Prims Algorithm Tutorial #711

Infonioknight · 2024-10-06T12:10:47Z

Change Summary

Included an overview, the complexities of the algorithm
Explained one leetcode problem in depth (I couldn't find too many and I wanted to leave some for the suggested problems that were simple and similar)
Included two suggested problems.
Highlighted any references used.

Checklist

If you haven't fulfilled the below requirements or even delete the entire checklist, your PR won't be reviewed and will be closed without notice. Regular contributors (with 10+ PRs) can skip this part.

General

[/ ] This Pull Request is all my own work. (You'll be blacklisted if you are caught for plagiarism.)
[ /] I've read CONTRIBUTING.md
[ /] I've applied LaTex for all variables, formulas and time / space complexity instead of using backticks
[/ ] I've started the app locally and verified all the content and all links (if applicable) are accessible correctly
[ /] I've included Complexity Analysis (Time Complexity & Space Complexity).
[ /] I've written my explanation well and it is easy to understand for beginners

Tutorial

[ /] I've read and followed the Tutorial Template
[ x] I've explained my topic well with 2 - 3 LC problems and no external problems are used.
[/ ] I've provided the full working solutions to the problems used in this tutorial.
[ /] I've provided suggested problems at the end with the given format. See here as an example. If the target solution is not available, leave solutionLink blank.
[/ ] I've given credits / references if I use external resources. (For an image, give credit under it. Otherwise, add a new section called References at the end (after Suggested Problems).)

Solutions

[x ] I've read and followed the Solution Template
[ /] I've formatted my code well with K&R Coding style
[ /] I've confirmed that comments are put above each line rather than writing on the same line.
[ /] I've included a meaningful approach name for my solution. e.g. ## Approach 1: Two Pointers.

- Included an overview, the complexities of the algorithm - Explained one leetcode problem in depth (I couldn't find too many and I wanted to leave some for the suggested problems that were simple and similar) - Included two suggested problems. - Highlighted any references used.

tutorials/graph-theory/prims-algorithm.md

Incorporated the requested changes.

Infonioknight · 2024-10-06T13:26:09Z

Incorporated the requested changes. Do let me know if they're okay.

wingkwong

the structure is fine. please add one more example with the same structure.

tutorials/graph-theory/prims-algorithm.md

- Added a second example problem for the same.

Infonioknight · 2024-10-06T17:32:00Z

Added a second example problem, also highlighted the solutions for the problems that had one.

Made a few modifications to the code, indentation to make it copy-pastable in leetcode

Infonioknight · 2024-10-07T13:14:41Z

I made a second commit changing a little bit of the indentation and layout of the code to make it directly copy-pastable in leetcode. Do let me know if it's okay!

Infonioknight · 2024-10-13T09:10:49Z

Hello! I just wanted to follow up on the PR.

wingkwong · 2024-10-13T09:26:32Z

hey next time please click re-request review when it's ready.

Infonioknight · 2024-10-13T09:28:28Z

Ah, got it. Will make sure to do that next time!

wingkwong

please verify locally once first.

Made necessary changes to run locally

Infonioknight · 2024-10-27T16:50:48Z

Apologies for the delay, was a bit caught up with work. Made the changes and tested it locally. Seems to be working fine now.

Infonioknight · 2024-10-30T18:04:47Z

Hi there! Just wanted to follow up on the PR!

wingkwong

please apply LaTex instead of using backticks.
for the content, i will review in depth in weekend.

tutorials/graph-theory/prims-algorithm.md

- Changed all backtick highlighting to LaTeX - Modified the introduction to the problems (made it an explanation instead of just listing input and output) - Changed value for TabItems to 'py'

Infonioknight · 2024-10-30T20:34:00Z

Made the requested changes. My apologies for not checking with the format of things. I think it should be compliant now.

Infonioknight · 2024-11-17T17:01:47Z

Hi, just wanted to follow up on the pull request.

Infonioknight · 2024-12-12T13:46:54Z

Hi! Just wanted to know if I needed to make any other changes in this.

wingkwong · 2024-12-12T15:30:24Z

@Infonioknight hey sorry for the late update. been a bit busy these months. will try to review on weekend. thanks.

Infonioknight · 2024-12-12T15:33:50Z

@wingkwong no worries at all! Do take care.

wingkwong

The subheader for examples should be consistent. Also subheader shouldn't include :.

wingkwong · 2024-12-15T06:21:23Z

tutorials/graph-theory/prims-algorithm.md

+## Suggested Pre-requisites
+Before moving on to learn the Prims algorithm, it is suggested that you know what a [Minimum Spanning Tree (MST)](../graph-theory/minimum-spanning-tree.md) is.


can you also work on MST page?

wingkwong · 2024-12-15T06:23:49Z

tutorials/graph-theory/prims-algorithm.md

+
+### Complexity and Use-Cases
+When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.


may elaborate how to get $O(E + V log V)$

wingkwong · 2024-12-15T06:24:59Z

tutorials/graph-theory/prims-algorithm.md

+
+### Complexity and Use-Cases
+When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This makes Prim's algorithm highly efficient for **dense** graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.


This makes Prim's algorithm highly efficient for dense graphs,

may explain why it is efficient for dense graphs but not sparse ones.

wingkwong · 2024-12-15T06:26:20Z

tutorials/graph-theory/prims-algorithm.md

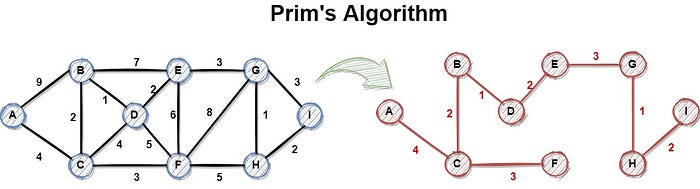+![Prims Algorithm Image](https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg)
+
+_Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_


refer to the post title instead.

wingkwong · 2024-12-15T06:27:40Z

tutorials/graph-theory/prims-algorithm.md

+3: [(6, 1), (1, 2)]
+```
+Where each tuple consists of '(cost, destination)'.


'(cost, destination)' -> $(cost, destination)$

wingkwong · 2024-12-15T06:30:36Z

tutorials/graph-theory/prims-algorithm.md

+## Example 2: [1584 - Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points)
+### Instructions: 
+You are given an array $points$ representing integer coordinates of some points on a 2D-plane, where $points[i]$ = $[xi, yi]$.


xi -> x_i
yi -> y_i

apply to j as well.

wingkwong · 2024-12-15T06:30:57Z

tutorials/graph-theory/prims-algorithm.md

+for i in range(len(points)):
+    current = tuple(points[i])
+    for j in range(i+1, len(points)):


i+1 -> i + 1

wingkwong · 2024-12-15T06:31:26Z

tutorials/graph-theory/prims-algorithm.md

+
+adjacency_list = {}
+for i in range(len(points)):


len(points) -> n since it will be used more than one time

wingkwong · 2024-12-15T06:32:12Z

tutorials/graph-theory/prims-algorithm.md

+        heapq.heappush(connection_queue, connection)
+
+    while len(seen) < n and connection_queue:
+        cost, current = heapq.heappop(connection_queue)
+        if current in seen:
+            continue
+
+        res += cost
+        seen.add(current)
+
+        for connection in adjacency_list[current]:
+            if connection[1] not in seen:
+                heapq.heappush(connection_queue, connection)
+
+    return res


fix indentation

wingkwong · 2024-12-15T06:32:58Z

tutorials/graph-theory/prims-algorithm.md

+        seen = set([start])
+
+        for connection in adjacency_list[start]:


include comments for the below code like L314 - L323. (apply to other code block)

wingkwong requested changes Oct 6, 2024

View reviewed changes

Update prims-algorithm.md

8545f87

Incorporated the requested changes.

wingkwong requested changes Oct 6, 2024

View reviewed changes

Update prims-algorithm.md

590a2a3

- Added a second example problem for the same.

Update prims-algorithm.md

68a45b2

Made a few modifications to the code, indentation to make it copy-pastable in leetcode

Infonioknight requested a review from wingkwong October 13, 2024 09:28

wingkwong requested changes Oct 13, 2024

View reviewed changes

Update prims-algorithm.md

a09a98c

Made necessary changes to run locally

Infonioknight requested a review from wingkwong October 27, 2024 16:50

wingkwong requested changes Oct 30, 2024

View reviewed changes

tutorials/graph-theory/prims-algorithm.md Outdated Show resolved Hide resolved

tutorials/graph-theory/prims-algorithm.md Outdated Show resolved Hide resolved

tutorials/graph-theory/prims-algorithm.md Outdated Show resolved Hide resolved

Update prims-algorithm.md

2d9bca1

- Changed all backtick highlighting to LaTeX - Modified the introduction to the problems (made it an explanation instead of just listing input and output) - Changed value for TabItems to 'py'

Infonioknight requested a review from wingkwong October 30, 2024 20:34

wingkwong requested changes Dec 15, 2024

View reviewed changes

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

Prims Algorithm Tutorial #711

Prims Algorithm Tutorial #711

Infonioknight commented Oct 6, 2024

Infonioknight commented Oct 6, 2024

wingkwong left a comment

Infonioknight commented Oct 6, 2024

Infonioknight commented Oct 7, 2024

Infonioknight commented Oct 13, 2024

wingkwong commented Oct 13, 2024

Infonioknight commented Oct 13, 2024

wingkwong left a comment

Infonioknight commented Oct 27, 2024

Infonioknight commented Oct 30, 2024

wingkwong left a comment

Infonioknight commented Oct 30, 2024

Infonioknight commented Nov 17, 2024

Infonioknight commented Dec 12, 2024

wingkwong commented Dec 12, 2024

Infonioknight commented Dec 12, 2024

wingkwong left a comment

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

wingkwong Dec 15, 2024

		## Suggested Pre-requisites
		Before moving on to learn the Prims algorithm, it is suggested that you know what a [Minimum Spanning Tree (MST)](../graph-theory/minimum-spanning-tree.md) is.


		### Complexity and Use-Cases
		When implemented using a priority queue (usually a binary heap), the time complexity of Prim’s algorithm is $O(E + V log V)$, where $E$ is the number of edges and $V$ is the number of vertices. This makes Prim's algorithm highly efficient for dense graphs, where the number of edges is close to the maximum possible. For sparse graphs (a graph with a relatively small number of edges compared to the maximum number of possible edges), other algorithms like [Kruskal’s](kruskals-algorithm.md) may perform better.

		![Prims Algorithm Image](https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg)

		_Source: https://miro.medium.com/max/700/1*7kpPIPcmXr38Juh0umM6fA.jpeg_

Prims Algorithm Tutorial #711

Are you sure you want to change the base?

Prims Algorithm Tutorial #711

Conversation

Infonioknight commented Oct 6, 2024

Change Summary

Checklist

General

Tutorial

Solutions

Infonioknight commented Oct 6, 2024

wingkwong left a comment

Choose a reason for hiding this comment

Infonioknight commented Oct 6, 2024

Infonioknight commented Oct 7, 2024

Infonioknight commented Oct 13, 2024

wingkwong commented Oct 13, 2024

Infonioknight commented Oct 13, 2024

wingkwong left a comment

Choose a reason for hiding this comment

Infonioknight commented Oct 27, 2024

Infonioknight commented Oct 30, 2024

wingkwong left a comment

Choose a reason for hiding this comment

Infonioknight commented Oct 30, 2024

Infonioknight commented Nov 17, 2024

Infonioknight commented Dec 12, 2024

wingkwong commented Dec 12, 2024

Infonioknight commented Dec 12, 2024

wingkwong left a comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment

Choose a reason for hiding this comment