Leetcode All In One: https://github.com/grandyang/leetcode
基础算法 —— 代码模板链接 常用代码模板1——基础算法
排序 二分 高精度 前缀和与差分 双指针算法
回朔法
位运算 离散化 区间合并 数据结构 —— 代码模板链接 常用代码模板2——数据结构
链表与邻接表:树与图的存储 栈与队列:单调队列、单调栈 kmp Trie 并查集 堆 Hash表 C++ STL使用技巧 搜索与图论 —— 代码模板链接 常用代码模板3——搜索与图论
DFS与BFS 树与图的遍历:拓扑排序 最短路 最小生成树 二分图:染色法、匈牙利算法 数学知识 —— 代码模板链接 常用代码模板4——数学知识
质数 约数 欧拉函数 快速幂 扩展欧几里得算法 中国剩余定理 高斯消元 组合计数 容斥原理 简单博弈论 动态规划
背包问题 线性DP 区间DP 计数类DP 数位统计DP 状态压缩DP 树形DP 记忆化搜索 贪心
时空复杂度分析
提高知识点 动态规划——从集合角度考虑DP问题
1.1 数字三角形模型 1.2 最长上升子序列模型 1.3 背包模型 1.4 状态机模型 1.5 状态压缩DP 1.6 区间DP 1.7 树形DP 1.8 数位DP 1.9 单调队列优化的DP问题 1.10 斜率优化的DP问题 搜索
2.1 BFS 2.1.1 Flood Fill 2.1.2 最短路模型 2.1.3 多源BFS 2.1.4 最小步数模型 2.1.5 双端队列广搜 2.1.6 双向广搜 2.1.7 A* 2.2 DFS 2.2.1 连通性模型 2.2.2 搜索顺序 2.2.3 剪枝与优化 2.2.4 迭代加深 2.2.5 双向DFS 2.2.6 IDA* 图论
3.1.1 单源最短路的建图方式 3.1.2 单源最短路的综合应用 3.1.3 单源最短路的扩展应用 3.2 floyd算法及其变形 3.3.1 最小生成树的典型应用 3.3.2 最小生成树的扩展应用 3.4 SPFA求负环 3.5 差分约束 3.6 最近公共祖先 3.7 有向图的强连通分量 3.8 无向图的双连通分量 3.9 二分图 3.10 欧拉回路和欧拉路径 3.11 拓扑排序 高级数据结构
4.1 并查集 4.2 树状数组 4.3.1 线段树(一) 4.3.2 线段树(二) 4.4 可持久化数据结构 4.5 平衡树——Treap 4.6 AC自动机 数学知识
5.1 筛质数 5.2 分解质因数 5.3 快速幂 5.4 约数个数 5.5 欧拉函数 5.6 同余 5.7 矩阵乘法 5.8 组合计数 5.9 高斯消元 5.10 容斥原理 5.11 概率与数学期望 5.12 博弈论 基础算法
6.1 位运算 6.2 递归 6.3 前缀和与差分 6.4 二分 6.5 排序 6.6 RMQ
2020.06.25
今天的目标,就是熟悉二分法的思路和写法。
二分法的思路很简单。小时候有个综艺节目,猜家电的价格,如果能够准确猜对,就把相应的家电送给参与者。譬如一台电视机价格为2000块。
我们第一次猜:3000。
主持人:高了。
那我们第二次肯定不会猜2999,否则要想猜到正确的价格,需要尝试1000次!
既然高了,我们又知道价格肯定在0-3000块之间。
第二次就折中猜一个:1500块。
主持人这回又说:低了。
现在我们就知道了,这个价格在1500-3000之间。
第三次我们再折中猜:2250块。
主持人:高了。
1500-2250.
第四次:1875。低了。
1875-2250.
第五次:2062。高了。
1875-2062。
第六次:1968。低了。
1968-2062。
第七次:2015。高了。
1968-2015。
第八次:1991。低了。
1991-2015。
第九次:2003。高了。
1991-2003。
第十次:1997。低了。
1997-2003。
第十一次:2000。答对了!!!
二分的威力,把2000次的搜索空间降到了11次。这也就是时间复杂度中log(n)的来历了。每次都砍掉当前搜索空间的一半,可不就是把原本为n的搜索空间变成了log(n)吗?!
二分的核心思想,很简单,但是难就难在,怎么去实现,或者说,把实际问题巧妙的转化为二分法。
那么现在,我们也清楚了,与二分搜索(binary search)对应的是线性搜索(linear search)。线性搜索对应的时间复杂度就是O(n)。
快排的本质就是分治算法,也是一种二分思想。
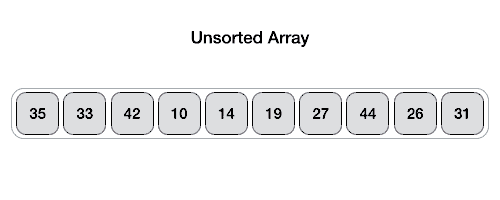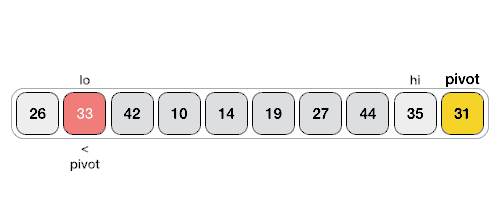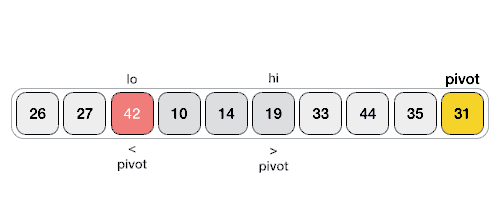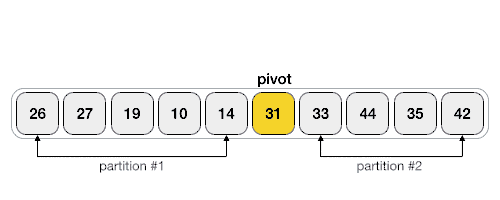
首先,找到一个支点(pivot),然后用一个双指针相向地检索arr中的元素,将小于pivot的值放在左边,大于pivot的值放在右边,最后,将pivot移至中间。就得到了2个子序列(partition),左边的partition都是小于pivot的,右边的都是大于pivot的。当然,两个partition内部还不是有序的。
由于每个partition内部都还不是有序的,那么,接下来只需要对每个partition再重复上述的操作,直到所有的partition都不可分,排序完成。
快排的步骤:
Step 1 − Make the right-most index value pivot(最右端index的值作为pivot,也可以选别的)
Step 2 − partition the array using pivot value(根据pivot将arr分组)
Step 3 − quicksort left partition recursively(递归左边分组)
Step 4 − quicksort right partition recursively(递归右边分组)
曾经以为DFS和BFS很高大上,当时实习的时候被一个参加过ACM的小伙子一顿DFS,BFS给我忽悠瘸了。直到如今,我终于有个空闲的时间,不玩游戏不约妹纸也不偷懒,好好地研究一番才发现,这玩意居然是graph里最简单最基本的算法。可以理解为graph里的暴力搜索,因为BFS和DFS都是遍历图结构中的每一条边和每一个节点,因此他们的时间复杂度都是O(V+E),V是节点,E是边。但是不同的是,BFS的空间复杂度更高,形象的理解是因为BFS看得更远,而DFS则是埋头苦干,不撞南墙不回头,因此BFS心里装的事情更多,而DFS则是干就完了,轻装上阵,赢了会所嫩模,输了下海干活。
讲的严谨一点则是,DFS是要用栈来实现的,通常就是递归,遍历过的点,就会被pop出去,内存里只会存储当前的路径。BFS则是用队列来实现的,通常就是python里的list,BFS每走一步,都要查看下一步的所有可能性,所以自然需要存储的节点就更多,内存消耗也更大。一图说明:
DFS:只保存最后的路径的信息:
BFS:保存几乎一大半的graph信息:
图片来源:https://medium.com/tebs-lab/breadth-first-search-and-depth-first-search-4310f3bf8416
当然这里的graph包括了我们通常理解的无向图、有向图、有向循环图、有向无环图(DAGs)等,也包括了二叉树等树结构。
总之,BFS和DFS给了我们一个基础范式,就是对于图结构来说,我们应该如何实现节点遍历(暴力搜索)。虽然他们的效果就是暴力搜索的效果,但是这两个方法也是两个非常重要的思维方式,因为我发现,在了解他们之前,给我一张图,我甚至不知道如何去暴力搜索!
接下来写个伪代码实现:
BFS(Queue):
BFS(graph, start_node, end_node):
frontier = new Queue()
frontier.enqueue(start_node)
explored = new Set()
while frontier is not empty:
current_node = frontier.dequeue()
if current_node in explored:
continue
if current_node == end_node:
return success
for neighbor in graph.get_neighbors(current_node):
frontier.enqueue(neighbor)
explored.add(current_node)
DFS(Stack):
DFS(graph, start_node, end_node):
frontier = new Stack()
frontier.push(start_node)
explored = new Set()
while frontier is not empty:
current_node = frontier.pop()
if current_node in explored:
continue
if current_node == end_node:
return success
for neighbor in graph.get_neighbors(current_node):
frontier.push(neighbor)
explored.add(current_node)
only difference is queue and stack.
注意一点:在python中,队列请不要使用list,而是使用collections.deque因为list的pop方法是O(n)复杂度,而正常队列的pop方法应该是O(1)复杂度。
今天完成了BFS专题里的6道题目。https://leetcode.com/tag/breadth-first-search/
3道easy,3道medium。主要涉及到了二叉树的层级遍历,基本上熟悉了队列的写法,注意在python里不要用list作为队列。
今天完成了2到medium的DFS,本质上,上面的blog已经讲得非常清楚了,就是栈的数据结构的应用,或者说是递归。
不知为何,理论上BFS和DFS的复杂度一样,但是实际测试下来,DFS始终比BFS快一些。
DFS/递归博大精深,不止能解决图和树的遍历问题,同时,DFS也是回溯问题的本质。
回溯:
LeetCode 10. Regular Expression Matching
LeetCode 17. Letter Combinations of a Phone Number
LeetCode 22. Generate Parentheses
LeetCode 46. Permutations(全排列)
LeetCode 37. Sudoku Solver(数独)
LeetCode 39. Combination Sum
dfs的代码经常想不明白。
# dfs 来做搜索的代码模板
def dfs():
for choice in all_choices():
record(choice)
dfs()
rollback(choice)最近有个感悟,二分法就是算法里最牛的思想,为什么这么说?在最开始的Binary Search中我就说过,二分法是将搜索空间指数级降低的方法。可是日常生活中,并不是所有的数据结构或者问题都可以用二分法来解决。所以本质上,二叉树这种数据结构就是为了将二分这种方法运用到淋漓尽致。
参考刷题:https://zhuanlan.zhihu.com/p/57929515
114,105, 106,108,109,589,94,173,145,104
二叉树的先序遍历: 根左右,在我看来是最正常的一种二叉树遍历方式,可以用DFS、BFS来实现。
二叉树的中序遍历:左根右
leetcode 94
二叉树的后序遍历:左右根
二叉树的层序遍历。这个是符合人眼观察的遍历顺序。一般用BFS来实现。
binary search tree.
字典树,或者叫前缀查询树。用于word查询,每个字母是树上的一个节点。可以用于搜索时的自动补全等功能。
实际上是一种数据结构,而非算法。一般包含如下方法:
- 查询:简单,就是hashmap+树的查询。
- 添加:简单,就是树的节点添加。
- 删除:困难,如果要删除一个非叶子节点,需要考虑补全其他已经存在的节点。
- startwith:简单,天生就是干这个的。
堆,一种特殊的二叉树。
特点:父节点的元素永远大于子节点(最大堆) / 父节点的元素永远小于子节点(最小堆)。
LeetCode 23. Merge k Sorted Lists
答:插入O(LogN)删除O(LogN)的优先队列就是用Heap实现的
因为在做链表的题目时,经常因为各种switch而丢掉链表头,这里有个小小的trick,用一个单独的节点root,来作为给定输入链表的表头,这样,root节点在所有节点变换中都不会变,所以我们计算完毕后,只需要返回root.next即可找到原来的表头,非常方便!
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: ListNode) -> ListNode:
root = ListNode()
root.next = head
mem = root
cur = root.next
change = False
while cur:
if change:
tmp = cur.next
cur.next = pre
pre.next = tmp
mem.next = cur
cur = cur.next
mem = cur
else:
pre = cur
cur = cur.next
change = not change
return root.next严格意义上来说,slide window更像是一种技术,而非算法。一般用于字符串处理,对于一个连续的字符串或者链表,求一些最大不重复子串或者最大相同子串。这些问题都有一个核心共性:单向的滑动窗口就可以解决问题。
一般来说,这种字符串类型的题目,如果是暴力搜索需要$$O(n^2)$$或者$$O(n^3)$$的复杂度。但是通过slide window配合hashmap来让算法记住一些迭代过程中的关键信息,就可以将复杂度优化到$$O(n)$$。
目前这部分的题目,我做了2道,一道medium一道hard。总结下来2点最重要,第一,设计好hashmap该存哪些信息,怎么存。第二,设置好滑窗的步长,划窗的一个特性是end节点每次循环后,都要+1,这是保证$$O(n)$$的关键,而start节点则可以根据所求解的问题来自定步长。
来一套模板吧:
def slide_window(s:list):
ans = []
table = {}
start_point = 0
end_point = 0
while end_point < len(s): # 以end_point为主循环
table.update # 更新hashmap的内容
if condition:
table.update # 更新hashmap的内容(如果有必要的话)。
start_point = xxxx # 更新start_point
end_point += 1
return ans # 返回结果并查集。用于2-D数组的连通域数量、大小,朋友圈关系等问题的求解。
其实这类问题也可以用BFS或者DFS来解决,并且理论上的时间复杂度也是O(M*N)(M和N为2D数组的长宽)。但是并查集是一种更好的数据结构,或者简单来说,BFS或者DFS在实现的过程中,如果对Hashmap管理足够好的话,其实就是实现了并查集的功能。
OK,接下来来看看并查集这个数据结构长啥样:
并查集的实现,只需要实现3个函数:
init:首先,初始化父节点list,让每个节点的父节点都是自己。
find:输入一个节点,查询该节点的根节点。这里要注意,根节点的判断依据是:该节点的父节点是否为自己。查询所需要的时间复杂度为树深。
union:当满足一定条件时(依题目而定),将输入的2个节点合并。也就是将输入的2个节点的根节点合并。首先用find方法分别查询2个节点的根节点,其次,根据2个节点到根节点的深度。更深的作为父节点,另一个作为子节点。这样就合并了2个节点。当然,这个合并方法不是一成不变的,也可以单纯的把第一个节点的根节点作为2个节点的共同根节点。不过第一种方法考虑了树深,更优化一点而已。
并查集总体来说也就是一个O(n)的方法,理论上来说,没有比BFS或者DFS优越到哪里去。。。不过算是掌握了一种新方法吧。
什么是拓扑排序呢?一开始听到这个概念的时候,我以为这是一种新的排序算法。后来,查了相关资料才知道,这是一个图算法,就是对一个有向无环图(DAG)进行排序。可以解决任务调度等问题,最近正在用的spark的相关任务调度的算法应该就是这种拓扑排序。
在图论中,**拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)**的所有顶点的线性序列。且该序列必须满足下面两个条件: 1、每个顶点出现且只出现一次。 2、若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。 有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
一般解决拓扑排序问题的步骤如下:
-
根据问题建图,图的表示方式可以是邻接矩阵,也可以是邻接表。
邻接矩阵:
邻接表:
-
贪心(BFS)或者DFS进行排序,时间复杂度O(V+E)。
贪心:
- 找到图中入度为0的节点并输出。
- 从图中删除该顶点和所有以它为起点的有向边。
- 重复1,2步骤,直到图中没有顶点或者入度为0的点,后者说明该图不是DAG。
DFS:
- 维护一个状态数组:visit_state,当visit_state[i]==0时,表示节点i没有被访问过;visit_state[i]==1时表示当前节点i正在被一次dfs访问中,如果此时访问的节点状态也为1,则说明图中有环;visit_state[i]==2表示节点i已经被完全访问完,并且无环,如果访问的节点状态为2,则说明i之后的节点都已经访问过且无环。
- 正常访问节点i,并且递归访问i的neighbors,记得每次访问时更改visit_state的状态即可。
做了一下LeetCode207,感觉这类题目有点难度,但是难度并不在BFS或者DFS,这两种的本质只是队列和堆栈,而真正的难点在于,如何根据问题建图、存图!有一个高效的图数据结构至关重要!
Leetcode 11. 最大装水容器,非常经典的two pointers问题。
Leetcode 15. 3 Sums
Leetcode 16 3 Sums closest.
总结一下:
大体上,two pointers可以分为2类:
- 同向指针/快慢指针
- 左右指针
主要用来解决链表型数据结构中的遍历问题。字符串的很多操作也可以用快慢指针。
实际上,slide window也属于同向指针/快慢指针的一种。
这类方法的特点就是2个指针同时从序列的左边遍历到右边或者右边到左边,不过2个指针的移动速度不同。
主要用来解决有序数组或者字符串的一些问题。今天做的这些LeetCode 11,15,16等都是属于左右指针的类型。用好了,可以帮助我们节省一次循环的遍历。
一维DP 入门,用一个辅助序列sums保存前n个元素之和。 问题变成了: 如果当前子序列之和小于0,则抛弃之前的所有序列,以当前节点为起点,重新计算,最后记录最大的子序列和即可。 时间复杂度:O(n) 没觉着这个是DP的题目,可能解法还是有问题。
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if not nums or len(nums) == 0:
return 0
sums = [0] * (len(nums) + 1)
sums[0] = 0
max_sum = float("-inf")
for i in range(1, len(nums)+1):
sums[i] = sums[i-1] + nums[i-1]
st = 0
for i in range(1, len(sums)):
pre_sum = sums[i] - sums[st]
if pre_sum <= 0:
st = i
if pre_sum > max_sum:
max_sum = pre_sum
return max_sum一维DP. 类似斐波那契数列: 转移方程: f(n) = f(n-1) + f(n-2). 时间复杂度:O(n) 还是没看明白这跟DP有啥关系,就是递归而已。
class Solution:
def climbStairs(self, n: int) -> int:
res = [-1] * (n)
def dfs(n):
if n == 1:
return 1
if n == 2:
return 2
if res[n-1] == -1:
res[n-1] = dfs(n-1) + dfs(n-2)
return res[n-1]
else:
return res[n-1]
ans = dfs(n)
return ans这题终于有点DP的意思了,依然是一道一维DP。用一个DP数组记录第i步的最佳选择:
最后返回DP数组的最后一个元素即可。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices or len(prices) < 2:
return 0
dp = [0] * len(prices)
min_p = prices[0]
for i in range(len(prices)):
dp[i] = max(dp[i-1], prices[i] - min_p)
min_p = min(min_p, prices[i])
return dp[-1]非常明显的一维DP,这也是第一道自己解出来的DP问题。这个其实可以理解为是背包问题的变种。
输入为:nums数组
假设有一个DP数组:
dp: [-1, -1, -1, -1]
dp[i]表示nums[0:i]的最优状态。那么状态转移方程为:
dp[i] = max(dp[i-2] + nums[i], dp[i-1])
有了这个,直接递归:
注意一个trick:dp = [-1] * len(nums) 将dp状态数组保存起来,避免递归的时候重复计算。
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums or len(nums) == 0:
return 0
dp = [-1] * len(nums) # 将dp状态数组保存起来,避免递归的时候重复计算。
def dfs(m):
if m == 0:
return nums[0]
if m == 1:
return max(nums[0], nums[1])
if dp[m] != -1:
return dp[m]
else:
dp[m] = max(dfs(m-2)+nums[m], dfs(m-1))
return dp[m]
ans = dfs(len(nums)-1)
return ans遗憾的是目前的dp我只会用递归写,还有一种非递归的写法,后期需要学习。
比较典型的DP,第一道二维DP! 被二维list的生成方式坑了: 千万不要用: [[-1]*m]*n 这种方式生成二维list,因为这样生成的是浅拷贝。 正确生成方式为: [[-1] * m for _ in range(m)]
时间复杂度:O(n^2) 空间复杂度:O(n^2)
- 递归DP
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
dp = [[-1] * len(triangle) for _ in range(len(triangle))]
if not triangle or len(triangle) == 0:
return 0
def dfs(row, col):
if row == 0 and col == 0:
dp[row][col] = triangle[0][0]
return triangle[0][0]
if dp[row][col] == -1:
if row > col > 0:
dp[row][col] = min(dfs(row-1, col-1), dfs(row-1, col)) + triangle[row][col]
elif col == 0:
dp[row][col] = dfs(row-1, col) + triangle[row][col]
else:
dp[row][col] = dfs(row-1, col-1) + triangle[row][col]
return dp[row][col]
else:
return dp[row][col]
ans = float("inf")
for i in range(len(triangle)):
tmp = dfs(len(triangle)-1, i)
if tmp < ans:
ans = tmp
return ans- 非递归DP
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
if len(triangle) == 1:
return triangle[0][0]
dp = [[0] * len(triangle) for i in range(len(triangle))]
dp[0][0] = triangle[0][0]
ans = float("inf")
if not triangle or len(triangle) == 0:
return 0
for row in range(1, len(triangle)):
for col in range(len(triangle[row])):
if col == 0:
dp[row][col] = dp[row-1][col] + triangle[row][col]
elif col == len(triangle[row])-1:
dp[row][col] = dp[row-1][col-1] + triangle[row][col]
else:
dp[row][col] = min(dp[row-1][col-1], dp[row-1][col]) + triangle[row][col]
if row == len(triangle) - 1:
if dp[row][col] < ans:
ans = dp[row][col]
return ans这是经典题目买卖股票的第三个变种,据说也是最难的一个变种。因为这个题目有交易次数的限制:最多交易2次。
之前几道题做完后我的感觉,DP就是数学里的归纳法,或者说,算法里面很喜欢说最优子结构,只要你能找到状态转移方程/递推公式,一切问题都迎刃而解了。
从这道题开始,我对DP问题有了一个更深层次的认识。其实DP的精髓并不在如何找递推公式,而在于如何定义状态表。何为状态表?状态表就是待解问题中所有存在的状态集合,不能有遗漏。例如在House Robber这道题中,我们定义DP数组为:dp[i],表示到第i家时,窃贼的最大盗窃价值,一共N家,当窃贼走到最后一家时,最优解也就出来了,转移方程为:dp[i] = max(dp[i-2] + nums[i], dp[i-1])。
我们发现dp这个数组就是对House Robber问题中可能出现的状态的一个完备集合,有了这样的完备集合,再加上转移方程,问题自然很简单。
那么为什么House Robber是一道easy,而Best Time to Buy and Sell Stock III是一道hard呢?
可以发现,House Robber中这个完备的状态集合dp,非常容易找到。也就是说,我们很容易就获取了所有的搜索空间,剩下的就是小学生都会的递推而已!
但是Best Time to Buy and Sell Stock III这道题,你会发现,你甚至连暴力穷举的方法都写不出来。为啥?因为你很难找到这个完备的状态集合dp!
所以有个概念必须要纠正一下:DP难,不是难在状态转移方程的寻找,而是难在完备状态空间的寻找!一旦当你找到完备状态空间,转移方程只是告诉我们如何去遍历而已。因为定义完状态转移方程后,我们的搜索空间就不是像链表或者数组一样的线性空间了,而是一个非线性空间,我们需要用递推公式来辅助我们在这个非线性空间里游走。
举个例子:
对于线性空间,遍历很简单:
arr = [1,2,3,4,5]
for i in range(len(arr)):
print(arr[i])或者我写的更直白一点:
arr = [1,2,3,4,5]
i = 0
while i < len(arr):
print(arr[i])
i += 1在线性空间搜索,我们的搜索空间很直白,是定义清楚的,
而且线性空间搜索,其实也有递推公式:
上述函数,我们已知定义域为[1,2,3,4,5],也很清楚值域为[1,2,3,4,5]。
那么对于非线性空间呢,我们下一个需要游走的点是根据略微复杂一些的递推公式计算出来的:
但是对于这个函数,我们通常不知道定义域,也不知道值域。
这个函数的定义域是什么呢?就是问题的搜索空间,或者说就是完备状态的空间。有了定义域,g(x)就是转移方程,就可以得到值域。
这样,我们就可以继续遍历了!
综上,可以发现,DP跟一般的遍历解法(brute-force)其实极其相似!都是遍历可行域内的所有节点!但是不同的是,一般的遍历解法(brute-force)的可行域我们一眼就看得出,但是DP问题的可行域需要我们自己定义好状态空间来确定。此外,brute-force中的i=i+1其实就是DP中的状态转移方程。
好了,回归正题,看看这道题的状态空间是怎么定义的吧:
拿到题目后,我人是懵的,我甚至不知道如何去遍历。但是https://labuladong.gitbook.io/algo/dong-tai-gui-hua-xi-lie/tuan-mie-gu-piao-wen-ti这篇文章给了我很大的启发。
对于这个问题,我们的变量如下:
第一个是天数:我们用i表示第i天。
第二个是我们买股票的剩余次数:我们用j来表示当前剩余的买股票的次数。
第三个是我们当前的状态:0表示我们当前没有持有任何股票(j>0时可以买入),1表示我们当前持有股票(可以卖出)。
这三个变量就可以刻画出整个搜索空间了,这是一个完备状态集合(怎么证明,我还没想明白,但是你找不出一个不在这个空间的状态)。
所以这个搜索空间有多大呢?
假设我们一共有n天,一共可以交易k次,那么这个空间大小为:
我们的DP算法也就是在这个状态空间内遍历,所以算法的时间复杂度为$O(n\times k)$。
注意这里我们已经把搜索空间从一维的输入list转移到了三维的完备状态空间,所以如果你理解输入空间本来就应该是这个完备状态空间的话,这个算法时间复杂度其实也是$O(N)$,其中,$N$为三维完备状态空间的大小。
现在你应该就可以理解,为什么说DP其实也是Brute-force了!
回到题目,我们的dp数组就设计为:
# k=2, n=len(prices)
# dp.shape = 2, 3, n
dp = [[[float("-inf")] * len(prices) for x in range(3)] for y in range(2)]我们的递推方程为:
dp[0][j][i] = max(dp[0][j][i-1], dp[1][j][i-1] + prices[i]) # 未持有股票,可买j次,第i天
dp[1][j][i] = max(dp[0][j+1][i-1] - prices[i], dp[1][j][i-1]) # 持有股票,可买j次,第i天注意,持有状态不一样,递推方程略有不同。但是本质上表示,当天的最大盈利,受到前一天的状态影响,包括前一天有没有持有股票,以及当天剩余的购买次数。
最后,我们来看看初始状态赋值:
dp[0][2][0] = 0 # 未持有股票,可买2次,第0天
dp[1][1][0] = -prices[0] # 持有股票,可买1次,第0天dp[0][2][0]未持有股票,可买2次,第0天时,我们盈利一定为0。
dp[1][1][0]持有股票,可买1次,第0天时,表示我们第0天买入了股票,剩余1次买入机会,我们的盈利为-price[0],我们要花钱买入,所以是负的第一天股价。
到此,这道题解完了,代码如下:
class Solution:
def maxProfit(self, prices: list) -> int:
if len(prices) < 2:
return 0
dp = [[[float("-inf")] * len(prices) for x in range(3)] for y in range(2)]
dp[0][2][0] = 0 # 未持有股票,可买2次,第0天
dp[1][1][0] = -prices[0] # 持有股票,可买1次,第0天
for i in range(1, len(prices)):
for j in range(3):
dp[0][j][i] = max(dp[0][j][i-1], dp[1][j][i-1] + prices[i]) # 未持有股票,可买j次,第i天
if j != 2:
dp[1][j][i] = max(dp[0][j+1][i-1] - prices[i], dp[1][j][i-1]) # 持有股票,可买j次,第i天
ans = max(dp[0][0][len(prices)-1], dp[0][1][len(prices)-1], dp[0][2][len(prices)-1])
if ans > 0:
return ans
else:
return 0这是一个新的系列,Jump Game。第一题我目前只想到了回溯法(暴力解空间):
相当于模拟每种可能的解法。
解空间有多大呢?
具体的空间大小其实和数组内部的元素值有关,但是我们考虑一个极端情况。当数组内的所有值都
大于数组长度n时,每一个index都有n-index种选择。所以总的解空间就是1x2x3x...xn=n!
所以,解空间的上限就是O(n!)这种水平的算法,是完全无法实用的。
即使我使用了mem来缓存一些中间结果,依然超时了:
这里的代码完全是根据回溯这一节里的套路来写的,只不过加了一个dp来做缓存:
class Solution:
def canJump(self, nums: list) -> bool:
arr = nums
dp = {}
def dfs(jump_from, jump_to):
if jump_from in dp:
return dp[jump_from]
else:
if jump_from == jump_to:
dp[jump_from] = True
return dp[jump_from]
if jump_from > jump_to:
dp[jump_from] = False
return dp[jump_from]
if arr[jump_from] < 1:
dp[jump_from] = False
return dp[jump_from]
for i in range(1, arr[jump_from]+1):
if dfs(jump_from + i, jump_to) is True:
dp[jump_from] = True
return dp[jump_from]
dp[jump_from] = False
return dp[jump_from]
res = dfs(0, len(nums)-1)
return res实际上这已经是一个backtracking+DP的解法了,复杂度已经降了很多了,但是还是不够。这种方法,Java能勉强通过,但是python就会超时!
O(n)的方法,从最后元素开始往前遍历,每次记录最右边能跳到终点的点,作为新的终点。
class Solution:
def canJump(self, nums: list) -> bool:
last_pos = len(nums) - 1
for i in range(len(nums)-1, -1, -1):
if i + nums[i] >= last_pos:
last_pos = i
return last_pos == 0