chinchilla

chinchilla is a research toolkit designed to estimate scaling laws & train compute-optimal models for various deep learning tasks.

Features

• Scaling Law Estimation: Fit a loss predictor based on multiple training runs.
• Compute-Optimal Allocation: Train the best possible model within a given compute budget.
• Progressive Scaling: Iteratively update the scaling law estimation and scale up the compute.
• Simulation Mode: Test scaling law estimations in hypothetical scenarios.

Expected Use Cases:	Scaling compute for Large Language Models (LLM) Vision Transformers (ViT) Reinforcement Learning (RL) Embedding Models Knowledge distillation Evaluating compute efficiencies of new algorithms & architectures Researching the neural scaling law itself
Probably NOT For...	Fine-tuning tasks Data-scarce domains etc.

Important

This work builds upon the scaling law formulation proposed in the original Chinchilla paper by DeepMind (2022), with some modifications detailed in ./docs/changes.md.

Installation

From PyPI

pip install -U chinchilla

From Source

git clone https://github.com/kyo-takano/chinchilla.git
cd chinchilla
pip install -e .

Prerequisite: Chinchilla formulation

Just in case you are not familiar, here is the formulation of the scaling law estimation:

Variables

• $N$: The number of parameters

• $D$: The number of data samples

• $C$: Total compute in FLOPs ($C\approx 6\ ND$)

• $L(N,\ D) = E + A / N ^ \alpha + B / D ^ \beta$: A loss predictor parameterized by ${E, A, B, \alpha}$ and $\beta$

  ---

  Intuition:

  • $E$ corresponds to the irreducible loss that can only be atained with an ideal model with infinite compute
  • $A / N ^ \alpha$ accconts for the additional loss coming from insufficiency of model size;
  • $B / D ^ \beta$, insufficiency of data amount.

Objective

1. Optimize the parameters ${E, A, B, \alpha, \beta}$ to better predict losses $L_i$ from $(N_i, D_i)$
2. Solve $\underset{N,\ D}{argmin}\ L(N,\ D\ |\ C)$, which can be derived from ${A, B, \alpha, \beta}$

Usage

1. Fitting the scaling law on existing dataset

Note

An example of this usage can be found here

First, prepare a CSV looking like this and save it as df.csv:

C,N,D,loss
1.3972367362937152e+18,73824672,3154403320,3.405928
1.7656304230443515e+18,89818214,3276303602,3.325255
2.0558971596900728e+18,105811837,3238291053,3.300442
...

Second, define a grid of initial parameters to fit like:

import numpy as np
from chinchilla import Chinchilla
cc = Chinchilla(
    "./",  # Assuming `df.csv` is under ./
    param_grid=dict(
        E=np.linspace(1, 2, 5),
        a=np.linspace(1, 10, 5),    # a: log(A)
        b=np.linspace(1, 10, 5),    # b: log(B)
        alpha=np.linspace(0.1, 0.7, 5),
        beta=np.linspace(0.1, 0.7, 5),
    ),
)

Finally, call cc.fit() & you'll get the parameters fit on your dataset, which you can easily access as cc.params

>>> cc.fit()
>>> cc.params
{'E': 1.7004437920205586,
 'A': 185.388090185727,
 'B': 1627.0012474587165,
 'alpha': 0.28923265350161337,
 'beta': 0.3556020928031086}

By calling cc.scale with FLOPs specified like

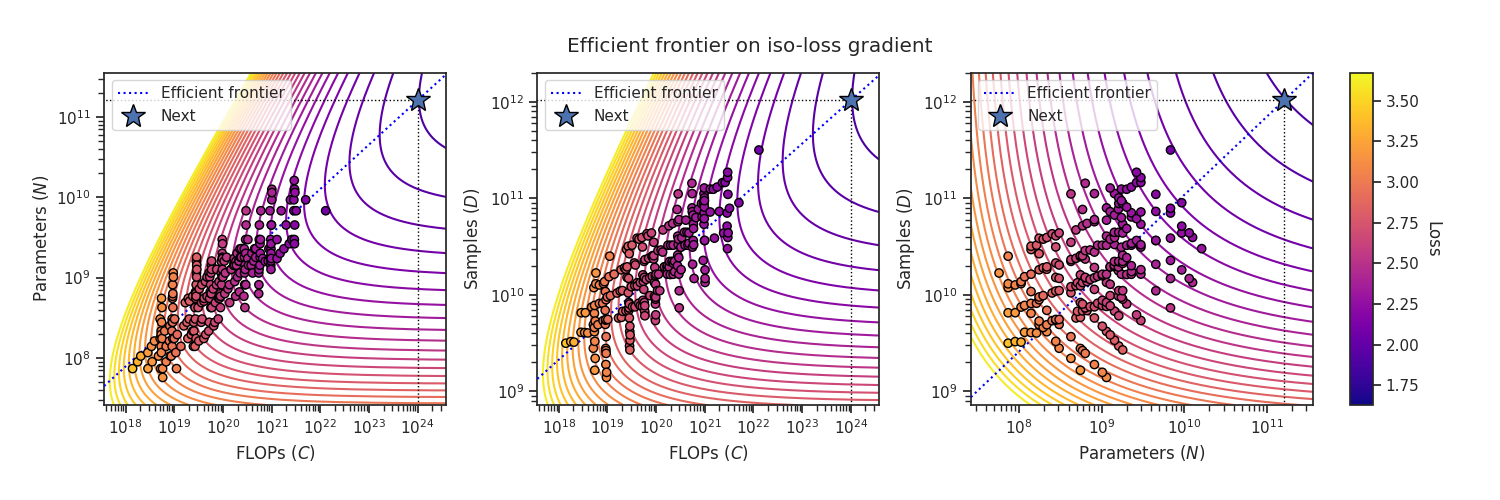
cc.allocate_compute(C=1e24)

You can get an estimatedly compute-optimal allocation of compute to $N$ and $D$.

2. Scaling from scratch

Note

An example of this usage can be found here

Procedure:

• seed: Sample X training runs $(N_i, D_i, L_i)$, referred to as seeds
• For i = 0 to K:
  • fit: Optimize the scaling law parameters to fit $L(N,\ D)$ on the training runs
  • scale: Configure a new model with a scaled compute
  • Evaluate the allocation by training a model
  • append: Add the result to the database of training runs

Below is an example to get started with chinchilla.

import numpy as np
from chinchilla import Chinchilla

cc = Chinchilla(
    "your_project__dir",
    param_grid=dict(
        E=np.linspace(1.1, 1.5, 5),
        A=np.linspace(200, 1000, 5),
        B=np.linspace(200, 1000, 5),
        alpha=np.linspace(0.1, 0.5, 5),
        beta=np.linspace(0.1, 0.5, 5),
    ),
    seed_ranges=dict(C=(1e15, 1e16), N_to_D=(10, 100)),
    # To search for the model configuration with N closest to suggested:
    model_search_config=dict(
        hyperparam_grid=dict(
            hidden_size=list(range(64, 16384 + 1, 64)),
            num_hidden_layers=list(range(1, 50 + 1)),
            num_heads=list(range(1, 40 + 1)),
        ),
        size_estimator=estimate_model_size,  # You gotta define a function to estimate & return model size also
    ),
    # Parameters you may pre-set
    num_seeding_steps=100,
    scaling_factor=2.0,
)


# Run the scaling law estimation and training process
for i in range(100 + 5):
    # Sample a new model
    (N, D), model_config = cc.step(num_seeding_steps=100)

    # Define a model
    model = YourModelClass(**model_config)

    # Train & evaluate the allocation C => (N, D)
    loss = train_and_evaluate(model, D)

    # Finally, append the training run into the database
    cc.append(N=N, D=D, loss=loss)

Ensure you define functionally equivalent versions of:

• estimate_model_size: Estimates and returns the model size.
• YourModelClass: Your model class definition.
• train_and_evaluate: Function to train and evaluate your model.

Simulation Mode

You can also visualize how chinchilla would perform under the given setup and a hypothetical scaling law, optionally with a noise term:

import random

cc.simulate(
    num_seeding_steps=401,
    num_scaling_steps=1,
    scaling_factor=10.0,
    target_params=dict(
        E=1.69337368,
        A=406.401018,
        B=410.722827,
        alpha=0.33917084,
        beta=0.2849083
    ),
    # Add exponentially distributed loss averaging at 0.1
    noise_generator=(random.expovariate, (10,))
)

Examples

Find practical applications/examples of chinchilla in the examples directory (more to come):

• Allocating $10^{24}$ FLOPs to a single LLM [NEW]

• Scaling Rubik's Cube Solvers from Scratch

Documentation

• API Reference

• Tips

• Math

• Differences from the original Chinchilla

Contributing

We welcome your contributions. Please report bugs and suggest improvements through new issues and pull requests.