Skip to content

Home

Jump to bottom
Jyotirmaya Shivottam edited this page Aug 31, 2020 · 6 revisions

GSoC 2020: EinsteinPy - Null geodesics for Schwarzschild and Kerr Geometries

Final Submission

Project Details:

Organization: OpenAstronomy

Sub-organization: EinsteinPy

Student: Jyotirmaya Shivottam (JeS24)

Mentors: Shreyas Bapat, Rishi Sharma, Sofía Ortín Vela, Ritwik Saha

Project: https://summerofcode.withgoogle.com/projects/#5023440827842560

Project Description:

The main goals of this project were to implement Null Geodesic calculation & plotting in Kerr and Schwarzschild spacetimes, that would help visualize some important aspects of general relativity, such as frame dragging; and Radiative Transfer, that would lead to redshift calculations and obtaining black hole shadow.

Project GitHub Repository: https://github.com/einsteinpy/einsteinpy

Link to commits, made during GSoC: Commits by JeS24

All my GSoC blogs can be found here: https://dev.to/jes24/ (N.B.: I have posted only GSoC 2020-related blogs here)

All the resources (papers, own codes and generated images) can be found here: https://github.com/einsteinpy/GSoC-2020 (This Repository)

Project Implementation:

I started with a survey of the existing literature, to know more about the project and to find an efficient implementation for calculating Null Geodesics and performing Radiative Transfer. The papers, perused during the survey can be found in this repo (Direct link). In consultation with my mentors, we decided on a numerical scheme, similar to RAPTOR (Bronzwaer et al, 2018) and Odyssey (Pu et al, 2016), as the (then) geodesic module was structurally similar, so, we would have minimal API breakage. Also, a numerical scheme is easily integrable with radiative transfer calculations (See Sec. 1, RAPTOR). More details can be found in my EinsteinPy Proposal for Enhancement (EPE) here (corresponding PR).

To implement this, I first had to refactor and fix some errors in some of the modules, such as metric, utils and coordinates and also add some new features, such as a BaseMetric class and 4-Vector support. Related pull requests and issues are as follows:

  1. Refactored metric and utils, and added a BaseMetric module: https://github.com/einsteinpy/einsteinpy/pull/512

Relevant issues:

  1. Refactored coordinates and added support for 4-Vectors and 4-Vector operations. Also, fixed the math-related errors in metric.Schwarzschild, metric.Kerr and metric.KerrNewman (partial fix) classes: https://github.com/einsteinpy/einsteinpy/pull/521

Relevant issues:

Then, I worked on the main goal of adding Null Geodesic calculations to EinsteinPy.

  1. Added support for Null Geodesics in Kerr & Schwarzschild Spacetimes and overhauled the corresponding plotting.geodesic module, with new features, such as 3D animations, parametric plots and better 2D plots: https://github.com/einsteinpy/einsteinpy/pull/527
  2. Added Jupyter Notebook for geodesic and plotting.geodesic: https://github.com/einsteinpy/einsteinpy/pull/536

Initially, I was taking the approach, as suggested in RAPTOR, as can be seen in the commit history of the corresponding PR. However, the results, that were obtained, were highly inaccurate. A simple check of the 4-Velocity norm (which should be 0) indicated that this was due to error-accumulation. Moreover, this issue plagued the (then) Timelike geodesics module as well. This motivated me to implement the same code in another language and I chose Mathematica. I present the outputs from Mathematica and Python, for the same initial conditions, below.

N.B.: The codes, used to generate all the plots in this Wiki, can be found in Notebooks. I have provided direct links to corresponding notebooks, in the image captions or near the images, as well.

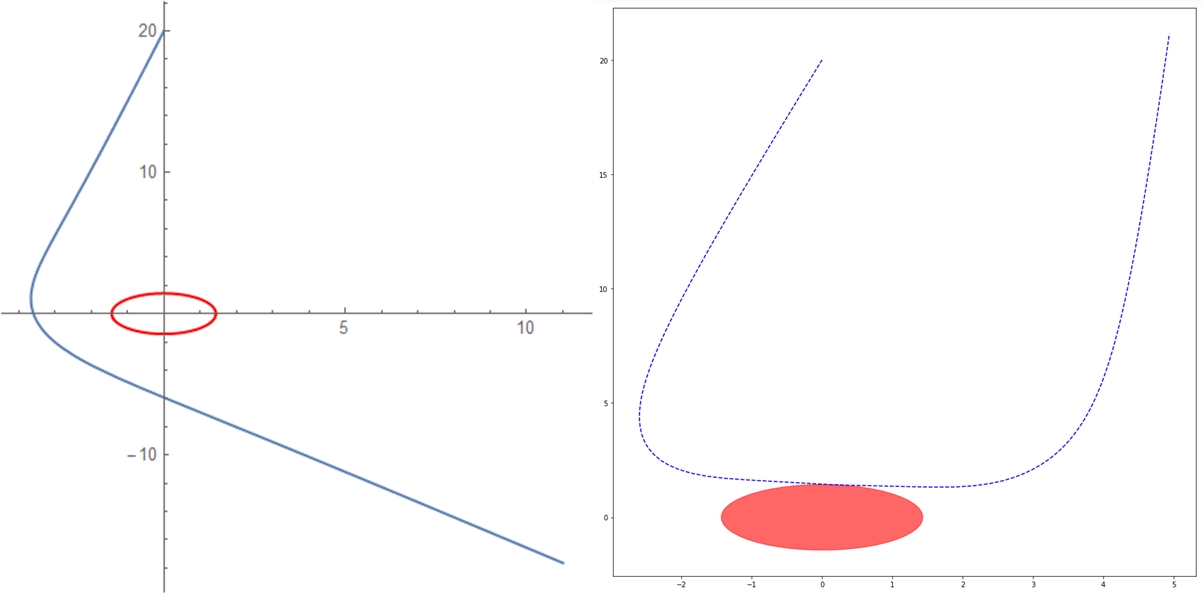
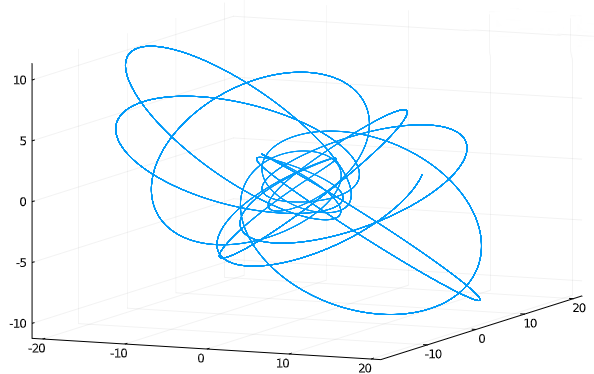
Mathematica (Left) & Python (Right)

MathPy

4-Velocity Norm; Mathematica (Left) & Python (Right)

MathPyUU

Note the drastic increase in the values of U.U (U dot U = 4-Velocity norm), near the black hole. I tried multiple solvers and even implemented my own, with adaptive meshing, but none helped. While researching for this, I also came across a nice derivation of the Kerr Hamiltonian for massive & massless particles, in Chapter 33 of Gravitation (MTW, 1973), which gave me the idea to take a Hamiltonian approach and use a symplectic solver. Unfortunately, even with a symplectic solver, the issues persisted for long simulations:

Kerr Null-like Escape (Code]

Py-Bad

While for short simulations, the results were fine:

Kerr Null-like Capture (Code)

Py-Good

Even with the inaccuracies, the symplectic solver did bring down the error by around 2 orders of magnitudes, which gave me a hint to look for other symplectic solvers, even in other languages. After discussions with my mentors, we chose Julia, due to its excellent DifferentialEquations.jl suite and "closeness" with Python. Another key bit is that, the HamiltonianProblem type, offered by DiffEqPhysics.jl, immensely simplifies the process of solving the system, as it uses Forward Mode Automatic Differentiation to automatically calculate the partial derivatives from the Hamiltonian. The separable nature of the Hamiltonian helps here. Considering all this, I combined a simplified form of the Hamiltonian with HamiltonianProblem and wrote a Julia module. Et voilà, the module worked well and even produced nice and accurate results for some peculiar geodesics, as shown below.

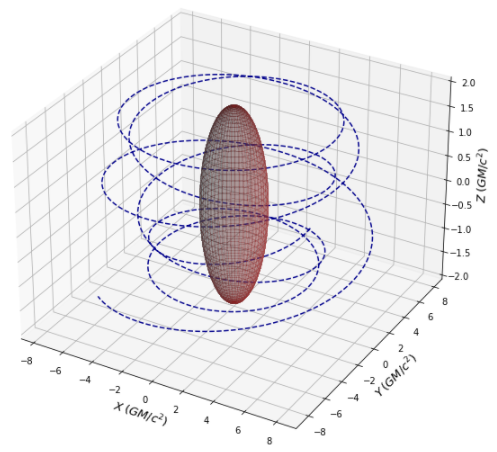
Kerr Null-like Reverse & Capture (Frame Dragging) (Code)

Julia Null-like

Kerr Time-like Whirl (Code)

Julia Time-like

Then, came the problem of integrating this Julia code with EinsteinPy, for which, I looked towards PyJulia, but it has some issues with installation on *nix systems. So, I opted to write my own wrapper, using Python's subprocess, and, with the help of my GSoC mentor, Shreyas, packaged the Julia module and the Python wrapper into what is now einsteinpy_geodesics, an add-on module to EinsteinPy. Since the Hamiltonian is general for all test particles (massive and massless), I rewrote the entire geodesic module, to incorporate Timelike geodesics as well, for a consistent API. On top of this, I also overhauled the geodesic plotting module (einsteinpy.plotting.geodesic) and added support for 3D animations, parametric plots and choice of spatial coordinates in 2D plots, in both Static and Interactive modes (that use matplotlib and plotly, respectively), as can be seen in a later commit to this PR.

I present some of the plots, produced through the final API, below. The plots shown here, have a mix of both Static and Interactive back-ends, as well as time-like and null-like geodesics. The corresponding code for these can be found here.

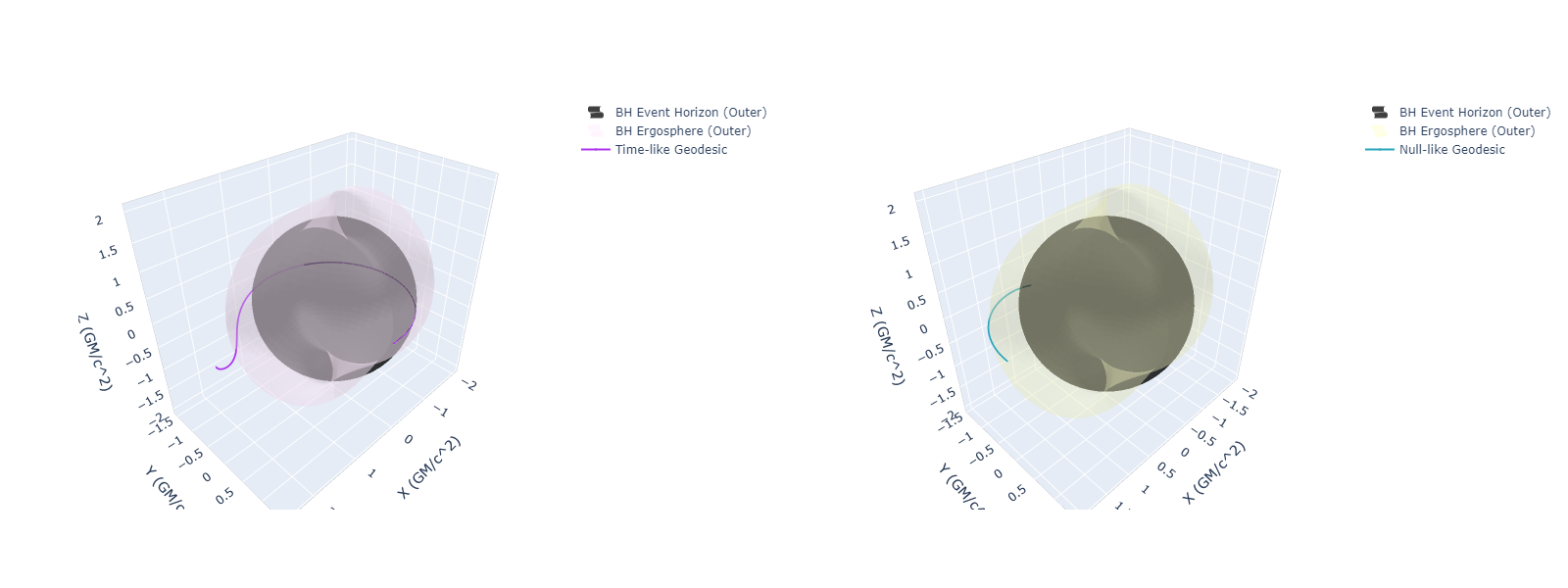
Kerr Null Reverse & Capture or Frame Dragging (Left) and Schwarzschild Precession (Right)

Final Kerr Null

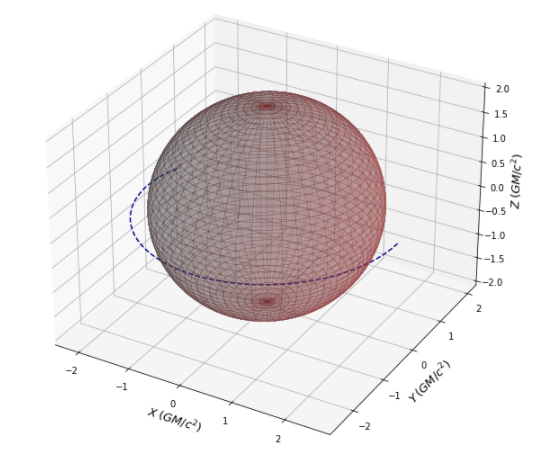
Kerr Time-like Capture and Null-like Capture

Null & Time

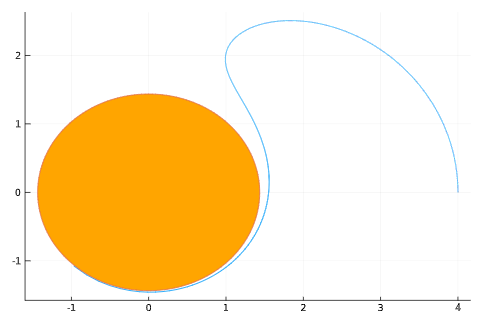
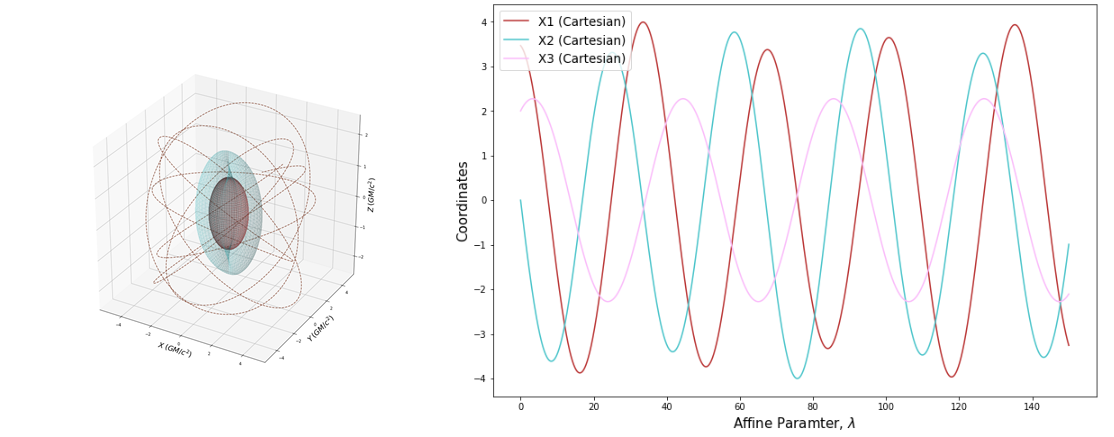
Kerr Time-like Whirl & Corresponding Parametric Plot

Kerr Whirl & Parametric

Kerr (Extremal, Spin = 0.99) Time-like Constant Radius Orbit Animation (60FPS):

Animation 60fps

(Open the animation .gif in a new tab, if it seems glitchy.)

Furthermore, I have added example Jupyter Notebooks for all the new changes and additions, as part of EinsteinPy Documentation, which can be accessed here (all notebooks, under the tags, metric, bodies, geodesic, coordinates).

Other Pull Requests and related Issues:

  1. Introduction of a name parameter in Metric Tensor (symbolic) | Fixed #449
  2. Mechanism for altering "tags" in tensor names | Fixed #454
  3. Added Alcubierre Warp Metric & related docs | Fixed #532

Project Experience:

Work left to do:

  • Add support for Radiative Transfer (RT) and redshift calculation
  • Plotting module for Black Hole Shadows (that uses the RT module)

Since, the discussions regarding the RT module were held in previous meetings, I intend to open a PR for it soon. The design will be partially, as discussed, in my EPE here, which in turned is based on RAPTOR and Odyssey. Only difference is the Hamilton-Jacobi approach, that we are taking, instead of solving the Geodesic equations. Moreover, I have some improvements planned for various modules, including the new geodesic module, some of which have been opened as issues, as linked below:

It has been an absolutely awesome experience working on this project with EinsteinPy, and with my mentors. The community has been really supportive and easy to talk to, in all my interactions. I would also like to thank my mentors, especially Shreyas, who was patient with me, while explaining a lot of things about code and was understanding, when I had to take a week off, due to my semester closure and submissions and then, COVID tests and procedures. He also helped me with the packaging of einsteinpy_geodesics, for which I am grateful. I would love to continue working with EinsteinPy, as a member and a contributor.

Finally, I thank Google Summer of Code and OpenAstronomy administrators for structuring and managing the program so well.

Clone this wiki locally