Categorising free polyominoes by collinearity of cells as well as size
A free polyomino is analogous to a simple connected planer graph where nodes are points on the lattice.
Free meaning we do not double count the dihedral symmetries (rotation / reflection)
The exponential growth of the number of polyominoes of size n is known up to n=45
We are considering just the Square and Hexagon polyominoes
For hexagon polyominoes the analogy to connected planer graphs uses a triangular lattice
We are considering cells/nodes/points that are collinear in 2 ways
Using the centres of the cells as points then collinear points in the plane means the cells are considered collinear.
- For a Square polyomino that means cells in the same row or column, or points on the grid lines of a square lattice.
- For a Hexagon polyomino that means cells on a line that runs perpendicular to the hexagon sides and through the centres (or for nodes/points the triangular lattice).
We are interested in counting the number of polyominoes that have a maximum number of cells collinear (k) for the 4 cases of (Square or Hexagon) x (Lattice or Plane).
See OEIS
- A377941 | Square | Lattice
- A377942 | Square | Plane
- A378014 | Hexagon | Lattice
- A378015 | Hexagon | Plane
A377941: Square Polyonimoes of size (n) with no more than (k) cells collinear on the Lattice
| k
n | 1 2 3 4 5 6 7 8 9 10 Total
------------------------------------------------------------------------------------------------------------------------
1 | 1 1
2 | 0 1 1
3 | 0 1 1 2
4 | 0 2 2 1 5
5 | 0 1 8 2 1 12
6 | 0 1 17 13 3 1 35
7 | 0 1 39 45 19 3 1 108
8 | 0 1 79 182 77 25 4 1 369
9 | 0 1 162 607 363 114 33 4 1 1285
10 | 0 1 301 2004 1539 593 170 41 5 1 4655
A377942: Square Polyonimoes of size (n) with no more than (k) cells collinear on the Plane
| k
n | 1 2 3 4 5 6 7 8 9 10 Total
------------------------------------------------------------------------------------------------------------------------
1 | 1 1
2 | 0 1 1
3 | 0 1 1 2
4 | 0 2 2 1 5
5 | 0 0 9 2 1 12
6 | 0 0 18 13 3 1 35
7 | 0 0 37 48 19 3 1 108
8 | 0 0 62 200 77 25 4 1 369
9 | 0 0 86 678 369 114 33 4 1 1285
10 | 0 0 78 2177 1590 593 170 41 5 1 4655
A378014: Hexagon Polyonimoes of size (n) with no more than (k) cells collinear on the Lattice
| k
n | 1 2 3 4 5 6 7 8 9 10 Total
------------------------------------------------------------------------------------------------------------------------
1 | 1 1
2 | 0 1 1
3 | 0 2 1 3
4 | 0 4 2 1 7
5 | 0 3 15 3 1 22
6 | 0 5 50 23 3 1 82
7 | 0 1 171 126 30 4 1 333
8 | 0 1 506 710 187 39 4 1 1448
9 | 0 1 1459 3520 1268 270 48 5 1 6572
10 | 0 1 3792 16617 7703 1948 364 59 5 1 30490
A378015: Hexagon Polyonimoes of size (n) with no more than (k) cells collinear on the Plane
| k
n | 1 2 3 4 5 6 7 8 9 10 Total
------------------------------------------------------------------------------------------------------------------------
1 | 1 1
2 | 0 1 1
3 | 0 2 1 3
4 | 0 4 2 1 7
5 | 0 2 16 3 1 22
6 | 0 3 52 23 3 1 82
7 | 0 0 169 129 30 4 1 333
8 | 0 0 477 740 187 39 4 1 1448
9 | 0 0 1245 3729 1274 270 48 5 1 6572
10 | 0 0 2750 17578 7785 1948 364 59 5 1 30490
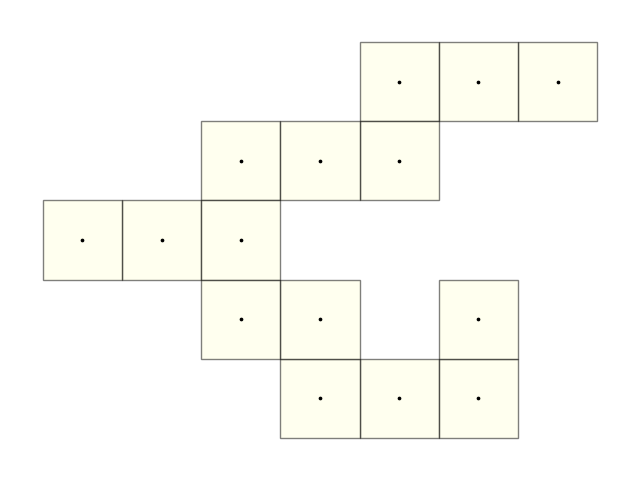
Square: n=15 , the only polyomino is
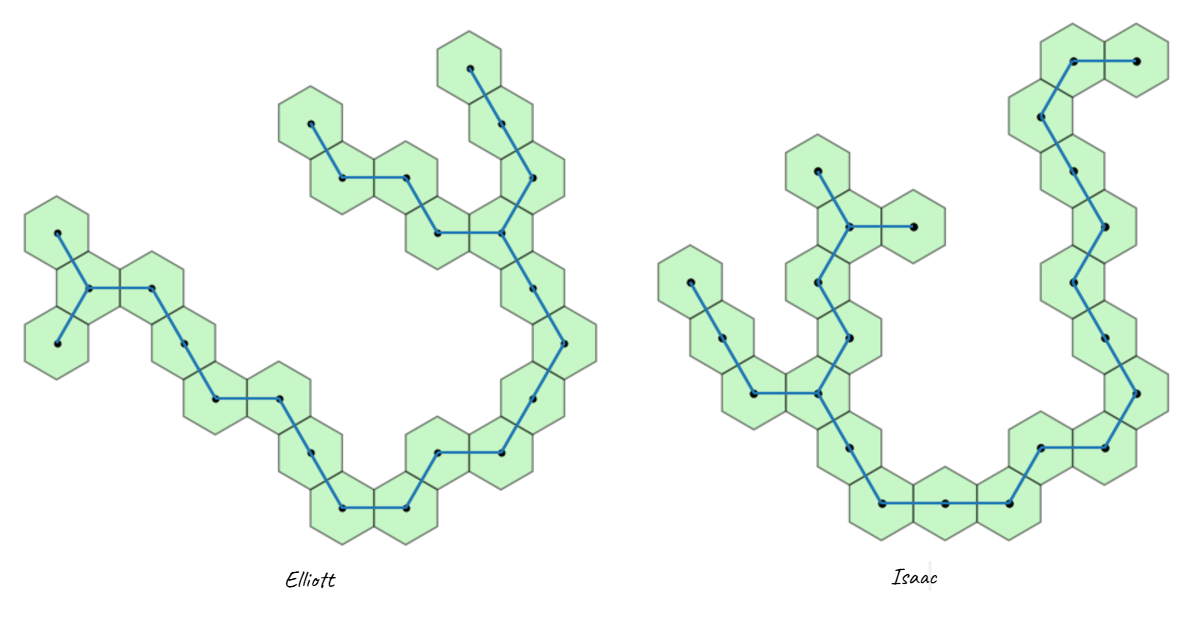
Hexagon: n=23 , the 2 hexagon polyominoes are:
The enumeration identifier is constructed by observing the pattern on a row/column grid using the usual coordinate system. This gives us a binary representation of each row, so the whole pattern is represented as a tuple of integers.