Skip to content

Commit

Permalink
downgrade to v1.0.1
Browse files Browse the repository at this point in the history
  • Loading branch information
@RCmags
RCmags committed Dec 4, 2022
1 parent e8c315b commit ee5049f
Show file tree
Hide file tree
Showing 9 changed files with 702 additions and 748 deletions.
23 changes: 9 additions & 14 deletions README.md
View file
Original file line number Diff line number Diff line change
@@ -1,14 +1,9 @@
# vector_datatype
This library includes structs for 3d vectors and quaternions. Both vectors and quaternions can perform basic operations such as addition, subtraction, multiplication, division, increment, decrement, etc. Other operations include the dot product, cross product, magnitude, and normalize.

Quaternions can also be defined as unit quaternions to represent rotations and can be used to rotate and scale vectors. Vectors are compatible with quaternions, and both types are compatible with arrays. A length-3 array can be added, subtracted, etc, from a vector or a quaternion, and a length-4 array can perform the same operations with a quaternion. See the examples for a complete list of the operations available for each type.

For more information on vector and quaternion operations, see these links:

- [Quaternions and rotations](http://danceswithcode.net/engineeringnotes/quaternions/quaternions.html)
- [Quaternion operations](http://graphics.stanford.edu/courses/cs348a-17-winter/Papers/quaternion.pdf)
- [Vector operations](http://emweb.unl.edu/Math/mathweb/vectors/vectors.html)

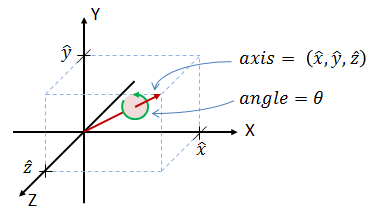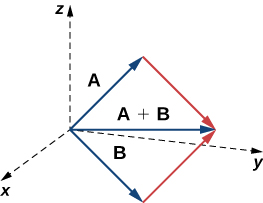![alt text](http://danceswithcode.net/engineeringnotes/quaternions/images/axis-angle.png)
![alt text](https://opentextbc.ca/calculusv3openstax/wp-content/uploads/sites/288/2019/08/CNX_Calc_Figure_12_02_011.jpg)

# vector_datatype
This is a library for 3d vectors and quaternions. It includes two structs to define each datatype. Both vectors and quaternions can perform basic operations such as addition, subtraction, multiplication, division, increment, decrement, and their analogs for multiplication and division. Vectors and quaternions are also compatible with each other.

Included are other operations such as vector dot product and cross product. Quaternions can also be constructed as unit quaternions to represent rotations. They can also rotate vectors. Both datatypes are compatible with arrays, meaning that a length-3 array can be added, subtracted, etc from a vector. This also applies to quaternions.

For more information on vector and quaternion operations, see these links:

- [Quaternion operations](http://graphics.stanford.edu/courses/cs348a-17-winter/Papers/quaternion.pdf)
- [Vector operations](http://emweb.unl.edu/Math/mathweb/vectors/vectors.html)
347 changes: 163 additions & 184 deletions examples/quaternion/quaternion.ino
View file
Original file line number Diff line number Diff line change
@@ -1,184 +1,163 @@
/*
This sketch shows to perform operations on quaternions and how to convert arrays to quaternions.
*/

#include <quaternion_type.h>

//======= Display functions =======

void printQuat( vec3_t vec ) {
Serial.print( vec.x );
Serial.print( ", " );
Serial.print( vec.y );
Serial.print( ", " );
Serial.print( vec.z );
}

void printQuat( quat_t quat ) {
Serial.print( quat.w );
Serial.print( ", " );
printQuat( quat.v );
}

template<typename T=quat_t>
void printOperation(String label, T input) {
Serial.println(label);
Serial.print( "\t\t(" );
printQuat(input);
Serial.print( ")\n\n" );
}

//========== Main program =========

void setup() {
Serial.begin(9600);
Serial.flush();

//-------- Quaternions --------
quat_t q1 = { 1, 0, 0, 0 };
quat_t q2 = { 0, 1, 0, 0 };
quat_t q3 = { 0, 0, 1, 0 };
quat_t q4 = { 0, 0, 0, 1 };
quat_t q5;

// 1. Basic operations:
// Quaternions can be manipulated in the same way as scalar values

// Addition
q5 = q1 + q2;
printOperation( "1. Addition: ", q5 );

// Subtraction
q5 = q2 - q3;
printOperation( "2. Subtraction: ", q5 );

// Negation:
q5 = -q5;
printOperation( "3. Negation: ", q5 );

// Increment:
q5 += q4;
printOperation( "4. Increment: ", q5 );

// Decrement:
q5 -= q1;
printOperation( "5. Decrement: ", q5 );

// Scalar product:
q5 = q5*5;
printOperation( "6A. Scalar product: ", q5 );
// Reverse order
q5 = -3*q5;
printOperation( "6B. Scalar product (reverse order): ", q5 );

// Scalar divide:
q5 = q5/8;
printOperation( "7. Scalar divide: ", q5 );

// Scalar self multiply:
q5 *= 10;
printOperation( "8. Scalar self multiply: ", q5 );

// Scalar self divide:
q5 /= 2;
printOperation( "9. Scalar self divide: ", q5 );

// 2. Quaternion multiplication and division:
/* Quats can be multiplied together to generate a new quaternion. This can encode multiple rotations */

// Multiply
q5 = q5*q1;
printOperation( "10. Quaternion multiply: ", q5 );

// Divide
q5 = q5/q2;
printOperation( "11. Quaternion division: ", q5 );

// Self multiply
q5 *= q3;
printOperation( "12. Quaternion self multiply: ", q5 );

// Self divide
q5 /= q4;
printOperation( "13. Quaternion self divide: ", q5 );

// 3. Important operations:

// Conjugate
printOperation( "14. Conjugate: ", q5.conj() );

// Normalize
printOperation( "15. Normalize: ", q5.norm() );

// Inner product
Serial.print( "16. Inner product: " );
Serial.println( q5.inner() );

// Magnitude
Serial.print( "17. Magnitude: " );
Serial.print( q5.mag() );
Serial.print("\n\n");

// 4. Compatibility with arrays:
/* In operations between a quaternion and an array, the array will be interpreted as a quaternion */
float arr[] = {1, 2, 3, 4};

printOperation( "18. Quaternion and array addition: " , q5 + arr );
printOperation( "19. Quaternion and array subtraction: ", q5 - arr );
printOperation( "20. Quaternion and array multiply: " , q5 * arr );

// Operations with arrays are not converted to a quaternion type. These need to be explicitly converted.
printOperation( "21. Array conversion (multiply): ", quat_t(arr)*3 );
printOperation( "22. Array conversion (divide): " , quat_t(arr)/10 );

//-- Compatibility with vectors
/* Vectors will be interpreted as quaternions without a scalar value (w = 0) */
vec3_t vec = {1, 2, 3};

printOperation( "23. Quaternion and vector addition: " , q5 + vec );
printOperation( "24. Quaternion and vector subtraction: ", q5 - vec );
printOperation( "25. Quaternion and vector multiply; " , q5 * vec );

// 5. Vector rotation: a quaternion can rotate and stretch a 3D vector

// A) Rotate by angle about axis
constexpr float angle = (PI/180.0) * 30;
vec3_t axis = { 0, 1, 0 };

/* Can choose between LARGE_ANGLE and SMALL_ANGLE.
* Use SMALL_ANGLE for a small angle approximation (less than 30 deg) and faster excecution */
quat_t qrot; qrot.setRotation( axis, angle, SMALL_ANGLE );
vec3_t vec_rot; // rotated vector
vec = { 1,0,0 }; // initial vector

// Rotate into angle
vec_rot = qrot.rotate(vec, GLOBAL_FRAME);

printOperation<vec3_t>( "26. Rotate by axis and angle (Global): ", vec_rot );

// Rotate away from angle
vec_rot = qrot.rotate(vec, LOCAL_FRAME);

printOperation<vec3_t>( "27. Rotate by axis and angle (local): ", vec_rot );

// B) Rotate by unit vector of magnitude sin(angle)
qrot.setRotation( axis, LARGE_ANGLE );
vec_rot = qrot.rotate(vec, GLOBAL_FRAME);

printOperation<vec3_t>( "28. Rotate by unit vector: ", vec_rot );

// 6. Axes projections: can choose between GLOBAL_FRAME and LOCAL_FRAME
/* GLOBAL_FRAME projects local axis-vectors to global coordinates
* LOCAL_FRAME projects global axis-vectors to local coordinates */
qrot.setRotation( axis, angle, LARGE_ANGLE );

vec3_t x = qrot.axisX(GLOBAL_FRAME);
vec3_t y = qrot.axisY(GLOBAL_FRAME);
vec3_t z = qrot.axisZ(GLOBAL_FRAME);

printOperation<vec3_t>( "29. X-axis vector: ", x );
printOperation<vec3_t>( "30. Y-axis vector: ", y );
printOperation<vec3_t>( "31. Z-axis vector: ", z );
}

void loop() {}
/*
This sketch shows to perform operations on quaternions and how to convert arrays to quaternions.
*/

#include <quaternion_type.h>

// Display functions

void printVector( vec3_t vec ) {
Serial.print( vec.x );
Serial.print( ", " );
Serial.print( vec.y );
Serial.print( ", " );
Serial.print( vec.z );
Serial.println();
}

void printQuat( quat_t quat ) {
Serial.print( quat.w );
Serial.print( ", " );
printVector( quat.v );
}

void setup() {
Serial.begin(9600);
Serial.flush();

//-------- Quaternions --------
quat_t q1 = { 1, 0, 0, 0 };
quat_t q2 = { 0, 1, 0, 0 };
quat_t q3 = { 0, 0, 1, 0 };
quat_t q4 = { 0, 0, 0, 1 };
quat_t q5;

//-- Operations:
// Quaternions can be manipulated in the same way as scalar values

// Addition
q5 = q1 + q2;
printQuat( q5 );

// Subtraction
q5 = q5 - q3;
printQuat( q5 );

// Negation:
q5 = -q5;
printQuat( q5 );

// Increment:
q5 += q4;
printQuat( q5 );

// Decrement:
q5 -= q1;
printQuat( q5 );

// Scalar product:
q5 = q5*5;
printQuat( q5 );
// Reverse order
q5 = -3*q5;
printQuat( q5 );

// Scalar divide:
q5 = q5/8;
printQuat( q5 );

// Scalar self multiply:
q5 *= 10;
printQuat( q5 );

// Scalar self divide:
q5 /= 20;
printQuat( q5 );

//- Important operations:
// These are useful operations that are commonly encountered. They are explicitly named for clarity.

// Conjugate
printQuat( q5.conj() );

// Inner product
Serial.println( q5.inner() );

// Magnitude
Serial.println( q5.mag() );

// Normalize
printQuat( q5.norm() );

//- Quaternion multiplication and division:
// Quats can be multiplied together to generate a new quaternion. This can encode simultaneous rotations.

// Multiply
q5 = q5*q2;
printQuat( q5 );

// Divide
q5 = q5/q2;
printQuat( q5 );

// Self multiply
q5 *= q4;
printQuat( q5 );

// Self divide
q5 /= q3;
printQuat( q5 );

//- Vector rotation:
// A quaternion can rotate and stretch a 3D vector

// A) Rotate by angle about axis
constexpr float angle = (PI/180.0) * 30;
vec3_t axis = { 0, 1, 0 };

quat_t qrot;
qrot.setRotation( false, axis, angle ); // Unit quaternion: true = small angle approximation ; false = exact rotation
vec3_t vec = { 1,0,0 }; // Vector to rotate

// Rotate into angle
printQuat( qrot.rotate(true, vec) );
// Rotate away from angle
printQuat( qrot.rotate(false, vec) );

// Axes projections
printVector( qrot.axisX(true) );
printVector( qrot.axisY(true) );
printVector( qrot.axisZ(true) );

// B) Rotate by unit vector
qrot.setRotation( false, axis ); // Unit vector has magniude sin(angle)

printQuat( qrot.rotate(true, vec) );

//-- Compatibility with arrays:
// In operations between a quaternion and an array, the array will be interpreted as a quaternion.

float arr[] = {1, 2, 3, 4};

printQuat( qrot + arr );
printQuat( qrot - arr );
printQuat( qrot*arr );

// Operations with arrays are not converted to a quaternion type. These need to be explicitly converted.
printQuat( quat_t(arr)*3 );
printQuat( quat_t(arr)/10 );

printQuat( qrot.rotate(true, vec) );

//-- Compatibility with vectors
// Vectors will be interpreted as quaternions without a scalar value (w = 0)

vec3_t v = {1, 2, 3};
quat_t q6 = {1, 3, 3, 3};

printQuat( q6 + v );
printQuat( q6 - v );
printQuat( q6*v );
}

void loop() {}
Loading

0 comments on commit ee5049f

Please sign in to comment.