sortingAlgorithms.md

Sorting Algorithm Cheat Sheet

Updated: Jan 22, 2025 Author: Navdeep Singh

1. Insertion Sort

Insertion sort is a simple sorting algorithm that builds the final sorted array one item at a time.

It sorts the array by inserting each element into its correct position. At any point, the left side of the array is sorted while the right side is unsorted. We choose the first element in the unsorted array and insert it into the sorted array in the correct position. We then repeat this process for the next element in the unsorted array.

It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort.

::tabs-start

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

public class InsertionSort {
    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int key = arr[i];
            int j = i - 1;
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j--;
            }
            arr[j + 1] = key;
        }
    }
}

void insertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

function insertionSort(arr) {
    for (let i = 1; i < arr.length; i++) {
        let key = arr[i];
        let j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
    return arr;
}

::tabs-end

Time Complexity: $O(n^2)$ Space Complexity: $O(1)$

2. Merge Sort

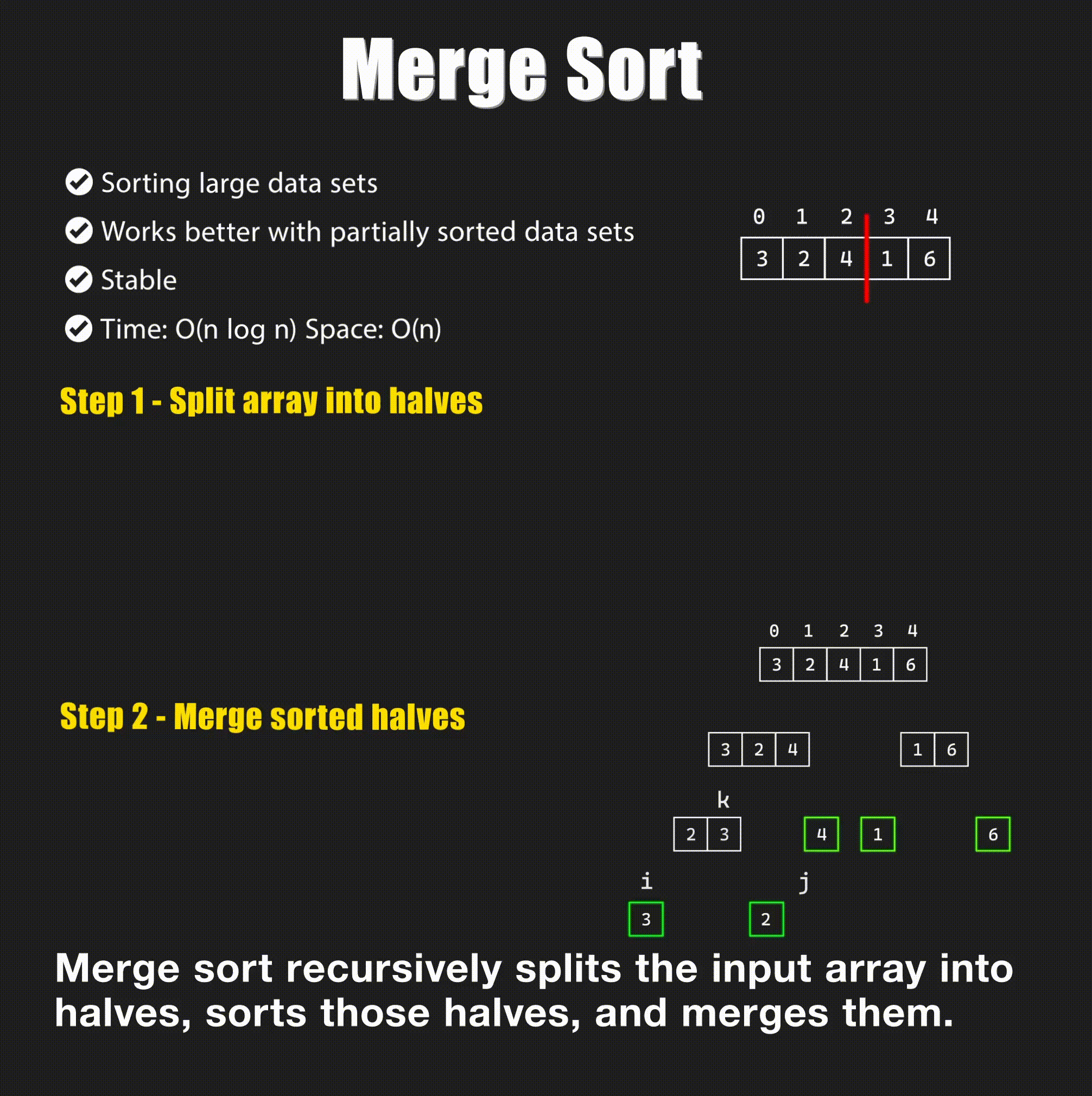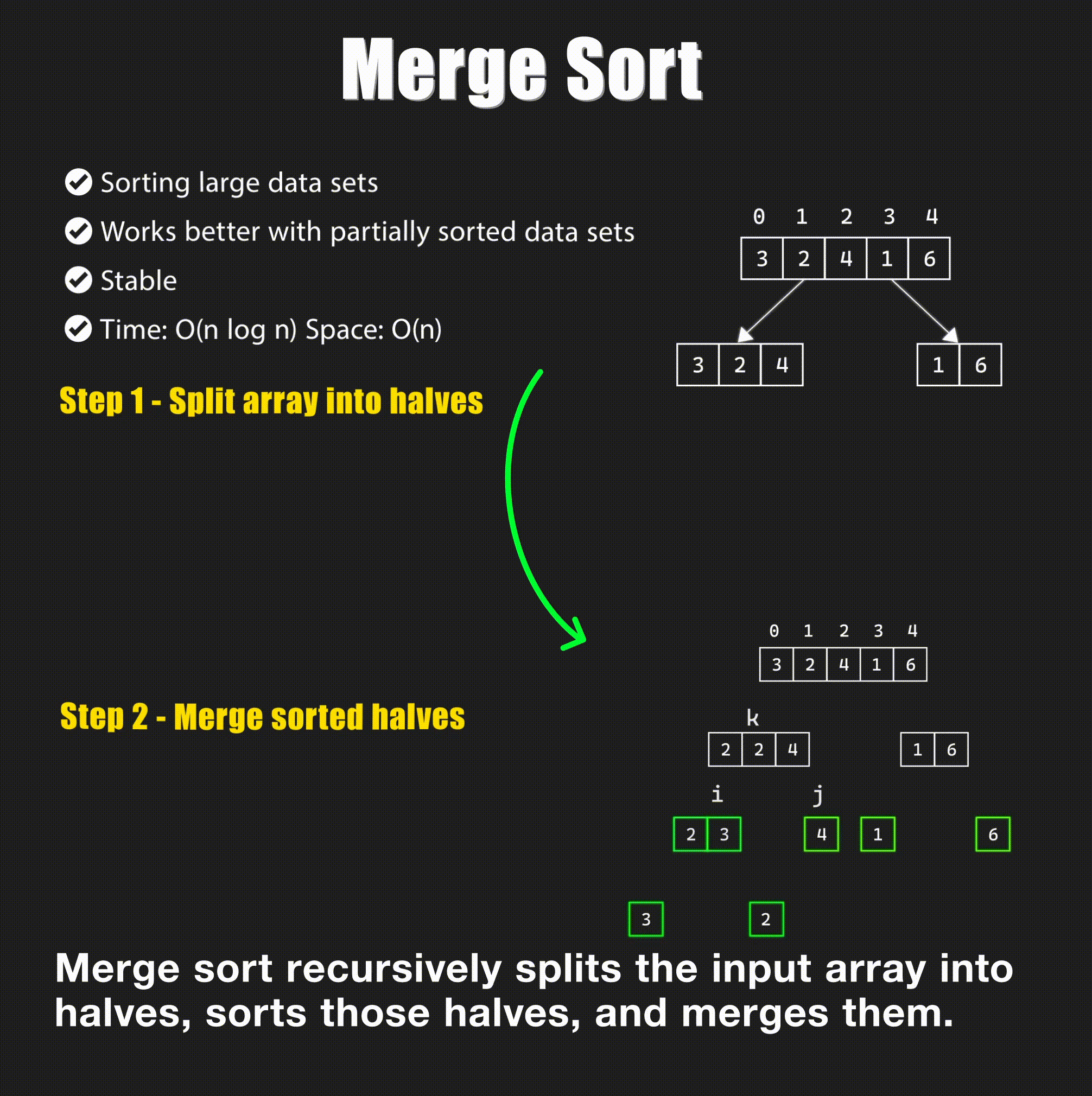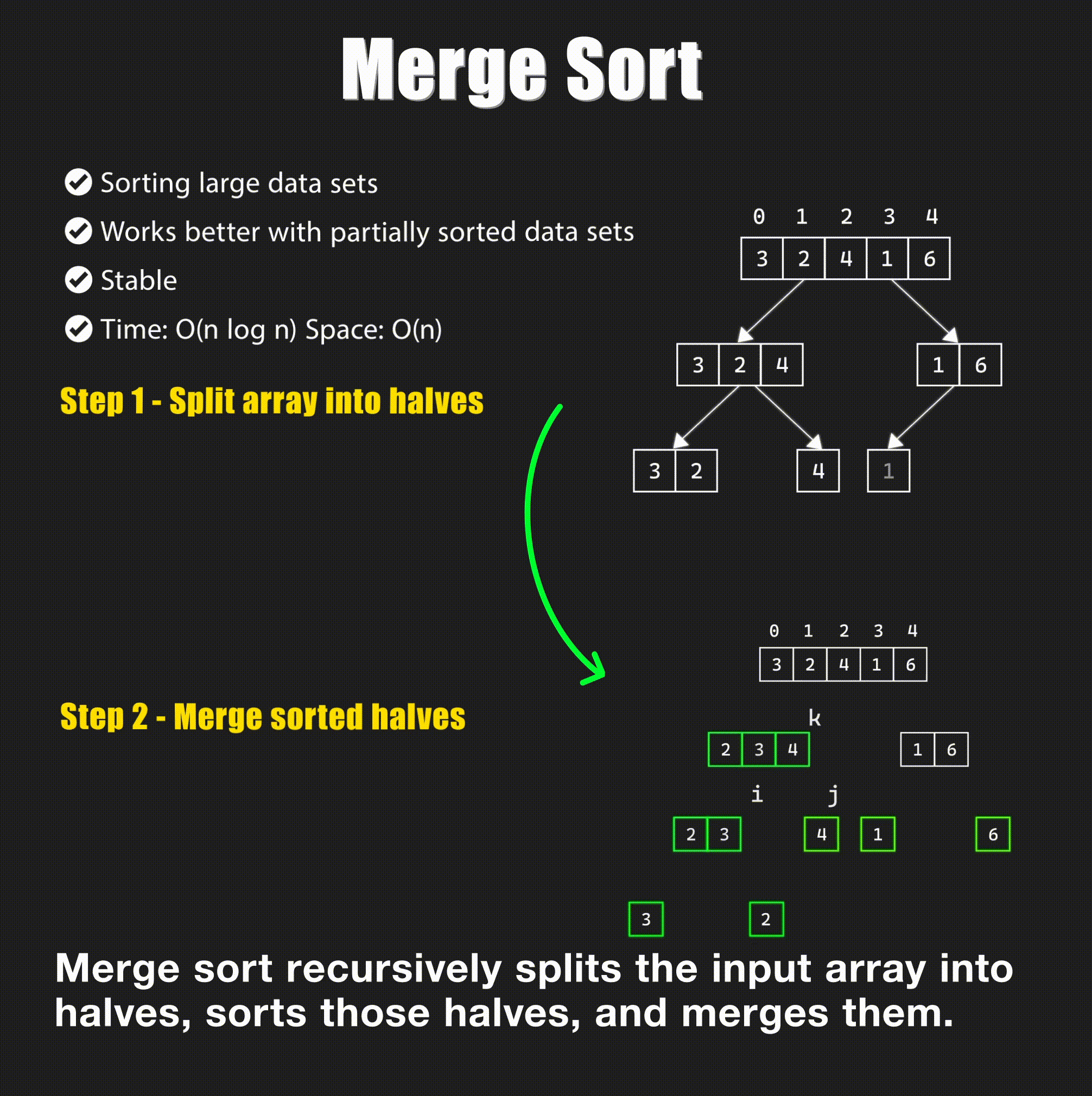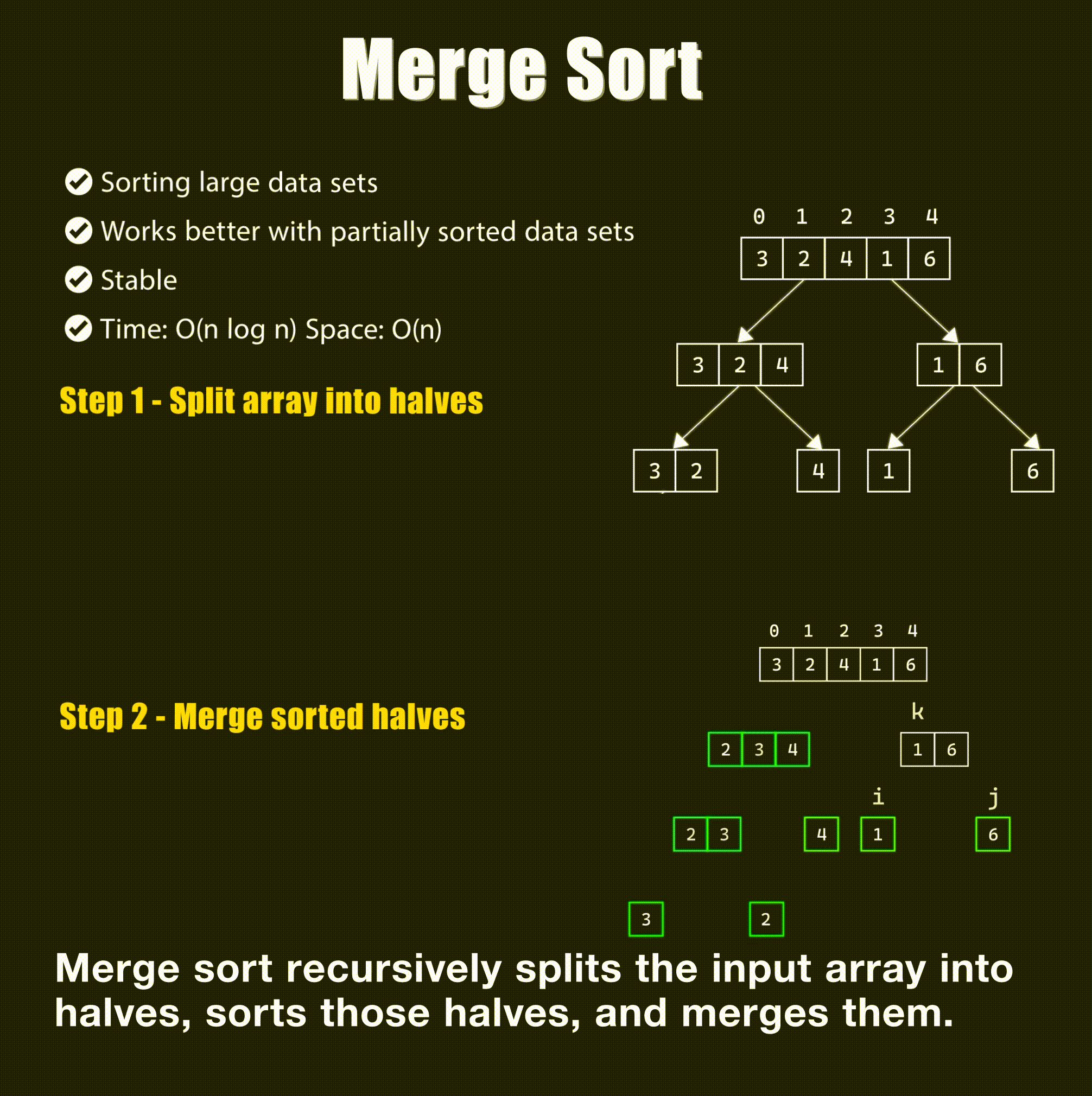
Merge sort is a divide and conquer algorithm that divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves.

::tabs-start

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
        
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    
    return merge(left, right)

def merge(left, right):
    result = []
    i = j = 0
    
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
            
    result.extend(left[i:])
    result.extend(right[j:])
    return result

public class MergeSort {
    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);
            merge(arr, left, mid, right);
        }
    }
    
    private static void merge(int[] arr, int left, int mid, int right) {
        int n1 = mid - left + 1;
        int n2 = right - mid;
        
        int[] L = new int[n1];
        int[] R = new int[n2];
        
        for (int i = 0; i < n1; i++)
            L[i] = arr[left + i];
        for (int j = 0; j < n2; j++)
            R[j] = arr[mid + 1 + j];
            
        int i = 0, j = 0, k = left;
        
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }
        
        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }
        
        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }
}

void merge(int arr[], int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;
    
    int* L = new int[n1];
    int* R = new int[n2];
    
    for (int i = 0; i < n1; i++)
        L[i] = arr[left + i];
    for (int j = 0; j < n2; j++)
        R[j] = arr[mid + 1 + j];
        
    int i = 0, j = 0, k = left;
    
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
    
    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }
    
    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
    
    delete[] L;
    delete[] R;
}

void mergeSort(int arr[], int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}

function mergeSort(arr) {
    if (arr.length <= 1) return arr;
    
    const mid = Math.floor(arr.length / 2);
    const left = mergeSort(arr.slice(0, mid));
    const right = mergeSort(arr.slice(mid));
    
    return merge(left, right);
}

function merge(left, right) {
    const result = [];
    let i = 0, j = 0;
    
    while (i < left.length && j < right.length) {
        if (left[i] <= right[j]) {
            result.push(left[i]);
            i++;
        } else {
            result.push(right[j]);
            j++;
        }
    }
    
    return result.concat(left.slice(i)).concat(right.slice(j));
}

::tabs-end

Time Complexity: $O(n log n)$ Space Complexity: $O(n)$

3. Quick Sort

Quick sort is a divide and conquer algorithm that picks an element as pivot and partitions the given array around the picked pivot.

Unlike merge sort, quick sort is not a stable sort. This means that the input order of equal elements in the sorted output may not be preserved.

::tabs-start

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    
    return quick_sort(left) + middle + quick_sort(right)

public class QuickSort {
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int pi = partition(arr, low, high);
            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }
    
    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = low - 1;
        
        for (int j = low; j < high; j++) {
            if (arr[j] < pivot) {
                i++;
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        
        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;
        
        return i + 1;
    }
}

int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = low - 1;
    
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            std::swap(arr[i], arr[j]);
        }
    }
    
    std::swap(arr[i + 1], arr[high]);
    return i + 1;
}

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

function quickSort(arr) {
    if (arr.length <= 1) return arr;
    
    const pivot = arr[Math.floor(arr.length / 2)];
    const left = arr.filter(x => x < pivot);
    const middle = arr.filter(x => x === pivot);
    const right = arr.filter(x => x > pivot);
    
    return [...quickSort(left), ...middle, ...quickSort(right)];
}

::tabs-end

Time Complexity: $O(n log n)$ Space Complexity: $O(log n)$

4. Bucket Sort

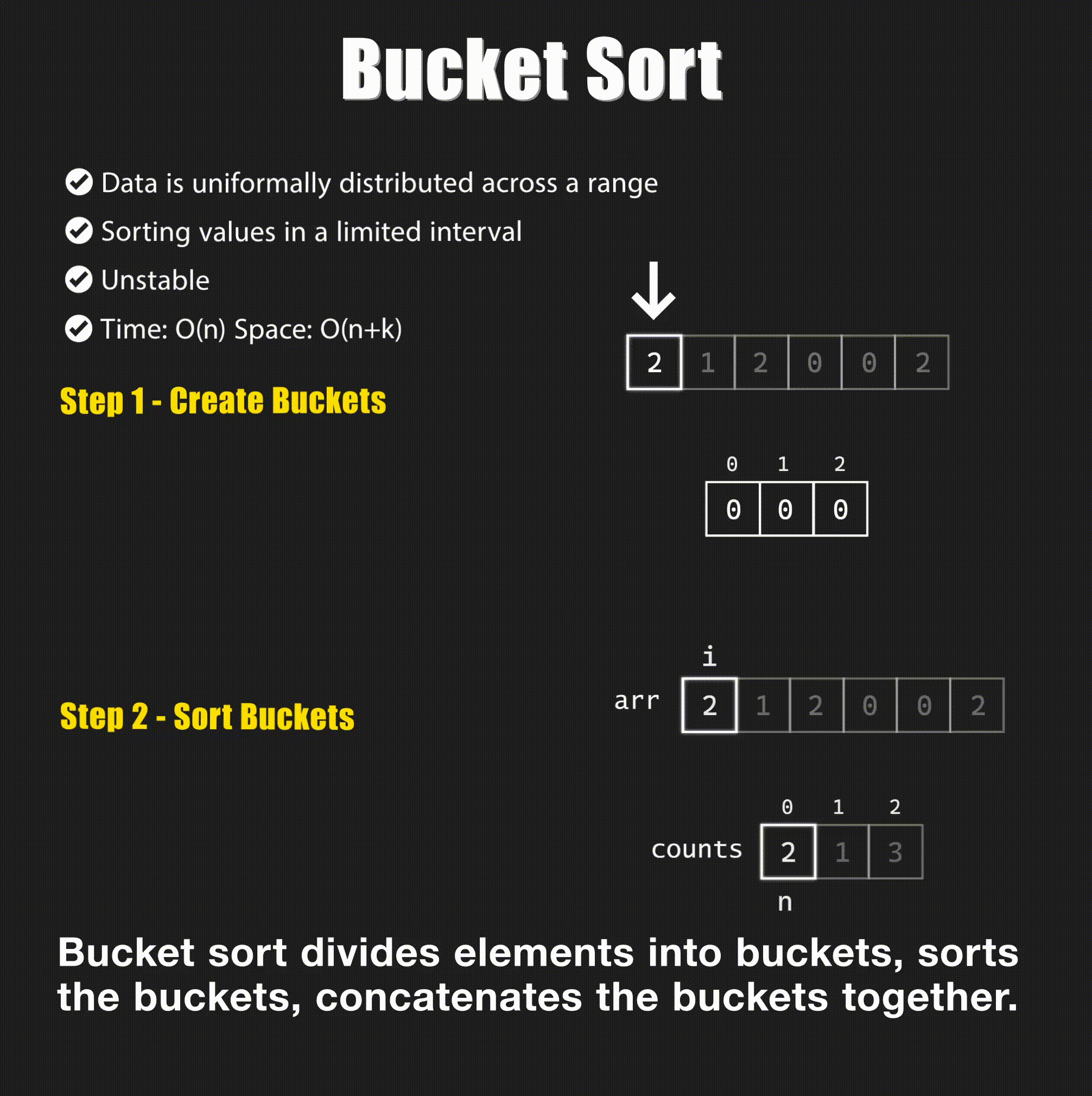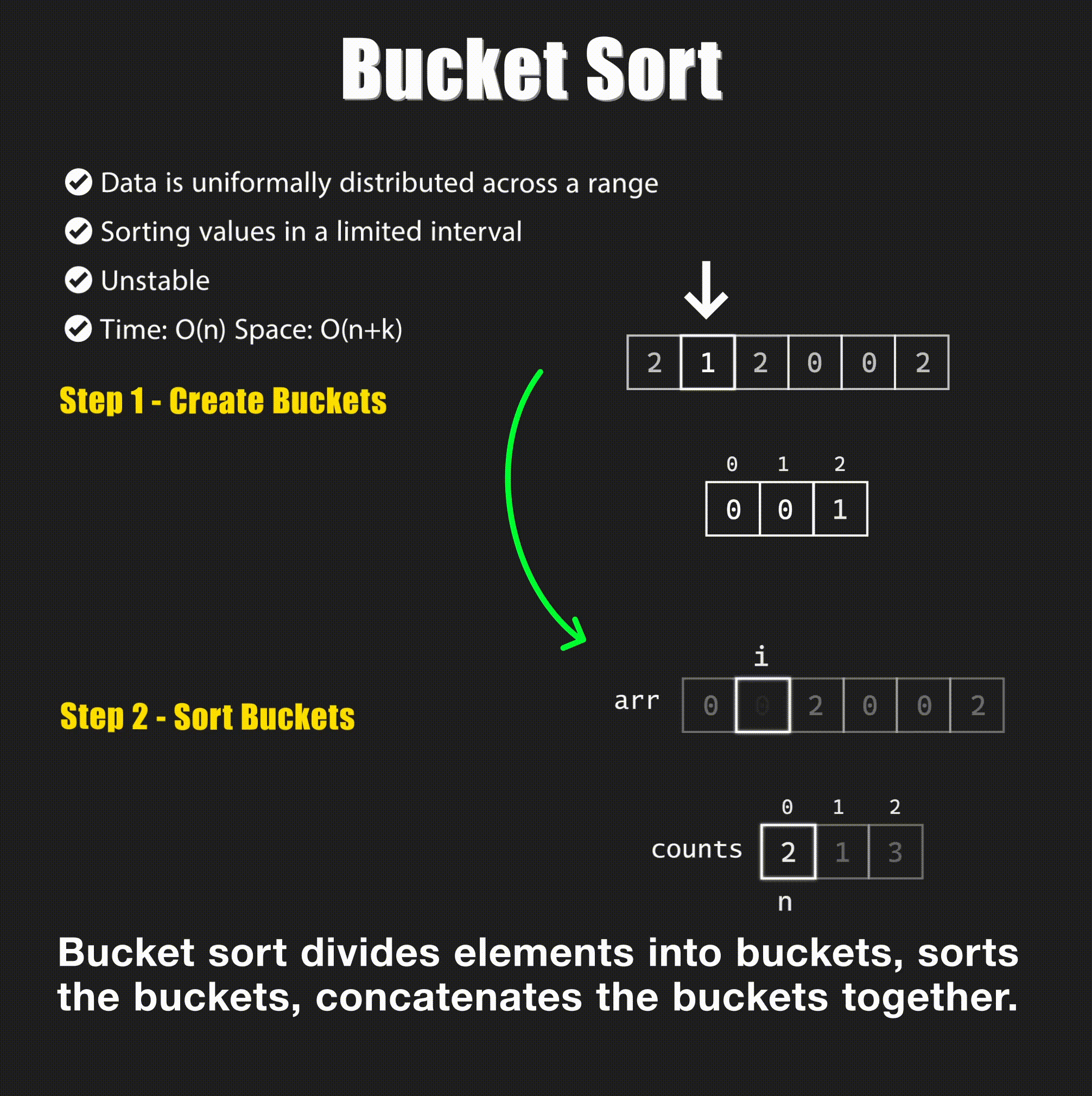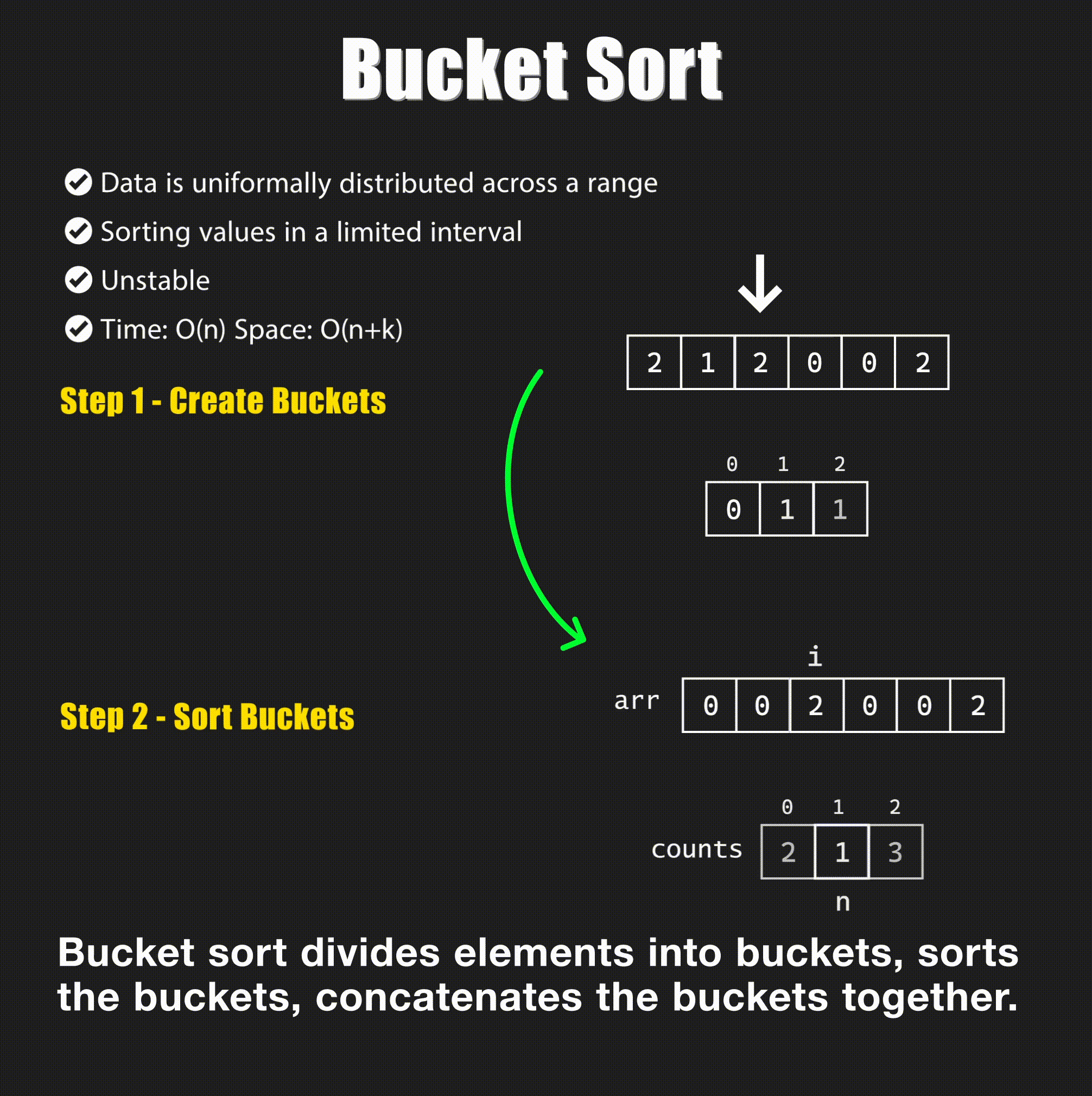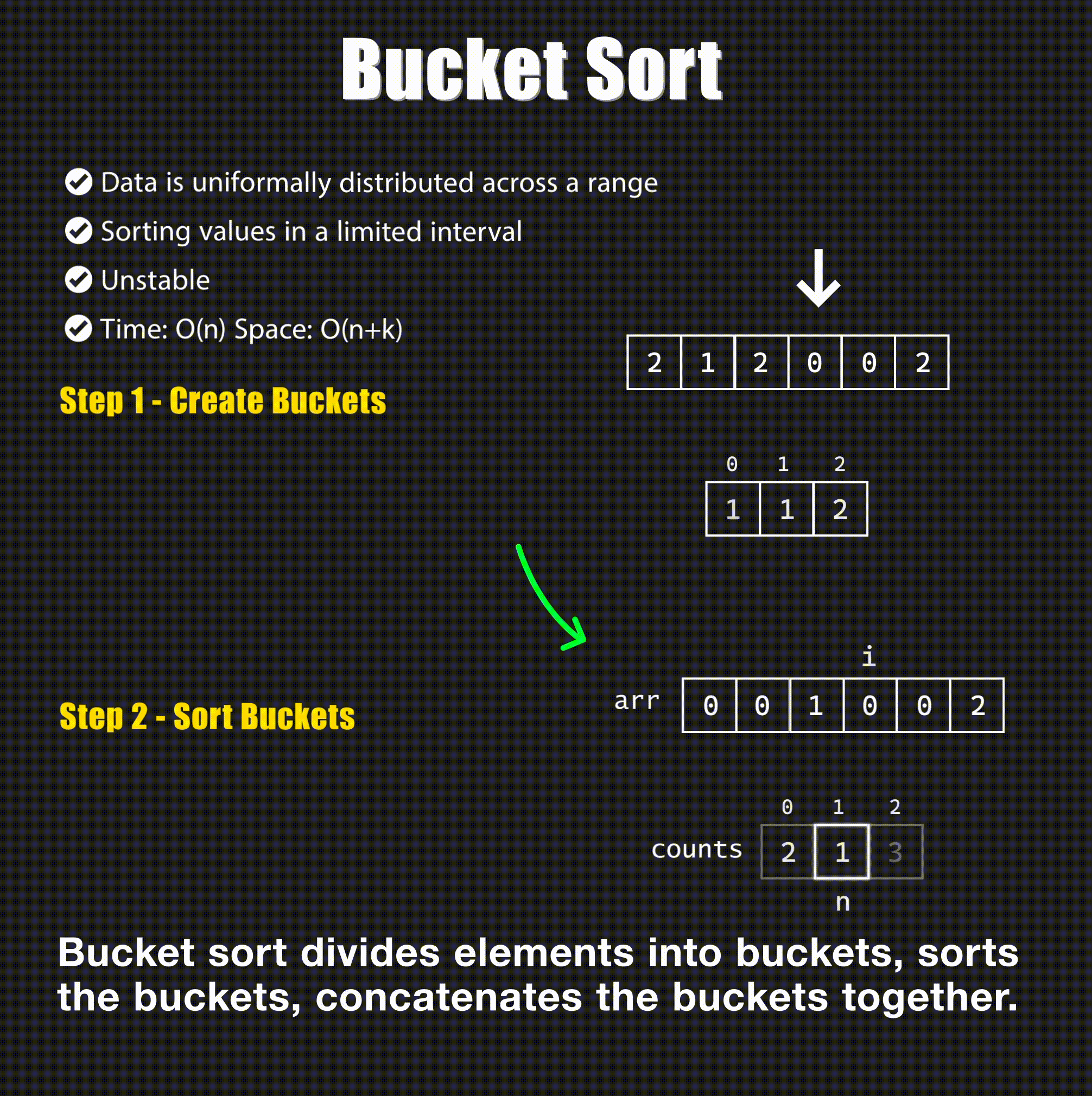
Bucket sort is a sorting algorithm that distributes the elements of an array into several groups, called buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.

::tabs-start

def bucket_sort(arr):
    if not arr:
        return arr
        
    # Find range of values
    max_val, min_val = max(arr), min(arr)
    
    # Create buckets
    bucket_range = (max_val - min_val) / len(arr)
    buckets = [[] for _ in range(len(arr) + 1)]
    
    # Distribute input array values into buckets
    for i in arr:
        if i == max_val:
            bucket_idx = len(arr) - 1
        else:
            bucket_idx = int((i - min_val) / bucket_range)
        buckets[bucket_idx].append(i)
    
    # Sort individual buckets
    for bucket in buckets:
        bucket.sort()
    
    # Concatenate all buckets into final array
    result = []
    for bucket in buckets:
        result.extend(bucket)
    
    return result

public class BucketSort {
    public static void bucketSort(float[] arr) {
        if (arr == null || arr.length <= 0)
            return;
            
        // Create buckets
        @SuppressWarnings("unchecked")
        ArrayList<Float>[] buckets = new ArrayList[arr.length];
        
        for (int i = 0; i < arr.length; i++)
            buckets[i] = new ArrayList<Float>();
            
        // Distribute input array values into buckets
        for (float item : arr) {
            int bucketIndex = (int) (item * arr.length);
            buckets[bucketIndex].add(item);
        }
        
        // Sort individual buckets
        for (ArrayList<Float> bucket : buckets) {
            Collections.sort(bucket);
        }
        
        // Concatenate all buckets into final array
        int index = 0;
        for (ArrayList<Float> bucket : buckets) {
            for (float item : bucket) {
                arr[index++] = item;
            }
        }
    }
}

void bucketSort(float arr[], int n) {
    if (n <= 0) return;
    
    // Create buckets
    vector<vector<float>> buckets(n);
    
    // Distribute input array values into buckets
    for (int i = 0; i < n; i++) {
        int bucketIndex = n * arr[i];
        buckets[bucketIndex].push_back(arr[i]);
    }
    
    // Sort individual buckets
    for (int i = 0; i < n; i++) {
        sort(buckets[i].begin(), buckets[i].end());
    }
    
    // Concatenate all buckets into final array
    int index = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < buckets[i].size(); j++) {
            arr[index++] = buckets[i][j];
        }
    }
}

function bucketSort(arr) {
    if (arr.length === 0) return arr;
    
    // Find range of values
    let max = Math.max(...arr);
    let min = Math.min(...arr);
    
    // Create buckets
    let bucketCount = arr.length;
    let buckets = new Array(bucketCount).fill().map(() => []);
    let bucketRange = (max - min) / (bucketCount - 1);
    
    // Distribute input array values into buckets
    for (let num of arr) {
        if (num === max) {
            buckets[bucketCount - 1].push(num);
        } else {
            let bucketIndex = Math.floor((num - min) / bucketRange);
            buckets[bucketIndex].push(num);
        }
    }
    
    // Sort individual buckets
    buckets = buckets.map(bucket => bucket.sort((a, b) => a - b));
    
    // Concatenate all buckets into final array
    return [].concat(...buckets);
}

::tabs-end

Time Complexity: $O(n)$ Space Complexity: $O(n + k)$, where $k$ is the number of buckets