forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy pathcnn-fp.md
108 lines (53 loc) · 6.79 KB
/
cnn-fp.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
# 卷积神经网络\(CNN\)前向传播算法
---
在[卷积神经网络\(CNN\)模型结构](/dl/cnn/cnn-arch.md)中,我们对CNN的模型结构做了总结,这里我们就在CNN的模型基础上,看看CNN的前向传播算法是什么样子的。重点会和传统的DNN比较讨论。
# 1. 回顾CNN的结构
在上一篇里,我们已经讲到了CNN的结构,包括输出层,若干的卷积层+ReLU激活函数,若干的池化层,DNN全连接层,以及最后的用Softmax激活函数的输出层。这里我们用一个彩色的汽车样本的图像识别再从感官上回顾下CNN的结构。图中的CONV即为卷积层,POOL即为池化层,而FC即为DNN全连接层,包括了我们上面最后的用Softmax激活函数的输出层。
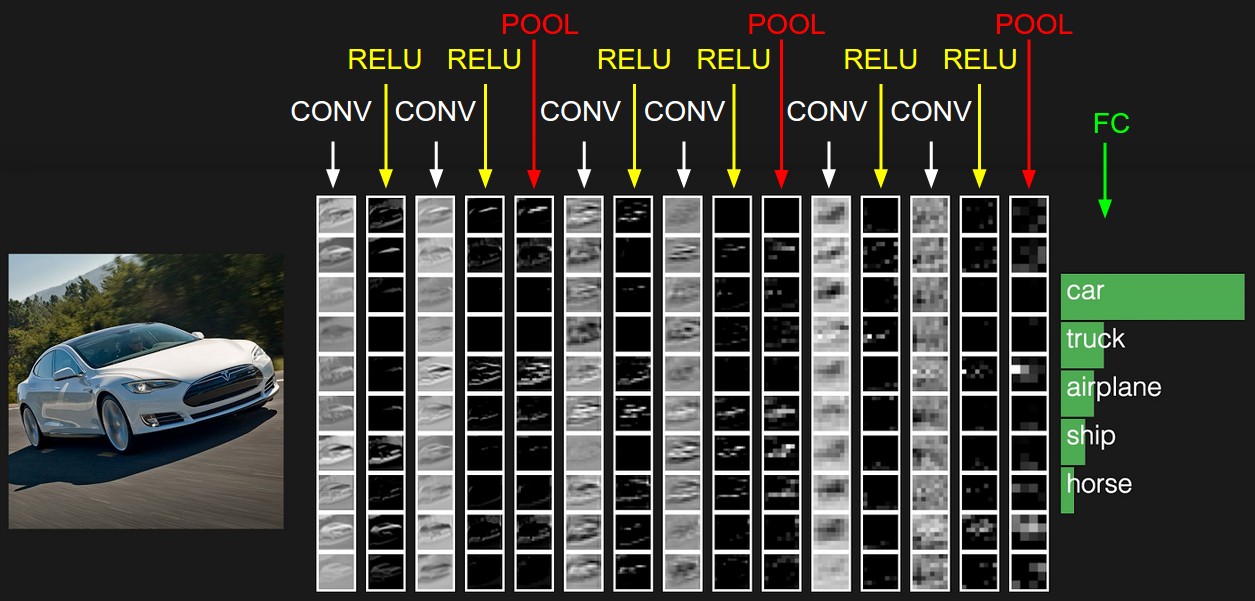
从上图可以看出,要理顺CNN的前向传播算法,重点是输入层的前向传播,卷积层的前向传播以及池化层的前向传播。而DNN全连接层和用Softmax激活函数的输出层的前向传播算法我们在讲DNN时已经讲到了。
# 2. CNN输入层前向传播到卷积层
输入层的前向传播是CNN前向传播算法的第一步。一般输入层对应的都是卷积层,因此我们标题是输入层前向传播到卷积层。
我们这里还是以图像识别为例。
先考虑最简单的,样本都是二维的黑白图片。这样输入层X就是一个矩阵,矩阵的值等于图片的各个像素位置的值。这时和卷积层相连的卷积核W就也是矩阵。
如果样本都是有RGB的彩色图片,这样输入X就是3个矩阵,即分别对应R,G和B的矩阵,或者说是一个张量。这时和卷积层相连的卷积核W就也是张量,对应的最后一维的维度为3.即每个卷积核都是3个子矩阵组成。
同样的方法,对于3D的彩色图片之类的样本,我们的输入X可以是4维,5维的张量,那么对应的卷积核W也是个高维的张量。
不管维度多高,对于我们的输入,前向传播的过程可以表示为:$$a^2= \sigma(z^2) = \sigma(a^1*W^2 +b^2)$$
其中,上标代表层数,星号代表卷积,而b代表我们的偏倚,$$\sigma$$为激活函数,这里一般都是ReLU。
和DNN的前向传播比较一下,其实形式非常的像,只是我们这儿是张量的卷积,而不是矩阵的乘法。同时由于W是张量,那么同样的位置,W参数的个数就比DNN多很多了。
为了简化我们的描述,本文后面如果没有特殊说明,我们都默认输入是3维的张量,即用RBG可以表示的彩色图片。
这里需要我们自己定义的CNN模型参数是:
1) 一般我们的卷积核不止一个,比如有K个,那么我们输入层的输出,或者说第二层卷积层的对应的输入就K个。
2) 卷积核中每个子矩阵的的大小,一般我们都用子矩阵为方阵的卷积核,比如FxF的子矩阵。
3) 填充padding(以下简称P),我们卷积的时候,为了可以更好的识别边缘,一般都会在输入矩阵在周围加上若干圈的0再进行卷积,加多少圈则P为多少。
4) 步幅stride(以下简称S),即在卷积过程中每次移动的像素距离大小。
这些参数我们在上一篇都有讲述。
# 3. 隐藏层前向传播到卷积层
现在我们再来看普通隐藏层前向传播到卷积层时的前向传播算法。
假设隐藏层的输出是M个矩阵对应的三维张量,则输出到卷积层的卷积核也是M个子矩阵对应的三维张量。这时表达式和输入层的很像,也是$$a^l= \sigma(z^l) =\sigma(a^{l-1}*W^l +b^l)$$
其中,上标代表层数,星号代表卷积,而b代表我们的偏倚,$$\sigma$$为激活函数,这里一般都是ReLU。
也可以写成M个子矩阵卷积后对应位置相加的形式,即:$$a^l= \sigma(z^l) =\sigma(\sum\limits_{k=1}^{M}z_k^l) = \sigma(\sum\limits_{k=1}^{M}(a_k^{l-1}*W_k^l +b_k^l))$$
和上一节唯一的区别仅仅在于,这里的输入是隐藏层来的,而不是我们输入的原始图片样本形成的矩阵。
需要我们定义的CNN模型参数也和上一节一样,这里我们需要定义卷积核的个数K,卷积核子矩阵的维度F,填充大小P以及步幅S。
# 4. 隐藏层前向传播到池化层
池化层的处理逻辑是比较简单的,我们的目的就是对输入的矩阵进行缩小概括。比如输入的若干矩阵是NxN维的,而我们的池化大小是kxk的区域,则输出的矩阵都是$$\frac{N}{k} \times \frac{N}{k}$$维的。
这里需要需要我们定义的CNN模型参数是:
1)池化区域的大小k
2)池化的标准,一般是MAX或者Average。
# 5. 隐藏层前向传播到全连接层
由于全连接层就是普通的DNN模型结构,因此我们可以直接使用DNN的前向传播算法逻辑,即:$$a^l = \sigma(z^l) = \sigma(W^la^{l-1} + b^l)$$
这里的激活函数一般是sigmoid或者tanh。
经过了若干全连接层之后,最后的一层为Softmax输出层。此时输出层和普通的全连接层唯一的区别是,激活函数是softmax函数。
这里需要需要我们定义的CNN模型参数是:
1)全连接层的激活函数
2)全连接层各层神经元的个数
# 6. CNN前向传播算法小结
有了上面的基础,我们现在总结下CNN的前向传播算法。
输入:1个图片样本,CNN模型的层数L和所有隐藏层的类型,对于卷积层,要定义卷积核的大小K,卷积核子矩阵的维度F,填充大小P,步幅S。对于池化层,要定义池化区域大小k和池化标准(MAX或Average),对于全连接层,要定义全连接层的激活函数(输出层除外)和各层的神经元个数。
输出:CNN模型的输出$$a^L$$
1\) 根据输入层的填充大小P,填充原始图片的边缘,得到输入张量$$a^1$$。
2)初始化所有隐藏层的参数W,b
3)for l=2 to L-1:
a\) 如果第l层是卷积层,则输出为$$a^l= ReLU(z^l) = ReLU(a^{l-1}*W^l +b^l)$$
b\) 如果第l层是池化层,则输出为$$a^l= pool(a^{l-1})$$, 这里的pool指按照池化区域大小k和池化标准将输入张量缩小的过程。
c\) 如果第l层是全连接层,则输出为$$a^l= \sigma(z^l) =\sigma(W^la^{l-1} +b^l)$$
4\)对于输出层第L层:$$a^L=softmax(z^L)= softmax(W^La^{L-1}+b^L)$$