']}]
+ elif key == 'RawBlock':
+ # this is needed for the cells that have embedded video.
+ # We add a special tag to those: ``` {python, .jupyter-code-cell}
+ # The post-processing script then finds those and genrates separate
+ # code cells that can load video.
+ [format, content] = value
+ if format == 'html' and 'iframe' in content:
+ # Extract the video URL
+ video_url = content.split('src="')[1].split('"')[0]
+ # Create the Python code to display the video
+ python_code = f"""
+from IPython.display import display, HTML
+html_code = \"""
+{content}
+\"""
+display(HTML(html_code))
+"""
+
+ return {'t': 'CodeBlock', 'c': [['', ['python', 'jupyter-code-cell'], []], python_code]}
+
+
+def process_images(key, value, format, meta):
+ # Add https://tutorials.pytorch.kr/ to images so that they
+ # load correctly in the notebook.
+ if key != 'Image':
+ return None
+ [ident, classes, keyvals], caption, [src, title] = value
+ if not src.startswith('http'):
+ while src.startswith('../'):
+ src = src[3:]
+ if src.startswith('/_static'):
+ src = src[1:]
+ src = 'https://tutorials.pytorch.kr/' + src
+
+ return {'t': 'Image', 'c': [[ident, classes, keyvals], caption, [src, title]]}
+
+
+def process_grids(key, value, format, meta):
+ # Generate side by side grid cards. Only for the two-cards layout
+ # that we use in the tutorial template.
+ if key == 'Div':
+ [[ident, classes, keyvals], contents] = value
+ if 'grid' in classes:
+ columns = ['
',
+ '
']
+ column_num = 0
+ for block in contents:
+ if 't' in block and block['t'] == 'Div' and 'grid-item-card' in block['c'][0][1]:
+ item_html = ''
+ for item in block['c'][1]:
+ if item['t'] == 'Para':
+ item_html += '
' + ''.join(to_markdown(i) for i in item['c']) + '
' for column in columns]
+ return {'t': 'RawBlock', 'c': ['html', ''.join(columns)]}
+
+def is_code_block(item):
+ return item['t'] == 'Code' and 'octicon' in item['c'][1]
+
+
+def process_all(key, value, format, meta):
+ for transform in [process_admonitions, process_images, process_grids]:
+ new_value = transform(key, value, format, meta)
+ if new_value is not None:
+ break
+ return new_value
+
+
+if __name__ == "__main__":
+ toJSONFilter(process_all)
diff --git a/.build/download_data.py b/.build/download_data.py
new file mode 100644
index 000000000..cc07c7256
--- /dev/null
+++ b/.build/download_data.py
@@ -0,0 +1,136 @@
+#!/usr/bin/env python3
+import hashlib
+import os
+
+from typing import Optional
+from urllib.request import urlopen, Request
+from pathlib import Path
+from zipfile import ZipFile
+
+REPO_BASE_DIR = Path(__file__).absolute().parent.parent
+DATA_DIR = REPO_BASE_DIR / "_data"
+BEGINNER_DATA_DIR = REPO_BASE_DIR / "beginner_source" / "data"
+INTERMEDIATE_DATA_DIR = REPO_BASE_DIR / "intermediate_source" / "data"
+ADVANCED_DATA_DIR = REPO_BASE_DIR / "advanced_source" / "data"
+PROTOTYPE_DATA_DIR = REPO_BASE_DIR / "prototype_source" / "data"
+FILES_TO_RUN = os.getenv("FILES_TO_RUN")
+
+
+def size_fmt(nbytes: int) -> str:
+ """Returns a formatted file size string"""
+ KB = 1024
+ MB = 1024 * KB
+ GB = 1024 * MB
+ if abs(nbytes) >= GB:
+ return f"{nbytes * 1.0 / GB:.2f} Gb"
+ elif abs(nbytes) >= MB:
+ return f"{nbytes * 1.0 / MB:.2f} Mb"
+ elif abs(nbytes) >= KB:
+ return f"{nbytes * 1.0 / KB:.2f} Kb"
+ return str(nbytes) + " bytes"
+
+
+def download_url_to_file(url: str,
+ dst: Optional[str] = None,
+ prefix: Optional[Path] = None,
+ sha256: Optional[str] = None) -> Path:
+ dst = dst if dst is not None else Path(url).name
+ dst = dst if prefix is None else str(prefix / dst)
+ if Path(dst).exists():
+ print(f"Skip downloading {url} as {dst} already exists")
+ return Path(dst)
+ file_size = None
+ u = urlopen(Request(url, headers={"User-Agent": "tutorials.downloader"}))
+ meta = u.info()
+ if hasattr(meta, 'getheaders'):
+ content_length = meta.getheaders("Content-Length")
+ else:
+ content_length = meta.get_all("Content-Length")
+ if content_length is not None and len(content_length) > 0:
+ file_size = int(content_length[0])
+ sha256_sum = hashlib.sha256()
+ with open(dst, "wb") as f:
+ while True:
+ buffer = u.read(32768)
+ if len(buffer) == 0:
+ break
+ sha256_sum.update(buffer)
+ f.write(buffer)
+ digest = sha256_sum.hexdigest()
+ if sha256 is not None and sha256 != digest:
+ Path(dst).unlink()
+ raise RuntimeError(f"Downloaded {url} has unexpected sha256sum {digest} should be {sha256}")
+ print(f"Downloaded {url} sha256sum={digest} size={size_fmt(file_size)}")
+ return Path(dst)
+
+
+def unzip(archive: Path, tgt_dir: Path) -> None:
+ with ZipFile(str(archive), "r") as zip_ref:
+ zip_ref.extractall(str(tgt_dir))
+
+
+def download_hymenoptera_data():
+ # transfer learning tutorial data
+ z = download_url_to_file("https://download.pytorch.org/tutorial/hymenoptera_data.zip",
+ prefix=DATA_DIR,
+ sha256="fbc41b31d544714d18dd1230b1e2b455e1557766e13e67f9f5a7a23af7c02209",
+ )
+ unzip(z, BEGINNER_DATA_DIR)
+
+
+def download_nlp_data() -> None:
+ # nlp tutorial data
+ z = download_url_to_file("https://download.pytorch.org/tutorial/data.zip",
+ prefix=DATA_DIR,
+ sha256="fb317e80248faeb62dc25ef3390ae24ca34b94e276bbc5141fd8862c2200bff5",
+ )
+ # This will unzip all files in data.zip to intermediate_source/data/ folder
+ unzip(z, INTERMEDIATE_DATA_DIR.parent)
+
+
+def download_dcgan_data() -> None:
+ # Download dataset for beginner_source/dcgan_faces_tutorial.py
+ z = download_url_to_file("https://s3.amazonaws.com/pytorch-tutorial-assets/img_align_celeba.zip",
+ prefix=DATA_DIR,
+ sha256="46fb89443c578308acf364d7d379fe1b9efb793042c0af734b6112e4fd3a8c74",
+ )
+ unzip(z, BEGINNER_DATA_DIR / "celeba")
+
+
+def download_lenet_mnist() -> None:
+ # Download model for beginner_source/fgsm_tutorial.py
+ download_url_to_file("https://docs.google.com/uc?export=download&id=1HJV2nUHJqclXQ8flKvcWmjZ-OU5DGatl",
+ prefix=BEGINNER_DATA_DIR,
+ dst="lenet_mnist_model.pth",
+ sha256="cb5f8e578aef96d5c1a2cc5695e1aa9bbf4d0fe00d25760eeebaaac6ebc2edcb",
+ )
+
+def download_gpu_quantization_torchao() -> None:
+ # Download SAM model checkpoint for prototype_source/gpu_quantization_torchao_tutorial.py
+ download_url_to_file("https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth",
+ prefix=PROTOTYPE_DATA_DIR,
+ dst="sam_vit_h_4b8939.pth",
+ sha256="a7bf3b02f3ebf1267aba913ff637d9a2d5c33d3173bb679e46d9f338c26f262e",
+ )
+
+def main() -> None:
+ DATA_DIR.mkdir(exist_ok=True)
+ BEGINNER_DATA_DIR.mkdir(exist_ok=True)
+ ADVANCED_DATA_DIR.mkdir(exist_ok=True)
+ INTERMEDIATE_DATA_DIR.mkdir(exist_ok=True)
+ PROTOTYPE_DATA_DIR.mkdir(exist_ok=True)
+
+ if FILES_TO_RUN is None or "transfer_learning_tutorial" in FILES_TO_RUN:
+ download_hymenoptera_data()
+ nlp_tutorials = ["seq2seq_translation_tutorial", "char_rnn_classification_tutorial", "char_rnn_generation_tutorial"]
+ if FILES_TO_RUN is None or any(x in FILES_TO_RUN for x in nlp_tutorials):
+ download_nlp_data()
+ if FILES_TO_RUN is None or "dcgan_faces_tutorial" in FILES_TO_RUN:
+ download_dcgan_data()
+ if FILES_TO_RUN is None or "fgsm_tutorial" in FILES_TO_RUN:
+ download_lenet_mnist()
+ if FILES_TO_RUN is None or "gpu_quantization_torchao_tutorial" in FILES_TO_RUN:
+ download_gpu_quantization_torchao()
+
+if __name__ == "__main__":
+ main()
diff --git a/.build/get_files_to_run.py b/.build/get_files_to_run.py
index 80f958f50..bdf4562a8 100644
--- a/.build/get_files_to_run.py
+++ b/.build/get_files_to_run.py
@@ -2,7 +2,7 @@
import json
import os
from pathlib import Path
-# from remove_runnable_code import remove_runnable_code
+from remove_runnable_code import remove_runnable_code
# Calculate repo base dir
@@ -11,7 +11,7 @@
def get_all_files() -> List[str]:
sources = [x.relative_to(REPO_BASE_DIR) for x in REPO_BASE_DIR.glob("*_source/**/*.py") if 'data' not in x.parts]
- return [str(x) for x in sources]
+ return sorted([str(x) for x in sources])
def read_metadata() -> Dict[str, Any]:
@@ -40,27 +40,26 @@ def add_to_shard(i, filename):
)
all_other_files = all_files.copy()
- needs_gpu_nvidia_small_multi = list(
- filter(lambda x: get_needs_machine(x) == "gpu.nvidia.small.multi", all_files,)
+ needs_multigpu = list(
+ filter(lambda x: get_needs_machine(x) == "linux.16xlarge.nvidia.gpu", all_files,)
)
- needs_gpu_nvidia_medium = list(
- filter(lambda x: get_needs_machine(x) == "gpu.nvidia.large", all_files,)
+ needs_a10g = list(
+ filter(lambda x: get_needs_machine(x) == "linux.g5.4xlarge.nvidia.gpu", all_files,)
)
- for filename in needs_gpu_nvidia_small_multi:
- # currently, the only job that uses gpu.nvidia.small.multi is the 0th worker,
+ for filename in needs_multigpu:
+ # currently, the only job that has multigpu is the 0th worker,
# so we'll add all the jobs that need this machine to the 0th worker
add_to_shard(0, filename)
all_other_files.remove(filename)
- for filename in needs_gpu_nvidia_medium:
- # currently, the only job that uses gpu.nvidia.large is the 1st worker,
+ for filename in needs_a10g:
+ # currently, workers 1-5 use linux.g5.4xlarge.nvidia.gpu (sm86, A10G),
# so we'll add all the jobs that need this machine to the 1st worker
add_to_shard(1, filename)
all_other_files.remove(filename)
-
sorted_files = sorted(all_other_files, key=get_duration, reverse=True,)
for filename in sorted_files:
- min_shard_index = sorted(range(num_shards), key=lambda i: sharded_files[i][0])[
+ min_shard_index = sorted(range(1, num_shards), key=lambda i: sharded_files[i][0])[
0
]
add_to_shard(min_shard_index, filename)
@@ -87,8 +86,8 @@ def parse_args() -> Any:
from argparse import ArgumentParser
parser = ArgumentParser("Select files to run")
parser.add_argument("--dry-run", action="store_true")
- parser.add_argument("--num-shards", type=int, default=int(os.environ.get("NUM_WORKERS", 20)))
- parser.add_argument("--shard-num", type=int, default=int(os.environ.get("WORKER_ID", 0)))
+ parser.add_argument("--num-shards", type=int, default=int(os.environ.get("NUM_WORKERS", "20")))
+ parser.add_argument("--shard-num", type=int, default=int(os.environ.get("WORKER_ID", "1")))
return parser.parse_args()
@@ -96,7 +95,7 @@ def main() -> None:
args = parse_args()
all_files = get_all_files()
- files_to_run = calculate_shards(all_files, num_shards=args.num_shards)[args.shard_num]
+ files_to_run = calculate_shards(all_files, num_shards=args.num_shards)[args.shard_num - 1]
if not args.dry_run:
remove_other_files(all_files, compute_files_to_keep(files_to_run))
stripped_file_names = [Path(x).stem for x in files_to_run]
@@ -104,4 +103,4 @@ def main() -> None:
if __name__ == "__main__":
- main()
\ No newline at end of file
+ main()
diff --git a/.build/post_process_notebooks.py b/.build/post_process_notebooks.py
new file mode 100644
index 000000000..81f51766c
--- /dev/null
+++ b/.build/post_process_notebooks.py
@@ -0,0 +1,97 @@
+import nbformat as nbf
+import os
+import re
+
+"""
+This post-processing script needs to run after the .ipynb files are
+generated. The script removes extraneous ```{=html} syntax from the
+admonitions and splits the cells that have video iframe into a
+separate code cell that can be run to load the video directly
+in the notebook. This script is included in build.sh.
+"""
+
+
+# Pattern to search ``` {.python .jupyter-code-cell}
+pattern = re.compile(r'(.*?)``` {.python .jupyter-code-cell}\n\n(from IPython.display import display, HTML\nhtml_code = """\n.*?\n"""\ndisplay\(HTML\(html_code\)\))\n```(.*)', re.DOTALL)
+
+
+def process_video_cell(notebook_path):
+ """
+ This function finds the code blocks with the
+ "``` {.python .jupyter-code-cell}" code bocks and slices them
+ into a separe code cell (instead of markdown) which allows to
+ load the video in the notebook. The rest of the content is placed
+ in a new markdown cell.
+ """
+ print(f'Processing file: {notebook_path}')
+ notebook = nbf.read(notebook_path, as_version=4)
+
+ # Iterate over markdown cells
+ for i, cell in enumerate(notebook.cells):
+ if cell.cell_type == 'markdown':
+ match = pattern.search(cell.source)
+ if match:
+ print(f'Match found in cell {i}: {match.group(0)[:100]}...')
+ # Extract the parts before and after the video code block
+ before_html_block = match.group(1)
+ code_block = match.group(2)
+
+ # Add a comment to run the cell to display the video
+ code_block = "# Run this cell to load the video\n" + code_block
+ # Create a new code cell
+ new_code_cell = nbf.v4.new_code_cell(source=code_block)
+
+ # Replace the original markdown cell with the part before the code block
+ cell.source = before_html_block
+
+ # Insert the new code cell after the current one
+ notebook.cells.insert(i+1, new_code_cell)
+ print(f'New code cell created with source: {new_code_cell.source}')
+
+ # If there is content after the HTML code block, create a new markdown cell
+ if len(match.group(3).strip()) > 0:
+ after_html_block = match.group(3)
+ new_markdown_cell = nbf.v4.new_markdown_cell(source=after_html_block)
+ # Create a new markdown cell and add the content after code block there
+ notebook.cells.insert(i+2, new_markdown_cell)
+
+ else:
+ # Remove ```{=html} from the code block
+ cell.source = remove_html_tag(cell.source)
+
+ nbf.write(notebook, notebook_path)
+
+
+def remove_html_tag(content):
+ """
+ Pandoc adds an extraneous ```{=html} ``` to raw HTML blocks which
+ prevents it from rendering correctly. This function removes
+ ```{=html} that we don't need.
+ """
+ content = re.sub(r'```{=html}\n\n```', '">', content)
+ content = re.sub(r'<\/div>\n```', '
\n', content)
+ content = re.sub(r'```{=html}\n\n```', '\n', content)
+ content = re.sub(r'```{=html}', '', content)
+ content = re.sub(r'\n```', '', content)
+ return content
+
+
+def walk_dir(downloads_dir):
+ """
+ Walk the dir and process all notebook files in
+ the _downloads directory and its subdirectories.
+ """
+ for root, dirs, files in os.walk(downloads_dir):
+ for filename in files:
+ if filename.endswith('.ipynb'):
+ process_video_cell(os.path.join(root, filename))
+
+
+def main():
+ downloads_dir = './docs/_downloads'
+ walk_dir(downloads_dir)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/.build/remove_runnable_code.py b/.build/remove_runnable_code.py
new file mode 100644
index 000000000..037017d8d
--- /dev/null
+++ b/.build/remove_runnable_code.py
@@ -0,0 +1,58 @@
+import sys
+
+STATE_IN_MULTILINE_COMMENT_BLOCK_DOUBLE_QUOTE = "STATE_IN_MULTILINE_COMMENT_BLOCK_DOUBLE_QUOTE"
+STATE_IN_MULTILINE_COMMENT_BLOCK_SINGLE_QUOTE = "STATE_IN_MULTILINE_COMMENT_BLOCK_SINGLE_QUOTE"
+STATE_NORMAL = "STATE_NORMAL"
+
+
+def remove_runnable_code(python_file_path, output_file_path):
+ with open(python_file_path, 'r', encoding='utf-8') as file:
+ lines = file.readlines()
+ ret_lines = []
+ state = STATE_NORMAL
+ for line in lines:
+ if state == STATE_NORMAL:
+ if line.startswith('#'):
+ ret_lines.append(line)
+ state = STATE_NORMAL
+ elif ((line.startswith('"""') or line.startswith('r"""')) and
+ line.endswith('"""')):
+ ret_lines.append(line)
+ state = STATE_NORMAL
+ elif line.startswith('"""') or line.startswith('r"""'):
+ ret_lines.append(line)
+ state = STATE_IN_MULTILINE_COMMENT_BLOCK_DOUBLE_QUOTE
+ elif ((line.startswith("'''") or line.startswith("r'''")) and
+ line.endswith("'''")):
+ ret_lines.append(line)
+ state = STATE_NORMAL
+ elif line.startswith("'''") or line.startswith("r'''"):
+ ret_lines.append(line)
+ state = STATE_IN_MULTILINE_COMMENT_BLOCK_SINGLE_QUOTE
+ else:
+ ret_lines.append("\n")
+ state = STATE_NORMAL
+ elif state == STATE_IN_MULTILINE_COMMENT_BLOCK_DOUBLE_QUOTE:
+ if line.startswith('"""'):
+ ret_lines.append(line)
+ state = STATE_NORMAL
+ else:
+ ret_lines.append(line)
+ state = STATE_IN_MULTILINE_COMMENT_BLOCK_DOUBLE_QUOTE
+ elif state == STATE_IN_MULTILINE_COMMENT_BLOCK_SINGLE_QUOTE:
+ if line.startswith("'''"):
+ ret_lines.append(line)
+ state = STATE_NORMAL
+ else:
+ ret_lines.append(line)
+ state = STATE_IN_MULTILINE_COMMENT_BLOCK_SINGLE_QUOTE
+
+ ret_lines.append("\n# %%%%%%RUNNABLE_CODE_REMOVED%%%%%%")
+
+ with open(output_file_path, 'w', encoding='utf-8') as file:
+ for line in ret_lines:
+ file.write(line)
+
+
+if __name__ == "__main__":
+ remove_runnable_code(sys.argv[1], sys.argv[2])
diff --git a/.build/requirements-full.txt b/.build/requirements-full.txt
new file mode 100644
index 000000000..d66c029ea
--- /dev/null
+++ b/.build/requirements-full.txt
@@ -0,0 +1,61 @@
+# additional requirements libraries for buuilding tutorials with gallery (aka full build)
+# Refer to ./jenkins/build.sh for official tutorial build instructions
+
+# use `make docs` to build the tutorials fully
+
+pypandoc==1.12
+pandocfilters
+markdown
+tqdm==4.66.1
+numpy==1.24.4
+matplotlib
+librosa
+PyHamcrest
+bs4
+awscliv2==2.1.1
+flask
+spacy==3.4.1
+ray[tune]==2.7.2
+tensorboard
+jinja2==3.1.3
+pytorch-lightning
+torchx
+torchrl==0.3.0
+tensordict==0.3.0
+ax-platform
+nbformat>==5.9.2
+datasets
+transformers
+torchmultimodal-nightly # needs to be updated to stable as soon as it's avaialable
+onnx
+onnxscript
+onnxruntime
+evaluate
+accelerate>=0.20.1
+
+importlib-metadata==6.8.0
+
+
+
+ipython
+
+# to run examples
+boto3
+pandas
+requests
+scikit-image
+scipy==1.11.1
+numba==0.57.1
+pillow==10.2.0
+wget
+gym==0.26.2
+gym-super-mario-bros==7.4.0
+pyopengl
+gymnasium[mujoco]==0.27.0
+timm
+iopath
+pygame==2.1.2
+pycocotools
+semilearn==0.3.2
+torchao==0.0.3
+segment_anything==1.0
diff --git a/.build/requirements-minimal.txt b/.build/requirements-minimal.txt
new file mode 100644
index 000000000..6de5b47d5
--- /dev/null
+++ b/.build/requirements-minimal.txt
@@ -0,0 +1,24 @@
+# additional requirements libraries for buuilding tutorials with gallery (aka full build)
+# Refer to ./jenkins/build.sh for official tutorial build instructions
+
+# use `make html-noplot` for htmls only (without evaluating sphinx-gallery)
+
+sphinx==5.0.0
+sphinx-gallery==0.11.1
+sphinx_design
+docutils==0.16
+sphinx-copybutton
+sphinx-sitemap
+sphinxext-opengraph
+sphinxcontrib-katex
+plotly==5.14.0
+torch==2.3
+torchvision
+torchtext
+torchaudio
+torchdata
+networkx
+
+# PyTorch Korea Theme
+# pytorch-sphinx-theme@https://github.com/PyTorchKorea/pytorch_sphinx_theme/archive/master.zip
+-e git+https://github.com/PyTorchKorea/pytorch_sphinx_theme.git#egg=pytorch_sphinx_theme
diff --git a/.build/validate_tutorials_built.py b/.build/validate_tutorials_built.py
index 46452cc18..eb027929f 100644
--- a/.build/validate_tutorials_built.py
+++ b/.build/validate_tutorials_built.py
@@ -10,6 +10,7 @@
NOT_RUN = [
"beginner_source/basics/intro", # no code
+ "beginner_source/onnx/intro_onnx",
"beginner_source/translation_transformer",
"beginner_source/profiler",
"beginner_source/saving_loading_models",
@@ -21,11 +22,16 @@
"beginner_source/former_torchies/tensor_tutorial_old",
"beginner_source/examples_autograd/polynomial_autograd",
"beginner_source/examples_autograd/polynomial_custom_function",
- "intermediate_source/parametrizations",
+ "beginner_source/torchtext_custom_dataset_tutorial", # not building with 2.3 RC, might be able to turn on with GA
+ "beginner_source/text_sentiment_ngrams_tutorial", # not building with 2.3 RC, might be able to turn on with GA
+ "beginner_source/t5_tutorial", # re-enable after this is fixed: https://github.com/pytorch/text/issues/1756
"intermediate_source/mnist_train_nas", # used by ax_multiobjective_nas_tutorial.py
+ "intermediate_source/torchvision_tutorial", # disable due to RuntimeError: DataLoader worker (pid(s) 20092) exited unexpectedly
"intermediate_source/fx_conv_bn_fuser",
+ "intermediate_source/_torch_export_nightly_tutorial", # does not work on release
"advanced_source/super_resolution_with_onnxruntime",
"advanced_source/ddp_pipeline", # requires 4 gpus
+ "advanced_source/usb_semisup_learn", # fails with CUDA OOM error, should try on a different worker
"prototype_source/fx_graph_mode_ptq_dynamic",
"prototype_source/vmap_recipe",
"prototype_source/torchscript_freezing",
diff --git a/.github/ISSUE_TEMPLATE/1_TRANSLATE_REQUEST.md b/.github/ISSUE_TEMPLATE/1_TRANSLATE_REQUEST.md
index bac5e213c..ca4d033eb 100644
--- a/.github/ISSUE_TEMPLATE/1_TRANSLATE_REQUEST.md
+++ b/.github/ISSUE_TEMPLATE/1_TRANSLATE_REQUEST.md
@@ -15,4 +15,4 @@ _(반드시 지키셔야 하는 일정이 아닙니다 - 일정이 너무 늦어
## 관련 이슈
_현재 번역 요청 / 진행 내역을 보기 위해 각 버전의 메인 이슈를 참조합니다._
_(특별한 일이 없다면 변경하지 않으셔도 됩니다.)_
-* 관련 이슈: #660 (v2.0)
+* 관련 이슈: #799 (v2.3.1)
diff --git a/LICENSE b/LICENSE
index f0d2e189a..d63c3b121 100644
--- a/LICENSE
+++ b/LICENSE
@@ -1,6 +1,6 @@
BSD 3-Clause License
-Copyright (c) 2017, PyTorch contributors
+Copyright (c) 2017-2024, PyTorch & PyTorch Korea User Group contributors
All rights reserved.
Redistribution and use in source and binary forms, with or without
diff --git a/Makefile b/Makefile
index dfdb067d4..bee6ab630 100644
--- a/Makefile
+++ b/Makefile
@@ -38,21 +38,8 @@ download:
# Step2-2. UNTAR: tar -xzf $(DATADIR)/[SOURCE_FILE] -C [*_source/data/]
# Step2-3. AS-IS: cp $(DATADIR)/[SOURCE_FILE] [*_source/data/]
- # make data directories
- mkdir -p $(DATADIR)
- mkdir -p advanced_source/data
- mkdir -p beginner_source/data
- mkdir -p intermediate_source/data
- mkdir -p prototype_source/data
- mkdir -p recipes_source/recipes/data
-
- # transfer learning tutorial data
- wget -nv -N https://download.pytorch.org/tutorial/hymenoptera_data.zip -P $(DATADIR)
- unzip $(ZIPOPTS) $(DATADIR)/hymenoptera_data.zip -d beginner_source/data/
-
- # nlp tutorial data
- wget -nv -N https://download.pytorch.org/tutorial/data.zip -P $(DATADIR)
- unzip $(ZIPOPTS) $(DATADIR)/data.zip -d intermediate_source/ # This will unzip all files in data.zip to intermediate_source/data/ folder
+ # Run structured downloads first (will also make directories)
+ python3 .build/download_data.py
# data loader tutorial
wget -nv -N https://download.pytorch.org/tutorial/faces.zip -P $(DATADIR)
@@ -67,10 +54,6 @@ download:
mkdir -p advanced_source/data/images/
cp -r _static/img/neural-style/ advanced_source/data/images/
- # Download dataset for beginner_source/dcgan_faces_tutorial.py
- wget -nv -N https://s3.amazonaws.com/pytorch-tutorial-assets/img_align_celeba.zip -P $(DATADIR)
- unzip $(ZIPOPTS) $(DATADIR)/img_align_celeba.zip -d beginner_source/data/celeba
-
# Download dataset for beginner_source/hybrid_frontend/introduction_to_hybrid_frontend_tutorial.py
wget -nv -N https://s3.amazonaws.com/pytorch-tutorial-assets/iris.data -P $(DATADIR)
cp $(DATADIR)/iris.data beginner_source/data/
@@ -79,14 +62,6 @@ download:
wget -nv -N https://s3.amazonaws.com/pytorch-tutorial-assets/cornell_movie_dialogs_corpus_v2.zip -P $(DATADIR)
unzip $(ZIPOPTS) $(DATADIR)/cornell_movie_dialogs_corpus_v2.zip -d beginner_source/data/
- # Download dataset for beginner_source/audio_classifier_tutorial.py
- wget -nv -N https://s3.amazonaws.com/pytorch-tutorial-assets/UrbanSound8K.tar.gz -P $(DATADIR)
- tar $(TAROPTS) -xzf $(DATADIR)/UrbanSound8K.tar.gz -C ./beginner_source/data/
-
- # Download model for beginner_source/fgsm_tutorial.py
- wget -nv -N https://s3.amazonaws.com/pytorch-tutorial-assets/lenet_mnist_model.pth -P $(DATADIR)
- cp $(DATADIR)/lenet_mnist_model.pth ./beginner_source/data/lenet_mnist_model.pth
-
# Download model for advanced_source/dynamic_quantization_tutorial.py
wget -nv -N https://s3.amazonaws.com/pytorch-tutorial-assets/word_language_model_quantize.pth -P $(DATADIR)
cp $(DATADIR)/word_language_model_quantize.pth advanced_source/data/word_language_model_quantize.pth
@@ -107,11 +82,27 @@ download:
wget -nv -N http://dl.fbaipublicfiles.com/pythia/data/vocab.tar.gz -P $(DATADIR)
tar $(TAROPTS) -xzf $(DATADIR)/vocab.tar.gz -C ./beginner_source/data/
+ # Download dataset for beginner_source/torchtext_custom_dataset_tutorial.py
+ wget -nv -N https://www.manythings.org/anki/deu-eng.zip -P $(DATADIR)
+ unzip -o $(DATADIR)/deu-eng.zip -d beginner_source/data/
+
+ # Download PennFudanPed dataset for intermediate_source/torchvision_tutorial.py
+ wget https://www.cis.upenn.edu/~jshi/ped_html/PennFudanPed.zip -P $(DATADIR)
+ unzip -o $(DATADIR)/PennFudanPed.zip -d intermediate_source/data/
+
# Download some dataset for beginner_source/translation_transformer.py
python -m spacy download en_core_web_sm
python -m spacy download de_core_news_sm
+requirements-minimal:
+ pip install -r .build/requirements-minimal.txt
+
+requirements-full:
+ make requirements-minimal
+ pip install -r .build/requirements-full.txt
+
docs:
+ make requirements-full
make download
make html
rm -rf docs
@@ -123,6 +114,7 @@ docs:
@echo "Build finished. The HTML pages are in $(BUILDDIR)/html."
html-noplot:
+ make requirements-minimal
$(SPHINXBUILD) -D plot_gallery=0 -b html $(SPHINXOPTS) "$(SOURCEDIR)" "$(BUILDDIR)/html"
# bash .jenkins/remove_invisible_code_block_batch.sh "$(BUILDDIR)/html"
@echo
@@ -130,4 +122,6 @@ html-noplot:
clean-cache:
make clean
- rm -rf advanced beginner intermediate recipes
+ rm -rf advanced beginner intermediate recipes prototype
+ # remove additional python files downloaded for torchvision_tutorial.py
+ rm -f intermediate_source/engine.py intermediate_source/utils.py intermediate_source/transforms.py intermediate_source/coco_eval.py intermediate_source/coco_utils.py
diff --git a/README.md b/README.md
index 482b29eb2..a34a66979 100644
--- a/README.md
+++ b/README.md
@@ -4,7 +4,7 @@
PyTorch에서 제공하는 튜토리얼의 한국어 번역을 위한 저장소입니다.\
번역의 결과물은 [https://tutorials.pytorch.kr](https://tutorials.pytorch.kr)에서 확인하실 수 있습니다. (번역을 진행하며 **비정기적으로** 반영합니다.)\
-현재 버전의 번역 / 변경 관련 이슈는 [#660 이슈](https://github.com/PyTorchKorea/tutorials-kr/issues/660)를 참고해주세요.
+현재 버전의 번역 / 변경 관련 이슈는 [#799 이슈](https://github.com/PyTorchKorea/tutorials-kr/issues/799)를 참고해주세요.
## 기여하기
@@ -22,7 +22,7 @@ PyTorch에서 제공하는 튜토리얼의 한국어 번역을 위한 저장소
## 원문
-현재 PyTorch v2.0 튜토리얼([pytorch/tutorials@9efe789b](https://github.com/pytorch/tutorials/commit/9efe789bfc3763ec359b60f12b5e6dda4e6d5db0) 기준) 번역이 진행 중입니다.
+현재 PyTorch v2.0 튜토리얼([pytorch/tutorials@6537199](https://github.com/pytorch/tutorials/commit/653719940f7c4d908811da415f190465d8c3189d) 기준) 번역이 진행 중입니다.
최신 버전의 튜토리얼(공식, 영어)은 [PyTorch tutorials 사이트](https://pytorch.org/tutorials) 및 [PyTorch tutorials 저장소](https://github.com/pytorch/tutorials)를 참고해주세요.
@@ -45,6 +45,11 @@ v1.0 이후 번역은 별도 저장소로 관리하지 않습니다. [이 저장
해당 릴리즈의 문서를 내려받으신 후 빌드하시면 해당 버전의 문서를 확인하실 수 있습니다. \
빌드 방법은 [기여하기 문서의 `2-5. (내 컴퓨터에서) 결과 확인하기`](https://github.com/PyTorchKorea/tutorials-kr/blob/master/CONTRIBUTING.md#2-5-내-컴퓨터에서-결과-확인하기) 부분을 참고해주세요.
+## 라이선스 (License)
+
+파이토치 한국어 튜토리얼의 라이선스는 [원본 튜토리얼의 라이선스인 BSD-3항](https://github.com/pytorch/tutorials/blob/main/LICENSE)을 따릅니다. \
+자세한 내용은 [LICENSE 파일](https://github.com/PyTorchKorea/tutorials-kr/blob/master/LICENSE)을 참조해주세요.
+
---
-This is a project to translate [pytorch/tutorials@9efe789b](https://github.com/pytorch/tutorials/commit/9efe789bfc3763ec359b60f12b5e6dda4e6d5db0) into Korean.
+This is a project to translate [pytorch/tutorials@6537199](https://github.com/pytorch/tutorials/commit/653719940f7c4d908811da415f190465d8c3189d) into Korean.
For the latest version, please visit to the [official PyTorch tutorials repo](https://github.com/pytorch/tutorials).
diff --git a/_static/css/custom2.css b/_static/css/custom2.css
new file mode 100644
index 000000000..4e263b677
--- /dev/null
+++ b/_static/css/custom2.css
@@ -0,0 +1,19 @@
+/* Survey banner .css */
+
+.survey-banner {
+ margin-top: 10px;
+ background-color: #f3f4f7;
+ padding-top: 15px;
+ padding-left: 10px;
+ padding-bottom: 1px;
+}
+
+@media screen and (max-width: 600px) {
+ .survey-banner {
+ padding-top: 5px;
+ padding-left: 5px;
+ padding-bottom: -1px;
+ font-size: 12px;
+ margin-bottom: 5px;
+ }
+}
diff --git a/_static/img/ExecuTorch-Logo-cropped.svg b/_static/img/ExecuTorch-Logo-cropped.svg
new file mode 100644
index 000000000..9e0ef52fb
--- /dev/null
+++ b/_static/img/ExecuTorch-Logo-cropped.svg
@@ -0,0 +1,57 @@
+
+
diff --git a/_static/img/distributed/device_mesh.png b/_static/img/distributed/device_mesh.png
new file mode 100644
index 000000000..2ccabcc48
Binary files /dev/null and b/_static/img/distributed/device_mesh.png differ
diff --git a/_static/img/distributed/distributed_checkpoint_generated_files.png b/_static/img/distributed/distributed_checkpoint_generated_files.png
new file mode 100644
index 000000000..b32dddb7e
Binary files /dev/null and b/_static/img/distributed/distributed_checkpoint_generated_files.png differ
diff --git a/_static/img/distributed/fsdp_sharding.png b/_static/img/distributed/fsdp_sharding.png
new file mode 100755
index 000000000..9dd1e3c11
Binary files /dev/null and b/_static/img/distributed/fsdp_sharding.png differ
diff --git a/_static/img/distributed/fsdp_tp.png b/_static/img/distributed/fsdp_tp.png
new file mode 100644
index 000000000..e419304ac
Binary files /dev/null and b/_static/img/distributed/fsdp_tp.png differ
diff --git a/_static/img/distributed/loss_parallel.png b/_static/img/distributed/loss_parallel.png
new file mode 100644
index 000000000..b5cf9a499
Binary files /dev/null and b/_static/img/distributed/loss_parallel.png differ
diff --git a/_static/img/distributed/megatron_lm.png b/_static/img/distributed/megatron_lm.png
new file mode 100644
index 000000000..38f7b0663
Binary files /dev/null and b/_static/img/distributed/megatron_lm.png differ
diff --git a/_static/img/half_cheetah.gif b/_static/img/half_cheetah.gif
new file mode 100644
index 000000000..b61ff47d4
Binary files /dev/null and b/_static/img/half_cheetah.gif differ
diff --git a/_static/img/hta/comm_across_ranks.png b/_static/img/hta/comm_across_ranks.png
new file mode 100644
index 000000000..2336de3bc
Binary files /dev/null and b/_static/img/hta/comm_across_ranks.png differ
diff --git a/_static/img/hta/counts_diff.png b/_static/img/hta/counts_diff.png
new file mode 100644
index 000000000..34575c145
Binary files /dev/null and b/_static/img/hta/counts_diff.png differ
diff --git a/_static/img/hta/cuda_kernel_launch.png b/_static/img/hta/cuda_kernel_launch.png
new file mode 100644
index 000000000..e57c54a2f
Binary files /dev/null and b/_static/img/hta/cuda_kernel_launch.png differ
diff --git a/_static/img/hta/cuda_kernel_launch_stats.png b/_static/img/hta/cuda_kernel_launch_stats.png
new file mode 100644
index 000000000..33a160fc7
Binary files /dev/null and b/_static/img/hta/cuda_kernel_launch_stats.png differ
diff --git a/_static/img/hta/duration_diff.png b/_static/img/hta/duration_diff.png
new file mode 100644
index 000000000..050d491c8
Binary files /dev/null and b/_static/img/hta/duration_diff.png differ
diff --git a/_static/img/hta/idle_time.png b/_static/img/hta/idle_time.png
new file mode 100644
index 000000000..782bfe9ad
Binary files /dev/null and b/_static/img/hta/idle_time.png differ
diff --git a/_static/img/hta/idle_time_breakdown_percentage.png b/_static/img/hta/idle_time_breakdown_percentage.png
new file mode 100644
index 000000000..3bab5946e
Binary files /dev/null and b/_static/img/hta/idle_time_breakdown_percentage.png differ
diff --git a/_static/img/hta/idle_time_summary.png b/_static/img/hta/idle_time_summary.png
new file mode 100644
index 000000000..101b696b5
Binary files /dev/null and b/_static/img/hta/idle_time_summary.png differ
diff --git a/_static/img/hta/kernel_metrics_df.png b/_static/img/hta/kernel_metrics_df.png
new file mode 100644
index 000000000..53eefb58b
Binary files /dev/null and b/_static/img/hta/kernel_metrics_df.png differ
diff --git a/_static/img/hta/kernel_type_breakdown.png b/_static/img/hta/kernel_type_breakdown.png
new file mode 100644
index 000000000..29a29cf89
Binary files /dev/null and b/_static/img/hta/kernel_type_breakdown.png differ
diff --git a/_static/img/hta/launch_delay_outliers.png b/_static/img/hta/launch_delay_outliers.png
new file mode 100644
index 000000000..9bb455ade
Binary files /dev/null and b/_static/img/hta/launch_delay_outliers.png differ
diff --git a/_static/img/hta/mem_bandwidth_queue_length.png b/_static/img/hta/mem_bandwidth_queue_length.png
new file mode 100644
index 000000000..9df5383b5
Binary files /dev/null and b/_static/img/hta/mem_bandwidth_queue_length.png differ
diff --git a/_static/img/hta/overlap_df.png b/_static/img/hta/overlap_df.png
new file mode 100644
index 000000000..ef164a28a
Binary files /dev/null and b/_static/img/hta/overlap_df.png differ
diff --git a/_static/img/hta/overlap_plot.png b/_static/img/hta/overlap_plot.png
new file mode 100644
index 000000000..acd449bc7
Binary files /dev/null and b/_static/img/hta/overlap_plot.png differ
diff --git a/_static/img/hta/pie_charts.png b/_static/img/hta/pie_charts.png
new file mode 100644
index 000000000..fa9137109
Binary files /dev/null and b/_static/img/hta/pie_charts.png differ
diff --git a/_static/img/hta/queue_length_summary.png b/_static/img/hta/queue_length_summary.png
new file mode 100644
index 000000000..639a03fb6
Binary files /dev/null and b/_static/img/hta/queue_length_summary.png differ
diff --git a/_static/img/hta/runtime_outliers.png b/_static/img/hta/runtime_outliers.png
new file mode 100644
index 000000000..1e2dfff90
Binary files /dev/null and b/_static/img/hta/runtime_outliers.png differ
diff --git a/_static/img/hta/short_gpu_kernels.png b/_static/img/hta/short_gpu_kernels.png
new file mode 100644
index 000000000..ff382a3a7
Binary files /dev/null and b/_static/img/hta/short_gpu_kernels.png differ
diff --git a/_static/img/hta/temporal_breakdown_df.png b/_static/img/hta/temporal_breakdown_df.png
new file mode 100644
index 000000000..dce1829d1
Binary files /dev/null and b/_static/img/hta/temporal_breakdown_df.png differ
diff --git a/_static/img/hta/temporal_breakdown_plot.png b/_static/img/hta/temporal_breakdown_plot.png
new file mode 100644
index 000000000..9c5f45c1d
Binary files /dev/null and b/_static/img/hta/temporal_breakdown_plot.png differ
diff --git a/_static/img/knowledge_distillation/ce_only.png b/_static/img/knowledge_distillation/ce_only.png
new file mode 100644
index 000000000..a75037165
Binary files /dev/null and b/_static/img/knowledge_distillation/ce_only.png differ
diff --git a/_static/img/knowledge_distillation/cosine_embedding_loss.png b/_static/img/knowledge_distillation/cosine_embedding_loss.png
new file mode 100644
index 000000000..ebfd957a2
Binary files /dev/null and b/_static/img/knowledge_distillation/cosine_embedding_loss.png differ
diff --git a/_static/img/knowledge_distillation/cosine_loss_distillation.png b/_static/img/knowledge_distillation/cosine_loss_distillation.png
new file mode 100644
index 000000000..81f241eb0
Binary files /dev/null and b/_static/img/knowledge_distillation/cosine_loss_distillation.png differ
diff --git a/_static/img/knowledge_distillation/distillation_output_loss.png b/_static/img/knowledge_distillation/distillation_output_loss.png
new file mode 100644
index 000000000..f86cbddbd
Binary files /dev/null and b/_static/img/knowledge_distillation/distillation_output_loss.png differ
diff --git a/_static/img/knowledge_distillation/fitnets_knowledge_distill.png b/_static/img/knowledge_distillation/fitnets_knowledge_distill.png
new file mode 100644
index 000000000..407d9de89
Binary files /dev/null and b/_static/img/knowledge_distillation/fitnets_knowledge_distill.png differ
diff --git a/_static/img/onnx/custom_addandround_function.png b/_static/img/onnx/custom_addandround_function.png
new file mode 100644
index 000000000..a0c700016
Binary files /dev/null and b/_static/img/onnx/custom_addandround_function.png differ
diff --git a/_static/img/onnx/custom_addandround_model.png b/_static/img/onnx/custom_addandround_model.png
new file mode 100644
index 000000000..793d8cfbb
Binary files /dev/null and b/_static/img/onnx/custom_addandround_model.png differ
diff --git a/_static/img/onnx/custom_aten_add_function.png b/_static/img/onnx/custom_aten_add_function.png
new file mode 100644
index 000000000..d9f927ce7
Binary files /dev/null and b/_static/img/onnx/custom_aten_add_function.png differ
diff --git a/_static/img/onnx/custom_aten_add_model.png b/_static/img/onnx/custom_aten_add_model.png
new file mode 100644
index 000000000..e5ef1c717
Binary files /dev/null and b/_static/img/onnx/custom_aten_add_model.png differ
diff --git a/_static/img/onnx/custom_aten_gelu_function.png b/_static/img/onnx/custom_aten_gelu_function.png
new file mode 100644
index 000000000..5cb573e7d
Binary files /dev/null and b/_static/img/onnx/custom_aten_gelu_function.png differ
diff --git a/_static/img/onnx/custom_aten_gelu_model.png b/_static/img/onnx/custom_aten_gelu_model.png
new file mode 100644
index 000000000..6bc46337b
Binary files /dev/null and b/_static/img/onnx/custom_aten_gelu_model.png differ
diff --git a/_static/img/onnx/image_clossifier_onnx_modelon_netron_web_ui.png b/_static/img/onnx/image_clossifier_onnx_modelon_netron_web_ui.png
new file mode 100755
index 000000000..0c29c1687
Binary files /dev/null and b/_static/img/onnx/image_clossifier_onnx_modelon_netron_web_ui.png differ
diff --git a/_static/img/onnx/netron_web_ui.png b/_static/img/onnx/netron_web_ui.png
new file mode 100755
index 000000000..f88936eb8
Binary files /dev/null and b/_static/img/onnx/netron_web_ui.png differ
diff --git a/_static/img/optim_step_in_bwd/snapshot.jpg b/_static/img/optim_step_in_bwd/snapshot.jpg
new file mode 100644
index 000000000..50be55e7b
Binary files /dev/null and b/_static/img/optim_step_in_bwd/snapshot.jpg differ
diff --git a/_static/img/optim_step_in_bwd/snapshot_opt_in_bwd.jpg b/_static/img/optim_step_in_bwd/snapshot_opt_in_bwd.jpg
new file mode 100644
index 000000000..65d53d21c
Binary files /dev/null and b/_static/img/optim_step_in_bwd/snapshot_opt_in_bwd.jpg differ
diff --git a/_static/img/pendulum.gif b/_static/img/pendulum.gif
new file mode 100644
index 000000000..a7adf181f
Binary files /dev/null and b/_static/img/pendulum.gif differ
diff --git a/_static/img/profiler_rocm_chrome_trace_view.png b/_static/img/profiler_rocm_chrome_trace_view.png
new file mode 100644
index 000000000..cff7ba98c
Binary files /dev/null and b/_static/img/profiler_rocm_chrome_trace_view.png differ
diff --git a/_static/img/profiler_rocm_tensorboard_operartor_view.png b/_static/img/profiler_rocm_tensorboard_operartor_view.png
new file mode 100644
index 000000000..27effb91e
Binary files /dev/null and b/_static/img/profiler_rocm_tensorboard_operartor_view.png differ
diff --git a/_static/img/pruning_flow.jpg b/_static/img/pruning_flow.jpg
new file mode 100644
index 000000000..bd57158b3
Binary files /dev/null and b/_static/img/pruning_flow.jpg differ
diff --git a/_static/img/replaybuffer_traj.png b/_static/img/replaybuffer_traj.png
new file mode 100644
index 000000000..64773ee8f
Binary files /dev/null and b/_static/img/replaybuffer_traj.png differ
diff --git a/_static/img/rollout_recurrent.png b/_static/img/rollout_recurrent.png
new file mode 100644
index 000000000..2ce24d40d
Binary files /dev/null and b/_static/img/rollout_recurrent.png differ
diff --git a/_static/img/seq-seq-images/attention-decoder-network.png b/_static/img/seq-seq-images/attention-decoder-network.png
index 243f87c6e..d31d42a5a 100755
Binary files a/_static/img/seq-seq-images/attention-decoder-network.png and b/_static/img/seq-seq-images/attention-decoder-network.png differ
diff --git a/_static/img/thumbnails/cropped/Exporting-PyTorch-Models-to-ONNX-Graphs.png b/_static/img/thumbnails/cropped/Exporting-PyTorch-Models-to-ONNX-Graphs.png
new file mode 100755
index 000000000..00156df04
Binary files /dev/null and b/_static/img/thumbnails/cropped/Exporting-PyTorch-Models-to-ONNX-Graphs.png differ
diff --git a/_static/img/thumbnails/cropped/Getting-Started-with-DCP.png b/_static/img/thumbnails/cropped/Getting-Started-with-DCP.png
new file mode 100644
index 000000000..426a14d98
Binary files /dev/null and b/_static/img/thumbnails/cropped/Getting-Started-with-DCP.png differ
diff --git a/_static/img/thumbnails/cropped/Large-Scale-Transformer-model-training-with-Tensor-Parallel.png b/_static/img/thumbnails/cropped/Large-Scale-Transformer-model-training-with-Tensor-Parallel.png
new file mode 100644
index 000000000..426a14d98
Binary files /dev/null and b/_static/img/thumbnails/cropped/Large-Scale-Transformer-model-training-with-Tensor-Parallel.png differ
diff --git a/_static/img/thumbnails/cropped/TIAToolbox-Tutorial.png b/_static/img/thumbnails/cropped/TIAToolbox-Tutorial.png
new file mode 100644
index 000000000..76f2bcaf4
Binary files /dev/null and b/_static/img/thumbnails/cropped/TIAToolbox-Tutorial.png differ
diff --git a/_static/img/thumbnails/cropped/knowledge_distillation_pytorch_logo.png b/_static/img/thumbnails/cropped/knowledge_distillation_pytorch_logo.png
new file mode 100644
index 000000000..3ce407815
Binary files /dev/null and b/_static/img/thumbnails/cropped/knowledge_distillation_pytorch_logo.png differ
diff --git a/_static/img/thumbnails/cropped/optional-Exporting-a-Model-from-PyTorch-to-ONNX-and-Running-it-using-ONNX-Runtime.png b/_static/img/thumbnails/cropped/optional-Exporting-a-Model-from-PyTorch-to-ONNX-and-Running-it-using-ONNX-Runtime.png
index 426a14d98..00156df04 100644
Binary files a/_static/img/thumbnails/cropped/optional-Exporting-a-Model-from-PyTorch-to-ONNX-and-Running-it-using-ONNX-Runtime.png and b/_static/img/thumbnails/cropped/optional-Exporting-a-Model-from-PyTorch-to-ONNX-and-Running-it-using-ONNX-Runtime.png differ
diff --git a/_static/img/thumbnails/cropped/torch_text_logo.png b/_static/img/thumbnails/cropped/torch_text_logo.png
new file mode 100644
index 000000000..3fe736d60
Binary files /dev/null and b/_static/img/thumbnails/cropped/torch_text_logo.png differ
diff --git a/_static/img/tiatoolbox_tutorial/read_bounds_tissue.webp b/_static/img/tiatoolbox_tutorial/read_bounds_tissue.webp
new file mode 100644
index 000000000..5a1ca81e0
Binary files /dev/null and b/_static/img/tiatoolbox_tutorial/read_bounds_tissue.webp differ
diff --git a/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_001.png b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_001.png
new file mode 100644
index 000000000..fafd95768
Binary files /dev/null and b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_001.png differ
diff --git a/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_002.png b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_002.png
new file mode 100644
index 000000000..fd6f7aba1
Binary files /dev/null and b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_002.png differ
diff --git a/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_003.png b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_003.png
new file mode 100644
index 000000000..8feda69de
Binary files /dev/null and b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_003.png differ
diff --git a/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_004.png b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_004.png
new file mode 100644
index 000000000..8feda69de
Binary files /dev/null and b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_004.png differ
diff --git a/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_005.png b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_005.png
new file mode 100644
index 000000000..e17e03812
Binary files /dev/null and b/_static/img/tiatoolbox_tutorial/tiatoolbox_tutorial_005.png differ
diff --git a/_static/img/usb_semisup_learn/code.png b/_static/img/usb_semisup_learn/code.png
new file mode 100644
index 000000000..fdc7b798a
Binary files /dev/null and b/_static/img/usb_semisup_learn/code.png differ
diff --git a/_static/tiatoolbox_tutorial.ipynb b/_static/tiatoolbox_tutorial.ipynb
new file mode 100644
index 000000000..35cb4bc56
--- /dev/null
+++ b/_static/tiatoolbox_tutorial.ipynb
@@ -0,0 +1 @@
+{"cells":[{"cell_type":"markdown","metadata":{"id":"YWsXrOQGyiNu"},"source":["# Whole Slide Image Classification Using PyTorch and TIAToolbox\n"]},{"cell_type":"markdown","metadata":{"id":"yLUSqCAMyiNz"},"source":["## Introduction\n","\n","In this tutorial, we will show how to classify Whole Slide Images (WSIs) using PyTorch deep learning models with help from TIAToolbox. A WSI represents human tissues taken through an operation or a biopsy and scanned using specialized scanners. They are used by pathologists and computational pathology researchers to [study cancer at the microscopic level](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7522141/) in order to understand for example tumor growth and help improve treatment for patients.\n","\n","What makes WSIs challenging to process is their enormous size. For example, a typical slide image has in the order of [100,000x100,000 pixels](https://doi.org/10.1117%2F12.912388) where each pixel can correspond to about 0.25x0.25 microns on the slide. This introduces challenges in loading and processing such images, not to mention hundreds or even thousands of WSIs in a single study (larger studies produce better results)!\n","\n","Conventional image processing pipelines are not suitable for WSI processing so we need better tools. This where [TIAToolbox](https://github.com/TissueImageAnalytics/tiatoolbox) can help as it brings a set of useful tools to import and process tissue slides in a fast and computationally efficient manner. Typically, WSIs are saved in a pyramid structure with multiple copies of the same image at various magnification levels optimized for visualization. The level 0 (or the bottom level) of the pyramid contains the image at the highest magnification or zoom level, whereas the higher levels in the pyramid have a lower resolution copy of the base image. The pyramid structure is sketched below.\n","\n","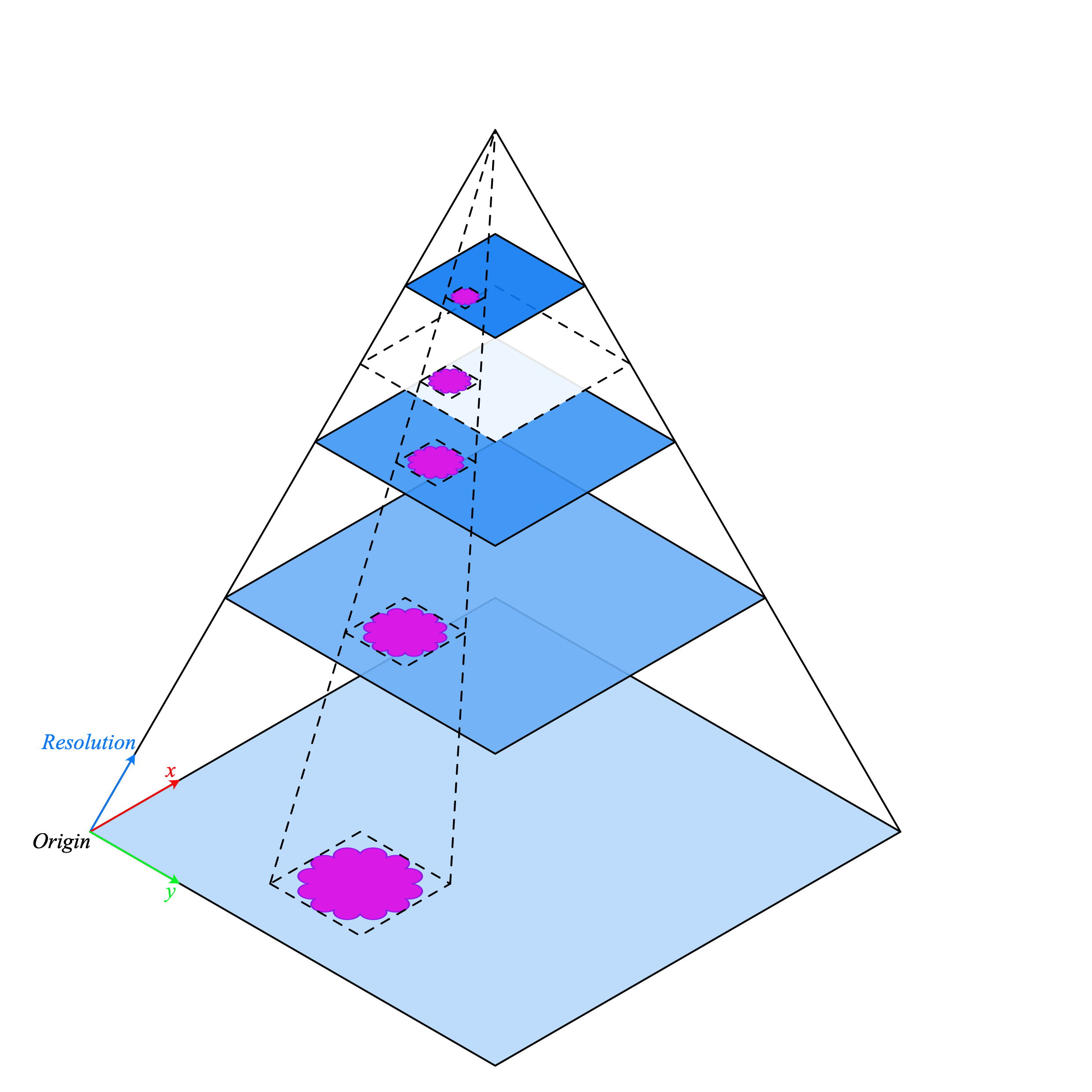\n","*WSI pyramid stack ([source](https://tia-toolbox.readthedocs.io/en/latest/_autosummary/tiatoolbox.wsicore.wsireader.WSIReader.html#))*\n","\n"," \n","\n","TIAToolbox allows us to automate common downstream analysis tasks such as [tissue classification](https://doi.org/10.1016/j.media.2022.102685). In this tutorial we will show you how you can:\n","1. Load WSI images using TIAToolbox; and\n","2. Use different PyTorch models to classify slides at the batch-level. In this tutorial, we will provide an example of using TorchVision's `ResNet18` model and custom [`HistoEncoder`](https://github.com/jopo666/HistoEncoder) model.\n","\n","Let's get started!"]},{"cell_type":"markdown","metadata":{"id":"EPiF6kU5yiN0","tags":["remove-cell"]},"source":["## Setting up the environment\n","To run the examples provided in this tutorial, the following packages are required as prequisites..\n","\n","1. OpenJpeg\n","2. OpenSlide\n","3. Pixman\n","4. TIAToolbox\n","5. HistoEncoder (for a custom model example)\n","\n","Please run the following command in your terminal to install these packages:"]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"end_time":"2023-11-10T18:40:04.895625400Z","start_time":"2023-11-10T18:40:04.621790200Z"},"id":"oCOSzUCUXnfh","tags":["remove-cell"],"vscode":{"languageId":"shellscript"}},"outputs":[],"source":["%%bash\n","apt-get -y install libopenjp2-7-dev libopenjp2-tools openslide-tools libpixman-1-dev | tail -n 1\n","pip install histoencoder | tail -n 1\n","pip install git+https://github.com/TissueImageAnalytics/tiatoolbox.git@develop | tail -n 1\n","echo \"Installation is done.\""]},{"cell_type":"markdown","metadata":{"id":"seaUmzYoSANq"},"source":["Alternatively, you can run `brew install openjpeg openslide` to install the prerequistite packages on MacOS instead of `apt-get`. Further information on installation can be [found here](https://tia-toolbox.readthedocs.io/en/latest/installation.html). You will likely need to restart the runtime in the runtime menu at the top of the page to continue with the rest of the tutorial, in order for the newly installed dependencies to be picked up."]},{"cell_type":"markdown","metadata":{"id":"bGp2XDMAX1GB"},"source":["### Importing related libraries\n","\n"]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"end_time":"2023-11-10T18:43:40.489228400Z","start_time":"2023-11-10T18:43:39.434913Z"},"id":"SNbdWfvnFtG5"},"outputs":[],"source":["\"\"\"Import modules required to run the Jupyter notebook.\"\"\"\n","from __future__ import annotations\n","\n","# Configure logging\n","import logging\n","import warnings\n","if logging.getLogger().hasHandlers():\n"," logging.getLogger().handlers.clear()\n","warnings.filterwarnings(\"ignore\", message=\".*The 'nopython' keyword.*\")\n","\n","# Downloading data and files\n","import shutil\n","from pathlib import Path\n","from zipfile import ZipFile\n","\n","# Data processing and visualization\n","import matplotlib as mpl\n","import matplotlib.pyplot as plt\n","import numpy as np\n","import pandas as pd\n","from matplotlib import cm\n","import PIL\n","import contextlib\n","import io\n","from sklearn.metrics import accuracy_score, confusion_matrix\n","\n","# TIAToolbox for WSI loading and processing\n","from tiatoolbox import logger\n","from tiatoolbox.models.architecture import vanilla\n","from tiatoolbox.models.engine.patch_predictor import (\n"," IOPatchPredictorConfig,\n"," PatchPredictor,\n",")\n","from tiatoolbox.utils.misc import download_data, grab_files_from_dir\n","from tiatoolbox.utils.visualization import overlay_prediction_mask\n","from tiatoolbox.wsicore.wsireader import WSIReader\n","\n","# Torch-related\n","import torch\n","from torchvision import transforms\n","\n","# Configure plotting\n","mpl.rcParams[\"figure.dpi\"] = 160 # for high resolution figure in notebook\n","mpl.rcParams[\"figure.facecolor\"] = \"white\" # To make sure text is visible in dark mode\n","\n","# If you are not using GPU, change ON_GPU to False\n","ON_GPU = True\n","\n","# Function to suppress console output for overly verbose code blocks\n","def suppress_console_output():\n"," return contextlib.redirect_stderr(io.StringIO())"]},{"cell_type":"markdown","metadata":{"collapsed":false,"id":"X8dSUvDHSANq"},"source":["### Clean-up before a run\n","\n","To ensure proper clean-up (for example in abnormal termination), all files downloaded or created in this run are saved in a single directory `global_save_dir`, which we set equal to \"./tmp/\". To simplify maintenance, the name of the directory occurs only at this one place, so that it can easily be changed, if desired.\n","\n"]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"end_time":"2023-11-10T18:41:51.192871200Z","start_time":"2023-11-10T18:41:51.160504Z"},"colab":{"base_uri":"https://localhost:8080/"},"id":"YibjAicoAVS1","outputId":"0006363f-003a-42d2-ee34-25105b6339a4","tags":["remove-cell"]},"outputs":[{"name":"stdout","output_type":"stream","text":["|2023-11-12|17:47:11.792| [INFO] Removing directory tmp\n","|2023-11-12|17:47:11.792| [INFO] Creating new directory tmp\n"]}],"source":["warnings.filterwarnings(\"ignore\")\n","global_save_dir = Path(\"./tmp/\")\n","\n","\n","def rmdir(dir_path: str | Path) -> None:\n"," \"\"\"Helper function to delete directory.\"\"\"\n"," if Path(dir_path).is_dir():\n"," shutil.rmtree(dir_path)\n"," logger.info(\"Removing directory %s\", dir_path)\n","\n","\n","rmdir(global_save_dir) # remove directory if it exists from previous runs\n","global_save_dir.mkdir()\n","logger.info(\"Creating new directory %s\", global_save_dir)"]},{"cell_type":"markdown","metadata":{"id":"TlgYO3n0FtG6"},"source":["### Downloading the data\n","For our sample data, we will use one whole-slide image, and patches from the validation subset of [Kather 100k](https://zenodo.org/record/1214456#.YJ-tn3mSkuU) dataset.\n"]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"end_time":"2023-11-10T18:41:56.177054800Z","start_time":"2023-11-10T18:41:56.104412700Z"},"colab":{"base_uri":"https://localhost:8080/"},"id":"l7CzZGFHFtG6","outputId":"39bd40d4-9f0c-4f0a-e18a-e7e982e8364e","tags":["hide-output"]},"outputs":[{"name":"stdout","output_type":"stream","text":["|2023-11-12|17:47:11.797| [INFO] Download has started. Please wait...\n","|2023-11-12|17:47:28.245| [INFO] Download is complete.\n"]}],"source":["wsi_path = global_save_dir / \"sample_wsi.svs\"\n","patches_path = global_save_dir / \"kather100k-validation-sample.zip\"\n","weights_path = global_save_dir / \"resnet18-kather100k.pth\"\n","\n","logger.info(\"Download has started. Please wait...\")\n","\n","# Downloading and unzip a sample whole-slide image\n","download_data(\n"," \"https://tiatoolbox.dcs.warwick.ac.uk/sample_wsis/TCGA-3L-AA1B-01Z-00-DX1.8923A151-A690-40B7-9E5A-FCBEDFC2394F.svs\",\n"," wsi_path,\n",")\n","\n","# Download and unzip a sample of the validation set used to train the Kather 100K dataset\n","download_data(\n"," \"https://tiatoolbox.dcs.warwick.ac.uk/datasets/kather100k-validation-sample.zip\",\n"," patches_path,\n",")\n","with ZipFile(patches_path, \"r\") as zipfile:\n"," zipfile.extractall(path=global_save_dir)\n","\n","# Download pretrained model weights for WSI classification using ResNet18 architecture\n","download_data(\n"," \"https://tiatoolbox.dcs.warwick.ac.uk/models/pc/resnet18-kather100k.pth\",\n"," weights_path,\n",")\n","\n","logger.info(\"Download is complete.\")"]},{"cell_type":"markdown","metadata":{"id":"qdaSTKE8FtG7"},"source":["## Reading the data\n","\n","We create a list of patches and a list of corresponding labels.\n","For example, the first label in `label_list` will indicate the class of the first image patch in `patch_list`.\n","\n"]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"start_time":"2023-11-10T18:40:05.791111900Z"},"colab":{"base_uri":"https://localhost:8080/","height":886},"id":"5sF4Q-6Px6IV","outputId":"4c474a52-24ca-4947-9cf0-08dcfe960702"},"outputs":[{"name":"stdout","output_type":"stream","text":["|2023-11-12|17:47:28.276| [INFO] Class ID: 0 -- Class Name: BACK -- Number of images: 211\n","|2023-11-12|17:47:28.276| [INFO] Class ID: 1 -- Class Name: NORM -- Number of images: 176\n","|2023-11-12|17:47:28.277| [INFO] Class ID: 2 -- Class Name: DEB -- Number of images: 230\n","|2023-11-12|17:47:28.277| [INFO] Class ID: 3 -- Class Name: TUM -- Number of images: 286\n","|2023-11-12|17:47:28.277| [INFO] Class ID: 4 -- Class Name: ADI -- Number of images: 208\n","|2023-11-12|17:47:28.277| [INFO] Class ID: 5 -- Class Name: MUC -- Number of images: 178\n","|2023-11-12|17:47:28.277| [INFO] Class ID: 6 -- Class Name: MUS -- Number of images: 270\n","|2023-11-12|17:47:28.278| [INFO] Class ID: 7 -- Class Name: STR -- Number of images: 209\n","|2023-11-12|17:47:28.278| [INFO] Class ID: 8 -- Class Name: LYM -- Number of images: 232\n","|2023-11-12|17:47:28.278| [INFO] Total number of patches: 2000\n"]},{"data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAA5AAAAK3CAYAAADzkqAeAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy88F64QAAAACXBIWXMAABibAAAYmwFJdYOUAABtNUlEQVR4nO3dd3gU1eL/8c8mISGNhB4gBJAuTUIRKQIKCChIExCFRAWxUi9SlKIgICgoKLYLhCKX3uEiwgWkKIoUjfQeJCCdFFqS+f3hb/fLmjaQ2TTfr+fJQ3bOOXPODLvZ/ezMnLEZhmEIAAAAAIB0uGX1AAAAAAAAOQMBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGBKjg+Q33zzjXr06KEaNWqoSJEiypMnjwICAlS3bl2NGzdOsbGxqbbdsGGDWrdurUKFCsnb21uVKlXS22+/nWYbSTp69KjCw8MVHBwsLy8vBQcHKzw8XMePH7d68wAAAAAg27AZhmFk9SAyomHDhtqxY4cqV66skiVLqkCBAjp//rx++OEH3bhxQ+XKldOWLVtUvHhxp3aTJ0/WgAEDZLPZ1KhRIxUtWlRbt27VuXPnVLFiRW3btk2FChVK1t/27dvVokULxcfHq0qVKqpataoiIyP1+++/y9fXVxs2bFC9evUya/MBAAAAINPk+AC5c+dOlS9fXgUKFHBafunSJbVr107btm1T165d9Z///MdRtmfPHtWqVUtubm5atWqVWrVqJUmKj49X27ZttXHjRnXs2FGLFy92Wmd8fLzKly+vs2fPaujQoRo7dqyjbNiwYRo3bpxKliypQ4cOydvb24VbDQAAAACZL8cHyLRs3bpVjz76qAoUKKBLly45lnfu3FmLFi1Sz5499fXXXzu1OXXqlB544AElJSXpwIEDqlSpkqNs2rRpev3111WhQgUdOHBAbm7/dwZwUlKSKleurMOHD+uLL75Q7969Xb+BAAAAAJCJcvw1kGnx8PCQJHl5eTmW3b59W2vWrJEkdevWLVmbUqVKqUGDBpKkZcuWOZXZH3ft2tUpPEqSm5ubunTpIklaunSpRVsAAAAAANlHrg2QMTExGjVqlCSpbdu2juWHDx9WfHy8JKl27doptrUv37Nnj9Ny++N7bQcAAAAAuYFHVg/AKuvXr9e8efOUlJTkmEQnJiZGLVu21AcffOCod+LECUlSYGCg/P39U1xXyZIlnepKfwVS+2mwISEhaba7cOGC4uLi5Ovre9/b4+vrqzt37qhIkSL3vQ4AAAAAuNuff/6pPHnyKC4u7r7a55oAuX//fs2aNctpWbdu3TRp0iQFBAQ4lsXExEhSmuHOz89PknT9+vVk7dJqa29nb5tegAwODk61LD4+PtlpsgAAAACQEYmJiRlqn2sCZL9+/dSvXz/duXNHp0+f1ooVKzRmzBitW7dOy5Yt06OPPprVQ7wnbm5uKlasmM6cOZPVQwEAAACQS6R1EMuMXBMg7fLkyaOyZctqwIABatCggR555BE9//zzjltr2E9bTeuQbWxsrCQpX758jmV3n+6aWlt7u7+3TU1a4TCj/7EAAAAAYLVcfY7kww8/rAcffFBRUVHatWuXJKl06dKSpKtXrzqdlnq3qKgop7rSXwHSfq/J06dPp9muUKFCGbr+EQAAAACyo1wdIKX/u17xzz//lCRVrFhRPj4+kuQIlX9nXx4aGuq03P74XtsBAAAAQG6QqwPkxYsXtW/fPklShQoVJEmenp568sknJUnz5s1L1ubUqVPasWOHJKl9+/ZOZfbH8+fPV1JSklNZUlKSFixYIEnq0KGDhVsBAAAAANlDjg6Q+/fv1zfffKObN28mKzt8+LCeeeYZ3bp1S/Xq1VO1atUcZUOGDJHNZtPMmTO1bt06x/L4+Hi99NJLSkxMVMeOHVWpUiWndYaHh6t48eI6fPiwhg8f7lQ2fPhwHT58WMHBwerRo4fFWwoAAAAAWc9mGIaR1YO4X5s3b1bTpk3l6+urmjVrKjg4WLdv39bp06e1e/duJSUlqXLlylq3bl2yezdOnjxZAwYMkM1mU+PGjVWkSBFt3bpV0dHRqlixorZt26ZChQol63P79u1q0aKF4uPjVbVqVVWtWlWRkZGKjIyUr6+vNmzYoHr16mV42+yT6DALKwAAAACrZDRn5OgAeeHCBX399dfaunWrDh48qAsXLujOnTsqUKCAqlWrpg4dOuiFF16Ql5dXiu03bNigjz76SD/99JPi4uIUEhKiTp06aejQoU6zrv7d0aNHNXr0aG3YsEEXLlxQ4cKF1axZM40YMUJly5a1ZNsIkAAAAACs9o8OkLkZARIAAACA1TKaM3L0NZAAAAAAgMxDgAQAAAAAmEKABAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACY4pHVAwAAZJ3SQ9Zk9RCyhZPjn8zqIQAAkCNwBBIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYIpHVg8AAAAA1ik9ZE1WDyFbODn+yaweApArcQQSAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgSo4OkHfu3NHGjRs1aNAg1alTR4GBgcqTJ4+CgoLUtm1brVmzJsV2o0aNks1mS/Pn4MGDqfZ79OhRhYeHKzg4WF5eXgoODlZ4eLiOHz/uqk0FAAAAgCznkdUDyIgtW7aoefPmkqSgoCA1bNhQvr6+2r9/v1atWqVVq1bp5Zdf1hdffCGbzZasfY0aNfTQQw+luO6AgIAUl2/fvl0tWrRQfHy8qlSpooYNGyoyMlKzZs3S4sWLtWHDBtWrV8+ybQQAAACA7CJHB0g3Nzd17NhRffv2VaNGjZzKFixYoOeee05fffWVGjRooB49eiRr365dO40aNcp0f/Hx8ercubPi4+M1dOhQjR071lE2bNgwjRs3Tp07d9ahQ4fk7e1939sFAAAAANlRjj6F9bHHHtPixYuThUdJ6tKli8LDwyVJs2fPtqS/iIgInT17VhUqVNCYMWOcysaMGaMKFSooKirKsv4AAAAAIDvJ0QEyPTVr1pQkRUVFWbK+ZcuWSZK6du0qNzfnXefm5qYuXbpIkpYuXWpJfwAAAACQneToU1jTc+TIEUlSsWLFUizfvXu3hgwZosuXLysgIEA1a9ZUmzZt5O/vn2L9PXv2SJJq166dYrl9ub0eAAAAAOQmuTZAnjt3ThEREZKkjh07pljHPtHO3QICAjRlypRk10zGxMTo0qVLkqSQkJAU11eyZElJ0oULFxQXFydfX9+MbAIAAAAAZCu5MkAmJCTo+eef17Vr11StWjX17t3bqbxs2bIaO3asWrVqpVKlSkmS9u/fr/Hjx2v16tUKCwuTu7u7nnvuOUebmJgYx++pBUM/Pz/H79evX083QAYHB6daFh0dneqRUwAAAADICrkyQL7yyivauHGjChYsqMWLF8vT09OpvHv37snaNGjQQKtWrVKfPn00depU9e/fX88880yytgAAAADwT5XrAmTfvn01ffp05c+fX999950qVKhwT+1HjRqladOm6cKFC9q5c6djhte7r4uMi4tLsW1sbKzj93z58qXb15kzZ1ItS+voJAAAAABkhVw1C+vAgQM1ZcoUBQYGav369Y5ZWO9FgQIFVKRIEUnOAc/f318FChSQJJ0+fTrFtvbZXgsVKsT1jwAAAABynVwTIN966y1NmjRJAQEBWr9+faozpaYnMTFR165dk6Rks7GGhoZKknbt2pViW/tyez0AAAAAyE1yRYAcMmSIJk6cqICAAH333XeqU6fOfa9r5cqVio+Pl81mSxZC27dvL0maP3++kpKSnMqSkpK0YMECSVKHDh3uu38AAAAAyK5yfIB855139MEHHygwMNBUeDx9+rTmzp2rmzdvJitbvny5evbsKUl67rnnFBQU5FQeHh6u4sWL6/Dhwxo+fLhT2fDhw3X48GEFBwcnuwUIAAAAAOQGOXoSnZUrV+r999+XJJUrV06fffZZivUKFSqkDz/8UJJ0+fJlde/eXa+++qpq1qypEiVK6MaNG9q/f7+OHDkiSWratKk+//zzZOvx8fHRwoUL1aJFC40dO1YrV65U1apVFRkZqcjISPn6+mrRokXy9vZ20RYDAAAAQNbJ0QHy8uXLjt937dqV6rWJpUqVcgTIkiVLavDgwfr555919OhR7d69W7dv31ahQoX01FNPqVu3burSpYvc3FI+ONugQQPt27dPo0eP1oYNG7RkyRIVLlxYPXr00IgRI1S2bFnrNxQAAAAAsgGbYRhGVg8Cydlv45HWrT4AIKNKD1mT1UPIFk6OfzKrhwBYhtf1X3hdAynLaM7I8ddAAgAAAAAyBwESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYIpHVg8AAAAAQO5UesiarB5CtnBy/JNZPQTLcAQSAAAAAGAKARIAAAAAYAoBEgAAAABgCtdAAsiRuKbiL7npmgoAAJD9cQQSAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgikdWDwA5R+kha7J6CNnCyfFPZvUQAAAAgCzBEUgAAAAAgCkESAAAAACAKQRIAAAAAIApXAMJAAAA/A1zP/yFuR/wdxyBBAAAAACYwhFIAAAyiCMVf+FIBQDkfhyBBAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACYQoAEAAAAAJhCgAQAAAAAmEKABAAAAACYkqMD5J07d7Rx40YNGjRIderUUWBgoPLkyaOgoCC1bdtWa9akfV+uDRs2qHXr1ipUqJC8vb1VqVIlvf3224qNjU2z3dGjRxUeHq7g4GB5eXkpODhY4eHhOn78uJWbBwAAAADZSo4OkFu2bFGzZs304Ycf6syZM2rYsKE6dOigwoULa9WqVXrqqafUu3dvGYaRrO3kyZPVvHlzrVu3TlWqVFGbNm107do1jR07VrVr19bFixdT7HP79u2qUaOGZs2apcDAQLVv316BgYGaNWuWqlevrh9//NHVmw0AAAAAWcLSAHn69GmtXLlSZ86ccVr++++/q2nTpsqfP79q1qyp7777zpL+3Nzc1LFjR33//feKjo7W6tWrtWDBAv3222+aP3++3N3d9dVXX2nOnDlO7fbs2aOBAwfK3d1da9as0ZYtW7Rw4UIdO3ZMjz/+uA4dOqRXXnklWX/x8fHq3Lmz4uPjNXToUEVGRmr+/PmKjIzU0KFDFRcXp86dO+vGjRuWbB8AAAAAZCeWBsgPP/xQ7du3V1xcnGNZXFycmjVrpi1btujatWvat2+f2rZtqyNHjmS4v8cee0yLFy9Wo0aNkpV16dJF4eHhkqTZs2c7lY0bN06GYeiFF15Qq1atHMt9fHw0ffp0ubm5acmSJTp48KBTu4iICJ09e1YVKlTQmDFjnMrGjBmjChUqKCoqKll/AAAAAJAbWBogv//+e5UvX14VK1Z0LJs3b57Onz+vdu3aae/evXrvvfd069Ytffrpp1Z2naKaNWtKkqKiohzLbt++7bg2slu3bsnalCpVSg0aNJAkLVu2zKnM/rhr165yc3PedW5uburSpYskaenSpRZtAQAAAABkH5YGyOjoaD3wwANOy9atWyebzaapU6eqevXqeuedd1SxYkX973//s7LrFNmPchYrVsyx7PDhw4qPj5ck1a5dO8V29uV79uxxWm5/fK/tAAAAACA3sDRAXrlyRQUKFHBa9uOPP+rBBx9UiRIlHMuqVauW7DpJq507d04RERGSpI4dOzqWnzhxQpIUGBgof3//FNuWLFnSqa4kxcTE6NKlS5KkkJCQNNtduHDB6TReAAAAAMgNPKxcma+vry5cuOB4fPLkSUVHR6tNmzbOnXp4KCEhwcqunSQkJOj555/XtWvXVK1aNfXu3dtRFhMT4xhravz8/CRJ169fT9Yurbb2dva2afUhScHBwamWRUdHOx05BQAAAICsZukRyAcffFDbtm1zhMh58+bJZrMlm+QmKipKRYsWtbJrJ6+88oo2btyoggULavHixfL09HRZXwAAAADwT2HpEciwsDD98MMPql27tkJDQ7V27Vr5+/urbdu2jjo3b97U7t279dhjj1nZtUPfvn01ffp05c+fX999950qVKjgVG4/bTWtU0xjY2MlSfny5UvWLq229nZ/b5uatE7jTevoJAAAAABkBUuPQPbq1Uvh4eGKiorSihUrlDdvXs2YMcMpfK1cuVI3btzQo48+amXXkqSBAwdqypQpCgwM1Pr16x2zsN6tdOnSkqSrV686nZZ6N/usrfa60l8B0n595+nTp9NsV6hQoXRPXwUAAACAnMbSAGmz2TRjxgydOnVKP/30k/744w916NDBqU6FChW0bNky9ejRw8qu9dZbb2nSpEkKCAjQ+vXrU50ptWLFivLx8ZEk7dq1K8U69uWhoaFOy+2P77UdAAAAAOQGlgZIu5IlS6p27dpOk8rYPfTQQ3r66actvQZyyJAhmjhxogICAvTdd9+pTp06qdb19PTUk08+KemvazT/7tSpU9qxY4ckqX379k5l9sfz589XUlKSU1lSUpIWLFggSclCMwAAAADkBi4JkJJ07do1bdiwQf/5z38cgcwV3nnnHX3wwQcKDAxMNzzaDRkyRDabTTNnztS6descy+Pj4/XSSy8pMTFRHTt2VKVKlZzahYeHq3jx4jp8+LCGDx/uVDZ8+HAdPnxYwcHBlh9dBQAAAIDswNJJdKS/bnfRv39/zZkzx3GrjrCwMNWvX1+S9O9//1sjRozQsmXL9PDDD2eor5UrV+r999+XJJUrV06fffZZivUKFSqkDz/80PE4NDRUH330kQYMGKDWrVurcePGKlKkiLZu3aro6GhVrFhRX3zxRbL1+Pj4aOHChWrRooXGjh2rlStXqmrVqoqMjFRkZKR8fX21aNEieXt7Z2i7AAAAACA7sjRA3rhxQ02aNNGePXtUpEgR1a5dW2vXrnWq89RTT6l3795avnx5hgPk5cuXHb/v2rUr1WsTS5Uq5RQgJal///6qVq2aPvroI/3000+Ki4tTSEiIhg4dqqFDhzpN/HO3Bg0aaN++fRo9erQ2bNigJUuWqHDhwurRo4dGjBihsmXLZmibAAAAACC7sjRATpo0SXv27NGzzz6rr776Sr6+vnJzcz5LNigoSJUrV9amTZsy3F94eLjCw8Pvu32zZs3UrFmze25Xrlw5zZo16777BQAAAICcyNJrIBcsWKCgoCBNnz49zdtYVKhQIc17IAIAAAAAsh9LA+SxY8dUt25d5c2bN816Pj4+unjxopVdAwAAAABczNIA6e7urjt37qRb78yZM2keoQQAAAAAZD+WBsiyZctq3759jtlXUxIbG6tff/1VlStXtrJrAAAAAICLWRog27Ztq+joaI0ZMybVOmPGjNG1a9fUvn17K7sGAAAAALiYpQGyf//+KlGihEaPHq127dpp3rx5kqTz589r6dKl6tq1qyZOnKjSpUvrlVdesbJrAAAAAICLWXobj8DAQK1bt05t27bVypUrtWrVKtlsNq1bt07r1q2TYRgqVaqUVq1axTWQAAAAAJDDWBogJenBBx9UZGSkIiIitHbtWh0/flxJSUkqWbKkWrVqpZdfflk+Pj5WdwsAAAAAcDHLA6Qk5c2bV6+88gqnqQIAAABALmLpNZAAAAAAgNyLAAkAAAAAMMXyAHn69Gm9+uqrKl++vHx8fOTu7p7ij4eHS86eBQAAAAC4iKUp7uDBg2rQoIGuXr0qwzDSrJteOQAAAAAge7H0COTbb7+tK1euqEWLFvrxxx917do1JSUlpfoDAAAAAMg5LD0CuWXLFoWEhGjFihXy9PS0ctUAAAAAgCxm6RHI+Ph41a1bl/AIAAAAALmQpQHygQceUFxcnJWrBAAAAABkE5YGyO7du+v777/XhQsXrFwtAAAAACAbsDRADhw4UI888ohatWqlyMhIK1cNAAAAAMhiGZpE57HHHku27M6dO9q9e7ceeughhYSEKCQkRG5uyXOqzWbTxo0bM9I9AAAAACATZShAbt68OdWypKQknTx5UidPnkyx3GazZaRrAAAAAEAmy1CA3LRpk1XjAAAAAABkcxkKkI0bN7ZqHAAAAACAbM7SSXQAAAAAALmXpQEyKipKs2fP1qFDh1Ktc/DgQc2ePVtnzpyxsmsAAAAAgItZGiCnTp2qF154QYZhpFrHMAyFh4dr2rRpVnYNAAAAAHAxSwPk+vXrVblyZVWqVCnVOpUrV9aDDz6odevWWdk1AAAAAMDFLD+FtVy5cunWK1eunKKioqzsGgAAAADgYpYGyPj4eHl7e6dbz9vbWzExMVZ2DQAAAABwMUsDZLFixbR379506+3bt09FihSxsmsAAAAAgItZGiAbNWqkw4cPa8mSJanWWbp0qQ4ePKhHH33Uyq4BAAAAAC5maYDs27evbDabevTooU8++cTpNNWYmBh98skn6tGjh9zc3NSnTx8ruwYAAAAAuJilATI0NFTjxo3TjRs3NGDAABUoUEAhISEKCQlRgQIFNGDAAMXHx2vMmDGqW7eulV0DAAAAAFzM0gApSYMGDdLy5ctVvXp1JSYm6syZMzpz5owSExNVvXp1LV26VEOGDLG6WwAAAACAi3m4YqVt27ZV27Ztdf78eZ0+fVqSFBISoqJFi7qiOwAAkAuUHrImq4eQLZwc/2RWDwEAUuWSAGlXtGhRQiMAAAAA5BKWnsLq7u6ul156Kd16vXr1koeHS7MrAAAAAMBilgZIwzBkGIbpugAAAACAnCNLDgPGx8crT548WdE1kOW4xucvXOMDAACQ81g+C2t6rl69qm3btqlYsWKZ3TUAAAAAIAMyfATygQcecHq8ePFibd68OcW6CQkJOnfunBITE9W7d++Mdg0AAAAAyEQZDpAnT550/G6z2RQbG6vY2NhU63t6eqpdu3YaO3ZsRrsGAAAAAGSiDAfIEydOSPprUpwHHnhAnTp10sSJE1Os6+npqcKFCzMDKwAAAADkQBlOcqVKlXL8HhYWpkaNGjktAwAAAADkDpYeCpw5c6aVqwMAAAAAZCOZPgsrAAAAACBncsnFiLt27dLixYt16NAhXb9+XYZhJKtjs9m0ceNGV3QPAAAAAHABywPkv/71L02ePNkRGm02m1OAtD+22WxWdw0AAAAAcCFLT2FdtGiRJk2apBIlSujLL79UixYtJEnffvutPv30Uz3yyCMyDENDhgzR//73Pyu7BgAAAAC4mKUB8quvvpK7u7s2btyoXr16qVixYpKk5s2b67XXXtP27dv19ttva9KkSQoICLCyawAAAACAi1kaIPfs2aOHH35Y5cuXT7XOu+++q2LFimnMmDFWdg0AAAAAcDFLA2RMTIxCQkIcjz09PSVJsbGx/9ehm5sefvhhbd++3cquAQAAAAAuZmmALFy4sK5evep4XKhQIUnSyZMnnerFxcXp+vXrVnYNAAAAAHAxSwNk6dKlderUKcfjmjVryjAMzZs3z7Hs3Llz2rJli0qVKmVl1wAAAAAAF7M0QD7++OM6ePCg44hjq1atVKBAAX3wwQd65plnNHDgQD388MOKi4tTx44drewaAAAAAOBilt4HsmvXrjp79qyioqJUunRp+fr6aubMmeratauWLFniqFerVi0NHTrUyq4BAAAAAC5maYCsXLmyvv76a6dlbdq00ZEjR7Rq1SpdvnxZlStXVps2beTu7m5l1wAAAAAAF7M0QKamePHi6t27d2Z0BQAAAABwEUuvgQQAAAAA5F4uOQJ58eJF/fvf/9bmzZt15swZGYah4OBgNW3aVC+++KKKFCniim4BAAAAAC5keYBcsWKFXnjhBV27dk2GYTiWHzhwQBs2bND48eM1c+ZMtW/f3uquAQAAAAAuZGmA3Llzp5555hklJCSodu3a6tGjh8qUKSNJOnnypGbPnq2ff/5ZXbp00datW/Xwww9b2T0AAAAAwIUsDZDvvfeeEhMTNXHiRA0cODBZ+euvv67Jkydr4MCBGj16tFavXm1l9wAAAAAAF7J0Ep0dO3aoatWqKYZHu/79+6tatWravn27lV0DAAAAAFzM0gB5584dVatWLd16VatW1Z07d6zsGgAAAADgYpYGyEqVKikqKirden/88YcqVqxoZdcAAAAAABezNED27t1b27Zt05YtW1Kts2XLFm3dulW9e/e2smsAAAAAgItZOolOr169dPDgQT355JN65ZVXnGZhPXHihObMmaPPP/9c/fr108svv2xl1wAAAAAAF7M0QLq7uzt+nzx5siZPnpxivY8//lgff/yx0zKbzaaEhAQrhwMAAAAAsJClAdIwjCxpCwAAAABwPUsDZFJSkpWrAwAAAABkI5ZOogMAAAAAyL0IkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMyFCC///57HT582KqxAAAAAACysQwFyCZNmmj8+PGOx4899pgmTJiQ4UEBAAAAALIfj4yuwDAMx++bN29W6dKlM7pKAAAAAEA2lKEjkP7+/oqOjrZqLPfs0KFDmjp1qsLDw1WtWjV5eHjIZrNpzJgxqbYZNWqUbDZbmj8HDx5Mtf3Ro0cVHh6u4OBgeXl5KTg4WOHh4Tp+/LgrNhEAAAAAso0MHYGsXr26/ve//2nEiBEqV66cpL8C1uzZs02179GjR0a61+eff65PPvnkvtrWqFFDDz30UIplAQEBKS7fvn27WrRoofj4eFWpUkUNGzZUZGSkZs2apcWLF2vDhg2qV6/efY0HAAAAALK7DAXIt956S506ddL777/vWLZ9+3Zt377dVPuMBsiqVavqX//6l2rWrKnQ0FCNHTtWc+bMMdW2Xbt2GjVqlOm+4uPj1blzZ8XHx2vo0KEaO3aso2zYsGEaN26cOnfurEOHDsnb2/teNwUAAAAAsr0MBcg2bdrop59+0vLly3Xq1ClFRESobNmyatCggVXjS1PPnj2dHru5ue6uJBERETp79qwqVKiQ7BTZMWPGaMmSJTp8+LBmz56t3r17u2wcAAAAAJBVMjyJTo0aNVSjRg1Jf4Wshg0basaMGRkeWHazbNkySVLXrl2TBVU3Nzd16dJFo0eP1tKlSwmQAAAAAHKlDAfIu40cOVI1a9a0cpUus3v3bg0ZMkSXL19WQECAatasqTZt2sjf3z/F+nv27JEk1a5dO8Vy+3J7PQAAAADIbSwPkDnFqlWrtGrVKqdlAQEBmjJlSrJrM2NiYnTp0iVJUkhISIrrK1mypCTpwoULiouLk6+vrwtGDQAAAABZx9IAaZeQkKDFixdr06ZN+uOPPyRJJUqUUNOmTdWpUyd5eLikW1PKli2rsWPHqlWrVipVqpQkaf/+/Ro/frxWr16tsLAwubu767nnnnO0iYmJcfyeWjD08/Nz/H79+nVTATI4ODjVsujoaBUrVizddQAAAABAZrE8ye3du1edOnXSiRMnZBiGU9m///1vDR8+XIsWLUr1Fhqu1r1792TLGjRooFWrVqlPnz6aOnWq+vfvr2eeeUaenp5ZMEIAAAAAyJ4sDZBnz55VixYtdPHiRRUtWlRdu3ZV2bJlJUnHjx/X/PnzdezYMT3xxBPau3dvtjvCNmrUKE2bNk0XLlzQzp071ahRI0lyui4yLi4uxbaxsbGO3/Ply2eqvzNnzqRaltbRSQAAAADICpbe9+KDDz7QxYsX1bNnTx0/flyTJ0/WG2+8oTfeeEOTJk3S8ePH1bNnT124cEETJkywsmtLFChQQEWKFJHkHO78/f1VoEABSdLp06dTbBsVFSVJKlSoENc/AgAAAMiVLA2Q//3vfxUSEqLPP/9c3t7eycrz5s2radOmKSQkRGvWrLGya0skJibq2rVrkpRsNtbQ0FBJ0q5du1Jsa19urwcAAAAAuY2lATIqKkr169eXu7t7qnU8PDz0yCOPOI7YZScrV65UfHy8bDZbstt1tG/fXpI0f/58JSUlOZUlJSVpwYIFkqQOHTpkzmABAAAAIJNZGiC9vLx0/fr1dOvFxMTIy8vLyq5NOX36tObOnaubN28mK1u+fLl69uwpSXruuecUFBTkVB4eHq7ixYvr8OHDGj58uFPZ8OHDdfjwYQUHBye7BQgAAAAA5BaWTqLz4IMPatOmTYqKinLcF/HvTp8+rU2bNlkyC+vu3bv12muvOR4fO3ZMkvTll19q9erVjuXLli1TsWLFdPnyZXXv3l2vvvqqatasqRIlSujGjRvav3+/jhw5Iklq2rSpPv/882R9+fj4aOHChWrRooXGjh2rlStXqmrVqoqMjFRkZKR8fX21aNGiFE/dBQAAAIDcwNIjkD169NCNGzfUrFkzrV27Nln56tWr1bx5c928edOSI3XXr1/Xzp07HT8XL16U9NcEOHcvv3XrliSpZMmSGjx4sOrWratTp05p1apVWrt2rWJjY/XUU09p3rx52rBhg9M9He/WoEED7du3Tz169NDly5e1ZMkSXb58WT169NC+fftUr169DG8TAAAAAGRXlh6B7NWrl5YsWaKNGzeqTZs2KlCggMqUKSNJOnHihC5fvizDMNSsWTP16tUrw/01adIk2b0m01KwYEGNHz8+Q32WK1dOs2bNytA6AAAAACAnsvQIpLu7u9asWaO33npLvr6+unTpknbt2qVdu3bp0qVL8vX11eDBg7V69Wq5uVnaNQAAAADAxSw9AilJnp6eGj9+vN59913t2rVLf/zxhySpRIkSql27dpZMngMAAAAAyDjLA6Sdl5eXGjRo4KrVAwAAAAAyGeeRAgAAAABMIUACAAAAAEwhQAIAAAAATCFAAgAAAABMIUACAAAAAEwhQAIAAAAATLE0QJ4+fVpRUVFWrhIAAAAAkE1YGiBLly6trl27WrlKAAAAAEA2YWmAzJcvn8qUKWPlKgEAAAAA2YSlAfLBBx/kFFYAAAAAyKUsDZC9evXS9u3b9fPPP1u5WgAAAABANmBpgHzhhRf02muvqUWLFho7dqwOHTqkW7duWdkFAAAAACCLeFi5Mnd3d8fvw4cP1/Dhw1Ota7PZlJCQYGX3AAAAAAAXsjRAGobhkroAAAAAgKxnaYBMSkqycnUAAAAAgGzE0msgAQAAAAC5FwESAAAAAGCKSwLksWPH9NZbb6lhw4aqWLGi3nrrLUfZzp079dVXX+natWuu6BoAAAAA4CKWXgMpSbNmzdIrr7ziuH2HzWbTxYsXHeXx8fF69dVX5enpqfDwcKu7BwAAAAC4iKVHIH/88Uf17NlTnp6emjBhgnbu3JlsttXGjRsrICBAq1atsrJrAAAAAICLWXoEcsKECTIMQ2vWrFHDhg1TrOPm5qaHHnpI+/fvt7JrAAAAAICLWXoEcvv27apbt26q4dEuKChI0dHRVnYNAAAAAHAxSwPk1atXFRISkm69Gzdu6Pbt21Z2DQAAAABwMUsDZMGCBXXq1Kl06x09elRBQUFWdg0AAAAAcDFLA2S9evW0a9cu/f7776nW2b59u37//fd0T3MFAAAAAGQvlgbI119/XYmJierYsaP27t2brPzAgQN68cUXZbPZ9Nprr1nZNQAAAADAxSwNkI8//rgGDBigw4cPq1atWqpQoYJsNpu+/fZbVa9eXdWqVdORI0c0aNAg1atXz8quAQAAAAAuZmmAlKQPP/xQX375pYKCgnT06FEZhqHo6GhFRkaqQIECmjp1qsaPH291twAAAAAAF7P0PpB2vXr1Us+ePbVnzx4dP35cSUlJKlmypOrUqSMPD5d0CQAAAABwMZelOZvNptDQUIWGhrqqCwAAAABAJnLp4UDDMHTp0iUZhqGCBQvKzc3yM2YBAAAAAJnEJYnuu+++U8uWLeXv76+iRYsqKChI/v7+atmypb799ltXdAkAAAAAcDHLA+SgQYPUsmVLrV+/XvHx8TIMQ4Zh6MaNG1q/fr1at26tgQMHWt0tAAAAAMDFLA2Qc+fO1UcffaS8efNq4MCB+vXXXxUTE6OYmBj99ttv+te//iVvb299/PHHmjt3rpVdAwAAAABczNIAOXXqVLm7u2vdunWaOHGiqlatKl9fX/n6+qpKlSqaMGGC1q1bJ5vNpk8//dTKrgEAAAAALmZpgIyMjFTDhg3VqFGjVOvYyyMjI63sGgAAAADgYpYGyLx586p48eLp1itevLg8PT2t7BoAAAAA4GKWBshatWrp119/Tbfer7/+qtq1a1vZNQAAAADAxSwNkG+//bYOHDigCRMmpFpn4sSJOnDggIYNG2Zl1wAAAAAAF/PISOPvv//e6bHNZtMbb7yhoUOHatGiRerevbvKlCkjSTpx4oTmzp2rX375RX369JGbm0tuQQkAAAAAcJEMBcgmTZrIZrMlW24Yhn755Rft3r072XJJmjJliqZOnaqEhISMdA8AAAAAyEQZCpCPPvpoigESAAAAAJD7ZChAbt682aJhAAAAAACyOy5EBAAAAACYQoAEAAAAAJiSoVNYU3Pz5k3t2rVLZ8+e1c2bN1Ot16NHD1d0DwAAAABwAcsD5MSJEzV27Fhdv3493boESAAAAADIOSwNkJ9++qkGDx4sSapWrZrKly8vf39/K7sAAAAAAGQRywOkh4eHlixZojZt2li5agAAAABAFrN0Ep2TJ0/q0UcfJTwCAAAAQC5kaYAsUqSIChcubOUqAQAAAADZhKUBslWrVvrhhx+UlJRk5WoBAAAAANmApQFy5MiRun37tvr06aPbt29buWoAAAAAQBazdBKd4sWLa9u2bWrbtq0qVqyopk2bKiQkRG5uyXOqzWbT8OHDreweAAAAAOBClgZIwzD0ySef6ODBg0pKSlJERESyOjabTYZhECABAAAAIIexNEBOnDhRU6dOlYeHh5566imVL19efn5+VnYBAAAAAMgilgbIf//73/Lx8dHWrVtVs2ZNK1cNAAAAAMhilk6iExUVpUaNGhEeAQAAACAXsjRABgUFyd/f38pVAgAAAACyCUsDZPv27bV161bdvHnTytUCAAAAALIBSwPkqFGjVKBAAT377LO6ePGilasGAAAAAGQxSyfR6devnypWrKjly5frf//7n2rVqpXmfSCnT59uZfcAAAAAABeyNEBGRETIZrNJkmJiYrR58+ZU6xIgAQAAACBnsTRAzpw508rVAQAAAACyEUsDZFhYmJWrAwAAAABkI5ZOogMAAAAAyL0IkAAAAAAAUyw9hfXFF180XZdJdAAAAAAgZ7F8Fta02GdoNQyDAAkAAAAAOUymzMKalJSkU6dOae3atdq1a5f69eunGjVqWNk1AAAAAMDFMnUW1lGjRumtt97S119/rd27d1vZNQAAAADAxTJ9Ep2xY8fK399fI0aMyOyuAQAAAAAZkOkB0sPDQ6GhodqwYUNmdw0AAAAAyIAsuY3HjRs3dOXKlazoGgAAAABwnzI9QB44cEDbtm1TyZIlM7trAAAAAEAGWDqJzuzZs1Mti4mJ0YEDBzRnzhzdvHlT3bp1s7JrAAAAAICLWRogw8PDHfd6TIlhGJKkp59+Wu+8846VXQMAAAAAXMzSANmjR49UA6Snp6dKlCihZs2aqX79+lZ2CwAAAADIBJYGyIiICCtXBwAAAADIRrJkFlarHDp0SFOnTlV4eLiqVasmDw8P2Ww2jRkzJt22GzZsUOvWrVWoUCF5e3urUqVKevvttxUbG5tmu6NHjyo8PFzBwcHy8vJScHCwwsPDdfz4cas2CwAAAACypRwdID///HP16dNHs2bNUmRkpBITE021mzx5spo3b65169apSpUqatOmja5du6axY8eqdu3aunjxYorttm/frho1amjWrFkKDAxU+/btFRgYqFmzZql69er68ccfrdw8AAAAAMhWMnQKa1qzrprRo0ePDLWvWrWq/vWvf6lmzZoKDQ3V2LFjNWfOnDTb7NmzRwMHDpS7u7tWrVqlVq1aSZLi4+PVtm1bbdy4Ua+88ooWL17s1C4+Pl6dO3dWfHy8hg4dqrFjxzrKhg0bpnHjxqlz5846dOiQvL29M7RdAAAAAJAdZShApjfranoyGiB79uzp9NjNLf0DquPGjZNhGHrhhRcc4VGSfHx8NH36dD3wwANasmSJDh48qEqVKjnKIyIidPbsWVWoUCHZKbJjxozRkiVLdPjwYc2ePVu9e/fO0HYBAAAAQHaUoQD52GOP3XOA/OGHHxQfH5+h4Hm/bt++rTVr1khSivehLFWqlBo0aKCtW7dq2bJlGjp0qKNs2bJlkqSuXbsmC6pubm7q0qWLRo8eraVLlxIgAQAAAORKGQqQGzZsMF1369ateuutt3Tjxg1JUrVq1TLS9X05fPiw4uPjJUm1a9dOsU7t2rW1detW7dmzx2m5/XFa7e6uBwAAAAC5jcsn0YmMjFSbNm3UpEkT7dy5UyVLllRERESWBK0TJ05IkgIDA+Xv759inZIlSzrVlaSYmBhdunRJkhQSEpJmuwsXLiguLs6yMQMAAABAdmHpfSDvFhUVpeHDh+ubb75RYmKiChYsqGHDhun111+Xp6enq7pNU0xMjCTJ19c31Tp+fn6SpOvXrydrl1Zbezt727T6sAsODk61LDo6WsWKFUt3HQAAAACQWSwPkFeuXNH777+vadOm6ebNm/Lx8VHfvn01ePBg5cuXz+ruAAAAAACZxLIAefPmTU2ePFkTJkzQ9evX5e7urpdfflmjRo1SUFCQVd1kiP201bROMY2NjZUkp7B79+muqbW1t/t727ScOXMm1bK0jk4CAAAAQFbI8DWQSUlJ+uqrr1SuXDm98847unbtmtq3b6/IyEh98cUX2SY8SlLp0qUlSVevXnU6LfVuUVFRTnWlvwJkgQIFJEmnT59Os12hQoVMnb4KAAAAADlNhgLk0qVLVaVKFb366qs6e/asHn30Uf34449avHixKlSoYNUYLVOxYkX5+PhIknbt2pViHfvy0NBQp+X2x/faDgAAAAByiwydwtqpUyfZbDbHdY6tW7dWQkKCduzYYap9/fr1M9L9PfP09NSTTz6pRYsWad68eWratKlT+alTpxxjb9++vVNZ+/bttWHDBs2fP18jR450uhdkUlKSFixYIEnq0KGDi7cCAAAAALKGJddAxsfHa9y4cRo3bpzpNjabTQkJCVZ0f0+GDBmixYsXa+bMmerYsaNatmwp6a9teOmll5SYmKiOHTuqUqVKTu3Cw8P1/vvv6/Dhwxo+fLjef/99R9nw4cN1+PBhBQcHq0ePHpm6PQAAAACQWTIUIENCQmSz2awayz3bvXu3XnvtNcfjY8eOSZK+/PJLrV692rF82bJljltihIaG6qOPPtKAAQPUunVrNW7cWEWKFNHWrVsVHR2tihUr6osvvkjWl4+PjxYuXKgWLVpo7NixWrlypapWrarIyEhFRkbK19dXixYtkre3t4u3GgAAAACyRoYC5MmTJy0axv25fv26du7cmWz5mTNnnGY4vXXrllN5//79Va1aNX300Uf66aefFBcXp5CQEA0dOlRDhw51mnX1bg0aNNC+ffs0evRobdiwQUuWLFHhwoXVo0cPjRgxQmXLlrV2AwEAAAAgG7H8PpCZqUmTJjIM477aNmvWTM2aNbvnduXKldOsWbPuq08AAAAAyMkyfBsPAAAAAMA/AwESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYAoBEgAAAABgCgESAAAAAGAKARIAAAAAYMo/NkCGh4fLZrOl+XPz5s0U2/7yyy965plnVLRoUeXNm1dlypTRm2++qT///DOTtwIAAAAAMo9HVg8gqzVo0EDlypVLsczd3T3ZssWLF+vZZ59VQkKC6tSpozJlymjXrl369NNPtWjRIm3bti3V9QEAAABATvaPD5A9e/ZUeHi4qbpnz55VWFiYEhIS9OWXX+rll1+WJCUmJio8PFxz585Vt27dtHPnTtlsNheOGgAAAAAy3z/2FNb78fHHHys+Pl7NmjVzhEfpryOVn3/+uQICAvTzzz9r/fr1WThKAAAAAHANAuQ9WLZsmSSpW7duycr8/PzUtm1bSdLSpUszdVwAAAAAkBn+8aewbtq0Sb/99ptiYmJUsGBB1a1bV61bt5aXl5dTvZiYGB09elSSVLt27RTXVbt2bc2ZM0d79uxx+bgBAAAAILP94wPk7Nmzky0rVqyYZsyYoZYtWzqWnTx50vF7SEhIiusqWbKkJOnEiRPWDhIAAAAAsoF/7CmsNWrU0CeffKLIyEhdv35d58+f1/r161W/fn1FR0erbdu22rx5s6N+TEyM43dfX98U1+nn5ydJun79uqkxBAcHp/oTHR19/xsHAAAAAC7wjz0C2b9/f6fH/v7+at68uZo1a6b27dtrxYoV6tevn/bu3Zs1AwQAAACAbOYfGyBTY7PZ9O6772rFihXat2+foqKiVLJkSfn7+zvqxMXFKSAgIFnb2NhYSVK+fPlM9XXmzJlUy4KDg+9x5AAAAADgWv/YU1jTUrlyZcfv9pBXqlQpx7LTp0+n2C4qKkqSVLp0adcNDgAAAACyCAEyBZcuXXL8bj/ymC9fPpUrV06StGvXrhTb2ZeHhoa6eIQAAAAAkPkIkCmYP3++pL9CY8WKFR3L27dvL0maN29esjaxsbFatWqVJKlDhw6ZMEoAAAAAyFz/yAC5d+9erVy5UgkJCU7Lk5KSNH36dA0bNkyS1KdPH+XJk8dR3q9fP/n4+GjDhg36+uuvHcsTExP12muv6erVq6pTp45atGiRORsCAAAAAJnoHzmJzsmTJ9W+fXvlz59foaGhKlq0qK5evarIyEjH9Y3PPvusRo4c6dSuePHiioiI0LPPPquXX35Z06dPV+nSpfXzzz/r+PHjKlq0qObNmyebzZYVmwUAAAAALvWPPAJZo0YN9evXT1WqVNHBgwe1dOlSbdy4UZLUqVMnrVmzRvPmzZOHR/J8/cwzz2jnzp3q0KGDjh8/rmXLlikxMVGvv/669u3b57hOEgAAAABym3/kEcgyZcpo8uTJ992+Vq1aWrJkiYUjAgAAAIDs7x95BBIAAAAAcO8IkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkPdp0aJFatKkifLnzy9fX1/VqFFDEyZM0J07d7J6aAAAAADgEgTI+9CvXz917txZ27dvV926ddWyZUudPn1agwcP1mOPPaYbN25k9RABAAAAwHIEyHu0fPlyffLJJ/Lz89POnTv17bffasmSJTpy5IiqVaumbdu2afjw4Vk9TAAAAACwHAHyHo0dO1aSNGTIEIWGhjqWFypUSNOmTZMkffrpp7p27VqWjA8AAAAAXIUAeQ/++OMP/fzzz5Kkbt26JStv2LChSpYsqVu3bmnt2rWZPTwAAAAAcCkC5D3Ys2ePJKlAgQIqU6ZMinVq167tVBcAAAAAcgsC5D04ceKEJCkkJCTVOiVLlnSqCwAAAAC5hUdWDyAniYmJkST5+vqmWsfPz0+SdP369XTXFxwcnGrZH3/8ITc3tzTrZLZz125m9RCyheC5eTPUnv34F/ajNdiP1mA/WoP9aA32ozXYj9ZgP1ojo/vRStHR0XJ3d7/v9gTIbMpms2XoP9YVggKy9okfHR0tSSpWrFiWjiOj2I/WYD9ag/1oDfajNdiP1mA/WoP9aA32Y/bj7u6uPHny3Hd7AuQ98Pf3lyTFxcWlWic2NlaSlC9fvnTXd+bMGWsG9g9hPxrLfssY9qM12I/WYD9ag/1oDfajNdiP1mA/WoP9aD2ugbwHpUuXliRFRUWlWsdeZq8LAAAAALkFAfIe1KxZU5J06dKlVCfJ2bVrlyQ53SMSAAAAAHIDAuQ9CA4OVp06dSRJ8+bNS1a+bds2RUVFycvLS61bt87s4QEAAACASxEg79GwYcMkSePHj9fu3bsdyy9duqTXXntNkvTGG28oICAgS8YHAAAAAK5CgLxH7dq1U58+fRQbG6t69eqpVatW6tSpk8qVK6fffvtNDRo00OjRo7N6mAAAAABgOQLkffjkk0+0YMECPfLII9qxY4fWrl2r4OBgjR8/Xv/73//k7e2d1UMEAAAAAMvZDMMwsnoQAAAAAIDsjyOQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQAAAAAABTCJAAAAAAAFMIkAAAAAAAUwiQyJDSpUvLZrMl+/Hz81ONGjU0dOhQXbp0Kd319OnTx9F21apVpvvfuXOnXn31VVWpUkWBgYHy9PRUkSJF1LhxY40ZM0anT592qr9582ZHP6lZs2aNfHx8ZLPZ1K9fP7niTjd377fFixenWq9Zs2ay2WyKiIhIsTwqKkqDBw9WzZo1lT9/fnl5eSk4OFjt27fX/Pnz0xx7Sv939vZPP/20Vq9enWrbUaNGOdoULlxYd+7cSbVudHS0PDw8HPXnzp2bal1X+vv2urm5yd/fX8HBwWratKn+9a9/6aeffkq1fZMmTVJ8rv/9Z9SoUaba+fj4qHLlynrzzTeTPU+zEzPb/PefJk2aSJIiIiJks9lUunTpNPs4efKko+3Jkyedyu7+f+vbt2+a65k4caKjroeHRwa2OuvVqFHD8ZpM629oeHh4sv3v7e2tokWLqk6dOnr55Ze1cuVKJSQkpLoO++vZ/v+WE1j1vLAv37x5c5rrsL+O//76vltUVJTeeecd1atXT4ULF1aePHkUGBio0NBQ9e3bVz///LPZzcs02Wk/3rp1S1OmTNGjjz6qAgUKKE+ePCpUqJAqV66szp0765NPPtGFCxfudROzzJEjR/TGG2/owQcflK+vr/Lmzavg4GDVqVNHb7zxhpYsWSIp9c9Raf3c/Tc1pXJvb2+VLl1aXbt21bZt27JoD2Scfd/8/TPQd999Jzc3N/n5+enYsWNpruPVV1+VzWZT48aNlZSUJMn5ffnpp59Os/2iRYuc9u2ZM2cytE25Rc5+h0W20aBBA5UrV06SlJSUpLNnz2rHjh0aP368Zs+era1bt+qBBx5Ise2tW7f0zTffOB7PmDFDbdq0SbO/+Ph49ezZU//5z38kSUFBQWrYsKECAgJ08eJF/fTTT/r+++81evRoLViwQO3atTO1HfPmzVNYWJgSEhL03nvvafjw4abaZcTbb7+tdu3a3fMH3s8++0wDBw7UrVu3VLBgQTVs2NDxx3TFihVavny5Jk2apOXLl6t48eKprufu/7tr165pz549WrlypVauXKn+/ftr0qRJaY7j4sWLWrlypTp27Jhi+axZs5SYmHhP2+ZKd2/vjRs3dPHiRe3Zs0ebN2/WRx99pMaNG2vGjBmpPl9r1Kihhx56KNX1p1Z2dzvDMHT+/Hnt3LlTn376qWbPnq0NGzaoTp06Gdk0lwgLC0u27Ny5c/r2229TLa9UqZJLxvLNN99o4sSJ8vT0TLF8xowZLuk3s/3888/69ddfJUm3b9/W3Llz0/1wX7ZsWTVs2FCSlJCQoCtXrigyMlJff/21vv76a5UqVUrTp0/X448/7vLxZ7bs8LyYMGGChg8frtu3b8vPz08PP/ywihQpopiYGP3222+aMmWKpkyZokGDBmnChAkuH8/9yMr9eP78eTVv3ly//fab3N3dVbduXZUsWVJJSUk6fPiwlixZokWLFqls2bJ66qmnXDYOqyxdulTdunVzvD83aNBAhQsX1pUrV7R371599tlnmj9/vjp27KhOnTrp4sWLTu1jY2MdAbNjx47y8/NzKi9UqFCyPp944gkFBQVJ+ut9edeuXVqwYIEWLlyoyZMnp/s3JCdp3ry5Xn31VU2bNk1hYWH6/vvv5eaW/JjYt99+qy+++EJ+fn6KiIhIsc7atWt1/vx5FS1aNMW+pk+fbvn4cwUDyIBSpUoZkoyZM2cmK4uOjjYqVKhgSDI6duyY6jr+85//GJKM4sWLGzabzfDw8DDOnTuXav3bt28bDRs2NCQZxYoVM1asWJGszp07d4yFCxca5cqVMyZPnuxYvmnTJkOSkdJT/9NPPzVsNpvh5uZmTJs2Le0NzyD7fvPx8TEkGZ9//nmK9R5//PEU9+/HH39sSDLc3NyM8ePHG7dv33YqP3DggFGrVi1DkvHAAw8YV65cSXUMf1/3nTt3jDfeeMOxn3766adkbUeOHGlIMmrXrm1IMlq3bp3qtlaoUMHw8vIyqlevbkgy5syZk2pdV0rruZqUlGSsWbPGKF++vCHJKFq0qHH8+HGnOo0bNzYkGSNHjrynftNqd/XqVaNRo0aGJKNWrVr3tN6slNbr6G4zZ840JBmlSpVKs96JEycc6ztx4oRTmf3/zf5cW7hwYYrr2L59uyHJqFOnjiHJcHd3v5dNylZ69+5tSDJKlChhSDKqVauWat2wsDBDkhEWFpZi+d69e42WLVs69snKlSuT1bG/nhs3bmzRFrieVc8L+/Nu06ZNafaX1ut48ODBhiQjT548xocffmjcvHkzWZ0ffvjBeOyxx4ynn37a7CZmiuyyHzt16mRIMqpUqWKcPHkyWbvz588bH3/8cYrvR9nNuXPnDD8/P0OSMXDgQOPGjRvJ6uzatcsYMmRIqutI62/i36W27+Pi4owOHToYkgxPT0/jzJkz97M5WSqt9+3Y2FijXLlyhiRj/PjxycqvXLni+Bv61VdfOZXZn4f25/2ECRNS7P/06dOGm5ub43kvyYiKirJk23I6TmGFywQFBWnQoEGSpI0bN6Zaz/7tTt++fdW4cWMlJCRo9uzZqdYfPXq0tm3bpsDAQG3fvl1t27ZNVsfDw0PPPPOM9uzZo8aNG6c71jFjxuiNN96Qh4eHvvnmG7366qvptrGC/RvB9957T/Hx8aba7N+/37FfJ0+erMGDBytPnjxOdSpVqqSNGzeqbNmyOn78uN58803TY/Lw8NDEiROVL18+SUrzlOIaNWooNDRU3377rc6ePZusfOvWrTp8+LDatWun/Pnzmx5DZrPZbGrdurV++uknlS9fXufPn1fPnj1d3m9AQIBGjBghSfrll1907do1l/eZU7344ouSUj8KYv87Yq+XU8XHxzvOrJgzZ478/Pz022+/3ffpjzVq1NDatWvVpUsXJSYmKiwsTNevX7dyyFkqq58XGzdu1AcffCBJWrBggQYOHCgvL69k9erVq6cNGzZo4MCBLhlHRmXlfrx586ZWrFghSZo0aZJKlSqVrE6RIkXUt2/fbHmWxt+tXr1asbGxKl68uD788EPlzZs3WZ1atWpp3LhxLh2Hj4+Ppk6dKumvMxnsZ43kFr6+vpo1a5bc3d01YsQI/fbbb07lb775pv744w+1bt1avXr1SnEdzz//vDw9PTVz5swUyyMiIpSUlJTj31dcgQAJl7KfTpHa9TcnT57Uxo0b5eHhoR49euill16SlPqbWExMjD755BNJ0ogRI1SmTJk0+/fz81PNmjVTLTcMQ/3799fw4cPl4+OjlStXqmvXrulul1Vat26txo0bKzo6WpMnTzbVZuLEibpz546qV6+eZjAMCAjQxIkTJUn/+c9/dPz4cdPjyps3r8qXLy/pr1OL0vLiiy8qMTFRs2bNSlZm/3/MKX98AwMD9fHHH0uS/ve//+mXX35xeZ/214iU+usEUrVq1VS7dm2tX79ef/zxh1NZbGysFi5cqODgYLVo0SKLRmiNRYsW6fr166pataqaNm2qLl26SMrYaVQ2m02fffaZvL29deXKFX399ddWDTfLZfXzYsyYMZKktm3bqn379mnWtdlsatSokUvGkVFZuR8vX77suI6+SJEilq8/s9nfMwsXLpzFI5GKFy+uggULSkr/vTwnql+/vgYNGqTbt2+rR48ejufRsmXLNHfuXBUoUED//ve/U21fsGBBtW3bVgcOHNAPP/zgVGYYhiIiIuTt7a1nn33WpduRExEg4VL2SUmqVKmSYvmMGTNkGIZat26toKAgdezYUQEBATp48KB27NiRrP6mTZt0/fp12Ww29ejRI0NjS0xM1IsvvqiPP/5Y+fPn13fffaeWLVtmaJ33w/7t9YQJE9KdcMgwDK1cuVKS1L179zQnA5KkNm3aKDAwUImJiVqzZs09jct+lCK16wLsunXrprx58yb7Bi8mJkaLFi1SSEiImjVrdk99Z6VWrVqpQIECkv66UN/V7K+RokWLOt7okbIXX3xRSUlJySZUWLhwoWJjYxUWFpbiNS45yd+P9Nj/nT9/vm7cuHHf6y1YsKDj71tmPK8zU1Y9L65evarvv/9eUsrXAuc0WbUfCxUqJB8fH0nS1KlTHROd5FQhISGSpMjIyDTPvsoMSUlJio2NlZT+e3lO9e6776patWrau3evRo4cqT///FO9e/eWJE2bNk3FihVLs31qR983bdqk48ePq0OHDgoICHDN4HOwnP1Oi2wpKSlJf/zxhz799FNNmDBB7u7ueuedd1KsZ3+jsr+Avb29HUcAU/rGfdeuXZKkMmXKZPjDdqdOnRQREaFixYppy5Ytql+/fobWd78efvhhdejQQdevX9f777+fZt0TJ07o8uXLkqS6deumu24PDw/HEVj7vjPjwIEDjiOWKZ0ifLf8+fOrffv2OnLkiLZu3epYvmDBAsXFxSk8PDxHfai32WwKDQ2VJP3+++8u6cP4/5PozJ07V2+99ZYkaeTIkS7pKzfp1q2bvL29k33AnTFjhmw2W4450p2aw4cPa+vWrcqTJ4+ef/55SX99w16pUiVdu3YtzRmbzahVq5Yk1z2vs0pWPS92797tCDs54dTK9GTVfvT09HScYjhjxgyVLVtWffr00dy5c7V//36XzITuSu3atVOJEiWUmJio5s2bq2nTphozZozWrl2b6bPIbty4Ubdu3ZKnp2eWfEGeGTw9PTVnzhx5enpqwoQJatu2rS5cuKAuXbo4zuBIyxNPPKHg4GAtWLDA6VIie6C0nxkHZznnUx2ytRdeeMExxbG7u7uCg4P15ptvqnr16tqyZUuKs6atX79eUVFRKlq0qJ588knHcvuL1f6t593sf3ytOM1l+fLlkqQvvvhC1apVy/D6MmLs2LHy8PDQtGnTdOrUqVTr3f3mY/bbRHs9M29c165d0/r169WhQwclJibqnXfeUe3atdNtl9I3eNOnT5fNZtMLL7xgapzZiX2Gu5SOCL/77rtpTq++d+/eFNd5dzs3NzcFBQWpe/fuKlCggFavXp1p193mZAEBAerQoYOOHj2qLVu2SJIOHTqk7du3q3HjxqnOnJtT2F8/bdu2dTr9zf76yuhsgGk9r3OyrHpe3P03NTecepmVr6+JEyeqX79+ypMnj06ePKmpU6eqe/fuqlKliooUKaI33ngj2am12ZWfn582btyohx9+WIZhaPPmzRo+fLiefPJJFSlSRDVr1tQXX3zh0tnJL168qMWLFzu+wP3000/TnI09p6tRo4ZGjhypxMRE7dy5U8WKFdO0adNMtXVzc1NYWJjjrCnpr89CS5cu1QMPPJCjbm+UmQiQsESDBg0UFhbm+HnyySdVsmRJ/fzzz+rfv7+OHDmSrI39vPQePXo43cKiTp06qlq1qmJjY7VgwQKXjdk+uc5LL73kmDI/q1SsWFEvvviibt26ZfmtQ9L79vbu8B8YGKgnnnhCR44c0dy5czV69GhTfTz++OMqVaqUFi1apNjYWB04cEA//vijmjZtmu49ALMj+1GFlE4RrlGjhtNz/e8/9tNf02vXtm1blS9fXkeOHNGAAQPSvAcl/s/fv6zIadfZpiYhIcFxHfHft8X+N/L7779P955naUnreZ3T5dbnRWbLqv2YJ08eTZ48WadPn9bnn3+ubt26qVKlSrLZbLp48aI+++wzVa9ePVOuS7dCxYoV9eOPP2rnzp0aMWKEnnjiCceXQnv37tWrr76qli1b6vbt25b12bRpU6f7Mz/zzDO6cuWK1q9fn+okMrnJ4MGDHV/kDBs2LNX34pTYPwfZn+/z5s3TjRs3HPfZRXIESFiiZ8+eioiIcPysXr1ax48f19ChQ/Xzzz+rcePGiomJcdS/cOGC41q+lN6YUjsn3f4H+M8//8zwmNeuXaumTZvq4sWLeuyxx1I9cpRZRo0aJR8fH33zzTepBtq77/1k9oJ4+75K7YL+u8N/69at5e/vr8TERL366qumQ43NZlN4eLji4uK0YMGCHP/hzX5PrpTegNq1a+f0XP/7j/36l/TarVixQocOHdJnn32mw4cPq2nTpjp9+rRLtyuz2d940/sS4+7y9N6smzZtqjJlymjx4sW6cuWKZs+erXz58qlTp04ZH3AWWrNmjc6dO6cSJUroiSeecCorWrSoWrduLcMwMnQvvrSe1zldRp8XZp+jdz8/7/6basV7UnaQFfvxbkFBQXrllVf0zTff6MCBA4qOjtakSZMUEBCgy5cvZ3jug8xWt25dvfvuu1q3bp3Onz+vX375xXGZzoYNGxyTAlrhiSeeUFhYmLp3767mzZvLy8tLN27c0PPPP39Pk+jlVO7u7vL29pakZPfNTE/ZsmX16KOPauvWrTp27JhmzJghNzc3hYeHu2CkuQMBEi7j4eGhMWPGqFChQoqOjna6NcecOXN0584deXh4qGfPnmrYsKHTj/2b+B07dujgwYOOdvZreE6cOJHh07B8fHy0Zs0aPf7447p06ZIef/xx7dmzJ0PrzIhixYqpb9++SkpK0tChQ1OsU6ZMGcftMHbu3JnuOhMSErR7925J/7fv/u7u8L9mzRpFRUWpadOmiomJUefOnU3fXsT+Dd5XX32lOXPmOE6HymkMw3A8D1x9arPNZtNrr72m0NBQxcfHO6Zczy18fX0lSXFxcWnWu/tU9fTe+O1fVsTHxyssLEznzp1T165dHR8ccir76ak3b95U48aNk/1NtH+pFBERcd+nvtn/FmT1KfuucL/Pi3t9jt79/KxZs6bj+u77vc1KdpMV+zEtRYsWVf/+/R2TtO3fvz/FM5pyAvv19f/5z38ccwvYL6WxwpAhQxQREaHZs2dr/fr1On78uKpWrapz586pW7duOe5a0sz24osvOmbm37Vrl5o1a6aSJUtm9bCyLQIkXMrNzc1xCuOBAwccy+0flhISErR9+/ZkP/v27UtWV/rr21F/f38ZhpHmvSLN8vb21qpVq9SiRQtdvnxZjz/+eJaeIjN48GAVLFhQa9eudczudzc3Nze1adNG0l8hPL03hJUrV+ratWtyc3Nzus40LQEBAVqwYIEKFCigU6dOadKkSabalSpVSo899ph++uknnT9/Xs8++2yO/FC/du1aXblyRZIy7ZYQ9muL7n6N5Ab2o7GXLl1y7NOU2D8Q+vn5mbpfqP26Hvs9SnPqkW676OhorV27VtJf+yqlv4knT56UJJ09e1br1q275z4uXrzouA9cTr/VSWru53lhf44ePXo01TqGYThOHb77DIP8+fM7bsuR0m2McqrM3o9m3P2ctR9Jz8ns2+PKbSlevLgWLVqkPHnyaOfOnfrmm29c1ldu0KlTJ+XLly/XvK+4GgESLpWUlOT44GP/xvGHH37Q/v375eXlpStXrsgwjBR/7B+o5syZ47g/Xr58+dSnTx9J0nvvvacTJ06k2X9sbGy6RxW9vb21YsUKtWzZUleuXFGzZs2y7NvkgIAADRs2TJIcs3P+3aBBg+Th4aHffvtNU6ZMSXVd165dc6yjS5cuKlu2rOlxFC5c2DFz7ocffqirV6+aavfyyy+rYMGCKliwYI6cuezatWvq37+/JKl58+Z66KGHMqVf+4eqez3tJrurWbOmIxAuXbo01Xr22UWbNGliasbekJAQPf300ypYsKDq1aunhx9+2JoBZxH7UUX7pBup/dhfz/c6mY5hGHrjjTd048YNFShQIEe+Ns24n+fFY489JklasmRJqnW+++47Xbt2TR4eHsnu4/j2229L+uvLumXLlqXZl2EY2rZtW7pjymqZvR/NHBm7+/T+EiVKpFs/K93L9gQHB7t0LJUqVXJM0DZq1CjuNZwGHx8fhYeHq2DBgipTpozatWuX1UPK1giQcJmEhAS98847jm/Y7Kds2D/8PP300woMDEy1fYsWLRQUFKTz589r9erVjuUjRoxQ/fr1dfXqVTVs2NDxbdHdEhMTtWzZMtWqVcsxm1xa8ubNq+XLl6t169a6evWqmjdvbuoUUVd4/fXXFRISop07dya7sa0kVa1a1XHvyAEDBmjChAnJ3hQOHjyoZs2a6dixYypdurQ+/fTTex7Ha6+9ppCQEF27dk0fffSRqTadO3fWxYsXdfHiRVOzt2YXhmHov//9r+rWrasjR46oWLFimXKzdcMw9Pnnnzu+5Hj66add3mdmypMnjwYMGCBJGjp0aLLXlGEY+vrrrzV//nzZbLZUvzRJydKlS3Xx4sUUXyM5jf26xvTuJWi//mv16tWmbwfw66+/qnXr1lqwYIHc3d01d+5c+fv7Z2zA2di9Pi/69u2rvHnzatu2bXrvvfeSnR588OBBxwfw8PBwBQUFOZU3b95cAwcOlCR17dpVkyZN0q1bt5L188svv+iJJ57Qhx9+eD+blekycz9eu3ZNoaGhmjNnTrKZ1yXp+PHjjqNB9evXv+ejl5lt2rRpCgsLS/Fe1oZhaOnSpY73ZPv1kK70zjvvyM/PT8eOHctVR8pd4ZNPPtHFixd1/PhxeXl5ZfVwsjWP9KsA6fv3v/+tzZs3Ox5funRJ+/btU1RUlKS/vqWtX7++08yq6X1Ycnd3V7du3TRp0iRNnz7d8W2Qp6envv32W7300ktauHCh2rZtq2LFiqlWrVrKly+fLl26pJ9//lmXL1+Wl5eXypQpY2obvLy8tGzZMnXs2FGrV69WixYttG7dOj3yyCP3vkMywMvLS++9957jOpSUDBgwQB4eHho0aJAGDx6sCRMmqH79+vL19dWJEyf0008/yTAM1apVS8uXL7+vSTO8vLw0atQovfjii/rkk0/Uv3//XDH5xt3P1Vu3bunixYvavXu34/6aTZo00YwZM1SqVKkU2y9fvtxxVD0loaGhjqPkabW7evWq0/U83bt3z5QPE5lt6NChioyM1IIFC/TII4+oVq1aKleunOP63OPHj8vd3V2TJk1KdnTnn2DLli06evSovLy80v3/r1KlikJDQ7V7927Nnj3bEVwkadu2bY4JHxISEnT16lVFRkY6bgtUpkwZTZ8+XU2bNnXZtuRE5cuX15w5c9S9e3eNHDlSX375perWrSsfHx+dOnVKP/74oxITE9WkSRN9/PHHKa7jww8/VIECBTRq1CgNHDhQo0aN0sMPP6wiRYooNjZWv/76q+O1P3jw4MzbuEyU0f24Z88e9ejRQ15eXqpRo4ZKlSolwzAUFRWln3/+WUlJSSpVqlSye1RmR3fu3NHs2bM1e/ZsFS5cWDVr1lShQoUcf/Ptz4Xnn38+U84GKFy4sAYMGKD33ntPY8aMUY8ePZQnTx6X92ul0aNH64svvki1fNq0aY77NyOTGEAGlCpVypCU7MfT09MoVaqU0aVLF2PTpk2O+tOnTzckGUFBQUZCQkK669+7d68hyXB3dzf++OOPZOU//PCD8fLLLxuVK1c28uXLZ3h4eBiFChUyHn30UeP99983zpw541R/06ZNjjGm5tatW8bTTz9tSDL8/f2Nbdu2md8hJtn329atW1MsT0xMNKpVq+YY68yZM1Osd/LkSWPQoEFGjRo1jICAAMPT09MoXry40bZtW+Obb74xEhMT0x1Daus2DMNISEgwHnzwQUOSMWTIEMfykSNHGpKMl156ydT2GoZhNG7c2JBkzJkzx3QbK6X0XPX19TWKFy9uNG7c2Bg4cKDx008/pdrePv70fp5++mlT7fLkyeP4v1q2bJlrN95iZl5Hf7d8+XKjXbt2RokSJQxPT0/Dx8fHKF++vPHSSy8Ze/bsSbVdeq+Vvztx4oTjb0ZO0L17d0OS0alTJ1P1P/74Y0OSUblyZcMwDCMsLCzZc8vLy8soUqSIUatWLaNXr17GihUrjDt37qS6TvvruXHjxlZsUqaw+nlx5MgRo0+fPkaVKlUMPz8/w8PDwyhatKjRsmVLY9asWaber06ePGkMHTrUqFOnjlGwYEHDw8PDCAgIMGrWrGn07dvX2L179z1tY2bIDvsxKSnJ2LlzpzF27FijRYsWRvny5Q1/f38jT548RpEiRYymTZsakyZNMmJjYzO0rZnl+vXrxvLly40333zTqFu3rhEcHGzkyZPH8Pb2NsqWLWs8++yzxn//+98012Hfz5KMEydOpFnXXu/uz1opjalw4cKGJOOLL764j63KGql9xvz7j33bzXyuMYz7+zxi7ysqKioDW5R72AyDaZkAAAAAAOnjGkgAAAAAgCkESAAAAACAKQRIAAAAAIApBEgAAAAAgCkESAAAAACAKQRIAAAAAIApBEgAAAAAgCkESAAAAACAKQRIAAAAAIApBEgAAAAAgCkESAAAAACAKQRIAAAAAIApBEgAQK5RunRp2Ww2px8vLy+FhISoS5cu2rp1a1YPMVX28QIAkJ0RIAEAuU6DBg0UFhamsLAwtWrVSklJSVq4cKEaN26sSZMmZXj99qB68uTJjA/WhcLDw2Wz2RQREZHVQwEA5BIeWT0AAACs1rNnT4WHhzse37x5U71799bs2bP11ltv6amnnlKFChWyboAAAORQHIEEAOR6efPm1WeffSZfX18lJiZq6dKlWT0kAAByJAIkAOAfwc/PTxUrVpQkx6mnFy5c0JQpU9S6dWuVKVNG3t7eypcvn2rXrq0PPvhAN2/edFpHRESEbDabTp06JUkqU6aM0/WWmzdvdqr/xx9/aNCgQapWrZr8/f3l6+urChUqKDw8XDt27Eh1rEuWLFHDhg2VL18++fr6qkGDBlq7dq3pbT158qRsNptmzZolSXrhhRecxjlq1CgdO3ZM7u7uyp8/v+Lj41NdV5UqVWSz2Zz6v/sU3mXLljnG6u/vryZNmqQ71sWLF6tly5YqXLiwPD09VaJECT3//PPav39/ivV/+eUXdenSRcHBwfL09FS+fPn0wAMPqGPHjlqxYoXp/QIAyDhOYQUA/GNcv35dkuTl5SVJ+vbbb9W3b1+VKFFC5cqVU7169XThwgXt3LlTQ4YM0YoVK7Rp0yZH/XLlyiksLEyLFy9WXFycOnbsKD8/P8f6g4KCHL9v3LhRnTp10tWrV1WkSBE9/vjj8vT01MmTJzVv3jxJUv369ZONceTIkRo9erTq16+v1q1b6+DBg9qxY4eeeuopLVmyRO3bt093O/38/BQWFqZt27bp2LFjatCggcqVK+cof+ihh1S2bFk9+eSTWrVqlb755hv16tUr2Xo2bdqk/fv3q2zZsmrVqlWy8ilTpmjy5MmqXbu2nnrqKR07dkxbtmzRli1bNGXKFL355ptO9RMSEvTcc89p4cKF8vLyUq1atVSiRAkdPnxY33zzjZYuXaqlS5eqZcuWTvuxVatWunPnjmrUqKFHHnlEiYmJ+uOPP7RmzRolJibq6aefTnefAAAsYgAAkEuUKlXKkGTMnDkzWdm+ffsMNzc3Q5IxY8YMwzAMY//+/cYPP/yQrO7ly5eNFi1aGJKMCRMmpNrPiRMnUhzH6dOnjYCAAEOSMWTIEOPWrVtO5efPnze2bt3qtEySIckIDAw0fvzxR6eykSNHGpKMChUqpLX5yYSFhaW6PwzDML777jtDklGjRo0Uyzt27GhIMj766COn5fbtt9lsxty5c53K5s+fb9hsNsPDw8P47bffnMqGDRtmSDIefvhh4/jx405lixYtMtzd3Y38+fMbV65ccSxv2rSpISlZP4ZhGFevXk3x/w8A4DoESABArpFSgLx69aqxZs0ao2zZsoYko3jx4kZsbGy66zp06JAhyahTp06q/aQWIPv162dIMtq0aWN67PYAOWXKlGRlN2/edATS06dPm15negHSMAyjSpUqhqRkgTYqKsrw8PAwfHx8nAKdYfzf9rdr1y7FddqDZ69evRzLLl26ZHh7ext58+Y1zpw5k2K71157zZBkTJ061bHswQcfNCQZly9fTmdrAQCZgWsgAQC5zt3X/AUGBurJJ5/UsWPHVLZsWa1du1a+vr6OuomJidq4caNGjx6t1157TS+88ILCw8P1/vvvS5IOHTp0z/2vW7dOkvTyyy/fc9s2bdokW+bl5aUHHnhA0l/XVVqpT58+kqRPP/3UafmXX37pOOU0MDAwxbZhYWFpLr/7mtBNmzbpxo0batCggUqUKJFiuyZNmkiS0/WhdevWlSQ999xz2rZtmxISEtLdJgCA63ANJAAg17n7mj9PT08VKVJE9erVU8uWLeXh8X9vfUeOHFH79u31+++/p7ou+3WT98I+yU6lSpXuuW1ISEiKy/PlyydJySb2yajnn39eQ4YM0dKlSxUdHa1ixYrp9u3b+vrrryVJb7zxRqpty5Qpk+byM2fOOJYdP35c0l/XNNpstjTHdOHCBcfv48aN06+//qr//ve/+u9//ytvb2+FhoaqSZMmeu6551S5cmVzGwoAsAQBEgCQ6/z9PpCp6dSpk37//Xc99dRTeuutt/Tggw8qX758ypMnj27fvu2YPCczubll7slBPj4+6tWrlyZMmKCvvvpKI0eO1JIlS3T+/Hk1atRI1atXv+91G4bh+D0pKUnSXxMRNWjQIM12dwfvoKAg7dq1S1u2bNGGDRu0fft27dy5U9u3b9fYsWM1btw4DR48+L7HCAC4NwRIAMA/0sGDB/Xrr7+qSJEiWrZsmdORSemvo5P3KyQkRIcOHdLBgwedZj/Nrl5//XV99NFH+uqrrzRs2DDH6axpHX2UpBMnTqhGjRrJlttvkxIcHOxYVrJkSUlSxYoVFRERcU/js9lsatKkieMU15s3byoiIkKvv/66hg0bpk6dOqls2bL3tE4AwP3hGkgAwD/S5cuXJUnFixdPFh4lae7cuam29fT0lKRUr8ez34bCfhpoVklvnHYhISFq166dzp49qxEjRmjHjh0qXry4OnTokGa7OXPmpLh89uzZkv7vmkZJjtuYbN68WX/++ec9bEVyefPm1SuvvKLq1asrKSlJv/76a4bWBwAwjwAJAPhHqlChgtzd3fXbb785TfYiSatWrdLkyZNTbWs/spbatZMDBgyQv7+/Vq5cqXfeeUd37txxKv/zzz+1bdu2jG2ACemN8259+/aVJI0fP16S1Lt37xSD9d2WLVum+fPnOy1bvHixlixZIg8PD6f7QBYtWlRvvvmm4uLi1KZNG/3222/J1nfr1i2tXLlSBw8edCz78MMPdfr06WR1Dx486DhKXKpUqXS3DwBgDZtx9wUKAADkYKVLl9apU6c0c+ZMU9dA9uvXT5988onc3NzUqFEjFS9eXIcOHdLu3bv1zjvvaMyYMZKcr+WTpM8++0xvvPGG/Pz81KJFC+XPn1+SNGjQIFWsWFGStH79enXq1EkxMTEqWrSoHnnkEeXJk0enTp3Snj171K1bN6dTOe0Ty6T2ttykSRNt2bJFmzZtcjqyl5Zff/1VNWvWlCQ99thjKlmypNzc3NS2bVu1bds2Wf3Q0FDt2bNHefLk0enTpxUUFJTieu37uV+/fvr4449Vp04dlS9fXseOHdPOnTslSZMmTVL//v2d2iUkJCgsLEzz5s2Tm5ubatSooQceeEAeHh46c+aM9u7dq7i4OP33v/91HMUNDAzUtWvXVKlSJVWuXFne3t46e/asY0bWHj16aNasWab2BwDAAll6ExEAACyU0n0g05KUlGRMnz7dqFWrluHn52cEBAQYDRs2NObPn28Yxv/dm/HvEhMTjXHjxhlVqlQx8ubN66i3adMmp3qnTp0y+vbta1SsWNHImzev4efnZ1SoUMF48cUXjR9++MGpbmp92TVu3DjFPtKzbNkyo0GDBoa/v79hs9kMScbIkSNTrDt48GBDkvHss8+muc6774O5cOFC45FHHjH8/PwMX19fo1GjRsaqVavSbL927VqjQ4cORokSJYw8efIYgYGBRuXKlY2uXbsa8+bNM+Li4hx1586da7zwwgtG1apVjQIFChheXl5GqVKljFatWhnLli0zkpKS7ml/AAAyhiOQAABAiYmJKlu2rE6dOqUdO3bokUceSbWu/QjkiRMnVLp06cwbJAAgy3ENJAAA0FdffaVTp07pkUceSTM8AgD+2biNBwAA/1CHDh3SxIkTde7cOa1bt05ubm768MMPs3pYAIBsjAAJAMA/VHR0tKZPny5PT09VqVJFo0aNUv369bN6WACAbIxrIAEAAAAApnANJAAAAADAFAIkAAAAAMAUAiQAAAAAwBQCJAAAAADAFAIkAAAAAMAUAiQAAAAAwBQCJAAAAADAFAIkAAAAAMAUAiQAAAAAwBQCJAAAAADAFAIkAAAAAMAUAiQAAAAAwBQCJAAAAADAFAIkAAAAAMAUAiQAAAAAwJT/BzhhaCH5zxh8AAAAAElFTkSuQmCC","text/plain":["
"]},"metadata":{},"output_type":"display_data"}],"source":["# Read the patch data and create a list of patches and a list of corresponding labels\n","dataset_path = global_save_dir / \"kather100k-validation-sample\"\n","\n","# Set the path to the dataset\n","image_ext = \".tif\" # file extension of each image\n","\n","# Obtain the mapping between the label ID and the class name\n","label_dict = {\n"," \"BACK\": 0, # Background (empty glass region)\n"," \"NORM\": 1, # Normal colon mucosa\n"," \"DEB\": 2, # Debris\n"," \"TUM\": 3, # Colorectal adenocarcinoma epithelium\n"," \"ADI\": 4, # Adipose\n"," \"MUC\": 5, # Mucus\n"," \"MUS\": 6, # Smooth muscle\n"," \"STR\": 7, # Cancer-associated stroma\n"," \"LYM\": 8, # Lymphocytes\n","}\n","\n","class_names = list(label_dict.keys())\n","class_labels = list(label_dict.values())\n","\n","# Generate a list of patches and generate the label from the filename\n","patch_list = []\n","label_list = []\n","for class_name, label in label_dict.items():\n"," dataset_class_path = dataset_path / class_name\n"," patch_list_single_class = grab_files_from_dir(\n"," dataset_class_path,\n"," file_types=\"*\" + image_ext,\n"," )\n"," patch_list.extend(patch_list_single_class)\n"," label_list.extend([label] * len(patch_list_single_class))\n","\n","# Show some dataset statistics\n","plt.bar(class_names, [label_list.count(label) for label in class_labels])\n","plt.xlabel(\"Patch types\")\n","plt.ylabel(\"Number of patches\")\n","\n","# Count the number of examples per class\n","for class_name, label in label_dict.items():\n"," logger.info(\n"," \"Class ID: %d -- Class Name: %s -- Number of images: %d\",\n"," label,\n"," class_name,\n"," label_list.count(label),\n"," )\n","\n","# Overall dataset statistics\n","logger.info(\"Total number of patches: %d\", (len(patch_list)))"]},{"cell_type":"markdown","metadata":{"id":"r8tg66bu48Vh"},"source":["As you can see for this patch dataset, we have 9 classes/labels with IDs 0-8 and associated class names. describing the dominant tissue type in the patch:\n","\n","- BACK ⟶ Background (empty glass region)\n","- LYM ⟶ Lymphocytes\n","- NORM ⟶ Normal colon mucosa\n","- DEB ⟶ Debris\n","- MUS ⟶ Smooth muscle\n","- STR ⟶ Cancer-associated stroma\n","- ADI ⟶ Adipose\n","- MUC ⟶ Mucus\n","- TUM ⟶ Colorectal adenocarcinoma epithelium\n","\n"]},{"cell_type":"markdown","metadata":{"id":"UxBdhIE-FtG7"},"source":["## Classify image patches\n","\n","We demonstrate how to obtain a prediction for each patch within a digital slide first with the `patch` mode and then with a large slide using `wsi` mode."]},{"cell_type":"markdown","metadata":{"id":"N8_S93fSVaFS"},"source":["### Define `PatchPredictor` model\n","\n","The PatchPredictor class runs a CNN-based classifier written in PyTorch.\n","\n","- `model` can be any trained PyTorch model with the constraint that it should follow the [`tiatoolbox.models.abc.ModelABC`](https://tia-toolbox.readthedocs.io/en/latest/_autosummary/tiatoolbox.models.models_abc.ModelABC.html) class structure. For more information on this matter, please refer to [our example notebook on advanced model techniques](https://github.com/TissueImageAnalytics/tiatoolbox/blob/develop/examples/07-advanced-modeling.ipynb). In order to load a custom model, you need to write a small preprocessing function, as in `preproc_func(img)`, which make sures the input tensors are in the right format for the loaded network.\n","- Alternatively, you can pass `pretrained_model` as a string argument. This specifies the CNN model that performs the prediction, and it must be one of the models listed [here](https://tia-toolbox.readthedocs.io/en/latest/usage.html?highlight=pretrained%20models#tiatoolbox.models.architecture.get_pretrained_model). The command will look like this: `predictor = PatchPredictor(pretrained_model='resnet18-kather100k', pretrained_weights=weights_path, batch_size=32)`.\n","- `pretrained_weights`: When using a `pretrained_model`, the corresponding pretrained weights will also be downloaded by default. You can override the default with your own set of weights via the `pretrained_weight` argument.\n","- `batch_size`: Number of images fed into the model each time. Higher values for this parameter require a larger (GPU) memory capacity."]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"start_time":"2023-11-10T18:40:05.805638800Z"},"id":"dlQu5878FtG8","tags":["hide-output"]},"outputs":[],"source":["model = vanilla.CNNModel(backbone=\"resnet18\", num_classes=9) # Importing model from torchvision.models.resnet18\n","model.load_state_dict(torch.load(weights_path, map_location=\"cpu\"), strict=True)\n","def preproc_func(img):\n"," img = PIL.Image.fromarray(img)\n"," img = transforms.ToTensor()(img)\n"," return img.permute(1, 2, 0)\n","model.preproc_func = preproc_func\n","predictor = PatchPredictor(model=model, batch_size=32)"]},{"cell_type":"markdown","metadata":{"id":"xKUJrBKkSANr"},"source":["### Predict patch labels\n","\n","We create a predictor object and then call the `predict` method using the `patch` mode. We then compute the classification accuracy and confusion matrix."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"P_NpnknhSANr","outputId":"eadde29a-8fdd-44d8-d238-8498c87edc59"},"outputs":[{"name":"stderr","output_type":"stream","text":["100%|###########################################| 63/63 [00:04<00:00, 13.15it/s]"]},{"name":"stdout","output_type":"stream","text":["|2023-11-12|17:47:33.576| [INFO] Classification accuracy: 0.993000\n"]},{"name":"stderr","output_type":"stream","text":["\n"]},{"data":{"text/html":["
\n","\n","
\n"," \n","
\n","
\n","
BACK
\n","
NORM
\n","
DEB
\n","
TUM
\n","
ADI
\n","
MUC
\n","
MUS
\n","
STR
\n","
LYM
\n","
\n"," \n"," \n","
\n","
BACK
\n","
1.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.00000
\n","
\n","
\n","
NORM
\n","
0.000000
\n","
0.988636
\n","
0.000000
\n","
0.011364
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.00000
\n","
\n","
\n","
DEB
\n","
0.000000
\n","
0.000000
\n","
0.991304
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.008696
\n","
0.00000
\n","
\n","
\n","
TUM
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.996503
\n","
0.000000
\n","
0.003497
\n","
0.000000
\n","
0.000000
\n","
0.00000
\n","
\n","
\n","
ADI
\n","
0.004808
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.990385
\n","
0.000000
\n","
0.004808
\n","
0.000000
\n","
0.00000
\n","
\n","
\n","
MUC
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.988764
\n","
0.000000
\n","
0.011236
\n","
0.00000
\n","
\n","
\n","
MUS
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.996296
\n","
0.003704
\n","
0.00000
\n","
\n","
\n","
STR
\n","
0.000000
\n","
0.000000
\n","
0.004785
\n","
0.000000
\n","
0.000000
\n","
0.004785
\n","
0.004785
\n","
0.985646
\n","
0.00000
\n","
\n","
\n","
LYM
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.000000
\n","
0.004310
\n","
0.99569
\n","
\n"," \n","
\n","
"],"text/plain":[" BACK NORM DEB TUM ADI MUC MUS \n","BACK 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 \\\n","NORM 0.000000 0.988636 0.000000 0.011364 0.000000 0.000000 0.000000 \n","DEB 0.000000 0.000000 0.991304 0.000000 0.000000 0.000000 0.000000 \n","TUM 0.000000 0.000000 0.000000 0.996503 0.000000 0.003497 0.000000 \n","ADI 0.004808 0.000000 0.000000 0.000000 0.990385 0.000000 0.004808 \n","MUC 0.000000 0.000000 0.000000 0.000000 0.000000 0.988764 0.000000 \n","MUS 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.996296 \n","STR 0.000000 0.000000 0.004785 0.000000 0.000000 0.004785 0.004785 \n","LYM 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 \n","\n"," STR LYM \n","BACK 0.000000 0.00000 \n","NORM 0.000000 0.00000 \n","DEB 0.008696 0.00000 \n","TUM 0.000000 0.00000 \n","ADI 0.000000 0.00000 \n","MUC 0.011236 0.00000 \n","MUS 0.003704 0.00000 \n","STR 0.985646 0.00000 \n","LYM 0.004310 0.99569 "]},"execution_count":6,"metadata":{},"output_type":"execute_result"}],"source":["with suppress_console_output():\n"," output = predictor.predict(imgs=patch_list, mode=\"patch\", on_gpu=ON_GPU)\n","\n","acc = accuracy_score(label_list, output[\"predictions\"])\n","logger.info(\"Classification accuracy: %f\", acc)\n","\n","# Creating and visualizing the confusion matrix for patch classification results\n","conf = confusion_matrix(label_list, output[\"predictions\"], normalize=\"true\")\n","df_cm = pd.DataFrame(conf, index=class_names, columns=class_names)\n","df_cm"]},{"cell_type":"markdown","metadata":{"id":"6rmVxHVmSANs"},"source":["### Predict patch labels for a whole slide\n","\n","We also introduce `IOPatchPredictorConfig`, a class that specifies the configuration of image reading and prediction writing for the model prediction engine. This is required to inform the classifier which level of the WSI pyramid the classifier should read, process data and generate output.\n","\n","Parameters of `IOPatchPredictorConfig` are defined as:\n","\n","- `input_resolutions`: A list, in the form of a dictionary, specifying the resolution of each input. List elements must be in the same order as in the target `model.forward()`. If your model accepts only one input, you just need to put one dictionary specifying `'units'` and `'resolution'`. Note that TIAToolbox supports a model with more than one input. For more information on units and resolution, please see [TIAToolbox documentation](https://tia-toolbox.readthedocs.io/en/latest/_autosummary/tiatoolbox.wsicore.wsireader.WSIReader.html#tiatoolbox.wsicore.wsireader.WSIReader.read_rect).\n","- `patch_input_shape`: Shape of the largest input in (height, width) format.\n","- `stride_shape`: The size of a stride (steps) between two consecutive patches, used in the patch extraction process. If the user sets `stride_shape` equal to `patch_input_shape`, patches will be extracted and processed without any overlap."]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"start_time":"2023-11-10T18:40:05.805638800Z"},"id":"9Kp1kx7wmOYq"},"outputs":[],"source":["wsi_ioconfig = IOPatchPredictorConfig(\n"," input_resolutions=[{\"units\": \"mpp\", \"resolution\": 0.5}],\n"," patch_input_shape=[224, 224],\n"," stride_shape=[224, 224],\n",")"]},{"cell_type":"markdown","metadata":{"id":"drn9RF4-SANs"},"source":["The `predict` method applies the CNN on the input patches and get the results. Here are the arguments and their descriptions:\n","\n","- `mode`: Type of input to be processed. Choose from `patch`, `tile` or `wsi` according to your application.\n","- `imgs`: List of inputs, which should be a list of paths to the input tiles or WSIs.\n","- `return_probabilities`: Set to *__True__* to get per class probabilities alongside predicted labels of input patches. If you wish to merge the predictions to generate prediction maps for `tile` or `wsi` modes, you can set `return_probabilities=True`.\n","- `ioconfig`: set the IO configuration information using the `IOPatchPredictorConfig` class.\n","- `resolution` and `unit` (not shown below): These arguments specify the level or micron-per-pixel resolution of the WSI levels from which we plan to extract patches and can be used instead of `ioconfig`. Here we specify the WSI's level as `'baseline'`, which is equivalent to level 0. In general, this is the level of greatest resolution. In this particular case, the image has only one level. More information can be found in the [documentation](https://tia-toolbox.readthedocs.io/en/latest/usage.html?highlight=WSIReader.read_rect#tiatoolbox.wsicore.wsireader.WSIReader.read_rect).\n","- `masks`: A list of paths corresponding to the masks of WSIs in the `imgs` list. These masks specify the regions in the original WSIs from which we want to extract patches. If the mask of a particular WSI is specified as `None`, then the labels for all patches of that WSI (even background regions) would be predicted. This could cause unnecessary computation.\n","- `merge_predictions`: You can set this parameter to `True` if it's required to generate a 2D map of patch classification results. However, for large WSIs this will require large available memeory. An alternative (default) solution is to set `merge_predictions=False`, and then generate the 2D prediction maps using the `merge_predictions` function as you will see later on.\n","\n","Since we are using a large WSI the patch extraction and prediction processes may take some time (make sure to set the `ON_GPU=True` if you have access to Cuda enabled GPU and PyTorch+Cuda)."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"tUZTP0bKSANs","outputId":"723a5ee7-7f0d-462c-ac59-c6acfb720c85"},"outputs":[{"name":"stderr","output_type":"stream","text":["|2023-11-12|17:47:33.620| [WARNING] Read: Scale > 1.This means that the desired resolution is higher than the WSI baseline (maximum encoded resolution). Interpolation of read regions may occur.\n"]},{"name":"stderr","output_type":"stream","text":["100%|#########################################| 629/629 [02:14<00:00, 4.68it/s]\n"]}],"source":["with suppress_console_output():\n"," wsi_output = predictor.predict(\n"," imgs=[wsi_path],\n"," masks=None,\n"," mode=\"wsi\",\n"," merge_predictions=False,\n"," ioconfig=wsi_ioconfig,\n"," return_probabilities=True,\n"," save_dir=global_save_dir / \"wsi_predictions\",\n"," on_gpu=ON_GPU,\n"," )"]},{"cell_type":"markdown","metadata":{"id":"noAAy35oSANs"},"source":["We see how the prediction model works on our whole-slide images by visualizing the `wsi_output`. We first need to merge patch prediction outputs and then visualize them as an overlay on the original image. As before, the `merge_predictions` method is used to merge the patch predictions. Here we set the parameters `resolution=1.25, units='power'` to generate the prediction map at 1.25x magnification. If you would like to have higher/lower resolution (bigger/smaller) prediction maps, you need to change these parameters accordingly. When the predictions are merged, use the `overlay_patch_prediction` function to overlay the prediction map on the WSI thumbnail, which should be extracted at the resolution used for prediction merging."]},{"cell_type":"code","execution_count":null,"metadata":{"ExecuteTime":{"start_time":"2023-11-10T18:40:05.805638800Z"},"colab":{"base_uri":"https://localhost:8080/","height":1000},"id":"WF_vY2B4i1yi","outputId":"04feef1f-6754-4181-c8a7-20afb35b345c"},"outputs":[{"data":{"text/plain":["(-0.5, 6039.5, 4703.5, -0.5)"]},"execution_count":9,"metadata":{},"output_type":"execute_result"},{"data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAAxcAAAJvCAYAAAAJJiwkAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy88F64QAAAACXBIWXMAABibAAAYmwFJdYOUAAEAAElEQVR4nOz995MtSZbfiX081I0rU758WtV7pUVXy+nG9ExjMBgAS4DgAgvSdo0AzEijGWn8gf8A/4D9A0iaEWs0LHe5ywVWgDsQA0zPoEd1V3V3dXV16XpVT+vUmVeHdP7g4REeceNm5hM9a6TlKXuV98Z17cfP+Z7jxz2ElFJyTMd0TMd0TMd0TMd0TMd0TMf0jGT9T92AYzqmYzqmYzqmYzqmYzqmY/r/Dzo2Lo7pmI7pmI7pmI7pmI7pmI7pudCxcXFMx3RMx3RMx3RMx3RMx3RMz4WOjYtjOqZjOqZjOqZjOqZjOqZjei50bFwc0zEd0zEd0zEd0zEd0zEd03OhY+PimI7pmI7pmI7pmI7pmI7pmJ4LHRsXx3RMx3RMx3RMx3RMx3RMx/Rc6Ni4OKZjOqZjOqZjOqZjOqZjOqbnQsfGxTEd0zEd0zEd0zEd0zEd0zE9Fzo2Lo7pmI7pmI7pmI7pmI7pmI7pudCxcXFMx3RMx3RMx3RMx3RMx3RMz4WOjYtjOqZjOqZjOqZjOqZjOqZjei50bFwc0zEd0zEd0zEd0zEd0zEd03OhY+PimI7pmI7pmI7pmI7pmI7pmJ4LHRsXx3RMx3RMx3RMx3RMx3RMx/RcyHnWAv6L/+d/jpQSBAgEQgiEZWFZFrZt49g2IOm0OzQaDRq+T6Phsbe9zWg84eTJkywsLtDwXNI0xbIdFhZ6WJaNbdtgWQhhIYTI65QSQCKEso0kkjRJsSyVTkpZaROAeo76yHQ8ZjIJWFxaxLJ0OXnhWT0SKVPiOMbzGqCboJNk5es2VH+LoxjbthGWoMhsfioojmMQqD4jSu3I84l5uQvK+4gklTJvnxDqk8zaqr6L+rw64UzZKZPxmGarhWWpeR0O9hmPhqyunUFYlspYzZuNkx6j6piVqqupd4aqQ5DlSVM1V67rZoM1OyfVPpuUypQ0SdQciLpByEeTJEmYTsY0fB/HcUllqn4Rgu2tLQBWVleKaZRqzBG6nKJ8zXfFGEi1FjK+rPKZQCCl5oeiFLMuI2NlrHQ7BGkcE8UxXqOh6s/WjC5UrzkpsznNfjPXmBCCNE0h46c0TeaOrzkPui0yK18CpDLjiRoeAsIwxHFd7GxcpsEUmUo8xyG+tw6dFtZSN1s+ugw1LnrcCl5U/CyzOmVaVJhKmY+HLLWlGGNzzOWc9HWfhRBYlkWSJqqbUpIkSS7T9HirfzqfNNY1RhryOnUbzPxIkCWZZUxins9Ij9EXox7zOcbcS6nGLc3zy7xPMh8rafRNZDwly32syNzSWjCYRrGtyLtitoO8ZwVP5avG0E0IUZKFZRlR8LnWOVkWVVamX4qx1FS0zcoyWEIgrOyvEAhhYTt2rrNEaUFhpDP/kX+2LAvHdYt2Zfl0U0Qm061M9wohsGz12cp0su24hTgwZEpeVy4vqm2wcllj2bOQQWURxedSOVkaQ4enMsUSVkk2zWpHYQyPIE5i4jCg0WwjBMg0zedYjV+5vJoW/qVTSYOYothgnaOou7wIYy0/Sb40TXO+LFNlzedrz5AHqURYihdSKSFb72k2/mrZp0U5QJLEilezWizLzvlB5jK+vO7Vr2T5ExzHNtarxa2bN/mTP/kR//Af/WM81yVVBRSyxdCvosJ/QiisIit5SvVLmeGXQu/pz8KyCKZTJOA3/Gzk5AFcJUrzPZ2MGY8nSJmwsrqmxsGYQXFAXlHi6yoAzfpY+rmQDcVDSbWWeoBnPM/GoN3uzO3lYfTMxkWv1zXkvymMBDJN2NvdZjye0r7cptFo4DcaeI0Gq2trrAkL13XxPA/Xc5Ux4rgIy2YwHNHpdnBtB3IwpQYqCAIGgyErK8sKgEnKBkIFRBbNK8CSsCzFwGaqyninaYpt23gNG415itQSIQVSM4KhJIUQpEnKaDii3W7huG4pc1ngKEbr9/dJkpTV1dU8hcn8CtCVcteSRBIGEbatxmM8HtPpdPL5UdWKrLs1gAWwNPNnPKmBihCCZrudgVuV13Ub2E5IsVjrJV8ZLsjC2JAQRhGO4yCsrI+mkVMhPdZlKKEoCKaEwRSr082UuPotTTNjyiq0caHoChCq06ZpRJIkmZK29ODMAFTX9UjTlCAIFFDNBFy71QYB0/EUmQteSutcgZQCjObCOkuWyrSYo3xIZT4+OcAvATWJypbm6fLnFN81L6j0aZ5Gj4UuU2TjY4JVsrY9fPiIZtNncWEhB4gpCmzKrO1pFezmPCKM71WQWAGlOZ9KxuMJjUYjM8AhiiKklDiOQzoNkJaFcGxjvoy/xjiWjKZ85vWHAtyWlV+eOc9vGsz53Bm8W5ZBxRqqKnnTUAMFnDDaaYI/kTtQCp4sxqy8ZITRVt1LIew8UWHjmQaAel4odgPgCoFlO1ga4AuR7X2rObWyR1oh5msl+2zZFratDH+Rj5vRFhOAaWCQAXTLsrBsG9t2ij4ZRoww+4PEsmyklFiWwLIycG07WLZdgPN8WquKvmIYWMpwFrY2DiTlUc3mJu9z2Tggy29px1ENFf0X5QeAlCmWZefgp46iwQTH97Bcpzy5s1+ORGEYKicNxnpJE4Rlz2JUg8wlI2oSpmnKB++9x+tvvHUwcKmsTcdxcRw3/7nOyCmyFnr4KGSuvWoZURTiOE7mTHsyMkRtmWqNqnK95XyVVIICTBc557YhCqc0/FapHdLQoQUoP5hmR2C2Tikl+ztbtFqLOb+a8q3M33XtlYTBBK/h52kl8NIrr3D1xRcz7CZwLTs39HOHFMLQeWnu6LJtS7Ull5dGA8xnppMkGyPtgPI8F2UUpHm6VEqiKFLGlOPkY6n1EyjZM52O2N7eJphOaLV8hKX5ONN/aUIcx5nDSTvsivmdTgMs28L3fcOoK/RUmsSkqRKCTibf8jHP5KDpMEu1gVcxruIwJI4ikBLbtcF2+Nrb36qfqCPQMxsX3U5ZQJjeIduyWVhYIEkS2u02zWYTx1HGhNfpYFkWcRzhui6O4+A4Dna2kNvtDrbtGmCInJdd16HZzCzIivVbgAn1uew+KMjzGjQaDQqgUwAAXZ9lWQao0rAv+6RQeF5fFIYkaYJtOZmHStDtdRDCyoCnOUa6fQU4GY8nJHFMuryU11FGPQZQkbJQZBmlMiUIQhqeh5Uh8CSO2d/bx3XV2M6MgyDzPKYkcaJAWgYqS17XnFG1klHM6WQe/mazxWQyIUkSoijCc72ModNi+E1Qm6Z5f9I0YWt7h163g9do5CAnTVO1kLRn2ZgHsxtpBsQUmFULf2+/T5qkuTGw398niiKWl5fVc4MvchCfzZHu69b2Nu1WC8/zVP1pxbubj7sJ7tNCKEjDo2sAXA0KNbg3wXw+5obAK7qdgchUlgCyyRP56JjMU8P72htTZIaqwpPV/EKDTgvLEsqTkyZEYZSDIgXCyA0TtDLRiisDdZbtYFlKTtgZCMv0QqaAKgpAZaXbbmUeWScHiDnwyfJYFeVVeLHUHwVSnbwtIgdxMi+zJDNyYK9+KAPcYnDL3vNinKuAWXmTKwYQio/D6YQwDOn2Fop5EgXQBb0rrDxxJu/kNeTCKet9qQ0i8yKqtqdxQhLGOE0vZ7QkiZUS7HQL40QIwskEx/XwfN/ooWkgSKZ7Q9I4pr26lI+v/p8Qeiwt9VfKOtYsgXbNM8UfbSwVY1+Wk8VP5eVhTsKTA+2noRILGdWagDOOYnZ2dzhxYm3G4NXjF8cx21tbLC0t4zUMw8okKfG67ZmuaXAlhGB3Z4vewpJy3h0CuqWU2LZNGAQANLI5PwjQG7nLu64VEkLw5ltvq0gAI4+RApBqx61iMEsjibneqrnNfhyV5u3aTydj2u0OUhwWQT6nLqnLFkaqurSFbtnd2cZzXdqdLkAOBotds6Kds44bqdVLXp6UMBkPS3UlSUqSJIUBXHKolOVamhbGgdrhlcRJovgkm2cNerXzY3PjEWmq6ugPhuzv9/F95VwmA+Cu46g6tQ7XYJuy0ytOUqIwYjgaMRyO8H2PTqeD53kg1RpJpeK5NEkIw5AgnBKGscJhnQ6O4xLFMWmaoHf4hBDZrrHS0VEcZ9/T3EEcJ4kC7oDj2AoT6nFNUybTKcE0wG80cF03c5CqMRIIHNdlMhqysb2DbVncunM3m09ysB8nMdPplDCIsCwVvRLFCbZlYdkWg/6Qht+g6TcVLsp41cowhDJM1O6U1/BKc6fxrcY55s6vZieBkhXBZEo4CbBti0bLR1j2/7TGRbvdKr7oRaQ9XZYyMHJmcl1s28G2LezMo4RtI5OEwXjEwuISIklzkJHEcVZsJkisYjQ81yWOI3JUQgGsSkBN/6JH0QTsuSVdeFBNBif/W3gGtfBUXjE7L3B3d5fpdEqv21Mg2cgXRSG2bRvllsvTJATcv3c/D7HRXmBppC/ya++1FiApYah2ADTjjkYjFYK2t5MLCDOMQCIJg5AwVEqk1WqRZMBfCZUUbaDlMifzmqRSFrtFWZnTyZj9fp/V1RMIBKlMKE0DkMRxAWyz8Y/CAMdVinMaBGxtbtBo+KysrJYURP45k55CCOI4Uda6VRHeGUhP0oQP3n+PMEr49re/jddoZMreyoWqbovMFq7rOERRRJrE5GEMBkAVIvNiInKhX/CRzL28dgbMEJYy+LT3V1hYjlPUXwH2GoxZGRjT29K5B9gq8pseU4ksgH5RmBKkGvwLkYUcOqRpQpLEhaIveXR1u4owktxpYBfhHabRmSYJtuOUMY4BMrVXV/GNKNeXz94MvCzGRc+BsJgZtJK+NhBcOWWpTaqGwjiptqacp+7LrBH0NDQZD2n4TaIwIE1Tmi3lsNFrOgymTIOAKAyYTCbYloVME5IkYmdnj2arSavVxvM8BNBqt2k224AkikK2trbodHqsnTqV9ziKY4SUpGGC2/aRMiWJY2zHJU3UX5MajRaWDlUwyPT62qhdZqepFFwOMk2gmLH8ZDKm2WzNAl1ZnjvjB3KAZoC1nLdEdU7yX0tG3HxgXQP4DJ1RB2DjOGI0HNBbXC43V85yRnmZS9JEYjsOi4uLRp/MMlSbbcfm5KnTuaFQTZcmyttpObOqvDBiU3zfhzRBpgKseWpfGnkNoCJTLU4royArWYvvqr3VMVUj4LkuUqbEUZIDySRJlczT4C1NkGmKZdul+dZjoENgtZdY60BVi5g1ujNdmcQxSRLjel6hD9Mir94J04ATYDQcEMcJcRLn7U9TSRRHeciR6XiSesykJI6TbI1UwGxWF9m4yjRBosK7tre3EQI6nTZJkjIaT1T4quflMsp2bJIkIUkS0iTJy04SXY6Sk0mivOJpqoC/nTlMoygijCIVvm5ZpKYDVGMLlGERxwlpmirgnBkCURwj0xTXc5GpzPulQHvWuwz4b+/ssre3T6/XpeF5xHGC57ll5662/ytOhzRNiSLl1Q+DgOl0SsP3aTWbmbErSWLFR67j5A7ORHvzUbgmzdqonFM2tm1lxk+a6/QkSTKZpUY5yRyUKmRd5M5UPWd2pveiOMLKonDibD7SVK0Zx7aRacpwNMK2bfz7D0nSlCRNcF0v5xmNqRxb6bYkjpXzPdE62lO7rtr4KqYqw4OFw1bjkOJfsfxMZ59+bAm1U5LGsdIBtoXtOHDATulR6JmNi+l4XCxkaViekAMfK/O25X9tC8d2EELF102nU4IgZHmlb0yeDptRVrbeGq4CZJW2WNjlMA5zcBUgTdPMm67N+8zyM0F5WpO/1tgQZRAXRyG7e/usrKwURo5MePDgISurqzSbTXJDh4qiMxhASpkrDVuDSEN5aqEqRAGqDbZSwjVNmUwntFstzDCFHCRnHuA4jnj0+DGe6xFnDN30/SwUQc2DtvKBIkRACCTKEyukUkaB79FoeCws9NT8Gu2xbIvpZMJ4OmF5cQnbdRXIti0G/T7D4RDHsfEci+Gu4PyZU1y4eCk3FiwDZAPKe5wJSgGznrJMAa2vP+KXPw85ffIk33j7LeWFk+B6jUzhqEVpWYVBpRWWGZZSXpiqZ8JyckGMMT/5fGhvc/agCBNRBseRIKkGwlKSJhG228jKF8wroNiNitnf22FhcQmv0axNm6bJkbf8g+mYYDqh01tEI6/pdILvNwsHwCFeUdV2jLabgNF8XIi/Mt58NiA/046az9KcQwOgzgLectvzp0fwDOutawDLchDCouG3ilKFQNn2Et9XxoOVnV+LwogoChFCcPZ8ZtilaRY2ospUXjQLL2nQaDQZDvoqXaKM+/FoRJomLC4tZ3WKPD7fygwLs1e2W1YVcRRm+Wy1hQ44vkcyjfI0UTCl4TcpVJnI59K2ClBYouz8TsmbIRRPyyTFcpSCDycj0iTBa6oxk0mWL3MQ2I6Tez/1jpqwLGTuuZN58eUdSaniylOJZRdpteMhSRT40LtXjYZPMB0bg6X1RDGCRR/VmaQ4ivLwrDRNGUt1ZlA5zzTIq/CblErZS6O9qWRva5fJYMSpS2eUY0gqD2ycxNgCxTOZrrKys39RrABL7hzKHU9pvmOsAGkKSGzLRgJJqvpv28ppmEoz3KLMMSVwY8TZgyBNEpJsbnRY6WQaYFtkoR/quRBqZ1iBR3I9pnd8kzTRE5iDW+2V1l5zs1V6Gix9hiBVnmmZyjxKQaK98GmpD8E0VGe+HBu/2SRJ0wxEyorMKvhApilxouZE6S4FFpEyczammPu0GpxblpXzW5omTCZTkiSh6ft5HZZtFaA+xyTFLoOOXtBjrMNmRK7r1PjY2S5umhs92tjTIUV2PqZlA0rmnn2Zylw263HTjjTXdWk0XE6fXEXpi4AwDJhOxwpnaS9+1YLPcFKaqjH2/QZN32d5aQEpYTqdEARhbhRq3lK7vGCe8RkOhxkOFTmvW5Yed1HMT4ZrVESJWm5CCFzHUzvGojjraO5+SNSZRdfRmEQ7ZVX/lTNnMWdC3a5ms5kZ7SoKRIdWaZmjDCClyxuel4cFmmGqwlK4yM6MRMuy8jPPVsZz+Rms7Lta82mx2+EpIyeOIuJInVn1Gi7iSDuV80nIJ9k7rKF/+v/4z/LBqIKGPHQh76z+Z2dxcOrMg2VbCjxmgDUvQS/WbOE4jlNYuNki0dv82nsLuSzFbI5lWdy6dRPXdTl//rwSTklCfzgiCgOaTR/f99nY3OTsmbM5UxSgvBxHqw7oOcXECcFg2Ofhw4ecP3eedhYuJpBsbmxw4uRJFfObAVUFrAtLWOuSNE3Z29uj02ljZ4faoyhkPBrRbDXp9/v0eou02m0s2yIOIxzXZXdni6Xl1dJugu63HssyWBb5b1EYlcbXtuxs+zDzQohqrKQgjkKC6ZjxJMBvtlhYWMgFscgW8Xi4T7u7mCuKOPOUxFGA3+oShAGe18ASgiRNc7CfxglxktDKzi4gyb1Ge7s7tNsdmq32kfgzTRP2drZxPY9OdyETVkoxKOBzdBoO9hmPR3Q6XaVgEsnmxjpnzp4rgdNUSibjIbbjZd6ZbOhEoeCOAkCT7HD5aDTCdR28zCAKA3WWw2s0az3J+7vb7Pf3OXvuQg7i9KUCSkEqYBRFIUmS0Gj4OfA4iJSXLMZxvbLro0ImcD5y3HOmXIrkovwbhVFX/X2mrKpIm2eHVfWZ+VMaK+PxiJTEGjA+ubcnTWLiOMJ23NyIzh0ZHDDUhrOj9NgYe+1BNneaNBAUCJIs3lc5EzJnRQayFMiImYzHpDLFb/gkGRBLMm+d43lF+GIGUJU3GhBKmsdxTDANQECz1Va4PgOuuRc6jBn3RyRhpHjRs9UupwTP99h9tMP9j29z4etXWTm/xmBrl4df3CVKEpYunGDnzmOi/hSShBg49+YLPLx2F8KIRq9Fo9uis7aI3+vk7YyjJAtjSLP1loHKVJJEMbbrkEp12D6JY4IoYjKZ4rgO3XYH23FyIF4AbNBnnsxwFYm+RMA4DJuNWZKmpFGC5TrG3GWTKQpngSk79C6gWjOKQzTQD4KAIAxxHHXORMpCB4PaSU+TFNd1jcP4KIeMNjAy76ve6VRebLUT5ft+7ixEO6wyeaXBroAsrMMmzXRtHtKhAa8sQhGjKFIjlHnbi3Nbad5/rfclMj8PY7Y/zT3PVgaYlYdYZgaKEOSyT49xFMXIDMiJvExKYTkaUFp6hzYLDTJ1d877Bng015r5vAg3BDP+y7yQJgeDGWC2s0PR2uiwbTs/b6pCmWUGgM3zTjLPbz7XO/1pDmrVWSCBDgVXRpFjW/gNT10EoMG0IV90uI1UdksBevUZJ0vgOi6u5+E4dm4saINCsUKa993JLjzQQ2Pbdo4LHNum0VD6z7ad7PKVNIvy0P20sr5Z+Y4MQgFvx3GxLKF2gsOw8M7r/mSOBtu2sTOArh14duYIt4QOiUrR+FbraYCGpxw6+pILIUR+MD2KIrV7EsckSQpC0m6rnak0VfznZQ4hzXeWJUhSZeypC4UK2ZwbKRkeE9qgMhyYOoS06pNLpXJQ6ZByLzvvLNPCKCLr68rKCZ6Wntm4+PSjX6G9q5DLO3S3hBCEUUgcR/R6C+iYbb2DYVuO4X1Xyq7f77O4uFhYkhrXGrdWFPHI9gx40OOjNfJoNMD3m2xubmLbDmsn1wAV82rZNmEYMBoOQaa4DZ9ut6sUrSEkyrsHRXuSNMkAc0QUhoxHA7oLS7iex2io6h2Psq1zrRBKbZVMxiMsC7xGK/cQlHc1VJogmNLtLSARaqdFpkTBBMfzkanMF0uVpuMhYRTjN5t42bZkEEzzA3VhGGThavrAoWTQ36PZbONmB5myhhQKVEqSOCKOlUJpdzpGm82wr8KosLItvzCYYjuO8ppkpGK9A1rtDjrmUStWIWArizsOgyl+s1XaqajuYmkjkIIFSuhMeaIm+M0ipO+wcIkkTnh4/zZrp84iLCs77CiytlqkSZyDy9xblCQ4rst0MsJxXRzHM0ayqLe6fZ+3MZjSaPjGb+QKlwwwmOXNB6GqjRrc6DqCYJrd6ObM8OUMpSnpZIxo+k8EumcQfMnAMn825jAtzsvo7fn8twyU5aFV+a/lemQaK5CQATy9flXdWT4DmBReVqWs4ijEdoozXwowl/c0tNNDypThcJCBLgczlDH35KHrUpJR15cmCXv7e1kIo4/rOLRaTRWOkHk5NXDMlTLaA5cq72gYYbl2fuNVmuXJzbEMMEoJcZIojx+Spu8zGo0Zjsb4DU/FQ1uWAgAZoI7jmN3dXaRMWej1GIynWJZFu93CElloRgbgMoyZAdQiPDCOY0bjMZYlaLbaRQw3xa5wf2OXB5/eJpqG+H6D7oVVHMdi884GrU6TnYe7xMMxzRM9Ln3nZR59cY/Na/eJ4pgzb15k89p9PCx8z2UcRJx+8zJ3PviKXtMnShOCMKJzepnzb19Vux8SgvGENIpx/IbSQVbBnHqm0uwmL8uxM/Ca5HJWX/qAsLKdZnJdVuV/veuqvbqm40yfA7Nsa5YfpfZgyzw0Sh2sL0CQzAwcHbJY8ABZaLHqjW0rsF8KzZGz60CtzaK9mnccxy553PVtVGqe1UF3HYqSH8TPdk7ycih2F3Q9tq3GNsou9rBtJ1//OVCCzPgFmahwHH2O0MpupdRg17HtbI5EhsfUurYsC9d1ckPbEhDGSXbTJFnYtl06OC4y77AGq1ov5SGruUe4mHfbtnOPv36uHat6jM1bvfSY6/MLKnzHQgiZAVsLN7tNM45iJMoRqM8c6B0X2yhTC9eijXp+sh0LS+1gSSnzcxCaVxN9zkCAk50R0577JNt1cmwnu72srHU0vpOp2kGT2VmIAhSD63n5WJg7TvqWRrUjk4VPa9wvJUlmBLqOOtuQpkp+Rll4vOPY2JmDRGSRAWkWkuS6jjojGCWEUUyr1cT3/WJ3IJP7Qlj5PEjmO8pylS2yXcfM2Y2xrtU60HNsnCGJ42z96NDkFIEsjWeSpPmaLRmredmGnBFl404/qJFE2ZjI3MkK2S63Bu5kui6rQ4dtPg09s3ExGo0OTSPTlDAMkFIShgG9hSWiMCQMp7Q7vWyAE+VJSSUPHtzjzJlzxqn7OY03vJzFoMPO9mYG+mxcz0OQ4jfbinFqykxiDQxVWaW2S0kYBDR8vzTJqu8DWq1Oielm82Zbmq323HRxHBmeoHqSmccHoW7y0KDTBJfj0YiWvs3JWPA6fk9YFtPxEMt2mEzG9HqLCCEIggA7O1BfpRnPeMGBPH70kOWVFWSa0vCbBrhVjFncLlJY3FUwXbC8rhBTVs22Z+bnrMY0ZTqdEEchvYXlyq9PTxrAWZllr8NKqocbtZevjvp7OwghaXeUcY3Qc1LcAKM9pnU7Efp3bbTp7W9heChysJom+cEwx3VLnjMTOOUAN1P42lBCmkBaA3bJ8PMv2f3Ju5z8T/4BTrOpAK6U6DCOVINoA1BLlAc4zG51sjIPWph5ES3Lzj2EGqQiJWEYZbs2VmZEF7MYRTFBGKkYcjUwuTdJAxv9fBoEhGGEEBIvMwbTDPRrsK4vAUgpwge0kk6SwtOKAbR0WJtpJWmlrrz4SQEIkxR1wwiGlzWT/HmogrrRZDKZqrKElY+n6bXW4klkdYpsjcUZyC3C21Qd5fCObF6TJPNqq5hnbcQ62S6s5q9cWWVx1mmaYjuO2jUDHNvJ4qEjZJrmt7For3y+LjK+1u2OdTyyHtesX4OtfR58foc4iPA8l8WLJ2m0Gjz44i6O4zCZTLGSFL/X4vzbV1i//pD+wx1S4Pzrl3j8xV1828axBP0gZO3qGR59fpeVTgtpW/SHE6QjuPLdV5WhECfs3NkgCSKavba6gabj015Utx/KzCsaDsZICe2VBRrNBp7nkWY6IUlT5RW1HcKxOgzZWVlQTpRsDEkl4STAbXo0O60cqDq2o0JKKa6PLf6J3PsujPnMr8KFPIzCyozBNDO4tadUgzzNAyr8pbjqXHtV7Sx8VeRhFCLfPdPRBBqcOq6Tt0efndQ7ATrUSYUBKWeGvkhEn03URgrIPOIgzWLKgyAkBZpZPL2OYChknL5IIiCMYhzHpun7hNntNkKo9RVnssX3lSNNr8nJRF2W4GVASt0eZiGlMn7jOEIIi0ajoS6LMb2kkBs6xTPDM2J6lLNfigsz9M5HWU4Xa1gbgoVDTJ+RyK81zuZVyuKGPMsSuRGkQWLu4DUN2ewXvesSBCqccTDoZ17zlG63qy5zydZzFIa5N14IFQ6nd4qiOMa2lQOk3W5l/CfztLouhfVixpNJttOu5lwf6vYannJgJMUNSWrdGIfD9TNA7ywC+a5NKtNsnar6rWxONQmhzmROp1PCKEagd3AlzaaP47p5CJp2xVQxYK4LpXmepLipMWcByjtTs9Bes0mxG6bL13pA81keagh5ndowy/NgBtQVBq9e27lxbvRkBtuWvhRzaMrvhYXFmX4clZ75zEUVcFd/m04nSKkW+/bWZg6gneyGKJXOAlT8pGUJzp27UJkoSnUUderD3xljZwuq0+2RxnF2s4kW1OSDXSpHFh7/OmAnhFCGhc6XMVUUBPh+K/dk5CDfGAZVfEKr1coaiZpRHSeYeVDKnhJyhp0Z56x9pjfbTKd2GQwDIAOVKj4zZdzfx2s0sG2LXq+be71cxyFOIqZRkG+/yTQ1+iaMcgt4v3bypBIGhKRZ2JJEkgQTUiwEKZbjUYSKyBKfaEtcoPtseNGkGrv8ez43emEqQaB2nCTNVps4UQpid2erEOJCxWciZXaIrwDnSX54q3yjghIoao4mkwlBENDrdtWNXNNpFg7nFPd95zc4FIJIex11O6fTQsBqEIcgv30jjLJ3TrhOCYhqnouzA2pSKo/2dDLFzjyJrqNCH3Qc83gywcu8cGnpUoAiJlcac6BYsQDLMjcQyMcwGU+IGg3sn/wMMhBrGdvw+RzJ8vqSmcLSMa0S8rM9OQ/INIthTrM2KwDquV5uOORlZjwmVaVoYZoDMAMAlIGu0Xcz5KIit7SySZJEgbH8nJd6FoYRChwVN8lpZa4PE6ZZXL6beRZTafCI1IclyXZgRHbNppJBcXZjSZnXC6NEv4tFe/qiSO0euq6D32jk4Sdu9k4E/Q4SfX2sQIV3xFFAFIxzRR2Hcd42DEBpo85U2RYIGdNuNfLwTuWF8/Jxsu0szNWy8nL1vNvZIUpdvpWt53gcEA7GTFci3McR0+GYVMCFE2fxHIfmYkpkCdxlm+lgxJkr53j7r32Ha94nPEruYLd8vvHb3+K97Z9wotEgkpKJZ/PKX3md99Z/zKWlRRbbTfqWxeZwxG/94Hdor/Z4dO0eP7/+E5Y6bWxH7eY6aZPv/c73+fKdz/B9j6g/5l7/EUunV+l1e0ghOPfSBU6+eIY4TQijCFsIHn16nwdf3GcaDfnWd77H8tkTfPjDXzDdG2FFCTJOGEcp3/nd32RhbQksgeu5udwZD8bIVLKw0lM78dphkq2pNFHODb/ZzGRJQJx5+S1LAagwirAygwFU6JLt2MRxwng8Vrf4ZVfBC1F41zUwLnSYRjllXaj5IUkShsMRSRLloTppKomiGFdo77sklWQ7KwrwpGmKSAsQ2Ol0cFyHOIoZjca4DfUOm1azkZ3hwnBukOsizwuI4gRkSqvdxA1jwlA5U5IkxbKTLM6/geM66rByKrEdj9FoTBTHkEoajpO9o0itO3UIOMVxHKVHDU9utgLN0cnlZDFAxYODwSVaeqFBan5xaSa8dLhTMRVFrLwllAzQYTsSiZ1dL63lERThUNqw0eV42Q5Ip90mSVVIZrPp5/K44XlMHZcwu1wijrKdL6F2odoND8/18LKdozxErNJRS1g0GgLbFoTZZS25sWsYXFVnrz4/UAL52R+VVDuT1ABZtq1uwxZiZsR1hEer1cTPDrpDIZ+khDTRWCw3zcrtMcFd9XdpPin4Rera9XxnxqCUGLdfFmNlwKNiJLP+lI0dzYOzbTXXbr5TbupEs2WGTSLNPhjDLeXMrD4xPbNxkVtvaUp/f5eFxeV8oqSUNBo+Oq5uZbWI3xLFyCGEyE/O6+95+QY4KD2TWfyeudAyfOO6LrhuvkBlWjnYZaxcwewg5nXmYEsvIMl4OMB2bFzXJ00ikiTKt1wLUJYZITJFpjGjQaSWe9atYDpRddsO04mKn/cbvto90Qsws2ZNj3PhiTSMDanf1ZAW293KjUMUR0wmY1zHJU5iHty7x8JCj4WFReWJFyqca3+/z+bWNpYlWFlZxnUcptMgF0a25eglnbVD70JY2QF5HauqPQ4wnUzVjoitXv6ELOJsNeMmWTiAbRUhO9q7pby2iVIGUmbXh2owSg7qtBfIsm307Q/mHJa29im27ZUySTJPlpXxsTR4t44nilAX/YJC/bw4OJUJLGMNmFe06gOTxc6DeqtIHOvt7vJuQ47Zpdoq1vOdZDdZ6UNdOr1WEnnctMHD2ruoyjEFj2E85gLS+Cxl7r3m9u18PetwBe1dMw+MFasq85rJ7NaR6pV42Vo0XyKmwW0+7gbo1WeWNM9pD6uuOz+8q8GxGS+edVUZAwBZLK1l595i27Zzj6Fj3HCn2lYoRc/LXmgGmbGptvPDKFJK07Lw/UYer56rA22QZbyo8+sdGt1ffQ6NvC/6PQk5FsRxHMIwzG9u67SaBFksrY5RTrP1mF8ZaYA1O/OcayPZsixc80VvmafSPNyZi5c0xXX03e/68KOVG9vKkFCHfoPxlDRO8JsNRo93EU2P9lKXL3/8CdP1kDtfbNNa7XG2e5JAjlk+s8Jrv/ktfvXv3uNC7yzuQodmy+fhrQd87Y23+e73/grydoB9P8Vf7vLqS69xTXzE6eU1AgnWQpNLZy5xo/UFvYUTrDqCYBzy6ssXeen1N3CaHnf+5DqrzWVe7vr0Gx12R1OufO0lWkmT/ld7nL90hunUY89b4tU3X+f9f/dzLpw6we2H19n6bIPYSjnz4jmW1pb48o8/48LZU2xFIf27fS6//BJ713dZ7rQ4t7LC1mTKo6/uEAwS5KrN7r0tNu9v0lrocOblc0hpEUUR42kMxJk8ybzElkXDb9LwfHxfnbFKU8FoNGUyCbCzcK0wihCoiyp8v4njuop3HSVPbUe9+8hreNlug5U7c4ylOgNXiq/FLW+2batDslk740yOC6RyjmT8E8k024VTPK3j55utdh7CYnk6bKRZeOMzVKbPDZjkNTxsO8Z2bCzLxvMErptdrKHDREVxVkHLn0bDy2L4k/x8Uf7+g5y3CzlTdTrMeoEpwIMet0POW8k8rQaiJXSa15TfsGZUlxs3lpVft631oEYzeXMMR6RpI0q0c0vtekVxjGM3sYzQcukox2+aNgt5lOu3QkYrPpTFmOnWa6Msk6ueZ+G6Xt6OJE3VzVtxjGOcMdLjoj3u0hwfw9AyQJzCFLp+LRQpdAdSIoUKP8pDsLNBUljEPAxuVlImM7ztUBLlsnSImW1nuyq6rXm1GktV6qP8MP9uOAZnqjXGq7BdZI4lNZeU7GZB/m6mEo/XAeMnpGc2LgZ7u0oBxTFxFDAcDJQ17TgFcCt5HmUez5e/3RWyuNM0Px2PBpjZMzN2GUkuqISl4zVDwlBtqSOEumFCprnHrvAmG6EJxmDmRlLGsDmQzMIONIhNk5gwUl5kz/eL9yZAqf06xCXRgFfqg84qTZTFyEZRpLa4dQw/smLdFtZmmibGYhZGHHY5jlWNs+KOVMosDlGdC3i0tQ/iYbaVqkJhgumE4aCv3o6+tYttK9ACqCvQNGjIjSyRvxsjSVMcx863VfV7MpJsTvRc6Tu19eJXh8O0cCpAoS5be/RlJgRUnLk6oJd7S8xVWfIamRuHeqVpz335BWX5/MvixgtzXeUyLRPwGjxpr6wmffOVvoVBH2aUqaH0MAqVhQclQ9tKUWcKXBjPdLyrhVo3jm1hZW+M11u52rix7WI3oXSVrR6LrDMiA946jro4yKZjicvCJgfIQuTpNbjQ53XUGapyrHGh5ItDxTqcQ7tItMFnO05mlEsjvpt8vvSViaqfTmZsFDxVntdsXLLD0YWHTYcMFLs5tq3er6ND4JSRqtrQaHi58yLJdmHyyxiy8dTrLo4TwjAodhJ8H30GJ3cSZGOjbpJRcfqOY+cH+fTVlfmL6igMZGVY6gPEKl8q1VWNyhBymE7DnP98v5HLWr3TkGSOCw0U9JrQ136n0ojblZI4kSjbQsUEW0IQhgFBGBOGCe2Wn8k5dahdhcikhEFMOFUhKx/+q3fZ3u5z8ewKo89v8cj2Of/Kee5+dJOldpO9acBir8VkrN6Vc/G1K0SDkOHmgMXFBZaXl4iCAAuLNASBerllEES0hU0aSRzHI05gFIQsLvfYu7NJFMTYjQaR6zDcn/L1b7/Kwokl0iim5TYIpjHJi6cZPN7BsRxe+tbLfPgH72ELiyiM2Njpc/riaRW1ECUsxVNCv0trmnDz3jrtZpt2o0kcJjSiiCSReH6TaBoxHU/Yj1Na3Q4PH+7QazY5dXaNaBTx/v/wDovLC9zZ/Ypeu8WFr18hmobsb+/jd5o4DTfbffLwGsoLr2//EkIdwOz1uozHY6VDEDQstQZVLLlKry8MabVbNDP5ZmU3P+UvaqyRdfUgqwjT6HQ6CEuwt7tHlOkJbXwkqXoJqTJ4bVKhDmLrHbRWu0O308murFYg2PO8vMpCP9e3RWSXCGhfkDa4c1lldEjt0OqrRi1cz8KVbglc5cZVdsZBY4C5wEqAfu29QJaaJ/WzOSA1T2R+EKU/5TbVZpelb7n9Jcnl9kF1S6HDZUTmHMick8auknK0HPySwiQ3LKqtz1optc4oDB0NZ7RDpdxxURhpeerK4NZRbYeNvBrz6bo0dDB5TOu6alFVg2Ye4K4aP6LQnNopdWBHRMEE+hzavImcZ1iosZ1dyQr+iHzcEZVdE2MccuM3K/Co9tQ8embj4t/+4R+rkI1E3aUdx3F2gDtRLyAzhEXh0Zd5CIfMjQhJ7RZbRsWwFR5d7ckslH+CjrGMoji7JcAxvKSqJOXFTUvCFoqtRF2GusNaedWV9061P86UqDBjnDVTCVGelByUZtIwA2T6/ml9o4EG7+bBoiIkSIPIAmBDcXuB0OtCFF5bZThkeTWYFyK/UYMsnZ3F7vq+uvWlv7ebezsFMMyBueqHfluuNkxAeYYc28acvVIImkyxhcyVoyXAcbLbaTKPiA6j0O3UYFIfrM9DLIQ+KGgeJhR5O3TftbdXzPymKA/bwPTGZMIgu3BAoG8IKdLonSHX0Qfgi/F1HFvtQEg1No3snnh93qWI6QQpRcZ/ljK+4kSF0mRxoJrn8/nMeEamMnvTcd15pEKomTs3aldJZrHxdv6SR5kqXtZeaxOYF0ZtoTKB/CBhkiTs7+0xnU7xGw2arWbu4S8EXXb7lwGM1XwZhwtTFZ/t+z6uqw5Qh1HEdDrFEuSGh37BprqGNcJyrFJ/NZ9r0zDnRX2ltcjWvdSODLJ59PBbTVxXbfEPRyOCeAqZ0T4aj9UBwOwyBOV4SJFRlNeuWEytTZnK3CiaTIJMsRmgxSBtOKsYd2O9AwgL13FUeIdj5/HkaZhmMeIJIpBF3L2UDIYjojBU68lv5vHVhfwtximOsxdEZTfqKL7VZy0yQ9WxCYIAEPgZ4I3jkOlkwnA0odHw8BsecVLc+GQ7Krzu/hd3+ezHn3D1xfMkH33Bw1HKou8TOU2G+2N27u2QBCnSS5FxysqpVW6m0Go0eeHtl7j30S11cYCw8No+URAhhUUwCUmihOkwQOi5TFIcrwGOTTxOcREkgbqaV6aS7eGE9kKb81+7jOu6hGHCmTOnuNO8iSdtBv0xzW4baVlM9lSYZWRZbA8mnD+9xGBniHBdBp0F+jt9eoHNZBrRW15E2A626xH4DaJknzgI1Y1XwsZ21XW4e/0By8s9fL/B44/vwiim6ScMYouzL17ASgQf/vfv8ODWI5ZWe5x9/RIX3rhI+9SSAuGZvE2zg76O69C229nOWPl2Gcu2lV4Q5Lu4puOpCt5ntW0JJWEm1GdrLMui2+ngOg6D4UjdBIY67xXFcSY3i91E21Z83Gz5eK6LPhuUSh06CiXlMY8yHVTF18oOnpM5MySkTBFS6ySj7/mXOtBntKn2s5hJfqBhUZNaYwdZY2QcXoK5+1vFuHPe26PHsJSrKFEZgaYsLWVV+E3PQQWgF39EnkFHBORDZwkcyzHkYXXU9OAeYSSMXYBDdxZqDAUhBTLHTpUahdGy/If6XQNdbj6H2Y6JuqJfRxeYpRfOw9nuCPQ5RpFjj6yK3LFcGAhG03IsWGqWtqT1GpHFRQn5vFQMorzOw9bjIfTMxsWXX31VhGJImV8FlqZKcZlxz7PhTkXYR2kQ80RmTbI8SOibPGThSTU895bQB2Gy9ywYoFUbNwLl/dMDrEMFVNy1WkR2dqsV2lK3BK5jZQeu0vyFYvo2CQ1680Nx+rMGzPoKuWxynQyk6t+1sVT2QFs56M2v5csAbm5gGWnsLMxD/2beXqF3Q5TCsXOFpPqpmFmNX9EeBHkoj2UYbHEcEydJHj4i0YBJKw0V86hDL6zMi5ykSX4ntLqbXR1Q1IcYi63Y4go9U2AhKN+UVAVt6qERqiZzGVEcPitCcLJCciAocyvfENVZFdro1LdS5HH32dgrozFBoEOcZKlfes1qQaEM2SR/wY+dvZzPfNcKmQwVQiBFipSCJDXu4M8BQ6E185CHjISw8RpeBladfB1E2fWaQRjmu1kaLNuWmlfXdfLx1gc7Ffj0SOSU8TQ7iGyEt+kZyw1dMp7Q2ECCsG0818P3G+qMiFO8x0b4vgqJE+rFQl52naHrOIShTZKkBGFAkoFibfiWDKzsW/ESQrU2Xc/L+U3vuql1CZ12S71EMY6Jo4hJoGK6kzih1+vmu4W6g1pQa0VU2pI3Dls7xntZcqEnsvWCxM3OLOjdJ71m9a6G5nNlELaIs4PypsxJ4gT9Nl/Pc2d4U8s3zVBpWlznGMdJHkangaHjOMroddTB+0bDZzwaI1OB67WwkCpcx7IJplOsIGX39jbd5S5XXnuRr/7oIz7+44+5tLjGgpywsrbGdGqxP0pZ7S3A7pQ4lqwuLHHuwmm2X73Kzv0tWgsdrCC7ojVN1HXbTZckTWgvtknCiL3HOzgNj+H+gCRKkNmZLyEErYWOumrV94mShL3BkJe/+xrNRXX146Mv7rJ1b4NYSjaHI+JUsnb+BMk4YHdjl1bTZ2u7j9vwOPXiWX70X/8xTdfBdR1OtRrsJylus8HS2RWSIII0ZdwfM5kEWEIw2hkSpylRkua87jQbYNvc+OAGouHxaH/Aygun8TpNPvvh+3z2Fx9z5YVzLODQ/8V1/vTPPuK177/J2ndfwe+okCH1EsMEIZVucbMDyyXZJwsZVQhLkDPoKWPhQq1STlAH1mRuDIPA95s0Gn52DkiF4QZBQBSG+L6fXR1a8LNJ1YP/z0RHLKYKvmfyVQ2IKhm/V8OBnpaUrJ9/GchM/ZrKNsFMc2sNizrAWOqvBliZrDE97rKabdawOMwg0Di3qFObR9XWVsqpGgZkeqUyBxpHHtwIVY7AMCwgl4daj+nEeTja3MEvVymMDkrdTktQsLrWr5RCo0tli2I1Kj9cFi6WG1NFw4sb94xxmTd+Qr3qobozlo+hqMyDeLb1+czGxcsvvpCBFdVvDYpTzaep3o4tAHeh6OtvytAgQN8uY95cYXqwzVP8jm3lW6RaMStBq16jrp9pT3EUqTcRNhrqwLEWdPrgTX7Ay7Zyr2YqKR0A055mMw4xn9zcIi7CfcxwkSR7AY0KiSrAngaGeVhEzpUiZ0gNRPOXrlQ8UTqvOqyk4yyL2OrSeYQ4yQKmydugwXW+RDKFpV+6oq+UtewEO7uKVwhLvfFXpIjsAGK706Zh3N2s+WE6DZhOJ6RhFsvt2CRSkCZqGzsHmEIAhpLMewimZJix1nOwra38rCeGYtD9L3aaFAPrHTXDKaKuOnScDCDaCCmU1zfKlHhujeQNQAiRv8UURDEGFJ6DfDeKAnDG2b3r+uakonMZFwll3NnZDoSdzXWSJsSR8mgr/lHGot4B8lxXHXDUMfWZZ6Rhebiuk91Rr3fNZtdnQZnR6VgsLy/S6bQyg1LfcpLmuyRF+mIshb77PANrxW5VcQWz1/AKcJyVoXeQHMfF99UtR0nuvMjCEbM6dWielhdFHeR9q+4w6qF2XTe/YEHKlFZL7QA4toXXaJAk5Vu6NB8V/KSVhczbZAmRj7tpXOjzU9oQLmLGs3EruF3xoWWBpUIKGg1JM7sSVPOSeR6r2K01lHfJSFeGirBFsSaydtWFmOiSnHFAOlKHiTeuP2IzijnRbSD3Bnz24R2+vPaAE6dW+Wv/x7/D3/7f/4f8/n/637IbCRxh40gb23LwbQ/HdiGRTKOUyy+c5tZ71xlNQjorPZI4ZX9/kMlugWULgol654Xve0STkOHmHq4lCJIUYnXlcxTHWJC9AMrC9RziRL3l/OzrF9T6mgSEuxO2HmziNlzS6RTHEpw8d4Lx9oDxJKDhNxhOQy6/epHh3ohgHHB6scfmxjaO47K5N+DkhdMsnV3h4Ye3QEqG/SG2ECycWGTz5mNIJM1mg3EQkErJ6RfPsX1rnf3NXXq9No83B/zGt15k6/4G7/2bd3E8h6avzrolacLu1h6fv3+NR3c3OHHlDGe+eYXOcjf3bCKF8kqWxE4u4NAIpiI+ZkkvzsPArSF+U7KQ5EwW2MLGtsB1HVrNJge9mFOH/R5KNUC4ul5rwXKlvYfZC5XGHZyoDpA9I6lzEM/2JuRaQ6K+sko+c2xqyjDHozLW4qgjK+an0LhIOZ7EDAsW3zMZpS3h/PfD6zW/ykoniiTZbYGgdh2kRGAd0K2DGK9wbuZrS2Z5KvyrIlXAtov3vZDrFWPnSRTjXVwFYJSjDaA6w4JinBRMkYUDUOiw4up4zH/yJPTMxsUPfvA7CCGzeOjslehCxWFrz3qu4ExmEGYIj3428yEf8OJ7MUlJkmRgjMxDKBSIcuzsgK8kDEOCaWAAAlVKnAF0twLQRab0bTfOQ1VUTLabHwqTMiUMY4LpNGuVYszcIi55jFV9OsZbH9LUID4iJZFxbtJrEG8qBplvZRnjIFScc1FWAbRy0Jp5dMuLmBzpyRxMFEOeh5xVFmH+SJhMbHrHi9t4XLdBq+njuU5pN0l5kVXMcBRFhKG6B1vxizAOfBfnSLQRMSNISoexKC1Og3NQbzFnBiyr8VSKLsoO4eo3Vab51XTFuQhlmJb7rcFjHreencfQgiQHbLrJ2SDqxa13nMyDctowiqIIibq9w84O+usduPzwsjFxOp/5xtJ8a1sLJ1Gc6cmmLN8lK945MqthtbDMt7hldmbDdmg2i3wm35hOScOZX7TLmE8JM0avGcqhy9a8onfVHOfZlHK+U2WAHTM8TAibdrtDu30Y6nhamgPAjN0ovV5zL5g2YBCYHi+lv4qYa2n8kHsZ9WdpyLsEEII0VnyTxDEI8qsiAZIo5vavbjDaGRCPAgYbffZ3+nzrb3+Hn/yzP2Vv/T4+MO2uYjkeu9sDvvzzT/n6f/hdaNgMxhOmQUgQRUjfYX88ZDWOiOKQVreDY1t89svPmE4nrJ1awW17TEbqCtiGZTPd2CWKlZHWXurQf7jNZDhh7cQSk/0B0TREZi/ebDQcZJyw8WCDtt9gc3ObF9+4yoW3XgAJo819JsMJ+4MxfssnRjnEuqsLBJMpiUwJk5Ret82lt17gxqe3SeMYd6lDurXHYBLgui4X3rxEs+uzd28L0hTPtmi3mzTbPp/+yYeEccxip8Xd+xu0ui1e+M5L3Pn5lyqcrOXjeR69k0s8vHGf4f6Al65eJLZshmHIcH9Majl4qcNos08UxEymAa/99a/jNRv5OtbApQTxlFLNv+Ry9AA6KjjNV0HGR0XZ5RLqDIt8J9XEZDk2mNMuYeidrKWFPqtmnV2j1XT5OhBFH+aC6mohVWNGzEk/j+Z09cCxn6lvtpCnxL9Fsnm8Mce4K83HAXkrCM6gaqP0nBjzN7fY8hX7cymvv44fxIyRorGWBtpK/+j2ZLq8ZBDXtEFjKrM2iRHuVuHPXBfOtlvBsjrdVsaEutzDRqSouZKy4lR4Xrtxmp7ZuGj4LZJE7QI4Qt8cYmehDG7hkc/pKJ05mq/BcZQXN01SnFSdodAHaRVoU9esSk8doNY3BKSpzF66g7qDP7+HvRxCYTvl0BDLzl4EJ9U1a66jXyJVACN904xuvRmGlfdIe31Ms1Hq+DdZYkMNKsr/mAGXGtzHcZzfCqQ9uNpKNtlMh3GpWzesHGSZc6JvX0rTJH9ZXv4WUoobmNTNGw4N36ORXVVnhmGVDvRn4RadTgvf12/cLF6IZs57eeEZvpKZ1VSjWAxDdfZzWTPo0KzZdlTTlsupdziZfag2dJ7Er4D5bK4kqJtBjrDgC8BeD7hzb0XJ4KS441vXoRkm/1NE6OY/CcDMl3sxi77k+MboccnzmFVQjQHX/Z8bMiElqa5HmKpZG1GVOoqO5GUeFI6RphXjTOhy9bosG0WVDs2VXAeGgBigPzfiZkgY81ftZxlklus3x0UW5VSg1WR/yIMv7uK6Lrc+ucnauZO89P3XSZKUn/53f877f/Qep5aWaC90ufPgMS++cQW33WA6mrLTXGIvSuhIwXQyRgKfvfsJL/72a6xePMGtD2+oN2dPJ9y9foe23yCaBHgdn/3tHXa2tomjiDiWnL58Dtf31K1AjkWrrQ6Mb/WHOJZg6ewyX/zx+whgsdNic2uPZBzieA5xnNBb6nH72m3srNOtbps3/4Nv4jYbTHeH/OSf/pAgSTh59gQP7j6i3W5hI/A7PlLK7AIL2NneY299T72wzbbZ3+0jLZvpeMKFq+d44Tsvsnd/h3s37iORjOOUVtMnHE4ZDye0Gi7DnX0Gownf/OvfxErhy/e+oLvYIQkiFteWaC+1kcMAr9GgtdzDjyLsJGY3SUksm4ePNhkOBiydWODqD97A9dXVzPoQZj1H1ayAOTsTuaw/SLyI2o950am+blsnyBFouYXVzd2noXz91hZUFjhV2VObXO9+zxPTNcBPP5PV9OZXA1SWyjki4M+pVs8dgUTl75GLyBpb6msNPx3UjznAfn79qrB5gVFaBxUOn3kYoJJxLlV0TVZ3CY+Zekynm+mz8eUg2a6TVnlECGxtQIhZ3TlDFYYunMfzqGyIHNjCvO4nYc7D6ZmNi3bLz0dDIrMXghQA3QxPmQWA8zjh6GJIHXCzjI5o72/22nhXHQT189fFKwWtb8UpDjGaYN9gdWECNx1yoc8xOLjIGd4SlQ8a3JcE8JxeFt7f2W3Co4yLPkQ/CzWMdgrQuxtHI5U3lTI/R5NmLwrTuz9lz77uiyQP/dDlpIDQd/u7NXX9ZZMyIKvPNBUgOP+WJyl20Sogt/bzQc8qKWq8gaoZhQH6dGQKmXLp+sra2rL1T3p6JXk8rpRSHYw7cgvm1HGknCJvorrZpSw0TQBzoAI6ao16l8bAS7IybvP6U32SK0kARGHwmDlqLZN6zjLbmIQxlmtjKgiZ8edsbLlRSZqSApP+mF/+D3/O40/vcubli2zfWefO+zfoLHVIgff/8D3sVLIk4NrdB0jUjVDRJCTIzhk0HZuOa7PU6zAYTxn0hzz+6gHLa0t8FUXqYLIU7O4NePmFRR7fX0c46uxMs+XjdFrs7Y9o99pMtvsM94a4jkuYpDSnCrBffeUyrudw55NbdNotptNQvY3Zsmi2mwz7IyaTKe12EydJebC9z5vff4szr10EKbn1k8+4e/sRliW4fPEsaZySTKekUjIeTPB7zewl3Wqedh9u4bd9kOD5DaZ7Q1ZOrfDa73yNeBzywb96l92tPboNh0SmtJe7JLHavXSF4M7DTS68fImr332FBx/eYjIJWVxdYOvRFt/5rTexLItbH97EazYYTQL8OGII9BbaLKZAktKwBOvru6QU663kDMhnVeZ8ZWqXg0T8XK+5idMNtW2swCoXFuutuhZKPP0Eep1stVQX9UHA2chcQhs5ZiwKknVlzBPdpvwzn80xTHIgWrVwRM2zp6VK3TX4daZuPQXzZWMx0Xm2GSVE0Y+avh85RCsvbs7u0Vw6HAQ/WQsKg0IA+QUgFNpyprtVeFWh0jqps4TzBIdhhZqfjIYIAVIWxlkRtFEZURNvZo6GGtv54DY8BT2zcWG7RhESsLUQZO6ORelJiXuLvPNohrWkzOwZc9XKygIR6pac0tWW89tVR+ahWS1DRW541KRHR/gJEDqmrk46VfqXMV3dEOgwprkDJMxQs1nJ+aQ7XkULVV5biPy+/APzVcaqUFZaeBn3Uxvg3AzfqGtL0ZMK1Qja4sMhUjwTiAe9YbuWJAZwO9Jm7Uy9T1JX/jFTtjWmRympgBleN+zWilCfP+7z2mEq1/rel9dyEfcpj7D2snM/1T3jw5pWxdGlhj49lZdbuYaSo7a+VSArs2UUqJVQDna04sozHNR+VY7t2pXZZ2ZetBEkJYy3+8goprHYIYkS/vw/+zfs3dumu7LE7qM9rGlAEkZs3t+is9jFwWKp1yawHCaTgIbjEI0CvGaDhaUeO1t7XFrq4fkeZ7ttBrsD7jxcJxkHNJe66swX6n0EnucxHIxx/QYvvXmVcBpy98vb6oYl2yKaRoTTiChQt5g1bIskdUllSnupTRrGyFiSWjHjwQgbdSmHPpPn2RaeZfF4fYe106u8+be+ieXYrH9+lw/+6H1aDY9Op8X12/dVSKzrIqcR0WjKyoUTNJtNXNsisiP6m/ssug6OELRaPnaUkDQ9Hn9+n3vX7rDxYAPfErTbTQZBzOrJFfbX94qbt1yHN/7G1wn2x3z4p7/Ca3qM+iN6Cx1e+NaLPPrsLpv3N+ktddXVtQ2PfpLgyJSm42BJAY5Db2mBKIzrMUnOR4aENXchNQfVsZEpNyuqaYbla2TOPL4X5qcDEG9efQ1IzdMJQ5bNGBkHA81qjL2sPjFkt6haJHmfa/DhQXLSBH5mEw8a+6M8P4TmSUqzr9LESE9Zj+aDksyvlVtzslciWUSFR0q8g6zFLIK60KaibfOopBvLS6T4JIw21WGKaqU1WKxoQ1GIRCB0JElp+0X3v5bBK6Vkn0wDo2i0+a2+jTqqRspS6c/XpCjo2V+iV+OpmFF0GIutCu5LK6ECdszfS5xh/laEy+RJZfVDJQHCGO9Ka2cEq2SGoQzgJOs50ExlfK8vp56yA0bVqTe9qVXELY30M0Jy9nkJzFee6wWWC15jrOtbSx62YRZ6kE/bPK9Rp2SqQSbaAMnbVC3HAKQFCKdURl3DdezwbJ6D8pbbZp4XqNfYlELO8nM0Rk8PWuSzRvFsjhlZW6tl6lr26yAx2waqBsMBuQ9K9iTK/ol6Wj9vB+aQ874YRWlkV9vOOfKjiu5KqNJUzho01CjbvFkSmaQEwwnv/r9/xKPP75BECS9+93W+9j//LvtbA9yGx3QaMhqOWfRdkjBmtL2P53u0PI+TK4s0hMSzHSxh0d/ap/9gm2a3RfRoi8e7fc4ttmksdIk6TRzbYvv+Dudev4DnOOpQdpxw8tQquzt95HjKdDThxIWThEHI7r3H7I/GPLq/wYVvv0Sz7cP2Ln6jwaPdLVpNn2a3xXB9n6XFHnujMTQ8vChVVz4KsJKERttnMJhgCYtv/Z3foLPaY7Sxxy/+2Z8x2h/SaDaYxjHtTos0zq7ijdTZL3UZCQSTKTKKCIZjpnsNwjjCjlJ6LZ+769us33pIEiestZo0fBc8h2g45cuPviJKYpppyvZwzEvffIWzr1/kF//tXzDqjzh5aoXNrT1eevMKzYUWX/3Fp8RJQtN38VyXKErxkQzTlAaCja1dxnFE7+QyyTRi5+4mSZKwfHYFt+HVTrfiNInpvawCuHL6Wdk5Q6JIm7mvssdHcarIA76Vyy8DpkqTMx6vmgszhc5dujVoeq5OEyDMHaB64VlneMgke4mk6xQgXI+fLN71I5DlUJtUv3hVlMejpLZNsHpAN82vJcwja9PUlVGr6TVPyYqB8YRGSq4D9YNSzFy13lmgX6Q7YAWU9HH55+qclUNds3xSlNkr+5+Cg2W8oqep0B41eqSqrkXl95m+GX0x2igrNVVvdJrd0Sw3rm7Fao563mbGMxsXR6E8Xo5ZJiqdu9AAubQLUUoOaA98GcTWga0ZT4tpQcw8m6VqSIGYQWtlTi28slXGf9JJK7hWivI2d6kd2TiInAFlKW+eSBaQfJa3JGmcKMFhV65gq4IdUWwU6m6qRVY3iPWXzKHTl9zpdWTE+GPwSGXdlgRmjSCZq1QrbTZZTpaKEqV5LcLbKrxWq5irPFA2REo8/aQSulKLcSKlvsuiWsezC5KcB56m6fN0w+E/zkjzpx+5cplSy+qnGZonNHBM86DeRJwFhHX2xkHVSinZu7/Flz/+BLfh0mz7fPxnv6LT6zIeT9i/t6l2B9pNhuu7pOmEVEraqwuI/pD9eztc+farxEjsNKY52efFC2e4ff8xaZxw66fXOHP1NOFwwsbDDUS3STOKmTZcpCXob+/jWDaOq8517T7e4cLLF9l65yNcS7Bxf4O97T32d/sI4PTCAo2WR//+FsJz8bIXcw7GU06cXWP18ik+/+H7bG3t0Vnu4TUcBvsj4jSl1fbZXt9hujdi2B9y4aXznH7rEjJN+fyPPuD+7cd4rs3SQpdGp8nO3oD+cIy0bSxg8cwKg619+oMxrWYD1/dJgTSMmUwCtrb2aDQ9kjBiqdkgzt6T1Ou0mcYxXc9jdzhiaXmBYDzFabi89L1XCUZTHt98TLfbYjoc02o3ufqDN9m+vcGXv7hGp92kPxgjpSCeTFk+sYgMI7a2+0zimMvfeYnXf/A2tz+8wR//V39MHEWcvnSS3/yPf4fTL50vuMvUqxoI5bpyHoMUH2di3mdwUQnlzqIWqumN9lTSVLFztYT8eakgreGkoTqM3EZ7Z502RwDlta3VmveIgwgI20LYVt6HfE8+A+TVq0Nz0hEBMwB0FtXk9VZhkiinM8N68qem861KGn9RwWW6Gq2L9bjMyP4nEZxy9usMs2YNqj1kU9P+Q2W3PDydTlJ3DW+NYZEnqSYX5UQmQjMxG8zDDnkhM0+qq+lIRn4Jd5dx9fM1KQp6tutWID+PYAJevRtQvRUm74nxbJ53Vd+UUrtxUKFZoFgcxJRCl/XkEKSKV2fDvOYL5OL3I05dXV6TD0T1n3FHssjqzjwfMmfcw4SiGuObP/0po90d43FhQpQEqyx+z8c0M1ykLA6E13ap1L357Zo3V9Xnxa1Wqrhq0Fk5b3XuyuVo7VwOJ9OfTaV0MA/lN/xQDGPxr36Lt6CqVin/K9ZSHV+V50saT2brqOPJbPQOY9c5v82e8TmIjmoRHGHdPMHyOkpZz+a5qSzUfAtaFOtmpnxp/DPLUJ+LM0taEBZwZ6YcU3amku27G9z4i0/4k//L73P33WtEo4DVF87QW1mkP5nk11K7foMTF9cYT6acXFvmzNoy0lbv8dl8sIklYPnUEnvTiPXOElKmuLZFMJ5w+/NbfPaTTxkPRnRtizCK2B9PsJKYpu/T7baYbA+wbAfHsunvDEjihBNry0Rxgi9g3B9x8YXznLpwmkEcsbC2yCc//ojHdx+z0Goy2R9gOzaXX7tEMArY3RsyiWN8z2HQHysZLyUrJ5bwGy5kVypfePsKtueyfeMxN375FZ7n4DYcWt0OnaUew70+Z8+cBCS+79FbW2T//hYCdY4wTVO87IrmVEriNGUcRghhMYlidkZjPr//kIePNrm/sU0/mHLm/CmiNGU8nvBb/+AHnP/GFR59eJud9W0822IUxlx84zKdEwt8+ePPmE4Cep02o+GUldOrSEuQhhH97T381QW++/d/C0dY/Ol/+UN+9q/eZTIO1AsE1wf8+//7v2Lrznqxbk2+yOTZoewsyrqyNoG5KrQ4rADKslQ5CChVZauoFpUnmQWtunRDJur/myC7IldEzadCUorK06KGokCzaP0f+beD6zRKEeTyW4uGoitl2Wv2sDq6ukJRKny20vxmrhkQPF+/ljCnqPTajErI9X6lXlFTYQ0Vt+CZeVV9s217UplcDGIVtOtzpubjWaNaM+ABVcgKL+T/qzFIqHlkDCXMMfQqLVfp6uZJMVP19sXy0BacXpouUcNfz1GnPrNxIcvDrJ4dxGOyNLMcqSeiAGnlzPUg62h0iEQwH4qD0tS16Skoa07p5UJ5E0VJKJjAOgcWpTGXM3+kLB7o2dKeoRe+9106K6sGwBRVvFLuXt7NQtAdeutIHdUJxPyzSjBroBZ5Rc1LXmYNifqKtZCxrLKKEUIagrXc1LzYw3Yp5vJ/BhCNPlWTzSqxw2n2LE/2KeeTJ5wYUe5ifkOZLir7p7tpiWfg+6ck03B7rvSkQyUqHw4biqoMk+UMxVKeL0QrkK+k89Mk5fZ713jnn/wb7v7JJ7Qcj6V2k7sf3Sachvz2P/w9Ou0mnuvwwjdeJgkizr52AYkgIaXVarC5uateUDcc8/irh7zxg6+xs7uPlIJH6zucPLnG8vIiaRzTQnLad7m0tozXbBEEAePhiDSJSWLJx+9+gutYLLQaardkc4+Tp1ZJpboJLYlTSFNOXz3LhSvnuPaLa2w82KTV8FjotBgGES2/QWupw3irz2g0ZnWxA1IyHIw4e/E0i2dXeHD9Ps3FLlOgt9DhzBuXSMKIaz/6kOHugMXVBVJhE00D2r1W9jLCGMd2aC12cJoe6zcekaQp00lAGKrQKRmnuK6LhSRKYlzfo9Fu8r3f+w5LCz12gwndc8u8/TvfIAoigtGEV7/3Oi/94C0e/Oo27/3bn2OlkmAS4Houl7/9Ehtf3OfOJzfptX2m04ALV89z7+Z9es0GQRjjtlt84+98l3tf3OXLdz7j4a3HSASObeN5DSZJStfz+fm/+HN1dbDBPTlAFgYQf4qlqeWoGbo6jxdNvlX/r+7DmhDf/HwAf2unpe6FCchnGlttu6yVfWUcXqyy8u+FTitHps9rZ/nHwkAp93nWjDGBXbkDpklj6gJ5kFQ4GNceSnXn2+rlqyjE1vOi51XWXAOlTKYtMDuedRq5KHemaAOjPXFHqgbbAekOcuDNGBja+JMmR5M7PnWe0tEEQ1Q8r+l4DmFR2eIwramnFGg168ywt2bFgB4NHeeuo230DVX18M0sTmcoJyvH6xUhQL9+qr5xUpg/5QhXN790KNcYopkt7PxzZTSz3y3byTPnIVZC5MJMgPHOulkhBBg7ALq5RXkz2WZ6XWfJlI0E8x0QebkVL4QurchT5K2nWVCeb8VLIN+Bg9IAzytNmEacKD036zF3XFTXRc6Gh1K56CcjY9nMzA/lZWHKzJnY2sqwPZkye7aFpKeivIlYfTC/1iq2r7egDy+nAG2m4DPaMSM0iud6qZSmUmbgQRb8OptGIo3wNv1/gTIq9h5u89WPPuDOe18ihE3qpbi+RxAEuInkz/7zP+Rv/Z/+Hv/g//yPGDzc4eSr54nDiGl/jOPZWJbNYBIQJymrvS7BcMyXP/mU3/nf/E1imbK33yeNE06cXGJna48olTza6SOXF+imkvZCB5k2GMUxCwtdbn5ynSRJsB0X4hTbErTaTYIwxHZsWp7DKLD47KMvWX6wwZmza7zwwkV2t3bZ3tonSlPCKOHyqxcI+xPWrz8kDiNouGxs7NJpeLzxH3yTvXub7Oz0afaaTEdTvv/3fwt/qcONH37ArQ++wmm4RI6F7dlMxhOa3Ranzp0k7g8Iooillk84mrL7eIeGaxNGMatry5y8dJrde5v4jQY0XBrCwhcW+/sDvIUm3/v7v43lWDCJ+PLdz5BhTLvb4pt/7zfZvbPJR//uF4yHY9aWujze2uPFt67S8F0++B9+oi6QCGMiz2F3aw/PEoxHUwLgN/4Xv8m1dz/lzoc3GAYhQljYQMf3aXbbTMdT7KZPEqds391g7YXTIARp9jZ4q+yaPZxMXVjJV81eWna5ISHK8nJexTPLoRzQWzZPDqi4rlwjk1KTpiBH6Yo63ZWvxXLd0ngqMgU4m3+2Uc8ing8mQ6/NPqqnp4RhZUFfxXb1z5+EZl9PUP7t6AVRgYK1Uv4IVGM0lPpnGKEZBjtq84rPNcabwWk5GHjKGZtZp1lR5hvD0bXOrHMDx5UePeUEZ/TMOxdzwfthdCDe028JFgZC1LVV6pPlv/PCX+oEW0ka1azYpw2nOjKJmn9zZkRbmpIM6Is8mrNoe6kfxffS1rcgd5ZqD30ShcTTaZG+rp3ky8BoU/Hb7EvsdB4DmFb/FYmMPtYzhmnwPdmLXo6WtuSlmTPlpug6GpStlK9/Ndd2rYH0REWXnpXmyFg+uf+rBu8eSHVjoos5xCB8sorqqTo2xRgWnr8qjk/TlCAI0I/N6KQ63nmS4TekQ70ny0w4T4Gaf4U5wMV5sqJvNQMgRTHPEsZ7Qz78l+/yp//X3+fR+zdYW1rEbrfoByG7u31ubewyDELSwZR3/9mf4bUbnPvGFRzf5e4nN7n1iy/pLi0gkIwmU2zX5vLbVzh98RSdls/GjYdc+dbL2LZFkMQ8erzFyQsnOXP+FJ7n8mh3n/v9IbGERrNJb2mR/mDMxZcv8Y3f+gYvvniRKE5wHYf+cML9e+sstn12+iMsJGdXl5kMRlz77CZJkvDiN16i02kSjsY4tmA0HHPvq3tsPXhMr9vCangEYcS5Vy7QO7PC/Y9uYDVsZJyw0Gtz5s1L3PrJ5/zij37JOIxoLnYRYUTT89jdGzDeGZDEMaGwiOOEVq/N48/u0t8f0m01afgNTp05wY1Pb3Ln7gMWF9qQSoJpyOPtXVqtJr/6w58T74yIdsZ88dPPmE4Dtvb2eetvfZvh431++f95h/u3H9FuePSHYxqdJpe/cZVP/uAXPLj9gMVmg0EUc+HKeaaTKb7rIB2H7/zN77B9f5Mv3vuCQRBiWRatlk+n0+bExdOsXjxFa6HD/s4+Lb/FR3/wHoOtPkD2sk1DgRwVa+lFMpeVC0GvVbIOwy2BrhkFdBTK3xlcrlMY8sr4V97o0/kKpaXBr8huDyvJdEk5XCgDXtVQk6qJ8+uEAGarZ59Vn1fCWKrYwUiT6+ODqpurSzLZk4deH1HvSq1HD/a0q3oM5VQtJJet8/OL6hhQYI3ZmzmreQv+Pbgv5fBvEyQcxuXCGMdCEdfPaV5h6S+HjuGB9raJ44ydjZKzt6o4Z1r1pGu5TM/nQHe1l08CWnQnS3nqAEAd6jWSarBthtbML+4AMsGe5MD9v3k/ydKfuWB9brFVpjcFhyj/kPNHRTjWgr+SAC4+JeMJbrer8tXO3Zylqq+7yOsXRv2ikqy4gapqoM/ERuqdqBKLG2almT8r73nJ/6rvQMydxCrNMHFNPrPTGpgaLwiiejRLzoxlXdkCURxAOwjslrLOWU9zq9FzwoH56hVQzXoWuW4/kOr1S8HIdYfZwjDk0aNHXL58eaaOksI6ZMh0XHHtDRz6w6FjWGWgisPDeEeIGuFiZ2JeefrXNE4Ih1Mme0P2b6/T7nTojh5h704RXpfRZELTsnEti2mc0O40Wb+7zr1f3eTKd1/hvX/+p9x+/yss22Y4ntI6s4ZAMB6M+fLDL3nhjSv0t/Z579/8lDNXzuI5LpZlsf5oE7fhcu7CaXzPJYoT1h9vsT8Y0m21cDyXJEoY7PY5cXqZzYcbWI6g47psPVjHE+C0mljNBu3FLg9vPWS51WAYxDy6t87K+TU6vQ7pdkSn2WD38SaeY7PQahA5Dju7A06cXuatv/dX2Ln5iLs3HtBa6BLHMeffuMx4b8R7//IdoknA0soiJAlMQgLPRToWk2mAZQmCScDS8gInL53izq9uIqTEdx3GQcTDW/chSjixusw0iRkOxpxcW8GxLXamU1ZWFgi3B+z3+5x5+Ty95S7Ll07iui6/+tc/4/rnt+i2mgzHE6Rl8eLrL7B54xG3P7tFu+WzOw04f+EMwhYQxUTA4tk1pv0JX7zzKa5tM4kiHMeh22qxeHaVF752hc/f+ZTRcMzKYhdGU2IpefjVfV5e7Rm7WiavHX2dl/jS+DA3u6zlauYtDFn+3xy5Jsq6SxqrQ5C9QLDQM9WqZKbE8hhzUW+8qKyytDxz+asWvX5sNq1SwGzvn/Tc1mEllL5VEpvpSmM7BzQXNxnOucoVc2RFaegLh0f9geYnpycHzfMuUylIWxnzx8BMN0djg6w6jjSTlSfAxOYHYT0DCZUeFJeHVHdyTAMjS1vTnbmjIOb2rLBzoKR76sp8NtPieexcPDWTVaLKj9ITc37nJZljtZqGY8kaz/8z0pgVHiRZq/xQkWFHaG6lxDkW9yFOgGraw/GOaplEQpoyvPeA7O1RT9BaRQKRvek0E0tSqlVjjjcYcfuC0vZ53thyJ5UAk+WFbiaZAcvZX22hP+E5AFH5q+so27yFR2huyeaPotKuvOFl7fAsO2RSSqIoJNF36x8gLuoEn1YcOiSnngwwn/fpSXeQqu3mqWWH6VGa4QvA930uX7781G3T2lOmkiQI56fTMjz3aumHdQkxGF6vF/XXhDFlSFNWSyZNBxN+9t/8iH/3n/43DG+s89r3v8bCQo9BajGJEvw4YtnzSKKYluch05SV0ydIpWT34Q6//B/fIRUQTkLWN7aZTKZsb+6QJAlX37zK5sNNvvrF5+xs7BJNI7Zvr+NagobnYgmLZtOnvdzFsiwGewOm04AoCNU7MKQkRTIejIkmEeMgZL8/ZJqktHtt7KaP6zeIgojpYIwFhFhYtoWIIj5/50MGm1tYAnWNreciPJfYstnd3ieVku/9x7+DJeD9f/FjbM+j4ToIYDQYc/tnXzCdhLieSzAcM+6PWDp3EiGh4XnElqC10KG93MNp+3z8k094cPsRJ5a6RFGI79lYts0EyaPtPcJxwMrqIhffeAG/2aBhW3RXenz56XUe3d/EmyS0sJjujPjJf/0jPv/4S9p+g7VuC891aXsee3cececXn7N0YolTL13kO3/jN2gtdfjw3Y/oNtRbwaejKV9+eJ0Tq4u4tk0Sx/i+x4vfe40r33qR67/8kof3HtNoenR6bSzLoul6TO/tcPeTWwYPMsM/T0SS7CrOio6WlX/Zw3rwri+3KB98Le4QrDNLtIQ06810VbaTkeoyS16wqj4RlTJ0STWhTSUXrymXzZsfTQQpK5+LfZ0Zr3BFFxykOERN64pWSbO6cvszI+BAJ0ze4DnK02xfKb2Z9QDAOqdqM4D7iFlqSUp1+UQ10UxzSyGp+nH9Dli5v2YGU5bXt2yehK8+L57NyaHZJcNFpcPkpfqfRlEW4KvYacTARaLAZnPa/6z067mKVuPU0tkFDTz1+jdAWhbQL83FrYFDHm5TLj83Juc3YW4CWfPpoEe1ZVSN40PWnrllV1RUXfxZQfPlbomq0ddz22HwrDmWAsCyWHrz1aKsmT6UAU698CunFmaFlfoVYtfzXaSpWv6zXvw5dET71Lz+dVaEy/z5zM1jHMpq89uU8W/5J704yEPVDjs0Ob8eSRzFBGEEUuI3GtiOXeIfiRFiWGlJmkosYVUfl0jHx5aOEzyDUfH/E5QtEmGB0/COlBYwxk6UGEZUfirRgVMuIZXGeScYbveZDKdsfnWfmz+9xkqnw86tTdbvfkIUpSy5DkIm7EiB67q0EURxwng8obPUorne5MavrjPZG9BZ6tBZXWB4f8qZMycZ7A+wgCvffBFLSr766CuunlpFZPU+3tghCEKkEDy+95jFlR797X02d/ZoNRtMwwgxmRI6Dp7jkIQR2IKF5R4IaPe62JbN9mAP23Wxk4TB9h5BGNIfjlhc7LF4cpHN9R26vkecpERpiuM6bO30GY8mKmzqrausXDrJO//k3/D44RYrJxYJ0wSn3WR9YxsnSvEdmyRKCOOIk5fPcOLUClvrO5BK0iimt9Dlwc2HLCwv4MQpZ1eXGE4DJmGClwqclsfFSye4f/M+qYCr33yFe1/eZX19i3OXzrJ9b5PxNOClV6/SO7lE+9wJ/v1/+YesP97k8uXzXGg26A+HLLU99vpDYhv8dpOo4dLudfAX2kzGY0SSsj0YcXJ5URk2CLyGRwpIITh35Rytbouf/6ufMhqO8Rouy+0mURDRsC1GkzE7n94hvHaLpVPL9E4sUrxDx5BcT7tkTeFXw7vzdpcLO7usiUtnGWogjblWSnJXZnLHEkYpGPJVGxizV6DP200QlU9aP+WQWMpSXr2rMW9n0dwJqQ1nLFdaW8JsotrRmCFBvVye5/kWMP/l0bIYC3PmNOY5BOoccn6w3I95QH0GwswJyypcdnPA0iEqVUHNsv4tZzHnpOAQE53McLCofK98roN3GvOq5wYHy/JvB+7IiLqPxfqvzWkMdn6G9zmp92c3Lg7ltOpnUeIv9dEIt5jhETmTxyx3ZvEfpU1HWugH07wbjGbqyJ7XLYvSx+pbfPPnRtIarlQLudLhKrjMHta1QZpbyDO/FkK3tv1ZtSYjlzxK88a3buhMA1SWx/dpwGxlNz0v++DFIw/nnSduR/mkSnFgPvutJDRnKz6o5+oguMCyLGSaFvw/p/2liwpkcYZHq/jabFrgSfPR7B3oT0zPeZwPqyt/j92T1PmkfZwzjXLmg/pSugMhG4+c/y2R2+FSSvYebHPjnU8ZPtjFXWpz7pUL+I7LcsNmOBjTPb/K5pcPkcJisrjC7Rt3SVKJJQSxTImikDvXbnPxlcs8uvGAxZOr7G7ush+EOI7DwpkVRuMJjuvQWu2pF4FZAq/l409DwobL5VPn6G/u83hnj/29AZ++95k6E9D0WVvuEQUhVpqy4Nikp1b58vod1m885JXvvKaux320jd/yORmdZLQ35OHdx0yDiJOnTrBwYpHVcyfYubvB+qMtHAmu55CkKcPRlGazyetvvcQkjnnld9/m3k+/4Nant1laWsC2LKZhQjyNcBybME544cXz3Lv9EJlYnL10hv2tPaIgJJyG+I7D7U9v4lgWMkkI4ojd9QHLy4tcfuMq9768SxSEPL77kIQU2/X48uPrjPdH+H4D27bZ2dpl5cwaraUuH733KX/1lbMI4PKJFa50WzTGY6YIhsLCaXaYyhRSyf6DDbbub/Ba/CpXf+s1Hly7x+N7GzzY3GGp22a520IEIU3XQVgWj++us35ng0kwZW2px/LKIlGc8PjxFnt7fQSC3mKXtfOr3PzwBm//9W+WGa/uxS2HeEs0dCqAvSzWwozuLPRHWeXV60dT05Qu56jmnVFpZWOhyGsUXvpkwuMa0M1s3VXoJyrpTSA7FyaK2fry9E8pM+u1s/G7KHZqirRViKx/KZ5XSzy69jHAtahJKY05rI6FzFpTCt2pfi7042G6RqexLEFde2cPL1PDO0W7j6ogqudPZ/CoqDGQqnyuFbABcct4qq6Rc0jU1VBq8IE6t4SdnxP9enYu9ACVmL5iec4YGMW8ahB4NGx6JP/2bAEVwZWLovk4b9Z4MATJTCtqLYWiav22ztzKNwfArKOuEdW0dQtClj/Wj+UBBk2luqIHusoyUM+FxrxZ0wCvVBHZoqrr6Hyhku+AVRVebWLytPqA32xIpjHpNVNw2CFz8jT16LXOE2LGc9Y6Jcz5E+rBrBIG27HRvnXLPmqUoxoAUZ3Zmjjc3BCirNTNNjyNjfDEYL/KPxqM6wZoZVXPSgWUELJU56/NxqnRm2maggDLspRxV6fOjX5oZXPnZ9f4+L//C8IgwfI9lhwbu+EiLItkGhGu75Lue6RS8mgS0XRTsCwWmg1abZ+tnT1c4XHi7Bq9tUXufXiD7TRhmiQsLXQYTwMG2wP1Ar3lHpZjkU4CfNdlEoQ8uH4faQn2dvoMhyNimeLZDmkYqfMVScLe/pCTK4uqb0nC48ebpEmC3XCxhGD90SZb9zdBqHJs1JS9+taLLJ9fw3Ysbn3wFTe/usNiu4lrq6tXR6MJbc9lY39Af6fP+a9dwW04fPrvfkEQx5zqNtnfHbB6Ypn+YESUxFw4f4pgEjAeTThx4TSe73L7i9tEYcSp02tMByMmwzErC13WN/fwPIeXvv4SV//K68ggZrixx+7OPkJIfMdlMA4YjiY0hGBhZZEHdx9y+sp5zpxZ48an19nb3SccTUFCFMfsbe1iuw7YNvv7I85ePY/VanDzo+tcPLHK9YfrbN15zNnXzvNb/+j3eHztPvc/vs3Gwy22+mOWXcGJXodWp8V4GuDZ0G04WGnKeDjh9v11eos9Xnr1CpP9EZNxgOM4nDyzhkxS9RK3KigzlcBhAELLAVGsG11GFS/W7RDo0Njyd1So1YGL5ZDGGXK7tG5/DYs4B37593I76sIW5vevknd+rTXJq8bPPMOouN0RvdNsZFSQQVaelTsljN8Owj+mvq596eicYThK6G9d3w6jQ0OgZ+wAYyRNz48enzqccgCKMtNKUS7/QEPBrExW+KmaUcw0rKbc2TZqXCvqrJ1SERUwfkB1R6XnY1zUNKY4GHVIniJDztP1V7CWH5nFFIdDjYQV3DnD/6aUzMB6vjDnro66R0cwCGb6Ko0Y/Eqjqsinpqiq3Z0L8fxH0/ydiTKtjEnxpCSsq03GMCZMcG4uzgNo7o7BTLY56YyEUgtyoQBb3TmbHBA/d+RYNijKIQjPVFyNYCt/Nb1neRsQOK5TFoxzmnPgQa9DSCunmkILZfYEReu5qbZorqeqajfI6t8jVC7lQcNzdDoIC1XXgyzWTMn4M+WPNN5Gnws0STwJufXnH7P+/g2SGNYun2bj3ibhKAAh6I8n4LjEgDUYM5oGCEsgJxOiMCR2bK68/SIvd3xAcOU3XubLP/+EKIqwfI+11UUe3LhHp9Ni+/EWnu+xcfsRo50BnfOr3L71gL2NXRIpOXXxNN1em52H20wmAeEkIE4SApkSTAP2hyPiOObEqVU2BxPCKOGVKxc5eeUMTrvBzY9vsLfXZ3V5kaVuiyiKSIVFMAm4/v4XhOOAnZ09VnptOr5P6tiM05TQsmgIgSsEt27dx++08BwL4Tq0Ok3SJGU8mbL2wil2f3mNNE7Y3e2zNxjRbDW59OJ5tq8/JI1jVk8ss3piiQd3H9Fd6LA9GHFqdYkXvvMKKy+fxXZsrv35L7h//zELLR+ERWwJXn/7JT7/6Ct8z2FnYxvPsdlZ32FvfRtXQtNxEELQaLjE0ylhKtkPYmxL4DsW2+vbnLx4mnAyxR+PONXyefhok/5/+6f0lhe48MYlzr92iSRK2H68id1oMrYFVpLS8xwsy8IVHsQx24MhfrvJN37vmzy89YBTJ06z/3CPnfU9/uy/+RPe/Gtv8epvv4Wl3xJdNXIFucwqyRNT5Urzrxb4RhE1ILqk6mvB5myeunMXObicB9TzigxJWLuYtXYrzl7MC5WqBbSy9Cdvz/zdYZE/nu1+BYwcQLkmltTLwdo8Rfq6CyvUzzWKpbb4zFCqynORN+twjD2XqpK3ikzMxtU8rivxCXaDZpxKNYZFWY3MQ4/zGmOwujQeHMUuyQwRzfam66no4uHtqMMIT0zPCTM9s3FRF5NYTaF/yxdo5hkpeb6r2WTN5wPmWjDnBoQ89qBAxcXFOrLEZML4/8F0ALccaPWJMnauyPWZhVvqryg9KrkMDpCyddhHGp6NWqB1EHg6/IdSMWLOt3kZ8rGonNcxR8kU1jNnBqotrKvygD5VT3ocJruex/mD4oV69ataIAvgWUcZ4yjh9BSSQYNuUc+21Z2emfjd7IEQs56fgzYUKklLZf06qSpaDjU2zESC2TVa1ZGytHAhranEHCit/A1BMNoZ8OF/9xeInQmTccREppx4+Sx3bzwkXd8lmoZEUcQkkfQWOqxcXOPj9z4HS+C3fdrtJqkUJKnkte+/DkIw3OqzfusRKUrwX/7mVXYfb7G4tszq+TU2764zXN/h+juf8hv/8HdxfY+tW+s0mw1e+MZLrFw9TRzFSAmT7QHbt9cJR1PG2wO2NnfY6w/YiRKSKCJOYh6sbzEOI160HNZOrbC31ydOU5I4IQ0jhOPw8KvbSCHUAeiFDlMp2Q9CdjYGRGHI5UvneHD/Ma2mjy0Et67dZn9rj0kYsdDrsN8fsrjQoXtqmUa3yXB9Gz9u4DiOerP2aEoUxlgIJqMJ17+4heu6xK6FEBanL5/m0m+/jhCCW3/6Edc+uQ5pAlIyHAW8+d03eHjrEUkU4S90sGwb13W4de8xy50WwyDgwqVzkKJewJem7EUxjVOrbN7fwE0TvCjh9he36bab7E4myESy1nCI0oTBxja/+vfbtFs+TpKw2nDoANMwYhBEjMOYaRjScl3OrCySjMc0Wj5xFPPRTz6k02wjHJuTy12cKOFH//Uf4zY9rn77ZSzbyUSDAZ613s35Tn1QsrJu7cnZTzULRj2qAelax9aUXM5tyvwDE88C/0PLLtc+E9Z0BHVeAowzY1ITWpyXabTSAOyittKqxpy5/D37/6wAynd0jAZXd2kPphrjT5itF+X51UOXhzHXl1UDYQ4Ev+YoispgPs2uhtmI8qiVjbD5h+KL+uvbqj6I6gQIyob9UajicH5SVV53TtUcT437jt6gZ6NnNi7m9X/WcDDAsSw+z4Q6VMquN9oMTX8IeMm3gwT5xNfZLTNF132uNLRsWOlfyrGIs83XK7HOEKiwRmk1VM8LlCs4dAfFHDIx2+45jTUeZX2uvmFdFr9Xr0PVCqc4ZFduazksp1Zb1TbuyPhTFmA7b/9heUXWl7mSZl7D5izsXAhXUtcs8uoOSJUXcgUuDy67SoVQmUM5W+kPZcGr68jnr2pB6GKEYeCUkEh9emXoy0qP/3IEX96EJ0lU1elk/D3jZTUFn7EmzHNFFENdVXST/RE//qc/ZPPmY86fWmOnPyKMYxqLbcbjCSLxePD5PS6+cZnP3/2EaRjQOrvCy997ne17m+xt7bN2YoXdvQGu55FK+OD3f8rm9QekSUowDZmMp8STiN/4238F27aJwojPf/YJy60W97+4S+P33+Xqb77GhbdfZLy5TzSa8NG//AndpR6Xv/8mK9+6iohTtXN4FRbvbfLRux8xCUJc2+L0Yo+HO/u4DRfbtbny2mU6vTb7/TGe59Drtlm/+whbpmA7BFLS7rY5v7pEHEe0tpp4nsfrv/cNVj+6SbA75Padh7SbPqNgSsOxiKWk6XlcfesFeqeW+Nbf+i7TKGT9ywfc++w2nROL7O3s8+DhOnbbJ0pSFUqGxE4lkYA4Sdm/vcH6Bze4d/0BAN2WT38ScP7CafYe7/L44QYrvQ6T8ZQoTkimEUtNH8+2cZZ7nH7tAruPtjh9/jRf7faZTEMunVql4Tjc+eoOjabD+U6TveEYD4tQpoRBhJABbsOj0WzgxhHLu4/od1cY2DbDSUBrdYlTSwt8+sHnxEhkHLOzO+DMxQ6nXz7LybUVbByCJCKOYzb7I5ZWVgj6Ux5+fp/Tr5xTFzzk7tCyX9P0jua6eN6CyPi3Kh7q0xlfZfGDqRdzICRNYFZZP1Xla+gw0xYvPa+h6t59CbNm+Q86T2HilEIGHmIIGY2TOXotAPv85h4IZg6z0qqVG19FFu2mO3IQWK+T2cWOshJrVYOtSC5MJilc8ZVxLeWseV5Dpsw9RJGXLiGZiRKpH+PZ4Z3HWLKQ5znviNlkT6JcTOU6sx4OIWOoDzS8/hINC3guOxcZ6fkSZSBipqnDu3P7KqqLvPybKlCCFAffkmZiYUO6SYNpyphhTuMrj6rYST+TcxtjIBTdjpmy61njKApgxmqtK2hG5pQFqqz0JV9DNS3KGdkc39kljEWxo1RVbfqPMBZHXpY0fnhaMqei0onywbJqJmaf11l9JcaZbWvxpGoQydL/D1vueZhC3W+H5J3XvHon5cGlHV6XwS0Za9QZacVaqZUIR6a6lXb4XeizdGQuMxeDAZLmFjQj+GTpsf4ipHrD9vbtdRbPrHDzJ5/y4MsHSCBNEtoNl/WtbYa7AzonetiDgJvvfMobf/0bnDi/xmh7wL1rd2l2W7z6W2+xfusRdz65iYPko3c+ondmiYbvsr2ziyUsuq0m2Bbj3RE//4N38BsNTl46zdq5UyT7Q+wQfvnDnzPY2OPV77/FjZ98zJcffcX+aMy5i2dpLvSQUhKMpnz2zsd4zQZ7W3s4tmAaBjT9Bk3PY2FxgfMvnscWgtFgzHQaMtwf4noug+19mhJCYbEzHOG7LtOtXabDCUmaIJFc/vpLWK7Dha9dJdjps31/g9FkSm+xQxTHCMdhOh7yiz/7gN8+vUyz5fP5n/+K0e6IpXOrrF0+ze1ffIltWTi2TX844dXXrjIZjHn8eJM4TujvDrj5Jx/x8PZD9sYTFttNtnb3OX/uNO1um49/9QWubdEfjuieWKKRwu7OPu2mTxBH9JZ7/OwPf4rt2Fy8clEZL1Ly6P46L333ddJUcvfmXdrZTkncatJJJY47ZX8aEEQRyJSRBE9a2NMxQywCKXjtzRfob+0jpKThZmdskpjR3pDhxj6X37jC3sNdHq1vMgpiLMtm+eQSp186x7/9J/+Sr/3O13nz975RODJycFsFV5mZcRAuMcCoKcVN8VobiVADeEqXxIpCL9QevE5Vu2YMkGzxlwCy2aca4WC+5wGqThCdrU4fyNLSL5dfvEejLoqjzo+Yyz9mQ1jKKqsyyrWCqgqAjTbIahpK83EkuVequmQ9zKarAXTPZyO60MlHPWErdJugGIiZM5qysPQOqVsVU+iWUqiSoNrtetJjpP9Wp+4Z6bBinjlc6gnpObyhW5E5X/VdkJTf+EgpYRVoHIhzKgwh9CKuFmoAAFHhAJEBvnpoWU8zWKH6pYLtzRpl1eKaKWgOSUqvjTiIRO1/VD7X9VkUjC6zsS9kkdGf8rdyilKB+Zoz21Wqb07ri69H7PQhNE9pCVNhaZonaKRWBVotFgN16Dsq8uRF2nwLVhrCTRZfs4YfKJh19uo8HZXythgFPqMpl/Wr0EbzhuVZ6zmIxGEDV5vnGRNW+Sa3zOvCErQyKhSdlHD755/z4//8h4y2Bzz+8iFRkjCZBEQbj3HimK7j8Pm7n3H2pXNEYUiDlM9+8glf+xvfZuXMCtPplP7WLu//wU859+oFLrz5AsK2cW2LX/3he3SXutiWxenlRVq9Nm7D5d5nt1jqdui1m+zdXWe6vU8chkRByKVL5zh9Zo17733Jra/usdDtcvX8WabjgLuf3ebP/l9/xCc/+YjxaMJwe4+Wa7O2ssSC36TbaHDSdWg3XD55/3N+8Rcf8Oc/fIcPfvExuzt7MA1oWRaJDQmSxZbPYsPDEQLLsXCaDYTncvfzW/zxf/Fvef8P3iUNE1ZOrRInCZZlkcQpIpW0VhawPIeta/cYD0bsP97FcmxOXTnLw49vEycpwrXZ3x2w2GnT8Fz2dvdxbYum63Dj2i0+//wGkyii7buMpwELiwucffE8mxvbOALSJObCC+e5+voLBEHI2toytm0RxjH9B1u0Wy082+He9bu0HZuFTotHdx8T9Ce02z6plAxHE5I0ZTCaqL67FpElwHFwsZAI+s0egd1gHCdoebP7eJs4VX0N0pRLp0+yvbnNw0/v8MJbV3F8D9uyaHoew+GI29fvsbe+y/f+3m+ze3+baBzOsGWx06ZB2zzmLgRwjtOMlHKG8esWRh1l9SLmJCugbDAKSKK4eFwD1Mu76XPaJCBNE8bjKePJBCnTGb1Q39qq4WNoVFF+Vt9NkV8mosDx/FEpLhsRFd1UX35h1BxMIhPus76Pol+HvlH7CCR0XQe0eV6uo9dRr89NKhmveUbNa9JMOHuu5MC6KTBj9qXAnbOYr7aAqjExA8aeAvDklR7F9Pp1at8y/drCoko0V3gZSSqDOm/bqwTwa+XhrPSZ8TvUAbJczom5qGj2aVZuzUHRmYUstOWrhXX9wRstVmd+EzOJ6n+vHTbdzmL0DjeijJVQJzdL1qTZ8zltxjQqjB0DjUVnvEjzFE+ZysqOfO5mt9prMuhHeZiKqBnnZ1+MhedwtqzaeXiGg9dPTPKovqD5NK+1pXmppDQPHz5tb2vzHGQA1KR96r7PA0S5YVE8ri4VlSTNnw029/jqzz/D77SZ9ses314niCKklGwFCT5ThG3TX99jYbHHOE5IBNgEvPdvf8pv/y9/h/d+/x3u337AgrD48Ee/5Af/+PdYv/uYaGfAZC/k4c2HNNsthtMp/b0QKSW+79KwbCIJotEgReIALcdiY32TOE2JkoSW18BuekwmAZ12k529Po1eE8t3cKIIESd04xQ/TomAvWnAaq/LYpISxDGWbXF2ZQkXOHPyBOMwYH2vj+U5JEmCYzvEro1MLPqjMe1emySISDwXmYLnNQgnIXt7fVzbZjwYc+H8aR482EA4Nq3FLtev3eXujYd0Ox1WLp9kvLXH9sNNpGOzutDj/Ksn6Sx0eXzrIVvbeyyfWkGGEe1OE0uqG7zCKCQII06dOUl/p8/m4y0cSzANJX7LJ5hGbG1sEXQ7+L6H1/DotFpMpyGOI7Asm8E0YKXl0PAbxJOAxw821fW4SKaTMUuNBsFon6mwEI5LI03wLYswDJlKCGyLWFq88o1XCftjNu48giTBtQSDwYTNfh8pLB5cf4Dnuuzv9dVB8jDEti0c1yUJE1Yvr7F0ZoW7X9xh5/EOl996gRPnTxphojV68UAmr9MZovTcLK26pqu/FSXU6ZfC+PC7zbqfCl1a9UbLyvesZoE6f5RKSRKnuHaM63lFG5jTjOotPqU+6bJn6TAA/Kxe5Fw11QDW+os3eAphl82Nvu2rWp5RpKj+8MQ0W9I8g23eFcZ1RZVSzNF1qVThnZZlU2CvYk+svjmmlfEE9EzTbszHnDY9G1c9X3p+YVEaOz2P3h0IZrUgMLyCovyLompjqjC0HnyWAVEVHpVXaMGGmcGQ/zxrvRQO3YpQrKGyB39usiNSTVmlFSaRaYqw7dzsKZi4isKfsk0z3oF6cVzTuBmhWI7TNQHdEelwq4p5HZ3HWWaO+kLLBs9MvK5mF7N+XYkgD+c7yAyY98vzNlPq3hUyB2fPMcaLcubmf6IGqf89iZLL5+9p5JWc+VDmv7lejyJtSWakCdd+9BGEKZNpQLAzIgwjoiDkzPIyruviipTd3T6+43Djk5sstHwG04CLr1zkqw+u8dm7n/L23/o20382RFgWWw82ufnel/y1f/w3+OF/9q9hOGH39iMaQD+MuHj5LIPBkL3NPc6+eo7Nh5tcee0Ke9t77DxYp+G5tCybyWSKlBLbsXjp7Rf54uef0XY9Go4gmEQ4DRcrhbbXwBYWoeeSCkiCkK3plNQSdFwXkaYIz2Gx6eMLQeQ1aPe6pDYEqeTspXNc/u4rTIOA6WhKGsXc/eA648GE5ROLvPY7XyPuT0iTlKbvkaaSRtNXayOVnFxexj5hsb23z2g04cLaIvd/+RWtXofJaMJCr41IJbsPt1jf3GF5bYnzL5zj5ic3CCYhjuuw2OuSDCQdT/D48RZhFNJueqRCEEQJtmPT6ba4cO4Mjza2QUCSSE5dXeOzz66zvr3DubUTnDi5yv7OPq7nEAch48GIrt9ASknswnYSsz1NCKOU3soS21vb9JpNmpZFEMU4vkswCemu9Ni5v87e/oC1k6skacrd7R0cx8GxLDY2tlldWyaaBtjAzmCI6zc4efoEH/zRLzPvPOzt7dPrtbn30U3+5v/h79JZ6s6GdOdMWQf0qzKkusIO1mNSr48D1tnM2tW+MEyZWwBKCfkuABTYoN5hV3y3bRvXsXFsS51Fme1cfcMOpCcTIgceZn4Cr7VSo/UYxiwvD/+lOONSO8c1dUsd/y/q5rr6xPCmGOD8cLg7v03zktefdZ01qupvfipXC6rvtm3nxkfeE6mHuKyrxIHNLcZl9kzLE+q80rgcPEBHNyuOku5pgV6Znut7Lmbi/ss/1o5ocajskCu0SsC9zFwGzKxkmv2u6jv4bEPhOZaVH+s9AlWDNpeMB8zRvJ7Oe/58pruuFoGw7OJrIsEWhw9lLtc0YK4p2pyqQxt+0HJTBUmpr90x2l7jjaid3RkDh0zAGGakcbOYwoiyAKEVBlYKDuMcTz3n1yngGUE+09wcgR7A20ejJ8112EuLSjtOTwPMn5aBD8xbPQpf+mn2kUY7z7SYdI2G1JsjI8y3w+tKpZSMtvqEoynT/pie6yDDmA/+zc9Jo5iVXgfbgq7v4gYTLvZajKSg22riddsEm9sE05CG3+DBJ7dZO7vGy995le27G8gdi89//BGdxTY/+Ie/x7//p/8W13GQaUoqJWEQ8NJ3XyNOU068cJrLm0OG/RFrCz4b99YJUslkMqXreSRRRKvhsnV/navfeZX3/ug9us0mdsPFkYJewyNMUr7a3QckJ5YXSRLJ3t4etm2z1PGxE/AdhwfDMf2NbTzHodNq4rg2rrDYXN/G/vAm/d0+48mE8e6ANE5JpOTMS+fwWj7rH95itz/ghYtnWN/c4YvPb5CmKb2Gy9JSlxhY39ljeWkB33GYDMY0Oy2E0+bWnYeEcQxC0PB9BPDVr64hk5TLF8+yfO4Etm1x+6v79Le2sUhxhGAaJog0peE38BoeyTQkSRIajs14OOHypXPcu/OQOAzxHEcZELHaZUjSlLtf3UPGMTGSaZrSavqkiSSIE66+8SJLZ1b46E9/yfp+n3Ory7iWYDwJWTu5yuKZZb76xadEpNieQxInOJZFy/NYWewxHE/Y3tojngSM4pilEyssn1ji9o07DAdjOp020yBgxXOwkpSHdx7z+NYjrix2KDu2jBtk5qyHGrU7V9aZZr4AQz6bOls7iIrnIv9F1GJm06GhZXL1IsGD8IM+BNxoNPLOVCV26TC3IVAO0r3PRx8/X5p9cZwx9ofI9xmqXhVoPp/DM7M3PR7Y2mcaRM1zhweHGaQZOje89OOqnjbTMTOW5udaPU8RBmfyellN1AErU18chhd+HRw4V5s+ET1H4yJHWvXtqoIDM+kB41MyPErKWddZ9arIA8dFH9gui8BSL2Y+ze9E/aMDf5r7YH6jZ4yv58VPZtWa421LzaOcU1ctbj9wwKleMFUH9GvZeeZBtoRLwrMyg4YDRZazlep4HkOYpvLAq3BVMw7mR7NhZjTUjNPlL0mLzbxjpvTjnM9HLrz89YkU3YHJNMg30srST8Xnwws7uJo6i1mYSyYzdKRpEppySa2WOIy5+e7nWJaFDWxt91nptdnY3FZnKlyHzdGIcRTRsG0c30cgeLw/oBEEtJo+9766h2NZtP0Gv/zhe6yeWWVheYHx3Ue0bZtf/Muf8P3/9V/na7/3LT74V+9wermHkJL1B5tEQcxv/K9+wOnXLxCOAoLhlMnOkDRIEJ6F227g+Q127m1w/aefsX7rEedeusDZS2e4fvMeF5rLylARFtKySLIwr4dbO4TTgJPLi7S6baaTKd12k/vr2wRhiIPg8X6f6aOQS6dPcebsGrv7Q67/6kvSNKXR9nEtB6fj0lpoc/LKWSaPd7l37Q7tZoN2w8ve+wCtdou9acD61l52zW1C48QSWw+3wLHZ2RuwfGIZ/1ybyWBEu9tie32HcDim2/B54fUX6J5bZbDdZ2drn+FoRIIkTVIG4ymWbeEKwfLSArZjc/fGfbbWt7Adh5WlRabTKQ7wwplT7O0PiZCM+wOaGaBPgwDbUaFSr33nNRqNBp++8yG253L29Yuc/+YVwsmUT376MQ+2djjdbTOeBgTTAKfhMtwfEicJ4TTEdWzWFntEUczu7h69Xpc0DGg7NmmS4DoOGw/WiYOQRsOl2fQJJhN2J1POXz7Dt77/Bjfev85X71/j+//Rb9NdWaDg1qMviXIAcL1ELWOf2XUp0DcLGpBMr53DfEy1lWQ/G/KkZM9nH8q3sh1cUZF/vtb4yw5COVx3HTIXHBXw54nn15c/1PNo6uQDdF6Noj/IGKntcxVr5684qGSqIzmbpspWEsUeSZJg27bRLs0UVUAzz1w16sj9luX1VnXImyN+8I2Vz4/mcfez0nM40F1mrPoYyoxq3R0K2c7Logc7x7+lWmVeu9kKkbWjfAiL4qnM/h0wnJXlUjydZ3PU9O152wBP8+vRy64oDWMAcgOw1rAwv8jyWAhdlMz/Ufo3p5w5rZw96HYwzfBGLiMKzZOXWbllQPNQlih7UHCWbs9zmWRtUNQMQrLbZ/AX7xc/zuG1Ulk1vx/l7agzVF5Qz52eyzst8nmpeW7+nclzSLlaw5j/yA7vz/wrpy0OtRf5SsoslXz6r3/GrZ9+wfKZVZbPrjCeBOzv9ul12rR7bSzHYXl5kcUza0yThEEY8+K3X+Xt3/0WTsMnDSNanstwOiVG0vIb7G/t8eiGisWfxAlxIvnZv/gLTl05w/L5k2wO1G1IUkCz6WM5FpZj0VxssXB2idZqhwvfeZHFC6sM9vq8/4c/5fYvv6TTcPE6TW5+cosX3rpC229gWxYr7RYt22Jiw9JCRw2rlMgkYXGpy7lLpwkmAVEYMZ5M+fbvfJPf/Lu/xctXL7HQanF/Y5Obdx8hPZuFtSXOXD5LNA2YTqa89PUX+e3/3d/kzFsX2fjqPnvDESuLPR5u7DDeH3H19Sv0lnpYtsXe9i6T0QQZp2w/3uLxgw32+yMsIbh09TynT61iOTaP763T8Bu0Wy1OXTiF0/G59Ysv+eL9L/jiwy9IJ1NECgsry7z06hVsAZ7nkArJo8dbbKxvKYOj7bN29gTbO3u0SYnjhJ1BnySJGY7GrO/02RtP2dzdZzwN+OZf+xbnXr/EtV9+gSUsRsMRu3c3aC62eOvvfpdLL5zHcRyEZRMlMZNJwO7dDb7+e9/m7KkTbG3vMp4EjKYhnW6HMIpJ4hjPcQkltDstBnv7SClZWFnm5bdeIZpM8TyXl3/jdV75jVf55b/7BTtfPiDaHfPv/8sfMtjpZ2wuj+4AMbTq7GUh2ow+YHEZdVSNGln5Pc8ii2s0jIVZUiP5mjSW3Ewr5que7OeK0jKeH+UQ8fOmuotCzJZVR6XIOL/MJ9Of8hAxWUYOZYBcX49ktk9Qo5tKfFI2EI0BqMylnD3LL2vkNQWvVDow07tUpll9RYLathyRlJpQ9ZfxqqjlsZn5qgKaQ+o3eeigi2d+Ter9+YZFaXBaeCYyOlBwHd6t0uHhKs0whSgdWivd7VyzHE1L0WS6uU2e+cHk9gojyEI4ze/m0UDfUYVbxcbOvsypQxYhaUWuWpOqplDjYZYgnkY4vlsGe7llYhRWFRACxExbykUcmfm1fVQtoNTUOXN2pPJlUU5+OveIZOqvuqKZLc7qtPAuni4yHdbceWU/LZD/y9WpB1N1/HJEIso/ygPyHNQfsyhtjVYDxkU5fdGEWRmivbZ57DKSNEp4+Nldbvz8OjJO+dm/+DFv/81vsnZulfs3H9Jt+YQyxXMd+jv7XHn7Ko/uPMC1bR7ffMh3/sH3afZafPhH7+MJyYWVRQhCnF6LJJHIKKbbbdMfTThxdo1H9x/z6Z/8ijf+6tf48T/7ESkC17K4ffcBzXc/I5Ep7eUundUeURBx65dfcuP9a5y5fJZ0FCAcm/XdfU6cWGJ/e5e7H6WsLS/yaGuXBoKu6+C7DpPplKW2z+bugG6jget7NDstbMdiNAk4feoEJ188x8or5+ieWeHq1j7D/oilMyu0l7tMt4cMHu2wt7FDGIQMdofs3lxntL7HvZsP6HRbrO/sM+qPePHSedxui2BzjyCI6LSanF7o8fDxBt1ui/39IafOrnHqzAlSKXl07zH7W3vYrsOZy2eZbPd5vLnD9S/vMB5PsAT4nssojCBNubDU49SrF1hc7PDZx9dJopitx5tEYcyJtVVavTZREGIh2N4fMrXH7E3GRGnCC1cvsnpujclgTBCEnH3zMp3FLj/+5z8imIasdZqMw4DP3/uEF3/wOt3Ty3SWe3RaLSxbsOQ36A+HfPInv+LFb73E7/4nf4O773/FF5/f4sqViywsdtjZ3UckKbcfb7C4tACjCZ5j47SanH/xAjc/uwFJQm9pEVLBn/93f0av6ZPYFoPxlJb0+eCP3uf7/+AHWLZ1iH6qX0rmEistmSOQnFmrsmp/lyssFT5fP4mjyOPK+tXPRL7Wje/zO/DrJ40f5nn1awf8OTm78gYcLZ1GfYdxQX5OsjJ+llXxcR8mo/WHuTaxLI1dHeabBxEKXgLPdUvptUqYp0rLMFXzUn3iJw5Pq0Kq2cdHzm+W8+tU78/lQHfdFJa2e8zZ1GDyCXp1UNhNGUyXUcWhMkCCnMPw1XRFw6v1G0xk3BqVIeacyedf9/esVPRcUBd7eGjHSOMEKz/gVgZr5nZe3QvxzCqcpnfEFlfvBD+4nU80aiWbVrW0Nn/WiTq8PyvQJeaLH3V6c+v9KLx2lI5UjUPhOjQunjk84xNSITDVpyO3/6kk23Oian3mmipdPjDHiquzvEXN51K2chkahJT4oDQu5UHKwzelZPPmQ27//Bp3Pr5DPI04s7LI/nDMX/yzP2VtcQFhWQRBhCfAtQXhJCCVKRdevsitz25z/8Y9dv5vv8/3/t5vc/GVC3z87scsd5ucSAMsb5n90TR7aRoM+0MGozHnLp/l3ie36Cx1eO27r/Ppu5+y2moiByM++PGHfPqzT2m2m7z63dd4/XffRkYJb/zVr7O3uYu70OLrv/st/uK//xO2dvZZ6nUIwpBxEBLGEYPpFGE1SWyXdqvFeDTBtSxWl3osn1olipUXvtdrMwkChOeQypRGt0lztUt3GtJd7nDtzz7m8x9/TDiaYDs2XrPBJz//hEd3HxEOJwgBqZSMB2NOLy9x4sJJRtt97j9YVzdRXTpDGsU0dvaQluDC6TWCOOLe7UfEScLe9j4LvTaxlHhtn0im7Nx7hIWk6TeYhCFRKhFJihCC9kqXh9fucv3zm9i2TTCeECUp58+ewms1uHX9Do7nYTsOSZoyHA45cWKFt7/9Bue+eVXtCLk2QsL2zce8889/RH+vT6vXYdeSdHodNja2ufHu53idJr/66Ud4jsMosYlTSdd1ebS+ycYfbHNidRnbten2OiQyZf3+hvLPCIFlWXS6bYZbuwSR5Mrrl7j2s0+JgwgLGOzsEQzHLLVabO3t01vssX79Hldff4FbH97khbevcvbFc6jIzkOA6RzbvbQusoRaXZr2uQmkDjp0fZTHtQnr1m4dqjzw+2yFMzcJ/mUYFkZ9tVfY8+TOoqMer87TP9G5CQPz1P2Q6z4DQz3NOMpy2+rTyDxNrp9Nu7HKvzVFiUyo1/Y8j3A4rKnFbt78ptYbGOUzelrnVBttDmJ9e8pr7i+NdXN6DlfRysP6eADNseqgcnyjYN3qvTBlTFFGDwceMM/zHGHI5xoGVYFcAFDd4icekhrgY5wzLtIY3GLevjdb3yxbVdPlhoVZaY24qL+yzyj/IA4W5sfZEuqQ34EvRzwyHYDq59yOMktVBDo7nofC9EPqOVxUPDuZdRR/n2CA/6c0LA6j0gAajSv5Gyq8cJQ+zOHBEreaniqzqnyBQhLGXPuDn/Plr24SSzjRaSPWH9LyW0jH5d6jDYSAxLaRTReRSOI05d4nt/juf/QD2u0W6/fW2Xm0xXv/4094+3e/QavlEyew63dphhGe56jwquGIfhhAkhL2x5y6eJLrP/uCv/J3fpMTa8uM94csdltEaYLVcPn6X/060+GEyd6Yky+eZfPmOq7lcOaFs6Qy5a//b/9nXP/p59z41VcsIPF9n9MLPRq2Q+RYhJOAME6wBDQci2kU0Wh6xJOIpcUeQRCQpJJbP/uCV3otbN8lSVIWTi3x83/+Z1z74Bone12GaUrLb7B2+gR7u31GgzE0XWzbZufBBk6asrTUJRpNuHbtFnGa4DgN7t19RLvpk0jJcG/A2ReWCPYCokmAsC3WTq4QJQlukvLg+j3Ov3yRq29e5c4Xt+kttBF7A2zLYtAfcvXKeZpLHT577zMsBL7v0V3oceHyGSLX4rN3PqHl+6SAtCSTUcCFi2dIXQvbtnjnv/ojNh5tIoWg0/SZJgnj6ZSFhR4RKW3XJyZioddhe30HsQ6u57J26gRnXzjHw5v32dreZq2zxHg4IUpj9vfH+A2XrUfrWBJWei2E67Jq24R7A5pNn0TAtZ9+CrF6J8QLb73EtY++ZLHb5tH6FkunVuj0OuxsbmPvTxhPp5DCcHdAd7mHOPD13BWMWFpOVaklDF2VAdo6UH+YnjCNmWwtPfHu65GR9LwHFUtFmg6Zw9LPpjD1w5EjESp91r6KJ32/7EFQd961+KANwyery6i0MrZzLNO8DTrTU1KNYWE8zj+XsFTWxlk7s3giK8lrfyhlPsDYqmvz3Ncu1Bgeeb2HM0DZeDmySf/c6Pm/RM/4XsRlGpTNbMnDLosCTNBTemFZ/r2cSUiMWDtZ+llWGbv0j7yFOkZQzPlttoxKMbpKYRi2YjbL09IMQ9f8LpgnsGYzPHVz8ozVeahpTO33ymiaZxbq2eHp2ljXhnkkTR4r2qXfw5C/XCgrMy+6NNdFGTPTbaL5eXaHOHBEnxs9Ubl5l+RsxoPAwV+2e6SO8naX5cHRhH3NP1R5slpmLjuYURDVncrHn91h+/O7nOl26boeC0nEdDhAxhFd32Pt1AqdTovmUpc0TonShE6ryfbDLXbvrvP4ziN2NnZotXzGwyF3PrzOm9/9/1L339+SJFmeH/Yx16HjaZFaVFVmqe6u7mrdPT16ergzs4vZXQCLxTk8HABcEIeHIH/gj/yNfwCx5CF4ABIECSzEArM7s7vY2emZVtPTsrpLZqWWL59+8V7ocG38IZS7h3tEvMysXsJOVT4Pd7Nr18yu3fu9Jl/H9n1URcENAgCOO116rouiqhiGwclxA8WTvPmZaxhByMbmMr1Ol8C2KRg6ds9BBiGVCys8fP8+ruOxenUd1VA5+/pFpOOjqIIv/N1v8MYX3+C43sEyDKSu0QkDeo6L7Xksry+hGgaGruF5Pt2DBr7j8spb11BVldB1ufn+He7/4AZCERRXK3QPm2zf2WKxVKTRcyhWSlx6/SrrV85w/vwGvh+gIJCuj+8HLFbKdDo2D+49od2zyZXymIZGr9HiYO8Q0zJxXQ/F0hCahqIIPM+n57osry6yvrpEs9bg9i9u8fT+FoHv02t20A2dXqfL+Y1Vzr55hYfv3aPZ6VAtFwgDyUKpgN2xufGjj1CA5eUFLFXF79rousbK8iLHWwc8fP8eTx7v4voBQii4no9QVQrlIr7nsVIo8eobL7OxuYpu6iytr1DbP8HQNZaWF+jWW7QabVzbo9nscNJs0Wq2qVQK+EFAEAwufhMKBJJ8zqTjuNRbHcpLFSo5naKpoxgaZiWP57jYtgOqwsr5NR7ceUQ5n+fx7iGvfeV1FjYWqB/UsdvdVP2UBm1io8YjGU8BwKNuk7E3IJpBUmdPKMPJwRwZfXje/+MlHMH//r/T91tkkMks6mRe8yvMUVyZ8m5GulOepzQApc8JXBLtKCXx5fKnITVlz8BEnqfJQiYSDHHgoPhRTCeSsxYvEp3HWJhnb4wYObvZUcQE7V9meDF7LoZgI6l3YFxAkR59wpsaVtjE6GOC+KifydHLOOaZdEkzQXoGGpxskzhYSeCHbFmTcWov7NSnaRU5ESkaoV/J4eCiLgDVNNI96JS2nchMiGSEjJASZ0K5v6AgI/Uc6YSp1SQZLI8bfs/gItr8kSoV6VHiH6c6ONmf5q3ZZw2Z9EXiQTIpC2mV+kkPh5wiyMG/0ZZ9DkIp2Gew0jihn8Y2sD+CFro+j77/AWVVIRc65GUPo+dwaBYwrDytTg8/p+PIAKXTJR8E+FLQDUNs1+XGt99l89waoePSbPdQhMLOo12cwZGjx+0uC+UCrXYX13YolwoUw/4BCsVcjoUzK/i+z90ffUTb83EcF0tVUQydIOzidh2uvnKeI9PEtR2aRw0effgA6XhsXNqgWC1z43/4a26+e4t8tYgdhvihZPPsOlIRqKqC3XVQhMC0DHrNDu2TJsuXNpGOSymX4+jomJWVJT746w9QEFz88jVEKFlaXaB73EIKSWWpSmljEeGH5Mt5CpaJ5/l4no+uqtTaHeo9G0URVCpFQNCst3jz09dRFMHt2w9BgmJo9FwPqWtce/0lalv77D7eQ9NUNLV//O3a5U16jQ54Pjv7NYSqoeYtHn34kJ2tPZaLBY5aHTRV5e69xxRyFk67g6EqqBK6PRshJdVSkU6rg5TweHsfw9Ao5HPoAnphiOe4aJpK6AccnzQwH+/SarZBQO3xLp1GCyS8/86HeJ6PZuiUS0Uuv3KR/a09Hjx+yqMn/T03CgIvDAmCEEVR0Ay9fz+HlLiNDoaAo7bN4rkVmsd1TFOn3mlz5c2rPLn5EMUPaHW7XPnidV7/6uv84i9+wcMbj3jjS6/x8udfobhQShP70TKRpB3JtneDRTjjs7pT+1OU3LALpdEUsUize3L8LqQJYjMVajquG2iR51TGz7MxPD1tOr2oap5V5CyeXsR5G/GQjYZjy6SnLsnKkqdTNkxUlCWgJE41GzgYMyb0TpffiPY4fwnjo9GTSQbvx6uzB/ZGRNs0zbGPXAQon0/mnie8gD0X8ZX+WSAuq3h9JTQ97vCIx9i3DAXQr9LxAp6Y3IlRjmPZmsg7e2OxGErbrPU6kfzSRxamQN1p+mMqQp7FTNwxCv2Ah3/yz1HLBS78xm8M3stRY4xKmNaXwxAx2IQ1vswoWSeTdZSGs4WIXO5DpE1GTmY6D9NKGt/EH889+X6awk6fzk+51zbjDLwo61GTPHnyu+gvS0jRvfMVPXsBYEKXTX4RpN4VkknoWfXUM8nuFDpz0IqVPW36ObPQQ80v06PK1Md0MsDxo328/SY5z+EkUHAVE183sWTIwVGdo0aT6mIFzTLQNJV216HR7qIrCpVikXy5hOZ4XH/zJVzg8PE+x0d1mo0WzZ4DQlAOcuR1DQH9jcRn1rnw5mUUVUEGIR/+8EMOaycUdJ28ZbGwusT20RGFnMWVL1+nsFjk4P4Oiu1hFXIsbS7z4MYj9p4coAQhquOzVK1w1Gyy37bZXF/h5OiEVquDQn9PhKapFERIIZ/jyc4+hcUS7cM6j59s4/oeoQrlYo6Pf36TwPW48NZLrJ/f4MbuESqiP9NQ76IIOHywQ6fbo1TKI4OAcs4g8ENy+RyBqdEOfFTbxtI0yisV6rvH+I4LYYjUVDrtLvlCDiuns7a5QqfZptW1CYOAsq6xsrFEN2ex+3gXXVNRTJ29gxqGoaNqKl4IMggoVIo4rodjO+QMA6kqSAG+7yOEYGlpgZNul4KuYakqqP1jeR0Evuvj2g4nnkuhkEcgaR43CIKAvGVxfHTCytoSftchDDwkCt1uj26ny9FejVd//S1eCt5EKILyYpm9Dx/z+NYj2u0epWqR7e19mq02UkK73UEIQRiGXL+0wYMb92l1Orzy2eucPD2ifdJCUVU2rp/j01//NH/yD/8Yp9XjzQubbH/wkObhCb/y934DoYgUA8z8K0iHIWv8LKnPTwvW5xikGQKwqSA1g07MHkQHVKIZTDhY89dMdN/ii4B9WemTun6ySRP7Hk+5xyItxOx4Cp2pM0Ap+Y/3u0RUd6q8yNGfDI2diC0iUFCAiC7dywCj864PS7NP0Q0fsbh9mmkYeOKi3ciPkSmeys+cnviU9PNMFE0LL2DPBYxcvHQ8N+cA51AbTQLUibipQCXdl4uDwPGb0XnYEXrj5SkROpH7HqKnTqWXIdlp01snqqvSHJyJiFMEJFaOqfAynqnf63Lnu99C0TQ2vvwVzFKxH3uKpx4EIaqqjByLyc6TAWBjuWcOXYzaJ1aWUwj49H4kIxIyPSTcz8l8Mo7ZG34bT9+mrDcejiSkWF05cF4mv2S5LcO/U87Xznh+lvqNxX8WpfWiHIushkx6xBFD1++XQ6chmxcpZxyJMAE0stgYSHEQ8uCvb3Bw0ubwpIfnByAEqqYShpIQSaFYoGiZeJ6HlNBsdykMLktbXFnAb/Wo1Vps7dboeD6lSpEwCGl2bEIkRV1HCwEFhCIIQ0mr2UExdKSQ3P/xxzTbHUxdp7JQptnu0u72OD5u8IVvfI7FC6sITWHtpU2cRpfSepX1185x49vvcfz4gE6tid218W0HTdNxfIen23vkTINCqUilWqJ5cIznugjC/oV9usaH792iaOXwZMjm+gqqooIKZhhy+73bfWehnEdVFXRVsP14l9ruEY7rUj9ukDM0Oj2B7we0uzae66H2bFaWqhi6SrPeoprr7+FwezalchHXdvCDoH/BYM7i6a0nXH37Ghc8nwf3t/rH/S5UqD854NHjXRzPY3VjhYWVBe7ffECz2eHC+U3MYo69xzscH9X7swRAIZ9HMVTarQ4CKBTyKKqK3bVpuy6lgXPn+hJFBRGEFCyLrueieT6etDkJAjRNRQ1UHMfl4LBGgORspcp+s4Hn+ai6RrizR+NPGpy9vImZtxA9j0tfe41r3/ws3ZM2ucUSH337XR7fekLjsI6m6UgZouga51+7hN/zuPbp6xw8OWB3ex9D01i7eoYrb1zhn/+nf4rqh1zYXKG3d4CxvsHjDx/Ra/XIV3IZnoScia+G3WpSPyYAe+JV7Oe0Pj6v/kiulkj29yRtkYiTqVueRYHFC5y+b/EFhim6bRQlsWE4nczp3Z957etMOjEbOsOxHar6qN4f6t5EMccgPoLSEvWVVX39AaqMj9PCCNPIePqpwC+SPMPpy2JFTPz7bOFFtOOLvUQvA3TPApzpQimmfp0M2fBKRnyfZLWn8yoSL6I38E4PaZ1xPLofFfQUZ2yqyMxwVGLUE1+jrwezLk6jzs6tGwjTZO/GTc5//rMIRZlaTlVNOBWp7A/H0J9BPGMO3HOEWHXFapy4nCa0VtqoA2nfU5RTRK+NF+hF2nMKKI+O0Mz2NKPPL0IFzBkmFOMpQ9KAP0vIHDUYhIHwJv0zgYw54dmz7VG3NuKgpAKTjL6W6EAnjw+4+9ObuB2XC1fOYpTylFeq5CoFgjAk6LmAYPnsCr/4Z3+N7XioimCxkOfytQscbh+ye3SCFOB5Po7v09rroaoqbuBTzVmcLxVwAh+JiiIEoZSYhkZ3/4T8Yomu7VAxTTTLYOPiJs337+B4Pp96+w1e/93PI9R+WfILRfILRRRNwRSCz//hV/Edj9ZBg8c/vcP9d24jJOi6RkEoFAmxdEH7sEY+CBCaAkLDCAKEoqIoKj3b5sz6Cs1OG9N16bg+0g+oFPM8+fg+pqGTU1UMAR3bQ9oBipRsLFexPZdms0MoYX1xgXK1RLPZ5uneIatLCwihcP7qWayFAo1eF2mo5BSL3XtPQZF0Ol0Mw0ToCqEMsbs9rJzBk/3DfuupCkbO4OjwmPpxnV7P4cKls2xePYN0PIoLJQJCwjCkurZI48E+tu+ydXeLIJSsrywR+AF2t4cmJV4gqbVanNtco9OzKZSKnFlfYfngmEfbTymWyqCplEsFNE1BaAa7HRvbUvGEpNWzsXSdkmmyXCmzc3TC9g/fQ9P7S6LKxQIbFze4/vVPYZZyvPGbb/Hmb3+O1lETu9VDVRUC28dtdCkvVCAM2X20g6qqrJxfY/PSBn/1x9/DUhTOV0t4zRaGZaAaOvlSgeP9Gvny2em6b+oG1PnfZjoOs/r4VDrDPphihZP6N8Xwpx7MlFS1M+FI0iB8AuE59Wja4NYLuXMobTBt3pQTe9b6DTKuxcGQzUTVyrjujjkboxhjEskQGQiMVUvCXp32slc52KsYk8Qo7zPIjS+DHFuj9K4RWfr0XE2Y3GDwvPReqHMh5+AnfUxfTrxJ+x0jMzuM8J2YGMjIjpseaSi7c/uDo0KOy5t0VLNGr+M/k7+TXE2zAiLKyEQ+uZUV3vyj/4Azr7yKLJYTWWXQzih6cqRhvpBlimLdJrsIs6gnNjOlu72kANE+GJ2ogoS2EsSNbDK/eCaJ5wjdSSWYHDmf48Sz5whTfai0iC/KOXjGIMOBnslcTy1GJ9+MqzpuosbE4jU77DERHzL+dxZvMv4sgPajfZaKJfZ6J+w83sMJQ3RDx7RMjLxJzjSpLFU42a3hBSGq0l/GlM9b6KUce7tHtG2HQPbX2kvR7yG+50IoMVSVtudi5ApgahieR7fVJvR83JMWR08PaHa65A0daTs8ufsEQxEsbCxz9UuvUVqr4tkebtfB69oUlsoYmkkYhgihoJk6C+dWUBDs397iYK+GpuvYYYgW+CidDqZVQDVNDl0bIUNKeQvP9TlTLXEUhvQ6XSpmjoe7++Qti431FU7aHXICtMBDkyqBlBhCUCwVOGm3MTSVk3bAhUvnWFissHL9HArw6Ce3OW608YKAaiHPmbdf5sm9rX7ZhYJ90sJtddEtA7fnUDmzxsGtLe68dweHENPKoWiCIAgJXIeNM2usnl3j4Z3HdDs2hCFLF1Zo391F9wPM1SoULPYebHO4f0TOMOh0upzZWMM0dGqHJzSbbQqGTsfzKFgWjuviuh6BGrC9s89xrYai9JeOrZbLNAKbT7/1JrvvPUBRlf7GdRMKho5pWVQWK5iqwmK1hGFqmLqO6/vsHdfZPalz59ZDNF0jBC5dPEu+nKdRa6JqOvliHtfzcQIfu9Oj0+lSKhZYXF/iZ3/+MwqlHJdKhf4le74Puo7aanHlM1dwHT8iwMnOMuwk6Z14GmZKJZUc1ImAvDnxV0qHTQf1MXoyndeYJpg4rzSF2FSmktTTyGSf0DQzTEs2LzbKDFMOrX1GWzyTlzQHcQ5bPU4xH0MT4Dy6QXsI0MQwo+cH19FMn2mf7ZQZpqGPPzZRzyFPRPyzF1HmQXgh91zANHkTKU/JFC+wRLPYSBuJoO8hyiBE0VWS4dTep0wI/FBW4ztxptOIJU5mHE2YwUxMMPtpoxQ0y+Ltv/fvQFToo0p6StnidPsv46fjTOY3dMzicpKBxOUkxJ47jDIcWpFhzn1uxk7G8KSOWUaAiGMZDSIyaBI58m1U6BeknH7JjkX02yc49vbMQSgzKnXgYAwfSTwBmQWbcComPcxJWhmDIn0bJenVu+RMk/XFMuHJCceBoBNIeq0OnWYbO2fRqNVBCExd64+2qxqqhOZ+na7rEoaSkm4gNIkvJY7vo2sGuqaRt0wcx6Fx0sBRwLYd8opKMZ8jlJK9g2P8sL9XQdg2mmXQDH2ePniKqmlYpRzNp4e897138RyPsy+d4zN/80vkqkWMvIEMJSdbh+y9/4h2vY3neoRCUO85YBhI3aBYLeIJgeiEHHV6HDQ8KqZBLgx5eXmRJ6rKk4MaXc+lWshz/vpFLho67/7wfQqGSbfXRdN09h0HYRoULIu67XDp8jmufuEanh9Qf3zA07tb7O0foedM/CBk8/warZ7T39weBoBg9ewywg85PqyjB5Ltp/vIIEDP6RDC5Stn0U2Djz+8CwhKxQIC6LQ6CCSPHz4l/8McZ996ibDVY+/pAXc/vodVLXDx4hluv3MLUzf6IL5nU2u1KOQsKpaJ8Dy6tkO90WK5VARdRVTzXLyyjl2r0zvusH9yzIWXLqCpGq1uDzsI0I2+o7CysoAiFPYPazxyXXK5/j6aoX7dXF6k67hITcHuOfQcl/v3txCA6/uU8nnWz2+iKAq9VpfD/UOKBRMrb3H/g/sYus7ls5sc7h1gOC6FhTJ6u0mwssDTBztsvHIu1o+m6YAxGJGxSEPpF8jRIRnTus34U2ZvJfNDig0fqd1pY5PJLk3CxifSxtifoRifZTnRXCEj31lO3RAHvJCZiRkG4Zn2bSTretgeUXM600xHK2eW1UoM+MY+DYHa89fVC6nvwexNYhwzCmsYTuVMLJuSp7tbTczTcU4ZXsg9F+nsDxtcRuKOv8xJfJRgHjOfykKSWOoI82B2Y7jsJw1RpvZeMckUKZ70sCpO5bUmeZCxPyPSE8URTA6Hy1EdxplKBJH8MWWfwpCdyG3oUyinSMFkjNmOx+wwFpk0LiZlMjOMKjYxohZfXxehG/2ZiDCl3fujD2JwYkSUx/HjbAc+QTMRPy6i0a8iEUGO8kumPX1rDOspoRXn8A2eLb+sRJFMh2AoBchET3iKP6U7D9G00d/DHjOMFYb9U4Icz6Plh+SqRS5srGBYBn7HQbUMth88RQhBr91FDSVLSxU0TUUuWLz2jU/x5P0HBH5At9kGFHRNQ1MUkCFdx8XxA3RNpWzoXNhcIScVcgtljg5O8FwPQygI26HjuDiej/Q9TE3n9ge3CNpdEHCwe0jXdWm1OqiKymf+8MuomsrOrS3e+eMf0K41CWSIquuULJPlQgFNERTtDo2jA/zqIj0JMpSEQUDdcQilRG+1qVgm+bxFoWdx8ZVLbHz6Ct39OhcuneXgyS7VYgm326GiCbq9LigKjhegmjqqqXNwd5vb793hpNWmVC6gFfM47S5110E+3sPtOgSGSi5nYJXybL58ljdXqzgdm5vffg+n3aN1WGd9bZny5hL3PrqPJiS2H6JISX3/BN/zQYLreXTbXcIgYO/eU+5/fB9N17l89QJ337mJ7boYhs7+9j6B79Ps2RRNgy6gmQZVVUWRoGk6vqYguy6qanDrxk0WihUuv3KV619+AxSBYugUCwVs10WoSv828f19FheqrK+t8OjpDidNl3I+z0qxgBMGFEoFTNOgsGZRazZptNp4vo9QBLbrsPVoC9PQMXIm1WIeNWfiOjaWCKmsVNivHeP5AYXFKo5ro545w5Nag5XLq5SWSzGhToNr/RFTmf4xkrLfy4ZgLS3OmOBwNm5qEEPAlKJXYwymJp1JO5Y+xaZPo/8s4dTOR2a+2ahqNM4yNW1c28uZvM1AcafF1DMARlQbD7H2JC9DMBLXzWlbZGJOYkQ+k6YhzlbyJNLJA4ziv0S8mrKOlpw3JOFF9DniQCSdu+gKxolvCZaFiMZ5Bh5TwgtbFjUpI2kSM1A50ZJNOcY0DW6KxAbreTvpxI2JsbYe7MuIb82fi25aXxvusYidWvRcqGl29nMTThHUmAuRKM8E1WQ5Rk5GErCN/52Hs9GBoTE2Eu11Cp8gxmuEVHQGI3PPxYzTReY6pSHjbZbLk8l4rL6nV0By0eF0BRjpP3Kitqeknx2klAR+/94FRVVQkueDp7GTJW+nYUDKkSzH/fnIGS1yLFsjvR8LY0GbXf5oLnGvrK+sBcvXzmP8/A5nLl5i6coG9d1jHn/8iEcfP0SGIeXFCpoUWLrGke1weXOd3PllHt7dovvd97j2jTf59N/6MgQSTVNQNA2hKIR+QBAELKz3b3DWDQNVUzj8eIuP/sVPeLR3iBsESClZyOWwCnls30fIED2fR1EVyprKo60dTMvCdl1yqka5kOfp/aecu7/P0qU17v70FnbXxsgZHBweIxBYukrJMgm8gLZuUtB0erqK40Apb2E7Dl4oUVSVPdclaLcxcgamYSD9kNAPCCUEfkCra7NaLuIVCpiqQPEDbNujYOmcHJ5w/OSIdsfmuNni7OYqtpSYqko3CLB7LvmDJq7toasKoe1x9GgPq5RDswwqawucvX6e+z+5iVA18pUiO/d3aNZbBIFkcamKpmtUq0XOI3nwYIucZaEqCh9/+xfs7x1RrhS59NJF9j5+xMFRnWK+f4FerdlChiHVfB5HSC6+fIHDnQNodnFlSLPdplouce7iOdBVdCmwXZejgxq3fvQhn/s7v8KnvvkFtt69x60P7+J4Hq7nc/HKeb74b/wKB7d3cByHp7v7NO0urV6Xar5AEYXQsemVoJzPs7RQwZMhAVBRFHqaoFCvExQK+KZBu9UhUFVWV5dQNAW3bYMANW+iLpe58XAHJafzxb/xJQrV/vG+Q7WYJvfJueehnEc6YfxxmkkdDD7MY2mzbqqO0hXzbrie4jAM1eyz4qvpd2LImXGeKUwZtBnfLB5RTMNkUfAZ+fdZwzON1ieyHNNIoD+Zwt00djN82oHIjdHJAJxHlznPKkXs5uu0kxajvMo4xaxN4VNlY86j2mJuohAx23a6m9bnx21TacnTL5aPhXannfmt31GTPXUMZpLgbqLeh40UOUFKDBvrefrnDOc7KdUxJ5ShKKb4+GLI8/xVGttoOneqlExnvstKnX460+iI2Fl5pyit6dWaGF1IjzR4TGr95wyRHj/hXMzZABOjZ3PEh2dUvDFC2XIlEmuEJ7fB/RKDBClDglAiQ4kiQFHViJzLyXqPMnvKvCbyHpIaavHBqFHM0Yg6ABN0Jnt7TDhSNrSOR9Qijpvs/yNDiXPY4ODeLu/84+/zdHsfU9NYqJSoGDotP8D1fHq2TTWfY/XiOrc/foAIJULXMKtFGsd1dEVDMzWsYo6Vl87w2W9+geNH+yxcXKOw0D89au8XD/j+f/3n1Ds9qqUCeU2j1mxTLubJF/L9ZThhQM5QafZcpCKo5HKIUOIHAXldJ5czqbU6LJ9dI1fOoxs6j24+BD9gbXMNz/M53jmgnLM46vZQFcG5pQWOO12EqvLmr32G/b0j7v7sFiLoOxg5QyWvqZy0uxjFEm9+9U3cnsvJ/jF3b9zj8tk1QgSX3noFIUMOH+3y5N5TWo5DtVLGsAx2H++wUi3ihZKDWh1FVbh69SKqorC9d4AQgmbPYX1zGcfzyKsahCFd28UXksD2IAzRVZ12zyav6WiGRq9nU6mWcR2XRqtNKWdhByGqDPH8gOuvvUTvpMmNOw9YrVaQqooOhJ4PUtJ0XKRpUKwUcJsdNFWh2eqwVK1w/vwmR40mJ80Wdz7+iGK+yOr6Bi4hlYUyn/2tL/Cjf/ZDfEVi6Sog+K3/4PeonluhsXPMzoePqD3e5XD7kON6i3a7g+O4hAgs00BVFUzDQNP7Y4SKlIRAEIb9pXCWRThoW9/3UXWV5fVV9h5uEaiC0mqVysoin/nGp7n+5dcGSw7Ho27JLjocBEk/jCSuaZ5/g2mC7LzjORl+zsw8kmmehc6M8Ik5F3NlPmmnZyYZ/J2Ug6wGyW6oZ9kTEIWm6VhBjhT4UP1OxyyDrcoTm3BFVOwznOoseU45slVGBq1S8EVqE0R4idX3cKnf3GdBz48k5zG9pVIp48vs8AKciw6ZvS9SwcmCTPbh/ttpYht9GAKDibixjFJEJUpo2ua0SdSREsTkz6npkhorekFKNtkMaY9nOkZVUxJlh3FNnSZ9Ul1MturknQ7x9BE4FvmTcENeFDoeZZGi5DP747O7fWMS2bI2P42k4pzsReM3n6BzMWd1hEGIlBJFEeOji2N9Q2QpgtPxMu33kO5EtQ1rKT5cMMHiXJmn1PrY0uHbHj/9R3/Jgx/dwnV9CqpCyTJpuz5d1wVFoVLIkTN0fM+nK0PKl1ZoN7vs399GDUHLm/TaPfIFi1BI1i5s8tbvfpHDj5+g5g0q51Yory9w589+wY+//VPW11YQoj8zcHJ0wlq5hDA0jlttCoUCpt6/ZA5FoCBoOS5BEJDTNUxDRzN1eq0uXddDqgqKqpLXNXLVIpffuMrP/+KnFIQgn7PY6fXYXF6k2epw7QuvcvXrr1FYKnPy5JCDW0/ZvvGEzkkDTRGIUNKyHbScxcJylcXz63QPTqg92SNXyvPSF19DzRsoXsDjjx/x+MFTpOfjOz5FvX86li9UhKpy7dolSmsL3HnnJi3Pwet5ODJkY3WJjbOrANSe7FPvdnH8gJxu4DoO5ZzJfq1Bq2djqio5yyQEVjdWEMD21h6a2r+gToYhpmFwfFjr33EhBF3Xo5KzUARoQiBDiTc4oWu496qUM9k8v0Gz3ubR1g7VpSonhwfsHh3y6U9/mlAVHOwesX5unYOdQ4yChVGwONre48orl/nt/8MfoudNoE/fd1ycVo/WYYPWUYNOo8PT20+o7R7j2i6tk0Z/NgsJCpg5CzNvUVwq90+mKlhYxRyqIsgvlXn43l0W15a49uXXWLuwjpEz++ppPKQbkeyBbokOAs7qJAMwFFlkkHhI9JPUj+l0TxVSxgYy48GcyvJ5FNb/HEJsGIY42I3/npb21CENqkX30JByaExEz44djOTQWuRp8I9ICuScLMf6Q+xl9ixLuoM+JYNE/cpTOxcvKvQ5LpXKz0zhBS2LSrPgxN4l60Vk/Jpa74kIkzROAaOmgL2RAEgR009j0ZrC4KjoKSP/Qo5mXtL8+GfvmpGyT8wUpR+jO+oiSWMy8wzsZ4Or8XocvkzJS8Q/pfIyIDaaQZqXnUjbnDYMDWpavc3O9xlaVcoJBRWvv7EEDWVzlkub5ZpMCxPx5iyKqioZ9KMoZX56U0lNAzvJtpZRp2LcZ2avTc76nNiXJKNf+v2puXXEYj5HrmLQtR0OG01836daKlKsFOn1HA6bbVrdHlJKjupNdF3D0g1828WzXSxTZ3lzheXr5/j0b7+NUbCQQYCiClavnae2fUSuXGBloUqv18PMWVimwfqZNWr7NZYLi5i6jhSC/UabIAxAUXA9j1BKDF0n9AM0TaPVbCH9gKKuE4YSw9BwECxvrlBYKnPx5Ys8uf+UsqqyUiqi6RpWvn9PR65SQNVVFs4ts3RpDQn84s9+jBQKqqJQNg1c16W2d4RZzKO4ASFgt3s8vvGQdr2FkTNx/QDF1JGKoKSqGKpK6ApMQ6fZ7vH0yR7aQY1Gpwu6ih8EFCsFAilZPrtKrlqgWC3R/ekNQgWuvHaZ5nGLJw+fghBUinlK5SL4IW4QYFkmhwc1LNPg2mtXebq1R6fZotVoUrRMmj2bXD7HmbVlDo7rlHIGQShBVfDc/ilRK5srVBbLSNvj4LDGzkENVRXk8hb3GsdUSgWufel1Pvr+u1SWq+zvHZHLWywUyzR9h8APufXBx5z/yyu88c23UXQNoQlMPYdZzFHeXBwBl8/4X8LtOrSOGjx57wGtwwaX3n6Z0moFq2ihGjq6qaOooj9S2/ceAPj873whxaBmdcSo7M+pNYYDIZHxovHyqUnLlzgNdCrdGKuxTpeRUibjkl0MGY/6/+/uQ/ZswClKMKi6tPX2IhphLopzOohZ7CXaVSQGh4e/J7YnDrDa8BCBiavSIj9G5Uva5DlsUboVEKnwN8mDSEuaEmKORdaH/5mEF+BcZPTSX1YPHeUjJxVIgrehkouHhGRE+RbjDjY8+3eMY2S2Fzo6rSZj9CaqdGNJMsYG5qnDDIWZfXxb/9+hR5zsWyPgOseFO9MZHTA2BHViCkPRShqVJ6VtBs+jm9vTaE7pyBPLYZI9erRpe9jmydoZytopnYysTpGm2BJykta+8TGaqAscfZeMOcnJNJ13ejeSWPWkEnkROmHuJo/uwogyl5V48uOp2B9VaN/Y6TmDL//R7/Dxn/6EnY8eYzsOedNk4cI6nZM2T57u4QEFy2JzaQHDMgiRuH5Az3bpBJLA89AUgdO2MVWN29/9gKOtA0LXZ2GxjGf76DkTU1fYvLDJ/dsPcYSDj4suBIuVEodHdXKWThiEmLpGId+/NDMMAjpdG8cPKJk6KpKcUPFEiO25FC2TqqliC5UnHz1g5942nuOhqYK274EfoAkFS1W4+/Pb2D2H13/t0/2L+RSF3EIJVdNAEZy9ssnDG48oGhply+Rk+4BWq0cxZ2IZGvdvP2JldYFWr4eiq4QKOF0b2w0oFQsgBe2ejaYp9Bwbv9vBMDQ8x+P85iqHtTp2ELL7cIdz187Tsx3IGZgCHnx4D1VVCcOQYqnQ3xQvJfWejQQOdg5wfJ9rr7+E63p0Gm2ECkXToNZqY5kGr33mOruPdxGhjyo1mq6PrqhcvnQOVYBRzKMj2Hqyx+NaDcMycNyQR/ce49ouG+ubHD8+IPQCWp0ugR/w0vUr5MsFHMejcXBMzwn47n/3LRbPrnDurasDxyAuXwIQmoJZymGWchg5k0c/v8PG9bPololQItHHaGqs9wb7HCY3x8Yd/8mtFPPo7owocmh7JxVdGs5Lxoy9m2DjFAolfaRmMlqW7npW5ZVJ79lDNifDUf70JbzTb9IWGc8puGRKyHR8ZpX/Wet7IFtiOFCUEmEkf8nvo8sx5sddY9iZMaiXBYWmhZR+9KzLqUf47pmN7fMb6U9uz0Wm95jKBuPqmJYkpfYzAFdi+3aqNzlBI+qgTCiDhIc67brGiCIeAeAkEJzL+ZrUgCLlKZ2FvnKZp3XHIwST94dGnYs0/RgfPR9wPHFqQQTupuobGWvaTJFMe53p6meECKPjy+tS2jbiiY43Ps/I/zSZp3yL+nGTrT67cNNGsV6gTTt9yCr2HKBkLrqD58kJ8ajEiokkw1/TWEifQRteoDh9xmNo4JH95VF77z/k/f/2u/QaHRwZ4rgehmGQzxn95TlC0O310BSFwNAJPZ98Mc/x4Ql7xyfIMETTtP4FbgsVVENDAXwJhCHFSoliKY9hmeztHtA+aWIoKoqAtfObPH26hwglC4tlDo7q5PI5Qs+jVMqjCxWhKQjbZuukhaHrCCSLlRKNbg8vCDEVBQVBoZjDt20aA14NRUGoGgJJvecgNZXrX3yV13/jLepPj/nz//f/xPJylde+8Wl+/u2fI2wfXJ+lpQoSiS4lQtO58egplUqRUFdwfb8/o9Hpodo+5UKBjmNTKOTwZYiu63gyRFEUnGaHK5fPYVgWd+88orhYplIu0qjV0QczMmcvbWJ3bJ4+3Mb3Q0qVIoEAvWSRUzWePthG03QWFsrU9o8Iw/5R1Z1eD10IXn3jZYqVMh++c4PAc/CkYGmx2r/MzzK4+dFt8qbB5kKVx3tH+ITInIFue7Rth4KuQsGke3hMz/XIVRd4+ZUrbF45gxuESAE3f/IRx60mbbvDV371i3zjf/03+m2S0a3lQAYPH+xhlfOUlsspzkikJ8Q2oib0uIh/n5T55w+n2qs2TDPoujEVkm6IphM7bTmGaeYdhfklhBe3ZyOOC17MBXpR6sOHFOdmDDVmJI7+SBj5tPGhac5vlEaWwzwhSynxfwkhWl+xPSdp5yf3v2TSmrbPZd6u8zx7Ll7AUbQZzJ2qM6ZBqXGjRwH16NyX4RGokeMOZEIjJKHF7BHIFK82k82siEMvJgnT5/eKh+ojrfpmVemo7oYdMEYoCqIHzoQY15ZIiOMo/ZS8p+uJCFoGoqf5xDke/xl1qGijTZOlKRUy4m3WvLtI/E3EGzsWEfg65ykn6RmlMBqp9ckiDdsq3Vkc+6/D+h5U2CmM4elt51C+5zi+YEj8tAI0PxuDx0lnIhlJDD8DaZdljY/W7jM9moqPReoDz5g9G1vUJEEANFPHlyG255OrFBE9B1XVMC2TUtFC11T2T5q0ujaGaWC3uiwtV/HbXRZLefywv8G42+kgheCw2WKhXGSxVCDwA3pOwOHeIU8eu/2ReV2n53oEon/j9eNH26ysLRGGIbWjExShcP7yWeq1BkcHNRRFYOo63U4XI28R+j7NZgdd07B7NrlikVwxR3VlES/waW7tY5k5jDBAQeKGYX+JjxD4UnLnRx/z4P17XHr5Ar7jcbR7yPvf/wW/9x//bepbh/zwv/423U4P27YpGTqFYhFNUTipt1hYqeDYDgGgaCq+EXJid1F0lVavh2bolDQNU1HoSh+pq3Qdh2K5iG87NJstbMdBDSWvv/0qDz64T+O4ydrmCr1uj52n+/Q8h1DCl/7NX+H4ySFbD7YxBJwcn3Du2nlauyecnDSQoeTSSxdYuXKGxx89RAkDup7PQqnE2fUVUFXu33+MoaqctDt0ew5SSkqlAt0wwA0l1WIB13WpFovsPX7C4UmNNzfXKeQsel2HdqsD0HcsdY28WqDX7BKGISqCtNNipAwZou6l86sIVaHfG/syF50lmOwJw1471osS+sdhv2CgOVLhM8gmLUJUFUOi+BMAVKS8j8aQoz0gM0sn53g+dYjXc//p9GFuizNTp4rY0aMvOow05hSINApRXjPZiUbKsDhDeU8KUtI5TNZNmt6WEQw3b4M9p/M5y8GLI7P55GCavPwyfOUXsuciKR9RAz61QycaLm6nRaoMjsfWJ8G6kEN4HKc7apJIPiKRNo2fieeU7xMzJFFQJzLqJsn4RDNPA2wzGBq8S1KInnaQVr9x/k6H+OI6eKhUUsolkrGnhGQ/mtZGaYxEo6TebTK7Q08NUZsWxfRzJBs+xFttsl6S32fagpEPNCZ+GiUyf9znqLcswzKDn0zeJrtOZntHsxzWU7Zdm/AaEpHiPV9G3g9bc2TvBpjNKuVQDB2jWCBEYAgBYcBOrd6/fRuJUDUkCheuX0a3DHbuPKZ90sQNAhYXKqxvrtJudvBcj/JCmaOjY3K6hqIKlos5pGUQAp7rUbUsQKKrKlLC4fY+QtOw8jmk43H/5kMKhRzLKwsgIQxDCqUCRt7sA/mTNr1Gi5xp0Gy3MEydykoFPW8hQ8nxXg3XkZQVQctzCYOQQNEIPI/FapGiUHn089sUTYNqMc/RQYOP/uIXXH7zKl/+u9/go2/9nEajjQT0bpflfI6m6yIkaKqKVAWKInB9H90y8H2fwPYoCgWn52AP7jvVNI39rUOWShUKxSK+9HCaXc6uryB0jU6nx2G9weHOIYQhRs7EtEy8rsP73/o5u092sCydc595iVe++gaB4/EX/8kfE4YBGyuLnHn9Ent3tnhy/zEylKiaztrZNaSm8Hhrh45ts7pUpXvgoci+o3XQaFHO5ygvVnF6PTRVRVME+8eHVIoVKvkcuWqRXs+m9nCbduBj+x6KrqDpGse1Ol7PRdVzqX1ZKEr/sJwg4GDrkLULaxEkH5HSNDAlBvohsgwk4otEXswRZoCvUS+K8JGq96YAhWk6aWTFMh2LcT7RY+w/cWSVGWah1TnQ7Cz+RbRe+7+zgOYL9iUjLIyRxIAlYi+IfEi1AzFNHbkUblbGEacgdt9XJHESpCasb//I8r6DIRPpp95WMI9cnUL2hlcafFLC+gk1/Si8sBu65/2dTSXD0IsM2cukNKnBkrKUedLUPGwO6IxEfwZgPp2+nlfysuOMwGX0hYh7vikDtiOas0+EmD/M29fGuTM6VjXTvRoRnbzYZgpSjGd22pDKjyRts/DMvKbuVM/MPjXEyp88QEDG/jxzHtNin8pGDyNHO94cxY8mS2FhGntEQX50xizVfEcdxDnse/blof2EUdM6jLd0ZZOXf/1T3P3zd6k32gRBgON5oMBrb79GgESXAoGCFLDzeJdGs83G2XVK5SK6ppIr5gkEHG8f0qg38f0AVdfo9Ry8MMQP/P4xwKqCpemEQuB4Ppoi0DQV33UIwxA9Z5EzdYIgoHF4TEB/428gQ4rFPLqq0uvZaJpKKEH3fXb3D7FuGWy8cp6Ny5t0T1rsNZrkciYFRRAGAV4IZzbXaLQ77NVbLFZLqIOzes8sL3Lne++z+8EjLrx8jpdeu4jhePQcD4omy66LtBVcIQh8n1AqSF1BMTRC0Z/9CYG252N3PQxdRwKKoqCqggcPt1AUKOgmpgg4+9I57r5zG6/nsLy+RK/ZxSyYfPHv/zr7D3a4+a9+gde1kW7A0tVN3vjtz1HfqXHzO++haSr4CufObXLyeJ+7N++jK4KO53Ht0jkUTeXurQegKmiDu1wqmk6902b93CYnrQ6+45G3DOxuh2Ihz40bH+P7HtVyhW6rQ9ixMRTIFfPs7x9QKuZRQoGqCrwgpLl3TK58lvG40MTB4TRrLQrl/AD0jDt9//Aqid3s0q41cR0Pp+dg5kyKSyWKiyV0U88W9FMYSDn4Zzb4k5G+KRK9I55nzI5NeD7zBzE00s8GTJ4R16UpkHELnjZlLER15zy8TWuUyMDHJxkmmi9ZyIwyxZdXy8mzarJzi+eV6BvDfGI9KSl7sQfiTksWzhBEwFXKRxGV5+jjtFINe8npGmkOE/aCE06GF3aJ3kSYy8scPoyVzjMc5DNnnvFaSzrMkgiwSBWgaPq05yl8zKExJkB2OuXE21NVcvpbmeHazSKdcNSSlNPdxXipMssoBmY0a6h+oCymwbvThszZhzkUeCoXEwpmMlbaIrHTZP384xlTnPo5QkRPT4+Q9j7KwpTkpw4xw5E06dkWLgbOYjxFXJOYUYiDovQlawNmBlH1nM6r33yb8nqVd/7b79I6aFBaW+DyF67j9hze+7OfUMrlQFEIfJ+cZZIzDQq6Qeu4jt1zkBLOvnyBytoiW4+3KZk6LdsmDH0MIXD8oH/3garS9XwKpSJnLp+h1+1x8GgXoWqEukan10Pr9tBMA0UIAgGu6/ZnChyXveM6EoGqKP0jW3MWpinY2d5nb/eQXCGP4zhYlolhWrieQ9fzUBWVR4+eUl2qcv7SGR49espytYzi+piKwsX1ZULbY+/GQxp5i3NvXsFudHn4cBvTNNB7DrbnoSLQ/BDf0AmFRNM0FiplQi8ARVBvNOl1bXTR1xNeGGKgISW0Wx1ypkUYhlSrJY4OajidHoHvUV7foLxa5Sf/3XfQVJXOcZtKqUTgBnz0P/2MRzcesbhYAVPHRICusXXnITnLoNbusFmtUl5f5P13byJ9H6fr07B7OJqg0axzbnWVYrlE7aTJ0kKF1bPrHNZO6Dou3U4bXTf41MXL1FpNwp5DrdXmoN3C0jU6rQ6hruJ2ely4fI6Hv7jN6ktnIse6RoZSJHQOG9Qe7LF+/RwAgRdwvFPj5l9/ROgG4AUcPtonCAKOanU67Q6qqlJYKFNaLnHx2gXWXzrDxqUNSsuVAQhMDlCkAPNEF5ob+8cGPDJ69xxOzam0/vMqyVONoKQlOm3ijNJNK3SKzZobjH4CjkVsIDMrT5ni2MQci+hzZO/G3Eu55OC/vkCJ5IBrkpkYEIw9TJqDKVmm7sUd7XsSsajZZGZa1rnCszTtxAFEz5P/827obkU3dCdA9MDfjGYX/RwPQ0EQyZhp7uGzBhknl3VMRTQbGRWzcQEnLgObke2Y5vgKvnhGaUzM1rXxGpWDe2WiyzLGI/xxu5Hd7AIRu/QsNYzAeLJm0rqEjMXPvq8h6cud0gA9ryEZ5hlD20PlMx7WyPIVJ99PCtTkcrXnZHs4IDIYHY6Pc8RbZVZPmu3YpmUvJhJM3YXxorrzqT2arLRxRT5xzCEZv1MIpl2kl7UZt33Y4If/2f/E9u0nXP/6p3jp62/y/f/Pn9N4coiRs3A9D0MKwsDHRWB7LrrSP85V5EyWz6zSOm7QPq4T+D5eGKCJ/r0VZdNEqCp+GNIOfL72t3+N8599iaNHezx+7z6NvRN83+dk/xhFguv7FEsFzp5bo1ApUFpbwEfSqrWoPTlgb/uAXqeLoaqUcxaKpqEr/b0Vhq4jpMT2fOwgQCDJmwa+hK5tEwYhhbzFomUh8hZ+z0EbpvN93CDEzZmgKuQIcF2flm3jSDAUQRtJjxCrkGOxUsHUDay8SafVpdPp0mg0cHsOCgJNVbAQyG4POxQsLy5gmCYdp0e5mMNYLOEcdyCn09s7QSgKay+fp7jav0Tv6c/vYZkGYRDgy5BGu4tlmfSO6zRch4VCkVc+fQ1N6TtZYddl57BGq9vFsEw0IXj11ZfYfbKH47m89uY1ntx/gt3tsbWzxYOdx1w7c4mvfOWL7D/eZuX8We7v7qMs5uCwQ6PVIrdSxbNddFXFMlT+7v/530fLGSiqEtNLvVaXuz/8GMvKsfnaeYQiuPWd93h0b4sbP72BaZqYut6f2cobNI+bqIqCrqpUF6qECnS7PUIpKS6W+Mrf+hpvfu3Nfj5DeZ9l3+YcJDhtEGI8sBSzlonOdKosn1fPiIznZwmp6ft6KHPTdpa9ywDns/IeD2xluyHPuoE8cyNxgleJHM8speUdKU/09K60Yk5cVitl7CCZ7MoZHzIzPH9j6CBMOs1z4D2RhvDiicZLvLKJjfYWj+76+AS8wDnCv9YN3VlBRJ8ieG34MAHERo2SqPLhPgqRkphk5GTIWsku0/OKR4nwNfw9BlKjdFlIM0kvwtM0fpMMPKtIjfnrn/3cpz5xBcwodgx+zpPpXIyluhkT0HeS7IxNwjFhkvH3MxRs6kz7QBBkrK1JiTgryMi/CVZJcyyiLvQzWqtUppNimd4Lhk/JvKP9YhpXI9pJh2u6Lp8L/08NWbRHl+PJyPK6IU8yYsTi7TTaO5EtkJPPmRUz6SyL5HsBxZUKn/t3f53Wf/JPuPWDDzHyJr/67/0uH33r5/TqHYSUHD05pHviYqkqhmFw3OlQLeRwWh3uv3eTzWoZU0DHD7B0Fde2+xe9hSFSVTFNExFK/tV/9S959cZDLn32FT71zc+j6P3NCm7bpltvEzg+nVqTfClHKOmP8vUc1q6e4fKXXqVba9LaO6Fx0qRx2MDvOdRrDTwvIOzaKKqKZRhUqhVCASe1EyzTxPE8VFXF0HQOTxpslPOEusp2rcFKMU/guSyoGsIPcBwXWbIwNElOU1kyc/hIOp6N4oYQSoSm4jsedihRdY2Fahnd0Dk4PMLv9FA1DS8MUXWdvK7Ra7dptVvkFstc/sanWL20wc/+h+/jnXQBCAQ0ThroBYPDh3tIGdK2bQqKSt4yqPdqKELSC0I2Fpd46StvsrixiH3U4vNfvMbWX9+k0e3RaLUo5XLYPZvDgxoyDCiWC5ycNPrH/DouQavJtTMXeftrX8S8vMKjH/2MnmXiBT4lVLoqhLqgO9iDkisW6LW7+LY7uFAvHnq1NtIJCRSPndtPeOef/4j6Tg2rlGOtXKbluvRsB01VKZgWpTWTxaUKK2uLNJo98qtlfNfHaXVpNjv81T/+Hktri5y7fn4+xyLWFZ7nyMv5w0hPDgZTkr0sqkcnr3eN98TEx+yyJp0KEs+nUNvDMaDsjD7BkEJ+6M5k5f2sbRoZzpya/+iglNgozKD90gbx0hyLNHsey3QA1mRWg42ldxwtKTsDbudwLIYURy8Gh3/EHAQxHJyeXvcjTk8xXjYqZdLZ+tcQXqxzkfQuBRGDP/4Wranxz+hIxYCcHDfUJGwbEhifeJTUAxPLZkbJx07KqMPLqFAMOUnEiSVPcXTS8sro1M8cEsh1srwpS21i5ZbIBHPD+MlyytjXFxASIHjsZCTzECl8jI+Djbd1QmnMyW58ZGSsXOIgUBAfyk4rzzB6eqYy5emFh6FzFGNqkodo3xoZ4Rn1NVaIUYWZEi/S16cW9XmrYZa3M1QoUaMTa+vsOz9ishP9m6xSOU3MxtIZ1+uJjiskC+dW+dTvf5n3/9F3ufu9D/BaNle+8AqljUXMgkX3pMP7f/JDHr5zh3qzRSgltu3R7vVHnB0/pG272K7HuXyORRyswCXUBa1cf8RpM2fg6BVqNx+y9fEj9LxFgMTKW5gFi1K1SHmxjO/5NE+aeI4LCBbXFlA9n95Jm8rGEm67x2LJ4to3PkVxtYLbsXn43Q85urNNdXOZ6sU1zHIO1/Y4uLPN/ffusLpQxSznkbaPFEX292uYOYtyqX/RHprgsN4kL6CQz2EEkqbXv7XcKhega7PkadTUsH96lO+j6TqhDAl6PqGmoGsai0tVth0b3+mRU3WEqqDoGoqiIB2PQrHAw5/f4e533sdu2aAolJYXqW3vcrzlUC4V6TU6qIDi+my8cYHCQonGUQ0fKBYLnH3lAmc/dQm72SPUFFpPa5wcN+m0uxTzeYQiKOVzEIQ4vs9qpUyrZ6PrGoEMefXqy7z6O1/h/Dfe4P733+Po+ABPBpSXlqnv+SyVK6yuLmFIwf7RCZ1ul6JloGgKQknYGgme51Pfq9FutGg+PkAFzq+u0A19jKUq+WYXVQjKC2XKSyU826VQLWDkLTA18pbJSbNH66RF3tApbqxy+907nHn5DIqqJpzxlD4wYuUUHXpuUyJHNn18FPqQgX7fiaqbESdJ/BjFuMML/KYdtysTaaK0XoD6zr47I8rKKcBgMmpa0owBE4FIVuDMMAfGTWcmRX/Go0bwYBrES0sz8S6jXads4h/jzPEAbHYWs0ufJpPRx7GTkUU/xSmW44Gy6Ke0vbH/+tyI9PCCnIu03siUThQHmHLsiaSs+Uq4DInGi6ictNjpLEQc2slPE4h9JDQiHjHJ6DOFeK2JeE+al/ZwOYxIqwWYFOF45sMsxwA7jcv5FFGGJERmnpKuDaQeLheJJKKxB43Rd4TEeCnKnCyO/QWRrnCSHv9Mg/DMcw4vOIjECbSTXE0e1Tzue8k2mJAYOfklQfw0rL74ENEhaTI2ixU5Ub4J7zb11fhD2pbx9Nz6Mtg/WvjSF69Te3rI1g9usPXeffbu7dBxHFbOr/Lab36Wt//er3LlK6+yd/sp3eMWzaMGds+h1+oShCFXXj5H6Ho8uPWIE8VEV3OYuknXdpFSIoMAS9cIfB/Lsgg9H4IA1/Gh1aO7f8JhGPb3eQQhIRLTdbiDgqLrVColTMPg+OCY41aLarXM+WsXOffqeX7xg/eo11ts1Opotx6DgHwxT6GY5+ylsxwfHXPljSvUtg7pNjs4vk/j4BhV0yhaRQpCo10qEHg+ruuyaKiIANqACELQVTalie4I9qVHqIDn+lg5k8B3+0vEpKSQy7O5vsbhQY3Q85GajqJpaAroukHzqI5m6HTbPcJAcuHSWVRTRxUqZjGPJhRarQ6LpTwXXr1MZWMZ33aQioqh6+Qsi+WL6xzf3+Pk8QFuvUPbsTncr7G+XCUMQpq2QxCG+H6A5/k8frqLJgRBKFEUQWjmKWwuoeka/nYTWwYcPr7Luufy0kvXuPTyBfILJR68c5PjkzqlYp5gcMSSHI3sSmQgadea/PSf/hUPbtynlMujyb5jo2oKeAIfQalSpFzMo5s6dstGz5t0uy7dIEAN4d2ffMTO/hF+ELBQLfPy9cvsPNkl8AIURR2L64wONAGGp2KwcT+Z1ktGl8eIxPjOuAdFyCXxRiLzqBqfdxQ3C7FlGbfThH8dxiLTMez/k7nP8EXp6bnr7TSVkyJoMvo+9RzPbEqR48wmlm3P4VVlIa9ZqaZVS0xmxSBWH/hM9LsJ9v41zlgMwws5LSo2QzDDK5/YbSAiR8TRb9joiU8xZZKae8bbDHw+ISdi/GUIfdM9y6w+l8FbliOdHnt+nZXK/BAs9hXyafY8DTH/5CBVooPNYiVONuNdsrOfUtMmPSMZlb9TdOlp7r5gMEg/VlKjeMksntNQjOXpeQiNHavsek9/I2PP6eF0NTtHSAr6lO6TOTBA1se0WYmo1pGjFh25WVFnPpEyjUHBGPsk48rRxzSaCWd18EM1NN7+u9+gWCly65/9hGK1hGobsNvgW//wn7B+cZ3zr15kYWORK5+/hlayMIs5Qj8kDAI0XaN73KL8r35GffcYTVVpdjq89ZlXWFitsnXjEQubS9g9m91bT3A7Nq16B6dn47kuru+jaiqqohAEAZqioocSVVMQQmK3u7S8Jj3XZblURPg+D96/y8MP7yHDkNVCAek4tHv9/RXNRgvH81leXSJwHLY/fMC51y9jVS8jgYPbT3ly9zHNkxaOpqEi6fkBXtBl2+7v6SgIQWg7aIaOpahsGCahDw3bRTOs/syFHAD5MEBVVSzdwMiZhJ5PKCAQEi8I0PvIgU6nR7VYpFop0aq36Ha6BAIuXtqkflTHHJyKhZQIP6C2dYgfBKihoNVq8d53foGUknq9iaFphEFAPm/Qdlxsx+PSxbPkFQXN0Hm8vcdRo4lpmpy/sMH2012O2x2CMKS1dcTh00PKxQV6nTaOb7O2skjQden6dRrNNkJRsLs9rrx5Bb1gAWC3euze36W8UOQn//i77D/YodPtYTsuqlSwfY+lhQpmCE6jiy/g7tYeLpJOt4ciJWfPnWHz0iZ7j3Z5tLXL8tIiecPAyOl0bRfVEhztHLF+aSMOXtLAVZounOWMJFcxZEWLasbR3ovJEOuLo+417umnhlfzjkSkxZ1VKJH4G00TVRnJDcExW5QS5lHOkeSjGetnODnnmeHqnAlPZWdkWq0M7x6SM2fkh2xNuh8JuZHRuOlSlb6qZRbSS76dXUlyAIhfjNswh8f0nOGFzFzE+4tIfT98kXou9ahzidjqi1mZzV89Y6WWOdIixmA1I7txZJEtaLO5mPYuhYF5KEaq9LQcZavueIifdBABpcnbuE+V/9QMR7nFX6RwLBK5zu2ppWU77L0piZP4UI5SpDpPsfCc9mFa+ITuQurTzng/dvrHMiiHSw9mpI0QmBoyVbSM/E30xUnfZc7KiU77RAxEzBFJ42eGFzQEQDGtOPotQQpUVeHqV17nyTt3CY/b5DUFJWdwXi3TeHrE/aMWIpR4AhYvrfOl/+B3MQrWqGzlM0t8+X/528gg7NdHKFE0FSEEl77y2ijbMAgJ/QC36+B1HZxml4NHu8hAEjgemqkj/ZD6To2te1ucHNbp+Q45XcdUBG3b7h//KkMIIK/riMDH0DR000CTEqmpKAi8ZgtVhuzvOhw326yeWePM1bNsXD/HwvoiB493qdca1Gsn5A2d0HVoqBJkQFW3UBQFIwQhJYGQ2IaGrqmgCPxQInQVq5gj7PQQUqAKhXKhSMN1KWgGtu0hkXTCEEVKcqpOp9PBdlxk4GMKyFcrGHmLRr1FPmdx9s0rNPdPqP38iGa7A4qCYebICclJrY4nBSIMEUIiVIXDegdVEWxWKlRKeaoX1th67y5HJ3V0RWVlsUKxYCFdD8syKayUCXs+ruej6wamZvDS+iaLywu0j5vYts1xq0Uhb+F0ulz/2qf6y6IQhH6AqWts/eQWge2jDGZtfdfDl1BrBmjVAnsPtjA0DUUohEjKKwtohkrQtnn44Am1oxOKlsXq4gJ+GBCEPqaeY2dnj1/9O98g9IO0JfDjMOgMoQwRyRHUqI6LzC4/a4ie8JN6OEKEt2g3fOE7QKYZ1lMM5M36NvQjkmvx+78ymJhV0Cm8Zx5IM4GunwHRnnbc8NRGLMUYJxV0GpgbKuOR2RpfJzmBXBMDQVluwSj/1Pfjb6epwii14QDYafrSVB//Gfh5lvDiN3QPGk4k36XFewFZnSZmfB1/tIJThEnKOK4dAMlxVJH8eIowy4OajDn8NV1tDpmTowsFp8dNquO4QovmG5/Pmew4cXA9hnqTHIzfjLulGCPkNI80xnKkBkbFnXJrZ+T16TY5ZXsC0U2DUTk6PZj+BL2CSLafTC59ymOlHPn3BWQ6V/JEX4z2qqSETkrsIO7QKZpYXjGU6IFpzwQXMpkkxsnw/Vh9pFh7AWYlz1f+vW+y9dPbNHdr1J4e4nccQgSYJoaq0rMd2raLDCdPGxEKCDFYzqImshicGKdqKqqmopkGLBThzBKr185NVIoMQzzb5fjJAY9/eof6To32cYvmSQPP8VAQoGmsXD6HAHqdHq7nc3R0jIokDCWa2j/ZSpEBwnVp7R7y7tM9VlaXOPvyOc5ev8Bqs8vB9iEHT/bIF4vUOh2OWl20qoaFZCGvoxRNnOMWnhLi9RysvAqeB5qg23XQ9f5yJ0PX0BQVM5+j0+yf8iRF3xnwHQ/X7x+Tq0sfXRUEQYDb7XHvowdIz6N6cZNKtYzbttl7uk/JNNA1FSkEngwJDZ1CvsDG6iJWzuTo6R6N7j5F3aKctwi6Dr7vUzs8xnV9DEshX8hTr7fp2S4vXz1P88kRfqOHqikEvstiZQFLt+g0O9QaTQ6PT1A1ldALuPjKRdbfvDTSN3a9zQ//0Z/T2a2zfG6VxnEdTRGUjTx5y6SwXOH133obu/4GxeUKZt5EMTSMfP8krtrDfd779i94fHeLer1OsVhA1xQcz+Ph3j5vfOF1Vi5ucPB4n9JimfJyJV3eB3KliMipUjEklIg6a8RrChicGHiL2qfEXrjsbCLx0sep4iFLd6XxOUtJReNFnrOsv0h520/6HGBpQtWkAedEhmkEsuoqmfbUTtiMSoyO7ETznPB3hhhvArSREi22PFpMCG2M4sT7aATB+AjyIa6YjJrdfpmYJGKPTu+fz48vP8nwwp2LCadiljc5DDL2J/Eg+oB5qEgSF5ElweZ8fA6Zy0r0STZM3EeOA/O0mMPpvgHMz5S2CMQedL7sAYGs/JI9eXrnH98imckJKfAzkeekyzGGrpORY6028kkGAHDKCEhWtfWXW2adpDVfmB9Lx1yqRLlfvBvwrBRncTPRNjLiSspPoiRTmYGMvOPbkMYub2y0avQtw4ImlJogsjdseJrdKHVcsSd8gNiPvsxKhrfBljcXefUPvggS3I7N0a2n9BodtIJFYaGIYmgUVysYBXPS505cFBbLN/J+tLQ4Wd5oWlXBKFisXTtHaaXC4Z1t3I6DYRm0T9rcf+c2+0/32X26S3Ghwtmr5wg9n8bxCZffeoWXv/o6B/d36TQ67N58ggwCOrZHGAbsPN7m6OCYomly7qVzrFw9i1EpcPcXt8jnLKQQhAoEpkE9CDGaXTxD7y/3CQNax3XK1SpWMYc52EehmhpSCGzHwfV8pOeBrqMYGgSg6BpeGOCpCpqioYYSUxHoIsQPPUJdQ9U0jvdq7DzaRtEUuo7L619/i8cfP6B5eIJimFx85SKu47L1YIvaSYPA91HU/qwCon9JYaFSRK03UBWF/doJjXoTzdBBKPzkn34fQ9VwPY+CmcNBsr+/j2/kaHS7LC1UcNs9NFPjM3/ra+i5/ilRneMWf/6f/gnClSwuVmjt1OjZDksLFc4sLXD9N99m/a0r5BZKfXkfCL3bc6jvHlNaKrN95ymf+ebn+fzvf4XdB9scPj2k3myytLnMy29fp7xQZuv2E5Y2l/FcL1UuYiEN8KV2vBnhFGqv382TkQfgTI77s4jmP1QL0e6RxXeyv8xyjIZhHockxlyEcFbZBzQn9ce0kGA4jf8XqZhnlTnlnYw+zeIlOTIzB0NjUyAn6m4CdaW122CKLCZDMYY+KVw4H+353IZZX8eo8nkwz6zw/M5FmuAknL2YzkkMJCSLlQo9E1Iy6cnP0FCZdZfo4GLyU1rUuFvyfL11ChSOMRZlZxK+ZGuoIZBKxpo1GjIJ7hPDLzF6KSgmQQsiTmHahTgJzT9ZomhdpEjOXEYqg78Za/Gypmzjb+e1kjLxNEw3XRIm8xvXxCftlKT2YyAxFTj680mp3+wQr8nYl5jw9w1HsjnT0o2cVZJYI6rwxj1kNHVNXILlQNGJqHxHCPd9i8jcy2B5plXKcfbtl4Z+x4T+SZZ+8jLLlIjDeFGvaojKUrqAEIL8coU1TcNt9zBLOaxqgau/8gZ7t59y8wcfsHNni+ZP6xTLRWQQsPXRQ9qNDlYpR75cYP2Vs5iWgZCCg0d77D/cQfd9eqrCxx/do1QpQRjiegFLpQKhDHElFHIGPdelIBUC1yfnezR1gSIEQgWna+P1HAIpUYXADXw0TSPsBDS7XXxdY7FcQIY9HMcDVYAf0NQkplAp6BplTcdzPISmcbx9gBcEKKEPEhY3VnB7Dn7bJhSCq69exnVdbr5/CwU4t7HCztYetUaT9UoFTdcI2jadVgfD1NELOWQQUCxYeIHk8dNdPClxlQBdSpRcgY1ikZ7r0em2WSxXCPwAxVD58r/1a6xePzdqkuZOjePtI9YWKzRliBcE5HWDly6f462//xuUz6+M+qOUkuMnB9z76U1u/+RjQiH4tf/VN/nT/+xPKFg5qstlzr15lfOfvsJb51Y4c/Usqq5S3z2htV/n1S+9RuAHY+nNulUrQ+XMA1gm+1va2TeTiYYiGx1LSLIzEuPhOiox7psTDodM4TLddxkznixI2nNa3cRAbhriTQAjGXk/7OAzQ4pNTIuSBgimhojWyWLjVCZoDscim4OMCBEDlGRpkDhuswSpA5FT61kkoiR/nz4M9XGyfKNl5lmX/z1HnsNlxJ+0nX4BMxfjaklldtioKRUjmHw3V5hQdCnIJpJHqhxnIbZkSCzXGZb0lw+gkjwMQwIVxAB8xAufSJckPf46fdX85LvkieOTHCYPBX4WMJyhyWP2IoXzudp5ztZMHl0S09LPCvDT6nPyV9oszi/rnKpMKZARICGgv2Ttl8PTzGwymjRVP8tJPTE8qnhiZm4gA1EwN3rNpOMyzSkYJhz6tnL4HNlDJAAUEf+dJDHwV6bX/biEMZ9w4p6UeE0IAbmFArmF4iidtVDg4hde4dxnLlN7vM/evR327j7FWsjTPGrQbXYQAup7x4iuS6vRwpeg6hqGpuF5IZoJlqGB4+IEAdVSHlVR+vtCHJdus42uKNi6jiIlS6aFpwt8U2KfNPAMk0KlQN6ykLaH6/q4nku93ugfQQu02h10TcM0DUIpkTLAdn1US8XWFPYDn3VdAyHIyxC1YOI7Ai+UYGocbB/Q7nZZv3QG1TL4+J2PyVkmeUPDWC2x6Di4e/3jdTVD4+nDbXo9m4JpYkgQikLbtnE9D02CIgb7RUyDi9cucf2rr/Mn//D/S8FaBD+gsFDk83/4dc58+jLd4zaoCr16i/L6AqVykS4QOC7NZosrZzd4/Q++QvncyqAdIfR87v/4Y370Jz/kpNGCQLK6WKJQyHHt1St0ujZHu4eEHz7gYGuPg71DfvePfo9XPn+dynqVr/zh17FKucFeiqF8RI7CzBLAiIjNs1E4TeOlp4rIbMq78eOkkh/qp3HCSe87tq8kzUjGvBgx38jJM6q/GOlnBkZzhii+Jt79J4+pn8OxiH4bmcT0YZDRp9OyfKpqiLZZgo+UkaXJCwunZxbfVzxPx5gRpiSNXig5wtKZfA37SprzmnyVGLH6BMKLWRaVVuKkFT9N3ae1l0yLkJX5OFocGKTEmcnX9AhJt2ryEMwZLZd0BiKUTheyh1wmHKxIlqMzslKHcWblEac9XfBTIrxAvTkEe+PMJpUIKa/nspkRuumt0q8FMXh83g3WcXU4j0V77kxeDD1grG4/QSdjgm8xbvOpZYo7P1G7M4/djCOQjL4wwwCMqETt3bSPybwFo5mM+DHMUUc3kS6JWpLreWXfsZkAUwnu5CD+8ItmaKxePcPqlU3e+K3PIcMQ33Zxujb7j/f56Lvvsn9wjCrAzOVwXY+O72FKSaPpo2salZyFqakIS6dl9/BDiaGpmLpGgKCnCAqVPGqjw4Kmo5RKPLYdXNvG813aqobTs5ECvJ6DkP17KaxSHjcI8MIQ13VRdBVNV9GBUPY3hHc9h11Fcl4xKOkGXSlQLBOkpHvSwu10yS1UWL1yhq0bjwhcB0yVtuthdF023rhEp9klnzNxOj32do8oFfKcNFpsrC2z+fpl6od1jFKO3EIBs5hDz5voloFAcPsv32H36JDzZomWsPnqv/tbrL16AbfjIIOQJz/4iHf//Kf8+j/4A9RyjtxSmdr9HVTg0hevsfjymX6rhP2N3R9+6+f84l/9jEBVWFleQNc0VAFbNx9TubgC2ye4XYflc8scHZ8QIGnVmvRaPfKlHFY5H3EqUnRQVCyT4pEGzlOSp2qFzA4TiT2awhskiK6DisYZ9YcUhZ+Vz9T3p1CSUYCeBlqnhLnjZlbiFJ6mgdcUWpm3J6SPP6TkKTOzfdZ9233bOx7USSMmB1MAIzbF0BIN96AO3w//JuicxoMZDQg9rxmd3vKnutg4nUA0q8G7TxxdAC/AuZD0R9vS9gGk+gNi8uvplneMY87cnBRJkW6uxz5cJswU0/mamHJN8Dl/mIwfl4vI8qZ5LgSag5PR6M5zhdNqbDkRS0Y/iZT3pwinBban6lgTTA1dy/Ea/tMwnek7J8JzzVBEgGjMVr4gjTLRa0Z7o8aVJTOPZ50MMx3UaMSk4pSTdRqjF7GkSWc3u46jVCa9yygbMhpFTMYZSYuIUczye0cu68SEmYjkETmhS45SwXgP0WRp+t8jRCNYLRZTDNsxyVc/wbClR06HUNDzJqqhcz5ncvH1S+zf2+bHf/xXHD85IJT0lx4JgQxC2p6N0PW+8+F5VKslgp6LnrcoVIuEUuDbDu2eQxlB3g8JVRXDNOj5Pr4f9GdJFIHbtdENnXK5hG4ZGJaJ3+6hKAKEwHVcfEUl9HwUVUXp9o+m9RyXI9/jfKGA1XMJTA3f95BBgEQSeC53f3YT13EpVEtYuoHvepzUmrz8q59m6xf30Ep5br1/G6kIWq7L2vkNrEqBh/eeIEKJaLZwH7qEXtg/JjcIaNcaiDBkfXGFymKV1778BmfeuoJA4PsBD779Lj/5sx8hLJ2dG4+wKjmWL66y+3ALNMHG2y+j6ioSCP2A+tMjPvizn9Jqdjh3bpOtvQMMXcNzfYyfWVTPLPHg8QGHJye0Ol2qlRJvvHGNi69e4uDhHhffvBSHlCI63zz0QCPydZowxHBRWqdLSqIHjdlJU7rRd1FsNg+SivozQwmft8iptkvGTrqa5ySrqSdRPpcpiNCdqLdh3WbkG1diM4OIykxUfIaZR52ACT4jOjFSdyIZaRBh/BjHhvFJizEjqbU7b7kizMT07QsMw4He0aXBMl0Okz7RrGWFzyM7zxJe4LIomTCAKR5vLETAR9qnrHfJadcRYkrJJAo4RCxBXJGSEPzMkLDA8fUFk8SmtPVI7lOqKcnb8CmOC59DqDOTithTrHXSPOCUn5MtkUg/pVePzl7KsmNz1Gu0bqaC8vnx7gwCae/nIxo1l5Pf5qExR15JxXwKAzFPiM0FJAWaIYCdH1ZMfI/tyxHxCDFjEo06LmSMNzlZ9OliEFnmlHQWksY5ZsnGAjxW/DHUMjKAQ/wuUzaU90nIGJ0J3odVPFpSlSxZWpoUeRvZrozFVRG6qUv0QsnBnac8+NFNmrUG3lGDtQtrtLSQz//Nr3Jwe5s7P7yBIgS9Tpe241LKWzieR97Q8X2fRsdBNQ3wfJx6G9000BUFaWggFQwp6TU7WKbJSbu/9EoRAtM0yZkmoZQYpkG+nMcLAoQCqlAIwgAhQRUC1dCxHRfFFij5fiVrhk5TV6i4KouaDkh6UhKqCnbPRslbFPMmtcMOJ10XEYZITcEsWlTPLNNodTCqRUqLRY73apSqJW58fJ+Nl89xsn2I0FV81+8fq+v6oPblqtfpQEHnzd/8HC99+TWEELS3j7n5Zz+h5tkctptsXrjEnZ/fZOmlMzQP6qiahlqwMEv5AZgSKJrK1rt3qR0ek7NyBN0eeD6251HKF1BVDWyfiy+d5/rKGyyfW6G0WkEK+vtZivmUpk5qppTem+YZT9UtGRpgTns5Xx5p2WZjkfHBDHEWk3rjtHmOljqOso/2rhTckGbpn0FPj6kN8kmjMeIt0sZZtnbit5zEYBMhgQdTAF5/2WkK/hvWf5SpNLCUTADx5XvR6MNGEPQJJ9tTiFiSSQkVmVX5osLEXqUhj2JQrpTcT70NJ6WNP8kyvbDToiYHwCOdJm3ubSJudjFlIs6wqlMgxDycTvgISUwgEu2bekDFQNiG8tw/HnL+psoS55gsZCnTadkk0szUi7HlWPO5WNNDZN9DGv+xd/HdGvPd6zMYCZra2+dwKtJ+ZyWLVOJwDX6czMAcRCxSetMl63dsRIQ8vTsRn++bAt2fvTHjNFLqeyw5MmZQ0zh6JjYSmzCT37LPR09DEXK0eXrIW1+W4nHHfA9nBMYGSUxGGvOZdDgmqEbipcpu3IOZiCJSHgd9YbgUY2pI43n4KrIOJtmO8TyT2rgf9m9t8Rf/2T9H+gFm0cI7btFp9qhUinQvnPDS19/AKOW49f33cWsuZcukVC5z0mjgdDqYWn/vw/LFDfbvPcXzemg9m2K5hFAUHEsh6DhowGqpQP2kScO1MQ0DJZCgKnihjwh8ej0Hx3HQcgae7RG4Pqqh4Tguy2tL+Ps1UKEduniBR0lVsbs9Fq08iqEhVImWNzAcg0atzmf/4Mvs3nhM9fo5Du/t0jo8wQ88QLB+9QzbHzxELRiULqxSqzc5sttUNpa49PIFlo0cajmHYeo0Hx3gD2Zugp7DceBz7te+iKZpvPvPf8Tn//BXuPcvf8a9D++jlXNce/kqgRtyctLBvr1FdXkBv9bh0rWLmKUcQukfB9s9bnH/p7foeS6LiwuQ11kIShQWF8hrOjKUfPyzj/GQ5A4KdH2H87qC3e0iWza5lSqaAssX1xOAbPAnCe6yOnVcOaWEKY5FmlBNpIgwdaowGK1O4UlMPDDue1mb2ScoQ3x9jIj0pSkGZy5YdDqPSqQ8jd9EyiPHpn/o/EgZ9vNUBJO6gtGyo+cCpCn+aYzHkUER6YdURPgZ6+T4INDE8IiIxIti0YS8JVemR/fbpZV5AqsPL+97phoanzooYs7ObIQ7mumYAK4zs3wx2CAjvJDToqSYNtknJx+nKJ44/EqUfsLTnTTUM8H0jDDp6EXLNqlsRv5mWqbz6IWoUYfYjaSjckom6jfqBE0Ls6PMKV0ZgpgFiVOBUWZWKR8ye7OY7auOzpsee5FpQGkqFpzCS/IS1UkRTzsxZRLAZnxK5zMzqphetWlsnM5ezYg7rIxhb5HToz9riHbBmAGIRxmeXR41PuPyJhT1PL6YSPS8gQXqLyOKuCETtDJqQI77+TQbINI6eOI+l2gRM0OSxkSGQ6cwQjsVU4313BhwDttaYNfbOJ0eqoT1q2c56Lg4jkuv3ePJdz7EPWxRPbPEr/2D3+PJB/e5/YOPOD6qUchZqJZFdXWBJ3efsNSzyS9V6OwdkbM0XAUKikogJb6lkZeCcjHPK5trHDpdDo6b4HgUNR0pJGbOJFcpEhz5GLpOebmC67kUKgW8nofjuaiWztnrF+jWW/iEdPMahGDrKqam4rsOxdVF9g6P+c1/8PusX9lk7fIGd358A6OSo6iEHJ+ckKsU6LV6ON0e5z/7MuViiUapjCzobG5UONk7IVfM4bsBu0+PONo7xPY8ioMN3yf1E8Tdp+QMC9UL2P3wIbc+vk8QhChdj04O8ENKlSIBErfWRlEVzn/qSv+uEkCGIVvv32fv6JhCPo+RN3CC/kV4ruPSrrdottt0Gw3y5RL1gxPq9RYP3rvPH/xHf5Pjp0cc7x2j5HSWL66RbPlRj4no0QndGQXS83T8CSIpHsUUfXMaTBQ/HW0e1sYynQawx7HEOB5TMFBWJ5VM9OUMhlLyT48zG4cl7i+PtGkYBLiuSyjBNHVURY2nzsbkg++Denueo5NSaKdTG8eamEGOjvJHiA0x/1BGx44AEYdg5GnNyD8jvEiv6zSkh0WOm+Ix2SRM/gQdimh4fucixnHcKkUvGUsNKSAnRa1NZicga5h7ZvuexhUdvpzaqeVkg4ro97gi7stugomh7k6uCY9lFQdtk+B1WhmSRCfbKjPu7J6eEjJGUkf6Ogt6R7T5NIMQka9x2lSIFi/moCEi5mNyJGPeMMNgxW1CtF2zCxWBqrE3KXZpREtMvP2EQ0q5x2MusZfj+JFXGa0UIz2zJLFIwz6UcGpiRxOKESCeVBsp7R+RmajxEhObH8bpxiwNnyIVFV04PNGxskqb1rfjp62M5SBL10bvAIqAiZjMi7GTIOOSmsVLrPoH9WOW8kjPR9V1FKFw9VOvcLRf4+DxLmEXjv/qA1QJZz91lbXr5/id//D3qW0f8eGf/jX1kybn3rjIGfU82w+ecv7qeTqKgmaZ/RmHUKKF4Fk6vmrgtXqohsq6UeT1X/0MH793i9qjA1bLZbo9h+W1BVr1Bq1eh9WXNmm323RbHTYub7Jz5ymKqVFeKpOzDLp3tyiVizjdXr+UiiBnGRiWwcqFdaprCzx45w5u26Zba7F1/ynnlpdQQoXWUYObP7uJ7gXUHh1QeiWH6obU9vapa4dYORNh95cn2Z6LqvT3pCgoPHryhE6rxutnv8bJw32crsPDGw8w8znyRYWN6+fZvvMUN/RYqJbZPTyi221z7c2XOPu5l0eN4Nset7//PoEfUq6UaLTaOLaHoqqYjksoJUoY4vo+K5bFZs7kvt1jf2sHu2tz9QvX6bQ7KKqa6CMyIqrx9s/unxHZztKPMvNH/FUGNphHy6XCw3ltVzTfqJAnTsyKwp5T74kbYoG5SjQH4wl7OJGXiESaNtMrFJAhowFPOXSj+joirh9S2BgZ2ZRT80aR5OhPhs8VKdMU7BURlHGzJHBFLG0Sm0YoDXTYEE086+zD854h+qypo45iagPJcXXOdW7PCwov7p6LSaTI7CHm2SG6pjvVKY56nRl89ZXmQOhHkGwKOkykjXsJURgxXiITpzbSHtE/CaZl4jH5OyOMOn0W7elBIkdLQZ53lKGff5bCSQNPk/nJWGGGIG6SVqrOj1BJD9mnVsR5irfXVJJZJAZp4u7AWHrGau80LRd3m5JlH13mNg+vyYpIIvrThih2HvwbZWN0zHzCX5zFWmqcYf/Iktdhvxz1o3i9IcPB1LEyyiwqtzIeOcLvGHhHyzQM0apPgvKR2yvF4Ne4hFFHLCkrcaOX3kfHa4vHcjuasRnSmZj1iNTJsA4iwChRY4kQLd3gAI9hSgFIwcL5FdbOr7O4tkTl4ip3/vI9Xv/GW+QKOe5+cAdDV1ELOe68e5t7793BKJh84d/8NX7tP/7b/Pgf/SUP3rvDl/7t30D/2W0O9o4oLRbJWwaqUHEMiesGVKsl8qqGIqEcBPRMhTt/+j2u/drb7BWLaAsFPv7eu/TaHYySRdCReK5LoVwg8HyK5QJ63sTzfJ7e3mL9/Do5w0C2enTrLTrFEtg+hD61m09ohCF7N7fAdpGeR6PnUirmaZ+0KZg5mjvHaELg+T66qhK6Ppqh4gcBuhB4no8kxLJMVs6u8uT2I4pGkTPnN9h++hhN1bAME++kzX6zxeWLq6h5i7Vzq7zxN75I57/5Do9vPcZ2PSrFAtZKlS/90TexKoVRm25/+IDt+zvohoY3aIucaVKoltjbOyRwPcrlIvlCnuNaHWOxQrPZYnlhgeZBg737O7SaHRY3l1C16yyuLUQlLVNtDAVptGQwKn6j48ySgpsUqYgCybTtyVdpGjYZSUz+nFOfxzc8J+ilo9bpemlE7tkvLBsNhz3L0UQTrEZeRMqoqCq6BFDQ1D4s7I87RPIUk3AlSjd91nqKgUlZShqto+yN7YK4UxHnLx4vI/tpBxANnY3YMbCf7PUDWdRH+EicznnJqrtflmMBL+K0qJGXGzfEAiZujY0nPE0mkWeR+JDId/wljmjiJlSOBWhgZbNBzfSXYvAqLqvzNGEcpZx2p/+sHLL06bC8M+v/lymFifxk8iFjRme2CCWXtAwTjkHZeEnIfBSTvE68n2B+/EskuB8q0rSlLmncpP6WZJ4mEcl4ksfh+2SaWc6GSPydKwxKOjwaMKWap9b8UL9MCVKGxKCHDKk9PuDeL+5S2z6kkLd487ffZu/OFksX1li5uI5EcrJ/gtdxcXoOuXIeGYQcbR1SXCiyfH4FzdDRTR1FVfv8R3TaZLtJZDjQh6lOgxw7DInDIOSA+zH59EoayVF0JiJD5tLrMf44mvGYeWpcxOwP/oma+Fy1wK//7/4NzGIO33Z58sEDtm8/4eUvvoaua2zd2yK3USU0NRQnxBchP/0fv8+X/p1fxyha6DmDfLXApbdfof7nP8VRQoqqhizn2Nneg65HfmOBoN5DWBo5L0RDoZwvYu/WWaiUkZrC2uoKfr2H6oaojqR2f5/AC/oX/N18itOwUTUV6YU09k/QhMbBUZ2CopFTdRQ/xDBMPNdDCSV5KXABqeu4XYeLa0s8ureFFRrogWBjeYm9vQO6rS6dkxZSERQXSlTzeY7qTfwwZPHMEodP9ymWipw7t0G5WubM+gb377a5/4ub1Ls98uUijaMmxVyeS5+5SmfvBEVRyOUtjo9POHf1PJuvnOk7FoPGczo2d378MaqpY5XzhF2HvGGy32pzeWOVsmkhVAWpKDx8sIWuwVG9RTGXY311ie/9j9+h3ehvnDcMg9vv3+Vv/2//kGK1GEPkMrL3YBLUJ53vKGCMClzfAw79EEVTGHrEI3WTBuaT6FEMM5khrslRgNOG0ySdhvdFHBymq9bpCvg0MOnUIQZBBJo2hoOxQb9huw6fM8mlfJkodESWJo4wHCcBZgx+iiFjJNe9jfdfxJd/nRbTRPfzRe1yWoudlvy8y8jidj0i1zNVfXpbxHjNAokvKLywDd3JssjBCEbc851cPjE6Zz1GIzrykVBjE5UhY8BjjEMm1WC0yqMrnserOIcCO06a4Da7QbJAWaZjNCUkQapk1Ilih+dMIZgqM6PiTdOIU4idwoEaV2FScUy2x3wbuZ8hZLRJ6iUzyUWlJJTLvMZqSodNf53uOGVGSyvPNN5SnIGpRx0+Y1uI5FPsTPphvsPv6Up7zgxSEkqGMxGS/ok89358k5vf/wg/DHj9a2+w8co5vJ7D9t1tbvzoJq997Q3OvHKOd//0J3iNHpoQVDYXWb92lgff/RAf+stZfI/P/NZnyZXzXP3MS6iamvD+xtzv393h9vc/RFUV8stlqmuL5Mt5qmeXMfMmTtfmp//dd1EUlfLaAle/dB2hClRNQzP1frsoyf4Sb9+xuMpxhEQNTjRhRB+O+5uMH3E7AQqjdIebYcUo6pCH8WZyQWGpDEhUXeXsa+d59M4d6sd1Nl45jyogWCrQqtXRDZ2cpdM+btBut3l67ym6Lzneq0EAG5fPsHPnMV5VxfddpO1x9eWL1PbrlCwTzXZRFA3TCbA8SfvBNqGZR9F1FkKN0DRYUnR2GzbtdpdO4GGVC1h5i/r+McXSApXFMp7nEyJxXY/zpQLSC/F6PWTewrFd2n6AF0jwA+rdLkIoNOttdFNnYWWBsG1zfNyAnEGn0+HmB8dsLi/x8ssXEQI812Nvv83ju49RQskrb7yMIQSN/WNarTZ5y2LvYI9ceQktZxLaHh3R48YPPuD8tYvUD0/6cuO4dDpdNt64NGqW2uMDfvLff4f2cZvKUgVFChrdFo6uYekqQej35SkI2dvexw18iuUSmqZiS8nB0TELuRyvLVVQnB7u8iq7rQ5Pbj7m1S+9NhaMkZMxcHljjuxk743JZUQQPduhtlMj8AOWz65g5k2gf4yuMpT5wQZ1EXUOonor1u9mhRSFOYEKnxF1pmU10nHRfjl+/0zj3hG6z8xhFi6ZiCaTL6b/npnp5O/xmF5kECUFpk29UjEiGyLFsRhFHNCUsQHvSb02b4jvkJvtIr6oMDEbNFd7Zt94n4SWn2R4Ic5F2kzbwH71NxlFJGmaB0jK+1nlT6/AyJRZBvCKbtIem91E7s/AYJpL83wh6ghMm+iaM8dT9YJpkpy9e2D21yRDGbzPJBEve2rHSSvCBN0p+T9DQ4oBgksq7DG5KXxnEp0nwnzMvojlcMkQu7U0ZjUi+SJioyf9dJkEp4ne4G/UaPUJ+z2H9//FT+g2e1z/+htUVips33zEj/6rv6DXtemedFBCUCXsfPyYvVvbaKrAdz1quzUUQ6VYKVCvNVG8gBwKvaMW7/3Fz3F7Llc/fQWzkENRxAiL90/blXg9l8ZWDadn4wF6OUe71qS6UOarf//XKK9WCXoO9ZuPOVpcxJeS/Ye7dA8aVNer+JqgsrHAZ3/jbTRTj2nL0X0XgzxHTSiI3COSqLPU43HkQDYHtAeyOl5iJ6akHw/6JF3imE4XAqEqKDmdg6f7lF69yuLFTUTZ4MnPbuMGLgJY2Vyjef+Qgm4Shj6H93YIbI9P/e4X6ezXeXjzET3PQ0OhuFwmCCUPPn7Euc1FXMemXC5AADnTJMiZyI5NKAQiCMhtLmPqCr3DJp0g4IHdxTV1KstVUAWdVhfXdlACWMgX0BQFXYZoOZNGp4frepw9twkSjg+P0DQVTddpNVo4PZvV82vUdo6QSFSU/kV2nk+70UIvmBw93qfT6qDKkFK+wMbaMroQNE6a3Lv3mEa9CQhkEGAYOt12l6VqmV7PoeX6fPD0HVwp0S2d9fUVqpdWWbywBgK8nssP/ptv0zmoIxVBu93GbXbxfI+SUWFxeZHqcola4NE9aOL7HoVqgeNmi4IULFTLqIUcmutSc3wM3SRstGg0W2ialm2f05SrHJ/AFvgBJzvH3P35XRqHdRbWFnjpsy+xsLHIkw8f8b3//rs4XZvNyxv8zj/4fcy8iRCCg8cH/VmbhSL5cp7KavW5wFrU334mVZdUSrP0UCI/GY7TTb+xPK2mxfhLbEXGKQoiEz9Ou5wqTSmnwIzRIFViIb+MxWCkZuJ5JADw3HAhTafFfwxrMHt/3bNLVxqCTaM2a2ZibhsswbVdDMs4hd3OWLEx/Jmshk/IyXhu56J/fPDQWMG4l5FQRhHwARP9KV7+scAJGd0ueorKHXo3UZ5mpc+INjxPfPos3UikJ/iYXHQ1ro/x8tQEOEzLKzP/LOmI7zlIjjVlTmNm5ZX4NuegSCLMKtizS3p2ylmcCmJLxYbi94zXb0ZHaNK5m+TnGf2YFxOSggHPNxSTlJOotZ83TCi+9DYcAvs+/xKn52K7Hpuvn+fxz+9wrGj4jTbVXIH19RUO723TcVw0Kdi7uUXZNPsgU1WxNJ0b3/uQSrmEFoRIqdJybD78/kesrC7y4bfe5f7P7/D273yBjZfPDC5oG/NRWilTvbLCzvuPwfNYWypSWChw/95TfvYvfsxv/4e/x8tff5P3TzpUVpdoPD6ialr49jG1u7vIkkmxESYSwgABAABJREFUmOPk8SF3f/wx1ZUKZ9+8TGG1OpjZ6BvyMAhRVDVeT8OKkvRv26Y/yDKKNGrf+HKmpKkcD8pMaZSYrIjBcrH+Kzn8HQiUlsfxwS5XXr1KbqmMampcvHKB7QfbeLbDo1tHLLXanHvpAqEAa7GIIqGwWOKtv/VVwv/++3TaPXZ3Dnjw0QM+97/4Ig9uPKRR71DIm+xs75NTFBYcQflMDtdSURD4PR/nqEl+scri+gJH9/dpuR4NxyMMQoIwpFtvIwUUdBNT1QiCEE8E4Pp0bYdQCkrLVe5/cA9FhXyxgAwl3V4HPwwxTYPHhyf4YcBiqUin2SZnGDi+j1dvUz9pohg6JgWq1QoiDNl5usfT/SMIQ4rFIgd7OyyaixRMk56ESy9f4P69J7QaTTrNDq++9SqPbj+Grscrv/I6Qu07dgc3n1ARKlo+R8d1cTs2vu9zdnOdc1fPs3L9HDKQXP7S6yiaysN37uA4Ljd/coOTozqdoxMMz8GudxCqgmWaBDLklc9f58LrlyItnXbsdrTzDSRASpoHDX7xL9/h4cePKZoGRcvkzq1tbv7gBpc/fZnP//6X+Prvf5WtDx5xvHuI0+5h5k0a+3X+9B/+U9bOrLJ0ZZ3D+zv87n/0+xiWwcRZpLOUZDrKGwvzRNr5Ad789nioE6JLVdMIzLYH/fpPMD2P0Y2ZnfltmITsbbJJNiLTSCPzMazqRNzhYFsU5YxZmh/wp7KWsbcsqedeTHg2xPO8wbCMSTamhoTenxUt9uLFle8FnBYliDsOEemam89ZLlTcu81YqpcIM1pgXu9NZoDwOfNLf5voWjN79bM2eJzz4fP8R2fH630+5TwELcMRzbFbmLIFa/xNpsvMNJWczm/coRxX7fQON3nUr4yTO0UQ0YfEtG2aCZGRf6eGF9T3J5zl5N9T55vh+j+rXk+3IhNvwiDsAyvPp7FTwyxY5CoF3vrdLxD6ATf+2U+QqHhdm0DvwZMD7J6D4/s8+M6H7G4f4AchxZzF4lKVrudRzeVwWh06g026hlA4Oqqh+CFSEfhthz/5v/wxb/7qp/nc734es2D1uRNQWq7yxb/9DW6vfMD3/utvgeuxvlRGRSI6Hq2dYyprVQLf49H798nrOp1ul1qzRS5v8dt/7w8I3YA/+7/+E6QXopsmH37rPcrrVT7ze19k4/p5UASKqjBqlCjIT62+VGGPjyZGVfac8jVeUhXd2N3/HQaSgyf7aJrKSa3OydYB5754jdDxqO0dsrd3gGEaXDy3wUGjye13buJ5LptXzrN2eZOTR4eUNqp84W9/ne13H3BSq+N3XDRL59y18zz86CGtnoOhKFRLBRxF0H14gJ7XKLx5ifaTI9yDJsFhiFwtsfb6Bfyfu5h+wJH0aHa7+GGArqgIKTFUBUtT0A0DiaBr9xC6xslRHdu2MXImiqlQ2ztGCUJWVpdwbZfmSQOzkOPMpQ1u/uImpqHR6NocHDcQApq9LkXTYL9WBz+gFwZYxTxuo0WvZ2MBpdICiq6yubwOpo7re3TbXS6c2aB90gZVIBRYffksAHajy0f/9K95cP8pasFCzRuYukaz1WbvqIbd7tHtOewfHlGrnXDp6gW+/kffJF8p8ObvvE230cHp2IShpHPU6G90XypTWC4TKgJVU+O9OboMJSJbMhzscRLQ2G/w3f/qL9l/tMvGygJlzUDRVcxigVarw8ff+4DiYom3fudtLn7uKvWdE8orFUBycH8XAonasSEIuP/hPfbvbnPujUsJvTMc/EmCSRjumUwbDJKjMvR7yOTZQtOEnGfT/1FwMhyhn4UzUj6LxPtsfhNDiM84KHaaso5nUfuDCSO5iNGIHHkjiMzifHLDaPGBktn5RI+hnX8MbFblDjeDz0NrRk6RTeXJ5czxcy+H7+J8zI9fX3x4AcuiUjbDJr1cweTdAPEY0z5OfBmKQkyZTODWNFgd5S0jz2SPHj0OANks5mKkM6QrS4OkhukRZnfX+UcGZkYTcX2b1i6THGWNysyHlLPLlVHxUcCTSkMS35cboTOyB1Nqc56NWKmfZpV1Dkv2AnVE1klEkxFnR0nbDp8cbphf3WfxkHA+Zd+Q3fvRDe7+5bsoboAnBF3bxrAMFs+v8sZvvc3973xANwwJOz18z8cs5JCOS+2oQalcwgLUMORg/xChaTiej26ZqFIQeD4t2+bC5gb5Qo79ozqdbg89CPnRP/krWod1fuOPvolm6IBAUQWKpvDSl1/l6bv3uP3eHRw/pFwscOvnN9l5ssMf/B//LXxFJeza7Nl16p0ulq7y6a9/EQOFP/9//TP2T+q8dHYDDYljexzf3+Uv/m9/yrWvv8Hrv/M5cpViXGwHhj5W/1nLBwZdZLxBM3JR4LiyU4IY5yWT72XiCSzDoKNraIbO4aNdLnz1NWQgWT63zpMH21R0HUURrK4toUpo1eo8vfWIh7cecvneBc69dpkzn71KdXOJq9cv47s+vhvwqd/+LMsby+zf32Fv9wjX0DA9n66U5GodGu/cp/yZy4ggJGj1sA8b+MdNls+voOw26PZC9EKJhtND1zXybsB6uQiKQk6odP2AXLmA33PY39plcXMFS9Oo1Y5ZKuaRmsaZs+vsbh+g5k0WKiUC36fTs+n0YDGXY/38GkeP9tg/rtNRPArFHGoIqgxp1hqIIES6Lmapip63CAPJ5uuXqO/0b/NeW1li6fw6d2/dRzd0zr1yjuJaFSQc3nrCzpNdXBlQNnVkz8PSdDYqZWxgeWOVnYc71Go1QkWwe/sJD//qYy5++RpmwSK/UOwvuRs2fzjY5zNo2PGenzhgjALInbs73PnZbYoLBT7z62+x9cFDHtx4wMvnN9A6Dodeh0KpiKYqEPiUNY27P7/L69/4FEbOoHpmcUBX0j1ps7CxiIWCEoCRt3h6+ylnX7/EcDbZdzz2H+1TrBaorC0kgLpgeOHa/GFOuPVCMHDKEpU0J2kiVZ+BYd9MhTXDEPMtxPhd2vepIXutfhqHQ1w+FZSnwLDYMMicvGWdAp6dXZqdjmQWyzNCOEsNjn3sucMnsPo4jr1OCe1+2eHF3dA9+Df7xIBxwyZh1LAjyWSaeISUj3LUmZLT/BPAMcGnlBIlea5kVhCn8P5SOkB8U86LlYRYx05VPCmdKVbsMdSfR5tOixGfmYj2UhlLPNxkNbFsI5FJclY8mdvEMbiDUaKpG5aZXWfxI+gi70dcy3QllKYoB4VI5SkqrM9syNL71MxUp9mgPiOk5TuuijmtR7Lzx+olIikRcgd3trj5T/6a1kmdM2trWJqOIUKaTZu7P71N0HU59+p5gptPaOweoxk6QRCQ13UqlSIhErvVoe0HuJ6HJfqn87iuh+u6rFVK2D2H2nGDXrtLTtcJvIBe12a1WuH2z25x4bVLXPva64MJ3D5jZsniG/+b30P8P/4599+9x+r6MiuLVba397n/Vx9x7voFfnDjIXa3h6FqlHM51l85x/0f3mC/doIE8s0T9oRO0/FYLhRo2S4/+dMfsn9nm6//+9+kvL6QPpCSNIJpIwCyrzejR1k8D5ISkT4hpMAPfDr1Fq16i0BKcsU8br2LVrTYePMSlw9O2Lr9EKtlEKjgqCpGTudscY32SYuP379Nba+GWbKwinkuvX6JnRtPaGzVqH7+KsXlMj/6lz/E0FTQFui5IbgOPd+n3Ag5+eubsFLBCEG1DMJOl1ATlPIGq2HAbq9D2TAwDZ3rG4sYORO8gLDrgAyxciaqpqCbBp1mh4NWh4VSrr8HQtc52K/RbrdRgMWVBQ62D/v3Sug66xc28dyAjusTOh5CVen2bKQfkM9ZmIpCU8AbX/0su4/32Xm6xdtf+yKGqfP03hZrL51hZXGRJzcfopsmoedx5WtvIBSFwPH4+C9/Qb3VRtM1ZLOLoqocNFssVUpI1+fpk23CIAAEOcNkcaFC+7jFw+/eYPvJLk/297n2+dcolHJsvnSWynKFQqVIEAQouoqmqJM9djT6Lgj9gHf/1c9RgAc/vcWZq2cpLBQpFfOUi3k+3jmk1bMp+i6WUFnK5TA9j6ODY7onbQxrAc1QkfRPjmocNlAMjdANcWyXSrFAeaGEDEOEIvBsj+//N9/hznv32bi8wVu/8Rk2Xz6LbgyhS4LbLHUzeJ9pF2apqWcFcqmKeVpmE0NhCXyUNsApYiQnYn7S4HOq6pgJrLK/Dr2Xocsjpg/8jbPLQlpiyi8iMtLP/Nmx+2lSzLaPp9+3Md8NKv3c5cBmRDHbiwnK85MYgEc5KNIcLZLiFGYAFDn6KgcOwfBm2xidoWEX0b0fgy4px/8PDe9oY6mU01tgWN8DAv28I/wk+ZVjbuNkEpvGReR/plRVVsXEvj/f8MqY32ehM/QWZCYf00RWpjylf5/Bw1gER3nOmTKlFVMyHtIf+RsZOWT39fTvA6Ec3htwuq49WbPzOsBCnHak79nDuLekfpiUcSkn6ptB3YhomSXc//4HuK0uVw0FXVUwFInhtJGh5NzyEsdPj/jwL95h784WPduh3bFptnoc9mx2Tpps7x5xYjt0ev1ZDU1TyVkGpqGRNw2k77Nk6eQ0lWazhe155E2Dc+sreK5PTtH56Z/+kO2bT0b6ZegMWeU8X/ujb3L2tQs8ebKD73msLVT58HvvsXx+lcVykZyuIww4qR+AH3DwcJcwCBFCsK+aqKqC6wd0HQdDQtd1eXTrMT/8L7+F07Ej3W+of1NGy2J8DU6bk8PFClGtNEsg4gMEk171IAgIPJ9mvU3oB/2lZapKa/sIu9bCKOS49PYrWKU8T/YOsNs2Xs/GcT0cGbCwucSr165wUm/yiz/9axRTRTV1Fs8ssnB2CaNooZk6F166gFB1jg4adBwfT1NpS4krIAglykkbLwzx6010JLLroiuClcUyr62t8qUzG7y1soyhCBTPxw8lnU4PNwhxmx2anR4HR3VMVVDImXTdALVgEfZ6nBwes3xulcXVJaQQHB3V0TWNsxfPUKoU6Rw2OD4+wbR0zpzb4MyZdfKmSafZpd7tcuHyWd76t3+Njn3C3t5TDh5t8eG3fkKva7O0usTB413qhyfYtsPK+jILVzYAye6793j04X0qlSJmzuDCK5dxBSwtVlFVhYKlIwOPtWqJADg6qfNwZ5df/PBddu5tIzseje0ad37wEd/+R9/iv/g//ef83//3/5A7P71J4PrIIBw1Z6y/DkCd2+zQOmiwd2+bTruLFkp+9I+/R2WtytkLGzx4uk/eMpFBQKfRpn5cx3dctht1Op0u9YN6v3uHcpRXKCXNgzqKhHajzcLqIvlSHhmGeI7HR99+nw9/8CFrC2VUCbd+fpv9h7tTZPQZ7eEs8X9W7JVgJ4pf5skmOvQ3lQUxiBdXkacKIoJU5g/ZuYjEj3koD0/pjoNdEfk+i9A0b2X8v0i+QPTtYqQCXzzczmLqk6M8k3pG8w2x9vOEF3aJnog8k3wexxgDwMQxcDJjz8F4x390jH3KSTzR5R7Jjh35p3+qQ4hQ1YkNp1O9vmF5U1ptzGqahc8KIjPOxGi3jLxLZjEL2M4K0exn9M/TEIw1c1LbpGY+I5MEn+ltNa0yEgRSyz2xvT7BwEASwxAJKGK2jz6UyTmreY4QpzRberPl7JMKMvFrWq1OpBEM1ujK2GjUEPn4nk/7pI0KeFaenqKht5ss9Op0ypu4SDzXQzo+pqrihJJqOU/VUGh2eniqirQsQhnSsl2WlhdodnrU97t4roulaSj5HKFQyZcscqqK77m0XY/S6hKLy1U6nR7dRpdv/ef/kq/8nV/h6udfRqjKSGnlFor85n/0N7H+iz/jxl9/xJnFMrV2l4++9z6ltSphu8ex6NBs1+ntN+g2u0ghKFgmdc/DD3xA0nNdVoomCtBzXR6+f5/iH/8VX/n7v5m9/CmtVuXQaMYHaIZOybPZkkmwpFsG5kIBp2NjGDpB4NM9brF7a4uFKxsUViq89Rtf4OFPbnDn4WOKuRyqZbCUK9LtOghFcG5zjVqtzvb7D9l88xJ6wUQ3Nfyey9LlVT638CXe+6c/BqGgWzqN4wZCqLR9nzBvEbZtDEMDQwdNwVIVfMvAMvqncJkCZCDxPQ+patDsQhAQqApCqmh+iG079CyDIJRcvXaFrSfbtLo2Z86sE3Qc1LzBSb2JmTfxw5Bmr4caSJ483UXRVdRCnnK1hK5rLG8sganjd23WXznH4+9+wP17D6i7NjutJhWhkDP7y/Ee3XqEZZl4tsPFL1xHtwyceoeP/sWPaXW7LBQrFIt5er0enW6PnKbhOi5WPkeoaPhCcGZlASWocPfwCGyH3nEDJW9h6BpnCzmk67N9cID0A2qPD9BQyS+XOHPt7KgdwyBk794OmqGTK+YIm212Hx9S36/hSp+NQoHju9t87//5Z2geKF6I7XmsVisUDZWSqvK0a+P5AWEYsvXeA3oHTXzb4+VffxPd0hGaoH3SxC5YtJsul66ep7xSRagKdr3D+995l+WFClcub3JUb9GzXY4e7nPm5bMxnTBWEc+uVafMDUTV/qnoJftnFjaJxIh8TIDrmfkP+7cY4KlTMJ0xxjbdFEcvJGZgj5MDXmNio9nNoQaaWgfZYVw+4lWVYVwzOJorTCyDfsFmdNYqi2GcaEjbYzHpho2/T6P+SZwcOQwv7p6LaWHkeYgRVogCjYHfSCRWeo1EPmQfyiomanRyM9XgnGVFRM5NHvMzj9zMt6k8zln2l0iOEWmZqeRm4IoXDiNlrArH/Ilki85J7FTx/3/M/eezZEmW2In9/OobN+SLp0XqrMzKytJVraq6e3q6pqcxjREYDMRALkjQ1hYgjcYPS9oaaWvGv4A0fgDXsMsx7IJYgAtgMTOYnenpnmlZ1d2lZVZq+bQKHXH1dX6IFy90vJeid/ekRb4r3I+7Hz9+1HUxCkOPZzvJMjrs/x6B1OMNDw7QwYb0fnXuHAwpAKEoPQ7r8Ws9UNrQm8eD//mch2NB31g8um59e5cfDjBJz2cjAMKmR2OngmmalBSDnGUQezr3UzPkMw5W6NKIJI5lt9dhaCqNVgsn0Wh4Pk1CNEDTNZIkodloYQC5XAZFSmzTIFXMU92votgmm5U6KRmTlbC93V48rgsFW1VpVup877/+j+xvfImXf+OL6JZxWG0rl+Jr/9u/gt/0uPXhTWbnp3nw6R1e+rVXSbYraKpKTqoY+TTTxTybpTK6riN0hSAKMXUVW9VoxgH5tMNeo0EjCNi+vcn+/W2mT8+PIPVkedPrWPT3z1EjWHYHQw/Gdq7uQ0URLJxdYm2/RuCHPNjYxtzeZ2pmivLaLo1Kg1Q+zZnXniWUCXfurTKvaoTNJuuVGr7nk0k7OCmb9374HpebHlEcsvr5fXRdp3h2gcUXT/Psb7xCc7+OX3PJL0xR3izR3KvgyYRAgWzDQ1EFDVtH6jphEGNECYahEbZ81JkCetqmVarjRyG6aRBX60hNEIcBC1mHQFGwbAPDNmjWW6iaxuJTy1R3y2zfWUfqGnEQgaZQ3a+w6wUgJaZpkfgB1b0qpd19wihi6fQSMyfmWH3rM258dosgkUylc5i6ji4Uzl46w/btdRJFUG+2KOQzLL14Bgk8eOsq5Y19UmmHKErwA5/ZlVm8egsUBcPQiBFsrG5ScT1URcEyDGIpsXQDkcDubokgiLi2voOTyXDq5AonLpwgnUrx83//Y77we18FuXzY1WtXHvC9/+ZPCcMY0zZZXp5mb32XSq2G6hi4poGqCHYebBKGMYmU5LJZbNuiHvlY6RS7a1vk81lcL+DB5w+48fPPSWk6+eUii8+eJJ13aDWaVMt1pG1QXJ7GmcnitXwefHKP6n6V51+4QCMIKO9VcVamuX/tPs+98eKBI38oOLo8Omoq8BCvjxobTySqNhnHOGP4qMIesvyH/gIxoj7jMPQdDHhcddNjL3QOWzx05sYaUqM7rG9lSN95SiN06ygeOCYca1bDE4AjV7ocBrQfhQn7sR9nzahsJ3hsln8C06KOC/1qr+NQ9H39kozfNOlhiunjLdn9J9pyp8vUnU9hwzwo6Naxt+MH7yeVfRyY+JF0EJ/oLL47Dt6joa+NgmPVX/Zdd6eJ9b/rtcyPxvkkYGJ75cRboJc7D349l33GWMfW7dw/NL8elDTikLlHB4no6YdxaYbfTy74kaslB/4eu4D+aJvsedyZFgmQxJKND2/R2twnKyOk71Pa3kMkCb4QmI5F4mSxUxaxkKiGTspJIVSN3SBBNWyEojBzcgHLtsikHVRVI5RgKirZQhbbNnFbHoapIeIYxzSQpo2ntU8zJojxGk3sfJqVS6fREXz+o4/5s3/2hzT2an1tN9M2v/KPf4Pls0vs75XRVI1rb36GOTfFpS+8wlf/1neIwgQ7myaTsqnU6mhRQt5pLzQOheRExiCfTaMZBkESU9+rsXd3o0vIXl9siL79IYfBoR6H8cGBeBO6BkFnHvJYCXgwNoSicPYLF4glZAt5FEWjVKtT3dxDt0wM28TKO9hzBc699DQLU1NUfJ9mHDOddsiYJlkJ1XKVKdtm4+Ya1969xsb6Dl6tydr1VXZvbZGazjB/eYWZC4tIAVbGZr9ap+IGBKpKWQEvlhgohIAWJShGe91Moqskno8wVVSZoCoqMmnziqIZGFMFFE0jlgnT01NEfoCUCZqicP/KHbw4IgKIIpxMmuXTKyiaRjabQjd0VBQSCfdXN4kVQRCF3Pz8Nq1SjVrLY2O/xInpeRzNJGoFTDkO+/c3qWyVMHSNOJGsXFjByjvUVve4/oMP2G02cXIZWrUWjmWzu7qDF4QEUcTm5h737q1iZxyy+Ty1lodpmuTTaeqtFnc3N3GbLSzTZL44xcJ8kXTa4e4nd/jRf/gRO3slvJZ3OMUuaPlc+4sPmctmeO7iKRaLOW5+cofyVomUaTBfyFNvuTSRNAKfYsZhenaKMAiolitYqkap5ZIyTfwgRNdVZBiyXyqzWyrz/v/4M3Zvb5EuZDAMg0RC2PKRcYJhGyAlN97+HNvQEIbGZ+9eY/XeFnEcU9mucP/qA6Iw6sroTvyhX0ENyKDeIJ4cOfXjYfTIIf7B3+FwEP3PHk78HlsnPxF4CD3WZw0NqMzjIeiZKDvWsRgqtFvO4X63kn4CPSyx2jjGas5Bx1Uw4uyMJwwTppiPejxgPg/x8ziKPIlpT0fBE3MuJjnhRxriR9lFgwW1qTgUQRtdhui5PVCsnTnnfZ7MiJHfswUfvXnak+THNGxMQ0bWeTyM5uGBpwe0EMOPjgVdl2BMSGcEMtH3chDXiLxyuNmHg0AOJu2uaBkLT0DgDm3B2rk+rsfQa7SNHLlH5e3xWA7rMqlRRzsBjyYmxufq4JxY8lG+zKRn44RCj/QWHebpQNJeM3D3nc/5+b/8HmkBYauJqmvoQgGZ4Ho+pb0KzXKVqOVSqjVAQsv10ZB4fgCqYDpjE+yUabU8Gn6AoiikUykiKfEqDUI/wq02iNwQLUrIplPMzc+wMDOFbegkUqKpCkGlwf6dDWIJtqpx870b/Nn/+w/xaq1um4QgPVfgG//pXyVdyNBstEjCiNu3VvnZ937Bz/7jm2xeucPchRWee+UyM1MFKtU6oedjGDpBIrleadLwfYqZNFHSntNevb9LZ7enQ1E2SaT1esUdeYQ82Nq2/b7DhV3HTh72Rb+cGdP5B4mSKCHyQuZX5rn4pWex7RRlz2Xr3jpBs0WmmGX6/DxTz5zghW9/mROnl6m2POotl0QV7S85mobX8nDrDVbmppEStrdKKF5E4kckUYzf8DAck9mzCxiWwVMvnKe4OEtDQCuKqKd0XC/EDGNCPyD0IgrPn8a5uIw2l6e1tktSbWB4AXgBpm4ghWDp9BJBEKHEEsM2iaMYoavEMqFSqaIYKs5sDi9KKBTzOJaJriiopsnsygKeH2GnTOy0RSP2MXQdS9WRDY9GvUkunaJUr1HxW1iWRalS4/b6FvU4IIhiUobOma8+h19pcudHn7K+uYuZtlHiBEvVMGoB927cZ3trlziMEIbGysoyS6dPUC2VsRAYusYXLpzhi+eXefbMAos5B8s0qFRq3Lp5j621LRQZs5jPcOrcCqefO4ugPR3q/T/+Oes31nAcC8exmCpkOX1inpX5Iq+//hLTs1NMOVmef+kSs8UifhyjKAphFFF3XdY3d4jdgJViDsexOH3+BLl0ivmpAkEUsb+5y+03P6cwN4WTsvGbLvVSjfpuFYDGXo17V+9x6tQSrShs7+ZlmVT2aii2yR/9sz/mxns3+s5b6LD3aE+jV+9Mlnt9eXrTHtdeGeFo9L17GHhc++/I/A9jMfTA4+jfzr/OGodend6n33sKGbRDjrsAebB5fVkm4+gNPneSHdcXOi4c0mJk/QYTT+inQ3k+XEIv0k6bJtfpyTTx8Z2Lw1pIEplwGM3u82ZFJ0k/jOr4Pn4aSCC7XyGGYZLA6F+o01dYT68eMtPYRUOdMEnnNy7N+JqMqu2QjzQO9RgY63XLgevHFVR9DmF/O8UI/INxga7t3k3Y1QH9jNB1Nnr/PUZ7jmCZvnHZu53fxHyTDayx0HF6h+bjjhA2k8p5WHgINL2s89AOxpCS6Hk+mP6Y+gEEqApIydpHt6HpEXgenqIRJpIEQSwEpq5Ta7ltw7LlYZgGqqHjRxG2bbI4M4UQgpYX4oYRVhxhRwGWouB5Hl4Q0owlAVDxfKrNFi6SppT4YYQmQVUEU2mHZhBSqzeRTZcskrxtkkml2Lqxzvt/+CZJGB8yuACKZxb41j/5LXRDww1DcrNTKIbGTqnKvRv32by3gaqpLMzPcHJmmlq1jq3qqLqGk82QCImmCHTDaDtD07kD+jzcYOgYWa1Kg3vv32T98/t0dgTqQOSHVNb32wtvO7uwSXl4ZsyRsRUhiGRCGIaopo6mqliGwb0H69y6epubP/6YoOHhzGRY+spFXvnbv8pLrz9PJp1CR1Au1/AUhaxpEnoBO6UKOcvAyaZYW9/m7jvXqK7tk4QRkR+imhpRHFPZKWOmTPKZNImuo2oKrqbguiFay0eGMRvv3Sb0Y3w/JlB1hK4RhCFNPyBKYhq1Grc+vYWVsjBVwfbaNo16i5bvU6k3CMKEnbvb1Lb2UVWlfTaEImi2XDTbYG6+SK6Yw/UCkjhGhJKm59HwPW7evM/2xjbpXI65mTk0oSBVELZBdr6AH0ft7WfPLlM4Ncfqz69x7YOrhEKiWwae55PLZMicmKHZbDCXzyKFII4T1jc2ufX5DTIyZrmQxVEUmp6HG8SEiaCQTrM8lWOxkGUhm2Z5rsDrf+cNnv6tr/DVv/8tssUcIKjv17j+7nXSho7lmNy7s85Pf/gOjmlSPL1IupgjBmSSsL9dxm200CwD3/URccxicQpH19kvV/AkzM5NE3gBkZRk8hmmpvLUGw2uv/M5uzc3WViaJQwjojBif2ufJE7Yvb+LEIKUpSGFZH6+SBSG1Ct19ndKKBLe/e67eD0bGxw6GKPsjEH+pyOeRkeHhqaPjHLej4JRqAefCZBCttcQjJKbjx45OoTuRjQTKtlXr6ML7NVR/bJggix62MDgOD3S+/5R8g7YmI9kSD8pC3wEDKlI0eOI9aWTfc61gCMdh0Gcv0x4IudcdPaH7PEzhqO7I/jtqMUsw4uZD/AdbfKMhkPF11/KxMF0rGK6LtTQIB5Z5ggnVIxPe/y6yR7B2rubtKT/qTw0oOVhufIRB8sA/eRwmd3ng9vHdvpRHl72npnwyNv/HiFHx4KQ3cOeJ5X1EHQa5PFfxnA+tu45qvAxbRvrvI7Wy780oQttg6a8sYvv+6iGga1IQsui3miSKRZx6i18PyCMYtw4JJUYJEmCkJIwlljEJK6HF0ZMzUxhhCEFqbMjExRdI6b99UMmESKJ8SVI1ycMQxQhsGbz6JpC3PI5sTCHF0bUGw0cTcEKPRZSJjcbdd7+7ttkF4pcfuOl9vziAzG4dPk0r/31r/Pmv/kBQbWJ5Vhksw6VUpUPfvExhmFg6jpREBDEMU3Xw0lbNOpNVKHgKSpxGKGYktZeDTgYJ0PGQQ8XD37Ll5KP/+QXfPaDDxGaRmF5mrlzi2iGfph078EOP/qD7/Klv/l1Tj5/tj0uxfBGGkNwkF+3DRRFBUXQqjRpVGvEcUJaNxFScOWDz4mShPNfexYrncLIpnjqN79I4cwin/7pL9je2UNPWWyVa8yl08RCUGu65NMOvh8QhxFv/fc/IDOTZ2p+ipOvnidVSHPr/RtsPNgik8/gODaQ0IwiUmkHwwtQVYlI2ex9voZpmyBjtJRJ0vRRLQPNMjFr4LktnEIOQ7QX0d+8vkMr8Hjp2afJZlI8uLtGJYhIZU0aexW2NwMSITEtEyWRTGUcKpUqUghStg22TdJ0EYZOfmaKrJMmm7FYX7+PIsFruBiZPMQJU/PTnHr1Keqru1z58UcEUUR+togMIvwwIuM45Fam8d90mSlk2Gl5TGUyqMUCm3t77DVdalFCZX0LP4rQTQMRJyRxgqqpKICTT2OoEj+OqVfqnEifAaVrsKRUnZmUgamozBfzRK7Pux9cQTF1Vk4voiSSlKbiNZtEmkR3LLxSndnpAtPz0xSbOe7t7bK7X8bMpKg1XWzbwmu0mCpkmDI1bq5v8/lPP2FmoYiiKiiKYH99FxkntKoNhABfqNSqDfLZFKfOLFP3PfbrLk7GobpZ4upbn/Hit15pjwEpqe5XWb+5xlMvX0A39YmyqKNpxumZIVH2sEb+UbJwILDat46zN+9Dy9OezAcIJ6MY81bCyHUMPa87Ru1QvE0M0/Xw8NaJdRlVh4fJMFiPMe8HlPzIZI+sxx7WkOvJJY/vIHRtbzkUqPxfAzzZBd0HkdfueqpBpdcD44g4oV8Odxl4HMdixIu+xUUTkh4VRBhlxD9scP3xWGTEwJUDzw/uj4mum+Xgqk/uHZ6O2GO/jP3kLHv+7yLv/N95Ozmi1F+vkT3yiFGew205e2SyFLI74vuEdW8O6JwQO1QVKYmjGE072Dv+OALgKCZ7nGyPJvOeLPSWPcjwsv+6vz3dO1VR0AyDWhBgaRZJq4meMgnDhNxUnvWNHVRNYXqmSOhFeK0WliKoNptkCzmCJCEGtnf3cZIIWSjQjCKyjk09CHBdH5mAoiiYqsCII2I/IIoSyip4XoihqvhJjGFoLMwU2d4vU675zGUznF5e5NbaBj/8N3/BzKl55s8vHRoNQhE8+1e/iG7qvPeHb1EvN0hsk1zKwp6bwQ98yvUmoZBksxn0tIUAFE3F0A0UoYIAL465+8FNzr/xIoWVGfpO5T2ka394oTNVWcYJ5Qe7xEFMyjQJah6NUoP8fL6NR0ruvHMDJUz46X/3fSpv7HP5jZfQTH2oK+Uh9oH+UwQJsn26dmMLtfP1Q1OZKeQp5LPcvXqXB7dWWTm9RH5misKpOWaeWuR860Uaf/42keth2BaVIOTU+WWuXL1L4PlMOTZb2/tEYUi51qBeaZCeKzB/fhEn50ADUqZOtVIn51iYqkrNddGlIGl5aHFCYhpomkA3LcIwxlV1DE1DiWJy2Qy+6xKGAQhQk/bUoY1ygqoqYKiYqkYChH7I/fIOpmng5NPEQYTumMQbIaqikLg+6bkicSugVG0i/SZLy/PMLM1QrVVpxSH5bJpyrUUSxni1JrOvzjL91BLv/bd/wfbmHvMXV2hVGtSrDWQUIwwNggRFSFa3S7SSGNff46mzp5iZLnK3WidoVrANk+UTCziZFKZtoCgaWsoiO5/jqS9dIg5izJzTPu+pM01VtB0PayrNvTubFJKIRrXJ1l4JTRGErs+Da/dJpUxqbosLJ1cwTBPphai6RqqYZebCMg/eukISx8RxjCZBjxOavsfO7j5CgYImWJqZYndzF7flIeOEIIyYXppBURUC1wNAVxQKmk6z3mLt/iYt3yMO2ttGT6dsfvpvf8TUfJGVZ06iKgp3P77Lz//oZ5RW9/jKX/8qqqYyeA7EEBxa9d0x8zC2mjzE3bEh+oOiPWj7oddOGkzzBGX0w8RS+3KMrMOgHh8Dh45Jf6OGUE7waw7jnZP67jECXEdN7TwWjKLnsQ25fuYQSGQP48khb7Ofgr8cNf7kooOP7VwcrvTvjjCUPsV2QJhexfdIBXXQTGL8I/L3lj8QNRilHwcNn/F2+XCjxjLuhPYPrVPqTT/ufizecaZZ1z04/OL7MIK05+9wlx71yeDg/aDkloPpBp6Pa2snqnLg44zsn1FVGqz8SAk2yCCj0fTBCEGTxAlSU0fmH1vMwfgRPRb2qGYMi+ojduwa8/Lw8Rg+GJltFKkEI+g6BkaNw4GX4uC6z3ETgsWleeq3t4mEwlYsmZUSzw3wFJWsDioCr+WjqiqOaYKMkEKlFUZUqnXcIMDQdBzbxqiX8BNJOpNGFRC4HtPTBWxdp1Rr4EURbhRh6Dp1z0PsBMSxxFyaxmu4NPwWpqZi6BpBJNkoV5nLZVku5Nmq1fnuf/WH/Pb/6W9SWJ6hE2xRDY1Lf+VVFp87w9Xvf8C1d66wu1dBbbTIZNMUpvMUVYVKo8mu56NaFkJR22tLTIPZXJ69apXVrT0+//HHvPb33phIZ9lzjQQUwelXLlDdLuM2PFpumbWr99vOBZJWrcnG7TV02ySjOXz+o0+o79b48t/+OpppHPZ1n5nR048yThCJRNM13GqdoNIgkZIYiaVrbK1tInSNfMpECJX1O2vcvXaXS+5lZBAwc26BL9pf5YM/+TnUG6gpg2bd5dnnnuKzK7cJBZxaXsD3Arb3yhimwfTJGcqruzTrLaamcgRhzImnz1B5sAkyxkxZqIEkDkLSSzmCGMIowggiIkUhUgUyCCGMkEh0XSWMJVEQYJrt3ZaQEPsRqWKWfKlJK4oI/IDcdA5L0wlVaDZd3GoLNU5olaqomobQFISUVBsNlhdmmV6ZJZNLs/NgA0mCrWhUFQURJaQNk8ULK+zdWOfujfukUlZ7HUIUE4UhuqoQeQGJH+J7Lp4fcvHpsygZk1Qxw8yZJc7vXsRvtFAMHWHppAydIIpJ4pjGbpXNz+5RcBzsmTy3379O8eQCoR/x9OuX0C0dzdR49be+zJv/4ntcv3aXRCYoBweLZp0UK+dWOP/aZf78X/wJ91bXOX/xHE3fxzJ00vksc8+f5v6716nWmqR0g0a5RqXWoHB2AUPXqFdq2PkMzTAi66SoVqoIwDJ0Zk/N49VaJF5EGIZsrG2ys7FPLCEIQmZnpsgUs5T2K8QCdFT+7A++y5e+/QWe++YL+PUWGSm5+uan2HmHl7/16sHmGQ9rMT5M8slGzZMz18bhH/xKMODcjFNrHOP5+EL7ihrSIWP0zOQHvfiPGQkbpZwmNL83zeRvKBP2cBqs2pBtdtzeHu8Z9dmPQk7on8llTdxeeWTJT45TH9+5gPFRWTnQ82ONxCMKkd2u7iYf9opHZhxV4VGpJlllAxHVsYbVqPvjZBqqUy8zdZ2Bh4N+D3fYAeha40LIY3TFgeUo6Wd82TOW5PhpE709N+ioDZ5x0mntoF8/1lE4Lozqx8FuObYi6jR8wLgaqHjn0/zYT++DUwr7QBw6Pl0adB20TmRDAFJ251Ae+ko9zeqiHOUIj6L3mPwPA+NIObYfxzvknbmxQkBqOksIOLpO4Af4cYKhKjQaTYophXTWobRaRVM1plM208Jjz5mlXK0RyPb0ECdtYsUhhq7RCH2q9Zj5+SJaRYU4QXU0vChEjSWKIoiCgOnZKfbrTWwvpLa1j5NxSE3nKG3skc+nmcs5bG7ssl2p4tgWU2mHvY0S3/3nf8Lf+L/9vTYvdHpSERRWpnnud77CM99+het/+QHX3vyUaqnK3s4ee6bB3MwUSeKjqSpZTaXV8jBUlalchv1KBSklbrnRv3PvGGJ3xZOkurbPz/7ND2lVG2iWgZFOIeP2lMA4jHnvP/4Cr+Hi1ZooUpAr5rn34S002+DVv/Yaqq52ZXsvnx0Mier6Pvv3dwj8ALcVEdRanLl4hsWnTxN7Pu/96G28UpMwnUYX4KRTaJHk5kfX2V/b5px3iezSNJe/+QqffP9d6tUakRfQ8gIsx6LSbLG1X2Zhpkg6lyGbcwibPiBIZIJumWSLFo1qAxnHaKpC2PJQDQtNVQnLddTZPMKXJK0A1QtJpS3Q00SbexDHuG5AooChKsRhQOhHCCHYWtvCKWQoLM9gpUyu3biLFKCaOq1KnSSMUQ2dTC5DyjCQmorn++hJwomFWbwkIZSSUrnGbqmKrZm49RaqriGkZPHUErpt8NmfvUMsJamUzcxskdU7DzBTFiJMUFSFVt3Fl5KYhLv31nCDgDiKyObSnHzqFKZl8vE771FtNilk07iuj0CwOFtk+sIK5aaHq9bJz01TW9ujUXNZPLdIYbGAqmvMX1zmm//kN/n8e++xd3uDwvIs+YUpZs8vUTy/QJJIvrBT4sf//gesPdhgdm6GVhRx49PrzD+9QqvWREkgbdsoKNSaLaYQpA2DCEk9iEiiiMLMNC3XgySm0myxcfUBMydm8OpNVKC6W+XZVy8xd2GZzXvbzJ6cw9BU3v7eu6ytbuI4KdKaxkdvfcqJZ07iZFKEUuJYFh//8GMufuFp0lPpA14dp28fDx5x0tExQPZK/n5kE8yqJ1R4P4JB7+HA4O2PpPdo/7HlysPgWV8RA6L/2FODjlBOfXQbpf8fRbl18h3Xfh0JYzIf1xk8NhztLvQX+eRc4cde0C3lpOqPMe4HjbqB9/1rpdu92M4yEO7s7eCHhb56yOFnI/p8oEojKj6hsL48AwOrF7Vot7Z335a2Hu8s3jn4DW7B1Fd3efjr3y52DN0OCC4O0B6i7/mN24Gjg29yV4xamn1w1Vu1geb1oO9rQ3tb4f5lrIefEwdxTYKebh882b3N1T0L/AeYQiAO7PQRmwUc3PbtiMEQikM8R0H/BiedaYe9To14iM/4g5UYVX9B57T7sSQcFK5i4PmkMT6uWhPedeqYxAlhrYUiFOJEknccSq4HioKIYtxmQBjHmKaFoqmUa3V8qdJwPWQcY6gajuOg+C3SjX1cw8J0MgReQL1SJ5aSRsul1mgSJwmmphJGMS3Xo7FXoVWuYqgqOdOkUqmxv7mPHwSUK3WMlIWTdpCJpFxvomg6C7PT7K5us3btwcjhky44ZOcLvPL7v8pv/1//Hk9dOk3WNKm1WqzvlpifnkJPmexWaqzu77O5vYsiQFfbO2QZBwc4igF6tfuiyyO9vlt9p0K9VEXV2lu0rlw4RSrttBd5Vxvcfucqjb0qc8UiT7/yDKraPgvk5k8+5d1/9xNCL0QgSaKE2k4Vt9pEJvKwTNXQKT3YRddVlCBmem6aEy+cJ71QQOgq6BqWpmNaFugaXpyQmimgxAnV/Qof//B9bvzgI4xsihe+82WWTy0TAmEQ4AUBlq7T8gI2tvewNZWdzX2uv3mFjetrKEKwv77N3c9uU98toRoqIZIpx0EVAlVCo+ERugGZuTxqwUHXNRSZoCoC1TJA1zFUFUURSCHQdB2hCGansuzX62zcWiWWkuxcnlOnlkhaPvlUiulcjhMnF7HSFjEHDuRUnlaliW2ZSCkp5LMYpk55q0QSxuTTeYIgxLEtiCWLF1bY/OQu62vbpAtZFhbn0ITAD0JiVZAkMb4XIL2QJIlJmybZbIqpfIbidIFyrcGNT27SqLlMT0+hKyrFmfZJ4ucuneGr//g7ODM5muU6G7fW2VvdRY0SbEtn78E2t967wf7aPvX9GoUTM3zpH/4ab/yf/yav/sM3mH/5PIGUaJaB6Vi88DuvcemVS9RbLm61jq4IPC+kfHeLvWqNJE7Iz0/RCn0iEmzLYGlphoJtUylXsTWVB+ubxEmMlbLRVJVGpYFVyKBnHKani6QcmysfXKdRa/Lcr77A4rkFKrtVWvUm2UwaVVXJpSyQcO+Tu8yenm9vO6wqeA2PnbtbyASSZIQkOxgfXfd7knvef9X/9lGMkEFrenzKo2r12DABVUfXDibr6LZ+EH3/Rig7hnZFnGQ6dmwBxoUsHxMmIhXtQ1yPU/Dj2KGDZYoB2nRsiRELsI+zkcdxVLA4wDbgxj42PJE1F4cr1nvsu0HnVB4Yr71p6Im2DbNvO0E73WCzh5l6KO+gYzipD0SvIzt8KvaoEttc3xsJGbMaRHTpM1wVeRAAGFyh0TufX/TO/hnZmMNyh5yX0Y5A/2XXSen0SdeQlXTmq/ZNnRrsR+j3Bo4Lg1+2xsAodh+cHnfY4rEoB3qnt4t7+q/zqpcEjHo+iEYMEXZ05UfwZR9pO3090lrk0NCW9K8VGoLB/hp63UO4wzIHO3U8SDl8+uwgvrEwlj0HiCI7Iq+bsLlb5ebPP2NeV1gPAtQ4wrQMKo0Gpqogmg0CNAxVxYtjhKqyj0AqCqqi4Hk+cSJJ2TpNcxoVcGwTu67Scj2yWYe9SoVEEeRmCyitAA2IZYIfRcg4QdM0wsCn1qiTdTIoqkKCJGoFnDy9RLlUxfND6o0Wuq5RsFP85b/4M/72f/mf4OTT/bTuuLaKIL0wxev/+7+G8d/9Of67V6j7PmurWywvL+BYFuV6HUVRyM0USJdrRGHY3oUniA6+ivTQdeALVXf5kCRs+SAE2YxDud7kk599yNrt+8xfWGTnwTaqFDz/5Rewsjb3PrtNbb+GH4QYlsGVH31MHCV8+fe/gUwk9z+8QxLEzJ6eoXhyFiNtYaYtajtlssU8dzZ2Ofv0WTTLbC9c3q8jE0km7RB4HnYmRW52mtxCkU2gslNC1prcKN+kXq5x9gtPs/ziOXwFKht7TKVSoKlUmi6ZdJpqy0UT0ChXoaGStU18P0RxdBJFUJifxt0t4esKSZwgACfrEPoBSi4F5TqimMHaqmDZJuUgQk0SlJSBCEMUTcOwTCIJmlSZsi12S2Xmt8vEtk46k0JTVLa39nAyDg/urlGt1Sjkc4QSWtUGpmNSb3mEB+tO7l67T71SJQpCTs3OEyoKCmBrOpnpLB/+hzdRFEEsEzQp2dsto6kqjmaw5daYyaRZfPUCzwd16mtVlDgh8EMSJJlsmsp+heufXsM2DRanp5BZk6WT83zjH/8GwtJxNvbaJ9Pf2yLQNcxT89S3K+ze30G1DdauraNrGkuXVqjtlFE0DQWQioK/XycMEwxTQwKv/b1v0Sg3KG3vkzN1Yplw/9M71IOAMIqIowSpKkQyYe32KvPz0xiqiq5pVFyPU0tzlGt1rGwKSmWiIKSytk/19hZ7eyXOzRTZ8jz2N/Z57tdfIfICGqU6SZIwOzuF6/mYqkYhl8JruKRyKTRDI44iLNvEbbRo7tXZvr7OmdcuIBSlJ/jRo1F7dfQIudbdPWqEzBqp+AcRDKYRw++HQAyJyt5lgN3pXhMKP07djoKxNtAxQYy4lgN/x+bpTSiOp196sx7H/huV7yh4mHqMRTDittNM2V1fPNIu5cBWEOPf96U9dKFHlNsx/AaeP+4xGE9wK9oDkEycItbvaw26FO2B0rsZ56AP/Ehe/DGI1MU/poOGBsiwqzOU86CxnfoPO8KHbwaMxO6A6mwj1x/x71JO9tBw1G+oPke1TQ686B3bvUhlb00ejQsPBfmAt37Y3wNyUw5Up7d4Cd2vF+PGmGAI56iCxsj5fmV0kKXb+h7kYxiiu0CLPrINRWYG699DokH38zhfPkQPTQfJLXvaMjb/qGeTDnMc43M81Njt5a8eT88r1SmXa7i+j6Mp1F0XS9URmoqq6YRSxdJ0tCTG1nUCKZGWTdN1sQ0d3dBJhCBJpQlUjTpK+6tGEtNqeRBEpFMpDFVrG0cJBHGMrqhoQsEyTJphSNowMKIY2zQo5nPMzhZRVcHG3Q0Cz8dQBBnbIo4TctN5Sut7/Phf/vlBhH/0FyFFVUhNZ3j9n/423/pHf5WVhVlc38OrN0hrOlbKJBSS/WqNOImRgOFYKMqBDOkn1YjuaAcL/IZLmMQEro+ha0Sujxa1F3k39+ucffYpUsUMV3/+KfVqncULKyydXUJKieaYfP7TT7j6o49RNIUzX3yKxPN58NE9mqU6UoKqa7QaLYKDrwzOVObgjAhJnCTksmkqrSa2beK5HpWdEn7LIz9fxM6nCZOYrKFT3t7jnT/7GZvXVrnw6kWe/tJlFNuk2XBxFIV6o8mJ5Xl00yTwAgrpFPUwIlZV8tMFbCdFZb9K6Ic0XZ9mFEEYkcQxZiSJ96roto4mBEJRMG2TOI5xXY9ASvwgpFFtEjZbKEnC+n4ZD1CBq5/dYPXOBkIozEwXqDYauK5LPm1T2SsTN13m0w7Nloepalgpk7nFGaq+i+aYCEXB0DTUjIVqm7hhSMqx8SsN9kplMtk0xJLN3X3WtnZIWyaNRgtD0zjxygUycwW++pvf4Ff/wa/z8jde4ZkXL1LI5TBNg6dPLpPRFdwwwhMJX/yNL/M7/8XfJXdihjhJ8PyA9FSOr/zeN3j1d1/n7Fcvc+G1S8yfX2bpqRMsnZ5DC0Naa/sYioISJWSm8kyvzLL4zCmSlo+VsUllUmRmcyw/dYIgitGFgud6XL17nySJWZqfIfLb09kUVaXR8vDjCM3QUYFGvcna5i5KAkm9iUBgpyxUVWHp4glSls12pYauaShezJv/7V/QKDXIzuTwPJ/7d9dIp1NYjoXn+iRBhCIEqqrgRhFRFJHOZwhcn+tvXsGre/1iZ5TqEsMyaZTcHCWv+u8HpPrjGvh9YZZOYOcIpBPVsuw7a2ocdGyx8UcATMw8Orj2UGgGNmc/Tt4BO2VsmseBx83PgX47tAckvV+aoWv7tm3qQeNRHur1TtqJIMb8xr17AvBkd4uCw4oN2Ucjnwt66Xtko7qW1dHpRzm5I9Mf4doKOcor6K/WYL3GlCEOyxmgguji7/VAO+JkhK058P9QjfpK678YSPa/IHS/hsiJfTky+DJCmPfx3ghHro9iAwZ29+F4D0weDOjeGEFvDtGXdgR20cMBvQ1KesbHGMO8ne8xwlCjmWiAS/q9zC69jlgofgwYqvmBdyiTg1PnJyiB3r3I3ZZHmEjQdFJJRNpJIcOA0PVQTJOyouL7LVQhySkKTRlTa7oIRZAv5mjVmghFodlyUaUkuziNv1cjr2vEqorUNZq1GqqlkzR9Sg0XU9fIWSatlothGZiGQStJUHUNO53Cb3nkpnNIXaG54RG5kmw+i51JsbexQ2Y2x8qpJW5/cJPqTpn8whR9uzt16Hxwr1sGF379ZZzpHN//5/+R9b0SC7ksWdXEsCy2HmwSRTGKqnDi5fMoujqyB7t07z0jRhK4HnEcESSSCy8/zea9TdYerHPrBx+x8pVn8JwWtz69wezZRU69+hS5+Slys3k+/8FH3Hv/Jq5t8sH/9DZLF1fIzU9RPDPHvY/vouhtdaJoKsWlae5/fIswTti+s8721h71jT1SuQyLJ5dJaTqlchXT0Aldnzuf3iSOY+IoZq/eQACLuSwpRWHt5n3Wb69iZhxOXTyFUODGRzdI/IDt3RIp0yTWNRp7VVKGQbnlkvIDgjAkk7FQFQXFNFASiVZtodsWhqLg3tnEWZltf9HwPGLXRxgamuuhJAlSETgZh8D1SHQNxzY5c/4kN6/ehihmr1Ylu71PdqaAtrHNzMI0+YUCwUe3uHdvjblcFs/zCF2PmWIeRVPJ6AaN3SoijHnhtef5/J0PaQkFQ7NwUhb17TKxjEFVsA2D2n4FxzZBU6i3XC49dYqF58/y4z/4U+7ev0ekSBbmljFTFnEQYigK67UKoVCZXS7y9b/7BideOn/IGIX5KV79ra/guz66oaMbGghBKpsCJM1Ki82GS25pGhHFzJxfbp8D4kUgJXGU8Pn33+XZv/IFFi+fIg5jLnz9eT77+aesbWwxn04jCzpO1qHWcttTCpstOoc9GqoGnoulKMzkcwhdZ6dSZ2G2iGFo7S8//9/vceaZM5x/7jzXPryKoWt88v4VDNNAMXWe+vJFMj9MsVercufuA5566gyKqqDqKkkiiYOIRCacevoU6UKG1n6DqOnhVVrYudRE4dRZNzScoFcf97rr8mDoDmQS3ffHXSQ7afFt7zeMYy+6nSC0x8ryI8yhsemfNBxpU02AgTaM7IMjbMe+Ojxx6Oze93h8cSw+ONTzEw2LUYU+dtc+mRO6O97OUV7psb3W3nUCPZnFiBYfJBtFiMOI8qE3NmyQiyO5eAxTHofyI73Bo/HJgfbLEb/DRo+IwEi6FDya5k9oBEm6R8ofs597V5YMvBh6OIzugEKiO/j6cYiegXWQ4wjPfHJdun0xSOxRbDmRCP02/IHDcjTBho/RGQ0PHRwabLl4OByPLoTaEeMJb3sUd7uUVsul5fvs+iG1RMHWdQzbIp9Oo4n2qcS6EDSCkP0wwo0SgjBE1TTUICYJQgxDRxUCU1Xwmh6eH6BoKmYSY+gahak8MpFomoKpKMzms0gkCeAFIaVm+7Rsz2uftoyE1FQWw7JIpMTQdLQgxKvUydomJrRPIXYDfvZvf0TohUD3q+QoxhNCsPzSOb74m6+hKwpuHLEyP8PC/DRZOwVCsHhqjoXLJ3vyjKCh7PRQ+6XX8Cg92MVUFJqNJp+8+wnLz5xi+fQKW6vbrF25S327zImLp3jmWy9z58ObvP2HP0GoCs/9+iu88Z/9JinbAgFv/cvvE7oBs2fmsWydGz/4iO0bGyDgwteeJQ4jAG7fusfWvQ3CIGJvc5c7V25TDwKkphKEMbFMkGGEpioszhaZSafb28cGQXuHIstg2jLwm02uf3idyk6ZlZNLNKMIlQS/2cJrtjBSFrahkDd1gloTS1VIkgTd1IniCD0BVVVoNVr4+xU0IUgtFZGKgnBs/EqdlGFgaBokCYkfEnoRqpPGqzUJPZ96y+PMxdP4XsD0zBQb69ts75ZIAFUVWKaBabR5MrsyixAQRTG7mzus31unXqujCnj21Uvk5osgFRLaijiOIoI4QdE0oiBk5sQCp8+dwg1CSvUGi8U8l3/zyzx47waVWpPp6RmCJCIhIZ9xEAJ26zU0VeG5L13md/4vv8/KS+f6eCtJEuqlBoZloFt6V7YdCDEnn+LUK2e58KvP89SvvUjx5DTF5SlmTxVRDRXF1Hnhd79OejqHaqg0ay7puTyXXr1EHEY0wwgzm0JpNLBRCBouLddDleA4NopMiIKAOIqp1uq0fJ+0aaCZOmYhQ34qx87GNm//8F0e3HyADGPy6RQ5xyaKI/zAJ5V1yGTTSClJ4oRWvUmUxFiZFKXVPdxaE01XKczk2b2xwec//hTPD4iCsGdk9Ei4QV1zoMs66Xp26aU/cDRJnYjR8vpxLbaHVdfHKm+U/uzJKxh5iBswvGbyGKiPBRP09MPiGL3D6BiNO6otT9jJ6LPLDnEfwzAZDEY9LDwMTZ+A0/jkv1zAmFBz58UA9Bj9gzHk0Xk6yOXEVKPL7I9AHD7p2+e6J0uv4T+qgB6HYZRxKQelUB+u0USaEGwYwM7htOpH2fa2W4N2Hbo7D/XTdsR+FWNh3DbB3Tb1xl/62z9idulhDbp17U3Rvy6lE6Ht3cFJINoLv/v8sF4eE13HtK8vu2nGsnJvVYceiu56iF5eGqXLxEBbjnAE25G1yX3xBORCF8tB/aSUA2+7/HFc2Tsx3eD46x0Ih9eCE8+dZf7iSfZubxLpBrLZQhMCS1PJ2zZSJtgiQDMNNNsmAXRVAQG1ehMUlVbLxU6nCJFk5gu49SatKMGMPEr7VYSukAhQvJDZjINba1D3PHQpMBWBD3hhhBvFhK5HpLfPVFDCCFs3qPseZhIRaDpmxkZNWQT1EsvTU9z88Can37vO9PIMM6fmhhvdowCEIjj71cus/MV7XL15F7fRQgpBlEiKuTRf/N2vYdhml0gTmLVDQsMyWL54ko37GyRRQtzy2bqzznO/+iIf/Pk7NEs1nFSa4vw0hqFz/93rJEnCtbc+4fKvvIhmG1x8/Vne/48/Y/PWBu//0Vt84W/+Cudev8zO9TVSeQcE5E/O8crvfY23/n8/xBYqqZyD0HScnENpu0Qqm+bZF88jYolba9HYLbO9v0+z0WBmoUjG8zG8iFYU4TVjQlVhupBma7/K7oMthGWh6Drr5SqGojCddrAVpe0wODZONs3W9h62kycMY0wJViGFW60TRyGKraPN5NDnC/if3qde99CjgCCMCfwAw9AQUUy6mObyr77ElTc/prK+xeaDTZ5+5Wkuf+kyt6/eIfQ8qpUqhXyGVCZFaX2POIzRAKkIVE2j0WgSRxbFxWkuXDzB9NlFglqLvc8e0PQDUBWSMMa2LKSigakTS9jZ2GFmtsjK8gKqqXLxtctsfnyH65/copDP4GoSUVLwPZ9qHBKqcOLEPK/+1ldZevk8mtWzU90BA7g1l1TWRje1dkDogGH8lo9uaCRxws6dDWrbVYIgZP36fbKpFCsvnaN4cpbAinHyRQzbQCDQ5nSSKOHZ73yJ8uo2t2+vMp8I4kShVm9QcVsIIbBQOLe8iGlpbK2WIEnQNY04jmgiUMo1tJSJsHRmFmYI3YB6uYpAUKrUSTsO006KC68+jW4ZSJmgC4VTJ5bYLVX40mtf4dQLZ9j4fBWRxFi6zr0bD/A2q2Tm82iGhulYkwXTkJMhu7qhT2/3Jj5K2g4inZRyBK6BMT3xK+9Avq61I4Z2JRTj9p8f5yBMVIJi9K0c8WzY1Hs4OK6BNApk3x+OaFh/mY8Lw+bN8bNK8XjtflR4zHb/cpwLGJoq1B6k/bUd7lox4s0YBhgaHKO8g7G1G74cUUxff4oRz3pe9DPs5LK7pBmUHHSN3WNia2frGnoPA73l9Busk2g7CdmA8yA618OCc1iQDrobPc4fI9xJcehO9FfiwAjt9pfo67vR9R6siuiiGqLpUK8N3xw6EeJwp6+OMB/uowGOOkL49q0DPqzv6LSPDEMO1/9McCA0kjhBUZQD56zTzwe9IQTzK7PM6ym8uksSx2zsl2iFCTvVGlIm5C2LfNamGUUEYYjUjbaxmLVpVproho5tW/h+gNfyMLMpypv7nJydYX+3jIpBmETghZz70iWa5QbVD6/jJhLdMphKpdirN4hlfHg+F0KQKWTZXt/F0FRSK7N4WyU0BOZ0jmS9RKaQQaQsrv7sCsWZAl/9B2+g9H65GUFvK+fw0l//GuU/qFMv1wjihOlcmm//H36X5ZfO9zDEQRigw3uiK4O7LCMIgwhV10hP5VANHW+vRnm3THltj3wuy95OCWVWRSII6h4KAiEUfvKvvk9+forZEwssPn2C1U/vcu/T21z9yaecefkCds7h/NefRVEVBKBqChd+5QXmzi7xg3/2xzQaLVzPR9sTPPviM7h1lztvX0E3dbKFLJoqmS9k2Q5CFp8+Sf7ENG/96x+gqyrGVAZFUylV6pimAVGAEsDK0gz317dp+gFxIlEzNrOKQLdsfD9A19uLukkkhh8RbVfQVBVbAS2fJojb8xE1Q0MF9HQK6QaoYUxNkSRCoVKr0ao0mD+5SGlzF1tXufnJLZ7/+gt89ZmTNCsNNq6vEtQ9arsV3KaP7/uc/+IlZs4ssHzpJEkcUzi7QGo2T32jxLXvvU95q0S9UiOMZXtDgChuH5AXxURBhJpRSZKYzfUtnv/aCxTPzLP69nU+e+dztHQKmTJQPI96s8lMYZalE3OceuEcC5dPY+edkboWJEkYo2fs/ndxwp1P7nLyqSXe+6M3ufbONbymi1QV8vkst0s1Pn/nKqlcmue/+SLTpxeZOT2LpmsoioJiCOypNM//1a/Q+Hc/ZC/02NneIZYSXQjsg/UlpVqNxbllBBBLiOKIXCGDY1rYhknd8/HKdRQEsZQUp4ssXVgmv1AkDmMy83mWLp2gulUmNZXG2tZRDI3pE3Oc+8IF0sUs9z+6g1QU6pUG87MFYl0jTiSmZWCmLbpaZMAZH6H7OxeiZ1w9Dhx95sA4L4fReuGIOvXFZ3rtJTHwcoQNMqoaQ8aPmNSWgXzHquUxYayjNwIm2HXHnl72EA7BgPkxDB1b5GGa3Mujx813VD+Oun/CdsQTdS76phEPVHSUizC+r8YbuiO9TjFsZo6s3yDGgYHSvejz+SeO54n9MsoAFEew9MBq275q9YV0xzlcA4bqYzLM6G8yY5zCHoNmZOE9HdCPQ/RiGQldH3D8SB80pkYUe9xYRZv2YyxsMXTB+IFMDw0Fw31ET6VH8uPIko/1eGJrJ/FFxyk83CFlxLaDh5GxESPgKCJPGlASSBJkx+juWu8I2jsdNe7tUt2p4MdJ++Rqy0QmCbNFG9/1ccMAr9rAMnSyukpLJnhRDE0XQxFkU+0dZXwkuqKimgauplGqu4Rx0l6IrKqojsXSS+eIGj65hQLv/+W7WDmH0I2YSqcolzU000QDVKX9dccyDLwoolVuYmk6TsoiP1vgTnCD0PeZXZxmu95gdadCeX2f4srMAFEPnNcehXL2tWeYO7fE9tUHlDf2WHnxHPOXTg4ZkL3ucN+4FZ3+kkRewNqHN3n6Gy/w8Y8/xBIKlVqTt7/3cxRdw9Q0DNuiurGPoivYmTRhy8VOOXz0l+/ynf/s99Btg8tvvMTO7Q2iJOa9P/45r/39bx6W1SlfCMivzPDlv/sGP/xv/iem8lnMXIqbn94g8NunLNs5h739MkkYs3xmidMvXsSwTJy0w4u/9gU++fN38Cs1ctNT+KbB7IkFAtdlb3WbqN5kNpthvVJFAqZloKgagQBNEWRSFkbKwtdUKn6NbJhgqQqRrhK7PjlLp3l/G83UUeIEmUhUQyPRNYjbBycqMuHBZ3fIzRfRbAPLNrHDhI9+9BEvfftVTr96AaGqXHnzU6L9OkJXeOWvf5VTX7h42D9JEFG+uc6V/+Gn7O2UWb+/SRjFmKaOnXGIhYpm6ext7yMUBQ0FPwrJ6gb7exVkGPGTP/gzKpUGmqUTKRLZdKlVajx/7jxf/v1vcea1Z9Gt7gGHfVxxEOBw6x6GbaBovVMR29PzpmdyfPAf3uTu+9exLYOUohIqgsJ0Ea/WIoxjWpUaP/5X3+fspdM8950vs3Bppb1dL6AZGvnT8zz7tRe49tENyqs7GAJMXUcCbhSxtbHHytOnUIXA0FSajQAaTVq1JhnHwUjZFJwMDx5s4NgWrXqd93/4HrlijunlGQqVKdLFDPmlab78e1+j8V//Kdtr2yycW+Iv/uBPeeZLz2BZBpppEHoebqkBSYKta6w8fRLDMUfLm4dQDMc2SMdYPJPslJEqZFJxY/V7t+z+7/89ZsS40nv191H6SA7cPMyx5r1G2MPYKH1pj1feqNkXvftzHrnL0qATNVTfQVt0MojBREfo4r6+O65NN0rHHtmHTxaejHPREy3rwCi912NfH9/IY7j9bRvtaIN0EMZ7k/245Mgo/uRe6KY6ovcHGz5uAPd45p3LfjExPJj7F25OrO5E6EznGTf9ZrS7MfblSLoft9+GHcF++o40rwbo2OsjPAy/HM2j7boM9bgYcSn6c3TqJPsiML1pu57a2HocS0CNyX08tj4WyDhGqI+4fGuEUyU07fCxV3cxHeuQFzVDxwsjpCJIC6V9AJymsb29hyZUTF0nkgmGpuNFIRgqBUtHqCroRntxbhITRTFhEIAb0Gy1AKi5LpFM0GMwTYNLb7xEfqnIR/+f7zHzzEly03kCP8KPYjJTDpoCiRAITSeOk/YpxdkUXqWO13AxTQMzZZHKpkjiGEVVyc3l2b9RZ6/Z5J0/+Rm/9o+/g3awELpvzPcEIRRVIbs4RXZxqq83x+ny3ul+kh6HP5HsX1/nwZ0Nlt94niSMqYY+hqGSSWeQbogUgsr2PnejGGFoTJ+YZ/PaPVbv3OVkTjlcgD99Zp4Xvv0qn/7lB2zeXOX2m59x+a98AUM1++SGEIKFZ0/yxj/5Ld7+1z+ksVtDoJCEEQ3XA0OjOF+kVaqzsbbD5t0tgiBAM3RmTs5z/svPUt8ts3V/EzWR7N64x/kvP0fihVTLVaYzaezFOSLXZ0ZouH5AznFoJCGJoVJb28Rw0himTlzz8MIQLVSxZqdRVAV/t4oQbeew5QfEQYQhIeOkaCURieezv71DpVylUMhQqTcJghjL0Ljx9lX0apO5yyeZv3yS2AtwprPIKGHrg1v4dbftDG+VWf38HvulKjJlkDYN7KkULdpntszmcmzv7bPadNG09pccqUB1r0wukyLyQ0qVGrZtE9kq+WyGtdsPyGXT/Po//WvMXTrVni5zMH6GRryUREGE1/DIz2ZHxjE+/JO3KN3dZmauyNbaFinbhkSyvbaJTBLSuo6ZTqEaIXev3CWqtHj1P/kWc08tgWjzqJm2OPPaZXRFJbmzg+v5xFLSRBJEEal0jptX7kIUUSwW8OIItZBBd6O2sx8G+I2QMIoIPJ9MLkNhukBlv8zm2hZOOs2Vt69w9vJZnvrS03z197/JL/79j2mU6gSux3f/+R9RmCmiKwLFMNgvV0mhUFycZv7yiYEBM2BxDcVOxHhb+RgG3ii1frTFcoR26i13goPQDY22M03WY7156COLGE42GUevrh1RqER2p/g8NEyykCdAr/If+XqS09DJKxkizBgHY6iko5zX3vejQAJixCYCslOVRyJmF/cvEZ7slwvGdKOkPeev4xxLQfuAtwGj/uDvsL8/DMch6bg+O3zex+e9Bmv/rPtePEfxwdi3kxhsJCZBr7swqg6Dh0k/KV5pj8feXhkxoB6HsUcR87gdOgml6EffW8QhrQbLG1W+GMg7udS+skfa7IO4xzmU46S5lH3GZl+SiXQ7BlEnMPTx1nZIOJgKI7tsOwy9dB4os7ubx6DjKLDSVt/apY3P71EuVbFcl7xt4Pkavu8zlbJp+gFeHGEYBrWWS9o0UISCmbKRUqL4Lfa9hFAGWF5ARhOU9ssYGbt9SJtMiJP2WQjVpsvmrXXOff05lr50kRv/4S1mC1laVkQtaRJLiWLoLMwWqTddqqUamqEhmz6aqpFKG0SAH0akpzKkMym8IMKtuWRSNrfv3Md1PXbubbFwfrnfCZWDHdsVVMf7nD56gmTgBfhugB9GCGDx7BLXfvYZxbkiM2cWqG3ss3lngySWNPeq3H73Kql0CikEzWaNt/7yx1z6yossXjjJ1NIMF775Aulill/8q7/k+pufcfrVi5gnZ/sLPZATcxdX+OY//S3uvXeDrc/vI92AqNpgY3OPjZZLFMUUF2eJ/BAlbs/HL63usHV7nVTaZvnCKUIvYO3qXW5+dI3LX3yGK7+4gmJoiDDE0lR2SmXmlucQCFq7deaXF0gtmDTX95jKOPhRjGYZhFFEqphFtgKC1V10u33AnS4U4rSNaHqYmoauqdSiCGsqj2kY1Bou9f0GS6cWqW6XCLwAs5Chem2N5W+/zL2ffMbmlVWqdzZYvfGAQEgUBImq0qw3cUyDOSdNU8b4qsSvNJnJZBGJRNNUpqdyJFKg2Sat7RJeEPD868/T2KkiVBXdMTB0jd2NXexUim/8o+8w/8yprqzu3Zuyw0u0pxnuPdgjO5NtBwF65swJ2eaL6uoeMohYv7PO3JlFLr32HG/9D39JYb6Iv1+HIOL63fsUUw7FbJpqrcHOp/fIzhewsyn8htv+AuQorHzlEtKPuPJnv8Dz25sXRHGEnXNYv7OGGrUDY8VcjtzyHDc+voEWxaSyDnreIR9LlEQi4oiUhOz0NBGSZssj0TRufXaL6+9c4dwrF7nw8gUMx+a9P/s5xZSN67ooWvsLnDQ1wlZIcblI8eRMD216NjsRcnjKEEeb5CPlZh8acYTxMe6VpKP3R55rcFDvsSJW9t8LMRy1l4dbYg3sRPlYAUkO9BTj13M8or3wMDtuHVlqH/3FcELZr1bFcKbxeCYZqo9KkhF21sTzrf5XBE/GuZhA274kose7HZFawCManoMJJpr5fc5iJ3Lcd45AjzUzOE4ea1POcczXG404ZEY5IET6WWw0qq546kvw0NUdgX0EjnFbo47trpGW92Toc/wPbgZFzTC6nnqJAb46TmXGRW+OUdm2QJ+crEfHtds2mn276UcgHBpDoiOEO8+HDwU85I9HYN+jhuKxeG4Uyft4/MDgORTy8tAQ6kRrkigmCEIWbRNZyFKJoVVrYZkGsUyYSaWohAHzuTRRAo0IKtsV0omHbhjoeoqMbVGt1Ah1g9D1MWnPCUcIorCFAJx0CkvXufuXn2DnUix/+Rm2PrzN4pl53MYDarU6lWoV1/XRhUCmbRq7FcIwxDQMNEOnUq6RX5nBzNiYtkkzCFi7vYGlqRScDEHd49Z715k7vYCqqV2aHCza7Ab5Ro+zoX4cx68HMs5r+CRS4rouXrnJzKl5DE3j+d/4IoZj0dir8s6/+TH3Pr2NG/jono+zOMuZZ8+ztf6AzfIO//K//H9x4sxZLr7yHNm5As988yUyi1OU1ve58+YVsgsFNEMj9EJKD3aRQYRVzBCHCY2tEudef5ZLv/4yMpEEdZcP/9UPcKazfP72Z0hdEJQ94igmMQ2kAoah4zU9bn50neJsEbuQx/N8qpslBNBoeRQyDpvlKrqu02q02A8Csikbd3sPL5ZMmyY02qe4a7aJ5kpSxQy1OzfRYokbQSQlxsIUIo6JSzWkpmKaOkhByrJpVRv4MubEiUXSpsluEKBrgiRroaVNZCwJE0Frt8b6rTXCMMQyTYQisEyLad1EFwqNKKLhe6SxSQmN/HSeu3ceQBKjmRZZy6LiugR+wLMvXiRVyLD6+QOCKMTSDXa393CDgNe+8xVWXnmqzSu9nX9wUF/nS0ar7tLcb5AtZnByzlDg5MGVu2i6wekvXub2zz/hjb/+K+ROzlJd20MxTZI4IZt1COouC/k8+axDFPjU6h63PruDYmic+dplPvmjt5k5M8/p158m9EOWXrtEc7/O/Xevkk5ZmE2DsOEhE0kz8Lmzt4ulalyYTrM4N4NAsLVfwhSgGSoyiIh1A0yDer1J4IcYQkGTkpnlOSp7VfYebHPnw5u8+htfZnaqwI29CoqUSEtSqjVRbYtpJ4OMJYqijjGkxwvrI9dIHMMwfFjd2xnvo7ejPZDxnS3NO7bLhMp04xQjcB7qq8kV7R6SPKh3D2yUYd9sJPTqvYeBx4rODxY+qexOMyciGMAh6IsFPWxNE5kMTzseY2v10mHowNuhgkccyTwiZjWyvEew00bB429FKydXQsLh8fFwQMSH7IGjDmt7FNaTA+gkYzdGPQ62njoeA8dgU4aSixG/MUmGDMxHBNkjRIYK6kk0dCnH/AZej4NOO8akG3L8R6QbRa0hqomBxIfPe/jxqLoeEw4jSGNwHXVoXbduI+7FgTAfMY7a0TLRGXR0N0M8+Puo7ZMSIeXYKh97xPSWf3Atk+TgYLlB3pKH173rDxYunSQ7naekmdzeqRLUW1x46SJnnz2HF0WoxExl2qdgVz2fjKEjgNjKUEsUdCHwfB87k6IexqRtG01RiOKIOI7QtfZhecVCFkuqhHWPyudr+Ds18qfmcBammJovEvg+9UaNaqNBhCDj2CATCmmHKcugXG20pYEX4TVchKVhOybZfJb9RpNsymb12gPu/Owq9d3qgKMgxjsKg30uen4TSJ/ECdXtCs1aEy2JaNYaZKZznHjhHHEckyQJTjHLs7/xBZx8GkOCkDG7a9skMiGXL3L54jNs1svsbO1x44MbXHnzE777//h37G+XCIKAnXtbhE0fKSH0fCq31wlqTXbvbFFf26fxl2/x4C8+ZP3De5Tv7eI1fVa+eImTrz3Lr/8f/wbnLp0h8AMUVWHuxDyGZRFLyblnzzE/V8SrNpB+wHTawWh6pHQdpOTu+jaZmRytMMR1AzJCgxikrlOYLyKnM0RhiKB9xkeggqZqiJZPoCpEAjRNJZVLoVvtHZPiMIYoQdE1Vs6vYGXbhnmr1iCstkj8ECWlsXlrnevvXCfyQmo7ZYJqncAPmJktohccUvNT+DKmEQYoKRNTN1BiycLMNCdWFjDs9ta11UaTOAwRjkHT9XjqhadYeuEct966wsZ+CVPTUaSg7no8ffk8z/3mV1A6UxE740V2dpNrPw68EEVRyM/ncabSfXJOSmjsVXn/3/6Ue+/cIJVL84Xf/QbTz5xEsQxuf3qH9NI0bhQSRjF3SvtUAx8/jGgZOtNTeWq1OvfeuUpjp4JXb3H3netUN0oYpo4UgqUvXsAqZOHAQZmfKmCiIBSFlGkxk80SNT229vYBOHN6hbRttb+USIHresQSYs8jJSCra5RqDTY3dwnqLTRdozA/RaVap1Spth3Wlgt+RJJIAi9AIHEKzsAAEj1jpie6Mdm+Gzn+RoN8TF0yvpB+AxO6Yv0oI4zuVvGHDw+uevfa7eiY3jIPjN/uUXo9ZYlurcatUXziMMHcmJjnId916Dpxu105bG+MPXBwlBk37mCrETaCHEf/hyH5YTtkNzo1mP8J2UG/lN2iOhHUXoUpD7xnaLPi0Tsn0NPoh2PYwQ1PHxrGFjfK2ptUh4cof5QNP/Ss50XHXR6aJzE5CjEOjlfTMSGKocjHgFfduR4hxI8NPYrxkJXGetjHCSOMdfkPH3eLGHT5e8sZFLRHw2CXDW8bMFDFw1SP3rNiXAWPiXCQWm2csh/Foww2RYyY6jMekZ1JMZVNs1XZYnZ+Fq/eZP/BFpEfMZXLUXZdokYZXdOQiSRBtk/YTlRUy8JPEpIkIWXoZGwL1/UISZBRzHQhSxRFOBmHbC5DIiWl3RL1epO45VO0bcJWe1qToeuoQsFvuUhFRe4Kpk7MU9+poEQxqqbieiGe6+FWm9jFDF65SeC7qJqGqaksTuUoN122b20C7TMYMnOFYSkzaPT0MILsvx3WEwcvant1kjjm3gc30WwbJ+1Q368R1l3sbApV05BSkpnOYmcdKtv7JA2XsFSn2WhSnJum5dZRFYVCxmFhZhqfhN2dEmbGRtMUtu9vsvnZPU6//gy6aUAUkTu9QGY+R+gG7BkCFA2v5lHfqIIi0Cwdb+cBuRNFLnzzRaSUvPvnb3Pryg1M3SCRCffvriJbIZZhoFkGzUYLbyrL4sosn39+h+xUGryQZrlGpCi4toVmtB0MpeURaQopXSU8WOw/f2kFd6+GG4ZgGogwxpjJk2gK2cVp3OtroAoCNyIOI25/fIuYhFw+w/q9LUqygucHxE2XnTtbkCR4DQ/DsXAbLlEck0QxIQm5GYdsKs36vXV2qzWEpiBJqDaa4IXE+xLbMkmZJut7+8SqwvTcFAvnlrn6/Q+4s72DY9ucPb1CVYYszU/z6t/6Fcxcir6trjt2woGBJyWEfkgqa4MQh05HZ8TGYcT1H3+KkJLN2xvk54vU9yoYBQfdMthc3UbVFdRYsr69C3GCYuooYYidzhJ6AYaqoaoqQd1l6bnT3H/3Jhuf3ufiG88jNEH+1Cz5pWkau2WkoaAIBccyCeIIIQSegKJUmZ2dZme/TMp1OfvceSwpeLC2RSIl9TBmWhVomQxbe2Wano+dTTGTSTN3eokb1+61v0poKo6uESoOLc9DGDqWonLymZPMXjrRNXyHROB4XfFQEfPeATh2WhCjRdtgYGEUjNF1guFtwh8XOjjbJBuycHtI1kvPEemeAEgph6P0IxMOV2Fkmk7CEU4CMJbOhzDW1Onas2P5po9HOEw/Mp3o+dtT4FhbYURFB6fNj63TL8kffDKH6A1Ab7R01D+Y0AkjPLHJbR9rNg3Uod8hPPTGD73ytrHU+X4xuvTBd+MN1In7//e7uV2LYaLH2G+pj5RRg59jHgY6oZyBesruKBjyqLup20pu5GFyx/WKx3ngg+n70oiRyfoOEBxZUE+GXsE8tn3HGH2j6tknwzpq/VGjDrLrWB2n/J5CDr9oAIfhrmNDu1DRmad9GPEYPuZyIo4x0FZQorfzBhN0UiEQqIYOjo6parT2K+hC0Kw2SRey7QXcMkFVFXTTIGXqeEAYhTQ9v72bk6mjxgnl/TK+6xEGAVEQEUcRhakciq4idIW11U22t3a5e2eNjY0dmn7AeqVKoKik5/IsFvLolkngeUzl0u2dhjSN3GyeVpLg2BaOabK1vkPp/g4nnz5JLp1iYbZAIZMGVWXxwik0Xef2uzcob5bYW93v8mNfUGmCnOx2x+G1PODr3ihl6AbMnp7DTttEUcKDD29hWQYffvcdfvAvvsv+/W2CVoBXd2nVm0hDo95ysSWoSYwfBXg1l1mngJlOc+nXX+XCK5eYK06hSlB1nSQMufnmZ/i1FpqpM//KRaIgYvfODlEQsfSFp1h6+QzTFxdRMzaJTIi8gLDl0djYo7pR5uK3X+W3/vPf59wrF7BSJs16E0VVSeK4fR7JXpnI89mt1EifnufMS0+BSGjWG1gZk839ffw4xkjboAhiBUTNJfbD9iGIAnILU/iVOrx8HlFwCIIIVwjcUgOj4BAJUOOEXCaFoimopkJ+No+dTXPm7DKFU3NEhooWts8J2V/fxas3WX76JHrKJIxjqo0WxBKv1iSlKCwvzpLJOjQaLUzDoLq7z617q0hLZWo6xxd//UsU54r4YcT82UVuvfUZt1bXQQhStsW99Q38KOTp15+lcHquO5VCiD5+aD9vr6MwLKN7+Fl/Mlp7NW7//HNSmTRTszmcqUz7vJHtErqmkbEswqZHq96k6Xk0Wi4Z08LIOCRRjGGbBH5IqVxj48Yqt9/7HMPU2LuzSWu/ju1Y7XUsqkocJ2imjm7qyDjBVDUunFjC0nX8MObkyiKXL5/HMHVu3bxPbmWGF197gRNL8/hBSAWV3Uqdqu9TTDucWpnn6W+/yst//5v8zn/xd3j6tWeYWpwmVATNICBWBMvLc7z+21/lS//gDbTOLlojB9DDvGH4oNhBIfgo6nfIOHkEHA8LI+rZW6wYsAfaOlV0+eko6BjHj+Fk9DlNvabW+M5hZHR/qGITcPQkO7RiO7q8o6YG+ql3Xeyx4KFp0t8PYgDJSHQj9eh4vL8Mnnuiay6O83zQ8Ws/az89Fs2H7PlB16sbqR3PXr3e3+BmbaNcht70vV7kKJxyFIJjwIHxeeCpC9ETkRA9yCaOjUmtngzjnIIR/saAH90Pfb3xyxKSg3jFQF9MjBw9HH267ZEcbiP7EFvuDToo47ah6zxvR4wO0nTmTwsmR8MY5N4JfHCc5k+gUdtu7YkmjcPbywgdT29cBEpKkiRBJu3zLTrzxbvZuxkUTSE9k2X949ukTRuBJI5CLF1haWWOwPWplOu4vo8iBKmcg9psknUcEikpV+sYmoauqkQyIRYKKpJASva299vG6f0QRVUp5rMolg5RTMvzAcHdu2vkzs2TzjhM5TLc315nZmmRtGOz/2AH1TZQNJ2o5UIS40URW2s7LL9wlnQxhxlL0mFIuRSQmc2R2cjw4S8+RM0ZEAmmT8+RmU73jKyHH0SDOZJYYhhaewpOxiaMY65/dpMX/8ZXKZ6aYe36Gj/8gz/l9AtP0ag2iVoeAI6qg1Bo1FvkZ6aIFbDTGU48e565C0vUtso0KnWqN+8ipcRJp3hw4z5bn93n5FeeJrswhRAQeiFxFB+KsdxCHsPWeedf/4j9Wxu0ZMTMiVnOpEw0x8SZyvH6P/w2Ycvj3vs3qG2W2FvfI6h7EMbousrS8hyapWHlHS597SX2724RJBGltX12qnUSXWUq4xCGEU4iiQ2Nmu+Tsy2ErpE+t4iuabh+ROzFCFUljgICz8ewTaIwQUGlUJyi4bp4rk/KsVFVlTCMufj0GXRdpbq+h24ZKEJQ39inuDTDzN1N6mGAF4QgJdOFPI6mYc5NQ5xQ2itjOCZF22LOdoiaAWHN5dv/9K/hV1vc+qNfsL5bAk3DUBQ29vcpOA6nzyzzzG9+GaWzPmdAz3Tm4CexpLpbZXZlZoAXOnJBsP7JHSIvoLxT4st/81dwZrLMXz7dTpEkxHGMBJwEAsMkrRtMTefxo5DSdpmTJxfwS1V03cBv+WzcWCOdSjF/eonQD7GFoLZVobZXIQlD5lZOUb2/i52yqZQ9ivks2YyDiaCxX4GUxez0FLdWN7h/a410xiGMIhRdI7R1wv06Fy6c5sSlUzz1ay9hTaVJ4gQjZTHlWHz17/8ar/z2a1S39lENnamVGVJT6YNzZEZsRtqzjuBYgwgG9PEvGY5jU/U0YbzIPiI0LQ50zwHvTHYcHjLM/Th0kj3WxTFVdlfNHNMOOoaDcawZNr3I+nTeY8BA/knlH+U3jLKX+uyJx63rGHh85+IhGWhkxH3I9R+FdLIr9nAToIbL64t0DwhrxvRDf03lEF8dh8UPnQjZvW/jePgef1J8PRrrBNw9hBCDCQcjDQ8rcI5MP4LKR+Tpc+COoNagczAs3TsOx4hyhq4G6zpwL3suhnTfQVm9SrET5O7QuDf/QPXGVGzk8/G+cRtZh0cP/J/hhEN++Pjx3GnOvV9c4cb717j09Rc58dzZQ00h+760tBNffuMV1q+vUrq/y5TaFrsz5xbRsjZv/49vUq3VURQVW9PYW98hSRJqzdZhvWMpSVSVdNrBShLcIESXkp1KHdOwmJ2fY2t7F1XTCBWFKE5I4oSMk6JZb1EqV2m2mhQUC8/0SGk6tmWS6CqNahMZRcRx3J4Tnk2jqypaSqe6sYdqGXh+iGnoePtVZgtZ7iG4c+UOptS4+tMrPP/N57Ay9sD6tPa1GLAihrqy0ykHX2OlBEURpGeyNPYa5GcKxEgs3SAOIhr1Fo1qHcPUufvBdUJVkCCxUAhkTKwqGKbNzNIcpb19VF3nwjdeJLNYQGgKxVKD/b0yld19Ik0llrD2wU2WXz2Paujt6LWlowu9r64bV+5y74PrJEjCIOT+boWt62souspzr79AeqZAEsfIZkS+kOfk808hlIMQjh/RuLPJ3laZa299iqYqWGmbxWdPIVZLnD5/kspuGb/ZgpSF9EOIY9KaRkpVEKqKVBUUKbHSKeq3tonrLmbWJA4jjLSNu10hiiOwTDQpMA0Ty7bZur+J4ThslLYJ4oiZXJY4SdobDfghMy+cpXZ3i8AL2K43IYy5dfs+S7NFjChmeWWBE2eXDwMH5fU9Vje2sTe3OfHVZ9A1le2dPVpRiARaYUgSJywtzfLc776O7piHNOwO9zZvdA5vrpfqZKYyB8ZRr1HdlitxEHLn/ZtEcUyrViMJI/ymh24ZaLpG5AXUK3V8YgqpFAuFKW7v7qEIgfAiDF0jiGNQFFKFDPnFaWI/pOpVmDs5j6oqxFFM2HCJmi523uHtP32TlGkxvTTLfrVCEEaEScxOrU7KSZETNtVak3zaIRZQ3i9hGgamqrF48SRZzeCVv/0NjEz7lO3K+j7Xf/oZ27c3iOII09CZP7PIiZfPMXNmoe2AjRHV/QNIdmXpse3HERG33g45pm17LBgnjEeZQyPLPEoZghQdmT4p7aSA3dHFDKGSD2O4D5TVg2O4hgN6+ihzchzdBEO0H+/vPWFvc0Sduuw7QLPj8Fon80gbZUQfPGx/joFf2gndx4LDdQO9Dwe81T4eGd3i0Q5LL75x1BcDaQdxyGGi99RpVGmDJ5MPeCr973oG2Ei8o4zyI4XWiBUnDyvsHoGx+vjxl+QJjy51NIxqcufr0ujTyMfgGvQFJiUY7PuOzzFQ3nhuFEgxekpXOzrVW9Yop2QyHM0G8jDdqCfdtvQ7P304Bx2cXoyH/pE8VOoySRACZk8vsHD5NLpt9o+Lg0WqHTEhEMycXeT3/u//Gz76o59x5bvvoigqt9/6jCSRpFIWcRCSt8z2/G4JduDiCo0QqLoevuehqBq1Sp1sxkEiSVSF+UIWJYypNF1UVUW3LWSSkDIMdE1DVRU0TWkvKA/vEysCw7CotVo0fJ8gCPGikIyTou75pHQV2zLRTR3TtoiShMD1qVXq5GwDGSUkXsjphXl2SmViwyTyQj74tz9j+dIKyy+fRTX1A/LJQy9yzKTIA+LSlVo9/Ci0dsQ99kPCMMJO2wSuz8LiAnt3t9na3mUun0d1bAKZoCkKpmnSbLWYn5knXcwhhMC0TIQX49dcVF3DSJkIAXbKwpcJuqFz/+o9nt2rkZ3Lt8/3MIy+BedxnHDz558jpEQ3NC4+9xSNWp1b1+6RTjvcff8GRDHVWh1d0xBCoOk6URJz7tWLnPnyJTZ+sk9AAqpKdq5AXGtBK6TgpNjZ2iNjmcRBiJ64KFFCGISIlNn+ypAyCBsuStrByDn4fogaJ6jTDiKWhE0fS1WJTI0oiJASzrx4gSSKKW+XSGdSNJtNUqZJrdquo2Ya6JZO5sQ008+e5voPPqDZbJLOOBiJ5MHGFn7L5+TKEimzfS5KpdFkb69EuV7n5Mw0ABvvXMf1AuI4Jj4YX3OFPKdfewYzlxrb7Yf9THtKVLaY7huHUoqDsSpp7ddp1drOtpW1qWyUmJ/OE3kRmqOxt7qDSCSOYSAQeFGEL2NiIUERWBkLoSlt1FJgOSlShQzS9dle320vJG8FICVxEnP742vYmk5LxlBtMJ3N4iUR9SDAb/poiWDLD9nZryA1yM0VqKzXUITC4qlFXvjGS+QWi6AIdm5u8ODdm1Q29vFcn5tXbqDrOgpw47PbFN/6hJe+9QVOf+kimbl8VwIdyKkuuXqkYe8q+MM0I0Irx9kGsFPIE4SRBmBv9Xuf9T3o3DyqpdhPrSOSHL/EYxjDD6N2h1L26hlG9KUccz0S4xN2HI4LQ2ZnT2cPKOhjOWm9+Y6i/xNq8v9izsWoL4yy76rPAu8mHtvw41vQo8sZgXGSMBlg4LZgH3R3jylpJnXmkaNsxPtHMDyPwn9UtGaUfzhU/iMz7TEFZI/B2w+iy0YDSmTwarwDOQomL68aH+mYcDdm+tPhdCn6TxVtX3fc4H46tZ2Uka0cUcCk2376DOHpPJAjXh5Yub0smYRRe6ebzvd8oeDMFw8RSWQ7jaZS26mwc2+bMy8/BZpy2EYzbfPy3/g6ipRc/e571GoNppZmqO9WEICqKDwot3dh0hUFVYnbpyJrKrZt0YoSbMugFQSYhoaXxNQaLrP5LFO6RrGQJjJ0bF0lVcjieyFN14UoYevaGqsbOzRqNfK5HFGStLcydQyKTha/6pJNO9SaLeIgJOdNIaXEDcL2IjdFEPoBfsNDBRZni3hRiBfHRI0Wimlw671bTJ2fJzObo3+wiYG7gSEmOjQclp+aoRK1fAxNQwki9lZ3KS7P8OobX+Dtv3gbTQoIQmzDZOmpFfYebNHyPM6+epFmvUkkEzzXY+vBJvNnF4iimJ07G1S2S6i2TuL5ODkHTdepbZXJLU6haOrQgnQhIJtJs+YHiDhmb7fE3Mocz2TSbK1vU94voegamqYRRtFBGxPCJEGmdHw3JFIF1a0KlmOTmspgn5ilem8bBUHa1Il8HwTYiYoSx5iqgqEopHIOum2SNFwikvZ0MU0hMXXCSLbXjwiFWAjiKML1WtipNNkT0/g7NWwnRbXewExZeNUGiibIT+Wpb+6z/tFtCqfnOPmtFynd3WT34xvs1epMp1Kcn5/j/toWt+4+aH9Jsmy26zWiKELGMWbaxiqk8fbr6IqCraqkLIt8IcvZ1y5z9hvPjxUoHanQ3uZ9nB5s84Ffd1n96C6JH5FO2Uydmaflemi6jltukp7OEDRchKpgCoEWS4LAQ1NU4iAmkAlBw8OLJIV8FtM2iZo+vhtg6xqNeoPGbhUjZaKrCinDwPV9iuk0xswUe3sV5tIOvgKl3fbC+DBJmElNoSoKMgyZL+Rpru0zuzTHr/zvvkN2ocDOzU2u/eRTVm+s0ihXieKo7dCZJvlsGl1TaDVdGk2XD376ERtX7/P1//Q7pAppOgvaO9u7d0h0KOpH6flRKmfUgJsAjxSZH8QhhgM+DwfHyzlewx6he8e96tjCYnyyR6XLcd0l0ft1vzePGHwwDsEjVe+Qt56UW9K7C9eRNsUAf048I6Rjs47gZ9k9M+KR4Qk4F6MsyTEuUm8krf9iAJMYoNaB8GRo5uQI5IPlP4R1fWzjvdfY661Bb4cMGJ1HGdwjq9lvOk6OSMgBphqHc0ydJr3rDJbjWctPFHrXuozdWWGoDv1cIgcSiZ5nw314fBB0jLjRnvLEgd0jfLs+YW+dulKxS4FeR2HQaZCHf0cWJyeNnb4q9T8YiqBMytD/WNDj2/RMP1B0jc7YlHF7K1rlIBIqpSRwfYK6i9BVmuU6H/67H1Pf2OO53/oKqqoc4tcMjed/+zXWr9xj7foDMpUGSRhj6zq1OEE7mLMeRBFRFBGFIWkrg6LraLGPlbKIggDD0IlrDepxgr8bYpkGUau9y9TcqQV8N6Tm+QRRRDZlI6stLNNix/cxXA9HSgxVRYskzf06ds5h5sQMGz9+nySVwjZMFFUhFJL56SLq1j5BrYa7U8YLArRMmkwuTWN9G9MyUG2ToNZCUVUOuaHvE1GX8zqisstpvTzel5zqgz2iho+lG0RRRG2vSjNIWL50ipRjYysa1WoDZ7ZArVJje2eXk+dPklsscu3ffQoKiDghFgl+pcnalfvc/PAaapIgvAiZSBqNFs++/jxRK+jnth5eEorCua9e5ua7n0OYsH13g9L6LnYhx3PfeoUwCLj70S0sx+L082eZOjGLnjJpVJvMnl3Er7lYKQsBOFmH5k6F6XOLNOtN3EoTTVPR4rYjKb2IEKjoCsVcCq/uomZT1D+6Te6Cg2IbaPk0fr1F7AcY0zlIt6dHRb6PDBOKizNolkFcSCMMFTVW8LerpEwDj5gE+OQvP6S8s8/CzZNMnZrl5NeexdurcXNjk/VSmTiMmS0UWFyc58qtu9RbLUQcoysKiariODZCVXByDjPFPAVg5eXznPr6s2SWighV6XHQewzO9pICkiihtlujsFBgZnn6YN1SlwsiL6R0f4erf/4Btz+9RRQEXDh3gt27G+hLWU77IaquIQRUtsuoSUK97rHrBSxlsyxOT1FuNRGx5PS5U2ytbbanrcUJbr1FkiT4XojbdNm9s8nM+UXQNfa2d0nbFkGSoPoRYRCQmiuyVq5jaTpRGFN1XeaB5dkim9u7uHUXCSw+expnJsfV73/IR99/n1bLwzR0CukUMZJIQCyhHvjM2BlMTUOhPRavX71L6//573n973yT2QvL/evWBmIgh3ZF3+nRY8zDYzsW3aH32DBR+Y4KcT2EB3SYY8S5CEfUvnvOxZhwmXj09g/7dV3deCycAwZ+R+f321H9gbpROEZWZlJlR5oCj+hkDjqzY30EMfigW4+hqQWTcR2+fgKM+4S/XIyzoAdgaNxOtLAPUhy3tQ9LlYcbhIel9OzScayhPOQYTLwcSjsqPj7pFNGOLH14MdMttmOmdIVv55Xsa/9ENGJwgD8cjP2kOaHcvi0aO2l7GiCHUk/iv54CjznYu8V2ldlQ+gGjXdBREh2aieF2PAYMTZYboRRGZDre+yEe7vx/EBhIEpqVJulCuutxHHy1EKpCq9IgDiMaezXuvH2VreurVCp1nnrlIn69yannz/PJ99/l3OvPkpnJHZYtJeiOxfSFJXbubOAHEYrS3u6y0nJJwgjdsTFMHeNgYWelFaBGEa7v4+1X0KSkLFpM5dI06i2iRFJ3PXRNI+dYJGHE6tYuGcsmZVtgaGS9JlnTwDB0tve3mZ5fpBX4GJqOpqucevUprv3oY06dPUFutoDneTQqdfymhzhtolYNoroCkcRZmqVVaVLIZlld3WD7zgYrF04wc3YeM231s4zocdYGRtOorupzfqWksVXBD9vrQXQhWP/sLssXTqKaGjOLs6xeu0+90SQgQbHbC98vfPESq5/cIWi6yDCi0qi1aS8Et96/jqapNJsuM4szhKU6ke8Rtnw0S+9Kp4NqJkm73wUw8/QKX/tHv8HWuzfZfrBFpVLHqze49oMP+eLv/yqFuSKVnX2CMKK8XSEzm0fTdapr+9z+8ads399C0VUyuQy6oeLvVpk/u8Tm1fvoioqwLJJEImULNUogiVj42mVab15FeiGqbdG8uU7+1acQeQfVC2mV6wRJjJq2kNtV3CTGc9sHv4UNj/KdTVrlOmbBITRNYiUhZdngB+yXy9RbLXbvb/OUEMy+cAZvv47/U/j89n1WyyVacUzettqbF9Be+6MIQSGTIWWaNNb2MYo5Ts7lWfzSRZylKRRV6Tf1Ot050OmqphJ4AaEfolv64WgM3YDta2t88r332bq/hQJMzeQJg5DV3TJuvUau0D6oUFUEYctn6+Yqpq5TqrdIBJTiiIKu0Kw2eeG1F0nlHLZWNwmDkPjgTJA4itpnpWTSlNZ3CFwft9KkEQSkczlCIQmCEF1VqHk+ulQoTBUINrdoRCFX7q2ysjDL1Pw0YSwxsw5nXrnAjR9+ytt/8jPCMKKYSePGIV4Qksvl2N0rkXZsTM1ESyDSNWZnCtRKNfLZNPfvrNP853/C7/znf6u9xbPSJtqgSD3k0cFAiuw68ONH2TjoCv2uNHw0i22snO6La3VvHnq9pmTgC0M/MSaqu0lF9WV8Uu7WEQ5BDwymGOrGQfPpcXTtuLyH4nfEJihPqoxJ6ca1cZTpOGiTP6bt8djOxbH6pi+U2ZPzcErRhBCp4Ah+HPaax0ZYjx6jI2BE5lHSaAIcnvvRW9ZxGHuwyN5kfdGMUUZzb95hK7B3gHbrNWh2d2rfEykbyNVva/djGazPRF7toUcvabpz7wdo0CdUDyswHunEskeEGw4xiAEF0w99Btzgi95qjIHB8Tzof/TNkjq4EaKfWJN7f7gg0cc70Ddn6WGhp7PdhsvVdz7j4qvPYKdTkCSgHByalbHZub3B/uouxZUZ/IbL6id3qO2UqexVadVbnLlwkrsf3STwI4SmceOtK5iGzsLTp5g+s8z2nY2uc9F1v4iaPrppUHNdLMNgs1zG0gwUoFyrYwqFpqLgy/bXDE01yaQdTF1HKlAuVxGKwuL8DH4Y0Gx5SGB6vkit0UI3NMyUSalSw/INDNMiY0kcO025Wsb1PQrzMzT2qihGiqB5EPGensLSdHZXtymt7bWrrSk0ak0iwI8jTAFxkuBWGqQMk3qtQXo2x8kvXUDVtT4DXQ4RfUyXDPbnQX9nT0yzc2sDVQi8wCfc2kd94Ty7N9d58dtfJDOVZevGGvvbe+h+zPTiDLqmsvb5XWQckzdM3MCluVfj2s8+o15vkFuYorxXRkiBZuuoqmD33haXf/2V/uEnOHQsOr238sp5VF1n5/4WYRChhiHWyQX2r6+xu7pNXcTs3thAJKA5FqEf4qRsdEWhkM+QGArVcpWpQhavXGfm5AJ2xiGsNtvbC0tJJhEEYURgKtgr0wRLU7hbZVInZqh+eJOk5WHNZom3q2hCobFRwkhZxEh0w8DQNUobu2Rtk/uf3sb1PJI4wc7byDhGVXVazSaWoqHaNneu3uPS6i7F0/PMf/GpNn+Xa7iuTzqdYnVnB5nAQjrDviLafFfIoysqcRiTXplm4ZWzqKbRVpGJbJ8F06Gh7NJRdtYjHRgulmNS26tSXJpGIqlulPj4j9/hwWd3CMOQqekCqqVR3a1AArMn5tm5HxC5IU7OobZdJnF9gigmTBIuPnMeRVPZuL9Oq9liairP/DMn2V/dQRGCWEpmTsxR2dwj9gMUITj54hkatQZxEFLa3ENJW8wuzFGpVCGBjGlQbbicPLmE7dhIAVOBz53VDRKZ0Gi56JrOS9/6IvWtCp/+4H2qtToL01Nsbe9x8emzZNM2qxu7RFFE4geEioKia5x57jwtz2dtdavtMM9O0fACrr19lfMvnKNwau4hBNsEGGUwjI1PPZ6F9nAOyUHFHiWK9wi2/9DOh0ekfhzoWh2PQ89ha3pQ/z4SyL4//Whku5RHdiyOb2Y+6cyP7Qf+0tZcjN1e9liOQr93MSrLoP/xMJToBE+BY+wYJMZwTdfUPsq4G4o49XmWExjg4NWQwTlUlxHlTZSAwzj7TjIbspO77gS9p633JR3u74eXccMHvg2vJOjUpDNdZKAdfTdidNdNqt9AwpEyYcDb6K3vMAXo0mx8d4yEIUwHc4ZlHxMNtOKICEqXEfu5dlAgPhy0M8RhxPkXLmCnbUCSRBGKruM3Pd7/o7fY+PQu5c19pKYQBCFBEAACXdFImSa3P75NVjcJNYOa66GpKrVaHSQ0Wi0eXLnLmVcvtiOQ8qAZcYIeQX66gFtuomjtg72q9QamrlPMZRGKQqlWR1MUMrZNK05IaRrNMGxPozANhK5RqdbQEGSyDq16i8peFUVTWVyeY29rHxlLQilZr9WZtUzmi3m293fwXJf0dIbaXhkpYPPq/YMFxRE3bzwgnU5R3a1g5x0UBItnFtm8eo9WnNDcLKEaBr4fUMg67DWa5E/NYh4slB7XKbI3qionfcPs9m96JgtBiJJIdF3HVGD91ionz67Q2K1x8evPM3dyjh/+93+BbuicfvkC9z67Q71axw0CTBkzncvz4IPrpHN5hJBk0g6FfJY4iVF1nTCM8FwPv9qElemhOvSCamgsv3iG7esP2Pn+e5iOg+f6/OSPf4QUgvxCkemFKRqlJqalkxgaGSdF0PKID3iLMGL15gOmMg6Ve+tYtknccNFMA7vuoQO1OGYjChGaQmqugF+ukVk6heHY1H/yKTNvvIx7fw8lCPD3GqRVhZSqEhsqLcdCKPDBzz8h9DyyC9Pks1l8t4WKwvZeCd02sFIp3JZH3PK48qOP+Oqpb2FNZTj/nS+Q6CoiiNDTNuYvPidoemQyKeYzi8xdOsnU2UXSi1OYuRRCVVB19bCPO0ww1L89USaZSIQqMB2L5vo+URCy+v5tPvv+B2ytbpOxLRTHYq9UIZVOceryOebPL6OoCvVShb1SCdXQSE1l2Ln2oD1FSzc48epF3P0aGw828BoeK+dOYBfSVN+7Rst1WVicw8mmuPvZLSzDYOGpk8hEUl3dJnYDauUqaVWnvlfGrTbIZDOotoXvhkydmMNIWwR1l6Aak7ZMDFVlZ7fE8198Hh3BB3/2Nru7JQrpNLv7FRZniyxdXOH6O1fZ2NwhZRgkqsri4iwxkvtXblNruSAErhfgBgGOZfPgxipxucmX/sEbCHX4aK/uBgiHRsGEkcRo+ThGZw7xfY+4Hj9d5vjR+VEwFJQaVUcxTj8PZxwZXJugI8bq5InQw+ETaHTsMzaOA73m5jHzTPbBujr1iS0EFwN/eyPTgx04VOSIOoy1Z3rg8fzhQ3hs52KcYd5ndHaseTmQ4pCXBgz8ProN7J4zgjhjaTGG8HJsovEoHotVOhHnTlv6Bo94tPltEhizs1C/E9BNMMkJO27wenjBoODwULVj8vIYxN26dG7l0Kv+5McInAy6fr2DXnYTPQJMcEkHGzAmSafoI2VbZ+iMTDSk1Y6l/Lq2Sbv00cpI9l22dyvsTSi7Rj6Qzqd7+FGi6Bpe0+XP/6s/Jtqs8tSrT3Mvuo7bcKkngjCMMVUNS9dpui62ppFOCYLAY91t7/wTJpK9jT1WnjrBJz/9iNd+/5sYlnlQetuwSiTUmy0soOF7pHQdy9AhkeyVK1imia7pxEiEkISBj1QVHFNHQ9KMVVpu+5C9essjabkIRYF6C8XQqLZaZGyTTMYhCEJ2Wi67LYmdSNK6zonpaSyhoKsqqiLw6y4z6TT7pSq1lovhWKR0A8sx8coNEj8glbKxLAMtjAmR+GGM6aRQwgi36Q71lej0key0vNPdYjgAcdiZso9vdEtH6Bp6ysItldEsg6jWYubcApsfPyDwXKYWp0llUyiKwK23+OzdzzCEQsPzMA2NKSfPzvY+tuXgFLLsbexSXJ7F3dpHk+AGIaEXcuV775E7MdPe4ejwkNIRIllVeOY3vsD6rXVqa7s0dyoQJaiGhpAKcyeWaFRu03AD6o0mSSJpNloEuyVWTi/iKgmZ+SmQklbDRwoFNQHiBMfQCb0QYRsYRoJu6oSGRugFBPUW1pkFmtsVmjfWyE5n0byQwI9oWRrC0gk9HwWBqqnUmy1mClmm54pkCznW765SqzeYKebZq9Q59/x53A881ERy/5M7XLy1wdyFZVKzOV78u984/Jp05lefx6+20FImRtpCd6w+IdAb4VRGHGx6OM+9p/+FKkBCs9rEMHQ+/g+/4MpPPiGWCZm8g9QU6ntVVk4s8cyvvYQ9lSVsBbh7FUIvwKs2CDwfM2WyfXsdt97ixPPL2FNpgqaLikCkLM6+dhm33GDn7gZSSgzDoFGuU9ktMT1bxFA0rr7zKbqmcuejmyydWebjP3uLrGHgJjH5lE0jlji5DLqpk14o0NwoUW7UMVSVOEo4e/40mqpy5/2b7G7tkklZNFsuxVyWC1+5zObtdda3dsnbFoquU5jKsfZgg0gmLC/OMX9igd2tfbb3SmiGTpjEKIrCjY9v8VLj9TE7bh2Mk4O9fIf0seRoh2METFxzNwh9g2NMrt404xRHj60BA+NNiKE6jS7nGM5Nn7Hb//zRXaJRTwejfWPK7YWHCeLJnr+P6Q881PawDws9jq+UR3DVcWg0sownQoZDePwTumXPb/DZ8M3IMTrKTOsOjQPDta+gJ9BzB8dJj8R0eMxtm9BDW0D3VOE45xTLwzb05z1UEoNNG/jJgd9h2ZOKHkGuLiXlseo9CIcxNEmPs9iDYwS6J9RbA/U4WloMtXLooksUKXvTDlKp/x/I/hNaR1dwXLUOGEr2bc35pAbzI0FvRYbaNCIEdXBCrd/ykQl9NO1M0UiSBK/uEnohN37yCaobUt3ZZ/fqA1KW0Z7HXa1hqjqmplMPAsI4YSrtUPE8GoqBKhRIEoIoIvZDVFVFSEHoBX3859db7K7vEB6cGmxbFqZlUpyZIgLiROLFMYahoSoKuqZhqAp7tTq1IECXCTMypOhYpFSFtGUwO5VjOpMmnXbIOQ4k4DU9gigkjAL+/7z915OsSXbgif380yJ0pM6rRenq7qpWaDS4AAYYDoCZ2RHLMa7gcm3JNSPNZh/Ip/0Llg98II1mS9qSayRn5XBnMLMYiF4sVKMb3dVdXd2l69atqzPvTRkZOj4tnA9fiojIiMy8VYXxa3kj4vtcHD9+3P2c437OsQwNISX9MEYKwSjNePZom7JtUauVKJVswiQlznJSRZBnOWnP58b1y2RhQpSmDIYeg3YfmabkMifTVBKZoykqw93uFE2cHodTR+3jY3e8Xh2ZPxYLXe/pAd5BjygMEaqKaVr4fY8szRge9Lj0lZu4izWWrizT6w24//Yn1E2LNJe4hkkqBZaqoeQ5ModLL15DQSkY1CxHMU1efPMVHNfiwSeP+PiP3iZP89OkJSc+sGsuv/q//W3shSpZmiI0HdMtcenqOo/uPMEPA0Sec+3yKlmS8/ovfQWhqjimiaMbxFmKVXJQDB1vMIQ0Q1MUhlFCkiQMsrQQqgydaBiQeDEyiKi+dBnzyiLhk320pLAH0BBoPQ9NUXEdG0MouLbJwkId0zIxTPM4Wn15tUHf8ymVSiy9sM76zSsEYUjihbz93/+A0cHgeI4pqoJQFezFCrVbK5RW6xhHsUyAPC9sF8bHb3y5Gj9pn1ATSVm4y81yZJjy6Mef8sFfvItlaJBl9HsjvP6IWrlEr93D63r4BwM0x0SzDOIgIhx6xH5YxLsYBuRpTuqF5HHKzp0NsjjBLbsomopMM/IkQSAwLINgFFB1HKxqmdb+AWmckGQ59aUmpmPjug5CCGqmjQSiMEZRFbxD3KRZxmjgYZoGmqEReAGjoUen3cXWVEZhQK3s8rW/8Sb9/S5Pn+1h2SapAqoi2Nncwvc8fM+nWq3QbXW5/6iwu7EUjZJlEwQRcjwo7akkjiNPz7y+cmGt9skV4jMLHg7hRLTrz7NJnpY9Tzdy+Hfq+rCY/i5nrBun65yMvTPZjBTyDBw/Z5pufpr/Ov56gfbG9vgz2cgLVDXd/XntnfnuC6JobkiScUHpSEo4j1WagmW+o/znT19cuLiINnUs3yTxndeRsckxEYN9hlRwptwxxQxOMJrT+abhm0eN8nSWiarkMSN29HN2c2PM6tx0+uWsa9VnHj/MaH+cDT8vnSyCR+R3muGZhdLz6Ps0PGO/hCwWrMOF64Qc5ESlk+LA2IIzZ2zk2O593JdDhvVo2xbjtHf0eUR7X1qaJsg50tms75+rnbPrOYW3sYxCFu4cw1HAg7fv8PTO41N15mnKzmdP+cv/4g/5/f/Tf8u/+j////jwD9/G2+/TqNcwECRpRqs/xNRNbFUjyDKSJKPpOGhZiqHroOtUDIPOcIitG1i6TrfdA0Ugc3ksWwD0d9q0W1000yBJEoaeT28wotvuoxkGFcdliZQVxyBNUgaej2Wb6LqKN/LYDRM6GCQIwjCmpEoUJKMoJpOSLM9Jo5hUCAzDRAiVlUsrqJpGu9dlEEfIQ/e2QtUwVI2Va2uMkhgvDKmUXRKZM+wN0esu/sAj8GO8NCUFhGlgll0iL8AKIyzb5PFHj8mzfHJkxPhcOjrtnMMwTIzoyYwY7PZRgCRO0FWVPM8I/ZAkLJjwxA/RbIPVG+skcUqa54RZhm0YrNXq6LaD4TiEiUeWpWx8/BCvP2LQHxHnOd7Iw6266JaFXXJ58O4DBjud0yyOYGrNE1TXmrz+m18nlWBaJrVmnfZ+B28wpFmtslyp0u72EZpCf6eN74fs73XIoxRL1yk1qwTdEUYOnheShglqnpOpCsM8xy47yCTD7/voMkdRBOkowHr9GpEi6W0foGsK5BlYGnkYoZo6uWmgGAb1hTpmycZdqNK4sYJpGCxfX0URgiiMyOKE61+7gVUpYWsqm/c2+Pk/+yFZkk4OSS7J05xxhUU0injy/gb333kwNe6HY3h0MiyLk7rjlVvCqDPkR//Nn+L1RwSdIQcPdzA0jQyBW6tw84XruK6L74ckYcT7P3yXZ3c3Sb2QOEgKt8hBSOgFyDQjGHj4Ucig3WP/ziatpzvEScry5RVUXSu8aiUZZJIwSui0OkhD42CnxbDdQwLLSwsYlklrc5eyZdGs1fCFSioloyAgCmMOtlp07j4jDmOCsIh+7igqNVNntHeALiCXcPPqZV75+sv0nh3wybt3yYKYsmOhmwYjz2MURhiGwZtvvIZddej0BlRtB0PXSPOMbrdHSah87W+8gVm2pyfIWJraUCaHYMbDebWccypwRrMXbGA+qBdhjmcpjOC0lDKHr5twMjJb/rhYel4GXE59Tnw9r+NT2ozpdMwOXIwX+txpVtVje+3cto/X+jmC74x1/1w45Fh/J8bzy+Nvvhybi2OgDqGcI05LKcmyQjujaSoX6YhEHh7zz6DoI+nsLKI5+jKTv5qWz2dPvGlvSacynAZ66r2cDacYh+BoAswQjWe4yJu5FkxrFM6hseMrTtMgHPo4FlN9kGOZpJg68hXj4zSmdpuoW4wBOyMdjefMBXq6cydlJrp6Dj2cCFRjOJ26/jMGMIgTWf7U5P+c8/AkYsURqzjepDyZP1/aOndaDTTL0uisEyGJZO/hNnd/8B6X37jN9a/dPka1TDN272/x3h+9xe7Hj6jkkrIiiMo11FSyYmnINKE38nmy2yKMYlxVJ04zgiikYltIVWGQZCimRp5LeqMhrm6w6LgQpxiugasbJEEM9QLy1uMdHn9wH9t10VUV0riIqp2kCAFZmrJgqFQ1jb3eEClAU1TCUYClQK1ZJ8xzoiSj6lgMBjq+qiHiDM0y0VTBQqNK9izl8q1LtPY6BGFC3hlw6coyhPsMB22iJCGXEkNVsLLCG1MYx8RRglkr4Xk+w84QrdwjDmNiIbFskyCIKDerPH26w8jzsbGIgpiuAmmSYmjG+ACMfchTD489w+WSPMtRtUm9UZ5mGGULYeoEcUzFsUFVi3vuD7cxbJNwGFJaqdO4usjK+hKOayOAtatrGK7N3Z9+gt/rU3ZsJDmKprJ0ZY3Wsx2SNKVUK/Phj94nDmKEKgj8AL89pH5lcRJeYCIY4+Fac+XNW/z8ez8hl5JgMKTTH7JUrxeG7p5Hf+CxvrzAoNXntdduoVRs9h7uYEcp2UqKrmtYqoYa50RxjEgzhGPiJzkVofD4X/2MzAvRHRPVLjT3ualT/coNeu8+xFyporZHxIZKsNUmH/qkSYJm6iRBSC4kum1g19xCmI4yDE2j3/cYbXeorNVZvrRC79lu0cWqRRImZEmG6ZrkWU4SxnQ3D5C5xG6UydKM7tNOYUwtBL29Ho31xth8lCcB4OThValDXOZpxuO3PuXTH35E0Bnx0rdfwbQNdFNHCMHN125Su7zEpSDkJ3/4V0RBiEUF3TT5xR/8iMyL8H0fFIU0ywr4ogQdiAY+jz+4RxYnlMouSy9dJhz6DNsDNF3HSxIQEHoBlmsy2j6g0qgSyZzaShOv7/H4o/s0ajU22z26aYwtdaoll2dPd+haJv3egCAMcRwTb+gRKQp1XOIgxI8Srl5eY+HKEu2dFhuPnqEiMBWJF4aMvIAojLi0sMDVF67h+wFPPnmEzHJMIUnCkFgTXL26yrf+/ncLd7SK4Dh45ynvPcebz8yfs9dEDpfrwz15eiOdVcH4onuBPXp+wzOamFHfhW9zTbBYgjMVleNwjLN9z7MhnpV1zrvpIRGn+Kz5FV4o11nImh7a50lHgI/jeGoMZ1Y7Bc4xL3yuUHe0ts7Je5xrjrAyDd/nTF/85OI4nQ/NiR5NzKDd2Vg4ueM/Q0SbljnGB3Ca8MaLCw6PJC+WxETlU1XOjPZ89HNMBJ8WbuT0/D2sf2xwT+UZ79N51DhvOGapOsZkACGKDUw57vXhoikOj46P/mYwrIcIOd2nWWN3Cix56tehvm5MozD+hIm/U7BMjz0wfeogTuU/6jEnPZeTb45p4VR3nmNhlYyd4J3ui5w+5noeIeZCe8Lz6WeOQK2vNfnlf/dvcuONF4r7u1LiH/R5//d/wk//8z9CfPiQ20lI3TToaSZalrJethioOkPd5v7THfI0p2xaaEIQpDG6olAiY+gHdJIUP5MMvILhcS2Ttu+x8ckGpZJDba1J52nrGClBd0T/WY8kzRCKIIsilsouhqFhVx3W1hYoyYiNSKEbpWRpCnlOGsfESU4SxWiiiC4toIhFkR4yWUmMoWns7rYxDIOtzT3anT5pVmhttx49Q9cr6JqJSBLKikJN1VF1ld5giGUayDzHMgx0VUWoCvXLCwziiNgPkVKiaSrOYhUlzzFtk0gopGlClqZ0ttsn2v38SKCfM0Bicv6q2mGAwrF5UMQSUcmlJMkzgigiyVJ0y+D+L+5iGAaD7Q55miNMnZVb6/zqf/Q7/M5/8m/ztX/313jtH36H13/z68S5JMgkGXD726+RJDFxktKo11i/soYqBeWlKlJVUFWVPMsn9tP5dCexqg43vnoTxQvpDIeULYs4jHi8+ZSt3T2ULEMo4EU+T5/tUl+o8dKbL+L5IZZrIzJJCiRIFCBTBWGeQZrj7Hsk223yJMGoOCi5RCs7OLUydtnFzCWppqKULaKnrWK9SzJUCYNWF1NR0TWNyItQDQ3dNOhstYpTIMukfGWBzm6PLM3IDZWVlRpv/Na3MByTwX6PcBCAlGiGjlUtodkmmq5iuRbX3rzO7e+8iGHqPPt4k2F7MDZPT5QbytidDJlL7n7/A97943dwTZPuxj6oCle/9RKKqiLjmPvvfkrU7qNmkpe+8gIShSxOefyLT7n77h22njxl6A+QIqdUcgn6PkmWIXLo9oYMewMyoLnUKGKcqILuThsF0BWVMIgQmoKfxOimQf3SMrZl0by6UkSf7wd0egNyRWBpGrppUq+UuL7YxBIKvudh6Bqm49BYXiJEcHDQJc5zbt28imbo3HvvHo/uPiFLUparJXKhkCY5hq7zyo3rXL19lc5Bl/v3n/BkZw9/5JMJiOKYpXKZqy9dxWmWCYY+2REtHgkW08QoT6+507qmWXNvtpRwgUV71l58Tjq9u45d6Tp8KJHjU//503k3IM76/bxNPcduNLc7Y2P13OBcFEdfpJ9nsUQz25/H1ZwB7ClmaHbe4+th8+D7EtOXKFxcoDGhoAiBqoiTyT1j9h5pBI7uVZ/aVGfKGfNG68vD3CTfLE4W/gnDu5NMp+bohMAgj0TvyStTclbBo/zjv56DQZxCzbQQffx0rE+T5D0lJE1keE78zsleLJJHr6cuJcnxK0li4v3sysahH7vWdAyAOO7KyaPJXk+Tpzysd76tyuzRmPV0WpQ5hm9ccDvPaOvLTmMdTZOCwT36fQSraZvolkGeZQxbXfbef8Sd//r7JB8/Y71awS25jMoNHkU5B2HClhfzsOfj9Qc83W2hCoWyruOaBrHMSZIURYAnNBJgsVYjDkKSJKFsWeimjqIoGKbB6OkBV1+4Qnt//3iBqCzU2L7/FFNR8cKYEWCnAesElJKEYOCzLW1CURhD12sVojyn3qiTAGGSIaMEVZHsbO7iODa5kCRpiqaq7O+16Q89uiOP/YMOihDUyiXsko1QNUZhzDAY4egaQtM48H2CKCU3FBQkqqqgRAkChSBJcZplNFWlcngiYBoGUWdEo9nArZYRqoqqaeiqxs6DncM7+JJw4BcDMUmws8fxaC06vG55lCv0oyL+gaLgmCampjEKI0ZhiJLm7G/v093r0NrYxXZs7v38Lj//Vz8qom8bKiiC5q0VXNfBth38OGT7sw0OtltcurrO9TdfwrRMQt9HQ8FSFAaDEY9+cQ85fdXniKamFRFCsPryNSQKagZJlrHb7RBEMZqmY5gmvZ5HvVSibhl88IP32Ly7SZ7nDJ+1yNOULEko6Tpl08SLE1qDAU3TYkkzCBVBdbWB7I2QikoeJeRRTOfDhwWe0hx9tV4IWIpKnOcIIUhkTqleRhUCf+gV0KpKEckagV1yOHi8x2c/u0Ov1UGVkqzs4pQdolFEnoNm6SiaitfziPyQNEoJvQjTNVF1Fbvmsnx7DaFqPHznEV7XOxlpcXTX/UhQzPnsrz7mnT/4KYZlYJQs0kzy1j//AWkUc+tbLxKnOUqU8Oi9eyReROPKCksri2Sex6g/ZKVRp2lZlHQDRVfRdB2/OyJLM0wh8HwfRYBmGKx95UZhqzII6O600XSNMI4J+gOEBDMX6LrG1qePWFpfonl7nSRKyIKYUZazvrqMaRgIKTFch+YLV1i7fZnFeoU0zbj64jUuv3IN3TZAUYmilP12l93tPbzhCNswkapGlmQMgxDHsnjjm6+zfGON7e19njzdoe8HqJpGybEZphmplPhBxPd/7y/53v/99/je//VfsPnuA4KBT/vpATKfunZ4kTXyKPfYdedjvdWEwujzrNznlDncsI+dSx5uh5O85MkGf26Pppubk/3EVmG2kvSLpjGx6PMUHtOqwJnixSymfkazksPrh58Pos+fZimax97J8Uxna1bPTcekchYT9UWE08P01+OK9ow5pqrqybsz6GD8W+GB8ySzGJ9Rx5NOzmjv82J+dpIzf4nTz47muDxNM9N9gymhZbyuE1XEHMDknOdnJDEJU+GtqqDSUx5Txxap8SPfcbZ9boyIybkx8ftMiI8ly9OPi/VDHMMwV+ifmBhySiElTmWfHjfJ7D6dSU3jL8XpRxN1iekHU3UIZpPXeelLWRElQiin5qdEMtjtsnvvGc8+foIRJpg9Dy/J0C2LWAi6qslmt0OWZdRsB1VVCMKISAhGnsdKo0F/NEImKUESQ5ZTcx38JKHulkmSBE1RyZWM6qUGYRBjBCrEKaPuiEUhsVX9GKbAC6hdXsSIJJYfgq6xHyX4uYmCyqg3wLRMVlYX8IYeB/0hWZaDouLUykReiGPbpBQGtdVmhdHQIxUCXeZYlgFpDnlWuNFUVBRNQ8mLOVtfWKDWXaS8UKMz9EHXGHYHvPzSK+RbPWLHIc5yTE3DzOHZB4+RQqBrKlGqkGY5zmKVJI4Jd/fRNQ2R50RBxML6QqGBlrDzZJ+V68vY055ujpUUs13Rjq8rQddDt4o4FHmWoykK2iEzliiSKBgRiYQf/NM/5h/9J/8Bq9fX2Lu3xffu/S5/4z/6O6wcXivJsoyq7RJlKdsPNrl0+yo3vnabg6e73H/vU3IBg6GHoSmousbB411iL8Ss2DPXkBM6K564NZdIgaWVBr4fUVGqXLl5ibWXLlNZbTDaH/DpTz7BTAT1kkUe+Ny4vETuhSQSpMxxUdGkxFZU9jLJDU3HXKwi0wzd0BE1BU1RyOOUeLuN7PqoJRuRZIgwQS07KNKjaht0hiPSJEEVglhI0nafNE5xG1V6o2FxSpTlPLvzhF63R6laBsvEMosTi9p6E9Wok2cSkeb85X/5PxGMAn7p7/0qiqYeCw6qobJ0fRGnbPDgx3d5/O5jbnzjBk7VOVE0iOIq1L0ffMRPf/eHxSlJDjLL8Dwfv5uwfe8p1964hV2y8boDRBAyGnqUSyajkUdmaqgCSDK2RyGGzMiyDKlQGHXnObpjsYxNJMCtupRXG6RpSm+jRY5EsQwuLzbQamWG/RFm1SXca7NwaYWbb7yIWbbRNQWhq1TKNcxqCWWvRcV2qF9fZ+nmOt2nezx5p4/MJV6rT7fbx0pzrIpLQ9MLoVfTuHzjCu12j6zXw4siNNPk5svXcaouH/7oA/Z6fYSicH1pEdex6UUBaSBJZU6UphiWSeRH7G7vc/Cf7/Pmr77BrV/9KsEoxCnbTCzW01u5mLP8zuBdZh2EPHc6mR7PkY4vbR/PdzHriPOLaqrE1OdJ82e38TlYlM9V9jycTb+fp5s5q9lz2jjNK10wyaLMTJ3yFB8z6cPjhGET08Q6rhUd69SF4218CbzEX1uci+M0ziTN6vy8NKYSmM56vBcdcu9ivMCXxGAdkcip6p6Lbo7qkBML0pl84zHjeRzf+LDQFPE8x7Wu6epPT57JgTn97kRE/jzonegHp93hMfZ+4qTgzBzPwewft/s517njzZ3CsPyC6ViZcvzjOdJhg2JKOPprTYftqJoyYXsiJbSf7fPn/4/fJxuErFbKSAl+miAFPN5tkUlJEiWoqkbVskmThE6vh2uZDKIYV9NJAT/LgBwhVC4vNQu3sLqBa5kc9PuAxE9i/L0+9uUFFC8ll5LefhdhaNz+7mvHJGmaOq5jkSYBIKmpgs08RzF0ZJrRqFUJg4Bg4HEwGGLqOqWSQYRCueSQBDGxlJRcB0Uq7O+2cEoOVs2FXJL2PdqdPpqukeoqg2GAKSRxGFGxTASCmlXBH/hYlonpmPT3ewSjiGGa4dgm3f6QimURjAJWXRtD14iTDHQN29JQDY1+q0scxtgVHbNaJlYV4lGIUAThMGD3w8eM9nu8/KuvoRk6x/YKY8qHY/KaoWARgOGaGGaJUqOMFII4CrEVh/bAwy05BFmMqmuIGPzuiBe/+zo//K//J2zD5L3/8ef8xuUlkjhDAqkURGHG7ZfWuPL6Dfp7HR6+d48kjlFVlaXVRXYfPzu8DqYSjUKsijOmCDqCf1qKlghNobpYxR+GZFLgVl28oc/2Z894/P4DBAqD/pCVkoVlaIzSGMMxSIYhZBk1FDQF8jhBixMaloUmYGe/g+UWHoswdcKtNq3vv48OGLrGqDeiXC+hmAaGlOSKShZE6AjSNEfVVGSUIDWdLMvRLAORg1Wy6XcLD1WO6/Dyd1/n8SePGex0+Pnv/YiXf/0Nlq6t0N/pYpctatUS6TCkvdvihW++yKg7pLJYK66+KYLSUpVXf/tNhq0Bew/2KTVdqktVDNtAZpJ7P/yYd//wbUzdoLpWQzd0slxyyTQYDAa88N1X6e20ccsOnVYHLYnZfvSU20s1kiQtGGpdp7vXReYZlqaTRil+3yMNYyQS09axVcFA1Xjhl18HIUi8GK/nkVPAaS83qa0usKIpBH6Iv9spTqgUgXcw4PF79wiyjKsLNQzbRNM1kizDLNmkYUT36T6uphAZGk/uPylO84QgSXMQKbmicvXSKnmesxvHVAyTQRhy7dolGpcWufv2HXbaHdYbdRzbRDV0+kFAmGU4pkGWS3phgKqqVDSVhXqN1kGHn/3pz0nSnK/+3W/DsYH3/MV5cs844gtOSx2fd4me2AvPquTMzesCe/N4+bmb65xGxrWDZyiFz23jedNzChZnZr+wwu60PetzpzOFhDnvORusWWg/QfW8knN4xzOyfpnpS4nQLacp6py+nqpgZt5zJswYrR8bIH1pnnzmrByzJo6YzjRd9PTzi7G5043Jw8k7IUqNvRpXz4tT72cqaE6pOo/+k8fyxLFgdFj4FJFfGOVi7NusQmPalymN+XSuKXYExHSM7AvS40zYppKEXMpjQ8q5sE9LEvKM05WprBP9HTOUP84iuLiAcdbif8F0cgIuQUpa93d45/d+QPfJHjfWlsnTjEEUI3s9BkLFT3N0Q0dKKDk2ZDleFFExDaSiUrFsypUyXc+n7Do4uoFm6IgkJkkz3HKFTOakeUoUJ2iqwovffJn79zfIvRFZbGDWS2iqiu6YgEDKHH+/z8HjLYadIctLiwyjiDzNcCsuaZKiC4VIVbFcBzMIsSyDfhCAUKgJB9c16fYHlBYrODWNsD3Acg16zw4QpoZbKZEPCk9IeCFl1ybNU2xNQ1EFIy+EXBZ++Bs1pBfSXKzTetbCKlmUTZOhH9Dq92ksNUhkju1aiCgmU1XyNEMOfQxDxyk7uK5DRkYsJcP2kIPNFr3dHssvX6a8WOXJuw9Jdltc+7U3yQ6Nb4+Y8WON1NTYH/10GyXC9ojOs8JmRbdtAplhaAZ5mlOvldn5ZIMsh4/+5Be88htvsP7SNR69fxelZZEmCYoiyJIEoSjUGg2al5fRdY2NTx7S7nSwVJ1LV5dYu7ZGHIYEfoRbdQtXqYf33I8Nz4+Ak5OQ7j7aYdAZYpsmiUyKgIb9EdudLikCJZc0GxWiMKBcK4Nq43khipSUVBXdi0grNnKYkFsGS6ZOIgSKYVBWFYJOn9JKE3+nTTwKyXKJ6hZMpmpqqK5J7lqINCf1i9grA9+j1erhVsqkusJwv4eiqziaTjj0WaiUSbIUwpQszlAB3TYYdQYsX1/h2fuPGBwMWVips3R1me5Bj0svXebJLx7gLlapLFaLGAuHaDAsg+blBWQu2fhwk/JylUbDRcYpd/7kXQI/xLUsdp5sIZCoFYf121f4W/+bf8jwoI93Z4OdZ3usXFpBUWDQG6JYGo3lJnF/SBwnLC02aXcV4uEQVSlsPwZqYasziAsjdE3TKTUrqLqGWbIIBiNUTSUKE669toxVdjBck/2ffUqepcRxQuRHHDzeIewMuPmtV7n2+s3idCIMybsj9p7skvohIooQEpZrZaTrsP7mbTo7bYZ3nhCIDAUVKQQbm9vIMEJoGiurSyysNNm884SdrV1eWVlCkTndMMLQFMquQ03XGPo+fpoSpilkGd3BEAOVtaUmm1t7vPNnb1NbrvPq73yj0HkebxfjQu/pOXREtKdk4uN3F2DiptLs/eTzaqQ+ZzruoDi1dc7Pe7I3T/RBHirgjniQL5Npnbe3HT8/UlzOyXsGOk8pPI827/HPWfWKE77zXJsI5uBsJozTNFDwOZN5xDEI0+1MZLwgGX3uk5c56Us5uRhnzU7plWdxaxechPPo8hQjKTkkjTF27rnwc3pGTbKb8yjrYtUeX4+amARFe+cOpDxiNOXUkdhEdUdkVjDC8+AYb+s8Mf9onWWawT8D4llr4pnr5Bx8Tk8wOeu1mOj3qdrE5PN56WTkT3w4Tc9PMfF+JqAnv8cMaMSsLOfAMe3KsNjPxp+efR+0uGd/dqMz+3nc4OTb3U83ee+f/pC9R9ssOTbacEBoWOwf9KiUXCI/QFUEaZaSSrA1h/aoi63rXDIUnsQ5i/U6Xd8jyzJsw2QYBKhRgqMUkYVFnhIJhZLr4Icd1q6vYdZdBltt1lyLodAQuko0CA49vkAyDIi7Q268dINPfn6HvU4PIRRMxyJKMwIvIE0zkixDMXRyIej0C0NrQ9fpjkL0VNIol9nb2GP5xgq1RvX42qYChAMPkeXUSi6WY7N6fYX9x9v0o4BwGBVXiupVAJL+iLJhoGSSIInA0tjeP6DmlvAGI3I/pv1kD5RC85nnOaqikPpRIYiGMUa1TBanPNnZZ++zpwz2+6zcXmX99ZsYtkFlocKuN+Ldf/5DElXn1ndeRNFUys0yytF1U8Zp+iQpQrD5zj12tvbQAUXTWb+8xsGzHfIoxO+mxFmGUSmx+MIaD39ylxe+8TL7j7fxugPCYYBm6qDpGKrC2guXGR10UVTB3rNdDMskDmMUIRjsd0jDGEso7D3c4u3f/Su+9W/9Cs3rS2O0eWqXBiS97TYiSwn9jCSDrWe7CMAfBtimiVlyCLOcWq1MHEegaSRximWYmKqKMHSEhNjQyAwF27RIkgSZZqiqgaGp6CWL7a0WlfUFjByiNKNScXCvLqO6FsLQsGoloizD9iN002SUxDgYqFlOMAowbBN0leyQnp7tdwjzjHu/uItjajQvL9K4tkQwDLj/zmfc+KVXCb2A3Se7fPMf/ArN9SaRFxHHeXHdQTltR7ZwZZGgM2LQ9UgqDn7HY+XVa4TvP0AguPbmC1z66nWuvH6DoO8hVAW/3adxaYE4idnbabF6ZZUoihnsdagu1egNfaIsYunqKqZjcveDA3KZoZkaaZwiJGRJjERFSFCU4spWlqgEfoiiqlimycLNVdxGmQ+/9zatzR1UBNVmDaEqtLZaVGtl1l+5hrtYQWaSlRtr7H38mGSnTZrnCJljGRoxCgvVEtKPyEcBqsxxcugGAfc/e4glBLZrkysKvU6fUX+IAtysl9HLDnkQcKlRZ71RQbcs5ME+MldpOTXaQUimqnh5yqA/IkxTHNNAUVQ2fnoHVVe58Z1XMMvWoXB+uKtO3z+ZTrO2rHEjvS/Mm32BCuYywVPfx5jdyXg5kx34PB6gLs5nPGeaZvRntC8O+cHnq7ZwD61qJ2voufibbPQEvlPvz3xxRprCoRzD65dCY7Na/HIr/RKEC3Hq11xW/JB5OV3D5OicyE9HLkNPOe2cbPVYuf55kDNrKx7/Naa5nyMwFf2cbntMCjxlzABnCRbHxmJj3kHmOc09wXHxRJm1KB6tmUdtXhRN02vE+MXS6Qn2uVQU55U5oYHJ5uRUjsO6xodKnFCT5DT+jk10TuH35NxgUqFzFtKmaedIgJ7V8kmdp8ucXfsklmfgXFBcrzjvXHdMiJhoeWpjif2Id3/vxwy22+R5jqsptIXAkAIpBIORh6aqKIZBmKbkWQpZXjDPwMMgQdc0hmFAGMc4hk4UxaRZjm1ooORkqUTPMlxNZdsP0FWNN/7mN7n3gw/QNQ01iUgNDUtTGT8L0ks2Qz/kg7c+wNQVoihFGAblRhnhJyi6QShSTMNA1TRUGaJrGrduXSOIIsIsY9TuU1+sEbUyLMVgq7WHUyvT830WzEJoqNk2qqZiWSb7j3bpDUbkWYZ66HnJMm3UNCFMUqJc4mYZAom7WCXu+9glm3LJJc1zCBPyJEVRCtewiqEhXOtYQ6BJCLOMOE2w6iWSMMKuu2iGilAUrJLN5V99g374c/Ye7lBZqGCWLBRVmaKFgk09cjcsJezffcbmx48YeT4yzzFcl8uv3UQzdB7ffUgWxNiKwLEtVl64xIMf38GpuKxdXePeh58RDn2cSqlw52vo/NK/8+v8/Hd/gNcdQS4xDZ1hf0Rru4VSshns94jyjKEX0BoMybOM3/zHfxerZM+hXkk4DOhu7JPkkusvXGftpSvc/8Vdnjx8iqHr1EolVq6t4XshaeShlCyEUMiRWEIh9iPsioPwI/pRhOKWyUwdxQsI8xy96pJpGqplFtr6tSb2C+uUwoTs7hbJ433E5QVsx6S328HSdOJoiGObRCOPx5vbvPzidcKehyhLkiAqXA7rGqquU1IMnIpL0O1jlm3e/K1v8dnP79LrDjBtm3DgoaQ5wTBA1TVWbq3x6MNNsjRDN7SJuX6EpLXXr1AfBNgVm2HVQrU1rr9xkyzOiQc+1fUF3v3jn7H1/iNqi3We3t+gslDl6is3Odg6oD/0CiE7iPE7A/IsxbJtDMvEMAwURSE5NG6OBoURd1Xk+MIgy3I2f/YZV779EmbFRsly/JGH1xvy9L0H3PrV12msL7D3ZJsszVi4voo/9EmTDHWhjOVY5GlGEiQE3SFef0izVmbtlatsP9iiu7uPrSg8e/gM+fAZhm1SK7sQxqRxQsmy6Acho1xSrZVYXWiQpEUEe98yiD2fSsmh4ZjYeUqcRGx4McEwxM01rpg61bUFMm/AvTillWSYJZdIUfn47kMebu3yt3SNF3/tKyebwedi3MTEx/FAzqpnOs/0s1NEMCfPdDpToz9/hz61Oz3HnaC5blFnZj78PAfO509jNidzNfhjz2bAKxCTgsU4XM+TZuU/bvNI9T2HPztVxxjfIqezXkAp/Xlg/9xjMDt9YeFikvG5AHQzJtese+zy2J5CjnX6rFk3ZWg8AdwYVZ2a0F9MDDyr5Djjf8L0HjoYnLgfMFXuohP8aE07C+3jzPOsjOcI1RdzWzZb6Jr3bJqxPzsdGZyPT7ITQWBcHC3qlmNaqHEIz+joDJqYnO/PQR9iXOB5nnE8o5WxhflYOJQnL+SY5wChKPMXiXkauSON29gDmWV89sfvcP+9+4g0Z2WpSV/XkFmOF4TkWYYC9MIARzqgqKiKgl12UP0RSZJSrlZR0pRBEKBKIMuIkoRqqYyl66iGipJnhXtYCXGSstSs4jYrdPa6aJqOYrmQpAhVpbRQO1kzspz9TzZRVA2BpFpySDJJbbHOo48fHXdL0zQM20LmOUFvQJomxd36MGJ3YwvTt8mRRElKpVYiDCOWKmWQMDqMlbBQc4lkxl67gyYlqqYw8AOu3lxA2e8SZgmuaSARpICpCAyhoOga3cEI0zbpD0b0Wn10BezFKvHAx9A1siyl1eqQ5DmjJEGrODTzJm69RH29yaVXrhwOWUGTiq5y7ZuFN6CDjX1ufOPWqeE+2W6LlHghv/jvv89+f4AGGKZBMBrR3thh+cYaSXdAq93FiyNsLyQKYwI/IPIjnGoZRVGJ/JDKYg1N18jShGDoo6oaTqWEY1nEYYwqBL3RCKPVodysovZHdD2fLAx5em+TaOBjOGZBo1MpzyUP3/4Uo1mmHgTsbu0TRQmKpuHHMauNOqnMae+2CZOERs1muNvGXahjmiZakqKVbOIoIQxC2nmK44dYpkG57OL6PnG7T+mFNbRmCcVQEVlOda1Jstcnu7qEd38bf7fL0I+QuSRJE5Q4JVKhVHEJgUF3iEwkZDkl26BRdmm3++iGwYvfeZksy3j67mdce+Ua93/xGXf+5F00Q0MiCb2QzY8ec7DfY+32OnbVpdxwiYOYxI+wynZxgjE2R48ieyMl7/7eW/SeHWCVbFZfvUa5UcOpuQy2OvT2ugSdPmuXlxl0BqSGRRyEoAgajSqDdo9g4JPlkOQpRsnCjSu4tkMgEmSSEw59DF1nqOmEQUQY+4QfP2A49PnK3/42zkINs9Wlfn2JylqTUXdIqVFB0zR0XcewTayyg2ZoJDInjVPyPGfvziaduxtkUcy1X3qZ6q01Wrsd9EzihxFuo8rSzUtsfbbJaBgwkhJsl9Z+C8vQcWsVrt66wsqb10mjhP7TNn7f5867d+hs7aOtLZGWHPb2Ojx4uksUhmTZDiXb4lYUs2SZrLkmaqYQlEvEUiJFTuegw7Of3MXQVK5/95UCz5ysq9Npes+ajIk0rQCbV8GMR3L+kn3S2FywZqYTo+6TgqeUSeNAzN0zptod24rF9O+jh+OfTJU/S8g4L43XOcYLXIgvHi/3POyelMiL2LeeBcAhrzdRx5l81zSST/KKAqTJOC2z8HsWjPPyfMkCxpfgirbgTGYJFtPs3QwuZmZ949Fb5Yy/03WfVevsEmLsbxrEme/G8oijvzn1CeaY2BwzkcqJb+qx2BHjlRx7Hhz7/QVkoDkjdH4ad5U6VeHFCHFq8I7d8M7LN7duOTkoEmYZIpyc9pwexfGenI1PMfFvfi45e6zH6GNeaSmLYGcc4+OiCD1u/IQ25BSccwVFjufWzFl7iFMpJTvvP+Tpjz8lzXIUXSfIUgbDEbutNlvtNpoQxHlOfOiy1o9DVGBrZ480zUARLDaq5ALqJRfD0BlGMTW3xKVra0hdJY1ibE3FcRyCJCGTOQtrC2iWTpJmJHlGapiUaxViL0I3NY4cJYdDn4ODHmXbIkhiEglJLomDiMV6lbLrYGgqMktRLY38kC72d9tEQYxuG4UdSKuHpmuMRh4ik2QyJ5eSYRAUQdlci0bZpX/QI8+yQniwDbI0pd/qIbOM7rBPlktMQ8UydII4LWIVSFhs1ohFjsxyRiOPaOhjLVQIvYDm5SVKS3U0XStsVnLJ1/7ud7jxtRdYfXGdq1+9cZomJFSWqrz6618lT+VhxOaZ2Y7H+90/fIuH9zewEJQMg14S44URj+48YPvBUxbXFmk26pi2TRJGZEmKWy+T5zlCV1E0lXAYYNgGTtnh5i+/QnuzRdQPMUo2juvgeQEq0A8Cdp7tsLC2gBfHlEyDLM/RVYUn7z0Yo/cxWKUki1NMy8TIJau3LiNUaG3v0trYwdY02qMRUZ4Shj6WkqMLgVRV4ihCTzLMLCcLIpKhTzuOiDXBIAwQWTERKys1IkvHXl9A6hqaY5J5ITLNQEj0a4tkikLa9zF1HdU0SUcBuaJQLTnopsFSo0aepIy6ffY2tomyDNUxCJOMq69d49qbNznY3GPoR2x+/IQnb33Gq7/8NSxNBwlpJjFqLsPOAK9XuJot1V1kJvnshx/xo//qT/nJP/0+H//Zu7Qe79LZ2CcNYjRd5eM/eZfde89IopjdrRYf/+AD2pstsjTn1jdeRNVUTF0n7IxQM0nn2T4ly2BhoVEEpdzrotk6RtlGyCIYoMxzkjRlcX0Z3dAZ9IbkSErNGikSS9NI4phH9x8XEeRLThHJPU0pL1Q4eLjNL773U6IgRKoqQlPp7/fIwpjUj9n+8CGf/cW7tD5+iBdHxboADLfaxEFMbhrohsHNN15Atwz8wRBPCCzHJgwCHNOkXikz6g158ME97v/lR3Q3WkSjgDROyJKUOEmIgoi9Vpfd/oDecECSpSiaSt8P+OTRJu893uKen6K7Dk7ZwbQNKqUSpVKJnWe7vP9Hb7Pz4eMpF6SnOf6jLWc6DNHknJtcVSd+z2BkZuh1xhqa2cDpQjNhGY8HNf59jCEduxkxM50lcEy1P66/Hf+U02Vm4e6i2954vim4z2SNBLPYgTObOZFdzua4j/MeK4BmIeaCSUx+mYhuMKVgnNuNi7HY/1rSl+Mt6gyJ6KQfY0yenFFEHglq54hPYwLdMT3LOXrfaVXD2M/Tgs+8X0eF5Mz3xZtZHWL2szOI+8S168kCcExT8sRQ6RR8F5gwBZ6mcHu4wMjZo8TscfgCXpeOy51T+tTrsxj8yQWzkOzlSalZNDBdwxkLQNHXMYo7olMhzp+jY4g61iaP7xmKmKAdefj/ebfP5hp3nwWQnK5PTr47dqAg6Tzd5xf/4ocMhj6GomJoKmEQoguVLMsRsjByD+KYJE3RVYWabpNJiZLmKKqKbhrkuSROUoZJgoJgZaFBxbZp73UI/YCKY9IdBYy8NlESoysq1775Eo3LSyxeXeLpvWckeYptWASDQpt8BPWTX9zD641YqVbZ3N2m5pTxsgTfC9BKJsmuT64K3FKJ1uYeCLAti+7IJ3q0xfoLl1BdEy1OURUFb+jjNmuIOKN90KaxvMjatVX2nuxysNspDM9LJVIki5dXkGrBjJmaxur6KjIXNFcX2drYQTN0ZBiT5zmBH7JQr9INM8I4QUki0lxCLrFKNmmac3l5kZ3hCEXX+PitT6gu1Vi+uYaiKeMEBEjuvf0pne0Dvv63v8PijSXSwys1p9YkeTK2cdcjTjOyNMcuu+j9nPWlJYahT2t7j7xSplorM0piksGAzU8eYzZLyCxHyhyZZuQShgcDtLLJ5Veu8eFfvIuIElS9uLKVZhmWrnF5qYlasvDCkBe++iKbnz1B1XVGXsA7f/xTrn/zRZyqi2poE4LG/oMtPvzTdzBNnf79LYSuoZkm/XDI9bUVHrYO2O10udyso+gGQRyiKoI8k8S5JE1zUgG5Kmh7IVEK12p1lDRHdzSMepmSbWOt1EAIykt18iQj7nsoWY7QNKKkuNYnDZ1MgutYeEFM5ofEuopTr6LrOkG/OFWTmkI6GJKlGVe/ep2g59Hb75PFKXEUc+XVGyRphkxzdOvwSmAqScKYUWfEwtUlVKEUSoY859knGwQDH80yqC3VkUHM9TdvkysKT99/wMLVZTbubLC0toiqKnj9EWmS8fTOEzRFkCuQpBmqKrAMjSuv3WLtKze49xfv8fDuQ8qLNdIsJktTejttyqsNpIA0TfG6I6LDgIA3v/Eyw+6AoD/AMg0al1cwSzbd7QNMw6C/0yYNE5aur7H94WMSVWXpyjIogtFBjzRNMRKV0cYuB60OaQ71hQptr8eTn35KEMWonoeFIDY09u5sMBh4VBWFtufjeT6WY+Mu1MkB2R8S+T6PPn2I/tkTADJAxglX6jVsUyfXFOLRAF3T0FSV9WaTIIqQiqA7GOF6JXZEj0qtTOiHaEYh0G/s7WOOhth/8BOa11cKT3HFAn/mtnG8Po8zIYjpm6XPn8SpL19KOuK5BHLsZvoULzBPYJkhOIjpBWdeu88B4ynUncFXznw+zhhO5TnTWHmqHTFVz6mbJDP32bENdnw/lzPAn4Xniwh5p5iB5y3zrzd9OUH0zpAIp4XGWcLYeN7iU4zlOQksJhATAdXERBSZyUbOx+m0hoGTGG0z8s7s0AVamPNitmYCebioHVHkoRg65jlrssgxhmbicnI9mMZ8gcMTSXgS60WDRZ5jVn2cQT0TB3MEvVmEMD5gzzMRjgUjGFeJPK9Qfm6TkkPXmecrBWYJfUdBeWaVn9f29NojT7o3JQZOIfMM2jwew1nXosbLSGg92MbIBaYoPPNYjoUuFLIsp14uUTIMgrhwW2mbxb33MEnQNYWqbRGmKRLBXqtNnuU0azXWFheQQmGr0+Wg28cQMPAD9jtdRr6PkkuWm1UuvXYNs2Txa//hb7O4VKc38klHHiqw/2AbJKRhwsbPPyNOUtAUGo0FUkA3DQa+j2UZDPwAoSqUSjZf+dYr6JaBqiqYpo4fxcReRBokKEIgpASlCAR24/oVLNdF5jm6rtP3A/aHIzRFQVUKzb/IJZpuoKoacZLy9NEmo14fPwwI4qgI0CUUZC7Jc0ma5YziiDRJChenaYp16C437AwxaiV0TYU4ZvPTDZJcHtpRFANyRD3hKOSd33uL9/7lj/jsrU9QFIU4iKeIBdIo4cFPPkHmxd3c13/7l3j5lZt0ewPagwE20B0OuXrjKnkmebbfYhSElEouOYLWxi5XXr2GZmkITUUAlcUqg90uw1afH/+332fnkw28QRHnYeQH6JaOaxnUSyWURHL/00c8uPuQhZVF3JILQmBaFg8+fMju492xuEQF4Wm6xqgzJGmPMEyDKIxIgrC4PqcK1psN1hsNVE1HaiZRUgg8tmWhZjmxoZJaBpuhj2oaLLslaqUyiiLQ6i79fkgoBVmcolg6xkKFPIpRNRVtoUqWZURpTqxAKDOGYQBVF5BoUUw89AqDcSGwXBdFU9A0FcW0MMoO7/3+27z7L98iDEJKlk3QHbH1yRO2P3yIoWtE7SGdpy0aqwvEaUrkhSBB0RQ6T1vs3t/i+ldvs3ZrHVSBP/KpNSp0tw64/9M71C4vkgUx1WYVoSkouoqiCvI045Vf+Qprl1eI/Yhh4DMMfdBUGleXgcNo1UsN9nb2cWslNFWh1xkiVAVN1yGV5HGKzHJ0TcN0Daq1MmGWY5ccLr1yg8iP8XsDJLC0uog/8Nj66DGkKc3lBdZevYZpGeRZTi4kWZzgBxHXvv4KpWaVNE6I45R3P32APxyhqQpSVfGGI/af7UGaEOkaKdBYbLB2fR3SDG84QsjCpqfsmJQ1Qb1ks1R1aFZc0BRQVbpxTK1epV4qsb64QKVa5sVXbnL1yhqurtM+6KCjEHghlqZTNg0WF+rcvHoZKXOePN5i4517Y8LBrP15bLkc5zHG2QMxuRufd/r9udNzVnmyA4ljRmcCtvM2zjFlxam8Z22MzwHnqawz97IzAJ3HUB4Vm/c3nefMZuSEZDUe+JdD/nQShDH8noWnM+Ebl1Zm9I3zn89F4zxcTLf3OdIXFy7O47hmFThL2jhmqsfyH0aJPIoWOX7Id/6oMSOfHMPt0TWsk9jUcqK+0+zczOrh5GBgSuKV0wN5XNt0EidSjhxvUTC5HIxdVjrOcvoiz1EVxVoyLkhN4/Do6SkgD6Eah2cC2jnonyGMzUxTCHueNMF1T734MgTAMQhPRAvmXqeS44+n8kyS9CTxn/onpkcYjiKnnwgHgvFxm8DBOSg51ecJwUWS+CHhsGDMVUPDVCDNJXFWuJPca7cxFAXXNFksV7DtwqA4TTO8KEFVVWxVJQgCkDmmZbKw3MSP44IJBVYtDVtVaA898jzH0DR0TWXlxhruUhUEVK8s8kv/y18jTWI291rINC2uhfgh0cBH9ROqNRdNUyk3qwyiiJJlosQ50tBwdY04SthrdXhyb5ObL12juVCnUi7hODZJmGDZJlmek8QJzWqZzmDEvbsbWI6JoqvsbbdwLZPVZp1axSFH4kcRve6QOIowdBXLtbl+6xqt7j4yzsgyiQqESQJSYpdsIj/ELbks1sqY5RJee0h1oYKuqJiuhTcK8KIYCXhDj8VLiyfDc7gWSGB40Cfsj6i7Ju/+6TtkacbmR4+O16+jAb3380+589YH7D54Rp7l1C4v8N3/8LfQNY1y9TDORRyjWjqXr67jmBbd/oB2q40QgsW1BeIoxq7aSGThdrXq4HUGRAOfNIjQgDCMUBSBHwSga6CqHLR7iDRjtVZjbXWRg519MkVy6Y0b/PK//xvc+OpN1l5YP/b6BSBzSb/VR1d19JLD0I+wSy7XXrvJS99+BS9JcQ2VxZUmt775CpZrYdsWbrWEmuU4ikLuWAzJiBRBlCYIIXAcA0soRQySskOW5sgkRSgCY7lW2FUEMcLUSKOEQWdINAjobR2ABP/RNroEXVExJOxu7bH9bA9FVRmMRqgSvCQFMtr7HVqdHpZlYqgqwSggSmN0QyXxIzY/fIiMYvzBkDzNCLywwK0i2Ln3jL3Hu3iDgE6rh9A1ymWXIMvo9IakWYp/eA0w8EK8oU8SJ2iWzv0ffMzG+4+5/etfo7rYoFIpYelGcbqYpDz+2V26nS624+CWS9RWmyRJBqpAKtD3PdZWLwGFoBN4AXsPt7n06nV0QyfPJe3NPfbubxF4AUmWUV5pIBSFQWeA5tpYZae4erXTpd/uFfFZohCzWqa20oQsQ80yViplbqwuY9oWMYKuH6IrIAyN1DQpNWq4lsHBfpuNe0/Y3d4jCSLcSglpmrS6Q1phwnZ3wE57wCjLyIB+GCHTnE6vT5plrF9a4cor11h55SpXX77GK6+/QCZz2q02cRjR7Q8IwpjED7BMnbXlRSKZ8fT9R/jtwcS17OM1curnZJYLbjbPq0A7bmzGj1n7rpgsNrs6iSTn6Prrqb7OK3wRuI9B+5x7+kUbmPdqnrBwaJ8wffX8vD95xDvNqHICH3PG9WT/np/nVB0zBaSTh2NdmiSH8T1gSll4/HEOHMdyzJc0fF/aycVcpvsUsOOS3OwenBKq5nR2enJPE7WYen8mUzf1boLRP93dGTCM0YGYzHkeTZ2fjohGjqFvxop3/GwMCDkGxTGtnzCy4xf7JvF1VI08qWTGRPvS05RcJ+fQyOdJE+DPEJZOns8WFI5FvFPC34yajtFW4PjExuZEPjgRDCXy6G8MASdHuYeCr5CFln1ihpyGfUxaOBYajv+N41NOfomDmLf++V/y+K07GK6LYloMoyL6r8xz4iTB0HQs22IYhhwMBpiKisxyqobOkuOgKyqWYVCyLGzXJk4zWjstBiOPkqEjdJ1E04lF4b62bNsYmoap61x549ahxr7A1+U3b7NyfZU0z4iCkOHQZ9Tqk8UJ7U4Xr71POvAZjQJ0XS/iaDg2lZUGYS4p2xa6ojIc+Ow920dRBG6tjKmqdNo97LKDoqqIXJJ5IaZjoiKpOiaJHxaMjW1yMBiy0+4TRzFxEJCFBWO4/OIlvvm/+C4rr11j9fpl2t0BihBkUpLmOeZh/IA8TouNKooYhSGdnTblpRqGKkj9kDRNUYQgEqCaOrXl2kyi7bf6eEOPWEDqhSiqwvpLV5BS0N06oP1kl3AU8uAXn/Fv/Hu/xS/+8C2efvwYBAzbA3w/IBTQuLYKCmzcf0J5uYmmG2iGQblSolGvUGnW+PitD4vAe45Jeni1Z+fhNghBpVFBAGEUo+gqtm3S6w+I85ROHNEPA0qWzuigj6IprN1a49/8x/+QhUtLbN7ZOJnjh31Lo4RP3vqQKIlIyGkuN/juP/o11l64QhokJDmohg6ahlt2CT0fMkkyDNAVAX7Is/0We70eWDpC1Ui1gsFHFNHXFcdEqCpZnJGHMYqhEYmc6GBAHiXousbSrTWkpqKqKoZlIjWNTICuasU1HVPH1AtBwzYtEiHQbYvqUoPmtSWcqoOWQ5ymZJpCrgpknBYCt6bg1l22NnZxqy6Ny00EoFs6zUsLABimjshh1BvRaw/weiM83ydJc9rPWvjDAKlAhkQ1dYKez8adR9z92Ue0n+xz+1e+QhzG6LpWOGT46R0efHCPKE6QpoZm6iRJSiok4aEL6Uxm9Nt9RvtdnFqJTEjaO23segn1MGL8xr0NNt6/h+2YlKoV1l6/hqZpJGGEMHQ0U6f9rEUchMSeR71WoVKrYVg6/e0DZBQTS4V2muJaJrqh04ozOkGIqmgY9Sov/9ob3PjWS6y/dhPX0Aj8ACydWy9c5/K19SJQnlDIsqzwQJXlRHFKqzdg6AcoaU7NMEERPHz0lM/e/4zeZouw77Py8lWW6/XiilYQY0pBvzcgTjPSHBYbDRRD48H9DT77k3eLk8exdfF8T36z3p/BsMza9Kf5pJk8zzkc6vGcOps7fG5PQ9OM9CyQZuyTz9XIvOxyOtOcjPPKC5h5Wn+BNJvXP+ckat7YHr8/3OM/j6ABBW2O8QDjbN8EC3hemikMnd3286YvLlyII8Z+zrt53mmKDLOrnGL5xzs8LSIwJo1OEvWYtne67SmCPZZqz8HqXKFuVj/HhacTkGZMxhnGuBNgyGMJ+oSc5rmUFRNljzF44eCCs6fTmZQ29/UXoPKJt2csJsfEMa/cEZXMXhCOaWg6zSbmGc8+v4gvDssf+g6brP9IqDoSDuTh+I8rmcYl7yntkzyVaQ7ox1kk7Y090iDGKbsMRz6jdh9FKPhJgqaq1BpVrt66Qs11cHQdW9dplssYpgGqig+INCHNMiSFZlyLYzQVOsMRjq7TGXkF4w0EaYpjmIhD7Znj2izeWp+YR6qhc/Nrt3EtmyjPaC5UyaMEr9XH744IvZBAysKoPJdoikKn16feKHPtxcsIXQMBtq4xHAVsPdsjiEKSPEMIgYFAtw2yLGO/28OsOvhxzMHAR1NU4jRlMPRIsgzbsjAMDVVRSaTAdG2++ltfp3ltiTf/3i/z5q99m+EowDV0DF0nS1LK9RJus4znh2i5RFFUshysXFBbqBFsteg/3qXbG+AFATe+8QLLV1cwXau4hz9GE4JiY8lzidQ02vtdRt0BpUYZkPzsX/2Yf/af/ld88ie/oFQpU12qc/sbL/PZWx8VQcx6Q2QuCTtDbn7lFi99/SU67R7PHj0limNuvfEiqqETJym5zOntdYorQ7qGQHDwdI/u1j5ZnvHCd15BUVTyPGew08EtOViHbkOXl5ooml64+o1iRkHEwvoSiqpQqZd56VsvFacWYzTYb/XY39jFH/rYZZfhYMSf/ZM/5q1/+UMefPKI1atLGCUToQqe3H1CniRohooqFEqppK9IAl0BTcfSi+suaZKQJgmqqqAqClGUkAYRuZTINC8Y/maNuDsi8SKIEnRDQc9y/KFHGsT4rok8dJ2bA8O9NjfXl4jSmMgL0FWVvOvhtwZFzJIowaSYM6quoSoKhh+h6gpZlGDXSlTKJaolF+3w2luWZDg1l1TCzr2nxfgCpWoZu1yCqGCmm+tLlGwTyzIoWyYH+23EoUmOUAVP7zymvFijtFgnihPSPEEzVeqLVYZhwu7WPtKPGHWGVMpucT1MUzE0g/5oxM+//w6jzgBDU+nsd0CAaZmksthJHUfHGwWYJYvufodffO8t/JGPahTuXku1Mv2DHrpQuPnaLUoll95um707DxFAEMaQZQRxjFIpUS65lBSFWBGsX1tltNWivX1Af69DGkUcDIeYroV26PJ5d++AyA9IgxA/jIjCkDiOyYEYyb7vE4YxlxYXMTSNTqfP3uYOsUwpLVZ45buvs7q8QGYodDp9XEWlohu4QkHxY0zNwAtCth5skRxfNTxUHE3t7bN3nOl19jm5s+l9f5zneZ6YG4dKr7k2qFOCwtyqz9r2Py8DOsH7zFOMzSjzvOksdI3tq3O3x+n3s3A8R783s82JWyOH8E0LmhP1nN7Tj7IIRYzxusXTQqb8nNfv5o3ll6DT/XJOLs5LZ/KsM04QJojwhPk/1rQf/01XdsJMzmxshhRcjPP0Nasz4H6uNHb9aKaNxXjbEw+POcRjaXSc0QTkWbCeyjOj4Yv266L88yxB50KVz/g5vcCetRDMAW6873I2lo+v2Z1V63ENY8fI8zyCTPybOIk4DRkzhIoj+n+Obk53iKMj4Fn4L+7gn644TTIe//wz8jzn9d/8Ou5ilZ2DDr4fkuYZqZTst7v0e0OklGwPhqRSYuk6EskoCsnynCiX5FIS5xmaouK6JdySQ921iLOUeq1Cc7GOCigSLMMgyTMURaG23qS8UmfiNFNA5dICMs9Js5xud8jjdz9j75NH5LmknybkqmD58gqaa9OolMkzySc/vUNprUa5VmI09EjSDCXJaNZrGKaO5RRBsyI/YrFRBcNAVVTiYcBCrYJlmbRHHnGcEKYpmqKQpglpkh26vM248Z2X+MUf/owf/b//lNF+HyyNLMuwDI1RFBdCk6qw82Cr0ITHCaHMiaIYoUJ6MEDVTYSp4fX6LFTLXHr9Ovv7u4RhhNf3TgTHw+EXmkKSZoRhjCMUHn/w8BhVX/3Nr7N8aYV7f/URncf7BL0Rl169xtbGNjuPt5GKYBQFxHFEmMRc+9ptVFVlZ3MLRVNZfmmdSq1MHMVFHI9UYh1GrjYci7/8Z98nGHiEfoAE4jwjT1I++vFH9AdDao5dGNnmOa995yts7bXJ0xQvitn85AmJHwGgWybji1WWZuiWzt/7P/wjlm6sEQ0DVq6vcP21a9TqLpam8vjeBoPugMZKFSUJ8fs9wiBiQSgEeUK8WEFaOqqtE8uMcBTipwnDJCEJIrANrJKNs1TGsA1AolZsSqsNlCyn+9ET0iDGvbyAdamJpSgkAoIkBT9EjHxyP0TXdXrtHn6UoB46LPDTlKuv3iDpexCnyCxDWiqKo6NkhZesNC+MzR998ohys4QXp2RphpSQRAn3f3oXTVNJ4gjb0mg4Nlvbe8UpZZqjA5ZpoDoWmqYcBkoVWLZFbWUBpCTwA4KeR/PyClmWkUg42N0nSjM0Q8PRdAxDYzjwyAUkSYrf96jYFov1CqaqYbs2VslBMwzsiovlWoDENA1My8R2Ha6+eZvUjwjimNX1RUb9EfuPttm+t8lwe5/GQh1VVei1ulTIUMOQUq1KybFxdY1UUQijCBmFlA69cD358D533v6Ix+/cQfohhmOx3miQxSkP7z3mYL+NgcQtuTQrZS4tN7iyskgcJzSbNW7fvsqVS8uga/hRxJWv3GShXuWzhxt88MP3ePT991l67Rrf/K3v8NLrtxgFAbudPq3ugIdPt7m78Yxed4Cqa8RJcoGFdnoFHd9pLpj5AqlQKEhymZ+tBJt3teOsiifl+7/e9IX5qM/RzjjvcJTkGcrEM3mMqedi7OExHuWcPsqJeo9tho/ezhBc5rCKE6rSk2enFfCzys1NU31+fqvV+ekLCxdn08w5jO0hEz3NBs6q54TBYwYxTHLfx0yjnPqbAOHCy8Hpbsxre0ZHxVmjPlGfnMDBiXAwXePY59FxxnTz4oQQZ/ZOzP1xZn/mMr2fkx4/rwJkNhhTQpw8Ae903tnPJBwb9c8U4MbSiR3K+IQXTF7UnC1Vi6OGJDNd1l5c7ju5ODX54jS9Ayca46ms2589ZenmGh/+xbt0t9t843d+idpaEy+O0W2TTOboioaSSXIgyws3sb3hENMwsCyTkm3jRxFqlqMpCqauEQQhuqYDgjTPWVhpIhGoQlA1VCxTR1ULe4tSs3LoHWkyVZfq1GsVyFJUIRjtdXj7e3+C549QNR1PJtz8pZdQTZ2FpRI3lly6u22SQ42vaxtITRTXlfIMoSg0mzU0XWXo+4ceqCQV1y5cbFZcSg0XS1OouA5lx6JeK6NphbGpJqDcKJNGCcOdNq3tPX703/w573/vHVzLIFEUZJZjmga2adDZaZMLiaYqpLbBYr3CS1+9Tf/BFnGSsN/ps3B9DV3X2PzkCYPekEq9MnY14yQZhoGmqGioVBcaHGzskycZAli+fYm/9R//A6xamfaTHf7g//K77D/epVQq8/inn9Ef+NiOQ61W4cE7d/noBx+AplIydCxVQ9c1wigmy3J6rR46KoqmEQx8VCEw8sKgX1VUNMegVC2hKoLIG2EpCqQJNcNip9Vh9/E2r3/7qwhdY61RYdTq84P/5/d4+KNPyJL0mHoBvO6Q7/1n/wN/8U/+mCRIwNBQhUALEg722+zuFzENvCgha/XJ+z5CVXHinDBNidbr7PX6WK6N5/n4ng9SYloWOQIUhfZ+l26rR+RHhX2FHxL3fdAU4jRFCWO8x7solk79pTWqtTKLlxZYvXWJVNOKyOW6jqprKIaO7dq4roPMZeEowNTJssPVQhWouoZh6Ci6RjuKyKRkY2MXEeeMDgZYmoZbKxVYyHOGoxFRmlBpVnGbVaq1CjXbZuvpLnGakpOzdf8ZpqIicsjCiDSKSJKE1ZuXMFSNLE3Ze7BF0B2iqwqmqqDrBiLL0RA4jg2WgaMVLmNVtRhPq1Khn2aga4RxzLA3xLENsjQjCWMalxZxyg69zoDG6gLLN1c5eLJPtVljFATYmsL+5jatJ1ugQhglbN3ZQIsiLBRErcby1RWkAraQODKDwRBbEWiaShTH9AcjvCil44cMhx5pklEp2xhZThKExJ6PW6lw5do6bc+HDIZeQNW2cUoOpVoZ17HRVBV0lb2nu7T7AyxVw1JVhB8hkxTFMnAaZWzDQOaSzmjEKAjwkxhBsUa4hlWcZD3HYcHZD+dsjjOYyumtN88PeZn8FAd4+ud5zPHnTedtRn/tQsOJKu4LJzHnbyKPvGA+Jh6KcV5sKuOEUfcsmGbWK+bnmc5/zhhciDTHeJkvi4a+hCB6XwYkktkYOqn7RAidbPF0qXMwLS4yH+YtCBcqfAKGPPk6oYEfzzOjXTFFi+MC+OTniSb6VAxzcYip6a7MafOMDJzo2L/claQY9bHxnAGbhAIhcjwq5Wl6mQfbrKcTz6bH6CiPPGwXeegtSh4PjJhjBzIN0VnprFkjD/t7dnl5ggY5Tiln1z6xnhyWS4KY9/7oJzy9/5R3/uAt6s0KKzfX6Gy3MISGVnHJwoQgjKmZBo5hIRRBZzBgr3XAUrNBKiWxUCipAkWoSEUhkTndvTYL5cLwWhEKaRTjGAYijRkOPfJckgvJ5VevM8taPs8ykjhiuV6nWna4/etv8qc//Sv6uy1cVeOb//bf4PJr1+hstfnG3/4W2z94h2d/fof9py0qrk2pXCJHcLDXJiNj6eXLPHrnMxRNxbIt9vbbuBUXNU4QWc7Bboely0u8cPsq5eUmuZT4XoAz8Ol3h4zCiFRKdt57TN1xGHYHDLpDIi9gablJnOVYtolbtpF5xigIqTgWXhphN5rYfkLr0TbKKKRybRUhBHGYUtEEj99/yKXVNVRNRVf1iREFcGslytUywXDEwqVltj7d5OF797n9jZdAgFN1+ZX/1W/wR/+336XzeIu/+H99jxyIWgPCMGLBsjGtIuL4cOShKwpRlqFnGaPWgCzJMG2TeBDgOA7th7vsP9qmUikRxwneYISqU7hPzSliZoQBUlXAtPjG117i/qdPuP/oKVeyDMN1qLgmYZTQerbH4Pc7NG6sUF9b4GRVE1Rq1SLAXsUgCCP6ux2EIpCaxte/81V6T1vktkrz1jpPHjylalvkChwkEcNn+zj1MuHQJ0szTFVlf9inWi4zkBllTaOW58ReSKXuko7CY29LhAnECdLQkFIS7/bQGyXKl5dobeyysL5EstKgdH0VsdWiLyVPWl1u3b5MMvJIs4zhwGO41yXPUlRDwwtCnJUqSpCiOTaBqRP0R6hCww998lyyuLZwfHpmOiblikutUcEs2eRxSuIHNEsuJcsgkzlZFJNrgjgIscsOgR/gWBb+fo9suYlh2yAC2jstsiAsBHYhCPOcimPTrFeJoxQlyghlhuM4dDs9/L6PqqqEvs9iuYQXxkhFYJdsLNdC0wSGY5ElGX4/x2oUAlHoBeRSIhwD3ZAsWBp+lh0KjgpPn21TtwyGqoLUNDbubRAMB0QSsjhBMU0WKy5ZknLtpWuEw5AoiLj74DGZEKgVB2no+L0h/eGIZUXgLpUxqw6xlLRGIxRVwdVUDvbajAYe/shDMzTCUUDqBbx64yrBYIRpmVz+zsssf+UaS3nOYKvD619/hd5Om2d7LRIpUVUF3TBYXVlk9YVL2PXSmWvv2el4UYYz9qujx1LIUx6Gjl8ebgMTCvgZS/uF9uVZW8O4Dux52bjPow2bVce57R7xNXMaOYUccfr9nHSsmhtnuGaNxbw6pnFwvA0f8V1idvmxPp+KKi5O+L9TTB9zKWnM/f7zDMZYbTPG4Yvau345cS7OSLOm2nE6Fw+T1Hch9nF6YGbP6Qu0e3bmguEWnM54cb3zJPGN1TbB8M6H9pQJ9hSSBccK8pn0PdmePJ5XE2LK4RBIyUmk7EkgnrvnF09jPZyQuC64ABy7u5yX4YxXY+XEdKYZF1WPMXMWEuYIlidYvcix+mSOo4t9TD0dr/1UjkNVl6Awpt354CG7j3fQDg1ZgyDiwbv3SPMc29Qgk3hxgmXotDyPLMtZrdaolcsc9AfkaYpmGcWdfSmRMkNTCq2wlJIky1BUlX5/hKKqDPsDYgm6VjBcZctl4erKzO7atRK2qrDb7nDrN7/Kp99/H2+zTZ5EDNOYMI9prC/wq//B3yyY5ldeoPGXHxJIiVEyeXavT5hkSHKErpAkCXmWoWlaobkvuzQW6+zstNAGAWmWsvHgGaZjwdYBuqHjuha1Zo3hwCcRhYGvbRk4jkWpMyA3NNRcEudFUMQ0DNAWqjx5+BTf91mtuLSChLoi8IKQcrWM3qiw+fAZeZoRxh7NxQauLrA1hzTJ0I48zY2N5qg7JEtTlDwnSTM0AT/9Fz/Erbqs3b4MiqB5ZYmbX3+Jd7/3FkYcY+oG8Sgg8jwaK4skQlJZaaD5EbkVoiMI44SPvv8eQmZIXWe404Ms57O372A7Oq3hiCTNMaUE0+Czv/yINIrIAEXV8cKIOM95eH+TxXoNt1omiVMQArteZfvBM4Iw4MqlVbzWgPpaE4RAZpKH794j8AIwNYIkQVcUFFUDTdBcafDo7mMkghdevMXeZ0+xDIOy0Bgpgm3fRxM25ThHZDDIMoySS5qk9HyPZdtBNTRElKIbJtUbyyR+iO5aRQyWPEcvOXgDj8Vrq2RRgggSksGIbBiw+WgLPUtZuLSAt9shDhPqbond7QMWqi66qTAcDNn47DEyTbBLLkrVxVmosnp1nSxOGR70ihMPoVKqlsiFQHEt9MPrWYP2gNbWPrqqoEmQcYa2WGX91mWGncJO5mBzG2EalGpVvMEIveKSBBGe5/Hog/u4C2XSzRFZFIKmkqEg8sLuw/M9jDyjVCsz6g7RbBu35NBv93h89zG2pSEHWWGMbugkkUbihcW1vjxH1VXiKMawTRYuLyEl6JZFnqVomkbseXgjD3KFsmMhpWT15hpyENDp9Uj9gIppUrdtBlJw48VrGIbG5of3qV9ZYenFy7Qf77H580+wpSTIc8qqTn/kI6RA03V2B0Nef+EawShkoVZlsVmj3x+SygzbNIj8ENsyyfOMr37rdRa/eh1FCkbbHZbfuEHlxjKKpuD3PXJD4dv/+99h//1HlH/4EVJR0FQFq+rSuLHCyleuFYLnmYzL1Fo6h4c8s/BxmTGFpZzMIAQo6tjzKSbz6Mup7WjWhnzexnIRRn8cznl5j/Rwhz9OtuspoGYxrp9HyJnC2ews8hBP8wfy5A7Al8DFfBFcn1N2HnQyz0nTDMMwLlaAE+XuXwfnBn8NwsU0qBeZn2e/HWMq587TyRdy7P/pms5i1ee+PcXgz7PrOP/RybuzMXJ0WjAN3TiUuZQoZ9ZzwhZPuZWfAdqcaTWtOSnULaeEmJkFJ1aj6WB9J8zTF03zSWOOZCnmFjgG6BSsM4WXww8xXWI2DKepVBzJdZzrQeK4ksMxHe/0KWcCk5CcVuxI2lsHDDtDOg932Hu8h6nrVKolFl++jFt1ePrRI57ceUIi9CIonqKgCYFrmuSaSq6ApWsoqoIXp1RcB4GkFYXIJKVk22imiUgyLFlEI9dMnTRJMTWNMEnwkhhFKLhlF7Nsz+yu06xw4+svknxwn6Wb69z7y4+4Vl/mrvcEIaGzsQdIVE0BJPUrS8TNRbK+R9wooas6SZyBoXP92iVMy2QUBKw1qqhIPD+gtSdZXV8mGgQctLtUVMiEQtsbYaYZXhjR7nukSULTMel6AUNNpbnapOTYDOIYSRFAq2KaUHLoH/SJ0ozrty/jxilDaTEaeJQNg/WXrvL0s032Wp3CHa1jI2VO2S6x2WqTRPGhbcD4kEqGnQGmTBHRAKdW4qDVhjjjB//Vn/Fv/h//LdxmBQSYllEYyds6iaUjBhn1hSZeELD84hX+5v/u7xAOfN7+5z9g++4mzYUKUmZEXoCzUufSi1fZfPtTFJETDkYsrS2Q9jySPCPJJQd7e8Xd/1yjYmr0w5BISQiCkKFQUGyL+s1lyo0K997+FF0ImisrPNrYovaDj6itNUiznO2PnrD58/toOaRpRmO5QRSEtDb2sF0bu+JQb1QQqkLW6nCw00HPJE9jj0RTQNdwDQPRGaKULeIkoTcYYKY5QRSx6QUslEpUc4ni6thLNZKdHlLXSXoexBnZIECNc9IkRZg6eZKhGBqVZpXe0EdWSvQPBmSAZRtUFuv4wyGKBL3kcOvmFXzP59nGNiMvYnG5Tsm0qF1ZJOyOKNUrhFkCaU4aq+RxSqZClueoec57f/YLIj+mWSrR2Tog1zWWl5dpvnqJS9USsRcR/CuPQaePYZsMByNKJbew+9A11LKBZejE5TJJEGICgzwBTUFKyGVOHEWMegVHGPSHJF7AwmqDPE2RQUzj5lUMy8B2HToHHUpVFxQBKBhlG0XTEJlk84NHiCQjDgIMXcOSGqptEXsRaCqqZeANA6pCIdZVFhpN/DDA9CP6QuWVX3qVhRsrdB7tFVfueiN27j1j+8k2w24fRVNZu7RCvV7h3sMnqKrCQr2K0FSWLy+RejElw0CzdPqjEWmQEQdDLq0ucvObL2FUbUzDoHp9GXupWiyNaqH9krlEJhmxHxKnCYtv3GDhtaukYYLumGi2jmZonLbnPG89nlp6Tz9iYtM9a8ObZt4FY6caJ4a74y09lyOkWe0/zwZ8kbxy/GPixxwAzql/nmaUGc/nptnjOaGcvbDTm/Obmum/9oLpKP7PxFUqMd7hSV5KHPJiiqJiGOpYg2JSAT4DZyc8mDyhtbEhOtORwAXSly5czFcCn8/az2NAYVz6PPp9Ngzy1NnSkQ53uvQRXFM1TgzGVK9maQQuxBjOeT5dh5js+4k24Gh5KbA0IVicrSCZD96ENmTa4PdkzCaUDxeSdieFB8GXpBU4T4abOl057pMcy3kK/NPnUM8L0vi1tGnqml1mhkB8NKmB48jp8xbcc9IpspQgjw0DBYZlEA48SmsNkiRm5dY6L//mG1z72i0Egtd+/et0t1o8fvsuj372GYph4AUBhlZo6aUqqNYr5IpCq9dH80NKpRIiCEhyyTDwKZkaKyUXhMSyLdIkpbpQo9PrU3VMhKrg+QqNlYVTzPQxnlSF8nKD137j63z6ww/pD0bomokuVBRFMNhukWc5qlYsrFbZxqi7dPd7KM/aOLrAVExCVWHn0RYvLr3GS6/dpr3fZRgEREGEqqmUlir093uUqmXMPEdJU6zFGqgqetnGXahQdgyGu22Gj1tFrIPuCC9JSKME17WIshyn5LC7e0DPD2jUSrhCJUiLwHqxl5C5TmETkmVYpollWWRA6IdkQHu7hdcdUV9tFP0fcxVdrpXZ6Y5omGVklvPS11/m07c+RAli3v+Dt3nz7/8ypmtxsNViFEWsS4X1a2vozTL3f3yHcBjQvvuUj/7sF7zx29/mm3//u/zL//QJuqKSJwmDNOP1r93mYOuAMI4RcY7QNfx2H6vkMOj1cUsOZU1hOPCpui4bB/t4SULZNCgbJv0opLFU5d/49/8muqnj9T2evHuPYX/AtRcu8+Y/+A6aZfCj/88fM9rv4ZZchBQEUYyWSraeHnD91VtsfPqIJEkwbINy2eLZ/acYioLMc3oyLzZTyyIRIGslRsMRbtklD2PMahm1naKbGh3PY319kXLFRRoaQleJ93r4gwA1SRC6RuwHJNsdrEsLqCUL07UprS9iPD0gyDPCOCazdLKDNpnMMCyDzA9IQx3d1Al6CaZlUatV6I5GLCDIs5ywV1ydypOMYOSjm0Zx3cuPGXWG6KbO3qNtSq5d0IxXeClrHXTIgRvfeAXDNmhcW8E76LL78ClJJqndWsMbeSRJgppk9A8G1NZX6O7sYQhBJYlJhcJCqUSUZ4RBQBxG5JqK41hoqoKqq6RBSBiHlB0ToevEUUQYRsgFjSwqTiNN3UAKgWnqpElMFqcImdO8vM76C5e486P3i9MYmWNXSji2TdAb4uU5eZhgWCpDYOHyCk7Zpf+szeOPHjAMQ9Qsxf/0EVEQ4VTLrK2tUFuqEQw9wjRGTXKuXl5FLzuM9ntUlxu4zTKqpmA0S7z3/XfJ4oRBd0B7q0V416e+2kAq4PdGCGC01yMe+JCDt9vFXauTtkaUVhvUb64gLB3LNjiKE3WieHoOAeNoiZWT83Xuojy3gqOPww1qptvww9qFOL3IT/OgU0kcXu+d2Mb/taZJte+F0DufobxocxcTwC6AwzNPN+TU59iPSaHwgnBM1XJSfowvmIJ53G/UBJzjMI19z/P8xA4z54wrep8vfWHh4oTVPS+dlWe+z56LCNoXtvuYdg17Llzn1Tfn+xzhQ47bDTzvGIpDY/YJYUkeLopTzOlY3RNKgznNHrHWs20axNTvSRjOBXtuq8XzkzksJ3A1K11EpJnOcbFJPX796uRj/pXDGZDISdF4UoExH/nHMs/0PnLWfcczF77Z7+MgLDSdWjHly80KL333NaSExnIdq2RjV1yklDz82R10RWXnwTO2H24Txmlh56bpCE0nSWLyPOfR9j5CU7lx6wqD/pCBF6DkkoVKmUxR6HkjVBJMQyPXCqbmSOjPcslyucRGktLa63Ln+x/wld/+BifmLYfCqZRgGNQWF/joBx8i04xcgK1p9KOANEgOjZ8L4UJRBLe/egtLqgzafXLDIPE81CQhTFI27m4waA9QFUG55FAyjMKQWYVOp0u5UqZSdSmX64R+QHjIvFj1Eh/+5FNe+NZLvHJ9neF+Hz2DOCqifFuKwjCI2N1rE0UxJtAbeHT6I1YX6sTDEE3A+qUlAj9m0BlQXW0SdEdkSYJRdojj4lqQXbIm7wGLYk6vvLjOytVV+jtt9h7vUOpVkKqKqinc+fln7D9tceXVq+w83qNeqXDlzRfZef8+61+/xdf/wS/z4Z/8gnwU8P4f/hShqXzl19/gV//X/3M+/qOfYWsaTsnmzl9+QByGuKaOrhUBEkuqRt/3Ic2xU0DR8DSVA8/DixNqtQo3qjUCkUOQ0d/r8M4fvEW1WaW1sUu55IBr8I2/8x3KC1Xu/PADkigm90K8MMIxLdI4wusXbmGr9QqNRo3WXgvDNjjYbrE/GnK52aSbZlQdl4HvE6Qxlio46PdxFQVhGfhxitRVUApVzCiMube1y2trDWSWo1Zswu4QLUnRJFC2cKwihoZ39xn2jRXMywuFobyA5a9cZ++P3yXqeZBJeq0u5bpLEIWYsUnZ0kmiiCRNccsunXaXYbvH6OkB/f0uMpMsLC6w2X7EwrVVtu5s8Gxjm2/9w+9iVl3qSw2C3R5qLliuVHFME9XUefrRYxprSyzeWmfp9iV6j7bp9zxykZOrgvpyk8FOi8gPQVGL+a0oCEVQby6gG1oRMDABxTDxkwSZZuAIdNtk0B9hIbAMsxCEhn4x7o5DHCX0djokSUrohcRhjFUy0Q0DwzHRVBXTNsnilCTLqNRKJElC0B8hk5TRYMjSlXX2nmyRZZLc0Njb2Wc08hBpjqJrrLxwlWDgs3n/CRXX4fKNS5iqStD32NrcRolySo7Fg0ebpHFMmuZopoHj2hi6ziu/9jW+/Tvf4fF792nttLj36WOGBz2U9wWVn1YQucRAEGcZZs1FSEiGAY3BKnGSknZGvPa3v83KV69j2gZHbPexQevn5bGk5PmOE+YxrdNa/8N0pCkbZwIvwiSNtXMOMLMZ7bPyXTQdbYN/LULNDIDOgu8MGCbHY/zE6IwKp1/J8VcXR9QppfKcPHLWFXXJCZ94jOuCK5FHgQTnVJzn+WGMqS8v/Wsx6J5Fhyda8vmIl8c552UTx3PtnKqeP51xEnBmj0+VkxOM/0wd+blwjzGO0+0fLmaFDZE8ZooLLcwM16MT3GyRBzk+Hqf7c5Yp9QQ+LqJJmRLsJlo9Bw/zYLhQGj9aPPQ6VoB1+mh5WiAbFxmObLUm6WBSI8NhvbNgPS2DyqkB/XxpYoTk6SHYebxDpVqmfmnhEKgCD0LAwpUlkjDm57//Y0atPrFMePr2PVrdIUmaIZAsLCwg05yB5yGlRE0zUARV12Fru4VtGGRSkuc53TihbBhUbYvhyEOkoIYRSS7ZbbUpqwphHBFIyVK5xN5gyIN37vLyr38V/XCjL4AvsOisNRjsd4nDBMd2sNaaPNvbZsVy6A36xHGCZujHuAiihIP9DpWSjW4a2JZBEMfInodQiuAAqqIy8gIsw+Dmy9exMoWl1UW67T6+bdDd2icOYyoVB1XRSAcBmqJy92d3eenbL3Gwscei65AnKZalEWUppgLdbg8pims+1ZJLeGjoqxk6i80qvYM+o2FA3VBBVXFchzxN0S2dKE4RCujmoTH31PUMr+cRxzFmpYR3aFRbqpZxyhY7G7uEo4BP3rpDybFYblbpDz38KOb9P/0FzfUFXvv2y+w+3KL9rMXG25+xtLJA0PMIkgQNcKQkkTm6oSFUFUUI/DRBFYKKoZMKMIUgyDMqpkGeSZbrNWxNo+f75JZOqVom6A959ONPUHWVxaur5FlG49oy9eUGf/7//R959skGumlQ1nVknpEhcSouxAm6adB6vMve1h5O2SLzQxI/YqlWI0lzkiwDKVEUhThJyTQd2zaxNIOW5yMkRF4IQMWxIc1ACpzFanEtpjNCcyzCIMZZbYKpEe/2imXB0unv96guVEgGIVl3RNr30FYaVLKcRUWQuhaB56PrOkQpXjQqrjzJnP5BD5lDMPJ59ngbfzCkXCqh6NrxGh2nGcOhR9gZsXhthV/7d36DP/nPfo/GSpPb33mFUrOCWbZ49v4jBq0eKy9eRjN1FNNgOGyhGBpBd1hcUayW8QdDNAFZt0/ZsbHTDD1MkH5xVcnVFEzbwjB02oFPkCZoqY6laShZRqnkoLoOrV4PGUQI16Lf7tPeaWMYOvsb+yBznLJLlgt0TcWwTfaf7rJzbxOyGKEI3LKD8CNSTaFcdYkGQxqWgS9yRqMQmUlEnFKulbn+3ddxGmXa97fZebpDmsZsPnqKqiiQZcg4RiYpgyRDqAo5AtMq7DniMCaNEt77459SXWmycmONxlqTwcEAESbFyUuWEUQx/TRDUxXCTkaqCmI/YvR4m8alBR4/28H/w59w+2mL1/7eL+HUSyDEmGxwyMA/50ZzpBi6yJWSefqjY6Z2hsLyZD+5ANMz7ujjov2Y3twvku+8PHKcTWds8/wiUtx08Xmb+JwmJniSSVxOVnni6nWC1zxuZpZgONWw4MTgevzEiXNG8YhFm1JbinntiZPPU/a4QpwqoygnwoSqqnzZ6a/doBvmje3Fqf3cnGfNr8P/jxB8RqZz60IWdg7iiOgEMxeAafZzkrf+vJPpkLqlnCabsV9Tk2P6iGuetMs0asTpd2PrwnhmOaPYdPVn9/j5F5gJNM9sdxL/M/VCR26NhUQI5bjYWbYPMx37TqthxHje0xVNZp+7u8zWWF1ICJmRUUpWrq+h6ScLSBGkrbhaJ6Vk84OHvPfHPyNPczJNIQoTmvU6EgjCCIGCVBRUyyRLM4RW2GEYmspgEJHlObqmIzSJU3ZJw5hMqjSrVYLo0LVjHGGrCpqiUHZKeElGRVFwDYP9nTadzX1WXrzEoUR73Au9bPHBf/mzglFIU4RpkGQpCtDa2aHdauOUnOO+VRcrhEOffqdPc7mOZZnkacbCUp1MAX2xTrfTR5UFbu5/+phL11a5dHOdaBQSBTGVSglP+IyGPlJTqeYlLl9d5f5nTxi2Bgw7A7KhVzBeuk4kJAe9Ia5to2gKV66ssHn/KYquopccrDAmSxM0RSPL8gKOXNL3PExFJdPA9yN03UBRx+7OTtyDlay9cIkrL11n1Bry/p+/Q221zm//47/Hn/8Xf8T+xi6XVxZxag63/9Y3yKXkgyhB3nuK2vX55Pvvsf71F6hGCUmS89P/7i/Y6/axhUK5ViLzi9MtU0pKzToH7R5JnJCWdSIErqYT+AERkgxYKjkYuo5QVfYHQ9Zfvcr69XX+6p//BZah0otDXlyrIqOE1k6bm3lOWTdZrtewbBN/MMK03eK6TZKSJAmWqbG3s0vFtZAI2p0uV5wyvSwhUAC98KCkmwaqZhX2BKOMWI+pLtboHHRRVEFzpVlcL9MtLKuIMj7abCHyDNu0EbZJ4sdYZQs1TZEUMTcqlxfJowTFNclUhYOf3yc3dJJOj4VamUjTwDRJ4hjV0NndOcDSNZaWG+xsHxAHEYtXltEVSf3SAgeP9ohziaKqeEOPfn9QCOJx0SaaIM4zqvUSt/5nLxMMfAatIZVLTe7+3qdcfeM2wrUoL9bQNnZRVY08zojyFNt1KNcr9HsjVislLE1FySRZzcU2jMIO5WBA7IcYqUSzXAIVNBTKtkUkBHGa4fVG+GGEY+gYpslBe8iz+5usry+w0+rTrFfIZE4S54y6w8LgOU+AFMs0MQ2DXFXxhcTPE9YsB93U6YYxQZRSXWjQbFTRNZVHdx7T3tilt9th5/4zHCnRbYskzQk9D1VVcSplVhbqmJZ56P5XI/FDZJKTZym+HxJGEeHA586PP8LQVCzHolGrIIUgTJLCCF3XMMsuUV4E7LQ0nSyKUREsVSuE/RF33rlLnmR87R/9ClbNPdnrpk4Oz/w+M52/r51so3MY47kc53OkL8C7z61vHr809wTlRPf/BR0QnYbled6dBft5hefBPWus5uJh1ruZDNhk/hMZBXkuXU05BhJTz+a18deQvgTh4sJczxer46ICwIyavxQYJWRpih9GqIrAtq2CKT21Lhxqjg+5yBMPTIeSyNHzo6dT/TpxcDRORIIT92aH7RxpR46zyElhYiL/Yf/P4GXndnq8EyeNcyFtyHiWuQz7+MnArJE6mU6z+O0Z0M78NdnKeB2zBbRT+Bqb/OJQAJkS5SabPSWszerV7HfzSXVKypur/RnfAYvfpm3OrNHrDQkHPokfYRkmkYypaiZJqYh9oNom5aEHesGgdYdDkixFaCqmbdMbeiAEw5GHbdsgczIJhqqiAZ00xVQ0lDTBMgxknqGaBqZh0hr1KBsFo9M6OODgyR7LL17iZHbAqD3gw3/5Y7xWD922IBcMNg9wdJOeNyTJIjYfbHD5+uXjPpUWqziOBZ4kDhP2nu2jqCo7cYxTcXEtk1fffJG9zX18z6PrR/jtIYNWnzzLMFyLhWvLdN69B0KhZJm0Dnos1qromoaiqei2SRgnpIe2MXGSFW48HYvLty8hgwikRFdUEi+iVi7Ra/dYXGmiDnyMWoVUETiGSRRFRLmKF4QsXFvGrjhjI3h4ZVFAY6XJ3/6P/yFCKQIAPru/yajvITSVV371q+z+k11WX73O6tduorsmWZzwrX/vb/DB//Bj/I+fUE4pDM2FgmvpNJs1LF2n2x0QpQmuqhYxGmybJIjIFYEiFMKhRz8MWa1WiXWdKAiQAgIjJ8wSHMek2qiy89kznnz4kExIbv/GG7z4rZfIgrjwJPbz+3z0/feJDvrFVIpjdNMgjWPCJKFRbRZRl5ME6UUMgwihKCyoOl6ecZAWzHwRjwAUTUERhTchBRCKIPRDSpUS3sgnz3RM1yIJUlxDR/gxSW8EmkbuxwhNJZAKYn+AqunEcQKqiqKqiKqG6AW4N1bwP95gqAkC0yBr9ZCGTmppZFIQ7ndRk4wgCqmaNdYuLbP1bK8IiBfGmIZKqeLg9Yc0Vpts3nmEoahkZhFYT4gCv+7/n7n/frIsyfI7sY/71fc+HTIjZWXpqu6uFtMzPTMYgRnIBbCYpbC1XZC2Rv7C/YV/Av8E/krSbGlG2zXACJrBCOMuFiAwg8EoTPdMT3dXVZeuSlGZGTri6auvu/OHG+K9iBciq7IH9LLKeM+fa3m+5/g5pxGwv3VANslIRimTYYolJEWpUKrCiNppoe1IppOYoixYvbWMwGAJya2lHmFRYVyH1jsvIbRBjdPaNOxaG9/qUQymyL0RvrTIhOFgPEUDWVnR9HxaQlJoRcPzCFyXViukLHLWV9s0mw2M0jzZ2eHT4YTVGz2yqaK51KWqKpq+z9P+kMwyuEiwbLJKUwQ+9+7forfeo8pK8nGMkYKn732OZVt4WtOIAlILPM+nd2OVqBXRWmry7OMvGQ0nZHmOBmzbRgjwbBvf97j18i2qSvHoiycYAVIZqjxlMokpQw/HdpgkKYQlBQYHg6o0YatJNkxJ0SwttUmmKR/8+CMaSy1e+Z1v4XcbLHwadRZYvMiwsLyraJaLOdf1tbBAenIF43RhmrN0lzmNPsfkO5t/ll45Q79cnPiSRl5GwJ8Ni2iURUS/gOeRUJ1dFieSiCvac7EpXXEh4ppV2j6WXhhm5vUsX/OK9XlMeb5olwIXhRciuTh11vZVd90L3K0zRQlx9hX8Jekv2lQz8UprQFApXSvDHHG853Wr5jke8zTm/OzPV2nObdxL7Q+dU6w4V9miXPNtmeXQXFgRc/aOTxg7CzOc9UHy/Iv4fI9PAdi5zfMcZ+eCYo+GTMzHzXyZ7818I85CkjriIgBn5pIu/O2ah9MiJsi5Iq/i0AiQlqTKCn7+r/+Szr01br19D+ff/hjXdggCH3nk3yGwbVQYkJUV2ii6jYhWq0FeVWRJhufWzuKWWi2MJRkMBuRxgvY8fN/FAJVrYxWGrrTIlKYoSow2RLbNs9GYTujhSotklJz2VQDG8ODPPmC6O8BtNBCWwNWaWAlKKRFCEArJ44+/4Nf/1t846WfQCsiqkqwoaHYatQM0Y2i2WyhtyHPFp+9/gec6eJZFr91iNE0RaHrry0z6Y/JpQjPy6Q+nlFWF0YbhYERZVQhb1tKQ0GO4PwBt8H2PLC8YHAxYXumw9WwXDfhA2A6Y7I9YurVMlSts1yGPMxpRyGExJgh9/NBj9GyXN9+8SzJOaa/UzgeFoPbSS22PvyqrmjALPe598z7v/v5fkY4TsjSn2WsRrC8x2RuTJTn5JMX1JW/9/e/zwy+e4WUVaVLgGsHyrR6jwxHStVlZbpOOJ1iNBlorpiim/TGu62C0RkpJGPrkRU5juUdelpTGkB0pKWdpSp7nOL5PUZTcfOU2r3/nNYIgoHJcPv+LT3j83gOsSmM7Nn67QSgscl1RTTPysiIejVHmaF1qjeu4rCjDSMJ2lWNsiRN42MIiK2pJmbQtHMdGHzmNLLKCsB3RbEZEnQZpnDIexuxOJtw1mvbLN5hsHiAsmzKv8LOK1JT1W+OiQkQ+ye4QaUuy3QHSCNJxTJTblELUHthTRSQ84tBlOBkRRk0afqOWiDQCXvvWKySTGDcKefrJU1ZvLNO70UMpzcq9DWxpkaQpha7vEK01Uhmmwyk7nz5DI5DSpsxyeksdoJaUq1IR+T6jcQplhSctUIrQdfGPpJDhSgvHdWi+vIYUAuk5fPkH74LSrP7m2xz82ceU/SmiLAmCEG1b5EaTpgUNxyPJUqqyxA8D3NBHBPUa7E+nBIFPFPm0u23yssAPfVqdDo7vMNk5JHclLWGxutLGlzZbgyHaaDQQTxLGh2OefPIYhEHaEt+28DodbN/DylIi16d3c4VnHz/io599BEoRuS650piju1ZrhdYaIwR7h306N3ok45j1dpOpqmiu92isdtjbPkDYgtW1LqM0p2s7FKXi9q111u6uk4xjHnxRMkhSjC7xpc1nHzykLAre+V/+DSzXnj9Ez70AuPq8Pjmjz1r/OZfg7MdT4m+2moWMrLNtWti8mZwnV83pk/RzNMZljPHLrrHjcuft2S/MuzhcVuliYvrCYI5zmcVzt6isOSBURxz3xYgTVjALB+g51sPZcI6WO9smwZm5nf1y0svTWb6kHReuoa/R/svCL/ZZ1LWpn4viTou5mAae4TWfM8H5nCN2RXtt2z55kzn7Ru1SQL6w7DMKxObkhzkS8nQfzL/1v6iKy4M5P4hHm2hWMrBo7x2Liq/mLZz31XHyFGsRo/7CvXDmjeYl9X2lXSG4llWEY27BCQ5b2PMzbRAXtOpkcGfm9iIscj7TvDGA02KYm41FXrmPouNxTNSK5hqnyoqw22T05T6rN1f49m9+h8///CM8yyZPc8qyYjyJabcaBAgix8FthChlqIBOt4UtBFVVIW0LoQ1dZ5lUKQ7TAuE6WMKrG+BKJkrRdl1yrcnLkmboM4pTAsvGxTAajJj1GqUqxf4XWzRuLJE+2kMajdVqYiU5QloYQArJzoPNObPMjU6T3s0lxOOK4f4BKM00ywmMoRICvxEStSJcS1KkBb2NHodP9gkCj8wo/MBDIkizAozGtSSD0YRCSqLAx5GS6TRlpdtERRHGd2h0W2huWpMAAQAASURBVDQPR3jU0pZOp0WWZqy/cZvHHzyqzWo2Qp48eYLjODiBS5Fm+K7NeBKTx1PCVkRnpVdbzprZq+kkYfvTp7z8/dfJpxkHT/ZYe/kGjU4T27IZ7Q6J94aEoY/fCOr1KgTSGLJJSpGWSN8jzxWOlDjSxl5p89ZvfoM/+x9+n1Cp+jlNVZJVFaasOcVGAFphXLu2nhU1GE1i7NDDVBokmKoin8b4YcB4PKG7tsIP/tGvs/PxU54+2GT78Q6ObdPuNHDbDp7nMdwfkmclURgwLQqkYyO1IU4zGkGAazu0S0Ul4FBVUFVo16LKS7KqVlyujMZ3bMqyQkpJWVZgNFksWVpfJggD0jgjQ4MlkUJSTlKIMxLPxTbgL7WoDsYUcU4xTfGFhHZIkRSEG0sYwB9OqcZTWisdhgL0MEZkOVbogesQl4qmo3FCF7RG5SW9boenT3Z44wdv8eSjJ7SMRoQBSmt83yOwIwZPD+hvHqKNpr8/oCxKdr7Y4vY37zOd1CaaizwnHkxBS/L+FC/00QK67Yh8mtLwPLy8QuUF7Tfv0HjrNqIoKQdxvfdLRefuGmVW0FhuMW4GONLCOBbZOCY9GGHbtTM6LQUy9LGFoCEltjY0HZeiUNiNiHboMx1MKMq89kpuWVSjKXqvQmc5K35AqA29pQ7D/RGqKAl8h+1Hz7CEJEszwtAnjhM6QUDU63D3V9+i6E9IhzHBWoeP//hdnjzZYiXwaIcBaanoD0aEjkOj00RaFqaqqIqqdtKZlxijebK7j+175EWJ57sEjo0qFVlWIpXBawW88sZdlu/dQE1TRvuDGoxOUxxboiILU2ne/7Ofs/TSDe78ymunHOnLmG8XEOLi3CV4jfzHvKvzbKvFlZxPNFfuKZNzhu07U5eZvYCeGwgsTivOVzDXxAUel64s9itx2Y/B3GUEi7jgMzNjPoOTDBfRIzNc5HM4zVyb1lgUzurcLfardo4n+vzhMkD5NcILsBZ1+vdaRDZwjqq65t5ZPAYzm+eq8q6mji/OKGoFGM9zr13G+TFZHHOeyJ4nGM8Biuvu0ZN0ZoaaPd4x87DYnB3HMxyVs6Dj+s5XLkD75xs5E85M1DGyOofkvyrcXgC0LmnaMc0+q49xmvt8G85C3NODylwDUMwWMn+4mONBOJ5DM//L2abPJgkbwfyP2vDJf3iPh+9+TjKMybcGkJREls0kTsjjDK01qiwZHhS0m02yqmIynKK0Zm84ptmKePWV2+RxgslKgnYIyuAnCW4rQtmS6TDBtSymSUp3vUc6TXErxSSrIMu5s9JDK01Phaj9EbqosI4UmjGG8WRKZ6mH3wwwZUk8zdhY6zEYrrOdpcS6YrjTpypKXL/em8KS3HrtNuXhlIlrEXkB48EIXZSsNhukpSJOM6bKICuN7E+xpSCexJipYGW5w7NHm1QYGo2QaVHSboWooqLVCBjujWgFPn6nQX8wJos1zSjEsS1EqYjHMeOy5Na9dTY/fYLMK268cYfdZ/toCVIp4mnCenuF0WCCI2BSVPhRhB95+A1/bh3sP9zmz/7pv8eyLaJOg//3//mf01lZImpEeJ7Ngx9/ilAKIQWWbdWeqhs+ju/gNAJUriHySUYJchTTakTYvocTeJRFiRsFOAbyMkNaNlVZ4DcbiEpjCwsjwXZDSs+mNBU6K48sE0mMNEgMo/EUJSVpf8If/nf/ht3DPkJKbm2sEDg2aVFSpBlpOSbNM6SGOEkpjnRnLN/HP9Jl6GhD5ruM8hzfdwkqi5GpaqbOkUUkV9i1BTNdc8eFVkjXQVWK6WiK1oYsr59WWaWiGiVYgYtEQK6ohCDbG+F3G+RJhjRQFBVOmtVmjZMCY0uqJEOmOYFlE758k62ffUYqJIPhiND3ebx1CMBar8lwMsEuS2zbQmnF63/zHVo3l/ngD36CJwCjKcYpQSuiHMRkwyl7T/YIbZeJZdHfPGD1/jpCWHieAClwA4e9z5+SZxkrt1b5tTduMz4YoffHiEphGgHL37mPv9zm8PEe3VtLuJ4NRYVca2OyAvbHjH76EMd3aH33Pt5ah713H+M92Sf5chedlSAERgi0ZYNjYUkLT4PtOlhaoHdG3PAC8jjHtRzUwRhRKoRl4dk2Mi2xmwGTOAUBLddjf5qw/sod2t0mAHtfPKN4khPHKVlekfzp+5RxSnepy7g/pn84YGOlS5XlpGXtPT30HLQRBO0Gy+vLWEWFzkssz8EKXDpOwOHhgP5oQprlZGXB2nKP29+4TbTcxglcykmGE7hMnuwx3Nxn++CQ0WSK7zhMxxO01vQtgQ385N/8BSuvbRD2WlfTEcef5whA5iKu4YZqBlhclGBRE46ZVOc5dAudxl1ETC+6fs/GXdCMi5WZr0WlXRpO+HBfh+h9YQTzeWbn+TGeoSnOro8XFsyMuePn6dzxqlwAj8zM3xcMMF6Ytai/jndcV+716zbhooG8ao9c9ajtbDWzNLI4ijhTd82PPnc6zNR/QadmUfV5yv9Muss7ex1jwub4baA4wiWLylxU/zH35wpOwWJ48Rw78wREXbUIzqhEzYEvMVfOCTH/Fdf2WV2Sk+quExYg6tNxqiMXKphfVNyRmbnjZaiUor3SobOxjIOFGicMxwnasZimWW0aNC9wLRvH86AoOZwmlIDnuliWRFWKh188Awm3b68hQ5+D3T67gzFh6NMLA2wJWoDtufSHUyy7Vsp2bBu7qnCNIdYKS0qSZ7vkgynhehcQSNtm+e4NPvqzn7Px0k3yfk6lNeNRTDMIeCQMru2QTuJagfMYXAAbb9/j8Y8+QRqJlhLbcSgMWFFAsnfAxlKbMi8ZZFOQFp7n0YgCgkbtd2L4ZMKtuzcYDCfYjkM6TaiUwSsr0jgjcB3SJKPRbFCWOeloynq3zcFgzCTLaydjzZDp/ojexhLTYc1N7kUBxrLpuA5+KyR+kNIIPOI4YeXuBsv31k6ZCUcf9h/v4Dg2f/RP/z1/7//wD3nj/h129vqMxjHCkmx/+LhWsL61grQlWikQYPsu0q79gdx551W+HPyM1BLk0xTbs9B5SZbmlKGPqUqazVbthM52KJOcRhTS8H2yJMXVBtvzcFbaZOMUkWZM8wIr8KjSnJXAQUqLZwdDKq1ZbUbYtqQYTiiMRgtJdQQOLCmxkGhdETkucZ5RZjmmUri2Rey5JGgyNB3LJjCSAoE2YDs2pVIIx0IYg2XbSMciqSqENghLMhqOGY+m9eBVim67SdCO0HGO3W4iNw8pUCirgWh4WJGPFIJplmELD20ECk2eV7Rev4V6tIcpC+SNLtHTNskkwSo1fquBP4iJi6LWJ9AKx/YoqhJVKoabfTprXSajKW7ko7IcJW08DFWSc/jsgDDwad9cprIl+5t7/GC9S+/uKkWao//Nj3n60y8IfR8/dDG+jVEKq1D4lcERsPyNuxirlsqkh2N691ZwOg1UVuA0fFSpsD0Hc6uH3hshXJvicIKaZoRrXSTgLLcwSUG8OwClcVwL8gpzOEVEHsK20KWqvYgjcIxAdJvIQmFKRYnBsi2CdgOrGTJKCqylFk3fZeXuGoPtQ3a/eIYjJK985w36m3ukhwOy/oAqK9gcjjFFRbcVYUcBK/du0d/aJzkcsOK5jFTFcO+QyWBMp9umHQUEnkP31hJ2WhC1Itr9EUVZ1Yrdaz1ufedV+k/32Pv0GXtPdvCjgPHhkP1p7eX+3uoquTLYDUOuFSrJUQb6ByMe/Ohj3v573z9vmnPRJXVMT57VcZiVIp99wnxd5uBsOHcFHXO+rpF+wX07xx5bZBv2Om00FzjxuyDvyXA9D3P0FxmOGrTohjfHVjhnktZNOg/YzLn4o5jZJ2KXkBHmxEjQmYIvavYFlqfOpJop55rU1PF4XAh2ny/8tViLWhjOtfyKrp9B0tcm+c4i8ItYvDPJZ+lxAzOWyi7byS8Qoi46GBYR7tcJpiZyjy1cLc5/8gDo/CabNWcrZjbLTM7T5n2VMbgY2NRjP8v5vypcB/AsgsELUOWJkEKcqf95uC8Lyj1ZKrMNW1ymOZZanbz9PNvW07xXrkAz94edh1t88MMPGO0NyfsJN9eWyZRG2BLHsnEcg7BtHGFhG40jwJGCOM/RxuC5DkYbAtsmr0q++OIZS8s94iShyAqkNjweTlhb6dGKfEaTjLwo0JVBeh5pnCBsmyRLKYxBS4lRMHyyfwQuQEjBN/7O9/ji3c+xLEk2TSmVxg5dyolBK0Va5fi2opjG0G6eoCcDHE5jnMrUz24QVEqRFwrX9ckrRZpkrHY7JHGCZdv4UcjocERcFnSCAFcIiryku9Tl7iu3efjBQzQajGY6Tbj39j02P3lClpV0Wg7Ctek2GziOXUtK0hoMpaOMQhg8x6Y/nGD7HlkiybKcZhhQVCW2bbP2ygZBKzxZ97UqgeHw6T7ZJKGS8OmPPmHlzds8fLxJaNsEQf0MyheCKAowBmzPOdI3A+HaGG1Yf+sexcGE7c0ddFzSu7nM4PEueZpBGhD6PtMsJ9cgLYEpK/IsZ6Kqeo6BUX9EcdCnu9QhqSp8y6LICixtqPICS0q6nk1WFMiioNJWbcrYsrAdC6so8K3aBK9dKYRlI41hQ9TXUN5pMEhTsjTBEtCuNEZl9KWgFBrXchBCYrn1/qwEuEf9sxybqqoQmcLyHZTSRIFPWlSsbizj3eiQPdylGkzwHYvSttGRjxN4mE4DXb8lQyDQeUmKrsveHyNtC1od4ke7DHf7pFpjIpdikhBEPv3+iCoPEcaQiRLPd1jZWOaP/9kfYLkW4dEzvHQ8pcpyyuGUrafbVEbxjb/5ndo8tDBsbu3z8Kdf0Lm5xEd/9AFlkmHd6OJGHpWuEP0Y0wgIDqeISrH0G2+R7Q1Jtgaw1ET4FlppqmmG9B2oNBKDiHx0UaJti/HnW7TurNK8vUSyPySxBZbQNHsRbpxSpTlRo4Gz1qEcxug4pxrFOJFfe47vNnGEoAo9PMemOpighaFMMmgHGCmoypK8ysn6Ez7503cpk4Lbr95m+eUNJgdjstGEqqqoEASNkLDdZLI74I3f+g5SWghLUoxjnj7Z5KUo5G6nzW6e4zoO48GQaRzjJTFbOweEQrL20g0szz4yRuAT9hrsfvyEZ1885WD3kFboYzsW7V4L13MZHgyYTmMSY5C2heW43O602ZuMSbOMz37yGbe+cY/u3TVO3kGbBYcpp/Enfnnqg3v+iJ69WcVMvHmOS/2shGQRg++kivME8CwhYU4LOF/HgvLORx4xGc8ihVku+GVFPyeZ8PVc3F5c6iL9yVMDGmcJwyNfEXI2z/n8LIpZOC7muNh6GenZbNeYiLPSkYXg8yuEY9rkmCn8NcILAxcvkLS+Vrj8Wc4ixeIjNaYTOnEhXj0TI46I29Pvs2mv5EdfNjfm9MNc7rnD4OwhdSbv2TPvkvrq1l42Zme27zmX8+frrr+eYa0vbMuZeufKOKtyf5pu7vtV5/B198HZchbQ/5cX+jU23EKrEBcAi4vqO5d8EWA5zmfOfTwuw/M8vvzwS1RZ0faD2iOzLUjTjDIraIchvla4WEgpmRqNY0mWm01GeU6Wl3SX22ilWV3tsrV9SDqJ6ax0KLOclXaTrCjZ2+szDj3afu0YzrYtmp0mZSPAqkrKwyG6KrE9nyIMePrRU9a+8zKWUx9NvZvLfOu33+HRH3+AEYJOK2I0jCkLzVp3if3hgCovSOKE3kwXV+6t8vbvfoeP/t3PiNMUG8ndl29TpSUN30NEHkYIYqOwbIu7b91h5+EWRZbjhx6lrugPptiWzXA4odWJsGyLvFQEnovlCnSSk8UZnpAoy8J1HZLhlDzN2VhfIeg0EHtDsrIkigJSUbL80g1kUpCkBeM4xZQlWkKv3eLG6zdPPaaeLBlDmeQsbawwTVI++uGH/PLf/T7SsmivLVEkOcKSZGmKkUdcLQNY4vQiPLokrFaA9UiTZDkCcB0bR0qQgjhN0YCpKoRtEwYuruviWbV+hdTgCHAtnyrNQGmk7RCFIeM4gbJAKYVxLFzpU2iFa9v4AizbxQo8Qs+nqwyyUmSVYSQ0zUozdiW5Y1GmBUmWMS1LbCHoGwO2RBjwLIdC1RIuhIUferVyu5Boy+BZHioXGEugjo6byXDCq7fWWfvmPfLtAaLhQ5Lj3+xBqaAqUdMUrTVVUSEbtclibTRWWlCVCqcRULkOTisiKkoaN5aptg/QfoCpKtq2gxEC33MJLYupgCQviHpNbi/dQSUFUTNkuNen6XgM4zFTHZPmOc8+f4rSijd+5S3sNOA7P3ibj3/8CXvPDpj0x6zeXKLZihjvDml4Lo7W6Ee7WK5N67WbJP0J2bNDrMinmibEBxXOOy/jtkOK/RGl71BOM6qswO+1sG9YqLJCuzZe4EJSUAU5+aSgUhLv7gpBXqGGMbo/pYo88B0s10KWGtH08VybcpJR7g0xro0OXKpxQpWXpGlOGdcgYJTUDv/C5SbJMKWsFA/f/ZyDL7co0hzLstm4t87GN+7RutEj6U/wWiFVXmJUberaa0Q8yQtuZgWRZTNNc0phcIuS5CCnsB2mUtCtVlm+u157W08zJrsDDjb32d074K1X7nDz5Zv1M7jBhCou+HlR8GwwQClNJwzZuHODG2/cY0UafvYffsJoPOXhDz/hu7dX5/fjuTv4GuDgRFJxbXbo1WUtClcWvYAdfTV/a0E9Z4DENTN+vZ5fkvsKEuyicDn1eEKanNRR6z+cBxxftWfmzH18/Pcsjp2nys6hy3PRi5pzOkTXm2hhxGJp1nOGFyi5OLPoviqxNxs3G/8VkNmp1Zmjb3PlngcW56s9JsnNmbgL2n1a1FEVp1a0jkH+SR2LTJCdI8jPt0zMtecagywWpLtwT8yilqN6hJnvw8LGXrUQz4/1afwVvbjk8LjWubII9F/TydFJ4S+EaXIGRF5R7kU8kQvPBwEn7q3P1nZyeJ3cdDS7DTburfP4sydoQJYKKo0NWK7DcDLFsSy8ZrPmMuYFGIMLCCEJPBudV4yTlOlkysb6KtM4IxlPa6dra21utBo0Nw/Y3u2TKU3kOWSlZnA4Ik0zvvO3v83O+w8xO30ix2JQVgz2BuSjhHC5ebJv3/ytb/P0/QeoSUKSSULbRphaAVhpTWVZlNrMDZft2KzfW+dZFCAjn3KcsPrSOk8+fUY6iVkOXb71t7/LT/+/P8YKPD7+yWf0JyMcLXnr7gbdjWU++6tPWVvv0p8kbD7aprPSYXevT5kXEAb0R1PyqqIXeLjNkCTOmMYpy62Q5mqH7S93qKqKyHIQlcIC+k/3sW0bx3NqJXhH4rkWWVrQWevOTWkySYgPx2TjhDwvSZP66VAyzRC2RdCOaPg+cZ6RxzFqmiG0Rrr1sW6Urk2r2hKjNekkxQsckswinaQ8+OAhFYAQlFIglKYVBnjN2nyqVgo7DKi0wTMQNiPGwzFeIyR0HHScoIXAFmC5PsY6Wn82hFLSsWzcQqExZHHt3KySFo7RWK6DWxTsOxbToiBOY1KlMJbEsm1KfURgeh5FUaBtSZYkhI6NrRS6rLBti6IsKaoKy3VOiLiiKDDKEAnJy2/fJ1rvkiHI90c4S03KokIlBY4jqZKcCoPdCkmyHA7HSN/D6kQ0VjroosLOS4Q2mIO67y3fw/I9bDuiKksi36csCwqtCRo+nUaIEjA5HNNabnO438d3HIQCx7axKkWv26IsNVU/4b0/+Bl+y+eVd17Ba0eM+iPWbr+MC+SThLbtIg+muJ5LEXi4nkv8eBdjC9pv32E6TTF7E6RlSMcx/nIT7dqowwnGkjieW/sRSXLsZgB5SZzmmLzAjTOsTgPtSzzfwb/Rw19tkz49oLIE460+Oi9xbrW59dZtqqRgejhm+6efEwgbZUmC1S7xTh+v2yRJS2JTMMlTjFYwSZiOprXjPynxHJeiqGitdLn3gzfxmiEGQ57UFsCKtODJu58z2hvQinwIfapKo9OMvSRhqdPCO7JKluc5oePw5PEm61lt8riqFNPDEU+ebtMKA5ZvrpDmBZHjktkWyrfp9NpMdIVVaBqtoF5HecmdX36VzUdbxNOUB+9+zjf+wffxmuHpAXric2bBIXyVZ+6F1+XXuFguJSIvyHARwfhV6cjnASVfI5zj9y0izJ+7zGNqbl4qslD5ehaXzdCTV4eLicRZ+uPEetdCS5TzQVU1M2yWbrpqCMyCT5eGRTTjVwgv/lnUV1lwX7sf5yudAwLXqmj2gc8st/wUGFwmrZhrwUn2y6b1DPI0Z4qfSXbsbXthL64BcsxcH47iDHNxp2Rn/e28P8cXGb5CyRfveRYvupnRn2PaiBOQd5zrvM7JGeB35m3pC8Qbsw07H646PcQRUDJnkhiOzDfOcFuOvZILKNOcrY++5MbdGzz5+HH9vEEpjIFKCPI0JXQc0qIgz7IjxV2BwSKl1tfw3Fq/odFqUGnNYJLg2ZIkzZEGhjsjqlwRRD4rrQb9SYwjBdKWlLnCsiy+/OgJv/S/+Bu8/9//Pul0iu35xAcjtj96wv3fePvEU27Ua3L7G/eZPN7HUgotJD3f51GRUVUlQjgko/gMWBdYtk1RKdYaEdvDmE9+/CkrN5bJxzHj4ZRnP32AozXNpRZ5nLHuLhOnOSAZH4xQVYVjWehKEwYeyzeXmPTHpElGZ6XF8o1lRlsHWJ7D3t6A8SRmqdVk9eUbbD3cxvJc/LzCE4Y8zXAin3GW02rYtFbaTAaTI+dxFe31NlG3MTe96WDKs/cfsP10h5t3NrBsm8HhCOlYtHtNdh9vI20Lz7LwA5/D3T6Hj7dZff0OSul6HWBAa5LDETrJCNoRh+OUMs5JBjE31pcxUuBKQx6nTLIM1/fwPA9TKfxOk2qaYSPIqwrbkuRphm3btJpN8qpi2VIIpckcC0tKdFkxSTNsR2BJgQVYRpDZDqnSjEWtoJ1IQ6JyMlOB1hgpkJaspS9S4DgORgqQgizLyMsSWZU4tk08neJUGiUMOWDntV+WoiiolKIqKu5s3ODmOy+T7gwoRzHqcEIxmOLdW8OJXIwQJOME/0aPuD/BcSzkcguFQCpqj/NlAVUtMamA1r11CjT5x1+yrzQ3ljpkWYrj+wjXQVo2WZqxtXnIWrvNwbND1jZ6bH32hF63g2NbKCnwfQe3qEizDFsETA5j3v2T93nrB29RhSF5nFEpTTBKkeMEbVvQ8GlvLGFJwHfw1rsE3YjxX3yOFXn4wmf6cA8rLTG+jd+O0EIiAVVUeI0ApEQGHpFtUWgomiGqKtHDjKyqUHGOyQqclTaB72AKRew7iNAl2RsxerKPdC38VoPud1/GCT02f/9dKlsSGUHjzgqjh5usri1BUrCzO+Te2y+z8eot4sMJH/7Jz2g0QqJek/GTPdxmBFLw8Z+8BxLSJEOUJct31ojjBJUUCM/GLS18rVhZ6rG01sPvRuw92OLZ1i7+NGPr4TO8TgOTVzx+to0rJTeXu+RxxhTNYTFhtdsin6Z0LYF78wbD8ZThZEpQaZL+hHh3RFlUFFnOYDhh8GSf9bfvcnJTnJzTF7Ehj2IuY4ReSN+fYRjOnv2LylsAFC4XJnxNFLAIHJ1t21wV836lr00JXxWuyP/8d7O49Ot1snzdhHPuC64oQkp5jr99nepm6bq/rvACwcUpEfP82S5YeXNE+mXDcpZLK+YH+rnG86wnSbE4/xnLAM9tbex5N9msctA1ue7nwM1CYnYGLZsFXZ0VZszmumwXX0o0X/LjOSxo5qKfb2OcWqWerW3uu5nt/aw0Y5EUa0FY1JVL4hYBUMwx0DvD+fq6d4GcfwRnOPKZgGHnwTb/8v/yL3np5Ts4SBwkruOglcYXFmkUIYSg1e3WDtOKkspoAsvCuA62bSGkpNSGvCyxLAtpCfIsJ7Ascq0ZxgmZ0mijWVluc7sZ8uWzPbqdCMt1yETFZHfIeH/EzR+8yRe//1d4QlBpw+O/+oKV127SWu+cjMlrv/5NPv+j92m5LkoJhnlOUWUINFJrHn30OW//yjfnxjBohWRFyeFeHzDYwsZzbTorXZ483GSS5rQbPnowpRP4NCKfYZaztblHFid0ug2cI+/eQegz6U9J44y1myvIrGD3w8c0A49BmnM4GmMZ8NsBB/sDDg8GdFd7bKz2mExitC6YjGqrVDfurfH4s6e1REAYTODxvX/06ydPwY7XicorNt64R2/tQ/IkJy0rGoHLcHdIa6WL6LT45KMHhJ7HnfVl0iRj7+eP8AIPp90gHkyYHoxI44z+1h5REOAHDkE75PMffszBwZC7N5eZjKaorKQ00Go2GKUpzSBAIcjGSd2evESELo7vEwiBqRSB5+DFGVZRUQnBUjMim8SoaUKMxlSaMvRIyqJ+PpNXHJqqVr72HFylaXouQltkWY7UGl1pvMCjUgpdVeRpirQsqrICKWsne0IgLElcVViA4zhUZS1dq4xGG0NDWrz6S69jZSVWMwQE5TTDzivE0VMhp9egwDDc3MW2XLRr4wQ+xhhsBLYlkUttqsEU49i188LdAY4WBEsdGqMpXprTSDNcaZH7HkWSMlGK27fX2X66Q9SKSA5HmFKRpwWWtCilwHNdZENiVSWe65FNMwbjKdnuEGMJ8oMJkedgsoJwqY24vUy03MLtRWSjmMHjPW7cWcHrNZDG4C41ifeGDMYxxmj89TZ+r1UzFVwb4dkIKWsQRy1p8kIPu9fA3R6QpCmkJY37yxhg/6PHhEEAnk201ESXFU7kEax1mHyxi8grzMEI6/YqwUobXSkmownBRpc792/y9NOnDA7HpNOM9fsbSKt2etjqNvECl+0Hm2x+/pRuu4XQmixJaC53WLm/QXu1S9BrAbD/4Bk7P/mEsNWgVSqmeY4zmuCvtFh77RZlWbG9e8BS4FP2J8Ra03Q9bnfb9OOE+MsSrxng+y5VXmL7HnazweHjLbwgIPQ8JoMR49GYw/0+g8m09mFlYLw7YO2tu6d3xCXU3OzddGrRZ9HBzBm/URdwBWcvCsOM7qOY/32enX5FOCphhun4XNzgc5ZjLst6TUcAiy7or0L/HuW7hMe6mIz7ClW9kHANkATzdJYxBqVqycU5EHpFmKHy/trCi30WNTOLzwNUz6Wd5eRzzLl/Ma28TjgDwM/EHwOda+yCiwjNRcDnMu71LDI4EcleMSZm8bExC5zMBRyQOp04qdyc5mRxqfP1Xh4WLI4L+3HBlli0zi4oS5yJW4CrjsZqflIWvJq7sMzrBTE/+GfKXHx5XdyGk1wnjzTPz/SiZ5m60my/9xBZaZLxFK000zRlNJ0ipYVlW7Vys20TZxnStvBtmyJOaDYikqqikIbRNEYKQVmW9KIIlCZwXIZpUivsilpyIDFMxgnrt1fx9weMpwntKMCyJJ7jM/zwGd/4X/86/c+eke4MMELR/3KLrXcf0fy730aIWrmudaPHd3/v1/mP/+wPaNoOroTDbELXbRE5DruPt85trc5ah9uv3SJaavLFjz5mGmc8+6JgZa1Ht9VgmqQcDiYoA9oYXNcmcmy8dkgZegTtBv3DMVppLN9FFRXSshiPprRCDwG4oU8xHONJi2YnotFp8OzzTWzLpmE7DOOYw+EEx5IICa0gJB1M8VsR0hjG4wnf/q1vsvHm7RlmCqSjhJ1Pn7H9eJveao+qUqjDMbbvsv3ZUwyCTq/Bd371Hd7/0fsM4oSu7xOPpnz8Z+8z6I/ptBuES22iXovbr97mwXsP6XSbhE7tW2O91yLNyvo5kxQ0GiFu4OL4HraUTI+eIck0Q1sSu9TYvodv27gqg/0RFgLt2NiWhYpTqDQ4NkZodn0Hy3eIhzkmSTkoC7QAB4meJijHQWcZ6shwQVUppFV7BLd9D9ur/X1MigxJ/dTN87xacVtLbMeGSqPKiiSOcTwPrTSh4/LOt17jpbfv4XQjDIK9RzsEtkQYDa6NHXm13ojSuO0IPUpryUnLx7MtpvsjRGYjpcBqhySbhwjPJoh8tNasvXKLKskpdg4JqwqZlXhdmzzwKLIUS0rCZsTa7RUmewPanTZBViAArxnVvkOEwChJFIagNPdaa0ymMQoIypKmtHAbIY03b5PGOdP+lN5Sg+bNJQqlGe8MaN7oEjQDgrUOXi/E9zxUluN0G1iBS9Gf4EceRVEiK4MpStKyxHddgpU2biugtC2cUmGMoRrFyE5A7/4GRincpSb5tD4HsCRuOyRYboDvkGUF5uk+oqhwGgHJwQh/rYMb+FRpTnupRWUMn/7lR7UvklGCiRMmeyWOa4PSGNfGbQS88b3X6W4sYbs2wrFqCZbSrL96m8c//4Km0vTaDcqyYmtrj93NPW7du8nyjWX8wGe3PyAbTVnZWAZa+FGIB5hJSjaMyZ2ETCksx2Y0TWj0Wqy12gzihGdbO5RoXM/lzq11Hnz2COm6TMfJ0X6cMYgyd15fdoHNs3bm083kFbO/XxIMFzuSvrZ5HzOPW2battDZ37mr/mtwvC7KerbNX5XOuyTffzIAcVG4xjCKcx/qdaiNxj4m2///rmPz4RdmLeq5GfMXomFzSjsJMa9nDGhVe5C9kkh/AeHEQsNl1OW5zXgB0XgGQJ0Wd0L5nwhh5kCqmU13Fdy/2O3b2W9zXTvDORGzCWZLuApfLWL/H1nymbWuca6I50LjF/BIzMmSuSTn5fUdg8mzZ6zBIJHzc3jZ+hOn+c7Fm2t29yxAfa5wah9bVQor8Lh5d4Nv/OY7bD/Z5vDzHWRcUAlBWVUUlaI0BqEVjSBAGYPrOKR5QVyUZEpjWzbGaFzLoshzVtstNNBb7WIhybKSsiwRUiBti80n2yytdNndG2A0GK0YpRmNwZT+oz3W3nmJh1/u4kU+CPj8T9/j9i+/QrTUOrrcBS//xjd5+KOPGT/dR2UVlQAlNJbjEe8PaxBgWSdj5QYu3/u9X8MOXL746efovCDOUsI0p9Vp1s9nlCZNM7Iko8hKlle62K4HomJr55AsLZBGs3pzmcOHtUnYNM3wpcByXL7cPgAh2Li7zsvvvMzW55tM4xTXcUiMYhpnSKVp9drc/eZ9Dj7fZPvpLp2bK+TjCY7v8sZvfmvGaRdMD8b8/n/3ryjjgsHhiLWbK1BVhO2Qv/9//D02P3vGn//zPyIdxTTeeolf//u/zvt/+h47yYjldsRkOKXdavHtf/AD3EaAMQZTafp7I5zIxepPWeo2qCYJxrapCug1GyAE0zwHIHJcGmFIYFlYrSY6K5GOxHJdgqRAa8Cy0NpApZBAnmXEwuBvLGEpxfBwSJTluI7L1nSCE3q1lKEocQIPtCGfxmBJqqrC8z2UMViOg1IKVSmEY+MJD2HAFvVTKc/3sITEC32S8ZSszLGEQBcVnmVzd6nHN3/jW/i9Jm6vyYM/+4j+/ojVlQ6OY1F5Ns07q6TbfdylJk7gMzh8iu0KCq2R22OcyEW6NkV/Qm40fjPA7jUxRYWnFEVRUdkW9sYydl6g8hIzHOMvd/AN7O4cIJRGIGh4Pm46xS8VUylw8xIr8BFNn8lQ0z8Y4dg23TurpDsDfK1xCo1xDdHrN1n6/n1GTw+PnqlFOJHHmmtTJgXZ3ojG3RVsx8L1nVrvJvRQlSIe1pIyATi+ixokVNOE4OYSrmtTxTlOw0NbgjJXOAYyNK4x+L6NzgxOIwBLIoRAuja2FDS/fZ+qLOk/2MZb6xBsLPHsP7yHXyrsuMDrtVla66GUwZrkHAynJNOYhm1RIaARcf/br9JaaeO3QqQlcUMXXdVSJ6U0CEGeZOw83GI0idnoeqyv9JhkGU7qMo4TPv7wM1ZXlth45RZvvXKDD//4Zxz2x0Seg+y2qJRmIBWWgKJQbD7bpdEMcbVgf3uXO6/dJTwQrJs1Hj14hGk3ORgOcXyXvFRM90b10XvCVzu9m09uhwUE/1XnuYBzahtXcZbP3eSLuLfX5eSevZcv4lUu4EwaA0Yf0VxXhEvv9q+BU64dvqoU5Kr8i6QtLEh7MVl2NdhayEiUuEfPkf9awtecoxf7LOocF3x+FOdEhzPxl/fhPIF8LBoCrlzk814NZt3en7bwgmovaNkclDxXW132DCdhTgR6nOx4rC6hRMWCJiyCswu/n4m6cCGf566cNndeXsG5lIuhy9XK0ougzcyXs8T6JVOwuFvzJPyiFbmoHednwxwpd53P8Tzn1Wm551hGC9NeWb45++H5Tk/btWndW+FX76zhWBYf/+xTnj7bRQBBUHtZXlpaQitFKMBJM1xh2Kk0OYKsKGg1GzUn2bYYDSeEvkeiFErr+v257VDlBa1um2YrQlgW/cMB7V6TeJwQFyWhLWmudCiLks33H/PKb77Nl1FAkiTYjkM8HLH1yRNe/fVvcLwZ7MDlzb/9Pf78//FvCbpNXMdFoBmnU5aTDF2dngvHY7N8b40iK7CDWqnVMbU53eloSqvTxPZs/NBn98kOURRyuN8nUwqhDdKS9HoNbr9xl/7WAU+/3CYtK27dWMJVGkVt/crxbJabDfoPdxkejrCkxHbtGjgqg3AdNl7aYPR0n8ODEUVVQZIxnCa88kuvE7Sjufn98E/e4+F7X7Bya42oEdYWf6qK5loXN/J5+fuvU4xT/upf/YjHHzxCG0Wr3SBJMwptuPvKLR4+2ORw84D1V26idW3nUGuDcS2C5RbT/hQjayVpRwhc18XvRBQHQyZxgi0VgbbQqqSapmjXIcKB8YjcgG2gUBVZUdRi+kbAzd96G/v2Eo8+fMzmTz4hjAL6o5h4OiZoR6STFK00tusgEUit8V2XEoM4FvVrVTu/sy1cW1JWCiklptIUVYnv13oDrufWej+NEJlZZNMUzwjura3wy/+r3yLsNnGbIeUkpb9VE/qB6+B0I4o4x254SCnQWVlz7jFIz0aUFaXRBO0I6TmQlahxhpYV0vcgsLA22jjPBpSeQ3O5hVtVTPpj7LxCj2Japlakx7JIvtylUSq8wMN/7Rb68W5tvvdwRJXluJbE0Zoo9PAqjR4nWErj31zCe32DynWIhzEG8HtNiqLE8mtTw1IK1KTAsSX57hBlS4SQGMANPYTW4DlUlSboRmjXYVoWkBY1o86q82kEbuihxinRehchZQ0AWwFlmiMQFHGGnhosIbECC6E1URRg+S5OM6glSFnJ+Nk+OitxpIUaTtDG0FntYQlJO7Cx/ICd8VF/2hFu5GE5FkVa1MyPUlHmJZYt+fCH7/Pkw0c0Sg1tzfBwiClyVtE43TZO4DMejRm89ynf+LVv8YP/8nc4fLrPg3c/4+c//4zA9wmaIYd7fZqNCEsKyrKiLFUNXB5tceudV+gZqKpagre3c4B07FrP5uQOOrqYFlwmC+/Ao3/ECefoPDU5/xrjLD2y+Ez/Wj7FxAWfZ9tzVb6jr2KW5rqEUP46dP2VYXbALrtXj0DhZTTLhWGGBjlR/J4nCU7Snei1Xlb+MTFwVXuv/PEFjezXBV9XhF+on4vz4zhvd+ls6hOy/AradJ6AOCn6tNIzpc63aGGyc0WdSimOAQMXqzrMEv1nD5wLieRFrIJrhJNBfRErQ1y54K/PGDHUis+n4Gg+0/zhPPsu1RzlPc12ulXhVAlpYY/PzftR6hN9DXEexy1AS4vn9nRwTj2BfIVwtHhObYfNhDPtuh6w4My8nZ0Zc6qwf1zNiSUKwft/8BO+9Zvf5ot3P+fwix2WlzpUShM6Dg3XJc8LXCmQvodBMDUGx63nrChLqqomvm0BDdcB28Jr+PT3B3hBwCROcG2LNMsJfJdKFxgEO5sHLHVbqMPaPCujKX7gU00yklHK8lv32P35QzQGz/V48t4jXv6VN+d0EW69c5/2Sq0o2/Ui8rIkwlBNJ5RFgeOfcnYE9bJyfJfXvn2fzc826W/2kVmB53ss31iiudxCaUNruc3O589qXw1RgO3a3Lh3g+ZKh72HW+xtHVIYTbcZ4lQav9Pk2c5BrVDtOIz2h6y+ehMO+kjLotmM6qdCVm32c+fRNnvbe2jLotdrU5UlWVFx61svz609rRTDJwe8tL7MpFKURUGmK7QlCenU/ZKCm2/f5T/+iz9mFCf0Ok3CbpOwE1EOJ6zfW4OVJh/88c+wMLRur9UKyZOE0jY0fZ8QwdiSBEfK25bjIAxIAcutJkFlyMoSr6zAshCOg5WVOAYKoBCGqqrIJaz/yqusf+81Hn7ymA/+X79PNsmoMFRKM41jHN9BmrrdRVGBFCRZgee5GClQ2tTPZooKy64Jl7KqEKaeSylErdht2Wgp8ByHIi3wbBfHdihkieU4eJbNr/7eb7B0Y5n+h48I1zr0f/4lDS1othswSck7Ia5TMXrvIVle4tsOlmORBzZWy0cPE4KNLv5amyRNEU0fNU6wvACNwe1EuDsFXjskKDVlXtC6uYz30jp7//FD3NAl0gYzGONYFmleA9tb/9n3ad5Z4fE//SN4tkcV+vjKEAgIXA9rmJAOpjhLbbz1Lstv3EG4FqMv93j69FM2XrsJWuM4dq0HYwy6HyMdi7Ismez2CVY7KM8h6oSYUiEKhdJQbg/Qqy20JfCW24hCUU5SDKaWxKy2EUd+QpywNj2sygpVqlpPwbGp0gIn8snzArt0EFIgbKv2lO05+LeXa2d+u0Mm+T4iCKi0Rrg22fY+WmsmloVORpiyZPeTxzx9/3OaKz16G8v1s8SGTzZJyEcxqigYfvaMFWnzLB0z3NolCgPysqTn2EQKmp0my3c2GE9TPv3pZ8SHY+5991U23r5D3J+w8/kWFoKD/T4Cw62lHpvjMWmWkquCv/zxXxF0mqy+epNv/Z3vM90bsbOzjyMEURRy8+27Cw7es+fxDNv/0iv5BVBxi+6ps3f3RXf5wjvwqMDnadpzduNrUSnXoaWvwV03+qiYs329bvliwd8F6eZoRDPz9yJe8HXAxgXNeSFhQUFz1rO+ZkUvGFzMj+x5ILF4FGcZ1n+t4cKZmuU3zxO9zzXizwM0r0p7ZhGetOSi9DMH34WqVea51/aipszEXpD4+IM4rXM+iZgvdMYz5oxMenENVxzmJ2P03KD/PCida8HxBFzKqDDzEyUuwAJnalzIoTqTx8z/cw5niKNxO3bOMzsNb//6N/n0hx+idyas9tpoIQl8F1WU5KLAMgYpBFSKgVLkBnzHwSiF77rcWO2hyopGK2AapyTTjHRSe62OkxiL+vmKqhSjacyNGyukRUGcFZhSEXoOh3mBv9SmmiZUacrg0R7Lb97j4NNnVEmMa9scPNhmvDOge3vlpO1O6PG9//K3+eF///tEUYQZTlDGkKQZVVGeG8vjoV++v8EHf/g+kWXhSKgcm+nhmPFgzOBghOPa2BruvHob23fJ04yD3T7j/pgnj7coyopba0uEGLJSk2cZke0QlyW2FhitMUWF73tMrZg8L0iqirv3bjA+HKONobvURWBYakd8/GiTl77xEnffeWluER083OHwyz2ajZC2lOzvHFIKQzsMWLq5fOJp3Y08Gt0WZjghjAL2nu6CJVhb6lEaxS/9ve/z4N3PeP+P3+Obv/1d2utdqkqx0mszeLSDraEyijXPZaw0hcqwtME3gmZlsAyEtkOR5hD46KwAWevR2KpiUlXkDY+Vt+6QRA7/+v/+P5JOM3IMtu/gIaiUxgtcjIHB/gDLd2k0G7iujWWgVApVVlh2/ca+EtRSicDHQyAtm9JUVKqqPbC79XOpyXiC7djEWYIuNaPRCJUV3Hz7Nu2Xb2CyEj8KyXZHjPpTvG4TeThB5SWZLbEaPnla4SiNXI6wIg9732CVmir0kZFHqRSu5TDZP0QrReP2EiarrVpZYa3kL6oMI6GIM9jN6C53UKFL6xt36Y4TymmK47sEa12M0ZCX+HdXyUcx0a1lorUOSV4i+xP0IKa51mH1V14n7DaIN/tII2ndXqZ8WGEHHgawAw+ZC+K9Af56G4lAxRnt1+9gSUFRlAgNVVoiBZikRIYu5TSnqhSO72G0OZJoVODXfjr0kbNDU2lUnCFKhR0FJMMpotIIUwPAMPBqsFcqqqyknGY4zdp5nm2gNOCtdHCQqPUOPNgityx0I0RXBlFURI6NUhqjYXow5ODLbbwjT/LlkSUyZRRLqz0cJLltURhY21ijQlOlOZu7B6jDIZ5tcfPWOusbSzz97Es2H20iK8X9773O7XdeIug2mY5j9g76hJ7L3eUeu4MRJkvZ2d/hcGsfKQR3vvcKw8MhluOAY7N+c5Wll2/Ut6cRZNOU0eGYpY2lWl9k0cF9JszS72fjxZmYWSrjXBkcXzViUeZfTLjovvy69Z/Jf6k05rJ6nqMNs09OT+o1M5KIixo3U885pun5Ss58P2KYniWWzvMBLx+DBU26agq+zhS9yKX1C5JcXNXERfKLrwgtLqlq0b6YjT+lv+dXwCxyOwYVBnGOu36a4Aoi/jiTOf14vpUzthsWFLMIoi1iRiwq+ypR4FkgPVvL6Zidb+c5ov2qAT/JM1PTLOK/AihcHS6CSuaMd+sFJtkWchjOoLmTKp7nZJut91Q6d3YYZpt/ndKFECdP0Iy5eOUtksiUWQHDjJuv32Lzw8c0Ax+T5BRlic5ylJC1pRwhyIsSISUaqLTGsW2ePd3BsSRJHOAc2d23XBgMRriOh+c7tTMsBNpAGqcsL7VJsqJ+omRZtBoRkzij49gURnP4dI/O3RWat1YoP41JMCijefbBEzq3lmcU12HtrTss31tl8sMUVIGxXIq0JIlTWsvdhXvCWJJKGypL4AFNx2Zvr0+mSrKsoNNsUGoNT/fI84xKU/v3UArPd2k3Wkgpa3OdVcV4Z0yjEeFZFgZQUtDf6+O4Nq5rU+Q5t1/aoEoLqkojhMFxbHb3DymmMVpK3vl73691D44aWiY5f/kv/wyhFX4jYH8w4a1ffpvHHz1iOklYvbfO7hebrN6/gSrr50Lr60sEgc+B0QSOTzJJGD09wPUc/sF/+4/5n/9v/x/+9H/8Y27f2WA6TVkfxLhIHN8hylIGSYqwXWytodQEZYWSEl0pVFEhXAfLgCkrwKA8l4GEA1Py+r1bfNkf8OQvnyGLCrfTwKo002lM2AzRZUWW5hSqwrNrj+5JnJDntWNGPwpQVYUpKmxVK9QqS4IxteUyyyLOs9o3hDGUSlMdGRIo8oLhcESZ1z4tbq4t8xu/95uEnSbF7pAyLZk83gPbImyFVAdjvJU2xnfJq1pRuUpyLAxW6CHbEWVWIH2XbGuAtd5BKs1o6wB/tUu+3UdNM6QG4di4Gz10VqCfHaIsieqGBK0A0Q6xHZvG23ewI49ykpK99yVVVnDw8TOEbXHvv/ldgpUWxTTl4D/8HG+9R++d+zTvrFCkOf2HO7jdCCfysY1h9c1bVGmB1/BRaUZ6OMYKPUShsJoBgWOTH+n2OJZAAiLOQSlkw8O50aVKSxylyZ4d4t1aQlqSwA9QlaKKM7AkepSQIUAI7MBBCLC0QXngRCFqmtZPhoSAskIrRZHmhBisQpEOYiqjUXFOrjRCVaRG134kihogJQm0A59hmhH1Wrz+g7cYbPd5+JcfEbgObadBJiFOC0ZxfqJI3nQcDndrCUheFCitiRoho+mUx0+2ePUbr3Dz7hpBI2SwO+Rnf/Iun/74Y77zt36J13/7W8gffczDz5/hN4LaUlm3w437d8jSmHSScLh1yBcfPcAC8tGUd/73f5/Gcvtob2q+/PBLNj/b5KVv3+elb760QMH7/NeLgjEaIeTRZzNHZ1xZ0Bzxsqjw67VhrrDrUqMXXjIXp1lYrJn9/a8DKZ1vyLyfiatg3XxsrXNy/A7h1PTNhXVeRBfNJT2mXS4ej6tSnHVH/NVQxoubj6u1cq4KRyKH4wE++//ZpAuy/sKCOfN/HcQpn0DML7LTPAYjDKf/zZdmmCXmzAlKEcf/maP/T/6r6dT5MTkzQuL4SZFY+N/sqM7GzgZx9osw8xWfVHncg5leiNm+nZ8VM5NrLvIrhcXw6vJwncoWA4uTeow543F9pgEXng4L/r8UCHHpwjZn/i5MN4u0rjE4QlxwRJ+drKO+L99ZJTUVn//sMyzLRuc5cVkxrSoSpUjznL3RhL1p/TZa2BbmyJqQ57lIS9Jpt8iqiqjXZJLm9JMUy5L4ocuNe+usrS/he/UTq629A/JJjEpSlK5Iy4rQsTHKkBmBLkvyyYT9T5+x+uZdFOBWFZ6Bz/7jB0x2B3PdkrbF9/+3f4u1V2+ym8WUWnEYJ8ST6eyocLxXEPWzmHsv36Iwip1JQn88pRF6rDYa3Fnp0W34RK7FNMsYJRlCwMb6Miu9No7toIWgxPBkaw/PtmnagrQoMQIUMJxMmI6mWJZAVJpeu8ng2QGbz3aRVUmW5EymKUiLRMOtV26y9urNU1rBGD76w3fZfbhNuxGwtzekmKaM+2OEZRFGAZ1eC11qPvj37/Ln//xPsBybtbVeDQTSnE4UEZcl6cGErZ9+wdKNJf7J/+m/4bf+d38HZylgOfTIB1OC0EcAYSOg4fg0NYRpie/Y2K6Di6AEhOsgjOBwPKZSJZkj2fUFu/GUqN3i55vb7D3eqYFoM8B2HIwEx3UAKLMcy7FxbBsjBXlRUKkK13MJQx8D2I5DZQzKttBSooyufTFYFsa2aPg+Rmscx8HxHGzPwXJtSqNrZ3iVxvUcfvv3fovu+hLlOOHgZ1+QlyWTwzHpJKGaJFh3lzG3l2trRIMY4gzfkpi0IHuyj+c4SG1wAw+726AcxEjPxQz7+K0AsrJ+AtQMKLWiKkuEY2OFLqZU+L0W7p0V/PUulBWTj54y+WSTLM4wN7tYb90k/KVXiF5aww1ckq0+0we7BI5NsxHidiImj3ZRg5juvVUaax20YyECF+NYNO+sEK60wBI4yJrwlaIG/kpRqRKVFeT9KeU0hU5IGtgYKTFxhu1aCAzB7WW8ho9RCpMWOL6HdGrLVU5UO0IUgYO/2q4NJCAImrU1OCfysQK3VhoPXJwjZWxdKIQlUVrj2jaqP61NxD7ZIR9OMEfK4EgJ2vDpl1uMR1MeffqY4XafoBGwfucGk6zk881d9vf6PNs9wA98Xvvlb+A0Q5RtMxyNQRg6rYj7L9+i6bms9zrcWe5xw/UJ2y0SA7376/zKb3wXO/T40b/+c/Y+fsJrv/Y23/yb3yEbx+SDCRJBJAOm+wMEMNwfsLW1QzxNee07r9G60cMYQxZnDLf6mElMa7nFdH9EkRbXvvqOffXMnvxSfH2y6yuF88TQLPkyH7/ojjsbdxkBd0LfznBUvwrdetVAz/H/jiiU+eG+siyx4NNFXRMc6/lehfKu39nT23tBHnE25dXlinMf/tOEFyq5uKZl4+PEdRDXy3dM4M9NqTmamK89iLPQ4/Tfc0hwhrN8EUo8BxYXcTguacW8Eth82+Z8w1+ryAWJTB1/RlizYNGenZXz346beTo3Zwz0XtRGccHnS/v2VSf5VKJ03LaLS7oE6l9V/YK2X3wQzCyki+q54OyabWEttZjp4Una+fU6h6eMwfU9TFHRcD20gUpK0qqi0oYMQVZWeI5NIwyZpBm+6zCdJKzdWKLUhjjPmeQFlpSotMAYQ6EUSV5wZ6XLqD9hPJwSeC6h9BiNxyRlyYrv82wwxG42KDFEjsNgErPRi0iLiuGTPXq3Vwg6bbI0RWhFMZry4e//jF/5r38by7ZOdCv9ToO7b73KJz/+gFjXRGaR5adjNMvmETDYPMCxBS+/fZ+th1tUwP5oiqoqWs0Ineqj4dH4tk1VlDx5so0yhpfu30J6DvtbB0RhSJVmOI6kt9xFaZAG9rOMm6/dIUszpIFkktbKyEKwNxzT8ANc2wLfYzyNeemXXsfxnKN5M+x8/ISf//F73Oh1OBjVz8LyouLZ50+wLYnje/zb/+v/RFaUJGlGd7nLnfs3yIVhGE/pdprcubtOo6gdwj34o/fZf7xN584qXlrRyDWWY+NaNmlR4itDmWlUkmG0QakKN69qL8cukNZPo+Ik46AqySKfg9EQmTisvXyTJzt7lFVF23XJi4pJWlAWVU2EIsmyHGHJ+mXAkQKo73sgapARhD7SMUyGk/qZztFzL1tJtNbII+VeDHhOLfWonNrfhTKa0PPQacGdV+/wO//Fb7PebnHwJx9S6gpZGlJqDuPt12+h+lPsRojlWExGMaZUSG2wl5qUB2MoS6Rj47ZCDKAFWKWiOBiTlQbLtqnKHNsAtkRVCtu1cRoBbtNHR35dR7O2rGR5DkVWkFnglBUmKfAjH6EUcVGidocErRC7FdJ0bXAkwY0u0a0l8v1RTYgLsITAdh2E0tihWzuznOYYYyjjDCv0TiwrRa0GWmb47YjRg02cRohXGSrLELaimlhKC3RWkB1O6nPbktjtEMt3KCYpWoCMXJTRSNuiGkzReUk5SVF5hWwGWLaF0woxjsRybXRZMX2yhwac4MiXRKnwbRuv0walGU4mdKRNOZqSC0PLc9ifTnGF5LMffYA2BkdaCK2wtWGvPwIpGfaHjPYH2LbNvTfv0uk0Mbbkiw8/r807S0noOkSex854TKI1lYTD/pCuH7C81EVow4c/+pCtp3u88s2Xeec3v82nf/kxWVFSVpo8jml0m+wfHBJaLr7r8NbvfpciKzn45AlPfvI5q3fWePRwi/RgzHLkkX/rJdzQPT1wjw+cBdfHiXT65Lg/k+Ac+XLBt696/Z1p0+xd/XWLPlfPmQJP7qQztMbzFFpnv6SFl92hl31+AeF5pS5znrhn6IWqLGs/MNJanH6GGDjNdr7u6yrlL2jYLyS8MHDxXMDiK4TTQTYnoOKr1rhwky9MdwGSvIAuPCl10WY64mDM06CLDpJF7IIFYSGKWUCJXlTMsbvm44TmTMdmGnry1vOCIM79e0m4AEDMrp8FTVhc8myCS4DJXPsvPehmaxZnPl2U/gJJyEU5zHOu23Mg8GxY4AWV0zyq0hgDtl1bkTHG8PhHn+LaLs3AJs0VGEPguagkw5L1M59SGQ7HE4QQpHHC6nKbXClEpfCd2sdAXil2dvvYroONoNlqMhlNGcfJyX1bJhmdZoPBcILTEzTCgMPhmE6zSbMVorRhWCg6jk1VFEwPxjTWl4g//xLpWAQWPHz3AauvbfDyD96cG4eo1+LexkvsDA7AVKijTouzg2AEN964zXv/81/SjiJ63TaFUhil0FlN1KZFgapqi1ee64JStJsNUl2/Rd98uoMp62cnlVKwvITjuJRJTjyO6TQiVF6y9cUWRoragpI2aKVYXu4RhR5bWwcURY70He5995WjS8aw9clT/vB/+He0Ao/JJOXW63e489otfv//+W/ZWOlRloq0UvieixTw0iu3SZKUg2e7LK8vc7hzyO/+nV8lDDzKwYR0mmL7DnsfPUE9PURLG6eiBhde7QTRGsWUeYlvWeRGEXRa2KGPzktEkuKVqn7u0/BY6YQMR0PufusVbr1xh3d/9glGShqtJnGcIFwLU+jaX4UUJEWBE7i4UlJVinGZI2yJa7sUeYEuK3bjjFanARo0hqqsJRppkeP6LsIIkizDlhJl6meNruuhK40oFRu9Fvf+9i/z2pv3YJwR74+YpCnjacJyGIFn0729ghQC76V1CB1EXhH02lRhgCkKpCXxek3Kwwl6b4Ruh1iRj7AlTrdBMY7xN24gfBe3HZLvDQmkRKS1NStTVBhNreuzNyQpS+Ryi9BzCZeaVI6ErEIJKCcJtm0hS4XfCjBG44Ru/cTCd9BFrUCtSoXjWOi8QtqSYhgjZC2ty0YJSmn8W0sIKZjsjQg6EX47ROcVWTbBaQVEt1cxpcIKXZxOg2J/hPRdZDvEKI3TDDFlhRaCIiswlcbxXdJJTLjcRleaIs6wPBcBtURkkta+J8oK6bvke2Oy7QH97T7RWhcZeqRGE3WbZNuHVAcjlKSWfgmJqUrwHDwMyi650+tiY1AYHG3IshQlYG21x7IAU1QkccqDn36EHXgoYO2VW7VksKiImhGHBwOePNsknkxYHXXQzQAQtJoB5WDItNTIRkCjWXuV3/vgS2Tg0Oq1mD7ZRqkS15Y0l1rs7O7TiEL80KOqNNOn+3TvrrD+8k2swKO7tkxTKdzDA5zAPX/UXmYl8fJLZOZEO+aXv0Aq+DyWWVz+81R59gK74PsJIX1ZuICJdvzjNf0FnzKaZ8s8ijfi+F4QZ7Kc13UxUD/2uAAsXlz94jpmgyo1li3n+2RguHtAo9PGj8LT9h9xBGdNHZ8yEK8wMHS+cf9JwtcGF7Mg7Pkyzny+jAi+JOO1B/eKwr8KsJ5dd6eLd6a0RV7YnkPqcGGbTn6YEZUAC/UDWPAbJ+vz6ImQACFmNseZNprLgOMFhvhmdRIWYaWF9Pg5Fs781+eR2FwLSCwuc9ZawlkoaGbEA+K86Odc4S9kT5+ZVnFc8tFhKo4I1JlfTttj6sNZlQociTBQ5CVPP/2SyXiKdB20ZTOaxti65hD7RkNVWw5qBSE4FpZrU5QKD0iUwkFiMKRZjmc7WFrjOhbjyRTbsfHDgMFhH4nAs6kdeCF4urnNN19/iWmpMFJSlBXd5Ta7B0Mc18MUMdOdPp07q/SfbFOVBQqIHMFP/9WPWH/1JtFS62Q87rxxn487P+edtXUeffmQ/a3dmcGaQ8e1bkjo8/TpDmHgE0Q+r3/nNbKDCXbg1mZmh1PWb6/huy5fPn5GY6WNGcXs7xzWBJhjE5QFue8z7U+4/Vsv8ekPP6TdadAKPDYfbJGXJe1GgzhNCQKf0GsQLTUZ7Q6QlmSa5/zS736XRq+JALQ2vP+H79ILQyxtGCoNxrD81h1e/tZr7D/d49b9m3z24CnxJGajEeHEGX5VoRCkk5T15SV+9B/fxws9UIb11S7lOCWIwtoMqSwJbMmoMGSTCc2wQZbVCtIZBhH52L5LMZpi8hLZCZFRQLTUYjoYkkxiOvc2UKHLj//iQwaHw1rqUigoNaWpsCzryIOsprvcYTqNSdIcLIkUtTRiMp0SBkEtmUCQpwXySF9IYyjKEqENlqgVk6Ut8WyHSZaBgWSaQKG4u7LM9//er9CMXEaP9ogch/HugDxy2Ptoh+bLd1m6e5vy2QFVN8JaaSGKCm+5Rbk3xl1uooWpLZ61QmTTJ98d1eZsAaU0WVESrHXptqJaetIIkICapggD8cfPCG708G4vE/aaVI6D2B8TLrWwfZf4YES6c0jz5gpSgN0O0WmBJSA/GOM0A9Ikx0oK3MirnxcpjfBd4lGM7zogJOUoxm0GDD98QmFJWktthBBk+yOaKy2S4RTHd6jyChm5GF07ytOWxEwzsnECaUH0ygbl3hC7GSJcG2Fb6DRHUL+Nlp5D6NSetlGGqtTYvoPtu2STWs9FTTNM4CIqheU6BDeXWPIc8oMJqSUwgct0OEVVilJV5Eh8YfCVwQQ+RVXhWxYTDOs310imCcODIdOy4PabLwGw/fAZthRYWtGMfELXoT+c8P6f/4wwCnnz+2/xrX/4A8q0wP7wSybDEYPhiM+3t1n1bzLaH7HR69DodWi2HEypGCYJrmPzdHuPZDypfRTZkiRLmBzssvfpE/b3D8EYbty5wdYnTymV4nBvyNpGD6U0tmORRQ3e+M9+FT/yz5/Tz0G3zMeeJXhfDLRYyHu8Tqaz6V8w1rm0zuuEi8DIRbhOLKZS6iyz9/yM7oQ4STDTzKvBw0lpZnE6y5YL27m0sT7fZmMWz8UMAD2n3P8i5+kFgZEXILm4FHr+QsJZQDNrqvQ07miSjr5cLsI604czBc2Z55oLZoHDZTPzzvJ8cWfzX7QizJl/zx4Ui3Ke47cv6Nbx5jmL2I9VjecEGleEi6HaBeG4AedOveutnYvn4XphzlY1nDPXWrdGLPw829LrteBYRevoUDJnFP4vmsBLS5z/ezp0F4+htC1cy+IIjYAQ+I2Iwe4QQp/pNGE4mGAJiePXln2ENlhSMikrdFESFDaWkBD5+KJ+91mYWuG20gqBqK01lRWlVoiyJPRr521B2CCZxoyHY7IyYzJOaLYalEVFpTR+y0dtl4xjcG2LweGQ5ddu4XoeFpoKMFpRjBL+6l/8GT/4J38TrxGAAdt1WF1dwncC7touO59uHSlInlndBvzIo9Nrku0OKI1mOJgw/elnqKLk1ksb3Hv5Fs3lFvHRE5Bmq0GlFbYUZHmJ61gERa1DkCHoLLf54i8+oUgK7G6bp/uHVNpgWTbGGDzbQWjD4WhCOk0oqoqqKHj1nVf4pX/8qwhZb2JVlGTDmMC2CKVkuREy3B1Q5hUbr99hb/MAVVa88dZ9TFpgihK7FcD+oHZk6Ds0GsuEowTXAgtNZDtMfEMj8MkmKYWQEIWYfIoThKRJBk7tGdnKCqq8RE0SnHZEcGeVshWwt7VPejjEsSWNThO34fOTn36E1qZ+nqYMicpwHBvHgqAyGM9mNBizv3uAdB2UrAffWAILC8cSoDSuU7+/D1yXPM+xLImQtY8GKQ1VUeGGPlVVkelacV0rjWsEd27f4Du/8Q5RqUifHoJtMZ5MkHFOQyuWO03anQgORhjPRvaaJI926bx5u9bd6DWYfPKU8Bt30UnGwbM9erfXQAiiG0sU/QmlAiEl2eYBMvIRk4TRziFGgN9t0v7OfZIvtjGBA5Wi6k9RylAOJtjubeyGz+SLHZS0aDkWdiugSnKENrRe3aAcJ7WCdjNENgLEkallleaQ5ATLbYQlah0FpXCXm6TThOaNHiovUdMc4VjotMBxbHReIqWkMAapNNG9NbI4Jf5kk8b99VpHQteeyLElRmuEJbFDHyd0qdIcozTCluj8yMy0bdUK/QicwMOUFf5aD53mYMCKPIphjDYaf63D+qsbHKx12PnRpwgMO8MhVlFSqYqGEdiZIMtSjNYErotlSW69epvVjRW2vtymt7HM0p1Vbr55l3Qw4dnPv8ACMJrGcgsV55S64if/7ke8uv86L//qW7z6W98gbAZsfvSI5HBEb22FZH/I5vYuL3kuESEDKqZJjBMGGN/C0iG9bhs/8Pnyi5wv4glfPHpCuN4jTUe0VrroNKex1AQMZVrQf7jJ7mDKy99/neW7qyfPUWcP5Dmi9OyZfUIPfA3q73mYa4uSna3+KoauuYRx/Dwk39clek8u6eNLe0H5Z8Nz1ifmOjSHKE6+Xm0UZ6aMC8ZHXNCH8xIvccoQPsOnNWeSLfz8dcMLKusFgIvzHoznf70uqJ8p5bob6ST58URctHuuKuaKtOZkhV2r7OsJYi4AK1x8BixMPaPMO0sWnyfgLyBO51LNLH5BDTeuOkgumqtrL9DFBS/aSAs35wIuw0XhHFg4ZQTMHCKXjLngyLHefJ6rIGL9aUGpFy2UM404ppePJScnh5GZH/wZwcr5io6YIeODEYfPdolHU/b2D7CwCBwXz3FwpIU+ehM/zfPar0VRIKFW/IynNVDRGsd1aDUifMcm1xrZDNk7HDKcTPBcF8v1cGwLx3NoyQZLvTbbe33G45j1RkgfgeU5aAO2BCMlrpRMxlP6mwe0b64wfPSU0HVIKoVvGfY/fcrP/tkf8b3/ze9gBQ7ZzgjfDSkNdHpd7r98/+JLQAjirKAy4BpD5NpMKo0Wkp1n+7SSgu0nu5i8JClL3MCltdTi8bOHrDcifNuisCQxtTfpva0DLCFYX+4QT2LiSUoUBnTaDaqiRB55Ru61IqbjGG0UnZfX+N3/9h/hNwOMgaQ/4ZM/fI/R3oDW2hKlJamEYOnWGk7osvdsD6U1lpRk/TFRu4mSks2tA6bDmCDyWevaaAl+O0BohTx62lVMUpSuncTZroPOq1rxv9K1s7I4IY1TCimg4SN7TVbvruMuNymSHL3Ww/FcpuMYRykG04RK1dIbVSq0ZVEqRX4kbbClYHR4SKkqjDI4pvaW7khZE8nUyttaaQql8CyLXFdM04wgCkBrlFFUlSIKotp0q4Eqr/CQ9Dpd3nztDt1uEzlOyBshw0rhhT5e4GOUIR+MWV7pYQIXq9sg8BzQBrcZMn52UEsfhMC/t0aZ5MikoCHtmrN/b5V8f0Q+TQlvLeFYVm1KttfA5CV2NyKbpLjLLcqswOk2iT/bpFrv4bRCxCRD3l3FaMNkd0iW5LieVetoFBXSUHtDj/PaFG5WEvpObcUszcmGUyzfxY18OHLCaIUeemOJ6XAKzZB0d4jpT7Fud8me7NN65QZIQTqYEm308JxG7bTRsQl7LXi59ngtPZt0Z4C33DoiGgXpswOMY+PYFsKW4LuYkiOFeQeh63WiK0W+P8JdbSNtSXlkllYN4/qduAL/RgvhWLgNHxdBPEloWDbSkbi2DUWJVopkkrKXJDR9j3I0ZbBzyMb9m9x/8x7hcgspoL3Wxg89pDE8+MsPEaELZYnTCJC+g+vYfPxXHzEajPn1f/K3WH3zNuloSuh52J7L/Zfu8ODRE7aGA1bTnN5yB7vRQDQjDvcOMUoTNiPavo//5utsPXmKF/k0bZ9o1UYJQzxNCFbb7D/bR3+xidtr4kYh0ZGzyxOm5RFj5yJgce5cP3smz53d5ojv9iKpxCuqnv0+y/RbwGNdGJ4HZMxVd00m4eXEzxW0peFYcn/9cI4geq5w3K8TLHnuN7iOpcnFD6ePpCtzjjSuKOtskuvzcV9I+Nrg4qouXtr9c8TV2d4ffZ+Leo4RmgOhZrbEmSTXmezF4bjvi5jHs19PlsMcRjlPlc+P5dmdO5vuuC8LWmbO/D0+NJ6T8zHbirOjfemGPgdsLs44x9s/M+1Xw7dL6jlOcc7W69WDcD1mzHUV4mZV3M1c+aexZs7M6uLC5iVkp204LfXEbvdM0Erx6L0H3Pvmy1hHCrO99R6rd9cYT2NagUs6rrnqSZaCMTiuh6BWUlZaEfoe0raxLQttDProHX2e5RyOpyx1u0SBS8P3uL26RLfdZDBNyPICrTWu45BXmr3hGK/ZwAhBURmQkKcFtu8SBgFJkhEEDkIYDp5sc/PuBpmGhmNTHCkHV0XBo599ht+OePsf/4BiKwYhqaqS17/7Ot/5u98/BYmzN74AIQXrd9foP97FCAvfFliWJCsLSmAyiRFVrUCcZxm6VPQf7ND1PTzPYVKWOLZDw3GwleKwP8ALfZprHUaffFkTvbZNkZeURYE2mjtvv8TO42200GTS8Hf+q98l6NQESpWX/OR/+gsevveQ1XaTSoAjJMaSLN1bx3Ysth9v4/kuw9GYZrvJzsGQh58+5KW37vO7/+Rv8ei9Bzz9/Bl317vYWY5wXOJKE7kW7SDAKjWu0pRFiQtYUJuVlZLScRDtiKjXZCoNrXaD8KV1dOggd0YsdSJiVbLUDNj+YhMmOa5l4foeqUrJsgwDFGmG77rkaYkGXNetCfiwNnM6Hk+IorD2WC1qnQxjDGmaEkZB7aCtrE6sHiEFWmu0giLLabs+N9aXuXVjGafhowDl+4wPx9z9tTfprLZ5+sOP0FLArWUs38FrRqiDCe7tZaRfP/FzpMBuBuTjBI1BFIoqLXB7DaxuiIoLisEUWWpMmlMKgckK9Cih3B6gJik4NomC1qvrVDLBEha2ZSE7Ad5Sk/xwwujBDsP+mBvfe4Xi6QGOtMj3hpR5SXh7Ba8bkfenNG4tofKylgL5LkIILNdGICiTDMtrMt3u1xaaqorgyNN2XinsaUGw3sVog9ON8NsNpO9QHIyRnoMxhirOkb6LUJoiySmHMXGc0rmzBnlZ+8s48vTtdBsUWV5betKadJoQNSOq6ZhCmFqBW9Vgz0iBDDyk0uikqC1BORZbf/kph+8+gjgnNhppDKCJ84xV1yfTBSuBR9tz2UkzrChEZwWPPnpIEPi1VGe5Q9hrEa62KYuKaV7y0p01zPYBe0WOaHqsfvdVmk8PePLZE4ysn3N176yxmxZMBiNcpfnWt97g8dNNtg4HjMYTsG2WVgxNBVMB20+3GLge2XiIJSXpKCFyAr75u9/h8HBIrxURthuoxzuUUqLTAi/wEUIw7o/J04JmM8BrhghZs1fFySU2fy/NXkFfmU56rkRfMcxfU+evzeekY0/C1yFuL0Bt9Z15RD9cyMm9nD5YVOYpRfL8Q32OeThDus6xdheRI2fqP5/w9Pu86eJfQHiBAOSFKHRf2JaLfrgCzc+L445GcpEJ0ZMkX32oF3KU50AJ85M551NgMYoU5nSxzCkNiUU7l5POLlIIey6rANcNl87LUV9mOl5bsBInBOzFnqrPooIzaGv+w9dYw9cFhIs36Pm4Bawacc4e2AVFmPMHyPFFc85d54JizBmAsWhQjsQW4kx5c+1bJMM2sPdwm5uv3kYevROWUvDdf/xrCN/h8Y8/A9uqfQVUFZ5tQ1Xhuy5pWdH0PLQ48qBMrfhtWZJmp0U8TbAsm9F0wjS1KJdarHY7dAMPP/B4srNPlhd8/vAprWaT0PVQtkUnCmgGEuP4FElGpRVu5JFlxdEYKMrhiGmvjeU4FHGGUerIsZbGDTw++rOfkycFm493ycqK3lqHN37n2zXX96KJMjDaPaTbDEmV5iArsBB0fB9hOSRZjjjyFm1ZFt1miMlSLN9jP05wHYcKRTaIObIrxa2XbzIZjHEaPq99/3U2f/YI4zk4vQYH2wMevvcAbTR5VfHq33ibpTurAKTjhL/4F3/Kg/ce8tqtNfKiQoQOaIExAr8ZkI1ShDK0Vlp0hSATUMQ53/7u23zrH/0KzdXay/fTT55QVZpK2ghj8F0HkebYRYXUpn7+4thIbdBFSaUM9kqHpddv4TgWQSdiRYAJXCgVZlBiezZ25KMziRmPiVwPKzCsNZtsjkZorVFKUakaFGRl7bzQcR083wNdK2iXZYnv+0cSsBIv8MjLnCDwccKgdtCnDbZbAwytNY7loAtF03N54+4t7t+/iWdg62BI1fAobUn/86e8+Xe/R2elxfSLp6Sbhzi2R+dGj+j2MmKSoVshymiKShP1GiT7Y4RjY+IcEbiMDw7x4hLdicjygmp3iBCSQgqcUiOqCiv0KPsT3JfXEbbF4ec76GGCfLxPNYmRzQCV5KgHKfZLq1i9CDfJWQ1cbCkp04JynFJlJfF4SuPWMtnBGLRBZQVGabQl0UmOjDykZaHSHLsZIG1J/GCLpe+9iuc5JJ9uUk0SnLUuShua99drD9hS1BKhSqGLCjvyqZKcMs5QQuC4Nk6ngbvcIt0fgwHZCPCbPkZpkt0BgefUUgjLwtIaL/Kp4npuRFEilppYloUuqlraqBRkFcIYjNbEm33GHz4lORxjfBdtFBOtaHkBTWOjjzx5atfGAMvGECcJfrtBt9Ng2h9TTlJGkyniYQ2ykknMdBozynMKKfGMA3HF7k++oJL1Uy2EqJXy2xGrb9xh9GgbleQEvSb3XYdheEiW5+wdHLJzcIinoRUGuLbDKM/59JOPaHVWuHFrne/8F3+Dzp1l+GyTqNvCawW8JDSHm4fcfPMOjU7E6HCK67n0tw559sFDmitdbr9xBy/0T4+bRVfMtajVKxL8IqjJ52E6fkXm5KIynpt+WXCNngzpLxJwLWrDbANmfhMXSSQWActLCeZjbvDZxPMFzVMAF4zpWWB3aZil+15M+AU50btmWEBwwmz/ZonTsyusJtYXxJ58muGLn/z2/GN32a4ymKM36GZhq825f7/qXrj23r5sE2A4+87p4nLPSBSEmY2tl+KlIPHsJrko3ZnwFbJcnvASmH8CAhb9OK/JM6vmfYaqvxxoHZ+AJ8N+csIe/T0vRp0dd3GcdcZp3tmVvBh3G6Qleed3vosbuDNpDcO9PkIYkklMMwpxLJs0zSiKEoNCHl3+UkcY2yYvCmzHAQF3b60RNQKGexZ24DLYHzLJMva3Dxj1J2ysLuO7FmudNllZ4nkuG6tLGA1JnqOmE6Z5RhYamktNRodjXn7zNu/+h/fQvkPD98mKkr0n2/TWVigGQ9rNBpXSKD9AGY2lFV/88H2+PDhg9fZNfukf/oDuzaWj8Tp2KjhvvUVIQdBusP3FDmHg0VtqMTwYs5/kOI5GVhVRPqEnK8ZWA5kmFNKhKitCaeEEHp21HrtPd8nzgje++xrt1Q7DrQOW7q6R7Y1RWVF7nVYVGo2uSqZlyS/957/Gt//+L59w7bfefcTeB0945f4tVJIhfQshJH7Dp795gElzHN+ht9wjjmOCRkCFIE9qHYfHHzzis598ynB3wI3VHtKS+K5DIQwtLIp4ii1qmZmNwBMSaWo9GtbatO7fwHZs0AZ/qYmxakVDIQXNjR4G0HlJ9eUeJnRZWu+RqIqkyEmyvDYjajs4dm0ytahKdKXxfA/bdcjTnLIoa0CMAAntIKACPMfFpBVCCaSofS+0vAAnkLRbEUGvSaPT4O5rtwkDlycfPuawP0XbFmVZovcneMstlm8tsfX7f46IOpTTEms1Iuw0KAZTzGYfux3hbHQp4xRTKryGTxWn2N2IahDTXG5jdTXBrSUmhxP8TkQxTGjfCdBZQbDeqa1AFRXFOCGrNKWUICG42aOKAygV5AoqhcorVKyQliR7doDT8DGuReWC2wyIxjF5WmDKCidwsUIPlEZpTRJnVPtDmu3GifUo5+4a0asbFNMUr9ek8fZdikmC5btUcYawJL7vovKSfBjjtgO81XZ9nhyZQJaAiTO8lTZlXnvqxqmd0hltsDyH6MYSuqrtrBmtkZZE5SWmUjjLLZKHOwSOjR16qKTAwlDFBaKs0FmJG3oMH+1Q9KfYrlMzIoSgg4VVaPKq9hgelxUJmtByiMKAKo2pJglppWl0W1RBQJUXJNMYiWG9GZFGAZbv0bsdoSYZqlQ829znm7/zXd74zW/SXOsgLYvunWXKrGB8Z5kyKejcXqL/eI+1aYbJcjZ/9gUZhs3PnrBzMCDyPZSqCByH7/3qd1n77n0m+Zjdv9jBqSy0hpX7q/iRy+YXOwy2h4x2BtiBy/7jXfrPDinTnNHOgOFWn5tv3ObGKxunN8GVAOOat/kvinBeRHR+FaJynhT76m05K/VZwCRj5toTF6X7GuFKwHNmyuZeL1zUXq4/LheSKLM8ykV1XUaDXU6kzaU9tzxfwNr7+taiuGSOLwFg8+GrCaJmx++i3AJx8kbyeRwrz+afq/O4rjOFzaY7iypP0phLGnphMDOlXzJOsxzwC8N5Tr6Y3dRzP4mTjTFrnejKMMtOOJmfeYJ8tkcXNu1rh0sO+iuyLIo8BQDnfYTMQthTweoFIPls6c95QBpz1RzPVxl2GvVXrSnzEtu1iJbajPdGNIKAMi9xpMVqp01ZVoymMUmRo4FhltKMIqQQhIFPkmTs7fax9iWO7dCJAgQGz7LxgtrizcHhgPW1JQLfwRYgpCTPCwaTBMexSQpFs9Wg6XvsPNzBj1xGW32KrKBqhCAtLNdAVnKws0/k26gsqznaWqONPtLPEEwP93nzu2+w8cbtk5XMyR4w507mtZfW2f14kzTJaEQht26tcbg/IElSpOOQ+W0qSyJdm2maY6qy9gkiYH9/QL8/4sb6Ev76EpZj8+Ann5EntYJrIwpqR3tas7c/wXUskrLie//wV/nuP/iV2tOwhv6jHXSc0wx94jhBVor28hK7X+7Rr/q47YD3/92P6f38EXmSkSc5ZRiQT1MyVfHuu59ifSC5e3ONu2/eJ8tzojDAcR38JK85856DLSRaCFwDKEVlgVzuItsRyhiqUYxwbRoYZOjitILaiZrSVKMYtMZ1bfRqGz/w8NMCRxscxyH54FOKqkC6NpU2hLaDkAIPC1VBVml8zyOQNkpAI/LxtKDhe5SY2hxuO0QYCFoRvaU2QbfJ0p1Vwk5EejBm8uUuH/70c1LfJokTmq4DRpPFOd/8zbfo/+lPcIKQ0ZM+rgZZKKrDCcU4QRYl7o0uaprRbEckzw6RrQDj2MT9MaFlkxyOkJ5DoA1u4CKsCq8XYUU+KsnRZUWVlZhSUWQFSVohbZtopYm0JNWxMnXoYksLYzTFdh9pW/idCOFYyIaPowXF7gAZ+jCMa0lH00PGKcQF0SvrdNa7JOMYx/dAKZJHu4ylxFtpUUxSzGCKGsZY7QAjBFavgakUSht0VZusLbMSIUX9XCnOMEWJt9xGOjbFcEI5zfE7DYQjqcYpIvRmdLfqf6pSYfICjKAYxsiGT2O9i30k2ciS2qSwJSRW6CPaEbs/+oTRg22U1jihhxGGRmawLIPyHZLEMPn/MfdnP5YleX4n9rHl7Hf1Ndxjzci9svaqrqrurppp9sYmqSExJMjBYERBC6AHAXoaCIIe538QoBGgB3EAjoYCW+KQ1FBkd7P3quqursqsLffIWDx8d7/7Pfsx08Px5br7dQ+PzKhu/ZCI9HuOHTM7ZnbMvr89TiHL0QJsoMnzHFVYhJYUxmAnU6RUhN0m6194CVsUBO0mZVFQ5iW9vR7+ehdjLN3JhO//T9+ludLm9eU2whG4gYvjuwTtiKqoakHCQhN7lOl95Sv3qZKCzT/9GXsbe6TDKUIJ7n7lPkuvLZOmPQqjufXG53CUQgUe2x9v1YKFdkh/5wCpFP2dHt3VLu2OR55V9A/6pNMJw96I5bsrdU6SE+HRPHHdEV6aEdhdeaaek47/tdNl7c87sz4t2D955hKgflVfntWnT0nPlG9eZUUzW8E8xu3ScbpMRHkRJx1XcQGbzsF3c5u50P65Vl7QWnshPhcvhk7Nh87yIfZMmdM712n5xWffOOmBmDOZJ9zqRVj5qXiKuqGLDVxCF8KTzT5yjjU9E1aV0w/mDG8wB0QjBNYcR8QS515wfh6P81volW9xhAevxbDOe/jSMqcDMS9UnMWeRHQSR6KYWeMvMVvuAjN2WVyps7+PnzsZ+0tecnYOzlwXZ/vz7LV9JFKygBQ4vsv+413e+Q8/YP/jTTCCNC+YVClaa3zPZTWos/dmeX7CmDtKk0uBiARe4JPlBXGa0Hs8RglBIwyZpgl5UWCVZL8/5taNBSaDMX4YsN0bMElSfN/D8TRVnlNicZVEV+CGHp7rYpXElhVWCrSE0PeRriJLUkLPRVlLL0vxA59SK5YXF0n3hjz+/vvc/87nTyIwcfxtnuPcbn71FQ7efcrH729wsD/gzr0bOAIiz2Wc51R5gR/4qLLOEj2JY2RVoi2IqiJQLvHhkP7BEPFIoAHfdXBCBy/0yOOMPKnzUYwmE+584SW++ve+gVSSIivYfW+DH/w//4S4P6bVahAGLpOsgIMx66/eYffBBtFCC9uKGPfG7B0M6HYbDEZTdvcPWe92yUKP1kKLZhRQGoPjusi8Bmi2LHGoJddCWaRWFKGH2wpprXYwRUWRlwSdBuqOT9QOEcbiLrdQgYfJS/L+FNOfUPUnGMCGLtn2gOnTA8LI597NVZabIZ882aHVCEEIpJaMywKbVUzLnJuqy+RgRLfbJIxCGoFH2PBp3btBcGsJsLiNoB7vVoSJ65C15TihSAsOtg55+nib3iRG5IoyTskdB18q3HbIyvoiqaOZPDlEFGOKsqJzo4O31sVGtVO0VDWI1r6Lt9QErShLQ/vGAuXBmNadFawx5P0p1STBW2pSlYb08R7WdSi2D9GtiODeKna3B0WCkYL23ZU6pGzgYX2HcjCl6vWhqPDXuuhOhLfUZPxgB7/bpBxMSXb76MUWyUebOIGPdTSqFeDfXgIEOnRxxgl5f4J/o0vra68wPBzijlOynz7C3rtRm+yVBqssJs9xtcaqOpSx9BzKOEULSdKf4LQCvKUW5XCKu9hChR55UeG0AiabB+h2hHIVxliEqp22hZQoJakQlGlWRxOL/Dp5YVogiopiOEVoSdBtYsqKw588YvT+FkWSUTUDqsij7E/QCBJrqMqSdJrU2dilYpok5ElCww/YGYzA0SRFgdaaRiNENTy07yCbPo3VOkN2mReEiy2KsmC0O6DRjui2m/z8D97m4ONtfvmf/kZtDimotTWeZlZYZo1BuV1MWfHSP/gWt9MCJUC5mkc//5D+9lNuvfka+08GPPirj7Bpwd72AaPDEe3lDl/5ja+y/O23+MkfvoMpK8YHAxqui618pCNBOXU0s7ICR5+e15fDgxcudf9UdBkTdKkI/ez9KyX3vyiaB9Y/9fPXSND3omge5j+/Pi5A28sEyeKSiJ7iVAh8Yt1wRX/+Gubsr88s6vrC1kuKnmUyxBxsdunz11o/x9LO888cg9HTa89ckHNs7S+oneYtnk+r3Tn/3Ixk5OTGHDBc13h2FM+2IhDi1Jm47rY94SkuwvNz9YhZf5P5XZ9HxhxJn6/7zFxG7PjeeYZjpswcdv0s42AvFmOGAbmMxElN1OvnkvLnL133gz+/9uduuketzzCR6TThnd/9M/Y2dpiMY5ZXVjClYX15icoYDuIEoSRYSzpNQEpcRyMrgxDUjt1S0FpsI6VkOJ5gtUQ7DjLXFJVhMpqSZDlFafBUbetfFlWdOyDJ0I6D8FyE69CoYBynJElOuxnQH06IfI0ChLTYyYhpUUIYIhoOrpSE1mKVwrOW1ZvrZGnOz/79X6EjnztffRmknNEQnrK4FvCbAf7tRRafHpAmOcP9EePxFCUlbSVp3l2jN5xQFgW+Vix1anMs5WraUYA1lr2DAXlpWPRdlCmwwiGNU9KsRAcujcgnTlOW767y7f/qN9GuQ5mXHHy8zV/+iz9GlIaFlQUqLOPxlDAM8bTGPRqnyWCMJzXjJKW73CZqhiTT2nl6YamFyBIqR6FMHcGLcYJJMizgVIa8LOv1IVzQCpaalFLiKFXnX0hy3MWI1r0VynGCcjTCUeSDKcnDXXTkIxv+SfKmfDBFO5r2rWVMkiHTnPZCmy+9dIMSi3I0WitKYDQYgzGUk4zmr3bwQw+lJMGNDu5Ck3yaIpVCAEWcEXQbmKJChi5lkiNDj+H7G6S9MSot0cbgD3OmWiMDF4tl5dYqvfe2mGz2SPYGRNbSemkFWVaYaYrOKoRvUQ2PfG9Idjgm709wFhq18/goxu1GOM16Pqu8ohxOyZ72UO06r4uMXAg8ZDvEX+sy3jpEHvmWSCUxjkQVkjLOoD9BWEvrm68RPz0gzTKKj6dMn+zjdBu47RCMYdwb1Q71UoAjka6DbPiowCPb6VH2xshGgHQUwkKjESKEoPutNxFakoxj8tLQ9OrEe8JRCKVQkSJLMnTgoVWdv8EJvVoosNDESoEpKpo3FzFFhdcMKfOSsqizqRd5hd8IKJM6aIJuBlgsVZwjHYUpDUrW2dIrY/C0S7I3JE0L8u0BZVXhdptkvkYUFeFKhzIv8bOc4WhKuNhGVIZ4ELOzN2Ah8HGswu+2eOmNe6TjhCTNGBwMefTeE0ySc+tLL5MOp4SLTbxGQKJjPGsxRcXe1j5+5LO1ucfO7iG6HbJ0e5mXvvoqbuRd2NKFqte+8By0o9nYfEJvY59pmkBV0l65SXdtnXhs6dx0ufnyOuPeiPFgysZPHrH17lNuffEeSlgc38H1XHS0SLvjoMcZrudy4/4N8qzADbxLNnbOHTtHwit7BNIvkyZ9CjLWIufVN3NGzPWZvO5ZdHKcvjhQfgWymdv2i2holrE4xUHzEc2Zd50jmLyyPS5Ue3p93vuc1+Sco/NTeyYK1Xme4lmM4i+Y/mZ9LubS9bUNpyYiM7FzjoHXMfd2AVxe3u5ldB67XUzCbs/cP4U0F6MFXaz1GY3Ou3Atdchpn87rgmbf4GzPZ+s8NTSZh13FaeUzV2bLX9G5C1KQc9/EmVCrYg6nf/zj6MaV43Dx5jwe5OJ+PGcLeT4e6cxKvrCq7ez1c209Y37P5suYGaNzFcwOmTGG7fefMtw+pBynVKWhKitWFru4CCbGMk1TpIBmGBH4HpWtzWCqsiLyPVzPZfdgQLq1RxCFKAGuq3Fbim4UkqYFrbWQPCtqsFeUqNDHN5a8qnBcB11USM9SFgVFVVEUBf29PlHo45YGz3fIkgQpFYVWaD+gKkvG0wlhq0mTkMGoNjvqOpKhExCPp7zzr79LPk155TufR8ijwTse49mD3dUMRlM8JdFK0Q090qzEaEUcp7z0yi1sWWciN2WFDjyKomSwuY/xHPzIR05zxpUhCKM67wMSRwiUEEzKEuMqfuN/9Tu0VztYaynSgo//5Of4WtNYaVFpSZkk5KOKytP0hmOSNMM6isDzSNIEP3BoLLUoJglR6PPyzVXSLMOvJH4FuSkI8hpQS89FWEsZ+ahpCpWBToA5kvJPpzFJkrKwtMz6W7fRzTryjdsKEFJSTlLix3u1zT6gIx+n2yDZ7qO7dbK/eLuHt9LBW2yQbvUIVjoYCcknu+xv7BOsdGjeXKDRbSCMQToaiQDfqTUHUuI16gR6pqjQjoLS1F+xkgitKKcZIvLJhxMyYxhOU5Tj0AoCUBqvtKhewnBrSL4/JM1zvJfXWLmzTPpoj3Kc4K92iA/HGC1xl1rk/UnNwChJEaf1ep5maM8ln6bkaY5s+ggp64zb1mLzCmNB+g7DB9s4Sy3MaA9HKeKNfZRWyMrgNHzUQhPlaKSjkF7tl1QMpkgLMi0oRYq7ugDjGLW+iEwK1GITUxlsUZI83kN3I2ScYZSgKiu0FmhHkx0M0Te6JMMp/kITX0pMXtaRxSyURz4YbuDVCfgAM0rIhjHe+iL5NMHqWiOBtXVSwsUm7tG5aasjR+ujaF1CCOLeGMd3aazXOTWEFJR5iamqmvnSClNW5A/36ihYjsJ6tZmZ12zUkcOmKVmS8fijx9xZXaZxo4sXeYSBS6klqSNpNAKaK21aN7oorcmmKbsPttjfO2TyZz9l6eYyw8GIPMnJkhTtOSzdWmG41aPMcjrNkCTNefTRBt/7d9/lb//T3+ELv/W1M+fZ8TlyvN9rV3Hrc7cpi5Jso8QaycLKKoOdAa7jsHJnhaDhEy00qT7eYuPdR3zjd76Jdh2iThM3CKiMBc/jYKtHqx1x7/P3aK+02Hq0y6T/MW/80uuEzZBT29nTzedsgtZnbOFX0uVwXF4jS/hcgd+xEOpTZ0XmVHJ+2cvMg0E835n6mWkuc3QxBcAxXSoUtFcc0vOk3r/Il7TXEHj+DZCwzzQgu5om08kld553RC9Zec/7/KVS/Gc8fs1ylyrTftELaBYw2mPNwFUNXgSYM5fP3DvviyLODd6ZoTlu++xOdaHOK8fzOmN9npOZfZHrzumVlV98+PzV47c/G+RrpjMXuK0LDx8VO69qOL3/zE1hhje1x4zUVZ/JCdd4qnGzWPYebvN7/+d/xXqS0istj4dTHKm4sbJEJ/CZZAXboxF5moEQmKqqJbumQimFqx2kFJgjJ9TAcbn10i2kEuxtH5BVJd2FFkEjwA4nqKKkdF3QDtuDIQJoeB4OYIXFaUV1mNWdPhpY7jbZ6o3odhpIYwh8B9sbYlsNSHJGRUbL80DXZg+jNKHp++TTmH5VEQiQvs8X/u43ufvN12sTKeC8Q9buw23+5X/z37EQNvE8hzLNCR1FVhkKa2kEHs3Qx+02OXyyh98OGQwm5NOU1nJtwy7HGTkWRykqAXlZ4rqaw9GYxZfW+NY//k9YvLMMCHY/2uKTP/wJw/0BZVlRVXWyOUVJ0GpQ5BXJOKW50oasYDwc17kewhrwSmwdRlXq2tk2yWk4LlVZ4uYVwtPYVoh75Nxb9kY0by0T3FpEOLUjejlNadzoonwXqWXNPLQDbGVI9kdUu0NMwydYaJKMY/xWbS6V7QwY7/TJdgdM9/osf/1VWq+uE+/0qdKCoBVgPIfKGsKlFo7nkuwNcEOXcprhLjRwOw2MsZRxSpXkqNBDHeWfyMYJBguFQYce6eGIeG/A5uY+8f6Q5HBMJixTDHdu3qArHXRpMKOYoiwRyy1Kz2X5Rgc/LwnurWDzEtkOSeOkzp8hBPnBGBm4lFWFzEuqaYpe7dQOzlnJKM1ZWl+kTHJEZcgOx7X2tKooixJnscXBRzsALL20VIP4JEdIibfaRkhJFWdkG4dYYVHNgPJgjFqo805gLNlggh2nuOsLWCwmr2h9/jbpKKYaTHHbETLyQEv8ZkQ+nGDSnEJKRFYQ3l5i2BsQKhe3EWCBvDfGW27XUZusxeQltjKowK1D007S2nH/aD8QWmFLg/IdbGWwFkxZMxZYi0nz2tHbd6lKQ/L0kGC1DU79nBCC/ifbyLxi/68+RrkOsbDk05Rwuc14PGW8NyBYaiKVwklLnrz/iNufe4lev94Dxv0x+C4HO4cEjkuRFzQaEbdev8Pi7RXG+yPef+d9smnKwmKX1mKLsN1gOo5xA5ewGTI+HCKl4N133mfp3hphw+dX/smv0Vpqs/9oh09+/ADHd/j6f/YraLd+f1MZHr39IV6zwXQYs79xQKsTIZQmzws2P9pEK8lXfv1LrL22znQY8+SdT7jz5ZfYfbSHrCpk4LH50SZSCsq0pLnQZOPBU1rNgKDdJEly7n3+LnfeuH1h3zmh83kKZkDqdd0lT86laxyAVybFvUzm+amZi2f06yos8Dz0afv4HM/NPZfPgIPnBCHzwMUl/bkgs71W9fNx6XUyi19FzUbzUz0Hv9AM3c/7Mi+AsZj987mqu8aqO1lLx5KH57M5vBJEzpOwXtL8+XKX04l8YmYdH/fhNDmePalwVgNwOR9vL/NAnhn+zzz1grN9sefH+Vz/LmE8Zje7M0XsxcRHs0zRSTIcUT99liM7+ozPPGtPK5l5hct4j7PXT9cTdg7DeNVCmPf7+B3s2d/bH22SDMegwXddljttktEElaZIR+AbQyuKSLWu1fXGkOdH4WGFoLJgZT2OxlpQkkY3Yn+3R24tlYXBeEqr28Qston3BkShj3U13lgxSVMKR4NUaO0gLZiiYmFtgfxgDNOMCkOj6ZNOU7KswGtHiAqE59LWilyDJ2vzK2Mhk4Kw3axBUVlSZDk//td/TpFm3P/2WyjndHs7HsaVu6v8g//Df8Ff/os/5vDxHo7rUmBpa4HNC6QOOBhO0NMEW5Xsb+7jtEKWF9tkRQlaMS4Lqqqi3Ypqu3Br6I/GvPqtN/nGP/w2XugjgNH+kL/83T+lHfhoR7N6b43KWvY2diGrnZMXFruYwmDijLI/Qkko0pysMqAkKyuLCCWRoxinMEgrUUkO1qBdB2trKbYzzUizjOadFVTgIUIPOc1QPqjAQzkK1fDw2mFtOqYkxSAm3+zhLDXRzZB0OMXmFaXOmR6OyJ8eohHkk6T+JD2HfDRFGUtwewmb5Lihh2gGJ4riaH0Bk5dwnDAu8Em3elgtKQYTlJLohSb5/gibV8imT34kmS9HMcPdPuUoplla8sBHjye0XBfZiymUQhhQvkOw2MC7vcTS524zeHeDqqxwllvkW/168fcTCIOTuPCVrwj9iKI/pUwL0sMJomfxtKa52qacZnWiucUGjZdWKUcx+STFizyyrKAoSqJ2gLfUJj8cY6VERR7l4QThKJTjoJSizHOyR3t4d5YJ763WZoZaEWUF458+wV1pY6uKcpwiXAfX9yjaNcNdZQXKaqwx6EaADTwoK9zFVm36JBRCSUxWoCKP8OYiZVYgHU2y1wepEFmOClx6G3u4QiKjkCLJwBq8xTamLCGtGQ0hBOWRpsQk+ZEwu/azquIMFThUeUkxnOK1I6Z7A5RUHPzwQ6wUxHnOxJT0e2OcSQIWFm6t4irFzuNtVOSw/q038doNlhYbtNYXKK1hYX2J6cGQD7/3LgdP9+kNx+x/98e8/MY9Xv+VL9B9usvWdIvD/QMGu7tIJZmWhka3iSgt2nd542tv0Gm3yOKUzlKbJz/4iPbaAt//t3/O4cGAu2/epUjzE+ZCSEFjsU0xzZnuDXEdyWvfep3DjUPcyGPro6coR2OwPPnZI6RW3P+lV9n4YJODzUPKSczhfh8Az3cI2w3G/TGu77F/MCEcpTSW2uRJxtzAKmKe0O70zL1wZF5xhorZAs+ALvOSP19Jl9V1lWBv5sw8oxG5Svj2vPQLFdzOpysx21kAcGUddfFLzvU5wODTvOrVzMPfwODxgqJFzf71WVyo538nn4GVhmtG15mRCD9DA3FeiH5y8Rl03m7vsrqPl/T8e5cxcs9o+1jbcBrX9ARIn7Y4U/dJtj9xynOc7GVi/gYDGGuQdVaho4E62kTndXdms7VHZc+P0dk+z7y2mGchefou57s2Gz6XC6zGUZUzjMsZwH+u6XkkxNlQxCflZ5sQnIzrhdJzlviJg/0VuTIu79TFG52bi9x86z7DScrh1iGhq1jP+7QO9nH3SuT6KyxFHaYIbFWRpCnj8RglJUpKmosLZFlOYS0LrQZR6PPBOx8ipWR1dZGqMkTLLaLlNoOtA4S1TOOMyXBSOx5LWcf3p5aAOp6LqUpMUZJhMQiCKMQUFSgJQpAAjjG4qn6WCoS0eK5bz1GSohHoylB5Gi0Ekyzn7f/xzxju9vnC/+xbeE2fWS2bVIrbb91j5f94g513n/DJH/2Ug+GYdJJRuZKi18NthIwmCa12hwhJXlZMqgyDQYcuvThGI4gPc5xmyL1fepXf/M4X6Kwt1CY+R2N+uLHPaLdPdGuF1kKbhdfW+fG/+wFhkZJJxWg4JYlzlJJ40kV7DkWWkymJoxW+6+IjSA/HeKVBSoGU6sjJXqGVpLIWMYlJXYfGy+vkjmQ6jBHbPRqrC3gLDZRbOxDryEcFDiYtmby/hSgNXreBiAKSvRHV4RjrKCYfbVFmBUVZItOSMk4hCurM3r0JQimKOKvD3eYl5mCEjDyE1oh2SPxkmyrJcUKPQiqElDjdBv5yi7w3ITusw8mW4xjRCtBKMhpOyfeH7O326ZQgtIOYpGgka46PLCqoLIWjUAsR0WITO0rZ/WiLldfWGX2wSZkWZPsDGusv4bYz4if7VK4kXGjjL3VInx5SDqb0h1NMUdHxNFma12FqPQetJeUwwbQjskkCroPQCrOxTyfPsIkk3jrEjBOcboTTDJlsPSVcX8BUFaW0eDe6dQ4IIcn2h0jXwe1EdbhXp04E2Xp5DelokILh3gAn8nECt86l8YMPcb58H7RCRx7VKEZoiYkNaZzRvNGgnKYUByN0t4HSqs5v0mlQjBNSYZHDKe3l2tzIZAVe6CJdjS0qhKjD0ApjKdKMIstxux7WVZikQPoORZxR5QVOK6QcxrjNEGsM4WKLeHdAYSwi9EjTlMEgZvXmKkVR0tvcYfvBU+598RVuv/USGz/9GLnaZXI4YLI34nB7n/X7NzkYbSCl5Cu/9XW8RsD4cMS7f/ITNt5/wvQPM9748usMdw8ZTCY4UmKEpLQlSoBMUqQ1bH+yxShNibyQlz5/n/f/+Ccs3lqmt9MjMTmb7z/he7/7x/yt/+XfQco6s/Hq/fX6nHE0m+9toF2H9mqHMq945WuvUiY5j3/2iCLJcUzFox9+RGoFr339VX7yhz+mKg1BKyBqRfihj9QSpRWj/QGq4REPxyTjVm0qKc9u76f78nnEdPavS7fwyzDG+bP4WczBZdft+d7NaedY6HeJ8Pbk7J0n/TyWyH1aQ5nPInu+oo7LGIjnimZ5BUQ9n6bgs9LzaiLmWphctUZeXFdfvM/FpxnMeWDulK5T17kyMx+MuABEn8E9XN5JjjywrhcK9JKuna/z4nxekTdhpsSVozLn5tXfRt2LWSh9oV+n6o+5PT2W1pzJHH1VozPTUDMv4tJprMsfs/WzbNZRJTMFz0dUmtvuuWfONnqeIzgq/gzGc75CZ2bAZtKzX0gcztFYztuTL9uM7UmBI03FjBO85cwKMVVFZ6XL3V96nb0H2zz+8BF7w5iF9gIblUEJxbIOiceT2j4/y/AdB9/z0KI2hUoGI7TWuNaSpxllaWi0IrSQHA5HTNKManefqBWxvr6EbkfE0xRTGRzXwRYlVZLSbDWZxCkm8onaDYrRlKgbUeQlLc8hzwsyY7BVBb5LTkXkOLVTeVmSigpPSHwhwPcRcYprLdIIlOvh+T5CwuO/fI/J4Yi3/vbXWX5l/dRM6mgOvMjn7i+9RnO1ww//33/O/niXLMkoHZ/1G0uYnQPGkyntMMATgjTPQSm+9p//KqP+BGMMQTNg9eV1om7jzLqxR/MRdRpUSjAdTnAKw89+/0f4nsJKDx+B6/s4SlJVBpGVWOUQdAO6QmLzgjAKKIcxobHoIw2SDVy076BcDZMMmWbIToPw5iLR+iIyzYg8j7Is0CstpsMp3TvLOJEPUpD3ppSjhHJ/jLvewShJVRSYomSw1cNiie4ts/LyDZKDEZvf/wChNW7kkQwmeFLiuA6qqFCLDZxORJXmZAejWvIra5Oh8M4y0w8361CqSuALyMcx3kqb4N4KWX8ClWX6eI9ynDHZ3McmBctKU40mKAF3Gw0mOsOVdXLB1FpK36ETeKQSqqpA9ieM2xFuI4SswL+1XEfA6jYwRYmj63ws2dMe+c4AZ62DX5bkT/YxEmiGOJ0ImxXkFoppwmTjAJIcvdqmjFO6X3yJkVIUWVFn9Q493GaIsQbl6JohkQIin+HjA0To4bVClBBkG4eIsPZDaLx+k6w/wVSGLJ6ipEAHLuUkpehP0Q2PcLlDNU0RgUtcliglkUoShD4KKPIC3fApBjWDZEuDrQx5f4zQdYLL7GAIzZAqzUDWzwshan+JrEDqWgMilCKMQoSAMs7QrsNw8xAJqMClNAZ3qVWHZt44IO5PmTzYxXE0B4MxozTn9ut3Ge/1mR4OccI6upSWkt0Hm/VelxU8+sljwmbEwcf7HD7cY5wkFEmOpzXKddBezVi//qVXGE9i3vvBz/nSr32FT372Cf2DIeVREk3l+8RJ7Yi+/d4DuosdvvJb32Dan6JdzdZ7GxRJStQMwcKN++ucWEce74gClu8sUZUFyShm+4MtBPDKV+/z9OdPCNsRVVHS39gljXPyNOO97/0MY2H1pTVuvXGLwdYh03GC62huvLzGzicbGAPRQoPXv/EGcpazON6qZ/f8cwyBmLl4euvcYfAs2GJn/zz9ccG64hImZEaXcm3gOktncd/lor/zvz4FEns+OmrkMiHzp/ZTeA6tzNw2ngngXsDIzKvmqnZfIGMBv+AM3bOx5/9GaA7T9ky1xHUqnFfYXgTUx9DyQrVnBfQX6rlY/fEXcvzLcl7feTLOl2gJLtAzJCNzZ+z8xZkwWrN8x3lmqf7vaON6loTkUpr3xNlteTanydlHZvUyM9KVM9N58Y3nRSQ7ZbLOMlbnm6xv23MPctkgHV0761g2l1E/PqksWAPj3oh4NKXKS5burOD6LieJ+Y44mTwtMYXlzV9+ize+9TluvnqL3//n/55Bb0Sj3aBISjZHA5bWl/nS119jfDAgiXMeffCY0lqQAuk4SM8lz3PyokSWFaM4rvur6yRub752n6ePt9l4uMWNG0t4roMX+ezu7tJx/bovRX6UNyAhDD2qvAQqJBAPYnzPw9Ea42qMBeu5JBiMlmihCcqKnBJjwNeKMvAwk5iqLJFCEFTg+S6i2WC6ecD3/rvf46VfeYvXvvN5vGZQRz8zR2tACLq3V/j1/93fZ7B1yNOfPKS/dUhjuU3mKEYPthkmCa5UJFXJyp01Vt+4xe3AO50Vay9MLeKo7puL3HrlNvloytRULC61IClIqpg4ySiqlIbroq2g6TjYskJXBdp1KAzYSYqsKlzXwe02cRablJXF9MdMdwdEjQB5a4nN3oBwPKY4UBgLLa0IF1p1iNOoDjE7fXKAChxsnGPLCnW7i2n4qNIyebTHZGOfaL3D4hfv4TUDTFEi85xbX7lH78E+ZprheS6Ne8tUo6R2hhbglQaKkujWEklvzOjtB0Qvr6GbITL0MNYS3V6mLCuU65D3p8QbB6SbhxhjSUYJoZSouED5dThfKyVxnuMpSXexhfEcJtOEzmKLSiqaawsc7vboTxJWXl4jH8UEjYCiP0F3G1TTFKcT1RGZXM3kg038m4s4613cboMF3yU2FmEMpasoxgnVuE5WJ11dR9CKfITnEj/epTgco5sBWIujNd5CA7cdke0PcVsRxWCCzUqSpCDeH1KELtH9Faq9EVZJtF+DZ5vk2N0RRSNARx5Zb0K6sY/TadDb7rPw8g2cyEM3Q4SrkWVFvjugyOtcG86RHw5KIhs+1TQl2e7TfvM2uhliTEVWlIjApRgnOK0A7XtURcl46wBVmFroXBnC28u1I/eRH8Zx2FnlalRl0a6DE3hUaUHcG7P17gYqK5kcDMjGMXFZEQQ+T95/TORpVtcX2drtc+tz95gOYvqDETdeWqX0FEILlBQ0mxEIWAkCVtZX6NxaYu/RFvtP9xnv9fiwP6TSgpffvM+Nz93h7q9+jr2Ptxju9In7U6bDCW5hmCYpQgiaCy1e/eYbvPt773D/G29y8P5TEII4Sfn7/9t/wOvf+QJnz4j643RDnzuffwlbGYaHA7yj6FqVNWx+8BTXc8iyEnc4oPADpoMJQdSgs9rhxr0b3Hz1JqaqNYm1EOFv4fguSksc3+Vk67/q4L+4qZ/+eRlweJ6D8wQizAUUl9KVpZ4B466ViG4GKFyrR58FZz8HA/DXTldqCWakzp/l/cW5/z+DXjSz95kduqfT6ZwxOjq8LzAXl7DNl16/Ll05U5+Onu+bPDMzF1RtF+o6JyGYvX9Vu89gCOaWOe6aOO3XbHjSeXWc6gbOo6Y5jc8+/xwf83Puk88Q2lzVT04ZsZmlfmlEi9lWL+HVLtY/09Hz185VOffvM2Xqt539bsTsLWopDBY++sH7/N4/+w/YoqS10CDstoiWG/zaP/l1/Cg4aWd8OGHzg6e8+o1Xaj8EC+P+iHiU0Ow0KLKCqqjY+MkD9j7eIk8KlJCMtnvs7R4iHYfjUe4ut1m8tULUiuoEb1mBdBQLSx1cC49++ojd4Yi1G4tQFuRAlhc0rKAcx0yKnDAMyKQiaoZEjYB0OkWWJVprpkWB67oE4ZGtuxRIa4kKgzJAWaFCn7Io0bIOvUllMHlJ35a4SLqOCwKyqmRYFORxQufuDT73O19n9fVbZ0yXLIA5HWtra+ajKkqyUUyZFQghkI4i6DZwZrKdH2/+J0k6jy4ngwkP337A3oMdJrtDrK3wgKYSCKk4GE5oeB5YCKTEMbbO8nwEeAPXIakqnMDD6zQxjqoZpt6YPM3B1QTri4hOxMajLfK0YPHWMlEQoPKCzlIL2Q6Jx1OssYSdBqKoKPOCcpQAUKhaEyJ9l/BGG78Vgq2QSqFCn3TngMPv/ghnoU3itsgHMTrJie6vEq60sUWFsrX/g7fWraMVHUlsq6wEY4g/2QEElavIhzHZJMGxkAymmKxE2fqEUIFPWhRYrcjLCjmKqaoSvdKh244wq23SUczS7WWGjw6IPI0pCuRah7Ks8FwXN6+jewUvr1L2J8jIJzsY4YRe7d9RVIhWQHB7CZPkTH7+hDzN8ZaaiEaA0grr1BHEigc7BK+uo5oB8eYBJs4Jby/R/2SHRqtBMZygFxsIBMUwxg6mFFYQ9ycko5jo5iL6ZhfRm+KNU/S9JXTkoSMfK+qIUH63QT6Oybd76IUWhx9vs/qFO7W/irG4i02EkqjAJRvGxPtDlLWIwMVt+GjfQ/oO1tT5TE40c7bWVJqiqn8bS1UUKM9lut1DZCXOQhMVupi8rEMDS4F0NcUgpsjr9a4cBRYGmz3i3SHF4YhKCvJRzH5viJaaeDjCj3wWVjpsPT1g+3DA+voKoiyI1jqkRYktKxZvdOnvDRAI4sMx496ElfVltO/w3g9+jnY1n//Nr/H5v/UVkuEUN/DqNesoqspgSoMpSrbef8rTH3/CxnsPKYXlS7/zTb7y21+vTfjSgp/+m7/gp2+/y7f/0X/K69/+fP0OMCNsOSVxtJ/mccbWx5tM94Zor87A7bUCSiz7T/YIWg1aXZ83v/NFombIcKfP/qNdnMBj6d4KXujhhR5HEoXTsLJno4AcdWP2vJ8nBLvw45mXr03nIdJl5/Zl1z5N++fxjL1cg/D/D3Rl366JtV4ozQE+n9pB+1nzfQl9FofuF8JcHNPlLMSzmvhFMhfXbfusBBp7xByJeSWP652nPaj/OuObML+5iw/OGYaTONgzZU6j614FkM9JVI8qqRPFwanW4Xw987ib44rmcD/PYiJmzJkuFL0uA3fJpni6cq+xbs4tkfNjdx7MX1rjpZvu0fheUfTM5J2/ac8Px9mEhGfPI0s8Svjv/5t/xsHmAV9qe9Bq8miYcOtzd/nN//Xv4Ec+AGVe8v7332dhfZH1V9ZOzATr9uwJQDZlxV/87p/w3u+/QysM6xCqFsZZRl4UeEoTBB690ZiqKAkCn0Y7oqwM7XaTdJISJyllZdCu5s6tVYosoxBQ5YY0TjFZxvpql/tffY0HP/iQAtChR2AskzjGC3zGcYxSqpb0pgW5q9BK4JQQOhrHwKQscYTESjBZgaMUVgj6ccyAirUgpGEEoqoohEAFLqPRiHFpuPmFl3j1O59n8d7qqfnC8dif3wrFyT/1Tzl746isgSIriIdTHM+hSHL+9F/8IYePdllaaCGtIC0Kul4dLlQJcCuLawXGWkxZoayhcur8HhJwtQKt0Z0I4WqKwzEizVGOxjYCGm/cImhHJJOEajAlsII0yzF5gSsEphUQ5wVS1f4ZjcCl9By8ZoDNCtL+lOhzt/A7ETKJSR5t4t+8gdEOSoOUkoM/+QGy1WRSuhRJQRgIvGbAZFyw/o3XsMOYbBgjTW2WE7y6jteJyHpjimGMSXLyzQMA8rQgTwqs1pCXIEVtTuQqwtUOyWBC+/4NssGU0YMdotAlF9C4u4IaJkSvrJFlGao0bLy/SacV0mi4eOuLxHGGKmrwKfIS1Q5pvbJGvNWrwYKxUFQUeyNMNyRY79bast6UZG+AbvjQCgmWWxhjEBYm330f7/YS4StrJJuHxB88xbnRZTqKaa8tUY6mWCXQvksxSsimWW0aleUUFmzTr5mJcQZlRbDcpPWVlzCjFKcbkR4Msf0pZVbgL3coRlP8O8vk/TEy8pBC4i63yMsCz/UopkkdEjnNoTT4i62aQb4APGZWp7VUSW2u5q92QMraKVwrqmmKtdT+GlqdLPG0N8aMklqrMkxQvsvWTx/DNAUhKAqDqirSJCUpSnwhqRzJ/mCIdhyqJIeqIitL8DwWFrr093ukk5hJHFOmOXGW0QhDPEeR25LltWW+8p9/m6jT4OGPPkIayxf+zjdQjj7Jti2UQKqaURjvDdn46UMW7iyzeGcF7dblpJKUWUEeZ0QLDeTMe4E4Nfc/OvfE0QULWGM53Dhg54NN0sMh0WoHpx3SXu2AFcSDAVo6vPvnP2fz/Sf0ByO05yKVpLPY5lt/91u8/I3XEEc5XGYjRZ0c6Ud7yTFTc3xW2Jl95lNB7s8q1YYrDjueTwp48si8RLNw8UDjGYftBTHsMzs5C74vwIsz+GoefpsRCl/FjJ1v+hdFlzEXlk/PoD2nHP5vOFrURU+J5x/vs6D+7IBegOwzrc6LGn2eZlfU1RMy37HnWfXOu3Luyz3yJ6izQB/1ZBa4nF9AZVVLAYWYWeyn/Z/bpzNf0lHZmQR4s2MksNgZjuXUGOe8c5M9Kn18b844X/iCL2Ep7cw6mWVqnkXnmnwmL3wZw2Kvbu/8yB4Lns6sGnE8Huc3z3Pr95mdm9dVe9LY8XWTl8SDKY2lFifGw0chZt///s9JhwlrS12c9RUOBhOUU3K4ecDjnzzk1a+/ilAKa6G11GLl7jJn0YglnaSUeVHHswfWXrvFu3/6E7Z291hfXmZtucuCMUzjBE0NLqNug8loSjxOiOOcIs/JkhylFW7oETqaQOmTPBdOM0BrS5YkGGtpry0wLUt6SYbrOIiiIsfSVA5CayrHoVAC5bnkaZ3LodQCzwhspKnyCinqw9oqybQsCCuD63s0lGZkDQNpsCWYJCXUmlJJ/EaTYjJh6+ePOHyyx9K9NdZeW2fxlTWiTvOsT8bsBB2vVTH7254wZFVR8b1/+WfsPdjCWIsoDaHncKsRMRxPqYQgUhpZWbwj+3iMoRSCUlD7kmAxlSFqBJRSogMPZY/Ctx4WyIbPREmitS64Cht6xEkOjoNTGMhLRF4gtaX0JUyHKKExboisLMYYXFeRFTnBSgchBGaa4Sw2GD98SiU0u3/1kEIp1n/5Naa7Q/S9+5isxNkeIKzFCSKSgxGO9ii3+1Ra1qZHjiKfphSHY9JHu5RpjqgsRZwhpSIbJcR7Q9zQpywMeqmJClz8doj0nDrXhqs5/MkjbFbU/ita4XVC3KLCv72E2w6QqWb43gb5JGHsKhqrbbKtHv79VaZPewhXk4xiFm8u1JqncYx/c5H8YMTwLz7AX+7g3erW4LkToW75pKYiWl+k9/EW1TSleXsJGXro1Q4oSfzJDt76AtXn7lDFGY0ooNgdYGV9uBcGJodjkklChIDCYGWd9d7XEi1Aeg7pMEa8t4nrOnD0XdhJimqHFNMEXAWuIri5SL43xNiKapIitQSv/uZNWeG1QqTWJ2vyStmMECjfBd+lmGZ1EkwLynMwiNpELi/J4xQ3qM0TpYX48R6db76OaoX0fvIYvbVHMZ6g792mc/8Ghz99iGoEhMYwHk1QlcUNfZpKo6KAwWRKNjTcuXcLtKSzvoAbeeRxymQ8ocoqepv7bD/eRnmKpZfXeef/+5dMemNCx2Hv6S677z2h2W1ysHmAH3g0F5pEnSa3v/4aC6+u8cavfYGqKHHcOiO2curIV27k44YexwE/ZvdWa+Hh999n9+EO7dUOr/3q59Geru9LwdKdJdLRlE8ebrOztc/CvRu0Og0ev/OAjXcfs799yMHeIVYKHN8lryqMMSRxyh/889+jv9Pjq3/vm0fRqWbB7uxmfzHR7Pl95lKc8mmZiM/6/Kd47ticVxwDnQtn+Pyj8xdBZzxu7dk7F8tekDZe/vt56LrPXgr8z33pn4LhuzZdk+m7Dn1m5uJ52r90TK6sZD5kvwwoXj7uzzkb15WmX1XuvOTzBMJe9sJHDJOWXDm7z3wVcfL/uaHobM14YGdbOW7rPAA+RdnzgPbFLp4FsKexmebMzDWnZDa0nzjvGH3ZGM2Zn7mObufv2Pkjb8/+cyJBOFPiukvs/FCLmf/PDNOj77/Hz773Pn/3f/8P0IELWOJJwtu/91fsv/uUW60mLVmCrVhsNTBHdsMf/NFPWb93g+ZaF8fV3PncnZNKj5uMe2P+5J//AbubB0wPhjha03B9vAJEGDDMMnpPd2r/B2tpNUICIepkelKigGanRXFknuS6Dm7gkk5TjDGkVYUT+igLlRBMJwktz6N7Z4W9J3vkeYGUElMaeuMxnW4LkgQMSGPAM3hKUpUVbmrIrCW0llSAQlBUFZFSKD+o37so6Sx1yA/69KoKq13S0EUkOUEMTujVoVvLCt9Y9j/ZYufnj/C6TZyFiM5ql4UbCyzdW6WxUEtrhBCImscnn+bkSUZVVPS2D6nSksc/+YR8kpKNY5qeg2MgswWUFakSLIQhurTYNMelIDUVbmnqnARa4FRHJlha4bga7bvIOKM4HJJbi2gE5A0Pd7FJy/fo9YYsRyHV3hhfydovoqyZMysMRe8ApxUgOl0ay0vowEU0fLJpAlUtxT98b4Ol+2tkVcXhz54SDyzG5ugSpIThZg+3FWDzCqs1wfoCo70+2eMDHCkJb7YpsxIdhGSDKYONA0ZpRhh5kOQopfCEpDgcYy2UQqDWuoS3l1CBizEGL/LZ+9EDorUF9j/eorHYZOVrL2OLiviTHdxmgOO6KAneepdyFJPtDXFaITfWFvFfuYFQAlFWKK3Ye7RL2IoYbx3SurlAPoqpEGRJRvbxNv7r64S3l0ErpFuD8zzOkIFLtjtA5hV5bogHU5qhjwhdiiSvtUpJjnI1dhRTHo4pJgnBjS5lWeF0G4jemBCBKg0VFtdxcBoBaZLihAEmLWvHayD63E1sacg/2iL84j2ko0g3DpDtkCrOsEqi2hHZwZDi422i+2tUboXRCjf06+zd57aOWRLn/5aCYKlFPo5P/CmEVlRxhkmLOmv5UQbvYhQjrKXztVdQocf+Dx+w+8EWqrQ4r9xl9RuvsvP9D6mUJslysBbH0bitEG0MQWmIB2OCKGCaFfz0r34GFnzPRRiD5zooKemuLvD5X/sKX1Bf5XBrnwdvf8Ty0gIiCtn9ZBNXKHY/2eKpMRhj0NThcvOq4u5PPuHX/+t/hBMFFFmBc5wR24K1BiHVpRLduDfhB7/7Z/TimFBrgiDk7jdfrYUKRyD4xuu32NvYwxkFrN5e5j/8t/+Wp48263n1PfzARyrJ2lKXjYNDSluRF5beuOKHf/gj7n/9VZZuLzMbvOO6JDgVBF4tlP6UyPL8gvlM4PTZ4OfEC3POQr1208cCwWvjnZlzffY4njFR+xtLNncdsH7p/XPv94tkLK7aYJ6T/lozdD8P9rooP3+xbTw3zQ72rHbgup07s7gue25WTFr/vpiN+ViKem4De54Xn2F6ZnNfXGAWxMyrHpU+mwRo5r0u4x3E8bd9TipwboKttfOlxxx9UCfMjT1rnTVL170GZ/N1nJesnLtmxZxy87r6nB+kmB07zkwLFlj74n2WXr+N9h2stew82OKP/x+/z+RpH5Qi0A5ht4nXjFDGcsPVHAwm7G33+N7v/inf+V/8FkGz9r0wZVVLQoXAlBV/8j/8Pps/eYTTDJC5IYljSp1RWgh9H20tRZbhug6FsezuH7K5uYP2PExZUlnLeJIipaC70CbOc6rDUb1G8wytFJ21JQogGYwp8oLKc0kGUzAGrMUVhirLwHXoT1MkltAYfNdBIMiKEiklWgoqV5P0JviOJnc0FZCUJXFVgLUs+gHpcEor8EnjKVZXtKKQPpbQSKy1tGQdx15rFxfL0Cmxacb0acLo8R6PjaEQ0FldoChLHK1pLbaRStDbOCAeTdGei6NV7ctgIfAcrFK1BFhrdFki8wp5lLFbWo7CaYInanOgoqrNeJKqQktJU2t8C8VwSoZFtkJEt0nYaWL7Y6a9CQ0vY0UozN4AmjlF4NVmTo6kfLqJXmoRvHabojA0XrpFdHsZ4SjKcUq2PaAyhnwwpdjpM60gxuIKKJKchZduUPhJnVxvtQNZSTGImYxislGMyMrax8VRBJ6LkpIqryAv8YXApiVKKmTgU5aGvKjIlKT9+ds0l9p4rZDhk30mG/t4rYj+zoBguUPjzhLuUpNooYnXCphs9QhudPDbESbJ8da6OA2fbOuw9gkYxQQtH5EVeEtN8oMx6c6A8XafeHtAa7GJBtx2SPxgmwqLcTXt126iAo+sN8ZgKfMSshIlBarhE2rF9OE+5f6QtB2ifBfhaEySU/Um0IlAK0Tg1qGNmyFyHJMOJ4QLDZKkYFoaZFogJGgHIll/NzrLEbr2OclHCbrh4d5dohhOkM0AZ7VN1ptQTRK8xRa2KHHaETbyqazB9TROw7+Qefm6272UAjcKMNWR6dBRBvdimiEjDyfysWVFstvH5hX+2gKDjX2StCAMPEzDZ/mtO+z91ceU/QkoiYekLDKm05TxMGZhoYEJXPRyh3KSUBUFS8st9rYPmQ4TRqMJZVFiLXSfNnj6cJM7X7zPrS/e587n7yOk4P0/fIfBfo8oDGrtjhSUpkIUFVla4Oc5Tx49ZfeDp7z0q5878e8BatOpGW3F+cExZcWTH3zI/n4PpxXgBB6P3v4Y4SqyJONwY5/WYouXv/k6X/rNrzJ4esCD777L5sOnLK8s0F1ZoNlq4BnLJMvZ3N5jZXGR7f19PM8lydI6TPVR3hkhL/bhOnSNnLinhc6fRVedPVecVZexCSeh0E8wyfkK7aU/L2vYzvx1LYD/WcCcmP3jFHD8jTEWZ/r0Weu7jmS7ppM3vyB5OFdoXpm/ac3FC+jDBW5pxgLozO3P3sBMI+fp+vM1p+AzRuEFcIEX6/sMurHzG8dJdZfVOYt+7UkVz279aFyOULQ1HEmW5jEyp4vAMjOi54b2RQ/lGbqs8quYls+4OM86aJ3aAAME7YgAsMbw4z94mx/++x8wPRiT5zm376zjhR6bewPcaU7UDum2QlYCl3Sq2fxoi4++/x5f+K2vYssKM0mQnQZVUfLxDz6gmmS8vLrMsCixzYpQadwjm2FrDHFeh3wU1mKMxXcchOfiHoWLbTQjTGkojKXZaYCW9LZ6qLLCIPAdhyzJCDshxtVoKcjLkuF2n9XP3eLhTx4ySUAKWfsZNAJUZVHLbYpJgoozZOBRTtIjp12N4zqkWY60lsRUJLIOThCGAWgHYSxpWbKiPQ6KjGpqCRdbJElBJCRlkuMgUGkOxtIMAqSjsWUJAkpr8XyPbJzhepoyr4ifHpKnOS3Pod1ukpQlnu+SD6boypInGdpRdCoBeY4H5JXBrQyuVqQCirKCUmC1JpMSLeqwqi3fQ4k6VOhUCkrPobm+hA49ysow3O3BJMakOSJcoJKCYL1N6WhSBGUS47gS97U7CM9nkpe0b7TQrZBinHDw7gYkBfm0NrFRgcfCV19m8MkuEkvmO5RAXBRYXxPe6FDtjdj/YLM2yYtTnMAjTzOCpTbkJePemOpJgjVglETmJTarKG1GmVdUWY72XW5++02i5TbWWMYHI/Z/+pju+gKkBdKAUpIqzhHTnHRyQAE4S01KX1NKUYPeo8zT0StrZAd1NmrKiuk7n5A4Eq/pMx0ldO6tUo0TksGEqqg1BcHNRaTvoHwX5bvYtM4nUkmJ42ikozGVwaQ5WV7UUaMmGcGRCdJop0+00MRdbtfM0mhKsNAk3umjpaLoT0mnKe7NJawUiGmCRCKkQ5WlqCwlxSdaalMejmgu1JnmjSORUkLok+8OCdcXENYiigodeTidiGI4xUiBu9BAuc5nPv+EkmT9Mfk0xaGu15WSyeEIHR5FE+tPCVbaxPtDTF4hywpVGbzVLipwSQ5GUJSk/RjruqTCsNcfY6WgzAsc16HdCtFpwc31Vfa39tCORLoey82QIklRWpOXJaMs4Wd/+TMe/vhj2stdpsMxcZoiHc1hfwhZSei6SN+tNUDaQUtJoiTj/UGdJ8fVpOMYx/dOE+Wd/HNuj60sm+9t0PR8lm6uMR1NefLhEwa9EZkp2Xq0SSsMWVxbYPm1m2jf4eff/SlgWbu5wuKtFYqiRJaGp59s4EUh4/6I5YUO3WaTj5485XPffIt8kjIoDuneWjqVE3K9M6s+855DpCrOFbkK4lxVlT3nZ3BZW9e7eCWJOX89D505cp8LeJ4Dk58WRLxAqf6VNG++Zvp98fZVYOQz4MTPuPH8AjQXn2YGjkHoi2n/VCZ/TMefrn02Lr/s3rzJPvPQVdVenHwrLosoda7sDMI+dZMQl2sMniVdP7pxytjP7E5nRPanYPekuWsD6jPswclvIY//vKjimN14zu+Xs1qGY/7mub/vecvysr+fh84/95xrWIjj8Lmn63X30TY//rMf8/Xf+CW6q12efviUn/zR25iiYO3OKtPRhLtfegm/GbI+zdl5tMNgp48pClrWsLTaJSkrfvQff8Rrv/I5/EaA7DRBgFKaoBEwGUwokopW1KC5usxwEuMZg/RdfM8h7o84tIbeNEEphcCClZRxQhRFVKU5WjKWrCgY7YwIGgErN9dId/okSYF2NKYwOIHP4nKXpCjJJxlREPDL//A7DHcHfPyTh6RZhqoqlNJMhzFSgCtB5SUi8pBxjhFHBnbNACkkYZqRmTqpnWdhkhdEnkuj6TMdTrjZ6DBKUnqTGE9IHFeTaPCLOmdEgCWZJDWAKUtKU+EGHm5R4QqJMTDJM4KioNNqYypDPE1xyoqwhJZQZKpO/ieLCpnXEXlQCm0tlVLI0EcqQV5U6KJEVyVZUWFcF2+xjZWSSikGeR1mdPnmMkJJkv6EahyTDkbgKHItaGhBHufgKKIbHVorLbSU5L0JyfaQqirxWwGZBdGfMt44YHwwpnl7CaEFnfs3yKcZ+X4d7jNwHORCk0fvPUZsCpbvrZBt9Ui3+7WTfKdB88iMLLyxgJGScjBlnOQQuCy8tk77pRUk4oR5KbICpKS53Kp327LCWMvejx/itgKywZRotUtzpUWVV7ihS5mXKEdRGguRh2MNfrdBsTeiHCfknoNQknSa1kzdZo8szggs4LuUj/bprHfprr/C5g8/rrNOTxKEX4dO9pcdqklKvN1HtGuptTWGIs5P/A+klriRhxxb0q0eSgjc0MUJPcpxXO83eVF/r0oirUVLQfPuKnF/TDpOUVJiigrtKhwbkzx6QtVZJvZcnFaAWu/gLnfqfBr9MViLjuqIYeH6IqNpSpYXyCQnn6QIqH0mZveVzwCKvGaIzQvcTpPkcIjfaeI6dTbwMi8xQhAsNRk+2EVkFenOAFFULKx3SfdHFP0J6uYSZZrTn0wJ0oJmkiF8Fz1Niftjkq19lnwf1YqwlaHl+8RFjnAkSQIizfEcTfPGArob0Y4CsmlGXuVUwzGNRsQrb77MnS/dJ1poUCQFg4e7PH7nIw4Oe8iixG8EmLJk58EmH/7F+3zpt3+JhbVFgJp5Cr0TDfiJGbIUtBfbBF9/g6ys2Hj4lOF4ynA6Jew2SJOMpW6HLM0xleEH//rP6B0MuHNnncoaDnd7ZJOEyWha5+2RkqqqaPk+ozhhcWkRMsO/+7/+G1bWlvn2P/0NGksthHxGPqpZOhHuXbh4dg3M3rpivq+kmbV0mRnZi5DwfwZYO5fOfAJz3v+ZJk+f4hs68w5nhJxXtDULf66Q1c7t13mcMge3nEA/Y2pBxRXvfC0zqheiIbhIvwCfi+v28gWJfs/UcRaknW3iokPxmR+zHryfsRcXb4gLr3v5RyAu+XWOVz2f0fp56DqPndnTxNlLly38CwN8dl5Orl1r6s+k45u5emnxq2nevv3CyV5kns7yanPpTJYQY/nwL9/nk7/6mKcfbvL5b7zFl379y/zj/9N/RZnVfgrCWuLBlHe/+3OWby7zxn/6Fj/8N3/Bzsc7pKGHNpYyzsj6Uw4e7XLr83frrfBos7vzhZdw9W/zvX/1XX7+/lNcpw5p6Xsu5XhKltbJ7wLXpRv6BGFAZesgAHle0B9P8MIAF0EQehxsH9AJQrQURN0GNs7YPdhmpRPVIMrRrLy8zuMPNtjvDeH3f4znOzRXOvgNH6kVVZYzzHK+9K3PkQ8mfPDuY9rNEJEViMjDLQ1FUWGVoFKSKvKhqEPoZnUsWVTo4YQBHV1va5FTh8uUgSbLC8ZZQWwrllyPclqiHQ1JRoAAKdBZnWfCCMhKi2OBAorDIdZCU4AQEpnkWFejjIEkRbYiCmOx1uAIhWn4CCHIfY80ySjynMhYDoqCTGl8oOE4dNaXyIxBTpPasX2vj05SnKpC2QpH5MgcjBXk2z3iVh0y1Ulzskf7aATDpwe0Xl1n9c2bHPx8g+nHO4ytxVaGyhiG2z3a7QgtLL2dHmZvTKlA32yw9NZtqkmK1QorJWmSIJeaLL1yA6/ps//OY5LhhCJVoARWCLSjufXrn8f3agd8qKXI1kJwFFjEGrAYbFkiHY3TjahGCc07S0jXoSoqgm5Um+QJQTlJkXmJ6U8xgwnJMMFf6zIdTsn2hkx3egShx1RKgmnGIMtJNw9YvnuD0lEEWqGkoH1rkdIagiOTGSkFtrJMnx5Syjovit+NqLKSJC1QWiIK0I6mLCvICkRhSA/6OLeXa0Zgb0D4xm3cUUjpO5gbHWxSQmGYPtjFKEGe5bX9v+cQm4J2GqOjEJWMKA89UulQvPMI95uv1TlEKot26oR2ZZpjshyv24SsJM1GBDdqbcG8LeTTkICagRvECAN+O6KaJHVQI2NByTqnTF6SjRNGjw9QZYXb9DHG0vvxQyopyKZTJklKe3WJ3Y1tRlWFGoyJRP2s72p6ZYmbxGRSoLVCeT4VFl1ZdF6Q5yWDJ3uEByETWzHJc9rdNl/9rW/y8rffIlps1R02Bqk1tjSMf+8vcQMXx3HprC8x2Dzkvf/4NmtvvFQn6DwKHz0b/e1Y8AE1c/Hlf/KrFHHOn/3ffx9hLHmWk+U5QadBO4pYWegw2u7RXGnz0+/+mHa3hduJmGYFTl5yOBjR0nUI7O3dAzwpsUlWa0pvrfKDP/khUivGoymvP94lWmy+EIBev449EsBdwmjMf+hi2efpzvOUvfRc+4wMxpyFf3Vd5zw7LZ/G/WUOFzPn6ate7FnjPY+ZOKl2VpAqLpafuXCZGfm1abYP56t6Afjor9Xn4ixdwYa/SL7jfPUX6jx1On6+Np/zs7ku93i+2jlS/mMVwty4zJctkmtpN2aTuM3ofa7KEn2SFfqK1TiX/X/W1ntNdvpFi0c+M4n5H+15ZQ5nx/XkFYTg89/+Io/efcJ4OObxxxt86de/jB/5WL+Wum796Tt88PEue493eflrrzIdTli5v0KVV+x8uMnq2gLS1iBv+/0Nbr5198yGV+UV0UqXX//f/A4//Lff5+DJPqoCkZYc9oYYY480HCG93oD94ZjKWnzPo9NqsLzQYWF5gfFkinQUTllxOBqRHGTs7vZoNht1UqkjXwObZaTDGmxgLIdJipNkbB8OsUpSGIPSCh9Fs9NAdxuY0vDw0Q7twMWWFVXgUVQJZpQgPZcydJBS4lQWz3NBK9I0Q2pF1GpQDsZ4WrHabvFkMEAaCHyXoiiZVCWOI8lthecqAqXQkY8yltH+AEcp8B2042BdyzRJsUpRSElUGbCQxCXSGnSS4RYlbivCX13goChIJjEmywmVQgmJrzT9KkMGAbfWV0irktRYJsMJjgB/OgVTEjQcSjHB5hle6MBSk2ycctjPqaSgFYYYYzBJjhSSIitp3F1m9Y118o0dIt/S/Np93FZIOYnpPdgjPhxj04KDj7bw2w1Gn+yxcHeFaH2RcpTQXG0z3R5Q5SXd+zfQgct4d8D2jx9Rxhky9EjHMdrW6UCE7zDZGSBvdHEqe+QgLcAYks1dTFnSeP0eVZpx8Mku1TjDDqd4DZ9CgD0cIQKXPM1pxBnOUhOnG9V5M3wXGfnEvTGukgyHU5jm7O8e8MrXXiMUkv7bD2kttrBK43ZCiqJCT1LK4YR4MKax1CbrT/AXmiSbhwjfJU8yoluLRMttTFbUoY51bQKoQw+KCpQkK0vcPMceRUFr3L8Jfp1nQoY+VV7iOw5VnlK1QtovreJEHps/fog/SjHGYsYleaOL0wRz2EPHPdylJZJhzPTpIVVYfxejaVInH5QC62gcV5EXZe0gHXonPgWXSWqvKZ859ReTogbf1lIVFU4zREhBcTBGdUKiVoC0AqUkzVuLZE8PaL9xk+l2n/RghGr4VFmdByVJUpRWNH2faTFlP8tpeR7eYpv9nX18IVFaMB0NKYQg8H3G06TuizGYPCXOM1ztcOfNl3jzN7/K8itrdahlY0gnKRjL6OkBj37/bVJh6bYaGCNornYZHAxZvHeL1XtryNKw9b332fvpJxTDhOUv3OPOb3y5zmB/jM2UxNEKpRWdtUUaG7scDoa1RtYaWo7D/a++wu1ffoN3/u1fUKQFq68sM6xyyqoiyyrW12+wvNTFf7zNo6fbdBsRQis8YG9jh1YzYpjEoARucJxI71g98MyZekG5H2ZWxfnq5v2+rkDuDB65xnPzmp05B699ZD8PA8X8Yb5QxRxNwNVdmN+J+fP1HGBEnIpPZ+erTn9gj+XhZ8pz5tr5nj1H2/Pe/UVjbl4Ic3HZbB2DLHu22AunWbnvudC0M104BuJnv43zMPr52v3F0Bx2e3aTsjPrYCae9oU6OO8MzpwP7+xonOb0uILxO1fDTLfOXr6gzTjfh6P3vGIYz/fvbN/s2T4/56b3qZ95ZoUz9BzaktlbnbUFfuN//ps8fPch08GU4cGQpXWXIst5+4/eZrw7RDka5ToUWcHP/uht4uGUX/kH36H3ZI88L1m80WEyHHP49ABT1Q7UQgmkVGx9uIHre+w93Obul18mTzMe/fBjfOUgpah9C+KsjtaiNUJZ2p5LnhWUWUZRajYebyMEBM0QP3DpRAHRQpPKWqo4Q4r6kDVlSTrJwUKrEYJWTAYxUgoiJGEjIJeQlhXT0ZR3//RntDsNdF6yFIVM8xxfCeI0o9ACpIPvOxhj0cZitCK1BsdImp6HTAuMSqkCD5OkOK6uc0wAkZAcCEGa5qRS4FUW7bvEniZPMhY7TcaBg4Ra+yEsshMhXEVDKBytatOovKIscgSW9JiJajVIpSRUmkJKSqUIjiJfpdYwKnKaDR8ZuPhGoUYx3miIHO3jLrdQkUOxu0H4yj1Eo032aJNif8rIOATLK3iRf+QcrqjivPYdkIK8P6k1K2VF+sEDFn7tl7GTmHI0YXIwwtEKE7hkaUb6eJ/KdxBH72sDB8fRNO+tMH64y/BwjAHSvKznth1BZfADnyrJsNaSZyWHP3lMOc3pvryCJwXFYR8ZhYx2J8TjmNwLCZZaTB8fEIY+EoG/2KQc1iZGJi3AQpYWJPsDgk4D69bmeuPNQ1SW43dC7n31ZaZPe6gsx3UdRJxhLeg0A9uE0hB5Dul4irq9BKVFFAaTZ8j1RWxekdmMuD+gdWeZcpJSpTnSrzN3jx7tEi61kULgRz761gLl4Ri51EJPcso0R2qFKStsnFE5imKcIvaHlK5LXpQUWYkrFbId4WQFjvTJsoI4tfhSUozHNG4skRlqMwYhmPbG5JWl6Wt0K6TKyjoyle/idRow66x89M9MIviT65aL187sJeeEVMGd5fqdlEJ6upb2N33KYUzgOwhrKacZeZLTvrtCEaeMP6pDLGsElTFYRzA+7BG4LqUniUqn1lJJwfL6Mq6jefxoC5tX3FhcwIwGMB3hap+XXrpd+2dVhgpYev02K2/dwWLZ/WATR+vajHCSMnpywGinx+MHG8hWwGi3R+fWKtKR7H+yw9qr6zBJ+NE/+z02n2wzjGPansd4Y4+F127SfmVt5tXrgZBac//rr5D0hiAgVBqnGeAsSNa+fB+E4MnPH9FqdZjmOWWcUPkuVV5QWIOOfLzAx2IJmiE379xgd+cAU1YM44QoCPjm3/4mK/fXyNIML/CfQ7p8Obo7yZn1zKqeA5Ncde5ddm4dL7rnBOgXy86GkTmL3J6LriOwvbQPV9C8cidY4axp/ZX9vkqoPQ/WnK/z6H9VVdUWCzMMzVmEVvumyWswsRfa/AXSL1BzcX1OasYb4kQafrp+58z0me/wYjsz/GA9Z+JUwn9WgPxZkOUV6rLTVXKmwxcF+KdlLomAPUN1r2dH5nI6en97Oq6nSf3Oj+jsgr34TvPam6eImPeR1a943P4xLzEHgF+5TObcFOcUJc85jaeZyj/DxnbNlq56udOMrWdN9qQQ3Ly/xvrL6xR5get72MqQjGI++sGHdMKInSe7dXbYyGe8N2L99Vt4zYBmp0kyHHPva/d5+vFTBodD4uGE3sNtVl67RdCK2Hj/CZ3FDm/92pexQDFMePjOQ5KyohuGiDShUpIszhDG4CBoKM2AvD5oRR0dqBmFlNOMSVkwsXAwnLC+toQ6cpjNJgnKWALXQxqL0oJBWVGUJUoposDj5W+/SRznfPT2x3ihj44CDsYxRZziHTFQeZ6jkBi3zqLsex6yKgGJNgaUpCkVwyzH14pkMgGpabiK2JTkstbWVMqgLERKY12JF9ZRn/KioBkF7PeHhIFH5NQJsrKqInAdFjwPVwqU1vQjn93eCFUpGsbQVpqsrJgkKbYqUcbgFRWOcurM20qRKIkIfIJuC1tWqNEYnwyn2CN7+C6m+WUgoswk8cMexsuorEfqh3hhQGupjb/YxGpFJiCUkqKsUGkBk5TB4x5ey0e/+jr9J4e1Y/M4wY+8OuM1dR6RaZ5gHYfx432CUYJ3OKkzkDt1eFLXCvJJgjUGHbiowpDmBY6jKauKyoLvOVRFSbo7YLc3ZvWXXq6l+tOE5t1lOoFHVpRkwxhTVkxGCRUV/uEEURmsqzHCkhQF1ndRmWEyTeneuklVFARaUoxyimGMu9BEN3yiVlRLoqVEhx6yFVE69WEb3uiSvP+E5NEm+dYeSEEpJMVgSrk7wCw3iW6v4EQ+6eZhnWTt7jJWQLjQRPoOQkgqYygPhzjLbcppLZm344QqzSnjvHb69xxaNzuUjoPZ7tfRoazFsxb3lRtMNnuExiAbPsJXNMMlDv7yJ9ioAWWJOIpOlfQnhJGH040wWNxuVGf2XmqBuiLZ6NWX5m+DsweesWjPrQUNFqq0TrxY9MYIrSj6E2xlad3oEnQi9j/cJB1OcdoR42lM5Wh8oRFhQCVhUUcMSkMD8PKcp+89oKgsSggKpRiPYxYch954ROBL9vd65GVF6Dq0lztUWcGTv/yA4eY+/a0DkumU5kKHpD8iS1JUu4FaaqGzgsE04du/8WUOn+4TdSOKzR7v/96P+PH7HzPJM4w1lFVFO/BJhxPap9sppqqAOhHf0qtrfOfe75COEsppxvhgRNBt0LjRpfdwh0lvhBf55NZgQg9JHZBBey5lVuL4LtM4RipFoxXRbjcZ9kY8+fG7eJ7HBz/4ANf3WHv9Ju1lgRf6l+7/z03z+I/nEFg/N80K364rb7xWtZ9R6v/XQDVUmrEMOYanx908z2jB+R9XXxYzmOyy1z66V/tVcCRYPp2QWbnqfPR2TZp1pn2BwtYXkkTv8kF9jp7ay36eB7fzxc3Hhk3XwZzPO36nY38KRi+TM1jmAeiZiT+Zv7OqrzqU3qmG4gzDddKWmOFHxKno6pnSf2aG7dNC6VM5wynrdkrn+b3zs2EvlJ6jtbgwqHNYwEsm+IRRuIZ6+ZSxOCsh+DR0km11brvXrfh8sAEBWtUhI9MC13MZPD1g68EWxSDmwSe7tBsRN15ZZ/HmEl/4na/TWWjSWGgyHk8phhOUNbRudCnKkh//xx/RiFzufPU1RvtDPv7zn9FuNXnpK6/gt0Ne/fZbTCZTHrzzgI2fPsJYg+toiqygGQQoLdkZDCjLirIsaHXaWAHjeIrveXS7TSIh2TjoEx8M8DoNAitQRZ0grlKScZ5jY0MQeCw0fOKyYuvgkKWdPlHo0vI8NodTQs+jGQU4nSZWCrSjSAcTqqLACXyEgEhrTF5SagsSPCFJ0wylJLkUiNxQmgITaopxjiMkhSgRQoGwrC62wZRkUnHv5gplkvPx/iFZklIZj8paPKk4nExgMGS5EVEkGYvtFhXU+QCaISLOEI5mUhakkwypJZHj4Ko6OlaZ5aSVoaxKwkaIa0AMhrhmjLIZzuoyZfYmWaoRhUQ2b6ADj0pLtLW0VheR7QCnGdafe17S8pwj4OPQvLVINM2okpw8yeuISMbihx7Cc1BKUfgOsjLYYYzjalRZUShBOk4gLzENj2ihgdcMyJOcytRRcdxuhNYS6TlUkwR3VDE2BlyFyXNkWlBVlo0/fQ8v9Fj9wi2CRgOhFfbpNu6NRfL7q4w2DzFZRTKeopWupb6ug9YO/iChcBTj/ZQw8NBrHSpPI32XKk4pHU01jnEXGyAFcZLBahsn8kniBLREhS5CGibvf4TUtamKboVYY7Chi+PUmc5l6KKbIZUUlEmOt9Cg7E1QkUeRFuRlSXBrCZPkqMqiO/6RuZLGxgVyuUueZlS9Sa3dUJJkkiG1wFQWJysJFhrIgzFaCqTj0Pj8PVQUMNwcES51a4f0/oSFO0uUeyOchSbVJMFKSXNtAekonpHk4MLucrm8+5wABks1TlHN2scp6Y0pB1OSnT42K2m+fKP2odGSYLFBPojJ+xMqa5lOYjAVVVYSVxXtm0swTfnowye8/No9UIL99x/iTwe4WBYcD6tcYmMxVUm3u8REGEIK0seP2KvAf+hhtaqjhJkKshTVXWBqSxIt0O2IzFesBj77e31W1pZYfPUmg50+gSp48odv82hjm3GWYqzFdTTLzSZhIyLrT0+OGAtsfrTFaK+HqSpe/cab+FFAuNiEhSat24snI5SOE8qqwlc+ke9htWbQH6Jdh/WbK7QWmmTDMa1mHfI4SzKkW0fFu7m8yKPNbYZpQvknhqVbS2Re/JzMxTPmfp4w9RmPnOgIrgN6LtNYzP79gvH/6cl3LPz9rAK/mYk/beRT9Gv+g2fO+efVnDyrzDy5sT2L4YQ9wi7CzuwVc/KZzdJ5jDhPvvsL4O1ekObiBbI7Z+o7qzo7uTdncD5F1TN0tTZAnP/reMLnCdUv5UJPF4OYLTjT5PkP6lN9YFdtAldUd/JRz5xIVzNns/kxLjZ/WX9ON49n9PXkxmlW8yvppCv2TL1zmb2ZDnx2rUXtPIuSL8hutq4TBEIKok5ENsn403/xR+w82KYwFY3Qp7AVX/ntr+H4Lp/75bcY7/UZPt2nmqaEwqCxDLYOuP31V3BXQu5+7lWKrOD7/8Mf4qWWw7jH43ce8PIvv4nWmntfepnmSofbr90GA4eb+2x8tEGWlFQCPNdFi5LMWqqiQArJ7bs32N06oIwzBlVFu90gaIRoz61txh0P6Th4job+BFNV2Mrg+R6tRsC0E/Hg548JQh+blYSei8DWvhkAWY5Bk1cVrufhFAblKmJTUGpBgEC3QpJxgqckgQWnGSBSh8wYfKUpw4CD0YSFMOBeu02FpZcXPDrsc2d9Bc91aGmHL7YifopgvzcgThNy10UGDnaS4WuN78N0GrM5niAMtByNlxeMi5wcS+h7uGVJVFaY0lACIp6wUsVEaQr+XRgMaC66VNMcp9Um3R1hglWsrDOTSyGg2wStsGUFSiDjnLwyCATS00yzAk8pQkeT7wyQvkPlaSoJYcPD6TQwUqAAM0kR7ZAyztCvrKF2+yjPZdwfI+OilmT7GlyNthZbacLlNjkC6Wv6cYJIM+JJQmEtvu8yGiY0mgG+q0lHSW0nX1l0IyTe2IJGE6M9bFrSeWWV5r1ltn78iMpaXARVeRTauBlihajzJqQZo90BwlSEjQCiABH5ZMMp+f6Q8M4K1lpUZWi2Q1RVYQ7GUBmC5RY69Gl+/jXs4YTCQvOl1TovxiRFdULy3SHac7DW1CZZ3YjkcIwKPZTWoC1FaSirDDfwYUWRFwUqK7Ba1kyMr3HyHFMYksMxpQHlO9jKYJOMfGeAs9CoNR9xhnAMk2GKs7RCvjnFb9baR4lFpCXZ/hC36ddmUVWJq3yu2vFPpZOf4qy1UI4ShJZU04x0f0Q5zUgOx4wOeyy/eofg9hImL1n5wl2y/RHZJCXbG+LdWqLYH1BUhkGSsLS+QpYWDHYOkQIGgzq3TaYUiXC5v9RiWFoOkgKBoXIDbrx8k8AYdj94ROg4LKqKkTBMhUCGPskkxvEdpnmMNylxpUa6mmXXp7nc4cFPP+Q/+ad/G68d0ga23nvK4KDPKI7RSqGE4N7KMmsLHRp3bxCtLRzFUKmhazZJ2H1yQDYc0VpocvdLr1ELhKgFf0dnh7WWvCxpui6T4ZRwqU1elFRpxqQ3Jh1NefxwE8fVPN7aI1Fw784a8SRhIWrg37vLVjxlNBiTJhkH7/X44nLnTE6OS6fIgrggjL24GmZgxMy1GUA+R8NwITLlZfRMYd8LoDmy4dm+Pdd5fJVW5UX0+Rp1vPCkfM/8vO3ZPz87fDldN/PG8TPQL9Asar6G4dJ7Yl75y7bSS5DzrKjm2oP+KT665yVxhUT9ar6mHoFZpoTTUbl8Uc/5wq6r4ThzzV6o6YJSbjapnj1X6IouHUsr5vJ4lzx6FZ18IMcMxnGI10uH/bNN6pmlpuS52i6O/7M1K0edF0d/H2mZrLX0tg/ZerIDxhJFAfE0obncpr3aPSmePtgkORghpaBwXTaf9giaPot3V7n15h06y10ON/bpf7zDq5HDw4nhf/xv/xV/35G88a23WLy1zOKtZezX36j7ayzT3pif/ce3+dkf/4zJNMbRirbXxPUcGmHAcDBF+x7RQot4PKEsKwb9MYGra3McLbGug8lKAsehUoJmFOBHAVopVptNqiBgXJVkQiBKxTRO8SIfAajSUFY5wlpUVdWhM4+cuEPtUGmJSEusp5lOU0Ip0dMMYyyBEIg4x2BZbEaEkUdDKWyS4eYVh56LKSu2Dwc4VqC0ouU4TJRCOi6VMbQWWnQWFG++dBtrDKPBGPF0l8FgjJMW5GlOUpU02008z8HLFRYwShFGPmJninm6TWjA5GtARRpbtGoymkj8zk1KKSiNodQKowTthkc2TZGeg254qMDDlhUNzyHLay2WUnWkIQIPcTiuJeCVZRQn6GmGkOAhUZHH4O1PGGcF3UZAPs1IkoxMCboLLbyGB6Uh3epjGgHTcYz2NNJ3MOMUVRnyJKMd+Cgp69wHCy1WfvtL9D/YpPz5U7SnKQTsvreJUpLJ+5+AEGRphvYcFl6/yepbd6iqiviTPcJAIrVmuN0jvL1InuY1YHJUHbXsYIzyHbKDEY2XbqCkIBvH4Gn8boPDd5/Sub+KN0qZ7vRp3V9Fhz799z5Aej50O5TjBG+1gwkc4r0hgRCYsqyzanciqkmK6zoQepi8gKxAWygGMWl/SvDyGtnHm6AdvNU27loXY20djvjpIXFaorQkHcXIowhujGKimwuUWEosrueSPNwjE3USO+05tQP+SgtbGdpv3iYfjKl8TXS03p+1JZ0RzFzYYc7tPrMYpKpq53zXYfR0j3KS0lhqIScxjRuLeGudOlN8WWGKEiNgejhCOYo8L9nZ65HkJWu3b9DbOWD5zip33nyJrYdPmez3uHFrBaslXqOBFQ65K1lrtHj4ZJNP9vbYPOxx6+4aq6/e5clHG2SmYLHTorAlWVWSK4lSLo4xaO1QFCVRqVCVxTRc7txdY/lzd7DWol1NEWf4gc+dpSX8wMPxXbq3V7j5rTdY/NxtnMA5sw+n04wiztCeTzzKOLEaONl2a5v1pVfWeP2rb7CzfcDwYID0HILQB6XpD0cMdg7pH/ZZWF1i7e4iB70BG0+2udnpkown+EoS+g5JnJDGKYlNKMsSR82EFP4sZC85t47PvTngcLb8cwPhZ0G4c219mnovxzLXQM5zYeCVIOdiE9ekYyzxfLjhxaoD7AlD/JwPHmOuqzDI+UsvoNu/4GhRl43EeWn3pcj6tJozNV6HPb2k7QuP2ItlLwDhi4qOz7xsrqO2O9pMzvs9PzPpzaWS+mt06iRs7vFCnOmqPR2p2Y2qLn7Fqj/T3VM16EmX5g2mPfO/OT8uoRn93pmP6NgM6gV966dVX8LoXij/HJzTzLWqKIh3BpikwPE8It9HGbjz+i1c36nBbFEhHM27P35MnGSEkcc0jtGdgCxJaTQaQO18XQrLTgWLsqIXhPz5v/xjbr16m2ipdUY1KiQ0llp84x9+m4OdHh/91YdkQF4U3G1GCCBwHZK84OGDJygsrucTNII60/BoivIc0iQHLWuwKSQHaU6Y5iy0IpSj61wVQAX43ZCo6eOHPkWSUSmFW1Voz2OSpORYvCTDtEOsFIzjFM9zsKUhiHyKNKfle5R5gRUCAwRaURQlbuhjDZBLPClZiiKKrODxQQ838LFa4VgI2w1kknOYpESVxdoSmxW1o3vgc+fGEmQFEknUjFBZDlLhBB5G1j4R+gj8VyrEf/MbqEaA0g5JHCO1JklyCgnTNANpEe0GbjNCV1XtryAtjimZHg6h0yRTgkmRs7KygJkkGC3J4hKnqpBrXapJilYC2Wnghi7FMMFUhnw4xZGShfUF5CTFr0q8xQbOSgd8B6kV7I8R7bBOZBi42MpgDsYYR+F5Dm4jgGmGI2oGqDCWg7cfkg6mtG4tUZpacm96U/KyYmGljQw9xsMYyopsb0iycYgxBkdLgtdvMv1kD2exUWf+HsYUw5hgsYnb9HGXW0x3BpQWWlLiry2gRglpf0QWj1G+puhPke0Q13Mx06w25xEC4oTx4ZDO67eID0doC05R4ax18ToNnCgAY7B5ifRdksEEUZRUo5Rkt4e31MK/sYBJc7TvUR0MyU2FvtEl3xmgpCSfpJhJUoeF1opKSXTbwwQu4419wuUOVBVFXIc0TpOMxlILKwTuQlQn7rNQbPUgTmneW63nQZ5Gh5q7UwieaWV8qaa5skz2BvT+4IfEccbqb38Td7lF3hsTrS9QFCX5o12k54Cx5OOE6ZN9iDxcIbi51OVgMCbuDxkNJ2x/b5e7925y6+U7bEvFcDglk5ZSQ2ZyXMejP5kQFyWB67LUbpIOp2wcjlBa4Qrn6JuyOEVFwwhyY3CMISjBIsnHCZuTKb+09BbR6/dI4gztuwgpWP7SS8T9CR0haN9ZpnFrkfa9Vbx2eKKxOB6Q0f6AwUebqFHK+ldeobO6cEYyNHu2bf78MRsfPUE7DrfvrHNQpERKo0KfTuBRacVQSFpRxPprt/H3Grz//scsRg1sWSKEJPQ8trOM9777M/7Wf/nrOK5zYT7mTu/M+VCHmZ+zEC6FNGfPtcsA+6cVqM1FW59FQ3CkJaoD7BzhgQvvdq7i8/cvSjvn/30VXRuoW3a/9yO8pQW6r710rorLB8Ae/Xvtcb+0LzUuE8dlzjN2Z2DOWSbIHgl9LwYzOnmB5+zL9ekFRouCsz16Ab2bQ+fZkku7MitJf+bcXt3X68HH56czoWSvrHCe/uBSkfw1rl30nZg1i5oH6K0427w4X+CSn2fqqBuYuXj1KF76IcydrjnagpMrR0zTC5YkPIvmSQqsndkoztGREO2oYP2PFJLxYIqQClNV9A6H4AiCTgTUicq2fvQBf/n/+QF5UtBqR3Tvr5BlCa//8ud57ZffQh/lffCiWpPx0V99wP1WxGLk83inz+/9X/41f++//se4gTcj0as3fakV3/5H3yHeG/LkwVP8RsThZEon8BmNx0iluXH3Bos3l9jePKC92CQexdx/6yV6+32G/THTNCf0PBYCl+WbS3RuLjI6HLG31cMJPFqtkMoClYU4w6QlDlCVJVVZ4VmN72hKLEprVGXrrNJKkNsKLRVJWtAJg1oC6XvEWFIlUVVtVjfsTyhdl6XApUSQ9IYUWtFBQ1YyNRbrKnztkFQJ7UZIVBoKAYfbO3iqIsdlOE5pC0mqJKVWtaNu5GOtAN9FOAq/MjhlhVjsUFlwogjraRplSak1oeuSegrVDJiWJXtPdoiygryyVL6DSTJay20WVroIBJ6jEHnJeBQj0pwqyVBaMd7oY4VE6Tp0rhd4lFWJdjXJpKDRDCiVRDYDUAITeYg4R2nFcKdHJSU+EmENxTTHFCUoiVxqIkOXsqiYHo7p3ujiBS7J/qhmPvaG2LwiFhLPczCVJfJcaCpE6KGsZXGhiQgczJEzuBDgBh6qEyIOxoQLDRpLTVpaMvhwm3x/RDVM6D/eo9Cahu+Q7w2RgUM+mEJlaN5fwwv6DN57grixQJnk6FZA97WblMMh8YePEWmOUJKgFWKaIXmSk2Q5cjglO5wgPU3z5TWSrR5SStK8xJYV/p0VbFZg4oz46SFet0ElJFZIbG+CbgaMNg6o4oyqKCmtQaQVjqPI0hxRVcRpgdEKURnKgxFojWoG6HZAlqX47RCRFpidIamt17oXZziN4PSbnxFonewJAObyfePixnN2Dxk/3GHv//Yvsc0Oa3/nV2i/tIypDGqphQhcVG9CDni+S9qfkmz3UFKSJBlUln5WsHBzldFgzHoUEPeHJIMh+xual776OunhiL2Hm4wP+1SuhxlPcEvouh6NxS6pK0knKUVlyOMErGEsao2KEYLYGJRUOEpRZjntdhPXd7l1c4nbb97F+9rruJ2I0f4QSkt4a5HX/4vvILVCexrlOTV4EpxKfSyUecFP/1/f5cd/9g4r7TavfOk+sjLkk5RimtbrpNtAKIk1lp//wY8oxinLt9oQuPhFTpblRGHAgu/hry7ydK+HavlsfrJJd3UBbQQ/ef8Bju9ispLKUwgh2dvYw3XdqyXpl9CVkmVxlbR/to5za+HTkjg6P48r/az1nVR12vdr+YScv2/PjcN1oOf569eeGsHSV96aOy9XzcXzMHOXBpc5J4G14pRZmO3FSeG5qo3j8Tnnm/GLgegn9DeY5+KIrmIA5l27LsPwPAN3niOewfvXruazcPIXKjrLcFxcpHMamYOb7Zkbxxao56U2V7JrF+q/yKfMjNJVgyXm/jmnkeMS9uLlK+mqMRGXl/kMVEsFrnCmmvudX7J5HH38Jw4mR89mSc6Hb3+EVIrOQpN+b0RVFqzcXwdg9N4jnvz8MY6uTV1Uw6e/c4BuBqy9fPOEsRjtDnj7f/oL9j7exvN9do2EJEcryd7OUbhaMTNk9lQi1lrtEnYbICVZnCIDn1GWYcqKWy+v8/rf+hJ/8t//R5ZvrvDox58wGo1xkQy2eyRZjvActFb044Txwy16vWFtSiLqJHyVVnihT1VUiMAnxeK7DqIoiPf6uEAQBciyIjFVDVaLirws8HwXq8FxJK7WuFqSpAVTYcmNYDROUAK8wGUwntI/LFBCUjmKaZLSlZLkxDlO4MFRPgmLRiEs9A7HZKZAC43nesjlNmZ/iBAS4bm4nQY+girL0WmGlBKjNbKqMHlBrhW68pCNEIVFuw6ttQ5xfwrKIn2X0SQh6rZYW12gmiRoz0PlBifyKcqKLMkhzbFC4CiFmuZ4QQCy9s3pD8ekcYYnBEKCsgLhu8jAQ8QpaIkcJUx2+hRxglNavDQnD3xkw6PIC0pjaa53adxdRipBY7lDMo7Ze+8pyThBhS6mslgl8XxLZQzCWtrWUmhJWVb4lUEUJTZSCFchSoMsKkpryMX/j7j/frIsyw87sc8x1z6fPsub7q4209MYPwMMhgAIGpBcCssILVcMhRhSSKFQhCIUob9A/4RCK4UUMkvGMijtEsSSWBIYEJgZDDC+e9pNm+rylT6ff9ffc/TDzcx6+fKlqe4G9nRX1X33Hm++5+u/guLtXVAKK8BZaYKBtW+8yJPvvV8Fpau5ROkE3Q4IjKmMv2seaSLQNR99exV90I9iFOPUfaTvYlwfkReo0pBsD9DeGJsVCGGJumPKXoTnOSghybb7ZHtDdCNAWUuc5EglKcYxNspIywIxnOCstDBpVqmoLdThkx1KY1F5iQB0zccA0oAT+sR5Sb47wqt5eM0aWZIj8qJSyQkctJR46x3ySYrd7KEcRTmcYFfaTDPD7Dwkxh4EzToLFs6Cz4Nq8v4E+eorhLcu0f7C9QOQKHBrPtHOABVnoBXROMEgSMYJphmQZylllIG1JHGCE7iVWtD6EjZOefzgKas31wkXm1xvhPSe7vL0/hMmSIQjuPXKLTpXl+lt7rN1f4PX/vG36T7Y4v57n1DmBfV6gOe6tFY7LF5dwWuEuKFLuNLBbQQ4zQDnICAlFtprHQCySUq0P2K4OyQfx7TWOizcWMEaw96jXZrLLZqrbfbefcSDX94lN4ZBFPPOH/0EVfNQjmKw1wdreeFrr/CF//zXEVrR2+njS8H25g6JsLRbbbIope35pFmBqyQLCy2Ep/nozY94zX2V9WvrvP/eRxRJyqA/ZO3aGu2lJl/67a9U3r8ukp6TAJnrmXGKUXlqsL3nQmiOt1g1MlOn/bT1TaVDIkHM9Hv6+p9ypHPi+ykSjKMYEmfN7by+nzJHOnhmmD+Nav11eJqcJVjs0fOzsMLHGNMVGjKFus4Qbues+2c3op+f/uaJi1lE/tOWPZbmkOlTFJ+deimms53T/pnn5tMSE9NdPNfD0Pxo488EXDOHframQ8T6CHE9ewM9o55PqdbOvrsAZJkD547RQeKUzJ9D+jT21dOH9jw5xzG6Ze73k9TYSeLs6K9njwcPZV5y/6277DzapuF77DzdYWFlgbjIWL26wminx/s/+Yi0NPgotNIUcc7K1XXKsqS53EYAeZbzx//nfwPdGF8qOosdepMYqxQdRzOROVmW4RNULirLkixK0Y7mwS/vsnxjjdd+6w2++Pe+SjyMePM//oyNu08Q1uAt1Pn45x/R3e1BWmKKgnanycajbaTWCK1YbDVYu7JM3J+QlwXacQjDgDzN8S2o0lIYQ5pkWGOo1XwKwBjIQ49uaaibEl2WGAG+0oyNJZQu0lRuZsPQJ41TEleRlQXtToNQabaSFFlatFAoLLtxQuh6dMIaWmtMXpAlKUmeoUuJ77rUXAdB5dffGINo1vEPkM/CWnRaUm/V0a5DYW0lcUlSbFGgXbcCqragLCzeUotxb0jgOxT7Q6znMvJyzNMSZSz0hwSA2wxoOBrZj7ANn8SRZFlK3YEyNTiBi27WKEtDOphQFIagHkDgkHWHVdyBwqCMIRpHuI2QVAkWPRfykmJrHzwf/42b1NMCZSzFoz1KKSjzylVn+wuXWX3lKsrRZHtD8u0BYpJy7Y2bRMOIT773Hp21DjgS7Tq4cYaTFqhmiLEG67okRUG97iFchYkyIlF598q7EXmcM4wztIXlVy4jEAhHYrKCpS/dYPPP30NZ8KSi2BqQGwF5gR1O0EtNjKnitXhXl8l2BqQ7A1CSMkpY+8JNHj/cIRlNGG93aV1ZJh9MkEqRD2PqN1cxpSF5ul+Nd5Iiri5gspJ6pwaORgAmK2kutShLgx0n6HYdOjWG2wPKJMcMIwpP4wUewZVF/KUG2nMILy2w/Yt7ZA92yQW4y02aa20m+5WUJi8NRX+COLDdaN5cQUjQrXolebLAVEyEYzihYMoo+HRMQYhnks/pXM5ig+DmOtbVJFFCUAsgKyoHAuMUUxTodo0n7zw8ghkZFoqS0lhcR5LvD9gfjOjHCdtPd/ClIjeGrV89pL3Ywu806FxeImiEfPjmB4yzlCzLWbi9jlvz6Q9HPHz/Pt/6n/8uv/ZPv4M58N2PrIgcqdURQBUA8vgsCMFRBG6/GeB4DqP9EXGWs/OzD3HfvotXrzHoDXjtO18k6Y356Lu/YDAccevGZTCW7v6A0e4uo9GYxXqD3FpG33sLv1njpd/7CmE9JB5FxEnGC2+8xGB3gKM0ge9Ra9XZerxFkmQsXlqkf78FEpqdBtdvXyObJDhS8lu//x1uf+NlvNC7+AVk7Yzq8ymMsunPM79nXaYe3xhz6phX72lptjunlHluJPWIYTmHWJqp60SO2XIzdId4DinLsWB2F0gmSTF5gdOoHZWv4kycb7h/Wjo+B6ef8ZMCnIN5Oidm2KkVzG3/80mfC3Fxcu+e1VF7PMvzjOkYRnoROdj83s3NMsUwPkMMMNOPc95Nl3ueMkflpjfM9AGw83r4mdPxA2bP2OJz0mkZp8Z/bMXmnIUTtjcHSHalSfT5b/7jbVXc69kjPicjczfvc03WYZMz0pnjdCXDnT5/8d/9ANd3meQ5QmuyKOXFr79EkRf81b/8Ux7/6iG1TgOdlbhK01jtsLnV5eZXXqw84QBFVkBhsVISpzmFFQgpCTyXyXDE/s4+d3/+EV/6O18Da4lGUQVsTE4yiPnB/+tPaK51uPGlF6pItq9e49//X/6AJE648xtf4Pv/4ru0202yJEMIyUKnheO76MAj7Y6oNQIePN5GGIs1UNgI34vBWvRAILXCcytvSe2FJkJUqkClAK/WxtWKZG/IBINnJXGSYpXAKIEf+JgsZ5Im+EIRBi5xXrlmjfKYpuuxvNSiiDMG6ZClhRZlYRgmKZTm6CJacAMiW5ILKAMfVZSUWY5q1HCNQZaWVOdVGSmQgXcQFE2ik4wScHyXUghKJStbDM9h3B0gHYWVAm+lTTZK8EqIRhFl4GJDn1JXbmtTIai3auArhLVoKTBKI+sSpxEwHkSUaUEtrLi5haM5CD5BrzugXg9JclO57+2N0XlB6XkoYzG1EBoBZqtPVhiCZkjhVh6UrLG4TZ+VFy5V8SRKi677GNeh6E1IN3pMPrlPQEmyPcC/vUKpJOUowgs9ilDjBi6N1TbScTDjhGJ/WBlWhy55b0TeG5PlJf5ah86L6/idGtZYsCVSSYJ2ncVfu8n4/Sf4nSa93S52oUHem1C/vlzFiNCqOqfGkPdGhLdWMFmlyqRrASvfeIWH3/056SginsS0XrxM9MkmeVGAgNpSk0JKVN1H13zKoqT3ZI9au0Y+TkAIzDiCzjL28S5CCpxOjXgQke4OKQYTjDWES23cbMzSnTWchRbleIJNE0jzSiWqLFl55QqDe1u4CzWi/oQyy3FDj2IskVJQf/ES2XCCOIwkfZbK05Qkc+bHsSzTcOgZU0qQj1Oin39A+MJV/NdvVipRNY/4wQ7C1SgtEUqxcH2F8XafdBwjvMpwuswqNbuhglY9oKEVWZwgEIzKgs3NHXr7fZSjqbfq1OohGEtdO+zv9ejd38Zr11COw9aDTe5+/13WXr7K4q3VyoZiDnPJCg7svyrYb00ltZlGoKWrcB3FpDvCFgVpnpNlOY2lGu21BT75j7/g/t1HdNoNGtdX2d/pkkaKwK2hrcVtBDSsZHc45JNf3uXWb7+ONSWTvKDmu7z/5nsErs/qlVVarQZCKzpLHdaLsgoOqiUbT7bY3djlyotX+c1/+lsg4NIrV3E8l+e+nQ/xj2Pcz2dzctp+qKbpHGzgrM+n3VsX6v7xip8bQT2BYk1hkLNqU7P5z0LnDnALK6bfiaki9njTs0GLZ3o1+8GUZRX35libn56wmG7pqL6583qwWAJsWQXFPY/BOVXJyUam6/8U+Mt56XMhLi5MVBwhmsdHMrspT47xJL32fMkefzo4wCcNng430uwunhOg5Hlx3WPA43yu+FEzBxmPi8rFceO+0zgL4jSqfJrimUXp7fNvtAsCp+MHes6LuW3+Nez6uc1Msz4OWSrzKMNTVs1OP1xscxweg2NFDx6stbz3g3cZ9ca0gpAiLaiHAY3lJq9+53V+9m9/yJP3HqCbPtoYOtbilAWxsPQ29/nGrd88IuiEEPRHYxjnaMdlfzhEKYWyliRNEaYKfHUYNKjeqh8N4eoXb/LjP/ghOw92+OTHH9G6usjr3/kiv/9//KeMdvv84j/8lP52H99zScoS39VIIRn0J9jumDTLyAR4jgvSomXlZnYwjpCOIi0Mi506y9eXmPQi9nb7ZFmOKyX1RkinGRLUQpTnkt7fRAmLUxiUkOSuPgiaJnDFgYG1EEjPJcoKyiitEO44BQRu6JOakqQo8VyHMs0pqdSUCixrnTa4mjLKyPMCHbrorECW1bwY3wNP4xhQQCEEQkky30EVBlMaRFmQYPEcjVQSN/TwaiFpaRBCoXwXKQUd5TEGxr6DdARe4NFe7lC6CmnARAn1ToPxMMJxNMk4RWQFwYHRtbfSIo4ztFY4ysdLUuJBRKcRooVEtBuYOGFnY5+F0qKBrO6jWrUqTsYkRmc5SkBpLe0Xr6ADF1sYTFZUMRHqHv6NZeInO0RPt0ncBovLberrCziOxiy30AdGwLYosXFO2Y9QC3X822tHx6UYxoRlST6I6T/YoffWPfRCg9aLa4SLzQNpIdQvL7D/yweM9/pVZOxBhG6HmLLE77TI9kdgDCbNUQt1LAK3GTL+ZIvM7lN77QYrL11j+/4GaZzi13yM57C41CK5v41ZTqhfW0Z5DuUoBiEIsEz2h6AU0q/Un/IoIc8KtK9JuiOyKENkhizOaL92leJHPyB595eMPZeFf/gbmCRBtRuUhcH6Dn7NIxnH6NAHJRgOJzSlxGmEJP2IcKlBmWZYJXFr/llQZQ58OfHjGc0x76WF5s1V5O//JrrmY4WgTDLi3QHFOEEKC/UQFbi0G8v0f3EPqxXS1SR5ycrNSzz98BGeUGReBVCkkngCpPXJhTyKYt7v9tnb3CVKKs9UnhS8/cO38Ft1rBSs3rrET/7jjwm+9xYrl5e48cXbLN5aw2/XcHyHMi2IuyOyUYQQgjxK6T7cZjycsPTCZa5+/SXCpVZ1Q9vK7ky7mnSYYxGs37rES998hf79be794iNsltO6fZnR/cfsZwWbW9u03YBkErNcCzGOJMtyBjs9yrwkbIRsliU3Vpeo+w5rVy9jtaLmOozGERpoNWr4nkcepxgMC406Tx9t8ejDR3zjf/Lr6DMMuM9ic047CDmm8nLafXLE9Z/CZOZdVxe5ji6Ky5y4ip8V/CzMzs/MwDwn66FkQcz0dy7edGIiT47KqYVQe1b3cxNVp07WnAWcyXskyVEHhPghr/6cLlR23hUDde48/jWgWJ+ZuDix306M9vyR2GPlnqPxmbU4bc1ON5+9+DtxVpYLps8QQ/FZKXv4z9mb+hmZNG+jngKspj/NLuz0ctpT8pyTjsetO4+gPCR7Ko7VcYD7N5Hs3LN+Xhl78O95AOdoPOKA8yQO5sdW/056Yz786QcsNZsUWRWTIGj4/L3/3T8ijVOirT6Xbl8msSV5P8FZamCvtHnw7n3qnncUK6IsSu7+9ANu3bnJx299jMBS8zwW2w2MsXT7Bt9R1DuNZzq7U/Nc6zTwGyHDnQF+LWC00ePP/z/f5dcHMU/evc/dXz3CczS+6yC1RArJk609Xrp5hdf+3pf56Ecf8PD+BnlRslCrsfzKVTbub+GWHlmWIYDxJCH9aBPfc8myHO25lFnOaBIRxzFOb4i2At/30VhMHhE6PqnjgBCURUnddVGCyksTJeQlfj3Aq/vsDSvEwBGCMsmRrgNaUSQZzdCjEIK0KCnTHFOUOI7GlRJtQBSVmhELDcgsySSl7mqk66GzAoSEosAIgSclpRA4aYLREqslydaAyV6fxspiFetBa0pHEx8SNo5LUUKzVSeJUkxkUEpTFgXj/RFlVhCn40pCUBSkewPi3ojebp8rL11l7foq0ncJjCUKXMbCkE5iGoGPv9Khv7GL0QKvNORFjlPk1AKXMi4QtYogLC1EO/s0r69gs4JkZ0CyPUR1apg0ZXT/CUnYwpce/koTVysMlSTAlAabl+R5SZblZN0RxVa3ko4oBY7CadewgBGw9KWbpN0Rg4f77P38PmvffBGn7oMVKFfjdGoQpZWtCRZZlATrHaRTIfqyKEn2+xSeR22lXUng7lwm+niD5Mkebuhw+Qs3iXZHbLx5j5U7l3EDj8kghnHC6J2HiE4NP/Rx2jVE4GIHESIvUZ0qCKCu+wz2R5i8QBpLutknHyUEKy3CwLD97tso5SACj3RrlzKKEK7GXagx2u7jrbYq6Y+jcNfb9EcTWteWKdICt+bhXV7EAq5bEaCzjKfPNYlKMhgut0gGE8afbGJLSzmO0K7G1g6CRjqKwYMd4uGEou5BXh5x4FevrLL3ZAclBU5NQ2mI4gSVFTjK4gUe+90hwtGV8XPo0QhDNvd7lXaTNXz1732Lv/pv/pS6oxHGcO/9+zz5+DHtRhXlWjuKaJIwiWLyoiCZxBhrSYuCxaUOH779CZffvMvX/ou/xcIL6wgErUsLXP/iDTZ/pVi4tkzn8hKDx7u89wc/ZOPBUxZWOvSSmMEkIUlS8uGApStLFH5AbzBkYW0FX2u07+AEHisvXOa9n3/Ag5191kIXk2UoJ+DjB0+JJgmB51JIQf64zqVrlxiPxuxv7eE3QzbvPn0GO6dw0mNX5OG7E/fqYa6T8PdYRact8YmHeR8/ZZpGWU6965/7ojyWDlmcF0XSD/POlnlu7GpeATv70x70cd6CTnH9Tyl/9Hrai9N0HUe46+ks+lPVzex83PZEfgsnVe/++tNnJi6O7z0782UmnToye/xRnNzT4li+k5M8u8YnWjgvzsBzUvfTkS+PnudsmuPlxJyni7U3O51nHsQLb6JPFZLpdEb+OTBGnEFwnvhij799rov3LKkOB6O2c/bCafTEOfUd/3gxIPnMw8VUZO6DFI0m/NH/89/R3d6nGYbESUa9HvLiN14m7NTZfLDFpTtXyJWkf2+HVBUEVxZ4srVHnObc/sI1misdsDDY6vL9f/EnOEZirEUFikBJBqMJ/fGEPEsJ2nWWLi+fnCcBySgiHceEnkeW5TRdl6Q0vPWnbyIlGGvJTUlvOGZtbZGtvT6mLNALIcFCg+7OPnmWV4QDli/8nV8j/sMfsfGrJ3haY4xBOw41KXFcTRIneEVJDhRlSVZazDhhabGNdh2EsMjcxTqawHXJyoKWH1RxKIYR5AVaKaSEduiTRCl5VrmLzfICV2vqNR8xTlCug0KiCkOoNZG1CEczGscoILSgXI1cauHkZaVXqyWu62KEgKIALAqwWpL2x0gpsYBjQMYZdmUR2etSdruk7Q44mgSD0BKTl/i5wXYCEILNDx7x5N5TXN+l1qjRWV/g0itX8ZOc3sY+YauKQF27tMDlO1fo7fTY+mSD1rVlVKuO3huSlzkmSki1oowgXGhAXMX7cLRC5SV6wcc1MaUxBEVJJgXdjSHxf/g5djQB5VTSlq0eZZxiSkOj2UQ1fIL1NkaA1/BJhhHDdx5ic0s0jvHqHg4Cm5WIhkealcikIN4doYyhLAxjV+Ovt+ncXmV8f5vtH33M0ldvgxYUk5TFly4xebTPaBwhSoNYalb6+ECw0qIcxYSeQ++9h5h2HYtF1X0ab9wCY/GWW5g4w2/XSX92l/7DPdo3VwgcSVIayjTH70XE44TJ4z3KZohwFOnukCBKCC8vUmYF7lKL7MEWw2FUqeW0ApqrNbIHjwi/+BXS4RB9ZZl8OELWQ9LtfRrXlxn86gn5JMXdGyF8B6UVi6sLJP0JTjPAJiX5cIIIPZx6gJDyNAbp8bN4fpaT98+Buod0FMpzCDp1RqMYhcFdaiLrAePeiGxviN+qMX66j1QK6bnYvGB1tcPmh4/YH0+oBT4aQT5JKY0BRxIZS61dp98foT2NcDR5klFv1RgNxpS2ZLA3YJ0lyEouX1nn7kf3yE2JUxYEjmKv22Nzr4tSEqUUoevgSEWrXkO3azi+R1APKJKM3v6QH/zf/ogv/Wff5Mo3X0a7mpVb62itWLq9ji0NH/3oQ3Z2u9Q8l2FR4Eag4gQxmHC51eb2KzfpDkZkmwKhdeUoY6mN8h1uffUOv/qzX7K5vUsWDVlYXqLXHzGcxCxfXuOjX37A8pVVlBHUm3VWrq6QZQVO3aXu+ex8+JSFGysErdoRZ3l6WU6s4Twi4qwNMLvGZxW98J11TpsXKvvpndwe3pZH9+FxOmu2mWMI9UnNkwv27izG6dSL0pQIKocZs5HOy6JEqkq9eGo456ez8szDSaa7N626fUY9c7fIWTY5Z/Tns6TP0aB7juTheQjaExThvOezN8nZZ+GAPHkeDvgZ/Z+vE3daNcc35qmEwzQVa49O0untXPREH1R1JBqcYnVMcz2eqVBx1P6x/WXO6PsFujAtTzmR7JwDMf10UUA3W8kFuBNnVTMXbk/ZSszupedyP3eCGD8gTozFpgW+0iRJilfzWbmyzNUv3MAaSzFO6G30aF5fJt7t4TZqPHy0zWCnj6Mk179xB3lw0f/ov/0+q7UaC2VOtrBInmb0o5TBJKJWCxhh+N1//g9ornbmDZTHb99DG0GzVWe3P0Q6msC6OKZSbWrWa2ilcKQlaISw3cWTlSvQvY09tjf2CGshC50mveGEn/ybv0Tkla1DLgzxOKLMC5TvkZeV/n2UF7hasrreYeXqGp+8+4Drr99gsNnFTlIKIQCDDwhjkdaSWwtKEvghOi8ql6iFwY5iFps1mCTkSqGUwiY5ntZ4olIJklYijKXle+TGkCiB63sQZVghcdMCETgUvovKCkRZVuxHrdGOwtjKW1WhFE7dx/dc0nFM4WjkZIxaXkZaS4IFR7Hf61MLQjzfQSiFOuCeZmmGrxRCa179zhe4+sWblFnO/b98n+t3rhCuLhD1J2SjmMZ6m1d/9w1+/P/9C8gKlO/SurJImebkQaWOQ5KhtIu/GFAoQZkXuAaUkhC6uEqRMcEpK2PEPC+xjg9CEDYC/KIkcTVKgFptsXBzDSkFSImNM8Z3N0kmGTYpkBLSUUIhJSbOMJMEsgLrqIr4MhYDOBbSezukzQCnHVJuDXj6p+8gXIWjJMF6h9rNZcqn+zi9CSbJMGmB8h2U5yBdB1uUBJeXSCcJ9cNzJwVIgW7VoBWiFxp0+iNSK0jHCdp3cXoTHM9Bt0LcVo10s0cep7iOrtTexkkViBKBzEpkzcdElQF6mRYIU6BrAeXaEt7Ltyl7PVTg0XjjDtFOl2ic4zRDTJJVBPlCjSJOUVlBmRfEvQmekuT9CY7vHgKQ8xknx+65eRfsbJ7j301Rko9ibJpXgSXzArXcYvv+Fo3FFo3VGlmcUXYniNKgtGLYG9DtD6k3awhHoTt1dh9tEEpFwwq6wwgtBJfWlunXQx7ef4ISAmNKdt/+iCDw8ZshWikC12X33Yf09vsYAYUx9JKEcZayXKtTr/tkvkeaJKTjmMQaFlaWyJOKSMxcSSodFoIleg+3+eH/73t8I0659btfQjoVYSEE7Lz7kCc//5AoSQkQiMKQawNJwWsv3ubq11+ic/MSG//iTyiznF53UNk21dzK7ur6Cn/rn/9d/uK//mMePnlMpjU1KehJies4hPUaAsuTtz8mBdaureFohTACk5X84g9+hGh63PnGK7zw668glTy+JDN3nJiOtyEOFnGWUXoUCHbq5ek8utPvu0+D/T9HmeNxr6Y456e0PZetOZch+/x9mZtmy5/XxqEWAQaBOpFV6tnAuaelsyUfz9ZbnDHGqQWfY19zkll6SkyM+a+mOvQp8ctT0udkc/EZSZzD9BkPwFl2CIeeNI6JimbzzXl37rm8wKZ9Xrr+2SGthH9H9R7EoJjWzzzRz7M6fM4tdtDEwfPJi+uYut50O+Lku1MJwmPUoDg2rtnPJzp3XroooTNLxU8P/PD9KXM83cgJ1a5zo3BPNzFdD1QRxavq957sko4SnMDDC3yW1xf5wu++wcK1ZYqsoPd0n6d3n5IKi9+qEXfHdAdjwtBn5YV1Vl+9xqQ/ZufBJpvvPeS2LOnpgGic4EpBdzAkcD0Ka/ECn8XLS6fC2tpik8KU9McRsiwJHUWBS5RnCFvpX6d5jvQ0jx/v0F5qcf3OVW5/8xV++d03EVISem6VVwiyKOPJ3adox8FxNMuXl1i/tkJnuYVJCvqDCZsfP2UUpzSU4oN37uFJxcN3H5BjWW43kHlBehDozAt8hDFILA0lqzaynDRKcOsaG7jYOEMJQb1W6Yin45jMq7w6eYc60gfec4yFeuAhJylKyErVSisoDKUWlNYgDQil0KGHtZY4inEKhXE1SZbjKQlJivBdWOpQGsskzzFpwfZ+n04jxJaWSZLSWGojsEzGMfV2g5YRDJKM0e6QSW9M0h8jQo/apUUmOwOyJCdYatBe76BczerNNfbvbWO0ogxdTJajjEFbSaYUejTBRBlqoVEhUvUQO84QeY4oDKo7pgw07uVFgtJU8yEFxnMY9Ma4rcrrkfId3LpPkWRQlPR++YDBg12EU+VXeYkxhjwroCiPmDglB15+jAWtMG5lcK7Sknx/wsIrV5h8vImt+YyLnMBCEaXowEPEOa7nHHhREgdnC9CK1itXyAcRxTg5sCU4OMbCIqxAKIG33KK20mbjRx/RWGpgtMK5uogoStK9IWmSgqswk5iw5uOttCniFKdVI++OKVKQZdVfMymIY8Hqd76GsIYyzRh98oja6y8xetJlcG+buDuuDDtdRTaMaQQu9eU246ddsqzAXWgQLDUp9od4zRriLARlGgmxJ6HQ2cDlGWCz1hI/2MbkJcZROIsHLqXjjGR/gut7hIsNrBRkZYk5WCupNSbOeLrfpe5oBlGEJzSDIgPPwxMBZZZTJim3vvwi1964hSlL4t6YnbtPSbOcfm9Ikedsb+/S6w/IMIQLLdwoqc5TnLA3mTDMMlzXpen73Hz9JZZvrmEmGVsPNrj/0UMa11ZxkaRK0lxs0t/u8uaf/Iz21WUWXr6KkJBHKf1Ptuh3B2TjCfV6nVroE8cJL1y7QqNZY+31m9z7s3fY397DcRzqtQDX0dz59deP1Jmuf/0luk/2uP9fb5DHCZ2lFmvri2x8/ABZ5KzUfOqdNo82dhmOJ4xGI4JGyCdPtxBIZN8lywvWX7lK46KuaE+s2+EG4PR7b842sABijuT8HGbmX2s6p43n7sIho5RZRulU+izo6FRZqSS2KJ+1cwwlEifyz69rhqg4Z8Dnxc2wB/9NvTw9zcVFT+nm+V177vQ5EBfnyGdmyeznGsnUil6QGDi9i4eHzh7jIMxF/GcZ7J+l7el0GtFyCmYnpj/OEQwdyz6PCT63vvmpKjJ9gqZiYswswXH2y8n2niHL9ijzcfe5xxH5cwkLzkHcp4iTM9fz1MpPb97O9t8+G99F0mnBcY7c3c4ELbTW8uSjp7hC0X75Cs1mg8WVNp3rywglefTOPZ589BjPd/FDnycfb1RqG1qhheALv/k6Ukne/bNfsHxtlcVrq2RPthgrhyLL0IFHI/CZxCkCaF9dprHSnjseC/g1H5vlFKVFSsV4PMEIRaPTxPMcsJbu3gAtJKUxfO0ff4srr99g6+MNHn/wmM5ym8DxeLyxw8pSB60VSitC38MYQ3uxRbI/ZHO3T2ENYbNFox6ysb1H3ItwhcKvBUxGMdKrbBVaCw32R2P6UcxiqwJhkyjFEQKpBFlpUEpiXadCPMcJIi8pC4vwJdZzUMbgdOoYa5GFIYtTigwcp1IdUkpVCK6WpEmGU5TkRcG4KIjGESoIqHstyv0hkyKn6TjEwzFioYlIc4QQDMsSpzQ0Qx9TGKQvkcKDrACtQAgG+wP0YoMSaKx22N8bMh6Nefj+Iwa7Q6y1rL+wTvfRLos3VrAClKPw2pVFYRqllEmOo1Ultchy/AMVEy01EyXwlMIdRUjPxQzG2JUWWnvY3SHBQp2dnR75h09YWG1XApnQh9IQ1jwcR6NtFQU+nSQU44Rib8To4S5lkiOkoL7YBkeBpyvVsTgnHcd4rRpplJIPY2yUghZk+wPKVo2gERAnKf0neyy+eoXRo11UWhCPImyUkHsO9YU64iCiNlOGsrYoEFLitmrVVVsahJSYA69CFgtSIAOXycebZMOI3NfgSJK8oB76pOMU3QyxxuAHHl67Tvp4F+fyIvnuAJOX2DyBQURkJFlR4qc52TghWGqSDyY0X3mB7bceEj/pIaWoIs0bSxanSCBcbmHyAvfSAuU4JY4zaljUcvOZpxemGDrz7pfz4MsZ+a21xNs9SgvKd6o8xiAlFIMIJQVSCpyGz+TJPqQ57kKDvd0u4yhmMogRUtMdx2gkpQUpLEOZUa8FFGXO4609YizxKCLPMtZuX+bqr71APklZ3OnzzpvvoUIXz/cQeU6yP4DSQFbgBT63rl6isdxh5eVrNNY71NYXGG12uffdN3m6tYPQirI/odFuI5XD48ePWGy2eNrt8smfv03r5hrS0Tz54QcMH+9itYSyRAYeYRjghQGe0Gx+eJfa+5dIo8orWF7k5InC+prFFy49ux+FYOWlyzQ7LZ7sdgk9l/3RmFAJ2p0WwWTCbmZ4+HQLFbo0mjXyNMdxXRytqTdD9vsDHrx/n9e/88bpC3d0DYqD/0+7w2aQhtM2wdFmusC9NHMFn/w8TcpeYCMKKleoc8pfpI0LpZluXAi5f556T2EKiwOPi59LO2cwY0+8n5emvh/iI8/lSfOU+mclTtPvPkv6G4hzcZFVOQ2q2qmnAyRt6kCe1tIcVXoOT9SpfpMv0LN57X3aJThW7rQNPm/qTqUuPmVHppqZVdM5FQbNIVxm6xN2tuQh3396A3/WEzuvY7PgcI6O4tQhn43tcZRmFtcyk2/O4s/VlxQzDKmZNmbPe5mXbP7qEc3FBrXVBUrXcPXLt4n6E+rNeiWaL0oKDJv3tvA8l95gjFIKB8isIRpOCFo1Vm5dYnf7P1ImFkWGNCVSKwpj8YMAkSU4NRflHAcD1hgQAlMa9p/ukxUlSmlC36U/iWh6kvEoorefYYG1pSajYYzQks61igj6qz/8IbI0OI5DmqTUGjWGo4hhGnPz5euMdwf0BmMef/yUrMj4wlfu4ErFaJRQisrb0q0v3qK3uU93o0fguYzjjE67URm42woWpHFCp91A5yWjLEMKSVDzqUuFHieQJIhmDSsgthaVVa5c5STBKyyFgMJYTN3HAnmc4UuJFtUejtMC13dJ4xQ3zdBxgqqFaFHFJlCloRYGRHGC9lykBfIS7Xs0tEIWhrI3xg08irzAtRZ54AK3LA04ApGXWAnWUTRurGBCl4XLSzRW2mTjhP5On93He7z7w/cqN6a1gNu//gra0+w83CXwXExpKrsKxyGJU4RWjIYTjDEUWhHXfeo7A+LeGDmIaF5dJteSMitoNGp0JzH5OEU2AgpjKKKE0HVIswJZ8xClYrjdxy0sxd6IdJxglKRz5xIrL1+pvHYlGV6tUquypTnaT3lWMHq4y+6vnoBTRa0uBTiOJutOSNZz1FIDMY6RlsqovxlgBFVsiyk3kgIoeuPKfe5qp4rMrFQlKTnUc7dgS4PbrrPxFx9Q7O0ilpvovMCmOVF3wngc01luobTCRAlJlELdR1hLmWbkjsK6PmUN5CRDUJLsDsjiDLcoiQYxxdMB5fawikFRlCAEpbUU1rJ4cwWlJcUoRi/UseMEW5REgwn+Sqtyw6sO9c0vhhNe/L6pGDuTB9vET/bQjZCsFyPbNZx6gM0LGpcWqN9aRWiFFYLxVmV8HS42EN0+piwp85x6GLK8toLbqpGNIvpb+1grSbvjA4CVcu+9u+RZTm5KNrd30VTrr5QikIpyEvNoc4/6YhPXVOOouy4L19e5853XWfviDZSjKbOCweM93v+3f8XT3V1Gk4jOyiLLy4s0wpBBt88kSlhsNHG1ZufeJuNHu9SvLVPGOfXFFoO330eVhkYYoLVmb7/L4soK0nXY+umHtK5dpdFuYtOMeBJR7yyifedo3gBWXljnS7/9Vd75wdt8/HiLF65fZhInlKaEeoN7H97HCVzKosQKiNIUk+Zcu32Npw83SCnZfrjN65ZTnfPMjYF0jBl76tIebIaTu+EEL/ccIuK0ZEzlTlmKA/fP59VzgTbON9g+n1t7bMSfN7t9mqF83njOIwIu0tYp9Zxquzv9/ejHOSTALEFjT/t4vB+fl+Ocz5G4mMKiTuvbqRviYtQx9sDf0iwFePjzlHarAz7Thp3593Bjndb2nHdnbfQjVck55Q/R7OeiDj/rep8y90cw6JTpObOumTqmf8zD5avnaZ9ZF4OA9jxIImZc857Su1lJzKcz7j+Dqp2b7XDE89iTU9kroQjdjT2S/pheklMfJ9z4ym2aK22axoAUWFuys9uj1WoyGvVZazY5BDky8GgstRBS8sLXX2a0PYC0JGiEaKkhS+kPRiRFyUKzyaSQ3PnKy5W++tQ4jLEILH/5r/6UBz/5iKbvI3yXbn+A53m4jYBskpIVJa0wACvJBSxfWaK10uHBW3dJ+xM66wskw6QKxKUUMtQsXlpgcb3D03sb1EOfSZRw5fIa2nVRrsIvDUWkuf7aTXYf72DykizPiLMcYSw72/ssL7TQvktQC0hGE8r+BK0kvi2xSuMhcLKCzBoyQEQJnuviag3WoAFVC8iTjFJJjKsoqFzcOsaiPI1xNFIIXFsiswJtBcJx6GhNlmSEjYDRJMZVkkJAriQS8OMUXQ+Jiwy/2SDujfHCAAU4pcUKiwk9sBaFIS8NURTjNUIEEK62CdcrVSorBe1LizTWOlAakiyjyEui/oS7b97DWkutEdLsNJBKUXiSqD/BlJYkLyiSHC9wWb19ieGTXaQpSdY7NKWiv9tn0h8T+A6OFDRaDZTvoNOCkkpNy1loIq1l/GiXOMuJuyOkFbSRhPWQwloG7z6m2Bux9s2XUFqR9Udo36v2lNYIJfEaAc7Ll4ke7REPE6SrcT0Hf7XN5OEu0d0tmr92k8VXPPI4J98bIvMS5WhsP8IkOar2LEKu7tTJB1EVZVFKZiP8WmERjkIWGu1I/HaNJEqpBy7ZsAp21lqoIxdqpE+7qMKQP91Hr3eY7PTBc4iynKVLy+Qbn1CmGbK0ZEVJ960HxDsDgsU6+f6YQgmycYQqDNJzCC51qEtB69YqyXYPpxGiAg87StDG4jVCwuX2cThwAAIv4s1lLoExw4+z1mKSDPISt+6DlhD6OK060tWodp1ikqC0YrQ7wPNd0lFMmRZs/+ohvdEQayuj/X5vQJQleKMx7Uad21++g+Pqyp4GUDWf8WDCoDdg7/E2/f4Q13cQvouvFK7rcu/pJg6Wl25dZ/H2JRzfQQUundtreI2gkt5ai1PzSfaHFElKWhTUPQ+Z5JXdh5Q8erJJqF3KOAFjebC5zeK/+Uu+/L/9B9SX6jy5+5h4OEErxSiKsXGG6/sES01WnOv072+RtibESUrdGJLC8Bu/+9Up97HVRLqBx9d+/zcok4y3v/cW27v7XL+6Tj9OEGnGjZVl9pWh3x1QRjnNZp2bX7nBwqUl9vd6FJOIWhichPEHf1mmmFqnIQlnvp4T52r2ijztWj18f8ZGs7a6jAwWeSAN/MwINfMJjKNuH0PsOFVT4cjr0l+n58izUBIx5/msvLO8cjHzmzm/Z3E0exy+fT4E1TxG6Oc7p5+/QfcFvpxBmJ2aKoru08sKTiLy04jteRT1BXt8we6J2XrmdW222ilOxexletE03b15sKh6f0F2x1RF58HHqt1nH59x80+Q5fObnoeXW05kPnsHzicKDps8f8RTgO/Em8P3h9KN48j6qV2a/Wktj+8+prHcodjukSYpa7fWybMcUxgef/AQX2lcR5IOJ/iBizUGz/PxPI0JNPWFBq7nkowj7n//PRp+SAGUZUGRplghCQMX13MYJoKnd5/y2m+/UUkvDrqttCIeTLj3s7sEUpO4Aq0V6zfXGe0OiaKUy6sLxHGCQdAdR8RxwlfeeAEpBR/9+AOkUhWBbQxKiEp31dGUUc6HP/0IpKA7GIGAvZ0ueztdXv36S3i+g22HtNbabH6ywc6jHdZvrrFyeYWtD56ws9ul2W5UF5+0WEdRKnA9l1pekOUGLQpyIC1LrBAESiOLEqE1JQIV+tiiRB0EZMtMSa20WGPRgUdWlGAtwnfQoU8xSfH9KsifyXKSKCWexPi+S+5WRt15DlZKbF5ikpj9OKblKALfpYhTZDNECovjOcRpXsWa8CRRkqEKhS0ti8ttTG7wOjXiPCfqjYl6I1rLHZSWhKGP9BwWVjqUaY52HYw1FFGGcWSlLiQE2hqGvWF1lrOCIssJlML/+h3Wry5h4pwnP3gX0QxwF5rIfoQYTtB+mzzLUb7DpCwJshyRl+jARUxSOs165QkqzhG28j5lioJ4o8fWjz5i9esv4rbq7H33BxT9IdLXmDRj8TvfRC4uVfPrOZjSkCcZtaCNUZXkJvpki9aLaygpIFyqjNGtJS9KijTHwR4hztn2AN2pTR2hmWBSh/DCd2i/ep3HP79Lx3cxAuzGPmKxiR3kyMUmNskw44SyEUCcIZWgHMaEtYDRdo9yHJNmOUWUglak+4KkO2YSukhrwUC9WUNicdc6aEeh6271e7VD8mgXpxkSLNYRvoPTDkGeVImyWV5x+0PvDKBBFZvC1UhHz/Ap7BEgyycJ2d6wUoFynMprlQdlnDLZ6uH7Lu5SE4yhc2OV4b0tkk+2SOKUzUEfGfrkk4Q0Kwh8Dx16RKOIYhwxHo5pLbZoL3do31wlWG7SKkqWhzGXrq6xt7FHNIoY9Edsb+3gYHGU5vLaIo7WrHzxBuFiHaEktrRHUlKpFdH+kI2f32W/X6kDttotoiTDrwek44QkzVj7lTMXAAEAAElEQVRotyo7nyxFKEH3yTa9Xz2qXCJrRZwm+IFPnCQUCBabiwQLTVqXl1h69QZ3f/IhtiwpEBS2JFxsHl0s0yDZbwZ8+5//XaRWvPXnb+H5PVqhT2wsuJqFTsikP2J5ZYGv/8Nvol2HH/+7HxEPJ7z0xm3e+J0vnWCyncaXqph785HpUznY03t9+vmsO+fkZX+ibmEr70jygNIVh/ZOp4rfz0kH/TsXVzmwOTyNcXz06rz4H3PrPqVfTDc4/X5O+TPwkudKs/f+zLpb7DNC6xCOydmNdMF0FiEzD6X9DITjvPT5qkWdQXzPEKZV1qPBXRCh/ZSExVwjmVmM+FTus5hX+txund7TAxbVzMaehRHPZuT4388E6cwFDqemGa7YiX13xPq3z4UUX3RJjkmOnueg2kPCkpnxnqINOuelFad8mK3jzAN4BjCbs33tAfA6tl6npKOZt5bdh9sM9gY0Ow1+83/xt1m8ssTWvU32723x4N37RKOI5aur9D96Qhi4FLkhzzJqruLWr72A67lYa/noe+/y6INHlFIQAHFh8MOQNMu4tLbIKMlZWGjz5L1H7D7aYe3WpaO5OuytEYK0qNQb0jSnGBjCZsDmxj7WGJSrieOcZitECrjy6g2ScUJ/q8e1125w9627CCNoeS6tRo3t3pAoSSlKy4tfuMHTB9tkSUat7jMcjLGOQzyKCZpBFdtEwAtffQlZWOLegJVry+xu7GGzgqIoMVISuJpSCdI4Q3XqqN0hwkCZZoS+QxFNKOshPqBCjyzPyeMUayy5MZTW4JUSV2uUq0myggJLmmWYQUKjCPAR5AdqPpExFK6myAtIM1Q9QGU5TQNJWTKSEAYuDU+TFSWlhEBBYEq6eYaIU3ygttjAtRbjGaRWJHnBZBwj8pI4TrACbFkZSHtqRFlWSH4tDEgOVIDSKEF6DnmaYTIo0gKZm4rTnxqCVkhalowe79G6tozuNFCNgHC1zaXyVfb/8lcsv3GTzV8+oNzoUhiL62gYx3Q8j83tHgurC4i0IM2KKsL1MMbiIo2lNAa90EQYQ/K0y/ZffEDz1Sv4t2/S//HPcNwGenWNwft3qX/pwHOSrOKSKN+lGB4QaP0x2TCmyArcwMUTgkl3hLApNs1Qnq7sigCkINnp01hqnvDkeXjmppPMcoL1DqO9ASs317BigDUGvdigSDN0q4aJM0ZRFRtE1QJ0bsg2u+RSoZzKnSx1HyctKr8xoY9Ic9ASd6mBXmyA1mS9EV7gICSodr0i1JohNi8QDR/dCFE17wjEHrsPtTru1vKUpDyn4vQfqOQIKTCFqWJyaI2QgsGjXSgNjaUGCMm4O0QLgWoENOoBWXdM2h3hrbQoo5TeW/dxPI+dSUQqLIueR1FYlup1HMdhEsfUw4Bef0je7xOPR+xv71N7vEX76gpu3cf3fPKipLm2iNcIcUMfZS13Hzzi+tV1usMR7tYerQ8e07yyRLjYwK35CCkRUlAkOQ+/9w6PHjxlp9fn+voq+B6+sZRxxt3371J3PTrLHZwkx0jYGwzY7PXZ+eV97vyX32HcHbK00GYUJdjSgpZIKzCyUs1bfv0akz97kyLO2EliwoUWrctLJ/ESqsVxfIdv/bPfobbQ4Od//FMe7u6jlaK22OTmlWWuvnyVl77+CmmU8MN//X36+33W1pb46j/4OuGBTdQhXD/hyecg+vjhRjidaTxzyc9jyh1eTbOX+jlMy3nvLZXnOKmnCa7PGetkPk52fB3OvzMvjA3OzWyP/XPQ6Onl5z2f1+ZF0tGyVrjCcQLqOeu6aJpHwH3+S/w3YXNRpaNxnIoQn05gzMoODvnrF91eFw+iN9vu1IJ/inQIVI6LA+eT5vMQ/3muiZ+JyE7W8Rw9m1N21jPVOfvtOQ/P+eWPQuZVv2YNoc874Hbm4WCIlftd+emnaoY7OJ8YmV2N2fmdht7zKJGDf4wlm2Tsd3tc/8aLLFxeAgSTwYTNh5tsPHiKjXNuf+UOke9DXrIdR6x32rTadW5/7Q5Y6D7Z493/9BbSwGQcIQIPKSUFEAY+jusy2u/TXGjjJRk//rc/5B/+738f7eijfvuNgBe+doeP/uJ9PF1xFvOspCxLfNepvCIJxdJKh353wPUv36Z5qcOvfvAOSkouv3iZB2/fJ/RcSmMwxmCFoNkIGI8TNh9s4yrFlZevUmAYjyI+/vnH2LLktW+8TH+rR96LWPv6y+TjmL1PNmnfXKDhOqjCEmcFHpY0zrBJzoKWlDUPlERiK3erBvxWndRaCFzSqFIFERwgZ0oiC4uqu6RJit/yGZqCySgiTnI8R1LkOaGQ+KKyTxDCkhmDkxeoMEDYA8TQOoz2x6QKijzH9VwarocUmrhM2bElO0nMYqtJnmZgCsyBfr4qDcpCFidIY/E8jXY0ubK4gUdWliSDCV5eIEYV5zpKM7QU4DrkgLQWISXSVkb4RCkizqg1Q0oAJbGlIRuneIGHaIaohTqbv7hLb7vPqnYYxynLV5YoN7vo0KNTlAgqNbm8KBl0RzRW2jieQ/TRJiQFZGNsUEkFos0u6TBCANpbQ4RNojglfriNfyepPEohKNOCNChxJynWdyq3yVIw6U8qrnxQSXsQEq/uo0LvGQcVCK6tAJZ4o4e/2sYkGboRnDhXAvAuLRAMJqhOo0LGX1hH5CWFENhBjCoKEmtAO5XHMCXJpcSUBpK8QnClIOtNKmlBXlDsD1GeQ219mSKoIpQ7SuBdXcRrhwgLyf0tRODitOuVp6Y4o1QKpxke7+MhmFCSOR4vZ8YjEI56BjKsJRlE5HsjXN9BLjUxpcXkBYHnUGYFuh4QLjUpkwylFW6zipWS7AzIBzG7v7xPstnDu75MOehRa9RJsCytLbJ+dRVKSxEnfPjOXfK8oJSSJSWRRcqkV9AbDBBCYbKCLM1wg0oNKxlHDAcjtJRIR1PvNNnc3Obxv3hKs93CbwQEjQCtNK7vkEUpm/eekuQ5d65fQdcDRklKluW88+b7THojbly7fETkayNZ7HQo45RkFJFPUvofPCU/mNAky1BW8/j+I5qLTULtEPfHbG9skGcW13H41n/2GzSWW8c3zPEH3MDlq7//69z59hfYfbyD6zrUl1rUO3XSScKHP/wVhTXsbeyyen2dr/ze12hfWjh2zctDT4Cf+hLi/Pt25mI6YszPY6ieVtcUonus3s/Q7dP5cWL2Nn3Oap+zUyfwzvnln7nj/yyD5ix0dibb7DycJaU4jiPN+Xy8/Xl9Oq/c55g+hwjdn22TVOk0bHF6mech6J9jmkPlC3tAGFxAVDlvXcVpMj4x+8Oe/D7N1Zjt6xGn4hRoMY+AO/ZuPmFzRMSdy+F4DojzPFvj1GqrD2cZhcWjiMHegM5KB8dzyKIEoRTeoZrBnLrtvHl6jv49m45nBN/xKk+u7axh+JHUojQIIfjmP/k2ay+u89W/+3WEgM27T/nwz9+ivzNApIa97oCXPU2j1SDPcmxagCnBlZi8wBQlH/3wXfZ3u3iuh1aKKErQroPvalyt6Q/H1AKfyXCMozVPPnzK/uM9Vm6tHWItFecu9BhNIkSthqMkQktyDAvrC2w/2kXInHgSkxU5N7/yIr2n+7z5H3+OEoL3/vSXuEozSlM8KelNYsAyGE4QCLQQtJt1UIKNj7YoSkPN0eSlIR5VAdmWr68w2OpCaXBCn/7DHertOpkA13dI+hO80Ef7LllRYMYJCks+jglXOuTjGCuqGBaZtei8oCzKSu3J95DGYKwhjWJy32F/p4+jFYHrQQGlsIzjlJEpCYWi2WrQjyIcJVFLTURSUFpDDjhu5Y1HS4USkkU/oLXcJqj55FnB/f0ey1dWUK7DpZevEg0nxPsjsu0eaIkYF6AqxNpRmlqjTlGWmLLEqfmknovMCoxSRFmO1ZoCixKV69w0ykjTnHo9JI0ThOcgBdi8wMaVdEhohUlzolGM47s0r69y74fvEboOQmt0aRlvdGmutjHG4Gam8hImBJmU2Kwkur+LcjWitDiuIu2PKboDpOdQBh5FkuFoTZ5b2BljpWX4dJ94MCQPHERRcaKLOEMYcCVQFGhj0UmBjXPcwKO9tkBRlNRW26jA5VB6aS24iw3KSYLbrlXG1Ac6+/AM5loLRZQQ7/TxXQc3KQiuLVOOY/KnXazjIDwHb6lBtz/GBh6mKDFJjmsFLDRxmiHpRhdHiComR1ZSxiky9DC6ihWitEIJ8C53cAK32oOBi7PcQtY8bF5SZgVO6COaIckoImjVDvp8ACUuDEpPAtOiN8YUJTYVJBs9hBKEzQCR5KhWiFAKWXktwCQ5tmGIhxFgGW91ifdHxFHCZHOfWrtJ0R+STGIGScbiUptLX7pF1h3T+OQpoyxBxjmjpKDTaRImKbIo2R6PyPIcJQRJkeE5DmHg02nX0dpBpBmZMcgwJCWht7NHuW0QWuFqh3qjhicllxfaSEeRa0VmSpSSNBZatLC0aj47VI4GdGkxpnJgILUkG0ak/QkAjtJEpUVbmBQFWEiTDMqMyVblBSvwa7z69dd4+e9+5fjkz4qTOEDkpKC52q5cy4pKbSgZJrz773/GJx8+ZPXmOq9+7VVe+9u/xsK1pRN1zKm2qvlC6/454TrzuJez22n68voUKN3zRNme7dLztvMpyItn5e2z8seIiVli7LOmTzmP89IzrOGMCo9t5QsQSfPwuc+R0Pgbk1zMpvPtBk5y1p+j8pNFzpSYTGeY/SrOKPus6NxqpwQB87p4SDTN54YffD8T0bfzMFrOPuYnBZL2xN/npec8gOdxTA77czgWMUWY2emeHYeQh2Rt1J/wk//wU778O19CKsmjn39E78EO3kKD29969cCDDSfmyZQlk8GExsKhP3J7/CaYpRifawvaudvvxG9rSbZ7xLtDPn74FDf0ef07byCUZLjT54//qz8kmUQM9ke8+vodHKXAWMokw3U0a7WAZrOOrzTdx7u49YDeVpd6s0YcZdQ8l9RafO3QaNTY2dlHOZqsMCwuL2CBurBsf7JZERdTPU17kyq4WlFQ0x7UPGyU8tpvvUHrg8fce/Mu0STm1W++ypWXr/LTf/tXDHtjfMdBFVX0bi0kBsjznDiuuOZ+3ceTiqdbexSPCxaaNYSE1mKDzXub7G/0uPb6NUxWVgEFpay83/RGtK+vsP1kDyUFgRI4xuKHleGwpFJ9koGHCV1KLSjiHBVVno1ya9Gui3YchBQoR9HtxXiOT2AF2q306KUj8Zaq+BhxnFJYRZJm9Pf7aGPxXRc3kEhXY6m8PunAY3mhRRGn+I0abqvGKEkp0oxamXJptcPj3R7GWBzfwS99JnvDKoCeFJi6T60R4rgO2TAm6Y4I6gHBSgevXUPXPKL+hNHOADGOmYxiPCXJsoLcWJSsvFcVUVK5xpRVjI48L5GSChlfbVNmBTXPQXuaSEl8pSsPSb5DvTAMXc1ou49X95FphmjXEcOImpZkvkO/iClHYxatpKEkYqFO1I8wRYn2HJzAwxpTxTUpDLKwLF59ifGjAVhQFowUqNwgXYs9CBroOJVdTPlwl0xUZ7PsjSjb4Vzuqwxc4ke7OKGPtQZVD47O7SG8iB9sY7MCJQWpI5m8+6iyNZASpQRmHJPs9CmVRliI8xLdHyMWmwyLnMV2DVn3SO5tk2oXbXPo1BGeg1ayCl4IyE6jiukxjLBxyiRK8DyHfLOH/9JlzDih6I8J19q4yqtA0YFOtS0rRw3HYN4p6RhqccB8yiYxXuAzerqHrvn4q228er0iJEtDMYwqyYmtHBXEUYpSgsJCstlDlAbd8BjmBbsbfaL+iMgUXFtZ4r0fvEX3/iZLawvUHYe6dLHKstHts9Xr0/Q8Fhv1KjaJlCw0mzTbdTJhK/VFLJcXOwRC8uH2Jv3eGIGl4QfUwgClNY6UGGOIjCEdjDCmxABZWdJZaCG0ZmhKSs8nSTJsmuP4Pve3d9ENn8VWA7ce4DQCnFpAPfDZ7vUo8xwTuLh1n43NXUa7Pay1lFojXIdLX34B5Tkn+HzHbpmZB6EVR16aBCy/eBkdelx5/QbLL6yjtDzag0dX3iFu8FmNZS9S/GhziBPjeu46L1rmGL5yRoVzL8NPNydi2gXXLG4xD9c4s1ufHzHxXDaX8/Kfkxumx34KJ9Y++9cKqOKeVK0c56YeQMln2/l4nz4H4+6/eeJCHP5zAYrqc1v3syi+UxbpcH8cLORxL0cnS53c2/PaOy7nmZXF2KN2TmPhHydJpgkfC1Mek467Xz1GalhxQuDxPAT2pxIbXpgatmcC4Wcr8Izc6G/1+NG//UuufuEGfj3gj/4f/55sa8jDJ5t84x99i5cDl2cn7VhxpFI0FhrHWnjW30PCTZw9QWKm2NwMZ0+Aqod88rOPeP977/LSN1/BFOagpMDEOTKHVqtJ0huRTBKi/TFJFFfuG4UgzlK002D9lesIVamdlLmhXa9RZhlaSoS19Psj/GbAt/7Z3+ZH/91fEKc5Qkq01ux8soX5bVNdkEAWpew+3MFxNJ3Ap7CWeBTTqYd0N7v8zv/67/PC2/d4+PY9Lr9xA+UoBBB6LsvrS3Q396sgfY5Dkmd41iKlJHAdTFoyFIY8z2nUwgqZSAp2n3ZJS0NeFOjApcgK0iwnCHwWrq8QN0L29waV+g9QFIZAWZQQKFm5xzWtGmjJaGcAvqahFJmUOHmJdR2ysqhiMjgSVRY0fZ9MCIy1BL6LgMrY2HGJ4pxmLUQaS1cIcDQ6yxFaU5QFjuMijKGcJFhH4yOJfA8JiElCbg3KdyizhChJiPIcJikf/MV7NJp1rn7xBk/euU+SZDiOjykrO4bm5UWEEGw+2Cbb7VNfrJOnOS987SUuf+Eae/e2ifZHqPU2epxUMS2sJZWQmRKjFVJJTFEi8gLpaOJxQvOWj78ecuhRQR7EbkgxjBzNonIwWz2KRkiQFciVFirO6boKr94gTHJkq4Za6eDsjyn7E4jKiijQClcKvNCrjI7zgizNMUVJMpog0wwZuEjfw3U05aHKlZIoC3nNQ6020bsjys0eed1De27lKnXqErZFiYlzMAa3UyePc/zFBkd665ZKKnDw3TzZJ+mOGI8nLL90lclOj1qnQfxkD+koLJAnBu1plOtCnKAuLzJ5/yHugy2clTZOq07Rn2ALg+tqULIyvG76yElKUZQIR5HtD3BXOzi7Q9RiQDmMKHojBAL30kIVGVt705Cm8gB3UP5CaQaU+O065TihdmsVC8STBNMdo0IHx3WI90aMN3vU2iGtly6RdMcMHu4QbfWx/Qg8h1hJEmkorCEvSxaVg2MsozSDjV2UMbhaI23lnSvwPa4srtLvD3nU6xMoRV0qJqMRSZ7R7DRZWl1gd7vL+/cf8/riAjeDOr8apxRlSavZYOXSSkWEAtJ1UEoiy+puUQCOoj8YEo8isiQl8n2aSuF5AYM4JqPav0HoE7ZqeO0awlX4jq72vRBIIWkstInjlND3SOKUW3deIEoTmleO21rMEgXHNAamGUsH+fxGwK1fvwP2pWd5Z+uYWrLPjMrMxYlmaj4NZfi80oWYhKekuRzUTzkrZ7U/79sMoXGMOPkc02cmVE6bXzGPYDmlrSmEUtjKJbUV09jrVOUHsHK63/nOAJIc99rS6W1cMH1OxMXzoKdVutD2uiD1Obc7s4XmGo2fV+kBsmsPiYVpxH+KN33oRxSO86uPtfls1Q/firlfnv07q4snjr17RqbMD1B3vI5jF7S9sE+o0w/r50T4HQsgdYTUHz/8Yqa3h0+mKPnFH/+cUX/MS195if1Hu+xu7CFGGZeurfP6t1+fisxun03PYf3VjTBV6dTa2sOu2KmmD0l8iylNFXl4ZiKOw4fzJ2n/6T5/9i+/y/6jXZIoZrTZY/uTDW5+6QW80EV5mjIt0FKxu70HStDd2EN5Dlo7aCnxgxqu7/LkvQcs31ijv9unoyRFFGEDn7I0FErS7Xb59u/9Nte/dJvtp7v87A9/TLNRR0jJxicbPPzlPW5+5YXqwleS0ppK5cJajFI4QjBOMu6+eZfX//avcetrd7j11ZeOxvLab32RnV89YrjXx/VcVFlSr/sUoxJtBQt1n0Io0jzDdZzKc5C1ZHlOWPNIkxRXKiajmI9//CHNxRaT7ogkSrlye516q4amCgontURbzSTPaCIoigJZC/DHCeRF5ckolxhfo8oSpRU5UGDwpUs+SkhF5W7TZAbXVG4X7YEBuyhKfCkRrkMuoQUYCV4YYIqCfhRjtcIpLUEjRB5EyFZJjipK8qKkX2R06ovk1En2x4SeyySNSZOMJNrHq3mVilJp8F0Ptx2w9NIllJb85N/8FfEowQBP7z3FGNh5uMPylWUWLi0wLgoWXJdcpiR5jlPzqLU75FFKOU6wpiK62u0maRTDKCHpR2jfRTmKpDeh2B9VSLrnVISchEBJ8pqPSXNkb0LpakxhSMoM5TpcubpIGfqMe59QNEKspxGTBDctyAcxeX+CsqB8F3tgNxF4HtJ3qb98maI0RFt9BJClBfXFOjYvoSipr7YpHI3WCjOKsVmBnEK6LVRGzwKK7hjn8gJBMySfJEhrUa5+huDJiossXU2Zl9i8MiIPVjok/TFWVB5x7EIdsTWgzEuMo8HRZKOIsDS4pcH2JthJStgKsAfSgKBTp3AkhbCIVkgYusg0x5EKR0pyKSjHCWWeEz8aUr++hvBdpNYnAL8QoiJ2p8HPTDoGgmfxg9IceI4SOIFHOUnB05T9CBYbjJ92CRcbNG4sk2xXEbOFBTOMMUXJyBRYoUiGEY4VpHlBvzSI0YTFWsgkz/n48RbKWpphiGqELPguWZbz0qsv4AQOZZKx82Sb3mBcxY/oDihKgyMEa0sLaM/jZqtOY7FFXhQ82e2yu7XLwvICtXqI63koYyjSnMVLiyjfRYcutbubZM2M+/ces7m1zWK9gee67EZjlKdZWezQ8QPqV5dRrsbxPQLfx3dctNZYY5iMJrQcF+s4YODFL7/I7e+8Tm2xwWwS854F88H4EcInZgocr+BTIZxTd+H0rT6Pm3zMNvG0S/3T3Nfzyvw1IOTnNQmnvJyHyl2cQ/o3k6b7PQe3P7E3Psd+He6HZ+5rD/GcaazzUOX/WT+c5VYV5PJzQPDOd09xTvq083HamT1Z/2e36Dis6fR3p7OljwEcW70RB5fC4Riqd4d/qnU8NAQXR/9V5TlEWqeej/2BucTRM/Lh8L/jFOe0xGN2NPNsKJ57TqeB5acVmU2P8eidPfgz09ApBY6IpdLw/l++z0fv3OP1336DdByzv7mHyQ0ryx2KScof/Vf/PR//xfs8+sVddu9vVYHGjH02IUdtV+1Uj/ZIaCFOdKFyV7r/eI97b35SBcKaWbvp7Pbg12lzbYqSt/7kFwwf7OEKied6PHz7Pn/2L79LGqW4gcf1L94mCL0KeXY0vuOQT1KaYYjUGukoHK0YjcbUFpvsb+yikgyNQdZ8Qt/HcRyiOKbebnL7ay+DELzxO1/izldfqgy+yxIlBG//p18y7o6wtlI1KyZJhcgJwTCKMMYgsKTjmB/8y/9EkWbHlqu+1OQb/9PfRErBYDwhKw1aKlbDgGISUY/HdDo1PMfBFmUVVdoalNYEThV9W3kOzaUm8ThlsDfgi7/zBms31+juDXDrPsu31qoozFlOaUo8pcnGETr08PIqkrPxnCqYHZAXJcFCC7ceEAALYYBTlGghoO5XcDTLKdOcNM4QToVAllohA69y2+k4BIsNPKVIJwm2hKbnQWEqA3IpSYoSmRToNKNEIEOPwncwjqxsFISg4/ncWl1mvdWiVQ/pbfVQvksCNK8s0r62jOM7/Pzf/YQ8Sivk2hiW2g380KOzvsjO/W3e/vN32H60ixHQ7DQQSpGOEkxWUE5i/EZAvV0ncHQV88EYert9du9vMdjs0X+wx/CjLUYPdokCl7weIEUV76PRCNFSkjoaVBVgTQpoNAJ0nDJ+uMvo7hbK0YjQA6WgsORZTpHlVQC+LKcsDbIWIB2FrvkV8TVJUX4VydgIgWp6YCxuM6QYJex8tMFoHGNtFRMk6Y6qCLnTB0gKVM3Hu7FMGiUHEe4to71BRaRMceLijzco0wLpSBquoNwf4l9awFlq4LgKGzhVPAxLpcY0mlSeiyYpYbNeRXL3ncp2IfQwNQ99dQECB2+5SVAPEY7EThLKKMW/vkIxSiooHHro5TbeSqeKUdIfPYM5s2nKDeWF0uGZM5Z8fwhxRjaMGW7so0qDyEuEVsT7Y0xWULu8iPAchr0R2Tgh70XkScYgy+jvD9jb6XL1xmUanSatMEAI6GUpJtTU2jWarRpLrQY6HWPylMJTlI6ku9tlPIoJGjUu3bzC0soSbr2G8RysECy2GjQDj1qnTj/LWazXuba+yhdevMm1yyukk4jHj57y8JMHPH28wXCvS+/hNuPBmOUv3uDKb7xKfW2Rq9cvoRA82Nvl3t4upaOQQK0WgLG0X7wEFsxwgkIglMIYg7RgsoJkHJOMI4qiYNAbUl9qIA9j+0xhIkfX7xmUxYmrbx4ic871aM/DauzxZzv9/tgfcYR7nKSMPiPWdKEr/jnbOJqrmUk7hT57rnSRrnxODNFPlWY5yad9P+33sXTOYOfiWfN+z9vfolL/+xzS5xtEb2YEz0NMnih49HhGHOdpKlAc5rPzM8wrN4PHWmufBRSbV+Z5NudUG9NFT3gGmFNIWHH890G+Z3Nhj717Vtv8d7M2a58qTcfZOHBIfYIGOq/yecMVczIcSRGYs6bPyi4ud/g7/+Vv49Q8pBCke2N0Dt3epLpInoz58R/8Jb1hFU/h9/8P/4S9p3tcvnmJlRcuTUk1plo4CF6GtRRJhvbdI45RkRa8//23+cWf/oJwoc6Vl68ihMANvQNR69SApocyL1nLxz/5kIe/vE+7HmKznI1xXPmVV5WKEVJy+8sv8sGfvYmUmuUrq2TDMa5QZGmO36pT8yrD5MhYGktN3vmjH+M1QhYur7DzaIv+YIRT8wFBZ6FB0AgRovIodPsbd7j39gPcwMOxluFOnz//V3/OtVeuEgY++7t9mrUahbX4vl9FbBWCpU6Lvad7pJMUx3OP9rQQguWXrnDzjVt88OMPqdV8uqMJPnD18jKdtQWy0EM4msePtlGxoVYPaXbqTCYxC0ttsqygvb7A1pMdLr1ymfblRQDe/B9+Bo5i78MnBzrqApOVOL5LudhkstUjDH2yOME7mHwVevhSkseVZyUpIM6KipNvDaZ0iOKUmrGV7rnvUpYG5VRRaXWrhs0LVFoF8FONkNJYtKMrVZaiJB9FFZJdGqznorXESMk4z7FFye7WPnXt4NZ8UmMoKciLElcqvMKQx3kVY0RJhJC88ydvkYwS6p0GQzPi8vVl4idbCFez+3CHsiiwBhoLDRaurzLY6lKrB+RpTnu5RdmqMeqPUYFLbgzj4Zgyz4mKgnJzHz1JaJQCu9PD8VykH6AQWN8l7NQhzalJQTpJUZ6mdvsqZruH57sUeQn1kOjeFrXAA8/BjmOKKEF5Do7nglYYVRFuBRadV1KhNMmJNnsUW30810GqSpUtT/PKPkAKbG+Cu9qimCTVfB8Gg5sFHwLKcYrrVK5X3XpQGUzLZ0hi0Rsz2Rviry9gGjWMgHijS+F7lHleXaJxTpkN8VthRZQIS1EaCt+hvtam6I4ReyOEI0EJ3Mtt8DTJky6hDVGtECkEYrOHu9rGZDnCGnTdR3kORZTitepYT2OipDon1h4ghc/GcsBD5AiTPO2emQYmxhDd26oQaSqPRH6rxmCzd6Ce5pOmEZkSmCilt9lluNmj3alTjCImeY670KLTrLP7cINhb8ClW5cIAo/9pzvUwgDT9OnvDzB5jg4Dmi/cIDcGOY6ZGINRgizP+fCj+3R3ujQ8n/VbVxFaYtOc/b0eeZTgFIZOq4GVEpNkGAuB0nRqIcZY/MCjHvg8ebyBEdDIMh7+6S8RhalcThtDs15nmGUURUlzpU3ZHVHzPIQVSKdisuAoyjTD812MAVGUlCKntJK8KDG+y4tfe/mko5UZ5PZI8XfG/bg4QIwrUP/pkfd50owTgdJm2rxQmuKVHsMT/jqQasEUF/yC6bQpm/f+UyOPnz49L4p3oQo/bd7zaM9j7o3n5BEHDOwjXfmZvH8DhNbnQFycPguf1964kITjvOjgp1Z4uKXsfEMhOMkZOLczx5+PMxXOqmgGsDy7eWZyXGCjnHJSxBHFOpv9dPGGPbr0pqUlBw2cRVicT0edeY+eOVNKsvbCOkJKSmNIe2OefPi4CkTlObhaIrTDi6/dYmhSNh9vsXl/i+/96z/n8uUV/s7/5h+wfHMNgGyS8sGP38dFcvubd9CBx/6THb77f/8PXH/lOkvXVghCj1/+4F0+/PkH1AIfX2p2P95E+JrLL1+d4gTY+ZKd6X1l4eHb93nnT9/i5vIiGQYhLCuU5FZw/dWbR0RPWRjGcUKjXmfSG9FsNSgGI6RUaNdBlyVJUTCKJgeuZA3KQDKIaIYBeQFllqO0QiZ5ZRQdLIKF1VvrhJ06eVYiPZeatdh+wlv//qd8+5/8JovLCxRRitYKqVTlVlKBKS26tMS9EbWF4+oFUkp+7fe/RaElT39xr9JHrwXQrCGW23zyi4+xBpq1EO/ABSmeJu+XlGnO0vVlth9uI63lyivXEFqx9WC7UgNTisk4IZCSQkp8XzHRgpa11fgCD1EPyKOKwPAcTWot1hoyoZHGILFopSi1g5vmDKKEKIpYWeiQjibgO/j1ENsfIwFjBfk4rrjvB6pGqRRIR6GUgrLESokyFptkaFdTFgV7kwmtVr1iIkkBUYZwDIW1Vb1KURiDMBYZukz2R5RZwc7DHVyp2Nvoog/ctPYKydqNFTpKMtgbYQ6482WWox2Nu9QkCH3iPMP1fPQkhtJSRimlMZU3qLykllucx13yskBpjfI0nqOQuQEtEO0QR0rojqjXfdxmgLNUxx1V3niUsRTbA1SSg+tU9gI1D880scZUMNhVVRyLA29FuqZINg443L6LUJKiNCgrYJBQaoFp16i1QhJj0FGGQGCMrTxQxenco2SzAtXwn8EjScXwsBW8KpIcvdTA1jyKvT5uPYR6iKMUtaUmcVoQbfdxPQfKFOl54Dj4t9fAGJLdAfVmnaIfYQYR0vdIN7q4N1ZpvrAOWlLGObLm4r96FeFo4qdbqIMggYwTvFaNbH+IG7iESy3yrKjas7YikI/BhgrGnhmle+ouSJ52yZ7uU9Z80vGYIk7wGzX8Th0pBWVeQF7SWm5SlCXDJzuEvkvvnYfEEmIMw26fa7evkk1iNu8/RSlFZ6VD0Kqz8dEjGrpOSyhiKynSglF/BL6LVppmp0N3r0cyivB8l8srS/T6I8bDMQvLHYzNuXRplbIoGY0m3N3rslwLWe+0qGlFbxzRdhXNlSWkpykwrN+4THdrD08oent9AqEoshwbZ5QH9hlIQb0W4ioHWRicRojXriG1xF9uYn9V2XblaU5QCwgbddIkY5KmfPnbX2T1tWtT03hwyxy7bGYojXnML06qFZ+kAQ5zXOCehPl3xskOzE/22f09q0L815Y+jyYuSkjPSzOM4WePZ9iEnoNU/A3g28+2xVmMVgtzl/EIZxIH2/Z0tz1i3p7+G06fu0H3KXTSp0jT03aKEHF68j4DJ2E2za4zM7+P1PDnwIzT9s6paS6Umnr3aan6uR2wHBeKzDR2Rr3TNhHiIqIQe/zh+PIcl62cUfh4D2faElph8wKTFXz0V+8h8hxHSTxP4QQeW/c2+OmP38Gtaf7+//L3+Mkf/gRfu+xu7vP9f/Wf+Dv/q98DY/n4L3/FT7/7c1wp+OStu3zx736ZyShif6vHYLtHFKe0goDUWlrNFv3hED1OGO10efsXH/GV3/0Kt7/84oGo/UKkMMZYXv3WKzSCAFMaHtx9zNp6C09Itjb26W3us/bCZfI4w/M8wjCs9OO1Zgi4xuCPYyZCsNntYusOo/0BL377dTbef8zw4S6TwQRPO4zTCUEYMopy3vrTN/nOP/sdhJIE9YD1m6s8ees+WZJSa9Zp1gOEtbz/vXdww6DybhT4latXYwgXGqRxyrg/4MnHT1i6vX4ktTncUm7N50v/4Ovc/9VDsuGY0tE8erxLPMlIowpZtKFHmpaVBGLP4ijF0mqdqDepVIKAZH/M437Eg/cfUvc8fvnHP6elNc5CE+m7iCSnKSCMc7RSaCVxtGIMECWVpycpkKGPpyVRaQmkrDwp5Rm9cUK9HpBoRT/PSYYTWp0mZlFjjE9alHieiwq8KtK1EAhrCYSgBHJbEo0TpIAg9EnKgjwqmFiDsVX08KAZooQgijJIcwIhIc5IHYMIfQyWLMko8oL2Wof1K8v094aYJEUpycaTXbyaz8aDLe5861VG3THSWna2utz7+V1ufekWm+88QocuTuCQ5yWlsRhRErRqiIkk2R1QSIGbFQBkhcVveDhXlwhKg0lz0u0BdhgjX7lM4/YqKFm515WC/PEumbGIwmAKi18PyKMMWVSucg9tBlRhEcMEkefkUlSIYacOgUsYZaTDCaXn4DUOXMgKC0lBYQyBqwldH+lpslGMKEuMgDKqVO9muXSqUz8CENaCycsq6vOBPVnyeBftONgox3UVWZKD7yL6YygKzGBC0K5RAHYck1HZ8sTdEX7gEXQa1L9wjeRSh8mfv4soS7zVNvHDLbi8VMVLcTXJJEI4Chdw6gFWikra1fCZjGJG+yMWfAdpLd5C41i8jmkg90yttaIwToTDmUJ283HM6OkOTqvG/sY+0kCZ5OTZiM5CHbdVI++N0KFHfamJbgbEmz22f3kf4zoUpqDlKCbGsvVwk7X1ZdIk4eGv7hO88RK1dp2XvnyHzQcbpGnKxs4epbF0agFep8mNF24QtkJWLq+wu7lLd3uPpWadly+v8tHGNspRtPyAxfUFOncukQwitt57xJN7T4h39llZ7lBvt5BpSlgLsUrST1KUtSwtdYiyjMHWLg4VYd9abGFsiSlyHK/yAOU5GgqB066jAhcQNK4u47guvuMyGcXUCoOxILWm02nx6u9+GaXVzDUyI4U/murnxGCmUJC5dMI59/UJPPAAmJ7Ap84jUqY+HUnTz6RYP6f0nIjfPG+hz+vK9iidmJP/MZDpeVzp03Ied8Zzoop5VYtnZauq52+ySqlkZjf/j0Nb/PWqRR2lC2Pbx+uwU39P55n2uHRSberilPszqdFx0cBJQDPzW/DMZuKQ0XFCuvCc6QAOzCM2T85AlYytfNAfS6cO/bhx2NzMpzQ0raZVzdl87rw9Iao7TiQcb3fWIH1ej6emYZ5gxVqKNGfz0TaPv/tTyiTFWVpiFCUMNnYp0ox6WGN5ocO4N6G71SNwHLCax+8+4L/5P/2/cV2XhcUWoigolOKTDx7SvrrEys1VWsttJjt9jIW4LMmMIcpSwlpAe7FJISTdrX3+4l/+J8bjiJe/cgcv9JDqDJ3Fg0vDDRy+/+9/wgsvXCHdG5JYwyBN6KwvkvQnuJ4LQOfKEo7vYrIMA+jC4CLwPI9RlhElCTrwqLku/Z19hHC5+sp1Ho1isv6EYhJhAccYcin45Bd3+cLf+iJL11ZACjqXFrj/049otJokccb+7oD2Wpu93T75gYFlnGaoXsa1l67wq3c+od6ucfPGOkUvejauI4OxKuZA0Aj4xj/+Ft/9v/4R+4MRtVrAfm9I4DgIaxmmlZedTrvienv1kKBTRwoItSRr1fjwpx9SpgXK15RSkCU5nStt8FzKOCNcaOAcRNsWByo6xtWU/RGFdhCextEKayxJUTBOM8ZpgRd6RElKHsVc9l0avk+S57jtJn49pNjpIzyXvDTItCKqjKkMho216CQnT1KsENQXG6isIE9yTF6SWkOfktZqh8svXqGxvgDAZBzTe7DDZGeALwU1JJNJzMiUeDWfcpKy/8kmr/39L9N9us/P/uinTEYTVi+vMOyO0K7L9oNtJuOYIstpt+oMemPKwrB8dZn9+1sYAQoBxiB8hySvvBAVoUc5iYmtwfdddCNAlAbhaBoNh6ww5JOKEDNJjurUkUIQv/+IcmdALCTxZIJMC8JaQGntAbe5khjl4wSMRWqFdBTSVVgJxTghjTKcdg0buqi8wJOKIi9QTjWXylGUEvIDb1PS1cj1DirKQFjiBzvU71yuvDNNnSFr7JHevACUo7FYbG4oxgl5b4JT84nKknGUExSG/e6IZi3ETmKYxLiBW8U68Rw8K2h26kR5ga75lK5msjOgiLNK+rE/Qqy2qXdaWEejEOR5ie9qzCAiD6tAiBzEF8nHMfH+GNd1Kq9uoxjTCA+Mzo8zJ49Bv0O1zLlwA0xekDzexxEKp+7TroXEWUFtpUm8PUDmxVGFerGBDD2inQH77z+CpSbD3hAlBJmF3FoUhnsf3McPPBxfs3H3MWuXV1i6usJLv/4F4lHM4s8/5OnGbmU4Dty//4hrt65SC3yu3lin3axz/+MHdI1hbanDMEm5v7PPKIqI4oRLb9zED1xW15YZJwkf3X/MqzeukAiI0xRcB9nfw5skhFevsxB6TEZjSmCwtc/jjW2SLCN0XdphDVcpRKCwiaV9a62aUyz+YhPfd3Fyw6QoUEnCStmgH8VcubFOfbU1FySfEDica1MoDv4/VQwxr+aLpRNVnkKxnPgpprLO3NefB3J5HlFzkTamkIB5d/6phMUs73M+inF2Haf18QLo4kWInrMxmdkmpwiLE+0ftHYu4TGvTxeNnXKB9Fwc8vnpc5dcnOjPiUmZt0vPQudPVmjn/RJHf104nQAqJ5u6WJfOyj5FNJyQbsyBQRWCPl34Wc3THJUquN+zMmel6bbPyjntdvcwt50GWAcVHRJ9J/VDj8hrjlbGQtIfUxQl9cXmlDrABch2O/PWPCNqrLWM9gd89KNf0Xu6jykL0ixDWMizEt9xKIQEKWhfXSYfJWgEWinGWcalSyvcf7oNdsx4OEEpRVmW3Pn6HbbvbdLb7HL5pSt8uD+iHgakpcHTisJIyrzg+hdvghS8/ltv8Bf/7Q/46R/9mLw/Yf2lK6zeuoQbuGdOdH2hSangzTc/JPADXM+ls1RHWEP70iJ+vYo43Lm6xBt/+6u89Sc/gzSn9B0WZAvbCNja3qUUsH5jjfG9TUZPe1z78kv84n/4Ma5S5IKK8PAc8rKCFo6Q3H/zExavrSCAlWsrlFIwSRKw0EtTcBSXrq2iEHiOYjCKeLjdY/PBFl7gsr83IPEiXvlHXzu+/hwyyao1uvnGLV79zmu89We/JCtKpCPBlMRJRlJUags1rai5DhJBvDtAaUl7fZEkyymHE1JSyrygyA1Xbq5XnEvHoR14WFdjJ0kVIKwoUWsdTFLph+uwMhaWScZ+nNDNMoqiQOUGZ+KBoyisZVwUWCWQgFUSIwVSS3IsSZ5hpIctiio+Q1QgtKL0NLIRUg7GlJPKqNuvB5TjCK1dvCJjsdMkbARV/A0laSw20VoRDSMya3GVomE1gQIVuGSTlL3umMnukNu/9TqvfusV0knC5VevsfnBUx5+8BiTl/i1ABt4LK13KID7b9/nztfv4G72SLMSGbq4UmPzEl3zyIYRbujhKkWSF2SOxq/7lKYyKtWexgsUzStL6LoH93egXSNJc+LNPtneABFnJK6mU/OR1lauPpVEHUS0dsMqKnOOJY5SgkaILSsXtTovUUmK9F3KS22KSQqTBLvcwCYZsSOxcYbvaFToU8QZ4VqbLB/gZAUm9CiLCnG3h0BKiGe2cbP8EWNJn+xT7PQxawsV8ZNmhEqRFCV0h3h1H68eQGkoDUgsHga7UIdJTFaUlP0JcqmJv9JEf+k2w59/TG0Uo1bbFTFUlLhaIaUkS1OK4YSwVUMUJdHjPagHlFFG+/oS0nWqwIGTBOnUyPeGiNA9soWq7giLLSuOlZgBfKY0FFmG47pEG/uYOMNd65BNUsK1NuMPNioXtFmOClykFBVBZyz5KGb3Jx9TNgJ63QFZP8JdbuN5mvF2jzDwqXfqZFkVgwZr2drcZbDXZ/XWJZpXV1h+7QZ4Dj9/831qjoPv+7zz47e589qLdFYXWH31Ks3lFhsfP2FjYxtPCtbCkM3Hm8RRTG+zi+NqlOsQ6hCvFnJ/Y5uVyyvkZUFHe6S1OlkmkHnO2tIKzYUmw8EIz3VxA5etJ9vVGba28vwVupgopbbWPpIGNa4sUbu8hP90m9B1wXW4u7VFLQh59Xe/jOO7VXyRmStnGo86Fyc4AfGmfl2AJnmGCzy7P0/D446x5uzs2wsgJfZTyQFOduLi/Nq/hvRsdj5VF84T3JxX6Ynpnr9apzNIT6ppncc0nR3zcex4lrJ6TuT0onk/hzX/HIiL84iFi8h+ZifJHns8hoifebaebzamqeBZ5H9ercd6KGaQa/GssxbBLOl5jCASxwqdzHUKu+HEMZuWnDAtz5l992zyjr+bzX+8T9OapUd2FzwDkGctswUwlsHDHX72hz/mwb0nfP0//w1e+/brSC2PA86jNmYrOOinrYic8sB/udIKIQR+6CPGGd0Pn+J3FlFuTFoaWq0GV26usrO1T5akXHnlGj/819/H05oojWjUQ5Ikw9cOaZGTW9BSUmt4LF9d4f4v7tFebbNybZWiKFlqNWh3GoyThJ29IV/89qsIT7K3ucdr336d4aMuay9dQqQFb//BX3LrN7/AK7/5+um3jYDmUovf/p/9Dj/6199DpiUbu12yPOfKnSvkcczu012utWtIKbj9jTu8/f1f4khJGsU0lzuM0xRlobW2wKg3pFX3ufLyNaKdPnufPKXWqDGeJDQCl1a7QbfbR/seQejz8L2HfOn3voZ2NcrR+J6HcxB7IDeC8WDMZBxRb4Z0WnXcouDS9TU++vAh62uLXL19metfvs3qrfWZ3XUcKVJa8Rv/xW9x49de5K/+2x/Q3+qTa0WnUaOIK09USEGaZiytL1SSASF476275GlGo9OoonN7DpdfuFwZQD/axV9sIUKXfJxSSoXCYLSizArSvMD6buWKtSgg8MiLgpZWDJOE1WtLJFHC/nAMSpIIcCyYOEV4LuM0w9OSPMnIc0tBhuNoHKUQAowQNDwH6TmMTUmRFTiBR1EaRLNG4DvsPd7Cqfk47TqTJ7u4tQDZqlGkOUEjoEAQTxKoBcgoRWQxrqjctw57Y/Yf73DrGy/Re9JFasn6nUukUczeo10mcYbCkqU5X/2HX+PRW/fobnZZfuMGj9+5j6cVRBnyIJgdSmKERkjwoNLFLw12ocno8R7ljiZcX8T3HLz1DizUUa2QyUebbO70KbWi0a4z2R0QNGt4SUFZFIgkx5aGBAOBi8hBuIpaO6zsX7SLcTW+1qRZjk1y8uGEbBzh+AFxb0RcGrzAIxSCbBiTlZbC04w+3sBbapKPI3TdJxuMEVmOFYLxJKJzdWUKMav2nDjE3KzFug56bQFTFJTW4oQee+OIMs6Qnku42ERqiTEW3RthJykTKym3BqjQZfjJNnq1iUpzoge7OFLQ/o1XiB/voZOc0mhKBUXDR2cldn9EcGMVW1QeinS7xt52j5WXr1YqO3mJDDyk5wDgLtQpioIiraJaZ2VJGqfUW3WEkkw77sDYar1yg9UWt1kjTnLiOKd7b5uVxQZh0ydPMuq3VvDXFqoo16OI4Xaf4daAPPr/E/dfv5YkeZ4n9jEz1+5HXS1CR0ZEZmVlVlZ1qa6uqhYzPTM9M5jBbGNmltwBiQVf9okAwT+ArwSfFgRIgiQWIAHuAk1iMbJ3u6dldU9VdanUOkPfG1ffo49rc+ODXx3n3ojIyuqxRMY97m5m/jPhZt/fz34iIxaa7t4IPwwYbfcJmj5+4FGVGlspIi8gEYosSchyjc4Luj//iMWtfcJWxL0H60ySjDROuGJb9Tpy9zFe4LH8lWuMHu7Sme+ArXj82SPIcl5SGU/29nm808VuhbQ7LXRRsrm9Q8txmdEVlYCs1GgsbN9nPIkZ9UfYrZCyLBn3R6zcuETQiLg2nNAfThhPEmZCl6oy9cnSgcxJ2oq5166y/d49lBDML82z2x/iLrS4/JUbnFR/mo4Uni3Y/GXFuWdh8kkdjOcrfErCNz1Ng1yfl+wvShJ+SMc5D2oSzztaOPHTnKznORomTncbZ38/K4mzdB0KWV9Q8nyyhmlY9qgpZ6XRp0De5wP8Z6H5s+r4gsb8V2TQfeLeFAHTeTzeU5cn+vTpR5+TaxNTKD78VqcKw848PAHmz9b/lK7b4eOTvMYZkk/N+QuCuzytFXqI8E+A/xP0iLN0ikPGxxxnOkXA0wyROGJyTi6Gz5LQHJ9YbH28zo//4AesP9rCcmzu/fQzVm6uMHt5/lRLzk8n+9iw82ibzmIHP/LrcSw15doOVa5JdILV8OnYiq1Ryts/+RApYfHaIp/87OPabayUaGA4nuA6No0wYMGyGGQ5AsPrv/kGe2t75FkOUiClREiBkBJTlgyHY5I4xnIsPv3hh5CV9PYGfP13v86jn31Ktj8maoWs3Ll8orOmt0sIuPbVl2jMNvnBf/dHLDiCeJwT74249sY11t68y6U7l1G2hVIKKWq/+vvDIXbkk6QJtucQzDXZvfuEV/7X/wDjKH7xRz+mGCR4ro+SUBQlve098qIknGkxnCQYpRjvDmitztaxJqoKJQWFMSzMttnv9rF0RTpKeNQb43s280tzLK/Ms76+Ra5LvvwPvoYX+sffTDWFXTS1usqVV6/SnG3wx//Xf0en02JuaY7s/fs0mhGWMfgzDUpbMhhMyJIcXWo81+HmS5fob+xD5CHSHFUJrFZIkRekZUHhu7hCooSNleUkVUWSpDRDn0KAMzODnCQYwG+GaEdRFJp2p4mqYFLktFwHFQVUzZAkL0gHEwbCsHB9ie7dTRoLHSpVu1MNA4/+4z3SvGAyiSEtabg2KQYlayN30fSRrYDxYExHa7QxWM0ABMTbA+ZvLiOMYf2dhwxHtdG3THIEICqDryS7n23SWuzQXu0w3OojpGT+8jzrn6wThj5FqSm15t7PPsP1HLY+3WDu8jxLL60y2O6RTxI8KeqDPl0ilcCSErfhIXoxepRgXIfIGOSk7m//8myt9uI7lElOpTXNlVlGuwP6WY5rKSb9MSoKsCqJbASQ5XgS7HZEKgx5VtKP09rtrIDO8gwqzvCLktJ3SAObsSXQtf04QeSiRymjNGNhrkUVuggMyneolMBu+Oi0YPh4Dw9ovnaVoBliSg1KHa+34hieSMcmiVOkZ2MKyYiKvDsh9D2sjsIyUPYnRF++yuiDR1BobCC2JPb+ABIP5Vgsv36NYXeEXWiqYUL/7YdEV+bIhzGlAIyEUYLVbuBcX0KXJcp3qWyJSDParQi/HZGPYqq8xGQlWApjKuzAw3JdjNYkdzdxLs0RhPUp1+HOBoYqLYDaZXW+1Uctz1AexBEZD2KCVoAR0FydIY1TLFtRTJIDddEStxUS5Zr+O/eJi5ygGXL51mWefPwI6Vg4rkU2jBEI/FaEm7sMpUQnAzqzLdJ2xKcf3GVxeR5d1e6qi1KzMx4y01rBM/Dgg7s05ps0Ls2y+cFjbCHpNBs8Xt/AL4bMBT7ewir94YTH+wOqStOQFu0o5P6DdYQxzLXaJGnG7t4eUSOs3UBv7rG1vs14NEYnKY0ri+iZiNWkJDaa/miC2Omz/ZNPaV9fxG76ACy8cZPtt+5RvHuP7s4+87cu8ervfxen4T8tQDyz3Z5y+T9ln/6l0ql6xdHWPU0oeIqeqWJ3wanGXEToL88PTa/3sO6L8l9Enzl98wKfoC9W//Mkc4yaXvhs5yB7deCyXk5TYTyVfcrzaczfib+nVNym4EzghHexKfU8NdFfIH1R84Uvgrl4zkacwMHPR/w5H/nxrefvgZMfrzj4WJ+/9HQO51xe+zx6z3nhU9+HOH5yxNOccPl2PPbi/C46BHynOv1ZaUq+k4zHwZ/jI/sLVhsD2SjhZ//mRzy+t06j3WSm4RH6kuZ863OQUoPxxWtLB4Hr6jxKChZeucqgn7K/3ycjpvIc0BWNKGA0iXEcm7tvfYYrbYRU2I6DL2tf6HmaIamwLIVlC2Yvz/P+X72PshQLVxfZuPsEXZQ4noP0HVAWs80mqjIMukPKtCTd6xJUoCcFaZHzpW9+jeZ8+3RbpvGcpmYmZy7Ns3r7Mu/8xdvgWIx7I0bbQ25881bt5cm2sF2bsBPR3drn+mu3uf3rX+LNP/4po50+fn/E1ddv0Lm6wFt/9BOCXGA1IpLxBN+xScqSKIooxxPy/ohmp8X2/oCP/up9vvUvvkfQDJBWvbT7vodSEsu2SZOMwHMIfRdpYNQfsbAwQ5LlDPpj9jf2qQ4kz17Dx/ZdskmKzku8pk+ZlxRZjt8IULZFe2mGf/K//+fsP9hm/aPHJElGe3mOOM7YWttBru+S5TmNMGB2oU0yTtl4uI1lSxZcG2ecoR2LwlXYWjOpIDBguzZFXuLOzOIeGJ0LKbEMFMM6bsHy1UWKSQJeg/5uD1FpClPRDHyUEFRaYyKfQpeM8gJMxZO7GzTaEa/85mt89JfvMR4dqHcYEJ0GMjaYtKjnh6WwZhuMHu1h7Y3wHIfezoArSjFz6xLGGPJRzQw6Ue3haPb6Is5Gl6w/gYZfA/60QNqKJM7Z/vldrv+9N/BaAfkkQzp1vAfPdxlu7eM4DoPtHhgos4KP/vp9bn79Ngu3VtgTYJK6rkGcYIcOtmMxLDWRq7AHMX7TR7Z9WOuiJymlruqo2usDRk/2KbcHiHFKpA2OkMhmSGk0FYadOIVxTCvyac22Ea2AapIw2hvghR5hocm0ob87wNYGt+kzGcZ0n+wyrCqEgUApqsxhvh0RHnggMpXB6oQYXZHc3SK8MgfDmOjKfK2K1J9QbA8o2yF2w8PuRAjHQg9idFZgdyKqvDbW1ntDzGwLPUyospLFX7/O5g8/QVkCneZke0NUoTEILNfGLQ2m0mgB7ZdXybKC1vIM3Uc7tG4t0x3EkGsaN5cZffoEIg+pDRQlxhiyzR7MNaGCfG+AagQIS4KUVHFWA/48w7NV/V07NhQad2UG6VgnInTXi1+Vl+g0BwTlOCEejZGhA1qTWop8nBLMhJiDExCTFlSWAmMo4pz+w11sJeh9vMagPySTUAXw+OP7+I0Ax7Eo8pI0y2nOhfgVPL73BGXbtDst9ne6XH7pMr12i8F4gi3r2BKusrh94xqlEMS6ZnLf+8Gb/Ma/+l3m71xi69N1FALLskjCZeZc6Ns24UyLRdclGU/Y7g34dHubUNlcXlpk9fYVmpdmKbKc0XaPJ4826xg7VYUtFfc3t1kcxcxfXSZRgmYUkFByf3ePzkaL/t1N5r92AwDLd7jz+9/DbgSoyOP2P/4mlucc9OzTUP7pXUxM3/Iv2sR/yTQ1AN4F+OdoU/nVkPP86eT7zwPM0/KevDbnZXg6+ynt73MxyLMqeernOQzP6XS0jR/kkSc8iJ4y0D4k9BzPo1Ovp73sGWmqG9ozTIUxL8A8PdW3v3z65ZmLv+UJftx301mskyo/U6X900o9d/8fMBRnF4GjSXamOjN9vXgx0A+I49OA4/JnW3Pm1AFx1AtHuYQ5/YGe1+4LSRPnvPJAFmDqn/HOADPJiaKQYKbB9nDEd16+WvvCP7/maVWCMeiyYrC+ix24BO2IfBCT9saM1rp4tkXTdelnKdJxUEoR2jZxkvLZu/e4dG2Z5ctLvPfjD4naEaP+CD8K8FyHYZLSbASsfuMmg70h8SimrCpas00+/smH6KJACbAmKWVekI5jhsMxURTwYPMxt25cwS1gP07JXJi7tnBBg57uN6kEneU5pG3jKkUY+qx98oRSGpZur6KLksZCi9/73/5TJr0xc5fm6T7ZY/PeBo5rUUpBc6bJ2vsPSPsTXNtmUMZ0fJ/t/ojlq0uYvEQXteGkbQnavsunP/8UhODV33qNO995hbs/vYsoSiZxihCgHIsg9Lj9rTv89I9+xurNlSP3roXjkA0S/ujf/BhXWdiuRWtllsHegCLJ6Sx32N3YI81z2jNNbv3abeYuzVPpivmXlvnkJ58glGLUHVFoTSPwqaqKMi/xI5+Va4vsPNwhCj1avoeLQDs2VeTiOxb+bIPqyT5uYZCFJp/ETLTG9WyC5Q4iLcnGCSIva29bgQOVwVa1apClDQqJryETFXmWY7k26SDG9g9crGJwOyGP3nuI8h1C16UbZ3Q3eyxEPtJ3GXZrA3V0hUgKOnNNBv0x7abPSEkm3RHRbBNhKfo7fcLlNkpJyqxAKom0FWleUIxBKUGpC6yqxG0ExMOEz/7kba7/5qsAhJ0IP3Dp7Q1wbRuhoL3UYW9tDydyGffGvPOnb7P80hLNTshwMMHJBLIy2JlmLxnj+D54DtK2KJIMuxNhAgdhDMXjvZoB2BnUjGZSQKExhpq5RlD1EywpWWj5aNsiL0qSJINxggIWm0HtCjoraXkOfceit9Vnf6eHJerYCyuOzaQsadgWnpR0rizQefUy/QfbhAstkq0+yrOwnToQm7vUoehPcOZbKNcm3R/WQDzySNZ2cRfalLsDnKuLCEsiTe2VtlpokcQZWVFy+Vu38SIPMIjSoOca6CynKHXtnMJzcJeaBIsttDEYz8Y7iJ0TdiKGm12yvSEiy5GmQrZDpDFYUpKPE5y5JtFLKxS7A/Q4QQYuvf4EdxAfeLACuxVQGTAHAe7q99q1MfKZNcLoCpOXVIUm3x9SDGM8qWqXrEXF6PEeTuTjKQmqDgQoPAfZieoYLKpEJBn7W116umAkDMJAmWTYSpIMhuxPErxOC9d3sFyL7fubJOOEhZUAV0rGjsXmk02uXF/lg7c/xGuGLHZaTPojdh9sMsgywkaI0/AQrsfj9+7za//it8jjlL3Hm8RZRqoshp1Z0lLjKsn2bpf94YDZhVlWV5cJGgGXv/oSq9+4jdsODpZ6w62HO/xP/+3/j8Zsi3R7j1JrPny8ztW0Vp90AKlAK8HOaETw1+8RXpolmG9iEPiLLV79V79NpSss9yzEueCs4OTJBVP283PSUZTsF7GmPSmFPgAKpzwnHWz4p+6JC9ysnpemZf28Uv/nwQ5nsx/g7GfW9wKv/qWSOPnzRcDrGYbhDAgyHLfzqVORaVD1GKa+0HBOU30/c2P678Pr8zry4NmznOy8SPrCDbrrdEoj9uTtL6BmDmqe/plNk+cfqxu9ILf/1LiJix4fUXYM+s2ZJyd+iBccwGd+XdPrOnX3rIHX0UGDeerei6YjpsVANox58uZ9hv0RXlGgu31ERe3a8umS0+urquNZZAzv/vHPefCTj3nt1Rt47Ygnn6yztbZDPpoQWoooDDDGMI5TpOuyOxwx225hFtssXVtm+9MNfMfCAJ1GxCCu7RFKYPbqAl/6jS/zV/+fP6fTDOsowbqqdZKLWpo51BVZUWIpQaMR8eFWj06rievY3N/aptsdsnxtibAVXtRLPH0EJrj2jVusfbbG3V98gh5JWlHE2kfrvPWnbxF1Am68cYugEdTGqlkOxnD7SzfI85LFVy7Rf7RDU1fMLM/y5MEueV4QmwrXc4i7Q5zAIWxGlEJgNwOaroOV5Hz21l12HmwxuzhLa6ZZe/HxHa6/tIKyFfuPdymyEiEkju1QFiWdTossK0ge7eM6LukkYTSakOe1FHN+vsOkN2HYG+E4DunehHf/7B2CyKMoKq7eucTi8ixMCnqjCb5lYUmJ77l4vosGujsDglaIozUOkA4njG3F3NIiAQIZOBRlhV0ZdKGRoQ+lriOWFxp8C08FtWTYs6mSDGUpPNfGLHRQOwOqZkjRm1C2fPx2RH8wYThJsFyLxmyDqqrYuPcEu+Hx5e+/zs4nTxhPYiwpSHsTmpdmcTsNsoOgc8oARUmzFaGzHNuSbN3fJNitpfk6K3EDjyLPQVcMt/v0d4cIS1JUFZbr4s40QWv82SbjQUzvwTZBK8RfnaE136Ix20ANEybDCYHjk+yPKauKyLbwGz5+p8HM5bmDyNYKYwSNIMKRklKAi8Q1hjxJabZCJo/2cJp+rRpkSdy5Jv4grQ2PD4yrjQCjNWqujRs6lIMYMc6wTIrXDPCUIt4fY0yF1fSx5luUlaHqTfBsiYwnNObarL52neHdTSa9MZbjEHUixqOE4SRBbffI90Y4toVlSdyFNlWSo5TEmW9Sfli72hWWpPGt27U9iTFknz0h3urR+PaXEAcHmkiBtG3S3S4ldeDE5lIb23exZyL07oB0lOLPNbFDD5OXiNCl89VrKLt2gzve6pNbFt5MWAfIBDLXxor8A6cStX2Msm3yUYzeG1LatfcmpKRIUuauLjBc28dtB9iRh/JdZFqAqt2rYsk6AN8Jw/Qyzeo5bEmEU3tVs5sBZaFxZyKye1v0sxLpKGxbIkOXMi/Is5wizUnXdmldX6ICho93yEKXKoao1SLw6+CVe1t7jLf7eIGNBbXL7vUdLFvQmG8TxxlpWtDyAvbSCf3dLq7vYzkOe1tdxklCN0mwlGI5CFCidsk76k1AgPQscq2xLUW7GVGkMXaRkTsuWVnQcny+9JWXaa/Osfrt29ihh5DyaDkUQtC5vsjrf+fX+Jv/8EMu3brK408fE/k+s3MdEJL+/hB3oU2uNf0yZ/PxJuGfvc3t3/+NI49WKIlSx/UedvJZF7+nGIgz3MTnxeBT0xRgfnjKep5b0VPpApz6zHf+UgzG87JY019xCoN/EYLoaSD95LNfwhbivHQgUj6XoKcwqHjOCfQ5GYznTRcGUJxG2xdMw6+IubgwuP0vl8TUnxemkydop6UWF9dw3P9TPCM9Y7IdTshjvvb0k9PEnSHnWYvCOenQM8HUvv+lBmQKQeZk3xykytB/tMt7//PPuPvuPYSQaNumFUR88/e+zrVv3D7/DebMheFI3XS4O+DNP32TK1eXqZRisDdkNIwxWhN4Do5UjOMU27YxZYGV59y6dZl7d9e41F5k58E2kyzHsm3G/RGB62FbiuzA44tRsH13g417mzSjkCj0+eznn3Lj9Rvce/M+lm1RVoYoCJiJPPaf7FFiWJ2bYW13n2tv3KQoK2avzB0xULVK5BH3xpFC78kF5aBLncDh6//4Wzz5dJ08zklkglSCR28/4Hf/N3+P/sY+c9eX6O/0KJKMm1+/g/67X2X38Q6WJdna6tGYbdWuVz0XP6wNI4WAZhTQXJ1ntD1A6IIqydFSYgvBXCtCWBaj7pDGbINRd8BXf/sr+J5D1hsT3HJ4+O5DPM9FF5o8K2iGHpNmyPZ2l4bjkKUZvhNwZXWeLM2wHIeZlVrFIU0LdKm59fpNrtxe5c0/e5e1j9aRGK7cXKEsagPsJMsxVYXfDpm/ukA2TKjSnIbvkSU5hWvXnnksRZrkNKVPqx1SPa698ji+jfRdqrLWr8ezsIQgzXKi0KVUipKSBgKRa0zgghQ4oYeOfJStqLKcIPDwZmoaHr77AJFpoGD743VWvnyV/v6AMinxGx799T38mQaq0GRVVUu1ZR1ro0hzqsBi9vI8G5+sMzPbJOw0IC9JtwaM9kdkgxgn8kgHE0pT1UbjxmAsxTjNSHoDXM9h/5MnBHtDGt//Eq/8zlewHItslDDpjhk93mP84ZC5y3Pc+e3XiLsxZZyQTDJUoSmEIDAKYyvCuRZ6u0fmethKke6PkDMNtJLYSYZ/dYGtn99DFiWu72IE6LhCa4NVGbK9AZUS6CTHCTyaqzPIQmN0RXOhTWEM+TCmWNtHew7YCmu7x8rCLGqhhe4O0UmOZ9sUtoXWBlPVQQWD0MO+ModUEp0Z9Dil/fr12gBaQmuhzYkF/AgIRt+8zd4f/ADv9iWcuSYg0JOMKslwA480zrBcpwZwQhDORGSFxpaCQlc4803EKMWELlJJTFUxvrtJtjMkVnt0vnqVoB1hHIuy0HiXZvGaPlVeUiYZ0rcR/Qrh2MR7I2QnohrFdVA31yK6NEP/wS5lmiNkbTvRbPiowMXoCnuugVKKSlforMA68DCn47xWkzOGbJIhMQw/XMNbaOEjCBdaVKOEKi2wXYusO8GkGc0bSyhLsffxOsOyxHEiXvr6yzx+9wGj8YQ8y7EdG2kpkkJjMPQfbRFaLvu9AcK3ac63cUvDaDBh2OvxZHMb27J46fIqSZpyeWGe3f6A0PNwPYdmq0FsCsokIxlMEEphOzaBspCuQ9zdYa4c8VDPIpUgzhJkYKMFOA2fpzb0g3Xx2jdf5hf/84/Jh2Nut32SSwsYz8WzLJK8pBwkOI5Nrkv2tSF45z6dl1ZY+vqtIxHyUXTro6kjjmWM5rSrEw7VXC4QBJ+XnuvEYkoWechUTdm0z3PV+tzIakq2c+MrPG86p5lPndy80InEFEn5iwDfk3lPAL2nvDQ9z6nLuYzLFPT/opzn2SqedcJw6v0nH4mn23ZRuWe997x59wUwGmdZ+8+dvmhm4nT/mCnHQWcyG875oI4zHKtSnT7/OHln+vWUQTy7EB3RYA503U4TJTjJctV5njrXMIf3j9Wgjq5EDbZPMitPJ3GwfEyl+oiO867Ou3XY2ANnLBwRd4aawfoe7/zrH/H2j95jkqQ0Z5tYtsXC9SWu/NpL2Ae6r8+1YMsDVswY1t57yGQYk40T7r53n81H23S7fZI4phKSWEBmS8Z5jmVA6op2UhDYDpvre2xs7mGJekRmogDbtggcC1NVKCHZ2exSZAVlUUBVUZUVVugy3h2QjGMqU6EP5kprpsn2o23mOi0mcULgOOR7Q9ozEd/7Z7+JZdW608fSCwEnJRlnJxogLEVrZZav/NZX0FpjlMCTinwwIUsyGnMt3vkf/xOirGgttBHG8Pi9+8xcmsOPfExekhcF+/c36Xb7dJoRthBUAsaTmDDyyeKUsqgQlkUxyRCujXQtpCNptUJsx8Kybd75k7d48t5DtGOx/uFj8jhDVBXd7S5+6ONZitXrKyzfWsFpenieQ+g5lKMJoiyxpEBkOZcWOqxeXcQLPPbX9phs9Ql8l4bn0HJdNh5sMZzEGAwLq3MsXpqnGXjQj5GjmEhXKCHAdzCRh4w8ultdSiWI90eU/RgCBzwbp1kbgZrQQbZ8tICyrHCNIN8fozwbuxOSS4EXuFSBhyiqOvhbmtffmWMRtAPyccqjdx8y6A5ZefkyllNH+x3vDvA8l2AmQlO7BwVDagy2Z2O7dh2z4SCIm0hL4r0Rs4sdKDXj0YSH7zxg7+EO2SihOIjRgpKEkQ+ejYx8hGMh8oqg08QOXOxWSF4ZPvmTtxk/3Cbvx7Uh/2wTrSTLN5Zxo4DtzzYRGCa9SR3szlK1x6qDyTbujSlEHVFb6grSDO0qmjcW0FpTjBJ0ViCVwmBIe2NMmiOrisJUmFGC6Y4QWlOOE8ZbPQicGgBXGqoKyxgsx8apDKXrYmwbGgH97pjeRp9MKoZ5iZGC0e4AvxLEO0PScYYbeViuhZQCb66J9OwDvCeOV7STgjgBwrWxl2cYffCQMs5r25buCD2MEVmB49hEcw2EEFRVRZ7mDJMESwmUZyEKXRtmDmKoagPqsjvC9+uTlcl6F2FJhFK1EbljYaQgHyfg2uR7AyxbYYYxZV5S7o9A1EH09DhBZgVLb1yjeWWWcKVDc7GFu9SuTxmGCUzqU6wyL7GD2hannGTotEB6DlVRYluKapjU0eVDj9bqLFWhKYdJ7ZXLsQkW2yx+6w7ObJMizug+3iUzAsqKn/+HH7Gztkkap+RJRpwm2JGH5TmUWe262zLQCHyMqE/g4knC3mjEaBQzF9Ye23a39wg8j7nlOa4sL7C6OMfKrctEMw3mF2cxk5y0NyHfH1KWBY7nMhGGruUwXr5OCez0+yS6RDo2fqdxfHJeVbVns6re/yqtCedbfPuffp+9rT3MZELw5DFb3R6b+12KsiAtCi7PzeP7PsM0ZW88Ye3HH1Gm+ZTNTBzthuLEs6P/xEF8ACFOl3xq0j07PY1UDu4ac3rbngY0zns25R1Tbp7++4WlE0KxczDWcb7TRc57fEHJ58p/Kp1Dz2m/YM/RKSeznSkiTs6BC4D/OYQcVHfBmJ1HywUMSA01zdM0vSjDc1h+GmP1S86lL4y5+AIYnan1HQ2K4RQgf962H8JscaIHT997+p3PTAcg+xBoG3NI5zFF9b3j95ppNJxqwEmqxNHidpLO06XPa+vJtpxcQA8B78neeIEJf/RwepmqKHnyk894+NkaYRiwsDLPKMtQkcun793jD//P/5rBbv8YUHPMOJtp1R8wML2NfX7873+M7zlIWzLoDdld32bSH1IKRT/L6aUZSV4Q2hZzYUDoOOzv9phVkkDAajPEdWziPEcbwWAS4/gOZVWxvbeP6zvYtsWtW1cQUlAB8XCCtBRKSXScQakps4xBb8RwOGam1UA6DpMkIRnGKMfBC9z6iF9wxBCeGpzzBo16D7vz3S8zvzrLZDhGCChNxWCrh7It4iRjtD9g8doyySghHUzY/nSNsNPAOIrh3pB0b0A6Sel2eygDc5cXCFoNJt0hw/0epakwhabMc6QArxFghGCSpKg4pxMFNGcaPH6wxWd/8zF5nOGHLqHvUSQ5UkksS6FNhchK7EIT+R6OazMRgl6pyQObbnfIxtoOyWDCwuocyra4++kTMqOplGSUZXQuzXHz9RusXltirhUSWhJfKRTQlgrHthgLQ/jSMu1riwx7Y9Dgtxvsr+9jKYk118SUdayFZLtPtj+iGqWIYUo+mJCOE+LtHtXuiGyS1pGKs6IGM8ZglESWVR0sz1Jc/soNknGK69qEUchwf0hzeYbGfJNHP/2UjY/XKErNcKtHELrYgUuJoUgL5IE3MgOoZoDWFf37m/QfbJH2xpRxHWTPbgVIz6EoS6wDl8pO6FNkBcYYlG3jKolnWXVAPykojSG6NI8KfOLNLvvvPuDxf/oQyxjCdojpjek/3GXz7gZloSlyjeNY2ECl6lMqR+taBcfUzKwoK0xvgtuJMKHPZH+ITAuSOCXuDqmSDKQgnyS4lzpYsw0qIxBGUCpBGWeM1/YpSk2eFmRxxiQryNMMQqf2nmQrtOcwGiUYIbELjVdWVL0xAYa2Z3N5tolTakxVG707M02sVnAM7i5IAkHjG3fQ+wPy7S6m0BQPtpEzEWXg4nsuraUZemt7jHcGDLZ6FIWm8D0caqPpkopqGBO/9YDRB4+xBVi+jQxsrFyz/8Eawyf7GMeCoiTrjvGXOlQbPXReUW71KfMCZzbChLXqUbnZo3iwQ9GfoOMMN3QJIh8zStC9MV7o1SpUAvQkqwUfWlNlBZZjYUUexThBxzmm1AilcC7PY4C8P6bsj5G+TdkdUQxr4QcC4q0e63/yNqUxWJ5i7aMHeJbF4so8C/MzrF5ZxkVRpDlSSDxlYynJ+s4Om/tdQscm68VUZcVcq8Hy5SX8ZsjswgyB71KZClGUzM/N0GxGrHz9JW783tfB1DFhHv7gfe6+c5dhnGAHPrHRlFLSy0sUUBpIyhKnHVLE6SkwX+nqAIAfCOOk4PLXb/Olr73K4xyS5cs4UjGaJOwNR3THI2wBnVYDjWFU5oz3a7e7yTAmGcTnxn86ZhxOzrHTjMWBnJCaMThZ2kz5/+zjM2JDcwB2nwUwzpMGnsLtJ3DLydcfgthDUDGFQXnqdOA5Ac9Twt0zTX8KSR3iIo6FpUx5fkzTNOR8IUHHeNBUxxQeMnBHf0X9/4n6j/O9AHI25/x+kXLT0kkANG06HUFfM30uf9Gg+wtOvyK1qGekkxzTlEenMdl0021x7sWvhraTt0/K6y+eP2cD/h2nKWva9Iwn3nOasTjTK4apXusOc51V7Dq6Ficr4GQDj6g/y4QZDFSGbJzSfbRDY66FyUr63SFxkrJ8bYU4TnCVwpSGRjOkPdfCj/zpjP/JBfkEp1Hpivd/8D6m0LRdi95njyiyGky6joPdjFCVISsKyizD9y0W5jvs7/bYiGNMUSAqjTI+RVXVbmjjFMeSSCVI0wLbVtz+5ss8fO8B6092cWybLM9xLQdZCZTnYjCIrCRJU9bWt7i2ssDucEy3N6IyFaWS3P7KzaPou8dDc3p8pg7O4Q8h8Noh179yg437m+RZQavlQ1WrTX3rf/Hb/PAP/oLt+1t8+Gdvcvm1Gzz4+Sfc+PodtJJYgUsqBGVeUCqJ1hVL7SaDvSFbj/foLM4zniTInT7akYz6I5qy1vuWSpIUJU1hY5UVVitimKRkpaa7P6DpOAgJUknGvRHeYod+b0RWGVpLbfY2eiRJSpKkpGmBsgW9/phGoSkKzWw7pCwrKiFprsyiy7JW3xIKW1bovMQSgkIYJuMEE3jkEvKiRO70SSYpzXbIzI0lxltdIiWoZG0/YrLaO5W7Z9eG6xhU0wclMWkBeUGSZDhAPJggEEjPQu+PkVaI7zoUgCgq+ut7tOda9Pf7NBc6lFrXtgyey8vff423/vgXhO2QySTD6kR1YMWmj57kFFmB0wyQWUmRFfjzLZInO2RlSQpEekw8mlB2IowRhK6DcGvj8TLNMcMxVeChPBvSHKEkju8iigIrcLE8B2+mAe0IJaBxs8SkBb0n+7Svz+M0PNxWQBFn7PdjLKlIeiNGw5j2TAOnE9HbGzA7yTDjBGHb2FlJOUkxlSbd7NdAVkooTa1mpjXNL1/FssBZmsVb7jD4bIPm6hxCCaq9MVlvUttHSYm06kjJ9CYIXVDokvF2D5OVaJ3gBD5GStx2wNxrVzD3d1CRj+nHaNdGBi7ubOPgmzjzsZwDvFQ7JHjlCslHj1GRTz6cYPkuylaYwYTk7hZJnLMzTkirEgsIllqI3phqb4gKXYrQxXFtWNutP1+nRLYkKvLY/sV9cCTBTINkb4QZJ9iujXt1nmKSUtkStxlSGYPujhCeg+g0KPeHiKyg7E/YXd+ldXWe6M6l2rB6GJOVJZ6UiMpQFSVSgLAthKwZN51kNYMxSVGOTTnJEGWF2wkZdicURcHClfnaXa1jke4O2fqbTxBLbeKtfSYbXYLIR2vDeJJAXtsDtTsNxvsDsrTk4d01TFVx48oKVuQz7o/xhMRrhXS391DaMIljZuba7Gzu8dKNq4RB7TLXSEGeFZQbXdbWtpiZafLwo/vYvsOVlUXGcUpa5XiRT56VzIQhRVGyPRow7A5ZWl2gTLLa7XFlUI6FHThHBvBUBq8VcvU7r/DRzz9gkKXEaY7je3i2ha4qKA3tdqM+Ua1qT4AIQTZOGe0NWH31Csq2OPLec2bZvQg2HO1T5viveCps8rSCJzbQE5U9tTc/CzyfvXE2+N/RgcLJPfocYeF5Qq7nBsoXWIdeCLzF6Y68wNX+M9M55YyuMAiqsqw9sD2DaXouO9dzuvKF0wnB4TSiDgWQpzxN8ex3PyVgPoPbnpm+iLY9R/rCmYtpAPrptk8HrSfLnHvv8GMXZ55N67ApDII4+tecWGWeHtXz9BsvkIWc+3Ra3rML3LQF72xt5mASilM0Hxec2ncnBBknf4jD5l/AwZ9asMyxPcdou8/b//4nbN3dYNAb8cbXXsZBsH33CZZtg6pVqGYXZnADl7womL26gOO7577reOE57onh3pBPf/Epc50mejyhygoCAY14iJQN1vf7OI6NLQQN26IXJ1Q7hvQgOJOxFJjaGLmhFEJVaCWJApc0L/E9l9e/+hLx7pBP37pLGIUIKfBch8k4Zbg/wlYSVymUZWiFPu0orKXDwOJsi7gquPO9L/HVv/vVU7q34rBvL9LHPere43HVwlDokkmcMDPXYvRkH11ohrsDVAmD7oCXv/ca6x89wvEcyqyo41TYkmSckhQ5jmPhCoGrK+LugEYzAmPQWU7YCBmlGW4rIM9zPN/HUhJXQN4bY4Sg4XsQ+aTjhHa7gSk1c4ttVGVIxilOkJCmOa5tEccZcysz7O310UWBRJCNMvxGiHRsPN+lPRMhJGxtjfAcCx+JyDQmr1BZjgpd8jQn8x3sRosiyZn0JgShx+ZHj1Ha0P71V0gnKSu3V9nfHqCloBjGFGnOpD9CH0j4bVtR6pphcT0HYyuyODvoJ43l2RRFibQP3HZmBarhURUljz5dw7UtmpakSDN0XnD5zmsIW/HOn77FZJLQbIXo/Qlhu0Fe5nTXRlgGlJGoJEcKgZICU2oWZjv0drpkWYFAoqsKd7aB0AbLCHSaYYceVuDhLLZr1RglaMw3KYoSN3DRpcb2XZSUpKOYPM1pLnYI200A3NkG0pJQlLgNHwmUAtJRjJECp+HXgQV1RRT5IFVth5BrpNYo10bOtyg2+zVALkpkw0fEGZZt4Xgu0lVk/QmdO8t0Xr18sBlW5IOY/Tcf1O5eyxKUREuJqCoq26bSGkdIgk5EWVYY10JZPp0vXarVfS7Pwv6IamuIu9Sicqx6XKg33ufR/xUIwjuXqYYxyY8/oniyj7y5guhPUL6LyguULUkrjScEoe+iJhnWfAujJLZS5EVB2avdFmsEen0P6dmoxTaN5TbWTITJCkognGthxhlFlSAPjOFlO6zVsRoelm3BKEY6EnehVdsgeC7D+1tE33oZhMBxLGRWIB2LapwiXbtm6ky9N+Xre+i8IE8y7FZINUkRlg15TqUDxvsjOlfmsAKPZJzWNkO6ojKGZBgjc0OJpNIlfqdBkeRkSUp/OEYqSXN5lvWHGxRFiTEVpa5QRclcu8Hebo9kP2flpVXS/TGbO7so00IduLlVvoNJM8q4QArBg598yPgAzOss49HWhNWFWWxtuLq6yGQ8YTcpKEKHq94iSXnQrsAl3ujWkeIF9fca+YSLbYQlMbqei34rwvUc7MDFdx2Eo5AGlBHovEJJC8uyqCYF7kwD5doM720SzDYOjOWPd/3T6SzqPn190a54jpjwzNVJceAZIPh50tNgoN7zT3AtT+Gps2U+pxD2KUHuc7bhGNscEPsi4Pc5aZWWhSk1yraPHAMc2YBMI+Z5WMtp/WZOPn7x+BinmMATwscj1/7nMYCHZc425jy8+8swDl8UU3WQvnDm4iLm4Bjgnj/RTjIiJ2H4WS8PJxmDo4jRZ2t6ink4SdM5lJ64LaYGsDlJ5WlSnspyotopP8+++anC9dQTJ66fZs84ynGCnz0hEZ8mBDk3mbqE0QapDkUApynLxxk/+O/+I5999IAyK7CU4sHHjwk8h929PvM3VzCV4dLVZd74p98inGsdROSugfbzry+G0d4Qk5W4Xn06USmbpmujK42Qiku+gwFyramKWsdvkCQYJXEdm7wosJG0Ok2KSYZjlbWxoe1gKUESGR7f22Tw5pDA9VBS1q5WC41nO2xt77E41yabxORJwWIropSCtW6fIPSZvzLP6o1l7LmIIsuxXedwzTg9584ZdMHJeV33zLXXb/I3/+7HTJKEx+vbiKZLmZes/ewzXN/hsx++z3f/5W/XQbMcizzOsF2bhx89QumS+dkZsizDuDbbDzfryNKORZkV2EA3L2j6PtJ2sGyHQtexCygqqqygKGoQFWSSyHGYWeww6I0YTxJcbXCVxGQFQTMk7Y5o+BE4Fjdfv857f/EuFgLL93j9t15jMkx49NFjtneG+IHLUujj7Y9BStxWgEkKKtsiF4LYsSgtwZ1v3aG/tkf3hx+ydGeVbJRQ5QWb7z9k5tYK5SSiEpBj8CpDqSvSYUo2SsiLkiKBYLZBu93Cbvl0N3u4kQ/jBJ3kdRwFoCw1Ii/JSo0dOyjfwTWa1RuLuBt7ZFcWWf9wjbs//5QkzZn0J1y6tUqcFNgzTXbXdvA7Ia1GQBnnCLuOW1ApieXY0BsSuzbSc7DbAdoIit09wlZE1p+gigon8MiNwbEV0UKTd//sF7i+ixQWoqoIOw0G233C2Ubt4tVSRPMttK6oDlS5LM9GCFFHr94dMni0S6Urxrt9Ou2IaiaiiNOa8YtzlKVQhUbYCqMkpqxwA5eyKGu3s7ZVxzBQguZ8E6kEbisk29hl7w8/YfGf/g4y8DBlRevWMsKx2H7rPnJvXKvvhC4Ygz1OccIApESGHikVzeU20aU5pIB8o4+yJPkkoyxL/MhDevZTH8sZecPUz0kohWqHxL/4DMtyyEuDt9RBjuu4K1oKPCWpSk3QiTBlxWSrB1Jgew52XjLWFXbg4lgWutDoBztMehMcS5Hvj5CRTxXnZNs9jBGYm0t4UpI/3q1PG4zAciRO5IPrkKzvIh0LXVb4EopmQLE/ROf1ySvaULVCVCtET9JaJaodoXsj8if7RF+9gdzsUWbF0fcrgOzuBk5gE85GFAegvnNzBUcIpIHe/U1S6tgnYTugKmubDolgfmmOwV6fXJd0mhGOpXDceg0gySm05vJXbnD1jZss3LnE9tsP2N3cYW+3RyPw2drZRWUFjfkO4ULE+OEuG/fWybIUSs3Lr96keO8TxmVO3B2AEVhCMCMlWV4Q+x4NP0Bndfwe6Tm1yikCUxn0gaG8HfkYU6ELDRgaUcgkzpGOhaoq8qxkbq6DO85wmj4Gg+863Pzdr2L5Dq3VWXYf76BcC2UrlKUwBtzIxwncg5O2A1XlU/zF8+xR5szVWSD7ORH8hcWfIaD6PM8uauRzgszn5QFe2K3peSDy6QOh+q+lTt8/JSw+g9MMPLfL4Bc9EbggnWIqTq5jZzHms3ifowXxGYzk8z57nuefM/2tqUU91WcX9M3prjsAzRd0wPRxeJoxOAG/Lyp4mqCp43go0zfnV3H2weEBwNHRw8UfnaFu80maTzC8x3PenPZI9UvNkwNJSO3W8emvygD99T02H2xSJhmrnQ7NwGdtt4uUgpVrK1R27c3myuvXaa7MHEiPprRzmiTGHLahZgx72z0c26IVeOzs7uO7LutJxozjEbg+YyHoFyWtwMMWkA3HpIXBsi0aot7YbNdhOByjEBilGOUZkefgWjYzc03uf7aOa9kUlSYwiihw2O2OyPIMpVQd7KsyWKFPf5JiOQq/1SDoROyMR1jdgOW5ANd3T7fycwhIAGYvzfPGd17n/pt3mZQFq1+9wag7ZLTbxwQ2D9+6y41v3GHp1iXW33+AdG1mV+aY7PRwlWR/NMFXkqjThMoQ+D6ZPjgyDn2iVoQTeMfjLSUmLwiURepY2K2QoigolMTFMBrGZEWJqyygQnZCdOgixilawN7aLsO8oNMOmZ1vMxnXaja763tkSU6rGdB2HcIKZKnJS43tKswgZiIEO2lM88oC8bjAVzZuI+DxJ2tMkozuRpdeb8RMKwRLsnhtkXScktmyjlGQTLAshZQSO3QhlZRxht8IaIUeZVqi8wI7cNGRj0hyNII0yWqjUddCaU2RFbgNn/EoJs5Lgjdu0f1kDaflU+qK0VYfjKG50sF1XAY7A2xbUWUFepKxeHOZMs1JnvTwGwH5JK2ZW1vRXJphb7/PMCuRzQabn6zjColUkjjLa7ei4wmPP3jI5vo+M50mt9+4ycyVBbY+22BzfRdnp4tl1ScuYSNgbm/I9a/exGv5KNvCCRwqrZl89ISiqGN82J7DqNSorKA112Kw3cdzHcrKYByLqgIsi2R3gDvbYJDVKkNpVVHkJY4RkGcIIow2eLMzpJMJvfce4i/NIhyLbHuf3r0t3EZAlmuspECpWtUujRNUIZFRgMRlIup1M9kfQV7iuQ56Y58qSfGW2uTjBNtWB2vbeUKd878kd3WekaXAspCezfDBDt5MhD6Ir+G3IpSCoNPAFBrbVFSjhDwvsYqKaKVDmZdM7m5AWqCMQHbHGK3BVkzygmSvz+WbK+j1fez+BNEOUKFHNUqIbi4zerCF1AarFYBjU8U5KvJRzQAzjKmKimKY4i+1wRjy4QQ/8qiqClOUYCp0XuCszlFVhnQUU41SvKUOqihrN6uVwW76pNsDLMfCCTzKUcL2h2sMH2xSmAqpFFeurbD1cJPFq0ts9MdYrs2lG6t0woAnjzbI85wrd66ys7FLuxlx+3tfZvnLV3EbwZFx8+q3bvPG+h4//Dd/gSgKQDDWJVacUmDY2NxBuTbFYMir33yVl3/vm1iWIh7HbCiHrf6AqtC4ts1cFGFsG68R0O+PyJOMsBUe+7qQAqqKrDdhtDPADlwsz+aH/+//yPrmNu0ry5iqopGWlI0IBjHD4YThuuLWneusLM3RujJPPk4YbOyjigLbthj1x2Q7PYyRLL1+DWlJHv34YxqXZlm4uXK8QD/Pem2O99+L0zn7neAEkPklmZCjSo/rqvdN8bRmljiT/XmrPZkO6zSnbz1V9BmH9Z87TaX9GS86A9yF4XziLmJozkAYYT5nAy+SvE/DQ2fLPA+TcDb/RUyKOC/PCxwdXZD+1piLkxL1aQcC07H44enDFI3Ck3WI0+U+b7ecKivg8Jh6Gmw3Z/4+M13IiU7LfJ7ficPJ/fTqcZZff5r1mS5lOdW+U6vDwXtOvKoYxpiy3jCElPSzlIV2q9ZxLguSXo4XuMzfXjn24T6NuKkt44hqA1iWRVlV5KUmLStwJK0oxLFgYtnslxo7CCjdOmCe63lEBxvwUAj8ICDPCzJd4QsBuiKbJOyXGstxcDsNLCEpqV22hsZQDRPmlEXmCVzPYdgf0fJcsgOPIlIYQkdhqKjVfismeYGy7afnz+nOfq4klGTu+iLr7z+kc3Oe1ZdW6W3s07q+yJt/+BOWryyzc3+br/+jbyEPDNO8+SZhEJCMY2yjsYVA5AXaUuiyIAp9xlnO3OUFXNsmzWovNVUFuizq2BFVXVdWFFieQ15qGq7DJMtxAxc/8PAqA+OEpOmDrWhYgrTh0bCbuL5DPk4xEmY7LUyS4yiFLSTWJKNQEiEljmNhlGQ3z9nvjhj0BggpiVZmGe70efPf/JjdtT2Wlmbp7vVpLLRwGgHjUYIbeWR7Q0olsTT4voOxFHmSYaTEFCVBwycv66jJstC1sexBhOtKSsw4wW2GEBfkhQYpCTyHwsDc8gxVZfjwhx/UUuCtLp2VWSoE0XwD1/cY7w4xkwwbkEiMbREtd0i2B8S+S5Hm5IMJTjMgkBI1zmhWkr3KELYj8qJkZ6dXR9zOS3JdcfnlywhLceX2Ze584w699T0++dGH7KzvsXRpjquvXmPrkyesrW0zHsdk9zbpLHWY85eImj7KVehhwfBJl6zIsQMXkStGownRUpvhk30CxyJKC7K8QM42Eb0xehyTP9rFbodYcw1UP8EqyjrAW1FhJgXFbo9ynFH2+pTCQqY58b01jNFkY0OZVygrqT2DOBZlXqKLAm+2ibQFsjTIUjM302AwjPGSnKATITBoA43vfgm7HVCOU8zhifahmxFxCAie+dWgQp/Wb7/B6EcfYUvQnkOcFKjQoVGUOPMtyiRDNXySBzv4gUeS5QgnQBclIi/RwxhV6vqFRYFKNCYvcRoBFBNa8zM4rYhkklL0x/BJgXBtRODWEcKbIcUwRvkO0UvLDO9tInSJY9sQupRpjr/URro2VV7WKh26QgUulRR14LyyAt9BDxP09gBpK8phjLAtjCmxApdknDHqT5i7PIfXjtj4wfuMdvsMlaA0NVDv7vboDUZ4/ZC55Xl2N3YxEpqLHSb9MfvdIa7rYEnFr/0X32X25nLd3+JYsqsci5u/8xW2PnjAZ588wHUsym6PidaUAygswaA75srNVb72r/4OwWyD1//rv8fGf/qQztoMTz59xF5/SC9L6MUJqzMt7E6TOEkwUiCURDl2fQonJdJS9YlCWavrffpHv+D+J/e585WXyUqNqCrIStQwZTiO2RmMuD7b4LXf+RrhbM24B62QhTurWK6NqSqixTbpUociKUjGCZ/81XuMtvusVIbZywu10AWOPIUf7vkHIu6nZtqh0O/8OXnOw/PAyoumU+DxhAj8rHT2i04HzTKVuVDy/9Sjs93xAozOxZ/+6cDCZ2kyB+MooPb0puRxvLMXAexn6X1K0HyRitRR2OXjOsTzlJta1RSinifvOelz4pMXSf9ZDLqfpz2n4TLHG81hOmeSPHc0yIu+/6P8B1SYp55Oqf6CET3n0aFnh7NtPbx7bB8yjcYTBtkn6TvRT09TfOYDnEbYUx/pIXU1k9FYnWXl8iJrjzeJi4KoEbI/HGF5No5VS4tvf+0W4ULzFE1nSRDi6KDi9LMa42Kqiq3P1knjhL2qQgjFysIMmxvbDLFIpY2namM9Xyompa49Srk24zQnyTU6K8iyAirD9njCzavLhFIgdIUtJeVujxkpcD231j/WGrcZ4bsuozxHYwhcB1dJcl2LrWRR0rEFweoC9lyEE7m8+t3XjkbtaMk4Gwr9oulzYiAFgsuvXUMPEq5970tUGAb7Az7603ewjGQ4nOAPxuw93qGx0CEeTpi/vsyTtx+gyhKlfaRlkSVZHSF7aR7bsqhGKekkJWhaeAYmpcZTFloIdGUoLQlCkmvNKM8IkLhW7ZpyOI4xRYnl2BSWJBlMwIClLLyqwLIknq4IQheNwQ88yspgaYNMcwpRLzRGCobGkAhDPJhg5yWNxRl294bkShIPY4aPttFVxeyleaS0aCy0aQU+hTEopfA6EX5WIJKcMi+xpKTqD7GvLiMrKPOCQNdME0lKSyp6aYq2FPg2KtNoCqSBsqpwqJkQN3DQk4Qy1vhI2lfnePk7L1PEOR/96CMajZB4b4gqKjwpyURt4F7mBU8+XCOyazeqInRRcVa7qo01WAoDOLqWKF977Srr7z9kZ22fqqqQCB59vIauNK98+2UevfOAT9+9i+M4dWwPbfACh6AZYNkWealpeg4ceMk6jPCcDGIA7AqEZxFnOfOdJlWcUcYpbuUiGwGFUrVRtQTHcih7I9LtPp3bK+z/+FMs10YnOcJWKFl7FhJVRZXqWo9/UHs0MrZFqVO0MVRQe1UrSqSu8DyHWEI0ySiMwXFsJAYJ+JGPlZc4Ly3V34hjUfZj4t4YrQTubPNYRGyO175peODUJyXAu7lCsT8i/mwTcWkO2RtjSUW5M0AnOcZzoNS1Sl5cIIzAbkeIuRZCCqSQVGu7VJZEOT46Tuo2zTagN0SNU8reBDsKKLf74DoI10IGLlWhcVoB6Sgm3RuA7+Ivdmqj7EFce7VxHaq8oEjqU1Hl2rXHG63rdhWaMi8waY4IPNxLc+iipOyN8W4uIYWgTIvafmauWRuc/+wz4mGMdXUeubVPozK4rYi0KJh3lth8sMm3f+/XuXTnCjorSAcTWvNtVnXJaKuHjeBP/5//ge/9L/8Oy69eRViqdud6YF8RLrb42n/1d3D+x7/m0YMnbO73cMoSLwxwZxqErZBv/Ku/SzDbACHwZxpc/71fY/BwBx2nhMpC7O2zn8Qk4xi34WOVFVVVYfk22TDGafjYvkORFiRxRjTf4rP/+CY//Y8/YfXaJSgrxDhlOBwxHoxID4JVvvrqDb7097+B167tu5ZfuYyy1YHr0ONdNZhp1kL3ypCPa0cjwVyTdJKy9/4DhJIs3bqEG3pHUtBnCX0xJ55PwaxTC70QljwU9j0NnI+SOM6NOOOz6YsRPp8l6sWikHOChs9By8X9eWwVeyy4Pt1oQe3pq9jtoxpB7er7sPjnI+mgrDnqi5N9ftYBzlNRx6bIWs+/MSWdZSLPq2NK5efO5ePOO7jxvMQ8O/0tMReHkoDPWfRF0zlc5vMWA46OFqe6UTslMHiOl5ydFGekGGfJPcx+CFSfQ3B34aQ7l/E5++LzeI3DExxT4TZ85i7N0+8OScYJWZZhO/UGmwpDqxHQXOogjkLmGkx1WNfxKlyvBSekRIcqUQc0ZHHGo4/XkKbW81+6fYVRb4I2hkwq7AMD3nbg0xuMUECsKzzLoRIlnqdIJjGz7RadpQ53P3rIbn/MXCuiGMW1TrKlsMsSUZY0bIVsReSWoqtLHN8hlJJC1jY9RRrjKYWd5yTGZvXqHDvrO3z1d3/7qcjjR+6nzyKiKYvL0Zp4ou/D2Sa3//5X6T3a5tG9dd768zexNKSDFNuSRKHLcL/P2gcPuPHNO7i+hwpd7LIimu0w2e+RxwmB56KM4dOPHzI7P8P8yjxP7m+gAoeGZWNVFQ7Uqj95LX0eVzkWNspRZEbjORYLwiHPc3aHE2zHwrF9wkaAlxSUeQGOjZCiBpKNkFJrlK6w04KyqD1DlZYkqSrW1jZxLBtZVvTzgnbTY7YVsb3VpSwrfM8FS/LKd19l87Mn9Db2cSyF2w4pSs3Opxu1z3/HwnZtdFpQPnmC1YzwWhHZToYEqkyDrvAO3AlbjkXRG1FKge1YCNuqxzYvyIoS0Y/x55sUO33mry5itGbwuMvmo206ix38yIdxRjGcUCFoL82iJSRJjqsNRZZABcoo7MCtT4YE4Nq1OkucsHBjAVNWzF9foioqhr0R+iDOQRAFrH+wRjyKcRyHLK+Z4vE4Ye39R+hJSuDYpGnGcDAiH46x3No7WVVUJN0xtmNRwlH/B8tNklFCs90ky3OqqsKNXAb9MSrysV0HM5mQ7A7wFzvIyMPKS4wlMZWhqDRGS5TlkJUpxmiqrMTKCiolsJRECYUVuli6VpmjqmpVqMG4BoxJin15DmUrluealOv7yJmIwfoecqdPudXHu7WCG3pM+qMp34upmYyzcopTgqaDCymI3rhJvtNH7w/JLQvXVkglsRs+2rYILs1RSUEy2aOqTH2a1R9jzzbR4wTrxgpikqL3h1SjCSL0kU0fkeeUo4xikmAHtRBD+g56nCJbPhVlvVYtz1DEKcMHG9hS4S12KLICK/Ap4wyrFZI83kEphSsEojKU4xTdrdvuLXRItrqUukJGHuU4wb40h7Atst4EZVsoWTPik8d76HFGcH2BjUc7ZGmJG3ng27QWWozX9rnz9VdoLXYYbewhLAu/FaIiH68V8Nm791h6aZVf/NWb/OD/9cfcvHOFuZU54s0eInC4/c9+HbcVMPfKJX7jf/dfcOfjddbf/BQ39Jm9toQdekjHonNrpQa3B4MjHYvO7RVu/fPvce9f/5CVoqQbx5S6wleSuDuhu77L3NVFUJJsnBLvDeqI76HHB//2x7z55z9ndmkGzxiefPYQJSSNRsj8jcssvHKF69/5Eo1Lc0cegg5V6cSpCXJaFCckzN1YZvHWJZJRTPfxDlVasHl/C78RsvDS8oncz5eehfdOZTyVzBkNDnEmuzh9indBOo/ZfjYNxxWc5xlyavlTDf4cMP3gfadOEqbArPNJNozuPsRbWsBuBCdynWSujom1Fzogj4Wxx25dn59ucyDwEFMWolOnEyeSOEXH2Ve+OLA9KVx/scOp8/1+vmBFL5T+lpiLX64Fp20bjqNsnvgz5WIKs3DiwTT9yalMHGe+qRMX9fUFIz5FYn98efHketbUOxlt8ykf1F9wOpLJC8HuB2usfbZObzDEaEOrEVKqCl2URF6AUhadS3OnSp5a8Keem0LNvJije3WQMuiEPgsvXWLpzmU2//An2I5DalnkWY6UkqwoybUmy3Pm/Db9/vDAJWZdpxu4bK5t47guge8yTDLaYe3VZbc/wjgO8w2fAni008U6kPpLS+F6LvOhz4wtCKnwbIc4A3yHapwye3URy3MwlWF/bZeZ1VmkUlPaOL1Pz8slhMB2bSzHZrjVY/XKCh/97EOWV5aI+yPC2Rbx3gjLceg93OHyGzd56Vsv8/7/9HNUqfGiAF1VyApGwwTynHY7pL/bq1VlAhutNZM0o/Jc/MrgpDmxYxHYDs3Axws89vZ6VIUm9F20Y+Faiv52j5aUTDDEpcFFYuKUyrZwdEVgW5hCH7VPG0NlSdzlDn7L58n2PoNRjJKS21+/TfPSLG/+6VtMDlx8SluRZjmP3r6H7TrovOLRJ2t4zYDAdxF5gTSG3FF4WmMcC++llxC6ojycbEnOJCvwy4Ji0kO6DSQBKIWUAqMrsCTSGCZZQTv0kaVGJrVxvCg0buSRFyVL1xfRoxQGCZP9AVEUEK7O4S+2iLtjVAXVKCExtdGs8R00BtexEJYiNgY7dIkiH+VYBO0GpdY8ee8RlhBIpXAaLmEzYOP+JlmWIZVica6NF3jkWX7grl3Q2x8gD1zXqkaI5dlUZcVws0+xM6TMC1R/wtCqo253RzG61Hj9EWamgZpkiMqgLHWgElYQXZon647Yv7eFuzJD+WALuxWgRyllXiIyTZ6PMVWFpSyMEpR5iSstlGNjsloVDd9Bugc2HL6DHAqkZ+M3XKQxqIaPyQvKsiKab1Jt7AOSYjAi/eAxcqGF7dlgKjgUTByqaE7bn0+JIMXR2l0VJWV/TPjaDex+TPZoBzPTJI8znAUP41lUgxhlDFWhSd9/iJCSandI2R1hX1nAujyH9F30JEV0IkgKvE6DdJiiypKqm6INkOQo10IPYvBd4u6Q8PoyQhukkQjbQg9j3MU22c4AUWqqOINhgrXUqdduXaGzHGu2SaUrJrv92sWyrkj3h4SLHfIkI+uNMYA/3yAI5uDRLvuPd9GFxgk9pJS4novW+sC9K2RaM17bRpWaxZdWaV6ZRyc5k40uO588xhzGPtEVo+6QR29+Ru/TdaSlGCUp/lyTl/7R1xFSYkcey792k+Wv3TzGg8bUajJSTl3ymtcX+PJ/8w9Z+/N3efwHf8p+f4Az2yRohHz01+9w/fWb+DMRVVnhhC6j7R6f/OmbvP+T92nPd5AGtta3sR2Lb/3edxCNkNmXlpm7vXoakBo4dH9YVeYgAKsAcYAcjiQ4HHgsFESzTbzQIxvFtC/P074090yh5MlXnpyDp3DDWRBxmOkc8HzAGU3HDucKJTm1gbywwfSUdKR4PhXom+lAmYtPeM5kPVOK0+P3FD3PqKssybsDLN9HqOkg7ii2mDx9sPGUChWn3OFMTac9QU7PN/X+Rdzn82K1g2qrIy9Yn3e8nxYzHzFNJ+fhc3PMF6f/PHEuuIjfezo9HaGBA1B94us+y1WLKd85HC84JzOa42en33o8SU9Xfvi+8+4/IxmOg938EsmcbMMFkofz9PvOp+GIc3rqibIUoai/Vk8pCioGcQaWZAZBq9OgudQ+3T9nrbymce8CKOuNwRjwQo/2Qhv6E67++isU/UmtB60ENjC70KbXG7G1s0e72cCxbRzXJi9LbAxpqWlGAWVRMpkkWJZFELgMd2PkTMQkKxhPUmxL8aTSrK7OkzzaJLBsFpZmiEcJUiqGZUngOhRZSqYkGQIr1Wgluf6lawhRb2hpnNXgTlUo92mvN+f08uluON61EVIQLbaJuyNufvUW6ShGj1PmV2fRVcXHP/6Qm2/c4spvvU4008T/ise9v3yH4WBMs90gaDXQ+z0oNGGryfraLvNXFpifbxNaFiDIESS9EbOuy0CI+rQm9FEH0bEvzc9QZAU7e31ykVFlOSrNyPpj0qwO9hYXBte2aFeGMPRQSYFQkkQJcikoWz4rX71OON/ip//fv8L2bazE4spXbjDz0jJ/829+RKUNvuuS5TlJfwi2xb137jO7PFv7Ma8M84sdxg93aMw00bbg0us3YJIy+GwTO/RJRnFt9GrVLlulY6G6+1TpDloEGM9HVYZSghYgipI0ThG6ojcY0hYWFYaiLMktSTmKsRyLLMtxHQelFNFsm9ISjMcxaVESzjbI8xJfSdKdfn3649i4vovxHYokh6TAJBnCQJEVNVMjBI2lDv3Hu1RpDmXF3mBMI3QJQ4/JJGHp1grRAchP4oxxfwJKIKXk8o0lGq0Ay1GUWclkfR+d5rVnpNDDV5JJlqOTFEtXtEzFYJzQqCQyr2NwiKxAxTmVqTeBchRjL3VII68OdBfUDHShKywhyIsC40rcyMMPHExZR7wO2iGub5NWGpIKd74JZYHj2VBWVELgLrbRZUnRnyCvzmF8B8u2KEOH6OWXKXpjqnFK2RujxxlW0z/6LmrVhmmSpClJgAw93MsL6Me7iJkm/kyEtBU6crFbAdlGF7M7opptICwJOWShT7XTq09lqop8bZdCSmQrwlyaRWkDCmzbwnTHVLaFjhzc2ZBiq48UYLUDLBkirdotrCkr9CRDNvw60J0uEUVJMk4oc03g1BG+bVPhdhrk+yP0gTqSpWp3q6IZUo4ShNYYXTEZJTRvLNUCjKJkvD8kurbIeH+I1prOQocHnzxCFxXSyUjGMZYU3P/wPkWleePLVxCtgGycMHd1icFOn97dDWRlcF0H28BoFJPokt5kgvfnbzH/ymXahxL9A0bvUEVWCHHgden0GJwE1Hbgsvq9V/lWb8wv/uznDDb3WLi2yCgv+Lf/x/+eqy9dprMwQ297n0cfP2aic2bmWri5Zmu/x53Xb3H7d76KO9fGsi2UJSiLAilr9a3HHzwkHdcuqY2B9U/XCAKfxmyD1/7u1whnmug8x1QGlKxPmQ/2PeXaBG6LI9n3ifW3/nuasT11WHb2xplMtVB+CmQ9wvDnVDzt3rR5/7z48iT6vwByHKGxkyj8qC3nisGOyZgqiZ1O69S4WVPun5uEoBKCd//b/wu3f/+fMvcb3zgGx6deedh4cfCWF3ch+xzEPJsROg+sn1fwvHE6Vc80TvjFWngqzsZhobN/f4n0SzMXJyH4RclM+XWx/Pa8F56Y9C9W8rCCg3Vj+hdrjja0p5aSKenM/YskDWfzfY5Ur9vHMTpOcptHi8O0us8ebAgzRQpx5k3HHNypVIxT8qwAA0oK5qSgaoRUVu3WcuHmMpbnHEiRakO90wwc0xc8c8hYHCw0SnL5lSts/uIzvFbAox99SJJnOI6DKyR+BZtpTug4LM002Z8kuJ5DXpSEVOz3J8y+tEI2Trnx8hV21vdYf7JL1AqI5loM723yla+/zO7GPrvdAY7nEDUi5maaRJ0IbQx5lpNlmq2ioOHY5EWFJRVxb0i6PagNX41BSsHcpVk++Itf0Oo0uPr1V2qpLuLY+O/MwneqW5/aqeox7m7sE7UjRv0xV758ldFmj9nri9z7Tx9SFYbtu094748V3/ovfxPLc3j9H32Tt//DT7ClAmWIA4+wrFBKIKOIpm1TIUjTnDwryAU0fI/cgJyJEJZCFQXaGJTyKPOSXpzQnmsyGidkWrOwOMveYITj2ChjaEYBstTU1uG1J6JYUpe7scSt77yCE7i8/Uc/p7s/oMxLXv7N1wjbIW//8S/I0xzbd3GVotWKSOKYcZzyyhs3CDoRTx5sMPfSEte+dYcHf/QW1STFu7WMqQz97ojRKCZya4Ns23UwusKSEqsypHGCHHQx+w+RL71MPE6wZ2pXpP0DjzeerRjkOcoWqFFCYSp0WWB7NpmKaLWb+IFHquuI0whBMk5It3pkae3aFSXxLYtyUlEMx+jAxys1tlJYvoOVlxRJRjZMqBYrnMBl7toCg60ek+4YL3KZC22GBRSlJmoEhJ2IIiuI05z7HzxESoXl2NiWYmW1TefqPAjBZH9EsTNAK0lpTB37JC9otxskZW0AbLICf7aJ3u6jswPD2KB2A5oOJoSujRlMGD3pEi62KXaGWJVBehaekBRpSRg1qUqNbanaw1UnpNHwwRjKcYLbDBClQYoKbIti3Kv3hqiNDhzksEQFLgQOyaNd8kc7BNcXMZ6NcB3yzS5lqcm2eqjmoW70wb/PWKpOrSNSYi93iPtj3MUW1eVZzOM9KiURgYsoatUuM5jUrnkbIdiqVu0zUKYFVWAjQo/w5dWa8SlKko19qtDBMgYRZ4iZCMt1UDcWqbISd7aFHiWU45Ryb4hRAiXqfsIAvot7eYHh3Q3sZnAQgTvDnWtR5WUdk2S+RTlOwFYU3RHVQZyTMisoJxkzt1axA5dilDJ+so+Qgt5oTDHJyAcj9nVFnqSgNTovKJKcdrvBjTvXWHrlKr0P1mjfWcFr+KS2wrEVvcGIYRKzGvmMkoxhHJMUBVJK0iRj/8M1mtcXMYCUgiPL56NF7CScmY6gnKbP7d//DlmS8bO/+AWD9X2WVuaZJAmP7q3z8JPH2LbFcuQydhoM9vuMC83X//63uPqtV7CjAFNqwsUWOi/45E/e4tGnj1i/u0Zvp49t2wgEnuMgLYlUip3dXfYebfK9/+rv88M/+EuePHyC34lYvrxIY67Fyu3LbN3fYOXmCu2lmQPPW+5RFPuTal7nTsBDtd6pj8+APHHO72clY55icur7L1LHxe89wjrixP57tvyZG0+Jhs/WLY5zTmGxzmR9UUBkYJxilwbLcs7pfsEpu0dx/nu+eIbjVOWn/55M58HfU313nEEiTsC26QVfpCW/0nbzBTAXL3iyc+rX06cK539BJwXpz9psTmHXE0bTJwH4eR/+4YdQz83DEieP2ep7U20xzqZnMhrHi/JJwHleVPLDOk8Htzsuc/qdp1m+U/RW5xF85lVn+Stj0GlOIQxVVdGZmyGPfNqhQ641NpKVL10+khrIA29RxpjjKJUnOfkToHraVAhnolrl6O4W65+t0YgihmVJVpbEaUGjETKOE9KiJEkyOp0maVZgeQcRd4VgPIoZT1IwtU/7hcUZHt19QjlK2NvtsvZ4i7AVoXRFpTU6K9l+tI0XesRZwY1Xr3H/ozWiqIGVF6STFN+y2bu3wdYHj4nmWwA8eOsu6++vkdxcJNzYZfHaylPjNm0tPh6uE1wikKc5P/r3P+T6K9fYW9/Dc2ySNGMymICs518cZ+w83OLjv3yXW7/xJRZvXeL7/80Cd3/0IZu/+IQginBcB601vhGUcYopNYUx2AZsbcitirDdwAQO1STBch2kMRSTFAkEMw1G3RGCmn94NBrXgDl08RBEdh1nYWIqupVmvDcmLwouf+MWt3/zNQTw4Kefsv7eQ6QQfPdf/ha7T3Z5+49/jtAVjdDH2BZoTXsmQhuNKkqufv0mn/7oI0RlmL+6yHh/hGspkqLAMYbxx09qiS0wnqQ4BmScIZQCy2DGKcr3KT7ZRdguVV7geA5W06dICxRgyopYVphCkwcSR1eM04LA9yhDj+ZsC8d1sF2bKoFMGFzfJh+nVBjG+0OEJVi8sUzcj7HDgDxJcVt1rBQncCHJsTwHJ3XI9kaM50Y0HYXl2izdWUGYinSS0x+nlKVGS0U412Dtg8fkac7lV65w6c5l9je6lGXB9Zev0PnaHdzZJkl/QlUaaHrI/TF+4KECB1GUiEJjBw4KAWlJ3B0hmz52UmLvDsgXO3ieQ2kEVVlhOzZCCVqrs2zvjRiOE4Rn44QuVlIi0qJ2+2sM9myE34mwmgE6znBaAWV3VLuTnaSI0AXPBtepDaLTHCMEMtc4jkUaZyjXRrUDpDGUlkB1IiS1N7oqK1GudfzRXCSDmiLf8S/Pk7zzANMbUbo2ZXeIE3gk7z1CVBXScSErMZ2AynVxhaBcnUEMYqRnk3kOrRuLWK5N0R1RbPUhLfBW5tA7fdwrCxgM1TBGLXVq+5q8pMoLdFpitUJkXoIUpN0xylYEV+YRQlIWFdIY/JkIZhoI3yHbH2LPNjCTjKzUZJtdrNCjHMWgQTV82ndWsXwXozV5f8zo0S5DKRCTAoSkGXrEZcFMu4E8iF8x7o+QCPY39tjb2sNCsLrZBSEY9IeUGDa3dim1pjceUxYlcZoCYAsBZQmlJh5M+OgH73H7O1+iudg+sbceLlmnrQOPdicBGMPug232H25x/e9/DV1p3vlP7zL+7DFB6NNybUobesMxj0t9EHvE5vv/5d9l6Y2b6Lzk4c8+YW99B50XlFnO2r0njOKYLM24tLzCeDxGKUVelghpYZeaRjNi4/4Wn/zlO7z7o7cRlUGs77Lz0WOaC7Osf7DG43uPEUAYhQTtiPlLc9z8yktsrm+jk4LXvv86M9cWz8cb5waynVLgRZiBp2b0L1P+xMnAOXG7njqZuEhIWktmed6TgOdWFTpz7ymm5MyG2fjKHX7t//R/oOrGtXOGwDnOcPL05aDsISapDEhxpt5fom9/qfQsbH/64OU/G5mfN/2K1KKeh80WT02Yi/I/awqfLHP6W5jK1hy/5pmT6yQsP/w9pcBT3Io5Nuy9oO7DP6dx/Im3XLipmumLxbnvO3h23np1kl+Z0sQyK9h5uE2cpDiWQkiJVdRu3gb7Q27/9ht0rsxjDMT9MVmc0lmZu4AZPNHwqgJ52nrt0p3L9N59xHh/QBqnGKFqg0ZH1iDTsYnjlPlGgEAw2B+gDlQ47rx6g/X7GwjLxvFsqqxkbrFDXlXEowRXCPq7fZphHcG4TDPCRoA2FX7gMuyPmL+xxHgyQRcFxm/SdB2kAdeyUFIx2u1RVQapJDOX52g+6bDxaA27hPlLS0hLHZ8AnRiVqdPu7A0DRaYRacWVG6v0trtYjs14b8T3/+t/wJ/+3/6QKi/JBzHv/OFP2Xm8zcvfeZWFl5Z5/R9+g5vfuMPeJ2s8+OmneL6HEpJ0klBqg6sUnoLClrX3lsBDJil+poESY1tMpMByapeZjdkWe2vbzM02EYFLoivcAz/8eRVj+w5PtgeUk5Sm7dB+9RK3vvsqldbsP9rl/b98hzzN+f6/+h1G3Qkf/Pm7tNoNmpHFw819KgRLq3PklabfG3Hj5StUumLr3iZGCIbr+2wPYi4vzpIPxiT7Y2zHxmp4lL0xSki0rpmEyhiErbAcCzEzS3njVawqQwBZqdFpQRFnVFIiTElRVijXgawkU6CkIvA9TOCjPBdpKbStQHqQ1IELZ1ZmcHybPM5Y//AxfuTjhXX0YK016SjGiXzMQZA/Gaj6pKeqiB/toEuNG7g4gcu1X3uJ3uNduo93iSc5jq3oru9htwL8ZsiTjx7jhnUshLAZ0r46TzTXZNIdkQ1qehzPITdg9UcUWW0rUuY5BRrXd8l9h7bnUPguAwStrKS/PSCYjZAHKlAq8sgGIxCC+VcvI384oTSGuNQElsS/1KEqNJZrI10H5do4kUcWp7VLUcvCaQZQaOxmhPPSCsVgQvHJBtUoRkhJdneTdLsHnZDgtau4zYCq1Dh5STKIMZOUXAmUo4i+fK2WIl+0mB0JKI5vGEAGHtZcC707wkiB3B0gZwWlY2FmGrXdzihHdSIKC5zZFuwOQFdYsw0sVzJ4sIPBEAYuwhjkJKdKMqpSU2Y5lWPjVAZRVeQ7fYpJigZUUWEOTlAtS6LHMVbDY/JoG6/dwIjaZsUAZZqjH+9gzzaRSlGFHmZ3gBwn4LvIvEIELu5sAyf0qMraq9T+p08oywrpWcwvzXH//XuEoU8jdNl/8AhvZYVCCsIooMwKJqMDQ3DP5eP37oIlacw1GHR7ZGVJy/eZb7ewHZt4MMZCIIG5uQ5zr13Fa/gEzZC7f/Mxr/29r2L77vEqJsSZ/fbEcmYMu492eP8v30FWhsF2nyvffoXZ26s8fvse3fVdxqMYpGT50gKXv3ydxlKHztUlmquzZOOUH/zf/wOPP3pIkufYtsRGsjca0Zpp0w4blEmC5/vMLMwymcRIJenvdlFIQt9nsNFFIbiyOI9n24yyjNLU6qDNKKLVarK7uU1RVrx1d431Dx9jew6yNGx/usF3//n3WX3j+jMkmpyZp2eR+RlJ/zTw/nmR43MJn1/AQF2coHFaOivMPPnIXOym9pnf8tlrcd5zgbAt4p+8jcgrrO+9wSnVqoM996Q7WhAH9kFTCDnV/8845vlbTL+yk4W/JYbqC1CLOiMVPzfXYTJn/vIFjONz9NSUTaieg8+h1nXeo3MHacrR4sGdk/11xJmL43Jnme5z0wXPL+qNc589NRwneuXgWe/RLvc/fcxwOGYmikgmCTr0iHd7XLq6xEvfeZnBZpePfvghbuBw+9sv18cf4jTTcGisjYGq1LU7zad80wqimYjbv/MV3vrv/xLHsYlsh6zUKAHDomShEeLaNsMkJ/RckiTFci1spbj7/n1s3yN0XSLXIljokGQlGw+3kbpi5eXLzMw0uffBI9LxhCwvsUzF9k4fKQSeY3H1S1d4/6/erSV6SU4QuhQYskmCUQL78R6j7pDWfJvO8hwTnWFFIU47YDQY0p7tXDAS0wZEcKgP7PgO3/ln3yXrjilGKbZrc/lLVxjsDnEjj3C+yc7dJ7VBsTDsf7zOzx7u0rg8w0vffoWZS/Nc/vbLhMuz/Mn/498RCIUwggLBTCvCkxKlJEWlycsCP/LRUiIAK3BRSYaSkkYrpESg59v4nktlKvQ4RccZ/f0B+mAz0QcR3cVcg6/83jfIxin9jX3e+sOfMR7FfPdffJ94nPLTf/tDklHM6mIHuyxpuDajvKTICva2ujRaEZe+fI3GQgs79MgmKQ/fvc/K9WUK38aVESWQjBNs2yJoBjgIMq2RUtSxAyS12kdvjGovkXk2MisobIVd1DEwbNuiMAZXGhozTfob+yAdlKqNU4NmQDGcoC2LYKmN41pUdt3GyTDGshQ0fCohGO4NCFYWyMuiVhmUEs/RZKrEaQUYS6FshdSCMqsYrXcpOiH5MKZIcrSu3aM6nZBke4C0JVWS0x8kpEXO/NIsnqW48+svo00dyVgYgZSCpDdmvDeiFOArhbvbI3YsbCEYjSfk44SOtJBxjvQcGjMN4mHMbCtCaE0xHmM3PIrNIXZZMnmwjb/cwb42T/LxBnlWkjsKUxS4rk2alTibPUTcgqxEhA56lCIqgxQCeXmOstRIJSnKCufGIvkgxp5vYc23KPoTRFaCrkAKlO+gPBt3e0DmO/iRR3J3E3tlFne2eaFr8XptMqfyHApPWt95hcFff0AxjqmaAVoJVOCQVRV6HGNXgJJYbh2AUO8NyPeG4FiEX7tOSczkyR47m106cy2cwCPL8oOo25q4MkAFW32cpRniUYzdDKgQiKLEkVBOUmRWYOIM3QkptKntOg7tgixJpWHnwzWCdkQ1SbBDD12U5HsDhOsik5xsq4/bDMAYjK7IRgnCURRZytajTaIoIAh9kl4fu9lA2Ra99T3QGltKfCkxhUZ59VpRoBEbewxGMbaUzDRC5mdazFxfAgO2ZxMstJl77RrBQhtEPdf6G/sMtnvMXVs6PQhPGciCLkomvTH3fvoJrueCEAy7Az77+ad89Z98m+Wv3aIqdD1+UiIsiVKqjuuRFnzwr3/E/Y8fcfe9z1BCYirNZJKhqwolJZeXFhiPYoosozSGhaUOTrDC9sMt9spdwlbEpasr7K7v4Hsuy/Md9tOUbq/HQqdFkmRceukKVVUx3NnDMnVbet0BM/Mtbi0t8fb9x/z43/6Qf3JrBSf0TkywC9bxc54fCfUOGeKz+V4QAz23dr15Nl90YeEXIOyF3dRe8N7z6jqJNe2VBVTgH0ToPhbmHqt9n+zsc+o0Z3+fEXpfENTkV2PDcYamw/RFMKDnnUb9ihiNL0AtahplXzC1Jz/c8zhaMT3ryXT2DMNMuXfuqYRhyvvFSROQ02WnDqR5ei5Pe+dFC9SFd07W+PRpzvMwFtNuH+L+3U+fkCQpQRDguA4IgdXwcIqSG1+/zf7jXbob++zc20DYFku3V4nmWhy75jrgHw5ONu6/eZeth1t8+5/8Oo35Foef6xG9usLokvW1TXy31q3MS81KM8CPfPa2enRaETvbu7TmZut4C47DcDjBch0aUYBvKoIyozswbO32MYUGDPE4Yf/xDpZto5RFnhQMeyNcpRBa055rMX95kUYQ0LkScv/xFu3lGTzXwUiLSZ4R92Oe/OhjGv/wGygpWVlaYjRJKHRV+6PnhLrAOSdMp9bAk32O4NLtSzx65y7dR0Pmbi7SnGvRmu/g+g63vnmH3pNd7EoQNULipI423F/r8efv/hHNTkhzvoXT8Hn5N17DsSzW339IubnPsKcZCkV7tkVWlrha1Ua8CDxL4VQG6dgYS1FlJbIy6HHK1uYeLdcjbIUMVU7lWFSFRouaYSx0ycqdS3z2Nx+z9sEjRKEZ9IZ891/+JmVZ8dd/8JcUSc5sJ2I8ybA7EQuNkDDNGQ5j5hZmyLKceBIT9Ca1xFgJZi4vsvzyZYr9CZYUKAGTNMPYClcp0sGEAoFUAjsvEFKgpaAKa1BDqaFMkKFHXhmsps9wcx9fKJCijscResjK4Ps+RghUqWtPYI5F+8osXqsOyNjf6LG3sY/nObiBy+LleYzW2KFLaQy+bWF7LnmWo0xFLkB7NtbB+LvNACdyiZY7oEtGm10G6/s0mxFZmmPaETLN8DyXyrPpbfco4oz5m4sko4QK0HlB0h1TjFMm+yNKYyjSDL8ZMNY+xDmgsR0bVWgsozG9EV4jYJzmeK2QKs7JKo3JC9LH29iWQkhFcncT49o0r8yT7Y2wJzl5VSEaHlYnooxT0uGYan2fYquPngtpv3yZdKOHnNTqYnK2gakqhAD9eJc89KiedFFxjndtAWxVuwtO8tp424DyHfxWgMFgLbYZf/gY+1t3kK49FRQYgKo29j8EFyc/IOFYVGVZe1LSgjLJybSBUmO0wSQl0rUpk4yyO0YisCKPYruPszskHSZMsoJWM8QWCi0FohVg+jFW6CHijL17T7j6vdfJt3tEKzMUeYn0HbLhCEPtjUw5FpQalZeIRZ/scZfopSWMgHxvxPggBkd1EENGJDnStVG+S5aV2FLghCEYQ1VW7L/7kHirh2gEuNKgpCKJ0yMveSJqM1jf48rNVTqLM1iWxPIc7NAl3tjn/ffuUZiSUkgKY7CkxHcd2lcXuPmPvwUG/E5Y96moF39dlDRmGnz5d79Ka3n2aIWqdIXOCgBsv94PjoV28Oj9R8SjBL9Rn1D5zdpVsRf5PPjpp2gDSy8tE7YjiiQnTRPC2SZ3//JdfvTv/prucIg29cmiLSTLiwvsbu+SFgXjyYTZTotHvT5plvH4k0dkac5Or4dr2fi+x7g3ZnNjh6WZJovtJh1nhtXVBWYaER/dXWOy0+XJ5jZKKdK8pOW5FEDb9RkNJ4S+T3enR3+ry8LNZc7dmLn4Uf38AHOcliVeWP4I2055/kxQ+2J8wTnpVyQ5fyY8FOfSL04ALvfG6plSp4GhOAAuJ5mA83nAKVzYtOafAFK/Mp7tLBQ9A2rPMjWHYuCnseyZ9/wtH8b86rxFPePD+cLS2flwQvRfz0Nzat85mhtnmJFnTnhx5u9RMXP2xum8U+s95lIOeOpzspqnrk7nOwTtJ++eQKvn8DoX3+SUUdcJ3Ese5ziWTVakBM2QuNJkGOwK1t+8x/qTbUDQXmyj04IP/uo9Fq8voQ6MJQ/r0XnJX/0Pf8HHP/uYNM+Q2vD9/9XfwfZOG2cZXVEVFX4UUpYlJYZG4BEXBY52aqmnY+MEPkpKlBSMB2M68208pTDGMIkL+kKQxwmdMGT28gzxOGH93ia2lHhC0O6EbD7ZI89yZjrNg2BPHu3FDi+9fI3d9V1MqckdG08phjs9pKwjID/8m48pypIv/+Nv8fK3vszDd+/zzl++iyxhZnnuwE2e4SLPIyfvHB+d1xK9pVuXiDoNmgsdPv7hB+x9uk4xvsXL33+NpdurbHz4iI/+6n1QCtu2KNMC27JIumOkUMi9EXvJE1ZevkwxyRnFGV/+9dt0H26zs72PN9tElBpaFtKxMGleG79aCgqNFJDmBTYw77n04oTKtxkMxgTNgNEo5tLNVbYePCFwfd79s7fwPJc8L3CbAd/+/e+hHIsf/g9/Adpw/fZl9rsDlKMIVmb5xQ/eZuHyIlWp2d3a48pXrnPt127x+Gef4XoOq69e5fKXrjLZG2CEweQluRB4votdamzPRQcu494Y98AgPUsyrMgndm1UWEdPRklUXjJMUzwq0qwgLhLCZkhvkiDzAtu2iYWmZdnosiJLcxzjsvn+Y5orM7RWOhhdETgOUkqqrCAIfZCCKslRjiJ3LKqtPWQrwi5KZK7//8z915MlS57fiX08tDj6pM4sfauuvrdvq2kx090jMTPQC2AALEDQlmtc0owvNCP3r6AZH/BCs90lzQhbW8EFAQyBERhMz2Bmunu653b37e4rS1elFkefEzrcnQ+RmZWZlSWuaJC/MsuKE+Hh4eHu4f7TX1RZkNX8CgskTll+eRUMA+G4rMy3CNshs0FEpzaPMgRFXuA3AtzQq77BovJFjycxs/0RZS5RSlNIySxKKvcc20TnEqk0hWNhlRLDMPGRFLZJGbi0Zgm11jzZLMWIUwrbRgYetbRAC7Aci3KWkDzcx2kGePMNknKEpcC0LXKtMTwHd3UetbGPZRkUhxgbmgqvwRhHGFs97OVuJUQ4Fo1uk1KAaGqshRbZdh/ncI4VvSlm6GKWiujBNsHrFyk8G9WPSTYOcOdbWK3gXH9xJVXleni0Wp1c7zRYjbAKFG83IHCwl9sYgxllWkBWUD7cR1kW2rWx1+bgYETq5eTjGA3MXV5AH0xgNMNqV7FBSgh0ISkECL+yeuRbPaTSCN+l2B4QXFsinqWEK12Sh3voKKH55ReJN3pIs9qXrJrH8PYOjbkQaTSZ7g3xLLCaNcz5KnVtvV2jLDXBUovp7ojo3h7jm5sopZmOp9SaNeTBkE6jhqpbTAYTZpMIbQj6D3axS4kVeKSzBK9RAfyZjkXbD5nu9JnNYta6bcJ6yGR3xP6H6/RvbhLUfOZeq9zWaqtdVKkIWiH1pTaWYx3vDYZpIByL/mYP07aozzUqgEUhMG0TUytq7RCvUSOdxYSNJks3LmB7NjIvGO8OqTUD0t6EWW+K47vYjkU2ihhNpzimSbveph/HrC3N44Y+8XiKEDCNE/I4xQt9Xlhe4Pb9TYQQrC4vsLDQZa83oLe7T7vmc/nyKv1pROIYVfrdKOfCXJvvvv1TQJColLQoaAchlmmyc9AnjhP8Woht25WF5TmYmCfptx/995Tg5nN1tIceFqc1mM9Pz7znE0ggT9DBPrdL1PO+x9MsO0dbqlTHAvARG1QJZOJRmxDHyk2lFQLxuOuXPlHp2U36ubJJfEw6Tyf8GfDIx/kFTrKD52nYf06WirP0c05Fe/i2Jzvv6FsTp5mp89noc+h8JfDjhY6Pnq3vPz55jpxw9ui0BeMJ3PvROx75/D02mI9G/mhe65Onn9Lgx+fKkVvXkZhy5Fp12MinfNRPluIff7zWGl1KdCkp85I8yxmVOY7hsbjQIspyhGly7RdepNYMeef3foAVxdz/8W2uffnlKopKa4abfQ5ub3P/nTusLXTZPOhz653bvPFrn2P+6tKp1hi2xd5HmygUUirSMsfzHGqWjSs1PaVxFIRelb6z06g0bmmaEy60ufjKRT76/kcV0JUAz7VoBQH7D/Zo1AK0EDRrHuP+iCSKWZjvsHh9GSOwufrKNe597wOG/RG72wdIpdCGgXZMau06MpeILMOTis3v38T2HF7+rS+BVDSWO1z/xVcRp2JIHhcwTnfyI1HuyNAjBPi1AK/mg9KENZ9xI6x+C2gtdWgtdbjypRtEg4gP/+xnHHywCRpKwwDbJk8TCinZu7eLUgo/8Nm6s0XNtiuGUhjYlgVKV7gLlkme5uA7BLbNZBaRKUXNc9na7zOYzJCDMabtsLDQ5vUv3+DuO3exlKRp2tiLbcbjmCufu45f93ADl4/+8gNMYOWFVabjGZ12EzTs3N+lKCVJnCCVor3S5ev/4BuYVhV38MLXXmblxTWGW33yUQyWSWGZ2FFOYBgVQ1eU2KZJ7dD/3w49hJQYWuOYBkpqdFZgmiaDKCF2BOlgQl6W+M2Q1KhidBxDECUxKjNw2wa2GWBok+nuEEpJtNVn37ORQmC6Dr5lYiLQnk2W5hXCs1R47TrKd7A0FOMIR0qE0oQYqFnCVMPs4QHdl9dQugLSql9cZPFV/zgbFfrQX/iQqSiSnLg/wXMd8nrIcKNPrRVS5JLAdVBaYwoQuSQIPLyGT7bZoxV6gMBwTMrQIx5GuHFOOEnIypJpb4J/eQHLqwKFRVqiS4k7Sxn8+C7uahelJIbjUCQZNddGexbTgzHWLMau+fihj5wklYbesWCUVjEJuaRoBhjNEF0WiCjHaIUYaOjNSOMcc76B6dsYoYsxV8faOKDYG+PNN7EuzGO3aiTrexVaeOhyOsOdxrDN0+v78RpefUD+yxeIb21Sf/0KeppAUVIGLmWrjqsh2xvAYpug4aMMQTmIcOcbVXyC0pSTGLsZUiZD9FYf5Tk4i21ULrEMQf3qKsV2H1EPMEwDb7GJ5ZgU4xjSnNwUyElK/ZVLYFtoqXACB2EZJAdjdJZTihAtFabSWMLEW+kiApfRzgAxTTADj/hhDzmcMXmwxyBOKE0TZZkkvQFlFDNGI0pFJktkqVBFyWgSMTgYgADDdQCNVwuwaj52XhL6Ho0wZHc4YuegX62hoYUtFbvvPWDzh7cIug2WvnCNtV94hdbFBQS6AketNoSqyy2TxmKL22/fwrq/x/KNFRqHSS7mLiyQRuvkcUI8iXnxq6/QWGgSjyKSJGfu5SXqSy3KaYrjpNRX23zwRz/kB3/4PYqiIPCDar7kOWVecPmlKxRxxnQyxa7XcfKCV66s4jbrzC90EVoxKwqkVMy3m+zu9YmynPdvP6Du+/SnFVZI0/MIw4BcSrSGRhhQr9XoDUd06rVKUSUMJuMptUZ4mFr8mHF59P7i9MZ8rj5VnNxnPx4HeYpZP09/+DzVnbjnmNn+NHS2Dee19Wn3fZrnnuBlTmFlHG2WRwLOGZ7nCMtb5xLhPo3lPaupPlk/pzWtJ69/WnoiT3DOdfFIeDpd7PH3Ppf+EwkW8JkKF2dnGyc+xHNKn2G0zuuuI3qu7+hpnXaGu9dP/PGc9Z3RkImzk+DEpH68LU+p90giP1vsKVLA4wB6Z4yDT3kP8YTJePwxnqpW0FxsYxqCoiiq4EfDxLAM+nt9Wosd/vr/8e8StmqMdwcYQoCCH/yb7xE2ayxcW+budz/knd//AZNRBEBY87nRWGNrd8CP/u1f8Wv/+9+uUIcPO0IWkkl/QnN1nu1b6yx6AZZhMs5y6oZgqeazM42xTZOGrVBFgZaSmucSxwn3f3YPU4CUBaZlosqSnQd7rF1aoUwyptOY2azKJtUIfX7h7/0iwjL46Z/8mL/42TppklfWj6Kg3ghxDIMsLxn0pxjCwFISGbgUccLmTx9w8UsvsvLSRRZeWKXeqXOucP1UOlwmTqQKzpKUwd4AN3BprHVZvLHKbDRjOphSa9URBvihj18L+No//CYf/cef8dPf+yuEYdLvjfAtEydwcQ7RfpXMyQuD2LZoNOuUWY7hVsBvRZaDlLgIPMOgKAqSWUK9WWMWJ1Ua20JiGBaWa9O6MMdHP7hJOompuR7jUpAlKQsLbYrxjJ1bG0z7E4o4Z3mlci3KRjNGvTGjWYQsqhScBzs95uY7hPUArRWTnTGTScQrVxYr7BDLxK77VUaeOAOtySwDJ7DRcQYC7NDDzEqsstIg57MELAPb91DCoDAMEqdC6tYywaz5mK5NmRXYQuA5NqVUuIZZab1tkyxNcLt14t6EwHWQeUlNC0xD4yyGxNMYpMJ3bLRhooVATiZIqQ99zqf4tgmNkGI8RRQKN3DZ+mCdsj+trAlXF2gstdFaM9qqgvbdhkcyjKqsXI6FHTg0vS4Ta0xQVhnNlNL4i028uTq9+7sYnoNSBWZeVHFM9QDLdcgsE5oB6b1turaJEbrY4wjbdUlLiZymFIFLmeYYgYsTeJS7fdxmiBQCt1XDlBojcLFNgzgtcFs1imFEkeQYd3cwhCZp1pCeg1NKTAzEXAOnU0fUPAyt0emAYqsPeVmln11s4sw3wDTQumLkzXad/GCCKCW6HeJ0G3hr86Tr+/hXl9BwIknCiU/mvP3FMDBCDxF6xA92sRc76N6MMskQpsFkGhMKjai5mDUfbQjEXAMFmEnB+DCVMrOsiimxTUSSo6cJwneYW+2QbfTQNR+7XcNb7pLt9GGuUbVxb0g2ijC7dZRpMfneRxiWQZ0K78RthtQ6dbL+FCN0sdohRVZQ9CfoiY2dK5A5+O4hE6wpBlP2+mO0MCrEeNdhSk5gWWhKhDAIXZfROKa9soBhCKJJVAlOZYkhBHu3NxjHMa9+7iU6i238nkGSpMzSjPF4ii5KooM+3TAEoHd7gwtfeaXCtOBIKfgoN5QGHM/h+hdvMBvOMESF7j7rjZn1Jlz/2qtsfrjO2ksXCFtV9j8TWLq0QLjYpN5tMslKGpfmsWyDez+5xXg8wRSClXYLv1GjPd9l92DAnQ/uMY1iut0mL77+AkaS4+xuIh0L0/cY9yeMoxRbaXaGY5qtNu05h60Hm0wnEZcvrtJoN7j54R12D3o0mg0a7Sa7O3vYRYFnmdRqActrSxwcDNkbjPBcF7/un7+GP2VdP71ln9iTxRMLnX/u5DPOzvvnbMvR9cf5kY8haJz9zp7CV1Ty/RkE7s+CTtQlEGCKY+tOdfJ0Ix+l6tcgNfJgirHafiQsPCr4SHY829wntl0f81vPanKl9P0EnfBJ+u6zEniOnv8p6LMRLk5oi07ReR/FWdHvPLPNs0+dquokGNwpbIXjQqe/3mOz2bltevzn0xohTpZ/nsF41oQ5q9w+tdiclQYeX2GeHVx/TntOHT/BxKGhsdqh02rQH4xJkpT6UptSKporc/zSP/1VwnYNATSX2nzrn/wq/+H/9m9xagHf/1ff4cu//RW+/7vfYWtzj8W5Dq1mg1mSYpSSpudw/6OH3P7eB7z0zdePU6lnk4jafBPp2ZgPdphoSUtZ5IUidjSLpkVc85klGUWU0643GMwisvEU17HRIqGz2IUoIdFUwF1RSjQY0xtPCU2btcuL3PjCC+Qo5i4v8of//F+xtzfEcBzCwCVwbEK7TpIW3L+7hS4ltuvQqteohXV2DwZ0AofhTp93/ue/4I2//zVai20qU+3JxfXRwJ7//etT/x0dZNOE29//iIOtHgfbPRrtGldeucwLX36RWquOLiSjj9ZpvnSRZDRj7bXLoBUbP3tIOk1RSpFNY0LLImzV8EOXYW9MkWSsXL/A3sYe0ygmixPCeojnVlp3dGXCn6vXiKOUzfUdpG3hdpqsXFhk6/4Od35wE2UZvPHVV9j8YJ0iyQhsm+ksBqC10IZCEvWntK4ukcU5e/0J0zjGd11cx2Zuvs14MqNVDylnKVvv3OPBT++zcHmJwb19ZFFi+Q6GY6FmKVYpsXwXJagSCsxSAtdBuDZW4CKyAl2UOIcMs7YFzlydLMkwc4MyKwgbATbgei4GBo5jgVZ4ZQGGibBNknFMPphRW2ojTVAoHNsijTI8A9L9McY0IRlNUYbAnWuQJDnmJCK3TIxSoS0TaRp0lrvIwZS4VJiBS6MZkBUlopezP46wv2whaz4qK4kGM7KoyjSVJzluzUPmJYZpUJur44Ue060BRZThNH2cuodnmWQAliSLJclwhhu4ZFGC4dq4gxkTLZikGQ3HRNV9xCiiFnqMspysViHWZ8MIvx5gKY2uVdmJjOGsCspOc5Rt4yWaxNSUzbBiLFe7GLaBPJhWmY2CefIsxxrGGEpjt0KEaVD6DmqakEcJIi0x9kZks5SsLLGW2pUVqT9jJiW1/TEojbuUYdU9vLV54rs7+JcXwLaevJ2cOFUOZ6S7I6z5NjKKMZWqEG7zAif0sBs1pGtjDmfMNg8IXryAu9wm6U1IBLi+i8wLjCjFXG6jTIGexMg0pzSqmBxsA3u5w/TuNnqaopIMY66JJTXhQod0GlOOI5CKMs1RkxhvbQ7TtskOJpSzFK01s/GMfJywstKh2BsS2y5uw8cLXErTwLJNNn7wEYbvMrcyR/9ghOvYdBY7FHHK7r1tLq7M01zokIwj6u06RZqzuDbP/HybOMnYvLNBPMuwihJPakLbJgpdBE2W3EVUf8z+7hB3sck4iam7Dg0El7/8Kk4rPNPn+nTXC4ETuHR8p7KcKEU0ivHbNbzQ48qb1xg+2GP9+x/SvryM3/BZeGEZu+ZTJjmYBrW5Brs/uY+McnzHoZSK/WlEoBTNZp3FpS5lklJv1ekuzbG9vsNLX3gZ85ULZDsjZqMxgWtjGBZSafL9PqbWdBshar7D7QfrjEYTut0Wtm3jFSUXVpboDUcYSrO2tsz2fo/9wZC93pBCKbwwYGFpDjdwObV4Hx08hVd5zIpxnjDwpDn8NCHiSfQs7fenpfOEnqPfjykn4Uww6sd4zKFF7FlS2xPprMb68AZD4Ky2D/PQPlLenWeseJ7nPhKxn6c1n3IQnvTO5zESn5FgodFP9wh7Dvr0wsUJZujZcClwbotPdtJ5fP7HQLN+5IpyJEQ8/rzHGfAnqPDPXj4qct7Hf4YpfPzGw2vi8TaJE5/UI4n48Vsf/4offYjHQvSnmFyPgotPmGOOFxGN69kE7RpKgO17mKrywf7GoWBx4oXo7wzojad4eYk/s3n7X3+X3sGQpW6HWq1GrjWteo3ebg/fAM91+OidOyy+fIH2QgshBHu3t5l7cY3N3/sBpmVR5AWlqJBY8yShJ8B2bBzPYTpU9HsTLi7PYShNrgTNTgOpwa+F1Hyb/t6QQlVaZSEgSXP6uwO8mkdY85nuD+i2mkzjnMWVeYRS7GzskirQSmFoWO62iLMMxzZwLEFgGIzTnHbo0X+4y+ZP7vHyr71VpdU9GY131sB03q+TVqvD0/X5Jr/0D75BWUqm/Qm271JkOWVWVqk6DQu/W2fw7n0++s77GIWCdsj8tSVGt7bQoYvVWERkJaOH+/iWg99qYOSSnbtbFFIRzSIsy0TmJZFlIkOfjtaYrsMsTRmpEqfToNZtsXlng3F/wtKVJUb9Ca/80mts3dokSjJkVqCygpXXLrN5e5NoEjEZz9BSsnN/l3EUk2Y5pmEQ+C4LS12mkwjbtikEJFHM7R/fpbnQImzWcEMXpR3iUYxhVpmFaPiQHlrOLAtaIWYuMWwTpUGEHnowoShKiijFFlUKUtEMqDkVdkKyO0Q5FlmeY9U9At9DmlWAqoFgOpohGiHKEIx6Y5RSKMNinMYYrk2UJoS+h8pyar5HEU1IHu4ggoDSNAksmzKJCNs1ptPqne1GgD9LEUKg0xwdemijxIhS9t9bZ+mNy0T9KYP7e1iOTX2xidvwKIQgjyptu1AaJRXBUovZ3giZFRRpTqmqDFIUBYZtkkUxngCyEjfwMFSJbVs0lMLIS0ahTX1m4CJwipJkNMMKPWw0hmfjmnUM28DKCtI4xejPcFyLbDTGDrwKq0IIdsczFk0Dt+5h133sZlhp9x/sIRsBeneE4TlotxIMjUZQWR98l3L9APelC1hZhVsikwx8m0ZzEct3yPdHlJMYq+ZheDZKQ/LggOCFJTiOs+AxF4HDrw2rFaIeVGlehZToJCcfzTBMA1WUKA3eQhOdFpR5QTGYIhpBFXcymGK2Q2wNxlIby4Bkq48uC1Spqb98ATlLKmwOpWjMtVB5ifvSGtk4xmnX0FqTDmeYjoVd86h//gVG33kfbUAepUQ/ukV6+xZ4HrI9R+21q+DZqKKkLCWeKZht9hENj3ijRzxLCJa7hJMZ7qUFRgcjth9so7McVypGgykd00IlGQBJmrJ5cx0NhK0aQeizv91DZTktx6a3dYARONi+yzjLWF7p4kxiRsJAKkWpdWUtvbJ4vEoJnrQVHy1cVTxJMo6Z9acsXF2izAqGNzeRWYlj2sQHY7SS1OabVUB4KakvtqrEEZbF1//przPcPGC8NyAZzNh5uMv61i6XrqyBZ5OlBbfubRL6PtqqYj56+wOKQhK0G9hpSdM0aWz73H+4iWGZRGnG2soSvd6Qmx/eRZsGSin6ez1mSULLthChyyuvX6eYRNzf6RHnBX7og1G91xO13eKxnji+/KRl/pn0pD4+KaV8nPqei0k81tSihT79XX0cwejscz8BP/JxtPyVA8yTFMk8mpcatKGfLPh8lhr/j0tPs2A9z31Pq+dJ9T6pi/XR5U/fIZ9euDghyR835yS/dDzu+lH58zrlOd7l7CQ6zwjwtGl5JG0+9q2Io0XzCWlpP6Z0+Gj8NKf97MWpDjr12kcc5fNIqSf7/Jxufe5pcabfjz68U/cePiubpQynU2rzTVzHZjCLqAt4+csvEnZqp15caIFhVllIJlGMQUCJptGss7wwx637m7zyC6/w+rc+x5/+P/8Dpil44cI8jeUOW+8+oPnLb2AaFnMvLJNNEspRRNN1kUrjBz6mlMi8JE1zWkJQKkGz02QwGDMex7TaIWVcEEUxk8OUqiIvmL+yxPbtbeJpzMJCizt3tkhUibqzhYVBY7vP5a+9zPDbGUmS0d8f4AceTc9lNo3xawHtlQ7Rw12G0xm9/ohGM0RIxQxoBS56Ep+JtTjslzOnHrdUHPXdyRJHWhcDyzXoPdxjuL7Pm7/9C1A3QEq00hzc2WJyd4+D3oBymDJ6L2H54hIXvnCNy1+6znt//A73728xP9ekHKUM+hNqjkOW5diWSSlAaU1UlphSsruzx9WFObxagPQdjHoNIy3YfbjL0qUlJsMZk0nMm7/xBXZubdHb6jEbzbhy7QLD3pCDO1t4nkOapORJRikluVSgNJ5pYQrB5Zcvs3F7E9+0cC2LWjMkmwla3QatRohpGCSzhLBZwwHyrMCuB2il0UKgTYHrOpiuQTmMsfICoarPTRsGVpRiei7kJRkaQ3sUWYHl2eDYFU6G1pSFQnmKPCogdChnGUHNp8hKwlbIeDhFC80wSQnqAa5UxLOMOC1otxtE+yOKWYJHhpIucaHIAbsRkIymlEIQDabUfRe7kFXK3kJiTiLMwMNCI/sz9n90F+XbkBXkacHUMgnm6himgSwk2SzGRJDFCXboEi40KJMcXUrGeYmnNLlh4NQ9GgKaWlM4JrmUSM+iNDxG+xmNcSU4CYC8RGmN5TrVnF1ookYRuhFC3atcWIRAZAXpNIYsp5gkyIUWgW2hXJusKLD6BfblBfIP12Gxg73UQW7sUypFvH5AcHEeah46LbCyEgIXljvISYx5oUp6kA+mmL5buaolOXGcIXYGaK1wuw3cZkg5ipi9t05wbQmz7ldgoIZ+zPVTACiNGboV2njok20dYDZCStcinabUApds/YDw2jLlxgEEJcZghlhqIQ1B2Z9iBh6u72A3fPK9EaM4p+Y7SK0psgIRZ5jCoNjsYb+4ynCzT6fbqIRArRFaU2YlWmnkNIFxhL68QL55QHGYxcaII9zlZeZfu0TRn6ByRQjkm4MqNfQ0YXx7m9g0GN/fQrk2lmdjqCqo3/VdelKx0mwwvzpP48IcCoj2R+TThJ0HO4wGo8pyZwgSYaCEgZnk2EKQuQLftpCmhd+oU+YpBgLbsln84g38uSaP3EsEUsoqvkic3I0fbSKykPQ3+mSzhJ0P1hGmyfLVRfQ0ZuMv3icVmhd+88vE4wi3qOKDlFTc/PY73P/hRwy2D3A8t4r3uLZGZ2me/v0dDsZjrr14iXgSE2/t0az5VYapOGOwP2R/r0+apvzi17+A5VmEvkfNc3mwuU2RFziGgZQSKSWXV5fY2e+hHAPb8ikVqCQjKyS7owkoRdO2yYA0zSmyAttzz+Vdn4TSfVrX+EgwEOeW+njmCX1Y33mC9bl0Xruf8ghx8n0+rWb8Y2q/P27w+nECn3OUtqeef3KIzgpHn4CPft40wKfacPbZz1P+0QMP17mnuFh9nL5+0pw41RefznTxmQd0HwvXx4zmyZNPp5Pv9PTS51hIzmW+eQRtz9FHox/n4fXZxeDoQJw4OjsaJ7T7Z9p2MmPVE2N4z072J2krjgqfpy0QT0kE/KQP5rx+OlP2UZD9IwZ4sLHP7v1Nlq4usfRuh83+gEJK5i/MnyOLaZZurOK6Nh0hkGVJf7dPZ67FbJbg+S4v/9JrOKFDkmYo28Lp1rnwuavUF5qYVqVh9uoB6z++S7vdZLg3oNOok5YlvufRz6YUuSQpZRWo3aqR1QKU0mjTpLFSZ7w3ol0P6Y9m+L5Db71X4SCgGU5m+LbFS29c5e5799EaBsMJhYAv/52vkCU5hmHQ6taxPYfZrAo6dn2XzzkWeZrTX9/nZ3/yU0LHQRWSmZDc++AB3Y8usfLq5XMG+kSfH43pk1Rc+uQiX43E6vU1bv7Fu/zsX3+X7c19li4v4fou9XaduS++SPP1K3z4vfeZfvCQ8XBE8c5d5q4s8tbf+AWuD17hh7/7feIkwzZNirKkKEuiOMGxTGr1ANtxmIymGEqxNxhhFznd9gq3f3wTx/NwQ5+DgzFCaL7yt7/Cwf1doo09Ls3VGddD0iTFMAXTNKVd87FKiW1b1GsBzWYNQyryKMGoB+xuVGBymdb4rRBTaQLHxVEgbItkGldo29mYoBlQq7mUaUkyS7ACB5UVECfYjo92bczDoGphmWSGwC5L0IIMQRyllFrhWxa6UFi2jWuYmJaB61iYnkMxS4jHM0LXxfNdhCkp4oxWGBDnGcl4ihV64NrULZOyLMhkSV6WaMshcUIcwySs+2ilSKMMXJcyyxGWSQ7kWYatFG6rTt4bUUQjqAXoLEcUkmg4RQUujmNjSMno1g6WaWJYJmWckeVF5Q42iolliafB0qBsgyTOWbi8RLjaZf9n9xFSY67vYncaFfhaVuJ5LnuDCZ5SuOMpWkFY95kIKAtJSaWtFkpTThOMYYTpWhShi9OqkW33UarAmqUIpwLNk6ZB1g4o90fYoYfTrZHd262QcF0bt1PDNk0Mz4FuA6EUpWFQJjlFmmOvH5AZAtEIyHeHJHGG2wioX1kk3h/BRp/Rh1s0Vtqkt7axOnXiu3sIz8K7MI/lVci8Ki8phjO0Y2GYBtlmHwGUVoVl4S52UFmO26whHRsncCh9GwU4q3Ok6/tIz8I0BHmcYShV4ZckGXRrCNvC6TTBtZne38V1bXRaIGcJWlQxKX6cY1gmRZSRjmeUowSR5Aw0FZCnYZLlZRUw3GkhXn4VIaD5heu4zZDo3g55XuIKwDJxHIvJRxsorTGCKnNY4LpkaYpUApXnaM+g027it2u4jQB/voFV96lfmicbRjQW2kSzhPfffo9kErPUmgOl6cx1cCyTWJZIocmFxrYFYlxlm2s2QtrXVxCGcbwPCCEql+MzwXrH2mCqeJJpf4rvu4z2Rlz8/FU83+Vn/+Y7BIHPbGMPv+EjbKvKWmYYjDd6/PjffpfN3T2klLTDGvE04cFH63TqNcJGjYZlQpTQnm8y36qTaU28PyJNMiypiaKEXEn2t/aZb/qEpmBtvsvNzW2iJKbR7XLx8iqOYTIdTSuLt2VRjKb0o4hRb0hYr1WuksJgGMc03RbRJCYZRQTN8PCVz2rjnoPExyv+xEpO7hf69KVTdJ5W/uy1xxrz6Vr3PHTudne2bR9bWX5oaXnK9fOPP/ZjHtGT+vdJbT/54uLMueNrz5AANWglH1dcflr6OVprPjO3KC1O/HiMxGN8+LH0faJDH+PVz9PicnZhE48lbjg5TucGMR3LGOdZKB7/+s4fcvFYG8+T+p7rGz4ZiHSe2eC8cmcfd5aeNtGfdv244tPt8Zo1PMPCDBz80Meb2NiWiT5C0T1TXz5NyPIc33IQlKR5iZQK0zLoLLSZu7LIwZ0dVF7QvDiP4zmkUYKXBdieg9aau9/7gAffeZ/5tUWccUQmJXFWEuVlBarnmAySBEtraq6Lueyzvz+q3FpGcaWNNxIkilIqtAbbtqAsSWcpncUqDaNtOTTrAZMkYbo75i//5Xd44eVLjHb6dDoNnNDjZ+/eZjiIcByLRrtOo+ZTW2zxlb//i6TjmJ/+8TtVkK3lcPfP32Xx+iqma58vO5ztr3Oi7rVWTPZGTCczijjHoLJcTHYGTO7tMctzRvf2UMDnfu3zGAiCesAv/PVf4JVvvIHXDKkvNNEaolHEu//+R8S7I6SSIBW5ARdev8L9H99E5wUWgrIoyLMcOwgwOyG6rNwWGgstakHIwXDCyvVVXvvW69z883e59fZNLi13GE0iZgWURQFKs7g6T6k1/YMRKytzNBohva0ew9kMy7KQcYLt2NR9D611BURY86kvtzAMA9OxqNd9irSgmMYM4xTHNLBqPqCRVhWYrSyDcpZgCFH5wRcl2WAKgUMhJUIbYJvUaj7SEsisxDNNCAPSJEOWklozoLlWac8tDUmWo2cJZqlBlhSOizKgLgReVqBMswoy9x0oShqLbXoPtknyDFOWVQYxx0GYJpZt4uZFpflPc0yoANRmCZZtUwynFGmO4XvooiSsh5hOhb2BEAipyWYRWkCWV+l0XWGQ96cE8w10lFICRZbTXG7Tff0S44194jhDWyZu4OGYAqsUGIUkERALyDYPWKrXIPCxWwFME6aWIAemWgECBwPtWQgFRn8KgQe+C4bArbnEgwgjsNFC0FruUpg26u4Ocr2HUVRxMdK1EGmBFDHpaEpwYR6pNaLmYzaCKog69MAU6FJhGiaOYcA0xqmtcvOHe7RzRbtdr3zzmwGqKLAApSDeOIAopZwmhNdWKHtjzMUWVreBaocYCLRjkb1zH3O+EmzkzQ3yTh11YQ4rzNEHE7QA+8pSNXeUwvEcorwglGBaBmoUgyGoNTzS3TF6FCHW2uDbaK3JZwnGj++ilzuM90dkwxmtSwukP7xbCW2zhAufvwbNEJ2UWIFLTRiw0qZ2YwW7ETC7vYUoFc1ODQyBGMyId/oUs5TEMskKyY2vvoqBAK3IRjHT/SHT/hhlZuxt7jIejfE/esDCq5dhmpH2xtSvLDH/ygUuTmaMNnsMekMG/SG+69C4skIr8NjfPiDOqxTUs+kMAfidOrW1CtOiQjY+3DcNcbxmncenBq2QF3/xZbJJgt+pYyvFu//d7zPujYhCj6U3r5HsDynTAn+pjaZSLlx8/Rr7gwGuXcO0bRq1gJWFLv3hiKzIuLw4h7fQYTaJkVJiFBIJ6LwkHUckeUZjvsV4NGHt2ipzYZ07P7lJw/OwgOsvX0UIWL+zQX84xnEcMiUppaTmeaxeWKJzcYFoNGPam3AwmRy7IWZpdmpvPM0GPlMTeqhgfZKa+DnplEwjHjt3btlzqtdHfzXPB3p3lil+Ap0y0DyjqnMa9Cn5/mcNAOf00/kWpyfe/7R6n8z2PrtOcfbEmbpPnjoEuf3Y9Cxe8OdEn5nl4oiVfjRXHmnuH9GjARVanDuxtD4L/3aW9JlfpySJJ0iVJ8qco6E/LiGecPvJdzvPgvCk3+fRUy0UJxtzXrEz736qzLPE52fTKSH6DLWWOgTf+gLZKCKOE0zbqnzDu41Hjz/qIK3Zfe8h00lE7BS8dHGVO+vbbKzvcOOlK0wnMXmcsX1vG2EIFq4tU7/Qpb7YJmiGyDijt9Vn8nAP2zCJehMkkCQZXdshUgock1mU0nQsDFUyPhhgtxoYBliWRZaUSK1ReUm7VSeOM+KyQGQK0zRBGHimxYN37zOezpCGJo1STGFg2hUK76A/QRSaelehkpJO4BNnBekoZnQwJn3/Pnv39sjLgsuvXubOu/c5mEa04pjZ7pDmxQVOoYWeTJN3cq6eWKTUIeJw7+E+//6f/yuSWUJ7cZ793R51z8PUimle0u526HbqbK3vMB1OaS51iKYJg70+0TSuGO6DAZ4E97WraNPArDksXrnA6osXWbi2hGmaXPzCVW7+xXvoaYrbCLj09VeYX5vn/T99h/3bO4xHD3npV97k3o/v8uKXbnD9ay+ze2+HnVvruMLg4faQ+lyDtStLHGz3yNKczfs7BGFAaDtE4wjHNCmpUm3aponv2JhSYpayCrItVYUlUki6V5aRSkOSIWcJXj3AqfkoKSkLiR245FmJZVto20KoApmkWL5XMaiWAWlRaXstgek5BFJRFiWFVVlshFQorSiByWBK++I8tudgWBZN06pA+ZIKFb1IEgzTxGzWyRA4RYGdl9jNGmlRMtsb4NcC9CwhlZKaaaFcg3yaUndqiMDDsSzqnkOqNdM8wzMMJjs9gmadXGhq15dQswQhTHSaU5gGrmGgogRZlhj1AABPCExduYTZQpBZJp5jkQynhI5DGWekH+2gRzFJM8Bem8c6GCHaDWRskSQZl7ttNrMCudolt0xkWrmMBFFcWRYsk6KQuP0ZRuggujV0lKCVwgaMUgHg1j1EWSJDn80f36XRDPFDD2Yp9oV59CQmW9+FwEc5JqZpIscR5WCGaVkYCw1SpTBmKdoSYFnIQmI6DtZ8nfH9PaxcoxynSuNqW1jdBu5cAzWYEe0OCBdbWI0QfTAhvb2DjlPKNMPybNz5Jvlmn+nGPnYnJJ/MMOKc8Poq0cM9Dn58j1qzhh0l6MDBKgqCbgOj5pPtj6g3AkzDwL8wT/pwHzlO0AKchQbZaIIWAstzKmTytXmyn9zDcCycbpMszhjf28Nf6RIPZzhCg1YYflVelhIElHlJ/NEmpmMR96eoXKLSklxrko0e090+slWjiFMs1+LOD2+RTCOWVuaYv7jAhS/foJwmRBt99h/uMM5TBvsDtnf7uLWAUisWhGa14ePaNq35FlmSsL2bs9HrM7+2QDFLmFtos/n+PcazCVv9CZeXF7n49VdxmyGICs/isb31aEk7s4wJwHZtrHkLmZf0fnKbWZlz4Ys3WHzzGgcfrvMf/i//A5/7G79E83oFguY2fN74m1+jmCZ0lud48LO7bO/s89YbC6y+eoV0GtNqN5BpTt7wCQKfbJoyG08xSkmWVa5cUZoynY4I34Hla5eptRr01jfJleS9H71PISWWZdJsN+mGIaNpxMFsSqMWsvzCKj/49tvEeYHjOqwtzmPaNs1ug0a3efiCZxSGz2DOT/ONnwkX/fjx06o755HHb/BJmvGUVxBHfz4p+/FJ7ztuy1M0/+fWfY5y+Ek361MPemK9z7A9PPURx006q3x8qqL8kLc4fhX9hHIfrzH6qI5PKXx8BjEX52vT9ZnzTxOwzzUgHBU4PhSPD8Jj95w2YYhTzLg+ftbZWOXjEuc08pn9+6QPSutT8+SZWoKzq/RzkzheK07lfn4aPVHAefKEEkLg1DyivRGTWYLtWGjDwPHdU3VqoMwK7vzkdrUBGwZeI+DGK1fZ29yHXBJPI8a7Q3bv7eD4LvVunWtvXjs2mAjH5uDONsOHfSZS4qcpSInvunSaddLBmCzL8W2D+TBkWhbYh1lktFS4nTqzaEBWKgxZmRLroUdZVn7KYegRhC4b93eRZUmr02RptcvWxj4aAXnB/r1dZFawvt/HncxIpSIwDRqBRyoVS80as8hjf6ePb1t89L33WFiZZ2PrgE67TjacwcWF43l5HJH0mJ/c4eJ16Lt79+0P0VKT50WVwlMqBr0heZLQj2Lmmg20MBC2yWA8JU1z6u06jmsTJ3mlrQ59hu/eJzwYsPDXvoxzbY1pkvC13/kGXjM8tSde+cINLr15rcpIZJkkgylv/+vvsnNnp0o9bFvs3tnml/7zX6a10ObDb/+Euz++Tdux0C906e/1Wb66zODhAWVZglLUawFFUeLXPdIoodcbIaVEAbgWVuBiSwhdh95gzCvffJ3lq8v87He/Txkn1Johyc4IPJtJf4I6GBNNY1prXULfRilFKTVG6EJR4oYhwhSUWYnZDNGFJO9PMOthlb5WVKllC63Roxn+fAeJJNvp467MsfHuPRZevACH7kWmADP0sfwK5X06nKIDl1xq/NDDTIsqA9Ikxa8HmLaNGwbIvECnOZHS+IFHmqXYtk0uINYas1TIKAPPxfI9IiWpLXeZf+UieZyy+9P7qCxHSQWOXS3OholOCizTxLIsJv0JpYDmhQ5zLyyRbvZhq4fsT9n83kcke2Pcmoc2LeJZhp0r7KKkiFOi0YyBMAgNE0NUgkLp2phaMx2X+HFGYpo0ah7FYgMnk8hSYgqBsdZB5BL10SbSMFA1l+YLy8Tv3MNzLNIkx48yjHpQTWVDUJYSYzjGadcpNBVQnWGghhFys4+z2EQrjRpMsRY75GmGGbhoU+A3Q9pzDaa7Y2auQz1Kcbt1MAVyEiMGM6QE8+oi/muXGP3pu5jLLRpr8+gkJ9kZUk4TGstd5CQmTzJUmqOEpvvmFdbfe4gUGif0MUuJYVrkpUTMYkzfJt4b4S91yNZ7qFGE0a1TTGKMNMepBxTDGU63Qak11ihGduoUwwht25RAoxWy+/YtFj5/HVFzyJOMUZrh+YK6Z6MDiyLKKjT1osJlsesBMs0RaU48mGAutClMgVIFSRwThgGWZ7F+e4PAczFNA8OxMHybxasrlHc3GStNZ67Nw7vrtBbb9Idj7v/r/4jIShphwP7OQYXyrhWxoXDSkpZtkkpJP8m4srrI5//Rr7D4hReeqFQ9OimOFuwnbC2qKAlaNS597jq3v/Muuz++yf5wxpVXr9G+sYbl2tU9GvbubbG1scve1gGykJU+xjExfIdazcd0bIwoZX6hRXBhjt3NA9orTfz9KU6WszOb4RgWqW2R2SZmmXP1yy9jCPjprbvERXno0mVwsHeAbFfWWtuySKRk/b0H5HnB2nwX4XskWY4XOHzxb36FcK5x+uXEmTX8CXEXZ+kTM59nO/Zj3HTMKB7RYw14Wqueav54dP3TCBXnPlU/uc1PUuieVSI/9vMUN/bp2qdUNeamcaqd59b6tH45q2jU55x7alMfn3Pn6fJPXfw4DO2n66bPwnLxOJd/LMUetk6fKldNnOOkqYfmguNXOhRKzurhH6XGOhLjjjTCj36etJw8oXVP4J/PqmHOEUROTeKjNj5e2WPCknhOSfLjfJwnVv2jb+qpt59o+xFA23mVnqt9ODXXKm2dEhqVZCRZwf23b/HKr755LDwJDbP+lK2NXRwEnmGSTmPcesDCyhzTUVQB0pWSPCtoteqs3lg77meVlxw83GPnJ/fIipKv/P2vc+cvP2J6f5cgCJjEKYlSYJjYQpMLELWAWEosqXAci3gUYfs27Wad4f4YAxgOppiORasRML82RzpLWL04j22YtOZbDKZTWp06jU6d3fV9trYOaNZrBIbA87zqvaKEduhyaWWeaZrTrvuobUV+iO462RtiKE3pOextH7DwxhVAMD4YYjkOtXbtnM4/+kaqOW+5Dn/6L/49Xi3E7tS5/to1OmtdugsdPvr++9z54S1cBIOdA6RUXH3rOi9883W2fnSbPCvw2zVSqVj+xuvUuw3qyx201rz0pZcwLJPRVg/Ttgma4SGmSIUdIAyDnQ/X+dG/+R7aMPjF//xXWHv9cuW/HqVEwxl//i/+A+OtISiFf3WN3uY+FJr9OzsYWhM2A2zXYXdjH8910JbJ0ksXufrF6/itEMM0KKKMjR/dYevmBqlv88V/8Ius3Fhjsj2gVIrkg3sUkxTtWowPBpho6nNNHn7wgNIRNFe75NMUy/MwTRMxiqsA70P0aGkIlM7xfZcyLzCkqnA8TIEqK9AsUykavosx10JJid+oUcQZQgh8t0J990KPLK5Sd9adKqtOgaaYxBRJjofAQ5AnGbXAQzo2KnCQqUs8npKOZ5hxjNXtUK9bpKXEEAJTGGTDKbIocX2X0a115l5YJhlGGEpTzGIKqUllRLsVYAYetTBAmoJ0muLVQ4o8xwk8HN9hnKVoy6oChk0TaRko2wADkklCXiiaOyMc16FVC1BaIw2DZBBhLrYQUiGFIPA87LRANh0iqZklKTXDINifHfr5apAK0QqRnbACoctLEgQOINOcrFPDcyzULMaeb+Am85T7I4q7W1iXlsh3B1jdOsV4hn9tEZUWKCFQjl0Fd3OYKbJUGKXGr3kwp0ikrjBMxjFFb4rhWLi+i8oKioMJzvVlrFYdDqbI1RTv+koVVD6JKQZTwqtXmbx7n8K2wLbRnoOyDFRZkuYaIUuIcuy6h7HQxGmFFA/3MQSY7RBtCYJry+RbfWYP96m/dIH4w3XigxGebZONIkToIZTEqPn4gUs5SXHqAd5iA6dbo5jEqLTADzzGD3ax55vI0RRZaIJ2SBYXmJliNpxRTCOiWYxTD+n1hiCorBq+xrVMnKbPrXdv49/26Hab1BoBTiOgvdBma30HL/Tx6yGYlXXXKuGgN2Rv54BClmAZlHlBEHiYjmJv64CXfvEN5t64jGGZNC8vnEA+5ymby5Gm9OxqVh2N723znf/7v8Nzba689SKNSwtcqgV0XrlE0G1ULlZaEw2n/Mf//g/o7R5wZXUV33NZ7i4RdJuIXOJ0fNTOPun6Br57g8n2u/jtFnmhOVjfY5znpEWBnGqUVswvzHPz5gOmH9ynLEoklXLsxsvX0HnJ7Ycb5EVBUkpq7Sa+aaKLkm6zjtMIufjaZS5+4Tr1pTZBp36a7zi3T04zmI911xEP/hiz+BRt6Sfm7E5rKJ+KtfU0EKyjgqc06c8SNj4jOvuYZzHZh+NTAY+eEEzEY4WeUdETK390qCH98B75fp/GL3/58XY/R1XnopmfbdbTpsOTFMCnuOZzhN0nafjPuf6YgPcJ6OeM0F2ROPH30bnHJdPzZMBzBW2OxI/Palaf1fgfJncVJ5bP4zY+3bzwKJib40n/6OKTH/1JmguacxNGPEVifSw25QkP0OeVEeC1a6xeWub+nXWa9Ro/+sO3Wb6xSufi/HGxWW9SpRhs1MiLAiV1lVEoTtBCYNgWMpeUacFLv/w56oeIrlChco82euhcYtR9mnMtLn/5BjfXDxhHMRSShl9hJMzimKmSJJnG0BrPskmTDCf0qYU+k/0R5CWdy4vc/WidUPjs90bYvk3gOIwmEcksZWdvQH8wQpWS7mKHpYU2flhly3Eti8kkpiwlgecymybEdzZod1uMxjOCmk851QwmU0qpMDyH+lKbeGfMrDemNt+i3mmw8f4DgsbVatM+Z/c5Wmwuv3GNv/df/2N66wcYh3ERZSlxfZelly9w8foFtu9t4TguSzdWWX3zKrODMdE4ZvHlC/R6I+6/c5cizfna3/gqXiPA9h0efvd97n6wzqA/wTAtuksdrn3+Ba586foxJoRMC772z36N5nwLrTQ7tzZZf+8B/XvbTPvjijl2XBSC7Qc7lLkkrPlkaYrlO0yjCCstWL6xxivfeI3GUgs39BCmwWx/zO3vfcDD9x8iSsnqm1d45Vtv4PoucW/C7T/+CVbgETk2yW6PQmvmFjscbB1w5Us3uPmD91m5vsLC5QX2i8rNScoSZRgIqRC2iZaVdtIxDKRtoZWiLCXClAjLRvgOhg7JLQMzzQk6dfYe7CAUlEnlDuH6lWuSOctp1H1M0yDKSwwpqQkYJBn2oUXMCwOEbaEKiRASITVSCBphQGyb2GUN07LRpkmcZxhZiWMYDIsS17ExQh+kZPyDmySOhdsMsC4tEfUnzPaHYFqMRzNmSUZjsYXd8FEHE/zQJ90a0ljrYsQlqdaEjomHQMkqpiahwDUFRt1DmwYyqywyoLEcG9IckWQkcY4/jQkdm+JQ6E9LSatdR2iNBMgOXcE6DdJpTJ4VqLzAkQq3EyJHMeHaHLPhjNI2sW0bOYhQrsNsvoU7SyBOcJwu+TiiKCXmZh9dKvAdzHYdJ6iy8RT7I1ScoYoqGYDRqaH6M6aTBNM0qLdC0oMKY8RYblOkGeObW5gX5ygOxsg4Q+claI3ZCDDrPvmDfWrXVxk/eIdiq49+uM98p0E0SRCug5FIwqYPgYcoFNlmD+vCHOXBGGe1C506Gkge7FVuWUrjLLQppKQYR4jhGDHXxmmFGFoThD6jYYS/1oVaFaeSDSNqdb/KNGUIiHMc00LvDRCNALtTJ93uYZgCK/Cw2nUyVdJpNUkmMbmS9B/u4zo2tm9TX2wx2h8y24gIDYsL1y+ghaDRqDE4GGDaJrbrItMptfkGnm1x8/Z9TNOg02pRZAUP3rvP8oUFbj/YBNtg+asvUVtuI8wzQaNnNX0nL5zchs/sRUtvvcAv/bPfwu80sOebODWf2XBKON/CMB8VNk0TWxjUHAfbMgl9D8t2MeIcf6lGvjPCDxvUvvkV7E6N7f/xR2Q7u8Rek2nQpZQly/UGgyTh8tISZiG53xuS5jmGaWIbBpdXllhcnOPdH71PrRZiOTayUGRpTj+OEUJg+x6XX77AF37nG5iOhRbifMHizNp90jNBn7pyoqeqQufcfbqkeCJ78XS+42SpZ+jST/E5T6/riPsRx7/Of4NPqeI+Q0/18jhP+fnY8fP11cemw2q9G5dwr134+LUfK4HF6Sae19xP1fQnzbNzp+C5938WPfeZCxfnZ0c6MQHPMMZPfo1HPX52HATnIGqcGKTjp53XljMDqZ8ovR9ZJx4J7c9eaE484NMKEp/mmz1HKH5q1rrnkdMOr9u+w5Uv3uDOhw/IsxzP93j7d/+SX/2vfhPTtdFKsfXeA5p+wPx8m1FvRJZlOJbJJM9BCOYbdb7/+z+g3W1y6cs3KnXlcSdDY75JqRQXXrmIXfPov31QacZNwHLwPYdplFIaBsq2OOiPCR2HqUoZTmbMWQZO4CK15OobVzAdm9Cz6cw3mUUJbuCxcX+X/mhC6Dg4gVUFctoWWZyxsdXDciw816HdbaKUJk0y3JrHbDhlGiUoDJRW1BZa5KXErHnYnoPQmnQUE88itt9/wI1vvUk0iemuzVPmBY5pPnVchRA0lzo0ltoAKCn5/v/yZ1x+5TLjgyGLV1dY/vxVQFDrVOb6TlildOzd2qY916b1y2/xV7/3PbJZgswlxXhINI2JxxGqKKDUjPdGvP17b3P7R3dYubFKe7FJa7mLG7rMdvt88Mc/Zfv2dpVVKs1oNOtYNRetBQfbPSypuPDSBYSUTEcW/f0RjYUmr/3qW1x+40rl8qAhncTc+4v32Pxwk/HBiNZyh5d++Q3ayx2CRkD//h4/+//8gJ2tAyzXwjQMSin51n/xm4y3+zz44B7j3oj6WpeLr15mtDugttCg/2AfUVaxE55tIOOsCrLWGu1Y2FONRCCVxiklo1GGdi3KQiINQa0eYJWKdrOGYRjYoUcxS1C6wKkHOE7lTmfUfGqmQM4yjCTHCn2MUqF8F601ZlYgXYcsK8mHE8y6T71Vx3QszFIihEAi8EcJMghQGuaurxENJuyNptQsi5HStCwbTxhVvEeW4TfDCv3bdUhLSTqKqHkuTugSlyU6StGlxr84zzAvKTp1VH9CrRVS7o7o24KWBnu1yyxJ0Y6FsExatYBxlDLVYE0TyHKyJEMWlauX05+Q10Nm/SnpOGL++jLGJCGdxRgGOI6FMUrQTZ8iShGejVX3KfIco+Eh4xwrcJF5iZ7FeK5NZATYaIRp4M03KGYp5kqX5Ee3MfMCgSa9v4f3wjKm71JkGcKyoCiprXSQtsnk5jaTWULYDAlurDCJUuzBDOfiPNqzKO7vY3dqlFIx+fbPkHFG8MWreFeWMLt1iu0B9koXZ7lD+sEG6uYGtmNTtupo08BzTTBhtjfAUJrWyxcoPId8OMNZ7SAPkcNt10YOZ5i+S5lmGEtthGmi4hRKRTSaEbRq2I5NKktknJHsDtCzDBoBIi2oLzQpsxKVygoV3HdRUiI8F7k3ZNKfMBaKMoFoliJLRZ5mBIZFx3WJJzGy1Diui+vaxP0J926tU+YFaV4QLnWwPQuFptVpUmuEPNgb8ubX32T5ygqGYRBv9bl3a52Hm3v43Sb3bm/Q/c77XPmNz+MfpRZ/bM9+9v5xjHalK0XUxd/4PDIvUVJjB27lYiSotOaHzJZpmbz8zbd4+/e+w95gTG8SE9ZrPNjY5dUvvEytHlLWPdpXFgmW28h/+LdZ//ZPGGzucXtnh0Xfp9ts4vlVpredgwGWbVEzTWqey/x8l9Zch9vv32WapCyvLlIUkgsvrtG4OIfbrjEZT5m7MM+Vz72A6VhPsDCcPvWIRz8ULI4C38+h09u5Pn3/ueUeeU+ceMQz6Vx+6hPyEkfD+ohlOlvJZ8y8Py89gV85znKp1DFY3tnMl58F2yxsG2Gd34Zn3nvYmuNfz1vHp9Gjn8uTP7n+z2pUfz6paM8y8Kd/Hv94+kCfL38fCxXnaVMOJ91TO+ex+w5vOnfwTogwJyo9EkiOJexzTKSPhJbTDRQnOuhZhqfHnvMJ6Znz8rkmrj52Lb345eu89O49PvjxLXzPY/PmBjsfbrL2xmVUKTl4sEtg21hKYNmVwKEwcG2LF1+6zK076/RvHfA3/vGvYx1qLI+zj2iwax5SSfbv7zJY32e23ccU0HQc8jgny0ukANex6Ucphoa8LDGBleU5XNti2hsTeB4PPriPGfpoUzDaH1GgiaOE4bjy0bUtk7wsqYUBRZqx0G1y0BuBZ1MUknv3tsnTHM+1EUqxdmWZQiniWYKhIU2zynXHcymkYm8wYTRaZ6nTYGFvdLywB80Ks+DcPn/se9HEoxl+Pag08Wje/dffRTkWP/m9t8G18AOXX/svf4v2xQUAgnYdb6HB3k8eYDc9vvq3f5Fap4Zd89h7sIsWBr7nUcxS8iwm0bryNx7OePijO+y2ggo3I4or15wCmottJuOIWqdO0Ai5/rWXEa7F+GCMEIKdnz2kt3FArjUvfOlF3vrNLxC0a2ilGW/2efjOXTY+3KBIcqLxlLmL83zh734Nx3eZ9ifc+s577H20SRblOEHl5qJ9k9/4L/86nSuL3Pv+ByRZxt7tTb75v/p1vJpPOkvwmyH9OyWZ1Ji+gw5c7HrFuBVphixKpG9janC0xBQmtikwmyHpJEaUmrSUREqSFSVN28DJS4TvMhlMwLIwrMpVQsQ5spQYVCCSrfYCehxDUWFEKN8lTXNQGmmZtGs1dJbjKI3yHOQ0Rh/ODZ0kGKZFOU2ot2qYUiE0GI5F5pgkUYYnBI1SofOSLBT4NR+tQEQF2jCxFxq0S40ZpehSEi61Cbb6zIYz3Dgjb4QI1yLMc6aWRbNQ5OMUhMAxDQazGM+yKyuUFuzHCa5ns2jbuKZBFjgEnofbCkgtEztVFMJAZCWzm5vUFjqYUmHWA+JkjOhNEYEHUuK1Q0TNh1GMrruI+Rb2YEJDaUTgoeOMoiixgWI0o/al68S3q6QOhu8iDyaotEBYgsxTWJaJ1a5hZjlOwyMbJux+uM6Fr7xI46U11GBGOUtRvQrLRt7bR+QFqlPHQFPsjbDnmpihi7i8QLLdw+/UqH/rNcbf+xB3e0D79YvMelN0VmB4DjWlQRiUcYq70qHoTRFaE93apEwz4o82KxTodhVkL5UiTgvCWoiUJUYJwrNRjgmznOS9dVIDXNPCrgeUowgVJYQrXaTnoJKMYpaQTxJmG/ukpaRsBQSORTSaIZTGNwwMz2EWpeS7+6RJysULy+iixFtoY6IxAp9Zfwz7Kf3tfVavrOGaFpPdHolj8Y3/zW/RWOzgtwIM22T3ezdJBlNu3l9n7coK2/sDNh5uc0l97gQzeoYl1rpioIXgKO7gOEX7MaDro/VMAwiBMA2ULE/svVUBWZb0bm8TD2cEzZBf/Z1fx3Zdot0R0c6Q92/fZ/PmfRqNgLl0hXgaceHrr1AkOdq1kaaoEkR4LtMsJcoySq1wzQoDqFWr0W43WL6yyrs//oDRLObKCxdo1ULuPtzmg5/exLz5gOVrK/zq//a3CTq1E1z8SavFuZzsY3rE8wSL42IfZwt/Ytn/1Mz8iSyf5/Egn8jrQp9f1zPv4wmv/3hcyVG6Vn34T3AS3ez5eK+ntuPnRU/Tcz9WVB/3yVPRzAVP7ruf57vwn8wt6oyF4ejgk1ivnkd4PnPupHHiaL14dOrECnGOu8qTsP/EUcD6GcHifOSJM/WdlI3OmGWO3LGee1X6OVkAHyNxjAOOW/N47a99kZvv3iWLEgzT4L1v/4S5K4u4YYWHsJ0kNBo1bMtGC4iyHK8e8Nrf+gqb/2LE/mDAw5vrvPKbX8A60hQdvkuZ5EynM5SqXJ10oZCWwSArCaVEFjlBs0ZhW9SUIs1LtCxZubhIHqfs7fYJGw1C16XMCuJpQqtdR6YSy7GwNfieQ7MWMJpMmU6mrKx0kMpn9Y1L7Hx7gJ0W2I2AhbkOQT3ggx/fZtCfECcZhZTH+erHwzHNZoPeYIzpuoS+S+f6JYppwmw8Q0lJvVUDYTwSLPWRTexxwRVg0p/wzh+8zS/+zjcxTQvPc6jVA6JSg2lipJI0jfn2f/eHfOl3fonV61Vw5MKVJRzLosxKWqtdTNdCK033xgo5mvlrK/z0D96mXN8iTQW56yGiFLtZQ8cl8TTCsE1e+42vUO82GO30aS22sAKPPM1RSrP1swfsbx5QpiXpNKFUiutfvMEX/85XsFybaDhj6yf3ufej2/S2+xgCXMvi0muXufylG/zoD99mtDvCVGBIhSglnm8xHEzxGh5f+wffoHN1iTzOSJKUC5+/xqu/8nmaSx0Gmz0GG/tc+8rLrH3+BfZubWHbFpbroKWi6E1xXIcozdGlolQK4diYCtxSg9TUDYNpWVY4DlKCZVKaBlOl8AOXucU25SSpcvqbJoUpEKVGGQbSd7AMgap5lNME0/WRvRF5IRG+Q6MxV6WGjQts00QVJXGUElgmweoSUit0ViBMEy8pUK6LyAtc36PMJQoNtolwHbRlYStwhIH0XUqpiJOceOOAuuNClJH/+B7tS22s6ZTEdsktg/pSi1mUkI8jElPi9ieUhqBj2TRMkwkK7bsEjkWRlfiugxu6eMJEKIWhBaqQMMuwQ49Rf4pXDyjbdezeiLLhYzs2wrHQpoBuA7sRkM9iLM9BSoW11ERlBYPNPt2ah9mpVTEhQmAIA2maWIGLcG3s1W6V8tNKEKaF2QopNnuVe1cjJB9MMRTUF5sMJgnRNOPgow2Wf+FFZN1HbvXI7mxieh6WIbCaIYlSGMtt3OsrJHe20f0J9V/5HMFLF4jee0D9izeov3WNaZpT7I6Q4xm5EoSWiRG4lRA0SpBpAXFWAfD5LmKkIPBwV+copMIwBI5jkm8OmPYnhBe6qFECro2axDiejS4k9fkGnudQDGYI38VMcopxjMpLZJYTl4ro/i7aNhALDWZxjE4KkijFs2yWLy9zsLVPIwwwLIPRxh4HB0PCuRZxlmO6DgKBWSiWGzW80CePMzqrTV765Tdw5xq4jQAhBMIyKOOM4a1tQOC4Dgc7PRbWlnj5Vz6POkw/bToWRzGFGiiLEtMQTO8fEF44XFukrtLmnl3EBMiipH9nm/pyh8loRnuh/Sj3ixAkwxk3/91f8f0/+C6teoO7Gxu4wmBxeZHA97BtuwIh1JqgWUcLg/HDPaKdIUErBNdheWWB+UaDnX6folDMz80xTGOaZUG3HrI/GtOuh2RRwnAyodWoccmzaS928YuUvQdbFF6D3Qe7zIZTgk797KZ3vPedYtQ4XMfF+WzdYyzKKcXkIe8g9BHk1mN0zHOICsPh/Fr/E9Fj7/0p6SgY/tPUd+beap6edk87W/ysqvq5evMsU/4Z9MEp3LXnacSTyjxPW/5/NGWO6LMVLj5O5z/JJniSntWxT5DoTgP36TPXn1bnE2INHnvcaXPWY4LKM9aDI//L8xjL0/eLR3bJZ02U88p8InPo0wbxkfTfWpvj6tU1bn/0gO5cm90Huzx4+zYv/fLrrFxd5oMffsA0ivHCgK3JBD/0+Orf/UW61xb5+//n3+F7/8OfMOpN+PEf/ZDP/8YXK39wo/IN3761AYaJQYVfcOHiIgfbA1IbbMvCNQRRllNaJoPBhDSKsFwb07MpxlWediFA+jay9KgLKLVinCa0nRqT/oTpaErgueRFSasZ8uqvvcXKK5exHJuFF9eYTCIsw6T3cI98ErN4ocv86jzrmzv072xjlvD619/gw5/cYn51jrm1OezAo9GuMby9zfs//oj+cEJZSFz7xGd2Np3hOVYzAbz5K29hOhVOhrfYZvvDTYaDKXGc4fkeSMWkP+WP/pvf58Kbl/nyX/sFOitd3NBj++13iXYHaNdk/fYDbrx+AysuaV1e5Ov/7Fd5+NN7xMOIYX/KrD+lLEukksRZzutffp0szpjsrmMYBg/fX2faGzObxXiei+VYCDSzcYTpu1x6/TKvfPN1hBAMH+zzw3/3A8a7IzzHptEKmU1mpGXBZH/Ev/9vfx/bsgjDADvwQCkmvSFTLbny+Wu89ZtfornURgjBaLdP++oiXiOguzJHb32PP/1//AGq1AStOgsvLNOYb1CbbzLc6KOEIDMFvmnjxHaVZWl3QOJY2I5DkWTYjoWJwDdM3HaNrJTYUhHaFqUhMKQmyatAa9uxSLMCwxQYYYUuXR4G7iIVehyhW5WfdhsD07NRtokClGlQWpXbXGEJyAocw6QsSpRnYwUuTiZJJxGmZWJ5LvksruIRpMRuBEgtkGWBHk0pCgWhj1aSQhYUEuzAZXIwwTAlZpaD45EgcB/s4dQ8/NmMol7HFwaFY9LbHWKszDHtTbHKAbWVecxmwKLfxszLCvTO9zGncaWhL0ssITBNUIeZy5RpkW/1MXyXbGTgeQ5ye0A5S7DaNdQ4QdkWGolT90ArtGOhsgLhO2AIioMxwrUrIausQCllnKG0RocuahqD6+CqEp3llHujKlNQKll+YYn99T7RKGH/+zdZ+vrL6GZIPt/Gsk1M28JsBDQDFyVADSPURg9rpUpqYM81yIdTkBK5N0JvDyi2+nBtBWUJslGEpTRllCFMk3KQ4y61EMqGVojsTxC9MeVKl3gU4bUCVFwibYvSMhGFqoAFRxHefBMLhVpsIaIUmeUUk5jSMFFZgW2ZlLOEKE4poxyz6VN0Qob7AyaTCFOD1wqZbg+wHJvLr11j885GtaYutjGTKlA5nyU02w1IC+YaNdx2QJKXvPC5F+i8ehHTd0hnCVortBaU45jRB1sM1/dY39ihttBk0h9jWyYqK0kORmilCOcbVWzOoSYsizOE0oRrXYRpkMcZRVqgpaQ23zqt4dYaYRjYzRClNHOr85WrEYDQ5LOM3/u//r+YbQ0RhsksillemMcyLWazmN39PkEtwPEcuksL2L6Pr0HPpkR+jYP+kHgW0+8PsSwb0xDMdbvUm3XKAewOhjTrNZpFyWAwJkoyPNfl2uoSxnBEjMY82Md0HKYGfOXvfJ35K0uPtMBHG8jJhfrs//rZDt2nThxbeXiMTXgS6SPlojjFmZzaJ46OTjOtT9n0Py5j/9z8w8cQgk47czx+7mNRVcGR0lbrR4l/HrlEfQr6OWv3Pyl9LG+W8wSk/wSCx8/FcvEo7uL5udtnlXxk/Dry6nxkDDs7/udaJQ5LHmtj9KHJ7BS4xWPY1E9o56PrWukK2GxngGFZ1BebhHMNTMvk/ACUp3zdh+0816PqeehpwtkpqekpZrSz1ZzbXIEdulz72ivcvrWOlgovdPnoz99l8717RLsjQDBIU1ZbdUzL5Nf/i7/GyssXQAt2bm1y9737+LbDB3/xHm/96ucRvkM8mtG7s8POhxtYpoXjubSWOlz4xVeZ/cvvMB3NmAiFaVuo0CMtS3Recv3KBRKhmbuyzOb9XQCSKMGyTUReMH9thSiKCHwPFefs9Ed4vosyNd3lFp//G1/l4htXq+wx04QiyZn2J2ihWXpplYVLS5iWSTKJuKFfY+vWJlv3tlGeyd/+P/099u7tYBSS+x+t8+F338cxDGzHxbEsTNs8NsRWG5I+3oDPGzMNbN3eJp/FtFa6aKA530YVinq7TnNxjmFvSKkU2jBIo5jdd9f503sHvPjN17n65RfpvLKKKQU7P71Dc67NZH+ASDQP/7JP58UV3vqbXyGPsirQejhl79Ym2+8/RMmSwfoe6SylVIrpYEoYVmkgLduqQKuURmrN0ksXefPXPsfclUWEEMwOJvzgX36HeBQTuA6lVFVaXM+htzdkb6eP73msXl/FtWySOGU2nhEudfjqf/Y1Fl5YOXYbK7Oc3Xs7XHzlMrf+6kO2TIu/+t3v4SmDUmm+8z/+GV//h99g4eoSwhCE83Ue/PAutm2jEBhCkJoGrmOTFgWFa4PvopTGXGiihzMsBQqB59hYlgmqShNrCSiFxvQcZmhsqbCkRKQ5UgBFiV1I8Bziw0xRZZKRTCJsx0IqjddpkOwNUbZJFiXork9SlBhKYoxzir0hXqeBUUpM16bWrZNOInzHJp7kZDt9gm6L2HPQrRrx+h4dI0C6LiqtYhcMpcGziIWBY5iIsqA0TUrTwji0ds3Myt3IkCVeM0Rv7WF5Hmmh6PVGGKaBFziYuwNUqQi7DUTDo92qMdvsY/suSgKyRGuBt9BG7Y8Qtom30KI8mOBcXcK0TfKtPoVj49V9sof7GI5FY6VTITynOWqWgCGwltoUWYHjO2S7A9xOA3uuidwZIp0MHXo4zRq6KMj2RyDAqXso28QyDbpzTXqbfcp+RDFNcFY6NH2XdHeI3h1hXl7AXe2QPjwgevsOpDG1b72Oykry+zu4y13yjT5Gt45zY43og3VKQ2D5Hsm9XcLARXTqyDRDK4h3htihC7MULBOtFXmcokZjaPgURYEnFdq2KJUkqAWMPtqk89YVtGlUmaRsk/T2DhKTeHcPaj6yHoDnErTrjN5/yCSwiR720KbAFSaOVwljpm+zeW+Tl375c1xrv8zWu3fZ39gll4qmFyJyhZrEWJaFrnn89J1b1BfavHRpHtN3iIZTvLpPGWXc+pOfMlg/4MLFJdKioBTgeg5N3+HB3XXkf7T42j/5NfK0IDyxLmWTmHQwJR1MaV2YRypNPovRpslob8ALnQbCOnT5PFzXDNOgvdJ9lJ3w6EDDtDdi/eY65AVvvnKdtSur5AZVyuDegMyyyYVAZzl1S+ALwbQocObmMfKcnY1dDMNkbW0Vy7Z5cO8Bo96Avd19mpbALEumWU5Qr2FIjS00b964hmmZDJTBYBiznwiWrq7wjb/1VS69efVREPvHYbpOxWuKcw9PLeyCY+vN823tPwfO9jOzQDyhro9z/nnMPs/17Edz61jveyIj08eWj554+VGm06re56n5dOlP5OL+vNaTjyOo/ScQmj4z4eKEkP2YCepcEuf8fKz46QwFR1PlqVm8njp4xzOvMhFzlBL3cPiPBY0Tzzhh0Th6t6NxyaOMD7/9E2595wPiWQqGwLBNFi4tcOMrL7H2xhVs3znTyOPV9thE+uSg8kdNeJRt4pNoCB7vxWfccJpOfLgnzY8Xv3SdF9++yd337lNv1Yizkv7ugGa7wYXLqzimwWQa8+qXX2bp+ipKaVQpmUwiFpbnGB1M+Npf/+pxStRkmiBsk3a7xcWLqzz48AGO75BPE7BM0jjF9B1s20IKg95uD0NqijQnlZK3/+CvyIsCWRR4gYHWmnQy4+5793jxrRfYuLOFiYkX+Bi2wVt/7YtceOsatu8SjWb84F/+Obs3txgMhmRZie+51Fsh17/yClJKfvKnP2Zhros2IOw0KNyC7/zPf87w4R6eYzOJUxzDoJ+lzC/P05pvnViATorbT3eeE1qjCkmZ5dhu5R8/m8XMXVpCl4rxcExnbo72XIP1u1tYCgqp+NG//yEb797nxjde48IrV/C6NSb7I9bfucPDH7xHnmS4f2xx7Y1rLH31VTpXVumuzdO9sMCLv/Q66SRGZiV2UKVx7e8OKNMctx5UcS1RhulYeM2A9nIbN6gwTma9Ke/8u78iniSEnoOwTJIsZrw3w/UsuvNtJpOI1RdWCRoB9392nyTJcEKHb/2vf42la8un+mPnzjbttTm++y//jGa9xqg8wNIGyjRozNdxhMmDn9wjmcRYnsXqSxcPgzCrdK1GXoHsSdem49kkGFh1hwRFOpxRTBPSQwHBcS1KAWWp0ErhKI1hmUTDGbZtYqUlKs3BsbBtC10qCkOQaY2nNboZYCqF6TXJ4xQtBDLLcRohpVR0G3VCxyIrShLToJjFaA1FUSIMgenaZEqSTxMsrRBK0WzXSWcx0XhKuNTFdp3KxUubFb6HJcm1gRt6ZNMMs92gVQ8YPNhl6ruEWmO0m5W2V4MPyNDDmExRaUptrknvvbv4hWQa2FywbApRIpTGSksM26LbrRMNpritGq6AzDCwcwmujRn6GPtTpvsjassdZJRgmYKwGZAPJqg8w//cFZysoCxK4lJhOTYiywGB06phNXyyKCP9cBNzrYt9fYVss4dhWyAV6YP9Km0uohqnRkAepQR1j6ATYNYDeh9tsvjWNcyGD+s9hDDI+xOclTZlf0w5jbE8m+jH9/A/fw1zvlVhHwmYfe9D7AvzSKUQUU4xjGk2Q+wLXZJpiltK8tkUqxEgswLLtbHmmwghsHyXmeeR7vZx6gGGVogkozQMRE2jai5mzUOaBnYpiT/YQ1sm+SzBlAXCb6GBpD+mvtSBQpKMc5SGxYUu49GUXm9IvVNnvDcg8H0e/PAmy5eXWby4SNIfk2h1iLdigWMRS1nhvxQlyxcXKaOcmAmWb2MYBvf/+Cf88Pe/R6NeoyFhlmYIoZnujXADj8WFOfpbBxiuRXO+hXnC2uqEPnWrsgwJ24SsxKt5+O06tW4dYZ7cU04rTU6pAfWRZlmwcnGZnYc7TMezKlOT1igDCsNgPJ4SxQmNZo20NFGTCBn6ZElO6LtYlsVCo4HveWzt7ZPEKdNZXFm1Aw9Mm0vLi9zf3CEwDbrtNr1ZzETmhHMNWpcv8KWvvcLqjTVszzmh8T5KZ/qI13jWTnmKb/kk3gVPoePd/tjT4ckVPJNpfR7G/pzyxwrYZ9V3VOHHYVrPK/tJ7hcCIU5kzjyrnD3b/E/KWGtOuKk97z1HCsVP5EZy/Nzzbj1OnvCsvj/ZD8+yXH1cy9ZT6DMRLk5bCj5GBz5r8MVZ1uwkPX7mvKefx7hXzLo+1ZEnA36exOuf5NXTccQP/6c/Z7TewxIGnmNhmAZKKvZvb7N1c5PVF1b43G9/iYXrK1WQ0eHgnqz/WYLFo3c9q+nW5wpS54+AeOrVs4956vwS4hic0AldPv+ffZ3h/pD9vT5h6KNNyFF4wiRKc9oX5vncb30JhDjOpjG32OH7Wz2+9re+yrWvvQRGJQg0l9v07++glcIQkOUF/Z0B3aUOou7T7NQxtUIiUAbkWZV9aVoUhM2Q/YMBwoALV9cILIuN/QHjOKYWBNx/7yHd5Q5JnHHpykU+97e/Qq1bZS7Zfv8hD/7qNqLQCMtm5dIa0+GMeugji5KPvvshSRRj2y67O33Cmo9ruQxHvcr9AkEqFZbr4PsOoVWnNDSmZ58I8jvR92cNapycE5qVG6sMdwYkswTLtek/3CfLCizH5sGt+zTqDdCQjdNq4TcMkGAqweatLSbbAwZvbXPlCzf4/v/0Z1h5yWqZYQ0fVtrzrQ/Y//Z/4KPLr/DCP/1NLr31AqZrE841TtgCxXHGqpNT6Mht4FDOJJ3EfPd/+I+Mtof4tkWcVjEpQmlc02Dcm1IkkuULC9has3NzkyIv0I7g1/93v0V3ba6q95DxKLIClOaj7/0MVwqi3pThep/AsknzglIqtAkHNzeZ9Mb4vkN9oUVrqcN0OEHbJmWc4xkSu1snHscoqbDTvAqOtiHQYJQSO68EB+naRGVJp9VAjWZINJbvYNc8LFm59hhAaRpE0xjPrixSwrIwlALPQZQK27HRhqAczTClwl/tMu6PkHYVIG4UJZbv43gOyrWhlKRpTnJnF1sIpNToJGNmmhiBT8cQ7PfGWDUfy7Yx8wKnXUOmGcgSOUswbYsozrE8t0oBqzTxNMYUAisvkElGELj0oxjD95CThFEpyQMfx7Gpt+sQZdjNOkqDFecUP3uA98ZlXM+BvMRd7uAkOcn9PczQQyqNTPMKU+ZgRLNRQ2mBkgr/tcsUe2OUZaLyknJ3hLBMZnGGN55h+D7oCdR8/EcoFwABAABJREFU7E6NdDSDKEW0Q9wXlpH9KcI2sUKXIi0qXJ04Q20N0aaBWGrRWmxRlApvrU02muHNN7DqPqXWCMchW+/hrs2T39xBXF5h2hvBz+5R++orTN97SHhtiVroojXYiy0Kx8TKCrLAxkpzbM9GzzVwBRTjGTQDpIAsylCFIhzG1G0boQ201JSzBNt3EZaFtgzaL61ViqPDmA2UpjQN8rLAqNfwLBMdZdR8j97tLbAMhMxRAra39gk8l1arwf7GHpZhYRqC4cYeB/e2qYU+Qiq0aVDaNoUpkHnGaKdHOolpN2ssvXgB0zEp0xytFHt/+RHjD9aJooh6p8HtvT26c22GwyEXLs7x2j/5FazQY/P9+xRpUc3tExuvYR6uCkrh1XxEUyAMAwGYh0B4j9a3R0qU83aR7fce8Af//P9NnpZVrFFRkGY5RikpC8WdrX0G04iagIVkxLbw0Rp2JzMWui2uXFzBdG229w548+oK6f2HeLZFqTRXrl/m4YMNXEswTmLe+Prr3H7/HuWFLr/wK5+jvdrFrfsYpnHIMJ/Qmp3WUD7B6+DUNviU+8+74dzu+Jj0CZnT57z9WMl6Ej/sqQLWOVk7Txc4o01/AsP3vP3ypD48Ugg/7d7PgmE+CdD83Pd8rNJPprNGMv20N35OBfR5/fkZWjQ+E+GiCkw6n9n9JHSukHCiw8SJ36c7+IxGWJ2T7vbcZj7i8J7F62ul6d3b4cPf+yFqGJEWJUop3NAjTwuyQmJaJg3TZufDdWYHE9749be48NZV3GbwSMh4TnpsOj+jjz/N1Sfq1J+kpUDQubrEr/0f/hY//d2/5L0ffsTaxWWSoiBOMl7/6iu88K3X8VsVaq9hVu8+2hvh+Q5zV5cOzdHVAwzDYDaYsnF7nWR1EaV1lVGuKPFch1QphNb4WpOmOaHvo5VCl4rh3gjLdei2QlzHIZeKJK1M45ZlMUtzakXJ4sV5XvzmaxW2hoatD9f50//+T1hamkMphZKaIAwqDb5jV4yyIWgtdFBK0eg0aDRDsqKku9jCc20MBHlZUsoSy7YrDXdR0pxrHWeuEIgT+9UZLZTWxz2vSsnevR2anSaT/SGeY7P97n1My2b3/i6L3RbTKKaUJSqHuW6Tfm9E13Gwag4vvvUC+5v7DA+GfO7iPF/7R7/M+3/yE/b3LWTYQmtwDYGPYjyO2PnoIRfevHqIXntalFdKksV5xVAgQCnKPMfyvaqYkuzd3mK8N8IyDJIsJ0lTysPxsh2LlQsL5HHOwcGI/d0DbNclkyXf/Ce/cixYaF39iccx7337HUYbeygNhdTE4whXCaRlIKVifqGNYZrkacFrv/wmmz+9x96dbV782qt4dQ+Vley9cx/tO1gawppPMZhQ2DYqSSk0hI5FojWWBgOQSlMXgnQ4wW2EmLaJnCWI/RQpjEMgPhvnUJAUSmPYNkaaUQ4kyrWxlSbN8ioDlOdgL7WZjqe4YUAmSwzPwRIGRjKFoqQUAZMkp2YIvNBjOJ7ipBn927dwO12CtVUUGlH36c8iClNUTJ8JvmVSxjGtbp1UCogyJm4ClkE0mNIqFE63iYoSrLxi3rKioOZYmFqj8wJTQwuNm+REroNTSIRtoQMXaUJ2ext3rkmRZBR5iTJNaIfotEBNI+xaQOBa5GmFJSC6DdLJDL03xDAt5O6QyDBwljtYuwNanTql0ghVYtRD8izD2O4j72xivXYNpilaGJjNEASUroOZFpRRguE6GO0AkRTk2wNm/SnFfJ3W1UVUkiJHMQqFM1cn25+gyhLHNAi+/jJpWkBZkt/fQ15exFtqo6TCWe4ghxHCsQkNk3GeIXuSsBlCf1oJB6aBaRroZg3bNlHRhMg0SEtJnGY0HRMxmKGLHN1t4jkOUW9Mw60Qry2vSldMPYBRjL88V6GdCwNjvs7sp/eRkxjVCMhnBd50iNVdYDyJsITA0NBq1gk7NZI4BaVRZYkCIlmQojAkWLmBh8WlaxdZffMa9qECaP8nd5FpQf/WJnfXt6iFAe21BSxDkPYnuIbJ2pdfpHllESUlRiEpovTc/cL2HEzbZHoworncOaX000ff8DGA2eMoVFqDzAt+8K/+jN3NPTrtFs1WnbWVeay8wHQcPrj9gCjLuXppjZsf3ub745KFlo0yDXqTCa5tIYqSuusxLIbgWliGQX7YjqtfvMF+b4DIS/r7Q77wd77OG//wGzihV7kpn2nz2b3slIzw8bjH5yJ9SiB5jvKnnnKaN3lUy0lHnXNadfLgfMbqcd2jeKT0fBrL/phT+pMY/1ONOask/Rj0aSwOnM4P9axMnCdjN47ok3K3H99m8Qzh4OP2w2kW+VGLnmTh+f8Xy8XJVF+ax9j7M3S08IhHP4/rOXF0ZsD1EwufLnccjHV84qyH3Im6xUkB5XQLzz7m5Ce0+dN7fPRHP6a12KEIPFYEtOZbKK2pzzcp0pzNDzbYvLWJ7zlEoyl/8b/8OYvfeZ+5a8tc/uILzL+wfGqxO49OLcw8wTR54vozJfdPSs+QbAXQvrjA4pVlHnzwgFIp0PC5X3mLlVcvIMzKH18rhbBMiiRn9HAfz7T4o//m9/n1/+q3WX3xAgiNVtBpNuksz7N/0CdNUhqlJJ3EFFqhypLQtrAdm5rnMI5SAtujM99kfWMf13OoNWo8fLiDYRrMd1tkeUk0i2g0QvYe7tFdaNBYrWIZene2+cG/+h6+YTPcG1dzRSrKLCesB9R9h1a7hhe4ZEVBkRV4oQ+2QRxnJHEFwFdkJWWRV5o8yyLLCwLXRdYdXv7mG5jW2bzpRz33+Lfy0V99wB/8t3/I2tUV/t5//Q8Y3t1h/+EuoevhGQZGnCLTnPpCh35/zHJnjq2dfeYvLdBYanGw22fxxRWuf/VVdm9usPjCCl/7x99isjes0rZqza3vvEchC8TDHhs/fQDGX9C9tMDC1WUaJwANJ/0pd35wk8//1hcRpoksJNODMe0LzuG3Dos3VnnxSy8wvL3Dwwfb1FwXw7ERvku9U6/iN7SqGHINpQHf+Eff5NJrl4/nkywkWx+u894f/YgyypBlQXdtiXiwT7PTQOQZZZ5jWw4X37pKkRVs3d/hvT9+hzLPqc3XUbLCIIinGe5CnfWf3OXK4hyOY0M9OBwbg8FGD92uo5QkySVGwwepcBAUlsFsluBJhSoVuWNCkWEbBjqWGLaFkWTQrqOjFBo+GYfZlawqXatjm6jArc5FOcKxMVwfEBRJhFMLoSgxhaDp2bimSZbl2K6DFgLHspgOhngryxXQV1mw7DvYzYAxGlNo4uGUmmkgxxFivo2FRqYFQanx/YDAV/hCk68uIPoTDNdhyalhFgUylzRCl9nqPJODEc5oiuU6WO0Gtl+lgLZ8B8t1yAcTRKsOrovhmYz2x7ijGW7o4vtOJYyXEmULRJzidZoUZYFwBDotyA0DOUmrWI5coptBBVSX5tAKKaWEKysUk4hSSoxxhLvUxuzUcC90kXN12OqjLANtmpihgSgkZs2nsdLFDhxEzWVyewe13sN69QKWa6GkYrQ3IowyzMDFNwTZNGPwx+/Q/O0vI+MUK/QQApJcUYgEZ7HNeG/y/yXuv54kOfI8T/CjxolzDx7JKZKAA4UCCsWaTbNh28Nu5nb3ZB+OiNzDPu6fcCL3fHIPd7MyKys3MzI3vT1NpqdrmhRDoVCgCZacRGRw4tyNm6neg0VERkRGJoAqdJ+KhIS7uZqampqa6vf7o4w2hximQN5bA8fB8h2SXoCquWi2gRxF6K6FY5kUcYqW52iOgT1RZ3x/g2wwIoxihG1Qfekc6cIm460hmm2ighizVcFs10kGAeH2iMLQ6Q9GjMOUIFRU/Ixqo0qeFcy4E/T7I+ZOzKC5Nveu3SHSFFmSIzMgz1CmTpakeKYFhWTxnRuMBkOmTs+zvd1jdXEF27Kx6hXmzszRWdmm2+kzHA6peC7xYMdML0qZvHyC5vHJIwVYWZKRjmO8idrRAq4DIZEO7aI7VgKL1+5y56Pb6LrO7NwUx+ensNMMXdfJipwwjIjGAY5tMD81Qa8/oF6v0OsNcUyTum3zwfW7JLLAQCDs8t0xLJswicG1aM62SbZG2J5DMAxx65WD1sQHykFUdSSMfBIy/KoA7FcEbE8+/Ss2rOAxweyuJn3/M9ynlHl6EUd+/ML6X1T3q97Wnjnb0Q1/ubhe+375GsFUmXdDe8rVvqSm4UuXfc/1yCbFU79+Xd34lcnFfkB/+BWFR+Rj9z7VEx/+vk+HxlqUDT1+3aPK/nN3mOeumdyTVLWP9+JgnV2y11veptKu0X7mGO2ZNn6jAobGh//xbUScsu05TJyf5ZV/8gYn767xiz96G5kXuIbG+tIGyw83uHftPscuHeOlv/8alckaT3ySB9/7Uqty4EV+NK5fJ7F4LB704SF5woXcVoU0KzPjOr7Nxz/6kI/+6n0000AUpS2wpmtkeY7tODieTX9pi2wQsvsWqKIgGpeRY5IowdYEo+6ARQThMChfUgChEUcpk5UKYZax+GAVYRq4tsX26jYCjfmTM0ydmOLGu7dKwB+nuJ7D7NUyIlQSxLz7R28TdMc4to1CYTomMxN1mhM1kIo71xeJ44T2dJNuZ0gSJVSrHqNxSJbmpd+OgJMXjjEcjmlMlImcJk5MUpms05hrkSVZSS44+v3YLWpnkq3fXUcowfbyNp3lbYq8wJMSTRWYuskwS7E0wZlLp7DvrzIeBdQ9j43FdYI0oTHbYunDu5iew8XXryIMHbPmMnj/JoZtcveDO8RBSm+rx3AU4Fd97rx9gwefPqA23eTF336F6dMzRMOQSt3n0uuXSDpD7r5/h/Ew4OLrl8nzApnm9B5uoGWKsy+fpzfbotcd0GzUUbrGYDCmtz1A5gVpliPjmMmTc1z8zhVOv3x+x3lbkUYpH/35u9x66zNEobBtC6lrWJaBW/PZXu9w/NwcWV4gk4yPfngNUzcIRyHV2SaTkzNUJprcfecWJ549he4a1OZbbC2ts9XtMz3ZRug6Kk1JhYFV9dhaWENVHGzfo+Xa0B2RA3bVhTBFBDHC0Eg0HbtRIR+FkEuciokC9CRFFQUiV1gaKM+CIMauOOTDANvQKcjw6hXirQGFUpDnpalPmqNLiREmSE2QmUBaZu7Wkox6q0Xa6VF1bTqyYLs/ImxW0DtDTKXw61WKho87ioiGEabQ8Dyb1LSIwhgbRR6MEfUaZstGxQ6yH5CZGZapo082MGROc77NsMjJ44yqbeFpApHlqFyi+xZ5UaCqDrIo8GydOC+oNzxo+GgKilIvj6kJ+r0ATRPk3SF1z4beCNHwqRaS3qCHJcAyNcwTk8hBiGaXTvSFJkgbFYZRTF1JrGqFvDMme7CBfryNf2yCMMoQqsCdb5Pc3yQex3iehTaMCO+s4Z6YxCgUsaFhNiuQZIhxhNMLyTtjRN3DvXwCveIQ3F6mc3OJqRfOshtv34hipOZg6TpevUKeSyIhsHwH17HIhcIwdVScgGtRPT6J6I/RNY1xFGNaGl7FJR0GkBd4jomSUJgmMkyIhyG5ACPLsRVohkGwsMloaYvOVo+BbaBZBprQiC0LgoRcCNyJOlYuEUVBd61Da7bN1EybhYcr6Ap83yMfRZjo2HWXcRixvLZFnGSkWUrvRopp6ri1Cn7Fo8hy1m4voQrJeBygaxpBHPPw4zu0r57AqLg0T0yWmuRDgk2ZF6x9tkiRSTRDx625oB/UBDzy3H60x+9pYwtFFka8+0dvkUuFV6vS6Q84Pj+N6bnkShJGMXGcYug6QT9AInjmykXW1zfZHo04MTPNIEkwDAPP9bnyzSs0ZtskScrkzCThVorMC771L3+d7sMtxr0x/lSDg53cv+AesQbvVhX7jzx9f/7q5YtMI57Qtjp8eFdYujeVH7e62D12GEAd3suPIF+PCWp/lXKUxHb/8aOG5EmE7mmKn6+gInhEpJ4EbMrvT4rC9aWjc1FaZDze0aOuuV8b9TWUJ/Gpr0kz8UXl648W9RgxOAipxBPqfak2jzj8KI+dOizuf8pJT67zxNOkpL/SReYFSS9kabnPqB8wd/UEz//+q1z/Lx+SxQmrnz/EtE1OfvMi3657fPKDD9m4v4bn2ViWTZak3HznBoPVLufeuMSFN688CtP3lPLoXvfpLvn63v/9V3psDPbUZ6qMslXInZdL7GlgJi8f5+o3r3L7ozuYqYlrWWimKCPOSIVmapgIEIpYCKLuCNMwiEcJeZqjGwa926ts3VoiHgSQ51T9KrrnIiyDTClMXaMoClKhGA0D5mfajLdiZuan6A8CLFNjLBWWbRJ0x2xIRWuqycryBkWWYzgW9ZkmCsUv/uhnrD/cwjZNkrwMR2vbBoPekM31bTzHQtcEnm2TDEIMBNgWrm2icodMz6i1q1z4xkWOP3cKu1ktw7QKkFKhpKTI8jLqy17Zx5aP2AiKtGC41qfieyilWL+/jl+1iXQdOQ6RSUEqQDgmt96/SaXikYwiKp6D3fQ5+8oFPvurj4hGEaZrYddclFKlJDeMsYOU1XurYDlcef15dENw890bdLd7OLnP1NwEv/jf3sJvVOivdLj0rStEgzFBZ8BgENKaaBCu94gHEaP1DpNn5ijSlK3371M7P8uzv/YiN39+nShMy2Rptsm5585y56M7ZI5NfzBk8uwMml4OQDyOef+P3+HmW5/i+R6z52cJBmOCUcTq4gaWY2KZBp3tIVomUUIw7I+Ik4xjJ2fwLBOjENz48Sc4jk19skbv4QZynDB77hijjQHhIMao+WhZgSYEli7wWzVyATXTQPYDhAJh6og4wwgTMtMAXSuzqYcJSZSSxwlO1UWzDESak+yERNYtg0yBTHKMVoUsTjHiDFVIGIWlZLZdR5k6yjTICkXs2dgCDNcmiBKKikOx2cMYjvBsm9bUBJYm6HQHCN8iE4oCsF2bfpLiuiZBu4q3OSSPMizXIc5yDF0jy3IczcSQEi2XKN9FBTFWb4iseVg1H2KJOU7wPQeRpghZUPgOel5AIZGdEVrFQWtUAEEyCMoQu3FG5fgEaWeEwkIrJEYh8QV0soIijLF3MqI7nkO63sUSgmGcMntqnjTNEYXErHtkvRFmxUVkOUac4cy0SEcBRSqxPItiEBENlxCGjn9qBmuiCk6ZNDMNY/xeQaEUo48eYFcchr0R1koHA7BPz5A82CQzdYyKU2pXHBP/8knSzojxZw+pv3IWre7hXpxn+9YaRiVDCAmGjkwzKmdmqT5zjM67t5G5BFWgS1muYYZgexDROjZBtNGDpEDqpeYS0yDLc/T+iHDdIg5T/JqHDFOi3rgkYcOY8VqHtSgiSATNegXPc2hONRhs9hG5JByHaDUft1al1+mzvr5VBgGwTZyKR0W32BqMufjcRYq8oLO0yWA4RhMC0zDLJIJJUq7Zuk6jXePsq5fQ0Hjvz9/m5tIyShPcvrfI7C9ucOK3X90z4dyP4gSCYHvIqDuGvMCtu4w7ozJ63jjG9mz8ZgWxQzYE+8C5KoUvmqGxfH2R9YU1mtUqkzNtKl6ZlyRI0pJYpBlRFHNiZoo0z1nvdLEdm83tPrOTE5w+Mc/1OwtcevYcp37tOWaeO8XDn36OZVm4uk7N9xhu9nnuH7zO7K5WlP3BXw5Bc6FQ+zUsB7D0PiPsr3+DPVgOA+IncZkjsLDaVR8fFkTv7S+P1A/lJ7V37mFT8cNt72MlvzrIeBoW+7J1j/x9n+3JE3KO/KrlSwXcUV9gWXLABOsLmNRuokr9ICH58nD5iAnxd0QmDpdfnVwcYqJHkcejyOpTy4F5/wUPlq/I876w6tGMQ0kFmkYyDiiSAoTGlO+yem2B/sImE/Mtbr13m6bncP/9u9SmGzSOt3njn36bH/3rH9DvDLBNSZplOKbB9vIW6/9+k6gX8OzvvvIoqtTBGzt4aG+SPoGiHyWlOPJpHBYlPFq51OGqu9lUs4L+8hY3f/IZ/c0+zZkmx6+eYvr8PKbvUGlWePmfvYmmC669/SkjJSgKiefaZHlBJgtmJpokssDWdbobXZ5/4zlas03Gaz28do3OUqe0Z85S6pUq/kybk8+ewa26bNxf48HHdykENCsug1HI1maX05dOsLqwieNZFHmBbZqkacpWGGGPQ3xDR88luVIUssCqumRRxvrtVTzfBaA1UceruqRhShpnuLZFkcvSz6MoAVeWZeRpRhAKvIbP5VfOc/GNS2i6xtbSFp0bDxFRyubiJvGOI/b2VofX/ptvc/GbVw5JgnZFTQfHerg9pLfWZapVpzsYY5h6CZosE5HmpFJScWySTDJMAgbDgJNzE8y8co6JszN89KfvoGTBhe88y4VvXibsj9l8sIbMCxZ+dh23XafSalDEGZ+//SmaqZPmBdV2E8ex2V7q0PQ9Bnc2GMYxYRBz6fsv0FvbZvLkDE7FYfGT++SjMfXJJt07q0yenyd1Lcb315m8coL26RnGg4DhRo/+WpdbH91mPBzTnJvk6m+/SGWqjpSKzbtrfPBn77JxfwXHcXBdF9t1WF/aRFNw8aUL3HznOrbnkCQ5py+f5Mw3LjLe7PPTf/cjNrd6BDLD1g2KKCWLU37y//0xahDw3BvPknRHWJ4FvRAZJwjHQuQFZsXD0XQKJbEUiIpLFkQoIRBBjDR1TE0rHbjTAsvUEa0KVuYS5gWmrkOWo2nl/JY7/j+VigN5SWCyIEQYOipJQdPIB0Hpz2DoCMvEEKBnOZqCStVFuhaFIcrEfUrRUoo4TXF9ByUow5wmGVIXOBUPO0ox6xXiuo+jlfkZNEOQK0HV97CEQPguxSCAZhUx1SCNYqzOAKFr5M0aqmJjJyla4ZNLhUwyrIqLEpCPwlL6PIzQshTz1DRGmKA1q8ggRTgWuq4TRDFaECE0jaZtIAuB0Q8oGh5JlKApheuW4aQpJJWTk2SbA/LOCN0ySfsj7Mkmua5RCIFh2xRFTBqnEI2RCsyaR3h3jTxOEZqgUnHo3HxA4bnULBM1LsmgqPksf7rIzFQdc7KBdW6WaGGLvFCYQUy0NcCr+0gBanNA1hlizTRxZptUOiF5mGKoAiyTPMrIRzEYGla7Sra0jVAKYUjyKEFvVvB1geM5FM0amhDYMy360Tp6xSEfhehpCkEMo5i0P6TwXJx2jSyXBKMQzTBonJhg0jKRUlJxPSzLQhvFdAZjVBjjjWPGUUqWF6UjtwLLcTCURh4lXHz1EhNXTmBWHIZ/GXLMPsbMiRkQgmAwxqk4VGZbNGbbGK5FuLTN7R9d48JLFxBIwihhslbFtiwqE/VHWHIvhOfOf03D9mySIGZ7cYul64u0ZycIOkNM16Y222D64jEM85D5595epOg+3MLQDObmp3nm/AmW19d5+xcfl5pZ26JZq+I5Nmsb2yRFQbvis7a5jaFpTM9PY7kapmsRBhF3fvopMs1JRzHtdotmrUqrVmXQGSKlpMyQJA5YL+ztZ0dumo+L6p4GE54mcP/K5UtCl8cTWz/qtzogVxXsRnQEtQ/Q7piu788K/HV07As7/hWaUo99eEJfdlVrpbCSHcFyKYD9qv1+kork0bhqR5rpf8VLfIWTjsr0vkv0v9zFvqbyK07wr8HnYv+Xx51gdo+XZR8TFiWU3YtMcEADsS9K1G5Gxy8oj6nx1L72nnzSY0z4SQuH0ASmbfDg9grHLx5jsNYjH4a4SMabfcZbA/K8IEpSLNPg2p+9xzf++bfxp+t845++yV//6x+QpDntuUlsz+HBzUWqjs2nf32NNM544fdfxam5B8foCeWg89zB+zkUBOtxycv+KBj7GPlj47SPWITdMR/80c+4/+Gd8iKGxuqdFe6+f4d6u8bpl89x4dtXsWser/yL7zJ35RQ33/mc3lqXcWdYJoqSBXlawa/5bK9sMTc3xbHnz9D58AH1U5OYFZdwFO0GPsJ0LOZPz+LVPdJxzHh7SJ4XOAKyccjEVIPe9ojRRp9+f8iJY5NEwzG6AL/pc/7sHLmUrN1eJhvleFWP+lQdx3PI0pzROMRWOnOnZoiDmNs3FpBZseeQXWtVCUYhliYI4wyFxPBNXvydVzj+/Bm8us/mnVU++MF79Nb6DHsjpicaHLt4nKXbD9nudHGqLkKqRzvD3kK7N7v3Rl5JydqdZWReEKUptbrH1KlpsighnFsjWtpGKAgtAwuYqXhsDcfUT01Tb9aoTzd56R98k+HWgMbxSQzbZLQ1IE0yGjNNmnNtslGCmRcEaYpuGwTjkNpEi+mT09RqPvc+ewCWTq6D41kMtvssfnaP5VtLvNau4fgOzZkWMs3xGhWcmTrZKGEwDrHClM77d2m/co7WXJvZqyfprXaYf/EMYRDRnGkxdWaW0Uafmz/5nDsf3kVmGZZlkRYFVpaycncZmRbEsqC/8z4Zpk3Yj3FqPqONPtuLm1ieje3aMIjZjGM808Rr+ARbA6oVD9H0ufX+bXzD4MS548hRjF11GQqw8xypC+xqFT1OiTtDMq8k9lLTEJqGkWSl6Y5jIQToaU4hIc4yDEegLAsNRTGKcHYShhVZTp4XWJpAa1XJBgHC0MmzArKCVBZY4whlaNgVF2Ua2NMNKhWXwUaXfpaT2BZaEOFkOV7VZ15ZfLC+QbVdJwoiPNtE9cbovo0XJ1iWQaPiMo7TMimdZbBVpEy4NsNxhJ+kmHGKqQqQBVvVCo04IwkiKqemGPcD3KqHFmWoYUgiNMIix1IKleVo/RFGu44WloSi2A3XudEnsgxCDcyqh5nmmFGK0a4h7q9hVB3Mlo/wbaK7a2Bqe4nmijQnLxR6kqDCFDWhIC3QrRy9XSWNEirn54mXtglGEfkgwOmMiFa2qf3a87hTDZx2izBKsRY3cOtV4n6IYZvUZl2wDNLeCPf8HHKc0O8OUa0KNqA3PCzbItd1guvLGI0K9mwTsx+SLHeR44w4GuNYNmprQNYbY821EGlB1h1SdPqkaeksrimNOIpJBmO8Y9OQ5jt7l0IaBpmpI1AIA9IgoxgluNNNcB2KrCCpOwgNvKpPEMUEqiAZh/TGAYauoVyLgQGWV8UKUs4+fwZ/uonmWqWgSyrqZ2fQLYM8Trn6+6+RRTFZmJKOIk68fglvpoHMC3qfLLLwh2+RKMXKg1U+/ug6l4/P0RuMWO10mV3vorICHHNvbVI7+0ORlblYjj13ivXbqyx/vkC9UcFyTCa/cR7dNug+3Gb58wVOvnD20J60A/oKxcbiBkoqDENne7PL7ZtLNKsV4jBiHEZ0+kOaFZ88zzA1HcvUef7kaaQCPJtBloNjcuvuAjLP2VreJBoF2I7LEEVlrsUzr54vgx4c2D/37YaHiMaeKdGBTfIRGD9ie318j3xqhUM/if3A/yuWg1vGPnxzuNLhRMDqQL++FPh+pLj61cvTLvcY5FB7z2X/z7tG9Qd4yu44fhXy8hWL+JLakMc530EmeBCbiqcKiZ/0fP6WPGqf/px/xUt+DT4X+yfB0T09cmDUEYTgSXWfVJ6mKxKHAPNh1d+T2jqqiPKhh70R3c0+U8en2Hy4ha6gyBVZJtGEIk0SumnKuakmD1e3+eRP3+Ub//vv0T45yau/8yrX/vw9+ps9Tl85TXOyQbA9oKEKbr9znWgY8to//zZes3LkvR1YK4+44f1k4hFnEHvmS0fGyBZij4wcxUFAkAUxH/3hz7j97g1s2yoTSWmCaqOCtHTGg4DP//pjojDmG3/wJoZrUp9v4boW20mGVIqG72IYOolQuGlOHCdMn5mlfWaG8fUlxpsDmldPUJ1qMOoMaMYJaZzSWe+wtbJN0BsTD8ZYUiFNkyBOsHYkp4YQNKs+o/4Yz9YZpwW6gpOXTxJlGVe+/xz3fnEL23c4//olUGW2WU3uvP8CkijBtSwqVZu8kAyGQ+YvzhHnGb21Ls9//wVOvHIOy7WwPYeV6w/5+S9usrmwyamLx2n5Ptev3SGNE2Sa4bdqNGabvPS73+TUi+dKQMYRqtN9r8tweYt+d0haSILtPpe/8Qzt45Olb0KQcPcnn7N+a5FgUODUfSbaDSacBnGSYrd8Hn54l407K3g1n+PPnyENYookY9gdIJOMIIrJwpDmRItIgWmb5EXOxGSdequC59q8+QffIhqGnNRKO+tK3WV7pcPsqTn+7P/+H5ian6J+YposzThx+SQTp6bwZj3C5W2Goy20ccH4wSbSMrDaPuuLG2iazqlXz2G7Dh/95/e4+dbnmKZJq1VjYrbFx+98TlZI6hN1UFCECUrAwq2HOLaJbdtUbAsBfPo310oTOtuEokDZJu12BUPXMJWgyArsts/F7zzL0vUFlm+v0p6ZoOV7yKzAVJJCaqi8IE8zCgWZaWCEKYZThtTULIMgycikpIqiyMt8ArpjoukaRpohTQNLCGTVQeaSrCiwEaDrZKaOvRN2tsglplPmdinpS04xHJNKienaFHmB0AVmUPp0eI7FrV6fIk2ZEJIiLzjWqLEexuQohmFURjIrCtJhSN22ibOChqYxMPQyc7smsBo+Rh9s28QSghxQ4xi/4pahVm0TGWeYugE1h8KMyT0Hw9BwhwloIMIELAs5UUO4RpnfoShIOgPIJZmpiAYRRqNCkUsKx8FJMpQmYGuAffk4qgZyYQt9skZRKIIHm+itChoKveGDZVCEKbkQyLRAhAmuYxNcXwIhkHFG5FvoWYEWJAQf3Ceve8RRgjXZIFrbwtzokDeqqIk6lmZRvTBH8OE9zLqHPlnD743JRyHOiUnUKCrDBzd8VJqSdUfYcy0q8y30ikPvw/tUWjVMoJ8lVJIMZ7KOfLBBIWUJjtXO2lh3y6RyEzUEkMcplm2BKciGSakJkjYShW7bWEZB1BuTBAmjLGNbZpw6NsNGd0Bnq0urUSEYx0yfnmO4PSDXITEEZOC3azjtOu5kHatZwXDLyE1FknH/Lz9k4ZP7RMOAYBTgmqUmZHKqzcnXn+H0b79M+8XT9D59wP2ffUyaZygEny4sUfM8HM9l/jdeQvesg7uAUgS90szKrnpousbE6SnG232mT05TnWvh1D0AwmFEf2WbNEywfeexNU5oGrV2Hd0yEHlBfzQmTzNmL5zg3Dee4eEHt7n38R3CUYBfqVD3fTqjIdqgS0+3WVl4SKVaoT3VYsZxGMYxmZTots2xy6d44Q++RW22idDEvhCzHCFZO6KIHdi6QzIOANynGAgcWZ5mMLAzpo9ZBjyp7lEd3XfS0X04IkrXl22eR3jpl0r09uRGn6gcODKU7ZMuvUumxNF4+Kt3+QvA41OK2OlH2cRBDHtIVv6FPfhbogwHy0GQ/mRS/LWo4h6VX90sands9wHao+ocLmrfbHlsYhyhgTiq7L1mh6NT7DVzKEjbU1eF/RB730u6T0IgTIN6vULeGeGYBsEgwGlUcBoew16A57n4eU6aZjSqHiuLG9z7yedc/r1XOPPGJVauP2T97ioPbyxy4RvPsHp/jc7CKjUpuffxPQxN8OI/fp3KZP1Ad/Zz4AO9Vo9C/z0mtdh3w2LnbXgUx3p/20cQFfXow+LbN7n78T2qVY/eMOD81TPUqxWuf34PkUvyJEETgrQXoGR5zqf/5V0++JsPmZloMTPTJleSbn+EShKcWg1ZSPKsQOgaJ//+qxiWjllxmLl8jHQckY1jPM9ha71DUUgqnkO74kGS0YkTDE3D0QXtVpUgiGlUPbS8oNcdYuqCXifigz99B9d3eFh3efn3v4nfqkIh+fRPfsHJ1y9S8V3yJGd5YZ1ao0LTqdLpj3Btm0a9xtrNFeyaw5v/4rsce+40RVbQWdrixk8/ZXtxiywtsB2Le9cXcW2T2dkJ8rxge61Du1XjzLcuc/rFc3sqzqPp4KOjqQTTtSjyHF1AKvM9e8/7NxZZ2+piTrTwgoh6zcfwXDobXabPHWPts4csfnyH4SBg9tQMKBhuD6jPtTkF3Pn55/gTDcYF9LsD8ijDRGDpJmF/jG7oZLrG+sMNttc7aAVMT9RYimMMy6Efx/gTTYa9gLzYZByG3P3wHu35Ni/+5ou0r5wopTzdAOIy4ZhQsPjJPXqdEWt31gjHAYt3HmKbFqeeOcmVN69w4yefAYLpqRamEmRpgW4aVD0blRYIoREMI05dOcXKZ4v0t/oYuo7p2YzDmErVJ+uFxEjG4xBN02jMtNEMnZmLx1n6bJGtzQ7102WUIjvLoOohoxSFQlkGTqxRmDYizREChG2iBgHDpEBrVdFEaUqn1VyKKAEJZPleqFwjTLDGEdK3UfUyElTRG5fgvekjNJ08zYg3+yhDIy8KXF1nNBwjNwx028Caa9AWiu4gxTV1As0iMjUmdPBqPuPUQMQJlVTiGxZK13EyielrBEGM36wiemMipWhnBSKMkVmGW/PJ0wwRp5i+Te2lM2jDmPTOCnk/wLLLfBvR5hDNKCNVWa6NcC3y3qiUkI9i8jhFm6ghsgJnpkURpphVl9H9dbQkw6u4JYHoDEuTqzglXNhEWQai7pH2Q4y6j6y5mJTgJR9FGBUHre6iU2ruZFYAArNVY7A5wBxFSE1D1T2yJENb3UaOq9CsYlcd/Mnz6J0BZj/APjVBYZls/PwWwtCpuTaabZEtboLSiB5u41RdzLaHnmYwVUMVBSrJkGHC4PYqUkn0PMOcaVGJEvqLW7R8h2StSzoYY1km2nSTbDDGEoIsTMjDhKLZQHNs8nGE5ddwGz7Gww2cYxPko5AiDcg3O+humUukVnFJUp3RKKC72cU0dGr1Gt0oo1WvMDHR4OG9FQpVIJOURCqC7ghNQBYmZEGMbhm4U3Wu/dd3GfeGCCEoNI1BPkQqxVZ/QKfbp3XxGI2zs2g1lzDLGKcpaZoy3aiXOYcaVSonpx+ZYuwTTtm+g5IK3dRRCpyKw/k3rxBuDUqfop31q9qq0V/cIh7FO+TiEDIX0JxrUWQ56DrVmgeaRrQ9ZOH928xcPkH7/Dy6ZVCZbvKTf/NfiDZj9I0+K9KlEyUMggjfslnq9Lj85rO0alU+/8V1NlY2ydLSZO6gY8LTQOMOclAHgfrulvvoqHg6AjwM1J4iBT7y8JdElnu9/lI5sb74Gk/2ETiEBr6C9kIdGihx+MPhcdyPyXcVS4dMhQ/3Rex7Uvur/p0A9J0ipdzJ8SIOws4DffmCHj0Fez1WFOxFJPqyd3p4rA+zzcN1j/r+NQzq1+DQvTMDv4BxPn7W0044+Ip/8dWfxOO/gFg8gX3uB+JKKbIgRuaS0y+dwxAa1/70FyRhTB4l9IfBzoKsMEwDx/dI8wJ0ga4Jbr5zg+lLx2ifmeHKb71MZ6WLyjLufXyfK9++il/1Wb67gqEV3Pv0AXGY8PI/fp3Wycm9fj3qutob6l3O/+genzxSe4vSvonzyPRy9z73N1N+KZKc1U8XyqvZFmcuT/HMd57lb/7ND9DSnNrpWV79B6/x8V9fwz3WRtM1wu0h3btreJbN7OwkK4MhSRzjWxaiyEAVGIaOqWtsfrJAHKccf/UcFgK75jL33Elcz2L9+kOUVITDMd3tHpGmoesGiczJxxmGEHj1CnbNYzQMQQmk0Kj4NsLTiIcRnufCMOYv/x9/QvvMDK/9wzd4+PkD5p49yezZGYbLXYIgIYlT/HaNKE52QmwqxqOAURLTmJ/A9hx+9u9+xPV3blBkBRPVCropyNMMXSlM2+D+4hozUy36YcTr37/KmVcvPC5OUYffk3Kc0yimPlmn3qljmAa6rnHpm5cQmiBPc/I0Iw0S3IZLYhqg4MHdh7QaDTYW1qlWPVozLbJCkiYpuqlTm25iuhaNuTamYTBxYobOcpcTV8+wdGuFOE4Ruk4wjkiSFHJZSp0RFLrGRn9MEERMztoYUmMYhGgaVFpVwmGAaRiouODaf/2Icy+d5cRzp+l9vkTWD6g3fSqnJvn1/+Pv8fb/+tcMVrcRjsnc3CTVisflb19l2Bmysdqh5rpoYYj0KlTrPgwUYVhmu3cxmZxuY5sGw40ek606lkpZ6Y5xfY/trS7NRoVBd1AGDigU/dUOWZJx/Oop7r59nXEvIJ5JsKFMwhalJbA1dQobNNfCMnRSPUOzDGwhcJsV4gerBIZOo1FBWSZFlKIVkjBOsW2LTNOQo4hMKaxKaWonCoVeSPRCorkWumMhRxG5VJgCVBDgN+rEhUQzTMLtETLKqJ2dwTkxSWVzRCNLMcYhiaGxVuR4onTu86tuCcoLSVHAxFSjTPin64hGm9ooQp6ZweoOSUYR1lSdKMmwHQuhgd6sYAwCiiRHN40yf4ySiEJhUJKYJMlQpYSASEG16qNXSz+MdByjJSnSEMjNHoZjMlF1kIaBPd/CnKwRokhyiVNxAEWuFFEQY/dDjI0e2lSTrDtG743QpxpQcRCGjtb0KLbH5FKVWbWlQhUFo04foz/EPH8Czs5hBRHhjWUaro0epBhBgvftSww/uk9yaxU5UcPVDYpRyPZPP6dyZqYE3XGCoenkS1vY7QoCQbY5wD4xQXR7FevEJL5nIX0b39bRjk9iNCoEGz30ioMy9TK3x5k5tFPTZLdTVKePZRkUpo6yDWRRRgETWc7U5ZPEpoE53cAcRVD3sOqnyUcpcrNPZmlgCTTX4tTxaUQmMXyHWrtCZ2WL+aunmT0+xe3r99E8i2FnwN0PbmLpOnbVo7OywaVvP8/qZw8YDUa0Wh5GxccwbCxDgygmd1x6mz1u/OgTXjs5RfvyCS4+OE8YRoT9EbamUZtqMf/dZ8v8S7ui+l3EtCvJlxIFpFFC2BnjNn2qc22yMCHujdAdG7GzG/VXu9SnG48ryIGzr17kzl9fY3Orx7GLJ7icS+7cXiC9s4D1i0+wHZvZM8d49V98D79RQdN01uuz1CXk2og0K+j1R7gCasMxcSG4cPY4D9e3uP/+bSZOz+x1/3FkcVAj88Syz7HhcR+HL1F+GWD2JcTXardDX6EL+w98OSRV1im3qKMEjmoHjjxFlSP29fMoLf1j5Qgx/+405CgfA/GUb1+1/HJn75lKPek+v9SVS3x5kJB9QULCw8ePIhDi0Pv7tOae3sGvRa3yNZCLp09adejTYQ3MkyfQF3DAfQ09ndfsoegvydrUvpdZMF7v8fa/+UtGg4AXfudVzrxxCbfpc+snn6HnkiLMGHeGDEYBShZEhSQeRxQyRyhJEma8/59+zq/9X36P2lyT45dPcPvdm6go4fO3PuOV334VFKzcX8G0DTYW1vn5v/0xr/zj15m6OH9AovT0zn+J8phYYl9bOwuDLOROmFAItgasr23jV3wEcPn7z7H0+QL93oBWs8GFNy8zc+k4U+fn95rTdA3HNKnWPDpxhI5EJjm5Ca7vUqQZ8/PTrK1sUW3WuPfZPZZuPeTb/4ffJA5i3v3P7/Ctf/Zd/FaVpU8WsCyTOCzV4JoBOQqh6QS5ROuPMXWdlm1SaBq0fIRlYChFN0yIeiPmZ9vUT81iTzVwah4TJyZZv7tMZaLG3ffuIHSdOM9ptqpcuXqGu3eWsRWcuXAcaQgczyYNExY/e0CzXkVJxXA4LkMiejYoRW9ziKfrKCk5/cwxLr12GSF2kyU+fYFMopjB9oDJY1O0p1v4rolVrzJ34RgAumngNCskhWTyzBRb791G5TkzM5NEWYFQiv5ahwjFiYvHGG4PALA9GwDDNpFZgaWDU3W5//kizapPL0yo1H2qfpmIcNAdIuwyQpZm6jRmWmw8WGXcG3H84gmC28u0ax5xZ0QwCmlMNpmcbeK3anz+k+v013u89PuvkfTGjJe3iUcRznSdy995jp/9+x8iAolf87nwjUsYjsm1H368MwISzfcIk5TRasCxU9NsrHWxTJ04TPDrHp2VDpW6j2FohJmBZduMhwFCKY5dOcngp0M0pWHbOpZULFy7y6nnz9KYaVJxXaRSGHFGqguyrCAOIqqNKkYuyYVCpar079AFojdGmDrVySZhEJI0fIwkxTZ0knGIlhaIOEe1q0hLB9eiUGB4ijSMKDSt9FewDLS1DknVoxRXe9RqPmMU49UySllum9hAstwhqrm4FRe/VUWrOGRxyjjLSNMMv+bhNHziJKVZ9UEqKlWfoQZGd4w5USW9v45ZFOjzE+gf3kXYFmiCrGZjmToqy8iWtxGTdbIwwjjeJlnYwKtXqdRdgixjEKdYtok5iJCORZLlFFGKJUDXBPp0E1kU4JnIMMZuVsm3ByQLWySrffpRhGubZFGKWfdIeiEqVWS6ThImVPMcpWuoiouMEuRGH83QkFKCbZIPQjANRmFM2h3hNaoM8oLw4QYzDQdVdSHJMEwDbaNPXuREC5s4c22C/hKju6v4zSr+dJPhWpfhJw/KUMLbfYzJFsUwRv7sBuapKaRSqFNTuBfmide6uPMtDMskWNzEzHJ010IfhMQf30ekOcZEaYYl0ox8rYNZ88hcDbPmEVOa8zmFJF/cIK176BWHYhggxzF63UeNQpSpk45DxhWbwtAwNMHy4hppkDDNMTRLJ4gGjH7+GfZOososl2SeidOsEAYxg80ueDbb69uMV7pUplsUng0FJFlKbzsgixJ022Lm9DxKSeLOkMal47x4aprx4maZr6fqYtZ97HYVdLEHph/l0SwjAcaDiCKXhJ1R6RMoyz3CqXvEo4h4FCKEwGvXGG/1ybMc43D0QwFOw6dxaoreB0PyOKU90yIcjdle7xAmKf3hmM5HNygMeP53vkF/o0+hNCqaYGqyjWaZhHFCrUhRg4CtUYZmGtQmmpx9+SIH8cLjKOPA8vu0rXOXVDwFNB5u/ag2vhCYPUma/HdBaA6cvF/bcCQz2/nxKXL2/fvcfgKyq/w5UlNyqOP7o1MdEJh+8Y0d5Da71hpfYUAOOLkfJfIXh6qrI47y1RnpPkHu02/z0Y9KSZAlBjrQRyE4UpVy5GWf4hz+NREL+NsIRXuoHAgFd5TK6wvm3GOLgXhU6StrCZ+0sOx7yLvZgqHMKPrhf/wpeqrQcnjvD99CBgkn37jEm//9r7N2Y4kf/b9+gECQFjmapjFV9Tl2fo7VhXXWVzexfZvOWpcbf/kRV373FY6/fJZb793EQJV2sr0x0TDAsE1OXz3D6t1lemvbvPeffs6Lv/sKs1dOoO3GFP8lH/jjt3301AoGYxY/ucelN55DKcXiL24RDANqEw3cZgWvWeH6L24wOz1BYZucfPY0AJqh742ZpmuYtoVuGGimjiVNdCGYnGoze36Ou5/exzINPNtisNIhz3LCrT5ZlOI3K2RBzOqtJU69eA4pJavXHtBsN0iznGAUUEiJ7TkYps2ZbzzDYLXDYK2DURQ4qShDceoas9MNhmnGzeVNLF3jxdk2QWdIc36Ce+/c5MU/eJOXfvMlHt5YIghjHNMsI/VM1Flb3CC+t0KeF8T/XvGtf/4dPM8hGIS4VunYOtWsUq963Ly1QBLFTLQbWEKjNdME5AFlmJKyDC23L4Hj7gMxHYvJY1MIIWjMtLBaPp2HW7z3n3/Bt/7Jt1GZRE8KbMemOd3kuTevsHT9If3eALtaKR2+o5S0KGifmuXSr72IYZt781opRV5kzD9zgtvv3CKPUvqFwjYMwsGYaBxw8eopTlycZ3triDAFlWaV2mQDFWesLW+ydHeFLIrpFTmTcxNMz7fZ2hig6RpLD9ZJkozhSpeVTx+AqSGQmBt9skFA68XTzL54hns//oz5s3N4vsPDjxcwdR2n6qMXBf1hRJbl1Bsex6+cpL/ZR2YFjXaNcXdIZ71LreKxtdEjQ1EUBQpF1bE48+pFVFywcHMRKSX9tS4f/vHPuPPeTV767VexbJtP/8NbuKfn0TQN19Cx8hwNhZCSAoVjmuBYWJ5VJiiTEtOxUWlGd7PHbL2CLBROWjrqKMrQs3ahkGEIQpDnBUUYYaY5quKSpCUBEUpQySKCrGA1y7CQ4JrEo4BUOhimhitAezhmXKtAHFOtesQqQQqBqvlULINoEOHXXIQSBKs9rAnwDJuiKtn8+D6VszPYrSpys495cgZ9oopMc4xxhHNhjmQYkt5cwvUd9JNTaEqgkpQiy9HaVSpSYdV9ws0+rmdjaFqZa6bmkm0PMV2TfBCQBwmGbYGUKEOUYaKhzByu69gK8maFOM0wHQOBotsZ0a67qCBBb1QRtoGMEnSlyNf6UHcQUuDUPAabPdIgxqz5yCCiUrEZhTFrny7QrFcZ+g5KKbwwwkpzwnduQsXFa9eo9hWyKIhMHd1zkFFCpuuQSTA0lKWj2TZynCJdg2hpGzXTRJOK+P4GqRDgWuRJhrIMtMkaxeYQpekUlgkjiBdXMZs19MkahgIMC8K0DHNcc6FiMb6+QOXqGdIwQ0NhtXzUZJ3Rg000pfBqFXzbIOyPkIXk3MVTDIdjIlNg+R62ZYJlIGSG7duIxCALYoTQMIVCxRlL1+5iORZCExhRThCEBOOQyWadl773Em67TrDZY7C6zbv/zz+jcXKa87/7DZpXT+yt/o+EbwdNkxVldMAsSsniDN3UQUE8inE1gVvxQZXx+03bpEjKfCm6EES9Mf5EbU9AtVt0U+f1f/XrdNd7fP7hzTLJ3Tii6ntcnJ8mzSWfP1xm7f4qv3Zmlt/7n/4FSx/fJ48yBhsDkmGILgS9VCeoulz59hXchk9jro3Xrj7uk/3o1viyaOnL4vQjYcdeJBWxI0HmyUDzKGJxANP+8lLxJxVxoD217xpfbmy+qMbujNrjCE/jB+rw18NgXezT8h/Eel+rP8gvWY6EkXvWIV+SYBxq4AtE6Xsl3uqy/db7HPtHf2/Hl/MpWPqLL3t0+ZqG+GtJondYO3Gg/BIC9v3nHjhd/CqNPaEv6vGflFQITXDvxx8TrA84OdnCKiQLQcTbf/Qzrr/1OcefP8X57zzLqZfP0b29SpJlyKI0YVBSUat4rEgQeU6j5nPn/dvMP3uK5rE2E7MtgvUuOhrrC2soS0MmKYPNHjPzU2xKhRxFfPhn7/F8nDH/4hl0c+dRia8+pI8raPa/zI9mkuO7nHmu9BMYr/VZ/OQ+aIIgiLjwrcuMNgeMBwHt4zWctl+C2B0VJlIidqTecZYSjgIaDQ93oomZK1aW1wnHAbOzk2gIdE1js9MnjFJOPXcGy7dJRxFTxyb56M/fZfLkFJNXT2DYJuO/GIKuIYucJC8wLRNdE2zeX+XUc2eZPjvLyqcLJP0hRZahuTY+Am+iTlBxWV3p0FvrIm9YtM7N0lvt8Pkfvo03UWfuxCSW7xKsdjB1jYmpOqapsb68BQXcuXaH2mSVc69f4kf/7ofEjsOZk7OILGO7PyQOAoo0Iw4jJuZbPPfb38B0So3G7v5SSImuaQdNgndWBW03GpoC3dB58Xsv8sEPPsC0ShfgLEnpLJR5Oqyqy/HjE2TDmOV7S8g4IcoyMgGO6yBsg/p861FsbgXDtS6drT43fvwpSZphejZFllOYJrW6x/lnj9Prjllf7fLgzvLe3DdMg/ljU4BAJDmNepXJ09MM1npYhWTq2ARBf4zvWFiGQZTkbC918Cd94u0hM80GRZbzzn96CwyNqbOzDHsj7l+7x8P7a1iUJhdhlCJR1CdqaEqSjELC/hCr4nPyyinWbj4kTVPS1GD29CxOzeejt64xNTfB5FSLGz/5jAc3Fpmdn2DcGRLJApkXrN5Y5Jv/8FvoQrC6vMncRBOrUQEJRqta5l5R4Pg2eS4xpEQFSal5KwqkodNqVsm2+mj9MWPdwG9WoB9g2DoySZGqJNY6ijSTWJ5DXNWQjoXZD8i2U1TFQ5kWGRnJcIQbxYwVVCQYvk2ykw9Ey3K0NKFi6CRJhl3x8fsjpG2Db5VLX5pDHlOZqFGdrJF1RmhhjGFbuJ6DHMdojQp2qwTweT+g2Owxunaf6guncb91iawzIssL8uUO/ssXUVlOvDUgNzR838GoexTDGLKMXElcUwddL31gCkkxDNFtE1H3ScKknLhxhqUURpYjC0Ghu4w7Y4zBgKIA3bbJNUFaSMQ4wq6VIaBlEINjors2AsjSAllIzCSD7RGkObrv0PBsBoaBsEzaCOIoxjg+RdQfEycpMkyo2SmabVGkBfQC8jxH1zSypW1030UNI3TPQUzUUcMQlSvy5Q5RZ4wxUUUJKDb7ZKVVGEbFQeU5WpSgRzHCNSlaNVytlPIjJSoHw7HwfJfk4SZpb4R1apI8d9DqPpahE3T6yCCiyAUqyZGaxmC9w/ZojKZr1GsV4ihhZrrNxmaXpEg5fuYYpm8z2OihopSq4zAexUCBVvVJs4zKdJ3+4iYTlRpnnjvH0o0FKjMNZs7Ns/TxXVZ++CFZlBAVOXGWU1/e4N6NRb79f/p9ps7NPlr5D0k7FexIRgWGbVCbrpOnGU7DK5+Na6OkIgsThKIMTGAZmLpGlkuKMGG4sk39xNQeENx13PVaFb733/8WP/u3f4NWKDQE/eGIM/4kxDkIQWuqienZeK0ajeOTABR5wbgzJB3HpElGc6aF2/D3C8t3rrOPJO3Hp4fh4E7Uk8M+mY8ol3gkSd8nyT2wj+4Hz/tARBkBk0NlX1tHlceOf0mUKL5c1f3Vn/zrweseHJcvizYPjf8OgDsqquX+AT2q/SdpOtQOeD+KSx593hHNHK7yRHT+5H7t4z1PuMjR5z/e4NPaebw4Ey2mv/t6eRV1xM3s79iujeC+KiXv/bshaF+L5uLA+ByheXhc0XTUK3+EeujAGOyeuQ+h7fPq2V3Anva8n6oO2t8FTRD1x9z+yeccm2yhdbu0NR3t5Cydzoit9S7LD1bprnZ58fdf46d31wjHEfMnZjl2bIJK3adIM1zHIokTdF2QDVI++a8f8sJvv8TEbJvN5W0MDWzHYfbCMT7dGrL+YAX7wklwLML+CC3L+fDP3ycahZz7ztVSgvS0RepXKCorE1w59QoUirs/v8GgM6Rd9+klGdPn51n/ZAGUIh8HYOulg96OtMIwDUCgOxYnXjzH4v0Veps9wrRgfXkdNI1YaDxMM3SrNJ3wfJf2XJvnfvtlNm4s8d6f/pzzO4Dn3T/6Gd/+l7/Og7dvEKUZQhZEO2PqTzWRaU5/ZZtP1rqceuYElZrH2kYHSxcUaU4oQR+EOI5BreFx65P7ZJ/coTZd57v/8jdY/tkN7n16n/6KzoXvPofhOzTadRZvPcSzDC5cOokCrn/+gIefPeTlv/cypy+f4u4n9wiTlAd3F8mznDPzMwy6fXzLpHVxHsMyKdKMu+9ep9KoMH/1zD6fl0NSjcMblICTL5xl6uwsTsVFaFrp85NL2jNtnIrDpz/6mO5aD8O1cesuo8UNNF1nOArI0mxPsq4UPLy+wI0ffIDIBYufPoACgiTh9DMn2V7r0h+M+fi9O9iaThKnqCiiWqviNStsbvTobfXJkoQ8L3jlD94AJVi+u4KjNGxymq06ySikNdtkZWmLex/cZeb8NL37K1S/+yKN+Rbx9ftMn5/n4j/4FqufLlKpeNhVj9sf3qWmCYRrceqlc9z54A6mrrNwaxm/WcOv+WzeXWHl4cZOPhLF6QvHsOo+SRDy8M4yoe0wWtmiWvWIgoRRf0ya5diuwcmrZ1i5scT0mVkMy0BmBcH2AL9VQ8Q5qaljjmMIYoTvINOsTCKm65huaRJkZTmalIhmHX0YEW8N0AytDDOq6yXYd20YR2i2RSI04iTFS3JM3yFKUlQh2QpiLEPDUwrTdqgLQVbkmFJQr3hESoIuQAhkIXHHEfl0i55jU4xj3O4IreZTCWKYaRIOAnqrXZpKYcoc2W4gxxEqTfG+cYF8cYt8vY+OhkoKjOk6RZiiT9ZxLxzD2OoTdkaorQHKNAANyzQRNQ+x0UOhyAWYUUJ2f6PMs4HC9GzsE1PkmkBlWZlZ3DSRCLLOEIFCmDqD++toQkeLU2QYok9OIXOJLsDyLMIgwbEMlK6hNX2yBxvY5+dKsoditLCJrkC4NirOMDQdrchJbAO9VUcYOggNt+JhhSnKsUiCGGHqyKKg6AwxHQuz4mImGbLiECuQ4xF+b4y0dSxdQ4YJ6Brp1rAk/3lBpBnIOEepmHgQYhcFFooiTsiyHGumCUlOsraNOTNJOgyxJuvYDY8iy6icPYbnmkTbI/Q4JQ0irFqNtDvCNHWsrCBPY4gztoZDJi6eIUwTGIwQpkE0DugPRrQMHdexGG91oaqYn2wTDkOGaUzz5BTRapd4FGK2m/izTZ6ZazJa6/Lxn/yM9Y1tJuamaNQ9nDAiVgJp2QRBwsYnCzg7jtOabexhvL1VSUqUKv3tNF1DtwyScYRh6QjNLJNy5gXZOMafbqDpGpoy8KdqdBbXydKcIs/xxhFWtQytvl9qPnlhnt/7n/45658u8sN/8wPatSof3V5EM3ROPnuW1/7Jd0rNmFAgSu2HbhrUZ5pHSckOfzjwm3i84qOy42MiDpuSfAkB5h7OOOzLuO9qZfPqcfBzlIZi7/hXlBx+OaXDXp+ffmB/t9Q+XvW3CESf1vRhyf4XmVV9FUAPHDafUvtI4pfXjqivetm9InbDEn+FZwggNA2rXf8CBcmhH47Ukvztl6/NLGqXLjySij+SA6i9T7vl8JFdevX4myWO+LT7Xe0cFjvsWO2ytscv9fSOK/Xo3ZaKcBgQdkYUmSLMJZFmYKQpumlyYrbJ7FSdhZUt7n1wh8nZNs//zsv8/D/8hPW1LVzXptcZ0uuPELDjOKvh6bBxb5U8eY7WmRmsT+6Dgoe3lzl29SRX3rjMpz+6xuriOqcunUKfn+T+9QWKOOXWz28ipeLC954tw/l9idv6MuUR1RIIXdvLCpmFCas3lgizjIrfwjNSqu0qd7b6pQ+IbbK11eOd//ATHF1j7oUzHHv29N4Le/LFM4xWO9y9dpdiHDE7P0V/u0/D98iUIgnTMqyj0Oitduhv9sHQkLLg2g8/5IXvv8RWp0c6DFl7uIFQCs0oJZ+WZTIx0aAxUafb2OL+jUUeXF/A9hwKQ0MBKQqUpEgSZJriuDZDQ6fZqJClZfhPq+1j2Tqz544TrvXIBWxu96hO1NA1jY2tHsLQOX7xGOMg4eaHd3nu+88zXOsyGofoholr2+i+BUMNKhbnXruELCRb95bJl7e59tb7uFWP6lQTzEemSvuJ976YdggEtu/shXMUUIZI1aCma/RXOsycnqUx3ebjH10jz3OUbxIPQhoTbfyqt4+wKFY/fkB/YYMzz51ntDVEqQLHMJiZn6BIcnpbfdJMgiE4eWqGlWWBY5jE45h61cd0TbRYEHs+EyenuP2T68g0R/dcRqMQkeXoUrG2tImQCsc2IEhpzU8yWN6kNdciDSP8ZoVKu8bcM/Pceus6D68vkqQp/e0cwzTwqy7nLp1g7f4aKstpTDbY3uyThTGObZGkGcfOH6NxYQ5NCOrtOtbyJlsb28yenuXUSxe49+5Nmr6LMgRbnT5u3SeXEs3Qef57L+APEjJdgzgtwaqmlVHLZIHQBEmSEdkavuWiFSDTDJlkpPUqeneE366RSkXhWSjLRAsTDE0gxyHCNAmUwogSKgjQNUxTp97w0Q2dpJCsL2/iJhnCd6mYBlvKoG6ZqKqDEcRIXSPvjxGeDb6LrgnqroVhmuhCo2jX0ObbiDTHzctxL2wT0zDIhIbrWGT9MYQJmmUAikIV6DMNJKCSgrwfojRBeHcdmUtyQ0PmOXlRYI1z4u4QVfORno1lWaiGj+oOMafr5P2QoD9GM43SnKXh43s2hSrD90rDIEei8hynN0b3LFKaOIZBYpRpzUJDI+0HGHUfXQFxRrYxQEmFDFJUXpAtbmFqGobvomwTTROoLMcuJFohGfTHuDUPS9OQgD1RR+qCQgjIJFqRY2mQBdEjAJnmYJuMkhQ9TBGNKkKGSNvEsgx036bojlFZhvBMNFnaiBe5IhpGmCrHnqhjeA5anhJFCWYBKohRjTIcNFGMpST5KMYwdcQgLMG571EocCfrjJa3Mes+1dxkOA6YnWpRm2pg+DZLnz5AJRlZljLa7JOHCXGaYbsuZ07P4Z2ZpX9nFX08Ypxl5EFMmmfEaQZScetvPmJ9bZsiS5mencCYapDlEr3VIB0FVJWAKOfjv3iHT//sLX7rf/yntJ89yeF9dRfv6qZeCiqkwq645EmKZuhEg7BMIKkUmqHtgXhdg8mzs5i2iW4ahN0xqpDY9UMaBlFGxZu5eoIL37rC+v1VXv+tF5k6N4+mYOOzh7SOT2H49iEgflhKqQ5BhiPEhkcCUvHofMVjeOXgdRRHxT7dlcgrqYgHIVmckCYpjudgORZmxUGhPbrn3bZ22zmsAtkjOIcErAdyUnHwM0d8PnjBQ8eP+uHxY7sh03edjZ8MRL+4xlN9OB4183dbDpPHff4TR3VFPSl322MV91/jqLr7WchRbPSoMw4L1Pdf4kuwkr8rFvGE8jUk0TuaFn2ZVDGPhuerz7BHmSbFkyLRHujPkeq5vTri0aoqBNHWkN7yNudeu8jtn99k0rGIdYtaxSNXZV6E6dk2RZrz4Q8+4PIbl3nm5Yvc/uA2m4srjKMMQxMIQ6NiGnhhhLIttjtDugtbnPu1Z+kubPD5L25iScXKp4tc/b2X6ax0WLq7zP3P73P+6llOPXOClYU1RCb57G8+RhaSZ379eXRLf9Tv/ff8Vdnznr4H0LS9doo8R3gmsxeOYVgmtnTQdA2Zl4Sg0DR0pVi5+ZA8Ttnc6IEQTJycQtM13KkmL/93v87MuXk++euP6I8C2tNthmHM8WMzxHlGnhRsd3sICQ8/X+DZ71zlt/7Pf5/3/+NPmb10nAuzz9G9uVKGxiwKhlkKMkcpg+H2gErFY+L0DKbvcPeTe8RFRpykJFIyVfWxTZNYgNI0XMvA8CwMy0Ri8M5//Ckv/d5rvDjX4v0//Tm26RCECRhlzgy/XWP5wTqnT8zSG4W0T0yiGwbv/MnPiaKEerOK5zo889I5Vq8vYgmoH2tTaVZZvbvIjb98j5lMYMQFb/3Pf8Kzb77C6d98+fFFZ3dzE+xJ0A4vPbppcPrVC9z/xU3G1+6WIWW7Y0zLJB0nPPtrz9F9uMXGyhbWDqgkL0jjjNU7ywjDZOb8MUzP4e4n95lo16jOtmhGKb3tPo2qz/Z2n3FRYFU94mGCQtFoVtA9m5VBCEnO5r01kiAmHIdkRYGQgmbNx6k4bKxskaUZloKelMycn0EJQW+9y+lnz5Vx8jWB5lhoFRt/sgp5jlQKx7G4/tZnmLpBGMXUGhV026RS9RgWOc12jc5qj7lLxzE8mzzJWF/eRDcMkkLS2+4T/vAaw+GYNEm4cOUMjXaV3maPq997gcpEnWi5g5mV0iItySjSHEMYaFWH3iDAloooSdmK0tJPwXEpTJ3Mt8nTHN800JIcu11FswzSOEUJMHSNQpkUWYEnJZqmQ8VFGhpZd4Btm4jNHvZEnbHnUGgjTMskySV1x8LzHMIkQ+k6WaOKvrCOpRRSNylyiRyNkY4Lvk3eGaJVXBzXxinKQAOqVUUfRVQtA3uuhWFoDP7qGs58G+HaaHlOvrqN0WqQD2PiW0t4L5zFnm0R9EMoJKZnIaKEPMvQbIt8EKC368gsI9UEWtVDLG8jRxEoid6soQFSiDJbtWUhc4nhWgQLG2iOhWWaqO4Qr+ISWw5pkJInBdZEBZo+eZigql4p3OgFZBRocUKhoIizMllfmpXZxB2DQpUZxPVxjFUTGGGMqHul6VYYo2UZumlCvUKIjpVn6GGCnqREQYRT93GUophqITsjHBRa1UXPClSUlCDZ1LEvn0QfBIyEIh1FuFmOZhoQpagwpvHy+XKr+MUtdNMkDsLyHR2ExKaO0/BBKOQwQqx0CKMYLBO97ZOsD0h6YwoBg2HA7IVT9La6pYBgWPoAHTs1R6Ik60sb2L6NVnFI17sMOwPCLGflwSpmqwrjkPp0E0PTyOKcrU8W2Oj0yNKUuRMzjHSFGoc0alXqms6m4zAcjqhrgtvr25yYnyLaGvLx//pXtE7NYpsGeZxheDYTL5wumcLuXpBmKClJBgGGa6OUIh7F1GYaj4CyAM210Z2EYKOH266B0BksbcNKh9rxSZyadwArm67Na//iuxRpgWbqCK3MdeJP1jE88yhZ4oF183GMdhhsHVbJPKne/uP7q+wDDrvfd6TbRZqz/tki3cVNgo0BKQWzl06w8tkCbpTTemae+W8+g9uqooAwDHFdt8Qg2qGbUfsGca/n+9jY7k8HiMVXFHezD94cxUwOJ3zb9//JYWv3Y7f99/OUThxFjg70phzr/VnFn9rYAdyzn7l98diIx+bPQU656zfz6P7VI22BOmhOt//8J86ux4d6TzD+y/Grp9zjV58efyvla8vQffhZPWmA95Pyp7f69NF5jCiog78ePHxYynHE5Xb+53HK53/xPvE44eV/9m3uf77Ag6VthGlwb2WTLMtwTRPPd2jVfCLH4vZ7t3EcmzhKcAxBKiUIHa1QuKZBbDuMOgM0TWC6Jmmacfabz7B8fYkoiFi8vcT81ROce+0iW2tdbENjZXGd05dOMnN8mnu3HlKxTG68dR2ZFZz/3lWcmvf4gB8atqPkNkd/33mRshxh6Oi2yYu/+w2klLhVr7QJNw2kUhQapHFSRjia0jFdm2wQ8tP/+QdgmygUzZkWx66c4Pxrz9A4N8vCz27w4NpdEILVtS1MBJppYGg6ZsVm4uQUbt1nuNHDa1X54f/yA/7e//UfsXV/nVFngOXZ6JmkVq2RZhmbC2uMRyGu7xKNQgzLBB2KKCrDyIYR0lEI0yTNElzLoD3TYLA95OIbl+isdnn3D9/ipT94g9aZORY+fUDQD1Ao4nrMM+0GlYrHcBjQbtWI1vu4zQqmEFi2RZYkDHo9th9uIZWiMt1k5tJx7v/4E5ShmPeqZA/WcQ2N+UYD0ywj4uh7ER52R/2R1OTRXigQ+yIVCE3jym+8hF6xefDTG6x8cg+3VimTZSnFxsNtXvx7rxD/8dtYuwmsDJ0iixj2x1Rdjxvv36LRrnHxtWdwKi4b99e5f2MJ23NZ3+piWya12RbjWyGObRGnKaPBiKI7RBUSTQhuvHWd57/zLHFnyNpah0a9gqRM9Hb69Dy6azLoDmjNtBC2oL/SwctzjKrNwmf3OfncGSqtGi//3jeI+gEbCxvcv3aXZqPKyucLjLaGaJbJi7//Gus3lhh3hkwfn6ZS99ha66E0iMYhDz9ZYGN1mzROMXWdLMkIggjPsVECHi6sM3N6ChnHaKaOYRsEnSGa1NBsC2kaCKVQWUZumRjNClohaXpNtDTBcywIEpRuIMOUimNhNKrkWU7WHaGSFN2xy4R5aY7aCRes5RlFxUPPc8ZJgR6n5OtdsizHeLiJnUsiTWMUJtRMAy0rKKIEpRS6BrbpYEy3MCQESpH3x+iGgWeb2K5BEmfoWYHUUnQd0iDBSBx0yyALY8SNh9inZ/CfPYMQgmiji7y7ivvKBeQoRnQG2JO1UjpvGihLp+iOEKGJ0A3cs1NkWwOqzRrpMEAYAnMUExgGVD0MKP1kwhi36uKaBrrtkPfG6LaFjDMq8+3SD0NBohSkOUmWUwVSpVBxQUqIJspn6fk2eQjCsMg7Q4RlogHCMNCFoEgzdNvErLiomkfRHUOUgdAwnDJkdF4oCtfGyAtkf4zh2SSOiWfnZJaBHCqyOCPpDogbVTJTx7FN6pqOpoOhG4ggwZppkK31QYBrGmRClhnkdYgqPnoQosYx1lyb6gvn6P3X95BJgk2p/TLTnKI7IlzZRrctNN+nKAqSRJFcX0I4Nna7Rr7Rw1SSybkJsiTd0QTauK0qW/0huQ5OzSUKI8Iwxp9u0k9TwuURhqljJgVzszOkowBh22wmKTfvLSI1QePYBCNNoesaeawwdIPVNEbaGtXjM3Rv3Me3LC698RwP3vmc65/cxrZtXMvCEBquafKK+E2mXjkPlME5sMrQ14ZlsvnJAlbVZbTVRxQFtWMTpKMQtbNvjjYH1Go2uqmj2wZaq0pvaYvg+hITZ2eo7uRv2lXYCl3DcDV2bUN0W0e3q3t1nrRvHdD47n0+vOGpA9jkIEIvv+8TrR2o+ejgftCgkGnOxo0lHrx/G6soiMYRg1GKbmpkvTFbC+tE/REnNrdZ/uQ+L//vvo9ZdVl45zOMXMObbRL2xsxeOYE7Waf/cJPtnehdZ1+5gNOsoO0kqRWHB+CQluZg+TJ4ST255g4we2Rq84gFlN+POutJgtojurZ7XIESTzZNf/QovyzcVo/+Pen2j/rtCYBeHFFB2wnPvpcTZY/cHV2e1A1xmFXsXudpyp1donX4HnaFkmpfu09o/v+fJONrydB91OdHR/YBpacA38fOU/s/HvEwv4icfIX5ud9fI9gaEPdCup0hg5UO3/yn36a/sIndqLB07R6DlS5plBKMAh4ONrBti4ptkWUZdb+MCT9b9ZmYa1MoxfrDdTY2uuimwdTsBBOnZ/DrPiLOMRWMC4lIUtY+f8iz/+ibXHjhLAufL5IGIQt3ljl3+RRV18HKUqICPv7RJ/TXe7zwD75Bdab5+Fjsm1BfSaEhQOxEBRkud/jRv/4LskIye3aOcBDw6//D30MzdYq8wNR1XNdhotkgU5L+YIBnmYzzHNM06DzcZLCyzeK7t7n06y9y5Z+8wezzp7n+k08JuqNScmkbNBo+eZLS9G02P1ugNtemNlUnf/82t9++zvxzJ1m9u0R/e8iFFy7g1ysoAUkYs3J3hdFghO849MMheVFQCA3dgCDLsbQMy9AxLZM4y3BtF/PUNPc+vMvpy6cZrXYp+hFnX73A5W9dRSY5WZZTjGPCzojzz5zgzs2HfPzZHRzLYmKqycREg3EQ4lkWulKMlzbRqh6XfutVmtNN3vp//wV+NOT41CSaY5HqMHHhOFNvPluGpt3/MPYvKrsbpdrZdA9IscpN+JlvXmH25Cx//H/7dwihsHyHcDhmc3GDNMk49cw8tenm3gUM06BRr9HZ7BGnOePuiOn5CWZev8ztd28jpCSNYihynv3OS0ydnmH1+kNGo4BavYJhW4x3IrR4VZdkELL4wR2eefMK81sD7n54ByLFYBgyNAYcOzHL7IlphGcxeXGOs9+6im5oGK6N8+Edkt4Ic7oFCNxGhVPP+5y4egpN13jmu89x/71b2L7LzOXjpFHM4OEW86dnWLi9jG7o/M3/568w7RK4mIbB6UvzRFlKf6ODIwxM1yIeR0yen+bFf/gG4+0h9eny/ShQ5ElGJhV5ltNoVpFpSpHkOIYOukYWpzQsCyuVZKaBkKWzrpKSSKrSXt41iccRucjQkpDCtRFpgZSSNM8J+yMaFQ9TF6i8oCgkhVJYeU7muVhJiu45xGmKjoalaziaIHAsks6AWrs0yasECWkBmqnDKEQKH8s0yKMMIRWaBC3OyVa2kVONMpeFVOQPttBaPhQSEaVYx6dBE8j+GG2yAXUHzTHJ+mP84xNEi5sIy0LTNIowRYsz8qxADcakjoWh6dhJVpIppdAKSaIJrDhHFhH4Frquk0dJmSfFtXHqPnKcoCRoqUSPUgxDR4tiCpmDViVOM4SpY7kOjCN03wHfZrzaQWpgZDma6SB2slCrMEGi0LICvRsgJqqILEfoGsUoQk90sAysqkfuWJgNjzwrn4kz1UArJNpgTLVRKSPvSYUUAsPQy6hWWY6+OSCLE4RSWIBVqzAuJDLNMafbFKOQ5OYS4YMNQFGMYjRZRkWj5qE7NkXaIzcE2doW1XqGyjMM0wQbzKZP/HCbrChwGjUWPrlLkeW4J6dJwgSlCdx2hSROybpj6o06RZgRrHWpz7epVz3asxPUWnVEltN59xaFqdGYn0R0RmRpThQkWFUXUUiaFBSjIZbnkqAwXZtEM2jV64yWtrnz2T2kVIzSlP6OUMaxLY7dXWbqlfOPQqDv7Ce6qWNWXTY/uY80zTJS1Xqfzsf3qJ2YQBom1ck6ml7uoW6rSprkFEGC7lhs31oGAdXJ+uP70R6AOmKn2pHu7t/eDp6ndgDrwZ1O7ftQrqlHILQD5xwFGPaJ3wrFyo8/48bbN0hkTs23CdKcZrXCdn/A7Q9ukYcptWYdb7ZFZ2vInT/+BULTWVpcxXNdKp7DMMtY/OAux589xfjhFsZsg9pUk5t/+DZ2xSE1NE6+ep7Wufldl5ODBEo96rfiCJOdJ236e47IR2Ojx4nFvs+/Ckg93NxTFUf7SNURGp3y8I5A7imS0z1rgKM6ovZ15Avua7+m7Wmy6cdP3Gn4yOR3h8b/ECHef2A3GtThd2DvRLFvjL6EomfvEl/qHr5kvaeUX93n4gmTeR/35cv29EljfmRSl0N11eGjT7ns/kzVe3IJBTIvuPYnPycZxiRJytqnizR/60Vuvnedy7/1Mi/+8zcxNJ3x1oDunRX6az3W7q0Q9AIKqZBphm0ZREFIf9ugPt3g9X/2XdI4RQDVmSbeZI1ge4huaPjNCr1xSKtZY3O1Q9Qbc+LlcwyWO6yOQqLBmMXbyyRJimMbyFzimwYPri+QpBlv/re/hlP3vnB4n/bzAQXfzgen5pU26VGKSHP6q10G6z1OvnSWOx/eRgFSKaYuHefO+7eYmZ+hfmyC/naf4WYPU2iM+iPyKOXH/8sP+P3/8Q+Yfu4kU1dPILOcLEpBCOJhyHC9R39zyGCrzzjOOP3aZcajkLXrC4y7A2TVRu/rmKZBpeHjTNZJByGWbXHrw9soq0CmOTPHZwj6Y8ZJRJEXDNMUTynqEw3GaQqjCAs48dxp7n+6wMbaFmeTFG0z5a0/fw/T88A2mJif4OxzZ2icnmLquZM8+OQBDz5foN8bIoRiYrKFpcC0XcZZzvGqR3umhWaZdHp9bF2hz7SJ+gMMXWd4c4n665fwJuscLY7anatix47ysQeEUgKh66UzcZQQaQaqKHMPKCBPMs59/0UMuzSLyrOCu+/fLpOp6RrNWpkbobPWpYgzdNPA0HVG45h6tconP/wY+TfXQEnmpppsbfdw/QonLh5j9tJxPvvxJ6gdh+jxw1XyIMRxdCbPHuPGe7doTjYZjsb0On021zu8Xv025791md2oHqd3fFH2AiqoMtqM6Za5ONyGz+XfeKm8XQHzz51m7fpDPn77M5IoJYlTHMPEq1cwLZN6s8rW8iZJFFNIhdeokkQpTt1ne7VD3A/JVLE3frquoTRVmipWXTIEBQIxGCOqPrqp41kmaVaAlJg1DyNKkVlBmmUkloEERJyC75RrWpZjJAnKd7FQxIWJCmKinWzJppIoz6GS5mXSSAEj28JwbeIwJipSfF1D1DzMOCVJC7IkR7NM9LqHHASkSU7NMcmQiFQSJhmmayI8C2NzJ4/OMEI5kvpsi2wcko1jVJwhZKnJYx1wLIogQrON0rchzMCysKZbECTIYYhZcZGeXUYBygr0zU2EZWLUSkdlo1GhGEV4pkkaxYRjRUWrYiiFluQUhobQBMUwIrm/Tj4IUHmZMFMiyITCbPjonSGZb2NFWWlGputoUUohNEAgdR2paRRFgaCMKFSkGWbDBwkqyTDygjiMsWcbhHfXSCJZhorVNFIU+oMhtufitaroZ2dIPl/BrVdJkhw0DV0XZX6OrECreUhTQwRJaTIXRORNH10qLNcmTzOKrQ5FlJJt9NByCfUKRs1DSEm+tIU4NY0+00K4FtblY4T310mHKVRszP4INVFFxBmqkBRBjGh4tM7OsHF3FdMw6a53mHA0PN2gM4ywLQsjyzl5Zp5kHLHV6SFqBqofUgiNrbVt+kmE3q7g9SLa8zM4vsM4Sbh+8z61qk9smCV5dV3SIGDUGzBxfJLt5W3u3nvI5MwEjWqFURSTjUOWt7ukWU5/o7cjUD0EWAW0zsyUJKYzBqFhV13cmSbNZ04Q9QPsiovhmFSPg6YLiqygfnyCqD8mixIEUGT5o8iHh9a5LzqmDv+2C0iPOPXoZtSBf+LQzqgO/b6/rH14l8/e+pyq62EoySiOKZIMxxfoUiGFxkSjTmAoulnOOIhhrUcmFNLQ8DyHSr3CaDBEaIKtO+uEW32S9W2OnT9OPI7prvcwKjafr3Q589JZZr99BX0nIuP+u9kVhpZC/iNE34KjzZl2CZyAx+x01D6znyOK2qlzoM09UxTxRSDj0cfDptxHXujRSbuKgsfMmL4IUu5ur0fez9EnH8SUO8SVR/Pki/D54dnEgfF8IhjlEVF42uAfLIfJ9FM7tvvb37EW428tz8VjYP/I38siDv1/7MsBAvPYFHjqdR4nGbsh6HZ/3umpgP7SFt27GyA0CqlIoxTLdwiCmJs/+hhh6Uy0WwyXSzvSyZfOcKZ4ET2TbN9YYfHj+yzfWy1VaXLA1soWK7eWOPviObyJKlv319he3KS/1Wf25AyWbVLkOZoQhMOAwUqH4y+fxfcdChSuprG1vo2pa4SGThAnNGsVZidqDLpjRhv9klw8bXAfG9gjqh6q7zR8Tp87zrV3P2e0XUaBufGjT/j2//BbPP8bL/HhD96lkJJcSc6/eYWf/vFPqa1uMn1sklPPnmH+udNsLqyjpGT2wjEc36FIczRDJ4tTnEYFUDg1j9pME0S5EeVpTtQbcfU3Xubim8+yfn2RlbsrxJ7J6v0V3JqH6dtomsB2bZCKaBQxeXqOU8+coEgyPvvFdfAFwjLJw5jxKCgTXY0iNMMg6QW0jk0QDcd0763xwj98nZVbK2zcWkHYJkujh2zfXaE6Uac+3WTm4jFOXD3JeGtEsNWniDKGnT5+1SeNEhbWNji+vMHJiyd5+bdexby+gH5/nQogPQfDd8mSdGcd3r9KioOr1f5Feh/JUAoGG10qrRrbyx0s3wNNYGmCOJMYjsVnP/yY+Ssn9p5jf6XDe3/ycwwhwBCEUYJtlyEzdUPDsU22s5RGu87zb17l4e0l7n72gOmpJvPPHMd+6LCx0SMYjpFZzvkXz/P+D97Dbvtsd8bYjRpzlyfprneZPTeHVArLNTE0nXPfusSxZ0+Xb1ZekA5C0kFA99YyjTOzWI0K/dVtPv3xNS7/5kscu3q6nKJ7c1Rguhbf+Fe/xnCzTzyKuPZXH7B5bw2lJP31bfpr27iew8zZOabPznL97Ztl9DHHIM8l2wubPP/3X91zTHQcG7sogaWyLKIsx3EsxESdwtAxNK2UsApVZq7OCvJCEmcZoyTFM3VGgzHZTshN4hRcizgrMCyTdKtH6FjYNZdwLSSPUypAEqc0BRSGATLBsy3MOEGaBg0pEc0abPeQYYzv2OhxRloUCMPDExLRrpZmR0IgKja2a6KNE7AM1NwEQtcR3WHpeN4ZlJmkN3tono3eriGAfBggPBuz3tyThGq2gdA1NCHIlUIUBcUwINNAxim50GGiiSEoJfkSckMnMw0MwNQEhmWh8pwiTtCbNYpRzGhpC69dId8elIRuB4zkeYHKM7SJKtlyDyfNQUoSIlzTQrMMiv4YK4wZKXD0MkytbpZ5KZQAmWQIQ6AKjWxrSHGyTWWyVibgEwKtkMTbQ7TcL/NFZBlKgjtZQz9fMByFqGGI3MmlU7gmVc8tQ4cnaRkSN5Nojo0KSv8PDYk11USMxuhTJllvAJ6DW3Fw6x75WheRp+QKos4IJQvcOIU4Iy8KbMtB+Q5avUKxPUb2RmhSogcRA5WhWwb9zS6u76IcC+PYBFlnxKDXozZRx6m4FGGCXfWIleTerQeYEmJZIBoujSCjWq8y8c0LxCsdgptdqo0qVs2nu7xZ+hMNI5I8x/FdEiGYPDGF5jkUWU4oC9xGk4ltRTdwcWwTr10rlyGxD7bv/NNMjelLxxgsd8izAjTBxJWTaLpGoSSWb5emVAJULjE9G5PSzGs3QWsWJYDYiXz49HJUHitVyD2hxf6KjxQfB8HrgfDfB1s6Qi66X6r8CHRnw4DNa/eZmmww7I2pNWuM18rIdJoukElGLqAyPUG43SMtQqqGySCOEY6Or1tMTDdKrdlWTqgykmFAEiXkMmfrzhJZlFOYOgSStu3y4Ief0RsEXPztV7B8+8ANiP19FepIrcORW77gsXveE7R+QYQkcWAwdw+KQxX2laeB2afAtcNRnA7d1gE490QlzeFPSvFVrV/2199/K0/lNEfc864Z1dNHdweDqsefxdfKB75KaKqvpKo5uvzq5OKXvPsvdZo69HF3Bdknan/i/R+Ygfum4Y4JymPcRcH6pws4lkVnMEIDkmGAUopX/uEbtI5NMl7c5sYv3uP2+7fIipzJE9PMnp3j2PNnmH/tPMffeIaVj+5x8yefsbGwTsV3kEnGnZ9fJ4oTPN8rVflRwt3PHqCUwq9XkDv9K00MUjIpMXQdTSvNMY6fmMV3bZY2OmiUYQKVko+41hcN5heRjX1SIFDolsH57z3Lw+sP2FrvMNtucPfT+5x+7w4XvnOVu+/fRAnBw9sPufL9F3j+ey+ydX2J3vI23dUOD64vMnN+jpnzczg1r4y8Ukg0XSeNM5y6osgK7r99g49/+gkTc21e+J1X8Wo+RSGJRxGViRoXvv8Cp9+4zMadFW78+Tt89vNPOfHMKUzXYjQMyZREahqmaSCT0l9ESYnKClrz00TdEclgSKXq4VU9lFKoQUzleJM0SvEmajy4vkB3tceZS6e5d+MBzckm1brH0r0NHt5eJQwihCF4+ddfonl6muXri1R8F6YoQR8Kz7ZZ/MsPqbo2yXOnGH94n3arSZoXVF88g1P3SYbhDhE8RCwOjP/hUmozahMNKApUVuA5DkKB47lEWYZjmqi0IBlHmE6ZG2PQGzAeBli2gaUEz3zzPN3NLmGYEI9jxsMxRVZgWxZZkjFzaoaHt5cJRxHL79/GaFQpspzleyvMPHOc9TsryCJHGbB4exWsbSzHIo0ThFZmGrY9m+ZcC8O3S9maLNj+bJGt64s4TmniEm8NKNKczu1VTr9wnumzc4fmqSIJIuyKi27pNHZydsxcnGft9hKLnzzAUoLl64ucee0S85dPcvtHn5Yhk32HYBQgXIe7n97jym+9iOlaZSQiqdBcG6EJ0iQrc3l4dkn6sJFJQmHo2EojFxItzRCiNC2r6IJCF+gIZJCQWxZSgR5EJKMAR0mKNCMLI4RjkwzGGIZOCDheBUNKiihBNwyUSomkwkNhTDYRtolx8TjZ0iaZ52BqGkVvBECiG1ijECyDPIiRYYQ2UcfwHZI0x3ItzEKRCg1l62TdERg6esXGnGuT9UbItEDGKTIvSIXAmqxiV13kcgRZvuObk2M2KqhxXGoVKy7SyFCizNCsWQZpb0DY66NsB10ITFE6+oKDDCPMyQZkGfpmnygoNYe6riEqDlKBaWgUsnSmpzvCmGkiXBPD1JFoCH0nfHJSYMkCu+qDJ0vH8bRAaRq5VGhxijBNit4YzTcxXjyL6ZiorEC3dESck3WGJJZOVHdhtcDeHuGemmLwySLYJlqUkbs6qjNE6gZG1UNognwQonQdDYkmgbzAvHqa+NYqpqaDAaEE+/wsw4VN7ChDTxIM20aYOramIU9MY9R8VBTDYEScjHBPzjMME7L+iCLN0bUycpZhOci8jAilS8nKg1Ume0Mmzs4SX0/orncYbPaQukBaBirOcD2vvFckWSZBg3EQ0bu1yubiBtvdHjgG4dImcRBRjCPiYoTu2MS9AKWgL8pAI7ZjUbF0nKkJNsJyrE++dIHn/tGbCG2f0G4/gJSKPM6oH59AScVgrYdTddB2zE9VUYBRkgZhHEyiJzRR+pwJG5kVFEqWvnJPWvqOKPEwoAgTdFFmRtf38iyVC+hjkven7YtPEiQrBbL8K8KELEyIVrsIoaEDozCiapqIOENoiuHWgCRJ0S0T3dAJRgGOadJoNehsbeMaNtWKh+toJLkiT3IyQxFFCdNTLda2tzENQWhpGFWXpDfGq9VZ7Q1Jri8x8+xJJi8cOwQM94ludzBRee+7mhfxOBHYHZzDeGiPpDxlrH4ZjPdF7T3poT+RkBwkV0cpMR479Sh2+kuWI1vah0P3NEJfsb0D0/VvWbOwO2u+dN6SX7E/X4NZ1K5K5+so+11cn9zmYV53kGMeqqQOnnHwt0eVZJ6zeWOJRtVjdXMbTdc59vwZjIrDiefP0ruzxs/+7d8wHgYUQKHg4d01lu+u8eFffUi9XeOZ7zzLuW9dYfrKCe786FOWrt2nv9VHKImuleFecxRS15ioe+hJjJioMdjo055s0jjeZrzRp7/Vx0xiWiLHmpml0qiQ5wVpllOzLHqDEVbFRf0ys/FLnuJP12nPT9LtDYmyDN+x+fyvr9E4Psk3/8l3+fA//4Isy/nsrz/Ccmwa822KKEMDxp0hS+/dZvWDu+iuTa6B5hocv3SSxkyTYBjQX9zig//tZ2yPA+TWkB8vbfLSG88y88YlNNNg/fNFOksbnHz9MvNXTjJ9fp4H1+5y7/3bhHeGFFmBVkgKNNYW1hh1BqU2Jc+RotyIhCiTy8lxjGvqZL5DPhiT2Dqv/eM3OfH8Ge6+f5ve/TXSQYDQNPpbfcZRzPHzs6wvbYEAr+EBgs9+8in95W2UITh+eo60HyAcg8axCTwFds0n1mF1pcuyplE4Gl7TQ99xjLz7znWmTs9Qm2lxIKLBrvpWcXDqi3KOCgFKCBrHJwmyDJXmpEqRZAV2VpCkKe/+xbt8/1/9BkII4jBG1wSmbaHSgt5mj+ZMi87H99EMHde28R2L8TjkxrXbzJ+eI0syXAcIYgLDxHAdmpMN7r1/l6A7pDXdolJx6VsBlmUye2yKzdVtwv4IHJuZuUnufXafjU8fcObZ01Tm2xSDMdtrPeZePIvn2ug1F73iUpmuo9c9TMdme3EDWSgmT02Th8ke4EDB6s0lvFaV5nSTuUsnmXvmBHmSc+F7z5FFKR/88TsE2yPqVZ9REFKgGA+GnD87XforUIIaKYC0KGP0xyV5zzwLyzDJhSAzdJQuiIMEghit4pGogkwIHNOg2xthWRZxb0yWjXDqVXQBumOX0aXihKZnE45D3JqHN9kETSPZ6CKqLp5UhEJgGzqRYWAIgTUKkEKRxzHpKMLRtJJsTDVLnwDXRpOlZkpqgjwtSPsRqRHjeXZpHpdkKKHKRH+WRaHrOP3w/8fcfz5ZlqTpndjP3Y+8Om5olVpWVVe1FtM9M42ZgZgZGBcEsaTRlrZLcmH8RBqN/wi/0IwfaDSSS8DIXRIwiIUagdEzrburulTqzNDy6qPPcXd+OJGZEVlZ1d2DxoJulhkR5x51/fhxf8XzPg9FvEcVeCBBhD6eqyjTgvThEfLGMjYtKLJaZE4FLtrU0DFXOmgpKJXEaI3INOnpGMoKT0o81+L6Eh14yEmMzAp0GIKA9MEeojLIJMdvh6AkuqgweUGlFCr0qI6mlNpg4xRhfGSSIOZ6aN8hOTOGm56LLSuqrIDKYJRElhU0fHKnrgFBStLDCZU2qOUu5eNDKt9FKok1IMqS0gRIaxh/7wHVtVVmcUpQaPxem6DSnGYFVctBzhJMI0A6DpUEM5hRuR5OVpB9sIUtNVVW4TU8/Lk2vutxeDxENho1fbYtMcMJzRuXyI+HqEsLOC2PaC/C6c4T3tyg3DrB77aorCA5mWCVIJ/EXL57tQ5iJXnNemUsyemU5WurCMchmkVEx2MWwh5rb1/G77fJj8Y8eu8h1nc5zRKW57o8e7SN1wiRDZ/odEKZFbz19k1aiz1QgizJUWfvQXw8Jp7EDEcRxycD4lzTX+rzta/e4frf/SoqcC8uBBcw/rUTqPNatbu73EPrWvhQuc4LWN8L8kVrau2Ys9MIQCpV159Z+0IQ7Wc2a2uHJM5RjgJbMzYp372wpFlqC0LwSkH0i2COfbnjKzaGtRadl5R5yQf/9C9o4jDeOUYLQZwVdJf76LIg1xVJVV/bsYZJklJVVS0mmGQYQR30MoYiK8AaSscjzzTDKCevSqxU9LstpDW0Og3UwhwLnks8njEtSvZORnjNAJFX6MMx9uY6GIvF1FHt1zgOFwt/La/Cpeokx6texHMK/vM9+Jrn8SkR+VezCp+Ao/wCCIqXu/z1LfRXL//qtv+o7TMctNcldT5x2IXjf4EMw89zwRebX89y9R+r/RJgUf9hN/uZR58bva/OFS8PPu+JXezV54U9Fy70/Jz2XN7DQj5NSE/GLJUJy70OB6Mpz95/SmtjnsWba4weH5Aneb2Aex79XpuwGZDGGbMoZngy5S//yZ/z+AcP+PLf/Tp3fuvz3P6Nd5gdjogOhqRJTnw0IRtGRElKNhjSLmLybA5tLOt3Nwm6DT7+Nz9iMo7oSkFRagZHQ0YnI7AggbFImeUFd29u0F3r87qJ5Gd2+M/zkjuSu99+h3Qw5WQ0ZXG+x+HRgO//4z/ii/+Tb/Kr/8VvcPRwnwff/Zj4aETlOPgNH4Og1QiZzWKGaUorD9lcXcItNNGPnrI1fo9Gu4kBHNdlrt2qo0TjlP0fPCI/GBNcX6W93IP5OX7y//1z+it9OosdNt+4zI2v3GE2mHL8eJ/3//X3CVtNyqxgMpkhqSdZv+EzncxqldmipqkcaY0vJVZJgqxiuj/kqBVy62t3GD09Yu+HD2kv95FKcTocs5+WrN/agO1Dmt0mVhvW1hZxZxlZUXJ0cEo/COiudJlbX6Ca76I8h7/4P/53zIYjVAbtTpvhzgDh+4wOB7iBi98Kf47Of9XxqMerKTVB4KOVwyxNa+O4LAl9l9HjQ8q8xAs9qrRgrtum3e+S5yVbTw5o9losL/WwQGUMeVHxxjdvMzkZs3N/l6AZ0i4S5nTKOFgABMk0QRclwnMIe01GwwipauiRVZL5jQVUmmKt5vHHWzXsLCvYurdLbzDlrb/1JaKkYrR9gn9thcnWEeFij8Z8l6osKeKMR9+7h9Pw6XQazMZTFq9vvAiwLV5eJs+LF91gjOXB9z7Gd1ze+70fMRnMaPkOK67lUVEyvzzHt377S6ze2azpRc8WOKM1prSIwKt1JAZT4pMJCNBZgddpYMsSKSSVgSrL0a7CCz30JMZrhqAtuh1Q5Yr+chdvGpMZl2lRkhoDkwgpJVOtaTkSmVeMpaiLpS24zQBlLW0LVkl0biCvhfus65JOUpyWIawspbWoho9oBdgsRYc+qkyQSYZYnoPAI5slWN/FrSydfo8iyXCMRoYeOA5FUSE6IRiL8ly8dlAXn59MqbaOCG+uYVuNuq5qllEoidSghKSIUhqhR5blaCnprsyjyxKTlWgNpCVus1nT1wYeJivQlQYhcEQNB/PW+ojBDEndB7bQYEtkw0ePYpQAGrU6uk5ySHI8KUEbSHKs0SgDnhQ1I5cA6Tr1XF9pfK0pDkc072wwuL+PykpKC8JzCEqofI8szQi1pjqd0Qs8pKiwZUWZF/T6PQqjyasKphHGc7Ghh19ZVJWjVucxGGxRYIuSrMzxUFTv79DtdimaAU6aolwHU5VEuyc4jsBqg7fcR55OMdqQTiKqwwGtuR5pT+BVGjWLKfKMw8e75EVBVWpCJSmtwHFcjneO6a/OE49jQrd25MO5JsKR5OMIpxOgrMFzXYpJjO86hEqxfzxGBR437l4jz3PUNGLjV98GDFVRIpSimMZ4rRBzBmuyFlrrfYL5DtKRZ8Koz5fWi8a/zgu8sM6OGmMQsmbbQtTMUqOHezSWerRX5rDGIL2LjsqLJVgKrIGqqFCOeqGv9IlpEEjTlI/f+4Crq5u40qFIC6qyorXUe8Ww/SQi4eVnryx69iIk6jkc5eAvP2JwOiYeRZwez2h1mjQWOsisoMxyRklKieXZ9gFSSjq9kOPBCOFIAhNitUFJSZ4XJFmO6zq4UlFlBU8e7TNOM2TTx8xSlu4scbh3ig4dJoMpfjtEOIr2QgfrKIpJyurmCrPDCdkfvU98MiGpSuYW51h66xKt5V5ddP/auorXdmf9fcXzvjrb+Xwm41OPe3nSF/baJ9MEn/Q2LnT5LxAxP3fMi3t+nbfwqmPzqjP1813k5Z6vBvbO7SLFxUtf/OM13s25j36WhXzBwXjllH+tZl/55TVUw/9DtF8CLOr1/tBn5x4u7vf6v37eTqiv9Nlpq+d/f7rfdnBvl26zSZ4rNsOQSZRy8OSA1p98QKvfotlvU5b1AnZpZZGrN9cRTY9illMaTXQ4ZBaljI7H/Mn//ffoLXbpr/ZZuLqKF3ooIVm5vUEapbRPZzyYxOTNmu4UAb1LCwyfHLH7aI+sLHF9B6/dY9l1yfISYwxVWTKuKtpBQBwlxMMZbjhfp0MvCPGIT3blp3zx131krUVISffSAr1OizjKODgesLS5zOnRkD/6v/xb/FbIwuYSd79yl9neoI5iZxmNdoMyK5if69DrNknzEmM1RsBcGFCkKeIMCNbzHQolcJSk0prMGEScM3l0QDSc0e21uH73KqP9UzwjOf7+AzZ/4x26iz083+Ppjx9x6+YVHN8lS3N+9Ec/JHQUjlRUSmONJsNSJAmecnA8t9ZomMUsXFpktH3C8rVVfuV/8Rs8uLbC3vvPmA0j5hfnWFpbwJGCyyvz2LJg8coyf/qP/5A8L5lrhSTjhE7H0l/qIaXACz2Odo55+ze/wv0f/pTxo2N0qdl7fMi9Hz7CCyR/5//wD3DPFucLs9+5B2CNoYgzvFb4EncqJXiCnQ+f1dmrVpPRZEpRlKwv9hlPIq5+/lqNd7Yw3jtlbW2RQZzScEA3A4aHI5pNl717O4wGUxylePb+U/KioNNtY/OKKQ3ybg9la8hXaWompC9+600ev/uEhfV5gmbE4dYJhztHuK5ijopZZQg73drgEAK3FZBoi2h4XH7jEmlZkkcpnu+jpCI7nmCAve/cp99o0L26jDEWNwxqSI2rsGcFtXma8+zDZ1x58wpCSZZurDI5GCIDh43NJcrxjLQqkL5LkRb0ludo9FoX1tzO5iLqNKY4i6wLJfGrWmBPugqlDeS1Qr3vuxxHMe3QRRYFNgxoBz7pNGHZcymaIVleUVSG0Syj5TlYIAeMBKMUx0cjfATzvQ5WCpA5QhvKosT6PoUQpJ6LH2U0fA/b8En2BvjjGa2ra5RpXmtx+C74AeQ5cr6NFAIZZeRpic4LQm3xAR2neIFHNU0wjoPqBDRVyTDKKEpNOkrQShCELgJBEIYkP32Ks7GEWughVnuEUlFNE4o0J/Q9PN/HSQryIsWba1A8OqDaH1K2QppvXYG0AK3RWQ5Vhao01nWwvoeNU8qjEV6rgSk1wndrKJoQiDPIZzVKyI3FbzXIZgmVsTjWUgUuojK4UlIZjQp9immMkgrf1qQb2Brqpicxwa0NrCNBSUxWIK1FSoGapehOg0JrilmKzkvcKMX0ezQuLVKkOeX9XfR8hyAtMHlZixK6Dk5VUSUpFoEEMgxgaoe1sLhZgbs8h8xybBSTxSXNuR5uv2ajkgt9WpdyZj/8kGrpGLKCIi9rKJlSOELS8mtiAOk6uA5Yz6cazJiba6N8h6Ss9TecCqJxxOxoyGwWMxrNkK6i02jgOR5ZmSM0ZOMIaw0LC3Mc7B1xvHvIF37tSxy/+4jTe9scHg2wUjA5qxfrrfT52n/1t2u9kqwutrbGMnp2RG9zkXyasvfuI7JpQn9jkeZCl+6V5TPH4Kxu8czBEELiNQO8doPR1jFFXiKKgmChe+YEfHItF1IglaqzHlJ+cpczQ9VxXfK0BAs6zjBC1A7rGUXuyxXMnjPQfs6MyLm5t4pSnn7nIzAgtEXqCl9K4pMJp1GME3gkp1PAYj1Jq9um1LUOStgKalVzY/EdhyzNMcbQEoKy1DQXG+yejFAtjzIv2Li0Qp5XpFZjcsP0eEx7aY71SysU3VYdiBICP/B4+OOHOK0Gjqh1dY4/2mX/6SF+y2fj5gbzt9fxO+cCVi8yGPZl/5yzfcVrbKCLAfPXAnbO+R+fBkJ6jYHOeSzKz2FlPz/mhXDd+Y2vtfs/+zy/6IevTSm87NLz+1j7Okf2zBI2dVbOGkt0PCLotfBbAdbWrIWu7/EqjOr1ztAv+o1f90WeP5C/hlPxH5jk+CVR0X7SSvplJ19+4XTOJyzmz959+OyIfDKl023hNgI2l/t89Gyfve0jVj/eY+MrN1m5tsazBzucDCdcypfr+ocoxfgukdE82zum12kSeC7FOGZrMOPJT58ipcT3PZTnUmmNlJJup8FsHDGNUpZWF+huzPP0zz4kqyp67QZ+4HN6PEQ4qo44FSUai++5OAJOt4/5i3/0R3zjP/8W89dXLxTE/sy++KyPLJRZQVGUKCEopCDTdYRVS8HC5hLRyZjJcEo0S9h/tEd4xvqTRxlZlLG4PI80ljgqyLKCfBbj+T6P9g+Zm+sRVZo8L2pq0KIikALfd5gNp0TLcyxvLDI8GnL/3g5WG4ajKaYy9ObaTB8d0r62hOsqPvdbX2T/ew/pL/Ro9lssbCwy3DthYbFHIys4PTwFKygFiKokz3O8VoO80oy3jmldXWL3/Wdc//pt3vwb73D7G2/w3X/1HXY/2GL47gMW+10u3VrH2gZPv3f/hcFbCoFUAqs1jue86Pa55T7zK33cpkvy5ow/+3/8HmqWoJSkfX2V4b1t+rc3cQLvbM4/e/GfT/7acvThFpMnR1z/O1/C8R2sPoMWWEs2jmn4HsPRhLXLq0ilSKYz5q8u8bX/6a+9uJdWt83uswHj0RTb9FFBSJxkOEowPhjjKIXRml6rQSEbFHGttxC2GjVNaqnxFUxHMxb6LSSWxZU+KEX3zia7Tw6xk5gUSFyHIPTwHYfmfJujrSPGxyMu377M+AePaFxaIAh8RJwjCo0jJaYVMD0a017u4bZ8TJRRNOsi09OHe1hPgJUcPT7g0buPKfKcVq/JwsYyC+tLSCsQSnC8c0RpLO1uGx1PuPntt+lfXrqY+BGCxZtrTNJtvEFEFGdERYlfapYDH9GpnQVvvkM5jtBK0Ah6qDzD8TwqKZFG40uBHceUWUnQbVFJQddRuFWFbDZAV5RpxnzDR4Q+KsnBGMpSo63AsRbXd/GkwCQ51pFozyU6ndCaaxF8/jqMppR5hXJdAteFKMe6CltoMgNuo6a+zUazmn42K2pNhW6LKk5xlMRfW6DMcnRa0JWCykJVllSNJlop5Cxj5irmNpeojIE0w4xjrJCkxiA9ReAqsgc7lFGK6zrooxEYjQ1dRJKTbR/VdR3SQU8j/FYDo2SdvYjTuv6gsiTHI7xeC11UgMU4CpmXSEfh2BoGVmY52TTBKzXCGNxCv8jWGaUoixK/FZLEKX7gQ15gtIHQJ9sZ0HnnGkGvhdVQNQXKrTMpgefSchTZOEZHOWkY1MXbEphrEb37GJsWcDwhtnVhvjOJISuosPhSkiiBWwhczyWeTJE6wV9dwogmahTXzFta105qXpE/PmC2dURgwbYCws1V3F4HE1dkAnAkMs1xtMFBMJ3OmE4i1q+vMRlF+KHP4yc7SAQicJBSklU521v7+KFPPEtodlvMzfdYXJvHawcUp1OU63LwwVN8z+P08BSv6dObn2Pw7JCHgzGjyQxHScIgwOk0wfMYD2Z897/5fZ4+2mL5yhp/83//D2gv9+itL5CdzvjD//M/Z2v/BABPKdqNgLe+dId3/svfQroO1mhMXmLLErfbBCHoXV2mvblANpwRLtdZUoxFqNcbNtKpRQClNuC8VLR+4R9gwcCdG7eQRVnr+DzXPwm8V6y+i3PpxfaKxfsct3UOk58eTihnOZ417E8TQs9hOJiwsLqAnMzI85xut4XvuewPR3ihhyCg22wxyVI8qbCAshZdVRyfjljudzDa1jow1tLwXKaDGhq4u3VA2G1gxwnri/OUrsR3XZJZhCk0RWU4nUQYJWkttPEDj3gUsXJlhVLC/e98zNN3n7Cyucjnfvcr9K+t1AQWLxSnfwE0w2tbbZBeYJ36lCDlCxZAXv/5L3rNFxf7ReD2r3FGPvX7P89WvHBOP2XfV89xbrxYbWrh4XPNVBWjj3d49oOHxOMpK8sLfPjTR/QvL3HtSzcps5Iozej1O3TX5+ltLnyGE/wf0pGvZo/+mgPhPzDJ8UsT0fv09vPmMD79Ai8dcPFiIFv7M875qr9z1skXvXR4jv1stRrsugE9Y/CUYKHhsrm+zM7+Cd/977/DVxF85R/8KqP/0z9nEkUMJzNCV6EmU/LQ49G9LVZWF7n2xhUOnx1STKc02g2CdoNoXEMmXN/FNQIjJUYItBVcubzK1V99k7KqI5WOEDRcRaErvMBlYb7P0uVljIBkEoOFBx8/oTXfYbB3yl/+oz/i1//h36G7Mf9atoyf66W58EGtnuoGHkWUUgjLNMnodloEvsfh033WV5eY7/eYTGKmSUKa5VRZjud5LK/Oc+WtK/itkO0fP+Jw75jHhwNuX17n1pVNtkZTJrOU1dVF5tbmGQ8m7D3Zw0fSDHwef/gEHMXaW5eRwOP3n2Ct4cnHW4TNgCtRRpkVRIdj2psLiIUmDx8848u/+3W+9b/6W3z///OnTPeGNDotOvM98jQnT1J0UaCNRVQGg2U6nCCLkmypy27TZ+3OJm7g8a2//6uUv/t1pidjHn73Y+7d3yEaxSwt9XjjnRs8ebjLdDzDaI3tNVi+e+VFZ3q+g7Wwcn2DSXjK+htXefL+EzrdJqdPD3kvylh9dkx7qcPy567hN0OkElSlriOks5TxwYDmXA3DArBlBb6HrTQLt9Y43h/wN/7zb7F8aQmrJFmU4ngOYbuBALI4Y7Q/ZOnKClGUMp7lLDRaZEWBE3g0GwHD4QQv8CkqzWA4oddrY4Slf2mB7tIc44MhZVqgQofFuTZaKh493qfIS/q9Nrffvk6W5ZR5wen+gJOTEYHvUlUVZVmydG2FpUvz6ElM9+oKOi2IDwaIWY52JMHVFaqkIJ2mNBbaNVtTVlHEKVmcQsvjwz/5KdPDMZPxjN5yj52Pt5hfW6TMS+5/9yOikymddgPhuxyfjAkX2lz/9bfq7M25l99Uhr/8Z3/GjUtrOKZ21MqioNltoQuNmcTg1hS+Xq9JrA0NKRBliDgZ47gKnRdIx2Fi63fDqTRoTSYFNi0olcTRtg4itEKC1XnM0QiRlaAkWeDhOwpZGfQ0weZ1oMC5tEgO5LnGiROc9T7ZvT1saSh7CrfQOK7C8b06M6ANpihQnoPVFif0SJMMv6xwPIfKQjmOMFpDUVG5Cs/3UEqSDqekgDvfoTvXopolqHaAjhJkZcmnCabbJOj1iN59jNQG13FASrLjCaoVIJICpKQ6miBdB93w0bqO9LqLXdzBDK0NuTGoSuMKCZOkplGeb6NnKQLQSmG1Rk8zpBS02iFEeQ3d0Qbpe2hdYYVAe7WgnidlzXwF2Kqiig3lTkE5TVCuIh+McJshQhd4oia9SD2NONPnEEYzTjKWv3iddOsIW2q0PTMGDfiBj4hTpBCoVgNchdtrIdMCO5zgNkKU6yG0RYUSrELHMVpYPN9Hj6f4l1aIRxFECQZDuLmIvzyH6/lMHh1gVvpUsxSZFqz5PloaVGeB2SxhaW2JoihhFmOLiqYWZHlJHKV0lucooox2o8G1N6/hdxs4gYfw63FAWqCtpdFuUCnJyrVVho8P2Nk9ojKa3nKfVrsJ2lJVFc1Wg8P9Y5482qHTaXGwfcThR1t0VuZQnsOjP3mX3d1j5oKA+VaTWZZxNIvZ+fEjLn/jDfpvbCLUWfbAVdhKIzy33uZIvLX5Fw7i62y+VzfMDod01udfz1hkLbosMHFe15AZU1Mzf4K56DWL3WvxJvU5X+Y7aiYyeQZhNI7H5mqTWGvGScx0e7+msHYcirJiaXGO4aTWVZoOxwyOByzNd3GabbRrkUVGnuWUxtBf7NHptTk4HuIFDk6liaYx2493aHYaVJWm2WkyimKWbm1weHTK8HDAXL/LtErYPzyhuzzHrMg52j6mKko6GwuQVWxurDCbzQiVYue7D2gv9kgHU1ob87Xzh0VYcUG07pzZ/krffTq+6BMfvcZp+YRjcd62fQ7ZfmFvvXrxi2eqr/n8fsXzxwXP7b5Xw8yfZsv8HDb7SxHFT8mqfOK+xQv0Sx3wM2Q7B7jLi5RZwfH3HjJ+f4toEjOOErKjGavzfXYf7ZMdjHH7TbSSbB19yMaXbvDFzW/9zNu9eNOvyW28hmHqwr3/J2y/ZCraX/AbvQZj9qlj5WyQvipP/2kn/tS7sC/+e+GI6rLi8U8e4boOT8cRxemMXq/F1SsrADzdOeC9P/gRv/pf/iaXP3eVD79/nywrePzkmLsLLaKdIYHvceXOJUaDMYPBmFboc+nmJniK21+/i3AVJ0+PGB0NicYRaZrjOpLOUg+0Qc8yFu9s0PjuPYZRBhjCVkiUJHRmMb0ryyx/7hLFNGVv64BoNEPnJdk0YbJzSne9Fih78c1fM7G/2tcv++Pl7+eL7JzAY+X6Gg8+esJ8t03H83iS1BogN794k7durDI+HDI6GOAoRavVoLnYxe2E3P/Ddzk8OiXOC4Kgpo2tKk2jETCYRMxmMWbvzLELA2Z5Aa5L4Cr2H+wQTWI2rqxw9coqh+MZs+GU6TTi/sNtLpcV01kMT/b54j/4Flc/f52g1cBvhtz81lv89E/eZTqYIXKDIwWZAURN5SukRHluHWmuNI1pxsG7T0mmMX6z5iLvLPeY31xifnOJLM74k3/8h4weHNDoNLl8dRVHrvPed97jxq+dRcpfdGPt9D77ySOe/eABx7tHrN9YQ2nYeryL53kc/NlP0VLQ/NMf88avvs0b3/gc0/1TJh9vM3f3Mle+fAuURHp1QbIMahpCKyVX37nG5beu4DeCF5N+s9d88dwslg///btEhyNmzgzhKKQ2FGmOMJbZJKY91+bSyhzH28eMxzPa7SatXoul6ytc/eINHn73PqP9UzZubrB+6y6j3ROevv8MkRYIa0nTjPjpAe98/TbJwZD1L94irjTHBwPAcPPmDeaWekwe7lJFBUtxRufKEt/77/8SczJleXmOK1dXaCx0YJqAgOHjfVorfYJei/hkwuKNVfpLcxw9OaDZb/G7/7v/MWGvBbbGdq/cWGd8OoGkpOG7LL25ya1vvkVrvvuJgT7YPmZ4f5/DVoPN+XmUtTinGjevKLWlEfrYJEU1fOKqIs9rjQgHUNpgrSHLCjLloIxFS4lxFH5ZIbXFuB7N0CUtKxpOiC0q8sf7OGWFCYO6OFkqmnmBlJLKmJo5R1tElKBcl2KaotMc0fRQq32K+7t1oXmUguvg9Jo4vkuJJby9ht4eUB6NyUYzhKtIK41a7KCEQqcFtAJU6KPjlFFUY/Kbc20aWYEeJwCk2tDUGqEUOksx1hD0mmQP9yArsK6DsRaUhFmG9Rxk6KMrjUSQbB3j3FmnzEuSosJRYAVYIfBcB1NWNdtTqRGiVnBWWqPnO4i8qjUwigo9y6ATUlqDlRKhNVVZ4qkariaUwGZ5jWdv+CRlhe8pbJwRGof4wR5ipYc+GIIQuEmKdl2sIymsxem0UGd931AKE6VEP32KJwRe4KMrw3OaVB0GhM0QXZbYWVpniuZaSKMhzxC5xgYeSgrKaYy70EMkOTZ0qFSdTfMcRZUklLGGvECnmsbnr+GMZhTDGf5SD1MZijilNz/H0WCAzQpCx6HZDMhnMWmSceXGJlWlOfqzH+OHPo7joFynduAPRzhCoAKXMs6Zbh0yi1OyUOEIQXI8IWwFbFxdoxAgPEVTOMwtzrF4ZxOyAu97HzOcayO1Ic1r8VMElEnOo588RALzvQ6NZgNfKk5mEbOqZlrjDP5ohYAzopIL64kEo80ZLe2rahIXmxu46GZQ076H3ifWLSElJ8/2aYchQbsBSuIFPlWa45xlzF9nR7xY518YFC8Nw+fbXzgYWjP+eKcmEWiCNdAJauIUv1M7mlWWM57NaCctjBCISpOXBfPzfYqqJJAgWwHFiSQIfRSCWZTSX1tmtndEu99CK8nyUp/pJEI2PERlOTw8pdltMR1MqKYpsjKkRjN/ZYVsVjOvlWlBWzmcVhk6LwiMqJnlXEXluYi05ON//l127m9x/St3uPW7X0Y6qi4UeN4X4pPd9MJkfaF58bon9BmR/U/Z9bXbXv3582KWXgOx+sRnFzBLr0btX7f/q3bqa857wbF43o/25bgCTFGy9U9/n53Ux5EOptDoyrC8ucRoa59SyFpSoBHQmuvgdgKm45hSKqI4Oxvz/otnIz7tHl58F/sz+u3ct/nMGpe/JkzqF2y/FOfis12KX8x9+vmd0J+zzuL5vuf689XzlWmBLxS5qPA7La7f3GDr0Q7vffCYtZUFmmHAYDjh/p9/yNqdDd7/qw9rXYppzIfGcHl5HicfErYbjE/GSAuVNrz33Q8o8oLefI+V66tsvnWFq79yB11U/OCf/gXRKGLr4S5PHuzQ6jS58dVbfPG3v8z2Dx9zsH2I0bXxfe+jpzS2jti4tsrGF66xdmmZB/e28F2HyXjG4OE+61+4eqYoXEenPN/7ebv8Zcedi/7orOTBv3+PYprWjDUCAtdhsdNme/cQKSWbaUF3vc/1r9xmeH+fk0cHnDzY49q338b13bpQ/fIKrqOQZck0L8DCfKdJkuaM0ozQc2k2POZbAVmpOU0q2g2H/WeHjI9HrF5eZmOuQzLf5XDvhPEk4tnHzygrTV6WVP/kT5lNE1rLPW585TYbdy7xm1dXmA2m3P+j99CzFL0/YpomYAxJkdcwF8dhMoupygo9hjzPWbixjskrjreOCHtN5lb6zK3N85v/y7/FT3//Rzz8q4+5eecSD773Ie58ixvfeONlaOds4dKVZuvHD5lfXaTRa4O1bP34Ib7vE0UpqhVSFAX79/bIhgnH9/a5/NZVvv+dD9mcxHzj730T5brnxmg9oKWj8JxzUfnzmNpzK6WVlt58l4pa3yLPSwLXo9EIyJOa+rLVbiAkLK8vMj4ec7x/yu31PunRmOhkjNdt0Oo2uffjhzz96BmBVEhj6S91mQ6mCKG4/95TvMqivIi1y8v037yMCjx0VlIdTVm4vs5H//Y77H/wlLmba7jdBrsfb6N8RfPJHqtvXK37C0tzvosQAjOOaS/P4UiFSHMu3bnE+jtX6S73a/aVWUrQbXLtCze48rmrL5hTxHn86iuZyvnNJX7tf/13yJKM7lIfPtrB+i6VsTS0rlmGmgGzskTFGT3HxboSKUEP6/6aeQ62KvFchas1otmm9DyqJCXLy1rJOqhZbGSS0fBcct+jtAZlTF0onhaINMc6Tm1YK4kdxMiGh0oKjNEkH+zirM5h2g3kKMZgsdEZpagUGK3Rwyn+pUXivMC3FpOVGGuoDkY1fr0doo4M7mIX7Tqo0KWM65oUrxVihjOIs5rcAIWz0EG1fKqjSe04xRk46uXyI2uH2Q4jhKNwpULrWlwwdGWttTGYUeq6gFyWGhMXOFLWmh1SoAA7jtDWIrLa0MeYutA7r8jzAvfMOdZK4uiaGrUyFjGYoY1BOTVMyK00QsmaxlZXlA/3CO5s4jZ8jLUYS60zZKHdb2P3BhhVQ0u1VOTDCE9IbFmiPQ8ReLhVVWcK59qUvouKUyrfISgqROhhS4Oc5RgD2qRUVVkPNddFzXkINNJzcQuNiZLaKZUWMY0xFZQHbWxR4KqaMMApK/Ikx+01abgNplXO1sdPKSUMD07J84I4jllY6FMpgRu4NFb6RAdDnn3wGJMW9Hsdeitz7D3cA88hcgXZdMZSo0UgDVYKCm3IhKFtFMl4ypXbl8mHU9LDMdPxDF1WTKcxX/zVL7D2hRsYbTn40WNOD4f0Wg280COrChqBR0itLbT9eI8n3/uYu7/1BRqrfYSQdQ2Gqo335+xQ9YN4zWL7muY0fKYHY3rr/dooPndMWRTs7G1z++YtiihFKoWV4PgePHcuqKF/AoF01eungrPpUscZRZrjt0LkGX3u6N4e9/7iA1JjcIQkK0qG44g8yRCexNEOWZyiEDx5sEWn36ZKUgLPY2N1hcOdfQQ1bFEFAYFUuJXGVYq9h9t0Aw+hDY6U5EXF3NIcRZrTQBGEAbNpTJwkrHZ7ZBbarQaD3WMC6RBLQ5FXOJ6PagVIpTg5GiJcRbjcJR7NEElBFCWsXVpi7/4ejW6TMspY/fINGqv9+jm80l5rWr+MK9Z/nlFCPUeKvDQPXpOp+LkyE6/cwwWT4xcMs593Hj/LoXj11Od+/zTwhgVsqRGOerFRnN2vMRqhLfkwYro/YHcWYOOMXOSoZkilJLNRhBWSUkBcakQjIJpEpMMJsulTVBVb7z/l1q+9xfKVlRfhcnv2AD71lbEXv4J4/h1em/H7tC/4P1z7pdRc2J+x5TMPPmv2wm8vO/glY+frz3leEK/e8Drv9vVie8/vtC4SBAO88ztfZuWtS0T/OGEynLG1f0Kz2SBKMyZ7A9749tt0ex2G4xmNMMAPA4ZxhqMUB4/3ufTWFQYHAxwp2dhYRirJ/sEpTz/aYu/BHl7g8vnf+Srf+q9+iyffucfOB1tUs5gyUbz7735If2mOxfUFOt0mW0/2UMLiz7WZzhIef7zFbDRj883LdHdPiNIMR0m23n/K8t0N1r58AyFrjPDrwzkXuviT217YqBbpObSXejz98UOqsuL9e4/ZerbHlZUlpKN48myX0WjC6sI8rV4LlEAqiclzvMBj/Y3LxKcTDnaPuX51Dev63Ht2gKcc1teX6G8ukwxnjMYzolnKnZVFtEnwPZd2r8NoPAOt2X+8X9Nk+h5+4LGytkDQDBFSMjkeUwwSQtchPZrw0R/+mIP7u7z57XfoLff53O98lYd/8h6DZ8e4SlE6BlOWOBZ812VcFpTDmIWFeSgMo4cHFGWJCFycwGHvwy3W717i0ttXufvttzm5v8vTe08JNub51b/3TVrz3YtRtrN/RhsOHjyj0e+x++SAZrPB/EKfg5MRtjJ4SBrNNq1mm933njHcOmZ+qUev2zorlnzN83n1oZ2Ppjyf/Iylt9zjx//2+1y+fZWl9UWeTp5RVRqn6WFLgR8GRCdTlKdIohS/6VNMYvbv7yFvC9762l2sEvzg336f09GUlZVF/MClmGWkowjXVWSZZnI6w3cUcZwyHc0wlSYripoFTEqWFrpIz6W91GPr3UccfPQMtxnQubRMd2GuFj/zHVwlMImL3wyoZhnlcMbMWpqtFmu3+/TvbAIWCbX44tlCVBsh5/vg+c/nafi6X6SrWLiy8gI7XKz2UR9t19oUUkCS4rkuoRAI5dTRPt+h8l2ioqIlJKnrU0YpDUCUVa3FkReIoiR0FLqqDRuEwGsEUJR4FoyuEMYimy7yLOJd5SW1jILFwaKwGF1hEJAVlDun6MVuXQNyODwLGBi0MXjSoZykcH+f0HcxxmKzsl7ItMGzFpMXgKDaPUUL8Jd60PAoj0ak4wjpOhSLPZzAwUWg9waElxZwrEFHGUWcUeZlXdhsLeUsASVxdE0jarBUgO952GmK1RrVCRCDqDbAHYnb9NFZCdaSa43XCBBnsFAbZTjdJkbJOniiNVWhkb6LsgJHCqq8qL/b2TN1WyE6LzFJrcWhPLcmgbAGMc0phhEycLGzjEqKOrOgDY3AJR3MMHOtOjOkNeJogvXdmmmnKKnc2piVeYkvanhBqg2VkLUitzW02yHmYIhjLTrWqNU+utLkgxme1VTtAG9tAdVsYKsKxhOskngr8yjPJ39yCFGG02phWyHeQpdsllLkBXml8ec6jA9Oa9psY9BW0+522Ns7Zn5lAW++w2Qyo8hTfCvpdZosXF1ldjxklmf4YZMqzukKj6t3r+I3A+LjCdnBCbLM8RoBRVzw/l/+lOZcm8npuBaF1BVXrmxw/VffQkjBsz/5Ke/9y7/CWMN8s4FnLP40Rjs+vUaDIs354F9+B2MN5nBE0G8zf/cSq1+7XUOksC+yGLos6z6W58TyPrGE1xmjYpZSpTmDh/t0ryzhNfwXa3PQCPiV3/4NksMhQkoKa/Cqi9OiBSb7Q7JJyupbmy8cnHQSnUFPJeUkZvbkkEd/+B6D0ZSFlT6Xv3qb3o0V7v+bHxD6HqYZkMwS8rKklJbmfAcXKCpNNk0IXY+5Xhu/EZDECZ5UdXLAWnSSMnh6wHy/SzPLEUVF4NTvWCnreeHgZEC33cT1HNJUM5zOuLq2wtO9Axq+z+7RCYsbSyTjGSIt8bo+lefQW+6TlxUrq32qomJjpU8ymdXG7smI1aW5muHOWKIo5d6fvI+1BpKCpS9fp31t5WV26TMMTnHB1hIvREgvbD0Pc3r1uf7MbMQnjY6L1t7PPs/FS7/IPb3mWnCB7t2e337+bj7FrjyrEzKVBmrbxmrDbPuUh3/wE04e79NbXuBkOGVuoYPUomb5qgp29k8wvsQgGA4nXH7rCiePDuq+cwX9dgtbaY53jglaIb3F3rn7fMXDO3eHn/7oLvbtpzocF/c4d/TLLMeFAvz/wPbLhUV9Znrts9v5rnld+u6iqvbzcWMvHPupZRj21TNe+JBsHJOkBZvvXGXtC1d5/O/f49G7D4mynND3GecFynF4XkA2vzbP1sMdAs/DDwPCho9UioOdYxr9NlfvXub+u48IPIXfDFld7ZOmJbYoiJKc9//dj3jzV+5y6298jktfusGDP/4pew/28H2XNEp48tPHSEehjUEGLkopegs9yjjl+HCI53vc/todfvrn76MdxdFgxHv/9kc0Ftr0rizzUlTnMzr8fLrRmLOeeXmAVJL1L10jOZ0wOR1TRAmDyRRHSq6tryD7czw7GTDf66LTHM936V9ZZu7mKvksY/jsmMqCqxRVXqC1YW6uQxZljE7HzGYJ/lmEvtFpkjsCv+Gx3PCIpjM8BbLZwMkKDJbJdEa7DCi14WT3BMd1sFIQdpooKemFAYXVHL63RXY4obve562//WU27l5m6/sP6toE36VCEDiKrCjxHEXk+4SzhKYQpECFhfGMUoEvBI8nEdsfP+OLv/1Vfu1/8zskgwntxR5VVV3sz7O+k47izjc/x3f+uz9lNNhDIGhvzjM6GOAqSa4NrpAEsoaw2KKEUjPcOmE2jCnLis/95hdxA+/leH917rXPMcdnE4KpI4ZCCjr9LvNzHeLTEUUFc+0W0zhhcjTCWIvsC6SniJOMhqkd6la7QZpk3PvxQ9751udwrWU8jmg4Tq2R0WvjNUMGkxk9z0cqS5bUhtzCel3rc7x9TLcZEhclgzShGsMXf+vztNfm+ehff58bb99k7e4VgqaP0woIFzsExhDtDZkcj+hcW2Hx7Usc/vQZBA7Xf/Ntwn4b5Z69d+pcdoLzv7/m3T4LKFhrKaOEIslr1hqgdXWJcKWLSCsyBF5WIJSiqgxS1kxXpbFMTifkfg0DUlkdvTWzBEIfHXgkxhACwnMxSlJZiyMlSVnintVU+UqA76GFQPkOZZSgAheblC+WVV1VeO2QYjBFnBmXjGYw18abb2EHEVoK8By0sThKYEwdVVSdAFmUOK6HOtOiKI0BXTMqOdqQ7w0IN+aRSV47KZVG7p6gbq6TzlIaSmCmKcGblxh+7yFev4MtRggEmYDKd2mFHiQFaVWBtfhW1GQMRxPKwMUcjmqmKG2wxpIVJX6/jTNNsZmFosJxFJW10PAxUUpZFLWDYgyhNmSVRhqD1BbpOlTW4lWaSghkqdFCYLQhbIToqi4CttZQ5gXVo33CtXnsIMLttjBJhm03yI4n5GUFJ2OM56ACFyNrut1KCFwlcV0XyrKmwC0rMmMJWg2qvMBqS3gypZiH3FGIwMefzRBGYzsBtBrYaYzr1Fm3SkmCwKVohVhhoBUSuS7thTbV0QQb5zUcrhHgNUMkkl6nwShOCHptnMClW86z1gzp9Dt0Ly+hBSgl8MYVVIIiz5lUlvTeM7I4RToOZalrCBmCYpZg0oKTnSMqoVFSkI1nKFdhipLpZEaSpKxf3WBxZY6lt6+QjiN2f/CQh9//kP2TAWmWsXd8SsP1aDZCmkKztjyPaIbcu/eEtKp4/+E2Vgg6H23xTd9l4+u3QagXr6Mb1uw45STGec58J+rAizh7lmVaYIwhjzIQAmMsx48OWH9jsyYyAYq85HB7n5ODA65dvYaPYvdoj2x0wBd+5WsvpgGvETDeHZ6xk9WGdNBqgICd791j+w/foxE2EEVFPpohwwYf/+sfcuWrN1l98wr77z7G5DkyrwiVoqpKdFExGk5pNgJ812FjY4W9k1OMrsi0wSs1u9v7dDsteo6Lg0ClBQHgtprQCggCj3Q4w2YlfcdjXBRkeY4VFq0N23uHdbF+lKC1oUgzAkcxjiNs22d5fhG0pbU0R5oVNHyPJEpIhxEaiykrDkZT2mt9qsKw0m1RaI0uKtyGz/bvv8vy12+x8MXrr2hhvG71et32s7j6uWLxz6KVtdaAkJ+0sl5jj1ysEzgLa/4Mx+Llnq9e4HUffHo65XVgvRdbtEEXFVWSMzud0t1YID6eMvjRI5Jpxu69HTwpefJ0F8/30K5iMp1RDUtUL4Smi+MrtLUEKiRNM3r9Lp5UHMwmjLOKhcU+o4Mh/dU+3fnuC1ph8dobEq9kLV7+/7OU1f9Ttv9IBd0XEj0Xd3wRlv30UfRqd53Pur16hRenP++ZvnLNl5d+ed3z96U8l80vXefmN++y+1f3+M4/+wuiNKv55oXEcV3m55qsXqsVhefm2mwLge84xIMppmgw1++QTCIOnx6wuL5Id65NXmqi0wl+6GGsoNVpkZYTyjTngz/9gIP7e2x84Rpv/e6XWbyyzJMfPCQrSooqoxf6OL6LtZZoluC6DqW2BJ7D7tYh3aUet790m49+fB9RVexs7RP8i+/xK//136xFrM4NyAu996qhasy5CPC5fhIglOLqr70FWcVHP7rH08c7TKKYLM1xPQclIElSFlb69C8t4S11OL23TxKlDI6GRJMpjYbPcJZgtKHZbhI2Q8qsdtaStKYF1cZwkqQEQuAL8AOXqtR4roPTDIiORzS7LZIowxhLy6shV9bU11euiwhcykJTZjmDrSNc36kFl5Tg5hdu8tFf/JQ0zmsISFnhOE69yEnByBhIc6Tv0RaCQimaQCUgbDVory9y8mif/sYCVhv8Vkio5IsuvjAuJSzfWmf97mWefbRVi6/FWQ1RKEsCbVleWUQoydbuPqHjsLq5QpLltPttnvzgASYp+OLf/2YNATh7Ls9HrZDi3BXrrUVWYzcFgoUrKzRXehzd26PbbbO0ucSz3UP6C3OYomIapeg8wwmDF/ARx3Vo9lqc7J3gNX3KcUzgOGRVRbtRO88nh6dkWQG9NjopcDyHpuei8pLmlWXu/MY7TJ8d8OQnj3C9Jl/6H32Djbevsv2XH3P7W29BaTg5HfP0+4csLfeJhWHn4Q7KCIJ2k/2DAQtXltn42i0Q4qww+xMv/MW/PxE9e+XdFvVCKL0zmI8A6Squf/ttRh9uoycZUZ6jxjNMoxZbnA1H6Kqi1+sStOvCep2maMeh6LWQpa4ZoxyFCn3cvKyL312F0IZkloLvgueBNrWxg0VOErzFNtnR9KxWQ2GEwBYVwveoXBenrLBSIJQiPRrR2OhDqSlUzbJkTYXWFoVAlgaiHNFuYOIcFfhUxqCyqoYAaV2rbFtLdTSt6yccB8eAFZJs7xTHc9HdJvnuAHd9Hq8VkgwiXN/FVAZXG3xtUcaSVRXKWHLPQRYVllqosnP7JvpkgjGWsixrKlprsZME60j8TqNWOs4yLB4mrrOthB5CSEQBIisI/Fr12FqLcwZ7Qhukq7C+j4yTOltlDMZSq5FnJZUjUGmdbZSei0kzcmvxOiFuuxbwxHOQtk5q6zP1bcTZ3FfWwmnCcfBKjeo1mRhLZ2pxlURkOTiKcKlLMkkolcKcDHDKFo2717CexFYl5cEQiaX9znWqNGX+G2+QPj2iuLeD92ufQyHI7u9idIV0XPzlHnp/QKvpE24scXQ8xLiSZtUidD2iUUyoBG6nwfEHz7hy+wrtdY+jvSNGk4ii0tz4yhtU05Rnj7cJei2yKOPJ/S2khUmW0+p3kKFiNpihlKLZauBoy6CoQECZljz50w9IogTpKfKy7v/SWg5nU6QVrOgeB2WJM3KwCGZZjq8kjnXIrGWaZjz64/dY/cL1msHp/PupDYP723jL87ieg9cMmB1PEUqiHInXCHB9BznXQkUZynM4/XCLyf6A3uYiIMjjjMHpKZPBGG9DgLTICj58/13Wr11maWUZa+pMZhh6mKJCeU69iklRw1x//IjJ8ZiqW7HQ7+IpxajM8XyPw/e36K32a42eKCMtCjYvrRLvHxNKSSxg89IKj5/sUhQl7XaTwlR0m00o6vM1rEUGLp7rYrWhkgI3DFFSYCVoR9Bot1FFgDgagfQ4ThPOSlLQWcHqwjyj8ZSoKMkmaR3MxJIeTygLTUcIDh7t4rcCnLTCbYXgK9qX5tFALsDPCoyUVIGD43scPj7k8HjI3mDE1xY69C4vvmYifV17/T7PnZPndtTrsg61E3GhVPrFsZ+F1HkdtetLKNbLHMOLpPSLLbyyCNtz6+XZvZiXns2F+Lyx5KOIKitwWwHFMOL44T7xwZhyHJOmBUd7x7z1q29z8nifNC24fOcyvYU50jSl6TlUwpIVBY3AJwhCBkVGZiv6zTZFnNaImMrWc4zQlHmJ9RzuP9zi+tIdsmlMOktodBov611fx8PLxeXuQodfCLb94u38M/xl6mD8cjMXF8Q6ztpnpsp+vva8a1+OoZ+hNPiK0fHyXj75kKqsoL3S4/N//xuYUrP90RZxmuP6PoFyyMuShluzpjS6TR792QccPNpDScUkSWi6LraqOD48ZanhUmhNfDwk9F1SKVm7tMT2/W0WVxZYWV9kNJyx0G0wmMzYerzHzuN9Nm5ucO1XbvPV//mvkU9Tjj7YZuvBDllWEJ5FLC9vrhDOt3nwkweQZDz9aIv5xTl0WRE6ClMZhgcjRk9PWHn78ksf7nx7bcTieZrz+QC9mHR0WwE3/7Ov0ru1Cv/NH/Bs74hMVyz1+jTCKVGSUWYlRZKTPjtmsD9kPJ6SzmJ6nsez0xHKUdx98wa95TncdojWGuW72EqTTRIGTw85PDhlrCuuLPQoi7oIvIFE5xUL3TZYOIxz3vzSLXrXV9B5ydGjfQ6Oh8zihDzNWL60zNK1FebX5uluLiIcRW9jkemzE4qiYvPyKrMiJ01SoiQjFAFCCBJhKcucOSx+EKCMII3jOmIsJG6cE9xaQ2pL9/Iy8iyq9pJz5GJ/Og2PN/7W5znZPWb1yhoHz45YWV/kcOeIZugzLUuq1OB6LlIorOcy3D6iKDUry4vsP9jnc3GG32m8TFee8WbrvEKnBeFc68V7UGYlXujX74cSXH7rGsU0J56kGKPZvLHBzpN95rptNq+vsnV/hzwtCDyfoOkThB55nOEFHkHgcXq4Q1WU3HjjCiu31ohOJwhPkT85IIqSWq9AwMKVZdbfucLi1RUme6c8+f5HJFlBONch6DT4vf/rv4SThM99/hbBap+jD7e48vmbBL0mXl4QJSnr19ZxfI+PvvMR+w/3uPKF6+eiMa9OmufCX+c9iOfj1j6Psr08wu82XxnwgrDfJvj6HZLDMdFfJWSigLKkyAucoqJw6toDvxmSYHG1ZaZLlK9QSmLOovc6zVGVQZYVIssx2tKwkHiWdllBmmN8B6qKqijRgwjZCqimKaaq6oXHWvJZzfiFMShjMVWFClyK7VO8ThPfcyhmKegKpRRlpREKvLwmSVChi9UWUVZY10E2fGRRYvIKqTVlWWECF8cCgYs0Fsetv6POS2QzIHt8RLg+TzyKkEJgy7JOlgvQcV47tdrgJjkohamqWpdiMEUudtGHo7qmQNdZBotA5hU4BuE5WGFRgFCyhjZpU0dYPZfQ8alU7WzJswxCVYEpKtzQQxclsqww3SaMI5wwoJrFaNdFNQJslhNtHeGamh7S8xySaUTz5gpaW3xq/HNhDF5RIbGY0ANTaxNoC66EqhMisxK/qFBFCVhsM2Q0TRBVRQ8wzzOGeUW8fYg0Fs9YhOdjLTi+S56UNGa1mrQjJAc/eEQbC55D2PLJHJeyKJErcyTHIwb7J4QrPXJtmA0nqEaLRqdBNktxXAe0YbJ/il3tE80S/HaDZhDWUKLTEZUrqdKMjuuysN4nznKeffAI7UrK45xWu4l0XPZ3j9lYXqDXbrK7s8+etjU9t+dx6cYGvfkecRSz1l/lcDAkK0sKXWHdWtzwZBaxsNjnzRuXOd07YZRlpEX58t181XyUkubmMtJ1KdIcmZXMXVqgiDLiQYTOIjIBynNwfBcpBfO31jndOaW50MUNfRq9FmtXNrhx9SocxxB6LPot7i5t8vT77xF3+7i9eVoLXbzAPXMs6vuZbZ2w9Xs/Yt4NCG9scnA4YGfnCO05NSNbmeG2Gwy2TphlNctT4Su2946I45Reu0lnrs0kSVlYWeD4dEx/sU90OMF4LqsrfbpIZMMFKfA8B60NOstxk5QoLzhKEjKj6U4TdmdT2l5A00j6fkDL85nkOZMiZ+/giMqVSKvoByEnWcp4EhGnQ5oLc8jhjEsri+wdD+p33mnSWZ1DFHWgLB5MiZKUsN3AbXj40sFXkuu9TXaf7PHhP/sOX/2Hfxu35b+EC70atb0QAH4FjPMJc+vMxXihSXE2975Qm3seqXyNTXih2df89vzQl9e2VXUWHZJAzQIY7w3Z/+lTkllCf3OJ1c9fo0wynvz5hwSOQ3OxQ3NjntZqHytARxnjJ0c17XTTY3Bvj0ffvw+Ow8a1NU4e7TOJYoq8ptBvdFvML84xenKILjRJkpEbg6Mkpa7IXFkHLYQljTPWrm8y3T3Ecz3KKMVxFKVwyKOUNMkoZhlO28NzHNyGi0hzpuOI4Xc/5Cu/9eVPFZP8rPYi6PhLdAp+We2XqNB90dB6zVh8zTGfHNuf1UWvelif6mCcv5XnA//VzIatlXu/8//8AxzhID2X2WhKb7lHs9vElS6ddhNjDcPhFFtW3PvhffIsZzyeYkytObG8tojf8EinERZBkmQQp7QbAUmUseov099YoiwrhqMZVaUZTGIcKVlc7KGBg+1DDneP6c23WbyyWrPlXF7k6fcfsL93Qifw2Nk54nLoceXWJT567xFZmnK8k+NJQVpaTFkisBTTGExd0CcuTCKffNmBl4wSLx7CWee9gjZZemODL/+DX6P6f/8xO0en4DpcWl/idDhl7+CEyFTEkwipqxp64UqCdoNlJSnKkr3tAw6eHaCfvw5S4HveCyyjlYLQ9Um1JZeSotTE6YzKVBRFSbfTAiF49OEz/Md7WGpsfyglhXBIxzHHts7o5AsdGvMtTFmx//0HOKIWuRvPIpY2ltjZLciNoVEZlKRm3cAyyDNyY+mFAbLVgKwgG06xwxnR1hGTh3t8/h/+NlBnTZDnh9p511fQW5nj7q9/jj/9b/8Ez/fJs5wsKyjL2qjs9bpkmaLQhuMHO/WCgeBw/5TWUge34b84X5XmnD7ep7XUIx7HjJ4ecftvf+ksyCFo9du8SClb8HoNZtOIpbVFBkcjRCvg8o2Nui4iSuj124xPp2RFgXAllDULTNiuqXHLtKTVaTEZzUh/8oRoEuGImirYugq/4bByfZU7f/PzUBlGTw/53r/4c8w04/Y332L+9iY/+bN3efTjx6yuLPHg/hY31uZY/8ptfvKn79HyPFbWl3jzm2/jeopSG8o0Z/D0kGa/ydKV1Zcv6flk+KeGvV559z9tn3PzgnAUzfU+t/6zrxE9PWL0wTMYTcmFxUY5pW8otCXwXRxX4WlDaSHQFqlLkmZAUJRUcVafVFKzrhiLj4UkO2ObsihXIudaiFFc61gAjgUlBUbIOjpfGbTjIPMCpWookAk8ilmKiXNE4GEzi/RcPMeiTU2pbCuL6gcQZVRKYgGdl1RVhXAkrjEY30UZizxzQFECWVYoW2va2LRAOhJ3sY0fuJhpihK1yBmVrgvJrUW0A8wsR1iDcBQeUDw5pPnFG4jTCUVlatxxUSEdhes4NWVz6CCqCorqDNJl8DwPTY1Tzo1GGolRAlHVDpdy3TobM0twHQXNEOG5lAiKLEeewZqqM4eiKjXSd1CVoSorlC4Rlrqm5+yx+9TBJNdxEIWudTlcB6UEbugRTSLkKEbOtbClpsJgXZc4LVibb8P+CWK5h5e4lGmOPZ1S+T6+BFlVKCE5/csPEccnOI23sUWISlOM75MfDfCaAQpoVBrT8HAWOpgkpZsVtVK5Y1m7vIYtNeUZLW90OEF6HoPZjOPhGAeQZUHppuw+eoZshhTC0CwNN752h86tNcYf7ZBOYg4HI7q9Lm9++/PMjsbkWUFiNKLp4ltN2GpgBUSnU1qtFgGS3ps3qErNLE1ZbfbZPTzh7a+9RXw0IilK1ubnqCrN/mhMbg2u5zE9HpGPE5orLwusrQUha3G9bJpSJTmNXgtTGbJpiuNI8llCMYxB1GPT9V2aKz0a3WYtNhZ6NVWxF+ArDzMHk+GERtPnxpWrHMwm5DnkR2OavRbpyQi3F9JZncdqw96ffsDTD59x68YlsjirYYFuLTSq0wzlOIwnM6QQ9BZ6HN0boJoBaZbR9D20tVgB2SRimuQ1PfxkytLyPHmc0i0tftOhSHOU5xIWJaXrMtEVB0XO0Swiqko6YcBxEiGUJMpTPCnxlIPQGiksnlLYThPjK7JpwmGWEHZbzLIMpxmQmor8eEiMxFto091cIHBdpsdjWv0WKvQQpk0eeLiOgx7FDOOczmKH/uYSSkia7SYnP3jI8tdvowKXixohr9hhF0TsXhpSr7PPXoXlPOcZuUCLf34aPod7EucMv0+E6ezL/Uf393j45x/RaAQ0ey2iOIG84vTpIY+f7XHn9hUGuyMcK5icjNn90SNmUa2L4zc8rnzxJstvXOKDf/IXHO8ds37jEu3QZzCcshCGHI4mHD49JE7qgJ6Xu5TG4oUueeCQxzlFWSEUHDw9YKHT4mhEDc90FJMopnVGdKHzEqTL4e4R7U6Da7eucLR3TLPTRACiKpgNZ5RVRVFWOI7Lx3/+HhuXV1m4tIh3bt3/RdrPsp3/U7RfMhXtL95+/g45P7hfdSvEy1F9/sSv9XBebpzsDSh2xhxGGUVZUmY52x9u0WiEFFlBZ65FXpSsBC7tVoOiLIlGAqqKju8jXAc3cFFlSVkaMiHYvHsF8oonD7ZpeC6PPnjCrbdvEIQeaZxx+53rmCTncPuIKM7Ii4qg4eNYSzaJ2fnwGY9+8pDbX7nF1S/dQAU+R9sHOBI+/sl9br15lY2NZR4/3MKGHkhIi5ym61IkGXmUXbCjXklG/Nx9ff4gYyxKSda/fJ1vAO/+q+8xOB2TJzm9bovUaiajEaHnU6QlWVG7EM8mR7iugwp8lKMwRVVH363FFgZR1cxWylW0m3UWYTCNWV1bJAg8zCRi5/CElaU+ynPwHRdZVjUVa6kZDKbsDke8/flbtPtddp/skwxmbE8ekQynvPW7X2PhjUukp1Pmbq6iHIfdrWPyrKxpJh2FSjNCKakA6zikeQ5CEAiBpyQqDBBlSegFyFlO9GifubevMvjuhzRvrOPNd89BeC4aw9e+fJOtnz7j6UdbCAte4LG40EPriiTKKdMMmxYY3yXoNBkPxgStRi3QZ1+er4YRKOLhjPRwxOrnrryYmE1VYYytYSRY9j7epjfXYXllnm6rgclLRicTfN8nmcZ1BHalz/BkTBg4CGPI0oKlS4us372E2wg4PR6SRjFGaxJrqXQtmOV3m7z5628zv9ShmGU8+tMPmByP2Lu/RRZlrF1ZZeMrtzh6sMeznzxBej5CSLSU/Oj3f0Q8ScBoikbI6GgE8w06K3P4rQCtYDCa8OardLKvi6y9driezQGvHvuJc507oaghkd1b6zhzTcaOAzunUGoSAY3Qw0oQwqNtLZkAqyyyrJjzHfIkA2ux2uC2Q4xbw+ucOK8pYuMcx3GwjkeW5DWtqzHIyuA5CmPrSJ9xXYTOAYFyXYy2aAlUumZ8qipsXoCjENYi2iHMUvBcbFFS7g3JfIWyILXB6zRq1eO8JNca2W1g0gKeHyfANoNa0FOArDQ6KUifHeG2fPJjwHFBawyWsqxwQh87SaAZ4OS14J1wFCI3TD94SthvIwZRDbPzXUSl0UWJcB1MlGGMpjIWqTVOI6SwNeTJKzV5rhFnTrcUZ9kBYyg1eNbWWCZtSKcJnudiygrHcxFK1sxTVuNLB6cRIOKM0lTkxVm2SNQwM2U0pZT1+Q1IBFZKtAAv8HEWOsj9Ue0UOgo914Y0hUpj8wpzNMRxJKaoMFIiK43pNfCVg8lzmMww/RaEHt6dy3gLXVQjwOu2kAK8pT6m364hpZWl4TjocYyNc4LA51SXoCWlscTTmJXVefaf7LN5fZPh6YjJMGN5bYmF5QWefPgInVdcunUVU1Vs7xygpKIqKqKdAcc7h0zzlCAMuHzrEmVRcXJwShmnlHGKdBStRsjgaEhvqQeuIk8yNt+8jK40P/2r92mEPlmUcvWNq1z+4m3+4r/9Q1q+D1nJ+9sP0MaglcSXksB1z+r26nerhqHU75cpNaYoay2SWYo1hmwa4wDFNKZzfZnmYpfodMrujx+xUFZIzwULw/1jptEULwh48vgBm61FAuVgsoKtrW26KyvQDGnPt0gOhhjpUOkaglINIvbubbNy5xLHe0M0AuMoSCqssHUt5PoiW493mVUV+mSErjSeNijlUFrL6cmIXq9FXpX4StIMQnqtBj3fww0CHGNq479ZZwrLyhLrinvRDO06jLMUJSUEHp6o1bpbnRaz6Yy0zJFSopTEEQrfc3ErTeE7ZNpiMVhRO/9txyNXAuO7dPstJgenaKNIRzOqNKdhBFFZEC52yQ5GrM33OJqm5EnB0d4JWGg3Aybvb+GGHgtfvXW2wl+s3XsxZZ4zys7bXOeBRZ/aPovt6NXp+Hmg5zUfmEKTDWZkw4h3/8X3EC2fOCs43B/QUBIrBaUj6c11SbGYrCA/nTLdH+EGLsutJviqhqmmFeU4oao07TAgGsdMJjGLq3Nkx2NQktFwQoWls7DI4OCUCkuU5CgsZZzRE4Ki6TGdxSwtztFtNNBlSlqW9XuX50xnKVmWI6Xl2q3LHB8cc7h9hAWyaUKZlkhhWV1dAmNpLvbY+niLluPx4R+8y5Vv3ubGF26+HnXy2Z3+/5fexX8EnQv4zKqcV7Jtrx796X30Wb13zrF47aXPvyIv29GH2ywtzOG4CTuHJ1ghcISoX+hmSENKTpKEwHeZpilpnNLwXdrtJtF4Stjt4AnByWDK6Tjmja/cZePmOvf+4kPQhm6nRXwy4vG97ZrdpKzwWwFKSpqLXZZ77VpgbJowmcWkcYpUklbg8/FffMib33iLlSvLTE7HOA5MRhGlNmy8dYmg6bO/fcxsFoEQVNowm0wZPNzn8jfv4rUCOI99fFFR9Wo/vqZfX+lD9Vw9VUrWv3qD/s1VHv/x+7z7Rz/h8dY+q4t9pAOZFUjH5YvfeJtwqYv0FG7DO2PvqBWtdVGhyxp7WBYV2ThhsHPC8cEpjq2dGD/waM93OE0zlFR4UhE4DkZZMq3RZUWpRI0/nbm0miG9jXmO909IsxwhYfuDZxgEd3/z87QvLfBr//XvkKc50fGY7Q+3ePreI9KiJAx8dJ7jOQ5GCIqGR1xVSNfD8306noeZxvSUQxlnjD/Yon1ng2B5jqM/+D6tL9yltTKH12l+QonW8V2+9V98mysfbnN0b4+nHzxhMJqwstInzQuEhbu/8hbv/vlPWFybJ0pSsijh6tduIp2XDovyXDqbi+SThHjnlM7K3IuwTzycEQ2mrN7ZxFS1GF/YbdK7tcr2X97jxts3iMcz8mlU973WPHu0Q6PT5vKdyzz98BmOFJSFptFtcvxon6Is8XyXLM3o9jukacbilXVuf/ttyqxk67v3Odo+ZhJndNsNPOnSWGux8s5Vfvzvfsj0sNZ9yc/ogg+HU1phSOBIlOOBtUyiBGstc+vztJd6/O7/9u+hlHrxvV+MyvOZx3NJjE++5/bcyvjKqmVh54OnFEXJtc/fQCj18kRnzkZzsYf/t75A9e9+zORhhucoQtdBlhWWWl3b0RpdFRTGMhlHBK6Dqaq6mD4r0WUtmmeKAtn0cKSsDfS0wFcK221gxzGO4yCloHIUwpFYU0fIvapC+G5t9GsDhcZIjdEWxxNYz6FKC6osx20F6LNiWWktDakoVa3+bZIakmMEKAQkBcoaGEcg1YvvJJVC2jobomcpVVXR/sJVVGFInh7XgoNlifJc5JmhLvMKXIcy0xRFgesonExTklBpjS8lTjMgFhI1miG1xlYa5TpIY3AbYe0c+HVNijUGx1hUVoDjoGU9B0ttEKGPrAyqLCnSDHe+g51lCGOoDFjPxZMS4SoqY8mHM4QUOMbiI8i2jrFS4rYCRJRhpYDKossK4zmUUYrsturspdaookT6HonWWFPRyEsCqeg1Q7StMLaeezAWKQVe4NJYmUcPJ2eOlCLstIi398nubSE7LYQvCTwHTmM8K8iOJuSOxFvoYeKU3s11pvd36Tkup0nG4tU15LatnaJ2wMFgQLPh46X+i2L2Ii/ww5DFS8tEwxnu7iHWU9z76QNcKUnyjEpb3CAgmaWcHI/Yf7qLKxV33r5FZ32eZDAlfe8haIMX1EXCu/d3GB4PyYVBSoXXavD53/0V7v3eD9g/OmWh2+XJ4RFvv3Gdk90jduMYAC3FBfFKIV/Og14zYLpzgnQdlJDgSIJmQGetT1VWFLMEx3UIuw08JalmMZ3NBZCC7Z8+5PBkH+tK3rh2l8BzQTkQtijTEcufv16P0SRHBR5u4MGZGN7TP30faWG4fYxPTbCQxQmra0vkRjMaTYm1RjkuVZ6jXcX85hLJNMJF0u12sAii8RQn9Gn32sxGE8ZG05QSv6zw5lp4yz380ymNrktcWY50gU1dTF7hCEUQ+IwHExq+j85yyjNIrRSi/mctpbBUVYmvFIHnkVcVWhuqooYPJpMZXr8D1jJ+dkyeZZRS4neb6DinNT9HMitxlWImLMdJRnOlhzyjZy4dybMPnpFPYw5PxrzZ9Fl88/JL2uCL8ZYXf7+Mb52VPz9nJvzUIuJPYX8618S5dMWrZuJzmNXkyREP/+injHcHNXubMbQ6Pk6/QWAF6f6QVreN48Laep/JeIYrBOk0pYgzjmcRi3NzZFmGKSqSwazOADsOTitgOJpilcR4gmQSUeYFKvSYnEzQzwRZklLFBafDMauby7hna5nWlkJaTo6GBL6LTC0OgmanTZGVPHy0jdfwcJWkGEeUWcHMWtq9LmaWc/XyGvunA9K8QCJgGBEEHjvTI6ZJykZxnSLO8FsBr7V1P9V2PnPqP01Q76/bfuGg9MX2y3MuXnVDfx5P6lM664Kc/Ivf6wH+cvDai+f4eW7x3O9Ga8aPD/CjnJanWOx10NYw12rgS8E0y5jOaorNJE6Qvk87DNB5RZbmHM9iwkIzGk9RUnHtzmWufv0We999wMHuMd1WAyQsLvWojKHQhtZcE8/3KJKcOC+Ito8Ai5KKS1dXcZQiiVMOd4/xGz5PP3xGsx1SZCnSdWkGPr3lHo3lLsueQ6PT5OP3HoKpMKWGEoSrOE8gLTgraJLyJeTpQiT4dY7FS0/tZd8/z10KwrkWd//uV1BK8qN//V32j065dm0DXWlOT0ec7p+y3q2pC3d/9IjTg1MwIF2HbJbghh5hp0l3qcfC5hKtZkirEfDw/jOavsvO0z3co1PC0OfS5VWs1pzGCSBwqBVVHSHAdejPt3n4cBd/74Q8rR0LJUBLyfYHz5BSsPHmZZ795Uc8errH7W++yfLtdZZvrXP87IidD5+SH2RIAa7WuAW4rZCwEeAKB68wKNetGX+UYvzRNurDdS59/iblLOP44R5P/vIDljaWmP/idZqLvZcKo0IQdpvc/JW7rN3cYHQ0poozjo5GLK7NsX55ielwgvI9ciSLmys8ubfN4qWlcznjGg7kNQPc0Ke52EU4L7GZjX67pj9FMDuecPjuE+bW5um3ArZaDs+e7qN8n5P9Y4CaL91TtDtN8jSnvzLH7r1t/GbAve98xO7H2yyvL6AxOJMEAsWXvv0VTFY7YNF0wtNnh0yOxyxuLhCGIaenY975+js8+eF9Vi6tkg8jMr+iEjXkTRvBeDStC/GlIJnErN9Yp9dvo4sKow2u5yDEy+/1iQVKXPz5qnv8YuOnhMPSNOOH//KvsMZw4yt3nu/88gyiFo1c/PptillGPk3RZYkrJGYwI9UGi63HXaeJUTCJMxqA6ztoIbGOj00ypAEV+uSTFF/UMAxlDOQFRTOolaqtRGFrnZUsx/peTUefl0hqyJT1nxd5199Luk7NOBTnlFmJzAqs56CtxbWAUhRVzRRl0pxK1BT3stJ1PYOwWF1h0wxTONAOsVmO8WoKXpMWTL/3kMab68jQJTMWtMCUtVMqHVVrVuQFshFQRQlGSoytkFmJJyW6qgBLaA0ai86Kmvmu20COY2ylMYAwBm0tuqqzIFIKRFWi1hbgdEIlBVYYZFVRGVNHs6MMc/adhJKQZmfOXInruQT9DmVZkk+T2nA7jTBC1MrepUYHYU3I4Lloo3F9t05jCEE1ihB5SSnANn1000c0A4rTGU7Xw87yurbkaIQDWE9hhhNiq/GEwKzNIcoKfTquKUILTfLjB+gsR1QW3fBxVnq4822ig3Hdj9Zi4pwqymq9E2k5erKLZwXpqGJusUc0rqO3nlA8e7BFY65F59oy6cGEBz/8mHQW01nokuQFRhg6813WV66x88ETorJid3sfz1U4rsOdt27TXe+TzhK2PnxKleZ0GwGuNIwGIw73Duj323T6XY5Od+l1O2z/5UdsP9qlMJrT2Yz1uTkWrq6ys32AoGY7a0pxxur2/D18ucAo36FzaZF0kiBDlzzOCVsByndJxnHNmIfFbwX0r68yG8zw57u4TZ/55SWENBSeR6PRwOq63/1ei8WDFmYww1nsMtofYK2lt9SrC8EtVLpiFiU0PY9uN+RkFkPoEud5rS6PZW/niCKtBRpFpamKgiIp8D2Xo51D8F3WFvskZ8KRoe/TbIaEpcZpNRBSYktN4Cq80EM2A559/JT4dEJWVTTCoM6iVBrVcnBKTRbXwnjWmDoeYusMRRAGpNqQZhlYcKUEKTENhwRBZSrkKKHXaaMbPt2lPmG7wcn2ETsnpwSLHYqixF/q0gwC0kmCOB7iznVpX17EKQ0hy5STmA/+xXf49ZtrKP8MHiVezIIXps2LdtbPNrRev8enR5OFuLiLtTB+fMj3/9Ef0+t36L91idHBgGZpmE4ifAzCWnyl8EvL4TgiLku8rMRb6LK7fUSZF+isYmv7gN5qD9V0iacxGkulICoL8qIO7JmyQV6U9buaTVia76ELQ6otla6DoNksRrkKhcIPfSQwiBOuLKyiT0dEcUwkBP35DpeurRG2Q7a29yn8GmpvECivDiKlZYXRlkmakMcZi02HxuUmq9dXKfKSaBbXAZrXPYy/Zu//p2z/cWBRFzNtdTs/xixYU8MJhBQvPejntu8rFGXP+/lllYXgM2suXntDF1s+jChmOa1uC601fUeC6xAYQ5JktcJrXDDfaqAbDaaTGbunR1SmFmma63aQjqK/2OPyW1dYe/sKO9+7z+P7OyAFftNnHEWIwOfG1+6y+c7VWuBHCKQS5ElOPIw4ebDPwYdbbD3apd1p1hzyoUtfWmJHkU1mCFHTOzqey9GDA7Y+2CJNM+zZ5O6HAY5nyfKclbubuM3ghZNg6zAJL3MYvH6ieG1XPu/7c0Crs2ejfJc7f/crhN0m7/7r77O3W1ORNoOAvWeHTMcR00mE2/Rp9Zo0e22iJCHs+OTTlA9/cg/pKNY3VlFSklcV7X4bV0q6fYegGZCOZzgCHK9mgplkOXMrfUxREg9miKKi32yghUADKRYXhSo0xhhEw+Po3i7lNMVqQ3I8YftHj3j83XssXFtl4coyd3/9bXbff8rBg12kMThW0pUKkxYIofGkU1MCG4ujFKnvcbR1xKUv3KTz1hXSvKTaO8SxcPCvv8/c1+8yf3ujXnjOjbzmYocv/PaX+Mm/+QFqluA7CiUl0UFN+2mLitlwBkrQmu98IgUtRK0AjKPOHlb9wIwxxFmMG7g0+y36b1wim0YcPDmk12oiXZcn7z2pHbskrQvluy2mkwghBTe+fIPh7jGzwYQ8y1lYmeN475i3v/15PM+ht7lEdjohGsVUKyVPPt5ieDTEVJpms0GWFmcOYgNfuSSzhKAZcjKe4bgORZrRbDeJ85JZnpNMp7QbAaPRhA9/8pDf+sKNMxrdn7OY7Uyv4qJv8JpAw7nfy6Lk4Y8f4PgeVaUv7vDKuA+XuvQ2FkmPJzhSYA9G2LxEGo1VdQEf4wgjoKEkXtNHaIsIXdQ0qRWcHYVOCvyGD5VGCoGSEj3LkAtd6DbQJ2N0pTCBjzqD/lhX4Whb08mKmi1GWkvpKNAaO4oIWiHFGduPcRVOkmMqTSkLbOG8UMm2UuAiMFWFdTSiqlXeK22QzRCKEsd1KC2IUtfMNY4D2pJ+vIe30sPbHVF4NWOdAjA1M5lwVE3F7EhUpRGui8KeiU7VP4vhDKPr7AhSIKMUt9ukmKUIUzsdxndqeJh0qByJnib4wwh0XVOirCCTEt/3EFpjKoPEYh1V641YS6gNhauwRUmR5TTDgNxEKMdBpwVSyboOVAiIMpTjIh1FVZY4vl9HMKMUGh54LspaXMch6LSQW8ek44gAC76L9Byk42DLCjwfJ7VIx0OfTnCudQlW2gx39rFphnUE2eEAd3UOM0yQ7RbJswO8O5fIjiBshYgoQymJ9B1MqVnYWCKaRUxOp7hhwMmjfcJmQKffo8wL4llMFWeUaU57aY58OOXWl+7SWZtn76OnnO4csXn7Cl7gcXR/G1VWte1Yaqg0O8/2eHTvCWmc0vQ8PM8hznOarRYri3MMjobIdgNTacJmyOHBMaPZlLAZIicKpOQ0jvjBv/8BJ2mCUIpACnzXOdO5OPdqvYApW2bjmOH2MZ7vUmQl7bkWRZzVzzIv0GmO0wzwmgH9VlCTMAiYX18kcBUfPHzAXlJwbXENowU6SplfWUCFPun+gM76HPE0Jug26/dIGy5/7Q6n7z+j3e9SWQjbNRvPeBYhjED6irARkKU5Dc8DUxflhq7L5rVNTo+GjJOYQlcIY5gNR1zuzxG4HkoagnZYz0WuJM9ymo6ELmxqwdB1KbDMohrG57gOk/EUV0iKokQIgdIGrxliBLR7HQAcpdC6zcnxgDwvkEIgGj6qMnganH6L/Ow9jA/HJOOI/sY8xkJuNCK36KMpbsdQzVKOk5QWEm9UwxUjIXAqQ2+5eyG79JmG7LlA2We2T9ht56bXM7PhopsheKmYXu9jipIP/tX3OTweUmYFc90AXVUMjsbIQuMYQSENnlsb+YHjUmQVxkJVVqS2Ik1StNaEQlLFBf5SiJGKucUeDz54jPEkUikW53ucDic02yGzdIKtDOFcm7AZEj3Ywvo+7bBBUlT0Oi10lhONpwTNgEpaRmfrmy0qlONgLKR5wdHxkHa3welwRuC7FHnF6cmIhdV59vaOMcJy6fIqpbHsbx8SzDWJBjPabsDseEI0mBA0g5rp8tMCbJ/o5LqDP63O5ZMO3s/pufwHJkB+ec7FL3gjVptajKrdeMVb/sSeZ/+Lc1s+w6l4LWTi+Uf2xWA/ebSPJyShNZiGj0oAYUkrTWQNvuMyLWP2Dg9q71NJFpcXaC90cEOPpasr9C4v0lzokA1nPPmzD7n/k0f4nsPm8jK+IyDPufV3vsLVr94EKS/UUjfnWsxvLrD5uctsXVniR//0L5jGCUHg0Wo3SMoKeSYgJbXBlYIqTjk5PsVWNc2kEYI8L2sctxD0Fvo0l3uvTBwv3TEr7Msi79c9kxeu2/mef7VzzwWoXMWVb3+O/tVl3vvn3+Hh+48wFroSrLC0Q5eqrBgfDojHEUs318B3mXunS8NzGZ1OSNIMay1aa5I0q7nwteHW7U0MAq01lTHMshxPKhYvL2FLzaPjCVhLUylyaWkol9FwxrU3LtO/vsL0YMi99x6SKUk6jJicjukt9ADLQqtNvjPip+8/o7vY5eqXbrJyaZndnzwiHk1JraElJP1GXYwYWIvjSDJHYTxBdDSsI8lKsfTOdcyojowuf/UORWUY/OQJ/bevID3nQo9ufP4aizfWSIZTslHEh3/1EVoput0W0SxGzODK21dpL3T4jJnklUciKJISMS9xAo+NNy+RRymf+52v8d6//T5xnDF/dYl4MCUrUuavL7NyeYUHP3xINo0YPjvmG/+zX8caS5EVfPf/9cdcvnuVoNPAdxTZyZgsK2h2Gvi9JoMnh7R9H1qKIspp91qsv32ZH/7+D3GVIt45rdP6tjZsfdchzwu63Sa3vnyH6TTGWkt3bY4bX7+DF36akvzLCfATWYpfMEijpCKQLoufu8blu1de9Fu96Fmw5zJzgAkUcr4JR1NsVWF8B6EFJj/D8AOq0jiOwu01sEmOnKakRVnXDiiJTeoiT1vW72osTR100BVquY+Jc6Suo/jGc1GlrkX+lEBagS7LWqFaCmSlKasK13WwRYksKpxWWNdRSIGUAqfTRKc5JTX3fSUEWld1UKY0qFaIjVNkI6h71nEoxxFWawQSvLpOwhRVTUea5mgl8LWpoUqeA6UG6SAEuEVFJkC7DgHUGaiixAqBV2jQtUNilcAWZZ2x8N16HdSWvKpwsGhjMdbgLHVhJhBFReEodFHTVDueQ5UV9TxmLUKbOoMS+rjGkhcl0lU1/a+UlFmB77pURUEFtJottDa1U27rrE5V1Bo11lrKoqwVn5VCKIMWYNKclhIUx2OsWwcX/KoCz6XqNHCjGCElVeDj+g6Nmxs125W1lKdjbJEjGyGy36IczhAViDTHD3okP3qCF7oYIRCuRGU5jfUFkq1jyqMR3Y1FZrOEoBXijD2a3QajOEJkBd35OTZvbXK4fYAxGlNpotEMQe30Kc9l54MnmEozGE5oNEI2rqwjHcnx/S2KqsJrNujNd1HGogKPhbXFOnumNfFgwuRoiBWCZDKjt9Dl7pfe4MlHT1HHDlYIXMchBxzHRQhB2/NYvLGOCr1zr6x9Ca3RlnSWEg1nKFMijaQ510Z5Lsfbx/SXe0i/ngOsrmgszTE7GiGVJOi3qTCszBYJK1XrlChBnhckWU4vdDk6PODa1XcQRoC2fPR/+318BIvfepNrX7jF9v1dXCUpiwpHCQLHpT/fY3fnENlvU5mK5aUluu0GW8aQRTH7ByeUxmCBzlyLrWcHdYJrrofUhmCuSTjfQRcV02GE22nWsLhGyMwadDtADgqM1oRhm6IoULWHWwvrNULavTa2MqAEVlu00VS6oqo0rutQndGbllmBLS3Cc3G6DcpJTJmW+K0maZJin54QTSMWN5coBJBXlMAoSfEDFx1nbNy9Sp4VDA8GWGDjzibpwZjG5sIFm+T1Zqn9VMfhQvsUqM4LNkouBoefz8HiOYOngGh3wP+PuP96livJ8zyxj7sfHfJGXI0LDaTOyqrKkl1dNa22u0evzc4sl8KGQ74s1/Z/4RMf18iHsRVm5OwOlzMc7rSaltVZOrNSIaGBq0Xoo4+788EDwAUSVV3dXTbrD7ghThxEuPyJ7+/73bt/SDcIaAnF5OExfhwQ+QoPyfpwhYd3HpFuKNK9IzxPMj2a4Ic+nc0Bg/UVlLQ8OtN0Oh1QkmKRUyRuH2n128wWKdJTDC+sIj3J4dmYSll8P6KqKtbXVuh022SLlG6/S09KZmlGqQ2hlLTbLcqiZDSe0m638DzF1uUtyjRjPp2zvrXG/uEx7TgkikP8fkBVuyxWeGWTMivJ05yyarh+/RJ52eB5ktF0RrLT5/0//oB3f/drDLcGz59zP6/7n6y1c9c/lxX63Nj9PCtbvPji37j9xyvofuH3SE8R9dpLX+Dcj/rc736WnHvx79/0a1hgdP+IduBTpSmN0RRZSVk11MYyW+RMp3O0NvRXenQHHTZf3eHC25dJ1nv4SYAuG2aPT7n/Rz/l1nufMJtn+IHP2uaAeZozm2bIIGTt2qbjeDYGXTt+9aZq0GVNa7WL1ZbFyZR8ntFfG7CYLjCNoReHVNownWfMRhOSOMIai+cpVBhQ5zmDzTWGO0MGmwMIFN2Lq6xc23zKD22XGyTWUbc1ZY0uaopZRlNrlKcIWyHRoIMfB8+ySufG4Xk0in3hDYGQlu6VdX7l//J3ef3eIePHpxw/OKKYpfjtBAUU84wH9/cYH425+tY1xMVVTDemBUyPJy7zIiVxJ+bunUcMex3mi5zFLGXhK9Y6LVqtCKMt7//b91Chj1SKKPQ5mqcs0oJOFKAEpIucvrEMb2yxvX/Gg70jZpM57VbC2WSG6ISkZcnFS5uUWcHRvUNmxzOGl1a5+tVXuf1nP8WUFbVUmL6HUhLhe9SNxrMQVZrZWcH0aExvc4AKPdbevcns0z0W85zW1XXGt/fw7h3Su7ntor5PohACVOjhdyIGl9fZfOsKi8MRP/6f32P/4wf4K23e/Qdfd9HeF9eBseiqIZssaK25rBkI/MBj/cL60nl0WcAiLRlcWOVX//lvUxYl44MRi4cnfPwn77M4ndFc3+ZLf++r/OX/8qeMT0ZsjjeIBh3SaYrRhk47dFz5hxPaSUgxT+l98Tof/4cPqBYlvq+Io4BinnHx9Yvc/fOPyCdzTBKzKCoQgkAKojji6//g68yOJmy9fpGtty5RlzVe4CGUevl++XSKPcvVW/HMQT6fR3tuF7Cfe/D0KqEE/e0h7WHHacA8MYCe20jcEyEF/S9cYfbDu5SHI8eSVNWYpUCcSAJk2SCVyzw18wIV+mhhAB+pNfrJrasG/WTjj3xCDXqSYfIa4Sm8ssKy3IS1hl4LP/RReUVdVPjCZWmaRqOMc7rrqsFXEorKqVJXDcbzqJTEVy6CLzwnmCYal21RFmxRgVI0whLOS6x2pAsq9B1rkqdo5jkssyzmeIZc78PpHN04o1vUDUQhchnc8BpNE0knQGgM1rqCbLvIUJ0YM15ga5wRhaYezQmvb9HcOyT2FEI4SJXn+djKFZdX1mKtpRWFGN85FsK6PcyPQqg1jdY09RO2J+UyL1GIqDRVUTg8s+chjaW2YJREljVN6KO0xfcUoRdQlSVCWwdN8RRSNvjaYGKf6miK8BS+cdnfKnTUnnpRIGcZIvDxkxCpoTyZUk0zWlfWCaRisshpspxguEI+38f6Hn7ToOsG1U3QoY/wFaKokEFAMMuQScjpPCXdPaaxhsPDI5QS1ICJFTKMWZylHO8ekc5SmqoiDEP2P3sIUYBV4PmO8VD6PmEnYdDrsnplExX56EXO7tEJQkHciqjmGeODE7I0Z3/vkF4rIfR8LlzYYOPmDk3dsHJzi9Fnexjh6lSU5+FZuDwYIKTkcDKlpRTt60sF6BcWtLVQFhVFmhO1I+oUxidj0o/uYW5epKka7vzgM16Tgu6VDUQQIITATyKq1BXWt7odkjChG4ZO5T70MIucrTevMHl8wNrVHfwgQFZT0rM58/GCxydTptMc6/v4UYjXNAx8n/00I25HjKdzxw55PKUTx5ycjJhM56RZQW9jSLXICJXEb8c8enRMEPisDldQBpS12EpT5SWmFdPKc8LYxw5aLA5G7DYVeVXjeYq+H6DnKXZZc+iHIVHXkZsIa13k21qsdP0rfYXvKVSRY62lKmuM1ghPUeBorlUrptVpo4SgGldsbA9QUmKNpbPep45LTouCcOhQEDqvOD2ZUGlN69Iq2cGY2+/dwvvgPu/8898gWmk9NT6fs62s22mFEE/335+F6f+8qsX5x0vsw3nK2mXGwlrrMorLy6pJRuh7XB6u4LUjpvcP6G+vQhIyP5ty59P75EWB6QZcuLxBYwzRouDy5W0Od08J45CsNniRT1XVbG2vsXd0SjFb8OCTh1RFRV0UKCmZzlPilQ7m5IwoCkBbJqMpYeDTG/aYz1POxlNu3riMH/gcHZ8St2Pmkzkq8kjTnCIr8JVHd7XP6SIlSSK2Lm8ymc4cxFU4mmUpoCor6qzC2Ia402KRl+inhfuC1rBNEAYc3z5g784ug83BzxdBPt/OB5PPYU1eHJG/uv2CmZJfsP3HZYt6Mej6wgs/s0OWE/15JoK/uVtljSEdzVlXiiKIODqecTZdkOcF0nPY0Xa/w8bOGje/8yYr1zdRviIfLTj46UNO7uwxfnTK6HhMoy1SSTxPEnqSs/GUunEFy60w4rO/+Jgb33gNYSxVmjO4tgU0NLXm6M4Bhx89Yu+jh8StmC/+7ruc3Dngw7/4kHSWEXcSLlzc4PLNC46CbTwn6SWs39wm2RoQdmLHeiTFM2SINsyORhx/tsf8YMQiLdi+vMH+3QOKtKCeZqRF6UTqQh9PCla3hqzf3GbjjYuEvYRGGtrdzrKXxTNjjOcdvCejJbB4kc/q6xdZfX2HG9o+dXB0rTn+yT38P/H4bBk9q4qK4nRGt9vh8jffIh8v2Lu/x3w8Z7PfozKWyemMjY0h03nKNC/xCsHZPKefxHjSCSSlVcPodMqw3aZGoDzJ3qNDhDEML66xurPK4/1j8qKkajS9QY/x2ZStt6/waPeIsqzp9zt4QcAwbvHgR3fZvLHD0b0DtJI0RqMwGOswxUYKhLZcuLLF4+9+ivnyDXo7qwSrHaq1Fn/w3/wbNjbW0U+cusjj1W+8wfWvveYC5RYObz/m1h/8iG//n/8+XhSgPcnb/+jrXPnaK6xe2SAZdp9N73P7czHN+N6//EPKRcYbv/lFNr98/alYlPTkU6SUEIL+5sAZA6FPmERsXd/GXtti5coG05MJZd0QDztc/9rrXL15FWYl44dHSOWRxAFNllPOU+Z7x6Sex6P7+3RvbjslXV9iG8NssuDitR1GuyccHZxhLMzzkjAK8TzF1bevcPUbr7B18yJPGZqEg7j9gqv06fx68tQ+99Q+u+QFx8JUDcXxxKlEtyKEkLz7977uPvsS9NWTqM2T+3hSUN87QuSl02NRkqYoXUHg0vhVUqKFIBCgQx8N+KMKbSyNr/C0QVqL8BXGU8SNpTYaJSVV1aDUMvKtXGYC5e5nJym5p5CVE1tSgOdJGunS3sJa0JrGLh8b5/SouqYUEAQ+Tejj1w3aU46H3ZOYvITQQ05KtFpSxBpDvdLCn+WIrEQYg3ni9FlBPV2ANe634KBKtm5AO+YlrCVqNBiL8T08KdF1Q2MtfhJSjxcI4zI20jp15nKaIlsxdp5RK4sEtG4IRbzMECt8rbGBT2UM/jzD1I1zjOoGpTysNRitHdNcK8RrNKapUaXGLJ0gL4meOkXSgsYp0zfzEqEUddPQaLdHhb6PaTRNXmEx9L50heqzA7SQSE9icaw+wpP4gA0CGlMjazC7Kaau8S5uUd87Iuy0aHc1lJr6wSHNZI4JQ2pP0Skrkp0hLU/SNBq9FCtUvqLutwiLkiKviD2n8FwXDX4QIU/HhIM2NqzIJnP80CcMQ3YubbLYyth9tI+1llfffR3f87j9o0+J45ijvSOmhyOEEhgscTfB1pqwrEFr2kkMWnP1+kVm4xkb25us7qyS7AzRVcPo3iHTowmT0cxll5uGuYDD0ZgkiQkFvP7tt1lbsg891wRgLFVWgTJEwxbz0xkGN98PP3sMvk82TTl4cEjn4jp+4DQByqqmt9oHnHG2sbGBzkoQEIQ+UTdBeh69i1sIC9nBhMXjU9qrPTprfbK8YlaUsMidyKp1jIc29tFL0VajoO2HbO2scfvT+2gBrU6ENQ1Hoymrm6vuvF4bIK0lVh6hVIh+GwT4UcDp6ZSVXuIM8MZwOp4RDTus6RZnj48hgKas8HyfKEnQWtMbdBmfTVH4CE84UTVtCXwfjYN0ZXlBq92iqWqUJ/GFpIdHPlrQ6rSo6xp8BaHH491DvDjAZCXZR48wgWS4PST0PGqpmFeaszKn00rI05yeLzBxxPhkQro/Iuq3Xnaon9scn+yO9txLn7e97Ll/zyUrnorqPZsWz+yI550Uy8prF3jrS6+Q3t7n4f4Jst8iO5nQvbZJ0msx9U/QJxPmh2NOPY9eEhAmAccnI2bjGVIIWv0OIFFJwONHh0ymM5LYBSa1MfT6bTwhOHhwQNU0lGXpBHqriiSJ2Ht0gFAei3lKO4k4OR7x2tdepyorHj7aRwpJ0onpxAFpVpFXJfPJHL/TIp/MOHx4SLeT8PjgDL+uCZuGfFHSSQLm04x2r0V/I2LoeTx6sM/wwoBYBWR5wfxsAkKgG7eno3gu83O+i5924i/SzmcUf4bj8dLE09+y/e2di7+Zi/RctuKJQ/uzbmFfeCT4m2cvrAXTGEfT1sBoNCMtSobbA77whav4cUh7vUdrtUvUS6gXBfs/usvjH99jMV5wcjSi0YYo9InCkPXQR1vLZJHSVA22akjLEl8ItBU8+stPuf/dT/BCn3ClzYU3L7E4njDdHyM9RXo0xk9C3v0nv8L2V2+w9uZFLn7lBk1REa20iboJ3lPGJZBKYBpNOS/IzuYcff825dmCYp7ihSGmrDl8eMR06sSwpBTsfvqY4caAw8dH1HlFEgYIKfCNR5FXPPz0EQ8+fUT/zz8i7sSsv3qB137nXZfNcKFjnnT8C/P0ubaM/bragKZx0VlP0trss3946uAiUtDMCmZnM65cvsDg6gZZv8XuvT0e7x1y88pFsJb1rSG9YZf4bM79O4/oeI42tSwrVtb6jKcLwjhguDWg3UkQqVPmnZqcOw/2OD2dcPWNK7z6+lXu3t2jUpbT0QRbaaaHE3oXBnQ3+5STjPkk5fhohK01927vsbnSQ9UNlYGg38bOnKpwFAakhxNMa4uo3+F7/+0fcvmtK1z81htsvbLD7/yX/5g//L//W7pxm0ZAd7PH4b09rNZceucGQSti4/oODz+8z+R4zOqldcq0QFvLpXdvPiPzOjfdn4jnFdOUk3v7+Mrn+Cf36V1ep725QlOWzmBfYi6NdSrU1rhomWlcxBEBK9sDhtc2l2tA8/C9WxT9OWuX1pG+Ynx7ny//+pfI6hp9PGX12jbTomBTGlToMXh1i4/f+4g4ignimCIrKXCCb0nUYeXCkPUb21x47SK97cGyxgisFc6YtbA4mqDLmqAb017vn0NRWGyj3e+QYllX8cyxeB5u8ZKdwlrqWcbi/hHpR49oJindr95g8LVXeZqlOB+ceM4h+fyOXU0XCATKWIRS+EFAhUUISbP8ahbQrQg7TdEY8BVBA14rdsQDeUkaKMKypjYWKdyB6i8hPrUnsWVNqaRjPSobV3hdNwRhgDWGRmsqa58WX1pjqHE+UqM1nu/oaJ8UiVZFiWxCaEf408xlJAR4AprSFV0b7RiulOeh0wqqmsa46L0PSzE8g8ob6EXQGMq6cQJ4xtWQmGUhdFXWLoumwZjGMWQ1tdvPpUAISVGW+ABCIkYLggtDqGqoG6e50YqxdYOWrm9sGFKUJUKHCGtRWMdQ1TjIFr6HbUr8wMNaaBqN8YQLlhQVNgxoPIWpG8LK9am1FlNrAs/x0Utr8aPA1aRIibQCAo/w8ipmmsEsx9QNtRYESYD0A7z1Pv79Y7S1GCwiDLBKossav6hoJMi8IIpCpIEqjgm7bfR84erePEVweRXPOGhWg6A6GFPXDUE/wc8rhrXm1uEJNlAIKems9pgfnaEnOf3BCkd7h/SjgMmpKwqfj6YYT+ALye6H95ChTzFPieOQK29epzXs8uB7H9FptZmP57z2q++g4oCDD+4Qddvs3tulZw26rhnPF4xvpegP77IYzylMDRbWBj1Wg5D90zEsayQ7/RZv/da7bH/7TYT/TLjuPBGFkBAmIcoqmkWNH0UIBMOL64x2T6hmKdVkSrkYUKUFVV5x8NEdtt68jvIVWGiykqos8TsxSjhoorEWm4R4vkc+WZDeP+TwLz5m851rNPtnZGcz6Ldo8oqVVkypDbUCvxXRVj45JXVVk5UFDx/sU1U1G1c2ODsekc0zhoM+22tDxv6MbD5ndW1Az0qqNMMPFNH2KjbNGXYjwnaEbQzGGo6PRxTWUrBkJAOCVowXBgRxQJ1XyMAxSJW5E+3rr/bI5jnaaFToUc4dfW1ZL2szPEVd1pSRT51qWmVD1dRIP6Gz0nHF6VmJX1vam20eno4g8JnlFSGa9W6H49MxCwtBoVlUNVcuxcStmHqRc/z+fVbfuuSghVZwHjX9N7Yv7XN/3Gx4upe/PKAMAhUHbH/zNb73kzvEoU9VVOhFyVlRE272qIWlSHOu7GyRzVJSTxGvdlkcjPF9l+2Pg4Bep83h0QlJ7BOJLouqZvvmRfJZSjZfcDqe0lsb0PESkrrBYkiSmJtvXOPsdMzp3hG+knTCAFMWHD86ojfoMsxyV/sa+VgD7a4iabkzOG7F7FzadOQTFq4g8ZIQL/Qoq4b5aEq7nVDXDVXTsHFpg86wy/69fQabPaKVBKNg/doGfuhz8OCA7WvbnzeKf0HD9wkEzS77/hm87Rccw79l1gL+Y2cuzn3h5wTeXmjPOxOCF/nr/7ZOlfQk3QsDsnHGG1+/yeDyOp3NPtJXNGmBrjWLoyn3/vQj9j58wNnRmLxq6PW7rAx76LzAaEOR5cynczeIShJHAWHg01/tgScRStFYS5EW+FFAu992dKFKkXQTtLF8+Z99m63XdhxcYxnxG9zceupwWRyFa50VZMdTTm7tcXJnn9nJjEZJ0lmGH7ioofQUZV4QBj7rmwPquqHWmuHWKoNhj8nRmI3VPhuDPqcHZ9R1w9bOOlbAtMg52jvm6MhytH+GsII3/uHXyE+mCKWIVzvOwTmvE/DCeJwjnlgWHrsXWxt9uqt95tOUuGrIP7lDmeWcHJ4xeP0C7fUea5c3OD6bIJUgG8+J37rCha+/wuP3bhHck+xNZ1xcGxK3I04XCxrdQC0JtCafLaiBQCh84xZTukj56IefEsYhcSuipS1CBWSiZHY6ZXo2Je7EtDdW2LqwwuJgxOhghmed0mrUbzE9m5FmNUPluxqXvECt9Dg6GPPFL94k8X3mdw758P/x+1z6jbfZ/OJNfuu/+k+pJhnDqxtIJVGBR13WS0MLgsjnW//5bzhHoDEMt1eXTtznJ3Yzz5h/co/+V98k6iYEvueifnf2uZ5XANSLAhMaglbk0rDLQ/lJ3Y3yvOUwCFQcPh0n6Xvc+JXXme6dkVcV7a0BRZZjiwbfWta/+bpTr08rJlJw/MFdXvt73+T+H3zA+HTG6mqP7Uur2CSgLGqufesNeheGqMDBtawxVNMULw6Z3ztkNp6TLnLWrm9TFxVCwLxqaM7m+J2EqtEO424cs9Pw+ia9a5tPaYyxThyumGe0VnvPNkwAYxj98C7F7UOqsxk+4AlB9viU3heuoqLAkUc8mZMvzNyn+/Vy8qooYOXX3ubs9z9A1dqt96WzY7F4nRbUNRJBVVaYvCQIPGwgnSheWWNCn7Ks0GECdUNQa5peG6M1phFQN0gL1lOQl9gooC5LhHaR7BIB1oC1ju1JG3SgXD0BTjiOQmM9hQp8TFXhKeeAN+USGhV4eNriSYlA41nrRJ6UxFqozfK0MW5NS5zTWYGrYcg1TOaowEEyaynwlwXx0lq0FO5TSiGMS+/X1gUj/NI5GrUQtDzP0X0Kg2wUejQnWOsRH46pBRSzFOP7RFJimoa6cUrkXtM4ljZPYbdXUUcjMFAviUAAZO1w6p4IsVKgq/op3EtISVPVTrXbV4goQNYaYUE0S6FR5QIwInTZHNFL0J/sYZUETxFiMQhEWWFGC7TV1IGCsnZ2krZYP8RkBQhBdnxC68ZF0v1TauWx8vZl9Cwj+/gROi9I//wTlAHRb5EejvGkxPN94s0Vcm3Q+yM6/TbGkygpuP/xXTrdhGZR0VntMh1PaHxJ0I05GY/ZubhFf9Bj7/4exoPJdEY7VE7Z+gvXqYsSGYXITgyLnOneCVG3Re/iJqezlLqqIYoIum3yLKcoCmzVkGcFyvd44+tv8urvfoXxx49Z+8ldvHbMhXdvsPLKNvGwe85YOZfLFs9sSOVJNm5cwGrD0d0D9CwlwFBXFTIKWH/tKutXNpy2j4AszYi6raf3lIFH2GsvC7Utpmwopyl+3dC+MKSZpOz/5C6dmxc4+uAes2lG0G25eZj4pNqJG1ZNg2o0J+OFO5u0od1tMR5Naa112bv1iE4YkWUV+JpHjw/oDLpEcUAiFH4U4IU+ravrhFsDitsHjhq3rJy446wk6rZYjKaUVU2lNZHnI5Tn4DqzBWVeIndhfX3AwljyosRa8EOXOUvnOcYarHbUzbHyyMsKP/Ad2UMnJq0atrbW2H90QD6VtHsdsjRDIcibmqSTUOQlUkgoGsLEad4EDVy6tMHu7jGnWUGZV3zyRx9Qpjmvnn2BK7/+tiMheWKA/sJW6PPt533qKazqc288exiuduiv93l4/4DVzQFr22vc+fgBounQaSXYzQF5mrG1s8HD3aUor3DrUHiK8WRGID2aomH/eMTGShdhLScHJ+xc26E0DXFR0O60aHcSDveOWB30MVXNyf09qqJi0G6xkoS04xijFNnZjKqsWF3tUUwWGM/pm7WTiLbyqLWm3XE1b0VpQDntF+UF6MbgK49obYUmq1wm2/eZ7Y/wOxGdXoujwxOGO6sUoxzdCRkdnLF5af1v1MnPZYMs1FmB346XGZAnsDb+9kb0L9D+9s7FL8HDOd+ejyGK5Ws/Ky/0V9zguZfPpeyk5Ev/7FcxtSaf5Zx8tscnv/9jZidTZuM5VVG5w7TWSCXodFr0moasLBmlC4SF3sYKN794nbVrW0hfEnQTWoMOXuSjPIX0HduL0QajnWCUF/hPD8W6qDDWEiUhRlsO3r/Hgx/fxYtCom7C+vUtOsMu85MJD//yFid392lq41QdlUurB3FId6VF3TRgYJZmCCmYzxa0tcZqzfU3r9O/uIovJddvXOTeg31WNhWVgHlds7XS4uh4zPhsTtjt0A188kXG3ocPWd1Z48F3P0EoyaWvvcLmu9cRSj7LOll7bpSeb08muQW8JOQr//ib8P/8U+7f2eWVd18l7KQcHp7Sv7XHxs1tdl65yHySki0yhJSM9054c/UrrL96gc++/ynaGNK8YNiOSTptRqdj0vkCPwpJ4phKN+hFyZuvXEILwdHeqWNXqWvSvKDfTnj7N7+ELmrO7h8xOpsxnyw4HD/GBJLLr1/ijRsXMGXN9OCE3YMJaPCNZRF6WKPxl0ZYMq85uLVLp5uw9Wtvkny6x+K9W+yXDetfvI5/ce1ZvwieY36oiwqtDdk0Zf+TR6xd22Ljyua5qWuf+tQy9mm9coknhW+tKGAynlOmObf+6AO+cvm38OIQszQ+pZRLns7PLSSeW6jLhxs3d1i9skWVFex+7xbb71xDBT7T3TOCQYdq74xg0GZ1q8d2FBC2Qn7tv/6HTB+d0L+yTnu1izEOlyuXQlzVIifsJthGs3hwzOxkSuApwqKitd6nmRfMRlPawhnFi9MpXjcmQmCzmvHRBCNBTpwORrTSoR4vkHFAOS+oshIaQ7L2jPGkyUuKBydQ1ijfo/QlSlvsJKVe5KgoQHiSZzPy3L5w/ukyGo8QdN++DIuC9L07S4SHxUpn6DZ1ja41YRwQKkkT+o6TvuthpTPQm6zEeh5RViIb4wrBFxnC95FmyYYUB9jJHFs3FFIQGuOcqbLGKonfTqiaBi8zDpqlDVVdoHwfax3bk9AGhKPIbZ5Q+jYaWTSUOEY+0zSO+cpY8CR2SfmrPIWyllo4nQLzpF7DGGRRIbBUeQlh6JiBlHS1P57CFqVj/GvH+FWNwdIAfqOpG4MtKoKNHmp/RI3bwz0hqJsGkZZ4r16gHi1cYbGxmLLChIErqNaGEEfnarQT+ioeHzn4UlHQCEEgHbufJwReJ3H48skcCXiewjSu9gVfoYTEKOWYraYL5EafZlI8hWvhSYehr2uKO0f4jUEqiW0EzbJ2w9Q1+ekEHXjQNPhh7EQQk5hmMcYKjZEeybVLlFmGSDUrg75TWtYG244Q2mKyHKFdVLP/1iXyoylmtCA/PKN/fZOT0xntoEOmG3RZYeqGyXRBFAYcPNjH9zx6vR67JxNU4FPphsV8QV3VFEbge85QPXt0RDX9SzcXfUVlwV/tMRnNaA7PKIRwbF9JyNnZhCgIiTsJKENlNCudNslqj+vfeRu/k7D9rTfY+uZrqNDHi/zn9vjncTDnoLRW4IUBndBlwJOVNrf/4kMOHp2gK401NXQSjh+e4McRYTfGD1qulmZ5b+l72LJBBU5TRqc5waBDIy3leMHee7d47Z99h5MP7nMwy+i2IxZFRW0tnVZEtBTVS/MKUVoiKcilQQK9bpt8njnmQQOdQZek0+L4bMRKJ6HOCzrtFq0gwFQNnYtrKKkwswzZipzuzDzDH3RIFzmnoxlPmP/iJEJaiRKuYLvXaTMXEqUUBouZZ0gB88kCf0l6kbRiJiMXzFNCEghBagxx4GMqTRyHGCvQFqJugq20YzeLA4aX1pmfTBGTDNIK20vIJNSzOb0Lq6Rnc8bjOWG/hS4bBis9jo/P2L6wxuMf3mH7S9cIB51nTHw8N6Q/s/08H0R87iB6/n4v+6hshVz6jXdoft9w8Wuv8vjH92iMpckqZxdtDXn08JA79x6TlyWXN1fYS8d0W21XVzka0R0kCM9iy4LDecrV61cY7R+z+9PbxFKy0247hMnjY7bikDiraPkemTI0SeQynipEW+FsPT9AxDGB76GHPlpK/MCjzgqk0agkIOhE6MgjMpawnVBjUKGPqRqqeU4DqBXxFAhigFKCjWOSTouiqZygohKcPDzheDigO+wTxP7P6Kmf0Z56h+5jfjvi2Sp9hgT4j+Bb/K+o0P1Cf9mn/zxvC70IifqF7vtXXFpMU37wP/wx2ShjfjKhzCu80EdKgRSSXhxhqpqw2yZtNFlWMK1qNi6t87Xf+iLDy+tEvQQ/Ds/Rfy1NwxdQFuqF36obxwrjWHIE5Szjk99/n4//+APqosQKQeNJumt9h4EuGwIpkbVGCUuUBMTtBF03LNKCJq+csFOj8T3F6tYqp0cjiqIi9Dynlmuhs72C9CUn0wVWSTavbtHNcj67/RiF5Nprl7n4lZs8+MtP2X9YM53Mufcffsp8umA2mjI7HpOezth85yrJRg/peS8M4RPT7YVo8LIv1t+8xNfEd3jvv/1DfvLdD7l8aYuT0ymP7uwSRAG2qJlNFwyHHdJ5ShAG6KqhLGpmZcmw32VjbeCK1LUm8D085VFWFWnLOiPXk9x6dEi7ndBeaSOMIZWCuixplOCzv/iEt373K+xsD1g/nrH747s83DtG+QF7H+8iNksmRU7QieisDUhPJswWc9AGr9/BC3yaokIiqT/eJX/nEtX9Aza/dJVFN6aYplhtAGjmC1QSOxXjJzPYAo3hj//7P0CWmq/+42/Su7CGrhuygzGLwzH5NKOYZfQvDGlt9F3U1sw5/dFdmnlGWdUIKZnvjqimGQioFznp4YjWxlLM78UJf24gjDauRkPgtEeEIEwiLn/9NbwkZPbwFAH4sU/v+gZFVdIb9CkmC3RZYxY5IlQErQjdaGTg0aQFyvg8+P0f05wtCIYdwiTC1ppimlNIiHttzMEUawyRp/ATnzovabVj0rSkigKMErTWugSNphpPOf3LW3BpyGClRxD4xL0WTVoy+uAB83aEFRLrSTqDNt2vXqc6nlI8OkM1Df5qlyZwsMNotfd0bp53ij+3UZzblIUUtL5yHaMt2Q/v0ixyqnbk+jB1Ud2mbhC1g4lYAXJeYLoJhafws4JQa+rlwIt24uojGo1OQsy0wp5OnYK1cQ6AUC77qGsnouVPU/ylA2UbR8BghYWmQQFPSHVRSz0RKZyitLVYY1yAI/BReYmwoD0P22iktFTW4mkHscQaTO10J5TWSOkKw62vMAjyuiZuQCjHcmSNxViLryS2rqmtRVkIhEAqD2Mb9DzFv7aOmaYwSbFGU6HwPOGcqdEc00+Qx1NipZwDIqHJalQ7wRSlUyVXCqs1stZY30cFAaHWeL6iCX3yRY5nXCbjSa2TzAsqJaHRqF7HZYsbULGHNi5rYXwnXqiiwL1f1Y61yljM0hF7Uni7yAq8fp/o4hrZR/cRSYDVAkZTzMYAG/qI1TbKSOSgDbsprSikPjhh+u8zysmE4OoFTFFjjCG8sklyc9NphQiY7J8RKonaHxFvrjD55BGil5BOFmzsbKJrTT6f0+iGrc0NwiSk1W2jYp+qrGi1E3ZeucjxwyPagy5rF9f57AefMM4Ll+lqGvR8jg58orohsRCFPlMlCCTEYcylK1tEgw5BP8FLQpKNPsGwA8Yye3DEwQ/voK3l+m9/ie4lFzx5ZiUuLaaXQTjOPfECj+1XLpKezCkXOcVihlUNg61NRkcTkmlGOwoxZfPMSFpmY3VRu9qesiKMArzY5+P/7o8Yvn6J2UcPme+d0d0YUo2meFjIK2Z5QXtnA08qZFVStZxW1EoSMh/NuHtvl7qsSLotZFlxOpqyubPB6N5DBv0eRaNZjyPqWUo2S2nf3HKJvrM54dYAPZnjNYbFeIHOCxqtMVK4zIiAqtG0goA8K8iNy1B4vkdRlFhfESmFhmUtj0+aF67Oz/Po+B5SSWIToLOSGMUsnTDsdzneO0K2Q7q9BAvE0qec55TjlBtXtskWOYezxdMi4WKR0diGqVBIY2kHHq21Lu2yQBtLOsv49N98jzf+6bfw2/EL++H50O4vYuS+6Do8b8id33U/b6YJhLB0b25xM1B8+j/9BZN5jqegnqQkww7GWlb6XRovJxl0WFQNl6/ucPD4yGXLs5Kg0mwmLfprkrqq8I9Ouej7BO3YIRnaCQtjkP02rTCgwYI2xMZBc/OiJO61UVGAtNBYFyT2WyF5WdPuJmgliHK3R3pKIuqGSIKWCluW4CtsoLjwpSuM7xyQnqW0twZUTUOzKMlnGX0hSIYBDVDXNXlQoX1gmvPo48cQSV7/+hufiw0+Pc9f4tk9w5U8H/QVCFerZjRSesvAwC8u5vA3af/rORfw3Dz8PNDmSRc9S6fBs/48b7j+1f+PPWfsWu7+6UewN6YvBZ0wYGwtOc5LbaxmmpY01iKqhu6gw5vffIf1K+usv7LjlK+ffrEnX+IlsK1zHqTVhjorKWcZdelEppRS+JHP/e/eYu/Dh/hKsrqzTl6UXHztCvGw4wSUsgJbaWZHExaTOaHymM9TTG3orXTZvrFDOl1w+PiYIs043T9B+YrN9RUWWYkwls5Gl+6VNayAizcv8PjeHq1WxOnhiNXVAdtXN7n8a2/ixT7t9R7BH37AnR9/xtH+Cd1Oi7JpuP9gn9OjEWs/uM2Fd65y/de/QNBNeH7zsZ+DxTfzFF1WhKsrrFzb4PVvvcHR//in7B2c8PaXX+Ng95h7H95DG0M3VsT9mPq+prXSRgjoXRwSLqPzaVlgI59qmjKvNFHkE3YTSmPp+AEajbaGxhimi4wmcvzrvnTRq0Wl+f7/+Gdcf+c6K1c22HztIsejKYssR0jFdJERhj7SCsy0wPN84iCgMZrjszFbnS5xGBIYgy93d5sAAQAASURBVBWK+YePGbx1kf33bjG8toWKAspxSj1NmX22S6MkG1+8TtBzaf5qnpM9OuDq5oD0LGVy/4jp3UP237/H/t19ahy9sPQ8PE/R7bao04xO6LP7cB8vCGikoNtKKLOC/HBMvNEnf3zC5PY+Y2UYfusdok6M1wpdFNxaylnu4CFK4ocButYESUCTlQStiGw6Z/r4hCAOyU4mNJ89Ig0iRqHHeDzj1a+96WA3s4rpnV2qWUZ54THhZo+Vd29w+NM7bL1+DbkoYZxiRguq0CcNA/yVDiGS470z+qtd+mVDHflUD0Z4cYCWkrgVIaWkqUt8T5KdzpjXNUErwJsVNH6INpCfzjFaEwQ+xen86fLLH48IVxLCyCd4ddsVCRcVzTTDa7SDRD3HZnMuh7GMsD63WS/f8EKf/jdfIR/NCe8eI9McIQQmCiiVxItCRF6grUEtqaZl1eBFPl47wiyAukEriVikqCikqhv8SmGUgqpGWoMKPAQCLSVCCGrfFXI3ZYVnJVoKV5C6pKm0UmIal5kUSrrIv6cQ2qCtwVMKdIOqG+c4GIM27vUaF3FOlCMoAAvGFfkpL8SUFY01KE8iEPjtFjryEE1F1Wg8oKlrjAUbKChqRBziCUnTOE0Aq42L9H+2S+/dm8y/f5ti4uolQs9RtpIWxOt90r0zAAc7kxIVBMiyAoSjxfUVtXTq3nVZ4XtLhh0h8bSlMgZd1U7dvW4czAwLvo/WxgncATQaLVzBu0lLjBCowEcgnLNhLJ4UaGMdeUNW4scBpqxpBY7m1pxO8ZbOn8lKRCcmFeD1W9BPUKFPfeyi4FgwVUmzu6CxNcl6D10a9PHYZUjmOcX79/G0JWon6H6bJi2IBi0GvTZH0wXtJVS2KZYK1FIyy1KyoxM3RmdzNnc2WL+6TT1ewFKgcHw8xi6NrvVrW8weHnPro9vIbsJKr8/WtW2krxgdjzgbTdnfP6G/6NO9uUXrwhDbGKb3Dln82cdMjyccPthn7+jEFdPrhi/+n37bkUm8UJD7UgfjhdbbGnLxnes8+tFntAdtFtMFddEwP51RxRGtxIl8nl+rqpugR3OMMah2gkwCUIobv/MVxncP2PvwAY2SVLsnLKoSHQbIlRZh2TAezVztw9YKxXiOqDxm4zOyqqJlJa3NNcaTGd1+h8JYTk9H3Lx5mUYbZnsjvFYLX0gY9pwDXzYEvRbl6QxPCXJr8bst6lkKgYcvJXlaECifTjdBLkkB8kVBYC1CSSbjOaHvU9QNypOES4ISXdVL28DV5+RNQysMKRczBtur6NGYPC+5uLPJyXiClZKo7TStlJLk7YjHj4+woaK13sMKKLKKlU6LbLygDnwoaoySzB/sE0YB4/GMKis5u3PA/o/vcflX3zxHY/qigfWCwXbu/edciuW2cl6V7EX8yUvbUhtFxSEP3vuMfFGANnSTGK/bYvfjR6jIiS+2WzE6ryl0jRpoNtcHjE7O2AkgO5tyNJ0z9H2GYUjQTki2V532TxwiioJI+TSLDGsN1SKn8F0QMBIQrvYcZDQtEO2IjgHTCtBZjickdpZSe5IAgWn5yKxEZBX5SpsmCvECRRx4TPePufvf/Cnbv/vbmCigvd5DjxbkQtC7OHBBmtTpBo0fnSDzhsbz0CsdajR6nlGXFUEUvqyzfnY/vmCDuaE0zOdzJtM5SRwyGAyQ8olm1rkB/Pxo/o3bL9G5EM8m2wvR/Je2l70lnsjHuwtedslLiAr+6vuea1VWcvbZPjKJOZll1NoSbaxwcWtA1Inw48DxokvJYGdIf2eVuBu7b7UsmrXWoouGfJKSn84oFwWj0wlhEjK8sEq1KNGFk5Q/ubtPdjqnbAynhyPqokQIiScErW5CEIVce+MKOqu4c/sRxoCvFLKoGQy65HFA1IoxRc3VVy8iA597nzwgLRf0hj06611WLg9Zu7zG/HTOnY/v4wnLIi9QwMM7u6AEi5MZi7MFx4+OyMZzMBqjLYOtARvvXCYatMEY2hcGvP67X8Zow90f3SI7GaGFoFxygJ/eus+ndx8xH835wj/6hvvcORCfeOF8UVGA13KHpIoDLnzjVb4yWvDen/+UO589ZnNnzam7hgqvqTBK4Qce2XjB6N4R3QsDfve//kfc+8FnnD06YTrLKfOK2JcY09CWEQ8fHbK50uOVL1xjNk0p5ymLRY5pBRSzlIHn48UJs6xACPjovU+IP3yAMRajBFEYuIhuVZOnGXEUEnkeKpDQaaG0oWka8kDSMoa6qp1xpwRmlDF49QLZ4QhRNFR7Z+hGU88zdGU5Olmw+mtvYYTgoz/5KV1g/OljPv34AY0Q2KUYWb/fRXoe3Y0V2isdPKU4fXyC9CTjsoZWzLyoHLwuDPB8RXoyo7WzCsrD6ySMj0+Y/PH7dNstmsDB13pbQ4pZjvQVF7/6ClY7qIwX+uiyIR/NOfr0PsWiIswr/PsHCAvVZszsbI5eFJy9d4uqLFkbOg7wdL6gPBuhY0U0mrM4mfP4/g+YH48RYUAkBHUc0JKeo9XNcvrA4mSK12+hujHJ5TXaWys0xpL+8DbNoyN0N8EczVBKEhpLPcsJBz1sN6Y8W1DOM1pCYg+mqNpRlxqsK2AvKkprybEk/Q62KPECDzkrKI5GxNurL98qf9b56WYzwlcMvv06s1rT3Np1jkrgLw0BsGVFKCV+FLpaAWMJPY/KGkQrwj+bQlVjAx+hNX4SYTKnCK9wEXK7jOZLFaCbBoF1BqoQVMJFQp3N7OiIhbXUWAIE2joHQ1QGX0inG6FdAENrg+9JaIUwy52AnnROg/E9zNJJ8JZ1F6LRVAICK9z3NQYlBaofU48WeEGAMRYfEEumowanTdFoDUGALiuEJ1FWoScZ9dGY1qsX0T+6g5SSvKqRytVdtF+7iPTUU0ifEoJKNw6SuqzhkELgGwPGIrXBhhJP+ksq5iejZLG+QlofbXBq6ZWridDLTI7yFMYImrrBVgbdThCLzLFwtWJoGoyURHFIk5dI6bQRhOeECaWnqBYFwcYQM10gtKUOPCyS3taQqm5QSYweSurPHpIW7jcZD/zNVcKtAemDE0wndoJ8eyPCxlCVFeFqlwWSppPgpSXxpXVaH2WkRlNWNWVVE7djpO9RlxXGl7RlgPI8TscTjv79Hk1ekWysMFksqCYNYeSTpzl6mZERvk+Dy1xiLX43oVs3zPZO6W4N2X10wOM7j+gP+0hrKRY5o/GMRepoWdtBwCjL+fC7H3LzH32D7tbgc0vmRV/jpZAZAcMr65SLlMXp3Akoas1wveeCHp2QKi+J6Tz7yNLwC1e75MtzxGX/Q+wodVS/eUl3c4A9mTAxDXVRMowTSix5XSPPFkRSMZ/M0EWNbIc0xjHLJUnMoihZ316jmKZMJnOiOOKtL7xKlNe0dobUi4JopUMzWTiWuJU2vrEEnRa6qEhWWsxGMwbrK0SBT1HVFHlJFMWEy+BJBZg0R3mKIPKxpSvallIym83wQx+NJvR81qKIIKvIPMGREhydjVBSYLRhOk9RSlHNMigaJosFaxtDIjSsdtDGurOoqkn6Lfd7hUCNc9a2hozSFD/2sY3h6iuXuPvjzzDaYrPKZVfV5yn1Phf8/Xl2ln3RenvJxS+zX62z70xds7KzRrU/ZsX36N/YZrx/RlNU6LrCFiXdrSHtdoIBzhYp9z57xPraCr4CWxhsENBa7dM0hqJpUIschcMjeaFPWZSuViYvUGFArxOhspzGDzBFSR0E1N2IlrHoukLFPrLrajBMo+lVDTbxKYqaVhAw14JoOsdmJSYIOJMwWBvgb38HWxsCazj74W1sv40ua5LTKcn1LbQCI2HtxibJ8YxinKJVQ52EFHlJUzUEUfC5EfhZ7Ynt/Cz2LZ4FeuuGsnI1au12myhaBsqfM6qfUL3/dUSqX95+Cc7Fk2jfS70Ffu7EOvfx89c/4ZF6KvL5pKDbPn/dX+c72uW/+TSj0obedp+3f/1NehdWaa12l7Se5/+fZ4/tMjo2OxhTL0pOHhyyf2vXFVUvCmqtyeoKPwxoBwGNMa5413MFWdJXdPod0BqhDdZoGizH+ykqCFjZHLCy1ediXXPno3t8+qNbDveMoNYNvu9TNw3jk7HDlM8ypIQ7H9/j5OiM4eYQPw6YHI1R2lI0NZ1eh2KRQ15y+4M7rgC2cuwfXhzgWafuvRjNn3oEYlnoGQ07XPzCFY7u7TE6HlM0jaO7bRz+uawq7v/0HoNBjyv/yTtIXzmozfkE6tLJEEvq0SejFQ57vPVffIfejQt8+Ac/4vHtxxS5ixLuXN4i7Pus7qzx8O4uZycT1jaHvPbbX+Ldf/xNrLXMds/44b/6cx7f32cjkKhuj14csUhzHt/bZ2XQJeokVMDxdOZoKYcxO29dZf/2HrPTKa1uTC0Ek1lKFIfQWEKhGHRaVALG05Q8TxGhJKsrZBLhC0ELwbip6BtBVpYcmprTT3KupAWXfvtLmLKmubVPVWuwgmoxpy5KHnz3Q84+3uPug308qWivtGmt9zEGiH2iXhsv9IgNFFXNeDJ3hcRGE4QB0reYXDHYXiUUjtq0u7PKymsX8NsR/bcu03lli87ZnNHdQ+pZhtCWh+//lNd+8xvsfPk6CIFUiiJNqYuK048fkqz3GFzf5nIrpDibM/v0MWnSwnZiGt9j48IGex/fJZ+ltAKfuwcHnIxOeHVlE6/U1JOcs/du04ym5H6IabXpbq1gx3M8IenkFYv5EU3d0O62CYymKGvMJEWfTAgbjbq0RvutK3z0//szwoMjVBwj4hgVRfidmDDwyQ/GWG2JADHLUZWmscZBdJaOntdYrISWBXU0cWw81lLunlLcP2Lrf/NtZOQ/nYkvrxR62dYiiIYdvL/7ZU7yknLvDBF4qCzHLx2csllmRYIwACmpisrRsQKq3aKZTKGqqKxF1Noh0pQEJVw0uCqQSewO1tJpH9hmqdBrrXvd95BV7YqupcQToK0zuLEaEQY0pdMYaaxFGgtSUFcNshWijXbGrnaClWoZAJICGmMxwuJbB5MTWHRZIsIAIRVWN05kTmuaRtMg8AIfVVXIOEIUJQJXXF1bpxWipMRKS/rgmOHvfAX1k7sYYxCeh7EW2Vi0hRJHw1lXJWHgoZQCYfCMwTxBqS2hhsJT1EogSo1WlqauiZRwDC3C0XEn3TZNVeFJx1Cmq9oZp77EBh5CCpoGVO70MGQrpHkSVQ186qJc8sZbMCACiZECI8BvxRhr8boJzWhGpBRlXRG/egn70/voWQ1ljddqYeZjRBiiZwuCzS7xhTWyjx4RNJbOF6/S7I0ofnqfptTo/TM6qyvoKKLKcsJWRDsMEKFHXZQkrQRfQqMN61vrHD7Yp7PSJerG3Pnhp1y9eQmKiqPDESLy8HoxUaop5yn3vv8plbDMm5K+CEmrivu3HtLajaizgtIY4m4PJRXF4YhHD/ZomgYpJUkYcGFnExn7rCqPT+/v01ntE3WSl6+dp2hD+zTAeD6L/2TF+YHHpS/doFwU7N/a5ej2HiYv2XjlAu31/jOCi/O3FgJdN7S2hwjhIG3Hf/6JEx88HrMoSwd/ipyYnx/6nE6nWN8nkJJLG6vsPzzE+B7hao84iTg9OuXwdIRVgo2rWygDB4envPmVN5mcjEE44gJbVIjY1R1p6WimgzikOplSSYWazVl/8zIdpZicTtHmWbY0iXzStMQag9FOs8bzFFWjWcxSkm6CBJRyEDzbGMJIMatrNnxFXDf4YcBKv+/0sZoK4wmidpv0bIbUBqEN8zQjakWYssGvDNs7a5TacHh6RhEFhP0EldZU84zaapJWhM0qmixHKMnmtS2ktQ5W1Imf6/tfxKx9Drrzi5hmL72pW3cy8Nn5tTcxe2c0i5Js95SDR0eIyCfpxOgVw8lkyv7uMXE7QYQeSa+FjHwm85LAk2ytD6gE7I6nGAO218ZrNH5Z0u20HbQ09LCtGOrGOVe9NkFjoKqJqhplLTIOKLRF5SV2pUNV1bStCwY1oxo57JB7iiARVMWyxkFrOssMrRr2aa32aOY5/miB1oYGQ30yx+tGxFsrzD96zNwYOjsDgpUW6UeP8AvLNMt48JMHvP6rrzsGzpe1F5y0FxMQT5G+QtBqJS6D7Sk8zztn5opn555Yno2/BLzU39q5+Jx/8zSK/Qt8u3Md8mLXPXntaUJtCW16rhP/Gv7Mk/u3h12++S9+k2TYWYrbWdLTGX4cUqcFunLFmqaqyWc5Z7unnD0+wbfw8O7+kq/d1U20Qx/ZCpHGonRI0o4RFkJPUtcNVhuSJKSqasJuwvrGBcI4IJ2mHH62i0kLdF7w6NYjWp2Y7bcvEyQh9z68Ry8JmU5SVBBR1zWeUuRVA2XN+saAxljm0zl1WvD40wd4vueibdqyc/UCV756k9nBiMN7h4yPzjBSuuhV1dBSPicnU1qBx8nxiFu//z6Xxtfp7gwJ2jHFZMH0eExv2OPkbEKn1Wat1+He40MCC35dc3Z4yvu/9wNO906IV3v0NlbYeGOHaNB5TnfjHIz96bCowOPiV2/QvThEL0o+/Tff4+NP7vL+Tz7lwvoq1968BsZQZxWffnSP0emUjasbXHj7ChtvXGT9yiaP7u8jWx0WWhOGHlJI0kVOnhWOxaMVIrSGxjAdLUjuHTK8MGR4ZYOjz/YwWcEwSYgQTKqSSzd2GF7ZwOsm7L1/n/2DU/IipZZOEE43xull5CVJu4tXNxRFwWlp2f/RiKoX89bf+xpsrLC4f4j34Jj8aARCsLLeZ+/TXRoBnWGH7uaQ+SRlcjpZcoo2DIddhlfW6a32mO2fsfh0j3ndkGCpBKz3+xgpUYGkv9bjtb//FZLVHqbRHP3gM5KdVaaPTvCMJei2sL6ktb7Jwf0DirzglV/7MgB+ElFMFs4ISSLS4yn5yYx6npP7PvmgRdBKMOMZpiqJtGBR1izyEouG2lIiiFcHRFfW8cYLEB5zY53uSuDhX9/Gl5Li8Aw9yzDtNsWgRf/6JsX9A1RZ8zidMP3xjJXDEYvJlLysqQY9gsYy7LVRSYCXRCAEtnCq1EXVkIQeep47ilLPwXwCA0ZAYwzKWBptMFXjinlDp5JdpTlR6J+LhdjzG8zzM/Rzh6TAa4cMfusLnP3e+5RnKUESIbIChMTTZjnfNabTwlQVvq8wZzNM4COjyLErLRZ41mlCiLykFLgsgB8ShoErPhcCXVaoVuSoaZsG3xiaqnbGhwDrSYTWbupYg+f7DhIjpGMlw4kzySV9tc0rlFJYa921QmAsTvXbU06jYokrDhoNS8PI1A3CV2TTjETIZZ9JZzJag5HSFTUq6RyX0gVYGq0RSrngSFZRFyVqY4A4nmAFTmTQOOpgU1boto/wfafibR3FK8vidqMdzBFPEQBSSUqtUVrg1zUaCFsxtTHUUhICNi8QSYQRIPttZF0jPQ8b+k4fJPDBWipriJVElk53RFhoAKs1+B6ialxxfCfGeIpqvKA2lsHrO1QnE0Rdk44mjL/7E7KzGUm7g/F98BXhxgqi30V4kuSVbcqHx6hBl/TuPtHxBHMyRRQ1KgmJ37iE/ugh5fEEG3rYOKAsSgd3s5YwDphP5rQ6LdqtmND3Scczl+Uy7vwtl0X1nV6bdLag025z4Vtvk++dsbt/jEWw2ukwXO+TpwWnWUYZ+xAoSAsiBHQSLvY7Tx3mqnQ1gJGQnJxOaaTg1W9/Ab8dPXdmP3d2P31DPP/4cweyIOzEXH33Bpe/eM0txeci5ucCVVIQDB1b4XlK03KyIJtlbH/xOo9u72N9QZGW9IOQQhu8VkIQBGjgbJbSBN4ya1LQ5CX1JOXipS0i3+NoNKMKCrzAY//+HqFSbg8rK6TWhIMuxWThoHfCMTc1RyO8RUauKzpxwMpaH53m1FpTVxWBlSzmKcr3kaFPUze0+i2qvHRwPOUgVE2tCQSYsmFjY4iuG8eKl7TJlUeMoVwskMoDDavDFc7GU/rdFvM0p91p02m1ODw6ZbC9ihSGdJpSG0OrnZAbjbSgVtvMqwZqyOYZK3HA491jLn77DfrbQ9KTGdaYl9r9L7PRzm+R4iWvvez5c1vuS9rT8VUu4zq/f8QkL8ETRMIjlp5DuKyE1EnNbDylWTRY3+fg8THdbkIKeLVmNpnQSSLySnM6T6nzgkgJxmVJr99Fj+bI0Hf2Qp0RVD46CtCB77KEiwI8jewkLsN8NgdjSEMf5XkEKzFR4KFbIVZbhLUIKdGRTxCGDionBN6gjYwD6rTA8xRBO2K6e4TVhvxwDFlJaA16PKe9NeDKt19ndP8YNV3w+Kf3CXsR19+59rwx9Vyn/YzOPDdyFgijmNUwcMH7c4Q7T3wLzt9egHiZKNRfo/1SYFHuyyy/7PkMxs/60eLlT+3L3uTZZPw8wu+v8QWXWRAVerTWem6SnEz57I8+4NGP71ELqPMKUzuYQZnlNMYSRSGhhCLN8eMQGQYUNY4CrR0jrODSzW1Wtge013v4gUvZN5VjrvGjgCLNGVxac3SggfMY57un/OW//CMOHh2RTebcff8u69NNbNXgtyJOTydkZc0rb1zDa4UuGhMHmLwmG885Phmj8woZh6xd3mI2npGnOZsX1nnlN95mcH2TlevrDG9u4QU+5SwjGy8IWhGThydM//IjTN0QJyH3PrrHw1uP6K31SeKQdJ5xuHeM0Rov8Kiqit2TEf1Oi47n4fkeZVExmi74yXc/xA8C/ChgfXvIa995m52vvYIXqOV8EM8m77nhlZ6itdrF3/a48OUbpLOM6tEeeyeniI8F25e3aG+2CZOQbLLg0+99wuG9A97VhrAbU5QlURyyezTiytVt18/zjKO9E8bzlE3RI2kMC2uQscedRwfUDx6zvbXGxZsXmO2e8ZOP7nJpbYgATkYzGikRxrL/6ACNIWjHeMZQ5yXC85mlBVQ1ZaJpScFa3KKscha+4ZMf3ma4OWD7yzdQUuDf3KZbNxSfPoD9Y77xL36Hq5/ucve9W8z2HNWvKhp85WF0wYQzlC/xPYUIPDqvbrPZa2Oahjt/8THGGKIk4MqXr3Ppa6+62h8hkJ5i8OoO2SJ30a9IIoFZlnH1q2+QZymP/+yn9HfW2Xrtiuv39RXm04yyqGCaUxxPyU+mzBcLfCGpRymRNpw2mrDTIe7GtGYLvDQj6g/oW4nNciZ3dwk9nwaLEo6cQEmoJgu6YURmcDz/VY3ohYRbPTonU8omxWQFjQppbQ9pFgUXNi4QSumMRCWpsorhsIue5vgHUzxt8bGIyMf6HrpaYvjjEIHDyTdZgS1r9LK4OTAWKwS2FS5Zlc5vJJbnSN1/XkRi+Xa4PWDjn/4Kiw8ekr3/gNKC8CRlWeE3DU0rRmS5i7BXDTIKaIIAu0jxWgmyqrDG4BtL4Um8usEWJcL30Oly92saF5mtG2hqZ4QIgVUSWTVoY6BeHmRh4Fh0lpkSjSDwfKhq51j7zsAzZQPGuD6yBhksi5g9R7fq1UvKV2tdkbrnYZc1EFZJ6tBHlA26ap7u80o7J075nou8AvVy/EogaJyWBIFPsXeC2BmiT6bY0MdbGvPZ41OiKHSHUBgs60ic5kKjNS3fQ1U1pbWgDTrw8ISkDHyQYKVEIaizkkZJgiSiyl0k9okhqpaOnEw8AiUpBARKktcNqhVjBXhh4DLK2sHAqDW1FKAd1a8RFmqN70vIKprZAlGV4PsMFTRpBWWFGkr8JKYsEsILG6Chvr+PCHxnzM6cWnO1e4aywulrlDVBFJCv9VEPjxBBTHkyQXoetTWuxgaHx/cCxdHDA6q8pNINMpTEaz1Oj0d0Bh1uXn+NxTSlMguKoiA9HFFMF6RVhQk98CVeK6IfBdTWMtY1syKjFUec3N9nOl3Q77YZXtqk8QV4EUFjCCYLbh2d0e932PrS9ZcsjhfX0DMEws+69OmZv9zDftYSfPKyXFJsP31BSbZ+9U3y0znC94g7MdPjEXlZglo6R9YSWUu5zDZ5LZ/xg0MS6RF1E5Ik5mD/hE6/jcbQSdoESjGaTFm7sIWqNFGnRZzEpLMMGTqYZ3U0I+gl5FWDUQFWOohSWdZIJUnigHyOM0iNRWoNUuJ5inrJyKaNRvqKwAokzs6oa808yzFlTc9YVNMQKIUvpIMpCqd/cXpwisaSNy6TGAsHC7XWUltNECmOqoKW7yPSip7vk1cVeV7hJRFebRi2O2gFX/7f/Rp1XXP8/gP61zYJ2vFLx+DFeMvT59aec/h+xrT4hdoLgy8FarVL5kuaVBN3WjTTOWVV0fY9NIa80ehac+nqRVorHXbv75POF1x55QqT8Yw88JlnJYOtdYLAY9xo1m5e4vjeLtnpGb1el0ESodMCUTeYtGQuwPgKq5csXU1NWtbE3TZ5UXI0WxDEIVHkI04n9IddujOf7vaQ6AtX8CIfEQXovGJ0+4D5o1PKSUrke5QnE5fhDX3k2gCd1diixtvoI3IHpZ88Oibc6NO/sYF34GrZFodj6tdq/DB43jP7mX3t3hBPPLmnDsaT4JCbm44Y8dlN7HmmqZeNyV+z/fJgUTz/VazWCKnOSZP/gl/0uZD3uazIix7GSzrWslzM4md4XOe+wuThMX/yf/ufybKapN/BM5a43SKbpRTWUGlDkWVsrA3YaAekaUgehlRSIBYFYSdGlw3rl9b58j/9FUflqI1zLLISL3bCd01R0d1ecawsOJrKYrRg/OCETrfNrJ85ZpemYf/Du1SV24iKWrO+ucqlrzhOcakkn/4vP+LRrYcUpTMeVBTyyruvkvRaPPzsMelkTlOWTPdHLMYLOms98nlO2IWVG1usx4FjDKgaIt8ny3NqC1IKWqFPPplxduKiYWvba7S7CXErZno65XD/hEqCbUXUaUmjDVv9DvVSUTTPCu5/dI/Dhwe89ukjvvBPvkW80nbqnE+MOLtUnlyKuoVxgLVw+Ttv0Lu0yvB7t9i9f8DR4yPu3n5Eu9PCD3w2VvsM+l3uPThgdP+I4bVNOkmCv2SsWkxT1pMYkcTESUQUKBJrkVZTRyHWClcEXGlGZcHsLz+m222xtTYgq2s6gUSfjhhNZ6RGECQhouVog/O0oGoqoiBirddmPE+Z5Dmx9FFL48bzFKMs5ft/+EP+wVuX8TdXMGVNdG0D6Uma0zFB4HHtV97g8rs3Xc1OWXPvzz/h0Q9uM52lmCJjujigOVogjSGdLSiN5ou/+UVGDw957Ttf5K1/8A3CXvKs7tgYB8XKSsSipLvZR5cOTrW61qGpNVuvXeb4wd4St+mWV5M59fgqLal2R8hJSqvR5EaQzReUdUnc6RCvdGnyilA3jISkHQYOB1oWjGzNStCnFJbYl6zsrDM6naFCn9FogqcNrTgECdFKm8k0Y//PPsTmjm/+gteGVsTZB/fx4xjP8xCFE5myStBut7CecurLgYdOC0fd3OlCLyG0UB1PMK3I6Toso8BCKWRaIJeGoVdpTAJeJyGfLIi6rWcCfU9hHL/AvvTEqG5HdL92A9a7yB/do3xwjBKSuq7wGpcpo9aErZCm0Ahr8MqK0lP4SYyYzjG6xI9ClxmQ0nH4Cw2eh5KOctbTBoOjWbW507BoTIVWClFWT2sBmrx0onZKIT1FLSDyFRYHn3qi4q2VJPA8lJBo7eqFwjCgWrLwCOP62YsjyrpBPsk+RB6H92/TCoaglGOssk7cT0kH26qlU6+2VY02Bt9aB80SwgmfTTLab21SCJDaOXyVBTHPsYFPoy0qLxzxRegTI93vWzo94ATyrBCYeYbve4g4hKIEA5WwGAuhktTG1RTFtSYE6vEMpS1ZmjlByU6MWGpweMu6Kb3U1RDC1W5YJZxejifB8zG+Ilri/pUx6GkKEvyVDrIVku6eEG4O8IKQ+PoW+YN96rRAtVqE/S71Z3t4/T6czQkaixd62GmJvzWg9aVr1JOMRVrBoINf1fhxSDjsoI8mtFY6TsAw8sklWA/iYZteO2Z0NqZ/YYgY51y6eYlkZ0hyNGF6eIYexNy98xjfgBLgVZrFYkKTOV2WWVURxgFlnrM4OONg7xAlJGnhmG5WLm3gWQNhQF1UKCm5/u5N+jurTxeNPRf2fP44foqveLZ84HNr7XO26Hk0xnMxypcYPNYSX1nn9f/yd7DG0j0cc/rDO+x+/IhGCcLQZ8XzqYQlWBr1ep6j8wrb8YkRrK8PuP/4AJRAaDh4fETUitFF7SDCRU7jSSptUGVNU5Yk6wPotahxOpC6rohCD13UvPmFm/yHv3gfVSrKoiRKIiyWqmxoZgWdOCJd1ERhQLLSJVCSRZpSl8t5uIRFrQrFtY0BlA1NUeEZS20sRVPQ7rUgr7GNodPtUOkFaV0zn+b4oY/NKmZlRZBEyEQRCo+da1ucPj7h7GRMP4qZNpqVfpvHu4d88K/+lCSMuPj2FXqX15/Se798D3Tdf96i+xy81D536Ysf/Sv9j2fvC8IkxK8aVnttHp9OiDsxaVYykhVhKyJsRWTzlKIoSXdzsizF8zwe3HmEtYYgivAFTI9OkLjM6+Gdx8RKkBsYj6ZMxlMaA+vrK4hFTqvforSCk6MzrHLBldZKj+OTEaod0h8OmC4WzEYzmqIhw3I6zzCfPGRwYY2dL1yhf2Mbrx0xfHOHepwiGuOCRr02om7Qi8wFQ/dP8fptqGqMJ5AiIPQ95gdjwtDHSEH/4irZyYzdDx9y+YvXnCN+vgNftsbO96YVPD9i7qKnlMPnzsBfFhzqSfvlskWdK+gW6knB3Yvf9uef5s9NVvH8tZ/bYl7osydS6efVv5/7CsvbVYucW//fHxI0INotDBD3W4yPx+6yRtNSikY4NdtaJVRJgpQCM5ozGc1olRW9ftcJ7xUVQRLSVDVR6DIXUrlJ4IXLmgNrqRYFZ7cPuf1nH/Lw3j5NVbPS7TAYdllkOWEUYiLB6sYAXTUMtod0L62CtZzdPWT3k8cURUm/32YxTcFTjEczDh4dMT2Z0Oq2GB1NOPm37zmlZqyjITSGresXeOd3v0LSb3Hne58ym86xSnLtrctks5TDx0dYa1jbWGE+z1jfWePq118l7rfIRnO+/6/+jEVeMJvOSFTAvGnodJzYTM+CFpZsPOdsNOUnf/w+80nKr/zz33R6BMtCfVcQL2BJlckThh1PMrixycq1Tb5YNaRnM8aPTtj75DF7d/e4f3DK2rBPEPrc++Aew0trXHvtMvc/eciw32EymTEZTwnj0IkINTU6CJCBU1LdvnYBXTc8uL9LtcggjpjmJVVZEccBu6Mx3VZClCT4QH9jhcU8AykwUYjxFbKwXP7qVfIf3WFe5hRak6HRTY3CCYrpoubxT+9z4e2r+FFA0IooAh97ZYPxDz+j9eYV2hsDN61bEW/8w69x4++8xfGHjzi8tcv4aMLseEJRVWhjiQOPtStbfPNf/C4rO2tEveRcZMGy+8FdbNYQdmJWX7+IwFLOMvY+e8TH/+77aAS/8V/9Q77+n/3GU5Xv/GxBnZXUoxn7Hz1AjuckUUSn02YjDDltGqJ2jAwDIiUpqxKtBfOqpGsEsRcRrq/QCQWVUHQ7Ca1WjCcV4XIN7mytu1qX0Hcq1JWGkxn71YyN9gpWQ1o3hGlJ4HkO4mRcgXbQjmh3YqdVUDUQeERXVok3VhwGfVFQLUrSvTPqRUlcarxGIyIfao2pmyWVKOBJR2X71iVUFKDnKXVeEiQRT+lofya+kmfXvOQ0DFs+4d95nUkvZvHj+65WoKrxfN9lFyw03TbKaLxuhxqLlxVoQPo+2lNgDMZTeDgldWmdVoRKImeoVxWi8p3hbxxNrVmuH2PNkp56WQ8gwFQ11lqa5QEklvUPaIvylaOflSAbg/I8bOAh0xIReE6lu6rRQhJJQY2CsiIYrLMzW0EVHkYp6rJCeT4GiwIqAb7WTqjNa6iqahkhc8aSFJImcxj+KIkpiwqjhCMVsAop3PlXLrUlEiFp6prA9102QYKgceQLRmOWzospqiWDVI2XxMjGQFagpMIK7cThQh9bN05B2VeQCPxF5fpaOQVvhGPmeRJdLrMSA3jaIK3FaytUHJAJQVsKvM0V/E5IeXyKdzoh2lmjiqdIAzotqRc5SOfAhe0IsdZF392lOTpDVIY68En3x6iVDn5akn/wAGsMQTfB60ToO7s0xuCv9ZBnc4qTEakvkFGI30AQhHSHHc7GMwYrfercUbMq32P+6S6np1PqssJOc1bWh8wPTglqw9rVC7SkhFZMaRpaB2c0VUPU73D48IBBp+NgO0nMbLJAG8vVN6+Rnc54PEnxQsWNX3/nqRjocyWWSxvm2TIRz9aWeP79z0W+ecny+rkGzjMYgikqdFqQ7p9hhOTS3/sq3Wtb3P6Tn6Ib7eh2D0fQdoQGV25epJhn3Lu36zIcvsew06LUhrQoGfQ6qOW+p6QCJdFFSZnmxL0WyvMQZY1Y62KEpduPKS3YqkHUDRffuc7GrQdM0xy/08Jqi/IktQZfeehGE/s+lTGcjSckcUT2hDwAB328tLXGUHqEayswTrG+4qLfZn82p5loenGbk8kJKvQYT2YgQVpoDTqUecWFzVXm05TReIbtOL2hk0cnRJ0YfXBCoBSyakgncy5d2aKcpuQYOl+4TDzsvmw0nhuXz737knEVTx89j0X5+WHmZ+PqnlnaG302b1zAH7QZ/8mHlHlNT/kIJbnz6IjuSgerJGfjCTLw0NZRUSMl25ubnJ2MCMIQqxwcdDGZIqzmJK25cGmb8dGZg1ZqzWg8RxQlc2EwSnG8yIjCgPWdDTqrfcRsxnSSsn51yOHeIesbq2RlSVoULLSh3evyePeU8njM+t0DNn/1TTqX1lC+Ij+aoirI8wq/mzgtorxCepJ6NMfrJpBXyFYEoUe/3SfLa7xG025HJN2Eg0/3eKjvcvnd606fR8iXD9XTBfWyTPwLC9cuw/d2mcE4vxh/CU6GsM/hmP76bZGmz6bRi0B74K/7LZ+v4Pi8c2Gfv/jzn7fnOutz17loy4//39/lwZ98TJkVBJ02oaeYpTkXrm4xvLaO73s8eu8Wtz97yNbGkAubA+Zak04zDg5PWV9fxUhLVdRceP0SX/vf/x2kku5ALWoXSRWCpqwoFgUnj085vn/IaO+UYpaRBIGL+gH5IgNPOcrYfps0L9FYWr6L1L32nbcxtebBj+9yenTG2qBLY62jtq0aLBYjXGQP44ocwzAk7MZ04pDR6YRGOwGwPCsYbg0oFyXZdM7K5ho3v/oK1XhOVWvu/vQe2TyjE3iMi5Lhap/Xf/2L7Lx7nbt/8AE//sMfYSQMVvuUkxQT+k65VAi0hMga4qxmNM85XqRcvLHNN/4Pv0nv0jpSndtiznvMz42RfTqFLDhM4njB/seP+PhPfgpZ/VRbYa3XYTpPORxNubC2Qt5UhAgWVUWlG7phhPJ8TucZl3Y2aOqGWhiqqqTJSuIoYlGVYCyJ5yGR3HjrOmfHY+ZpxqDfYbCzyu69A+Z5QTHPWF/pMZtnZELTtY555kxo5mWFNZotC/HaCu/8p99i57XL6LSgmaXUWYnfbXH2/j1WvnyDZLX3LDP35PdqTZNVFKM55aJA144londtc0k28KT7xNPN4/ZffEg9LVBJwCvfehuwfPzvf0CZFsgwYHB5nbWL6xTHU4RUlLOM+eNjikcnqLJBS0k3DsizHE8o8iiAuibSltQ0jqmoaYiEYGwMa70ujbD0pIdc7yOMoawq/ChE+B7lwQTZifFbIcQ+/jhFhB74HuPbu0SbA7LGMM9yOo3B93w8XxH1WlhrMUrSnM2QqROes0t2FK8VIbBLOlbjcOih08UQQjiDXBts3WCWBnqVZgxfv0jv77yJ146fc8p0WrIYz2kNu2hrCJPoZ2xGL9vPlo+N4xvVZcPi9j7zP/8ETmYORlSU0E4YhT7DwMebpg5iVFaINEMbi10KHtqVHnI8c45B4OMphWon1LMFEouUCi0EhYA49LFF/ZRiWNcN0lMI6cS5dFXTNPVS80XhCVeMrMsKjcX3A6yxeICNfbzNPs39Y6f2LZeED8o5PRIneBd/5TrVg328sxyAEolSktJafM8V1goLMgpRjSbNcnwlUZ6iKlwNhsEy/MffYPTvfgilo6vVUQBZgQ4kge9DtqwLUa6frO+jXS6aUHkYAfV8gYhCIlzdhzUGXTd4cYRtGvKmIVAeQgmEVM7Jql2WwsYBar2POk0xWoPvWKqsdE6bNNZlnfMcL47QhSuOt70EFfs0eUEY+oTfeBXOZui9E+q0ILy8ymK0QMUh9e3HxNcuUIwX2NNTkndew2u16Lx5ifQHdyiPxpjQqcVL5REoQZ0XNEqirm8zuLHF/Pu3yI8m6HZC9slj5NYKh1nOeLxgc2vdCXJpV2tSLQp6vZi6alhfW+Hos8dMtWZtfYWtK1uE3YSTh0ccffaYN3/1C7Re2aJJS2ToEfZbqCXFd5MWnH2yx+nuMaJpyMYpD+/vIeKIoiiJI59v/Be/xvVvvw3Lc+tzVsOTbUk8WS+fd8pfNEJfCkKwLzvWnwQC3H5pG83Ze59x/88+pE4LDg6OaaTkjXdf49V/8i1u/Xd/QpoXaPmkFstS5hVNViDyioVuWNkcYKRgcTZj+9I2D+4+pttvUaUF3V7bZcbTgjD06N64AEsoWqvTQXUT4s0ui9v7SAHhzhr5rV1al9eYBR7v/d73OTqdklclK90Ooe9RNA1Ju8VkPEVrg7WGTq9DNs+wWJJ2TB/JpdUVulEMrYhivIBJSp4EjJuKMi2pq4YiL4iTiFboMZukdAc9gijgbDQllAqhFEVVkSiP1W4boTW1hSrPyYuaWmtW1vu8/Z9/m6jfQiYhfhIusxbi+e3u/CgsyR44d0Y/N5ZPh/y87WVfmrH63PCeH/zl8/JgzO7//D3qSrO/e0INJL7Hoq7ImoZBv4sfB9y7v0sYR5SLjNpoLBBKRVaUREnMxoUN5qMZ2mg8z2O+SLECkiigvdJj/+E+3U6LRgiiyCdpJ0xOZ1y+voPWhsPRGOVJ2knC7GxGkkSsrPa4d/cxrWGLdq9LPkvJs4Kw1oRSoRvDF//+19j+xqvorCS9c0i0scLieMLkbE5/vU9gDM1oThUqvKqmFgLRiYlaMUo6e9JoDVjmWc3Rh49pX1/j2tdecRCpF7r6+Szgz8sPne96uxy3l1/faXde+vov0n4JmYtz2Mq/+S3cn+Vtzv9Q+/nLfm4TL9nU3Gfdp5uiImknXPnSDR6+f4+yqmlHPn7s8+bfe5fFyYRP//2P2Xt8RANsrK+ggfR0yuODU1YGfXZubrN6dZPv/dv3OH54zHv/8o9IZxm+59E0mrJ02OpsnqE8hR+H9H3Fiu8xTUKqeU5R1a5O4eoWnV4LpTwWJxOaWtNqRWRpzmQ8Z3znECtgfDphsNJxGNUgIAoCAnDRFGPxI9+xAPgKoSTjkynzozEVMNgaMjmdYOqG/XsH9NoJ3V6b6cmY9//oJ8wmc9a3V3n922+zf+sxJ4+OaQUB45MxP/5338OPfFYurdHptTg8OKVqx0hfkZUF0/kcFfisX9pgcjplVFd4SrDVaXF4/5D/z//1/8UXf/PLXPnKK3S2B8/Srs85Fi7T5JRdn0U7hJK0Vrvc/M5bbL91hQ//3fd5+P49VFHyuChBCNrdBBl5iLRiYR3DTCdJiJWH0paLW8Nl9N2glTtohJQs8pwQy9w4eIdnYe/hIZXRSAmP7jstkFe+fIMPfu+HpBgenZw+jdLXFiI8ykVOEHoIoxgD8zTnoz/9gLWddYJW5AQCj8YEwy7dq5uM//Qj7FdvEm0OnmKNn/zWoBMRdM4bum4um7R46rzL2HFeG2Po9vuUMqO70UcstRD8doLVcPndm7SGHUaPTnCltVDePcAfLQg7bSqvpKMtngGRJBSNRghQQuH7gn67je4l8OiELFBcacUIIZGBT6EtbamcboOSzsgKDDbymU9S/KrBHje0o4CwG6PLmnhrFd0K8EcLBmGElo4FRYSec4qPp0htiC2UxuInkdMTkAKlLbUAjF1GQAU1lsZAIHAwtkXxtPbAF4Lw5jaD/+SLLir/JJJjoZnnTH5wB7HRo04CSq0J4+i5Ln/2+MWN5NzclRJTlOQHZyTXNok2+pz967+kPJrgI7Chz1q3TTWe4S3JKFQc0VgLTQNxBOMpLFKsNVjfcwJ4SlHXDSoKUWVFnURQ1fjWOohpo6nbISYrQCmCKEQtsbJ+GKBaMWVeuGLuqkZoQxi4FLuVCltWrn9xULHaWkTToFuxc9CWWhmNNtiqcgrWKsCQI6UkVJ5TDbeWRkMsBI3WFLkjUkjCgLppyOsGA4R1QxMogiREKrHU1hD4QpJaSKSPMAJrtGPCUwopBcJT+NoZCmXTEAx6yLpGtUKavMFa8LCoMKCpaoxpSKLYZTuUc8iEAmU9rNYYo59qh2gpsLV1NXS4IIYQAk+AlRLdaNRSP0QOO5gkgLki6rToXNti79EJfhAi+z1MXSMagz2e4HVaFEcT1M4a+vCYyQ8/Zuvvf4ez3/sx6SwnjAOC0ynq8qZjnCoqPCxicwV9NqfyPed0BAFaKapOQmOgKmq6/Q6X3rnG8e09Hn3ygKtvXsMPfB5+fI+Lb15i/6OHNJ0Iv9Gsbq8RdBOstnS3V/ns/Vuc7J6w2D9jVlXUdcNwY4W1Ny+Tn8yQAvprXdZe2QLfw2DZ/Pgh45MZUS/h0pev090ePucvPBcE/VzWgs+dwS9Gr19yybnXz0uxLv8ug4aTTx6TfbbPwU/vMytK+isdtuUmZZqRPTph+v59Nt++zO0/+4hWK6bMS0KgqBrwFP3NIeZohGmM86mVYrx3QjuJHCOVdDpDobbopsGgCcoa43mIMEDmJbYX42/0qR6dIs4mmMfH6MBjfv+I9tUNfuf/+Lu892++y53bj4jbCdL38Ksaz/PQtaaqazr9NmBphyGdOCCIAq53uyR5iXdhyOl47s7YrHCOhTZMxjOCwKPdadFttdjdPaC/0qHIS4pFhjEGr+UykpEHgZYMNwesfe0Gi2nKgz98nzwvWdta5fJvvUNrZ4gfhecG4uW203Nj8AKaBM47GZ//8MsSw8/d4UXH4skzbXj0h+9z+9OHhO2ElUAwB9KmRiUBofaZTOeUpzXddouL13eYTRbc/ew+w26X3kqX/f1jpKcYj6ZUVUUvSZa1dwIlwQsjt4+EAd1Bn/l0znS8oFqUXLi4iS4qHh0cE/dblGcpsjbMxjOSOOTk8IwoCqgnJZPpKWleELQjbOQzLQoCP+D41h4rN7Zd9mKyoPPWJXrdCOG5Gp1g0Ma0I1g4SKgKPYJeC23BzHPqvCYctpEIeoMWi5UWzSgjm2X0Vv2XOhDPutOee/vn2efilwqFOt9+ibCo8zmznwUzWP79Gb/1c14v8Nfi2/0rLrPa8JN/9ecc3z1i89I6K6t9jg/OOD4asfPFaxx8+IAP/vAnpGlBr5Pw+o2LdHyfRwennIzmrK8OeP0br3P9736Zgw8ekOdOhXf3oweEvo+Wgna/hWzc4be6PcTH4fYPjyekeYlUkp1r27zyK68zuLQG1jJ5fMbp7QOiVsTp2QRZVkRRQKfXZvfBAX7osbU1wArBeDQn9j3a/TZ15bisF4sMr/So6ppWErnI4iLDNIZ42OFL/9mv8N3/4Y/xw4Ct13Y4+PQxs9GcOi+oypJO6DM/HvPTP/mAa+9cZ/PKFne//4mLFJc1f/bf/yH9lR7pLMPUmsTzWcxnFE1NkER4QlJNUpqydhFlW+NJxYbvk0vL9/71n/P+7/+Ir/zOV9n50nXiYQcvfsLdbD8/dC8krwTQGrb52v/217j2jdf4wf/0F4z2zxhsDaiLmse7J8ShTxD5yMCnEYLKE3STiIvvXKOYpFRlQ5WXFGmBFwZkacY8XdDSmgYQgaKsKpSSWCERSnD7p/f48mqX13/lLW796BZjNEVVO4pKP6CSgo7vY5WkkZbKWEpjePDgkA//w0/40t/9uhMUKyqKLKN9YxspBKe/92OStRX8QYvoxjbhWvf5TNuL81Y4kaUnUMOzO7vMJhl+7YpqgzjEaEO9yFm/uE7rS13Kacb0/jH2/hFpO0CUDUpbFoGi001Ikoh6msIiw5cS4ymyoiZpxa4Y1vfxpcdi2GOwNaCZZeisIkdgPUFR1uiiRBgnVGY9SdCJCToxRVlTZgVp4xy1Ji8x3QgzywiMpfAUQRA5yOAkxc4LlDbUwqlO+0mIrTVaCqIghMBDWhBpQVU3mG6CrxReVlI0mqCukb6HCTwIPcxKwsZvvH3OsQBT1mSf7ZPfOSLPK9TJnGZ/QrTWpZCe02txnf103gFUqYNFRJ0EP/RclP+J6J6SNMYQWghWuwz/yTc5+9fvoXdPkXWDDn2iVkKj5/jTlAZLLqAlJSYvqBCocslkZAwqjjBC0DSNY40C5CJDeg5SIaxFS4l6UhMRBvj/f9r+61muJM/vBD/ufnToiKvvhUYCqbOqsqq6qnU3m2T3UAyHs7Ncs1lp+7Rm+7DP+1fs89qOzczD2trakLThzLI5bMWuLi06qyoVEgkgAVytQkcc7e774BdIIBNZ1WxW+wNw74kT4p7j4f4TX6EU1SJFxCFWCsgKPITr4PoePlAL4dYkDNZTbq4VzgfCKuXcvvMSi7joqHpUpnKcCwt+6AjANcIpKUmJBTzfc9CzoiLSGhUGGFMgpCIRkPtQlrW7lsZCbbAXVdQgzfEFLLKMJPCJuh2sdXLD1vfJioLAc1XYUFiUMc6tOwrQaYWyxiW7uM6VlQqEYFlXTrIY8IMQg5Pq9KKAKi2wZQlhgO/7UFQY33tq+iebCRaBKZzeP90mctBCj2Z4UYC32kZGPt5oihkuKK+s4Rc1s2lOo8iJN3t4YUQxXaIGPWJds7z7mHpZE+Q58bV1ZCNBXVkhvrpOfTql3DtH1RadFRTvPcRqjW03QBv8jR758Zij3RPagzYP37nH+PCc1SsbNHtNTKWptSata3ovbTM7n+DnFXffucvWzR0ans9kvmTr6hYlhulwjteJ6bYTjh+dUpea4YNDwmaC32+6YLs2tK6tcfMffAWEUzRyxGRDtSyQSqCi4FPM9rPj6bGLB16cffzi8eT5L9jLdVZyeOcx1eNzWht95p8ckWhDqS1GKFJjuPet9+hvDQiCAC8KqK0lbCWExxqvEZKez6hqTRIEBHHoDFPzgkWRs9JfY2Wlz/nRKb12h6TfIYg8zGiK6bWJ2zHNb9xyyUK/RXurx6woXSe138JUmuJ8jl2WvHVtmzduXSJvN3j04WOH0S8qbtzYptNuus6/1ly5scXgxiZKKpbv3EcrCcawujFg+eiUpaco6hpT1sRJhNYarQ2zxYIo8DBAluaoQDk37lzDYkmjnaCV5fHdx8wmc9bfvMpr/5vfYvjgmLVXL9PYGTxfiP0l8ecvO+Xihn/6BGs/F+49+d1+0QPPDgnJRg/fU3TbDcqixJQ1nnLO58JT+I0IPa0YNJtorTk+OiXwPEIE8+kcYw2B8MnTnKSbkGcFrTBk0Gwwz3KWiyW6yOkN2qRpytrmKub4lNgqrDEcHp9Tmwq9kBjp/IuSVsx4MqW91qVZ+6xc6pJlJZ882GdyOKTuNvGCgKCbYGrDYveM5qVVgkbk1PqaEUmvQXFwSm5qhKcIVluY8xlGW+qJ822Jek3qeko5zwnigHqypL3ZYT5asjif0ey2UE9EDsTzl9EYVyz5RTHFZ27t38n4FUjRiv/0xOfZLtrTQy8IOv8mr/PZJ1ykzgIos5L5wZB+HHFw94D5IqMd+dQZqLzmJ//LT2h3Gty+sUOr3aCcp9x7eMBoNGPn0jrXfv1Vtr92EysFK7e3ee0brzLcPWW+yPCVIlaKbJHRFDWm2WR6OiZfuoSi1WmxdXWTrds77HzjFn4ccPizh9z/y/c53DtxMpChT+ApwthVbUNdk7QbNDoJJYJ0niGVJJ0syOYpKvCJwoBmEhAoRe1J8rygMAa/GWJCj/l4zt4799F5iQg8bv/em7z+R18lmyxYnEw5fXDE8Z1dRsMpa4HHox/fJRi0uPV7b1EMF3z43fcgL0iF09Te6DSZn40JopDVMGBxAcWwQrLi+VQahFQsixwlFNUF2fpgNOU7/+Y7rH3nA8KVFoNr69z4xit01lzVXSr1vHjPZ28hrrq/enOTP/i//hPe//Of8uF33yed5xRFibSOuKd8p7JSGEMhYL57Ruf6BpESNAZtPCkZv7/LkTZuoR6dM49jTKDwwpDrb92guz1g72f3Ge2dkWYlZ49P8MKAyIfxcYbwFbaqWGpNJwyYFDkmCbFljXUeVRzf20f/7pfQ4yUi8Ag83zkj39iiYwxn379LdTQi3j2lt7NK62svIUP/hV92lYRUk4Xbu4OA+nhIPi3xBm1Wb2xQZzmzRyl1UeP7HuN3PsEMZ1TnU5SnyBsRUVHjWQh7LSZ1TVBWmFAS2xgDiNrQaTUIAt9xAfIKFYesrHXJPemUObSG2GPrazc5+u5dfG1pWwOzJXq9h+1ENNoNotyRCutpynxqaAQBelFAVqE6DRq+h2nHyLM5auw2WSslXhIglgV6maOtJYgDTHUhjRr5VK0I4zfwFgV2OKH2FJ7vYS34WUleVqiVJht/+BVUHLqZc5EIpA9P2f+X34FKI+LQdU2Gc9KzGZOPDxh87SUal1YQT6li7k6UWcHdb73P+OicN377dQY3t/CbTudf+h7dG1vOafUCrtf6gzeZ/U8/xkyXhK0QnTnYmFzkAMRx4HwTpnP8KEBXNbqu0cYio8DBovLSqUX5PlpYpDEE0ilGiQv3bh04MYR6vsQTwsm2GichK4zzsiixhEpRehKvqPGtojIWzxi0VEjlktZKClSlqY3DLMuLKr8VwglRhAHC99374kjcXruBzQsHKSprbFWh89K5KFtDbiD0HKdCdxpuaa4NwliU7yOsJbQSlXjI2lIWJbq+MIwyhjgM0cKZJCopwFiCOKRGoeMQm5VooymkdeRsYzB5QSQkvu9B4LsuV+hhL7w5xCzFkwJCn8oYAoC8xBNQa01V1XhKYkqL7Tfp/6OvMfrRParcGQPSa4EQtN96iflPPiYKfLK545jUYYSZLlE9RdCIMGVN0B6QPtgnWO1TWwdviN64DIFCpzmLe/v4q13Cfov04BwaMWVWuORGeiAkjXaD1X6XWsL4fIj1XVJ39MkR6TKlf2MDnVfMz2e0O02KXNPY7lMJy9lsTtRrMtgekOU5arVNmhfkUUggBQtdI1bbNPttwn6TOiso5hm9m1vIwAME9qKj+WQNLmcp4cU6+/x2+5ko1T577JkK9pNDFz4sv6hQ/tkik9UafT5HdBsc756xutpjMRyjrcQLfdR6hyItGC0y6EYwz1nMlgxPx4hOTFkULBcp/ZUu4/EMb+kRCYUJA8xyydnhKc1mg7ARo5cp0ZUrJM0IfTLCa4b0/uAtZOi5z2Xc+iSKmlRJvKLCX3McmGyyRC9SvGaMnKTcaDfw+21nvjmeuS7j69eZ7Z3jdxIal9Yw85xZEDgPmVnqlKEWKbIZ0tAeeWjoRBF7jw7wPY88rZBKMD+fcXl7HWstB2fn+FGI0ob1fofWZo/JwZDFaMboz97hS//8N7j6+28iPPU0sbA8KYC7C/7kjry4DvwkyxDP3NAvHs+87At6Hc9BFz7/fkKw9tWbHL37mKPHJ+xcWqO32eDwk2PiUCGSkLrULM5nDIcT0qNjcgVKCk4Wc7zAZ6XTdmaDXo5QCmNKPN9nni1BCrbXVzg/OqeazFmUNVXlIKXDxYJ5mRM0AlQhqSvjDEMlJL0W6XyJHwUsj6bkacFkvqDTbzPLlggD125eZjybo5OA9GRCa6VDsjX41DC0GaECj3izj1kWBBs9Sk9iD0eYrEBJQVnUZEVFkgTIJCAgQGExvmK2N6TRjOnsrLwwgVDyxZLOn177Fx3/1Y9frUP3c+MFE+9Fwf8veSXBCzLdv+XwQh8R+CQo+klA0ggQxoJSHD08Zm3QYbDa4XQ45YO7j8nSnEYc8vpvvsHL/+DLNNa7zE8mHPzgI2ZHY+JWwmt//8vk05TZ2ZRivGB8d5dOt8FisiTLSi5vrRE1I3pX11h78yrNjS7SV9z/s5/z3X/9HUyt6Q+6tFoJVVVT5gWT6QI/8FFRyGyZU2nL4fmEUCkuv3UDgeDg/j6y1hzNRlwa9JybrLWU1jkWC2NQShIoxbt/8TPiMED4ij/5f/yPdLcHXH7jGnEz5uZvvkpn0OGv/uVfcjpbErcaFIuMuz+4w9rNLb78j7/BvR/eYXJwjhSCeWWI2jFZpdFLB4WQUqEXKUUzIV2mFFX11PiqIUBrQ9cPOJ2nfDiZ0dwPOby7z3t/9R7Xr23R6zRZff0Kjc0+Ua+BH/lO59paBPIz3T/nzPqVf/xrvPwbr7E4n1NVFTorGT46ZnoyZXjoyJMlJVxvkNU1e+89pi4q1ld7zE/GZBaML6hWB+hlildrZsWMD370IVtbq6xeW2fnSzcw2rD7ySHj5YJFWRIHgZPJC3ziMKBe5jRERA6ObOt5SCkYLjIe/vXHrCqP9lduOD36C9m+zs1tyuMp54djdCCZ3j+iTAtaX79J2HBSgOJJhfli7qswcBKGteb4YER7tYdX1dz/9z+if3WTCOGUKAoN84wizRFS4iHw5pnzoYgjqqImqTVRp0l0fY3ZO/dplrDUGk9r9CzHRCEK4fgLqYOfVcscGq6lO37/MXV1YcomJTNP0Tw4ZzyNmEnpEm1P4QeuAmRHU2Q7QYQ+lcTJ9S0L9HDmvtyeAk8hfQ/RUdjQw1/rQK3xlyWmqNz2s8zxGjHFaI7yFKEUVNqRmnXk0f31WySv7KAi/5n5YqlHC6Y/+Nj5GGiNyQpsbajTAj2cEvVbLI5GaK3xIp9wpYMXeOjK+cp0ug3y8ZwyLakrzbOvDjjTON/JVDbiCPtbrzH7459g65o0LwmTAN2MsGXtCMzGuEC2rJ3vhJTQCtHaunnieyCcyrgfhGRlSSSl898R1p2vJNpahHWcAfIS60lMFCBqjcg1Ca4K6gURtvLQpca3wjm6S+EMuGoDvqI0Bl8qjHYSmWQVlXU8BGNydCfBjJeug+Z7SM+jpnTuv4CJYyeb6nvYsiLUhqKq8BFO3lIIKAqMlEgsWV4Q+YogbmCXFegK31OUCKrSdR/wFKqqqcMQb5nh3d5EPjoj1JZaWIQEWzlDUlXVhEkCnqQsa2zoFKWqsiYUlkAprC6ofR+/GSPzijr0CJ8kco0ImxXknkfUjOj8/ltkj09Z7J2RdFsERQWTpavIXnQ5w+GYZaEZDNrkywwbB9RljVjkeHGAEcYFQVmG6DacI/jjE4q8BqOprWX68JTwcERQ1fieJGwn5EUBeeXctP2ArSCgaEeczxdoYxg+OsSEHkE7wY9DFsdjNtdXaHcbLKOQ+/ceoS9gcenDI+YHQ9Zub9Pot/DyEC8M0AbqRU6nkZBNl7SEYvDqDv5Ki8alFZfUA+VoweThCV7s07m+id9uXEgSu3n3OeTF5+Qs3XewmGUcvveQzqVVdF7x6Ad3eO0Pv0qy1v3FCcaT17RuTSyGc06OhmysDZiczwiaCWpZoNOcapZhFzlZ6BNEHqPJnE67SRwbzoqMdr+NHdTM5kvX2VOCNMupU0O326YVBZQGZFbiGZBl7czGBi16v/36pz4c1jLePQMpibd62HmORVGkJXVaYCsNnk85mpN6Ps2NHouTMT4Z3umQWlri2zsoqwkt2LJmuXuK12tQnk/RlaZeZNSLjKTdYFGXFIsZ5SIDa/GQrKz0ebh/RNyMOZs6z5NWt4WMAipdc3/3iMbROf2VDu1Bh2a/SbKzgvC8C2TT88nEk0zgs2H/xe37goNfNJ5BsdjPh7P2s/NDPAOpeibYy/eGZLMlnSQijAKKZQFKYiuDKgyRgJWVDtPFkqARo+saX0DuSZTvM5wuCH2Pbq9FbQ2pcMZ0Bsvm1hrtQZvFZI7yPLLFHGM1rSjm0tY6o/GMShquX9mh2Uy4e+chvY0Bsedz6g3prHVRvkc2XbC+sk4Q+awLB4U/Ox3R3egzmcxpWUhnS7o3Nx0kvLbUc+dnJH2P8HqP7HhMVRlsHCIqja01Rea6hF7gYecZXrdJnmZ01rsUZwuOP9on6jYIW84O4dkL/IXh8qeZ5NMD7tb+3SQav7rk4hmlqM/88OSEZw5/cT/s07z50+z4b5iTvHg882R5gWs/vHdCXVUM50sacQS1IY4C0qJi/4NPUELQ7jR543feZPtL1+jvrDDdH/Kj//7PefT+I4xxDrZGOOKiVNK1wJZL6os3jQKfyPM4PD6nrCr0B58w+PFdtm/v8No//hrTsymT2Zwr66tstCJqT7G3f0qzEXPlpUvsvH2T43cfcv/DR9S1YXNjwKVXryA8xfx0iu95lGmOrjRHR+cMs4ydXpdRkSOFYGOlizaGsOlgKsusQJYST0nO7x1y9OFj8ryk0W5w5eYOnnTEymuvXsWUNffef8AH3/o5L//Gq/z9/9t/weJsQj5NMdYyuLbh+BsfPubkzh7CQrYsON47Ic1ylO+xvb1OsczIsgIjBRNdgZJUWUXSbLK9vsIizbjz8/vEQYD6649ptRtsXl5n9eoanavreMrS2FnFS8Jn5otwJFIpSHpN4m7z6UM7X7qB1ZbF6ZijO3vs/+whu+/v0ho02byxSXY4YTZbMtKVu0u1ImknTgN+kWOFoihKPr7zkIcf7TJY6/HGH77Nl//JN7j7lz/neP8U63koJenGCZU2RHGDOAk4OjkjtxfGZdYRUc/vHdDbWUcgnDu0seBJhITua5fIq5pimrqK1zxl+L27KN/Da4SO/6AUzZd3XAUsCtBFxdHPH2ByQ3HvmOjaGs15gZhnqG4DXQtEaSD0yApLq50gw4BESeQiJ/Q8SgERAs8Kzj/cpekHVMsFhdU0pKKSgmqxoPZCzFLRv7pGrTWJ5+HvDEhPpuh5Rez7UFWk1joTOeUcfe1siS4rJyvajKAonemedcm9yWsoF0T9Nt6bV0BKVBIguonDiVvrSIunU7wLOVOsJZtllEdjVOZUgox1JF1pLeHNDZqv7hCutJ+XUrSQH40Y//9+gkQQbg6QB2cOU68NGovUAltUiKImGy1orLQR1pIP5xTTlHI4p+f5dC+tobRl/LOHlJt9Wjc2kJ73/NImBEIJkltbnL/XJxgukEJQLXIaG12qh847xmjjHKw9D22BKLjQspcoKSmNdn47UmB1TaQUpqzwkpDCWHTm4HtKCLSUGGORgUdtLamUNNc7iNkSU5TYdgN14RZbVEs8KQh93yUEuYN0SG1cN8Ia6otztRB43oWxXFnjJQH5ZImyltD3sVmOwiXUpdaoKCKvalTgI6Tj5ng5yLrG6zWop0syIEGgK02sJLWQqFmB0vqpV4q6kNn1g8A5Z0u3Zlkk0fYKk4+PHHeirAilxMPh5o02mLrG1s79XAqJMLiOjlR4nkIjHGlymeMHPl7uCOy1tUh5cS3Lkugr1/F6DSZ//i5+MyYIPIpZjnp0Sn1jg3DQxjcQxAmd9QRvkWFPh/gbParJ3BUZkgRRV8RXt6gmC7ysIJ+cwitXkVEIpxNkmdNY6RF4AtFrOT+d0ewp5yRMErIkRE0bqGVGMVlQWLh84xLzycz5MAjFx/f2SF72aG30mM4WLMZLrnQ6JI2Y5OY2Ukkef7xHa3PA8mjsIGJFwep6F2MEnZVVBl+7ideK0Wnh5rJ03bB6kbP77fc4Oxnya/+nP6J1xUF5y8mCpNf6jPHdi4fVlk++9R6np2MW334fP/A4ubOLH3h86V/8ztNg87mI4bmKolvz08MRy0VGc7NPXTt+XY2gFiBaMUVREoc+OvDwPR/bTJinOdqT+KHP+OExNEIwlo1+h2GW0VvtkeYF2WyJnqdMtSWQgq0rW4hFhtYGf6vrzDiNQSAp9s/J33kAoVN9a6+0UZ5HMU3R4yXKEwgktfLxywpRVPSub1OVJToMCIUh3xvhZRqjl5z+1fvoeeYKFMMZSyDpCIQxzIZTKmtRxlJiaa92sUXNaD4nCQM6UURlDEthXXGhNth5QTtwqnXD8wmBkpzun9J/+wbxZo9PYWqfidFemES86IZ+emdedPyXPO3zBy6CY3sBdXQZiWV+/5jhaIaUkunDQ6eKFvoM2i38yOdg7wQ8Sb/VYloUtKVHN0nYn44dumSly6DT5OxkRGk1GysDqnnKpHZKkQ/uPGR7Z53pbEFLNgiVottuIYx1hce0pkxz9sdT4l6T2PeZjmfky4zFAyft29nq42tLXEGnmTBY73N6NGL28R7NOOBsvGDrrWsAmEpj0gI/DhFXNxGeRznPmOwPaa/1qKxAaeMEUqRAyBjp+2AN5TzFi1zXrLXdZ3k64fzeAVtvXgcln+k+vegifzbe/rvvWsCvILl4Cl56wed1cb199sTnnvWFf+Mz+BjnJvi3SC1e9EWRgitv3+Q77z9GWNc+mi1SSmMIdE3cjPjqH7zNytU1elfWSFZapKdT3vsfv8/9H3/MfJ6xeWmN1c0B5fmYutVgcjqlzAuEtUStmEu3LhG1nFN3Ol3y0fufsLWxwng0ZX//lDwvaa902HnzGis/vMM8L2loi14uqI2hv9Jh++UdqmXGnZ/do5FExM0EFQXsPzikzivKoqSua7wooCtctaFpDbXRlHXNRrfNclkQhz6tVoOrr11lOZqhK838fMrp8ZBWO4Gyppouuf+ze8SNCD/wePTBIwYbA5qtBnmac/+HH3Hz115h/fbO03v2JNO9vdnn9u9/CaM11bJg/50HHLz/kONHRxzvn9CMIzrtFrUSbF3aIPAUP/vpR7SaCZGnyBBsxxHDumY0mTKZzzk6Pqdz5xG9XpuVzQGXv3GbtTevPIfxfeKs/tFfvUe5LByUR0J3rUdztUPSb3Hrd9/k6tdusf+zT/jor95nMpyz3ms5LH+hiYKQdr/r8KpGQCOiOptz/aVLVPMMLw44PB3y4//5+7z2zdf40j/7Jtl4yYMffsT+/glnZ2OqtGT7yiZ+4NNJEhbTEk846EqgDVWpKZVicTSk/dL2cxUCv9Ng42svcfLOffKjMaodY7OKGofpD9c7VMcTRj/7BOtLZiZHDHOY11BbppMpO7e+TNRpUB6PoDZ4voeJDXUt6MUN8Dzq2hAlIWrQwhuneMvCJT+zJXEjBF9QdJvY2QI/8ikjj8jG6NIF8XaakknQ1jC9d0S/lTj8f14RJyFmMqfSmkUSEQYeYr0Hx2NqZUB56G6MTHMC30MXFVYKiryi+vgAvxW7oHeREsU+vlKkuXOn9roNVBiwrA2FtZRFhR/4+I3QrSnzDKE1za/fRK138bqN56tlxjD/2Sec/8V7iE6T8FKfxA/IBGSPjhF1jfIUOvSIVjpUF9yAYrLEb0aUowXZeIEoHTF5MV3iz5ZEgzZ1WnD6k/vEvSY29lEXGFkvcD0NFQVs/f2vcPbf/ilBtwPaElxapTidomepI3h7DuuP5zm4kPKolKQuNcq7UH/yFLKqnGu15yEsiE7DrYll5aRTpcQADU9BVpJEwqljJRH1yQgbhciywlMKfUH+LrQhMJbyaEIQhdi6pjZOJlUKiawqtHUE9FJrCiFo9pvYgxHGGOqioDQukZZciEoIgacUQhtKramLi3lmLd5Gj+psSux5CCGd4V6p8RMHAzRC4ClnLiouuiraWMq8wJcShaXuNbGL3HkuKEWolHMvtzjTxQvzUlNr/CDAFtVT/4JQSsq0wL+oFtqqdoG8UhhP4sWhI+gXFWEc0PjyNUZ/8lP0IkP1m0jjNpNyNMd86wM6/9mXSW5uYU7GrPzay+jjEeVoSjqdopY5fr9PmefI6QKSEK/VQvse+WyOryu8OEIIgbSCsBXR/NINyken6B/fw7Yj1HiOHbRRRtMQgirwibXh0tY6e2cj8smcIHBqWvNFStxucHR4RqUdtK3f67B9bYugE6PTisVkTp7m+Kczrl7bQrQiHnz/A/T1hOJkwsrtHayx7P35uxS1Zu3WFr3b26jQp3l9nevfeJX0P/wUK52rdrHIXVfl+SLoRR7w2YMuBpiXJfd//BFlVtBa6WCU5NGP7nLjt9+ktdl/YSzwbBNEKEFZVgSDFr7vkZ3P0L7E5gW9Xovj0ZSw36TQmsDzkPOMXivhNCuIuwlmktFZH3B0OiJuJ4zmCyptqLRmOV2yubnm1NvGMwatBBUGqKIgfOMKra/efCqkgbWUoznxoEVxNsH0OmTjJYEvnb/NVo/i/QfE3S7RWo9095R6smSxyAlW2tRBQDFZsDie004idGXAs0gBZjhFtJooJaku9jihDVVZIj3FYjzn0vUdCp2R1yUqCpBJhFmmRIGPqA2+r8CTGF/S7XRQShFYZ8Abr7S/qLH0dDwLbrPPPnQhy+2e+yuKxz4T7Ipn/cmEILm6SrvTJPF8Bptd8pNTztIS0RXkxpA0I6RQrF3b4NG9PWxlHMTWWhIp2ei1Wb25ydnuMXESsrk54JPFEqkN6WSKrmoO945IkoRW3KAscibDCX4QoKyg0YippXBclnnK6e4xXuCzvTKgKmtmjZCwGdFsNTjZPaGuNXqR0o49iEPuPdiHvuOSycjHVBrViKiXOf6gxeTRKViLEhLPVzQ3epTjOfU8I1rrUOyfo3stRBIgQgnaKbsl7Zj0eIwSElM7+XU/Cn65QNQLBEr+LtOMX7HPBc9MoOdp2H/TBsxzLyE+RQL+wgn9ooe/4I223rzGP/6//wun+56W1HlFXdWEjYigERK1YhBQznPu/8W7vP9n73BycI4X+Ny8dYXGWofhyYSiNuQH56ysDYg6CX7kEyYBw6Mh5/eG5GmB73sslyljYGt7lfF0QZbmvPetd3njd9/kS7/9Fu/8h58xGs1IAse3WL+1hdeJefff/ABdawadBkWtmRyeg4AoiRifjwmiiGuvbaMrzeM7j+l2mpRas9XsoazFs1CWFaPjc473T8nSnDIvSCIfiSTNKlqrfaosJ2gmBKHP5Pgc5XscfPwIYQwtAadpQXmBF/9c10kIB98QHmHH48bvvsH1336dYpFzfnefD//spxze36fRSlhUGuNJet0Wq50W1TxlWZRkVc3VjVVSU+NVNZWFOi+YnI05Pjqnbl64EFc1re0BUb954b4Li9MpD3/8McoY8vpCkceXbN7YYvulLbrXN7j6a7dZubrO+3/8Yx5/coSuaidRt7mKlIKbX73FeP+cvUf7tNe7SGBwyamtnM7mjKZzfvDvf8TOnQ22b2xx+3ffJPufvs84LBBJwMKULDODsU5XvdSGSCoWZUW2yNFCMH58itdukKz3XOP5YhNWoc/GV19i/uEu2e4ZoDDznOVowXRvyODNyxT7QxpG4Z0tGJ/MCTpNRFHR7/fIR3OCdoJZuha6LxRqrUNoDUxTdK5RFzr/erigzkp8cD4MZUVma/pRgh8ExEFAJgV+p4muNGHQJhsvyGZLvEBRCkErDqFw0rQO32NRgSQPIiogLiqEtcjQRzdjrOfRKEpM6FPVBk9JglKTFRovChBZSaQkkR9QzwtqLH6tndzs2YzSU9TtmODaJjov8GqLHi8oAREHJK9fovvGVTc1L+amKWvmH+1TvPuQ9MExIgoQniR7fEJjpU3jlR28q2t4xiB8D8oL52driTpNvHZMvSzQxiIWBVlVOpO66ZIqz0jvPKTz2k2kkhx/8BjViCHy8RoBG195ibCdgJSEKx3sN1/C7o4cQXu0INrsk47n6LJCBf5TyIAXBKRSIpoN1GyJFgJbVYjQQ6jQVdQF2AuFORuF1KdTROgTVTVFWZKnmtD3yZYp9WxBFMfIrYGD5+yegbF4vkdtLChDleb41sdojS5LB1dSCls7wqi64HggBbKoUHGAbwy1cMZ8fhDgWaeoI3yfoq6fGvZJIQhw/AzlK+KNPpN3Hzs1Hhwswr9QtWOZOSWeqkJEIUo6M9JagPIU1Jp0mdG6ukpxOrmYdpZaSdAWrRRKSiJtkM+4GduiQmrjnI+LElU4Dw5lLXnoEyYhoVTUeYEpSwwOQhq+sk367iOqx+eI1RZeM4K0RgS+M7NbZFAbOr/zOnv/7keYb/0MaQWe77F4uIcIfTqbq6gspxhNCRYefiDwkiYqTalGU4z0kMagBaiqJt8/R0U+wVqHKlD42wPq4YzqfIZOC9qdBrOixJstWY0DFkXJcjxl49omWMMbv/0mp49OUFLRTiJ2TyccfLzL+qV1xgfnHI8mVFVNcyMi3Okzfuc+pTHUwmKw2Kpm/y/fYzZZEvdb7P/wY7w4oH1jA+Upel+7Sf/OY5eQIRzZPPQvuoSfqYa+IIg02nBy94An/kbZPENYyzIrWI7ntLb6T5/66T7+TFHRFbJpbvRYjmbk4wU7nTbT2EMLwyh1cq4qLSnrmjLUWCMQoU/YbbCcLMlHCyZW4yUhJq+IpYdAgydZubzOcDgj8D1k6GBztZKIyKfx6mVUwzn4YC06r0le2mb58QFmkRFIiN+4Qr3IyO8dIssa/8oWuQWVFySRR5mVEEjqOw+xgy51mtE0NbosCMIAr9uimC6YN2KMNfgaB4dRiqSZEPQSzo/PifOY4eGZ87WJQ5QSFEWBinxaK12q4ZxWM2FcGWaLlCD0UZUh1YZr33jFdXaf3pUXVLGfb/p+wbB/Y3j7c+OF8Zj43Os8cUYQQPu1y9w+GPHR9+/AZIEtnafO48MzukmEChTGGE4eHJFmOZTOK6cThrQbCUnPoRo8TxEnCWd7J5iiIBCSyA+dIIQ2XNla4+RkiAB66ytu/Tmf0F3vEbUTTj7eI69K2r02QeRzdj5CBh5+IyRb5AyPR6Atg5UexpOkiwXdZsSN9RUuvXIZ2U2wFmToUZ7PKM6neI2EfLwgikNCX5FPUqwvUaGHKUry0wnCWGQSOj+f2mAqzXI2p3dplWStw2K85M5f/JzN1y/T2xqghPf8PXxRIvmZW/l3mV38CgjdbtjnjtjPnPGMRfwvgEQ9ffT5/ugLf/xc1eSXfsqLSSsljdU2AGG78anbsXUmVJO9c04+2OXj737Awd4pYRSwsrXKzpV18jRnMpoxWyxpthoUecV0OmcynSMRLOZLhNZEFxr8SbfJy+3rhL6irmpacYQMfMqi4uDuPq///pd4+WjM/Xt7SCmIw4BGFDHcO+fkaMjqapdZVhC0ErYGXYbDKSYvAcG1166ydnOTT35wl16vTZbnrKx0KfKS+WRB3Iqp8oqGJ+lt9ByEKi0osJyP5rQiHy9QoGIGm32WsyWVsVzaXiFfZDzaP2WaF1x54zqrNzc/7aQ+d5MukkXhoiSnagRhO2b7ay+xcmub/R/f4+Nvv8/x4RmLZUqv3aAoK6eatdbnZDxjPJ7RXu2Qa03DDxguUlpxRK/tU85TSqP5yf/3W6xsrXLp7RvsfP0lhJJcefsmR3f2HE7RWOQF+XDvoz32PtzDDz1e+earvPT7b/LV//p3SUcLTu8fcr57yv6Hu6R3Uo4fnxAlEVmaoxVMlynx+YgoDCiNJpIKFfscn4wYnYxY2zslWWlTVSXnJyPmaYZSkjLNafkBnucqTVZCKg3Z8YjulXX2/vJ9rv/RVwjaDTffaodtl6FP50vXqYdzimUFtaF5ewuzyJl/dEC40yc7n+NHIes3mqSTFC8OUHnpSNsrbVQUEMQRZppihwtsM8QmAUEsYZpST1MWZUXUaaBq/VQOtOuH1EY7D5JXd5yL6DSjcTJDbg1QKy2K0yn+ssT3Q3RdE+308a0gvXcM85QgTYmEJBg08ZoxWhtMZPAQ1JM5SIUWksAT6LMJlQVfSUQUYC4gFaaosFVFXtWEvSbhWhcTeo5orC1mNEOfTrAIcimQoc/aH7xB88oaQl1sUMaS7Z5y+uc/o3h8hjTGQX8kmAeHGAHzgxHa3yfa7KPbDbw4QJfORdsGHq1+w7WsQw8xzyjOPURZYdOCqNPC31yh6k6Z//QOtNuYRgzCIzCSosg5/95HCGMJ+00a19bZ+MptsusL8tMJ6XuPEAKS336V6sM9sv1zIt93m6kA8STY8xV6nuELQZk6oy/biIlrjUFQnc3wQ985uFpLBXhCkuc5ZVESrfcJV7pUtXb382RMfTZCJjHFRYWrsgoRgwxDR0Y3jh/lW0t9Qa7HGExdOUhSUWGUQivpqmWe77pkletEWaMJpEAYMIBVEi18grKi7kSowKc6naAv3svH8WxkWTlIk7VUgYcvBNZCWTv/HkrnTK58hd9vkX2wSy0lnpTICyUj4SnkhTKNERd4bq3xMWjUp34VvuuI1GWF32jhFzXVMnWu5sYSJD4mK9HDJbPDx07OeNCm2B8itUVcW8McTagvFLJE4NG9tcP0z/8aKSUqCAjChOjqFvlkQu+lq+iDM2QUkN99RPy1Nwl2NvE7PURaYRoBvvWdPLC1EPksx3NEr0Xz5R3YPaM8n+JZ8AKfRhySnWl0r8nGWh/le5w8OGAymbF2Y4vZ6YTrr9+gsda5MLoT7H9yxOR8As2IVrtBY71LNl5ydD6l+9pljLXkeclH3/8QP/KJN/poT1GNF1Tj5VOpbC8Oefm/+i1UHDjemFKOp/K5jfuz2677birfY+fGFucPjwgDJ1UsEPjtkPhiPXxuPAl67DP7toCg0+Dm773FnT95h1lVU1QVCEPSazlos++TlxVGCHSo0FiYLhk0ErI2LIVBBopYCza3VsmLgrt3HjK4sUV3tQNCECQhVBq/nUDok80WeKvtpxFEfjQiWu/hNSIkIJcZ+mhIfHUdlQ4o7uzDWpegqimORlhP4ce+E13otinKCowl9T1iX2GynGIsqGpDOwqdKtpGj+n9A0xZcbxcIvIU2U5oXxh16jQjLypWNlc4Oh/RWOlQL3LCwGd4NgZPMei18UuDzArmUmCSC+nSz3Ueno8wvyiUeq5j8QUh2Wenwi8My17w4LOWaxYQvmLj771BYTTT4wl+t8XpnUf4AggDFD7Mp5SeT1M7SCZhwHS6ZD5dcv1rt9j9yR2sNXhlRTqbEcQhm5c2KNKCyXxOOl2yd3iCDH0C5ZMul3Qvr9LZ7tK+vMbJnV16mytEy5zCVeboxAmLssQEkigKCPKCWbbg/HzMxuYqWvkkleHKl19CrbaJVzrOFLXSTA+G+EqxeHCEto6P4Uc+ngQtoF4USCmw05RoZxXpS6yGIi2oy5p86f5HOG+z4SczynnuTJv/Y8ffMTrqV9S5eBaP8FnI02dn0TPVCJ6uP19w7t/sr/+cI/cvScmerl3GUCxz0rMZj35wl9NHJ0zHc2bjOQK4dmWLpJ0wz3LqUpPVhjItEHlF7ZfURUk6WRD5HhoIPEl70EE1Qkxt0GmB5yuKvOL8fEL/2gaNToPDj/Zob/UZ751zfDpGKeebYIRzq47iEGsNutakWcErt684YuZkSWFLVtcHtPot9t97zP7jIyJP4Xse88kSlGB1e5XtVy7x6J17TIczVgKf8fGQRVFT5SWBcolQuszwAt9JGPoe/X6L5SLj44cHGGN54xuv8c3/3d8jaEafu6ovWo6e7AcXTU6ibsLNP3iLzTevcv/Pfs5HP/iAo7MRi3nKpV6HJPDZvOCEIASTzJGQj+YLmlWF5yluXd+gBh4fnnJ8OmZ4MsILfTa+fI3BlXUaa12WZzNeeesmk8Mhx48O6bQblFXNYrbkp3/2DuVkSWurz+rtbW785qtcM6/w6nDG/g/u8bPvfUB94YTpJwnt9Q46r8nKkvXVDnEUEkuPR3ceI3oxZ7MFNq9obvbpD5w2tu8phNZQakrrOjRJHGMDn2lZsrXSZnY24+R7HzH4ynWiXstpkksfBBdVkIgyq52s7SJn49de4vQ7H5E+Pqf98jZmlqLykrkU2MBDSEl5viAIA/yywn95h8qX2MwpD4XNiKAZYxoR1fEYYWosGh35iLzCSNDLjCpQND2P4mBE/Mo2NBOYZ+jHp9heE1WW5EGAF3rIKGD97euU04zp7jkyK8i7HTxPkvSaaCUojkfOqkRKpOchVtu0FiX1/jlVljut+EZCaQwi9FlMFq7bISVRFCI7DWyvQXU+pR7NCSqNXOvgX1unPpvSGrTpfu0G8Wb/6fQzlWb+k3sc/8lfO5NKz7lRC+H8S0xdO+8DJSmqmvpgSDRJ0VGADH3kShsZhWTzjKKqHbyh1wAM9nBIbaFMItpKIfpdgs1NRK+NFwfI2EdqFwhnpzPS+ZL6bo3+1rus3tgkrSoGX77B2j98m8XjE6rYI391G1uUzI7G4HkEwLIRk+0d01of0DAO3qLLiqxShFWF9TzMRbBnnnSjjEH5HoGAaNBjqmtEpVnunZJ4CjtLycqSJArxBh2K6RypPMQio7IWL1BIv4FKFWldEyKQSiNq7VSatgaU05QqDPDbCVXgYWqojUbVgtpY52WBk89FW7SniKVEaEONIHppm/LxGbY2RIHPsqywRYn32mWq3TNEVjnoQVUjPd+R6ssS7XlgHRSm/aVrjoSflyTGoiMfmToFGH1hXiqcjpW7JljnTdFMkHGMl1dk4xmhlBD4+IGPSEsqo5EWrFKYvMQTgmq8JEAitnvQDJ3EuAf1dIkoKmQ7RlzA35o7qxzXmrjlrq9f5Og0pS4KvG4T6Qlks4GZLijPxnhRRHE2pfXaJcpPjrFJSD2aI/LKBcpaIyYzsv0hJi3A96mAYroA5b5PxXiBGXRodhqksyVVUXLy8Iju1oCTx8d085LFeMFy7KRPu1fWaTQTBpsDpIWDu3vk1tDSluZGi6gVc/74FLIKfTrFX+/ihT7D+0c0tvo0rq4BEA4+NdPyk4Aqe8H+/GyZ9JmNQgh49Q/fZnk+45Of30cJ535946sv01rvfqYc+SwW6umu4v43BrMsaHVbqGXBoNXg4HSEF8es9jrMTyf41ikPymZMdjZjtdUg7rUoJkus1XhJRJ7nnB6egYAqLZiP52zd3Ob44RHmfMqg3ULrBfOVFu1Cf7rLWUu6P8QMF9STBaIskUFAfu+QcK1L/NIWOiuZ7w8x4zmMjtFZCWFEHsZ4qysk6z3K4RLfl2RpQSVr551U1S5eWGmT5QXp2RQR+chGQJblDKxHVeckjQibhPhpRSYNvY0+xbIgjAO2twfYXofSGCcVLqEWhjffvsXgzav8srjoix4Wz/z7t4JE/aIheBozPvFOedZDRYY+V/7hV5xcdFHS+9kG5/cOWbm6gTGGvR/cpdaaIElYvb7F/v1DLu1sEMWei90OzrFSUBeS/uYKCEHcTZicDMFa1ld7rLx6BVsZjh8d0WgniLxmnOWc/NUJ4+kcrS3tQYf1a5vkB2M6K22W+6e0+03XlfIVG5c2CBAsxjM6cUhztYPqJqy8dgmbl9S1cabNzRhZ1si6Ri5ylmmJ2jvEayXkW5v019rUZYGQAq0E1WiBLjV5WuI1Alp9Vxiva40ua8IoZHg0pH91jagRf/4eWlzx9+86k3jB+BVxLv524/PdtWeTlCevLuBFnIvnDonPJBhfcCEt6KqmmGUc3dnj4+9+wPhwRF1UZEVFEPgkScTNS+uEEmqlODw+BwOz6ZLOoE0YB0SDFpXRXLm+QRyHiAusbz5NOds9hemStKhoBj5VLqiMYev1q9z6xst88s59hLHc/d4dyqwgjgLazZj5PKW72qW5M8BvxaytD8iyHE9JhLDs3z8gLypajQgNvPvtn6M8jys7a8zmGaoZc+XWDtPRjCorqBYFSEngexSTOcPpkle/dIuiKDg+GdEIA+csGzgn3VmWsyxK4m6T6196ic2bW9z+jdcuJAl5ftLaZ2gxFicRWNYIJVH+xflPJrSAxnqHV//zrxM3Y4Lvvc/BwSmfjKd00txJxHZaKK2RZUmkLCudFhiLsYYq9mg2E3Y2VlhOlxzsHeP/8Y/o39wkaMfc/vVX+Yv/5x+z99Fjrr5+neVoxnQ0o7fRR1rLfLbk3R/dQSpJ/CcB2ze3ufz2TVZf2eHWH32F7rU1ju7ss3dnF2tBX1S/ylnGUMzoX14jK2q8yEcvK9rbPYp5hk5LbFmReAF6kROogELmhEayqDRBwzmij5oRspOwfmuTs09OOfrRPS791muuMvYMkdFfaSOHS8Jek2yWU81SGi9vk//wHvMHx6x+9SaLx6c0GgF1VZFEAboRMnt8SmOthRgu0MMZctCl2XDETLXaQq60iBoBapmjtIOa1IuCSgZUUYAvBUQh0dmM6t4x4ZevMW+G+EriFzWZ7yOigCD0MM0IKQSzwxGltUSdGNFKUJHP6dwRIqMgQE8XmLwk2lohKDXFyRiwzlBKKUBQIZAbXTIPwklKsjXARgGi36B8fIq5IMF6W33iGxvIvEZt9Ri8dQ2p5Kerh7GM/up9Zj/+mLA2eIJPK6NhgK6cm7E1BrR28pfSfYZymhIEPvWyIN42jCcLtNY01zssj8YURyPEeI7cGtDuJOizCdLzCTZXCEIf24pAG7Kf3se/uY1a6ZBcX+fs7h5ipJm8+wlBEnK4e0JzZ5Xuy5fZuH0FvZNhv3KL8798l+z+MdbzCAZt9MRDeILJbE4UR/hKkhYX0oTaILRCdVuYRYZvLKoswWhmF93StlIYJckmC/KqxhqD32th8xLSgkQqROCTmyVSukQr8H2CXouGNuizCX4YkskS3Yxpb69QPDjGi0Nk6Du51lJD4OPhuAyVBX0Bd1KBT1DXCC2wnqKyhvVXLjP6458QSInWmsAYVCOieXWd0Z1dpOfjW4sXh9RF6fDJgG+scwhfaxPd3GH21/cwhqdEdKdiZRGRj6otdV4gpXSBv7bYRoReFqjSUFcVoQDpKZR10C/re0Shj7EGkxUIIV3CBahmSPjaZfKTCdQGbS3MNMKTRDt9J0sLyCSku7FCPV9ilinCGsrxFNlJ8FbazHzNykoXMZohsgrTjhBVQX4ywhpD0G6ij4bIZYrwBD4WPc/Qw9kFPt9H9Vt4GuplTqvTxK8Ns+Mxe/tntDoJjV4bM8vpX15jYmF4Pnbww7UO9fGEdq9Nq9NgdjBkdDZhOpmxtr1GYgTndw9o76wQS0Vvu0tdVUwmczrdNvPDEft/+lNe+t//PioOnqkCWqzWeIF3gUZ4Bl7zZI/43PYrCNsJX//f/j6dQZuTR8d0Nvq8+U9+DXmxXzx9JfEiB/CLddKTWAvhapv57BivrAiTkP7OgPRozNVbO9RFxdHuGV5gKPOK4bJAnU9ZljX97RV0IKljn+HxiHSe4g1aNDoNxoenmNrQaCQIo/E2e4SeJOw3n342PcucH0G3hTCgixo5Lwi7TcwkhWZMcGODduix/OGUap6jZmMnfd3vQ2sbXdYs65KmsYRKsjTgVRXxhbO2nedkh2eUaU642gM0+bKAjiGdzKGMHFeo0pS1ptFJiDsJurIUpabdb9J7aYNwrYPfipGh5xAFQjx3j56tAVueGK59Wul9IZzm4km/KOYTn/n56bkvjG/thYH3M15mT/LKZxJMFbo5YuOArd95nc1ffxmkpFxkJNsDbFZydu+A8fGY9avrNFY7TH58l7vHZ1hr6K+uYKqao8eHXHr1OsVkQaIkeVbQv7lN79IqRz9/iKg0xTznaO8YbSy1ABv57GysUNY1dVowS3NGiwwZe4yPR3jSQwUBKgroWsmVl/q0X9kh3hk4qWIlqacOSimlxJYakpDmzS10WpCUNdNAUT3cQy6W6NgDT2GLivJkjIpCzDwjaUSYyjA8GyIPzokbMenZDOspFvOUKi8Jk+hzxO7PX3b7mQf+7pKOX4lDtxsXJYonicGTtsQXnS+e++8zwx19Ahl47vALZvaTEO0X5WcWSMdz/vK//RNOd0+pZjnFhXZ/4HtsrvRI2g2yLOfofExeOCLl9ks73PjSDfo3Nog7DYqZu5HlsuDk/hHHj44xtWZ47DoQrSRilmaEcUhZ1nRWu7z+R2+TLTP+4r/794R+gAw9mo2YpNeiLmpOJ3P6WwNe/wdfgdDnwXfuYCyEnk/YiFhMlsyWGWv9tnPjzAp8IUE42UU/8inLmtMHhxzunyKUZHo6weYFfuBRaIMxlgd3H9Fb7XHp2jaT8wnTqsJXAm0tb/29L7N2dYOgEdHd6jvd8MCjzAu8iwSjyitMVTteCoJqkfHoBx9x8OEus/MpYRLSXeuxenOT7TevOfz5xQT2mxHX/v5bqNBH/eXPOTkbMS9KJqUlNpZVbWm3Wsx1TdhQlFnBYpGji5qwGdEZtJ1CzkxxfHTO6Yd7bH/9Fhu3t9m5scXRg0PS6RJPSoSv6K51ufzGdX78b7+HqmriwKPShv37B+x+vM/a1XW+9M++SWOlxZf+y2+i/t8Vjx8fEwY+65fWWIzmlLMcW9ZkytBba/P48QnTe/skGz3qNKctPKJWwvHZjKYfUBYalMMYL2dLMJaD/RPyqiRc79DIC8rhEl3WBM+qGgnnlmyKilJIqrzk/M4+a2/fxBhLgGT64T69L19j8fEBSSOiyComwzlN6SGlU7tSrQQrBdV4gdeMSIdzRG0w8yXKD1GJ5whvrQhVaaZVTVXVrIU+tGOsrqn2hjRu71AsMqgs5vEJSRRSaUM5WrL7o/uYeeECNCWIAkVRVsS1QSfOT6NQCt1p4gc+xf6QcpHhKYkXOUM8tHbme8cTgtUWYmNAOl/Sub7KfDQn7CZUkwVyo4fuNSiOJ3R//WWHGRbCST0KgS4qpu8/ZvG9O9RVjSegjEKwjhJSFuVT4QZjwUti6DRcwGksWVmBMYRB4jhGcUi+qLGHYxgvsYuU+KsvYaUg/eAxVnmIWMC4pAaKoaR1aQD9NqXW+FIy3T0j6jSdc3Q7xM4W9EpDeWeP458/YPbOXdpfvUHn9jWiV67grfddYi4k8Wqb7L2HjmheOjhPGIaIKCSJQmy/RZlXeKFGZzm+UpRK0mk2KD3nLC1Cn9hELPeOCAUUhfOi0MZQKUUU+LS2VtBLt/4Ja1mmOVEzwY8CsqxABgG6m1AM5+jAp9LGXXMDgVIo38fgAn1rQVhDeLHKauOM+kxd0bq0glgWMFpSKyejrIQguLxGMVmiLfhlhQ48llVFpI0ztBQCU1UEUUjjK7fIz6bISUqgDZk2GCxCOK17FYbUywuFJSmx0qmxydog8xJ9oQxVG4tF4yNcl2KlQz2aO3+Si91DNSJY5nC5j8Ri94boonLwK0C1IqJntOWtEBDH6MMjwp3rmLrCZgVBnFCcTWg0W4Cm8cpVyg8eoNMlbG+gd8/w1np4gYf/pesk19ZBSfL7R6Q/+4Sw3yLcXmH54T62cPfIljVev4X55JjmWofzvROsEtz62qvsffSID374ISuDHiJSVLpGSUGj22Q2mzNPU0RtEM0QOxM0ek2KsiZIQhbzJc2VFod7Z4iixmsnLBcZQTMiK0pM6fg2z0b7RrsNXlrzNzLqehILBJ2EN/6r3+SVskYIgQq9pyFCXddIIZ7CO1wu8yQSfualJMi8xgI1sLU2oN3vsNgfMV9khGGA8hR+6LF+dYPxwTnGUzQ7PnWlMYuMbL4k7Dfobg+Ynk8Z7Z8zWS546bWbiKqmG0WOZFsbVCu+eGPruFSNkHSRUUUBVilkmcPpBG0M+dEQf6VNtDmg2Flxhbm6oDg4RpeWqJ3gKUU8nhKtDxxmU83w0xKx2af2FYv9ITWgEJyPpmSeIIx8xucjotAnLUp2ttbJlxmj6QwhG4TdBuvdDqN7RyzHM6IsZ3Bj08EEpaB3dR3VjJC+ecr1ekGc/0wRVzwb1T39+/8mheQvPOeF0+TZcvAXzaOL4vLThpZwe4iFsJO4GAPovXGZ4b0DOpfXWO4PGT3YY+XyKmtvXaMYzvGTkKsvbROvdBh9sIsf+Ni6ou42ePCtd1kuMjzf43w0IQgDVnodFmiWaUatgDhgeDamKDMqYLy7QBh45a1bBIHP8mxM8+o660/2KQtGa4pJ6hJTLD/6058wmS4JQ5/VTpPNS6sEUrL29VuUb113xazSccX8bhOaIdlwgQyUi/GqGpWV1GXNdFY4B/l2SFVU7N/d5+bbt5zR6+e6F+Izv3/R/fjVjl8toRt4PgP4G/Y1nvljnzQsBDgpxs++xi/qztnny+vPVT+M5fFfP8BOCtfS9zx2VnoEvodvDKP5kvPJnDAJufrmddprXQZX11i5vsnyeMzwzgEHH+9z8MkhZeUWR20svW6TZqfJlasbkITMz6f0QmdAdHp0hpYgA8WdP36Pep4jQkNvvYuygpPRDFPVvPxrL9MetLj37fdZjJcoIAw9CmvZvLnFvXfu0WsmFJUzVmk0EzZubKE03P3gEzq9JjYrSGclG+s9qrwk15oKgVIe59OU7Z01xtM5o6Mh45MxURwQNmOMELz69dsUWcFw/4zR/QPe/me/TvvKOlYbTu7uk02WnDw6YvfuLpuba9z6B18mDkLO3n/MX/7rb9HttgjikCIrOT04593vvkdn0OaN3/0y1795+yLJEKjA49Jvv0Jzq8fj733kFvXRlEVZsns+QgpBN4np9Fs02j6h53HwySF4kmvffI29nz3AZ8j+8ZC73/6A9Tev4scB17/xMiePTrB5gQ0DdFljK017o8vbf/h1jh8cMj4cspgsiHyFF3gcPjhC/g/fYTxb8M3/+vdY6AJbVRR5STrLCJKIOivJzubUCrLrCZ0rq3hCkk6XGCWZpTkbVzYo5ilxHBFkMefnQ3RREkdNpvMZtTUc757y0tu3XZKWF9iifGbOX7SElaCYZ/iLC6L4ozOS7T7aGIqswC8qlodDuq9c4vzjA5pbfTKjOTudsmoFSTOhKgsCpSBR2LImaMVID4rxDBOAl4SI8QKEYFnUhEWJHwXOcbyq0d0ELQX+yYzm7U3S4wlJHFKPFoTrXeoyxZzMqKuaKA5Q0hlT1rpGXpjIFVJCMyGOAurhHJUVLoBPIlQcUBQVnnWy0KoRUZ1MMc2Ixus7LPdHLGepk+68+P6Wd/epmzHlT+4RbvXxakP6o4+xAubTBX7uDN90UVH2Wtgowl+miPnSJRZhgJHKLfBJhExLUmPwhURg0e2I5NUdst0z5PkUkxVIISgnM8JrW+jTGUWao3bWKKTzofDTmvk0xZNgsgoTeuisIF7tkpzPsLMZ+XyJ98oO5eVV6DSoD8+pz2aM7zxm/tEjRusDvJUe8dYA5ftMj4bU44VT02kmKAG5NnieT9RvUdbWBerGsMxzxy9KIqwx6KrCzAvqvEAcVmRFgUQ4szrPSaw2nvikGIPfCKmFRS9yfCkJW7FTRgp8LBYd+oSBjyxrGvEFNGc4Q0iF9ITz/1DSuYX7HlIIdGHwhIMdVcYg6prmyzvMv/chee06JGEYUNc14ZV18oenxEFAlWUIERAJiVICoTXGWOqqwvQa+JdWGf3bHxMuckyt8cLA7Q2B55KgReqUdowzG0yEQAuLuuhlV1pj8BDKcTRMVUOFc/qWzpFcdptYY6krjfIV3mobW2rn7SJA1DWyEUMnxu83n2mqC0Tk41/aJGg3me2eOBWwUCGlpPnqdeqTCVIFqBuXUHXtXMpXOqhmTP3JEf7rlx2HQ0hkM3JdFgm21qh+Ew5d188GAfg+za0+Wila7SbLNGN+PqHKS3wLoedxtn9Gs9di4+oaDz9+TNxvEvWb9Fa6eHFI/GHE6aMjGmtd1KBJlaZkywzSgk63jddKKM9nrL+8g+rGnLz7Cdu//tozHg+gLroW4tm9WHxmE38aBnwKcxIASuLHwYvDgCeV8Wc37mfWSISgf2OLve9/RNcKxqdDsIazn6RYJJSa8XSMjJWDlCxyiqykd3OLQCoWozkrlx138tHeMdFKh9lwzs3b1/APTjg/HbG12ccLA6wnCLdXkUmI1catD0qRpjk2q0ikAOVcwcNeCxE6755idkzQSmjc2GSR5pigiep1IK9BSiptCMOAYrJEpCUyK/H7LVRlKBYZ1hMUkwUmDqnqmhCJkJqsqkkaCfN0xu7hEcmgQ//KGvl4Sdg2pKdTcmsJS01+NGY5SZESRqdjbn35FrPFkqAZc+333kDFATLwfkFgb5/O72eTjC+o7f4KxrP3+0VRr3h+r3wWKndxTIYeq69fASB4ZYfurS2EJynmGQff/YDACo5+co9g0CbuNdGeJEwa1KdzNl+9yvTxKcv5giBQ1Lrm6GxIq92kNWiTVRUNv8HsfI4UkqqqaAchVkqO7u+x3e+wfXuH7d98BT8JQRt0WVPsnZOPFnx05xEPd4+Z1hVhHOLXFefLlLM043q3TT5z3C9V1OB7iGZEYS0scrdmS0W6LJieusSnSEsWunRwX2moCsPe+3uoUHHl1WuEcfiZmNo+44XxTAPg6XX9uxm/guTiRSC9v9k0fNJke64t9rnX/cxr2c+c8tw69Pxneeo2aS11XnJ294CdXpOt0EN124hKc3Yy5PHZmKysePXrr/DmH71N3GsipGB5OuWD/+mHPPjJx8znKdZC0oi5tDOgxFAVmqgRUhvLoq7Rpxlx4DOezMnTAuV5bFxeZ++dTxjun7O1MWBelGSLnOUy59ZXbzPYWWH0+IR3/v1fE7dilHALkO973PzKS5w/PsFaJ8u4yEu2r2yAp6iUQISKMA44OxoShAFSQtKKmaU5/bUBndUO6WzJeLqg2YxI0wy/03KkvAuVlrqu+eTHd3n1N17jld//MveFYJ7mqNkS/0Iu84f/6q8IPY9QCBa75/zlf/PvCJRPIjzCJKa/0mV//xSAOAoZ9NqUleF7/+Y73P3+B3z9n36TzbeuIX2FqmH9zSv0b24y3T3n/KMDRrunnB2cMZunZEVJejykGYa0mjGBEYz3zujuDNj9zgeEkSM37j0+YvzolLVXdth5+yav7p5z5/sf4tWGPC84/OQIPwzoXFrlld99C10b0tGck/uH7N3dRUjLdLLg1q+/wnK65PV/+FW+89/8CYvRjFB5TLOC3s4K6WRBMV6g9hXWwkJYWqtdfCWZDWc8/PAhnXaTs6Mh/ZUu1A6iIrAEoQueJqdjRK1pX1lntj9CFLWTGXyGg+WvtAnigGo4RymJJyTl8dg5rZeGKi2Ii5rh+7toaSmKis7lVbSUSAtSCjzPQ1iLiALAQ0owniK8sk6xLBDGoMdz/K0e5XCOTkv6vSZVUWE8QVzU0G9hHp1i1tpgwcMirEGeTmnEPmalhZHCuYCW2jlMz1M8JSkqjQo8pLGYWYodzjEX3YEsy4kCD+srvG6TcLPD4vGZk5RdaWMNzE4myKIknOfUy9xVy7VF+j7Le4dM7u4TLHL83LlxU9d4/a5zWfYkXuBRlCWUlfvsSYxFIAVUVY0Zz/GCgCSJqPKCZKVDuN3n9IcfIRcZFokvBKIZUZYadTTG5McE/Q6UNWEnwRQ1uqjoRz66qrGTBb4FkxbUUUp6PiGsagIhSD/YJUwCbOgT+x5xM8a+dp3Z0TnF+ZzZ/pDo7h7C9/GbCUEYEEah41v4PqLS+J6Hd+FgXdaaRqtBGAQETY86K6AoqaTEl9J1DdyC97SDgNbIMEDXmqwoacQhOs0phzN8QCoPVTtvlKgbEzQCRtMF09Gcbr9JoxETdJss986QnQay0FhdOyUTgTPTy3LHr1EKWxmqusYbuOpdejojjALqyklE2pU2/qBN+v4eBMGFR4fjMDgKtnJqWlLQ/ebLzO/uIcsarTXSGgLloaV0Jo4mh7yE4MK3QxvqZYpoxdRpic1y110xFnVR7awtTjnLWjws9TIn3BxQnIxRCORah2jQInt/30E8haSsazxribf7T7sYT/ZmT0m051McHGOLHK/dwfcjTFXT/vJtskcnlIcjbFZggxCZp4QvrWOXOdU8gwcn2JtbiNCn2HMBbDXJKD7+AJmW6GUKvkI0ImRtUb0WxfGQQbdJhOXs8RGiEdJMIrKiIN7sYivD0f4xdZYTmhan7z5i4nt0b2ySns+4/uo1Dh8ckGz16KxtcfbBLu1+m+5ajyAOsY2YxfGI0fcOWf/yTbdfPLP9fqpCI37hNu+w83+z6EUpD1cQtF8cYAL929t8+b/8Tabf+4hO2uDByQhRlly6us3pwRnJ9Q3n2t5tMa9GlO2IYVXQbiXkVcH53ilZWWEDj6CsCJoBk/GUK9d3ODo8xWQVuhcQJ6ELFIH0wz0WD45QxhKGAcJK8llK0Irovv0S+d19Z1zpKazWiGaEKGqIfJQnCTsNxocj51djDWmp8bIFGo+o24Q4IF+kRCstzh8eAxLpe0SB828plxVWeQRRiACSVpPueo/0aMLAC7CjlON5SrvTQHUiiAO0sXhRQFiU7D84pJinbF5a5+N//X1s7PPqP/9195144XV+8U392yYWv6ge/LmTvuixZ4PhZ4kZF3C9p+/xJIb2FGDx44DujS1OP9yltbNKev+Q0/uHJK2EbPeUpJUwfG+G302grmn2O4xHUzabTVSvgeo1OX58wvTROS/fusJymfPRvcdsbK/QUR5rm302f+020WbPqQ8Kiy0003tHLEczvv399xkvls6DpRkRxgHZIkNKyelogqxqXgk3idfaxIMWInSu3hjXhbbGUmmDGS2xi4J5uUQrQRQFLDKDKDWT8QxrDe9/5wPOds959TdeI2kn+IH3DNH702zjacL4d9y9+DvoXLjx/BR9NlviM5CoJ9nTM1PwmYzrP+kTCC5ckS9SGG0gT+mtrTBc5nx89zHj+ZJWv8OVl7b50j//Bp21LpPHp/z83/6Yw48PmS9TGo2Y1dUeVa3R1jKeL50qioU8zQmjAIML+GQYkk4WZLqm220zG844eHDI2lqP+SLDT2KiVsz1K2vMTsb86N/+EIWl02tCbZjnJdduXyaKA0aHQ04Pzmi1EnaPzvF9j48+esTmoMv+/X2k7/Hl3/8y9398l+UsxQ8CfCkRQrC2s8LR/ilHuyesbvSZjBc0Bl02r29y9viUaZYjrKGz3mNlZ8DV33gVrxnR2Oqzdm2TdLJgNptw/ugMaxVWeaz1WhydTTgfjomFIG80WN1aZTRfsrY5YGtnneMHRwxnC9qrbVZ2Vjl8dMx3/+V3+IY2bL9986IqJfCTgMHtLfo31lmezTj9+SOG9444PThjPF9ghODB4Sk7awOOv/sR619/CXV1wL0/+ym1tqRVySc/+IjV21uo0OPmH7zF4b19DvdOaUYBRZHz7g/fp3WnyUtfuUWRl3ixz9r1TU4PzlFlRX4hz/vRX9zn1tdus/3aVe799D6L8ZIyLUjaCZ3VLpPx3BFbq5puElM/OGEuwV9p0b2xzslH+wgrmE8WKOkhdUmeOtUH3/eZnk4wlSboNhCbPSph8aoKXwVP5730PYKLNmiRl4hGRH66wAsUuhE60nBRk5/P8ZKQYC1AKMH6Zo98nmO0JtjoOkxnWmCKCl0bZDdBNkL8WlOfzhGBR3nvgNalNc7HS8zjU4LVDnKti0hLiklKPUkxP7yHurpOoRRirQuzjBKB1ZpQeFTnC9QsxbMQexJqTWUh0A4yVGuDwFLWNcIYhPGpa41/dY0qK6k/2MdeqF4oLONHJ3haE5xNKQNHdFetGGUtZV4SKIU/y6jSHMKQqKwprSAvKlcRXulRdtr4vsIrKyddmBZIa8m1QYcBkVKgDXlRIqVkcTYlG86dX4JQaCkIPI+6rImT2MnYSkk1T1FVTTVaYAOPUEjMJKWsNbJ23jKekmT7p9iipLBQK4m0lvrC+Ex5CusrhHJQJ9rSJYOBop6n1PMlc2MRnsLzfFrNhtsgtaGoNNo66dz6gviL9fCbCaXnyMh5VaGCgLzICaIIYwy51iRxhBf6iFaCX1aEvSbRpQFxNsAA5miCOZ2CsVSzFFPXeFLg+xKKmlQUxM0YWs4ZPbQaaS0YjTYuoKcqkTIiLR0pOmkkeJc3WPy145cpaxypUggGX3+J2XsPsWUFWILAI/A8dFlhpKSqK6wAudbBW+sx/flD6qKkEQQURYmtnT9GAPDExd5TCGMR2lWH09qghMDzFXgefrsBxlClJVZrZ3o6XqCFwAS+U25LIqpFhgglMompJktsWaOSCA/lErZngjFxAdWILq9h7u+jJQQ7G5h5iggC8qMhFoUez0m2BkzHU8icG3j6+IRwrYsdtCjynMk79xFSoYczVKuBORhisgKDe0+v26BWktBTiKqmvTWgOJ5glaJxdYujkyHLiwDm8qtXWM6XVLVFeh7z0ZStzRWKssbUmjIrOHl8wsLUyOMJcSPh2u+8wcNvv8/B3X0aK218KQi3eqhHx7QGbapZRti/MCs19ikE7cX4Gp7Zvz+71//i7fpTwMMzCcZnuhjC9+i9fZPGpRVG3/2I9dqw8foVgn6L2bffZ346pqoNerSk9iXtnT7CwizLSbb6lEWFkjCIAkRtuHR9h/OTMQ/uPcbzFZ12kwoLhyOCN69i0oLJn/4IL2lS91sQReiTc0IpwFc0X7tCeTbFnEywzditK3edIIrNSgqr6b+0TZTV6KMxxTJHaif3bDzQ84z8+BR/cxXz+IxqviRqNSD0qLKcuNHg9GxMp99kNJ0SBD6+VIwPzmm3GoxGCzqdFkEnQWx2KCcZcVoznMwZCU276VTxyqrGjwPOHh46mOCyQPreFwSYn4fRPHsvPzd+Cczml6NwniSp9tNJ8GxM+EKUyjM/vuDFrTFMDs6o04xyltK6skaj36a8ts7o4TF6mbN1dZ3zd+5BO0YDyUafxXBGt5GgWyF+N+Z89wQhIKsKHtzbpaq1M8qtNCuXN9j5vTfwW4lTLbz4zMXZlMm9A3720UNmRUEUhSRJhJACY6yTccaZlC7qmqwRsHljA1PWFMuCNM2J2wnjT04pxwuyZY7UFtuMiLd7nJ6MqIYzrARjLXVZgYB6VjN8fM73zr9LmVasXF7h1//pr7u9h2fBbr/gXj1RL/wVtDR+JcnFizPTF3U0fslrPNeqeb7t9dyJf4ucQ/kS6Sv8ZovT3SPunozRxvLa117hxu+8zvrtbYp5ygf/7q/58D/8nPF4Tr/XZqezRllVjGcLlFLceOM6/curDG5scHTvgN0PHtNoJahCs/vJISrw2L6xA2VJVdcsJnMwMJ46ZY9+EhEnIY9+9gBdaxpxSFFWLLMSUWuUgKOHh858SgpajQhpDUkS4fseg1ZC0AiRnmSeVZw+OKLf77C+tcbhowM8IfA9xScfPkJ5ipeub1EvMw7ygo21Hnd/+CFVWdFc6fLyb71B3G/Q2eiRtGN0WbH15nWW51POH5/y+P2HnO2f011t05QC4ymyShNFEa1mQqfbRAjn8Bs0Em7/o69xdZry8Dsfcufn96mykisv73D46ITv/A/f5s2jEdd+6zVUGD71qhC+ornZpbH+Fltfu8nRe7sshzPqRcHux7uMJ3NOzsbM333Al//w6xx/sMvR7gm+57H30S7xv/0xL//+W8T9Jl/9X/82d//Dzzl5fEq5zEk8J0X53vffpyodhyYIfIRSvPTGDY4fH3G2e8av/aNvcPrJMQ9/dp/+WockSTh5fMx0PAfPyc0JJP2tFfxSc+0br5COFxze3Wc8PGXt5W0mhyOy0wW2LGmEilwalOfhYTk9G1OXFYEQqF7TVVjHC7y1LkKpp3C+YL2L2B26zVsJPE9h0oqo1yJdFixOJzTWutjxksD3qApH1PWbIdQGoS3EPqauCdc61IWT/JVRiB8E5NMMZimyNPjLghXlEtHqbIoX+4hFTmgFUSNioQS1NYSDNpxOGU/nRKsdAs+jnKfINKWWoGtXPdECqDWmrDFKElWGyvcwUiCCkHjQRuwMMLWmOpkgmxGhMah2g6rSJMMZjOYYpRyZd72D1JqqqgkXBZXWeMoFfjXOuO2JM7OII4q1HlErcRXJrCQ7n2GrGuV5+MrBJGqtUVLiex56kWJ1jZEKrEGEHpHvoaREtWL0PHNQ1U6CX1QYTyHTArISkggTBVR5QSwFvhTk1mKlQEqFMoZKQJ2XGCEJPOcYTaUp0gq/CtFlReh71BbiKEbXmsQYlPLQWMo8RwmBH0VUwjh/C9/HGrBRiGhEUFR4rYQ4DlnOU0xZYVLLwtSOIOr7SO26Xsu0dGTuT47Jd88oixI/dEREL/QplznlMiVWikgpQgtFtUStKJjn2GVOUVaYZkwwS11HSDn37Np46KpGGo0WAt/zKD4+xGY5QRg4ZZO6Jt7sIn1FvXuOpxTlhZ9GZYwjPmoNnkIZn/ClHRZ3dgnbCd7U3f/clzQqS6U1SRxSao32FL5SCGXxhPNwkXGAn9dwAaFSccjy8AwvivDxsMbgxSFmmWGVpDyfOkdyC8n2KtXRxCUWygXQShsqKZDwXLnPAl6/iU4rfGFpvXGDsz//a/z5EgKf4u4eVJrxnT2nKmYseBJV1kQ7K+TLHJNqzGiOiUJ0rR0HSTlFOOlJ/KzETOeE2xuIQqN9hV1mqHaMnMzxKkO7lXBwPmU8mWHuWDaubWJmCydtnkScHZ0T9dqoUuOHAcaTDDp92q0GD//qPQY3N4nCgGigkN0EYS39Sw4C+vin9+mOZ9z4p998io1xnYwXIA3E5448B5D+5QnGF5xx8WTxJMiVEKx1Wf/HX6X92iWWx2P2/uoDSCKixENPFnhKMj4Yku6eIwVkSmC2+g6SdDSBUrOoSvrXN2kkIcKDjaSJH0cEnQbNSyt4gxbFY9fNMDbHtpvIswmyqlCtBH1wRvHRPsL3sL4HeYUIfKpFjldpWBYI3+KFHsFmD3N36fxdrKUIAurKYhshQjTR1jB7dIzyfMSgjVcWyLrmcP/I7QPaYrKS9c012t0m9+48xA8Cgm7CebokikMmh0NCI/FaMcaTRFrQCALmaYmKA85HU9o7K9TTFF1UPB9jiS++Sb/sxv3HxqFPEokvyFiMtcgXQXbs5395kntaa53vyjPJaNxrI3otTtN9pLUsH5+RbPa4+huvY41Beort33kDoSTLsynFcMbso0NmpxOyRcnRwWPSvGT72haZXRI0Q+aTBUkjZr3TYus3XyVoJ/BEUj2ryPaHHLzzMT/+eJdcu84zwikWekIhfBAXXkFYaHVaPLy3x2I0Y6XdphgvqMuaERatDfge8fbACZfM5kz2T6nyAqTv4ghd0UwSsiJHSkGe5XjWI59m7M5S3vztN+msdD5z2X5RIP6rA7/9SnwunhqfiOeXnOeT31+U9n76hE/n96e5k332NAHPP/BLPt9F+0wqhQgUuTY8GC/I6ppv/NNv8to/+AoqCpgdjfkP/69/x+OP99haW+HK5gpplnN2OiJsRNz+6stc/tI1DDA7nyKk4NZvvcbt33uT4w93+dZ//+dIBHGv6ZQFKk1RG668es0pm+QVs/Gc0dkYrTWmrNwk8xSdKCSKQ+azBfPpEmtLkBIv8un02yxnS1YHHdJljowDCm2RniLwNcPjEYvpgqSZkDQCRmlGFPqunW8t40XGeq/FauCTD6f0Ww1koFhkBfe++z6qEfDV/9Vv8eB/fpd2p4kVcHb3AK01LSkRgy55UTKbL/CkT3O1S3p8To1luswo8opW4LH/6IjjD3a5+Qdv0truI0OPB+8/Yu/jAwYbfbKs4Md/+tfc+cFHbNzc4vIbV+lsr2CxxIMmQinCXoPL37zF4myGF3psffUG7//5Tzk/HtINfI7uHXDp9iXe/N0vsfvzT0jP5wwfn/Lt/89f8Hv/h3/Aykub9K+tM3pwzI/+1Xc43DuhP+iRCEupJMr3WcyXeEJQlBVZWXF8NqL/YI23/uFXUcB7f/UevYFGBB6zxQJtLM0kJjbuOUcHZ3QeD+hd2+DG125xdu+Qj999yNqrl5nMSkqFk6U1boEsi4qkEbOcp8SrHeJuk8XeGeGgSTFZOFnaosIaS3xzA+/jI9AXtpFSYKxlvnuGQCAjhecrdOi7inBl0FFAOZqgLm9QG4OXGUTggbEOY15r59oqBO1bm6QWRG2xShG0YtKyJGwk+HmFTgvwPLQxRHGEaicIKaj7LaLMQVDULIPIp2xFTuIzz2l7IYUEGj5LkZMEAYvSdSzUoEO73yK+vkk+nJF+coINfTxjwTp8sY08R7DbWWWhHYeiHk6woY/v+fi+xg7aSAnsn2MrjW3EJJUmrWtsIyZsJ2ghUNqQVTVCKfwopKy16+q0G9hZjrEWspzY95CBQgvh5AGrGhEF6KLCFBVGSbe8LDK8ooLQJ1AKG/pobSi1wdOG2vewoY8qa4TW1Bi05wJ022xgtEGnubuOxlDVmiorLyASAq82zo1aSvxeh3qZwoUjdO17mMAHJRFrfZQAezpxHiFFRV1WDjbTTEi6LUpdYwOf0BpEWbvNyWhqC6YqCQIPGYeUVY1sxhD4T8nCylp836cWwiVl5QXsaVFQeYp6siC0FjNdktU1MonwWg2kNshqhjAabTRWKnRRYoVLPqoL3wwlIHn5Est7R44bFQT4F50ZKwxWO0iXrxTSd+IRndevMP9f3kFqTR2HtPICCwRxSFbVSGtRyvlcaCxWOgiT1TW+1uTG4gU+i2PXqRRSub1TWMwihbJCtpx8o18Z6tjHX22T3jlEhgHWuGuDct+7sJV8dudDBD61dGaB5cf7+O0m0vOwWFQ7ol6W6MpHjOeON9EI3XWVEjFoIXyFGU4Iui3keg9/pUXx8BTfLp1oQiOEokIsC0zgo2vrlGd8RevSKvnuGStX10nXc0qrHXRzvKDRbZCfz8hmS6KGc5z2K0sy6HB2OsSTisnsnHitQ2UsZrig0WnSQHL++JjDtHRqNnFI+/Ia2dmUaNDGaP0p/+IX7buf+f9vGq688Pwne/5TNIzLNISvCHf6PPrOBzw+OWfz0jp6WlFnBakn6V9ZY3jvgDiO3PdgtiTXC9SipL/WIx1NySdLByE0BhUJkn6T5vaA+OUdVw1eZFRSYUdTVFZgfJ/g0hrGc/DJ9K/vUysILm1QDmcoJR0ccVlgswIyTbF/jqoMYJGNCNPxsadjbFVApfCSAJ1VRDtrVPtnxO0GZdTBLjN832drZ4PxaEotCo7PRoxGE7Qv0QryvMAvDJ1WwGI+p/AlXuLjERL4Dt7rRGt8Et/HU4rZImf+8JR4rfMZ1MivcPxSB7fnTn7uNykuumJPBX2eTxqe5iXPcGxdYvHp43VRIYHlcIE+XRK2Ex7+2U/JPbj9+2/Te3WH+d195ucTete3aF5eJVlt07u1jckrFsdj3vmTd2giWNlaYb5IscrSiUO6ns+Vb9wi7jdBSWylST/Y5fjdR+yejXlwcobfbRJKSej7DLMUz0CpgNQZEtdV7VRKs4L1bgdmBdPZOXnlvH9KKYhbCZXWzM7GzEZzigtF01oX5KWmv9JlOUudkFC/wXKeoZTHcrRA+oreVo/Z2YTOoA3PxeafgRA9vWVP/OjE09//U8Z/uhTtZz7Ai6bT0zOe6p+9GCb16dywTxOM/9g/z1687pOk4umQgu7WgAff+5hawh/8n/+Qq792G4Dhg2O+/d/9KcdHQ1ZX+1TGuUD2Nvu8/dtv0tsZcPLolO/9q+8wPZuSFQX9lS6/8S9+h81XL+EHPr6SzOcp54dDOv0W6kKetshKlvOUfJ5S5AXGWoq8ZOfVy6xf2yBsxSghMLVGV5rFcEaVFkipePTeQ5ZZQW0tRa3Zee0aJi+pas3HP/uY1dUeUghUp+HcbAUslxlFobl+6wp1XfHwwSFR5KQjG90WsYC9T/awcUyZZmxeu0GxyNj78ce8+fXbNG/tsH5rBxX65IcjDt9/zN7hGVGnTdRs8Nqb1zj8aJ/du48ZbA6wec10MiNpRHz4gztsffk6jZUWr/8Xv8bqjS12f3qfs91T1x5e7aC15cMf3+G9b/+cwWqf3lqXnTevsf7aZZqD1lNTrbjXJOo22Dg8QwsYrPVZv7bB+3/+U1ZubvI7/5f/jGKekfSbDA+HrlUpBOf7p7S3+/zG//EP2P/ZQ3yh+Nl/eIc4iXjtt9/i5OExn7z3gON7+3RXWoShj5KKfJlz/ddf5WzvnOx0Qq8RYQMP1Qqp0oIS4dRueg1+9K136LzbYXWtx7Wv3+bNfpPHDw4IOhHlTCMqR0jF1MRJSKPdAM99PmOcV0o3cATbam8IrYhqlqKaEZ1Xtxl9eICKfKw2hK0YWdR4niTYaCPaCY21LkVeOL35ZUpyZQtZ1niDGD8Oycdz6ukSqy8qwpMFwYqrGtvIw7++hh0tqCpBc62PaoTYRY7Y7DsZ16wAJZCdmOVsSX0yIkkL1Ms7ZHtDCD1nIumX+KUG6eHPlmQFlJXGH7QJxktUp0FrrUt1PmP27kNsViCEIIhCVF4i+k3McIrpt6kvkgJV1niTOV5pKGyNlpoyUKisoBpNKRYZMghQi/Tp95qLQL+QEl9JUIpSgLIWpbVzps4raqMdzCnyCFe7qMkSO3a8ENVuUAUeZeChWjFht4EqNeWjY8rZEiuhMv9/5v7sS5Ilv+/EPmbmu8eee1bWeqvu3rc3dKMbTbAJkCA5M1w0Q2mOZkSN9AdI86K/RU96kI5GGopHnDNDihwCJAECIBq93e6++1J7Ve6ZkbH77mamB8tbt+7SDUDAnJE/VEVERnh4uLmb/ZbvUiMCD5tftqEB0Tg8vm+tC+yTEIszk8O6BLGJfGzTolvnQeIFATUWIySt1YSBTxQGNGXtoGNCoD1FiyURDqplzqbUUoA1eHWL9pWT5hQeRdOgwBGem4YgCCiUASGI1oaofko9XiCkpDTOxdZai5KCqtHgCUzj1J/assLGIaoT4/c7ztEY6xb8JMLgZGYrbRGBR7XKHba3FcTdFD1fIQAtBQLhoKJYiDyiG1tM37yPJ5yqE9aNn/J9EBrZthgLjSdYe/0a+pKT0yhB2bbookKmMX6tHeRJg7UVRmuauiG8lMI2RUPbGAIloW3w4gisExEQvke5WCHzEi8JUQbaqibwPIKNHkJKzOkMtNO9tb7nfIhChb8z/ML6Jj2FapxMbTOe4QeKZrGi9gzdwRXacU7s+ehhD1PW2FEHsyhY/eRjZBpj2xpdNjRNS1zVyFpDUWEvpb1bcO7pkxnB7joi8qhKRTPJ8AYpUgjyp2eItib2AnRjKFYlQRJilYP5dHoJfhphiprJxYxg1KU2GtUN6KQxRVXRNi1awqpp6NzZpZ7n9LoJBIrjNx+gf3qfV//z30QGynV0vqzK/dxrzy/1z1bhz0FtvmTx/uI+v8w747kXjLV0t4bsXd3GBh6Jp5hNFtSywqwqokEXL/K5cmWN5fEFzTzHG6asPOhs9JFKcL4/Zm3UfXYt6vMZQlx110wSYmNnsOhJgRf6ziW+tZgshzTCRAoVSAIB5eEZ8c1d7LBDawzStrSNJTuZ4mMxykPnObZt8YSls9YlL0rkqEvx4VOkrxhP5qzKHGM01hgefvQIBHT6XZq6ZWdrHetJDo9OGe6s0dqKrCidH49uSfKanheQ5yVFXZNaSS/wODs4IwxDGqOfrUefgaX//5JjfFmc+qydwBdiuy8O5meThs88eFZEt59Dx9nPxnZ8koe42E83muJkhp4XTD8+5ON3H/LCS9cJ04SjszE/+xd/ymvjr3Dws4/IVgWdzSdsXdti/bWreKMOH//rNxEGRpsDxpM5T54csZgtkVHAbq/LnW+/yODV627+bTSTXzzgzR9/wDQrWRQlra8ILHQ7CeP50hX6Qh8lJU3TPvN0EnGEpyR95VMUJUvfo6kaymxOf9SlrhQm9MjmGf1Bj4PHR2ysDTg6L4jC6BIuBf1uwmy6ollVhMOU0PNRnsd8suAnv/smG9e2iNLoi0Nnn5Mg/rLtL5lz/k/Gufhl2dHz1/CXNFYvr8e/GKTqVx3B8xWU9RevcPfHH/H9/+3f5Oqv3cG2hnf/Pz/mo//wARcXU3q9Lo3WXLm1y6994xZSSsaPz3jvn/4x+SJj0EvZWuvz+PAM3WiiJMRLQtZe2Oab/+A7fPD7b5EvC/afnpBEIcO1PhcHp9RVQ1VUeErwwrdeZvvlq8xPZ9z74Ycsx3PaukV5ChUG9EeOcB0mEVIKVllJnVdsXN8GYDZbsvfadV4KFQ/evEtTtxgpkEJwZWdEUxuu377Czleuc/T+E4S1+BbKsuHq7StcnFywVB7f+NvfcEonoc9qkXP7d77Owc8fkjw4YfsrN+i/co2nf/ohJ+cz8kslkMWqRAvoDzr4nRh8xYvfeok//ed/yvrWgIODcw7ffcxLv/UVhJQMbm6w8fIVpveP+eG/+CFHT8/odxNuXNliOl2wf3TG8dEpp4+PufXkjFvfeZlGwb/9P/8Lbrx+k6//w9/gxb/2Ki99/yvOGMmTfPV3vsEP/rs/pjPqsvXiFRCCjWtbfJKsxr2Ud/7g52xc3eTF336Do7ceYRAs5ys+/OEHbF7ZQCpJVtV0lKKh4cFbD5mfzfjq3/01Xvn+G/zgv/0DgrLh/qNDruxtsvviHpP5gu2dDfK8oJvGzA+nTJcZqz/4Bbe/8SKJ8pk2jVvE55lTnfEUqyynqmuCKKScrcgulqjQx4pL1ZW1Dm3hsOTF41NEGpFeW6c6nqFCH1HUlMuC9TeuIZIAnVUYJfCigKZuCZIIq7XzrxgvsUNXBS6xRMMUXdWoqgFrsa0h2OjRnMzxhwn0DPX+BXHkYa1BJAGRCNFLF9xwvkS3LUFVI9OQ5cE5RgqCQFE2LflkCYCnhCOz1Y0LhmvtvCRmK8qLJVIIV5lWLvg3WYlIQmTVoIddTF7hT1ckrUa1zp+BYZfYGOyqwIYBVRKi5hme72G1ptWaqNMh9T2WUlIvc4o4oJWSJK+QeYmR0mmGS4EtHexQ+gI7y1hdLPF9hdocwM4QG/gk/ZTBIHEyvR8fsHpyhpqvnMyq51FKgT/PnaGlseg4RPoezWKF6rlAT1hDmZcIC4HyaIVA1g1lUSKNJgK8S3hWYa3z+7hs51tAKEVrIbAW30BbX/IMhMAPfdjok2yNHFxos8tqVTD/0V1U3dAJAqogwHqKyFfoTuxkgbOS0Pece3FRg6ccMVVbgkvomilbjO8RRiFi0IFeQoOlNtbhy5XEjHp4UuEpgdHOH0I3DgpiPUVcNQRxRGuN68ZJgRIgGk33xevk53PntxKF1EriXV6Tbatp2gZ1uQjbXkzQ73D+9o+d2lMQEpY1JvSRStIWJfGd6xQf7KO0pm0ssZJUxokooDXWGiyCVip84+6JRleIqnZQLt1SLWriOERpgxaaYG8NXdS0qxIhLvkkUoLv4V0ZEPSTzy4wCBDCQWR8hdwJCAYxzeMT5HyOuunTeD4UuTO67KbOpLJssa3GTBcOp9+JMauC+iKjeXwORQVVA0lIEPo0ReUUtIoSuTGgfeceDAZwMSe4uY3NCpKjMWptQLbIkOspddsy2hmSn86p5ksaY+jvrmOVoDmcEOytEa91iaUkiUOaJCYddpBRwPDqBgbL8S8eoIsG31dc/e7LeJGDYpi6QUbhcyv2Z9foXwqs+CVI52d/44vx5S8LBawFtEaFAaPXr5M/Omf/+Jxga4C/1iGbZ3STlMViSdRPOH9wRCcI2VofcXB4xtpgC103VHWDlRAE/mXCqgk2R27cgfroHHNxRnL1BgQB+vQcX67BssCuclhLmbzzAcn/8nfwB13qqqZZZBgEshsjraa+mLt52mrkckXeaKzW9HbW8boJdjxjeTKjbQ1sDdBZQTFeIaPQzXeJ4MruJmdnFwSRz/R8hvAvldoCH7mq8TwPHUMQSKplTtLvEiIJ+h2arKbGGZVe+4orUPaubVwiRayrhIjLuOv54OzPirns5x4/C7a+/IOfGfrn4Si/ZNCf5Q/WYrUBKTBN64oEUmKNdRURwLaa1XhOPOiAsSze26ecZFRtQ+QpxscXhGnE1tUtlosVTz96SndrndyMoW15cv+QkyenjK5vQNXQKsliPKWua7eW+R43b+2R+oK1b95G+K7rOrt7yP1HR+xPZwzXhySeQGnroKCeIBl0CPwAbVvyrIDaHWvVtES+RxKGtHlJZjSq8dCVJl9VNLVBBSvyrERZF/clg4TTswukJ1FCYKUg7MVOkjhQpJ5PtawI1hJE6GEuMlTscfz4hJuv3fjyIbwcB/HMC+X58frLZRd/xcnFl1GwP+1CIIRTDMF+Ft703Caeu94+zar+/P2L52+QzwGr2Li1zX/0f/rPCDoxzarinX/+Q97+w3co6prR2oCyqLjy4h7rt7Z49/ffYnoyo9tLGfZSrm2v0emETBYF3tmE7b0NRre2HKY38Ljx3Ze58pUbnLz3lCc/u8/x01OktfhpzJVXbxD3Y9JOzPRows//5U8wWuMrhRf4BIHvMIYS6qxEt5pqVdALAx5czFDacLx/Sme+IlvmjA/OeP17r/Odf/SbXDw4Rmo4O53QFiVKSuJeyvEHTzndP6OXRownSzxP8e5PP8ImAd/9x7/NjTduPjMwMsZgjeVoo8/P/skfMfujd3mhaJitChZ1w9r2OqtFhq4rqmXJ1d94jbqsOTka43citq9vUxclURqx/+E+t//aKwRJiAo8PF8RD2/z15KQD/71m5wfnHNwNGZt0GVr0ONkvuR4Oqf5xT32vnqL04Mz0k7K0cMTlv/Xf8Nf/69+h/lkweatLZJ+yvWvvcAHf/Ief/r//hP+7v/x7xP30+eHmO5aj6/89te599OPMVqz8dIVNq9ucvbokOnZBePzCUEYMPQVTVbRH/XQbUu+yvnhP/sP3P7uyyyyHIWrGB/vn+GFPruvXePJW48QkcfW1Q2Mtjy5t89w2OOdP3kHlCKNA6QwtIF3CfsBXznSXJiEVBdL0n6CHLoJ0BrrFEWw6DrAq0KK0xlRN8azA6pVCXlFpAT1eEm81kH6HsXFiu7VdVQc4AHV2RwiH68TOddobQhGHfQ8QwUetrG0WYHVBk9JTBpiswqvGxG+ugfa0rz32N1pV9dpejHqYolZFvQ7EXZjgOmnqPvH2MRHTDIXTG4OqLKScv+CZK1HFPpIKZFZjckrmsaRf2Xoo6IAm4SwKoh8Hx16lEriFRX+bOWCXikxusV0HcHOL5ypmh50yLKCqNfBDwOsdpCdpm7dfFLXBIuMqKpRdUs9XmCURIc+QTeiOZsTBj7tZaUzUQr/9jbB3objVbQGWWuahydkVUs9XWHzksBo2igkK0p3L7cGk+f4QmKiAHt1AyskshPSGEv/zi7BIMUvaxQCfT7HazSNMQRVQzFZoIoaayza95BKEBRO9arxnIeExh1fK4Rzbg9dwoRSNGmIGHVYFiXl0QXeWzW1scTaPCPthYlz8EUKZ6SYOxM+aQyRBR36ToYyCLBljW1btCdRnkSFIWXdEqwK2vnKGd99QohPQ4IkprEW1bS02uA3jeOURAqzKigDj6isHc9HOohaYwxxr0N4a5fVh0+RFgfzslDVjfO9wHJ5uyDTkOSFHdrTGbUBFYX42uGPTRAimhbZifA6sYMtNdolPp7Cs24F8oVAC0HdGlQoneO4cPygxgLWEPgeNgqo6obAgtwaIAYJ+mSBvYTJWF9hfA+JIFjruu+xrln2yaSTfbiP10sItwas3n6IXeuSXN0iK2tkFBPtSfS+w7fnUhDMVniALi7PU9WghikG8PaGCG2pnp6hhl38zR7+7gjzs/uYvMQucrxRH60Uqm1p6ppEKrTv0Q8DTouSIFJuDbWCxXhOlARQNHRHXcbjGb4UXHv5OhdnE5YPTymqFt0agtDn9P2nbL90lWZZIkKP5cdHXPvGbaJRxxkT4rT7PeXxmUn32cJ9ueJ+DhHzmWX+ywrVn3/TsyTEQSe/+H57GXBqkJLDP36Xo4MzVBLQGIcWiIUkny8RsU+xKpzr8jwn78R0NnpUeYVtDG1RsnVlg1EU4yuJbFuS65ufxhBRiEpSqs0h3W5CO52j2waxNQBhqM+n+HXrCixpjLc7wkwztFL4ClQj0NoiPYv0A+woRJ/M8Ac9jKdoiprmbIFOI8zOkDIv8Tsx+cE53SSmaVpS32MxX9HppMyWS4J+B5NV9Nd7tHWDMJZeN2Wel6hIMrw+dEWotiFAILquyu0POqzO5nS3+vjdyAXs1pJPloT9Dn7kf360np1uAV9KnP78+76wPRe+fZpbfvrCp4+fb3W5rmu9KLi4e0C9LCjOF2y+eIX9n90nXe9z5ddfJFzvgTG0RU12dMHhO4944be/hpCS5WTF+HTC1tVNvKom1xp8j0o7A81lURGnCYQ+pRTUTcPZdEEtYf3WNuXJhPHxFFtrersjkjSmXay48Z9+1/mXWEtzseT4zXvcPzolCEKy6RJrLY21hEmMMYJ+r8tkPCdJI+rcCZNYawkin9D3WRceq7KkqTW5dep2gTAESUi1yukNukhtqT2LaVr8S7PP1XRJmDj0gzXWQYk7Pr6UZJMVeJLOqAPCI0o+K037JUPz5x7Ov8j2V5dcXGbBXzgg++nv+lUQPPslz+znzT++5Ds/8+E/47mUgrCbUC5yfvj/+Pf84o9+gReEjLodyryk1+tgy4af/sufMEhjrl3ZYG97xGxVUBuD9ANmF6coKVnbXUN6Tk29Lmv8wEd6ikc/+Zgn9w7odhIWq5xXv/c66ze3OHn/KR+8+S6rrKATB2StdiZSylW3m6alM+jiNy1hGNDpxUzHM4ZpTNRP8aIAoQ2hktR5yQc//JCt3Q02b+9w9uSMPMudmtOjIz76xT0wml43Ie6lfHx/n96gw2Cjz1//3/0tBrtrTh+/bnn683ssjyYYJdm8fYW9r99m/0cfcfjwhKJpqa0lvFTBGNcNZVawOp8jhKBcFSxOZ7zw9Rf4+b95k929DU6OxizO5gz31lzV5ZKsuXZ7iyt39vAazWyWcXIxY297HS8MmKwyamD65JzF6ZTNF3bp9Dt8+MP3+dk//xEb1za595MP+frf/RbD7QEv/NqLvPN7P+fjH3zI1/6jbwLOeb1YlaTDDnE34Y3f/vqzwX/xt19n+v86J9WComkJQh8jBK/91lfJp0uefPyUG6/fYH5ygdWGb/z2N1g8OEbrlqqsOXlywtrWkLgXYyU8fPsB/bUB3TRmZ3uT8XjKYNRjcjHHWk2/ExNqWGUFXugTRyHl4QWdqxt4SUh+MkEmAb6v0E3rNNIFmKLCk8JhoJsGpQS6F+NlCqSgtRBGPuKSA/AJJMgfpk6ueP8cO+ygAx9pDEQBXq0hwAWrnkRFIYFSVErgdxM8T7J45wnEIZQNqtXQtEgDNqswVY2/1qMsG2LAbA7R5wvCowvqjR6BEuTCYjyJl4Q0h1NsXiGUQoY+ptWOpB2HNIFHG/kUeYXY6qKKBnnZ4daBh4oCF8wJgZm5iVqt96mNJZIK0YlpyxrrOT8Fv3F8irRsabQhjWMqrVGjHoxS7HSFOF8QWBy/KfBRAmpqzMWK1dNzB1PyPLytIcl6D44u8CKfZVnhKx9PCESn4xyxcRj/xhrklQ2aoiYQAuF5eMDqeIZX1qx97Sbxeo96mpGN59jJkvJihd938BR7saKcrYir9pKkbZ1krFKIXkTbWlpfooUzhBy9sO2C2rzC1C1yWThn9TSk302xy5J65gzv2rZ1ROo0olrm+NJBk7QxtNY6/kBmkVHokoSqptGGxpPEynWFhHBiAgutSdIEk5fI+dKJDwCBdQTFZtRDdSL8IHDB+DyDXopuWnwLVjrVJjFI0HVLc7bAVDVxGCKqCtG2jpxuretotZp4Z4gadVl9eODI7HnppG8BWVZY5RFe38RcrAg7EVUpCBzFCdG26DBEtQZ56SLubQ6ojy4w2sHPbKsJ4hhtjYN/1a6rnKYBSEF59xDPWNpLroiUBuMrvNjnE/foT5YUWzbU+2OiF3cI1roE/ZTy4AwlFD6SZr6EQhMq6dTivBbZNIi1HjIOaZ8e42+vU2kNJzPseInspVgpqIoKczxDbfRpswI8RWUNnF8Q37mBWeY0CKqqAilIex3W4pAMy3S+Yuv6DuOzCXWjCZRkejol3uhh6oajwzNM1XD9zh4CgdeNscuCev+UsmloyhKv9cjqhvt/+gH97RFXvnYLUzUEaYjFYtoW6Uk+v0DbZxh5nqEUfkUT4kuXdPvsQ5cdvU/Ius++xF1/MgiwbUuelXSGqVP8ajUoD2sdb6etW6qiZC3tMJ+v2Hz1OqZpGR+PSZMELw7o7o6oLzJGe5vEo9SZ+10eQri7jre2hrl/SLvWQ2wMXRd2vnKHsiqI9rYJdzeY/+I+tmkcaX+6RCt5if236DaByDIrGyJPIrGYrGI5G5MZgw49irqiqUvyFWxe3yFbLDHWUNatg2UlAcmgQ1M2XLu2zWqVo7VG9CPOs5UTtJgX1AdThO8hW0tvvcPkYoHqRPSCgIvzGfQi2rrB951oQJhGmNpJ535m4PjMKf/yF74MfvKFzaJbN79ZazGNfgbZta1G+h71LKOcLolHXY7fvM/anV2yiyWP/80vSEZdokGHt/7FTzDA9GyByRo2v3aD7q1NZODRu7FFurtGWzRYrelsD3l6d5/T6pCgk1K3ml4cMcsKVramVZaL8ZxaWYLQdwXHNGJpWlb7J5SzjKt72yznK5ZZwe6wy8t/86tE20NsXjG/d8T+m/e4O55gBERKoqWgrVu8KERrgwydC7gSgnyeobWm1K6wMex2SIQks5bVqiXxA9q8RHoSEQQoZQnigOV0jvJ8kA7u5XuSQAiibkIjLG3VsLe9yeH5BWkUUBlD14+I0gjRCfnt//JvEXzOV+bP24/4S6Ki/gqSi+eqOL8603FMik+6EV/27k+zY/GpMsSnf/llu/1zHOMnwE9LOc/49/+X32X/gycMBgP6nZTlakWcxCjg4NEhG+tDirzkZDxlM4l4fHxOWdacnVxgGg0CZgdjymlGtNbB832EctKW8+OJI0P3U6JRl3KWcf9PP+T44TG2bvCkoEawd3uPrds7JKMOxTRjfO+YIiuwjeb0fMrg+iZenpP4AZ5S7D85wdOWvCjodBK2Bl1OT8acnU0Q1jLsJxgluHVjl8ZavF6EaTT1qmIw7PHtv/fr3PzOSxhjKJYFj376McXTM+S8YO3qJkWpeetf/ZjulRHrr12naFqsD4kQrG2PmE8WVMfnRMDP/s1PSUddpJKkvQTlKwyC/rDL/lMHGftk2D4h/3lx6Az09tY4u3vI7KcfkdcNSRIShj4WuPuL+ygl6G702fnWFe6++TGnT06psorTg1NUA9/9x3+D61+5yd0/+ZBHv3jAi995maATosuaP/4nf8A3//a3WLuxiXq28An2Xr/B+Dde5Uf/40/xlSIQ0OkkzMYTjj84om4q/CTk1rdf4f0/fJuNm9tcee0azWLFcdUSe4pHHzwl7ka8/GsvcefXXuKt//FN+p2U7lqXjavrPPp4n+HGgDzPXRGv1WhjQEOvFQTdhGDYwbaaeL2PTEI+MRbEQrQ9Am1YFGeUeUmy1iUKA4rTKaI3wAYKG3pkhxPifkqxcE6f/pU1iqMJ7aIgfuUaXJJuw42+c19+6xHh9Q2kANFa8sdneGmIHS/A95DrPfwkRFtoxwvq4ymelJi6ccWCNMTcPUS9cpWsE+MvnYFbrTyktrSLHL+TopC00wy5yEFKJBobeIgkJNAGk5d4nQF+EuOHIba15KsS1VzKfQYebV7ixSHNZOnkbD2JXzXIyRKRFQQWKgEqdfCUOs+Jowjpe0igiHyMHxNojbzsvAitsZ5HWzd4oY+NAkwcoIsK63toIaCfEvke5ZMz58guBEk3RUuBVzcIAQqwvQRjB3hS4vk+QV3jD1KMkpRVQ73IqdqW+VuPyEddBi/v0bu5RfDGDeplwfLJOUZA/9svUhcVdlWilEQGnnP4VgoReAiDk9wVAmks9cmEep5Tnc4IfY90refgblKQT1Zkk4UjJ2uNyArKpqWJI9qipDLGnQMBeD7+ZeJg2hZjLdpYjDX4RU2uFKHnYT2fstUEoYNYqcBHKec/IbWmAOe5UTb4QlLkNUKAv7uGqlq0ta5rUDcoX9H97itkHx8S1C1aebRVjQKE54QHLIa6aQiVILy1RXU6p3l6gbSWOHb+PEJZEBKDIdpbZ/Xju2hxKc+qNbWSBMJHRSGiLqgseP2UJq8QdYOnJMpThEI4BTMrUIGCqgZjEIMUv9TUi4K2rqmwqNDHE069RnTjZ6vQJ0uOLhu0J5FKovOK6M4O+Q8/oLY4n5P9c1QDRmhs0yJ8hb7Ur6+nK/xRH1qNJwR2VUAQOLjkMMVULctFiX7zAcUiJ0liwmEPGSg62yPKE0XQtqhLVbiial0hQArCTgKeglYzvLJGsSoo5xlhawnTGHOppT85m1Esc6SSjjfTizGeIAoD9DzHiwP0siAZdUlfuYL0pStoWIHR2nVfAs8p/z3rVnw2MP1Vy/Ovrpy6AKApaqcIpzXZg1OCYUo46uL1Yj6Bc6jI42w/o5/E9NYH5I9P8PspphuxHoUuCFeCa199genxBUkQ0vVDZpM569c28aYrfOXRYmGWYxqNvJQLrZc53qCLbQ1i1IW6wdQt+nSKwOINOqidDdrxwrlfI7Gmok5jlJIo67iQOo4wwqIEeAgIAsqTMeV0RdmPabOSptGMj87xk5iwjSizEixcf2GPIq84OhuTSoWXSs4nM5pGE/di/CQkuITvxVRs7K1zfjKl5RLqYixkDbN5wejGJlXuuqfSc2qB0lcuKIdPvRCfzwg/01V6ri31Z5W9hevOCyEQBqw1AE4wo2pY3T/l5OEx177zEg//3ds0vqCTxJw/OaVZVvT21oivrDMYxKwWBWEvpmkNzSpj/+kpq1XOTSnoXF+nrVrayZK2bIg2+wxvbRL82GNZVgRJ7BL2qqabhCzqEiMVZVFD4FHVDZOLlZuTYo9QJnhxyMMH+wRxyN5mn1d+5+v0X74C2jJ/7wnvvnmXhbCobkx1NCYa9ZHG4ieuCBEFnlPTkwqVSmaTOVJKjDb4gU9dN2STJbIBG0gm2RJrNIENSEcdyrJxxS3PJ05D2loDCu1ZpFDkZUGcpui2pihKhLU0TUNn0KGiphKGr3/3NdpWO1jv5+7JZ08/h1X7BK3mxJn+cr2Lv4LOhX3u3y/ZnrsOxWWC8Xnt6uf++/TxZ+B/f4EfaT9z6p4/RAAW53MWR1O2NtfxrUUDRdMQixgt4PWvvciDewfc+fodHrzzgIcXM4IoZHNng/sfPeLOlS3my5yDJ6f4/+wH3P7eq2y8cgWA6NK4RGuDkpLZ6YTTw3OC0EdIgQh8Nq9t0N0YMD4a8/Cth9z61m2ufedFVrMlH797F+X5NNaSnc/oDLqcHVywnCyQUnDlxavooubidMZ4kTNY6+KjkMK5yxaritHWkBBL3jQgJafnU0aj/jOi6fRgjAoCLh6dUu+fs7G7Ti4lWeZM86ZPzhiNRjSrisgX1J7k0QePee17r7E6XzCdL1jrpXjDhDyvoGxRn8AwGo0UgmKeAY6kLr3L6o1SJOs9kvUe/evrVKuShx89wRhJpS1FXrC9MUQbTX6xJIgDXv3Oazx67xHL+YIg9JgcXnDy3j7Xvn2bznqP8cGY9//t25S0fPcffhfZWt7/1z9HxB4bL+/y4rdeYro/ZvPWNlt39pDq5/Q6Kb3tIX4a8OGPP2aQJrz69Tus7p9w/ME+x/ePOXr/Kcmgw0bHJyx9QiTagqc8PvjB+/yd/8M/4Pb3XuHDP3wX+fAILwqo6xrTGrTRqDSizTOMNmwPB9zaWifa6AOOm6B89dw1L7DCYS1kHGKz8hIeA1WgUFfXsKsKZdxC6zDgClnUBNtDdN0SDDuo0Ef6Cl012LymnSwJhh3CG5uoToSuGoon55iyhizAzFbUoY/OSqJr6+T3T9G9BFE2mO0hFDUir1GDlBooxkuCYZdyPCeyFr8TsQKCJKJqnfRqaJxpn241rZD4l2o7tbVUkY9SkrquCfMKZQyhce3v1hiEsWiLw5pjiZuWVnhUFzMSz8eAU4aSgrxpXJcjjZ2sZxyhrIGmJVISYcAsC9Rl1dNrW1rfR1vQi9x5TWyPWDYtcV7hFzXtosQIgQh9YqXwMIgkBJWiQp9aW1ACQh/VWhgvKE7GjmSchNC0+Bdz0pev00wysv0xerpC9mJEL0F1QsJBQlu15CdTfANNVtAsCkzrOCSUNU1eYdvW8bAaC3XrsP/iMhgedpk/OXfmbXnpOg/GgaZ9a9GBT7cTIwddbF7SLjN03eCv98GALh2pvslL6qbFXEKPAiJSX2G1IUoicmPRTYtXOjO6Uil830MEHoGFoJ9ik8i5pAuFJwT1snSu8Jd4ZFlL/OtbLB+dQeUU9IzvIaVEa43ynYknWiOsJXrBcajM+/v44Ij5deMUqawFBX6/46p4eem8Fi4r2n6rqbXB9yTWGPw4oMoLZKMRvkfdarc2lBUmUHhSYQ/PaeoGGfhEmwPMmQsApHEmpl6raa1FewHx9oBPxEI+2ZqsQIYeIgqQSUj1aIrIG1TkIYYdAm0otARfIHWLN+i4Tq42qEWOiAMIA+x4jugkqF7qoHuzJSJNSLsxOquIux3URg9Vtuh5jhUX+Ah0J6ZdVdStRilJ0o25mK2oipLTx0d01roUVYWuNN1hl+Ggy+lsigx8Nl7Y5uLeMSr0KBMPWTSMREL2eAzxApNXdJOIwSs3GH3jloNftIbscIK1lnhrgFCKpmgIkvBTGNNnopYvru2f377sb5/EO0YbqlVF1Is4/Nk97v+7t1ACdgY99v7et0jv7CCU5Nr330C2knxVsKorRBJQFCVJr8PsZML6oMfx8Zj0hRRfKhbThUuwrVMmUnFMiFPnMZWDdNqOI8DKRmOFgEEPczjG2xnRnM2Rox7kBarfxQrIH57ALEMXDVpJaAykIReBR2+Zo9KQrNH4SYhalazmK1bjBWpzQOBLpgdjWgFhN0H5kqooMNp19D7+6BFeHCIt1JMVQglM5BElEcWyQGQNrRQQ+Yi6RR1PqazBKDg8dup6V1+9gchrJhcLtl6/6jiTOMEc6Xn48Sfdpj8LXiI+E4x+YeQ+p+p0iWBzCkwHFxijuf+H77LW61IuCxa65fxnj1hmJRuv7jJ7eE66M2R2MiEddigXGedNzWKeY1tDZ9DDKsimOfWqQP9uyY2v3kJYePr+Q2bnC179299k+PIeo17K4fmcjVGfyFeMlzmRtaylKYcXU1dIkYKiqOknMWtbI6bTOYtFDlKw9+I1ZNNy7Y3rDF7aAwvLD/d5/+0HZL7A831mpxOu3dwhDCPyumF2sSBKQ8JL49KyqFC+YjqdXcLfoSpLfCEIGneSvCRAhR60Gmss2WRFXdaEcUh3s09RlDRNfSk/3+AFEgMEUtIoyflkSpRGWC2osoZkkBAMEvqjHkHof+mY/jJIonju+f/snIvPkPb/jGP5krD/s69Y+4W5yT578ksSjM9Dof6Mg+htDtjcWWM9iWlXS0oUeVPT3exx68oWRV1jBFz/9h2Cfsx7f/QuSSeiKCu6/S5BN+Hq7jrTeca7b37E/r1Dvv53f40Xf/srRIOE0dUNjs8mtMYy2tugrmqKeU6R17zy7Zd5cu8pD99+wCIv6K0NuP76dUzdsHZtk73ru+wfnLF7bZOgn3By/5hev4uvFLd/8zWuf+M2+z+5y/gP3iaNffKsoswrh50UAisgK2v2bu3g1y3z8YIkiemv9+huDijnOQ9+8vGlJJ1HvT3i3Brs2YWDeCiJLz0Gww5tVlJVNYGnCMOQKq+YL1ZUrUZ2HZH1+q09Rre30VVDr59isTRty/xkxlWckoppWsARQOWlolW62Wd4fQP74WNUENARkl4Ucng2IVTKyXY2mt3XrrL54i7v/ptfMDs+Y5HlXDw5Z+vVPV77jVf5xb/+Gfd+dpd4mLAcz+kMuxzePWK1XHF494Dz+8fsf3TA9//xb5EMukRxAJ5CFw11USGsIIgCpocTpLUO12w0X/utr1FnFU8/fMywGzFeFGDA5s4A6b0/eItv/Wffc14gHzzl5u1dQuthtcC7rOIFvseLvU321gf0r66jQv9TmMDniVOXYFa/n5LujqjPFkhjKU5nxGlIU7UIpFNEajXVoiDY7FHPMlQnwpzMMMai44BgvYc/TKkmC6fkZi12WaDS0FVJkxBvvYfqJojIp5msaKIas9vHHluqw4yuEqj1HmZVgq/wrm1QPTjBzjLiQULZOgWmIC+pi4qmbAn7KdparJJEvZQ29mkXObZqqOuazt4a1bKAsoLAQ4Q+flFhhFPhCrXBSAG+C9bEKifCmRC2jcbGETKyqLzA9DtOtanfpT2fUvue4zAZ4+BcAoJRD1O3FFlB4DnJWas1QmvKvKFtzrHWoJKIthNCax18YVViA4U36lIDwdUN1CInEQKTV2grMJMF1WSOKEuqcYO3u4leFXh5SfnRUyopQUgWixzlKYKtASoKaC3kxxMkgrKq8ZrWqVcVlSs+WMBTLl72FDaJaJrWwQuVxCJoZhmhUvidmGK+op3O8bsptefR+orB69forvdojXWyoVVD3WqqWUZ57wjRGurm0rzQ85CeQuPuAxGH+MI5ffvWqSs1dYPwPKQ16Eu5R6skKvAIuwleL8EPfJe0lA26qKBu8dZ7tIFHpYHxwkH5lERd8jhqbUmMIfQ8amMIogDv9g7Z3QPMIkN4Hm1do1uNJ8AGPsqCd32Ldn8MUiI86Xg6wnVKVRRgGwOewgxS5GSBaDU2iRB1hck0fifGaEtb5ijADwMqX6LSmPztx5RliYkuoWqNpvIVoa9QceiqsNI5dJtWUx9c4PdT/J0R+nxO9eAED4HtxKjQwxiweY3JWmTacferL9GrApTA5AUiCSl0S9LvYCKf5Mo63iChOrigOZlQD2JKrYkvYTh+N0EXFSIMIQrwlwUqCsgIqR8eEfmKJPQRxokAlKuKYuUgv0VRkhUl28Muy/0L9q5tsVzlnB6NuXHnGqPrm5wZSzVbsXn7CuvfuIXXjdFFTf50zPQn97i4WFJUFbe//xU2vnUbP/BoxgtUEqLS8BlnEvFcFfwvsFnr/ikXGX4UEsY+9WRFqGHnyjqnB+ccnU5Yv1iS3tlBVw1iVbF4cortJVRLTag8+v2I0/GUeLPPNK/obg9RnmJ2MaPf75KXJbdfv0U+mZOVJaEKqLMS6XvkT8Z0kgjVCalXBTaraBcFVljULCMIfYq8IOgmyChy5pYnE9plgUWgNgZ4iePapb6CycJV7luD1/GRVDDNCAddjsYzGgsKS2/QYTZbIYxEKlAYbly/wuHRGSr1yRcl11+9AUXN/Qf7yG4K2jBKY3pXRpyeTFC7HfJFCb5LmoSxtIuSdp7TWMPui1fY+Mp1txZ/EpFJcelG/2wUPh3EXzaGn5cpvexUmNZQ5SVhHDK9e4g0EAxSTt96zL137rOxOUK3hlZJvDigmpUcHY3JdctyWTC6vklZVuTzgtV4SVW3NL4iHPVo5zm9zT7Fk4JBGqKi0CW8Hzt/sdXRmOHGkMmjM3o3t9h89Tr6ncd0uwnRIOZ8tmSea9YGXcSJprvRc6IpsyVWa6e01U05u5jRYonjJVfigPXXr4MQrB6f8PCHH1DFvhMzmeeM1gYU2rAYz4iiED/wsK2hakriNCK3mvHJhDiOSDzXYTeA1IbpbEGy3iVf5QyCmFXW0KDZ3d5kNlvQNDX5dMVqlZOmKeujIcen57Q+RI26VLDy8RpFtszZubFLXdas5ivKgwkXTy/4W//7v8Vwc/BLk8bPJhC/upf4F93+ajgXz7fS/swE47JNxpfzLL6w28uXn2E5n//rJ5m0+POfkKgXs3ZnG/PkgsGdq6S9Dv6jI86PLnj3nQeEoU/q+/zgn/4xO7vr1HnJCzd3UIFH7CvG0wXdTsKtUZ+n+6ecXcz44A/f4cpXb9Dd7LP7lRs8/fAJ49MLWqMJk5BWG26+fI3FbMny4ILRwMnPRWFAMuzw+E8/5sFP7zKfLRmu96mblvEHT7j1xgu89De+wpN3HuF3Q8p5xkc/eJ/5aomveswXGbdevkF3rUuTVZSrgulixWw85+jgjLWNIWs7Q2795qukGz3+5J/8e5pFzuJSD9nvJARR4EyJNPiewsQBDz9+igdEoY8QlqIsefjz+7z+6y+jsSzGcxYXC7burKMiH9No0jRGSImUylUuL8dIKInnX/ZWP8mIxWU3Skm0EKxvjdi5tU34k485zzM8BHf/3ducnk95/buvsXvnCqvpAr/VWGD84JTezoDuqEuel0SXbsvbL1/h9PEZfhAQJRHV2YpBP+X840Ne+v4bbGyM8OOQwajHw3cf4vs+OqvY2NskSiNms4wsL1hVJV/7T77F5HSKxTBUHkfjGWngEUcxd9+8i+/77Fzd4v7bDxmfLfCjAD8EKRWDMGJz2KPIMqzRrsL2yTn5Ipz12etIQVM1EPnOYTkvUWVD0wkxeUkahvhSYusGVTYIoC5qvKLBEwI6guJwTNsaxHRFdb7E3xygZ0v8axuEt7dpDyfOI+X6gOyjA0QckL/3FH+Q0uY18dUN8qMJ/taAzsu72LpFn84JtwaYp+fYoia9uUV9saTVLSoKaI6nrKZLIm0JjKUcz1BpjGw1rdEoz6M9mTofmH4CxpKfz4gQTu/fU1RSQBzSxgFh2yLCAO37aGvx0pCmEzmJzqJEzla0G32CQcc5o65KvE+6JLHFk5I2c54WIvCoLdimpWpb5wUShaA1RrfUWelkcZOIsBOz9GpkUdOczPB7KfUip8lL0qlzjZdFQzuZI6xB9hOX9GQFFCWt1piipNKGOE0IZYBuDfZoyvISXmWNRWvNsqxJ49C5fVtL2xoi3wX7dVU7OE5egnR+GyoMqPMSWVbk2tBtWgyW/is3aLcGdEYd4mGHYFlSPD1nfjpDz5fYpsGXilVWkHRSWk8RJRGttYS+j4icAZgxBj8M8ToR7XSFKWvifkJdNti2RWalSyqEQluLnq3cvbc5wvgK2YlRvRTRtJjjCdXFAqMNYRhAVlC3Tq6V1tAqQYwL4I11i5D2JHKY0v77Y3fMQtC2GmUNjZREStFWNZ2dIav3nmLKGrHWxRYNKg5ASrRwi7ZpWuz5Ahv6YBsoK6IkwVY12vPxtYY4QlvHHeh85SZt3VCczQmGXZpVjgp9TFm7DkHgIZR0cteANYbFvUPKoqb34i5SCMp5gcbAqINMImoDceITnFwgjaDe3kD6PjLPkK0m2Bxi25aiqBzJc5k59Ze9F5FxSHUwxhpL98YmmedRZQVpoEAqwo0eIg6wlx1DfbHAC0Maa0mqlqIfU+e5E0OoDWkn5ex8wvrmkOGo7+6/skILQdW0eFKCNcxPJs4vREC0NcDrxkx/9oDHb36MSGNWxxekm0MS32N874j+C9uYrOK9/+b3GVzf4M7/+vuucPBsTvs0OHV1jsviofySGfD5gre1rtiVxHhJyMEPP8IfL1HGqZfFgUc06tDMcz76p3+ErXHmjZ0QU1QUtsGiiIcdl7wtckTZ0CDwAp/RaEB9cu6gJQKiOEbkFWQV83xOtxNxUTf0v3INhSBa76C1oZktMV6CmRfEWwOCF3YgDNBNg1zkTiltOoeiRAQh/maPZlWySkOGeyN2NvosP9wna1pmkxlmo09lLUhJut5HG0tRVFy/fQ1PSh588JCTyYSybvAFBL7i8OAU30DcScBaZBoyNjXFeEYjwFQtRglUZVBo5nlGkkasbMti/xxCxc5lp6mtWpSvnDT1J2Mgno+rnhubT+BRnw+17Ke4ElM0rA5dodK7vsHjH3xIIwR+a5nNV/hBSJ6VxGlInVdEvYRmMsVPI9rCdX1W5ZJykaP6ESdHYxptyc9mGCHohD4mr500v4JBoIh7KVXV4i8LvCSm6SU0y5zV43PSF7bZqTXVNIM4JFKKyWQGjRMCWC4z1pM1iqykFYbFvkscO4MOXuRxrdfhxrfvEA5SmvGcyc/us4oDJtM5TV4SJbHj4gJJN3FQy7pluN5nNlkwnc452D+m3+uSJhF6WWBCJ+JjhGTthV20hHK6pC5qrAIPj/F44niFQjGMEqqqprPZpY0E179xm/nZjLZZYmWLiH1i5SNKyJYZAL3tIZtrknyZU65K2PxVQflnuwOfcYv4S25/+eTCPvf/57F6f65M6HMQqS8ipp7Boj7NX54HStkv/ewv3wRXv3WHd95/Sngv47HwOT26oLfV59obNynLmsnxhPn5FK9sWK5yJuM5N27tcv/DJwRhwNOnJ2xvrXF1d4OmaRifTTn4+QNe/jvfYO/bd/hrgcfphwc8+fApnfU+1XTF0wdHjNZ6jhzYS0jyDi9/7zU+/tP3OX544trWu+tki4zhoMtX/zffZOPOLkEaclXC+f1jfvrf/YDpbMHe9W3aSvONb71Mb7OPtZZssuThgwOGoy6LiyUvff0Od37zNcbjGZ2NPuePz5gcnBMg8Nc7HD04ZagN26SMXr5K/8o67/7LHyOUpLfRJ19ktACtZveFK0zO5gyvrhMPUt77d2/RX+/z4S/ucXjvgM1b2xitwXeu20nX4WHtJ2S8LyHmB3HoSJaex61v3WbtxV2KWcb0vQdEvsfJyQW6bXj/B++SjvoEoY/Wmnd++gHbB+d84+99m6svXcMTktnTIx7/wTt0d9bZvrpOm1cURU0YBfSSHvnFgqfvPiLPS3a3huRF6QjpZcna5ojI9xi9cQN1MOZsMufo/jFf/08Eb/zdb/L7//d/y5UbO7yw1qMz6tDmFatW8+C9h5SznKKqeOnbLzHc6PP2H76DFyqUNrRak24P2X35KsGo9+er4FloS+dZcLrKMZGPqVr6vocchS4IWFiauqZuWyLho+c58c6QZp5BXtGezfHXe9j1Pnqeo5sWm0ToogZjCW9to8uGcn8MrYZ5RnBjE5NX9AJHttahk4lthSXa6lOezFDLgmqzj5is8Izz+zCrHK9pCAMPuSiwWUlrrevMZAXC82isRRjjdL59z3WAsgr/chYr6xovdkmTDH3qeU6rzaXJnMH6PstejDKWVBtsJ3WGd2VLJSBKY7yyQQuwnkccR+jAw2qDbp1vhtGaKgpoMkfqxfPIVg2B9DDGYoXFLHPqrED4zm2askaUtVPcMpqsaZ3BG+73aCkQViHjGK/OaC4N63wV4l1W4z8x6VstcwLPo9GadGNAtSpYH3adpGejUZ7vIE7GuO5LU+O1glI6OF4QBi6xulS8Qmu0EsR3dhm8cZNivEAuC8rTOYvDi0ut9NztW0qMEMS9rlMkCgNqY1G+hw48jKcIQx89z2jKFq1bAl+hwoR8kdHkFb4QNP4lLMr38ITAXAoLNOMJZBEyCkl6qXOW3x4iVxHt+YxaO4lbU9b4SYRd5IR+gLl0lJVSYJGEu2vo0xk2c7AtYwzqErYqEU4fPvTxR110VoL3abCvW+PUeoxGVw1t6/xM/Mqpick4wnxCmJcC/ACDwBQlxljCOMAsCrxG005XrvpYOriZbFrCOERIp3RYnM6o7h9jPEnn9jZWQDVbUa8KZC+lqDQpgna6pBYGJRXKU060Yb5CaoNII3QYUC8LZNVgfB8ZB1itnenixZLmaAKrAmkMnSsjzu8f4xlDqxTRK1dpj6fQUVC2SN9DZCV61KdeZCRWUMeuG9dWDU3d0JWSptXIXFCVLVrA0dkYP43xBwkH+6dESUi3fymNPV5w/qMlx28/cue4aRi8fA3tS4rJir6F6uCCwz/5gGhrwHKRc/onHzL4ynXCtQ5Sqc9iLLDoqiY7GKPikHR7+Ewg4PkJ0BpLk1dOROSSr1cVFUf3DlksM/K85Oqdq/iDlJN/9VPnX1M0yH5ClVf0B12OHx/RubLG/OCU6mLOII5JBylPHh+xeXuX+WxJ2InJ5wW5btmuakeWXethqgYuVhCHNFmFFRL/2ja2aJCLFe3FHDXqEbxyFX9vnbCb0C5ylqczLBBe3aLNK+T1berHZ8i8pHttg3hvnWa8JDudMXl8guh1IAkJMYTacnF8gd/r4EcBT+4+IU1jpKeo6powCdjo9WjzirPFinTUo5zkKO3m0CpSEHoobbHzllIaAiPIVznaA1u2iMgldsMr6xhtaFYlYT/9dHg+l0uAfdZR/0Js9VzM1+QV2emM2f0TpvsXFPMVRhtuff0FuqMe4WaP0w/2iX2PrevbZPOMuWmomobVyQQhJbV28rJV3bC2u0E6SDk8GlPplnKZYz3B4nyO6qeIHeN8YUyL6XWoraZYFQyiAJKYJivQQnHx4T7rSrCYLckXBfV4RtNqWl+yqEvKukYLw8P7TwmTCF1UdJOE4fYaTx7u8+r1G6xvDul+5Qa6arj4ycecXiw4bZwXjVSKIIlcEG4cSV1Kp5K3nGdkWcHRgUOedNIY1Ri8OMQoQRQELjbyJU1e0B90qVY5nlZsbm0wvphQ1TVKKRaq5cY3b5P2UtqiYX5wQdKNqK5I9HSFsZZZlaOxRIFCl4ZyWlD7Ei/w6A46vzT2EOCq9n+B4vxfZPur97n4cwVRn9rk/Xne/3zrRjx7xf7Z0mjPf+i5jGy4u0b/xV1W+1OOHx/T6STURcP9X9ynuzHgxhs32Hv9+8RpzL0//YB3/+Q9zn/yAVdfvcbNN17gR//sP3B6dsHmSze4c+cqP//FXe7/5C43vvMS1lg+/qN3OXl6ymhnjU43Rm8PmZxNGJ9N6Aw6FFlBb3NAmRWMjybs3Nhmcj6j1x1x89duc+vbL+JdYuVMoxlsj/jg3/ycyfGYnetbZLMM5fscPTzkox99gG5bPKVYX+8zm2X01nt84x99j3itw3qzw5OfP6BdFmxuDDl7fAqRz/f/87/Bz373pxycTBGdhKSXsrO3wVs//oC01yHuxuy8sMv54TlnD47w0pj9tx6xtjNiMV3RH6aEgc9inmPuH6NCn6ZuSeOIdNh5pptsheMKKF+RnS/w0pAgDllMllhjWC5XTE5m7H7jJsNbW8j3HpIkAUZrbr52g9U842z/lJ2tEb0gIC1rirzk7P4x+cWS44MzPOUxyxse/+IeGxs9er0ON37tRZL1Lif3jlldzDn/6BBPCOanM1c9GaQMumt0tCBc62K0QfkenV7KZDzlwz96l9e+/wZb17Zo6hqDoj6eUOYNNJZuv+sC2TOBKFtO7x0R9iI62jroh5Js3tyh99oNUOLPxC9aoDy+oMprZOSRdBIUksZWWAQ28mnmOb4vCXo9ilVF7TV4QPnxAbKbYiV4/QTiAGGd3CUCB1nwPZpJRnE2xwxS9DLH9zyqjw/wr26gAh8RBXgnuYOE+B2kdIt/tLdGdjjBxD7GV+TTFWE/RQhBqy1FWTGAZ4mFVA4TqpQkDENkWWPqFhuHBIHvCOeBC6ZiIZBVQ22tC0ytRcyW1EIgPY9aCTztwLsVIIqKKokIswI9rfF2N6iaBq81CARmkbmOhXEuxvg+RiqwhkRKpIXq0sHbYMHziS4hL8YYjLUEYYitagoBom0JAh/VSZGtpikrvCS5hBNLqBrU9hrNYukctOOAQmtMt4PqJ6zf2CZ/cobveeRVhXdrh94wRQDevKQcz508b91QTZf4FkSSULUNXt0QeJ5LZoRwSiW+IlnvEt3cQinF+Q8+JA18iqJGA8ZYAimotblU2XEwnqqqseBI2UIg0oSibiAvaC34xmICDz1rEGmE8JTT/r+2gRco1rZHJOs9RwRV0pGiW+1UymYZJqvI7x+jpznBoIPsp4gkQpUVzWyF2higz2fIToxX1rShB3XrpHzReLtDVm8/RHpO5tENucGzoIVxMJ/tAeXxFLvICW7tYI+n6LzEC3yqpkUag+d5+JecDqSkHXSgabFVReD5KGtpPIVvcUFB6BMMOtRPzrF1jZWCsgGpXbDgC0mYhACsnp5TH03ovXTF/T4lqc/mzofEU7RhgJevsJ4k6kYwW8Iio+2kFOMpQV0TpDGm+USm2ZHOUR5V1eALQ/bRPvG1TeSwS1NWNCdTsmVNWNXUqxwTKLIP9hFVi2g0Zp5hjJPflZGPrzrIvEYaQ5blZKuMwfYIWwjSbkpT1eRlRTLoUJcVsVQUViCGCSKN8Db6MM+5OJowOR0TRxHrm0OOqgI/VNhGo1uNUZLD3/sZs6Zl7fUb2Kzk4Y8/YmOyYnhzi7WvXkeG/qeTG86bR0UhYTfBtOaSBO64eUJJhBRUi4JqVdC/svZs3V7bW+fwZ/fI8pIX97a4+jtfY37vmMMP9+kkEaUUqLUO1emMZpETxjHLwwvaZYW0kOuWZrFi4/au44HFMedHY26/dIPz6QwvDPDCgDgOaa1FxgHFMicpKuKr65QnM+q8RikPlMAOEkzdsPoP71Gv9RGdCAt4exu0j04IBz28wKfuJMheind9g+Z0zsWPP2J2NMZ6Hv7OkHL/nH4voQ0swdKjk8SIKOKoOCHoxnihjy5q6tYwXq4cR8BYunFEZZasrw/wPY/T6Zw8KximKUk3YjWesMgLwjii54Vs9brkywJfSNJRh9m9Yx7+yfu8/r/6a0TDzhcQ5X92ndZ1N6wxXLz7lCdv3mf7zi79nSGdfoSNAg7ee0oLhGhKzxlvrhY5VdM6zkHkUxcF1pdUZUU86BD5Pr4UeFKRRhGNNsyPxwz6HbY3RyyWGWXTIqOAdlWxyDNC6aHr2kEtPbC+AiG4mCwJ9i84PBoz2F1ndrRi/8kJw6trVLXzfVIoCBy3LA4jyrZhmS2588p1+ptDutc3sNpw+vtvc3Q65aitqYqKjvTwug4CVeUVgaeIk4gsczww0bZki5UzHm0M9SInCH28OCAOfURtaOY5NvJJehFpJyEJfc6Oxlwcj1kVBZvrI5ZNxY1Xb9DkNf1Oytn+IXtrQ46OxnSuDgnikPLpBOMHtIGgLms2egN6gy6TMue1771KOkx/WSj8rFD/+cH/K2haAP+TmujBZ3qi8FyWLL7k6r382V/SirOfeYe9TC3g8+fl+d38qiNCCl7466/zi//nH6OUYrkqkViKLKfJKw7v7rP+83v8x//1P+Rr//A7bL+8x9Nf3OPV3/kmSkg2dtb48P2HRGtdOkJy59YVPrj7hOOPDvCUZP/RMTtXNwn6KadnU+qqpjfoYlpDMc+otOYbf/PrfPSHb3Pjzh4H+6dcf/0m3/xHv+HUgy5/g9EaFSjOPj7k9NEpu9e3GZ9NqVYFna5EGmi00z6uyorDgzP2XrrGN/8X33HW9AbG9475+A/eJu7G3Pz2SyyzgvlkyS9+901e/OodTu4dcjKeUv0449rrN0l7CWEaYj1JWzfc+tpt7r55l3qR8fBiztHjE1osgS+RSjFa71M3DVdu7XDy9BShJEEafuac+7HP8njGn/zffp+gHyM9ST0v3GTuK56894ib375NZ3vAcNhjtVzRGIvfjblxbZPJ2ZTIk1z5xm0+/vFHLBcZzaqkWOZkZcWVzSEH51O0MVSNJh722PrqDaJBytpLV9j/0V0evf+Y3lqX2XjJYpmxs9Zhc3NI8+icIA1pshIroDvsEEjJ+//hPc6fnvPKN19icT7n6f19lvOM7/7932B4dZ23//XPOHh8zPr6gLsfPiZZ63DjlauYe2fUVY0xilqJSwjAnyORtpbyeEptoF4UhH2FEK5l3gpIrEWOOo74bSFaVbSTFerKEH9vjeythwgpMFKiao2IfCpPEVkg8DDLAolxHaazmfMhGXbRN7YQvu8Ul7oxshMRaEOT5WT3j5DXNqA1cGWE9+iUNgkwSjqZ3V7CcnFBd72Pvz9GaIP1PaynkI2mbhrSNMJ0YnTPVSLNdElb1ni+R4NFGoP2FJ6x1ELgK0nlKchLQiFR2rhJOvBouwle0xIWFVhLLBTeIqfuxDBZOs33uqFsaoKiQm4Msb5PW9cErfMuaADfggaskISBR1O6JMzzlJOu9JyDKlmOL0H4UC8zQl8htgdIHFZfRQHJnV2Ktx9irIWdDfxRn7ZtiTdHJFfX6d7cQt7chHlOst5zFezITbtR4BMVNUIb6rIm++AAIQRVUSKrhlhJyrMZaTel9BXe7ojuRh/ZidAClkcT0mvrNMsKISVe1dA2LUVVY4XE2kvDs9AnUgqrJLUFbS2+MXg4idRGSQrAr1vHe2tyGoHrkBxfUEjJKnbBl261U8tpajwpaRSk6wPSK+vEr1yhfnxO9eAEkZeIjT7esEutDfnZFIyBtgFxOYsnMVKAjCPq8RI7ydz3h75bOFcFqqzxkpiiKIg3+6x++jFeL8LrJxQPT9ytozWibmkEWE+5ca4bYiEQyxzrKYS12Kah7URYAaYosRJII7xuTDleXio6OVy08JRLWFuN6MVUy4Lp2w/Z/v5X8J/z1vH7CW1ZY4rKQbyEoJ0sEVWNHHQweY3txHSHXVqt0RcLaFo4n6K6MUJJwm6MChR2VeAZgz/sUMc+TRhSVQ665YcBXhohkwBTt1T3D0h/7SWqVUkQ+9BqOsZSBT7nZ1NM5DPYWadsW6JejE1DZvMlTVFz9c5VmrLm7OkJgVKYJKQsSvRqQd3C+it7nH74FG9zQEf5rFY5QezhX3qLlJMlj997SOR59K6sU84zdBoQrHVYLTLmP/4YrxMyfHnvUzjN5YNovedgdr6inDulqnqZY4UgHnYoxnOSrSEgsMayvHeEb2E46lPMc7rrfbxewqP/4UfY2PmUVAKiRqPWO9ggQEwMQday88JVJscTjs4vuPLqdYpVQbYqQVs8ITg9OmN3o4Nft4jAZ3584XgyxuBHHkEnJtjsE+wMCXaH5O8/pXpyih4vaTsdVBhQPj3F29vA66XYZYENPLwwRC4rVGuYTOZ44znNIiPPCpo4pFECW9WsQsWTh4d01vsEnmQ1ndO2muHWyPmyNJr1jRHj6RwdKFazjDQMqMuadL3HwdnFZWcSwjRgVZTMpgta3dLzQhROnWxZ1sTGUHque9Usc0TdPuv8fSY2sl8GiflcBGahzUqmHxzw0Q8/YjFdcPN7L2GWFWdHFzQyx3ScgpXNaqdY1QlYVRVSCOIkoDWGaNihbBr8oqKaZMi4IfcDehs9rAA/VGztbZBNl4RxQhQEHD09pbaG4Wafqm6ZTRd0R10qqWiFxVx6OS3LkjVt8JXH8dE5Mvb5ym99leUio5xmrArNjRev8eTpEUZrdq/tcv74iCtrA4a7I0zZ4MUBp//+bc5OZ0wDBUZRFzV16qSmw8CnWBYEaYynJOJSMjkZ9jDHZ3S6CZ0ouhRiEfieh9dYVO7EduZNDRct/VYxLwp6oy5aKbplQFaWWGF58uN7dNf6dPsddNkQbw9JewnteEWUhjRS0oljVrS0TUtelAzXeihjCULvC8Z4Xxp2PwtBnqvA2y+9EP5C21+e0C0+B3v5Au/CfvaheO7B8++z9tO3PBePfRYAJb7w2pdun0swPjlpzzM9ultDNr5yjbPTKVujHn3fQ+sWv9fh/sdPOXxyxr0ffcwrf/11Al/x9b//XbLJih/8kz/kyd1DblzbuWx3OQnJKAiQQpAOO/T7KU3jFuBVWSKNRRvD6f4pvUGX7/z93+Dejz+ikyZMp0uMkLz4N153icUnx3zpD9HWLW/+Dz9ESkFeVOxur/Pk7j7H4wkvrvfpdTu8+O2XmI/nyMjjpe9/BT8KMNowf3rOD/6bf0uZV2TTgNODM7q9lK3NEXle8NFPP0QpheqEXJQF4t1H7N3cZXqxpPElhwenFKuCF964xdP7B8TCkI66KF9RLQpqXTJbZMRpCJ6kyEt3jq1AXzppfjKYXuiRVzWLpyvasmaa52wNeoRRSFnW5JMV/Ssj0mGHyXSBNZYkCfHSkNZYqkY7Wc+3H+JNFxw/PHbylZ2I9avrHE7mCOG0zXXl+AjWOBK59BW+UmRNg9Ytm7sjXvveaxy+84jEU8g0olqVGK2JO86L4Mb2Gm2tMa1mbXPAyeNjfN9nejbh2q+9wHf+i7/O2//qTU4fHROmkijy0GdzfGMdvCWNsJUL1r4UY/y5zbYaU9R00oCLSYXEOq+CS+MdCajIRypnvESgMEWFiAP8zT6d775Mu8idGV3V0pQ1aehRj+eQV0jfo408dKsJ0giSEJ2XRNc20bMMykvPiazEAtIYmoslq8Yp76A1eVHiS0F3Y0DVtKyWGdZXrGZLp4BjjZPltGA9SbDWo4oDAm3RgYJlRXY6RdUtamNA07TEjaZoWzxjMWlIU1bOdVZbaq1RcYgSuOPWmjpykBaswQt8p47VNDStxpMWXVeobgKbI2wvwQ8C9MMjtDVu8rcWg8DTGhsGeAinT641onGBtwfYukFoDcbQrFpsEuK/fIX+r79EvSqpzuZUWcXFwxPi6xt4xhGHEZLRVp94o48FTFXj9WOKtqWz2cOPQ+cuax1HRIY+UgpEXiG+cRPqlrBuEUIQDFOK2YoojegpiacUuqzxe06fXwig1uiHZ0jPo1hNQAiENi4gvSQQWgSNtWAsvu8jtabRBlNWeGGA0obAUy4REYJStzTWEkQhxoBvLSKrsGWDFRJjnRoeSJSGYlaQjx/Tao0yrtug5itH8k5jorU+0vcpHh9BXlFjERYi31WJ9arEzI5cF8MT6MiniXy86ZLGk3h1jRXCEYeVpPf9N1j90fsIYx2MrdVogePaWFfFD6TESklV10TGQttiwtB1pVrtVIEMhL0YsyppxjPnK2MMom3wwhAjXbFL9BLy8wXhWg+/l3y6CAMyCpBlQ7WqXGdLCLxW468PnHJc6CN8RbDeQx6PMaFP3TT4oYdeZhipCLdH+IGH2BnRns9pViVCKZQFM50TaYsZ+NSLnN5Lu2QfH4AxWCFZtJaBb50CXWZASAIh6VrByeMjjDUcPj1ld3eTpJews7XJyekEG3ms3XBd8Hy6JBGS3evbLIqSZVmSvLBD8fiMyWJBaw0xCdnhBbZqUbUm3hjiS8n50TnplXXKokA3LXfe2GP66ISnf/IB6faQYNj5zLrshT6EPtZawl6CEAI/ccWd6eNTwm5M2I0cusEYFodjTn/xkMf7Z3R8j3Cjx+Ldx9iqQfuKZr2HwrKarPBi51+0cXOb8w/3OXp8Ql5V9LaHWE9x/viEK7tb1GWNTp3h6GxR0g8siZL4QlDvDMiOJqRVQ7vICbcGICDeHuJ1Is5XOf75gurpKV7P4ez1+cJxd773GvVFSH00RyIosoKqrLDdlCqvqFYVQSdGxD6mrBC6xUicmqPvcX48JvB9lmcz0jRBGcvZZOLmO6FIOwl7e5vsPzkhaxrWux1GVza4OJ9SGddRunrzCtOLOaps6I56zPOccBAjM4UuasJuzOiFLdZfuYrXiZ4FkbpqMMYgPc/BV+HL4TLWwQA//u9/xMXxlEVV0wlDHv/eT9FWUFgBQhINU1e0OFs5A9lIEQ8S2knuPJqaFuYlntZoa9CV84A4U3Mm89Wl87YhSSN0VVGUDd31HtPZnNBXVHXD/GxO7PksFhlWWmzrYNhh4IPV3H33PlZJSAJMUfLgvYd0eill4Uwi9x8fsVws2L2+RTubc+f2LsMra8imRa51mf3kLifGMg0VFxczPCnxA/9SdENQLAviOKJuWoq8JUwjlouMex88whhLr58itGG0u+a4kllNmVcMdgbkyxVDzyNZtQRxRKAg6YUcPDimG8SYOCD2JD0VIgMfi0X2IqYnM9aGXTp3trl4eML54zPK0knpx1EETevUB5cF/qXc/a+MOy67h1/Y/v+BcyE+nyTAs8D+M4nCl+UYX7q/L+7/ec7Fp+/6FbCoX5F7iOc+e/Xrtzh95yk7m0PIKwIs2hoGgw4nkzkXT84JkoDhzW0e/vH7/PRf/JDZdMXLr7/A2taQk7MLUit4enjG1t4GG3d2WZ7OGGyvcXFygfUFAZJqtmQlS3aub/P633iD47tHZOMlYSciHHT4O//Vb9PbGtAUlZt8kc/O0Wx/zPhoTHfY5Wt//9c5/9kjtBTsDfucHZ5TVzVt2/LN/+I3kVKyPJ1x/tEBF49OGD88YXw2487tPabLnHyRo5RHO18RpjFpzznD+nGAUbCoDdV4ThKHLPISGXnMJjMWy5xOv8NsuaI8HBMnAbq19DoR3UHMalqQzzI83yPyNcpXXNw7YXo0Ye9rN0nWOmSTFbY1RKFPLQXd0MNTkjjweHw64aM/eZ9v/MPvOAigJ7HaqdX4kTOYy5uWtqi49sZNZpMlKvDoxCGTPKepWjAWD+G8HU6mfPDf/5AX/843iNa6nD86xe8nNHnBK7/xGmcHZxTLjNV8xVqaOmJ5WWMA0bSEQUDTNmDAZBUihTgKEYHHg58/YH19yOjODrbVeJ2IXhoQ1RpvWWE8yXB9g8oYbFnzifHW89fql122Oq+wnsSrWtY2B3hKYITA60bIVUF885rzNkhCvGFK04+dHO1l29MfpPj9lCYraJcl3sGEbJmjkhjrCbSEIPAdNyEK8NZ6hP2UNisRgGkN86enrnK61qUta5p5wcX+CZ00IQl8vOvr2IcnmCMP2Y0IuzHnT8dsXd9kMXlMaixx4zDvtZQkeU0b+c506mSGthAGPkJK2mVOscoJRn2kNRhPYhcZoqhIR64q1WpD0GqIFFSN896QEs8abNW4SrWA8NIV2gAyiZFVS+N7eEJSHZ4jKpegtRKU1rTaOviNdI7drXQO1UiBqixeqxGX01phDP6gQxSHVNOM87cfk+6tU8xz/MtrlaKl88p1bCckO50hkwhxqZ4jY59OEtFZ74MxVGVFlDg8NUphtaZd5ggBvd0RcEnKzEqspwg2+njd5JlfzLOrxzgCeLCzRlvUCAP+fIWZgLLQCQJaQCGc74jvYXHu2sr30cZSW/e8aTVWayeh3ba0QhDHIU1RUtUNnShw6laBhw1DR+r2Pewl7yESzvipvvTUoG5pqspxWVYFVrdEW2ukL11ntX+KWuaYvKDV1im0BA7GJ6MQ4UlML0adTFFxhC5LF5wbSb0o2fg7X6fMa2xWuPjD85yhohCoooKypgaUUs61vm1csiWkU68rKvQqd74gAuLrm05sIApAKWhaPCVpjMFyqf4mBHq6ZHipGqOXBSYvUYMOMvCQvkc4SKmenMMlftwqgS1ahOfhFy3V4YUzSkwiTF67Do6Uzk/jbI7vK6KtAc14QfXgkPZ8jhimMM3Qy9z9VmvIfvEIvcygl9CeT+kNOtSzJXES0RQVRAHxzhrqdMr1vS2eHJwS+opykeHFEaf1Eiudl8V8uiSOQjprPVTmlGkWixW+hN6tbdrpisoYdq9vM9sfo4qWrRtbTI7GBElEvchcUp4EBMagTMjTN++iasNoa8jJ7/6czldvMnx5zwkvAJ/cWM5FHKx2XSYV+S5x3ho8mxPboqbEcJpnyKZld3udeHvAgz9+n7xtnPOwAW0MYdWynC5Jrq4xOZ6wdmObVliC6QqvExMg2Ly1y/xiQRBH9JIY4SvOH5+S3rxC0E8xlyZoQSfCy0vyg3OS27ufxjBNi601shO5DrLv4213aCZLmumK4vGpM6edZRjfI6tqPCEoJwsW5zO050QJSgxhP8JkOWk3ZjadE/s+cRzx5PEhV1+8CnlDJwp5+PCAsJ/gtxbhKR4+OEAEPkk3pm01vrV0khg5X2LjELMq6XcSTi9OsEKgpaW6WDGdLhlc3yTZ7CF8Dz/00Y2mzRq80HHP/CikKZ0Hhhd4XxKYuuD9yR++x/JiyWB7SFy1bO2ucfb0jKytsMbSC2OqVU0dulhLaWjnObPzJRvb6ywWOdaXSGtZW+vz5OScbhLiBT6LVY669E7R1lBnFV7gkemc/HQK0pLVml4UkKYxW6MBp4sFGENtKvJFSZAmSF8RdWPGZ1OSQCGEYJB0qBYlQmsGkSKzLbvba4yMYHBzm87WAOoGoQXVyRQb+dg44ODnHyMB71JgxPddcqw8ZwoYRQFH51PCMODk+ByhnJ+b9BzvYTFf0u0mbF5dh2mO14vxAo+kE7M4nNJiufXyNVoMxbKinhXUeYkWirHfsLbZ4WK2QPmCXFumB2dcXUu5/Tff4Po3b3P/j99j/8ERt+5c4eRgTBD53P71l+is9X55IPwl22eTjL98dvFXR+iGLygKfObwPh9cfTGL+HR/nyOHP8OrP/fBZ1/7ZdCoz+/6C6YvbufpqEs0iFmtKvq9CHVyTlvX+Mb1SNLUaV3ruuXJm/e4OJuysbvBcC1l//CU27eusH/3gMZYvvmPvke9LPjpP/kj8rwi7ITE/ZT2IiPsprz6W1/FGMP+m/d5fO+Aza0RJxdzXnzxCslaB4TAj8NnxymUq27ODyf4gY81huxswVs/+xCpBP21Pk/eu89ob4P1Ozso38Now+LpOW/93s9YTFcIY9nb26LBUNUNW1traCxZpsmmK5rGVShbY0g7Met7a8yLBlvAxuaQs6MxpdHQtrRNTbLWo84LUj9AeYJQKJZ5CdayOJnhRz4nRxc8+vFdJk/PWeYF1Tznpd/5Ksa4SrRvBaG1JElEP4lYlTWjQY+Na5suiVhkSOHw+8uLJeu3d/B9jywvWTw5Z+2lPcIffMBktiQIAmLfY3o+Y9BJ8YHz+YKybrliNEdvP6KzNWR2PscETmLz/T99n71bO0wenuL5Hq3vJlaM4VJKnytXNnl6/wAZ+Zwfjtm7tUMYRxRZxujKiHd/8C5fUZJrr10n+9GHJMMu1dmSaFnRubGJGCa05zPW37j5hevyyy5Ti6W5WFJcml6prGR1GfQnUYCKQzAGr38pMdtoytMZXi+mPjWoTuWM3tIIL4loGk0VKSKZ0LQtfuiD79EcXEAaUeYzdFnjRQFoS3OxQC9LitbQWMsgr1CNxlsURE3Dol6g44ReZ8BZtiTcHDmVsemSRBvMwQWdQReROaUq6XlIAXVdE6QjinlOHAZkyxwCD9k4F9P4Ui4V37t0aVbUnqFe5s4l3Fqayyq0ryS1lPgClLHgKTzPEYWtFC5BaFqstOiyIjib0K4PEHmJXevhbY7QWqNPp+hlgSclQeiRVw0oQX2pmmM9iRwk6LpBBE6ZJ4wiyvMZVejTbTXLgzF+4BGvdxGzFcvzOa2EAOdUXhUV+mKBPxEEm32U7+FFoUuE/MjBeJQEa50C1CU05pN5SYYeMuy4wOtkSpPXBDujzyz21kK4PQSgs+2kbk/OZ4RAczjGILC1C2BN04IxzmPisrNmPUk8HFCucoQW+FtDkrUO0XqXMI2RSPQ8A2ugMSyOL1jdO0JmhbtnmhZtDUEaUyIwWPKqIQ58RFVTGIvShjQOsRcLlkqhuwkbr1ynOJsiHh4hG0MQBNRGEwUebPSpjcEeTS7Pj3FOxtrQGEPv6ojwyjoX/+0fIsoGGQVOwlcIR+A3FgnEoY82gKcIDE6YQkm41LX30gRLjvUVatihHC8h8lFJRD1dYZR0RpISpO+hzxcMv/8aMgkdV6YbYzsRuqyxrcE2rSskBB6i0NiyoZ2uaLLSBSJxSNiNKS9mGGNoy5qg42FWGZ6QmDCgEgLef4LshMiiJb69i9pZI/v9t6lMS9oZ4C1z6kXuXHrvXKE6mdJIV1gQTYsfB7RxRJKG6MWK5XRBGPkYJakbzZWXtnj60RPqpqEqSvwgYNBNmUzmMIjZf3TC2vVtismKLJ4Qj7oUF0vOn5xC7NNmLU/v7iPrlnyyYJEVxNfWaeqWOApYTZbYsmV3Zx0r4MmHT5Ef7/Ot//ofEIy6fIJWcMUWF4BZDW3dIgOf0e3dy+Iaz7oc1eMxAy3oXd9h48UraG3Ii5Lk6ibVsqDNCoJ+QufVPVRW0GQVAji5d0iIwLaGSXbMoiy58coNNLAYz/BGfYwUXH9hD5Qgm2WITozshPiB7+yEkpBPgNhcqjp5kY8RAVQNtmoosxrRSfBDn+qtB8h+Qri7hQoDAmuZPDiinK3wgoB2lJItc7LFigTjOuPG0B11GB+cY2vN+tYIo1tsrJg1NdGoi/QkgZVcvbnLweEZIvbJpxnalzw9OqcbBoRxhBFwcXKBHwRs7q2TDFJOHp9x/ddfoj6f03/juuOaaYOwgrZunoOeO/K/H7mk4xkc/fOx3GXh4qTR+N2IqlqSL3I8KZ2kdS+mbA2rrEBYRdiNWOQNMvIJg5BOL6Eua0oPmsukxrOCBkuv32F1XrEcL4l8n1JofC3Is4owDfATRVUUTM7nCCHojbqczRYUeUGRl4RJSJrGbO9tcrh/RqU13UGPpm5RviAMU4S1nJ4u6XSHbAU+w7UB669co5qt8HsxemZYPT7FS0KEp1BSunVGG6fqlUSUVUW3k7JcZQhgPl+ChPHFFG00vu8TRs4tPog9ojgkW+aUW0Ouf/0Gj//4Q7a2R6zmJWt7a+QXK4qzJW0o2by1zfHjU/xCEVhJVVXML+aYZY0Sgt7uEKUNJ+88YXky49ZvvMTr/+l3uH46p7PV55YB6SuqleskPruf/mfY/mocur+kFfF5BNRn//hnlHH/Ql/8uV1by68mz9pPD0lJ1m5vs//DBwgMwdkZevcKFxfntFpzfnCO0YbJo1MOHx0jlGJ9a8R0keNHAXnd8ODREa/8xmtsvnSFu//2LZaLnM3rm+RtTbusWC0y4iTm3k/uMjufIqSgk4aowKPVhrXdtS/HPgLWWC4OzomigDiJeev3fkonDkl9j9PxjBd//VW+919+n6iXgDEsHp3x9u/9jHKWceeFK1Rty/TkgtnEObxO5wviOMKTHiUtYRiSRD5x6HMynuEnIUVRMSkKwiLm5e+9SlO3nDw6YZoXzBdLWmMYyR6JBoqWfpKCqpGez3KV0V/v8c6PPiTtRbzw0h6PPnzK1gvbhKMuSRTiYVC1do7OcUTSTTl/eEiUhFSLgnxZPCOglnlJ2Ino9lIujsbk5ws2vxagQp9OoNCNoW1bvCghNoIk9Km05mwyo9Zdjj4+JHp6gcVw/OCE/taInRvbDLZH1IsCQo95VrOZVy45q1uQ0OvHvPDyNR7fP+T8aMxwrUfciZhM5lgJaze3eP+HH7B5ZQNPSDcZLwqC9T7eZh+E5eo3XriEBIhn3lL28tL/LBrQUp7PaU6mdPfWHXRlkBI0DenGwEGhAg8CRXF84fDsgxTVifB7CeXBGFWUhGs9RN0i/Jakn+Jd4mJlXoKBVl+qVUQ+qnWGWDqvHCwnCWnrhhRDHQXgBShpqOMA0bTE0sHzsoML+l97CX9jSLI9cImFryhO59jMVem01kSB77oCrUHfO3Y4dE/hX0KyxNoAU1b43QRxCX2ydYPXTahbV7VvjCEMfHQcYuKQarpApTFVWaOqGi8MyLMCPwzwWw2Vg37pqnbO0o3GTlcoz8O7tYtSCrEqKKoGaS26abCxj2lbVKkJ+ymyarBRQHR1g/5rV9GrkuyjfcIb287wzPNQaz1Eq2GWs9i/INkZsrYzopzn5IdTdFXTBD7LowlB5FO//4jN77xC//auuwDqBhWHjsQqBGE3dtedhWcykALnqVHU4HvPXywYa7HaIKWDH5iqxmiLrBo237hBuShYAna6IvQ9142LArwowGDw4gB/q0//pStEgw750YRg1CFKY/KDc6qLFc0HhzSBh50ukaucGsl8uiDE4u+MqE5nGANBGkNR0yqJaFq6ykGrUAKkoixrlBUkaUzQdU7mxSJ3crTDHt4ixzYtYS+l6kYEVQPTJcJolAHTOI+NVhukNXS/9xr53QPUJHMyssJJz4rQh6x0/iifOGYXFWK+cjebMUgvdEWmTzxInKfzAAEAAElEQVSBlMJ6Hro1NPvnaCkRSqCw7vuUgk+Ci17kjBKfX32EQEUhGIvOa9q8RguBMg53LXyF5ymil/eweYMeLxEGtGlpejG2rRGepK00TOaE22s0QuKfLpy3x7AP2qA6CakFr2lAggoker6iPp/jdRJsYQj7Ce2lX0I7X1EfnKGNpet52DhgkmWcnU/wP/Kwdcv1W1c4PTqnWBXonZGTvYx8/r+0/eevpFme34l9jnls+Ijrb9rK8l3Tvtk9w+bMkEtSJFe72F1IwmIF6Z0gQP+VIAECBKwgEWtIipyd5c5wenp62lRXd5ms9Hl9+IjHP+ccvTg3s7Kqq8ZomufFzci4EXGfeJ7nnPMzXxONeoRhQO4c25MpYSdB9RPaokb3YnQY0BGSQSfh4sk5sRJ0kdhVgXUQj7rkRc1stSU6HNC9uUN/2EX3ks9tbu7F9o2v7qa9BGu9/GxTeKirjr0p6Nv/9e9ja98N2v76GW1tcEL6osPeAFdV5NuS4nlF4CQIME3LKEnoxJpsXdCYkKyqfZLp/AF420lB0I2RFqrLBboXk2oFjaGuW9TWc7uEECCEF8aIA2QaE9/ZJ//xfVy+xWhNrQV61MNKwXS1IU4TqFqfgGYl+nCMlZamachWW27eOqIMIx49fEZRVrjacOv2EXXVsFpvsKFGaYVqDP00YZXlPHp0gtQaUzV0kpidUZ/ZfEmlIDCGnV4XOezy0c8/JhmnEAYMdwf07u0h3zn28srGQ32DJCS6Lp4iBMo56sIbwb6ERblXLxgvk6zO0Zi7reX8fI6KNLPZEhl56E5TVKSBprPbQ1gLoSLdGVCuvSngybMrGtOi+jF12/Lk8akvHHRCpmcznHSM9keMBj0++fAh490xnV6H09NLNtuMtBsz6PcYjfpUxlC3DcPdIdHKSy93+gkPH52w3WTs39hjNBlRZyWrzYbFdM52tub49gGTbsruvUPC3QGzB2eea9mJmf/iEToIsA7sOme1Lmiq2hP069orSxnDcrFiu8kIwxClFLPZgiSOiNMEY1pMa0g7MSCIooC2bpieTImkYvLeDRaPruiPB9hAEaYh49u7LM6XZLMtUaDI1y2udpBomqYlCCTOOKqyZhDHZG1Ds1jxi//xp7z+3TeYvH7A858/8u7fecXD9x/y3f/t3yfqvjL3+M2o+UshUb+l8dsldH+uQfCCi+5nsvhK3PmrLQu+NNn4TSXTV07PFyvDX0oW/+y17gtvHR5OKIenhK3ltDCcf/SUVVnR66Tc+eZrCATn7z+hbgyjvRFGCl/xeOc2m+czpBC8/fvvUW8Knv3iIVoK9GxOjSTppHR7KcUqoy5resMONZZev0e9KZFa0dvp++TC2c+fCwfr5zNOPzmhP+xSbgra1strNhJe/923eO8ff9u7owJnP3/I8798gGktWd2Q5SXdQLNYbOjujnxwKTymOMsL0k5CL4lxClQ/5XYUYsqWgdDUXU0r4OEvH/ljUpJ+v0tbll4CU0pCBJVx2KykqwRFW5HGIWGacuetG5iqIa9qensDVmdL3HTNtig53BlwsZ0z6ac8v5iRKMVms+XRLx/xvbv77B7vcPrknF6vw2hvDFLQ6XfYXi1wbYtQgkAJtuuKaV4SaMVx/4C2B3fevMH2xx8SbrZs6hodBeRZTpBEvPe9dxjsj3j+4JTZ6YwkDEnSiMUq5/SXTzh49yZJJ/abh1YkRU1bt3z80RPOHl+Q9FLSfopar3GnU27c2We1Kejs9pDzjFgp6iQgKmqccCTHO19CjPqMn+Sc85umVugkgoMhxCGurBGBJp70MVlBc7XEVg113ZAejIiPd7Ch8tVSB+nRDsGoS/HJcwoBWkkv+ZmE6K4ngArjEEWNuvaYKC8WmKyiuH9GdDhEdxPKszkqr+gOOpRVS5HX2DDE5le4q3PsrbsQxCRB4ANIKSkvVwzfPEZ2Y7KnM+Rqiy4qAJqq9sTnTkJjLW3poWvW+c6Cag1We9leZSxGa2xrcEXtuxJCYaTEVZV3OQXqxYYwCmhu7OG2BUHmnb2btiW0Dte0NFFEW9coqbxUqnM0q4wQqE6uAEc47GCrxlejrMVor1TTtoZ2lZP95D6nP/6QG//8e3S//SbbT09p45CqqLEPL+gejmgFxJ2Y7bMpm8YQR5JolJDoPsuTGdUy8+IF1k9tW7feKyHQ3n8gr2i2BeUqI+yl6DQi6EQvN3aZRD6gvb6H3PV9JKRASv1yAVNJROhg+ekpkXFEhyOC79wD58jNtSt17eVKV08uqSJNVdVUjy9IkhXDI59ob99/SrPYImZrmm2BCwPMaktTNV7mMNDYuqHdFJ5zZZ1XAbvu9onWgHW4skQKAdZ6uFNV43aHhIMOxSrDzlZIIYjq1ntqLLfURYWpG5qm9btGqKnyEqEVUTdBrHOCt44JJj2u/j8/8pAmrbx7uVKenxCFftlPI893u0447PU5BxBRgCwqvytVFZWG7mIDtaFtK9iNUFJ6UriUuLrFJiHRjZ3P5vCr+4fwfCrnHK6sCa69PMxqS3A08uam1tJuMmy2pbmcwc0DImchiWG5JQgUovWcFtEUnjCvJe7xBdXFEmEMbpNj0sjzN1YZYtiFdYFOUlabLWwzmtZ3bpxUyF5KNV1ityWd/TF1mqJvBYQygDQm6sQIKairivNHZwzu7IF1hL2Eqm2RxvrO9fmUqqg4evM25ycXdAc98m3G8mSG7UQc7B/Q6SZMn16wXmwI9/qM37oBywxbGQajHrf+V9/GFA3OOFQcvLLFfbapl5uCelNgG2/yWRc1xlh0oFBxiAw1249PefQ//4rupM9wf0zmDEIp5KJk1E+5vJyzszMkL7xnjY0D5mVNfDSim6ckB2OqvGRyMGGwOyDsJ8wenSGtV1ALHNTWMNkfsnr/MR0c5eWadp0TDD1vRAQKPewijCWIAoT2XTM7XVJfnNPevkWsFMV0RSW3RHFIvckJ4ohWSi4endEaQ5xGnJ9e0Bovjb08WyCs5eL0irib0FQtsrHIKECHmsnOkFgHrDBI47BVDd0EK+HGzQOuLude1a4bMXznmOGzcxSwOV9w8I076E6EVIrt+ZLsdMb4rWPf7fsCZ1dKvw6+2qawrUFq5QUYBDgp6NzbZ/n0imqdE4wSoiQkLypMaxBZTSMV08qrUyWTHtXFOSIJ6RwNIQ3pxSEXT8+9xPPegHq+QUcBtW3AWZqq5umD58RpzGaTobUmy0r2d8YUVUWrDP1rs7sbBxMu52sGkz5ZVmCUYDjqMtzzPliryyWubNjtd6g3OYcHE3b3hky+dpvNfMv0188YHY7oHo6xVYMzFq0UqhvjtpbdbszC9D3vMG8oTEMUBJi2pdftkOUFnV5Kt0qRUlFVFVIpdKAps9Ir7mlFXbd044jtdE1+tqB7PIYwpD/pMVtsWZzNAVCNIbaCfhB6SFvd0BY1g16PRZvT1CUyShDd0O97zvHLf/9L3jWG+bMp8+kalQTsv35EZ9z7XHH/S1ETX0J/frnO/R3zjt8C54Lf4D6ILz75uYfiC2JRX54JvORrfOmrvrxr8Zu//rIz9Fmg54DB0ZhP2pbESS5FwCJbE0ch3/kn3+Hdf/JNrj4+4dMff4SxluG14kc8iFHA/HRG3EtQWvLpv/oJZ08uGY+6hE1J00hc2TLcGTB54yaz6QojBFprVvM13dTLv6aT3udO4gt+ibOOJ3/5KZv1llG/w+V0ybs/eIdbv3OX/o0JyaiD1BrXtCwenHP54QkPf/kIHSjqpuH+wxOGvQ7dOGYzW2NwbIqCNIm5efOQneMdeqMOsmjYZgWLvIbWYmtDW1Q0fTDKJ1JRoIh6Edt8i7KCxlkaIzxhOg5IugnxOsdNuszXXpFke7WmlQ5pBIOjMeePztFRwM7NXW5/8x7biyXTT57inKOqarbzDU3VUJUN43Gf2sHJg1OKTU6+zbGtoXdrF2c9Rn58MOb802c4C51hh6ZuOfnwKeurFYFWRElEuNvxELPGsndj1y8QmwLSkE2ZUU4XpL2E+XrN8kcf0ummdCY9xjd2vBLY8ZjRfM1quWFdVdy8c4ALNOtthv3VIybdCIfCbUrCozGVMawennDwu+8gpPAVj8A7drZZQXG5JEojpPaLU1t7fLctKtSo6wnVndhXTJWANEKNvalXe7aknm3RSUh4NKKqW4JAU12tUL2Y6PYecrklOhjjjKV8ekn7+BJ9cwc17qHrBonERhIRamzRYIDt/TPSmxPCnT6iqGlXGYFWyH5EvsqJv3aPbLZLksaE/QQjJFEUIgXYJCSMAkIlsTcnsMo8wVqAEoLaGLSx4BxKCqwAVzXXbseWhuuA+VpZqlECGUgaBLGAwjoiFeDaBqM1ovbmamqd01a1VxurGxohsEGAahpUWSE7Kc4YVF0jtcReLmjLGtUayqqGa8Kz1Aq9NyQ+HpF9ckrpHOp62egFIaZqmP/5xzQXc2yvQ+f1A+qiJp9vUFpjGoPqJtjWeEOyeUlzdYEsC6LNgnYqCI9vsvzRhwhnSW/sEKQRzsLswSnFH/0vNGXtITwodKTp/vA77H/3bc89aLyeunMOqfQ1yfGVZU14RppOI8bv3ATjAxIOhgAk1yTu6nSOiwL6bxz6KmWgsc4iET6wn65xe32CoqLNSsqyItzmtGXlfRXiiMZYgjSmLWuM1iRJgDMtwlhiramuCxcISWMMYSchNJbWWvLl1ruFz9c4B3Z3iJr0sJsCEYVQ1IhQI5WitQZbe3fpum48ZNFZ0m+9TnOxRM0znPJyk9JajBK4qsHVNVYrMAJpLJFS1IEmTEKkA2EtbpMjRj3axQaEIDreoTpb4AKFvlZJs9fKUqJpUVojtEJE+uUu/KqYiLher+W187gTPsC31gsHGOPYPjghGvRg0sOenpMMuwgjEFWOPt5DaoG72vrPiTRu0sc2NfLNG+TPpkRKoyPvPG5rr3QkqxY97MJ0xcAYmqrGdmNqFHEUYmcrdD/FpDHSOnpJQrWs2GxXtEJ4aeOi4c7bdzl5ek43itGhooxCgrLl6eMLnp1cotIIWzUslmvCfoeqbenvDiieXyGMYXa1ZLHNaDR0BgNCrVl/+JzuuM/h79yhdzDk9I/e5+qjZ3RfO+CN//L3PjNYFZ+dRb+Hely8ujYsBM8Da/ISGstH//ovuf/8jHtNy87tfbKTK7KiIggVmzxndHuPxliMdOg4JEo8pKlYbnF1SznfMDrcQVjBg59/ysFrR3R3h7RZRTFf09MB/d0hYaj9vdiNqYuG4nz5MrlAQHxrl8UfvQ9A93tvsvwPvybt7UKg2F7NEElMsM6RowFpGrOuayohaWxDc514p70h/XGf+XROb9yjXJfsH44oqopagewEpE5z4/YBF5cLLhZLTNEi04him3HnYJfMGk7Prhh2UkZ7Y9ZXcy7OZuz93lt87//8L9BJCOCFH6Rke7Fk/viSdJBgG+P3xZfBlbt2nxcvi8B+z6oQkX7p5u2sL95WV2tOPnyKVopYh4RHfcpH58SbiqJpqOsS4RwHNybMthnD2BdNliczXzjQAUEYUiy2WARHt/Zo8oJeP2W7znDGYiUEkUZJycmzC4JIkWUFOg4wWE7OrnA4NqU3L53sT6hOLlDC0dsfE8QRSaSJixodea6n7Sb0uh2KKODy03MiLVHSoYTwggtKIhxYKTznLVAkCG/O6hz9YY/V2RSpJYHSlEWORFzz6GJMY4gjr6jXlDWdboptDY1p6Yy6mKpBDbrEww6XJ1eMel1mT6/oRCHj3QGtFMimxSYJbePYZBki1oQyJKtrrBCIqmVVbok6MQMdUWDYe+uQ+emcnZu7bIqK3o0RybjnC89/RWLxcjP5Eh+y3wLl4rcBixKvhOuf/fzs158d5QtTli8jYn8xDfiyx+4Lj/8GB/dlh8urrpJhN0Z3Yx7+8imbvEAKuPnWDd76x99ASsWnP/qY+TrDOBhOBqyLgtHukO3ZiicPTnnnh18j6ac0lcHiiKKA88wy2unx7g/fJd/kfPSjD9luSsb7A6anMxpjSQ5CgutW4ucIJNePi0XG84+esTsZcH614PZbx9z6xh0m9w4JUt/ib/OKkx99wv0/+5C03yFOIgajLsuiBOtYrLc453jr1hE6DdnM15zO1zSN7wAkSUT3zj5DYxleLHn68TOKqmZvf8T+rX1OH18wz3N0N6ZY57SNQccRKo2o5zm9GxOCfkLSidk+uaKebekGiouTGbZ11G3DZHdEOd3w6IPHjHf6bNdb1pstIgjY3x8xGnQ5Pbsi7aZMH5yzXm+5uT+kcYKyNSynS0xRkqQxQRhw+fEJVknKdc57792DbsRyuqQ3GrC8WtGTkqN7Nzm5nLFZeZOZWGg6B0OibkwgJG1r2d3xZnp5UyHHXR9o9jvMr9Y8/egZYaAZDDrsH0zItjm9vQHLPKNZbujEEf22wZkuZrrFpZrKNOwd79D/B+8S7A+RWqGA7PkV9WKLm26w4Fubiy16p09dVEQ7fYwEVVRI63xlWwrQkqCb0DYt5nJN0k8I4hAhBM3pknaYEgeKeNLHtb6CH+2OfHU8Donu7FM/vqA5m9MstqRHO9SzFW1REXQTwt0hAtg+uaS8WtN0Y3r7Q8Jxj2a6wnYS8k+f0Rn16d4Yo/oJohtjV7nH268Kejt9TNmghx3UMkPd2aNdZv4YwwBVOYqiJBl0Ma1B9mJkNyU8GlN8/Aybldg0JpcCndXE/RTdTTDrAisEUShxrU/A2qpGBwFV1SBbi2hbr/JU1mhjENZSGuulRIsCGXqeiahqmrb1WHshSALtlbLSPioOKc/mVL96DjjCQENrqJ1F9brkD89J04Tg1p4397pcsve7b4NSzB9dsFlsiKRX8lpeLlDGkbcNh1FC+fghbrugnl7Q1DXTJue1/8M/99CmrKRcbjHLBbrXw52eYhdzmF0w//gjZPp/Yuedm1jnUKH8bA0VrxRVXmLXr//rHCIOX656vjgjEBrim7u+a9S2tMbQZAVRGoOS6CikezyhaQ0rAW3doIwla1ps4L12lm1LKiSVlIjEO2sX1qujBGFAoDWqNVR5iZUS7RxWCFykMMZQNi3hcos0jibUyKJCFxWq9t0rkUaIqsFUtZd0FGA7McH1dRM3dui8ccz6j9734gDSCzcYrXyQZA0VQGuQrUF3E0/Orxtkr4NdbqiKmiSNabcFrbF0d0aYNPZmdGXtCe1p7A0UA43ByySLJPDqY6/uOteFqxf1q3q6wlQNOo19d3XQgTRCLLZQGmqL77bsTlBtQzzsY5+vkd0U1xpML4ZAog9GpO/eZf3rp2weXeCq1gtaDBJsXvsEKQnQUuCKAtN6CHDQtIjZCuKY8uQSIyQkAVG/SztdgRKEONLdEbUUJHFImRWsr5a0ZUU23zC8vYssarKqIdnzRo8HuxNWUlFoQRAq7KIiPe5w1ZyhOiFhEJBtMuptgV4WWK259703Gb17k3qx5Zf/jz+ispY4CDGFJwp/2RYttSLsJb/xKyUFKlTY1nL0w3c5u1ywmK/p9NJrAnKIqxpk1lLONlgcPaG4fHiB6Ea0jUE0hp3DCWrcZzld0QrH7uGYMi+QrqUsG8I0oskb3OUa9sd0Rz3sbI1qGqiaVw5VEO0OCG/ukD+7AiUJRj10GjN87y7mw6e01lFnDXFrscZSWYcad2i7IZMbE0bjAevLNcvzKVVe0D3YQY861BoiG7A4vyKe9HBac/r8itZakkGKCELKuiZIQqq25fBwAq3BpQHzyznjsYfjLp5ecPjdN1CJ3yts04IUhL2YZLdLOur7LmHpP8vBdRFDogKFM5bsbEH+6IruvQNkIajrlnDSQ4ZeSSreH/DuP/8u+cWKYpWzeb7ANYZOJ8aVgiJqCVuL0JLAOLZtQ1A1VGVJ52iEVeAag7CCjtbML+aEgaZtDGVeEccxxrZszjOiNGawP6S1LeWqJFuWTEYdjFKM0hSRKIRxXDw5w2Q5+zf3CY0j3JbYStFPEvRBCqFG5TVCSEIc0SAhEBCYkO7NXcJRl/X7D3FaeklqGUBtCKTgTjfleVNTLLYEWoMWhEFA0wToQKOu9yElJXXTECpNYy1CgE4jtNKkScTWWNy6JKgdt968yfmHzxiECQ5YXCy5/f03ufmDN8DC1S+ecPX0isV6w2aecePGPvMsZ7lcEqQxSgiKpiba8R4mxSLHGu8VtXw2o7hcc+u9O8Td35xXr0w9v3/8zYLpv/X4rahFvZR6/QIJ6PNZ01+RCr3IosXfPHX4TEXqlff8TU/UFxKi4e1dfvVnH2Jx3HvnDt/5r36PsJewPZtz8usnVEXFZH9C3I0J0oizD55y/uSC3dv73Pz6Xf7iv/sxYW2IOwmFtazykjvffp10d8Bf/vc/ZrbOOD6c0BYNnW7qmf+hIs/KL2RM/ltVecXJzx6yXmyIooD9W3t883/9PboHI6SUOGPZnM559pNP+fQv7mOch110uzFSK958+zZPP3lG08Kom9LgiALFcNABIVgt13z684zNwYSDO/uEg45XibjGLy+WW/bvHnLz3VuIR+dcXS0Y7Q8QzlHXDfP5ir0oxWpJUXlSmB4kmFVG2Fh2ugly3MWFmvnTKfd/8Snjm2PWqy3zla9E3TzcZTjoc/L8giDQxFHI+YNzdBLgegknD05ZZwVfe/sOhYNtuWb64JzZfE2iFZWUtFnJ7rjLxdWSwm4QWhInEZNbeyxWW0TiN3tyg460r+ZoiXQC43x1RKcx1bYg7kTMn0/p7w3Ze+OI9eWSy0/PuD3scu/NWzx6eEo0SOiO+nQM6MkeZd2yqksOdibc/EffINkdfC6ZNnlJ9fQKoa8dVLVGdWKUtcgkJAm8Y7AKNXZb4pTEKeeD3qKkbXwLXQw7VHkBvQQVBrR1i11m1NYRpTHNfIurWqJbOx4CE1uUVsR3D6jnGyhb2uvATw68wk11vsA1Xm8+jDQ6idg8vKD/xhHh0QRrHebZE2puoKIY8pow9lj3clvR3D9j8t4twn7iN526xaYh8sYO9nSGa63vwLSGRoC1FqoGmRqavMQqxej2PtuzOaGxCK1xjSWvcpQDmgbK2pNw8dUlrCO4/izbtFgg1IpWCKhr30ERAqukV/JSilYquFxi+x2CfhfTtLTSy062VyvP6wgDT36TghawJbR5SXo4olYSLYDdPjqvWP7kAcnbxxx++x71KmP58Qk60nSGHbKPnzFQ0quvTfZoXYtrKu8vMc/IV5nHOVvHzls3mW2+R3N+SXt2idhsPEl7NGB4PEGFGiVeMV98FZXzOdLO9dIXBr/R3v7ccigFMtBowC5zRBp7FSTTIhFsrpaU65x40IF15rkoQiCdxUiJCRWdOMRojXSQphGyMdjWYssC4hCjJVx3XBSOvKqIOykdPE9EOG/wF6YxXC5wVQNJjKlrbN140mtdI/aGuKpGlBbjKg7+ix/QrnPK+6egFDLUtFUNdQNCoMF32/DdVPISNxmgo4BWer+EcNzDtJagalCBpqxrKEr/HZT0WPbmWvs/CrF1g3EgXnCeXpzsV9drC1hLfjLH4WgbbwrokpCm9gpc0jmfGHdiVFFSPbtErTNs2eCURPRTXFGhjGPz8Bku8s7Q0bZEJglV1RKutljhkEGIEAqGKaJqfafwWt1NSInc5EQ3dilnK1SngwkDbBii8gqhAipnKYvGKzUFiun5DEJFZ9DBtRYVhVibsX+8x+zZBUEvRm1DxCajtQ6hFA9+fp/JzoDJwQRnHXkQEu6NSfdHRIOUztGEkx9/xOM//zWxcegk5nQ65fib95Bavth+P7dNf7Gw+FkM4Z+VWrL/tVv8fhLx+E8/ItvkiK6vygYIXKBZ1Q1BEmLCgNGdfaJhFyGgziuKqzVV21Jby+FrB17JJ6+5fDon0ILkcIIcBF60YZWh4hCrBPXlEh3d+3zooCSj77/F8t/9nOLj54T9FDpeAawzGYJwVLMVOg5oNjlSKi5nSzptj+WqpNw25JuCOI05uncTYSybPKcxLXlW0Nsdsl5nNK0j7iZYJa4NIRW2MHTGHdZFhbhaMhgPyPKCoBtTlDmTW/t0b+2+hAG+WAWEEISdmL03jqnzCmcDgutCBM6rMgopaLclT/6nD1hdrRiOejgheParJ6jrjlK82+f1f/pNymWGTkP6d3YJTxZe9lnA1WJJnpd0Jn36RyMuPj1lM10zOR5TKQlGkV2taIqa4cGIKAnZGQ3Ynl5QNcZ3SnBM9kdkDzPG4wG33rrFx79+yMHdA3q3Y86enBE1Df1ulyDQCKUZdjuYukV2E5Juim5bytYQD1LKTUmR1dTbkkkU0ApDb3dEti4o64adb94lubFLs8pYffQc1e14rkhR4SJFm1cMleJy27JqW1QYUDct26pBIsAZ+kmHqjHYUKGCDmVReaWo645m1TbYmTe2dJMUm9WsH10R9BKiOGGbl9iq4sN/9VOSSY+jb95h/N5NimvYbBsFXnK7MajQQ+WaqqUFzGxDgiLohjTKoa5VEF//3bc9b+zV3UC84CS/8pxzv4EQ+i00LYD/CCZ6nyNTfyHJeFF5++ocwP3mez732V/xnr/DEMDx79wh/Jc/oh+E/OD/+I/o7Y9wDp7+/BHT2RIVBRzf3KNtWqanU1ZXK772e+/SasmP/9s/pckqlFaMeykXsxXj/RGv/f13ePKnvybLS0a9lKZpqKqG8e6Y2WJFVTU0Wcnlx6ekw453iI78Bvf8pw/58E8+8CZVreXdf/xNOntDivmW5eNLTj94wtWjC8rKb1A3DieYpibflmTzzXXFUqOlog0DZBwRxBG7ccTB4Q4NULWGxdWSx79+go5DLxUYaRqraVcZn/7yIUk3JctLT44tDQKItKQoC1TaRUm/8FVbw87rh746Ol2j51tcvUKNOtx864jFfM1mumTXtOSdiHpVMzqcUGwKaB1t2/Lg/hO6wz5vffd1bGs52J9QPDrh/q8fs78zZLQ/Yr7NCZKQd//g65z/4hFPTy45f3hK6xxRFBGkIaZumT678pv6qkB2I0xgqbOSdH/I7q09HvzsU2wkqSTQOKI4JO2knD+aMggiHj655PAbdzh485jFOscVDUJAFCjCVqBbS9W0BIOU27v7HP/DrxN8sULgoL5YEg26GGB5OsUISc9YWgkurxDG0pYNMg0hr5HGIEYdbKtRQnoSshQgBd3jXcL9Ia5qsQLCqkUmoZe6HHVo1znN1RLZiWnma1QUYFrrvVOSkHq69MlFoKizkuhoTPnkgqAbU65ytKxJRx2WHz4nPhjSP5owevcum3/zR+Tf+D0O/+n3yJ9cotoWsOh+zPSjZ3T6CcGg47HhSiFu76DjkPbhObaqCbWvhgnriIHycglFBZ2YRgk6xzvUj89p8pImDLypWr+DJKRNY0zdoI1F7wxoVhnWGKQOqMuSoG5QQQCbjFb4xUzgwOAlId0LbrFEbbYYAe2w5+Ff+QYVaIwx6Gv4i3VgA02sJMI65Kak9+YxtYRqW0DVEO8Oye+fkox7DG7s0JY1sw+e0h33SG/ssv3Tn1FdnqCiAP3Gu9iqwpkGtzMkDBRSSow1JJM+B3/4bWxRU/3B92gvrqCq6X79TaKd/ucKIC9Wqs8R8fAbhe9IGB9QvFw+r3+K61e+SDqEQIaacJD6+S5Aa+3diKOIZDJEIn3wFoa+G2IFsVK0VUPhQGpDlMZYY719S+116m1ZY7MC6RzaWkygfaIQhwS9DqKXYq3FzdcEgIpC6ta8xLs31mLLEiclbV56E0TriL9xl/jWLrM//iVtViGjEGMMkfCGkSYJacvGJ6TX3ifWGC+JGwTIxRrSCN1NqXLvdm+dJbg2y6sqP7etkl7K1jlUa5DWl67M9Xl7edZfuShtloNxtHlFMEgRxmKaGqoKZq3fCycDxGyFQREGIXYUUDY1QVnhegn2colSkvSNW1z923/PZltw9A+/T34yJYy0VyUCxGjgk03nMIsNwaiL6CXY+YbyckFyc4/om6/5RPOjZ7iLOVL0UPtD8icXRFVDvi0Y3din20+pigpbVES9lAcfPODW4R52kLC9XCLKhs1yS1l4OeHASdqmpXSOvcMdDt66iatbzh6cUmYF2himp1PMco0KAvKm4fXvf436dMF6sWEw6HL6iwfsfvcN4r3+Ne/x8+fyq3dx/xvdiRm+d5PJ0yse/8WCuBfTKkEVWKJejyQrSQa+w5SfLthcrVBRQJWVHO2NabVkvtpweXqFLi2DgZeXXsyX7Bzv0FofVrXbkv7BCNYZYjRAv+rT8WLUrYfi5ZXvvAWautziQkUx35J2O5SnM+q6Qe6P0VmGTiN6vS5NXTG6vYetWs+1q1ps49isVoxDRSeNMTg6OmB3Z8TFxdwHzhF0OhE7OyPW0xVlVVG2LUkUYoqKztGI+GjE4Mauh5Vdn9uXifE1Mf0FR/NlcVZco0ucY/r+Uy6fXHLrB2/y9C/uo6Yr+nsD4t0+xWJLtcgwRcX9/+4n/l4XPqnoDToMhl1W0xXh8YTNbM3qp3NGxxNCKel0O7QYdKLZnK24e/uI6XJNYy3T5QYdaLRS9HbHPHtyynaTY62lLivqoqLfS3FNS28vpe130dahCw85jqIAHQS4sMUFClM3uCQkHfWROEzHJ5JhGtO9tYvZVMzOVgjnGL22S+d4B9e0ZPdP0EpBVXkoZKCQXS9rnr5xzDc2BX/yFx9SOOuhh1g0gts7O7iyYa4126oh6sReRS8KCJ0AJ1AIjG3RjaXFMdcOLS1Jr0NpwWoI+zHh/oD8bMEH//pnfPs//z618xyujtbUWYHBoHWAy7yMdqgDsqLABRG6FjSXa24c73J2OWd8NCa8hsb5WfRZbP3Z9PtN8SPxOZLG3y22/q0kF+KLHYcXVbaXx/ZF4NQX0oTPwH9fmjl98SuKl6988YIvSVe+IoP5rMvy2YbR3Rnw+//NPyKMQ3rX8o5NVvHspw9ASHYmQ9JQoQrfGnPG8slP7+O0ZmfUp2yt73Qst5jW8N4//DpKK56+/4iqbTkY7/L82TlvvHPXV/ZaA01DT0ve///+DCUl/Rtjmqzi0z/9FY9//YROLyUva17/9uuMbu6wPV/ywX//E84enWNqTyoaD7q4QLKer3h+PkMo7SvhWnJwY4/BoEfSS4lSb1VvLheoSBMpRawlvXGP+fMp9x+fYgTcun1I0g+5LCqsctRVQb8bMxp0eHo59yo1HlZNU9Uc3NqlcpbFB8/IF1uiSQ8CRTrssnw2xc22uH7CTq9L2rRY43BtQ5U1/PR/+hnBqMONt47o3t7h7Nklk2GXqJcQSMWdb94jiDTltiCvKnLboJQk1Iqwn5CVFeOjMUKCWWVcXswJpCLpJVzOV4jW8sYbdzg/m7JpDflyyxDYe+82F48vWBUlpmlJBl3ypiYVHYJuhHOOYZLw6f/8a+JJl6Qf09nvcdTb8w7CZyuckjSR4ubXbjH89r3PcMSvjGa1pdwUVOcrXNUQT3rMr1aoqiHpxtRZDVHog/KzFQ0QR5rFoyusc0y+fpvkeOydgrsJL/Xho4Bu/7NExgEYS7A3oF3n4MBWDdXVGjvfIA9HOGtJb+3RXK1wQlBtCyIBetKn2RZIKVBxiGsNyTAlu1iRphGDH34XOdqhTSIWv3jkg3AgkKB7IboToQ4nL1WgbFaxPV1QNDXytX14ekWzLbz/SRJ79R9jYbFFGIvsp766ujNAXFniqkX1UjLn0H0vGxg1Le3WmzO6Toy5ntoiCXwQusmxcYS4rhzrQNNcS9yKpvFzTUpE4INQY+1nnAPnENZhjKFtPOk5kBKbxAhrqFuDvZzTe+2AuJ8y/aOfI4uS5I0bLO6fIrRkdHsPUbRMP3hKEGm6336P4ueC6vwpoqyJJkN23r1F+sYRRNedMyU9fC0KCLuJh0HcPURIiZB8Fsy+8u+LdfGLVDLbGmxZf6Fa+ZsLp7s2cxRSonrJtYKZQyhvDCWGKeZsgVluKRvPedBSUbkWqTVBGiPCwMMsEGhjvceBAHNtmqmuA/7KWNptgXSCsqjpTAbEOwOWizVy2GVxckW/sTghCKXABgqU8JAmKSiaFiUVLtUMfvcdirMFzcfPvZpXVyOF51y4MMRIEHWGCkNq580fVRzhlhku9nyLtrWoKEAut2AcTktqY3CrApWEPljfHUBZY7SkkX5/kKEmCvRvdIRenFrXWoRx6EgjpUCGAbqxrDYbkm6C1BK39X4otqqwjfdziKMAIzqIbYVOY+QgZfOzTxkcHGOs8aIHRYXYFoQHYwQSax22yDF5jewnFCcL3GxDg/Dd7MdT2vMlO//kmwy/+wbr/+HHsN4SHk7IrJ9bSRxQLDesL+eURUkUe7n05WzFcpshMTTOMF+sCZTyJO9BjEUiTIDaFAwOxhTLjMvHp4hORP+1fdTzOao1fHR2SVhb3rpzhFjlPHh2QSW8u/bp6ZTDv/yUW//s23yuVPrXjlc7d5LDf/Auxcmck0dn9G/s0ZYtqQqQpWW5nRMYx86wx0lZE+/2SIYdcueoXcPkzh4Xj85xqWJFS1039EZ9lquM8c4Q6QRNXlIvMkxeewK9Vp87Dtu0LP/nD6guV37NCzTOWe9LkNcUte9WCSnIpWS9XKOTkHK1oa5KgkB7eJ6oWV8tkAhCregf7WGkY7vI2FwtEZM+5+czOklCXlVeuKJpKRZbDvdHrIoK2fX3d3bpvWrGrx+95Ex8sYP5Yg3hurvXmtav587RrHLKixXTh+d0ewlBGnH3+29Rni2YX62Zny9IowBjwJQNcT8hDkMyPF/yYr7CFA2LxRpd55is4mhnh83VhkIYirJGKMkwCVCB8uuqtfR7CfPFhjDU5HlJ3RiiTsT8akEYeqU2s9xwEISUs4zt6hmx8Q72OEc0SNFC0pqGaNjFljXFbIVtDDvjPkhJ3E2Znc9J4pCL+6f0Bx1UJ0TFmt5bN3Bty+ynD4j2h4RhSPXJc8QL41vrJ3qwMyA8nvD6o3M+XftkqKlKjpIOprXMspygNAR5Q5gmOCFRrSBqHE44TOTjhXDQpVzlDOOEfFMhpWR5sSRUiuXVik6aIpzFtY7Vsyn3fv89hIB2VfDRv32f/U7ExfNL4k7KNN96id4kwBiDaixCenGNNq+o84r4JZzzS8YXClF+jROvxObu75pb/PY7F8DLm/iz9ucXj/KLNTheZiJfte785tMvttqv7mf8TZcwIQS3/t4b/k3WYeqWT//4l8xOpyglGe0M6EYR/WGHvg64/+iUR2cz3vvH36SnQv7y3/+c434H62ByMObo63cweU2axHTrhtV8RWssQkp23zxG/eJTLuZrjg52uJqv+LP/15+gIk2Vlcii5LinWRoL1vDOH/wOKgooFlue3z9Ba8ntW3s4Z72Lt5ScZeW1xjwcHOwwOZ6go5AwDKjKiuXVknxboISvKrZVi1ECLTx5sRt5HwWTV9hIk6QJpiwJujH22nxstDugWhc0ypEknvMRjDqITYHsRJhYs/v2DeafnFI8n7P7vXuU988pnkwRt3dIq5KqbjFSc/PrdxBhQFvUbOdrXv/GPca7A549fI6KA+YPL7Grwk+8nQ6h8QZqEQHTkxl/+f/8X0hujNl744h8nVFEIXHWsDvsM89y4p0eHRT91w/Y5iWzpxuqTYlUgmy2xiiJsAJhoSxLVGtZihXpTo9SKTabmiqAtLG43NA7TrCzHNYVop9QNS2Hd/cYfus1ZKh40V58MZrZhtVffkq78PJ47SBBOccgCb1mdhTBqkK4Bts0GOUTzqa1GOMDvnrhHWc7t/deTgpnLCj5mxvHdbAaXpvmBOMu1fMplZbQGGgt1bMpMg5w8w3hqEe5ynFlTed4B7PMaBYbRBSQ7g49ZvRsgYgU8b0jXKAJDRTTNfpogtlWULRE+33cJoduQjZbE1qHjAN6u0NaB+b1gCYrMauMapURDLskvRHNusCY1kukSkWmBPFkgDmfU6w2WK29ok3TYqKQNg7INxmBgNg67Db3XZlJHzMeIIoKs94iW0Nb1Ugh0FGI6HVpqxrTGqI0QZgWscogjdE7Qw8Lsw5pDA5om88UreR1JdzFIfk6p3djl+6tfYyU5D9/jMWxmm5Q/+Bderd3sMKxfnSJ6qWE775Fu15gPn6fqtdh+qv36Xz/Wwz+4NvEgw4OqIsKshK9N/SVMuvxTZ5Y+WKh/+wav2hCvFjYXlSfnLXYrMKlEa5skJ2I4pMTglEXdQ2XAYGtGuQ1xvqz5VP4+yaJGOwNmT6ZEvRSwryiqht0a2ha453STYAEotAnoSbU6E6CLWu0dH490orAWAKlqALntffx3aBqkxMg0P0OzeWCtsiRSmGtRQwGyKzAtYYGh2otTWvo/97bhL2Us//pzzDTtU8StwVWSlASpSQi8xLE1hhQisY61HVw4JQ349RRAEnkvS6u10BxuIM9nWMag04T1LrAakVTVChjkdKb7ulBen0OeYnncfZaECAJaZ5MkVLhlKTIa5J+QtzUUNU4a6nrliBQnvj/bO09NA53sWdTzHyL3WaIKPQk8IslwcEQLaFGEFiD2O/TPJtir66lbNMY1zikgUprZKgRxmHzEipJ/v4TRv/46+g3j2meXlKcXNE93iF7ckEnTWhwFJuMvRv7mKJm9uySOAhojYNlzuxiwdHhDjt39ig3BctsS3w8oVnl6LLhyS8fEg06MO4QjbuEraBtLYv5GuUE73z9HmFjKBa5h5AUBednV7xxvMfu1+98Cf7ps/vxqxENL37h0L2Eox++w/JkynaxRvcSyrKm7Wh2D/eoFlvm64L9O/tkCkxTkq0yyqJksr/Da+/d48mDZ4RCMe50aXFYDb1+Sl2s4GwBrUVVNcIZjHUErxysrRuasvKqUVWDDDV2UxANffdY9VPi/i7zxrCaL+mP+kyvFgwGKd1OjGkdWkrqvGKyM6I37GGdpSprpmdTbDei4/rcuH3I9HJBZht0FGCxuG1FOOmwKWsO37nJ4v6p717sj3jtP/kGQTf+TJXzuhvxWarhPltDpEBL3+nMn89Y/OQhZdlg25b+awc8/ZMPqQovhrF/uMM0r7zf1bYim27pH++wfnqFjZTvwiWaVlr68YQqLzDGYEPJ0d0jHj58hpOO3cGA2XpNf3/ExdkcY1qctSSdhMXUJ1mDNCTp93FhQDnbMIhCVNlgiwodB4RxQNpN0EWFcwZRlFR5TZBG6CTwRa1OggsVZV7itEAjSHa6sMpJIk2w22d4PCHsJlTTFcuPnrPNSuSgQ7nMIAxwgHKOtvFrJoBdbBkFAe/ePOT88RlaBdR5ybPHc4a7AzLTotKA7XSFaQzjvQGNMbRtS1lbUIJV3ZIkMY01oKBtW+IoZDzoM9+uScLAdwtDybP7p0xP5yTdmN03Dnnzn3ydj//ol2BhvVyTDhJkEIEU1HnFcK/HYrni0wcntE2D8Sohf8vx2Y7zV9s5/M3Gby25eJlQvPrci4BL/JXLxl87PATglQ32lb/4GWHj8wfzVafmc7q+7tWT+dknnv78IT/7H37MJi8ZjXrcvbGHag15XpFXDafTJQg4ev2IT/74A7rdhO0mpygqXv/+WxhrmT085/xqST9ULNdbjHUUiy2hUvyD//KH/OpPPuD0fMbhwRipFXVVMxgPSDLJ89mataj57j/9Lv3DEaZuef9f/yXr5ZrX7h6y2WYoZ3FI+v2Uu7cO0FJQtS2r1ZrG2ZeVCuk8Xl1ag7EtZRhh2gbnFL1OSJTGnNx/xuv3jpnc2CXsJuTrnJPHZ4jS8OxiShqFBGlE2k8QgaTf6xIjMVVDkERMjsaez6Ako9cPMXnN6mqFHHfo7vY9GbY3oDmfYZWlXGToKGS92VAut/zsj39KJ47Ilxuq1ZbB7V2e/eIRnb0+y6JgnCT0b+2zc3uffLbh6ac+Cfn43/yMYlvS3xsipKRoGqJeSO0ck7v7iEhz9vySzm6f018+IY4jHvzsU6JuykB3WLKlcC1xGtPi2GYFu0c7HL12SBgHPPv1U2TVUn94QthJMGlA2AnZv3PA6N2biEDxxTutXeVsPjmhOFsShqGXQr0m8WIsxjbIvCboJzSbAoLAQ0o2JW0/IRqkmG0BrWV7/xxTt/TfuuGr2i9dmv+a+SIl0a09olueyNsut2w/eApbjz93V2uC3T61dax/9ZSgn6LSCOGgaRqSeweYxYb6ao3NSoJJH9eL0UWJWG5QUYQTAc3lGqMFnV5KOuxi1jmUjW9PzzfINEFfw58EgvJsRnwtDGCA6s8/Iul3CLXCbnPaovS8lKKkfXbpHaoPxl7No9dBFwX5fIVuW7QDeTajBkQSEgQa17Y0ziKjCBuHhHUL1xAZk+cQBOgsx0Xe2EzvjzzfpWxwsxWcz6nq2hvpRRG2ddjzBU7CxZ9+SJNXhLsDoiCkxVE/uyL79IzB1275rkcnopUCk4Y0oxEyW9FmOWq7YfWnhvT127iyJj2cgHD+vLy4feR14GrMtTrLV3Rwv4TYVl0rYckowNWG8sPnuDeOSMb9l4mpfKVF/sWl2LYGjEXv9BDrEp1XyKyArIC2RTtHN4nJq+Za2dZzKpxWtHWLEtCUFaHWSK2pnFf1asuKKPLmgbW1hL0UihrtfIXMvfDtWG58wKUlgfTKOmoyoP+t19jefwYPzrBSItrWuwdHIc4KrLAE4wGmLL2XgBReChJL2OsgHNThtYncfA1F5V3cjcWcz1DGq5phDE0roDUE19dAhRrbjXHXRGP3uf3CeTxzIGiU79oE14UD2VrktXpZVZaIXooe92gvl9QKNA77+BwRalrTEuwOEFnl/54UuLKl+OUjelIiBx3qi6WHQkqJSwKvrlUZTKC96pqSXlEsCtDGUF+tMWVDeLhDM1ujnaPQCt3vEpU1UT+l6XeYTecoJYmCgKibMtwbMT2fMtobUTUti/M5xTojPhoRNF4mfefWIdOrOVVz7RWzKimjkFw4lnnBN//+N9n9g/eY/fH7qMqwm/qiynBvxNv/2fdJDsdfcld/1SL2VU864ls7vlItHJ0bE7TWtBKq6Qab18hQs94WLJ9ccuP1Y3Ti/XHKpmG72vLwg4fcPN4nUwoVaqI05MmTc0bDHu0iI6pbKuvothZp7PVl99ferHKCboqLAsR8jZmuaZzz8uFvHFPmJUJJNjhEN+bqauoh0AtDEGiavGI73wCOTV6Qzle0beuV3iwEQUKm4Gy6ILWO9XqL6kUMBl0oGk4/fIYKFcIabv3+e1gc8cEQnYQ467DC+sKEtbRN47kVr3JMX1GGyk4XnPzJr1GNZXTvkOzhGfU6ZzTqs7Brirbm6mLhzfVUhNWKer5FXhtSVnlJk5VURYFwAlNbhHD094YUdYNZrNFSY0zNOsupihp3sSSMA+Jej7axDPpd1hcLhoMOw24HnESXLV0dEKYxVaBIx11C60j3+iS392ina7j2Z0oWW1TX+46keYWoWm+IqhXBqIMpatqyoR136EhfmGsuFsx/9gCma4SSRGFAczIjXOeY1tC2FhEH2G2F9JUewoMRQaDp91JEr8s2r6h6MVEW0zQtcS/xsPfhkDgOuVgtkVKSJDF9ITmbzegfjGjrltJeC+oEAbUpOTm7JIwVmyKjLhrqpqKtGtbzFf1Jj+mTS978g/f42j//Nr0ff8rDXz2mzis6gz4y1Gy2GYvFCqE8KqHb73zJrPmS2SS++Kq/eUH+bzJ+K8nFF8lZf/34W2QDn3vHZ2W768Lbb204AGu5+uA5H/3R+2TXbeM337qNrFukcAgL56sNVdPyzT/8JmZb8vzBCXt7Y7bbgjtv3uD1f/Aurmz49M9+zSYvGE326IeapDE8P7vi6l/+B268eYMf/td/wOmjcz75sw+xtfGSkNZ6N85xn3/wT7/Lmz/8GipQLJ5csTxbcLw/IdSKygiqrSdLbtYFYWy4fWMHrRSl8UTaKE3YrjIulyvSNKHOKhbrClEWdJKQxjoWyzU7oea1d25Tbgrml0tGDjq9hP39Cc+fX7J39wBTNQjj6CQJ84VvB0/SDs22RA07rE6mDF7bRwiB7iZMfucW7X/4mOXVCtlL6BwM6b15QHdzhPnpQ7LZhuqFTvm1rGllDZ1eytXJlMm+4+CNI6qihlijDHz0Zx+hP3rCt/7Jdwl7Cfl0y+vfepMn95+Rb3OEhZ03D7F1TSAkzz54zOLJFbWC0U4PO3T88s8/5ODuASLStFVDN+yhmprWOgLrCF3LdrZh9vCSQEtGUhFWHsM5rwv6ieD2H36XYJB+PtN90SazUJ7OKLclLggwOIwAaR1N1RAo5Ul7cUS1yjFxQO9wBI8u0bd3GX7jNu26YPnxCU1lWJ0uiK82iFDTv3f0yhQRn4NqfJbE83ICihfHpwTBuE/v26+x/vEnntx6MMZmJWGgaAapl967XCGTkGDUJXt2iTIG1Y/J7p+xXRUMj0ak2ieUzTL3G4xzaK1R6XWQE2oIFMXjK0Q/xlgw64qmqjDOItKEVkiUsMgwIBaQbXJCJRCOazdUj3dtex2fGF0siFuDDTS1EARKomqHENJzTvKSojG4XgctBXK99fAZpSm0JGjw5ndAXlREYUC53Ho9ekboxhGmMSqOEDsD3GyNaVvvon3t3dDUDcJ5QnQ1XUM3RfQTklv7ZO8/gSRk/O4tQqWY/fQhTVWR3rpNtd0ip+eAQE12EHHo5YBbQ3it+PYbrVp3XWN8cX0/p7bnXqJkX+iTq0iTjLuo0Cs7ubohvnOAG3VoqopQJ6+sreILf+r6ZrEWIQXhIKVMNBscnTgkdFCFGlU1LMsKHQYY5x1ghRBUq83LY1VSohEYPHnbaUWMIHRQ5hVJmmCnK2xWYDsxumoQTUNtDLSt51oIUEqhrKX/rbsIrVn96a8wWYmIIoyxyPEAV9Q+MWm9r0ZoLLUAc30/Sq2woaJd5jitkGVBU1XITkJ7zeVo64ZQhdh1ThSH/py2rb8/tUKECiUFsvN587wXk8u2LVJqz+EAmqImHXZwVUteV4SrNcGohxp16L57i9Xlwt9jRYUUINKYpJNipIRYoZIurp/QTlfIxZaolyL2hoiypJz58yzjGFu2lMag8ERnW7W0siVsHTIJsXWLySrkIPXKN9fETzXqop5fYbKKnfGAIA9AgiwNy6xg9esFo/0x7ahDt5uwfHTJztEu04sZ8aEin665KBuatiUd91hPV/TvHhB1EiqpuPXOXdK7Byx/9QySmP67QwZC8MakR3Rnj3h38JtYnVdbc1/y9BfhBy/q7zqN2f2d2zz75RO2z+c0wmIdjJwkigLO1lv64x4u0tfmeZaD2wfk0zX9Xsp733kb4yzFpqAbJ0ghaKXg4vSS414f27RENyZUJzOyh+cM94Yvj8PkFU56eJCKAvTR2N/zC6+AWM+2LK9ltqNI0Zvs89FPP+H1t+4x7Heos5LF1ZJsuaHOt6zna2SgGY77yEGMCxSDaEDZ1CzKmizLCbBorenHAV1gtDNkmxU0TcPgzWMfErWGOi/R1x4M68fnjN6+9RvrS1vUSK0QTrL48DlN07JcFwQXSz+HpeTk2SVIQbrXp8wryrxlu27RYei9XxxYJRBpyOrppRe8CBWTvuddLJ/NSYZd1qs1VeGLDsQtQRQQBpqd/QlPHjwljCNcawnTEK0ETVETKUl3d0TWeHnpURoS3donmvSQSYhKI7Knl+i2xWQFQb8LxrH6k1/7ArSSoAV20GH5/gN02XhzyiTygg3OQWsRSvoORWtxyiIvl9TOIpOYQEncOkcPO9C0BP0UUzVICTIr6UwGtKyR/Qg1XdJJOwghca4hzzPysqA/7qKc4PLJFYNBl0BpIqkwVcXu/g4XF1O2NkNWvpik45CqsfSDiG3rZcKHoz5XVwtCqVg9vkJLyeHXb5MtMp58+ozNakucJgwnfUzV0hQ1UgomBxPC6FW+xWdFdT+lvoxo8Nsf/xFgUa+sGF+KcfqqvuhfM14ES6+SUv6O44vQqen9c/79/+3fsV1uMMBrN/fphsLjAQPFxdmUZ88u6XYSxscTfvI//gW9Xsp2taUz6PKt/93fp96W/Nn/9d+ymG9IkxAjHEkvZTcMMK1htsr56OcPmF8u+Ef/l/+Ud//w68yfT8kXG3QYEA9S+vtDrypz3X1YPLlEWkunE3N+NmNbNTRFhWWGDhSj8RB1OCFpGrZ1TdJLyeuKrCwRDmZXS6q6pW4NUkp2+h0CCevlhmy1JS0D9LBDKy1Pn557D4KyptPx7sG2aUnGPepQEA9SHLDJCuxsQ/dohBGCOq+9LryAsJdy9MN3cH9xnyj0ZNnN0ynxwZCb332d7OmU+aMLGqXIsYRasnP3kNP7z8iXOeWl57WUxnD89TssT66IW8fZxyf82Trn7nffpM5qHj88AeDWzQNWyy2Xj84QCL72T77FI2tZZxVv/8HvcPLhE+Jhh5vfeY1AKubPZ8g0YJVlaCkRVYtqDDoImHRScgtmmSMThTwaUxQVnTDitX/0TYJ++vKu+Qyd6MA66qsVxfnCQ3MG3v8AgTeDsg4VaNqrmqJsaYzzlciipnt7l8HXbnjZyb0+3Tu7WGNIn14x/9GnbH99QvfGDuqF1Kh48cPfwUKIa5lH92X7tV9EuynDP/gdzLakOl8Q9FKq6Qo9SNleLlGRJkxDqkfnhHtDTG1oiozB33uL6uEFdr6FNCBIu6g4wM4zmnUOCprl1geoSeQX4t0+bdkgyhrnDNJairJECIuLAqK2xRQlLtBIHOiAsJfiOjHFakMolK/K4qCsMHWL3eYopTzxdjLAlTWmKBHWkhiDnK0QUYDrdRFNS9O2SB1iohBhLdY4lJIQBMSBV7fqPJ9h4pDmYoFwjrJpwVrCOAItKRpftddRgHkhE1xUNEWJzguWRUUy7LH94AnR0Zj0aEwvr7DG0OQVum7IpULEAeN/9kPSUQ/VT6mr5roL5TBti7r2bXDOuwvLF0ouX1z0X1Qg3eefc9edjjqvvEt7L0FHIbL5ktb4q8HaNVdNKIk0ksHxDmxKhhbMdE27yAhdiJKlJ+5yneDUBulajzKylrptEVKw1Q7pFEkc0TqHuoaYJcucZpFRW0sSh9TGSwlb4Z2yI2eQzhIIhXEWBindb90j++Q59nKNlL5DKLQ//+qabI2xtKF3sA2jkMpaRNNSCwgb4zkmTfvyPtNBgKwNRlri3SFmUWCVxDpwRYWwFoHFCIhu7VGfLzwk7RW8OgDW+wFJrVk+uUIh0J2IdpVjrCVOInDOE9jzgnq+wUl8EtOJsa03C3SdCPKK/GJFsjfEtAZVGdqioBr30U2LWeXobop1AnO+9OplcUSQhLTO0TqHFJKGFt3zvCezyWkvvVu8TDsQhoS9FNWJWH30jPqqBS3Rwy6FqpGuJRIJ2aZgeDSmLUuQgtnVgquZXxvSfspysSbqprhlwcHBLlcfPCW8u0uy22f6+ILwZEocR9gkYPzmEemtXYSUONxnxY6vuBdf3Na/AUz4wnDWkv36Of2bO9wMAq4+eMLVck3Qi8mkIIg0w9u7JEHAXigRrcXNtsw+PWWxzeh9/13iMGCz2JJvCkId0FSNRw6MejTX7urCOlS/S/5sSvfd7DOvC8BVrZd5zSrU8Rgx39IaqI0lDBWuhTIKqJDkRY1SmsX5nGyd0eYleVlRluXLudw6Q7/XZXBnl0gHmG1JnhVkOqDbiSmLmiYQtFqTpBHRpMfdH34PEQXY1qBCRVPWzB9cYK03Ydw52kFfk7nF9bpRbwrKx1PioxGtNZ7QLiTd4zFPn17Rn3QprlbEvdirBW4qXODV96yxCGtZnC1IlKIqK+rAsTPqQWMp6oLZdMF2WyKV5HB/h4vGMeylTFdbxjtjNpsttjU8/uQpVlgqY+gHikGvS9QYxvtjWmtRCkKn0K1g8PYt4rv7bB9fkJ/PiY53GH7nTcx0TX61ojiZwXSF6sQExxOigxHxvQNA0P7JB7Sns2vOIlgrEK0j6Ce4MKCtGupNgdx4+LKMQt/JLGqM8F1G1e+Q/eop+eWSpnXQ1BQXS5xWdI8n7N4+YHHq+Z7ZOqc/SLEONtM1w1Gf3eMRRdUw7vcoVyWBlpw+P0dGGqUFLlEM+ym2NCBaKuO7s03TcHF2ReMM6XDw0kwSAQdvH7FZrFnM1hzsjzmfLtjZm2Cd4/LkkmcfPeHOD96gM+l9xfL/HyeZ+OL4j8K5AD5rIf9GguF+8+Hf5rtex1QvGn1fzun4G37Ui2zu+lgv75+QFxXbqkIA3SQg//ghH6xb5puMUGu6wy7f+qff4fEvHlEWNWnkF/nf+WffRgaaP/u//ysePzlnZ9gjSWKWlytqYzx5Lo1J4oAb+2MeP73k8c8f8rV//C0O377BF9n8zliE8t8ym29YZTnroqStKvYPJxx8+3WaogYkZVZy+vySYRIy3RT0eyVHdw6pleZyOWcy7nM1W2PrhjgOqYqKrKwJAk3etEilGDpBvalIOrFXKYgUJBFXD04Zpimp1KwXObIXMTgcIac5/d0+Oo2J+h2Snb5XoMFfctWNOfzeG7im9QvT1QrTeJdKO+pwPLnH2U8fECqNbR3bswX7R3vkm5zVyQKEpQZaa5CR5jLPuPf2XRbTJdW2wMYKl1WMBz3QksYZWinQ1vL8l4+5/foRrbUsL+boKCRfbMmmK7QIuHh0weTGDmmoqYuaqLbExqGsoTlbeH37fkLveEL3eIwQ0DuaEE36fAaAd7zQPTPLjPyDp5isgG5KMkjp7PZxjfFt49kSI0IoGxTQICiLik4nYvyDN0h3PTa+bQ3yBSFPK7RWIAVt3dDm1cvkwjlHVRTUTUugNVEcvXRc/fL7/PqBUuhhBxmHZE8uyY0jXBW4vCEvaiwC7RzZ+ZwkjdGJJ7i/8BxoW0NwOEbIAXZUIBZbr2SSRlQPzwkPRohBiujHJPtDZj+5jzAGncT0GgNxSA0UYUBQNrSNIQwUppfQdFNkYxBKU+QFHWOp11tUUWHldaFCgHYOVhkIRxsF3u1ZCNDCCw6EAUYKdOvIlhvvy7IzJAw0br6m2uYkxtJKiW4EyoIVDgsEoUYjkMMOTVZ6mdu69Wo5107MMtSkbx0T4TDTFeHxmFIK5h8+I/p7bxLvD1h98BQrYPCffIPO33+HzuEEoSRmtkEPO95lW8nrTV9gihp1zWNSof5qRMjLteqztpVrWs8pEAJhDO0qo51tcALCcdcnfS8kCb/4wdcBnwiUN7IDBq8fYrKa5x8/YDjZhaxCa01XePO1xhi0lFDVhKHGCShaTw6lrAj7PS956xz62qxLKoVMQ9La4KqGAIEcdDDTFYESVNYRVxVNGCKVoPP2TYTWbH70ESqKMbJFAGEY0Na+KyWVoGla33VzDm0dgdbYuvUkz7qFaxNLYb2crrvW/FdJgm4dIgpQhU9YRRTgAgXbEtVLaUoPAZO1+fwFsNbLHKcRpqjRShAfj/28jSOq6dIrYBmDayVuWdM8uyS+dUB0MKb40w8Q1vlz3rSEx7tEZYObbSgDSbXcEBQlrirp/N67lA/OKDcl7XRLE3pDTqoG3UuIo9D7N1wsaLWkag2BtYjWUq9zwmGfDZowue6UnkwxrSEwluW6wdYt45s7iLLFKkFZN1SrjHJbMN6feJifaTFAf9CjXmSkScLBrX22Fwv0qOOr3d2IndePsEXN1WxD09QIKek8nyG7Mf3XfOX5r4Y4XO/kL0UMfnMKeEdpwebZFcX9M/StPbZ5SdJNCIZdjDGIsqG+XHNZFXTGPeqrDaNBFzPqku722SyWdKIIHQcMhj1oDL1eB3pdnITMNPSdI6panLPk8y3F/RP0d99ECEF0NKb4+ATTeBUv8+EzWicQN/fIsKhuQtI4OJnTv7VLucm4efcQd91Z7B4MGbTGG/tVDRZHMuwiESzP5nR6HeymopfGpB3N6cklvThARBHbdUbcTdlcLlk9uWLytVsopSgWGcJaOsOUMq/YefOYIAo/3wZygsufPEDnDeFen1//yz8n7Kf0bu8yf3bF0d6I2TZjXVRoqSBQTLopz+YLwkFKr7CEgWadl2wdmLKikYamMlTrAikcOo05PBiT5YUXUtlm7N/dI2lb0iQiW26QScBeMiRQEts6UgTKGLpHE6hrhHPIRJOGAQZD8eAEYo0OFOJoB1U3bH5yn3yZoaII0bYw6DL6/XfRkz71xYL8yaXv3llLuD+mWeXkZUOURuhB7HkKm4KmbKjahnR/TKebkJ/OsbXnAkqrobEYV9NuK+ogxCovAyuKGls1nJ7PsM4SdiPyKy8/vMkrjvd2uFquWc7WCAlJJ/EwzuvOc6/fpWoalJOkSYwLNN0opSlrtk2FsAJT1zgc+3s7FKbm2aNTnt8/ARzv/uHv8PY/+jpPf/4QFQcEQpD2U4pNTicMSG/t0t8ffdku8hvzCb6iB/BbGH/n5OLV/MB98cnfeNVXja9Chf0VL4fPsJBf5Y/xt/zYFgdKkiQJB8Me4cUlzwrLpqgY93rs39nnvX/xHaaPLzl5cMpOL2W2zvj9//0/5M7vvsX7/+8f8ezJObtj7wlxtVjT66Z8/Qfv0BgLjeGjn37MO68d8+z0imZbvqzo+EO9TjBaS/H0nM7tfYRW3P3772AjRRyHJP0O+2/eIOon4KDeljz6s4949vOHnD0+QwHbpuWTT57iyoooTQiUIggUcdqnLGquLhf0hj3auiXpJhSbnJ1Bj3RnwORwzHpbcPb8Aucct9+9zeJsjoo0RzuHPL3/jLIfM9ABrrEIIZjc20d14s+dcAEEHS8lGoYBQb/D/OOnrC4W5P/2TxCrOemtO3B0g3qeIS7WiNoQaUln0iVbZSRINpcr4ijg9a/fI1vmDG/uEgYBs4sZt+8e0uQ1DZbR0QRVlZhtxnabc/nkku1ig2tagl5Kt9vxC4HUXEpBu8yYdLwZUxgFREmI0wo36TAadklHHdLdAdZazwMINfXFknB3gNC+klnO1zRPp5QfnyK1JA8CzHRN1A1Z/fLXuEGfcHdMURqGd3dZnUxBSrQQ9LpeWrF3MPTJpLUvK1kOMHXD9Mef4jYFyf4B7aYgHHWvkwhH23qyqDGWIAg8BvxF4i34XKLxucXDgYwDwkmf8skVwaCDEoLOqEurBPmmpDfuUG8LVFERTnwFtW0aRChRcYhxEB6MCfYG2MbQzLeoTkT95ALZSQh3B1RNS+9oQjHbYq7WEIWUl0vfxdEKlwTQjWkdxIHGbAvMckscBt6Bua5R14ZpRkqkaWnLmkgJjFIEYUhc1JRKUg06qCSima6Jq5q2qglwdIc92kAjiopysUYc79LvdzBljSy8AovMSwIcrZLYozGkEVZLyAqUAxUHyCRC5AVhY4he26f7e28jnKOarsmu1mSLrVdWWW/4xj/7e968b7Zl+eCcNI0oakMjIQk9bEUG2gdKUni8fCheRE6vqNP81Yvfi26VF3VQ1xCpwEMARl1cY1idzOjoXQ+xEV/8jFfKMlLiipr8/jnhnV0m37pL994+2dMrmssNrTUkxuE2OfHzKUVZY62juRapUGlMgEDJiFgInBCIfgcjBWJbIvMKUxnquqbnoJGCVimfvOIhiY1zoH3y2/97b7J5/yHmbI6KY3Qc0eYFTdOilfbwn9xXSOuqRjUttXXX5n2g4hCx3CIC7X1hrEFtK1wnoUlC5DClXeUEReMTRu0ln2shENZg6hqz2hJYhxx1fELnnJcfLRtkN8aUFaZqCHf7mAeXFM9npD98m6SbUqy2COUTSBVF1OcLQqFphzWtNbRK0L29j7ncYOqK7nffIvv3HxB2YwInaNc5rmxpl1vqbYErGrKLBen+iDCNSMOIUEqwFqyguztkO19TFQ0YQ3E+x16u6H3jdfJ1QTbbEAhBtDvE1gYXKMbTFYu6pbkm63Y6KSLRbK/WHN3cozWWxdmMOI1xjYVAIQNNuck5/fgp89mKwVtH6CQi1BrRD6mzgvCgj8hKZlcLZg8rmqpm9/E+9/7L372GUn5JJPNVwc2rrYyXgYZg9M27RN2EJ798zPBgxLauaauGcrYhiWLaOCTpaqJuSrnOWVUVCEG+yel0U0pl2axyhr0OxtRsFmuKqmb3eBcMZDjcfE0y6WPThOpqQ+/6WGQSIjohXHmjToND3tghvnfA5R/9BDopKk2xqw2LDwq2+M5ZtG2IlCKv12RVTdSNSXf6OONdyBtrKVeZh+EIjRRw6w+/xvDhLic/+QS3rhC1YzvdMryxS7HwvI22qmmWmfex0YrJnT10FHiBhdZy+eP7KK2YfPd1Dn/vLepl7rtWQpBNV9RlRbXMiG8fkrQt6+WGQZxysc3JNrk38pSSunUMB13WFzMYxIgAiqucMNTEOz22l0uGOmB2MiVNI1B4vshzQa+f8vzRKa0x7A0m1KuMnZ0hZVaSaEW3l0LT4KQvqsnjCb2dPkG/Q3u58EWtJKZ5fMHqZEYTh+RBQGQMgVIkkaKYrhGrjHadY/MK0xjKiyXOQRAGXqBDCIY/eBMhJJd/cZ8wMWiT0H/tgGR/SF63iK1/v1RerappWtzhhGqZ04v93rWuGuqiIlQxQS9m1WYMxiOaqmZT5lzOF2TrgruvHbNcboi6CZurlY/vpEQK381TiYft6dKwFYZYSsSmJAlDZL/LKsu8ellZUevS89caw8d//Ct2X9tn/41jFiczVsuMuj0jW6xROL7z3/yBLzh92Xz6q+bbb3n8lgnd8FlVzX3+N1/2xV7scV/EJ33FH3j5MvFZt+HlNvkq7vz/z3H0tVt8/Ce/xjUG5RzRds2qDdg/3OH1779Nd9LjwZ9/wsOfP6DfS6hay97dA27/4C3avObZzx4RacVk3Of0YsHXv/cOIgl4/NEzrk6naK2Y7AxojMcG793Zf+WAr9W1nMM5h0l9a1Ih6B2M+OZ/+v1XCpafVS7jYcpb//Rb3PzWazz8s48wmwIRaB5/8JjCOV773pvc+8FboLy51ep8zvZ8iasMVVmTzzd8eHLJYNsltobJuMugmxC+dpO6KMkWW2KlOX9+ie4mqG5EWRlcXpKWY6xzlOvcu3N+Hq8BOB98bkt0FDB87cgrMnz/W5S/vA8PnyLKiu5rr+H0NW5wWxJYSzTqoUcpsXGU51dUUYzb6TDYGeKKim4Scf7ohDTtkGcVRdkwGXVIwoi6tbiiJmgsWgYkWYtdlNRa0Bn3uXdnn96wR9CJ0cOUYb9DMEhehlu2ExEGgcfbrzNEbaCoKRdbrLNEuwOaTc7sJ/eJw5DkazepsxLxfE7v5pDmck7TG6PHQ1ySsHfvJiavkJuKtmyogeDODsPXDxDX6k8vyNrOOax1ZM9myKqlVYpqXaAvVyTHE9+yRxCGAeDQgb6ugr9y2r9wFV79j7vGm4bDDvt396ieL3xgHSpUaxGDDqWDqJPQzFZUZzOCTuITs/0R9dWK8Bo/LQLv2CqEwM7XmDj0ld3ZBrfKWZ/NiW/uEbUOty2pjaPNMsIkhrJF9lPaskaOvGqLkhJXexdpGyhCpfzjKERJQRRo7wejJBZBKSWRUsj5BhfkkCZULsQo4d1zhYAopC0qVFagrhYUOoBBipFglltP2DPGGyKdLjBK4roxOolxVY3VknadoRpL8sYBwc0dMJZ6WyK0Zud37rBjLPl8w+zJBfliS+fNQ8rLFdVsw2K+oZ+V9N+5hctr0MpzAlqDDrQ3fZPC85oAcd36/qrxG1Wma8lQgZdCjYYpiw8eku6MoawRZQMdrzLm727/86WEhQCMQ+/0cY3FXK2pZxvC/SHj925ha8Pm2RWLiwX93T71bItqDa61BEoDDqf9v21V44RElAVGeB5NC9ePLYGU3mG9mxDtD6iVIFjnXgNea5ySdL73FsbB6s8/QocBQnjPEQNIIX31TwiqayPFKNQYIT1u3lpEL3mpqCaMoa1B1A1GCs9nQ5Cvc0LnA5kqb5B5CYFCidC7fDeGYG+EPZkR9FPstsSsC3Q/RfYTXGtoZxtIIpSU5I8vscZSPjgnfesGzNdILbBaYTYZYp1Rh5ry+QVqncNuDxEo4q/dZPEXH7H68Cn9H7zN9qf3IQ2xywwhFev/8GtcqCFOaAEdh3SDEG0dWMMLNaBIgOwmZM7RtmCNwa23FI9OSXQAWYFUkiaNaK036ezuj3BZyWaVcfL8kvH+iMPdERfrjNNHp/R2hh4OGoUYAavVhs6bh+SXS4p5xuCNQ1SgqS5X9O4dMV+sSdIYty1gXRCHIeFrQ9qrFeV07ZPqOMTrW76aMXxh4Xrx1JfBwq+fC/eGhMMup+8/Zn25pLM/YrHJ0L2YlRR0d/t0i4aknyK0oHw+p9NJKYsKFQc0WeVFBpxl01Y0ecnRLb8WL+YrVD/CNY5OlRD2Eu9gnhXoJKLNK8KDEWwr3DKjNQa53GIvlxz/3tfZni1QZU18MCKebrHdLtmmYLQ7IBC+2xZmBZvVlqdPL33hq99hsNtDaY2WkiAKmV4tyP7Nz3jnv/gB/df2KFY5STdGhJpo2PF9c6XAWeLr/9vaF9LadU55tiA+HHHxwTM/L6wjX+YszhfsvnZAr9ehG0V07uz48zj1SU9/3GOZeQM5EWpcUdPtpszmKx4/P6fKSmJpCXoxOg2hcayvlsRJSByHvP7WHZ4+PEEquPvGbYq8QDhHpxuhooB27Yt6YdUSDjp0W4Msa+xen847N5Dd2MuiFzXrXz0hGHVoLtc0ZsF2saUadrFNS8c5jG0Z3btBemeP7NNTFh+fkNc1G2PZLDdslEClEcMkZRhE7HQTzv/8E+R0gTs9J3z9HnbYIZ70kWFAcmuXxUcnhMKLehghsW1LPl0T9VKibkI+XVJJP7dVqLB1Q5s3LJYbLzPdi+l0UqJ+xWy6oGwbzEYSqIDJ/oBnT84oBoKiKJGtQ6UB9bomTCPCJGXv1h7PHp8zCDvcfeMW62WGkZAVFfvDAZ1uwvMnZ+S/eMjwcMzevUPuvnmDj37xKbv9LumNEb3d/ufhr18aDHyx6PjKziB+O1nIb8fnAr4QWP5tx1/z3s8hqdznqh+/De7FC0OZ8a097nzrHo9/9DHzqqG7fxMxXaCF5OLhOb/441/grKU76KCA2WbNe9/+NkoriAJe++4b8AvFYpOTpDFxN+ZH/+4vieKId/aHdLSk6PX5+JOnhJ2Iwc2dz+ViLy6sUJJitkFrRWd3wIvE46uOHhzRuMu7/+zbSC0xdcuN79zDCRjefIG99NX24Z1d3LVyVZPX/PJ//AsEjqenV7z11i1OHp6zd7RDGGqCOCDZHbA76ZO3hvOrOUGgMXXt+SFas7lYsHh0gc1KlL5B0E1wxlJN1+RXS6rphlZJkl7Czjfv0T+OiXsJj9YVwd4BMltRPz+l/4ffBetwdUt9tUFeLnHznHTSJxgM0aFC6uuTEGpG3S6VDig2GbEOsbamma5Iuh3GSUKwqihqS9R6xaAg1Ih+l97NHcZApQTVMmNyY0KQhCilPG9B+Htqezr3cVft26LN5QqZRrDOKZ/PMdftY5FE2KZFhgEyDqkri3Uh0TgmPp4Q9jz3YnU6o1qX1MJXncuLFdvLlb8HXtzHDoqrNasH58x/+og0iUk6MZTe4fdFIi6EIIxDzw0AX1W9/vflXXH9PV6qrF0PZ4z3UsCR3trDFDUuq6gcXnHJWpJegnNeXCA/nRFGEeHhiHZbUlsDszXR3gghfaIj45Dw1h42mHsehrUEOHrDDrqfMH0+I5LeSdlEIY0QqKbFLLeIMCCfrb1aEA6tJNJ5N2djDI0QxAJa5Q2b2tag65ZwEHsZTrxJnq0b5HyFUAqFI3AOq5T3Y6gbXBIj8gqtWkxVE+4MsFojAk27zX0Qbi1aCLDgQo3pRYjGQ3loWsoH52SfnhEdjIj2huhuRGss1WwDSnL4xjHF8xmDt46JjhVxP6HNKrbPZ2TTFWqnh3QW7STCXXerXiiAKYnJK2/kpK/n9Yt46xWkiHt13ZfCe6wY9/Kaq15C//Ub5J+cEu8NXvqXIOULZBmfW7GN9feEVgQHA8z8Go5XNbhQozoRnd0hzfkSnYZeeML4AN9YSyy9P0UtBDKK2DZeuMDlFW1Z0RhDnKZgLbJpvb9JXmJX3jtDVoYMSHCoTkz67i0WP/4Yt/adCqWuYU3Gd5WxjqCskXh/B9EatPCyjkEceufu1kIUXruCg5AK6Rw20NBa0m4KlytMFBBFAaJuEE5RrzICqVCjLu5y4Y3qtMJuK4K9gS9oCUGzyrwUaahpPz4Drv1G5ltM3XgonwbViTHX66F1DqkEVCUyD7FljWtaQq1pyoZmvsFlJepwjJpt0ZMe9ZNLT7Qfdek8uaJ9ckl+a5++fNHdur6G1qFwFHmJ7MdefjpNKE+nPuGc9PweokC9cwthDKobYX/5BKUke/sjwk5E3tbsv34ATtAd9rCtYdjtMF+s0FqzPZlR5RU337jB2fMLklGX3d0xZ/dPGL1+SD1doy83TI4mLM/nRAcDtmVNt2pZP7tieO/Qdy8+N6738y+F7H32kpdwVHe9kwWKe//Z9/j4X/6Y8nKJMJayqgiHXeyyJGwszz99QOMMu4MBy9mK4c0JSSdmY9fsTTrY2jKfLRGB4GI6I45C0kHC5dWC4mKNM5bhzgAtFPOfP2TyjdfAWMKdAW5bUTctsqhwFzMaPJ8rLSqicZ/m1gHLq09IAoUe97harXDW+QSjaq/NOxWmqmnLALY1/bt7iFVJsynZ2RmQ3t1FOIdOI4aTHlIrX/EOA9qiwlQ1Oo1ojaHOSjr7Q3COh//DT9g8nfH2/+b3CJKQ4eGI5+8/paprOvtDnn966l23gfGgy8EbN3j24VPSTkSlBI1wDIOYLCuIejHz+QoCSV4UjDopwgjKTemTW+mI05hyU3BeXLFzHZEFaeT5IFpx/I271KsCu8gga4ilhE5IJ9R+3gwSBu/e8p3wqqG5XFI8uSK6tUvv7Ru0N3IPN5uumf34E2RdE93YoffOLXQ34epHH3L/lw85KQoIlDcXFpBEEdtNziYrOVOK272A3/nuW1SfKNaXC9jkJPtDZBxgqxq9LYiwuG6Kma/RSYRF+OJSoGmdY/7wHJuEZKahmK6REg8B7HfQaUBZN+TrgrgbU5QtO6Mem8LL9Z+cX1K7Flm3xFEELdTWcbAzZj1fs6633L19l72v3fKy6E7Q3R/y7P4JUkjm0wX1ZsvNr91i+3RKv5Ng2paoE3B0MGFzteDeG+95l+4vmUZfOT5X/3cvmuh/5/F3Ti7+xsijLx7sF4vcf8247mrxIvp7afbxFRXbv+0BvghSvvWff58bbxzx4//2T3k2X5NEEfPlGrvZopWiqhs61rHe5hy8fsSNr9/h6Y8+JukmvPXPv4WrDT/7X94n6aVMz5eIIOD2rUPCAIqq4fHJJf39Ed/5z/4e3Z3B5wMG8FCH1tDdG5LPM6yDMIkIO9FLvfUXF95eaxkLKdFSIwK/2WilmLx+8FJR5jMAhF+hpRJ0drwnwrf+q9/j8Gu3eP/Pf00WCo6PD3n+7IpmlXv4inXsHU5Ihx329A4nj8/Q3YhaAlIQdmJ2371JOu5RLjOmnzwn1AGmqLz52XZFsy7RNw5pNznhsEvYT7nzL75Dm1XU8zXNdEOUREgpsMYSKEk8TCmv1uSzDcJa2trjNoO6pMwrAuPoKkFLhKlbhmmCVAotvaa/DjTDUZegF3sDLSVZlzXb6ZrxzR3ysznRsEPcTynP5tR5hXQgqha6Ea0QiLqB+ZamNiR7I9TQKyuZTeFxm0A46ng1mySAyMuaBr0YPe6+dHI11tIuc4yzaK2wjUEUDTTmpZlZW7fkZwu2v3gKtaEz7iECjasbZKgI/n/M/enTJEl+34l93D3uyDufu566+qie7p6ee3AJBAkCu+JquWZa2ZpJpn9Ob2kmGW1taVrKtLs0kAABEIMZzExPT991P/eTd9wR7q4X/lTVU9XVcyyGNPmLqsx8IiMzIzw8fsf36EeYTmMFLpnlhRPCS4mFfXGtPLtcXprjgQdCICVYaYlvbuHP1gwGKdZTlBcrZg8uGN/dJp70aZvOuWALge46RGfIzy9pGk3/1vaVdwB4w5RQSmSwonpyjj9OCdKIdpUR7g7p5hvUICUAqFpEEqKvXIK9wHPV91ZD4kEYERhLGwYO/rFY4+9OqLMS1bZIIWg2OTIIaAWOfBkFhP0E6gbdamzgYdY5qutQcYREONUnY5BG0l6uUHGAWOcoz3NqIpvC6afnJZ0UFBLCOMBrOjoLddU4V+gnl1THc4Tv01W1M94LfdTBmN64z+x0gerHSCUIJn36hxOinRH+KHUJrLF0VeNgJMMUPwqcsV9bOC+TV8ezU/ss2bhSd3pONJbCVYSvgjR/3KP3zVvIXvTCofd1OwRM6zgFel3SVg3RVh+dV+hOI3HSxP60R//dm+SPLxGTAfZ0hsWpoHWR01pXWtNpg5SKxlhoSrQ21FWNuYJGejh1FmEt5DWmH9PWDX7XYbCE20Okryg/fIBqNZ11VXivaQmlBF9hPA+zcR4ZXMEdOgvWUzTW4gkJRe28KHzPSaZ6CtV0rsKsfLztISYK8TyBzkqslAht3DwHrOfRXa5Rt3bQVYM/6WMtdJcbROTj9WNkFGAbTX00dwT9MEAbiy4bzLiPnC3oAkPRtiRFjZUWMx2AHjm38M+OaMQx8qqLuv7okZOXXGUuIfKuRASWBd47oSOaImizAhvHoI3LP9PQQc9Cj8HumCwvaGcb7DAhigO6RkOrUUlEVbeoXh86gfI9khtTmkdn7E6GbIqCOAxZLTOauoXGMNgesb5ckS0zDrfGBMrjPK+cB4rvYcsWPRDOY+BiSXu64tbBNsZausijlRCNe5z+4hH63/wI8V99h9E3b7/wYrg+H68nGPaVvz1bvfSVt5OnnMGZEAzTmMpWjEcRT08u0VdmrR2C6Z1dqqJCBx6T3SHzkzlxGOH3YpJRjyqvuPH2IaXuCAKfZpFjI5/mYk3TdVxscgeVbjrGZU16MCV9Y8+pod3exhumlMcz2kfnbr3VHaUCnRcMbm5TTYbMNjk69kj7KWVVkaQJw35Kl1WUVc1qnUHToaVw/zctdd0gvD42b/nif/4J2SpndHOKRJCdznj3f/hjhKfcsejHCM8ZtEnfx2pLnMaUw5SLv/6MqqjJHp+zXqzpDVOKuiYaJvi+oq1aVo8u8EKfoBfRGlDW3YO1diIYddfRZBX9XkLje05WvWrIs4Ib+9sUVY23nRArH5RgfukSvSy31HlFQsfmZ5o06jmZ6STAi32UBVG3iGFC784OJi+pvijoZmu6syXBW/sEkwGbn3zpZLL3xrSXK4Z7I8IbbxIebNHVLfO//Zj7nz/lqHM8pKqosdbiBz5VUZMOUjaLDTIOefLohLwo+YN/8Xts3dyiejxzqla/eORgVKvcEaelohv2kMagpUBp68R5yoY2r2AQk88qbtza5/T0Aotx6AEjsXnLYDxkvSkRUrBzc5fqk8dEYUgbd8TS+Wg0XYuIXEd+neVUXUdZNcyeXHL+t79EJSEhIJIYrxchkpitvQlH94/YHC+ZTIe0naE+X9MVFd/8736I8CT9neG1e/6VuuCvyxTEMxTQi6KTFc9f/t89/vMRup+PV6P7V1aQ3ySxeE1h46V9vPLw6zb5lZ9x9b8XBex95w3+eJhy/z9+zPnTS7b3hmzf2kF0hi9+9BlR4DOvG7773/yAJz/+gr/+H/+a97/3Dt+/u+P8IOIIYeHk6IJeEjGY9plfLJivS7Q1/NH/7Z+w++5Nd2SMu4GKKzMU22maqkFKSTJISLYcXKhaFU4+rdME/Rgv9J0DrLHoxhntPEM5PJsq1hh0pwHrXFyNRSjhgtOrCffhf/gZpx8fsXVzBxUoag/u/ukHXD4+Y3G2YDoZcfn0kvJsxmadUzcNb44P8WqDVZKoF1PjEh0Bzn107W7YVluC3R3q7hzrSS5/9pBwktK/tUPQj/HjgGRn4DDjz86DsXSrnM2XJ8jcoz8YYa0lCXxaY7FasxX4NNYQxRH1xdqpZpQNKvKhqAiGKcGkR9t06Kp2cm+BxzB0C2B2tsRrOgZ7Y0zV0p2vWB8vCBF0wnFvpt+4QXW+RGpLcriFlybYrsPONs5XYdJHGEtzsaZtO9iUBKEPSiJ7ITL0kL5PnVXYqsVLIwZv7VPPNnQXGfU8w7bu3GyOZiw/fIK5yFCRj0gCvE2HaRxp0Bv2wFNUZwu0hHR3gnqOqfyN03t4ZaHR7ZU54f6U4ukl4faQcJgw2B1QrguEtWx9503Kh2dknz4lSEPwFeHtXaqnc/JlQfz2PiqNEAj8XoyfRsQHU9pVzubvPkEEPn7b0khB3QuIVyXKV7Sdxu9FcL7ExiFSCFQgCIcpuhchViXdkzPwFH7TIZ6cI32PrpdgOgPGOlnBtkVbC1qDbDCeQuKq1XZ7jI1Cusslftc5ZTDlYbXFb7XrFMQhXVE5dSNP0WiDzBs8pRjEISarsEriXXWnGuPgW8pTThrV87BAucrYGaa0E4jvHdDfHblr9Ery8FlyJq3jVVgl6AwExjjISOAhBzGm1ahX0CLCvuhsIa4gdM+XT4HRHXjquYqYkMLNzayErMJaS3QwAd9/Xph41rUQSmK1oVuXdKuctjNuzvVjulWBBcxWH2+UwFOB2uoTrXPyqkFUDV7bUWuX9BpfIbfHrPMc1fmM0wi53OCPeigD7aZC1B1aSrytPnqVY6sKoY0TY3hrn/LLE2xeQy/CKxqkNgjfQwMo6ZLKZ61e7Vp5VoCUCqFdQiSsRbdOkUu0nevstS2d5xGGErPOqTc5fuihtQYjkGFAuDOiu1xhNyUqCvD3RnS+QhmN6Fwg7w3i57yn+nyJLmt8IVzHYhCjlKSxEMUhInaBVHN6gZj08ZMQPdtAoyH0QWuSgy387aErUKwLjPIwVY364hg/UOhZ5r77JMVflC6pqBoH2TMtIhnSnB0THt6A1lIvM8JejOwsop8iNwVdXlNeLumSlORmQJNbbNVRl7WDgJUtwgiSMOJode66Vv2U9XJDPIxJjGa13qB9yf47h/jDBEVHPO6hwpB+6jNIY05WBZd5jgh95P6I9cWKKPAZX8mlPvj3v+DdvTHxzvDq/iN+86Xr6vy/MImDep5x/uiMTkpUXZOOe1hPoQOBiELKizVh4ONHIfnpimq24cIa4mHMep3hpRFN1mKVxKwr1idzvJ0h4Tilvzskr1uSpiPvWmStMH/5Ebc8SXJrh2Dax45S1DBhucigrtHrksG37pIfzSkfz0gOtyh+uiTdGVEFCoPB9xRN2+CPY/omhsCtH11Zcfb4lGEvxR/EnJwvCcsK4QlM6rO8WBF5PtuHe8x+cp/V6ZzxnV12/+R9LK6DKaRg/qMvOf3iCDUdUCU+0xtjPv/x59w42KHTmk3TMF/O6SmPcJI6GV0M6d6YYlOyOJkRCEknDNq3ULSgBJusQIUeFg2JIgn7RFGAF/ksFhlYw/bWFrPZiihURMIjGqT0fQ9ZdXi7Ccm4x+zoEqEkye6QqBcjd0eYTUlX1OjjOXqxRgUB3XxNN98Q3Nwi/eAOaE18MMFkJcXJgvzhL6kuVswenfKkKsm7jt1eQitb5x3VaLq2ZTVfA84gtbkyKnz4ySPe/8493nv3Ls0yx78xRa4Kmk2JqVqUb7FVQ5NEBAjC7YTs/glt1VEHijzLiYYhR4+PGQwSynWBthpPKLqu42K9RkhB0gv56McfE4QBZpNjtaFpWudjdGX0J0OPqB8Qy9D5dqQxnTbcefOQpw9PuPv2IYvLFeuzCySQbUpuvn3I4mzJ+eWCKAxI+zHxMCGa9F5pOVxD+Dy7d3xNXHD98bPl9R87fmewKK6gRcC1YsPrfspvnlS8vP9f98I/7mhYY2nWBeEwRSCY3t2lvzNkc77k6GePOH90xvEXR2DhtKp5/0+/TTrt8zf/6j/QdJZf/MPnTO8dML45JgidJfsbd/YdJrhqOXt6zs7bN/jh/+WPGN3ceVF3Fq5jks/WjmDdjxnsjJ6TCIUUeFfZPs8kRy1OpceTCOlgUCrwr7og7u/GWH72P/0tDz98QBgEDPopq3VO0I+58703ePuP3gUhmN7c5fwXT9mcrbDCsjxd8OUvHrgWvrUkYcje+7dpVjn5OkcIQbbKSKSHVe6mqvPKOeMKgWgNJnMmMOEgpq01Nklpzi4hSRBJQHa+ZDJKEd5VJ+bZsbAgpKu8jr//FoOiRnfa6doD+cMzslVONO2hLtbooiQeJ840aruPnmd0WhOkAbpxxkT6ck2dbdBZhb+3SzhOiVuNnfQJlSJ/dOa8G+qWZpNBUUB/SHk8w7PQ/84b+MOUtqxpT+fIfoS/PWL9xSl1ltM1hniSIDpNNdtAGjHcGWK7jiKvnB66FA4ulDitbRG4QDAYpawenLP6yUO6oiYaJwS+T1nWDuLSGnTsEw9jhO+RH8+olzn1gwsG7xwS7o6u4SNfXApff2m9vMKo0IdhDxn6xDenNOuSeGeEn0ZU65KLz46QnmRw74DgYEz15BI/CRG9CLE/grIl/+VTotvb+KOeu9ylQIQ+wfaI6N4N2l8+JhASGXnUQoDvU80yZNPR1S1eGr/4el1Hc7aACwGTAepwG3O+pDHGwdYs+FeeF8JYdFbgCYH1PXTXgXcF/5MSWTeITUs9SOm2huiiImpaPAt0GmuMq2pr4zwitHHnJArQ1oe2c4TvyKfzfbwb2wT9BD8r4GJNuy6QUqCEoNPOo8W7uUXYiwi1hbpDXKk4SSmctGPZYKVEX1Xe4ySia7UzSLxKVPRVcP+8RGBfrGyuyyWex2UvnXTLi1KTpxBpRBT7MOrRLTKax5eOyLkzQiVXcDohnMKbtXR5ia1amou1q3eNE4IbY7p1SXW6JNoZ0t8bUSjHb7CfP6VsBEXToIXAUxLTGcx8Q+R7xKMe3iAm3J/QHs+cHGtW0AkFSqGOZth+AmGEj0VKS+/NA9b/20/xtcWUDb4UVFeKUKHnIVqNMAY/DJHG0Bp3zmTgkvq6ap0ClwDjeXiAeXa+lUJGAS0g2s4pwrWdI1hiaaTEXiwdPK2sEcOU5I09vGFCPd+gBi5RfHZPs00HBnReu86NcB4wpmycoplSBHGAD9SHOwzevYUJAvJF4XhFF3PEsEf++VO8R+c0lyvCm9t0RUn41gH6y2OsH0AvpnxyzvDGlGr+hDDy6S6WVOs5dZvBo4L6yTHe5ps03oB41MNagxCSNqsx0mno27xEeR768bkrVkgJUuEPErpFxvFsAWnA3t0dmrqlrTvCKKBuWsLtPhJBfbFhfb5ke2/Azt09VsczVkcLWq0J7u6y//vvUC0zNvMN7eMZw8mAOPCYL5fU0jon8Vdv08J+jdLdtY7F9e7r820tw/ducjuvePijzzj89hvkZyuW8zXNeUGp12jlDBNDz2MYBTSTHr2dgRNsiJwxrPAk5aaCRLD1wW3WeUG7bmnbFosl8yEWPisP5lmO/YtfcPgn79O/48RWvGGC14/oitJxGxD4W0Pyh2fkhSa6vUv15IJ513F0NkNby90bu7TSkg5Spxrkee69VpBtSpIgoKkaVKDoNJjW0K0r2jik6TpU6LFze5eybqk3BbqsicIUqw2Xnx+z3lRM4gQbOdGJNI2dP0kasTzPCUOfWPoURUMvTZi8scf9//ALNOB3hr2bu5yez7CdJlUhaS8g9y2qNiSBz2yxYjSIOTq5IO0lZOscz1c8/OwxkfLINwXIip1Bnz4WP/RRSqCtZZBGqDggPtzCn/ZpL9e050u6yzWmakBIOtM5ifE39uh/cBcsrB4tKE+WyIfHdMbStYb78yWP5ytII5SQLBYblHKFH6UkXd0y2hpicHDgsnSmnlVV84t/+IzF+ZLvfvseW9qSV53jiBUN3k6M/0w2umrIfv6A3FqaumWB5vLJklvfuoOMOmpriXp91puMRmqC0KMVgDBklxle6BGFIf0kJcsL6p7roIdhiNQgPEUviMg657cTDhKifkqRVXiBT1lW3PzgDnVR44ce050RyTDhwSePiaTi4O4+u+8fEo5eGOddj4afi68JnsM6/0uN37GJ3qtB/m8T8L+2J/rKvsQ1cM8LKVD39muPX2qUPLs7/4qDKkBIgZ9GNGXtCKqt5t//P/4X8vM1bdWim4bE89jULd/8k2/y7p99m5/+679BNpq33zjg/oNjTr44Ifrem2zykmEvYX6xxLOwXK0Jhylv//G7jG9tuyqmNq7KNEgw2hD1Y5SvOP/pA1bHM6SUpFtDJu/cYPHpEU1Zs/PuTYJxz6nNKIluWqzp8K+ChXZTsnxwzoMPH/DOP/0AL/RYHl2SRBGL4xlIiVpsyOqKuz94G+V73PvhPbKnc55+8gQ6Q2gF/Ugy35RMDybMLxaUF2s8TzB+64Dz4wt8KbDaOv3rTmPzGuUr8k1J4DtlKj/w3I07UQ4HPRyS3NxCAeLKBEvKF/jbZ6iOZ3PIGfJFboKOeoAl3h0RHV3SzDZ4g9hVolcFQT92bsG9kOTWNnaVYzYZJgposxWB0th6RbOI6L9/E1M6F9f6cu2CCU8y/cYhyy9OIYmJ0gg/Dul/cAdaTfXgBBtH5BcbrOdw/HVZE+1O6IR1v8kYfCsIJz2kr2jLBtMZwl6E13OeJe2yIKxbWinQviQ7WZB/fgadJuyFrlpSOOlPi8BEPv5uH397iNmU7nshsEXD5osTrBJE28PfJk//6pDiRYDWbjB5hfAU8bRPnERs7p8R9WPCnTHBMOUZFVj3Y/KH5/jjEdmnT5wholJ40x7euE846ZPeu4m9s0/28WPXUcIdg8D3aLXBbw2662iXGYG1CAuVtSgL5nSO6cXogwl+2yGWBQpQVzCfepERBq76q+MAawNE46RGaTUo5XgERUXUasqmpQk9bD/GzNYYKYgDpwylpaTtNNL3CMMAmxW0gWvdB60zLBNx6FSspgNa38NisesCYwwdEACLXz7BMwbpK/zDLYKDMcEoRSUhqh8TDRJ3yKMAoY3DTHsKId11pMLguTs38BziBi6oEq8zaBe4JN2+DK+UsetsCSXxtwZ40wFdUVEeX6I8j3Br6FSXrty507u7GGMR2mBb7fhFgNeL6C42tLMNKg3pDXapkoDs86doAYGUjrfSaXoC5CAm/M5dwjhi8ZP7ZIuMtBdRVw1dWeNHISoKaOsGjCWOQ2zTkr65S7vI6I5nEAZ4WLQFhYN51lWFNAbpB+jayeZa7ZIGYy2eNkTTAawdZNFXCjyFVc7wT9cNpu1QoXSYZKXohFP/kVWD0BrjOagVTed06JMQqSTRdOAI91ecD6RwXh9SYKqWpukIfc/5hQQeIqswgxBTNXS+M4VU22Pax+fYqqUUEA97jhi/KehsQbg1JPnOmyx+fp9utsGMUozVyNAFhlLgHN0vLll+9BNk6OPfvEF3kSOSmPyLj/He+A6hN3CwSwvWCkTpfFeUsciqQguLyXKCOAZjCA+nCGM5yAvapiVIQ1To0eUNbVYRj3vURUNxtmQQhKhxShiGHP3950StZZTE0At48qPP2f7um2w2GdvbU46+PKd3c5cgDLj57i3avEI2HUHvmaogdG2LMRb/SpTiBZ/IvpRbvHYIgZCS8fs3Cbf6fPG//Jyu7RCtZiuKWGQljZRUi4yelayqhsndLdbLDf3pkKZoqDYlm6oCzyPwFJeXC8IodBDFziA8WF7Ji3ddR6c7vlxv0D/6lPdvTBFXnK3ozi6b+QY6TX4yp1IeSkGvlxLf3mVVtURPzrlxc4fNqsDULSfzJb3ZhjiJCZSkrRvGOxMGUQhSMq87dOAELUStSUY94q0eXVHTT1OGN7d58uGXZKcL0q2h42NULT3f451vvYlMI44eneFZCMKAdduQzZwyWGAlG6OxUrC+XDPt9nj7n33A8Y++oDlesDqeobuWQHqoOKCoaiySDkO2LhBW0AmFl/h88cl9rNYcvHObKi/ZZAVxFLC3NyGtNHEvJp72aKKAar4iwNJ/5zbhjSldVpJ9ecwgTWmjkOpqEdNRQP/NAwYf3HF8xb/+mPzJHIXFtAY1SDjb5DxuakQa0zSNk2wvK8IwoN8bsLhckgQhtuooTEtXdyS9GGtAG+tio8WGX3z2kD8efYAuauqiJlLSwa6vChaLoxlN1TpBhXGPoQQCj7bTtJWm2dTUvkdRlPSDBKsthwfbnJ5dunUOqHRLag35OkemHjEetJbeeIDuNPM8w1OS1nQ8fXyGJ2B97lSxPvq7j/n+IOHeP/smxTInVIrZwwvKvOTWvVuMb0wQxl75nfjPbhsvQaKfix/9ponF7yj/+B3Coq7d2X5XydH1XOEqeXhhZP+sX/JVv8GXxzXw2K/YUCBQvrq6uVuqqoGs4ebWGICLiwUn53O+8Qff4P0//zY/+zd/x8nnR9y6uUPai1gtNnR1y5d/9xl1UbIWgov5El8Ibr57kz/+v/8poxvTZykks6NzhtMR0vcQQrN5dI4fBVx89IQmKzGLjHNfUV9uQArOf/mYyx/fJx712P/+mwzeO3SSc1eloGa+4eG/+TsePzzj/pNTynXB+3/+XcaDjzDWsHUwcReIpyiqhp/+v3/E3R/cY3pzi7d+/x2OP35K2XaINKK1mnCUUrcdyShlvc4JkLRHF5RFzdgPSOIQaw26ap3yj+8xeesALw4wVYttWtZfnCC0JQwDgu0+ZVbRlTXDvRHtpiAY9l5WObJce/K68wjJ3phwlGI6Q1c26DhArwuUr4gmfWTkIeKR412EPu32Ds1ySbd3SLQzxUiB1wuRUlIrQSAlfhohjGV8Zws8QTQe4A8S6rWTR413x2QfPqLclPTv7VFfbhzRPvYIIx+9zJGRj9c6/XvlK1qtiX3plICy2pki9mPM5RrRGvyLNfmnJ+7GH3kuMvQ9JAKlDSZQmLJCHy0oEU6q78oxWngS2Uuoz5YE/QQZ+b/5JffKhqbTzsXYU8SHWy/9bfvbtykeX6CLhnad4w2S5++XUYDfd2TV4Q/voZuO4uMnmHVB0xk6bUi3h4jAI3n7BsX9E9rzJUHbYnZS9KqkqTSxMag4pGw7bC8iCXzX4Xlw6kzSVgXepE/bt3SbEhn6dFmJtz2EpkUvMkRZY63AWINII3To07SaeGtA12n0piCw1illLTKU79MFHihJ23SIrHR+GZ3GGwbOuK9uqAMfkxfQtNhNjri7D/0YsgrjKQLfo2o7lAA5TF1x4nhOmVXEx3PkukTvjUjf2ieI3ZzjyrND+J7rZLQa43VIITBV7WQXfZdgiCs+y9deEs/+JF5i3zy/lK7fTIRw0tDeGwd06wLhX3FvfA+Cq+TFvtjHcz1jIYjubNFebGiOF07tZtonnA5o8hptNMUmozWGdG/C5GCKKlsufvKAOq9AStZ5hR32SN85ZHB7B70pWP/iCfYKYx73ItLvvcnyP35MldWIwEdqTVs6pRlZlkRRBEqhOwMeroLrKbRU+EArwG81eJ4zUdTORI+rDoV5Jv9onIKdVBKrNW3TopRwbtzWUjUdIZYgDp7Dz4QUqDhAN63jubWGrqzpLl1A6UtBbS3xIMY0LWpTus5vP0BtSopVTvbJY5rLDV4aMj7YxpQV3WKDlBJTdRRHl86zY76BssYAXCnfqWGK7FwxbXOxwFtdYm+9g2x72DSgqjuKNGXS72EkmCDASoGKQmfY12qCRkMMEoH1JappkauMcNyjFLCzPaYdDRBxQKcEy6dzB7VZlYRxQDfuYUcp0ahH9nTO5niON+hRRiGmqti5d8gkiRBFRV3XTD+4xdnFElF2TPYmVEWJ6izbZePgkNbSNC3GOmhbqKJrIO/Xt1+/8pIEP40Z3g25+4fv8OP/8W8cSbjVmKYjGQ3IsprLvCCc9lmvcvxeQtN2HH30iHTaR1xJDddNQ11UCASe8tjkGb7v05QNuecSWCUkddPy5HzBrQenDO4dgoVwb8w6cMmlqhuCQYAx0NUdqZSod24iY5/T8wV6khL0Enptg+gM4+mAUEhs60QViqahFqAGEXVe4itFVpa01pB/kXFwY5vQCjZPLpluT2ifzGDUp8lrgiSk/81bXPz8EavzJVjLeGeMFwc8fnAK/ZAEn7Zs0YFbh8q248Fff8rN797l8I/fpVpmrBYZUilu3tim7LRz4p6t8GpN5wl02dHNNog0YPfOLnpTYfISP3IdFVO2eNoSTftEOyN0XhEoiXd7l/GtLcJhSn00o71/isorzKBPHXrYCqyUTL7/NtGdHayxLP7yFzTHc5SUiDhCCwlxwNMHx3ie65LIqwWvaRyRuz6dOTNHT9EIR1BWvodUijD2qevamSc2HadPzpm9n4PWzkenc0qhxfGMttNQtsj9MV3bkFUt1lg85UHZEAnFYHfMMltzMJxQtpo6b5hdLkmmfZqqxtYtcRpzdjHDk4LIC2noCKXkcjan1+/hCUFjLbpq6SUeIgyY7E05fnrGrbcOwVq27x1gOsP9f/chlxdLxsMBq8WG5V+vME3D7/9f/wn9w+nrOXaCa3HzbzB+B5Ao+C/CuXhlvFqRuP78a+Rkr/MIXv/683o3z4kH1/f9W2A73T1VEA1T3vqn73Hyn76g2BScnM/59j//Nu/9H7/Hj//VX/Lo5w+4eXuX3riHkgp5ZVR0cjpjd9Dn6XxJPwr5/n/7e7z759/Bj/wX318Itg93n//ms7/5hAd/8wlh4DPdGnFetvi9hAh4/OFD3vjuW9z5wTs8+dFnHN0/Znm+4u2sYvIH9xBKYtqO9YMzFhdr3vmj9xB/ZTi5f8pbi5ydN/b48peP8LIK0Y/AV4gKjn/5FGkEvqdIt/q8/Uff4KMffYJOfKIkIQgDdN6gDPT90OHcG4unnLEYYUi7yJ0wyyghvrv7XKNfRQEWGMYB1eNLmmVG12nCJMCzhvZyQ+l7+P3khVrOrxrWouuG8mTuEhdr6IqGdGeE2urj3dwCC/V8475D42BOXi+mtz2kSwJUEjn+SVEjJz1Mp/EjVymWnkR6rupupZO+zB5esP7imP0/+zZWCjol8QOfzaMZYS9CRh5eGhFvD6mNddyAG9t0eUl7ssBPQqrlBqUNXWfxxn2XHGARgaR/d5vV2Qovcl0e2xn3O7WrvklfYj2JJ8BTkvidOw6fWzWUj84B6M6WrI1h9M078BWS5OtwluLaH8BqQ7HMsE3H8HDrhVfG1ZChT+/NfcpHF1RHM7qTC0Zv38JeGcBFN6bPK7kqCvA+uMvmJ18glKI5usTTGm/UQyUh/XdvsVYSe/+M6miG3BujvIamatDaEFkwykM2HVJJujTC1i1J3cLlGq9psVJSSQhvbmMeXzjZS2vB97EItBBERY3wJCYKEUrhN5pmMsBYTVwbjBDorCBsWmzgo9KQyhiStnUB6TrH9hKiTYFXVGhrkEmI1Jb2/gnFFUQHJdGRjzJXMq/rgnbtnF49T9FsCrpNgZ8ViM7gxwE68BCBhxf5EHh4o4R2VVAdz53Si/eiyu5F4ctN1+s8jK9Zt15zpl+7oUpdJw3xumqWuLZ8usLMMyUpC7SfnVCuStTbB9j5im6ZI5RktD0mHaSYsiU7mtMtMwJjMV2HCQMyT7Lz1j6Bp5j99cdU64JeLwUhKBCIL04xUiJHPSQWsdggsARRSNd0dIDqOloLxhierRrh1fzu+jFmU2JxiYKx0jl7Kw9lLNoTeNMBZpahshIJKGNRAro0xJfO2yQwIKIANM5HwrE4rg6doNoU+IGHP+6x+dvPIQpQ2qlx+YOEeuUgb2ZZ4vdC2izHUxL9+BzZdx4r3emMdpk7/kAS05U1xhiqL47xtkbozqI8HzpDVzd44ZBOgCcEbW+I+u4fIwnpLKi0T9x7FwXEkx7C851pq9b4fY/O82lFRxkF+EWFyHJEIDFxRBT6yLYjPpjSPJ1jigYQ5Msl4SCmLlyHqKpq/CTAZA3r1SUGwzf+5FvML5c01jjybFZycSWSQeBh6pZ00qc/6WObjuzpOb1e8tJMU9J1gq53sH+j8fzG74QpjBH40z5R5FNvSqpbW0Q2xu/HNF1L5HsYK/CSCHoBxeM5e/tbmEHIYpOzc2uH2/cOOX1wysXFks1ig+kMVhmapiHSIdPdCUVWEIQBWMv5w1MGbx+6rm8ckL6xz2a+RnSa4HIBcYQRgs2jC0TosTy5RMYR7bKg8hS7h1v0DiZUq4LVqsCPPXTd0glLU9SMRgOaTlMUNW3ZoDoIlGC13FDVNREd05vbqGGKn4S0VesEVqZ9zs4XJP2YoOfUkorTOWhNWzd0xtDMMrwkRscKGfiY1vDoP33GW3/+bd767/+Q+Rcn6EVOsjVAPLxgfrwi9H2GaY/FyYxOCHb3pjx5fEqlDE/PLnnj7ZvgwfHTc4bSY7K/Rbo1ILQWmfgkH9wm2HMu9OXnxzSPL5Cl840pL1aIusYTEL57SHRnB4DNz+9TPTylQyKVRxBLtJIcPTimsBpPSaIwoK5rurKjbVrqqkYKSVVWhEFAf9TDV4pOG6I4IFu1SCmduIeFumw5PZsjLjaMJ0OSJGT58Ay9LmgBr5+gQ8nxpydE/QRfKmzoEQYe63WGXW7IqpJgEFOsS3Z2tpiv14RKUG8qtscjZlmG8BV7kyldXpGHiigNnFiFcvLcofKQoZN1l5Hv7kVAEIVOjCSv8XsR/RsT0vmGKA4YbQ1ZPZ1xcXzBo//15yTTHm/+n3//5aLU1cViXyrM/5cZv0Mp2uvPro+viep/zc3y1Q/46l5fvvO+hHx69SN/k8TiFYSVRXDnD75BEAV88Vcf8cF73+WD/9PvcfSTL3j60SNuHWwjA49103J+dEp85ZC4O+4TpTGJ7vjhf/tD7v2zD567Lpu2cyRD5STlLv7hAeXZkvOfP2Lr7i6bVcajL49ptCbaHRKjqI0hm20YbQ2Qw4QoDSjmGauHF8T7Y6dKpCTJ7phQSWY/u0+QRNSrnMd/+xlv/fAtkn7Cw18+QiiBF/h44xRh4cnnR5w9OGW0P6Z3a8I3//m3efTLR5RZSYTCl5JmlnHzjRsk0z5F1fLxjz6h7yk43CJUToI3fuvAQTZeaV75/QTvvVuknaYtKqrzJf3DKc2qoNuULtj+uuTiyu+jK2tM3SI8iT+IEZMeXhq7iuuzuXE1Fbxh6t5nLOGBa7vaqsXWPYqjS2g62nWOWed4W0OUFHBVlZKpM+uyAtpNjgGGt7cdfEtI+u8dkp0siNsOlAtQTeMcgNUgwRQ1+YcPHdZ9Z+SSja0B5aNzAk8ipEVEPrZ23RbvsM/0cIInlQvAljkC594tlhlSGzyg9/038cd9R2a8KiYH2yOyjx6hVwX1PKM6mRMdTF4TKDqs2QtBhBcXnQWq8yV2UyF9RfbZEeHBhGCQuMr6s0tCCsK9Ed2mpD6+oLpcEu9OrnJ4AepF4q6SkMEP7zH/+CGy7ci+PAYlmP7+e6Ak4cGUcl3RScH6eM5QKsLYAy/BdpZQSqwK6E4XyNhHbA/pzhbQtMjdEWHd4QuJrjvq3RGhBZ2XBJ1BBR4midBXUsyqbjFHF04ieNHhpyGtUKgrGFDdtHhNh9d29LeHBPcOaM+XtA/PsYu1k2qMHETKKyo04BlLHAfo2Mkw67rFV5JWSbqiQgqB7jQi8Nz8tBbdabr5mrN//wts2zF67xbhlUQsWlNfrpFJiK5arOda27buqDYlwWTgOgqe/I3XymcO3q/rgFvAlg3NbI3aGuB5wet38qIG8gyriEAQ7A2xdUvx5Rl+FLL7h+/TbAoH+dob0SwzysczdNMi6pbaGNchrGomh9u0nx4x+/QIKwRpEBL2Yqp+jO40apY5h/VBStC0NBOBt9qA84lDBj5WG5fMddqRJI2hbjrCyHdGfK1xCUE/RuclXicg9DEWokEfNR6gK9fJ0ldrjLEWmZV0SYQMr0wOlUJfK1tZY2k3BTIKiAaJSx6Kmvpijc6dp0eQRhB6NFVDYKEtG6TnI7ZGiE3pYFlF4xKN2QoZRQhfEb+1z+WPPsUWFeH2GGMMNo2QCprPT4j3Rvh7Y7wg5PLDR3RSEgXD527xahChkpikdtK2dV46Sd5lQdNoTF7h1ZrKato4RAmPSAm0EcjAo11kNHHo5k3TUkhLrSHtJZTzHH9rSH864PjTI26+fUhTNXz+888Z39jC3x6gz5bUFxu2pkPaumPx2QnRzSmdNfjaIpWii2Drzi43//AbL5y6hSAIA6yxyCvu3UsI51fm7VceXwuehJTEWwPe/5e/z6N//yHTNw7IZhuatiVOIkTRMkqdmSWNoTlfke6OiSd98rJifbnmoj/HSonRhrif0HQdVVkReD7r5YYoDAhCnyor6A17LM6WTv46dEXD6NY2618+Qucl1vcRWUlyY0q7qZg9vCDYnbLMc/pBRFa3VIuc9SK7KiqB0R26NVRVTYelrRvKsqZpNKOtIWka0g8CkjginfSYvLPP+nyJN4ivVBtDxyOLfHZubbOerVBNx/i9QwabGoD58Zxat8g4IA58LpYZNgiuFP8ET//ucwZ7Y6JpHzXp8+TvvqAsnOSstnA6W1JlBSJULC+WNFqTZQW3Dvdpmg5bNNzs9RlNR+zc3aOdr4m/eZtwd4StWrpNSfXonO50juquoDxGIFrHqQze3Cd99xYIKD4/pvj5QxSOjL20sJjNWHctUjpDR2WhsAZtLL6naFtQ0qMz2qmGBT6rVUYYhmhruDidIwT0Bz0CKemsodoUPPnFQ967c4iZbTg+vkT0Emzos+laRocj5g9O2HnrgGqVUzcdbbaha2M0hs6zpFFEPs8Q1qCbliqvkb7C8xWz9QaAnYMtLs/WGCHYn46dlHrnutPr5QY/SajKhqCXMDzcYTlbMzqccvrwnMUyY3hnh613Dtj74DY73zhEKkFbNpzcP8FKQZ6VeOMEe+V98+wae7Z2X63+/MY3kt/B+B12Ll5OMV688tXXv7LR13YcfsWwX3nw23y13+g9UkkOv/cmB9+++5w4/fDH99mZDrFWs1yVmHVJWTYkUcjt23scf/GU46Nzvvff/T73/ukHCCHoioZyXYCF3u4QcHKz9//i51TrguHtXfLlhkqA6YWsnl5iRjGthqaqyfOSfi9Gly1V12D7Ia0UPPiLXxBO++x9cJtof8SN77zJJ3/1EWqSMpz26doWP/S5/Z27KGs5PrpAXFVeYz8gMoIw8llcrtjM1/S2B0ShTxr42LJDFxUSgZ+GeEnI+ugSqQ3DyYDBdAjLnPjejRdY8FdbSVwVSAOPMEgJx450ZDpDebmmq1vElTvuS6e2M1TzDeViQ297SDjuOW4A4uXL49rbXhSzHDZdxQEqDp/tkejurtPQrhqa0wW6bKjKGi8K8HoxbV6i2875H7Qd0nREb+6ju47ys6egJF7ko8YpddkQCFfcbNc5WkCbt+TLHG+RU8zW+MOEaGuIUpLozi7NxcoZb6Uh+mKFrVqCaR+kRWxKzOUarxcRpBHe/hhv3Mff6iMCz/1u+0xWDvAkyTs3qFcZNispHp6hm45w2sdLwucJ2wu4zPWD646TrhwGPRkm2LKhrBuKz09YXh3D4Y0JXi928IrQx/qKeDIgGPZeJl/aa+m9sYjAY/L+XQCyjx/TXq5olxn+uE80Sgn/4B69RUb68ILmaAFliaeAKES3xknIBh7NpkI1nWurLzNUEtEuZo5rdL5wqhpNQ3s1f4K6cbK91iI6jeqniCutdW0sqmoRbUXrKTyl8AIQxjgp1uM5TV4Q/8E7jH7/HdY/fUD56VNsUaME1E1LZyyBpwjKGi0VtdLItkP2EgTCJRttR3Jzh1ZJzCpH5zWyF9HEHqrV6MsN6589xD+Y0Htjj2h3QHxr2yV6yxxjjIMqCYHBkl+uGR5ugxJ4/Rhx3fDiVy9dr55ybNmCgG6VI5MQ7zVQutdCcq/BsgSC4GCMDD3W//CAIAoYfucuapg4WelPj8m/OIGqAQFR4NMZSz8KKM4WnM3XbA0HBGmIJxVV0xIfHCKjgPJyRXtS4K+cHGjlK2TVoOoaGcUYrQnDAKkNgRCYxhUcRD/Gf/8W+U++wEdipERVrXPYVcoFRkmI8BXe+dLJiCYhojM0eHhCII3BKIkWAtVqhOC5EWNXVZSXa5K9CdJ3xpUC3FzXGtOLCDuDSELqsyXJzpDudIU1IFuDDpzRpG478CRCX8lPO4t2ZC9mtDOienzuFLqWOeG4R/r9tyiWBRqJudwQfHub+HCKOl0hQh8/DvACDxv6tK2DgFZVDZGHXRZQd7TPODRpSFA1WCVdH2a7T7ozoT6+xC43JLqj2u7jly1FXgCC3tgpHIrYIx6m+JHP6ZMzurZlcjBFAmEUcHk8J79ck4QBSkmIfJq6QdctYRySzVZs393j/HjJ4//1Z7z5P/wh3pU/j5Dy+b3DWvN8otlri/z1KfnaW7hD9xDEAf1bW+x9702e/t1nVMucIPTpj3rkdYc/DVivM0QGi6KEPCQ/A99z3MDF+RIhrmDDeYkxLvH0PQ+F4ezkkkGaIJQgSSIn+9ppx9HBqauNvvMmm7/4Gf5kiE1iik3tuGutIxPPZ8srJEBAbzhwHklAtsoo1y1V0yCspes6ZmcLRtMRu5OUXhQyUB5xEtF/a59wf0inBDvv3yac9qlO5uiypf/mLrInufsvv+86/NrQdpr1l+eUlxtEZ1xHxlOcXCxACka7EzZ5yWCUsjxfsr5YIyOfw3cOafISGQiiSUy2qUh2BnjDmADB/MkFm6xgMOkRxAG26wiEx+G33+TGH7/H+tMjoltTkoMtmpM59RVhuz2ZI+rWQVSjAJv6RG8f4u8O8fcn0Gmyn3zJ8qNHhJ2msXBSt3x5MaezhvHOiNnxJV7g0V2Zqo7SmKKsMRbatnGO8VeQRm2cx0wUOViqbjvqwsFa0YYbvR7TMEKsC4q8ZPDdN5ivcs6/PHW+McsBnvRpypZWW3b2dzg7vwQhnYFvXTJK+ygB66ZiURZ4qY9vJWHag75Pt6poNw1b0wFlURMoRbksieKA85NL0jRGG02vnzDcGlOuSkIhuf3ubW5+45bjzvQi8vmGdNpHBQ4h4qcR7/6L79JmFcm0TziIX+bsPb9u7K+7ZXx1vf/aC+43H//o5OKrsKTrf3vNtxPX1XRf3cuL3Oo6KeVVJNVLu3tlm6/+kd/iIL0mCxHO2RUL1aakySpGvYSLVe4MVozhcG9Cm1d88cljqq7je//V93j3T79FW9W0K6f3riKfdNJzgfSVCtT7//0fcfmzhzz6+DFt6pNXDb6SJMMEr7MQerR1R143dLFPlpfUVhNOejRXpNXl0xlBP2Z3lNJ/ex/vH77Eli3xICZOErSFaJg6bGRrWBYFUkmkJ3nr99/BCz12ztdcHs/oLOhNRTBJaaSEskFJj89/8QAvDFC+4vbeBKsk3bpg+3tvEm0PXkQlFl4i4710hxDPH/q9iGR3RPHw3JkExSH1VUDix6HDNlctvTu7BKP0+f4t1kneSgfLeaXzd+3/l+E/SJyyh6fwehHRtE9zvmLz0WNM2XC22NDbHuN3BtW0zk24F9NcLNBZia5bV2muW0TfotcZnR8Qbg2cPOblmqYx1MsC/84O6f6Y9cMzRODjCSi+dMZrpqiojmbY1jkct52mWxeoYUL6vTfxPA+Zhs9dmsWzlp11ECZxbeGQUcDwu2+RffgAuy5on2j05YrO90i2hwRbgyv85ctVbGsM1dmS5nzpqrZXbp5BEtOWFZEQmKLFLAsWDy5Zzdf005Bgx/FQ8qMZwSDB78fIwKddbKAzeOMe1lhU4EiOYOm9d5vF33/K6kefM/zum/g7Q3cDn/SYjFLqW1uU5wuajx7j2Q651acqW9SkhzLWdZqqFjkduDlrnOFbFPrQaZSUSG0cV8F3VeM4CvAiD1030ClM6NP5HtIa2rpFOZEfjLGgDVIIRwac56z/5x+TH4wY//Pv0Hv3kPp44cj4WlOczGmblt72EKKIepFRf/aUru5Q2qm3NcYgrhy3Veu6cuXpCnm5wdPawXnajrpqaZc5g28csjm6RClJvDtG9UL8fowKfZpljt5UbD47ov/OjSu5Wv9aVeprVrDXZQjGorMSEfn4eyParKKrGvznyfdvPoTv4e+N6H/nDqZu8a8Sf68fEd3docsq8i+OsdpBXhqtkRZs3dFPY6cIttHUcUQsJc18g7czQkgPP43oLpfYtiVIY/B9tOfhhSGe1tR5ge/5iDiiAjyrie8dgOdghTr0XGfLmuf8FiMEJg1pJYhBjD1dOZx/pzGh64aIOEAXDTZQGGMQShEOe1SbgmaT09+dXHVKX9wbdNMipSCoWgzgjRPaU6fPX9YtSgjqqiHqpzRZAYFHoAQYiVEK6SsaT2E/e0LQj9GDmC4r0NmG5PfvoUY90n/6AYv/119Rny0Qnsfg23epD1Z0pwtUZ+FKXUwoSbvJsFJgNyVd0yE9DzpNc+UfYzyFLFt04FGdZ+562hqgrYZVhr/S6NGQNCvQccDpw2PicUqeVzQPjogHyZVpoWF+OqO4XDPMcg6/dZemrKnLmv7hNrKqqWYZ68cz1O4EZRrO/+Mn+JMewZWM7/MKx0uT+DXwhF81Xg0fBPj9mL0fvMXON29TnCx4+jefkp2vuFyuuJyvuPnmIQGC6SBlksT03r9D13Rkm5z52cIpjpU1bd3i+x6DYY/lfIWwoJQi2+SkgxTVarYPd1zXQvC8WhwdbpFvDdFZ4eCCvkezsESDmIujC/KmRfkeVneYdUt2Ocd6ErTFV4o4jthsckLPY3drwnTcJw586k1Bbix1pVj88jGDxZj9P7pHOO7Rrgru/39+SrnOefufvI836RHfmLjCmhQUj865+PSJ4xwkPsMopp2v6QUeTd0yu1hR6w4bKYywpJFPEPiU5yuSXkLetSChykrOPnvCzt6EeHtEOuoR7w3xk4j5yQW9Xsx0OOXwTz/ACwNkPyIc9WhmG+YPzgg9iVnk2LpBBSHYhjYriH94DzVKQUo2P7lPd76kPb5E+a6DK8d9YuUxbFtKq9k73OHk8RmxUiSxu4ZaAE8xHA9YrTYYY+ilsTsv1snva62RQhAnEevFmkgIJsonbA3zpsBXCemNCY+enJFfZMRhSIehvFxRrkqsr/A9xfnRBV4gEIGC1tLUHaZv8aykrVvapiNJY7SCWnfsb+9Q6DXjfsp6lRFIyeTGhOxizWy+opembB9MeXj/KausoD/oU5QVQeRzfP8EC9z7g3eYP76g2RS88+ffds7suDBnsD+hyUonlCCux1vXrizxdQHys8vHvtjudzh+Z50L+3XPvpIZ/Bov72et0WsvvZpMieuvXvvPPtvit04qro9rCcaz/Rj3qSpQ4AmqQGEDRb0q2JsOENoyW2bEScQHf/wu7/yzbwIWXdSEw8SZS3WG5cdPwFPE2yMe/tVHnP/sAdv3bvLWP/kmjz984G6ERtMEglgIgn5M8eUJwWxNtSrohHBGT4lLNMIgYFGUbHeGrqjx4oCDu7tcPjqnSnwWXYP/0SMO3jogOhhzIAXpImN2uaauGz77u0/oTYfcfP8Wb9zdwWhDdrbky48e0lYNQexjhSJf5Yxjn4HvEXaG4daA8buHRPvjV8qdV2fnawMfF+/runOL3ShFtx3lPCMcplC3dEVFtDt2xjlR8OpJf24e9tWy62vO9ystjme7EQiCnRGjJGT10SO2t4dwZZKz/umX2KolOZgifEny1g28KMTUDdL3XEt5d0xTtnSnS+Q4RXdX+M9pH+UrjIByU6JCH78XosIA63uEt3aJ7u5D43wJbNs5yc2tvlMQerUVc+2x8NXLP9k6Q7zet+7SPrmg25R01iDLmvp4RnG2INkbOxJ23bn5MUypz5fUszV+Pyb0nOeDLZ3juuwlbq6nCfiS7nJNHIdUeYu+f4ne6Tv541ZTnS+JdscObnS5prp/gr89Qvq95ydCepLx9++RfXbE6u8/pfetu0Q3t93vlIJoa0A47dPtjFl/eJ/mdIkXR8hBhLWW9nwNVUtjDHQGO+ljtMGTku5y6aRgrxyIm1YTBTUSh+SxVtHmJd4mQ2uDjSM86YjU0vOwbQu9HqKoEF3n8LUI9PGK2b/6D/S+/Qbem3vI0Gfz8WPCUcrw3gHtqsDfGTvi6A/edNXLVlM8uWT24UMuH54w2Rkz+uFb+FsDspPZlVxzTVW17thdrLBHNeQ1i9MZSRwiT1fIgzHVOCUcpjSrnNoaelHM5pdP6L1706nEXU/ksb/2hmCNpS1rbKAcdOcKZuXF4W/VJLfXLyAr8AYJMg5ASLAWpYUzw9qU4EtsVlMczwhbjb5SY2qsRQUBgRQUeYE/6COfXKKPZ5goQDQNQgj8kSNDBr5H0LZoDLpp8MKQJvAItCEQENzYJv3um8z/p//ksMqjHnqRYYVThPGlU7RTQtAlEXXTOpdw5a4lv25ASppWo7Um7MSVIpSh9QR+6BOPdp93TK8fDKsNGtAC/CSCwHvewbHGOJUqoyGNEFmBXbf4d29glxt067gjvqdQmTMs9IY97NNzbNOgKwdjQSm8W9vYoqL8yWeUgNoeQ14j4pC2arCRj+wM5CW6sc4ELQio6hqdVygpsU2LlhJ/kELkI4qG9nxD//Yete5oLxcgFKZuUElIfjYn3BqhpGCxyeiPh5weXXLrzUPmyznR9gBvkrJelXC+pNqUhHXHbFVx60/eZ5Y1bLRhMErpH0ycJPFWH3/c+xpTx9dMxKsDbr9ugr663turLrmnkH3FsL9P/40dsiczHv7Hjzn+/Ig6KxBpxBt/8A1mX57AsgBhCYQkHffwfY8sKwnbjjCNHEQqClnMV0S+z3y2oiwqjO8z2ps61bBrSZKMA5Jv3GT9o08RoY9Xt3BS4L+1z8GNbcpByNnFkqJpSccJvdJjvSwYjvo0bct6tsSPAoZRzGSQUmQl61Qjpgm+FTSbimSUMr25hS0azn/+kZNJbzr8XsyXf/0JZdOwdXuHN//F9+jqltmDM3o7Q8qsQoU+i+MZMglYns8IhMKEjvOXX2wIrUCmCbP1hq5qidOIxWLjDG2bllT5RMLj9OGZc/OeV7TnS/YPt4lbw5t/9j28MABrMOsSg6B6cIbSGn2aIbICOUrpWo2nLepg7Lr32pD/9cfInREIizcdYucZFZbaU/hJTL+oqNqK+794QBAGBL4Td/B9p9xkOoOfBCS9hKqqnvv3WBys+ZkvUVM3pEHAju8KOZuyoloW7Mohx4/PXHGz02S6YOfN3Sv7AYEvFE3VEiUBTd0RBQJ8eOPtQ7LLJaumQ0pBf9BjMuyzzDNk4hMEHo1SbL+1y150E101tNayXmTEgwRfQ1O3hJ5HMkjIZ0t6WwMIfOJexPpowRd/+Uukcr5nVht4pTsR9F/IuV/n3j2Ph59BmH/b8Y/MNf7zqEX91uNFNvA6yMvrOhfXkzH7lS1/x+OqdxsPEt77lz+gWhV8+/Yuxz97wIMff0FXarbu3eCDP/uA6R1H1HaTPSI/mrG+f0r2dMbJF09Qccgbf/xNesMe58rjyZdHbDUtW9tj/FWGTnyyrCDwAzos4TClLGrKvCJUkqasmWwNyfIZaRIiTzXKGGzTUW9Ktn/4FouzBVHiZNA2bcf58YypAJSkP+0Tj1Jmp3Pi6YCyKPnw3/2UG/cOSYcpQRTwzg/fYXm+4vTRGcKC5yukNqQa4sMpWlmiW9vPIvWXDr219lq+8eKMCVxiYdoOvS4QkQ9Vh3eVZAjl8Pahr1CewkhBM18T7k2cFv/VXoR8+TJ5rgHw2gvhaxKdq5dVL2b8vbcoHp07RRhrkftT1DAlmA4QvrpS93Ft72fvlaGP1zeUnUZ7kt6NLfQ8o25WNHWLyiu8OCCa9Om9sef281wqWVxv5Lw8fh168NpmzfmS8mRGfLhNcHsXe3RJczRD5DWMEpSU1J88oR2m7pgvMqSQGGsRaYhMI+wipygatJL09oYoIbB1i206ROTT2xk645+8JExjus6QnS2YBAHBMKWdZ879d5iiepFTc0oiZOi5Nc26pKj/jUO8QUxxPKe1kDzjHFydN3/aZ/In36I+mZM9PKM7X2HbBv9gTGcsIiupVjleEmKMRfYChKcwdYcInIGi309owgC6DtoWsS4IpMQI4WRujXOdVYCVDnok6oYqjQmzgtB0WGsxQYBpGjZ//wXVjz5j8OYu6XfeJH3/ljNa27cvkttnc8JCdHOL4XfeYPX4nPVnT6gvFnRlSTwd4I/7tMYwwRnoGYtTestKkgdnlE8uWc/XRJuS5NY2UoO/LhGxjxkI/FFCvczw0hDheS+vjfbr5r77W3uxoq1bor3R866xf5VY/KrxLJm4Xgy73pCUiauMPm9UehIpfaKbU1QS0q6dpHHx9JKu7eisJQw82sAj8D3CVjmzOCXxrKRbOYKzZ3F8h6p2JFTrpGjtqO8w2r6HzStE2xG/c4P8wRksM1ASm5cIT7mOFmDjADntsT5fQ9OSRMFVYmEx0i1eVmtkC0JJOk8hG/eD4l78HL7z6jJigW5VYHoR3qpAjVPMuiR5e5/q4yO4qpJK33eeFp6HDH3sfI3tOtSVt4MnIXjvNvVnjxGdYeVDoBTy8xP06QKbNwz+7DuYqmH9V7/AG/QcN2JHok/m0HZYT2LSALE9Qhwv6dY5SIloGvwoQvRirBCYokIXNWiDEtA0hvJiSdhLsElC3XZEvQC1t8XRk3NM01K1LmCqu46tvQl5nqPGMdXlmp7nk8YhddtBa7BxiPA9Zl8c00oYvbXP7HRBdjSjWq4Jt8cc/vF7DN+7+dzf6FdOwtfM6a/Uj56/IEDY553eZ3r+0vMY3N3lvf0xdy5WSKUcJK8XMbyzw+f/9sfIVrP1B++gN4LV6YKubBCJT1dWrOYbx8NoNXVniJOQ1nh0nmL16Jz03gEyDK7FLIL4zi6bT57ihR5d44wHm2VGMOrR71pO7RzbalZlhV9rBJbNJgNfkXeaofIpqpqn8yW97SHRpIfMW9IoJNmOGQwTwp0hv/jX/5GqaHjzrUOMhE5CI2Dv5jbZImf98REX90/Z/96bnPz8AW//yx/y8C8+pK1b6nmOZyx7eyOenl5gfcV2f8BitiLSlkXTUdPSG6V0eUXjCdI0Im81O7d2Kb54Qq01h3cO2Fws6VWG3R++5WT2gfLJDDvfUJ0s0LqjazUsM/xpn+BgQvTGAeVPviR4Y5dgb0L94BSNRUUeNhfoMKCMfLo4oFUexrOslEFZhewsQaxI+ymLTYZtDf1BSqVqUILO14QmdAgHIZ5DSQWCtq6JkAziiDaQ2KqhzmryoqQ1hrZ0cEprLdoYyk1J6IWEgU+eFezsb3N+fsF0e0pbNqzL3PFjoxDbakbDIVlecHY5I/B9mnVFlZWo2Ofss2PaTlPXDWVV8+a33+D04RlVVVFozXB3ilACEXgY6Tqb8/MVw0mfbJ2xc3uXw+/ceS7F/nXjRcHoN4+FryMk/v8KFvVrv8VvnP28pmXxml183eOXX3nl+7ymhfpbjWvB8s1v3gEcaXiwN+Ktf/YBumkJ0shZwF99hFSSJz/6nC/+t5/iGYNF0puMsGVDOh7SrAsmu2Oens45P59zWrfs39ln8XTG8HALg0VXDdPb2xx9/JT1OifZHpIfzxAI/KFTgwimPS6P5qxPl9ispL87JNkbsz6f441SokFAVRsef37M9s0tgiR0AaYQzB+c0dsfcesHbzN7csH58YytG1ts395h68aUKAp4+NljdrYGjLXAmySEocfg3o2XIDpfPVRXLQrxAqtkAV21NOuCouvoyRBtLPJKV18lIc3FCn/ap7vyD9Bl4yAKu6Ovj6Bem3q+/NrXBfPiKuEyV6Z14Z0d/Ci89ke+fsJJiT9KIa8Itod01pLuDKEXo+KQ6TuHV6oN19R3XrROfrPxdXPVQpOVdIuMxSon3Z/SXaygbBDbQ/zAo2taTBxSX6zwkpDknZsQeHR5RXe5on54Rny4RSJCukBhZmu0EIiywT+YXLnW5lhf0d8dOzKtpwj3higE5cmMcDpwPg9PLukWGWp7gH58RrQ/da7dV9OgyytUL2L4zdtkTy64+KunRIFH8vYh/tbAzSUhCA8mhHtj6tma9V/8HOlL/CjC7g7RVUe3yvHWhcOg39xGL3NYZAgpsWWNiUO80EeHnnNsblrE2jg5017s/C+uSJt+FKKrimiTY9vO+WLozn2mcGpn1A3F/Qv0yYriJ1/S++P3nHjBs7n/PLhx800lAZNvHDL5xiE6r1h/+AApwOYVuqyprYUkwtOGptVIKbHjFCEs4TBBFA2bJxeuUu4riqM1apnBrS0MgvxkTjQd4CXhFZ/mehfja+a4ksQ7I+dj8jVT+XUJ+uuumZeaJldJ/nUaiJWCoJ/iBT6qX1G2LfXJDF9Ker2E4kotjcBHSUlZ105NyViE7+H1E4hD5KZyBni+grqlVYpASFoPZ7RV10T7E7ztIfYvP8IoD0+5yqIIAyIhsEogb23Rbkri0EeOe/jWYGcZRgiaxkFQn5HujacQZY0nJa01hPvj5wfhq4fXOu7KxQbjKfxpn+rxBV4Sopc5SkjnlSCccaLXaefncjJziZfv49U1pmqQviT45hvkf/0LR+CvGsKDCekbBzTnK/Tpgq6sid/YxzuY4g2dWdr63/74SrPf0HvrgOKzI/ydMSIKqTYlMgpJ4oDaOqUyqSQ0GttpGixSCvLHl5g7W8hhijy5xOYVfugznY44z3M6KekNewgkVkASR6yXa6g6bKC4mC+JegnhMEEpSbo/oe5aymVGGAd4ewOqdcn0/fdoy4anf/sp8eGEcNJ/+Z4sXhzX55ncK2vfVxKLVyfzdbCEcVCYZ+/34oDBVeD77GPGb+/z7e0/ZX7/jJOfPaA02smJK0FrLdmV8luZlwgEnTYoKQhiH/oRq6xkcrkmubF1TTADZBwy/MHb5J89dUWX2Qrqhs5a4loT5y068RGbAu0F9PsxjRSsLpZEUYDshQw8gddPqK3Bnm3YubGNCn3assab9qnnG2zj5N/rVlO3mmTSo6k7LlcZURDx9BePqdc508cXeJuaB3/xIUoITNMxmQzIVhnz8yUeEj+JEFi01qw2BaZomJc1w2HCdDLgfLbCS0OSfoJpOob9lFZa1ssVkScZvLHL7g/eAiEwdcv6x19gsxIjBHJ7gFwuXMIvIP3mHfxJ363JcUjz+JzlT74gvDFxLvWeTz7b0GLRnodpW86zNZunl2xPx2jPw16JdthWE3iKbJ056fG+87EAUFfKe2jhJM3pmPZ7+FFAXlSE1pBlFXt7OzRty8XxBXXTUNY1t/d3Wc7XFIsNnTZks4LB9oDLixnGE8wuF3hKEfVSPASedgp2ZV5S1w39UULTGkZBTDcraC3MNgVpEmCMZbo95unHTxjf2KKMAihr5hcLtu7usLU35HSZ4XmK8XTI4Qe3mX9xzM3ff/u5n9lvOp5HP79pwiCuXXS/gzr9f34p2v89wfxvsevXvvpqDxtefIlf8V1+DWDr2hBgDdKTBCrAxgHWGMDSZhWrRxcUZ0uWnzwl7SfoKCAKA87O57DOOfvoEY9/+YjtrRE932PtK/pbQy7P5qyWGwg8ojCgnK/xBjHRMOHycsXtXkKURlisq74aS38y4OL4Er/s8JXk8uMnqH5CnpfY8zX977+JFZZ6mXP0xTGj6YD+pM/qZMn8eMbjL54yubnN7t09Jje3qKqGz3/2JaZs0FIQBR69okWlEXGo6B1OSW5MX8AxXjq/wnlf5BUy9J20qXT+AvnZHBqNP0joTQaO0KgkutWo1KmVBPtjqrZ1ij6dRgLF0YymaUgPpkhPuUqEeOVcYL9CMnbbuAfPq7DXbl7Wgr6SLQ12RsjIv8KgvzxBXgJEXH22BawxmLolmvSdvvnN7atdf80EE/zOMI2mqGgvVnhpTLA7QtUd/tsHFI/OCIc9VBqhqpr2coU/HaCGKc1shUa4yq0RaCGpjuYEwxSxycFXeGmMf2sbk1fUp3NM7UjAre9I1rSGbrZC9mO8UY9mmbuEY3+CvzWkWeeUeY1abDBFhb89AsDrXfljSBi8fYPerR2q0wXtpqCar4j3pvijnkvEpCDcHjL9b35A/enTK2+FFhEERJ7E9kKMiumKmqAX0SwziH28JCTqOsgrSCJU4tFGHloIdFbSLTOklPgCVBxRG4MfR5h+DEcXaO30gXTdOG6EkIS9mG5ToOsW+3TG+b/+G+LtAdG7N4ne2CPYHiL960n2iyhH9SLGf/ANkK49n1jryHYCrLbUFyuKB2eooiHtJ2yWBXVW4CnJrK4ZjsZUiw3y0YUjp273mb55QBsFjqeTRnjRlRfDlXfGVwI2a52MbvRyYnF9PC/8Pnv+tchG8coS+qzdzvPPFgJkEoCv8KVg6xuHmLym+fSI5dmcyPcxnSbvNkhr8YMA0sS9tslItUZJhfEkke9B6OHXHV1nMNIifYVSgtZTBO/d4uL/+xNY5HhC4Pse+goq2DUdXuA7DHRWYQKF0pribMHAOllGZS0aHI8nDPAD33lYXEn1hvvjF0fIut/4vFSiDfX5CpoOkQRYT2FDny6r0IGHF7tkuW46oq5DZwVBGuPd3KW+f+LUAoUAY+hma5L371Arj2Rnig0DdFZiAoXYGULZUP/95+jYh3nG4LtvOhneVlMBaEt3tiSYDsi/PKPNK2zbITB0smSTd/TbBC/tO6dnKRDa0ilJoi3l8ZL+3gg1X9NdLskfndAbJJzlBb0oZrA1ZD1b09Qt0vdJej02ywLjS6SvuPz8iDvv3sH3FWc/fUAw6eGNE6qLNUEnCJOQYr5h+sY+FxcbZ/R1nbF97fhen5S/Cib+2kTj2tufk1pfuQ9cLwRgIRymRP0IayybixVcGSZ2TY3RBiskYRyCEHR1i/KdSEC3LujCCL0q4IZ9+Z4kIJj02RSN+0lxRDNbEd7ZZ3Q4ZXe54cvVkmgyQNaaBIVnDE0vIrKWcBATJQlVVRPUhu3JgLKqKZcZzaZg97t3WX96RF7VqDSh7jqqpoV1QddpjIDIEzSVRYQ+m6MFKI+LXz4l2Rm45LbrmO6OefjgGCuhmm3IraDFsNKNc+A+mHA2W7GzPeZmFDBbbFi3LYuyRAUeftcQKMn0xjY3/un7rqJuLZvPj9F1i2xa1K0d55D+9g2aR2fE333LuXKfLOlOl4Ag/+QxqhfR/+ZdqscXrB9eYhtN2GmKJGKQRKSjhGqW0QsCtLXkXcvZOnMFQd/HZjmdMUiV4nmKnemA8nIJcUxRNWzvT1kvM7KuhXVD3/dpNxXWGpbLDUEYcHmxIAh8Eik4Ob1092pPILVld2+CwJBddV8FCt1qvECh647NKiPqR86Lw0iyvEIJRZdAMurRFg15VrDJS7b2t4gGCRenM/zZhsHOkMHWkJv3Djk7nrEsGmRjqZuKWz+8RTLtkUzv/cb8uF8Lf3r14rn+3F5ZU39dNfa3HL+D5OJ68P4rOgYvjevbite89tuNF3rwX33/86DTghD22qf+hgfvK2WrK2jLM23uZwR1C1/8u58y/+VTjBTUlxuaoibdn1AYTX6xZKNbosDj0YMT1j6wybj1zbusnp4xu1ggqo4gCJASlpdLxqMBDQ67Oj9dUDY1k90R548u2H//FvmjGUpKbnz7DqdfnCCTEDVbURvwo4DdG1ss7p8zfWsfPwlYnSxYCSftOJn26Q8TLk/mrGcbPn7yEfE45d0/eAekYbg7oFmVeOuK4c6IcBQz+uAOwfboavJdOzD2xbFpFxnl0eVz8mm4O0bXzi9D+J6T3DSG7nSJbTroRS6g2xREB1PCyKeLBJ4MncKNsVSzDXpZEI57yNB3SlBJ+ILYdC2BeB7xvJpgCnihXObUl/JHZ3jjHsne+MWpfQVn8up8efa8K2pE5OA59srd+WvHr0xof8UmX/c+z0nxdXVLULdoA93aSWLiKweBqFq8OKItKihrVBIRbQ2ey9qaykljdhcrjARZtzTLHHMu8Ecp3rSPCgPq40tM1QI4WctehMQRqbW1iNBzXYxJHz+NyM7XzKuWdBATNR1eP3nu9ix85yEilSJ9Y8/9FmMpPj+ieXhK/I1byDhE4CBr8ffeJv6OM9LLPnmKvljQdR0yifBGCSIrCQ9G6KNztO5Q4wGmn+APU8Qix54vUBLyyEMlgYMUVc45XXUaqpq2bQn2po5sv9zgI5DKVcxaY4n6CVVZo7RF1h31wwuax5eslMSbpAT7E/z9MdHBlGBvggyDa0uae1AvMletfRacS0G0NyLcGtAuMrIPH0FVM37/FkJJiss1q188IK8ahIFR21FmJQvPQ6zW9HYntKdLlLV40z5SSYJR4kjQzxLcZ0lC4L++SPzrp+av2eKVi+zqqVASqQQySOlWBb2bU7KiYvfWNvXTGc3l0hkHCjBSIIxFCUE/DKmNBmPQRqJGfVReoXspvu+jywrVucQgurFFm1cwcyZ2JoloPUmgpYP0KYV4xi8JPGRR4bUNURJhiw3Gk84FvNNOXUobRN04GJmAcDzFi18j02uha1rnRbIuoesI93bo6ga51ad5fAnGYBF0gYenBP7OiG6R4W8N8HcnVJ8+Rl3N+1Z5qE7jpRGjP/8eIo1Y3z9Gf3lE+fEjdBDRvzEleucmapwitwdYITGbEpFX2EYTH07Jq4bBpO8UrBAYBMJqdJsTdhXt6QzhecjpTZR0mv9hEKA3OUIIsos1oe876OByg7+/S3i5ZF3kdJeCZJhSnVWEvofttMOR5zVREMDBlEp3jnsy6WFiD4Ul7MfERtLbHnL02VMe/cOX7N/Zu+r6XZ9Trz52c8oaeObFAr9BtPBacoa9ev3afoxl8fkRy/tn9LaGPPm7z2hiD9KAKAzpGod/D6OAFktZVo6XBiSDlHpd0LQdl+uMvfMVyd1dp9B3/Vco10nVxiAjV3js7Y8ZbQ958vAECucDsTi6JEpSzOWKOArR1tI1mlU5x08T2k3FibEE0z5KWQaTAXqRsbxc4wnY5AW9JMIqgekMcRiQ1yVl3SA6TYuhkpLAU6gwoKhburajKhqoO5JBQn86YHO+Io1C8q4hGaaEvZhAKCphOLqYY6uONI0plgVGG8qy4u7tPXrK4+D/8A2ioVOBrGdrsi+PUVmJl4bYVYE2Fiulk3rvxxR//yXLz4/dNbopEF1L8MEtDILlJ08dP1HAzp99m/XFivzxJcdH5wyDkDaQdJ6k2bgYwgsDVmUBoU+kJH2lmGtDuSyoG43nO9nx85NLgqtzijHIzhJHEZuyYHExJxzETLaGJD3nOdNY5xpfrwpu3jrgdL4EbRjtTCm6mrZoODzY5cnZOVE/Zrw3xgaK8nSNJxXpqMe012Ox2nC52lBtrtaKMGS9yblcrNif9JhvSu792bco5huOPj1iMVszHfd5+/feYnC45UQjPPmce3otHf/KeJ1f0fO45wqp8typ+/o1dy0+tly7d/wOxn85zsVLxYrrEKhf39r4lQHYr/nkF0Hhs+rF9c9+3ba/qn/x7Aw8C0Atum4pL9esPz9h9vf3Gd/dww8Dlv0EGfrkbUv++TFt2VB6Fn/UY1k11BjKqsQ/cjCIdVkx6aUc3t5ns1hjWk08Stkd9Xhy/4jB9pDNImM4HaLrDt1pGms42N/i4nzJYNLn7PNjJntjQk+xenxBXdQc3N1jebbCG8VMdkeEvs9yleOFPkhIJj3yTUFjNaMruTPTdJhNRxp4TH7wJsEwoV1k+JOB+9mvXcctpu7o5k49CDpIApr5Gtt2qF5Mu8pRvZhqscFWNSqO0Nai/ABvmLK5WDG+s4eZ5zCI8QYx1dMLvF6MP4opz1fYvMJ0Gq8XE+6P8fsRKgxeDupenNCvPnlWEjMW/8rgqZlt4KrqabXBH6YvX8nX93OVwNimw+/HrqLZdlj/WrWMVy72XxHdiddt87rnz26O1tKcLJwzelFTNnNk26GmfUci7MW0WYmKBeHBlFg5nP8zk71nyhEyjbBJhL/VdzvWlnaV08436KrFZBXNqsCuC+rTBeHuxKnp5BUysoh+Av3YKUPlFdnnx3i+x2B/RL0oKE5XiF6FiENEXrvAfdxD+d5z48RnxO7k3iF6mVE9vcDfHuLFIc3xzOHnxz0Hqfrh27S3tjFNR/nzh5jFBjtMEP0YKxUgaVY53jChPV9iQ482CvA2FbazKF+gBBQ42dDGGGJhUXUHszUK6F2R+Yw22EEPz1o3H4RwBF+nVUlb1vhYzLKkuHiE/rvPUKGHGvVQO0OCSR+Zhvi+M8urji4p4oB8vkE2LabMmfzetwhubiE8RXrvAG97SHW5wVYdalMRdYYgCmiyitoIWOVUv3yC2hqwPNsQDRP8QYI9XdFUDbnuSHaG9O4dwkvdFPcbnkkzvjr/XioNvWZpfFlJ5JUqs7i2nj7fyVWyLx1PKYhD0skAk1dUWqN9H9s0GCFoy+q5TGQgA2RR0nYtkdboosJ2HaLTTtkr9GkDhcpq1O6IzU++wBMCnThJ4lAqF/h7CtW2iDhAGuPI3H6IDARcrJxjt8bBMrrOXb/a0BhHDiWKSO7deF64eP7Drle9tYG6AynxDsZs/uEB8Ru71BcraDWeL1wCrxSe52GlBCnJfvwZwlhMViKGCSEGW9TO9Xd3SLvIqR5f4EchzadPEGHE4sMvife2UJMepunwkojsaIbZHmAXOem9A4LHlxSnc2pjnOxt1+HXFfriAn+Qoss1ILDJFBOn+OAEEpTCq1tqBWk/oi1KbOsKFePtIaaqqLKapmoY7Iy4PLlEGRhujRhsDckuV3TWEO+NMJ0man3KeYbZ1MS7Q6SQbM7mbN3doc1Lpm/vfz2h+/qcezYPX0Mo+tpY4Fe2M573nKiO5zz4t/9AuDPg/P4J2SJja/8Wqh9TZCV1URJGrpNlu47Ihk5tqOtoyhohJAZoWk25LFj+8jFbP3j7pU+VoY+3N8Y+vUSOUppFiEhDVBRw8PYN5lnJ6ZMzDren7Oxs8dOLBX3h01gIfY8KkI3hfLVmPAzRaIa9lGJRcvTJMY2x+JMB5cklF8czzCgiNmCEpdEGVTq5Uz+NqPKKRknm64yg9Ig8j7rTHM8vCYaRU0L0FMkoZXGc4xntuvKeYNjv0SaaIi94+uicna0xjTTs7YzwypZb//K79HZHtIuM9nRBtS5ASvA91I0dukdn2KzABpLet96g+NtP0KdLpKewaQRlhbq9Te+tG9RPL2mOzwhFR/Tt9wkPtygfnlKsMoQ2MOrR1C1+oBBK4oUeddu4zpKFpm0pO43yPETkkBBtq2m7DmkVnYUwDlEGTNXSKIWfBEyGqfu+xnUkZRoR1hrlKRgmdMY87w7rsqGqa+I04ujoDL8XQNmRjBOWVUk6ulKY61rOLuYIKUgmPYplxv7+NkIJ5usMXymWpfvuQgkGNyacPzxjuNWnNZagF+HHAX7yeh+ir5TmvwYRcZWmP49Fnq/xXxNIf/VK+8d1L/7zwqJ+q+/29SH962sS1378r/mcZ/na83e8umD9qozupZbqi5eMNiw/P+b+X3zI6mSGry2+77M4WSB2+5RtQxAoVhdLYs/DTxVlU7HJS5q2pbNO9ebRbIY2lk5r+mnM2eNTdnamzM8WLGZLtm9sMZwMuVyu6PUSNpucvdt7PP3kCds3d1gtM3wDRAHDMCJoLbOzOaObW5yezCFUTLeGnBxdonoBm9M5otGUEowvwVdM7+2TzBPC2GGGJ3FMkoaMv3cXf5RSXa6J9sYOt/uaM2O1pp5tsFWLGCSosqHKS+JRiqka6qbFPFijrCUEVGfQrWFxfknkQasNw28cQttRPr2knK3xNzFhP8EzFjVKMNagswKbV8g4QghB+eCcTaCIehEYCMcp/nSADP2XvTNe5T1gMWXtYFa+5xy/N6Uj52mDKWvUMHXVy6tg/HpnrMsqaDpM1zkugu+kMIVysoLPAnn74uNfnlevBnhX38nt/irBFS/PR2vBdh2bj59SzzfQtvTu7oHvOS+HTYWoO4oHJ4g4INgeOVz8M9dt44JM3WmaoqSrGjhfY7RBJSEmq/B2R1Ro/MsN/t6Y5GCCANpFRn0yoztbkr51g7ZpqR6fE28PaS9WRLd2EKGPPlvRrnICKQjSANN2lF+eEOyNXCBcNui8pt0URDe3kWnEs1zVG/VQ/ZT8yRn1bEWyv4XVBpPXtLMNRD7+1gBPCgh96genLojNamQvpv70GCVwPAxfYdqWOPDpsPjjFG+YIs9XhAaUEMTjHpWAyPfRq5ymqJBZCb6HF/gYa53ppZAOm99pZODgLl7gQd2C1s5LIQqRStGer2gvVtQWsM7wrbNO+pamQbQ1VkgqYyk/PiPqJeBJrNHYNCbaGuL1EvxpD+/GlOWDM5CSdpU5vLwusK1G1i1ZVtGsS2ptaIqa/du7iNaSfX5EuO88SqQnadYFqhfhK/n1yjvP5+CvGM9c3XkW9H3NZtefeIr0zT3ivTHrz54y6DRsKqqjS/y2oyhKvDgk2h6i0hA93yCyClO2NFkFgwgjBX7T4XcC1RnCrSHlg3PCMALAFCWA83qQAisEpZKk45RuvqbIa0JfYOYVpjWOr9J0NJGPX9eYwHPJue9Ra0OEIdgd8exKBGdC6YonLdZY9CJDn8wgCvHGPaga9KpAlzV+GiO2Bo7bsSkxWYlnOkzTYrPKObinsUvgTY1pOrpNiT/u4Y96TH/vHcoffUbbs+iiQuyNSP/J+5R//znVxRptQZcFURo7KFReE28N8dqWQLd02joZzTaEtoXZJaLr0HWHP1gjk57z8Ql8J75gWoTu0KVTqJLDPu0iIy9KTBLwxjff4OFHD+iWBUJItu7sMtwZIn1JvSrQVcv8dMZgMiR7PGOQRPS2x8xPl4jNhvEP79HWmgTB9jdu/mrq3LXb+fOl8Gu2eT7PXo20Xrpvv/zmzZdn/OL/+ZfYqsP2Iwb3buDN1yyeXpBdbhiP+oRWE/UlQkmqVY3NKnbuHRIKj/OjcwajPn7oM04TBv0Ye6UO9hzJAE4J7+Y2m5M5XC6hF9OVLV6nGY96vLM1Yd20TEd9kkZz++YeD5+eEvsBKg5cUFZphttDwmGCVNIVdhIPHfm0laZrBH4ccna2YHsQ0FQ1VgiUsaxXGb7vMxkmLEvHKQvSENUYdnZGqE2A34ucu3VWYazh0aePyZuGrdu7rJeXlF1N1xkePTymqzu2t4eURYkf+fSShOn3bzC4u0N9vqb49Ij+N25gjGX18JykH6EiBQdDmkcVqh/RzDK6vEUkEXJTXBn+efT/8F1s3XL5ky8h7VN6kmhdcPajz9h89JjLdUnRaeLAo6oa8rMVwShGeR6BEM5zKg6cGpQxGGMI44AyL9yaZSxR6Dn5/LYjTCLKWY4NFVZ67O9v4SnJ+nKNn4Ykvofe1ES9mHmWcTJbkAwSemnEowfH9AcJYagQXoofKFRrWOcFwhPkbUNtNUEjSOKUpqopNgVeHHB6dunuK8byxjs3OXl8Tl01tHlNf3/Me//1dzn9/Jh0lNLbHb0095+vQ88LPbyIFX7Fmi6u/fvsja+//r7uwvrHjX98cvGbJjhf1wl9vpPfbrzoMbzSLHolCXj+cc/7qV//Zb9qNvIsqrx2Y0VgjeHpX3/Mo7/8iFAKF0RrzaY1GNuhT+cMBilJFLD2Fen2EBUGnP3yCw5v7vP09AKEoOlap8bQtEhP8aQ5Y28yZvbhFzRljQoUx/dPGE4GyNmSaKvHZpERdx2J9AmSgMXTGdv9PlXZEO0PmQz7bN3d5fx4zmRvQlbWqFXGYNzj4f0j9m7vMX9wxrDfo2s6giTl8mLJMPBJrCKKFdtv7dF/YxeRRs68atzH5BW6ccY80lNITzqjHmvJj2Y0T2eEW0PCnQFyZ0QUblEuM8rlhvpyRf9wlyANIfQRZYPxPUJr0I+eINMedbZFYKGa54hxH5tXdBTIgcNk46kromhCWzRQtnSdRhpNvnD4y+LxGeneBDXq4fcjvJ7rLCCdvKRpWse1yCvKqsaT6v/H3H/9WJLleZ7Y5wjTV7sOLVJUluyqltvTM7O7M1wuSHAJPpEgX/l/EQT4QCwIPpDAclYMsDPTM90zXV1dKisrRegI1+5Xmj6CD8dDZmZVVlcR4AHCw/0Ku3bNjh37ia+AukVPgm9Dt9jQHM+RVZB4jMcF6c2doBl+JeHprUPGGr0/obvc0FysGNzcCcE70Dw9QySaeDbCVW2QKpUywDMSDVqi8uRK3hj6ZUl7skCloXujs+SK4Bw6+q4PmO3+bEl/uaE9WQSYURrR1g1Rr7GdCfO77VDO47WivVzRns5RBCfc+tkZXdWE9SiJiPIUUzY4JYl6B32PfXaKsI667nBpFJyWrSWejRl++zb9zoR+VdGWDb5s6FoTHGLrDhXHRDd3WD45xSuByoPbuTCO7miBKFrWixIbCYrdMdXZklwrZKxfX3NSUNzex5ZN8IrIc9QgIxYvYW8hwIuGGW5nRHM4Rw5TpLjiSohQMdbG4qXAGAfeIy82+LZH3tohOl7QLipU25MMUpho4tvb6NWG9kgiV2UgWscxKpWYpkdEETpPQ0Lq/RVyLjgce0D0BieDX4uv25AwxXHA1W9KYq1okxSpNdIYMqnQeY7SERhD3xlEX2HLng5C4SFLSG7u0ucJ090pi8+eBaWXzjBSEpFEzM9WREqhBwki1VSbGtfbAIHRCpHFaBXU14IW/5dvRq/jsavV7es6a1d/vISgfm2MaC3d6ZJolCOv2vmySJj88D7+O7cZr2uW/+kLlp8+JxeCdFTgigQjBckwo77cEOUJcrlByRzx0Q2a8yVxb/HzDeXlmkTrsD5KgbI2QIUiRe9C4iOMJUkjrFKkRYpqGlQTEoPeWkSkSJ0P3JwkCiRxQGiB2Bm/Si5e3gOED5Kj3aYmGQ9oFxV9Z8LrPJhIEbc9Kk+xsSJ2jro3qGSAma9C0SKOQkXYeUTXByM/D8pYms+fEf3ZRwgJ8c6YNk8CFyTziLJj829+QX8yx8YxcjbCNB1ikCIWNctfP2dlPYmzyGGGkh1UPUJEqO1rmJPHqEGOLS/oL09IZ3soKTHWEbngneObEmMscZxgBllI4jYVXWd48flzSBT5/pQhgsvjS8rVhr6siWLN+PqMQZYhO8NglODzlNPFCqkEjbdszpZsHp9z91/8gGR38vak+rrb/svCym8NnH7zZt4ctjV8/K/+jg7QWcRAKhZfHNNoaJQgOxjj1h25kEQnG9abivP5CoMjHxZUzrC9NyURChJFKiT2YkW0O/pSTCGAeGuEnA4wj49Qo5zm0xfkN7ZQSpHHmjTSOA9//ckXXNuZsXWwxfJ8SWwdtelRAvLpgGvv3+Tzn3zG+nLFcDKEyiGVIioyuAgclrzI2JytwHtmN3fIqo6yaWitpew7fNsz2RnQXJT0mwZhHcODKaLuccaS6Ij1pgLjOPviEIHg2vVdXhyeUoxyMq+Ioog48sy2x9z/X/yAbHcM1tMdXjC4s0f56IT5Lx+j8xg9LCi+e4f6xTlmUZLePmD144fEWtOVVSjSRJrh/+pPUZHm8q9/RSQUcjKkr2qqowvaB8fUeUQnJeM84ehiFUwZq5phHpNmCV3TIqSga3q0UljvyPIUvCfPU7qmQzpPPhmwOlsQKYWUkjRPaaNgmLhebPj+X3yHp+YpIpLMn5wiDSjjiRNFsjumXJTYPCFOorCma4VuDMI6klmOqxo2ixodaeJhTt8bijxFOEdXtmztbdHEDU55TNUTxxFRnjAoEspNzUwIoizmxvfvXCFDvrwI+6+s/rzmmn41n/NLGcrXXDDvvO7/v2BRX1Vi+B3GV/U6fwOU5PWDbwDGfo+PfxOP9u7731RSEQicdbz497/iwf/0U9KtEcd1HSpMHqzwpF4y0DE0hn7TsL23xdEXh5gmGOiU6/IqsPQMJkPWizV9WZNqjdKaRVOTJJphMaK3llVVXe2IQNU9s50xl4dztrennH1xzN0f3efwl0+ZbI3ojeVysSbPU/bv7FGVDYfPTlisNtTzkrJu8L1l66PrnDw6RjQ9w67n2taIbJBQTAtm379DtjOGlxAyEWR1bRJh6w5TtWyenlIMMtpVHare1jL61s3XFXtjgmmVcfhVzXBrQjQdBJdhrdDjHP/8EqdEcCUdZCgReCzJQKNijRHBTMzXLaujC7SUZNtjuscneKkQxhFPBsg0It0aU61KzKrEbGrspqG8gjl0F2vi6QAvBeViQyYlRkr0bEg8LYj3p5hlRXV4AnmCj4P3g4407aMjzPML/CjFIojSCBlriveuBVnTPCEzBfUnzyiP5yTDDCUlZDFN2YBx2LbHdQa7roNZV9sx+sFdbNXRL0rcpsFtmqCMlceILCjp4B1qMgxVa+uQeXD2FniKm7uILIJIhXOyXgeTw0FOvy6hbNCXK5IPb2Eu1/Tnq2BeVyQ4IbHGYsoWlSekRRpMCaMMmSfBnLFs0EUwj+tXNeayJHvvADnOSaYDYmOxy4rqyQlCSvqLVQhgJwXJzoj103PiMviuSO/xStKsShIFVdNRvZiTbQ14+v/4t2z/6H2K+9feUh9TeYJt2qDp7YOS0MuOo8oSyBLUMEfGEctfPWMx3zC6uY19cUm8O4HFBt30RHmEqVu8lHSXm6DcMxmghin0FreqcOdLeq0DzCiJYDII+uhXpnekMS7VtB503UHX4ZQOPgbWoQErBfQBJuOSGNV20Pf01qHjoDzluj6QD6OIHvH6OzmPvAr2tPaIOOCHu3WF+uxZqI6/d40ijqk7Q2UMl+dzhsOUcZ7jhyleXJFIP36KU5D4CeJsiYoU8fbodTbwcsn8qgRDiN8Uy72u0Hwp5ntnsRUCGyniNATTvrdX4g0K8ESjjMmfv4ezlvNfP6cVIHuLVILl8zNc12O7nsI7OF2w2AS/mE5IdNVcSfEGF23XG2Qaoz04FM6ZQLi1lmZV0eCwdYm6LPFCIq1FtR4fBzlR3/UoqdDDgr5siASkH1wL5mjO4V91aj39chMUaLSkO1/ilST/8DrNs3OSNA7JW9US7Y2xFxtipXB4fNUS3dgOuHwTDBZJI5LdKd2Lc6TwVF8ckn/3brjmhCD/wT1W//qnqCwJHAkhKEcjiqYhe/8AJaFdlXgpGIxz2qZHrEqirECNCszzS4R1WDfEqxQ9LDDPD2GzpLs8JL35HlxxAlQc407m2L1rmFWJPr3EjIck0yHgiUc5C2Ew1uClIk3CNVVVDUOVUz69JE7ikNhPc9JJQW8MsZbs/vCHwTBQqgDb+o8d+3/xrdBVfneyide/fFWc9GYn4+0u9Mtn30EXvJzs/gpKOt8wm06o855OOZbLiqJ3oXOoJPn+lH7S0pctddniBinbsxyXRaxNB15g+45501N5w61v3Q/z9N7+W4Hdy9+kkug8Q4wGVGWJr3rMsiT74Bqmapg/OsMIj001F6bj/W/f5XSxIt40pEoiEslsb8Z4NmQ4yilXNZvDOcQxvfckWwXaeYajHGstTd9TFBl90weoU5Gyulwy3R5Tr0qsdTg8l1UoZja2ZfdgC7tpkEqR5RlxEnH84pzrN3fprWWY53SrJU4AVcvujS12f3iPKE/olxXVp89JdsY4Y2m+eEHctJAoomuzwIsEsu/c4ejHD3CdJUvCmqekYPwv/wgpYf7vfompLVYIytUG1/ZUSnLetDjb0ztHtSzpTM9okjP44BrSCzZ9h09itHP0dUeSJ6H72PYoq0iSGOEhn45w1pHnGVIpkiiiNQ4robM9wyJhsy6pm5b1kwXNfMNgMuRyuWF8MKYqW+58eJuHnz9hnBU4PKZ3jOMYrwReSqI45tp+QV4kHJ3PqZdrnpUtgyIlSmO2dib4Lcfh0QVKWRyetu3IJgXZbPBq3XyrCP7uZfFqeb2a11+qqb8urn8p0fjaa43fOVb+XcbvnVy8+UX8Gz/feMVXPPaHGq8bP29CYn/n8VV5xasKZfgE7z2bxyec/uQBj3/5mHSQYTONaMDXHTu7M5pNjekc+SynKHKePTpk59Yu27tTLs+XVOdrFsdn6CTCGMuqrCimA1SiaZqG3hqu37/GzvaUo8fH6MYiPFSrinJVM94ZkhnIZgM2izWJ1KxPluzf3efpLx4jpaQ2PdO9KYvFhr3be2zvzHj2+JBbf3QXKSTzyxXDSDHMIoZRTJ7G5Hd3mN7ZDSpQV0HP60MSjKU80B/PEUrSLkuWL04ZTsZEAkb39tGzIc3pAt8bbN1jvaP99AW91NjNCrloQnC+OyK7NiGa5JBq0oMpcRLTHl8iigJRtnTn6wCdmmYkW2NG4zwQNY1HxFe64rtjdBxjFhUqiSm2xpBnAeI0Dw60tu6wkQqVPgQpAmc9wlrExSZAL9yVws2VnvnFfMNoawyTAj3IWJ4s8EawOlsz2h0y7i2bj5+g8hRTtQEWs6xQrUHGPV4EMp8vG/pliRzl+CwQyey6wtct1cfPAgk8iWFVBefwYegSoRVKSHDBrE5UBis8QnRIJVFJjJmv6A+7UCXanQQn1MOLQGLNUkzVYHvH+c8foTvDYH9KMhmGgKLryXbGZHd2iUZ56OpwVZH2EFsXHNIv1vgrE7BmvqH+m1+Tvn9AvDsmShLi61tEOyPasyUqidBFRvPiHG0c04+uc/LzJ0gPRaKJIoFoDXo6YCAy7LpCVC2D69uc/Xd/w+b6DpO/+A7J9W2EELi+R+jAf5GR4uWFGDqLV9e8hPT2HqZqcGVDvL+FHBe0z87o6w7tPE3VoLseGUckk0Ho1JwtEd4T39nFnK9hlOOaHrOsEELQWBsSGBekDqUQWAlRnqC8w12ZkkWRDpVo7xHWBV8FPHiBT2J815MkOkjxilBRt9YiVJAJjq3Fq1DBM50ljjSm64JnjQwSxiiNtB53tkJHiiyJifKM1eWC/sU52bUdxDSnXFWhu3exQMzPKNMIvz8N3KG6C47mr5RAvjqF+O3N52/WJpdSkm+NaKuGpAhVRKEkXHE+hHPIQUq8O+Lg5g+oD+eUD48pqwaVBIMq2o7zukELSeIhy1JcHuMWG2JraTYlPtYoJQPp0QuE0nhrsUpimw4vQDYWX3dI4xDSB3iac4iqxScarTQ4B84GiFscoHfN2RJdpMGd3YOtW/QwDypPvaF8dIJOYpK9Meu/+QxRd1C1WCXRggBFmxRoLXEmePnYZRmSvdkAs9hg1yXWOWzbQBTj6zYY7gFqOiT+4Drrnz0kzjP8bIjfrDDjnGR/EpCaP/4MF2vE7pjRKKf820+h7tFNh5NBray3Hj/Zx7g11naosoFnn9OgUaMd5LhApAlSSOQkIx7ntMuS5rjH2cD56dc1Ox8c8PyXTxlPhtz46DblfE398SPiQUasNJ11gYfSGbwSdGVDfbFBdY58b4LME84/eY7pe8bvXSN/2cH4huOrao9ffvbNv8P92ruwqAnAblomexO6L47p+pZ4mjOflyRCojctm4endIkgHxUMt0cBduI8F6dzIikYj0eIRcWJMnznzi0SY0j2JuQ3tr+8Nx6akwWiN4jJAC095fEl7fmCwdaIwXdu43TE5nzJRx/c5vHjE5588RzX9szrjv3hAJfGHD06ZrOp6TpDMcxoy57x1ojjo3PkvGS9WDO7vk0Sx+RZQpYnNG1L5DzJFUJAJJrJzW2K2ZDVyYLDv3+A0IpMDXB1T5xoPvv1YyZ7Y9Jxzo3kOjrSXCxW5DoiSRMm44LrH9xktD1g+t071KcLzLykuHdAf7mmfPgMWza4LEY6T7+oaF5chs7+4QLnISoSou0RKBj/2QfoUcHmb3/FZlHjlML1Bmcc60hiJRglWF2uef9P3ueTv/sMYyxpkdE7w2oT7oUSMJ0lz1KKLGW9qcizFNMYeinIi5QkT5mfzkMi7RWqc+hhiu8atIpxveX446fERUrqJbs3DyixxEnMZrWht57DR4fB8BKFFKEY1FQdPtHsz0a0dcdAaHoX+HrFeMTWZIx1jvlyzcnxJddu73Lr2zc5fniE1pL3//g9tu/vEw/z18n0O8nzm9nG28v2G8mseEcp85uMryvcv3uh/Z5h+/+PHLq/2TOvxj8C3vX2VsXrMsYfMo95mV14T3005+/+r/9TMNkZ5thRDsYQZwlp5zm4vYdte54/PGJ1umTpF+SDjIunpywWG5I0YjQseLEOxis61sz2ZrRty871bYpBznq+5uzFGdWm4u4Htzj97DDo1McRddmyXJa0bcfBjT0Oy4ZMx8xP5gy2hzRNQ2dCdWL98JD737/H4ZNjxqMB12/t8/TjZ2zd2OL88SltnrCfp8y+e43xt2+RbY9eZ86vGCrwkr3tjcOWLb7p2Zie0f6MiZvRdT3JOMe3PbZq2BxfYC/XJFuTgDd2Av/imGSYEssxfbmm7XuSUcBLY2wgErc9Mg24SZdofK/p+4ZEKboXF+i7u0F6F0GabOOsxxlLNEjpsdRVQyZS7LrBOoszhlinuN6FCmLb4yAY1HSWPo0RsQ6qVtNBgEu1PdFswJ0/uo9M4qBZ3xv6WCF7jxcCLT3RKMfM13SXZXDJTWD0/bvIZ2e4ug1drDSGzuFVC0WOMYbYgRrm2CLDNi0uT1B9j+wMPo8Bj+89cZ7Rdz0yUShPkP2LNXZTIaZDSDS27YnGBd2Lc7AeNR0Qz4ZQpJhFSd30xJMB+mSBnhREOyO60yX53V3yNA6yr29wUl5CEATBVVvKGK4HB1q8J7eO9tkZ68NzzOElUkrc9pBse4QoEkQSB37HFRzLz1eMbm6zeHHJat2QyJzhuKB8fk7x7Vvo2QB7sSYeFYz/2R9R/vwh5z97THG6JD+YEm0Ng4u5FPAmAdSDF28kGEpQfHQL3xmaXx/hsxjx3jXi4zn+ckW8Pwkcj6M5sVZIZzEehJD0lxuiYYafV4g0DlCoLCJe1/jOoF66lxuLvFI8sabHxRFymAesNQGuZYQg9i7g6b3HenBa0RmLkhKFQEUxaIfveyIh0FKGCq4xWK1w3iMBaQxeKVQch211HebFKW48oFGCqGkp8gyUoi5rCg/7P7qHTiOy+9fpL0dERYbZtAiuJDRjHVyklfjmMNbXi8A3eJF/60+BCInF1TPOOvRLzoeSaCWZ/OAu5bNzGiVJdscM9BbtukLWPRtjsXFMFF11GJQk6i2+7+nLKnRzhCQCrNJBvanrEFrjnCPSCnflSGw3Na31aB8SnGCuRfDXSWKsEkGBrupC8iEE8bgI3QvAd31Iiq46a/XTM9zTc6Lt8av1xpYNYpThe4t9eo50nujGFt16g2paqo8f0A8GRLiQZMgwB+Nhhk0kvjX0iw16a8xLVET+3du0h+eYizXipCfPJHZV0q9rkv0p1SrM2+aLE+zuCBFrIqWwmxo9zPCtwXuLKib4ugJv8FGE9D4YUcZXcLBYome7wTH51i4aQbxp0VUoLKybCnkRuqcXp3PqpqE1PdneGJFqOmOQWhElKXKQcvHigvpowc54SFz1yE1Lf7JALsoAQ3zpdfIboBm/yRjya+ffW8iDwC/r1hVRnrD4+Dmf/fc/QSQRIo3omp7yWUU6KWhiRVNadGlJfIRxJQ8+fUa5roiUIh/k7H90kyJJaH1JlsUk65rRn30LvTV4JU7x5jBlw+ZXT4ikxPc9ojVk22PMlTqXSmMm376JfJYxOF8zGBY8O7mgP/L03uGFoFrXdKuG86dnbN3exameKI5YLYP3ULmpGQwHtKuaft0EdauupxjkbFYlojXE44J6vub9//pPqDY1Lz5/wWBrFMwo84T1fMPurV3273TM9meU6w0dPdODbU4fvcB6y52719j99k3Gt3cwmxqkJNub4vKU5b/5BRaPjDXDj26x+uwpVmq60wV+vqG62CDGA7z0uNWadJqR//kH2M6w+NtP6A/nyDgmiiSLywo7KlAayosl0xtbRHlMta547zu3Ofz8iPXZik6YYMDqwfZBPnw6G4f7lgqiDm3XI2NNIhWsGmKlGU5z8mmBOFmzkZ5YKuIkpms6lmWJTzSzImeyNWJ1eMqiaaB3xNMidOV6R+V6urpjd3cPPVR0qxqzbqnma/KdCSeH58QSZJ6SDVKkVmyaFplHPH12wr0f3OWH/82fB0ntJHq70PPGr78Rdnp17Yg3MpK3rpWveuPvQl34GjDQP2b8gQndv8ce/S43PV4eh6sqxe99JF6LlH6pBXLVVn34b3+Jbw17H91m7S359pDTp6c0pyuKIqXrDM9+/ZSmNwz3J6xOl2zf3AmqBadzslGOLnsGgwyHoO172q7loz//Fs26AeO59/5tnHc8+OQxi8sV+TBHOJDGcbA/Yba3hRGO7nwdsIbeUhQ5R588Ze/9a3z817/i4OYupJpP/u7X/OCvvke5LNkcL3G9ZX50wd2bO0TeceNPP2D44c0r8/HXLeS3Z5i4Cg4s/YsLZKTpGwuNRcogedgdzumNJUki0kgidma43oDW2LNLqidfUOmYdJTj968T70zwTU9XdQFK0AflqyhL6MsWYQNmGiUDLGWSUT48Jj+YBiLx41PSySBUhy5LVBG/4q3oIiFOC9ymxlcdemsQqvB9hxzmUHaY1QbXaKJ715AHW3RVTb43xSeablGCFCRbKkjWec94a4yMNYPtAc2nLzAvLpCDDG89LEvsdMDljz8jzlOc9/i643K+JDKOIi9QRYI7Lunna+SFwCmJGOS065a47YinQ1zVBdJfrlBth7QOqhafxqhhGjgVeYK3Fl+7ABczFiVUCCIAIRX95YZka8hklGPrFjkbhOr6YsP4+3eRRfr23H4Lcf/G4y/hbS44EgktSe/ukdzepTmZU//sEe7ZOeXlGg8Mrm+jbmyT3dpFTgtWv35GdHzBwc1t6qqnulix8g4faXh4hEBgVxXJzW0SC4O/+j6mC528/mePUFsDhvevoYYZtuvRccRXrS3hewsG37mNmZf4zlFerEgJUD5zOCe7v48epPhVjen6wA8ZJjApsEdzfBITKwFSY4wn3t/CLzfYpqPRijRPEasSsdhgLdhNg2k6Iq3wPpDDhVYhEUliXNOhrcdJhY8EbdOi8wzbdmjv0VFE7w1GyHB8pUJZEyqsVx0LYyzOBeEC6SVSCNyqxEQRlRBYPPkgp+sMAxW4T/rGFlHZ4AQY55GdoestyXTA/BdPmH37Fnqc/46FnG/w4q+qcl0lGMCVOpD4EqxFZjH5jS209xjjiLcGdBcbzgcJzacvcPMVybDA4KnXJZkNIgdRpFGRBiFp+h7pHXKQoYiwVYPqAl+qaw32YkksFERgjUUYgwNiRICJNB3Jd27RHV7gnCPOMrL9aRCEuNpXB3jvwpXiPPVPH4GUyEES4CJ1j6ga4p0RdtPiDFAkiFjh2x5RdtgIslFAw/ZVixrndN4RJxHMV/jG0B5ekN07eGXyKJRi8Kcf0J0tYVFhe8vyeMXhf/qC8ThU3YcHEczXNLZnsD2hr3rUAFzX0dcNskjoyy50a3WEiGKEUKSzPfpII72nq1ukgLYzyCen+LpFj4aU8w12uaG0hvZihZdw+/4N6qZFVjWryxXnnx+yPRsz2Z1y+fwcOc3Jd8fk37pBebFitS7JlGfvWweYnQGrRydff6d+p2r6Te7o7yIWvPOYzgQ+lJYIIeg2DY//9hOKaY68NqPvDblWtJclnbeMr29RDlKakwVda0mjmFGS0s9LbNfTmYoHP/mcv/jhtyiblskwY//+daLd8SsjyXe/RrfYoIsseO5YRx9FKDzdi0vc94OiGbFifH+fUgmyR6dst47NzpTOe7rOkVtInaTteopZgekMx08PSbOE0daQ2XBA25tgztj2pFIiBinluqJZ1eg0ZuejG5jzNc2iZO/9Az7961+SFSneOhpj0VqxWG1Qw4S9D69z8cUhR5eHnH/xnGRds3fngJ0PrjO9v0+3rlFRWId927P+619h2o742hZcbmi+eE7vPMQaX1W4PA9rYNMhViV7/+X3SSdD5j95QLWuUH2QhIWek/MlejbkyVFAdWRZjFSCruqoNzVbB1v0xuIXNekkxXYO6yxaBGnare0JaRrhpeDzXz4KHWIbigmZBJdKtIPBqOD5p4eoSU7z7Jx+krN3bYfRVLHwPfWi5ux0DjpIrQ+zjFVZE6Hp+550a4BCUp2vmcxGFEnEzv09bk7v8+BvfsVwlONEgLhuNuF+EwkZCtJS8OzXz9l57+AqsfgGE/zVjBKvkop3H/+Gb3/7728y/hEF/3fHH9jngnduMr8HJOo3fbk34+DfI7F4pf/7xke+tfsyEPnK4wUXnx+STgY8Pb1gsD2C1qAtHMwmXFyuOHpycmVW5ai6ntn1bT7/2RcorZjMRtx87wbHz8/oO8O8LlFKsr5Y86v/8Ak37h4wno549LOHDPfGTLbGLC+W9L1la2/KwAgSBHHVYfqOLonJkhgRac6fX9C1LdemBbc/uolZNAjj+da379GfrdmZFMzuJJhNg7CWbJCy/0++TbI1egci8XZS8XK4tmfz2QviSUG0P2Wr7lCxZnEypz9dMr61jc4S8J4ojUApnLGYTcP640fI6RjVGPx0l+j+dcZ39+irlupyjcMRJTGrqsVXNQezMU5YdJoC4qqy60hHeYAhlUviPIU0xsw3EOkQtuQJkdIgCP4P1rBcLhnkW3SbCrvc4I0h39vCZxH12Tm5ADFIiNMIa4L0XFSEaoM3Ftf1uLJFZklQdFnVkKfE17boji9D0th06EVFGwvyUR4CeeuZColpWtjUWO9AR8i94HrtP3+Od5701l7wA8hT/KJGzgbIRNN9eojMYqKdMTLR9HUTjLoc1OcLkt1JILlbh8oSnBbY3qAaQ2QsrunwmwY9G4ROTW8RaYDhxe8mzdZcVWTf7PpdrUaCAIdzr8uIQgmya1uk22M2j44xR3Ns1VB+8YLmYkk6HRLvTpl++zbN5y/oji7J92cM7u2zOF3Q1oY2j8jxQRHodIkoMkRv8M6Sbxrk1ghTJJQ/f4Qe5cS3dhCjHBG9VAATryrqr/TfYk32ndtc/sfPSKSkOTwjkhJhLe0nz4PB4SBFpBH5vAqKP8sKEWt812GsxQwCNt2VDa4NAUDcG6JYYXfGNMsNwlgiKZGdwUmJ7LpQuZMidB6ans55tBJoKRBeEicJ0lqEEMR5ilmXJFoHjoNU9NahEDgBQqlgIhkHJ1eMDcde60DStpZBlmK6Hl81xJHGbyqWhw4poF/VkGi6tsd3PX7ZUv7yU+K9fVZ1y+SfvjS7+nLF7Ktcur/5uDonX9Gff7nGvCswJQToPEG9fw23qTGLEgTM7u6TjgoO/+0vqJoOJyCLNOBIdUTfdnSrNfFggAVs18HaQxLj+x5pDCLJwFmS1mCMRUuJVJLee6T3mDzDbyriJKa4tYN9fBrgoFl8lYC/cRmoUGiAYLrZHs1RSsIkxy5r/OUG6xzGWlwbvGV8FtEdX6KVpFERsbXIJMH6NdaGbXlrIY3Q927QPT6h+uUj0v0Z6fs3XlXD4+3gTG/XHQZJ3HVY09OcLom2J5jeEBcp0b19zPk6BIBJ4O4pJenbHiUFdr0Jl3bdwGxKbx2iNxjvieJgIkoWYz57jtwa4RNNujXm2eE50/dv0NQtm7ZjvVyD9wyKjDyO0dd2uJyvWDUNjFOMDF2q7nRJKhVqkNNVPS/+5jPG+1O+9b/7S+Jx/vbEe6fr9dZ4GRhd/f+l2Oqd/6tlST4uQier79F5QruusdazfW2Hk6dnCClRrSHNYry1HH9+yOpyRZbEzG7tUF5uGG9PUEIyX67ZubdP3xvatmPr9j7TQYaxjvJnjyh+dO/ta4DQMTGrGhVHdEcX+M6QphF9b0BlNEcXZDd3EVIghKS4t0+yNcRYy+AXcy5SyXlbM4hiUmcoxjmHj4+Yjobs7UzxuaarOsY3D3j28AXeWQZFShLFrPsOvOf5yRl7kYAHh2RC8eJf/Zgf5H9JXCS0lw17+1MePDvm3rdu0ivBZrHBNT3COG6MhqhEs/3Pv4fsLLJsaR+cIHaGCMC1hvk/PKQ8WzL66AbNwyM4X0EUiNK290TDgs28xmtJsinZ+ugWxZ09Vo9PWbeG4e6E+vExm7bnYtWx6DpsWeGcx7eO1aZhlu/gpWB3MqNa1WzdmFEeL9G1o+s6iCTZbMT0YEZiPe3pismtHbazjLVWuNZSrku8V+SDlCSJSfOU+GBKf7Zid3cLv52jWks8ykicIL2WMj+6wFqLjCJWXYdXMJuOqOuWznp2tiYs5iuiWNM2Dce/fMrNP3mPa9+9QzrIEEJw/sUxy7LGacGtuwfkVx0uESmiLP7yGvs7F3z8N00twov+AInCP2b8gTsX4Ys755CvpNl+hwTja46Yf+PnK0jEb+hXvEwaftfx7vacdbSrCgGkSnF0ckk+HWJOliwXNVGkma/WxKMMHyliHbN/54Cm7YOqRt3QtoaJdbx4eMj2tW3aqqXrWnol0LkiTVPmx8G3IBlmnB9fsn1tC00gr1o8C+1JLIwOxmxXQaaxqTpMBjfv7DI/usRebNjZGtPpiH7TkFU9tqwxbU86G7B1fx8vYPThDeJB9kZi9nV9tPD95796QjYuUHmK9w4pwRvD+NoUdaXTL7xHRhrbB2dtgSeeFuTfvkP1MCGejpj88X1MWbG5WCHrjkRrmrajrFtirelNwOuqIkdqhVlsEEYQ7Y7wxrF5cYYwHpVq1tWGJNP0zhNdrJBKYa/w0f26BmuRaYz1kEQxviiwAuxqQ5QkRFlOPy8RqQ561r7Dyzh0TIynO1kEWb8sxq/rK6UpQ7epaC+XRFmC15J4fxbcsK3FS7BVCIZ8kZDtjgN05iqoMjhca4j3tjDrEv/oCFek+EGB2h0TDXOap6dwPCd6/zruYk2bKNKbO9SbhmZd0StPc3jGNL5GZywZ0D6/ZPitG7hliXcRajKgOV/hDi8D5CyS6ErTnS4p7u0TjfMATRlkb5Co34HL+ECW7asWHSm8FMENWgRoi0gihh/ehA9v4OqO1a+e0JzOoeroNzXJwRbpBzfolyU6img3NdnemLi3lKsSezBl+MENugdHmKqhXm3IdifISREw+0VGGdXUJyvWZytirRB49Cgn2RkT39gOJo1XxQsBpDsjioMJ1c+fBl10rUAGYzB6i19scFJghcBVLfHWED/O6Z6fIXqHWlao3gZVNOcQcUQsBG5V45xDKIGcDPBNh+tMMANMY3zb4XwQI5B40jTFd13w3jAGqSStc8gsDToOeY5rWhDBVdpFBDidCAmKtQ5hLVoIhLN4BDaOg4eJlCgPiVL03tF2PfWnL9DXt2g1uMYQHWwxmgyxTYdMYuZ/87e0TYs9TnFasvWffRsRq1BGl29GbN/YVvQfNV5ZYog37wjh4pCDDNH2xEoiRjmLZ0G2UcSawcGU+vASOZngn5yADlr9xlhE34VjIkNl0mqNlRIlQwCGhziOcFJC24XjLUVQ44ojooMprjP41oCSyK3hax8G8XrHg+AH1J8+x29ahFYM7x2w+De/wDYtQsngfg3oOMhbi+kAc7EhSmJUElEdLshu7eGfn+HjmGR/GuaeqFCxRGUJm7//DL03DWIFV12sdHdMbz3ti0s2SpHHksqC1xK1aeHWLtntPS6enQP+ag3yQVGPMCdZz1HGhCTetGAMRIpEK0gjSiEYcOV9U9asy454e8z0+jbnp5c0zpLGMTpLiSKNlILNakG1qpi9t4/QQSRCF2nwA1jVxE4w2BkFye4ip7g+pTiY0dcN0csE7tWBfqO48W7O8eZN+d3swof/TNPx9G8+JklT8j//EIRAak19vsTWHUkSsT5bBF6AkBSTglRKiiJFVQ2d1uRpQn++QcXhmLSXjvlqzQfj96DtGYyHjPYmgbdWt8id0ZcKwgKBa3vM5RpzvkIkEQiBjzTKWsSqZv3kHC8U+fUZhHoYepQzef+A211P9fSIwY09ymVJ6T1R2bFVjDg9uiQbZMy2cvrehXUiUrx4ds50MkB5yMcZURoRJzFSCDAW7z3VpubwF09IpwPKykISYY0L6IBNRa4jVp88pxhmzP7FD8i3R6x/8YRoNmD4rRsgBa414Bzn//FTVmdrxlsDTFkHUYRZQBIQxdA0tGWHlJJoUhBlMcn7B/RPzlh98gxZtXRK0HeOC+GhyBimMWcnF2ituX5zh+eHZ/TLGiGgXpdMdqccvTgNkuJCMiglk9EAESna53Nq6zDC8tH/5s8wq5r2Zw8p9qZIKYPITpFiOsvmdMkgjjFFTjzMyCYFflWTJjEXl4E0bjtHNAwy3oKebFJQe8PGdBRFwWoTuFJt2xMlEeOdCb/8n3/O2fmcne0pk70ZIlaMdkecv7jgyReHjC4G3PnRXQZ7k7cli99cZ17+Kt78y3/ta//R45ugXPnyR/9jxh8guRCvfr4sXL30Q3h9eL6qKv7Ve/914a740ll4Y7sv16Z3IU2/dc/Fy/vbW+1VZx3N5QbhHSDRkSaKI7RSjNKE/T95nxf/8ACZxTTDhGbTIntDbS1aKrYOZiRZQt/1rC7X7N3Yw+N4/MkTBoOM8bAgiSNO6grrLUIpNpdrvBB01nDx/CzAJJSgLmuufXiD5mjOP/zsU77/xx9x/Y/vYauO5YNjqrMV22mK9GCXFYmQjLbHDHZGRNtD5CCh2J+i0uR1WfK1UPIbh+v1au69x2wa6kenxEkgO/fnS6ySiM7gnEWOCtLtESqNXmm1294GiNQwQ2rF9P0Dhh9cQ2cx5nLN5sUlcRGcSPGOwcGMcaTAX3lECIEuUpq2Jd6fQtVi5iUuiYiimD529MaREiM6g69b5LCgqRr8ZUk8KqDqqOcr8tmI/niJt56uqSlPLxCjnNF0RixCFZ66xxlHpSzJiSPbn+LaHiJNv1hTni/IBwU+DjK40fYodAnylMh5XNUhBwnUHV3VoiKFBlyqeHF6TmI1aaTIpEYpyEY5BkFcpHRfPMdZQ7w7w56vsOug+W/HGcYapPOo2YT4YMryp4+QVU82nWCsw60qNqsafWubaHdE89lzfGeRgxRjLDZgOZDDjMS7cGp7x+bjp7irG87kzz4I3atI8VKC2UPwlmh7kCKQzaTAGUu7qYmL7ErpRbwKFmUWM/7Be6Snl1SfHQaStHGQRCT7E1QeU0wHAVIiJOKJxZyvqbUmmRT44xYpBf35EjkZIMYF3brEZRGHD5aMtaJXEvf5F2T3b2LmJeUXR0z/6XeRWfxGDCjIb+9Qf/oclcYBGuE9KIm/XCM8RNZjhUddm2E7gzcO+dEt3NEcsWkwq+pKsjUUL5y19HULWhE7RXeywCn56lrJ0uASH1mLtUFRLREC24UE3EiJNobEObwxNF0DcUqbJyTGQdujnA376TzyCmKF8+ggGEbvLHa1Js7SUEU3BhdFKKXQL6P1eUn63jVMDukwxxgbWu8uFAPcyRH+3rdYfnpEfDBj9P51bNUG+E/00uX+y+OV/88banq/sWjzKoN4YxvOY8sGmUavFbLeWIFfFjmi2RAz3wTewyhj+599m+HBDK8UL/7bv0ZYRw9gLU7JwE2RMqxJ3tN7H6SqiwyDJescnRAI71He46/cpZWSOA/CWNSdXZrDC8TVcU/2p19qwHsXIEpYS/vFMUiB3Btj1g3mbIUSAn8Fj9GxxuGJtgqsc+i6x9aGPo+RvcWsG0SRIIF0Z4ZvespVSVI1RO9dxy4rlj/+NZO/+j4iCRVOkURE+xPisyX2com4NmE4zamWNb2XRH2Qg86+dYPmHx7Qdi54sjgwTROOcprhFgEuRFyAdTgPqkiJ9obkkwI332DiCNcFhR2QcKWGBnDz23eI0hipJfSWyMPRcoMzjtXnRxRZwvxihZgWzD44wDWG+bJEeUHXdyx+8YT0zi6tsyTjwRUclzdu+L+lFvtmF+ONE7T47AXnD495/uNfU+iI9nLNjb/8dpAYXlR8/v/5OyY3d7BWoDc1dpSw7A0XyyasE86TxEmAsuqIpuvJt4bs3D8gnRZEWYLtXSjS5Am+M4HHNsxCV/fVTA7FTrNpELFGZTHCaZyv8JOCvo7IfDDgW//8EVoKkhtbr+ZYdnOH7Ujzo50xjz5/wbI3tE1HXVXk1nKwNULvTSjP5vRWsGpbRBaztTdjMh1Sryp0HLP/3dvUvaNqGqZbk1A8O7lkeb4iySN82/HpLx6SpDHKeAYyRtUdw5vbjL97k2J/yvrBMcnBhOL2LlzBy3COzX/4Nd3ZkijWJDtTqs6gt0fhxBiHm6+QowLbOIqbE7b/6iPWv3yCGma0hxf4kwXJnV1WT89xg5RiK+fk8Sm2MXS9wWvB88MzlJCsjuak05y6bCgfHdJbR5RFqGFKMcohihCtCZL/WUwyzlGJ5u5/9QOiWUExLmianmJvRJQmXD455fzTQ0RjmO1OUQIGkyHZwRbPf/WMYlhgT+bcubbHyWqF6S03DnZZVBXGOwZ58CoRUXCs11Zw7b195udLip0R+aig7w1924KMEV3Pze/c4sUnL2irlihLXvuEvdGNe3c5/HJ8/DK+/jqUyVdt4w8w/gDb+b2TC/8b/vrqx37DQfFXMe87JYG3/hSvD/ebiQW8RGGJrz8w/qv+fB1ke+de4Ta7TYPAk2+NOPyfP2a1LpFScLFYU/3iATIW7L23z+pnj7j+3nWkh+VyE/6tS0aTAekgZ7msKFclg2HKdDZkHEXsDQsu1ht0EuEltFUDcYzWKhgg1T29t0gTKk/Pf/WU4e6YtnH86qefo6xjdmOb8Uc3GN1sOXlwhJaSwThFKkmxP6O4NkMmmnf1wv3LIvVXHCcPeGNpXlxQPTwhngyIZgOkVlhEqMTmCf3lGtEbmuM5CEE8G+KrBrNpibZHSOuwVUu/qtCjjHqxxh4v0L1F5hkylsRXUCqBoCtbIimIRzneWNI0xRlL3xokBE37SJFHCW3ZgvBE22PE0QK7qUmMxdct/bKi6w2D2RAxLpBpTL+sUJMRW9NxwMsbh5oMsIsaQVCKktIG2NHFCld3JKMcoyQX1YqkyOnPVojpANd1+Cv5VxxBGtYGrfjLasPQSi43G7LJmEjEJAo0IWEUBkyeYmKNX5SY7Qn5bEhdN0jjg4qMdUQHW7hBGhLFUR5muZJ0WuHmVSjIb4/pj+ZU5yvyOFRppfHo1NE/OUN7j0wiZJEgshg1yHA2+ASwaVBas/wPn6J2x2SDLEB6tAzntu2IJgOy/dmr+SEjRSQSmvMlOomIxsXb8EElSPe3SGYjlj/+jPXTE7LJkO5ihcMzun8NmcTEiSb5wT28sVQPjrBCUPzwPnZVBQUSY2hXJel0yGCasLvZoX56ESBggwnVT36OvnWf7L0bnP31x8x+cDeQv5VE4Im2RuQf3aBunmCXVagaKhWkfHEY58AJ+lUVoCCriuG9ffx0RHexon90jN1UgXi/aYJzq5L0dUfvgvRwVAezKuFDwmCtpY9DIG+8I+5MmFdChuq6EAgPru2IVISUkhiBnA4QqwrXS6xzoXnkrzjXLgTSUmuUd+je4K403UkSosmQfr4kdp4ujQPx9uk5tYLxvMRrhZ0v6J49xl1eYFSMvzym375Odby8Oh/vGE2+uQh8xcO/vRPsv3JpF1IE1aU3NvoO+i78ogR6NqR6ccGNP3s/+J8oSbOs0EVKNd+Q5wl+0SGsx5kencTYOEJ5gQSE9zhv8a3BekAplHXB1zIN3CwHKAvRMCe/u8/Zz5+gtKKXAr0zevvLe7BNRzRI6c5XVI9PER7i61tUL86wfTjX+qoTbI1FTnPUMMN8doxf1SEZacAJiS9b4v1Qza8evMAZi9y02M6iBhnJZMjqp5/TPD2leP/6Kz8VryX9s6NgIHi5ZmuiqKRAH8yY/fkH9A+OiZWgTiNoGrpVie/6UCWNI/TOLfr5EX61hMkOHoHSEpGHwpAQAt/0qPEA2XXIYYp1AlcpZJbw3ke30VJQXq6Ji4Q0T2mujsvn/+GX3H/vNt5ZRKTJJgWmt3hjUFJg1hX5bIAtYuKt4Jf0G+fcb0o2PK8I+UIIfGd4+u8/Ye97d7j9l9/l6BePWT294DJ9gK16Dj9+hDeWxdGc3Q9ukI9ucfSLx9g0JtseYqSgtw7ZSq4f3Hw1L7MoonQ9g0Ew/hxOBuTbY9qqRdQN3hqa8wXTreHr+WxcENN4fIKtW8QgwZ2v8J3BHi+JRhl+kGCeXyAWa1Z4puM8yLNLia1b4p0xMk/4cJyzf7LAVi3pIGVzsiAZ5qwWa0Z393n8959jyprhJGc4zMiSmMmooHt+xOLBC25+cJ2qbqk2JZOdCd//0w+pVjXJ+YrR7T26SKPSCD1IyWdDknFONM7pz9dUD07Ae4q7e6Hg5z2u6bn89x9jn50jlUaWJeo7N5mNB8HLommxD44Qg5SmNgipSLSge36O6AwqicKxmw4oj+Zsmo42kgymYybXZyghSddDkizCVYbV0ZxiUtAZS1v3TKdjamfIJwOEh3XZMJxp4mtDfG2pe4c3lvknL5h99ya3/urbb8XpAhjsjpnc2KI+XZEOUtJxwfLBMb/+m09I84y+7dBCstlUpFpSVx2rTUmUR/heMEBTmfrqPpawNxujYk1X97TrktneDOthVVZsFzl9afjsbz9jd2fM3X/6Eem0eL0zHt5UPvz6i4G33vPu+vmVS/KbOclXreXv1vh/w/h984s/LOfid9ibrz+4X37d2wdM4MVX3MW+7v2v3LdfjnebmWE4Y3nwt79m984+n/yHj+nLjun2hOHOCIMn1pK4yOgAYUGmms18yWRvxOnhObPZhJ39GcOtEWdHF7x4dBRkNZ1FKcH2eMDsvQNWv37B88s5zzdrei2J4wSlLd55NlXNdDpCJwJpDcY7lBM0dYs7X2IB0/UorVg9OaVd10RSMjuYMrx3QDzOkZHmS1fWG+PLR/wqxfJgNzWbh0d0q5pkd4JLNMY5VBRRNj2j8YD+coNPY3QaB4Ku94hYgy4QVUf16BTtg5qTU5Lm8AIvJTLSRNdnCHWlKrTYEOUBqkEkMZua9nSBVZLlfIUWguHoyugvjXFtz9qUpHGMHGR0FwFH7KTCpoIojugWJcJabNvRffoUncZIpWmtx1kBm5p4d0K/2rCYL8mv7dEbS9O1xF5wcnTIne09+t5QNz0TH9FtKpIkolkHF06pJf5ixcoa7HxFUjakkyHbUYZdrkgaC+uStLP0kSBXMepKprc+uUQOcuwkJ6XAawWPj4gmA7plSRwFYnAUa2SR4KqW9mJNYi2i67B1hxpl4D1b12b43oTTpxUyEgjjgzxv2yEcqNpgNh3yeIVPFVzJuvYXK1xvUauK7nITnKgjjasb2B5B25PujK5gU1fZqHVkO+PQ1XgJqXlniDhi/GcfwjCle36O9Io40pS/fo6NJfndfdqfP0TtTcnfO6B7eobvDUJAtG5Qk5zubEG7aYi+c5vpnT3S8QDKjnWRIG7ugYDNfM1gkrP41z9F74wofnSfeDoEKYPzdxyz/je/wvc2uDYrhYxTXNVg6g6dDzBnS5LtEca7IHH42QphLDEi4I+7Dus9LopgXECWEI1y7MMXSATWerS96j5UTZD07Ht6YygF5GmGJPBZTKwQxhDEoVyAO9UNapgFd/vOkiZXvhBS0vUGjcdJidYazcI1qwABAABJREFUF19JJXcGqXUw80MgTI9eV/TWYrVifDDBnV1CWiCjFG8iRDYNqkoPHqO8wL1/LSgQZRFqkL5OGt7ELL08n2/36d9aL7/qoa+7b3khcJs6mOpddWZc24Xg5aX09dWbVaQpn13Q1y3j9w6ovjjGOIdLNE3doLZGyJNLojRDDDMiRCDN1k1INrxDCUFnDLFU4AzCe3zj0ULQdgahJPGt7eDK3vQ474mUJt4avfVl+qoJqlFC0D8+Q1qHLFL0/oT2F4/DZ2uJNwaMJZoUxLtj7GWJXVbBBNO5kOCkklgGHoXZNJiTBSZOENvT4C3xswfYnTE0HZuffEZ2c+e1CWGkGfzRe/j/+Dmmd5jzS8bjArcdEuuu62FREhcZcl6hkojNckM0HqKTBIbXUfV3sM8/ReQDxCDDvty3LIZNHUwnYx34ckcX+NEoqGh5y+njI9I8YXl8yWA6Is1iojSmXJR0bc/h8Tlbd3fZ/dZ9fNWzenwW5kBncFVLcXOPg7/8FlGeBjGOV/PKf8WEeXm/fwftIEJXta+DmML8p49IZgNE3VOezDF9z81v3aI+XnD88bPQkdUB+nR4eM7p4yPufu8+09kIrTXLxZqTyxXZzhAbSZIipS5rTF0TkaMUiL4n0QlxltDNN/TWsXNzC53HlL968kpRDKA/WbD4yedBVXCQIr2g2dTIKELqKHSuliWiM0ihEKcryl88YvQXHwVup/PoPEKlEcl0QHF9G5FEyEiFGFGAtx6hJXs/us/5PzyknpcY53HGoaRk56N7uFhTNR1xFEEhMfOKrEjRaUJ8a5tr//UfY8oG03a4qgswPinonp1zeTRHRxplLMN7Ya21m5by46eUR3NUliAQyCSYySKuTF6XJT5PQrfIOaKmZ/OzhzRnS8b/9Lv0pyvWR3P0ZMDqYsXxxYqs6Tn84gXXbuyyLitsGtGuKtIkZv/eHutNQ7cuySYFOzd28HhOTi9JRhnVssauW8rjJcPJIPD1tocc/uoZxjkO/uy9V/PmJaNWCMH4+hbja7NgiFl1pNtD2rIm9p62bLBaB/jrICVRAVIl8WRJzOaypO8NqYvAOFQWcfzoBO8cxXTIfF2RjnNG2yM26wqdRigJMlbELzvsQrwxnX9b7Pv1CcZb2/q64V+WzsXrXP2dy+y37cLvi4z6A3IuvrwrX7dzL9kSX0owxFd/5zcfe0ni/P0Vol6e4LClJz97yL/6v/z3/NV/809Ihim/+jc/Z7Iz5e6Hd4gSxfi9a6h1y/JyzfHZkmmxQ5ynLG3F1gfXyKOI44cnmN6GCouHsiy5f+eASRyjnMc1Hfn7+9Q/mSOymCRSIQOVEhlr7LJltS4pxgWRiCiymKaskTLox//RX32fvdu7ZK3FtD1bHxWAIN+dBBjEy6P1myZOaFuEfewt/bqmX6ypzpasjufM52v6ug8V5EHG1s1dJvf3yYY5tmyCu3RvIE8xnUFLSX14iW87fGuQRYrtuiAZmsbITiKHeZBT7Syrwzk6i8ivb+HqjvXzc+y6AqkYTIcoIZntbYU2qQc5yhBFGuANZc3lek3uwvcXDnpjSWNFZ3rEJMeJDD0aIqwJ0IciQ25qVJHSXKxDhWhrxMx7mrJmIARZEmHSiOuDm3TOY62nM55muWHLa066OV1VI2Yjdrdm9JuadVsRNT1Pnz2FUcG9D94LbeQHz1mu1syGA05fHJLsH5CUTeA4yFBB1edLmrYjmg6xo5xukKGyK9KfsXSHFwHPf2YQ6wrRGcRiTZpEwYAwi7BnqwAL05o0T/Fli8EhOovSUWhXT7Kgdd4amrqDqwBPzUZBPak1CCFRswFyOiCZDdl8+ozyk2e0q4rpH7+HzoOxF44AI0qTMI2svVI3en3tAgitmXzvPt2NXfplSf35IU1riayn/ofH6KsbcvPomOJbN+mfnSGUJvrOLY4+O8RVPSOtWX/+gsGtXeI2mCmN7+7grGN5eInVir7qyGZD3Kbh8q8/Ibu7x+DOLiLWJDe3sd+7RfnL59SLNXGWBNyzlBBrRNmEm/XFmm7TYKTAbOpAcu1NgBtFV2T43iCsRTYdZlXSdpbIe1wcrjfpPWiFaDukUqAUQ+exdY1IY1ykEX3gcIi2I8ZTIYiFxG8ajHUIZ+itIBISby2xFFipkFGEyFNwFokIPgLWYes2YKakDK6zTYdsO7qLDaMPbtAtGvrOkP7p9/B1RzQpMJsKZwxylOK1fH1eXy2jX1Ec+m03oK9ILN76/Q2IlEzjVzdEIcWrwPnly17eO+OtAV3VUkwLXG8wbR+MDJsKIRW+M8gsC6aNV1X3ru+Dl8TWAFW2+KYJpF4XFLjqukFIgRICaS3OGqKPbtL8+jnSGGwcY7IYOcpeBUzuKglRsQbnaR+dYBGo6zNUbzHL+pWqlJcyuLOva1ysqT89QvQWlydX7ShJcmsbi8PGEX5xjhAemUY0tUElMQIHZY0apOjdGa7pApT1asR398mWFSpPWf4Pf4d9/Jytf/b9QBjem7B+cU5ya4/+bAVtj8gSvHchgZAx8f3vYO5+gJEaeovING0aoQcZ7nKNRBB7MEmEdhlVb4gjjV70+FjTNh1CaTZlRb415PJiwY1v3WK2OwtQzE1H+2xO7OHeD+6R7o3pLjdEo4z89k7wrXFBrjnwSd6KlK7O/puPvdkJCzfU+mIVfGeU4vHffkqcaHQSs6ha+r6nvKywdUeUJywvlgxGBU3dkyQxSZJweXSBLjLSLKNPY2587w6LkznJIGd+fMHpySVKSLa3HUkSBbNQa6lOFmx9+wZWSkgj0umQ1nqE8/je0n5xSPWTh4hZgQayW7v0qyoIAUQqFG2iKPitxBFiZ0J2MKU5PKd5ekp2J3QJhABXd4hYo0fZq6//so7zEq+fzIZc+y++H8xZjcG1Bukcchg63d3FOhjbLTZB6GOQ4LOYZBJEQ5J0SOLfiKCcR49zhr0NvMCdIabtkEJS/eIx3ekclaWYRCGFQmloLjeYTYMva0xZk93axSwrpAN7dI5pasYffh+7rDj7+y/ohGDz4pKV6RGxRsSKpuo4enKM6S27u1sUWcZyvmEtJHbTspUXlKrj+PyS3fGIcZxS9Zad61vosieNNELH9Nby+MefE0ea0Y0ZXF331hge/8MDLp+dc+Pbt9h7/9oraJLpetS04E//D/+cn/+3/w6dxGzd2sURjH11pGnLDlcbollGNAoKbyDYvbHN+nJNvSoptkeUZc29P32f8wfH9OsGo6A8W1IMMsY3toKB5jfhAL/RtXvZtfzKBfYbjN/UoPhS3P0NEo1/zPgDE7qvxjduvbysmr3+8+1uzhtdB/Hme97tZvyGT/gmJ8jDs58/xPaGj//9L/kX/8f/gv/8//xfM39yytNfP2fv2g7Xt0acPTlnZ29KsjOhtD3Z1oi678knBXESI56d0W8q4jwlG6UMJjnJMAtwCCVJpgOy6zMOTi5YfPKYSKtA9tRhwve9CUZ46wrTGfIio25b8iJlsj3m9vVd+nWDnhQMbu+9o5X8uuLzsrPz9uF/nUjZxlCdLrDrmvX5ksdPDrm4XNHZQDp+CTOJLxfMmw7/+VO+9f33GSQxozu7wReikfi6C07UVxeCKDLapsErRTpI8E0X/BZmQ8rjBctnZ8hBiu0N5mRBGmnSLKGLJAJBNClQkaa+XKONwwPdvKE5XxElMTrWDNMCOUjRkwHaemzvwBjUuqZeBKfq9mROXbeotkVPR8gig6Yn3R1jV1Vwlc40yXRE3Fm60wVmVZEkGvIEtGS5Luk7T7GuMK4li1NU4zj9/AmzbMDW7h7NxZKbwwFpotFVz2l5SJpE9KsFpYXr+9cY3D9AxlEgxXkPxlE5T3N6TtnUFJEM/IoiQzY9RvUhcfKg96a4rkciyN6/SX+xwp6tYdMS9Q4nJMI5vAO7rjDuSgQgj6FuuXx8iokUg3GOsRYVSWQk2fvOLRafHeIWFb0AVxtEvcB3lmR/hpKS+vklD8/+npt/8j7pzd23qnQQjNF8G4JdmcWvL9qr6zGaDIinQ5KtEf3JAqSgfnJCeTwnftSjZwX95Rp9MMOuKmzVMNsZB/lXrXCLDeXPHpJ/5zYiiWjKlvbZBaNBShNr2gfPaS6XTG7tozNNdbZGSkG8O0GlMYM/eQ9jHPaT50H5a1kSRSEhEFIGB2brcJcrpBTB10KpQGo1weDOKxVI3krSdD2Jcyjvg6O8dZiyRmoNV90RZy0qiaEzaKlxxoG34IKMqtMSEWl0b/FX/KVYK0zrMcbQT0bozuBMMNXrTVD1iZTENy1eqyvycA9ZFpTClERHMbZskbGmXFSI3uFenNMnimQ2QmpFOhvitcT0hm5ZEU0HvCzV4B3B5+YblrK+Cjb1VcvrWzruIsyVl3y8N1SkeHO9Uop0b8Tlx8/IhhlRGirHcZ5SPT9H9ZZIK8gzKCvY3yJPdeBxxQpzscZ70EkUOqTLEiUlHo80FpvERJOCZDpg8/g0yEcbQ7oTYA6uC9dfPMiupEYF3apk8+wM0XWkN2ZsPnkWDPu0CsWKQeAiiXGGLZvAFfMe2bSIQYr68DpN3ZAqgc4TKmPwTY+OWmQcsblsKCJJsjcL4hjjAnu5QY+KYD4IICX5D9+jW2yQdw+INjXR1gjf9iz/5le0p0v0zT0Gd/eZf/acuLNY43BNG/bVO4RUIIN7sxzEaCAuEvrzNa7tya9tUV+ssVnC8Mqs1DysUbMROtLs7W/zxU+/oFxssFXD2bxi7+Yu9JbNhcGdb5h+9xbF7W3i2YD81nZADvhwottNjYo1ItJvzQuEv5pS4u2JdIX/MG1Pd77m0//u71FCcPuvPmK4N+Hi8BzTlWSDHRQCk0esTi+ZTnaId0Z0UtJ3PdF0wCDP6I7m9GXNvLdIJXEbRT4dkExzll1HXmREXpDIiLPjOdu3dkijCJ0nLOclKdBJz+bJCWqUIbOY+sdfUP3yCRxsobM4VKqvb+PsGS9pJdJ6vHJ467GdId0qMATvqM2nh8SzESJW2EWFeXqO3Bnhuh6hAlSVSCGzGG8CiVsoCVKg0ghJBEU4YLZssdahhhlxGhHNCuymIX5DGVKIK87YG/woIUOxYfr92wEKaC39fMPmpw/onl8gxjlp0+JaQuc8iulPL3GxBuMQgww9KKieX+INaGsZ/+d/RLQ94ei//wliXGDOAmdzkKXEw4y4SLmuBN5amqZnsy5BQmt66A1d03Jwc5dh03N4PufkcsE0yRC1wU00cpISe0UxyIgHGTvDnMF7e2S3tgOMVgo+/re/4N/+3/41e+Mpv/wff8L7/+w7/On/9i+Js4R8UtDVHZFS7H/nDlJJrv35B6yfX/Lg77/ASdjdHrMxPRKwSiF7x2x/ymhvzMnDY9arkhvfvc3mi5qLRyfEccRgZ8zZoxPu/eg+W/f2SEbZlxzcvyoMffMVL0vvr8Y3TSzeqtN/DWTFXz33W+LmP8T4AxG6f0PU/hUPvfri4re9+rUl+qtex+8AifrqPXp5IxNvfV5ZN1zf3+H8ckFbd9z98w+5+727fOuvvsP6dMmT/+4nCOd58OCQaJCz9e3rpHFEVTVkScLZ50fYqmfvxh7ZIKXvtpifL1ltGqbbKa43rE/mDO/t8dG//BFEivPlhuWqwqcxbdmQ5ylVWdN3PUpKlv0anSj6tuPavWvoWNNfdEQ3dr4msXi7n+Pf+uExTU/14pz6fMXR6ZzTZ2ccXsyJBxnlfE2hgmFbuSwx3jMYFmyqkrjt+Ye//SX397cRzpGMMtpNA1JiqzYoouQxXdtTZBmuN/iyRTjHarlBHi6oNg1d15ILhxjmZKMMu2kxq5p6vkZ1Bns4p+oti5M5o60xSiraixVymFJVDamSCOtJsxSfaeIkJi5S9LQg2h6ixnngQDiPqVroDZv5grS3+Ca4zto+dFuaqkOdlUxuzkjev0Yqgd5RL0rcuuba/g62bvFVRxLFjKIUYRy17TCpRjRNwJK3BrU9ZLVYMZ3OEF5w/vwBxe6U4e1roTrdGdyyousCFjwepKRpcWWw1NPrGOYl3aYmsg49yiGSHH3+GGkE+XTIYDdHZgkiiXBnK9QwRwgPoxRftbhVgrxyG+8lVMs1RZGEhKkzuDRCZQl91XL6d58jbYCzKSFQgGs6zNkSYz0uDbyKuDOc/eIJxdmS4toWOktRwwwRSfAiQKlshzehi1GXFSqKiONAqEZANAp4XhBk9/cZLDasfvwF9mLFer5BjQuyGzvYTKOzmMkgxa1q2pMlSEX36ARvHfrmNtPv38afrYhWFe29G9TnS5reEucxKR7z4gJ6Q/7+dWQSMfrT++hBwvIXT4iWAQpAGiF7g1GSTCtEluK6Ptxo2x4jfIC/XClOuTxBGotOo+ABIAWiD07qZCnGOpQN0BsFwanYuSCd27bBWE9rTFWjtKJDIIxh0RhmWqFVjB8UyLLClzUqibFKYuoGLyS2vVqrvAuQKCGIxiOckvRKYLdGuEhjn57C0Zzm4REyixh9/z7+fBUgAIsKMUpJIk0Sa7q2IzMWFWmcMbir5UNH6nXQz1fkEK8ClDfWlzeffnuhfb3iOk/74BgvIXvv2pc26XmTMA5RljC9s0djegbXZjjvWH72Aq8kZAlxkZFc3wrO9XmKqxvM8zPcWUjKldZgHaZug6+M96FbIkRQ4rq3R/vsDJoepEQA0bQAITBNRzzK3zgOnu7xKaIMFeVoOmD5P/w0CAYYg7syeuyNIZ4OsBcbnA0FIy8FyYfX6JdlCGKvT2mPLnF9cHTvDs9Jt0Y0VQt5RHd0Dk0w6koOZlRHZ4z+5MOQsL68noYZMo8x6yZsq2wwlxvM7ozNi0t2/ux9hlqy+fljRGtxdRt4HzoOfjFaom9Mkb0h3ZtilyVyVcH2mP58hdlUQTFLKRCC0d40KPEJycmTE+JRSrepqU7X3PvOXZSQHB+dUq1rpBR0v3xM+ulzokHMjX/+XYobAX4WZQlJEbh0CIJKl3GvuDUeQL4RG3jwznPyyVPKh8cMi5y6rNm7u8/Tv/41e9+7zfxkQbSV4yJJ3bQMxwVxktDMK6L9EaZqGdzcplluaAGRJihvGQ5SLi7WLC7XREJgJaTbQyZbY5pNTW0t050Z7bxE3cgZ39mhenKO8A4loes6Rj98j+bxCeuLFeXemMhZsk1FdG0LGSkQIIvAdYt2Rth1TbS/RTNf0axboonGRAGzr3/2BFUkyM6wOVnCYkM+zlG9oV9VmDwiTRPIEvQ4Rw9CYhOKgFfQFxG4cTKJsOsajESlMSpNkJHGtR2+MyBEOL9vdBVfx0TBjb67WFF/9gKzrBFbo+DRk2i0ErhEIeIIvCOejWgPz5n86D796Yq+7BDOkf/JB8T3rzH/m19jrUP2lqZpcVrx4vACGcdMJwPqdUWUReg8iOU0wpFvDclGGXJvwsX5kjGKa9sz5usNZduyszNj2dR47Vg2PZ13FMaw973b5He2efqLx1wez7n/p+/zs//p79kaFhxc30ZFmqNfPOf//cX/kz/5b/6Cm9+9Q5zHkMfc+1//cbiHacXWKGM1X4N1bN/b4/E/PKKtW+589zaHn75gencX2xuqtkPlKd2yxhlHs24o9qcMt4foLOLa925frSFvJxZfWlLf/E3w9cIZb4R6Xzu+SQfinSahv3Ks/FJY/QfoZPzeycVXV6z+ERt5Y1vinedeo8deP++/7mCL1xX8b7azYUy2JyyfBDOlpz95iKk6dBEznA0YbI3Yur3D8588oDcGHQ8oNzXlo2Ou379Oc75mebZgkGbkWYLwYOqONE949uiQcRoxThLq55dUR5dMPrzBD/6Xf8rls1Oe/uoJVdWwSWvWWuGdpSobojiit447+wfc/+F7XL9/nfLFBfEoDwvymzv/7nd6mVA4T3u5pj1fUl5scE3L46fHPD6dUzYt4+mIdDJgfb4kzTKiJKJeV6AUsVJYAbggaNh1HYv5hsnRnGiUYZWkqzoypXFa0m1qxPGCTd3RCsnwzi5l09BZR1HkRDYiGiXEWUxzvODk8yO63nC5qgLmXcBEwOXlinQ04PnZguEkx0VQlmviPKUXknq5gdUGLQSj6RC1isiP5xjr0AJ8H4iFjDK891ghibWmtg3xbIi9WGC0otjaot00rJ5eoBcV2TjDlRXZ7gybx7QXK7QHlGSYRIimxy8rxklCOhggrafpe/pUkngYFQU6SZmXa8a39jnY2qY/nodgYVmhz1e4LMUoQe89Td0RyWD0I+YVRgmSYY4RYNc1znsGOsYMFNI4mkcnSCWR3iOmOV4pqqZi7FOM8RjnA89CCdplyWQ6opuXVKcrVKTwixLb22AmBmAdYpCgEbRNh8pjZKRRgwy5qkL3KYowXRvMny42jL53OyiFRRo9zF9NtvZ0EVrrkwH6ymjpTXzpy4VTCEk8HbL9L/8Iu2moHhzSPDun+vQ5+mCKGOXoO3vYPEH2FlG2RJOc/uSc5vASP9+QzYZkt3aI8ox0EKBu5bzCW8dokNA9v8AcXTL6y28j0xixMyJ//xrd03P85SZU/7QKogNCIBKNGqb4pockJolCR6G7WELT4PMrnpWxoeonwXcdiBhhDJF1eOfCDdy60PF46XlQ5IHcCkFmtumQQCQVEykRbRfc5PMs8Cq8p9lcSSnvjhEywq9KrDWgNLbrUWkSgumtMYwzsoMZrjP0+1PEszOwEU4qqicnaKB1ltkP7kMWE88GtOsaYcL+qUhhmy44rL8Dp3yNdvOvzt+XltN31uA3w5XX7WaBW1fUj04Y/ZOPXr/xjeDm1ZL9zlJWjAehm9Ab1i8u0L1FIdDfu0vbNNh1jfzVEzpriIqMuG+wxuJjjbYO6zy5EoFfAFgZgrDx9++w/H/9R2zXE0ca4z16b4JpOnQW89aX9bD57BBpLdGHBzQPjhBVi9YKI0A6h58Ec0KfRjRHc2QWyPL6xhZymIUAvWmhs3jjMA5iIZCzArcsGXiDtxKvBFQNygVYZlx2NE9OSW/uoLIArRBKMvnPvs3if/wH1v/Dj5HbY1SRQt2ihGf5n37N+C8+QkSK6pdP8DhkEuEHGX57wOTDG9iqpTtZYltDOsypxAV+XeOvzTDekSURdr6hXFVBKv1yRa8kstCMrObRp08xVcf54TmNMeg0Yri1jXSePEmwdcv541P2f9SEY2k9TdmgrOPsk2dQtlw+OsFZRzopuP4XH5Jsj+irlnx3/Gpimabj8h8e4bWkfnJBfbGmvDGjiwTzxyfEStFlEapzdBcbauvRRUJuoOuDv4nrDfXZmvTmDuJajFtWFLHm+kc36K1jebakOVngjhacCc/Bd27RGwudZTQYB7fzVU0ugyy1STTDb93GlQ396RKfJkyUwK1r0mvbpPf36Y7mVI+OQ8SSxHSbmkRJhn/yHuYnX8CoYPzePptBgnl8Si+gPVniWxP4OGXD+ukZ29enqOmAVAissVA29JsaHSmivSl6mIVj1fYAdPN1KHalEa7RQTnNOYgDFM41bTD/dA4hZVBMvLoe+0WJq1rspqJ9doIcFoy/dYvq4TF+HuTeZR6jixRjgzJh4IkkRNtjlr94jBeSZBAz+N5t6sdndKcL5HTI5YMjzMEEaw3ROA+CNZ2h7wzJKGN1tmRUFCgBRKGYmlrPbFxQrRtG1rG7NeHw+JyqrhllKefLJbvXtzGdpW17kt0h7aqmutxgWsPF0zPqdc1IKbwMSm7X7xzQ1h3/8f/+7+B/77n9R/cAERS1rvyevBLc/acf4a1DaMl0URLFmvHtHQY3Zugspr3YcP3+AVGeEMWaOzt3SCYZOEiGGZNbO6+Tg68JQ3/Tg1/bdXj5+2+rr/s3XvduAf/NdRfxj7Js+KbjD6QW9VvSqq9qp3/Nd/r6r/qqcfq6Pv9VH/fbMrtXW/Kv91rA/R/c56f/6sdMJiM++dkXPPj4EUpLPvgnH3Hvjz9Eas10VLA7zKm1pFyWZEXM5ZMz/KJmkOfUy4pf/f2nQWM6VkRKkWkVVEDWFSOh6E5W+PsWlcZs3Ttg+/41XNvTV22Q/JxvaCLJ4aMjimHOwf427uiS9uk5cZ6glAxGb+8cK+9cIOZePdfNN1SHF9SHc3rrWM/XfPL4BYu+o+8MsdZUi5IkjUl0hO161osNvRKkSUISR4E0qjUkMdFyzbyp2VqsSRcltjPUpwui8YiorFifnBAVCjWZ0nWC56enxEpRJCmuaqkXGzaXG1pjoLc0CoqdMfPTOe/fv87TB8/JpwV13XPz7pTLszk+0VyeLhjMBmQ7I1i3qNGAKPeY3vJivWZIgdsag3NE6yZolG8qVN9hy6CD7/UaIs2yXZAmGtlajOqIhilqZ0R7vmKz6YiLArEOHYlIS5wxmL4Pbrs2KFJo08OoDyZnmxrtPdbIUDUSDTsiZjY6oHtyjqs72t0pSZEhumAsiFYID5lQV9MxSDvGBN6NjDWuM2SjHGsseZFTxwJlwRxeBgjOOEfHmvFs98p3wSKtw6cRqkgYbBrakyVd3SF6Qz9vIUuvyIUQyfAZ3dkGLwVkCW7VEI0zVNNRI0gjhTaeZFCEz7AuYGqtZ318Sbw7ZvDRLVSaoA7eDcjeDC7fuYqD1AtqlDP8wX3inTHlJ8/wraF+fILrDXqUE00yXKqQcUxy7zrRPBD47dma9eEl0bRATQuyNMKfLWm9Y91aiukAO1+x+ld/z/C/+lGA8V3fon1/n+rTI+qzFdI4WFa4poMebHNV8U41vgoeFGRpsIHoDa5qcAjsFV7cSxmSFCmQFlpAX2GYIyVxUmIluKoh8g4jFVGa4IUI/yKN7CXOeXSkoemQQuDThEgKRN/jVzU2NsR5jDRXVXhrcXgQEq0ExhOqvlKgi4w+1gEqNMro10E6mN6xfnhMkiVk0wGRkljjaS/WqCxGD4KkZiiyiVc3pJf87iC3+Uay+LUL61dV6MLjcpgx+icfIQfpG4+/8Zv3r+kfPnyejBWuNfRNT/3ZIaLpEUoQOWhXJc3FGv30mFYI0pvbmIs10nu0FBjAenD+CjoY6Vcdy+juLm5dU50uieOIzljkVUfCdD1pVrz1VW3ZYJ+e4r0jfe+Azd98isiTIFjRdohIIScFvrf0lxt008MwQ+ApPryOiDTrf3jI7L/8Pt2qCl2oVUM/TBBeYIWiuHcdUzbgLXJrDNahlKR7dEJ5tqR7cUH+0U2S3Wnw48hShn/2Iet//RP0/ozivWvIf/MxVZbSztdEv3rC8I/fZ/T9O9hFGQoYWYwpW5ovjhDWEccKk6gAbRmkMC/hYkUca0ya0usGZW0QshAw+vAaTdcTVT33vnUbmUfUVcsw0QxGQ9qyQXuwnWG1ati7fUBUBG+k8vCSflMjG8ODf/szjJJo4xhuT1gdL+Dff0pve/re8r3/0z+/4g8GRatYa6K9EfPekkVb9B5spKisZTFfk48T2qYh1xF+1dApKIoCW7ZB0SqNGU8HAfq1laMHMXYQJLaz8YB0WnCaKpafHTGbDINZ7vaQ/Zt7AWrYGaqzBVFvSQY5xfdu44ylO7zENyE5VVGMnA7QeyEx2jw8ot00xJHCLdbIrQnJ/gwhBem1GevjBfXZinZeIcqaaFbAJEGmY/rOQBukyPO7u/QXa1SkSW7tQKLxnaF+esbm4yfoUR7gf0XoTiR7U3xn8C/lw1cV2f40FNu8x+cJzjn6yzWu7okGKSLW9KcLmudnyDxFRAq9PUNPBqyfn1F//hy9PUJNCuRsSHMyx8xXxJOC7ukp6Qc3ufybj1kfzhF9D+kE0/QsvzhEv39Ac7LkbFPTH3sGw+DptXtnB6c1s+0dWmuCbL6XjEcFj54dERUJMnLs3J4wvL3N4tE5N39wO3SoNjXDSYAL5rMho50Ji6dnyCJF1h1b2yMm2yOGN7YohgVbReB7ikSiLUHG2joe/P3n3PrBvdD9f9mRvQq2RSwBgXeOW398PxR9VhXF7gSAZJCS7Y6D2p5z6CzGuRC4q1h9LTLnzcTgaxGm4jWf+Gthqr8h3H4LmfMm3PCtt//mhMLjrzoZv1/i8QfiXHztoeLtI/Cb066v38qXUGi/YQNf8xn+XdDQ2yOfDZFKksYBw9jWDWXVInxQDSGJeHp6ya71+GHGzof7NDiWj06IK8v+9W3a8RDrLNWm4fNPHnL7/VtopXj2+Jgs0iRZSnm+wv/yMTvfvRvap4DKkoBptw5/uaHYnjAbFmyeX9A+Ow8Sh6LHPTvBLBdUz64z/uH7REWKqVraeSAXiXVDHMe0XY9ZbMjfv0aZaR588oTjk0uaK07H1vaMrqyD9GfbM4gTpHX0uaTxFuU8oyylW5T0cTBRc8McGUcopXFnK9qmR1cV6wePUFiwLXJyi5PTOZO7t5gezIJO95NT5os1JDHLtsH1FhkJBltTOhsgI8vTBdWiZDPMsdby07/9mNn+NBjm5BmLozlRkdAtS0gTFvM13api99Y2xsPF0zP27uxy2RsEPpgAXa6D2oYOBE2/asiUosxi8iRmsa4YRgF7L/IIaTzWORrjUedrhHNEWlE2JYUQSCdQ+1PwPrivrivkpmPTBAUQEk279MRC061LWNeo3Sl1LDEuGFalW2OcDNK61ntc1ZBNBkSTnHRrFI6z87Bu8Ilm3dREC48pN0TbU9pBQiIlLEvc9hgtwHQGO98QCQF5ilWKtmyx6wpfd8EV3Dik8yA88f6U/nSNTCK0HqKvFkhTW5bPzhlsjyFWuDxGCEe9aYi9Bysof32IBoSzVMuS5XzB/g8/RKbRGyplV7mFhy/rSn/5Yk8Otmgv15jzNXES4y43+M4S3T8IZnadpTue012sUWnCalFihSdpe/KDKcmdHSbXZpjTBdXDY2Qd0Q4Lmt4j/sMnRLe2yd6/TnYwI9uf0Z2vaJ6e0V2sMYsNPolJkhhhHabrEZ2h73pkf+VOC1BkSGuxmzokAQikt4H0nUiSq0qg6w2y7XCRDoZt1mKQvISdv/Kta3qklthII5RCKIVzDtoWFUcwnmCXJcp6XNuTfPcO3bMz9OkCZNievVyTak1bB8MqqRXZbEhqHBZJ3fds5sExOpaKujPoh8fISOMTTeODMWB+Y/sVUVS8c27ePl9vPPilROO3tP6VfJ1YvNG0eP15Hv+mB48XqDSmPV0GNSkTCLZOAnVP//MH6CLDSIEsUpI8oX96Hjq1NhRZ4ixFiRjvHI0JHBdlLcUP74dOmVIoHYHp8XmCHmao/MuSud3hJf1iQzQugiT32eqVuo9SKsDUYo0bpNQ/f4q3jqiIye4fIHrL+u8fEt3cxhgb5KM/fo5bN2gtiScZZaTRtWF0Zx9ZJGz+7lOE8DiCLHU3KKjXNeZnDxne2CW+vRs4Z7MhMk8xx3Nq6xF5TNobVBazenyG3TTkd/dQ0yGuN1Sfv6B7fkEURci6Qd3bw2wqlPWhrRNFgUw8SKirmsEwwyw3xDd24cU5zfGSqmlQTUs/iMnjIYNhjjae458/xCWa8WSIqzrqqub5+YJ4q+Dm9RmHP/mM4XQcfIGSGNX0RIMMNc6JJwWrsxU604jOhtcoxeKTJwgUF4cXTFRQc5KjLHDpkmCiuPuDOzR9j/Ax63nF7t6MR48P8Z2l8w6tJFmWYbuO0ahgaR0u1dRdx+LXp6RFilOQ74yIv3ebky8O2R2PWF1UrPwZu3szoixBNA3SOtQkCwZ5/ZXEdBoHtbsipT9b0iwrYuvpzhbEwzyYFQ4yTG/wRQICknFB/fkLNr8qMYuKZJhC25NMh+iDGVlvYNPSX66pT+Z44XG9oz+8oLi3j/Oe9PYuMk/wy4p+WdEvNsSDhO5kHiBLWmG9Z3BzB6EDdAopr64xQbIzxq5rqvMl0TAnvr4NWtFdrDCnS0Sk6RYl8cEU9e3b6O0R6daQ5ukpfl1S3NjBrBssHtP3mJMF2XhAv9zQrdYsHx4HkZAsYfHgmGRcEEUKHORFxijK6HvD+eNTimnBaDahXJU8PzwDJJETRGnM8bNT3BcdUZJw/sURO9+/xeO//oTFyZzrf3SPkwdHLJ6cM727ixCC8myJyhNmN7dxPlyfj58dcj+9Q5IoRqMBX/z4M85OL7j35x+Eosa7pna8hiQF761Qhs6ujALDM5Ioi1+ZNQshUPorVr+XTd9XD39NbCp49fiXGg6/Kb7/uufeTD7ebYJ8Aw7y1zQ9fufxhyd0v3XneAca8frsfPltX/r5Zob1FSnfV41XL/uKk/x1u3v1Ix1lDGYD2rphMV9x7c4B7/2Tj9i+ucPFk1N2rm8z3R4jhgky1lTzDYOdIe3OiP8vc//5bEmSpndiP/fQ4qirZcoSWdXVWmIUMFjAMFgSBAFbcI2kkfxOM/I/4gfyy9JIM4IkSIMYADuz0zPT06q6tEidefU9+oSOcHd+8JtZWVVZ3T07bTB6W3ade0KcOBHHX3/F8z7P8qNjHj84Jkxj2rZldjFjc3eTeJgShj5SSi5Px5h+RDnPEY/hZFWRHG4wPLAGwCiNANz1HhiDjAO8XkR1MYeqxosjmqdHNNMxxbKmzRrcKKBBEzouIvZRCJYnU4Tn0n/zGj/56Xu8/9cfWtGY0Mc34AceUoAIPCukY6zzHSYxkYxwu4Y6r5itMtAKp9GEgz6LZYsjoHMkTVbZBf3pFKVazMEhbr6kMSH737+Jl4TMHp0zPplQqs7yUFc5YehSFS3GSALX5ejjI9zA4/jpGV1Rc37vhDCN2NhdZ3Rtg+nJhN0bO2BArWowgl4ccXz8gNDzCHsJpw/OaJuWodrA8T2Gm0PmszlF2eAYgZu4lGVNHMecLlYMQ4dsssATErdsqSKPwJE4AxvYRAjKpiFIYqyEoocUDtqxGVNPadydNWQUoHuKNA3Qy4JSd3iBT7FYQaeIBylo8M4W9Ec9xGafalHYBWaU0DUNy76P0w+QcUC9KihdQSgdHK1xNAzi2LIy7WxA1RJHAU2nEK2hXuaQV3R5japbRGxFevSysMxceWUVSrVBakvDKVwX4zmEd3ZpzpeIvKJrrfCjF4f0hIC6s7CAownGkQRbA9q8suw8QtAog/Fd/MBDHS+ZXr6Ns5YS39gi2Fv/jEFHXwkjfmEKPp/RV5lyYyC5tUfZHVlRQ2FpStvLBcGNbbqyRg4jPGXhWD1PoHox0e6I4mIO4xXdIscfpcRfv0F9NMadLFFrKS0OzUcnlPdO8LaGhPsbyF5McLCOvztCVY3VUbjSo3C1pqs7wtC1vTBPLvE291m88xA365Cehwp9XG0Zm5xA4gwT9LKwfS++S1PZgK5pOyLfu8puu2jPRcYhpmzosgLRKFvhvKIClUIgoghdNZi8pG1qjOfjtJrsg8f0vn2bznXppitM6KPrGplXiKzA3xyiqtZmVOsa0Tm210JrAq2QWYkfeJiioQ41TmLZ6/J7ZzhxgJNGuL77HLv9OQv6sorFb1Oa/0Ll6pnK9RdF9gCEvMLci2csJgauoHfdsoAkQJ02eL6LcST+tS1WTUcauPTePKT8qw9xrwI4ozRaQNMpK54HOG1rl55+jLc1oPn3P7dsUk0DxhAME8vm5jmYuoVnTbMG6ieXCG1wdkd0T8eorsMRNiA3UmB8F+M66EUJbWdx7n2rdZH97C50GnctsYq/xsCqwLS2WiKMnZsmL2kvZsTfuk0XuMhlgcgKjJQ4QqN3NqnvH9Gczgjee0j/j7+BvznEWeujjsa0lzN7PU1HEEbo0KfKa8zDc4aHG3QXc9oHp5g0pTYGkWVE1YggjVC1wumFtEqjywanqK3o6SrHRCHeICJlnerBGV7s0ru+jXFdPvrZJ2SLjNH2kM3dDTqlKY1itD2gtzti9uETlNEUJzPqeUl9kePHIV3o0Rv0KOuaVVsTCodwe0Bb1fSimNVHx4jQw19LOPn5Aysi6UsuH5whO2hDB28QQqsJ44gk8MjKGu0K8mWBH4V0niT0Q1TZkAYel8sc11fW7m8mrO8MyaVkNEjxPYdsVZM1Nbe/+yqP33tEqA1eq3B9F7nKUVVDdG0L40BxPrcQUN9DSoPG2L619T7LBxcEEsitiruaLa3A4rBHdjRGX/XTtcscT0p6t7ZpJqvnVS/iABF66EVG/vanxN9/nejrN1FZSX08trDIwKc5m1ptln6EtzMkjAOyt+/zjJlMGIMc9SjOZjT3TjF1i3YcRFljAo/0xhaulCweH7Px1m1E4KIcSxfPMKF8cIJ0Xeq2I7i2gc5rstMp7cUCVZZUyljtH9/Bz0u8QZ+yUXhpSrAe4XseZafIPz0lWB8QbqYQuMzGc8wYFrMVBoODIDtb0TMegQBGCZGUiLLBaNA4pL0e137/Dc6vqH9v/MEbLB9cMHpjj7W3DlBViww9jDbkeclP/x9/SbKW8vV/8C1krRiMRnhhYOmsm5Yo8On1Ep786iHXvnmLzVd2r+zZZwkO8bn/ewnZwFXS7FlfoeFL5u7vNP7HMjl9yW9+dlFflbX/ygqI+PWF6t9y/I6Ci19zJeaFF79mt88e4wsLDC+pNvw2C9tXfsbnD37xNG7g8ebvvcVP//WPSaKQH/7LP+DBp09ZXd7jzo/eILyiFZvfPSUY9ajKEn89Yf1gk+H6gMV8RRKEzI6nPH54yo03bpIOYlarksunFziBQ7QzxGsN5dEET2vaosbrDNH+CCcO7KLjObSzjLZuaTtF7/UD9KpEOgJv+wfUp2NQAhNbwTxZt6Aq2g8+Jv36HS4Ch40bWzw5H/Pxzz9hc2uElI4Vj7uCTElHIhRcf+0a1apg/PicrK4I45B8VdIqhe+7xGlEUVQ4bcdg2KNdWMYM44BShm5rh3hnhOu4ON4+FYbp/VNUXvPo6ILCaIajFM/18aKAZZbjIKAzXJyMufHKARoo6yF1XiJrRdiLyKua5SKjQfHog4espiuMgCCJSNds411vY0i9qiwv9t4GVVkzv5ixnCxIUruwlHXN7Ru3OKsUo40htVIQB8wvFtRNR+/NG3hKU5cNaryk108g8nE8h7qrCYoO43mUjUIXFaHn4K33aRYZrZQ4sY9uGp7kM3ZEiL/u4aaxbRR1HequwzeaZrGirSqC0KfxXc6XE7qiYuFpdtwNAlxkFBBLgRP4GASd5xCmITiS6nJu2abO5/ibQ3Rb2WB0kKJXFdKAcRy6qkEtckTZ4m0NoZ8gFzndeIXxXUQS0Httl97+OqrpUFXD6uEF5YMLRNFihKBrO7wgRACNlJQXC/woQFct+A5Op1ASnDTC2x7RtB1Np2geneM8vqD/1nXCjauS8Qt0h5ZA4YW/XyhFO3GAG4d0ZQvGioNVTy5w1vu4/dgyOe2s40Q+umpYfXLE5McfInoxIg5Jrm8xHy8IJPj7a7hpRP3kgsxAuSpI1gakrWHx3iOE5+BvDvDXejieQxh4NIsMx4AChIJmVeAZAb5HdLiOijyWP/4YL7f3WgpJHQVo3yVsOrx+golCSyYQ+CilbTDke7RVjTQGx3FRkyVaCOT6CNm2UJTorEQ4krbtcMsKrTReP8bNSpqiQKcJnhGUbz8gvbWLKRoE0Hk+XdPA8YRu1LcaJtrq8eiDDcS9EyRQtx2OH6AmK1qj8a9t0s5zjGMbM9uLJQqJ05cI1zbqf3kR+ooA43NW9CX15i80J36u1UIbC8m7OvTZr+FZgyHC4CQB7TRDei5CSIqytVStg5hep+gfXGPxZ2+jsxpXSiT2dynbjk5plFK4novn+1RVRbg3QlcNRdFa+uaqRkoHuTu6+toGndU4a1bwSlct5b1Ty7b1xiHVz+/jGLsfxqCVwd0c4Hgu9eWCK1wc/rVNln/5MeQVyQ9etYKUjqSdF1RFTRD6hIcbtE8vGACdlJTHU9RsZbV/YgOVpTNuLiak2yNqNMJ3UcKw+It3Gf3D79L7vTcpPn5K8fNPLCzEkSg0nnOVkVWa6Z++jbiipBVFjuMIhO/RXcxQUhIcbOF4LoQB+TsPLJXq5oC2qPBR6EWBF3iEgHR96vMMJw0oFjn9UcrewaYVVw09/F5MNs2pxxlxmmDqjgf//m2cMGBWLPGXGtYCpOtSrFb0gx5FVhGmMWaWIROf+z/5CDfw+Np/+4fUs4x4GFMVNSIJSFpB2AsZz5fkq4L6MiMeBqxmBRjDLFQsZyuG2yPbZ+aH5POcJAlYlQWrrECIjuHuiOD6OpOLJb4jSZII10gef/CYG9++TX2+YH3Ywy9q0B3x4RZ0GtNqq8BdN7ijPv61Ddp5RjvLmM9L4jS0/VhphK5bjBS0RcHwznW0NlRHYzIDYd0hr/Q+ghubOKMeZrpClzX+/hrZPMMdpHTjBcX9Y7xRj+TN63STJdmDM4L9DVReE28NqWYZzcUcmhaEoFoVjN68QVvUCCHJH1+iqw5dWXFYehHLnz1AVw0i8li+f4TsT4g3+lRnM6Tn4G8N0YEP2iB9j+psgVPUSKUJN0cIV9LWHYnnIo1BGYNRYNqWcHuP4mKBg0MxWyHWexSrguVJSbsq2TjYRGIIkwilNIvzOYtVzub6wMLb1lMb+BsYrQ/Y3F+jf2OLcHsA2hAebLB2e9euLwKc0CM7n/P4l/d49z+/SyAdW9E4nVOscobrA85OLtnc30TUFbuDFF02yMbSTT+zXEaI5zboN9o+IxDiC57pS/Lgv1354cvYnt8YUXwFtOqLAc6X4E9fddrfUVD0xfHlmtDfepgv/Pvitt9+2KKduDrTr9GyeNnzfoY9ePHvl17rF05jrHqurhte+/2vEa31UMbw9n/4BV3Z4EchP/2//4VVizbQG6W4RtM73GT79j5BHDB/dE5xsuD4vceMH5/zjR+8wWK14t6Hjzh/csZofUBV1FyeTizUw5XoZYOvDJOPnnL57mOK4wnjT49YfHqCqTu8OCBZ7z2P/rLTOWcfHGGCCJIIv9XoVqGEoG07vN0dWhkSuQ5OP+Lo/jFREuFFAa1SCEfgBz5BHOAGPkHoc/zgmLPH53SuRDlQlCWdVviBh+t7+L2QeJQgHIFWioFwqMaX1KsMEp8u8cnmGbXRzB9dUJ4taDrFUhjawCNOYvB9hCNJ+wntqmRnZ53dg02k1qzGC/L5imgtpbe/RiuhKRuGg5R2krF7a5/htS3CYcqd77zO9sEW2apg42DTqoPmJV7okfRidN3huJKmrBkfj9m7ts1gc8R8tqQpKx588IDRzohyWdg5JgTjuuLpdMlpXtIhyfKaxWROWdTUyxzlu8SepLc9INweYYY91LLEtBpHSPIipz6bMuj1KVcr8lXOZLWkQVE7ggUNjQvjbE7hQeHAfGFVvXc3t3h1tGdFEo3V9HDSCDXLoe5w246urOnKhkVT424NSL5z29KZpiHC8+iUthCb0MPtX6lwey5if2ThEL5jF8PAQw4jht+7Se9g3Tabhh7BMGH9G9fZ/kdvkXzjAHerjxf4trGvbnGqFsdY8bYOkI6DicMrcUhtaQ81tFlDvbK0msu7p6ii5ksW8Gp0y/wLM/LKAU0CVNdaGtcwsJS6yxwEyDTAjQNbfo58Bt+8xfYPX6XnAKdjyrvHOHmN9jxLsxn7JL2Y9WubjK5v4QUeIonwXjnAO9ymLBrqkznV+0e0xzPMZWYrao2iLWqaZUVVVLTGkH16RLw3Yve/+T36f/wW8Z09dC+0laCioq1qlCMsE1Xd0BQlbtMgDXSr3PZB+R7Cs8xcAoOzyq1CslLWSTXGVjV8D69vYTBKa4IgBMeyu4hOkT06Ifr2TQzQadvg6Vct3aMzWqVpfQ8QdKsSX0rCNKYRgrYsMY5E1h1tVmHKhnZmr02PV1TznJMPj2iy+nMB4AvG9KVm+DMr+mxFfdkawMvfN4ZneLHP6Eqf2WQrwilcB2cY428NkFJgpMALfLq8JL61RfnuA5iXtgfGkXRYWy46hasUwnFQeWEb5IUgem2f7P6pVUhHWAfckSS396xGCViJ9KtRnUwsLGpgG2eLB8cYrek6ZZ111yHYHSHymm6aoQU42wPUxYJ2PCf9gzuE17cQSQBGUN49QXgO6T/4GuG1TepZaRnpVvkVs5igLTv0dAlxhJPGFob05Bw3DnD9q6pm4FO8/wBV1sRvXif5xm262QqFwd8dMfon32Xtf/pDRv/kO8i11LJXeQ6e79v+gF6CuVr32ss5uqhxtIF+amE1swxVK9pOUa5yqvECH8nq3gl3HzxFbCT8vX/+exxupJhPPiES4GnB9JMTPn37HqtlTmU0lSPwr62jRhE68JhnBXE/QQpJJBwEIH2XKi/xhcN4skA4gvUbO7hJYIX92qv54UqmTUXdKTzfo2taksinKzvStZS9/U3CwOfOD95AKsPkwbkVU3SwsC/XIdxIqasG3RmcwGXz9X2CvRFPTsc2eRUGlpglDXG0QiYe7ihBrQpkEhLfOUBcNYr3v/8K0Z0Di7PvRfRch80fvEp8cxvPkdC0VrF8ewOzzOmOxxilCMoKaTStEMjdEdErewjfJXt0Rls2dNMMLw6Qh5vIOCR/OqYdL1G1DR7U2Zx2ssTZ6OH2Y4wjuXzvMSbwKKOI6dmcdlFQnc1ZfnyMrBWy1QTD1FJtV62lg/ZcKDuEcKiO5hRPpnjXtpD9GFMr9Cy38zKrYJ7RVQ3aAYWmmWe4bUuXlXTTjLZq6Uqb9PDX+5iyZTVZotKQznP49L2HOKViGMeszhdI12F1saSb5IRCEq4ljLOM1XTFYrykaxVB5NNUNU4vpMkrmmlGOEqsdXpmcrBaXV3RUsxyFosVg60B3/79b+D5lu0sWxaoRvPk02NOj6a0bUujLHwwGMTPV6Avu5QvSbI8t2V2+wuX8XnMzYsbPnfMS8ZXlAi+0vc1BnP176VnNy85398mePh17vzfcvzuYVFfVXr5LcZnRY4XvtVvebwQ4qox8beLEl+sjQjfQjkSz+cf/m/+MX/2f/5Txk/OWR5fIn0fYTRN29K/vctkmmMSn+HBBq7rkPQTJkdTDm/tc74oaKqadKOP6zs8Hi+5cecGKIU+7hgkMVle0AlNUCm68YpwFKNPZ5w/uSRaS3E8l1W7wg1dvDSiOptjWsXyYk4ySojWexSLnEaAcewC6fhDmrxCnSxou47ynUespQmXSYhqFVESWrpDFKpULPPKQrA8l3gQU6xKHClRxmLzdafIyorFZMH6+gApBFtxRNoP8E+OCQ+2LexASHRe0Do5Wacos5JgLUEbTRD57B7uMJ/MqeqGpw+OiDd6TMdzkIJ0s8/yeE7ST9BasVhmSEcSpxFCG0LPNmbPq4LRzoAyKxhsDCmPLyhWOaPbA+TSoyhqjh+fEfQjokGCajqC0McLrLZItbSsWEVQ0a5KhmmPnZ0tnjw8tmwpgcUYj9uKvb0dmqdj/FaTbA7xDJRNg5rnhP0YXdToOKBDIrTCbQSdAj+rYWPEsi4BQT6bc7C9w5rnU0UewrRkdUNgJIPBEJTCjxNk0xIHISYJaVxB0Cmqtsb3PMRFhkgjFl0HCuqqwxtICDzEsqQuG1iVGG2QZYOaLJ+H5VQtKm9oLhcIx8FEHv1vXCfZHX02vQSYTqGmOTJw6d/cpPnV+5jIQwYBqjWotsMpSjohoR9aMT+lIXRxqhapNXVndS6coqZ+MqZA040XDF8/wN9bw00sjaW5avJ2+8mXJ6U2EPhErx9QfHyE7hSq7ajevoezluIPe88n7bNr9w428A42oFHosqFbFdTjJcsqp7+3Rui5qFaRui5tVqJXObJuqHyHYLNP6Llk944QwkG4HsII6tM57dkcoTXKkajGNj3WZYPcGNiM5eE6vbeus3zvMd29U2g6mOe4QtA1Vj24cwR02O8d+nQIKx6YhFA1mKpGNQ3aaKTjQqcAgZQCJQWm6/AcC0Nz8xrlduB6qLqjOZtg9tYxD08xTYuSAs6mlJ7VB1FxSNG0JNJSsso0QtQtmTAIpXG6jqCBsJ8iWkVVdfidZnY2QziC/iAi3d+wa5R4Iff1QpP+V9IlvsQmv2h1DeaztfQKMmeeW+Nnu15Vr4XFOwvXQayntMMY93yO0ymGN7bofvUAfTRFOK5lBdIKZQweNhEihcDtWhQWoifjgODGNsW/+ZllgesUUjqofoS/v351FcIG70ojhUP+yRG0LcH6Fu3RGIO09L1th+k6RBhhPJduXmDqBrG/Bk1LczpFpyFimFItcpKNHu08Q5U16Xduk75xSPY3dyGvqX3bVB0YQVvUlP2EyPMxVUubt/idRF4s0KGPE4UIz6fLatpVRpcVDH7/60TfuAVK05Q14c1tygendFISr/eJt4cEP7zD8njK5NNTYikQRYErLa2vNgblSbrTKY4wGKUwWYWDwQQuQWDFT6M7e2x2LTE9VhczqsCn8UOiW69xMV5RNXMcY9g82GB4aOGRudB0y5WFESU+s6c5B1eVwt7GgEqAH/l0F5n9DfgOrhKsv7Fv13JHsLa1Tu0KZBugipbJbAlSEAwS8rxgc2uN3DFksxXD9QHlqqC3bZuK1aQg2RuSzwqW4wV7b15jtDWiaxWOgmJRWN2CPxjwqz9/h14cMzSSqKzx+xEiCiAvGf7wDh1QXi7tmv+Na3i7I1RudUxWs5wwsWQa8f4GrhCsPnyIdBz8g02irSHdJ0e0R+e4+9sWqjrLEHlN8+Cc+dEl9fmMdL3P5C8/wA1ckms7lMdjhIHibE5Xd6isxB1YoTzPcajun6LOZuz/8A6LX94FlbN9uEVztkBhYFXRaEN8e5t4Z2h7g5RG+lb/Jfv0DLUq8dMAk9c0E0mwHtu+l7pFdYpsvEIUJe5aD5GmdFWDcBwII0zbotD4WL0KJ3GhscH3ydML6jjAVYrXvnWbbLYivL7OvrOJo63WFnlL0GhqbasUaRLghwHpMGV6NkdKQbbISA7XcWLfJgOM+Zw/3hY1k7vHjPY3cEOPclnQbg9RQOD7RFFAUzWcn10QssVUGeqmQRmYPrlkeDX3PzNanzdHmGd263P1gZeO3wrBJL4MvXmWUP98PPISpM+z/PnLkus882ntTl9JZftfcPyOdC7gZcWdz8ZXh0BfLqr/hnDJfP7li9X5z4mV/KYgw0BbNbRlTTSwStcG2LlzyD/9P/xzfvx//TOO7z5lOBownS15+t4j7vzh12BRcPzhUy4enFF0HUEcsHG4wdn5mKZp2bu+w/EHj+g6zeJizsPuATuv7fHmH7xFuygZP7mgNobAcdhyJcGspHIlWimaaY5xJArsQulZcajAdYg81wYeZzO6vMKEAcF6Qn9zwPzBGfH2ALWsMFWDqBoCKdneWceTDl7gcXZ0aakyW2UViztNWdVUWUnST2ialqasEa4kiAPksmNva53tXo/QtWrBWoK5dYtyVoIqoNOo0EOHLsXKIFyffFFQ1w2+dJhdzAjjgI1rW6zGC+qyxokdC/1a1qAM0+mCZH+EFBJ/s8f0/gU337hOPs8t/j0KcDyP9mKFH3hobWiahun5jHyREQ4TfCNJ45CLkzH1qsIkAfc/fETYjwiky97hNmcnY5aTJUkv4fjJGbtvHFCsCi7vnpFs9BBpyOnZhMXlHE/ADelSGYMYhnhSoloFaUi3yDCtRoQhXhDgXdtFzTM8owk93zbfRynL6QxXSlYeJFHC1sY2XWeVnnXgXVGAuvS/dh0ZuBz/+CN0EqBbjaorSEPausYLA9AKHo+ZPh3T5KXVI4kCaqORvmUnyiZz3A78OKClAmV5/d1eSPD6LvFmn3aW2UAgDK6a0cDphahVyfT/+Z9QeUb/j39I1yiqR5egAnRRQdXijFewv4apW5zQpzMaPBc/delmBe7OkHpR0MsrHAOrdx4i7p7Q/85twp21z2RmlRVHFK7z2cx3rCCUED5OFLC6nONJgRNYbY4vGIjP5jgCfNeW8tOQ+sk5fhBy9uERu28dUnz0hLJqGG6M0G1L17R4WYNqWopGYVwXN4nRoQd1h1oUVhPhiq4xcB1UXsMnp/B0ghrFiKZjcTwh3R0RvHGAWlVkv7yHXpbW+FcNSgiM62CMRhiQVY1KQlRR0WnbaCqNQTgOrYDI9+nKCo1BBD6B6hCe5ZI3GBptKKuKWArquyeE33sNOerRnk8RZYXcHOJfLvDazma2BeSdInYkTj9h9fjM0rBGIem0QOwNEaGL40hO7p+xd7DGa7/3OkfvPebpv/sJ3/vf/3OcyP/yDf+1pvnXl/F/7aEGy2xibOBilLHK0kYiXUnSixltjljOC4wjLZ3u6ZzWkXi+R5OXVEqR+B5d214pQAtUq9COgw58nPUU6Th089zGfZ3NBMf7a7jJleo8BtO0yDSyTG+fniCEILm5Q/H2fRywvP2ei9Aa/9aOhaKczzFRQLC7RvvJMVppej94lfjaJt2yRDoOuqgxriT9xg1M09HcPbEMd3Fs7bJS1Noh6Ud0swKngVo4iMjB9RyboKoqhPbRDrAsaKqWxV+8R//33yL67qs4JxPKh2foTtM6Du3IoDwfuSppFjlx7NHrhZTvj3F6Mblw8DuFKGtE5NtAThlLVawVwncQnaKdZxgBvR+8RlI0nD445uxkyunTC779vTfoj3q04xnac2iM5vTpha1QSAHLGowh6kfceOM6RkhrOwIXL3Rppzl0mgzN2qjHxvqA/P45qwdn7H39Jg9/9ililOAmlvYzcj0b8LcNZVEh4wCxzFi1LUFRU7Qta3tDWt2x5seMjyYMtwasMo8ir9i5vsXkck4qXU6PLjh+eMpbP7jDG2/cwCkaEt+BtsXtx+RHY/zQoWs7uqJBH49xBhHh9W0A2sslBkkxz4gONyguF0w/OkJlFdHGkHpZEPdi3M0hzuUCfTq2dMdxQLfIqE/n5FcVRJWkZE+ntMsaz1fU4/vItT4aCY2hvcgQXUdTl9B0qLK2MMDAJ3vvISKNiD0XU7V0iwo6hZYSf7tP2I+ojie0oY83iPF6Ia4y+IGPqRorhgq4ra2gKynRvodoOyv2mUbguNSrkmB3RHJ9m+Xb9+iWHXEYIaQVmBNrCcXFjFobyqYhTWOOnl4y2OiRbPRZnc9pZgWO5+L1rP9y+fiS/dE6nRaEvR64lm5ZtYqDV/bYunNgGbSu5rR8EVqJwU8jdr55k9VkxbXXrzG+d8b0F3dJBwmrJsP1POq2w3Uckl7MydkU3/cIfZfiYv68KfvXmbWvZld6DuZ84e8rY/fScz5T3v6qM73w97Mg5NnOv8mGvuSzfquI4mXYqq9Guv6txu8guHj5V34eRb3w11ft99lZzOff/MrPewk67qs/4nMbBLYM3xYNJ2/fI2w14Y9etwakbHAin7XrW/zT/+P/nP/h//KnvPeX7xGHEb/6tz/j7JOnrA96uEoTdIbV8ZQi8Vl/fZ/83Ud0ywqnVQzShLxpufH1m4w2h+BJFidTsmnGcGcDozSq00yLklXVMOqnUHc0dYuQ1rGRnca4Ei8OmDetFTpb5JRFhSsk2hjiRU51mTE7uuBCadJebEXfXIfYc9hRDirwCXoxwU2XomlpyxohJYvJgsiNcAKPOi9J45DcaKQjSD2PG6/dwkegW0US+KA1FYLcdzAmQHWKTgqml1N82eG5LovxnP5aj94goc1ruqpF+B5VUTG5f4bqFIffeQUjBZdHU177+i0W5zOmD87YeOsaOquZac3H796naTvWfEF6xVQxO12i69ZScmrF5aMzC9nyHITrogX00pi9azuMxzN8IVGuRLSasqjIVzlO6PH440fs3tghGSZk4yV7rx4wnywY7a6j2o7lxZI8LzkrMvpJRLKsaY2grFucwKFpG3pJgu95VE0DdQUuiDC0InZnE9owoB2llI1tUszyHGflsVwtGLohnVaUXUt/d5PiwblVsw19TBTazI8DXqfpb43w1/vUJzNk1WKUxlEKsAxm0hH4vgedIu2ntLMMozRNXuMKaZl0vn7A5tdvWCGtyAelLR647SzjSKesMvf1A1gtUGWHvznEi30YDhh/corz6Sldp5F1ZzNfqxJ3lOBj+cOdJCC/XJLe2aebrFCzDJk41FIy+cnHDH50h2RnzTbJXgk/fdFOOL5HezFHlA04kjoOCaSwTYYv7v85tovPStpGCJw4wvU8wrZleTJF+h7xMIXAx08GiPkKJ43QWqOzivBgHbcXoxY51ZMx7SCGVllF1s7eZ0fauUZWY/Ka9mRBk/pki5zadfB31xn9199DjZe0Z3PKeyc4ywJHSmpdPy9jq7ygUx2y6UBImtCzuh+AvnqmtTJ4syUIgSkrPGEwUYRQhkBcVaqlS/3BY7zXD6gvZ4QIOJ8RBJ6tiBjw9tbw6pbKdWCVg+8RuA6O0rga1KygC31apdm4vonOKhYXS9plTq0FdVmTPAvqvmRfrxocv7hCPnsWV+8b82y/Z4f9ukXcPM8QPvtbXFVNpOfihD7uwTr66SW66Sg/OUYYQxhH1LM5RhsS38d0HU4QIrUCIQgch1Z16Cgg2N+gHS8xVYvRyuqKNB3eeu/5l1NFY4M6oLh/Sjtb4UQeTuhRnc9wjEFqffW8jG1QzhvMbIW/2UfOMsyqoIsD4jcOMVfXb7Sh+vSUYH8df5SSvfeIcpZZhrGVDTocz6O3s4Gbd+i8ofVdgtZA6NK0Cl8KTBzQKY3QIIPIsldNV2R/9QHhm9cJD7cswUDZoLKSxY/fR8YhypV4ShFIhzb2EIElqPAxeAqEb3sunLMpVaMJ+jGqshh7ISDoJ4hW4wNNEtD3fM6XFfvra1R5Qbq/gUOHaVucVlHlJXQdqujY39/i+NEp5apkdG2LbJnZaoVWyEZTXNGiplt9IumwOJsxPR2TDhJe/29u4P0MHGNwOoWzN2I1y4kDD1cbijbn6PEJievT3xmxWpSsxgs8x7D9yj66bNkfplwulhzc2kXXimTU4+TkEqVqglHMxadTqvMFaT8m7kUIYwiubTL76UfUJ+d4rx9iWoVaFBjPJTzcRAYezeWCyb1T6sbCsnzfo34ywZkVVrQ0tary7ekMp59YuGfRgFNgWksVoiYrq5quwFU14pOPCOZTdBQi9q6jh33roZU1rXQI94aoC42Y56xmmaWtDn2SNw6JDjYsZK9s6FYVl3/xEaJq4XLJ+PEFwXqC73iooyn11gCEsZXZK5ZKJ7DJjG68oPI93CzH6UXIosIZDTCeh2cM5nJBM0rRUqCloHEEsm6RaUC8s0Y9XiJ6Eb3rW6zKiq2bWyRxxNH7j9nfXGfY7zFdZuiipX9zjY2b2xz/4j7X37hGuL+GbjuaquHaeo+9b99CtQpPCtsvIsznAgsMlp46CRj6Lvuv7jM5mRAHPn//f/eP+LP/05+SL1a4vsPW7iZKGzaGPc6nS0a9hPS5VtMLXuWz0vgX/ckvL1pfPvbZRvH5XT+39coo/ma/3Xzhv1+1j/jCpYkXN73sAn/z+B1VOX6HsKgX7/gXEWN/R/DW5w7/7b65Xdy+/CswGLqmJZ+vOPvwKepoysMff0gwiBkdbnDwT74LgBcH/NH/9h+Trvf58K8+RK1KTh+ckQ1X3Nxapxwv8G9scXk5oylqAt9DDWMWjiTtB7hOQIIkm664OLpkuDlkc3uN8WRO1bQkcchkPCfppazyS3wh6YU+g60h3SLndDxF+D69YMR4uiAIPNYP1pG5x+XFgtHagAcPT0lWGd2qtuJMrqTzJYPApZiucFuNkzeoWYEnQKIJIw838Aj3Niiblmq6YtizzWU3dzbo8orED2iMxjSKrqgolH2eei1h2ZS0xioSt1VLuDakyAomixldUbOaLvjaH3+Do/cfM+qliNDF1C0HN3eZHU9oq5pgLcWNA9qyYThMWMxXdFmNIyWj/XWaqsVdFnSrGr0lOD+ZUM6XrG+PkEaAtAJW8eaApmrwY58OQzJMKZe2opLVNduv7XH20VOauiZc75GfztjcWqNVVtisWRQEB3282OfykxOMMBx8/Tpnn55QNJrWaylFRzLtcDpNsDvCixNcBKu2YlLMuDZcx5QVwk+QQuBsDkFrEqXA8XAlhK5Vhe7HPYTn4jmSoshwBZR1Rf4koyxLMDW+5+ILx7IGCauFQBqi6ha1ysEYqqLCSWPkeI7pp9aJkeBKhyarLFwNUEaT7n1WNbAZeYPR6nnGRpUNMnRZffAx7vqA6sFT3LUBzqBP+clDRv0Bs9BHL0vkPIfUR/gulTZoaYiyCqcXERQl5dGY9Nomi/EKr+nohMBVhvL+Katsxe6r1+2FPp+LVy+UsdkqIVCBh6gaxHiBt7/xWRn5pdmgZwVle55qWdJUS5zQRV9V/PyNPkirPB3srdNlFe0ko7h/SrTRJ7rpEVzfwlvrYZqGphdhJivcQtpGxaaFzmanZNMhohAnq9HLiiYNIW9ZnM3o7wxpPUH/T76DWRQsfvIRbllh2pZOG5ysxNUGEwS4rovTtgjVoJQCR+JKQRRGKKUwWuO4LirPoO2QYWiblFtLO0sraB+dIfc2kPMCUVVobeikg9Ca6HALPbtHNVuguxbPC1Da4DkOSinkNEOnAc4goSoq0vUegSOpjqY8+eu/4uY/+TbJ2jOn+wum96vq8i8Y2WcOgHnh+TxjVvnSUqANplNXQaTN1OnW3gOuFMOb8ZLhjW0W79xn9eiCZGOIMhqzWkHV4EcRbhjQ1gJPCkDStR21VsgoROQl0eEm3WRptWp8H2GgFobw1g4I28QvaoXXj0Br8nceIpTBu7NL+eQSpzNoAUpY0gUZOLQYxDJHK01yuEH18TEi9Anv7OMPUxtQBS66aWnPpshhhG5a8l/cx9HGTgWtEUrQeBKnbakuMlSnCDZ7mGlO53s4LRijUFWL43m2uuK5aG1ofZdmUdD99COaWUb6xnW8jYBmnoHWqPMpnRT4w5TOF7SPL6wWS1PhxQlO3lpo7Sih6TqCeWlpkD0XQg9cF1mUeMM+3emc+M4+envI9fGCi8s59Qzy1lLLqqKlKypMWTM+XXD79iFKa3TgMtxfJ+hFqKrF5BVyEKHqjtnljJ0bO0S+R1XWVNLgDhKaecnJn3/AjT96i0d//j6mM3SBi9cPaDyInJCDtQMuzscUk4zmfI6JPE7HU8K1hGY8wwtC6qJka23A5cWS3jBGdR0bWyOyiwWjYczGmz5uWeMYhQ48gv11ytMpeC7ycJvoa6+SVw2jNw+pjyZE1zbQTUv95AJZVAzWbANytSjQcwuLFb6HrjsoKxrp0PzqAbJT9n4acHwHvb2BKhuEFDhtSyN85Ct3kMY2URMGRBsp4faA8nRGMc4sPMd18EYp/lpKMErxBwlGW4HOap7jpyHhzpDtP/kmzckMVbcMezGO77L88Igur9Hnc5quI0agXQuVapqGKPZpipai04zW+zR1Q+RZ5jwGCd35GFM3qL/5GEKPOI4sLDQJwXfoFgXNVR9g3bZWQ8K1VOim01xO53hxSOh77L26z8adffx+RH9vDQkk20O8KHi+Xqmmg07ZwOJqqUBrmnnO5O4phC5+LyKOQiafHLO2MSBOQvzEJj8vzyf0ezFlXuHGHifjOd946zbJep+zsynv/OUHyI2Uw6/ffMaAzWfu+UvS9+Yl7z2zbV94+5mps379M+/+M0jpswTKrxvPqxzP1sqXfvwXfW3x+Vef4aV+fXH5mb/8/PP+jj47/yXYon6L8aWvYfisXPUbTi2w6refXYWtmz3LmvF8oQOjNdOnlzz91X2y6YrmcsFqWdBLQspuweR4wua3bxPtrtFVNV4S8sN/9Ye89Q+/RXa5ZHo+tQ5u3fHh//unBMAgjJgdTyiXJbps2Ly1S9O0RP2IrYNt3v+Pv0IYgwMcn1yw98YBSRxx9+37rK8Pmc1XuL7L2u4a08spgQe1K1gBqe9y8uSM0e4mBsNykbOYrdhYHyF9Dy8KuDye0B/2yVYrROyRrKWMx3Py8YrA9wkTnzQMqLISB0F9MbHc+m1LHPpsJhECh67p6K1aVAdNWeAAMo1wRz3wXbx+zKJrcf2IyLXNtcdPz+gnKTIxlIuc26/f4OnROR3Q3xpx/uCMva8dUjcdy/M5xhGsXd9iftXEfXYy4fDmNlEYIsuOIAlZTnPc0GNwuEVvvceyLAkCj9KRXD4+p1EKIQVpElGtKupVSVd19EYJjYL5eM76zhpFWVtMLAJcSTXN2NnbsCxRNzdZnS0I4oDK1SgJ2xtrTKcL5tMFo40hq2WOH/q0ZcNE1Qyki3p0TrCWog82SaRHPNrCGIN3aw/tSeSsoJSSpmpIEsu4pBYZYDU0DAKhFK4jGW1u0NUtLgKEJOynhI5rm6aNodIdGk23KvACnyr0IPRYrQoUmqRVdIBT1pjAh9Y6qXIQQ6tRjVVtfZ5BfmGeSd/FCGGZc37xMc14ZuFcyxw9u6Db2qLKMsx4Sdke0XW+zSQbcISDcQTxlZBc12nLtJOGRAjq++dE/QhvluNKQWs0TDLG40tEq1i/vmubIF3XLqJcGWcpCbcGNE8vkKFH50qqyxlhsY2TfCGL/uLkNy9YzsBF5xkqUzhJiOo0xf1zgs0BWkC4NcAf2cA2f+8Ri5/foz2aEn/jGvHNHQb/4Bu0k5VVljVQPTineHJpRSsbjdgYIhyJ63s44wXMc9vc2Isww4To+hbLxxfooiL+/quIVpP99YeY0ynSc9BS4roOEtBRQJcVGCHxEDaoWCxwkgR1NT9Je9RZjheGOK6DxMd0igIIFopwfYjcGdI+PMV1XdtkHgVEX7uOOL5kMOhRj1dIAatlTjjs0WljHflGEUQeg14f4UryozHJdp/X/uhH+FH0ZR3E5+vjiwb587X655X1Fw80L65tX7TndvUUnvO5ykjXdbhXvw0M+P3YPr/NId04Q7oSs7dG9GSMTq0woHQkxCGm7TCeg2lbC3fLcqv8vrvG8j+8jT9K6Bplq4BphLfWAwFuHCL7FqpXn82oHp6hXUlwuMnqT3+F9u3cFG0HWiN3N/AGPcqPjklubNFMMtpWIXyXtR/esWw2L9wG4dkmWj3NEJOVDQaNwZESMUzwPfB7MeVlhuu76Kqhq2uCa+tU98+Qo4iyM3j9GC82tHWDf30bUTesLhf4ZUH75IxV3dD/zqskr+zhpxH5+4+opysaQLYtXuQhhimcTdBVbeEzJxO8yMcfppTHUwt3lQ5BL8GgaX2XZHdEe77E8Vw2v3ObqBeTPrlgWlVcrjKaVUXq+HS6ZXa5JPA9zi4mOHVBGHispgt818UsSnTk4buOZWQT4PZCTKEotCbaHXLyq4f4VQtHY3b+/lu88b/4fbIPjigmGZ0nuZwuqIcxoyQg9AO8HZcnHz7BSQJu3LlO4Dj46z1Gox73332IupzT68U0WjE/GiMVrLs+fqMJDjbQ44WFKqYhZrLEaTv6owGLpuP0vUfs//B12ssFru/a32pRUT8Zo4SkWuSWjex4gtRgwgAdeyRKUzQdwcDHXR+gHh6jw8Bqq1Q1QexSFxW0mmS7T+w6qKs+EwNWUVsbxh88RboOzloKZYOThvjDhOhgw/bZTFeoqiG7XOCt9dB1i350QbA9ZPDWdesOaYNuOkxeM12VtjdnLbXib02LN+ohpcCVknI5I93o4SUe+cfH+GlEF4X4cYA3SOnmK0RrEL6PrlvcYYqqFWZV4416zCcr5qcTwlHM6mxKMS8R632Ghxs4vkOQRAz7CU4acPn2Q5L9NfrXNvHSgGqacfHkIetvHtqeLG0IhwltUTP75BizqumKmunJFH9ngBe4mGnBbLLi5OOn3Hj9kFdeO2Dw2j7z0xlREBBEAW1p+0eiJGZwa5uBgNG1DUzgsTyekO+u01YN/Z3hZ3bnc+NvjUn6yvGZS/rbJsl/yxM/Dzw+i0A+a9u4gmO9aH9frDQ/95EtNNUe/XcvX/ydg4sXL8K89IK++u58MRAzL976l0R1L2tW0cbYbKwxOC/w6tsDPl+1mDw64xf/t7+gmRfUqsV1PHAEWZGzc22X7GLG6X//Lsuu47V/+j0c30V6LslGn2Sjz84bBxgE7apAa0V9MkUJYJzxymsHrGYr/H7E/q0dnMBldTy1lHilYZHZZqsgDgg3eswnC5owZLQzwHNdjh+fsn9nj2hzwMXxmINXDjh9dErddmzubXDv3fsgDKONIUHg8/jRMQevH8KxY0v9juT06QWvBhZb2BUdWwebPH1wzObNXcL1Hsf3T5hlBWEas/PKHg6CcpWzrGpcz6FzQUYesoa66airAlN3hP2IOJCcP75g/2vXuPfBp6hWsfPaHk8+eIrru8RrCYtVxsatbfzA43K8YG3QI7tcEO+tIUcxYeBRjVfEjcJV4A5S/MhnuNajrFpW4yUXZ1PWRz1GN3ZoS8ttX8yXNAIuzmf0b2ziNoqD1/Y4P5tQtB3tpGaYhixnGWkaMRj2cNKQ8mTK7vYaC2nITqcspit61zfJjiZsHWzS1Q3xWsr0ZMx0MgffIR2kXD6+wChDO20IBzFGSAgj7n38mFeEYFG2DO8coDuNinzMIqfOcmRWoZYFZRLTOhK/7vCNwHV94tDCcZarjLjurFMsofZd2kAS1A6s962QVRywzDJ832acTRIiA5cg8pHKVpPakY/cO6AZZ3gGlPBhViCFoG1aVFGjm5bV0wnxFTWsAPAcKzL1+JLV3/yK7KOPwYB0XFrHRecFyz//CW4UYboO7fiYZASug3Yk5ioD7nmOdfJUQ5dXtJ1C9mJ0UeHGPu0gxgGL212VxEJQnM1wy47hnetXRs1YnnLPtf0JGILNEc14gWoVTV4THI9JXtu3duY3ZF/ctR56muFIiIcJ5buPaS/nZFLi7o5QB+sUTy7Z/mffZ+df/Ijzf/NTytMZ1Z+tUHVL763r+FsD3F5IN8sIjcEZxqhFSTde0pU1QRrRzTO6q7SScV3EPCf7m4/Rb98jvLWLN0pRsxzjwPq/+iPKT4+o/uYTulVBqzroJejOgOvgNg0YiQx8lOeigK6xWhmuMbi9FFk3CK0t+5EQOFmOHPZps4rhN2/hei7tyQRhDOmP7hBe28CRkvbDh/T2tymEwPcslz15iROHVmMDQdd0hEHM4mTG5lvX0P2UyeWCtcNN/NB/bqefZ8F+4yr7LPX1W6yKz0/8edQyjrROHAKksNn/vMJRBj8KKOuWRGtQBt9z6JTCtFaV2KQBxnFwssL20TgO4Su76LxCZyXewSb6wyegNcHWOm4cghA2gFQaXTeUnxzZKtVail4U6KJCeJ5t2haWvSu6sUVzdInKSsThJuZ4ius6pN97lXCjD3Clkmz1HdyDTYvLf/+xbVYG3CQgvHNAO8/p6gbhu3RljQg9zDzH3Rna35HStAZ8oemqGgfbt8NshVmVeHVDpzWe0nRPzpnNVsSv7BO+sk/qu5j3H6POZyAE4eEW0RvXWPzqPureCToKaJVGPLlEDxJ03dBJx8KaZhnBKzt0q5p8ukLUjb0ezyXc6FstplkGD45ZljXLLKNtWgZ76zhpABqCwGf/lX1WWUF+MkWXLVEa0tUt87MZnuNaKM+8IjgYUc8LXG0Y7I4IkDi+S/nwgiqrGE+XhElIEoUo32V6OsW0CoGiN0g4Orpk99oW/WFK3XZEccTNr9/g4v4pWVlxcLiPmuV0ZU28M0IuC8zFAjd0caXA8RxYS0k2hxilSYuaftuhT6aouiH97isgBF1WEX7tGurxJaJoqB8+pvnVT5E3XsP/5pu4sY+TBIhZRrKzRvzmNYrYo/joMfpyinz9ENF09F/bxd9ZA9f6LdXJlPzRJQpw0hB8l6gXoaoGlVf4oxjhu3hJiOu5iPCqKV9p/N01a8cF1PfPye6eWu0WR+JGtpet97VD3K0+9WSJG/pUkyVh2KebrmiXBVXo03ttFzf0yN95QKQNYpiQ3thGn0zJC0s2on0XUdXUqkNkFb3XD5h8cozTj5F5RTHPWY4X9IMQzw85uX/O8HCdXpwQaEN7vqC4f8HB928T7Axpqpp7/+lX6LyiKRsWRxPW7+yz/sYhXdnwwb/+CSpvGJ/P8OOQKPYJtWH16RnxjR1Wq4Jk1OPJ+w8JBgnp1pCf/Zu/RmuFaTp2b+5w8viCtVGCKmu237pOnITc/fP3EBrOf/UQhKBe5GzdOUB63suhn7/J4b5aE7601/PqwTPf9oVywucq8l9RGXm25Tf5+1+x3fy6ddM8O1R84W3zpff+tuPvHFyYl7z6qn1+u0clXoi+Xr75iyc3V5WO52Wk59HYZ+fRSvHhn7/DaNgnEy5qPOXWtV2mR5cUCrJZxu5owOJogtgZcPxvf8nu772BfzAiSOPPPtwYZOCz/co2x796RF3U7B3u4DoOOvQY7oyoqxqv6zj7+Ijt7XVC1yXvLLe6bGwJ83s/uMOyqJCuw9HHR5im4+D1a0jfZe3aNquzOTJ08Qg5eXiK5wiCOGbQS5gvc0a7awRpyI3Xr/Hg3fu88rWbTC9mdJ1tRDUYyryizSv+5j/+gm/9/W+AI9l/5ZC26SiaGl8LOiHQyjCfzsniko0bm4jE59OPH6Pymttv3mK1KJlMl2SXS9b31/FDj7PLObd6MYO9EUHks7a3TjFZMrq+xeWTCxwh2NgZMc1z4sgn3B5iZiV6VjDcGZHe2KGb5Rbe0CqKeY4P9OKQ7c0hXhoye3pJFUicomNtfYDqpyhprNMlBW3dEIYBWisaTzK6vUtzPCWva9qmZWNvw2a5XDCJT7A7IuiFTB6cAQJlDJOHF6zvbyIbRT5dsWo6rn/tBqcfH7G2NuDJ01N832dZQ5jGTHTLqHNY3D/DjGKiOKBpOhwjUcJAGDCKQwgDVFvieg7eVeVCN501FNLBkZZBKVAGpiVaQi0EVV2R6B67B/tUkyWdMUjfp53nyKugTMWWKrHJKrzKCg45COv8S4H0HWTnge9SPB3T3dm/cqKgu5yxeuce5aeP6eYrnMEm9PuIIMLxQ1RVoGdzdGeFxxiMkI7tzaiNIZQSYUDlJVpKvOAKtlG1aFkyXy4YXGXDllmG34IfBThG4TXQGehWBcHmgOV4xmBn42qCGosZrmvQhij0aJKQYrwguraFE/jWLrwUHmXNQhD5xGmIOp5ghin1PEMacDtNfTrD3+ijTudkv3pE/0evsvU/+T6zP/0V1YMLFj/+CLUo6H37NtoVyGGK12q8zR6m6ShnGXEU4kiBPy9pziZUnx4jito+T6OhaKnfe4SOAkQvJP7mTRb3jkiubeLvjJj97C7F3WOM0sg4xEsiBFjnTjqYzmL5pRB4nkfTdni9GD2ZU7UNjnaRUuK4Hs0qIzrcoXUka//iRzQXC6hagltbFKczVudj0tAj+cHrNI/PUU1L3TQEWtNWDZ6yfSd+2Ke+XNCtCi4/eEx8c5ut1/fxXsjg/a2WmC8GFS8KU33ZdH8OKfXstQPPdVJ024E2aEA3naWerBpEdqWK7nkWRiYlUihaDegOAh/aDqE1yWsHrN59SPDaHu3FEiMlsm1x1/vPxfIAuqqhW+QU7z5ESkn4+gHl4wucyDLjIIVlsdro4/QTyv/0Hn4S0T29RBrLNBW9dd326TQtOq8I0wg3DglCn+7xBc3RBByJIyT+9hA9XWGMrSY6voUEOmmAiX1c16U9n9ifvStx6xpZVLYauTEkf3BBELp4vYjSOJha4ekOczFnmVmK3vDaFuHtHdrQpblcIkc9u7zmViuHUFJooGnpRT56a0iXNfi+iy5L3PU+ST+meu8ROorwRhYG5PgukevgJyFRHDB9dEbh5Sz7iqJrqasWVTRcnExY2xgQ+C5HFzNuXtsl6FuK0qNPjwhCD2MMF+cTrt9Y5+TTI7b3N4i3BlRPptTjJcW9UyYnM8RmivIFF/dOiffXKJY2+eWNYg5u7+GGIUHkU2cF8TClPJ8w3FmHjSFaadTlErdVxGlEl1d4vos3iAhGPUxW0q1yos2BDb5jn/oX9yjuniL7Iev/8BuIyLeCd2czglf3MFnNqpigFjPE4gLCbyAdweZ3X6E5mYDnWgpXrZGutExxcYDBENzcJtpZo1uWrD58aqlctSEcppjE6gpVkyWibq3gbewTDHvEOyMbcwcequ2sPfAs5bjRBikF1bKgbRWXP7tLdLBuYdCbA3SrqKcrK66aV/j9GOl7JNc3UVmJMdDNVlTvPsXMc7TrQFmjTiaox+e4XYfyHJa+Qy8JCbTC3xoQvrpHcD638zVwWcyX7Bzs4nguVVERJRGOJ8ERdI1B1i1V3TB+dM7uzoCnf/0JZl6xaCq2X91j/viCg/U7mE4x+eSYqB/j767hDWIIXVxjGD+95OZr11icz8nrhmKWIYWgH4bc/4v3+cE/+xHT0ykXj8/Z++Z1jh+e4A8jRjtreHUHbkt2ueDj8xnSkXznD79OMcn48N/9kuHhBqP9DZLN/hcUvL+cDv9NFvJ5cf0KBvVZgvzlh36p4Vu8YFK/aChfPF58+arsa3O17QtV42dB0Bdd7ecF1/8/qFz8NuOll/nCzfm1Oa7Pld2/sLOwD8I+f/nlHsMXjl9ezBl/coTnBJimwdEwzwuyukYbw9q1Ea1WrEzHCMHo1X1mJ2M2hhEk8fMnrpWmmS55/V/9fQ6+9waLD56wfHDOk/ce4h+sMZss6a/1aIqKalGwEg6Tsymd7vjF/WO+/yc/YD3dYOou0LHP6mzG3u19zp6e4/gu2mi2b20jMJiFxJ1XeKFLPFon6CyOfnJ0gUHQH/XpaEAbkjhk3Co6T9B3PSbTOefHl4S+x8Zan/HxmGJZksYJ8+mMuAmIttfw/Yim6TBKc3l8yXD/SoDIQDpI2dxZ5+x8jONItl+/weJ4QjHL2bm2yexyyt7NXcJRwuMff2Sxp3mNCV2yWc6lEQR7Q6rLJb0gZO3WDkEaEt/ewQl96vvnFA8v8EMf3SmStR4XlzMm4yUn4zlB4lNKgckavFHCsq4I44DBujWUbVaxd2uP2XwFjmQxX1LNVowGIXJZcTHLKQKJG0d4jWJ5PMWPA/o3NlFZTVQqCt1ZcarOCu1lRUlbNTi+w+X5hIPXDsjnOUprtrf2uDy+ZOooemVNN5kRvXkDEXrIVqOljxx5mLykUx1+YDORsutwBz2cOIDLBiNAeY5V+jWG0EAruWrcdTDjFUqDl0YU88xW54zVNnD7IV7Yp5rl6FYjwgBV1Ail0K1CBwHaC/A8j7Zo4DJj8sv7bH73NjIMyD96yPLjx3jpCC/awDiOhVM1HapRCCfA3d7D8V2U6qzCcKvRvsSXNnjRGJqywY8CVN1hlGJeLumTEvkBrpT86r13GMU91qIBph8SebY3hGlG5Tj4az3SXu9zcBvhSIS+0p1xHfw0QhVWC2bzGzevNAg+M3vmaoI/n/ZaoycrGPQQgUf8yh7Nk0tE3eJLAWWNvzsie/sB/uE60eEG6//0u8z+/H3qB+dkv7hPdTJl7Ud3cK9twPVNZOiBMXQfPqY+XZB9fAyxh5GS6Lu3UMczmqMJUnq4QtAEHiwzxCxn9advI29sUxYV3qjH4LuvINMI8+AcWVYopRFa4Xg+dC04lszBXOmIuAYcZSCK7DYhUK6Lqw2B1qiTMZXRtK/sEFyz/SmqqLn8//6UnnAJttfJ7p/RlCVyrYdXNrhDjzAKcTwP14CarnADj/3vvoLSCgGEof87UWj97MF8OXX2Ik+7+Nwr87zKZsDCPDplxf5mGV3bkkgH0SqM69A1tqqjqsoGFEWF0zRXlRnQowSnF9GdThn86O+Rvf9j61wFAcEre5+7Vi8OKN57RHU6I9wcYEKP9qFNRCAESmtcT5C8vkf+9gMcoGs6nLYD3yN56xZeGqOajm5ZEm4Nn8M7uvESEXiowmqguPsjZBRQ3z/F6ce4o4SubNBSWn2Z9R7l0Rg6K57n+A5auVC3+HFANy9xK8vx72voDQJk6tMVAqFbTF6T//QTmvGS9Bs3kdrQHI1pT8bUFzNUUVttFUewFkeopWWs8lwXb+hSd5p62uCfTum9fkjluXiBS34xQzgOuuvQ2pCOUqTr0DvYoHd9i/6TMbOLGVnksvHGLe6+e4/JYkW/nzKII8qyQS4kWdkw7KcMtkfUXYfjOnR1i+4sbXDV2aboBz/+CKY5q7Im2unjJj5KWBrZ4faQk4+P2HzjgNmjMzb31wj6MU2W0xv2qS6XzO+dEoa+pY4tGyLfJRimCN8qUjtpSPn4AnU5t5XIOERpzeonH9OeTHETj/73X8UdJJRHY7rTKe00I/n6DdrTC4zrofMC9+YbiJ0dqFqKRxd0WYk7TCjHK7qffYLQBpIIKQVt3jDcHGG0Yf7L+8hBiggD2rMpzbJE160V+4w8ZD8gur6NG/n4SWQryFcTpssrurzG812EEHRlTTPLaDvFcrq0grdGW7az6co2+hc1gefQXi5oyho3jegenqKuthmjkZ2BQWKFWrPSPpcogEWHCENE3eHi4HbKVkhnGW7ToqcrPNdlbXPEw4tLgiTEcV0G+yN6WwMwkE/nxKHPYLtPtDPk0z97j0EQUYUePU8QpTHBjT3ijQFdVtEVDUppTu4d0SqFFwY2MVd3rE6nTIrCwnyNYuNgg2pRWnFLKfnev/g9pg8vSDb7xIOU8njC4sMjPjm+4PD163hpzIbrsJhleGmIbDrm98/JxyvG9864/YdvEvasVpjW+jlU/xkb3Wf++uc92OdL2pcMovkMJvq8ivFy02m+9OILQ/DFKOKr8m4YbUtaL/2oZ+f5Xdj7L4z/IsHFrxtffix/y/G8DHV1d57XgK7uttEYAx/+x1/CqiTsu+RFiTSayeOazhiifp+jJ+eEgUd/lFItSh69/8BCqR6f8+a//H2Cvp1sRls4A46k9/oeBsNHf/kB/a0RXhLT7yWURYXv+yS7Q2YXcwIM22tDzoVAGMPxp8doX5IMUyb3TtkYDvFDj9l4TpsVVHVLf23Aap5x/uicW9++RdcpqmXJcrwgSSPSOGJ+OiW9sUFnDEVeUq0KDAYn8Hnjm68yOZnQ6yWEkc/Tp2corbj/zl1ufPMWumoppgXrt7bR3ZSbb97k6MERru+Sjvq89s1XmJ5NqeqGTisCYyP4Mq/opTFtrbj9nddo65auaojjEN9zOVsu6aVreGnAZL7i5u0dZvfP8PuG9AcbxNcsq4WqOmQ/wtse0OuHuGcT3DhgtDVi+8YOZ8eXuJspzjhDhoISCHsxkePS3xzQ5Q2udPB9l7ZpyC4rojRGxB5V0UDVsmwb1nZ3UIsSNS+RvZAiK+mt9Tj65ITeIGHt5g5u6FEJyfRyRtKPOf/4iMHBOte/+yrVqsCPAuaTBaf3Ttg93GE6W9CmHrOzgvjROf1XttH9kFppTNuRJAmUFV2ncPohYpGjihJRCLQRqKICRyA8F1YlbVEiXQ9TtsTbQ0yg0UpD0+FLSXU8tg3wpsNUNekwhYGtTElj0KsCH+w5GwVNjdzs4zsOelnS3L9kUmvEIKKeVhAOaUqNF9hmPqE0bacs247n2n4NIejqFtVZdiPbZOhbpXADvnAQUiKkYLZYMM5WPFlMuDHaohOAFPzVvfdIw4hvOl/j5muvWV2NeU5T1LR5hd+LPpunz0boQeCBgHqWUeUN0daAepYRbPS+bCZeMKr+eh/je7S+h9d0+Nt9/M0e1UdHMF5Rn89Jv3mTWkqWf/4B/r/8EU4asv6Pv0V+74TFX35EdTzh4t//kt43rtP/1i0bXAhB8vohbhoRHa7THM9Yvf+I1dGY4LV9/NcOaO8eYzpFYKAOQwQGR2t4MqY5ntL0Y6JXdtn4gzdZug7tJ0d0eYUrhIUBNR3CWH2GNgjQGPzERy8ztBREYUhXVYiug7qxEDZH4Y+XqIsFbPYBg3QdgjjEvHZI9MY1ugcX9AIXJ69oBLR1i785RBQ17ckM+gGs9fCUYfDmNZYPzsiPJyTXNv9W682zWOGr6eA/s8vG8LkUnXnBbpsrVWCw3PldbVW5ldGIwEMYq8UgrhZ7WVl6XxEGiKbFcx1ax7GQu6YlPNwke3BK+vohAoGjAN9FAP7W8HOX161Klj/+EOF7hG9do/zpx7ZSLSw8Cw3OmqW0LU6nBPqKaviKzCN8Zceqrc8KpO/ZqgigtbGwrLIhHKZ03RJ3vUfxzkPSH76GnmQgBOXlArnRp5stEaczaJR1JmOr2UOjkZ6H0QJR1CghkKFPVTTI1McpGhzfw4QBYr5CdQr18ROEJ+l/8xXa0ynuNQvn0p3GJBH12Rgi73nTv5QCPctpHIkOXNonZ+Sei7M9RDoO9WRJdLCBDFKcRlGdTFBNi7u/RrJlKcXFZg/10ROe/uwjRocbNJ4glA6PL+eYVc6bh6/jtIpIOviRT1NoFnnBdqto2pbzx+fs3N4lOlijneecn08JPIfF0Zh4+zayFyI8l+V4QdyPWV7MLNzTKHwjiIyLulwROQ7J1tCuiXmFG/q4iY/XD2kWGaZT6LyGywX+zprVSFpLaZcFzcUcfxCTfOe2hRwBUgrKx+e4WyPaVYlyfGTTwuENjOfijxKEK0lubmGajslffEBTtXSLJV5R4e+uE33tJtkv7qIWGW2rUZ5HO89R8xwjDE7dMLy1g7cxwN9fx2iNxtCuqs/mzVUlb/bxU2Rhmf/KvMJtFdF6H5NVRHVrq+eznKp6ir+3bgUfBeQfPbHfp+ns+uM6oDUYgxsFGA9MGiHzkv63b+FvjVi9/4Q6b+m0wPE95NaA5umY5nhMnVV4nmPXrDAgHaRc2+jhbqbk0wzfcTl/cGZJQTyXaLBFXTbM3nuERrDqCurCwh6Xj8dc/3uv47gOsydjHr/zEHcYM52tSIYJi6cTxCDAzCuKusHd6dFNMvprPYq2Yzxfcv2bN9GLCtV0CFcyO5mwuT3iP//rv6LX76Ejn8dHF2zurtN0imEv4fiDx/hSMujFmDQkGaVQtzz54DHRmqXS9eOQ84+f4iYh6ahnm+f7MdJzfn0y5oVE+pcQUJ+zjeJLVYuXVim+dDyfc3l5Zk+vKha/MVH0svP+DoKN34FC9//4YaO3F//9bU/w7LCXYKWu3tbK8Ojte+TnK1rPp1AGFYQobfAdh8HGOlopdNdS1DXn0yWz+QpTNdRKEYz6zO6f2o9wLC43uIJcGGNIb25z4/feIJtnzO+dsHp4jihbsnPbFLqzPuTW125RZCXCc/jorz/koz97h34QsrY5pGsVH//qrlU9rlriJGXn9r4VEbtccXC4jdGGwXqfum6J0phbX7+FIwTZfEW1KtBdy933HxCGPjvb6zSLnMH+GvF6D9/3cIUEBMNhHy0Es8mSbFXw5NOnqE7R6yfopiVcS1mezJg9vmD99g6vfOs2D+49Zni4QV6UXJyNcVyH/dt7bOys0VYNJx89xYt8tISuqPFaQ308Z/vVfQY7I7LLBdU0Ix2liMi3WPpZwfQvPuL8p3epZhlogxcEFEoRphG6bgnWEuqmJWw1vThEtR3xIMZDIJRhfDymt9ZDKutQuZFP5Lls3txBKkNZlGze2rGZommGH/oMhglxFNLmNVuv7TM83GTx5JKnP79rMaJbA7JZxubGiHy8pJrnzO+fc/bhU6pFwf71XZwrBhukpNKGvO2onkwxjQLXNvtmyyUiDdGdQhtg0KPxPD5cnPO4HPPz0/ssiwxPSKLXDnCvb1uhurIhP51Qn03ppitYFLhXpXuaDq82uLWiu1jC+YKwbJGdpvUkjepwYx+hDY7SNgvlShpP0lYd9emC4oNjussKLwjx4hATesj1FDOKkaMEZ38N92ANZy1FuQIjJXSatm0tXaXnoD1LY4kxzC7H5PMlQZoyK1b85Ts/4zJb8fNP3mGxWnK+mPLg+DFDEWDKGiMFCmjrhtUnlrnki/PWH/UQrcJTmkArepsDnLqjOZ1+AepoPvNon0EiA48wDUl9F5YlXdOitSL95k2c9R5yUZL94h7pN68jfJfpn7+PrmyWML1zyO7/+h+w9gdvIpqWxV9/wsW/+RuaaWZNietYvPrNHaK3Dln7Z9+n971XoeoQsU97uI72XTTWQZOtQjounbKBoprlVG8/ZPqv/wp/f430D7+GvzVESgfq2sLFDOi2w5O2f6BuWpRrg7jGaFTbUdcNwvdtgqNtEMagxiv7+1PaUjNHPs3RBdIYuqFt8Jd5hduPCaKQ3hv7sNajrBuM6yINlE/HrB5e0K5KuvHqCqL1W5jlZ4/B6L+Fvebl2ORnG6WFD6i8ppmuaJYFfj+hniwJwgC3UxgprmiZDcGwj+P7GNdBPdNRAYTnEr+6R/PwguT7r1A9vLAOkAGDRkbeZxdlDMuf3sUpGtyNPkZr6llBJ4S1+4Ab+qAU3WRBtD1EX5EltEbjv3GIGwUIV6KNxhumPPMmTNOi8xqTV7ijBOE76MsF8VvX0POc6sE5buBTf/gY2TYIrsQUQwczDGEQ4/dSVKWssrjnIRqraSI6ZRWoM5tQaedLjGpxDjZRWtGscqq3P6U+ndL5HssPHtMuciuyFriE22tI34fAter2aUQOV89fwPGE+pMj1HQFZU24OcANPdCKrq4RvsTbGSAWBfX9U9sY7vvsf/tVvvFffZtdP2C9NlC1RGmEayD0HTZf2yU3HZOTMUopXnnjBn7o04sjEhyaoqY+vaBzBcaTDDb7RIHP5b0TsvGS/nqfMq+Ync/wA5/B2oBEO3C+gKLBcy0MR60KHAHuIMYLbYa/vljYCul0RXXvhK7pqM5mCFfSnM6oPjnCcyXxN2/Y3gcD7dGY7KefIjcGhPsb5O88RK8Ky/aUxji9hLXvv0L/9X3LSLbWQwxilOsglQ0S64sZxZMLVNmw/NmnLD8+pi1b6nmG7xp62wO2/uS7yGFKnhWUqxwnDjAGZj+9y/Lnd5l/9ATpOnR5xeDGjmXpOp4S5C3uqkafzXGr1gYAxlgIXFHj9yKk76KrFuY5SkiMkKgoxLgu+D5GSjohUVUN0znJzohwb8OSeUQewgE1m+PT0WEYK4V2Hap5humFGMfBBeKNPm3VcfTJ0RXc1XD+yTGp4yIdSYtGpAFZVmJCF3cjQaYhWV5RzzNaYbh8+wGrBxdoAcvxkiSOCT2fQS8BR6D7AW7oMOqlONrQVQ1107D7+gGm6TDasDiaIIVg7WATGbj84L/9I2Qv4PCtG9z85k0IHIqyZJBElsJda7o0YDUvaLOaR7+8z963btPbGTE/n/P0nUfkKwt1nDy95NHffMLb/6+/5sHPP6XJa8tu9ZJeM/FiUPFCEPEb5DWeVzmeN12/1NcVn/1PPItGxAsn4dd/EM/Mn3lugX8XTFHwO6tcvAwM9ht2gysM2gtYsefprxeOefGUv3Gh+8IOBpqi4tFff0IaR8xcl4NXr7G8mDFpW0bX9iiLCkcrWtcFbWk+Tdsy7KdEtaaqGppFYVWE5bPw0KCUps4rol7M7f/ZD9h4fZ+jP/uA7GKONoYmr4k8l57rcHL/hLJVDEcp8TDl6MExvZ0hq3lGb5DakqUxPPzpp1R5xTf/5Lscf/yUtX5KlhekG31iR7J354DzD55QXSyolaK3PcL1XG7/4A51WVMeT9k4WCd7b0mRl2xe3+Lk/cc4GtJ+jO40b/3gDY4eHJP0U8S21XYolgVt1+HEHg4S6TsUiwzPSO786E2EK2kP15k9HqNciRN4NJc1+WSFVyrO3n9C72Cd41/cp65qIsdjeTZFpAFJEpM9GSOVRvpWiIeqIV8WZHlFVba4gYvCIAKHYpEzX2aEO0OiOKRdNqzKkq6uceizmmXIVlNi2N8a4iYh3fklnRJURqPLGrdsSPspvUFKmZVopXEij05K6xikCa4j0UXD/s1dVmdTziYLoiTED33GiyWj/XXyRUYahQgp6QLJeDq3zoPqyKYt6wdbrKqKsGmRZ3PSgw3UZEkURYimo+00IqtZOoKu60jCiHc++YCtdITXaKsF8uAUrQ2eIxF+hGwbNNDlJW4a2R4Kx8XZCGnzyvZtOA4EHm1Z05YdLgIRBFR5hWw6ZByC0tB2+KMER0q6RYFnDNp1EFesJx0aKYxtvlyUdJcLmk7hbQ/xkpRWa5xViGegu1qsPVegJ0uU5/F0cobvB9zc2GGU9HAGKf/dj/8t/+i7v88wiLi2tUcYBPzVh7/kD4MfEfZSS2UoFEYImvHCBk4vzFchBf5aj9U8syq6swzdKTxf0FzM8Nb6cCVyZ7SxondS2rkpQK6n1PfOcLeHLO+eIs/mBPsj4ld2Wa5KUIblL+4z+P071E/GnP27n7P+e28QbA4Qvsfo998k2F9n8h/fQV2suPz//JTNf/pd/M2BvadSEGwN8ZXCS0LUJEdJCKcDVpVCn03p6gbpWqidIyUEPh1g2o56vKL8018SHYxIfvQa1S8eUD29wFz1WrRXvQ6yrJCBj3YkruOiyhrX81B1TXkVZPnGYOqG8v1HhK/v4e0MAUGwv8H8/QdM//t3CO5cx7+9Q3vvCve9yqgeX+L0AlxXQtOiWg8nDTESnEGMbhXZyZTe9c2r52IXQ/OyhkVx1QpzpZ77+TbAZ9XkZ9Ulw2fsXl8w50KANs9ZlkyraKaWOclNI7JPT9HGkJ9eEkQhXRjgYvugcCSN0kglcByDaqCTAm89pTmfER9u4qQR1ZNLHCEwCPzdddy+pfHUdQvaUL/3CGUM0fVNircfIMEy9RhD23YYR1hHbXed9u4pxnXQqiP81i27kLoSXXcEo56tNFytSfWTS9qr367pRajIh1WF9j26p2O0sNS7LqDaBhk4yLK1at+eJL21jX46xawK2p6P1Nqqs7sOUmn01Uc5WGHGrqiRjku4NsD72k2aVU5+9wh3mOJFPma6xDQ1emmhOp4TWEXwRU7y2j7eqrBVkLrCDHqowCqGa9dFLXLaeycoA7Lr0I0i/cFruGt9qnsnUDdIpaFTdL5H78YOcrqiRXP71i5N2bC8f4Lbi3AFxEmEO4rZ//4hZx89Id0d4ect85Mp7sGQcrIi9n3yqkb7ktnRmMHakLqobONxWSEURFdifUEa4qchxnNo6pZgFBPd3LEaSbPM0vlWLWItJbyxA9j+GMeRxLd3aZ6M8dZ76MCjGy/RZYub1pQfPQVtcAy4w5Ts/ilCadK3buKezxHG2OCzbimmK/rDBGctxZvlV44+CMeheXhqezDKhlZ6NGVD5Ai0lIiypbp7gi5b1v7gDerTGdXZjOp8Tu9wg/hwHXVFquHGAcJAdjTGvbKHcqNHWdv1oFwWRL7tR2qVZvbnH+Bd28QPHEQ/RVQNva/dINgd0U1XlHdPaSUofZUk6ydoBO3FnHZRUD+9RMQBXtXguh5ymrG5s4ZsFH4qcT0PZy1m9fSSaJDgPjrn2sEuSkKb1/Q2h+SOIF7vka8Klk8nuIGLLwVt2RK5HqoX0YYe2XhJ8cExyhF0Ega9FC0hX+WEvYD93RHtLMeNPfLpirpoUYnPxu4IIySLpxOCbYfqckl6Ywsp4PzuKTtfv8ZBVnL0zkO2bu3gjRLCS5/Ad1lVJdl0hUkC0IaH7z4gXktxAw8pBBefnrB+e4et1/Z4+It7tFpx5++9wbv/4W2mP7sLnSZOQgZ7a3hRYHWiXqBd/8zMvcyJ/S3KBC/zg68ikM/l3F6gxf1cn8VvWYn4HNPf33H8jmFR5nPBwq8d4rMIyTx749lZntHQfg7+YF78z2/kCH42ju8eUa4qllmJcByyvOTy7BLHkZydjFFtjVaaja0e6Sjl6dML4kFErx+znK5gsuLxp8cI4PCPv4kTeBYaVdUoAaYX4/geo69fJ9lf5/TPPuD00xPOxzO2DrcotaLyJTv7e4wGCY8/eMTg5jaTyzmXD8/xheTw2g5nxxdsbQxpPI+0lzBIYvpJzDTPyMoK14mosxrH9/j43XtEvRg9lzhNR75paLWmxXD68RGdsawqpuzwexHL8ZLhzhrNrCAdpgRRSDpM0Z4k9n0eTuZsvbKDLFpcz2F4sEldNXzykw9xApc7338dR8PBnUOyuubkwQl1VrJ15wDtuxRZSdGr6d/epjyesh5GdJ6HGaR0ywo/DtChhxv5uMKKQWnfJU4HnD66wAW8Z1zhgYMuNTJv0K6kFNA2LVv9PnWjkJ7DeDwnjEPcKGB8PiXyA8LYpapq1DSnnmWWLeRgzapyVg2HB5v099ZoFjlH7z7i2uuH9F9do7lYIHoxs3nG+OE5G7d30bFHf2+Nk3cesahaikXOxu0dNq5vMTkeM+j1GK4PiNZS5hdzsifn+POcMvFwXUHc73H2+IieF6JdoGkZhBFDHLZf/zbTqiCKI+q2xZEGpzNW00J1lvZ3aNVtF0XO++9+RITkzcNXkBupZYvSluZQrvVwFjld1VpFaNfFDwMapZACXCnQixztOMhRjCOlzToKqLOKMI6I9taojsY0bYvTi3AiC+eorhjE/Nij6zR+6NGpDl1ULLQmW8zY7m1gXAtl2dvY4Wt1ztpgjZPpBb3dayitUKqj1B11WVg9gzBANAoRarKTS/z1HsJzcJPQZo9mGe5aijfPKIRAoIkj11JmVi310SXC96jnGbpV0CrCrSHh4aZtNB3E6MBFH02I44AmCujGGZW8JPrGdcq7JzgGpv/pXdb/5Dv42wOm//ldwuubDL/zCvgu8a1t/P/lHzH/iw8pPn7K2X/356z9V98kfm3fqjMjEK5LsDXEbA1BG5pZRnhjm9X/8B7dOw/oys72BHg+oRSEV4rksqxQlaJ+OqUqGjb/6FvwE4f6/glKG4J+H5Xl1F2LZwyu52KE5Xs3RuM6LkYpXM+l6BS+q9AXc/K//pTeP/oGziCi/9Z1irfvUpxO6DV7hLEP20Oy0xmOgeLt+2RrEcO0h1YGkoDOlTRPJwxe32N1NuNzK9hvyoCJL7z4XK/FF034yzNEgqu442qoogatOT+eUP3kY0JlG9+7MMAJPNJW4QC1NjiOg8AglIWQeFrTaYN7bZPm7gmb/6s/pluVmPHyuUK8cyXAiTY4oU/2s09RywKx3qOZrqgXOc4gprtSXpdRgCor+n/vDbrHF3SLAg2YUUrv+6+y/IsP8V/fx322dr2wtpWPLhBtZyt1j2yPmcorwl5MoTQidi1LXGfFSKuswgt9urqxBApNR3O5wJECNS2QIweJwTgCUysEllmMWiMDF6c1dIvSamhoyJqW2HVwAp/oYJOqrPE3BuisYFV2hEYT7KzRZRbvv/nD11m98xDA9v44Ep0VCNdFGKv3gu8RvXmN+niKXpW4++s4g4T8nQe4jkBe2yQ62KCervBjK9QWuy7tEKTStF1HLwgIdkdMnl5w+eiMpmkRjiRMI7rlCuX5dPMVOzvrXF5M2b6+w5NPj1AGvvb1a6wNeziVol8rHKWQvYj4cJ1wZ0S1yPGNwe3F0HY2UJuskFrjbw8JX93DTUK8zQHt00vK0ynTB2c4s4zozgFiVRLsbWCkoHp8QbPIUQZ837MK6/MCRwiCUUK40WP283uM/+O7aGNIbtqgPNka0p7NMNJAUaMdB1wHOc9RjmN1kJTBTwMrorssccoG4UhWP/mUtm5QvsvwjQNLF+s5uFqj6pauqMk/eoIoG1rpIBqFvlLmbqUgjAJMVtmmbEBISXk2pzUazyhEEuDtjnB6EbpTpN+7jQbKxxcs5jlOmlB2mvwXdyGrUFlNnAb4aYQuarSQZK5LAISBR365ZLg5oHd9i/HjC3pJSN60KFeChN3bu5R1CW1Ldblif3udaVsTbwyYfHhML43BlwzXU8YfW5Vz4TuEo5jlyRx/LSYcJRy8dsDF0QWPP3rMcKuPqRRbWyPaxKUsa4QGL/I5v5giE5/933udbllSni54uPqY3vUNDIYurxnc3mVy/4y6U5RVzWjQQwLzqa2MCd/j7Jf36R9uMn9ySVu0jB9doDpFP0149Iv7uFIyGPSYn85Ibu7y6f/wIU3b0dvoce1bt4hGCdJxXjCCvMRBftmbV3CmZ/CmFxLxL9rJL5vTZ3oVv4V//Nwei5f703/HAsbvHBb10q/0rPJ8FU58tmy92PZivrw2ffHM5jfdsxcDFGyj6dP/H23/2WRJluZ3Yr9zjmu/+t64ITMjdZaualHd0zM9CjMAFliBBZZYGml4Q+Mn4Meh8RVJW5LgLgxrAIgBBpjGiJ6Zrp4urTKzUkZkyKuFa/dz+MIjs7Kqq3sG6NljlhkRV/j16+I553mev5gyHc9QlcZTkunpBMtxsCyFo+pEJmgGLNcxJ2cTCl2CgbPxgjIviR6fsxjPWZ/PgbpKKpVENQKy6eKFTxY43QbudodssWL/2g6N7S7hsIWHpBN4RFlB1QnYub1HmRVkZwv63SazswndXqvWf277HDw8IpmsODs4I+g1KPMCf9ghkRrV9WlsdFhHaU3+vSDBilKjApdxFCMuZFmjNCU6X9DsNkh1SWUJJuMZnufQ6rWwHIvUaDp7A/qXh0xHc3ILwk6D8b0jtrf7bFzeICtKjIHx/RN6G13WpuDmD1+hvd3lfDwjKytsISjQtG9sUUlouS42ArvtM9gbIGyFtBXKsbA8h2avRRplvPZ7bzIYdhGuheNYuI7NVqvBxt4G0oDtWexe2qR9eYDT9OvOiWORzyPOH52yHi1YXyhgBL6HlRTcvrrDtVuXSecRwpa8/luvs//Dl2hstDh87yH9RkD/1jbtV3Zpf+cajZtblMLQ2ewSNgNe/t7LLM/muOuMzXaDqqgoohTPd0mWEVIKRudTHn74gMP7h2DXmNVyFiOEJD+doNcxx/MRH9+7y8GTx3z85B4PyxlfLM7pNFpIz8EOnNqt1RjKUteyrWlGNV9jWYpWGLLfG3I2n1ImGevDU/7y8/fRaYZlW2A0he/UrXNtyIqSCKgaPkVZYrKsNlvq+Di6QlInxbLpM5qtmBcF0q4rnUaKGh7oORSlhk5IVpTkZcVqHTMbzVifTzibzalMSaJzMgds3yUvM3Ses9/fZDYfsy4TTmZj+o02geVzubPBZDbl3ukBruvghgE6KYjjlGixQnlOHR8qjclK0sfn2K5NiKDUUBio8gqrFX7pnC0kjm0jAp/lkxHxybRO+pMCp+GRW4pcG+wrG8jApTidUT4+J7i9W1fg44zZH7xLlRb0fv8tLMdm9scfUc6jevu+Q//33qDx8iWqacT4//vnnP+vP6GYri+U6V6IvMYgKoPVCen/k99g8//892n92ktYtsRSElGW6AuzNe26SKjhN08nRH/4V4S3dvFu7aIwlFFdBHHbbZRlUVKTuA2AZVFqQ1ZWFGmG77qoCwjN8qP7jP/XP8PkJarh4l/fRTg2RVpghEA4FvHRiHmUoAcdQq92claFpqBW9Ap6DRb3TiiKsnbs1eYZb/GvHXX7vv69Kqo6/mrzXMkPqLu/3xCtdZpTJRnPWvwYKFYpSZxQLCOa272ayOy7VFLSGnSobIVUkiqvHbeVMZiqJMMQlyWm5RM/OcfeG6A6IdV0DUlRdyIAeWHMZcqKahmz+PPPawnQ0CV/dEa4P0RZCl2UVNRQQ7vXxN4bsPr8EHGxHXenC1KSn8+xbOt5jHs+zxnQs1qUQaU5xekMLWXtleFYaEfV8TvOqKSAwEPmBUIpiiglPZkhK1Pfm7aFKjWi1DWPI07rxb6r0MZgKQtpWYhms+ZllIZkNMdreHR+/y1o+OTjOaodYpIMvUoJ7VoGuRgvkJ5N+uAYY0k6v/0a/m+9gu4E5Ela+4cU+fPTaLISbQTBS5coHp+x+Pfvkh+OKTyH1LYpJxHJF0dY7QArcHB9h86tHfq3d2lc36T7yiXswGf96QGcjIlPptgXXi14No1uC/eiSr9cxRhLcfr4lDTNaWx1UMbgGMG1rQHNdsDg9ctsvH0D5TnkByPMbF3HxcW6VkCartBJipmvMUKi/Dp5Wz8d4d7cQVweEuxtgGdTHpzXfIy8oIpSiuMppqxQLZ8qyYifjMjWSe1domppYpYJRVFSuop4HlEsE9afHyAWUd1p0gZ9wSeS/RaWgYYt8TsB0lLIJKv5RFmBs91Fd3zCb19j8IOXahd5KdBFSZHkKNdm8clj4s+eoitBlRQ1jC3NsbWh5bu0trpYjo1AYPkORhscQe3n0QnrhPovPmfyl5+THU3QGqyGT/jqPrmBoBnQ6DUQUuK0GziWQIcuVZbVJo6+Q2OVYCcZ69M56XjJ/OPH2C0fJyuxOyHWOuPBO5/z9Itjgm6I8l3ytCBZJxxPZijfIo8yoixjZQq8fpPFfE1lKxZVgdxq4XdCLn3/JjuvXKa52WK1WHL2+VOaYYjnehgjSGzYuLnD5iv7+A2fSgm2r2xiS0mV5pisRAlYjZeYUuN1GsRpTrqIyE3J2ckYqRSupaAyuIFLOOwgleTJ54dE4yU6L2kHPsQFZV53OsdPzpCAY1kUUUa2Ssjyks1LAw4+esKP/z9/xt0//pgiyf8GEfQXBdYvA/BX+Brm2fr5hZcJ8dVuxdcD7Td/wM8/9OIi/VcYf+uE7p8zX3r2ON+smysu/n9e53nxzV9HWT2TNfyFB+vL7ka2Tji7e8TBRw+pSs3aFAgB27tD0izn7Oicze0NolKjXAfbtlmP5jihg3Qk08WSQbvF7q1LfPreHZJl9Lxtb6TAH7RwLvCYSJ4nPhtvXmH9dMLkwSk6zhiP5yilOHl4ShHYdG5uYaSArERWhsd3D5GOTcd1ma5igst9bGkxzXPWq5irl/pI3yadrfGVhfYFy6zg0qVNNrd6jNYR/e0+44MzDOC4Do2Gjx+65HHGxkaHyWKF57coQ5ey0gijydMMv9ckejrFsSUqcLj6m68w3Bty+OkTup0WtpAsdEl7t088WtLrtVjPl7z2e2/hKZsHHz1k69V9xsdjzu8e4zV8glcHpMuMsN8km67QtiJohXUVTQhMVVdenEETnpwxun9ClmTsXdvh4NEJRoD2HOZHE7SsFVxqWUNJlWW465wqypivE4zWCM/C9Vxsz8YuNWrYZePXb1N+8BDteSgp2Xp9n3QWcf7+I668foXhW1fqirkUOC2f3hv7/GC3j5GC+fGEh+/fxxeSxTrBbQY4DRerHTA7n+D7HscHpzUZfKtHVRWIqqLIC5xU4Zia9P6jz9/lJF0ymc14Y/8lzqanuEbQbHf4ow9+whvXXiGJ1lztbtWuzUVFuY7404cfMM7W/Nab38cVikuDLfb7W2RJjNCafb9PNF/X3ARtMKu0liPshBhLUsU5tq2pQh8RuOiigDTH2+yRPDpBdhvo2ZoNSxGkBclnh1gYlNEsREm34ZDMa95E0Onw1quv09M9irzg7v0vSNOEyWJGNwyZLqZshA0+mxzznSsvsxF2+I3bb3H/8DFJkmDbDss0oqhyWo0WaRGhLAVpQa5LnFaI69SJEZgaK7vOkGmF8Bxkw8FbJCghEEVJMV9hN0PwHIJhh3K0xBJQVSXRo1OisyleVuJsdklGC1Tbp5iu8IZtknlEOVmTrlO8QRPlORS6YvGTu8iGR+d7t3A3u8z+6APav/MGTreBEZL277wGUpB8/Jjis0NOD84Jf+NVGje2cfq1n0GxThG+XS8yhMC/som/P8R7bR8TZaze+YL1k1O8qqorREqhpUBqTTJaIo9GmO0OrpRkdw+RUmKEqF2ChYSqxJICUVZIbfAti8oYsiTF2BahH1LMl0x/9JcUTRdvexPlO9j9NmIdkx+OSVYxIopxN/s1ETH0MOuMYl1XuPNVQjmvpTitXgh5iS5KlHT+s7vk8qJa+mW8vojvF/Kyz6P1BRSqlmK1n0fwKs7qGOG5eIuE+KMD5EYL3QoIljH5ZIlwHUyc1ETSZlhzoWYrrDgl15rKVjBd0vrvf4AxhmK2oixKXMuishXWRn3uhK1I7h/DMkbaNtXZAikk/rVtqj//jCDwQElMmmFttMken6PjDOE5iKrC2+rVCzutUb5TJxalrpXNBLW88ipBui7agJKC4mhE8J2bVFWF0BU6KcmdCNkKKEaLWlUuzZBSYdkKPVuRFSVWpRG2RZXlIEEVIC2B8W3iRYzeaONWoE9mSMdCeDZaglsZTJyzOl1QLZaEDR+hNcQJVaWpKoNrS0RlKLQgenhK+81reFtdrN98lXy8JD8ao5cJweUhWoERElkZrI0W/utXiP78U9jeoDIxjpLkCEBifnoX0Wvi7/QRrkVzf4MqLchP5+hhCwsokxZaKSohWecxs7MR7oXzdHery+kXR+zevkS+Trlx+zL7Ny5hJSVO6OButLBCF7OMyb44onIsmEdYLR+ZFWgh6ntNChovX4a8QJS1v44VujQuDcjOFzQ2OzWErSwopuu6KzOaUxnqwtJ2H2ErvP0hutS0jaY6m9WLytMFOspQeUJpckoE83e/oDyd1l5ZVS04oAYtzHINFVSmwMyWqH4bsdVBbbVxLQtn2CafRwTPvlepecbdEdpg4ozJBw9J751gewEiL3AcG1cJ5CKCaII5TuGBheU30O0WpBU6rygcC8cAUlHGaa1E1vKQAoqTGapZw2kHOz2iPMNkJSavMI7E2ujgXd8meXiM0SXujR3yjw+QpaZyFGVUkB6P6/ihJE7o084qNgIf2iGr8zlplrGYLNnY36C92WE1W3P8+SFu28eYivHjc+I4pb3Z4dpvvUyelSTLGKUk7/2rd7j+retMD8dUhcZvWNidANezaG33cBs+h588QRlNuNVhejRl69IQECSn8wu1RUMSZ5RGszydESUp7Y0OT+4dcamzU/NipcFCkBcZ2oJOt4Pj2jiWxWKyIDcGq+dxfjqhulBoLC1NJeDp/ROMgvMn52zv9vF6TdaLmPf+3c/47n/9vedFhxd87r7+yy9e1ooXfj577Nm7v75m/puOF177XL3q4sGfk8T9Lxh/68nFL9qfb8yono9fkCb9F2RPxsDsaMwf/F//Dfky5vL+HsN+n/PjcxzbwnZsTkczhjtDhsMey1UMFWxudxBpgXBUDd0pKiylODs4o9trE0/WNTbTc59/jecV1xeoIsp3uP6Pvkfz3Yd8+gc/Q+UFfsclKnJ86eBZtVJJsUo5PR3T2+7hVYJ1UWAFLp7vMR/P8ZsBVZQzuXfC9ltXyFYpWhtEWrI56LF7c5sszkij2rUy0JI4KtntdYjTgiIvkZaid20LzlyiKieeryAp8XPDdDynfXmDrbeuMRnNaHdbjMbHfP7v38X2XLa3B0zOZgShS7yKMWlBc3eDxAUXxU//+Z/R3K6rdp2tLsm6YLDRZXY8pbXdIV4kdFyXRVUSTZb0rm/VuuqCWlZvs8XmG/vMPj+m321iKo1tWXQGTRbHU6oohdAjnixRhca3JZ5U4Dm4zZCwLJGehXBtlFIkhabTb4GV4u/1sR+c0m64BKHP6POnJIs1u2/fINjuPldxMQbKtKBcp4wfnaGLimqR4AsLGdg0b2wTRRnt3T55nhO2G2SzhDAMKNYZYatBlRQ8+Og+V5oN8jhlejZlY3+TH1Rv83h2zvnTI4yuCG2P6zuXSeOIVZJydnwCUvMHTx8QBk08y8KTNlf2r2FPzzg6O6HfaNG1fexGwH/8+B2udIY4jkNHOuh2gzzOalWLsqJIc/zQQ18YAFVZjtYGE/poIaiWEdpWOGUNo/EcB5OUlEWJNAaUxBGG+IsjzhdTosmUeLnksxz6rR5SCdq2x+5Wh6Ztczg9p5lDaVdseA1EWZKsVvTCNi9v7/NXB3fYlj22dvfptNr1AsyS6DgjrwxlmZOXip3NTs2ZMBcqQVKgeg2KJEF6Dq4Ca7eHXqeAwO42MUZTjhYIxyIfL2hfHpIdjcijFG0MxWJN5zs3mH38hNIYjITGa5dZPTyFOCM9KeuKdZxit3wwFZN/8xPs7R7udp/RH39M8+YO3t4Au+XT/f03abx+hckfvkt2MCb66Rdkf/UF3u1dvFcu4Q476KyoOSBKPGfw+de2MEVF9NEjfMe6gDYZSqWwGx46TkEI4s8PsF+9jH9zh3IRYU5nNeFYa5RtU+YFwvfqYJ2XCF1hWTaiyGsFqCiiKnIs22Xyv/wBm7/+Q9bjJWUUYXVazM9mlGVJvoxwtrpo30Z7NsKxcDoB5AbdsmsSqgDbsiiMIV0lhK7zQgz/68eLc6C5uMkMwEVhoUxzbN/9MvGQF5VVeN7ZiA/GyMBB5xrWGWVeELZCqvM5VcMji1Lank1UFdhJjlNU6DQHy0J5Do500csUa9jF2exSFCXF6bxeqFe1P4Y3bNfJbKlJP3xEadtYtoIoxe6GF6I8Aoqibp0phXt1i/Rn92uzO6nAMaimhwYyCfLCdBBLQlV3F4SoYYOUFbLSdXdOyfrxvKSIM0xVUcQWji0R0yVmq4deJ3VnptKkqwQXgeqG5OsUldfddSkFVdOFeYybl1hJShaV2HmJURKDwEwjyjgnqu5QrAv8XoBe1bFAA1IJyjjDMxbl+QwVuKwOR6heg+bVLZTvYg1aBPvDi0LaMx6NwZR1oagYrygdFzWdY0UR2cETnMtXsW5eRt3YQ2UZxdEYnRbYnRCTl5RVhTvsEO4NoCjJ52uk69DNNumez0mXdRdYCUFj2EMkOYPtLgzb2A0HO2iiKo3wXZLHZ6iqQrk27rCNcS2KvCQ/m+Nf28RuBRSTWnLZ7jfJz+bE947xr2+iXJv13SMqNL6lYLLC3hng7W+yev8+ZZLjdBq4+0PICqxuA1OUNJQkSjKyg3Py8brucKVrCpr4JmFxf0qzG2DWMTr0qaRAa6iERRA46PUUqxVQSIE8X5DJ2sgxFdDYaCNdG2EgXde+JuFGC1MZ0kXE6tMDbMuhKEosJfHG5xBH5PMxyfycqkih0lhBC++175B2+qAUUlrkqr4xVVEipKD7xjXO7h3BaEVwa5t8mVAejmlc2wLfEC8iqidn6EGT5OExshmi45T10QQrrIVGhH3RcdOachnjDDuoLCe/1Od24PDoi6eYqMBOStqWy/mTEdEqpuUHBJZNZUC5Di1PICtDc6ONWefc/ffvsvdrtzj97JBBu8XRoxN2L+1Q5Sd4bZ/O3oD1aElnu8fDd+4xOxjR2ulhZxXStsCyiI5nnN87YTRdUihYLdfgWBghSOcxu9d3eOm7tynLkrPTY7pliZGC/LzCbYUUce0/0r88JEpSluMFVRazcWlIvlixTnN0nNIaNChNLSG+WkbMi4r9XoNWr8mDDx+xPpvTvlR7Oj3PEb4BDfWlRO03RNuvJxiYryQWRvxnGN99bW399ff9bUiR/y0kFy+mYebnuw3PnvoF7/0b5Q9/kxddvKYqK372Bz+lFzQ4mcW4rsNsPMNSkJcl09MJnWbAchWRZgVB6FGmBWdnM5ZxyitXrjA9PMdp+kxWa2wlCW2LbBGTL2J8z/3qx1aaPEpwGv5F4BUIW7H5vZsIW3LnX/4FZDnZKkYWmrTbpOr4LI7G7N+6hE4LdJ6TlSWtyqE4ntMMHLIqxfN9NIb08ZgkShlcHrJcZWxt9WheGnDy799DrlOO3vmCwU6f7WEHd7vL6cE5lZJEp3P8VLOerdHCsP/qVc7uPuXszhE3rt+mnEcslxmyWasMJQ/P6bkewnNIlxFpnGLHGUmSoYXh8aePuPF33+Lgw4f0fA89T7B6DZRr43RCmq2QKlG4rkPmFFhaYtKK1XTF7ts3kLa6uGoNylaElzcImwGLTw5rwl1Z0L25jd0JWTw6J1onXHv9GmWSY3UCTj54yP7rV9B5SSwMi9MpzYZPvErwXAVlheM7WL6DGziUQrA6n2OAve/dJBi0v5wcERhdYdKC1V894PzxGU47oEwKWpf6LM7npAqau11GD04JWgHp0YwrN/ZYjZZ8+sE9BieT2pPAwGwZEfTaZOsUpxkwDDvs3LzOo8Y9/vTDv2C0ntFZt0mylLJIOU1X3Lh0lVutFpP1nM3eBlGS4Po+r166SVlk9N0mH508JnA9fv0Hv8Pp4ZMaIjfoUi0jjJRoKUkrjcwK8qqqsdtRim6FqIZHuYzRFzAA16vb48q2KFcxWZERZTFPj47AVATKpmy65FHC9e42P3t8h9DYrEfnSKU4HJ9yY+86/SDkO5dvEsURRgq6zgYnozMuNwc8mp8gioJh0CbTmld7WyRlztlqQmlqeIdxbaxCILTCVAbEhVeFLVkna5rtNmtRYc9X2J6LU2isW7usn5zjCShmEdnxFHe7i2o3mD88oXv7Emq+RKclVZyyPJrQevkSizsHpMsIOwzo/PAl4vcfU03XtapQ4JEvUxzPwmoF9cItyXADj+U798iPpjTfvIKz0cbZ7jL8p7/J/MefEr/3kLLURO/cI/rgIcHrl2l9/2WMLBCe8zwyP5OR7P6D7zL7X35M9PAEu99BxAn5OsENfarlGvKS4pMDZFHivXmV+GyKFhItJNKqTaMKJSkMGNvClg4my1GWjS8tSqOx/RBpNMnkKfl0RioUTiPEdNuIoqAw4LablCczTDNEDVrED89qwzBL1d42SpAZg1zGSM+COEfrqla0El/jEf41oVprjaCGckjbqouvStZxEr7SwXhxlKsElMTtNWvxhG9fo/ppRR7nVIsF7AwxApbLmNCA59TxuJIC8to8r0JjFin+rR2Ekpi4JD1f1B/pOVhtH6vTqJPTwxPWT86RvoeqDKUB7/Yu68dnlGlW68NXNeSUypDO1lhKYlUVxpJ4VzZJT2YE/XbdubooogmlqNIE23NQtkUOKN9DpxkG0HGGt9mtC1oCinVCKjQiq/AwGMdCSUlVVZiswPZtinWGdJ0aPJYVmNBFxTlllCNdqz74aYaWiirLkb6Now1GQ55XGFfR+/WXWX14HzFaICpTW8c0ag6cKkvcvQ24/5TZx4/x2mENBbtIBp+bgD07V8sIu93Af32/7tB89gR/a4A97JGuMtyzKWpvA2u7z/rDB9jnhywnC3LPxe630auE9GTC5t/7Nq1LA5Y/u08aF7WAie/UcEPfQe5v1PCzvKQ4m1FFGVVWIsuKfHGKkZLgN15BC4HlOZhuQvb5E3SSk5/OCBo+Oi3IZyucQRvV9LG7TfLjKek6xg1srFZYczO0xtpos/zoIfmF70i1jFBliaMEyeeH2JsdpBFU0xVmHWOWGXmcUK0TpNulSDOsQQctqTsXfoDXaZIB+XSJmWcoqdBCYom6oo7tkq0iivtHhMM22XxN2GuRns8IdvoIIYgfHDP96BEoRakU+XSKNTpk8fQheC7Ot9/A3/s+ZZJRHJ5QfPIR1V/9Cerma4irN9FGo4VCJwUoC9tUZI/OaHWbzJYpi5/ep/m9GzS/c50iLaDUGEtgXd2kGM0pPRexjNFV7cGDtJiMFtgtH9n0sSZLRFLQeH2f9b0jVqdTXN9jo99mPF5AOyTNM/pXh8yfThgEIablY4UOy+mK1TpDWrW6093/+AFI2Lq2zePZA/KixFDxxXt32X35Ehv7Q8aPz5k+Pke6CisuaIY+1XiN8W3cZoCJc9Z3T1gvY1zfYXw2YfvlXZSQLJ6M0FkNIb3y5lWUpWi0Qw7ffYD0bLxc1R470kJZCi/0mC5WeL6NMYJsmRD4HrayKIwmjjPCTl3wW88TgqZLUZRkszXdrR7FOkWXVc2/eCGWPsNO/kIO8UUyYczXEodfkHv80vG3AHX6zxm/MufiBZbDL32d4QKnbF74++df9OVm/gsPRLqOWZ3PWC/X2I7Foy8OaudTpfBdm8ZWj4q6OlcWBdpolFNPrMqxOHh6RnThGu21AhwhMFnJhu9SXLij6osKW1VUGMAO6mqaeRFTLAXDb1/jzf/T32X7zet86+99l5uvX2V1/4RH/+ljzu4/hXlEQwuKNCVMC1aTJcVsTXFwTnI+Z2O7y+6VTbLRArvUnN17ioxSeje3cLfatY19L+SlH9zmxu+9ThmlHL7/AO2pmocAHB+eo6MMt9DMn4zIzleE2x1aVzZZxAmxL9l+6ypZnFJGKY3Aoxn6RKsEv+Gxszek4Tp0dwZ4gyYag05Ltm/ssHV1i2qVXcAAFPZGi36vxeTzI9JpxGSyoN1rcvO3X6Nzfeurp9RQ46w9C9l0aV4eEFgWx+89ZHE4YuvaFp12iPBtGlc3avJcaWhcG5JFKZ2rQ4JGQCvwa8WSfotsntC5MsQAretbLA7HGG249nfewO81KeK0NrRKC6oko1ynjP7yLuPjCZPpktXJjHQVkyxjZlFCoxkwu3+KYyCaLCmSjHyVcPr0nN5On8l4zuhsRrvfwG4HSNfG7jRqSTvLYvzgCZ8/ukMSR9za2ievSmzLZhqtUEIxWs7ptrrcOzlgNl+yEbRwkWhd0u30WZQZnuPydHLK3ft32Rzu8tab38a+vMVEGM7Pz5mdzRFpgeM52M0Ab7sHW12wJVVWICyF69pobSgKTbJKqNICrSyM5VD6DofpnH/50Y95f/yE0/mcaZXxzuFdvrV/i+t7+wzaPZqyXsh+9OAzHo1PcW2HdrPNw9MDjk6OeP+Lj/ls+pSsLHj34AucRsjNy1dQrsM8XrFar/ng8R3KskQXtTFS2GkhLFkrP11UuBu9DggIC7BdByEEydmC5NEZKslJD0fY3Qb2Rrvmrfgu1TymmCzJzpYkTydUaVHr55/Pad6+hNUISE4mrN9/gHN9E/fWDkZILCHxN9o1IX6RYK1ziocjymVE661rVOMlk3/9Uyb/6ic1kdxWdH77dQb/9DdQg1adLCU50TtfcPJ/+7esP3pUX9PGoMuK9ckEqgpr0KD7P/4Qa6eHiZPaLLCqSJZRjTN3bKwsJ/n4EarSBG9cr/kKWmPipFYFMoYiSUApKEqkVRtuPhOAVbaFUA45FuMP38MTFeraNrPZipVSJIGL9+Y+/bdfInp0xugv7mBWKRhw+01UwyMtChobbUoBVWXAUSTjFebCK+jF+Pz8zwtOhdGaIi++GrelQLp27ePB1ya/b9JilAIhBf5Gq+bWaEiyEhH6aN+i99o1mv0m9laXcNCsrw8loaowaY5UAuHalEmGMBrvyiZIQRmliLK6wLTnqG5QG2+VFcu/uo+yLhbmZUlVFNjDNlxwa54XBls+Js1xLr53aQzSd5ANn/x0jjNsX0joXtTXjEbZFjqvKKMEU1VoXcdJKQSWX3NapKwTSFVpXD/Acp36mCY54qK6nCU5RaUpjAH7glCsNdqz0aVGWAqhdW3UVmiKPEdbApFk6CyvTdDynI1vXUE5FsK2kQiM5wC191KeV5isonw6xtsa0AwcVu/coZitLzq9XxZlxMX5s3vNWkGuHdD64SsEv/VanVgtU4KGh5GKahFTPp3gWHbd4RktsOMM/eAYs1zjBi7pwQijwb20gV6smT0eIbIKKkOw1cULHaJPD5i9c4foeFLLLWNIZivUoIW7P0Q1fOSFwZwIPawKvK0ewraJH5yAa2Nma5Z/8iHJ3UOyC9M8Ag/RDtFpTnY8riXEk4xqEdfXnqjV9YJhhzJOiZ+OkK2QYhlhihKRlui0RI9PahPU0KX0XBxL1r4aRuC2A5ybWzRCh41ffxk2O2jHpqrAJLXXRhUnWI1amW9275hktMJIQbg/xPZdyrQAJeumWGUoMTjTE/L7H9Umm7e/hTZd4oOIYqyRwSbed38L3d+gIsG9OqSsKhzLQhhwmgGVZRE/OIYsY+uNK5TjJfnBGOW7BJsdgs0O3kaHqqpQnQauEHj9JjYanZckUYy31YKywFrH2A2Hch0T3XuKM2jR7zRpXRqwfWOHXughq5LOsI0lobfXJ/ElwU6Xux88II1SNl+7zNv/9DdrZTpH8vY/+13spk+UpfRe22P/pcvsvnaZl3/4GiCInk5phgHpIkZVmkJXNHoNpGMxPZ+yHC05P54SS8NstSaOEowSWK6F6zpIKfFbAet1TG9vgB162E2fEkO31UAUGtu2ar5LVRfllG0ReC7lKmV5vmRxOmc5XpCO1qSziKoo2drq4/cbFBgmi4juRpv1aMXJh48p01/Av3iGfhFfI1c/RzuJ5y97Jj3Lz0XVn08vzM/98gs+3nx1Rf6N6/P/zPG30Ln4WqviG/boRTTXf3an4pe84UVVqWe26sU6RWiNozStjQ7K82i2Gzy+d8DO/jbRMqIsKjY3e8xXEXGc0myGJPMIx7UQlWHYbbHOckZnU67tDGl1GhzcOWD2//wRr/+T36Dz8iWMVM8vAmkpKDXZZIk3aH95TIQg3O1z/fIG0pLk8xh3o8Hq/in3Hz5FAtu3d0jvlqRpzuDygL2XLzM7HLHh2Oz82m2Sh+e0b2zVrfiiJNjq4O/1QUp2f+dVtr5/k+R0xuMffczp41N008VbOihX0Ry00RjcZY6QsiaQN0NWDQvLteld2+baW9eYH4w5+eQAJ/ApgXi8xOo18IUgvNzn7NMVYegQXh6QpFkNY4hzOltdludLAmWReTbrkylb377GYLJiMV/RG3bo3t6hcXWjXlA966hrgx06uE0XpMTfbGMMXN/uMPrwMfEsovnqHsaSjM5mdPcG3PvzO1x6+wZW0ydeJ4RlhSgq/P0B6mRCOlqChmCvj1CCxqU+N//Bt7GDCxy0qVVhnvUjjYHF/VOO7p+wXEZsdBoMr22RAiePTvEHIeuTGduXhmRxznSxYn4+Y/HBF+xc3aEx7PCXP3oXSyn29jdpVJp8ndHc6TJaTJk/esQfffEeqS64srPP2bwWEmi32/zu27/FZHTK2XrGncMHBI5HXMRERYN1usQ1ClPW6l+fHj5gt7tB13KQcYS12Ye8YB3N+Pjxp3QaG7x8/QZNS6DPYozv4IQeTuChHIv4cERWlsh+uw6eroWQEl0WGCHpt/r89utvs9XZ4GQ15iyaYoTg0fiUGxs7fPT5Q7Y7G5iqoumFCCH49P6n5OsVJYJVGnF1c5dXd6+SrtY8OT5Ei4r3H3xOkqb8xo23OFlOeXD8hHUeY7kOTlGBbRFewHCeS/aVFVa/wfrxOY7jIHStDy8DRXW6oCxr/ohxLKxSo+MMq9/G7zSI750QffaU51Wg0MUZNMjO5shWSO/bN8nPZiw+P8B1Ldrfu0E+XZMdjnFaYa1GJQXFKsaaLigcB+fyAJmXxO894OTTA/w3rtD+7k3cSxsM/skPmP+nj0g/O6gD8TRi9R8+YP3eFwz+h9/E7jVp7gwuvpvB6jUY/h9+m8n//OeUx9OadyVkLUtp2+gkqauTf3WXxg9ewT3poo/PKS9inClqiUnKEq0kyvexC4sUg1I2pqqopTg7zMdPCU5PGf7Wt1hUtcTt3quXae9vkB9OaC0TUl2RrXPiZYTdDghCj7DhIS1JmheEWS3XqauSMikuzpNA2hZVUVJFKXYrqGWRjaEsSpRtfzkZXpzT5xPl1/C9zxaoXx/StSmyshYZcMpaAUyAh2C5zlFK4HcaVMdTsrhecFVlieO7ZFEMvo1TlLDRxhl2aqNCKVFZiRECWVW4m10whuj9B6R3n6IqjZQX58K3EY6NyIqa0H3hFeD0WmTTJebCpV5mBWp3D6EU6ZMzWm/f/BIOfWEIKJSkSlJYp8iypNAG5XsoDLLbIHl8TiXrfZIYqnWCKCqU0WRpBt0WoiyxigKlJUZZiLKiSjJkUWK7NrqK0VVVH19L1rQWKfAHbbKDMQYoygLLqrtBy4enmKMJRZSQNhtI28ZVJSarFaDKKIF+i2K6xsIQ3zmg9fZLCPsCL/5idvn8pF0kha9ext4bkB2MyH72BSBxrm8Sfus66dGE7LODWn2r0KBACoFphwgN0aMzlGfR++5NkkWE3/DID8ek904oZ0tKAyJwEUVJfjRC2g4myqhmEd7VrdrIzKqToCpOyUZzLN/Gv7qFCj3i9+5jbbQJXr3C6JMnpI/OCVoBVeCSHp0hk5rnYwHEGf5WH2u1plJgGh7lOqFaJsj9TQyGqiiRnQZ6tAadYbII0e2Ca9N0LLSuEGVJJQ3udhd3o81qvMDpNgjaAdEyQnk1z8hphnXXfB5RrNZo3yGNUqYYmlc3kUqi8xIVeDSv7ZCPvkDZFvLyDUR3Ax02EViUsl44V6sI4booEyBe/h56q016OEWUpjafFAKtK6qiwJIOs48fM/i2jfId4rvHNBwL+9omeZVjGh664ROGHtUixu6EuJsdkk8PsLQgTzKCqqLKCqqGi8BQrhNMqXGvDEknC6RjsfXqPq3zBdN1TKYBR2IcxfThGbeuX+J0Nmf7+jajJ+ec3T/m2vduo4zg7p9+zK1v3WI9XuL3Q67feJmP/vBd8jirY45rkywi0tmKSoKFIM1z1suIL6KM7m6fZr+NmaxohwFCCMJOAxsBvsN6HnH48ZNaQtp3aO/2WZxMKOOUxWJFoxkSHc1Yr+La5FBI5rMVaZZy5eouEsH5bE6n2yAp6y5taTRGKCZnc6pCU2Yl49Mp89GCb/k2W69c/vm17C+ANJkXzPCerXHNi3H1l41vgF19E2eDX7i9Xy29+JWTi1+a3zzPxi7+/grt4llvyHxVWusrb35GLjHookIq+VwH/cXnopMZTstn9eickz//HB+FDGyqskRKwfnZpF7cZzk6zynynLgsKcuKQa9Dr9/i4SpGeDbpLGa5iomkwXFdTFFx+OAIOiHpKuKT/99P+eGtPVCgLHmhSqUp4wxdVVhxWu+ZUqgLB+R8lSIdhXQsNn7jZbZ+81WuJnlt/ha6DP/+W0CdpAgl6X/v5vOj4PQa8GLl6KKU9kypt5iu+eD/9ScUq5jGVh+74bGaJwSXeuQKlBDEcUY8z7n66hVk4GBRYdmK4f4mRZxx+Kef0gx8hO+xXiVMVxGXrm7gVgYtBessY/LomLAV0lGSMPBQSUnzypDWyQxRaYKmz/pohgC23r7OsNK4/SZOy6/Jjc/Peb1YUs6FgdWFIZ2grqDu/s5rdfvQkjRvbTM5GvPkx5+y99o+nVcvY8qaFDv++AndzS7h/gZb84j52Yz+K5dQvnNBRpI4raC+tuRFrq/rz7Ncm/hwwsknT7jyw5e582efICxFlpcszxfEeY5XuCxOpnSCgPlsQXOnJjUn64Q7nz7gpnWTV96+TbpOqKKEKimwh13yOMPyXOI45rXNfZaOYrKY8Pr+TT44us/J9JztRg/Hdri+d5UsTTicnhGXOUo57Hkhj+fnWKnieHLKIGzyxfEThq0et4eXMFqTHp7iVoYkjanWT/i8yLh87Qab/R6y1LUrd9NDKEmwN0ApSbpYo89n5LlmvozoDtpEWlPIlBKNb7scnB+z3e2z0erTxKYbtnnnwackWUZS5AhLsbmxycaVy/zxx++TZxkv713nT++8x+bGJlJXPE2XfOf2aygjuDzc4/H5U9arBYNunyDx0UogHI/J+YhOM7g4V6Im50uJ02niNla1o1xZQV6QCIPX8BDarhdAixirE2LimtjqdEN0UWFttBBxXjvALxPwbAyGLCsw0yXOsEP/0gbF8ZT1dI20BMFrlyieTsnGS7QROL5DmRUkJ1PUgxPU5QHBr93G14ZqEbH4jx9SNTza37pO7x9+l/TlPeZ/8jF6vKwryodjTv/5n7D1v//tupr9PLYJnM0u3X/0a4z+pz/GrBOUbUFeUukK6XqoqiQbLRD3DgjevMo6L+oFVFFhggA7yy94woKqKMAYAt8lsRTlZIbEYAVNWsMr+N9+lca3rrF/ZYgfeMRpRppmdN66grPb5/zfvQ+BwyovWNx9Snwa4t3YRAUug2tbFGdzqrzEYCiiFGlJrLA2hqzPU+PL7oMQ2J7z5UzwHCH7rJrw4iTw9fnu54tTOisoswIhBV47QGx3cVoBeZpjThdkpzPyrCCPY5xmA6krdBSjbJtqnVJpQ7A3QAtRq6GtYnJjsJXCSIG3v4HOClbv3MGq6q5ZZagN9na66CTH5AUKqKpazU1ttMjef0xVlthGUiiJM2hRRQkmyWsFJsMFxE/UiwUhSA/HlHGKUApLWWigshRuv038wUNEVV0cAYO8gNGZQqPLCqcoEZ5NNpmT+x52L4DpAgxYtoWi3mejDUaBFgKkwFKS8nSOQSCExm36lKM1k3/9EyohUEWFcBRM5nhNHxP6BN0GYOpOw8EI5dmYOCP/4oRko1vPva6F3W3WwiaOQljW13DgAgkEr1wCz65VloqK4mwBjkX7736b/NEZq08fI7VEpBlVIyDPC/KDFZYtCbd72EVJ+rP7JEUJUqIu3NmtVkg5WyNliTEav99EbnVxt7q1s7utMFGGiHM6f+/bFKdTsqMJ4SuXaXz3FsV8TZXmhJtt8izD6vj4W32W4zn2sEexWGNEHY/s2zu1f0SUEX30kNWPP8G7toO8UCuUtsKsU4wUZA8fUCmJ6zXQlWY9WxGGNoQOelVSnkzJELiDNvEnj/GvbuPd3GX5+QHx4Qg39Gn8+iuUsxU6zqiihNarV0kXa+ZfHLHxyn4t190OCD2bxedPMXlF5boYZ4guS1wE0oBpeljrNYaKLClQrk36+SEoC2t/iFTiOSTRtq06WdSa9UeP0I4DpWH93iOk71AaQ3a2IGg3Uf1GLbX9/n2cVgP/lcusP32CZbsIz669PObr2ndIG6oko1onOLt98icjGC/wbMX+zT3Wi5jlOiKJc5RSxEnGcHeD40+esDicsFxHBIMmB+98QZbklIsMWUHVsJicjjn7/KjukhiNqEqGm32maYWyJcJzqJZLkqKk3Q7ZuLbJ+MEJYeAxX6+ZjudsbPaRSlFlGVLA9HTKcrzgpe+/xPDKkHg0ZzxZkFIxGc/xbJv5KgK3ltXNdYnbDqm0YR0lCCk5OZvS3GyzmCxotBuYTOOFHos45cHdA1xL0mgF2BfCFV+PgF/BAH2dd/G8HfrsDX9DQoT4yvTzZbv559rIX8beL1/+N/yMXzL+1gndv3yfnvlgfBW7+ZX3fgNWqljGzO4e4fabNPdqx0hjDOvJEte2KUZLosejWmVknbHZbKFbHpPzCYvRjMC1cH2HLMvRQtSKNdpQlZq0LLnzyQO0JXErRbDbozKa0LYR7YqzyQoROtgKlOPg2Tarw3OyecTwO3W1ygiBChxc18ZybbJ1Snw6w2n4uK0AXZTPc6kiy2kOOrj+l0RJdUEEfLHyZSpdV760AV2xnq7wAhe3GTw/VgIo10ntMColl7tN3O0uyy+eUhYlRZrW1VAqrF6IoyTL0zmD715jNV7RGjR59O4jvGbA5u4G8Sxicjph89IGYTskPZ2TL2K6g3ZNAhOCYhYThj7lOkN1fPqXBjy5f4y0Jf1hG6sTYDBYgY+8MDZDX1Qr5bOf8sKU6+K2ehbvhECoWtkDwG74XPrhK6wOx7SubpJOlwghaO/1WZ7PaN7YxAjD4O3r9PXFduUzuIWpKz7VhdOwrrev85LlJ4ecfPwEK/RI4pTtazucPjwhPhrjtgO6VoP10Zx2t8XT0zEbVzY5e3RCt9tm/6V9Th4egyXrQBEakvESopSsUdAKHQLHIwoFd48nbHhbpHmOj+R6b5vhYEjHb/DSYIdRvOL90edcaW+w198iRDBZLxBFRavpMVE2zXaLfn+D67vXqBo+2TRCCBh6Lf6r229zXqT8T3/xb3l1ccp3b77BxuYOrm2TnS/qCS/0cPst7I029lYPNVnXePvVmtH0nE7YxAt9pG2hhODqcJfFZMI0WfHjBx/Rb7YosoydjSHNsEUuwbIkP7j6Ck2vwU5nwJ3jR/zhZz/jO1du8zsvfZuXr9wkyjP+5bt/xNWtKzTbLeIkxtcuSZIQDro0up2a5G147qtm8gLh2DihT3a+qDHUgYcvoFqltZ9BrjFVRiVlnTwUJYQuwY0tGrd2WHz8BLFOSB6c1k62swjHsyjjguKLs/o+3+oS7HZZTyPi+YxGO8B2VO2ifJG4ePub5A9PST49IPr8ENVpEFwZ0nj7JvH9U6b/+qfYO116v/UaW//s77D49+8S3z9FuTbifMHkX/2Ewf/4m9jt8PmdbcoK79KA7t95k+m//inECUZKqgupWIyFU2mqxyPSMMC+uUP507vYFw7dBkNRVnVSUhZIBFWWY5cS4zhoakWpZjMkuLKDKCvaVzdJn044/cvP2f3t1xFKUhqNbLhk0xUNWXfJdJpjyoooSjB5hes7lHHtoC6VBNdCtsMaImN43ikRSr3o2/SsXvTlNPCMW2FemOm+Mjm+0Iov6qq80YZsvqaKbCxHYQcuquFhOzbL+6fICkxe4rh2vX3HBSXJ8qI2FlQK7/ZeLdMqJVWSQ16ABmfQxB52WPzZJ1Sny5qTUZaIuIacOTu9eoGtDZalsLUmM2A5DiJKUULWhQpZFymK6Qp1aYDda1LGWR3L1ZffU8+iuiDy7GtWGmuzDbaiHM1RtkWR5oiOj04rtKjQStRdiSzHJCnKsVHdJspRlGWFbIWYrESWGgnYSqCNJk5jgjyHVlh3xVQNmVKFhjiHZm0QJvtNLMtCeDWnxJSa9SJBOormbp/i0SlCecjdPuL+CckHDzDGkK8SvMBDN1xKbbA7AcHeBpbvYg+7dWerFWCKiuDykNRzkEpiMOTHM0SU1R3xG7tUT86h7VNoEEktRVycJ5gn50ijQSoc2yLTFXoVYXsO0lUoYTBFhQlt5HaXUkiKKKU4nqB6LSQCy7MRnoO6NGT9xx+hs5zm7b06KbAUTjvEevkybuhhSo1/eUhyNMHa7mGWEfkyIfrpHYRt4Qy7WKGPbgT4r+4TPzxl8eFD3EELU1bkZQmVxgkbyGYtbCE6AdKRVPMl7u4m7q29Gu5SVHiXNqiyHKfbo/nGVbLDEZXrUEQp5WyFVALV6+BeGeIWfUZ/9D6xbdF4bZ+y0lidkMH3bzH5yRcUpcY1hqioKCxFVZQ0ck3Z8JFNDxlWiLQk2OqTFxWebaGLAmUJxHyN3OnDeEH3jWu4O32Wnx2QTtasc035F/cQbQ+zTrG6TdZ3jwivDnE2OxTTNe6VIa3v3iD+5AnGCHSeobZ7SK2pxkvK0pAfntE0FeGrl9AbHZLPn8IqwQtdqCrsrEJbkspx6RcZcylpNMNatak0NIMAaaBKC/xGQKwrVkcTtnc3mCUxuzd3sbKKVZwiMRSrjEVSEi9iqrSg02syPhqznsU09oboJKLZCFmeTFFSYjsOOsoIrBom+PTeUy7d2CXohDx9dErYbTCdr4hWCVZgkZ2lBL2Q3lYXy3U4PprU595VQO3BRVUxvDLk0SdPSNOcZrteD/mWzZXX9mludn5+zftLxlcLNBex9RlS5yLG/LJNGC5c2l+MuS+usb/WyRC8oNz6K46//eTiYtSL7m9+5hfu9ot8i2dwJwPrpxOCfpN8HrNiTDioXXpFpTE6x+4GGCXJVgmO51BcKOVEacF0Msfb2aDMShp+rabT3OpzejKmvd1lfjyl121xdjohvyAqFcbgNAxVnNNwXdK8JC1ypDYEjsOH//f/gLYkVjugd2MHqQR+t0kVp5Rxih16iOmadLrG9l2kY6OcWkIw7DafqxXxDXOsAcq8ZPr4jNZmF6fhIQBlKZRrU6YZUqmLyj8Elza4dvtSTWxKC/Q6RS8TGleGlArOn45RgxBX2cxO5xRth/VsRZqktHoNLCFZjpaYYY+qKPGbPuF2hzzOKBYJjga5ymkO2zXuOy9ZzSN8R6FtRePlHdqrCGNL9n7nDaRbY5mB5xwbU5XUMAH7AlN48fW/qWVnXsjYlcAfNPEHTRDgdgKM1ridkH5W4LSCi1b4s2NYZynPYHhIQAuqvHquA/3oP3zI6ecHDK/vUFaaL965i+c5lJZAdjzyKGNz2EVqg73doS1h+XTCsNdh59V9siglXsU17GuzRyfwWZQavxkS2IL+m1eIHxyjcs2bezdJTcnNl7+NMQVN1+ZgfMqTouKz00e03IDNoE2JYTKfkvo+m70h7bDFeDLi9uYeh6s5b1+5RZrGPL1zn6uDTVToIm2LRqOF73XotVrM04RHxwd4pSZs9kDVSeVkdIJz5NHeGNTwMNfCGIHtO0gbijzh4Pwpnx58gW+5vPPZB3iuR5FXnM7PkAJspVgmEZmS+G7Ag4MHhJ7PyzdeIq5c3j26T8NySbKMa70t1qs1cRnz+PyY3a1dFuMxm/0NtOfTHPYZjUa4nodJ82cA9bpb5dj1om3YJpmsaix4WVItEiQGZVlUUMt6Ogon9JBuTVRHSnRcK4VVeU6lDWVRIPOSKsnxX9ohv68p1inF8Yz0fEH48i5u20csU7TnURqBTY13zx+fY221MUVBNVuhoozkwRn5o3OCb1/H7t0gfXTK5J//Gd6rl2n9/e8gBg9Y/PQuyqqdl0//xY/Z+qe/hd30az7WhWZ5+K2rxPePye48xViqlp7NayxuVZYYJObzQ9zffA170KIYLXDTHETtLi0uzOREXlCVFXalKYxGOTaB3UIpiVVqyukau98kizKKoynpZ0+xhWT56JTmzW3ynyxZFilulBNojZ5FyN0uaZLhOiF26FEWBWWS4XXDCwiqoUzyepHc8J7l8b9gkvwavvXrk9yL9zzUzsDtAJOXBP0W6TxCrwpE0wNtiMcLZOBhVjEm9Kg8B1kaZFmTqx1Re2aowMXbG6CjDB2lFGdzVGVqP4lOSPLwlNVP7uEIasK0NjXcCY2/PyT++AnCc2pfEimxfAvp2cgLydlKG6RS6Dgjna5pvHwJux3W3Tf11e9XFAVCCLSqq/qiqvAuDyjP5lR5RZmkSFN7DOTREsd10ElBlRcQeKhC10lSnGLt7pAfT5FZXi8CPAdCD72svRSyp+d4fgslRe1F4Ioa2z9Paodox0EUJdnTGabhI5suRkiSKMXrtciXa1IguLlL/uAEWj7y8gbF8Yiq0GjHolCCfB4jem2q1FDeOabKC8J+A3e7hz3sYLISq9eAokS1W1jtBu5On9VHD1l/8ojeP/we1aAFlUYtIqJHp4Seg9xoIY1BdZuYqiJfZVSzNa42NaTneI70LfR0Vauz9Rq1Ath0iTNoM3/3ATQDGg2P+HyGPWhTCol4Oqbc7KK2ukjPQama51WtU7LTKSr0qM6m6FWM7dp42z2qyYpitsAA9mYffTyt/TNWMbY2qLCWTzWWhbx1G8uxUEoibYXTC+F0gl7FNN+8imgGtW9GmmPyinKyxN0bIBwbf3+T8dmcMCtwLw1JHpwg5hHJgxOM61A1fJL7R1RJhn91CxOlKM/BHTRQSYZZZ/iWW6t+lRJ0iRu6tbiA65KLFJQiUHVB1mq42E2XaqnA1Oe0BILQw7EtdMNB5zCPMqyzBb2XdkmXUd3FOhjR+vYN7NYKU1a4Wz3sXov40Qm6LJGOQz5ZIRouVlZQRQnZ0wnJ4Yj2r79Sc50CD1HVMV8CYinJspxCKExasFitScuSPMnIbch0BUYzPxlx5bXLHN05wOpYSLf+t/3KPuUnjym8jHQRE61LpFI0PQ83cJGeTbUuMEDQ8AlsRbRMWMcJk8kc7VmEnkdRlpw+PK3XeJ2Ql95+iSpJOTuZMZ0u6BQB/WGXXBmKtMBSCt+zUQaCdsgqTsizAq8VUOQFDcclKwoc38aqBPs3dynzgqcfP+baD176Mg6+SIp4IXT8fHPiIn7+LXQUvr7Zr/75qycVz8bfbnLxvG3z83mPeSFzeEZGMd9ohc5XOxjGIKUgO5+TjVbIssL2XdyWT3NvQLlOSQ/OKZIcr9dA3NzGpAWju4cEwGCrh+u6GFUbghlTMT6b0mqHZFFCGPoEoYef5xSrhJ1+l+OzCevZmkHYoBV6rMczvGaAVJKnRyPssqCsNEfv3KF3fef5bivfrSupUuB2AqKTnOh0jtXwSNcJlq0Q65SqjLEvnJCVbWG51leO3+Jsxn/6n/+YeLTg2uvX2Xt1n92XLtUIIsd+jmcGkKHLzj/4Nta//4BissIRAldI1g/PcDZadBwXqxOwOBhzOFpwafcGVVYQT1asQx8/8NGdBo3b24ijKaO7T3EsRbJK0XmJ0IZoEaGzAqFEbfZmK4Zv7KN8G9XwuP4Pv11XxKxa6rEqylph5aJ9LNSXXZoXr42v3Cbf2LW6eOJFWJ1SWI3a0fkb8YPihczeGHSha/IksLx7zNFnBwwvbZAvY87PZly+fYk0Sjg5GcMMkvMF6SLC32xTzNcApNOIrVevMDsYcXj3AL/fZLvdYjqZM4kzkiRhr9NClBWW51AdjHA0PDx+wmZ/g1W14oPju1we7tXunq7Hd2+9yWy1oO35lAuNQDJL1myaAeezMULA5ycH5Lri/Sf3aDdafHf7Gm6vjUFQ6VqP27iSv//y2+x2hhytpmglKSxJIeB4PkNnGVe32pg0g7xkfb5ilWdYSjGenLGzscWVvT2GQZOn83OErtu+X5w85nhyxvduv8nNwRbzOOJgckpLWVzfvsTD0TFPzo753e/8GqHn82c/+VNe3b8Bts3h7AQD/B+///cp0TT7Da5t7VJJMLYk9H3cIMAIQbWuCebF+Ry718TqNVGeTXhzi2IWUT4d17KeRYE9cDEIstECk2R1l3CyrE2oQhflu3i7Nqsvjuh8/yaTH30MTR+9iCnGS4LX90k+ekKR5DhSEX10QDUMCTe6BJtdvMmaVaVRlQbHIl8kyEGrTuYWCSAoLJvFX95BtAJ637+F1IbZn35M8nRC+zdfZdDymf3hexRJhfN4xORfvcPgH30fq+E/v+KFY9H5e99idDKlOBmjZZ1428YgLAtdlJgKiienuK9cpnz3PibJQWuMgNIISLPnnYNca5QSaClrJ971muQP/4Lef/XrZEWO02rS6jThZE6108f3XGb3ntYOxabCygzGtagen6N3uoSeQxan6KLEch1c38YJ6vvNVJpsHmE5FlbD/+rcKH61qe9ZUaESXCgvGfK8QFmS/HCMdalHkpXYlcZBk64TsnWM6zgUQYBZREglCW7v1fjx6RShBOndI0xRoR0boSH+8zuQFER5juPYaEshygLp+ditAH2+gKKqydVao3b6lLOIXGuM1rU7tmVhLIVZRISvX6n3/6JodJEv12O+RkiByEss36HIMpzdAfnhqOZ1OA6mLCnmMbZt1YTkUtdclgvBkBKgKHFbIaUB14DWFYWparWiokBbFsQpajDE9hziPEKj8Bo+JqkVp7zNDvEnB7DOqNY5zC1U26Hh1mIlZQUsIzKjsXpNzDquJUa7LVCSYNjFClyK0ZKyMhSuS2kMVV6yHC2Rj07xug2Cm3toXWH3mmRPzjCDDOHZNF67ihX65AfnSM9BJzneTg9n80J6VSmyozHORpt8lWJrg3uSY4c+laUoi9q8zBpY2C2vRgQsIvxXriKUxG045OuIWBjs0Me/MsTb6TF5/z7rjx8SqhtYQV2sK6OU9HxOOV5g7h4hDfgvX8ZMlmSTZS0K4Flo28K9tIHTa1KuYizXIns6Jl3HCN8hcF2ilUUl6+RWhR5mPKcqC6x+u1bnU5J4vMBtheDYCKtPlZdUeUnrOzcp/vxzTHHhgVPkVFFC+tQh1RXd164gi4r5X90jenCK8lxkYNceTpbEHrSxAhdKTVmWyKykXEboeYSlFI6oOUlVSQ2J3u6iZyuMuvAbijLU0zHc3EVstNDHI4JhD8+W6EQh1xnNX7vJ9LNDqtGC9RfHKM+qzQAXEXanQXBzt3a3lxL/8pDsdEYxXVKtUqqzOSZNWf75pzhbfex+s563pgJLCCzHpgTyVYyMUvzNHu1+C5OWdLoh6mI9sXFpA1lJhFE8enTES9+9hbQt8jgjXqe0dnqcHI6QStLohsyXa4pK0ww9snREbKX4gwbNrT4P3n1IvIzot1ooIbA8izwq2Wi3iOYR508ndDfaNB3Fxm4fYUs2mi2yJCWLM4yjsCU4SqJ0LbEedELGB2OUU3NxA8/BarpUecVGt00WZxzfO6K0BHtvXPlSNe9ZwHgxjj5b03yt2SC+4Ym/Lt5+pfPxNxxfMYj9Fcavnlw8/9a/eIe+ng19Y3ZkvpaZPINKaIPV8NBK4nUaUOr630W722hDURr8bgOdFshhm8qStBYRcuGSBxaz2ZpsnSF8D8exEBKshoejHaJZzDqKcJouUmuOxzNUO8ApCmZRxDLPcDwbWRnCwMHrNwhch2SdsP+DVy4qrtbz4yBsq56QLIVerXG2BphS43g2XreBLivyOGJxMkVIweD61vPkwgA6L+jtDvjH/5f/HXd/8hkf/sf3uPfuXZrtBrbn0hq2ufatG+y+so/XCmoOQa/B9j/+Pou/us/i/il5WaKWFVlaEnZCGgVkhcbuNvG0ZHkyx/NtPGWxnM9pb3Xx9vpYvQb9+ZqH793HkorhRof2lQ1aN7dI5muqUqNcm96tbdzBhQnVMxiSoVa3KTR26H/1qv+Fd8A3XDdff+gbtvOVl/zcpfRlKdVUGmUrMFCsErLRCiEk07MpouWjPYvJbEG5TAhQ9Acdpghk00M7FtkyxtKGaBVxcP+IZLGm0pqW6zKbLrBtRZGkdDpNMIZgqwdFxZ3REeN0Ta87IMoytKx9FY7Gx7ilZNgPAcnhYs5sPSfJEn7v5lvcPT3gw4P62CsESir+u5e+h9X0aFg+lm1hkJRleaFTLlmcT9gPeviOy97WLm6psYSksATalCR5xuPxGXfOD7l96Qbn8wm9RoN5lrBczpksl2x3+6ziNZsbG4ziJZPzCTev3MB3fVwUyyTh7tFjGpbDeD5lVRa8tHeTJI34Fz/6t5xMx/zazTf5o49/ynx/yUJn/ODKK5SW4Hw5xXEcjpMFWVXw9uAWKiowJaAk8eEYUVWYSlPM1uTrGKdTE70t36F5c5fkcEQVJVCWkJe4bR9ns0s+XbN+/zFSCtq/+ypqt48QCqffRAOdH9xm9Zf3qOK6k1nMVjjfuYp8OiU7GKGUwk41yccHlAdj/Mt9mntd4rQi/uIY1wFRgbEd2A0wqwSZ5PVCYBax/KMP8d+4Qv+//T7zH33E6F/8OZ3ffp3+//AbLP7gZxTTFdUXx4z/4F36/+A7WL77vNPmDFp0/uvvMv9//wk6L6lnfwllhRKQliXmwQmm6ePtD8k+PaAyGktKKq3rDkujgQg8nMUKyoqqKtCOgxOGRCczFj/9nF7zW6TLjFxr7PmK2b95B/vGLk5lSKMUz64LBOQlotRUoyXu5Q0sWRcYbMdBNYLnC/+HHz3A14LNV/d5jmm7iNcXPOa/Bhn74uT49Xnh2R0syCcrbN9FhD5VnGGKkvZWF9d1mPzoY8QqwlYSy/coixLSDEcIRCug+f1bxMdThGfXyel0jZT1NFsdTWs+g+vUjvWiJl7rTKPaQX2dxCkYQ5VmlFVJuN2jPF+AbYMp6sm3KGs52Zf2akWsXxSGLkwCoVaYIvSw2yHJnaeYsqqJ5Epi0gJjKZTnYEqwHYcqrX1QbMdBhC6WAaUkZVkLIliVoUwzlJSYLIM4wqQ5RV5QKEVpOXirFJHmtSyqlJi0RBhTd2WijCpwsIsUpyFqjmLgIrKSqhlg2RJnZ0B6PkfEaS3167sIowkvDSjKitXRrBaIcF308YhKCZI7h2gBje/friE1798niVKCvQGt796GoiI7HpM8OUU+HeHd2EHnFZZnQ6lJ7x6RHo0hTmm+fRt3p0d8MkUsIsrjGfb+BuFb19B5hfRsjJLkszXCsQk8h3QRobZ6NUfIN4Q7A7J7h+QH55g0x+o1sdoNRvdOkAJco2ne2sW/vEGSlViWrA3jPn5AmhV4SYo/bGMNWug4JT2Z1JDLoqJSFe1rG5BXpFlRe5KkKboosJoh0UePUBdQn1VW4O8Pad3eBaA4nWGGHZQwuBjIC8plDEJirxMcJYk+f0oRJbVZqJKgK0xpoxYRjVcvk02XdZJVatJ5BEVJJSWyHWIPO3jdkOpCaUo5NsX5rHZbdyykUVisKeZroi+Oa7XDnT7rKCcctmgM2uQPzjBRjmr4WBiy8zmJpbAdVSdp0yUq9MhHS5ztHk43JLi6idkfkp3PiYxG6drwVVgK6dqkh2OqRYQuK1zHxo4ympc2MK7FeDRHjZeIrKQ8nBIikKGHMoJindLvt9jaG6A0FCdTzqOcux/e5zt/5y0uv3yJbrtJaQkcIfDbPkoKlGuDJdm+uUtVVizGSywl6QzaZLKWb4/WMdu7Q87OJmxv9kmlRrcClAHXtSmLkuUq5tLlLcbLJfPZmiDwMKHL5NE5/qDBRr+DUVCkBfP5mnCnQzJakXoBJ0cjAmB0siSZRV9NLl4Ifl/SKr4aRb80tzN8JW6+GEq/3kV+Fpcv/vib8iieiST9qk2Sv6XOxXPA1jeOZzpRL1asfz69ED//6wWUxQ09LK9m9pdJTjlbEy8jgm4tO+a3fLTW5GmO1wnRSuJvd4nHS2xtU2hNs91iejrBDVyCRsDxgyMCxyVeRNihi+O7uI5NoQS2b2P5Dmml6SqbwHE4OhphZSW+rTg9mbB3eZM7/+Ydbv4336d3bfuFiwKQEtt3yB2L0LUokryeg8uKbJkgtMZvuDVXw1ZfHkGtSZcRQa+FE3i8+ltvsndjj0//+EPu/eQzxPmMsyen3P3pXTqDNpdevcLeS5fYvLGN3wnp/OAWwe0dwvunZKMlxTrl9GzGbLYmWceEgYeVFnSkQqHIDiYU65Th795E+Q7SUVz9vddpftZBSknnyhCn3wQp6V6cj+cKXVL83BJBSInlO994Ifzi67S+Gr7xmhBfeclXH/qG7thXbi4DZVYiMJy+94B8nbI8nRM0PVaWoUgy3G4IeYXUcOWt6+ii5OzpiMagyfJ8Tq/dZL2KaHabgKEVBkwXK44eHNHot9Al2EhCp8a7ypZPcjrlo6MHzLKEvZ1dnk5G+Cj67TajdIkUFu8c3WOxXvD67g1G8YKXdq+xyFNeu/Yy7z2+w5OjA17eucLLW5dpNZu4QiJ8l0pJiqLAMgYTuMi8oG8H4AlGRYw/3MYLffQ8IkhzXrl0HaEUoyjiKJoyWYyJ0xjXkcyWM4KgSbfVwuQFx+sZd0aHjMYj2kED1/W5d/SYtMho2h7NsMVaaKTtcHN7l/VyxX53yCxZYsqSOIn4zq03CYREWwEPxyd8+Pgu37v9Bg/PnnJ7sMdwr1YNS6OYcG/A6PSMVrdDdT4luLKFrgz5fEU5XqEshckL7I02jVs7rD87IMkKZFGhfIkV+kR3ThBFTbhd/vgO6u+/hd0OcBo+0cmMxv6Q9u+/weIv7lI8nSAuD8gPJ7iXB6heg9WdI3Sc4/db5KuE6O4JyrNpfec6zbdvkN5/SjVZgRCUMVRCwipBleVFV0yx/ukXpJMl3d9/k/jDx6z/8H30RpPGW9fg/YeYVUL+6QHzXoPO927X99lFhTu8vUf5268R/ehj8rJ2xHYtC11VdUUbyD9+gvq127V0qhBQGVSR11AbDLIsyR2bPEnw/aB2gLYswnYXd2+LsjDEh6foB08pfQ/WMdk6oXAdTL8FRUESpTiWRZkW6MNxLVtZVmRZjioc1CJCORZ2OyCJMjzXIZ0sCba6dYX9P3sS+uZC1LNGtrIV3kaLijo+rmdrSluyvn9C97s30Ld2WH7wCBxFEWVIrTG9Btk8JryxXcvD3j+h8dIei3cf1N58FzUQdN15pZDgu+g0Q5cVtutiXxpgVikmybEsRVpWKKVwtntE989RStbO4JbEaENpW3iXNl7AMHyJWK67FzVHRqoL1SlABR6q4ZGfzZFCUBgNtkIWFdpIrHZIeTSr99e2KavalV0qWXuGAGVeoERtwlf77BjKNEboOknXQiEdG9+x0WfzWsgisKmWCaIoAbCVpNRVvWAVoJIMUZRUZYmwFPrJiMoSFKsEe6OL2hkg0oJsvCS4toOyFZZV++ekpzNKCbnnontd9GqNshSrH3+CfXkTa9gmzELWH95l+eCQwe98p4ZQ9Zs1mX6VUC4jiier2jtCSOTeAFlc3Gdxhn9pA7G3QRTlaKXAsdBZfTwoK5x2AMMOzqUN8r+6X6sXZQXJ+RynGVA0QvKz2iQwB2QjIKgqirQg2B/gXduhWESQ5biDNrLpk28P6F/dJj2dkn9+iOPZVK0Qtdkle3SKrQ0mzYmenEG/RTRa4WOw+m2qybI2gFQ29maP4beukY2WrD54SOQ5+INW3SHb7GJtdlg9OsG/to1shuA4FEajS0OaFgipsERVFyyTHNV3sNYJdugjew2kEBz+0QdYWYFoNyhLDVkNZRaejYlSRJyh24LsfIHnO5DmaN9BtELyCpYHIxrdkM73biHuHpF8cYTjuzS+cx1jNI2tLsoekM4+xak0ZJrVew8QlsLb6RG+ts/6/jGIunAilMTb7qFcm9WDE9LDEY425KGH9mw8ERAvIqLJsvakKCvcjRYDS8K1LaqiQk/XmHVKbimyKKGSgk43JD4a14mNJZG54da1XcQqp9FpMB/P8Act7JZLuooQlUZWFfFyTTSaoaOARq+Bqmr+a2bVghVewyddJ9QKfgbHd1jM1lhS1vyKJyPa3SZGQJpkFElxURTI2ex3KBsWVgHaEizO50zjNXbqEScZjw9OaDY9Ks9leHWzhvV/09qFvyaUvkAbEIKvYqfE137+3Da/Yctf65j8wuf+C8evnlz8jXfi6ynWs9+/4ekXhzHET86xfJfOdo+i6WOkIB2vapUOx2Y6WjA/nmGATlEyuLFD1mtg+bWBURVlDF/aJo1iglZIWVZUaUl7MCCLUopVwqXNAVmaMY0iRFZgey5aKHzfJY8zuq2Q0mhSYxi+us+TO4c0Ao/GBUFHvLjzNeqLsOlj+TaWZ7M6mbFKasKf8hwcz8aya4IZ1InH+uER2TomOZ7Qe2W/VkwadrjyvVu88x9+Stdxa21mx0anBZ/++GM+/OMPCFsh3WGHzWvbXH3rOqLr0dwfYNuK7mjF9P4JjdmaKi8YPzmjzAos1ybcaHPthy/T2B/Wu6wUoumz9b2bgLiQQatLklVRIm2Frur2rbDUc5WnryYGf32j7hee769n3t/8zp978Fm38MV9ENSGbWQF048fU4Qutq1IpymthofKDfm6IHUEFZrH731BYQyFLVjMlpRRhggCpJR0Lw8ZPTmjykt2X9knSzPiVcL27pB4vMBaRFiuhbPZZvSzT7k9vEZsG8bZEtsYNrpd1lmMNDBJV8R5Rits0/F8Lg23aPgBf3XvE+6dPyVOY3791W9ztTvk7vkhnaCBt7tTd+mKEkdJhGWRrhPysiKjoMDCHwzY2t8iSTLiNCcrCgLHQQUuPc/h97zvoizF8eScP/38fc5mY0oM37/1OieLKa5jw7Lk9asv8Scf/QS/1UAbzWZ3g2i9YhItGM2nbPWH3OptE3Z63D07ZBVFdNyQJInodbpstQe8e/9T3js7qFW9ZhNefeN19rYv1c7BVYU9aKOFpOXVcpLCcTDUSb10ezjtsF60PB0z//QAdzSntBXBbp9yldaKShfwN+lY2Hs9soMxkz/6iN7feR0LWUNM4gzVcOn97qvMfvQxq0enDH7wMsm9E2QnoPXmPunhhPx8geW7VGmOTCsWP76D1fKxNls0XrpMoTXrjx8hrPq+I8kQAnTgIfICc75i8h8+pP2D2zhbXZbv3GX9k7vIZl2dkgiiv7iD0Jreb79eq79dTAyNt2+TfHqIenIGgLYthBBYeUFhW4hSk9x9SmOnT3lwjpYSbAekwCkrsgsXY8d1awO/PCN0A8rL28jNLid/8TlquSZerqDVwFYKgUAjsIwmrTSOa1PKmqdhVQZ1Ad/p7G2glEAqRbZOsFs+N966gah0DWfLSqxAvrCk/hXmpBfigPQd9DKmKiuU8lGujb8/pHgyQhhwr2/hHM/Qq4TKKsFWmNMpaeDiN11G/+4dyqggPZ1RTepEVWuDcWy050Bcd8GyosCVAtu2qTBYww7Z2QxLKYQxeJ5DZUlsz0VGad2ZxeCGAdkiRjpWbRD4wpd4MZylT84pHp3VwhpSgdbYm+06xMUZwnUQVYntOFDlVFVVyxJrXZurCYHxbEgLjK5ACqo0x7h2XUkOXSpVb3c5PcdrtykvuIg6yfBDr+7sWwJvu4+5cBt2HAtdVlhNFyyF9j2qJyOUEFQtq/aAaXjo8yXlakF+tqLwFRs/eIVgu0f+dIyz2cFuNLGLCmt/k+X9I5xLg5qXErjoLEeWhvLpCHl9B+k4BLeu1uZsWUGV5KQHZ1SLdd2BuLjOZKeBrWzKZYKRkB2MqbICczhCGoOWUBycY293UY16LRDfP4UopbiAMxUPj7EvDamSguLgnLLSiDyHvCQfz2nd2qNarFFJRvH0CHGpi4lzitEMPV3hXd9m8e49jOvgDFo4/Wbte3FwhigK9HSFavo4vTaqFWBGC+KnE0LXodFv1BChosLqNikbIcIYsifnWJsduj94iXKVID2b1TxGH44I9jcpH5zghD7OZo8iKyhXMSJK8Bua3PVJNFhZiuU4JOsMv+GzPjirYaSORXuvj6mooU55SXBjEz1eMDmd41QlTuAhklodSacFsh2QTpdYjoVblJhCkJ9OiT49oDyd4tkW1d2nmEELrRTClmhj8F+7gp1XpE/OEJ6HXsXETyc4+0Nar15h8ekjjDG4/XZdZO21aIceq4ZPfjwhuLpJ+vgU7fj4DR8rDCnygmidsvrLzwgCF+/WXu1LIyCKE4yB1rCN12+SakP/6hbZaIbXbZLbiv4qIU9qo2JVgp0ZvE6XKsnJpwm77SaVoygXKWlSsrk/ZHEyQ3g2gWuxiDOaTZ/J+YL+pQGz0xluJfGUTZJlBKGHCpza92q+QleG3UtbzNMYz3FodBpknuTokyds3NxGxxVblzZYTFaUusJ2LOI0R/kur/zmK3WH7hvHL0cA1Wudr2GlftFmXohIAr6aiJiv/Xyx8P+LiN//BeN/M0L3N42vHrpvgkZ9w5ssSbA/JHp4Snr3Kc0rm2TzNU7br52btSZoBVhSkkU1ltwKHMLNDotmQLVO6febPL77mN5OD4OgFXhorUkoae71WBxOePL4BKvp0nAcdrpdRpMFzZ0u48MxFBUdKXEdh0VVEN87YqsR4Ice8jn/4avLayMEtu+SrmKMhuZmG6SguFiYmLzE3+yAqHXwpaXwtweoKOX0nTv0Xr5cLzI8h80r27z0xk3e+/EHXL91jcHOBsePjvBDD4zBMVBOVnxxPOHzP/ukNstxLFobHW68cZ3+lSFXf/gSbujWDsZZQVmUPHr3HqrlP7dSNBf/PcspnmvVP/teUqKewaD+GpWCrxyMv8lj/ILr49nnfGPi/eU7zFf/wwBSKeLZjNUiwpaCNM7Y2Ozh+Q5aCEajWQ0r8xxwob/dIztfMF9FGFvw9OQc23EoLYklJct1QrBOcAdNpiczzh+fkM+WXA4C/KtD/GZAMo8Y7l7CrJYkZcphXjBJ1syWMxZJROi6dPyQG5eusxV0OVhPuD89pbIskiLlcmvATqvH4XLMbn+TSZbgjaZ4tk1lasLvwpRoA2mekiQJ3UYHp9dmnWZMHp/RbARs7m/V5pEGqqKsjX4WS5rdLv/927/Duw/v8ODkCaPROXeOHrC/vcdOZ5NVkfL2q9/Gt10eVE9ouA3yomS71Waj0WW+mvFHd95lb2OHQaONMILv3nydduBjS4Vj2QzaXUJl89qtVxn4DWwsrLhAOBbVLMJt+vWCaV7UpO00x0NQzqOa+LrRBm1wuk287S6Wa1Mu1iTnUzrX9shOpiAkFQajBMZomt+9SvpoxORHHxFe3cTd6lLM1nhhHzyH3t99E/OTeyx+eh/nch/SgmIR493cQt7cJn1wijmvEBhEUmJmEcksIjsY47+5T//3v8XiLz6jGjZgbiObPuV0hfHdmlwapaz+08c0f/gyw3/2u0QfPWb5zh1qNo1BSYv4L++BZ9P9tZdrxSdjUA2f1u+/xdn/4z8iixJRVrWkqNHYZUmpKzidwu0mQgoqY+rbLy8wAuzQR8cplhDodVxjqZXE2xswe3CCs9FFFzmtqy/jbfUwHz8iXscYY2i1hqT3nqJ7LWxl1cpVcYaexzQv90nGK6ooJ68qbNum6GR4oVfffO2glt/OarnLr017/8XjmZqc9B3EIqaKM0TDQ64SlIb1k3PcYZtq2MTaaBJ/8gTftlBSEEY5xdMJ2ckcK/DJxud1l6HbvCAwB+jREmexRhuD7djUYnwaHIXdb5EePKzVCKWs+X4bLSgqhKY2Xx22KFcZla4Qaf7cv+fnaiTaMPvJHYr5Gtt163OKwN0bUC3j2k+i1Eg0MiuoXBshDUYILGPQStXJTKZBa1QrrP2BHAsd1JAu5ToIA2WWUqxXNLb2MHFac+OkRBQlxnewm/XiqBqtayO/rAAMKnCppmusPY8iKy4E9QzSCTGzuFb5kwIVl4ikZPIH79F68yrlOKI4X+Fc2SC8sU22imlcHhLfOSCfLLDbISWSSmc4lSC8skW1jMken1KtU8bv3cdWFk7ooY2hyi48O87nhG9cRfVaZH/5GYWpsFsNTJxRJhnVyRTLtpFNr06A1wmzTw8o5hFOkuJttEk/ewwOFOuI+P0v6Lx+leLJKc7VTZLjKVbDg0qTPjqroZVnx4z/08+wX76BVVYIXaE/uE91OKLyHWbwnOSdns7QUQZFiXd1i9l4if3kDG+jRbsfYuLaK0OnGSJwwbaQZUE2X7P+Yk5wdZvmVpfkdIYzbONudigXEWx2MEVFcu+oLtyFHlmc4xiD1AbyHOl5UBRIY/C7TSzPIZuvaxJ6O6iFYlohdqsuaEw/ecx6vMTSFaQ5le9i5utaDKLSWJWP02+RH5zVfiMxWP0W2ZNTROChHRvWKclffI58+RL+5Q2EFATtBkZA4FjMH5xiGj4qLykOxhSrBGlZ5KNFDbFqNdBZ3WVt394j9V1MVmICn/zTx8heC10USClw0KymM+KsiQO0v3WNcpWgP9Rk5wvy6YrifE7pOajQw7EsTFZgFSWWlISdAOFblC0fei2MrFXE1ouIhuchHEW2SqiyAjuv8DpN0lVMo9fCu+JSphk7lz0sW9F99QrHByPaDZ9CVzQbIdVGxfn5HCdwGAz7SEfhWh6+si+QoYbcAsu1uNCTIzCKlag7l0IojDH0trpfW8M8i3s/Fwm/0Uzv2e/PECS/FL30AizqWQH2608/+/+bVKl+1fG/fXLxlZLWl4fil4BhvjIEAqvboPXWNXSck48W5LOIaLLCsRTpMiFoh3R2+6wenpCnGUVWYIUu2qplBr3AZ9t1sNshk9mCbLLAaXjkaUa1yvH7TbygVpwxScEkTShtgasNYb9FNFmi2g3m53NKS9DotiiTjNkq5pl17VdO4AWcq7HdBwG6rNClxvIcnGZImeXYgxaIZxNTfRzsZoAV+mx/9yZcyLEKAbZn853/9geQaTzf4+jxCTaCSklEnjOZrxHaYLsOYTPAsyRow+JkyjtPx6Ak25c3Ge4P2f/Wdbp7fR786H0OfnYPg+G1/+YHVFV5AdGq1Zx0Vi8Ghbxom7vPDLLE84va8OUC/+fED77hTP6NVh/P77a/yYt/+bWjbEWw0+PKD19l8XRC9zs3QAiS8ZJ4naAsi25hOBst2b62zWCnj9npIz8/ZBnFFIVmc6vP+WjG5vYApRTKs1ifz2gELrPjEZuui/IcOrf2WN074L3TB4xOz7nWHXI4O8MIw9l6wmbY4frGHpPlhG6rhysk98dHjOMl7VaHMst5c3iFQEhOZ2M2wjbXetvEcUxVauZ5RI6mLAq6W0NMaRhNzlFFRdiub+NH735Go5IklkV+NkOkBdJ3aPRa2K7NrKp4/9P3eHlvn41Gi/7+bb6YnJHkCU/Pjti5+QZCWzwaPYWy5B//4Pf59PABjuexiNfMVwv2BttcC1vMl1OWacTu1iYoQ5yndZu4TOl3+kRhwF53wHmx5v/P3J89WZLdd37g55zj+92X2CP3rL1QKBQWAgQ3sVvqbmppqUcjsxmzmRc9zz8wf8i8zpNsbKZNZhoTW022mmqCJMgGCKBQe2Vm5Rb7cvfF93POPJzIrKxCoZoUIdn4Q2Zkht8Iv9fdj/9+v+/WR1Eai9KasB2TjeZEQYCxICuN0IZylRJ1GmSTBfVHT4g2e9RlRWVxQt2sQiQB5WTpkJvZCk9JCilQm228QZvBK3suIyFzzkvVImP2k/u0vnED1Yzpf/8V0t4x618+wcQ+jd0e1cmE9SIj6jXw+3sUhyNs6Zpvi4C0JP2re5THU9rffRk9X5P+9SeY2dJprWpNWVbuLkgLFn/6C8ofvELvh28gGiHTv/gQkRbYNAPfY/7nHxB0WzRf3X8+9Y5v79B4aZ/VI2efyypFhiFCCGRZIXyP5dNjvKTh3IO0wVyldmfjKYHvu5RnC1hDNpsRziKi/U3SQBHuDoi7TaplihASGQaYboM6CZwjlJL4eYGvLbUx5E8uyEOFJwQi9rFLJx7Wl3N6Nz43UlCBR50WyMAHYV9YD/4uN/mv3rvPTRjyEj8OsaUmP59TK5DmKnPn4ZmzXy0qbCcB33OF0zoneu06ypMIJCWWxq1NdL9FtSwo52vCZoQ6HlHXxk1jy5JaKULfQ210kElIPV2hfI8SULUmubODXeYYB+DibfbJLg+u6GBOr/GiXNAhqA5GtfMUT0qEtVcNg4fouKyGOnfBpn7oU9dXCeNtF0JmrgL9QLjCRUm8jQ72cu6S04sa1Uyo52usFNTWUFtQQqHCAC8OMJWmnCyQUmEvl7DbdwnkxrjPzFr8RoQ+GuPf3KK6ombZogKpMEWGrCzBXpd6liGLGlVp6tGScLPH8t1HpA/PyB+fkbx1Az8KabxxC9U+dy5PxoA15EXF+I9/gmgl1LMUf9hCGahLi28lxTrH1oYag1ca8g8f43/zNs3/5FvwrMn0nG5OrzLKw0vK6YL8oyfITpPQE6hGQLDXhbIm2O6jtdN0SARmuSZ55Tq2rEh2+2QnI1YfPsYa66xm93dp3tjCLFNsbdDrgnq2RnYaMFkijsboboPVdOW0k9t99PkUf9hm582bVKM5xeEFVVrg+T71yQjVb2HSnPJsTPLtl4ju7NEoa9afHjL5+UNEKwZrad7auop5Elhdk81ccKFJM0ILBD7tN29Rzddk53NsXWNbEcyW5AYXNJkVMF8jdjR2tsLuDpyN83hOoxWjrjQ4drLE83z8d+5Q3zsiPzgjfvsOXiummq7xNrrO8toYxwyZLIjCgPV8gf/JAdXhJcHNLZIbmxTzNfpgjJeV6MBDYKjHS/TpBCPcsAcl8dsNh/RKJ9yOb2y6JPTjS2eHPZ7jNWKK4wvib73E+NERwbBDZi3NosJrRrS/dYfZ//RzgthHN0KCoqJepYjQI2i6mi1oJtRpTjAcEirF+qkLpwx8RRT72EWKjHyarQgxaKGlQFeaxeNzss9OUJ6HSAKiYZvSWoqVc9JcrTKqWnP//gEvv36D8XgBniAIfWazBVuv77N8dMnlMiPabbF1fYPR8Zgqr+gEAe1mgyw1RMqn3W2SGZfr8WIh9HweKuBrfFRfXCSf15fPlpyvX2m/ojB7Rh6x8Lwue/FAfkPbb6i5+Lu2Oi8+er70mq9Dg64WcdEIiaIhXr9F9dMHrC6mmH6LfLZm4+4O8aCNPZsz/fiQzXfuuOj40ZywNIiNDvPpknKW04wiZpMFkRew0e1yeHKBhyUIAzwhmE8WRO2E9WiJV9ZEzYRlXqAFKAtlVrKcr/jGP/kO6dmUyYMT+i/t0bqxga40KvTAWCYPT/BaDv4TQXCVw2AJvAhrzJfe9tXFIiHe3eBz4aPFGsvyYoa2mgcfPKChJGsE7W6bWVbS7DT5zu9/i1/82S84v5yw321BEmNrg2+cH/34+JKTp2d89Ncfc/32Ds1uk+ErNzC55t/9P/6Y5XzFG3/wFnd+8Jr7rH2FrTUW7Wxv5efHaAGrjeP+vWgF++Xt+U1z9eVXXbtfugye//PveY07tOj5HwgcZUYGir3feY3u4YiHf/Ye+SIjCH2CwCcoNXleMui1mVzMQEryomQ6nrNxa5unpxOyNGdrf4OqqEnXGbbpU5caYyxJs0EjjtBxgBBw8OARp4sRnu/x3uEDlOfRiRNudnu0ZcDhYszLe7dIrUbWhqYXUidNJ6aOWpiy4KPZiJe399nrDCiynNFiRrPdY17UfHZ5iB+EDIRFFTmDRgdtLJfZAnt45fIiQ9aX51glaUUx0/EJrUmHRtJAIZiuF5xOx3z0+B5YS4Hmj771e4yLFZ+dPqWymkWR0en3mGYL+q02T0anfPvVt/no3vtstLucL6bc2b6OEZrxes6ff/wzdoZbfOP6S7S7bSbnlxgB/9+f/YgfvvUOcZLgdRqIvEDFAXG3RXk0QgYexleUaYGqa4yxNLYHV1bGFpPX1EVNaMFrJyymLqjO8x1tJdzpuQC88xl6niKk4/sGSQiA322wVpLxn39I74ev4vdbNN+8Tnxrk8mff8Tipw/wd/p0vnEdqS31MkM0IqrZCiWlC1Ara0oByemc0R//HP/NfXr/xffJP3pK+fAMHft4WAfBG4PISsxff4oX+rS++woyCZn/yc/dFNOCNIbZv3kXf6NNNOwgPIUIFM3fe4P8yZlrJrhySWrEyCikSDMwktKUNISP8D0MHlZrgsBZpAqpsJ5ARj5+XXN129PZ7IK25NpQrTJCIQgaCVp5SOk489IASjoLbynJp2virKS2lrgZY32F8BUiK6nzEi8KrnJ4FP5XCRP/g/fuVzUWbjNFhdHOOEJ6EuVLrBIIC6LWyLxi8fPP8Hf6eL0mdTtBC0FRa+TFBGs0SvmITkIZR6wOx4jAI0wigix3TmGBj3YJeXhh4CzCb29Tp4Wzrb6iRcluhN9vUh5P0RbCRuTWcAMI6xzrnsG8XD3driaFtq6xtXUicCGQ1oIU+I2I4tGpc70zBi2vRNpVjbfRxdYGIQVhEDhthRRIJYmub7J6+rFrDIx1JgBX9sZ1lqE8H6E8ZFVTKkvkKTQKkCBdQ6LXOcIYRFXh9xouV8RXMF87ByxjkEg8IZxDlYLy6Yjg9hb5k0u8K/vd4PoA78EpYplRH0xYpTnJ27cJe02Su/vIgwta7QaUFcUqZf3gGHvpAvU4qQg2e4TDhrtfO213bosas1wS7A1dqvbVPfx8rirAayV4r18nKmtW7z4g//gpIlBIJckenyCqCtVuuLTlRoQcdtxzoSyRUYjfb1Iv1oCgnC6pVylWCJJrW8jQo15mpJ8eYlcppqoIbm6BsRhrqeYrgnaD9jt3mf/0U+qLGcmdXUfL7DWZ/snPqJsg2gmy3UQYCN64iRy0MVWN34xovrpP+eNP8PKSxXuPkL5C1gZ9McVqi2yE2PkKpTw8ITGeJNjqQeixvpy7hruq0XmKl7hQRS/pQVmTn07QAjgaO+TEU5hFhjbGTc6jABGHJLsD7GYX86P3qWYp8a099OF72CggrTWirJFVi1BKwo0OnT/8JnqRsv7wCfnHBw5pySvMeM16mSFDQdhp4PXbsEiRAqLNDtnJmLLXQgjhkJJWQj1bYbF0bu+wyHL0aIFQEG50UWXN7j/9PusPnzhNyFVgsvA9ZBIikxBzPkFf0e5sUZJnBUIIKqnAk9SjOcFmF68V0drsouKQZLqizguKy6U77kWKNhZxRSWLuglWKcp56ta0siJpxIhGgBf7pJMVvX4bazRvfu8Vzk9GnJ+NUaGCsmKepoTNmH6/Q1FUsKyZm5Jaa04u5zT6DSLloYuK1n73OWX+xbrly+vlVw1pXkzq/nxg/3WL7dcMe37ty35zjQX8RpoL8auYzpchnC+x4d3298RdhAAJwgr8VkT7mzfwzjsU05RismR8/4TN1/aJtKV6esnsvSe0ek2Kyxi7dum0p09O2drZZDqaUdY1SeQxmi9obnZIxws6fkTcjliepNR5RUtKhvubjJYppdZstZusqpqw2yCuDdP3H/Pgrz4k6DY4/flnDO7uMJksuPX736C7N+Tis1OKxZr9N2/RvbvjtAvGuOmaknyOW11N7Gq3EDzbnn1C04NL/s3/839yE1klyXPD7bvX8MKQg4NjhvGA3bdv8+m//wQ7m1Mjoaip6hpRl7S7LVq+Yi4UaZrz6P4BeZoTBiFWOlGa9HwmJ2OkhVu//RpCyudhfi49WT0/DY668KW75NdtLzQYX/jvq4fyizjW33d71myLZ4fynNf1+R7PKGqNaxu8/l//kGqyojaWoBVTT1Y8/tN3WdY1sp9wuVpR5AXEHqmpaOz2SPOC+aMlWVHieR6RHzBaLUjC0CW0RgFJ5OOFHtV0xfnRKZEfEYcBt3rbLERFmeaUkaIVt5DKp+WFToQY+EgbwNyyKjIeTC54+9pdvrl3h0opSk/S9Ae0w4QkCXlw8pBes0NsBceLGVmQMilyhIA0zbi1fYN5NSfyPQ7OT+j1BsRewNPTI5Igot1osTEc8t7JI+7cuMPl5BJlSn52cI8/+p0/ZK8z5GByRq8omC2mfJY9oSpy/uC179BptjkKGxxcnPHg5An7vQ0uVjPyvGS9WrN9Z8jT0yPGH4/Q2nB35xq3t65xenHB1nZClXo0/MA1vElIaSwmLRG+QkY+orYsjkcM7u7i7/YB8PsV1aeHmOkKXVT0rm9TzVbUy5z8dErr7g7edpd4s0f64SGTe6d4O12a37hBtNtDKEnz7jZBK2by409ovXGd5NYWqhUz/Cdvs74xZPX+AcvHlyTbHdrfuUsjL5n/9AHrjw5Qno9dVfieosxz8Dx4cM5svKLx9i0aewOyx2eYozFB0oZlRlpWgGD5Fx+hs5LO77yBNYb5v30PU2lsWWGXOZO//Ijdf/HD59dycnOb+M426cdHVzC6wNQ1CIkv3bRLl5rSx2kA8sJd554Hxk0/q7JG+YmbJmpLlZfYiwXeZgdZamRRoz3l1iBjycsa0Wujsgqx10ccjp1wMi/RpzPCnR46LbHW4EU+Oispzmd41zao66vS9UoQ/A96LFk3QKnma4eUGusGA0mI9BTVbE2hLEErwkxW5GVJ9HaXuNdEdxpMy4pgq4eRArvOIM0pAw8vLQkAH4F8ckYxXREFIVXgNCfqynkrbET4NzfJxwuHel81t3Kvj4hD6tkKT0J4d4fCOoGnlcI5PdUa6amr9fDzrZqukHmFCAJMWWKFdDlKccBiunLrkrV42roMBK0Jbmyz/sk9TOVE+lZrlOfsQ8vximy0QOFyZ+pAIZc5uigp12ukH+BpTY1ExjHaQrUuCBOnu6iLAhOHqGXmGpuNDmaRoa5SrdHWaVO0oZ45HYTqJujZ+opGBVoJKGvS4xHB9SHFp8eYWsMkpzoaUU6WNG5u4vdbCKlQ3Qb+7W2ia5sUT87ILhyaWs2WWJxVuV2mBNc38QYN6CX4G11kHL7wSf7qNEoEHo23bjuHtMUaf2dIHAVOg9ltOK7/oIWMXJGKtSAVYGm+fZf1/SP0oxN3jM2I6uCS+I3rCFlgivLqeezOYXB7B7vM8Fu4RiMrQDgRenE8Rq8zzGTprJmHHdYfP8FPIsSdHcKbW87gxLjPtJytad7ZIb65Qfrg5OrZVCOaMSrwHG3U97BGIyMPVdSk94+otEEEAVVe4l3lXKA1Ni/ITkYY5V81/ikqnyG39hwiHPrufbcTbFFRpznLH3+E6CSI0MfOl6RZ4dLllyk0ImwrRhclIo6oa+Pu7zgCzwnTLdYZKZQFHhZsSXm5Jp9MCW/t4yEIr2/idZqk949dGOn5mKARuYbBGKR0VGSxMyRqRdSzlPzgAn9nQIzBHE8YzVYM37mDjAMa375D9svHLptE10TGR+z0XehpXiDLCmsUpTRUj0/dmnEyxhu28bZ6+Ns94msbVKsMs0ipriix68UaZSyBp/A3WhCHBOMV6bBz+yAAAQAASURBVCLFrAqiQLFzbdNR8EyN7/vs395h7Hmcn0yp1xXNTkJZ1BzeP2S4v8E6zRGBR5YVbN7YwPqK0/unyMDjrTf3fuV6/kIN80Jt7LQSzyCGL90OL5Q4X0eMEl9+Hc9e+xXBei/Q0F/8Pf+Q7TdKi/p1b/PzRG7x63d88c38mjclhHPKwFjMOiPQhuTWJpOypLHVIT2dutyIXgML6KzEi0Nnc2csjXbCaDyltdGmHi04uRzTbDeIhMAaODo6p7vVxYsCJIKlNaxOLmj226Alk7xCKNDHI5RUjM9nZHVFsNnF3454+O8/Jc9ztm/uMP/0CCMFJ+8+oh1FdO/uYHGJsbx4Yq/eq6kNQrzgk371/TqveP9//Al1WtLa6PDb//XvE4Q+P/7v/gyTT4l9n9V8RVEUbNzZ4eD4FCklwlhsWVGWFdPpmilQYRnubdDe6JBISblIaXRahLMZpfI5X+T85f/7R6wnC974o++6qVjuJolBM/rCSUuXGXEj+jwQ8Necry9fHb8abf+1RKpfu9kv7/QVP8aU9ZVfvvsaTxHu9vGukofL6YrL0Yx4o+MmpVJg0xyrBHVauklGbSnKmiiKXEJuUZJEAfV0yVangQ1Dmrd3KC9n/OL+B+wPtkltxfHojHde/QbVdEKtas6yOZ0oYVKu6HptwiDk/tkTfOERlDXH8zG/decNtoOEPIBC14S14OnFCbo9QFclmxsbeEHAwhTs37qLry1xlfH46DGV1JwtR5SmRElBc9DHFwHHs0sGnT4no3OMhWq55vjkmIvzU9ZVwZs3X6YZNfjpR+8xnoz59rWXmJslx+maYXcDFXl88vQ+s2xNp9lmOhkR+CF+q8vd7oAnB4/4b3//v+TD88dcXJwRBiFIyNcpW91dzKCFjgKePHnMG6+/jmcch1YohYoU62XqUpRnK4J+k3KxxoorV50kpHNtSJZX6OWacrG+cosK0FHIerKk8dZ1SEtEI6Q0FVwumf3b9wm/cY3ON266RN6tDoM//CbLXz4m++iA5Nt3iXcHNL9xk+T2Not3H5G++4TqYk73d16j+8NXsXlFdjgCpZzIGoEoK2SjgxeHLP/yE5pv36T3T77N/C8+oJqsEa2E0FiqdYYVkvXPHlLN1/T/8G3s77/J4kcfIgoX4FXdP2X5wWPa37ztLlYp6P4n36E6HKFHUyopEZ6PEjXC9yDPsUVFFYWwzlwStdZuEh14VMZlXui8RO52yLwAtdFGXKVdL2dr1OWMREr8q7wGM11iaottOAcjPwkx1rgU78maeH/gLEsrfSXeDqnnKbk/I9zqOK2CkohnFMYXc4uePQC/pvGwz6F4XIZHqRHBVVq5EEhP4W92CI3B9yQ2TihHC7y6ZvnwjMbvvQHbXdRojhdHFJcLZOhjaoOf18iLBWq+RgQe3qCDLBz/XHgKv9bUoY+qNHKzi60M9WiFh0BudhFZRuON685ydJFRFyVBI6T+6PBKjyYQSfC5FfmX3mV1MkGvMoyQSN+nLEtHg1MKb5VjtEYKgak12jr9g99KnMUtILICFThtmNodUD+9dK5PnkJ4EltXrhDGQrHGU47q5E6DwOY1/tWQUyuBWmTosobQRwqBbISYdYEMfcpV5sTzAoyxOCasoEpLiAPSyzky9gj2BnDqaMlxFDpKmDZQa+qLJbJVsJ4usFLQ+uZdvEELpEAlA8K9AW3rQg7zx6eYoiLcHThNjZSoZuSm1L4HWlOOFyAEpqpcxouQrlhsNzBFRXEyInnzFupZ/spzFF18PtG17rpCQHU2oV6mhNc3ERJkHOK1GoRbXbCQPTyhvsqG0HmKsKBubpAdXmBri0Eik5AEQTDoUDw+J/35fUwzQqwyR91a5/g3tlC7Q5Lb25h1jqlrymXG8sMDivGKzu0tdL+Jin2qkwmNb96mOHM2u+VkAbVBBAqMpS5LykVG0m+iIp/g5gZ6uabOCjAOLfXaMSqJsVai3/sI8fEHVCpA7u/jt2J0XqOrGj8OMVXtUITSrRvBoIPMSsrpHHV9C70oMB5oIaAo0U9OMaMZOgxYnUxpZxUaCPpNgpubeBcz1qMKgaZ1c4fZ4Yhmt0Hx5IJyskQvMlQzhDMwaQGepLqcY4uS4JnFtHHIm2gEyDiAbhMtJHaWkh5c0ryzQ7Dbp5yv4V6JSkE2YoRQVGdThNaYdoJQimSjA4GH32lQLdbUaUl5Mad6OkJ1E4wx1GWF9hRhL2HjxgbWQvroHL8ymNmUQEhMEhD0m1BosnkKpYF2g6gRU+gaGfgMe228Rsj6YsruzpDFeo0vBNYXVHlFFIQsZimt7Ta33rlDb6fHnbduP3cH/XLt/gIA6uple9VgPKPH/wrc8WvWVH5Nw/EfRJS/tFD/AxsL+E01F1ef1FdBPJ/vIr50wJ/TV+Bra8wvvEYGPtVoQdBMkN0WxeWCpBHhAampiTb7RBYWj88xV2nORinS8ZztW7tIX7Gar4hCRyfodzucn43o7fbJ4gBWBVsbPdbWYGOfxcEFBqiXGXG7QWAFzd0hhycjAt/nlVevM1muyRcpt65vMx7NmB9eoo3BKsVWq8m9H72H9CS7v/smJ7+4T//6Ju2X9r7QZDxzjfrySS2mK06Pztm8s80f/d/+BZ3dAdW64PWTCeNPDglPxzw5u+To4TF33r7D018+4GIypZEkBFGIigOmoxm7Gz2idovFeMlgs4O3mhNnS06XKVGjSax8hoOQqqp4909/TtRt8NLvveUauavE7RcpbeVsReApRBL+an3/7GT+aszkf3DCab/i6697zRd+t/28pbfmWdHi6AhCClaPLjj75SOyiePLt3cGtLf72Dhw2R9KMWh3mE8W5HVK0AqhzJytsDX4BhZHlwy7TYY9Zxfs9Rq0X97h9M9+xmC4jV6MaAUxYQ3pao0VgmazzclyzGY84Gw6wkjYavV4a/cW59MxUT+id32H3XjA+6eP+N7+azz463cZDof4SUTuW9ZVSWoren5CW/qk1Yo8zSjqmqwuaUUJ09WURphwPL0EK+i3OlRGc3x5Spw0qLEkUczvv/YdzhdjsIaWH9MLm8TtNlvNHktd897hA24Pttkb7LDQBYnyuX9+RGEqdntD7u5c5/1P3yUKQ3737tsMGm2+9co32Y17DJKm46Va2GoP+MXokL/59Bf8o5ffgemaOvTxmi4Jvaormtc3nFZjvsa37nytDy7x2gm+lK44kMIFVE7X2DhEVzVh4GOKiux8itCGaLdDYNrY2mDzitWjc6plRuuVfaKNNl4S0vvBKyzvHXP5Vx/T/+YtomtDvEZI5wevIKOA1d/cY1rWDP7T79D/Z++w+viA9OePMNogSjf1L46nkES03r7F4m/vk17O6X/zFov/+T1oBoRv7GM/PEDgtFbF+08ZXyzo/effxbxzh/lP7kHt8ioWf/oushHR2N9EKIm/2aX1j7/F+H/4a2Rt3MRda6cPCAJCpZyAU/kI3xWJuiip2w0oanyl0FWFn0SYtKKcrWl0G0RxRJWV+IGPNBVlUbl03EaH6XRFs6zo+gorBcJYSqNpeE6bYa8CB5WB/GyOaoTUqxSMJtrpf+mh9fnAxH7xn7/+/regi8o9RJ+hWJ4Ca5G+cjS67R7VuqD0K8LbW1TvP6U6Gjue9V6fSDm78rqoKHJJIwhR0zW2yNBCIEMffTTCy0oIfDwERVW7STyW5ndfYnn/2OU4WItZZTTfuu5Qi6zA5hWylaAv55i0wCqnd/EGLYwxju7jq8/fm4X6ZIL2lEsPF56juvRaTkS9zFxjoSRSCBc+dmvbNRYGhJRoT+EBSinCnT7rj4/xlEQEygWDJjE2t5j5nCxNae7doA58QqWg04RqiZEuXFH57jVkzjHJBB62cAWmrQ117rjg1lhkI3ACdO3SpGUzgaJAbPcwZ3PqVUrcv0n23lOoDUo6+opNC4SpkXsDcmNYPD4nqQ0qDlCRj9eKXcMYBSSvXcfW2ul/koLibEL5YAxWYD1J/NIu1lgmf/Eusqid5WzsnmXeZo+gmRC8tItqhF+8riwuBwLcYO3okvxyhvQ89GRNmRcEyxQ7WRDvDqmnS6rDEeHNLbKHZy4vIrsaKvVblBdz6o8eoGczzCuvEIs26UePqYoKJUHFThxuhUBu9ajTjKDdpMoLjNZUFzOslKw+PiDeHRJudDBGk59PqA8v8cIQC0jPQ3geYquPbCaUT05dKPDtXcrzGXlW4G10EHFAY2+AjAKqixnZ6ZgqjVyek5CEr93F3LqBLxy9UM9WiDjER2LWOQrQWUHyW684a27f5U7URY5dpsh+E6UUdZpTV44OXQc+5TKjsz0g7rZYjBcUhyM3cBw0iLsN1qnP6mINVlDVhmboIyZLZKdBejIl3HI6GC8OCHb6yDjElBWBkqT3jzGVRnoSdE3jzZsUowVqlVPP1sx/eg9/0Kb52nWCRsTixx+jLxZ4hcFmpbPzXziNmj64hO0u+nRG9NIOyY0tqssF2dkR0Vs3oKpZvv8EJQQMW26gUWn8nS6egergEqEtvUZIkReIZoyJ28i5c6zSoyVB4LE16LIMUoSSdLpN0qrCSMFHv/iMN3/rVU7un3D9zj7np2N0WXNwcMh0Mufld+5erQ/2+fAYrsqkv5PG9Mvr6P8KvFh8qVH5+xZcf4/tN9Bc/MNanK989RfaOvtCreqmWcFmB73MwXOQfOPWFgJQZUI+XdHc6hG1G84doHbOSTKv8HyP2WJFnhWk8yX9bhtPQO/6kDAOWUwWtJOEvHD8aZPmDIOQ3evbnD86QwQ+y1VGvkxJtnuspisOz8a0mwm+VGhrsIMmphUxvLnNkz/9OXe+/TKnf/ZzVo/OWe9tMH//Cf39DZb3jgn6bcJB6wUU40X6mMVaS2O7y3/5f/8/Iz1J2EwQgN+I+PZ//bvYWjN6fMZP/9W/Z+fOHtu3tvnOP/0e99+9T7bKkL7Hd/+zH5CuUhbnMw7ff0LT85hdzLDKo9nehrJmNF9RliVRGLC11Wcw6HHy84fc+q1XXZT9Ruf5eXlWNDQ2u8/RhxdO1RcuzF/tMb6CI3VldfsbaJQ//73gIOSrQEMhFdlowcO/+JCdN28weO0a2fnc6W66DWZZThiH+BYaW20W6zWeJ8hXGUrC8MYmo/GM4nyB1Ya4NMRbbYbfukPrzjbzBwf8xae/YL6c8sr1u4zyBd1mh3a/RzcOmU3n/PC732cxnTGQlr3BFptRi2W64u27r/He2SNeivsknTbtasDq8IKNbheB5bOnjzFCEIcxnaRBuljy5OKU/nCIJxRZUdIME2qtGWcr+t0helLT9BNKDOP1nDf2bmO1ZbpesNHqEllBHO3x7tNP0dZwbXuXQpeoJGR2esprt15isVgwK1IC3+dHn/4CqRS/9eb3yMqCn3z4U64PtlmVOYeXp5xOLrixtcvD8RH3ziqSIOK391/hPF/z/r0PeOvWK6R57qg+o6Wb1tY1XuhhpktUElFLgVYKYcHzPZrXNxGeop6vKU5nDtVTHv5ODzFZkc/XIAReEjjI/0qoTF5jJinR1QNs9jef0nrjOvH1IShFsNdn2Iww0zXnf/Iuycu7xLs9Gm9cg9qw/JtPmf3Z+3R+73Va37hBfG2D2b/+BeU8RUlBWZTYJ5eYxZrOD14lPRhRzlPi336Ny7/4iLChaf3+m2QfPEVMV9TWkk1WVH/8t2z80XcozmZUJxPn5FPWXP7xT/H/r/+YoJUgBDS+eZvFX32EHi+pjHYuTgJsUSF8n8D3qaraFaW+j2fslThYucTaCgKt8avapbgrj7qs8AxY7RBfTwlyJRDnMwZbPYIkIj+ZYFcZfhTghQrRa5CtU3xcwSeVoxCxLjC1ccOTwxHh7gD5wjTuuf5AfHE5+PL97YYBxjlO1Qa/GaEiH6Hc77LgpuLG0XW8YQu1zFjKBcGdLcy9U7KDEcPvvUT72hBrDPV0Tb3KqLUht5qkqvGNQac5xliXUeF76LzAthO8vMS/MSCbrckfnVGGHg2lEAKa377L8miMEFCuUsJBi+p87tY8rVGtBuFm1/G3v4Temrxk+egMapc74XsWg8VKsFqjMyfmNsYguy5gLHppj/zRGbW1hAKQAmsMXjtGlIZ6nTnUtzYOWchKrNHoMkdaQ5Q0CKTE6Bo9X7uMCGGRUlBO14R3tp1Q2ZOYosAsU5cZpQ1B4GNrg2kERC/tYh6cO1eyTgJSYApQh2PqvCR56yb140uqZeaGS1JiAo86UKggJL9/jujFyC3F8tMDSGL05ZSoGZG8dgMVeujzOcXpCK4ykfR0hc5KVBwgfMl6lSGygrDRwAxCZOCjkghdlGhdU43mECrCW9vIKMCWNeXJiGo0R69yqnWKjEI8z6EgxpTookDFPpyMMdIhfH4zJri9S5WX+Nc2EGGAki58NT8dU08zgh+8A1WBqDSiMo5mqMD4CqoafB8jFH7hEKeqrFwQYlkTvbLP+mxKcGMTb7vvEJkHx+RH5wSdFo3v3EWXNdn7DuFUgw74Cr/boPdbr1GN5qhOg+JkQvHkAtNskM8zkp0eyveIdgZwcEFNjV5lJDt9TFaQn04QnsBUGlXU6BCHDDUiGC/In1xgR3NMUVGNp5g4Rs7WiEWO3Bu6tSgrqMYLvHZM0m+yXpd4AsJhG1HWZCcT8vMlMlIkg6a7fsqUvJSsn5xDVWGmC0xZETZ2Kc4msNEl3OoiAu958HDzrVs0jUXnJcXJmCovwBN4rRC/3UB4imK6YvX+Y6qzKfHtHSqlCANHHzP7fbiYYfPC2QKXtcsLO59TH43wu02iG0OKz45pvnUb4pDG9U2qh6esDieo5Mr5LwkR211UElKNl86eV19R95KA2veglCglKVY5Mi2xRcXmsEPlSeYXc/av7TAbTVlM5yymXcajGcObGzSCiNXlgtV8TXvQ/uLQVXzp72f/fJHZ8vzLLwXhfUVq6eel86+hVX3d9ux3/YaajN8cLervciC/QpP51S9/Zd+v+p6UqFbsBI1bHdZnE/xmjB4v8SOfarIi2GhTX84IQh+9KgmUZHw84tP7B2zvb1DkNeu6oNQ1UknS2Zr+Vp+zR6dsXd9CRCGsC5aLJZ/98jNkOyGqXFiP9D3CMIC0xHiSdJnSvrHJarJE1Zr60SULK9FScPbRAe3dIVK4KVVr2OP0333Ek4dH7G302f+P36bzzVtfQqTs5+9dQNROHAz/7KO5goiE77H58h7/6d1/cXUxWt78F7/Na//Z97DGOq506PPwZ/f55R//BGsl5/M5dVXRardZZoVLuRUQN2KkJ1guV/SHXVToM3t6iR8HTuD9pRPs+c4pRoX+59fjFy5y8Ryu/uL29Zw4wdcCH1+4n6z9/LN60Wsf45K5dVEhPLcgBJ0GN965y9F7j5DNmKgRIaQiryqMsDS22+hZxnKVkWx3GR9ekoQh2Toln6xotBKK6Yq2VfhSMPzuS7R2+6w/eMLRR/e4f+8+g7BNURSs1in9RpvDkyNafsRWu8fjj+7z0t51Xrm+i85LmsJDyIhikfLO4BZBXnJ2ccHdRp/x2SXaWsqiohkmLEr380aLKQbLNF9RXNacji/4/qtv88HJIxpxghXw8eF9Xtq+yeX4ktDzaYQx5/Mprwx2ORifsk7XrLI1r197iX6jQ7vRwlchVZFCUbPR3WSVzWnFTdZ5RrvZ5ps3X+VkNuJycsEg6fD9V76JrTRJEBH6IZ+dHdBM2tzq7ZJIj6P5JTR8dmxAt9nm/Uef8Obv/+cYba6g+gqhLTarsbHvbGf7bYrRHGkSN7m+muj6vSbhzU3SJ2cI4ZKF1bBN3HWuO7YokUZQPbkEa1HDFtGtTarLBeuTKTL2SN97TD1akLy6j9+MEJVGNWOCrS7Tn9xHYBEbXbxGQPPtW6QfHTIZL2n98FWiGxu0fvgqsx99iD6dEiSRcy46nTP5k18Qv3md7OkFvd96hcH3XmLyp3+LPj6j+a1XqcdLigen2KLCjleM/+179P+jt5j/uw+ojsegDWKeMf7rD9n5p99zS1vgkbx5i/QvP0BI7/MitOGE00JLl/5rXDgUxiCFoxPpqkIKiZ6skO0GylMUVY2Rwk0Kq9oJQn2F12lC6SiP1TqHZYqKQ+paYyqLjAM8IzCeoDIGvczwt7qIZf7cycgIWB9cOEQk9PFajtoilOCKW/M5Nv1lFMNYdFahc1eMff5AE87JR0kXEJcWGCUJ4oCgGbNxfZP52QSv1yS9mDuEw5Po2lJj8StDkWWs8jVH0ykN5ZFYSb/TxniSyl5N21sxOvDItSYYLRxVbVWQWkv/jdt47YR89Ihk2MEXLs9HF5VDi5TCa8WIwMcsUmiL52/QYsken2MmK4TWjtpTawh8TBxSjhaOumatS1tPC2Qc4A/aTP7mUwIhXVNQ1s4RrJNQjuYYrdGlC1kUkaLIK1jnpNMJfhw5NEsIaMVEeYWuXMCeXucEwzbSgqcUStdUAvJViio18mpiJHoJjZf3yN57gjSWWgq8IqdOK5TyKKuS6NYmMvQpDp6iogDjSZeTgaG50ad8MkJnBSotqfOa4KVt9CqFMGA1XpL99J5jLKU5quHj56Wjf2QVwVaXxqvXqYsSoSEfL7C+IuwkyEaEAOqiYnE6xYsiZFkz//P3CDd71PM1+fmYYNBGeB6qkRBf26Q4m2I6LeqDM2RwJdJPYlQ7Jrm7h0octUsWFVVVO6c5LCqJMGUFzZCiNqjpCpOXiDghiHxUu4FcrqnHc+ywQ3J9g+yX96l9SXRjh+p8xnKZEu0NCZoxwbUh2eNTZCNGbXWRW13CrR7GWFYfP6U4nSCVQEQ+4d7QaVYArQ1Wa7xOjKocBa8eLxifjPFCn+ZWl9Y3bpMfj6jqS4rjESbLEYGPDAJEEjkDDCkRoU/rG7dY/vw+1YMjbFkjqhqV13iixA47qG7TXWOv7CMOLxHCUh2PkXtDkn6DdZbiaSAKsI2A6Eof6kcRZr4ibDs6UiElvhKukV0XpIcj58Q2Wrhr8Qv1gnDIdCMiubuLqWqq0YL8yRn1fIU/7BDu9DCLDD8JsWlJMGxjsIh1l6jTwHYaCO3onBhLPV7CKqOqK6LXrxNtdFi89xCrjUOP1jmq16SzN0DHAcXRGBX6pEdjuq/sI/cGmKxAX8xJdnrYomJxPKXSBiksjVZEHPms1wV6VdLoNkiubXBxNiZbpmzuDjh8ckJnt4fRhna7Qaziry1zf+0mvqKpeP69Z3XT1/+UX1tPffmAfuX7/7CR729G0P18+9WDebH446v2/DXH74pI5+X7laWo4DnMGvfazq5vt4+erSnPpth1xsar+6yOxlTTNUII8smSja0Bwlr6G10ml1NMXnPnpescPjlBRT5bL++RJBGr0YIoCtE7CrUuSQQEnmR0MScYdmgMOmSTJfnlguu3dzg7uMTrNpC1IYxDlvMVetBiUdQMeh0mj89I//XPSYUhCDy8wAcLj//1z7iRhPRe2v1CiW3z4opf6xZF95k4Yt5zk4BnTYa8eqUVCMmvhLTc/NZdomaMTkuevveQ9XyFHwYknSbd7R7NYZvuZg8/DtzDWimW5zNsWdG4NvyVzhhwVnOt+Fcb7y/xIb7ysv9yZyx4Ttf+usvZ6d6dGMk+/78rv2drMZV2a5UnQYMua8r7F+ApvI02URLT2xpwdjqiKErWoyXVKmc47JA0LKcXM9gfUGjt/OOzgiLLSboJdrqi00oYoBi+fo3m3oDFT+9TpgUHD54wiLuczcdkTypCP2CVrmkkDVASW9VEfogQHulyRSAkj5enTFcrvnX7NYT0KZdrHo3O6OcdYs/n8eSCJIjIqpx21OBodMqNwQ5lIGg0Es7mEzYHG3hC0QkbTNZLbt+5y+HBUz54co+NzpCb/R0+TT/jdHTGIGkyXy2o64qtjR2ejk/Y72xijeGDJ/e4tbVHID0GzS5bvSEfP/mE4/E5q/WKbqvF2zde5ng6ohmFKNWkLksiqait5b/6wT/GpgV/+tHf0G92eG3/FqvlmtIr6W5s0u72SJpNrJLU5zOUVKDcOas9BR2P2PeQ1mmfpO9hsvL5RNyLfCoDga9ASPJPjqmzEhUowt0eMq/JxJWT29mMuihpffMmXr9B+tkZVVaSPT0nHS1I9ocE1wYo3yEC7bdvsf7ZZ5goJLy1hWonSGD1yTGTP/457f/oTRqv7TP857/F5F/9jOJkivUUJvCQxlA+uiB+6zomKwl3+7T+6Lus/uYj5j/+JXJ7SPvtW+TvP3XOU+MVi7/8iNZvv8r0X/+CeraCKER/dEz+5iXxjS0Qgs7vvUFx/xB9sfjcxrQokVWFtVAriZSSwFNUVqExhJUGz0P5ilpb/G6T7GIBUUhd1/hXtAjh+1RKwHQBgY/MCuqydlzjsqaQ0N7oEQiJzgp0XkM3of+t2447Pj4iEMAqxwYe5ZVP/fpsivRcoRrGIf5GB9WOkeGVHuEFuqLJS9egWPCurEaFknhRgK40tq6RoSuWvXbyfJ0QnsQPA1qbXZZnCyLA1gaUQirF4M0bXByMqHTNuqpIfUmtBHgB7TvbmNxRKYQn8X0fs8yoQ8/ZfucVfhyRbLaJXt2jmq3xtMHMnaOQKa40GnlNjcUbtp3bWVl/cZGqDatfPnaoWhBglHTi21qT7A2oziYIY10OhaeQnofxFOLqeWCvErKxBiUE4Y1Nlu+6wigIfNAa2engn07RWIo8JW51saFPoTXKj2HlLId1VeFZhb/XI3t0gZCCrLL4SYTUzgbaCKAVE+8PyX/xyOk6pEC0InRaIbShqkuCboPGO3eY/rv3kb7nbGtrDRGAcfajxiC1xfMF+nLJuqzRgSTpNWlc33TZHvOMLPBRKsDkFaYZ44URcTuh+PgpJlBIqfDbDbw0xzw9d0ny7QSvrOkOWmQXC8IbG+jzGTqrqNc5KgoxeUkwTBDG4A3aGKlY3j9GIfAQqFaLcLuHtYb88AIVBRSHlwhjqEcLRyUKfaS1RPtDgnYDvzRky7ULWlSK9rfvkj05o9Ya0W7AbEkdB8jNPqosCYZdwhshq5/do+40EUlMeXDmnMgOLjFFidduUNw7dK5jtcZrNxDNCNYF64+eIDotwl4TXZR4gw7+Zo+g00Cvc6r5Gu/wHBV4rO4fUa4y2q9eI9jqUS9T6vMp+eMzN1wcLTFGU1ca2YyZv/8Is8yQnQTSAhG3Hcqyyt21O12DtRRHF1isW+MaAfp8jOq28Adtou0B66eXmNBDasiWKYWviKMQWddEWz3qdU6d1aimR63duuWnFtFtkD+9IHl5zw0fnm0vTE1l4BPuDlzzVWk3rPAk9FsvFAgWrCXY7DiHs8DHrDLK6Yr6fIaJfReCKnDDlHWO8n3KozHmcoHG0vn2HYrzGaqo0OOFGxoHPusn5yR3dqgWKf6wjdd1qEwzrRCrHFHVhIOmo8LN1hAFVJdL8vMVsZX4zRaNnR69bpuw32BZ1jz65WN2X92j2WnwBXHFV9VCX/5P+zmK8TlP5AvUjy/W2ILPNXBf/0v+N9/+d6BFiV+/z9e+1P5dKk1nBddtUExXSCnwh21s5XiagZJ0dvuUaYGer+mXCbauGez0ndA7rwhaitBzMJ3VBlFp0rMZG/0OR8fntPcGmLSk0Wk5a7iqxuia8+NLPE9C5HM8mqMl+FlJpQTrSuMZRWQlQSMmSzPSsoTIR/iKIvZhLvF7LR7fe0L6r37Kd//bf0LwvFi34Htuwb76t84rZPACSmBBqF/9DO0XZ/gA+GHAtTdvAXDje698oZUVL5weay11VlKtc1o7fbxAuaniV2y/7jK1V+eFrxIiPT/GF9AG+8KN8cJxP3Ol+nLzamuN8D931BLWid4v/vY+swen7Lx9i86bNxBSuETxrOTRv7+HaoT0t/soIfCsoLQWHXkoG5LWNeVo4QKA1vmVsFBhKk2j2+TifEor9ml5PkErpPfWTbJ7xxSfHPHg9JBPLg4Jg4AgCHn3+DPeufkaDamIpMKTPgQBtbAcjE45nVyyPdwi8nzeuvEySZRwfHbMfDEllD5HsxHD3gBpobQ1KgxotzucLqfMijXHZ+dobdgbbjNdL8irinazSSEtm70N0tmCMi/Y621wNj6jsoa3br/OLz/7gIvZmGvDHTY6fZqNJk8OHtFr9nh57yatRpt1mvLx8Wf4QtLwI169foezyQWptDw+PaTUmg8nl2wOt1C+YjKd4vsBVV3xYHxMJ0pQ0vHRb965w6OHjxkQ8Pq1u6jaYIXESEntKUJPUhQlXuBBVlLX7uFuc0WxWCPCgMhXmMkKag1Z4UKvHl9gx2v8wKNKMwoLyV6fxq1Nsiv0okwLph8d0Ly9RfcPXqc8HLP4+AilncPL+tEZjbdv0trfQLQt6p07LN59TH44ovGNGzR/+Br+9Q3mf/UJiz97j/TeIZ3vv0r3n73jmoLxGooSqhqhFPlPP6Oerxn84dv07uzS2t9ArzImf/EBi08f033nJbL3n2LrmuJ0hr13RPf332D+J79wDnGeYPGTe0T7G26SGgW0vv8ao//PjzCehxe4e1AYA1FIsFqDrTFCIoTA9xQa13QL6absYRQQVTW2rlHrHC7nFNaijMEva2gnyGZMnuWwyKi7LaSFxpWZRZ0WmHaEUZKNN687s4NaI9sxZpUjhaBe5WhpEaGHCBWlMbRaCeVkRa0NcXIVMPVMC1XVjru8LtxgIvZAP198rpyXnK7gOb1KOQH8c9qMgGKROrF5rV3zfrUgxf0m4UabbLWmt90nzhOkhHYmWDw4w5MKIh9/u4/AoqVwpghCUu4OkUmIinxsZfD7TawnWTw+pzYWH5zV+XiNthqaTkgsPInVFiHdwKs8n1EdjfEDH1uWoLVrfqQgvDYge/+JG4QpSW0tHhCGAV4rdpqj4Cot3A+cxXXgU4+Xzgk88N26GgfUgNY1tsgJ924QxhFGgCmvbJxdgAJaCUeHywqktvhX1Coqpy2QkY9qxeQPz9BaO8tkCWaRuQZCGye43u8jyho7WyOVCzBj0ERutNGfnVOvMmwcINPSIQRCEHieC9N7PIbTBer6gKrfoqUkdrFCxwEqUIjZkjxN8eOQWmtqY9GTFarWqKymejhyNMBOhH99gJxOMWnXCXnXGUJJTFoTvrTnJs61dWhA6NPf6iCUQA277vl2OqZ4eEbzh68TbPWQScTsbz5GSEndayHSHBkGVI/PkYM21hg6t7Yox0vEfMX8/Uf4nQTtOcRD9JpUZ1P87R5+r0n+2REmzVH9DnqRkj84QW516X//dbLHZxTvP0avMlQ7QViL0RLZTAi3eix/+QDVTuh+9xVU5LP++CnrsynlvSPkxTnBzhb+7pDwpX1WTy8QUYBf1qzff0T8xg3CzQ7Rbp/45X3K0wnpgyNUpV3jqpSzIq5qTFmhek0oa+pLh/6JIEBu9ghaMYU21IulG/LEobNwPRsjak1Z1DQ3OohGjC5ropMJ4VaH+M6O08cBs58/RHge1WzpghKB2lhEViIuUrxmTLA3/Jx+8FUUBSWdC9uXKg4r3BAVgcvXebZ7OyFuJ+hhh+Jsgilr6qKkPptSf3SAyDK8jR5CKYIkoryco5+cI6yEVuI+m7wmw9BrJ6irTJ2y1niNEKwhjjxqX2LKkqDTxChJhaV1a0icV8jTKVobQi2wnoe1guFGl53//Hvsv3YdpeRXv9cXKxxrf2WXXzegf3H7yjyLL+3xH9x+BSf4hzUj/7skdP+vyW79Aufsq3d43v1aY5BCuBtotibY7lEejikvF4Q7PYZ3dijPpwx2b6A/PWQxW6PGa4wBPw54+OiI9nYP4SlOHxzxxqu34KqwrsuK5rDDdJ2jU0eLCuKQ1XxNXWj8MEBHimy+otdpYLBoranygr3NAYvlinKVce3aFrOiBAvlokAOWhxN5nS3Bwz2N5C+opgs8ZqR4yNK6ab5VzaN008OiXstTF5w+O4jrDbsvH2H7ku7qNB3AuYrNOOLJflV4J3Wrl/TGuF5brp/Vc8bYzBlfZU2K4gHbZCuwPgVXQW/esm5Zse+8E3higYlnjdCL37r+eu+ALvZL+z7zAb3WQP0jCrx+Z0nMEXF6mRM0IgpLhess5xH//Y9XvY9kpd30YsUmYQ0N9qkVc3Bk1N0VpJrTWvQob/TJ5uu0GlJvkjpbnSYXM4orvznO0lCkISMLqbgebTaEbv/6C2EtYzf/4zalPzLD/6CEnhz5xZxq0Vn3SbyfIypWRYpvaTN+eSCbwz3+fDykChJaIYR22EbjKbK1pzNLmhHTTpSoCOP3e6QpheyoMYCB6MzNroD6lrTUhFPZ6fstvpsNLvMsgXzbEk7avK37/+MUPns9Tfotzv8/OFHVKZinq1ZpSnfv/stClMwXU0ZL+eIIGCWLrg8HeMh6UZNagVEIVIY0tWKlzavc+/4MUHkc3u4wzBucpot0QJevv0SG36TKstoXn8JoQ2nl+d0On1iLXl574aD3tsJpqyQxiB8hSkKdCWp44BqvqKzv4GygtW6IPQUnjXOBUkIVBJiypog9JFRgJmlVw9DD/ISpSTZh4f4d7eI72yymMwIwgg/Cqjma+rxkvjVPRq1Jn94DpMV0UaH6mDC/HRO641rBNeHdLsNlr98zOX/8BPiu9t0vvsSw//q+6zffcjq/SdM/l9/iXxll/YPXmH908/Inlw4QWdeYsqS8oMDThcZG//sOwSdBC/02fxPvsPlv/wRi+NLolsbFJ8e4WlL+YuH1O2E5vdfYfnjTxwa8/CM1aNTmrd3EEoSv34dtdnFzNZU1iK1cxUy2qD8AGM1yvPQ2llOSgt1USLLijovUIFLlV+fTWhoC57nLIuL0oVvRgGqrLBRiJmnUFV4zdgJvQdNpKco8pLmnU2kr7DaUK4ykIJU1zSlAAme8qnzimjQQc1XXLz/EP/mJr1+w1nKeu61AMKPqNaZC0bzFVZb1JWbmzXmc+2CEGDc/S/8K1TjKlNCRA7REJ7AV855b30+Jeo0UJGP2uoQnE2JIo/NnU1UI6a8d0KsDessxywzKjlzWo4kwt/t4kUhNGJ0XpKucwJjaFioz+bog0vCwMMoibGWwhpM4OG3HE1NhT75+dRpMhZrVh8+hUpjhKSutEMgpIQ4QHUbmOkapEJiCZTCWAvNq0yHuna6JGNBa/yNNtXhJdSa6ioRPLw+QEzWSClZT0dIAV7oCj3ZayIXKdb3AYsSoFoRMq/wkVirsZ7iuXujsYhmhDbGIRaAkQK9zpyY31o8T6GVpPHKPtmHh6godC4/WtPY6lCdzaCq0YsMEYRcyanRVU3QjDCjBdIY6qxEnk/wB12s0TTfuMnqyQX50QVR6ONvtKiVR7FI0VbQ0JZq4YInba0xvod+OqaarPEHEfMfv4+MHQ1PtRKCvSHp+4+Q7YTm2y+RXkyoP35M81svUa8y8sMLR307HCFWKev7R9haU2UVZRQhLZh1gVqkWAHG95CLNQZYv/8IudVHRj7esE114jJ6wt1tzCrHRiH1ycQVhqGPSmLKVUaQF8g8x8NSnI6pjkdoz0N7AeW6RHUahBtNfE9Spxl+EiPDgPLwDG/YRViDyHM8bWBzgNaG9k6faKuH6jQ4+8uP0ccjpyuarWj/7jdQTQ/VjIjv7qKGbWxauLyq2mUz1YsUvUydsL+o0UIgwgDTiPG0YXU8RjRi6lVBqGu3HlzfxB6NkZdzzConP5uik4Bg0MGLPMwyQ09XiHYMaYGpa1RWEu30Ud0m+fmU5NYmfhJRnk5Z/vIhvVaMbCc8505/JQea5zrnX61CntUJhnK0oJyvad7aRjVCkru72EqTz1aU5xOa2zeoR3PKsxm2qJDDFvHdHaKNLlVV41fuOauigOxkfFVzCFRRYo9T2Oyimu54oyunNZ0WyN0eXC6wi5TmtQ2SjTb5bA2VwZOC1WTJ9rfukHQSV0eJL45Qv7Iq/nJ99HfqCb5+pxe//8yhzx3Plz7SFw/sazCBv+v2v3lz8bVv++/yBp79gK/YTxcVSskrtwHlpjqR75wMrg9ZPz5DX8xp3dqi32mxWheIxZpPDk65+8YtTk8vWTUbbO72yZYZyUabujZMJ0tWeY7sNVBWYiOfoN+geHJJN4qYztcOPl2XhJ2Eo+kUAZwuV6jYxxfgNSLOF0viyMcsLRfnU+puTBj41EbTv76BLTWr8zlRI+bRv/oZJ58e8Oo//Tbt7R6jx+coY+nd3mL68Iz7/8t7xGFIFHisrLt4D/7HvyX6b36IbCXky9QJG7X7LLQ2SE+5z8U4NEEohcXRfYRyWRtSOm67DDxHL3rm/oFzu9FXTg5CCb62w0Bc2f49Ww3ElVMTrrjQFl5IAP/yKbXahTh9+ZoQVz9LiBcgQgPVKuXs5w85/sVnSG3Y3d9An85Qm12ywzHVKuf4l49ZXszY3Ohhr1Ae0YpoxSG20kzGc/rtJufHY7q9lnMVWqxBOTeZ0+NzgjCg3YgYNGI6d3aIdwfM/9VPmF9c8tHZU45nl2x0Bvzk4GP2h9v0kxapqcEaNoOI2fiSdtLgyeKSJ7Nzrg12uJhOWMkFe0XG9cEWN7ubzMuCXm+AoOZP3v8btje3CVVAM4iQSC4XY1pxiwejE1pxwvFiwo6/QafZZneww2y15MHxY9649RKL6Yw0W3F37waT6YzxfMTt3WsYaciLgkTGHF8ecW3rGp1eHwycjE8Jo5Ct5gZIOLg4RknJTx59yGQx5ft33kJZSOuSeb7GKsVylLPTD3j37DE3B1s8OD3kh6+9Q1uFkBXUpuZvn37Kd196Ez8IQRvKWqOFc7AJtUMzlKfQ85REG1ikiI021liy2ZLmdh9pXCFkjEV7rqCUeYknJSr00XFI/mRE463reOMFHM+ojEEkAcGtTbKDEZ03r+P3Gsx+cp/i6TneRhdtBZPjCd0/fJNws0Pvd1+ncWeb2U/vc/4v/5r+P36L1g9fI3ptn+mfvEv18RGXTy/o/c7rVOuC6nSMUgoZhVgJ1cMzJv/9XzP457+FbDp718E//20u/uJj5tOUZH9I9eQC1UhY/M09+n/0bbzdPtXFHBkELP7yY5JrGygVIJOQ+NVrzH/0PkHDex6EVa9zpO+jBRgBUggHFGLxhXQe+UJSztZ4gybhkwuE72MCDyEFkU3IrHYOPpFzfvIaMUm7iZGC6NU9dFZhAFNpol4Dq41DTj2JF/oOZfAktrLIyGnJTFqQjuaoZkSr33EhaMYhFjot8BqRW5t8J+T83Db06iGnP5/aCXBUJG1QUlBczgmGbay2oCShUuipK/yK2Qo9S5lPVjR3esTDNkUYYFYZ4es3MZcLZL9JtD+ApxekkyXd334VCXjdBn4zohgtSeIAnZXUnx4TRD71Omd1Oka2YhDSuf8IQRCH2CTE3+y4h3apWX9yQPR7byKkJH1wigKUcPQ1hKKSFm+/78IPlULFIaKsXFCdEIi+M/Uw+nPUVyDwtnpkD04dQq88LJZgu8/qbx+AteSLOSaKCXwf6ylXiAuBDD1HB6lq5LBFNV1jiwLr+xil8K4Wb20Nvi8cfSYrqWKfuBFSrXJsXmE9iQa8JMRLQqqzMXaycOfPVyCla0yVpMoqkk6L2ljnSqU11hOIde4amqpGyQRO5+g0Z1lp5I0NQj2gWmZE/Q71+0+woUuat90G5rykWheoQZNyuiYIfExaUiqL8BXBVeAiRY2erdG1xvd8qoNL/HaMuLHD4mf3scuU1rdfwb+5zeRgjIhDSgP6/ccuNFEo/P0BHlAcKcxkhneFBFkBYtPZ06soQM+WyMjlr5hFRtBpUl5OIfCQjQh8j+LoEq/XwkqJKUqqR6fkTy8ImwlBv4FoNygWKcyX5JnLZMFYPE+ANujJChEG+IMOrXaD7Ok59ToHbcjuH5FdzGje3GbnB68y/uk96skStUxZf/CQ5jfvIpMQhCDoNaHXfKGodetofjGjeHKOSEL8OMSrNcVkQbAzhLJEzJdQa8RWl2qV4ZU1upMgOjGyNtSrHE9F6JMRZV2jDFSzJY3Xb0Cpab9+neL+CY03bpCfz4jv7hFtdpHKiczz0Zz5jz6g9cPX8fotvmIi+hVF4JWxj7XosqKcrtzzZL4m6Dao0pLxzz9DCInqJDR2+8QbXaJB21EXhcW2YszlHIulPJsgOk0WT85IlGvIop0uW6HvqJDGYvMakQSI2iBD31l16yvnTG1YXc7xA98NHU4nhMM2rY2Oo7N1Y1QzJL+cQ1niJTFRt/GcAm5feGvP3peTAHxOc3JF/v+a0fyv2b6qkfi6/f6Bv/h/B+TiH9gC/QrtBzfNrzXFaE680XUhJ8UaPc8wlaY6HpO8do1ytkI1QoSvaLx+jfTdR+y8fI13ohATBdx59QaXZxM++MU9+sMug0GHxWrN8dmIrWsb2HWJpmKSZoT9FkIbRuMFNCJKYVhXBV4hicKAYRgzKjLyZUbbeiwXGaIVuYyEVgO2A2xZEbYamDSnvFySjZfEewNOnl6gak132OPy42Me//nHaF2RRBHHP3sIFra3+izSgklesHlnl/VsSdzyuHz/Kfd+9ilxp8XG/pDJ5YxGFJAXFRvXN7n+j7+J1wgdXUK4tFciH13UWAwgEbjwvrqo3KTx6qwJJamygqgdf+FEuHPwFZ2vdIX/F8791Y1jtKZeZajQx0vCz+lTVz9QXNnFIl9oYl7429lVSpCC2fuPuf9v30WXNde+8zJnnx5w7yef0GkkeNqQjZcc/+wefrfpQqtmC3bfvsN8nXN5NmG9WFPMU+Jhi6oo2XrrBpPjMaNfPqDZbpKXFZvXNhDaEkhJUteEwybdN69THF4ye3jCaLXiRw/fR0mPZZ46kwGpuHvjOvcOHnK9O2RzYwsTKsS65P7BQwZxi2aSYKXHvYNHvLN1k7QqacQJKopZmZKz8QW7vSHddh9TW85n51wsZygLSdjgzs4NTFXSafbY3dhili6ZL6dMl3MaccxoMib2Qz49O+CVa7cRniS6ylYIENzcvsY8W1PVGl2WnI/P0VrTabWptUZLQ8MLmazm7jXK5+7ebY5WY2b1mrevvcyrrZtcVCsWswU/fvQhRgqeTC/Y7g/pNJt4xlCamv/lwS94eH7E7731XWQSUi5T6tBzi47nkaZrVLNLUlZYz6P49D6UBdE/+oGjQZRXC7kUhBsd6os50UabfHmJMQb/1gbl2Yxgr09274TVwzOiRoj2PJhnlIuU+v2n+P0mK2NpvXObje0u6b1jqrMZ9cUc6QfM//jnJN+7S3Rzk2BvwPCPvs3qx/eY/vHPaHz7Dq1v3mT4f/gByz//iPXHByx+/Cmtb90mLStXXAmBVQpbpeSPTpn/9B6Df/JtLBav12T4+29Q/c+/pKoM+N4VnUqy/uUTknfusPxfPsDUNeJ0wvyn9+j/7psgBM1v3WX9t/exONtSk+WIqnK3VKggCjHrDLIC04jwYo+qKF2RNF7SuLVNfTzB1hqttaNgVRXhsE1eaQpRUk8WRJ5PpSAAhJAUj88JbmxQrwt0VpE+HoEEAkWZlTQ3ewS+R34yY34yoREFhHmNP2zhyxZCOspU0E4couo5RMJUV5kQV6izqZyZBuBSsSUOsbhaOuQVUqmSiHqe4nWbmEWKakVXBTjUkyXhoI1Mc9KTCX67QfzmdZZ/9THp+RSA+MYQ045pb96lrQ3kFUJJyosF9cSFxNXzFL/fxLMWnZYs5yleUbHYSKCyhKGPFdJlSRiDudJ5LT85oEpzdFGhR0vEbE2tDRp9NWAxNO7sk1/ROdv/6BtM/vt/T1Vr/CQCrT+fagrXVKGcBbOKA8RsjVAKaQ3+RgdbOmzAVCVVntHc2ae2IAKFX1ZUZXW1zivSwENHAXI5cSYE1qKMdYnnnkegBCYM0OkMaSGKfNdYKNdM4TlaqX9nG1M4a+NnqfA29imfXrhmpqqpp0vMTtcNq4TTjIjaNZOyGyNDH+n71KsFyvMono5oXBtigHijjT6aoOfO1SvoRBSHI6LdPuWTS+QsJRACo8AWmqDZxht0MPOUar5C1RUGC0lEcTIjv3fmro9egm1H+LuJy9YoK5Qw1NKhUFZKwm5AEAaoyKU8ezsd2O1hSo1VYIsSLwlRQjj3o1VG+NI+XhKh56lr+uMI6XlYT6GbMdFGh/rYWSXHe1t4t7bRvkJd2SKjJPFLe1TTJfnHT9HWYsMAW7mgu3K6xByeY5UH2tB4ZR9v0MZPIrxWjDEWM11hKk3/GzeplznF/SOqhxdMn1yQfPMOwbUNJ4S/QvdMWbm8nKtBXeOVa5STBVZb/FbCdLbGno1QSYDxFSKrYJGiqhpd1tTrHK+sEYMWwY1NRCOiPLxEGgN1jV6m6FWG1WCUICtqgtqZb5iyxmKxVhAOW4jXriGLmulffozsNUn2BgSbHbCW4mxKleZI6XJN4t0BCEm9zinma7KjEbUxBI0YL/QJey3CjTYiClj87UPSZU6kpqw/OSa5u0377g4qCoh2BugPn1whvYFbT4Sk0XaUNBn6mDTHWEPQjrHjJa0fvsb63Ycoa4k2u4DTi1ltkElI5+YW5SIl2eo6I42r/Ky61nhK0r2zhR/6lKMFNQK6DV5k+391P/X5Ds/ZO7/BTbzw5/Mv/4EIxa/bfoOC7l93hP+BI/97vrlnND1daaJhG6HczSKURM9TymUKwxbZ5YzWmzco75+irxfIToznK0bziv2b24zHM0brnCcPDkgaEf3tPloKvvfb38R6gsnRiFs3dxmfTchNRV4UNDaa5EUFoaTOK4J+g7yqMVVNFhonHqzAehJTGppJiDmaYeOadVXg54ZsXkAvhnXpfJYjj1Y7Jn18iQgl8X6fcLvD9GxKa6OLnefMDy5YGYvdbNGoGyzXGdpaxpcuJCqMIhq+z+XxmI03r2OXGdXlnIfvfkar32Ljd1/7nMMsBUp6jo5g3OVtrygo0nM2jKaqkb7CiwKyyRxTBQhPIoS8Eu5Zt1B94TR/8STa2gVv2brm+Kf3SacrVBzirQraewP8TRfwpY0l7CY09vqO5valxsJWmsm9Y07+5hPiMGTw8h6rh6fk8zUb2wO6Wz08Y3n33lNmShKufZaLNdaT+EqxKFO0sQQHIxpbXTzAD3zagy5h4DM9mVEsc6LAp39rn2a/xaOPn1DXmmYrIljmtPcGbP/OG8QbHVaPz/nJ/feYe4oAj1rX9Ls9Qs9nVaxZrJf88NYbHC8n+J7Pk+MjmlHCtY1tQGLLkqfTS8JOm7WtyasK7UFYaI5Xl+w3+1QNzcPZBa0gxrOCzVaX0WJGlqWs65LxYsINIfj06AG7m7vstfvsdTZ49/BTrg13OR6d4SuPdZoSKo+k3aUQln7S4Wx0xqu3X+G1nRscnB0hhaLUFZkwLBdznh4f8jtvf59+t0+/3aUbJsRRg8PLE261Bjy+OCH0AzaHG+y0Qv52NuFab5MnoxP2W32CypD7mk/PDuhGTf4vf/jPKUIPWdfIRuTsPz1XYCuhEPMleSd2zkR3buA9s3xcZKjrw+fXk7/ZpV7mBIMWWkrqdEWtS7x+kzorCK4NqUZzxFYH34DoNahOx8h5gZmsWaUlVVHTfH2f5rfvYivN/MefIJ9cUljL4q8+ZfWLxyR3t4hf3qPx26/g7fWZ/cVHFKMFgz94k+4/+xb+TpfL//k95u89ofXaPuUHTymmS2eR7XvUQPbpMcUbN4iub2CtJeg1ufZP3+HsX/+Cshkhl24IUp5OkIMG4c1N8o+fYmrD6q8/ofHqNcLNLsFWF//aJsXjM2QYIH0fKu0m2UIilLtN5JVgOFegEBRVhT9ZEvz266weXeCNl0glEVq7SWNeISIff5kRhD51UdPY6Tsbx8nSFUBlTSQE0/eeYj2FJ0D1EkKLK1QBMIijQ6puD1REuPKxm0033a80QkpH9blCKIR3laXgu9RkL/B4xn2wRmNLA1hnKSzAXhU1tqiQvQZCCkxWYivtkJlGhPYk6XjhLFe1watrWteG6Ns7bnLsKyopaPaaqNBjfTolPRqTdBKHyASe4/ZvdzDLnMb+gHCjxfznj5GtJp0kxq5z/GsblKMlNvCxWYlJS+p1werxBVwbgLZkT86d7kVJbFFC7CbDAoFSPrMPD9n8wcusdnrYp/UVWmFQ7Ri9yhxyDI4u5XvooqJYp3hRgKnBv7lB/eAMD1ivlkgBYdfReZWFcr5GCInQBqTES0IizyPLK5RSEAVu0l/WEIDoxthp6hpebaCTYJ6OUFdUWVHWyEDhv7zH8r3H1FlJGAUUde1cGS8WSN9zk9rNFhaBFjjRuScxszWyrOCioqw18Z1dp48oS1StnUA2y9FSYOZrR5tUErksEBtN6rTA1jU0QtecrAs04HcaZB8fIa8myrUvCJoNytESc2X4Ycoae7bAns0RgyZqkJAfXGCNxdsb0twZOAvrrKScLdHnU7jSLwXDDvgeOs2RnqA6HSOubWHjCIGgeHJOvlghpMJiSd66S5iErB6cELdiov0hKwMsU4LrWxitEYUL07NpiR0vHX1qu0t0d5/sk6fIMsNIRyVuvH2XKq/I05piVVCN1nQ3mo62cz6HVU45X189o33kVo/g7i7541PsKif94Cnrj5+ifA81bOPvDwmGXYQ2yDgg3OiCAK+doLMSW9Vsfu9lyqcXkOXI7RZ6sXamGuMFutSgBLLfwi5y50DWa5G8eh2b5RQHl7DKKM+ntL/7CuUiZTldYBYp0d6A/Hzm9CVF6bJRAh81aNMOPEZ/+SH1fE046RF1G24AkURYIbCFZv30kmKyZH02xfMkSkioNNUyp1KSqhGSno6RcYi/2cIXoI3A5iXrT06oTqc0X90nHLRIXr9BeXxJ9tkpuTYEpUZYy/py4RzbOi6+oF5meElIGLRJ3ryB6jQAqB6cIKIAM3Dnwo98Rx80FlMWqCRAhD4i9lFJ+PzeWKUF8RdS579U04pn2lP7ghvmVzUWz6Ko/55Nx9ft/utq7///okV9scn4Dx3bMzHvF2CgX/djv4xeWEN6OiYctAgCH11U2LJyGQQ7AwdbB85pyW73WJ1Naez2ab+8y3iVschymmFIWWu+9d3XiDfapLMV2WpFG8HEWuq8Il2sma7XJL0W1aogH6fkWuPvdqiXOV4Q0N7osl6lFELiCY+416IoKlSkqCMf3YmwSpEkAYGpXChQEqE6DZr+kCwtyKYlG9c2GF3MMOM588MxIvDIB02srlGNiPlyjfJALArXVHlwUczZ39mkvlwirWV4d5vpk3NMbRjuD8nKmvPPTlGDJv3XroEQzts8LRwS8+xCvppuSCWf8zN1WYGSRJ0mSCdaRLqLvy5q/Kt962WO1S6Mplzl1EVF0mty+NP7TE5G2KIiXWZsvLJHNl2yuJhTf/gY4ynCICCvKrY2e9z5g28Q39xAeZJivMJvRtSrnItfPGL29IJ2O+bi8JJmFDA+GhF6HsPtAfnJBD1bc/f1O5yej6nzAht4dKKQPC/p7G8gleT44Qn+2NFlVDdGBQFB6BG3E9KsII4CZpczTp+cEncbpIsVrdLS2RvSf+c2ze0eaMN0OuFvDz/D+B63dq5xOL/g9nCXZZ0zTVd8cPgZ98Rj/uNv/oDpdMLlckYcJRzOLtnp9DkYjbm+scd7jz/hF2ePKI3mH995C2Oh4UekRc79yyNKYSmLgm/ceJlRvqI/2GAyuqTb7fKNWy8TxQkPnrgGwutu8lf332W7t8F8NmO9XlGamoPTQza7feZ5xp3BHusqZ9Ad8vT0kKrSTJZT+t0eizyl1WjSajRYFWtUZbi9tY8tNZPlHNIlFAWPq1NaKmRmazaqmtMq552XvkFHBmS25u72NXyhmKZL1nXBb73yTbxuQqU8pDWUkyXWlygrkHFIHAbo2McucqyUBP0eHha9LqiSguBKS2TKGn+zg2rFVEcjot0u+dRDLDJUN8EPfOrLOeFeHz1LqU9nhDeGxK/ssfroKTaz+NpSnk65GC+JBg2Gv/cGvT94k+LRGfkvHjo7ROWz/uCQ9S+fEL68Q+udO2z8Nz9k+lefcPzf/YiNP3iT5Js36SnF6s/eZ/3eY8JrQ0xa4FU1tZCIJMGucs7/5V+y9X/6A6KdHghQ3Qb9332Ns//hbxCBwpMS4ynKT45o/sE30GdTyosZstBM/+27bP0ffw/hK7yNFuWTU+w6Q0SBC3BDIGqD9gTKOuchWbkAOK0U4CFLDXWNmS8w2iCjwOkqpKIMPYIoIh/N0VVNvNlFG0NyY4PFB08IN7t43QZ2mVNkBc2bGygEZV6i4pBimVEejfCtINzbo0xz4o32lYmCR5HmSAt2nbnU6StEUkhBnVdgLSp2IvW6cG5L8hnP9xlPwOBcpMKA8njiGoAkcp70ByP8QQtRaag15TrHWkG6TkmSkHqZ0nxjn9kHh8jYJ2iEoCSrsxnpZ2eorGJ2PHX3uS9othOiyqX3rp9esLHbI742YPbgGC7m0IxJz2fIVkw1zwgaEasnl8w+OaKYuufD6mSK8XzqKCCSzvKWZozotljXFjoRLHPnSJSVqMBHK4EUPsGgjV5mmNo4R7Wywhu00Ksc7yr7xSiB30wcIq412XJGJQRxGDnXqSu6kxEWW1YYJYmvd9HHU6QUGClRkU89WyOkwhh9RcFZonzPFbtCusbRWNQV/TB86yZBv8n0jw+Qge+SvJPQZShI51qG7wICywcnWFxqt9rvYqsrYXlRYZMQ0YqxpzNH4aoU1cUcrxNjlhmim6DnazwjqMsSPU8JdvouUDArkNgrJMTRAykqbOBRZQWeckg8+ipdXEmscg1s4CnqWUpZVQSt0KVZH0yYfnJCvNt3oYzaoOdLVFogPEX24WMXjhd4yE4DWg3EPEUKqBcpNiucJlJKct/HrgpipQgGHcqLJaun5zQ3Opg4ZP6jj6jGS6cJlQ7h9Cvt0KH7p7DRwuslFNMZVDXB/hbZg3O8XoPWbo+WVEwfnrF+/wmllGjhYS8XCKC0BuUp6ugIKySyERJ3EvxhB2IfFXjknx2RHl7ib/WIt3ro+Ypgu094c/uqWrPu+kkL6smSIs3h1NG8/V4D/9V9TKExn51QTVcEuz304SVVXlMhCPeHhNc3yR6foi/nzH96j+4PXqP3yj7VxZRwt4/wJYtHZ7RubDpULnTUa7/XZPi7b3L2N5+QbHQI9wZk7z5kdv8UXRtCJZGxjyk1ZV5hogBlDes0QzUbBFGIPl9SC+ju99BlhWeNu9Yij2qeYsdrJn/+EUEzpg7dwFS1GoRKUF7OiPaGSOmQ/ep4fKUR05QXM3ReOmcrJdAXC/KPD2n+3puoRoTOS0yaQ+QcNvWVoYOotVu3pLv+qnmK73sYIdx9HfhfKS95jlKILxe7n5fW9jfMAvr8v+xz2vnX7fv33X5jzcVXa0O+2DaIZ3j3C3997Q/50v9bLLbSmFpj5ylFVmKHNWaVYYqacH9AdTpBrHOm8zXNzQ7+Tp/66SXZRwdE1zfZe22f8f0jjOcRrDM6Btbrgsj3UYFAtRpknx0jEBydjCBUmEXOrVeucfrwhNrUBMuK3Y0hRwfn0EtoJzFZmmPO56wna8Jhi0anSX4+I+g28AIPbS0rCoJujO+5iVV2uYBmAK2Ig5NLWjtddKXpRhHLskRJRZ5VDAZtSmGpjGHv5X0uL6aIsubGrR3WeUH7+pBitqI4GdM0ksW6RDRdkN/iyTmnP/uMzs1NLIL1Eze9CbsN9JWIT3mKepUxev8p86MRiVTMLuc0eg22vvfyFZUB/EGLar6mmKU09wZ89m/eZXkwosgKyqJ00yVgp9XgdLyg3U0IhSDa6DI9nZLO19y4s0NR1aysIGzEJHXgpjTHE4KdHtUo4+jP3qfRSqhrzcmjE1oYFmmO0k4YWAqIei1OD84J45DR2YThsMvGzpDR1MmgF0VB0Iipi4rdu7uUecnl5ZSkGVEpRaXg+HyEWeRE/Rbady41sYzJlxm9RsTmjU2G33+FsNNApwWjjx/x+Kfv89rNl/jk/IAgafDy3k0OpueApdvu0fQDNjt9rJSs65I4Sfj48DOubV9D+x6JH+EbwcvDfXZ6Qy6yFSs0/ShiMTvl5sYO1+tNPjh+hPZ9jicXEARcTi9ZZ2vacYOLizMKDEhFv93l4fiYjXaf48k5DS8kKwpevfkyZZHRjVrUbc20zPCMpZ0kWFGyVjXtVodmq8NluuRmp08SN7i9c4NHR4955/or/PWn77LKUwLPx49C7nR3iIRgXGX8+NN32eht0IhifGHohA2youSXTx/w6p2X+P7Lb2GlIM9rTF0QRAFe4ONHAaoZo7OSKstIq4xuFLtAKuFRW005nRPd2qI6meLd2UZdWSurRojY6YF0g4PVyczRpxrOXjM7HdO4u0O6LCiejJCjJa1XrjP75T20VTDJ8VsRZpkzMR/S+8GrRK/sMdjosPzlQ/cwaW+xvnfE+mcPKR+fE7+yR++Hr7J8/ynjf/MuyRvX6Xz3ZYd6/ekvyI8nxMMWerREVzWqrt3DKtOM/s27DP/Zt/G7DZCCcKtL7z/+Fmd//iHNRYaXlxgBy5/ep/3WLfSPM3ReUH96xOr9h7S+/TKtN2+R/+wzlBJUWuNHAcJADQT9Nma0RPo+0vOQ/SZiXaC0hKqmuJyT7G9QPh2hyxKBQIc+nu8jlcC2E+RijTJg1wX55cJRjwKPfJXhJQGhEtg4cO5RWuO1Ysqywg8CEBavrF2KswKtJHLlchWM1lhcQ2EAa4ybmlunm3jWRHjBC48ga9FZibEuwKoeL/D6LfztrhtwXNGqbOBBUVMLMMscJSWlrmkM25jKUM4XUNQEceDyQQIPU1SkZ1N0UZKdnKKSHjov8fwQFQaYkWt8O69dY/reE9ov7dB/4zpnP/8Mb75G7A3AQrnKSF7ukZ/NYJnjBz6iNm6SPmxju01WyxS71cfvNjGNiFobSHM6dzbJD0boWeqm9FZglctsqp6O8KSkMk5Pp3oNR4kChJQkgxZ6vARtqK2lzDPipAG+j7gSPWvt0CItBUYKVLOBOF0ijUX4ElPULgnaOrG3qa5yUiyIdkQ1WSGEQEtQgY+1lvjuDuufP7zinQeI2mWx6FX+PFfA70TUZzNEbbBKgNEUaYmqDPLKKMRoQ7HOkNag8xolBVIbtO8TbvVZfXKEDD1M6XR3tigx4wXGk24S3GlQTC6QSUC1TJHNEK2f1QNgRYExGllb9xzKa0d9akX4wyZmnUNtqOdrRKpRtaF8cEb56ALbiRHdhEobhDWoThO6TcQqw0QBxckImZXuPF1O8Tf62KqiyktUHNG8tYWyFhv6eElA/WhF+tEBdVpTj1d4oe9E+rVxiJS1BPaqVJyswPOuNEcCWxiK+yfUUrK2FhoBNvadY1olsDpHdWLK8RIjJJ62eFmNQSCyElNr1qdzysw1psF2B6+RYM5nLC8W1EajLhbEixTP4JzIOgn6bIKxEG10MJ0G6fuPqacp2eElzTdukdzZoXx6jpmunHVuVlIvM/L7RygpiXYGlLMVzFasfnqP5Ju38aoayhpR1OQPj+FiSuut22QnM0AQb/WdgY0vWR+cEyhJfjDGBAFR16c+vaBeOLOeejqmwuA3Gqg4wpYeBM5soK5qNww2hjjwkAKSnS7zosITCm+6oJrMYbFE93tUzZhgp0vn+6+SPj6nzjNEFCJLTThoY9ox9SKlOh4x/vSQ5ndfcY6F7YQSSxz4Tn+TlVTzFfnjc+KX91idTpxG0PccFbzUqNDHSMHo46ecrVN+65/9Ft4LbpefL31XQ/lfR4Wyn8tZf23uxZdf8HfYxzUVX9pPfH48/5DtN6y5+BI15kvdwhUJhy8zv762H/tSx5Kdz7BV7WLto+DqtQI9WVFZJ1gyukJkJcuzGcP9If5G2/0uJWi9tIsKPGaPL0gbEV3lEbUC0skCGUWsZmuePjqi3W4y3N+gWuds3tigspaVMFTGsNNrky5Tcl+QBD7zyYJytKSnfKrAo7c7YHFwyUBDqi1JO6GoauKOCwhbTZeIRUE7iRlnhbsIA0XUiCnqmrSo6d4YUFpDWly5L3Qiyqzk9HhEHUiitMT4HtSaxfGI1kYHFQWUq4K4qqhmKVJK2rtDotDn/v/0c8wqpzvs0H39mrMXlGCNpZyuOPizDzh5eEq2WHHt+g6T6ZI0K2h/dsbpZ6dkec6d773K0QePmY3nvPa917j87JRhr8nGdpeDTw5od5soT3FwNKIuK0QukdsD9zsuJv8/4v7rSbI0P88En08c6dpDR6TOrCzR1aIaQEMNABIkZ0mardma7eya7f53e7F3a8blkjMcEhRDEoJAs3XJrEqdoSNc+5Gf2IvPszqrutDEEFhbv+iK7HAVEcfP+Yn3fV40ksX1gmVZsXfvBrK1TKYL9vs9snEXliXCh7ROpAwboFhRodFKY2kx3iM3VA7TWpJOSukd57MlMY68nxMP+5y/PKMtCtbrkvH+GC0ELlLMLmekWYro5ygEo90Rs6s5opsTacVksqStam4djdn5/XdRWUx9OmF5NeX//c/+Odcnp/TzHnd3Dvni+Ck3BlvM45Jx3ieTEZduRrc74Hw15dOXX9BNM3aHWxSmYqezhShKzuaXSOMovQuyqnxAxzjiOKWqG7I051u33uLJ6XPq5ZJWCm5kQ66EZjAcklWhkfv8+WMqL6ibinfvvMWPHn9EJ8m4M9jl7PoMncTcP7yNaRvk1HC+nrCsSoq64p1bD7i4vsAWJRfXF+z1hkym16zrik6S8ie/+Eve375BMbRcVysirel0Mi5n1/z+299jWa15fPqSHMW11PS7ff7Nh/+F7xzc48Zol2JZhiJJgEzikKUw6GKrNhgh9/pgLKNRB1c1yERgpit0kjB85w5pJ6V4dR2wyO/dRKYRtgjHhRcQjbroSFN8ckLnvRvEd3bI+inNdE367iHlkwvM6RT7s+eM3r6DXVc0X5zjlxVeKZpH51xeLhj/8beJtvqM//DbmIs5809eknxwB3G9xlzMWf7FI4pHJ6QHI8Z//F2WP3/O1f/zP9L7o2/R+x/eZf7vfk5T1iRJhIsjRNXgYo1uWszxhOLxCaPffTcUfa2hd3uP6q0Jy4+ek7YeZR1iWWGNQR2NcU9OQWkWf/EJnffvIntZ2O1qhcdhOylmtiZOU1SkoN8F4/BCoKoNKUpIvNZU5zOSGzv4VxPaukX2cmLvMUrSrArSbo41jqZpkVWLvV4SA21r0P2gkx+8fcjV2ZTIOnzR0EzW2Gko7tx8TbrdDwWlFGFYIYP8SW4kPtXlHJ3GiEFnM8Sogo/idVPxhu/KGxtyMXzYWkS7Q0SksKsSGWl8azFVg+ql1NMVupvhxwK3qoOMKwt//7ZuaaYFvb1BkHo2DrNeEQ9yTNFgt8bYlcHKKMhZXl0hViWiNVitGH73LtMfP2X4gwcMFgXtfM3u33+f4vkldVUz/PYtrhcFV68uyG7tMPr+XeyypLlcIL2lmS5Ij8bo/VGQzwqLW5fkR1vM//2H2MbglUQIT3I4RvVyipMJIgrHDVKihl3KD58H35u16G6CmZdh4t3USO/I8s5GAtQinPsS+ys2pYe0jrao8UohhjliEX733phAI6payFKMscRaI+YlJDGibpDW41NNtDVg9upnAYXbWkSsAj24MbgNMtg7j50XRGkM1mAHHdRkhU4TrFJIZ9Gpxl/McMaGrV3TInspdrHC5Qnr40vynT6REAH4kMZI68JW3Hma40mQEQtwqzoMGO0molFJZCxxtCA8xlq0FEgEtm4pTifBq7DdI8ojrCug8GGDIwMlqL5eEiuJTSOsqWjWNaq2QRq0nQd4gnOoRFPOVsQ7Q0TVEGtB88lLqh89Dv4i67C9BNFLoZ/hRdjOKS8Q3gdMbxqHz4fwJLd3qJ9dICTYNA33lQFTLATIdQOrEDroZBToVJ2YKIsxjiCta1q8lCjvsZMlRkckUuGNpXk5AcANMpQzqN0RJoqoPz9D9BOS2/tUnx8HytZ7t2gmK4qLOWXjyBKBi2ImP3xElMZ03r6BP58GIEwSI6saBh3csgqhoEKEIM75msm/+kvEXsAXvyameSFYf/4KEUeIPAElELFm93fe5fTf/5gpIIQn1hpXBc9S8+wRLBdw7x3SGzdI8pS6NUjjiFHQNiSdBGlaMu/RWtIuCqo8pndnh/LFNUL2sUWFuDzD/ulP8N/+gCaPsc6T39unfHyK15JmXdD8xQnx3hh3Y5vk1h5KSMqfPkXuDlD7A+qLWWjIuxlxPw9hrNv9cE7Gg7FY+JJ85104hpNI8/C9O0GeuKl6f0luYiOF+jW3/932i6894BuH9m8M+r++GfBvfP+/8/a3bi5++fK/uqt4Xfh/9ftvNBhftmJv0AzeuNevvJaAbG/I6sk5SgjQgRYjvMcPcurJiihSJPf38VqxnK0x6ypwqZcV5XRFb5CT7Q2JOinJuMvkJ0/Q0mGVoFmvkR4evHObzqCD8R67KCmrhtOnx3T3h7Tncx599pxkt8/O20eoSDLUQ5ZKUtRt8EJcz2hMQ1XWDG+Ex9gsYjDaYvrpcZgeZDFz26LTGDktySLNcrZCdWIOv3uXyeNTZBaT3xpTTVeoRNEZjYiVRkeK6bMLSuPQUpLlKf0HB+y+fYTwcPy/fYR18OzZKVuHY5yE2asrdo8Cy133s1/+Uq1l8fMXXJ9OGd/YYn0dBxZ8J8UD87MpVdOC9ahY4RtLW1RcPDkjizQ20UyNwQ9z1mWQt5BolBKsjCGLJKuzCVm/S9MaZi4Enu03JqTgnlxSdTtc//QZIolIdnqMdoZEw4yrT15hlWTrcIdmuqJq2pCFIATkCb5sWMxWkEbUjUUNMoSQ7A86RPKAF8+PQSguXl2S9XJM3TLeGrK9M+RyssBHmriTsh1pPvrZI+7eOWTQzxhudbnxD7+H1or6o+fonSHPf/YpJy9fsVwuuNvf5Ww1462dG3x68YJ1XZCoCBHD9mBM3umwuLjm9niPy8UUJSVbcQ9RtDyfXiKd5+HODS6XE271d1BSUVZrNJB3unz05GNOlsGYPdrapipKzqZXqEiznM24eXSb5XrN4e4BSZyyXC24mF5z78YtVqs186bggwfvMS1XLKsC27YU0pMnHcZplyZtibzgxv4NTmcX/MMf/CFPXzyj2+kxPT/mW29/AMZyVq/Y7vbIOh2q9YrT9Yx+1uHlxQmL1Zrfe/hdyrZh3O0j0oQH9RHffvdbxE5QeBsCvKyH1uGKhnZSAOC0JLuxhWkszfkUn0UIrYk6Ofm4T1m1xK3Fns2pPj2heHRC550j8nv7QXqjJCJRJPd2ccbSnEwBjz4c0Xn/FuUXJ5Bq4sNRQB/+5BnRwZD4/j7Vs3NsGaQ49nrN9f/nh3R/6wHd926i94eMt3qsn53TRJr0zg7yxRXmi1PWLx6x/PA56ds3EP0Oiz/5OZ0/fJf4u3doP3pJ0xh804YL56qALMHXDau/+JTeu7eIRl1UrLGNYfTt28xeXtEWNWpVI7Wm+NFjun/wHu3pNa6okZOAy8zvHSA7Ge2yQm2K+DiJQSuaDf7RXixQ3mEFCONwKqQxm+sl6ffuMzMGbUwoaFoLq4qkl9HiqNqWTGt806KyGKNFuABahyka4k5Gd9CwPJ2SKMl6vsScnJMc7eKTiKaxIAXpuIObrRF5gluVIeV4kxtk6jV6s73RaYT8SshnOM97ZzcBmWKDnAZE4Nz7xtIKQ5THwQ+QaChbbBKT740o7TUREGURzdQSC0F0exvRT+lsDZh9fhpwrFmE3Blgyoa0H5LEjbFkcURx9Qq5XmDzHi13QnioseS7Q9Ye2rMZybiL7uWk4x5xlpDEMVvfu8vgxjZIweQvH2ErE/JYliV+8hyXRIiqJc9iVj95RnMyDdcrLfGNIb67h5sVFMfXWBOKYuFdOFZai9KKyDpkmmKnwReAUpvwsBTTtqg0QUoVipWNHEN109C0eodQG7JT3X5ZjIskwl7OQ5aBlFA1WOM226QobCQOx7hliSsa7GaoI5VEdRLsosS1DqRHlBKlFN44WheONZWE1HbbGFoHytiArLUOEW2u/WlMJDV2WaJqg58X+CTBVg0ikXipIIuRtQnHrVYo6xGzNb5oQsJ9EqG7Mc4atBQEPGGQp9hYITaZKuwO8EVLc7FAdmNUpGg38qbm+QUMc0Qvo3lxHdK8+2nwCS0rfGvw+31s24AVDH77ndDgripcbSj+yyNs2aA7GVI4zLSgLWrEMMflCWk/Q1oLtQUHal3j6xb9YJ/6s2OoWkyewLiPSOJAbDQWpcLxLyxYL4gHOW1lMOsGtSFBmjYAAVSkgvG6dSSDGNE4GiGIAVc2cL3CpZrock6cpVhnKKoKmyb0//h7Ic9Kgt4ekBxtkx6OaV9eER+MKDeo2fr4GjnsBnz1dIk0DjFZIvo5LAPC1ywL2OoRbYW8CfkacWwt7eUC10nJ3j4K4X1ljbUO3c3Y/+PfwBtDOZpTffQSaTzp3j4i7+CMJe51cc4gTUveiRFN2GI6UyOdQciUfLuHK1uUgPb0Gjtuye9u0y4qVG2wWYJNAuDHtZZ2XpI92A9ULe+xD4+w8zXtyYTmfIY/GBO/f4cUmD0/J4s0qjXUr65IjrZoCHh8tRla6F5KfTXHeU86Djj/1WRJMuywNe6RbPffKGu/Ws3/zX0Uv3rPL6VNX6nG3/j3r1tC/DXf+7swk/+dbS6+6T2+bhG+bBW+8obf+O6v/CDiV7/cdFIyVnTu7GLXFbZqqC9mxDuDYG7KIlzVhs2GFMj5Gnu9CGvSLKLb3w4TMiUgUoy/c5skjjj9y0cMOwlzYLUuiTsJrXUoIZkt1lR1S/9ozHJdkO70yHZ6zOqK9WoNjQUt6O70mZ9do+YNab9D99YuZlXTzgpyJDWexWRJmsSUVU1/O6RLRt2MlYWiahiNuyznK04+f0V8XbCyBjHIcJUh2+7j1g2mLim1IOmm6NZTXF3ieim9G1usLue8/PETyssl8SAjTWOqZQm7mnzQpakNv/gPP+X21ZyH/9Pvg3Wc/edPmH12wmK2xMcCoUN4jYskWipW8yLofbM8THylwCcRT48vOby9T2EsUkmSwzHNosBVBpnHVJMVTdUwnW3May3sHmxzXRbQWKq2pZoukf2ci6sZ51LSHXZJ1iWDJCKylqqoKU3D+Ytz2rIm62V4pdi/u88Sz2Sxol0UCOlJ8wzrHGmi8KuKVEjiTo6xjtn5hMvza7YOtwPbvDFIrehmGadnVzSrik6/w7ppOEhy7vzj36Qz7lM8PiW9e8CP/8W/5X/5N/8r+4Md9rIhRV1yUS/5gwdv88nlC8qmxnpPOhoia8OLF8+IVMBO3ti/wbxY8d137/LpJx9ye3uP51fnRN0OYt5wd+8Gi7ZkOO4zO/kC7z2tcPzTP/hH/PyTn1O1DT8//pxYR+ynu0zXK64++wXWtMR5xv44Y9jt8bNXz6idYdjpEwlJVTcMsg5tU1NXFVudPrWqOV/N8MZhcFS25fOrY86m17x18y73tg7Z6Y+obMvheAerJNY77iQjPlks6KiEq/mcoqw52trDxpqqKblcTYkqze+9+z26VmOrgkGUhuLQeIQGbxzOeSQeWTuUUphpgYgV6daAcrkm6aRQVqEQFRLRTYmSCDNZUfz4Oc3xlMFv3kcN8vDZORoBnvLpBU3ZYB6fI2JN93v3iF5esfzxE+KjLcqXV7TngXMuRzmtX6NbgXJheDD7Vz9m9fSUrb//XeJBh+7DI7yxrJ6e0fvtB/i3j1j91SOa4wnmsxNEN0Npxfxf/5TO9+4iHx5SfPIKAVjvA/p1A0lwy4qrf/1j9v6n30fGAaQghh3y3UFoCioTMmZiTfnkjPTBIeXPn4JUzP/zh2R391E3dxGfn+CUCkhn55FShMCmnRHFxRzrw8m8lRI2hYnahKSJNMKvCijDFFtaSyE9iRPEkcZZRzVZEGUxWZwiPEHD7kqwlsHukOZsjisa8qMxpQkTXJSic3cHmcWsXlxh1hVxrKEkNJOtJc5j2nWFv17Q3R8HRK0nwCSsCxIpH2hRsJn4SRGStzdcWo+HpkFFfRh1EK1F5AnlRSj4ZRLD5QpxOEJKKNc1WRyRdrNQ5EpBujcIm5XZmiQPmzSndJDS9GLy7zykWRbk3TSY25cldVGznC7J9ofh7+k8ife0i4LF2ZROHBEjAknLe2QnI/vBW2Acy6dniFWNrEOonR92qI4n2Dbg070HdTiCbkp5OQseAu9DlokLZKlIykB/2mAqlQxoWKUUqID1DtC9sNmShJwKb2wgOK3D31vFmihWFN6HrcDG9Gw3AWsyUphFid3kbHgVIZ1B7Q+pTyYhANOD1EGa5spmI60S+FE3ZM8IUBA2RUWDVwrjaqQUqK0uflJsXk9h6g3MZL4ifu8W8x9+QRppMB6XgI40Po6wjcPGElk6nHeoboYrKmzTIqwn6iQk9/YoX5wjOmkAEvRShAXTWpyEeLuDiCL8sgpSFrfZdPWTQP5qDVpK/LqBQZg8iyzGL2tcHoe8q9rSXq7wCrK3bmAuFyz//S8wSqBv7aD2hyHbJFLInT7y1RV+VaM6KXECXCywtQnbk26KWZah+CtqvNk0SNaFa9lujFLBzyGcw3tPlCY03iOzGBVHSOtwxqHz8DO0bTAmvzb2szkOZOuDRDNSULXQOEQiaIoaVRtM1eAnJebJGeaox/4/+EEolnsZ3U7C1Ycvmf3oCd5ZjFbEWUIzXeGj4BvQHrR1wacpBbZsQtr7zoD8u/eJTqf46TIABrIY17QUzy+ojq+QV/PgW1GS7P4h0aCLUBmqk5J2MqhamtMprlCorT7xKGBc1cZv45oWlKazGVpEoy6uaqivJqitHmynUNQ0x1fIUY9sPKSIFCp6C1EbnBTh/PN6Qr/JVFJ5SnywRVY1lGdTZCRRWcL43ZtUnx6DCH8HOy/AevSoQ7sOTZJb18g0JsmTgJtd14EstcECvw44/bK0/Upt+98orsUbX7wutr/ymK8+gfibPPGvn+X/rW9/R83FNzks4E35k/+Gd//ayv16kyEIq8I3nvLrTwUEjnczt7jzOXq7D0ByYwt3MoW0RSDQ4x721QXGNGR5EiY9STDfsAlnklqR3d5m21qOf/6U3AoYDZFCEGURxXRFf9jFKyibBqEkVd1iraVZFUxmBVE3DaxorRHLhjuHe6xMg0pj+r0O5WxNYz1xHtEZ9SjUgg4ZqyfndJKEslPR3+kRjzq0ZcNoawix4sWnJ6QHQ+LSgnFYY3HLChlpmqbFXSzJhSTrBOb26b/7BbOzKTKJOXh4xNnpFZEISb3rZcn6bEo+6LBzczdQVBrD5YcvePaTx0zma3QasWxq8jwn3+rSyxRNWXP5/JLu0ZBm0bB6eUVVb4ghZYvVnrKskammmlfYdUOUx/R6XYr5msRJpPXIXopctWR5Qn05QWQxy3lB27SU2jPcGhAhcNbS2x5xeXJFdVxStk1IwVyXpFqxsz/m6mLBzQd71I9PsXjG+2NWizUdqbguS1JtEUqS5AndWczlfEq9Lun0cyJrcbFmWhSsFmt68Yj9W3ssZit8UTNWilu/8w7ZqMfq8SnpqEv1xTF//h/+M3VT83R6wuT6kruHt3l79yaTxYzWWQZpl+vFjM/PnnN3+4ijrT26wyFJlPDDD/8rUmmev3rBcLTNUWfAs4tTTN2y0xvx0yefMh5vMcxu8fe/89ssFwtUlrFereikOeuq5HBrj8RLdoZjXk4vubV7yPViRkdHjHVEN86o7j3ks6ePkEIySnt4KYhVwno1oVwXXE+v6XX6dLt9rhcT0l6XfZWiOxkVjixJ+fzkOc40LKqSs9k17924x8V8ws2H32bUHXCws8+gO+D4+BVHewf8h09+yO5giz9467tordAEhKVSEhXHKKkwm+mgVio0F0oGOUWkiCKFs472ekXaT6nPJvheRn4wAmsx5zOiXkayN8TNC9yLa+bG0vngbuDYx5r0aAs3K1h+cozuJhQfv0JEmmh3QP/33ub6X/+UeKuLX1aYxRpzZYniiDhXlKuCSAhcHGG/uOD86k/Z+sNvkd7eQ8aa7r0DqrMJjW/p/MZ9VBZjpaJ4eoGvGlSkWf/wc9J3j1BHI8znpyhpMa0JpBalsMZSfvKS8skZnXduAEGzvv/bDzn7538Zkm7XU5RW1M8uiX77LaJBTr0oUUVL+fELOu/eZPHFCbQGlyfocR8zWyFw+ESjN1r7ZhPWFlmHiKKQmuwd+e6IYlWF5gMHq0D3qa+Wga8fa9yqRCzWeA9tJIk6GU3Vsj6ekO8PibOYJo+Jt3qYJhTC3gOxBmPItnJMpjGNDYFqvRQdqxAG181QUuLMJijPO7zbNBRvZOMIGbT5Zt0EypIK/39ytI0zBmcsrqgRgO5nVM/PqadrVDch3h9QXywgSfGyDBk9RYMYdkm3euB9kJJcL0mOtmmenePPrzC1w4y6YTo67NI52gqEKuewrWUxXQGC/Lt3ULUhFpL5z5+HbYKS1Gdz/Ls3wEP/ncONrLOFWLH64WNM1aDzmM5v3mP2Jz9HWQdaIJ0jv7lNW9aIzcb7dXColkFH3iYR2oTwxC9pUj5speI0R+CD3M46dBxhpQ+DNRH8LM5YTN3gpUdvCrnIExCzdTCXOmODZNRY9CZ8zzYGtCLeGVD+4kUgMG3IN1Ir/DpMNp21uLIOIW+bjUmko833XMirEAJmRXgOHRoiFUf4zWPNoiAadSlPpjghEGWNtC2y0gHBuyyIxMYQWzeoKPiZkr0+0f6I6tNXuLrFydA0i9YipUJ2EnwaYRyoywVECr8x7gohUHhEP8dMV+HzmsSYskZ2EtqqJu5mgVg36OCuV7ja4DJNOu4z+19/jPSAtbjPTojeu0F0Y5vy2TlWetROn+RyGQrOZYWdF+goopkE8Ip1FmEtdrZGSYlQGiEhThSybnGba6EApJQ4IdA+mMlFGuHagBt2VYtpTRjGLMuQRScFNC1NrJFSY9YNwjmcMchBSjNdoqUMaexNi/CO6eNLZo8ce3/vN4MRWQR5Y7o3oP3oRdjglBV+VYfN2rCDj1Q476QxFhHyMKxDrKD66RPsdEnn2/fg1i5SSsrHx/iqgekyYGslyEE31AJ/9iHJ0S5N2yB6Od07+6g0JrmzQzJbb+hrIbfFLgpca3CNZX05QdSGOI0xdRukdDsDut++HY7X2YrVF6dorWiWBUmqkDtd5tcrOts9Ore3f7WoFqESlVlMdjimOJ2E45AQSOlWZZDRfXGC73eQeRwaVCHxVUPU6YMM2T/l6YTu4RautdSLgmwUrstf9hT+Ky/7zTfxy7r6y0f+qkXimx/4N759rbv4qtjov/v2t24ufvm2vvpOvr68+frO4sv/+jc3G68f93XvxldvQgiSYYd2Y0QWgEwTknGPerZEZAlaCvr7W+hOB1s2wZTswgTGm5DIiBDoQYfx9+7iE838R0949fgYn6fc/40HLCdLmrZlcjbn6OEN2rrB1BbZWjILlfTk/Q5FWbGarfBFw3y+okkEPL6g7Wbkuz2iLMHWlumjU3q7A1Q3pXo5JenlqERt0IoFrrWcfn7G6J0D8of7jHYGXH7yCpFG3Dra4tXFnNaCna649737bL17A53FYdLnoXh6wcd/9jEnz85pbEu1ruhEkr2HR9x47xb19YqLz09C+Mu//wW+Nuw8OIDzCVZLXKrJ4gQ96NAslqg8Ju3nGCUpm5rp5ZxGgRMK4RoaISjKmu1ORt7LuW4mWGOweFZVTTdS9KKIVVGRJyn50RgevwKlma7XpElCkkZEaYTFY65Krl5d4VPJrC5wrWO0P6ZYFJiyYV0ZSu2ZPjkjaixZkqBiTTLI6aQp82cF7boCrZCRIspitHGMbu2zWhdcX83JOzkIGA77zK7mPJnMEdbTV4r7339A99YOq0cn5A8PkQKu/uoRv793j//H9JQH23c5TPqgJH/+5EOMd3z/3rd4OTvn2clLbm8fMuz0mRUrXBRxfPEZo26fJ+eviE8Ud3YOeVk33Nu/xfOLV6zbit+/9226aQZNmMa+uDrn05PHbI+3ma2WGOl569ad4K+4OKGb5OROMhFwfHnGy9kVD4/uc3Z1SSfJ6G3yMorZFQu9YHu8xX7e5XI+ZTAYILs5nx0/oZd3uWqu6SUZo26Pjlc8nV1zMbng5s4BnTQjzXPeT7tMZtfcHO/RNi2+btnZ3WG2XvCdO++wm/fQWjOM05Ak31Rsdbt46zFuYzCtWqJYhwEvnmjYRViHrZqQAtwdfinbaOKIZLbCDjvEt3YwX5yBdehuiqka7NWK+Z9/Ru+Du6Q3trCtJdnu4e7tUR9fYycryi9Oke/eIBp32frjbzP7D79Ab/dQow7Nq2tc2VA3glRIXKbQXmDblvZ6zdW//BHx7R12/vH3wxTtYEwqtkLBVrebib6jfXKGKw3COqpPj5H3dkj2hrAscbHGtRaBI8pT2tYw+Y8fkt3eDdQmgmdk5/fe5urPPkGNu6Egt47lJy/pv3OT6oefY8qG1U+fMvzHv4HIYtyqwrWG1gcIg/UEv0SkaRGoqglEptdZEVLRXM5J7u7iJ0ts2aJ0hFAhaE807WZCCi6JsKuKVqogL9GaqJOw+uSYSG/OUauaxasrdKzRStLUbahD4jgEdNYtyW4feXeP6nJBc70gGXWw65ooCT+3a0KWjtgUeq/P5/DL4vpNYIp3PuCzN4WwyhNc1aIjTXfUw57PifNtGHeQ0zUaQfzuDdpVRXu1oKxbksMx9cb70ThHXLeB6mcc9XROp5ejhh1UrCAS1NdLSCPaZUm+M0BLFTYLScTgBw+Y/vwZtmmxHgZ3dsL7fO33cwGPOnz/FuZySfHoBLXTxxYNrqjDfZQkqlv0uBukYGWN0mqzoQCkQHZzVGvDJgIRqExszNTWEXd7OBukbngfcoBUKEQlYKUkyhOiOEIiQsaCEHjvgtSmaXHeI6WiWa8RUYBxhDCvIPWIspTZi8vwN9sE+1nrULbFC7BaEAuJdR4hwXiHcg4VxzjjaE2LkCE9Xmy8GRgHrQmSqfkaV7cBbY5HbYpVogBd8EoitKSVQR4WpwpTWvQwRx+OqT5+iSkbXGtQjcEmmmhzjAktEb0ccT4LvpMkCiGT1hJlKb7fwy/KUOxLgS0q9G4fZx1RtKkVmhZbt7i6QciE5OYudl7gqhobRagoChKcx+f4e7uIrQ52uqFxGQMiwscKqSSyk+LXJdJ5vHFYKZHVpkm3FudAljXe+tA8ZEkIn5UivJfWYAqB6me4qUVFOvgPpUC09ssaSSsZkMEyfGa9c9g6QCZk68JxqxQyVkyvJpQvX9A0FTw4/FqVJkjvHbD+s09BSFpAtwZrg09MZzHCOxwe3e9QTJZhWOxBerBfnNK8usI0hkjr8Fm3NjRL3ofw05NJyHLJYty6DOeUV1fMr+boJKIVEtmGJqv77TvocQfTSWgen+KMIdsfInt5CFPtJojW0q4KiqdnqF6G14p6vsRezEKjWTWkeyM6iUStS8rTCSqNiYcdVJa8UbWGUbhKY7p39vDWYutAcKuv5phVhe+k2Kal+vglYqtPMkioLqbhOUbdgPze6lF+/AI16iJHHRaTJd3be8hEf63OfeP37v3GUP1mPfxL24D4+v2/rJG/1oB8wzriV+/z37j9LbcZ8m/38HD7mzY4r30iX3YUf+0D3/Rj+DDd+toTiUiTjLvEwy5Yx/rjlyw/eoEwHhlrpFaogxHrz16y+PhFiL2v243sR6OzN4PcBMM7u2y9f5vb+9vc3B9x+dkLzp+fc+vuDbp5Rl1WCK1plxX7vV7QV2cxxjt0GpF0M6LdHqtYYBpLz0vK6yWr6RoZaaafvmJ/2Gd1NkMLweF7N1GDnGyrS3m+oDyZYSRs9Tu4VUVnmEOsyQ5HbN/aZfLiElJNEkm08cRtmBCXL69prle0y5J6XqKTCN+J6N3Y4sYH93n3H36A6qS8+ukTnv/8WSBrWM/JFye8enZGvNNn+61D4lhzcGOHYr7i6skpi+kSncYcfecOe4c79A7GvHh1DokiiSO2D7eIpSASirqoqMqG6nrOfLKkWBR08hTiiKvjK6QnBLQ1Bt1NaeqGwXaffKdLt9NhcTZlMV0SJzGdTkZVG3QUkUUxy8sFQitcGnN5fk3RGio8vaNt2lXFk0+fU69KvPf0+x2KpsUkmra1eCGoWsPunX1Qim6eM+zmfPHpM6plSccJ+lnKjd0x92/uMv7+A5a/eEr3/j7SWGY/fczk7IJ/e/4F3zt4wG8f3sdLyXEx47cevM8fP/w+4yTnre1D3rl5D49jsphyfHlKHEUMkxyE4P1bD+llHSrbEEUR9WqFF4o/+MEfcbRzwP72HjaJwBrub+/xe299h5udMe/u3uLd7Zsc9LfY6Y0YDcc8n5zzk5ePeHF+QuMh1ylPXj3laP+Abq9HHiWcXJ/zfHKOcYbFesnTyzPuHtziYHuXZblgJ+uz3x8zSLqs25qPn37Os4tj3t67QZyknC0m3D+6zWK14LpZM50vqNuW88WEYXeAcpK3xweMVcxhf5vd7oC8k6GTmCxN8DKYcl1rcXZzkW4MxoWMFLsOfy8Ra0giRG1oL2bYJMFtDWiQmPMZ2dsH6IMRYlVjm5ZkfxiKn1lJ+cPHlJ+fIpRA7Y8CkakNqEp/vWL56csQALbTZ/xPfiNkGlhL8v5NRBpBbVgXNXZdYYxBa02Yq4J7ccX03/2MZrIMryeDPCd9/zaqlxGNu2Tv3UQ0ZjPtFbSnM8hjWmeJhSRJY7wIWFFvHe5syuVffBImyhuTanL/kHx3gLDml1r40oTshb0ROo5pTieYixn6rUNqYxHWESkZirHNxFAOukgh0FpukKMxUmtca6g+ek5+ZzckH2uFXBUI5ymnK6Kj7SAPwuOalrI1mE1oVvniCj8vsI2lvFrR2e4TJRFuXWNXFb4yJDoK9DkfJug4j2sNWEcy6uCBdlWHQtIYXBMwrG1R4zYTdtu0gSzlfGDc6yDjeY1G/IqOeDPdF5tQvu69PURrKJ9fESURyY1tou0eAEpJpIPV52dUr67xccT5X3zG6uPw2Vd5Qv/BAVvfvkfUDwm/OoqgdbSbIM7y+RXbuyO6uwPmr644++kTVJ6QdzK81vT3R3QPRqEBEpvL1maCD57h7z7EHw4xZY2tQ9aDT6KQEbLVw2tFM11jvcBo/aVswiQ6EJ6sw8sNHlYrfOvwxqEiTTIIwV3GtLiN5t5t5FPG+TABF2Bt2HoT6UAsUoEsRWWCdMM6hLWbDCMfaFJCEN3cCnj3NhSyzodrsdBhu+QRyDiG2iCSIANUWiMR4DxxrDFCBPXb5nIfhmAe6x3kEmsCAVHEGmssfnMsyiSmbVpkWYffZ57Q1i2mdXjhg4/neBIkuEIghEQqSRzH+KIOYWhuE5a4KNCxRlkfGkilsImmWlVQhkY3VZokifF1+By6xgbTeBRB04IIw4f8cEz5+Awp9WZT42h92Ba1l4twPpBhK8QmkyGOI5QUAW+qBWa+ximJ0pok0kT9PPzs1mKrFp+HIY2tQ1hbWwbJrVMqNFwQAv0agwVMUUFR45uWTf8ZtioxWCXwkQ75JoBZlZBEIYukqGC9oF3NEE2Fb9uvFWQeH8mADe6mxCpsfoz3uHVNfTalXtXYyxXNT5+STEtk5WmWDaZtEc4js4z0vbuk37pN/sEDOr/3Psl37qMPthGdNPifNhuG+otjzGxF1O8QRTEyjtBphOok6FhTfPiM1Y+/oHp2FmTW3RTlHVmkiDoJ9uSa8vNj3HyNXxa0pxOa8ylSePxGwdG9s0d6Y5v0cAs16gXzfdVQnE1pFwVfDjh4rdwMWy6hFbqTEm31kDd3cP0cZ13YPG0kbboXqHT1izPMbEWSJeheDoMUO1tTf/QSP12x+OI4SD75Uo31VVeA+OV/xddaideNxt/s9k1Kob9mx/HmG3izN/n/9+bidf/15fvwX/3mV7ulX0Pq/Yaf+/V24ZtWVxCmWrqX4ZKI5npJOsjROkgtlBToOCIe9nCLElPUoCUyjhCRCr9Q9cvQNpWn9L99C9c0XP/oCTqSpGnohuuqpln4MFVxhkevThGdGCWhXhSkFmTHU3mPcy3FyYQqith57yamsZw/PqGTJth1TbkoWF7O2bm3T7QlaBYFkQy4vevTKbtJxmpesr0/ZP5qQlGUcLaktpb+nR3MvKTxnlc/e8r58wtaKSlXJYc3dijrltIa0nGXzu6Q0cGY1dWcV//lszA1s55+t0tpTDjJSsnl2TWudUxfXuN0wEa+fPSS/p0drLVcTxfQGHpbPaI7e9hYwawiTiLcBj2bbw9x3pIOu2gfvBMSWJ3N6GUpTWMwseLi0TGr2ZoMT12W2KLErVqG/S61kkSxpr/TZ/KiQDhHHEWM8pSrosBXhtmsId3pU6sKeaRQQBpHLC9mpFozGvY4Obni7Pk5N96/QzeS5NczmjIkZzotmFQVW4fb6DSiqwTtdc3uMOfwB28HE/smYGj65x9y8rNHXCrD9mDMIO/yk7MnfHT+nN9++7v8xu13+E8f/hWPLl+hoygU/50+z86P+aMPfpfaB8pSLCPOri95++gurbHMqxX/9dkn7A62OP78M6ZRwnff/jZJmnI2ueYvv/gFu70xJ7MLvHO8fXSHcrlkrzOi1++zNRyxrEq6ac58sSSKNFfXlxwfv2S7N8LheDDY5apec7VeYBcTchXzv338V3z39kOWyzkqz5iuFpzPLnEOdvtjSgwmltzY2iXXCV0U+WDI5fSahwc3mTUlR+mINI25ne7x8csn3OyNeH7+kj27y/ZgC5FESBGCmqhDkq9pDcoahFKYyqBESCJeP7/EdRNkawPv/vY2umqhaDDrEl2UVMaQvX+T6vNTysfn+GFOfDDErRvcdMX6zx9RfnHK8O+9T3JnB6TArCtWLy5wr65p52vyO3t03zpk/E++z+K/fEb5/IL43RvYizm8uAQXJnEWgYo0RBrTNNQfvuDyxSXDf/hdOu/cDCd7rcjeuUExWZI+OKD67CRMSYWAZUU7L9BbferjK5RWeK3DICON8XWD+clTitt7JDe3N4GVkt7vvMf18wtUHuNXNaJsqD9+Se/926z/7GOUlKz/6yP6/+B71B8+D2ScPMFWYeugiga/mUwLCIVgEmGKGuPBv7zGzNfEe0NmxTkJISBNTtfod2+QOE99MQ3n2cZg1xW1ACUkyaYxWF3O8cai8JDEWGMwEqJoA3ffnIujrfDZ8c5ji5IoT1g/OqVzZwerJb4KKcFtUZNt9xFKBnlHHYo8WzfIKEPGbxq+g8xIbkI/VRw8IqI2eGtRN8e0J1OKsxm9O3vIboaQguvHZ3R3R5hnFxSvrtn6vbdZJhHRaEhdNfTv7wf/1XRJ92iLTqQQcUQzXRElEUJKCjzt5YIWiFyF1DGuCo1ynMU0sWJ9PqNzOA6TchUyHkISKUS9lN7dPeb/5RHr4yvwHp/GNErS2e5RfnZCtD+gPp4Q3drBLUua0yt6bx1Sfn4SCDvOYb0Pk9zGBFmF8yihcHGKaRqyNMVFGmEa7IaohPNoazFpjCtKzGYiGibhHmMM8rUcWWscHuUcMkrC33rcDejaDTI1SiK8h8aErZH0Fuk8ltBL6WgzUNh4f9wmL0NWTZC/CUFtHVoroizBlQ6KBiVkyKlqLTaRqNogOwnxBlds13VohrI4NKFKoqSgna6C1l5IhAC7rgN5TSmk8pDF+Ks5xgQZpCAAD6x3iOUK6QW2dhArIhXSuc18TXxzGz9ZIauG2jpiC04Ikl4etP6LArlJ2xZKYYVHplEIVfQe302QqzpQvZzDXC1CobpYIzopbbHBEEtFm0boSKF0SKunDRheR5CQidfHkhToOGz+lHG0icYXDVoIRJagehl2vg4Y50En1FmzCufD59jXLdnRmGrzOdZSUdcrlqcntDZsMVVrvtwkfnkzDmk97fUibDqlDH4YawM+t7VhO5LH2MqQSEkmBBWSdJTBukAsSorpCmcseNBphHOWpmogT4jysBFSsaZ+fk712Utw4b6uCfJSH+mQcVM2+DhC7g5Ibu2itvvY6wXtxRQ3W2EXBbZpsEIE3PZOn3hrgJ+V0MsCHEBL5LIN29StHjJPaNcV1cmEdlGQ7g2R0essik1xvym+VRrTubvHynnqyZLszh6qsbRfnGKvZuidPqrfxb68wiQRdrIiu7WHXVXUJxPM+QwphjSLdTB8f7XSfaO4/SYTwTfffv02YmM7eCPD4pvu5//af/ztbv8/yblwbhNm82Wn5XntXn+9rPGCL7cG4g1t1Jebja88p/jqCxA+c+XJhLZq6N7ZpXN3D3uxoC0qolUV+NiJxksRdInGBoNNNyAWw8v7r7SNUiuGH9zHe0H9i6ccL9Y8vZjTti1RETSpfphjW0ucp9Rti7tecXiwx2y2Jt7thWliP6O/O0JZQkqjtZTzJeO9EbNP52w92MfULUkvx0eaNQ7XNLRlw+XlCrnb4+KTY7Tx6FwTxxqVd8JUZVXTG3ZZztcc3d+n10t59bMnPH92hpeC5GDAzs1dkizl8sUlFA03bx9wcXqFaS2T5QqVx4zzPOAgOymrkymHR9tM1w0IGByMmR1PKOcFw5vbzF9eMQN2Ekm1gq2DXRbzNW5dcfHynKKo2P/WTeLGcn12HYJkNkFhg70R87oC4Oz4Et1JaKylnJdkgxxPi/UO7wXWWqRSYdWexJiyJe1muPmCVgeTGlXLrLFszYNBMMpixofbXJ1ek+cpeb9D1bSUi4L1Yk2SJrx6eU6xLJD9Dm0sSLKIpqmJ4pg737rL4K0D8sMt1k9OyW/tMvvhIx79xU/5s2cf0skHdJOYw/4WqXF0Hn7Ab93/FiWGOM9IdESsY+IoZraes7+9GxqFkxfETpCnOXMx5+PTp9i65t2dm3xw4y3WvmXdVFyWS75XN6xXBbNiwWF3TBwnoBRJkrGyhpOLEyarOaN5H5ynbmvy3QOiVJOKUBg0tuXl5TEWQZ6m3Nk/opt3WMwX/OjJR+wNttBxRiqWDIdjZpMr7uzfoJt1cXXD8eScZy+f8/L6nN2tXa7rNR8++Yx/9P7vEKuYcT9lOr/mixcn/P7993n38A6Pnn9Otz+grWuwltpI+lGMiRWd7T6msSGrwAVIgJIqFD+NJarWRFtd2uMpKtYBP3h8gcsTzFYw7fqzCXXZMnr3NmQx5aMTzGyFPNoiOhpTPTuHF5dc/Ysfkt7fY42l1+sy+MFb1KdTih8/pppXmLMZvd94wOD330V1UyY//IL0cER+74Dy8SlSaxpjIdHIukVHEba1sG6Y/slP8ULQffvoywu96gXaWv69uyx/+HmQJmwmls28QHQyhPXozbnFNQZnHCwKJv/yh+z+3/8IudUDPNG4S/TgkPLjYzwQRZpqXgSc4cEW8nqBv1xgrhbEB1vUxxPcxu9B00IjaZVCawWdNJhvXZhgiySYP5f/9QuGv/8u1Ysr2jRGWUvsBe3La+J3jmiWBQbQRU1T1cg4wihBeTklv3uAtY71+QwvPL00wjQWOdKYoiHZH4TirrXU09UmTG9jZixL9G6fel5QX8zoHW6hOgnpoINKApFIbkhGSBGKqY1MREgZpGWvza1CbPJ2NpoBKaD1MCtQnZT6xTWdw61AkGks1WxNZ3dEPOrSytAYbn3/LovH58yeX7J6eUX31jbKweLDl+i9AcMH+8EMKgRyVaGGHbicE+0MKJ+8YPxP/4Dp5yf0DkYMANO2uOMpK+/JNsQZ3c++1K1756lna1rnkFerIInrZXhjqE6mdH7wgOLxOTpLiLcGVIuX2ESjRj3Wn52iXDDLCq3wkaY1NkytpcBHMa4qQlEvQ66JeH3pFISJ+rIMhW/dhJRzrWirOkha4ghTtUFu5WNUa0KoY1GFAtIRgivTJBT1UhJJAd006PvzFF+3we+hNTJSOO/wraM1Bi0EsqrxUgUzfBKjvYdNyJ1YNzitiMd91p+dECUxtYQIgWnMJjXch21ioqkbE4aBtcU2Nc57kq0+dl2B9aHZlAIvQ0ElnUeUDUqpsAWJNWK2Rg7yUJ8sS4QUQZKTRog2yLV0J8U6h7loiVSEL5ogPXMe1nXI8pASVDDXexUSo72xQeZkHU5JRBSFtPHWhY1MLydG4LI4FMtKYeo2SMayBJynpUGva2SkkXXAIvumxbQWn4fPhVqXwUS8LFF5B7feNJNChKBB55C9YBon1iFnQghM3QZq1qyALIZF2ICkSoFUITPkdQ7NpgBtl6EpdUIGn4aUoQnVGisgylPcskRLhco0bqMy6UkJ64bGOsyjU0zVgAjNd+Nd+JxHiqgwYJcUTy9xeUy8P0Lvj0h2R0F2dD3H1yYAAJTGR1XYAF3NsMeXIBW+DZs7LwQuVvjLMmwHlSKWwZxe22CMp7WYyzkYhzCW5mSCz2PS7QGiMdQfPg9bU6VASaJ+BlpttvBh0ye0ItKKfHeIGnYCaSoSyEEXWzfQ1tjFGj9dIfsZomqJdwZgHereHvX1Ar+BN7y5JHhd0/pNLSy+/s2vF9l/o+5DfHlO+IpI6mu19OuaW/yyAP/KYuC/9/Z3SIv65TuW8pe7njf7sG9+q/6rP/jm9mXj+GukU7qX0SzWLJ5d0LuxE3TVsh8+4MsSISXpzW18bfB1g9ofhc0FGyv5N+C2RKTo7PQZ7495KBUXJ5dkiWLiDa0Oq9ComyCkJEsylNI8e3VGPOqgLuYBUdjvYOclsoHJcoXuZXS6GY0JCNqyqtF1A1oxOZtQR4Io1qwXay7na+7cGtNTEdW6orKG52fXxElE73BEuyxCdkckma3WVGdXLK6WxNZTKM/W1k2qsublz5+jRCB4bL9zG3t6RdbP8VIEAkasWMxX6EQQI6jKmt5eH2MNqglc6uV0SX21oJ9nNHVLXVSIJGFxcs28rJC9lCSK8a1lcnKFtY6trSHWOLrDDuWqQbaWclHQG/eZr0vGnYSmsXS6WZDJSIFtLTLTVFWDSDRZlrAsK3wePB3CAYkiyyTFqqSz1Wc5X9Pp5VTzBVGe0Bt0efTRE4z33HrrBuevLphcTBnvjunuDci6KZOLGb24w3jQJ64Mnft7dG/ukOYJ609f0bm3T7laU//sMVppVJTw0elTjDXc2DrgyWrCZHrN8eSc7z78FqfX58RKc3frCOEto60jnk7PqcsaJRTv33jAx6fPGPdHTOdTxsMtRts7aCTn00synRDFMc+uTjnsj1lWK84X13SzLhrJ/cOb9MdjPn/yOZ2sw6Ozl2wNRtw7vM1suWC6muEt9IYDGttysHcDsy45X0z4xdPPuLNzg/uHN/m/bv0xkVQ8X004XU6YtwUP9+8QRzHD/oDL+YR5sWZ3Z49RW3N5fUkWp2x3B1w0S374X/8t7xze4e1b97i/tR8MlN7yW+99j0govA4pvVFQxiAXJc2iprKGtJPhXUgNjtOIpmqQxiPyJFyAASEDXQjnQ9ZJazBZRBxpmtMrzuZrhvcPGf2P36P4y8+oH5/ibmzDjTFM11DWrH/0hCiPKdpg2h+8f5vh77zD8sePWf30Ge3xNb3feovOd+7grGf+syfQScnfu0n17AJZW5SxSEJSs1Qq6Morw/xf/hBf1PQ+uB+a7/duMv/oBcnRCPViiDu5DhdaKamtIY40ELTCRoUUY2MMUSfDrmsu/+cfsvN/+h3iQQchoPedu5gnZyAVrjEk3lN/8orsO7eZ/qcpOs9Y/ugLsrv7tJeLYBTNN6x849CJxgPGE4z11iH6WdDTn1+jr1bU10vUMMcvarQLha+7XGBGnZCEfD6lKmtUrwObabmRGlM2gc5kLG3b4jsZkZAkcUy9DjI/7zxNUTP58AV7v/c2OoloKoNMEpIkZFOkccrqfMb4vZsIJXCtwa5rZBrhZcDfCq2wqwrVSXGtCYF5NshO/Gbb7De+Oec9RBqvBPX5DLOuaZYF2VafeJAz/tYtzGxNtN0lijS2qFFpzODBPs28QHczrLX0vnWD5fmM5mTK7OSa4dE2Kk9YfHHGeNiDNKWZzCmevqD35CnF1COdp//wIMi7liXt6ZTVxYJWeLr39si3+jjnWL+8Zv3pMcuiwmUR+bgXqHJlQ3y0hc5T2ssFjHuh6Z6uSKIIPy9JlAK9kQvpQAATrcFvMLEiikBHARnswoTZvdboEwrHdlUGWeHU0VzOiXf6mLM5Zl2R5gk4h3MOK0WAkmyGbVoImrMJ/Q/uofo5br4Of38pQYXiWvdTmtMQIoizGOM32RRtKMbqGqkUKoqCZ8CGIlgmEtu2eOdQnQQvBa5ownZACmTT4ktAK4TYSAiNQ7YG5WUIDSyDSbmdrxCDDuJqgfceKSQ0BtlNkU0IcbRSBAXTdg9lHY1zIfDO+6BkqEyoMVKN0Ir1+RRV1Kh+jp2uA20Jj9sMKW3VhM2a88SdhHq2okkjVBuQzMJD2svwQtDM1wHPqxWqaUEqdCfbeCHCcYQLyeNCQDwehPOnlDgZtkFOZuF8aAxSKowPYXkyjfDLAgG0Z1OiPMUnMWZZIlzYxLokQpiQYs/1KmwYlAy/S62IBdR4Whvu8+XmYlMWic2xJ5XEiVD7KOuRnZgoizCX8yBZrlu81oiNFEz0Usz1Gq8FIk/wzgdCmvPgA5XJlw2uNnhJkLUtG6rFKUJLVp+eku4OQgiiEhBrVAY6Uvj5KjSRjUUkAr/ZALdZTNkY8jxBWofQinq6gNkyNICzFdHegPzbd6nmBXEaoTYhkMWzc5JhB91JqT55Gc5LvQx9c4uomyGzmOZ0GrbCqwp6Kfn9fUBQHV+hRj3a2QrVz2HUI3ZBZmqfLnA7fbSWqHE3SDEPxpST5ZdeMgRfDeXefB16vE3B/7Uy9c1m4Bs3Ft9QN4uvf/HGfb4ivvrK0/1N9yfffPs7MHR/bcuw6Qq+SUb2y8f88n+/6Sbe+EqIN/qn1z//phOLBjlp3QchqM4nZIdbm6mRQA07WGOJ90Y466menlFFms69A0Skv/n1Njq35M4eu9t9sifnxJ2MerZid10wSxWnswVsPARaCGysiW6MsUVNX2hW8zV5NqRYFPiiYW0DmzlNOzz97AWjoy2asuHiw+dIL9B7fbSQKCHIRx06oy5Rorl6OaERjoNv3WJrd0zjLHXVkPZzzl5eMLy3G1bN04KbD46YzZZsHQyRkSRWmna+pjAto50Rs5Nr6qqlP+xSlhVGwvl0wej2LrPTa7IGVk3NvcER87Nrzl9csL27hUg13ns6gw5+vsb1YtracPXqGjoxeWvJ+jlVXdPpdjAqQqwb2taQ9joU0zUtnrZtYbKkG0XILMavKnSaEMWK+apCdcOkoa6rkOmhFbY2COE5v7wgG/fY39/i1dNTdKzwPkxn837O5WKJc56dW7ssVmvWRR3Mc9ZweOcA72ExXdE2hnJdk7YWvTdi73ffof/+Lbx1zH/0Bd23DtHDDrM/+SHCWDKl+f0777M7GAdEoxTs5T1myzmPr08pPm746OQJf/Teb7N/cMTPn37CrcEB96MDHp8+JdMJ/TRHOMft0R5bKkN3Mp6cveAfvv0bLJdLatNw//AWEYKfnz/jt9/9HmfzCa2wtLbl2ekreusl6AhXFrx3eJelKXj68gnjwZi6adgf7WC8J45iWudocQil2e6NKIoVnz39gqSTc2+8Ty/L+d7RW0zXcyarORfTC7b3DlmsFug44vZ4l9+5/x5Xk2teFTNGusOqWiF3DL916yEdERGXLc/WM27v30T0uzRti3IumF7L9ktja+sbNCHQSGqJSKMQvDTKNnKLYPD01lI46G4mp761iKpFDjPU9oA81jTLgvUvnlFdz4lubTG4vcfqF8/geoHLU0QUEWUpLAp8WeMEXP+Hn6O2u+Rv3WAxfYS8nDP91z9BbfdJ3zpi9PvvUfzlI1aPjlF5io5DkWybdnOC8QShsglG9T/5CaQR3beO8EDvnRssP3pO97t3WM/WIGXwX0Vh7Y/3oQD2DjUekApBa00w3768ZvEfP2Lrn/4GQiuS3SGdD+6z/qsvwoW8JbD8VyX5wZjmxSVuYajTBB/pYHIcbAK1Ik006GGjOLztxuA3uns9SMkYYydLqkfHyNs7pOsW+/Q8SF+Uwjy/In7nCJsmCONQbUtjg+nXKkW7LEBKolGXPI2I8oSqaijPp8TjHsXJBF8F30SSJSw/P0X1csqXVwFVaiymbtH9hPzGdhj8lE0Y7KggU1VRaKpEEqa9QkkE4TwuFF/6AGCzkdnIWVWskVmCBtKHh8S9bHMf6B5tcXEyQUUhF6i+WpDsDhFKMn7niFd//hlGwvhoi+FbBxRaszi9puzlxL2M/o0tpp+fhWnl1RQpBauPnuD3buHKFleGjKLXKNi1seA8zaoiG3SCt6ioMYTcCNE63G6On61J9kaIPGbx0Sv8RsLGusIoSdrJKI4nIafEeRwgU40vg6RM+CBF0nFEuj1kfTkhF128UnjvieOIpm6CFMf64APoZLSrEnbClU5GEV4pWueIhEAKia9qdK+L0zKEMi5LRKyQWyHc1PgWZRzp24eUn75CdlKSvSHVZIVGhOl8rDHOE8mwhfaA0xrhPGChkyLWbaDIZTFy1KW9mAXf0EZKFjDEBuEVvg15NBJC06CTkIeSpyHoTwh83YAPA03nHM60CJliqzrInxEB7Xs6w2x1ghRsUQIi5DTkEVII2mVFtD/GnF4hyxYfRwGO0DaQRqh+FoaUOmTAeOcwIbYH7Tc+F2tRcZD9SedJB12q40vU5rOF80TjHu3VIjSKmy1cU1SIWOMny2Aan7pAePI+YGSNRUmJGuY08zW2bsiOtjBfnOIiHfIlINCKsgSyBDVdoX04fkS0aVLna3Q3C5tUpSFO0V4grQGhwnDnS68rVM8u0Pzy38QRcpDjmwZ/tQqy18bS1i0iCh4wCGGbFvCNQ6aWqJfAuqUlfFa0lERShvJYCJwSCOlRKOxGnledLdBaIWKFE5JWFcg8JZYR1oUcFd1NifbHRFs9OnnCUIccLr8q8esKW9SUx9dQNugswV0tMM8vkN7j85SqNfj5Gjnq4aUkefcmZrLETFY0ixXmZ0+x+yPSO3uISKG3+4hxj2oTJBgNuug4xlQ15fmELI1AKey4Qz7u4xtDWzXE2wPqk+tNlkgALXxlPfEVCdbm1+3/mvr4V3uNTfHtv/rNr205vhyof+Pm46vjffErT/Dfd/u7S+h+3Vl8ww//5Vv/mjFDvPk98fX7v5ZTff013ngaIUh2h1+SMmzVhIt6WSOUwsmN0Wu7T/38AjtbYxYF8Xb/q+3PG39ID6AClWHwrZuBR+891bLk5Z9+SLy7xdlqtTmhBcNm07R04pj5qiLb7tOsaiha6EXIzfrz1eKavXsH9Ed9itmKTiuwSlLXhkiKIK/ZGlG1Dd44jq+uufvObWzVEjtP6y2z02vu7e3gXl9gnCNPY+qqgUiRNIZaeIrpiu3Dba6upshuysvjC/JuHrjz4y6uacj6HbJuytx6nj1+xd6dfV588pzRuE9/a0gkgrZ3va7Y7g9YzFb0b2+xupjz+NUp3/97H1BN14xv71JMV6FAIEKVFpRHekexCib60XgAjeF6ecVvHT3k+fUqrIRjSZwn5FtdZtMFSinW0xVF1TDYHbKerbDGkGnNtK1pjA2p3EqyWpf0x32SOGJZlHQGHXSecufOPirWmMkCV9aczBu2dgYkQjDc6XP41hFbH9wn6odU3NVnz2kulgy+f5/5py/45//xTxhkHX7z1tvY1nK6mHJdzHl0eczvP/g23bzL+6MhadZjVhd0hCS2hnt7B0yKJUVRhq3DwS3yvEOa56y152w9Yygdf/Tge2gdYRVclGs4e0HV1gihmFxd8gfvfMDPXnzOg72b5EnKo8sT4iji7dv3OJ9cYZcNidLYuuZuf5dFsaYRnnVbo6SirkqGvT7X8wlX02u2ByPms4p1U9MbD9Ct4/T6gt977wO+e/M+P3/1mL5O+ODed9jqDlg3JYP+gMIbOihuZPuMoxzVOCQt83KNqdsN4hKkcKg8Qdcu6Iw35lFvCNrqOnD6VSdQk9zKkI56UNSIboLoZjBfYHudUExsuOA6ieBySXM5R447iFRQn0xZHF/R3R6RPjwkBarzOe5kEqZ0QqDSBN80KMBfLGjcMamDZKsLSUJzOWd9/RmMO2R3dlDGUX92QmFbIqlQeRrOPOsS4S3ae1o83nom/+KvWN/eZfjH3yMedui+dcTiF8/p/NZbzP/r58TbfZqrJVIphJbYTVq1MxsO/bpCdjKiPKb+7IT5Tp/e9+8jpSR75ybLnzxBGQNahs/e4zN6339AfXJNi0CcTRFxDHGEnyxxUhC3NhSCeYJbliHBuDVILbFXC0yeopOY+nyBTiJ637/P8myKGnSw01UIsnp2QfbOjZAMvC7R8zWNCfkbCkgPttCdJBRCVYNvDOW0op0ViCTCtzYkqBuDnzuWzy/obg2QSlI5hwXiLEWlMaZqEFWLVxI9yENxYUKuAxv5idsE80kVzMP40JCIRIeCr6jRnUCNssbi44hk3ENtvBoeQthgLw/yGC1pZyVt0TB4eIjupey8fcjq2SW+tSwfndC5s8vyxRVNbZBU9B4eQKSYPjrBJil6awsRJ8RKkW730EJg1jXL2ZKd33xA9fFL6i9OiXaG4ZisGlZPz0nimChNWCxW1C8uyJOEouOpPjsmSSJklkBZYyNFfnMHO1kT7Q6xkxVivoZYE40HmMkq+IFaE/qy7R7G1OhVjSBcS2IX0MdREmONJdUac70iGnSRqqGdrIjHXZrLObZuQm7EukYIQd00YWvgZCieZyVmtia7u4d5eoEQQQpkGoPspJhZQe87d6j+1Y9wSm2Mqa8DAFPUsEM1XeKqliiKcMIjhA/SSGtD8zDqINM4SN6SGNu2wU+j5Jd2SOPCeUVvQvla5/FK4guHkJLWWFIpQG4cJDoUrk0TGhOhNVJJbF0T744C7alZgtiYnVtDu2oxzqGu58jWBRnYMqB/rfDE4y5YT3syDYVpa7AifPZUHCFVMMNbHbZratihfXwacisQqNZikwjfGur5aiML0iAd1jm00jjrQUXY6YKNeixQl6oWNmF6flaiIo1UIMoGi8DHOsiUjEEJaKREGhu8G0WN7WZEkQiN8HIdmjTC36o1gXxnEWA3m4tNKWSLmur5FVQNJDEOTzLu0l4vsesqDA46Kd7X6E3j5NsGr6AumtB0b9zKtm3R/Qy1rHDOY8sGtSHS2apGGhCb4yCSEiEs7UYmKaoW3cmgbKEugndLgex3cFVL8YuXyDwJ56pOgo0UcT+DToLoZaTfv8/sw+fk3qKkpvz8GNla2B3iOmmAIrw4xw+6mNqgOzFyu0d+OKK+nJNuhc9ee72gOZ4Q7w1Jb27jlhXVi3OyO/uIVUlv2EFISfXqAroZzjk8HlPWtLMV3ljqp+eYnT7xoBOGKZuf+Ztu4iuNx3/jtpmFCeG/9MB99ft/8w3El/4M8c3+jP89t7+D5uKXHc7rBuqXGwy+/N43WrnFmy6MXz7bV9uOr3cUX395gUrjoOElEGrayQqKNbKfBTNeJyW9vUv5/JzmxSXRuBdWUm88B7/SKQpEpIkPRgAk1tEWJc1PHlMvCpJuhnWWKE9w3uPwmEThRDgxlN4RKejvDFnNV+w83CbpZNRFyXy65ObuFpeTOZmDum04e3lJrBXxqIMsPHmWIpyDxjI7nZLcGLG9M0J3ElRds3d7j8nzSxbTEO6zmizp3tsnvrHN/HRGPh4SpzFZL2OlFN0s4epiwtbbh5ilY+fGDljHzu6Ig1t7PP30OauLGVEaI7xHJzHdcZ/jpycct2eoTkyUxBze2mO0NSTp5sFoacFYhxSSOI0p2iWNteiiYjZfIYTgwa0daCxt03J9eo1KI9azNWk3IeqkzK4WeC3p9ztczZbk3ZzaGC4uJyxmS9KtPlmjQUt2R1ssTc3K15RVQxRHFOuKavP1uqmxkylp25JEMVuJ4ObeFv2HhxBrmvma4mSCeHVN21qiUY/8/hHXnzzj5E9/ynw159XknLWxHPTH3N8+YPp0xls379Lr9vhB8oBLW/GXTz6hq2OeTS+4KJe0TUU+6PPs+pTfvvctirJi7RfsbG3x+fMnpCrm/Oqc6fYNPj55xsPbb7GznjObT7m3fcDJfEq1WrGvO3x35w6fT0/58PqE3f4Wj09f8OziFXe29nEiTHhiK0gHGfN6yfPTV9y9cQclBZWQ9LKM6cRTVCVt3ud37r1PIS1rW2HKkoOdPZq25Z/98N9x78Z9mqqidA3FesV5PceUFZ04wVQ1TmiOOj0GwyHeO9CSTn9InCTo2mCjIDM0xuJdaLiVEFhESIuWYMqG3DqqVYm1DcoRiqBuQnRnl+jTmrq1REoQRl4OvyhhQ4KzL66RaYSWAu8szcWc5ctzCmnYv32D7h++S/niiuaL06Dh94QgO2upJ0uUh+rlFVEWE+9t4YuK9csr7NWSZH9I57u3WX38EtPacJFuQ8hSLIKOOCZkYbiqxjy94vpf/JDR3/sWyf6I/GiL9fmU7Dt3aF5d0fvdt2k+P8VeLYiUCkSgdUUsQoHtELSLNUIpVn/xCN1J6XzrFqqXkd/Yon56Ca0N56R5ibGW+Fu3EZ+/QkodCFQCNBKtJNKH5GOVdsPjIo2KGtpliROg8PhxF5YF7mRKdTCh88E95v/ls2AO1op2vkYsSvJxjwKoXl1ivCeKNM44yhcXlFHAO1uge+eARGm6OyPWbUtVLclkEnj8QhB1M8x0SeQg6mfE3YS4nwVWf9FgBbTzQFqxukKmcdgY4XHLMpDB9kZUVwtEHiNtIIv5JkhYpBC4qsG2BpXFuEFOWzUkmzN3M1lSXsyppiuSfhY2DddzrBd0bu+gYkXnzg4ijlgdX2NKi3p1TWd/CMait3sgBb2HB0TjLsX5jNXPFO7iFJ0vKC9j8sMxdtriTfBFqCSiGYYiTBQ1bRXM1dnhiKZpiUxDsa6JOxlV3ZJv9Smv5ozv7lJdzIKErWrxicZPV4iyxqYRJlIwX+MiRRRH6DQJ3vthhj5vSTrBi6deX08jFXw1VUOtFXGkMK3BAb5s0HGE0ppmVZHvj2jLJvhbnKFtarxIaAFVNZQvr0j2RwExKwXOO9qXV+hhh/Zyhhx10fsj3PUSLyW2teg0DjkEpSfebN2MBGc8ygmMCjoQIQRqukIcjnFS4soKFWu8D+nstjF460LytLFhG1jWgYQUBWyvr1uiJNkMNAKJyisZcNEeRBKH6X/VIDxU59MwdPA+5K74jS/KhmbWrUq0VkitadcV8s4+LNZBCpMmyKJG6oACjtIY0xp805IOOshlgfACuyiQWYzsZUHi18sDyrcJG0G7qlGbrANpLK33aK2DJl+DHvaxi+vQ/HiHMRbhDTqNQyZK6fGdGJcmYStRBy+KbG3YLAiBMg66WTBNlzX4sIVUm5wvn8WIStHt9VlOrtE6Rqg3IQqhMcGYsEXUknpdkkYKV9SoNAokrjJI4ESe4nCYssF6SOIobCWcw8URovG01iBGKVFt8ZXBNi1NXSCsJc4zpBK0UpCOe/izaSCk5XEIvGs2fqJI4WsTznnMiQ53sFcrjKnCkMI1YCz2ao3LIqK39qFc0TvYwl4tiB/so5OI+qNn2LMpRoIe9QMKfFnSRhrdS4N0zzpUL2Px4px41aCGGXpviF0WlB+uUL0clSXYZfElzlYoiZ8sKc/n+EGHaLuPKRpUHCGylOXlHJ1oTNNiGsvwweEm++XNAlfwFeTsN3kG3qiUf1nCvjGM/9LL/Ppuf4174g3JztcbCb9pjv42t7+TzYXYCMde/2C/sqn46tria13Rr+uO/K9pKn55l/Dv1ytfTXZrBzy0V4uADKsa9LBDvO7TXiyoz6ck+6OvdY2v1+5veJr8G8+rJeOHN5hfztm6mrHaaOZW87AeBME4Tam8p3CWnQcH1LOCZlkyGPcplgV1WYcPq3HMFmva1hDbgPBbrAq6nZSO1syup7TLCm8d9bIklcF4tZaSdVHTNIbLR6/Ihj2IJN0oRu8ofJ6huhlJkuBai20stmyIdCCsJOMetmrpboggl6fXYeJytcY2lv1be6yXBbSO3rBHs2i4vJhyZi75H//Pf5/zl2dkMmLvxjbr5Sok3pogAfHGkOUpT2cz9va2iOOI2hju3DogRrBYl9y4uc9sviLr5SxPr2lmsL0/5vnzM7RWJGnEbLFCScWiLtk93KFZVZTrkjiNQmPVSVCLYE4ki6kuG0Y7fS5eXYKz9FpFrDU6iYn6GaODBJPGzM9nULdsvXuD7o2dQLyQkub5BU/+9GcsLq852t7j/tEdXkzO+c1773J6fYETkts7h6RJzEU543w65WI958GtB0xn1+znPdbrFdFoh9Niwu+9/QH39o7453/+b9nvDDgpptBaVnbF/niHWbHAeMuj4yd0VMwgzhh1ekHKICSPp2fc37/Fu5079KddHl+85LAzpNPvk+iEqm04v74k7Y55dX7KYW/MpLfkajYhSzOWizmvLl6FIkwp3tq7yVW9ZLZeMIxyrBSUdcmj02f87nu/wavLC4adPhcn5/xodoZC8P7RHbRS3Nm/QexAComrGtbSsfCGYbcbNPJCbDTVAZUpjUMKEEoS61AEVUUJicZbRywl1ijadQlS0k6XpN++Tb7eoZit8UkUMheMoVoVkEuScQe52OQMVE0IcYpAZTm9rQ6L40vSNMFv95GZxn5+irYCrCNKYuKmxSKweYr1nma+RtYt2aiPawzm2SX2dEp8OEbMS5q6IepkYQuzLDEqCjpy51BJwMuKecnsf/kx6dsHDH7vXbqdlPJsgn1xyeonT+g8PMQUdQiNai3xZh3eFhUqi4NJsAr4yNmf/AwiRefhEdm37lC9miAcwZ8Va6qfPqXzg4eYRyc445B5hFpXYaiiAk9faI2ZrmidRxYV0XYPdTkLRkcpw+91uw/nM4pHp0R/9F4wP7YW10lRkwVULfmNHcgTJo9eQBTh0xjlfTCvWk/r2hDwtixwWrM8uSbJY0Se0ODItoKu3S08WIuOE0yiQhM/L7AeVCdFaRmGO95jihrlPWa2RvcyiqsFqh/yCarTKem9XaJxH/C0tQlyo2URsNadFGct0TDHFA3V6QSsD6b3LCYmEAPz2ztcnFzjSsP8x0/pf+82UZbQORqRHwyxVUvx2fFGO65wow4uDRuZdLtHut0jBmafxhTzGbpqacsaby2dYYfydIptWvr9fpgQ08DaE0cRnbcP4WxCenJNp99FDQIQxGiwscY2BrdeBohT1gvbH+exShB3UrJ+Rvn4FDPsIJOISAj0nW2Kswl6o6x4LS/xgnCcdVPkW4dBSlMZ3KtzlHE452k3COBIyBDMpyS2qlGbbahO0oCttY7isxM6795E7w5pL2YoJ3Blg88jZOuon13Q/62HLP/NT2jblvhwiFvXoB3UFucc8aBLuwhhcdL5gIpeteDbzeVVkGQJ9TrIqLy1AaMsgqQQHzYSEoE1LmDptdxkdniUA9IYUbchW0AIXC8LPp6Nt8LFOqRHt4YoioIPKgm/+6ZtEUoRZRG2Nch+jrlaogFpDM55jBTgLKIK1EFrLWkSCHDOOVyisRtam2sM/npBerTNen4cho0++KGU9ZBqzLoi0RqzMcobY4P/xcqAbd7IP/xmkeA8wScRbY6XosZu9ZFSfpnM7az7palfSUxVE2lNUzU0UhJpHa7XjUHUDUJr0uEW68USvKVtws/yupqNtnvk37/P8j9+iKhbEimxyxIZ6UDk7EjqoiYWIqTGd1Oi2nwJZnCEDSoqqEyjOmCqvQafShAbsqAOnhabRMSNwVwvg0E+j8P504svSXHeuo2MSmOQ+HWFHHdwyzrI1FsDSRQ8OuuG+sdPyd69AVWLLxoWTy/I0wQ/GuLUOiShj7pURfCGquWK4pUnv7OPXK+JDkaoPMWcTajPJ9TXc9KdYQj0q1qigzHmekm0Pwo+xLJFDHJSoP75c/TvPCR/+yg0HVlMrqA5vsZMLGK7j6kbYp19Q2n75uD715THb5SpX3nkG9K217fXVfnXWpJfeXpnLVVVU5Qlpm3p9wa//g38mtvfSXPxpshJvLGN+NJb8TWd169bt/yaPcc33vnrPQYQfBeA3uphliVKK5rzGdH+GGcc6y9OwXuSg/E3rqV+5bU3eRi6kzK+t49+ekJzPmW8v0WsItq6QSURRivy2qCs53oyIxUK1TrKqxXVsmDV1uztbyOd5/pqxvjGVkDHJjF3b+6T9XLSNGL64pKtYZ+qqMk7GZergtvZIc3plJMXl2Q7fcb395m8uGTU6xEpCSKmszOgXhXB1JlGGByJ0ryYL6mN4ehbtyhXJZ/99DFRpDh8eJN6vsY1LaPdUWDzq3AmrMuKqq6IIsWNW3tQG7z1fPrxEw6KkvGdPYZDi3GOg7ePMMcTnjx9xnd+8B55a5iVDW8/uAlaslqvaeuWvTv7nJ9esZ6tePd7Dzl5fko27LC9M2S0M6YoS7wSfPLpE3aOthkcbnHWSYnSBCsFwzynrSsiPLGUPP/Z5ygh6HQzsiTGzpZ0tvqku0M6uwOyrT62bChag5KCtJeS39zZ+HLg7Ief4X/6nGFjWEWSVVXwP7z1AV7A06sT/urVp/zm4UO0kBTWcCPr0XYMk7agG6fs33pAsVpwPpswHgy4pXe5vX3IXn/I/+V7f8inVydc1WsejnZ5Xs/543/0T/j8o4+4PHvOaDDmO7ce8OzylA/PXnCY9nk+u+AH3/o+xsPZPFAlBjLh8fSMkTdYHXE2u0JFmo8nL0mjBB0pHu7f5tHpc66nV9zdv8n8xWNubh/gnOF0dU0cJWRKszcYomTE+WLC0/k5f/bhjzi5vuTto9tczib8ztFD7m3ts5110N0ukYpQcZAUiDRGC9jLOyAVwnmsc4h1A86xLlekeRdlw7RcJop2XRGraIN9bJGNAS9wkcI1LXpaUv70Gelb+wzfPqR9eUXz+Qn0M/y6Qi8MTkvUTp9mtkJXQYfvBYhVBWVNL5KsnpzSmJbtH7xL9fAGzSevkDLIG7AOGUdYH8hEvmyCp2exRvRydC/HFRXm1YRk1EFVYpP7EIK+Eq1wVYOrGrxrUFkeKHRlS/Wz59TPLhj9ow8YvH0DrlYsLuesn1+Sv3VA9dkxsnWbHIUyXHjjCNFYhBdBV1+3LP/dLxBSkd/bw97cpnlxhfKeyjri2lA/OUPf2cV+dhwKTwGRCLr2VgpifPBaRJpGelxVQ5Zg6xYVa1TdQj4KE8BlibleQRzBxQKVJURaI8omXCDnBWknpxDgrGNd1iSRDjSjZRFC7C7meMB6T5ulWGeDRjiJ0HnC6mKK6yR0O3nQ72cRLk9wRUBx6zxBZglNW5H08031JHHWE2XBkOlbS9RNiXo5EN5LlMbULy9D+nZrAQKgI1bEXlBeLPCLgu7DQ2zdYrSk++AAkWh2/+BblGczmlcTpn/5Bf1v3yTbHYZgvlgTHY5pHp/hiprF6YTtQY5bV4GylEZ0Hh6S3dkNGQgKRNkiBOjtHtWrCbF12LqlNS1pL8W1luG3bhJv94mGHcyrKXXZoBNN5Dw2VkTdDCsl6uYBfrUm7XQxpzPEVo/mbErUTRFZjG0tdrqmjCLkwZD0zg7q5RVq1MU0wQ/mRbjetkoitgaUXpApTZtJbBpD65Bli1Y6FHhqc43sZ0GWRky5nJPocSAE4WmOr2mnS7K3DjAnkzBt14rmeonSkurzU7rfvctq1EFezHDrClpL9OCQ9pNjzNmM+GCEmK1Ag28trQKcQzuBTGOUkLSrMmwUIHh0IhUm19YRCbdJ0I7wZRMm/FJi/abCaAziYIh5ehEGRpuNpbcOCMelsw4tRQjTPdzCnU5wzgecrCf4PGqz2YiFXAuVBZmhKBu8loiiRg872Mt5GLY04bxHa2FREA+7IeVeCERtEP0sND1NkHq+VqwIFYplLwJ5SW88HEIFOpovmyDREgIRCVTjw2c1jlAEH5f0EqoGNeri1xVCyrCxBdq2RXuNyFNomg2aOeRq+DIgckUUYa2lMgEA4MzGZtbaXxZpCHrv36T69BhzPg8+01VFTNgqkcfhvTuPbA110xIRQhm9lChjaSH4WqTAEQY+tnWQKsRbh6irOeJ0Gq4N0xU+UigdYSMNZRuOa9Nu4B8avy5pmyY0U85hpufIvQHp7S2iywVuE9jqJYGcJwTF+YwoirB1Q6wF1nni4Zi2acEL/DLIAo0QyCzFvbpkebVAdDLypiVKU+TuCJEmmFdX+NoQ3dyhfvQKfbSFGnZZ/eQLkhvbEEXIzbnE1C3r5xdkN7bRvZzi6RnZzpB4e0B5eo24XqLu7n+lxHxzCP83lST92hr5Kz3KN9e5bxoQ2qZhtVrTtJamaTDW/I3ew193+ztoLr7JIbJ525u9zJfYLf8NhoyvPNNXvRi/8rRvvtwbaqm/7imF2pAOgGjYDSmc4y5uVdEcTzCtJT/a2hgIv9YtvvHH9m0w64lEMzzaYXvUp2hbaA3Nqgg/oxKBGa0kaZYgjSF1Ai8Uo/GAs9ZwsD9kfj6nrRqiYcp8uSRSCgP0Iok3DevJmroJ6dpHRzcZjoecvjonzxKezFZMi4Kb+3dYXsxIopg41pxPZgz2BlxfXBFlCevFijxJMMZQm4Z3fvsd/LwgrQ22DvSW2cWao1v7KOED49ta6us5g3EXt2qoz6eMhx36928gPTTXC3aGA/yNFj9bIy4WZJ2UJI1Ja0crFLd7XTibUWtNN4uJel2qVYVvDUpIpk+P6aUJGZKLz57hELhlRa41zXRJmkSMdsfkBuI4wZUtB0fbaCFIG0tPSJo0wUtJHkVs7W5hjMVIyda3D+nvj0mHHXQ3DQnAQiC1pPsaCWos9WSFawzF8YTHf/ozusbTJeLuvds0AlZNwdPnz3h69oqb2RaLconSmvtbR5wUExprKeZzZr0Z//Of/Wt+661vc76cILXiD9/5gKtqyWQ+J+12OLBbdNOcajHn925+l3zd8OPPfsqLy1P+wc4hVa44X0x5fPwcefstVk3Fzz7/iPf3b7OrM/7ZF3/JeDhGxTFPr07Z6g0YZV2EDFjX/d6Iy+WULOny23feY1qtiZBs33kfYs3laoZpDfePDnl2fsx/evRzbu0ecD2bkCQJeT7AtS1/+fnPOeyOaV3LqNPjs8kJt7KbjJynloK5rRhHPbI88PTx4DoxFA1+VuCdp5t0wvYiVnhrw/GEJXUC+9rMLQSiqHE40iyFxmCuV6yvPwclyL99i+7vvsP6x4+R1qGVor6c01qL3uqiboyxZ/NgCuzn1ItV8AkUNWkkqT95SXxnD/1gn+liTrJoUaXBtS2RCsFcagN8kMYFg6YSiI0G1q5qpPe4skF3081cZMPk0JooTrBV/WUhT2OxVytm//KHDP+PP6D73k3a4yvq0xnt1RzdyzDzgvpyFoI9hcCvq+CL0AolNsFzq5L5v/kx0f/tDxn/xgPOLpfEiJCoaxv8i2vSu7u4LMYKifJhbe3WFdGoGyQKgEslsj+gWhfEnQjVtMhN4B4elJS0RU357DKEWfYz/LLES4VfV8xOrtCRCnjKjUyJvSFWCOyqDLlBox6uamimS3zZEGuFqBuoW+pIh9dqLdGyCv4FB+rSUjw9R3hC4dhaXBKY8ww7pLd3whS2bMjv7YVzb6rJjsab4ic0E7YMycUST6Yk5WKNLC1p3ifa75DuDjDrCpTElTXZzW1EokGA7iT07u/h7+xST1e4og7XJSFACpJBjr2zw+zpORKHbQzRuBskNkJSzFZk4x5xN8XULc28JB73aOcFUSelmq5BSbI8C3KdNCY5GuO1IokUox88YPmzF5SzNZ3bOwx2B8yfnCO2uqRZjC9b1p+dUBqDmK1QEJLeG4Pr56Q6BNl5BNKBxbM+mwTvx0b7T6TxOmQwpHnCel2GhG6pglQm1iHAbxPW57XEC6g39LDX+QU6Cn9T6Tzl56fkd/aYK4lChEBMIQGPna0pX12RvXeLycWcaF4GytJ8TXJzi/Wjk4BD3u5jZ8H9LFqP6qbYymCsw2qJkyLgnM3GawOBEqRVkP64ELwnhMAnOoTGKYFoPH5dhWZl3MVfLcP1u6hDsWg2n14B1nnaeUFcbybOp1OcVti6JVIqTJcjhStrVKRojYWmJUoTVFFhI01bVAFjX5vQjAM+jqgnS6JhNxCAkghfVJhVQTrsBhmgkkSVwSoFtQl5SlWL9iHdXBHoZ95DuS6J+hl2ViDKZlOOeIT3tHWDEQHJbmcB++zKgHFWaYRtBb604ZguG5wx6EGGX9ahIWgtMokwdYvAI60J5DljqIsCU9dfqZ9kN2X4f/gel/+vP8etm1DsKxm8cR4QEqHDaSLNU0yxwKlABlRK4hBBflaFRkEQzltMKzAviQ+3aYBY64D3tWATcMYhvEd6ESRzRY0STQiDVAI5yDbePGBSsF7XdG5tB7+b2Gx9IgmLGjdf4Q/GuHUTtrGJoPzkmGjn/8vcfzXblafpndjv75bZ9ngACSCBSl++u4rVzZ7mkByjiRkqYiZipAvd6lvou+gL6EajmAiFYpyGTUpkc5rN8j49PA6O2265v9PFuw4SmZVZXezumdC6AXDOxj77bLPWa57n9yzpTlcvBUG6Lmhjw/TOCant6UvH5ftPmBwvqV87kHPIckretHQfPiXXBe3DU8q7x5Q3Dhgen5NQzL7zNZQz6OMFft3QfnKKvbGHc5bNbx5JqngfsCdLtLUvjdvXloLPF7P599fMX1H85nHI/7nb8YqPI3++vgXBaq/XWwYfMEYzqQqULvm7HH9/hm7gy/cIr5hEXjm+7Hm53nnwhe99Tvv1xbXCl9klXjnSEEhNR3n7CL/dYZcz1N0jMXg/PGO1api+foxbTr6oOvvsRzjz8gGZScF3/tmf4P7iJzw8X1FPCplYjfjKza7FlY694yV626Oudpx/9IhZXaKagfl8ytYojm4fkduA6gZczEQLqulhWrLbNRzeOmRxMGdyvODr338Pv2kplOb+W3fwXc/6asude7d5fnpOfTDFGs1q57FW+OWXp5dYZbg6XaOHhO89P/r5RyyOltRlyeRGBbuePWNIEQoUvdIUO2GCL472sCERZzPyqHc2IXL39gHxcoMBYh/Im45dhsnRgqmGwhr6wWOT8Kwne1N8TCzHN3YXBPl5fLJPVKIVDnUlhWdh0YVj+foNTF3QNz2T6YRJKbjbkBJTa8h1RT2vKA7muEXN5PVj9MiUv3z/CZOygMqRQyS1A30/YJ0lXmzZXaywaHI3cNNVXIYd29zz5JP3Gdqe//aH/4Jbi0P+6LU3+Vn7iPOm5Z+89V326jm39o/473/5V5zsHeO3Df+H7/9Tfn32iIPlHgUKlSJVG7C15dHlC/4/v/x3fPPWfW7O9/jtww/57374L4l9z3dee4N2u+FnP/8FB8WEN7/5J9y/c49ZXXO5abg8P2e5mJKsYjGd8g+/8cdcri74649+RT2bcVzMGVLg7sFN5penFEkuEKtmC8rSb9d8/91v8/W7b/FX7/+ci/UV57sVSikePHvEreUhZ+2G79x5k9cmC/7s7ns8OHuKyjC0De/ce5MueZ73Ow73DjlKJaoqiSmTtz0YAz5iaqHOKJXASLGsjGa126ITaCNFuRmlLHY5kdV707MOW+rFDJMSDJ5sLLt/8z72ZMn0T99h+8sHhHXHRkfyrmH6xGOuGpLTuMMl7nhBfCRIQtt7Uh/FeHexIehM6zL7776Jrgq2f/Xb0SweiSmTBsE8aifFhRoCdn8qqMdNAwniqhlDMzO5H+knXYK6IuwazCCTT201ad1y+T/8iOP/45+z/PNvcPUvf0H2kfLtW6RPXpDON3ilMJVkMOiYidfYz1lNXDek1HH2//hLDv/3P2D/7hHdrx9hjRReqjR0TYc5msNlgykKMWCGSOg8prSw7SgLTV9KMZk0FPtTQtOTNKQXV+hrw+azK8zRQtKUjUwf03oHk1I2DAdTirM1oRvQMdOrzDBIIxGGwGA1w8GM4+Ml3cfPJb15WuF7j77YinwnJdGgF1bAW1a2XTolQpQkddX0hCGy23YkYO/uMd0npxL4tqiZZUXctJJDMCnRSsLc3LSSi/3VjrhpidMKN6/JUWRTw+Va5FdTCR4TPdYobzWK+mhOzvPxIiTSG6UV0xt7aBSnP/2Ydj2wm5W0MTO7scCTKXcFqi6xhSM5w7DZCTQkJspFTeg9zcUWVztSTrg8ymxjAmvIh1PK0nLwnfuyLZnVNJsGay2bD0+JRkswWga7NyU4C08vSUOgvneCu7nH6b95n2VhmN0+5Oo3j9kZxbyqpEiZViK1uVrDeB1qL9YUuw7tDFppmdiOhbRWmS5D6QwxBmJRiE6+G1+fkOifXDL7xuvoMfwwxEhZOHzXobVm94sHHPzH36H66w+Iu07ocE3P9J9+m/ZiQ//gBfZ4CTkTs0IPgSj9PeFiQ3FzDzuvCKvmswprlMXQDqiyoB8CttCUpZP05xDxVpCqyijUsyvq735NcMteNjluWpBaT85i/I4p4YqC+P4T6n/4LmnbEttBiERZJvf4gK6dvF+ibAn6XSvbtBAZ2p7p7SPCgzNyiJJFY8Yk9ZhQVUHqepEo7YRaF9tuJFnJBkKl9DKvRKFwCryXrYm1FhLoWU1atZCzmNFDFOJWYVGDYHy11oRTmbCz7Yjj+8xoLVLJDDjDcLXDLmaEqy3GWkLvSVphU6JZXRDaLdqVFGPY3svKbKx3ypt7TN68RfPTT8nrhlBJwWnaQX4npdDz+mWOSgbBRqMgB8m4iBllLHGUbcUYWbxxk+7jM3I/kOcTUhBfT+gjtiqJm5YcosgUBz9SpgwUBr3uGLoeVTvUssIVDoMmn65I0wprLeGqkWYVqTGMT/jLBrvrISTazjN98ybNxy9QCpxy5G1PN1xQWsV0T9HfO+HidI15cMbhjSXlvWO6R2eoERxkFlPCukFpRXHvBv2np/SPzyRX7c4Re4cLzv/iJ+ScqO/fxPpIDAm7nDJ9+/ZLbPTLOvN3VDS/fxj/Vd/7nS3Fy7v5YtUtFXdKkbZpSUlCLqvSMZ/NXiqA/rbH32NzkT/3x5d0Dp/rmH7fc/b55Isv6Upeuc+XiK0v/pzxr8pp/OkVdjmlONpjuNigy4LpN++BVrS/eED3m8fke8cSdvLyBf/8HX3W+GSKec3X/+kfMfnR+zx/eMrZrgOraduO22XFRfS4acV61/Kdf/YDNp+cUsZE7ALrTcNiXrHMhpATGoMra6b7M9aPz0hd4k//+F1STITTFVfP19jS8ouPn3LjcJ/ZyYJhvePGzUMuPn3KpC4wXaTsew6DpvCQK4czinTZEbYtw2im/trBHqYqyHVFs22Z+YQzlt5aglUc7M3k5FiXFHUBTUthDNQlaZwwxeAxQ49JGT0x5FrTRIXqehZHC2JpcUrRXzXU947Zu3vE7tMXhK4nZ5g0vYTNaE1UMKkKWpNRkwlGa/qhx2lHmtXkysEQmFaO87ZlurdHvTdlerIUI+rVFhSsfvwRu4+eUi4mFFmxHXnjShsuti0TZ8Ts6QOzuqJXmaqusNOa4TSTc+DR+Snfe/tbfOfZQ97Yu8lffPQTHq/P+dbtN/jNi0csrkreu/cWd8oFl7rldHXJ//L4t0zrKd+5/Q7HywVPr87p25ajuMfClnz/7js0ydPoxLt33+bJ5QtuHdzkxXbFvKhZVjPO2zW3773O/Nv3+Ol/9y84nu0TnWLTt/zg1pv0MdBerXjTLth/67s8adZ8dP6Uk9keDy6es9ltCV3LpthglSUVCTOt+ejiGZuHOx6cPWF/OuefvfHH7C0WXAWPA+zRAc16zWW74ursgj/75veZlxUfPH9E/uicyWLO6zdfx8dMVRbEkIgxgdGY2pI3HbJP5yXEIGsNKdH5DqcMNhuCNsSdZLrkTSsynSHKiScIjxwfxVy5mOCfXHD5P/2E+ffewL07of+ffkyaTqAsUH0iNQO79TOGYcDdPWTv/k1USJz/y5+RetEu+5mj1CPic9NQffOuTMAeX5IvNsKu7wRhSYgEMnrVEPem0kh3I0lHK3LnoXToELGzmqzA54pu11BpJyjHqsRfNWz/6rcs/8m3mLx5k92/+5D210+o3rlFLh3N43Ny50UOUTiy74khUNpSEJ1KwWZg81fvM/nW6wyfnKKVpu06hvmE0HmWt/ahETJc3vSSrJxFp87EoVKWwsMo8ArvDNYlMdY3PWpak7ftGCa1xqZE3LWkiXD542pHJnHVdUxP9qgGCf+caoOuKtosvPq6chSDp390TnXrgO7ZFTlnKmfRWaQePiRyXcDxnNJHKmdZPXhB7iN5b8pghGBjQ4R2wNQFzcfP6bYNrrDUX7vJ6nSNmVSUsxI9KVFA92JFpRXaWVTlSE1HXDVwvBQiy8UGU8nA5+X1Rstw6/PTvPyZ929M1s4+YkrL3v0b0AXS6Yr5pITHV9Sv7Qs18PE5xd4UezgXbXk34NsdelpQzWuiD4RNJ5Kxqx31jT2SD9QHMzFr7zr8tqUPCTsrMaeeOLTouqByIinZOsW0LGVTZTT1vGbx3fvYWcWLv/6Q5ukV1c191EenmIkDNEPbU/rIYm9C7D3pfCNp2U5TK9lQREAtJpghSLBgN1AWljRu5rI2Yyp4lPeM0SLhMxpTSFaIq0u8j+iiwO922LMNaQjiy/jkmfRqvWf9b37N4j/4Otv/+WfEZxckwGTxhmANSoNftXTPLim/doPwww9RBzPiVSPZG92AKyxx8NRakdtAXBboppekaJRgWrOYj7sHp0y+9wbNDz/EIMneZlaRNh3Xs83kgwS2/uoB5Tfv0v3V+2QUQYGKEZOUQCkqkS6aLMTE1AdSjNi9CeFsjZ7Xst1MY0XgLLnpiFUhMiAQr+PxHsPVDtV7KdR8BKtx1kgOiNbjFsmLJGvwGF3jFhXxCbLZ1xo10t+y0dicyUlyTBKKIiRS5Ui7DmuMSDqVFnUEUDgntL6qJCIeFOcM3ekVTSOTfkOmD4HQdr9bjCmo75/Q/OIhOUiyu3OWECLWGYaUUG0HKWOiDJlU7/FKofP1x2+snawRqaoCNakYmv6z68bQk0Y/h/KB4mRJOFuPVZhIyaK10A3oqqBwjjgktG+Ik4KwkHOYDQl7IJsNUiL1geZiK/4KY/Ap40qHbnqaR2eU94/oH7wgbluK/SmpjyRlSI8vyN2cw6M5m21H8+QKhiAKmPM1ejkRP9FqC31gePiC4s4RtixIT84k98RoZm/fpn9yLs9zhvbskv1vv/kyyPmzQvhvkEG9LEd/F4L0pcbrL9Th+ZVvqLGxzeP7oe97yTpRCq0UZVmgtPnd+/z3PP6eNxd/y+O6L/ncE/0F38WXbSfyK0/sq83Lq8dYwOx+9YD5H7+FW05F85gzofOEWY1Z7/CPzol9oLyxJ2me413F8cL38hgfY7GoePsff5s3uoHzXz7g9JPnzMuCo/fu8uInH+GBO/dusbc348Y/PsGUjs2vHzG92OKmJfObB3Rna8xyiq0c5c099i62bD98Dr1HF4YuRIanl6Te8/U7N3FVQdp5prbAuoKD4wMSEAePCxkfImndcKC00DnKgtmNA0KKVK8doKuStGtRKOLrFhuSBNQpoWHVs5JYGrqcyZVjfXXJoS6o5lNi25MVQpg53MNYK1NPo5kvawntKguunpyRu8jk/pTF7QPKxUQml7sWVQoy8vplDuuGcLWlvHeMmVR06x1qvWWCIaNIpcVvG6rFhInLuFKTz9ecP72AzkthYjXKGqavHTK5eUCxN6VrOqHOnO84ihGtNV2KKAwKkcP0eWCoHPPlHKUU318ssduWPg2sQsPp9pJpUbLpGoLRfNruuHHjNkd7B/zLv/4L3ju+w9HePiEEmtTwm0fn6JjZswUvNis2ceCT1QtuHRwxraecdxtCFgjAG8e3+cbBHerSsY03mKaK3Ecu2y37tqQ0loWtuHt0G73rUEZOpjeUJSjFBEvXd9RKo5cn3Lp/SJMDbT9w09R0MXDerkl7E947eU2wfr3okRcKJj5zudkwNA23ixl37xxw0Vzx4ZMHfLx5wX/5nf8AnzPTokBnRUigrKFwcrHPXcBUBckoIGACoBWrzRVdChyVcwmCyonUe3yM1NZKCu7QEZUWiltMBC9bpRA8CoU5WcBuYPOvfsX02/c5+qffoX/wgu2zS65UTz1kbIL8bEV4dM7Fh8+ZvPcaR//FP6D96Se0Hz+nvGrJe5b1xY7KB+IiMT2eY//onuAVXwimWKUoic45E7uB/KSjmFTEwkEvCEgzqQRxrTMpRLSPVFqTpjO6KMFWGI3zivbXT6AumLx9m37b4n/7jP63Tym/cZey87RPzrFWo8uCbAyp6WTjqRWMAWnhxYbt00vsyZJ4tkUtphSvn1ChCFcb1N6E8Gw1yl9EMhEqh7naCN9+05GcJhcGa7Sk8Q6Cwk1aEeuScloRml6kZ3UlWwVnBQ+57jjOli4r+v0pRTeQmx7nxFTJqsEyIefMdtMStMZW7iVZyhlNd7EWBv20IjxfSdF1c0r59i0psLYd4XSNjkL3UUbjjBh33bSk73rKkS5W702I1qDbgawUZx89ZXJ6SX24R3m8EMrS5Q794Iw4eOx8QnkwI/aeuO1QpWxD1RiG9vLko6TYTL1n2LbgE8ZZTGGZHsxpnl6Sc2YIkaKw+Mud+CzIKKPwvcdYI5TCeS1bG2tBQzGv5P2/bhmer9DLmuFsjR4C5XJG9gF1IJkFaEWxnKAKSzhdkY8WHB9O6bctxExY1hx94x0mtw9ongnNb/PbJ/i6GBORwd7eZ3h8RkemW+1whVCmyiDetM5mcpK8ADV4fAi4MfncDZJs7VMUvbtWqKIkDV4CTq3I0tK4fYnXG+YQyUk2RbuPn1G+cYPhyTnJCygjXu4YHp1Rf+MOzY8/RjlD9nItju2AWlS4YBh+85jZD95m99NPpLiZlcSrhsIYvDOYQTIeyOK1yjHhEc+4vIhRJvKPLzGzmul33qD98Ufiu2ilEFUh4bRsADSKfL4jdwP6ZClSKm1GdUUWSVWI0rSkjB0v+dpa8EnCC5MYlrWWpk2lLI29l0m7Dxnd9FQj4S6N0jsUqBBJm1ZQtNaSvEg1r43NrBu4ewSVk6FLSpjCMgzymqUErnCkEF8W+bk06PmEtG1JKqMjkkGRM9Y5+ZyNxWPWSoAIwdO3O9lYxEjWhuD952qc68O9foiZlTJQQo25JeCj5E2ZlCTZfGilQSrG4EQtYZkJaSrVeHuUJl5sKPdn+BcrGMJLjLnJWdDGg5dk+phk2zxK8txoas9RpuwK0I0nrzvswZy8aWVbc3OP4fklrnSyVaoFV0tMcDJFp4zf9qQQya0nOoM935KBIRQs3rvD1a8fE646qv0JxcGEoQt0w4aqKrB1SRw8/nKLmZTowgnMYDmlvHtM/2IliO75hFjv6M432P0px+/dESXMlxWzX/bkf/HbLyvePNoNPj+p/zJl1atz+s8GLBlyxvsBf+1f01rkiUp92T39ex8qf2Vaxx92bHfbv9MDAH7P85p/t7n4oiyKL3w9jzcetWqxG9j88H26ZmBy/4TZvZuQkhiEUmK43DI8OkdNCtEkOkv9xg2JgEeMkqqwn21IRjnDdcLiy6+nz16MHCLJR5RVKGNG7K2cvMJqR+wE/6dKJ2SHpkf1nlxIMaPH1fjuyQU5RlTMxBDpt52cxNqe7cWaqigoFhMJMtt5Gqux85p4tZHAo/kEd/uAMHiRhYQoJiyl6HKmPphhtZZCZ7WjOVuRq4JiNmV6siC1PeFyg61KkveER+eYssSeLFCLmtgHacqUJC5X0wkhRpwzmEkpa9nH57LW7bysdUMkNz1UhZgQY0ZpiKVDTQuK/RmF1kJ/ORNevEWhl1OGEMjbHt17qsMFzCcoqyjvHZNTlg/8uiEMgbxpaZ+e0+561NmGYdcxu3MkP1trzvotVxdrXqsXBKP55Se/ZmEKtldXtDrz/sVT3jl+nbN2Q1XXfPD0Af/1u3+KqixN01FNJ/xf/8V/y83ZHn/y9e/y00/ex+dAJPMfv/XHnK0vOVke8s9/9pdoDJO6JmeZSPYxYFEcn9ygyorT58/4R299m9+sTtmFRNxe8cbJbWbzJVNrUXXB4Cr++pc/ZrO+4ntf+wa1c/zm9AE3l8ccVlP65HEYZtqwqw3/6tc/ZjqpWdRLBh94Z/+Y5cE+2gcImeiDEHGaFqM0O5WpJjWmqKiNAWexs4q87uR1UgpjjbzXg+ifTV0IhSUnklakmNj2DW3bcWPvkNhJ3kTvxVichoA2hpgFLer7gRQ888kMU1q6sxXr0DLRJTplnDVE7zG39nE39yQA8oNn2C4Rgpg8U9NJgaeBScH0m/dZ/dX70HTSVE9qwnJCsT+hfucO20dnGGMZfvFAkKeLqZgh+0ESjaeVJMZaQx414D4kSSIe8xiGEMfAOk/cn1H2Aa0VMUTi4Jl+9x7mYE7z009Jq5ZQO/b/9G3an35K92ItybDj1DLtWqHoVI5clwwKwrzi6K1bDD/+BHW0ZLgpxuN0tcPt1cTfPiFcbHHTGgZPN6/R1hCutmigjBmWE2Jh0OPkOYWIi+KhUTmD1hQpQycyyKgUZenwu07SgJdTOquZ3djD/+bxS4KQQZGmIg1i1zOQ0UbkaUYpykLkD6EdRIa1mJDnFVw1gpt1FluJ9KQvNMpHqkmFriWgi0khuu6QUOuOOCpSzVwK8HIxoT9bCwnpYIbuZSsW2kF066VFdR7VB3qrUFpTnywp52JczlpJ4d8NbF+siM/WVK8fUk5rMFoIZ5fi5UkXO6gc1d0D/GVDv25wywlh17HrOvZvHFAeLkRHPhq6Qyd6c60k7C+2A6aScMDrTVhqepgUaBS+6XBT8eYMI02wWE5QdUHYduMmyqALS3u5Iw+B4XKHb3vSrkc7w8EP3uLFf/9jtLOEa227grDtJRekbyhsSVCasnLomCS9vDCC+R08u6sVZV1T7i9lyDdeQs29I/a+cZeL/+Z/IWfZfiSrKX1gd/YCqw31N7/G/N27bP75zxi6QeroDDFFlv/ZH7H76w/pX1xhlMYUhWxEaiuZNNuWvf/6z9j+8EP6Xz/C3Tum//hUNs+FFRphiChrsCdLeQ4fnRNGE7S+DhYcs2Rmf/4e/UfPGZ5eSnicD1hnUVk8d1pBUgpVWab/8F12f/X+WCADWot6Tmu5TZaBghmv4WHwMCvlGmIlzBJnICSSAqsllyVohXGaydu3aT949hlYQimikrA/Uh6HKgGdJN08+4AiU75zi3i+lbwUpSicFU9MED+FspqIUKjMrMJvW4p9waniA9SlNL8xQRa/RqqcyMAWNeHFFbHv+PAn/5qptmRl0K7g/v/l/8ytP/vutVmWlxKTnLn8H3/K9t9+QFaKBNSTUoz2k5J4tUNNC0wGv2lxixlpDHJUpRPDvjGyWdBK3tNTR3HjgO6Dp7JV0vJZtWMGSI6J3hncmHwefURNa4wPaKMZQhxlnjKJj4CtC1LTMwweczjDHS8YXqzl3K0VfRdwfaB6+ybDo0vy4FHTkn7dYqclcdehUbi3b1IvZ2x/+RCmFcWkEh/DvCTlSL0vcqjZ119HWU337ILce3IfsEdL2sen1PdvCkgkRIZVi9JQ3txn+tqhPLOfX1tIrflS1aNe/vtzkQlfrJnVeJsvgRJdV8+vNh/qeno/fr5TCvT9wODDSAoTMuR0UmJdAUoxm86+/Of/Acf/f2wuPtd55S9+6csbi1e7sbFwzy9v89kTqktH/cYt+PQ5zemato8c3DlE9UKF0IWlvnciUy+j2X38jM3PWtzxkvJgLhi0Vx7XmBaE0q8+NCVmpzHkQxkjBcT17V/+ngq7N8MCftsyPL1ge75C95HqZIldTMghMlztGDYtqpMpQGg6zN6UOjqh1hzMOL57hF1OQCsWPjJcbDFNh8+ZenHE7MY+SkH77JJ6UsJyX0xSvSdc7qjmNX7Xk8ZQpmAUh9+8R0qRs0+ekH5yShFlYqAmFaFpYAj4EOk/7UhkqpN9cIa0aXGVI622EmZkDe2DFwxdTwaMkaIgD5Hc9ngfMUk0m3bUiNuQUOuBcPWCnQ8oY4gKyqIkW8WwbljhufXuPeqTPWnmilEv3g7kqx09G8JHz0kpkwtDbjyzvTnxYkes5ATj5hOCsxz2BYdHR+TLhuw0f/Tet8jdwC+ufsyd5SFP1+d86+br/OL8Eb86/RRLZn9vj1IpfrO64pePHrHrGo7uvMmvHn8MGr5+8w2MVvzm2Scc2ikzbfmvvvvn/Hp9yfmLp+zSwHw65Rt7J9jBs+pbiqJkFUTLPHEFqrS4g0P29g4oQ+TB5pLmfEsoCt5+4x023Y6u7Xlw/pz7x68x1wWxMMyipB0PSjHRiv/iu38mScazWqa7zcDF2RWx6Si1ZlcotuuGO66m0IqDxRymNS4r0hCJfSCkDkJEV4VQinyQ1FujyVpBYcm9J/oMGow1LJky1QXNek1RVviMTISVISSPR3S3oQ2onFm1DVNbErYNOsPh4RHd5ZrejJPBCMPDc/oPn2Fv7GH2ZuxWW9xOYZNMuawX/bNutvTvP2L/P/tjrv6ff4VDPALqbE10lt2/+xBTOabv3MV94x6h7aneuol/fM7wiwcYrWW65j25sKIpRmGslsYqJaJSODN6IIxBbVv6wmJ6McIZo2l+9DF7/+z71H/yFt1fvo/2gc0PP2LxJ2/BTx4QLhvImWQ1djkjtVJEqpDEJ7CY0fQDqTak9RZ3MqfpB5FxfvKCvXdvk3/5UMLktMGerUl7M2oU2XtSBrPtpMGvCzLQqwzDgPEZYwxD34ucIydyzuhJIQhHJx4ZO6koJyWXz6/oDMwKg/aQfEJtWvwCVCn0LazD1tKMRR9FzjMEsg+kqx3hcksx4j/7DPQB3XmRETWesBGDbn56KXQdo0gxiwREK0m9PZpjjhaoIVAczGQCvutQ05Jyb4YeDdohBJTWhM7jIuJz2XX4mPAxYa2l37WYwjG7dUiaTyWJuirEZ2A0s8VEzuevH3HNJte1hAjmIdI+vaCeVC/9FMGLgbuYVBQp4VsxxoZdTxxN9Vlr9KRETyvitBIdeYhQOkxhYVJSHM6JTS840iAb18h4niss1f6UHBPzu0eo2nHxy4c4Y6nmtQScdYFKa9pWns9qVtN0A3YywygJTetywqYIhSEYQzYJvQ3YgwWUJYlMTBmnxgK7sOLbMQIfyLf2UQczeHqJW63oNiuqIZAU4pXJmZAzxli5/vziAeXbt+ifXxKUNADEhPKZWCbIitU//xn7/9G3ufj0BeFigzteEE7XkDKhsKM8KpCeXTH5wVv4lFCPzuXzOs71tJI/tz/5mOU/+Tb+n/8MOi8Y9pRJKQniNl4bngPtTz+h/tY9up98LA3GGMSXktCd4nWjYRTJJ1BybjTWyHt0kAR0lJIJuxWJaI6Srh3aQYrsLFQzyZcYMONjwWhM0mjNaJKWaiJpjTcGPRaXOYmKw88qzLpBL2rMrpMBaDOgkdA7O68Jl1uGXYczmmileVd1Re57nDWw6yknNV5ByJEhGwqt8DHg118xKFaK6t4x7S8fo5Pg7WMU34eZFDI4DAn2p6SrHXQSYpxHTD1jc6RSQlknv9+mJ8dT8UZu5Vya04jm7Qa0ViO6XF4vZwxxCPhhoCwL2UBoLYOtLJjbaBRRKyGPPb+iuH+DfucJ52tUN1AcLjD7E+JqSw5BZGmdp5iUuH3xhsYh4C82TA7n4mEpLHZP6rK07dFhELN/jLQfP8PNRc5dvHWbcLpiaFrm33lDpIlDkOaXhJ3UVMvpy+H0Z7XtOKz+wqLgZS37VcfYnHxFX/HZTT7398+vMVJMI6hPv/y60YrMKxCmv8Pxv25z8Tdsen7nptfPqHplY/E3HF+K7HqlCVFKSTJn22NRbC53vPj5J0xmFTpmzGKCm1akbYff9dS3DiX+/TdPCFbe0PZghpnXuMM5elahnR3fIK9sMsikTvjRse2F19/1kiBrjBBmCkO5nGJryWCwk1uUtw9JncfWhRj/lCLmTHm0kHAmY8gvZLLpBw+lpbp7RH+5JV7tSKeXbEOCIBsNczDDhEi8lBOF7iN6YUX/2MrkBSQls7p9IL/CEKgrR/tvfkNYN7gYybMSt5jRGTB7U2bfewM9qQhNx+7BKTorwXq2Hj2p0HUFzlDMK9x8ij6YoZ9ekBMUJwuGiw3KKNzhoUwMNh1mWlEey6Ss/9UjTOmw+zOK1w5pfvMQ03virhOc46zGmakY6z59gf/NI3JpUEpjbxwQLrbEpkOFiD6YyUocUJuOOAQ0iXx6Ra4rusJgnaWoSphneu9RXaRKGsoKMPzTb/yAISUuV5c8P3/Bn779XX785APu1Pt0OXCxW/PH3/guTy7OOKxmvH1wm0U14aNHH2Gz5WBW8/7zB2yGnlQYfnH2mPdu3+f+0WtUSXFgHbcme2xLy//u5BYbZ1B5wdGuI/nIxgeujOZgusfJ4oBdzsxMwf7EQQV3907AR+rSEQqLHpnpqq5pnEE3DboqQDvC5YbQ7NhuLpgv9un7SMZQVxblHP/201/z5zf+IXnVksYQRZKgl1PTS1FBRoOs6q0hNQNNHOj9wOF8SWh6vB/QMYkxTNsxN0DLe9jLhd5ZLea7GAkk6sMjeu+xlaOY1vh1gzGWibN4rXAhCk1FKZGNaFh+7SbuGwt2Hz8nPb8kaotKiZwSvouUg0dPSugDZl4SNi35dCXkoHLJ5SfPmCym2Fv7ZK04+I+/w8oo4qqlf3g2miglHE1Vjtx5hjj+/taAFt10VpIirUejclJZ5hrOsv5Xv2TxH36T6s/eof3XvyFf7dj85W+Y/fnX2f7iEf75FU5JRWScZYgJVxjs1Y6sFKErUEYT1jv8v/uA6miOn1T4tmf344+pv3ZC3g3EXcvQdEwaSUxPRr8M+kq9p3DS+LQpkKcldlLin16J7j5mkbqFRN60MtE3ElA2vFih5jVFkldet4GkwexNcDETUpKNpVJU85p+3UDvUdNaCrqywEwrkUL6QD8E9BCokmjGU84SLpak2YlGj2SoHkwhoWgj1SjuOtKnZ+Qnl7S9R88r7K0DyuOFaN8Lh5sUqKrABSH75Rt7pN4TNy3t8yuaFAlKMTtaUhwtqBYTab4XEwlhS5l4taXddRhnKZYT0UUbLU1FjFKYdJ6D777B7rdP6FcNti5lyzHIQEQXTibGVuNmtbx3VjvCuqWoC8xIDYs+4hYTQXa2PWEYMD4Qe4/NaWzOooTXtR539whKB1m28eHFWq5x247+bI2qSxkGaQ1ehltKa7JRGGdJZEwU+YMdqVL1rGZYbch7E4aupdibiX9FKYKGMCuoakdYNajCkjovshcf8d1AtgZtxeujRjMx41Yux0QGuqeXlG/flgZxGChnIq1UIaK2PWpW4p9f0T+9oLhzRPv+E/Rbe3CxRQFFVqiDCen0itgPtD/+iPmffx01Kel/8xjt7ChPUmAUakhsf/Qh8+9+jau/+i05Sz5N8hGtFCHLdipq4LIhX20xtw6ID8+ERlSXqDF0UCETcRWiDAuzQfUBPROssq4LFEK5MtrBdeOSE3a8rlpnCUOQjYIdG7TRA5Ni4toyq5J8prRWY7Ep/zZaggdtzFg/Fqt9kPtgbITGDAiaXorhTnCthIS2BuU9KSRsYSXnZFaRt1uy0sQwgBH9v991X1msFTf2MJUjbQOxLimcFX/mWuTOw9UGoyV8Mg0BSiWbjZSwStDvGWm8VE5QFcScqI4Fue9TEkR4SuicAU0YPEaJAVxZQw5C6QvXUAINKsnrZJUi+YiZ1RKaaB06ZcqzDSEkotKkVYMPJVYlqclSJu46MdKfLKShHxu2/nQtfpGUaD89lc+VgvJgii1LsGAmlYQ2Nh3pyRnWWVxV0j85x9Ql1e0juosN1WyCPpxjpgJe0F/oCH6H7vRlde1XKXZ+z3Etn3rpF/68goqM0LyEqCa3vvbHvCTp/R2Ov3tzkccH8lXrmz/w+KyfeiWd8HP//tKlhexf+cINrm903WBoRX3vBnHTyQfw4Ai7PwMyupDUSozgWFPv0bOKci64uPZ8TfPwVC7Cv5VVZHE0pzhcoPemKCXBUAC5D6TLHXG1E62xD7I2HQLF4YL+bMW2chy8fVvW96O3I1xu6Z8M6NLJiavz0MkHqB8NqLsnDXUC5Qz9zx+QUmK32lEWkqypBo9pBuFOnyxRSuMvt2hnaN9/Qt6f4C+2qEmF85FiOWH36CNBY+ZMOZ+AM1TvvsbseIk93hM/Re1A6ZfddjEpsYsp2mritqP55Dl6WuOqAp8kFMfMKq5DvnAGcqZ0VjSpIWJDT9KKftMybDti5aheOyDtOuKTC9h2qJSwfSCRmfzxG+Qh0P2Ln9E9PBPG9a6j2JuhVKJY1OTzFXpSkJqB9Mkp+ua+IHbXreigMaT1Dm8NbUrMx0mmG7W0RsOuG7h5cMIPP/klPIOyLHlt74h1s+PJ88c8XJ/xf/rmf0i/2fGPbr/HaW558eghtZtx09YkYzlaHPBHd98hDD167dg+fcj7Tz/luJpyoB2b8wuiNuxNDyhQdI3HFolJLlgmeLBdUZYV64sz2hRY1gsOFkuKuhBs4xCwwyCFWlWSFzMaleiagcO9uWwXVluS0QytJ+06oc8c7nN7MUNrQ5MzaYiUtWURM//ou39KbqWYiSaIBKou8BfbkfhkUEMgWUMxr+manherc/mIafi3Dz6hKAruL04os4YhQGEl5M1HLJpBK1KMlBhJ21UKrKXtWyZYdDHSaDqPc0JwGRANMylDVWIQItfw4TN2nzxj9p376OM58aNTwvlapAWrHc3PPsXsz0mrnWibC0fuB9j1xOEC+/qxTDC9J/ea2PZMv/sG659/Ao/ORjlEEETrENCFI8SELRw2JkLp0MYQRiJadpo4SiVt4eQimBVX/+NP2P9n3yPeP6b/+UOGVcvu335I9a3XacjExQR9tkGtG3wQfK9OCb1uyKsdg1G4WUn75JLY9LCYYLuBnKD58Bk+RKy1FLOatu0pfIQU8YUTOtCQyPWC3A5MQkYrTXe6Jscopn4j8i9SkpA1ldFa4Y3CKIU9mOGcoTpdE0fUqu7iZxLSnEiTkrht0bue5MbpYjeQY8ROpgQ7puqOoXmqdDIltqVsNWsJADPGjBuUGpPFP6ZIYkQunTyu3mOdI+8G/CcvCL99AimxmU/ICsppQXEwR58sqV8XvrydlJS39umfXgrFprCkXc/mySWDSpRGvABaKcobe8xvH5Jixu9akWKkjG86/BiIGNcdqY84q8l9RNelhLk5CUdLg0ePsjplZIsbrjaISl8M91QO23uISYJBrcbGjKoKuhdriBkTMzmO0qTSoYL8P0IkNB0pZyaHM3IrE9JiOaFXmRwyMzLDrqdYlsycodifSH6C7Zh87YTdR6dko2h9xCzmhG6FchWDD+hZRdi21MupFJAxE1IkaEWvMur5FXG1ww6BoW0pl3uyGTCa4D3ZWcmoKK34mowitP1I/pFGzVSFFO9KE7sBbQ3tzz5l+r036T9+TrrYYY+X4o0AWLdUb96i/+1Tch9Y/cXPmf9H32Y4W5OvGqJWuKIgeY9Oifj0Cn/7iOrWAf2TC2LTiTeqsJisSSqjQiIrRffBM6pv38M/Ff0+3UjD04oc0hj4KFkUWWtwEsinrSHlLBj7UXpEiEStpEDVmrRuJDsmZ5S14qUMCT2eG70PaGulCB9BEsEH7KbBzirJtBin67l04l1USqRiTozP12njIURJ5J6UsrnvhIQFgDW4BGZao6KsecJ0IqS/GCAnFJq8a3hFm8Or8nKzqHBHc3ZXO4z+jJAVhoAulMAACssA+Gtj9dgoxSQSNmO0SKJu7WG2PX7XMVxscG/cIH3wTM7RZTEav5NsI5TIGOMgAX3ZaPn9UkYxAkGCpJOrnHGFpR9rPvZn+HFDqAsJ1zMhCc54tSOqMcxTIRtPY2TLGAL+bIUuRsLdjSXpxRp7vMB0nr5v5LW47ChmEs5aKUNIMgiJMeLXDfW9G5QHc7onZ5IEzysSpms3wucK/i+Puvud2vYL9e1XHV8amffK/9FaAQalMzp/5uFQo0fm965F/oDj7yeh+6sexBfWPOqVP7/yvr7wrF2rnL54n/mLX3hFTvWllgytsYua+s1bxMut9CRjGIutS3Rd4I6X5JDIPhA3DWo+YW9/hj+YEbYtxXTC5sOnxIfndB8+w5YFelIQ60Km5H0k915kTxr0xBFTpDSa4t4x7rUD+vef4lcNaOjXDXnXie56kKlJYJxmjLHx7uYBMSWKnRik7HIqE5VtizUGg0JPCoaUKA4W0ozFRPfrhzIpOVxQ7M8x05K8nAlSsx2EdKIUdlqiD+a4/Rn21gHKyTo7D6L/5As4MjVe7ECmmNN3XkMp8Y+4EInbjrTtyTHIhXQ1ELpeTrpZEiDN8ZJiVjGpS/z5mt2DU7rnLco5glZcPD0nFZbltKaaFLSPz8ibTsx0LmO6ATWtpMNWGX+5Ed/IiyvUWqbveZw+kzLF3lwwejePaPqeuh+w0eBLy3C+EhLN3pzaGOJux+vTfe4f3Wa9uqRwBd38gP/bT/4lP3j3j7lKga/dusP+bI/2+UP+w5vvMSscrx+ecNbtmOyfoGPm3zz6gEPrePu1+3zv1teIg2e5WDKUJfiBddeyX8/Z14put6UcFNvthsOyZtM33Jsu+Z9/9dd8kDP/4O7b3Dm6SasVw3bLvitpFAwpUJ5fgNYsFlM22x1D05NyYkYW+YOzXA0NdV9gbUU5VSyzyMbOd1uKmLFmQVJCESEmKAtSO8hkTVvZviE0z6sX57iyYlJUzKdTUtszWVpcWTA93COmRDrfolOGfkBNSuLLi7QW/0VVSECZV4ScsM7StQPaalRpAHk/1T4w+A5VF+ghYua1hOkdLEgXay5++D43/6M/orna0a22YtqMifz8iryoUSEx7DaUxwv68wB9EOztx6fE4znpcE41r+kentP8L78l70/Riwnp2ZUYKRGNdG57MYYi8AStFPlgirlq5fFrjTqcQDs29/tzOX9MK1b/9gOqb96h+tZd4i8f4U9X5MdnTN66ge8lJFAPklNhlSaXQghyKaPqgny+EcSvs5LqbQx58EKqGXHLujSUk4rcDaQgxI9sDX03UDy7IsxrzEgQ0kpkRlglPplRr65R8vMHMbNGo1DbTs4XvQSJFc5KVsZVgyudGIr7XrTt1pAnpTQrfcAETRgihEToh5cZBillBh+wKeEOFlgzyiCcIWxa2QxF4dxHrUVq44zgX31CZZlAGx+J1+ShbUuOke4SukcXUBasrBbj8XJKsayZvXeb4ngpPqGQyNOKyghDf/Phc/K25erj50wP5mANk9sHqNrIICnPpEGqCvy24+Lnn6Ld6IkIMk3W1uAWE/ymYWg6TAgU+zOUgumtQ8klGdGYGkjOSN2mFNla2JvSbxqKvYkUrruenHqa1VZ8TUrhJhWqdlSLKX0/BsotJoRNR3GywI4DpHDZUB8tWL77Gt3TS/qux/vA4pt3qW4sufjwGfiMQ9GtG5TVWGfxVgZBuZI8lTgE8mUjpKxxAp+RvJRkNfrgAF0UxEJyirIxqEklvi4f0FUJE0dYN9KYV5YcEv28xh0vSU8uCG2HBdLFFnuxEcP4qkFPRKaWYiT1Ab9uiaWEPcYQ2f7lr1j802/T/OVvyKuGkJWYakcSYfPrRyx+8Db90wvZaiD5CTmnceotfj9jjeBypxW56UdvjBjf0+h9TCnjrB1D+ixpyKAEG5yMlvergjhu2rSVoYogYsWvdu0NUeMWOOVE6HtiGAMD+/hyTqoScr4ZDcvGGNmqpPw5j0n2QTZCSgawaQzfi0keT076sxRzIAxeNh3tQDWtKF1B3+yoS01C48dcjWvJzed1NYq0P5GE9SCfPa3EYJ5a8T0N6wZ7uCCuGjIyaElaofy4+UGhCiXZSCGJf6eX90r9+jHNx8/FaO3Fm2edFQiKHaXpSlEi5y2FIo2Dp2tz/RAi1mhMXZFywu5NRyP9KG1UQNOjYkQfzMmXW2lwc6aqS2IjdUeMkew05XxK7APNh8/QxjApLLkLxG2LsRYdNTEJYav3iVgoykVJffuE7nxF8+lzZu/coXr9BFsW49P6iuTolVpWfXVb8eXHv88W40sVRGqUQ4n6Jo+SRqWUbD3/jo0F/H00F3/gY1Bf+POLR4aXyLiveoq/2GO8+vzmL/z5pTdSClM6zM195OX87JvZj0SMEGWaUjhyjOiJo5ydYK62MET2371D2LZ0Ty9QlRMSSR/IraQYpxRJBzMGH+Bijd912DfviJE7Zdq2xT4LDCFg5jXVawcyzfMRPfKTh22LXzX4bScF87EErgxK4T96jiJT3T0i3dgjnG1Q/YAtHR4wjSc7TS6NbBhGBnZcbYnj2o6c0Udzpid7clJqBhQa//RSfu7lFnMwpTyYU98/kenAF1d341/1pJTnOCTi+Qb/7Ap6TwZaH3DrhmHX444XUFjc3pT63g1SinRXW3CGw3/8bZkYpETykbhuyKXDjA2hGjWteQhCn2gH+YAvp6RuIDy9REWhlOijJaF25PUO3XqGGCSUxxmiU5TRSHKqD/hdR10VkMBYTa4KptMpf/TG1/Ex0kRP7Bq+duce/5X+x/zi2ad8bAzTHDkpZrz7+huEySUK6PzAFMN0NifHwHuLmxwqS55NuLo656isuTh7wfTwkHXXse12nHVbsjEUITEta4xRzI1Gu5Jtu+XtG3e52q55dnnKOg3szZY8f/6YOisoCt567T6Fs7y4OGXSz1gu90gTTW0di+VcQrNi5Plv38fNptRBQSvmrSF4mrMX2MWS/WmmjIlsFCkrmf6NptR4PdVSmdV2w3wyRaXMLiu6ELB9YGoLtAf/9ILkDNViKhkMuw6Tka2EF7pJ37WEXcRlKIuCApFPOaPxIRFANOijkc9NqpcX1dD1kitxsaFwlt3g2X78jPk7d0ibDjY9pjQEH7HdQOw8TmnCqsXNanrdYoYksss+oNYNxhjWjy9Y/AfvEZ5c0D65FJ2/MniyTKBDIg2BgBQOxgdBuU4rUiMFV7raUZ4s8GtBo2atwEfsbmD464+wrx/BrESHgvjxC/LVjupogVpM6LIQV3Ql6cImJLnAklH7U/T5VqQainH0kIlkTIYEssFAjV4waeKSNiRr5bPTewan0Z2HnHFVKdNUPxZLWtMBBZC9x5YF0Qf05Q7vjHx+FHTeU5Yi6Qzbjk4h1KGYUEbJxipEATf4QG46kZBpaXby+FxWIxYy7jrJW4iZ4CUNNo2afVsWWKMpYiK1A6EdMMZg92b4qx0peXTOxCFgygJdleJb8UFC10JC5UA8XbF9fM72Z58K1eX2IfVbt1i+eZNyXpPrkqIu6Z5ccvXkHKU0qQusfvIpKXj2//QdyuMlft1iQsTOaw6/e5/1jz5BzUq0tfhNKxIqZzCzWrI5ri/YQc5pIN6jnLOQk7phPLdpVA5YqzFmBiG+DNZiXjGZV3TPV6iQCN1A8gPl/pxyVkmSeetx+zPxRViNvXuEuiWZQN57ihtL/JMLjLVURwtA4a1m6sWErEuHsYYQZZJf7U3JSuHqErwnGkW3aXEHM3KGQQPdIE2As0RnMCnjx9T3lNJLX2LWGl2XxNaTR6Q5bcSe7AnsQcsmIykleNachQYUIkpbEoJw1YUWudakRHVeACPbjt2//YDJP3ib9T//CckHiqLAGz2a1INQzm4d4B+diWRRK6x2o8HZYjovkpg+kist5MTSwnVjMRLMlJaCPQE6RBJCGjNYNCJHxVq0iuLTGgvenPP4/k4vfRy6sKg4fr7LQqhbZFIGFeW+h4sN1ayW7SgZneSxq3E7VNSV5NwYI2eD6w2KtSK3cgaTxLuR7bhJjqN0qrAMbU80BlPUdOmMIUUGpQmb3ecrquuibDyqm/v0+VOMNfLYvBfwwjXAYNdj9+ewbtFKSbE/SuViylJxRZGRq1FqmPcmpLMt+fVjcBajEDmkNUQfMIXUAddUrjB4jLMv6VMk2RrllCiVIgXZvqleaGcYOeeoEElIo5L6AHXEKE28nuYn8Clhm14GL31A3yjoti2mdFSHc4iZ9lyCGvMQJDl9PG8X04J41RC6QIehvneEX+9k45wzAU8xNu9frG5f3Vx88Su/e/xN4/nf8z9zfvlfr9VBSoG+roTHLdG1CukPNyd8+fG/vqH79z4Xn33zc83H557jkceUP/8/PrfNyOOt1Cs3+oojhUR/vqK6sc/nMF7OYJwhe0Ej5iRJomo0ZpvKyRtDa9K2p759KP+uCsKLK5le1AW+HUSHrBRxb0ZQmWI2wR0u0E1PcbJETUoWB3OKeY0pi5e/ah6NJ5OUCO/eZffgBfHhCwiRfvCoWY2elRAi7fkae7SguLmPf3wh3mZrCKsdXA4yQXGOWFnc3WPyaofLCn+5xt04gL0Z6fmVSKc6LytvpcmLWgKonq2gKiVQyL76Co0nzSHQPTpj2HZM7hzRPDglffwC5SM5BMy0op5UUJXkBP35miKD2tbEgzmqLiQUxyAbjjF4x0xKkZklQT7KkyMnVl1Y4tUOr2Hy5mv0j8+EIT3iTWwlRi8bM36QCWfZedJmB8f76C6QrwPSDhdUg0e1g8jhvAT1ZCT9VvcDB65ELxYEo/iz197iVjnl+OZtWgtxNscNETObEbc7cAV+WbHVisX+IbeKiub8ApMzt/aO+NHTDzHacPH0Yx7trvjG4W3u33idq/Ulve759aP3mU0m3L9xh+ebFfv1lLKoKSeB+WzJ5eaKy+0Vh/tHDJs1p92Gh/GSH/zxn/C9u3+CnlQjNUmRukFyDZzBzmr2/+TrhGsd8VVL3LV0zUD99ADTtPi2I4w0EzObitHeGEhRwo9ixDhHVSFSweiZaovug2z/Bi8newVq1TB0AXe8xEwrKbTIdCFQ2QlgGIaWQRucrqRALh06ZwplyIOQ06KCHESfGgaP3ZsRuh5nLLGUi8Y8ZfLjSy43PbM3XyNdbomnV8QQSUGIUhQOqyDueinknEGVluLuIeHFiu6XD3DTGmU1oSrQ37wLz69Ij86xIaCGQLRClqP3BCArmeLnDKYuhLYxqxl8oNibkB6+IE1rfGWpZzV53RGfr4nbhriY4nRJ3vR0F08pTpbkxYS86xnW2zGgTaONw8ZMbDxqVqF3PSoEQtujJ5XIKbsBWxaC1Fbi9dDWMuRMEUVXPHgJ6kyVGEqtNZKYWzgigWHbYpzDKykm1KTEjXjKkBI5KqrCCelpUhJDIHs5BzgvBY6dVyLN6D2hG0RyMgZm2WsZQ1mgBj+eRjQBKdAwko1iSifD0qbHWtFD46VxwylMUZDrEg+oaYVJBTklCesEdO+xzgpZZiyi0qRAKairEruoMfNaJG7blvWPPkYvasq7hxSTkvLeIfNlhQuJ4nDO+ucPyVdbdj9/SLwrBYaEg4k09uAfvCHEu9YLljtlwW82PXHTSbBhlAZDa0V3usLOK0l+B+y8/uxiZvU40Zbrmr/YEXpPXBQs7xxiZ4K6DU0rvrdBsmoykEMQ+UzlSG1GDwGsoihLbF2Ij60uxH+VxOdycryk++QFQxYUcJyWlFVBF0X+5Jylazqmdw4Yti02a4ZCUx3OKUIkaE3YdriZE6O1j6RtJyn0PhBilE3byR70A3qQZGi1Pyf0KzhdEX3EK/HzFSGjlxO2jy9wZYGuEI+Ek0I85YyOGTspidseUJiqwp9v6D89pfzWfYZfPhrfS5qsIjpluvefMP3Td7h6ejEW3nossBQhyuAApeiHAT0xaA1qpENmL/6JnDJ5bEzMOF/O1lC4UmTPYWymYiZbKwS5kWSlFPicsdaiy4Jh8DIEixlnDKm05KYXr0FMqDRu7WJGX0uCjIboiSiq0hG7LM/vSJxCA9rIucgaQuepy4I8REE4R8lb6PyA9VLHlIXDG0PhClY5MwRPXQlUI+csVCHF52UxSlHfPWRdSI2hrSC8GaVXOkSShtB72SbK0yxNFdJoDsOAuW48jSRylz6JNyQldF3Sbxppwke/mwqZaJRgsq+DE0dfavJBpF9GvBoKyf/QzuJjFAXI2LyqsdnPSch/cdujx89fzhA2jfibfMC4Qjwqiwk8PscuJsQYiTkTDKheHut18tmwagTUsGmxBzP8xQ5VWeL4u0zunQhJru2xdflZifoldeqrG42vPv72DcbLe7juM7SS4eHLe1R/4GP4m4//9ZuLl6uf/LmNxOeoUL+nYXv1dtdbjc/5MvIrHdbve87z2LmPjUqOccTNjvc0rk2Uu/YJvHJfmfG28jW9qNGL0WcREro4BGPIIeEUY1ee4PahrDZHk5tZTihu7pOGQQqBEXd7zf57uWhRGrucsvz2hPzObXYfPcV/ekq+2BBKh1tOcYXD/+ox+mSBSoFwtiVZg1tOiVcbUtNL2q4p8GcrKRhSpnrzNbJPxPM1ad1IcbFp4PYRsemonKGY1lAXmMM5eTRPAaJ59JHu2SXdR89gN0jjs2rQXqQzlJZcOeJqR9o2mPs3CANUrsZfrPFr6H/4EZpM9d4dQoaylAlAWLdyH82Aqhz2cE5cNejSgoK07QmblrhpWP31h8QRRxqsRdcVSg+kq60Uu4XFR095Y484KTDzmazUY0RfrUmzihAS5bTGrndi3EtJApKaDuqCqizJtRhTu8Hzzr3XOHt+ykEUaYCthUSy7gfMpOC3jz/iazde5/LTR5R1RX1yROx7np+fkZLi7vEN7hcV/8hYnq7P+X//6F9x5+ZrHC8OeOPOffZnS6ESbS/59eUjvnXnLcql4cbr93nnzgl7xweyIu+9SPlKR9q09JdbeHZBXLXEdStbuM6D1TLZ9j11PaG4f0Jxc5/i9hFV5eDb98g+0K13mJ0nXKxJ51vi4AneY3Jmtd1SuRL6QSgpSmGiQo9yEFPIidyHKNrdFLEpks7XRGvYWsXEOepOkUNkUjiKlBli5PnqnNl8gUNhRz5+5aTZjr1HGcXQjyjiECXQUSmMD2Qt6OE0DKhNx+anH2MKS31jD1aidWbwcuHYtqTC4ozBB2l+0y8fMvmzd7GLCcXRElsXVDf3OfsffyKpy3sz8sWaGAJqNGOqcQqnlCaEQM5CTFHOwP4cQJqPaSWejmREc+09ZvAkozG7Dhgle0B7tkEdTKWBVlo2RlH4+j6JF8FGGFA4bSi1SAmUs7jZhNh0uELkA3ZMIlbW0MeIKQtckqyGdD29zJCXU8LVDlNK02BTYrac0nWCLvUhorTG+5GEMy/kYu8TgxfeftZatNc50W9EoqlyxhqND6MZuTDsBi8s/W6QrIzxfK1zlkm3EsNqMeImjULADM7KBHNZQ20pJxXNpsWue4JRhJwpRo25qUu8asegsvDSjKjWnQTr+RWdkrCwMMpXbFXgjhasH56xf/+EIUTmrx9jpiJHqU6W8p4esdbMZDPiL3e4RU3a9sTdQH52CXtT0qSATYepC4q7h+zOV5TzycuJoDuYiVQwi5FXjTLR6/lW6gaR4OxkMJDagemtfXJM6MpS7dWkpiIZjZtVkBKxE3CBilJYBa3QY9BlbAfs0UIKNB/pnl7gphV2UjJ777YMyx6cy+ZhWWNQmMsty/fuSL5HSsxOlgynK7p1Q3Vzj7DrKac13ccvYIhizDcag2KTEnvO0I4IUp0T1mlMK/r/qJQkso8T56AUg1UcTAUGUPSe6mhBvGqIQ5Cgs+vguRhIhUVXFbGS4DXf9VAU+Efn1N+5R6oKUhT5ElpL4vi6xT+/YvreXbqPTqWwLxxUBYUGVjt88DR+IA4GEwYq42SbOk4zs9WjX0gRUxQzfIgEcy2vkq1B7AaiT7hRKhVCxCqFCRE1qUQ65AV9qkISeaUWrGuKCeMMQxulzGtEkmq0bJnwSu639zLB9zLUwWlUHP0eSr9Mgr9WZRgljVAegpCilJLmKSV0iuha3p8qJ1L0+PVW0LvFNQrz1cJsPHcgPpAwIpKNVqIoyHlEVUMaNz/jzluCFZ2hKAW3m1PGOU0wWszllzuGbSsZC0a/BCrFVuokcqbvA7b4rFxNMNZPCmUUWgk0RDUedTLB1gUhyGNUVozs5tpMreRzIgZuabrzrhvRxZFoNAWK4cUV9b0Tml89xL1+THFjKb6Wpsf0kThWtPXJEn+5FQzxVUPnFJO912h9oDtdoQuHm1XoxeTl4/8SUc0r3/nC8bkb/56q/4t3+lXHF2bw14oUmc2r373h3/L4OzcXv5OQ/Xtu+Wq9/vl9xVcc+foXz6/SZV/5mVKQf67hyJ/77y+f8P5qx9kPP8IWlvpozrrpqA8WMjXoBzHz1IW8Ga/XQmNqax7fiP58I8XYqiGerSmPl8Scibue3EmKZnQGNy0lSKl0sl4Oo19iXos+19jPiBq9J7UDqnCCHBxXfaLHBe0ss6/fpXr9hPbRC5EE5CRyk24gfPAMJiX1t+/j214MhtMa1jv0fIIaBphWchKbVOh2IA0B3w7Eiw00HepogVnU+BjIIeIv1hAS/eNzsBpzOBeuf4jETSvkl6ZDK427c0j1jbuolNj9/BNCzGKKT5GoDVSO4rXbqKdX5AenJL9De4++e4P0fEW+2tBOCuqTJe5wTk4ZH9f4foBtS/fknPjgjKBAbzqUUVKsJXnz5m0PywlqKwbMFCLKFuyUyMzsqsXMJsSYcIXFND2x7YR9rRJh06CdxWktZ6xJSadAJ8inF4Q0Q51eoOuKvD9jWc4ISaaVefBowE5KHpw9Iw89m+0VpTI8ePaIWVliExwt9jCHS/71r37EP3n9GzzYnbLc2+c/+aM/5/D4kG7i6KuMO15ydOOEd63FzGuslQILILU9/ZMLuienMp3uBvrTFWwlaVr5gMkQR71kSomYM64qqILC77b4Fxt21mAnpch2SotdTqluLNF7U+pb91CFITcDKUT8py8IHz3l8uqSnDJTU2CLSiRmRjTLcduhNRRG2Ouqmor5LmdM0zF3lsEa9LxGD5HU9HgNiUTtSth2eGvQdSU4xBQolXkpKzI+SdBa6dCdBKld5xUIMECmp4V1YDXbT55jlZYAxr6nvnHIsBXDtFYaYxS9l8nm6q8/YPH9t9DTGm00m3/3AeGDJyJ9Wkzo5jXGJ9K2lc/neFHKVpNq4fW3qy2uA7vrsJOK7LT8LCsyv7zajTriSAqBbrOlqGuK2YxsFHZ/SrzYEsapcqEES5iMxqEIIcr0c1Ki+0FkY86+zLsR6ZrUATFLEFyRM15pCFE4+VUplJicZUO1biTJvO+FJDSSpewrGmZXWIppSRwi/WonhVIhkrA0hoUpazAxoUOQyaszstUxIkGMIUqhUTp0hM4HbFnItExJYm3spBhNL6ULyImvdJghwNmGwQcxiSoFzuGMltDQJJP6wOgx2bVYpSmUJlpB6qqRgIWCEKJMJnNmWlX4sw366SWrj08xiynbx5eyGZ6WmElJ3psQQqSa1wxoBW7ZAAEAAElEQVSXW3LKpJQxhUU1Ay5mstVUJ0vi5Y60acl7U1TOFEkTVy3mYEbsBwkZu9hi5rXIYIJ4MHRVyITcR/zzlcjKfCQWIhMS6ZfHllY+Q4iZFURik8fCVBlDZTRMSrKPsDdOiIdA3HQkpRnIFCGRu4HZ7QPKG3sEH8gotqeX7H39NtXdQ1TKTJW8fqoumC4nGGPoLzfYxYTmyQVmWePXLeWQCKVhbzmj37S4gzlh20lTdno1knoUwWrKJBkZPidiTBRJURwvRQp8vpFgx/25IJ+XU7kW5kRQBrM3JTYiPc45o1LEFI7Ue5qPXoi0uOlHCRPowpAibH75iP1/9HX49AXZS0OfTpbYwwX9jz5A6UxOnqHz5EWFrSZUG8mhQiniGNpmrUYZSxhrEh1HI8M4Dc+jnKTPSRDKIZKcRU8reW+PqG4fI+XBDJ5cCKr12oOh5T2qjRTTcS1GdT1EWE5IV5IVYa1sX8LgZSAHEMFWJSaDmRSETSseJxAPWkySuTCIXDlrjQPmRwecvi+eg5QTzWpHHPzoqVRfKM8UadWSfcIr+fxaIDtLTJnsA9dtTRhzSYxW0vQgW9aidPI8qQxaUx4siOtWJGFjE2S0GeVLDpX9SwyvKZycU2MijmFvGcHJJqUwZpRepsTuyQWL796DqwYzym2vJXhRSb14HawZUsKOGRyM2Upq9Lh0z1cc/uM7tL99in+xoZmeM3/3NZrfPiWGVgznTaC6f8SwkcFoFxOlcwybjv2v3eD0J5/Qvv+EXQhM37xF/dZrLzcDf/By4HNdCF9d8+dXK+y/6fhs1P87d/f3sLWAv4fm4g9vlL74i6sv/eu1NOjlt8Zkzs/fzxfv//Nfy9fO93HiAJKeaRuPP12z+ei5BPRYg1NK0IFaY6YlFAbtLNYKGnE425J8JHQDOUSZBA6Bwlqay5YuRUwckzBLy9B7YmForZELWcpC+zCKISQsGX04p15OSH0gna5pR22ynZRYZ0TfnWQqqAtHcWNJfWuf+bt3ib1n9+lz/KenpKMZzljYn7K92DI8ukCVltgHqBzO9NSTUk62IaC6DaGwYjxteuxyij7ZE0nS5ZZ5hHC+JRVWNM5Z9HjD6UpkAZtG1tVXO5kMFo7+Fw+wztAXht3pFdqVVArU8RKVI5Mbe2I69An3vbcZHp8Tnl3gH53SbRvqWweEZ1eEOJ5ktx0XHz0mj5QHpRRu5zEHC0H/OQObTC4UKkKcVPSAU2AVcuJKkbbbUQBMKiLgU8AWJXl/jtnthME/eNy8Jm92sB1QZUFeB0og9wEO9wh+IFcFjox7fontPfF4KW+0pmez3VI6y71bd0hkgtFUMTOdTHBaPl5VgmmM/Off/IdMnWN2LOFb02/eo5iN4V1akY0hbmUT0X/4VGQnwOnlBbMeFJqiLIXBPnjctCYrSUY2QTJE7DhRYjS74iQAsiyc+FlCJDY9RmnypmN4tqL/8JkkNFuD2Z9Q3FiijxbU372PvX1A/s1Dhqdn0PQ4q2l94GJ9xaAz92bHtEOPSwrT9cQqEwvRcNcZGDy1kzT3ZBTUDtpOpvCTWpLbtSAeYxIz8S57am3Jo9QtxsiwadFBPALKWRklhChSxqrAOCNrc22EPFRIuu9w1ZCS+D2uddPWyn3nbcf6X/+ayf0T+MHbqElJcWOPeLoinW8oppWEwBkxERKl8C46T4riEdDOEFsvuvCmI+YsoYO2FMJMI2bHfDSjmNWkH/6WNJKhTARzMCesW3TOqFzIBsJaKdSjeD20UsS2J5JlE6o1SSMY0GuTbcwYJabJgAxGUhK0YNQKrzL1fAIxC+5xlBDGEDDGjdx6+zI7JsSMGhO0YzbSbIYw0qUyTimR1VwHWV2/JklAEbI1y+hphTFGzp8xQUZSkqM0iCkmnFYyzdUaazS5H8RnERNWM34+xDib217S3SshdhmU5NyoMRclJTAWm5IUhjGRSidAgSFSjmPRoff0PmBQOBQuJvyTS8Fr5kxEJG9mMREAxeuHYt49XcPeFB0S4XyDvrFHv71+bxqh/VQOaw1h26KXNXakCSYlAWLKGoxTdKsdhbMSwLhu6Zuesi6wi5r87IrzXz/g4N27GK0ZzjeoSYUt7ZjjMcgU2hppvK9lDqUjj42BG3M7lDPouRD84q5Hz+Q1MVZyItonF5hJRRsS6fmVaMPrAq0URV1KUNiuw1YF5d6Man/G9upUptalo1TApqe0hs4oYi2+hugMqXTYbUdIkt5uSiefnT6yeO82iz95k6f/979k3crW3DSdnMt6T7/t0CrjypLhaiey2eutlDbSaFROclO0RlWlGJ+1IjctOJFb+qst1buvsfv149ELkwhGyE95u5MBUcq45Qy1tyQOF9L4pQSDF1XCaMS1iNRJBxl6aCV0KJn+J8rFVOSKYwZH9FF8QcagyRgvjYO6sSQ8W4lKImboeimAtSgM/GWDqSw5ZEIzkGLETUqhd/kgABlrRRUxBHRKgu4uHLYIDD4QQxSzPGDG9534kQIpBlxRo7SiMBaltASPth3F/LMJ+6tHWEuIoxubmmgMagy5xVpiigSf5PyE5E0QI1GN6O50bTzPqMqiS4tq5dxijXiyxuUeKIWdyOdGjYOM2PQkBSZlXFkQlaIdpZY2g0/iZzIo8rRkeHLFENNnxvjxuUghiI+jdIJ/Hre+KSVU6eR6OvojUojoworMuPWE8w31vWOGszX9poXLhv7hOYuv3+HiRx/jasfs63fYnW9ws5KydEzfuglWJMqMv9ur2dXq+t9/SMPxt1kmvNpFvCzDP6uar3UzL20Ff9uf84Xjf5MQvZfrlj+0I7rei/0N93ktmPodsdV1a/jKE1QczKjevoH54Dk2lPhdhxoRhNEHCWlpNzKxjwljlMiBxpRLOxojQQm2KwVImdoaiAHigMkZRwafoJfppdGG3AUxZuUs2sPTNf7xhdgZ1DiBTZCbgb73hFY8EymPiMPzLf2Hz5l//w0m905YvHsX3rkjTcjVjn61o//tB5jOo1JmKA2OjN/15MsN7rWDl1MgqzRuUkrzcDgnXW7R652si53GHi9EEjMdCVhjwRq7DpMzaTnFWgXrToxjk4L2w+fY1/ZR2mL7QK8zqvfotiN1A2Yxxfee4nhO+ugpqbLQtrjCEJ9fkl6smN6/wfDskt3Zmr4ZsG3PkCLzqqY4lhwFVRRS9PsIbaLtBbcXNaQURW88TrSPJgv0EFBHC9J2h9625CEz5EB1uEdaTglNR161uJDE+OUsejEleo82A0krikqCq3LbsyoU03KC3TQkN/Dh5TPWuzXfu/MWldKch54PXjzkz9/6FtpYmt0O7ROkQDubsDxaUH3thL2TJan3+IsNuydn4CPhbI1Xhl3bjRM4g28baq2JBqp6ge96tPMyKeoGWEwEYTjqTWNZvDSEKgVlKcVqVsK6z72Y4UJMmKqg2TaUdSngAq0ZdvJ6DY8uQEF/c4/6B29y/I+/hV/t8A/PWX3ynDopbuxNyK0nrBtKreRkj/hnyqzZ9T2hqsbk6wa32WGWc8GmbhsqZSQPpnQy6UJhgsiAykktUIDrqVjWDLsWN6bwpsLhxgGCHqeIasQXKpQky2+EvlboQPRBCCAKjNIkZFoVjUZVlu75iv5/+BEvmo77//n34cWG4Ucfkbbt5+6bnCmUHh+vYYiSQ2AKJ/pirUWyoBQMATVmguSUyedbCYrcW6C2LXoYoCjoHp3h9qaksw22LOh9gKngQI1SIxM9Q2llcjo2Ew6IKCn2QyTXhTQ/OUvRiOQpGKXwPlI6CckzKHRdyHYkJmyCSIK6IMRIPZviuwHdDAydF8qPFTmYHi+2rioIvSR7h5xQyohxU4kfIQG6LjFtzxAiINtYYw2xbUlFgbFGXgMnORcpi1QojBSZa3lPUIqittLcGI3TWQL5lAIn535bl7gM2XtAwtxSltRfM59Iqi8ysdUp0WuNBYqqJCvFMIIkjJKCyahR440mr1ra1jP0ntm3X6dZlqgXaybGELXG1QU6I5jomChKR2wGzLxCddKIqbEh02SBZziZ0hZ1iTaK+HyNndcUjy8IzmDbgfTojMU/eBNjDcPjC9ks3YCUS9nolU420KuG4s4hkEkjbUsBPF8RTxZiGtcaU30WlJUVJDOGsw2SX7J3PKffdegQ8WTCamC6Pyd3nj4lXF1IPtOkZP7GDfyTSwmavGoYUiI7i1MGfdVAP5ArJz6pZsDMJ8QQ2W1bSqWo3zhh/tYtFl+7weonH9Ne7ShGLbruPUXhJO9Ga9CGECI771HWMtNaDLrOQhYjeNSZXEhx63PCmEKu1UreettfPGTxg7dRZSFJ908uSIiXy7mCqVZUKcHa05cBP6uwvZf3oBbaUxqv1eFaTq3ls5UZh5kj2jZH2Sx5HyTsbfDonNBGNqzaaoamh6rATUsJwbMGYqSPERcjydoxRT5gpiVukPNIGMTHZKyBpCSULgraNviIKa14HrXB1hUmRJFn5kQYc5D0dW1lNNN69lkhr2C3a2guVkyOD363VkuZzW8eMwwDlRM0dMoZkxVhRIsrI6Ga2hlyFK+DKQtsTPTX5m41mtoLAXkw5txco0/VdfOohAgVgmw7ldaj/ySSSXS9eFuNszS1NJjEiK8daiWb5uSsJLuX0iiHEKUGs6JO0V62S3HwhG33Mq/l+vWOQyD0nuL1I7a/eEgZM5sffkz1jdvUhwu6sw1qiATtyVrk8m5SMnnjmNl7r9FfrPFWMXSeYqoxdfF5G8v4Wczk332+f0c3xe8t+K8tA1/8ylfe+JX7/aqh/d/1+HtqLr5ywfJ7jy/YGmQCxvUqTb6byb/zZHy5BC2/NKlkFPr6SRu7DW0Ni3deI92/QY6JYdMQdj3aGYYXa8KTS/SsEkOwl8ZBlw4VE7vzNcYaVG3JORIePCdahWoH4bxnhTtcktYNqu/J1lEVY2E3kbUo4wquRMJelNUwyNrZJ09RimHcGAnaSyhSYXCHc3YXG+LZmqu//A3JKGZ3T0aKhpU1cDeIXCslytpRRFk715NCQmy0nNC0M1IgpESZEn61w2waUufJ20vRPz8vsBpUXaBiJvZ+nEwaQUr2A0lp3MGSPKYqZ6fpn13hYmIbM2roWR7OKQ+PsdN6JBLA2ScSRlO/dijs83WD7geGowOKBy+4+uQpKWcWxuJuzcmrnSSI+4Q6WghmNSRcaVG1xsxr+jhQIYjDVAgRJ68bzODRJ0spyjpLUYucp7IT0mpHWu0oCwvzEtWMKM7bh+Teo0tDqi1q05MuNrCYwrRCP7oi7y25JFD7zP2790bvRYHadiwGw/e/8R3ikKDrx0ldgbt/g707B/i2Zxg88fEL3GKKcY7sSlLfo6oas2npL9cc7+2hkkJNJ4IBHXr8mIgaUyJXTi5sKTM0g5w4lYwlXOWIY1o0RnO2Oqcyjio4qsKxC54h9NhoMBly10vx3PuXF6tkZUofTtds/l8/gnlJ/d5d6jdvYW/ssf3xJxQK7MGC5nwjYUSj7LFDPA2T2UTkWUFACX0ImO0O1fYUMdPZjK4tZRdFapSyYBtH02xoe6yzxJwl+dpqVOFomobZyQHxaifmx5ShGEMtxykmPuIK8ZvEMURKa5lERWvRiEnw8L/8Eygsft3Sf/Kc/Uee+OwKvagZnIblQj6jSsKG/LphUBo1Sl9sJ8WsNpo8FozGGEFmWkNOvZzPSivno00v4YIx44eAmU1QnRdtcBY8sNZyoTfjxddYQ9LSCMQQBM+ZM0obTEqEUSKlklzMIaMz+FF6FEWOjS4lJTcOguNFKcnkqAoxP2otDeblVmRoClxdorUWuaUxssFxhiEElBYNuJglEykntNJCsAmRuG3JhcWNAV/qmnFfFHgjA5oYxbQbtMImJbKSsQFmbFKSl9wVrZAsnd5jhojVClUVsp02hqAQI7iCwhqa9U7If7tOJvGjlEJpSzFOcVFKptBZjxkqCWUMSSEp1WTstKYfBvyjC9Sqpf7O66hb+4SLLcoZNj//lGJesx08e0dL1P5k5JAr7NH8pWkYEnHbC7CiLmAiWm9yZtu1zOf7mP2pkHhmFeb7b6IOFyL/eLHC3dqDWSlm28KijMIeLUinK/JW0skxSiRndUHxtWMxTa9bMZcnQItB2FaO0Hmsk4K1Ol7SrRvstMZWTiap21a8PYWhrifyWncDsS5xe1P0/kSK1VGU/GLbsAyBXFjMEMhDRO8GCh8kB6PpiRmCgkldsv/te/I57zyTvRmqGYje44HtaoublLhJyXCxxswnuLIQ+YwRdCuDF/lh6Ygp4azBYkhRrm9qxJEaI3kJw6YllwYdRu/RwxcUSqOsZlBKqGdZ4boBtevQavRDZIESmChynxQCtrjOfpKpOlma+hiTYKWVFN4embBj7fjYZcthRhlidrLNzVFgG4OG6ptfwx3M2T0+o7jYkfqB4P24HTASFhqiyBul6pEMCTVuK5setH7ZAKkAOmXCMOCmU1RloO3l8z2boa0baUEio2zPruC9L1ZnSFN22VBdwy0YM3LgJWHQFI5AJHuh+zHKw9D6pV9PaUUKCd0HwhgcGoeMqwv8WCfhjDQmWmOKSl6LlNHzCbofhFKoNb0P2FI8fKQsg4jjJaaU7Bimo3l6fD200dJsaQFKKA0EGeDmlNETyRhT7jP/mPaB8o0TNj/79GU9OfzmGdwPLL5xh+3PHpJR9OdbJscLducbkc+WVqSsu8D5Lx5x5z/99iu0zVf8tWOvl19+Z6yBP/vCH+Sl+N024m+pbfp77DH+HjwXf8Dj+Yrf88u/nMcOVr281atBetc3+X2P5dUX7nPffznBATu+8ciQ7x7BH12/yhKgpbUw3/1qy1xB+8FDhienDNsWpwayc2Tn0EWF0Q7beNRkQl7OaK42xN5LPsWkxpZOPjwXK9pdQ8oSZ68Kx9DsSE1Hnk4o6gJtwHhPXdZo51AXO6aLGWdR1vDbH36CMobpa4dysqocJshmJexNYVZRrFrCpEBNCtQQ8Bdr9LzGHi2YvH6T3c8/xfuIenZJ7Af0ckreQvYBt+sIWkFOpKqkzwllHcYIejDnjJoUxCxFjPIJ2oA1CuUD8wS5KshR+NftDz8klYb0+IKqtIQQ6Dcbilv7Euw01CSlePKLT5hdblkc7dFPS3w7yAlfiUabiy2x8/RNS3myP2I7E/OjfSZvvUbadTQ//IBBKdSR8Owzmf58LStQLdkgYVExeesmcd0SLtcUgycjshP//kOKN1+TTdsHp/LcOJG0setZzBYoNCcnJ5R3DrC3DmAIDJdbnJOUbDdSlkxVwnKKmZZ0p5e0v3qIu7HEOoe/2NL++AGxj0IjypL+rIzhZLqETsIGaRXd0FMsp6AMRI8eSSA5gSkkACf0A1pr+iRmOWsNGdl8HZRTur6TNGitqLTBGpFRuHLU249ED+1Ew+2Mxve9YCVLR3qxZvv057S/eMDef/IdFt/7Gqu/+CnTt24R2gH/4bOXdJWZtdiyIAND9LIF8p5iUhHiwCYGHMIrp4+wV8O6Qw1ywdApw67DzSeowmI2jQQDZlDzitJ7dOEEoUp4SWnLm1akS4uJkEs6QRGamCR1uh/IRhNUJh3NMYsZuzZQTSsOvvs1wlu32P3yAc2vH1PdPmDx3fs0j85RByX98yvCVTNKEUTKkzqPLd04kQZTFPRKEZuB3AdBFSolQY1DJil5fa2zmOmEhBRIedQMqyySutx5hpQxL0O7DDYhAWk+CgVmvC3GCHXGSkGslJjmfYhEMkkrSqXEI5MZg/JGyMw1/10pqpHOljNEP5JbjJbtmtUyFc4Z7aMY+Eespkoix8pavbxgW60Ef+mzpDCPzYeqSilOU5ZASB8I/UA1nwqzX4tUyiklht2UqQr7MhnX+yDbrGlBN8lMQsakTLNpKcuCtKjJKpEy44bPQoxSbA5e9O8ohhyxSpp0N8qwyIgsMYzD7hBwI+7ymt5jrMFve4Z/9Rvc7X1m3/saHC2ISgys08IxXGyJ7z9DHc5lkxgTafBUx0sxpy4n0liM15mwblBaM13OIGXs/WPyTjYbaX8qBK7Vjurrd+VClRQ5BOxy+vIiV9xYymZ124uOvJRzdPCR1A74bUt1tJRrRSnnzNQEGUa1vXjUhsjQ9rhxoqwKQ1GXFMsJMYmn0DqLnVeyQdaK6f0Tdo8viGOzcjAEXEycDh260LisqIZAHAIxBMmESAk7po5fF1oH//BdLqoC/6vHNA+f4yY1deHkvZKlgdSdl43lZifhbzlLwVoaCc7UepRBa6r9GbtNg3eGIgvFyJQF/sE5xa092uacqMf3ptWiKIhJMixSxnmP0vJ5Ypy6p5hwZYHRxeh1kE1Jvq4BteBmVUzEVt57zjmRARr1EuuNUaQ4Di3HhiuN2wVBpkaSltcpzGrUVUMxbqOj1iLDKh1sGzF+jzKj7ANRK5GBFZaIbO9UBp811WJCXMk2W41GclVYiumEoprgfZKNs9YM51djsfT56sxfbvEXG/msGBlw5JQlbNMaQhfla73IyDRS1EeyqCYUhBixhSCbwxDQRov8cl6TmoGswbgCXTiG8TNrga73mFoydLQqcYMWf1mSWk5HydRoo2deOpqLU2Lv8VE2XNlqBsD5SDctJQdoVlGlDGdrAStEkXMFK40FWZqNuOup7sqQJQwBrWRz5j88ZXrniPqNE/pPzkWyiZJN5th02VlNdWNJ98mpbK9fqUkVnwlsXvnjc3/7HcHPH1Rs/57ji1uTv+m2f8dG438TWdT18XsWNeMT/dXdVv6dF+GLd/rvsT251rspeeVUHkfr40/QztJ9/ISsNcXBHsooqjduw2RGPt+SZzvCuhVNckxEq8mTMbkTh5tMyNsOpcFvdljrSDsJkvPrK9ykpg/g3B42aZhMSdOKLmfKbc/6+Sl7R4cUd27IRORyy2JWs8mQVy3bH31C3LbUN/bFAGgEn1r4SNl6cl0Qdh1KJTET1gV0gfT+M3xdC7L15gFq1UBpKN++DRdbul89wm9bVjPB607QqJyoC4feXxBSJJ2uUKlDTWvUvCQ1AwHBnxZZkXYtdhAJTlpUmJM9SUKeVWAU2oipPFw1mGZgmFSUmx2zlHGzCb6QYLBqXmNLS9aG4WxFeHpBRlPsGnJSgtm7tc/knTuYWgKtfEwUezNJUX12ISjWTQMoklJU33yd6Xfuk1Nm9f/9lTQV1sLQY2pJng6/fCSpuYdLjA9ygmp73NGM8mSJOVwSxmLIX24gJcob+6hZxXQMocvj5Lb/5ScQAnl/TnH7iP79pwwvtrJqX7eSLKsNcehhUmGSnJzVOOFRWVFVlUjmVJJVb0yi0dZK0oABpw1+GHBa0/iGkCLTyZQyG3SCNmR8kPCpIQQKY/Cxx2rZCAzOUChFu2upi0LM0s5glJbUdWcwlWU433Dx3/wbindeY/mnX6f75QP2/uw92sWE9tePZWqGEl1vFhOzUZpiWmGGSIpQxTH8bEQ6GyPBU6aUwCXBhIx7kGu6h7OwqFEXW+qqJG1aYb8reR+4EX94HaqUrSFrL0ZFMm5avcxEKZcTeXyblvTknO3DU3Z/8TPR7fsgk7xZDVWBsQp3Y0F4+EJkUYWDWug7WvESk4mRi6XVWgyDhSX2nqSk2FYoshG9fWb0b2gxrefRSK1KR972pEWFzWJ0pvOowTM4i7NSaGcfKLP4C1JKYvpUBptHI6XW+BwFjxrGhPPr5rUuMIMYL1Ph5Jw6NkA2yynQjtko/Sit00kSmq3WJK1wmRFmIEFXCSHEZK1wo+chjf83a00KkVhYXO3kd9KK3A6ic1YKv95KRoU2Y16AlgYnJzlNW03fewrn5D3feMpZRceAsQ6TEiYrGElEWmuRWRlFVI58tSVoTRw8ZVHAEAhOCDI7MmqQCX5Go51IzNS49VOjZ8kVkh6eOg9Jk1YdV//iVyz/5C2m909Y/fbJ6O9y5G1LdbKU5tIHiqPFy2JYWSSctFSklYTXoSXXRsVEeLEhZQExpLrAtH7cxmjitsG9fiyF5LrFzCqRMTkrPpVBJuFRA1H8hqYucDMJG73ObIghSrigF6jHcLGhPl6yuLkvCF8lQ4lhGFA7LRvhQbYP/UiEK+YTquMF/Ys1k2/eEVISImc5iEmM+0ajjRkbVfGBVD3QeMKuE9P2tqN/tsIuJ6yzSH9wBj3IACL6AJMSrRKpGTCTUiS1vccYRbzaoLqBYDXV8R50npATldL0ORLH63m2RlDYZ1sp7LXGx8B622KUxo31QOmshD5mac4nk1q2jkh2hB5hBzpngUvEiKpLdFVKkwDobEbyoOBzs87S1IZAcbxH2LbEtif0kvUDIq8ChSpL8gdPCS/WVCG+DJ6MVYFVikIphv0paVain1+J5yxDIGNKQaNGrTDLKThN/6tPAdigmFeVyDbHCsnNKnLKlJMF8eqCRJZsp9MLkcvpsaYay6rYenJWYxDmSMpSCJo6ZRkAaslF0mhpNFBkpQUlPTYlSt5gZGuI4+YxLGp5nzsraozRDK7HJrwsHTgzDqySNM8jzCAFycIIhaEMmfDpOUEZhvMtoZFQU98O6EmJLy0uZrZHU8ysot6bslvvqHeDhCdGoX0pLeGdavS+pF2H1Rp/uaVwkuWSc6Z9fE5x8wAfJHvLWIOeC8VRARjN/ruvMf/aCW5Sviw/1e/85csPBb+/aP5Djy/mNvBKlfzF+1Zf8fe/xfH3YOj+m4v5/MrfRLqk/uYH/u/9i+XffR2+pPu6NtJ81d3nnBken7L9yW+Zf/8bhKsN2w+fsvv4DNULl92ArOQPp5R1hT2aE9qecLEBL3xlNS1JtYOd0JnCpsEZizu8Sd52uEmFzYo4r3DHc/mgXtNCjCM0O2zTsek9XTcwZU7hA4335IdntI/OmLx1k73v3MfuzzCHM/pnK2qnKV7bZ/v+DtV4IetsWmLwTBYz4pNzKW6co/yj+xQne4RNizlesomR1c8f4pRFzxcYp6mXe8y+/ybmUFCbV3/1W/pHZ7BpobDETogONin6qiQoJXrTwzn2zZtM3rtLXO3Y/fRj+tPVuJYORGWwrx0xafsRkzvSN0hUWmQ6m6eXTCqh9OSUKXPAHCykyLi1T58j6V//gup4n9ANmKM98tMLSSBGgnDCtmOoSsz9EybHC/zpFWHVEi/W0I7c8QQsJkyNQR0Z1Lx+SWlSMckU82BKf7Elf3zKznua1nNYF9jq/8fcfz3Llp/pmdjzs8uk2bnNMXVOGVTBNNCNJptNo5YozYgR0lwopNA/qxvNKELSkDHTw6HYbKAJ0yig/LHbpVvu53Txrb3rlAEaYDcZzIuqbTLz5E6z1mfe930c42dXYMSQr72hGC3m/82Sad8xfP6aw/SaasiUKHArUqJE0KuKqrKyNYhiEjbeMSUxueUxyCTcGowupONAyFlAaFkkAGUGCWVbaLTFFEPuAlFHotU0Vqa4Vlmhnd4VoVPA4bBakRS01QxXK0WMoXP8n8llluiIBCf88jnDPP09/PRjFn/yHtV7F+z/7Yek246pH7FG02pLbhVjjKgYcLWnDGKeK0bjF0vy9YFsNHazIu87oRzPUh+6UaQcK6Ff55jITYXyjiEmvPfoRUWqHPo4ovtR0m+sIXpDqB3m8QYWDerllvT6lqpypCjQuvJ6L4V2LqghYBYNWSvGz6+of/CWbC9HSUdSRRLcsjWSxoM0C/g50StlUponqlqI2iUlitLCUTFG/DFBjMtOKcpJS7zcQzcSvJOp3m6gaKjfOqV/diPvwSixhzlG4Y/MsqE7fXJR4r8gi3TOeSm6rTGyTbD6Xm8cnRzyrRNzZ7YakwtxDKJFRuRQ6TDI1iAXXFtJWIBzZGckVnOWGTjrZFNSZBOjtKTPlCBRxdZbYpSYaTU3j1NKMyekzOwBacKyUlKcZZj6gLMZpcWboZknn1pTbo8i/2sM/u0zwvMtGoXJmRxF8hXFHidgtWGUU0HOWO9EflcKViuikqSm7BRDTviY8F6mzlopEhG1qKC2mKkSMN27D3AnLXZR4R6sqG+OxOu9BAmowvT5Fe7RBnO2lJjSm6N42XY94epA3vXo0wVuXRNf3MKqIR8E9GjWDaUb8Mawv97j2pqisjA6akf46AXqdCkba2Mgi1dFLWpU62HbiXzGGTne7gfUZkFpHOO+o9x2tB88xqwaTEowTNJ0LmpSN2CXs0ejcsRxIueMaysBmG07MYZ7Kf6WHzzErRdc/dsPqd97wOHT17CoqEZJTLS5MIyBqvYcyNReisfh5sDth8/ZfPcxi/cuGD58TnOyRKGwY2DIGRcTxiiGJHRnf7IgTwKejd6imwq98HDssf3I8OIaEyI0tfhXjiMjSraoWnNSVcScqJetNKve4lAc90eSUpJAdMdsgHsKtoqJ5AylG6jNzG9AFAPi5Srobpwlq5FsNCmLmV57JwlmzpJzJt7uRQ5sLWZZ0+86FIXGe6FHxyTHkVtJmMulMMxx1+FijfYOc9JSulHSqLRGlYJuZHCn+olgNP2qZrWoGDYr1KLGv7whNpX4tKZInj1WwxdXVFXL0exlyFUQie7c7LxZJOkhYIwmDSNqHqaknKkqj6agjcIsK/T2gHbiWRJiuRyXslb3EjpmoGZIiepkRR4CnQlU716QLw8i3w7CyChGjPGOmWydZZNEnyThydxJeguxHxhilJCb7QDDxDYGjDa0QbxiQ61ZPTyhaqQhdPOWv8w+lBKTfJ4Qr004DiStmfScbpeTCJe8ZbrtqR7KACwMkuS3+d7DN3wMAqn0d83G12p8sb/8DlnP37exuL/976jR/wFlUF+//INvLr7t+fi2lc8fcvtv/P7NpkF9rRN78+v5izQFebPEyB3F9p7eqOcPUZEuuf/1c6ZnL1n90z/Gnq25/stfMvz8Ge6klYLDO0rlaN8+x61a+QzOhSg5SUzjbLjNKROvD4xXeyhZPpDPbijOglGURU379gVuVZOPA2PtmD6+xK6WsFoQL1/Dyxc429L3A/78hKQVUUuk4PTr12y7gH+0xl+syNtO/BcvbvFjRKlC9c4F+eaI6mEcJ6YvXgm8rnLQCUArH3q2H/6K8eZANYyM+yOuqWi6iTyNjLdCCPbrlurBeoaVbSEUJqWwjSXOqSfrh0tKP1HWLeHZFd2chJWnhA6zjGWK5DRiVkuGJJp5XUmR4jZLIGOCJLsML29Eu+kMsfaoVUtaSBJPnbLINF7dwqFHF0U8DETvJHdbK+Jywc3VLRfDhhISr/6XXxFuj7TeCUWYAq5CdQP2ySmhJPRuIAwR5TX+nQv09YH41x+RKw+bJXVKqGFk7CeOxx73i5+i3vsuebVAx8SUM9Y4phCY+p5+Gnnw3jtkhRBbc0JbizWKghxAY2NQGEyUoqaOidCN6KYhx8SUEs7MGvlpoqk907EnxkDlZzNklujRu2mStgaX5GBIhuzAGkPIsgbXs28n92KMh0JOQfT1RaZ14zBQJzC1FzmJgtKNDD//nNx6zE2HernD/vApJ//qx3T//jf0n7wmhiipL1Gm5secWRawlaOkQtj35MMg3gKtmHYH0c12I10YqB+ciqY6Fdh1YkTUWszJ2uCsIbYVYXekOVkSQ6R6sBEo1RjQiwb75JSyqIkvbijPrimVZbjc4pFmVq0aSi/G/aKFxZBVYRomqvce4H/wlN1/+Ij68YbUTcRth+qkGFNKoYaATlKga+Qko2wheysn4hF5v4Oky8ipVaQ4SmHGhD5dYg4j2ehZOiXHknR1wJ+05P0gUZZW41wtJ1wl0iM9T9DUnLB0F3KRi7y+xshGQ2fkmGTUPQGXAiFG6qom5YSpnZhS50lf1FApJU1IzCTvpMBXSnwfkzRxCYHEKSVNhdYiJXKVv9c6y7scSY2aAWvKCKzUlILyDp2zUKaVFCPGW5m0ByGj3zVweZgw2pAOI/ZswfXzKy5OVkw3HdoaxqOQvOM4YSpPcRa7auW2s3Qmz3rqu2QhbSxOCUugaCN+/CKyK2Vm2clBqNu2rhg/fs1tP7J494Kzf/oBUz9KalcumJMW9+RMtPHDRDwOEoOtFKEbUCHh3tqQtXA99KalaIV/61Q2J1pT+6U086sa+ijk44dr2a6dLDCLmvByS6ktdtUIkEwhf0sl/qO063AXK5LVDGQpgI8T5mJ9P313dUUwHWkMDHaQ5r+fmIZJvBnGMulESkKA18taos5DIt0esd4x3B44+eOnMvxZ1YzPbug+eiWv40kjr/MQ2Kxkezld7XFoxp98Snp8ilnWXH34nIrC0VvadY3dD5hFJalK3UTOEKwmTJHmtiOnhC0z4C7OkbRIuqKPifL6lpKSJIkZI5PzymGzGI2tFX9FW1XY2QcyWkOwGjVF4gxyvJPKMAWRsyYB5kUtUh89T+xzSiQvqXZGS2JdnKsYNbNknPdMIZGVRreOtGwgJnwpqDgnrjVGpuxak6Nsi4wxKFNw10dSP6ArLxJl78SvNIzkfoScmazBhUi7ahj6ifp7T+i6kd5o2spjdj1Gg3WW6XJH6Qe8sRyzNPGGTLreStU7x/HfxZuOL24gSVrfXRS2TYk4TtKwh4iunRT7c312Z6JWSgkNe5Itkz0/wVqRiOonpzhvCdsjh2dXNK0nDRLA4a3wrXQuklbmxFs1aSXypCxyspgLxUCqDG5VSzDOF5dMXh4PStFRWEwBu2glEEZNxMs90xiprZGBsVIkJYqA4i0qg1u2jNd7QozY2hOnKM2CUqTDQPf5NcbLZs49WLH+zsOvzLS/7B3e+OlXCvrfUvH+PkX/3yXW+UMakzce2n0j9F+bLOo+zeqbm5g3hGa/4/Zv3OT+ql+7z/L1r9/8p77lCRlebdn+5BM49Bjv0ZWjhEDz3gWLH70jJztkskVtWfzZ97HLluu//pjx40vq7zyg/e5j7EmLWjaUIbB/dinE51nCUj/cUD9Yo+dOWNUOAH++onr7nP7lLYtVQ/nRO8TLPcUZ7LrFrRqJmdz1mEMPfSBcGvaHHnc8Mm23sLbkcSIfB8iZVV3Tp4iNMFwf6G8OYBUpJRQai6xmbVthFzXFWdS0gOOAohCGCWOEqPv6//VXYkZF4b3FnC2os0wIpuKwm5bjp6+xGiZryf2I0gX3aEMxmtVJizaa9PJGolxzIby4xO861IMTwuutwK8qLxri272cTJ2FzYLu+oAJkdvrKy7WJ7ATUmYMAftojT5bYI+TpE8gKTBmkhV0vjliQiJFMe0Fb4nekZJQPF0/0PoK3Taklzu2h18zTpESRQdsCnTDkdfDC374L/6xaL2L4hgj9aaiOlky/MdPcXUF6wXKWraHUVgJvsLGRKOgPHiI3SyxdSMmQhRhjFRNhW9q6ts9bI+oRYs5a2C0mEWFPk7EMcJhIN8cRVLinXAfChijMCGQkxgJQwhYpWiUIg4DumRQBW2ASXS5zkgQQC7yWVRaCjprtGzQQBI4kNjCeBxEihIlhUgjngI9r68zcMiR5QCqrdGDZMDnmMTQrDTTcST+8hnhak/z3Uf49x+y/dc/E5CiMWgUS2aDtVJYjUyHg4QFxG5kqjyVNZSccMaTUqFESScqMaKcw1QOfb6SlKRdT+xGfCNbpqRguj3AYRD9cXZUBYkLvNxJkVM59Px+sUYzHUaU1VL0a6G82llvffj1Cx79X/85ftVw/T/8NbEbca2XmOf9ICyM8xWpHympSLJcQSKlZ/NnQbYATEEmVdZggeQ9eTtQugndeJJRcxTiHJ9NIYwRk7I0c5pZ04t4LGZ/i8jzxIiprUElie41KVO8kwYyS6yqd1J0GmcYhkkidZ0TmVCQJC3trBTW/YizVkyTU7iXPCVvhYqb5bNY5iz9rEHljK08qRtxtWPMWTwaM0djyInKzNGzlZOYWSVpME4JcVc5TUhlZmpYwhjmIlekTpNWaG9hFOO8GyLnP3ib9PmVcHCUolo04kGykpZV5ml0ykXiUO82gkYLF2ButJMVyYaZC3Wn5m1iKaK1LpKNbyrxNbTnS/yTU46/fgFXB3CGMAXsqkHV0ojlMaDXC5meh0R9tpKJ5xfX2IuVfB6HgD9diJdhfo/aWs5Ri7MT0vWB/qPnhJRQywZ/upRC9Hx5vy2V8165n4aG6x3p9Q7z9oVMrnNhOHS0T8/AW8ZDPw/FFNWqAWMIIYGRqGaRURm0M3grDUIOEg9b+gm9aqDyApicInYhTa/WCh5viLUh/u1LOI6YXEglUxoncpEgdPg7YzKl0C5quinSKBj3Hcu3LqCfKGOmjBFt5DjQtDU6ZVyBOAWBPiK08zIFolbk1hMHaM7PqReNDPbGwHSIoPS91FIZja08dphwTSWAtXVDGCZqrZlCYswFPQWaxpPa2deFpNPZRc0UtQRrHAf6IvLLhDBbvDPEfmTMBbdoGMaADeLl1EPAPTxBmSXsBoETakNKiaqtybkweYvVIsez8+ejtDXRKNxxENZEyrJtUoriHampqRTEj15yzIn2/ccynV+3KOS5bZ2DOKLGSPAet1xjjcVpSawcrnakEDHa3ddSYX/k9qefSNqcUpJMpcXwroyRUIRccFOa6zT53IV5C3DvedSK/PiUdL4WCvpcK6Up0HUjftlyeL1Fay0SNSVhNUkpqCz9OJEXtSQFGo3OM/PDGSarSH1EGZhSlIHMFKi8YzSaxhpGClztcbcdk7MUZ1hWHp1HidxOcpupFHzKZKXFt/SzZ/iZOeWMRG7HOXUq9SL1jEPg7J1z8cTwB9T15Uv1z1cbEfn5fQKUeuNXv6vo/09tCr72z3zzmz/88l/Ec/GHb3e+5pifn7GvPG9v2Ca+8qOv/0MF2idnKOD4sy/Ih5586BmPI93LLf1+4OxP38OsWjCa5u0HxG7g+OqW/c8+p3l4gn/7jJwz4bYjXO3RVpNvjzIl33fYh6fEqx3HXxnUJCfqYjWL9x7SPD7DNJ727XO6l7c0Fyf4ixNKTNLppwJK4U9XjK+3uJwJhwHXKfzZQ/TpA4YxQEzEYcTWHlWg0Y7oMsZqIWSOMyG5Fmq0shr74ARd+/mEc8CtGpbvP2a62RF2HfZsTf/iFjNHMqbaSc7+/FwWRNIydXIQVzlTP9hQ9j2LkwXm7XOqixOUUmx/+hH5rz7CVo70YEOuHWpdk19v8VNALRo5WDUV+qQhxELsBeK1fniKebJCX/X4InpVU9eE2w5Te6aY+Oz2knfPHqJ2/V34isgarCWYQtcPoq3tBhprWJnEuNsST86oFhUsGtKxwxx6/DChFw0uF9rlij/67ttwHJmMZihQP7lg+WjD7b/9hSRKHXvii2u00TRtTT5bM1rF5nyNebAiv/OQuBvEvKiNRJMOmRwgTgVTN7h3z0kvbyk3ElsYLo9C454lLmaexmQgZnlz6zlVKGuNsY40SuRdQaY5ORWcdoTjvMpWCaKiWIU69iSrMcYJ02I+SeGFAaBm6UfKmRzKvfdBKYEUBjL7aeDB+pRUFPswsoiSsa9jwixqKfyTQCZ1KnSvbzh8+prm3QtO/0//mMN/+Ijxo5dilgRcGelVxq4ElngYIitrsV6oyOZ0STwMWKPpGk9slYQi2DV6SvI+P/QEFPWiYjp2LOeCV2sjxYrRQiXWmv7ZNYyBxhhCpaS5GBPKFPJc6BdAp0S0YnQv84mSmLn+ycec/vhdFj96m/2//w1lmE+qWpgFrq3I3UhVpHhlnuSXIqeLrKSRU8ZgkSI/g2TbN46cy6zxl+maNpJxL4JnMXpmbcQ4ngS6FgoylfWzRKNIMksu4o1QKRNTRmXxQoxRpqn57oQc1VxUF6YsPhFlZIqurPzddp7aDUGkD97JVtFnuZ8cM6by+Dke0zceHRPDKLyJkgu11mQnBnPvHbapCN2IcxZbZunfJJIzChxLpkXNMZuZeBzQbSUsgjGgrWiw7zwdxmjyEMilcLSa1dmScn2UgtuKjErNxuGYkhSBzqLzTBhOGasVI7JRUdaSkfuNMyMiKZHMCQlYjN16TIRuomhF+yfvkLzhcH2gpERVe5FQFgRQ2VbyelNIwyRNh9bYzQLtHfHmyNAPVGtJQ1KLShrk2pGOI/GTS9LhiBoj+um5sEmGSbbv3t7LL9K8achjRFUW5R3VD57cm+hLKSwfncoUvghY0xiRvKlFLR6GOdVQWTNPjGUzkGZGTMkRt25F565At54wgNey8ecuGMJolg82BOcYP7nELpekXSdk60WFaaXxMoBZ1Iyvbuh+8RFps8Fow8mjczkOvd4Jq6Mgca7LBtNUuNrT74+k44DOhXrVYmOizxmutuSxpd6sYN9zs+/EiJ0zIUQWdS2fgSmgrSdQyLXDDCPVeoGKYoJOc+qYNRrvjETV9xO0Nar2hClQmkoYCVPEtLU0qVPEbZYkbzB9uKfFB0BniU+tK48fM4e/+jWL9ZKgINWevTOwj2LqNgZzvmbadcJfcU6M85WY7TFiuI/7jikE4UFojQmBQcngxVqNutrjK8eUC/ZyD1rT9RIpbwHb1CwfPOT47DMMEMNE3B3nrZ+7L6GGz65R8yAmzUwwchGvlVL4uybhMKBaURUQgrArtGxpY84My5r20SnKatnK5oyKhdINVLcdLhUZaJVMKhKlbhfzpqytKDnTpEK8i7td1kwxoWKgjnBVe5rNAtrAeHNk0U/004RxjjEmtFY4Z8kZ8hzrq42RiOJ5YKNXLTpKk52SeG8YI77yxJRliNF4yjCJFMsGTO2wlcWfLb8xU//WuvdOelPerGfvjvtvXO0bX/wnfn93oLiTSH19AfBtzcjfs7GAf0hCd/nKD792+f3bizLf51d/wv0L8uXzcXefb4quyldv9cZuyp8uKd99JNrglKn6ie1PPmb8xXNe73owhuatDc0759x+9orjL15Qaai/c0H73kPivmf8/JJ0dSCEDMNEQaFjQV0dCf2EdfO0DZHxHLcDw9++gNOW5XsPsMZw8zefUDS052vcZolSiuPnl1TLmvqtM1QpVA9OKIeRw4fPKCmzrD15UZHHwPj8hsNNJycxIxrpMCdaKKMJVuOjfN2cLcUEVznCr76gvHiB+affY/V4Q+4n0mGgfnyKKhBTFklIP5H2A2E/MO46jJds/bp2dLuJbjdRLyvatsaeLAQyYzVaaca2xiwr/OM1etEwPLtEOYeqHOPNlrpt0Loio5nCwDJkqqpiuWxYlpqbXZJibD4o51yw3YSLmel4ZDIHGieSp1QUL4eRaRx42ixZzRyDZUkoZdAXZ6zeecwQEvQDuhvY3+xpnKF5+yGqrXAXK+rGMz27lkmj1ywfnFJXju5//CmVFvOtNpayWUvcHgU3TVTeET+7pr894pRo7JXVuM0MUVo16DFgYyKFxPDZFXrWmVKkwEkFgRJ6SfmgAFESc/IkkXjZO/E8pJkuOyejaMAoJVKrWTqiQCaKU0IZO2t4J4oWgFNICZur2TAutFNn7b1HRCkoRuOKTK2rolFjQKXMqlnQ9T21c6hmLppyIR9HtNOz9MNAKGx/8QmHZ6+4+Bc/omwapp99Qdh1qFxonKWEhK88i5CIc6FoMqTrw33EqVs1VN95IACxfY+2sv5Ww4T5zUv6kKjWjaReOUdozWwWHoWfMQbcWOZNTZbPQUjCI5gSdtbU5zmvvaqF81AmeUx0I+qzS+xf/ID1P/mAcd/RffgSXeakpZyZbg6YhWe8ldAAPZN6sXeNGqS7A/rdFCQXzChmU4U0JQYBH+aYRO4wp6pkCiYVUpB5sq4cefZ9UeYI3DmJxnmLtUakG7MfQmnxh2ktkEZToISEVopJfSmXuktHcYg8TDuDCbINyVESarQTkzogUY1AiVnYDVOU92eWBLmSMv0ooCptzZwuJVKLIWdszjTMjaqzGK04mTK5sthGth8hJfQoG7aSC+MUqIxhnCOZUdJcEBP+dIXpJ9HGz8WhNpqhFGrmJL2c5TOLxPoSRLNeeSfpWaVAShI3mgUiiJLrZi3snJwzaZjI65qTHz2F2jL+5hbnDBToQkT1A1XrsczBAimTxohb1l/yLuaG2J0tMZeFadfL9mnm1VCQZLtuIG07mv/2T8X7s+soIWLPViijiftOmtG7VK75tmbViNRUK8IUUUYx7Dt0vqO7Z4oSuB5zIzzeHtGNp4qyIaHMPiuUNO/eSkgI3MtU9cwGkvdjkY3UsEehcIsK9Z0LVB9xTmNPF4TjQBgmFj9+j+bhBu3ledO1J9eeShtUP1G6EYZAU3vMumG4PlCGiTFlUu+ET2EMyktamQbUECjeoa2VGOCHG1bO8Pyv/hanDY126EYR9514bipHtEqkUiXI5i8mTBRf3MmiYTj00sArzaEf2bQ1Yz9gM4TQYVPCLRroBvz8uUg5o7tAOoxkZzFFtppZaVZNLa+zgrqRYZvLhbjvaTdLTOXn96WSaOSmkpStUYzqKPEtmHVLWtSkmAgKSZZKGW8Mw/aA1go/Rcpnl4R1g68rwuWWoBV2/ryPlcNZg9+csHj3PfpPP5HtYDcS+kGaLa3k/fv89n4DaSvH2I24WXqMknNTUfP7ZN5Up1wkLrdAP2+eG2OJNztsUQyfXaEoHIaJRkkMdgoSCR9ywRkJmuiNxASbIoltso1XhBRRlcFqyLXFLipOK08ZJ1qlSA8d8WpP1XiqLso5zlu0MYw5E48ja2/p+xGjJDmRIIMypxXjMElyWipErWYGTxLoLvI5YvavkcG/fYpbt/e1Z9n24oHy5o0a9avV/J38qCDvsTcK2W9Oyn9nff2133/9IkahbzYVv+3+/lM2H99y+YchdM+rnbs1jirqKw9Yfeuz8e2X337NN4iCX3ni75qM8uXj+ZaL9g67rMVo1VbEKVJdrNn+5a9Irw8oBYdXW25/+ind7YGTkwX1O6fUDzdMz28Ir3fsfv2ccNtLJ24NtvZ4rRmHTsy1RnS3vvbYkMnDgeg9ZdtxfL3DeMfirVNQMO17jp+/Zv1H79A8PKH/6AXT9Z7F955SVxb1EPy75xhr0VZOpiUmhi+uOP78Cw6fSlRqGGUK2ZeIN1amlTmzuFijjiN61VB/8JjHjef2rz6StJKlxOPadUv3ySsUUF2soXa0s9aUnJkud4RLedxhd8Q9v8JYSxrh6qcfsby+pX50hkmJ+JNfMxWYppEH/+g9qLzQRj96ydAPmKaBzRK/arn9yYd8sb3mjyohhI7HXu43CesgKvDLFnO9J6ZEeuuCH7zzTynbA/HQs729pb44Z9UVUpzQqhBOl9imwq7OSP3I4fVrpuPAab1ELSpUyJyfnaCNovrjdzAXKyGv7w747z4S8NDlLVzt2H/6CjUGbNsQS0G3DnOcxPTnDeN+oF1byphwRVG8IXY9tq4or3doN+eRwwzkU+hUmPpeTiDWErWGnPFGM3UD2WosSlazpVA7c//2vjNZ5yyFinWOKUWqeQpXtBa5wWwcNMhEJsREtGLIRmuG0LOycrBLUwCjScA4DnhlxCfQj7haXrtoJaFEJSjDRGMdpsjJLs0ejfshjIIyjOiUWRiHyZb9v/mPhEcnLP7i+1SfXdP/6nNUzmJg1iJByUYTQ0QhCVwKMUCbyx3mfMVw7KGbKJXDzoWGMxqfM/QjnK4YDz2qH0Szb+YJdYhkreS5GidJRvMWNOQUmYwREnaS40eYJVHFyNS/5ELYD0yvd9Rvn3P+z35A2g/E2w6GKFG4Mxm4aDOTocVHcJcqo7QmzSdzbSU+ETeTao0BVXBGjljZGdEoz5ugPJPVi1foMVIyogFXsxyhZCFGZ+FjJATk5pCGxmhJc6Eg2e6YWboCVF4M2t4xhTgD5TxJi7m5BHl8eZYQqSKEb6zBIg2tKhBzxHk7H+E10srI322yllhagCxMi2QUVV0JtTdGYs7UtWcMAjxzpTCOQXgBc8pVnONpSZnRmHuyuCmF4CzVomZxuqT/ySeUbpD4ykoAoMtZEhW6kWhENuq8o4yTSKRqj/OWsRvE2J2zSFpqJ4TueZOSU5JEntajT1oW75wx3e7pXlzjUeQpUj09pak85q2NwM4aLzKnmNCzR8S0/n7roKYo8tyzJVwd5PWPCTtvB1KB6gdPZiBZlkbzZHHP54hXO3QjG7+476UBbLzEnyrhKZSUhW9SCpWrpbHUGmUc3e2B9tEGXSAeB5wx1GcC0lODpOdgNRop/kvKDJcDxRkabdAG3KYlhygDptpDKfjTJceX11RTumeL2EcbYkpEVXBaYGjDq1tpoo4Ti++9y3R7FEr23ECH0wV5iJRth9ossIeBaQyoUdgZpakgRMZuoJo9P7auGErmcLujTolbAovHp/jLHb6VAR3jRFJg+0kM2t5BIwl0ysvxUzmR+iilJIq8gjo6EormZMXQDRI5mgr50GNXrQwVvcXdmZjPZIIftRJZkzaUfpRjBMKyKZWnlEIzjITbA1ReIpSdQQ8C19M5k44DOUbi9Q5beaazlWwnKsfF2xf026NE4S5rfOuxfaA/dhg0tg+ML26ZSsbX7X1DkksmxkidCqvzh6TLS4auw6ZC2B3h0QUA0+sdw29e3m/wZGsoQREF2fpRhNhdckFVhnQP2CyM/YTxjj5n9KHH5Tx7T0SalitDGKIEiOQshPqYZCCZBBape2HfmLoQ+hHzYI1P4l+pTmpiI7Wd3+4EitlUmCmgHp+K5HcR2APLZYO76bEUdOMZShZYptGM4yQDJ6OhdjitUDHfD56UUuhGyfF7HuZqo0kUQoqcfvDw3i8Hs0wxl2+pZ79eod5Vx28M4L9+lb/r+7/r8ndd/9t+n/ldxfjvdfkHkEV9+ci+ysr+ezy2N4wT39qwfasw7OubjTcuuRCu99KJA+H2KNKE1nH2f/5H9M+vZS04TOSQ2VjR/LpVy/Dxa6aPXpKHCW66r4C+dIF06ERi4eVAoZY1xEwfM8vKo/pJeBP7AdaG7pNL3IMlyhtyzIzbjuU7F6hly8u/+ZTVr56x+PF7uI3ItMosKVAzbbJ57yHN2xesXtxw+M1z4nEivLzF7nu8UhQNrq2E37AfOO6+oHpyTv3OQ04yXP30Y5aPNrBuaE5X9NcHhi+uMED19AxCpFrUmM2SUjLVkzPy7YH2vYfUb18wfvSScLPj5GxJ/UjkYun1jrA7sHhwzrMQCP/Tz3n8Fz/EPT5DnSzo/h9/CcYKKfpizertR/yJa8QcmzLDcSCsW9TtDXa9IMRAd3lJFRP6XLLk++sdyjusc6ybJTYVSs6MBa4PW04WK/L1UaITrQDOtKuE9qwUkUKpPfWff8B0uWX/7z+UwmscMbUj1Y5yHLBT4rg/smwbkirY9YKUE1pX6G4kh4RvGnkPITHAeZhkknE3oZ6iTJu8NGqSDllQ1jHlzCdf/Ia3Tx9J1v7JGuecnKTVbH5VipCKeOrSJNP8XNiGHgqcKsUxjfhc08eIVZBVZhg6Vu0CkBjHqEDHGVZkLW2zkBhBBWoK9CSGccCvFiIrKlka71QYD0cqbcgGsBaC7EZCkuQkPUwEBc3FCRwHcJZJ4i9kyNAHYRZcdcThFbkkPilHvt+cwyQU8RgTyRviqsXuRymGjMYyx6h+9AprJbmm3Hao6wPu0MvUX2l045mOg0RvjoFk9Jzyk7CVI8wDD+OsNC5KzWwYyTIvOZOdoUwzjK+k2Zdg7yf6N//rh5wvKurHG+q3zhh74VD4DKWyAo1Apml36Y15ZlToOZHIIScbbSShqcym/TJPxLJSlCmQazmGGC/3WyhgDHZREY+jFLhWNhzFymSaUtCVlRhgI2ZkM0/Ik1JQhP2glTQ/ORdMSiLJi0mAav0kkL8pyHG7QDcFXC7gFCFGMQt7kfyYOcnGKSmU7lLLdIEBCP04b4KypO0UkYrZqkYXyf0vKBwC5lOjhA+oUvDOzmZYAf5ZK4wNNW+L7i5RK3LtODy/oQ6R8OIGY+wMy1KSSBPSPPSR18BoKfaz97RaQH4xJinEs2TlRyMgPXKWbU0Wbsw4TtSnC4iJ6a8/xm0W0Hjqs5W8V2MhPWrwtQcFpvHkbmLcdujKiZE+ytAGa8i7HnUitHRmQ2t1vkJZkTeVKcrGx2j86VI2yMcBv1nK56uRAUC4OYj0qx8lGjlKslQaAyUl4q6TKHIjZGTtDHmM8p48jlJD1B4VE+NWthemFiIys9Sn7HpK62nOlrLdVErivlNiOvSYVBi/uGKcAs3ZCr9sKWOQCfD2iDcLUiqsn15QNiPdF1eYdUvYdvRfXIm0Zyq40wX5OGJOxHQbTkC3Dwg7GejVTQWThHCo2YSbU5IYaKOIw4iuKiqjKDc7hptbzv74fRY//oB0fZDXbFFxuNoxTRE1TPgC8dhL8lpwlLZCn7Sy9cmFdOyxSmMoMEm8ta0cdgiSZNTW5NpJ4+2snAsqj249upvI4yQN5ryVSs5SnJU6QsvwBq2Is69IG01paqklgpxH7LqhTYU0N5gWCMeRMSfCi2tMN8p7Zf48H0OApgKlxOx9vsZrRT9OeGOp2wo9BY4zgLVpWzbf+wEvfvofCMNI9/KK0++/S+4mjn/7XI6x82dBot3M/TmtKDkWm5xlC71uCJdxThacvTbKYHIiOSvbk9pJ4p5WVM4JfDMJBd7MBu0xiNF6ynLsoDJMqhBLZDKwfLiRKO/KkaPEU4dukKivQ08bC6UR6VunlZi4bzs55yMyZFUgGXCtAI+3NbRna+hHKh1F2uYdIUa8E/9LKUjTNysIckrU75yxeLy5X04rQG/ar9WnX63g70vcUu6wN3dT868O4++u+HX9/9fEPeVbb8s3i/Dfsyj/2n7gP+ny928u5q3F17cTf78HNo/clLqPgJz/qa9sd+5+Wsq3/fzLS46Jy198hq8cJz94G7dsKCnz8rPnbM42sK6YupH28Smm9oR9Rw6J7qef0n1yST70YpiqK4yBetnSzm/Y/upI2m4xvkK3S6zaMFkj+rmmZjgM2G0vkZ5NJOZE99kl1Jb24oTu+Q3j5Z44TqwWNfHf/Qf2v/gV6o++DycN9emCPEscFu88pDpdSdb903Oqt88lYec4MF7tUaUw9SN+1xP+/W8Ix4HqT9+T60wj/mLFuZYJw6QV+988Y7raoa3BXqww3mI3Cxgnwu2BsRTK5ZZGK+KhZ7w9Uj/YUP/gKf3HL+n/9gv0WpgeKEUeRh4vGzhbSkGDALZSKdjTBSoX+o9ekB6sKf1A/vglzQ/fpTjPcL3H7/ekf/9vcTFS/uJ/h/3uW8Ttns37D3CbBVf/37/BD5Fy7CBGXnW3LHSFRzMeDtjKk3eBetniFksxxf3wKf6tc1QlsqPhP35C9zcfyxp2CkwWusOe8wfnpBAJuWCdg6YlHif0YfeGlEkKjWlM2AwEgVWhECNy7cj7jqPVNGjydSfTjTvDqpLUkgfVGqcdlQYyxGMHWjPGwKJpmFImzRKNYjTKigTu1LfzJDrQ2lpOfikTSmJR1TRWqOrHNKDRlCIG3sp6SbzJWQjG3hNKolYOe9JgKWSdiWPAZWFOWG3Q3jKSMUmKZ2OMbDOmNOedR/K2kwIehM+QxGMwlowOIpUJhysWTcN7528xhCRhCsqiUsINAW80Uc2m4VIYrabWdt44iS5fG0089GAteopoq2DXk62RiVGWY5A1hgASb1uKrOqVgOr0Hb9gjGSr5cTXyxZGFSmYNV9O29GK8OKW42eXVGcrzv/ij7gukH/2OWpdCe169qqUIp8rZnO0ygVnZQV/B0ksMckGUsvES5WCRpoQbS0xRJEshYj2DodimCJaiexIKzkZajMDnebM+VzkfaliImmFnQMqYgiYymNGAYPFIkb9HCSxydRSDOnZY6GdoUQB5BFnenbJOGNJWSBhRklzEI8D1kvTqWZJhJqbKVM5xmGiajwmi0SLmAn9hPJClydnjiHSJEueItSeYRyp/cwTCBIwkOdpYBwm0jDen9yFbgzuas/2Z5+irCXoCbteCl0+zZR6jXBxxkD2AjdTSMLW0I3SAFqhyIPc953kr7whL9Nz42ydobQ15qSlef8RblWTbjrSsRc6+66T1K6l+Cziyxuys/hFjW7EqJ2GGbQYBNyWu4G6kdQ+7VaQM/XDtSTvpHR/7CqDIcUop0Y7x1RX0vBpaxGYQJRmBzE9W2tB6S+lkAWUN1RvnYpM8PYoPIyVnBNTyuj6jsIs2vSw7yShKCMguFlCZozDNxVh10kC1RTpr/YcS2btHO0Hj8lKGEjjoSPc7PFtQzaa4XpL+Pmv2fzLP8d6y+XPPmP5J+8wXR+I2x7VjZQSeXa7I46RzbJmsWyI3YDb9ahlQx4DlZHhQx4DJiUC4BtP8Y5HZyvK6QmT0SzffYB5cIJrK+wUSN0ojdN+QF3tiSjqkCR+dtsRlUIFia7VdmZXxCwR4UA5abl9fcvZyZIYRWaprEgQcVoAeUDtRTY29aNsp7wjG03pRmn2ThqGECmmZaJQZTFul6JIN0fioUOHKBN8ayg3B7pjj1q11JslKhemQ48dA+nQYUojMLw7poXRVA9P0H0gZklhNJUTHsi6hTESxgnTLmjfepvDR7/i8OJSKqspMX7ymqK1cHNypuQ7vsWXpu6QEilEKu+FvVK7WdqlWbiKkAslKzH+p0REBqBpktcMZ0hTZEwZ4iDyJ28lPbIUwklDSYnxcGR0huWmpfv8Gfb0lKresNqsKFPEn68pKWEbB7EQvcHve2zIpKJIVweSd1BbkpVEuaI1UzdSUqI+X1E9WhN72W6Vz64xGXzdUEohjQGn5PyYpsgQAkorTn/4VAYSb5Svv1WtU76qTip3detdY6LU1wrZb6nyv+V79W2/+HsU4X/fxgL+gWRR33C0/732FuWNLq3w5l3fvxBfuby5VvrmIwOZ2CxPl7K6RTLY082BE1PdZ9l3L24xS0lvyduO/pMrxk9fo1CMc4Fcx8DCWRbOEmJkmzK88wT1zhNSykzHEZMz7ZQJzgo/4mzJdLknh0R+cUO9aWhOlrKe3HbU5yu2V3vGEDg1Bv3jH1E++YIxJKbLjnE3cPr+Q8Yvbtg9v6F66xz/cIPZtPhFI/rSVYNdNVCgLYV8c8CcLJgudyz/2fcFbnOzR9cV/skZBai0goenHMw8sVaK8dWO8VfPZcVbWaq2wlysiSghfBtL9+vnlL/5mPzsEv3oAf3NkZV3dBjqxlMta7TRdB9+QTAaQsY4x3S9R5+vJYmqtJTvPGS72+GfXVN97wlDyXB6jvnBn1JS5OTsFF974uohyx++DbnQPjnj8pPPaTYNvhge2jPsqiFbDcdJctnjhNKGVLKk3fzNJ0y/fi5bIAr5ai8G2Jhof/CUWslztnt2xXF7wMTCiaskTSNMeCVazByjTBy9w3TC9gChk2Lu4GFQjED5inNUJws5gd0ZjSsH3ci6aoTIO+vYlffonKmNFV6Hns2rWos8BcjjJPF7WqGtkxhNBbVzlGxJU5AprZeo130cWfgKkAK0i4GqqrDGMEUpNpkTR9Rdoos3dEZTDwPWGFIqTEPPwtfyOELEaub4v4xNBebhfZyNu7ppYAzoMciEMxessoz9xIFErQ1VuxDJWJIUnjwIDDAWsIualZH0KkKcT+iSLIQ1kjh2FwGplEiBZv8IMYETc3HMCT9LU3LMQo3OhRRnqUhMMgVVoMsMLcxZJoBI8lAGsIZwc6R/ecvUjSw+eMj00SvyEGZTrSLXFjNJBDW5QCXFfQhJjlu5QOXQpaCsEHT1GGQ6buYJmFboCKHItDrNsENXZFKs5qjanDPOGlKRJCZyIuWCjhnVenTIpOlOQy6fgckaCgWrDclKc1WmKCd1rdBF7leiYjNZy7+pnQD1tLMiXQxRQF8lUznLMAbqZY02RgjWITLGRKXUvSxAWBGKMSVyyiSlqIzoq73RpBRxlQD9bFuLjnlpUYcBPQR0TJI8ZTR+LUlJIYthtAkFXUnggyoFxkk4ASHKZsNqAVvBHDlrSKWISf1uEp4ScU7iMkq2GWZml5SYKAuLOVmwXNWkcaS8PrD8s/fFu7PthQWyrKCIjwNrMCcSM5q6kdJWtOdrKdbV/D6zGr2sGfcdVA6zqGGY0IsalAwhMHO62hRR1khqEhC3HakgpvXaimQuZUKQoszWXmSL44RdtbNvJgn34jgI5O98TR4j+TgKd0ErqtpLYuFJS5qE4H1/Fm28QFHHILDSw0DY9Sx//C6+8WSlME/P4NUWkwuLbUfRmf5yi63Eo7WcNybGW5pVi20c41vnlD7gVy1P/uUfC7TRW8aCyAjJPF209Fahtj2r9x8xbY/kbY/RiuH5NVlD9c4Z3UcvSFc7ysKzOlux7Xrsco12luO+h8pTDyPaG1wl8uG8qBgstG+fEfY98TCQX+8wtaNuKroxiKwni4zZz5P1Mm901psloQhHxjQV4/Ve3q+dwqxarNUMW2FWuNWCYZxIqdAohX9ySvuDt7h6fsXydI1pHGl7JHxxTbw6UJwDo9FL4VpIfKpE0PrKkZyRIn5KDLVn7Qz5MJCsyJLaqhLzubGo3QBGszJiZi5A7ywNM9ATSYhrn77DQ2OI/UQeI7u//oR0fcQagz1dMh161B3zxwjE1FgD4yTHEKOwsaBSIlcaNx9zbeWpreJQxLNRzal0ymp0htRPwihB6ORTzkzTRLNuUW1FddKye3EFCpGrPz6l/c5D+hlqV+6YPc5gGy+NthVpcq8L0/6I8xZ30qK7iUkpdD9ROwHxJQX9FNAvd4x9xD9aE48jQSmWSo43JUnYQaQQZxiobTyLDx6yePv8d/Gf7+vUu3r2K7uMclfyfk0SdVfw/l33ez9V/31XEr/f1f4hLqrcUeX+Ey+H40G++LZ7+QP7izL/9+uG7t/1AL/Sz7z5MMqbGrZCPAxs//YLtNbUD9bkkHj1y89pmop21VKMotosCC9uuP74FeXlHj0GppTJ3rA5XeO3W0wl3ffYVsTTFfq0Jd8esScL4rYjXB5oGs8+SPLD8vEJcd/DGMiHgcpq7FtnDFNiLJmmdRynzGLdkHe9GMKcIw6BEiJm07J6ekp8fkt2WhKCVg3h2FM/PqV5dIpZ1JI8dfeczEkf+TiiZxKnUjBe78i7QT7wD1dMH79i9/GlNFtDgCjT1BDmhJs8JwFJtYVpaplQLj3m+TVh3XJ1ecuTzYq8XqJChFnb7I0m147OVTS1Y/3OOcMnL1BZ0U0Th+2OM1MJLTzK5ENrgb0po+BizXW/Z/PoAaFEbB/Jr3fY1YLUj2jn0N4QupHPPvmUk/WKBx+8I36Rm6P8v3FkqwkxEI894ThgQsFYS/X4FHJheH0gXO3Z9j1932PIPFiucU2LcVrkBUFSkXRl0d95SPz0CpVnXaXRqCQ6VmtkMnXc7rCA8RUqBCkqq1lrPmuUlXOothLt9TxxSyWjihjYcpphjEoTcpoPNCLt0UUaZNF4KtFhpyTXMzKFT6VgtCaQ8RjZmDk4UaKNvjPf3g4dtXd4Y8llXnWnxFgCy6olUQRqaPQc0VcwejbbOUurQKVCtureNzZ5jSl6nnAK4dtZS8gJFTJaG4IDb6QzCaOkf+SDcFcKotsPCtH0J9Hs67lo1VZOTmU29xZn5oAFpCicPSqmFrMuRTY8Zd5eKC3RmlorSsn3nAWipGepuREV/wvkymJWFas/fY/x+Q3L9x6y//nnhNd70r5HLSpc5STdzIjOvKBmiN78vFiD1iKLUFOSYr4gfp3ZkGutpEXlJGccV3mmEDBFyLcUgeUZowFpTss85dcUqP19jn+YpUh5DCK3KIUwBapVSyqILDRnynGgGDHDqzkIwuRCpJBm6UkBVMoSteoc1kpcb54Cpq3E8FhZ1EFkgwqk+dQCMQMpkvtxwmqDNZohJ1pjCPMwyeYitGElGxT37gXDp5cwRPm3QsR7J5P0IvwB6wzN+Qq7rFGNJ26PxE+vyLXkzifAzWlsZEmA0d5KQYOs/jXSSDLLlrSVzRJa0oya9y4olzvy9Z78aM3y0Slh23F0cPL4fPYVaMoc5UwBd7EiT0HOB8cRu2mxi5q7IAflLPH2wPb5NTklzr/3VLT2Vt8nOqEg7geG17fozZIyBvyipsyNvIoRv2jIk5jsY8qkfpSkJK2+DNqonGxHQiKXfB9pnLsRozVm1UiKmlZMV3t0W2FqByjCYZDPhVLEQSSsNB6tFfHVFhoPzorev61IR9lg919cU/qRMv/d1WYpz2tIDLcH/LJBKykkVZmTeyrLeBwkurafBDBrNfE4YlY1cd9jURxeb+9T76abA3GYWH7wmOmjVxilMG9tsMbw+tfPWL73kHEM3HxxzaLyrE9bJhBz+BB4+KO3obIM3YjtJkqB7tnNl1HoaKaUCGPEW0u1qCSJrnEwBJgiU0hUmwUmFbrXW0qRBCt9Lo3weH1g2HWsLjYYrej3R9YfPEYvK579/DOWpyvO3jpl9z/+jKmXOF27Fm9NGiZ53w4CpxR4oWwOdEgwM4LUEDDLmvjsklx77BhlS1J5UuMFUjuKpGsaA9ZoRsFuYozh0I3YmLEFKkB9/4zN20+4/Xe/keHXqia//wD1hfCzppJRd2ykMlPfSyEpUN5infh/GAIpix9jMAo1RupVI82ZM8TjSFN7dpe35JSprSXkzKShPmnxm5apG9G1Y7/rWFjN2QePMctWoq+dvY+q9daIzLT298Oq25c32Moybo+4TgCLu2dXNEpLIpUSBssUZcvZnC1R64bx+oDOCtU4Gd7NTVKZkkhEUyZqcCcNb/03P6I+XX61D1BvVKbf2iC8WdH+AduGr0mh7n/2d1Xw33a73/OyWq7+sBu8cfnPEkVbZgnIH3r55mqnfONl+LbNxbc+Y2+ul5TCLGsW71wwvd6irOW4PZKc4ebmiD9bYafA+Okrxpdb7IsdYz9RFjVpmLAU7OVrjsc99WLFdDgQHj7CPljDUUxugYLZtLghUgo0q5axGyjXB4IBNwykaSKfndHfHpgAq0CdLqiVNBL5OJAvr0EX1O6IUYXy5z8mHQbsSjK7R2vw3uCSZ/r555TPrtCbBX7VkmLAv32BWS1QzmCW9SwAVPcr7+HZa3i+RdeO4xgZXh8wy3qeQmj8XcRhzITjgGucpKuUgjoMqGkSk7V3uM2SzaIlbA/o61vU+QlGG6i8rIFf79CLmtWPfkj19Jx4c8CcLrEKmo9fM33yEm0tz/otm2hpFppSGVJMjM9ecVJ5+Pxa9OIJXn/+AmstD0/P0OcVadtjveGDf/RD/MmS6dNX5Je3qAcn5DhRYoEhk6736KxRlUF5mayEUlChkC/3KGc4e+uMaBUqRMx2okyBFBRJy5RwMoo0BMxhFH2+UsIvSJrsraS5GANToGpq9LyxGPtR9M3dKBNIPUt0YkQds/TAWSjgOUkMX5yzwVWQ3G5jzP1mwngrzaPWYkIuMzV0nqw4bYi9ALHIhcrMWw0yi+S4GrZ466i1yFNWVc1V7FBpYuNaOSAYQ208o84kqwlFkobIiYxiiInGWHyS3xvAohhTxBmDK5pJyzC31JajLay0Jt0eoSjaSpPGiKo02RkoFn0cscYSkZNVrBSuSJpWAdmcqIIOb5jkZu1+zkXkQEU8K2qWtqQ56ScrmYSqGWhHjHPikaIk0W2nIGRXbcX4nLNsdHLKhJywF0uW7z4gPr/l6v/zN6z/+feYPr8WSdChZ1RgWwcxE6PENao51SmXOVUJTYoZpSTuNispuv2sv5buI6G9ZZom0iRFljYKMCKry0VOhlaakrupfC6Qj8Ms67FoVWRjUuT3Wmmc0cQhCFU85rkJBRUTvqlIMZPibLbUMuKJMwAuaQXMED4FZQyyFYgZX4TLkYMUtGkSjXIMiawjpfXkAHVdibYd8FaaWZtEwz72oxyDchHQXOWYzpfEz65QlUMFYBLZWI6FUgQgWIVEvlihWs/q+4+5jUmkLiiquRlPScICKIUpZSprcCiymaNqpzjL6gqqcfhHJ/hNKwyU/UBxmvqHT5l2Hce//lhAjD98iv3+25KWFBNFeY43B6zR2JQxbQ2piAwmJhnKOEsIUTgJmyVnTias6Tjw+b/9KWf/+DtUVgCDNG72jxmJC7aG4YtrqpNWjhVDZDpswSpJDCtFEr6clu1PL9KvfHMEa6CyxJCpFzU5J+E81F6Kx5RRyuDOVzMQVrgS8dBhmwq0wm0W7C/3DK+3nDS1mNLbirDtCLses1lgG4cyGnfSit9Ma9RxJM1NI1pjZxhi0dLQ5SFIsdlnKYCHIFuVk5bu5S3HfmSRliwebZg+fs3yyTlZgwPqpZyflQL1wSPKzYFpCtizBnfSEnYd7mLNow8eoWKi3Bwpc5KYc4bx6gCtl+3Z2YrpxZbFDx6Tro+w6+ZmW1Ex1xKrmlxb1BgZQ6SqHfWyAaspOrP40VNYePKul/MlCrVpaB4sSUqhrWF50VIoHD69ZDsGlt5w/OUXjAlUW6OmIAlTc4qdWQj3IjmL95Z86ME7obobhRujUKRbT1nUqFVLPozoWWKpY0YvK0LO5MOAnze/LmaKNXRJYlYTE8UYSu2pqgVX/+bnshm1AlotXRD/xhjxtWwL9MwNSVZkd94YGS7GSNonqT8qA1NiipGlMzJITAkDpBgZBkXT1IyVkedoDNTDhHEaNU5UZ0tyyaxXZ7SrBv9ogxoiYx+xRsvwxpr7JkTPslScqFViliQ+9dBwfLlFxUSwCnXSoA+BY07U1uCWNb236E8vpTbYLGiVElZHzrLxLgWVMrr1+FXNyZ+/R3Wy+GrV+rVp912oxl05+q3ypTcvbzYN37jPb7vyPBj5UuTzuxcev63R+H2alD/w8g/XXKg3v5zx6V9/tN/2xP0ed3t3s7sn7c1dy+/ea7xxP0pRPTjBtBXHTy65/fQKpxSN93DsAcXw8SX9672sI89WmKZiutkTp8jucMRcXXK8vJQV98PHIi2xSiaCRktMZiuRsVDwxpDGSG4r0uRlAryoma72hJQxU4QnGlM7Nn/8HsOLa7Y/zXC7hbYmPXzA8nxFudyRVjWxctStE9bGFKkebqh/9A7jL78gvLxB1xXptpMkm8sevWzu9dDFGGxTcfrPf0iZAuNvXjJ9+JzkLG7ZYGpHUxQ+JOnMTyyjd4xBYF4xJqbjgLGOksEsW9yiRu97yqLGXI5wucOcr1G+IpdC8+CEfUq8/Dd/w2bZor2j+fF76MYT1wvCZ69IYWJ1sqabRko/sFisUBrU7cBn+y84fesJ3fUttq35zevnfP/pOyStCENA1Z6yPaI+fU3vDNlZquNIYEcYelmXDpNMtJTCTQp3vobzNYcXtwK4erxBNZYyRNztAecd+q1TwuVemCglQ12J8a725Ks9pZZmQjmRT2hjcGYuzIrQTomZOAWZaiqFdopcFHmaZILpHSVE+hCpSxFK7DCi9QxaM1oa0BBlWq0VyiqRJI0Txlhq4xi6Ae0stqkFfJgSxUlClHOiW9VKYbUDpVg1C/ociRR0kYL2vBbZxl0SUSpiQneIIf3VsONBu6YylpgylTEihbBm1nLLlNwrxWgUSRVyW6FPV5hFTT1MTEOgnqLo0UtB6ZnyPEMHyzwxNjO4zKYkKVcK0mx0VICqBU4Vp4SbmzVdpJHAmNmfJZuZZLREac7bt6L0l9NlLdIuqXk0SWs5EXl7PxyJRfwMrijizZHj8xty4xgv90zXB/SyJu56iaeNWeBuc/ACc5SpMpqkRe+eKOJZmDLMWyajNMNsyk9VhR4CSoFVArkstRdjdp75At7iipi1zZzYZZHHquaGpcxbL+Z4aqNEGlcKqMpJ7PAUQGuRw4QocqMiza1VWlKigERhmqJMBa0mOTGuqpzJ+S4hEOIYJHmlSPJV1kKLtouaft/LloaZtYFsQnAiwzJ3HoEknyFTCv2vntO8teG29VRZka0R3o9SYOZCBpiu95RXDebJKd3tkfP/448Ju479//wrkQcxN0qzYs1pKZZSFPOzc4b6wQp70mJXFfn6wPHjl9y8fE2zXFGcpfKW7qcf0d8esWNH7g/0n39K9/FL1j94h/aP36Z4kdqVWYJWYhQPj7dMnUzk7XqGY84+oVI5xmfX+MenLB6dEq4PZG/x6xajhSDu6gqUyAVjJ6EHymTKHA+rchGJmzHoVSs+ikPPdHOU7eUgWy3/cIOtnRTiWuOWM2X+7jOs3jhfZ1Da4DdLxqsdGdHImxg5aWvyfhCe0q7Dr1uSNRLZC5QhomqHdVpI0IdBZJ0hEYukiymjZ3K9kq3EMBEOI6WfiFPEtfI36/MFzejwXiJay7ImBYkfPu46nLekAjpl6vWC7nqPyWAXFYtFAyGxfXVD40W6lRtLXVdkZ4gvbjn86jP86Rr39JxwfRDTdh/AGaqTFmONsFyOA8o7stOUYaJe1Pj59bZnS8oUsauG6oEkEN5eH7C5CKyydhRrqJxh6CecUvLZNvD44QaOA+lsIfK3VMgHeQ30spbQBQX2vQtqZZhe3pKOg2wTjYY+yQZ7jounqXAnC4mln8NryhTh9oiO6X7zbRB/mWkrVgXGbsAqzXEKVG3F4W8+ZSrgogQ/5NsjuiBch7uo6wJxlk9OfcC3FdbJeYGCgDbHQHEa1Xry1cCQCy4WcjdSUPiThrwfGCikytBUjilIBHvT1uQYaR5uOO6PbM7WZAUmI/Kmyt57y4aUqFYNpXEim52N6lpr9jcH4Y9UTgZxbU1YeFQ3UmmFbzwpJElS++wKVg1DpVlbg8mgKyMSKyv+KE5q9KLi4T//Lm7ZfFMO9Vsq+/Km9OnvuvLdr+CrHcOb33/tmzebm3uQ9R96+VqD8fftNf7zQPTU71f033dbX3t+705Y39ZOff1ef++Ga5aCHF5v2b3esljVrB6coK4PKKO5/stfkoqQJcecqUth7EfMssFNkRDX2PISbq/BWNRuT0kPKCGyPF9Rv/uA6dWW4fJA7oT4mkPEt46m8eQpEdNI+OJazJ59z9TUwlIwBr2saZ5ecPjFZ6i1NDasGrg60PzgCdU7F7S7juE/fkqci/j2zz7ArBvytiOnTPPdx1Ikzrru8cUN/mKNO5XVVhwEcqWXDe7xBv96K/KbYSLFxFZrVtZQjxMmJxaNp+oHTFNzDBG1WRLGiJ4C8ebI/morhcJbZ5TzE/mAh0A59lTLlqASS2MoyhOub4neoV/c0L59jr1Ysf5vfkz4/IrDcOT5r37NOycXKJ/QqqAuNjyZU5LKyZI8Jf7Fv/wLnHV88uFHPAinEvs3jpKM0U/4hYXWE+IkjZzWqEVN0AZfeThdEG4O5Oe3qN2A244y9YkC2dIh0M8HAOctJUZJjGk8uR9FJ9/WsqrPmaQNVhf67R5rhDMwDiMFqI3FGYkfjaqQZ3Kz8lZMcEWmr23JqLM1xRraSrwJKQtjwM3yHFCzwTCQomjjs5ZiwDUVU5apikZJuk4Uw24OUU5EWoMxoMADhES9aESfnuVkYZTiGEb6NHKx2MyckUxTV5xSuI0d57qVolBrjBVKd55TZWJOlM2CcrYmVYZq1WILHC63qENPOwhkzWpFiSKtijERo8iIXOVlA3gUWFPOmTjHaOQYUEUkcyUZKeCZeQUKVBFeAsxbnhmaZpDiXhVmWVFGJSWTXCMbl1Qkvemu6ygxSQNkNCpIJr0C0q4n73tCN2I2LflyT/PuObuffCJND4jHCGTSpYR2ruc4wpTv6LYRFSOlchJ0oME5SY5rrCUuK5FH3oHvlCKFIAfqrO7Tj+7y3kuSxBKcIZmZZaEhzRRdrRRjP1J50VvHEPDLFjsEQggcuwHvLHkKkuIy6/PnECz0IIV/nlOVutsD9aKZh0dScDilsHfPdc54BXkSKd9QevLcMDgvRPBSOfo5Atc5TShCHtdkklOEYWJ8dSvBNKcLpqu9vN5aSOZFKXTtMUoRpgnzxTXLdy849CPhl5+zPFvR/pP36H72hVCMe0lOspUn5kzQYBqLW9dUq4aw7+heXaH/tiN1AxSJX54OHenY0XcH1NVrSn9gGrfCjfENul3SNS3ND58ILNBK3KjaLInbDu3FdC3yoxrTyDZRWaGAp6s9pnJMNweqTYttJGFrionaSeMrjAkpMpO3TPuORbvGnC5Jx0E2EBthEoTjwPDRNf7pufBQdh0xF/xmwfh6i90sGOet0J1cUGl1ryC+azRKTAwvbgQU+PScftcxbTuISTaNRjG+2lK9dSbneq3IfRQ422ZB2Pccrw7oXIglE/uJuqkIKdO8/4jp0OO8pb/cysZ9lv/oOTrYnS6FRTVF2tWS1I3Ew4BSiv3LG6pFjVvU2EVN2h3ZHg+cOUvz7gNSNzK8uMWctMRdR50trkCwimEsDIeB9nyJIlMRsd0R0gbrLemYKMc9+mxBP0R0jLTLVpKcKNiY0dbO7Kcgx9QxUG0WpGGi+/yKPEXSccA+WONrOQ9Xj045vrwlDhHfetS6gZIpORGVovKW6sFShoJACgKyvGt+95c7WjLm4Qq0sHF0kuPAcT/S5CJbo8rD1Q7VVKRXt6QHG5q2kuP/YZDPcSkwTKjaYzcS91spJD5WFfqYCItaNqTXO7wVtozvJ6qmolRCqE5a0fcDK2Nxs/QzFPFYmYVs7jOZcBxJc3R0DJH26Tnl1sDtERQYpzHeEsiSHoVC1Q7TeFS9wJ0uOD1pJWBilj4VNUfgJpHd1lrLOanIJswoGPbyfl1sWpQ2mMoRrg9MOeNzIY0JKkd10sr26uaITp6QMy0z1wc9N/OifNGNSLHP/vS9+wb422tNdf+7+/p2lqnCtzUZ9zf8u7cbv3MtwbcXw3/XbX7b7f6e7cV/EUL3/eWuE/hymyPflDdfCYST8eb3b2xBFF+umr68W/nBV56KwhtXkjvKk6wATzYLmSiHjL9YcfXf/wfMesXhdk990lJnMDnhmoYxR6ax4Lyn1AtyegVxQj37mPDwHPNghdr2qG4i7jtyilJA1ALzUY2XVXddMYXE7jDiP/yPVJ/+HPun/1uGhxtUbTn85gX6k9dobXHvnuKbCr0bGI6dAMSOYspqf/gOo7e4ty/Qd/TKlDhebnFvn4kW1CjsakH73Zrx09ez/tZiTlpySkyHDne6lO4+REpRqMZiimJKGVc5VD/KlO04wRBojaWyiqO3TEpJekjM8soMCd0PxF1HtZBJwGFK6Bgoyxq/qOBphS6F/v/3S+z0AdX3nuA/eIzaLKj++3/HSjv6cWSte6zWuIsT1DiRjaZuam5VEHPvq2vOisOXDPujTFv7kbyo8DGSpkAdM0kr2cisGqrGE2+PhGe3TEE4CzrL6l9NMgEkZyIyubfWUIymmwp5GPCVFbDfPFUvUyCkAjaThzxD4DJFW6ySwrhYTZ4yeRT9ZyEQK0ceJuycF26BYj1KQfP0DPfkjEXjMVpLiscXV6gHK9FRK8X4+SXdJ68kblIbVD9KklmIFNswBYkStcYIHTYltHMSP5sluQkFvqoYKSwqT5mE+JtzwfkKg53TjuRzFQGrHK2CQ5pokaYZxAeQ53SZdHFCWLZUbSWhAq93DNsjJkZa78l+NnLvR4zOsyFbjNq6IFGyKQtbocyRpFZBP4kRd560mwLTJAVb0lLU5iI+mkwhI01byAVTZPpb9DzlL4BSWO8gRjlJG80Uw1xoaZn+AzojvoRJzNaqKGI/8fAv/ojrytP/9BPqd4RDU5CtiNPcNyzcTcyt8CvUHRE2F9CGMImEjCIMDKxC5SJyxtqTpyiTuTQbt1HS7KZMHBOmdqhhkkmhUqKXdk7iR2OSLccsb7JeuA00wv9Iw4hSGuUtLkR0Fh+MKRBRpCkx5XTvFTFJBhZhCngzR8PO0gZdiUcmgwAgrSXmTD9OtJXwhEoSX0vUmkISQJqViaBWCjvzP8IUZmmVIePo9x21kma0KKi9E3mCd/K4jBTpRiu6f/cbqscb3NvnskVpPfUP3yLsB1xIhEOPyoXllJliZOiEjZI+v6SUwvZ2RxMy03aHPewI3R6VAwwHcgqUGFBzapyyM3xxe02cHtG/3tI+OYfGywyrl/SZNEoxysyNyCFS+kA4Dmxf37CcvRS2reWUNb8ndIGyH2RbV1uJK54i8Won09erA1HDft+zaCratmJ6tacfJ6pc6D6/JB8GkTJaQ+wmIcdXTgImrCY3HqsgZrDO4Ba1FPC1xzqDPVsRdh3bT1/Trlvs+Yrjp69R3QSHEXW1pxsj7nRB82gDVWZ8fo3tRtzTc+wYhBFzthQZTyo45zh++Bx/0qK9xWwWHK/2qNsj9cONJIG1NRSIvYBI8xCYSiGGTBonVk/PJeJVyedz9f5jyueXEqdsNMob+mcHfJFjv9/1aAum8pTugNWKyjv0Ow+JdUX2jsXFiTBIVgum59fo2qPGiF3Wkso2RvzFSpoJYMpJFpOVNBfxao86aUljYHx5zfQ//GuG/+6/4fTdR6QQWV6csHq0YffRK+LljuE4iBE+Z2lGhoBRGhuzxAIvHamy2DGyuFjTa4HGNo2DdSXhFccJdXvELyV9S+dC2HcC8ty0uIu1bJVqh42ZzhvSMOKCyOUIkXzbEXOG1uPbinToUVPEKkXQEjN+eH1DXC0klKXINrwcB6KCyjv6Y49ZLcjDKFHqZyuKVrg+sv/sFeVshYmOZVVRksT3Ryvy59ANVKtGIIq7jtpb0kmLTRJfvXl6LmE0M9/HLmtyP8nwRyviHFFcCqiUBFpnDePVnhwTVimcEigoVnOMkaqRKOLKWYwxEvk+D4VSnkGlQyDeDaUUVAuPOVtw8v4D6rOVxGL/tvr2y+Lzy4JXfb2K/UahKsf3b2qrvv1SfsvXf+jl2ybzb2xK/hA+3bdd/ss2F996+eof8M0mS/Gm5/wb+bt3Moj7ZkK90YB87Z6MJvcT1luG11v8siaNCtYLop2TFIYJ7T39oZMCLgRJR9CabCtKnDDGoW6u0dsd5XRJaDV2dyTfHlExEymoXQ8gE4hc7o2e69rCZ7+EfseUE0yBdl1TtTVj42jfPmf94/cYfv0c++Sc9uEJ00Empu3DDSiNPV+RxkD/4ga3WeCfnpHbiu3PvyAfBzZ/8o6sj3PBni3pf/UM//AUu24lctIYxpe3hBRlwgXEXcKerui3I/5ijepG4kcfEy9f4B+/iwCtJtqY0dYRFguC8ySlMUVhNyuJnj0OjEMgnVdU0yjQrV1HthJlSsz0Hz5nPPSs/uy7hI9e4PYTF4sN++7Ai+mah0/eRj2/5KATq+UJbFral7fk7YFIpjlb4dYt6uSxQNn2PXHXM4yR2DbYKYLXuLfPyf1A6kfCdiQdBkkJykmAfVpLgTIbFW0ZCbO5tQwBHzOBQj4Mop2eIhx6QkqzlyGTjRGzZBIgj4pRpufDRFSSUOOcIY7SkCgj8huS6KnLNGGuAofdQPzlM1ROKG/xD0+oH58yfvyCfviE6vEF9vEpD/7Rd9i9uqF7teX03Yekz6/Rv/xCiglrCcxxmlqTh5ExRzySoR5KInuD85V8RqxBFdFJ2zm6Vc2pS0llnNYSizozIpy1WOMI3SgFt/Mio/mjtyFn0s2B/tNXtEpAWTGnWbowcxD6GVBnNbayKG8IQ5hhREApWGvvtya6GPFUFPFRFGbz4HySdzM3IhQwKckEX4nshlzEo6GUUM1nFoOxljBMiI1Bi6YWRDJgFHGI0lzerbG1QmuRsRgvMp/mYkVat0zbTib9d8cXbYQ9gTyuO89FoEgToZUk/RiNSfJ43BxNaZ2mOA1XnUif5vSlMEVJw2KORnUOq4WAm2PGtV4kFXkG+HknBu1plhAphdLi7TClSFrYzVHy/BuPaisBBkaB5zEbikuam29vxWfhDN5oaXyVIjswRjMNk5gd7+CbXgy+m3rNpCBc7WiMIc2xq95a1JwrT5Skq1iKQNeA6A115XG6Jo8io7PeUqbIECLaOWo7E8JzkeStjGTjv9px9v5D9DGQu5HbL64wTcVq2VA/lO1gvNyjfvOSetmS+gF3viR88gr34hV5d4WfOsY43p9ziioUpDkvyxUqBvANpmqIzz9BPTjHuD9BOYNrPGrdkmZ/lV23sqHQMDy7BgVu3RK7gbpyjLueZtVgljXdvieVwvp0ltmcL4nHgbDvma525CGQdwN6WRMy+NMFZ48qSsgiMw0RlTLT1Y7SjTTfeYRZNehFTd71jDcHwus9flWTvKWExOgt7cVaPBAxEQ8DLibKukU7I3n+Y6T//IrSeoETDoHUOHh0QnXSoqdI+OQSva4pznL85TOaMdA8OsU91oR+EpnhFO4HHcO+xzWe4fVrgcg93GDXLakOlCmJd0hrmYUoxeJ0SYniGVRzAMJ4uSPcHOgXnuwMhkK42stntK1wzjL1I25V487XdC9vmCjoVctw6Kmtod0s0JWXKblS6GWFeudc/ILeMN0cZMNZO6IVLw0FFk/POcRLKqPYbY/w9AxDkdph2WAePiQcJqZ+wlhN9+qW0E2koxC/S4hsfvg2uy+uUHqCmNgPAyYrVrmgjiPLByfEXS9G/lVDGib8eoFpqvk4JIPFcHOUBn6Y0PN2NOWCfeeccdthYpZj2iwBzSrjvAAIyVluEwvjJHH5WinxCsVI6kda5zCVp3r/Eab2jNNEfrWjcoY4s6bK+RLTSVGejwNT69lrME2FPQ4opck24zbiN/GrhuikwWFdU5BwhnQcyVajHp6wuFhTaifKCDJYdS8LZD6+Tzd77OlKAHutJ4wSDWtrB4hnKY7izcgggMcXN+hUMIuKQ4jCYhoCjFHOE0ahjcU1nvp8wdkPn+JPFzLQ+G1Nxbde7ibjX11h3JWr9z+8K/DV7yjmf68G4suu4Jv3U771Pv4zLCu+cvkv31yo3/L1mz9S5Y3vfkuv98ZW483rfKPxuL8raVLG2yNOa9pHp+hVTTqOlJzR/UhzssBryGNkXQpjimAdOUwia/AVzBGepl1SNExjxC88+nSJ2R4xxlBZLWaydUt1viLcdPQvbrFjZJgS7tG7lO6UcPoAk0X6EEKg+ZP3CP1Ef71nvD6wfnpOQU7y1WY5U31Fv5qjTC+tsyhvWba1HHScxcwTNLTCLBv8ww3+rVMohdSP2HVLXtSkKeHP17Be4Esibo+Y2nD1+WvoJ1ptSL/5Od2HP6EYQy4JFTOmWaBOH6FPzuD7P5TM/pAwViQyiwcb7A+fcvz0BeN+YPn4jOp7TwjXe8JPPiZvD5TKcf3RF9z+Tz9hnS2tNSw350wUspNpw1QS6ThyeH6FfbCmeSzTGOUc2+eXDB9+Bt2EsZ6YRy6Ko9GKXCnUumG62dHtOvRQ0JNMR3UIZJQYRmcJAEV0y9k7UgiYLAcju2wwRkse9hDutw3eO8IUMd6JHnqWb+UQMUpLvN8MBrpLNXKzbOfYDZJDnguVVhjvRAerhOQah4AJmfjhc27/9hnVpiUdB44//wKlNcvvvIV7/xEn5yu6Vzcs3z7Df/cRu7/8JfHZDYyROIkfRTvL/rhlUS+oncEoiFqjSiamREZMrClHcsj0KqOHkaVvsdbS9b2kBsWEnqFxOYz42qGUJlWWPk6k37ygSvn+YJJmnf8yC+wpaU2sLHr2v+QQMc5QKjc3Mlr+9pxkShsS2jpp6q2euQhi2pbYZCveFqXEcJjmhn5OrilZdO0ZKU7ULJ8yWop96yw5J0KIYpad+RrGGrIVFkhRClMKaf7M4e0cZQ3uZEle1oRukqYni4ekKEkhAvnskWdQn5KG4i4RKkWB7DlvZ8JxJBqD3c/cipQxqxrfTcQQJSmrcmREWqC0lh7AKKZ9f689ppL3b8lZ/B3G3MMKtdFkKwT2XDvxktzLyubXTSFN4t2hc2ZbKGPuwXmoWVqhZJpukcYjxCSE9xAlxjiLXKtyVozdUWJacy5UlWxBmKeq1liYIs47XOUYuwFXeVTjhftxHCT5yRhs5STysoCaIk6JDIzWs/jeI7JVUDvSNLF8fCrnh7khOry4IcfE4ruPOHxxSdofCNevUIcjxgfi0pO6CMmgspiwtVMo78EnTFVB9JT+gIoB+/Q92j/+nhhX8xwk0A0SG1tbwu1BprL9KHGmIRDiHj1GlIJqUeMfbsiHgc07F3KumqVpx88uGa/34gEbAiwqckwM+47NH78r0rVtJ+/lfU/pRvKza1Tt8O8+wJ4uCf1Ivtphkmzo8RZ1HBmv9lTvnMOilqmuEjq5W1SUbiJ8cU0yWrTvJwtplhY1eZhIcZRm+GKNtYb+eo9SkJ/d0HzwUJLSQqL/5BXurVO5f60ZY8IZhbtYE6+PTEPALCrcLBU9fnEpspi2JmyPRKNwbS0DBCWbohIL/fMbqocn1EYTXtww3R5Ipy2+rule76gebygI5KxeOEwl8LfluiXOvoDqpGU6DBQ0zapm2HcS0hGTpC7OSWp6WYuEa1VTDgMTii4nFjcHkRBaTfvdRyyXLeM0cTz2LGyD/Vf/gsZbuilQJ0W4OcoxrUBaVCyfnOJWjcTQf/gC7yzrpw8oc4JXAaYYCSniisa1Fa72tE/PRTo2y2wAqrMl3edXsKhwyAB1HIOoBVYVHAZuD51A7roJGxPJOkrKmClg1wuoHWZTUxVIh5GUEnQZdbEWaOZJS9GK6eYgCXyLmpwzoUTU6ZK69oCihMw0RZp1i29BPdjAzR6NhGZMGvQ4QeXwD9bYRcWxG3HLivZ0gUKRnWZxtppjvpFtdSWR7aSEmYdVzlv8W6eEWdIbD8McrKDuoam4TBwnYhEg7epsRbg6kKwlaU0XI8uFDDEmCq5xqAxp5Wm+c85b/+QDkXp+s0z9esVKOA5znXYHz/vqmPzbK9k3flje/MHX/sU3v7379Zt3dncAv//f1/6lb+k1vvz516RYv4+E6ve8/Fewufja5a5z+LY/8Fv/6L9TpXZ/0d6y/t5bpJsjeMN0HGmairrxdL95jn1ywdhPxKKgqdHHnmmxEHWx1uiqIhmNe+cDxrfeIZ2sZRLbehbvPECXIrRrpfBvnYkJbYy033mErzzD//ohftVQ/uW/QkUpxqt1Q4qJ/nKHXdQYK9NBNQSZlKdMvNrjl6KRD7P5XKt58lzJS1hyxp+0mMoz3B7ofv0Ce77CVg4zCUCNmLHLBqWF+nr23/6Y/jcvyVqx/uHbjF9ccvuvf4avDaVaoGNDeut9yq//ClUy2nrU+hz1v//vKMsVYc7GzyHO5GaLrhzLDx6hNi3dryP1O+f4t85J1nD7yWuqJEWI+84jcBr14JRxUXN6cQqHAV9XhNbTrN7hxEkx4m62mDEQb4/kF7eo/Uh9vaWdV5e5O8CiQp3UqIenMrWPhd3nr7FYHAFWtYCrCpKrL4cydG3QVtNPkdpY6pTJtUd3AyVEpiwAsDuiclGKlDO2qYkl45WedepuZgskMcF7R+2sAKP6kXouQhvrRcevZi5GiHI/zqLSl0AynRNlCgyvJgEYFdApMby8IWjF+NOPqaxlqi32wQnVu+es/un3uP03P6d8fkXqBqI1nJiaogymrhjGgU9uLnm4OuWkbaFy5PMFxjvK5Y7p9SsetiLB6lOgaVtpQFLmeX/Lq9tL3qvPoNbo2hGDpJw1lUU3FTEmGoXQZ+fC1daSkU8f7ot2pYXinINA6IiZqGVGVWLG1dUcbwjkLFpeLbyKOzOoNrKNKGrm3eUingyt5H0pGFaRKCmB6+VcUCVTshxEnbVyO6PIKYkcat5iK4rAE7NE35YQ6f72Gavvv8XhoxeEfU+1aOR+tcAi1RwXq534XpIS4J2mkK3FpIxWmlQSMUQxQIYoscRKzcTb2SsyiozKWENOol9xWhOTROjeGTRd7WUiCTCMTDFhy3w7Z1CTxNxKbCVYbcTTMpPWmRKxFHxTMR06lLXoItG/0Vu8EqmkyqL/VlqLLHCIVLUX0GA/kZHnWXuHYmZvhCivm1OMMeKsNN5pCpL9HzJTN86JYcCczKJjIpWJ7C3WWlTKAgms7L0ESzUWdbHArxtMW6E3C9I4EW87tldb7ChBB+psQ7tpoXG4syW6D3TPbkj7I8SjSFxPFxQiJSdUrgVWeDxiNajjERUDKSXU4RZWp6jFCe7971P9s39E+50HqAL7T1+z+s5DUjeSlRIWyRgxtcc4x+Am9q+2LE5WBCMyvfqklc+7lQLGLCryceT42SuK0viLE/S+Jzgrm1RjKOtGOByTyHaUEjlFtWopqwH/QDY046tbhpdb4tUt6qTBPdywePqAsKoo/SBm+l0nr2vtyftehBspk7qR8XIrPKXzFSlGnJEiebg5Yh6sMGOAtiKEiF/VVG3F+HqHWzXYZSP69pe3En3ceNRoUcbSrhfcfHHNVBm0bagX4pezqwadCsPLW+IYaJ6eY71j7HrYHTm82mLamnpZY1Nm2Hf4VUO9PJOCentEOSVhCAX63ZHcepp2zXh1S71esDIVr15esVy3VBcrMW+PAW0U0zgxvrzFOYM7WRC7UbY3leOwO2K6ieWTC8J1J1tib/GnS9IwMV7t0a0np8wwjHJMCGDbijwE6AZ0LGJeD4lp2/Py5ZYyBPbbI4vTJSutcQ83sOsoQPv4VJqhVcv0/IqTty/Q3vClQUZeKwlpsPhFwzRM2MoxfHFF7Aa8MTTvPeLke084Xm7pfvWC8GoLGXSMZGvI08TZP3sfc7Yg9hPHXzwnXO9xT07lvJaKbElk5SowVavJSlO3sjEbY5LhSVvRKAi7jlKQ9+mqkfCPU4mPNa1Ha83i8QacPIdCI0/iG5yJ9TCzhmKaeU8iWTUzc0VZjS4Ob6RWijEKUBAoKVF5K8dK7xi7kcXJghwj9emCcdszxcz60QndzYHpOHK6bNBz2AOt4+ydi7m8lGPyG2qhr9WaslE+PrvGrhuq0r5xvXJfnt6J+tX9bX5XwfrGsFx9rbJVX/v/m9/cNZ1q7j5+G2b7Wybw8nDubnv3p//91hj/cJyLf6jLVzoy+cE3HmB549f3T+TXrvJta6CY6D9+RfzkFe7xuazgVy1p33H9v/yc4Bwqa4bDQOUdpe+hkjQLXQppd8T++qfoP/vnlPUCf9pSSqa+OGH9R2+TSuL4mxcMr2+pH53iUPSv5ADrNwt4dsv0mxfkRU1Y1qSY2Pz5B7jTlehgx4Dxhuu//g35N69QjzZ4pWi/8wjzeEM+9qRU8KdLSQUJkepsSTgOvPrrj7n4k3epN2L0u/nb5wyHjuXjU5YnCw5XW2ztad86Q1dOptsFDj/7lNSNbP7FDwjDRHh2w/ThM5E27Sf0q5eov/x/EktBVQ1854/JP/wx4zhB5b+MxFTgSqFuHWrdUPoBs2o4+cHb9DcHbj+7Qm8PVDqjjgPuj7/D6s+/T+pGuv/5F3C1xX3nMdlo+jRRHwLp5Y0kUoSEzoVh1+G0wuaMXi0oXgxeZr2ULO5tx/BqS9KGWiuGpmbSijIM2Jjx65rm7AT98ATrHcVo/BzDG8dAud6TDwM0tZgWP3zO+OKG3E2SqJMlkUggRha7qrGVg8pSvMVlwFmmENBzYlOaIjGK1Cb1E9PtER0j036QFXlMlFESVXzbiv6zdsTbgxTfpRCtwYyTQM1mjsOgImffe59ycySHQMqRxY/e4/DpC9JuRPcDdikeG7doKM4T+wF9tsY+OSVai1vW2MaTCxyvd/B6R/7sFdooKUK15vPtFTolPr59xdubB3xw9lh8LjmTlcJrhVh+RWJ2lwJUkIPTHWMlpSKFo1ESUTubteU8qcWfVOaEJ60pSQzBZobMxRAltWZOquJO5jT7CrBzEzg/P3dJPXebiqKYWSpzYpSREyVZWBYxSbFeQpJAImeIWSZeBYjIZuPx//2fc3x2Tbw+Mnx6iekjRRXiHSNi/rspoCsLQ0DXngQCYgzCt0BBSolcwNiZ1eENOsoB3mhNiJEUk4DI0pfPgcDzZq/GLMNkTnaJ/YhtKnTlCMMEWiafZor30bwqSVKScgIEi3eDh7sGx2hyjNjK47QiohiPPZV3pCxm/JQyvvIUoyUVTQFKCOjOGWK4i3cVevSYEmFmnqgxUjVeoh3neOWci/hqZokOlSPMMgTfVpRWsvOLN5jGSTOXYf3WqfwtShH2Hc47QhSicXW+AhSXv/pCtj/bI3qxIA0R5wxlGKEfSYeO0h1I2xvizbX4lfojar1Ga4VtF4TnL6XQevIO+kd/RPveI5bff4ypZlDjJClJCsiziVXNm9wYpPAJxwF3IgBJlcscMYykiw2BBMTtkRKFyZK1GPRTN4Ix2Fyo3ruQraq35O0RvWzoX91KtPC8hcqTsHnizE0qMbL6s/cJ2042I8cJd7bEaI1uKzQwfvxKIJ9ai8dv11H6CXW6pHiNbTzDdmB7u2d1tkJbjVnWqM9v0IuK6skp4fbI9PyGEgL2ZEkZI+M4MTlDe7LATBGlFXEeDqR+JMfZZ3W6pNz2DNcHTFuxfO+CfBzZf/KS9q1z+m5gmgLtZiHww5hI/UgMEd9UYA2urRhe3NIPI9XpSuQx1lJyIo0B44WsnEqmPV2S5yjV6mQhm70Q2T+/RPWRohSln8RToaCUTFPX2LMVi/cfsvvoFePtnmItvvXin7KG4/NrUsqEccQ3Na93Bxk2LhoWzs+gQ0cMkapyKC/NTLVqYQ7J6F/csP7unEY5FzxqVl6kkIQmP7NL+ps97cXJLMGU64XjyP75FYSEdUIIbx6dYJuKHBLjixvGS/El6E1LfbaSYUg3kfY9w/ZIdbpkeL3DbxYiFcqFcH0kBpEntsuG7DTeWsJ+QE2RfpjgtpNtXWUpFOKxJ/cTi/cfSTR0zuTWUz85wzknqpH5uFVvFpSYhUsx87lKki07KDiO8r63wmex88AupSSPATje3GKqGiY559rNgjIloir4AiEmxuc7wq5HtZ5DP5KPA947FMIQiv1EcIrmvQfYxrHaLDn94BFxCPS3B1aPT78swktheL1Deys13hv1/Jt6mjebkW+uIr5S8L7xsz90hfA7bvdb7uq3blTmy391nAvg25+z3+fyjb9WfnBnh7nbUZS7bus+cupbb/bVh1RAVQ53viK/vEY/OUN5g1o1PPy//W/oL/f0v3pOHAOawqQ13iiqRyeUMRKdJdw+JFcVy01L2HfY7z5m9b23UEbhjNBRD9e3eKXpY8K+3pOnRH8cxMz7+BTbBUI3opXi5icfs3hyRhkji++/Rdh15Jdb2j96yu3rHcuzFceffEy7/hG2rsSkW4v+386r8pIyJ49P5Q+eI+ZOf/iUdHvg8pPX8tj2A/HFDaPW+EcnIq0wivbdhxx+9gklSezm8gdvUT54zPX/+yccp0w+O8P+H/4vTGOGRStTWaPwFppKEWNkqgxVTNiTlrEy+GGienJOfXHC+MUV4zBRdnvMs5fw6Jxp0XLzs2fUT84p80nGLBq5bt/jjcgs1LLixauXnDVLfMy061byyhVCFl4txMAWJvInOzn4GCUmVe9Fh3274+TdCzbfe4pZtSgE8MUYUMbIOlOBaWvM4zMB5VUOVTkWf/Iu6TiQdh2pFwmMqj2mkTQJVTnyvud4s6dYTdM2+NPlvQSPmGbZTL4H3pUimtF4fSBeHxg/u2T7i0/RhwlVCuPhiJ4q8cwouByPnKoFNM094CzHSFMcfQk0y4rYgxk140evqZUlLQ3RQAkBs1lTQiTsj7BZUP2RxGbmJLGZWimYZMJ6rC0jkRAS+/0t3jhO6gWLk5ZXcWSz3JBLoY//f+b+q1eXLM3vxH7LhXvtdsdnZqUp2+xuimw2OTIjCBIgARJ0p++hryUBgm6GmLkYAaI4w6bvZrOqulxmVrpjtn9tmOV08cTeZx+XldVVEicu8uR+TUS8ESvWeszfSNXdGovPCRsyZIHT6JuHTuRoQInEqFKi836TbKgxORGJWTUalynp6ClI2tya4d1Mx2ZUI4lJOhl6XEyV0Wg02gmfJTmD9VEM3cbEIgzCLUohCMl2rPIYrQkhjmZ/llQYDOrWTE8pJe+lTOoDq599RS4six8/wX8umPGg5XeYkWMRQhz1/DPeaGwQychExjhRiRJBAfHRMIWlPFmwP1+hjSXFRDYim5q1zH1ikCgBhLnjkZGNJg9RNPBzRhVipunHCqitCikahITNGR9FicaHSGE1xXIiinnOyjUNQQjbGVF8KRw+BlThME3J+uyaxVzGeDt4rBODPutGP4fB49N4LaOQ8Nt+wHvPbFITC0ffDdAOUEiHxysojSHXBYqxOlkXco0MuOM5qnT4GCliEnNCL/wZpTTNw6XIhWrF9j9/Tmg7Zn/2sQS3nWd6NAdnUI+PiUr8U4xS9PtBOqLdQGi9+MPsdkSlqO8dYuqSiHBbbDdQViVu2aCcxi0nwvsaFY5UIfdtWO+xzpBbj8ojN6gqZNxPK+g9rilJ255sNKYq5DGpClQ7kFJmyGBCFIWb9Z7Ue2xMpIMpw/laILHvHeO1JnxxRu57mh88oT+9lgLGpmU4X9O8d0zuPCqLuWIayeKqsNAHojOEczH87J5fYY7nkshphVo25LogG0VQmc3pFUpZ7n9wTwoqWqOtZj+ryJ1neHqFOZ7hFg0Xf/UzeHjM8uERVhUUVUHsArkd6Hcd9mACQSS77UTI02rnSaX4RlTHU/y6JW86qkdHdHvpFMxmFUVViJTuyVyI16MUuDKS2FYfPmBxOy9ID1KUeoAsBOoc0m3AsPrmnHa9oz5eoHYDs+ND0jDInNUHwr4j+YHcDYQYqJYNuilZ/OCR3LcbMnDnQUPz6JAwhFs367iuKOsKVxW4LkBpaa+25JxoQ6B0ChuTdMZSkq6eUaKEpG9ipzHqUUr4R/lltOOqYpTafsk1tU3B9MnxrYjBsNqz++qc2UcPUUZTPjgQRS6rb00Vi7IhVT3q0QHVxYZ+11Hen+NDpJqJg3yaV9B5puUEMnIv9tItzRqqeUXfe9y9uahepUjoeyZPDikLQzGpBLnhxGxWutgagnSIu8stelKiSkcYhWqsMRjnYN+TppV0pncdui4kievkmTHOkMg0B0t8NxDjaLKXpIOeU6a73pOtop8XVHWBX+0pK8dgNHhBDwxtjzuesm17cZxHUVcFw64jB3EYZ4RT7z4/FS6ZUcw+uv8yCL1tJNzpKLwSmL729839VO/6zOsB7es2068d+C1/vrGPu//8kWBQr29/xOTizXzt77Olsdp1lzxz00p6ee1fvUC3H3r90Hdfy5C6AV1azPcfC5wpZXRpUbVgqZvHh9RHM+bna7a/fIo/3dCnTNUU4pcwKRlmM/LQo3Rm+cMntF+d0U9qtqcXzOczzDdXHCAumfrRAfbRsZhZPbtgyJBSQC0KCi0SjP31lt2+p+i8WMovpxz9139Kcpr7Hz8Qd91JNZq3iAlVWreY0qJH91tVZdTBBG0Ncd9jmgJlNWY5IX/+govPT7n/3jHNmLwQEmZeolC4kznlvSWrv/o7Fv/0hyP+VtzFVQ4ka/HLA+rS4Uct88Ypclmx6j2u61FOlKjs4wPMek/13gl6OUXtety9BXndkl9ckZsa5RxuXlPNQVcF/YtLSdJChrKgrmrhdqRMutzxeHJI6AeK5QxVOuLFSpRiDhfiurzdY4sCM2lofcJbA02FUjA9XnL85x9Qvn9C//SC/stT/PWO/nSF2nTifBoi3nscYKqSkCL2/gHlvSXl9x9ibjoU9xbkIKoz/npLuJbKtatK7KJm2OxZXW5Ju05UT5RCWUsYx2oagtwvJdKQ7mSBWjQ0//BDJn/xMXG1p/v6Av/5C7rPnqGKAhUjx7YGFD4FirIm+MAQAq4s+O0vfs2D+RGqsCzKBtfUxGHAn17iJjWDLWh3W9j3KFfQ7lu6z5/SPL5H0FDEjKqFpNdfrbCn16A0VYJZs2Q1dOQkULz3p0smxhGySCCGlMB3FFq4DYzSqap0I/FYSLwaqdIqIJDGToR8XuWMiVmUiaxBISTSzNjRATx3ZpYsuHWtDEqNHAA7clucAQ1KGVHUQVSbSjMqRiGci5ucRyfxighJOAWEIMULpeTc1Jgk3OB3k8gv3sCM7LwmWg27gB4NCRmFH5RWooalkeszLuAGRQoB4xzKaZIXJbHyZE6wChMzMXgJWEKky4nCaKl8Z+GcFNbKYp4zxihMFOWt4IVrY0uHvzG4a0pU50XhJSOERyd8CGs11Sf36X719BZ+NrQ91bQmdYOYu910SELE1iWqsMwm8n52hmJWk264RyMx+yYeit2ARoji3gufwg9eFKfGxDwajakbmoMJSUF9f4FylvXZiqEbKGc1trSk0jFpKqaFFbnvdcvi+w9JvYgn9Fcb0uBpv7xk96/+HaXv2dw/YlE5lA9E71G6FO+OdpCOTVPS1FP8pqU5meOvdujJCRrx9jClJFO6Gn9biLhJJYTVbkCPyfDdrb3cUORMv+9AIcIfo+xx9EHGSFOC0aRK+HHJR/LuRmpVFGvcSIAPzy4JhZEk5sU1adsSr7aEGEdPDU3c7DBNiW2KW3NFfb2jKgvYe1RKqMKK1GYhQVu/3TE5XIhgxXqPrxzVJw/JPuIOJoTLLb7PdKstyhlmD48oDix5P4gXRSuQNX+9E1GAkbtofKS4t+Dof/VnnH3+nK7tRXxjKZAbM60Esz9EivsL6bAkqcbnpqT/5pLpgyXlgwO6n35Be7XFtgXbF5dM3zuhWk7JVlPdXwrPhVeAJlK5tzcY+TvxyDi+lTOjNwxS/Mhw+MkjuqcX7E9XxH3Pi0+/oklQ1OJXZaoC4wNRydzT7TtqxEX+bgximuL2kCZDOcJ9pvqBfCy9NBaevHdMTmOMkzIxhNvfEQbP9adPmTw6RrmXY+s2VrwNRBV65JilOHYzbgNVgUveJLXDtiPveza//Iby0YEEyDdJepTrFpOUa1Pbo5zBNiKqYNoejcJnKI5EIjgPESpxdS+fHNJk6Dd7aL1wQnwgp4zxgemH98UDI0Sq+8sRlq2E6xriKAUukKgUE7kbpBNZOZKS5C0DaloRrneY0qHH4pLvBnSSed1NKlKI9O0ORcYqLXLs+wE7duPyvMEPHtsNhMZhVMPV2YpJ4bAkklEs/+J7NAcz8s+/JA9RYsIHB2wvN8xPFhTO0j27ZvXZC3TlOPjRY+ykfEd8/gom6p3bS/DQy4zgzTzj7k6+g9HDW08of4fP/PG2PyIs6rXk4m2Z07s6Qq+9lseH523SXXePol7/cs6vHOJOgg9Z2ojbX31DeTDFHc9J7UDqPHbRyAAfq0+kTBoC1//217QXGxpnR612xZASHNQsfvSY6v17+NMVadczfHkmD2cQAxt3b4le1LimIpyviF+dospCKqJFQbzakpqKpBX10ZR204r/w3wi8qVay0RZCt529+lz8TG4Nyedr4mrPep4Th6CLNizWjLrpqT5+AFojd917M5XpJB5+ndf8uTJEdXBDHc8l8DDiEhqbD3P/9XPOf7hE0xV0D67xJSO1a++pkTUdsTxN1G/d0IYAvvPn6MqR3WywC2n2OVUAksv8IyolChH/d2XxIs13RDQZ5fYuiQ0jtlf/pjcBob/8CnqpvUaEqnrZUIZgrh9Z0VyljQpsCoRz9dCNoyZYBS2LGC9g7okHC1QTUUxqSkqi503DBcb1v/6V8TVXrwqxuo5pVROzCBqYDfk35Qzxll67ykPZuScKOsSXxf4F9eobpBALSSqUQIwkMne38qY2rFFbuZTUoj4XtxPX+LJBZsfQUx8UqI8nMKsEs+QtqP/69/i9z0WsEVBT2Y3tAx+YFZNMDHzddySlOLD+QmTwyXeGagLur7Hpoy/2sKuxQNTrfBRJHqL+YxQWlRTUy9q/PWWuN4zsY4QAn03sO13XOxWZGBiK+7ND+hjFKOpoqCyVpQ4CiGEai2yoAmBNyUlCYJGvUISZlT6UUq00TWZEOOoriSSgUqpWyOoFMXQLwHBC98gZZELjgrKkSTsCuGAJK0x4/diFvnLeLMYjwTriECltBLfbFU5dB+ImRFuIwZfIQg5WafEkLIIAhw2HP1XP8LOa57/P/4NqhOYhVXqlgMSjcAFSFJRDFEq+kZr6RaNoUTMWcwrf/iQ9d/8FmeMJAA3CjWDBItprJTFmCSQR2BcGlA3SmVK4bP8C4jcbuWgHSQJS5kwumGnFJn+8BHDi2u6ry9wi+kYhAtxXDlRQANAKzGBq0tJALQoYeVCJGdViHgtcIKiKhk2Im+pUsYAXiu00xSzBnswEUhMYbDTisXHD7CzGr/esz29Jmx7UttTPjpkcm9Bd7Ulbjvi4MnOMXt8hE2ZsBVH6O3nzykPZ+BH2V5j2Z9esz+7YvrkBDcRyGMaPBgtHAVrbs2vlNECQRrCLVZZG4OqHLcGJzkLj+Jm/UmZlASHrkZlrTAEjNGkzgv0bhzD2olhXOgGcfJGgkxjNMPZith7OWzv0UrhlRSrab3AKU+vKT66j61L9p89xzYlyhl812NmtcTMvRDjD370PvtPn9GfrYlDYPreMfZgSt8NAjsqC4bo0TdzU0gC4esFQqYKix69I/IIEeRGrns0ZLut6QUxHWu3LXEI1Fq4b3nfU3x0n6Rg/82FDJ9SxAPC9RYSFLMG9j1uORGz2qZge7nB7Qb8Zy9wT44ZyAyDJw4edbmFkzkn//AjbCNu4eo17Mlt5fYWbz5uKQuZfwwTXhYpXnZX/cWG7mpHiomyKfjmv/s35FnD4//tP6I6nLFf76hmDcYZLv/jb9DLKcuPH0qicBuc5DuhzE3UclPZVG8GLTfHj4m460WSuXypRhS6AVsXr/yWN8KmnKVNcbOv153TlHRtsg9c/d2XEk+0gVhZ6oMpOSXxWHl+TXE0k2B+3xOsjFdtjfA4rrcU05qYkzwrUTqGbjmBnGnPrgHo2lEZMomkd7vZU5VOOjFaM3l4SDnGXIxwWX+9k4JoSuRdj5lUZC0FZrS69QXSSjgXceTBkBmltjVh32EmpXjE7HqUUrTnaxHvaMSAVKUsyb01hMHjssKXFn+5w5PpL3YYYP74kMUPHnD6d18zOZyhZxWHj49u78PqizMuf/ENReU4+sl7VCfzb2lK/D6R+93x8vK7N0idl9SJb01hbv94adtwp3Pyjlj79u939Ab+EFjUH55cbLd3Wndv39WrWTe3P+QW0aRe//zdD765zzev1Z0dvnbcu8lFzgJtCM+vMPeWhKstbtEQzjdgDXnbYh8folovweZIekvnG8y8kYpdYXBHM+KmFULc2HYdNi3lyRxdOGLv8Vcb3EykCOk8ZmyhpyHg7i/w5xu6f/9rKKy0uLseV5XkTSeV36og7FvUwRQXMl6JIZadVbDpCFdb0hDJXY+7v2DyT36A73raL87QRjP5+IE8wGcrivsH7E5X7P/zb5n/+YdUDw5ExcaHW13osGmZPhRYkF/tSZdbNp89JV1uCYXFaQXLGYsfPLqtbFbvnUjF+OZe5HHiTpn+Ys3uP/yatO8oP7iPuX/A9m9/jTm9Rp8smf7lj0nbnuFX35B8YOg6WO+FxNX22OUMFSIJmWT6MJC2LaauyLXIIqpFgyklEEjWCEFMG4ZNS9cO9Bdb7IuVmN+lLERro6USPRrnESI+iou1yVnImFXJEANl4UZHUsHcKx9AaSwCXcgpUTpHHyNWQRoG7GQiFRUj7fqkBcdux4A5BQnQh1FSTwM6RcHYR6lW2+8dc/TwAdu//g1Wa7oQ8ZXwB7p2x8RWOGPp+padyszqCdEYzsvIg+99IFj4mMirHflyI21nH+gH6dQE73GzCWVdCV9mVB/quo6Ldk0fAyf1nJRgXlXsfI9KmaIo2KeBedmA0sSY0DGhrcZqMddKI9FQaUUKaSQ0g09ZiM05C98hJeFapAxaXLIZuRIkgTHcBGkpZUIIt0+6ymCKEZqGJAya0V/CSLKTRgdp8UJQYt6XszznGYqyIMbI0HsKZ0bYhGie57GKhkJ+g4I+yW+KOXP0F5/gjmZc/79+KrCuGElRzllZfavAkxBehc6Cm7ejJ4Q2mjTij+sfPRY1tLMdubBAxrc9xXwi8CmliL0Xn4IhSuLhhNhsrGHY7IV4ivw+rYRQb52VY1tL8EHM9XzAFgXF947JJPa/eCpzZukEJlg4cXdXCrVrCUrjphVx2xJG122XoECJgMNU4BI+RMqDmVQefRCSt1aSpExKmntzdGHZb/bMllOqgynTJ8cjTjyx+fKMy//0BaG0PPlnPxSp8LZnf7Yir1ps7XBHc4ppRdh1nH/+guSE1P7wkyfkIRC6QbpSGtKmxVqH0tC3A9XDA4rDGcqK67ktC1E1Aqkc73t5FisnhPURupdjQpeSzImLbyDESDmKYtysK7EdiP2AdU4SiUIUkvLgMU0l0sejR47ykbjvRy5EpJjWhBEiZusC/9UF8esL4mhWZw+nKK1o9/2tuVjaSEdR3cjFpkzz5Jj26SUxRIrFhGJWM/QehkAyCl06YooYa9EghoZa4Vd7qvsHwk96JfAYV9m7S+sYu98sqakTjwdTOvSsEtW1bQdNIUIk246wbQkhSsejH+h1ZracM3l4KJDCznP19IKjwwXDsysJGmcicqKNopiL2qEaixKvrO/5Bi59d6GXzXeDJJxv+d7Nx/unF+yeXgl8rPec/YdfkkJi9sljintLnn/xgn/93/4r/s//1/8Li6MFu8s12hqqxeROgCH/87LSrO4e4uXaiIyn7mKDm9eybt18SN2JYtSb3739/su3X8Y2Kb8RP93wM8JOiPn702tm751AEj4OVkvBJYu7uQJUXUhhRSv6dsBGgQD5fY/WBjuvyWSZc5VCOTvCuAKbF1cUVYErHaEd2F/vYN9THs8whUVbUbT02w6cpj6ckbtA3PdkMr73An+alAI/Lqx0X1MWlc6qIPgosrylw1QSY6EVKYnviFUKjZLkRQm3whpDSNItV1rTb1uBke161jniIlRNyfpszbBuOfrxYyKZat5QLxq21zuO37/HSM2hvd5BztQH09t4Ut1Ndm9v0DsSizcr4y9fyHc+ND5j6m0F+r/H9q4o+tV84u2x+/8EOBfvTizk3XcnCe/+/Ov7flvL4x07zC//vJsTZoRkqWc1/qdf4N4/IZ1vRG95UsDgGL6+kMqis6jKYZuKOBnIMRA2O4rHx/jTFcMXL1B1iRsnPt17hl2LfnqBuXeAXreiQ10XNEdzkWEcPIlE9+Up8XwzBgoG1QrhL1yuRR0lZUgJt5gR1y3DppVg5HiOf3YlXh3WoA3Y945QKLb/8meUH96nawfSqNphFhNR/2h7mqMZ/UcP2J6vcYsJcfBSGQyJfr3j4KMH4vbd9qL7vagpP3nEs3//KTMU+wzDek/8q58z+cn7mGjpvjyl/vjRbZ4t/2SG55fsf/YF1aNj6h89IfWe4XyF7nry8Qx/ecXl/+evmfzgA4ofP6H91deoK/EXSd6jCkt2ljQInCcYhU5afEecEfx05UZ4ikAq2tMV/XpHdbpCh4BLiXR0QPHkmHy2wm9bjLJiuuYDafAErUeXYIdSUt3IWjEMHqeEtBpjwlYFxosCTg496xCo6lq6A4NUmqMPRCWBqaskcE0pEtPLyn1WipCT4J5HXwlG2AiTht3QUmGozlq257/FTBuyM5j9wPmw5n6zJOfE1bDj3uFDrroe9hFPppzUnBSK3YtTrKkYdh21UlxstsyaBq01zhpyVZC3sNnsSSh8CGQtRmQ6ZQ7LGV9sTtn4DrRmomtUzlTKkmOmMgUMEVeakVw9JgVIJS2nJDyohHhVKIF6SKdGqouFUsQxAVBaidfDKCOolHR0VEy3QgFaaVHMiuIpkcegVHwtxiKrks7JrXCgUqgb1caURDHLiFpRHj0mspJ745MY+eWYRmiJFVnVfriVc9VKyJZqJPw10wpz0OAvd6KVrqUqLX4cSngsGoFJRTF+S0nGU2ELbIbqvUPa1Raz6QkpYhASva1Lohfy601HzcTMYLV0N3zAVgWxG26ldnNhUUm6LWhRWVHOEvYdylpJqrRCLWqKgwmb//wVKopSUDcm30Zrkgb6QaqoIbBf79CDJ3pDsZigpwXDEHDNhFg7zBbwGTUpKKsCNSlGJa+EPpAOW7/ruPj6jOVcqp22dLcE1OFiQ3u+Rh1NWBwIsXZ/tWV6b0la7dGParKC/bMrhknJ9PEh9z64J4RlJzffTCp04egut6zPNyKV3DjKWc2sEmhTHnH3Nxjv7KwEyjljJpX83nGhCF2HrQpJLPJYvVcIvMsaci9+DKpyMkdcb0ezL5m3czavkNRtXcAQ8OuWvuuYLufiVTIEkbceuTpxtSMVFvPBsfBiRuhmv+8IXQ8Kpp88Zv7j9xguNpL0bTtMI7AMnSR5Vs6w37aiRmYUOMMwDGhr0c5SL6ciK7vvqR8dwQg9uc0lbjL415dbJWMcRI5YV04kzu+sv3paEVuBEBejolJY7WmfXzGcrom1pWtFta+Y1aT9QI0i7jsh5vYDtraUB1PKw7nA0ng1wrgttt6Sal+LAzK4qnylafD6lnOm++0Z6WpLPpqxfnbJ8h98j+powfV//pyf/+fP+df/+qf85f/xL5kfzUFBczR/RxTy9gO97dhh17F5fsns4SHl4UyKKm+c3KsNmLfuL2f8piWlTDGtXia7SCK8+uwZ4XKDrQuqac3Q9vStp6gdThnc2FXLPoCRbr7OUCymuDqQRon+4mAKo5R0ypndhezTjPNacThj+f49+p2YPlbTGncwJVzvRJWuFyhk6gbytscaTWc0zlpwRgqVRtQHCUkSkFERKltD1qA6L7ApZ0XMIyYY5cOLaYUavAiyWI2ZlKCUJPxR5PpvOJ2qchRNSVCKSYx0651IY5/MGNqB9nLL7nxNeTSlmpTc+8n7KC1XXilolpJUZoWIkmTIMWOsevsYEHz0dxgYb37323KUv8/2pu7Rq6ig26bf2zocf8/tj5Rc5Dv/vu2s7vyMbznpd3/7HcnL7YUYv5lffe8mI8vjcVUGf7UlrLa4x0eEF1eEvac4mpH7AFZhbCnwgKYQE5bLjQQesxozqfCdJ56u0NZRfnCP8PU5eTmRCum+RxmDm5SkwhJSpHp4iLKG4fklpi5xR3OGn31B2reUx0vSQSNyeM9XQlALkZwydlJBLRWhrh9wSCXQVg27SYGaVLBqRYGlD6S6wF+smVUF+vuPoHSE1Ra2LebBAcPZWoi5v/ya9B/3DFdbQgY7KSm7gagU7ZkkTfiAspZhCExSxAyeBkWVEvZggps1oqax6xljSlmEO0/75Sn9b8+Y/OAJcb0HBe1vvibuW9AQnp+hNj36w5m0RC/WDKfXdOsd5XxCcTDBLWeEeUNue4xP2LpALSaonNFVKSStQapm7nDB9hdfki/XqHWHbxPaGEw3UF5eox7eo/URhQSQPsaRFK7Jxghh0/ciMewMNkqXqFdQhAj9IEZyIwGNGKmqCucsIfmxOqyFdKZEZlMZIxh5wKYokChAF44iJq7WKyo0qRAZUVsWqJSY2FKC7klNHgIKzXa3py5KHhWHtPuOs27Diar45vlTqqrhs9Upf35/JvJ828CBswxB9PFbxE+hKww2amIIAjt6/wR9th7N5RT90HFwsGS/3TIrG54c3GPftpTKELynD4FgMrNqQqGNOIIPgTxqjpvR10PnTEJJh2I037sJWIySQDsDITPCd4Q4rMYKvZAAsygUhdEqIqaRSyHQKD3CqW6sglQSnH9yQpbPKd+SLLU2eO9vjxV9QulR0SkmTGEIY5AZYsRm8SOxVngOOSaiMeLRgMIoLYpFXgym9LyGq52oK8VEtgo9EsEzGeUKgbyAwIsSeA2sW6qP7xOWE/q//hyXRJ2KsYWfb5Lam2qyExlW1w0QE+W8pr/awY2PipbkS6UEyt76ApgQRQaysELYrhz1+0dsvjiF2gENAaiXjZConWHoJRhWozrREAWOpUcFMB0SIB4arrToo4lIW08rcusJWWBGSol5ZnFvwaQwlEpBYfEZhtWe6t5SfG96T3k8Z7GU/eSccaVj+/OvMJVjt97T/c1v8G2H+5MPmd8/YNj1GKNpFgLFJEuXuXILqgdLchK1KevcGJXKeFTGCIfmZowoSTZyCKSobjHwprC3yU/qvbhctwPtakf55AR/sUaPnglaK1JV0K932ImoKkkiKjybPET213uKaUXXDkxOliI7PAR0YenXe3TK7C82VHWBmVaEyxa964ndIIaeWVS14ljtbr85Jw9ROuhI0HX94hKcorBOqr/1yI9Kibqo0cZQ1KXIimYZj+5gNsKM3o0PuOnoyTMgv4eURIK2KSUqCUmEE6LMdUmN4ySI6lLsB1KK6NpRWk13tcXvelzlSH2gOJ6TCkv56IBSK8r7B692xN8SE7weCOSbTqhCJotvSSwASAk7rYj7gc2XL5h9/EgSLTL90YyTwyn/hz/9gI/+5Hu3SczbYsJXQp87H3q9y6AAjGb6vftMYuT6ty9IKdHcW6JeP9m31VPv/tqcyX3Av1iR9j324weYppS1OCY2v/yacLoSVTmf6Hc7cuHGIlcmXe/EUT5n7KQm9p6Uonh5xIRPmdh7pveXwp2qC2KIDLuOxfsn9J2IIOSU6b45l3VzUqOcpfvmgu1qSwyR5skxvQ+U05rkA82TQzan19irHaop0YWVjua+xSpHCIlsZB2JrUDD4vh7y1nDsNrhDqbE0ag2dAEzBCnIArEXrofAifIIRVTQBagT9bzBFNLJLXPGTBpiyhTGMBiw3UB9f4FRivJgKkWBV27unVv8xr25OwDGm/dKdfsdGeObd/fdN/47bW9+/7bL9S3b7andYh9/1wP0u7c/HufiTnz/znP6Dtct34YNr77ysvV45yC35ZaXadkbPybfOWjOoiRwvsbUwjnY/Mff4BYT+ssts48eSHXRR8qxbR9Or/EvrkWBBk3ctVBYiidHosgyBMJmj8tgTxbSkhxEGWb45ddUf/YRiYRZTG8J1+GzZxQ/eR+CdCtIGX+1QaNFHhFF8cPH+GdXEMWxlCGA04I/dFYqUrMJavCoIRD3ncCvDqaoaY05nGJmFfFiQ+wG9qsdzghGkRDJGbqLNZUy4o6pFXZSEUtDdTAnK0X//FKw07Oa4tER2hns4QxdlYAkaglx/d38+ms2X5yJ/F1ZUr13iNruKR8esf70KXrwlNOK4ek57sEhZjkjTRrCZ8+xtcOcLEQ1xAf0vSV+xNYziFSrudoI8VEr4osVeteh6gqVpS2ai4q8aolth0oyQVoL1f0FaT6l//KCtOtRZPLoXqxvfAPIBAXqcE6xaSEk8AMBCRYDmaJp8DmT247SaHKCboQEkbP4XBhxHc1K3KzT+GgpY4iDJ2oFhSP1A2bXkpwh9APKOfG66Ad0VWKXCwYylbX0MRDSKFmqDBboNzvaKKpH69wzWxySjWFaVVSFpR+EnIwPrHY7sjPUZSlKNSkTCouaVJTbjj5GslV4pXD3ZqTzFf/jL/+G947F5X1uLI/mR2JK1TSAyK7qkcAcBy8BYSEqSPKD1a1x0gjdFqy6Uags8L6RIw2o2+/feFooLYngDbRp1LK9VXwx1koih8DKzAhX0s6MdQYJ7jGGGCJmxF+m0ZDJjEpU2hoJnEf1NYJ4ixitiUqC8+heJhdKK9S0pL/YUj455N7/5h8wvFix/XefCqG1sCQFSSu0F9jbECNGi7Svz1EKFyFR/slj9HXL8PUlOA2lEPhNWRBaSdptXUqAOamkUtcP5MHjDmcMZ2uUyuAj7nCGbiryphVOiVGYRYNOSTDHRqR97aIZZaiDKCC5MVHMGTur2W5bpoUQU3vvKesSk5Gukg90PlI3IgOqR0W3IiW5F1ngBOpoJvyBXcew7wghUk4r8RRwhvLeUmCIWmG0EbWqnNk+uxJdfDL+6bXIYJJJzeilseuEDN0PpPUOdbxk+f2HTD64P2aeidx7wV1PSmzpCCPcyZaOHDN6hOv49R5dWuy0GR1/M4xmbiQhyKdBzApJch/VCEUjRNrVHmOUeA9pUbt7/uU3nDx+ILCL65ZstUgL+0S/a+lCoBkdltvTK1xTEYc7nJ5dT971qElB7AcGbdh+ccr8ZI4tLNHLPatOFtLNqwrh8vQeN62F29ANnH9zweGTYyEwG42rK1KMAp+qpKukjLmtyN5AiW9RUHcC5pwh9B7jDDHK2C3KG+jYqID3Gi/g7vp7d4lOvac7uxZ1viGSr7YiuuADs08e0Tw6lIRCvZns3ARzt9PL62s8r8Zu7yy+vgwD8C+uCes99mAKhcVN69v3w17knN/lyJzvHvD1c1Jv+exbrk3cduyfXjB5/+SlMMu7ftwrvzMT1i3+fI2ZVKS2p993TD64L7HIes9wuoKY2G1a2k2H1obOB5T3PPzTD0QgZV4zeXIiSnq7TmBoUbq5++sdylnstEBFkeo1VSFwUS9JRmx7ut4LBLsp2VxvWZ4sZXyvdnTbVgQwYqYoFLkPuNmE/dWWfrtneSgQ8tANxJBo7i+I+4Gwa287tyll3Lwhbluqo5kUX1HsrzZUdUm/7UQoxepxzhExm2401HNjR2dYiyO8tQZKS9x14CMxRPqYRI7bR05+8j7lrAJ9wyFUr+UDY6J/94beufF5TMb1nXH21o7EO/6S8XIT/77xBHy3YP+VJOYtJ/B7dib+y3Mu7mzfOeH5vRK0V1s4Kt+9RncP+Lbs4tW3Uoj455e0v35K/f3HpNWecHqNLkr0pMB9eI+4aUUv/HKN/+oFxcfvkfsB6lIqYCOe2O968q5j+PIMczzHzhtsXWKPZuhpTfeLr4Tbsd0Tr7e4xZS4bTH3luTVjrBtsYdi5pPO1zAtUXtxsMQYsjXE0TjHWcOw6Qh9oFk29KeX2OMlxcGU9rfPmfz4fdrfPCOud3C9xz06Qn//EeXhVOQOQchtKRO7nrBr8duOYtZg6hKC8C9iFFyuqcvXZvMxwbsZuEqRM6S2Z/tvf8Hm8zPCtMZp6DcdZfRM7i0kAdOa4mBC3rSk3ksVf1qTFjOax8fCA2h70Uef1HS//ho9rYnTBuc9w/MLOF+TvSg65CCk+NAPqDxOAoUjtwOpGwj7Dp8zVeHoVRYMsrPEwjE8vSSFKOov1krVvS5Eqz9mrJLqTwyemBJOG4G25AxJOCAoRXYWosj++n6g7Xtmsym2LMk54zvBVZdVSd97MSRSiqKpGNoO1Q8M3mMYScdKka0oYDSHB2JcNanZ7raEmCibRrpXJPrBc9puiWimZUV9sAAy8+UcMyuJKdN/c0nctvRZzNcGH5gVcpwQPfZgilGGQOL68orFyQFfdpfcb5ZsX1zwfNiw9z0fHz3mvWohC0uIJKMwvcjYyiodX86mSszobpSjSCJ/qqw0SH2Qz+Yo4zmNxnPqJtgfTe/0yEfwId52HG/mC30zIM1LGIC5kfu1mqyEA6GMoY8Rp5Rov48kbesMGENKIlXoh0HcoEcsetyLl0zS6g4uX/gfSY2dllnN9E/fw81qNv/uU+LVDt97XFWI4Z5CKmhBODphTHCykyBfNRXaaOxOOhE3crSkjPjlJVwhGGi/7yXoNUZgWsuGtO0IGaqjiSRahWDv2feEfS+meItapj1rMKUjG0WpDXk3iDmg1ZQZUX167xhdF+zP1xRGulXxbC0BeV2gVnvS9RbdVIRpiZvX2LqSMarGIkBdEpRA4vxX50SgenhA+80ldlazfn7J9Mkxzf1DKAwpJ/EXiJnNT7/GPT4g5yyyz9d7VOMolg3d+ZbUe2LbEa8uCS8ucCcnTP70E5onR+jC0q73xM5TTyrcXH63aQTqlHs/cqySwH9GQYWb4DF2g6h3Iddd5G0ZCd0S0ebWi7BGSiIvvO8loCkdfrsX+FM7YLS69VKwxmCP58S2Z9i2mLqkmIh2f3u1oZ5PbqFJKMUwBHQ3MKx3xE1HKhzNsiHVhUjX7nqKw5l8pxtIRlEcTLGTWu79uMilcKO8Jr9t2Lb4diCrTHMwFx6TNVLVfvsyKbCTO/P8TQz9CmyCl3IrdwOwDO9CVN0G5Tkk8Q2KaaxeO15mNq8G4neD9t83ubjz1TfOI21agZAV4/1+7UekmG7dsF8tdb48oBrXwLvvKPW2s3vzWqQQWf38S8qTBfWDA+D1QPYt382ZcL2n+/JMRA2MzHupdLiZjPvQ9sR1y+5qR/zmDDMMxIdHbLGw3vPoBw9pg2f+3rEkz1bmXGftLadsf7ameXjI+tkFtnCYqmD55Igv//2vsMZy8sG9WxfsOHY6N08vcEY8O+ykRFlDDInV80v8vpf5HiibEh1FJjxpjbECr1VaMVxuSFrLM2y1CJ5YOwpcFGNxRaCE+Cjdc6QIZSeV8DAQErjqPD5FUb+LWQx67y/o9z2q89jCEoZA2LQErTj8k/el0PHq3Rzvycs7dxMuv+1e3XYI1J3BenPDef3Pt+zgW7sh7xoXt2f6zs+8c3s9h3nL9j8BzsW4qVcnlre1CO9uvyu/eNmgeJkm3v38G5n+Wy7U6y2h3A3EzpONwT+/ory3RC8mxKeX6MMJ4WItEqLXW7Q11P/sT0jna5GxndfQJTAOvGDn87TGfXCPfL5BVZG0voIHS1KQgZ+vd9hZjWo9ebXDPjhATyqGboDOC1a87QnrLfHXX2HKgliXFI+OMSHhjCZNS1LXk4eBiKK7XIlD8vNzmo8fwjfnmIMZuf0CpQ0xZ9LXF5AS6UfvYR66W9UMZTR2UmGnFdV99eq1yVmqvDndTrivzZ2v3Njce7q//hTtDOUwUK4DfloxMwnjLOHsGnu8wKAI35xJMH4wRx/MUD5K0PtXfydqRYXFGBhmDbqpiM8vyemCrvcE7wUOlYMA8o2TCvhkSn+5hQyhjxQpYqclcd/itBCBrbPk6z1dzlCXKAXFtMZ0Ayol2q6jUGDqEt0O5NEHIeaMyYFBKwothLA4ZELXE8fVttCaYdtKoBQiOYRbkYJCKZIxMvlWJUM/YHMi7FuBDxSOejqqlBlNt90zuXeE23WYugLvIUSa6UyI6IAnc5l7DiZTjouCbZZztdoIoXy9l/FrNGo07svWielgzgTAaoWfNXgLIQiHxDUVk6M53/s6YHtNQcm9siZOFWXRkAZP1JpUSiCrQg+DOG4DEsxkgSUp/ZL7kLQiJiTIRkjbOYmZXsry/wmwtwnF+N6oFKLHinJUSmRcc5aKeRTju5uYIJGxhSOFgNLiqBqjLD7BaKzVUoEn30of3vA9lNIwBhEpJXRZiLyqE46U1pqsR5O9wlJ/cp+jv/iE7sU1L/7bv8ZlTU6C4c9atPZjjLcwMKoCm7N0CEKkev+E6tER5//D36G0wGqU1qh5Q2p74bOM55SRbo+1huws5awkTIVDYJ0mVpbJtCFcbIibXvZTGFzbo7oBPa3IpaWY1+hZjU7AMokHwnJKczwjFwa/7QibFq625LGDaJcT/PWOPHjygyWUDn21Fb6Kj2QzYDYdYRAIUgqR7WrL9GiOvrdA956UM8tPHrFb7ahOllQPDul7T2E13fWWnGD/9JJ4sebkhw/JXYtPLYt/+gn9i0vWP/uU/tkF5b0j+i+einv7w0cU33+MXdT4nKiNGLSlWsbYcL2jGGVKc0qoWqCHlNxGBGZcFHLKYoI3ri86K0n+buAUN7Ndae8sNgkzmg9mH9FoUHl0Lg8i2TlrblW9tLPUJwtC50VAQylMXTC0HTqDrgtSziTvpdvgE/XxAjutSLUTJavCiqJT5Yi7lqwV5YFIvN4Es3fXuTwG7aYucTnTXe+4fHpOPd9iteLww/vohX0lkHo1+I+3RPZ3Fk3vBiZ3F/Jvqe/JJZTC3I2Ua77z7htr+90tv6Ruv3Xfd77waoD42m6AtO9RVQHk2+7E3aQgg4gqTKpbiOUr+7oTOL4roXn9mHfPC2QdpnQMq510o8wdadvXi80jOXt4dimKeaWlnB3QbvZYpAvs9x3WWfrVns2LFearZzSzglCVuMrSDsBiQt96ymWNyoowBIrlgnpaM6x30vXTislDUWsr6oJuvac5mrP55oLl0UJgoWOhKWz2mMLR7zrqaUN3tSalxPDrZ9Q/eYJve+qmxGmD9oGQM+FKDPKSjyibqQ6mxN7TrURm1hSWTbdncXQgML7CEXYd++dXo0jKCFccgszxWot4Qu9pV1vq5UzEU0qLjcKPM5OK2AcxDiwNuRRZ5TQpyb3H1YV4+9wdQPntN+OVcTJmtDfj8mZ8vzIw3pWcvutm376Txy78awP7tYH2u5MK9crvupv855vf+LYk4zskHr9r+8OTi98R3N985I3L+B06HDcXQcEdC/abduSN4Nu7n+7XEwtANOwLSzERu/e068nzmm7wFKcr3GIKZlx0KkfadUIATpl4viEVBrVroR3wCqy1hBcrwXufXlKeHBDOVsSrHWw79Af3MIsJ8WKFPZrT/fWnFD9+j/JwTp5NxLH0Yo1+dEQciUim7eByTa4L+str6r/8ESwmmElF6SP+bEW43OAeH7L55ZeUT46kOuscIXRQGFngThaYRQ3q9SH4+pW/m2WPAdcbN0P+I5VcIVQpq9HHc/zXZ+TDCbYsMCmRS0c8uyTsdqh5jVaa6offw39zQe80PD0X59Cza1F3mDcU8wlmURGGQP/NObb3MvnmjJo25H0kdFk0q0Ng6DtcU2F9wGfB3Q85i6tpYciDJEj25p5rJYZdPohMndH0G0kgLRl1b87u02fMmkrw9Aoh7I8VqmQMWhWQEoU1gunxnsJaun0rbdS2xyvR+lZakYyoGSnvKbIoEEVnIQjmM2tF6wylc+jdXjwUUIS2w6DYhkBfWqgctu0p64oTJVCwTmuaosbFjEliUhezqCNtuwGnAKuFXL7bC648JezjQ07+wQe0/cBwueXrz895+L0PCL89JW97zuiYVBWFNhTOknsPyHUMQcEgylreaqwxxCFASKSxA6GswYDAjfJonDfen5gzWYkXhB7vi9F6JGYLGTzniEp6dCjWQnwN4ZbYHMYOkLYyRsPgISeBOmk9mlFJgmGNOF+LrK34YeicRYpz/L7SAmPUdSnfvUmi+gDuxtBOYbWFpmTxD95HKcX6P36Os06UpHyWSlsIwgdKiahHVbK+R1t7K2WajcEsGw7/6Q/ovj5H+ShqJmMlUFWJ1A4oq0gRdGHxTlEe1lQPlyLfO6tIo9Sw7wbx6YmROAS8gryocQn6fsD2ItNaPTig68QMbPnhfdyBkBP702vi9U6e+5QIV1vMtEIvGoqHh/inl2ANzT/5vvCNbngACvrPTwlXV8SLNXpWMz2Z03xwD+0Mw8Wa7mJDH/e4uqBYTjB1QegD7dWWYlKxf3pJUVrKP3uf4ZvnnP/z/zd6OoF6Qkia6CZUnyzJxjB/+EA8Z+oCfTDB71rYdoSYMU013luwPjFcbEXhr3TYeY0uHPqGR2E0cb2/DZKUFr8RRm6AndbStciZ7EUxLPYe7Sx55F4FH2XMX+0kIa1LGcdOEjlbFVK5TUnUo7QSZa+9QOduuwY3vIyYqSc1uq7ws1p8KdqRX7OcCFlWIV0XrSgXM+yiAaTCfqPOdhMI30J1NLhJxcH3H7H48D5+33Px2XM2v3mGPZoyeSB8wFuVtixKZqqwrxSV0uio/bKYd6f2elOkvdNdfLmUvCM4eHdR94315pUt/+6C5Bu7uD2XsUg5Xi9djnLXb6yN8sX+ciNV9aZ8c39vKVu/K8h7V4IDiHzqtntnlfsm+BvON3RXG5E4DwOqKvCbTgxA94NwMKwhhJ6UEm69pXx8QCotGk3QBmcVVeWIBgrNreJlvZyilKI6mOHHwoqbVrdqTOWiIaaIK510WDvx5OjbPUoJ18yHhPadFK9SRi0b/L4nDeHW40YVFmu0qE6lPML0HOv1hmlZiaP6tMK3PdVeHOiJidVXZ/h2oCiES5aVIux7dGHJ7YCtZM1RMTE7XgoE1BqiD7iqYNh3YDRqUeORLrrfd2QfaYysDUbrl7LQdwjcbx9Jd169E7Xn8c6+kqB8yxh4+37znX19hwD5O20vexu3xYfXz+jbBukfsP3ROxe32xsZ1lvee8vFe1lFeYk9y2987e95NW5aWjGRty39F8+xx0vMB/dgtSN8vkY/OEQ9ORZ8fkqiJtENIwwmoqsJ9t6MvO3QXsjXzXvHDNsWPa/xw4B9sSJdb0UxJUfy1+eEENn91X9mcv8e6WoHzknAd71Frzv6zQYuNpjjBfaHT/CXG/arLfWsYfjFV9iHgkmNq70sQv6CejFj87PPKR+LJKw6WdB93rJ8dCRBnff43zyj/LMPufUOuSmtw+0Vfnn53syriYk0eFSGuOsYXlwxfHOGXcyIhaX/+ozcir502u5BKVI/yILeW7jeke4f4j97QdyLrGSyWlqkjwWOES43pLZjOOvRTYUyFj8ZdeF1Ju0iYdPBaCBXKYWrK9gPIq2XIvFGa321pTQWrz3GGMHql47YDaIPn7MQtI2mnE5QMUoz5DdPmd5gxduOQmu0s/QhYMoCHaM4XisE+lc5HKIK1cxnog5FptvtcZMaMDiLEGTLsWKqFCYjZoSThqEbROmpqXGHC2LX4/seezCnGzyr3FN3BtuUmMKRxkBdKYGGOZ+ISYyjQk5yP0d4kRorockHivtzwtMr3EcPKX/wkOZ4ycX/7X8ghsSj9x6ijSV8co/0i6dMaBhUYlqW6KoQjf8oLvBqkMprtML9IYlzddZIix4JgLyS6rA2o2ndDT9iDNqwssiLjF8eMfGJmMGjsSiBN42dBoVwOHwQUq5WiiFESmdRzmGsJqUkJm5WOBI5SVXSKEW2liEEUSmylqIqCKNi2K30bAjETqrtprCEEHBFxeBFAEDPKsK+5/qXT6kmFf31HqU1wUAYEjZId0OVQoZOPqAqGTf0XpIXH9m9uMI9OaS+P0eVmua9EzZfneHP1uRKoAMplJicMaWFIVAvJ9SHM8y0pju9FmOoaUWoC4ZRX94uhD/gyFA4stXMl1NMWcCup/3ylNlHj/C9EGuHqy2x7WlPr1EhYhdTmg8fYA4EX63dWK1/dEiOkbDr0bMG52a3k4PWWt73EXsyx8zq2wDXNiWpDxIo+0DX9hRaUTQF5aIRM89hIG+u2Z+djo7RBWZxSHshst7FoyPKwtJtpVqvlw3uYIorHWVdkvqBsNoT1nvxmhgihEi/62mvduT1lmQ0dj6leXzE9CePxWyrGwRKpgUmFVqRjk7DOM6Vwg8yf2hrsHVJJpOD+I1YawiblrbzGKdpRs6OreWZwYhKTh7VuMiQY8Q5Kz4wQyCsW7LRqEFkyrerHSUyt9ALKdUUFjepMFUhsr59wIQgxNW2p6hHlSsUad+LV4IxIkOdb4J7mfe1szDsObx3QLfaMuw6ikuRYo+dQHFtVUgXb5z3bxL+lPJLiOBttfMtRb0xIVCvey7cvpnf/pW3ffQtn/y2Vf9b47DbVkYmtQMxZemM2le7N3c/Orl/wPrpBbkumB5MKUb1qdc/+7uO/2Y1XM4jp0yOIybjrd0KxNjyeieSzCHi2510XtatSPvue/qLFXG1pZw2mIdH9FdritjTqZKoCpSTdaOxEApNc9BQHy0Ydh0YkQ3fr3YCNxoCtrSszzqKsiCFSLzeUT88HCGxGh8CuvNstx2T4zmTwxlq37Nf7Wj3A5OlQ8VEvx8wbS9Jj44UtXC18iiY4IeANZpp3YBWVAdT+W0hUi0scT8wjIIwZVWAESU8E0RW2ViDPZpSLqcooxmutvSblmJWY8qS7MW13TaV8OmMQu09bfCUxuHmTqCOzrDbd8xD8/cI5l8LeF/r4L2+vQlhuvOFO2P+lYL5dyjef7ftj5At/J7bH5xcvNmsvNNu+K7bnSdU3f6veuXFu4Z6GfWyrUEeZ+RX7+qr09jY8xg1oYuHh/jLHXnawKREFY7pj97H//obdF1DJ4si61awfp0Xwp/WmPmE+PxazK26geqTR/jTFWbVYoqCofP46x3uRORni3sH5HWL8UFci6clueuJv/6a4qMHqMM5REV1UJMf32P4m1+h/+xDnFboxQR7MCN9/pzhN0/xWQJ98/CQkAS6oHKkP7+mfnLC0U+esDhs8F+c4T5+RNzsyBdbur/+lBwC9uER7r1jQBM3LbntIYhMpmqEEJj3PeHZFXHwmGmFv96RQqA4WjBc72ifnUtVYLUXeU0vyg168KTVDjNtqH/4Pupojo5yvUM/oI56cZodrxvA8MULwi+/koWMEVqw71GzGSDSeGY/QGhpB0/oB1xK9FHM2V5KZ3oKbTBVgW9F+clWBckn1GjGlFK6TTZSkt+ck1SxfAgUxghRPoOzE0zOtG0P/TBqZY9eAhpUH4g+yUIcxSfDWosqK4qY0GUpficZqqYCFINS5PFcXFUStaIvNJWWxKc3Cq0Sk7oidj1X22v6ScXJVBR9TGlFOQOwRlNmQ+8HyvkEv21R+wFXCIk85Yw5nsP1Dr2cYI8XuIMZ5tGS5QcPePH//CvsECEm7PMN5Q+n9NMSezKnuG5pRvLwjSywCpI8YIUXkH0gE2+fV2utVH/HCv2NIZ6QRJM8zSndkklTimJIhxKewei4yk0HY1Sw0dxAocRlOwFuJJHqnMegZ5yDcpIFRCtR67GIDntMt4mQQsZiUmNg7IxULseASjkD3UDadSLmkJIEZT4QrSFtOvG36YT8jc5kbXCTirjt0M6JT4rRaFuSNGhtiUpkeFVhcMcztNNkq7DzhpwSrnBsfWTYD0wOp6TKUtUFtnCUk1rMtlKif35F1w63WvMFopylCoNbNJiyIFUOYwwxBKwW+Vz3YMFkWxK3LVhN2OzZfnOJrQvKR4fYpqI+no+JwZgAjlPqsG5Z/4ffiBlf5Tj48w9xxzOU1pQPD16tWN/+mwmXW4IPVCcL4vmKycGUOARMXeDmDeWkpL/aMmw7jCvwlaL+h3/O5NGRkNFjwhhF3/eY0lGgqBYTUYoKke70Sqb2kBmeX2GVJipNyolhiBSffUZer6AqyYsFG6eZ/viRBPzHc8jib9FfbNAjj8S3/bhOJKwWUYDQDYRdh7HiUzGMmG3XlEzuzcUkDIE/UYkSjY2aYdeJauDgRcI6RnQUaGI5KUWmcwhgNMP1jsrq286KnTWYWhIFlBIeWBZfCddUFLOxQzE+J2iNmdak3pP2e5H2HD1T7q7NxeEEPwSm05L+ekccPMWYwNwuxZ04mDPCdJQ2uNtEYtxfuoOreI30rL5VnH/seKibtXkcNL+rVngTf905j7duN+f3Onfjzsd1XUhXPGfhbb2eLCGhhakcu8Hz03/xn/joTz7kB3/5g1d/193TVt8tDryNaJSSe2fFOVqNBY6bivkNl3H31TlxCLSXG4Ztz7Dp0CGSO09eXWNfnFKcP0c7R1aaeHyEnU0ID+9jHx4zmdUSp8TE0AdUjkwfHePqgmHf0+072rMVfixguJMFse2JwVPNJqQ+wLRm/fyKNJKl+7GjcX2+or3eMDw+ppk1lHVJ/biUxLZGipIJ6roU4vT1Vrp9tWN/5XFK02uo5xPcRMwt474Tb41tS3u1pZwKLC0MIgARoydnhZtJpzLueoZC4GumKWlmDaHrJRkvrcg0j9wp3VRoa+k3O1IhHLwiJdy8wcVIfTi9M4zyq+PtW7ZXOBivtMruDILb/OHN/b0qYPRdgubfp3f3B25/YD7yBycX38GI/PfZ2cvtzs26mSrefHhfe+XODZX/fX3iU1L5dIb6B48Is1qqi6XF/+0X5MMpaVphmkoww0oRrjZSdbzaoue1VHKNxnSBiOLy0+fw/Ip+CFQxYCYl1cMDzLQGZxkuN4KnnFRUn7yHDxF3/xB/vmL786+oD2ZEDcXBgrjvyN9/gv/tqfhppFaCkPel25Fzwv/mG8KLK1xdyyJ0vMBpI8GTVuhZg3nvmJSTuIUvG/JqT1aG3d9+hr3agILu775E7TtyTNQfPobKSrKhAG2kwrPeY47m+C+uZDGKCY3C1aVUnret+CMsJjT/6BPCaieQmS9ekC/WhNMrbE7w8BDz8IR0dk16fokfhNClQiQ7Ry4yYbunAFThsBfXJDNWtKuKtBfjupASCUVhrQQR2z05ZcrZlHa7I3kJqJSxpM2GrDWDK1FtJ9h+pQjWCsk3JHHsrEvqlMX92EcKZ0lK0w0dnsSsKum7ToiSTS3yiiGQURjbcN2Jn4QuS4rFlOgs+8srXFMTtIaqohgDVGUNRVWKeguKxorZXTlrqApL2OzEzdta7n/wARQOg6IyBj8M+LaT5MxqdO2YNILN1t1Afn4tk3RVkKymeXjA9oszOpup2p6QAif3vsfpP/939M+usWWJNhGTYfj1c4af3OP4xx+w+9svpM3O2PnREAkoMrp05M6LB0yMUtWMkdhz67xtCkPy6WXoEEV9J6eMD8Poup7JMcCoOpZDlCquFq5Irgpi76Uz0HlcYdFGnLeVGiVrc4acKbQmhSDP2CgxrIzIxt4EQlklISyOsLEck7TSg5xXsnlUCJOES9WlwMxCIiHfsVMpOlRHM1xTUuxbus9OIQt80lSFBHkhErW4U+uiEDhUEgdvPSkxJ3OG1R4LmKpg9/yCYtJQnSyoU6JoCna7jsl7JwLf23uSiuRBlFyquSgUoUSJZfLRA8GwVwWbX39D9pHt6TXOaIrFRGSwHyzJZGxWxM5j5w3zP3kfBbh5PeK9822gddMdI0P7m2ew7jC1ZfHnH+KOZsBLYuNtoJfku7EL7M9XpNWe5lAcebWCNET8VnwbUiv+HOXRFL2cCC9JK4yzuFFcgShwozJnbMxi9nm9pX9xTRwJo3beiBTxtJIEtQ/kqy3WZYYH9zClQVtNsIVIX454bcZ/YzeIT0BZENYteqyuMrpqY40YwKVM2He4ukSnJBDY0ojZp3Piu4IkrKYP9EMvBqy9F/EJMu2+p6wKnLVCaEaQleW0Yli3I6QvUS0nYpT6tgDCKCGAZ/GY0PVLyA5KiRpUVZBGYQtdutGB3IvaltZstlv65yuWDw/Fw+BONf2m22KqYoy1XzuHGwiRGREF+bUg/vfa3tL5eP3td8VRNx2ZV5d8kQqHWx+E/Jbv5hBHDxiRC5fG6mthn5Jo48kP36MJYmgQQxJ+1AgPy28GIy9jybcc91URGuj3Le3FmsXj4zuqVJmcIKz3rD9/QXe6ZrjeEU8vcFfXNH1P8gOq3aOCJ7mC/OghaQiksoTFDLNcoE+OqGc1qnSUJwvyvmc2FjIYFaEoDFU1RYdMGLwIHCiw05qpalBKjEr7qw0pRIrlhLRtmZaO8mTO8khMM5MTGKxRCFdp8AzXOxjn+dh58RbadCOyw0sicDQXj4nlRNAOQWICUhChHCNF6zgE4S8pIDr0mBBorYjTGoy+NdKNvScNkSHsQWu68zU6w6Ztsc5SzyaUStMGkdduCgfO0l2sRR1u8o6x+HttMmjzCDNUSr2WQLwyKl4xysspveJX8ravvCIGxds6Z68/NGNx/tuy3deS9fz6+3/P7Y8Li/qu2+snfWeGeBf7Pb/+BDM2Sm+vtHq5OL6x7/xK6zGOUmrZGlE2SBn3+IjkBG/KWFE104pwdi1GR1ZhFlNWv37B1dNzmuUU7z2zskQNA9WsxoWE2ffESYV/fgl1QXm8JHpP3A/krVTQ3fdmtJdbnq53vH8wQ4UbN2FDyAiJct+jh0D/8y9RQ8Q8PMQMgeIvf8T6735L+eBYJCSXM/zffsY2RuqPHmKmtfg5vLgaFz+DmpSE02vYtoSn52AN5Xv3cEcL9n/3FfrhAVSO8PSC4XxNvFiLpOSup//yBaobhJxsRd2B0jGEiKsqrMqkfcf+bz9HFVYcZAFnDJws0ccLwYO/uBJTrKxR6zVqNoGZKKaYrsfagpA0auNFVvbslPzoAH20pP/0lKEbBPcfpT07tN2owIRUKxRYrfExYfYtlBXx6pT63gPidCLysyEIX2MkVjpKNBAArxWVNoSY0H1PZQwb76ldQTaCQVZ9L7LBWTTVY4w4V8jkqBQ+ZYiRwhj6YSApTbSWkDNVU6MQyVv2/cjhADWfokNgt9pRLmpsXXOaW1K/4WByTNgI8VNNCvTJIfuYuF/X5P1AXlT4UtF3geb9Y8pJJXwGBQMZXSsOlVSbzjZrLn/6cx5aRxrdWE0yUBXE9R7102ek/8VS1Lcqi61KitKRZiXpfMPucs3EC4Fc5ywmh12PtVaSg5yl2unFbZxRQlZbQ8qiO56VLPgpIX4Qoya51noMZjNWaWhKYkw459BxJGFnbn0QtJX7kXImJCGDhxhvj6OMBm1QTs4jp7F7krNAl4wQvhUiY2vLkqz8+J7AsYKP4qHgA7opKO7PqR8d0Lx/jC4twSiqoxnt1xeEBDpBDOIBoK0laiXqQSmTjEY3BdMfPaJf7QjeY5uK7nxFLi3RaWbHM1RhcbOa2c10phRq3jBsW4pQYpuK/mqLUgpjNWpSMnQD8fkWXTjpMu4HwTM7gzuYkleivqQrS86K+uEh1dHsNuFTd+fPm3k4SGfJn63E0+egYfYPP8QuXq6+qZeANe97+crVVuBYWjFcbXFNSXu9E05L26PwRO8p7y8xQdylq1Iq+DFEujNxP9aFZXq8gCHQhyhGjfueftsKTOh4Lq6/dUFWina9Z/XsCj0tuf/ePemIrTvayYxityV2HX425WCEb+m6FB8OJ8mwqizdZkc1aUSaN2X63V7MTUOEXqQunRU56V3X0VQlpIyuS9QYjKNGx+reUzQl7b4TOc2YKEtHMSlRMeN3nQRUWlFUBUpr9KTEjQqBQnR+VYwyJwkABx9oFtNXim43wfHtmpchDYFuvRdZzTGYjF54S4v5DK+drDE5iwgDskYqo0e5z7ct0q9v6hZNcHMOd874ze+/GQXBqyv1a++P4/Fui+Adp/R63TffJJFZ+DLGGdBGJEhDFAU0q0mtJ3YDbjl9ebi7+9WKgx8+obvckEe54HI5fQf65WW1+y1Nl5d/ZKl2x02LdvbVZ8pH1t9csPq7bzB9oPIB/ekXpHZHKh1MCrRtSGtDCgEmE1JV0tkKc7DALGZEq2nmtUhPBynIhMKy+e0L6pMFKUa69Zb65GDsLgdUzKI+VTkpoiBFodj1+M4zfXxEf70nKqiXE4mljEED/bbFo8QwsSzwKVPfPyD2nlAKzyl1Hr1sSFZTNA2T5VQECozM+zm99EWKMWImAmuyE+EXxhBZfXEqqn7LRuB7St1K+AIYU4zS0ZJxnj8VuPbBk3vMhlr4TSNfz3hJLq6+uQBgejDBNtXtTfoODYtX7vfrr91GoGOB/Nt2p9Sd4f02Q8XXjvl6N+X1fb+SfGRus9q35vB/xL7A27b/vyQXb33Y3tGluJm05IrIi/m1J/nl1Ht3ln25wzcf/Jdk8BSjkKaBfLVhuNpg5xNCEmiLWU4Yfv2cFAKmXFC8d8Lwsy/RH90nnq9wMTKZVrS7FnYds//9DwnrHfiAmzXieOwT5mjBcL5h/Ve/wm9ENi76ALOS2f/sI+q65PGDY9S0FvLvumX3zSX+akcZAuF6h35yDCmjllOaP3mf/hffsP/FV7i6or9eU+97Fn/2CeHkkPW//hnDb18w+7OPBf6gIJ6vhE/QVNgHR5iTpVT4avEkGK63kBO7f/cLGAaULohVAU2Nv9hhux5lFHo5IWuDGQJ53xF9RI0Ox4FMNhajLXHbkS43ZGdw8ynlvSV93wvczGp4dkmsK1IUOUKnNbGLpC5jtBU3513PsO1w2hC9yHnGfsAqxHfCGdre42IkaYVVgre3swlq32GMQSWNb1tCPSfvO8zorJysJWQxYnNJKgVxSGQFTmuy1qR+wPuBelJz1DQCsRm2pBjpywITPFEbrDV0fU/KYGcTqf5qhaor8jBQOUs8mFFnLQZqQ2AwCpcVtioIMWOt+GIoZ2ic5Wq/x2nHvJmQtOju60UDVlMcz0g6snn6ggfHC5RRWGvRTlMfL1HOUtcV3XovMJnrvfimWEVzcsShgq7zTH70mLDrYRBintYKVTqqWY3ySQL5GHHHU7LSdKdr7BCZl5WQlK2GIYnDdV2S+4HkxFlajxVDQAzd0ISchecDmBFqkrVCGyeQkkqCxBSlQqiUInWS/Kk+jETaSNQv940Ca8R9+GYxN4COol1uR2O8fYzYxNi1QjoLVqOsHd22Re45aUilgWSwBxOGyx1MS7QzFIcHzH/4mMn7It3Yrnb0q70k9sczjj5+QL/t6L48J40mTqn3wn0B7KymXDbkWYUiU85q6oN7mMJRGUXoBqpG9Nh16YhjoqZilgRglIs0pRM9fisSo8ViQljtGb4+H4MELYldYTGTgupwzuT7j9BaE72HLDwIdQdnnpIQlm8rp6MKS/vlGeFiKx45IVLeX9CdrfBfnhFHiGDctazWW5YHc2xdkZXCIERM+/iI1A4YZ9ifrgSKpDJu8IRdR4oZNavE7ToK9MwsJ5jCEK92JBS5cthCAsKcEkUjEt8xJa6/uWTY9VTzmmpWc/jokN3Zmt2nL5gcTGiDqNXFuiZWDdWDQyb3l5jSEX0grPZoBeH6xu+ixtTCleifXmIKiy0ccd+LSV7rR1ib5eCBVJp1YUcxA/EA2V9vKIqCnBK73R6rlHAibqrjRqNKQ7IB33sJnFLCzJpRoU9w+LoY78+dWD2lhC2cmG2OkUO+FTR5dSnNWYpik+lLpSOy+AXc8EkIiQCsPz9l+aMnt94fbjF5eezvsqnR5BLERPaNFfhtL72jHfFtB75Z3yWLuflJ7zrSuKtxXigs+/M1pnSU8wkoCJu93I/CkretyMNPypedj/Ry58pqUfsKEddUr0ZvYzHz5iflKPOivjFvfH3LkH0UZaazDc3RVJLJnGlfrDj92ZekbU+zb1Fn53T7PXrRoL93Dx+E0+gKQ1tOKCrx6xkmE8rDGYWzGGco1HhttGboBsLTCyl+WY3vPd22Q3UDqhM5ajNtqI5mDLsOUwkkCaPpXkgnfHKykI57XbKxSDcvZ+woiOC0Zn+9I+62mCTXoG+3JCCEIJ5GzqInpXR965Lb2C5Ll3TY7MX4MQtPrpxU6G3H/mpHURds1jv0rKZZTqlPFtzII7+SdGbkWo5xycHJIRxE+k0LVYEm0Q0B5SNVaammjuefP+Pg8dFoYPrajXrn6Pq27dXI85XCzVvGwt0jvd7dyK9Hr9/2fNx5NF5JPt55+m9GyP+/2P7w5OJdrcu3vK++w8ffXjW5C3C6qbC9Pq3e2cHdTO2VcaJQzhI3LZSObrVF67FCVVhW/82/pfr+hxTff0LSihATdB4eLMl1if7+DPWLb8S0qOuYVfcI11voBtyjQ5LKpPUAKdH9m0/x2x5bFsRdR6pL3LSi+OFDdr89I2z2zP70A9j1nP+PPyOdbkXdpizAGPxqw+yf/ID9rhU1GGOIp1fkYaD44B55uxVjPcA9PGTxv/vHbP/jp7Qvrshtj57VqKlUuHEWP1aI/emlLJhJYCCZDFpTPLkv3hIjF8OWDdiZSGK2He5wjjlekMdrR0rEL07ZPT1DDQH98AQdE/pkjnv/Hv6rM8KzlrTrsJkR3iGERtOUxOM53YuNuHU7Q/LiBRCzQJSiNhTOYa0i1yVsJCBQxlLUmth2pAxRKwatMLuObvBoGykR8nRK4h7tR9l25Rx2s8HVtVT4QhTPD6UonCMZTZcTLmeC0uQwkIeW1W6HyZmp0vg71TqNwiHKQJRuJGQqBmOorcMqQy4cOmdsBhWCjGWtUSZz2u2xWVPWJbYumM7m+JwwWVHVBbl2bPOA1Y55XVLlTP3eY5yV7prO4LoEk5F8FwPTh0vCas8OULMJuvdoo5jfP6Bc7/HXOw7/65+wP72mf3pNantibTn6i0+E/JYSvU1MXcXmszNskt/qY5LKUc5ko1CzGna9cCycwSJwpazFZ+LGqVk7wY5rnV92GkZsfyJjlL6tmqpxsTE506aATRqVpVuWvXQdtLMjvAXBe4+dGqO04GhLgSeFkXjrsiiFZZl55Vg5Uc6n8gwYRa4dpilwsxMm7x0L0ddZXFOM5/9ykajnE8LlVpSVfMB3A0VT0jw+GBe9EQK276lG07ph1zJ0AwqRFC0ORKFFj/h6ZTRxCALbGkn7pNFXpB+ks4kot7hGcM3d5UYUbeoSNa0YLtbkyklHpSqYfvJIuFRKYSonMERjxrkxC+zBCCej/fQFed+TUmb//JrBB6q6xM0qTFOQjUAMcjvgKyPmcXXJUmuUT/irS8qPHsgUmzK0PbYqyCFRFY4IhG2HPZ7jRz6HU0qC+evteD0ksdSFpXt2iT4QoibO4HPCGcN2tWO43qJ8onAGV1j6y52Qsrc9VI5yCLimYAiRwTRoZ3j0vZPR18QQLrdsvzinnlYSIDlL23ZMmoLcD+KLYUQmOVuBzphaYG+mLkclKUhdL8IgGbbbHS/Oz3j/+D4xRGKKlFPpVCotpNkcZbzEKH4s5aSSwpFWoMbxnO74S9xZ2rQxd6qpN1GJJCS8Vu28IXi/vjrGkARmOvjbsUdODFcbqllD7jwcvF6F/d3dC31z/FeW4rvl0ze/821/vrLl8QPq9o9v/ygI1j+I6tuw2qJSFunxurg9lp3Ukkj7IOaDMdF/fYHvPaobaC+3olakBOqmjIhquIMJZtagjMB4CImw6+hOrymsZegG9LSmPJEgWrnRO2IIxMHjtx1516NLeb08mJGGwPaLMy4/e8Fy2sDXp3TbDX7RYA5n2NmEWFi6dYDDGqYVVRCjTFUYmsYxP14QbyT2K4udy7jf7zq6bUfjLG7eQJTnJkV7O8ZZ7+l3nSgt1gX1vAGlmD45JqXMMELslNFM51OB8jUV3aalW+1xTcnJxw9Zv7gith4Gj55J54QonWtTFzT3l3f8WOSeJh/EVHFUY7ONiF4MmxZVFeyuNtIBtobF0YJiFIx46bV1d7zJC2ZS0a12xE2LrQpcXdK2A3kzqlsNHjstUTlz+PBInhcf0aMXk0BCf9fA/Pb3307IvulqvDx39cZ3BBZ3I+n+hnP7t5zKq/t6Mz169Wn+o5IZ3n1af6iJ3m67HTP+d+zm90g+fq+P3JYu3szCbviImbv/GSseIdJ/cQrtgF42hIst5nBGOFtRPDig/ZvP0E1N0pnmzz8ibVr6n32B/eQhxclCuAirlu6XX8GklMnmaEb67Qv68xVUDcOvnxK8xxiLToleK1xVMPmLT+g3e5onR+K3cbln99MvpEJbFqjCkKzFEqk+ukf5yUOGFyv6F5dMPnyA/+acEAPVhw9R+57h2QX1X/xQ2uZdj7/aEnedVDkvNqQxYNDjgxy6HjufUDY1/eUaVRaEuiRojfcBnTOFtRg/EC83qLoiNiVNluq+33Wiba0VxaSi/tOP8esd6WJNvNyQrUEvKmxZki63pJMD9HpL99kXMETMfI5eTolXG3hwTPvrU+ysoUgJNatJL64kUO8G4qTEzSy5SwzbHnwkdGI45bwf/Q6EALwPkSZLV+qG7DrkRG0diUxrNbrtKZXGD56ylIUmd1IVDUqBD1CWpKLAAnYywbctebdFo4iFJa63RKWo65o+ZZmsyNRHS7IxJCuJhO+F3FucHIKVhMXMRZ5P78RVtPWB6aQhpEgxqQiDp1lOYFKK4WCMbHdbCmUoywpXOYHJhITfdqBBLyd011sm95YoH8BHUkxUhzPCShK72HuS01Qf3kP1kXbw2MrhqlLycx85v7pmMZ+SG4dThvZyTXO0wNYladMSfKB/scL/8rl0e2IkAAwBq8SnQSMYcqUkaGE0KzMIPyAlMVi7IXwnIOWEK0WFRY1yuiEmtDMEo3Bp/J5CpKDH+3tr0ofCllZIzaObcsyjW3hM7B00ymCNYRhkAdPWjGRsRaoszZMDotFMHhxQHy9E31+9nHDuCGC/3FLCb1upMo+t+GG1k65LTMR9J0F2zlLMGCFbUn0Wzxk7qUSVqvf0bS+dU23G7g707Z5ylOTN1mALK8ZtzuJ3Hf2La9oXV0wXU+zBlP2+w9QF03vLl8Zkdwiw/nqHv94xbPaEIeLmNUVV0L+4Zv/iElOXWJ/xbS+u2IAy0Nw7xKeESYloNcOupZrUmKzI1y1D10HnaT64hzqZk7tB5p+UCb0n7Qa01XS7jsIZ7MFU/CD2A7Y0AqOYNcR+wA9BcNtGY5yhawds5SgXE2xOPPtv/ntY7ah//CPSZIYLmS4mzLRkfiL8I5Uzpiq5/sXXxHVLdX9B/fiAjEKXlt3piuZ4Tljv2az32MLimlKUZcZgX5Uyfsx4/3TpRIlpHAe59/iuJwyBajEhxyTEdKXwmxbbCGzD+0BZl8TOMwSP1UbWSqMp6oLoA+16z+RwhmsqEccYIR831fqh9xTja68X527HZHo5993dYu/pdi2mEHUttCLuetZfnkpV0Wh8P7B877504g6nrxVIf3dk87bw4SVE6vet/L7yq15CFtRLWPPb8owMkDL9xVrUA62hHPlG5LGjEBPJewmoc2Z3sSZe7clezFOJWdTmKkdhjCh+aUXuPKYpMIuG7mwlrs9JxCQYAtv9HmcshTLYyhFTElGNwlDPG7kKWot/1WqHO5qRek9xMKW/3rH+7AVh21MB5sU5/XpN8cP38FnTdZ4MDBGmkwpXFeJ47wyqFq5ojFFMPksJzv35GvtgKXOdUujKSVW/sITrPWHTkowklyEl4rZnt26JCsp5zXwpRO5UWMJqR6wcrFsmhzOK5WRU2Qvic5EyXddz+OQEQiSMc6AeZZhzBrdoqA5mohR4p/CbfGDz9bkgDYwS6f/CigdUVvT7DmM03balbkom9w/eGN+vjpcxOM8QugG/bbGV8Eg2lxvYdsQwyjZbjR0LK8pZpk+OpGDyynD9LmM33/737UVxXn1Yv1XsQD6TRpEZU/zxhVxf+sV99+2/qInetyYW8B0qE/zOeejNPkZ+s5Jz589XmlHqZR4CiNvjoiGst+jmkHC+QZWC5R3Orin+9HvQe7wV4pZyFvvRfeykwp+uZBL66ozYe9wHJyiUcAnqCj1N9J+d4lAUywVhtwdjKYxm9hefoK3B7zuGXz+j/e0ZLkjApUfCUooJc1wx/cEjqeIqCKdXtJ9/hd5t4bKlTZ7ZX/wQqoG46eg+e0Z3eo2e1uh2IGVE5u1qg25K1HyCCRmVNSm37H/6SwZrifMluihEclNb6qYUA+8xiFMxotoW3fekWUMKHnqPGiJ6WrPxCf/Zc1TOTN8/IX//MbkbGH7xBf3XV2QLdj5Cer7/AcMXX6HnJTlG0n6L3U9wBxN052nXW/Jqg8synnLbYivFcLoFZUhdj1NOFvrCkveZLkZx/ewHmjFwVIWDGAW2gPAzYggUwaCUJiiFq0rUyM1gMiVuN4Src+rpghAjDkgx4smYxQxVFQSr5bcbi9235GlDETLDvkUZg5s0UkSc1gzXG4bgWcynqBCI9w9xhSOTSTsJxHwIUulKkaoqQSn0rCIuSqppg25KUJnlosEMkTAMqNLSXm0Fw30wQXfS4lVaSKsoS/29+4R9LzC8g4bi4QJ/usZf7ei/uqB6dEiJqFjpwhKswjUlx0ZjSyvkPGtQnRdISAa3nFBWjvJgyhrF7tkFZV2iz7fiij7iynPKJCXXXQEUFjV4Usoj/EYJGdYYgpIumlMG38tvczc+AkbjR5WxdEe96IZImZQoT1ljyUaBNbjSiSKPl6qxUaIKMyFBFjUop0VGFAX5oMYeTpgcCAzE1QVuUt0mpq9MK69PPgoJDm+w0uPnqnJUW/ORNKlkGg+iOhf2PW4+Ybfdoo1Daz3eM5k764Ukk773Ajk0Ck9ie7mjqgvmxwuygs35iqoqxUehLqgfHVE/ORYTSxidjpGqYcrErif1nv035/Rna3w3kEPC9oE0bxiqAlNausaR9z3zssQeTshGlIyUEgiWO5wKZGEImOmEvOvwT09RswnFpCFbMbpylYN9j/voAZefPefqYsXiaMFkUlEWRjxGMiSt6EJPrUsoLKdfnzGZ1kzfP8EWlrjZEtsWVxUU84ayKYjbPUYphn3LcHpO9b0JofdUBw1pteH6s6/xk4ajP/uQycGUw3/8EdlHwr4Ts7BZTQriQdKer7g8uybVlu99/5HwEU7XAkEsBOKnokCrlBNZ4bhr0WUhwc8glc4cAn7TAsLdyUPAFEZgzklgn8kLQdwkI47DTcnQ9uxWO8gJO3aFYikBXgoRWxV0+456UnN+ekY5a5gvl6PymcA6tdEE72VeG4KINhmDdRZTWPpdx+75JZvnlzz884/p+4EUxJUerbg+vWQykTG8e35J9fDwlTX0u+YFN4nEqzlG/r328e6d35zMu88rI/yf9sW1FMeWU3CGOESG0xX+xQqdMkNKIuc9PhvJB2LrqeqClCJ63mBDZBgi15drEgq0YvFgiUqZ/dUWX1j6fU9pDc3BlM3nz3BAWTpSSuwvtwytdIqb945QGYqlqKRlHyiP51IgyrD+7Rmrz085qEvyak3/7Ix4MCEdTHAPj9i+2BJVRqnMREO5aEhkykUl19pZsspoNHHoMcsG05S4jx5A6TBa0Z+t0Fphl1MxRiwsZtGw/uy5OGVbDSFifWB+NJoyZghjJ6c+nlM9PmJodgzrPWo/CMcxRFRI2H3PrCmIFxsyyDh0Fr/vKQ/lPlSL6W1icasBESLd2QpCQlmLndTY0jKcr+mHQAxROJ3TGlc6ESoxr3bo3jlkFNiqoO973FRUpRYPDgjtwO75FX7XC7fIGNyspjpZSDHk9cTiXeX/v+/2XbohSjqP2vxxEos3CxFvKQS89dU/zvYHdy62u+3LP961IL++ve2Iv7N78fbTVK/830s81BuwqDvb8PyS8OxSEqOY4WQB3YCZihqUMpr22RUmZ/K9BXXpyBcbwtMr8tEMazTKGrp9z+6nXzH/hx+g6pL2r7/Ahsjm9EoWlsFLIPL9Byz+6Q/Z/+0X+G8u2V1t0VqhjRDKaQrKx0ekILb09cEMlBKog1HEqw0pBWwPe9+y+J//qeD4z9cyUe46slYkPz6Qx3NMylA5jLP4by7pf/kN7S9/Rf/pL9DtVvw3lIGyJh6ckOeHuMdPsIsJVitIiYvdnrnR+KYSt/LjBWXh8C8uGcoSmzJxtSdPS3brLU1ZoucNetuR+gGmFW45JZ2tGdoBYxRqt4e2JflInM3RQyBuWkboLqrrCfuWpDXVw0NUu0Pngj5mbE7EYSCgsFpLIhACqeuEPH0ww7a9BLAhUMRE1hrjLIPWKB+k81CWhJxhOSNud3C9Irctpq7JQLda4+p6xLsb7HxKXm1JdY0OEYYB4xzBS6VVWYueTQRGMWrCB6vRdSlu0vMGbzV5tafoA8mJfn4c3YDLwwm5sFTzGreoSdYIZ2HVihRs5SSI6D05J5KPVNOaftOhS0N1NBMVspgpThZEH4gXW9zhFJwmPF+hSkdqh1v1G7dsYFZJq3k0mMv7XiqRMTEMYyKplBggTUqyMVz/9Av2v3gmsrxBYHUqJSFiI/wbyOgUyVFgTmEIEAI4JxwKIPgBY+zt9boxQgqjWk+2IxQkpFsDxJSz/I4QKapScOdaQWlx1qKzFDuzUoL337UUZUExqcXcblpgZwJPVCO23ZSO6nhxWzG+VexQjGS7l23st807GW6NuZS5SRh4uZJq8SRRowJRThK05iQwsRTERC+lRPaJYdviCktxMGX1/BKtFPXBDFcV7C9W9NsO5yxsWsJqhz2Y4ncdrikp7x+gC8uw3tNeb8mjBwRKCUG9GxiMcAE0YGYVCiV4fB/E0GtaioZ8FCPCDHiVKOcT4epse9qvXhD/5b+i/l//M9zH7zOcr6gfiBa+8pHq0SExJrbrHbS9dApDwm86clVguoEQE9VH9+h7T7/ace/H75G7juf/3b+k+/o5xaN7TP+rfyL31Wr63ktn4PkF+59/Snm8RM8nRGvp+8jsZE633jN77z5FU6JGDX+y8HME2hcJIXL+1TnLB0uWDw+FixWkIHEjGDD4QDHKbKdBDFSLumC1XrM4WEoy3Q23/J7QCxlVyNFKXIELJ92osdqak5C5VWHp1nuSQqBdZXGrYjUMQToIgB+7Joo8YvnluayWU9IgJPOcMyFEjDVs9luur1Y8fPQQWznII78oiAS0LizBRyHibzpyDJQHM4Hkna7R05Lm/Xsv+TffjdUK3xY+qJeqYr9b1vP1/bz6+Vf2k1+GSnHf0T69ZHe9Y7va0lRSoFldbZhOKqw12MLRdQNqNMb0+568G7CzmjB4un1P6AZ0zsTTc9R2Q3nvACYTQtNQ3z9gfjJjv+/pYmRiLTZlri8u6TY7lkWDMoazb66ozs4xXUd6eI/6T95n+t6xdCONSA2HTcvVr55hz1fo62vpMp7M8Zs97nghCfP3HnN1saWaVRRZEk43bxiSePtkpUTkQQkUldJRLKcUTYmOidj5W1iqO5iQhkjX9jijydseM61ETtxHIVtPK6KG+mDGsNoRhkBeicISdUG83oki3bQSnpvWAifdiqM3pWW/6yhLiy0LmntL6USo127lGJ4Nlxv6651ArCaVCKys2tHUUgpGOSa8s9SzisnJEvQduNG3jiF1O17uwptSTLSXa4bLLWEINCdzitEz51s7Dt86TN+RQb+yOHwbRPB3/ow/2vd+H3ndu9sf0rn44yYXv2u7+fF3kpB854+3/+xxIrnbfXhr++plVvFtiQVI5tz+zWcM65by8RFmWmHvL6WVv2nxX58Tvj6j/MsfkTZ7cYK92EKMlJ88lMr9v/0N/usrgoX5P/6Y/b/5Fd3FmqKpaE+vsDEwKE3zoyc07x+T28j6519BiJjaUb13TPOT9ygfHcrCvusJZyvSMJDbHtNUpMsN9t6BtK9fXLMfIs4PlB8+IA0DPmea+wf48w1JQbze4fcdrnBUx3N05Sg/uC/me+uW/sszhtMr+l99Q7q6ROVIcI4Bw/TwkFwU7HYtlRJ4i9IJ5Rz6/gFh16POVqBgbzWlB98O2MMJs5+8T9aK8NU5u59/iS1L2tWK5sEB8//lP6A6mPHi//4vSOstpnDU04a90eS9l+BmXNRJmbzfk4xmfbUCp2kmFlvM5b2up+vl2pRKjK5UiuzajkZbsjF4q3E3lYdSzMjsjbpQ16OmjbiGZojjQDKzBkWmfXZKcTAjPj3Fh4CrxQVXF45kLEZrigfHDGeXDOstduTH4Bw4h2pK4XpkGEwWpRJj2WSRZl1MGpTW9DljtcJZgwea947AaQqtcbPq1tU6j5APVRZimrTpCIMXFSCrRS45S8U+5fyS7BakVT7oTDWV5KG/3pL7wP58zS4k7n/yADspMY3ICt+4BicfBYJGFgzsthPls5QFB+8cl//hU+JqT4oJGzNqbN/nMWEmCskVZwXrP0IF4o1/hRJ+Rbpx21bcBvaY0d1cKaJGlIVG/ozI2oIrC6KRqrDIL1dYNXY2nBECcFWw3u2ZKI05mJFLDbWlmjVYa8RgPUSKubTt49j9EjUZ4TX4tqeY1mirRfv/luclAU4cvIzL0RAQO2LnlRJJ2xtcM9IpuiWDKsgxkwYvCiZaPhdiRCd5vTiYkUJk2LUU0+YlGT5n+k1L/+JKBATudH9zTgxnK/z5iuLegUgtb1u6lCiDEIbNpCKNnZPq/pJ+8DBEykZkTHNKoDTDvqNcTCRxsQYKe2veFYGw2tA8PiH3XtT3rMY0FUPfC9yvkoQvXO1Yn65JPpJDZHpvSfVwKfDUUtOdbzj66AHOGZ7983+BKgsoCsz9E+aP72GsFcjZpKSoC3LMxHZAF4aURRp7d7Fl+dF9EZQYPGEQFTlXWnl2QqSPkc2zK0prsRnKwgqhddHcqtyBJAFp8CQf2a7WVLaQRIHE6ekZD+7fJxIxiFy3HoUIhIDuJOFWSnxphsD+eot2BmvEmDF56aaauuDsxXN6P7Db73ny6DFWGdr9nspKxyYOkf1uhzaKXdtiEty7/wBnRY3OTSu00iP0RRH6gaoWj50UIj5ETMoM25bmwQExRMLgiSRK49AjPyitWnZXGxbff4Sd1xKAfJdK6+uhwxj3337rTnIhU/K3JRt39/XmcV9NLuRvf7EWoYFuEI+jbUcGXFMSvBduWifFCobA5mLDbtujUhbPpJzQux1mGLBNQdpuwAfsJ+8TT46FI9Z5FHD/+49IOYkamdMYa+mvd7TrFr3ZM/SJ9adfcxBa0nZP2OwI9+6TP37C8uMH6MoRh8D1py8oL68pC0X1/n38bk/56Bh/tiJsdpTfe8LV6Ybp4RQ3KRh6L7LlyylD3xO3HW5W4692pPWe2Z99TxLHbsCVjjyIKaQCUhqluQuBZ2MN8XILOQvkqw+YwpLI6LKQAtJ+wBuFnVTYwtF/fX4ruKFrRxgCri6kMKIU2kcxKHUWNykFWupuRCNuxtHL2CyFyP7FlZhqlmJCq7QYp/rVXgRDQsLUjnI5pTyavVRReqPM/m0J6Zt1+zQEtl+dowpLSpn6ZE7RlG8db3/U7dt2fyvMoN58fu5+9/XE4fXH5duieDUmW/B7Jzr/RWFRv18P9bV/852L+o493bx2I3x3FwP9ds/OO7t/x0VXRqPvLymmFWnXomtxUY0+EPY9sR+kKvb0Aj2tyNaSDZQfPsQsJlz+9/+J9HxN7nuO/09/weoXT0mbjmoxw693WKPBOKbvnVAez/BfXhCvdpASzZ+9z+IffYwdFzUyxHUkblqGZ5fk6y3lj5+g24C5f0CMifC1yMfa6HHHM9Jqx673mN6ze75ivd1TjbKN7t6S6nAqOOFqXDBDQjcF1eNjmh88Zv/RQ/KzS4a/+wqnDYX3KB8JtUVfXZCGnnR0X0xulCX+8hnsO2xM9G1HaTSpcJQfP8I5QzGtKH/wEPWT9/BfvhBX7mFg9YvPWP7TH+PeP6a4v2Tz5TPU+/e5RFHtBdaTERlYtCYPXozxup7KGuxyQWhbCBtMPRHStDWYlNhdXlBai64bUcQZK246JjG2S4lqMSNnGNZbovcYa/HrLcWkJmUlnhWDFyLoJ0/wF9fU947YXa5xKaNnU6IxhH1LsxAX7rxrwTm63ZYCwfUa58RocBBpV0qLXe9IKdOqhFlOsGMFMaVMMfo1UFgm80bcp6/3DHUhvAejcXWBbkqBgRktGNvCUhlDGgLZKkKK5P3A5npNVZT41Y6sxPDOzRvcfkCnTOiF4B8LT2M0s8JJK7j1o0a/wu93Qi62IrErRngat5ygJyK5OVzvsI3j/n/9Y1afndJ+eY6+2JELO3oVaOn2ZYijb4UhvlSDSmn0fYgiAT1eh+ilQ4JS4sidRcXK5AzOkEMecfhiEngzC2StcLMaJgUxJKYf30ePqijZB6Zri/GBQWdcVVAdTgBFv+0wWuOWDWHXsc/iHl4dib9FHgJx17E7X7NZfcP8x0/oVztcU7J/diXcAKuZHM2ZPBI4yY0SjxnFCW6Un27MzHzbY8euixqJ36aQKqo/X+NOFiKVS8YaTdzsyUpRNBWhHxh6cRaumhpXF6jDGZtffD16DkAcIrpwWOdwD46Fp9IF8Y5Qo9FhTKTOo3TGFAZ/vRVPg8pJd8pZUowMV1u01myvRelJVzW0XgjQWovD9OGMoesxWhOdER+PzuMQnkz/7JqhcOxPN3S7DpDFfb/a873Hh3TR053vRJrbana//By6nvK9x8RmwuTekhwTL37xW/rnV5z8sx9STkqM+/9S91+/tqb5fSf2ecIbV9z57JMqVze7qnM3KYYm2ZKGkkaaEQQNdGFdDHxnwzYM+9K+MAz/F4JhYDAej0YzGshDUQIlkmIPc+xudqxcdapO3HmFNz7BF79377NPqq5mtzDwC1SdvdZ617vSE37hG4YuWgj0VYtbNcz3N2CQpVYAXU/oevo+xSpFrDsSYD4pwQgmXGmFylPMSORaZQOKhFqq2EqJbn40AjVLrOXK/hWUgva4oigKIBLOE2MXcLGXrmXXs15XpEokbHWa0DQtf/RHf8B3vvcdvvrFrzLbmvMXf/WXfObzn+fByX1u3fqAb33v27Te8YXXPsvxyTHzyYw33n6TL332i2xtbbMxnXNwdMhbH73Dd7/3XVZVxSvPPc9zL73E5z7zORIXqZueo3c+YBI0fj6lfu8Oe7/0uSEYlDnjGk+xOcJow+ruMWliqB+c0J6tGe9vUL6wd+F78OzjYdLw2K475NdDePm0izwSJD1tg74MgThPKs5PHxTN7h2LceU4J6xq4slafqftCUWeUp0GVOehEfPVdec5PVySpJY8URQnZ8TVCm2McCydJ87ndNMp6Y0diiLFeU+clyjnaRdrsitzVGrJxgWhd4wnJfZ4SRUCXbeiLzLqaCj3tomLJUnb446OOT1b4aylnBWUriUqh/Ngd2a0xwsxrstzumhY3z9jfmMbFUWuORvWxPZogR4JrNikg1nnlU2RVS4zjNF0BwuCUfgIxgeRa040XdMSWkcxHmKO1EgRY5SDFriqSiz9spZ5teygc3ij8akVqN9ZTag6cbhf1CSbY7oBZlrMxyRFRjorL9T7zjsH58WVczGN+ngpHBGtxdyv6xkVOWHgtqgIzrWScEyKR00af2QZ/PK4efi8i5qONdhxLvO1d7SrWoj3F1yITwq9+eRHHMbyM0vnz+iIPxENP/70H3X78Yc/bjI/5aV+GlCpn4KJnvz/R7esPv54xOTjkQ86JBNDJSU+BCp8bIJxcZlL2eDFmUqR7m+KbJkPuHWLrxrMKEdNCrTfoHrzNkmWEtoVfllRvLyPmYw4+1d/QjhawWxMSBXNoqZ94zbWe/qqpl1VJFphb+ySv3qN6o/eINQNXsHW3/8q5eeeF6KZQnDRq4bVBw9Y3TtBvfUh5d4G2d4m/Z1j4rolf3kfV2Z0R0vUqRhR9SuZ6NoYfIxM0wQ9nzB6bg8zzQedb4SkfbISPoY16GlBqFpGL+3D87t0exusv/FX+PkIRSRNLXY6IeoZvszpxwUozfrgmHxdo5KU6B3VIFc3fu0GLk/JX90XImyaMPuFn+HkX/8Jpvc064rudEG+rumOV3gtWvGJV8TWi1a2gti2GGPonRf5OiCxCdYH0SdvPZgeazSuqeg2N0j0FjrRsG7ItRk2z0jiAy2QWwvLNV3XUTcNmbHUTUM5nYprbt1i0oTeO7q7DwTu1Pd0RwuSUUF3tkJHBD4VxUQrOofKM5QxpJubuKYl9RFVVdg0g1FBRDCuHoXtelRmQRvyPCHmFoMEoDExaBfIxjnRKqItMQp81ZEWGSYbqqB2gBshFXq3bLCTjO5kjULRq8jt5QHHx8fsb+1xtlry0rWbjLwnzVOsUZiiwNcdrfKMt8Z0lZBss40R7eEClSZoY4aKrcjAigpAJDhHUwv+207FGBKlGF/bxBKpe09sxYzvfBUPMQgBVimCl6RRawXGECLoYS7q88r7YE4Vh4RCJeJa69peMPBxcFdX4lVxboJmEoveHpNMC+ykYPbKVfp1Q//OHXofCHlCHIu/gNOKdD5GuSCE3RhI52Pq+ycUG2NRNwqBftliBoWTfHPC6nBFdfsIrZVwmYqUiBgyFvORVMWXohGfYCWZrVvxYhhwwq4RhR6FbKoRgYoZq8UILrGYNEF5T+h6qaI3vfBMBilepTTRi7fE6mTJZGfG5HMvUH34AJY1IQQh8A8dQG2ksq4KSchDVUtgMsqJmUWPcnRiMGlCtJp0MJCLLpDORgJdW1SYLEUHcHWLzy1OeZSO4kqvLGqcE4NnvagYZTlme0LoPRbN+qTi5PCM6VRIz7UPzG9u05+u8EcrepKgTwABAABJREFU2rv3KTZLlqHFzCeUzz+HxzLdmGCzBDPKmVYdfndGWqR0pyvaSjq7wXnSnSkmy1h+dEA6KjCJoa9b1nVNPh3hVi1d3ZKkiZD+QyTOChG5yFNUovHnBY0Q6BdCSKXz1K4nUYZ2WWGzBNf0khx2jlEhXgDBRaJ6SNpPy0ISNmMGaWtFWLU4Ffno3m3+7DvfZLVe8T/+m9/g+o2r/I2v/QIvvfIy/+G3f4tJVrCztc3f+MLPkk9Kfuf3fpdFs+aVF1/iyvWr5CbhW9/7Nhsbm6RFzle+8GXqvuOrX/wyf/kXf8733/g+r9x8gSLJ2Lqxz+mt+8TQM35xn8ViyfrwATt7e3RtS4yweHDMZHNGsTnGVy3ljR0W79/noz9/g/KjQ/a//ArZ5uSi4/BwT46PxyIPd+NPABm5IHvH+OxQ7jHowflNX7X0q5rmaIGyhnx7Sn+yxjWOetmgg2NrZ4pvehG3WNQku3NWx7C+f4gdpex/7ibd997BZ4aYz2lMSj8qScqcpEiZTnOSLEGjsIUQtP06oFKNbzrcshIYsvNirJcafKIZ70zId6aEqqde1oQkJQ09JgRGVoQZTG7pJwXdZEymYXXa4Odz2lq6jtnmmBGgghTdVJDOiTEaNRZ1MVykqRrSnSn+bC3mkkcLkiKjU2ATS15kLE9OUatKOIaDx0PonBRSvfzdt714x0wLiY86hxmI8Haci2hGHzBW4/JElOqcJ0wLXJDkJykzip3Zk8HrkGSEXhIQnYh5ZKg76TgriM4xygdvpokk61prVJFQ7G1IEeBjxtInTQLU0EFznSOdj+hWDbqX58cLxbYfcb2nJsQ/+vV/VFz8xOOXmuPPRN78WPH2szqEl4PsR+97usj1j3/8VGBRf12I2COf83xtuvSZLhdFLi8zT88xH17kWbCop35dMdIcCp/CbIxRiaZ9/z71W7exRtFPR0xu7JA/f4XTv3ib5s/fxS+WJLubTH/+U6z+4l38wZmQVJ2nXtdMd+eMf+WzLH7/e/i2HyA0luv/p3+MnuQXb6T56JD2/hnBalTrMFWLSg0UKbFucc4JFrSPeALWWlwI2DITnfQio+l7cqWJD86IncduT+j7wOrdO4RVi2mkikuRsPHzP4OdjUhvbksFwwW6Dw/AR3zXoUeF4HPHOSbPLqqi1YeH3P3vfpfueIlZ1/i+IytyNv/p36Y5XHLl731ZJBcj4AMn/+bPOPidvyQ2DeWnn2f+uZc5+8Z3pJLrekxR0BPBWKksNh0Jkabr0ADOkWzOaKuGJM/w62ZQ5fGcrSvy+QRGBfm6JawrUaZQima1xBQF5XRK7HvR+j45pe5a8rzATiaiooHIoHZnCzSQFgWxFKUZ7xwsl7jRhDwXFZnuvJJZ12AT7KgQOAHQVzXpqCBJEtZE6R7NxhddioX3pJm0ictrm2AMjetZrJbsvnQds2zwVU/oeyFqDjyI/MoGegiyVWLluwtRCNBa06wrogusFksg8vZ773B4eMT+ZIu9q/tszOfYaSHk68SK23cqjvHrwwVFkZHMBSt8Xh0yueC/+1X9kNysGBSUJGlIBgK67x3d8ZLQOvqDBeu37kHrRFJVKdJEuhkqFU8J76QbErSSANoYdGYlCOidzFujZUOxZiCIg0qN+MZYK4vqILUZfMBslpSv7OFWNdl0JMnCvSMx8cszqrrFoOiPl8xfu0E2KaTrA9QnK+E+uIDOhPAf2x6TJ1SLir7pyacFbtliMgOdOJNrpWnqFqMUSZ6QbU1p6oYkT0WiekiKjBZeltLg6k7U4Ab+RThPlojiUTEQjkIvruc2T+mbDptaumUthMaBkF4/OMWtG+hERjOdlNSLNaHuITGYCDEEkVTtenwU1aB0wGon8xF6VpLNRnTrBmsNrnV0VUMxG+HWjSRFWguxuG0Ji5rgA03TsDw+JeaG/ZvXUVHIk6r1dFUj3jdaUx8uKcclp4dL+nVL3/UU45zp8zvgPV3VkaeK6v0PKF+5CUlCHzVJnlFsTjBlijaGblkJ36B32AHed46j9k1HXzWYzIqC37rB2gQ9qPpk2xPS+YToRInPLyrxoGg7xvOxKOv0PQkyv7quY3HvkDxJUb28Zu89i3bNuBxhk5Q8ywjei9lp72RsOUdSZngVpaK8bsFq7h8e8tHBHQplOVsvefeD93B1w9beHscHR5wenuBSKNKExWLJV17/Al/69OfolmvcOKFVnnpd8dGDOywWCz73+ufZmmxQqpQ6dswmMzQK+p7T0zMiUExHEBV5Jm7kq7MlWZbhU4HGzDbn0HshGDe9QAPbnlQrvA+EpaicLU6XJImhuLpFtjsjKfOLLuMTScFjUI1HaoSPn6/ON/JHk4ZnxQ4RGcvdyYrmoyO6RU26OyUZZUJOt1bQBq3wKRQKlSfQB9y9U9K9GTFNuP/mXbpFTbCayWYJdSMytGWOmhZkeSqFikkOA+eqWzXUVct4a0LsHGmZEpqevm7R1mKiKEZ5AsqDTg2u95hM1pR+UQu5GwhWE31EGymi2DKlP6vREbJJTgRMIR4sJoordTIp0GlCd7yUeb45QfViMNdXjexHVUu2M4NU4Jz9SuCJWZnJ95EnIseeSkFID/9G5yFCVzXUizVFmdMuKuxZI2Z3Gux8NEA3HXaUS5dh1WBLIa+nZU5S5iJ6oNUjsdoQVkkypB+qnNX3TnDrQXq+EYn8i3GlEH6aMXgF872Np3TF/pqHEgWpZllTzEZUZ2tc2wnUdNUyfXFP9sEfpeZ0MTDPq9XqJ3p7PzJFeUQi7RNc6Cd4L5cvdfkS/8uqRV36Vz1+5+XjEySe6hnPjZeBaMMCpp4YeE9rrz5699MSzhjh9E/egMM1ydaU4tV9uuMV6f4WOjVgLcnOnNVfvkv/vY9Eez5ERp+6Rreq6T66D50jJCJ7aq0lff4Ky2++zfrOAeXOHNN2sD2RxGE42ttHnH33Ful8hC4KiqsbdLcO6RaVEAOtQU+mTKelBHx1J4FDanHHC5KtKTq12N4TFhXrVYWxCe13P6S9f0pY1Wir8UoLBv54wcm//jNcotj8pddId+a40xW67Sl+4TNivuMFl3m+KDBk9OULu2z8zS/y1v/n37OdJUTvWK/WjO4ciSRlCKCM6FVnCRv/6VcJRnP6+9/DHy5ZvPkRbE4w65a4igOuXzwpvDEkRhN6J3KkzuGB+vZdnE0IZ0tsnuOsxVUNhfeY6Cm3JvQYYtMSmoauqbFAqkV73StFvVpL8mCtcAGCJwQjleO6lirMeExIEtyyQhuDKXLaqOiqNXog0CU2wYVIsrMl/AbviXmK7hxpkZNtzDBGU1Y1JJamamAIkrNUKu7BKJarmlRr0kHv+83vv8krL72IanuIBlsITCMpJThQRSpO8sPsak5WpFlC17bYPOPw8ABtFEmasrG5yWg2ZWM2Z6OYEK2iW1XEpiMbl+je0570uLMK4yPNuiGkhlC3nJ6d8fadD/jsp19nfmULlOiFh66XYD5KlcmcV9EzUaTJNib0J0uSa5tk04Ll3RPCusUcrQla4xIwHpQWvkrwQVTIIqihi6FygSSGvpfNpUhQLkImKljp9pT2eAloUaYyGjvOmL9yhXRrgmtasmlBdIHF7UPyUYbRimxzzGS2CwiZTwHt8ZJ0YyxjAUTVZG/2UA2mE537bFKQlzmrgwXWarqTJemwkYbW0Z1WjPY3cD6wfvcexbigOlxKiz1PiJlhPJ8MOFdNMi7wnUMrjfNidNesa5IkgVWL12CzhL7rhqQDtNXUVU1Wipuw3CkwhW4NFCl5llLXDW4wmUvmI3zvLhS7otbioh3FO6acjWQcj/MLv4bqbI2xVro3ZYbvHIvlCosi6x12mnN8ckbuNEkf2d7dRecJ/fFKqotK4/pWYI11T7dckQ3wiK0XdglNJ14CKrI+WZFNS+Y3NgldT/H8Dt26Y7kQB3FbJiI0ECL9qqarGvIil8QiF9OusKppj5eEuiMmBl/JOtUrqYX0RwtClGLD+XeAUZBZmaOZlaqfC8SmJyYJrq1p6hobFaHusEXG/cP7hBC4fXCXV597mTTJLrhQoXfoEIkaIpKIKK3oXSPk875jUS+5/txNkiShfeNtnrt2k+99/7u8/unXuPore5ycnfLrv/HrzCZTnr96g+2NLd649Q6nyzMm0yk39q4Bhud2bzB/dc7O9g79osbrSG5zApFklKFCyu5sjK9b7CjH+8Di5JTRaEShBP4y3d8hND2n3/mQdtUQlRJScwgooxhlCePnd2BagNXkmXRv3MmK7sEpxhjSvTnp5gSTWVCDd8wwhi4nGRdbbnwIjwptj7IapYcA7rHi4aMNDwlofdXiljXVyZKzkxX6tGJ8ZY6BYR1q8XUHVuMDqM5h0xQ1yqi+8yG26YmbY/rWERLFaGuMyRO0UdjtCcRAHGW4zuFjJJ8UdKuKpJB5fnq4EB5H01FsjEhGBUmR0a9rKRaESH+0lI5y10OaoKLHLxtIE9IiIxpFMgTLPkhH1iCw0+L6FjQ92gVsLvBokxu6dSMcyxjg/gnp7px0cyzdRCe8JUekrmtGm2NQCrdqMFaTTEsMkaTM0VMzQDIfBkuXfxuUIhnnF/BDm6ewA13bSXdVadJpJnuAtaSJJZ+Luli7qgS2lCaop4k4nScW6mGc5tueelGR5Sm2zCThUkpU/jon8Cwr3jXUrRRohu73T3zEiG+ddIC0IiszkkQ8h5zSLO+dMLm6xePQ+2cf6tFB+3hw/wmD/ac9dBmZ89duTvwEx0/xUj95cnF5gXha3tcvK4EIZOmz3/nHpXAXecXlV1IPs7rHHnqiM3v5OSpKthm5WORUjKgioz24TVjXVIsVVkEcZ2TljLzIOPytb9G/9RHlzja9VmTP7WKuzDn799+WKoAVeT+jNPlzW5Bqzr7zDihFf7IiTsdc+cdfQ51rpUepBqc7MzAam1rqN25jjWb+xZfQZYZvezG0q1pc79E+CEmsdpgyo/3gAe7+Ge5oRV01sFoxv3lF1B9CxCrou54+CIbbWovrnbhQVz2rH9yiv3dKrBpO7x6SX93G3TkSlRkvzsKT156jeH6XdHPC/LWbvPT3f4EPfvNPmRiNDob+7jF7/+RXiFWHKrOHWvBasfH1z1O+fJWzf/tn1G/eEg+JTNSr7MCLSJTCdx0kCU4rbJZSNdKlUNMphfMioeg99B3Ge2LXUNeKjS+8hPudvxKuhRMoT1CK9ckJtmowWUbX91LN9IrOB0LdUiCGaqFphSwaRQ7YOScu5d6js5xUS/XW+YDRgb6qWNYVkywTH48YcTGg85TeBwnw8ozeGoL3WK2po6dMElQjSklKKwk8r27jlyX33niDZDaiPl1RjHKKrQlmMF5Da/rTNURxBiZLiKkoKLmqIfSGo4MjQtdz5/49eu/41a/9MkmWcnT/kA9vfcj25hbaapJ6SbOu2NjYZJSXMumrjurghHI0YmM8pUwLfucPfhcXAp/61Kvk45Kf+ezrGB+JWirS0Qs293w66dSSXdmQ23sbZDd3qO+fihRsmhBByLi95+zte5ja49e1mD9qaeGHQR1EOYcuM4pPXUWFiB205XWZki2lyqe0ls1MKSGgdw4zHQnheIBJYZSQrEMg9l6mewh0xyI8ETtH0AHtw1DBi1T3TsQ1ucxwS3l/zntC02EmucjfGk2sO2KMpImhWdVMb2wLKThPMJOc5rSiP1mRTgpaJbyXEL34aoSI82HoZmjycSnSuVbTLdaglUgWh8EEDIXyIlO9ODxDK8V4Y8JoY0LfdUQUt9+/w2g2YbQxJh0VtFVL33bk05JiMqKvW+k2do5kc0Kxv4kfKpyLW4f4k4X4gmxM0EqMwYJVTKZjmmXF6ekp6lS+v2Q0FuI5EDohC+dBCK5JLjyhVinSuQgmuKon1+CsJnEOnxrmz+/Q3HvAybdvs/mV12lOKwBGu1OCj0y2ZigU3clSpHa3prT3TkQp58EZoW5lfUvtkDyIWo7JEtJxjs4yUmsorfB9ovOi6jT4RwTvcd5hk0QKIZ3HNY5oNHmaERys1yt8NJx0Favlgheef5HpxoZ8P0NVu21FsUuMH2UMx3OSrILT0xN2r+/jvefO+7fY3d7h7ZNTJqMJ169e4/T0hO/84Lu8+KlX+eznPsdbb73JB/fv8Ny1G+xfv87W5iaTzTnBBQ7evkNYetbuWMQOEkNmE7KRcG8IEsA7Jx05ek9bN4yynGxrSjIrccua5Xc+pPIRPUoYTTNMNkdrQ+w8i/unnHxwwOzlKyRpQrYryl9+3RJipDpcEA4W1IdLlBdVOlWk+GlG7R07N/dFupgoRpxeuiNKKwhg8mQg5T7asYg+4KuW5sEpIUZMmYl60/GSvMwx1rKqWmJiGb+8TzmTxNPVHTpNMGOLTizpjqF/7wFV25O6IAlHkVAt1rBu2Cpz9CgT75xJIUnRoKaYRkVXdyxOljSLmu39hJjk2HmJ9pFqURO1IhuX4iKtFMXmVApxrUcdLjCTksXxiva0whvFeHtKs2poljXl9gS0It+dMbkyp1+1RCVyws3hkvXxCXksSBJDbDuUViSjAhUh+5mbKKvFWb4TmW53VmFyy6gsadsW2/R03pOXGeVMIJaXk4nH/5BEcCDWD+dpa8i3pgBkUbin5wIX574gYZB4V0Y6jKKMd6lge/kYpMcFjgTduqE5WWKtEfXLXrrb0QeU8/i+R2WpCBQMHiPOCa9NDCSfHfJ+UhWkdFqIWp8PAglbVHTOExJLUzec1+f/WvD+i/jzaVnzj3m98/CW83D1HK3zk3dvfkKU0499/HSdOh4/FNhR/uzHn/phH0tR1Hnd9tEWUbzUXr1UDDl/2Ys/Hg7+x15suNkdL+neuE0yykle2EUXGb7tMDtTTFAsv/U+qx+8T7dc0jpHNp8z+vyLVH/8JsYFYllS1y3KedSoIH/9OU5//69IrcGWBavlmvlnbpBd25YK7XlgNR8xRjL6UHckexuoEFl/9xbth4d0d46IVQutcCuCUugt4VW0Hx6x/sGti09qYsABnQ/o3Sm2bmlOpYKnUPRE0iLHDu7I7Xdu0Z2coZJEoEDre1Q/vIevG2ofKPOMcPeEsx9+yMGkYONnX2XjF15j+299nvV6zd1//UdMXM/q8JhtKxWQ0PYor4XwqRU6S8hevMLOf/mfcPw//RHrd+7DqhHn08TSG41vGhKFkNdCpA1BgrcY8XVDGyI2SaDrcE2NNhbvepqPzoh45l//LCe//ie0Ckya4b3H9yJFa8qS1BiMsfhKpCW9F25AHxw+sRdqKqGVoFEM3RRxqMq4EDGjQmRtp1O2rRWYSN+Tl4UYjhkjuvIhiEGbUixXC/wsZ2d3B3e6ory2IT4ISpHtzmCc4+sGExJ89DAp0GUO04KYWGLb0/mARYy/fIjYxFBOSugda9dw9/4BxhpeefnTvPblz0sVKYL3gWI2phgVvPPBB9y8cpU//tafo0Lkxu41PvXSy8wmE3GXdo7jo2P+9Iff5iuf+jz37j/g1q23maYj/tW/+3X+7//X/xtX9q9gRpl00hJLCAFzzhlSl7rDUQyoRjd3ZHr1nvbuMfSOZGfGzuYEv25oT1a4RU2zqOjPGkwQTwqVJ2QvbFFsTzCFVKlNltBXDeP9TTEJM1KNO3d0Fe3zKEpmWpFsCGG7X9U0ywq9bkiKTMjg2VD5bjrxBikS4irSHJxR7M4GE8ZAN8lpjpcYpZjuzeirFh+FhI/W6AjFlTmhc3QHCxkvPhK6Dq3BTArG+xsEH6junchr55a0LAQOpSWIj86DF0fuYjYWdbAga1zwQvq2gyTjeD4Wo7a6lQ5FmVGUJap3rI9WzHY30UbI3+ddXmU0+XQkktSI54zvHe3pmmZZE7MElySQGKY3dkQRqWrQIdD1HWmSYM2Yw4MHrKuG0mYkowLXOqqTFbPdGYkagnhraCupeK6HxDrmlmA02UZBXK5JM8XyB2/TFyNCOWH1YIEdZRRDJ0kbja9agjWk21NC08uagmL97j0pHOWJBKDek4xSks2JeKH4SNc0NKuK0eYUU2R0yxo7GAmeY7e1NiTKEqoGXWSYIsM3ncDAlIJEVMT++A//gFW95jM/8xo7O7sk1hKdp6tbNFqkgxXE4IhWk41z1icL7t65y0dH99i+usfx7RU3r99AJYbf+sZvE/qez772Oe4ePeBkcQppwtbGFhvTGV/90s/i2w6r5X0mZY7JUtqTJdkoJS8EguLqDgyk45xiYzK4P/eEzlFsz6XLGWHnyi7aitki6xZXNSjnCI2n3B0T7h9QfPoFgTe2LbPtKWf3Tjj8/kcQIckT0s0Ro2nJqq6x05x8Y4JRWrh/PnB2vCAuFhTzMf39wT8gRlxusUXK+nhBlmYk2rC6d8T0+T2SSSlBsla43nH24QHWi/mm6x2Ta1tYrSk3p6AU927dx3rY2J2JGlGZ09w5FiWjUY4iCmm57VGjjL5uUCcryBMJUOuO9OomusyIqaUoUuh7Id83LXouHYnl+/fQdcf2ta0L9SBjNF3XkSdWTPWUSA0ToVtUst6Nc0zdEa0h6T0qS6hjYPLSLiax+LojmZb0y4b7f/wW/f2FQLvGGSYR76Q0twQ8sRCPmUxpklkJIdAu1ug+0BFxmSFLM8zmmH5VD7wqiy4TkhgoNqbi88SzwtnL9z7KW724d0g4TGoxiQEU2mpc00uRS+uLru+5IlTfO/FGGiBwwtfT5/xtbv/wPVIseZZKEaYQCJr3omwXvcdmqbiKD9dJilQEQH5ah5KeBJ1HFQ8NFn3V4ntZh+NQ+LnMN/hEAb167EZ8MhL9hGCr4RlDN1BJF0P+/ml0bz7hm/gpJiA/5eTikqwWyF+XZcQeOfPS3Y//QDx6++FPdI7ffAiTUpdvPmXGnA+TJy8vA6G9c0JsHXp7Qr6/Rdc0FPsz/L0zqrfuwbpBNw3j63v4pmf6ylW6jw7pj5d0Z0tMlpHlGdFA+Qufpn9wSjipSG/u0949IJmVbP6tL4BWuLMKvxYylgQABhV7urOK8NEx9Tv3oO5EqtB7XF2jQhT8eNuR1g3Z1hQzLYjei3N0kEloFFRvfkS2O8MdL1FeWq6184zGJcF5tJYFrasa2QjaTjTzW3ksak2hFH3fo40mTVLSxnPym38Bi5qtf/g32PvSK7Tf+BbrB2v8D97Cf3QEr4+FKBai4J97gTZl0xI2Rmz+418i/Ks/Zvnd9/BNizs9I0Zo+x41HaNGBf1ihSaSDG7PHlnAmqYB32NjxLlOXJi9J5ytUcVYqqRZLuZ51pDoDeg7ei+YXKM1vdbSxVAaHwN2PBLDwTQRZ+4hYI7Bo9OUDki0Js8sAYhpQpql1GdLUmuJWrPqBqfiNKHvHZ3VqODp8hQ/LXHKQdNjXeRssWJ6dZt0WqKKhNgJrOL1r7xK961vE7b2UFfm2DzBFrkQmlc1/UAMToaqQ9922KHNfuud93jl+vOEVYPOU9anCwk4XWBsU3Y3tkTT3rXszDZ58/13mJYTTk5lvJejkoku6KPn2s3rmI2CX/rZn2M2H/Nf/Yv/li9/+rP88C+/zegXS2ZaCHthUGx61lp33laWboshv7lDDsQYiJ0nxkBqpyRZwuyLL+B7jz9ZCTxpcFjWduCZpAm+aUnPscI9FwmFzlPaowXpROBQCuGLqCG5U1bcckUiVoPRLA9OSBwkRYa3YKqAVgozqHD1TSf8mqMFeZbieif66yGIs/a4oFtW4sodIslsRPBeFFK0xq1q7KigXzcs33sgSd6VOdmk4OzWIU0icKHGCYyGzkMIOBWhEX+DyY1tklFOdbZCRcjnI+EV5OmFupTvHeONKaH3bDx3hdleJwpVnZOOTd3hQhAugo+oMgWkUtlXLdoa5jd3RKlqtUmzWIPR1MdL8s0xoRFFGNcsSLKU+WTO9m5Ke7Ri2fQslhVXr+2Qz0dSxdwYU7//gMSIG/A4RrpVQzYfkc1KuqMzuqajO1litjYZbc3JiwwQLLq14sgdfRB1GCcFBr8U3fvmbE1ILelsRFJIEKKGLoLWAkFK84QsEx+H6Ly4B3c9NrHCiVCpdLGcFyPTricu12KklQjWPahI37TcPz7gt3/vP/DSq6+yMZljtcBEvQ/C7bLS0VysF9y6/REv3HiOs3pF2zRsP3+V5z//aQ7v3OOtd97idoQP33qHgwcP2NnZ5vDshI7AzsY2r7/0aa49d0PWd61RkzH0wlmyaSKwotYxnk8lkFaQzUbij1Fk4kK8qDg4OGb35hX6szXN0ZLx/gZ+gJgs/vh9/L1j7KduMn5um+zBgpO7p1z94iuyoPiIMgrlHNs3dnBVCwHqqmF9+4T2aEXf9uAdserIZiOynQnN8ZL583voGOmajmpRiZGcC2RZSrdsMEbW02RaMn7hCs2qxtcdLkTioqLrHOXujKSU5P/u924R7x4z3dtAeemIbWzPUQO+nyhE5jhKqdsO7hzRNS3luBySLM9kd067rHFKkWrF6PomjDJRjeoEsotNOL57QJIldO8/oNzfxC0q5nsbZHkqlf8QGI1LZvtbotqXJcQQxX27bukq6Uqk05JkXqJbR6cVDRHb9Jx96wOSK3Pas4pyS3h+1nn84ZI00eSpwezK73peSEmyVNafZUWoWkyRkm1OhWd1tMDmKTpN6Z2jbTuMC5S7G/TrhvHODG3tj4gdnw4PuVzQjmEYD+qilItSwr26fP55EhDhwsdFHjyHC0V872kWlcCmEy0+QkFc5MXTyJMWGf3BGTFJQAuPzuapeH6MRYQkZgkmEU7cU/ecTxJ4D8VnPco4ePcW9dGCULWkRro82WyMq1vSSXnxhL9WQP9kMMvlex6F8z/6/p44+emXeupzL/KGx89/PKH4/9fOxSNB/DO+oMvD+6ldmo+BRz37e1GXzn/KWecPn3c34sNMJPpA/cM7hBgpX3sO37aUexus37xD9advMP3Zn2H1zbdJNibYCEmRk13f4uDX/4i4brGjUkzaMsv4qy9j8pSD//Bt0p05scwI2rDz93+ObG8DkIDZbk1QiSVUUm3t3ntA9f59cmUElz5Ugft1hQkB14tKUhoC9XKBf+cOWZZKOxGF6zqyNCU6hw+esGjpm04WU+9JfEC3LW4wkNNKqjI+IsohusQoTd+1IifpAz3xQtEqtB2h6Vh9cI+tGEk3p4yubFIfn9Ktag5/4w8oXr6KyVOilgmsybBR4BQKhRnn7P6TX2L2iz/D0W9/i+6D+yzvHVAAse2pu1NsYolK4/seGBSFmgaDSOu584ruoM/e3Tlm+ndfwezMsbca6dL0kTTLIEmhLAhKgfc4a0gC+L5DlwV93eGb9gLj6TuHTgtC3+N9EGJqll04TtvBV8Hm+ZCTRk5WZ5jpmC2dklhL4h2HoSXpPZPZlLTrUYsGPSuYbo8Y78/R1tI1PcbAaFqyvHNAt7nHyWrN1ChMluKNgt5Jh2BwlE1KwcibIsVkCdNugxdffYW9nT30uKDpOj788EOK8Yi6rvj2t75FcJGvfennyMqc20f3+dRLr/LS9ZtM85E4yPso8rTLis+//BnWTU2qDa/s3eD/8X/+v/DGe29zfHjI2f0jZttzmpOltM6z5LFJKrM+hiiVvQFOptTDUxSGmBuy69sQI25RibOxAjsvKV7YvagTKQWhdRCDdExG+VBh7QlNJwmJD+Rb04tO0UOZSvlXZ3ZQq3q4IpQKdOfpT9condAr6DWkhQTu9dmaNLECTXKevnekmUC7LNJhbL2HlSQGkzLFdT2sxAciGeX4ztFXLemWSDOu7hyzun/K5itXxcxyVYtpVjoS7wzArxrcWUVzsqZb1OSbE8qtCbEP4v4+8HNijKJ61fXUywXl1lSqm0dLurjAWJGRTbenmF74Mb5rxVgzlUpuOpZuG94TgvgjFHbC2Zt3qU9XLB+cMtqbErrAydkpG9MpyhjW909pXeB7dz/gSj6jWY4YDR3ps9Ml0UdK59EbY/S6I0ssat3RdI7Vuma8OWO6M8cUqRAnAbyXsXL+w1lz4aAeOocqUmLbYacFsepwZ2vioqY9WpJsjIiFBCRFlgmEpx8CF61oV+Ka7Z2TrnbTDTDwSLOqyCcFRuuL8eOdE28X7/j+977H9u4uf/8f/GdMVYFvhC/QNg3v3nqfl155GRc8ZJbr+9dZ1GtUbnnxZ14hxMjtW7d48OAebdtx79Ztvvzln+Xnf/4XMYllc2+X4ILAhLWS4pKC4GXurE6WpKnFrRru3rnL3ks3KcalSAgPMD/VO5xvMGWGHReUJwlUHQE4euMj8QbanlIv1pSv3SR5/TncsqX3nmxvBndPOPrBHTZe2CErEoKG6jtvUbx8E20TmvfvYpRipEWqOEsS1k1PtXzAyhrSK1NG28K9UD6SWT2oGAXsKEUX8nvk2UiMKmMkUYqYp/Sdo5iWhCxBn60xVtO3HVmSsLkxxk4KfNsNW3TEKQleVWJomw7deLSRoqAtMow26CLFt45kktMua4rNMem0AKXE9yEE6qqiOq2IJyvMuBBDVaNxXY9e1mzsbRLrjmp5jMoSTGRIaEvhQKwb1oO5ZTXM1XwsrtFndcPu7gbjpiVdNbTTgjSCqjr88ZLFyYp0WpLuTCAzpKOcdGuKGWXYIgUfCacrSBP60zXd0ZLgPdNPXce1Av9K52NQ0NctsWopi2yA+iXYUrrKxHjBM3pkef6YsOnxcElpRfQetLmA5nC+Jg/CCnqAdUbnxfvCGjGyPfchCpFuUdG3HaGTrkC5WUp30iYXioQi+d9j9+a4qhVn+SyRseQD/bISHpcdOo8/BVSQd46Pvvcm13auooKIRjQfHVIf12y8cuPh13b5xR4J0B8vnj/tuPSEx0E45/d97PHwST8WFOppp/6439nl+PunkIj8VAjdz34vj977RE/iiW7Gk/iypzlzn+sPPIrgfOpLPgqLig9/9EgUJ8uzFdnWmLZuSa1h8Udv0t87xaUpfdvRrSu0j3SnJ+i9DfoowZIaFcQsFSz0z71Kujnm5N99UybJzoz6nbtMfu5TTL/8ykWWn45zlNXEztHeOqB66y79D26D1ixDwALGGnTX4hToXtST1qs1RmsMUCSK9Z0DrLFoAkZr2qrCGoNSgWaxJADee3TfE5WibRpiIpMpuB6d5VLtJRLrRvCuEXqrCc5hQhD32TSFpiZ0Dd2Hd3EnK+z2jOKl68wP1tQ2pXnzI+7++h+y/w9/SbSkjXkYVJqH1QaVJuTP73Hln36dsKg5/t1vsfqLN/G1E7ywa0lmY7q+x7cdSYwkSYJrG6nah4DxnqAUaVZQvX0HVaZk+3OW73yIaxry0RhvE3TfQd/htSHJMjasJTQNNalgSY0my1KpRsYoDtuphbqGsriougWv0UVOV7dSvbEaZS02BMyoIDMJMUvoe09MEyZBXKZLpWlCFJWWScLeK9fQSuEWFYm1BA3F1ph8khMUjNdr8azwYTBiE0hQPCcBloJxtZOC2HvyPOe1r3yB2PUE52naVtzmW89fffe7NFVNUY54/713yWdjtuabvPXBO4yLgslehjGpGCqtG7JJjvGBtA1o79jY2YYQ2Z7MOTk45o/+4k/ZvLZLlmesbx8xffnqBd728nwLXS/BkrkU7PNwbbgI9JXCzkYks9FFF13maRyEBATCBI9WY5JJIbCZqhWDyKFi9kgd4+JaDwsO54/nk1IShVlJe7ZGt72ogYV4odLkOyc4c0QJhkwJHyREjNK4tWO6N0PnCauTlSgwoXAhUr97H50Y9EgSUJMlzF+8Qne8YvHGHUbPbaN8pFlU5Ftj6rtr1kcL6AUvXdUt414q1DZNCTbQ1x1JmhC8E5Uzazh9cEK/bJhe36ZfVOgylbHZOXRn6M4q2lWNtYa2EWWb6fXtCxdxk6f4SuAzSZYQjWb24h7+TfHk8G1PXuRMklyceZUh35mhTtf87Jc+z+nZgkXVoOs19emadDwizRJ8mYnM9DgjLXN0kVLkGeMY0IMiljKa0HacG1KoocqprBgMKqvpT1as75+Q7Yhr+mg8/O7D2tgfr2gPFuLHMkrI5oOZptIYH/AKgYc5j2t7qVCvRHErIopK0UmHAKNpuk4QUXlGOc4Zj0a8+NwLVFVFWhgmWlS99Djj1S++jkks89GIxckpfdezPS4xxnL71od89y++hTaana0dbu5f59rNG+RZTjou8ESB6D2+Cwbhc/WLSqRN85TqdMn2lSskxoinStsJVDNL6I9WmO0JJpNCw8Zzu6iowGh2Pvc82WxEDJFsXFCfVZCnZJOCflmzXFZsv36T6s4Jp+/cZ3Rzm/nzV1FKs/rmD0mu7dC6muzKFumoYP17f0lwkHYe03m8Tajey2n3tih3ZqRbE/L9OclM+ENRyxarrRETwcFHR2cWoxT5xoTmbI2KkdHze5z7ivR1Rzof4YMUPNpFRThd09w+JIwKmklBMR/RVS2984z3ZmAMaWbBB7oYSKwhn5boPCHJStr7ZzTHK+oYyTfHWK3FL6LuGE9KTCaGmjoE2qqFVcPRwSk9io3NMZOdGX4l8vTBeazzwoEKkI1ztl/Yoz1ds70xIZkUhGtb9LePKLwowWXTkvGrV6TraLTwqzpHe7yU7qvWhEZELAIQB36lOl1TfuY69emS2Pay9zUdauDyaRdwIUqXD+nSfrLjKRXfoVB2MRQHuGZUYsSnrb5Yd+KwfoQIIfRSTBqU04L3dE2Hr3uZVwqqusVaw2gywtWtiDIYjULRV40YzI7ziy4GIeCWNevTJekoI59NBzjjT5hVXPrMSZ7x2q99jfrBKauPDgina7L5iPzaFmbopj6SVZ0f8ZF/fuTrPPHcH6t7oB6LedWzux2K80VUinPPCsY/YQfkE5/7CY+fGqH7WbeBZ7d9Lj8cH/tmLmS4Hv+21MVz1KXb5+f86A7H0GOJ4A4XnL71Hvv/8GuYMseOc/pvvkd6ZZPugzus/ui7xL5D2ZS6rtgYXWHx3Q8IA3nY+kDx+efJX9zjwf/w+3QHJ2T7O3RnNXpjzNavfBYiokE/yFwqFCQWuz2l/eM3BeddNcQBBmW1JrYNJjh0mtH3Mll1jJg0o/noAANScRt8CFzfEUxOrGpskkoApzUuRoLrRaUjBIxNsNbQOydV/aalbypMmuOtoV93uBjJipF0Bzoh9CnnqB4sOfv+B2z98ufon98mfOc98vE1fNfT/tnbnO7vsPGzn3r4yzzys8SLjpHOEsxeyt4/+RUmX3qF+//iG/jbB0TnaY7PWNdrpkVOcA6vFa0xZFEI6pWLpEqhtKGvOtHM1pAmFqNHJEmCzjO8gn69ppxviKHXek3vHIwE09o7J2oYSULrBSqB1tjNDXn33tN0PXZUQJ6J2Z5z9KMcvW65Vy9IIszLnKg0fSFSsfgowWDVMrqxTXFzWyrUgzxrMsrQeYqdj6SLNeBas3qMHkQBFien5MqgoxrUTbQQCTMrmNfEMNqeXbjS4gNpl7F14wqjmPCfpL/ID2+9x9HRId9854d8/Zd/hXpdgVbMtzYw04K0HGERydmwavFKTMJCnpAkCaH3vHDtBqlJ+OPvf4sHDx7w0qdeEa+MowXZ5uQiiTzXENeFaKATgvhQXJ7NT8F7PtEiVkqwffHRc87/CAPm3STmkgPsM2b6x3RL1UBeDG2PXzXEENEWprsbdGuRY12dVXRna5ZnFQqY7kjHJun6i6C4r1rSqYGmhyKleG4Ht2qIrUMZMeJr1g3lbIQeZ7iFOJonowxfd+SbY8b7G3R1Sz4t2QiRbt0ITj4ikrA+EDfGgg+uO7yCPEtRnWN575hmWTHanBGA9bJifedU4AhtRzkbsXl1k/5kwYPvvk86H7H50lW8E6+Lc7z+OUl746U9MAZft2itWPuWtHGkNmVxdMa4j2QdTJOMdlMz395gfnUHMySURDi7fyrduUrgbLkWmVc3JOcKxPuhdaK5r5Tgy5E1khhxMZJvz8g2JuKSvhbltbhu6NaN+FJYI2pji47aNqDAx45RKq7CXd2QGCuGmplA2nrnaZcrdJpQbkxpm4amroltj0sU//bf/SZf+epXmUynfOWLv8T2lT26phU4mjUkqayrMXgWZ2eUkzFt07A6XeCbjs3xnF/+2i+TaAPGiFx4kV0UWJ620UYfBF5b1dhxwXRIiibXd9CJxa0b4roiOE9xfZv+eCWk8mxQ6YmKZFxejPH5C1dkP2h60kIMIZcPzoQY6yNFmlKfrEh3J8yLhOXtI05jZHpth429DXSaMPrMiyijCJ2nOF7g7h4yeu1FVt/4JvGt9ynrBv9DRT+e0l+9xvLqFfKbO0xf3Zd2sw94FzBGYzfG0hVynn4lkGBbpOT7GxcwPq8VITF0Z2vILLlJKTYn9GlCMi44uXtMmieQJYynJb5qScuCeLJGTzL0dEyiFGHV0HciVvDggwdUhwumiSWWGUe37pPZlD54JltTprtTbJZweusBi6ohtylHp0u8itgsI9+bo10grBoR09CK0b4oBdpjUZVr756Q5KkYz1lNUubMX7kq66HzklRcNoBLBP7nW4dKOkLf03SO0eYYYw1+UdOfrAiZpT48k06EC6g8IZ2NMFbkW02e4ZYVvm4Jo5wYw6OqSk8LZB9ZLONFwTWGQLeq8Z2TgtqwR9sslQ5RiLSna5lf61biFyNqV9Za8QhTjqigXdSUk4KQSbd9c1ygEwNDUSGiCJ3M+37dkG5PKTYm1A9O0Sj6dUN9tCCZluSbP+3EYvgaIuRlSfZcwWhvk7vfepM79+/z2kuvf6Kg+uPez1O2uKecEy+4KA/PffJZPx7X4yndqssh8yf9Cj9RIP/jHT85LOqRD/F4S+dpfYcnj0eTBPXEvU8mEpfvf7I78kgqoi49/xwaNWSHq7fvkT1/A7s1E0fjaUF5cwf37n1M3xO1bHZxsaQYFZgkx987GTzGFNnNbaa//BrLP/g+3e1DdFmI1GbbMf97X6I9WmJ6J4vD+WIzfAQ9KRh98UWqg2+SdBD7nrZpqPoea4xAmhIxg+tCILadtIMTgXSEpsaaBGs00WlRUrIW+k4qn2lGGgJ91VN3HWVR0HknbU+lSGwiCkaUopqgZDBk2khlTxsMUrG1SYJvG47/528x/eyL7H35ZzheOZZ/8D3cyqGqmtN/82eEpmPrl18fcKvxokIZgyhQnGtin/9Q5StXee7/+I9oPjrg4Nf/kP7WIUXf0p4eYmdb+L4nVZAZSxVlczRa03YdydaEfl1TvfeApCzxyxXGWtq2Q6EwSULbteSTiUjchgBJIrr3CoxRkjgp2RO7wdTMJAk6IhKSizV6IN3GLEP3QXgi1jKfbRLzlGA0QUVc8ORbI3SaMP3sTZJ5Saw6tPPo1KDzBDMqUImRMXiyQm1NBALX9SzuHUCE0XRMOhvTr2vsKKdZrMnGBX5RY2elBPBak44Kzkv/Jk+5UUpl1u1t8oufeV4MkLQiTRNOFwsmN/co84Lbx8dcnxZUXcW1F/bBi2+KMprlu3fxixo9LchMwdnilMXpCe+8+RbznU02tjZp7gscLptKtTIZ52J+N3QbLtQ7Ls/iS/tehAuZQpQiNB1h3aDKXGAUF6oy6pGuRnu6gtahxvkT++ePuw4qJMnVqWyQREl+i80J0Xmm1jCa5AQf6Za16NmvG1Kt0S6Cjcy2Z0JWz6wkFNagsoRYJCRpItU+BMoAkIwLqYJ6LxCSxBJ6JzLMbY9vOmh6ulUtwfd5tf6sRo1SksTivHCjUmNwi5rcWlTdkeRjpttzJpszfN3inBeitDV004L27dvEVcXi3gnl1kSSAbiA2iRZgu971sdL0iLF5Dkb8xlmKr4cW7kFJepzPhGCsbYGqzQxBEyeYdKEnUEPvzpdETSSFAzSol3dCS9qVAhsbSCa+6ZDJ+bCyTcpM/qqpT04w1ctROmA1vdP0K0jTkshLueWdeiob5/x/MsvDAp0AV+3co2ztXRKBg7K+s4ho8kYn2jOFqc0dU2S59SqxwbN1pUdmuD4yq9+TeCFVcUPf/h9Xnn1U2RFLso81nLno4/48N33eeGll8SnQCfY6QyrNCqV5N+O8gvIk4zfh0k4SOKIApNn4ju0PX2ijR99EH6Phr7pRenGaLK9DWyePDahhuc4jzaWbCLbejofszkRaE90XuCgvaNZNlitmL98hdWtQz567z5ZYUmDwx0cM/7cS+TX9tBEsv0t6RJuzlDXr8Kde5ijB+j1Eg7v49+bUt97GXdWMf3MNcy0IB8kUpVWJFlKV68wWlTF7Fgcnl3viCFQnYiJpwJMUKSTUsQ0ypz2eEU4PKV45ao4i3vh86gASZmiixxTiMKUnY9QvaevW3bKHZYRiiIlmY+pqgbX9thFxfrBGe3ZmixPSDcm5DKdmc8n6EmO3Z5QvX/A6KUrOCed8nxY6zrnBZ46ytFEwgCtc4sad1bREclGMjfyPHlkZfJNR3OyQm+UpLMSrQ1Z73HDe6sXa5KtkajixUi9bhhf2cJkVnhi3bB/Rkj2NwVa1HSEJlIkiagKKUkIzrvAEdBGSwd84CxEL3AmYqQ9W1MvKoxWJGWGigqvEYGMGEXAoxMzz9DLGqcRI1Afo/gGAcvjBcW0kG5MCJio0FphB2J26B0YhVs39KuGdFaSz8YAZBsTTm89QB0tSLYmjPe3LjocD1d4uLyJPBqcf8IF/5GbirTIufFzr7PvPi0mm5cLon+N44mnPrIxDfvZeRT7082ZPuEb+hH3/0foXPzEJnrL1ZLzSvWTidPTuwof9/4vv5uH8IqnlDOflqg/Y9BdVE8v3xci67fvcv9/+gM2PvMS4599hbBquP///g/0ZwuKF/dZ/Nl3cBgMgY3XXiEsW0IAHwLJ9oTtf/I1unsnHP73vy+T2WqssRRfepH0+pYQHD994+FgujSqYozgI+s//CEn3/guSe+ozpY419M6TxaFjJoYTYwI38B7tFZ0KKzRGBQhQhejcD+UQsVAmqZgLb5toGtxUYEfnJfTREhWAxbW2wSCx3lPDJ7Y9yggzaWVD4oQPNE5mqbiyv/q77Lz977K+u07vPPPfoNpH1gvlqR5BnnO7OufY/tvf0mqFlpdfOYQIlo91j0apOoIAb9quP///DdUb3/E8uAeIUmZFmOCUpjgCdpw5jpKbYnOMf7CK5Rf+Qz3/uU3GNuUfl1h0wSTDAoxxtA3DWQZidaEvseFiAuBMksIKGKSitmb1lJ9zzOBrdVSsQwDYbgPQaq6vQPA55ZyPiGEQNd7ggqk45zZ9W3MlmDm8QG3qglGi8fA9lRMlgCMFmnLGASLX7cEq8jKgtg5bCl4XrSiW9Wk40LGl/ci6XxpPiktMCrfdIJVbYeqZXLORxgk/4YuSYwB3/W8+4M3OTo4JC0LXr75Iu+9/Q7X9vcpughFKr9JCHz7299hXJYoNA+aUz7/6dcwyjDe3SD0TuB6QxBJkZJOR09wIB7O1csdrXiReBIGrsZ59n+pChd7j1vXdOtaCHdKkUzKJxuazzg+bs2JSBDnatHUzzbG4mPSC8G6O6tEujZEuhjQWlGMCuFzGC1Os20vCabzQm7MLMZaUfFZN4IjDxEzGGn1TYfrevIyp2s6svMK4GCY2a0a8vlIuAYo3FIqizInE/wgDakGOIJOBLakjcG1PUcfHTLanpJnqWzuvcd7PyiweNQgSW0QbkNAYB6hdbh1Ld3QEDBB+B3WJlQnS6Y7c3rnKG5sD90eccMOx0uRIzaiHBWcKF3FEC5kLJVS+LMKVaRi9JelxEERC6QLtDo4pZyWIm4RBC5jU+FX4TxhSFKU0Tjn6XAsQ8dke4OtzU2phpYZoe1xrSihaaNoXU+mjAQ5ueWsWjLb3OCDW+/z5ptv8sorr3Ljxg0hecdItVzh2o5RXvLP/7v/ltnOFl/72tc4Pj6h73t2p5s8d+OmvK9BYUzlCTZPSUfFABl8tJp4Dv87nw++7ugXK9LtmVRo48MZfT5HJEAEpYVr1i+qoeM0KPaoh/tsGOR2k4GQemmJvXj9c6NGgOr+Me3JkmQ6Fuf5ZUN9tKQ5q9Bdh7Ui+WzLgmg0flmhfKC/d4I5PoH1CnP3HqqqCEF8Vfwrn6b/4uvMXt4j25pS9z3jUUlzsAAFbtVA26N3pqSjTMRFgH7dsfzoEK0VybSESU42LihGOdXBGcd/9R5qZ4otc2wf0OtO3OHzhJBotj/3Am5VD2adjuasRq1b4RWuGspX9gkh4NctzeGCalWzqltmk4LTtmVWlpTGUN0/w08LkmlOmQl/0AxFAp0n4u4eZdzXB2fiFdK0sg42AltLZqUgFKxBJwbXyX7RLWp81ZBOR8TM0JytyBNRT/LrRuRWh9cYBONo1jXjK5vSuXbCM0vyFDvIVeOl62AG1/iuasRsM0Rc28v+O+yvUWrmMuedSMr6ocjhWkeSJ6hBqENbS7duxPxPS5LQtT1NI9KwRZlKF7DtmG3NWN8+pmsaprsb8rkHI9RsPqZertFK4DohBNqDM4r9TdJpeaE6xfCeoj/vwDy+Wg+TRj1+3+Mr+jNW+o879eOOJ6rUn+A5F9ePlybhs97EJ74Ysm9fJpn/JNf7JMfDD/+/qIne0474jL/U5bue+d08LgH28BpPv5dHHn98PDyROl0aq6OXr7D19S/Sna5xJyvu/8af0zvH9t/7Kmd/+D1CU5PkJXYyxmtL7FZ4lFSE/sHPgvOc/eZfonwgmYwFq51bys8+z8Fv/jn7/8UvPtK+ujwm1AADGf3Cp9FFyulvfYskjEidR1cVoa6IXU8dvEjg2gSrNSFqdIw0HjI7VACD4Dz1eWuTiGvEaVelGZn39EFShXa1ZDydETCoYdfLypKkaeidwvlA8I7gevoQCNqgg8cojVGa5u4Rse7Jd+YUr1yl+857qL4FIto57v/L3waj2P21rzz8viMwKIA81OA+7zlJhd2Mc2a/8nmaj47IR1PapsIHj04yGh9QwbOR5mAT+rqmeucOV/7BL3FnY4TuNQkiq4jSaK0IWmPLUvwimgaqNU4bfN/S6zHeJOhqTRiPaKPIgapeDJVcaimsIc4n+KZFdUL4VEaBNiRaFGd825PNRqRbY8rrm6R7M5qmoa0aUmNoE0U5G8Oqoa5bMq2lzT0d4Z2jW9SyqRYZ3cEZLihMKWS90AZsKuZ/3geMEnlfgOCk1XyZ04JS4iDdO5G1TMuhc6QGGVd94RBtrOWVz32G0ZsfYFOLTS3Xb1xjvLNJPK1oD06x2xOstXzhF77K7/z2b/PDd99id77FjckeXRJ5ocyxStG3PTEX3L9v+0f2AHUeJF1aZM/n48XcVEhiEQOu7sTLQIFVBhdEftYkhmw2HvgP50HSUypNT6mTqMc3pcdOUVpdbKb9qiYZF5LsND3GarzXWANGi4KP6x1mmDcaJNBtGhJtCFZkSn0/GDYNHAZVii+KTi1ZZuHeGQc/vC2O6ZlFWYtKDeXenOmnhIvSVy3WGNLZ6OIz1/cOWN+6Q1LmrH54i+Izr+COKpqjJWqUkxjNZFJC1dJWLfVRxFiLzRK6RtzSVTKUfVLpImapxbtAaDq6dSveCRHCqmFZVYy1GCf2zlE+vyfB7gBvYNmgvKgakRiiClJEsBoiNIdL+rWQ2JNpQZoYSdarFaYQDtPpnRP8qhITurMKaw2hanFWJJ7d4EbcWjHpnM5GmLpF65z5xkjgHJ0TudgYxXWZFud7/LpBWUWfKkgt6aTE1Qu+/4MfcP25G/zaiy+hgNViKcp5Hvbm24PLeeR//7/7P0jRpXXslpsUW1NAkWUp1YMTfNeigqLYmJBNCmIIInwwG19AA8/HW+j9BT5eZ5Z8d0OglJfHY4CoEZNJpWCIv5QxpBuyyYe2p1uLiqApc1kTlBqkWR8f/A+nhDL6ontS7m6Qz8bir4IihkixM2PrZ66LcMHJmvpkLW7ydY+yGV4F+umMLslJTk5QLmCqCuqK2DbY998TeJ7RZDszRhtT3FnF6nSFVoq47kTu+KMTwvaY0dUNlNGcfvuWdPxOarr7S/Qkw01y4vVtlNFMP32dvulJyozq7ftQtSTjguVHR2itWGSW6ctX6dcN/dmapPOSaBjZU5qztUBeoxQq6qbDO0+uDFvKYgOiCGkVSYhoH8nnI9xAXu7ungjMcVygtCItUpJcFOYm17aBSJ8IL8ufrnA+EsuU/mSJzRLxtskM2XRDAvbeUU6kQ2HHxUVnLzGGaCF2Utwr52O5Ztvig/CWQtvjvCTt0XkUkqgqQCuRcu6bXgRJjMaHQF7mBMC1vfhxJZrggsjBty3eeVQVoYTx1hTfdPjW4YmoRKNcxBpF0IHRZCQEfR2JxnJ655gk1UyyMckgkX3ul+ObDuWjkOuB6uAUOx+RzcbCy7s0TE1iJDZ4alB4uSB16b5nHueZ/MOnqCe2hR+zTP/MijVPBp2P3Dwvsf+I13lmsnM59r0cPw7JxuXrPvEdPXb/U99nFL7WU17zk5kJfvzxU+BcPP4GfnRi8MwjXrreRdfisW/tUkb4tMVUxYdV3af+Zpe+ZKUUsy++BIiz6+Yvv4YymvaHtwl3D7GjKeOrV3AhojNLVTeY6Zjyb30WMy24/89/n7CoIctAK5resfmlT1O/ew9O1rR3T0i3Hmt5P5Z8KqMpvvwSZlZy+K9EhSqPOX0MuLrGxEAeI7GtUcUIHaWinA0VvagUuVY0XYdJrCxgrbRFQ7T0rgfnJDHpOtzyjLPgme9fp6kaMmtwnRjKWe/xg9SqA2yMWK3oEJdvlaTUf/Uu3de/SHplk5u/9rN89P4B3dmCdV2TlyUGzYP/8XcwwNbf+vKQUAjJDxBIDPDkmI5kL1yhtRqbFfi+F76IUqTaiHeGNugYqZVCNz0H/+7PeOEf/Spv//ffYEtFtALvHTEaVJLQAunw2p1NsMYQgufW6SE3dq6hbYYLoF2H73uiNfgs4ex4id+cYBKNc5oYNNYJnMylmtZ17EynqM0d9DznB3ff44u7NwltT2YStIqyMc6FlJpYg6ta+kVFmqe4pkOlll55RuOpVKaNEcLg4JvhB4J0aBqSPBnGrCQLF86rQ0uub6VKnk5LbJnLcwW7RwyRqq4pjUj8Bu9RDlRi2Lt2RSRKm45RWRJOK5qPDtFTIbWfy17+rX/wdym+MWJzNCNPEr77V9/le9/8Hl//T/8m89n0ojrukVa7MYbY9oRBF14ZkSLUeUoMQSreTY9yXgwj1w2+aqVjQyQYTb2qMOMcFwJ5YgghkmbJozjmH3U8bYEgPjIH+6rBOy+VaC0ERt/08nmczDUTwWuFUUh10QfaWtyjI1GqgaXot8ehyhiOa+y8lGT1eCmyyGVKNh+Tbk8YdSJ/muYZWE2SJ7hFQ7doJCjWClAcf3hAlojgwMar+2x+4VP4qsYWItm4fu896nqHVlliZpluT5lsTcWJGSi3p6LA0/a4EAi9x/SeOM6JiWFyZQNXd6hWpFv14OURlEariB4XjIymdwE3SEQqrVBogjV0rad//4Bse4IeXN29lUKEyizlfBvF0LV0ga7p6Y6WmBjJ9ufkuSWGDJVYuqqB3rEKHYVNicP6qLOEIk85PDlj5D1nvmZjuilKVosVGoVNExKTSnCmIr7vSPKEBkcxHXN0dsKWKnnhxRe5dv06q8WSb/7Rn/LCc89jHezuizcEMUrH0UXKfYHJtccrzvqKcZagXKC+e0S2M6NdaOqzNePBQV1pTTZ/aDZ4efg9Srwduok+EI0ICTjnSYcEIQKE8+l+WYodTCbSqPhAf7YCpUT8gcdCpsub3/mbibKbKmtQ1lCUOURRXnODgZvJUyHSX92gX9TERIMP6DShOlpS3T2hz1N016OdRxlLnM5kXYmKoC3dWUWhtEhxA/XpmsxY6rZDGUN9+wQ7qCVpBcXeDP3cFs29M+zmmHjvlPVbd2XO704EevPBIaru6SPYnQnJWUW3aug/PIEX9zHG0Lcen1t077Flgd2di3iBC8QQyLenlC5wZXtCqFqKIqWtWnQihShbZMSqoblzTMgTivkIuzmRblkIKCKr4wVZkWMSQ3e2kmBfQ1x3JNMCg0KFQDYuiD6QFRlRK3SEdt1gE4MLIoOtvRc4aZDOko+RpBBRh3bdgNYEL9LMDKpJru4IXf8wiB94U6HtxX9lkIO3eUKiNMFHmrajWzYoIjERyWaMYuPKJrQ90QrhvF+3RO+YXNsk+CBBvxKJ2Kx3JONC4FEo6cwMkMbQOYy1RCK+FR8RlYk6HUB7shQvlv3NIbH4UWXiT3Y8Ws1/+iUfefRicj1rD3lKl+TjEovH/o5KAvKLzxfjk3HO045nvsZTCmjnT3nWdZ+Rnz391KcV6B4Wf3/S4yfvXDzlPchvGB9b7R79O1568Km505CZqYECHy89pi5dQRbS4Z4BQ3/5JeNTMrbLg+j8/HR7SjIdsfz9H9B8731MBH1lF51lmEwLgdYYRl9+mdnnXuD0N/6UcPvwQmnIOcf0xSvk+xvc+/U/QZ1Xqp7VwXrsvvTlfXb+6a9y8N/8Lm61xiuFsZZ122BiJDEG33com4B3tCFibEKSGLy2WCUbRxeCKMEQUb0Quq2Ria+MBmNpV2fY6au4dQ0R2raH0HCOPRdysSYgXAIfoAsREyNmVbH+/gekV7dIrswZffZ53MkZdrWi9YPbZh+4/c//HTqxbPzqFwQyoS7P6yd/lOgC0QVSI92FmKR0fYsNgSK1uIhI5AFWQVCK6nvvk01HzL7yAt23PkDHiEWh0oQwqGu1fS9+CeMRtC2TvT3SY8GYm7EQ5azJ8COpIqnOk+cpaUA2KW3o2pql78lHOZO9DWb7G4yvbpBPSlbrFV99/ufIkoSurwR+pBVYRXWyxJY5xVxcpE2WoMsMBpfQ4Jy0jqtexqlREMQ5WmnZ1JNRjrZW1IzqFpXaCwnN8+M8MI4uSJVqURMBmyUCeylyfO8kcByuRe9xTUd9tEArMe4iRsqbO5hxTl81Qrgd5yQRvv63/yZKKZp1wy/sTGnrhlQZnPOYoRIVey/J+aoW88idjcGjwtHcPsI7T932dL4jLwp0olkfHXLtlRcIM5Ehja2juXdC/+F99OaE6XNXsIMUr/o4LNTT7h6Sr6dvFsO1IpK0GEM6LWnXNdViQa4TvBJMsGtbYuvodCRJxaG8nI85ODgg1wlJksqG3XuSxEhHh4jvHNkoR/Weru1QIcENKinj57eHCkjENT1d1aIVBOcodmYEH2juHFMOgUxsHff+8A22vnCTfHOCLQvcsqLc36L68D5t7Vk2DcsjxXhnxvTqJu1HR4QPD2nvL2nqGjsfE9OEGCPudM3+F19AWy1GkoiPiFQ2PWZWMukFhmTGuQhBnK7p7p2iI6RX5phZSaE17V2R8OzunRCdg1nJ/dNjrr/4vFRdlcadrgU6klrMpBAyfdOLI7oLgjV3QRKJzqFzK6ITWYJvepIsZefqDipGytGIEAI2QlEWxAieQFM3F0mxTixV6DldLhhtztnY2MAYw4fvvY/veiZpyc///M+LihZKgkEl3avewGxfKud90+M1XH3uhihQNd3gexBIxwXF5lTUuoYxpi86s08OydA56pMVbt3QdR02SrKabE8xeSJmnl78FOy55CdcQMiUHThrUdZyXYrwRWx7umVNsjHCZglxgEqGwRleAWroel7sukoNJV2BsyVDwSJ0TgxhjcbOStnb6hbXOcbXtjBZQmMUC3+VkGeYg4Oha27pbl7HjjKyral4R00KzKqmMJruZE26OZGk+MNjmvtnlPsbdG1PoRWT/Q2m17fRiaGa5Cz+6hZBw/ruKemsZOeLLxBD5OCduxy9e4+5tYx2ZqTX5nS3j2nqVngXGkgsOk1oFmva04p8lBN76RJNJwWqdUKwtgZrNFpBNgTYauBHxhilcx88mih+JEaRFwJZrY8XaCWqT+k4J4wHSd5LJfO2c2RG9oMQpaPXNK2ohg1FChh4EWpYr9seZZR0edYteuiK4AP9ohLYrlKQGPyqJgZoXUt1cEYAzk5WpB/dZ//vfJWoFQd3DkmKDG00SS78jX7VUG5PCb0jHwjlrfN470iHsayNpl83uM6RTcuHMrGDISVI0a5f1pIYmZ5z/p9OoX5wRrtuSIsUT2S0v0la5p8waH1YIP7Y6rx6eNaT6/szjicef7ybrZ54+OOf//ilHlb843nrUMWHvKvh9T7WRyM+9pmeevzkwf/HXfZjdtpPfPxH8bl4aiyvHr3j8d6DBJ6X2kgXKd9j5zzxCvJ4GNydAcy5VOZQpHwiwVAPk5Fz50mA9tYDFn/yBk3dUsxnqMkY13QkVzaofniL/No2G7/8GbrDBSfffBcUBCLWeeLGiNmvvM7ij39I0kfM/qbACH5UFjx83kgkuTJn8+98mYN/+Xv4o5bQNqjgIQacixil6AaillHgvCNBNNAVit77wVvC0ystLXYl7XAXIihDkpfEdU/+/B7drTvExNIET0IktRbvOnndPMdbSx4CJngyrXEDN+H4d76J2p6y8dVPsfl3vsLi1m3M99e4GIhKETD4tuPWf/NviEqx+SufJ16WLz1fNhQPSY5na9q37qDWFX3fYpWoRcS2okVhi3LgcMhmmGmDQ3Hwpz9g7+tfZL05QaU5tu3xgz+IShJMmpBlqVRUkxQ7QBaM0sRzFZm+p1+sKcclwRqywamzXqyxShETQz5KWLiWjRubjPc3qbuO1DnKLBcfjKojHZXEGHAx0GtF3XWM00Qqk73HplYCBSOQtMloTAwRZxRhUOLo2x7d9vTrmrTMSeZjmS+D67kaDMfCYAh2vhF45wnOiUTjfARaXUjt5kV2Mea75RprE9qqgd4zvraNyRP6urtwLtZZglUKVzVCLvae6niBTiyrszXzyQQ9mw0biUXlCSZPSUMguEAyLihSjUda/mmZEUcZcdVgZwVaF4zKgvsf3qHvPG3VYLWmPV1z8PZd0kmO2dvElpngsM9HzTlZ/KkLc7z0/8dyiEcWoEefa4tUKpZhkFpsOiazqcADj1vW1QrnPOVkJNAn58nKnMVySeU6oo5MtuaiMd97ohu04hlEDILAAZeLijw60r4nsYZsLLwRV7XU79ylTROSiWDNCYH1Yk1fd2QbI3wIjG5sMmaH6B2+97hlizcpJkmx2zu4gzN29zaplj1ZklC/d5/upKK7e0R4+y3Cgwf0kymMSuJzN8leuo5zDn+8hNaRzEd0bUe3qijSDLKEUGaodQujnGbV4PueLE3wq4b2w0PM1pgI+FIMNOM4w6QjDk9OpCJrNaw62lVD17ak0xHaefzZGqcVwTnScUF7sqJZ1WJiZg06DlCJCIvVilGSS2KNEqlTpaTw0YpUtxqMQGMQKdpFtSIYxenijHW15k//8A/51EuvMh6P2d+7Qle1mAgYQzYdi1KVUgL5KHOiEzK1q1rWD06IMVLMxzTHK+gcqrCEEMUl22jOsUfP2pDdqqa+e0JzvMJMCtS6lURNgcoTcmOYvXQFY41AdEMQrs+A5WdIZIwxUq1f1dhcODTOe8YbU3Se0J9VEjDPR/iuxzW9mEkqjR54KwwJTURe+/I0iSDzeQiCwgDHyTcmdMuavu8Z7c0xRtG7wDIE0tmc1DuaxJBf2SLfKFnfOWZyQyStXS+eMY6IP1gw+eLztAcLunVLf+dIjEMHSdLV7RMikXxjRPbcDt2bd0SUYnOM1pqjb7+PaToKrTGTjMmLe3gNWIs1CmWUkIqdk8+/qNAIH81YSwheeA7OY7TCWfGe8p0n7QK6zC64EjoxwqnYmhFaJ89JLa7pcL3w4owWCCQhEpRcJw5ctXSUk2WJXKfrScscC9gh1tCpRWcpymqC7oREnQifk14U94wRLxqirH3JRPw7jA/CsSly1gdnHH7vfSqjSCYFOy/vU7x6jWI6om97dvY3yeeiOBdD4PSjIx68dx/3V+8xem6X65++TtSKYlgDtZakAoXA9owWSFWIUtgyGrdqLhIw1w7ww8F1Oy+Ft9jVMufJEiZX5pcSi2dF648VGy+f+0QbcPgnPnbnYzHmRQz5sXH4Y897JuSFZ20hlx6+9EC8+N8jucInIo5fiD9EBHz7Ex4PKwqPNO6fOOXxt/8Tphc/RSnapw+Sh/c9ZXQ8cc8l7adHPmi89Phj17/clrpcpIyP/L5PfStqeI7obXfc/5f/M83hgnQ8BmNQdYeZFPR3TyjGBdv/8Oewk4L7//bPCcsaUxZYrVGJYftvfIr+wRn1ew9wRKY/c+MCI/+0176MPX843jT5Z66zk/4qD/7l79Hdg3w0wp+d4fuOddeSWEkCTAwiiRm1VFeikLGMNvhhXiVa0flBPcJoYiddjDYrMDd36E2kWpwxKUaibqM0vetRiO+FCkE2maE1nxuDUwrX9Nz5F98g25pRvrTP1f/ib3L/n/1riuMlznuCd2BH+K7hzr/4LWKWMP/iK6Jjv6wu3HJVFNfg5RsfUP3F2/Qf3aV3nvLmddr3bw2mO0IaVkphJ2PCusLmBTiHUeBd4OTP3yGOU6q2YysfEeuGBFBpchE09EoxvblHdec+alWhNubYJIHNKfFshS5SYojkWtMq6M7WqO0x6caEdJSiIswSmN7cRVvDyBrx/ioz+fGGfFgr6Q4YayjHJbrpofCi9rNqMHkytLwV1lpsnrKuGtKB+1C3LcWkJFUIcdlKMnGhh950NA9ORVJzf1OqRnWHnZZDh+jhxDFGc3kERufxrSM2jlh35PsbMk+cIzadyF+2PTpNiFphyxzX9sQQsNrgXWDnuStoo+mOV1L1LjPB7QbB25+/ToK4eYcQufvGLYosQUVFtappjld8//ABOzu7bM+nLB+c4pUnS3K2XtgTZ9vNCcm0lAAyiFmT7510WJ52fNy+9YxDKeCcWBjChXEhgzjC7No2boABrBdrTG4ppiN0lrCRp8ymU/yqJmhNWopOel+12CJBZwk+RjGOG7xJ0jKjKEpC14vUrJZk0pQZsfeYGMWdOEuY7W/gtyf4RUN9sqJbNExe3GP13n2Wt+6Q+kAfI05DlqVkE1mzNl/YoPvokMX9BfEHbxA/eJ/gHUobtOsIo1301gbjzTEsG6luj4QTkuSZGHnWor+fTEXUoTle4jWYEMFYER24soHrHNEoTGLo25Z1U6Ebw2Q6QaE4vnWX+c42JkswbUc4WxPmY7pEQ+9IlQYf0VpT5Kksj6kl25nh6g6sVIZjolE+4KqWJjhIDdOtDXGr9x7ftJgy5/7dO9y5dwdlNfv7V+lOl8Tgee3TrzEbTYSgi6JzHaH2bG3PpBgzbBTiK2NJ5yPcumF9vKQYFwI1bHtJprOEdFoCauAxcLFpP77Q+6rl7Pvvs753ip+OmG1N6R4s6D48RB2d0j6/j+qElN8uKtIyQ6WWfCgauBDRZSqd5BBwbU/vPPnmBD2ICKRKCzQmRKwVUn88W+OHDrRbi1lrzKRj1be9dBo6h41SsIkxDryniG8HDH+WYIyhOTglnQumngqBcynNZG8uvI2TCptbsitzrIL64AyVWZqTJcmoQPkg/geNIzEKXKC8ukH9/gHu7hlqkpOUKcdv3mX59j0sinVmJfGaFvh1S7k74+yDBygrct7F9oRiJsp7eZbQ1h3ppBDPn6omhkCIHVZDaBxGKVzTEqsOUoseCfGfKFyMbt3CpJTA3ivSIiMC2XQk51sjv3+W0J+twRpBMoyEZ9NXDfn+Ju39U5TVGJNgrBGhi86hBsUkk4p4SJIlF5C/0PTSVc6sJBqATRNUItC19WKFCkjhsPMQI+2qZmNXAvZiZ8q1L79CfmVD9oiBn+WajsM3PsDkOdMbQycssaRlxu7L+xAjo40xCrCJmNupdOhuxTiYokbSQVQh+CGJ8j0qNfSrSowNiwxd5jgi+fZUFNvaHrMzZZZY8rLApPZS4P14nHgeFD0aHz5SfH7WOq4uo1UeP+kTBPHPuOZPfH48f3l1+ebD8z9BzB5DYKh//PSOS5SBpz/+U3wtfiqdi2d0Kx4+xI/3iz2eiMRLt+KlYXfZRE9UDdTjY/T8pZ9sdAx/qwE/LOlcN2D4lJGJ6J2HdYs3ivnf/gL5jR3W3/+Qsz/9IVqL+2jXO2ZffIHkygZH3/gu0VrMKKP4zPWPlRxTj8+x806L0eSvXOXa/+YfcPu//i30oqZJLOHoiNB3xL4lJokUNxAMfaITeqTxE0OQAPO8OhXC0LkxEkx7hXUJcVVTfvFTHP7G76I2d5mMx+KIaiydj+C9eEoohSWglPAZSFKRFWx67v5Xv8n1/+1/zujGLskvvkb177+JbftBkaYnK0ccVw13/+vf5Ozf/jFeR9qjM7JiREitaOQTSa/ucuU//0UWf/RXnP3lm9gkobVGAtp8RATSJJFqfZrinAdj8eslSTGSQVz1jICq7RgZQ907STC0KDOVI/GkiMUIn2X0ncOfnZFkmnpZkWTCeah7R5ImJHtz1sbTpYrZ/qbonWdCGo0xiklhltAvK9LxQ4nZECO6H4L3UUFQHd2yJt0YE7R4W+TnTsVBKlBZLnh9nGc8GYHW+GH8qSCup33XEzvBs4ZeFIwI8cJc7/Hhfr7exiDwnH7d4JuOqGVshOG69YNTkjLDlpng8ZUiNC1aiYwnRtG3snnno+JCgSjdHgimREyeEJU4HdtUqnV+UPZZ3j+WzSaVz7v/6g3e+pM3SDtL6ByHyzNKlTOeThiPhTCYz0eCY+4dphQ+0zlnJzgJxp7aXlc8JO89be155MuROy62vMSijCQYdd1QFIVIPTovQbfVtFWDOYemKOEChKYjKyQ4N2UmFT2GBMtqYtND55iPxzR1Q3CVEHHzhNg50lFOkqckvbsIKkyW0K0bqg+P6boenViKvRnH37slrsjjHLeoSeYjssRAIXNDLRuaN+9Q1472bA3KYHf2MK5DGYu6sk+/s814WqLGuVSpJ4WMWSPO6nZcEBJRjEnzVGQvB/+S2PQkW1PqtRBBm9hTH6xJqo5GB/7se9/iypV9rl25ymxjxvpsQX3vCNYt47yg6x3V3fts37xKUmSEppMxPGDGVYwEvyaOcnzb4RY99fKMVThmPpphMkvVNOzMdyUJM0aMvnTKYrng8OSIT332dRJrOXn/Ni+9+BLj3S181aDRmCIjxshsc1NgHkR877GDT0A499VwnmZZcXzngBtf+hRuSGrNULH+URC9UPfUD05pjpcs3vyI/OYeo5057Z0zuu+9R3J4RNyYirJOlmBHOcsPD0hGBeWkwGmFXzWoxJDlA8/IWKJryYrs4mVd1YrBYOfwK4Eu+XVL2/U0XU9pBN8/e2WfZJwLJ8J58mubKD9URo3GLxtC12MnBSZNUIODte870ulIZE/bfpAIBTPJZR3zEfPiniRCvaM6WdL4QFL3oCtimpDNR8Sqo00kcK2OV4yubuCPVmLQVqQYa2k+PBIpWQPZZIS1huasIk4yjt69S5pYiu0JFkVSpESjaNa1SDZrLrojq6rizXff5Ktf+iqqDyQj4RCuT5boMqWPkXKck4xyuqV4iKTzMbbMcOsGpTR+WaNmJWaU4zqBLGZlhveBWKQkiYFTGa/5zlw6TCFgx4UYk04lGXWDumC0wp1QbU+SCKyoX7coyVGxZS6KjEaKFFXV4I7PUL1HT0vGu3NAUd07pms6dp7bAwWubug7hx3l4n3Re3QmkGbvPMWVbfJcklMfAqwb8tkIoyFNU4JC4MjaERHe6blcvIhPPBwL2vmLhKNbVAStKPe3yEaXij2Px/MXFfhHl+EnyuSPreEX0KHHz3n8KZ8EPfQf+/gEAfkTDRV4aHj3jGvoAQL+4wT8j0KyHv7/8e/xaTW4EKVo8NP8On8qDt2PHj8iNXvaQ5f3/3jpS1IPv6JzuT6lLn9tl54bhwX/oh1x6Z088y1dupZSZJMRftEJ+VlrQhQX19nPvcL0yy/THi24/T/8HolNoRBVmfTGNpPPPsf6rTu0Hx4RrWH0N14mnY+5mG2PD6THmzjnb1JJy0FpMBtjrv2vf02kMZuOe//sX6NuP+D4zrtMlCLNcrpB6tF7j9FaWsDyJUGMuCBQKgUXMrUOhQX82Zrxyzco85xudUbMCzSeaCxGCQncK7DG4FyPUkZQSc6hLLgQ8HePOP7//iG7/+Wvce1vf4W7rWP1W3+B63rSRGQzp3mBUYbquGL28g32/+Gvkl7fxo6LQX5UqmQCOA+c/OWb0Dp81GhtMMETjcGUhei4K4VOE/Go2NjEdC16VMgEOTnloDmmznO2yikepBWuNSSWVddSlylt40kwWK1JrbT9sZaksIMHhiZ/aQ+1WhKBtuvROpKmhnhWwaQgWjEI0kZLlX+U45oOnJBmbZkJxKOQFnh0Hr9uiAOmVRlDVzVSuWpaVtExGU+Iywadilxnt6oxVqQt/cmK5sMj9DhHTwtsIm1upS8R5QcCN3roAHqBjnSLCr8SV1QSQzYupEvRdCTTktB0F52Bc8laPzgX91UNUdH3TjabAYaFTS82j3NIkR2M9FSE2PbUdYMOkTSxrGvB7t556yOqdsXzrz2PThVNXbN/8zqqdahMcNChFy7KeGsmUyZGugEKApIwnXs1XJrAT6wln+j25fsHxa1U5ehEEkkVpLv2w+//kBdvPo9fNWhTYEuBqJntGa5uofNSpe2cdCvyVBKhUY4uc2IIFJWo7riqQ9c9yipJoLJUqvC9pz1dMtqesX7/QIKNiRiHHf35OxLwjTJ0iAQisWuZbmyKDPHdE0KEpY/E3KKKjNHrn6Y+ExMsW6RkWxM2N8eoIhWpW++BoeLdex7cvc3O/i4mKEyI+LpD56nIpZqEmAkhP92Z0p+tWVULTJIQxyljm/D1r/8q5WQinZllxUY5QU0063SJax1v3P6A2XyD3ZvX0HlCs6qEb2FkLkUFuACna8HIe89sNJWO0rhAG8XETKXqm1i8l+88AsvlkqvP3UDFiPVw9YXnsGmKQmEmI/HSiFwopp1vByYRDlJw0nk7vHUPghBrr77+olR2tSIOXiR2XFzqDj7cWCJS2HFVS/vhIQpF13vGn3lBiLDrhvZ4SRJ74vaMuDkjGxUEq8EqxtMpXkG9lvnfdC1+0ZMsK2ZXNklGOdQd/Xml1ot8c1+1dPcX4rUSItEHEh+wXt6e6QOrH96hA5I0oZjk0mXsPWYq3Jf6wwPsKCPdnaOyhNHuHFe10s3rHK5qZb0bJDZ1nuCMpnpwTN4WVEcrmoMFo70ZG3szFvcXqAiZNYRxTqUU3krFXqWWYlbSXpmjVw3Z9kQKD0bRty3lpIC6pzWeMk9hUpCNUsxgHonWkFn6ofOH0sS2w6dSjNkoRnz59S8QtWLZ1czLMV3d0feBqHp819OpyHxnTr1uODk8pchSsjSlzFPcwYJya4I1Gtd2ArGuWpF8P1mCgmaABdUPTkk7gQWZnRlx3UjnclqQTEu6ZSW/R2YJPtL3Xtzs255sUshviBhuRufARw7eu0/je4rNsfBGfvgh0XnS+YRGQdd2JMuKrmop9uZYo/EL8dggireHCwGcp8gSso0RIGgD70Xh0EaBkFGL83cckgmTpySTQpSelKK6e0wyLqTg0HT0VUvddqTjgnJjKr/nx3IHeBjvXI57Pi5E/Lhg+imPPQlFesrxMUH8T348Xrl+RsbzWI3riRjw8Uv+uFH+5WTsPJTkse/nvID9lPel1dPgVz/ZF/ZT5lz8ZGecn/cQHPVwVDzeRHv0ulx69Cm3PsHL+tMK48T3wSl1EbBnr99g/MWXiN5z/G/+DH9Wk8+meK1QqWX6c6+gOs/yL9+Vd5JZps/tDhn4UwbSxxwPP5skJWZaXiRbO//k69z9f/1b+juB4HuMHhGjGKoFpcXhG1DGkBhNf/7taIPRiqg1YQgSu66lOjjkytc+x+jaNU7fH6ATWSb/uV58IWLERMEja2PwIVC1Han3JIV4L6y/+x4P/qc/4so/+kV2/+aXcG9+hL93Stf1GKuIxhBCoJhMyF68yvhLL0sicelzyiIUCSGiYqQ5PiUai85y2vWKJM0gTSGJ9M6LmZk1pPMptB20nbhwVxV7WY7e3UUnloWK6D5ijaEvUjhesNZgXSDJcyaTgr73hBhI6ha9M8UlivHWjHxrQjYpiYno6tssIXSeYBSrg1NRZpqPMVpwvtEJzn5xtuDg9j2mWxts7wopNDov3YXWEeoOPcrpVzWr0wXvvfs+se54+WdeJSkzXOewiRX+xbKmq1pU72mXFV3VMNoco4Ok3+s7x4z2xVW8O1lJ92Hdku7NAYSIWTUCZcgSOP8cTsjTq6NT8ulY5FMHTLbuBAbUR1EyKScbxAjV2Zp6sSbPU0mmculgDGUP8WroOuzQxzVlhj1dk5Q5zaIi14o8S5nsztm9uYdy0g3TmaVrOurTJWmXiWKO1sz2t3GdSLr2XT8kFGLa9mMvek8p1VwWnLjohmpFklqS1BJ6wU/r1FJVa27Od6RLlSbkaYKvGoGeaCFj6lSC1Fi30qmZjfBL8SZYnK0oxiUYxemDM1KTsPjoiDJRZLMJdtGgo3SA8iShvXuC9oF+URMSg4uRYn8DFyKq7nB1y/TmNp5If7rCr1vqqmU6K0nanj4x2HHOdFxQBo/eHGPHGapICVrDUPVN8hQahzIRt1hjz1pcOCVkCV3fM9qZE73HO48tMkxmhey9McJsjLjmtmDgP5jBiCoMgY2NmtPb91nXFWUmXKbXX3sdP3AZ+kWF0uLV47sebRQRJdr6AZJZSex6QvDQRvFScIE0SaTDYzT1conJM958+w3m+3ss7x3SJQnl9h7KWHwcOrB5IoZovRcuB2IEFoMMjjjgaUPX4vqOja1NslFO9JGDd24zmo4Y7W5gJ8XQcY4X4yoCoetpFhXaeUkyjWG1rLCbE6wSKJFve4KK6OeviCJZ0ESjSVLDaDpGWU02KHHFEMnyjD4E8mkpXRrAjHL86YrFwQkoTVnktLdPJVnNLHZaUm6O0HlC6D0uRnSMuHWLaXuoOrqmo3vrHs6Jwls0mixPaNcdPFhiy5QuS1kfLRhvTSFGdJ7QrmrSUTEIULSksxH9wRndgzMCmnR3Sj5O8IslEc+66RgnhlA1lC9s4z44YnR9C1KBV27c3Ja5HIRPNnpxj9XhAm8sqvXotsHlCa5zVAeB8dYUMyuFX3ayFshvDNhRSmo1fQhCRLcG1Tu0j8wmE9CaxOaUSomYRtNAltAuKoo8Q+9tYVtPp6A6Xf3/mPvPZ92y/L4P+6yw8xNPvKlzmOnBAJgAEKQAgqQoUhIluVyWrLLlsv8M/zv2G5fLLqmsKkmkSMOkSIIAQYRJwGC6p3PfdO4Jz3niTiv4xdrPc56T7r0dAHFVdd/z7LD22muv8IvfL9Y5smVD66dUOz16gyLkcZwv8WUTIIaVwrUWmSWB3DFL8dPABaKEoD5f0B/3kU2EjMPa4BoD3mGrlrjfGcoijcPTlBXSemZPTrF1w/BgSAz037lHeXdM07R88fljZCR4+9fe7ngjPLpLwvd3gge8Ol+wWFYkWUwjBJETNNNVyAlsWpwQmJMZ5AmyDgYlYbqQ28YgvA95dtZRnc6YmhZ1vgjEgN3anWcxUspbQpGul0vKx0su218Zqeg5sv3m/Loh/gbD703lhcnVLyHXftnXuaZsXHh/PHA1iVhs37R1at33l67+a/T0fAM5F9cVgZvLlePi+tmL8XpVfRCBgfLa7dd7ars1z/3sW5j4ZlEx/XcfUJ3OiOIIIk1TNxRvHrD/H30PmWjKv3xI9cFjskEP40E6R+9vfov+G4c8+X/9G9ouDCTuJUSjYC1A3IAWfNPHFVvN2fx9MaCEB90PqCjxzh1sWVF3Gqj0rpPvQviYBqzzWOeJtcLJoGhYYxF4IgGltUz+4pcc/tf/gOK7b1E+PaKpq2CFnM2IlKLtNtzWgU6zADXoPFoQIDtdwLpGCpZ/+iHTvTGjv/NdDv7P/4Cj/8c/Q35xhtARVqkQ/pSlVA9PWX1+TP76wUVH+LWzyVO+/zkyTiBJ0VGCjyMiKUiKHmQpab+gqmv8fEVTVnB2TtYraOuaSAjU3hi/vxsIsw6G5M7hHp2xbFriLEIhGBZZsFAZh81isJZeEiGLlCbq4FfTGN8Y5lWFqCEfFoHEKE9p6uDFcK0NFlWhqOYrfvnRh+RFzid/+T6vvvsWd958hfrJWdg8O0jSeLdP/fCUsq05W835t3/2x7zxxlv8xm//FpGQrE5mNNMlWZFiywZftvja4OqGh5MjBvcOyIRANIa4J5CRpDydcf5sQpxGFHVG9eycaCck2pr5CjddYaToLLgZURpjmha7rMkGIfFTRhrZcR4gJESKTMqQDOqCAN2LdbDmd+PoYpIJ5idz2kXJ/jv38AQ2WqEk2WsHAeZ1vsQLQTNfEWUx7aJicjQhyVPSUc7sZBo8IIQcliiLacsGCEmEURLjow7f3bMh4Lo0p15m2bk2ES/Q5bYXbNdZSEPSrCMd5uRFymq+xDtHOV1wfnLG3t4uzarGeEfWy3GxhiRidTqj38+QSYw9X5JpjVtWNK3lo59/wt39PWQsaGKNMIblqmJUFJTzGucclTHoJEIVIbmeZQXOowQkOwXeZsyPzxGLGqE1Zd2CDR6dNJJkCNQgxztH9NYhIo6oFytka5BxCAeKlWZ5OiVbWGwWoz3sxAW+cdi2Ckpd22LrmmePT7l3d3fDMm6sCflGSm44eHxtaOcl7fkCv6jxQpDFCcXeDm5VQaQC2dmypiUQeuksRuYJKsloqwYdRVRVhU5ijAfhQ9hS3AueyTVMs9QK39qgpNmaJZaBtdw9uEPa76GUgjjwe+A7kq6OxDN4KnyIgU8DWSQiMMVPngYW72Snz8nPvyCKNfWypLc7wKwq4ri/IaRbE3+FnKcKe76irgLSknEOIwWFlswfn5GNclSvC8tsDcjgVU6LmHiUUbctqYppO36UKEuQsaadLRFC0C5rGrsKrMdFijzXyNKw+OIpdAqKzWLEfo9obxC4SGpD/WyKixT5q3sMuoTb+mxO9fERog1KIM4Q5cGK3kxXQanW59SrmrxjeTdni5DPsCiDR9pazOmM7O4uq1UFy4Y8DnlYDHtI15DmSQg56+ch7+vemLOPHiMtnDvP4P6Y/P4YqUNe1uJ0TpIn1OdLOnk3IOpJgZfQRBFFPyXt95hP5pTek+30Qo6I9egssNhXqyqArDhPnChEGpPEEWmR0dYN87MGe7rAK4mblYhewhJJU9ZUbU1at5w0hjzbxx5NiBZV8PDlCcJosB7nHa1xoFoaL5DzFeNxASZ4LoWUwZvZIX815wuEkkSDnKiXh4Tz1gQi38mcSEoa78lePUA1hp3DMVVZc/z4lCiJMNbQKzLSfh7GtiAAGaxXMiURMibdHdAqSW/cZ6AUtmlZfHEMSpAcDBFa08wCnHQ9mWGqNngAlyV5P8esanSsaesGtdNj+fQpb733BkmahvDx53kp/rrL88TO26JjtiXsbS/Kcx8iXnDN1Upuv3htIn8p5emSILstK/nNycsBMV3d2+/oL/75auXrfe9vJixq/b+v0ZZLt27qE1vnL1futzp5Wx/Z/L0l/9wER7v+MLZuWXxyRDtZUK1K4js7qGVNPsgY/71fRaYRzdmCx//4j3FCBe4B50ju7TL43htM/u0HmJM5SiqElqTffRWVJ12O35frELFu7Do8aqvR7apGZBl3vvcd5v/2zzqlIixeBkhUSH7UXdK1UpLS+YAmhUBJiXa2O6dojk+oz+f0f+1N5n/0F6zmcwbeh1Citg3cEMailQoJxZ13IVUht8Bbg5YKT3BLn/3zH6P7Gb3feJt7/5f/hIf/t3+CnjZhsEcRsQhESmf/5EeIf/QDstf2Nx/KA/Mvjpj/xSfoNEdlWUhAVwrfL4juH5De2cFqRXo8pd0ZoM7niMZwXlbQzyhGfawK8Hy6rFl9fozME/ThGPn0jOhsQRtrosaiDnJM1aDyGCsJyD17fVy5ovnZh0xHGcQROgoJ0uVsRf8weAjSUUFcJJTHM9yqZroqyYc93nz7TWxjWNyf8ZM/+TPu37vP2eKc40dPyfKcO3fuMJmd86Mf/YhmvmI5nfJf/5/+G4QKRE7OW+SqRswr3KrFrcdZLyV6fZ935X18x7swWyw5SCKiQY72nv0iY/bxE5ytiA+G1OcL5o9PybIQW2wXFa1wxFHHF9Il6UmtMNYEL0KXfK3SKCD9EBQ+Yy2xVlRni7CB5zEyisAHZJGTD58grGf8+n4IOahb4liH3BDfMHt2jvQiuN4HOW1HGLW7N2IxW9KcrxjvjxCR6nJX1jkNYQwDIfzFg9TBc2HKJiSY3lqu7jyXJ/3Ga7GOCV5r9i6EeBljgzW/bkMiZBj6pGmCjCOMMWRpF9anJbmKcWWLq1p8rPGR5Pz4nLxIIVJEaYyXktmnR6RxwudPnnDnziHjQUEzX9J3ksVkgfEhKTJRgup4hnYepwRxkeJ8CKsrj6Z4RMihcZ44jUiTCB2DspA8OMB4h0wjJLAolyxnc/r94G39yY9/ypv3X6FvNHkcQWVw1mNXNUpKWmdwdwf4oxkrZchGffJ+irA+kENaR6tAR8HjNDk+QRqYHU+4k/aQeUJ0fweqlmZRBnZkD35W0gLRTp+4C+eMxj1cE/pNdh/IWUdTrcLyr4KHLB73EI1F5aEfJ5MzZmfnjMYjVJbQlwmJjKidQzQtw4NeZ2AJXBKmbklH/cBObyz1ssILKDrlsVlWVJMFysDg7pgoTzj41depT2eBNC2OMIsqhDe5EHMu8BBFSCmwlWFe1qgkIu3FtKcL2tpw/NkRB/f2Aoxvl0u0WtYh7DaWqCzC4qFsArR4a7He49sQRy+FAOdCXkIUFCpjDFm/YHb0jGXTMhgUkMd4PObxhMnDM0QSuB7W6FDTo3MQkv5bh7Ba0X9rn2qygrMFbRNgkjUC3cHPlnUb+BUaE2Bx8wQzM3g86f4QVzbYqiECkn5COatoljU+SfACkn5KttOnPZ0HgXrcI7WO4St7tNNg8Jh+dkx9PA/5c0KgIxkg1Ac51WzVhQkavAhkeHqYBejTyTyEGI4KmvMFCjCdJT0pUtJ+hhcdsl5Hujn/7BmVdSSjHCJFjGb5xRFZnjGfLHHA3jv3ePb5Ed5Lhvd2KfKEpvRBivcSd7ZE5TFV28Agx5/MEMuGcrqgKFKqVYMi5EG28xKVJWQHI1Zns0Bmt9PHGRu8yfOQd+WbltY0JDsjhuN+YIifrjg7mgRlJImIkoid4RjubskItxStNeO90eYaFUcM37q3WQoFgqQI62baC6Ga1jraxhAnEcm4j9SKrLv+Vw52vrJC8WUie76U0L0um4iHK8dedM9Ltae7dI029VXClLhQAS7yhG+p5Oo7+O1Yna271sLtVZ3ny4rez3ufr/iuN5W/Eobu55btQbFlsd8AbtyoZt2ue110vb/QIl7otthyGSmJn65YfvSE/JU9ZKRp7Yrx7/4q8Z0xvjZM/n8/Qc0DIonWClLN+G9+CzMvWf34E1BBDUjujdn59TcuuaNetohr/1//FYaZ8x6bBCi41gZiL+lBiECOZtfoIkIGnH0PqRIgJFpKrPe0CKwPyD9V21Cfzxm9+wp63CdtagBaF1BrJJoojkEq2roCZ3EyIGDEUYxrmg7yr0FlIU5z8ns/Irq7Q3J/h+F/+dvM/ts/xC8NWoqAWe8sZlZy9j/+KYO/9yv033sFBNhFxdn/5w8wvT7yfh8aiypS9LAg2R9SSYkpElRtqWINz86JzhfYOAZjSdKY8uwc1XZkZzIQGXnnqJaBuK6sGkQvxWtF25pgLbIWtd/H3dul6OU0Rw71xn3SUR/pHHpYoJynenYerK79jKyDRrXLiqZsWMwWmOmK0dv3EVHMG2++xft//nOePnyEwfHzD9/n+OgZ/+Gv/Ra5ThhGOd/6re8xPtyluLvH5NOnxFIitKJd1sFzphUqjYgjjVEikAOeLqgfnxHd2yGdVlTmmDaNyF475Pj4mP/l9/45v/0bP2Sv9wC7qCnSFKsk1WyFsZZ0WJCN+7i6DRbBVIdlT0hq7xkMi5AULEKYikoDQlYcxyE2uLUsjo8ZvHWHpmyIs4RmWTE7Ouf1v/mtkMTdmpDPoSTLRydBwV3MydKMYm9ElMXUpwFRLLkzYq8LjQhwngSLq7VhTMuQYCtkUDLWYVEST2DzeLkZdWUqXV4TOoIq3wbIRd8luiutMG3AfJdaQYe0EyzVHm0URRcOhPM0ttkAB5jpkqRD/bGtJd/pY6uG6ZMznh2dkI8L9u/u0ityeuM+c+exizlZHIX6yganPHlrEGmM6mXY6RJXNpSNxdSGREuKXhbMu96i6oDgkt4bI0cZ5fkC1Tb8/Cc/Y9GseO/b74W4bu95986rZE4jbefxdA5pBSKNoWqQDtAaOSyI8gKJZG9/jCB4zOpFydnpCanQ5HlOb2lZVTU7vT66VwTDSqypFmUIe6tbDA6fR5zOzhm2CeneEFqDM5Z6VSPqNljMBUglKOuKwWBANO6hihThwVLTVA0ffvIhf/LnPyGRmr/39/8+0ydHvP3OO9Srhta0gecBNuFPIg55NKYJ7PEqjsgGBcYY8J7qaIoqEpJhzvJ8gadTOJ2juLeDXTXINEKnScjLMDaQDeYBivP80SnTJxNG93cRjUFFmmSQ0stTFpMlTd2GkMlE4/sxkXdI6+ntD0iKBKsV3nn6d8a41mwSZo33wcvYhR66xkBr8a0JJGWppr8/RMUKUxvQksoY8n4WFG/niftBIK8mC1ZPzlk9PEPlGvPJI1oDUb8gf2uH8niOXDb4OOSPLZ7O2L07RghYnS9Rg5xkVCBUgBhXSYSVYd3WUUT/boYtG1QR8sxcFXIbZBpTLUp8pNCxZvBgD3vQsnw0wT89R7Uh90Mahx5m4MAIR7bTRw1DTmO20wveqnVujBJE/ZS2brocS3FBMlekgUiuEyqaqiXKYtJxQRxrFvOSeJgT6QDXvZyuEOcV7emc+dEZeZ4w3B/hlhWr0yl+mNMb9aA2LGYlVVmRIPGLCuE8tQ+5T3EcUZ3NyUcFPtLIXoo9X+KGBdmoj8mSAF/bGU68VtRljZmXDO7skvRy8HD69Ix61bB/fzfwTayXrksC/rbhZCs05qaID3H1+i15SQTZRyoZ9pyXWEJfrvgu2uKW9XfT7CsGoKvPusU+dGv7ttf2ry0cd2A4tylWL+kK2EhzL9sesf3nGrLoBmn/an1rgxnr79vhq96mdLxsn37N8s0oF89t0O1S/iW3jl/3RDf8hdg6L26YUjfV6W/+9ZzB4Izj5McfIyNFMh5iHk/Q37pP71dfB++Z/Lv3WfzsU2QcB0QmJcm/8yrR4ZDj/+lP8dYhtaaV0PvNt5Bbi8KtE2b752UHDZtMnPU1nVBTvHGH/t6Ayc8/wuNpnMNZQyIlsdYYBJFSVN3GKIUkGAhDKBSAiiJwCh+FGOTV50/Y/cG75K/fZXl0RuwDCZ3rPCKeIFz6VgYGTqVo2gaBDwK81DRNg/Ae5Rxu1TD/t++j/9MfsPfOa+j/sGLxBx/gFyV13RD5iEgI7Lxk8s9+Snsyp/fd1zj9139OVXmS995ERoqmNsQdAlJlHX7ZMP/gEVltkHUTUEK0IsLT3xkwF1BPKwoVktKySIfY2DjCDTNsrJHzEp3ExDs9SDRRkZDe20EmmuVkjq0asjwjeyUwSdezJVET8NLj/QFRP0cPcqwPSZuLsxlmMkfrgO9uzuZ8fPqEyAmWVcW//YM/ZLFc4I2lbWrEXkEkCt4ejzl873U8gmZZkSodYuuXFQxzop0+rmohi1GJpl1VtNaymi5JLESjguKNQ9qyRlrP6i8+p3hlxD/8P/4X6GcLmqNz4r0BapRjWoNKNEkc0XSIJkJJ4iKhLmvaVUO+06etmjD0RIDXVFLiGsPki2PGr+wHBLO9PrJIwubYYXDPjs7ZfeswJBpXgSOhaQzFeIBIY3Qv4+7hmHZRBaz/5RItJOnBMJDrdbkaovNQeLc146XE+ZBoKwiIQqYJwqPWurMlXAs6vGXiXZ57AhEgJKsGFakA+ygEKJC+4xqRXSJ9F+/elDVJGodnxjoIr8ai0xizKAP3RBd+41ZNCDOpGnwZoD3zQc4rbzwIFubWgLWsTmY4JVnGip0iRlkXLLfnK5ounNB9foLMU9ra4qxlp5/isph4kGEXJbYxuHFEWTf8/Kd/xqNHj+hnBaeLKc2q5O/87t9DfD6hGRmSLCGPElSkcGMVmMSTDO88sSUgAuUxctmAEBw9PeLwzgEiCazy5mgKRczOaCe8m5CQJShjAzSqdbCqEcsKv6yQscYSrNGLuuTp02OiOKavFGqQBZb2tWLXGFSRkj3Yoy9FIJCrW3zVYKqWVno+eP8XTKoFP/vpTxj3hvzwez/g9bfeQMcxxsxJVELWy0PYlIe6rEjSgIJmnSPJ0w1xmVYK7z3JuAjkedMl6SBDd+g6MhUhdyYL+QvWmE3+UFSk2NpQni9opyVRHFE/PsPFCtdYRKJRRQrnK8y0JL4zIhnmZLsDqskisCmPc+JejjUOCZRn87BWdyhxP/n9H/Pet98lG/bAeVYPT4J3YZBDHlO3AYFLJV34l3P09wfoPMG3bYCgXVZEr+yjBzntZEVbNdTSo+MCr6FaGcpPj5HGIXsJJQ6mc4bDjDjRmOmKuJ/SNE2w2yUiIBF5j440Vod8sqYj8ovSOCi7SmJlMGTFaYy0LpCv6ZAPmI5zsn6GqVvcqgmwwwLi3R42i0g7nh4lBebZDLusYaSom5ZEK1rhUHlMLIKnOkljRJHg5iWN8MSDnDhLoTYBfKKXIZxjZ29INV/Rzkp0LyMfKaIiZXTQR6cJURLhVjWkMQwDlFP7bIrPE9pYhvU3UkR7A8qnZ2Ase8Me0kNrDG5VE+1EIczrZMpyseLwh+8G731tUKMUby2+aiknM4av3SHu+G48sHMwDvkMcmvN+tKy1ZeRsL+kJLllx725+K0gliuN91v/Xmm2WFvjb67yBc28euMFjuhXzd14/n0vaNDVT/I1PsMF0/eXuHb96yUVoL/K8g15Lp7nJgjCsu+grhBroSDcd9V1tG1hvPAC+atdt7nrUhuEvzR2xdozcm0wXxRpLbpuGPyd77J8/zGml3D3730XIQWrnz9k+gfvQ5GjnUdKQfrmIb3vvU716TGrx2dEIjBZD3/wJv237n754fw8jb17CaEkZrpi8dFDmrNzUEGBiZUKRD5CIpRGSkWkNcI5VtaRygAv2TrXgTGFfnZSBYv1F0d4Af0fvsvsJx/hez38Yo6rqhA+I0SIMY7i4P7vyPpWxqKtI1ICHyegdEggd47VX36OtZbd/+w3GPzwHWaPJrhPnxE1Btm2UNb4JEJ7WP30cxbvP8GUdeDueHhM4z1WK8rzmKgN8ctSK2RraKyluLdHNJlhqgarg2CYeU867CNaQ6IVKxvuURLmyxVp3GehPEWh8T3F3ht38EJSz1dENiZGoIWALA5CZqwpyxWmbZH4gNPdxYzbeUlb1qxWS3oPDsgHIaa4Pp3z0c9+zmAwJNKa77zxLe4fHjBfLfj86Cl39w8ZDIc084rmfEmUxDTzJdIL5rMlvcMxxd4AnEfmCT7WCGBQZIEc7/Mz1N0xIo5QHXwl3iOd5+yXj9h57zXqvMWczjHnC1S2g9aKuJ/jBdTLBfJsTrY7ADrouUiFftIBM18o2Wm6Hf/Ih4/JehnZXj+ELal0kwQojGN0MEImCtuGhOtk2EOVNVIJkkGBaVtc5RCxQmQxzfE5en+48RJAxwrd4aojLi+RSqugJHbFLFaQRFvGrkumnpcuzrog4EUaqWXAyV8jn3gu4pq1olnW2NaQDjKWJzOM98GaKSUqDsn8Oo3xHtplGeKrvQDnSQchjlkohQLyNGJ1vmD28IQsljgi8kFGFIUwDrmokLXBr2oipfCLOvBlJIoszulngbTQrWrqyZxo3EMrwXw25f2P/pJ//M//GdPVigcH91CR4r/53/5XDJMe7UCSpgkgkeMQcqhitYHJ1XGMmazC+LeBHb6RHoVHC0m1LHny6efsD/doPKi6pfUW3wavWtLLLj6BdfhY4bOINpIs5nNOP3/K6eSUB4f3SETga3F1E3gAejHSeor7u+g0RkSBUwDvaFYVk7MzjicnPH76hL2DA4ZFn7//23+Pb7/2FiNd4BY1cj9lsNNHdsReYeF3xEnUGX8UAhnC7ZwPvBCi+x1r2vkKJWUQ9FTgjXBVG8JqtEYKyeKLU1xRIyPZVe959sETrHM8ePcedlZiY01+d4wpW57+9DNSBDIOa5QuUlSkiYp0A3vrncO3NZPZjKSEyrbkvZxk3OM3/+7fDAK8DZ60uEhxyxqpFNpY7r39CqJDkhNxyCPxqoNWb+IAZWlD6KKIFdEgx57MwFhs03b7okBLzVJblBYM4pQoi5BS0UoQaRhr+e4AYwy+akn6aSCnG+boSONsgFxVXb6aMSbk4zUGlUTISCM63g5vQwiUFBK9lxOL4Kl0szKEQ3brjnQeL8BbH5Td1uBaS6QVrbX0Bj1UHNHWLdGwoFwscKUJnBJSYY9q/LBPPMxBCMx0RVN29foA5azTCNlPA/P1vEJoGXKT5qugrLUucNwIgbGWiEDgWJcV5Z+fYg+GaBvWwbapyXb7tMsa+WxKemeHdKcfyEwJHh7X5V60VYPBM3r3lQ5tqVu+BAEZcFtYeeGa9jyp86vEt7xAMfkSAmsYXutokhuq3ISq3FKeJ1Jeu/Dy9Td6TZ7b0Jd5zpWbnssz8DI1+A0M9633fx1PzEv3319d+UZI9K4R222Vbe/D+sD1sKHrvXf9m4tr5y//DqrGRia/1D4ufbDteLbmfEXv199g57e/Q++9V2nnK/SwoDmecvp7P8alMXGeYM4WqN0eo996B7uomPyrn5NohRSC9Ft32f3b39lYYG8tNwySa4e2lKvtsvjgEavzOdK0pHES0E481ECuI5SSCK3xIuBSx9KDkAE5SkhifCDriTSmlqRZj+kvH2IXFcm799F394mTFL+cIbt6jAAhBRqFhbBJ6gjamgqBaGq0DKRDje+Yc61n/v4j2qpl9LffY/Sbb/PjP/sFb7/5KtY47GwJvRQXRZws5hRlTSsFPa2hrIklgc27NSykZZjnLNoa4QWxUJhIYHoJtkjw85LlKlj09dt30SpY8XJjQgL2Ts4v3n+fH776BnfujEOymnOcnZwxHg7RUSCn8kqGUJ807siKDEWc4qSgfDZh+fiY/qCP9MEK2zpL1O+hi4Tjp0cMkwwaQxannJye8ua9V3jz7j1kGpPvDLj74D5SR/gqKCvubIGJAtGejCT5wZDzyZx0t4+MJCqLscbiCUqAq1v8IEMO8gBB26EUCQHx/V1GzlM/OsVmEdGdMefvf4HYKUJ4l1aYpgUkk9MJURLx4fu/ZLyzx+69/VCXUt0iJzaoVyqLYC8n6qUsT6ak/TwghtVtYKt1DiHBNC1RkSGjYLmOeiGR2DtPnAWceNMG1vTB/X10997rMIFAgiQxbYOO4zCTu/AkIUXHRBvYY3Wefu2kQo/Hdxwla2Ez7hJ/15NRxRpvHe2qJkojojTgvfcORiH/SFxsaOvfAfkqIr+zQ32+oF6sEJULQpcLc09HmmJ3gJeStgnQk737u4z6QVFsPz8JiMLO4+sW0iiwyqswF8/bil6Us2wqvBbM5+f89Mc/5peffczR8RGq8ySmecp/85//V+zkBR5BFKcQadSdAauqxLmWfj5CSYVSBjddBUIvDyKPmJ5PsFnEnTdeRUUR7//kJ6RO0epAxCmBtLXEUQjn89ZhhcBpz8w0iDYiKxKmxycID/eGe7x9+CDws3TrUJzFzJdLvHfs3DsM5IVaUZ3MSHcHrCYzfvwXP+GnP/sp9++/wm5vxN5ghyJJeXP3AbZpKe7uEhdZh9QFQqkQIt/F8Qsh8YqAlud8SLKVEp0mHflZjVsEwdJ7TzbIg8esC5dTnYKPFOT3xthFhakN3pYbTqXR3THZqKBc1qSHI5bnS+x0hRIgsoje4Yh0b4CKNa5qAx9KpGkXJc10iZxX5LFGFjFxlBH1805x1WEdLuugfEuBz2KMgKgf4vXxHisEbWMoRgUIQb0sSfppCLFaVpjJHDkqyO6PaZcVfh4QyFSs0HFMvN9n3EtQXmCMYfXsnDhPSQ/HLJ+c8eknH7Mz30GmMZlKqE0d5vaqIjsYo9IEliWSwD6ttAqoc5HG14Hp2jtPvSxRaUycp6h+irU2KPgyhDHZRQkqeGacsbTLkigOpIXOByEsioKSIosUD2ghWCznvP/oU2bTc54cPSXTMd/+1nu8oV4NzN9KEg2ywBo9L7FVi1aSajkL3g2tQiifDMJuMezhZEBV0r0k5DqawB3lnaV4/RDnPctPjnCTBT6PWaSaojHEWm08u0mRojqUJhkp/GlJ0xqcdxRv3rmkWFxdoS4EgfXvqxLNX0X5UrE+N1++Ng5ddya8+BEvcECLF0qat9TxovIl7wmhxC+8aCPH+Rs6ZOOpeQGS1obv42XCs7YF3y+jVFwVtL9BheSvgOfi8on1Iiy2NdXnzJV1n1867DtX15Zl88KVtq5MXFIwrvXyVozURZ5HSJjc+Z2gGMQ7PeKdAlc2nPyTP6NtDPm3X6H8i8+JsoThb30LhGD6+7+A1mCsQ/QS9n/nO9fZuF+iiKs//OWmiuDyYfHnnzP7d79EmRYbRUQ64M1HcUSEwIpgwTJeBGWiI9BDgEGQSBEETNPiBEil8XFG9eyE2ftfsPPDd+i9fkj58y+wTY3sD/FJSuZDspeQ4JRCC4FsDVbHFL0U3zS0VYl1DrveVLwjixLqT4+YZRE7//H32b+7G1i+k4j6/g7WGeSyJRn2SaIIpksWZU0qJbFpUasaOSxwUtM0hsiLgO5hW2aLBaVWDIwg2ukhTi3s91HjgpPTU1575y2KPAUlWTUVP3j1b9EveizPpjQIhHUUvV4QpCJFdTYnLpJgfSpSrAg8Fw7Po48+Z7i/Q9bGqNZhNOg8Qq08SZJgZitSEVjRyRVYz6+98g53799B5gkVniyJiaOI6tl5h7MvMVqgOvQqioQs1hzNJrRNQ3+8g9AK5TztqgqhBnmKHvVo5yUyUiGkqBv+3oT8BakkbVWT3t3Brmrah2fElWPiW9K9IYP9EVmZ48qaO+M98vEQRWAv952Q3FQh50MoSXm+QKZpSJSMI7AO56Et6xC+MQxkf9KGjbdeVGSDPECRijUYge+SsgNT6wWUbLDcGoLADYGVduPBlCAI8MpKK5pFSZQnmzj6a+W2zezqb3+hDODC+3jnEY7wrCwJY701Ib7cOehCsS4eFZDCdKxDPVIGpV1KTGMC0WA/Jx4UtFWNmZY4azA+KEyydfT6OS5WG4IqjMUsK2wSIIiVHgUPGZ60SPHOE0WSQRWSVE/LGa5t+fiXH/Gjv/wpH37xCff3A3P6/+4f/md8/+33GCd5SNKvGhinpPd2WdUlnz38DC/ggfTsZgPaskFWJhgG8HgdU9mWwXgXgcBWNaLy7I2GASq1ahHO0VQtvqponYdYYXyAie0JwHvqpxNiKen3+9i6CbC9/ZRsWKDTmLZu6SeaJA/eMC8EtqxpmobVw6c8nhzTHw753qvf4u7hXUav3u2gcR1Hv3xIOy/Z6ecBg9/a4GV07kL57sK0nA3J7YKQbwFscoukEJgO9S0bFaiO/d05R1SEhFdnBfX5Ehkp5udzlp8eEeUZ+bBHL0+IleD04ycMXz1ExZpYK2ol2bkfUOtUY5n+8hG0lihNaVtDezZHNZbk3hiymOT+GEkHL9qR5DljsM6jtGJxOmU+XdEbFqRFWNusEMEzQOCTsMahYkWcJZSLFTrRLBeW8ydnjNweEui9skN1Og9zeqdPstNHFSntfEn5bIoe5qhxb4N65OsGOcwYvnmferFi8eyc/+G//8ckScL/5rf/QQg5S3QQ/rXGx4HATXfKmosCr4LthCScpzlfIhONbVpW0yXeeQZ7Q6KsA5LQElu1CIIhwQNJP8NZtyH6FCoQfJZlyenpKT/4W7+FjiNOj09pz2fM5wvO51MWpiIpckaHeyQ7fbySyFJjj2eBrV1J9E6vI3CE6uMjamdRw5x2UZLmcRgzjaFxDqllCI01Fr9qMMuK+N6YYS+lfDKBQc7unR1UGmNXdQeEEkAx8B4zXaFG+UXY063lJmHyJhP7bQrI9j3PqfKFz3zJy/2Vv28ScG8ShG87f8OzNmrF17XI36ToPKfbbrv91mtuq+uqM+WqwnCT4XnL8bNWry6q9DcPhxf0zTX80tuG1DdQvn5Y1GZMf4Wv/hy3j8dv3FvbyEtrxserXo/r33RbsQiNDC283M78zvhSTaZsOPmf/oTy8Rm7v/MrLD54hNKa5LV9itcPWL7/iPKLE1SXhLv7d3+VpGMr/lrFcwFH2ylN3oMvW07/2Z9QffiIKE5ofceroBQoHQQAT0jMiuKwcahgPZE+oABhHaauUXhsKzZWJulh8cuH7PzGu+jXDjC/eEjtHWlVU8QprdS4WBIDXghaIUh0sPYHaI+IOE3wdR2ERymxrUXVDd5Z/GxF+dETovt7nC9XDIoC8fSMua8Z6RzdWGa2IUk0ygaOgJXzGNsSLUuSu7tYY2inC9JBD7nXZzlbMM4zmo+fEu8OyV4/ROz1sHXLwdsPEEWMzmLqqiFXEcLB2RdHxHGEk4J0UKDzBGxQVpNxj9WnT+m/dS8kEscKXxvKuqZ3d5faOMa7A+I8CwqaF8SDHNUEl7mrQm5EczLjt371+ygtUYOM83JFvz/A1YZm1RDtDcB6pJaYeRniulUQspWQvP2dd/AdCy7QEeSFcCUVBySweE28ZD3OGFyXpKu0wsWSet7inpwRDQNkYfnkDCmgFRLGfbJ+HuKex31s09K2TfCMtCERVRiLswHXvrc7JB31Q1z/qkINC6JYB3ZxIQJRn3V4HxLAkyyQxnkIuQxrLHQpidKkG9x+Q3QZbYUhOdeREbpADOZNgHV2zoGX6CgIAreWjdXmFh/3WmnvJpi3PngwCKFXbReiQweHuw6NibQKcKUQSApFgEP11m36vm1MZ62FuPOwyEjjjCHp5SRZSnU8De+oNUIDStJWLckgoA9Rt8g4IlIq9GsWuDxU3dB6S5QlATEr0SzLkj/4kz/k9OwM5aBtLf/F7/xH3Nu/w9uvvclwMAjhKpHCTEsmfsX+wSsslgvKpuLpsyOePH7E/b07iEwSIajbIPyoXoJ0jp3BmHg0oJyv8IuKV3YPScY9XNmglEZUBtkCSYQcZqheQprGRGkYG7ZuSDrOASnlhkRyHeKJ80RJHBQzPPVsSeMMRniKnR5nj58wm85Qy5Zvf/97xMOCOEuQWqMyzYNfe4v5swmf/MkHHH7rFaI0AkRIKJYS52zIrfC+y0fwARJ5zTxdteAc7bLkbDln93AvsHdbizOWycNnjA92oDGBayUN4T1RkTJ48x40lqY1IZQrj1FaUZ8v4WRGXKRYB5NPj2mNDXC61qMAa6c478mVDPkFsUJFitXRhGpWYhpL0suYT+chl2HZ0L+/y52371HNK6qypKxrhjsD4m5O+TWr+KrB9hLssgo5PUlEr1cgO5StdlZSni9ovCNJg3HIljW2bgLzs4ToJOQoGG+ZH59gleW7f+OH6DjC73n+fHIKacRwPOLJ7JSB2aWerzh5NuHVH76DiEOIo1ByA/srEg1lQ5TGrM6XrM7myKZhVdfofs7e3YONYmrLGj3Ig+LXjR2RRLRNi1CC49MTnHP0hoFYEel567sXEQP7dw5YFT2ScsWnv/iA+rTmg19+wD/4R/8pdw7uQNXihSB9dR9aizmZYds2EDQmESssdlWx8IbB3THH53OGwz5RlBAXCXEv6/J5PMkbhxTfukfTGupVjc4TsjRmejZDO8jGvUBIVzZhvY4UxB2U8q3axXbYwstIeTe6D24+/nUt0i9j3fYv+PebKF+zrgv58YrX4MuKr9uegquN2/Jsi9svfsnHdB4bH3jAQsSCuAj/fFH5so/998lzATxfqV5fsla0XvJFr378LajfW5+xjTm7reWtLSAXxy8+tu8+nBQB8vLon/2Y+heP6H33NTCW5umEOI3p/fprmLJm8ofv43y4p/8rr9D/7quXm/Cc5r24dG3p7L44x+n//MfUHz1CE4TEOIoC9J5SwWIuBKmUyCiithYlBFpAWVYUSdzdB5FWAboSR20tUkckSU712RHOWIpXD5itY4yl7OKia1KlcGmKEpBqHZLq0gTTtoEdt2loD3Ywu0MiBPF0EXIERn1MljL/ow/pv3cf1YtIowzfGAZPz9DCURtLP0twVUuUJaymc9CaxIvwPnWNEAK9M2CFI+ulxFWLWrWkD/Y4V57Z7ISBbnn1u++QJDHNZMFyVtN4R6oUQknqtmWwNw5keAgWD4/p3dlDKkGcxJRJjD1bEN3bhSpYT8+fnLBzb59op2D52bPAGh5r2rPAAyKSmORgSDTMMXVDPMhxSqLSKGD8zyv8ZIFIuzj51hIXKdP5gnm1YK8Y4F1IfNQCdBRhO4UHH+L9hVa4jkAOIQIEZN2iswSRRSH5+GwBSgYc/ixBFynJqBcw8rOIdrJEd+NgHfKE9wjfWUZaGwjQnENFIVG6XpQoKTE4sn4RoECVvGbxMHVLeb4Igl8nREohIbngDwA6bwWdsmSChbaLhxdSIghKlLMWFQV0H9eE8KukiDd9crEBXLXIbS8Ot6ymm/U+EGRGabypTqdBAA1tFOBFFxp1YS1be3cCW7UMrNIuhH8gRAj9Mo4oiaA1SCGDQiAEyf4Qsyg3icsoSdxPQ99v4u87s4fzIXdqkDM9XjE9nbIzHBHpiP/hn/5jvLH88Z/9Cd9+811+9e33+NadVxn2eiE0LU8CCaKSuLol2utx2NullfDxw08xreGHf+NvIIVgJx+iLDSrJiSvJxo1LjBlg8pilHFkXjJ9NkONeqGnrMMsS2TdkhwM8IkmuztGdV6cdlV2ib8aIold1RjriFVQauv5gmW5Yu9B4ENZzqc8fvSIN958k+FgxOmzZzz99AvOPn/K3fuHHHz3Lvl4QFu31E1Lnl7k22gpSSMNjaG1Di8FUZ6E3JemJcmSkOPXxdmrDtpZdGNExppk2OPusBe8cnUb1l/j2L27h6kbfCc0VpMFq+MJVJamrMnSlCiNaacrmrMFXku0dcjWcvz5KVVjsHVAKuqNe5RnM6xW2EWDzuKQl+EsWaxx1tIsKlaTkqJIKGcrbNmQ9XKGBzsM7+/impbeIOf0s6eoNObkyYTB3oh0kGPbFqkkcpCF98xinLUX87iDDBaRQh322SsKaAzVZEFxf5f5k1MQgiyOaPGYSBCPBkRCkBd5UCZF2ENfe+tN/sv9PR5+9AlvvvEOQkcMDsek4x726TnRvd2Q96EvxAq/5ikRgn4SMzmdMT7cwT49Q0jN8nTGzhuHYCzOhDnloyCE+6bl7Okxx8+OuP/mq+gkZlWVpEVOkiSXIhmCp16QD3Kst4x293CmZXZ+TjVbUrpJSNbOE1bTFc3xlCzv+BuSmGZeYqyDPGHc5Yq88WtvB8TBDszBWcf8eIqbzKFqsftDpg+P2Xv1EFGkiCyBJ5OQzxFrqskikJbWLcumIcsTXGsoZ0t6e6Otdesi0uBaMrG/kGG2D26jbF5a4F6mPEf/+AYN1zdb8cXWuecYl7/UM74Jgfir1vFcgXR9eG3qvgGA5LkOJ7H56TrYYOkdsgMaEUIQRfralnjxs3veVj/flKy+zlS+6hn5ymSG68d577/Wp1ksFy83SK4+5RYD47XD/opLbPPKV7rkUhv8LZ19QzvWh63lyf/8IxZ//hmH/+D79L59n/kf/ZKzP/yA/NdeZfdvf4en//TH2I+PQsz54YD7//XvoAfZRvnxV17g+ive5JPbKm7d9kDyNPm9H3Hyez8i6iAQjQubhtYaAygd+Aa0DhC1HhEIuKylqSuSPO8sZo6mrrAIMiWpyxVSB4FS7u3w+v/1f489mXH8f///0liDy3L8oEBZh1uWNMuSONKofo4WcuMm9q0h7eXYLKFuGybAcG8Q2tO0YBzEgaBNl01o32wBUUAKapuWRGtkEhNFktZ7ZBLRe+2A5afPaJzlXMO9N+/z8c8/4M7eIfJsQZUr0p0eTSLo74zI4pjVakVzNCNyEl2kLLwhahyjcZ+n5QyvJXu9Af39MWZVIZMYncfBimwszcMTZBqxrCrQiqJXkI56LCazwFNQtph5CYlGGIeZrrCRpH9vNyiDXShG411AE2pC4iTWo7RE7g1oreNf/NPfI8tzer0egzzjwYNXiNKEbH+wCZPxW8nVtg4kd12eNe2iRGVxGCatQXQoRdWzc+KDIMTqLEFYhwVW5Yrh/i5SSVbzBThI8xQRR8HKrlVIwlSSKAthISHZOsQ5byAOb5ivzloef/AQKQV79/bwUhAnCdaYjfVeyhDK5H2wHqtIBQGvg5pd80zIjtnbNoFArpzOSfrFBi5xew6Jl1lMrpRgd+iWTRO4D3TnbRHigiAq5ICExFjnHLYJTMZJ55UQsksEXtfrgg8kCLIOBDgbxnacxmEuG0db1lSzBXmRB4Wk6z8pZFCyIhXmcN1SLkowFhFpVBoxP5/yZ//uj3FtEPitc7z+ztvsRjlRkiATDa3FVg2kEYwyUAK0ZNFW9MZDev0+v/zgA37yJ3/KP/rP/nN05QKvxftPglX/zjDYTFc1rksAnv3sY3wvozjcCbHkVYuZLANHTaxwkSYe5cznc04fP+UX7/8l491d3nrnHYT1/OiPfswP/9YP6aUp0aDAEjxFUaTxncfKOYvWgfn7yWcPSa0gyVLSvVEQHmUIsTHGkKQJ64lg6pBzEOVpmBd18JYhu7HafQMdB++uUF2oThtIzqyxaCURXd6Pt4FUzkGw8E/mpElMNCwQWlGeL1meLUgGKWZZI+s2IHu1nRKxO6R8eMbZsyneeppVjY7DNxUqWBvjPCEe58Rao2OFWVbM5hXCBkS/dKeH72CjEQKqFjXMqeerAH29LJF5ShSkfbwAlSckHaKUbVvq6ZKyralNQ1JkjHZ2ME2LUwIihShbsp0hCFhOZoGDpm5Yns+xqeLeu2+Efrw2pUQ3N+D06TG2rImjmCxLqRcVGId3oe+kEux85xVAUJ3OKO7tdtZFweLxGbOjU4gjii7MSyIQaeDesfMyhC/FASlvVocE6939/UvKxIuKaVpOP3yIrg3RqIewUJ/N8dYR3x2xeHxKJBXSWPT+kLhIaaYLVquaYlSQPdgnypKN7Hr64WPayRwhJcWw6CIrfSBHjTTxTj8AEXSQ2bbLO0vHPdrpkuNPnzK+u8fi0TE20dz9/jtXck8FFxA/NygSlwTDr6Bc3Cboby2l/uZl/uuV26ytz5M6r8nf/kK5utpF296Rb7zxzykvITVvy61b20/4jtu286tOiBu2N+fcBpq9ExFxLoBWbCq5ehObgfP8dtrAWnkJVKkr/d5Xj8r5a4CivXzNxoNxpfhrv8TWX5c9Ddeuf86Hvt2YefmLNiczvDG88n/422Sv7tOczpn97FP8KGPww7eY/fRTqo+PiLt4/N3feheZrj+sC7CMzj0nqfsFKra/+MeVDaf/9M+Y/eFfQodzHojPEmIhsECmFMZ7pOsI0LwPISg2DGojFYn3gYjOQyQlcRzTOI/McrK9HdyqRuuI9tmM0z/5JQsgfv0BTdWgx30MHoY9eHZGlCQ0dUUpHGK3T9zF4DvjkNaRpCl3lWQ5WeKLhPT+DssPn4LwqGEPuyiJ9keopoGmRWRpEJIjhW8MblSQ9TKUlCzLGnV/BzGZclgU2LM57775Bsb7EJttG56dn1A8uEPrHbqsOf/sGbkOMKXSQyIVIpXogwEP1JCmboiTGNVPcd7RrGqc9BjhmZ9O6cURpgqMxHncQzaG8ukZwjn0eEArJLPJjOFOgQJkkbA6ndOcLShePwA6wd+FTTvJUxQCHytUP+P3/+XvczI749e/+2s8eP1Vsl7O2dNnzKYz9pO9gE6TxtgmJJZfzBdPsyxJihBbrou0SxoEoSRNtcA1LSrRuFnIyYjyhPpsjkwi0n6BAMyyopqXKCHJRz1cl9yP9ygpg5C23uzkS0xoEUKE9u7u8uyLZxjvUXTWeilCXLJ1SKlCgrcI9W6za8suFMl14Sje+5DLACRFfokV9mL2bGOQXzciXJ9UWxt4ZwAQWiKaoBisk7qFCoKp6JLJXRPm3Wq6ACE6S3gIBbONQ2gZQiS6NggJvnNXCyWDMtIt+DqNOgGzg3u1DuMCQaUQweqOsbTzkrptmC/mjHqDkJuwKBGTkh+88i0kkjiOkKM8hFNVBlG12NawEA1fTI/Yze6gWsvOeJ+iVzB59Ig8D9efPznh1VdfDwhhqcItKixBYGylw1eWeKfAG0s5WWJby/jNe2BC6ByNJR4ViCKhqWrSccGzjz/nfDHj448/Zn//kLe+/Q67dw4wVcNv/O7fYLS3g46izmsQWLIhDDUlJc5aVtM5s9Mp2imG9/fQWRoQyLoP5owl7WBkpRRAUDilDtwqOE8UR5u+B/DCE2sZgAq6TUCIi3t0l7QfGLMF7bwMaEZaE2mNHg9QSYSZrTa8Dul+P4R/3dsNSr9SpE0LbQiN679zl2inh1/WWO+Dp4oQyqATDWkcoGJNSGb250tSHOleDx1F1MuK42dHDOpRUMojST9WiEgT7fZ5Oj/Fn844ePV+8MQ0NuS/nM6o5kuMcCx8S3G4w52dB3z+/i/xAtJ+j2LQJ4ojJuePsV88Ix71yNIAJHB+MmHha95+91c6CObNjNmsQUJcCHg7h/ucn5yynM2Zl0uKLGM5n5PKmN7+gOXJlMlHTxi8ekBzNmf56RPsoyPigzGzz88ofvVNdD8n7efoWIc8QK1Znc/x5wuiLAEfckeKcUF/Z8Tl/fOGvfTKTx1H7H/7NY4//oLlwyPyOKVcltDLqCZTVolgZ9jHnc5xTUuTaESekPVSevcC39WmB3zwKiohoW4xdUvSy4jSGNkhuNllhdIaVze08wofKaIkoj6eIpSiffQM9dZ95LMZ0Vt3AkEgYU2MIn3l3bZLeNdtaQheIqn4tuJv+RuuwZduJK1OsfFbJvLb1bznSPkva8a+JieL7Ve/ubywP15g2H3pa172eeGibbaKm+67Mbrphmasw6HWocS22z9CHf7itkuVPaez1h+7kyP+Kso347m4Ujy3KuHXj91Wrl17k8p6i9fi+j8vLHZVI+NoI1id/sFfBmH9zhhlHU/+uz9EieBal/2E/NsP6H3nAfmd8UWLOsvm+rm+g6+9aNzzlQvvPXZZ8ex/+mOqn3yKsA7hbMDG7uy1Qkh0EmOsRUMg3urii4ljbJHSnkxYSOgP+yRpSvXwKcJ74jSldY4oS4kBF8eoWJG8+4Cnf/I+yb099M4AX4VQiVYEZ4o5OiPu5SHGvKwRQJrGaCkpJwu0CkKl7WeoWEE/CzHFnx6H+HYpiIF2lEPr0B4wFoY5xhkSA7pIaUxghM3SBFc1rJZLojgiH/YDKo0QRJFCjApkFiNGOe2yojmZ4s+WyDjGSYGONU3Vko5zon5O1CXoFQ/2wmZnWqgt+SDnv/t//r95+623+c7rb0IX59vUDX5REfUzkns74MAKaBYllA2+atE7fbwS+NoQDwvwHjNbIRoTCLuUDKzSewNWy5LZfMawV5DJiGhUhCTopxPUTg/lRSDqGhXY1iLXvAs+MBZX8xXZIJDcqSTCGQvGUs9LWDUBtcnYgL+PQ+kowNEmEafzGW3ZMh4PUEWKmYW47b3X7yI8qDRGriEtnzNCBWxHHW5NQ09V1sHSX4c8hDRPN/kiyIsF0TlL2BgDz4RpTIC47UjqQvKQwNRtYCTuwsFwwcOh0zhYprmyuV2yjl0VQK6ZwcJ7dMm+3vlAAJYFRCjZkZo5Gzgr1l6VtfVMrMn9Oqv62oq49nj4jpzOWovUCmcsq8mc/t4I27TYqqWdrYLwIQW2MbRNSz7q80d/+G/54KMPeefuK3z/Bz9AymBpdtbReIuTgixPgwBYt0EhyyP+8tMP+NFf/Dl7d+/wve9/n/39fYqiwBlDUwao0P7+kLPTU376p39Kmhf8xne/h59VVJ8eo6XADtIQcrfbRxcJ9dmCqJcRCRGeU7ZU5wvy1/dpVxVqt48RjqPHjzk7O+Pd736H0c7OjdZl340T16GcrT9N2zT80R/8Ae/ce516WXPw1oOQS9B9Pmts6Hvv0HHM/HQGovO8dfKGtwGRC+cv8mM2D/bU85K4CKhBbRVya5wJSdxCSJQP42D16JTZqkbHmt1X9pFxCMGydRvCjbq6pVbBQ4UIYYvGIJwPrO5S0C4qZKRRayVKyQDDrjXGGJQKiELtyZx6WZLtDUJfLEtWJ1O0lKxsg9CSYjSkf28PFcecn5zy8UcfoaXk29/7NawxnJ2eslosEB7SJCXKEsa7u8RJ6MOTo2f0B32SLNt4IL1zLI/OWJ5OaZ2FuuW0WfCtH/46SZJceCovdaO/uH9LkDHG8Pmnn9FWNXhHeTbnW+9+CxGFcKdyssA8PGH19Bnq6Ag1HCK/+w57v/4mMtZk/aDIeh88PX5VYcoGvVOwLFcMdsckebbxal42s3ez+wXbqnOO8+NT5ken1E8n6F5GGwuifs6rb72BcB7RfZPwYuKayOKMoTyeUX3yDF83JPsDdIdSprKYpmwC18sgB2ux5ytWx4GcMX/1ABGH/lBlS3M0IXrjgN69vQ7s5qqi8Dyh/Xnnb7/GbykI1y59YW0XysQl/ohb+/3CWn4pv0FsnXvR818kH26e/VIYUjfd+NdW/GagXrTgpV0sl/a1F192K7fFDffe2BM33N/vf3XPxV+JcgHcoH12lsJrUFC3lBvmyQXfxc2Cw3oyXBwNAtrVK2994bX/0fsQe5zGLB+fcv5Pf0xzOsd5gZOgRgXxvTH3/uPvd2g4V160e4qzIVH1ZRRi7z3103OO/vXPKf/8czLoiIoUxjmqsylaKSKtkFJRdyFSaZbgypL2YBxCNMqGaL6kdQ56OfH+iOqzp0ghQ46B1iitsU1NoyKiwzHxbMl0VaK1DuEyxpAMChCS2hiapmU46tN0idxiHRNbtdSn5+hejq9b9N6A6M4IN0hYPpsQT2p0pGlXNcd9T6o0I1KyOMJIwdliQb1ccffOAdOzc2QWU1Ulo/0xalDQuJb+YMDwlQBV6aVAxYrqdB5c1gKqkxnmdI7MElpn0SZYSEUvw0yXqF5KdDAK8J7WMZsFS3/sBR9/9gl/+rOf8Hd/+++QFRmDXkF5NkMlccC9j6NA9oUIIStVQ2sdbdMyfP2Qtm5hWQc8ea1wqxqVJ5Rnc2rhiYuU+WpJJiMGhzshEVgAXZ5DezRB7vYR3hMVAS5RZslmTDhrEZ3wK4TANS3RuEdTNmAsi8+OKQ5HxKOCZr7isw8/od/vk8QJynmiQU7UC7wGQkqiLMbWbRBqhv2NUnF5cIprm8rVubg9nzaLJ/D0sye0VcPO/pi0XxDmothsbNZalmdzkjRm8sUx2f6QrMPLX89r2yVzqw7iFCE2nBhCiiBo3Ci9do3yWz9eMOkDLK0LcJEqKHSi4+DwPsTfyzgct43BO09bt8RZHMJd9A3oVZ0pyjQtAsHTTx9SHy949XtvdyzsFW4V+Cu8C8n53lp++dEvefjwEb/xa99nMB6F2PlFjTdus+7Z1qKLJDBeO8fps2e0seDDjz7inde+zfnTc6afHRMlEbv39uhpTX2+ZHa+QO/0SA8GjF8bM3n6jNfffBOO5rTP5qG3egnOO8jCPPPGhnCSxiA8uEWFE6DGgeDsZHLO0lUcHT/hb/zO71AUxc02yytjxrO2gnomR8cszibs5ENknhCPepsciRCWFmBb18n+1bwk6voeT2BWF2zgijdeC+9DPd3fqvtOawI92xrqsiItcmha7KJicXIOcURvd9AZRMBYR9rPA5JYEgcSR61pZisa58iLFGk9pBGrxYq0FxL0XcdNsSZE8x7qZRWMQI2hXVZIKVkuFxT9Hg4QzlG2NStTU4wG7Bzus5xMcZ1HDGC8s7OBoF4Pte1+vtz3YqPUAZdi9n3nLVzNFzjnKAZ9lNa3Q15eGt5b9fmLPXlxPuPRJ59S6JTBeAQmeNQXJzPyvUFAPMtikl6G60gXfWtxjUHlCfU0yBHLsynnVLzx7jvoKLqlTX7z/peUixvm+6aLvKeqqpDD19W77UUVW++2neBpyprZF8/QMoS4mfNFAO0Y9jCTBcU798IaUjbUZY0Wgvp4yqKsiKRg71ffAAT103NWx+ek93fJ7o7RSfxS/f38sq1hbb/tLdLkDbffWsRF9Zd0g6t1bU/sK896LpTqjYvFLW38kt10SU68QQ69shhda/vGUORfgKx0U91Xzl0K3n+ObnMhuz7nZb/sN7zlHmdt4M9R6nLI8VW7HP++KhfrckODv+xg+XJl/VWvS/TXX/TKyN2+oIvDffw//gnVLx4htQ5xlAdDomHG3d95j2RvANcmzoVlZ0vuemGTbVnzxX/7h9TPprhFSaw1tbX0D0ZgHbOzKXHjUEqiioy6aYiAZrdPM1lQtoZRa0iEpKlrmkjT6/dojQnWVOdIRn28dRhrsf2UvJcjxgU8myK0wjw5w7WG6arE7g6Jd3r08hT7+JRWK2ykyQfBnb16eIoUnukgQLCmMmK4N6L5xRe0sUY+2KFpHYM0Rg9yZD/h9P3PMcYx7BVI53lWroi9Z3Bnn3iYo5MI6yz9Bwd4JagXJa4xJM6T3N3F1Q0yT6k+fILa629gT6UQ1PMVzdmcWIUERhXpANGKCMnPSuGl4JNffsQrh3epFiv+xR/8K37z13/A7mAIUbBo1vMVSZrQyAC7q43HpzGuCUnkXgke/sUnxEXB+N4OWkmiWAeLWxQFCMk2QKjWkwVWQTbs4ZxDK43MY2xH6oSHarYiu79D72AULOhFuhk/3jnMrAy48IsKEUeYuiXKE0zVMD8+o3+4h5uvEB1jtExjZKQwJsRnxr0sWOXE2va0ZTu5LbToRZve1jzedpU/ffiUj3/yAb/+N3+NbNDDwwYSVPgubtR35HjOBWsvBHhdJa/MP2iqmiRPQdAp6uoG48QNms/6D3HT8e337Nrfhd40qxIdReg0Dh6kDlIT50MitxR463FNS322ILs73ng/2rohiiNkZ0Vf9+P8bIpvXQhVm5csz6eM8h4yjWicJUbiJDz+7AsOR7vYxpJEGpknRP2U1aMJojHoUY4aFzTLivl0yi8ffsJv/Z3foZnV/Oxf/YSjD57w/s8/YndnxMFrB0ROEDnB3Xu79MZ90JLjJ6ecLhc8+P59iqLgoI3BOAzgY9V5siLQ4ZvpIsYZj5gscVIihxnWGlQv4enJM0g0VsK777233aU39vOlL+ZhOZtjWxOE66YNXkdrQ6K/810OWfhu3lqs88FooLbCA6zD1i3TL05ovWXvzbvB+xTpEOKECIhs3uNtYEavZismD08Y7A7IhznCeejGqG9amtkSyrZjuQ/5FmuFtl3VZMMiQNy6ANe6Qcgq603ujHcwny5I05g4S0AKmmXF9LNj6lVFlKhgbKgCB0K1XLIkeED3794JRh5x4SWoy7LzPvyVbpxfrazzmAhC2dmzE86Oj5mfTBhGGf3xmP7BDquzBSrRpL0M6xxxpGnnJU3dUtYlOk8w3oY8kf29S0rUrQLDS4ouV+XeS8aRtbjgHNXpjGa+Ir+zEyDDp0sWD49xSUS+OyCKNMluH1s2TD94THV0TvFgF+EctXX4WUktPP37uxS7A6qzOdnhmGaywJwvsUB6fxz4h6S4/b1etlxPvLi9XLUR3SRYX7n+5dpw5Z4X1XfDczftus0I+yKh/sZGveAFXuL0y4yur6D73FzP+lN+A3VdK9sirvc0TRuUCylCHhvcLKfz9ZSLb4ih+6Jc62xxy99Xr93SCa4eu+ne2z/rdfXx9kHy/E+5/OSI2fsPUdaDdDgtiWLF3d/9FZLd/iVtdPOkqxaT9d+3rAPr65rpCs4WRB5EF6+PETRlzehvv0fhBQ9//+dIJckijX9WYrIEpGTQy8isw81LfC9D+IK4MchEo7IoWGicp8UzFYIWyCcLkJI0Ush+FmD5rMV4R+IhjzR+1cC8DDjl1iFdS20M5nwBiUanMeb0hDzPKAYRblWT7I3w5wtkY9EPdqE2uERjVw290ZCqCfkUbWvo0Wd/HNBmZKwDoVESYY2jXdYUO4OAGtQYpidn9AZ92umSVgvqx6fIXoKSisZaXNXSlhUmz8hHPU6ePWPMgExHAdUKaKzjdDLh8N5d6qoiiVKsBJdGiA6lpP/anZBcW7fBK9Ux6epexjpr/+3f/lWqecnpZ0cYYxnu9uiNBrRNG8KWnKWuK+I8IYoUuhPwfRXyHHyRoJSkna2Ik4jIeVxtAhtzWaOSGC9DOIrME3xrMVIQSRGQSHTIU+nlOaJpqU+nqMMxvYPxJmxI37DhXGK03zJFXVvLtzft2xLptn6uT413R+z1+syOJsRZhs5CKEkQujqBqWo6D5Qm6oRYpQNvh+imj3fBWh9gHx1CqvC90jRce61cea+bloZLpreLe9ZzWGlFnKV4YwL7e2tCHgpskoG9DQ10tSHZH27OCQWxDAnfAZ62JU5ihJIM9sfYDj1I5CmyakEJqrLkbDJlb2cciOYODnHTEjnOWNQ1Q5GwODpnVS8pDnfRRU7T1vhMMZ01fPrsMf9BElOtzpl/cszTx8843N+hGPc4P5mSRhE6jqg/eYz7IPCJWCFwicb7GC88Xkt82TJ3Lb3xmEQErhqLZ3p+Tj/bRcwDiZtrW2ScQ5RwvgjQ0Puv3CNJkmtr3W1r3PqwaQ2zozPGh3uAwAkR8s/jznouQsK2EHQJ9BLXNMRbcMembvGNoTqbBXIy0248T7D2kIcQtrZqAhyygOVkQd5L6Y2LwHIvAnO0UArbGGSeBALOPLyXswFFzVlHnKdAB5PqQyK+aVpsbdBRyI3w1mKWNcO9Aba1mLLGOcf80yPsbMV5M2c+rXhtGDMoeixOJ6hexsGdu2R5fiksaZ1XlObZC+XobY/CRRjTlbnxV1G2cqKEEOzdOWD3cD+88+Sc6fk57WzC7OyM3buHCNcSxRGnZxNiL1j5Gl0kZDvDAHbQKXKXp6u/VYB+aXtlBxzRNoa2rEHLkFuTRDjjmH38BDOZ44VECYkVMPvkCZFWZJEmUpJ4pw8ImqpFC0EyLJjPS2ZHE4q9AXtv32XYy1BKUB5N0P2cerqgmS7weUK20yPu5d+MYvFSL/2cW14kPd9ijLnx2PraF9W3/dq3rdPdubX34MZyizPB33j0q5WXtbhfUtSu1XELOtRt9XyVcpPR/gWNl1J2sLbPD4X+uuUb8FwsueoduPzBLzr4Vi3Pbym04gaX1pfpeX/5j+cp6BfKwcVXWSece6A5X1IdT5n96Ydkd8ZwOKQ4GJHtDrYec7nm25p8+d3DE+yqoTyf4xvDs//lz6mOpqRaB04G62iallhKGGSMfvc7nP+7X1I3LfGs7CzAGoPDlU1I7E5jrFZIrYiMxZ3NcHmCGPXQ1mOVZFItQ47DsMCLgHOv+imqtdiTGdJZXNUgHuzAokakCb4x2KrBtBavJPpwSHu2IHIeoQRUBtVLSd++izcGKoN+bQ8ihawN1bzEdMy+ySCjlaCzlHiQkRc5pjX4eUm026etW0xVkxRZCDtxjnpVsWxqRr0+7ekMB1TLirifBkv9KkDWIiW6lyGzmEefPKJqG9767jsh1ru1lNMF5yen7N+9g21a/sW/+tf8h//x3w9QrMYik5gQKuORkQoW7C52XqzRFKSkbRq01rTzFV5Knn34kNVixe7BmGxQECUx1jmiSGO9RwlJvSiRUoaEcucxVYNrDfXpnLi15G8cIvMEB4E4DzCNQQo6NAdJtShDEqF1OGtDyBPhvExvcbPftj6La0P3uRajq+vWdhztxsKMp5kuaeuWbNgPQkK3UcgO5taZkFOy9hY45wOOfgdXiwihUWtSOp3ozXyUnaD58uXybLzw21x5ue4FvPPYJgiptm6BAKRgqgadRrjadBwpLiCeERShtUAo1EWdvguPWSelO+uwi4r66BzjHXpY0CxXtKuacrVifzgOoVA6WOyVC2hdrbW01jBfzth95S698fBS2xenM/7ov/83LJ9N+fbv/Cp/+S9/wvTknCJOEUrhrOX8dEJvNODgnfvIIqFpG779m28yKAXivII0QowCEpwVoR+oGrwHs6pQStHsZZg8kN5leUbeK7rxdsNK9xxznvdw/Pgp2isG+yOcdSzPl/R3+pg6eBzXCFHQeaykRCgRCM26WJimrNFaBfSnDpjAGYvo2K29D98G7zf1tVWLkgK6vBgRqQBBGwVCQ9PxjUjZ5dNsxq0PyqGS1GWNd444S4LSYWwgimsNrg3rpG8NMovJxwNMY6gnc5plyPl6/PgJWkfsHO7hjCXruFBuynX4MuWScnGTUPOCe51zm6TRb6qET+VvVIxMaxCCi3DE7QVGXNy/LlehWLefcfn49Td3xrL4i8+pzpeQaFxjoB/RLCqyNMOlEe50Ti0FxDFt2wbWdGPJdwaY+QqdJ6heRv5gL3ixpivaZ9MOaU8hrEP1UrLXDmgmCxYPj7FpTNTPSAc5URJvwvO+dPjZi6592e990yW3uXWea9i9tSGX2hS2CMG1feW5VWyrCOL259/Uxm9YSr6UY/LlbnyxgvQydazLTcLk5s+XbOP2dtehQUp54R3ers93fBrw73tYFM/da17q/MV1Ny8el67peuvma7oR2ElWt774loLiPSHMQd68AF53tYS6N9CWF40CQtx8u6wpf/mYxfuPmD6boJMkEGn1cyhrACKtkf0E3c9on5zTNg1qvkKMerRH59gkRo+KsDG2FhpLNCoCakUaYxYlaRpRNia8r4T8lQOa0xn2bIHtp5gqCFDp/jBAc0qJUsG6OX96yt6dPUysUDbkg2gpQvx+HLE4PifSmt5797GAkeCE4OzkhHtvvxaw8qUkiSNs2eATjdeSdFAQ9TK8tSwfn9GuKrSQiNaS3xnTOkt5PGW5KBm/fogwjna2QvUSQNKczRBSsmobiiKlWdUU9/eI+nmwalcNdLkE5ZMz1CBDaY0EmmUVGGCXFbZq+fDDD7nz5quMDvbIdwdhYxYCX9bIpEselqLLm+kkZeewVUtZV8hlg07iIFhUDUQa1VlfZRaHvyONq8N5b11IDI0UAjCzJc2yxh3P0GlM9GAHPSyCpbY1wdthXCDFag3euGBt9Z6mblGCkDyaxgitXsrSc2t5WUvVbec3HjsfMOObQMwXJQEpyduApGZbg4xUyGfoGLe9dZiqDSEmUbBc+i5HppqvAvJWEl1sVi9dtpSLF2w+Ho+rLfiAJ67jiLasaJc1znuiJAoCQh4s4L4Lh5Lr3JCuBJQsi4o1tg18Gt57bGMwsxIzXbKqa56cPuPB/h3Ozs+Yzua8dXCf7HDEtFkx3t0J0J7GsCpLTqYTskGPB6+/doGS1b2etZbF6ZTP/vRjTG2YfHyEkoJnR2cgBG1Vk0uBEIqFAjnM+I1/+Bvs3hsgJxX24TlaSHwWBbQ7rTCtIdIKH2tEppnWK+ROwcH9u8TJdtL05bbcNC6uGlvquuGTn/2CN9/7FjJSLGdL8FD0802C67pfhZLBKKEkAmirFuc98RZEqGBNwhgUDd8aVJYEob816DTeJOuux9QGfKHzmIqOD6ctG4QS4V8piNNkA0nczEuU90wmC6aTGa+8fZ96WSKrFiGDJ0qrCCUl0/MJVV2zOwoe2nR3QLo/JOnll+L8gUtKxfZWfNNc/srCzguK934jCH1VYeh2QeqrSKkXdcLlvrjmldkKy9ouYuv68x9/QvXZM1xjkF7Qpop8b4AsEtrzFS6LcLMV9HK8lkTWY6qKeKdHNugx//lntNbSNIbdt+4x/O7rG7AG10GF27IJXEPjHuXROeV8hdofMD7c+UpepJdXLr6EBfZFn+em615WePNXD9+i8FyxUl0J1L35vq8sn3+9+eK3+nZ7PN24D11TrDo5cGOE+xJK4Jdto7/SnpvkVLZPb82nS46B6/31vz4U7XPKyygOLz99bliEEWwz824W66sWDbE1Yf1Fst9Vi4hAbDDxg+VFBMz4tXXTX/FACDaLh3ddM25ULMIRWzV88Xs/wjw8RTUGNcxZns7o7YyIYw1FCIMRixpzNEXGmv6vPGDyz39GtVwh2pb03QdEZYtrLNoJ1M4A6R31tLxgC94dIPf76I+PgkCbaOy8pJ2v0EUMWiGEwSwrmkenxIcjXNUiBxni7gi1LPHO8f7RY4Z5j1e/+wp13TCtloyLPoM3D3BJFBBv6priYMTk6Jy3//b3g0AZOpjq8SnF63eo5iskoLIYO18x/fQIrKP36gHJbp/68YS2ajCRZPitV8iWJVIK7KrGasGjTz5Htp693RHpsMe42MEsSpRzaKXwZY3xNUiB0nHAMx/3gqAuBfWyQglB0xpm51MiqXGxIotisu46REhkFVojkwgIrJh0Vkyco13V+KZFIUIS+bJCpjF6XODqFpEEEkIpBFiPSGTgIbAWK8BWDXERMNFdpyzY1lI/neB7SYCrTAJxnDM24PcjaF2I8zZlTdbPUE1LWzYoCCRm3JBc/NdVti2MCOJ+hluU1KsKgUcqHeB/Fy15P6dZVMS9dGNRlpFCdYKydwGlqS1DGIyMQqjcJaE6POjG518uW0rFy1i5fMD7Vip4UnSaoLRmeTbHtRZRqEtVujVCUNOiO08G3oewCQRxFmPXPBoImlUFBG6GNwdvoIRkV0l2Rjv4ssVL0FIhIoXBsZwv0b2ct1/9TlfH9ReQStHfHbH7xiHnT88wbUuSZ8SR5q23XwElkGmMq1p+9rMPOXiwz6vffoU4i1mlAVHMPJwgraVtLZQ1SilsqnCFQvYTirTHzv7edVSbW+xSV61hwMY5bFvDoDcIRG8C4iQoX3R5QaZuA5JTHRT3gBrmQEhUpANvTxtAJop+TrOsQrvibh7EGmts4NDJ084j1iE2iUA+VR5NSEeBd8Nbh5mXGOfo7QxCWyPdIZt52sYye3KKMJa8nyOFJUkEp58/JssyojxFZwmqnyEQWDzjOwOyIseuGmSiibL05QX3l9kMv458csPY/zpKBVzej29+YHcdX67pt7fp+vFtw59fX+KhrQ3nnx+TKYWWHfeJjvBpHHb7LEY5R7Y7RGYxxljs8RSFI0YGqOKqxU7n6P0h00fH1FXD/g/fCYadLiFWiRjXGhbPJsyOJgxfOQhhql+xfOP5NV/FJrP9+znW85vW0q8qRH+Twvc2I9pXqXcbIWtz7DkGvAtAgIvDIRJHbJSAW5txVUl7yeaKDYTjJe3m4p+rigdce6eLyjZaUPf8r+cK+gaUi+ebBG/toy9l0LhsndjWdF9YwYVecP1Ut2FfREUJtt/n0kDqlJarhzoZel3hJUuKsw5bNYGboLvOtpb2ZE6eJDAewLREpClqUUIWBxesUvimBREsnmpnwM4/+iF2usKJEPO7LEv8rMLOqkC4tV+QZEkQMaVA7/Swq5r8rcOw4PYyms+PSXcHuFjjy4bitQOWz86DNa8O5HtxP8N4kL0U1S+4Ex9S1w2n9ZJBr8ejzz+i6pfce/M15m2Jy3IO3nqNerbizoN9tFJBwWkMItZk93bBO3S3CLenc9qzOdneEJHFxIMcLwROS1QUkQ9yMBZFsDTqPCFPY94+3KGtmo4pGmzdoKwj6hf4ZRXeUUuicR+pFNYFq6VZ1bi6paxrcq3JBgWxComo93qauCg21kS7CjCSG/4S0XktvA/s1mtkBaVC2Eok0XEvCD3reHHng3Veh5CLZr4KuO0Q4E+dozmbYzorsYoDIaIc5uhBjqsajA0snKZtKRcrpIWzkzP2X73H8edPufPanZA8rhqEtZfG4kZB/gasJLdaaTbz4eYiEKS9jCRLsB1pWTuvAvlj0264B9Y8E2FRDkqG7MaOzGJ0lhCJ7Ue94H2+yutuLV9CSVxrkZHsYEYtXkD/zhjXBjI9YWVQNrt56IxFd16jalnhXYjXFxC8To2hbVuSKCKKNMZ5ko7HxBtLkieB86ANMNa9flB0m7ZlfP/OJsfkQre6vkMJJbn3rQccvnkXZx2//LNfEh/2+ejRE3pJynh3GJJRdWBzPfr8iHtv3SPOEp5URyxUycHeXlgPPRgcIk8Y7O0QZcntMeI3hKp42OTObPp26xs2dUVSZBhjSdOYalUjpWQ1X6K1DqScrcE0htnjM1CC4d0dPJ7ldEEx7BElIe+oXlUbVCYP1KsanYTQqRBqF0LT1mtys6iIpCQd9QKUNZ7zT57SOxyTRklHfObQWUxT1iwenbI8m5Foha0byqZFxop+noMHnSdM6xUHh2Nc22Kblr/4yU85fPUV3hiPiJLk9vlz01B8gUB5lXzrK5WvJy98veeKL7Eq3WZ1vdpH21ba7UPd7yiJyN+9h/34CJEqRBYRv7JL/mCPyYdPiFc1ViuaZoXGk796gB/kLE6mOGdpPn5CO12SPtijqRtUmlCdz2kmC9KDEXQhlOXZHL+sWM2WpHd36d/dWYsMVxr6zZUva5m/dP3/quPg4ufz+TLgm+i3r7wP+q059xL9tb1Eb2TUax4dgkdjLXiKrZu3/73No/QlvtuXfetL+sRmAf/q5RvPubhUbvNV3nDO08nmrPvQb91y/SVfuExtxuZFTHioKdzjmrYLwRAXbdvyStzYK5cvvfE9tm80dcv5p0fsfesBAO2iYvXwlJN//hOkCcKwBNSqprUW0ctRUmCXFTqOkK/vIXspJBHDNw4xx3Oqo3PKx2c08xXxvTE7772Cq1tOpucMrEQ1AU4ye/d+IKeLFe3ZEplGRCLAEz79+af0ihyxrDGDFCcksXHE4yKEWnUx/KZpA0lT3SKKmN5ogCFAmAGBa0MqqtkKhCBqLFE/C4mixoJxqFijhjmmrLHLmvLZFFdWDO7u0VgbsL+XJWVVkWQJK+8o4sBzUXrL0rfs7u0SAUIpsBaZd7kWsUZnSedVCJCeITZ6nSMBItIhv6E7r0QITbOdAFIuVhQ7g4Aw5Ty6nyG0Dvevw6G6sDi68AFTNago2oT1rL/7mh9BdVZsW7ed5yvALtoOScobgytbklFg4l09OSPtZyR3xkGgbS2+biHWrGYrVqczxq8dkPRzPvnpBxy8codiPAiwps6FHA0hNmE4QMgF0DehK10ZzzdZoNYGjJuUi1v3gps3gw3pZReSsu4z2xqEEDz94hHD4QgdR4FQyzrMskRGEemwd729X6c8Z79ao0JB4AJo65Y4TzolyAWySCVD8q+UOH859HIdUmfqZpOU6pxDisD3YauG5nwJzpEMixAm1iWJu7qlKSv0uCAqUhZ1SZ7n5IP+DXmsVxZRv71mAl1CuVKK+dmcj378ISefPcM0hqJfsPv6PsZ7vvNb7xElEdVyRVXVxEkceA66HBG5YSIX1x97U5++VGeHtp0/PaUYDdAdU/dqviLJky6pO4TRORNyWepVTZzFeKCpGtI8ePqaqiHJ4jDHO7Qn2ZGRCUTwjGwpjaZsqI+nqDymNZZYK2TnNVSxDvwT3bpVPTmjOZ3jI4VSkmZZUmUh58N4RzEeMtwZo+No8+3XidRN0xDHXx5m9DbYzkv73HP2zxfVvtHwXnDfhez3dV0k1yvehIt8ozX7S//cdLZZVjz7kw8RZUX+YB9RZOT7A5790fvEzlFriVzVpLsD5tJz/1feQDSGyR+/z+zzI8ThGB0pXBYhoggxWzF4sM/oO6/hAbOomH3ylPLzp+z8B79COu7jbMi5+ytVLr5EXsbGsr72gD5nHNz45a8e+IpS48srRFtB8F+167aWoK8UIvUi/ebGPrh+03b+yTenMt3y6Ft078tHXp4Z5N+vsKht74z31E0D3pMkMYItzodtpa6T/v1aw+DqIPBXPkrY9G6cBJdUR8Hmk17SGsRGmNgkYfqLNomLNfAGY2EXJXjb1+lMjKZqac4XJB2zrKtbpr/4gtmPPsFLiY9AHQzBe8zTc3RWIIzfJOrqOyPsvMRngfU0JJHKIJzNVijj8I0l2hvgGwNHJ7R5Sno4Jh4WIRQqjbHO43ND1E+pTgJz9Oj1u8TDnDiNER0pW72s0FnM5LNn9PMkJCXmCTJPKPo57aKimcxxSuI6L0G5WNEaS380II40JBHWu2CFFQJfN+E/HQSVeNyjfTbl2dEp8cGY9mSGn5VEd0bETYvw0NMRs+WCk/k5e4MRKQpbtURJhBeghgXZ7iB4RqJgiZ2fThGNIRv3CaFNBpEleOeplyVaKaQSyCTFty14jWtCImexP0KncUiIlvJSfsB6rPmtMOlmUQZr7la+wJpYTWqF6kjCBHR5At1YUQppFaZdIJUiGkbBw5TG+LLBrmPNI41pbRB8mpbe7oD+wQgPtKuKWMXEUYRZVqg0QhgXCL+6jcbWAeno6PEJWT9n78H+5bl0ddJsCxxXF6bbrIQ3lE0VVywv62cLCdZCM18h44izx8fsHOyE5PeqCcm5HT9AtDu63sZvorygHu9DOxEiCL4dL48zLoQqRgrv1t86KJ5rQr016lCUxF1ycOAmwQPOUy1W6DzE/5dVg5KScj6nl+UIJcOcjSIEgr07h5f7ctucdekdtgW1CyF0nRcxOhjxg3/4G0Gw6xTjcr7COU/cjc2sV5D1ii0Z6CUUyatNuHEtvOnmIIS3y5LocDcwGltLEmvi5ILTwLYGQrcFbpaO9A4R8h9UpEh1iqsDu7axIUQwyVN0Gm2ELtmNKWdMQLtKQg5UpAJQhG8MUawDaaYQCOMoz+eYuqEULcY2yDhi91v3EU3Fzt5eMKxcVbg3XSdIkuTa8ReXrdCJ51/29cpLWl+v/vV1yzaZ2jdlML+ce8FzLb662+OyPAsgHMsatywDr4sP3J1OyZBrJEFKgfHQTpbk9/ehbHCtgyzB9zMiIZFJFxKrFOXpjGa6wOYZ2bgf4JCl/Ca78MayTt5/WX/QJrT0BVbpFyqX36DX42rOxXYrtkSuF/flLddsjFtfJbn6RZdf2lb9xfj2V5fRW2bV1TbfKlO+4Py2ecmLS0evP2J99HL11+Xcr1++IeXi5h3G+44B1zmUtUT6gr26u2Kr45/3VpeH39pCd7tWuyX8iys91tEYqjS60TuxfpMbO/wFk3JTPJx++pTIQtLPsI2hPpqikgg97mGqluJgRLTfx3iPPRhx9vSUrHUoD9kre7jJkubJOcwqFo8myAc7yHFB9cEjdJqQHg7JvvcaUglIYw7fey2gIjUWv6xpjmfIJMIsKlykKL1nUVf4RJPtDXAEaFpZt7jWIJWgmi/RHYkY/QShFNXxFFG3TOcrdt65j1IyELHNlrRlA4kiSqOwOVsXvB5JhGkMy/mS/nhAM12i05h6tgIlGQ+H4DwRAjEM1lrRSxFFQrUqGZYxw/EQsWzCN1EKkUbEOwNUGtNWTcdKHjaHJE9BG7wLnhKxJmgyliiOUFlywcCaRGg8UWtC0nY3ltaoMH7L4rkd5rb+O4ojcB7X2vC8SIFnK1GzsyZvrJlsrN12uiJNE+qTGfLOKFjAnaeqGvRen+Wzc6IsCd6fLhnVNYaTL47RQtDf67NzOA6W5UhvkFYC0osISDUiIBxNTmZk/XwTevS1ywuqeHEyeRDYlVZ44PD1eyAEB0V2+zO+gU3spipvikEVBE9Du6iJBzm2sWAD2aGQAtftGKIDR/DW4wnWct/Bo7rGIPPOWikEWitsa6hmC2aTKeOdMWezKVESkUYJdWtANRRConsFxhiyInhrblTs/IvXyKuujrWNZb2C9sbPs0Rd2Y5uscxt9+HN+9Ht9jlrQw7K6tEpItFkw17IV3EeR1DQAyv3Ba/F4mxO3s8xVY1IY0wb0MRk3M09L8iGveBh6pQ914EEtNNl4H2RYgM/6oVnNZnhmhbTNNTWUrU19XLFytQMx2OGhzvcOTxAq7Ce9MVwC4v+m5Yau69zwxy6Mbn1S8+Lb1BR6Na3r5QTcNt2/bXKlQ654adtDHHrENphVACGWDw7RxiPLxJiERTaxSdPuPM33sN16IPOOnTjNgYCJgtEGjF6/Q6+bGgnwVCU5inNoKCt6i537xt/yevvd+k9X04mCZeKlxxDzzEyPO9x22274bqr4/kbm0s32zIujFsvO15fam7dZo3bOnXZcn6DcXxrLl1Suv3FP1cs3OvrxPZ1YbPZUtK2Y362ZORbA5Qu+HQuv9PXD6v+BpSLK43eEsSllCgtkU6gu1Cay1qduHzPSz3tNk1327+xrlZwGc3pekM3n0usk7wvLr+kYLx0AzvlJYkwx3Oaz0/p/coDPJ64yBh97w1OPnmCOhjgZHh68fo+NtPEWge3f91gZyt8pKENiE7l+4+RoyLAYe5kZO/eIdnpUdcNYtUReCUxdlZiywaKGGOhLmuy/T3EICfJY0zV4p1FKUVbNoH9mcDaKD1EiQ6ss6sGu1rg6hYbaXSRoGNNlCZ8/ugpn3zyCcu6ZH93j2GvhyoS3LLCeboNXaPXcdHe44Rg8vgE7TzOWdqnp2RFTlXW+MmC5N4OMkvQdUvy5l5g35UCu6o2HAlCClxrgsWTgIJVL0ukECGsJg3hEyFRGHSnVAQBq5t6ErxxV75pBxfaMf4KHZJIbUf+tibuMssKYwxRL8OsSlzZEvez4FFJIpppGZiw8/TCIyboQrYCmaFrDKqfBVjNLl7XBnMZOtEsT6eMB1nAYjeOtjUsHx3zym9+G6kkOkvxWwhWa8hMMytp5is+ffQFb737Du/86pskefL1FIsX3rrGye4Woq0FdTvPbAOyINb//BVoEdda9rwWXy9+rRgrFZL6hcCVNdY6GuuIk4h2VaMTjVsFJc534XLrvByBoF0EQrBAuGexZYN0cPjaPZYnU3IdkyQpXhAUaBfyeSaTCfmgH7wXNzXx2qb1zfTIBl3vZTff9XJ6afO8YS3efHd/6Zh3nqqpkRYGO/uBTLEO8+j8ZEoUa5IsJVp7jiT0dvqU50uq+QpjLFkvQ3Tssu35IvDoWIuONK5qUFpTny8QQqDSiChPsWdzlpM5U+05m53x07/4cxDwg+//gOHumPs794miCKX1Juzz2qt/00m2X7ZctcNdGgu3K3SX7vc3/P2lmvDlNYS/in67XOeVDtk+5cPcTnb7lNYhi5T6o0foUR/rPDaNUOdL/KIku7+PTCKE1jTzFd7YoGjEEbYscYsWm8fEowIrBO10SfL6IXZewqqmqVussRvI2Zsn8lcp3WS6+om319KrQv2Lvu2VPnrOky/W8JcdLy9Yqy5Dgr+wCXxdFcRf7ZQtGfSyoWQtlt9sLrk67cK2tn4bcenei/e5rBJsl5s9GhdtuXRH9/1vuuNFdW0bxW8Wha/K4d/MuP36ysWVAb+tIOMFcRRfPn9J4Hi5OjeHu07ywrP2QFzu1Ns2UH9pZISmbW16a+FnS8vczF9xMcG+TNl99RB3b4/Jn37M9N+8T/rmATJPUEXC/ht3cfMVjfWkgwKhJMMH+8jWILQiPRiwkpC+skf5bBpivWcrzJNzVJYiDwbk93aRWRISf5eBaE7kKWKU4SOBcB7VOopv3Q/WwtbgqjYkSi9ramNpjCErMtrzJSpPoTXoTilsrcPHOrBkR4p8d4CtgiKipORv/t3fxlctpmpojKF8eE5UO4o7OySRwreW9nyFGOYYIaifndEvMlSeMH1ygs9jRC+hGOaIWKH6GbasiEcdwpM3CMQFr4EgKBlagXGIOMK1hrTIwpfXMpz3HluHcAaxgQ/e0s5dZ4FWHYSo83jfQYlKga0NbrYMz1Fyw8DrmhbwgfHaB0XRCslsMqdXpLTeB1QYtY5p7ZJJW4uINWZe4gQkg3wzlGxZU81L+vsjIqVw1tPb6dOuKlxrqOYrWuPo3d/r4sptwOHX6tJa2S4rzGxJNVsyzoYIKQJpGEGYE2u0s68p018P3bj4dS2kw1/9099w8vqOdenIV13j/A2vJrZOXrkW6LxRJoAuVC0O0HmK9x4tBTrWNG0dcncS3eUTqY2FUwiBSjS0FtcanLGYqgkJ3llCtQhKsDMOX7YYLajqin6a47SiXtWMB3dCWNa1Bt7eERdx1y/qlCsbyOYT3GS1ek5ZG2u6D3XzmiuuGJDC6Dg/OeXpR1+QZVlAY1MCkcQggudw587OhtfCtabLYWmJspje7oC0l1HNlgEwQQhcHUICdRLRVg3t8RQzWSAcqFGBzyPmD59xOpsg8pgWz7A35qB/j9893GdVrvj2e++xzbNwaWTeZAi7uVMuWxpvK89TGm+t+XaB5yuV51TzpWL4/z0qL5oDsgNSINYkvQR/uEP7xQk6i4hlQf3wiOKHbxNlOeXpFCc8yf6I5NX9ANxRpNinE3xdE/VybNVCGhHFQ0QS4VtDfb4gGRWsZiv6O/1rivWLP34nVF6TjdYCcbcOXFMoxbVLbxxTNykHVx//vLH4jdp/ttCTXnwp2+oBt4rqz6viQhtb5z/4a+cuZNab2nBZlb3919Vl9vI1L6+hvZiz6kWa5Fe0HsDXuO9y+UbCoi5/+q1y4wjoRA1/pQP9zQvpy6aebAskl5TyS5LKlj65NYjELdes5/NG97j6rK0itq4HEYRMY1HKk751QDwscFWDNCGEJToYgzGo1kJrURGgO3KxqkX1cxSCvJ8TxQrrPasvTkn6Gflbh6gswSxK2tMFehTitsvZkjhJ8GWDyGJEGuGtxZctJIHroVysyPoFqm7p7Y+CJ0MAZY1oLNEox9qQfNu2DQjHoEhw0xVy1EN4UMuWxdEEjcC3FqUko2EItVpN56RJQjlZkO8PyR7s0S5KZLwb8lCmC3qjPlYIRGuIDkeY2ZJ6vqSpGxIhSCKFE+DrEBalYx2UhXVH6y4fQnTQsZ3leL0yqzje/PZe4FxIqPXG0i7KkIiuVEi4cx7VD7wbMokRxqGTOFiwZIAidM7i8egiC56cqkH1M6JBTs972tmKZHcQLF2NC+RciyqQDxqDSmJc3Qb8/TVRW0ekp5wj3RsAgupsRpQV1KsKLQTF3ghUB8GZRODXeQBhDNqmxTct1emcxemULx49JrWatJ8zup/QNgZX1uTrxOirA/dGU8wNf28ue9FcfMGyf20vvV7fc59wi9Hh6xcPSuIEyCRCaxXgcBcVOo+J0yRwlTiPQhBnCW3VbJibvQmhgN6EULnJo2N0pIIXQgqaZQ1a8PTxE/ZHu3jjEK4jffOe2WLKz/78J9x95w0u1qCvt8BvR/NdfdXt8pWE1q/YtOlsxu//i3/J7/yt36XfGyCURCqJFGHtWuerSB14YOZnM04+eMSrv/lugKVNIrJhD7uqMPMS2uC9NI9KnLGgFV4Lns3Pef/3/x3D/V3u3L+HGWW8+tpr9Hu9TSjhZYH0pk4SL6GwbZWXufZ2nfrlbvbixj3y5RvwgvJ15JG/tvK8Neb6d/SATjRWBaCU88mU+tmUfNRHRxKZRFS9lF6RBRJFrZn95RcMgHx3EMKCW4Me5SSyQN8dY+arAHiQhn1GKknvzi5GC5aTOb1R7xKh5ovbfaEg3fweFwYa8dxjL1Jub2jD9jffMqSKrdNfvdxmse/+v2nPbRvTzUVc74QbLrq5CbflP/j1uRsq91v3XfT5+vdzJsy1+e5veuiV/g9K1yZf74WVb7dx+9+LPeRGQJa/hnn+jSgXXxVD+LZy05AMHbatwFy9ansIXH/Wppu7L3DxEcPxy+pRN2TERc0XZ25vMxCgLHWIGZ58+BjTOuJRhrBBCHZaILRG9VKSzsIplcTVLa5uA0kaoFqLaww+i4PbNY8Zvn0XkWhsY2hPZ4gkpjmdIiOJR6CFgM67IMoWH2matkHUBuEcy6bBVy0zMyWPYsy8op4skK2hhSCYA/VyxdIapBQkSYytW/QwD9bY8wW9YQFtl6xvLSKOqM6XNMZA3TBhRTHqE+30Alt4LwvJy0WGlUF5mhyf8eDtV4iKLCRdWgumi1FfrojiIExIrQNx39akX09oqSVehE0DKZBCAi4gESFoqi60qGnxsyVSSsqmpXWW4XgAeYKMI1TX53iPW1SbMCjXGtZxcr6xrKbneDzpqIetg9fGeU+8Nwg5Gx0Sh5cC0RfgoHl2hgRErKnPZvjliqjIAmRvGmGdwleG1ekUlSdU01Xg7ssTZKRxSqLiaEP+BQTBt6pxZUN9Nqc8X3J+OuVw74B6tiQtUtqqQXYJ4zeWq4rEei26afF50fRe3/fCBfErlpexqN088V+uDgJClBQBinXy5AzpQQlB3E/xxuG9J+2lHYu3CSF0WiEjhXPuQnHtvGlNVaOEQFhorGF2dMZOfxTIFZXCLksKneASzS/e/4i9u3c6rozLDb15e94ykjzv22wLzlc2sevVXduFL/350p91U9fligRw9/49xq8dEo8zensD/KKmXjXoXkqcJsHTIxyr6SKgV8URUoApmwA3+/9v7816bcmx9LCPMe7xTPecO+VUlZnV1ZXdXeUqWe2GIEuW2y2/2IBf7GfB/8/wi94MwYYtCTDcaslVXV3zlJk373zGPcRI+oExkAySwdh7n3vLQCxcnBubQS4ukotrYJCLBQWSDOXrW+QeD9yQMwqUJTZJgt9+83v85tmX+JMvvocf/bN/gg8+/NC4Cm9MlxrvukY6UP/ZFhw7mOtDuxi2NcVQsVlL1sbVPviFmlgPb+6EU3QIW7Dfh8EJOf3sMbbPLrH6aoPwdIn5dAISeEBWYPn0ArjaYPrxBa5/+gdsihLJV28xn0ag0wjFzRrF9RrLDx7g5JPHKDcpLn/ye7D1Bmc//A6/G2cxQfn2BmVJsbq+w9GDI4cWiZOMGdiNqDl1pR3B4lgI0f7e3YerA7gwtqI9ekN9zYS/DW5Wv2PN/+0XfKaRdO1T87baGCE6DM07phxcr0vr/C3WluueXTG1Q/Olx8RqB4b9nQsiPvRLvkYQCI6XS7QDbuyL7oXcadryrM6lmaIdXdplFD3z2am8++0LhIspsrs1im2C8HgGDwCqEIskIKABX3EHIUAVo51vmZqAJjk/CO/xrT7xcgq2nKJMMiSXd/DiEFuWI5rECO62YL6H9XYLn3rIaYHl6THYNgWZhMjXCZhHEB7NsF1v4QP45dvnuH17hb/6wQ9B1wnCwAMrCDAJgeUEzPMwWcwQT/jh23KbIUtzpJsMESFILlfANgWbT3CbpzjxArAgQL7eIpiGmH/6FMHRjJ93qA6PeVHIw6+mGfLrNaLZBB98+hEAHjIynE9APIJgm/I44fGM3+cRR/I4MMYP3aYZ/0JTJfuLCQC+hYKAf0ng4Sj5pXPw+SV04XyGfJNiMZ/BowDxfeSbBEWaVRGgAiDg249QXebFGIMHgu1qg2Sb4ebFFeIowMVnT3Hz9gonDx/AD3weJre+RbHgjiFKing25fdXlCW84znSbYJik4JNItDLNf8iczJHuJzy252raFz+cgZQisDzUCZ8739YffkotvwyxPxmA1YyxBfHeHK8wGa1RYnKISpKeNOYf/EYAjoD1OZ0MMjbKfqM3aFSzXVRS6S7T+FojWvACwIkd1ucPDpFvkn4uaS7BAWliKuwpV51hiWIeaQylJSHD6aMn7MqC/hRgPkkwurqFj/5yU+wXC7x+UffQrTkZwXKNIfvB/DiAL/53W8QTWL81T//Z53zMbvakfLB40abtR3UTqj2r+oUqI+GPh0ylGEY4j//y7/EL/7fv8ejhxeYnh/zcyuEIEsSbDcJprMpAkJQFgXyssTxh+cokxQFIXz7ZugjKXO8Wd3hZz//BxydnuB2s0Kapjg+Psb/8D/9jzi/OBcMZZuXrDJ71R9Ww/hAalkzuKZtSeK+evmrPv/bdYiq3x0ldvij6CYYaqA634BhQGyKBlSnxacLvv0tIPA9H2wSgGwygFKE00kT4MULAgQPTxFG/BwPYwDZZIhmMdiU352S5SXoIkby8hKrl1dYPn2AjFHQMEQICF8h3Duh17FzQdW3CKOT4bpqTO8dyusLaJJ3FW6iDnHFMTS/UE73ZaI+D9F9I6fWi9rFNkGZ5JicLaCXQUQqY6LFmEO7JkTMoupwawhWOMA9FyuIpnvH+9OBMPeYGPVJ0IOkfi+ltI6C4GcbqmhdU46fQd5PJ67iqKFu+2waomcwxpC8ucPr//ArRFGA+ccP4U1ClNdr+MsZ/1RaUBSBxw8f5iWKskQUhcjyAvEkRJnycxf0dgt44J/6SwpvHoMmOY9WFPoosxz5KmkMmsgLQHzCI0alBT/0GwYgkxCk5IeT8yzH7e0tpkGM9PUNaJJi9vgBwigA9QhfgSFVtAvPQ7lN4IFHhwqmMcpNimKTwp/FWLMcs/kcJM3hn8z5loWLY35WQemt7XqDOAxwe32LkHiIJjFKxsDSnIfgrFbmyzRHURSIphMe6pUQZax55I98vUU4myCrDtySwEcU8zMYNCtQZgUCz0NxswGtrzKZxCjWCZK7LbLbLbw4wNG3LhAGAaLljDsuZYmiKOD7AT+UTcCNH0q5A1hFsbl6fom3X7/GbD7F+bcfIay20fgzfs6Bphm8KGqNher2Yf6S42IlBUtzfmP6csa/TPik+no1hT+JpK8VIATbmxWCOMTm7S3KrEA4m2D24Ai3zy+RbBKURYmLD8/5ofL5pNliomHgLtgEcE/ZZiaZHBC1niH4jflrg6srEzo4mfK/lIcnltuMO/qVYVkbK8TzqluegTzJEc0nAAG/0JEyzrtFgTIv+L0mHmm2fL58/RrXNzd4uDzBdMGjGcXzCb8/hgFZlqOIgbOHF4ginRMoa42OAaXxBQiYGuBMo0xUJ0Z1QIRsBkHYr5wEI7gi6ObqCtnVCv/w83/AZ+cfYLlYIniwBKUUd8ka//7f/zsEYYgnDx/hJJrj6uYayd0afgmsb27BIh9nRyf4+xe/xb/87/87TGcznD14AMYY1usVjo6OW7Ir2vXbntqWy7S2zgXQNfJ5Dv3KoTNY5sOwMw+68OydFTP7XFTqfz9wIGdNEmBmB4TmJbLbNdKbDYK8RHgyR/LmFsFyiuT5JRgBNkmO+UfnoDdrrF9cgiQlogDwv/UQPvFQlhTlJkU8m8AnHvxJiDxJsa2iIZ78+bcwW0zR/dT0rlw7C+xj2P8xgIs+OQTeQwID1yHV+dE/+iNNQp8ul7vfc3Eg5wKwWyZKeuUR1kJUEgeauSiK0VYNMAwV8XVTawNCF5JSpLhRzjUpRAnbJTStxlSmOW5/9RygJaYPT1FuUlAP/AKmVYLgeIaiurW4fHsHNo8wmU6qCEeUn8uIQpSrLRitQuaWfB9/CSAIfBQF33pVZjnKkiIOQ+TbFEEVEz4IAxSrhIdlrUKzFnmBVy/fYBIEmMQxbl++xfJoAZ948OYTxGdLbF5eIghDeIspspsVvLzk60kMSG7XiI/mABjKokT08AjhcsZX7UOfh+wkRL5LrRrY2jgr0xwEPGRnMJ8AHgGpnBlC+VeJZj80Ic1ZClaUKNK8uRiLpjm/28HjYVhpWSIKqxCDb24QMA9hdSB9m6aYnS5AC365nReFyK9WyJIUlDGsX1wjOj/C7MERSEERTiNskwyzWQwShwCl8Kcx/DBAkWa8X6cRbl5c4c3vXmFxMcfZ43N4gYf4jH8KV4UHvzivhBdWh8gJ4U7QNkWRlwhmEY9SEwVAdXlZmVehdYNqBa0oUWYFyjTD+m11nuVkgcuvXmF1dYvJcobTR6cIoxCsoPBncf8lei3jS7xvWArpBxfPvMe50BpYdk9fn6+vTuVlmZWN01KPVZnzyC/8wDaXF5TyO1BYde8Co5SvUBUlym3KKy4pUJ0byu+2yGmJu7e3WB7P4c1jRMRHRgscXZzyG6X30WwObWvBbnw5gdFAZZ0kcV8yAVDkBV7+w2/gL6fwGEFQMNzlW6SvrpHGHi5fvkDiE5ydneHo5BgPP3iK+WKOoihxc32NMAiQZhniOMbJ6QmCIFDqEwkcvnrc4rI5ELvjdeJbXV7tkNUOoQapyQCTppSmjWo9TpaBvPxnNOyrv3aNLRM62JEzHDRSZQpjDOUmRbnacjm8yXiY9DxHEgXwSwb/aIZ4McH2+SVIViA8miFbbRHMIhRFCd/jW3jJ1QbkbIHgaIbVq0vMPn6I048fNl84ZfhjtyotoONHDX/0SZedpY+lkNEWPJTfegAQv4D08rPOBq62Zw+xeKXpYNShOuu6zb+Pc3HAS/RMkkifLoau1EaVU5IYE3rI9Gm0+asPdik6DTxNL7zEPPKc6jpJYh7GqqSsQHgyBy1LkOUEURyAlQyB7yGcxSCvU5TrNWLfgzeb8q8b65SHnU1z0DgEfB/BJABlFCQO4E8ikKwAW6fcqQg9FJQhXs74anfMD48Gnodsk8Cfhjx6FOM3RzPfg+8RzMIQxSbF/GiB6GgOlubwl1Nexg9QrhOwbYYwCuBNY2SrBP7JDOlmBQ8UHqWInpwgPlkinMWtp8baldWmr+s+9DygpPCjENn1Cn4cVgYaQ5HxMyIsL1BQHvrV9wgYBfKyACso3ybBGDyCJqoPAg8sLfiB7CDgfbhJcfToDMU2Q7lOkK9T5LTkEaGyAt5yhmA24QdJ11uwgiIKA+RpDna9hn+2BHwPAaUotxnS2zW2aYqT02MQxnD5h9e4eXODD7/zIeZHU0w+fwJMQ1w9f42zTx6Dphk/Q1NfCFatYJOaMWi7QuxFAbwoQEirS5A8DxS87QAPDczvWOC3uGe3GzAA2TrDybcfI5xGuPv6DfJVguXpMU6enMKPQh7RyyPYvryCP42aw+J9QEzaYij0oXCQjU7C1+TI1MnMHLJaB17kg+YUZVnCry5FBGPY3KwRzWL4UcC/rK0TbIoUd1e3mMf8i9ekOmxcblJMzo74UBcFfN8DiwIEhYfo4hTwCbZZjtn5ApNJhCD0hUli6oueNhBFLjGxc3Rl99S2xvGVHReZAv7ODwMsPniIm7dv8Ztf/BJf/Og/w8n8MdL5HG+vL/H482/j29/9EwQhvwjP8/jZpygCZrOZlaBBrdIY0OK2HCv/qdt6DRRpMahGg22uqO86SIm5vLrAowGuUwFGmBTcZDcRwFfhRL2pJ2oY7w3mVMuSMFGyBbMY/iwGy0sU2wwIfbAkR/b2Fn7oIyhKsE0Kb5Mi/OgcQRRh9eoKZBqBFhT+IgYLA3hnR1hcHCOcx1h++gh+ENz/yvQ+onrowowuax2pU7cNrcZlorHeQWKU3xpP2Kk/JQtvQLl+jE4vGUAZj3SnM+StTnydVuXVzyPLfO+gUuxaJss3qb5D6X0NHMC5UIhzXtjp9rCuqNxN9XYkc2cQzVtR5emchUY5m/perqBz9krM64cBph+fA4QgmE/4Tb4MSJ9f8a8PRQkyi/lNsgDKTYr8Zg0QfigsPFkgv90gnEQoy5KfBzhdAp6HYp3wVemjKbySISgpolmMwvMaw76stud4IEhXGwQeP3AazmPEiymypOChVI8XyJIM8dEM2d0G0WwCMo2QpTnWtMDVyze4ePoYyw8fIFtvcXy0AHyf3wB+uhD6Q9hYRjQjQ5k0L7JthjjwUWxTZOsEvuehpCUPa1tQFHmG6WzKA0kwxg9qL2egSVptg2IIwwAkK5CiRLZNsTw+4gfi77YgCwA+gXc0RUgIojCAHwegHvDy919inaf4+DufAQC8aYQ8L/jFbgy4fn2DSRxgOo1RbBJ4cYjFdAJ6swZLch4NqGT8fMn5EvExj9I1Wc5AABRr/jUkDAOwStA022tifuAblPL7Lkoeqtav7qsoKYXvtbeDB1EEWpZIV1tkqy1WlytMFlOcfPoYhBDcPHsDmuVYPjzB5HgGL+SOoTeNUFytkb+9RfT5U8Ms6fK0ntmVZJsMOpBCtYbgM01sFyPNQF8Ta4VSZLdrhPMJKBiCIEAJPp/fPn+DeB7j6OQYX335FW5vrnF+foFoEcKPAvgegR+F8OMQlFLOBz4BoZSHnqUUt3e3eHt3hRdXb/Ff/8u/4avuDGgiphg0GRP+6hSa+KPbVF1mXUcw06KvAC4DbM5Tk744OQYJfRzfXGF+coRJPMFsOsWDj59Wirm+9JHLElM0Fn0buzmcvoTZoAlj3u9UvPOl0qEOSp1WtWf/A+I1EYZ5K+XahX+G9aXxsGuHNlL/A4l8ROEU4XKC4nbLzygup/zr9psbBI9OMH18hrzI4X/2ENPjIwSeh8nRjLOG8IXCLWzxAWCXMXOR4X34XRyTOp/G1q+sXAfHYhio55Ca5U27yLM4QNV/JoeLKf8L6c02f006mqj69oWBxkGr62VWvxnS3W/C/HYVR0TtqwP5GgfcFiVAX6N0zGgpys9PCFuiiHpboaF6C3M1SkfnITODSnPo+HrPs9SrlCF7c4syL+DPY77CTCnK2w2K6w28wIM/jYHAQ7CY8gPdjMALvGYlmvg+Nl++hn8842cVThZAmqP0+VaNcDZFEPjI7jbAJELkeSi3KfJNBhJ48KIA+SYFAwO9S0A8Am8SoSwpvJRf1Aefr5IzSpEVBYLFBLMnD3io1eUM3iwGqbbttA0WB0/pN8pQrLbIbjfc0SIEtCiRpxmyNAPyEvE0Bgt9fj9FUfLVylqhex5YViCYxkAYoMxyUJ/g+tVr/OqXv8CzV88R+gH+5q//W8yOlrxI4MOfT/hh9ozf5OtPAiR5hh//P3+L3375B/zFD36A8wfnOF0eg1TGH2P80Pd0MeFnXtIct2+uMWMeEIcglKIoSiQEmMwnoJRhspwiSzMEQcCdBN9D4PvwplUoXPCINiCEOw2Bz6NfgYch9TyPtzmsQhBnBd+PTwjyJAVLeRjbV799jtnDE5x9dAE/DJDcrPH2dy9w/PQBpkczwCPcKANQ3myx+t0LxB89wOTxKXxh64gk02sDQ5gL0mwgSoBpxktKd1JWK56M9IuQQTKrTymICPd0LupVnTLNUWxSvv1pEvHIUb4HAoKr55eI5xMA/GbnGB78uLqVHoxfvjaJ+DmiouDbqAAUt1t4kwhFnuM//vQnOHn8AF98/y8QDd0KxYSGiIau2kYRLCtjOtx1FTr0+oLDoOGmemtqUXKs1Zkg0rKY/uOARmeIK3Na8ire6KzO7wM2nhQIYYBsvPdVbzJkxHdDmqAzFoYaWQeBfgvn4Hd5DIKKH8X2M4bs1Q3y2zWmnzyCFwVI0xR5nmOxaBfW+pyJd31viNyPSr8PHuPdmE4upZSt9cTQuWhaUBEVmpqH1IY+7Ja5BtRIooNBoYeBART8Dp/A24nPTQELGvwwzB+XqixO1B/JmYsDgIafjYcNYZ+0DKz1PHX5NB50YyTZPHcXQ6YyssusAAhf/Vw/vwRLMnjTiB/+9X2UqwQlpYhOF2Bp3hj3/iTE9noNfxLCJ6S6H4GiTHK+L58A2TaFx4AiKxDMYsTzCWia88PfcchXsjcpaBW5qASAnBs+yHhEofU6xfJswc95ADxSESHwSoq7ZIPZ2THmj88QTuPmYCs/ByENQtXkSkhTxu+USDLu3KxTwCMI5zG2WQ6fAZOjOdIk5V8vki3mJ8fwfH4fwOXmBoHn4fjoBMlmy88cUODt65e4+OgJylWK22yDdbLFdDbF8miJ25sbLOdLkKLE6YMHiKIYtCyR3K2wzlO8/PoZyoAgS1P86fe/D+J7+ObLr3B3fY3PPv0cR4slaECw3SZYHh3B80h1BwFQXK9RZDm//yAKwXwP6fUdyoLCm/Cbw8ucIvD5wT5QBhIG/C4NVLc3lxRpmiFJcyxOFgiqcyXeJOIHe5MM6dUdVm/umvCbmzQBIT6yrMDy8SnOP3+KbJUgvV4j2WyxPD+CP4kQTCMQEJSrBNmbW2SvrjH59BHii2PutLgIHK0eUVb/rHrBMCmG6CdXKeS6eqamGRQRY/y+keTqDh4j8Kvtal4UgIJfKOlVPL99ecVvhI9CeJRfqEjLEsEk4l8gi4KfWYr4hYgsL5CnGX7xm1/hLt3in/71P0c8m2JwyM+elUTuizPBQodzn8tnbfqrNytG/YIMgWC4ifKzPfimhT57Qi1YSZ+WPhOP7wuqX9d82UDXgXF1KN6HTT2EBuPAmrLX4+DWwPfrXHRBNIlaG6NtSzckbpduPY4WU4vVMUqWAzQ7MSjfUmgEJ0djR+dE/BJrciwF36cx5C1Kqb74bmg/ScGChpTbhx9ZRTlRu4JxejyvH6uyqlJf8uwyizpfRQyFes8sVzjeq3Nxt77Te6kq1IpMiQAEcSC1nSrwtbB459bhbsCkZTu03KHOJtsEU2kvKOC3E3z95WsUeY6yLOHBQzSLUSY5gmnEdw4x7hQEkxCsZMiSDGCUHzRlDJPTReWsEHiU8sPGBQ+1GhzN4BPCY+8zBn8aAZ4Huk1Bqjs3aJoDhB88LZIc4XLKD4XnBcrVFmmWYZ1s8M3zF/jzP/sC4fECwZyfTxA7qj5wLraN5gXu3lwjCgIUaY78eoVkk6AoS5Rliel8itnRvNomFuDt5RVOjo/Akgy32zWu7q6RljmS1RoPHj/Cg/NzlHmBeDqFBx9f//oZbm9v8eDJGS4eP8DR2Wl1GVYrvsqyxPWbS1y+egU/Z/jm9SuwyMcPfvRDBEGAOI55mWqoyrLEL3/2M1xdXuH7P/gBvzXY81Cf4mcAX12lVajRJEd5swFmEYqyQJYXCHwPjHhAQRFVEa8YAMIYiqLk0YRCHkmqZh9altUdCQG8wMf2doPNyyuQ1RbsaIb4wRE/PL7NEFMgyUuQ0yl8QhASIJjHiI7nCBdT+GEAMIb8ZoPt129AVwnCp6f8i8Uk2kmwNoS6JTb8rp0c9+FcqOA8J9VXrClb3G2RXt3Br0If13uw47Nlc09IsU2xeXkFz/fhxzw6TOD7oJTxL0dV0IGipJgeTbFNUlBQxNMJEAU4enAC4vltVxzQjqrlV0caWupQb8iVtxYIhhG63Wg66GzTaTb7dPjiGjGwW60we7Du43gIZYu8AIDqIkDSvJQUNxErMCxyibhV0h0MhXcKNvo6if0E/zH4V0NBf7hWbontq4X1nYRFTHc3eLV5taynsb1UX8pSXsLDoLn4jQl/9bQ35zc6q1aCc7GjGmsCw+xQdmdQVaHOz2Lornez+j/R6N93dugqGgbLxft0LlZ3HFErSWvU1f91r/FOs29pYq3nJ6CQZG7jFtrpqmprkOiGqXsrZv0ZDc1WW9Mc63SazZBhDPndBnfP3iDwfMwfnyJf8djHLOD78q/vbnH64JRvmfB59KXidoPVq2tMjudA5CNdJ5gt+T7/PMsRTycgoc8vA2IAy6uINyWtok8xeFHAvWXfaw0Kyr1oWkViYtsMDAz5NsXvf/d7fPjJJ5g/OOI35VZ3XeSbFH7kI88LpNsE0/kMQczjfhfrBMnlHRD5CBl3NvKyxCrZAjlFfDzH8ZNzBFWb4pMFeMQk7vBsV2ts0gRBTjF7eIr52YkQ5agdhTrEp+SaCgNL0K4qUUqbA6EmoJSiKAqwkuLm1eu2bwi/2XsaTxDNJ/A9Hyh4+EEKBo8BLA4QzicAA1ZfvkK5ThFmJTxCUFCGAkCR5sAkRJnnyJMcszjihmjgoywoaF7i9nqFWeBj9vgEXuAjCAN4lKFkDP7pAvk2BaMUYeQjOJkjPprxaF2zCVhJkby4xubLV8iyDMtPHmLy6JQ7hQ6GZtOLTFAOpF5y0YGqTF2XsxxgRzTWlb8+5wK8ucU2x/qrV/BnMfwgAM1ysIKiDDwsHp6CEYAmOfJNwi/b8zzc3d5iFlX3s8xiMI8gXyWA7+H25ga36RpPPv4IJ2ensiFyaE1n6zelrs5Zb+iHWo1s0vl63DGsbIQR5UnpB9YtITs9XZptddnzEEF1EOUtc+dBwmV6WZRg4EEYPN9vrIiuaWfwEPQ+2rD0gbA3mgqBfsV5OPbulzM34/l9fuUwOwdu7beVF03LThmneWcAV+diQHkRDz9SoJNxTAiH3e94VUU6Brotm40uXvzAvGJTj4Z37deXOqMDPp0MFeSmlltUGoY2XaHl/W6LWq1c7X0n0PKTMZFY3pvxEwgMritE2gOOTtBxTZXX1SGM9ZevsX1xhenpEswjPMJTFKDIcgSBj5IxwPcQTSJu52YF8iRDsJzyPeCUIcv51iJGCHzPgxcH/HbgdQoKIIgCvmpeee1B4KPMChDCL6wjoc/zZAVKyhB4nHGTdYJ4GnMDNw65U5EVABhISXl/BD6KJOUX2RUUkzgCoRR5kiFNtvjyxdeYkxCffPwJrlcrFNsUy0fnWDw8BRhDttoCVRhaEgYokxSb1ZYfjttmSG5WyOc+Hn37EyGUn6y8munEB7HjXOwCjPE7LtIkxc3NNW5fvwUow7NnXwOU4uHTp3jy9Clm8znoOuU3gRMCEvpg2xRZWuDm+RXirECwzREwgvx4ipt1isWTE8QRAd0kSL96heJ6DZqX8EuGMklBFnPQPEcWRcDZCYL5BMuLI5DbDegiwk2R4OzJBZZnR4DnwQsDeJ6HfLVF+vvXSF9cw1vG8B8dIT5dYvLgyG2vaCOkCBijTaJHiMMZCtWgMP+0k2GQxgPmXhPSWjFSm+bZ5nmVu8wK3PzmG+Qew2w5R+AH/BwO+Ja1ydEMyMsmVHK+SVBmOfzjGaIoQnJ9h7siwcnJCTZ5hulijtlijiAM21pdbXFt4w1ypXnTlT2qSKzcc8XkFZ0IXT26wRwgbE1gYZ/uC518VstKQqC36qIosN1swBjFdDpFGMVA7UQ5sX71ZZNyue77fqsCXPrnEM7DUL9edAogzId6e5pD2ebZKaM7YeJyo+g4mAxqnXNx/+cbDsD3zvUYeH6f9Zwev9spVKrEAzv2h+iY2k8po/Je++vYd2gG6htelVtlXD/Joqqzo0B1BowLPpqARATtV59DsyZ779ui6jMX7QrEYdYVBNUpXDYhh9eC46G5dlZadXgNxglMmgu2OjXoogQoQPMCl79+Do8QzE8X2H79FmzCL2zDpoo09GAJTAL4Bd8LHp7M+fmJOrpSdakeI0DgB3z1jFGgcgDIJIIfeKCbFKy6RC3fJIjnE44ny+FVsfuLouQ9Um3bKdZbBGEIfxphc7dCPJnyMLeTEEV1aRshQJkXyHN+DgF5idXVNdIiw6u7S3gM+PTkKb8cizEsHp0hWydgSQ5/yu9eCMIAjADbq1tcXl4hZkBSZnj06bcwO+JfNXojb5htxZ48tQFBNGkyitXdHZ4/e4Y0yxAwgjRNcPHgAqdHx3xfq+8DBIgWM6y/eoPQ45cY0us1yqTA6nYDVPvvvTiEl6RgmwQoCh4hLC9AaclvC39wgvLiBMcPj+ARAn85RXQy57xR33sBIIxCJK+usf7dKwQgILMQwRPulIRTHjK103ATP4vpwuqS1bkw9e8Qf6QPHIStE25WO/atIusaIdxBTS7vqku2cngU/KxSlb+kFPEkAgjB9naFN7dXIJGPm6sbHJ2d4PT4BOsswUff+oRHgRLo6ehj0+pVp/GtvDLlb7YLaD5J6ERik6s2kGn7Tu+QuniK7ppdMhx7tcQ9GHPVgsR6vcY3z1/i+YuXWMwn+PRbn+D09AF4tDsHBwOovsAL9Ln7hIcDzdy419VaJwdjIAyRIRa4/3MbB+LHXZ2DfaFnareSxtV6268/3EprlM1QfSDwrXoqbKf7Jmo+E7dx2WjSVGHEoatfrRe9mz71OnrI/BXyvfczF2rvmgZN7hR9F+lSpTMRCrXaEIMGZpJoa7/VNWWb4lWsWdYWAphg8KpRkWR7wAi1IV+sE2TPr0BvtvAWE1AA8PmXDC/i0X3SPEeZl4h8nysyz6sMWo9Hecpy0JIi36QIJxEoYZhMp2AFN0K9wAeJQ5TbDKQs4c8mKLYpN3LjCKwsQTwPyfUd8iSFF3KHww/4fn8Gyo3aosBssQB8D/FiBgaGZL1Fttpgu90g2WzBAoIkSYA4wGI6xyKc4Pj8AUh1yzbd8sPbCHnbGKX41S9/CW8W47t/8WeYTKfNOFpXMw6gNxhlIJ6AzOptygbpZr1GkiQglOHN189xdnrGD2VTIIpCeISgTHOUGx7ha3K2BM1KFG9usb3dgKY5j0DEAG/Oxz3w+dcnfxIiWEyAwAeJQvi+h7IsedjdwG9vlv3qDfLLNchygvjxMYLlFPHJgm99M63y6PjStnLS6TQDHlVYuQrYfVeYXMszdGjSORc8nT+yskS2TpBc3SJPUj6nGMPNzTVo4OH11VuQMMD5xQWWyyW/LyaOVVHSAB8SAvErG/GA3ogpZGCD+xZL6jyiuGStkDPT1EfDEDPB7Fz0HjA8BFRjtN1s8NWzb/D7P3yNoizx0dPH+M7nn2IynTk7F4MVtS59J80r9JyGhnd6ONokUxydM16EtHw5qFz1d0DZIWA34HpXsN493Ifjp8NfAwOaE8tq+gDo/3qqoYMJZQnMkeA6pMkriH1nUkz09tIpLvZo9KzW0rgPNur1QvrLv+dL9Ijwv52z+hyLJo9g8LEaL2mZr1VUMirRTiRoDQjtKh6pcWiYQG1R+0euTCojOCRMZyRXLfEI36K0SuDNYh6S9ITfdM2yAtubNTzfQ5qm8MMAaZqhJHzrhj/hcfTDIsbmboU3L1/D84CziwssFgvkKEEohRcGoB5B4BFktEQcBqCUglWHsGlRIN8mSG7XiCYxQt9HmubIshRHZ6fIfQ9ffvklXt+8wQePn+LbF2cI/QCbqzu8ef0ar9++4hfj+QRBGOLzz/4Ev/r5z/HJ00+Q3mxw8uQRP5ScZXj52y9x+fYNvPkE8+kMy2CCNXJ8/L3v4OzhOXzfwoJagWbOrgWbMyrVQaDssWrK12Xmizlm8zkYY5jMZ9is1nh7fY3V9Q3OTk9xujzhZ2EWMRD4SO+28EqKPPKx/PQxv38j8FEkOTyPIDpb8q02QBP2lIGfg6lvLi8SfiHg9tUN6CYFAEw/eoDbcou720s8PfuEf0GBItBUplempypYdY6/Nv6Prf9NDosNpEnrYnD3Z5EWBVRaOhGKSFs1AeD5yFiB/+Vf/694/vIF/tW/+p9x8/oSOaGgDPjO976HxfGSR5DyiNahI7pnbr1XaS0NpnscTA02HqZ2mRcKe7Rb4MwysGEOEYdk0LlNSP6FmQhV7WiU6GSCK1R0T2czfPT0MaLAw916i6Ml/8pae6Nyc03yQvhtpIHJDtsu86ODUaBIIw919zztDH3yVp1fmopVp7KebFIYYUNZE00dku7LoLaT0fyRZQATzgbeA5j4rXN+9MBQG8b1FNbIvVoO2c5w8C4zh1XtgC6bKkNEPtTJ/Cp9F2fCikO36Kbtl/ZdswvRxLNaz0OTfk/sZaRhBzjQge6K4wbsezR9FldtIqPyrRSbgcdlJIbysm7s1iPr0XaECZOdU63zoSeYP1GG5JtLFLdbUJ8gmMfI3q4QhgFyQhFMI6TrBOndBmmZw/MJCo/h1dfPMD05xt/99D/BDx+WOUEAAC4xSURBVAK8efkKy+NjfPHFFzg7PcOjx4+R3q4xC2NExwsee78osbm+w+xkCS8K4BN+7MqL+CVeebUdJDiZo0wyZOstMp9vmXr+zTdYxFNski0ePbjAerPFv/0//k9Exwv89d/8N/AYQUYzXP7uS/zqq9/jv/yv/gXmfgRvEiNbb3B9fQ06DXDx9AnimIfT9QjfqkXEzh1iNbpOqr4VrZ2cFNaV4YwfDGeMIc8yrG/u4DEGQjyEfgDkJQ9hm5cIllMkb26bG9d930O62sIrGT9TQ6ptVVkBFCXKLAeykhs+UQBvGiIPGF6+eoVtnuLbn36KB08egXiyQUE6fpKiyDXt73at3ezV908P6O3i9sEiN/RDqaZqcmmUjBaEfFme4eWzb+D7Ph4+eYKyLBEEQRVNTKPULDRrGVfUvSbxa+LfHpnmQJC5H2zprpkl3csqY9BNH/DijsJcZ0S4gDB+jJbIshQMBGEYwvP9huaOATN0YaPRCXsYNO8TjIaTId8QOICT9f7hMOf96vJiPzidSdDQ0yLT4O8rJtKxizFb60dAEzVKg2vIuOtEwi5tsoEuj60PTE7ALjBwDgwSRXvKnPccLao6c9EwTI9XapkD4tmK9j8HXDXsMReZMqusdqnWuRhUHRil2Ly+Qfb2Dl7gg61TxOdLrG/u4BOCYDoBLXlo2RevXuPi8QXyLMNXf/gKP//1z7F8cILz0zNcXV1htV3jxz/5Cb744gtk6w3+i7/6J/jsiz/l4XABBFHIo0p5Hug2AwCU12skqwTrtzcoWAHveIbjJxcoblf4+1//DMEkxtMPPsDbV68xP17i4vFj+JQgvdvi1etXePHbr/HZD7+H5OoaR+dn8HKKBx8+QZqm2K5WWJyeIFrM5EOt6M779sEyeDtMEKv8chU2Yt2qc2EZe0Yp8jxHkWT43W9+DVZSfPjBR5iUHr8FdhIgX20RFPxrkhfwqFZlSYHQ5+FPfY9/hZpEKMGwTjZ48+oNvEmIhx88wenpaSPIfd+HeOmdfoqpDW49EO5k66yJPWFfx64WBz26amc6dsVhGPu6Nzk7q72vV/qt9LVrYz4qh7fEtIaMZn7o1cTupya6zoQpt9Lxuxi4hkmhOR7Z4ttFKdv4fR+cruUOOHVt0D0UPqCwzXfsWxA6BBwUPxPIdxwkh/b3OuW7tGGXxTmxrC1PhdtpS96AOSDJ010mDwP/cNh334VLW3cBiZ+rXTjKhZ6MQI7YJ4kk+4KbripTYidcsMpDqpFW6aaj932gu29xQwKNUd98yhWZoINQp/GUnwIjNXvjSK2W29klDO2wOSr4PlbD1QUIwAqK7ddvUNxs+LaoyMddusV6tcKjx49R5gXffkEpwqM5iO8h2WyRZxmKssDRyQlyViLfJvjVr38FUlLkaQYQ4MHFBWL4WG03+OSzT7F4cMp3hBAPrKTY/vYlbq5XuHv1FgQE5IM5Tp5cYB5PcbNd80v7yhyr1QpFWcL3PHzwycc4fXCOV8+e4//+N/8X/uIf/wCzaILTRw+RbRNsky2i+QyLkyN+Y7XSJzpfkBvI9S/hXceg1Iz/ritgtpnIAPn2GyGvZnXGOH2qMkVe4PrtJQgDJvDBCoo8ywHCMJlPQRmDRzyQKEBZlgADnn3zNf+SUTK8ePMKn3/3u4hnU0xm0+p8Cp/4tIpCFgS+dVuM8TLJzgoPk5otN4egbb1USD/5B8wDIxxM6Ct09oG+AwaUUxhMW9bNQtDmktALKl1Jr7xGm8epp1dMlupQnYFBkl/K1tm7bO0KpY4+A03Ms6tRryPhkIbHrmBZ1Gje72k8951/acM4O3j9TH7sXPYIiYN3JdlSsaztD38WZSBj6HhXZ+gZ+rU1uDXWoIvj3UeqC+/UU5bpzk0dbhyZ8NeGs5FOBJ3zFxIXvOv5Kxr3wt0GvV+kRJ4wyevWcJLzacfbgUcbG03sb4bl8shezgIHu6HbdiMlINhsTSYNssp403GC6B6IoEYT7wS6kdD0OBP1+As6TKfYZTdFg1NVdjqjqzLmts8ucfXLb7A4mYNOIxBGURAGjwIsDsCyAtPjOTbbLYJqKxNjAM1LTOZTBNMYYAwsL5CUGbJtgpQW+P0vfo2zBw/wd//xP+Dzb3+Oz//sT7GcL5HdrnH3+gpBSnH5zSXOv3UBcr7ABgUePX0CnxCUZYnLb17i5uYab68v8fn3vkCeZXj68YcgxMPN20v8u3/9v2EehviTH/0IZZ5iU2T46E8+w3Q+a7tetWUF50zsDvM5CDGf4HnfC7gZSQTtnlr9zFG+bgh5KC1RJjm2mw3CKMRkMePxwaszE2VJ+c3tZdmEx2UA4jjW9hGj/CshIbDvua/7nSjsyDQOgyqkBhnVcrt3ssdMDopOAZvql/Kok1BDlTqQPc6FfMWRQ1kdLp1c6AgcpmRz702joifK81CHSyu3dSPd4xCY8GtfaAqbqqvfqQpaVPSmvrG20ZD+PuAADoQNeg/X9809LS/31Xf/zkX3/X71SWGuiZJm0lMucstSH2O1zNcJDwfYgXeMPSnguo8xlJwGkEqnaMIQOzkgXXtEm2/IeRC1AulR5g3uiKFvZmmQEsOvocQZnE8hi65v3++B7qbFvOtM9Lt3Squ4VdO9OydI95dg2OhKtQfedOnd2AVQU6ovIYTJ7zqEMLQDplp+9U9CEJ0vMb8+hh8HIJQhmE1R3G3g+R5Y4CPNCxRJhmkUgYKA+AQgBGmS4e7lWzx/9gIn5+c4e3SC0mPwwxAx83Dx4RMktys8mMzx6utnIJTiKJji7eYWt5dX+OiDj7D45BjfbC5BX9/hB//4H4EQD9dvXuPl777Cg6MzsKLE8fEJZos55otHIJ6H9e0dNq+vMMsYwnmE7fYORw/P8fjhOd8CRcQJpJhG1SQTHQqi65eq39WJ2M75Pi9VweLklJBeoxIAWHPjJwGptiLJ5VqJK/nIBPC9AP4iQLSYgjFaCZ5aKxEEAf/aEwTVtAxDI6kAae4CcQ0dW9uA4pRtOJ4J+TuGW20gMiPLa8k8lBG0q76SBocJeBRnY6Cerhc6SPVX65z1gZqPKP8LDk9LkkBcVzxpHSArDBkbAzqzstQoM5sPIpkIDp6t6i/21eMCtjLi+OzM0weKiXWPjgWwJ++wnve8AshTpk+G81kmCVRFbIk5NZrFQMRhYCd266xJOBjntZGttfJ3q1eLRjKULduSrGrngM5GD680iz1N1wiKzhGvnK7wWh8KpnadwhHi9mMIfSPYJO2HjdZ2YNwraS4O1p31k5xZZU6Q2i5o9l718JZreF1H2Nu5oLSE5/lu+6ItBDOgNV4qN1PvTNiZVvyA36LknSuLHdkjZHISxGkl0ViltoxMRM7QUGxwLCrwJxGWnz9G+voGNMmRXa0RxQEQBiAMSAsGzHzkDCBFAVB+jmKbpvjxj/8TPvvOd/Hok0fYXN/i3/zb/x3nT5/g7ds3KFdbXJxf4INvfwuPLx7jbnWHZLvFB8dP8edf/AU8Wh0c/voK7E/PeHQiAL/7xS+RrxPMjo5wcvEQFx89gR8EjQ08nU2xXUxx/t1P8PDbH+Pigyc8DKrQNnFlV43K3NkCRcxsQaTn7vRt8RkQGPrcms9hQrV8UAcUYMKXO9LaVaSlXORKSilWqw08j2A6m8DzfLe6O/yppImV2JQ/UXpRsY0le5VpHJA++up8VEkX6tem24DVRVqOEle2nNve0NrR7t3fJoO6cpC9OvIUqyrd1ajVQSVQGylYh7Ot5V9XYMl9sHO96OUdsR7tl2KdgdmhqXZUVTkvfq1RK1QQmeg0OTAVuoOtrg5WwPcUIPYAhsAg2LUuojw74akkVTPV9ZOM1HlIrXXMW6A6YZAtt1/bvkRoF6xMRmlfexs5YsuicywOCK4OoaYtu3G23dmW7LQ+I4GJskjPH0YQcPddGi4laPCqtmWdKlubClImDD9r8xIA0F4mLGAW7WTV96h1hI4nmUiJ3LENX+/Ja3tvi3r+/AUWixkPTToQtGJC0SPyMVXSHWCV6esXpq8FQmHdzkX5qV8CSvaUaq/oGFAzYIwy3PzsS7A0hzeNQOIQQRyiTDKskxTT4wXyqxUmyxm8OATNc5QlQ5IkiGcTRNMYRZLhdnOH1WqFzc0dZvMZVusVjo+O8eGHHyGYxCjSHH7o8/MUqwTJzQq///WvUDxc4C//6T8FACTbLXzfRxhFcjsbuokgcPW/uz1q4VKLc9ELQ4xTV+gzEEVh1hBfm+qs8TpFvpDaR4AyL3G34udaFvMpojiCYPGb67SlD21/3zD1GduqI6EB9fD7IFnlooyNFTvi1+V3GIP63h2P6GSe2lGCG2firUFjZ7XYpfetA34gi0Rn61cvbEaCC1rpqXECeF/zaF1+lae/Duuq6SG64hBy55CyS52L9+FsDHGcbUbg0PJEjtCnN972A6sj4hQBU+dhDwQHeSrlFW1Ui3O0LwxeLxnQjr6vG/K52R1h5wUfwYY8eLdWRNkWZqylK2lb5XdeUyKwXPas76j3ui2qKPJe5dWqHrkBsofFE1j19aL5ysDEbQeaeO6NAa9YPkTOovNlu/NAZ1HJZUyjb37D5Mmh8/o9AraIsL29w2w5ASEE2ToBYQxxEIAUJYIZvziPBB7SbYqbyysEUQQ/9OETApoVODs6wXE4RR4vMb04xTZLcLu6xbNnX+PR48cIoxgIA7A3t1i/ucLL1Vu8CXJ8+vBhI5ym02m3v1Q/TfFs2ybp/Xgt+zdlmaHsQDiUQnUlgwCqE6uuLNULB5L7zgDPJ4ijEGAMQSjcqG1qQ5+AHFjGuFXMVs8ORvHhVZ0j3HPF/INF7VjoznEZOqavbxmTh0ArV/saRxoSDt4NRPlfdKZ1qyt1ZtXTVnPUznn9XshDaYmrqytcXJwPIHOHO1pMIK9ttWn6ih1lUGURaD73S13U50ea2nMfjoVTNr2xyIDuFy70izWe6TBcbDNkbUb5bvvvmWHuQprrUoKhjxmEezQ0HcYYQ5EXoJQiiqN+elUetfBsU93QLnDkF5ezE52lGmYeRys9RPujTWqJqtJ68GvWkJoLHpWzjO12ptqpUN6r9qETyLaHSzmm1iWBarjsD3s7F8vlvNpSYz4srXzo6YFaU7lEcupultELDz3YatCfzdAfKm/iXSnKx3hjsoa+xZNz3Ly+Qn53h+PpHCT04fsBfAJkZYl0u8UkioHAQ3y2xOkkBCiDHwZY390hSTIc+0d4+fwZvv7mGX44/UeYX5wiWEyxur7Fj//27/DRx5/g8ZMnSL+5xIvbV/jb3/wUf/ajH+LTzz/vUkk6DwbggtS27d9UjMtLA1OrCt2Ew0ii45KFDoe6AmhwaLldxYTn6hXr5pWAEEynk67kbvCy5rdViHYME8cIPJUjaZ1gfYaUC7j4mib8ffX2jZum6s7Y6Op3YBndsoQJnfFNY1gyKa2vy9r6e+SjWFCqh9jb6DBt2taQloelDlYqZ0LJvv5X6vd9H+cX54K95javtfNGKGoVHbpygHTYk1Vb1KSvV7YBscgRIyjyp/cg+iFAdKZ07zo/NQdgNeX1B2W7PDxEfx8Sdj7IC6AjhJzmFzH2s9orJiOfMQZGKYIoAKMUaO/p1OLqyHyTWcaUZNOUO7QTq8BOoY71iLTQaRYxPJtwikKEoHO21ijN92To9oxJ9zyvTTo6V3ugCbf3tqj1eoW6pzvKG3AjtNY/SjipRkVpojLwMgzdIVRXDcwzQ2samAwfazsGWmKGbLSkWF3d4Prrl9iuVlhO50DoI1zMEM0mmMynCKcTftibMjDKsLm7w29//RvkSYqHJ2cISoar1Q2miwVOHp7jpz/9e9A0w/nTJ0jTDCeI4XkEv33zDKcPL/DF979fbcvpbaTcXOmqyR5DVVe+0xnVPtldPkV2ut/BdDCNbWc6mOlRL6vbWwg2PgVrutW4z1ZjzLX78fcQYvu0o6/bdc6FWtaJpgNpup3a2rpvjXElWoH13BBo1EsgpmAx19d2W2PS99ixglxU5oQkMV35Q+sgO5at6xV9KIM1oxxbkt+qYl3FYRLBYrqJZtGAVw0rgx64nwhHduiuhDYvDlnJ4KxSX9UvBswtHV8frl8HuZF/FOC2XajajswY4BFDXr1sGTT/3Xz5w4AoqwhwqK9WIv073ExyD9CzjdTS5+ICovWwfQ+e3rxVN+2zLeogzoXWptPOad4C8RxFN6yjrLx1/7dGmNp3tYKXCenqhjpdPmzLUTCxqFqwA9yWqPDUn8UUisQHE1qxjYwypEnSNCOaTnhe0paQBDIDNqsVfvbjnyDdbPDVH77Ew0cP8YMf/ghfffMMn3z+GY5PTkAAZFmGMGo/n7rtJTUILtu9CSbooFKYZsinPr2Nsj90ruHW19uM5SGVfOOrKQ4GQ7tlkKgE7ACmsodwkval4b1DK6d0CoBSLtQ9Txd0oh9cfSqxQOOzOECjukQBqURAGRTz36leVVYohawXq6rSvynU4GqVsUEm6WSB2tEOok7K1uckC+UGg02/WHEatd7hQKfHIaTdC6ge3uGdi/fhEL5fkOfK/bb/wFxomepNdWo+NW+jS1VJ0urUTjnb3NtRz5u+MXdJN9saIh6rU6Ii7xsSU1uq8n88zoUBut8IRIeiTtOVq//Kw8DPYQBiBKguMr0Qbp1igTubRyZlFvfK6e0wFb+Sa0jPdvKalLXqjsj5GWMoihLb9Ro3L18jXsxw8fRpZVe4OBL6OtVAkUTMJpLjMjkPBO46vmeWqXR3ruHuqdyEZ29QlQMa/gWx1OciVGzOBQzvhuBxIaop60CwIYuzwnTUfc3hSC2TV3loVacnvHNgmUFwcIuxpy5gyITqIGjJVU9ROcwhqa59G14hEy+Y0tXZKeM4lrsqa135gc5F7fLeO2PojBTTbxvYZEnn3aEnUBer2+Hsw9Ze34k0oMQfjfPT2VLVk/te+bJnfmjvv5Dk+HsCVvWjQIN6JqNJ73MuhIP78rkUi93povMs2ZaL9+hc1JfoAWhXf4QV/GbFySZgbMDQOBKAC5NbUTX+A6scEIk2QeCZYtc7yVpbj/bJUGNZu5bsuBqMgVLKL9wxfjY119Sbm9jarih4C462zB8JDFWcatqQtuzbflN5V4HqyhKuDuOObe9s5zISQKT/3g8Q1LHH28WP4Tj06uUewSp/XQ07g0rrM5J1QrND02E2LPQ6my7OhQ32nTN7OBfvDMSFIt1aVt9CUl++XkMRgGBImcnstwnux2VxBY1zcfAFqPsDybnoidHaLsoY2iryk4Ef+DYvTV1Og2efw71biO4RdNPJuWANUrfyH/waCA8gpOk7Kxh4z+R0MwBH7/USPRGIrCLavzK0StmuRpj0pLnpgFWpjouW4kKkRB3R5Re2bwlbpdRFNqaWd1y5Ms6xug61Ihs+1u0CQgh83zfml3HLDbDdzSEW11IlDVKPaNchOMRKg1qtqxHvIvQPJZsOKePU9hHlnd0v3b9etPNQMpcdlWj/HuB3pBCcFD8DPMGx2MFQMMQyUmsxyM4dlaRxCmrwGeeggW4TKS4LKE2f84e9Rlo0bnQG7qH4q3aIVePXhRdMInEoH92XkaoKd6Z5pz43SYKetimJPucEcBgzNydU1mytZq/f6r6yHS60K+mur7Huz0NINx5VSjVQtCQNl8u2emvzS9U5tmedDSLOi6oZxMRD4pSrbZ/7+BrlOjhdE6qTob4QT/a9lO+QHSNOh4tDkmxxt9ogCgMslwt4ni8FgpFw9OBsglTUNjUxZBwIh3UuoGfIVne0UoUfSGoKNTk7zdHYHbUgMDW9VvxNOFtDDvVNM9BCbO322AwzFeukK/qyA0Qqwn8xfVYt5R2FZvJIG8GpV4BiiN82n96xqCe7zbjoHrwfyJw78nLHjtBbZbuDbrz76tDl6fXMHOow0SSm6ejo8fOsoPIX6b6U+dlghvbVbXt/SEPKxei1gpDR5Lg2HdJdvTRWQ7SPUiGn/bY6BIbxH3QXxCBLSHdoUSBCFehsqGPRWBUy6gYfumOzqyUn9l2Pgf1OYYj+P5QVawWNMd03P7RYqr8Hp7d2HnToBUJ76x0mTIduxzKGCrdAb/S/Fvm9wGAnWwRVtvUNgdL9jSNCKjNeYwgYw67rhlI3x/uGojefvlG9Q6x5zxhDSSlKypCkGWazEp7vu9NqeM/ttlZQ7OtcH9y56ABr/gAQvExmHk+eT9+wlidYxUxdEaF3KeTP+Iyx6vJDkQGFuolQxrRzTCc4lTkuxaiu3R4hDrbbOQ2hIobKQxV6SKdIm5aYZ7oUh0acoRp6tKOhVSRdN7ALBk03kJdr2dAsVjL1jSNO0RhxMfp1afsYzjvkl9ffWodaKuvqyOxFj1yJwn76rC4soqtfZ0AbnR6Hug8Bpr4l7UP3K78q+ZTD40x11zR9qx567XUgq3oqOSSziOarsA6NURMytEuYNXkE4tIja4qbcOjSq/KMCPdZKe02ORHi/8SQJv62kaIVVWZGsoqDPt53mas6HH3ldG0ytZ1p/ncly+hkO9I5CEw9rZ8IDQnStOl2zL37YFJt9yWY3g1IVA8e21raDOxzcfwEPm1kpnWOKZ4lEdKMZdzpMZXnZNZ/awvWdou8pEKkviWEYBLHoCVFEPgIguCA8+pwfHjYMxc60BkE0uv27gjZKWhTzKftu+4JA1GDRVkwQM5IVBpkOs1yQGER2QroytsmprbZmDdB7z7IocpJKGPdcmHgOYnvHQ29ffY/SjYU6XS1hThNdSqf2Pquaw8OhwGKuo92sziujdX6GRa+dSVKjNMzQFyYDItd5ZeuPxx5zqnrBzXNoBj2cYB6K207ULsNwoC7dij0oMxETaALLbsP6f+hDmAnYQ/Fb0DzrmGX1ejBMMSAl2LuWoW18rAj/V1VfY/wRzDgArz7g+T7gXW+Q+jdgc6nxrQDvziUtE4CWhtnaMhso11hofFdcgoXw+282+ccrDGYkMtiyYD5915v6AagGSGhK4iOWbvbKHTv+TYcpugWIuVqS6vpZsdE3IokNaCzAKeU7nMqTDWKyp0QQci4G/G2GptyrkavZkWPORfWoNIVtczavQ5saoRcp2LT3tNdnQIVbDj6FLyurIlWEwqrsVbPCGmpo0Eqim3BTZV4XnySBZpcxllK1Yj27XtdeZvR0ssrmvydlQB9vdamqC+HtNvKo0R40vC4iVbVgLTxpmZPYW9b++aVa/v7LJp9HIt9cFSOwd77uu/bgnGdjlWwDwDwPA9E/GJtMcIk8k3Tv0e+abvx4M7GH48Rrz2bM8Qgd6zFuc06eanQo2YRdYlsDynGvwGftnBl25H6At6BqkQHzltGpTKu9WoWk4aOIeEOJmPVfV6mBRqm/K+hQLtcrpar/hfPEDVnVN4B3NO2KGL5xVP08kVmHfWGCtF3kZ2Otje54VUPHJMYvT6kLdu9Sn1MqNdix7eECI6KtlGC2b6rcnKRHaoS3QWvLb64bpVC/K0qEFMdIlTGjOrqSe91dJjeiUaU6r/tIsybsgOE9xCnwpkO3UaabrX2WcdzcEVRP6tv5b/t8NYuiYq7p3Pft47v8LfwbDRwFAZzMPTtybJCkFbjWNu/zSyw9JnLec0K3XBjf4CC1+Lr43uL42cFUa6IZ7oOAO6zWjC8TROvB5k2SMYeBua+h465kQMu28Rbxg284bTqbpPzuiw7tP//93dV3APZg3xmnR7vhbaA1sBW8ZmcTqYm6QWa0Ygnmnb2yXSHuekCg/jNohoYY2AlBRGD7aj5NeWd6lfVsvR/Ze3anEtRVu8pn4BDORcHmDCiIdOgq7Vp1UhW3WshfQKSeks3SqztXNYOUotWz3lEKC/1NVP7nGkfWyQyWzTjZzRuNLCDIu6Fjq4jbkaCrj5XA55AORcho2dqwn2CzUnR5TE5VWKaU50VNxGBx4j63UisQMObWuHTB6rEUd+2FHT/2uthxh+m6nbZZmVqIdNncXG2tV1sq0exkhwtfab7paCz7k6t8upyqGc1pDKdH7Jj03nWVgwhowm/pg5jPodqjL6qxko1Gfy9VboIAIUuW/o7tnX32WLTXqCqlyVa0PWzXUzdG+xS1S5bkw7hyOy92r1LHfpM9t+9xSwWMwCRERpWEfnDSd64ATNtLVINZDHN4mA43Tehg4FswQCAEH742qXsjmwnHOkFAHgwnLw1mc4Hkmnv5EC3+CWgu1dMJ6NkK6FWn6QyzgipOlDXepOBQfqZiEl5K7oax8bYQjNOrRHKpNetwjfEjR8CUn2a2bQLs5j6E+Z0Ij4wIU26PIZVlyHeg7Q10NXbfqPgI23Z2ivtMzY6ye0LBnTudJBtJc2WPSnjfazb9UhgHdSO9mBiHEbdZLw2WquGdtD4U/W7jyYX56OvvE55quDsdOqQ9+MwGtxSuR45qTPO637WKWytTCB6PLZ61TR1bonOeF/ZvrROlnuWPX3wLqvWjBux8UYfnqHvTFXtYGia9poPMbB1ccwOCW7na+6PCi1mVbSr8ssGhzSENcZ+ewZVyGPDTer5a6nX5kwp7X5XX8Gabf61XJVeCs+md47pREmjGtHMszBZfncExX5C6t6cC5mHSJOmy4Mmb9sopuRsdDhj8CBupel2G+/cLg6100TBxDSnk1yUDxGexNCukvNDWOudMNGlEDZp7SBo7QTtOGF2ocNWVSPQ+V/VbXSGengGNssWkUHCrYKrMyFmJ60zqqPD9lukRXqjrdepVe4gGpOmVzogh2NbZ+CemfmVjh6DrOy0TWc8d5AYQK24d3A0lIpzd59OPQRjmJwvm9I2gauu2gW3K2jXWnatwDIrXMdtiPPrUsa1XnWuu6wnSMZgVVHPaptxS7MJ9xDYxSnRHvSwt2F3/tCE5D0gdjfoWaDokVfDtyASzZOmXk360EvzzFcMVNA3d6jw29XpIrrMYr7KwiGQQ/YT8EVUguYFP2tiaYGtz6RDE8SanwEApeCV6TKRir6aXnW09+PQ/Z0L0QMVkolk3JPGEBFBz++thpd/V6l1RxFuzpuJUnDXg6rJxYSQiR16TERLzoNAMQMoZaBV3HbP567QO10lsxpJDuBQrolWMxBqZ/Nd9Udv/G1XFpL4vLsyxfpwqQaWg9C1g8zNumJyVa17Z/BXzEKqbpxOP6uVH9qwPVDhzlzWLdIY5K8RNWsw6/MONSDdxVm3Phew0TTYOHUr13SzS1sHOHWcDIdO7nGSpAWmPoNKVequ5Nr6yCQPnMZWaP9wG3DHckp9fXzjsihkkit99DDdWNkFrPVLxy6OjgG/tv5d2qmW1xq9MlLJ9LZNEROvtiaW2/gOBlUh6h2/9i8gHjiTeniALNKSYJoPdXWK80DEnx3Too1U2tBdLyZXuoJR7tkwj5fSyxom/G15VY0IpQ1jLD5ShuwuQXQ8U1GrWQ+itlXY27lQ5bXYLXzwnSxVAUmNRbeJqXUr7WqlOwtrO2Bo4F2jIUxq884iZSVO7MJe68/qxjp9Bf1cs6NAtdJtqbd2GdUzHs0B/T5F7GIcCQLCik98Xz/byog+6JBh08zivjj5RiIEekVSuSDUGLmo1c0Qgtu6jfzv4sDqDHi1TOO47OMJt/SxzoP2pyCoBxinu2XoZtVp7T2NGre5rpsk+p/aKnSHiHU2gsKj2joIOsZ8y/dKsAEmGEySbWsgWqRFneM2cFRVnWx9RuMQw3qIcLFtJXlXUNuwyhgNDSOqw9lAn1weoMPkgAri/StVotnW69LmLBsEYe3qlNnQWdM0DWDiY5/NwbpbzvfgLVEv6aJk1nNeNaC5xhL6T6LBcM6sjxAdn+jGtspLpHRDvxr1uckAaukmndPVigXdqCimbWdt00qLLIotHR1N35ts2P/LhThXm0E3W4CN6mBqulhSYDStgW5WKk031wcznCWPPp9t+wov1v0A7HncJGsmjOLRtFPMaxLUkLtSHVpyLQLCSaAPtZANKHR16uYMZCPCFo13b9AaE4LEYIZ8jgqAeAOJrgWVesaEWPjLUn/9zsqbGvuvftVpYmXsmmaAPMcPAB3W6+nPhlh1gIQMDJLxPPguFVcDVC1jyi+SasqnGsH71tcL+022Rm7vYkxb6W71gvaebkO1FkLd6gakkJBqoEedEWZ1LFwnh6WMamx1Jp1OfhnhADLeBTqG0v3UYR1XSUaIhYSXmr4jYjZr9ZXR27MYoS7GNGTXhqJY7zuG1mzfvfTQ8o0tZnxP9L9NBr2mzHCCLL9tsszJuRMdJLEtldNW2w6d7qxt4uG7OmQHWQUi5LM5lkzJuz/s7VzI81vwNZs+7ErGrjkubIESBFXHO+04GkpHEaB7Alty2ytDj6hvDO3qN6eY2rzm9my9Y9GQoTMsG3d1uPHaljfQ2WEspW8PCUajqVXZ6hY1lSzndAm3LbMFgUluaou0TgpvB5GYgECj36oi4gqEfuw19ZjyNEaZZZtT89jVaI5yUqhOuZjPJJR1Ct8GzkNFesaDDeJl5wOg/UKi/73JgdDa0aJs0hhHDbg1thNIwJLXZMM2b4n+za66vpbzPDSjZ0Rl3aa0o/xiYACFfBFhLRKHiuChNFjy90YXcjKEa1yaMjZdUfenKY/G0BK3apBOJkt5HcHWl6SPQfuBqXPAQXHWOZUb6K15hQkvd9luBvpBwCY+q/e1cdvJZzH0nUDlKRc+MKjzzuHvPjwCjv5pLQfVacI1E00XDJQRTC1v0nusnU9yYV6hqf1O0dB0NDPRGVJI2dM4POyB7vrTaK00NJKxEUCENXu5ZdNMMMg7AoQIODTVVxKuvqVbL3/qOiofUWEY61kCm08jDYdmUITJJfJQa6SqGR2hyxGGbIcRaHX7mm1NfTR13nW3u6l7CXtxdATiABps88Uw+eS6WqeMkS5CvStp41pdIdbtCy3dBBoS9OV2NcSa5u5QuK+vDXXp82o0j9Z6ql/tMY/eI+i3oO0u5LtfyjoZDOXMGF3q6z+3gFbeejrClDK2uWlL20EOaOW/yZjYT//qwQWnaheL+qV5rmS0swOvpFvlePsfqxiLEWaKtWAH69yTrUKpuRaZVi/kaI+o6qznug4XfbKLLCXaR329LkasLb8O+ug9NB/bnGKjkdtmNMkP5/tWNP1TW2iSE8y0jzIOhV4G9Gwcqe9Ta5f+anS6c12icd+KetZduBbyM8pAPK+z07U+76379trdMSSkC3AoVjhwtKhWwnWbJoJ4ZkLs5Pqv6vFXf5nGdJf6qxZ1zCJ8mcQzak/K9do0kJCvRlQ1SmoX6eLRzbtdbT8bXQcXGBWRuzoq+i/K8nYcq3xntiYpyHdtu8GB7DV+jO8qBjUpCReEosARcw05L9D4b4Jw07XRJU0H78o4t9FjGzOVycQH1XhvNIGSVxgHHRHuXcDL6xxRndK5175VFGtHclcvWEfT9TgRGmgNPqHiBpPcG2IeJq3mDZQ+NuFKBk7LdwUdgkxCSZM0xDnYRdZpELUGu0Gm9NFiAnFwGt2qrLPa9J1S1gpE+V+lw/bbBUS9qfKjgq9jgJrk2D703Be4OsbaMZFG9nD1KzzYcSKaxy7/1jKxOYdCYHSg9VZvXRtpdqvovk6KH1DrHTxMk6fZ1aPbms0Aouyc2WVu7xSmWgOHdS4EorpkCSPc3HfQ9QEkNDAZ+MT4TrdSoV0Z1wERMVhiGgmEE6ktnAlbm0/wSE111sq7N6MD7Fq2qtdln/qu7GaSiUTJZGtCX/MGxTzvUzitTNDPcicClUqGjI+WFwSjrheXGndNm6U7AU0OBjTpHWgYyQ12YSajsKwNcWLOq4I5brAFv+jUMSmbdvg7SVX/EH1sdwYqFSU6Mhu90WcJKcaMpT9IVVSLk+nkgh6Zbe41/SZ0n8tc7eRx5Bu7H2rhE5ORagIXub2XF3NA96em1WTc1jJPTZdgwB0Nuiyuek7LbqZ1VpnoZhuTqR5Tuo0X9tXPfXV3sukNUfnhQLzR11eSqGJN9CMATfhVJ1IUf0ke4gO0RcO7Irc62wa6ZOLC9Qbjvmlwt3TjMLB20Z0R8fI759km1+nyTlI0UhP2hvu/RA8VzcKkaG22VgBIgccaBlRGmejdCn04OrMD0gGtnhEHVBh0qZr2rfSubrAykWr8Ku3Ozo8JhhpzhvykHQytghWv6+ilRZOvNmDEedb0nLS50YDTkj6461wmjxYpgZ4ZdpiTTkSbeNlUU9ehqUMtt6ebemjYWbgIg3tI3WcSfFrnC/IXHSkvU2TRDsAMMkXDCzYGbT9f85e18W5iOXewZNYpkr6itUBW3/UZWi7jf0Cb2Rm9g6Pljqwj6geX7wPjqSrTHOhzlFx431Um6O16PUrx8tiOEqkdbjJ4bjY7qE1OEaky1fildB3C7iPRvLsPqMeaDO6H/axB7izY9AkU/ATiERTSfd0lTSGREAWvAw8NAiL/2FeEWhcjTLVo1DWjFPC8Nrnpn/aYAG1soXZrVLuFn4joOsBcZJFLuQOMwztxLkRKxRCk3NgUDffawRBaVndoJSC4jLB3cNcfZvpFSi2/6LC21HXbRWQHQSrRBdnuqWKrs53kakuCAxChcqZb9iadh049TlWZug9ot49JGQ9lhdpWeQ6A3gFEx1R0TXXQMRpUgVyn7cwU3cKt81s5G4TojZc+PeNMRc3bgkNmw+eiYIxd2k4gZmJWJo6LK9/JhLelzMsWrdIVtKqytFfbOeIKYFtGxTdwjphFmGIR7IirlsdGqASaajS61GnKdzgx0Q86PjTQ9Q7Eir5qUzuGOHVD5rPOWNM5nCodwm/xvhzjxWm2sdeRpShOJqTpQhgb6dXUefCx7ZN/YnrvGPVQp4p/a3bhZUd1dPvOFZX0u/NpYx9hMAxMc6fPL++80Zksqk2j9rvqVHmk2XXQWL6CumKsLcOf+RtGqnKK7dae3RVtYnO/2XanHNp3fifOhaRkUT+yxluSjfNu4zsGEBO+FBDlfIao9ITqWjparFIm6Y2mm432uDhcstHSXveulmIV8wimytBDmzvMO0pLEEJA4FlMI41cU+uy1W0wIkX3sklWSCCaNB1tej9xH80vSlSRvnrrisYEt9KpxvypYy2JO4Zlk1E7/kx5EAq4RZtSHpVDK3WdRlwaRdE599JnDIi0Ct2rtUP6poBOWaplqJKnoyyV9tZ2v4BTcQMkAlrZpOE4EW3zssea7zFwFGRKOpT2i1pJraT9amOzAWWy2goUldbOVWIYCunTTMU0NsdBRaKOtZ1QGZeariurFyLu9bxT2CGcgq3AgHe2LhmEV8RY6/8+BH06TjXiGvRMSWZdfjLh0zVYTXd1EtQyDv2jk5W9uHVE6NpgrdfwY1+LU2qHUwcocvvQJq+mvu5jZ+xYJ4Pmt8pnBn4SF78YEca7rk76wiY+d7UOEfq21k46ia0n29K3B+h2wgZbtSOMMMIII4wwwggjjDDCCF3w+rOMMMIII4wwwggjjDDCCCP0w+hcjDDCCCOMMMIII4wwwggHgdG5GGGEEUYYYYQRRhhhhBEOAqNzMcIII4wwwggjjDDCCCMcBEbnYoQRRhhhhBFGGGGEEUY4CIzOxQgjjDDCCCOMMMIII4xwEBidixFGGGGEEUYYYYQRRhjhIDA6FyOMMMIII4wwwggjjDDCQWB0LkYYYYQRRhhhhBFGGGGEg8DoXIwwwggjjDDCCCOMMMIIB4HRuRhhhBFGGGGEEUYYYYQRDgKjczHCCCOMMMIII4wwwggjHARG52KEEUYYYYQRRhhhhBFGOAiMzsUII4wwwggjjDDCCCOMcBAYnYsRRhhhhBFGGGGEEUYY4SDw/wFujSWoDaSNSgAAAABJRU5ErkJggg==","text/plain":[""]},"metadata":{},"output_type":"display_data"}],"source":["overview_resolution = (\n"," 4 # the resolution in which we desire to merge and visualize the patch predictions\n",")\n","# the unit of the `resolution` parameter. Can be \"power\", \"level\", \"mpp\", or \"baseline\"\n","overview_unit = \"mpp\"\n","wsi = WSIReader.open(wsi_path)\n","wsi_overview = wsi.slide_thumbnail(resolution=overview_resolution, units=overview_unit)\n","plt.figure(), plt.imshow(wsi_overview)\n","plt.axis(\"off\")"]},{"cell_type":"markdown","metadata":{"id":"ruKBD5tSSANs"},"source":["Overlaying the prediction map on this image as below gives:"]},{"cell_type":"code","execution_count":null,"metadata":{"id":"RndmFblDSANs","outputId":"48969f6f-55e9-4d7c-bfc8-c286089cd268"},"outputs":[{"data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAA0UAAAJvCAYAAAC0x3pRAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy88F64QAAAACXBIWXMAABibAAAYmwFJdYOUAAEAAElEQVR4nOz9ebBtS17fB34ycw17PPO585vq1UgVxSwoIyQUwkZWh4S6UMuN2kIOWQYcRBiHFBJ4EKFuEw4TxlKIwFZpsKzQgDosMLSMkdzIAtwGFEAVGKjpVb3pzsMZ97jGzP5jzXuvfc4+9973Xr26+X3v3L33WrlyWpm//H1/mflLYYwxWFhYWFhYWFhYWFhYPKOQ73QGLCwsLCwsLCwsLCws3klYUmRhYWFhYWFhYWFh8UzDkiILCwsLCwsLCwsLi2calhRZWFhYWFhYWFhYWDzTsKTIwsLCwsLCwsLCwuKZhiVFFhYWFhYWFhYWFhbPNCwpsrCwsLCwsLCwsLB4pmFJkYWFhYWFhYWFhYXFMw1LiiwsLCwsLCwsLCwsnmlYUmRhYWFhYWFhYWFh8UzDkiILCwsLCwsLCwsLi2calhRZWFhYWFhYWFhYWDzTsKTIwsLCwsLCwsLCwuKZhiVFFhYWFhYWFhYWFhbPNJx3OgMWFhYWFhYWFhYWj4Ov//qv5/79+297uleuXOE3f/M33/Z0Ld46WFJkYWFhYWFhYWHxrsT9+/e5e/cum5ubb1uap6enb1taFm8fLCmysLCwsLCwsLB412Jzc5Mf/dEffdvS+8Ef/MG3LS2Ltw92T5GFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFhYfFMw5IiCwsLCwsLCwsLC4tnGpYUWVhYWFhYWFhYWFg807CkyMLCwsLCwsLCwsLimYYlRRYWFhYWFhYWFhYWzzQsKbKwsLCwsLCwsLCweKZhSZGFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFhYfFMw5IiCwsLCwsLCwsLC4tnGpYUWVhYWFhYWFhYWFg807CkyMLCwsLCwsLCwsLimYYlRRYWFhYWFhYWFhYWzzQsKbKwsLCwsLCwsLCweKZhSZGFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFh8Q7g7//9v48QAiEEv/RLv7R0/xOf+ER5/2/9rb+1Vpz/yX/yn5TP/It/8S/K69/6rd9aXhdC8D/9T//TuXEdHBzgeV7juS9XWFJkYWFhYWFhYWFh8SWI7/3e7+Vbv/VbAfjLf/kvc/v27TPD/9Zv/RY/9mM/BsCf/bN/lj/yR/7IyrD/4B/8g3PT/8mf/EniOF4/w+9iWFJkYWFhYWFhYWFh8SUIIQR/9+/+XXq9HqPRiO/93u9dGTZJEv7cn/tzJEnC1atX+et//a+3htvY2ADg53/+5zk8PDwz/YI4Fc98OcOSIgsLCwsLCwsLC4svUbz88sv8yI/8CJARmX/4D/9ha7gf/dEf5bd/+7cB+O/+u/+O7e3t1nBf+ZVfyQc+8AHiOOaf/JN/sjLdz3zmM3zyk59ESsl3fud3Plkh3gWwpMjCwsLCwsLCwsLiSxg/8AM/wDd90zcB8B//x/8xDx48aNz/3Oc+x3/xX/wXAPypP/Wn+BN/4k+cGd+f+TN/BmAlwYJqlugP/+E/zLVr1x436+8aWFJkYWFhYWFhYWFh8SUMKSV/7+/9PXzf5+joiO///u8v72mt+ff//X+fMAzZ29vjJ37iJ86N78/8mT+DEIJf//Vf5/Of//zSfa01//gf/2MAvvu7v/vpFeRLGJYUWVhYWFhYWFhYWHyJ40Mf+hA//MM/DMBP//RP89M//dMA/MRP/AS/+qu/CsCP//iPs7+/f25czz//PH/wD/5BoN3hwr/6V/+K27dvMxgM+PjHP/60ivAlDUuKLCwsLCwsLCwsLN4F+Mt/+S/zNV/zNQB8//d/P5/85Cf5T//T/xSAP/7H/zjf9V3ftXZcxQzQP/pH/whjTONeQZS+8zu/k16v9zSy/iUPS4osLCwsLCwsLCwsLoB79+5x48aNlX9vFRzH4e/9vb+H4zg8ePCAb/7mb2Y6nbK1tcXf/Jt/80Jx/ck/+Sfp9XrcvHmTX/7lXy6vT6fT8gyjZ2XpHFhSZGFhYWFhYWFhYfGuwVd/9VfzQz/0QwCEYQjAf/Pf/DcXdoYwHA5Lhwz1JXQ//dM/zXQ65bnnnuMP/aE/9HQy/S6AJUUWFhYWFhYWFhYWF8DVq1e5ffv2yr+3Gn/lr/wVdnd3AfjoRz/Kn/tzf+6x4ilmgn7qp36K+XwOVATp3/13/12EEE8ht+8OWFJkYWFhYWFhYWFh8S6C53kMBgOAlecRrYNv+7Zv4+rVq4zHY37mZ36G27dv84u/+ItA5bb7WYElRRYWFhYWFhYWFhbPIJRS/Ok//aeB7Myif/SP/hFaa77+67+eD33oQ+9w7t5eWFJkYWFhYWFhYWFh8YyiWEL3C7/wC3ziE59oXHuWYEmRhYWFhYWFhYWFxTOKj370o3zVV30VaZry5ptv4rruhVx7f7nAkiILCwsLCwsLCwuLZxj1maF/+9/+t9nb23sHc/POwHmnM2BhYWFhYWFhYWFh8c7hP/wP/0P+6B/9owDs7++/w7l5Z2BJkYWFhYWFhYWFhcU7jM985jN0Op0zw+zs7PD+97//qafd7Xb54Ac/+NTjfTfBkiILCwsLCwsLCwuLdxjf//3ff26Y7/iO7+Bnf/Zn3/rMPIOwe4osLCwsLCwsLCwsLJ5pCGOMeaczYWFhYWFhYWFhYXFR3Lhxg+l0yo/+6I++bWn+4A/+IP1+n9u3b79taVq89bAzRRYWFhYWFhYWFhYWzzQsKbKwsLCwsLCwsLCweKZhSZGFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFhYfFMw5IiCwsLCwsLCwsLC4tnGpYUWVhYWFhYWFhYWFg803CeNIJ/+e/8O+X3NE1RykEqhZISpRwcR+E6DlJKPM9DSYE2httC8HNxhJQSx3FQjkJKiRAShEAIQXGCkhDZZ/1EJSGK3wYQC9eaEEIAZuleFIUopVDKWXpW5IkaYzDGlL/r+cl/ld/e4zh8R7cLwOfihH8ezFbUmlhxnTLNVddFXjeN6yyEz39GUYgxht1uj+/u9+kAJ8bwj6dTolrA4mlxTr5a08qfq18v4slez/nHYGXFEWV4rTVRFOL7nfJePZfFT2M0xoCUBbc37AnBHzeCzUGfe1rzP86m6FrO6h+U7SfD17gef6jTWSrdYg0sfmuvteyq1mneprMHsnZmCMMQz/NqeV+Mqa2m29JbTn31k/XQjUrAxClGgFBysYEvPFHvS9mzWmc1LKUsq3S5j9Ta2lptQjT6gVl4V9WNpYJV4cvnTS2OZlhRq4fifll/rcnVZIHJ5QOm/N6IwVRPZe22EDImlytZpqpgBlNWVT2zWdgqrYW8muqzkdP8er0uijyuKmORRvGMNqZ6e+WzReGz7NXL0ZRdVZ4aVS9E4369/HmAst8XQbM6r9pR8Q7Kf3OxIETxXWR9S4hmGevhyN+/oJaeQEhZZKMpE0WVXiGHhaAas/IyzaazMslOp4OjFBr4H+dT7qa6TCvr+3XZVh/N6uUuvgNCriGlF/IrZF6OBdm1qk+V6cl66IX+2P5c9oyp2pkxS39FnNX4Xh9rq2euC8H/rd+v1XkW/nNJwr8IAyjGnbL9r8qTKD+/3e+w8fAh165d4+fCgC/E8ep6yN+pELJs/6YoW6NvZ/lrto8qWiGqfD6vFB/v9pBiOR0ArbM0VC5L6/pHU6SKsi9JIZZzX9Odsj5Rhc/iKjOLTjVCiqqtlx/1MsGVH/7h1vq1sPhywhOTom6nkwvyajAqBos0TZHCwXVdXDcjRtPJBN/v4PgOSiu0MWQSIv8rB79Kh0hTvaA8QjVUV2EbypfWzOcB3V43F0oLg4IxuK5XCeSWshUCvAiTpilCiGZehKkpi3l+k6TM29LgIaA2GtRVskqBqD3THBSr7+ucueu6XqNkwXxOuKAcNcp7xgB5FhafM4161hlZdtyaUDeYujq6MChJKfH9TiM0lOohwmS/TD6AgKwGYQFKqTLeQjHM2lb+rhrjZ5VbbXTWHhdKU6XdyPAZOkXeI0TWdoVoKucAjuOitSZNdeMZrVOMIR8U25SRWhq18biow8XPpq5sagQmq6M4ilCOgnmY5aDjN5Te5rstyEBNcT4zzUojrtddqZYvVmC9SDVStKhM1eNv7QZFGouEo1aKMukFgmwWv9fDLbCqhkK2UJTlC01FacUDteCVQlaPr5RJZW8ogleKX2U4acq8KidUylFJOmSDKGSPC1QR94Jszz4lQi4vNhCilkaNdIj8i5SqlXcbrZFKVek1ni/yV39pNX61NA4AxiDKsWWxAmrPLFdO3jdTXNddzmgL0iRBOdlw2h9uLJcN6CtJL0mXs1EL05bNpR54LivKDIpV3TTrbLnhr0uz8rBmMUcGRKbQA0gp2vtlGQeNPlbRyVp/MjBQin6vl3c9Q5okOK5LL47pqqLdVflp9s4MWqcZyc3bUtf36XY6dDodekrRT5IqXwtVUbaOVSS+XicsvhuB0TobnWp9ZKAUw7xMWbDqWWMMURgShiHdXhepFtSzVotvVXBRJ0ctekdmvGzDUqHyKPKBUkBrh7Ww+DLEE5OiTsOyXln4jNHoNEUpieu5OPmsUWdvD2OgYzTbxiCkRCqFTjUyJxx1m4g2miCK6Xa7y/2yraMW16Rk2OsicwV5MXxhfWnIwZb4MyVSIKUg1TrLr8ysYYsPdREkScLo9BS1MWQoRM3ySyWYcgWrSXIoryMygRqEIb1er6WIWb6b5KlFZuYWon4u3Dy/g5+m9MMAJ6clhfJYkcP8elE/xhBFEY7rIHMFbdEqXRAVU+SDqsxaa7ROUbXBK9UajMneTWkdblfsoyjCcVTNAlmlq/JkjAkRhaIuFUm3y2gUM00TzHxes47XFeKmYo+BmeNw5BVW3hZLfm3QbtxbUvTrqCz2ZUSrlHUBs9kcpSSe5y8o2wVBWIy/Mkg0UjWmvGQa17P2HAlBnKddbztiOl5+qMxfpSCs7DMLl0tlViyQkTIRsdSNC6XeEYIuohyTCyuyLGbekJWCjqgpwBWZWsrTgsW1sPLXlaKi7rQxzIzB5NbYgZRZX1GKWUtZFNA1ZCQzTwsgBQJASIkrBIXEFNIgnDyvqYBUVPkrSYuk+SJbSE7JbFioh3YsKmSNOM7AUpiF3zqfBWkjSkA5O7oqLZNopCNrHDSXhcbkpKoud5cLVRgYjDGlYSS7tdw/inCrypamKbPZlM3Nrfb8LsiUghC1xVWk1ReSDXkGET4DWmvSJMH1vPUeWGZ6K35X3zNip1rCL4QtyWnzupHV9+YEXV3yitojYkEfF2QDSTZGDlRBZvI6dVQuF6CvDUmSZPqCrIWhuWrBCLKxIR8DZarYv3SJIAgwUYgP2UxLEUaA0ZnxKNUpGHBcJ5st0iYrQ21mi9xQURjoinZbNC1ZG1eNMQTAw/EYN5cRFWESSAnj8YQgDBnOBw3dxWhDmiakaUWqjckIaBjFOEqhlKKcTc7zoVNNMfNUkqZc6FfGpvq4VY05SRyjtUZKgVCKS61twsLiywtPTIp831+6Vsym9Pv9LBHHyZep5R1XG54Tiv+H4+C4bkNxqgvPUhfo9xELgrocks4bY2ryu2H1NrU4coW9vkxOCAjCEG3A891MEXPdJhlZSFsCOkno+D7XkpQ/WZCIgjEsKs01QZSRB1MKySTV4DjI0rJYPauNLgW346jGsoMyxoXv43lQfv/DJptFK95dkzQUSnyFJIlRSiEQJGlCEueDc2PGpDkEmpxA1jJRKjmj0QlhGLG3u9e0lNXiKd5FHMfZoLSk4jcV4JrBkpNptmxRAX+0bskTLFjem3CShHma0lTUMyWzYbUu7pRNVtYs7tWSGiEkxuhqOU4to4XiW17NleDtre1GGoZqYK2HrR4XpSW0UY+w0GOqiwLBr0QR/2cctdaDaAZeSHc51rP06eYzNaWoRNu17Ln3uQ7/Zqdbth2dpqRpglebRSws+kmSLYMRMuvLYZgReZXPPCgpc8urIU1SUp3S6XSrNmoMSRDhdLw8V4ZZkvC/zANmAnpC8n/v93HihJmj+OezGdEC6drT8B2Oi99vLsF8I0n4+fkcgPcrxR/udBBC4O3FdK5n/TJ86BPeW1PhbUVh4qgpn2fxnMVG0hCNhiSJcRx3NVkq5Fn9Ur6c1Vma1c/gum5OattkOSUhKq/l4ZI4QiBwPJeVhTI1BXPhvSwvLWx5fOEZ13XZ3Nyq7plC6a2U3FK5XEhN6ywP9WVTAN/muRjjNlp8JStFeWFx5rGcQckJUbGksTBaFYaOyhhQPZwp6/WwC7mtKfaT8YRut4OUkiRNa+NRYSDL+lv5jG7Wic7fP2VuDEmSZu9cSuoKeJFbY6rZ6+y6Ic1nWFwpeb02bhRcTGvN180DptMpvu+j8iW/ruNU1pOl92rQ2hBoze/FMVEUsec4XMmXMGttIJfVOtUNAlIYqLQ2uW6Tl1dXJKgoQ5amri2DU2U7EHkffTVNUUohparVZ0Zw4jgmThJ8zyvfYzaOZO85TXW5iiCvFtI0xXGcyrBZEwMFSar3uUpXWDFSiKxNpkmK0RrlKIRUWFg8C3hiUmR0WiqzTdtRNihLIUnTBJkvtciEY67IxAndciaktqekZuWG9kGi3VKf318S/DpThvNw1SBXBlhQ7AuRbkjimFQbvJwEGGOYTqf0er1coaoGx7a0tc5mwBanyYuBSrSXlCSOq6Uboqbw5ErtfD4njuM8HyLbF1UKysoaV1jaQkT5XWJQSYLjqHIZVSF8MwUzodPp5Mq8IBaZYgKCcDJGCMHO1mb1rkW1z6lQ0I025eBRL18cxxzfu03X9bi2u40QMldcZWkRBoE2Wb21Lh8URfuq6rTUzPMRt1ofXVjes3/Osog3iYrJB/Om1b9ZnOx96TQhTTJlvcpjMXDqvB7O0lAhCgNczy+fT/OBsxz5HgNF7TR7RwZZzGJSNfuGwsfCkFkjie2D6ZlUrBGu3kXOIqlJ/r6K/u54Hg5emYM0TdEmm3H0HQejNXEcgwDP9/LyZLMtZX8TEhyI5hHaaJTJ2tF8Ps9mvYu61gbluMQyItQaJ7/seJliH5pMwcr6f0acU0eVpApApylSKVIgzNtKlCtBmRHIgDJ5PVRKVVlTuggHaRznVvFqqShNcZVZxbPIKORSXcZR+24awSqjStmXjUGnSS3yRV5RKeCmUAjzCMMgWVJOG++1fssYglmAALyuX5IErXVpYCjyEMVRrryaMv5S/huTG4t0npV8Nj1f0iWkbIZvFGXFOJK/q0K5T5IEJyfZ9aWdOtdC67OZi0s/i3JkxLGiRUW6Ih8XjTb14lHMMJAbvlKd5UMphcqVam10i9Ewe0YvkKKKrDVDF/L3OE8vjpPc6OaU9QnUCEw1y1Au5SzrIpMlQuThBWX8VV1nBKogg02ymcVTvLvqOqXBSSmJL0DEEdE8QaeaoNHkltte0abc3EiL1sSTaV6mKnxRVpmPt0m5xC4ncguxFwS1NnSgivFGJ5RDd2EgEtky6VonyOORed5qe9qERDlO2TdlbmCrWlD2LlS57LQ201zmq/0PUZSxPuZVy891TgozAmd9clk8G3hiUnQyGpUSouysNUt2MQtUduj8e4JgioHTEZ4Q9PNOGhmYag1C5GQijztXaATQkwK/rhBTjZMHB4dsbm4Qui6x1kRxTDdN6fs+URwTOi7SdWuG1Pq6+izNLcdB5tfnsxlxkjAcDsr0vY5P2us1BZAQeEIwyJd5RcZwFIZ4jkNPKTomWxMtpCBNUjrdLqEQzNIEhMSNYzZzJw1TowlzITgQEq+akqgNriZXuKtZAq01EwF6YYAUxtDXKVEU0en1mQAdDA6CAfngrxQjneJoQ18KBiZTCrXJpt7LDdfGVINlYX3UmjiOkFKtsbzD8LXDIUJIPN/PLGVaZ4K4Rfmvq+CQ7YGJ4wjf76CUypTZbrckfIZsHblONc6K/QAlcVnQ45sDfrUkJonjfEazmb80SZhNp/SHwzytrB3ofO9ZoQTo1KDq68MXimmMWYq/XP5TzrQUyvP5BKmyFNf7SJMcdYVg+yzr30XJWKH8LSxhK7NRJi3QJi0J91nol+kLjE5Jc4tzYZ2XQiCLpWoGyGeis+wsKEU1RRWg1+1lSmaaYAy4rpNZh8OUwpiTAL04xmhNB8MkSUikIBQCdzbLc1YpfEpKZqkmm6wyZbrTIIAwyGZKlMMkjgFwOzHT8ZQoiIgOHZJZtyRCOtWMH52C6NPf3md6PGJ2MsXpeeg4IZ6GYAyq49LZ1MSzMY7nIkJFp99HuQ4MyWapgXDik60GqpTl3E6UL82JEcEEx1E4nk+sOplCvaC4ldZrneLocJlUdcB4Bqkkeq4x8/wNikqRLjhBYRQqm0get9a6XBpVyL1iLEiTtKlk58qyLuOukaI8PqVUvuSyam+F3Cot+IUMXSA0dWidzSK3kZ56Q68s9oaCCGEKombK2ZtihqhYlozIliBm7a/oR5TErKlc15JcaOe1Cm/eExX5qBMj0bheKe9KCTBpbYZEIkX2/rJuKItIa2Np9mOkNchqKaRShVMJcrKUEUWlslmIcqzP21O9/utjrCCbEVRKIZUs331R9vIZKRv6gyzagwBHOWW9V23SlPVe6CyFMUsIkPnStCRJEIgs7eId5KSydFZQ6D1QawtV8yvImVQKQTXzVziq0WlajrNCCBzHadRX3SBQ9BulqlnWZrsQ1fsVVDpLo+HkhDsnQbLYIlC2pcXwFhZfvnhiUvTiiy9SidQFCAjnAZ1etzHwCCm5mab80nyOAZ5PEv7oYIDrunwmifmlIPMsA/X+WAm4P+B3+CrPywYVkXmzS5MYpRw2t7ZwPY//JQp5M06QAr7D87kkBLHW/GyacJhboArhWymaGTn7rl6PTi54+oNBqbQmcYyQglPf539OEhZtuy9Kyb+lFK7rcktr/r+5UPmw4/CHOp1yXbjMLS+/HUX8epRtxP+DvR57OaH4zSDgc7l16t+Ukvd4Hq7joLXOptZ9Py+7LC15xhgiE/NzUcSpbuasLwR/0nXpdHtMMPzTICQyhl0p+VP9Pg7wIE35qXmAEYIbyuGPdXyElJRqcy6EZT7tXy4NIRPqnufnM2fVdk5DpTSo2oxLp9Mt61tKiRGFtaqpVFBLu0CaJnS7vTKuYqbRGE3hmSnLXzZohcEcz/epz0gsK8z5eJHHuZh+Qa4Wn5NKMdhobqo2udWXIr7Ssld7tmmmJp3Osmv95v4x0/hmiv8XlDBKxa74XioWdSVhQSH8iNZ8pLYPYnGJUbFUo3gflZJZpd+0iuefKbX0i3JXs8BQLMd0VsRTKZMSeED2zsMwcwShpMqUhMLibpp5L/hgpnzqJrEzRV1RWrULq7jK9y8EYYiSmcdMDXxlMVtgNDejKFOapOKjSVLujymWwEjg9dosQoEoSfgYebvE8MU8L97AIfECppMxYgv8F/ooVxGM5iRxgnmP5uZvPY8+3uHkHkRTD6/fQScpxEnWp1LJy1/7OYZbRxgNJ//vCb10SHdvQO/f6WAGKUkoeeUXP0o0r82E5e+rcG7gpnOeP/0k0qTMRYdbe18H0qlmXhaWpvWDR1w7/UxZxiJa96MO3rd4CCmIfj0i/NdxLb3mu6obyooZlLqRpyQOCESuhBftqB6mlN6iUNCrPZFKyUzJFNmMbRm/IJM7iHwVQ9Xvq9mdqu0IIUqlMZO5TWWz2OdWGIxKQ6AQZdmz9FXDmCRktrSzkH06XxatVDYr6DSMKTVLf/F7oewF+Vr0JlbOUphaf16oS533R1mQApXto0kL5bwwOORp1ldA1OspNvCT0zEnSYI2mjQ1uI4qZznry83qMxcmJ+tKKRynUv7r47MxmiRJy/abkbdsNkVQOHtoyqy2JYNF20NQLkWH7B0V+/gEmW4RRxGkWftMNbiOws2Xluoa4a0vkytntgq5XL0eyMcioZv5IifEha6ji2XZqa7yl+9xrpbP5W0sJ1Il0V14J0uoxECjXgzLy7UL/L9ar1pYfHnhiUlRr9cvv1e2sgxaazrdHmEYkiQJvX6fJI4yqzgQkymWrufhuG4m2IxB1waORQgh0LkAmgdzHMfJLb0uUkq6vR4GSKOIJBcY0nEyt+CAnk6JyQa3QqgUgygYgnxJjpAShMyV+SwfjutmziMchzhJSGv5EwJSIXB9PxfOmphc+crDSCmRtZmUFEiLPUT53giVL7eJ8zSV7+M6mSMKAC9X0LNBq2b9F6BclzgMl/Y6ePng5TgOpAmxyWayYp3mimNWwkQIUmNIMEvT5U2Pe2DQJZkoBkvyOtRkS8qyNdNpZv12SzNguWG1dJ4AmAWGWdKqvChJEpfu26MwyL1U1bzOlWGL5Vm5Ah7HJHFcEjmtqz0+dWtcPY5iyUox05PqYildc6BNcou/Uqp6tlD0i+yXVshaey6sk1lVEt5/gAG8S/s03CPUyUVZzmw5hzGmsp6npubxyZRKenM2sdqkbky+rC+3tNbrvEi92KtTf/eFRbZOYIqnWgdeUyhUUB+mKwUozRUUWcaLaS6fLUhmsYlY5/2z/p4KRb1SUMiVyzRXQqmWogF1uVIuAZIyUwYp4s3zmmW4XApqTOXHMsxd3hfW/UIZKp6pl7eov1JpMaBnDmmcMA/n2e9Q4OEShDOS3PFMYjQGQWIAoVC+j9ERQuQKmuchlEA5At9xCTwPJppux6PTdTk+PSUNJeHxnCgQbF3ZydqfNiRhzGw8Y3N/SMd32GcXRcpUdJnt74OWTI6nSCnY2N8kjVPCWQCJphOM2N/cprfRq6zeQuC+7ND5gI9yFPE4ITqKSuW9aPFFe6qTIJ07Xyk9hQmJlPneytzgoUpCkynCWXQLBKEgKlD282LDfEF86kpwY1lSscSuMCTk7U5rnS2jTrP9FW3OIoTIVgAkaYrMlzMnuRdSo7M27SiF47nlrEUURdnMQ56+kzsS0KkmzYlRtq+r0U1XoxaokT1TXSjab86PyjZuBI3lauUSK4r2nfWBmmhdaN+mkQ6hm7XbOCYVGqmyZWHGQJKkpGTL54oliuWSNSkhd75kagKpkiECbQoZmJGYYvGbqHnsLPMlDMZU+zwrYxHoIq8SjMgJX73i8jRNMf5Kme2tcRSJqGWsUdk141P+r2hcMxV5bUjc/IliTXPGtCtZlfeZcodxXT616EkNmEVDYz2dKq9FmJRltOliFhZfjnhiUlT08DRNcyLRtEgD2SCSkwHHzT59KbmSX9t2nHLGoyME+2p5WU+1xlzQy9Po9Qcrc7UpJZfy6WmvptBv1860qenc2dIIIeg5DkoWI0aliOYFwugUB9jFoEUh1DVCKLpxROJkSzXcNGUnX6vcTVPSJC6iKGP0k4TtNMVg8JQkTbIlWX4UMYzCfM8EHIYBQkC33Bieebmb557VOrkb5UhrnDCkW+Q1z7YrBEG3hwbmxuDOZ2AMSsDRPEAaw0iACgIwhkRKDqadUhmvK6jF8pdsM2lz/X6Vpqh5MqpctVbKq8nrrNq8WyjvRXtaFMKZO3SZGw9zIlVTjot81F5tnpNcWa6SL1Eo5uW+oVqd1WdAktzZhRSyUgyaEaFLQrZoCS1ysZx2+WyhGNy+W9Mrmkszy4I10iyW4hSDa1Uf5XKJhfKIslZq8dWtz0W9CVEqibpGPFgMkysbRRpSioZjiULhEUKQkp2ThRA4wCaZVVJLOKVIolomW5QpUxpV/u5VmTaFtb5RR7mFO9VIMgu1lCpTaJUsz/8QJYmpylJYvgvCWZ1XU7XJYsa7uFfOoAnwfcXuTuFVKo9LZzLCcRQ6TjGmw+QI5odj5tEUJ3GRySkS2OjuEk0DhElg4BMGIdcuvcz+/lfxRvoFpsdTrr33Bo/evI+TGmJt2Hpul233lG46ZAMHPZwx2N9h731XiOScyUiy63Y47uwxiR2eu3SdO5+9yUbHZx5Ap7OFChRMEoLEZ/PSgJ7X5/ql69z6zC36qUcURlz98FUevnoPfWoYdHx00mM699l7+UXSJCEJE6Tn4HU7pGON2++g3BS1lRsOkgCXFMd1CB3FLNXMg6CcLSmJQK4Q+76PlNkexyiKEFLi5cc6VPKGtq5VktaiTUcRhFFQktbCqFHs3TAAaXNpnBDg+T6ekBiVGYuMzJYFKtFUviEjuUYKUiPzpWJgCiW92DcjBLJGqnVuADMmk32q6HO5g5Ys3mVZuBbqSnPtd/l1kdiYRmio9/mCUOlWy9WSXp8ASJmdPZiTynLPC+RE08mXZ1ZjSPFui2VrpmEpK+pQ4roydzBUGUCMyepq2ThTLY8vyZcQNedHlMbRJeTXHcdtaErFWLdc+PZ0F64uPVa0t2KWqzLArIia5fyWy7VXospvXQepxkxT9pnl1QWWEFk8O3hiUhRFYbksrBilhJT5koBig36OQuk0sIXhOwpFI4qYRNn69EsY/i81gVwov4Uw0VpjplOOalPfQKUT5orsR4APQ2YRmU55lCf8tWUecuXVGERuDUtzpwiHJycZCSsH0cIinSmcWhu+0Zgy/TQfLNIk4Y3CfSfwjTVF9FWKcaYS9D3g6001Df5qfn0f2M2fTeQJ93O31lKqUjylaUIwnwOCbq+bk4uUr5Squak4r8S75iBLR0m+gUopv1ObEfj63OuPAN6oWQozBXuZ7BbnMBTX6kK5aRum8VlkqiBYRcgz18rX2lChpDcGhlypLcmIFIVmVD5XRF04cCis+oub/Qtlv9IJ8k3DJiVbkVXbrJpDlU4lBMYIUFUYma9vLwbkRQLSKENN2S7dzS6sTy/KVreu1me76ktVy+UgWdbKpRGFNT7jFtVSm8UlQ1nVNQfJYvaqSreuaOb7evKXnaZpuQ/oWGt+ZT4jMdkhu/9X18OVkgcCfjkISmJZZhZT9kOZW5nrs0G5tCmbS+GVUcjaUpzcGUqaZoqHU9u0DCy3JWNKEl3Wj8ncyGuTzXpJpTA6W8YjhcB1sziv7gi++7u3s30XOmvY4wfHnDw6Zdj1mB+NePTwBjffeJloNiMcJ3RPuowfndIf9tl/8Qo3P/0GR7tDZs/tcvzwiA86Xa5f85DCQSBxXQ+jBZisjMooXv3fr+M4LzD0PUYy4r1f+yEebfZ49Gt3ufmZDfb2tpiczLj0/CWSaYSONcIzJIlm/8Vr3H3lNnudHrd7X83dwDA5iXjhckowCtjudYiQCCNIo5Q4StC9HicMES/+QZz969z63dcxqUYLw0vH70X+uiKcRxnp2Mss+5emr3EpvItyHP6POOJ3o4g4igmjiMLjmECgVDYTo3KiUCwzQ6cInZZ9+CyNsd42CiUvTBLCIKDY31POfJRtuzZbSeZV1RMCmS9jNoWgSgWYsJQdVWtdJbCW+1LRXgsZlLXnFOKasaQWeZOANRbKrq+vrqvfnlWMtmfF4s+sP2pM2X+KvTLFjHm2rFHRYvuskinCLt7LCUTZNwEhNNW00tlkZRVxKGTCkqyrh28OYBfHIpEq879exPUxqXn9nLYHjTG1Xs56XzornnOSsLD4ssETk6JXvvDF7Iyh3DKapmll9c+ltqkJ92KTaXm93jlZVpxLolNYpXNrHqWFyJSKJFTLyUxN2SmGr/ra5boQLASE1ukSAYDip2jmKf9E5ANdroyN83sN4WpK231ewGpJlaglIuqf5WVReZzKCV+xqdN1s9cXRWFeegFpMYjXnheQ5BekyRXZ/N0IIXKF3tS8vWXPqFyZLazo5eZ40SQGZb7bri1+ijKnFTER1WbjUvGvEYCKEIhGAymU70L5kVKUZ5VIleW19Pwmyqov6yQ7L4mGFbNe79U6c9ky3jbJVtFmGuvVKc7r0mX6FUkr/ilHqnIZYhAEJEmC67rl/oR6LyksfYWeVoyWOk/bcZxSoYzjuGo7QuAoJ1/nn7aUuVauOkxtZo6q7t3cOUSSJJnXt/zw2ygIkFLiOi4ImZEdrUmNJkpTEgOJlKW72iRNCeJ8j15NaSzq0xiDTKv9JEVbc/IlOZC9yzSFJE0hqZZlpbnBxphsX2Ca70eoar94b7qcsSsO0C3aQTFjAZlDBpGmpElCEGZnaBkpSbUmjAWpSRES7r15D5OkyKNTTschcm+LODWMT6bMTkMcIzFG0e0OOI1O2drbw8QCkyi0UQjpoo0ijg1pnJLGmbcqneZOSTDoJM5mKFKJRjJF093aoLs1RAiB53bxnQ46kURxCkoSzyMwhliTOa5QCq0NsesRhTGO0SjPRzoOQkpiKbOZ3FSjk2wfY5KkBGGM3+8TjkOCUYjvOHgbXbxOj4PX7/Po5kN6gw7DS1sM9zfpdLs42s3flSEFpOfgO6rqWqZaPqfzdwqU+5mWyFDNut1sr9WX4o7jeSAlURTl71kT64r8FrLPyVctKKWyZcDGVLL+TBZyjlK7qFznj4ja/fp+q9XRLZOmtdASthhHGyPORZX+pfDmrJur31n5hKnVc0H/mlKpPtOBKIxE1X6eJ8GZBGOduinkfO0lV/oPjTuLqPbyrJr1EQhR05vWZCrnpdsItyJdC4tnBU9Mig4PD8s10pkCL0qlf0FfbELUld3q99L3/LfJ3Y5WnlEgO54gUxAEghOyw9EyoZI9Wij2UCnyhcCpL5epW4YKJbkiA4sKf/ZccS97LvMAU/ckVCrlRfoUMw6Z4F/c1Fkq+OUsRy3/OdmqzwJk+yBqQq9W0UX9F2kUXt6kKjY2F0pu5na6UKKL+imIbbnnonbifbUuveXFimKOiIaArcb62mhekMvGO8/ul7NIovl8+ZwxjXtFW9JKl+Uu2mQ9lBE1pwQ1nlXEWVdMirKjF88FWVBgavWvlMJxVXkIsTGCRBuSNKnNaoryoOLsjI2qbQCEUhAag4xjZFpsKq7KUFkM85Ln8SmlcJREQrnsRudKrRHZ8j8lwRiZKXxak6Rpua6/Vv3VO6n9ZX1PVBux8/oxUqBzRyBJkhAkGqMTOp3mGDsy2RkuBkMM3DPZgacHWpf7+IoDC01h+c2JVtHvGwRdiGabd7NZhWzWoXr3xvMyYqUUteZWkvvcslGSx30pkbkhI/I2QFau0YXIrOAjcUIfgwk1G3oDISX9JObOp0L6mz0Gg/fyxm9+AZlsEGuD7u0SHU3w0l0cocBoBv0Og40B3UEPv+uThvlS2iTFSQ2zWNPrOehUE80zw0ccRghgriDouMw6LvgeQhuCMGL/vdcQAqJZwOTghERrpkGI3/HpDbvcv3uAoxSTWcBgd4PZaFou6eo4ktE8YXt/kO83M4RBmM3QpZokJ67FLInyHU4fnqIxzOKYa5euMDkac/uzN9nod3FjzfTNRxy/8QD3mkH6Pl7XJxEpRkcgqv1qTaW3MmydtSzI0C6CVsGpLdMu9swVjhGK2Uyx0AXe2r0UlRrfJk9K1EUYLd+fLAtn67xtaZ+HBcK2vByLprxZit80bq3MnlgQV2cVRFQfj/VKV9ZDXc8RtSBnELQ6BzW1sq4iiqV+UqVV12nWR5E/006qaxVzoWi/RNDTDt99//1vW3r/T/0Udp9YfMnhid/qB9733lxxz35XMw3VspZs2VCh+NWWEWUPLIWp4qk+6+cWCEFDSSr2pPzzMOCLuQU8zU9yLgbBuoad5gfTqcLjUH7ugTHZ/pF6fshK05AfovGl3T12Q4AtoLR+1/Y6VQMHpYKOAVHuh1lcW163pC2YolgeiBYH3WIZh+s4uJ5bkbn8XpwkRGGEoToNu4r3vJGURtr1/CyEqIRvyXDaN8QXZ1PIkiTmnpqMrpHwOglbKG8j1eX2ZYwh1Wmp8BdtVAqJVLXlbxRtUTcOUSQnHcJoRJrUEisZTJW/gstoUc7sUeQ3D29U4dyg8LJWK1+NDRZ9QQiBSA3k519U+4qaagOFM7DqxWScoFFH1SAMGcHCkMVdHy3LWZ2qr2AM2hEYo3LSVIMUeL0OIJgD/0u+lMnIzIvgypmqM1Bv50IIhFKNk+AvAiEz9/d/vN9nU0hS6XLz0jeSKL+snCSKmekpn7v8fxJEM3pxn63/fYutOGIeav6P347xfY/3fuyDnN59jtufv4lUiuNre0yPxxjlgM7O2+n1u9x/9V62l8Z3mY/maK25HGrc2ydsHc3ZcXskQUQaxtnhpvmm9zs9h9OOw2S3y/CuojsNUY7DxqUtjIZoEjCfBDiug05THOXguA5RFIMR+F2frUtb3H3tHt2OTxCEJCZbGrhxaZMkiEAbtE7o9DrEs5BgGtDr+gRBhNf18XodHnzxHkpK4jRlsDPk5u+9TpomWVqpZhaEpHHCzeMt7vtD+p1tJv4bmHBCOevfeKGVPBOFBnumhna+ItyGwgNoGbQSP01dsdZ/l+JeECoNvfkMgrPQI88ITLMMbYp5m3K7Ji6mUF8Ai/lZJ4+NMGfn68I8wNRjFCCaL7m1HkT7z+ViNAtXXza+OAY1omxrU7VhddEYUBiJzpKRS8Rp4V6TiBbGtRUGBwNCrDfOW1h8OeGJSdHm1g7FpnmRaYYoWdtsSlu3WhwW2hXmBkzlQhdDtaE7J0VJkpCGIXF5uF8WR5zqJeWtGvgESqr8rASJMAaVz6qkWmdOj0RRiix8oSuWHrLyc0CElOXyn2Jgb+iwhSJcEMIFpxQCqnRNtUZ6aUOvEAgDoqjfuuIvyNbfm8q5QLOGC8GaWf1d182WbIncg09BSIRAOQ5u7dqq/SVlAct8tAvZevilJXK1uMszHKSkSYrq6WXJKAV19Xcdq259VnDhTlmXqw6qq4x02ftrC2XKv7x9NBQYsRSWkmTWmm0tbLkU8RyU6RZ7Joqr5YyaoPAYWDc+tOZNNI0AjVptdVqRE/giDqnae7WAutejxjbqNTWdZSW6vZ+0Zv6sJLLKwwiDDmPCKCFMBMfRAf2rlxFScnjrEbc/exN/x+HBe+5iXMPOi3vMTueYFBKl0ClMJgEPvnifjUtbJIlGpIYgiIjjFJ1oPN9lPplxcnBMMA/RRuN2vVKOekqiw5g0Tuht9BjdP0YKgSMV4TRAyfxwYyU5vH/IRm7MufHB6/j9DsHJlEev34fcgQFC4Pou0nXKuoqizL9lHES4HT83CCVs728x2B1y/7O3s+WjUtLpdZidTEnSFEdKxtM5199/g2A0Yz4L6PgenV4Hx3FIg5jBoJ/NdscpqRGgXE4eneJ0XLztAcar1XnjFRRSuZAH2dVVr21lm1mrw5izfq4VX4MvFWNKW8NfuFYnTSvb7eJzC+K2FsX5pKOe/4sQqIvqwyvy0TCa1K9Xwi7/OGefVBnNsm5wZrZqhFcUsk+0k4dGdtrSWiBUWfz1B0pNY/ndFoSmPq7l/xY0SphCR2kZ+9YyGolaeVvSNy2yfzEGke+lXiM1C4svNzwxKboroVJN80HNaERaH+TOx3q6SyUchDGYfJ2/EJm1OXVdvJpFRNRHD8HSILq4/AYhqo3iUJGppcF3cWlge45NTSG9CM5T7s9TIIulZyZfelTMqghRnU7dVqbqM6sXd8Xhp28ViuVn9d+tWFE96yjWS+SqjLM2a/WEMG2azNK98kIjaEmm1mwzFbE6I8yippGT9uW22TRUXHSZSWO2sy3/eT4uvHylpcpK2raqiRgD2oAUhd0CEFyWMjuDrPGsYO5uoIVCacOdeyfo+8fgdbglb7Iz0wz2Nnj1U1/AMRCogOPjEVuXhyRRTJqAK10SIOp7zKOY24cnfOX13WwZpzaYRBPMAmS/w0kaE0tDV2s8Jem4PlLJzIObUmhjSGZzfM+jO+hy6/fu4fkuOklRCLTr4Ich0ktxhECmmuHOBvsvXsZow4Mv3OHR3UN2dzezGWwh0EmKkALHdYijmCROSHJnCJC550+2+/gfuMaD4zFH9w/L5ZHKdUjjLK3RaMxwe4ON3Q3ufv42jucQxjFXntsnDiJGQYSzPSAVhtgVxI6PTjXu3BCOprhdjw13g/3kMgIYhaeEadg6VpwpO9s0NrF8r+pPrU0J0WZ4as4rrDTZmWLWYTHytiwvNDlT/hZlPtsy2bA3Fffari1muF4XT0O7PYt4tdR7GfyMvm7qhpR6Dawglo+7X+jtVe5XGWjMyl/r5m2d5YHt9V2MKMvktE4Y107LwuLLGE9Miv4/UUgpxepyfcWa4VUDXd1xQYGGYF1TKKrHXDrTKjpXWunXU6Afd3nCmRbQNRRKUSqCivVqw1RWzmcJa9Rl+8ySaVVKSgVmqSmt4Slq0eJ8buAWTWRlpGe9WLPYdc9J+3wskbBaLp4s5iqeKrF2K3QWcMEIYgzf7Ps8XzsQ06Sa+TjgzvaHSHqbHLzxgFeOfDrbLxGFEcJoTg9HeP0OaEOv1+U0mWR7l6Ikc4ThCtIUZL/Do/0es3mIGs/4SpOdbZZEcX6WFZxIOHnPJZSjiG4fcunRGIA0SrNzr/LZ6kCD23Wzw0fjzMtdHGee/KQ2XJnG+ElW9DBKuf7RGyjP4eiNhxw9OGbQ63B6OskKKbMzdIQUeL6HjlM0mmAyB5MtoU1dxWuXB9wdnRLePeLlOKHneyRkh1WeHo+RUhKnhqvvv8740Smj4zGu56CkZPvaDoc3H3HiCY43XTwlibTJ3Ewbw9VTST9JSOKUF/df5sWtlwH4rXu/wd3xnXNe8nmNoHiZLHWL2g7HFapqnYyJpTui+tmSfnEQcJ7WIllZkcXF9FemYXLyVM9IPY22rl8bdltl+pnK82NALPRrU/u40HhS0Mx2UnFWVK37zhp6RB63aAZoXT4m2tpCBlOv3IWHFsR9S1uo2Ec7yS5q0eQGuqZx98xl62Lh+2KRWu1TJs+nWBnGwuJZxBOTokUF6HyFrrgvlq6sjp+6yKjk+tLGwIv37PqG/fNtShe3OS0KnyJNoCnAFiyHK5M/K53i6bMsei33ssPt1lGgmxlpbPrM1361WT7reweWlkzQrI9q6czq8Mt5aYu/eqbKZ62OzmmjzZnA1e+90ezM01P8z8biKPiYUZiW728h1k9iqVOUlxeXWGXXq5fV3Li8HJsgI0dxEIGB1z/1CtOTGbev9LnytR8lCmKQkiCISOMEz1VE0wCTanzHoec5RFohEcRBRDgJ6LgDZrM5XsfFkQLHy85gieYRfsfDJNmBs51uh5NUM5vO2b2yQ6ffxT8NCKKYYBrgeNmh1iLfo7PR7xDNAhylMEIglKbw2yJ0tidxPgu4/MIVBnubzI8m3P3cTUS+3831HJI4c/BhhM5nrfLjE7QmmYfoNCWNYtyex/x0QpimbArJVq+DFoJgHnLv5v1ytmnr0jbdjT53PnMT31HEccLulV0QgvHhCNdzEcYQxRohM6+XJk44HU/Z3eihE82jNx7g+C6blzZZbVnnTHHbJldXP1OpuatU0mZLadgomkFasniuTSIPU6j9KzteazwChGk8W5Yml01msQpSg1CVml0nbo20Fi04C/E0KWI7RP2z0vvXwtLKjbJkbW3ibDnXcHJQCfzaUyueXyn7lh0olAksEa7ldrVkF1pRJ2eNRRcxqjb3PVdk6qzwlXxs9qVWGWth8Yzgyd1nLMn1atahPhTVpebikobsTnVmA1Qkp7mnZ2GUKb7VLCnrC5LaMh5TJlhLQ5RhmlFehBjVFfXquZVLuErat4jl9K6mKW4c4w4G3EoSwqJMnCHMTG2QLKxyhhWEst0M2ba4qz6+1t2iNuItiFP5ilvelSH3DteS9TrpqZOxWp0ueaxbWEZZEvjac+eMVsv5oKjflufEct1Uka3PmBp7FdbBynjPaKdrDNhrozSVX+QZ2rWuNeNoku5mHAK4rBQbufOQubtJojzQhlkKn33lHvPxjCvvu87daQftdgnibL+i2/E4EhrHd3B7HToJhNM5ylEYCTpJ6He7XAr3iIOEyWyOs3eNuYFYpGxOArpKMYs1SRiXTkqCacBwe8jB4TEboznR+C7dZIbhiEFXosNjwiDCkZI4ivE8l/7eJke3DpjOAzY2B4RhRBTF9IZ9xocj0iBCCsHO8/sYrXnw6l2OSDE9j/3Lu8T3DjN34nFCb5AdxhzMw+xQ5TT3QKk103mIowQbUmIQ6PmMKMncU3uOQnrZ8jkhBdc+eIPZyYRwHmYH46LYffEyp/eOmU/m9IY+vWmMjhNc1yGOE4QjeeGlq+x7Pvdeu8v4aIySgs39TXov9bg6uA7A8fyQIA2ykWClXCre8XJ7axpQ1pHTBcloZwyt3SoPusgnmj9rLvQbkSwr6ab2XEnnSwMTjVbeLl1qoYpuqIoStRiAFofQah3fUqzNb6bxtcxqKQ1N87mzZF0LIWsq4rV6W1cetK1MeRxHAfX3e9HnVv0uX0/9PWQJtZHuxfZYeos7ryxtxtY1UOhe5f5hS4YsnmE8HZ+Ci8KyZnVoBih+LXe6xVmfcpNtY4Yl/8wHjCf1nlPT01sGgTynC4RmXSxNfS+M4XXyUE+vea8QozU30hgUgt/v+Vzp9sDz+MnZlLDcX7Uqn2b5p1gkfMt5aZapFk/OTtqXIBTMpyAjDda8lJXGUoEGoVrOe8MZQSNvzTCL95bcN7eWsMrzqmoRtc+Swi4R5/bnalXSUOCLa2X7PjuqZTzeWHhRHrIaj9sPV76EBa2kVrA2y2y9J4l83cpXux5f4bgg4O72BzgRWzz4/G1ujuYkpkPc05i9l9Bf9wK3v3ibjuvi+h6y3+HW8RHeVh8fiXjzEB3FhJOAzf1tpkdj5Fyye3gV33WZovm9SzPcbZ9Banjf4RwhBZPQkMwj4jjBdxXzecBg2GdXOuyeRAgl2b+cIDYfMp1MePjGMUn8Av1uh3kQ0t3oI4UgCCJcx8m8zhlDd6NPPI+QjiLRKf3NPt6gw/j+CScPTzi+OuTEaMK9Hpt3D9j2PeZJSmejTzgNSOIEz3VI08LlPkgJMtG8ONa4vksYw2gyxet49LeGJGFCkiS89DXvRbkOt3/vTYQ2hGHM7rU9hIBHbz7A91zcIKUXppCkOComMobnv+IF7n7hDl8cT7NtXrkjEz2P6dzv87Vf8w0IIfiNO79GML1fvvILN6eySSzL23pTqkI1e0tdAjUPCKjuLnKnM80gC6Tf5HJxlYwuJf6SgtxEfc9ieb/WlxZjN3lGF/XqTB4tGhcWKc7CtyWhsbBHcFEXWIFqqfHy2NEgCqa6vnaraBCj9R6pw+QKxuJrWnLQUAtwIUNWYyBYN/zZjzTG2BX5WPReusQ7V6lsFx6QLCzevXg6pKjRaR5zw3pdAJrGj5Z4i2GqIg+rM9bMzJITBrFOj39CtbFUepuDdTsxqpPG1WVzfA9XKZIFI9LisrWlTJQ/TSP8WdahtiUn1Vki7c+c1QbalILmeUK1b8UrFLkKsML5RWM/zwo0Z5vEku4NC7X0OINqbQBr1m3tXdbHr8ViP0FTu8jYVR/Ez3vuomRrnTRX2ANaAlQvoa6qLfRqah2geSfVTB6ecvPmQ4JxgOe6GMAVgpu/8zovfd376W31ITF0t/qMjicoNzunLIoiPNcldVIObj7k6vuuc3jnEa7rZh7WMBzPZpCfr+Q7EiViojhBAA/evI8xBs91MmIui/OkBNoY7t95yM7OnI7jEvs+SSpzpVgw3BoSnM6IowhHCmbTgMFmn43LW7z+yS8g8nO4Lr/vOvE04MErtzOS7iqIM0+dGztD4oMR2hi8rs/0aIzRmiRJ6fY6dAddppNZfsAxuCI7BPv6B55ndDyi1+8yenCMjmL2X7hMf2fIvc/cYno6xXcURhu2ru5w8PoDkijGVRLhuegwQhlDGKdce/8NHrx2j9l4Rqoz9/6+6yKVJDUQTAKC8ZzuRi97X9qUnjWfBFWLaWp3JY1YUBCzZ1aRlXo858vLeh6Wlq0thVlBqKj2NNVy3frEEgErry5+q9AgerVrzb5+wV5/YVl5hmS5qMBpi2rd/NSNLqJOMM6LYJ29oosCab0sFW10yRnUysAXQN2IV+gkdSViiQ1aVmTx7OBL5vSprE8umLFaTRjLAv2ihheoj4lPSHhWoWHtq5vw6ht4zz+Fu3mvGJqzOHScgOs0wp3n4lU0mMaaqNeVOSeNIqHHunc+sSnGr4tyiIxI1Z5b58GzLHONkbR+fbXHwVYVYNlQ+pYY5tosmdX7rBJ+znHopSlSKW5pzdTo2nN5CZofQOZ/8mXHxRWQAK8mCUltf4+hhUCf+xLPqonl2tzqbjPwhmBAui6PZiEPPn+bO8FtZHcH6TrMo5gkSTCApyS3P/MmL33te3F8l3Aa8OALt7nUdTCzmDiI6PZ83EGXaBqQRAndYY8wCnjYfcD2/ibuRNMfBRjA73RwHReUIkwDti9t4wjJ0cNjlJTM5wETnZJ0XYwU9JItTo/GOJ5L98aLHJ74TOYBWrlEacR8PKPrKhwNhoTdFy4xP56QJCnKkQw3+7gdn1u/8zrj0TRzBpGkKKWYnIzLYwKyg2slx/cPUa7DuOcx2BryyvEpoutky+kSTX8a4mmH8YNjusMeJ/ePiGYhwpVsX9vl9hfu8urxCW7fJUk121f3uBOFHD48ZFtJUArd9zkWKQZ44folTh4cc3xwipACVylcz2WwvYExMB+N6Wz4PHx0m+uXXuD5jsNe5APwRpowu6ibwpqYLaTqovSsmrKoP7JGxIsE4jxylMtYUfWBKt2q4Zvav2XMNXZiamNGFc+KNPPnHseWswrNBXhmKeJq3L44ixENZbsuRNuMcFn6q5dUVnXdjHHF3qBGqKpcbQa3pSfEgvxvZLT4WHjvZ0bYfqEwAq72wlpnN8vZWCLPZxojz8rsW6QjWVh8CeLJSdGFNbhVIrt57bxNgqYUS+cpTgtXFonXBXAxRfwMz3WLvy46pghBOptDr9ecdTgn5ZpGkP88m5BVyTUFZ6F0VCStRmbOrN7HF67nr55oqcQl3pK3mDrzWhjQ13WJ3fbK6rNnQpylMJ0R1+PoF2s8t6xnFBqkKVmmAL7KdXlOCBzX5X+OIiZJ/TQh0/YBZILkD3Z8BghmGG4lCQnL4VrzXH+3Zy67bZSIwqhQ3Ls+fI4Xt14mTRKC0ym3fM14dxtzcEpnNiJye0RxjCMkUZIgux1m4xnjgxGdfoc3PvkKcRizdQS9fpc0TRkHE3Yv7+J1fe598Q6u44BvuLn/OofbXS5fv8yHP7VJNI3Rsym620UqSRTGpIkmTSK00XQ8l2A8Ixp43Nzu0tvs494yvDcaEoWao3DI3V2HdAJCCmIdo7Z8rk8k8mjG3nOX6O9t8Nq//mx2WLaBwd4mD1+9y/h4RMf3SLVBxxrTkSRpduaRNobBxoBoGhBMQxzf4f7QJSJCb/oo1yUMI/b6QzZvHZeHZJ/cfURnY8DetT26O0OObj7ijQcH3N3rkULmjOLSgKM7j9ga+GzOUjY2B7yeBNza8HB7Xfw4onc8zhR1Y/A7PpuXtnAch4O7B7iuixwkJBsJQXfM1w4c+mEHA/xUMGOWLwm+GFb33qZ6XyMhC8/UjW5tsYlGyEUTXT2SyolPk0JV59IU96qxLFPuBdRmf5rb6FdCnEOamkGp9596qVbNXtXRtoSMpUstXuGo3kN9QqYakc7OdEUiF3PV/uQqGZ3l8yw95Gw9pRS3F5DVdT63TAfFUnHaTgoypjZm5/2qlezUv4tWntkIXJVa1C9bWDxzePJ1CmugGgBqnVyw1OvMeUKxhkU7oOAxNgi2BD8rB80UV4drcyTxdJDnwIBQ+VlDjYQuok2fF7bNrF8fjDJl2uR/5a3aY5WeK/K/xdgNi+kIWsbZQm/PzHgUB5q21nGDvwmq5QemjOixt8CY/JDgNG1tJ0WemksBsz9TKAGLvE2IgkFVWReNjzUzd5HA5E4pmvsBiq/dThdHvU2TyCtf5DKWq6+p2hptSOOYm5/6Arc++UXCwwkSiRGSCIUE+p6L52TL4zo9H4Hg+O4RNz/9Bo7vEYQRWmvCeUC332X70g5HD46Ic290URBmZ/5Adki1q4jmIbPZvNz3kxQHEGNAKqIoJko1fq9Dmkup6fEYYWAeZ57pRocnzEcTIJvVQSmCOGE8nuF6Dpffd537n34zIzauAimYT+aMHp0ghSQMI0yq2dzbLHmu1/WzWSApOLx7QMd3swNZhUA4CuE6hEFIf9iju9EnSVI8z2U6nhKGMR3PQzmK259+g7uv36XjOgx8DyUFrjGc3n2Echx2n7vE9fc/RxiEmRc9JYnDkOnJhG63A8bgOA6XX7oCwINbD0i1xvcclJAobTh47T6jR6dP1pZKIXF2kPq3uhyqjz+VhFlsnKIWclWY6rJpXGgLVh+3KstGw05Qj5D6eLqU3FIpz4OgfeRs1kYzlfYqbitfi5GqIAWmGezcg7cXheMaqZ8ZXUPG1l7WgpDOlmtf1Epl8hhXC7d1xF7bWFgfy7IqO7/kjWB5wqL+V2vHZ7RoC4tnAk/d+xzkQts0LTGZkF/QikXb86ssNKuSf/Lu2xyA1ovvrFw+Le8tq9IwwBeV4lGaoBPDfO010BXOz+Py/crGWo32xenXpZHzjFgaTsrKvUFrZ5nz2sZiU8qsarW8iyK95v60VbbMxbSNITsMVxukEI3MZ2XJFYbcereOU7aGgwio1e1FB+KngzeShGmep5GuZolaunkDKfDpOMZHEGPKWaInRsOOkrW1S1JxLT+PLHA3mck+85Mpp58/JHjfPsHJjL7nEsxCpqdTPEB6HuN5RJovB4zThPFownB7g9loCrnbbMdziS9tcjoLSIYeLw6HTI5HOI5ia2eTKAhBZgeijk7GqLGDE/aQSuK4DiJJcVwHV0nGJxP2ru1xxbtMmhOmQc/BCIiTBCOg2+8y3BoQTWfIUKMAEWqmYYLnOWx5c67e6BEcfoY3jk4x29ucSoFG8WA6RfqSKx2f9GTM1t4W4TQmHIe4rgOOII1TYpkw6rkcAI7XYTCLkZFGAkEYszNURHeOkEIgpWQSRnB1hzse7A18Tg9P2Rn2kT2fR1rjKQVhwmaYgEhJT0KSvW16W330/SnzOKHju8S+4lBIHiUuO9Jh9OiUk6MRrqMY9LtobTh5OEcfp3gdny+exPhf8RxCSZLoDUhnF2srldvJ5u+yKS0YdfLfovZvI7raM3V52dYPmveXZ+ALOlOFbs9b23P1uazK9U72qx57M556Xs9bEbAYz7oEpZZqYzyo8nbRhRlnypkym8t111Tkq1gW3XuvmlVZdEJQe6AlG1V6S6rL6ky3Blj0otjc87zinS2283ORv/0LjLXWLbfFs4q3zhycab60DQANmMUvb38nfJwUW8vUYADnJLZgKWtHOwkwwKei6MzkGxfXHfPOHJHy4cWQuc1e3KAsKB1JnImFIp2xLLqZ+gqp3vTy155c/YdZuCra3ploKiLZrYxIqdxz1vmZXqwjSu9TZz5VI1QXoUXnkZbFsMWXuppmMPxeHEMctzwkEGa1zTQBfjUML5DjFcitxkLWyWGt4Rp4Xjl8S8cHA3fEDr/3OjgjjXQUaZygXAeZpMT5LMt8NMVxHaJ0jhIye3U6e7+9zR7BaEaYakTuiu3ewGPkgbm2xY1JgjKAkowenaCNIXQCkjTBGE0chzhCgJQ4UiGUwBWgtUZrjes6KNdhcjLBGMN0MifqSnrDPlcu99mZJBzdfYSazHg+d54SpwlBnNLpCfavwcb+Q974jVcYDz/MaOjX2oZhc3PI5M1Deh0fv+PRuXmf66lme2+L0/vHdBzFNIq5s9VncGOPnb1NXvrXr5GczBBAGCXo0T16QuB3fCajKRvX9vn8psvxySkf6eyilEKlmjCKMX2fMEp5cXuLrVcf0HEcxtM5ExSX33+dl/YGjMdj5tM5p45k5kLU38I/njM9HtFRAt9zmc9DgijG7/iIVBCREj/3fh5u3EA4kmj8EKLpBa0m9WVnq3x7Fv8uEozzFMHVhGYR55ltLqpwNh15F/Ko7fiFdjL2pOaVRVnYJBoFmaDqr3XZdY5RqJlOE0uvvvW15O+wJZ2KQxXHNZx/ZMc6SZblXzmGN5dHNkeBIvgyabw41hk4i8wtEsnsX0t6LCyaeMtcclcK1xkdb0GQrNU9W6T8unTqS8r6sdZo9fj5bN0vtK6pbuUzgnIza4PNLM52rEi/Fn+dxDRF9jrWyrZ7TzD0r2hPdWR6lkApRd3mXOoEovm5Tjpl3OICRr8zsK4CtGSHoFGi9mdMc0no01C2GhkqIhc1a24bEa6ZaKePTjk4SIiSfbrDHvPxnCROSbVhHCXZ7E+iSXSKJiMqnu9w+cWraK3Z2N9iejQmjmI6gy6z0RQhBPPJDOE5nD46xt3ZI8UQTOdoY9jc2yQQHsPhgCgN0TMIkwQTG8Ioorc1ZBpkBoud3S2crs/91+8xHk3odTs4Qw8pJcqRnD485tHBlDAIGXR8jBBExpBqk800nU7wvRM8J0vbdR2iKGF7b5PJeIZONJPJjK0o5vrODuFohk41GxsDkihBSkmYpAwGXZ770Auw2WV29wh3NKEvJInRbO5sEMyCbB/WPABgOpoyFQ6qUIKFQGvNOEmZphopDGEQIKVEhBFDz+Hk6JTZb80Jnttl+9oO6tEp89EEx3WQUtBzHTquydZrJwlB4c5bCkg189Gc00enpGnK9a94vnrZi/rckubc0o5yr2aVoixaAi/PIqwK00y4jYws4ux7lcpcO9OtJDtVQc6T/sv3259YJ6amsWiZWNVRJwQGGtsyW52plE4tmsao9rDnZLXlkSzuFjqzaKQTtfwvPHMeWarGtRrPWMzE8o+F9leFWZXahQ5svUBdnU/4V7V7C4tnC2/NTFEpPdrE6VPobksa2YIwX6GxnZfyhXNXT+csE9M6YerhVt5eP3+NcOdosBcZixpusc9IoHWz7qJ+2zJuLd6rx9ianxoxuwi5KEhO8WwTTQtyKxZuZhxxVeIXow/VbJFpLk8s8t5SzqdGUM7K18L3p0aMziSSWUobnU0u9bI9KT0peeXmIya3HaZujwTY3OwzOh4zPRqjXMVsMqM/6OEMPQ4fHoGUdHwPhKTT79LbHTI/mTI+HGGMQTmK7Ss7xEnK3o1tHhycMJ/Mubdv6P6Br2B8+4jtccjutV3SniB46RJxGhPem6HkJsHpjMlkRuAIhKs4FZIH0Zy9OMTZHaCmM7Qx6NSglGB2MqY/T5DG4Hsuk47Lg9wpw42tPsnDExxHcTfocfNAofvvZe4McYSkv7vBMEhIJxPcROBp0GlKnM/wTSazzOOc60AKG7ubDAY9JgcTbn3uDiJNSUTmpttxFGEQ0el6KGVItSYYz9jFY7A5YBhq3hx6nBiDM+iyO4lJw5CuiDBxggbmzoTZ7oSplIyTB4weuXhArzNA6G3COCFMNaP8cNpB18eYCK/j8fDWA9IowXEU3Y7Pwa2HCCX44JYk8TwM8JkkLpd0NhtdiwW8mK2ohWgzzC0riee15IK0VOGeV4qrSmGA15OEh1q3crT2uBbz1OxR7c81rQfNYWVVasunGi0fVtuwYrZ4hWtRmBvMIDeWrajCatxq1nXdG2iZdi3uVm+ZlCKhJsPbGErTlfWTOpmt0+pz9z+V4atEW0nJW+X5tiU3TbfyVf7euv3PFhbvTjw9UtSw+ouGHK3Zh2phLogzHnisGZF14lnvofXDrDultTKax3iwqOxVBqK2W+fU3yqvPevI+MVzoipeYhYGiSK+BVuuyXPcklbbWLU0ZopMHTFUDnqX1ANTJdM422gxjUViYpqEpe6FqbAOtlVt67K/8mLTE5UwZIcLvi00aDUeKwfrdPx6mOIlAFv+Nh/Y+xAAx7ce8Tt3RnQ6z4OBOIyQXnYg6em9I/ZeuMTo8ITZdE7fy2aGpicT4iAkjlOCWYARcOezNzOnGdoQzUL6W31EEOO4LkIKlOvwWzfvMby8xY2PPsfg8w+5/8otRmHIcfIeNt/zEgnHPNgM0H2Xw/sJjgHfkcx7DtJRiP0Buylc1YL5LICtHq5KSBFoUhKgN+gxHvqMvR6dfofB1hbDjSHH9w6441/itN/NzhdKNR1XIZXkfdtbqFRycv8Id9BFG8P4dILyXUyq6fV7WXoCiBOc33oTHp6wny+7lVLi+x5HD49xpSBJUrQ2SGPoK8UggWEqmN06YHJ1i8nxiMue4qNOh4PTAE9pHCmQQpJsphxffUCSphhH0hGSXjhlpt5DEG2AUuzfuERy8iYIiKMYI8DreAy3BoSTkCRNmQYhnW6X/rDP3puPePF6B+E5vJkmTHXdelKo2eLcNnXu0u1CMa9r54UhokFS6mpu9u9LjsPX5cRtZgyPtK5l52xhv3pxX1ORbjeM1XLWanyszebUO2p5Nl327zIpW85umyGuKmNdyRaVjKpysALLRLRYHp2V6SzJUntpYjkfa8PkZTtr0CqWC4vaezmXEDUlY+uS8reNDFENaC0tru09Wlg863jq3ufa1eXlv0W0e7t5wow8SV9f93lT+zsvzDppXhRPU5615XNl/E9XKV8iPuWF2hr+uuJiFv9WxGsqFcVA6QihuGCqkWE5L6Z5bZ1ZqCZpqlk7V2fx3PhKh0hlHM2YnrSZNxN8gsgunNgZYRYahE5S7v7eG4SjGSe3D4mSBB0nuEKQRDHhPMDxHVxtOL5zyJWXrqExjE/GHN8/ZOtKdk6REoKHb94njWIQ4ErJoN9FCsGjmw95dPcRD16/C6nGaE0cxSTTkJPXH3Lrs28yOZkQRQnz0ZwHr9zm+P4hD2894OjeAY6SKCnwpaLnZqRoOppy/+Z97t6+z8nRiJNHx8hUZ7NGJivXyfGI0WjCPAxBCR7dfIBwJBubQ4zWIECTkYggThg/PCZNU45uPQQEvWGPyWiC67skUYzveXR8D6M1xhgO7h3y8O4BsyAgW61m2NzdZDKZgdFoAZvbGyglcX0PgSCJEk4eHHN4/5DZeIZyFJPTCdKRDLeGRHFCnCTMtcGVCtfJyJo0Aq0NM8fHaJhHMa7vZtLdGJTIHFKYRHN0+xF71/fxfA/IvAdGUYyQgigIefDq3XYjQm75Pl9G1z3FNUV14Zmy3u7qB2U2SVBdxW8qvUmUNNpqe3ZWdypjDFqnjbDF4ro272VNGlLl1zTyWCtTrWwrc7cgb88aqds835X7dQpzU7mSoOnbzrS536zJ4db7UHpJq36bM3jF+QN30yvpGriwTGx7b8t70d5pKlK18HfWwGZh8aWEt8Hv7jrm4cecBYHlPt2qVC1kYR0Z8LTCrJsH0RJmnbTarreZhNrunRVu8dqS7LzA+6rNAq0aiKqlEU3L7IIZd8n+erY9lpUyX9RurNgetVCGc6Nc8cjyMpAnQVs2F1/vRZJbCvtW6QkrI1gtHzb8Ta5t3AAD0Z0Z0+MJw70tJqcT0lQThBEqTfCU5PThKcp1mM5noFPEaMq1993g1udvodOUwzuPuPaB53jjd15FasPR3UNczyUNIibzACkErqPw+z2uhQYdx+g05UFHoZOU0fGYPSFQvoerJNObB8iOy0AKtsMEZQwdpZFSAhGe43AynxKnI/w4pascNgZ9HjiGIM0ONw19hwdbkkRrgq6TeX47nuA9mjDt9FAGhvOE/nGA7/s8SGJiV3F6OOLB/JQBgu0r24wenhBHMa7jsDEc0On4HD46BglSSNI0RQqBoyRRmjK9vEXYczgeG/bnmq3uALfjEcxDel0fo8BBYQxsOIrr4wglJSI2pGFCMJ0zdyV3fIGvFP3YZ+vuZRJtCFzJsScJjEEnQ4Tj0N8cMHnzADdJwHEIo8xJxXQ8424QcrcrSB2fzVFAGsfMJwFXv+obSYIpb0Qp2zJlZ6ePMYbXT14lSsM1G2p7Ky36iFgjXPvIlF15LUmYSglRyv3amUq1eaxG+CrVKvU01aQ6xVHk+xVXp7cKbfMAbakX5VwVW7tntop0Ud9XWE6crLJGtSS0FH1eFzWhVZC41XJ93XFnMYZ2gtdW20vLlYv4WgxbOne/n4Wrn5smyocbKSwk93QpyUJsovFhYWGxBt4GUrRGl1xXOV+l0L/dvX4VETsrfB2PIwUX01zHbduTkLYLx2HyLOUZNVmES0tA1uPIeZjzlZri+6psFhblYi9UFUFNQVjQWUpfEiviXMVDnwpReMJX+q6w+ZmlLy2/BQN/yMvb7yeazLkzfp0wiYlnIXGUIAHf9zECgnCOnMyQSiEdRW+zz+jolN5mn71re4weHjOfzBkfjnjuK17g5u+8TjIPMAhSrRluDphNZghHobXhxU6fcB4wn0cc9RzmswDPgFSK7Z0NTh8e81yiSCcxUgpElOBKCSIFZdBpipAJPa0xiUYISbeXkSmpwPFc0jTFubyJc2UbHUZ0tSE9OCWYBWztbbE1HDK6e8h2anCmCUPlc6xTuv0ebreLmY9AZmeVRfMQKSW9jo9yHWbjGYnW7O7vMD4eZ1Z8R6GUQhjDLZkSzsf0t7psT0JUfq/b9TNvdEaztbXBZDpjfDzi8sYAYzQ6TTGpJgoj9MDj0dDFCNiZ+Dz3cJue6zJ3DPFOh0RrjFQoV9EddhmdjLjiOhhjOJ3NUUoSRRGH0yn3fYFxFPI05fqwz+hgxG/eT0l1ShRGdLs+L37VFXrbfe6MbxElYU0+nD8rUH0/O8w6LvTruJWm3EpTqjmaSgFv2pIWZ32qFKQUgFwiJOuKyeYM1nloNz2uM2Mimv+0xFGbwVszdZOPYeWsX00Q141WF8P6zzSXKhbDwvLzC3a5ZhyLdVe+jqYhr73q6nM1zRZ08ZKf9Q4vqqDUcZH2ZWHx7sfTWz73NPtMffw4D2bF31lxiRXXV4VZFceT4kniaBvI6vlsqQNR7Gx9yppzeTBpPcFaXspBxdRe0eK7MvVZoiKAwIhmXPVSF4+f6STXUFuaQXFOKo3T6+pWvcesmwtwx9V4psadljm/WnsorLWTRydEswATJfRdh/tfvIsxho7vAgYH2Oy4dFyXnu/h5zMejutyePMhfq9Db6NPt9fh6NZDkiDm6geeI9EGR0qMMSRRzOWXrnLlAzd47iteoLvVZ7CzgRGSQBtwFMJRpEmC0Rq312E6nZFGCSLRdJVkliQcTudMw5hZknI6CwhSjVESpORoFnDr8JjRdIZJUpTMnEEc3Tng8NZDDm49YHI6IU4S+tsD0iDi9GREr9vBYDg8PMGkmYtv1/fQBgabA+ajKb7nIZVkNJlxdHxKEEd0Oh6nByegNXv7O1y6ts9wc5A7ZtMYbUiSFAy4notOUnR+lpKnHOI4QScprpIYnXUiCZwenSLIzjfycrfoGsHejUvsXNkhMZp5olFKkaaawcYAk6aEcYzjOJh8xqrneXR8nyAISaOEKE7Y2tkiDiMOHhwyn86Zjab42hCFMdPjCWmcNJvMuYSoamnVnykNNYb64jqWOv/6S7qrxVFtQ8ZZqyCklDiOk88wNlNvExarDDJvDxalL7VlaIsLDtdEuX659tyKMapYpnd+HtcZ4JefeixbpWguEWws9TNFLs7LRyULTR6JWByblnK7kIfacFb+nT0yromL1aPFk+HVV1/lB3/wB/l9v+/3sb29jeu67O/v8+EPf5g/8kf+CH/lr/wVfvmXf5k0TfmlX/qlsv897t8bb7wBsDIuKSXD4ZAPfOAD/Nk/+2f5pV/6pXe0ft4OPN2ZorMky+K99QxbGS5isr9I/GdhHVNdq+VnDdEqVnxfF6uIzzlpNXJ2ngHoAgai0reNWC5YScRaont8G1R9oUIewQrnA0tzES2zFEX6NxyH9zsOJox5QwleS57aEaQV7PgC1K3KpmGJ3fA3eGHrPQCoueDozYdsX98lihKkA0Jr5h2HW67A73YYjOZsIvAGXWbjGa6SxHGCweA5DndfvUN/o0+SZLMcd1+5xQsffZnOZp9kNEdJSTALCU5n7L3nCspR9JKU+fEUt99ha6fLdDJnfjBCGJieTNi9cYlJnpbwHG52FdPUIZmH7E8i0jhhb3cr2x+jFA/mcya7PQSCyemY/q0Dtjc3SFJNqsfZsrmOQ7jdZ2N/k77fZfLmG+hU40rJLEnZ3hiQxCmz+yN0kuJFKdr1mE3mREHMcKOPu+kxncyIozgL4zrsXdvHCBgfj5lN50gDVycxUZq5Lj/Y6iJ2OkwPTtnM9/N4votOEoa9LvNAIoFUp4SO5KCniFIYDvp8dDDk/oMxbpzSudZj89oOL0vQdx/QdRxmacKu9Nn2O9yONHMT0vFcXKWIohjlKKQQ+I6CBIJxgJOkdHsdhIHUAF2fay9c5vjeEQ/v3Mf9BsWly/uY1HD4mSN0pNsbGIt9v1K+V5GV834/PnIDD+t3/7pXvGVJ1RbuyXHxIysWSrTG6oVq1qzYF9Rm3FtWFjKy0C7fF2NYdOZThFuRWi0VSmcR5w3jS8u8ga4QfIPrIQ3MBfxGFKGLiFoSXibcphF31lxFKSlh2X9ceymeDHZu6J3Bj//4j/OX/tJfIlo4g/Lg4ICDgwM+85nP8L/+r/8rP/IjP8Jv/MZvvC15MsYwmUx45ZVXeOWVV/gH/+Af8D3f8z184hOfuJD7+HcTnsJM0YJV5iJk56K4yCzHeWHXievCpqPHsjU9xjNrJNVq4MlMV4XltzXOCxahFKBndZClUat+2ZQjW2l1rJnbqn/r16sBqSJdjz/9VRR7T0q+ynX5iqMRV+yQUOFxZxeLGbr69GCpTDQX/hTNp+v2eGHrJW70niN+I2B2OiNNNMPdDabzACkFYd/jsO8xv7LJzHcwwNblbZ7/yEtoIfBdB0l2ts6g3yGZh0hjkI6i0+1w7wu32X/+MrHRKCUzN9TzkGgWoo1GuQq356GThOSzt0l+5w3cO0conbmsPj04YTjoESSZS+qjvsvRhsd84APgSEF30KXT8YmiGN1x6XzNy3S/8f1ces913uv3uYLiKy7t8VVXLvPebg9/FuL3fLau75JMA0bHI1zP5WQ8xZWSzkafQZSyO43YD1KcMGE6mpLEKZ7nMtwagoE4jBFCMtwc4Hgup4en3HvtLsePjknCCKENz0mPj+7tcUN5nPRcvhjOuS810nPZ2t3KHEBEMVEUM57PmQYBRghiV3G/q4if32Pr/dcwr9xlbxrRmYacPjjC8Ryu7G/xkvLZD1Iuz1O6D07ZOpzy0Q+/l+GgR5Sk9Id9hsN+5lghjBgHEUopdJri97psbG2gk5Th9gabe1s8eO0ehDHdbodxcEr3aofNlzaRznnDV1161OXJRQaR6ls101RcK5wKLM05LTz1OLKk6h31uYi3Qyq1zcgsls/QNHYVzhWgPnt0Fs4rTXa/SQPaZj5WvEux/LM9tfytFmV+XFkHeAI+6vl8je/zfsd98ndVyEzqbfj8WM8qQv3dLrbbemu1o9/bi5/8yZ/kB37gB4iiiOeee44f+7Ef45Of/CQPHjzg3r17/Oqv/io/9mM/xu///b+/fOZbvuVbGI/HrX+f+MQnynA///M/vzLcCy+8sJSXT3ziE+X909NTfvd3f5e/8Tf+BltbWwD87b/9t/nrf/2vv+V18k7hKc4UtUwHmIXbFzFArXO/bdrhceO8yHOPO86tncDqWyK/Xq3Hrlm3zomuiEDIhcy3PVNwD1P7viLYuTDFx7J1bdkiunDF1AiXaXxk2Xp8LlTG0fwu8J6/ClEITzhRVKdvT0La3nE8blsXIIoTNE0RUV3Za75QgQANJ3cOGD08ZTaa0/Vdbn/mJv1BB4QgTVKMlkghiMOQ4e4G0fF97n7xNns3LnHtvdd589Ov03UdeiYlztuw77pMpjNEvg/n6M4B+89d4tHNh/Q8l9HJiM/92mfwOx57N/bpbQ+YHU8Y7mwwH8/Yu7bPnS/exsUg5iEGQZKmzOMYTRdPOTgqQRhDr+PjuA5zglwJAekq/GGXjfdc5cbmFm7XZXIw4uD1+4SzALXZ4fjhEVEQETyasKMkcRQjtGHr0hZRGBFGMZ1el16vw8nxKZ7nIoWLkJLRyYTJaILjKBzfxen6nJxmS84EWZ9PtQGj8Toece49DhTBbM6m4zLYyA5hdfIN/7PZDM93ufbcVTav7zDpuJgtj2gecetTr3J9HuB7Hp4SHNw/ZO/+MYe3HxEEYebYQQiSOObWF24z3BzQ63UBQafbYXwyxlWSIE7o7Q5I5iHKdeh0fU4eHiOA+WRGOAsQwDROCecTzMuG26/c5sUPvXR++8tl5PIwtHhYaSVLmrMXy3b5amt+/u3MvrE483QRLId+Sqf8nZFiUTLTknxLWRrnANWercW1Mo2iz6+YQVlcjLd6XqRl9mxNC/aiQ4XmzRXzJYXtd2EFRBVnM+yqc/guhJYZOLNQgcsqV3v+i/PvilmnxSJYMvTO4D/7z/4zAF588UU+9alPsb293bh/5coVPvaxj/EX/+Jf5NOf/jT7+/sopRgMBq3x+b5ffu92uyvDrXq2Hv4jH/kIH/nIR/jYxz7GN37jN2KM4cd+7Mf4C3/hL1ykiO8aPAVSZFb1v4vpguuEayNb5z37JLroYv4ftzznPbeGJBLAN3geu0o1rmvgV8OQsVm9jKQ1X6tHmQvjqXDEtYjueZX4eC+7yP8bSco/N3MADtI16/OceBe/vavQYJ882UtuEKMmBt6Ql3ffj0CgT2Pu/M5rhLGm5zo4QUxHOoxPpmitkUIgOyf4m8dEWrP3/FfjTvcYH4/53INH9DauM76+xcbhFKEdXASu6zALQuZxjIhj9vZ3mJ1MGAx79Ic94nlI13WZhiHb+wMufeAVLr1ngysfCHnt1xTDnQ2Up3jhK1/i8NYjgvEM3/foOC4SwdWTgChJ0Upwb6eL57ukQ4+NmctMT5HS5fThCbv9DkYb3J7H8e0D7r16B08pEIIrwmEYCIKTI3oAQhCFEdsbg8x73sEJIndOoFQ2QxKHEdvbGxwcnCCVxPNdhJAkYYzWhq29LU4PT3CUIo5jdKLpdH38QZd7r99FScGL05TNnU2U5zB78ABPKUIluN13cfwefTcbIl77jc8zMxrd99FJwkaUohyFkQIpHRwnZfzohLvTKaf7A7b3t5H3j+lPAtI4JZjNmU0zBwunx6coQDqK51NBdH+EdBQjV/EonCI2PN7r9QgfHeM5ilkQsrmzRXJ4xM5rO3Dgstu5yvj5K8SASWNGr/82Oolb23D9jDHROLOlKWzWdjiw8O2tJSu1jmfACFPrjs08sHCtPbbz8/q4Th+K9NvtiG3pGowRLcTootbTtvDnDXSsIZZbGVuTqZkqopmBXwjnSAShMegi6BM2jbPqv406r4flHmAJ0TuDL3zhC+Xenv/gP/gPlgjRIj784Q+/Dblaxjd8wzfwbd/2bfzCL/wC9+7d47XXXuM973nPO5KXtxJP/ZwioH3+tm3W+6K6YtszF5MB66Mu+ETL76eJNcogBDzvOHzIcRt/H3QcOgvnbSzl+dzI6+FrQ1dx7W3R6ZcZb7EMo5zyz5fPlYsoRK7wiMryddFXY2qfRzrls3HMZ+OYR42zQyweq83XK9cs3qiGes/xub7xHNcGNzB3I3pS0VWSjk4J48zdda/XwfEcpO8g5Qx/eIz0HjA5uE00D4nCiKjr8sXjE5Kr20SuwgiBxhCEEYnWCClRUjIfz9jZ3cIT2RlF2YyMxhESoxOufzTBHb7K/vvGKA86wx4SQXejz9X3Xkc5DkJIpJMZKDaDhCsotqTDqOfwQMFxmtAddBhuDEiimEd3HnF86xHKy87zOX1wjO+6REnK5u4WV3a3eE+vz26Q0ksNcRTjOdmBtIeHJxhhkI7EaM18NkdISZqkSM/JPOAJgTHQ63VwHcXxwyPGxyOMNqRJ1pZdR7F9eYfT/JwjTyp2E9iex8Sv3UdoQ7/fJUpSjn1JtLfBg/mch7cfMpsFuIlmMArYDlK2EJBqdrY32dgYZM4atGEuYb7d46FIOU0T0jglTVPmQYRUkjhJSOKEVBu01mymho1ZwmAcQs8j3Ohw1HUwPReAeRCxsbvJ6fEpjlTIRx0+uPsR5E0XI/foXXqJ7v4LCKmWmumSRGnRUJuzSI9/Ut7iEqSnAbOgDheb+p9GvOuW9OJlWT5wtg0r9xOtvNoeMqvvi+Wy7aylx8lFsXSyQAy8kiR8Lol5PU1yG9BTUhYWzuJbuUSxJnNXlrB9kqsRxbvUjPeuxKNHj8rvw+HwHczJ+fjQhz5Ufn/48OE7mJO3Dk+XFK0iQ+fJhbpRp222aRFnxbluHE8C0/LXlo+2fD2hacZoTXQ6Qpeb8VYIxrPydWa6FxeH5xYjT7O+Jnx19hanilbZHSm3qNRVhbeKI6+LVa/9XYmcbF6oSZzV9soAtV+1QXx+PEafTHCTmIFOEDpBScVcG4J5QGoMJtVIrYmimNQYTg5O8QVs7WwglUJrzdH9AwyGIIrRqSbOl5Bt9Hts72yytb+N03G5f+sBBw8OwRiE62DI9h0Ntof4vS5xEBHNQ8YPT0hTTTSac/DKHeI4IYxjhJR0Oj5CKQwQRXF2MKnWRGEMqUFHCXGS4jqKB28+4PjNR8TTkP5Gdu6OchR+z0c4CgQoKUEbHClItGYexyAE0nGIw5jhxoC9S7ukaQoimylOjWF7f5thv8fp8YgkSRHGsL27yc7+Nt1u4SUOTo/GTCczfNchiBOmszlHB6eYJAGdkkQJQoDnudlSRQNhfgCrkgIjBXEYk0YJaao5PR4xHU8xGEYHJ6ANo9MxBw8OSZOETrfD1eevsLk9JNYpfq+DIyVBGDIPQsazbGZWp5okiJiGMV7PJ5gF6DSlu9EjmM7RcUKK4YWPvMjo4ITbn7/F0e1HjB6dNNpbc35ANDpffV6l2QDr5GNVw12tSje8j7G6v5c7OFYcUrrqqVUpLl5ZR9JcdGfSusN3zZS1Mt1FMrZ4KOvTRZbzwqBW1LlZbChnojnIl/lffH1vbUHKnLTJzgYhbOw/Wp41XNwVtgrv6jHrXYj6zNC//Jf/8h3MyfnQulpBU+wx+nLDU1g+t2Iq4bxedRZxeRJSszhrbhaurfq+TpwXzctjzuq3ZiEvRxoG3Prff5lr/8Y3093dWR1/S14WfLatCtby4EUGkhXZWbH5Z+lqwziavaTVB75Wz6yamGxTd0T+cHl9rY1J602ZLTevXDF7mie4vm0olMqmxXoJrW267ZmFgMVhkDnDPb1zSGIEp2GSb+cSQEychsz7HqcbXYQQTKVGGMOw10P0E+7O30QrgXIV22nKdDYjOt4gTQcIA56jCJMUKSU71y+RBCFH94+YRTGulBiluLPpcxRqul/5Im9+JiI62MPEsH1tn+npHY7uHWYuobXBUYowikmSlHEcc7DXRwCzWCOSFMdRnI7GjEPJyWjMUAkGpxEYmEzu86kXLuFd22Q+GbM9jpiPZ0SzgPHxmCSJcV03tzJnrF85ihhDEscomTmQECZz5xwGIUopwnlIf6NHHMVMpnMUBgVEQcRsHtIb9LI9UPN5NtOlJEJHuI5DmqQIBI7vE8XZErRer0uYpkig5ypSBFNPcceDtCtwgogXEkkYhjhK4ShJagyDMOUDJiNqZhYyMZnzCucD11GbHUTP59I4Qtw9QrkOxw+OGZ2M0VozPJzREYYrw02IQtydDUxqCCZzpONw9eVrHN4+ZHx4yvbQR/FpDh8l7Dz3fpDNmd2i/rL2JRaaYnP2pXhCLNxr4mk4N657UVuXwFwk/jZUfa55qOzTmsFY4AO1ohmzILtr3f9inu5M7QypNjLY8sRivhaunTlTUj8aogi78MrK/J9FhtY5S/AiWIrK5P+b0kFRMe60n9ghIHeIcRHPYWfuvbJ4Ynzwgx/k+vXr3Llzh3/2z/4Z3/u938tf+At/gQ984APvdNaW8LnPfQ6Afr/Piy+++M5m5i3C03G0UHehuWbnydXd/Ecbk1n4etbM0GLY8xJe/L7OTM9bhSXh1F6I4siC2cEjjh/dp3frJp3tLSjOt2ifUGmfCzyjTpvRLAS46HRMPQYh1iQfNJpSq+wWC0PhEl8ph4bl110f2BY205aHCJo28nixUaGaAHkXDyiFInAuJ8rrumLAK0KubkDBaMajmw+zs3gGXXq+h9Px0KkmjRPi5/d4OB0TBRGpq9jtdhls9Tk5OCF1NKnWJPOM+GiV4nk9tjt+ZSnO34OOE5I4PxTUc+lv9Dk+GXOiwH/vdeLL25w8DPHiIUYb/KHipa97H+FkzvRowsmdQ8LpnE7HQ2qDcSWBJ4m1zvqiEPgGOkIwOh2jHIWnJExDkiQl7nm8cXyCN/PYcRW+Ixkfn2IQSJEd5hmEEcYYfM/DGJjN5niehysVnWGP+XSO4zu4jsPkZIJQktlowsb+Jt1+h+lsjhGSk+MxYRRny9biBJ2mKKXYvbSDQDCfz0mSFNdzUQaiOGF8MsLp+iipiOcBrtEkqUGjSaXDtO/R73VxDk7hcEqqnOz8IWMgSdGzOcNhj/F4hhQS5bnEQcTnP/sahxuZA4qvkD7v295isL/JznP7BNOAyfEYQXYuhtfxCIVLHCfc/uItpJJcev4Sh3cPiKcBW/0uOolxelMEExL9ECFa9gCa1dS81fjzNuCpEpKVWFXCt6GMZyTx+C581zNINdNqptmU9evF1TZcLbWlReLXlolz01mDYC09RM1pQvONi3qg+pWMka+ZrdpRCXbaaCXu3bvHjRs3Vt6/ffv2uXEIIfiv/+v/mj/9p/80kHl3+9t/+29z48YNvuEbvoGv+7qv41u+5Vv42Mc+huu6Ty3vF8Wv//qv87/9b/8bAH/+z/95Op3OO5aXtxJP95wiOKMDiYY4apsOfqKpiPNIUzFjtB4HOTuOxesXieDMZxYKI5qJGcDd2uLK13w9/qXLaG3Q8owitBCidWaLzsXFx6jssZrHnuZ6+bo1s0pCLGo1S6NUi8W3lORnoxlVbR284cnr50sd5/WZRbSaV0vT7eMpWws2lOBwjO84zJOQcB4RRQlOGKM8B1c5RPOw3BsjDAw3B8wmc8IoJtUanb/QVKcYY3CEINUaoRycjsd8PAOtCY/HTOYhqda4qOzsHmBzf5vhe68DEM9DCBO8fgfIltR1twZ0N/t4nsubv/saUkiMAJMkqDBEuS6xlESpxnEUnlJs9joEeZ5Hsxme54GSGKMxQYDSGqENHdcFmV0P4oSNzSH9zT6djR7Th6c8enSc7b/Z2QDfITiOka5DFERobTCk9DyP+VG2bE0DynUIw2yJba/XxfVcjg6O8Ts+ve0ByekMd9jHGXQI5xGjRyeYvB6Hwz53ophwHuIjCHWKnw/GBgjCiDSKEAi6vo9WsHtph9GDY6YyQBtwpEQ5mTc5YcDzDMqRJGnCnXsn6Nfv4/k+Qgk2tzZQriKcR7iuS5pqEq0J5yEGGO5scnDvEKM1270OxAnCSRFRwvb1rWyZ36qmW/6zcG1Fkzy7JV+046wfUzPt0szwxOm05fXpleLsSFYp+Y8jXx+HULWTjcWDxhcfyoe3FYSo0Ftah8C3k0CUpK8xei1lpxb0QnlrPYzd4i3Dd33Xd+F5Hj/wAz/AnTt3gIxQ3b59m5/5mZ8BYG9vj+/7vu/jh37oh+j3+29ZXsIwZDKZAFkfunnzJv/qX/0rfviHfxhjDN/6rd/Kf/lf/pdvWfrvNJ6YFJ2tHzd7UlMYrtnLLtIZl1lXZSTRZtkV9bppripg3ZLe9ty5EdTvNaYwannJEjAY/n9hmClQH8ynVeMQE8OoWOd5ZvGqjFbuU5t5q82XsMwA1yjKKpRFrEaNgiKvG51ZKfoXxqJ8pudLBWfl+XHieip0bW0ytEYGWjNUBFytJSw+FgcRHc+DJCGOYoJUcyIM9z2DKw2dh0e8EGdLyBw55BKXOJ3O6Y2nOFIioCRGjlL00x5RmmbnBAGuFPi+R5ykTGdzHEdxZ+ASdhzCRDF5dES60SH0Pb7wG6+igpit6/tEX/8SdD1Uqtn+4iMm94+z2RUlCeOYjuPw/CjG6TqEScw0zJbJdRF0XRfXdbkVzvn8hsPe9gbPX7/MV7zxkCQICRV8bstDC4GnJIk29Ic7bO9u4zwccXjzIePRJNtvlBr8zT6nh6cEUQRSMNwekIR5fYURQRhxZ6uD6XfY3BrSe/UBMozp+JkL7jRNGU1n3J+OGby4jx7P6b9yF52mbG1vcnTvANdxcOOUK/em7CQJeA639gckaYrju7iei+g4bPn7yNceEiUxg+EwW8IXx9mMF9DpdcDA6XiaNYHNMb3dKcYYNqMdvNMhWmuCeVSSn3sDDzpDvK5LGGnmWtPd2uC20cQDh52NAdw7ZlMIOkZy6c3rxA8drnzgGkfJMSnpUhPNbCRn9ZrcTFQYbFbMnj/JDM8qirM0i93I01n5OC+9Qoqvlj6PQ7iax8i2jO3mLPJSjXM1U9b66Z4Z9wrUGkNDIomWJnGeYF16eXk5yo2tj08cnuQQTJMbAZtjep4VU+kORTrZzFYZohlX7dm2g28tlnH16tW1ZoPWwXd+53fyx/7YH+Pnfu7n+Lmf+zl+5Vd+hS984QsluT84OOBHfuRH+Jmf+Rl+8Rd/kf39/aeS7iK+7/u+j+/7vu9rvffX/tpf4z/6j/4j1IIX5C8nPDEpKpTVdtuJaf95vtxcH6tGmoWkS0K0mMaK8Et5elycU6Zm8qvr0Bh4mKbN50QtdCnoVhek7eiFugtVUwv7NNE2HK6FVtewopxBW5nLNdbsizPe+3lNYjnmNvIvFr41Q5+XRhsWz6Y4D09MoharsdF+REvkpvVXe301wwolGU+mCEfRubTN0HNBGuTAIdEGDif0T2a4UtLb3CG4H3D1xvOk3YQkSghnATrVGG0wUYrb8cATDHwXz3cx84w8zOchwhg8IZk4gmOTggSlJPe+eIdhr4McTXHihPj2I8bPbzF86TLTe8eMfvc1TBiTGI1vYKvfy1yEBzPCNHOSoKJsKZ8xMDKCjpQI3yXxXdSNfWS/w/Vej4fHE9juMfHy/TdocCSpK5klCeHDE0ajcba0zXdJopjpbE44nmMkONJBOQ6X33cd1/c4uXfI4e0D5h1B98o2DydzrqUJnfxNpElaeqw6EYZ5GDB6eMj7o4Td7Q2OHhxmHuFMyvh4hEgS+lLCoEfQkwhjSBAYrfFSELFmNBpx9coVdq7s4vY79I7HpAa0NqQ6I6T7V/aJ5iF3k9vM0kN6nofjbOBIieu59LodojghThN032ckNU4a4nRdjN9nlO9r6m4MeBQn7LrZuUwxEB0Zdm7ssplsZedhLbaqvJktK8FN61nZzM/oVudJlLNcXdd2epShH4eUXOSJs/L71iyjy+XyOTLq7L1ElVxfuv8YWW49R2qlQGyOKSuOIVqK8+x2Uad/54xZa2PdFCnJz9JBvKZ6PUuzaaYijuvTcIunBc/z+PjHP87HP/5xAEajEb/2a7/GP/2n/5R/+A//IVEU8elPf5rv+Z7vKWeQ3k781b/6V/mmb/omPvaxj73tab9deCrL5x6vu68R/nFI0qrnHkcLvUhaj/143YYF1eCyEHCpDi6672W1iry28vyYZRVt7wHA1H3RceZ7Lgaj3DCWu6c9O5N1K1q7eD/DumfKf1bmqH62/Zn5WHnnAjCmnAlZtOStfOTCaXCW+fqciFeVt91OXl8PD7D53D6O5wKCg1sPeXT7IacdhyjpYpREGTBa0xv2mc3mhPOQ6M0HdDZ7oMmWtvV8tq7uYlKN1/czF9bGcPzqfe7duUOcpEiZachCyewgV2lQSpGmGqEkwTxzXNBXDsJ1OLl/jPZdksmcTUchtaHrudn+oDQlihN6no8rs307G1tD5rOAOIyIjSFJU4SrcJQgiWK0n5KmGg1I5eAPfXrDHsFkTjALmExnzBKBnyR0fA/pKqIgJoxjelGatX2dzayNUs18FtAddEmjhDiOMR2P05MxcRBhEPR6HYJZiNfzUVOFERBHMaObD3C1YXd3i9nRKUmc4DgOMj8fqeMoEimRjgM6ASGI44iN4QC/1yWaHKPimNFowvSzb3Dt/TfYurzNdDpHSBBG8cJXvszw0haPvniPLTNgpk6ZhjHj2RxvFuB52VlHrqtwOh16XZ+042CiONvP5XkQRiAgSTWu45CkCXMctDE4vuL6e66inWo/UUOWmVWybYGQQ1NTXMB5Pc2sFWqdjvV00CYZL+bYYP14qwSK2YqzTEnNPCwP05V59UJpr4F6Wquk9Sr76plXzpDDTaKdfRHmSdy+t+WkZuxdZXhtOWR31e+2VN+WvWgWrdjY2ODbv/3b+fZv/3a+53u+hz/wB/4AYRjysz/7s9y6dYvnnnvuqaf5P/wP/wP/3r/37wEQBAGvvvoqf+tv/S1+4id+gtFoxMc//nF+93d/l729vaee9pcC3jrvc48b1bqom3Tq6Z+XlXXI0aL0eVy+1zYlsG4Zzwn3ODW+uLa6ntDibp7ldJ42m6ziLVNeo44EnLM6rj4A1AyXj5/BhehXmBDfagiRc+X1zgG5MJ7YKChaf52pAtT6lvIcojDi8PWHBPOAvuvQwWFwHKINdIWk3+kQa430XUScEAdReQ6OOpIYIXCUwsQpJzcOSfYzxwKjXz1BaY9uzyeJYkwKQmuSJEE5Dq4RPH8a0csbliMkjsz2DEXTOTc/8waOUpz2FaIruPTcZY7uHyHiBM84XDkJ6Hseju9y6b3XcDoehzcfMj+ZEAcRW1rwVTND8uojOoMZxnUZbg55kDs56O9u0tsacPrwhJPjUw4eHHIpjHCV4I6jOOz77O5cIuh4HDw8ItWGOE3Z3Bjgeg46TgiShHjTI1ISE8cokTlOOA1ipBTI6YxuxycNAq7dG6FclXny0zGT6YyO6+XEQ+G7TvZetCY9POVlJUl1ysagjzdJObx5B09JpkrhuQ5ur8O9L9yhvzng0IXTSxuEkxnHHcG157Yw1zfYEy/Qi8YE4zk7zpz+IGQ6mnJn8yaT/og0Thk+vMb2rJeRVSXxvGz5oXAkUkr8foco1XgbPpef3+OD6g6d8f9JYDRKx2UzXmpk5xg4TF1pbA9x5t13RmW8WIddTTeeDsqx5Uwlex31eh0q8gRoXTtX5V8stZXH128MJpfZxRhLLscfkxi1vnLz1Mak5bHVkqEvJfy+3/f7+PN//s/z3/63/y0An/rUp94SUlRHp9Phwx/+MD/+4z/O5cuX+c//8/+c+/fv80M/9EP83b/7d9/StN8pPCVHC3XBcQbrWOpw5/TktfvkUyRmF8FTS7Ye0UKE7XP41OeYHntGrTWJFoIpFj6fVlULMGcynPooYMqp/frz5yZxEdejC65Ym606t26adkX/aVdNG4R8Ooc3tkde+/5Y7Wmxptp+1YM3VTSdpJzceoQrBF6vSxDFxPOADc/DcR3iNGUcRqQzjeM5CARSCNIkQSlFb6PP1o19dl64xPxowunOMfK6YXI0xt/w0CcCbQx+p4MhJE41SkoEgiCKcYIEESUkWmfOEKRCYIgShZQCnWoi18FIh2DgIy9tcfLomG0jcB0HpRTGkfjDLo7vcvWDzxFNA1799c+TzENcIegrRXx4SrjRx/dcdBQQTAMO7x5kBEQbpOOg3ISO52S8xHcJfMmx0aTTGaEn0YlGdTvMOw7DG5dIk5TRrQdEccLW7hbjkzHxPMR1FR1PIYxBKJXNxM0DbmxuMJnMiaOIeZqiZOY9z3UdojQtveBJnRHE7X4f381I6+mjE3ppSm/QY2I0m5e2iGYRsaMYHY9xdgdMJUylYXLrDurGDhuXtkF49Lqb9Lbguc2Q3Wl2htTW5S0eOfc4uXvEjTevc7X7HG7HxXFdlOcglawd4gzmoxopJYqUwaNXcaMAgy6NOg2RnM8Qn+sOv7GHM/tnlf75NLrfRbrXE4r2Gt4qybFGpeRBsgO4q5w0DXFnlfQplF40v69sEovMoDndc2GY2r9FhOYJ9YZlO+vqWc7HjbuJd8IKaNGGD3/4w+X32Wz2tqb9Qz/0Q/zUT/0Uv/3bv83f//t/n7/0l/7Sl6Tb8CfFUzi81dDsNKbQHN86mMUfC4Nac7KjHWLhe9vvRTKwKnxb3Bd9pg2r6tA0b1fZFQvVcZFMnhF28RU/xdF1acxZlPi10cuIhQBrt7PFAjTvVYf7NUM3W3WxYdWsrLl37dBhWFXoC9TvBdHYmGwQnuL617yMM+wQaY2Sgo2NAdpoTifTbJlax2dr2Kfre9mGf9fFCJHtYUlSklnIzd96lbufv8XJrUNGt47Qk4jOoIfjukRJwjw/VyclW9qGAcdRdDyXXsen73s4QtJxFI4QuIZsD5KS9ByJBxy8do/R4SlSQJSmKK0xcUI4nvHGp77I6MExAE7HRbkKqSSDnSFhkiCMIY0Sjk/G2VK+NGVyPCKKIuIkwghNEsdEOltil+oUKQxhMCeOo+zcoI6PEoIwCJlPZpn3NSlQnsPkeIROM29s/X4PR0jSVBPHMZPxhK3tDQyQxnHmQZzMQcX+ld18aaHGGEOiDZsbQ3q9Dh3fJQkjjo9HpFqTGsPx4TGDwZBgEpBEMXEU43kue9f32NnbpNNxiZOY13/r88RhAGiMSTE6RWuNxoCCbs9j59I2l67vs31tm43Lm3S3erh9F+nKbIRSEqMkKAlKoDGkJiUxJv9bYVIqNsFfAO0zy3mPF1Uaj9VNmrFdKPy6V996LJZ0tTfT4qDaht1ryaolWr6vTvnxZexZA3pL0DWCXRSGnBg+yUCx8KwQF2tNWR2uel+rsvY4yovFW4Fbt26V369du/a2pq2U4r/6r/4rANI05Ud+5Efe1vTfLjx9l9xrY4VkWNd4dE40F7J8P4nCv5bVpxlItHyrf7/o5LqpWd+asZnGv8Xq4DL22ibLZhWIRpYaGzWfpuZfKCCmIB1kG6ZbWUb9HJxa/p5wgGlrbudDVP8KLqx4fcnhiWeJFiyr5xnmF4Kehqf86q1fBgNbL2yxeavP9GDMbDrHkJEAz3XQQBBFnA58HvRdpOxwaZrgHow4PR5zcjTCUZJ+r0vvs13mn87OBnp1E8wLOyRxzGw8QwKO30F0ffQ8wFMqa3tCoJSi43soKZjPQ54/zPPgewTxLJt9cBV39vu5U4EYne8tcl2H8HTC65/6Ahv7W1x68QrF+VzdzT6q43F3POXRwEMqn60o5YNHIaezOd4lRbqZopVB7sXEiSEWgj1PsaUknuPw5txjFDtoDMONPoeHJxw8PEIgslkvbdjc3yKchYwPT4jjBNeV7D93lcnBiPl4xmwyJ02yo3HTRBOnKZcv76GUIokStDb4vsfGsE9iDIeHIzqTzCIphMAoidQax3HpdFyOD45I4pjOYMjW1gazziGdvQdscALTSaYUy5DwUHL6xgiAY23ItgEZPnYo+WpPMD2d8ZsEvJJ8oWEpEVKy/cF/A7e3hdEpR5/91yTBBDB4yQyBydrF29gHi3abySsu2FcuntaXFpZzdJaDCVMYr/LZvidN2TzG4aMZmoLtzNmiKtiXNIr6KH8veQ9qe1eFWc/iSwWvvvoq//1//9/zF//iX2R3d3dluJs3b/J3/s7fAbK9Rt/0Td/0dmWxxLd/+7fzzd/8zfzKr/wK/+Sf/BP+6l/9q7z88stvez7eSjyFmaJ3Mc4wgDQuL07JXCCeZgTVr8JiU80/1Kw45Yi7IkOtaeVUKs9Lm+G/mROz8GTzd/2/t8RQtKpOG4ZDQdvhtvV6Q6xjEF5IpKVilu2fq2PKNKFVNXx2LtYL9Q5ubV31rp/aTKEpX1jxzhKdMApHjKIRcx2QxClu18fN95S4rpPt74liokQzSVOCjkvY8QhNCsbQ63ToeB5CKqIkRc8EvajHFhuEYcrD0YjDecBUQugpxmnCZDbH87O9NEZrPN/LiE2UMAsikJLLm0M2HAcVxPTilE2p2N8YsnVtH+04SOXiSoWSMlM2ZLYfKTge8+ZvfYFgMkMaeHTrIZdeusr++64z7zocxTHzMGaYaPoaulrjixhfJLgdQdIF3QVtIjoipSMSXClAScIwQgkJxhCGEXEYsX1pG6kUJwcnJHGMECI7cDVOcTyHKI4QUtDb7nPjK17AcRTGGLY2N+hu9jk5PMnOTwI2Bj2MEJwen+K7DvM4c/SQYrJZM9/DcRRKOUhHMA1m9HsdpFLMJyOmp/cIkyNcP8TpRGh9ik5GxNMTkukJs/kpo/CUcTjCmYYMRjG7sfz/s/dnMZIm2WEu+JnZv/oee+6ZVZVdXdXdbFFsiZJ4RVLQcgeDGQnQQIQg6IWvowc+6FWABEgQCAF6EaAXPUigqIEIEBrceeFA0uDqkvcKvBQpspu9VHdtuWdEZKy+/5st8/B7RLh7uHt4REZWNdV5Clnh7r8tx+w3O3Y2OwedDelmHbppd/S8QzfrkkhH4ksST9Ar+vRGdQ+N4cBYjkZWteuCeZag8d9PtsmpFeQSMtkibf31wxnWr2dpWdzH5El2Btfk1TXWYNno1ccx63B9AzBvsgVXPk/FPMFSTAuJiztYdLa9FZe+eEiShF/91V/l9u3b/O2//bf5t//23/KDH/yAg4MDjo6O+M53vsM/+2f/jG9961scHBwA8I/+0T8iDMMvBd9//I//MVBai/7pP/2nXwoObxK+eEvRRZroC5n/BeXH219UZt7z6VPvCwd3/jReEo8rHRJfJgWcsihcqPlz5f8mxummJmgB437iz17KeBcfGAvnc/w1XZIZWrbUdTMvVzKqTc/v6e+L6rweJlIKWjebtJ/ukxuNdTBIC8IoJG5WqQiJrQWYZszBq0MK62i2mgShjwwDhv0h1pZR2Xzn0FmBVw0QFAghUUqNovgJFJD0B4TKw1eKPMmwtryzIpXCWkORZHhSYqQFqegPhgRKIM0KG1trDJ/vkWhDVQoKa0EIoiikKDTe6J6OkJJCwKd/8CPkgy0272yy/3gHmzusB3HoY5TlJNy8AxgJQM45cl1grcXoAjQ4a+m1u0SqFGzCOCJPMrITIW+Y01hvsbUZ0P34JbvPXoG2bLxzg7V7m+w9fYW2BhX4NFbqHO0ckg4TjHOsr62graXb6SGVJPR9nDZoa5GewhqL8iVGSQqjOWy3iePKKVMscAyHCcKTBFbgnGB4NKQumwSIieVU8reSQguMk0jp4Y3UdE5anABrLDrJgASBRViBkt7Uuizd6a4PRuvTjZjv02igZxbqkhy5M6uWWEh+JkBcWOI6YXq/zd7T1xGd7qy/WXA9gsh4ConlwZ0GF3RXIdwzm5yk09Pn11w2YqZUPQOXi40+Jx1fala/AHHwLVwSwjAkCAKyLOM3f/M3+c3f/M25ZT3P4x/8g3/A3//7f/8LxHAS/vJf/sv84i/+Ir/zO7/Dv/t3/45/+A//IQ8ePPjS8LlueDNC0bK77tICyClXe3UY73MBXZx4dEn8Tt0Glq5zyaJzmr5cEJpxXMcbnZ6YaellMQ6Xgln89qjdWYHy5nU5x3DGuQV22s6cjOQL+jjf4xel6b0euLxANPV9lvLhqtMwFYFpvJlK0eZbTeiuH/LJZ322/ftUmlXW72zy4uNnKASqLVl/6VgHGpUKAksySDgIIHtvg8PdA1wcYqxForCNR4RxHyklg6N3CMMtvMAj7ScIKUv3qzTFt6Vl0lpDURRIJbHGkuUFUpQuarHnUQxSan/4OWEcUaQ5SpXR0ZzR4ARJkhJXY3RWoJRg6El21ipY6yj6PcyzIStbq9hGzkf9IUIbqt6AFiCNw/kK4yyB7yODAOscWZqz4Q3YGIUZD49yxBCMdvQf1hgai7WOe4cJYW64e/82P0gGHK7HYCxfGRiKQcajP/6cz2o+g60qVeVT6SakSYoBanGM9D329w5RUjDIcoq4vI+0utoizXI8Kak2ahz0ujyJHK9WA969eYMjIak3PPpohJIYbajur7J5uEn0IuZnvxqzUs0ndRgOuvG7/GAQUt9s8q4nuZHmHO0c8nLzMQOvR9YZon/7uxTdMlpew4+or6xRX2tSW6kRVSNyW/AHL3+XXOdciz/bGJ0Y//4na8+f36BvThibDrI9iUUpMJ4kO319FC5b/eRMeZMels45JkNfX1Th3IfZFcXs8Z5N47zUwNcJb0WpNwlf+cpX2N/f5z/9p//E7/zO7/Dtb3+bzz77jOPjY4QQtFot3n//fX7hF36BX/7lX+YrX/nKl40y/+Sf/BN+4Rd+Aa01v/qrv8q/+lf/6stG6drg+oSiy6nJrqGTBe3PspBfliBemQ5cRiAqOxonaDOFsWsi5uNH5IlINCEQnQgSXyL9G08qN3k+iFOcRyXO1f0yjXyzsHqd5XdeWP0C4bRLMVvweU2UxNjfaS8T4QyBSVjfqiDWb3L8uU86SIlqMet3Nzl6tocPyMKihCDv9DGubKXjWzptiawEJP0CSxlEIFaa0M9Q0sNTDuMsd96/g1CS7l6bopcQFxLXS7DG4vkezbUqQRzihWVOoqSX0D3skBUFnpBUjEMOUjzKxK+p1hgHDosnJcP+EK01nvIoagGJJylGQoUwlv7uEYUqIx14vgQhCYRAel55P0aVyU195ZXR96KCPM9JhinCOaQ1qEKgtCld5ppVPN+j4hlWKjHHHz3nKIbcV7S21lhJLIOnezghKKoKE3gMtGHQH6KtIYpCVm+tU6Q5K6tNhv0hMi8w2lKtVhAITKFZ2Vyl2+5jpeNF75ioWsNbbZD2E3pYciVQEqSGSEUEOiLfK3ArlmZDTDB9zjmeveqTVRuEMmJ40OPV4x0O9g55mb4kbyQIoah1+0TDCN/zCEVEspfS3xkgPcWth7dZf2d9jIZ+Qbvfjf9155jZZY/DNwfLzsd1Mrzz3T/EjCKXtU4tSpA7//kksTo7X5bpcMH9pZMQ3nAuOeqlYAa6k2fgspa35d7j1d70W4HoTUOj0eCXfumX+KVf+qVrae+Xf/mXT3MNLQN/6S/9pUut45//+Z9/vXX/Ywxv1n1u1pyJOZ+ny8/jfa9jf85q4yKt95U47jmNzjZgzC63bH+XnJfFy1nMnf7rhnOWoZMxn7sJO6kPm31Z9LzNaxaIc4fJZUCAcGP5dS82l8zbBhdZvsYdRV43jOuFcNFau9Cqepkkf/PFPQskJ+G6axFbf+o+T//gE5599IQHP/UutbUGJtforODo+T4mycCVAQM8GzA8bFMNAwIceWGoeAI/N/jKYD1FiCTpJzz6bz+ktdGiubWCX69wq94kyg1CCJI0RwUezlpwII1lZavF2vu3KYYZeZbjkpx0kJD2UjJj8KKQKAqQnqJ/3MNZi5GSIPRJtEFrA0qRFBpfCZS2+FKBdKAEnrDEkYezjsQUWOewwmKcReQaKSVxFOEcJMNhOVNKlaG2pSNJBsTNKmsb6/j9jH57HyoRxpRCUyoi0kKDr5BKEQeK9LBDjiWqxGy+d5tQKuJWDZNr8ic7ODfEUwqtNbkQxHFElhVYa9A650a1xua9O0SbDbb/cIcYRyhKNzshSuGvIEd4Dq3t6SZ3UuGQ6KJAG0OqEw5+8Iruqw5SCioVj1iFWFMQRTFrrSa1Rp1qNSZNc4JqSJ4WFFnB3uNdwkZAeBK2G8gXqKUW5Gh9PZiphHMjK8kZnEYIFV+Mjv9iuB6BZHHrs4nLZdu7qPzp8/GXPLUQFvNx5/FcKrPSVRfUzGNozIIuxr0azqc6mOUMcdbG5Bkuxp6c1H8Lb+EtnIfrE4rGd+C1CxeXgGk+ehk4b0K5EpxVnZb8Lmhw0Zwsg8sE/V9+AOcEn9P+zxCaKRzNw/fKTLubyFckTpo+GcoUEpPWNDf3oHMzPs0rcVmYnutpCxyAO5OcZsCky8n5ZTt9ml8Z1dkwq71lf5sy8UzaOZfRTM+HF9rw/xoOAAgrmvr7mxyIAvPHT/H++HOqqw2CVpXWnXVW7m6w/9k2x7uHiMKw1s+pak3g6dL1zToCAeHRbZR3hxyJNYrQt1hbkB/toj9+hTaGF4gyN4/v8flqTKbK+yzKU8TVmLhweL7HcfuIyFf8uWaDtXubfP7xUx750NhoIUbht3XWpL13TKUWYwpNlhekeY4Qo5xGAoywCG+X6sounoC+1TyvRAjn0IWmowtUGHLT3qRlWmAsTgrCMMBiyTYzpLVIpbjvZaWroEjpPu5hugYnJbVWnWG7gxOCH4YwXA0JA5/qehMnBcNOn883a2ze2kCvNbn77BjbSUmHKXmW06pWMc7iEOR5gfIsehSMYRWPh401th7c5enuId9JBvTTIQ/7Db7ivkZjvcV+7SWPW5/inONr1U2gCsBh7R260RaD4z7f1r/PcfRD5IbDv+WVeaICj41HN3m/28APA4QUhHGEkRBUQvpHPbq9AVIIWmtNkoM2v7RWQVqPgXP8v4cDsjlLb6ljZwkF2amr8rRS57TIGLGaPl/Gys7JiDTd3RtnYd8kk3xOafKmeYAT4fvSmuwphN6I9DzZ20wUx+ZnUm5aJNDMx/WS3MhbeAs/0XC9lqLL7LZZhPEiGnQVGjWLClz0/TVo4QT/PjvpxQy4rDhzvs3JuvOlvOk+FuUsuNQLvaw5ZLqgOD9NpcLvAmJ/BQp/9UOhtBKNa/Vmtz0uvc22uX1x0afmwLxpnfcex5+56QN6ejOPsXFTa2BcCyrc5G8AGkfPltyrwREpSfP920gD7r99Tp4WDB7vcvR4l8pqnbW7ZcJWqSTGGKy2GG0IwoDhcY/dz7cx1iPXlmqrhud7JL0hfi2m6PRRhSkFDudwUqKtJSs8EgOeENi0YJAXiONumQ/JGOpIHn38ijgMOC5y2msR7Zc51rkyNLYU1Oo1+lnG2tYaVU+hC0Nn74giy8vcRVJiMTiRIqUkwmJMilSKwHPUhKDn8tJSJAQGixxNaxSE6Mjg8gLrK5Rw+LIM/V1kBYEXoHyPYW+Ic45qvcqgN8B6knC1UQoWxz2cLENsH/eHpL0h/tMjpHVorQmCMgpfFIXEgY82lk6/j7SWKApJs5y8n6LSguxVG6E8snQIIbQqLQIdMsiG5Os50jm8ug89hzOOfj+nW2g++84TDtbb9EQHJSS1KMb3JRZLXYbYDgx7GVprKlVLVI3oHfc4bHeIwxAnKHMwpRmhtkRKgijna66mZBnafuHWFKPALWOL+FyRBTictrLcQfPjoNO/rNB0YuEoTWLLSqM/OXDhdIjJUrOO0nO/jbn7zSfvb1/EW3gLi+CLiT43zVSN7+aLtEavu4enNXVXhSXwuNgysbitUx56GVxnqg/PT+a8qb7IoLcQrpGuLlLGlQLRFIM93b0bZ8uXHdFVRz7fKnVdfZ2fDjHGYFwN8wuX1Bwt9sWn8LwHY4248yWnuxZTBU63rDPYPAFg9VYTtRKh2z2U8hBeQLp3zMuDbmnhCX3W39ukeWcVIaAwFtVcpXK7UQo81qF8DzkSHoSUmEJjCkOR5uisIOkOSLOcejMkDhTOOIpeHzdIcMYRyhCDQBiDAPI0Iw48GkLghEBKhR1ZLm27h3OW42KPSqtOZa3B5v0bDI/7DHoD8jQl8gRm6BhKRxz5ZZ4kB8I5hJKnkdisdggpEErhrEUCoR+Qa4MSokxci0NYUMov3duMweTgxyFe4KELTaVeIdeabOeQJEkRQlARkrTdZVhYsjQjGAmGqR4QRwH1tZhARRzuHmIdhNWIoBrTz3OohmglSfOCivQQSDaaDWxq6B/3yANDqH3iWky10YReQp5mDPMB2ztPcYFF24KiKNBCQBai0wyMo7LfJurHRI0KWZIyHCTElbgMCe77CCnwq4J21uGdB7foux0IfTIHbjBjibsF7l+XNMWcKgTGicG4EWTChDT+/MeTIS2HPz0Jr2fOmdB1zggeMN375WBxHTc+/z+GcHauMXUAjisvZ50EYzb5WY4ES0Sim68jdnN6fQtv4ScLrlcoWsAbnft+WUFlHo1e1kIxj96/SVP+rDYXWsguF7duPpwdGrP0+fMFiNdgvWcZpy5o5sS9YZE1aNYdgNN6o46uS+798YDJMZ0Yp14HljXWnS84xnxMrVsxM0HLJRgcNwev0/ctSI+2efWHvwUONjyPn7sh6JhDds0qL+0WULq7eUqRGYvVjwm8JyDgo/0BLzrpGfMwwxI5jjUAERA5pBAEBfhK8PNfryPznOPnXTpHD8lSTZ4U5X0jKWnWavyUAVs4hoMhzhikLHMIlYHQUrJewaNOn1qjSq1VI67FJP2EYMdxe6dCqguSW12Gd46JfA/h+dg8JzcW60rLF1KgPFH2O4qEh6dwzuJ5Cu0cDou9USCERSIQQx87CsSglKK20kAXmuNOH18IwiDknb0+Li9Qnk91Yw0hHDvdHV68+5iVWkwuutzZfsgwSRn6ku2bDbQxJCJm80ad7WQAvuSr+0MUkq1uTuqgP0hoiVVa7RXe+emHtLp9cM/JekO+W/weO3dqJK2cYTGk4vmEYUhc/3OolQ2C0Of9DWhoUJFPMczYf77PwfY+Ra7xfA/tch7dfsLquyu8uC3Y1j4rWyvo3KL/1z4Uk6tLTC+Aa6D701r6eckzT9Qa4lzNL4cFnd6lYuz/079eHZatf5V+FuzkL+sQmBk29TyUBsSzc2+y9Oy6s8/JaanITSRhn9PS6Nn8+XsrGr2Fn3S4HqFoniC0SDCZ18YyQs+iZ/MEkTdliZrZ2dXrXspaNAKxsMK0CHQB0Z5TZilR7ZJzecL8TvYzqbUcPwimfcTHcfqTKhBNv7npef5CArzMfG+zN815jfuMygv3sDg3qImexg9+a7E2K0uIgDCM2Hx3Hb96Dz96QN5LyyAFgYfwFGH8FCF2ANA2Jzf58utihnbZOUEgK0Q1n/jhBtHOOraQhLWY3kGXgxd7DLo9/DCgvtLAJClhNWbj3ZvotCAbpiTdAcYTWGNoH7YZdAdEcUh1tUG91cIepFS8GC0SnK9InMPPC+QoSl2e5ghf4vkKay3WgfIkOssxxiAcCF+WqCuJFhYjHZ4T5Zw4gbEOpyTZMKXf7YMA6fvUVxuI7Q4Sydpqk2FvQK/bx3iGQuQUysNKi/LL5LTCU3SzjEIXKE9xcNwl3d5jK3eseQGuyOkcd3BSlrmaUsParQ1Wb9xADB6RJxmPv/0p6mfWMKpgqAdEYcD6jVU23r+LM+9i81UEjqo/xOwco4cZw24Zae7dbz7EOkeeZrgQan+xQuHndA87NDaaZL7AOjnfmDnv+zJ060J5f6TOmpSUxvj0KabZgVsgqL8pcBcP5EuA18PpdH6/yENgrLs3fPVorMsx2jvP5HPBGl30bFyN+hbewk8qfPHJW18X5glPs77P29+zFXpvCKYQuaivZc+HMeuSO/1hWa39mb+3m6ozrVl3V52jpYxOs1wErtLZ9cIXaXWa3Y84PWjHrUSzDJzXChMNj72Dy3R20sYFr3DmeT63jiDH0R0txr4tyGUBTQWAxoKwWK1RwgKMwnTPNmDOXJonAvqEcCQYFqUg4lD4GzHWKPAk9eYK8Z0avb02w91Duke76MKQpxn6RwXK90AInDZIP6Aa+uSDFE9bzCChP0hRg4Ia4EuJspK4CFBSINEYkxMIgecpTJ5jrYfyFJ5SGF1ao4q8wCCIfK8M8DCyUllrKSQ45fBwVBykIicdHOJhsQRE9Qr94x4tJVndWuG4OyDvDYiiEL8qeZl6eHGILz2SXlJapKRPaCw+ElOUd5oCBK4w+GFEc2OV/b0Dao0G1lrW7mxw+6feGb0jRU5A5gLSwpIVGk8q7t5Z4+7PvIvyPPp7kOWag8e7JH/8FHfY4+4H9+h3Bxy9PAAhqK3U8SKfjXfX2WpWyAWEaYDwAkxqMKldvPBmLcJlyc2cdV2u2xFrPndznghN43btL95iNCtk9ZdvHXidvt3Eny8NFvqBn31wuJnKwMVNn/cfObV8usknV7O7fbmWy7fwFn6c4PWFotexwiyyKs2zAs2iAPPOl9fY47PPtgvY0ZmBFS5BrWeMbaLHmbRreVNa2da05WjZ2leEpYSjsyILdVmjkE+zj4H5CVmXhR+fI+FEDXmC0eSh+MbO/6WMgfNMsScfzzThY+hPLuITDfklVK2fFJpHul9OzfAz3OGjGcjZ00aNdRMM6jgKJymLT1z7zwlHo4q5dfzXZ92xFfZ/TAntjnqg+Is/V8flmiKP6HcfUqSazkGHwVEXlxWIQcrdEUPsqzJCXeT7Zf+hT24MD/rr3Dl8AAg+bb7kcfCCKo6670NmKfIcRIC2Fq0NOi+w1hKEYSkAulKh4bAIKXDOcr86RDoIheOo8oJUarRVDA6/TjJMKLKM7fc22Q882v02X/PKMNmNeJWvPP2Q1eM6nvLodgeEShEauEtEfzBEeAoviPACD7/lU32/wuGLV+RFTpYVbN3d4ubX7wOQdoZ891HG6q1vsvugRb+5Q5Y/p1Wv8td+cYt3b+Tgcj553OOj/+051Z0jPCkJm3XyzoDNe5u4TJMNMyrVmG6nx6tPn/P/+PCAOC4Y4vg3//uAQV6+E6vdcsqly2z4BWUXhvkeD1N3srbGmOQ3BZcJoX1hqWvQwpyJgifKiquMfQ7zfp0EccKKvcCUdxkr3zgtv+IrnztfSwhYF8+5GCv71nnuLfxkw/W5z51j4mdJMG7s2xWTU17njp1vSBnRsVnWl2uARdYuN7voFwbTY56lGeXN4LXUq53R+YnIsIwcPd3PrDpfttIRppfI2QY7cS1cZu+c1wm/Bix46cuzOTMaOMffjFob5zJdmb8oP01Nb8p/Yw2MM4FzXT1PadTZ7J6ETT9nJHMCnEObceKmzzVnnENKh6oovDjCq65hLazeWSftJ7z8+DmDgy7SOoyxWOvIC7Da4vsegRQEnkfgBVT8eMRECwrn8Jwj8D1QClsUJINh6UJnyghrYRjiR0EZ2MFanHBYOyJezqGswQ98tNFoYQiEASmxzuKMBhzDNMUNHSLwkNKCMyjPo1qt43shncMOVoCTkkY1xjpLpRIiRiHPXWHIck3n5QHDbg8/DKk2qmy+fxuhJCYr2Pv4GQe7h0jpQSUmXmugjwy1zRZxLSKQGmscx4+2OXzSI6rEpFmGM5YkyYhbdZJewiBJKZzBU4qbd2+QHT+iGQYUVmALhy3Gds241O3E2QtbCpancGLq27mdOc5knwhHJ4K6WEZyuxqcie1ugnKMP5v+NleQujThOD+ua9JVjrXPeYWGcyOZc2xMCxOgLmz92t7MZMLY6zk9nRsnWm6mcHQmrL+pE/stvIX/8eDa3OcEZVSnM2Gi/HW6FNOHBnOKLuhpBlc8s9R4+RPaMbevmdzxDDXzQlPGgmeXgXln5cL2p1j9mfiKqSPwTH939rObqFc+PTtW3bQRYxznC3G8brgSGz4a9XnR6GIR44s7WM7YKya1kmOWsoswWgrbcQvOQnX4GS6LGx8r6Gb9PqWMdSN2bYpvPYkgNWmZmS/Ojr/PiXc7xhwvUuafa/KEmVgwiQ6wSBJVRUpB1nEcfvyIbJDhtIFmhej2KuHmCvtPdpHWkiYZkSjvvdiR0CWlokAwHGQoXxEEAU1Rx9OGWiEQMgTryJwuo655HtY5fN9H+Yosy1FSUhSloKOURGuL04bI9wHQUuBLQWgFDSS5dmgLdpgR+D5GWwptENqQpTn1jRbZUR9ZCZE4fKnoDRN8ZymGKcJT2ELjrMNIQS4hk4712ze4eecGfhySHvfZ/fQ5veGQLFTsdLpUV+sMBgkq8AjrMUMt6OQSkxv2nu2jCw9pDE4bCm2o1Wpk3YRGq87qrXXqaw1UoPA8S0808QlIcDj6M17QVffs8nVOKehlu5mj4Z9FRk+o02WTI8/sckFvV7ERzKIa04lDx/teto/ZAppYmHto3pNTweiSZ5TDTWRguCg9xCye5jwtugQC0/i4GYL0+ERPNXvqgn2JPr/Q4/stvIUfQ7g2oWj6bsrUwxLErB/nwNzzbInTZ0KD5Bbv9DnmhbkH3WWVe7PG/kYozwI1/rn+xt7WBbmUxp3Slmay3zRlFdNkXpzyvm5qwsUU1ufZ42U1wuNz8OYFpIkZd9P7a7zMa3ZyOpR5czJLczw9x5fD5kzQfp0RnNQfX3DnN5sb62lWTqUJYUqM1ATj9OOCtZyqCh+1/jzWOF789+9x58UBQeDTNpoXVUXdhax97TbpgxVeffaScLvNe6lDG4sxBicEUeDRQbG/3cZXkrsba3y1cQuXFfhCQjXmKB/wiTym5+cIBFaUQpUtSkEJKSF1yFEc7zDwy7DcEgprMQKUgEgpbnZypIgY9nNW723ihwFFVKGTHeIKjbOW6kqNwX6HqBFjjcVYi3I+qxsrmGGGjHyKfkqeZLQrPruxpD/0aL6zxe4PXxBWI/Z++IzOcZeoFnOwVuEzaREUxM4RCkV1pcH3DkK+fwDtlwe0X6XUvCb4HiEQxjFSCI72j8nyHOl7DIZD1m+uM7SW/8X7GQLZoNaKSPmPQHr2Yk6XhZj8bYl3ellwMz4thBPLwQxU5uvCLoP0HAXBBCyjTrm4z4t0d9PPrS2tnNMCxriL11Wpwiyh5bJWIoQY3eNcPgrsuR7OnU9zyl12QYqzNXNu/maR6REjdOk5eAtv4ScY/uQFWpgFF/BwV2tSMHHLfRke7ipq+2VOxVn1LxrnDHzPk/nzhaYVaksfUGOFxdgPc5nL1+CHT5X/C60W84PgunlVFsAJUz01qjcGZ7eIxj9djPf1iWszWprT+CwRafrjidZ+ERtw9mycNVq00MUETmc1zqtoxMQ8Lup91KxbMI8T2lmBFWV+Iq0tGEuzVacocnJnaR926f/hkEq9wq0P71O7vUn8/RckRz2kH1BbbXD86ohgcwWNQEmBdeA7hfYF0oLvBCtRxFajRZoc4bQto8EFHirwGPYGxI0K2miUp7DaYq2l0qriBz55J0d7Ai/wcbko8xyFAZXVOhv3tiiSnMPeEDyJkB5Ro0Jnr02R5VTXGniuFEyUp+gedfEQZJ0+WZaT5zkdHXBQCIwt6O53qCM4evqK3jAhCAOsdWR5gWhEGGPI84KVrRpho4Jx4Ixl98krAlfD9z2yLAMH6TChKDRFnhHHEb7n0T3sgoM7X3+A9R1JARFq/juaeLUjonGZ8+LyfOvC/Xe6dJZQHl18F+R8BrPlLTEn+Mwr/3oH6SzcrS2FawEoT031PalaOXWFPQ1H/fo4LV1djGNwAQU6R+7erAByubclZhyWb+EtvIVFcP15isY+LjT0LLNHFzK9c35fdODNUi6fVx6Pvs+wMM06aH+cac1Sczw5ySeixOQ0zbYiTBgaJootkW3p+rj3uQ2PCxMnMJ3Re/wWwPQoz6H4xnA+D+7079R8CyYSxE+jcyn0Zpz6Fb+KL/3LIzrd5mgCrbP08y4OUEKwJiQCsEKRe9X5OM3rS0CmU1KdjPVfvphxF5lJFmtG83Ne7jSbNo80nPwgsEh/gPQF1aYgPooxAuJKzO1myPGrwzJXUJbTPupyU3o8uLsJdzd5+YPHaF1QXatTpBlSSZTnYYWkXWiUFJggwDiBkYoIxbu3b9HrDrDA4KhHpRYzsH2U7xFVI5x1EECe5BhtqNaqBMpDCokucgotyH1FkmVI4Rh+9xE2zcmyHFMYJAKbFgy6A9IkI+8O8epVXGHKaHe+R1IYhACpJGEYUq9XyZMjqvUKnoOsl6AF+IFPpVWjvt7k6dOXxHFIMkxYjVf4yofvEeQRuZS0DzscbRfc8UJsDkVWRu9LkwThSovYYJjSqkRordFpaS1rKAlKEeWGVujhpIfF0c3Mgn3gEMrHqzQAUA5CUzLq0mp8nSAALX20F+EAz+R4prRCGSUwqnz5ibak2o6tj8UEQox9uh7l/Xk3teVrnsBse9XrBUQ43wuUFgspyrHPcl8+ocViqs44NbwKnNLLOUM5uZ9zJffBcyiN8gUt1ebl+lssGp9/KmZ8Wh7eClJv4ScTXlsoKv11OWe/nfh6Wco9T+BYtE9nnUfLqKUv+u0yMAvfKzbzZnjvKxB93OQ8Tr3LuWb7ZdG5klmKqZNzEqfpxiabnQxHPm1RYNH3y1wceINC81muikXmjMvBid/9V9e+xs36LYw2dPc7DDt9fN+jvtkiH6TUN1oIKciTHKtNGQEtChh2hviRT1AJkVIipQAhGBZD/uuz/w1tNA0h+VuVKj6Q+nWer/0MCDk1OMHMZIVje//R0af86OAHpxagk1m5WA5f8mVMGo1mNXTKZAkvI1r7IUIK3vmf4O7mV3Ha8uQPP+Wn4i2KoM7jTpvntxvoJCdLcl58/wl3vvGA+uYK2SDlzjfe4cUPn+JJHyUV+8bx6OUxcRxSDQuwDmUst9diGl1HtHkbI+HIHiDaPgN6pL0EU2isdQgpMLlBIhl2B+AgG6REvsNKnyfNgH4KQhd8rZeijCVNc5qNGoP+gCIpaFQqFN2kDOygNdJXKBTGWqQnqUQh/d6QOArwGjViEtJhSlJ4xMYQGUcQBqzf3yLtDvECj263T6NV5/3qbd7dbgLwuObz7IePyY6/gbUFgXAUQLPZIE9SpKfIs4IkSRnmBaHn40nF93/n21jn8Hyf+OE63/xGFSlCEm35Xx+1KcwMpdboB7+6wvo3/wpCCOq54Z3jHAHU0lfcbH8fgE50k72VDwFo9Z+z0fkUBHSais4oFPz3Xg347HDMZe/CzSguRQ8uw6TPKztO4WaXmdJicD0kZSaTLgRKzbDqsdgqMx5C5Wq4zGl4spOJMsskFp/b1GlAGGbG+LjM0TCpqpxX6/UOmdn4vBWI3sJPJlyLpWimrHLRzl8k+Mz6POu3q0gPlxHQZg3sspauK+B7/QLRfGTPUBrXHY47MSxh9VkWLpq7OfMzLowsPKQusR6+CBe464KTYZ26kIymwI0/fB044R9d+caLQc7eox26R13Wb29QX6szPB5w8Hyf3mGfzXdusP3RM2ymUUqxenedw6d7aG3Kuyexz8a9LeqrdaQqE4ueXFpWgAQ6Lw958fwxKg4JqzFBFFBpVVGBx+HTPdJ2n6AWs3JnHWddmaBVCoSUI00sY+to/Mt5S+a5BTePvzjlYOYIm6ea3zE7oiitRUJIokZMVI9x2lFbqdE9arN+a4P1UHLYCOnlmjBUCMqEpL2jLsI60mFKtVFj0O6R43BG43kKlCIpNIoy0IHMDVI50ldthFTUZYAx0FQeSb+PthYZ+qVm3EEYBTjnsGV4OkLPx+YG4yA3FoUg1xahNQ7IswKEoFqL6e63wZMkScagN2BttUVYjekeduj1B3SznEoUUW/U2BmmGGOwxpJQ3v0xhSZzjs7uEdmgFG6UV05xpdVAOEGR5Dz/7AXDJCGMYvyOochTPClBuFFOJstwmOAHPtI5rBBkScpKJSZ0BhPFtHeO0A9zooqctIDM0ticUDshOTG7CjeyYiBxuaHf7jGo1qApkFIgXblmcZx+FmKWreMiuOqheBmYTdlmBS2Yh8KJwfXHgy0eE4kWTPJCfGds/4lj+Y3fuZnE7jp7O1FankV6X9T6G9TUvYW38D8IXItQNK3H+dK23GU6/rGhHUtKaa+Fy5nYM33Bfdqd7Hr6vgSnfhXhclHRsbKzq8yahcvCErWvbe2cdymZwOKKg2gJSU2W3E/uVdAyBMAlhu2nT6lvtqg2qww7fXY+OibPCpy2yJpleNAlORpgrcFZR5EXRJWwtB6N7gwcvzigu9+hdafJSriKwdDCgSvAOUyhGXb7mKM+MvDI0wI/9Hn4s1/FCzz6u0fQDOhGXfr7Hfzcw7cRXhzg3/VpeS2Ur0CemS+LIEMHZdjsvJejE31+5ubwyWcuKKPZPhWMJrX70y6ZVluGB2kZ7CCTpcVNCqSS5EmGzjWtzYj37xl2TYfwwOGpEN3PEEHAwGheHBxzY3ONupK8/PQFTgpC32fj7hYvP31JNQ6wGPZjRSolMvBpFJrQgULSqChsryA3hoPcIaMI5XsUucYaAziiwAfr8KTC5AXWSlaadeRhikThCUGRF5SygiDLCqQUOGMxhcGa0n0uzwukgEalgh8GpMOUTr9HpAqULohqZWCGaiUi15r2zhFZluGvVNnwQxqNOpUogFRz9OKAQbuHDSXJYEiSJFSlorXSoNKsYpylt9/BDzysgCLLCaLSEplkBZkSMEhwgSXWgiBzGO1Or4JKqWiGrTG3yvKBHzSJhzmd/S4vnu5RHCbUV+vc3VQcpSGPP3nJof8EVVtj671bBIXgyccZnu/R6Wni2hbKU1T8gLU4BwGBHqJMBsChtSQzNuYJCktZLl4XTpbxTFo1rak7++vEUifC66J1QRl3Kpyd1VrQIGWjy4bfXoZkXqegNKlImYHPAqvUhYKOK+9qSSm52Cdz9vO3ItJbeAtn8NpC0fhGnrm5xmnBZXffOD1/HYvNvPKXFn7EaYSq2U8nm53Z9txJeg24xNjOH5HjVqHzVqPTWtNR6i75LgVzFLfTeM2YxNPs3UvAGS8y7qE+T3v6Jqxy1wlTg54Q9q6A+dia+FOBz58OArDwqvkBnfgmAKYwDO8P6O23KY6HZRhn5RGEkk7Wx+aG9rN9MBZfSvzIp0gLusMMJSSeEPS7A7JhhlCK7kGHO3fvs/XOFjEpav+/g9XU1husNDd4+clLajgakcfeUZf+UZfGRpPeWoPD6jG7zY+xlQL/eYX7vfdZ3Vih97zD6lGLxlqT6lqdxo1VpKfYv71Ne/0QIQS7v/+K7pMeJwToVJiZFnTGmOWzBTE2UePBVsb17aMFrQeal7+zDUAravHwzgc468iTAptphsc93vkg4C/+zA85WNnh2fdiXu485Gj3kOLuOjtrK1RW6sR+wINmFSUknf02x4cdHI5Ko8Kg0yfwPX4vSUgbMVGR8VeikPu+T95LEC8+pVFNKNKMLLxHYkNyo8uErw4CvxR6rDM458iNQfkBxliKvCDwFNY6rNbUGlWS/hDrDI1qnWF/iO8r0jTDd6CdRXl+ec9nkNBLUqrG8FVtyIdDWqqO9RS1Zo2jg2OGSUKtUsEfFKx2Uh7c2KSRGZL2gN7LQ7Rvsb6Psw7ledT8iGqzhhMgPY+733wXU2j67T7dg06Jp7U4UQaO8EKfm/dWuNl7hNfJ6VmHsOU7i72Yn739cyipJvZL2k14+p+/R9hPWIsilBS0n+1x8Bze/emfJv6//Cwuf8TB13bQNzP2Pg44Pthk7cYqnf0Bt6o3WLu7yZ2m406zbHOz/UOaw3Id/FaS8KmezGk1uQ1PmP4lrTeXAvFaQtekZ8DF4stVOrowsawb+zvakxdRu3LMP47s/eI5upRL9gwQQpQC0bleT07y80zB5Im/CH587IVv4S18UfAlRp+bYyFZdg9e5IFw2XJL4TBHIDphVr8I7R+MqRovJqjTgs7455Nfxs+gxW0sAzMmYYlD7dzcLTCgLdSsTSvlRkzwZMnpkb8BuIbzZJ449zpha8fbkE6g84Kjp6940e2ClHihjx/6VGoV9nfaDNMcJwTWWKSSdPfaOByeECgnyPOijCglBLkucIBEEAU+SZYjrOTFR0/p7LX5+k/f5mRi4lrM5upNkl7C7uMd6rUKSgh2fvQCpRRWSZLDDt1KmyTPuGlDbn/lNrufvuTw1RHNWoXui0OOnx9QWTvg1of3EHcoLTYjoeeULZiQbaYE7NFeEo7zUvnM9zf68VxSzrO/JwlWPd+j3+4h1TpepCh0TpEJPOXRjCO2+wmHaZ/j/WPq1ToblSqNrRYA2TDDFJatd29y8OQVeZpjlIcRgiI36HQA6y38RgxtR3rUI6hGtKoxEoUVFu2Vc6GwhIEHUuAKCZ7CFJZup8vDehWTZKXQ5HtUKjH9wRBPeYRxSOe4CzjCSBD4CmstKMmwKADwfA9jDGme4ocRSimqjRgVB1igEoZ4vkeR5YRxQHW1Ac7RebHP4cEh9vYKAkfke+TFkEFusXvQ7nTRxrB1a5P7f/ohzRur3B7pZpy1OFveZZW+gjxFdMQErTgllQKctnSPuoRxSFQJefb9p6TdAY0oLEOa+x6RlCRZzvbn27z/5z5gY/UmdqtMiJsNM7wgQA9zvMDn4MUBq7c3Rmtt9L4Lc2l90TiL+noBDRb1MUvNdb6v82LQfAv1onaWwegiGKfrSwXs+TJgWq8y8WFOhXlPLhLmTk2Mi8ud5B0UJ3XE+LO38BbewjJwjXmKLkuf3Pyvsxoa0xrNLbMI5pVfpp2r9rksvK41bNbzE95tQadnx6U7KzmzT8FE0YU4uUmmfeLDEtrBJeZYiAvuOY2p808Yj/mXjN/QcXEta8VNfJrk5edbwBY0M/ru6NcUe82A/c8P+OzjATK4g/J9hllOqgviepXNe5v09rtkvSEi8LHa4CuF8j10llMYg7EOlByd245AKRKtKdKcQEqSokA6GB71ePajbW7cX0XgKIIA5bW5+/U6Th9zuJ0SxRG94y7bP3rG6u11Bsc5gyTBV4rWxgppd8j+9j4mKkiiAT0DgVK0sza7331BY7VJuBafxm44Yeucc5fQJJ/M9OVfoFGGQaOHyTXDoIfoSpSS9HuC50cbDOOIbn4MzpLnOX4l4FYQYQpN59E2z4XP3a8/IKrFrG2uYLMCU48Q99bZ/v4jpI6paYfIC/rasZ8cIKshkWriVXxMXuBcjjUFOkvJnEVKwUYc0xTrOGvJck0vik6FxqKb4QqNEhBGEcNBgi40lSggSzIc5X2maq1a5kYyZbQ1qRQSUFgK51jZWGc4SMjTlPU7m3SPOlSaNaqVmKNXhzg3YOPOKn7YIesr9p69wlpH0Eup5Kp0uZMewgn6vT7CQRQEoC1HT/fRhaafJqzeWCOshsS1mGI1x0mLtJonxwXSaDIka9VNNILIixEIDl4ccLR9iLOGh996H6ylGocMhhlJURCEAbHnIWLHodijHWwgfKj1Gzjn6B/28CMfAdRaBVF1SOPmMVm/Sm8fnnzvMTvtF3ztYZ24UUXLfWDMUjSX9E3RyjcA5+neLGTGie94Xq/zZacFuQutPq8FS2jTLgETcVtep905jgvj6SzKYsscZsv1t2xBMfPz8p1NWpj+ZFmJ0qLN//KD/+cX2l/M1hfW31v4YuDaAi1cuvAyltvLdDSz/IioL+J9L7IsLTO4RWO5SNi7zOxN1L8cVRe4yYPgvFV9npGnPBxfWyl4hQYWyj3LtTduE5tueHmG5MfjcDjTCyz57uea/gTP7lbovFvnk+PPubW2wlp/1DgW6/mgLbufvsTkGislQpaRzQrPQZYDDmssQgp85ZUafCFQzhIqVd498RSxHyCAtCjY2+nx3bUHrN/dQMoBnvxjvJrjnZ+pkBdN2rttqmFI/6jL6u0NKnGIJyXaFQjh6B10MNbSa/V49WCfzDicdQSexyDPiZ8EvLP+Pq1ba1+AavT8BirCnO13n5ENM7ZXn3Nj7w6VOOTlbsjv/f4HeHGAzZ9TGb7Al4qKNlQGgigMUdU6nU6PnY+fcfeb7xFWI4QnOW5GPI8E+/11Nl62uTk0SOfYLzQDIQjaKe9tvUslUKjI8nz/98D0CJVAWlfmMxp6fNP+PLiQfprxudFkRkNhwJZCDr5HnqQ4BNWVGoFSdA7aKM+j2WogRu5yUkC9UcM5x7A3pCg09Vadmx/e47v/5fcQQnK8vU9WFGzcv0nn1RHWWAJvj9W7GZ5ss/vYI00KlCf5alSj3e4iRRnAoDCa2PPomZwkzSgOj8m1JgwCDvcOGRz2GCYJhGD/7xkbH26Chec/7KNTTexX+PkHfwZfBlhtcIWlvXOE0Ro9SNl7ssvqzVV2PtvGOYfRmsQYVBhyVG/z/PYzohs+t7nHzc/vAbC9/4Lj9AgpFbcedrj3zW1ufc3y7A/v8dFvDxkc9XC1e3xnWGG9tUYSFJAPZi+VcRg7nr4ImG01Yuy3M5FnHmU8oaeTqQLGLBQXwHTuuNca+wU6rTMhaEYvV43ceWp1PuMrzucqukxzr//2Z1qaxOz5vbC3GbzA67r4vYW38CcJrinQwgUwT8CZdmNZhkpeRWi5zJ6eh8NSSp8lIrXNEkBex4r1WjDjVJllIRovs+iAHytzruVljTKXtMpdeLl23GLmpptedmFcKNlOPb+eQ+SyeoH5pcXEnxMo8gKjDShF7vmookCZAi+o4JxFF7rMK+IctTBCZAnJiAuwozwcnu+RZwXGaALPwyoPqQSRUghdkGUZYRxTq1bo9wc8+8FT8jTn5sMGnlei6IU+7/3Zr/Lkjz7n8OU+ceCz+2ib+HaF2PM4zgZYbSgGGSBQnqRvDMKVcRakLOc8y3Oe/vFnVFZrE+O8zJ208+/v8u/TCz2kL1F+GcI67/Q5NjnxSo21VoObd2+y+2IXlxrCMABlGRQ5lTgiywuOXuzTurGK1YZ8kBKuxNx8/w61xFHTkGc5WhUUxuBGwRCE8HBSoZSHFKoUVj0xikQnEKKMrHYyJOlAa0OuDeurTQb9Idpa1tZWSPOMhAKhymhuwzTDFppCF6jAJwpDEFBtVJGewo8CDj9/SbvfI4orJEWB7/nYXJMMEoy2rL2zQlANSI/7HDxNUd4G2hRIT6CLYpS/powu6JSgXo0oCk0vy9FJjqS0ukVKkSAosgI9zDh8tkfcrHESXt8ay/6TPaIgwvMUUgo6+0c4JWkEIQef7+CHAdI6jINaHBMpgXZQ2DKC3tHzA+yBJsoqNG+vIqQgHSa4IMDzFdWVKlIKhu0+x6/a3Li5DsaSFYZ+uw+xO3PxvYrUMzqDXldomG1dngWTdH4ZRv2kzHVbuiZDiJ99mBtyXIwH7J4SdMaFlykQCNyJT+2MAYx7I0xmgxLTkzp7DG6OsPIGYJY3xCwqNl1ntrVLnC90khzvLbyFnwD4Eu8UjWCcb1tGUJgHM/j3cyqcK2qGloUJgeiSzP10dxejusSAxnAoz4fpOuekhJkNXHbaZgqGsyxyMxseI9dLDPFyB891EPbXjVz3BcLJ3JwgOyYZhkmE/8SjultBFXGpNReSPKpSjUKyLMNIxcn9oSQvCKRHri2erxBOIp1D5wWVKMLzYtQomaYxhn5/iDMONQqhjBCl0CTh5Y+eMUwrbP4Fhx/7qMIR2TbvfKuJyQ/oHBqkdUgXE4b32Ko4qvFdoliipCRIQla6q1hr0VEKfolDcQThoIr5SOPnwdg8XDxVG9VNfOWDc1SzQ4QzEy9ZA0+1xsyeaMYLK0/R3FpFfCrJCs1gv02DBr4TGAfDWy38QHD0dIfQGHShSYYJhRAo3+do+4Csl1BozcFxh+7NJqsPNql94w62k1J0E9RRn+yoh7WOg6QgLwz4gkGh0aIMt621QVUipBfgrAHPx+X5iMcpI9IJqfHDgOK4g+95RLWI/k6/jDxnHS702XUFeOB5HvXccnzUQWuNtZa1jRXy3pC9nQOqUQUlFRJBo1Glf9wrLYjO0rx5D2M0+5+1aasc0xwwHPa50bzFStLAAcZY+v0BuZRYqxGU0fwcjl63jzaGQZrTbNTxqz7H7QMOnxyy9qe2uFkJMb4lPUh4tb2NFIqsKLCtKrsmp1qtMZCWXFuCIqWWW2CUN8fz0UWBn/k0jppkg4Kj/Tav2CaoRYRxgNEWJw3JUUTef8De55LPPkvo10L2PcgPe7QaVXoHHVoPV08X3VFyQKaz84bFmcq9E3o82759ebisWHW1Hq+K5zzd44ndaRmL+Kxw3Zc5E8SZ6Yfpfbw4jPkF7hVjH69DNJoU0Kb6ng6CNAcdce7XSWFvkYLxixLw3sJb+LLhyxGKrsLHLmtNmSdVXERfr6LNW6LeTIvJgjYWoTmtB7o8Y37JGpcR7Ja19C3T0Czh+JqkkPm6tOVhca3l2rzmYV3c2YlSdPSO/KcB4jPD/eNbWOWhRUEoHQPj8KXEWciNxlceQkiMtWTO4SuJpxTaWJx0SATWWowG4RxFVuD7HtUohDgiLzQuL0oUjCGoVSlyzcFRh+8+e8ZX/sKHrGJ5J/kYT8HDn63wg//dkvRS2i80+8M71Js1+l2PzapjdaXJ4aHjRqeG8j1ebW6T1A+RUrLSWaW5t0KraGFvj/wB51o23WheyuhNH258g3rQRFrN/YPfx9fDieID5/h1M8DM1ZiOrSwBYTXCVx6V1TrsH1PfblNdcRR3V9l/d51iq4avBMXnuzhj8DxFNSzv8SAl2TDFCkGSZuT9hCLJOaiGqJWY9DhkqzCoQYrRlmf9FE8KYimoBBanLF6lgpSAttg0B2GQGIRSCAS11SrJq0PCKARrEVJiteHVzh5xvUraGRDFEaZV5QUpKEk8yGmaAm0NKvDQgwSba/SYVcMh8IXkYO8IFfg452i06oStdzl60WH3eZvjuy/prz1BGsPLnRryKMLzPRxQa9Rx1jLoD2k2YuLQI9eGyJNIL8T3FFmWkwwSvH2fW+E9Htx+SGW9SpHkPPr0E2QEzZU6R2nGf3Mp8v4GeSWi0KbMO3TUYyspIy3meYEpSoG9klRYP1rHl4r2UZeO7BJ9tsPK3XWUKq1+L78XEMXvY63jD3/wEdndFV4Wmi0lqGQ5Qgiipx4//c1vIZXk91/+Lnv61RmDPZlga8yiNIfcvgZNfXN3fd4knM3EhDXnwmonotRlehKnnyb7X672+Bl8rtbpD9clFo01Ot3pnKNsAoWRhf/s2fkxnxN8xMSft/AWfiLgfCzHK4CjJO4nWr3lKrCYI7zo+UUwbXma9Wz8n2M5vC7Z/5WaGsdh7PMZesseFGNtXNT+IiFy2UGMz+NFsMy7d0uUvQwIMfav/H7235JNXBMqJ8O7wEh3fZ2d9Djq8PjpHsODTnnvQgiEFFipkEKQFgVZnuOsAykojCEOA/zAL5nDvMDlORiDkgJjLcY5DIJMa7K8oLAWYx2hpwj9MvFqVmiyoy7KWSLfZ9AZ8OyPP8dqc4paWI14789+gBd4ZUJCpTjYO2L3+SuyvKC+2mCt1UQ4MEWZPLYQAucsvqcAsGZKVTtrLYlJAuEsFEnGsN0fPRanTILOipJ5dSe7b9bLGf+tFBStc4TViCAI0NZxsH/I8c4hRZoTNitsfHCXex++QxCV966SLEepMnx2luUESiKUJBmm9F+1scagU42KfIyzRHFIpV7BSYmTktyBzcu7Qtkgw4U+rhqhtQXnsIUGB0VRkPSH5bssNFlWUFjDMMuw2lFkOcZYgjBACCi0ptaoUWvWsKM8TFmW44Bhf0jnqEMURQipcAJyaxChh3ZlVMLVu5voJOfVZy/IRgKgtY5avcowSYh8Dz/wEVKSJClFklALfCJPEXuKehxSjQIqvoewFs9ZNm6tcfeD+zz45ntUGlUAdh/vkvVTwtDnYO+IYXfA+uYqazfXCeKwvF9F6aJnjCXNMqQUpMOUvChoNet4vo+xlko1xjnL0c4haWdIpRLhjGXQHWC1JekMsboci+eVFtU0SUmTjKPtQ452jk7XgkDA6fpZsEWZwdYL98budLiptfz6vSw6/5dvfdxd7WyXLj5YLkPDZ2F2nTMsxBk21yWYToxvdHZNPJsSaE54svL5F6J6ewtv4X8IuLY7RTPDUU9rMGZpNJalGcsoXKb7ukz7M2GGVDFLNXSx8ni555cQJq4l/PdlrWl/AiASgvc8DwEMreORKaNACXeiKZtaSJc0GF33FM1t7zqlr4lmSzeJpDsgNnWEL5FKMTAWPwzxAGcdmdY4IU9OV6x1KAeDNCOIQmIl8IVgYB1CSrJRaG5rLDkgUShhCWoxzpbBFwLfJ8tzfAFCW250N+gfZBz3BpgbNxBC4hnFzahL+DDijz7aZhB6KN8nMhk7z3aQSpL5ik4oMM4Rmzq1vRyBIKPArB3TbkiaKxGBF+KAvUHBMLfn5jVau4PyIzCO5997Ch2NCiThn94gCEvlc32Q8/R7HxPfXOXW5jqFAG01u71tHHbiZSnjWDnOEFLgCngVSFzkcWwLYm0QOPrdPjvff8zN9+8SeR6VB2tU77RwP3hO8nIfowQm11R9nzQraOmQtJ0R5o7Bi0PiRpXmVota4NM+2EUqSVKLwBMYrVnzb9NwCaIa0T54CdLgKQVKYq1EKgi8fQbWELY8EpFxlGYksWF96ysYK3jV6bEiBXmaMkwT1gLHRu5QUtNePUJYS0yV4ChEW4sX+sRhiDUF/X4fXLkmMJpGq05tvcHeJy8ZDBLCSoSwDikElVaNxBTEUcCw0FSiiLTIybICYyzHr4ZYyvxFThuklAgpCCsR1nOsvd+luamJq5bj56vYwlAJfDwpqcYRg3aH4WfbVFtVYiGoOci0xjNlrqNaJSaOI/K84LDXo2LK6HxqFGq72ajS6/Z59WSHKA7JpCRPc/IkJ09zasbhJaUSYLNWRfYSkiQjCHxefvqC1maLjeomkRfRO+ohBNRW6gDs9ncobD5ju07eDVmW3lzGqD+r7iId4mIaOU5PF4kAc022M5+f6+602PT8XN5CtCxmF8H12YCWf3uXec+lnORGyr+38BbewjJwre5zF269eVTkdSj6ErAU37vQf+Ga3Z2WFayuYq1Z1OcF5val6y+C63iH022c4nsxEjUh+CthhAJeFgVPjC5ZVzE++FntX2VS5sB1ekxcG0wiJKVEKsnAOOKiQPk+2jiCIKA/TAjjCJ1rjNHl3SFrUA4sjjTLcM5QhDFSSiwlk2kMIAQeYIoC7WCII88LKpUIkxuqccwgSTB9wf3iPXpJwuClYf9nV1m9vU6UHbLV/mO2mo7aV6v8wbYjOerjSfAqMVLAfgDblQjhKW4NCrb2YnzlsX3jBdsbL+iEe/yid5cPb9XAwf/5osewmGJAhaB+9+sEjXXIDXz2x0g0xgp+v3aP8OYKnoPbH7/ipUiQe5Kmt8rN9++Quoz9wSv0SeS20boJcsOt7TJCW9F1/H7NYzvpE4WCe32HUop6vcqzvODZ9z5nrxpTbVRp3Fjl1tfv0EgLesddhKewviKQEr3X4b0wxAz66EIjXvVZz6G+3qTneXiBx+cBpLGHj8fPiPdYRyACSTc5xIkhXuBRyFL4lTKntrJL4RKcc7yqOzwhOe5YMvUNFB4ZBfWdHr1hivIUD7RgtZsziHs8vf0CazS35F38wwBnLLVqTL1VZ5AMYCjwPUVqDLbQrNxeJznqsf9ij7BRwRQanRe4kcues5resHTPS7KElbVVDrQmzXLiWoVKo0Jci0veTpV5tJobLVAFH/ylHxI391GqRne3SWO9yZPn+wx1QZEXFFnO7YFDtlOiSsgwSbjdalI4C0IQN6rUV+vsP9rBOYvRBmEduXXkSUY9joiCgHSQlIEdtCaMQ4I4oN/u0RwWbHRyet0BaZaT5wU4hy8FOjU8+d5j7n/9Pn4z4PPtzxgc9Xh38yGVlRqdrE2RnReKyuV0ZtEV57funDqMPBOWFxKWZpXd+a/jdoo5jV/ZTWIhqXecusqV3cxQdM2osgDT5WFsTBdbxJbrzY2sYReVOhvv2edJ570TPkWc/rJci8v3/Rbewk8CvL773EjFJE5dkjgvQcyyiFzkPjWjj2VxOaURo3/j3kMz+56LjztfZHp8i3B1C8q9Lrxpq870u5zV/9LzeJ1IXaL0gsuh5w41ceb2MLvWuKPdBXhMe8AsV+yNw4mLK0C9VUd5HkJ5ZNahjMUYgy/Ke0JpkuErRV2VyUaLvCAtyrtBse8TCEAKpFLgKF25KnEZbU1rnBA4KUjTDAHl3SIBwyTB8xRKKQZJSsX38aTgsz/6hM4oMSyU76J1Z50PfvGb3Pv6A4JazHAwZDhMUVLSjAKctUgESpQCXhQGeFIyTHMOXx7MVypMrVMzct8rsoI8zegedoAyktnR9iFCSZQQdHaOeP69J1gzCsLgyuhuk805dFaUocytJRsOcQ7iWoU4Djk6PAat8aVEpxn7L/Y4fnFA3k/Zev8OjbXWKU6elIRBwCDPqVQiwijA9z2iRkw2SLDW4nsezfUVPL/MoyOVAgQKCKohFnBZUWLol3fBhB0JsWUmVAprcA5MponqFRr1GkoKwkpIGAaIUbAM6cDmBda50rWRUlDxK2XeozzJ8KTE6jLQQxyFhJWQvce7JcNeGGxhRhENy+9mFLChXq9SrVWQvuTBhw948MEDKs0qDhh2h/TafTq7R/T22gyO+uSDlOPtQ/ae7GGKMvxF68YKtx7epsgLdF4QBj6NZo17X73HV372Q6IopNftEQUBQkq0Nvi1mEIbBGWC4jRJkUqWbplF6QZar1ZKPLXBD3zyYYZJS8HucK90kxMOWq0Gd965jaUMtnG8c8Tn33lEkRdlctdc8+h7j+cLQzNhucPv7Ph9favAYjLuWModa+lzYP74Jp6c8hlX6fCaDqaxJsZd5C6DyTScnSfzJMAZQsnJNYXTYc3r8aIDfN6T8WdvBaK38JMFX1yghUV769L77iITyyXgIgvN63Z3Ea1eYMC4sK83Ze2Z1fYizd8imnyV13NZ5dRYPwmObxc5EuhYuwC1+RrOs2A+I42ccKOD6OQwPOmUifFN9jUpUE8YIsUJMz0Hu+tSzrnJD7eUx01V3rtpxwEvKwolIBjmtIAizzGeQCiJK0AbTSANqQhLC5AsdSh+nuD80kqQW4sUgjwrRgqI0vKQZjlxFKIBH8jTvIxypg1CSSpxSCcvGOQFoR9QGMP2py9Y/7MPOK7eQwAHwPPhM+yapX5/haAI2P3hU9rFHm3rUW1VMXXHcSVnmCZUsoiNwSZZURCuqsm5mDGfK4mhqjRHj/d51umiYkV1rUXYqOGAzn6b7MUeXqaRlRhnobPXxqC5e/M+KIEnMlaCp0gJIhIcrYUMjwraGDZ6GVpb7t/YYKtSZXjUhb0EJyS5MVQNrGcW/dkORyt1inqVyge3yF4G9A46OGeIpcNzjk5/QC2OsdbS3+sSxGV0vSIr8HaOaUlHIARx3SOQirzQmEITxAEit/gICDyU8Mv1Zx1YyWp7A5cZQuvxMu2ivJCNVpVGs85gMCSuVEYCRgBCsXl8A6cEhojhep0kKzCNkCLLOawG+E7THK251tY6nd1jkmGKbtWwK3UO9g8RuWX9MKMl++zhc9gI6AhNpZ8jDtoEvs/q5hq9gw7aGJRSOOe4/e5NWg8OcOITooqP2u0AOf3hK3a9F7BRo3Iz4Bd/cZOiP8SLGhw+WSesVjC+Ye3/usFHv/tdUjFkXW7RbXep7MXkusD3PIoo51Vll7Wb6/iHgmxXEijFoS5oV3xwHsfC4CvHoBZw1IjBOdZur3F3rUnVQnevg7WW3FgqcUieZPQPe1SaVdLjPiYr6O61+dDz0TbAAD8qCtITJlec/Dm/YL8Unf21ukichxN3wfHoamd58catI+MiwixXgvkwfkdp3txeAfELe7s2OHX9Pu2i/N9YEIrL9Hoy0/PgrRj0Fn6S4fWFonlKhdcRghYJCBMCipv8bRHhnmWtmn6+gOmfzlY9FxYJCIueX/TsuuCqfSxb74J3e+UM6BcJWKMmB9bxf2TZpZo+XUYTaImJsZSCzAwELhCYJ3NHuOlOZiBzEbZLwLk2ysl74Hn8hSDAaMP/p9vjqLVFZh23HaT9DF9KTF5gDXhKYZxjaCVGWJy1FNYSewqhFFYIgsCnP0yIKhFWF2hn8XwPLDhRXug32qDiCJMX6CRBCEFeaOJKTKNRK4MyaE0UBvQPuzx/2aN49yEA270XfLT/38E5mq0mm39uk9pXmwTf/hSv3aWQimylQbuaMkhTPuh/lc3DBwwGQ0L/eHaI2TGSsTEsaNkMdTTkBxWfLPYxJqXyYo/KzRaDoy516bF5f5Mizei1+1ht6Gy3WXFr3P/pdwloszX8Q+KaR7a1zn+5USFtSI53D7nVL/Clx5YfIaVAp2UgBekc0vfY8APeEdDZO+SV6PNJkbKiLM2HW/SaId3DDnc7GXVb3p/KCw3OMuj0GfQgUBJTFKwUmlojhkLj1yVaAFLihgZVD3BWl9Yu51Cj9Sg9hSp8NvZvYXNYUYrdwDLo9VnxPaIoIBumGG2IwpB+b0BD1Wm93CQIPNqVgCerClH1OPQsg2GGqYfcVAqnJcpBGAfsfvYCBKSNmD3P0q56vJ9A61WPm6LC47VNnhqPIA54p7DUrCNNcw5eHaCkpFavkmY59796j9V7K2z91CdovYtJDd5nKXk3pfMy40crljQPuHGjxof3+vjKkbRDPvtdR6W1gl01tL9yTCUOOfj2Hqsv1rHW0TvskuQF1WpMVhvyqrVNvjpg1bZYPbpBkmXkKxX2qgopJUma4UWKXs9yVPMIlORpt83Wgy1auSUb3SkKAE9KVOCT9hOqjQqvtMaPQ7J+ws/WwM8sshHz1GhSO6VScW5EKibX78wcOLMJ2JVh/Kg6S+Vz4uZ1/Szz+TNhttAzt+cllW9fxPF6vSAm/ox/mVCyzRKgR4LUSK030cikiLickPknb+7ewlu4GlxL9LkvHmaYw193115Q/7WJwjVZ8L9wmLbAi6l/cJ6GurF/U88mE+Et0d94m68F5+04E5aaiTGKiRQ/p7ahC5iO02kRJxpPcf7BFCrnWlzk8TCj6ARMr7EZhymAyTWDdh+sxVqDsw4pJQ6BNQ4lQI2irxnloa0lDPxyPMqj8AJySncjZy021/ieV95T8j0MDiEkUgiUlGjrCEcuU3EYUq3Go7slmiDwiXwfB8SViGffe0TSnQyH7cbmsbrV4uFf/Cnuvnvn1K0r8jyUp8gKPXLtEkhvylK0YP/pvMA4N4poV1D0EtLOEJMZ1u5sMuj06Rx3qDQrRNUIqSTHO4fsfvoSz1dUWhUGBz26r9qAQ/ke6SABKYgqEdJXuJHLmhd45TqyjiIt89dUm/UyYAHQ3T9m+5Pn+GHAxt0t/EpU3r8xFt/3CKMIozWh71M4h/Q84lqFPNdYY8iMQY/KKwEuyfGCci6CKCjfuTYYAUWhKfICX0j6SQZSkKUZ+zsH6MJQqcQMhglFUWC1ZtgbUAl88lwjpShDdjNyjXSWMAxwnsQKUJ6HTnPyrMDzPbIkpdPrE/ge2cgdsHF7nXe+/pAHX3+HzdubNJt1BILVVh3pbCksNyp88HNfZ+v921gcxhhW72xw66t3WX/3Bqt3NojqFWorZZ3koEMxyDBJUeZV2lyhSHJMUQZqWLmzUd6XM6Xr3sHhMb7n4XteeSdICpIso7BlNMMiL0jSDOlcGexhlMw4rIQ469AjN8eDR7uk/RQv9BgOE3ShiSsRzjmsNihflS6Ltozqlyc5+49fnQk0szb0lGvUNBk5ezB6Mr6+l40EuwAu0iMuA9MR7s73IU7LXRmWrHq5OKM/jjBJxBY6e8+h/VeFP8mz9hbewmXg9S1FS2ppJmCW1WeJfs51Nav+zDZnIDmLN581lstSg6vMx58EWHYelh77OWnpenCYO//ifLGR0DYnPcOFXZY8y5g1YmHFcQlxXEN39cXizn1ZoDF2jmHQ4rB+g8QNcPo5N4cG6xyxBacNRkoSIdDW4EuJJwRpXqCU4sZKlTzNUFLRHWaIOMSlOYFSSF+RF2V+onyY4pyjEvgUeYH0FA6BBrzAx1pHNQ5J05w0yVHWEMURySCh1qyQJhn7z/a49/UHNEKPDzYq4ByJdhz+4AgBRBsxd7/1FYSSvHj0EgFUgxAlJOkwweG40WrR6pUhqP1i1hw7lNjFE11c/hnrw5AojPFrFT7udTh6vEu1WSPZPUAowZ2v3aHSaBNEMfuPBhy+ith/8oq1zYjGjZ/hINumaCvWtkthKE8sGMeg26f33LFvNV7oU2m12DpoI6WgUljaaR8hBL7JibOUahCSVh2HL/ZwAtaCiPXbmxztHpKnGV7g4wcBRZrhSUWhNeSC0Fd4UjAwOzgKZFHgpMV0BwRrqwgcNs3xlM8Hw1ts5oY8c+xXI4wVZEHI2o01DvaPcNbR6/RorbZQStJYa2Ct5Wj3iGrgYwpNmGnuJYZBosnzAuFgfavF08MuO806NT+gg6bdCvGjEKkPuJMdojxFpfBZ/+rP8epJh+1Xn9KVMfV6g06jg7vV50AbaAnWb2/Q+maDe3af2OwgmpaVWgWV5EgpOdYNTLUOwmNrcJ9qkiNSw5NhDRUokh7s1yIO97vUErhxXKB8QRDVOBwMqQUhKo5QUlK4MiAItrTE6ErK0cYug1qCxNE8dMRxyKGwPP7+I5prLVrrK7QPjrCFZvfpLtXjAZv3t/CfvWKQJIRRyGCrj7mdkdaGFF5Os7lGWIv5KN2k3XTc3XiP7OUPwZ63bk/rlMatNZPUZIZV6TTS5sVOd/MtBoufXRf8yRZU3hwsO/fnyy3nJDizxP+o/MtbeAtLwvXcKZoWMOapmF6T9o3lW5yBw3y91lL7fNzqMUPyKn9288c23sZl4EsiQFd2Y5sHk/b82eOa/v2SQvF1w8XeJot90Kf5kAt6O2ny9Ai7VhhH5ry0BAKScIXD+rukYojHMd7REF8phBSowAdACgGFpXAObxShTnmKhoSgHuIQJLkmB7SxxBKyQuP7PnZknQiUhx1FZjPaUGDAlP+CMMDJ0UV7B8o6iiQjDv3S5SoM2PnsBa0bqzRXBasbFcDx+DjlyQ/KS+2rH6xQvRFz6+v36R606XcHNGpVPFEyi82VOjcaPq3OPs65SaFobA0quYuwAqUfs5neJ3+6R31zlVsPtthvdzG5Jgx8th7e5Nl3f4jv/RFf+fNf4e43qnjRJtuf7vLoOy+Rf/5r6Op9jp9/Tit9TPP2CvHaBj/8xJIXhtwUvGpFWGtpdXu8ZyWeExjr0LLMEXXXi1kZJnhas+cpisjHCUH3uENVC4KwjAoojQFjiSMf6xyBV94tctYifUU3fUZiu5iiwKN0YfMaMaYPOtf4xvJBdpuOM3SM4dmNOu3hkGyYEiYprbUWxV4b5xztThc5Stab5qXlxauE2F6fIM2RT/cJhKDWqtG6sULeHvDCCV5VfPqhjwp9DhNFGPt8Q1niF08pkoK1m3+BLLvN8YHihrTEwx4NkXP4oMuO26ZWq3Drg3vU7zXpymNWDl+wqstEtea5wYt8rBMc9FrkRgI+N/RdLB4Z8N2nEhF4yMAjrWeIn74PcsiNzlNsntOor5DXJOkwp1GJcVkODnJRIB3UqjF5MmRvvccgy2geWe4kMYHTuGZEIh3He0cji59Fje7pKV8RRAFSSpSUOGfprLbhoebVwUuiqILyJIfPD/lBrUq+9T69rXfJX30OxWyXXzdSdpzIOCcBLk529nzD8gz6fgWG93J3VRadKRcLZ9OluVSN64bF+F5uNNdVf9kal2j5rRD0Ft7CBLyZQAvTFO2cuf+K7TGLoXTnC03VnRBmlqG257jdMeP+l0+tx2DeMXQxyZ15YL4uzLOUTH/+oojwrGUyt8B1dLJsjSnLkjv/7MruJLMEoikIqhFb792m9/wQZyzaaFKtkVBaeSSYIMKYkuFTgHYOaSEcCU9e4JH1HVYwCriQY53DF5JKo8rxQRtnHZ4ncUKSao01Gul5mFGeGiVFWd+V4aqNLMM5V6OI3Uc75P2cW+/NE14FfhSw+c5NOt/+hIPjDrJT5d3aOu98630kz6GYnouze2GnLpFSUF1tECc1KnnMoJ9QbdXoJOV9GumF4CDrJmS2w8sfPeX2hx9QXa0T1zp0Dzq8/OEzbn9wj9UHN6jWjhFAbbPFez97h5fff0JblGHLq60aK1qwkpTzKpUkOe4xyFKkVGzdWOH4+R5WCHIAY0u3rVyX8y8FvSTFV4og8olG7opFXiCEQheGUBhkKBFaoAIPEYeIwCvDTTOSREcCry00fiVktVlh7+kOeZJRbdZYub+FHGyXQjECXWjSQYqQZRS9NWMRAhpbq1RW6+T9lP6rY/rtHtY5jC1zIwkpUSNhuZ8MubneorZeJx3GvPh0Fz8OMNage4ai0MSNCnc27nDj/bt4leCcJVVnRRk4YuytDtoDomqdnc9ecPiyR4Llk5UQbR2NzRart9aJ6jFe6CNTiYp8lB9z9+u3ePLdR2RFQZpmFMYgAvCEJIpCtHGkaVGuUyERUmILiys0Kg4Bged5hHGI5ylW/Zwb92+cWmia9RqFtdx5eBu1JTl+eURFCNJeQp7k6LiBF0YItST9cEy5744fRMu5TDg3+7T4cbQCXarWDDr6Rupcvcrc7heXWW4WXvv9zeLP3gpKb+EnFK5XKHoNQnOp9pftYJlic+jJhXRh0cOLKi9Spl0KFtowLtPM68NlrITL9ncZq9Ksfqb5hmub39eAsTXsRozONK9zJvi/zkYqw2/f8TweeuWdHbOSsn97B50XHCU7BM5HuzJfjC8E1jm01gycRBYFnVrAUJX5bVRW0HCCUAsKIUuXr8AjLwzGWfQoCp2MPFYf3kLGAQcv93BSEkiJUYoChy8lOIdUEmcdKhwJWUoSNKocdxOiOCQfpLw8aGN/NsILPDrGwnYfEAz3hux/ex8QbMU17r7zkM72AdGW5MH9kMrqPp/sHTFIUwAOrDkRiSZehLa3yPKQ/pFl5c5t9j/bR1pL9gefsOIplKd41hQMfcH+Sp314/d49cTSurVGVK+y9e4tku6A9qtjWjfXqK/7o7tMFilSVm8eEwaKj/7oBXcHd7C9I2TueDXIkJ5iGCqSekxlfQU/jigaMb1I0j1oE4YBxjmyMOJVkqGzgpsEqLbFAo2Kz1oU4AQoAoTvYZ2hcwwmyfB8D20snrWYJMfzFFKD8H3QFmc0Skp6Rx2itRa+UtzINfbRHq21Jg//3Ie0nx9w+GKfQXeIFwW881NbhNUjhIxJfMmO6/Fy+wlHHc0grSMiwcCLkFKRpRkiy9F5QRCF5EkN12pw8CKlfdjFUAVrOIr3SN/rsPW1NbKmh7AB7Y+7/KkgoKUkAojrBiscSMXvvhAMchBCshLdpdA5Bz88Zv/5PtaWe+l+HtHvDZGdjOTjHeLNFcIPbvB87X0QjkAbmptH3Hp3yIvDI7brOUpKTFzgBHTaPRq1CkpJ0rTAOgvW4YcK3/PQWY4QkiLLcVjqa01qa7XSqhb4+B/c4fNnu4TVCG/HoxHUsalDF32M1ASe4mZqWQljmn3NsXXosf2/rL7qMrRpESVZ3k3rIl3iskSaC1q6IsziP+aR0ZnKo+UOqXG11fyw3IsCU7yunel8a/N6WqryhcrDt/AWfnLgeoSiRZah66CDr0s/xBh5EtNeXvOpwEwZb5HFaZbybhFBvgwxWkj53On/l2bjLxLMriK4XKb8m7S0XcbLYBqfeeNZ+K6u95A7bfMqzY6NQwjBDeXxM34Zce5RI+OTjQOM1qSVBLTAEwIVBgyHaZkXx/NHQo6jG3kkFR8hFb3jDD3M8AqLNhalDXmhURYKbUCAH3jc/OpddJIReB7VVp1kkJIbi/IVxlnEyNXI4ghCnzzNS7esmkcQBVhrUZ7Cd4J9ndEepNy8dZtBJx29L0d6mJIdle5GN7eqvL/ewD1sjIbfATo8M32ejhK2jtuSx/eHdZsMDqHdbrF1q4IxFnBs5BYSjVaSH/qC9mCA3VqleZQyPGqTDFqEdUVtvcHGvS0Onu/z8qMnfOXP34HQUQbqyFBim/qG4+vfWuPxd8DmDp0XZSAE6WEbFV76DtIENxggjiSVVg3/zjppf0iWZBxJSevOOt2DDo12yka1QmEMtyoRjUjheR5agMlzhFL0A48iLy/3y9BDKokepEhPYIzBWYMQEAYBKkvRacbhqwPqnsdqP0Eah312QMcIqq0q8TffAecIKhE23yPpf7+8Q6NT/jjKKayFxg2MuoG2FgUI6+gNhwgpCeIQoS1FVsHZdQ72d/F8D+UrnDYMmz1u/LXbhDcqHPzXHQY7A6QQbMQV7ngeQkLwviV3OSLw+c4rOBiAJwU/f+8G+0+36e+FKOkQzoIx1A/7VEfufkpKikd7dDoJu3/tpwgbFer6mI3oE268Z0lrBU90l8JatACty0AVvX5CICW1KMJLfQSOXGu08dDOIDCEUYjONTuPtgl6BbnwWL25Dt+4jah5vNo5hGeOpx/vE0QhTVeQpRm+VNzxW2xWKqhhuYcWUwIx497jMgLI2d2j+Qz6WYsXwSyPhEnyufhQmfC2EMu4b198rjkcYtyncHYTZ2Vn4nl52r2cC/Si59d5ZkzO5ZXvgb0ViN7CW3jD0eeuwjBf58YUjCW1Kxt3p51MdnZtxpvLwGXN/RfQuNcWiMZhnJNc1uI2z4vjMgLWrL6W8zW42hkzs94MJBbOwdU6nhfNTpz7cAk4ySZ6qs8sQXlq5DrmSDoDBr0hXp4SCdBZGTDBOot2FuNAjvoWSiGxoAty6xgkGcIakkGCVJLCWezIKpXmOUlnQLxaJ+sO8AtLvRojpcQ4SyWO8DxFOszIsgJjLGEQID2FBaJqiPIUeV4QKI88zel3ephcnx/mjDmbVgqfLKfy2XikpnKOrLEUmaYoitMocXGzxsY7N6muNTDaYLXhePsAk2uElAyGAz79zg/Ze7yNKTSbD2+z+c4NTFpw/PLwFAE3iv4lhKC63uCdP/s+G1+5xertdTZurqGsI+kNyUbBKOwoOt3wuEd3/xgHNNdbWAft/WMaq3WElEgJoSrzQHmhjzEGYSxRJUblhtiVRF048KMAISSmM4DClPPg+yAFnpLlxEiJ55UBG0yuiaIQ4cBKgR6kRLWY4UGPo893+Pz3PuLzP/qEpz94zO7OAVleEAcBQkmMcNjCEPllhLs4jkrBC0me5rTWm2WSXCFQvofTlqLQPPjmQxq31kCOGP/ToCUl4bbWkfZL1z2p5MSmsMaSdRN0luOc4+b7dwnCoAyJ7fsUhabd6xP4imSQ0Ns+whQGk5dj9SKf9Ye3WL9/A9/zCDwPXyqkp+h0unTTFCklzUYNay3WGIQUBNUIL/DBWSIhaNWrVMIQieBwe59Pf+8jiiTn5nu3iaIQ5SgTtgpR7gVjqTarBJVwctueXJo9t7bd6X/Lw8Vi0FlJwbyErOP9npygp7+PHaMnedfGcXTu7LQda3Dy7wVwVnx2hcsy/td1nl8Ux+7M9XPegbY83stG8LtMa1M/vYW38BZGcL2BFpb9fRwuYTk4T7ov3s0nF1VnWQLGAzZcmi7MEwDGObHx35Zp78rE6Ro1UtN4LLKMTXdzESoLn7/WBCyHyzLWu+mKs9C6aLovBbPfz8LZmPdKz4X3FTzTmv/f6PfKseT2tiTtFhRDgwojEt8jywoqtZi006PieRgpkdayOjBkwz4BDlG40nXIGApLeW9ESpSSZchooFKNITe0P9+lutog6QzwIp9BPyFNU6xvqVd9vMAj7Q2RUiJEaWnyAg8V+AglKHKNyTRR3WfnYI/9Z3t8RTX5ZhgD8NRoPtGloLTdzRjm5txUHA7LiGiL3lWRFSgjKArNTsWj9/4Nbj28zXrucMMc/f3HWD1EWouUgubGCsPjY3afbdN/1WF9a5O4UWXl5hrSV+ztJQw/fA+/FhFzxLvB91CRD7Igqu5z/8+sowIP6fkcPco56m/Q+ANB0kk5MoZkpYYuCla1oH4wpNjpsuJ7CAqqKai0oHACbS0v+xl93caTkhu1AIwh9D1crst5lYKgEqLbA3Cw3f8YKRREMS+jlNT36IYgB3eRXkAx7FGrVfCsQxelNStVkooDYx1pu89AVOiv/wwO0J4kzH0KLRBdeC83+NJDJob9vT7VSkQYhfR6farVmPptw+eHH9O/k1GJIzq9Pjfv3yAPfI7++x4AWTvnJElysJURxpClBf/ngSBphzghuVX/gFv1kOFhn/azI1q3NoirMevv3SoFV68M8hEGPoXWNKsVDA6vsIQfvaBZgMwTtg8ibn7jPr4b8o3YsTM8pOM0BysVCm2J+hXqBy2UABn5RFGIJxXZoOBumiOFhFEQinzQwzU6bAcdgkpEkW2Sd/qkg4QH+PQ6WblHcssw19TjiLX+YzY7hxTOomy+cL9/mTzrbHFpDkaj/TaL6T7V05zIvOcsG2czMJ7M9QyPC2CJSXotZ+grHU/zrFuLnl4Nxm8XLzfOGcRxoTfEW3gLPxlwfclbp/fhm9j5M+BC5nGi5MwHc2HaOWChBWHmOEfYLWLGXxNmJqg8h8OiBmYUf513NosRXWotzNCSvqm1s2y7YurvNFzHGj8V2ictO0sxAYKJ+T6tO7beDpxl3xpw8LWBx50jD2sEx0HEccfiS0ulEhHFEWl/WLp2IcgKTQtBYUrhByVPXdtwpbVCawOuDJrgKUUcBpi0gNCju18y7NKLqFQj2u1jcgtZoIkDr0wmiiiTwhpDNihDeUul8KVimGb4nkKnOYPDLs2NBh86gRf4ZLhToaidaNqpmZiXEwZs7rYYlUl7CaJjkRLakWKw2WA/kGymBVHgsX5vC/noMVpreu0uw4Gj0WiQ2pwiK/Ms9Y579I974EmGA8tRtkJ9bY0Vq9n8ICRoxjhtGTx+hqwdo8IyLPnNb0iCz6vw3gd0d4/5g2cv6RuDEIJYG25bibESlzk8Jak7SR/BsCioNmsct/sY7fA9xUoloOL7FF7JTBZaIzyJDHxsmuMCj262jfAVymvwRA0ZRh7dxKG5hXIOL/AZ7PcILRhnyYYpmbbU15vkw5RskCLiOi/CiKhaoUgybF/j+R7V4ZAbCKSz2FRDZnFpn1oDmtJjbaXJR/t/zIvqNvWNKm2RoG5I6j/X4uA7R3Sf9iaWtRQCr6kRUUG85vHo2x47A1BC8hfv3yKyEc/2PyfJ+wQ31qhtrSCUon1wiBEO4yzdQUpaFISeRxCHhBL8bkrl+RG1W6scDlY53g5ZvR2xPniOH1R50jnmOPDwlEQWjpXjNSLfp+GqDPMUoyxbrTrD7oA0T3CA7ymktRxs9div7eOHPtKtIIxAKkXQTlgbFDhrQQhyIVBKsBkNaQz7FDiU0+V6XbDr33zY6kV9T/5deIxNPxxX1EyfDSdBT05o30w+/erjvqQ6cEb9Mbe0S5zdF9HwM5Fv/NPrvHt3iXHOac2d/o83zrS9hbfwYwxffvLWcSZ8CYZcTHw+cxE4/++spBCl7kngEMKd5rpjRlvnezmBOVRxvK1zMpS7FDG9EkxxfjMcFs7DRTjNamLWuxkfr7ho/q7Q51Iw09/k9en6RdagRdampft2p3PnRlHBztw8L8BthjZAiNkueYLJ34WU+IGHLyXSOYo0Z9gdoEaR4fKiKN+nEGhTBlGwI1SLvMCaMumnHSW4bLbqVJtVtLUMhwm72/u0u316g4RsmBHHEVEUUhQ5npJkWU5jYwW8MkJZ6HtkwxSba6JKSKAUke/jKUWjWaff7tPZPaZ/2Dsd9OloZiSZEoLSSjT+nhxjDJooI68FHkVWgJDkvYT27hHPv/+YtJ+Wv+OwODKtcbnG5AUOiFSA53ls3NliZX2lTFqLAOc4ePoKqw1BvYJTCmccfhyy+s2HNO6uYxAUaUGe5KTtAclBl8bNNd75mfdRkUIXBXmakWYZWZqh04ykP2SgNfFqAz/0SftDrDV0+300pTuMNgaTFVjrMICKAkxWoJsVrFJllD9PoQIPJwXSlUKG0QaHI6pEeKFPgqXQhnyQ0jvuogtNa2sFbUZ3yBBI62hUK6UrZJYhpKDX6bG3f4gVjvXNFVTgkaYZ9ZU6e4926PQGREGAw6ECjxtfuY0XB+fenRwFHrGje2jixP95DDo7R5hMY63BCxTDo17pnmYdJiswWUGuNdZa4jBAUoY9R0AyTBl2+viRz/CohzUG6UnCekQQBXhhmVxXOKiFYZl4tihYW18hjHz6gyGVRpXWWpNAeehC40lJokv3xGocsfHgBu/+mfdZvbWGH4dlEmQHxjnW1lo8+OmHhI3K+Q08A+aRsqXo/BsB8Rq0erqpM83FdLqL6060urz74Vm514mcd9HxcVb2OsYpxsjc2cu5cLTnur2Og/MtXAV+7dd+7fT8FkLwN/7G31iq3t/8m39zot6v/dqvTTz/5V/+5bl8wUV4/PZv//bccr/1W7/F3/k7f4eHDx9SrVaJooi7d+/yrW99i7/7d/8u//Jf/ks+//zzpfr8cYM35z53oXBz3kR+Dma5cY09XFx7huWBab51HIez1k6up57ynSfM1LL04py2bKruNdKd2caVS3RwbVas2fO9TLUvBcYXwrUIODPqznu4wPvkUjCG202p+NN+Ga74JEeQlJM6j92h5fdflFp54wIwGiU8nBD4viIIPbSnyLMcYy0i8BBFUVqHcGhTRuGygAVwjlwb8m6fJM2QShJHIXYU+jfJc1x/wPqNdRq1GkftYwqjiaOIzn6bIPTRWYEQMMwKhoOE+moD3UkQUuAXDb4hb7Fz8IrsheNHZpUb4S02ojb/N7kNCD7WBZ/p83eOZs63EPxsELAhFYXUqEaFl3GBKTTqoxf86Xdu8PR7j/m9/R7NW+sMjnvcHhqcNgROYAuLkhKlFPVWi5V7G+SDDG0M3eMufiWks99mcNBFSIX/hxHWWB4lfb7rlai0wjUanRpHT18x6EmkGCIrETcbMWtffUgxTBk82sVPCobtPozCl1erMcebNbo36xRpTvNwgDzqM8xyEDWQAlVYVhsfEOuM5nqdnnqGa8QU+93S9TEvkAX8Wf1VbOrRtvBfVUCW5/gofN/Dk5Jmo4otDLkQCDPAF5/TamxjB4Kbuw8IKznhpqR994BhkuK9BFihEvjo5pD2jT71u+sUSc7nj37A0Y0BYRoSfbJJ4Hvc/1rIhqsgng/oDg1dSin2f7oLN2vly0oTxUu/hnWQ2yFQWgOddbS3D3Au5+v/c5f19xy9ds63X25ymEe8Gkii+ClpkRISs9pukA0LKnFEmuaIKqM7YobGSgO/Yrn705LjxwWD7/mI/ffJ+ynHnQHKUzQbNYbVDjsbT0BK0jTjeZZRq1ep+FXY8+kbg7R3WF/5GhsPb6HCDUzhsxqH3ImrhFtrJP2E46063maTA1/yv378ES4trU19e0GkhSkadHL3aNLp7Jrzzl2Ez2WJ1Vid+Xhe7whmqYcuAjfxeWxOLzHmcaHqi7K9zHKdeyve/MmF//gf/yP7+/tsbGzMLXN4eMhv/dZvfYFYQbfb5Zd+6Zf4z//5P5979uLFC168eMEf/dEf8e///b/n61//Ot///ve/UPyuA15fKLrizrtqHpar12OC0Z2+a+Smyo4br67ErF620rUJB5cwtY33exWh7RrLCbGEkDwTXnPiZlUff3/zLGbTC2bJvi52rbhckyeF61LwVa/czoePt0mTjJtfvY/yzgSjwyzjRT/H4Xjv1h1IDclRHyEEXugTt6rsfL5NlhUEniIfpgjKiFwAyPJyvu/7eALyQpcX/RHUalWSNEV65SV6Y0orUjrMyKzBFppqEOFRJrY8iTwnAOEc8Sj/jAOSQUJhDC0ZcbffoqIFz3s9HieGYU3w4UbEfa8M5b1vzeRELJhdAdxVHveUwnk+n+eGMA5xQCPTNFNN1BmyXVXs7x8gHHxYOERSurX5UUBUiej1umze2SBqVlGBR6WXMOgOyEeMauflAbbSovhcIwQMtOAHyRAH3AhbVD5JydMYZy3WbnP08oBas0ZrcwVPGyq5JWrWaW6soDyJFIKin/B095ADVYYz/6lKiOp4+KGPzgtMoFDaUlVrVD1BvdmiP9hGYbG+R9Lrle6JBm7ZDUwCFedQwqGwhFFA0m8ThQHtXp8o9EfGtRzpH7F2x+E9LwhSie1lDMIBenOb+mrEirfGhljHaMOz7BEvkqe8WxO4imPnxQ5J07AxuEH9sMGt25u8u6bweuU9Ir+wo3cjuN+E99fKe0RPey06WYh1YGxy+g7zQUr3qEtUgcbWIa3bmmDdYzgI2Hma0w4da+sJgbJkwwRx7JCU0Q6llHhRgFWCrNsurTyxoHFHMjxMWF2v8PT/OyTwA+o0URK0MbRFj+PaIUopEj/FNQR93WFT3mQ9vkG1Vaf1Z96jv1XHGkv7eZuDF3skvSG2r7kZxazc3aB9d41e6IGz7NkyN9NFtHGmC9gpnz6uAvvxZ4EvcvN+3RHMs/Bcxu4z7TFyKhhd8ZiZrS8WkwWu6ey/tIVrfHGNfBdf10r2Fl4fGo0G3W6X3/iN3+BXfuVX5pb7jd/4DYqiOC3/RcC4QPRX/+pf5e/9vb/Hhx9+yNbWFp1Oh+9973v8l//yX/gP/+E/fCH4vAl4M8lbF8E8vmUJ5vwytOOM1syLq7O479Mkj8vSr+k2FlnPvizryEnfs/0xSrgWWrjcAM9bC8dmeM7PC/GbZf1ZNNZJZOb3eVEfy8BICJ+9BM77hIuJpxc07expOYFg5e4WQimEPFv7VhucPVnTgqhR5f7PP+DlD55w9GiXwVGPrDfE8zykc0SehwY8Y3BKkWmD0RqEoMhzfN/HOofyPWq+T1IU+J5PEAc4Y5HBiSMgWGNIi1FdY9CDpMz9IgRKCLSzBJT4+oFHkmblWIIyIWk1DKgGIUWng9GGnR+9JI4OaN1ZH5uj83N4dsDPmEsBQkl0pkuXs9yghGJ1c42P0h6eUkgBTkBciRgMhrSatdM7fM44dFrmq3HWIlWZoNX3fbpHXUxWLd+LkGcd4ki7A9QwwvPLO0vpIKFz1CPpDEg6g1GEM4ngEK0N1VaNra/c4WD7EJoBKgrwpcT1y3w3RZ4jRIArNNI6zOjel1cJsccafIGMfGxhStc568rIazLAWUNRFDRvbVBFoFQZPU8pWQoMXulK5qyldned3sERaSdF+T7SObr9AfSHyKFPdNRhkGa0G4MyOa/n0XnyqgxzPrp31qxV2Hh4E+EdzF7XoxdVJs1VOHtCH0aaCFcKRSBKK+NIWHemdInOhim+VHhCkGuDRZb5s/wyDLyQAmcdYRwx9MqIdCbX2KIM9NFtdxFmExOI0joYhaTGMEzy0sXUlWG5w0qI1gZrHRv3brB2f4snSrL/aJfjF/tYbUv3xyQlHTpebB9xfNjhKB9S/6kHeL6c6cI9H8TUtzfPsC7OszP282UUQmK6tTNiusyI5gqIb+w8vVrDl38/8w7ly7TgZujqlhBwTrs+b2mabOetkPRFwd/6W3+Lf/Nv/g2//uu/vlAo+vVf/3WgFFT+9b/+128cr9/+7d8+FYh+5Vd+hX/xL/7FxPOVlRUePHjAX//rf51//s//Ob/7u7/7xnF6E3ANQtEl2LdLENBzTU/0d3FDM0tcZA0Zc7NZmvtdZkzTzPabhFnM/Sw8pp+/qYPlxGXi3N2n0aOxAANXQeXazsTLWn7mLo/5UueiZqef1YXgL0URakGlTtPnk69UAYiHNV7ubU75DzucsTigu9dmh2fc+LkVlKc4er7Pwe4etmVRLYPY1/hBBZ0X/P/Z+7MY27K0vhf9jW42q4k+dps728oqqgoKKDBgrrHKrmsu1wf5CGPZl+baSMhYsi0/gNyIB0t+sGwj+QlZlgWyLGMk8wD3+li4fI9dcM7RAQ7gchmoysrKrGx2H3tHu7rZje4+jBWxY8eObjeZWUB+qZ2x1lxjjjHmmHN+42v/nxKCxgecn3thbPpbFnkCXsgMgVRwtXWeWYjkWao901mPyQ1aa6qqxijFbGdK1XUprG6uqGW9gmA9JtPsuG3uXL1P+0LNICwhXxcgBKNJxRu3wHuPUwngITpHlJJm1hyzsoeu+/DDdMgb/JttyxcFCCRXcke0HqUV7+ZQDTXiGy7zyh80FCOLE5HdKyvcsxbfl7x0dYV7r9/EKsmX6OgWMtz2BLG5Az6Qh8hLIxgsDeH+hP+lbYFINccuFoBd7nPzYo+2aVne3OIFU7B6ZY2u7ZjuThBKUgxKikFBiLB0ZZW8XyCMRkYgRMqLizh9Dz/sED4QvEOhiCFwr34daJjMrmBdhaBAaYU0CfZcaoX2Ct+lZ0MpST4oQUpuXxrinENNA5cmLbnRbF+fQFgnW3qZ7BsmjJa/xKipyXqSxaKgDYGN6h6jSxNa52hUTaEkujAIIDeaUimefwE+shDordzh7d1t7k9TGOde/cBbEpwnRonJDbfyj7HFCkR45fIMUTv27u7y+/fH1CslFy72mbTNPP/IE32qzZR5zdIbl8iloDMZbw/zgyLJeqlgtNRDNi0LMdI0DfVoBiIl1zqbkPuMMeyJyP31HqPxjLxdZPn1jIVhn/FkxmBYUtct+uqLjD/1PDdubzP7H3cwoxkXiWz0NKHQ6MxwP1eovkEYxe6te6xJuPqJ5/i+/8cCg0zgXORz/3nEZHwohO44g+ET7BsPhX895nnPnMSDnp9WqXtoOQ5N9bz9nnc53xdvSeShu/SkK7TP88Uj67G/AT8Y7+D748gJH6gl948X/eiP/ij/5t/8G77whS/wla98hY9//OOPtHn99df53d/9XaSU/OiP/uj7ohT9l//yXw4+//2///dPbauU4nu+53ve6ym9J/SMPUWniLVnKQbn5gLnMeef1P4EemTa8ZAgFR8Sqs7s9hlM55nSYSZ4evTCwZ8nnuL+bnOc5y1x/0eOH9fFqQcfeY6OYfzHnXuSQvy09+NYc/fTb/5GCF7UGhPn/e0/hnNQBtc5BqXhzuU+UYDeXaCarKeaPgLaacPk/h6T7RGDlQWIBSNnEW7KhWuXub+xxe5sD2LkIy+8ymx7h66xKUxMa2pryZRKtWFiqkPUeU/wHt+mi9ZaIYkJPa5ySCEo+gUOQTOZkWUGlWl0ZzFKM233GDiP1BrXdBTDEpVpRBtxFy3V0pQ4FvTzIZoEyLAzrkErTJE8N761ZJkiM/lD63W8p23fNL1/kyIbPgELSCT9UYWvO0IITIj4pqaX51wqCrqN3aRkDA21dTz/8hWmm1OCtTS2ZZxL9rRg8859nu+Sl0YrQTlpWFtehM7xjnMHz8LB4zIoWPyOV9l64zb2/ph6NKOa1rz4qVdYe/4iwXtMv8DkBmU0RBjf3cFbB4OCweKA0HaUl/uIqSUTGj3NcU0qaDqSY8q+Z7x7g2AE7M0wq0OiVkTrk6Lby6Gz6bORSCVp645dGQlGUmQapT0xBLa2ahSai90i+XNDygvvMLo+5v50Rj7VLAz6hNyzp3aT0isERTEgOE8+7LFW5gyvrXHVaoY7HYgdJm3F3Un3yDMffKSrO7JewYxl9lgnOs+F7Yb67S2accVotcANMm61FbO6wrYOZQqa8QzfWVxriTsZRV4gcs1sxbBy9QLbdzYJMRIyiW6hFzxKCKbbY0DQNC0my4ha0TYtvlRsiohe7CO3AmonwEyzXlwg7AFdTnHpCm/d2eL2mzd5aWZZD+A6x3iYM4spXM9mmloJpNFI57h7fYN6MuF//ja4tJ5jbSTLDoVpHX5cD+9B8RC7OwdfOVxbaJ8jPYGofeLRx2abx2oyJ8/nOC+HOPL3vHSc7+PBlE7r7TT16Sl4/JEFPH5+j9nviRvnccLLkSFOuh3zeX4YSvf+0rVr1/jMZz7Dr/3ar/Fv/+2/5Z/8k3/ySJt9L9Gf+TN/hueee+59mdfm5ubB5+Fw+L6M+UHQexs+d6xAeoIX5hzC+8O85EijU/jsuZn4H4V3/0l0wMc7/fQTjn5/jDWNJ51/5qSOaXTem37Wnni4zbkX50h1j3i+EwUPrHv7Q4YY2bu/w2ApIY+lzSwVwKzGNbu3A8VCSXu9xv5+RzNr5uFRkvHWiABMt8YUvYKlT69xd/sm4oX44DUTInkMtMY6j5SStkv1YmwICJeskAFAJCv6/mS9D/SKAiEFXWcRUpJpTWMtSinaueDd15rcaISQdLajAW7JVAABAABJREFULLLkkcozmvGMweqAbnGB2eYEHYsU1tZ5PJEgBSZTuNaSac1sUlG+2GeYLx94GY/WPDlQiA7TgU7+4F6YMiMqh0QQQmC8NaK8tMr6C5eYRsH29ghhPbkx9Psloy/dQvqAloquaRjd36WpW6KRCBcRWqEi1NOawfPLiJk4UGYPq0bDi8sgJH70JjE0hOBoJhW2apm2DfXeDKU0MlNIJCJGMqMPwr983VFeKpGdITYdUYARkhA9Qil611aor2+SX1qivr1JJhZQRUZwNd2kRl3UuGiJIoWJ1VsjZrtTXGfRRiNyjTYhIfRJiXOOnTtbrDy/xuKLl2jrFtc5oohUVY2zjr4xVN5SmIwyz7HTlmx5wPLFpRS+tlEfIBimEMRD78r8/VBG09YNulcSiVTbEzZev0X9tfsszHO6hBREITEmI3TpufVTz2xvSlSSwXDAWixoRhOcDyytLmF6OcwVNmU0zbSCEBmsLeHaMd4Gqqol6y2jc0PwKRxShMhwdYF+4xk2gbppULkhRsHqcxcY1ZaN67chBLxzGGVYWOlzCwchIETE+sDS2hKddTS7I/Iio6oaNm/cZ3XYI0hzugf/KelBAOJRT/3JStLZQvB+i7lH9rx88QRZ//it+70Txc8F8jRveXovT0iHRJ5H9ZBnedXPoK8/CjLRH0L6q3/1r/Jrv/Zr/OIv/iL/+B//44dAk2KM/OIv/uJBu/eLlpeXDz7/1//6X/mBH/iB923s95OeWinaZ44P/v9AsDvseDn55XqUqx7HwI/77SS2ljbe+WdxBs8+UZk6g9sf8/OThiu8p3TKJvRUdFYnT+UNPO95++LvkWdt/6fDysxZnsrDdFRnf9IFi48Gdp04noBSCL63KMiEQCjBzrohhEA3vMQs/0Yg5XfEGLn35h1uN3d4Z/pVohL4KpDFHDWQLE6XWNlcZ1AUjOqWGGA2mfHxnYzF/+NtPjld4H/Ujp39S7Seolfi6pYoBN55vPcUWYZUkqa1KCURUrK/2jGkULhAJFqHNgrvA23TYnJDFJGusyAF46alnxmyLCOEQNbLsU1HO6vBesq6pPiNBZYGBb3FRbx3DJYGjOoG7zyhEUQBuTFU3hGurLDTGyMQVDsSukMuykPKz0PIUYdo/6spM6yoECLQW36XWdahV1/ka9sv0//2l5m8u8G1t++xcnGIfOc+ddXQWUtuNN2kZvP6PYSCjeeWaccVQiu892gleX5lldWrnwUB3WiT8bu/BzHS7t5l+0ufhxBRviOKEm0MG+/exbYd+UKPXr+k61Jony4Ubl6cVgDTvQmZFCxv5lxkCdd2DIMii54KWBh+gpcuvcJ47wZ7+jZdntHeuM/g8iqjWUNMlXfRQjDQmlf3Kib3bmK8x7+4llZRSt7oOzyGgc9Y3RixfXuL1a11XuRjXNHPM1JvUpZ3mW6NqEeOLBfkwyX8C2vMPrKGyg3TW1Pu/J8bANzvAsalELFp5w9C2r5hrWS9nxSDJrzIGyNBz5WEGyPU22+x3lp2lgpuBU/RK1i4uooZFLS7E978319kGD9B56Ha6zBZxsK1i9yfddx/15JFwadUTntrD7ZmTF5cJ3iP6yyDpQWkEOxcF3zlf/0IN77gmaqWd698hSzPkJMh39i+xIrKaaLGak2RZdwTgfriIssXhzRfvcmL44oYAkOhWLq6zNbdLZo8Ivs5ZVFwpXKYN+/hYqQuJTWgleD/93sVXx4FVl+4ROXk/ImNBwK72Nc2zgmle5TOg0L26H51zEZ9nm3w6ADn4rWnz++4Y+fipQ+1f/j6DquH7+c+fbL482zCCY8d7ajtGU6+j8d5iE5r/yG95/SDP/iD/K2/9be4efMmv/7rv85nP/vZg99+/dd/nRs3btDv9/nBH/xB7t69+77M6bOf/Sw/8zM/A8Bf/+t/na2tLf7yX/7LLC4uvi/jv1/01ErRcRaXg2PHMtQTYqEOvZgxnnD8pLf0kXCD40c7F53luT61w68zhWifHnc3eVo6zzgnrfP5dzwOLJVfp3RYUTtxnvHBxqiAK0pTILAKNjJBkJpY9qn9EjGm0LlbX36X7etTeh+7wKB/n6bp6JSlGzZIKZhWhsusI7uG4ANRCpz39GpP3Gop392jXCjnCkTEO0/bWHIhsSGSZQl5rG5blFIopYiQQuWcI880Rgi6EAhA2zmE80ghEYCPFilgMCzprKPuLLUQqBAZFAVyjkwXfSAzmq7yyFlGHkqGgyET9mibDq1SnZpMCDogirRSTfAUeRIknT5hB3/osAAx9yAdEdhiBCElUYzQxpING3buVnRhiL60RPbVO+TjmtHWHsRICKlgqnUBbx2D5QX2rEWUJgncQhC8I1y/z/OffhVpNMHZg6l42+D3GiDy3LVr9GNJvTPFO0cEjDJIo8E6rPOIziKVYjSZEddKMCC0RneCEglWYWTCV0NJ+r1V+vkqnRoT2xtk64u0b28QpzV5bhBCpNwZJcE5BjYQbaA0mrpXYEOgrmpikWpWra4so3cqonVsvr7BtU+9TKn7rLwAWjnixVWC9QgpEEqxs1bQDYt0b+pAtZmQ42qOE54jC7l6oBS1QyZ1xs2vbbNzZ4tSCMpMsaEFNitZ/4bn0UUC8pjWO0zu9di9VRK1otq7jSpzdC9n2llmmSIf9FnShvv39iitZyZlqlEkFSYz7GxsIqRk90ZBvbvCPX+dycsjemVJXimWomBJKmZFxvYoxcnTK4irC9zcHbHSdix1Dq00F59bZzaeUdctplfSKwum0xndTs3VwQJBCm7GFi0kkchOI6mvT/HrEncMIvdxICFn0bmUnKP00B59SogGHLP3PTBKPfSzOEnQfzCfxzEgPiki2tH2T1cI9tkbPJ8E7vtkOmWT31/2ZzLOh3SY7t69e2r42q1bt56o38FgwA/8wA/w7/7dv+MXfuEXHlKK9kPn/uJf/Iv0+/0n6v9J6Hu/93v5vu/7Pv7zf/7PbG9v8xM/8RP8zb/5N/mmb/omvu3bvo3v+I7v4DOf+Qyvvvrq+zan94KevnjrWZb0k6z178WY5xnjOK/BcUz/uMKrp/Sd4r6f/ALj/pjPmp50nc5L4ph/p83l8NhHtdej/07r56z5PO5vjzvOGY3j0WeM9LLt/3twSkJgkwA+MNkZE2JMoU0ieUh8iEy3x2y9u8Hm23epd6dorbGTGikEs7ZFiQR13XlPphQIQSVUqk/jHCFAcIEgJM4GkAKhQEjBbGd8oBxACosTSqKVhhjJTbKdaK2IRGZtR+cDuVIYAX0tGRY5WkkSZFvEOp9QyISg3yuxztEETxcjTd2ipaQ/6BGFoPMeOVeAjNZorWnqlqrtUvK9ksSY8qq01tSjKUKBVGJuSH9wY1M9SMFJXqKD7wLacYOd1jjnEEIhkDSzFtdaegs9ysUBOjPU4xmlMQghKbOMgEASExy5ELjWEqTAhsilF6+QlwW7m3vs3to64SFKx1RmeP6bX0EXGUorykGfrMiYjWfgI1opQFD2SyKgIygp0UYTfMDVbULO8wEbPFXwqEzhrU1Igd6hexl6bUi7O0n3J4C0HhEjeZkjpKQ37CO1RucZ2hiKXoHUEqMU/ZUBC+tLEGHz5n223tk4eLgFAiElssggy4hSgkiFcZvRDClTnpVW8+Kp8/daIlIR2Pl98p2nGtWICNXmmJ07W0glE1KhTXDutu3Y29ihnVQIJQkuIee1TZsK0DqPrVvctGFybxcRIr1BjxgCrnOI+bjRB4QUVNOK4ANFWSCNwRQ5RhtylSGiwNqA84Fqb4b3ga5tUUqiEUx2x9i2I3hPZgzrl9eoJhV7u2Py3BCFoJrOcNaSZRpTGvbGI4gBQUBJsK0j7/cAiQLUfE0O1vUxCi4efrgfRfM88nX+76Bo6OPwuBP5ZyqN/qDXk8LTDnuHxMOHH5c3P0M6u7Dr6Yt01vlnIJE/XhTDWXTaOh4XRXH4tzg3SH+oOH1d0H5o3C//8i9TVRUAVVXxy7/8yw/9/n7Sr/zKr/C3//bfRs/Lfzjn+OIXv8jP//zP8xM/8RN89KMf5du//dv5j//xP77vc3tW9L5BcsdDG+mZL/5xitRZjGW//RNN7hm02TeDHiQRHLnOE4x2h404T8MQ96GCj6X3YrM5q8+jjP70PfJ8fRw9dl46j+fvqa1o+x2Ih77tkwa+ryxZEBIbI/+pqZnFSC7gfypKus0Rk70x02+7hh8a2lzy1gs9Rtsjdr70Ngv/vUJHya4SbK32yVcL4iAyntXEEFE6wV0rIVFKImMEKYm2I/jAsMgZ9S5x78J3IJdfQH1K8PzSLtOdMUwiappgi0MIhBjxgJGCoYDWOUIIWOtREpRQWMC7QFbmWBmIIRKlJFMSMfeMKSVprCPLDUVuwNv5Ky3wMaK0IkqB7SxZZqjqhnrW4JwjhqSYeSJSKdqqJheCIASiX/PyZxLQwq3/S8L902/0vkIlDr+SMcFXy9wQfMRPP0rdBMZyhRd34LmNKXm/4E6e0VqHjbC8ukSMkc3JlF4RCTFQTWYIIeiaDgRs3t7EdZYYI5P7e6y+eOGRJ+Tw96xfsHRllbtv30b4wO7mLnmW0SsLRtMZUim6aUNR5NyZ1bRBMxz0EDaQzwuy3tRj2kHgvmtZm73N9MtfJExmPH9tSn+Y0/UiX50IHJFcS2SZETtL6z1vrZXYCD5GikGJ8gFxv+GVWaDamXJBlRT9kpnRRGvZ3thm+YV15BznIobARrfA7f5HUJnmcn6HbxOvEfuRhT+5iPzOVRDw27894/d+L3mNvt1kvGo0IKjFy9y/Hbn52nWufcLjmg6pFHdXepgrK+giQ27v4nZHjHdGmDyj3p3SWMvWUoZZzimE4rmdGhkjg/oO/dGErMi4HBTRO7x15AGe35jQ1g2h7bDzHDCxvsjvtFPcUobavcDy64Z+ptkKit8pGvq1YLG2rGiVQDAkyODprGVxYciazqlnSSHSCEKMXNirWfSexcUh7mN7fE3fZnc4QWlBpiVSai6sfRdL68/hdgX/z2xM2ZvRRfhPTT1HKzwfzR3mh57tw4xSHNP4yKty3qHO2IcftT0c0/AkHnvc3nhofu9FqNs5fGgPTeY909cew/B64k2YyxuPlCU4dtKPceUfepbOpMuXLz+xN+gs+uxnP8vVq1e5ffs2v/Irv8KP/uiP8iu/8itMp1OuXr3Kn/2zf/Y9Gfc0KsuSn/3Zn+Uf/IN/wC/90i/x+c9/nt/+7d9me3v7oM0XvvAF/sJf+Av8vb/39/hn/+yfve9zfFp6ek/ROS08MZ5uizm7A45nICd5fU6yhnDM8VNJnHne4fylh8af//bQHhePnHN0rCekA4XoPF2cdM+epQfprPH3xzt87L22FJ52fc/kuh9cwNHuBLAmJZeUYl0q1PygRLAuFdf6Pb7p4y+iV3q0mWDStbz51eu89Qdv4vZGDARIKVnMM9ygZFrm3JnOsJ3DSIXznhAC+VyJGbtACJHO+ZQD4zxb96b0X3yZvVYjBj3y5Zy2rpCZRkpF8I5iHjrXX+jTE4FZlMysT/uj93jrkUJgjEappICFEPAhEEJIQrxL0MazWYPzAdcmZLosK/DOoWPEzL1gzjqYI3UJBEiBF9A2LQKRCm7mCd65jQmeWyiH7jnKFYEuHoTXnHpnDj1fB+aZOZKfDYG2zQh+wPiupRckcntGPwgGSwNe/OZX+eRnvoUXv/MbeP7bX6Uc9HAIPJHV5y4mMUMIhsMh0XmkUQfrEfdDo05xPC8/t0YuFc7bBPrgPLu7I9q2JcZA07VILbnyylWUVPiQDCAhxpSrIhwjbamEpd26x3jjJlbMKLRjMFQsLWfkZYYSArVQJnCGGCFEZkRmAmolCD6gMk1oLNmspR9gkGUEH5FGkxnFlW+4hlSKZlQlnh4i3hSM4oCpXCAfDnj5pSFrfSi6MRcvSK5cNgwG6uC6F6XkklRclJJus+PWa7uErsfOrV2GF5eSt8xbtuuaLlcMlhdQ2iCFZPfOJjfevM5kb8REBLrCMA2ewnry2uE39+hZz3pZUrhAV7XJOxUiedPRD5EiQG+hT14W5MsDxt4zth0TJ+nVPXrdkKFZoDWKza6h8g5tDCjNeFZjraPf76OUYvf+DjubuxRaI0QyFBQBnh8usGoytib3uF3foSlmRD1F6RmXny8ZXriEt31C12NVaC5KxQU15wunUTzmo9jfT/Y9FucQfA944dMxvvisNo2j3Txht+eVMsRDnx94lp9k2MPnHzvQM9pTH57bozM90fP3UNPjLLMPGjxitP6AvHcfUtrvf/iHfxh4EDK3//dHfuRHHgJfeL/p6tWr/ORP/iS/+qu/ytbWFm+//TY///M/z3d913cdtPmZn/kZ/sN/+A8f2ByflJ79qp7AVYRI4RIHbU479xTOlDwq4ohP+inf3Ie62o8vODrG8XPa34zEvEBAjCKZyePBjw938MBU/XDu1LOY++FjR71Uz0rhOUsxPYnOe4uOsxiedKufBcM+osS+VxQBF8GGVABSaYHRAmMEUSryhQFRKNpJy/TmDtu/fwM96ujrgpiV7LjI1AX2rKeuGiaTGSLEA9hsFyICiYsKITRaSZy1aKXQOoWm2VlLr1fQNS34gIyp1lC9N0OQ8AoyPAMZCU1HJTQdAqEkymikUkitsT6AT5DNXWcTAphPitN0MsNax3gyJcZIkWUoo7HW40JAC0AIGucJEkLwKKUQPgFIqEwjtCKfo9wpqVJtnn4v5a0IQXSBapK8DrF1GARakP7x6D+5H4p0SDFJAn1CGTNKsR/yF2NgNp4y3ZtQTytcjNz46nWmkxnSKEyZ0VvskylNdJ7p5i7BB1YvrdFb6BFtmk8mJJPtEXaaPBgP08MPW9bLyQYl0QYikUlTY4lkZYEPkdwYQtNx7+07KV+pbojWEWOkVAqEpG0sPanoSUU0Ci0FAYH3EVdbulFCXFP9AucsgYCPCVDD5FkKvWzalGsEWOuQuWG8M2Lz1r0ExS4lRb8kuABSglA4B+2kAZcAHJTRoA3F0hDXRnau7+DbgARMJsiy9DwFoRhvT7n+++8QYkQaxd7WiN2726xeW0cgaEdTqq0ReZkzXBrguw7fdgzzjEIpEKCNpqu7OR9KiihGU64v4axLoYhK4mPEd5bgA1pK6smMsl+SLw4gRprW0uv3UJkBKcmGfVaurDPol0QpWLiwQn9lgagkIUTarmM6nWHnOV8xJKS5Is+4cu0SQiu2tveYNU2qfaQ1jQ/IKLnzzgZf/e0v89bvvMZsd8Rs2mKjwAv5gJWeK3ph3++atqoHj9njMLNT2h7ltacZHM9Dx+2fz3RzehY+nSedy1kheM+aHrbyxENzOAiBO+d0HnpsziNPfEjvG+2HyH3+85/nd3/3d/n85z//0PGz6AAtFui6R8sgHKXDbQ6fexa99NJL/PiP/zi/9Vu/xU/+5E8eHP/Zn/3Zc/fx9ULvT/ic4EAoedp+9l/+h/s6Z8fnerGPuoXiAwS7Y5W9hzs+VDdz/n1utYtHrXfi6RjN44Y/PE6fZ9FJ1qjT2j8OYz2r3Um/n+UJPMk7dly7Z7y/eeA/1hUKgcngf/5/LdMfSnyrufe/f5T7r2/S7E54YamgDIFMvMz4jZa27ZhMW1JJmUjROp6/M8J5j1qPXHcpJM01C5j2FaoQWXQ5IXQpR6fQeCUxMXkC2mnDcGnI6k7D2mRM74092t5ztJXE5Bkz67AoorXECINeSd20tK0FIcjLPAn+maHpLComWOQQI1pLlBB465DaEEnodMIHpBQMF5fIixwPCC1xraMsC5o6FXbNtMbNWmzdIaREyJT7lPcLxqMpIsbkmfKRsl9AhFdmlktdpL88OEHogv+tbbixX4h2/3hIuSXKpKKwIgZKnadcIdfS2pZ7N+4x+sRVvvb7FW+8e4vvcYH1yytoH/j4yFF3DdoaJt94DZVpdl+/zkf2WpS2MFcYX3h7G7tk2TrqIubB4yilBKMwRUaMUC/1EB+5TFjssbZT49+8iyFyLa94+WKBChN6TR8RDEZIXq56LATDwGh2VY6Xjigkt6tl7rwbcbszQkz5YL6ruTv7Aq71zGRGyD6BkQm8gqpFri/R5YavXejjXSCva65Yy2BxSNd1TLcnLF5aQuXrNO0S99+5y+7tPT7yiSnlQo/NnQk///kUSvEJL3hpZ0aTd3zrZ1b51F9fAwTjL1/jS1/Q3Lz1No1U5DqhLLa+oxpXLFxY5pUuUu1WZFVktjCkbTqEkrw8aonTlkBklCcPpessCOhlhkYKbr+wQvv8Eq7puN/MCFmPvi/5SCdSXp33KOtYvrSG1SoprUrRLQ94IzgGmWH40kUGWtJOZuxkkv9Gi8Wilnv0ZMp3yvOcpZWC7Z29VKNJKVYurdJMK7a2dhFKstTv0/Rg1lku2MsMbA8pBTsL19mZ/h7vvFnwX9f/FAsr6+hc0vzB/wZdfT6mcjSK6mAvOoen6FmQYI6Sd8q83k894RnQU8RqIE5iQCfQieUDHm+EQ70dVgr3+Y149H7syyL7wSXHhd0f3kv/kN3DP0r0jd/4jXzrt34rX/ziF/mhH/ohQgh8+tOf5pOf/OS5zl9aWjr4vLe3x4ULF05uDOzu7h58PgzB/Tj0T//pP+Vf/+t/zd7eHl/4wheeqI8Pkp69p+iw8HsOz88j5z7JeE9DR6MNHo+vnfzbvvnuMFc5tA4PT/spuM6zVDbeazr8HDzOvJ/EmPgk57yHFrEIjGJkJwZGRJZWFGtrmqUFwbuvb/DOVzfxrSGPJdoZYquZbnT4sSTrcgqT4ZwnWktuA0tCI5xHSIlWikE5QPgeQiwSQ4YPgcZaZBSYLIMYsM4xm8xYfeEixkXyxjPwgum9HXAeHZOnIjOaXlmQaYWzDje3gGdakRmFlIKqbhks9OcADQKlVcphUpKOiBNinijvsNalhPwoaJsWrTVSSFzd4aXAaIULga5zuODJyzyFnimJzvTcwu9RUpHlGZGIax1t1cLelHLSUOzOWHSBFSlZFoIVIVmRklUpyY4YZPa9zcWwTJ4nUj0o6xytDYDAt55mXGNzjVgdUhPYub1FCBERQbWWMkguri6jjWbz5j18ZyldZH3QJ7eePpIyCjIfDj1YDx6y/SmFEFISv9bpWGG4dW+L119/l+tfu5VCCQWUmaLMIrn0aJEgrkMIZA5WZE4/apqmQ8RIEIJq3LH75hbVbouP4DuH0IqOms5P6Npx8pB1Fi1kKm7qA0JKnNHEwkBh6C8M6S0P8M5z72u36KqW6f0Z1U6gKJaRQWM6S9yZUO+0bG46Njcd7UyysrBGbgvq2zsUsmF5ELCd5+3X79OIEpWX+ODxAp776DWe/8aXIEZU6yijQM5quqpGZwYtJLmLDBDkLqBReOuTjUxAlIIgJeW1C9RSUBGpZKTWEpYGlMM+S5dWsE3Ks/PWMt7YYTKaMlxbolgewrCkyTS184zv7yFDoChzahFRawu0QuBD8pT1+yV11aBJRo/VlUWC9+xs7VEazUKRo7TExYSyuGD6FKJEeYOLFb1hpHUjfv+rd7gzjYzzAfGUrPwDljYvpnw0bOtBjvwzYmJPKwyf21PxR8UVcZ5rON+inATecOhuP9SXOL7RCUOfPc+DsT9UiD5w2vcKvfXWWw99Pw+98sorB5+/8pWvnNn+tddeAxKg0QsvvPA40zwgYwwf/ehHAQ4AIv4w0VMrRQ8sHedkaqc1PVfIwDnbHTvweY4dHeysXs+r7e0j8jysFT0IgIgHm925ujt+iPPR00QriCP/ztPmPd3vDg1yVnjm/m+Rh9s90fxOX8Tjwji0BC0FWgqcF9SV5d3//g7btzbp5RneWTanY7a7lt22QswFH5MZbPAYKegZjdEaZQzeRwqZk2EgQBAOKR0ei1Rp/NXnL9CMpqmYpE6haGnWEld7/MyhpKJxjnHrUp2ieThR3XWIuRJUdy2d99RdqlkkRSrYqubzwScLfAwJNU0BK6uLFJnGzGsYSZVyn0SIlFqBD0TAek+WGaxzVHszUElREjKhjOEDUsqkkPlAPWrZvT1l8509Fp+/zOC5NdoQuPfGu2ze2mB3c4ednTFtiLRAiA/uiZYaLQ2ZybBty+7uDuiAznOU0WgiwgXqvSloyd6dHVavrIOUNLP6AAACo+chj9DtTWmnFdEFBoMeRit6wx5lkbNze4t22qKlxkidwgGPPDfeeUbbY7quTdDczhM6i3AeYkSXGUFJhJFY2+FEQGrwKtAJhzWS3GiClGghkSEkYXw8JcqACC55+QYlssxQeUk+GKKkpmc00TqUVggSPLvUEokgI8F3N03DdHNEOSjRCz3INDv3dgjAeHOPtefXWLrUI8QWQcAog1EZQhqCNGTDAabsM75XM9u1jO+OCaT8sECgv7bA1U9cY/HyCqY0xBiZNg0iN6gip51WDId9tE/KyHBtmagkeE9ukqcnhoibK/XaKHSuEzKfS0rTcH2ZYn2B8d4UH5LiFyNMtkYMFgasvXiRwcVFli6tIqRk79Z92vEsKf1KsbS6xPLFFXq9gp4QKOcZ7Y6xbUuZaYSSTOqGzXvb9IuMQZkRlWCYlVwaLHPFlFwoegyygn5WoNB4L8lNQdNWbL17k3pvBEIhlEHocwRxHCSszncRIRBPHYn2GCc/Fv88vt+TsnHe82C0E+f8eBtWypV+XMvb/qfjxjpvX0fPPbSSER4K/z/umTjjEr/u6i3+MaYf/uEfPkB701of5Bmdh77ne77n4PNZ+T1d1/G5z30OgE9/+tNPDPcdY+T27dsAXLly5Yn6+CDpGYTPPVwmbj+8TcCDuhTHhZ3xAC3lvTdGnDRKfCSi7cxuDp26f/CkGgYHiHtzaKBH6yYc7uoc4XRPyqc+SP52eNmfZdjbiYOc95yno/PIA4eLGCsh+JPXhgyMImjB/3W35Mab19l9q2Z3UFDKDLKIHnwJhMN0Oas7z6cwuUhKaEfQxPQ8Oe8ZzPrkX34JhKBZrNm8/CWUkvRGK3QbQ1YuLM+ViohSAnuAAAk+PEeQF9ibLtLMRhAtXgj6ZUmoLTZGMm3o5rkrRmmWVhaZ1Q2usxRFTnABqTWttTTWkucGScoDyoqM6ALeBWIMICQmk0gizjm8kBglCT4QBJRG02lFsJ64r2DNi9giJcTkoQkhsPn2Kv/tl5YoF/uMsj1utTegp/jOH7jMpd4uSy+s8hv/LfDGmzOAOZpXBCH4povfwkq5irOW1+wXePe5twgBTP7dLJcr7Ny8R9NZ+iFSDkqEkVR7UxbXlui27hJ8wGrJG6sl177to9y/fp8X705Y2qrwzjPTad6z0RRrHbt7Y1a6Fb77W78HnWk2pnd47f6XHjJ+VLvTOUR2wXB1Ce5tkTctmda0V1Z5MxMoGcn611H5DplQbBnIlgy+sXzT5FWe0+uIpiF4Dwh0L+dSuMNwrUQuDXnnbo6bOEQdeHntu3FVwBeOK0FTx8jGpOYLi31s3ZHbwOXNGblSzCYtSkq8c9TDDPmnPsZv3dtFDwzrQhBD5OJHG77pf/oqzazl1lcGXL3xZwFBLuD6vre8itjfsyijaGvL1Y8Fog8QIsVSj92NHfbu7OBaiw+BvRfXeMd7XNvxka0Zq61gsttye7XP7vKQHRquvrvHN2w3bN+d4GLEIOgQzDZH9ItUeDh4T4iR3VnFm5dW2JyMcK3hm7M+PgS882TDHlLJhKDoA85a+oMSnRvG2yO0EEx2EvrdlTZwZdrRdhaBoBMCKyS76z12i+S5Uio950Vm+ORuj3I7MtkbITEsmgzTy5mJFW42DZ23LF94i4Z3ufF2wXMvfB+9xRWCa9j6g18j2O5UJhMhKUJHgXZOiqA7uic/sjWKYz8eO/Bj0eMz5DPPOGlbfz9Dvt6jfeZspeT4HejMwMkPdZ0/dHThwgW++tWv0nUdWZaxvr5+7nM/+clP8t3f/d385m/+Jv/qX/0rfvzHf/zE0Lt/9I/+EZubmwD8jb/xNx75/ed+7udYXFzkL/2lv3QqyMO//Jf/8kAp+t7v/d5zz/XrhZ5B8daTvx3QMcpE3AcmOOPUc0/gOIXlKRhA4qvHakHHtD1+oPPWmRBH/p5J51E0Tvvtcbz851HUHml7ijb8rMY9qdHj3POz1u5EweGUTWsfkv0gZOvBk1RqST9TeAmv3xnx1usbuEagypxJMBBqJBUCh/KWlRgIXpDnOS74gzo9eI/1ASlANpphrwc4dBkBRyDlEy1fXGFvYyfl52gNRHSRIaQgYnBdYLrdIYRGSoGIgqzIGU1rmAOjmCLHCpE8CFJQ9HJGdYPzHuc8w15BPWsojCaG5PVRUiK0YjSaICMEAirLUELiRaq1w9wjpSPEzGCdnwNGBOSsweRZCivTmq7tsHNvhunlZDFDmRUW1y+wOa4ZhwTxpi4ssHxN07UttsgZhfDwXYqQ64LS9Ni8fotN7uGyDoGkmk5ZGayztLyI2Wpw3uLalOvU1i2DIocYk9CbGTopaIh4rehrQ2U9EajbDt12qDkghes6JltjjNMUvR6Zyh/CXwnOs3N3m+H6ItXOlNloihES5Tw9kzFqWiZC0isMtqvoDRxZ9LSZpAmWmo5Z6OjmyIGlFKnw7aAgc4JMOMqVknySE2yLHdXEhQwtBTK09L0jyzRtnuHaDmYNurOslQXVpKZvMi6+cpnNd+5ilgbcHk+5f3eby0WBs57p9pj7b+8iVcZwzVAUAu0MSicPo5VzpciD6wyujdz4vbcRQD7oJWQ5o9m7u4OdNZhcg5C0MaPyDlMYVN0RRjOUC3QC9LBEFDmlMmQuIusuKech0lnL/Tv3GTjHyrV1tNYordC9nFnXwaAgGIUpcrI8S7Dv3uNdoN6dMr23g4iR1VcuY1vHZHuE845iOMCUOeGd+7jOI6SmmdUgBcN+j5VXrqCWS5q9GfW04d6deywKmNSC2bhmd2zxrkYpycLCgEovspANmEpPuVJQNRXVbMzujR3UR5YpBn0QZwRyzPlSMj4eMcwdZU8nseSzvOrHu3HO38fh8c8dTveAv54q5J/Cn5/VXM7u6llrGeft74S9Lx7JLXoy3eqptvAP6dnTyy+//MTn/ot/8S/4ru/6Lqqq4nu+53v4u3/37/L93//9XL16la7r+PKXv8zP/dzP8Uu/9EsA/Ok//af5a3/trz3Sz1e/+lX++T//51y7do0f+qEf4jOf+Qwf//jHWVpaoqoqvvzlL/MLv/AL/Lt/9+8AGA6H/PRP//QTz/uDomfgKTr+rTnXu/S+vXDxbGF7Lss+yBs945wPgmk8S8XxWfS7T4/ojvF4y+VZ1svz0sH1nDDxM673sauTn3d94qHL5+G47CgiXkmcElRVw72bm9hWQDQ01hKsp3UzlhfAxwAxYGXylIybGqQjywzKSGIDIkacDwx7yaIdfMQ4RRSCpnP0s0B5scfWvc3Un9Eo4fHK4bVHRqjHs7myI/HzULbgPGVRYK3F+4Cbe4qc90xGU/pLA/Iyx7YWpdQ8yT3irAeZILp7ZUFXNenSpcRoRdumUDvnPdpAmRuquiXYlE/SL3OsdwgX6OqWcrFPM5rSW1rGTxu00SAEqy9cpJrMuHRtGaUCuY70evOQNC8YLF9gujtFupaekBx+6AQpXridNdx8/TriZejlBbPOE1vHzs0NVhaGDIc9mtGMdlrTL3OacY2en++dR2vFxWvrKOcJnUealCPl516JqqpYXl+h3bQomSDLN2/c59onX3zwgMypnTXo/fWXgmaWiooqKZl1HdYZjCxSWKI0aC/JAgQJ1npan8IDRYgILTD9Aq8Cwmh0ryDYlhhCit3MDWEyIynOAucatMnxUlLmGbQt9XhK4TytFHQxsv7yZXSeium6UcXknmb58hrszrAA/YK69sz2Iv1lg8DQjCvufvUmQiuKYY/BUh+TG/Jhj7uv36SrOwRQ1x2dCxQXFyjXFqirBolASkFbtfSX+6lI8b0ZIZeoTCNdIJMC6T1ZkSOlpLOWmBm01oTpFGKkms5YCevoCKHpyKWk3p4w2dimFJKYaaZ1gw+BdlKx/fZt7KSBGJJHclRjpzWGlKc0XB4yHc+wIdApSdd2cyh7wc54zM5b0K0vABHfdigXUC7QNpbQtHTWYlQkRMfedI/72xG9skDZMxA1WpUopdje3KTrAs9/8wtInR2ExwX3KHLUgXI9f8T3n/TDNev2edCxgAjn5GkH9LhdPOGQjxO8ARyrpJ1LmTpn1+e9jKM62mn6pHhkk3oGllxOM9Y90vDR3z/0Iv2RpG/5lm/hV3/1V/krf+WvsL29zU//9E+fqKz8uT/35/j3//7fo9SjxQEWFhYAuHnzJj/zMz/Dz/zMz5w45rVr1/ilX/qlJ85L+iDpfSve+lh03At7+LezGPW5X+6HGdLhbo/lm8fxrWM9Jccce9bK0+kc9xmP8aSmtQfC6Nlx1/NgsydUdM6kQ90eW8/hvdwQBEQpuP7CANNT3P7iFvc2XiS0Og3rUo0eo1SCuQ4eITPeXuvhg0BlDWrxTYoyw4wy1t+8QqY0/dLgvWcynrKUL6D+IKNtO6rFCbvftcHmn1ynGBZ0/6nBWcfo0jb3Xr6J+Khg7d5Ftn7zXhLmQ/LudDHiYyCKiAuBwbCXYI3bDq0Vs6YljgUoCaSEc2s9w8U+2/d2KIucrMioxjNCiAlQQUqGywO27+9hvZ97qVLhzAhIKQjWYTtLkWdUtkaFgO0sIoJUCqEUg15J03XcfvM2H7sUeHn3NkLAy98uUd+yRld3/Ma/nfL533yJCy98go/ff4M/0d966Da4zjJSkhmKXq/Pytcuk2lJaz2DQY+uawn3K7JeD58Z3KTm5Z2G9e2Goge7IXl/2+0xrxaGvdfu0C9LZK9HmHsIh0VB1JKmbhgsDmiqVIx29+42y1fXsN4eep0ie3e2me1NwEWkEEQpIUQW+j3GVUMMKbywc5bL7RqrYpG+SspvbS1Da1mKfbRSSC0hM0iTIbTE9HLEuCZan9ZbehrX8e7kt7FVR9EKVsK3EGKBGfbIJMSuxWvDGz3BzJRMS8nF6ymkQsSIMYZmPMPniq8sGjYWDf3dNdb+v8+xfGmZ6W6Htw3KGOpJxWxUMb0/ojcocT7l95giw7WW4bDHrYWMvaWczaWccdvDh4iUAoxm/doFRAT97jZN3dDr97i2OeVCf8ba1DO1Hlt3uAgbL6wg+zl33u5QRrN69QJMG17ZmGCE5OJSjWsdO9stYXXIuy8ssXd3h2nQKOvpOseg87wwaqnqhvx+xYoSFAiu54qteB9BpO4ptktBf7iEEIKm7ainM56rWy68fhtkgux+VUlM2yEFTJUk04qF3tuURYt1AXZfoddKRJlxw3+ETgSEbxHDP6DC0javsv4tn4Go8V3F1u99nuDtySzmII6OY3jZ+yztPo0i9Uwn8fSDP9i+58rlKX2eR5k7zS751F6nZy1jfOgl+iNDn/3sZ3n77bf5uZ/7OT73uc/xpS99iZ2dHbIs49KlS3znd34nP/IjP8Kf//N//sQ+/uE//If80A/9EJ/73Of4jd/4Db785S9z8+ZNZrMZRVFw4cIFPvWpT/H93//9/PAP/zC9Xu99vMJnR0+vFD2usHoc53hcl/6hc88U109l0PGU3044tn/a45iPPmgLzFnGqDPn9yTcMT786RxjPDMe/AGu9yOQqIfIKQESOiK5LFKYUIAQPc45tAIpJGWWEXxGKyJOQKkFQXVY1zIUQ3r9EhkFVZOE5lxKbOexTUALjUbQf36RUASWn1+l/+qAm69dx/qWaTuhaie03SLdqEIoQZEVtM5ioqBrLZnWBB+o64beoMdymVPXLaK1CCERMVmjc62RRlFPG7QxxBjoWktEYExSnGIMdI1NNcqEREtDXVdopRLC3DxZXM1zk4RIIXzOeooyB+fxPtB5j5KC2awhywt0aAHITUY+zNibVsgqcPOrG/QXLpJvzegP54nnAtq64d5r11Grn0YNNC//iY/xxm9+maZqyIIgto71lUW27m1RN01CmROC0mhcpsmURCiJzjW2arE7U1TXEYWCfokNniIz6f67SMDTdi49E0axcGU11VmKSQGOc3O20hrfeoSStK0lLzIyk0IklwYls8U+dW6I3pKpjIGQKCGxWtLVllzmSTHzAp0b7DQQZEAIgR6WhNEeALLIqMZ7BOeZTkYp16wWZKXAWks7remCR+UG23Z0WY7LPHdv3KPcbdBS0TQd450RRivIM3Y396DM6PYk9VjSXzTYuuPOV29hyiJ5dkh1oqxzdE1Hb7FPUzfEGPHeYwnY0Yze5RVa51IuVvBoKZFKsndnmyUlUV6Rlzn1aIYKAWEdeVYchKtOq4bli0uQG7TRRB+pp1OWfKRXGmLVUm+OKLVGLg7YdJ5p22Il4B2DtRXKvRl6p6IvVAIDkRLrPCaTxBiRmUmKUGcJtqOr2gRFnxtC3SBDYj2ZSPlJgognEgUUecbySkm5aJBCEW+W7I2mDNQCXW2QRYYIgaWFnElTsbNxl2IgMGUvefpO5TnHc6BHvz0lPd028AyGP7+H/3w5OY+3Nucd+2jPx8/7tLv2DOlw5MZRq+95ZLEP6X2hH/uxH+PHfuzHnujcj3zkI+cC6FpYWOCnfuqn+Kmf+qknGgfg1Vdf5dVXX+Xv/J2/88R9fL3Te1sSNx769/VGh+YlOEFfeq+8CUeZ0Wn9imPanGaGOs8cn+Z+RN7X+/qQs0ocOXjS+KfNTZzw74loPtDBn8P/pW57QjAQgr6QyBpuf+EGTMFIjfAgW4e0Dmk9WXwADa2lQMiOnvFoHci0JjcGqSTeOpqmTRDFxqCUpHUuob5JSa41yyuLGBcRIrDyDeuoRUnTWagF7b0a2qSMSe8S8EGMCQ5ba1SZJcEXwXhviu0smTFkRtM2bSpWSUTECCFBfWcmwXcTAlpJfEghd7azuK5DZYqVa+ssXlpGF4YQIkoIWueRYl4vKET0PDm+ntVk/QIlZQJqIBW+jRLyYYlXAq8EXRRUVrK1XVNbh3cebx15LwnM9aSi84K7t0YMn7vKu196B9fZJMjGiDQa3ctpmxYfI2WvBARKSYoyx3YW7xxSK4QA11q6qmE/Mm8/1ynG5F2btg0ueIySOCkIPcOrf/obWfvoGp3qyIr0PAyEQFnP5u37KCMJRF74xItceeUqg8UBPoLKDCvrS2g8uQQRPSIE6rZjNKuIShFiTGhq8zUyZY53AWLEo2iCoK4cwXnyfoHIksIgEQdFHrUxSBERvsPgmd96TJEhy/TMaZkKoKo82dFia8ljxI6m6Ah6fjwrMiDljbnWUU9rvAs0TYdznvH2mM5bLI6gkuJ5//oGd968xdKVNXSeoVXy3oze2aC6t5MKB+uUp+bmBVpD8EQEvrNIo4hNh4nQNxmyc4xv3cfujBFCsHh5FVPmtBJ8mVN3FtdZgnUURQ4ITG7omharFDbTZGWOk5JJl7wzqlew/PwFVq6uk2Warm6JSrCytszC4sI8ny7Qtpa6szSdo+lS6KIK6R5NJhZbC3ynWL2yTGY81WwPRUvTToixQSrJYNBnWlVsvfUuggahDnkXj+FrDw4fF6pwiJ6K1x1DYn+k92eD/yAR0R5n7EfvwpPM+8k00AMsvPggvPIgYvckw+8HbbT9kD6kryN6ek/R0Wql7zWdGBoQH/pz8JN4wNAeDZJ79JQT6aQQvkNM5cACfNw8D0/zNO/aUdfXs/Q0PVEU3GOedMpcDxef278j8dBvDx3Z/3O0vyd9zM5jODyz/cM3I8b9x//4SUngzxcl61JSTzs23ryG/mpOtztDRsu0bgneU5YFbWsxLvK1C4KgDUpbirXXMAKUUnREggtooLWprkznPEpr5DycTYmkVF2Khm+42yG3Ruwud9z61Jix3UL8ruCVtz/OxXCRYlBQT2oUEbIkXEshaNuOi1dXCY2lqRu0EDR18sqoLFW4VgK00alukhMoLWlahxJg3dzrpXXyjASBD7B4aZmlyyvkvZysyNl46y69PKOxlizPMEWG3RmTK4kDVIS8yLC7E+ppTWsdCxeXUJ2lWjTcLlP/m65g552Cm1/L6UaBPjDeHlGsFYSJ543ffo3xtT9Bs/AtvPDJV+Ctu+zd22VxfQnbdrjO8cI3vcL96xuMdkYQI6uX1pjujoFANUl1FpRKeT/jzRG27bh49Qq7t7dwc0XMGI31njLPicBEC75UaAYrC2QfkfTWr+Od5+r9lv/3bp8IbLSB35p1ZEpjegV33rx9UFR2cXmIs45ydp9XswqjFMUcsr8WEebKr5/nNSEFQqYCvSEEgocb4wXqLiBva8wqGKNo5nliSkpcbkBKpJCIZsZ3XRWMZtu0Wc6NOnkLjdEJDTAKUOn+ax8YOvhYJ9jecygEer8IrhRIo5mOJsmjCGRFTlOlXKneQp+uN0UuS5yo8LIgzsC2LdVeqhe0c3ODF/ZaliaOqurwoUVpRVc1GK0T2IXWVLOGO+/cQSB4pbOsXd9lbeLoZqn4aZYZfASk4J23b/POWklvdYF8UNJVNYTA6oUVtu9sMb67BTKyu2iIwBU0z7eRvG6ZCUF/2KOb1ljrwAeqtmW4OEQrxbSqyNqO6FwqTBxIxgsUznlEhF5RUjUv4e5rBkt91q7e47kXN9je3oNBj0GRwCm0EBDAh442/BZmYYKJEiH8OT36Ry1HR35+JvQwc35EYTguMuG9Eg/O0APPd+J56WiB1PdilP17KA4+HScCHBfO96hYsT/bQ2efdS8+9Bh9SH/M6Rl5io57g0SSGI9YIsTB//df1kNtzvp3pP+jgQLHv8jikP3kSLjccQL3AWcRj83R9i2vx/Z3nJXvGAXu5M7P0ea4cY/SY1qGBA9j8D1yT87jMTrkSdn/8lB1h8j56j2cl1Gfdo3n9XI98vvhrSmZ4YQ4ZqAj5+UIshAJe1OkEzz/6kt4C7514FMNnmYyQ1hP23Z0PoUOISDOaw5F4VKYjpKYzFDkqZZLr1emELMYMfPESCEEw+UhRgiUi4gY8NqTLRcIBKGOTO6MGV+/R4zQxkDWy+kt9MmNITjPbFJhCpO8LvPE87zIyTKTEts7S68siEJCCBilyXND01m8T8ANIQRiSLDEppdgiN/5b28wvruTvCvykIKsJLO9KUIkxa5zHpNpwqxB6ATOIIksrC0yq6YJ+Y5AkOAitF7QIXFz79Nkc0SMKR/phU++RNcF9jZn7O1ULF5a5f7NewlaOwZCTErCcHmBpq4J3tNfHSbvT4jYuiXPsnT3heDGV6+jZKrRJI3COcfmzXtp7nPAhNVLa8yaFi9hNJkx2hvjhIUiIlSgEKmga+wsL3zjy6AkeZGxfGkZYxS2s2zd30UpQYYntjU6eFTw2H5GMAqhZcrRilA5lxQXQGhF1s+J3hOEQvZKnI00G7vIwlBcXCTTCpEbgg9gHaFL4Y2uqVFKoLTAhcDC6iKhdYgQ8QRUrhNsdYgJFGJ3ipjXptrnxXv393CtRQAm02RaMZlMIYJkXvg21widPJVKK3oLfYSQVOMZJk9Q2iJGfN0gIxghMcaknCQp8M5BhF6ZY7Qiyw2ZUhgh6OUZmRDkKtW0Wrq0kjx8MWAGJaPRhN3tPSZbuxRFjreO2HUo26LLElXmKK1wUuDaNoUyCsHevW02b92j2h0jlWChVxKsZXd7l65pKcsCYwyLgx79siBGWF1bYnV1MaE/GsVwaZnpzLJ1Z5fxzQ2Wri5y8bkVTAGTdsqkmbC1N2J3Mk38UDgQLilE56B9zvq0dO56eWfRe+2FeN89HCdVVYJnEToRH9pjHv/yjhbzFUdlq/NN4kOF6EP6Y03vIdDC8W9W3PflCjizStFp1vt4CvsXhw0i5xS0j1qcTkr4f9Z03PjHWWsen0P+4aaTvGj7dNLtOc0Ld5aF7NRHcV+dP6L1HvOMDoVknj5EVyq2JxVj6XntD75EtrrO0iuL7HxtN+XZKImMoAChFEYp6rYlL0qM6NNZiw4q1QWIgraRENJARa+gmtWUSkIQTAIoIVGDklk3AsB1nrwLDLXBSokCdG64c/8uTdsgM8XSeg9X1QxWelS7FVtbI/rDPv1+SWcdrnPz9UmFWQHatpsL0AkcojcoEQKKsgRgNp4RgBgiIUTGt7aJPnDnzds4m+CjXQhIKcgyw2h3nJQKI1CloOwbZuM9imIIWpNryejeLtFBnisy5VEK1LxaZZYZOtuQ5wXtrGVWG3q6R++5HpfWL7L92jZf+52vsHJ5DV9Zrn/pXbRU6EKzdfMeLkSyLEuvfYiEGAk+IDqP7CuacUVmUkFQKSJCCkyeoWYVMQS0EPT7PaZVw9a9HVYvrnA3tGRKc/e/v0M13ePap17GR7DKYr3l1jtb3MpKZGGYxYCuGva6lryX0zUdvsiwzQzV0yjn6cqMWdshlaJtWoiRQmpaEaiFo21rqsmMfEkSgWBTTlO0DiEEdlyhi4x8UBIAk+cEDAaVvIyhI9cG2yVkQyL4GOmMTEYMrdBa0zqPntRMJxUxRMq+xgwNGMiHGdZ7+v0SKQUygAuByjmEUbR1TRYkeIFzgi5aytUVptsjYt3SbuxQuoAwLqHoRYiUdDrl6Vgt6ZTEZprgHAKwncUKEAsls8mUcqGPazq6zlFeWWG0sUssMmzw5JnGWYtQSanc2dgmk5IgNUUvp91pkMHjrMMJwEiElmgfkUi6SU0vzzBzBDpi8uSuri7SjO7im8QpMq1S3Srn0pxtR95O6OcBRSDLJKbMGKwvstgEAo667pJiKyU6yyjNIsHmp9YEOcKkjvC905jhSV2cbS0601ty3L71ON6i0/SO035/H+n4qTzdxE4s7fEYbQ+f1BfiQMCbxpi8pid1eqaY9KGm9CH98aD3DJL7facjTPeZz+ooUz+vl+Sk8897zkl01gZxnM/9CejMKZ/FXB9RNk/oI57y+7Ogp3og5srPQ8mqAo6xpkrgz5UFV5QiCPjCp1fYsDlv/rf71NVXkOoNekWfda5Qks8LY/oE9WttUjpERlsLxPTj2CiRCJASR8TXjs51aJ08NvuFXGs/915JwVgXfPGt6yDg5VHJJ2aO0a0R3K8QGSxcWOZrb3yNtqow5Hz8YsNwfIe8X/CaXGb33YaslzMaTbE+4J2jMBLbOqy1lMMeXdtRDsqU+K4k486SG3NQz2hxdYF61tJUNcYHtEw5Op11aClRucHXLf1Bj7ZpabuOYZGz15uw/dItRIysLa2xfrvAWYuRObZqWVgYsJS3vLgyRihBXSg26KGMRmcZrvKIKPjiDcEr3/ppdKYxQnKhzrj5pbfZvb2FlJLxdDvlTSmJ1AkQINokDO9t7BDmiG2u7pjYEYFwYNCJQGgctu5QUqX6N0KQDXqsLg6ZtB3sTPlUpvG+YRPFjn6ZpbVvYBfF9QsN050JX1u7w81hngy582ff9pdSaJsrmF1bory/xxWl6ARMqwozB58A0ErROMvNfMpItwx6BWISKKXE1S26yHAugBBEJecgGcnjOB3NiEaQrRUoVbC5scPspqPoF8hM4ZRl9/4OQUa+dmkAWlIOeuR5RjfPK1NKJQ/Sqka9HMF42klFnmmUlsTWkfUysigYDQ03hUMoBVJAE+m6DqkiZmeMKTKuboxZjh22s2y+fJvNQYVG4etvoZlqZGYgQtO0yAXD1cmM9TzHCs/bKznT5ZzGDvjITgJyCL2cd64usNHMmKkCkxtC3eG9R0mV0P6UJDhH4xx2b4yIkQ6oVoa81u8QUvCxtTVe3hizvbGNbRvy3BOVpK1bnHOYzLB4scAqRZGbZDDINNNpxVsDzbSfMxz2+M7iLfKtO+SLPRZevIzp55jW8n9rMibVNtv3N1PBYgJmucfN5/4UvrpK11XE8DZza8ipJA4xu0cDrI7ha4+I9eJEBNADe+Y56++dMMTxdNz+eJIQf1yf76EYcjzy3NEN+Ek3rvdG0xPA9xYFV1UK6/2VtmHTn/78nHqrvk7EvA/pQ3qv6f2H5BaPfHj8U4G4z5gPC6bieN567k6ffGpPd95p9DTeov3zvw4sayfSSfM77iYe9aYdVkrPuzedtq+dctKBHHDw3J08TY0gA6bjmulkyp2Ne6m45jCnWOojOoFzjhgzpBCIGMmUopOCKATaaJpWAAYpJJW1EB2ZMQiSp0bHB6JPnFv0fQj0eyUqN7hq/muISB9ZWF6gV3qyCyvs3t6iRFOHiO8ctq7pD3MgUq4MEbc9Xd0ihCD6hIzWH/bZmm4hlST6gBSCECJFv6RtOqT3tDi6KiWLm3nYW64krrPkvZIsM1jriVLgfaAsC5x1TKc1vV5BrjXWOawKLC0OsHVgb3eC1umas8zQhED0HiljinAVSWiZjaZkwSJiQGU5s1HNjddv8cI3vZxQ5AY9EAKtJT4mNLDOe/qLfV76lo+we3ebja/dJi8y2llNcJbhpRXq3SkxeAQRk2sUkQBM9yZJkRKSnslovGM2q5BZTpFlmH6ePAV1R9Yz7O7VLN7YYe3yGpO9mo237hNI9YZ6g968P4nuF/imoxgU7N7bpiRSWYcVEaRA+Ygk4pwDpQg+MO4qssGAwjuKXobpa0Jr8VVH9IHoAkiJyDXRegIRLSXWOmKW4aYdWikGgwHOWjCC4eKApmmZtB1aa8qyx/DSCjFEmlmNaANZkaUQPC1ACaxtuX/rPkZr7KwFJektlKxcu4AtNVv3t6mnFeWwnxSHuZAWgicvMoyUqMYRAS8DTqb8NGdbglB0TYtSCl0YlPUsDnoURY6WEqEDGIWNAWUUXiSjxXR3iospT0u4mPLvrEAqmXKcyhzfSQrpENbhhGT92gXKxT57t7bo6oamapjujHBVnULkFoeMx1MKqXAa+oM+eZGzuryIMoqdnRHOpnpW69cuMFgq6fULVsoZgxcyZKYP7CvT3TG9pQGrr1xm8fIKwaUwRfpDJuuXsGhilI+1p6VgxngOtn+SZ+JwqMJhNeucCtHRTfg8kz+r/WkK03tOj17zBwn68CjFR74JRNqHhEAqdSRPYn5fD+9/4kFwzHFK4GMpwh/Sh/SHmD7QOkUnKjAnCqsPx9tG4CjQw6MheY+hJh0NWzs6/lnfn8Z49KwMRidtKO8XT3scJfNpFb7j+npSxXH/3HN7/h6EzglgQUjMXCmvYmAzwLjt8FNJ3pUs52usfNM6C5eWoIWL8QrTd8Zs37ifkrJDIBMKU+eUOkMC07qjyAoCEuccwbWUykCZ0UoBRqLKkm4yIzMFTCPFoESXmixmaSkGhrZQxKygvLCEGfa4/+49jNIpd8kHqqahG6aFM0WPqMbUowolBYVOAuZ0e8zK+gqTnTGdtTjrMUWGzg0+RFRMCoPRCqkVupegpX3bMR7VIAS2cwQf0EYhEHOPTUWW6RRO5zyiA1PlSKmh0ZjMIKXCOofoBJPZjGnbY7NKi90qTa4KBmHIqN5jGAVLF5a59+5ddu/uMFwasvzcWkKhc46FXsng4jLVrKbeHFHvTNjd2OHCS5epRjPqnQnOCBqhWFwe4KdjcA4hJWUA2cupuo6QZ7TWo6OknkxACAZS03pPf6nPC3/io4yrhq3f/DIuRi4tLXL5wjL13V1u/I+3UUphSo0K0FUtWZ7jOktTNQxKjXQNtq7RhaMKSTHVShHmYAraaESIqMzg2kDjHML0yTINUhBDpB3PkDEilMQ3HaHS6EGJKXKyfg83sdRuAgSabkJthiAUNQGhFR7IsoQmF3zKJQo2hVIKKajrhoWFAe2swY4t070psQ10XWA6q5FSUtUNpixwl5coVwY0kxmTnTF5v0DlGa5pE4Jh5xArBjdtEc6ijWCY51gdmE0rgvBkhaGQBVJLnG1hYOkyQeM9XiSACyklSj9IUnedJThPb3FAb9hjdyPVrpJKURQ5Xd1iQ0jQ4UqltSlyqp0Jk/GUKGD37hZ51VD0S4YLA6RSuOCxIjJcXyYoyYyAvrAISpBnks07mxgEsbGE+x1x0bGXd3Tz3K3gp+BdUh59iQiB/qVVpGxQSmCFwtUjnDT4ruYQhM/prCzub4mPzwjj0U8x8bnTMmnO6Oh9o/dyiztvvw8kEHHo2Fn+urOEjuPGeTiA8dFwxrQ3jUKg8J5Ayr188Kt4ODvgkAccQCFYkgKJwAO7Z0DCf0gf0h8l+gCVosePUj3XGfGQpDo/64npOKH9LA/GaXSc0H2035MUq5NC9Z50NziOBx/Ll0+78LPOfcy5HD7/uHmdds5J63e03/P2eQodLPmhcT9TFDwvU57B57qOO94jC813TD/BC70BvnTcHr5N3VRsvr6BvC6Z3pnRdR1KSpAKOrj05gtEYNUY8lzT7k0JPiSobCXZ9DPeXO/jlUJmKSndG8eqg0vWMx3PwMEL//fn02ULeEuIlIh/p2Rwo4UQEVJipKTxjp0yUl7UgMB6w/KFZdp9KOXYEH0CgbDbI0LnkEbTKxPrcDHQNS39XoHJDHSW1jkK02P73h6L64tcfGWJZmdKW3tgDsVtLbazyBix1mGdp5dn9GYDLr27jtQ6Jd4XOa61SCVQMZ372o7iP91MF/eRtRVeXn2F9dFlfn/6Rbzw7N7dASHwznPz9Zvs3N2hmTX0ej36q4tM7m6z+PwFsiJjtjnizleuUw5LLn/0Oe68eZsvSctMCN4Z7/DxK45CRTIp+WS1QNd5JiLnczEw84Ewa3h+Kljt9VJCv/dUe1O+8tq7vDnQVBf7rErNZ1ZXMZsV7/7eu4gItmqIpiT6FAbZHw7QpaTba1mWHYOwQzZMyiPG0DqHDR7fBYr90LWYwuiUUvgQ2J7OGOSKhH8RUFIgI4RMp9wv5+l2Jqhhia875ECx2XyRemOXjVbwpfXvQeYJfKCMEL3He0+vLGjalmY0S/dMyuQNUwmmfO/6mPAW9PUCvXbKxI5YGPTJMgNCsH17Ey4vUi4OmJV7NKMZgUhWpto8znmkhnsXbpI/P8JE0BJiEAilCCvvopwjz3Je7F5CWQWLnttXb9FJi21B7HyKrmqxncM2KR9KaonS6dqFlNjWEoUgLzOi93TeY63FzJUzR6Sd1dhb99FKsnhplegDzZu3iRF6vZLgAtPxjNBatpdKvkSNaxyyU2iTxlq7dgHx3CKje7tc2dhjZXcKQvB/XuxRyUUg0L+yC2KCKASf2LhIe6Pi0ssrXPzIHVQfgmvZ+oNfo52Hxe7D0p+PQR1oRufgZYdF6mPc3wfM7us05GA+pfcrBfhRerAuj+Sb7rtgHjr6IDv1Sek8KmoE/mvbHLT08WEF7bAs9WA+6VhPCv5S2acQgt0Y+PezGSeXDf6QPqQ/WvSBeopOpGfNe88S2M9iqI+j9DwunSd87CTvy0khBUfDzM4zh1N/fMwLO6+CdOgaHhrlLI/bk2yAj3vOKV6jg00kPghRkQJkCPi6IxQKB8gIRIFRBt84vvpbr9HoGrqIeLtANRoEFEonRC0gulTsUhpJPU3WdilSWJ0PkTLLUt8CvO1wbUrydzFQasW07djb3GNBDBFzFLsQAS3JVgbs/s42ymjMYo+9yYhCZuxNxlwWywcX17Ydk9GUoswZLg4SDHGItJ0lzpHlHNCTit6wj6862s5hrcO5hCjWTlvKIme0OaKtWkRjIQSUEKm2zrytVAla2pEQzcoyJ3poqoacBOSADxglCfvCnpDYuYwYg0AGyWyvIi8LtDa0VU1voc/CypB71zdwdUemBEtX1/AhYJ1n883bDFaGDC8sMdsacee1G+SDktH2CL/eQ8kEqKBECrmy1uKloMySguJjRKiEdrba76EQWAnrVy6ydfMek3u7uN4Kw7VF+iQF9O3feR3XOco8RxlNFAnq2/lIPa3mUOYKX1f0M42Qktp7FCClIEaIAoIUBwhhQpCE/gBG61TAtZqCn5eMLDO0lthZi3ceslQDKFqP3ZsiBiVSwUIvp9/LmdmAlIq2S6F3SEFdNaAk1WRGlAIZ07OISCh8IURc41i4tMTihSWqvRnPf/PLmHl43ebbd9ltOlguD2DdXWuJcyjzGAPReTIlyEREhICKkmg00np0pmhUesaNFGRaEYCs0Ezbmn0Q1a272wy1Zjqe0c80Ya4YKKVophW+69BSossMIQWddZRljnApf2zWpFBBYkAozXB9kWZcEbQCLKPdUTIoCFBSIZQi6+WYSCqwOg9hvXdjA50Zil5BvwwUrae1DqLEA8gE8qDyBJ9oa4fzkTtvbxDaG1z95EVinhODJ+5nxz8GC06G/3iukKeHt4oj/qhHGPJpe8GzCnU4QucxRn6gCtFJdLLqc/wq7qulj3qW9gs9n3Q/9++bOBgz/Q2nhcMdbHBHjyUFUwuR/n1ga/shfUgfDH19KkUn0jnim56QJ3vvEUI8ivRzksfhWRvODl/a0cs8zatxHoXquLk+TpjbCdN83HNPpZgqvz9WoMZ7tf5PQjEJp4OVIVQVRAhxjuBlPdXOBLEnUEoRLQwWcoqlHl3TId3c6zJ/BvM8xzmbvocwT2hPuUohwMCTaqIoSaclWklUlHjXUhjD/XsTlraWKAblwa3v6pad1+6h6qSIdbMWiaC2LRt7FS+U6+n5ryW9hR7TzRFta5nNakJIOSg6NyysDFNBTh/Y3R2RZQmmWUlBb6HPaHucUPe6jl5RUNcpx6iydg7RrXEhEIHh0oCFlQV2bm8iVbLqE8LBbh61xseYvBNGEUIk7+XIeY7R4Ru2fHGZ4fIQrTVvfeENXOu4/LHnmI0rynLGhZeXWby6QgyBzXc6Ju/eY2+qmHhDWOyhgapumMSAEQ5DxGiJKjyN6AjW07UtMcgEIqAmBAJZ35CHDCUloe2opjOQgsHqkOevrOGrlswL7s8q4rCksB7VeWIU6OgZmEghIl1saFVLiBEVO0BQhZR/JQToLMOH5BnqnCMrckJIIApKSWKXoNx93WF3J+giQ2qZCutKgwiRIATGGESu0VJgq4Ywa2i9h9Bh4gipBQRB16T+yyJnMq3QSAzQl4p6UoOHqRa4psGbQAx7JGzDGhc8OtdIU4OeUKyMEY2gbAdYBNZH4qyjHJYE3aIzh4qRxa6j7OWQCfApDygIQXQBVzuC0njR0EqPlYGu6xA+gFQUecZu3ZIXhgtLPXqZYdw5bt3dIVOCPAQGZYGUMtV6msN7Z1Kxk6WCyKtX1jFKEaxna2ML++YtfNexogRNaYhIjI+sLQ6ILtAUCi9lMj4QkTGF78lMMRlNsVtj3NQRnUdLwVCmvChdamwYgM8I1jH2EXqGTMGNbUf15oS1jy2iB2sJ/jx67HTvKRnUSXQMEz1y6Hxb3RktzuKvp0VRnEQfuMB+nk31aIvT2zyOF+nwfTms0B4d46zQvaP31wP3vCcTMA4f4s59SH+86BkoRe+Ruea83p3zMk5xMleOMeDnSb9ZJs/X737fZ4V5HaazPD5PK+SfditO29nOHDce8+nIgadUKh6ygp3mGXo0IuHhc06aw1nK40let4cOPRwv/hAanUj/O9jURBKQ6r0J090Ra8+tc+XLLyB8RGeaeKVD5QHVCtx1gfeCnslBJBCCCGTGIKWg7SzeOYLWFFHy0m6HJGILw5tLEheTQFZZS2EMvb0+l7/8PP3V4b7ZmLuvXae5WWJVQMRAcD4VmkRwXXWsPN/DaM2l6wZdZCnHSe8rY2k9XOeYhQqtEnJXwLC7PcJkBh9jgmAWCYKZKGialhACJtOYPDsEYSyZOotpFbPRDOcDWkiUFHgfycoc7xsg1f6RUmLyjNF4yvKVFTrfHFr0BDShM5MSipVk7bl1brx2He8CUkte/cyI5z61g7dv4NqOF/9kn82vbfAf/teXuR00CsFgoU81qVBrBS/pbRYyRRst75rr2NCSFYZvnq0hEEjdMVh6ExVa8Bld7xWkUNAKmhsN5UKPl7/hRaRW1ELwtfub/LYOqMWMtS7y0jgVjR3IluXcEnPYCHe5bzYpQsR0q0y7pYSoJ1O+WZgjC6ZHS+KsIyuypJBqRdO6VLdIQr7Qo6u7BB+uJK61BFLIpLeOGAKuapMXou1Selyo6PV+n1Aa6pkiTj9OZjIkkeXVxQSM4SJXbm5RFAWTQcYbVxbwnWO1nWHM76PVKlpqCJrx/RHPfXqTy5+8TTuZsfjFK3Q7F9jdrJjudVSzhoUmsv3KXZrVCcYHnrsxZa3tYRb7KC0JNjJ+e4fy4jLtVoWtK954KdD0NF4InHcUStHZiA2BsiiQmebl9ZwM6JwhbIyRxlAo+MRSH60l02lFKxWDLGNTKf6XuiIrckxmcJ1jb3uPIMB3HZkxzFYL9rxjMOhzufJMb2xSz2q0EKzHw7wxeWeGK4u0VTM3aKQ8rrpqWL4/5pLW2JnjHfESlZEsLgwZPW/Y2dpLgBD+W9ExZ/H+kMvf9BLKaHw75f5//xzBnz+I6QEOUfLoncbi5yaIY4Tpw2zw5B4e4YsnD/Jw54ePn8S3n5lY8bhWzMfflA+PcNKank3H+ZDECdN4EPx4du7S+UesYuT/U1cH3z/MKPqQ/jjRB+wpejxJet9JfBwU8tl08jlCSJQ6X7jBock8mymc51KehK8e3WzOo1yeax/Yd7yfMvHHme/TemieZOwnHm9f0ji+E+9SQvzhNs46hEvhQhevXmR0dwepJG1s6awlNxlaCPKymNdOiWRZCo9jHqJUzgtXNiEgtJ4//xEHGKmwIUAMqHkdIhEitu4Q890s+Ei9W5GVJcFVSGlSHpMQSCFoqoa2bdHGEAX0lwcprMt2KQnehaRwSI1QMgnnCDKTEzqf6rhECC4pc0oKrAs01pHNBU0BlMYQJWRFhmm6FOjuAyYzlMt9xltjhksDmrrFh4BUmuB8CumrWzzQXxhgZfKkCAHeBnbvbrN8ZZXZzmQOzW2QQtDOGkJnyXoZOm9BBGKQdLOGbJBhJcgoEFLSu7qKvSfptveQMRKCx0dPCJ4gkuEkCIFWilYEkCksSyGIrSMV+gGtM6688hxbb28wGc9SnstCQXZhAICtZngfDpTI6D0hBHQm6YkUHteEQBYjMQSsDwkFkIiSau6BjETrEUrQHw7SXEXEzvNOovMpHwhBLzeEqiU6D3jIsxSm18sTamHbkReKNghi8EgvUNpgY0xQ8Ptog0oSG0t/cUA7qQmdRPRzVJGRyZxqd0Jvscd0LAhuyHhrnAr0xjSu6yyusYTGYoxGZxoZIypGjPcIoHdlldwlNMbYJcS/3voipjQwLJFCUCz2cc6CTblNUQpkmePHEKUgVxqDJNMKpE+hqAK01ijroImYmNr1Bz02qwTfbduO3apJtalIIayZMSw9dwHBPNxPwOY7N7hYNywUOS5Exk1LWWTJyxkjwfv0zPpA27YI6bDOoYwi1xopJDqmmliDq2sUvYJ6d5Le/apFSoGWkq17e2TDe1x49TkQT1pj/Txhb4kOmXMOjhz+ftrW8ERIbOfhwfHoh8cf57BS93hnP51ysa+mHM3jOWkWT6PUPBj72YVOfKgIfUh/XOmplaLH9hOdl7+d+PtxMc+n9H9OPqGUevDlhHPOjAA4LDMfN6eTOjvLg8QZbY8b4z1y4ImjHYoTPj9ep4kiZ+/fT7o/PvE6pAnFQxv0UccVwOa89gnBI5Yy+irDt5aNzVv4iWPCFlmtESW0tiYEj4seukAuelRtqjlUNS0mz1gY9hAh1ZQBkJ3FaIW1nuADznuyPKP0UPgInSMulNQIfAs7TYvOFZmPGB9ouw6JJO8VVNOKflGwPFxgd2+HhYlncGPMykUDosJfKFHXBHYDStmnqRokSdmJIdI6BzGQ5RnEgGs9RVkw2hujtMLPQ5+0SMJpV3cUeUbbtHjryU2C9PYhMh7PKAcF9WhGpjUIgbUeTVIyTWawzhNVCj3MexlKy4N1b6c1t956F2KkHs24+cYtyl6JQLB1/T62dUl4DhFldIJrdgHVGnIfyScNeZaxGJJS0zjISgPSI/w8NE0qtNDsFlMakTHLwXYDAhEXFNOQER1EL/HesfOlt7Ghode39JYyGt1g3QwRoJUtO9oRZEArSRkSSmDpFI1eoI6Wvi7JvcTBAVNRSh4AZMSYakEFF2iqBh88MUZUiETviJ1DBvAxeYR0kcG0JrpAND6th/VJuQ0B5SILl5eJWYcNCXLch0DddSxmPUyVoLDlrGX91ReoJxWT+1v0gRgiRmfsdENC02PXeppeRtu1bHYlsVrD1n2c6yGrilJBfq1EG023NyPvGnInKC8uIe7MaGtHudRPYXFGo5XEj2sIkf5LF1m/2CfbGeO7GX7WARBCS8/u4bxkUBmsMcgmYjtHGWZgJdJGalUm5S5K8nIlPaeAmucZ9Rf6+M4x2dojNgHbWbZu3SeGQF4W2LZjaBR2WLIbAlnryYwixEh/0CNTCuEDupcRFxIgQ11tEWKHwLC0dInB+ipRCJyKdF2g2brPNGzRhZaikOg9hfKQKcHW7TdZfl5hcsnjIAkcFpDPi6B90rcHdDzjPSvf5UnpYQXiyft+trN6vJHPNB4+kxEefHtaxWqfnnVmwIf0If1hoqdWio5DNHmP5PEH/Z0VCvVEnT7cb2JoD67kEYXomPNOnMJJCyKO/PSswuiOG5v9e3TcRM4/7rFr8Dj76GOHPR469qy9SueiQ8LFKR7K32jb1FIInvvOqzy3XlKNZ4w39ti9s80oSi7tXUHHLKGAWZcs8QiiczSdQ4gELBB9YDquQMJwIXlOZnWDkpJenhLnEeAnDc/NJMI7Jrni7ZUCFyPeS+6HltFixsXGc9UFhmuL7N7ZITeaCARSDlcEnn9zwrf+HxtcfFHyP74lsnGt4G51m+HeAnlbopUikoRlGSOZkoSY6hQJBP1+jnUeESHPM+q6pShy6lmN8wFrPUJA0SuYTmYE51no9xJwg7UJ4th6TG7oWpuABYxO3izSuredp780pLfYh9mD92U2mlG6nBtfepcXP/liAm1oWkAw3dpLG7wUD/KQRPo+WFngY7pgZeKQ0XFt1HH7nW1s3WB6AWEUBJvq/BBxyvO7S28kHmcWcLufwrce7wPXQ0zw2FLSLFus9/T6gmzlbWIIRCGQRLTS+AXB3fm6L3WLLLQXCFJgwgJr1QJ4TykkNUl5ISYPCCJ5xqSSuJDWWsRIM8/ZIiR0NCMKoq2AgPCemGlkbjAx4mcNISTLQ0dAZQrTK4jWUXuf1lRADEnhraqOrOp4cacmzzK61rF5/R5ZkZP7mpd7HbbpaMwC/8N9khV9ge65jna5YWtjm252jYWNb+LO6zf56NaE71zICOUCX7pwi1vZBizUvHCv5tJeD7+5hQ+BWGZJ8ZMClSVPoVooidMGN6m5/LWO9arFNg5hDEoIut0pyK8QpURMHPfn+UJCSoo8oIxGaMWmD/jakeslXlj6U+gyA+eQWXonJjtjbNMyXBqyoJfYvrkBPoGM1OMpSgjslRV2+iXV7oTFG1tca6ATMBtNqOcFintBg/MM+yX93g4xbJEVBWZ4jba1jDf30NOKMjeYpuLeK6+zuq6JXnF14yXUFKzquL7+FuPRBpdeucaB2/ccFI/wqmehsJwkaJ8c2vWMxjvad3z0q9hv9z7uDfvjHlUgDitzDysph48/ellnKTJHZavjRt8/cno449kb8KNL/qGa9CH98aFnFj53nFPjWHro3Tql5ZMqCI/T/gSF6MFP8dimp/ZznnkcO9YZ9MSetZManzHq46z/s1LmTjr/ab1Rj7FZnrihHFyjmJcoevCEPNiM5keSrsNoc8TNr1xHAro/wJMETkmkyDIEAhUEDsi1ovWBGCJZpsmNxjnPeG+KKTIUgsJoZlVDXmRoJQlBIKVA6RyRCVxIHiSkpG4dtmpBJqjti69cYXx/j67uUmhZZ/EhkJs5LPJkmtDygCgivZUBjoizXUI5UwotFUIrnHMplCk3mDKjHldYa5FCYFuL94GszFIelA8oJSjynBgCIqQw1UCCjZZAZjSutXStRWcaco13Pgnw1s1D/WBhfTH9PntwQ7qqoS9LnPPsbY/RRYar24QiBijJQSI8iCQgSglIhhdX2L2V4JKVSqGHfo4oaK09QLtTQuCJ6bQo6JqW2Fq8AyUkIYYUZhfmHjJUUjoBlEAbg46QC5FyuWJSLosYCCrlhLU2eQpFiOzh559TCGEkJu/O/JqNMSk3iAgyKaeZlAzXFoj3784L9gZ0ryDMBWQhkpIBEF0geI+ch3mJfolWkhgdIaYx1RxAIHqfkPW8Jx+W2KajHlcsX12iEVN8jAnEY3uGjZELL1xEi0i7POTO2xvMJg07d3cZrC7ibXpuRGOhq1FaUlxapnljEwQ4IegXCRkOF/BNR/SeGEEWGbFzScEZSHzn6BqLyA16WBKrNhkuVgbEEAjTGj8PwYvW4a1DG0XUAmcdQYDtEgJedJ6ua0BIFpYWiBJ2723jvUdJw2B1kXKxj2st5dKA6APtrEn1kRCUeYbzAS9SmGfbdsQQWVldTFDrWQAhmU0a9jZrvPdcuXoh1YKyHVuDm2x3Y6IVXAiB5eEAtSC5Kd5ib2uPhaWFY/gQJ/PdR/a144Ta98ICdwwdZxA7T/t45O8xdKKR8hR6evH+eG/M/r5xFOEtHrPO5x0/GX7io8cOK71HjJ4P1K6T6Emv/n23Rn5IH9IHQs8wpyg+HZ8917mnCPMPS6Zn93XSO35O78ZDoXLn5RfH9BlPE/gfdx2PzvPI92Nd+U+zQ5zgATs4fFzf592bn8S79AzodIvd8b8dXdX9771hSb8eIDpB0ZVUwUDUBB8IIZBpgwpQRI9G4KXExwgxUlUNZZGlBP4YUSqhwuVlRjVr6HzAaEWM4Jynt9hn1UBXW2Kh2HWOam8GKxlS7lH04cJLC9x5bRNEAkoQSIiRyVLGjfWM7EKOCIGFiaW3sMimaVBZhgL6y0Omu1OMFCxcWWV3Y4fOOibTirZuWF1bxuQZ1aQiy036azSVbRAxIfG1dYJEFpnBd44QAoOFPt1cQTMieUa8cyiRlADrPVlucHWTvEQIembApcHlpOD5VMDUtx3jzRE602it0FHQOUuwltlmj9EwB6C/OsWUDqFEUspEUib3YuBW25AXCqPGCO2ISXcCAkZkXGgXUEhaFDezEWWpUF1ktVsgRIUAvBCgQKLQVUQCVkbIemQkb08XIlaACzmV7bAxJiXKB5CpSGuMkTDPbdJKIefeIu/nnied1se7gKjHrK8sMBxE2IoEoxC5AevAJwUozL1TwXpkjOjMYApD7BUJgrduWCsN/brBZ5GGPVwBxktm/T4qMzRKEqNCLZbc6xp0yKlDpOqgKHJ8Y7n/9l3KhR4rF5eRk5r+9pgra0tk3Zimq1Ctxbg9FguPMuA2tjDDkq5z0Fhsa2EO2x4am8ICiwzfOWQ/T6GjzmEiSeNVgqzMMReXCK3DWUc7axCFoX9xiWxYYuuOye3tJEdqhZEGZTTWerwUzNoGrTSyc/ibmxAjhRI0CNavXqC3OkQIQVcndMB6PKOpaoYLPe5NWvoiYtuGUkiM1gQbkAImkxltrwdB4qyncjuMTce1Fy8xlBkFmqqDPL9MnOXgInW/ZDLMWX5pmYVihdFkj9GdbS71e0QfcSGyNbPnF1E/CCP/0/Luc17ck1yWOPzhieR8ccI3cexSnz+U7dGzBRwgsj4SGneo6UWlGIg0/oZ3VMduvE9OTxuO9yF9SH+Y6OsXkvv9fA+fYKyHWNhxDPa8m9G5rX1fx3Ss5+uUXedxNqP33EB1zhslSB6TeGRKBxa7Q31EsI3FzTqe33sJsSnIMsNrKwVTGYkueQKUlGQIPhKnZFKkXBclESJ5F6xP4Am+s4gYaWcteS+nV+RUTfLgIEm5EdsTPv2JF9jZnHG/rRmv9hlv7CKWJFq+CcDq1Utsfs1g6w60ptSK3a5l44U+/3/2/iTWsm296wV/o5rVqnYZdZz6Vr6usI3fQ2nx7MdLnpBAljEWSslYpgEdJHopWjRo0YImNBDY+NqysmGJtAQiSYHJ5FHkMxjb+PoW554y6l2valajysZYsWPHjr0jdhTn3Gs7vnvj7LXWnHPMMeda8xvjG//v+/8XXx1w9KNr3Ly15I1PF3jnWXQCnacgbHG4QGlFU7eoeYMETJUmqTHPQSSqY0FECkkEimFJ1/YEHyg3Rth7B0ipqOsWax2jYYVQCtdZjJKpjsQlxCUSqcYDQt2ke6Ik1aQCAVeGV7k8uMLBrV1ut58idEw1Ss4z2hxzdGcPIRObHVLy/v+n5PDWNYSE9/6XbzIpZ3jrscsWUxj6pucD4flks2JQarLh+wQ/RymVECcnKHTB/3zwJfKQMVMNe+P/hteR7Tjip3Y3yAEvk54UITCtAwc7SyDiywnN5RvEmFKtuhhwRHrn6cIq1UsIoky1Q1GkgM35FMAgBKFNtNWWVTqglPgVScNg/1O2t6+gPp3j246waCHTCKOIMt1fVRV4lzSP0s9ZIJQkBg8hoH3k3YVgcb9hsTigyO/Sx8Cy2OTrG38GtKLpenSUiEygZEWYWkQwOO/IioSChRCo5w3LecP/en2b77epbmd/cYsHB98kCkHlSr5gM4Tw6K0NdJnR39pHlgkNanemCKNQeWJfjM4jtUromVKICN4opHWEzqaFhBAxo4pimCjb+65HZJr2aJnqyQpDdWUD1/b4ex6pNXmuiPMFo0GFtYGJEPyprQn9ouU7h0fU6wXEQDetCTGyd/tB0uCqW6pRxXy9ZDrMMFIyuevYVjnD8QCUZLY/xXc932y2qE1J7zrc8HfYuOm5t9Hx3uGYTZcTB0N+Z/EOlXuT1lk+GVr2h5pJcCs01dMcTPnRG5tkWjHvPP/2wyP8meBPPPZDj2fMnb869cJ1KOcsiB1/9qIRy1nj3mcxBrziNl9+iD67hdPaQ2fZj2QZX9YpBfT/Wdd85P2Fz/oqxGRf22v742QvSmtzhr1Inps49+0z7TQqdLKNZ7X1tIDjLEd8Tnvx9Itn9f9kn5/nek8ed1bwdfpenAddPK3di/bhacc8T3sn7fTK4osOWKf7d6G2PpvB4Oj+AR99/SNs0yNJk1gZI4VSGGPI83yly5MopTOlGJQ5WiaRUh/88cT3YfJX21mWi4beeSaTQRI/FSKRMUTBcn/G+ltXiCvhvfpwwfz+EawGPlPkbNy8hNYKIxUBgfUpIJnuHaQga3VHpJRIo2iaLolrhkhRZIQQmR7M0yDdWqo8YzIe0HUd0/0pJs/S5HUVpAQXGI4rmr1pEpkNgbpp8d6jy4zD/SMIkSrPEZmhs5bgPKPJgGZRE5ynrVuuvnedfFAc39/gAlmRM1wbHafaiRgJLpAPS1wMdNaSGUO/aJjd26eeLjm6t8/OB3e4+61PmR/OV6iL4sHH98lzgwse51IKotSpiD6uqKyDj3iXWM/yLCOTkkwIcutRIZJLRR4iqncI7/FEmhiopaAFDqNnHlL6nEaitUJImeqDAK0UEHHWHksEhJjQsiigjyGxwIek3eRX6W9bW2sURYY0GrQCo5IuUWshRrzzdMs6pfdphchMEnyVElUYMAqEINYd2miGg5LMe3LryH1AkVIdizxPaYQk1rro0+9KKIXJDLrMyQcFmdaJ9nvZErqesGyRvUtMddsTsu0xalLilMA6j65ypBJkpcE7T1+3BO8T850QRK1SjRcktrlck11eI18bpmOlRA8LbNPRHSxAQFZmx5/7ziYx26ZDITCjEtv1RC0YjgYEF6iXDdWoQsq0KGEyjVKSnU8fsH/rAYe3HiCVpBgNuPrFN9h46yqX3ruR0ulCYFDk9M7RNB1SK8YbY4TWeB9wbUeMMKlKjFYsZktc3YFNk1dhDF3XY6RCSclivuDBnQfMD+YE6/HO43v3bF/1RO2QIJ46Jq7+9/Adp7ae/Cye5UCfd9w66/VF9n+yO0/an+B5/JNJMSIJCD+nieeeeL221/bH214dUnRGjuvTLC0KnXiszwpwHmt/9Z9X+fy+bHraWdufBx163u0nx7IX6ftZaQ1P2/aCKQbHa5AXSY27WGOP9+tF2nkFJo51ieLJDx+9Xq3UltMB7ScLNmebGJnhY6BtOtxQ0dpErTyoe5QQ5AHylb6O7R29S/TVMQYyIcmlwsaQghSZWPCigK53mMzQ947MKHoFD7qOy+9dIZvNmSwaopRM7xxycF2hMoOpFdvvXWH64JB+uiTGQB8SwUO7TIKse7VletQBMLn5BrEbcu/bt+lsCo6qKqeuW9q2o1ulepVFxrDM8XmOC4G27SjKIqERUtDWXUr1EwJrHUWeMdma0C4ahEjis8u+x3aWPDdoY+gWLTozBOtQZcald67y8AsPznN4Z4/7H95DG00xLLHWM9wYsndnDyUl29e2Obi/z7LtGGYZRzsH+PuBN37EM1gfM94yfDyqOJwGjBRsFQGrA1EGjBij1ACCQC4kIUIuNY3dxQdYNh6tBMqB7RvulPuIFTrmhScYWJSWOtsG62l1Qe1TzVAMEZSkX63mxpX+UBLpTNTXUkpcSFTcRpvj51CZFCT3fYdWGiUE46riCzdgVPTYuubufIkWEiHAjIf4tkdnErQidhaURAmZhE/DiuLbBzApsBFa4UIk9o54NCfrG264HXopOPIOX2mG60PCwYKNuSV0PXqwTpVdIojIXLU8iAesr2c07YJ5E8hdIIqG6sYmtnfkdKxtVcSNkv19i+8d+XiAKg35KDEHogTEhKqqKid0LpFeGIkmBewMC8gUAoFvO/SggBDRVY7rEw128IFyc0QE7KIhH5YIraCzYD1jrfmC1oTxkOZozh8uOqTzLHT6DvJRRTEoyYqMYlIlltIVsle0loEpeHC0w7opqKJiUTfcb2vyyYj86jo6g2Y6oxyWCHUJKT2+s9yNh+zGGSLkHPUDghSMRgPWDyOLeoGysDG+wuzoACEi+28LhmsZyyYFisfO9WmZBuKRL35sh7hCCI63n+9IzxxqnjUOnvP5RfSMLqR5dLofL3r8H2E7eYV3vQPSAsriReRKPktE7nO0ckPwf/t/DD638/3fb/zx/539SbTPMH3u5Iz6aTPbp1hcTRpOpSa99OLGealqTwt2nrb/s4KH06jTs27Bs5yUOOP1RdGh8+xZgdZZX+c5QcqZp74omvYygerTgq9z7sdFu/XoBp3fUCTp3qzf32ZzuUXQjuyLBbe+/glt3SYKZxfQRnHtqGWQ5G7oQmDWO4QUaZWdiLMBJRKRAgGMTlTSUkFZ5DRNSzUs8bOaECJNqbg7Muy2DVeub/Lm/+/9xLilF3yjHLB2dcLm/YyNRnPlC9f59Hc/QK4WGYQQhN7hneeDg4b5nQUCwZ++OmYj2+T+h/fwrseHgPMrKm5Wejk+0LQ9qd7FJ9HXzDBaGzI/mOG8x2iFiJG6TfUik7URWki6ticS8YD1HmM0440xrnccThcUoqDve25+8XpiWFvd5Lvv32bno/soYxB4gnWMLq1x8/vfYrgx4vYffEJXd2xc3uDw/gHdqi4pCMFwe41qUuP7kAgsyozMe94YdETt6HpLJa6hhGaxaBG3DCYolLTs8NsgHLEwiG4AApay578Mv42QApFp5FqF14rl3ZabxdupiH/149Jap3vtPFqAjYmYQQqJX7GLRUEKXKRIOlURpFIYo5O+VdsRvCe6QFkWvPGlm1yv/pB103D/4B6yK5HVmNA7siqDEBJ7XQTbWaTRuLrFTEoIEddZ0BI9rlakAzbVHRUGlWeU1vLe7n/FScn+JOODSYnOMjZNy9vzOdF5xuEm14ttgtH8Hnscjj5kbWtCeH+f/d05qirQmyPGG1uE6ZIrm4Gt8RIpIMaSw2mPKUxCtazHK4nUOqX15Sbdo1xj5w0qU8hcE2wi8UBKQmcRVZ6IIQggBcro45XzbFisSDs8elAgegV1JHaOzSLn/1pVuGXLN4qMf6sFmoiNMNmcMLq0lvqGOEZMvUsU6OLTPfIP7vNu79hcKwgxInPD3bWcb3uLDpFLl6+wPSyYTxdMH2zQ5BnIwH8e/C4yq/FC4+MP09eeMBry5byiPmpp5g3xcEwVR3Sq5fb/ZhjeGNDNeuLvw8lUufOyGER8chExscWtVlae8H/iiX0fIhLi4ebnQX9O+d+nBisvuAD32HmedY6XsBdZh/y87Pes5ff6iwv7PmF/xIOh1/baXqW9uqBIPPJqT86Zz37qHvOD53icM+lEv1c81MVn1GfbRQeCp+33Ig7taUHaeQjSiwRZD9t/nv1eMo5+kT5c+Os7qx8nkKOHA7KUgsO9Qy5d2+be+3fo6pYACCmRRFzfpxS1h+dfac88vN9GKfAeVRiaugUhUlqOFBRZkQZ/IfHWU5U5y7pFk9CGftagt9bQK10VKQRH9w+YXNk4XjkeXVmnGBQsjxYoqXDeIb3H28cHVqEkOtOM1ga0jcEtO3rrGI0qqlX6nu8cs4MpQikyoxmsDckHBbPdKXXdoZVES5EmudJhlMI1PabM8T5gjCEzaZJrcsPycEHdtKhMI4gEIRhtTx4F3D6y3JujVsGF8x7nA4MQQMD61Q3uf+cus6M5ei7JBwXReYaTIZ2I7HzwHUaXKoRKZA/OSoosoS6tDxR5hpQKqVMqk1GK6CLCexQekQl8n1L8ghKE4LECRm9sYyYD9ncOOLy7S94XdN7jQ9Ja8s7T9zbRaq/Y9NIEdUWTHyM+huPJqhSCIGKa4CtJCCtxXqWQKybAd7/6DkWVE3qHbWpkZymzEV4rpNH4ZYttOpQQiNwghjkIUIMspQYCwgW8T2KvMtMUa0P00RKMpriyTtdb+p0pmVbkXU/pc9y8RgnB2lffpLu7j5wFonWoEBkONRMpCQdzBBGzNWFwZZ120XD48QMGG6MkuRMCLgRiZxFCEdqedlFjJoNHtUQ+4Joe1QkwGlXliBDxTZ8CRilQucEL0JnGW5+C8261cu7TqoNYQSJydV9kZZBe4+cNi6bjoSC4iJFgLTHPECGyOJzRLGqKYUUxLHlIi25XrHj9rQds1y11iNw7nIGAgRTItYK1tRHWOXZu7bB1fYtrV27SLVtmu1OkhMZaxoVEScVh3+M83L9zn+9fu8TWzcv43rJze4e+78nznKwyL+i8ztpBXMjpxdV/X5h2+/Q486zPxSMf+sR+z3OuV2zxOLi8yE04PWievvCHwejz1vI8ZdITH7b4qoPCl53gvLbX9kfPXjFSlGbY8bH3cJ7HeqYfe9mJ8atCJ86asJ+XyvWsfS6SAvYs1OdVDwAvE9R91ud4Ve2eE1g++toeD2xO28Nx8VnhfSSymMzx7/Z8+/7XuWaGbGyOEFpjCSydI7pIjqDzHkcSj5RAXmRIBHlu6HRKp9NypUtDSrvr2o48M0glaNqeTKXaFBUiW7UlcxCKgvrNbeZ3dqjFkOktQX1zjegiSt5DZrD+pwt2//AebZzjyh7nE23x8R0RMLl2yKXtSJQtX/9/z8lkiROS4COLwzltm1IAB6MBWZWnIMl5Du7u03QdZZGRq1QjFVb1T4o02SWEFXICbdczngyTSOzqeoaDgsX+Dl+4mnMp7mG7IXW2xvJgjm06qkFFvWzorUsitqMqdVslgdp22ZLnGYvZguGgIsTA9S/f5O6H36SvYeP6Bt1cYIyirVsW8RBKRyeSaKqJEjLHWHikhtA3KCOJtkdnORuHm7Qx4nNJ+d6E5bRl//09bPCM9YQsZoSYUuC6VZ1JlmeIGLHWEUNKm2OVUie1QkSJVEn81vtE8620pu9tEm+NMTH1WcfmQDDKW8LhAXMfmM08Poygi9iuRlQ5hIDwATEsVjTXgBLIzCAyjegdbtmSb48TEucDoQ8p0Fh9l6r3ZGWOWh+yNcwIZarBGgqFrCPZ5hi3bGmKA3SZIf2c7YVH5hmXb1xh1KYgphhX1PszhBQsXIayGf2ipdc5AgNKUGR6hVxC6FNgQ4jpXrQWMywSBXkkIXPmkfZUDCTR2sLgXdIAUyKwMQhIYXFBsOd80j3KSpTWRBwiM+jM0HY9uu1QeY6PkbK1jKLAuo6u7tndPURKwaB1FJ0DsdLdMhnLpmXb5BQh0lqH250ipoq1MierCupv3KZRknJY8t7lDfJxyYcHb9O0CybVgEaXhMwyPdjn3lrL+mCIWc/oP00aXhvrAy4f1oh5TbsM1HGbfFziouPe4s65Lu9hsH1yYfHx9LKzo5Mz0aOzHN+LojsvgwqdZfHky6f78Rex59N5Eue8ftq2Z6/yPgpQz2o3ffaQo+6cEeyZ53htr+21vYKg6Elm/Gc/eC/0aJ6HJJ16f3ZM8gwv/DQU5o+THzkr9fCsVMCTn7/oYtFFF9We1rfTbT1vX56jzxfaVXAsLH8CIHq8BQFHl/aY5QfUasaPFN/PeFkkQdb7U5adIwiBEtCvIq1ICrr6roeYGKekVsgV6YIQMjFlhTSlafueIs/QWuOsI5OK0Fsm3qKkZypmTL90hf16jvUGf7jF3nfWuX5phpIfpG5+qWCZzbkTbpGjUEHSdf3xlQjg0hfv8+Z7R2Tr9/ngvwxp9nLyXNM27XHtk1cStwzUyxofHk7AIplOherWJzIA6zx5luFJWkBd3SIkxBCpBmUKyFa1Ej4EZrMlg1jzA5st+fxbTKvrzMWIO9/8FLlCV8rxgCIElouGfFDQzht0bkAIhsMKKQVGStqmI9MSKSTj8f/Ct/7zB/jWoqRlPFoJd1ZHdHqBjaAAIyRKObblAuF6tElBCSEgrGR89yrSByZXx+x9eoRuA9vqClIp+rpH6oTAOe/S9xgCfdejlEpaO6TaKAlgEqEDIaKExEWPUAKiwPapFsk5h3OprmYwKHnnhiaf3qLfOeJ2Z3G+JDcaZIseFDjnEEaDCogIMs+gW7W1bBExMb1Z25P1LqXRRRIaU+Uwb1KQUWWoKkOWGXmWsaYTPbbfn9OHpAGUf2WTtprS7M/w0zlfWBtiTE5YOFwIyNKglGSwPSE4z9yVTHcdMWikUUijEEoSpCOutIxCCBBiQri0QjpPaHrUqESphK6G3hFkJHYeG1MNkZBJzJhMkmnBlXyGlNB6zW4wBJeEhEPdEYkE61IQ6hxBCmQICSWbtVxvAtY5xBtX+DiDo7t7rLvI1TYFP7fHOQebFX0t0EcdW21CBrcixMbhDmsuX9pESINSmmZnyfLDXYorG2z/0J/i7t4RD+5ME3qVS0bbE+6sfZPm8pDmsGPDX6Gg4PobV/jSt/4AGSy7Bz1TvszG5iVc6bi/uJdSBi9qKz8biSvE+dSG57EXRXKeZ2x4+rrqE/bdryd68j6eFF59GJI+/3B6sSPO2+vFpjLf7Xv52l7b528vzT4XYzxmrYJHE6pHodKT3ix9+mqWiuKpfw97EUkO/+Ek7ZWcKDX9dDvp8QSnb8iT75/WxlnHX7SNi9p5bZzV/tlf5/eGnf1DeA676A0VT8ZC4mQHkg23xnRNS7NsIAT6ELAx0jpH3XY0Nq02qxVaMlixaBlj8DEmhCAE+lWtzWh9RF4YpICm6WibFbNX8AQiuTF0zifyhLrB1h3ZqEIBMgR2P7qHbbpH3ZaC6z/4DmZY0AVH6zxd2x7fynRN6X7kmWE4GeCBZdeDFJTGUOVZIokQ4EPEaIVZBXNZngKguu3RAvJMEQRIJemdO243U4p20VAvanxv6TuHXDHjbVzdfMQ4F+HBd+7QL1Ifl4uaerpYkTho+lnDzof3+eZ/+kNs21MOCmxvwQdGkyHWevY/uEdeZHzlz3yVa1+4zqjMEC4kpI3E/pZHgbIeJQRKJRFWVulrs7bFishRcMxshzSGB4dTpPNpYi8l3qdJPSFpDCmVqKRDSDNQkxu0TjpEkUiQSZMHREqjfCgkKyRKa6RWkOSbCD5QlAXvfvktdBC0O0d00yXWOoJ1ROeQ4xJZGERrkZ1FaUV0Hr9o0EYjlERWOdiQhITjquBeSUSmcW0KjFNNkUEWGWpcocoMt2hoDxc45wmDHHN5jNkaEazDzmp8a6lGFXqQAykdLR+VKVCVEoQgnwzQZQYuHDPgxRgTtftq0cEuGqIUuLgaJUJAxHicPheaDmJMZAuAzDRRpICOFXGFlImAQZqk8yWMWjHVpfq5sBobpPVJN6xPhCMiksRevedwOmc+XzLdOcS1lqIsmNctewdHzOaLpB22NiQfJKr4IFKwVpU5wyLn8mRMLiRCaboQqNaHrG+vc7BzyM4HdxlMBmxc2UwphD5AH7BNCxFmhzNCCFx99xoq03TLhsXelHbeEENgeTBPpB0XsJNsc8+HerygrVZ5To7xT/T0ou72DH9+3PJncCmPs/O9yPFPzm0eirrG4z1O27Mv5KL9Om+fZ9ZzvY5/XttrA161eCvPmI++COpw4WNeIvh5ztWox475rOy8lbLzEPmztl8kVe+sz0+29Vle52eBPn1GJoR4LPhPH3IMGa3mtYgIo4MJ3WHNxs42fZ/xoLf0ztG5VBiuWLHIxUjoLUVukFKilFxRcatEQhAjCEkIkcO9KQBGa3Ih6K1jMqzo65aogZhQBr/q4vJwTjmqqGdLJIlN7P77PTffvo5UgmpRc9kteLvW2HsW2pq3316wx4h5ao7p7cCu9xzc8vgGNrbWWMxr2rYj+MSUFlfIlhAS7zxCCvI8AwG+d2il8D6SjSt0FLjeYpQirwqW9w+QShJ4lBhitKRdibkO3nyDw1FHjJE79zv27+yRGc2iMHTlkNl0xrqHyntuf+sWi8pgq4zMaJCC3lpuvH0NKSU7e0e00yWz//EB41HF2HomVYbWCkuk22tpWeB90orSWUSjuJS/hVLQRs9yrWPqe7JqxHiwzt7+nCgDnjSpDzEkjaYQEVpgtMaGQIxxFQgF2rrFZIYQIiGAVokpzq/Y5oJPVOwxRrSSq/0iVWYYjSVvXF/DhCnt3fvQLldBBYwvrYELiYSgT2lhSIHMNKGzaeKtFajUD5zHtj0UOVFJovVIIsJIdJUT+sR6KGYtYfXcSa2gSCmAIUToE1W0LDKklmTjkhgCQklUpiliw2jUpXTJ1XOiSpgtJb0QoNWqVkphSsXQLygm4JrA4TLgy/w4RU7kiYlwTS7RY4HQIS18xUhvA1M1SJTjIRLbngB0wbFXlkgt6Fqwyw43ayhLOPS3UiDSKcblNaRUlDZws/X0ncVFWExS/V7TNMzvp2A8qzJqNcE5z5HtWdzfZ21rjfK9G/im5/D+HtvxgDjfw7aR+WSdOleg0/qjygLtCJo4YnF7l/VL64zWR8yO5oQo2DraZuvgEm4fDJpyMqSuHbfsBsGVLEo4GN0hkzDcuAl34uOBw1N9pHjsVTxe+Dg9iX8V9vg0/MQay9Pt7FSPM1qPnKkO/iJj+WOHX/TqH6/hedTt84+/aNsnkaWrSnNdqVQ/aS1ZmUSoP/GOnRWD5ek+PDcq9L260PnaXtt3wV4+KPqeWWF43BW8NIx+XvBx+pTnbbuoPW+awFmDxnlBzUXPfVYbZ9nTsPmT2y9y/vP2fVY/zuvz8xx3QXv4i0qipGKV3nWqsdVoH5xHroRXRztr+N+3bDaX2MNhQyoMl0KSyUjrU2CQUqkSLbK3jug82mjaPqENaoUiOO+JQN/3Sb+FiNSag6MZk/GQurMYrakGBXXTYZTCNx1qY4zSKrUdAwd3PfvZmLXrWwxnHzKe7fOeKxgcVcS7+7z9e/t075TcW13awUeBbDewPMo42qkJQZPlGdtXt/Btj4+R6eGMIs/I84y6bimqghgizbKFGDExYpVCa5W0YiIMqoLZ3nSFniTh1azMU6A0W+K8o5wMMVeusbtCkt6/9Q2qLGNZt5gvXuXw0pB7X+8ZCUN/f4YS4Mcl03FB03eYxlJGwcF0QXQBKZJHuDwq2SgNstBEUhCilSTc7+h8h4OEbNgaFSTbl/40xXCNBY67aoei1JAbDvenxE2Plgq/KsWKIZElmDwV/YeQdIVCCFgf077BQ//o5+pDmthIuaL0JiL8KiFqxe5XGcONd28wnH+K/OTbWB9o+57l4ZzNK5uUZYY/WpBdXidCCsB6BzppLSmjCbnBLjtkZ9NcUgryqiSEgC4ygpKEpicsO6xaoMocozVOyRRsjTMIkX5eo3OD1BKZaUSdgp6oZEpN8wE5UEl7KuvZNi3CQLA+ITZBsmhK9GCN4NxK88giq5y1rGFtGHGio/Zr1E4QOpuQIJeC8EubgVwl5jkBSKOwXlAfCXqXyDbUuMI2Hd5F7uwlNAopEBnERUuzPGJ/eQfZe3I/pjKXCVoy6APXlx6L4IFSfHR5kIgVOkuMkXJYMa0bjnKFjBEF5MDRzgF1kbNxeYP8jS8y3vlt5Kd77O/tc0sM6TYnBOuZjAYEIYhCYne3Ca1j7/YOXdMhpMT1jtH9McNuzPqepxqU1NMlUUBdvYlZz5gzZ3/7v7Nxc4NgDoh/EC82ZjzhHx8fIV8sveoce1pDFx1znhoQPeXAi/r51fh58et+ck9x7paHnz8Mbs6bPDyqAjq7D4KbSvETeUHMYkJ2lSIS6dvIjvPfQ/Ov1/ba/njYK0CKnmMm/CIPsHjy5UlBuoeTVuBJ7brjfU5B1xcJZp7lvD/r1ZWHQc/pfpx33lfpHMXpN5/BxX6eq1MvCSCmDMyIiOKxAfBks0qrR6db0eU6H0HBsmmJPqZ94opdDoEPAWxiGtNaIXQKgpRcrfyFkOpIROqEkqn2QgFN0+K8gzjA5GnCqjJNWDZYH/BRYntLVhb0folAoKLj/vt3KYYlw/WEfhVlwWg0RG9p6sMlj/RPHl1dVubkuaKpI03T0fdJFHS8Meby9UtIo1KdiU8oges6CJFcpn57rfCto+s6yiJn2XW4FdKkpEQAXW9xvSMEj8kNb/3gOwmZiNDNm5TOJgW51hxOa8r3LpMPSkQb2dhaI/aWuswRCnIlURrGkyF9b8mlSMEhEb0S1JSZJliPkArX96AkRmqE98S2R2aGbG0E4yqlJUowRUYbPXt3dpAi9d26FJAGG6jKIt2ftieKR78DsdINevg70Von+muZoFgBqX5GJzay4FO6WAyRUVlw/c0rFEqlWqDeITtLLiJRKzIl8W2PHFf00yX55iilSPmAHOQEn9jltFLIwiTigt6llDQBKs+wh4sUHJU52cYoBdSDgmh9EoPtHbowtNOa3gWykUFoSegcZlIRfSBYl2p/Mg2kvgu3ohzXGl936FFBP29RxZjQ+uPFBiEgWAeFIvgePSqRvcHPWsxkkJAmAVIn1j6kQKuEBsbVOYIPSBLyBDHpCWmFXN1rmSfKb2U02bjCjCtmn+wQpWIWHLmV6Xnygd5ZQqnJckM1qggusJgtWL+6CQJs1zN/cAg+oETEOI/vOh58fJeNq1uUGwPG8gom0+yXgawq2d89TAKxZYHTqX5PiIIQA7rIyYuMue04XCzI8wptDOVogO8sqjCE3tF3lunygPJLI4aX1ugOu8cd0UUzAT4ve95Ft5P7vfLx4dRNio+f7mlHiTP3FGe8Or3H01o/PyQ96zghBEKpUx+e1/bzhrivNCR+ba/tj7S9AqKFF8jAvWhqGI9lKJ04TzwRAZ08+9kP97k9vCjS8zSf8bK+5Fnoy0X2P30d58UxL4RsPdnQE81f4Hs8t7nTY8OJe33mZZz88CK+/EUQosdUZ+OJurRHobUAvqQNW2pV8HGsGyLIfGCnblkua3wIaKHQSiJjJApB7/0qLSoVSCutkFYeByJFnpFpTQCUkizqBiHThFlJRZ4lxGZZt9iuR5clUUvcCvVAgBQwP5gx3hjTL2syrViUkTutY/c7t/jB719nPbtJbGfYeItBCRvbm3y6uobV/49vgwtpKaLUgt4HfITFdInUEhEivXWYIkvoCDDKDTEEugiud7jeUeQmoSa9Q2tNbjRdb5FKUhhN13Z4Ce/+2JcYbAwhRmY7Ux58cI8+UxyOcmwuGY0qtmcds505g7wg9B6dGcysYbQA5xy5yUEKssIwHx/gKofte8SgxMREBT5ZtuRdgODp6zkRizMKVWZUG2NUWdDEO3glsT6QqTFHy+44vS0SCTHSdolifbGocauUFqWTaxWRVY1LSoVLZBnQO5fqySTpezMaRUKbYggUyrC5PWEiWtT+LbwURN9STAa4gzm+6ynHA6KSiZVNCFRmEiV7bpCDgpBOdFxLZIYFzYMj9LBEEBOCIoAg4WHgsOpDvz9HD3JU1EQlcXVP11rkKiiJK1QGRErLCxGdGWIMCfnJTfonPVIKumqd+4cBRMFyHvC2w3vP5jhQVYmRsCwFUmqEllzaiIyMJIqG3d1IyFa1ZT5g6zoF1HmW6pAEXB53IDWu8+wuMrx1mHGVECoSGgWppq0cTCjDNmW1zqL1HFU9INBKcMUbpk3gKHqWRwv6RcNwY8za1hqCiMoMOtNIBAe3d0AJtICRyahaS/PN2yy2IxtvfB/lxpQb9iPsXsdmrahnNdg549GYtSbiRWS5bJmvVRR5Traxgbl1SG5MWjwpMqy1MFR8qj8BFbCTiMlTnZQqFFvfvwkBysZz83aDAA5D4BvWPsX1PZlu8JkTFDx0mhddY3uO4OizYJx72OHP6q48HEmehiIB3Pae/6Nrn9jjvvenjjwrme8CJuDMNMTX9tr+hNpLB0VnPn4XnnyfN5s+K0fs2c08cjQvMP9/3snzRYKTl7WXaecit+6i7Z9a8XvhRbznPPCzBJOeqnx+rBj/qDD5sb6sxqz3jOZL2uB6y9GDQzZvbIMQ3CoLDq9u0LtUc+F7S7eiGE4F4KkRo1ZsWQ+1ala0y/OmxWhNWeSUZU5R5CyaNk2+k/4pbduhswyhUwpe0/TkVY5aISEhBIL32LolSokLkVpFZgNN9I7sGzN+4MYV+voGzu0x2hRcefca2J6TgzJiNZGscmYtBCRGRTIiLkZcn1Kggg+EzkIMGG1onF/p6qT6KWst5WjM8mjBYDIg9EljKIaAHuQ0iwYXPJtvXWG4NQYB7bTm9jduoQE7ynkwyrBWsb0+ZPJgxpXaMRAOnRmmsyXae37sh94jhsDtb34KRYYmMptMsZs1OM9Hq2BUS8k77ZzB0hGFQAwU2WCAUgKdZ6gyxxOZuztYEZEmw/uKAkUDCCnpV7pOwQe0WKF8K2IFYzRd369+L2lbJCKlTJTRakW24FeirWG1PUQ2RkNGowFCK/zRPcL0Proq2LyxSXswo48RvTbEVDnKB3ABUZikK6UTS2FYoTf4gDAgtMDNO0AQ+zRhljLVEhECvnMED/laBTGlpaEkpsxxTU+9N6PcGhHrLgXBR0uElpjtSaodGyS9JJUbHC6lkqpUR9MvW6bNkEM7IvYrUgjryMcVa+Ml6yOLWtVG+WWPGhSMmDMYRAhwpEvmTU+uUj1FPhngmg5VpiBcCsGmahP9ubPshLUVMpR+v1FLJCkVDyWxh5bRrGQi36CtGm6ZGQjBJZFzZTxko1DUPvAdEj35/GhO2J+mNM+qIF+ReDRtx8bmBLtsGC87rquMXmZ0ewHx7jsEecRmv4ObHqEQ+GiYTVv8g13wBxSFJAj4eunY3z/EzmeMVs/UtS/ewHlPoXJcBUcbe8QMBpMhqDylpwKDmyV5lbN56PjxnYAEPnSWb9iXEPP8rOysRawXQZPOtGcdfPZi6flhz+N+//y1y0cB2ROXd84Y/FjWyqnPT6NSd73n7mqh5fHg7/TZxPEer2b6sWrpokHsa3ttf0zsFesUnWNnIRknAyBxeseH208cKJ745NSrs5/cMz+9iNc43exZDX0WCyynkZMX2f88R/a0QO5p+7wKu8h5zvoqn7bfs871cGXyrPOfdcjDlArx8D+nG3zU7sn9pZTkRfbY/uPtNerpksXOUdKeScwKyBMDmxIC6x1CJaHQaljRtx1KSZz1zBdLfJFTlgXDVYGttY4IrK9NsN6jvUXEQDEq6bqe0fqQndkcpRTR9jSLGpNl+K7DKE0Iqf6jPprz8YMZi7bn8qjk6pc204T+nLlU3/bkZSowtzagVOq/Dg4V08RUS0EIkhhDYqCrchbTJUIJ1rbXEi3zxoiqzJndP0IZTYyRerrEhcDw0oQr710DIWimSz78r++TGY1OiqeYIqPvlmijEAGUUuTG0IeIRnD9izeJMbJz6wHBeUDgIgghwSZq8ERIIZAIxIrxLN8co3KDyRJKgZaIuKotUhLqDlc7ipEhCk3T9yz7PpEqkAIh55OmkDYa75NQKyGhREImJjvnPHL1gwzBY7QhBn/MOjgeD9nYGiOsp581dJIUnPeOrXfX6faOaI9qIoJsWKCKDOoeMkXvPEVu6JddYpOTKbAXIaKrfMXE5xEqMdwdM+BJUGtD3GEKGnVnIVMQBX7WINfSL7YY5NBaYu/wuQeZiBds26c0MmmQmcbWXSLciOBFTxxEdK6hjshc4+qOYF1KzxMCM8hRKqFjIJBFQpuij8eL2NnGEH20KirPNKp4yC4qjuv4tJJEH5BFRugdcpCBSIx++EBwjhgC0Xq62RSHJUpJIC0gZMYcB6lOSYySqL6jqxvK0QBl0rV1TUs9X6JiSnvtpUAYTalgvjNlcnWDajJAasXo0hixeYl2ryaGgCkzTJGDjxwcFNRdj3UeNTGYTLFoGtY3N7j63g3MsCDWPTrPGF4pWN/cpA89g8kAHwLBBaY7B8QIw7UR4/jI/zwx0T9ztn7W6+8hi4+/fFovH9NdOl7Q4uyjHpt2PPvaLxJqnTu0nLPWezrweTF7cgH5oVLRyaDryWt8znSO1wHRa/sTZp9NUHShif1zrGnEk7PVpzS32uWFnuPngOuf2caL2KtEmV4mgDvra3nV4+bngbI9swvPPlF8KHx4zm/i67bnrk8IUBzl0CU63S0fiCs2todriHme453HOod1lojAmJSuJGRMn68m0qNBxWK2JBJxMTCbL5mMBpSZoTCaIs9Tah0S6wQyCvpFmyZLRYZetNzMND5EjmLHdABaCN6UkktR4AnsFYaPfMNUdbz71R9mtlUSgdZ/AO4QInx42HJ/kfRrKDaw05QCl+cZzbKljx4lZFojfSg6GsGsyB26tmM4qjBFhikzlodznPXYeUsIAdc4rHcQazauNbz1w+v0xSG3zDUWs0g9yCn9av1TSup5TSTyyd1djqRif2Q4qBQ+BJZOsPPBLdYclGXOjc0RG6MSISVXQ6BbbCKBw+YTnF8QfSBHoiYlMtP43qIyTVYaLo078lITouPBLCMogagMk3LBoHXoOOd2zOlPCLAapZBCJmY2nxjVlBIILclsizm6lxAqo9NvSkkuDQ1XtxWDtRGLfI0jv8F0b8qi7dAhEtpAXLSsbQzp7u/iOo9fWoSWSBewuzOkAGUGFGWOrzukkYkavLMQIrEwiS7cOtS4QgtBdEkTKtFvC5qDBTEKzCBDlRmiSal1oswI1hM7i5/XmPUhMTcIUkAaWosMEbTCxT4FxmVGXFFmzxaCfhnJtsYc9YGoAiLTbG0IBnmPUJJS+kTUsNLsEiohXfuLDGdKIDJiyXDk0YVB44lRE43h338cqS1kMvATNyPaOUSEG5sCVXU4L3gwNYSYEDqMoJvW2FmPWpdEKcl7Tb6f4QXMOseHzYwoBK0UvCVESnPsaqIUSCEwZZYEX7XmqNDMC4VVikUJfXTcamu+9MNv0U8qBHC5HbOxdpXgAx8etcy2MqQQXLuqkbXl8M4BfW1wteat8QZXtjfoXIPvBdNLY4JRaGDj3lWmOwcwEOyM7lFNKqSQNE3P7u1dTCeJYQji7IT2h6jI4/W3n7GzPWs+Hk+9P21nfHbxXj701c+YJ5y30PaCE4fH1nrPOuVqBe1ZY86zA7Cz0K5nHXuBAf2Ja/8eDZRf22v7HOzzQYrgnOfsZKrbxfJhz/ZnJ5UYXtLO8x8v2vDLTPYvguycRkXO6+d56MvzDgZPu56nL+c9u18X6dOL3s9nXOdZc4RnDWIfe8/H3h/DRnF1zI/UDe3tlvpgDhGscxRCJpa2zOB9Togr9iwh8SKhCdalCWJzNE8ojFQ46wkxUrcdZZ5h255WWuquR2mFkgJnbRI0XV3fMAry2iZBykJSywSzbiH4Ea2pbc9vVznf0VBnkU9rw3p+Na38z+4iOCQCd2epVkYIwfdf26Rtl7StZTQqybTC+hTkRaUSGhMDvXMEIPhUzO98oGs64n5ErwgPTJZ0W4KPeB8oRoK3f7hAmftMQ8/vfhCZPjjgkhJsdJ5ASjtUWqCNZGo99+dLYmXIM8GisRRrBcO5ZIxGSsmkyrhUmES73K4l1ETA7fktagKqzJDrhuA9qjCYcYkxClMatjd7DC39rGenHhGXFpFp/K2PUpBSDTFXb3A4q491poIUBBewwRPySOgdVVUkdMxLhoVCj4bHekZSK7bymmuDGVHM+LRXfDRVLBY1UQhsZykGBVEKxhsj3Lwm1i3Re7JJhSwzlJaJvGPFrCeNXpE3pPQ3oRURcHWX7kOm8fMGpEy6RcOSmOvECkikmFTgAmidKMLrDpxHjUqyzWGqz+ksobXY2RKkJMxryDQyz5DjMqE2ucEvO/rRiI4R/sDB0oKuEVpSqY61rEUpldIIPas6JU9wCTFaiA2WtUYqwZuDfYZjcG2D0gYhUjf/+73AUScYKPjT2x4pAjrXbGeeyJI2wN26QpY5BKh3pzT3DjHZOiE3BOuRXsJMY53FR+hDoHVJp2rkA11v8aQU0rzI2BgMUFpSjAfcGRmciuQx0jQ9SzdkcTRn+eEtLr9zjcnVdTacZBAlQkvuN569JiCJvP1WzziTjG+MuNK8A7JifjSjb5dUkwmH04aPMsW863BHS348Znz5za+yX+9xO/uYZjanGhhWGre43h0HljzN1X3e6VDn+euz+vF59euCwdizG/juBw9PjlFnYUMnZ1ji5K6v7bW9tlP22QdFz3jwHk4kz97ydP/1WLzyIg/48/i255nUX7TN5+3HRdPpnndwedF796JO9azrfZUO+kJI5QXbeY7jBYIYIve/eRs5E/gQyYwhNwYhBEtrVwX3SThTSImIKxphociMRuUZvbWoLE3Yzap+oHeeKk9dCs4TQ8RZh84zhFJoIbC9w1lPZlQiM5AgpSDaHh8CsagQRpFhkMGnlCEqpg8OuB8kl794PV20OP11CMqNEe52miT3TU/fp6L7Ks/QRUbbdGiTriECWmXpmusGoqBQiYrYe0/X9iAlWaZBS97+UzfR2Ue43vLgo9ssG0NW5IjWYV2PkpJMK6J3uOBREYSSFFV+rIEzHBQMuoDqBVIpVIBoXfoKQ9pHSkE0Gkye6mWMxhtFNqkSwmE9IlP4toflgqgzMApZSXznUo3UqCIEQVFkXNmYJMHOkJCs3ibqZhETY5/ONDLTZLJB3WkSiu1DYsEQKe0qCpJobV0TuxRIahcIWWJXK4qcdn9Gd7REdBYzyNFSgPXIEBMj1YrcIDiPKjNiiImIIDMgEl18WDHMIQTohJKoYZEQpcYSQkJFU811hN6C82RX17HTGnqHPVgcM8wF5wkkSnJBCurFCgXzswZ0qq0SAmRmiEYjjcL1lii6xN5ndPqt6YSqqswQdQAhkVYhokqU6blB6JC2x0TrHpw7vnahBNLopA+7EokVrFLydCKJcNbhZg1BCMQq1TWrCmQAL1IKrFQKu2hZLBsGK/HhzevbAPSdpVk07HzygM2rmyitiUONyg2htZjCEKVAac3h3hG9dSyO5rw5rpkUJ5b+BAghV4sDCqJk9/4S53q8tQzX1ymHA5Z94PIXrjGyFnuwwP7uHQiJeEVphTYamReUKuKsZ1zm+COX7ulTXNdxitXD/F/x4mQCTyU4OJlf/LBHr8ovf9ft0YWcVZd0+rPE0/P5RCCP3+IVuyN/xG/3a3ttn6N9fkjRmZYe14vz18VH2FI8EQx97yzcPGmfRZ9Oe7mLnuNVB2oPA6PTX594Djd8XvvP+/lz2JmDeXx8jzM3nbwn8fG/P2JytoXk8N4B+9Oa1pU4a3lrc8y4yLDe862dI/rerhjixPGglZsk5jmfJzFOY/SxiKiRkvGwSjUyziO1ShO7hzTePiQB0VXhftu0GKMJLiCImGpBsX6Y6ImXE6y9jDaad1vPplJIKZiqwNHdXYL33HzrDS4NLgPw4eF3mPczIK2U9yHgnKfMNLleFcbHiA6ByXiAlBLXWXSVM9s9QueGvMjxvcfJVR2LS3o1MQZsCLzxQ+8gNwd8pyxZ1jN2pvd5NyZ2s8wGZKYQUnE0neMmeWpD7THenBJi5M1+i2tiHRFgurXkgTxExkg27fELuWJGS2KlelThK0dZlPRdjyoNxSilzyEEMjf4ruf2TJGNLuG7AGWJcC0iUwQB/XTJ4Po2wu0QpyCMop8u6a1jvL2GynQKxmpQIUd4hYg21fIQIYpjkoWlNdzxY+yy5ZCCPgSs9eTtEXGxpFCK3Hd0yxm+6fGZTuKNPiRdrEzjnTsOPlgFf6F3KQAUKQD3PiCqHGk0oUk1P2iJXbSphkpKVIjYeY0IEVWkFDE1LNNPPMYUMMZItI4QIqrIkTEilWI4gvWyxgw8s1riqwEhREZ5z1ppCdYTegtGoycZpU4PUQRC3SHzDKVVErFtHdEFtgc5I5lqoP7T7cjCghKan3xHMJKQZ4o//w70TkCI7MwysnKEInB5UBNX9VMqN/hgqY/g4+xLdIVEioxbUiCcoy8kOwNNN+u4VBVsOM+QEqkkznmC88xLw3J7Dak2kfcOOXhwgDmcs/g0kpUZynvm6xVepNTJ61ZQ7ixwd4+Y3yzY+tIXCD7yRtVwfZjIR67Wd6iWHb0P3Pmhjns7OxgR+fIXDqHvWDOGhWzJq5KpP0JlAl0YcpOzcXWTznaEmNLhBpMK3ICv15poPfF6RWy+fb4DPOmen2tx6/Gdzw2n4qM9Tv550Zn5w+XRM8/3spkcL2XxzDvwtEXe784k5ezKIvEyC5uv7bX9MbXvclB0QXtWSsBF7GnoxFnbLurDXoVTuUgbp/tz0VS1p9205/HTZ8Jzz9r5nGMves9OByGnX5+0M4Ozs5t9yBT02GArHt8jBd3P+MWd2PyGUrzh4Rvv3yGWY6ZlifWaoYbNUY6znltFwbLtiaxEO0PEC4FbUTpHQCJY31rHtj2LZUPnOsbjAUYJQmvRmWHZ9QlpCkmU0nmPUpK8ygmtJcpIIJLnGSbvKUeHCKUoQoVYpP5ey3M2rSUvCj4wjr3es9w9Qgq49uU3kEZxd36beTcDEZFSsPXmNve+cYv5skVKgZES4QOuFykVSSu6ZQvLBgBnHUIn3RoRwDuPVILOOvSw4N0f+iLlqGQuJF//FJoDwSjf5q060NYdkpTKJUhF/XmuaesWVc2R+h6Z1lwVI77SJUa/3ytq7pYHKAFN17FoAtImXR49LMkGFg0EoBpVxxTUkDRw+sMlobO4vELUEu8DJg+4zuEWDd3RIgUdMcBsd0WgIKkGGZUAJRbE2iVEZNGhKKAB1/aEzmJGKb3MHi0IUmAR1Jmhnzvm0ZGVEKSiW07Jmz2yLEMEIARUlZNvjhLNtpKoKrG9SZMCTTUoiD4mAeAyw02XeOsSLXYEcpPEVXODEYKYB3xvkSbpIkkJqsyJvcM1HWZQJga7WQN1j0+SUWRbYxACA/hpDUJQlD3rpiHfLLC9Y+pBSEGhLRsDSwwB33uQEWkCtkuIKasALK6K4/tlm5DPQlL4JYX2oA3fvut4YA1Gwv98QzI0oAR8eTOloDovef9gQN1q4mLOlnEoRSJHmDW4RU+zEOxuvUFjA9Z5aNsVE2QkrpXIjYpl59n2kSxPCN5QSg73Ztw6dNxb5kzWJ3zf1Q3KzjPdPyLXhqr3IAVz06I3Bpi1EW9oB3f3yQcla+MbzPc1t775Cc2i4b0f/SKT9RHj3QfI+ZTFwZQHVzyzDc+lqxNGV3agXbK3u6S1b1DqdTauK27+wBdY7C1Y+iXNZkvTJuQxyzOOdqfU046Cr5CNC4J2Z7ur45nwI9/4fMPX6YHlgke/ZMAinjj3Gd35rgRHT/bpibsiTr14ynrh04VcH7V/9pnP6t2zxGHP78tre21/Uu0VirfC8z9hL5LnFR9/+d1+qM8LFl5FsPS0ts4671mvOWO/89o6beddw9PyxJ+2/Tw7L/h5FXbOICRWJ45p8f54RRw4oUt0qomTEwnxKENEHPdZoMsctz6hd4YhgkG/JDuokVlFZUxatUfQhKRVlArlM7z3QKQsM+aHM7z3ZJlBKEM5KmnnDT4mXRyxQpl8jISQdI2SHk7ql4ugM4UUEQ8Eo5E+IoVMk9GH6UJBgXWY1echRA7v7dM3PVe/+ubjFwtsv3mZ0caYvY/us9yd4UJAep/S85Si6y1FkdF2PXmeEYMniohdsdMRBdJkXH7nChs3ttAmITTNtObw7h5FVTLcmqD3auSyIcZIb3uKIk8oSO8wD78nF9C5RPqIth4lwEBCL6RMSEFrQSuyjSF971B1h8wN+aRKuk9VhsoN0fmUIuZSrZGPETdtQArqnRm2t0gfkhSVVomowDlElRgBRe8QmU7BS26ws4YYQiIp6B2qSOdxs1QvJFcpUK61+GVLO6/pZY4pBJ0QlFJR+ojqU32WHhRkVU4E8vUB/f4MIwXROmRh8HVHbxfIzKCGBWHREhD0jcU0qfZMGpX61Dqy9SE+WPSwJPQWEwNISbQuCZ2WWUJ2hEjU3Dqx9VHoVeQuUIXBNz3ESDYZUKyJlIqlQa+os+3hEXGiQUqE0Uit6Ns+pTJmmtBaRJUj0qODysxqgUCAUelZckloVzgBcUXIEMD1KcUUHxLrnFJ0tSWvcqKbExCE6DHDAfWDGeghnfW0naMaVeme4xlvTGgXDUEKVJUjFo7R2pByXEGMXH7rCsNcooPl3od3eTBt+P71CcvpnK7vME5iQ6DLAovdHp0ZLIZoHaMi4/DWLsOtMUe7R0gt2b21w2h9ACQdoo3r2wzXSg5nU6pRyWDNoZ2mcxJ3x3L3/TsU1lDeWqPISrrWsjxaIDJBMSwTy2RMtPDWWoIPxDI+4fZOPMYvb485wPO2n7CLjNHn+On4mB8Wpzd+1+w8Ou9zb/EF7v2rYMODx4f/89p8DRC9ttd2tr0C8dZH9tn7qM/RCz5vQPCq7CIDzel94hmfvwpo/FXB68+6lxc57mQQfFbw9UI/DYEQq/z6E+d6JN6a7Pr4DS4Pr57KoxOsLT+l7I8QES5LhYiRjWubSLeL+/ge0Uc+ufJ9fKArijJQ94lhzodACD6RI/hA6PuUDicEziY0xWiNdR7bdvTOMxiUqNxQt32a0CPAe0xmsL1lMCxTvUphCLlHb0R8dPjc4UjB153qgKla4ESiiJYRhPcsC0sbIkpJ3qqvsdYI5Md3eHPtKjevvImUgje7XYbtXSKC4VffZW9nwv1v3abvHSEKhkWG6Ho668iNwflAiJErb2/i+m8iREAMSj71PbdUw8F0ny9tfR8iJpQmRHBNRx8Ey4MZWkkGRrE5zFesX1OORp8ipETrFmNyVBDUi1vcm94FIchsx1uZRUUolg5hNHo96fnEZdKxEYOc4APZoEAoSegsvu7xyxZZ5Xgh8E1PN6uT+Ov6gEoPmd/ZJ64m827epmDWR/KR5tp6T+iXdHVgz24QOoswCnu0JDiPWTHSySpnkG0yidfwzjELd3lw7w+JEcq4j1gu2VAS3y3IVGLV85kmyw2WiGx6GiXJygJW9NNSK1Rm8N6n9LhFi687RG6Is5oYI2GQY4xOxfg+0M+aRM+daUyRwbDEtT2u6dGZRhmN71oIEec8USc6ajMsIMaEEKkhotDgAkuX8clReoDq1uF8l36jRhF7R1SJ1lsIgck03vrjRznaxIQXY8Q3XULAGpsm+86jlOJ//5KksREcjE169tQq9dP1HlC0s5pIYoK75zYQQeAWsNZ/gcHgOvddpHeB0caE+nB2jMoOAmw9mFOOSvbnR/y+kjR3p2zdUwz3F4llb5AzMorN3FCJyP79PbaubfPhcsktPD4EJlIxmvUQe7resT4esn55k92P7tGsfgdSCFxnCcD/t+/ougYpBV/5VPP2oWM4P8SZhuJSwaVrE35CO6yTzPeX/P7020ShCXnkzYMvMN4Y091u6duetUvr3D36lLs3P2VyeYI2hvi7j3u6ePrF8QJPPP74XETmtMWTL+NDT/rkdnGBfU/aGX78EdrxeC8/Tzur3xeqxDpvzH7h8erZ9nTtpTPsM+zLa3ttfxTtlaTPnbGmfsqZnWUPCwBf4ol8Hv/4qn3pQ//8vO1eBP05aS+y6nbWvqf7+7z9eB57Wp/Pu1/iKdvPCwKfpw9P3fHkoHfqFxlhlI+5MrhGPV3S1S1KKwZrQ270+4z94nj/pm7ZvL7NtpZsFZaP/vBjPsHjjeGo6xlOhly6so63nr27e0nPRQpYCX76GAgxEPpAiD1SKdbXR7jGspjOKQclRWbogkupa4B3DhciocrBJyFOUXl8ngRCVZkK4aOCA1lzpJZpdV2l9CVdKFxmISYa5iFXuG4q6r5n95MlYSLZfucKa919iv6IiORw+CaTKxuMtiYs92csDhdIKWnnNcuDOWGlkVOOR2y8sUFRDAHHvHXsfriPC5G1fI0vbX0FEJg8Y7g+om86nHMMypy+6ZFERgoypVhklmF2sNLgkUQfITp87OmygMwMufeovRalJSHPmLUdA+twy6RjZKoclSV2OrdoU52PDwmFGuSgFX7R0s8a8o0B5eYYIQW+7RlsDminXdLkKTOUUYncoPVUboEuFU1muPvhHD2skJmma6aYcUmUEpzHLzu6aYvKSrAeXRukX0F8fYvr56hBTpVpXFGgBYmoY5CzmC1ReYYMAWESyiLLjBiT/g9dxB0tUIMCtaqTEidqeR6iOnpQgPOIKk/U07tT9KhERIMEdFUQQ0Bqha87Yoi0yw5vPXJYInrHQyY/nWW4eklbe/o8TxpETaB3DfmoRGYGoUBoSWgtwXf4FfJDiIhcE13A1Q3Z2jARMkQQRhGcQ2UGIQU3i54oHdEEhFVg8qQ5FCRSa7xN1OgiglCaaSPpFg3+KPJmNYJYYAiI6FkczSgzTWs95WSAmzas+0geYKEU94YZLpfUteXG+oTx9hqLwxnmaEEIS7xRVKMB40trXLv6BtZ2NIuWzXszyvqQru/pXWDzxja6MKxf32K5l4Kw0eaYd3/0iyAlnzrH1FkyIfgz+z3rooJpYDarcesGkxvW/BShBKbosWPPtIehGXB1dp31bB2Rp5Q4IQXVuxV3vvAxptA0O83ZPvSsSbo4f5fns4sd/SJpXE+b5H/Wa5QP236lccNnHIRcODB6DRe9ttf2hH1mNUUXee6f3ze8Ivd02pN+N5zDRUegs5ARTh37MoHTWXZWv552vudBgl5m5H3a1/+i2yKPaRGJE8NJJB4fe/TgkG//9jfJicg8I0jB4PqC0WSViBcCXd2hjERnBRs3thhf2WRj+8fozRjvPXe/8SnTvSmpDqOgXjbH9RSRSDWqKFY0zjGCyRJd8qJzICRKSFABg0ZlkfCQAa4q6ZqOosxRHqJIOknOe0RIAp5eJhpjE0EJQUCAFIQQkoiqD7Qh/fMhUGpNJhUH9w749HDO2miXK1uJ5jkhbKC0YnR5ndGltdUNiwQX0qAsBFIrhFqlQ5HIIY7vrxC43vHgO/d5UDfYSZbSo/qAbztCCBQqp1QaSUR4v2KaiygVCUIkWu1KEOc1YbYkCEG2PkSUGfVsSVUWaCTaxcT05QPtwSJRmSuZUI8m1XgFmTR2VG4YXVtLyEWbdKfqj+8gBiUiM8Supz1ckG+OUIVBuA7hE1ohlKS4vJaIJeoOfKSf1njn8b1LQqqyhJFDQqLPHpZ4H4CIMqlWSJU5skxBiu89wXqGwxKGBbFzSAFxFVxE6wgrRjs1KPCLFjkuQclEFe48SitCDIkEQgjCvEFvjFC5pl/1y/eWrMyxRwvkiq46Wo9b/ZUCgnX0nUNaB3kKLtW4TNfmUkCuC4NvInL1mw7WIVWGHhRJF0kGQmchN0idtJCyMgMEaqCOf0eEuCLlEKhM42JEuMRk53uH1IroQwps3cP7mYKvelrjli1ZLBLrogR8RDpPlmmCEMwXS2zfo1xKMV3sz9GTHGUEUhnEsqdtOvzOAYujOcPNMde/8iYmMwglMbnhaJgxzgdMpODKZIzOcvZu7TCZVKxfWcfkhnJcEULganaNm9/3Jsqk7+KhrzleqVoJzV56+yq1XbLYX4CPaGOo1gpiISl14Mb1mwy+WbH70X3qeU21NqAYlpibhmJQnL9QJx66spP/5Xj6/OIu+RlHnhi7Xpzn7riJxzl8BIh48eHuRYbchyc6Tj88J8XvmSjb54rIPOd9fo0Wfdftl3/5l/nrf/2vH7//S3/pL/Gbv/mbzzzuZ37mZ/gX/+JfHL//pV/6JX7xF3/x+P0v/uIv8s//+T8HnsyAeVY/fuu3fouf/MmffOr+//E//kd+4zd+g3//7/89d+7c4fDwkKqquHbtGj/2Yz/GT//0T/MX/+JfJM/zZ577e8VeSVD0uJ9aTRKfedQfwafwPMTivIDh9P4PR5/zgoWTxz/r9jxtiewi53haP8/qx6tElE6POs+L+F0kxfD0+c54mwbUR6Pqe8bwQ9o81laM0AvJH3z7NtEFRqOCOqRjj0bvINdLhIDy9v+A4BM7GCnQUkaitERIgRaa0daEvU92KI1Jwq2Dit5a9Eq3ZjFbsjxagEwTdm10Sn+KkSLPUAJsWDHB2T6lp13fTqKphwuCC6mIvlZwX4HzDLfWyIaGKGGupjR5jQScDygBTogk7GkM0ns+yZYEPUc5z/ow4+p4Hesc798v+WCmWb+xjfEaodOX+DDAWV00KpOnvg+D9V8BEdAy8pXBEQf3Dihsye29T7GzGjPoMMP7SCXRQnFnLaXAzaTglpHIENFtzTu3lqv0uYfBmUXNGmzn0VWBHBaYUUWMkTc3v48Rqe/77XdYLvcJS0DpVHeRa2KRoaocu2gZXl1HBE9/f4et7YjOJNlkyEcfWdRkTD8PXBl9lXJzQNssOAofp6AHzQeHQ+RUQJbRL5b4pidYByFiFy3luuDSjxt8BDdfcPfu18nXBzSLI7RIaW5mXGG9p1obICOoUYVftiymM7IyozSGK6OeYrAkRNiZZrjeoXLNJXlIVUC/O+O+HOJUEm/VkwGeSDYsuJQdUo1zApKPj0jpgplGj1JQ9hA1SzpBltB7ut6iPIgQ8DqlqBkEIUZYdmRrA2JrERLszixpDRlFMa6AyFGT0YaM2Ci2h46RtmiVpdS1lV7Tf/wUPj469RgLwf/2jmA7Cymlb4Xwxcxw57DABoUInhvrLZpUu+XnDXJjDbts8dMloW7oq8hO+3u4tudIlujyi9gQsdYyGZaEEFnEwL2raykNse54a3dBvaxplOQPS4E2gTe/dI2NomTv0wfcrmvUl64zyEfM95aEKlGva6O49M4V1q5ucKm/zbD+Q2IN/6nveFAEKCK7uzsJ6UTyzvp7ZCqnn9fsaM1yWBKN5O5HJU5Dsztj7f0H4AOizPlT65eYH85ZfGvO19//H/RNT1f07Kh7yFqwYda4/MYlskHJibWc9Hf1JopHjvBROl189Px+lvYKJt4iXcSjD44Xsi5u5wdGp1cfxZP7ntP/CwV7n8N05/Fv9zn69Box+p6zf/2v/zW7u7tsb2+fu8/+/j7/8l/+y8+xV4/sk08+4W/+zb/Jv/k3/+aJbdPplOl0yje+8Q2+9rWvce3aNf7hP/yH/NW/+le/Cz19fnvpoOh0+tuFn/0XeiBfkWd5WSdwUQd/3oBzkfO/Skd10UDr87SzUvvO2/60z04e/9xLhvGx9yMf0R/cYePGFuUkFUP3bc+3Pt0l1JqtYYHKC7RNE8YP3z9ATr5IPixYW1tjUPhHtzpG2kXLx3c/YtpppBCEPq24112HYaU5IiVZblBakeUTuqZLtSHeI1apZUqlWqMIyFWhvo0RJVJK2PzuPr335FLSBU+uFXEJIihMr9E+Im2kNUuaPGIRSCI+gpKJkjmGQFnkuN6zK1oMsGYyhgFimXGrWmfpIrNbHeLOdyjWhgw2huSDgrzKj/VRgGMiiOgjIUS8LWjnDe28pXvQMgwlzAOeJqU8CUeVz5Ex4KWkqZIipZCrhMYQ2fCW7V4gogdvE7qhJLLKodLYECiEwC07hBBkuqAsNsmiZYpAyogsylTwbxQxpJlj8IF8bYBdtIS2J6ocvXiAKQRSO4KaECKUw5JRvo1pNRmGafcBsZQEH9k/svgYkT4RLOgVYhFjxMXIaL1i/F5ONq44+MBy/9v3OFom3SRtNGZQQIiUo5RWZ7bGhN4dB8NyUICS5NQUqsP3nnZukcUYrKccB4p2jhItZryJlykYjyRGOeE9eTMny1r0ZIQaZIQu0q/S7XzdISO4WZ1S8ZTEC4+wAeF9Qv2UJIhE0CFCxC874qBAj0v6gwVmY5COW7ZgUn2dC5LZokcQWavSPZeZRip5/Lg+WMJ3Dh93UVLA/8WBGOiEaq7qjoQxLBqJMwUSTwgt3lqEALMxxMXIcmeGny2Qw4pya8h85wHOeWo1IpLY7jIpoHN03tG4wL22QWnFVojckBq1ts5sc8BHA0U9r9nbmTG4N8VZx9LArfc/RaqkrSRX/l3KgvWvvp1os+s5A3dABBb1kl0fVg9G+qOE5Evb30fWGr79u59yYBQ3v3iT0Rsb3JuW9FKg4hrsWdysZrw94cH/+SmzwzlRCLxLqbGmkCyHM4KILGdzlr+/4Es//uXHXGV84s1Z7vACSMeL2HlZDs886ERfHvPr4sntZ5zqPHv6dnHi1fl347kSHb5L4+3LInKv7btr4/GY2WzGr//6r/O3//bfPne/X//1X8dae7z/52X//b//d/7CX/gLPHjwAIA//+f/PD//8z/Pj//4j7O9vc18PufDDz/kX/2rf8Uv/dIvcffuXf7xP/7Hf3KCope274XViosiD6fRjZODzVn9l2d8eBZ6dNa5ntaf81ClZw1Aj3Imzr+Wk/0UTznmae2/jL0M+nRBO5mCIRCPgA4lGV1ax1QFEZgdzLj1Bx9zlxuItXdBa8g0ldEIKeg6y51v3uLNH3qbh/kpD7vhfeST3/+AeVmxDAXeepRcTVS1xnY90WhChK7rU4eEwPuQhBmFJC8zuialkokQUFqRD0q8tVjryJRKKWs+pDS5GLEhvWcVJOEEBIhRYIQk2oAEglLHgYsFSiERHgbKoLpIlmXYTuL7iIxQKoX3DpSgtY7mcMZ87zD9LLSimgxW16bIy5y+7mhmibI5hgA+oIVAxJgEOVckEzJCFiJZSJNFF9PfICPRB1yMGK3IpULaFHyQG0SZoZTCthZjA3kI0DeI3KCMQpYS1y4RVUa0BqmGFFtjhEpinnZW462nny7JRxWepMWTVwZV5mSlJJY5Skqatsf3ARt7fAzIUiC0TmxuncO3fRI/zTRRSKz1eCko10eUg5xiU0Do6WcN3VFPvj5IdN9lhs4N/dESoRK9uZ6UyFzj5g34QFYaZKYTUuIXdIsl3bxFhk2kSC7GL1tCsBTXNtBNCYtACEnzBwEoidaGsOhwZQmyAAOx7VPwqSWxd8hhkVjhrEt040bhhACXKN+1BrxIqYxS4L1HA2pUHKeyyTLHz5ZIo0ErkAKhFSG4lH4oJSezOM4DjUNkRT/+SBzWuwi9I/geXaX0u9C4VFuUGer7s/SbGg2orqzRPDgi9CGlqPr0/YZg0UYRTUpHlSrStx31whKmLeVBiwDaoxH9u5e49MYltjc3uDrv2fnwLkp6hsOcxJQeiCHireNw75DDu2O237sGShJ9QhoSy2M4vtbjISME9j55QNt15Crn8P4+sTIcdAsa71lbH/Gld69ij5Y8eP8ORwczBsOKvMzJpcQ6z4E4wiiDj44QEtU5MaHYJ/BawgV84nNN9p/HzvXL55FFnxpEnjj+yWDoyU9ftT26O9/L4cZFe/hYzdFZ84/vpcXTP4H2V/7KX+Gf/bN/xq/8yq88NSj6lV/5FQB+7ud+jn/6T//p59K3/f19fvqnf5oHDx6Q5zlf+9rX+Lmf+7nH9tnY2ODNN9/kp37qp/i7f/fv8vf+3t/jd37ndz6X/r0K++4FRa8cvTjR4Fme8rsZfD3PNT5vutqzEJeLBirPSrm7yDEv811+zo74IcL5jtb8eJalCU51hemNtzmKkfen3+Ab6gPsFw3jWcZVU7Kc1UgXKKqc0miC88z2Zuzf3uPmOILzRCnZWfsid+7VHAw1eb5G33mCMahV9BVCotN++FVJmQQ9AYoiT2KZCPIyp122SJ/2lTFNppSSKCFwMdItO6pxxdHulM6uJkVSgtLETMHUQZsReseN4WV+cHKd4D27eceOapFCcMkNuCRKpA8op9FBUtee2ThyUNUYAZ8ObtPGVAPlVxPd6D1xxWS35wNRpdQqEUCWEXlJ4mNECUnsE3ISpCBzqTaImCaWm7Hkzx5+HzKkwPChOK0PgUxKpBSoIDBbkI0qhFa43uHbDh8txbBCxsA83ubI7hBiZKd5H2NKQq/oTYuuSrz1NHcPidanCX1uKK+s0x4tUVLikhotn3TrlCbHfdwztF9gKDSiUkQUZBoRYSt8H8F6lnnPt9a+jScQlCD4gC4zLq2P2djtca3lwR8cUN9PAqV9K4gxoEIkLDtc3SMLjXcekxse1mOZtQGydxACdm+G2BrDigAhX6vYOpoxGVcoo8lVBlYgM8W1MMVnAh/hLkN6L/HW8aldwy1aDBU+CPq6JV/VoIQ+6RnZuluxwPV4rRIJiE3isFFEylixUX0VUxYs6x0W2YOE4kD63lrL+sCxZo6Qgxy9QqGE0fzBVPOvPpKctv36jGczwv/rO5CrhDr+8KUhWd9htOTaZYeMixS04WlaixwOaO8vE6IVImpcECMsavhw/MP0HmQQXL47QyDwQ8v83T1MCBRrkvlsgfOecTWgaDdT7VvvUB88QH+4i89y7jQd1lncwNC0PZnRKKXwwSGF4Git5H9kkTe3Ku5dG0OoycucH/hDyY8fprq1f9e27IYACLwN1IcLqmHB/hd2+bT/gLwvONr3NHWLUTfB/E8APNg54N61MZNLGxRCcmO/ZjFbUGQlb374DoOqYLqseesrb1L9p4q3C8dPVFMAPvWO/9x1z3Sv4jFn/tkPkk/vz8XP/6I9fb4g8CXvx6tYLLzgOR6hfqdP/L0czr22k/bzP//z/PIv/zL/7b/9N77xjW/wla985Yl9vvnNb/Lbv/3bSCn5+Z//+c8tKPo7f+fvcOvWLQD+yT/5J08ERKdtPB7zD/7BP+DrX//659G9V2LfRaRo9cC+7LMaT7x40bZe5LhX5WtedInurGNOrvo8K5h5ns8veswfoRWmh+QKlRBcU4r7n+5wyzrED7xDVuQ8CODe3UBJydrhDcazdYZbE7q6ZbozJRpFnhtUkbHzyQPC9wXQiUXOZiPU5U0Wt2pE58m0xnqPIqEqkogIns6HlBYkZNJjkeBWq/IQ6ZsOJQXjm9v0R0uapieGiFCS4WRAXXf0i5bJ5TVGG2N2bu3SdanWKGUHCvo+YhwgDQNr2OjLJBwqW1qxwMfIph+yZguM1igt8NYxNoI9d8A8cyghOMhqgmwwMa08RwFOpWcuywyC9LkPHi0kcbWanXisJSKD1ie2Pb+qYSKGNJD7AZvTTYL3ZD7Q+UDUisyYRDkeAkFEikmZ6qqaHtH1mGjwGeQyX13zAVlZoTKNnbe07SEi04lMwkvsssM6Tz4sKAdDENDtzYlETJXjrcXVHZ0sE8plJVtXL5GpErtoUZnGW0doPDofMby5TrUW0BsNRI9cQSDKKOzcwk6XWNAsLHc8utKo3KAzndL3nCcqmSjHtU5Io/W41mKbDqkUse6xrU21OxOF0orx9pgsn1MaB9GhsgyygtD2iLYnL7JEwuAdMRoi0HpDINLPPEKEhKZJkRjmXLrfwqiEMkiJNIp2WiOkJMRIJiPhcEF1qYA4Iqt6yPZQuUmpdCERP2R5YKQlQVhUjATl0JViuRe4NSVd4wVc9c4y/ZUC3ts0DJE4ITDigFwloeAY47Huk697umkivciqnPZwgZeKWbHJvLaUXc+leo5RipYlB8u7ZEpCVJg8oGIgs+l3pJ1nYAxjaciKxIjXEpFIrrx1jeGbm+SjkmA9i3sH3P3gNr1W2HHJUXDc2tvBDOZcuTbkC7lmM1gwkkw8wkWEEmze2Kb3PR/ybfbFAbJTmMKgM48QM4L33P7mJ+l5mwzY9w7TWqq9aUKDOxiJIfSSdVXQfKfjcHnE8GbBlXWBlJJ5DBd0y/HUu/T+s0rF+l5N8TqXue05ApsnMLD4au9nXP33LBr0427Gh5n7T57vCZToycZf23fRbt68yU/+5E/y7/7dv+NXfuVX+Pt//+8/sc9DlOinfuqnuHHjxufSr3v37vG1r30NgJ/4iZ/gr/21v3bhY7/61a9+Vt165fbk0t33tD3M5zrHTqZ5ndpNPOPQV2rxxD9O9OcifbjoPs86/1mvz+rfs/49z3270H4XgaM+2xy6SFyhMcfJLPjeMd+f853f/QAQvPOD7/GFH/0K7/zge6xvTqhnNSpTXH73Kps3tuhdCmh8Z+kWLe3icRrcclzx7v/0FfKtEdOmpXMeF2G2qNk/WtBaT/ABtUJFijxDq6QbE0mIS9f01MuGwweHWO+JBPQqqMrLHKUV82XD7ic77H/8gBgjSqoVCqLZur5Blhl6HxNdt5II0mTcWYeXaeIUiQQZ8SQR0rxIaV0pPQ+cc3gh6IXAKYkDRBRkQpIrg+g89IHoIjpIRB8IdWL2yjzIPhADGBfQHrTUKVVOKoJSWCnxISBDxMZIMBqhNTLXyFJjCk0mIrJuELM5mW2pTKQQlrzv6OsmseuJSD9rqHdm9IuW8tKEamOIkgKESAX7SuKWHXa6xPeW0PQoBGaQMdock1UFelRSbE8Y3NykmFQE5wkh0NYNtusJMlJdWSMrk2iulmCUwBCR1iFTdIitO1Z6uuhRkX5nIf1uZK6RhUk1KS7gu4SkLecNi90Zy90p3jr66RIPiYktU4nGPYIsDNYHRKZxdQqWu0WH0BpdFQhjEvufEEiT6nhs7xAR/KIhSkEUItVYFRlRSuQwpY1GH4guEGRKLY1S0HvQoyEiWkRX45Y19f0pwSU9qsTWZ+mXLTFGRATXOcRwQFAqTex5PCA67SbPMyEA56DpjxczovUIkUhMIB5rMOlxSXCR/mAJUhHaJKgataKJcFC3HLYdnQ1Mm55u2RMaS2xd0jyKkc57Zk3NfDrnaOeI2cGMtatbfOEnvp9LX75BuT5cpQVKumV7rBs2WBvSzRtCHxhvTggu0EyXLA9n2D4x5ClACZBasPHeZYrNIVobYhB4F1BRMClKhuMB9WzG/oNdynGBjQHX98QYGQ0HSCnpnUOr9OworTg6mlH3PUdHc7xQeCkJFyBREE95d57Fp31zn9dY+xLnOP9Q8dhVXeT3eVajZ7f/Yh1+UrbkWSueYiVA/lwnObvZ783Y9Y+9/cIv/AIAv/Zrv0YIjyfAxhj5tV/7tcf2+zzsN3/zN+n7HoC/8Tf+xud23s/bPjuk6JlIysssSZzguBOPVkYebX110+yndOFi9jCweBFk6SLHPE97nweMf6FOPG7PKTf3XG2fafH0G8H2m5e4rwSHUjPbn7I+WifbLTh6cED3oKVfdAw2htz78C55nlGNK9pFQ5YbuqalPlzCVXXcdjOrsW3P5NIa+bDg4NYernMoKRFGoJUixEhrLRKwVqC1RqyQojzLcNahREZmFG+ulZgVFbDveiKCQwruLSzeBbxLNUtSgtQZvvfUR0tGw7Si/TAE7AUEIkEk5xoCfHN4h8bUZELyp5Zvc11vE6yjKDK07YhC8ba/TtOn2gVNImgISnGvnzBf9Cjv+d+znFKm9DfXOzKtEC4gQ8CHSIipnikfDxB5RmctXdNRYciFwuJpvWe0NkJqzWx6i6OdP0QFy2R4ne3yraQn5AHn8Nqw133CvNtBB40TqTZLxAiZQhLo7+1jqgKzNsA3Lf0SlNFYF5B1j4uBaqXZI0Igr3L6wyVCCqTOWdYztCoRheD+/u/g+hYlCm6oHyNsrlFdi/yv1xZEGVjcqfngP8woL28Sm576wRQRI2ZYEHqXAhvr6VqL0iqRDuQpAAydxRQZwyKj3ZsTtUJrRd87jFpp8AhBdB7f9tzeUbhsjMo0QgjcrqNfBKqtMdIZQu+wUeOaFpVniBjJBznROoRSqEhC0eo+oXzOE9s+BRvDAq1TIEPTo33Au8jMTbHL/5DqhyYDkAE7rSEGeuvJc43ODEKmtMn/sSj5bx+mZ3Len/P4nfrsSRcVuT5acGkjBT2ZAZ3lhM4RvSfPDd5FYoioTFEMxmz077E5sbTasDxwLNuaXgo+3C6xvUaoglLcxHUd9d6Mt5cWLaGOgm9MDIPhGlpJiKDKjPWbl9gZlewCIXps7egXLcsHRxzc20MVGdtHLT/QRub3jmi+OmE53+H273/EJ/tHFCYyGTh+3GxTLVKK7fvv3OPW6AD3piP8ly8jljfIROALh19na6S48nbGf81/h3vft8OoXOPNj68jnKQscoaTId55lk3N/be3OJwv07M8GuOB/Afe5N9uFUglme7fgQ8uks9/OjR6ui+9kKd90fHmosfFh38eITMvi8iclX1+8lwX6c/5537RtJDHjz3d/tOu+bnvx8kVi9f2XbOf/dmf5W/9rb/FrVu3+K3f+i3+3J/7c8fbfuu3fotPP/2UwWDAz/7sz3Lv3r3PpU//4T/8h+PXf/bP/tnP5ZzfDXsFQdFn/BSdGC1P+8rHBtITG195T54VnLxoKt3T9n/aRbyobz0rQPsecH5nAfyf9RlPDqAAWZ7xzg/epCjfQRuN8IL2oOXwG1MUkr5Nq9SLvRnFzW3G22PaecNgbcBytqBe1HSLlKrFFhze22ft8gbV2pBi3vDgg3uICEalWpyHqWVGSIxWWOdQIrHdZUbT9i4FEUoxGuRMBjlKKaJzoHUqso859xYWt6q92by2QZCCvXsHKC2ZzmriQ4YsKYjep4vVCpMZlOyRUlCbnjpvmftAE3u6rkdIgQshpb7FiHKagTB4EY+FY1sX6bsc5w2l1kzQlCEyqAocljIzLHpL11mECBiR7rxrBKJXFF4SY4ZBIIFWSkSeJWig79GhwS0+pm9bRsONRBe96Ik6x3uN1woz0KjoCDKAAC2yRC1tHd2sRZQlURvqgwW+Sdflg8dkJrGuaU0/q1OBvlZpkSUEhI2EOiBMQItIZ3t6v8CGhkxHRAj005qYWcbGIXBI7ZkUA+K8xy7blJYmQHZuJdKbVvUDAvpVfVW1EiJtOqIr0YMCM8zRrUwCrKv6LZRMukBKEvqebqnp+9Q/KcALiVM50hv8XgdKoCqZ6ssEYJKmEVJCnui3o/UE54jWEzONGZa4wyVx0SaxViWRawPcrCEzirbtCFWk2z1EqQJIiFff9GiTaNJFBkGArnLqqeT+4uJZvZyxXQC58pR5CnyApGEUA77uIILtO5SpMOOS0AVkZ9DFENs7crtAR0GtJGpc0LcdwToWe54oDLkdwLKlMpIlFl8JGiMpygKjFWpUsQievVs71NMFxJhQmrolagW5xnU9m5Mhee8JIVIfLLj94AMOZwtc8FRZhqVnIAXbUuGV4FtZS1cEKBQ3fvj72TiMiLbh7buHbGxl0DmO6l38xFOLhs0YEb0j1xkhRKQUdM7hhyVrG0PapufO/V0GwwEP6h7rxoksJateylOeb5+hj37OMel7KRXvrNS2k+PMhYVVX+jcJ2/cS5wjnpggfA/MD/4k2nA45Gd+5mf41V/9Vb72ta89FhQ9TJ37y3/5LzMYDD63Pn300UcAFEXBW2+99bmd9/O2VxAUPQVCf4oJxCMxqed+fuOZwdFL+5qLBhvn+Z6zRvSnvX5eJOhFZhVP2/68Du+8/p7TzkMNoGdB+Q9/B+Jh5Pu8XYqrlULx+OfnNXXMNhdTHYx9iDiKiCIgCTRHDdP7h7TTmhgi480xk+01YoyMN8ZMHxzStx0iJhaxEDy3P7zPG19+i7Zu2f/kAb7puf7Db1NuD7j+AzfZ+XCHxf78GNqUQqKVou16rHPoEFBaJ6FNqSh1hnWOdtFg10tEiEif2LR6H6i7HhMjwmj6vmexbBiOKjKt6K0jL3JUkaUUKimQKmKUJkrIpERHmV6j6R34KAgr0VekTjTTMRFDoARaSSopiFGxPhrQ9I5v3/O4AJ33tAR6a6l96lcfDAHocYyKDLzH2phSiaSnUAopUrDmYiJdKIclou/RoUdhUYMRQg/o60iYFChjiFKQGYkYFLRhgGwyiBEtwOsknit9JDhHsECbBE9lYTAkLR1hfaKO9iHpPNUdwSj0oCAfDVepdUnYVuUGU1WoNsNFR1CSgEfYnn7RMP34iGq7whQV+Sjg5jV6fUB0jnbRgrWJ+tynAFi4lA7Rzx1KSeQgRxSG6Dyh7cGltLgYIqEwZLnBe4/QEpVr7P4hwo6RWUQXiS1OCdBlYq4LnSXEiBQxEcDliq6xyEyDjtBaVG5SClgkMcaFAJ0Flyb2EcAHFKTgLEZ0ZjCbQ1SZ00x7iu0xoenJhgWh7tBVQXBLzFqRAiR5sUzgZ7mVGJOIrVil/Nl5i5s3+M6RbwxBg8o0IOjrDhcCIVhCiHSdRVc5UgkWy5bx1gS7bPBHU6SITCQMlST6SFYWKKORXctyscAjkLs6BXnBp5TbIiNKiCogjSJHUHvL+ltb6ZnGs//hXY7CEhsSeltlGVIqfGd5OOTOdxfsHViyoqJQMJ6U6LFme3CZLLQ0zuG7gFKaXGcobWh9y8Z4QDYsWC5qTJ5hux5lSmJvGRc589mCrm/JBwapRyCezj13kUzsMxR7nn3QZ2ZPHzQF4nh2cFaAcvFzvDjS9LCH+nghV+Be4p48G7U7OwB75rEnL/OCY+dre9zu3bv31Jqe27dvv3Dbv/ALv8Cv/uqv8hu/8Rv8o3/0j6iqirqu+Y3f+I3j7Z+nHRwcALC2tva5nvfztleYPvdqYIeTTu242ZU9kfV0avvTWn1m3+KJv+di6E9p/mQbL2pnXdPp/pzVl4ue90W+omd5yAu1F0+1c6pBccZnz2rxNNolTnf0Yq79A+e4v0xV3V+yn/Kj5SHeef7rHyy5307QRuN6y/qNLXRu2LqxzXL3CDtv0CIxx9m2Z/nFEXLN8GBS8vHvfEoeFIc7h8yyKYN3h4Q3Aze33iAcBKIPHO0cMd09wluPkDIhSBEUgjzP6JqeoCRCKaI2fLBfp8BGClAa39uk+6IkudFUg4Ku7dlvjiCAFhJCZL0yXK4MUUmic6hVnch6mzEShkxKGjshulQYP9ADMiPxMfC2HVPbgjLTfHP9Y3bjlP2m46e6H+TNfoMQ4aN1y3f2p7Sh47c2P0Aoy0BqqiKja3uO6gZVSsZGk3eGH7VfpjAG4z1ylVInvKXslmQrggWpPMoIhuoab4h1wliDKbBSQ5klimUlV/fe4XsLRqXr9jHRNq+Y7jAKlQkoTCJCWAXCsQQKg/eB2CWx2MQLprg5+hFEyIgbEpMN6KwneMl29WOIsSC0Dbf738MYAXfhevwx7MYIL5bUu/9n+uX5jnJrgh5V2KZD9B6xYteTmVnpGnnaWU2uFd5H9CrtEO8RJgPArOjfQ90BJWZYEoLjRu6RgwXFpsD3DmcdsXPc89vYEBEici0/oKg85BkfuwFNFxCAGuT43qKDJgqBLgyis/i6xzZ9upcAzuPnLXpcgvMI6+mXPQKDyHwiV5AC4QOxd/iuh1Ico/pn2UVd5Ul3/Ml+xUyT0KF5S7A59dRRTiaU441UjzbwiVxj1vCRCTTzJTWRb18akI8rlrMlsYflbEnZOW7s92wWGW1I9PTWOmJZMLq0Tn04Q/q0UNIJWC8dl+UShGBP3aYdJgHk4f+fvT+L0WxL77rB35r29A4x53zmU3WqXLarbJcpG1z4ayxQy4AE6gaEbcASsrhCXFjc+KrhEq65QL5AAvXXoAYL9DWf/blx+zMe8ITLQ02nqs6Uc2aM77SnNfXFeiMzIjIiMzJPnlOFyUeKzIj33Xvttae11vP8/8//KQosgaGUuB8ccMd69r9+k72bu0grKI1hVFWsrI4YXl5H31LJ4Q2CjbcvEhYgXM8XLv8BebTIDFb/akQNNM1M88pvvk7XaboYeXstpzWCe5VA0XGgLflKzpVv3mVza43QWgTQWMX9uIse7dEhGQzKJ15n8cgdefwEeDol6yGJ7aNdVJ/S8rF5LZ7Y8ul78mH7LxCsSclfKZMwzLYP/O9tsxTc/OiQoudi8ch9fUGl+7baj/3Yj3H16lVu3brFL/zCL/BTP/VT/MIv/ALz+ZyrV6/yF/7CX/h2d/FPpT1Hp+jkoPr4Nykuo/Mnm3j086eJNZ71/Tnsacapp5nxH+e8fRRj4+OQq8Pvn3WQe1Lbj2x+ZHUk0k6n+5xPvhCP+IZi6RhFEPLR/hyLnsX4KFoV01ZdjHRLD6v1lswuaGYN/bSBPOUWBCUZro8QAoILxFlNO2sIAiaTmnwZ6S+3CmyAdtFSiYreOr7+lW/xyVfeohxVVKsDsjIHYOOlLZppzTd+922aRYOQkirPyE1Su8qKjN5agg9Y6+g7hQsBISUxRjIpCYApMjIEWghUZnAx4kJSnIpCkBcZuUoXy0tJ8EnlLlOKIgq8j1RBEoNChIgRIqm1SYkKkJsSrSVID66lyMDUkYOdOShFgyeTErRmJlvKkURmElEqMpdTLjzz6YK5sAThyKUk1yrVGCKmHKseotWoIgOVEsSdgyAVejhM550bEIKgZEJNfCTPUr0Z4RWSpEKWBDRI0sxCYAEXI3HWopa1kbplgVHdO7wAMrNc+AfoIzIWKJFEB2hsQqB8ZCUbJXXBXDEZKHrbYXqFdiP6e5IWsLOOKCK27ZFGYcocVRrwEaVFQi+cR2Wa0HTI3EBM9Z1cZyk3x8TcYJuO6JMYB2WGKsG3PTKXNPtTFKCrDBN7lAwI2yKNQnmBrDKEc5QZ5JnA9x2xVtB4RJUjM53qNLmAHpW4pgMX6KY13jpia0GQrqdzqMPiqTES2oRCqcykPKxMJ5RuWBBcKjh8niTvs+I8J4eVGKF3gkXdU+9OMaOKvBogncQPB9RNINhAsJ6+7vAx0nWOyaKhyww1gYP9KStrIwa9oZnV5EaxqlNeVa41EcHubMZ017KjHUVR0IkkkVHkBhV7chmRREZZxOskkx+EJ6sy1jbHeNMSVcSPAuU4p5QlpswoN1cYXd3AFAZ5f59l0TDkXJLVksxkDOpbVKJLx6tKxFAQhWJr9SLb1xcICb0UMMjpFMz2p9joWV9f56qyzCcLVoqC2PVkUjIVgcV8j4tvXkLM7BPvxXnv02l2FI05BXQ4t31YR+Sho/aUdsp8eOZ89BTznxIw6ixGSVotTxzm0bP9qJ2lM3OLluPlI+/skwKxLwyAy5cvfyg06HEmpeQnfuIn+Of//J/zr//1v+anfuqnHlDnfvInfxIpP16dtPX1dQAODg4+1uN+3Pacruo5+VTPZPGUn+Uhlwvtox+fvf/pfz73Lh7r21Pa0f0Ez9bOk87vWc79kZXKM7QBLDlqz7rno5+JQyrcg18e2KHCXNpOpCjd0fDzKRaFwAtN34OzaVFNhCyTVLlEekt3MGVvZ0a7aMmrApUpBlsrjNfHqChQQlCMKnY7y0CC7gXX//v7hDqgpUOLHi16VHQMRxkvvXkRJQUhBnqf6udY72i7HqHToroYV5QbIzYvrTNYFkntY0Qvc0yEkTRdT7csoCkAIyXZMg9BitSvTElc8MSQxBYaEWiix8WIDyCkQkhJoVWiahkFIeKFADQmKygweB8JnaVrO2xnGZQ5WQQVQfmA7Xpk7VB9xDjJSOZkpqDISpTWRKWwWhGNRgmBVBqxtoHe3ITcJDk3LQgqHdsKgVs6h3Xf0zlPNBIvBEIoeiuIwuD7iPMS23p6L7BtQKIRKiMbDEAZpNHk44piXKLGJUWZM1gd0Ld9ygfTEqLD+57gevxA4iqJKwRqUKCKjKgl/c4MuztHZIqgQaiEeOVVRjkqGa2PGG6M0YWBzqGMQg0LMIpiUCS6l5BIJVFaYq0jhJjU8IxCBY9WkA9z3KIlyFTbRuQ5YryCQ2JdIAgFWQZKE7IMRMoXUoOcaAyuD/R9IAiBVwJZGNz+Am00ftERWgudS+p31idRjhAQy2cphEg7qfE+4OYtoU0qebrKEv1OCLAeN6uhbkAr2iBoXPIxj75uzzY0Rebv3Wb6x9+EridfGRAF6HGVFP4WHWJZH8tOFoTlS55VJdpolA9Ia5nd38PkGasXE8JppWAWA67vWDQtZVGwupbycJqmRSyRPDdvkG2PaBpC2+IXDXHRpXy0ELlwcYPx1gpx0cOsY/3KJpc/8zIvff51XvrBN9h69SKF1hgb8VJgtWD73i63vnED3/QML67RC0UnND2KPghsEOzeOeDee3fQItUrOwziVJnh4soQLSRGSZTREGHvYMqk65k3Ld469u7vI8M5HNQHKP3jtzuqNieOuUDxQ6+Zk0Nwyt0/b8PxaJ+O9u0Me8rg3rFtz7l+CEBrLXXX4yLkQpALyM64H+c51chRxdTTOnZaW6dHZeORz0+9Xmcsu17Yx2uHFLlf+ZVf4fd+7/f4lV/5lWOfP8mMMQ9+P1SOe5wd3ebovgCvvfYaAG3b8sEHH5zr+P8j2nMUWngO9qwhpu9k+6ijLGed/2Ew6jTU6ttky3n9+bb3NE2eDGXG43TNWXmJDza+i1t7NzgYbKNzQ123vFbu8dr+7+MmC3baNYbjDczaJjcWHXtdz+UrV7nSHlAcdEzuHRB2NnExZ+YlVz54he69nsvqMp96+Q/IRwvwgvqbFdEKLueSO4ViOg9Y72lJSM3WyxcQWjLbndEsGnbv7bJ1cZPFwRwbA1mW0Xmf1MS0WhaDjWgl0cKkfBQgSEGQgtj0mMxQZRnOe+6qmvuqIRCR+xlyoSi04tW1CqUELkS8D6gIse158841YrhMFIL377aIfoFXkv/L5oDcR4TJ+fUso48W1cL33rxGEXOk0kQB1npMFKgiJ9MK37vk1EoBiqU4gqdjwu35HyMEjNdfYaP8NK7t6OY1yhiqqiD2Do1CS8l6+RojeenBs6AOEQ0AKeidwywL48oStus/ppFTQgiIELBNR/Ae0fvkeGjFu81vEaNAbQy5fnUVMSrQveQH332FSpiUm6MkUiiabsqN3V9HxIgNAZEBvUuqcpmCHmSRIXONm9TI3KDXUtHVYm3A9L37NPcneCAoSR4ja2bOeP2AbG3Idjdk+06iVm73GZNFyaLXtPfA9CMKV6DKHLfI6HoHNAip8FLwXp1DTHkn3qf8ITdvUy0srVCDHJzHrFT0d/YJPiCcB6VACnznkIXBLwu4Kp2QRlySj5ZaoHJDFWasD3aRmeIbe4H/8I2Ehnb+0Xc1aXI/5o098VKH3uHqHrW5xugT11JekTTJiest8fCc6h5hNI0QfL3S1F4wznPevHVAnmkaAl/bPWDr1cuIl7a4OaqYHcwIwSMRjDZWCVIgD2ZcvrqFvLHD6u19tFJUxR7j4V3K0YDXDehiE1Pm6GFB1uWIu5bxrmWw8PjeIX8I4oVFUpP8bYW7GWjrlnd/+CIHecF77jbXG0WhLOO9fX5HbRGcJcael39/xuorI+7+yT7eGaTvqb0j5CVoSdZ7PrHfszmxlHHGvPMMBiV3p3NgWSdsrNi8skm5MqCp2ycMieeDBI4Wdz2ODn34Af2RNg4P9Yzz1VmoywO0JD7qIJx+Hk+BX52Yaw9C4P+t0ocbfc/frgZI4Jb3/NKSSvdoA+e3o8jPIW3xaK+PtvjwLM641ycYLh91jaoXdn777u/+br7v+76PL33pS/ztv/23CSHw/d///eeu+3M0/+fg4IALFy48dvv9/f0Hv6+trR377otf/OIDKfBf+7Vf+9hzmj4u+wiLt54YJZ56BXtWm0cbO6O9k0y+05o4y562n4871oe1D9v283CCvk0+bxJpeEi/O519ePakdVK04RH23LLA6dFLFIRm1kTu3JkhlKatWzKjWV0fIOoZe+/eQFwcMihUSrLODAWSfFAgJzC9vsPdP36PuLnKoFqhs45SlOAENGBER6ZqXO9RNjK5NUVUQ1761OeIecn+nT3uvX+X4D2myrj73t0UvQ+BLDPMJnOEhEIZRisD3FIiO9qAVgopJSIkYQTv/DL/SIGUuEOaU1gWTJVgZUAg8M4hHeAjrQ9oJRmUBU3T4awnF4rSaboeyiLDKE8tLb3zKOcoM02m04/FIZRmkK2SdQLhQGmNzBNah1JgPQKQSwcmEhG5obcW6zuaZkpQAmZTxrFDWYtWEmM02gZ8ZnCKJFmuFSYbIjOd8oPapRJapgldD9Kjo8D1FqEkNix5l94RXUSuDdERhLL4LuUi2dBRXFwhv1AiNgyd7wHBytV13E6LXThEaZBRIF0g+BaUJGaCAOilip3vE+0stpa+szjnyXKDMg9V5YoLK7T3JyiVCqk6rQiqxZQ+qdx1EbM5wh3UOBfAghqtEMoFi2kHgyHKp4KynY8Uqzmxtdj9BX3vUYOMENWDYwbrMVVOXNY7Ermh7+ySguaIRpOPS7JxhVASPciZX98htD1yXJINCqx1qCwVevVNh1SC0WqVgOCFYtJy7L099upJcfiCn/LOngIkC4lZGyMzgfceowyISOwdoXPIKme+N0MrtawBpeiVwCGYHEwZHczoXcBmim6jYH5vn6zIMeOKYZmxc3cHHwJr60NMmVNbS28t3/OFT/PSQZucQXWLvBgilHwwmIjDQcWmYERlYdCDEBo9kkzdAf20p/lyDbclNnjaH97izr097nU11dYKtjbcm85o2hajFEIGFl96n08O3qSLGo2g6y3DtXUkEaU1eZ6BnVNEwbgs6G2D1IrVjRVsl6TeL/25y+x97/3H+p4PxsFjSM+Tdni4tP7w+NBjO3Xiz6ejlp0lWX0qV47Hu4JPttPnoBBhtvR8hiJStT2myKkO62w95Tml3pxz8RJBiLOQo1M++04PLP9Pbn/37/5dvvSlL/HOO+88+Pu89sYbbzz4/Wtf+9oTnaKvfvWrAGiteeWVV45991f/6l/lH/7Df4i1lp//+Z//U+sUPRf63MOh8iTn6+wJ8Glb/9ANnRV5elp4+KxtzxqvPi7o+XwBv2dvE045l4/u5FJuwlnEjg/nYR/S6iKgEVQi/egYufWNm9i2x4U02WV5RrW1wnvv3ODG3W2mswVt0xER1L7DbGSEPOKVorUCKzN6H+itA0BJgbWO3RvbNDYy72DegxMZXhW8+yc32L21g+0s1z79Mq98z6tc/uTVVMR1yT8KMVKVBUWVo7OkRjZfNPTOYX1gvmiY1y3T2YLJdI71nhBjqhcTAiFCPkhyz10Eu0RlTJQYrdGFwkpLryyIlIzfNB0qwsq4Is8MWiuyPOUsEdI2hVIUxqTovVIYMjKZU2UDjFSoJR1PKJmkoJVMSMRSDS9KmQp/KoXre3SWColKo1AIpLM4enrt8UbQAS43+EzjEASlcELgM82i6emtR+QZVik8gqgVfYwEpVBFnlT0uohyEuk0IdPEpse2faIICoghosuMam2IFII8eqpMknlHt7NDd/8OvqtBgBzkiW43zImVIV8bUl1cJdsYo8ocaVRCrbzHNx06N5hhQQwprwQpKFYHmGGBXApjROchpvo4xIiSERUcMliy1ZLQOXCO8UubaBGwizkyUwizjG/5gBkWZOtDylc2USsDyBTCpPuQZLkTciiMgqWaW+gsoTSoPIKwyPU1KMvkRPrUXzOucDGickM7bwlNchYJEbM2QBQm3esz31tOHTIeOwRL8IsW0dlUOykEgk8/MtMIJSlXh4SFR4oMvMLa9IxFLSmHirKCLEvqhLPpgoOdfaa3tml3p2jrMT5S3z8gLDoMgm53zu637tDOGoSSyLLEmRInc4LIiMEQosEGTdNDbQWdMnQmp9U5ZOndjT7QO0fnLMNLq3Szhvsf3CPLNNmgoJdgBWiTHOU8M3Qzx/zWDO0NLgRyrdnf3kMrSVmmelpqWFKuDeklLLzjxs27NNby6ve8xif+zKeSguNDbvHjR8klrTj9PLwT8QkT48eJITyLetzDs3iIaAlYXhdOnMBToEEnlzhHXUoBpRRUUlAcHoclVVkKapb5q+LZUZjDO3IUpTuezfXwuE+cmc94SZ8XAvjCno/9xE/8BFqn8V1rzU/8xE+ce98vfvGLD37/T//pPz12277v+cVf/EUAvv/7v/8Rue8rV67wUz/1UwD8xm/8Bv/m3/ybc/fjK1/5yrm3/Xbbc0GKzvIRHo8QLyO2T3z3TrZyjkX4h3mfn3bf54HgnOZ8nOcYZ/kGH4MT9kAy4QlsmA9xAI6dyLGDPO0FObrFUnRhmWD6ptb8L0UBMXKv9fzW3T2MVHS9pawKrnzqJb48fo/3vssQvvsKl25LLh10RCd4u/oGq59bo7mywL57lcX9ETe3PyCqDOccuTG45YJSZBn/9stpAaVlwRcufz/ZSsa7d/+IfqdmPr/J3W/d5rXPvo5EcP2rH6C1wntPpgzWejIhqaqCycGMoswhgFyq1oUQiBHMUgfWOU9vHW3dsjNJCy6lFa63yBDYKBWfGa8SnOZLG+9y6/I2eWZ4af4mg2aV6ANGKbrOpf6rtCCVSvHaxuBwLUymJUVREJzjzx98JjmyzmOCBCOJsBRBSPtHoxA+FVj13hMEKC0RDqIL+CWdKWpJ43Z5d++/YrUkiEuY4tNE16U8J5+2cy7VHCKmHDLbWlSueXVrxGqu0TIhCEla2nBx9XP4riMPgZv1l6jVIi0IfUjqcFKQjQuElCjr+PPX38EUkiA07+7eZ7ozRWQ5xcUh0ijkIMlP40Oiek0bohIIKZHaIKocs1IlwYx5S31/gq4yqgurSJXulR4WzKYLdGaS0xMDelAQrGNTzVgR24RNxa7MmThNd+uA19/UaDxds8utfaBaIdcKN2vxraVYHyZhBq0RIWLrJOqgBkWq1SQFtD1RSmJn6bXg9mfXaL78x8jsCnr8BWKEgZ9x+fovo/KM4AO6yBBGEic1ZlTgO4veLIihQ+XmuS+mpFIMX7tIYSTeeULvktKaICnn5QbhBJvFD6AGQ3YWLe+sr7KzfYAvPO996l2UjISuINt/iyAkZe+5dm8KPuBjJMsMYrpH+GCPl7ZWaCYdzfu7vCMk1bDEvbTK/qU3kUqytrNgZXtGsI6bheRGcKAl65c2uPjGFXRu+OLK11gVU7qmY3/ToDbXcMOSO9fv0ncd5doK+zdm1I1KyodCEbwnL3Iuf+NlrvISw40VvmG/hqkUG3nObDQgasV+2/LlocINS2KmWEQLKwbVWTa3J7y8tYrjRO7AcjJ+ZE4+BqaLR3Y5y56CVPZ0djqQ89T2WBTrBHnlfFjQ6bS7Y/2NMJKC/3s1wAB7IfALTY0HtkPgf409wvX4eHpW0KOdPC0UeDp15CHa99BNOqudo58cK4Xxwr5j7cKFC7z99tv0fU+WZWxtbZ1738985jP82T/7Z/mt3/ot/uW//Jf8/b//98+k3v2Tf/JP2N7eBuAf/IN/cOo2/+yf/TN++Zd/mVu3bvEzP/MzFEXB3/gbf+PM48/nc/7pP/2n/N7v/R6/+qu/eu5+fzvtOdPn4im/8ZiQIU83wj5pzfu478/a50ltndz2wzhNTzvgHw66571GRwfpo+Pis9qxEfS0gx2F6c/yzE4JW52DBfCImlA80pkz9j8XfnRiYtMCKgR917P93k2i28RL0EqxfnWD0daYWxbE1gglwN9TsDJgd3+CWpdkaxleO3Z3puy8u41TGQJBrhUCaLsOISAvchoHCwtaCpzMUORElRNjj+8ckcj7f/guUghc70FFhEgLw0XdsHltk2p1wP7eFOs8RZZx7Xte4f0/eg/h09TmQ0T1Dq1VotcRWTQd03mN1ppBkaOVREZBqTKClBgNUqc6Q13bEp1HCYHJDfO6TTV2nEcbjZQy1QlSCmISQui7nhBBR4kWgohKCIpLSSXBaAgBQnKGghQIG1I+kU8FYhGSUC9A9kSWuVDepx8hEXlkujNjPpmnfBijyYoMBMwnSVLdu1RwNEwjl0pNLEZIKfHe0XWWLDNIk+OR9N5jG4EPkbzIiL1HaPAhsNiZgo/QLAjjCVZ4+j4wvTsgqgwzUEgtExVMCvrdGb536fmzjuADUcmkdrd8zkKIqDKjWB/SHyxo7uxTXl5DCNBlRl7kBJmcPIxGaIlEEeoeJQJ+1sB4E5Fr8mubSLlPuZJTDDNuvWNp+5pibYCd1sgoaW7tInOD1JpoFMFbYtOjc5NQrEVSt/Mh4l0g3xoRosdXJWF1BdclJ88IhxrkuMkC1TmiTshJVmbpHZUCkWsQPdKcozDR09jylRdSoDNFtzeHEFMBWylwLqB8oNlbsKYyZNQMyyHT+wepTpOMRO0JBFrpsM4jtUBKSaYVRZFTjSoWkwWeiOssW2sr7BzUBK2IzrPYn3K3b7izkyOk4NLMcmVhkUKwv1pg10pyk3H71oR5E7n06ZfwUjHeXEUg6T+TUe9Ktr96nV2mqNWSruux1hJbz7DIqQZDZnWNUZosGIbFiNFohaIs2JvNqUKO7S3TRQ1Scn++YLg2ZjQsGV1aZ297P6lGWodfvnOnOUAAx4frZ4vofWSL6A/tEB1iKOejpz2c2h6/7QMq9hOivwKohMAA9ZEgXohQx7AMIB5Bqs4438dO94dtnHIeh+dy2OdHz+n4DHn++/iRucEv7Jz2+uuvP/O+/+Jf/At+6Id+iLqu+eIXv8g//sf/mL/yV/4KV69epe97vvKVr/DzP//z/Lt/9+8A+PN//s/z9/7e3zu1rc3NTf7jf/yP/PiP/zjb29v8zb/5N/lLf+kv8Xf+zt/hC1/4AhsbG8znc959911+6Zd+iX/1r/4V9+/f50d/9Eefuf8ftz0Xp+hwEDpmH47h9Kg9zYB5nnf4w/bvnL7Ac3PUnuacTv7+EdixCOOpfTvywRP6cqpk9oldH7nMR5TlHh7xyTfz5LMahMKqgsY69vemCAPWe0bjASsX15IaVx2p1gd0+wuMzjjYWWDrnsHGCDMocL3j/ju3qbxCZgaUorOOpuvxxjO6usLK66vE94+HKRcHc0LvyTND7zyZSgIEfQwYrVBSUpQZizrJSavCsHd3D+89o2yA9Z7ZzhQlJTFErLMQJT5Ggo70zlEagx5kFIOCrrXkmSH0jqgUkUQfNE6RyZwuBDJpKIREZ5rQ9BQqLQ6DkEldLkSUVkQEMiZ6IFLSWpccmZBqNwmAzCCWKE2MMTlBCJQUREEqlGk0waf8JzkaErsWqUtcSMIHKNBFhlcZ1lraeYMpMi6/tMVoc8x8+yA5oeMKWycFudHFVbp7u3S9QxhFnmmM1umih0iZ50gpKPwKoo+YIsPGRVox9g7vA/P7E5QItCUUhcGJgByUqGFFPq5ACKSAdntKP2/BJ6pOkrEORJmKwgLIGJNP31q8UUm8oOmZvn8fAJ1psrVBcqwWHd6D9RKkgmEG1uPbCXXraAggBAuVIYoxIDDrATkH1/bp3nQOVRWoMkt5SrVDKIGve0RI1EkZoXdhKWsfkdGje8jH62SbG7j9BcVLV8hmSWxBTCB0FpkVCEDFiOuSWIadd3RVCiR44FQlsSPv88Nodjzx28N3NFci5ZyJlHsWbUgL+pgEKfrWYgpDsJ7QWtpxUqCbWEumFW1vEVrjnUFFj3QarRXV6pj+7h6ud8zbnuneFL2k4WmtmU4WNDHijKKvG0SMVCJjRSq8khjd0auWLMtQlcIMSoISVGXBYrLDjT+cMHkDFuMCRjm+7JhO9ziYLwgDQ3QGj8Y0no3xGutvXmGyv2A6X9D3NuUwFQZTZrz6PW/w3h9+k8Y7ohBIICsL+rYjWMfk3h7DsmCkDUUQ2GnHB3/wLdQbGnFZoo1CefUgqf/YNV4i8fGEcyTgCIPjaSatj8ZOCgo8rgdHp6HHzgUnHrhzOwdPmK8jMAsBGQKL0+azcx/m9A3PLm5+eG0ede6OiyY8jTt7/Gq+sP9x7XOf+xz/+T//Z/7W3/pb7O7u8nM/93P83M/93Knb/sW/+Bf5t//236KW4kSn2ec//3l+53d+h5/5mZ/hV37lV/jlX/5lfvmXf/nM7V955RX+0T/6Rx/6PD4ue070uWdcgT/Nu3YW4nIWknHaCPo0jtBHMQ6chuQ8zT6nfcdjvn9e9qT2H3cu5+ibWCafPn4nceSb0xs96SjF+DBy+HDiOo5AzYstPtj8HLvdNpPBByipGJYFF1+/RLU6oF90yC8rLpTXECHgF46ua8kyw/DVNepuxuTePnIvshIG1FIjQ6TpeqQS3Hr9Jpuf2+TmGxn2joXuYX+VVsQYcT6gRUrQb51PtLglda7rHcpoNq9uMlwdcvfdu0uHSeCC4ODeAW3TIZWkqAoGo5KyyvE2MJ+k/KeqMsymNVpKZp2lLHNYynMjNRd2riCaDaIUjFYGBC3pnSfXCg5Ro8zgvE9FR6VESwHycLUVMUYhrEeIVC/Ih/RdiDEl9KuUU+SsRbqUTxRjRPqQ7kmREYSgYIMr6ocRSjLLLB+UC/SgxE0kynhWh1XKE3KebtHSd5bRxgq26fEhMFgfonPDRBt2ru+hBwWvrJUMY0RLkeh6TQdScq38HuRYEUXkRvOb9M0B0Xn0qERKgZKSO3EFO0uL0myzROUGqRXRBdr7E5rdWZIyjxBjwLY2hYYPF5YyyVpzeL4kECpfqfDTJtVdAlTnkJkmast+W9IcjI6/V8UGv/vOPre6/XSNRXyQc/f944zNiyWLuwfoTBMBVWWExqbaQVKA9WSDpAonTaIUxi6ilvV4RBv5DOtQjZF7gVe3NqDxHOw1XN9fIIzG9w4tJSY3xHlL31vKjRGz1vF+M4ROslO3wOLRV/dINP3sd/yh/cCVERuVJjqP35niioeqf+20wfWOfJRyZ2rn+aUYaIOjtTahm0Jgg6SZfRqtJCIICIIsM2y9eZWr45rQ26Tm2DuapmGiJV+2c/yKYt1WXLQe1/WU04aXa4tSEvd6jf/Rni62tO9FmqlCFRnDtZsU4/t0i5b/z//3M1y782dQuUaVX+dgZZdbG9BNP0nYX0cAn7OwYTRlHfn/bR8kBCxTDMcDBmsjBILVlza5NKt5++vvoYHBqGJ6MEPEwCA3lB62buwn+XAhOGgTbS5rc16WL7N6aY3bk1vc4Al1VA69psOF/Dnmpucd8zyfPfmoz0w8+bBzaYQZkf9XvUhUXiE4Ir543B35kPP1aepwh4GGZ16Lndr+C4zoT4v92I/9GO+++y4///M/zy/+4i/y5S9/mb29PbIs49KlS3zhC1/gJ3/yJ/nxH//xc7X32muv8V/+y3/hN37jN/j3//7f82u/9mvcunWL/f19qqri6tWr/OAP/iB//a//df7yX/7Lj8h7fyfbc3CKzngJH4w0J8JUTztiPc0+T2OHXTv51p+3n+dFeZ5H3z/KUelxThdP+I6jvGQ4mVx07Lujv51s81yT8JEbE08/3ulNxQf7pF2OOkwQkXip2NuZk1UV2bBgvDaiWhsiBOzf2cG3nqKqqGdzXO8QSjFeG5INC27f/YCsyAna0gqN8x4jNUYpem/xOKoLA4Lyj5y4VKmmTBQJOXG9RecZupApz8UJWuu4/OYVLrx+iVtfv4EQgjzPWTQdeWaW6lgqLZSlpF+00DuQEiUlIYaUo3N4ZYTAeU+WVwQJfW+RQhP6nhgCrgwEpZKMtZboJXUuhpRXFJ1HG5X67Dx+WVBWLp0lodN3wju8czTOoX1AlQXKebx3qJhynmRuyAAbIyqCkQKkRuU65S8R8FESe48PIqmDzVu6ec10Z8psd5Yofnsz8lGJlOqBQpizHucCMkb6zia1OKnwMdBmmswHpBeI3hKHOUiJ1ArhAs3+nHKZexO9Bq2QIiEX0Uec7YmNpd2dEVwgWykwVQ5aJSqOS0IAQkpcZ3Hzhhgiru7IVgd472kOFgwurNDtz4nW4ZxHOIOucmKI+MMaMwKCTc9cyDNs07Lkl4JYvgJFTr83xy4apKzwMTlhznmk0Qgl0EpBZxFlhm/6tA52Fh8kvXdor5EuIo3ByIK46LH7U4Ttkcv7FUJgNCyIPqBXKvr95QIwN3gkIib1vUeG0FNIBGfFuA5NS4EOgX7eII0ihocOOD6gM43ODf1kgQBsppnOkpMspUrX00eiE3QetJaE6Njb2cd6GNyZMhwPKMcD8t4RgmcqlrWEfHK4Y5+kyC9srjO8sEq1PmLy6gF3V2+w+85tJrWAuE4WBbkU1O2czGh27s+obs4Yv7xJt7dP17Q4JZDCoLNqWXy5Z3rzHmZl8GAIdtZiBnmqbbX8cHhhheyDItFfY4EUMMxzlHXsHdRUBzNGq8OkrigEWiukkOx+sMv65kaqVXTGNU4qevGUKe98E87HsVg+vvB/hC8Aj/3+DHvEQeeJ89zj2nkwrUWW2Vwng3wfjz3qLJ3TpTkDOTsrh+mFPX/76Z/+aX76p3/6mfZ98803H6xnHmfj8Zif/dmf5Wd/9mef6Tin2Y/8yI/wIz/yI8+tve8Ee345Rac6Ex/RyPCs7+eHfa+fNTx2dL/vtLHlOd2is4ffNOIeRXiODroPBnDBuV5sOCWN9sEkd5xe8IBad9i5+HD7o23Y1tLsz8mHqQr96OLKA6c+BggyMK/nmFzQ2Ui2XHSKVlCKISZkHLR7dBGIgWAtPkSqPMf4jIEYYboMYlqCxBBwvWV6Y58QA0mKYBlZtI62SXSyQZERbWSwMaKrO3Zv7qClwnmP0pqu68l1wcbFNfa2D7BtT09ksD5OdX+aHqM1xaDAdZZm3hIBr2Ra+EmBEJIYAiuZpg8eoyRFpjEuEBpLXNLjYoyoQ8chJKpYUJKoBKGz5EvHLBxKWQmBDJECgTAGCcvk+CRPbDKNXCJIudEEaxPCoST4pG5nhCL3kmgTKOWzSHlpSGUHlFWJVhLvEzozu7NH9IF2Z4rKNH3bMxiWKCXRWibFPaDuO6SROCOR+we4zqK9IXqN7Q1GZwgj0FKilaS1NUkFTuAagbeevunISQ6SEAKRabLVQUKCpEjXSIEpBUiBXVh2v34f4QNohVGS0Flc3aNHJaK1S8cz5R0Et3QthECJgI6WaHtWishmlR7kaS/oXbrWUkvsooW2JVZFui6zJvXHKELT411LdAGVKXzb4bVCVhV+0aGkxE1r2kGBqTL6SUNd7BB8xPbz5PhmiqIsH4IJS7TM9w5GJW2XUMLOPSp1f9KGGRRHZ55TgiRaBLqdVIxV+ICocmRuEMDg4gouREII9E2fjrcsfBxjxDlLkefkg1TTCimSQIM2RCHo6jkLb5nu7mP2BNoHMq2RmWQymbGxtc5IFxSyIRsPWH31IvmwSF3N5+x96w4HBzOkWgMvGAwrvHP0XU9WKJA9kzvXGV4ymFLhakPXdWnciGB7S7HiwfXE7j5ZOSDzDt9bhlsaIVpihNp6GAi23tjkW3f3MSGyMaxorcV4gXI+0VdDQiZElVOsjtjd3sZHR591eOOWL97xi5yGxENkfXnRH2MnF9ynb31eXCE+QJKVfMKk+JiH6XBOeZIzdBqycigU9Fym45Pzy0k7zZf7EPZ4itzjDnzK14eB4Sdu+MJe2P8c9hHWKTpiz+JMPO17eNbA87hjP+6zk/s9D+fhWQMvZ53DRxWNetKq5vDwRybaYw7IMfj9NED/oV5OXEa9n47tvJyYT8zBkbjkyp8Sh44sFwdHPlva/GCOkJKD+wcM3BDzyWtIKenqFiHBDXtYj2RFgbmlkHOFGRZc3LnKVrjMvW/cwjeJ5hb6JA0dEHgfeW3nLV791idRmeR6f4OOHiEF9965zeL6dLkYM7Rdl+qQGJ3QoMzQOUdW5gxWBtx++ybVsCS6gO0dUkBRlVSjisneNNGhQqTIDe28oaxytJasXlyjbTraeUNW5ogQqecNN5VELXMprmSSly+NCG2fipK6gA0RHwNKaFRMye1EkCZRmsTycioXkUoTDhfL8pC9DlJplJTYrl/S9VJekY+pPpH2nsaT8lmEXCreyUQx05rSwZt+ldBGdk3P7ssOIQUXxYjNRYZGoIxGaQlLhyy4kOo8GU30IR3Xe+gdtndcNzP8WDMYFbD7ZVSZajSti+9ic2WEESL1ocygbfj69LfwtocQCb3D27TIDD45iVFAvz0lND3DlzYRUtBv7zG4IHnlBzJUkbGYlky+pbBSEonowmCdx01q8gtjzGqVaHdxmZO0aBMyJ2CrqlkdzEFK3ry0RBAR/Ievwjf3HtbLKTbG9J0FIVINn5BqUolhkZ53n/Ka/KQGSAIMi46waJMwhBQ09w7oCkM2LHlv9zeSGl8MZOMCZRQqT0WBYwwoJclLgzKKu33kD+5M0mu2VAEkRDis63PCvvgyfO5ifJh0fuxVjYQAH9zrWeQGGVJ7Qilc26ONWYpQpHOy+3P6JjLZmyKyKokrxEjvHd3uJIkprAww4wFmUCAzhe8c0/05s/0pxaLn6r0Z3nt6FxisDRkMK8o3LlPnmlYppoeIt5LYzuJ6SxQRLZfUx9wwqzuUTOIjevABHdfx3U3MMKOZLvA+0HkPXU+WCT71F2+zUU1YTO/w27/2FoKMgGfz2l2M2qFzgd+5MaHzgVwX/IVLb3HzazfYWAGjFbieXhfsihYRYPDSFntvXebd9+/SF5E3fnDKjdfeYXpjBtcfOj8nh7+TzLkPZ+LRX0+b8+JTTH+PnYc+jFPzFPueteGJQNsjn520DzFfHw0gni4M8QxX4gn9eaFK98L+Z7Tn5xR9p78/z0DZeqp2T2vvSYPgsyJPH7Wdc/AW8DBR9wFL7Qk7x8N9TkYun7zfIXpz6kdHag8dOmOPi2k+7EFkfjADBJtXNrjy6ZdxvaPen7F7exelJEoKtIQYPT4KjNKsXlhDBMH8zpSD63upen0IoFJtmpUq0Zja2rJ/Y4+t1y5wpJ4efWuXqmupjlE1rFhMF8QQMEZTtx1SCjYubCCEYH4wR0qR6gfJpPJWNy2LpkUbTTUoqBctzgfsvKEcV2RL2pGQgmxQUBYZWW5o5g3BR1zTozKNGqV6BLLIEH1ST5PysLAqD2hxIURCjHjS4lcG0EoSRVJNc8EjkGRSPHgk3BJRwnqUUUsEKKm+dTqplXkhiFKQi5Tz0zmH8YIsS+IIbqlaF4MnuoiLHdJr2ranWKq2CSUxmUEKQZLTE4TUUaL1S8lsiywki66D6Fi5MKbMPEppRtMVinyFKAR2Z4aIiojCSMli0ZMVGTIkp1vnhtikYrDEiKpyfNMz/2Cb8vIawVra23t093NUWRDkZbx1KLGM6vcOqSXBOuysRZlUOLRfpHpBD+L4MTlGfrYgWx8dqyonD5HV5WpWSoEqc3zvyHJNrHtEYThUbfTO45Qkk6lWVNyf4wKJ8qckyoeUItZ5bD1J8t2jMjk2ziNdQI0TlTD2jugCZnWA0JJQ+weR/wdxkhDhjFxdJcBEj1g+/4i0fSTV1uoXLbYWCFUS5fL+kYqX+rZH5BozKFjc3AUbaH0gBI+3CW3TShOIOAmLRU1b15g8pxwNKNYGKKlQVc4oW6ectoxb2N/dRxcZEbC9w1mH0BKlZMrJEgLfW/beu8vefEqRZcQ8R3pDX3e0dcv6pQoVIIueetEwuX2fKz/wCcr1EereTnIYvUfLDJlFBpdH+KLFWUtvJSZT6EItMeOIjy4FO1Tg4uuXyJTh5ts3CM4jhWCwtcLq5ioXX72EWxvwlQ/uUtcNl97YZPO1hiADQYQj+M1DZTYejI2njbuPTkxPvUB+XLOkOmUf1h4NfZ2OGp3+2VPYSQAsnrg+pzlHJ/d/Dvaw5tJxey7Oy8cVcH1hL+w73D4epOgoTPtxOQAf9iU/LRDzrAPFhz3nx0WqDu0jH8QeEg6O1jc4utAnwlDKB1W7ncrx0hCBXolUIBPw7Zzg7bHWBbAqJYZEMdsL4Vii6sNzPXGiD5Cho/pER3c6MoEt+22UpDISiORFZCFnHIh9tl69SFbm1NMFk+0Jk50DyrKgWCnwbUNdWwZSMtooGIwDrm+58/ZNvAs465BCoLRCa41Uis5aTGa4995dVi+vMsxTQVMtNRtXN7i1fStNaELQ1UkswToPUpJlBhc86y9vMdudQoiMtsY00+aBCICQErMUNfDWs7I6RCjJZG/Kzs0dVjbHaK2wdc/W6xdpDxZIoygzg1gKHIQQkxx4DKhBgQ0NIToEUKiKuBRISDkyKY9ISIEICR0MApwW1L1jnxkCyIRhw5WJ8hYDCzshA5QqyFWFEIKma5P6nBKoGHChow+eXkjISnRMi+pAQqyklpg2OboS6HpPkIrGemzbo42mVH0qUBp8EgYIic4WIylHKlpKL4gmQ0dJqSPGt+RFSbY+oL/b0IeA8HOariErJEwDRaYT8hdDylUhkq2W2IMa0UcyXxJNhWs65h9sI6RAro9p44Du9j4iq1N+CyCCwjBEZhJr53S2wy/peXGpDOe0pu/Sdd6sInpYptyz3iGUTEVXTzzmssrR0zrdr0wn0YYIsbFIoA0lAgVag1oQbIsQEqUV0nmiUumZOKxFNMhBCqSWqEGG0oqw6JIzXGZIGdGuRg8GZG049ioKBJzs45G+Tnu432uIUBmJcI5Q9+jCIHNFXS8Xt0om5IyHSoVOCKL31HcnNPcsolgjuA6d5wSp2dhYTWhd3bF3bxdjPbmUmNjjm47F3vRh8VclwUWmk4QUGSEZSUVzZ4fr9/cQgwJdZmitUErRL1paO6daWaPICxadoms75vMFo3VDFC1RRDKpsZnB9pZgPXbWLIsXtwRmNE3g7v1AdHCw08O8J+skr33yFVrex7WWfkn3RAgCkZmdUVyreGntFRYHSZZ+OBqwmWkObu8xn+2Q7e9z6coGFy4O6adTICblQU4gckeGxbNUP89vR12sb1907yM/8rG1y7fvPB8nH34eGfJH7JTNJbCu5HdcrPaFvbCPw56DU/RhvIUPaU+DtJzlJJ3mWIgzvj9Puye/O8sZPNb+kQOeRdv7ThihznBqjw7GnzUZn88yAG4Vr3HXrzFYGfLBUHNfRLIq4+Abv0W7d+tYGxL4S3nOJa2xwL9dLNgL4VxdevT5O+xPPPLJQ0rf1sDwZ64Nic6zv9Lz3vdHsloiZKD7RsOtr32QFh5R0NQNG9Uqdk/Sdxadv0+5bgndfeb715gdzBFCYJQixIgGlBB0XZ+C+DHirGO+PeHPvDZGoAHNwY7BOofQGiUkXknKsqCe1ilKDQzWhyituPn1G4Tec3B7HymT4yRkko4OIaC1RstErVos+6O1oqs7svURg5WKbplj0s27VMNIJonf0FuEKEArfGe5N/sai/4eusi5Wn6WSl8ghJDEA4QgiOQI++ARHqwE0XqEivzuyuAfsVcAAQAASURBVDepZYeykr+0+1lWTUXd1dyc/z4KT14PeGntz2J0hl6qslVFjhMzdrs/xDrHgR7g1j7F+MJqEiSY1PRNx4Yt+ES9gjSKSRv4oOsTCmaS5HCsOy6OMlZVypMiBDJj6HuLkoIQQSjFtW5AdJKiUAzWW0TYQVcVKMNk2xP7jjuLP6SdN6hMIzNB1qd7K4SglgLf9LSLJG89yEZczX+AGARtVfPB/m8jYmSxI/jW/1bTLSz51pxgJMJFSta4Mvw8WkoOwrtsN18n1h0IQV5keGF5LyjeeT/R0Yo34dKVLKFLmSa6cGxBKyBRKuctRklQoAYFoe4J3oOWCJ3TqrdQsYS2pzB/lOTFjSbMG+Ky3eADGEXQEqOTaIUZl4jlucsiA5mCIsPM8tJqQ1QtC2uOvowcMlXPemF/8zr81o305w9erbgQHIQyBS20gpjqTwmTpiepJMF5UBLvEkrVTTua7i1cnxO0pGsjZI7FdM76tS2UVpT39nhtapG9wxiDjhEbI/OuQ0uVnFch0EaxsrJBsI7V+zV9b9k2cN05mAm01hij0VIwMq9g5y8zX4hUPLaAochTXldvkTE58nGZx+PaHoFIiNPoHYzWBCT/5ctfgL5kMZ3z0t0p37M14KWVVf7b+xNa1wBwOPp1vuV3bv3mw2sYInjBBSt5fbehfec2b6wN+ezaiDW94Prbgf/tjxJNMj7gy51AfR47n3wnTDYP7fyx1I++30cVTR/066zlz3NcGh2XxDilX8utnnStzmZQxAdRjUoK/m9lRf6IKuwLe2F/+u1DO0XnFoF83uPV+VD/87Xz+FHk6fc5bb/H8owPVznn2P48x/pITDxMsj6SP3Ty7ksSa8b1jrs37lB9zzXaacvdWxPuabj05lUenOgJECe6gNIpMvoIMPTU7I2HbZwAs4CICBE7rblx+zb3Xh1z5Y2rxGnk7rdusdiZ0vWW9fVV2rYl9B5vHZkAYxSSjhg9tusxmU6rlxhTLSGl6LqOfJTTLjryIieXkvnenMuvRWRiXGGXCe6HfRRCYPKMNz9/jVtv38C2PZfevEI7b2jmLUarlCMjQEiJ957gQ0KmlKTrHa7pKDODJyYBAtsyXB8lHE1ANijopjXZ6gA7WSABLQQqplyh4DyUhiA1LR5rVJJ01gqWNDmpZKJ0eYFQghyB0GnKziuDdZYMhZSCuukQ3qOCRxqROF8ASlJlGUIlhbw2BOr5HI1DrY+Ztx16XqO0wpRZWmyiKESOUpJp2+F7jywMpiqQOqFmhQLtLHFJLYtLylqwnhAjRkpEiCnHKEsCDFIZTK5xSGSIqBjp8Yjg6DpH5lO9KGU0ru0pjKZ1HkekjBFlPXqU4WxEIDGDgugceE/oPZKMfr9DyCSmoaVCRZFkvIVMjk7vCKGBwiSaX5T4eGRNFSMogTtYILRCmZJDfmIUEL1PC+UQ6ZoW40J6V5WE1tL3PcGL9Ny0jphB7wNFmUGMhKZHKFIelVGJLuk90SiI4O2yKK51CB9Q44rQNkgRk/jBsXErLD2is19YfxgoItXu9T5CSMViVSURSiVannX41ib0qsoIPuCtx04bQmsRWmG9ZLI/J6wm6tu8ntJOa1ZWhlRZhgkLOuvpeptQTKWSSEaMDIoSnRvm85r9vSmrRU7XdczqhrrKECY5jviAi5EQBH2XEGEX/APFx4UU5EJifAoczJuGLDdkeZZQNykwWrHoaopMozPNbLennzgIAWkMw41xKkobk4z9MVQiQuBIgEgcjnAwvjCiql4hHxTo0iAQSB+TWl98goP6XOw540OnzIEfuatz2kRx5qZPrpf0wJ7Y3pMXEo8vxnq0X0d+iY9v9xjV8JjTvMwAjgK1DN+F3iFz/cR+vrAX9qfFPh763HnsNObT40yc9sczegdPS+v7qMaHx3X/WU/tMYVRn6Gx9P+p7aXvnCqYywHvfOWbZG9eI0b45pe+wYERmKtrbOY5MzOkK9Yf7CmEQBIplrLVIsJqodMCC0GIQ45ddCEQMVDYGRDxEbaD51Fc6WGorkCwsSxIti5zmkXG/VuWgwNLvpJTzitkkNjVnvn9KZkumO1PUYXB1Q2VUQilyMyQqhowLDa5O3PgI0aAXyq0dV3HYF3y2g9c5pu/+zbtPKBURjOpaWaacrwCUbKYtoQlmuGWPW2mC7Iq560/+110XQubEPpIdlGQL7KUh7Sc9ASpWKZSiq53RCJaK3xMdLPgAxJoFi3VoGA+acDPGW+t0NYdhVZkKgkFGAliqeaV+ZzSDwlCoIVJQnIh5WcoKVI+Q4wYrfARlErS0TIKttyI0ipymVOZDG0MMUryfg0fHYUeLRdtISnXhQje47qAyTcgBLQrGARN2Em5UqPNFbAtucyobaCoCrKNjMX9Kd3eDB88McL6lXXWLq+yCEkAwasAKiC1wjiN7EJ6F7RMi2IbqVvIRhXWKrp2j76b0zUN3llkjIgQiFqnnBIfsEva4mhoEKMKuz3F99DEKSFGrF9AZyF4lDBoSrwMhODwZQDv8bGn7vZQOqePCaUxZYbwAdtZlFYI/5DqGSOE1oL36NUhEB9EqyMkFEcrqAOu6QhCoMYlft4S6g4RAqIoUW6OwKFMixhkhHsT/N4MaXR6n8XyPmqFyCSF8cjcoYyn7gIy04hME9oeN10gNzOEPv7GpcCyeDAanD1KHH9HVaZTLtCwTPTBrkc0EZlp2oMFpsrAR/q65aAxtHNH1CVzremALjd0PlCEmAQjeovfn1IE6MsMbyRKKUyWkMPgXMobtB3C90QpsBqiCIxWhvSFQauUS1eVBUrrFAxYXu+sSEi4mB/gZvvM5zVZtsBkglnXE4FBWZCVOWZQoKsCs0RzH4xfIr2/xaDkrcurXFjR6H6KeDCKHR3vTrmQgAV2jESsVekDnwRQdkMaN1PxrMc08EQ7eRefdqJ8CjvKqngme4q+PetyYXmIx6JDT2XP8VoeO6fHOU/HMK5H+iFIMb473pMBoe2QKp305vPr7Qt7Yd+x9pzoc/AdgbM+rWPzuC6fp60nnfJzhM+f1Z7aIToRBjuaP/TgiyPndLL1veIyX5qtcH9Y8NbLn6Ce1Agp+aTK6O7M2fraHV4avIzafB1TGA4TrUWMDHd/H/oZUgg+f2WINQLQdO77iBTHjuNnB7yy/btUleYgBP7XxYL+xMU+RIsEcFEp/lpVIYGp3OD//ANNcyAx8SLVbxrcVyPq/6qYfGGXu/oGq7c3Wbu5QbSerfUBl8clUQqy/NNkVcVqsc4H/puUYh8vJUZreuvw3nPpjYay+hqvfmbG13+nJAZN38PNb67wyve8klCDeJ1DGe7eubS/99z62nVe//wnMBuG6594hyACcgjtf+jwPpJnhirXLOY1A6NwZok0xCSoQIwYpWisQ2eGZtbQ1x1rF1eZ3J/Qd5ZiULCiJZulBgEZpJpEQXJx+Ba+SIncTmmMkakWUkjOtQueYFLdHuE8IUSkVuig+MLBW8ilXHnMkwpaDBmvb/wwnhS9NkrjSUVMU5FDhc7GvDz4czjriBEyDN4H+t4jO8FF1pl2nttKklm4+83bdIvkVGqjsM4z35vxlZ0ZbduxdmGV8lVFa1qElLwWx6xlGRKQ1iOUxHcd37wekSsZUgj6g9+i357iVXq+hYQsz3BSJInspaqeloK46Aky5eD02nKj/gN80+O7nihA+EA5WOOltT8DQjB329xXbxOlYDHZZT79bTKXI2LEd57OKPLcYIRIdaZMAUI8iPLL0kDQeO9RStLNW2Is0+IaQWwtMQSEVpiuT2ITgxxCSEiQjGTqbWIMaBXwM0le5IhMIXxEVRnRBYRKDkquPa+v1ygZaem4MbqInXcILRFFRuws0XtCDKij6g8ciaSfskY9Pe6VkCoAa1Oh4KQ4t0RTtaLcHNPszvFR8M3s0xwMJV3wWB0oBxWLgxksGhbWURWGwmRJ9p7AuysKm5V46yjynGq0hgLms4bFfLG8pwplFBMlkQi0GmO0YtR2tF1P6PqUVwQYIQmZYfXVC1y6c5PR/GtMun3+ZNdzoCqk1mglybQmHw9SjltnE71VJPESbx3CeSQG27Z8av0+m9bT7oEO/Smj6qMmgP0Q+fd1fcqXDyeek+P/2fLNj27z8B49yZ6Ds/Ss8+SDUxUP/35ceyd9gUNH7Dzd/zbM50+Fw5314p3S6rFf4/HP6xj5j02dvpIgmpoIfPb8PXlhL+x/WPvQTtFzo9M+aTA7AlI8usk5jnQezPtx3z0rNe/bYsc7+1RT1in0hUe/jKd/vfwwK3KuvfUSMUT6eYNwkYVt8dZx/U8+SPkoSvCJz7/F4mDOhZcvIpRYcoHigyOliFxSnxImRVeDD+xc32b7m++yMtinfHmdB7D/E66EJMXX7793j36+yajImdQt3gZCnyK0w82UBB9joBoNiNaiRaJPZUuZZ2U0trH085Z8Y4VmVtO0HTo3aKkoRwVCWMabY4YbJc2BwEjJdHvK9a/fYrw+4mBnilaSECNKKRCQZ4b5/hzb9MhKEkUEGRldXEVd0ezd3CPGSNP1DMuCaljgM830YIHrPUQweUYIAZMZinHFYrJgsDZg5eIa3iXKXV93SQIMEAFiYbDWYWKi3SkE6FSANiFOEaTALZ0+tMRZj/FpIR4hiS+IJPMdXaoXIzKD7Wyq3RMjzjmIfrl9ory5mIrX1ouWXKkk+b18BnKdrndQAmk0Umm237+XhBVyk5QBXSoG23WWGFIB2Wp1CJnDZKkfVVHBJCXWB8B1PS4E6mmD7lqMD1D3RCORIsXqdZGhDp0+69FbY2LTowREo7GzBgUIJQlNT/AOmZn0kEkJgwIGBToKxELSHyzSonhJQfTeL6l9jtj2hLgUl/MBVIrwP6CrIgjOJRRHylQzZxlIiEC/NyfkkpgZovfY/TmxzFK9Jx8QIaJzie+WKnxZUiF00yYdTwpElYGWiS5TmPTT9ahhQdhNog8yN/jOpgKztImeFZYcvqNDxDnHvRhjqqeUJWqfVBLbOwgRpZMEt9SK7qCmmcxRJscJRxs0+WhIvzfBOcfq1lpCSa1Dlzlt1xN9TNRKJZG9w4sk+jGbLui7Htc7xmvjpYNs6dqO6DxVniVxhxDJjUYJwaLrkcv+1l2LDwF1U7KxqCEEjFYoGbHOMV4ZIFqHNknsQiyj7A9qdyGwLhCcp7OOjQsrZEWLsPVxCtTJQewkcCQSBfC0S/2o4MzR757sJIlTO3HWZ4dHfIYk/+dhJ0/12zDnPsvS4KOyY9S4M74/DwHwKGj3HRDufmEv7GOz54AUPX4x+tT2hJHlpBrm+Rtd7nh0/9OQ5FMPesbvz8ueByp1ctMji6rz7JAJuKSSZHIbI/eWIgdPO9DntFxdS0NqEx23dpPak1nW36mqEl0lZbU779xm99YOtu659umXaMyY6UHLvQ/uovVl8gtjZrsL3vmjrzJYXWc4HnCwO2Hv7h6Z8Ox4jZgq4saYvFhJ+UzRMXITIGJ9ZL9xRMBLQ52vs39nj71JZG08wCvBWAqs8wxXBqhOU02H5PsVpsuILhVJbUPPwhRYEZgwQ8SWlWIVl3l85zBG0zuPCBGJoJ4oilGi/K1dHjHf20FpgRaSbm/O7rylGpTYOkXCBQIpwOQGN0vCApnPqe81BOEJVvDGW6/iPezf3kVJhdcpYr23fYCUkiJLSfBoiWtS3kMMAW8dw7URIQTmBwvG6yPaaY0cFcs8l0iQgszF5JAUktg7jJS45bPkhUCEw7o8AlygtQ4fPEaQ6gKVOfQWKZL8s1g+PFKAFyBFUrGLMaIgIRtS0lpHrxX7KslzV71jXaY8Jy8eTt+2s3gD9cGCGCIuWFbWR3TOk48qSpOEJWzvcL0liIzeKJSS2F5QLhe6deyxyhJIfRcHdXJQyhxt9IPhQJQZIgSMD5gyQ41KXGfxXcoDEdYnZ0JnDEeXkwBCiCDAh4ARBXXch97TNHNKuU5cLvyVlKkosHGIEoKP0DuiTPlaAwUXR6lQ6cJ6vrUXiL1AZIcLbEGmNBdGSS7bxIAoMkLTIvMMMo3RipAb3KJNAg/5KqKQ6EzSiRneWrJxhd+dgXOEBuRKhR4UCJ1QI70xou9JiJ8PSGcZDiOubhkMkhADwCiDN9bSfZp0sL1Ig0qMD/MQN0pYPQ724ltLseiwscAvnWeRabJBQbAOGSJ6lLHfFnQmo592tEPwJAd7sDJksnuAFILxxgrNvMH3lrXGYXuLsJF6YNA65ffUiyY5MUqhM2ibluFogDaGsiqgXSCmd5C1IBuuEtQQISKXxyW5ClgBk0Wkbh3zyZwDK8CPaHRGr6aAJy9ytFCICGaQI6RAD3LYTucsY0z5dAEGQvHJN65yb/ce+97Tx4g7dXg+schdXtSTNVkfAB/xECE6DwzyNM7P8T6dts9HSLD7aOyRzj59WdfvpPM9u98nz+o7qdcv7IV959h3Tk7R4yEKHqyyjnlFJ7Y7bUR+ACmf47An7WkdoKNd+jCOzod0vB6oCy2jk4/tyvL6rEvFXysTveyG9/zCEjI/44I+uNTHLq+AlfoO1+wu3jq+sr+Cn+dkmUZpRTvv2ds9IJtrXvnu17j+lQ+QQnLvvTsICdv5mOm2Z3+hUL+v2XxpRLV6Cdt+wL3r99gWKaKstKb3gvtbn+WDSUfoMgY/+ml0lVP5Gd89/W1kDOzWlv/63oQItGbErY3PMRdzFnGX0aCkmdX4GBlXOYuDORd3rlDuDdl9dw/hIcrk5NzVDRNpiVLwvvyAWMGlay+x+plN5B/3tHWHJkWB+xC5+a2SavMttNEMVluI95foRkZmDIu6RYqEfgilUEtqmfOpls9sZ8rK6hq3f/M2PnjG+QqfeOnTXP7EFfbv7xNdYLFoE60L8D7gieBTNDzPMjIt6ZoOpST13oz5zhTbW6bbE7T3qLUKaRQ6RpTzKKlSnRrAO48NjqAkUiukgF6AXgpKtL2lzAwBTd9Z8twkZ0mrdA5KEpZOA5FU5NI6fIypvo1MdY2s8HgiszLjt0c5zgUu9pb/pU35N0hJNBLnQ5KiFoLNly9wcO8At2iYHczRWrOYLBhvraTipTGyf/cAe/llbt1tiCKypXqGMkk73xv2HLiarm4YhZ5SkHJyck02rnA+4PYXYB36wgoq0+AC0XrcosW7AC4JXIQQMM5wufpe0Ok8xbLY6NTu8sHt30BkihEbXK2+H3GIHsik4DeVd9hrv45etqWW6msvZYI3Lo4BwR/eWfBf3284NlRH+MLLJZ/YzPGzBrufctuEUgQb8LikVte7VFMJxcXh91DICrTn+vy/ISqJWR1g6xZZ98iVAWFa40clQUX6tofgibJC5oboAlUVuFLs4WJHrjIIGUIbXl+H15Ypgr93C37pWxBjGh0Oc4y+7zL88EtHhhEfqO/PubtY4c6OQ0hJ11kKtRSfCAGzUqGHFdezT3Gv9djV5Ewbn4roRiEoq5Lp3hSjVQps+MjLB5bJ9gELAourq4iVjGo0SLXAZjXNfEGV53R9T123lHnGYG3ItZHg0tu/x8G9fe60F5ld/EGkMazlliuDnr5puVOW3DEVXW95ny2sHCOGkkb8Mbncw+QGEQAl0VXyArNxhdEawbImWVZwcdKzVa7xMpr/c9GwsPXpw754igX6M9C7Tmv5WeKO4qldiedr56EFLjd8/El/lOdw7P48Z/fxQcz3dJTo+NHEsf9e2At7YQ/to3OKjg7Ox3gBTxpyHzeqx4fO0bN6Didpeqf5Yh9msDgrQPeE03qedvTQcalk9MhAGU/8GkkRcClPdPtReetH9jv6WUwKWPXBgtl9h28HxPEKs1mNs5Yiyyirgnbegk+KbVIIbnztOkhJmWdpIbVUWGumDWZQJOoXKQqPT7kk2aBADXPe+dZNbn/pm1z5xDXyMYjlY3ISKUsLNcHO7V0mUiKERGjxQMVNLWWIL7x8iXvfuo0LMS2YBiVWWdqup9ocsD/bwTlPPasZVoNUdNNbXEjJ0/2iY7ozY+3yekIZckO0AWsts3lguDIg+EA1Kuk6i6u7pEg1W1CVBcWwfHCBj17erMi48omrvP9H7yaBBWsxQtF5h/dQlTmZ1ixrp1JUBdWwpGktfdsjlpSbfFBitKaQqThltA7pU22faF1Kes8zZAg452hCwC5lwuWSppTplFeklw5RbDuiUklFbCmJDekmSEu6ZxFEptICflnjyOQ54/UhRZURpWDsI+LOBE9SMRTWp9o71jG7P6faHHHh1Qvc+dZtVjZXaBcdzaKhW6JuSiS04WBaU2wMqXdnxKUYhACiFGAUOjN4JYhGpcK0QqCMSovaCChBOFigNsfY3Rl2e0IfYurzYR6cTOiWMRqiIEpJ8EmpTQqdFNxaD5VAFVmqNeQDymSEGOldwEuBDhE9KpHOQ+/wdXfsJV7WRX34PC9pePiAmzSEuodS0NYdmZTUTUcpBToEVDREleTXiyqnFw46hbeWflpjNsY4t4/sLGZY4JWEYCmKHILH944YI8E63LzHuoa8THlY0S7rG8W4pIkd5hcdReUfDqqCmAI1kXRsJUErikrRtxalRDrZuCxSaRTdrKGZTnFmjK07dJHhfCB6n5zsGFFGMT+Y4dqe1dGAlYvrDIzmzt6EQGQ+mdG2LaurK4xWh+RlxmwviWMI75keTKnnNeWwYW3WUJQ5uSrYm8xYHQ9pY1KfE21NjDnVcEARA711tEYzP5gRc0GmFVoprLCo3GCGBSDIVwZok4IOXQj4umHNOtY+sYlYOuvxGORz3glIIMTxAfh4DtH5EJ9HF9FPnghP3+djxomOTEtPn3vDh+/qY5Yhp0pfH5tzj/c4Hvn3SefyZAfw0ftw6rYveHEv7IU9Yh+z0MJJHtqRfU9H48/Rzjn3eZYB8GlO7XkiTh/CDifXeHLEPaV/Wmk2yq1E+9qe8kff3Gfz1Ys0G0Oo6wdEgqPNPNpmRFcr6HKMkJKAYjptuXFzSpOVhLIiBhiPhwglaGY1q5fXmdw9SGpmy0Kl1nmsc7S9RSvJyoUV5rtzTG7Iq4x+0VJlhiigaS1b1zZwwbN6cZ3NRQ2rBjPdZX5zj3y9R2tJ0T3ssQo9w/Y+wzyy2FDcvtuliUkpRlWBlKDLBeOLlsG6YTrpabczhFKAxs8cmSzIJpYts8naYp16v2YxXdBaRxiVWAHWe8Yo9m7vsnZ5DSkFWW5obZuECpxnNlmQFxlGSUqtmAhBV7eMV0fkw4JybYCQgkvDy/gYqEwqeIoQbL20hVKSu+/epZu3IFnmwcQkfuA9WZkjlaRuO7pFnxSdlaTKFJcurROnNaUUqfCrD8QEMqU6MDEiiiTV3PR7zFyDtY4y26AsBilfQwpsjPgQ6TqHW8qC+7bDRRINSgjUsg7M+jAjorB1h5EqJe8qiYrLPK4VxUvFLUSm2ZCSTM1wix6/MOh6HeUDlRCs5Ro3rRmsCl76VEGMLaONAbs3BbZLjp8UgkvXNtmf1eSjkkGWYWJMKJgUDIJZ5ilprNK4HgqjyauLqFpgRgVtsYeokhRzDJH6YIEjqe+1LpDnmmiTDHZwLXuT6witU0BBCRSKVs6SxDVgZWCSW3zbU2YlurfJWfSR2FmCVsRZA3nqG0t5dBEiVXRcHWdJUr2LaJ+e6S3tWckCjayZZxJrHSo3NG2X0IhBgS6XznWXivu6zkEO3aQmZAl9c32P2RgTO5tiTiESjCQIiIsWUZh0Xi7QxEhTjfA6RwdLacIDClewHmVgrRC8OXZordhtBduLlG/SOsWkTTLbg2L5XmaG5m6DYADOIxHkGyNkZhBK0k4b+kWPk1DPG7yPdK4hzw3OefSS7pscrci8buhnDWs6x5Sa+8ESdxrWygLbOaYILqxcYrUUbLYN83nNfNIyVGvYumM6mXHdjMjyjIUr0JMZQ5VhnEMKjQsrBCuwmSOrCgadYw1DWFujzlapzYJ+Kf0tltL11cIxcpKAoVMaxgW99ZhrEfkpxUJPCco/oEWec5Q/Mi4//cR26Ag9vpjGOSaQM7f/mOzDzqtPs/9pDtBjCShnwVGPuEpnNn8eO3lnxLFFywso6IW9sKe1jyyn6Hzv43P0Fk5FpjgbuTm633nnlyegSg8Gtuc14j2DPeSSn+HEHIHvS13xfZc/z97729y+d5Ov2hHj/RVGW2Midx50/UmdNyuXKS99F+Wows4tt97f4f64YlF3qNKQS8mibhMCYRRt3dLWLQIIIdB0PZkxFMZgQ8DkhtHqiL1bu+hcI5dy10YpOudwzqIzzcGtXfbv7fPS977MymAPu2hYGwm29gJaBFx4yNDP7Zwr+3+CAEavbhHHV9m9sUPb9NimZ7QxQqr3eePP1bjecv2rB3ywc4G27zGTDFpFNioZ3dO8+rnPs/9be0zfn5BlaRq6oSOzTKCLitf2OtS8w3cOtaRLKSkIIVIWGW3TYYG2bsmMYjAs2d+z1IuGrdcuUo6SxO7nLn/+kUsvpGTj6ibDtRHv/PdvMBhUuM7SdRatE7WQTNF1jq61eOtZ31yhbzoub63wcmWQZoAAeusIUmKUTEIIIeCcT4ISWrFfX+fe7AZKay4XP4jJVlFS0PV2mZeheX/WM91vcETyQUFfd+hBjpKSPDPQdAxLg7OOTCmCPFRVS8VAu3nDejnjR9/8Q7JxyttxL1l0bph8uaT74zG51qxExXi9wnrPZHEDvblL31ise5lqZYt779/DZBrnAgf39rmYZ8R3dli/tsk4erzzKCm46DI2owERuakLejEjdJ6L629RhZKYaW7lf0jIHQiRBBWqjG7icCFCDPQxogSowmB9z7b7KkFogk3XjyUlL68y6B19Hnl3sKA1ljUXeF2MESEk6ekQCVqihEiIVpYocO32lKwwvL5e8gmTEvY3dz2DhQegHNXosWU+m3PjYMxuL3FNj1YaVWlwHlVk2MkC4Za5XdYRbFq0V5tj+rZHoXDzFl1mD4oBoxKSp8cVfUfKnSoN/SJwL64RDjwjWfOKnuMtqMygtCJax2um5/XPZKhM8F8/EPzqeyRK48Jwfa/ALlpeuWgZOZ8QRSTRB8qNIa7rQQh8b5P0u1EE6+h9S8SwurXKbG+aajWREOGsyBI1t+1QUqGGBb9/b5dyUNAWktdud+TTDjZWead07N/e4dVLhlenf4jtOmaNYbof2BSO+5sbfKVcx/ae9YXlM7WDW/vEEJlmGV3fs5cLFi9l6LZjfHOPwbRlY3OdO2+U5GsbeCWYLSY0ezO63RmvLiTDmeWiHjFVc/Z6y3B1SPlDFfe3bhNdxL3tiC1HReM4Mvgef/8fOxKfbsebPI5RnLZ4P88n57KnmffOw6o4q72nnV+fw3z8VMISIgUrY0yBq7M3O197j2JMx/c7Wqj8vP17/PV44WC9sP957OPJKToPXH2Ww/Kk/c463vN8h09r66NGox83STwRwVpGo5ZIztkOYaSd1tz8+g2IMBiUFLlOUtnn7p9Aaf2Q8gWYIqMYlPStxS4j4ZnWdF0HQrB3e3dZrl2gjUYpiXNJ5UwpyWhrzHRvRoxQjiom91MytdASgiDXBt875vMa5wPb79xGvuRxIrD6+mXkN7ZhKet7/CKmCyEkrF/dYveDbYiRvunwfUU+KIAFUkkGa0N0mbH5xmWc80y/cQNdGNavbOJDpNmdU+qk8KVVEhFQRuO7HqMVdtawd2uPzVe2yAcF3bxFaY1SiaIXYqSocnyfFOFG4wGz2YLFZJGuYabJyhykoF905FWecmaIFMOSvMp564c+Tb2/4OY3biX2o1ZM5g3MFkRgMKwIWtEsWozR5CEinccpiRLgIhgAKQlFyh0yhzloIeCdo1zWjtGZfpCjdEjRczEds/MeYmQxXTBcG2GqnG7RMZ/VFEIkSpYXeOvRQiCrDDtvoU8L2+AD5foIRMTPG7JBjlCSam0IWUIFpJaEziJkkq1u/QGDi2v4Wiba41KW0juH6yy27vA+IKTgpU9eplDQz1oQ0PeWvNBYEXFKoH3ADHKkzfB9T8girulxs4Z+2kDTk/ulIIVJ+S69AN90ZEYhc4PUin7RgBRkIeKdp3EhxeNLQbNosCQFP9tbBlXBwFTMaw3LYqVuUmOGBTIEZFkQpSTuL4i5RmaG6JLMeVgqtIU+Kdc55/EuUdeGF1dY3NoHwPep2KpAJREJ5xG5IlsfEgVkVY7rLLH3ROfJRiX9tEYiwHkw6ZqHuiN0dqmMJ5O6oE3KfGJJCTzM+VJlhjCKB0u3GFPxXOtwdYdrO1xtEaWhPVigs1XoE4J0SLcLLtLsLQhdz2JvTl9ZKCLzgyk6V8SQnDelNdIH6oM5Os+wCUwlr4oHjruSgvGgohMiSaLXDdPtOeNrG0yu30ci8FIRywFRKUyRUUqJ6Wc0vkV6z8pwwPrVLbJRidKRd0LP5P4+4xgJIXL/3g7+Yosde4os0UCn0xmDewfEchUB5CsDLlx7A9kuWHv9Mio3aRAVh/Tmk+PqGcPt4zY6w87a9+xF+LcJbThtvj9JLjlppwU0nzQRP4eJWhw95pkUugdkCoAHDtFxh+rc2VBn9OM4k0M8oaVHjvYERs7zYhq+sBf2P4p9BwktfEh73AB1XmfsCVG6x0awnmTniAKee9+nMnFsf60El4cZUkCuMrr9GhlBGUXrHKvDEqnkWS0drlsYZkNWy3VihOkkMr25y2BtyOzGPtw6oJs1lLnB1R1CRCwOrTVd07KyvkKeGfbu76OzDNcn5SnrI9W4ZP3yBje/dh1IBUnbuk2JyiEmmpRNCfXRB6o8QzvB9E5LuTkguJyvWQsxcBDCg8s2j5GvWgtAsVpz6VMH1Iua3fc72sk6870Zt78hWLmygjKKi69kZEIRg+X6l3dQUqaFTO5pxAJGnr5xlDEtNi9qQ+0j3kEuBcoY7rx7h3q6YPXCKrOdGcEH2q4nr3JsZ9m8ssntd++gCwM2CRTE3nPjazcQywWoUBJ8RBpJvWiQSlFVBcP1IUJIVi8l9MZHsI2lyAwxJnlgpSSllqwNMgqlkTGy4wN5XjAcZMhZgwTqZpvGzTF5xnD1Mirm+LYnKAkBlJRpgRnSgCFCxAsIAtq6Sw6JlmijiEok9bVM43vLbFqzXw9TjZzes2kUwgUyo3E+/d/ueeT7GyAgNAo5nhCsx+/k+BCwvUMZnRCLGBkUa7j5HGEqyvEKrspQS8lwJQR5lbOYLMjLnHpSs339PsPXtvDBo5BkUhJ6T8kG49EI7QKz6V3aLMe3LbaeYvuaxbxFh3S+kURBRAhC25MLAUYTl85aXLRkAnRhiHVPphU1gWbekhvP5eGYECJGW6zbZqEKwtAhyZBKQYzoZd6R1JI4b1GjEh9CynGKEbc3J5KjypyF8/heUPuKPkqstaxe3Ux9JNEhw1L0QXjPPO5QXdwgygBTidLLcaEl3esQ0qKtSLLiewuDyjUuN1BDdIGgJd2kJqsyvMiZRUnsIlkIjKoIWrJbw63dNEiECJ+9FAk9rGuPq5NU/GJm6aaO6DOiTk5UCJGoUn4NUrDnRyykZpqPaDEQoW86ZCeS41kWCClo65boAxtNcgDrbo4cV+zudohcUK9PaMM+1mrWJteQmUZ2HerKy+RrY9qDe0zW9lDDIYtMocuMtmlZXXN85pMDynFFIwbsNZ5G1ays5HxuVPD+fEa+AJSkazu273pkPiJWBfiW2i6Y7h5wdyTxW2tEwPqAyVdY3G5ANIAg+kiwy2Krj7EnLU4f1JM7Zz7SYVHvk4jH0UXzId/go5VPWJ7ZuamDT27qIzNx5h9P3Pw0KXSxdGGeV8cFR92Ys1DAp4nmfowUlxf2wr5D7OPJKXrW8e7ZQicfXdtPa2fNZE9z7NMu67nGqSNRviOUuVxJvu/KABUjk9sNN6/fw3uPjIHBsErJ63SPHOx4wC6yUV3gey58lsX+jP/29gf0/gA/bQjX97D3psgQUAKGmWHhLEor0IpROUJrxWR3ilqqkikpiURCjKxdXme6PcF3jswY2kXLeH1M3/Qpz0FKBlVBV3cIKdFKMW067IFgrEpmu5LfalvCMl/l8DLshsD/0bYAfHq4z9/8Ybj2Wcev/z93effXRyil+OBLkn6+STEsGK/t4to/wWSal956lTtKkw1z6n6P1csbKA9qLmj2LZHI1qwDpYg+onKBLwwqROb7c7pZS1HmCAmrl9Ypq5x6WtMsGqSUaaISgqIs6KYNhTE0vkMhyI3BlIooBV3TIYXEL/MpDran1PtzqrJAiv5BHSGtFINRhSky1nPFa6McGeHmrOXepGUoNddyw1ArYtNzYG8x6W4ie8llJKPhNaSUaZFepwWUWRZoFTo5bjEzy3o7gSgFK1srTLYnLG7uUqxUbFzbZDaZozLDu3cO0GVOESMrRYruSykxUtBbS6gHHPz6NfIyoxjuEuWv4nuL3ROJsqbTYjkvUg2mSl9Cx1VUB7Nphh4Y1q5uIISg3p8jfYQQMblm89ULXNoaEq0FBFGCMSmaf1W+lWoDWcutxe8yn84wMZJtrRC9ohCSaBLCEHzAu5AKnQaTEMKl2IQkyYcnVCRAZoiLBpNr1LDgwuWLrDcreBeY+rvcmv8JolOM87WUmySSqIAqSmSukVol+lhuUKtVeoBDILb7qZ5RlbPbZMxbQzPvl0EFic40yiiEkQif8mxUVYDzHKgPWLj7uKanuT9BD3KKjRHZIMcdKFSWJ5THe5w03F6MEPMl5UelGkV5YfARFrtz2kwzXSTEcH1gqUyHNJp39wX/+9uRGAI/+prkr30SfB+5O5Pc3RYE69mdS6xeIS8M+PR8ubZPo1WVE3rPu+ElDgYXMGuGrOnQMRKLnPneFFVmOOdpZw3eOSpjuDSx5H1gFj2/X9d4KQjGcffqTQKOsh3wvfcukTmFFRmL6Uu4eJFF5phc+QZtNcEsJshsQJ4FLmzCZ/7cBmuvXeL3/uCAP/4/pmns8BWfVhVXLs/4yrcWlOO3yKSiLS5x0OR0i4ga1bi4zcJavjHdZ/7mBmZYcvdXb9LstMdhhnOuOx9s9px9h9MdHvGY7571iOenmh3dLRIfoMDnO9I5cZeTXz/ntf+pQgsPDn0Su3v+i5FT/bezGCdH/z5J136BEb2w/8nsdEjgqeyQlvQx2Ed9KHHk5+jxznPck9uehVh9bGOMONKPyIPyphGiD+y9c5f3/ugdDvanFFWByHNe+d7XGW6On4SoH4tv7dzcwftA7wOLuqNte0LwKKMJWtM4lwohRqiUopm3TPZmKckBgV7m2ggEWinqecNsL6EqSqpEGQsR733KQxGCclCkoqRVkeShi5xqUHD5jSuPRkofwxAxVc61T1wjhESzkiHSzhrKUcV8e0K/aFOE3nmK9QFZmehGrrX0TYfJDEpKpFSJArW8MM46wpJSlC8Xk8Ugx7tAsz/H1n2iV00ahIC+61FKMhyWqbaJkggpKItDkYBIkRvW1sdkuUEgKHJDnhtwgXpWE3zKNdGZSeIUuUE5jwnJoYlKJkloo2nqjtC7VGtHSWRmMIMCUSypT0v+e3QelRtknuiUSThApCKigpSAL0BrlYrOdpa1C6v41hJ9IC8zvCDJV3tPFCxlyCVRpHyy6FN9H2UUwXq6pmN294DF/UlSvBMQQ0y5WUYhtUr9Uok2181aJje2KauC4fqIrTcuU6wO0t+b42VRT0/oHBIICOTyXQhCEHKDjBHfO4r14YPX1jY9KElwIRVY9SE9C9Oa0NtEIYPkJKmkLieWNZyi84TMoCPo3LC4s5+ohkIQlnQy21l8a8nGZUIvICnQ5SblzCzbSz/pWqu1EXZ3SrQpV84vWmLbp9pHJgk9AAijE2oXY1Lbi4BNOVJuVqOB0Fhc06d74XwSVMh0kkFfKjzGztE1PaHtl8p5Hq0E1caQuMw/izHR9HyzzI9aFu6VSiVBi96CdUSXhCn8okWvDxM1MgI+JKW2QUGxuYLUmnpnSh8j2mimOwfM5zWLec1iviAqkXLfrEMLQa40PoRUjLfrmB5McX0S3ejbjmpQsTIasjIcMFwZUpQ5hkRJPSwybPKMxntcUeGJNH2HdZZsWKRrARzj4sZIuTJg88oW/WzBWuhonaV1Dk9EC0luMmwIzBc1kw/uLwutniirel4Gw/Lvx25+qEh4qh2fjARnI0rixDL4yMxxbjurhtHpthw0nzQ3PsXc+cTNnmUOXqK1553XxdHzeopjftglzuHdO5U5fvZOxx2ij3Wd8sJe2HeWfefS574dZNZnHY0+akftGY4hheTq+BpKHr/FmRI0+5677+/i/BbloMLGCCHw/pff49XPvX6yJMqZnZrvzdi+sc3KhQLZ7eM7h+x6PJJFbxFSUghBnhn2jcBrqIeGcefRQtJ7h4gCqVJ7i7phVa5TDQqES7QpvMcImXKEfMpzsZ3DO08xyIltRztryMcVRVXglhS5xwUn9/c8v/s7KXcntBcYrkkWkwVFltHVLULAZDsw3LiKqTaY7h7g5nuUWyuIrmHx3gK36wjTgAykPBAlaecNQgpMkeOcA6OQqwInHVJGqpBhe8fe3T2cdZhME73HtpZRVRCESHLPUkCeIaSgs57MZLi6pas78kFJCIGdu/sYrdga5Sn3aqWCGMmUSgtaQPmAFnBn0ZOtDmk7TzuZs3JxjXpWszosEFoykltQJ4nsHVVzW1wnikDpc1bkZUKh0FmF79LCVgmQPtLjGW6tMNmfJ/TKaLquZ+XyGtP7BywOFuSDAt87slFJJCRUUsmULyMlQim6g5THpXODm2uk+DQyg9COgOToCSnwywKyvXPUDkIMLEJM9ZFay4FNPzHCtYsLVvtbCDSy+ATBlwiVRCUQAuFSLpdaonTCe2JUyEGBrTuECzjvUx6TEPgYmL+yim8sorWszJJTYwEhBcFaZNCs5JeRZYZtZrTs0naOIGsO5u8SrKf2BxQCZGZQy+cxOE9dFuzvt0dfL47/EXl9lDHYzKldjRUZYdESc5OUBQcF3bxByqTwWFQFg8wQuj7VsDqo6UOEtkeZlKNkJzUxRLwPZJFUMNUowrwlLqWxdWEgCmJviTNHLAx6ZUA+KoldcpakTPXDovPgBUIk8QQhQGj9wEmOQaDGVZLytp7gPWPdk4kWuZJRx4zdD/aSquJYsHd7h7LMU60spejqhkFtyZaveDNviCFQDUr2tcSXmrgyYjjYxkWHtA0buzUr4wE4hf/MNWzn2Xv7BnpnQl93OJlogd55FkIiSQ7WvjN84yCjUoZprln9RJKzr23kW3uJ+lZcuYY56Jn3lpFy+DBDIAi+ZVgUtCrSND3NZEH0gWIzI19NcuaX77ZkfSBEeNvZhM2fMucdrlUf+GSRh7mip4zJsKTSHUrQH6NTPb2dhRQ8jlr3tOhCJEI8C7MSRzd8uD0nHLv4DMdezhHH5NAf28aSbnhI9XvS3HwC9XqqTj2FPQ6VOi8S+afCphb+H//9YzweMP74DvfCPh77eJ2iD+vofFgH6ZzHf/ph6Yx2zxqMnofDd8aAfNh3JTSf3PwuCl0QfaBfdCwO5lTDKtUQWnQUgzItUgGEREmJzsxSBOEx/SZF+e+9eyfJSrsFZZ+cCWEyVDZIdYVCSAhImfOBidzUAREFb/aRwnt8iMQYKAtD01my3FCNSm5/4xZEcN5jrEDkGr2UKY7eM5/XjAYl87bD+4gnsnZl40HdmCdd27v3LL/4S2lldW28yuWLl5lsTxBZhl5G2y++9Vluff06PozpF7dQvI+Ra4RFjhIXcXcEMXqilAwHJfW0QWmNdQ5RdzgJoevIVzSyTPkdphbkgEWAlCzmDRqB0iqJAghwIRCkwJQ5XdPTdJbeeYSEvu3wMTIcVYgYqbTkE9fWIQSM0aiQaEuSlL8QYuTuoufG7gI96wg+MN4Y463DCFKOjlasmZcY51dwreW/jd7m1nhCcIEvqk+xUY9QRhODJFW09USW4gYxLtG0hI7p3KCMRknJ2qV12kVHVmRgPUGA1JogUq0plRlEF5JCWt3Sdz0uRBQVVnwWnRm0SXlLQkpC22OqHKk1c9twr01RfqElJs8wVU49NExHGcE6Pr34Mp8e3kIaDfmbLO5qQojYRYvwqS5QlCIhKM4jIsTOIpSgnzQpsh9ieqZiRF1YYe/VFWKZIQ4a1r+2T1ZkhGmDa5JqWm5GbA2/CyMlM3+fW/O7SUaaA7b9HN87yv8/e3/2a0mS5/eBH9t8O9vdb2wZkUtlVlb1VuxlpCYpaUYDzFACRtADAYKYIUGAfCQI8IWCSL6R0JvmX9CQGkgEBhKGoAANBWEaEIfFZquryarq7qrKyj2WG3HXs7u7rfNgJyJjj8jMyOoqdf6QGffec/y4m/txN7Of/b7LpQllHOaK0rrPXKym4KQN/NHx+rmPfHFtyLVfOqD7+B6m7wjrHm109hOarfEx4WwW49BGIUtNnK+QRhMLieocdI5UCkRlSDGx/OQEWeoMX4uRcnuIGtb4tkc3ZTbhDREKTWh7ZIiEtWW9XDPcn2RPJhJJZhEVQoQo872lJLHPnB+3WJPCAESusAmjaVvLGzcSY9UitOW9my3eRbyRuK5HFTVBgO8dWgcKpbg07aG1tG3H/qCmHtSsL1o+uDSirUBLS6o/ZNAo5KLnnVOJWXcsleH2O5rZck1qDPXdOQgY7zWcKoWWieAjRmuGZcndFfzuJ4ItV5JSZOubBqkl05/O+fjjOaTEt/Y0k0tDjj64zUgFRgMwSnJHR4KSlJUmtW7D0UxUlwrqrYayMPz2dy8Yz3JSfTME+hif2Wc9Oa99wSz3CcPuL1oaeVZC9JJ4v5eMlzJcfeTXzfab5O9zT/rTU35Pue/MFgzPPvfntvW5CcjLzSqebryannvkBz6C93O1h/lZL3tt/rQkTl/H1/GC+PmtFD1YInvKa0/b9mnxBZOPn4vK8cvA9Z544cmO0656Pvn+h8zPMib+8sEu6+Vm8iUFRhl2Lu0ijEQalZXn1rxwhalbdfizwLAwdL7DCKi8haRZ99mPRghwPjBftbitMsOtEpSVpFw7hEyZa0SGxW3vbXHy8TF9ZxkOagQCbz1tSBgtETEyqiuUUizWHVJJdvYmTK7tsv/a/st7Hj4UAlCFxsdAbx2lDfTLjhgjWimS2JDnN4aXUtZ0bZ/hXwkUKatzeU9RFvRdQBmTzR6VyomhUAgSvu2RXlEVBh9TlqwGTF2QbOa8RCUggg+e7cvb2E/uZR+ikBiMh/lrk+KB+EGRQJNhW/gMh+tjhKagakr87B51U7I4nSO1xNmK4fYQucw+VMH5THInJ7ps4FCmMBnW5TTReYTQCC2JDsTGzFMWOiv3AQN4oGpXDqvMC9twn0IEUxqIgZjAJZDOI6QgOU9pNMJ5khS5wqAz4V34jbKZ0ahBlcFHQlBOGlRqs2x0aRBAt1jTyQqxXWHKiqYao8VJfjLyJcWuuyxmoQTeZ+EPETfKaTEhhEQ2FWmRYZNCCOLmPaUzRNItW7YORow7g7CBtDNkdfOU0FpiymIBQUgQ2RzYlFlpUFYFZquhHDekdU/CE+ctZmuQE7fWPUR+f/IeffB7oTF7E9ynx0SfoNDZANkFhMw+WEZmMQkSyJ0RSgh87wjLDlkYYmszTFJLqq1BhgkCBkGYrRGDMgt9QPa/KjUykWGLwzpPumMi9A7ZlMhCoWQWBRGKB2WN5GPmGQoQpkGEPNwk6/Au5MRaZ/VBrTMs1PaO6CKp3MA0jcL2Fuezma8ZVKwX6wdwsRSz+qNzjsH+mLqB07NI9OQ2p0iKIGTCLTvOj04pO4eIkdlqRSh6Utsyrms6HF4KhoMBs7bNnDnrid5npF+X8OtsghxjyqqJo1yhrQcNfZG/Q1MUBG2zlUCIVNujPJTFSPQRdHqiOvGseJmtPqva5Lvl4Tvoq+GrvGCfX3ax7zlj/mdrgffLPF/iWJs9CQRJgFDqkXN77vThaS8+3pbP0bb02G8vkk1/sj1fIFlLz3jvC68Kfx1fxy9+/GyToj/pB+3x6srj7fmqS81PO+4rON5nykP3d/jZAe799A6nR2doIdFKcnR6wVmtqV/bYeYje1d3CW9eIrqO9b0POT87Y+VWT21XOSkYXh2QEph7Gi0kMkR0lMQLg0OjrEGLDDURKq/EdzEyXEuUzd17GRVKKSRgVIbGpIHi4mJB2kykpRQP0OwxRhQS63x2jE9ZHnmwga0VwTK++ICyKhCuRbzkhIMNRHxysMV4MqRfWxZty2WjmL5/jPOexcWcy28a+i6rafW7LWf9J8Qy4NptjJ5wnmB3UGVulBAMa81BXSIKxSf1Ma3s0QLiXiRGgRGKrbMdlM6chZGCQZm5RHc7T987ZILVxZLRqKFbW7QRHL5+yPJkxm6lqZRiKEB0lmQ0NgTOWkesC/reMmwqyiQ5X3b4skBqyXhvzu7bU8YHW6gPDMGWSMEDdbNIlqtuDhsKKZEzgSx0ntD5iKg2fkMm/4wmy4trrRlf3mExX9MuW85unmLXPeP9MabU7DYGBBRaUVfFg8miVBLlPFZJ5KCi957eepY2UHhyNUWA0A5lNKe3T3IlrG6QdcnZ7bMsMqAUyijKNKEZlGijGTQ52Q3W003X+K4i+IDUCkpNDAkZcoVIRGDjiaNlvqdTSiSRkzRVa6SWmEGJ73vaW8dEN0AJSKVm9vYO7axl3FUb8QWJ8AGREqVWdAJ0YzCDOickEeKyQ5SaJJ/HBXkyBAJZF5uktCBsrmXSGRZYNWVuQ50rcCQQSiJjgmFFWvcZBHSxAi1BSryWBBdQAjAaOahACMK8pRgZJlxQbA1wdKgyglasXGQpwF2sCOMAReZeXd02/Nm9NXrcsBsDp3aIqAvW3Wc8LJFXSyhHNdOFZdoqSl9y02/zibOsQ8SrJmeyG5Pc3YMd2tmKI2EpL29lntrZCl2VbF+Z8O+97tADRQie29N3OPv0lFJpfuoik8mYVA+Z3ZsSY6SLAf+ta8S7Z6zKc9bO07kFWsp8bxeSoR8y/GSL3bTPUs5YDReklCi3DOM3B/lah4LpD85IQH/uKNcJLyXqACIeMx5yXZS8M5wQ77XYFOgXmZP2o6KjGifq/QlmmRiGSNGUm65bkHxk9sGMGL7oAPFlB9tnzfpfYr9fpskvmVi8umTvs1Ty8VDALxlDs1H3/KGz9E9rz4tgdI9s9KJ3v+B5pcf/eMlq0YvQLF/H1/GnLH7+KkXPWyZ92t/Pi8+z7avoBF62g3nFHU4eRx/uBHOJLcVIO1shUqLecA/WJGZ7A05MhqXV3zjADwvsYsHJ2Y9I6RnYuQTldsnuL2fp5PQD6IVHSkFcK1KriSKRlKbdkCUKlblAEti2kR2fEzMfA3YjYOCdoywMpi4JG+JzUxikC5RCoKVEbXgyZgO/IiVMoTMXSgmc67jk7qBcJoN/3gusy1wtO/30mO0ru6QYqbYHzD68S/QhixfsjLPU9RXL3E3pu57+vEHLArRmNHeYzlNPhrx2aUxjFDEF/riYMlMLCiHxlyNJSWSQTObbma+iJG8cbFGEQKcV9+4t0FJgXUD0DikESoDRivnROeO64I1xlR/cjfIZKXG+6vnBzVOacYMsDIWf0a97nI2I0COlpD6c8fq/01JUUxbzS6RbO1n5L+YkQEAm6OMQPmYpahcyGd95kiBD6QTIjRhEYTRWSk6PpwTnsV1OUoQQmKpAxMRBpTf+Polmd5SFKpYdqrOEEFFaooQkhsQ8Jm5drPF2lmFz3oOSDEYNi6Vl7/IuSUraWTbZHW6PcK1luVxjrKdcdOzfOGBQbyqAqx47XxPiNlprbO+yt1BKmLCBzJQaZom4tqSxR5QGEXIlQADYQFiucdNVFoxA0t89R4bAUsCnr49gtyDYmjjlQbULoxAhUNUlMYFdtBSlIVmLnDQZwvfwcyyeyQx4JGRZYA638edLgKzEOCgppESN6gd9gdHZNwslIUakUviQjWxlBGy+/4RWKC0xk2E2ez1fIKoClKSuJQesMUVEXJaEbglaUSbD/MyhqgJZ5n2kGLk6hivfLpEycXRquNcOcXdWxHVEDTYJoABdF/TLjjOrUeUeyx+f8ZN0naN6iyAEZVXiF2u2D7bpO0uIkfHOmIsQcCFSlYbXtyZcvn6A0gEj/wDZORIlW1vf4YM//gmLFPlgt+KuL0itILDCOc/lt6/hv30DObuEOnqPPXOH6fmULuSq6aAqGMldqh837JlLME6sh0sQguawodzxiELTfm/B/PaC8e4Evw6kRaTUCldYpvWSt968zLu+ZvThBUJJ5m+N6MYFuiy49Q4EH5Ea2mgpSsPu69v5vgFCF5h/soCNgMojXfED/szTbpavejb7FZYR/oQm4s9SrJMC/kxRsCclfYKfek//sKrpK24Fm1a8qF0vjj/p1eev4+v4xY2fv6To8Xi8r3gVfJzH9/3zEl+0UvXISrN45PXh9ojlbImLkSQETkT6EIgpsn24QzGo+FwXc7NpO28JNtEKgdH5NnLB4zd4dqMzdEyobBzZWgcxwgbO4pxja9TgW0tKEJctjZQorYkhT8TrwmA33BiZMrfEe48mMSg1ejJAFIqdSwNEd/QYVnwzeD/v1MRmwBGCyaVtTKHZvrHP9HjK8Ud3Cb0jpoTrE3WdeT/19hAxdeAc0hhCn40pQWWoWIjIBHKjiKUioASBXNHrY56QJpWhhCEEvM0TdWezqhhSUhrQJpPxoxDoQhOBMiVkiFklDOgF9CFge4s2hq5zVEpxfnSOc57BeEBMieHWgHpYowqHMgrdVCStgUQKWf45Q5LkAxWxAiBGoswTteSzl42PCZVARSi0xllP7DzlsGTnUvZ8Cj5mPkpMGIoHX8N6tqK4b2AbZK7q+XxvipQhT8OdEbbts4FvzN/97HzBcHtA39pc+VQSoxXDrQGtFKzWWeo4uVyNkJvJpduoF2olCUQaU+B79wAS57XGa7InVO+wF0vK3TFdd45AImNEIDJ3rbcE5/Fe4Pqw+W5y8oTcKMv5gFGKaBRpHhBaIgFrPVWZIYkIkHWJIGHX/cbsdHPbPvmoPTENFUJQXN4ldo7k8gRdCkFaddnotsrcroz5SohaIZuS2Dmk2AhNaEFMWU5dkDCBrNBXGlK/SQyLrAioJyV+vkZtDZClIVhHsvcTHEG0jug8agMHvc/PiAGidXmfkDlQWwNIiRCzmp+sDOt7U2xrSbsFwmuqIkt/C61YL9dcunEJKSW+tTSDmsVihfCR07vHjAcVo/0mw/mCQ5qCZnfMtV95k08/uE0fPH3XoUsDRjPeG3Pw7mtIo6h3x9S7N/Dr26gQWazWLPueynm0Vrnf0RtOWZFNe4MPqKpgdTzl/L1jLo2voUJWL+y7noX3uH3PleuXGO6OKW1PqT2q0NTjAXGQ4cLNzpgEuHWP0gpTFnjnaU9nFE2FMcVzOq6H7pUNlSSJh++TLz44Pn8i/nM42X6pKs3z4jnnu4Hvh2UHdfFg2y+SFn4mhnAf6Pjoce+/9uhI/lVDV76Or+PreDx+/pKiL93JveQxftb7f/i152F8X0mkBz+qUU1RGWzdkYpsxOklmMJQVIL5J9+HGAm2fW6V6MHPjVzz9HjKJE0o65K6LLi4mOOlfHBqEuhs9ifSkCFTKSESjLYGXFwsaJ2nLA3eerTM8tySmPkbhWblQxZ/kBIRRRZe2EvI5PEjSXvtgmZnSD+C9MeZGP+iePzST7sLfnzyh5BgOBmyOJlx+72b+N6RXOYrIPe588GMgzevsOMK9k7uIHzkmC1mKaFlTmgW85b9K/vcPFtiCkWhBGE7oWIipMjEbuOQlEKTYva/KYXk3qwlCIGSgms7A5QNWQpYZq6H0gpCyBAoF7i36IlK4SXMpgtkErTWZ5U2YD5dIqVEScXWpW18nyWKp/cm3PrBNrFzNKcFAxJKCHCO1PforTGvr/e4Mt1Fx8TEVUgpiVJwuviQYCP4yLi6gRIF0XsORyWdVcjtBqTA9Y660tTDGhkSwjqUlJSDCrvqES7iN/wXuUkYEpB0lvc2OlJdKpAtuKLHHntCSkgh6Zc9trMAeB8QCObHM0SMKJH5KFWhs+DHYU2YNARtEaFArLLC3Eoes2gvUBt4nDQau/QMB68x2X4D7xyreJ55TN6TQk4+k43s3uvwvc+T4NaSZDasvXxmUUZRizUX6SOkMNgwQ1Ym+w81JaNSk5Y9MQRi2yOmKyaXanaHLbLy3LNPdsWPT75uznpmXYAE3zaGw3rC+uN7zLZL7CbxE1qhCoMaVrhFS9wklbHPsuKiLtClIczXeZGiMplntOxI3iPgQSKAC/TAXd0g1AB3r0ekhKpGWJETOSEl0fnsq6QVuERs+1whLiYZgihBGIUwWdwi2rCBNgbMbECtdgmXND9qK5IQuRJVFRAT4+0ResPNM3WBKbMENypxvHWHs7ufsOtGNM0Fdr1m++3rlIfHpCuS3V/f41uzBc46TFkx/2iBriPL2z98cGV3C8evDwYs3Ihb857vVZkvNCexFJGikqzVNu2ZxveOHaVJH59w/JMVu2GX2Dvm7ZJmULO1O2F0aYd3vvVt4jaIhaCIlqQSPsL4tKCe3XfB+GygO6yvkUKifW9JuSzxIbJ1bZdP4y0CT1aKXhwvmranx7b4nPyVF+3/Gci7F1Y+HuqcHzeVfe5x0ktu/1h8SymGZxeU+3v8YfBM42fjXyIbIH/PWWoNwTu6hyUAX+JYzz7fJ8epZyezP4eJ6NfxdfxvOH7+kqL78Xhy9KIK0cskFC+TmLyKeFHC85Ucd9NRp4cuWYws703pnCUdOMrRhjfhBSIlqoFm+fGPNpCzTTyrX76/LLnZQCpJ05RsXdnFdRY5zUTVGLKHTGstCdBKYa1HKomPEW0M61WHkpJCG0KKlIOS+bIjxciwrmg7i1vmFf48eVaMqgKTPHE74lJA78HF7gnqHcWsWzM7vWB7a/TQ9X16lSjx6Fe/sHMW/ZxE4o3JmxRtwe6lXY4+vENVlSAS7bwgxOt06122mjE3Ys3F7VNmew3CRPCevu0ZG81itsT7QFEXaBLrzhKaiPKJcZhQ6wGFUDgkhICXgntdVnErjeJbjaYqNSIqpMzKXnWR/w4psWwdP75YU+3VOB84XWfS+mR/wnDUcPzpMcEHhMnnf37njGbUYFvH3Z8KFvdqSjPm2rhkdFgge48YDYirjpjgqt1BnSt0itAucUVCyIq1v8cqzhE+MSguQVSUWrGnIIwrEjl5S8MSZ11Wc/MB3TSUW4MsnhAT0nr6jYBCYTTCaAQJlxLGaHTpkbuJSpYsZyCOwWyku21vM79MSibbI9SGCxNDylLsKWV/HyWJE0O/JSGVxNu5GhZj5Gj+MevVPczmTtBKYqVmd+fPM57s413P9OxfIIclaRZA52qJdIHtW5vKldEkKVEIVIgcXjjMSJFkz3n/EcorRG+zv5PICUFynqBzcuhXPVFJ9OyCvX2HqmqaruZZa8P3b+O7C8fdRVZNfLeCcecxq4Q7MIS2JRWa5Dy6HBDafiMeAf50htAaOoscVohRg0wJNosPosjqc/SZ98OwRrpAImExHF9o9LCiW2ZBFNnLrF4X+rxI0jrkjiL5CEYiyoLoAmHlUEWT+wejs2+RC8SYqMYNSUqa+S6j4RWckQyVI8wWFGyEIWLg/OiU4daQ7esHSCFozxZ0q45yqJnvnOH8kiUaZRVdckzOj3jtzdEDb639lABFP11y8aPb+FWif6hf2NWab9QNMGT7as1P7W0Wy5ZQRla1or91l73XLyH7Ldyq4/yPblK8v+ZKdQ3nHCEFLr1xmeHBNqo0DPbH4IHjz4RLbEp46yhXikFpHvhJ3e9T78MmU0wE7RGFxJ95RHw5G8EHXfNDXd/DA93TpuSPuxG9Ulz6M8a358l7P9JkPuujn3ukR47z+ZOHt4uC1+qG1Fk+KRTTh3Z8v27zR/ctHh450v3qzv1tn37sp4slPEc++0vGF0kMn7YPeJWcra/j6/jFii+dFP3CFnh/Xhv9rEWlF1bQnv5NiJA2ktuZfxI36lZlXVGOapYPdvoCqNlDjRBCMNoZoeuCwf6Y2z/4CCUEISUmkwFnF4vMIVECYzQ2baBzgCRLaAsJfW+pBiVRSqqqgJSwLlBUBW6xZudgm9V8TUyJ1nnqFLI8tRas5muadwYolaWim8mA1fkcV70k7OSJM8tQIJESwXv2r+7TzVaMD7e599Fdyk0VRpeGndf2md85Qwio6hK3jlRGgheUZUFdAiEnbxGyVLZRKKEpyCIUVWlwXmZlLRdRCfQGPhacR5ArG2WZeTlJChyCOK7ZPtgmxMjxH35CTImtw22arQF33rv9IBElRgiBoCTRBkII7FzZARdRISLrgmZnRHe+JLUWn0BvJG6j8/gUkeslcTGHS1eJPhBVhj7azlIXNW1vKREZUhYD5n6yYDRKKVJpCAJW8zW6LLJ4htFI6/He4ZXcSOAKxMYcNBaRGBPaSJqtAb2Y5QpHjBgpkIUhkRjsDgm9o1/3GQ6nJGWhGY/KXAlxAXu+JCaIUuSkIGT1L6XkRoY7IUTCDPM94zqHNgJhHVQiewBt7ocHGCWVn5Ni452EUVnRLgSEMujKZChbL0jWI/dGCCUJ3qPGNaF3hBgpr+6ikibae1n0INWPPWUvfhRlk8U5ElBc2iItOxhUxBCzgp7JXDxZl8T73631pMWapBVyUCKq7IElAOECMSXEoOS+UaWqCwSC0PvsfyWy0MN9yG4IgZAShEjoLHprSPQeQV7QEAEUIhv1AqFz6FGVleNCxLUdvoZuvsamiJSS2ekUUxhiCGgpMzwxJtSgRFcF490x89MzbGEpS02MkbZ1WO9JJ1O275wzfuPwQV/1YJonBEl8BoG6f6HTZrtyq+HG9Xf5+Pd/wvJiTVkYzo7OOLt5gimyJcClleNyVdC3PWVTcuVbN9BNlflzSrCeLulWHYvTGRfH03xvxISzuQq3fWmb67/6JvOTWX6ORg2mNBR1SfAes/EnS/cFFr4YVuszaPBTbx3xtM1fSTxvYn7/vcd9dV6ulc+PR1O8l5jYb95afPQJ7dk56c/91lP2lq/MZ/t79EjiC125V5dsPAGrfQX7/joZ+jr+tMeXTorSIx3IF4kXpFVf5hl9XjX65zUpela7Xqa96dHNUkjEFAkuUc9rpDMMpOR1l9jdKtlzBZf3f5WUEq1b8eHF+w8GgKcduz3vOP7eMQmoZw0pJFZnS2xrs4FlStg2S9FqpehD2KjI5UmHVjLDiWIi2kQiUlQF09MZk+0Rs/MFRZUnYUYb2kWL1BLfO4qypLURdZ59bkqtuPTjmsvldYRO/MHlU477FeVlw97BHklK3NJx8ZOLR07lia//odNdL9YsVy1FYXDeUgyyYln0EZscxx/dpRiU1KOa63/mG6STKednUwSCrbJCC48KAVLCxYSIEZ3AKYmuSi6dN2xRE5Hc7XuCSMhCo5zH+UAbIjenLY3RlFpDTMS2JWz2V+8OmVzfQ6567v74CGsdBzcOsb3j7odHqA18SqvsObVYrdm6tJ1Xq53j6tU1ZvoT0toyGn6H/qymna+ymIPK/J5ZuIPtLhC9YzKXGCpETOyNvsFWDd2iQ6uaQPZUkkoRQngwbSjqEm0SMn0fjyWmkluz17HdHCUF9daQuOwR1nGlKHDBUZTFRsAhINYrwqdHmElDnRraYU23aIkhQEh4YLw9ZHY8p6wLkhAEIZBS8uYbLa+9cROpj9B3BvjuW5ASi/mCbvlDRExsDS5h4hVSbxFVgbIeTElZDxEhPbA+wQXKSUN7PCMoiTKK6HKVihAQhUI3ZeaaAMl7kg0bKeuUE4OyIIWs1qbUhuN0PEMO6yzYIMkKdCGyrwXfuTQAAXcWluPlkyvUT4SU6GGNCIF4HxLV9iBllo1uXeZKKYlMiViZXM1tCsykyUa4Z3OwHjGooHMZquojstSgN9yvzmXIm1a52hMiIiWKvTFutqZLJXdWNcl51KIiWIfUioWXeJuFMmLvQAiKrQFmWJFSwp4v+DQesF61SCGYOUeKiboqSDERXaAYFBASZ+/fYXSwTQwB5zy97emxSJ1ofX4NQHnF1k+3GfU72PWC7cM5QiQWS8en6eHJeL5jl0PNH30rV5jnBjyOq7/8Ovf+lynm5jlFaTIfrXc45xnaQL/u2b28x+E3X0NIyXq65J68xbpacHp8QvyppFrXFMZwtzH0hUJoye7C0n18RDMa8PEffYR3jigE070h42v7zO6d8zqaYV1Rjkpu1K+ztmuUkoz2sidU5zs+OH+P+Cyo83OSoWfFF58IP7pi92L/os8SjGelE+mhfT4PFPK8Fn+e85m8/RaTt7/BryvDN7UkCvie7ZnHyGdp0MPn93DS9wWv2y/sSvLX8XX8bz/+BOBzX9FKxNMqLF9Bx/MqV9VeZTxxqgnsqqPvLCkm1EqjvQEtOBTwxvYE7SSuuIKUgkW15MOL9x/bR3pkf27hmM6zOWRTDKkGJcuLOSEEFAqhsnSplALnsgpZ19q8MqgkZV0yn63QRb7txpMh62UHMbGcrTLkKkS0UXQkpBR0bc/WpW2WZwsigoFvsK2lMoorpxOuT/fwW4LffX3IzVSiRMeVA0M9GdKddUzfu3jkNJ56rTbhOktwgXLQIBKs5kuaasjO1T1mR+f41vLxH3zA3o0Ddq7t8fYbl+l2J6yOpyzPFhR1tVkVdijEg+Qw1SU6whVrGFNhE5yqgE+RqCC2PYNRgxeCJTBf9Gjj8SGwbi0GKHdGXD3Y5mJtuffBEYuLBVfeuYa3jvNbpwwGFe26x1nHeGtISAktJc14wNFPb+VrsDhmr/oATCTYq3h1uFmVjoSQUD6y7E9YdrdRPlKP3qWIDSQYlJeIWlHVmdzfbyS1I4mQEmVZQGlQpUHIHsFHyLBCqzFrcQNXFMzuXdC4iFGKWshsHKwUCYg+oIzGrB3q3i38sgB9meHO21RNyep8Qb+2aClYXiwxw4rVbEVZF5nHNKw5vLzkcHw7+0yt/zz24jJx2bJe/AHT/i7eB17b/22G5T5Ge0RT4n1A+4h3EqNyYi+MJrk1pinxgwoxX+OlRFe5KgRZMEFXBlUVhM6SdJb5pneoQYUc1pl3tOqg0PiTOTQFcntAMWoyLDQJYmtJApr1kje3dhBK0rr44qRocxPryYC4PieVkjRdIptseKoKjRAZIpeMRhUaZut8bkZil22ufEpJWFvkJMuDU+QkTShFWPfE3uVDxSyDL5TArztkaZC9I4bIuoNY5mRIWIlqxuAFdrFERA+FRiIQdUE5qnOFqHN00xW3JpJlXbKYLrIqoO0QxqCaAlMY+rbH2pxQrT65m4UrUmLd9VS1ojSCuijyMycEI1lzyA3q2YTj9xfU6ynNpEJ24ZG56P2JbVsrPrleE0Pk3od36Zct9bDm7V96g3JZsbxY4PoOhKAeVAyu7FBPBowv7eCt58P/9ccspgvuXPmE9mDOOlpeH7xDEytCiNjdERcyC09M1p4madqLJcF7todDbAzcrAyzvifWBfaiZ3qxwm5UC5VWpJjQneTqL91gHVd8dPH+05OiBwPT02vhrz4e3+fz05H7KcbzqkmPQtNe4qgvscj5vOPp0QD74W3efO0SojBE4EfOMSfy8Gj/1ITvieTmJWcHr3Be8vM6H/k6vo5f1HhF8Ln02CuPxysi1LyoB/gZrL78vHZATxsbpnfOmS1XlErhXSApT/Bw45dfJ6XE7T/+FF1q9l7bf+La3RctiJuJq0A8tI2gaEq26h1ufv8jio3SlRTQx0hhDG3bUahsiqqUypOnRUthDLXJZPC2s3Trjqou2NoZMzvLCRYpYa3FdhZTaJpxw8WdM5JSmahNyqvFvWN1OqPY2qIZD4gi0YyGtKs19WTw8hduc16j3TF74gC37JBSsnt1H+8D48Mtzm6e5NV/Kbn4+Jj53XNGh9uM98ZsXT9AlIa7P72Vz9kHSmMoVCaZ58pWQVIKokSrrLRWbhTlYllQVgVp1SJColvnSViuxEhSVXDw1mVcazn79ISLexdcevMyIQRuv3cbIyVGZOPXiMT2Du8DW7sTmq0Bymjsumd6dMHVb2R4V0gC5z1Sa7RKRJEhYlKKbEDqI0KXhHofQshS6DEnqkFJjBRoo+nWPdIoBGDKgrDuYZAoKoOIBcFCCDGbAktBu2opt8fEEPG9p6xycqRKTUKgdFa/s4sWWTvsusseOlpRT2rsqs8aAMsO6/3G+FOxfWWH4O/CphoQ2iwukUQ2iqXL1UzbWXywlEJkVbqyIKpAURhib/P90DtE3+EWLcW4xi5bQucISlJpidQKP18jekca1ohSgcuTbjFuMkRVyszZISuTidJk9bdB9qLJgggVSpQkJUnHATtdUuyMnnmrfuZH9tnTLuuCYjCmXS4zp0iALDQuBHSIyCJf9+QDbr5C1yXF1g6hc3SzFaEymEnzAF4XYiRGEMsWuUkaZZXhiHJj2it8INksgJF85sR46xAI7KIlLTMcT8kMrcwcGgHLjjQoAQidzdDGEFgv11RVkblwQqCMpp+3SJEhpdookhC03hO8R3YOHwJ1UTAaGgZ7E4SU6FIzGu9S39lCuszHWV0saCbVk8/8Q79GHzm/c5bNfQvDarZiaVve+M4v4bssiy+kACmQSkFKnLx3m5OjU2ZnU5RUxJhY9xYpBJPRkHARSETq0rAzaViczwkxsrU9oV/3FNowGTbcW62y+I33jLZGmFVE9A7nE+26oxlUjKqao0/vMtwdoQ/KZxu/3q9yfgXxMnyVlz20eGS0elZy9Ori+TA6gdqZIMr7yomfferhytBTgX5PfA0vavWrTWGeSA4/7/zn0VWCz+LrKtbX8ac4XgF87vEn6BU8UY/v4uty84sjPfpNpBDpZqtcrahK7oxLfCFptOGK88w/usvibI4ymsnhNno4ZOebf5ZIovKJ/VnP3fdvc3b3nGvvXGP78g7n7RmfTj/O+4+JGAO9tdhhxUWhKIxilCRM1yil8MEjZVayCjFXE4zIctWrdU/X28xDiYnTO2d58iQFy/kagUBLGE4aiqpk/9Iup8cXtKuOuiwIzvPJRcvpD2+yr+HwW1fQO5rFesl0fZFhS0+7TM+5hKum4Oxwh9OP73G5GjCwEdk7hjsjdq/vsTpdIGL2VwrrxPH7dzn54IiqKZGlYWt/i+gjs7vnJKNZ9Z5vLl5DuMSoKKmokDKT1V/fbjIszkfeny3p5vm7ClJkSFiMOenoLeWo4d77d1jP10Qf2HttnyTg1h9/itlIT3shEGVBsYE3KSWJItEv28yjKQ3jy38GWVpC55BibyOZnq+/9YGiUkzMa9RqDzGAZXfO+eIuQkh2Jt9EiQE+JcQmOSImlM7mrUIIRMyTcFUoiq3/A4lImFmujBqkUlx+6xDXWuphTXSe0ntEjMQ+IoTIFY4twZV3VV7BbQOn7x9hF2vUesZ2bQmTLKxQDioCiZOLPTrzJv2qh29XuBsN/Rz6D32u+oTEaPwNtDnM3kTFBBMiISXmZ++zbhJCSg74BjoZ4qpDbPyJ+tM59dVdyu0hat4SYoLKZK4OEO9XUoYlxaghzdYQYubkkHKS5SM+ZSNIszNCaJn5IhqWrqBbjKA0tAb8dIlqSq6NCsZVPsYnFz3HK5fNZDfCIwB/4CzveY8QcKVKGClQusiJisj3WOocosqJqhASM6zxrUUuWlyIKKMwEYTJMuEIj9SK9nSGubRNXHboQZkT5BgJGxnzFBMiBmRZ0LdrimGFNIrudJ6viwuIKns9idJsxCkksipJIdHNx8xvNdgwoaj2MTKry8WUSEVBv+4YjhqG28M8aS00obOEozN25h1i2TFZO8R1TTUZMLq2R4qJclxjQok4guA9O3tbXFfb6FPPOCb+z0WF6y16IKivBRAJiSd+74LbP77F6nDARzcMpirYH6241n2Xi9MzRu/sU7y+Reg987v7HP+k4eZPPuG4ucf6+gqpFbtih8HNIT4EpjsNq53MHZzPF9jlghAjZ1s1fSVZz9d8e2tIaTSXD3cZqZzwzW6d8FH9PmoMygkOjq9SCMXSrzi9cRcx8uxduUz6JD29I3vmfPuz6suLp+1P5+N8NVyTP6Elxs1h/8BZfiokDApS3z1Y4L2vQvfwOSsh+PNFSSMFNsH/r+8eMnJ92WTnKzzf+014FNzx4LcnkroviQD8Or6O/63GVwOfe9rqw5eNp8HjHn7vaYnUs7b/eYrnAac/RzzeJ6aU/VPSBvZyr5KZVC0kRx/dRcTI5GCL5emcex8esffrb1HvvU4Chp1ncPs24p5i4reINyMHNy4BPEiKhBTYpUUoxVLCtDEUWjLoE0pKlBL03qOExHlPMx4ghcgcj3UPwGTUYAYlZ0fnKCkZDCq6rqdznrIqEALqyZCyLuh0rlZFJYla4XrLysJqveTi9z7g0t5Vru++wXt3f4wX/qXkuR+/gr0SLCY1xa/cwKwc03/9U2LvaLaGXP+VN7Gd5fzWCd28pZ+3m1XmAELSz1uCtujC4FNCVwVi1TO5qNieNAxDgZK5ChJEYrs2xBhZ9Z5KSharFp8ScVOFKwYV/bpnLBPdsmUdIkVdsHNtj2pY88kPPqQqC8q6yB44o5q7N48ZTIb43jHYHnLlm9dYnS0YbA3YurJLVWucjdlkNyQqtVkJVRJtctWqKXapQkQaySf2DvN0D4Wktq9RxoJgc7KhksjiATHRO0dVFsSY8N6RVh39vKGcNLjesdeEXDXwAa9zlSkVBXGdcvUpJcSqQwJmlDCHnsGhZj2NzG9dUA8kIxw3dl3mrsWEEC1CSEazMbcuJtkQVkXSYY3ZNnR3NeJCgJYM/Db11h6pc0QtUdETS8l0cYxNHcJFJoN90nAPU2UYoEgS0Vq60zlm3BABofJEV6gs5Z3oUFoR5YZ3kxKsWjhfIMcNSUnMoMgGsbXJ/JxlVoVLnSU1JWvf4BcWtTNADbMwwpDIZJL9w87WnntLBwhEVkwB4FYIsJFr3tmpMbM5bNVooxBSPJAMD7M1oi4RVa6yKiACWklkXZAWLZDl0EW5gQDWZfYFWrW58qRVrk4UGlkY/LrH7I6Qhd5UmCBaj7ee4eEWq3tTdAjoUUOUIieaWiG1or9YsjyqadsdbIz0q0RkhWyyka13Ga43P53SzrJhqthU1hCCS2j6haX0kWPrOD86I1WG9d0LqkFFrYZcaq9SVUPKYc14JhApV6C2jSFqzbo9Z2Q66nEDbWDxiaM8DRyP4CNg68o2hxVMPvoplFOGWxa2Zvje0c0LLm6v6a0lHlrcwQrrPW+G15ncVljv+GQgWFaKSwd7VKs1RYzUw5oQItOuJ04aQgdn8yVeC5SL7Awa1hdz7OECX3nCOjFxu3ibaGXL+esnmImgHg9APLtSlDa3iLj/92Z8EaSHhpoXgdxe9WD5FYK8vkRTb4VASh5ihjk87/oo4E2l2VaKNkV+1wr6Bxf8JeNnsrj72bV+uB73xDfw8zof+jq+jj/h+Nlwil6UsDweL1OF/qLH/nmOL9HW+2K+DxaARFZ+W8eO4EOWe00B6yPD3RGXbhzie8v5rdPscH/rBHZfo523nP7wE1YfnFCXhuGgYtX2XNw+hf2H25po52ukztA4valuiBDRUuB9xNyf0Gz8a0a7o2xWSXqgPhVax872mNW6Y7Vs6bueZlBx7ds3WE4X2FXHR3/wPl1ncSEybsqM09MaH7KPkG17Tt4/4rXffIutgy3i1bQx7/Rf4DqygRBFDt+6kuGDG8PNoim59PZVUohc3Dnj7o9v4YHQ9rkKoQtcZymMZr1s0Uqhjcqr9invN8SE2qz2922foYla0fUOmyLKGCZbQ9pVi+ssKUZ0U1FsOA3ze1Nc5xgNa1RV4NY9wQVObp/mVeqzKU1TM9odoYxicTZn63I2pnWthTrDRGTKSmL3ldO0ybA/lMwJj/VIBDIkEAkrQG0MgFWhiZvqRxIpJzvKUwwqhMscI2k963tTtBDopkJszDCNyBCkkHJVKTqP72zel1II51EB5kcXxPUQt5KIQUm1PUBonwU7jMjVCiUxTYnpisxJUoqw8eMpK0OnBCSBVBnKFswGJlcaEAnhHHKgMH2k0prQO2gMwUdQCpEcTJc4m803BVnBER+Jgsyfcx45DwQBqSxydURnnlTSimQkdIG46qAqiDGipURu4IRJ5GcpLTpUXaCairBqia1FVkWGRD24OZ/sGAVk492qgBhIdrMYkhKu0OjOIoxCV4awaAFQLhIEYPI+w7oHEnLUIKVgOKpJvUONG9QwJysoSWr7rFRXFgijCbM1JqXMPZQCbRT9xQphFHED5RIxJ+AxRuKiJfWOdr5m2lXZsDREeiMRPitUppQIffY38zHm/SiBCoLQWVazlsm4wc56Vm1H73vMcsxquaJfrPGi5/TkJle+9TaqNKRNgvAw9LCeDIihxbU9OpXYdcdwb8ypElR1wXBrhOgWpJAYHYxptoe4YU05rDn645Zb7x8RQ6QxJbGukc7RnXQMigmVUVw63GUlAipYtrZHWOtYrztEgt56tFKcnV8wCInxeMjaWdrzaX62jMan7O1VVxWjasQiSG7FSFFnGOALh4mnztVfLil5KkzsS8er2d8rS60eWkEUCJA8kjI+7WhpAz9PtXz02go+yzxfUbM+dzyBo3v87a/LQV/H1/Gy8eWToqc9yV/FM/gEWf4xjPMvSmXoVUfK/yTAIPgPqpKBECRhuOeGrM9bnM8mqX2Cre2S3ywuKOwUpyq6Nw85+uAud35yC3tpxK2f3MTfOWfXJ2SVZWgrozn68C7fbEb8J3WWDnZJcDqs0euOFDO8x8X8/8AYVjJgu55CClKMyBjozuaY0lBqhQsxK4rFhBXZYHJrZ0RSYwY7I9bTJXd+ehukpDCaojSoBG3bs9xAzQZNTe88USk+Oooc/XDO+No+J9/7AIgEG58QWXhqiPzPuA/cOO+49+ER56dzzuct9aBCvpsovmGQUtJ8WDFJe4z2xvCNy5zdPsP1HlLCdZaqLlBa0LfZm+W8TxyvF2gEpjRoIai05rVtSWkMbW+Zz1ckrWiqGu88F3cvkEaxtTthejYnuUCQgvn5gsFkwPJ0TlFlWNJi2eJDQApB02S1vKossKuOs4/uMSmPeGP4I2II1FvfRLjrSOvyxF2A7R0q5om8KQ3S5cRIxsTe4G22B6/jvOfISIJeI0PitTRBOT6TopYCoSS+s5mkr+WmGrGRhE6JuO5J1mO9RzclrnPIGAkbJTOAqinxqy3Se7+R972K7K4Dphgw2u3wl9/PyVqhH0DJJudHVJwg9gTaXcAPlqhSM1/f4nh1kxAi+/IGKk5QRhFcyL5BrWNr/G3MzoCicpSioScnr4fjXwHvUKPE3bN/gyeBC6hxTSTLpscENJnfocsC4Tw2JcywJlmPCJFCSmRdEmwgusxvEi4QO0foLKIpkUplXtmyQ8aIbErUsCYsOyKWN3YqDkc5kf3pacvp+tFEP6WEX7ZgNKG1mPGA6HxulyDD2HpLDAEzyp5B/n6fkWLuQ4cVWE+0jlQW6EKTQiCECIsWlIRhxWik2dUzkgtYPHfOOlSTq0qhz95UMUVsZxnUJX66wiuFNhleKQvF4vYp0+2r3PQDUgK9O0bMl/jW0mwSMC0kRPLfITK+c4FaLbG95XatWRwMWQwik/1tvFvQz9f0MZB8oqwcq99YcPz6EXHd84NbGdL4cOybxP9pbwwpcYbku++W1JNdJkXgL3Qn+J+csjuqqDcLD7fakh/dKjFNyfFPF0ghkTLRrnZZnR+gjeZIFMihZLQ1oteC+vIBftXjeouIkbIoWLcdWikmwwHDpsNPlyAlZ4djTuZzdncvcXg3gbdoobBrz0U7p9M9RmvqwWPcqOd0Z18FWONnEs+ppnyRc3kmF+rJzOaxIzz6Ga8k/9/kMV2WoO9eamB5tB2kryg9+YrnOvnK/GmZUH0df9rjZ1MpelbC8qwO8CUSnEe6l59JSfqzI/88RXroGgrgutZsCUkQmuWgzBUTAcTEYGfItXcPGb33ISY4ejPEdobVuiOqmlt/9Anz5YqDpkb1PWbjx4EPIAT9nXPe3Y6UVcHNVc9iVJPunJEEhJSNCoPzWAtKCZCSrncMhzUpJFSRjQu1AV1kZTlPnkQ7axFrGO+MESGhgKIsqQcVwfncxpRno8OmxnmPUoLkYe4jC0oWn8w4KBWrOyt4WJ3pJSGKRUhs28jW1QPipT26VUtRldzc+oj19hIhBEUhmf7oHovTOVHAYGuIX/eIQhNJ+GUHAXRVkmLibLrEOk+KkaquEAK2m4qro8w76WLEDCq89QTnqQY1PgS2Lu1wfuuURCL5QL01YL1oWc1XWUjBeVwMeO+RQjIaDYgxD19RwOpiRRwnDg4D29URMUZ8OCTyWvaZ2Xi/SK0yN2jjd4NRpN4RvaeSw0zeH2ju6HOWsUO4gO0Cw6rCaJWTmi4byEoE0UeSDxitscGDlFhrUTGhExQx4C7miDJfH6MUxIBP2UNLMUBMBwQf0IVm1ARYR5KPhJFmebJChUAxqtBGoRczVFzmCs3G7DJM1ywW95ivAyklJtUBVRgBCZEycR8pmVT7KDUgjBJyZSlSou8DhdlDy4CsFXL5I6QJuHWH6HRW3LsvWS0ka2tppEcXOpvMCgiLdb7pQiSlmMUJKpNX8KWAzoJRyBCz9VFdICYDQtsRe4e8b6g6WzHeGjAZZR+lWzMLaaNKt6kaCZH9d7Jwgyb1lriRwRaAqgqSD1lGeyM2kVqLLHSe3O8OSYuWECMIgW6KjWiKQKYApSaVedvSJAa0iEpgmxFqe0TacNb6W8eE6YxkDPpgD1llmF1iAzENgf6sp28t7U6BlQ0+RPxyRYoB31mCNmitiEJgvWV+ZpFScM1FWPYU3nM8LrjnLXJUoUiMxwNiiHRS4qNDFpLwhmA5nuOk4+PgiD4+Ml7YkB5UkBbWcvdwnBXqzk749ukpKSWU64iDEiVg3iVOqiHuuKfa2uWNXx7TrTuiEdxbrhBSMBwP6GXPue0YGkGjFT5F+taiK0NB/p7uHp+hEPgQaKqSi4sZJ/WYZVMQnePNi4qxGtBMhoi9yMViRdgIgdyHeL0IhfXI9P5LlVdeNeztJfb3isfyl01Dnr3VJiUQgk+Dhyi+xHTg+ef/M59ZPIyve1YD0s/bjOfr+Dq+2vjySdHzEp6H//4Fj4c5O6+0k/iS1ycXOTLX4X7FAyFYTpeEBsq6YLFcE5zn4PJOVjMjPRAcVYXBKMW064ixoalryiCwYc2b37zG8QdHdMuWvb0xo2ZFDCdZQnh7iOhBhUhVabTayBUvLdZ5iigpjaaNkd76TXIT8DHgfURIkRXo1h2DytClhHWei+MLAHau7rF9eYf1bEUUsHd5B997pFHUg4rFbEXfW2KMqELR+UBVFdhF+5Bh4wuur3jo58OXD4HUitX5grm7wOxpuj6ra60vFgz8kLbvaBcd5aJjsD9m98YBR+/fRlQGbzts51ECYswTMKTEx0iKkePTC2ZDQzUoCUrSrvvMz1AZMnTw+iEnn54QQuZCJCVYz1ZZlWsDqQuAERKlNfWwJqU8+dQqV9ZiiNRlgRQS13uKqiDYiKo0xCyUkSSYQhNCTmTEBlsPoEW+jzrriBKSTJvJd/6uU0yEEHMiGPOkLcWELDKcsnMWozWFkll9rdCEGHE2ZFG2mDYcqvxEhXi/spjNLpESOovSCpkS7nSBPZ5vki6H0hqtNKEPhGWfExAlME2ZEwafoVjCZ/hhqUq0y2p1Hui1QHgo1h1qUBG9z5A3k7krqSpIts9JYQqZQxRj9t2xjhRKzAaW50JASUNatVAWqLokTpf4pJGdRtUFMcRcYaoUyYUHalexs/k2DQHvAqw6kg/ZmDWBPZmjxjVqUD541nN2tcGnbUjh+IgoC8JshRxUWB8xAkJr0YOSNF2RQkQOKmJpiNZljpBWCKOxMVGUOifWqw5pNHHZIXaGJOsxdUmKkRizyl40AfpE2ijxRaUy5FApmoNJfqRsQMWcFEYtac/mOCGYXSxw2wcEa3NirhRKawajhmpriBmUuHWP7yyLkwusXVIpiUARlcpS5j5QG0OUmbdYCImXksHhNsWw5uG17YcFKrh/DUV+XlazHj/sOV+0XNsqUEqxODpDDSvKYRYGUY0mdJ5b3/8A+UPD7t0DVGGIr+2wu7/DcrpAC0kxGtC1PfWmH+oXLbPzGdY7Xn/9Gs5bxk3FbLlgsWohZL7WoKxIIpJiQGhJ5zxy2dK5rLanlSDEhO8cDJ6yZp/S/Y7rs5ce3eApycHL15IelvD5k4VifZ761zNG6s89L3msevQFx+uv+rqlzb+v/DgPMvCvU6Ov409HvBr4HDw9OXrWc/TsKvXT9/34Zx9fqXnays0zO6+nZW0veuC/tF3bVx4CQZSC7//amKrWnN8JdOY2y/Gc85sXXJ+WfKNNFBcd/2y9JkZPFTSXJgOEgEmS6NszyqYG69i9tEOzNcD2GfajmxJxSTItBkgtmS0809tn1MOG/a5nOO0Bge4jEknnI40B2VT0naXvLSSB3pC2tVQkH1FK0XcOAexf3uX87gVCwPnROc32gMtvXiK6gAK8FMxnS3yM7L+2j5CCvu1ZTle8u+hJq4BYXaD+jzvopsDOLSf/9uS5ELrBpYadd3dIJLaWE9I0bSouiWYy4PYPP2L5TxfY0lFWBd+8fs61b3TENwM/ev+Aadsw2BpSDiquvH2Nex8eZRljQZZF1gq3sgyGDUJJut4iUuLHp3NGcczF8RSkpreealixe2WXk0+OqaKnHFZYF3C9Q2iZDU7bnmZQ59Vm74lB4F3IfjtKETfo+KoukFoytVdZnY5RCfbGe+zWGyluJRExgvVImVexkUBIJJl5OOH+YOgj12JN0gNSiFRoiqpAlZr1NFfQfIzcnnY45ymqkkOT0CqT/qXaSDIrmb8zJDJGtM5E/ZQvNwKB81n6+QGEa76CqiSd7sL3fz2LBWiFByKCtHbEpcWnrIS3WgqkgG75Kd4f00wGjK7uwHn24ZHLFrSk7CNozTp41HzJ6uL7+MITlWFn8qvEUFHIXO1k7bIpq1ao0mCtx2wSXmEUsjJErRDLfAn9us/Gp0WWPyfEbLIK4APResS6z+INhc5wukVL89o+i+MpcdnBLJt24jyp0Nje8VatuWpy9TesOpJRiJgYqwyTi+s+84tiRKSI2h2D9eADapilxVVvH3B8fGghRqIQFE1FtJ44XaGVJG5MaGvpOZwsISWsl3x8XBE6j686YtA4oKwKzKAhDRuKjQ9Td+8if/ciJ7l3VhPujN+kVxJ9cIUBBaEs6BZ5wcZohbUO1XaYUYnZVDP3XrvEllWsP7mXfayUwjQVulDY2dssZaQQnhR/gFYR01Tc+e5dgg2klBMiKR/rtQcafnWMiJHxh5I3vv8GQiuK48Dvv6fx1rE38tTR49qe8so++9025//6mO7C45OnKgrmJ1NO14aqNPyaUrxWGJLK3DNah7OR71+0tDFxePOc1dsXnLQnyMaizrfY37tKURrS8ZytGEFH7h58RFCOUTXixtlbhGVgul5y5YPr7IYDdr5xwCfp0w0cKz9WL9Lh/uJj1pcb7Z6Ern3Z0fPJzz9bKvwZx3rmWPAF2/aiJOlpZb0Xlfq+kob8bHfzdXwdv6jx6uFzz0pSeOj1h/OQL/IQPq9TeeH+Hu/8fl7TnM8biSgEF1sGMzT40T5h3WFtj512jC9gEiG4wO2QKzaj4Bkez2h7y/ZoiOh6vF0yGg3ypNh5+s6yfbidUQOlpq9kFmg4n2IXUNYlwnoGcVNqkZKYAlpkRSozqPA6J0Ag6DdS084HYggPJsSDQc16tsZtfE2UECxO5ggXWE6X7B3uMJsuWS1bInDy6QkpZNGIsinZb2oWF0sSjs63jA8mSPUcJPTmDVVp6oPMk2rvLfnxv/xDtDHYtie6QLQWmTQ7jOinLcX+nHp8jNSSrf1r6HRA6C2rO2esesfqPHNamsmA8cEkiyB8dJfkPCAZHW5T1SXTu2csjy4Y7E/oLlbsXNlh+/Iud35yk262olcK5RNa61y5CIlu1UECoxV9Z2nbHm0UKgp0ypBDaz3eeExh8upyGtD3BUJIBq4mWI8uFGEjVJA2kEeFyBWZPldnQowIYyiAGCKFMAQLMUmSzNfVVCWmtEgcwQUWiw4XI9p6Dg+GyMSGUwRSSXzvYHNfBQRIkT2MigIlBWpT/YgyV5eidUijcSSUrxHzITplBIsCnHOgNYGEEiA86NKQRCJxQoqJalhnE9JlTmDKqkABIiVWIVAajV239KPA2s0pgkRHTzICJyVh3UFKGf7WO6J1aCURRiNcQAuB6z1KKURVkDqLHjek1hJ99ncSIWzuf7LAglE5CdUyV3hCRFcF/XTJar6m0Zq6LkAIZN1ATATvGZaCerFCKAUpoiYj9KAi2oC9WJJCJIXs6aRcYHUyz89n2yOUwAzr7J20SYRNXZCUhNYiUswZXesQozqLoyhJvH3C4FsbI1fRMGs1tg1UhaGoNNqnfMxCZUEHrehPZ4TOoQqDjwm3WLMQB5wPDsAojFeQPHVTMdwaEjrL+mJJ23V0fc/F6TQn+CGyc22fetxQ7W2xWK6ZLleMhyWmGFJXh6zO57iwpq88ewcD6t0Jpz88ItqszMem4vlIR6AFbBVIKdhyE/bfu0J/vuLo+z+laHaYXNunv/iET3/nuxz88luoRcne4DL+smOWzgDBarHi4LVD0rhECcGBKbicQCidBVK8w/WWce8RQH90hv7mGlkukHZNYbazkIzLPkjbZUnbOdb1ksnlAVLBxfszpFM0pkS7knG/RbWuEZ+D2C/u93VPfOTz7OPzj5GfDfWPJi3PXIJ8eEx/ygLrsz73aisjrwoH8tCJPG0A+goSj+ddh2ee1ePt+Doh+jq+jiym9KXiPsj5Ra/x2GubyfArPe5XHGmjtPSked7nJV0+Jb7Q+WyADQ/t8L4YlDKaejzE9h6ByFyeQue8JVMqIEbO755lM88Y2d7bolCZY7KerVjPVnjnKJuCy28eYkoDQtKvLMujKUGQ4VwpMaorCqkgRgotGVZlrkaESPABMyix3udkKMZs+CqzKWIzrOk6y2K+oqgKmmGFi5kHYNeWEBKnx1Pa1qKUolCKwmiapmQ5XXFx55zF2QwpwPqAX2SlJ4FA5bn3M290ASxP5yxP51wcndNfLFiezVlOF/TrFjbXTlU5yZCbT7k+QEhMP75H98EtitpgasPVX7rOO3/u21z/zptsXdll98YB7/y5X+L1f+dd3vx33+XSW5c3Ro4gCoNznqvffo3tw21u/tHH0HZU4wZhMmk7bZTEsk9NxGhFu+4yl0jmtgklKasSUmJyuMV4b4xrO3ShievslRNjpO962nVP4LPHTxQKo3T2n0Gg6myumYR4MKNSSmQVsJDNZEPvcNaxni4xTZmrPTHCBr6miwJpDM6oXOGSmYCPSBR1RTNsaOpiY55q8N5nqW1yFShu7pEYIl4kyv0xg9f2QGej12Dd5lnkAexPImh7S4qeatJQFpoqRNxszeLogo36OF6pjXw2uN6RQkJLCYUmIUlG461FhuyhJOsKtEZojagMcmuQKw/rDqEl5bCmcJ52vs7+PGrzcElBmC8zJFFI1LiGEImzda46xURa9bCBEIpSo8qCusqGqd5HhNHIqiBZT5q3JB8xB1tE63KVKUTCfE1ctoiUkEZlXt+6o9hA2ELvEEoh5EYRL8aMuusscdMeKTMXLJus5ntNFBkmiVb4s0W+D10gOc9wf4KqilzF3CgWJiWxnaM7X2aTWimJvSe1Ftc6xLAmKkHfW9rlmvnFnNXFAgGYQUWzNWQ8GeF6R4yJ2WyJS7l/uv3BLbp1R7tqSSniU8Rvvh/rHNPVmt39bS7/2luoYrPO93Ay9PisMEEMEEOuCksBIkX23rwMUjD7+C4n79+ingwxTfGgb44xEVNOUGPKFbZyUFNvj9BaUjcFw4MxZmdAszeiacoskQ60wdMtVmwf7LA1HmOtY7VuCSHivcc7jxYSJRXBRc6PLlBCZB6i0hSDgr3r+w9ESR50Xo90/E/2bZ/98lXPeB8d0PMl+8z29KU+/viunnGqn69Vn/e8X8V1Ek/8KdPmPnsE4viiY71MW77w6vDX8XMef/tv/+0HnNHf/u3ffuH2H3/88Wcc04f+N8awu7vLm2++yV/4C3+Bv/f3/h7/4l/8i5dqw1/7a3/twX7+tMSrrRS9CPL78PufBx788Ge/9LP+WSLxYAHxwaCZG/b4ylb+5aEO/4kb5PPdMC+1avOSexIPnUgKiaPvHiGUQEvDdy79JulDqD85xgXH/N6U/W8M+b/9X3eRyrM4EvzO/32FFgqRMuxqOGzo+0zIDs4zSSt+WX5AfX7EuhpzbL7F3Y8+pbeew3eucfbRXZQPxJSwG7K2FBs/oc0kSymJt56qKXEuy4O3bY9SksGozupUGzPQsi5YrlrGW0OiD8ynC4zWSCkxUtJ1lqrK/jxoRZqv6bselQTReqQ37P/xNa5UN2j0kj//1k8pSs1Rp/nn7z95mZv5iGvvvcYnP/yQIjUMDhsG22MGo5rTmydcHJ0hgOnJlO1LO9Racv69E8rhkJWIjK7vU4+uUwxrdO9IPtIuWqQUlE02tVRGUama+fGU4w+PGGyPuHHjAF1obGtp52s+/tGnBBtoxoPMMwmJ1cUSoQT1oGa9XGNKgyo125d2qMY1Qgj6Rcf0zhnOOnbePGTr0g6LexfE3tHePSfqXJUTAlyp+eTmCVfffY0dLdkZVXny4jLo7r6UtIjpQZVHyE1lKGSvIaUUoi5yBURmbocyGiMV375eZR5UhEGhSFpi1wuOpv8GaQQEzeu7v4kuDAkD0mJ7C22Pamp0kWFbQpDll7tjzi5+ilpXHFx+m2G4QrCOEBPJOnRdZi6TFAQXWPqbHF+cMB7tsbD3Mqxv0RJHiSBBSoHtHDpElIByI0MupeKw+DahTAgip+c/JrSWUJTsDH8ZmSS6b7m7+LfElBOZVGiUFPiUJaeNgqBknpSHgBhUKDsgLlvUMCchclQRFy2qyhyjFEQ2io25z0k+UFQGB/Q2oIpAmmYiv5Qi76PKiVKcr2F3jB7VbJ861HKNbBrumAWuLjIvq9BE53EBZEyIEJCTJnOelm0WjRiUqEGJ7DVu3lLsTejP5giliKuOVGlEqaEwqKhBJMykQRYat2xJncevOkRp8vMnJWkjtz8Ql2jYJ+5K7sQC5z0xBFSpqErDarnKZsxVQdVU6NLkxRKt0UYTUiKse1xnOVm0xBi57iXbas2WrPnxcsnOtQOuX3mT0bWaYqzwbXhhr3nv2PP/+MdnAByEJf+79Zyb//KPWHYG/c1/B7Mz5vK3AlevJVTZ0VpLe7Ti0x99iBaS4XDA9njArKkeeK+d3PkeprJwq+XoxjbnROy45/3JkK5tqKqab90d0r43ZxBLQg9aa3Z2t5hezHDBk0Lixq23UHcgRah0zd61fbb3B7weP8Ksf8CF97mq95SxYPPfk0NJ4jGI3bMGm8878Xl8EH8yGXhsgH1BPeMpW7yCuf0j1arnIlTEZnbwKrg5n31+Vwj+vXvnlK9d5lgJfqfrNls8/xgvV7d61nmJx7d4+XjsJnpV9bOv4+XDe89/89/8Nw/+/t3f/V3ee+893nnnnS+0r/Pzc87Pz/noo4/45//8n/Nf/Bf/Bd/61rf4L//L/5L/6D/6j15l03/h42ejPve0eJmn7PMmTi954JxI3N+9eAySLXjir/sJkXjy/T/5eCiBS4lumo1RCxkpRxWHgyssuiVFbTh6/zbbr93g6hWDNJKjeYvRBVFKpJTYVcey7YgJhlXB4nzJ4ZUttusLsDOcbohqhF9XyEow2BrQbg9ZdRcsup5KZw6JCwEbIi4ESq2xztNUDbbNhPjh7oSLsxkiCtrO0gjBet3hrEMuJd0GFjYY1kx2x2R/GMFysc7QsT5zlEyZDV6l0XTWgpBUVU25LPEfWYavl7yxV9Atl7h6xNO+O+01+/Vltn9tD9v2FHVBCAFdGK5vj9h7bZ9+3VOPGurtIdz9PsmWSDGkWzrunt3k2jvX0FVB6CyffP9D2taCyEnR3rU9ti5vozYGqa//+ttIIZjeu2B6dE47W2YydVEQU2S9zF4yRWVIKWGdIynJ/o1Ddq7tootM0F9PVxx/fMR6vma0M+byt1+jqEtWp3POPz0hacXKuryyPxmymi0pBgXBaGiqXClMWSxBkCstYcPLQQqSFFkyPSWi2FQMfECS0IWhXbWZ8C5z1U9qKH1A1TVJCrzzGKCPAeumJCkpaIgxoYhEH5BK5QpXWSDzU4kPAZEgKYkTnlVaIOYzajlisHMJM2oynybmCmRvM/dKG4X3a9bhArWC6C0uRupBhRFgfKTDoYXIUDgBad1jZFbdM6FGaYXoOkI/pw1LQmoox0OKoiGZlrRS4C1qVGOXXT4X7xF1gUmJZDTOeYySJOsJVUksDFiHllm1LkmJny5z9abMZqhyI3wQYkLrnHS2q4522dGMa0LnSNajhjVu3uYFhK1BlmpftOgW6qomTNeUlwfYk3NCazM0MCaSzJatqq6IPuJti5oMiG2PaCpEoXHHM1RlQCt0U2Vp9Y2cuipNXggKoIcVGJVlv3uPaQrsuoXeoWJExkQaZUlxY2qaYpdegHYeLSIxRfr5Op/nhgO3alu6VctgMsz9WIzZ7FXlxZrReEC36jFGs1VXuFlL1HNWZaK7d874xgQzqDJ+8ol4uNyQO33bJ27fckDC6EhTCd749j47Ypu7l66hSkPdtBQ7EkFAkLmP2W8s4rxHCEPoLHJSQe9RV7dQxTnzHx9z/Mlt7mwP8UnAcJsgSsrxiP7ODHfGRslPs7M9ycqAKWGKInPsXKLvLCjJ1lv7HL77GkWyDE7XKOtZx8DzMoXHCy5PjhI8k2N5f4HtM0+np336yf0/M915ygT98Q3yhFs8+PmsvX/ReGbi8dTs8f4nHi5TPZxtfLG2FEJy483rSCXwPjz70A9FeuS3lzjuF2zeE/nyM9vxdfws43/8H/9Hjo+PH3ntH//jf8w//If/8KU+/5//5/85f/fv/l0gzwsXiwUnJyf8/u//Pv/0n/5T/of/4X/gRz/6Ef/xf/wf8/f//t/nH/yDf/DKz+EXNV5tUvSih/LL9G9P++zT+s2Xeoo/68YfHUTyCpF66LW4gZ1kea+XkHl+rIHpvvbry37kC8WTJ52Hm8hwf8hoq2ExXVM3Nccf3MWHXM25uDOl1FcQwpA2Xh4hJcrC0K86nPV88zcvk9o5kIntotBELTFNxXK2YnE2RwsoVVZs661HaEVrHaSEc54YA946hJJoo0gktJJIJVFa0bYZ1lVvZGeVAImgW1uisGilqKoCpfNnTFTYzeCidFa9k1UBm8n4crZEForL17dxvacaNLB89iqmJFKUClM0ICTTT+/Rni1wzlOOaoSSjIcVSivK0YDm9cvMji7YOdxmPVNoAcl6+o3Cl0iREMC3lrvvH3F265SiLmgmDWa2ZHE6p1v1OB8IPjLcGmcC/wY6NBw1tPMVXecY7o658vYVqmFNipF2tmZ654zZvQtSShx+4wrDnRFSay5unnD2yclmRT5SNiWv/fKNfLy7HcWg5PI3rxFDRDUldrHOZqhaQIoYmQghgBTImDlqUmTxgyiy31SsNxLeQmCkBKNwbY8pTBaCgPwdFgbhAqosEIUBckIlpMA5j7eeelhlyJrMfkcpRETXk8oCU5doUeEX2Rg4CoGKidRZlN9weJQCEYmthcpgxhVyCsREsTOiDwm/WfRQKSE6nyGblaFddVlRT4H3ARsT0QW87XAxq/4ZH0giYVdrTJ0hYn7tMrTMehg3BOsQKSIKjZCZO0WCpCXS+wwtbMoNh0iQQhZmCNMVQmXjVDXYeBuZLC5R7U3wKdJdrHFKUh9uYVMCF5B1QVz3YB2+c6RVRzeD8rVLiFENrsNsNejJgPbDe2jnSbvjDBeLiRQTsXeonSFomc2XVz3JutxjdD5DCUOAugRp8Z3LQis6c9Dios0mrlJm3mBhsrpg7zKKywWSD3TdCtM4glH01tI5j3UeIwS4hJEFLkZUWRCtZblY5YUTrSgGFRKBEoJkItd/7RsMd8fIlLh4/4i7J+eY13eYLVZMb50yuezQDaSY/Zke9NQPz/g2GNqUcj/3cLdZThrqakI1qhBSYMqClHLCHEOGI1//pTdZHE+zCpyUHB2dIBuNKjS2EMjxgPLN1wl2zrRfkHygUZrSaDpnscGjjaEuDJOtEe26Z7FcMZmMsN5TVgXlZMDW1R2KQYVpCpJIxBQIJBJpI37yeGefPjvPh39/ybHi873/WbwqPs+TCVHe+1cej0wAHm3Fs1Oiz599JBJeClSC8JLX9wud/efNYMRTjvMsCObX8TONf/SP/hEAe3t7vPPOO3z3u9/lv/6v/2v+wT/4By8FZSuKguFw+ODv0WjElStX+LVf+zX++l//63zve9/jL/7Fv8jHH3/MP/yH/5AbN27wN/7G3/jKzucXKV59pehVVnc+zz6+yJJGyjLDD3OEKin4v1Q1lRC0puK7b/4mXmp8t+T8j/8FKYZHjyfEpuj+eLn6Ibxf2rz6VfUwT8LJESJg1B9Sl4o3fqXnh/8yEZzn1seO/9fvfJN6d8CtH77HKMxpNpLWxIgpDJffvsqPf/A+TSpZ6TGf7v0WiMRFVfHJsOaj7SK7wZ854thw0CsOZx3BuexST0JFiXeeQV1mxbHOYZTCt45p5ygKTQopVyJipCoMPgaiT9SDirKuWK1ajJCYyuTJdErYZct4PHggKpD6SCKhpMw+RkCMgYEL+JXA3tsiSEHnAtA9caEG3QnXT36Pbt1zbEekt38doxWz2YooJadnCyDRni24+qtvcDa8wbS5SjtaMbj3U/7dvYiS5xRbv0Y33ONKKfnj9++yOJth00Zu2ApEYZjeOc9mlHsT9MYksxo1SKPRpWZ5vsC2ltndKd4H9m7sc+mtywgpaKcrTj66x/x8gQSUUey/eYkQI/c+vkc3W2dhApk9UHRpuP6rb1CNGo4/uotpCnZe26ceNixOZ8wGFT5J2nnLa1s/YW94TGwtgl/H+n0oMj8FHx5UuaLzedKaElEKVIyoILJcc58rWkkIoss3pDCSomzQq5Lge5Amr4LrgqKpCAikd1AYgnWopiKwWbEOiSJBZTSSLF0chERq0F4RU0KnBBt5cO8ifedILtBNV5g33iGoa7iY8GqX4EvSxYJWK8q1hRBZdH/E3E4ROnOq+rbDpkijAypKrBHcXfw+UincscWLSJASZQOyKlBFVirL6n1krlBpECFlERGlqKosGJCsf9DfoCRye5j9v8jwK3wkyiz9HTe+YEkLlrM1qtSUB5MMJTuZIlJOVrGWYDTzb45ZCo+IgStvACdnmL3Ip3KP5ScXyKbELdqsnte7bKbrAjIm3LzNcMCYiNaj6o0hrVZ0vSeo3DypFanNRrv2bIEa1WglSTGfmxAiS46HSL/q8KuO27uaW4VEkrjXWerB/c8kuq6jtw5dFpixQSrJlVlPdd4jhEDNPWVZUO6NWfy7NzipCy6M5MbpGiUlWkm8zWIOTVnyW793waBIpAhO1ySVO8ZoAwjQI0n9RosQiaOl4J/+RHBfryBDGSPG3uPKcoqpC7p6ix+5/z3dbMXHP7hN1/4xi9mc8faY0c6Y0FqkDyymMyZbY37S73DTK6SAZbBUtiU6z3wtEERCipxMCuYlbA+HvBsN57fvsbuzxfZowHK9Zn4+ZbFcY63l+m++xe/d/le4aBEkCr8GEgF4AiD48CTpsQnTk+CGZ9cpEiAemvM/PVl5lfEnIPD9cE7zVJwh3G9XrhflhVLxYFT//G0+DZF/sl4hAJtejuX08Jzk89I5fn4k1L+OLxLn5+f8s3/2zwD4y3/5L/Od73yH7373u3z66af8zu/8Dv/hf/gffulj/MZv/Ab/8//8P/Prv/7rzOdz/s7f+Tv8pb/0lxiNRl9637/o8bOHzz1tCYbHXnve9i96/YWHfyyDeAxLIIFdKamlYKU1xWALIfWmZ3ryYOKBPxBP73Dvj0o/8zp0QrJGCEUzUYwnA2bnHUmX/PgHM67/xj6hOKC1Z5RKk5Sk9YHDNy6x+8Yhv9KUfPyDDzi9N2fv+gFKSTqlmVnL1DmkEmgtKSpD168JUlJIgScRNolmjNmYNdrMJYhGI5oyr8AncDFQRE3fdmiT4WKm1Fx59zXKUUM7W9GuOwQi+6oIGA5rVl3HarFiPBxAKQgh0IwaVGGo64KLO2csl2u8DWANkUR8fIl1M+qp6CncEt+uGI23mJMNL9GKvu3xKVJIxeJiyU9+90ccvH7IwfVD1M4Abv4h6fgMqwROHdLsX+fam5eYlyWffniXsvd0rcXHSLvKctWX3riUDx8T3bpndnoX27nM7wgB73KlbfvSNodvHJJi4viDI6Z3pxveV8L7QFEXHL1/B9c7yo2oRdh4/4z3J1x+5xrVqMK1Fj0o2N0fM9gecvzxEacfHyN/9U2qUY0cVOgmgJwSlYOUBRzoA13wFMaA8wghkT5S1EVePd9IaiPzvS11NjYNZENYsam8oHLVAB8QJlGVBUpvqnoxkmQ2gPWA2UDPkJKkJTplLpmSecKdFdDyBJ37YgzWk4wmhZhNbWMiLDv8rEeYCa4y+FVEGIFynpBAFIYQA61b0XZTZIpUwwZZSsqUcpmhMMje0cYpUsosbKE1KEWwDrTKFRcloct/Q+YFSZkrmi5GEDoLIChJWluoiyxAYiSRTfXGqCwX7gMkiMsOrSTD8YBWtKymK6RWFJMBfr4GF3KCU5ksT14o4nyNIFIUJcVOSfQtwpfQWcLdC0JV4G1HsVHIi+s+W1LJXP1NHVn+e9wQN1VYYRQ+ZrNYoSSkRDkoScMKqTV+uiSJTTXFBUJv8SESOgvjmgvvOWo7jNF4oxkOaho1YDFbUhsFbsNFbHvKwlD3gYPhEJSg3h7SXN4Bo5iWir5U2BCZ3zxjPc2y/MGHDGutK4pPljS1QhcaZJb9930WfBBKIkWgUhZlJH1Qm8Ww3BVEH3CdpWhKSm0R3tH7CUc3PTf/7S2cdRB7BJL52YIzf4EpDIwLmtEwexatPedLgUsR2ydsLyEVlFVB09TMF0tWCqIUnPUd83VLVZaMJIjVkkGKJKPoq4L91y+RRGLpFljfvRjf9CL4UwIh0oNNnwffytvfX8BLj02wP/vtAcQOPv+s/XPHz4LVIj6bG4j7idD91z87+hdphQfO4tN4YM9tzheeM3zuROhVLmR/HV86/sk/+SdYm/3r/spf+Su8++67/M2/+Tdp25Z/9I/+0StJigDeeust/rP/7D/j7/29v8fFxQX/1X/1X/G3/tbfeiX7/kWOL68+93g8PXf46kPwUsd+WochhEBLjZYGLTRRKLqV4+L2BYvbZ7hFiwwRLdVmO41UBqkNQukHe30g2LU50v0B6bFfXm08pUp0/3UfEz5EopTsvLGPFx5pYDVd8vHvv8fF7VNCSriUVZWuvH2Jq9+6gpSJ+dkMKSS33rtJcD1CRrrFiovbpxliqBWD7RHbNw6IweOEp8PjJVjrKJVi0NQMtkf0G3EFZ7PfS9mUFE3JoCnpu56YACkYbg958zfeZuvKLkpJlMlAxiQSW1d3ufFn3uTwm1d481fe4LVvvoZqCq59+zqX3rrMaHuI7Xrufnw382REVmazKWFTThY2X8uD65P3LYhSM7tY43y2Ei02q+VlU1EUWbZYSIld9xy/f4ePf/89FqczzNYQUZR0sw7vI/2y5eLmCdF6XvvVN7jxZ97inT/7LlffvcZgq6EqJd3FjNXJBce3TrIKXYj4lLLvjlYMtwd84zuv89q3roAQHL9/h+md8weqd0VVUFQFy8Wa6CM7l3ZoBllCOdWGa995kxu//g2qUTawnJ/NGe1OsKuOex/c4fj9I4RP3PzDT+gWHaY0lIMBto0EJ0lpozSjFSrk+yJpRRIghxViA50rNknQ/YQnpUSQWXLdb0xSQ4wEH5FCkVAImbkp0TlCb7OMthIQc2UlklXuQteT5mtwEY3CVDXFRrY7OU9q+zwRL0yGX5F5GhqJUgYlNS5tvtuY7/8Yc3VNKIlWma9CZ5FREBx0rSckiegCftmSNqanSglEzCITImb1PaF1TqjrAqREbw0gRkJrESHiT+eIzmZ58JRIrSOtekRtEEoQ73OEqgJhHUkI5LhBNdUGppvQRqOMYjDMpq1htkLIRHN1G7OVPY/k1gA1aQhnC/zZDL03wXeeGCFGkWGSW8OsQFdmiGxsLVHr7E/UWkKIEFJWzIsR1/Yk7wkhomLKCZ6WhEWL1Ao1akApYtuTbMDNVrh1TxACjAZjsNqwbAMxSZSQSJGf5fl0jhnVbF/aQcRESBElBUXYQANLw0XbcrpYofcnpFJnmKyUXHx8j1v/5gP6VcfSWlRhKJRkeT7j/JO7KKMJLhvw2pRoO8tq2WJXHa53dPOWxaJnetHiHqLlRCCWBj0ZkApDkrn/j0jO75wyny0YD2pu3LjMjTeucuVwh0sHO0y2x+yMh1RComJCKINRkuX5nNB5Rs0gGxS3HdPTC4y1+N5SaENdZFn4/e0JQRecezjqAnFvm2t/5g0GByNCDDwwZX1evOxYmx7kOS8xCr38WPWVrPU9ck7pKa+95GfFM/5/ieOkRxLCR5PDl437lSYe+vmiT9zfTvCZethLxReZcz3epJ/5wu3X8bS4D5179913+a3f+i1GoxH/6X/6nwLw3//3/z2r1eqVHeuv//W//uD3/+l/+p9e2X5/keNnXyl6GnT4eQ/jsx7251WVnnj50aL3g44m5fe01PzW1d+m0hXExB99esL5R8d01qPvvkeSgmZrwHcuf4fB7pi+VHy8VZIE2PkZFz/+l0+R6X5Kwx6McfdXpJ48iUeHwZdZIXv6cV1M/ItP5whAV4ZLf27EanjO2dFNYv8rXBzPmBjD9s4E4SNVbbn65h2kvEvwA6QaAPD6N8cMh3+EkAIlhwgO2L+8x/m9cwBCiEx3L+jrOxSlZnx2SPzAoMoSUxYcf3qS5XNTojElfdexXrfsHOzQtj1CKYaDiv0bB2xd3iGGyMnH97j70zs453AuGyUu7k3RVcH8dJYd7OsCqRWf/vhmNqUU4oE0tJCC4XDIaYz8L+sVkVyJSE+5XMtyn0/3f5nj9TFlPaQmQ/q6zjLaGecKjw9s70yYns8QCdbLjo//7QfMdodcefPPES9FFhct8x/9FD+f40NkuD1i8NolqoMddq7tsXt5i0v3/g3aTcEUfDz4Fl3UpELzwVaJTYlBcvz7d/4tJTPsvOTfXhwwvTfLktFC4LzDtZ6yNBRFwXhvjLeZQ7UYGOSf/SZH+xPaznN5YbHrHqkkxx8eURhD21qkVLnqUGhOb56gjeSwfIdx+SYu9AhXIEOW1y6qgkDmyQQBoXPZd8hopJb4kL2nREqIGPF99vCRIQ/uUkkEJVcnv41IEV1XyFRmdbkNwVzGhCw0VYwYIXDkJF0ATbHHm7v/PqIuCG2Gd6aY0FVBt26Jvc0KaxtY2vbgLXbFGyituKUsbSMpYqJfOpzwyKJAJyAmjNZc2f1NbNtCVdKezTDFhLqM3J7+ryThoHMUw4q47olaZf+mBLKzWdd+bXMSIQQ4jy6LfFNpiZ4MCOs+L0qkiIqgEhs1P7KUdl0itkekziILjW97UogEkSuxpMTlLUc9yWpVmp5qZ0jQLTd7yXrVYyYNYblGlCX27pRbaoJQQ2Ln6M5WeaIPWVRCSPSgzPywVTaPlSkr+Ym6RCCQSuWE9f53Gz0pQtQiq9S1GhUC/fGaqBXJWdRwkCF/IXCS9vnp8DoWMM0QbTNPbTVfYaTk9NO7jCZDhuMB8+ki+zRpSZDwQS3oR4pm3NCNDKpWyEnB/HzO7T/+GCklP6xrVnsVIkS+ZSVa1nB7RnWjoJCKVUr8v7s1fUwMdOI/KbIf0Xk0/H8+GGT4mfiMc3QnBP6f6yUAB4NL/PLerwKCvg8oeYQpCxoR+ebBkBQjfzhU/MHFnBgD153jzdszpNH0G6jw7nnPqJHE9Zqzs1k2j1WSQklMUVI0kdVixaCs6GUWrhgNtrh2uE05Lvn9o39N90lHImGjfUHf/+rjwZrRZnx65vD7VVaHHumjxVNee8nPfq5J/n0Y/NPf+TLx8s34Ekd6KhTwSXjN54L/fYlq1dfxxeLHP/4xv/d7vwfkKtH9+Kt/9a/y3/63/y3L5ZL/7r/77/irf/WvvpLjHR4e8tZbb/HBBx/wr/7Vv3ol+/xFjz859blXFU95aJ+sBn9WHnha7iIQNKahoODs47vM7ixxoiJITxkz1MmfLLh3smD3imX0y6+hq2Emf/drXqb3eMLZW9xfjXsKBvwp7X7auw/v6mmLPmuXh36tPb4JHPzGFdbfu8X8PYcpKgC8C1RVwbVfOkQVP0WIBCarVA22h+y9sYuQp0CibMbMP5oyGA4IMdKvO+qmQo8NvgxEAkWyNLLChYiKER8DUkkmoyE+BDrnqYuCi9MpW/tbQOLqt69TDCpC77j5h59QVSVSKZqywG0gSu2yx09XCCEJBITN6lfaKMqyeIBQNHrDNykLopJMY3zuKl2UCqsa6sNDYky4ztJOV8QQ6VZdVg2TiXaxRqvsOZJLW4nZSUe3PuLaL73O6b1jQh8wMWFSxJ2eszyfcrKzx1v/3q+glaBUniJ5ooBqUKJ0jVcCtZ0V27RtKY8sxlvOjk44vRAIobAuEGJWApNSEHykqAra6TJD5mLg6q++zfmlLXrAiwxnamcrTj6+S7QRu+jRKT/wUmeI2nq24vDGAWc3F+z/8g2E7glrS1j2GKXy6n/vICakllkwwXtkimAjaeOTJGU2XJWQhTRsrqwkKbDWU5pBrjAFQRIZnnYfdZogG5e2PSFFEJKiLLPhaWHAKbSXKBGIwZHalj4lTFVhQ8iCHkIidcKUDcl5dBBoIt2q3QggSGLvMu/F2mww7D0i5tX91guqwTZ1NUAQUVWBiwHpAnG6Rk4ahPWo0sAqJ0gCSDFmX6XeUWhDDBHd1Aijc4UKcjVKSlLbkaqCZHvUqMr7DzF7l9Tlpsqcpaxlo0m9R4SIahy19kSjqbdLCBZdgR4UJJcIqx6zv4UPkb61iKM55toewQeKG4fEzhLWPSBwwaJkTiioDCrFDCc0kuhytU/YkEUsQiRZCwOJKQ3JyCzBvupJfU6iCBGaGqkkujTYaU8PrEz2JBMrS1lXuGVPoRRaa5ILXNw9zwIKAjCKTiRSb5nP1wyHDVtvXyMMyyxGcjZnfvMY5xyDrRGrUiFEiY7/f/b+7FezLT3rBX+jm83Xrz76HXvvzJ2d005wpo8xlnwOOnAKoZJLwlQJQ0H9A1xwzQWXlpBBiGvL2AmohBAgkApxVIdjwC4wGNvpdLa7j3b16+tnN7q6GF+0OyIydpO4Yb+hiFjrm92Y45tzjPcd7/M+T+TV125S5pr1vWNCd44oU13hPATamGCmXjrKQYmIilnlcA9W4jdDqYsw21Bc95B0ukcMkbd+91uc3z0lK3LyTJMRCcD5csUseGzbsr1qMXWksRYQjC7t0RMSt6wYbo9Z+6S1tn95j7PDM2LdsnN5h939CeVkwGh/kqCgm3Hdho7KVjSufvGY/xHsQf3UR1tie2qjeEbNy2OEQi8+xYPq2xfv/LL7fbL99HIBwyN2vuetzD5q+aNa4x9GEPmiRdPnff7YMR/rYfjUfhj2IEskhOCv/tW/+vDzP/tn/yyXL1/m8PCQX/3VX/3EgiKAz372s7zzzjtcXFzQdR1Zln1i5/6jaH84gqIPM168xBj47E1PRg4CQb4ZxzWCbtVw8va9VKMgEt10VmbECNWiol7VSO85u3vKeVUz+9IVevtjVASjzGZpLSI2ZbA+xqSn8kTDn527/8G39IMmkGd8IMDIRN+spIaQBABvfuXzrG97ghcIFxgfTLj06iWyXkcMCkTEO2iWFVJI5hdLti8bEvORJDOG5WyJdZ6e2NT6BEFoIc8ytNAIrchMEjtVWjMa9qiqBu8DZVkmLRspWZzPeeWLr5D1C4J13Pn2bZbnS2zRJVpsrchyQ240RZkhlSKEkNjmMo33Adt2eBfw3kFM/R5DpK0aBnH0WLwaH3lC8bFOilDNV7zzjXe48tplJgdbXNw+QUuF6DyZSM59jJGizJnPl1y6uofKU71LPiwRWvHqVz/L6nyBrTsikXbV4DpLO10xvXfOcKePixItNV6mtp8dnjK+vouOMTFaBY81AoQklIaiMdSVTVpAQiCNplfm+M7RNF0SRZWS61+4gd4Zsdjce7eoufvtW9TTJbrIEUokx7yzWB/Y394h6+Wc3D7BO89qVeNjRBpDyKFZVIQuUmhF1Iogkh6R9y6t6scIQqKEwDtHpxQaCdYlqFZMzHVIiY6RKHVi5BOSEFMZEs6nWpt+kWo/tCaqhG+JnUvsZ0oiRWIga2MkOk+9WCDajmw4JGYaHQNeBVoBomnJpEKTYG46SkQQiK7DW4/ONcEIcA1CKZSMWOcoNnpFfrkkKmg7h1SRYBTCeVg3qZZo2RC1xLYO7TxmWCb2ts1NiY0eFzESG0vrPMWgRHSOsBHFRUBXtakuSFpCqxOt/LBETPrIpiOsG8gNZBpfLaljS365JAhNCA43rRHlCNGGTd8plBCQm0TE0M8R/TLV9IkkzKq0wiFQVZfo2NdtYhnMDSiFDI4uBJRMtWmqcyBB9Quq2RxtJGvvIO8TAe9TXaDqZeheD+8Ftl7iMhAeysZCqRKxRgSdJ8Y1HyPrZYWP6d2NrUdJCT6yOxlRlDmLt+5RjAcszmb4zrKuW0ajAUZrqvWSqq65vLuFGEi8d8Qs4qKmjo6OSFEmcodSK6yQtFrghEB6+VDEN7hHNR5PLGlFWBxPOb13mmr7dicMhgUuQhsC81XFeDSgso5l67iS9ajaDqUVs9WaytrEXipICzghUIz6yNMphU4Mkze/8jouOjwJYvrArE804U8EBJ+kLx2flwt57gFPqFE83kdP7cazZrHHoWBPmni49XlhiHjyii+wT66D4mal5uk2fZyw60O5Nj8w2NqcMbJZVP3wrfkh5vf+h7TDw0OuXbv23O1379596XOFEPjH//gfA/AzP/Mz3Lhx4+E2pRR/5a/8FX7xF3+RX/u1X+P27dtPbP84NplMHv48nU45ODj4RM77R9X+cARFL7LnvftPj1QvGCMen2AeKIJrAT9b9hhLiXVwp3OYfs7w+h7KaC7unFJPV2SDkv3XLxF94P6b93BVQ7hYUfz691F5xnh/xBs3/zRZL0eKKUa9CcC9Rcc3DldPNTc+WrKDR+KxHy6p/cz7expxYKThf7r+0xS6wCnB+/M+nRCo2vLFxbfoqgqTaapqyXuzFUpLXJeKwJ3tCF7hOsfdk4K7n/8pEIK2dujsGLusCM5RVQ0xwvBswMH6s+R5jg8KbwLOp+yGUopqVWF9YPfyNtWyplrVKCmRStDfHQFw9NZ9ludLtFKpJqnI6fULhID5dIWUAqUD1bohyw3d1OKcJ/hA0dswZmUanRl64x69ySDp7Dx8AB7v3ycfloujC1bTFWd3z5gcbOHqBiUiSkDdtgwnI4TRrB/oJFUNmhxbNUijEOM+UkuKXk5oO5p1y3q6ot4o1t/7zm10YTiZTLj6xhWU1jhpGG0rRN2x/XvnIASDa33+81dHNNWKrB1x6e1r3P/uPXCJytqFSNsmBz96hy5K9l6/zNbVHWIXeOOk4vzOGSdv3kW7AFJSGk3nO7rOMhyWCOupqpqm7bCdZXGxRB9M+O3vHTLcHeNaS9tF5rfu85VX9hn2spQRUIpQ17g2wefyfoZsLVFtWOo2MDKfa3RMNNdaCfAgrEMouWExkwjnk9aOS9TXyujEvhaBGJIwqk1Bu1QCvwkK0Ypev0/nPVmZM28ajouWqV4iheCVfJuiEjjrubwyXFY5toGzxTe5Wx+RSUnoFVA1+BjRUuCVQjnwQtCdLNFGYTIQxiRYXp7+DzFiejnOOcQD4oQIxFS3FzuP0OohbTxaonzAVh2ZEohRmeLyCMpIvBrSdJa8S2QA/mKFyA1qa4B1PtXuWMfxokSpEnmco6tUO9acgjkoEbJGtDbBGononRHej2hO5hQ38odPfHAejCIrcpzzRDbMgUISXUCIFIDqPEPGiG0dEJBaU3eStxfDpAOlFGY30m1ggUoIlJB06yHri33W1QG60XxmsaauG+bjiDsYUvT61Ms1trX0Rj1s3bJuEj21fgC1NILJ/Sm9dYd1niw3DENIixFFTqxqmm7K21e/T7bV4HoD3pqckY966DcM3/y1Nb51DEaSv/pXdjAmcnR3wX86GZGP+0QluRF2iEAzbbj/n46ecOYFaeHDW8e9793iIpNMD0bMtkvu5hm/FR1117Fa1Ly2DEgpKMdb1Is1Uggudvp8R3hM1uNrOzu44zl6Q7Gucs2Vz92gW7ep9il4fufov7LsFk+MQzFC69pnD/Ivg6R+kT0LO/xSx7ykPfDVnxF2PQ7aejTPvcyM9wfgwj+jnz8Q0omnnY4nFztTVz8Z4DyZWXtOICie7r1nh2NxM599GuD88bJ/9+/+3cMg6nHo3AP7a3/tr/GLv/iLxBj5R//oH/G3/tbf+kSu+zLP5v9I9gfPPvdh93k6AviI47wA+kIwEILFssGGFt96zm+dIJRifHmLeetolzVndcelL1zj+o++ysm7hyxOZvSVQvrI/NYZblqxe/OA3RsZmZYIIFPPuUHxYNh8HBzwcR7EZ6+oCQSFKshihoiCYJO+kJaKyzcvc/it9wmNxW+EW6MLIHKSfxQxmaatWowy1F4jtWJ+PKNZVgTryI3BGJ1WOr3AWIOQGt85jNHEjdinUpKmdhitWU3X5L0cqVqc8/TKEpVrFiczTm6dIkWCYfV6BW3bsZivUHJD+xsFrd0EOSGiEAil2Lm+x9bVnaRroiSIRLFLhIVffKBfHvXZxmKkXTTkWUa7bujqDo9IjFMqMaktlmt6ZZnuO8swgwIpJauqxYdANthAEWOkqTouDi+ISPavXaKpaqYnU3wMNEXGe989oussvbKgN+lRzVZ0nWM0HtD1Isf9C8zI0NqOrVXD/s1LnN89o141+BDp9QuCCdTrgCcy3EvZsOg80/dPUkBkNIPtEavZimpVI1X6jperBpMZqtmarrUMhj36wx6r6ZpmVeOBdrFGa01xaZs2BMpNvZAUApVpgvXkSiG7DStZjCjrN5mhxBIXQ6DbrJ6jZGKKi6k2KUByxIuktyM7l6B11qHL/KGuV6dlGpyUJKqY9IDqFqOT4KlzDhcjnYzUeDKlqbuO2JsQVg2y8ehSE4mEYGldk4gWYtK9EbMlTklCvyTapDOklQUcQZdI78EFsCB6OVrKRAARwWwylYSIiGBioBOCuu0ovEYDuswI1tHGSD4apkfOeoSW4EPSTdrUU4WNppcEfGuRmcGMesQYWHeOdtVgoqNp1ojM0HWRfNlgCoNSCrdqEEUifRDDApNp3PkSdXkLWRhUv0haQ7kgKEkIgWxvjCoymtM5+IAIaTIIIu2jjAIfCDYQgsJ5mWB3iwpvfXr3W0vwAdd1NHPHvAVhoMgE/dGAWiY4ajqfoakbqnWdmPxyQ24M7apm+2Cb4DzlrEW6hlJIhPVoEtFDoSSjnQkyExzJNzn1DbN1x9ldzcGPvQ6ZYBUDLgYkgsFQEZsKLSwrHLXrUELjOkdWZKh8o0QXnxwLhBCszucszxcMtgasRz2i0axjwLaOqm4YKE0PyXS+RPVTlmh/Z4sLDeO9LXZev8xeXjI9+v0Ndbimqzqu/tirD8eeQKD1LY1rHhuHnhy7n7A/IBiTeHxqEQI2tX5PTDmbnx8l35+cj/4ouO4PA5EX1FC91HmeJvN5wX7PdT6fmwV6cs5KH4mHh/zgyz4j2vsUHvex7fLlyx8qG/QiewCdK8uSn/u5n/vA9i9/+ct85Stf4Rvf+AZf//rXP7GgaD6fP/x5e3v7EznnH2X7+EHR4y/Wx17JesY5nh6AP449XlD0+CQkBba2RB8xUmGrltO3DumPStazjlwrzt45Yv9zV7n6+ev41lEvK5z3ZJmmXtbc/v33CW2PK28kVi4lPIVOnGE+RGyIT7ZBPGOQerphH8huPGOF6indg0ylFeJQeU6+f4/VyYqQa6afv8zg6ja6yJlc3UFFuPvdW9R1orwWQmC9p1fkKKNoVivKXsHkYML6YoUaFLSLOmV/tKIcD5hc2k5O8doSFh25knQbqFlWZHSdRevE9uW8x4VAcI5ok3aIyhRSSuanc4QUaKPp9YoEZfIhffU+kJc5Td2mlVwf8DowubzF9o09TG6YHc84vXcGNlHrdm2HdY78agH5B3tYKyh06kYdHPWioiwyPJEQPElnU+BjxMjE1LVYrJhMBmzfPCAQmd47Y+vqmIPXdmjXC6pFx+p0wepkjlIKbwPHd4439RYZWWZoVi39IlItksjrwWevII1icmmHGCP3795i8Lkx9WxJqXt0ocXoyMGPXsG55Bxf3D2nvmjJy4zLX7iOzjXNoubo7fvMT6ZIKTFZgul4n9jpFmdzhEzByaXXLiOV5NY336OuW5rDM7SQxBi5893bKBfYvraL7Bxyd0i0HrGppdKFIkqXiB+kwIeQ6tk2ekxCQAwRoRX0S2yI6E0BUQyBGAIugtaK2FlcaKB1ACiZQdOBUSDSs4CzoDfMb0YjQg9pPVJEnEjwVDZwvqhEWkINDtsz5Ej8BsooYgryo4C4rmHYI+QmERysKuJ4gMo0ssiSdpZ1iCLH6Y1T17pUzzXuITevbiJ3gM4lvR8VIz2VdIBCrvFd0gPqjXup70Ylfl6nALHtUKMe4jHYXQRC0xF8QGaG7ugCNRlgcsP6+IJgzQaSmrJY64slg2EPsz1ADktc51CtTdo9Kgns+ukKeWmLbGtAPF8mbSIi1kNsk/isVJJoEw1JcAFRGIwQiNykvs4zYkhkCTKSRF6bLgUgWYYwinbtsLlGFSotiIgk3qtdh+scIjYQI53z9PopaBNKIUJg59oeg/0JQsBgbdk72EFnZqNBpDG9HC8svmk5fu8u218a45YNUiYorykyCIKeFAQh6QmB6DwiJFhzWEbWJ3PKfk4MXYJEohj0N2Ozj9T1oxG0mlcoqdidjGhzw8nhCda2GA1lnqGCZbZs6GUm1TkVBVmvQElL07Qcv32Pq/1RIoPJDD0FsVmjfUtD0hiKhA8S8zy9tiWe8/MLDvmk7XG1iYcBEY9Po4lk5eHMtAmIHkDf/nD43E+34vElyfikb/HgXl56tfzJ/R7Xz+Vlz/MsN2Dz2csnB1/GQfoBkLxP7Q/Ulssl//Jf/ksAvva1r/Hmm28+c7+f+qmf4hvf+AZvvvkmv/mbv8lP/uRPfuxrf//73wdgb28vyWz8D26fbA+8zFv8Mu/fswKjZ/3+oUbdBzCJR4c9vgi2OFswunqZ5fEM71JGYnG+oG07jC6o5mvON4HRlS9e59bvvENwntH2mIvTKQY4enuN7fY5eOMqO+WUP/vamyDg1rzlm0dP0Sg+pzA1xk0LxVM5pMf3f7jC+WQHaKH5iat/Cnfeceut97jwZ2hjCJ1j9Du34HfeJ9vfIn7hOuOr25TjHqfvHTE7vGBdNQ8x1cTk3O7d2EeeLLl5tKB3bQex6FhoiXCSsswJzlPN1/SqNgVi1pFlmrZ1+FWN0Rq9ocQe744YH2xRLytmR1OUVmxf2QHAdg5CpDcoaauWal2jtSbEwHBrQLWoiCEw3p/gYuDy61cwhWF1vuT+9+8iI8zOF/T7BcWgZHoxpxiWDHfGsOID9toEfvZzEL3nvffn/OdO4oTk8muX6Y37HNy8xPL2Gc26xsWIFIJer0AVJlElFwb9ygHavE1ZnEGzJvhrFMMR1dkCrQ1r16KzVHC/d32fLNOslzWCyHY/CdouzmZUqxrfWQbbY7aGO+zfvQwCqm7Bm1d/F6Kn2B2hywwzLFEzw+fe/2LKwsTI4ffuMTuaAmAyQ123KK8JrSWEyOx8QXCpnsYUBtt0rC6WRJFqwHxn8SqkTNl8Rb41oNgacOf33uWVQcawzBFEWh9QyKQDA9iqRWxILZRSeOcxOmVQggvJ4d84HVIngVU6l9oNtHbBveZ3CU1LyYjL/a+kR895aC2yyFiFU6bxfWSIiPWQvd4XWHeWKRXToWPWdlQhYDeU2ff1mnPTkgnJZ8WEYZtU5J0EZxTOegygF2ukdTRao0WC8dHLcEajVUzZD5vqmoRIpBWqXzzwmwjOE1ubMoMCimwTQBgNnUVJidmf4M4XxFVN3NQsRbmh7peSuKGpV0oShSa0DpEbbGOxTUu+jongYthDZhkuRvSqTtkbo8lHPURmiJ3DjPv4o2kiGFESURhsBFt3qHWDGfdw3mNnFaFuMVrhq4ZMTch2R7jpmjBfplqiPLXVeIXMdBJm1ZLoPX4TyAijCG0k1B2RjAsj+N64T9YvsK3Fx0C0gbYRKKkJuUYIQe4C4/0tyu1BqmWKJAHctqOZrtCZpps3NLMVg+0R/f0JaMF33f+P4/Yu1dWW+cmKyaDHommYOEcMgVJo/lLZJ5MegUf+lyNUJpjUBde+cxOEYbAjGY7fITYea+d84f81wRSG997r+Of/YrpxZBM0EGCw7ti9f8aNXklRVqyn36RpO/BXQVwnINgZDQhSUDUtcWRw3lFNa+7enbLdBkZ7E97oHbE/nGFOp/yrpuJoI/5tvX2mT/oEP9hzfNYP68J+pOnyGQd+8PjHAp8HqaKHjfuDyxE9cEPiZuHiwWfw7PjjwQ+bZNjHNPEc2aZH8/UT25/+bh9m2h4teD59vqeDrY/e08847ocdaX9qz7R/9s/+GVVVAfAf/+N/5Gtf+9oPPOZXf/VXP3ZQdHh4yHvvvQekgOtT+8NUU/Si9/pjv6TxhecIIa1kd8s6QcZygxLgW8g3wpAmz7g4uqAYlUyu7XL5javc+f33WU4XbO1vMT+Zol3g9NaUGDRXvmDIiwTn0vIpqNyzgiF4KpP1ggY/KkZ67Lzph1h5zt48Ig8KS6TXL6mqjWq9C7Qnc5pru/S3hizP5pzcOkJJxbCfCBCs9xiZIDblZICUiRGryDTj3RHZcgER5rMl4XxOphXbQqAQyZkyGu89eWaQQLdh/VrN12SZQZUZr/34Z9CZQUrJ+myJlknLZLVINTtZlqG0TM6nDwy3h5hezqXPXCH4wPx0xp3fP6GuWrRWGKMoNwxevrXsXdnj8uevUev6mUGRktAz4IInNwIfIsFb0DJRVvdyapF0d7xzDMcDWuvReUZTNZx//zYiRG78WKRbL9GZwNUNIfaSNlTTIiHVikRolxWyyOiPSqplRegsZa5ZHc4ISnB47wJtTpOAp5RMLm0xen2I2SpwTY1zNd46Vucrpt+co84zBpMhh+/cxzaWrf0J/WGP++8doo3GGE3jOqQSRJfquoKLjLZKTm8d0zYdWZknZr9MI2IiHIgx0tsa0NsaIJViOV9zaTxIorpaEaUkErGAMAk+ZiIpS6MkNVBsICjapMyRCCnIkFoRfYDOgQBPxNkG31TkvQGqzImdI2z0a2RnabuKSi8pCk1f9lACWu+Zm8Csq+lrTScVziahWGsCwVnIDJV1bGU5befoiVT/E2MkKzOCT0xiuszIAkn7qPPoMie0Dhsdea5RLvWfNIJoUvZH5BkqS9kQAFY1yECQAgUEBCwrRD9PdOZFhhyWdPM66RYFjzAGkWnwSdtIGZ1qxlqLbC2hl6fs16JGdB6vFVmRIZoOaT1qZEBrnHXgPGZ3hMkzovNEo5EhovsZMusRQkzEFiHilcAoie4XtMsqsdJ1lrCsiJCILzZjj7IOH0j6RTGAFMSqRhYZDqBNjHYOiEZShzS+nM+W9HoFEtg62KJtOqqmSedXCml0CixtqicLPnDnd95iOV0SzmuGbdLnye6dsTdbcelPvkp+MGJ9WrFyLQhYNS2Z0oxfu4zMDaKLFEKQb84nA8goyLRh99IBXRUock8mNuOxUejY0evnFMWTHmoxLEEIMqWQLiCtZ+fGmMtXb7A4ucBzQFvvcn58DvNzjqzAhoDs7yOMZOvyDqOLFnWxZu+1y+yZll57Tggdznd0m6Do+QHPU178c+y5m58ZaH14ezhXbeahH3SOD5dzePkcyIc/y2P1S08ED49D+h5r7QPq1geZmZfKEr0I1vLBfWN8cN505R989+LRfy/15X2CGZ9PA6I/EHsAnfsw9k//6T/l7//9v0+ePwMO85L2y7/8yw9//nN/7s995PP8cbKPHxR91GDmecf9UF7KR4FIoQqEkBjAq4LWR9SkZKK3Obu/xDuXGJOkeDgoGZkmU2cUd++cku2PGexPGO6NWZ0vqBcVe68ccH40pes67t4/w4bAq18QmF6GUAKdyk4SrbBtX/pWn0BUPBq/6W8CEYg4ldqqhGR5OKVrLEIr9vYnqfZltiQblEyub3F2dIbJPPiK+d374CPDUY9l0yCEwJDwzlJK7LpBaEV/b4g0iuH2gEsDzfxwStNZ1sFR15ZORNYiIGLEO0c+7iVNHMAJgdYSXGR1OkcYxfJ0zuhgQq9fcHHvjN7WkOpsiY8RoSQiBqzzGK1YzdaYXsbnvnyTZlXzzu++g206iixDkYrwtRQ0XYfRmtY7vvilS5SlwDbdU524meCDIHSC0EqUyjckDobh7ohIpFnVdHWH0gZNpK5afIhUyxrfOjKjadYNrY8IJMpoepMhzSrBggY7A+Zni4dxbVu3NKuacDIjxEjZL5lWa7I8w7UOoRQmMwSgWTfMDqes7IL+/7qFFTl2VaHGhnLcw7ySU729YnW+TJnKcZ+d63uc3T5BK4VWgugjZZnTth0xBoiS/riP7xzBBQaFoWo6hFJ0dYsQAh8ThbRtOowx9PdGOOtSpjTPkA+KgF0gaInSm0ADUuAsBX6xppOCzGgsLTEEvE/1SNGDaB05WaKyN4rMG6LqkxWJsjtICU2TSDi0RjoDy4AXimJvBxNzSucocEhT4KTASPBSkEmJQGAyjQKsrXFaQvTInkZeWESvSKQNSkBuyDINmSFMV+neNoX9WabTfgi8TA62BITS+LZDGk1oOtSgpMizRLKxOyT4RAUtZYFrOnyICBfwqwb6BWFZpWGoyJCmSKyGdYcPgdimgNBVDcp75GSAGBSEeUUmBcoHsp1hgpDOK0Rm8KsWS0CWGUhSrVZTEzKN2h7gqg4zKPDzCmN0gi7mGr3VR+iU3dOZwVUN+bgHoz52viQj6UihdHKKm47epQkxNyl7tKrxkwEygFs1RBUwhSaKyO7WELQmeI9rOgZbQ9yJo/WOtmo4u3VEXmRJo0okopXlxYLCKAaDkmEeEd7jheD86ILRxR75QZ9xsUVOSxMr+mWOGpaorMCtHZ0NLIOnDQG0wNVpYlutOmpbQ5FR2zX9oUNlEqxgtnDEkaB2T05E44MtTt+6x7Lr2Lp+wOnROdV37zHIDimGfbau7yOXQ/z9U2qdkZmIbVu6ZQ2FZLQ1pMwysqzj6J37XPtswIUUhPtnrmQ9Y6B/6uPnIq2fZZ/QSn+67oeHwD3IuH0A6fDwvPG5nz8r4/EInPfguEf7PLtLnvfps9Mz4jmLlJ+cPfaFPMQjfogLiif74Nm9+uiznhDozeZ1jPhPg5w/9Pbee+/x67/+6wD8jb/xN/gH/+AfvHD/f/7P/zk/93M/x3Q65V//63/NX/pLf+kjXfedd97h7/ydvwPAzs4Of/2v//WPdJ4/bvaHJ1P0IvvI+f8nTSL5k1d+gmE+ghh57+45p+8cMtwbs/e5a4jBnOndMxSCZlnTdZYoEjPV0lne3MqwPnBydML/fP0KOzf2WJ4vaKoaeS4pX7/EtxZzQgycVR3hd/tc/dINzN6A/VcSPfbq7vdZvP97H2kcfjAtSAH/l7Lk0qZw/WhX4XNJcIJ3/ssKbRTKaLau7fLWb30PJQTb1/fYf+0S+5/Zosi/RXQdubxNUb5B7ZIWTQiBPM8QxE1B/grbdJzfO+WVr7yOOJvzaowMxhPePp/xbilYLVaclIpDU0IIKK0RSqKHJQJBVBKhFZcvatTFmlGZJ8Y2H8mHJa6x5GWqP4oxYq1je2dEVXd0VcNo1CcbJ+au2fGUaD15nvZXSpEpRVN3qXg9l1y52uNz7bcRp4HMO57k80m97peai98WaJ0j8wl5HjD9knJQAoKszHE+MNzuMTudURYZKAEhsF4kRkLTy/nWyYzlbIUAvjx5FTuv6E0GzC+WZBsyAKMNZZlTVw3KJE0fqSW5zqlXNYPJkLCqkELQ1S1aawbDHqGF6l94Xvn8F/BDy7vNt4lUDHfGZOOC1fmKQb9k95V9qsWa1WyNjBEhFW3XkWeGLDPYLtUWmUyznq7IM5PqQ6SkazvyXp62LSoyrXHrlmqxZrw3od8lSKW0Di9FqlvZ0GT7jS8RBMg29XOeZ7jO0UrPvdl/ouuqBD3bEG8Y0ePVrZ9CIjBOcHX8U4lsQAg6QEiBzDRCa5p1RSm2eWX8pynyDFqDHGjyXs4Vq9j3Q9ractbvOB95QojkmUELCSFwdvY9nLHE+Rq5lzJf0TqiVkSjEZ0lNDYFeS7VuImqQ2caJ6AJoGVymhIdfUR2DpWpVJSWKULbkZWGUHfYsyVdiAgiwUUwitDZBMELgcwndj0VY6IcXzdEKUBIXNshtMROK7TRtM7j52v6V3cIszXKR+QyERSo/QlRCtrjWSIXQdHcO0eXGbFuIc8IF8sECdQShiWyl+PWDeXuEDddESKIwsDFMmW4yhxXpSCWuiMUBmk0XomUQfMBdzrHbI9S/ZH1D0lNog/Y8MilnV8sKPolupdTrWuaw1TX5f0mmM4U66alazp6gxJ3eIEuc7xR+LrFug7fdujM0B8PaGcVVw5f5fLWK7SrNbdeeZM4AZEZ7v/GMa5KNWnvPeb9ud9yIASuqZDFf0RIyeUrGT/+M32Ujpws+/yb7zhGVUZ9/mRSPu8XlJMB99sWe33CrIiUx4Iw3WK6CJyerfjMV68z3p0QOk9fCMajEftEVBswt6a0UiOMZnxpm19r3+OsWoEA+2AQ/zA+8XP2feGU+Ak5+R9ruv0A6cBjGbDnwsue9al45vYPBlHPz5a8jObRE/f6IiKEp8/zxH0+/a2Ix3Z7Khh8iizhBzcsvqD5jzb8z8bwapYTgH9VV9z3jh/8QLyYHv1T++Ha17/+9YfPx8///M//wP3/wl/4C4xGIxaLBV//+tc/UlD0O7/zO/zcz/0ci0Uio/q7f/fv0u/3P/R5/jia/KGeXfByA3R87O/zjv84I3SEBzpCSii00LiV5ey9U5TMOLp1zv1vvU/Rz7nxldcISmCtS3osEcoyZ2dvGy8EItPML5bM7p1TjvuUwxIZIt26oWtTAXIxGVAMelTTmnvfvk89axHSIFWWCt4/oomNiwaQCcgQiKajmS7QUtCeL6nmayKCwd6Y1fmS6CMqM4wPtgBQWiHwCBlQOmGulVYYrTBKM9waIjNDr1/gqo6u7rAbh6k3KJndOiEvDNvXduiP+/QHPYKUOBEJmYYiY3RtDzXqYx84zs6RCxLTWWeZzlaoTd+a3LA4XXDls1cZ744ZDFMxe6+fJ0KD+Yqj2yccv3uI2QQa0SdI2HBQEmOkqWsyo8mMYrA9QEaHih4ZU93Gwwll8zdGyLICpQzaGMqtAauLBdOjCyASmi4xuE367F/fp21tynpYh/cR21ouf+EGxWSA25BotK2lGBYQI8F5OutI6p0RZST713fJyxxTZPRHPXqDEqUkq/ka11p8CJS9HIjMp0vmFwtCHZjfnuJqh/UeO13h1w2Dgwk+eIp+AS4wP5pRFBlFL6eziaa8N+qRF0k/qzcsWc/XeOvTMxoCbdshBAzHfcb7WynjoQT1Ys27v/MW1WLNlS+9wnpdE2Qi4sgynUgPNs+glIlEI2pFRKA29NWxbXFtA7ZDRUf0FlyL7BpoWkLdIuoO2QakNHidgZaYEGhJNOhRQLAW5wU2CKgt3axCtI5CKYoAwzynl2UYH8k3tN6uapEIhBJU8zlhuyQ6hxwUmL0xsp9glmp7AGWGzDRq1EO5+BAmlgg/MrSATOsN855JWTfrUi2NT/oyQZBIJ0gU7jqCLFMGUGeStrOpf5xH5IZoUvYlVG06R0x0613VpOAxkoJZ61jfO6dTkgponcMuKta3T4ghkpEgv05LhJQ4F4gkkhNRZBCSZpWdrfGtJdYd7nxJcAHXdMSNgG9w6Z6DFLhllejQM43M8/T8+pDqxLzHtx0h4RAxk366Hx8QKmlWuc5RFAVlluGaDqk15TjtZ8oMnRu8D0RAK0mzWFMt10nvSySqe0nkyutXOXjlEkrAxbuH3Pr336Y+WtLbGjO4uku+PUjPmg0P/7Yx0oZA3TrqLtJ6aFykbRuC8Pjo0LnAFIoYA0EoqlWHdU9OLFJJbvzYawQtuX/vhMo6hDJc3t5hd7SFbR3BBz7z0z/ClR97jb3PXyffG2N6BTHPkdtjrn35Jte+8ho7rx5gBXRA9wDB/bz58EP4o8+bLp/c6SNMmJ9QVkGINF6IJ86ZWiw2f9InTy9XfVKNe9a+jzI2HyC5+Mj2Ufs4PvXBs8/zbHDei6E53e376M6Si5d37uJLO2qf2idtMUa+/vWvA/D666+/VI1QURT8xb/4FwH4t//233JycvKBfbquY7VaPfx7eHjIN7/5TX75l3+Zn/3Zn+VrX/sa7733HkII/vbf/tufZokes4+dKXrkIsEfSkBqfOI/IFE2H3/vDr0sQzmPK3Mu7l9wdu+c8f6Y/dev0C5q6CwmMyitkEbRd5KmtfSl4uT9Y3qjHpODrRSIxIizqZB8NV2yPxigM0O3qLj49h2iEQz2RnghiBtK2NalAvaXv5UP9m9WZAx3dmid4OLuMT6MEN4z3Blx/v5xgiIZmdi8YqLcrVUflKcthnTHHX2TERDUzjI9npL3C2rvESpio+faK5dwraVZ1ogYOXz7HtmfeA3tOqRWSOdRYVMvEALLszmT/S3yMmdxdAExEEVA6cCgzFgtYX66YL5Ys311h/XhlOntE7IyZzjpI5yn84Ht3TFN1dK2lvvv3Of1r3yGrF/QLBu2JgMWixVda9GAt5bezh7lzojFQhKcpcs0W5UAKbFElpvJsIuRixgggPUd169tU8aGYT+9DtU8FTyafkGIqY+FSNAyFyM4SdYvKF3JwAywnWNxf4r3feplk+ovYiQKQVbkhBA4O5zS1C1SKWbnqe4CBNE79q7tEYHl6Yw8Mwglk1MjJat5hT2xtLFhsjumO7ecvHfE5TeuMb93kVYaN1m+IAVZmaXvOUSqRcpAlb2C+dmc4B15WTDaGXF87/Shg3L03hFFL8fVnigE0TmadY0QgqZucUWBKjMkgqAVMsTEWgaJulqmWhUvBKVWxK5DxQKVZdA5hDFEQKkeMjdED3EDF1Q+IJqWkGXYmNi5dNttJupAlA1tW+NVhrHFQ3ggOgUX2nVoGlQXiVKC0ZhmjWoatNFIHwhCYLYGROuQMbG8IQT5pS1C02HXDbgukSOsGkII6NwQfEiEFdahrEX5tOYcvUdIknaT9UghEK1N7Gwx0m2elWhbpNTJ7QkbFj4lkEImraPE741SBjlbEdebgM558o1obp4ZTOeI4xxXNbQhUHQeVBKWjT6xQYamA60SQkcpopLp+Vo3uMYiMk2sW0IXCFLiO0fsLGbTNm90qn2MEd906KIgGxRJpNU75KQPxmwgsRBWLbFzSAG2apjZOUpJiixlxHNjaJqWLE+/L85naKMJXQKRxSJDD0qqiwXjsmB8aZvdvGQSBUf3TqmXNUZCZx0GSfXNd7kcX8G8ms4XbMCUI8AjRGTEChE8sRAImWHrDtl/oF8GfelYBYMOkqBgWC/IDDSLjr1eWiefZI7Mr8kL+MJP3GC1mtNMV7CytFbQekd/lDPYVmSFI14qaH0gu1ISXEjC0kYnWnMc1lp8cM+Fhn0UU8BYJtmHKCRWlURScN6p5AbLEMk2bKcyOExIcG0vwW+kIpwwWJlv+rIhdO0n6Be/IB32MGEUH4YpL3fZx7Iuz+zPZ8Pj0m8fzDY9nct54ogPodXygBfpMcTgB6//+PkeLtB+SHupJgnCjavMNvWb9iV799Nw6A/OfuM3foN3330XgL/8l//ySx/38z//8/zDf/gPcc7xT/7JP+Fv/s2/+cT2X/iFX+AXfuEXXniOL33pS/y9v/f3Pq0leso+EfjcY6jZze8PVoI2/z43Xf50iv1DXeSZMdizB8xHOwYfaJsGu04QI9+29IucMs+ompaL+xcopdh9ZZ+7371FlmfkJsGKvri0LFcVg15BvW5YHE3JenkqGA6R6AO7r+1z+NY9lhdLro/6NOua/GyJ+U9vc+Vz1xjtS/TrEwC+e1Lx/bP6JW7+ORYjMQpc/CKLi8DxUSQvCoIU5L2cZt0gY6StWhYnU5RSyJ0+7+/9BEEK/I9M0fe/xWpdk2UZtuvo5Tkz73h/p0RIRb8WfHbcZ3E65/Dte2wfbDM/mTFa1ZzfP3tI1xuFoDfqk+eG+fGM43fvM5gM8CGgpcBtWXzuQVhyYVgdVohakPcLiu0B1apOwYSPyNwg6w4hBOWwpByVVFXL8btH7F/f597371C1LVXdMuiXRK+QQjK5us0yg99+HWYnc964dIW//HtJu+S2d/zrpiYCd7znn1SJDfAL9h5/ppjCpchcFJwyRhhFv8zp1g3VYo3zYeMEgwwiCY8Cn9/9Im/sfIHD799hvZzhtQcfiD4xzs3O5qyWVaIwz3SCUZlUNO+DB2dRRrN9Y5d7370LpMJ+H1J9i5Dpd3c/cunwGpO9CTIznMdztq/tMt6bsD5fspyusM6jlWTn6i7Toynr2YqsTHC22ekca5NI6NaVHYpBwbZ1nNw/Y3YyY7gzRAqJWzeJct0YTJaxnq3oTwYoKQguoDbvnbeO2EWESuxzQStyJYjWI0Mg6IJXt34yZVqNRmiJ9CkIFS7ihEgscyT2saglSsokCNp1CCHJM8Nxfcp09V0iMM6usF9+gShM0k0yGu8D2ek9evIeKkSigK5uUSGiBYhBiV815Hsj8B5/tgClkEWCcIbWIsscuawJzuEWFR6BjJEQu/ROK5XovBsLg5JQt6AkPjOJiluKFOCESJACgifUiXmQukblaahygA6BqFJfBCkQtUOMFFhHXNRItYHmieTYeuexRsOmTirPMrJN7VeMIFwKSAGElAglaWJErhpkv0CLFKTJDQuiEJJIghoqH+h8RDRtgrNGEsxuVSe9sJAypjIminAzGaaMsQ+JjjzEdE2RAmIVAkFAf9xnvapxTYcLnrpqCC69g6Ux9A92WJ3NCaWmWlS4ztJ1Fplp3hWB5XSOywK9N/aIzpMBbxxXqDawvHNB8a8yrv3ITWKmqD7/ZTopKWj42fhvKPAQU5YwuE3w5DxCes685D/c7+OFZKta8b8tD8ldRhQC/UWNLjL8/ILu9n8FBOJqyfxrA2594110rXDn19m6conh8Iwi+z2MyXnzYs3b549pDX1gtoEQ/YsDoh/ktz61fSwl/49eDyMErRlyZ/vHCRGWSvDOVmK1HNvIzVliBB00J1yafRuA9UBysZWm/KPiFW733gABy1u/z/L2t1/QiI9oH7gv8dRPz+uZF3fKx3Xin03AIPhgqPRs+wAU7mXtWcFQ5Kkg7ClPavMOP6tLngUL/A+2RWxqlj98PdGHxHZ+ah/bHidYeBno3AP7M3/mz3D58mUODw/51V/91Q8ERY+bUorRaMR4POaNN97gq1/9Kn/+z/95fvqnf/pjtf2Pq33soOhZ2YuXK8/8EG/ss8aq5xz+gWE2Lak9zGd562iXnmxQUFcdWumHMKCyyJFScn73DCklO1d2mR1NOW27hImPERUC2jm0ECzPl9y4scf2lR3O7p5RzdZk5VW2r+5i3zmmqtdMdkYs5mui9Rx+5zYqRravPIAYvHwXPPtmxQaOJ+jWFmEMqsyRMaRAzXmiVhADd75zCykEk89do9sfgJEUkyE3/6fPc/q9u8ynSwbDPtHHBIlTiU0ud46L++fsv7IHIWA7x+s//gYnLjz8DjxptTk6Tz7qs3Nlh9nZnPWqTtowIaCVQCqBj6kwX2YaU2hW5wv6r19m99UDLu6e4Zeexln6vQKTGy4OLyjKnKAE5bhHtayQUkKE0XiIiAHvIN/uUQx63L9/i1l1RlWvuPOtt/nx8z6DnfGGlOLRo2Pjw1wEMvoN3CMAiYGqPl+yvliSj3qs5hWutYz3R9SLCp1plJIIkQQtq7MVyhi2D7Y5vnuKloKiX1BWLW3VYH1yhstRH9e6DTywZL1hxuuqLhExhEAMkJc50mjWqypBIKKivz0gOtC5YrA9QhmNbTqmZzMgafEoKZkdT9FK4iHRPWtF5zvyPAOZ+lBshHW10bg21ZOtVyt8CGztTlgt1wx2hvQnQzKjifM6OcLWoxGgNZ214ANL58A7lMnwkERZG0shFLqXpWxKCBAcQpJoqENACknMNbFLNWXCOkJhWFQ1RoqUfdISbQOdFHijCF1iW6MsE/GBBGU0qnHIXo70IQVZRiNDEmQ1wxJ7NkcoiewXROsIbUcMhm5RY3ZHoBVBSFRuUE2XaoGkSqKjhUnBkQ6odQOtJRQZIVqiUQ+fK5EbXNMRfMQoCc4SBz1C5/GtQ/VyvEgMdcQIVYcXKfh16/aRPyIArfBNh3SCqDU6N4lJ0PrE3iclItMEIZHWE6NPmSityLTCbZjqKLL0rmzY/+jlKVASpCA3pOcGIuWlbXCeuEqaQlECPuCkTG0OIJY1oXOJobE02FlFFAIXAvmwRGqZasykoN8rCDHSrhpkrolKoiP4LkFBYxPRUjIYDRARqtM5pycX9MqcrJ9q+oqiQDpPLQXbUnB674TxZMhod4mVYMUWLQGdOcxQYDaBcRLV9Yk5UEp8Z8kHfXwUG50gQdnLiK1NwWtncU2LcCNETIGVxCNV5MaP3aQ3HnB1dhMhJX5ZIfUcQSDEgI/+g+Py89BbH9jv5Zzwp00j0BG6zlMdL2iWDTMRWNyYUJ8vEUVBLPuoIpHRqJBqZFQUm0A5QV+F3LANPs5b/Qn4xA9kJZ7O1zyVjnnuJdNnL+qbl2tkfKINzznmmZd5UUc8+eV+4LDHvJ+n2LWff9zjp3hsPyEeBV/P85aebunHI1b4NCD6722/9Eu/xC/90i996OOklNy/f/+Jz27evPkJQkOT/cqv/Aq/8iu/8ome8w+7/dEgWnjcPsJ3PsgGKKmRCJZ3L4iLyM5rl7jze+8SA/iqwXuPkYneedAvmd4/R21YlPAxOSBSoFRyRmwIZJtVnK1ru8yPZ8Smo37vhCuvX2J+ZwpVzXpVM5oMmJ4vwDruf/8CfGB8dYvhMHBFJ4ri+dyzXj+C0r1wIIxw/kDcNCZBzHLS5/qXbmIyjdQ6DcRCEEOgqVr6vQKhJWdv3+PudIpXgnGes1/2uPxjrzI4nHJx55TWJQd9mJV0LtBXkaLfkRUt+Y7h8K0FNA1zIrazm5Xi5FSu5yuc8ygpCSGijaJrO0IIrNtAoSQ+RIyQxHFJS2Rr0OP89injq9uYYcnseEbbdHStZWd3gtbpe9NCElqL3dTCEAJ13TAaD0Ao9FXD8fltOpbIxpJHSRlEKq7n6cW4R5NlHSPHIfW7dy2FXXDlUoGOE05uz1m+f4TUGq0VzgZ2vnCD06MLqkxRRIjeU9ctZVGwWqzZ2p+gMk21rKmrNgU6MWB6Oc2yRilJiDFRc28gLtPDC/au7HB672xDixxTBmlnTCBp2chMYTuLGmUs5IyRmJAdZFzZv0Y9XzG7c0ZpI9V0SbV09Lf22Lq8w/mtE/rDXhLntQ4fAs1FxfRsjrcOKQWL6QKtFB5YLWvyYUlXt3jZsFieoqwjN0OEVkS/gW5lBgGUShJVom1/kOkzmSGGSGgtMbRJqHMDLQshIkIgZInq3jlPXNSEGBDrBoPAxgSrM5AySgK8afBlh/UB2zWENtGEoxOES7QJLEIISB+QWhIbS1QSNeghBLh1A4sKtTcmrhtkBLxPcEURCasaoRR6a0hoLEoIQmcRgI2ATpA1KZKDp7VKwqutTeQiucHbFKA4RIKXhZCozJ3HAyEkQVSCJQpBWDXgU1ZQsOlHrdD9IkHibBof5KBI9XRaJciidYkmXEuUD4QAwgd822GVwmWGQqsUHMYU/CTSE4lREmc9KgbINN46jPPoUZ/YWLrDM2TTgVTIGPGzNbHpEBG8DzgpsBcrpE76Q4TIeGfMYrpA+Ig0KtXeiDRg2y59D5V3uPMpSkgKpdFSU/nIumk5P59jyoxoFEIrsrqjrwKt88RRj/l0RZdpiht7vPmdd1nWLfN3+gQpGJeC5U8VhKIgisiqWxKQxKZj7JPGWZCKkeqwraUMLbZqyUzS1WJgcI1lfX+JCoq8XxCio5mmFfcgA0uXCpJVCTYKaBytCy8cp59nMT5AMzwdKDzDRKoN2ZESCQyUYWqGrE9mnJ+fczo6Z1VZmkLh1gVnh+eIICi9YP+Lr9B5z/LemrxXUM07pBxh+jmLo4ozcUR/MkDIHD3YephBedAk16wJrv2Qd5cCmuculcbHMzXPhhV+GKjhIza7Z53nZWzzDX6AGOLhBZ67GPs0cOXBJ+n2RDot8TmIlueEe2JTFygee7Ke85i8KM/2vL791D61T+3F9kMMij7kdPHxF4ae0wrBly99ha1iG9c57t1/l2pRsWU91770SmLhqlvW50ts1VEt1zRdcoiicxR5hnWO7Z0x0mi6tmM9X1H0CiYHW+T9AtfYNGHZwPj9C64PhrjtCWfLjnpVYzJDkRvs2uG6bd77VmBvsceP/t92+N++fATA//5vF/zWf3sk8PqspP7j2/6PJsE2lJD8qRCo7s24+849tvYmdK3l1R97LVElO1IWrCxw3qNi5ObxalPnMOdYKeaDkr3XL/PKT7zBxe1T2lXDZG3RRQZxSt+8SXMC9vLnePdgyNvLBds3D1DzOdFHdi/tIJTEu8DifE5rO5QQiVEOQEpuVYZTaxBGIUqJGGmCFLw+bShDJNSW0d6Y8f4EQVJKDy6gjeb8ZEo1b9BaMRr1kVphEFSLNd26ZfKlHc6/dsK7v/MdJlpi0Cit6Y1LemHwAhSH4D3veL9ODFZfcXf4mfYMgMH2TVTvOm/95rfplwW2c6znFe0w4+LgGm6vx415y7CGzGjqddIS6uqOg1cvMT2apSyAdYmQYjxgPV0l9rwiT7TUWhBiYH2+pHd1hyuvXWZ2MsM2HdUiUXYPRj2CEAz3J5SjHu24wV3ueD9+l3IyfHhLozdabtxNbZge5WSjGwgpE8QzNyxmK+p1zdu//SY6MygpGO2MaduWalmhywJnHb1Rj51XD8jKjNP6e8ym30WsO67t/BT9bBtdJLY1bXSq15ACFSCqVGuEkikokGCkxtUt0aUAgM0qvosR13QURiUq7g0VtiQ5BcpoQoy4EFK2xijmq3t03SlapQDDhnRtoSVKSbxPdU7CR3y1JvYKVG6IVZeEqXKdWNP6BfFBtsVs6n06l4IQ65PorA8Im/ah6YhKoSHRxcsUaEtpEntdphLczCYIqTJJOFe7RLNN3JAxx1S3E4AgPaJzKXDTaeFAxpgcKJGEXUPTpSxPYxFlltjefDpnlAJVmhSESkUIFvp5CtiajryfMmlJjFlgrUcHiNESnEeFFLi6kGqa8BF3MsfNk7grAcSiTrTgQuKNTpmUlERBSknMk5ZY6xyml7O8WBB9oNvoXakskUtopdCZYbVYEXND0S8ZTIZopeimS0IDxbBEtQ7nAzakDNZnZw0DOjqtef9gwCIHuzYc25p5HhF5zmdOlkjryI3h+9e+Qn9vTO1qfuP2v8d6y1Zu+L/vzhDO0RsY/vT4ArtckQ8KYm5QmcaXAvGj2/i6I9uvCN86Qu+OsYuc2//HRXJe4x0eOLmIuMlipLwyAjYL+o/G6echseLjuYsnilCebxH6UvAXyx45gkXW51+o1ziVc9RliYtghjmttdj752ip6CYl37Oed07OEhFN8Tn6ecFg3XHtG5bB1oAT22F+1HDx1n2U1njxWXZeOSCfDNhI6jB98zepjt57ztj5bEvxwAaZ8YyJ68lbfjJ7/9Gm+Sermp/Rmg9c4SFt+LOuGR8LKgRPzBUv487Ex/55cOjzPKEHLXoIx9scIMQTDXnqVp7sqee7TeID+z7TPkpU/6l9an+M7eMHRc947/7g37P4GOOlQJCgTrM757TLBu8DzWyNzjWn90+59MZ1rv/J17F1h60aqkVFPV3RLBvaukUKwWK6RBvN5PIW+69dQmiFkILpnTOyIqM37OFmS1SMVBdLdm7sszqeYduOxcVmlVEKrAtkRnN694L5fc+1r2za+RyqmGcPpkn3Io29aY9iUKaV3NbRrRuadcPBa5e5/e33EUJQbA1Yns1RmWF3ays5ccDsZEqzbqhna4a7Yw4+f22zcJZqpKItwM1olzUBuPLl1zi/d8r86AKMJDqbrj/uJ/w+cH50jvWO8c4EQmS5WBGcow6BMipcTPUKWZlTjHo00zV63VCMSm5/872k72IUW3sTxvtjRle2WE1XzI4uiCQNHtt0mCzD+eRw6p4hKh7SkSMl9nyNazNUmUSixIPuEk9OKg+elfRfeMgK5pxDImiaLkH+BLSNpX9zL/V/iBy+fT8V28u0LuesJ1iHNoq27SjK5Gzf/u5tskwz3OqzmleU/ZL9Vw+YHU5ZzpasLxbkhSbLFL3xhNnZAp0bmqajbVqG+0mg02pLMSqwbZvqFYSgWddky7Siq4xk69oOzhdEYOuVPc5vnyZxUOvpD3sPRUxXixTcD3ZGNKsWk2esZmt2hUAXWVqxTCRlaCWTPs8Gqhd8QMmNexgjUipC9LjO4jefp6ySRMiUxUBKhE6ZheAcTbURuVUJoqVkcjyEUnQ2aSoF55E+kG+yICJLNUqhcUQhIYqU7bWOqFKwp3KDA4TzqEGZCBPWTcoIhfjICQkBETbiiibBaOO6TZ8ZRWgs0YYUmGQ6sa2VOdL6xHQXAmoTrAgh8CEADnc2J27ESYUU+BhRvRztQ4L0dBapU/bMdw4ihA1DnVQRIRLtOVIgAojNtURuCNUqBZgRfKExGwitubqNO1kgrMc6hypyQtMREEiTCq9FDImcIQaESP0erAPvCa1PZBFFhujliM4TOwtFnoK3/oCwStThomkRuU5wRh+IwaP7GXbdQUjkG70yZ1VbXIwURc7u/jbL+YrgAu10Re1TpleVGZmLDK/sEdqOs4tFela1gShQQqQMaZnEcK0QTA52kCGybyXrWUWIkWbV0duVxCjxAXxIRCfDqzvYiwURKPoZJh8hmwiDBM9lO4dJj3zSI4oMd9SlxQrvCUE+Ni48Gfk83xHnwQ6bweWx3x9fu386IHrB6UQERdLKqo6nXOgZOiuwztF5R66SkLKWClVo2hgJjaWVjihAZxn5qI9oPB7L6mJNjWN664RoNwydWnL2vXuMr+0yvL7LUxHBY/fwYnvkDoiHA258rD/iS8aCL14lfbpJz4e6PcojPQmkezgNxBeEDo9v+AGwpBeFZS868vFtL5QxeirwflEfimf89OIGfPSQ9FP71P642Q8lU/TEJPKy9vQk8pGvnAbzxwcNIVYQBNXx+4Sg8SHS1Q361RFSSbpxzdF0ztmtY/JhyWBvzPizO2yjcLctp+8e0awaRIycvHvE9O5ZwuX7SGMtba4BgTGKfoh0VQtElFZEUi10FIJer2TVtJhMQwhUU1iejBKzWdUA62fd1HPvNJ0cml5N8WpBca5Y3FtQ6pyjN+/x2tfeYHg0YnWxoGs69j97ldvffp9m3aCNYnRpmxs/+irlKMGrfOcS9KVqyAY9YojMVw5fjBi+ep3Y5eTzQ1672kOQsbxYMrszZ33vDsFfxZQZ1idKaKE1vWGJ0opqVSGV3mTaWsZ9jdYRSUdDxlJEEJGxUgz2JrSLiiignq+ZHk030CTNYGtIf9ijmVepsH4A3jmiEFSnc66+fhV//5zhWY3QijIbcl7so7WmcS1XuxQ4VDFyEcKTK7vAKgTuek+wHucc7aohL1NwEUj6QqvDKTuvHaSMQd1xducUQURJlQJj54kxEXqEENjan5D3cu68dS8xAYZInhuqxYp6OUJnOunkDArmq45iUDI/mqGMIoZIMSw4eOMK5bhPJFIfz1jn5zSzJdmwRJU5F/fPyWVO7tL3GGKL9VMAemPB3o/s4K1jfmI4v3OKjJHVQjLa32fr6g6Hb95LgY0PRKmolzXDvRGFdsQ8MbYZLYghIpQgZul5F+nxSwH9JiCOIgVJMYJzKTCQJJpypTJi09HFmFjLmi5B34ymJwXekwIn58gBlxuyrI+vakCitE41RZki0wKkTLU3mUYVJgUZmUYbg1hWSeh0uoQYkaMekUTwEK2HIkNt9RM7nnUIKYmdTxC/1uJjxEEKEqRIArSdpYMNnFOgtEwQRO+Rwx7hbEHY1D5JmaBqMWw8HSWIVXq/Hiw4CCmhtQkKpyQyPoIWhRAQIX0fYVWjhzl6UOBma6RMsL7oHK1R5L2cWFuyK1vU6wbZ2vQeEskRiRUvJOf3Adwt+oAc9xCrBqkVft3AMFG8C8SD1YOUseoXULXEuk6ZsTLHR3DLCkJEupCovr0ntIkqPCiFyA3tYk2fJIiMUTjrqOerVOujJUXnkRsyCXv/nLJNAaNdnrCoKjzg6x1CVtDLDdIolPVorTF5jhAVW3sTRgcSIeYo1VHuFuio0Tpwd12j8kliF3+vxfQyzLrlspLJs2zB3wsgBPVUcG4L6OBsnWCQUsrnrvJvlzDaiMnHEPHWpUUhq6nsi4KeZzugAjiQKtX9IGjMiCgEpZSc9XvI1nJsl5TDglVjyZSibj1O+QTzlkkTLjaW3Ggqa1GZptfLUSJigbmMBOuwhaFd1+lZyAyicxR5ztFb9whKMr62gy5HZJP9D7TTrmdE1z3zHp683cdqeh57tp937z/ok0/O4qMFsoefPLqqeHLXj+ySPPO4l4n1ntOuJz99cTj48hYfO9un9ql9ah8/KHoc+/oHbptX+8GSS/LQ0PIdYtVi/PvE8HlELMnHBfMvXxC/5vn93/0vLJoZ3XZSlVcLRdYatvrb/InyT3Pza28wvXvG+a2TVHzcOYQAXeR4I7m1m/RpttEUh0t6wx7eepqqIY+BICT9rRFaK2prIULXdJy/e5k3/89LCCGYHVtgumn/k7fzotsNInJ8/R75OGMhpojDDMiplhWzO2dcfuMad771PtWqwt52jHfH2KpFxMji3jmzu2fowpAPS4SWjHbH5P2Crmo4ffM+3zs+5XB/i/F6ix+5Jvia+D5uaqlmKwb7Y/gMfGc25vcXa/z5jLBZDScEFhfLFGz55JD1+wW1c1xRFbtFwAnBO+2Q+kev47aH5G+fsrp7RtEv8M6TD0qGkwGrxZr1bJ1ooGPk/N4pWZ5RZKmA2+QmFdn3MvRkyLX3G6LwcGObX3/lJwlCsnVyh79o14gYecs5/j/1B1n/3vKOd+oE//mMc+z1C1rrUErhCZggGB4vOHj7lNHemKbqCCE5/hroj3qcn8xSkBMjWikuTmZsXdpKtMchUM8sVhuyXsnyYkm7qjG5oas7mrrFZBlCCNp1g+qXrM9XzI+mHFzfIxv2mM/PWG9VlDtDdG4AQW/cZ18N2Pm9BcEHTG4J7n7KRkiR6I1zw81SE14PuNZyO15ltX3AyTuH+C7VydStxQuHtwlOeNBfE0dzdBHx0SZYaZmjIkQpcBsnMDqPUCoRByAeQszCps5Hab2BfnUI68ikwIWIyBR5WWDbDpRCOU/KtaRifRGArkukDCKmQFFLIoKAQGmFDhHvAiGkonkpBL7rUibPOqJS6TyNBSnTs6lSvUlzZMm2BuA8ISbtIZEbhPUokUSbfYzICM46QmeRSqbn0KgUUGlFNAq/qmHVpJV5ozbw1LDJfEmoUxATc52geUVGMAq78kjrkSZpBcUQkrMWAhQbSvMYcfMKc3Unfa41IoIIEddZnFaEszl5jLSdxShFhqBrXQpOYANfTN8LccNuJxPJhhKSmBnkoGR565giMyiV9MWyYT8J0ZYRdzYjiIA52MEuKmSepazZhtRla2+L4Dz1uqZbN/TGfYbbI6pNXSE2Mtoaofe2qaYL1m1HFzwqSJo7J9xcWbJZhWs7DnbOMHtLfBAcuANCLOiWLZ1taNoEz23zjN1Lu1z68lV6/e8gpEWUkqs/uo9XAruy/L//91v4NkEV/X+dI4Tg+hj+n18MKBPxx4HqP9WA4C1r+Tf1g+yxAsKD2PCZM81Xr8BPXkvTjW/thlFR8C/flXzvQj13enqeZQL+QlkyFAInM97f/irT+wtsF/jXMVK3FrF9leBDoipXCi0lTdPiQyArUraxtZai18O3DXQROejhI1woON4uyEQaR7PcbEhXHN2yoRYdSivsbA1Xdxhe/xLDa1/8AATw7Fu/Rjs7ev6NPNVpQvCDEi0/JHtGVU18fOszEX4v3P4HbY/iyk8qlPnDeJef2qf2B2c/FPjcR7aXXD15KYup3FNsXvp6tsJ0LT0laW2kWtVUy+Qkr87ntN5jMk1ZFklrpLOcHZ7z1pvfZf/KJfZfu8TW1R2aRU27rLGdxa5bquAhBPLgCDHpxAwPJkxvn9DUHb3gaNHMpovUkpAU4GWmKSf91M741KTxYccpkdZ7xtd2UFuC5tzRK3Luv32Pa1Jw/Ys3WJ4tmB9PqZapxklqRZ4Zlqs1XdeB9eRKcXG6pLU2QbU6R2YMIgrWpwtmqxVLc0y+1Ud2jqNvvU9/3Kd36YCbr38mUX8fT5neOUNplepsfHK4pZYsZstUZO89bedQxkCI0HlsY9m9tgv3p3SrhqzIaZYVymgGoz5KSXr9ktA5Sm0SGQMJcjU82GJwYw8bLbe/8Q6j6RIdJNlozWq8xlrPaFMULZ6eKJ8KQMNjH0spkQ9op0PAk2Byi+Mpo90R3nkyY8iLnK5zzM6XlGWemL5EEjCcHEyYn8yQSlG4jkyQmMOAtkr0zlkvp60tSmuEkhSDAtF12LZLdR8+cHr7lOH2kPLmhLZ6F9PPk55Mv8T0csLSMT+a0tUtu1d2QMnknMeIyVRaSY4KKQVd3RK05/bvv4+tO3oa2hAo+wW7r19i68rOY49hJHpP1KnnurolizHpThmdHEEf8DFRUiul8M6nzMtG9HPQzxGNoIkJ5hasS4FPnmrMQrsJHDbfpxCb2p06ZXWiEPjWgUjnjxt4mBCRYBSSmHR3iiy9XxsmPi1lqv/ZUGY775I4KQLZy1PdYNUS5mvM/oSoFLG1hLSWkl7KmIIDHyKmXyQYoA8IJDLLUkbHGNxisWEyTNAt1ctTdmVDX431BARxVSMHRWK0sw6sS9dynkhEhtQHQSY4nlQyZYzqLpFb5IbYpexolBKtBB0RtW6QUpEbjQgQO4fJTMp4WZuY05RE+YgMAYoS0Xbpu3MeKRXxZEHWK4mb4AzncOsaJYpEBDHuE5oG31n0JoCEiHACb12ir3cu0XWLxHBnuw7dy+nma3b3t8mH5QMdbfSGsc+7lFlTIQkjb22PQEI+6lHuTmjtZUIc4ttUZ+V9Cj6yYZmypSaRmYgHUAORMFpxk7FEyUREsdFuQkS6qiFai4xDog1J2ymm4ejhkCDlJqMnnolXEgLqao2tWnp5kQh5YkBE8yEG7wdjUCSxpKb3zi9rTk/usF57Whtor40IGybBurO03uEWFqElrrMEwASTmOWEoO0sclMH06wb5nOPl0Dn6U1GzBYrlFFgYxrnCoMTkMfEqLm4fUpXdwQi/a0h5c4w1bU9zlT32Lj5rL55KOLzABb2QnzY8077/At9GP2np+t2XmZ+/aGECi+Axm2+rue2RTzdqI/sdz3Zp58SMnxqn9oj+6PHPvcD7BEl4aPRI4Qhq5M5WXaJni+onWR6/wLxPc/WF/YYrMfEdc3u1phRNkpMUSUE6yiznOndVENT9gvKcR9lNAJBMeoxkBC7Cqc1y1VHO+kxyyT3z+YY72hVhlIKNsXkzienrQAulhXu0gShxEPhvYf2Icep4AO6yCgGGjtd0XaWrMy5//b9pBg/KBhtj5P2zirB00QIlEWOD+HhXJVtnC1CIJOCPpEdF1OfCMEFI+y5ICt2iFvbnDYd66XAjzr6oz5KK1zdMRz2QQiObx8TrWMYBcJ6vLXMZcD6NAEPbGDXBGRj6YY52z/9BaZ3znB3z1FeMhz0MEaR9wryMuf+0QVda8m1pqmSiGumFOMmsl43vHrpCvpoiZ3WtCcwPX2HvVcO2Lm6zbrZTfh8WfFqZ5/oO9d0mH7x8LNto5nfnSGlwPmA957caHyM9Cd9gBRQlDmdD/RyTd20ZJlicTanrTsEMD+dIRBoJWnJ6KR4KJgZQ+Tg2g7L2Zrx7ojzwwvWyzVaK0oJNSTHdgMR9ELQk4obgxFu5fASuiLgW8vFouN0JMmubnM6KvAhkvUzTJdhqozl+YKia9keKYpBgQwKqQVFkSGcxSNQCOIgct6dI7rINeXpM8Z3zUOiBNE5mrggCI8IqSZF+UDdeMbFDkST3o8IuZQ4pbDWPxS3fCj+iaCzDpY1eWZSFmeTdSAGvJC0KomMqtwQdIKRmVGqXaNzkCWWRbGhHqax2A1hg9kQPiATLFQPe2gfaFuX6NibDqEESkiklNijKWpriCgMWkp8a5EdSV8pgmgteljiTheJVW5nSFL/dPi2g41Oz2qcg/MY4Sllqmd84BtKkr/uqg4zSpTqxOSURpFqRoKIKfvkPApBLvsYmSd4XdDIfp760gckAaJAFwYfw8NshYok/aVMYY+mSSi16Qi5QW28wug2tSRSPKKVjgItk+MrvMdaT1bkiWFPCLLtMfXbS8KqIjoQuST4iBTpOO8DSqd9Y2PJc0PYeMRKSpp1Q7OsaNsO6xx5njMqEsGHEIJgLZlJCx7LypP1RqzerJiev4MLBW3dkhcZW1d2GV7exrYd2ahH8JF6naNNztFbx9yeHZNt9ciygt6lHgDae3bbGiki45HmdLxFt6zIG085XVGM+88OfKRknAUOhun5P6/g/GGSWSCFSn6/dSBkWnSR4rFalA8xhgvJyXCXldKcHB5yXFV4ZWhlQEZo6paoJa5uEzGHkklDa/NsPfCcpUhyCoaUIRRKYjf6X/1+j9ZahFF0q5ooBdu7E3Smqedr8l7Oar7GLyqMVgTraGYV4fYJw0mf4cEWk2KbOEg3JsWClNuFs8rhwgaO9aCW6PG+fNjG562kflB353kT4csGRPFhIPboVM8jmvthWQFcVilz6GVGk40AgZWCtYwE6yFCtVjTm/QppUJXHTrTuNJi8wRV7JYddmUfO/PLQkoetyf7/lPo3Kf2qT1pnwB87sE/P8QU7Ic49eMteTDAWneTrhli25r+oM9YdDQzh/lvJVvVDn9C/RTvv/8u+q7m0qUdok8wnovZkraxDIe9JDK4bqhXifUtyw0RwSqTZPt9qjoVH598do9ZIZjnks+FVI9Q1Q1FUeBjQEmJIq0ef+/wDD82HLxxlUX+HKaFl+ygB4O/J2J9QCmFylMmxltHNa+olzVaSax1xNaytTNOJBKLNU3TYXoFnUuTe90msU9tA5erFb0sY9plfOfgT5IPShbnC6plRSQyqAf0T+bJGfCB0f6E2Z0zxvsTtq/ucnHvlOtW0l952tbxTsy4ZyU9l/HnlOFS1WGU4v+r1sQbe5i9m9zYHbO6dUJ1vmC9dPSHPVYXS7RSOOnpvE/1KFqSBXjlbkWIgaB2WX72p7nze+9THVXcUGu2xRTjJLcnn0fnGYP2lJ/1Veq3EJnfP4fOM97eevj0XEjFN2JEaslw0qccJo2k3qTH1tVdIEG8bIg0VUss0vPgXFp5h5jEcqV8WF+TFRlCSYIPeBfQkg0RSBId7Q1KVrM11qUsmNGCojDUVarTMlKiThbctGt807HMBfcnJeSG6TZ883+5jABkpmnXDcJE+ncL8u+VLC8iV+KCr35GkxUZ0iqC84TOYaXEes/lm1e53d3h8PweArh20eOg7hMXGn0p4nKPI3A+/31aXRMQKVvjA0LljLKfQkSZ2iDAdV0K1rOUUdAx4qREkmi5+6NhIrVwqSYibBw4EyG2Duk8XiZq7WxYIrb6uHmVMkaAcEnI1Hmf6vc6m2CUGwpsaTTBWnS/TIKrjcUIyCJ0MeKkIMaQtL18aoNYWmIQOEESeL1YP8xQhKYjbqjG/GwNO0O8kIi6RWhNR+DW5ZRV6a8cN2+tiFKmjEPcUGNvsojeJx0dFUDETWZNilT3FEIKRDrLpH+VSX6doBQX69t0/YJuViGzDR228xitcXUFncNrRRCCclTS3r8guECsWqwSiNamDAopSOkECX4YQHiLGvSIUiFWNcH7FEA1Fuc8vrWoIsPsjDHbI7rTRaLPjhENZAhm6zVFr8T7VIszX64SFXuT4LRV2z6s0ZnsblGMeujcEOo2EVMcLfDek5UGnX+e+7cdddOgtSbPddKvQnB+/4z7799HKMUbf+pLDPcniOzLvP/bb3P3Iuc43sMfnpJrxc0ffZ3R9T0mXcP/evw+ish5r+T/3LlGQLB7WPET9xeJ2MK7D8whCPjcTuTPvZ6esf9wC/79+49qZpSQFHmODBsx4xAQ6jl4ux9gTil+65WvIE3JyfQdmvmaxnqiUKi6SeO7TxlAoxWrtkUqhZQJsqwynQJ076lby3DYT9+zSzVYVVWjhNiMT9DPczqSqK+tKoiR5bpGKEk+LMFHfJAUuWZ+vmB9sWR1uuBPHVxn/8obQCRT30TKBR74tXdmzNtn6Da90JJb/vww6Xm03S9nD+ixH7y3/90twpZS/F/LHirCOtvm3u6fIEY4nC/4vcWCxXzNsN+jCzUmDti3koPWwsoRvhppfiRF4ae/d8b0exuI/Ut0wAOf4Mn+e/LATwOiT+1Te9I+wUzRk4HRC8OkFy1wfNz08MbJfAhJgFTf01iUkPjFiqws2Nvb4vjkgjvfvsX1H7mZdDYulqzXNTpGVNdQrzv2Lu/irMM3Hf1hn2LUI4RA11iadRLc7JwjywxbB1v0tgaEEFBGEdaWGEFrzXgyIJ/0iTFSTVecnUwRfc3J+8cMdkYfO6RURiO8IB/36NyUSa8gNJbgQ6LMNor5xRLbdpSDktH2iHLcp56tUIs1tfMsm5aD0YDzqk4rpFsjkILVxYLWOoQwTE+mjIVgMOrj6o6qs8ynS+qqZVtA11jyYcnklT2kUoy3BjjnWH/vkKGUqA0EKgiSqKmIhOjxqwbnHLN4ymBrgNKKq5+9Bp+N1IuKk9snLI+mbO9tkTctbdXSNA07r19JzuFmtTQISbuoUZlJK9RKMj26wHUOGzzjy9tcGzuIkWa6ROeGrMhQ/Y0M52O8qJNre4wv7zDaHW30I9hMMqnG5OzWCXlZ0LUO5wJZlhFiRG8opQG61tIf9lBGsX1lh2ZV4xqL2dLkuaGtO1aLikgKtA9u7BE6y3rdUFcti+mSsl/Q3xsjOpcILHZHnL1zn7q22GWffH8Lt3FeY+fIlEQIQVZkrKZL7EViHDu4eRnBKTEk6vSmzSm1xobAzrVdtq7vcfvsDg8cFe8cd79zi+3dLYZawgYK5mMkdg4hIrJX4KRAuQABlHM4B0EInJBIncglknYPJH4EhdxkT8VGRycgcEqShRRk4dO9iEzh24ioWmS+qSlqbNI7ihFZ5hgh8TFAbohVCz5s2AE7ZGbwrUUQE2tdCESZxC+xniA3GRqlkt7PgwBgMsBPV8SmQ+oEQ/TzKgVKMT0//mJFGJXEACZTyJiyTl4mUeBE7+2gzMEl/aEYE2zuQe1REOB8qpJ6AJ+KeYbc6Gt5sXkmfcCeLxG7muBSTaMIEYTEtpagNTok8WGkSCQIbZcYAjeosgTFi4mKPAayXmqXkRvEGRIlUtujDwnaKGIKluySdl2R9Qqi85idIc10DYMCXwtyrRhvjai7jrIsyPsFq/kKGaHXL7g4naZ6L+sZbY8oekWiMm8tMUTsqiEIQW9YYjKTxuoY6RfD9DuCrWEPrRWHt44Yb41Yzte0i4rhwYR6tubs+IJ+z7A3GLB2FYu2ZX08ZXRtN7EoapWeg8fgcDJLrIOP29NjsZSC0HYovYHfPbajENDOVxT9HlLGFNh+EKzwaEn+hQN9Cg58a5OGF9DrFdgYqK1FivRed52jKHJ0Z2nbjvVyTZFnBG0S/Nd5XAi01jGaDJlPF/R6OXmW0dUteT9l3aquIxuUzM5nuM4lwp2YFta61uLWLSHpZDMa9llXDSY3NOcrzm6fY3oZezc3sLRn3NcH3O9nBibiA/8+ufV5TsBLh0U8yEDF+MGv5AP2SadOHkwnm4vV795itrpMcJGL2Qq530dpTdV25FlGNa+Yd4FdL6mXNWIhn5yXntnOp/F3j2XHPk0FfWqf2oeyHxp87r//usxm7e6pCwvA1R0K6Hyg7JUsmg4jHKNBj9lixel7R4wPJsxO5zRVw6pq2J8M0NpTDkpO754CUK1rFvMVw60B40tb7BZ7zBW8e3GB7RyroynycMb2tV2GN/aZuxO6tsNkmtlqSeY6DnbGjPfHzKfLtFLvoJ2vKYbblHuvJCjX+gLfvjwTnWvHqKZPdb6m5yTaaPI8gxA5W89YLpcUXywZvTFEBkl8y+HqDjfuc6eqaAtF2R8x9JHGOsrMUDcdF2ezTRAjyTNDZwP9VUdYH9OMevS3B5TOs6oaqqrh+NYxPkT0hWZ8MKGzDqkE+5+5wn5Wkt29IJzM2BKK0HSoaFkMHUWuCHQYJ8lma5RsWFuwIZINSuzukNHe6zTvHnHx1iFbkwF2ueTSoOVSv8ZXC+7GhhAD7aKFswlCSPZvHDC9f04IML9YglbMvvUe3URhdjPWs1RzcfVzr+G1YmpXLJo5AMt2xqrIIROs16uHfb1VKPqZwncV0a5xlGkF1wZQiTo5GEXWy/GtJXhJU7WM90ZoKVmcLcjLjH5/wMnd00R6AZjcYJuO9aJCdI6yzNjem+BjyrTE1tGGwNntU0Y3dvEqcH7nHn4APdmnz4DYQDev8J2HcYJrmm1Jc7Bm58Y+del4+25AOoe93mdydYBA0JMClWecNEfULhWdP1hh3Lm8i8wMetLHNalGaJjt4rNtIGkJlTGg8wylDaHtsEJiScX8QgrIM9SmlkhojQJkDNBaYoy00lM3Z1ghyNouvcox0tkpomsQAhoJjW2RuyXmxFOuWnyMULcpyyIg2x+noK2xlHqMViWiU6AlshOoXs6yO6dpViitUWWGrDtE0yWnI9PIMgW2SEFsHIPyMiKKVAfmAlIrXN9ynM1onaUYG/qHDX7WIkrFaGmJIVA2if1NCkHcwOTo5dB0qdbDBbwUyM21Qowk2d5IYXOM3E5BSXQs7DHRe2wzI4z1JqgBQkSoVL+TZYkiW6pEJhGWdYIYGoNUqb7GSZkEUtsONtpMSPGwTiooBTaxmKlBDwEEJYh1i/Qh1Vata2IEtT1EKZFor5Vja30PX2bMnGbeeqy1rOarDYNbgpQF7ynHA9aLNe2qQkQYTAZU8zXWOYQR1MHRQyFyRZf38ERUhK3dLbphwfJixWpUsAyena2O8YFFiFPur+8yH14w2u3RqYhBI5oGiozZ3TPK4YBpcxUJTDtYrJap7SufYJ1SMpSSz2nD08CvfROQWcA1lv2e4Uf2kpe504Ou7ViuVng9wDUalGDHSd7Q6vFp6SnHVFDl23iRpt+ZIul8aY1Asrx/wWq2ImpFY+2GydIjM5kY/pzj/HxGXhiiD+zubFGtK4SWSKlRLuOSA9V45MmCfRGRtWPRWVY61apppbDW4ZZretoQNxBJ23REATHaDfw11Syt646YK7rOcm+2QtctpjLUY4XWPbLtAXpnRM+mrFV7cZ+wybw97Ij4A3z7j2kfBIb98E0JOBhkSAFeaOZ6J8HPH2+GlNzRhtBa7iF5/9YxJs9YGklrfaplJOm3FWWOi5b7zmKNwJ60HKwPUm2rWz47FnrsYg8ft4flW+LJrZEXsgB+ap/a/+j2sYOiD5EfevKgj7LtB500ghDxA00ILmnyDHZGXPrcVY7fvM/54TmZTquE1aJi75UDtFZ01qONZm0DSkiaVc14d8T0eEqZ52SZYTFdsV5UaK1QN3a58eWbnN85Q96bcuWihsMFze6Ai9d2ca1luVihVUHTWmYn53yxSKxqoq0TTv3OGTd+/DNsX36dGCKzN3+T6vidx6CJz7EIRIld3iD6CW5ZsTx9E+8Dh0dn9PKMUa/HxXrOcftNel1OT/S51r4OrcdnitUXrnL43n3GSPbXgfPFAgQMhwMika7psN6z3SsJbctnNgUSp27NfW9RSqOMot8vU+EugnpZUZ8t6Zzn/rJmtDfhxmjE7muX02r1vXOGTQcELgZrFpnCA/0Q2M1KYtPQSkFrJKGb89ayZnD1gMGfuEHvYsX6YonpKb56qaY//w6zEPjt9QobI7rWXDubMd7fZnY6J8szjIm0G9YtLQ1Lm/Of35cMtvfSavn4OiYzvDd7h2/PN6xK7W3g9ge6/E9eHjApcmTpcN4j1RWKXsF6vsYTk/ZJhGZRJXa0zCSnYrrGaM2Vm5do1jV3vn+HoszpDXrY1qYagRhZTldoKVmuaop5hXOOEBOVcq+XI/WA9epVzg4FmR1x+WKX0XvJgY4xEGrL6mDB/d57RO9pBw36ZwzNwZrffWfFme8QQcD0vQRNeVBj8sQ7EyEmcozt63tEBPnukPZ+S/SRnd7nEJlBaYVwPmHlpMRLgXcNKlN0m5oG4QJee4R1SVDUJ6gYQiKFByHp2nPuT/8bVmsym7IwcUPxLUgwtmVPcW8/Q6jI7qU+V99z6dpiAzcT0B1OkzhwppgUNxkV15Io7AOGzCCo69/ClBm+7nCLKsH8egVCCYQLqExvMgOW6AW74y+Sq4JAciakEFSm47e3v0EXLf0847XjpGGVrS3Xm8RGGJ1PJBkyyQNIrWHdIDJDDC7RVvukMSTCg5Xs5NQMs8vsDD6LCIHD+e9z3n4n9TEgTwtUP8cv6lQXKAQyM8RlRRQykSY8cH60guAJKtVA6hARSuJCTDVaszVmMkg03NYTpYdeQYwO6gQJVYMBIJJGVAeqzBFSEs7m6Rq9ki25pJgeYlvNLX2Vc/kqvm7pNvCuxXyJkJJyMqDzjhA9sYtsbU9SFr9twWiOcslkbxs7HtBVLYt1TRcDhda8Wy8xsaXtWtoCciX50qWGsv8u57fP+E6c4j8j8MM+quuIQpJrzcXtEzrncP3L/NbRjzC6vMu6aDm88+snDSuUAAEAAElEQVREAbnWRJODFFyWistlydMTiFEtwdbYdcPrvcAXvpg/HJeDL5nsbXO0yLloSxTwBZHz1Txt76oW23T0t5PQcgiBiOTu7o9QuYzl8YzfbNfEQcn42g6u8ly8d4wuc1rnEnQxRjKTqPudtcgARWYSecYGqqiETFIKecZEaW6sGzIlkCJlRkPtuC0CjAd0XQq0iiyjc5bluqIc9tLxUmGJZL2CQKTsFQghsG2HQBDXLRfDjK6niFLyzpFGiQE7co/+9W2KwhC94+S3/w2hXj5/7trYo4TGy5MmPN/SuPXEaZ7jjjzXU/lBGZaHA2XaaLTkxy8PyJSgUT1+f/xTeKkT/b1MMgbV6Zx/fuuY6CPrfg8zTm5XVJKuaTbZ600mPtccOcvxQFGMC0Ib0beuMNjq49sFxPupTuzpW3xeIu6JWxMv5V89/l08rvT0qX1q/yPYJ5cp+mFWLz59zufmvZ8+aANhqjuiEOx/9gqr0znn90/TCk2IhBgTqw7QG/ZYLdZIKcmKDK8ls/M5e9f2yPIMbx06MwwHJV2Xipqn986ZjzJ2b+7T2x5R/s5t6mVFV7fMTqZJO0JKEJAXGaptmJ3O2drfYlgOEG3FalVx9L07XPux19DFY8xFTw/wT9zuY/oCmx/yUY+9Vy8RpitmbcdiXaGVYlyWvFM1ZANN8Jain9O/MmbtA82yJWy0S2xnyXKD7Rz1uk4iqIDODFZAkSdBT+s9Mi9QSuKDxzUJ2lGvfaq9ABCS3AhChPndM+60ZxT7W2xd3mF1NMXbjYDlhiVKSEkrJaZLAYIHQuVxCNpasVxbtnfHfPZHXiEuG3o5mPP5w6H7wb/FsKRnB8xP5kTADFLAsqnfJ1MbkcyYMohd3XH01j0uf/baplsfK/Z9gLl4/Hna/C61ouxnVHOLD5E809iNQy+VBClo2o4sy1KfxMjZ0ZSrr1+mWlQoKWirFlFEpFF0bZcyHhvoS3/cp16nGrBoHbW1mGHBlc9cZ308Yzjs0795GaUkMtfIXNMtatbzNfYgku8MaVc14+u76CJLGYQNFOvBJPoArvPkO/QgFEnsYW1dkw97CCnpX9nGdsd4pZEPgpyYWPqCFLRNRzQaESOFlEkUVKUaGpQkE4Lw4Pn4/7P3X0+WJfmdJ/ZxddTVITJSl2yFbmAgieEuzXa5S5rR+Mfwj+Eb/xE+7NL4tja7M8Rg0INuoLurukSq0HHVka744CciM6uyCt1Ac2yXSDeryoi498a94ee4+098BekaCyHQSqEyMwoSSBhs6tSMcmBCy2Q8GhMHLDYDojCIJhBCTBLbt10pH4llUvFTOqnO3SUcISAGhx/qtCZ9UoQTuwYWk+SrtO/QRzO6VzfIwiQBAARBSYxRhN7hbmXKgFB3iVM1KsIRk+CCyjRqcHfeQHfdJ+uQ42vVuP+omLo9UcikDEdKvlyIaQ323MEW2bewmibooTFjcuWJvSPGAEqC1qn7ROIOSSmTj1RMsE+Z6SQ7HgNxWxOEIGYGZS0iBuK8hEYhlSDUPWJaoIxCzipEnmOBcjXFnq2T1LpRqDxxnEymMTonCqikwGhFMSmxI5+SziOjwFrHer0DRi7OKJARrGdoepptTZTpeocQiEIw9AMuBA6PD5gflLB/wcU/POP87JL9A4XINX7tKTJDpgXLxYy66Ris4+z8muy3L1lc7Jj/8XFyJH5jLYchqRsKlZQPvUuGvMF5ZO/AJtn5ftcipMCUyaDI9Zarq2usrpDA1c01pSuZVKv0u0fRDsbCRuJUCW6+eMXV2YDOM7zxhAiXv3rB8vER5bSk64ekIKiSKfLQOyRJ3XA2m1APQ9rHpKStG7LMUEiJRJDHyLTIU4KvJK7pCSFSqPRZYgwpMbrzaht5Rj6wD5bZao4SAlnkWOswRmObIW0L4/1mcoMRkn4YhR06y+UvnnH0s6eI74gq/qnQ4PsC8MSP+UYyEONbXY+3g35xd0Z+1+d4KzG6i1/eyIri+P03EqE3P+vdL4jp3nVNT13vUVnaB9uXN3TtQLOu05kGyFzg2gEfAqpIJsUQkSR473wxZVs3dCGdx/W2ppwU319vjm9mc7cf/Z8XjL1PgN6Pf83jX5wUfXudjgvqXcYEv48e5u/+hndvJ954/EOtmI5qQMvZDH08JwyOZ7/4in6wxDEgNEazPFoSfRjx94kE3uwaTJmzLRTb3Z5yljPZdjjvcb1nNpswDI7cO+Jnp9TPr5kezDn5wQPqyx2DHYgkud2F0ph9hzGaKckjYnu9ZfLJCYUK2Lpls37G/Lzh3o8eIXXH9x4h8TUUIRJoL79G7i6TV86h4KM/rXj1mzVnrwTWWoqqIPbHdLuSarZif7Lk6rqhHyy6aTnxDgZP76GaVkn9apShtt2AtY66Hyi0IoaAEoJZgIAiWMtOSmotWMwneB/oB0vb92TGYIoEC3OdRWcGqSWLeyuGfYcXsAk5rg3JbNVYah/IcBTG4Enwoqy4wsxK8pnjMgjMsURUGWqf5Jnvbi8EQSvUHz9l/fOvqIyh33VJ3KB3zCYVUUm2my3TSUW1mNB1A7buOf31cw6fSP7EZG/cZqli1ucCaxIsqYgppBdSsnp0yPpiT5FnTOYT1us9ZuQydXWLyXOIkazMUzI5pEQw+GSQOVmU5Jlhc7MjIm6bARS5Ic8NRx+f4Jue089fUEjNg48f0O9TolTNp9yc3SACFJOCy+s1EsFkOaN91rJ6cg+lFbvNlpuz6/R33PS/xwITfBU8OyWQ1mIuv0bkE4a84dh7fLtDB0GVnRAbsN5TVRUqzwnB460nFBnCp8BWG42NlufyFCTIwVPuhxS0uT3O+ZS1Wo8oDDQ92kyZ6MNk3msUplEIBGbY4OszzKQguABjMlqoJYWZI4QkSMu6+TrdV3FBbiqQgml+ggkTQozU+owQElzP71uUVnijkH1KHJz3vCgviVKjheHJcJggiV7wpD4kEKDvyGYhJQ9vBGHKaZbTx0SflOJQEnxkoKELNwlWdisT7ZJkdorTI13csW6/JviACpJF+UGyDrCXuJBgcUIlmfUgJdkkT6au4tbDCaKPdwlw9P4u+VJGM4RAHiNy5H7FMkP0Lr2u7dCZxhfJWyo0PWpaoJdTQm4QzjOcb2A1Q2SJmySkRk1KqFtyISmqnCEGhq6nKAq6fUu5mtJc75gvppipYn2dihark0Ns27Pb1UQlabqeruvZNx3ltIQQUDcNE5ksBJ5ZS9t2uOcNz087Ztmc4BWLm4iTJGhYnmO9p1OO3bIhzzSayPbghkbtGPxwd6/LmcT8kcHtEidPKonQGrEbiNc9spLsFobN6hBCZC56YmjQJznxHPoLR3+pYSLARAqVcXH1NQ+OJFobro4mrFcz1gcF0/0SZRW2GbiwkQsFUgaClPTBY5Rm++IKZTTOOWwITIqcvrEYJRFKoyOvPYqc4yOpKLXGmMA+XKIAbSTZyZIIWGeJBQilqIaBJ6Wnc45ehYSqCJHaS3bWoaMAJRj2bRLq8YGubumEoNAal8kk2S4E/a4FqYhGIo1hf7Oj2j0n/KcXPPijJ5QzSShyQoQX29Fa4HvGNwPxdzdqbguBY9lKfI9Aw1hoIEI+P0ZPFt+53UUfkgmzVok/GAJ+cAglk70CvK6JjUUO3w3Ul1uiNOxeaNqLDbt6R1P8IzZAKDL2k4y27VmerJB7nWCtQIiBPDPjWg9oo5NlQG/xKtB1iV+rc8O2bpj6FbvrLcX0kMmDH4CAYXOObbbfmptvTAJ3xb1/5nifIL0f/9rGH65TdLsDfV+/Gr778X/x27+uDEngz7OMD5Rmc7bmVeGpg8cPlkAky5JMtnMOKRRd3dHsGvbbOslTK8ViUrAPnqt7UzpgiuDDTWSxnLG52hBikvvNh8APeoFvO+xFzbPccPDokIPHRzycGtavrpGnG55se0yesThectM52qbj6vQKmwuQAp1fEsUpumqR5g3YwZvT9WYV7LagHyPbr/9zgoYpgfp4yeSBpJiCtzOubzqyoDDux2zOPWKYsc07Wt9j+p4fbloyJJumhUk1SpqnqrrJM/IixzY9282O2gdmZU4gMus9VZ0+56tK449nlKtZIphvGpT32MGinOLgyTFP85JSG2zTJ/6M90xmE77WBadti5GST2cOpePokWLJlcZ6i8y/IARHeyV4frzg4IePcF4Qfhv4pkWiVYKrpyvqYLn67TmfhnAna91Yi7ACKSTWeW4uN2it0SZ56zxRhr/Ikyy3HyxSKfaXG/oPFzT3ynFeXh/D+awinziijzjr0JmmmJZE55JHi3WUkyL5qoSIHj1mgnUURcZsOaWrU7Lc95aoJHmRcfzpA4pZydD0nH32HJMZpvdW3FyuefWb55wcHzA/WVHOJ8kHSmvuP72PLjPc4Ki/qpn/YsXkYEZ903J2cfF7HIyve29/e8sJ8Bbx1c+BhOL6b5/OMbEhrDsehwUmFnipiP2Az0zqdvgAAlSMhCiIUdDGhr9dfI7zlio6PtjuQQiMT348t4ZdsbNEISnEnPvTn40VT8EndeqYXA1fcCHOcbsOtLqr6C7KRyzLD5FC8HL/c3bxlFh7Hs//glzPgcjB7FNECFgCzzc1nU8wMCmAzhKswyPQqwl9t+Xnky8YlKAUBSeXc4w0FE7zZ7uPAHBux9fhEgqDaNP+EiNkxYwH5U+JOnVBhEvdgG33nNP2kqBESlpE8n8SIRBjksPfNS/Yi5egJPfLn/Ag/1G6p8Qv2AyvGOoOJcSd+txdFf22uO09RDGq3qXPIyKQa9wuwTpxydi2d6kDl1kHRhO9xe9aQmZQauxyu4BrOqTLEWWOCIH980uM95jFhGgk0UvkvGLYtQRjQUGWGbo2qXUOTU/wgfXVBqWTSptWivX5NT5GbPTkQnL46IgQIvblBX03kBvDT2cLhlfXRGnZ3KuoR9+ounnIvFxSZAM/qgec8zRt8oaaLabc9Ne0y+SPtLnacProeerULC1xmyZLHkqK/1MOIRVvgo+YwiDPBMPfbgnO87me8h/9Amk0f/Y48uNFi8s14VwQzhWLRrE2Go+jzDKOP5nh1NdYafj14x/xSpRURzOefvUx6qXg+a9+w9mHU24KT2dt4lO5gPMDwWgQgmEUAdns9mipMJlhsA4hFV3Xk2WGZYD/Y5kx04Zdd87L+udoCV25pJv/gNZ7ap9gwyEEfBZZKYXOBYRA6xzOOV7KCdcNo0myom47sjLHNIFMaXoRiaWhKPPUoZSSkBv8iIBwvWU6zfiZv8B++ZyH01eUx3OQUwYfOd/bN6S63yg4vbEnfVOMO0UTr2FctwXP+OaT3vjyLR+i2ybO+G958iGThz8CIv2mwXcWPXqa+Wbg8utzbDeQT0uOP77P9nTN9vIanSdT8+WT42Sw/tU5wXkm8wl1uyXIJa1TnH/V47oKfGS+2VNNK4au40qBCwHbWQQCSxgtHjwyCMqyYGgbul2bPBKrkqZtiSH9HXYUiAmD5WpT8/Djhyx/8BQkrH/z77+RFH17vFnYez/ej/fjdxt/gKTo263ld3379nP/BeM7wcDpwTdrR946rn/9kq+ef85ezQgxUJQFQzcwm1ZY58aqfWRoe4iRSZ4lHkqm0TYyIJC5xraOGCP79Z6DkwOkELRNh1YV7a5ObfFRbvnii1PWFzdcPpxz+PCQykHcXjD0luvTa2bLKX1vkwQwGut9MsT0nuh/B0nT752DdEDks5LH/+Zj4t+94KZuYJlR5Bl10yK6DhUjziXVtBgDk6okeE+9rYmkQ1QIeQcHyzJDBNrBkeUGZx2DtUm5zSTPle3pNRJBNwwEKe74MvvzDef9DQdP7ycCqBTk04Ihevq2H3kXAukDRoOLSfDhdjsXJCiXj5H+eo/dtcS8wF7vMJPqW3MjhODwyT1On13Rtj1GO4Qc4VQxHbZt3VCVReLsEMlUmRS9hCD6QHu9Q2XmNayGsRs5nrrBeYgRYxTZJGN3vaOYVqmz1vUpmRxs6g4JgTGa2cEMlGQYpZGvT29GDghkRca9D+5xS9Fdv7ji6tkZwsPywyOiEDz7hy+RytB1A/1Zem27ayiLnMlyytEn9xE6dQdvzm6oVtM3bgq+vSa/tXS/E6s5Fh3HAEVJJscLWC4wuwqxE8iuxyqFCgGtJNnIXYmjZDNCEG1SXhOZTMlMSJCqMEJ3YqaJI4SQGJFZ8hGKo1pYiDHRlxAjbEuPsKbkrSOlTNydmEQm4uDwgPfpHo8hAQajSjAjkRtiK+6k5KMU4EIShBhc+rmUCAnCx2SAiyZIkcQXRvjOcL1HLUvoLEqKBHPzIUHmXDKfjeNcCJGgeJq0P4lRiVExJklSJGiikozTQAgxkfBFkhCXSiEzDTbtX7cCC2F8jygTnFDeym1JgcxUqlI3Pbowae5ixLpAHpO0OkYiosbfzl83IKwlVjmu7akeHiK1TmbMSiYemxDIziZoVhQYmWB3kYjSOnWWR1hjURXUu5rc5BBh6HuUTIbCcfAUVY4ucrrNHkFS7Tx8fIw8TUIn3jnauiPkmkgyf40RVicrbGc5e3XBtEzwvoNHR+y+3jArcjbXW/ZtR5SCQilcN0BM/Mc3YVPRJe+w6AN90xP6AT9YWMzI5iXdrqXfDcRp8q6yXc8wWDCK3luESF0GESIxy8jKPCkrhphsEGJk+/UlKEldt3QiwakiqaA1qUo2uzpB2UZVRiGSMELb9mRaM3Q9SkBpNItSk8d0LVRVEBuS9PlguQqWtk8dsaoqsO2Azg2NtQlSOl7DTOfowRCUpBNitDlQSe0werzRlPMJ0Xraiw1mUiRD5bGQVAlJ11taGan3LQfzCe3pDcoostXk3efUO7YZ8QZ4Lm058Rbhe3d9vivAf+1N+Mbl5E1oHAmCfLnj7PPTVAGJIEYfs91mTzUtGTpLe76lWdcoKfEu0FzvMcagMs3+7IaoFLZzGKOIWmPbnqbtqao88a6cwBPpRrguWlDvG6ppSbfd4wjpTFCGYbDJmsFohsGSZxlSCAbnENFTliWegDCa4XzL5RdnrJ4cMjua/x6hlPiuttv78X68H+8Yf2D1uTfxt/z/ZiF+52bwBpYW0EuH32+ZPQzcVwU3vSHEwJcE/KLATQzZeqDINN57ijJLHj6DRWeaoe3puoGPHh6QVTnX52cUoyrb+jJxWeTYXi9mJcYYvHW03UAgyRn3u5az377iwwfH7E56hq5HbhoWWnF0suLKDUQCIUKxm5B9ppgspmy7BtiNlbLvmMy3wNXpnxAiX96MBFvpeLTc8ul/NeXquWP9oqGzgbLMESoFaSdHKx6uZOIGGcW6SkFGcMkXx/uAbgeyiz1t3aYkIM+YLqb0dcswWAqpMEKgtUwKOYC3KTha3luyvdrStT0X3tN9+ZIHP3nCYbnkw8MZth+Ifc/Ls2uGricrBcJZjFI4Jem8x+ikjCaFwDiPtJ7u1TWzjx5yNezYYmG54C8e/jgFg0YRu69BwMMflSAfsD/f0rc9WW4YeouSkmI2Sd0gnfx6qsWE89DwbEgQs+yjFSILRJshP57TFxLb9BzuNzyoNMO+ow8D84cHbL6+ZLpMqlogCCGw29VM5pNEUu4GhBRU84rdxQZESjqNlqAk09WU5aNDhm3D9ekNTdujpcL7yOrBAU3TU1/vECS+Q+c8qrNE65LMrnWovk/+OAdzjv/4Pht3w5frz7lqL/mdTsVvJNpCwP3pQ0pdsb3c0J3UZIcZAnixd5zXFi0Ujz+8jzjvGZ5fIpXEaIWNjufVFVYGYu+YXbUYIen6PQe2Q2hBZhWHxUdILUGljlTUChs7tpwi/cjpGJXLIiJxb7QiC0tW1cepsaRGDpdWGDklGgWdZ1beJxOGYBRGlhBGJbhACrgEzOUJZTlHRNL7WAdENs0z3LqmOJ5xsOlxISBwfFmdoaIcDTETN82Gjs1xjsejD3JWNz06M3iZ7gMQd4m0Uoo8zjiuPib6QGfXtO7q7gKIGJGjmSw+IIykdlcEZ0GA1hOOJ58SgW33ChssCvC7FhlCSgidv+MIzidPEE5ArqnjGb7r0h7nA5hI7jyl1ikwH5NTSUQoQVYaRNSEXVLck0VGaDpEkaNKA71DmQzXWbz3qDxHSEFW5WgE1geKWUWzqUEpuqHDaI02mnJS0Tct3gUOHh7irMP2A3XbYb8+pe97nI9keUa/7/hss0GqwOr+IScP5uy2DZubDZtFwSAFebDs2j1xVRLqjp99/ISbL0/pakf2fMa8ypiLnpfVOQiSHPx4v683nv/539UgImoPx8UJKtMUMmP1Q09uFKYryMoC21vsq0toLeJgzubFc65vrpgtV+hihZSGaBSthAcPDogRHlxYJtIgty1qU1NfbogiJeqYdJ0nVUnTdASV9K9tDMmw2DpUSGIHXTcwuKSY+sQ6Mik5xLIbThmqCUPXc3LwI/oQufYeP65lpRR9b5HittAlkpy9SN49Q4xMteNhlXiPSereUyDZm4ohCuqrLSpGpNG4pqfIDMMosNJ7jy4zZK64LB6x6WridqA6v+bk4QSRF4Qv3t577gQBxOtCU3wzm7ndgN444N6EzX1r6xrX15u/YlUesixWuHag+8c1wy//gWA9+UTjZ5OkhrjvUblmni/xIaSOaG8Z+sSfEkoSbEjc06ZHFRldN+DqFlNl2K5HEHmuEuTbq8CgAjoMiKrAjl3y3jlym8yYY4Qiy7DW021rTJUhIxAi+32Dzg1lkaWOsxSIILDtgCeyW+8pDiZM3yx2/ZNjTDbHFtt74bn34/34/vGHSYper7rf8bnj+H0X6O/8FhFzNBD9JeX9hqei4NguEUryQkYureXaBz6MEdX1aK0IPtIPlq632JsdUkoOj5YclCUXn70i7hvUtKKs8lSxNnrsPES8D7i2J4ZAZjTVakZQ8Fw4vA98fXZF0BEx0RyHElMm4vtKVryq98TgmV3NOV6vOH7wgBu7h+9LiL5jPkKEf7xMRm+ZEjyafUlRSh5+kqHEY579/QvsbmA2m9DULbOgkccLul3Lxb7hHxcmBUfW3f19HyxnfBySv1BdN7hh4ObyBqU1s/kEHwJDCAw+oEJECUFZZHSD5fzZBT6kKv1lJrmUghfPz/i3qxXhs1N2TcvywSEP7h/Ttz1rc0HfDsgYUR5UblBGopRCeItQCuE97fmG/fGS4U8esX1+RXd+yZ99+JdMTo6hdHx58z8RCUQ9Y/jBv2Ezm/D8F18lOE6ZsTyYcfnqEqEURVVS72rKecULv+MXfYL7HNybcPTTg7vOE0AMBR/cNNwf9lxfnLFVn6aKv0qiCs567DCgdCL6h1EwoWu6VMn+4pRu11BMioRN15LVySpVhIH11Zb1zY7pYoIUgiKviEIk3xwpU/A/wkT7rkePnQUhYLaa3QUWrWj4x+tfvn2TvKs6K954xjvW1tPFhxxXJ7zcPuPv7X/k3k/uoY3mi//XM7qbnkxp/vpJZPVghat7bNMns+Bg+Xn8FV205CLwSdfhe4ewjnu71NHJ5IyT+Y9RRuOriPSJFFj3Z+x98lK6rRYHm9Qjb+WjJ2rFbH6YRAZiTB3N3EA/EJoeEQNzcwL6ZOy4BKJNhrq3yk1CSQ7yD9If6j1RKyggesu+O8N1Ne5sw/0qw25bBiX45Ydf4pRAjiaiUctkOjpP0MpJG1hed0QRUaRuEVISc42wqRZe6AWFXhBC4Kb5kqa/SKIRPgUvUUAchQWkD+z7U3buOQJ4uPxzFtOnaY71wGbf4X1ADamlFG6V+3RaMwflx+SiIsjIV/vL1FkKETINRUaIQzKJ9R5R5Yi6I2WNAtumfZHFhNAPhMGCj/QvL4ky8ZQwEr1c0O/apJ7o/J2YhdCCdlsjY8QNqaPsmgElJNcX15gqx1Q5Nxc3RO8pJyVtl0RfDh/dY3N+Q28d280Wn0um946Jiyld07G52WK05lwKrHeErqc8rHDWgYw8fnnF9mZH6AXL58fcf3jMWXvKyw8uIESMlgiSyMDlled/+B8TDOmkOOGns4+QSnLwwSmH/12az/A8EIdIOZ+grwTyZY+qaxYTgfqjApMFQgd1L1FlxsTnSKDrB+5/tuFxCOSzCb/NA9YluG0mS7bep/02RgKR3b7BBk+yNw5E59FKsdskrmKeZxTAvzUZU60JtuGl/QyxUUzMAR8f/R/oY+Tm1XOetWukVGN3M4mZWDde/xjHfTmiM8NEOLKYFBGlkMQ87eNDr2kaj9QKVeXkRU7fdLTBI41CKIWSKlkPtIGz2ScwF+Qikk3/hqtuy9GTJ/h3mdmOm9I3pV7eNd71jHep1b353b3pfT6afMTz3/6Wgwhiqui7gUELLvcJQpoJAdbTOosmCQpt1nuGwSZofabJipyhTQqsXookMhRAOoV1yf/tYpGTZRl11+F0St/yXCC9R2qDF4HOO7RRNPtkeF5VJVlVYkMS0UBJQkyFVu/StXHepr9r1zBdTunrDjskj7bvnaj3ic/78X78s8cf3qfo+yA6YxeCsXX/L0qQvvONx46RC3SbhrzIyIVB6IwgBb7vklqVD2iZAtfdtknwKiVZHszJqpzl/RVZkXH2m5fs647ppMRZi6gKHv3oMeWiGnk9qeviesv+csvlF6esr7fsK4M+yDEChhiIPoyKWoGLr87wPnA+NbiJRimF0RojNfmigrG4f1cde/tPe8d8fXOTFG/9VEjB6sMTTDnl1T98zXazJzOGdtfgBkskIqc55WpKVDJVbpueq/Nr5PmGYp9khm+TwOm0JFiHUZIwejIsTlZoo9merxHWUeUZAXDeJ8d3Keito286rjdnzKzHt5b180t2WmFmBfOfLLAhY3exQfiQbk4fUN6nQzAklTqnBM2mRmYTyntLZL1Ocupna8J85LW9AU6fnyy51w3sLjZoLWl2DdEnONXQ9qn7UOXQvJ47Mc7bmy2UECPDCD+Z3luirzOcCymglxLnHSEGtIDpcpbUsnrH/GieyMuZSt2U3FDNK4ppmQjLwDA4tpcbYkgdBT84lg8P2F1uCSNXLpIC5oBM1VYl6UZBi5vrLYej5Pm718U7bhfx+p/vCk2CD9TbhvJh9Y7fnV4sjCKblYgYUT5idy7Bfwivyfo+JIPhUT5bhDAG5DF1i2J4PfPOI6YlsfN4HxBKIN2tKhuEkKreY5k5fT3YlDwLwJNgayESvHyNyBGpG8M4j8mokkSsFyRlrVvFlhHS5bVDjvydqEYxhJCuRvAQJcgASogEyxn5T2FwxCoZw8beIoscP1iE9wkiJ5LkedAKencHvRVK4UdFPu99mguR/ujbgDaIiHc+cXO8Typkb1ybaD3IBI8TWkFMPDakTIa7kWQwfL0jSInWMqmuKTniuUbVO+uQVYGsCtpnW3Iivh+QRQaDh8FhRYcLYVTJc+giQzioimQ62rU9SkqGukcbnQRthEhrRgm8gMOHx+jc4J+dUUwKtB4ljWOCFQopqLc1+00NInkyRSEopxXTTLNb70BJfB8I1tK2KQlrncPGwPnpJbusIwK5UqgiI9K9fePHiO0de7+HEKiOe7pNkxLgMH4eJdCFIZclAijmE6KIXJxfELIVhEDsLXqaYdseZRSqMGircdsaeU+wvLeiXtcErcZExTP0CWKrMo3tB6qyoKlbJAmCLLsBFzw+ePp+oJrOyKXElxk6ZngRE09lhKou8qR4aa3FmETwdyF1/wH0CDO9VWgUgDGG/b4e4ZkSEQUagSyz1LW0gWaoMWWWzm8hiPWAKXPC4OiJZD5QFDl12yByx2K++ta+8nbPOr6GxX1PC+PbHaL4ja/FndDSa8hcZPPsks3Vllxriiytp7525JMFXWuTwAEgfeJ/6jwjKoFWEm9BC5l+o5EUZcb19QYhk3F523RIJbG9I8szqvmE3lpkBkoleGcQEd/25FVB1ydT4+gTXC4K2NcNQkmsc2iVlFitcyiZErjZrMK6gG0HTJGBj9h2YHe5eQsy+MZEfXvcTfj3BWbfvjLpJ+/5SO/Hv77xh0mKfo91I94VWP3Bh+D0+h7FRlFKgVUK77rkkO4cq97SNR196yiV5t6Te0wOZ5gyI5+WxBDZvrzi5W9Padue+bxK3aEgOP70AZOD6d0OnIjMkXxakE9y9hcb6nVN1jsedRlKgBsx5cF75jbgbDqgyiZyP6ZDflGWHN4/QGrFyfQBpanugr7bUv4tLwEhuJlm2G9W4EJg/+o3RDfgQ+Q3V0nAIDLg469BK/yPDbJ9yvXVDjrLcecQMeJvHGZXk08K8vsr9o+OMEaTXeyTbwkRZ5OynDGJPO69RwrBQmrU8xuUUmR1h1ISJxy7QtHHSDUtmR4vaK62XJ7fcC4jV8LjFzkqN8wnFevrLf43NZN7UybHT1Cfn+K2gVxJfiKfgutBBD6rTlHR0+8aKCp0kRGeHvBL+SX5/SVD0yNP55SHc3SAg/pLAA4PISwlMQSu1oJXxQGbiw22H7j3w0fozIxJURp+mDHsHhFj5LE85URcEn3g0A2gBFmZsyxf8LOfHlM/qnlxcUhWHbK73JBPC8pFib+2dPuaex/cp/z4hBfxC84/f8mjHz1hiC3CB8RMceKecPnZBSLCZJLw/6v7B9TXO5p9g0AweI8Qkjx3TMpLtFE8+fF9pnLAFIKNgF+tP4cacrvj32ZJRe+V93w18tTelVsDTB5OKFZJYvg2uEDA4e6Ko/2ezfq3zFVOcT0QI7x0YwITA+78t7isILYDMj/CX7fgA8c3A71tMTLjXvYRWii8sGyGZ2A9Xo2iFTEiHHdFg0GlTpjwAZFl6BGCQkySzV4rpPOEMVk4N2vO9RqpJPeHA478nJEclswsc0NsEyTS+5FnI0TiFOkERxQ+IFwYBQnS49H7JDdeD8TSYAbHyUVHIOKU4PqwQEUQLnKwsWjnya3hsPgEbTRtDv8weQZCYFrLwTomWXJXMC8fQkg8KqkSh8rHJJ+NSv9Zl5KxJHueOtO74RS7qZG5IddzCqagAtf7r4nSjddY3Knzbodn7AeDC57B9ZAlc9YYAnRDki+X3HG2vBQon7yMIgK1mOH7pIwnfMC2HeZwwXBxg8iSOh2tRY/wRUFkHrZ8OHzBcObYrB7yIpQp6MsUXqbrnFcleZmxu9kipOT65QU6y7AxYq82NOs9/WBZHcyZHi3p13s21xtknjrsQz8wn0+pmxa6PomXRMizjMnDCSdOc/r5c4L2bI5umE0KvE4KbnmmyRYV0EGEgwPFH/9xMmBWrWPSfgXW0aiWn18kk9xX15a4DAihuJzM+DlpjX44iyxiZNl0bINOfKwQ2MsZ9c2abDHFzp/SXyvOfvUFZ/Ul4cF9ttETtLzz7jJG03X9yH1L3cJyWlLXLU3T4kNMBSkiPlqu288pe4EoAS1TJ2+qeFF0tL3la90SXTIDFpAKE0JgtEFnOilkxlRYCD51zMLI74shdahCBB9jglb70ZQ6BLQXNE1LMa/AKOohQbsQCaonjcY4w8HmPrNfGaqbkr9SBWQDFvg7a3Hx++Fw//S45Xi+Fmu4TYjuEqMQ2V1uqTKDX0342lv0qmTwFm8dvu3pFORKg49kUhG9T5YU1uKMSrDGrqePA1WlxkKPQBlFOSnZ7fbJzNmnTm1R5rR1m9ReY2TfNAmuPn7Irk1n42w5x9Y1Mk/+WBJQWpPlGd0wUE5LjNGEsZhaFEnFdPCOSilefXnGXy0iq3GP/8w5LkP4rql6a7xOhb45999MiN7x4v+Vj9qu+H/87f/9v+D7/d+Y/Bd7t/fjv9T4w3eKvjm+EYl9qyL0XdWNbz72O0Lnbl/y6uKYYn2E0ZJ2cDTdNc4n8uoSmEwrDn7yiMnhDF0Yhnag39SsX1zR3Oxp254QAnmeJRM961BaMdQd4WCWgjIpkEqlTlFn2by6ptk2zA9mzCNcv7xOsCetknCD1tjoyBcF06M5j4uMcpECeyFHtSgfWIUFkz5Ph6GStNsm4Zq7IfF8jOLiyRz5YEV5ML3z1iB4mouv8G7AR/jNVffGxCWlOFVOOfnf/V+ZodD7ng/P9gkqsW1ZfnXGzdkOoQ3bg4quHThczVgETd92WOepsoy26TFG04bApMgoOofadmgpEobd9QQXqBcZYp6zvdkluEKRYaTkpUtzEGOETHEpA26eMwyS/AqyveNn4oBwswEp+aS8R+EDVnu+nFyhREAOnqbZMZ1NYJXxq8Wal1/9IwfmkMevPsSsM44mgafh1wgC3gXOPnvO/U8fUS3vEx58TDYtEEpy9NH9b2GtbV3x8m9TQvonH3p+ll+mgFO/vhHvLS4Q4hKxVKjFB8wfnbC72LA+vUIYzcGH99jebFI38vyay49O2Tw8Jz9M19Rozf6iYRHvsRshm846posp3b5he71N3SGZ4FDlrOThD6esDjuEhEV1yQfzDQj4xYXg1yM95WfG8L/PCwTwN3ZISdEYbN0tkngbVAimj6YsPpq/XmghQaEO/9MVR3XP/MPIpRDYi5YQQbvxAI4Bd/45VkhAEWWO7AIqRg5f7rFxIM80x4tP0SpjCHu2/hVeSrRLnyfExBVCCoIQCRIYYvL/qQJhDBoQgqgU0oc701KE4CLb8A9VSj7yaDiyyWyUEIlEQjukbpIUyOBfB04hED3gUks2eJ/EB5KMQ8KijpK/DA5C5PCsRRDpjeRmmeGlIB8cJ69qpA+U+SHH8x8glOK83PHL6u+IMTIfety6QS4mzIcV8+JBCkRjHN9HokiNJk9MwXIEocQo5e3x1rG1L6m1QlrFo+mfUxVJFauxN9ThJn3emIwgfQhct1+lzjxjMconU9nscJq8ntTYcdRqTA4j3gUIARkjdt8gjCG0PTovEsSv6YnWEwJIJLIyyCofVfBg1l8z8Re0XUd/5ZGzH47Np1Flr8gY2h7vHDHCpCyw2tEPA0opFvcO2F9vKYyi3TVJYMUleJEbBooiJaOb681ImI9M51Pm91fI3KCdZ/jlKd55rBy4undGP8kp8oxikKye3kNPirs1fHCg+W/+2xnEyM2rK2Ksaa/3/PoC/uMvJiiTeIgHYcf0eMlFPuFcgppIZsOaQ1Mzmc/YblMXCSFolcFXFdIp9v6IUM3Z3S/5XEO32+EyoOvTfWaSWWpQEhNhuZyx3uwSP6vI2NctxegXVJY5uRjY7D+nNgIjM/zoiRYNnOYtN0NDM5eY2kCf/Iek1giZ9t/gU6CdjEVD6vgIUFIR2jEx8qmLqyyEwSOVQkmBtZG+Tx0w29sUzOeGIte4CJ3zhL4nyzMOXxygTiPmq8hfPiwwuaSOgV9ay52Jwl0Fhu/tfLyZ8Nx+99bT3/laweJwQdd7Pouel9OMYlYgzAS3bXCkLk6xzFBeEl2g33WJWwSYPKPteuxg8dbS7lsCkTw37LcNEZKNACnRv75aY4zB+UDbtBydHBJiYL9rQEBRZPTtkNYnkSDTPqOUpAsROwwJWeEcm4sNUkkmiwnOBfp+SDxhREI2+MhjF/mTPBWy1iF8d1L0epLentR/4tH/baVD78f78Ycb//Kk6H9lONbbzdN2Fo2mbQY6a5ksJxTzClNmFLOSfFLgB8f27Ib2pmZ7s0+yykqipGCaZ/Q2wU68czifiJhXX5xx/ewyVYuWU0xh2F9uCT7imo5qXnHyk8cIIZifLJI87yTh528hLmI0m/TW0W4b7PkmKVEh6OuO7fUuVXOFQGea4AN926fKsUyH4GW01KdXVNMSU2Wsnt5jcjAqscVxFu7a5rcZ6e0siQQZmxTk84BEYKqcy6/PkqGcgGHXooVgfjRnimb/+Y5usEyqgqIsKKucvh3Yb3ZJuldI8swwOIdUCqElZZmxU5LeOs5fXrJYzlgeLbi+3CRnex9QzpMfzcEoVK/TQeMC28stS2MSZ0cKglAEEmQo9o783pLrvzllHy6Y/uQRk48Ome0bdp+t2ZxvMGWPzAf2esP0YJqCPqXY3+wJRVJtO/jwPjrT30iI0oFr24GrV6ep6l9t4DGE4N/qdKbrOUIVYzIPnR3OmR0vkuJU29PfNEwOZlg7oIB7Hz7A9wOZ0TgpMGWGIUcYRehSoGp7hxdJZSyflFSrCYvjJZOjGdrUCZ4RAiE4+m2TgqJQpM8y4uxiiHcqS99aHN9RYAiDxa5r+ovNmDgkQm9W5CgtcYi3A5A3vhQkI1MRTfLcURIR5N3TAgliGF0gBItQFVJIRK4RPuAkKJcCNikF0cek3KUkIqTgSYw8iCgEqW6ezE+jkim4I6G/CH40Zw0jp4KUXBiFHFzqjMSkIChvlajGn0XvCb29UyIUJOVDYdT4++KdzPUdrHH8TCEmuWIxJnkIgY9hTApSoifnRUqEpEgS2O3rare/vY9CSIa4IXJryBrd+DeRRFyETMp8QSZ2jAyROOodx9GwVoQRPjeqbBEjosqQeuSBhNQpEghEmaO2DUGQuFIi/X3aKGJvUUKgsyzBQKcVrmlBS+SsIJtXybgyRELTQ6bRFFQ6xw0OaRTVfEKz2adrq5MPT4zxTmQhKQsG+ibxJpQUlPNJqpA3Fong4P5h2guVJPYDeI/1ARsCV6dXuN5Cbykvaso8Y2UqTqXEhYCX8OiPPmDx0X269cA3hxAJUuh6i9SafGLIuzIVpPqevukpB8dQt0Qi0+MVDInvJlUSooj7dJ8IIdDa0F5u2X72kuLA4PcdThsG7xJ0UCcxGSUgUxpnHc57Yp+k+5XRDG1HnhkmVepKECOV0QTnIM+ISmJCQFZ5Ujj0kX3dEmTiiQUJUhn06ImjM423ySpBa5WEcXy6r1xv73x/GL16ohSEwaOFIAiSmp4U+MFRSEXd9egqZ/ABIxXRRwYcond0veOozEFE2qstam5gRDbcIRa/sYd8a8S3t5n4jU3ndYH1dV8jvn6Q+QfHdOcbvHMor7CbBr2sEDpJ1Vc6p9025LOKwXZ47xECJpMJ/TAQQ4JwBwSTxYS+7XGDJQiBkpI8N1gXmC2meO/Zb/YQPEZomrqhnJR03TDygwJFkSWRjTurhoDSisrnoCTKKIZOMITxWghYHC3S+/aOyawiKMjnJba/wEeP0prfJ/i6Vfm77dS9YQH/frwf7wf/JTpFt+Obwdj3rcN/5hr9I2M4VjL5fVQTtgMcHh1TzCt0YQjO4wfHUPfcPLtke76m7y0mMwlXPwZxznnsKJeblfkdD0SIJLfbxsDlQUW5rMh8YFlmRODBjx5RLqo7NZ35w8ORnELysukG+l2bIHY3e3yIyTBQJPJ2CEnGs1lW7FRyWv8gKxDrGhEji9mE/bZOJOrVjBgd9XbP0amDFxsO/vxj6uUn9FVPNi9ToCcgOMv++S+JwRNsz+aLv0XIJE995JM8cG1Kbp6seNW3HIjIvedX7BvLrJySz0qmqxn2co0gBWGLJ0dsX1yxWW9x1rGYTeicwxcOPU3v22MBlar/3rO52Sb5WKOphEboSG8d+8styihMlVNOc2zdcTHRNFpTVBkTuacQAaMSZE9khqbuWN4/QOw61n/3JVPb8SePj+gfFBzMM7LCMPSef/+1RPU9B1rxx58+QgDrCLOjxbc4MkeV4UdywKxmyDLnWW3BD+y+LHk2/2OCdexXW+xyIALbL3f06wTN+nj5FY9nl0Tg//MSbroExfrxgxuW+Vfog4Jnc0UtUwIqdQo2bRgYXjY8+OQhX/3yM7qPd2T3Ihk5/yb8gNWDA6Jy3HRf4u0F2gtW8kO67Z7eXvNyXo2B3Ir/enqM1IoVgqGzeBc5NpL//uEcoSV1f8G+P8fWPQcHH1DlRwDczBquLi8ZTtf4pkMCQUluYo9ZZcQY+dWmYxsSvKezqSrpgf/QD+QjNOcvnhzBqxo5eA7LH+LxhEzxy8MzCB4VBcf7j9FCoPIqQTgibETDr6fnmMFSajgWPwPrqXP4+fwrxOA49HMetQcp0FcyQXaQPGgXZF6BkhwPs1GMIXVghLy9vvE1p0+KlGRJgYwBfOLo/Kp8SW88wTt2WuNDiQyRo7VDWQfDgFAaAeRk/Jv6g4S495HV1CIiaFUk4YeY/MsebloCAVMPKTGxno4dV92vCDGyH9Z30tk+Jgl8eSvOYPSdD5Ef1cJETLLgUikiIiV8Uo0JVLom0iiQScEuDi7tRVKkQowbA+hNm/hV4i6lJ3YDYexY3KqDRZHu0TD6hoUwwSOYPDhAbWv8psFf7RhuasgMtu1QQiap7DJDtoJMG6RR7De7O+WzvCxo26SEVncds+mELM/Yrrfs6wYtweSG6fEyyXMbDRH6XYMuMmRu8G2H8Cnpa5s2JRRD4rJ1H58w++QB3ek597I5swdLzEzT33zJ5d/f4Fp3dxZdXjn+x/8hCS2oSjN9smTfbtkMybw6EKmWM/JxzXZ1S7Wc3iWyMtNjoSDt3bYeUJwg1ILd+QvWJ/dZr/cME401KpnlypTw+5AgoPXQAoIsz2iaFmUUru4gRnx0dPuGpwPkg2VlPKbMyVeTVPhwPhULhEhw5lFB1YeYIKJSoqSkbVqiD0wmFVGN0NCRK+dtMvcFkHfrQxKVJIz7dXCevu4wmSGEQBcj0qiU9MpUuFBKEYOnqkrOZ44bJZI/1zPF4WHF6of3+Wv/W0J0dDHyN8Pwumv0T4xvQn/vRGLiu4FeUlyTZZrZ0RnzF5HV9CkiwFfXNXFZUU5K8IGyGPlb4rXPVzt6a9W7mr8qCwoE2nrMtKJe75KH05jYZ3kyBnfOE3PFTfgK5QViX7AYPkBNJ/ixEJMX2V3AleUZ+/0Vm/plKnhoRbTJ1yiodC+JRkOTYL5N3VCrx6zFClEZfq2WiJOHKKO4efEb2F7+0/M3ivQkA1rSXvk7zv/78X78axn/8qTo91lV76pS/wE7TR9rzQ9Mqpx8PZ1iphO6XcvZb17QbhrskFzLBSBH35pi9Nzxo8jB9GDG9GCGykwiymYpOBG3EUSEOhMMh1Uyb+09D6/bkTMqqC+3vPrVM6IQ6DxjcZyC7+3pDc3NLmGGZOIPxBGzDTA4n0xEA7zyA7sy5+jhAdJJ5lozDA6vJNJohFG03tMMA5P5lAf1DnPTYH75inZm2DvBweyI+cOjZLQ3tNQvf514Es5Sv/w1ALmULKtJqoZNVvCzvwYFp1+e86dkmG2HfHlDf2/JZDFJUAAJQ9OhMkW+qAjPUkdLxkiZZ7TFwDCxZHmG6AWh8SyXU6RUtPuWbhiSt4fWnHx0nxih3dTsrne0N3tEppjMJ/gPJlxZix8GMrmnFJHMSPpRwlzuOvpWUU1yjucPaD67QF20HD+5h5hdA7Bzjp+L1H14GgOfdo52XbPNIB6kKvntIRF9YJFLDj89QWhFv4ehHugHx/leMT95jMo0p4vn1MUOISUvNz27Zz1CwEfLV9yfpibAZQNfrUHLyH//Z3BSeHbXe2aHP8a6BFvRmSaWGcV8ydSt0Fbz6fFPeP7TL5BTReUKfnD1gNgHttdXBPcFOIffaMzkL5nIFU0x54vTU7yDo0nJn64+ASJaCHyWOpwnQvBIVegq59I3XIWIryT39Zz7xz8AIfib/HMu96epkyAT+V/EyE66hI8Hvvxy4Kpxd2s1kpKiv7ep6l5G+Kv7SzIy3MsbDqYf4aWg1QOfZX+DE56FmPHj+U+RluQRNHoSdarni+w5aM8Dc8gP7ceQSfb6lN9UvwVl+aA54XFYpXU4QuikEhzZOUd+TrztYsnweqMZg1VBKjoIF3BjciF8vAsSPPD15IqNaRJPZqKIQaCj4OB6g4pJ2EDIpMKYYfiwewi3nbCZRlqXIHo+EGJShDvae3zTJQEFkSTzu/oaN2nxmzp1mmIkCEFAoEMgulGeuB8SXHBMRG87nYIRatgPiFIgQ0xE+LsMJwWiUcc7YRdJ2na8c8R9hxo5YWHsZkXrCc4RZeq44Twi04ShS8mT1pAp/L4hRyFcEsBACaJzRJP2yvLoiP50g28HzMEUnEZrkzypmgFHSHChpmW2mNJsa6JWdH2PszZ1i6TEZJqubjn/7UsQILMES+sHR9/2WJF4UM57Sp2hJ8UogiPI5xV8+pArrQiTRxwUH6Fyg93fcPPrvyOp670+c9Zrz7/7n2sAZk+mPDyeEsqKsxcvsU0/djYDbd2hMkMxKfHDay+5WxEMgSD2FjMt6P2K3ZeC/OiPqFXktL0im+WEfYcC8lFIwrY9MjMERq+sMXn34zxMJyXb7Y5cSk46y0wbdNOS3SsQzoNMXK7oPWiVhCWsJ4SIVip1HUlFvjzPR6VGkDYZ93rHHUc1jPdQJhV9cImL6jxSpCQoKoGKSQxEFwakQNmAdJFBOHqdDGZlkDSDpT2o0Ah0hNZ9zAvrEf6AP8lfooJlEwP/yVp8jAnW+46C6dshgXjHz16Pb/Y7pNig1MDig4GP3ZQoDFcvrygPCpwQVLOKelvT7WvyKk/zICVlkWGHgaLKMa7kwwiP8pyu6cgHR57lIDVh8GRao6RASIVTiq7reO5fEQTkccoH5Q8xeY7PPNLo5L8GiFyjlGRfBF7al8RCIcY4o9u3iT/2RlPe9Q6rAl/KFWuWEAO/dSV7dczieMnu6tXbSdE7mj93PxICqd6cyfdp0fvxfrw5/st1im7H77IG/4WJUvSBV//5S66bIuHxAaWT6hA+4qwligSrUFXO8ZNjDj68hykMCPnGe6fS0RtfJhjP6OSd1K1eH7JXX5xx+tlLRq44wQeuX6SDXMvkDu8GhxAyyYD3lmKSYwdH9JZASpa0UgmGIwSmMJRZxrQdGPqBYlay3dTEkPPgowcs7q845Dn11xesz27wZknTNLT/0LK/3LJ4dEixyP7JOQvWoXLNyY8fs912XPzyBQcHC+pdnZSxbEraCIGszNNBSoIrLacVUQq8tYiJoswElmS+KJVivWtRMkGeZKaTkhZw8fU5B4+OmD8Ylf6eneN9pN00OKORhUGJNG/eD/TO4UdFOBkjw+UWpiVZbqie3iOO0KbQJtPFqPO7+yn0ls35Dt9Zln/8CS8Hx+7ZBc1NTd9bvPMsVhvy7CV5mXH9smboDmCEZnXXe6aPDvB1y+6rM8p7qwRtuj1uYiT4iPcRP0SiF4QIwaXAqVgmCJ+3FtFbBqtp+56D5RHDvsWuPbv9Fe3JFu0MhZYJqrN3tF+es958jcwVRXFMMJ5ORgbfI9shdQX2DVoPeK2JWiJzRa4Ebt8wXHusS5LUuIDvLFZ07J9d4nxgf3yFX0T0yYJoU+cyELGfbYhF6ly8tb7e/Oo2/wAQguLpEV2E4dV1yhBjUg0MWbqH4vhc5Twul0StUoX2TXPTGEGNQXvv7lTjogClJd4mjpSwSSRkpP+kAHU0aUXe9kCSOp2UKdlQIiUIYjRrjXArgHXHQ0pNKAHuVtyE5EuEGJMY7gRWlJZjF0oix89PSNwbvayI/UBwHhch04LQDXAwTdBRwR207lbmm+DvuEwiJiNWNT7uBen6hAh5IHqPRyaVuru9L0ko4wNRjWbFQiBsSo7kCPWLEbRMnJNYGmSeuEMR7jhlocjQswIRIq7tyKTE7xv6zxuiAvPgGL9tEGWGXFbJ1NO5dE03DfmiQO093WAxRUZpEjdRjgqXUSROZlnkTA/mDPuGelMzP1pyM7hUdCoy9tsarwSVVFSTCh8DXQj0LjA9mDM9WaKrfPSV8Qybhv3pNdurLZPVlEd/+cN/cv97c0gpOXh4yM3La/p9Q1fXSKXYXe/IjCaf5K+frFKy6p1LXTut8HuLyir6iy17lfg59a7BR/AeZEyctmxR4p0nM4ln1ezb1EnXKiXQ1hIQCWI4WGRMSIUg0u8QPiUrMSQYojN+hGaP5sdKkRlD3w9JiKLIaLshqRCOq0OOoh6R8R4UJCn2wVNoQ+yT+XAIkazMknJaBDuqcMaRC6t1MnONPjBoSRwsxZj8oSTdpub0F1/x8dMeVSR1O+BtlPc7DvzXlq7fCAri6+/ehte9OQSqyjCzkvNfXaY9wwVs3WG1IliPkpK+t0ymFVp6uroll5LYWIyApVRUPkHkVJ4lbtW49rWUSUBJCGQIKF0irQY8Js/IqhwRSKIkWiWOYKaRISKdR2YqQU0F9H1HWSiqeQVSoguDbQec9yivKLWiFIaJKXAi0lvLzcWayWryvQjEb0zmuN+9nufgPdY5jDEJmv9+vB//yscfNin6XZKZ3zfh+Z1X/OvnNzc7fFNiVEkfJF5EjFF3fJBMFpTzksW9JeVyQtSSs2mOkyQPEJvUrWI38LD1ZJnG9xapFEPT03QD2WeObt/RWM/XQ8DkhlYK6o/vUe8bvPMcPjjCVIapiyz2A/XVLqHppGRztSEvclb3DwDom579eo8dBrIswXTafUuYaWyXultfRUvIM8JhxeTJEdOP7iEE2D/9gHaWcfHVGdX5ltw5eudQ5zv6X71i+fSIPzr4CVIJnBScTg1RwNz2iMsvIAZcveHm1/+eQKTQjtmkpG46VoeLdGhKKLSiH1LSaZuB2dGce0/vsbvaIQNE6xCbCE4SA1RDzQ8XS/re3gVrvfesK0MrIj56zr84pZyWyJGHEr1LB2YIxKZPRpKZQkpNsD0HL/dUIkIQhMljXFWSHZR0r75AhIBvekI30O87xPyQnx7+Mc564uma7QLONud0f7tmx9/iQ6ApDPXRjHxVsWkG5pdH4APDkBFGDHxmron1Nco/wO/P6eOOerPn0/4hs+kjUIKX6oLPby6YHi/5kw/3/HTTYnLNFEdz1bI+2/Jk+gknW42SU3YSuqFkUebM1g2FNFihOP7VDLGqmN0/pn55g6pdSmisIxAIIsk3+94lRTESB8TPI5fVM+zFhkKtmJePoRvY2UvW9SuyOKGYLln4TxAmcq0Hfmv+AQxc9FvcZkCI1P3RI1xmc1Lh5zkyzxhe7aF1by+0Nxay9Y7/9+d/Q6Y0Okj+cnoPvW5hNHmMt4kEiVzsY0SFSNSKKXP+cvcJIgSqWKSig/Mc+Ql/6T8CKahcCQiCC7zK17zILiFGHtojHvarMS+97Q5xJ5QggM+rU9a6RgCf1g9YiGlKnHwYuz+Kn7ZPGbDE6Lmsf4OPA3E0XBSjgWwwIs1BCMkMdky0Yki8nyTPH+7kvd3NHnNvSXhxlSCJt6pbSiIkFOogXaeRA3Ib4O3sGc1wQfSexeQpE3OA0pqr3Rfs4zUIwU37FbvhHKkU1u0RirETMCZULuDfgEjd8QikJMnbh9RDGz93aHpUmSeoT4y4PEOROFwi14R9wG7rBLciIqoCNS2wdZdcdbYtoemQRhHzjBAiK3fJH8Ut9b7havaIM7tAjfvwMO4pygb6rse9vEgFo0xzeXaFCIHZakE5KbBNTxNS8jA5mifYz/kaqxXr6y1t01FOS1zbM2wb5hc7dDcwDwH1cs1qsUCtJBfjHLw2xX59CAmgv+45+w/J4LU8KqgWFUKAc2HMk0VKEPybh5JAGMXhIlCqATOXXFU33MQbNrsLdPURejB0QMw12ifuoRcS39kEo+scNqTOQ1Fk7OqWYlYBqaBQSMkPjjLmShGVos4MeEtUozS2UmijkZnGj1Aw7z0BsLc81BASxDDEsbsxFumsTXAqKSiyjOPeMPEZbdeyvu2wItIZODi8TYmXkgIvI8LIxG2LES1kMoTtLEWR48KtqIMkU4o+Wv72kWbyYErbe/zf1UT3Jvzttp/x7UP/9SO3z3/3827Hi91APaS/N7/Q5HJKnhlW9w+4uFnj2g4CzFczgg80TZdESLQmG1o2XqKI/OdCkctIqSR/GgJlarPciZ/IUdI8KkkuCo6Wf0KWKUTXcbX/RTrHTDIIV0rhG1ARrPMENSQunknJaxgcsoTQ9ngivrfkRRIyiRGeqj3TfYLefl3co9ET3GD5aFVQ6ikR+PyqZdP7d87Ju2Z1sJa66chzx3RSfWv+f9/w6/14P/63Pv4ASdEbfd43fwb8TkvqzeTozTgr8s9ekd2uIxpJcXLAajGhWExQmXpb+e7uI0b6ZuClCmz2DduLLf2uTZ2G3vLTjWWiDYO1GK0YhkRy1pkhGyzEyDYkwrc9nLF7ch+/Krl8ecnVZg0bONgNPN4lwmWWmXGDj7R1y/Wra6pZOVa5IyTxJwTQbGtePF+z7xzeeXb3KrpcMfSO+1omSWFgM5H4Hz7A9T3lL1+iBocLSWnPxZ7QeeY/fMLyo3sMRrE/rvACym4HV1+OnjeR5uxzPJGyPOajv/5zzn79gpuLNSGkpE8vJqgsKae9+vVzZqsZ9z95yIMfSYZ9x6t/fM5+vcP0ieBbdj1T33B/WmIjNPuBtu8ZigXlowPWlxsiga4f6K1DaYlEoZEYpeitA+8ZnMXIdLgutxZjB4zI2D5cMgRFbDVHR3Ni2+Gu9+nAtA5x0zPpDM3asb4W/MoohuwkQQgyTVXmDIXmepbgIMd9xUw8RBUS7xKMwWhNVlxQHg5k1RWTexWzsqLdNDzoDnkqj9mv1/x6HrlcVKyLjP/GNxyWkX6zpsxnyGqK1jnl2SGuNcTCEJRh32zJ6tSIaW1NmRkW9RFQoDYR23fYCGpSQJuhYqBwHr9OPlPGenofEM7R7W7wRSBMLfsXG6rpkiAFnd+z86cYV2K6igPzMcYGnvMbvlAv0tK1EeFH/oEA0Tlwnmsia9sx/fETnBavl/k7Cho+BH5x9gUAk6zgv/qznyF/ew3bsTLdt8igESROkCR1VEKMZF7zqX9I6HqCAIQDIZlQMuuTUlgg+RUF79mYhi/KU4hQxZKH/ihBxm73jFszI1KX5CLb8LW5QCB42B4wD9MktjBy+ESMPGpXYxfL42/+EeeTrw1jt0aKN9zgQ+IA6bGDJVWCMEkh8COMVoyJhriXEoHgUscakRS9glJk2ZxF8WRUsAyIsYNqY0vbnSOEpMgOWBUfEKVg25wjuAIhaNwVEk3wkRA8iKQgJ02qzodISkiFgCIbvYxUgmZBSuBiquJHQYK4GY0MgeAA6ygeH+HXNcEnkQXXb1DGEO1A9vAAQVIOzI4WhDpJY/sQMVISjKEa1pQCer+nHmZkk+MEX4sCpTVucEwOZ6wvrsnKIjUyYyRmCiMlzc2WdlvT2HQPDc6xuVgn36O2J6tybD+wu9lyc3FDiJEiwCdDpMpLhAus65bjIeC7eHes3N2+I3Tsdgy1Zfjt5g4ZcPJX96hWM7bna5pNjSozpoczTG7euPPjSNq3TI8VQvXs2nO6Z6eIXUvTVQzlCUprfEimqd6lzzDPczb7mpgbirygazq6zT55GxnFfr1nupwju54Hq5LKB2wuaYPGjT47IoKXSeBielJx+upqhE2mtpTROokEAdgkLBIRDF1PUaW1JaUgJJUPpsHwcMjZRMksN4iuH++PlFhpBG3XJ9EFJcEGqklO3w9YXOoaKYUKSTxF5xozBJxWqGXO85OW8kmJrR3x56+3k9fX5e1DX7z5hLfG9wcHN63jpkkJ/k8fHzGLSaC8vd7jiKjM4ENgu6sRIZJNStoh8YsHlVEZicwMP29aooVDrfgkCrIsI4jUOcYI8BEKgw4B+sixeYhSii7bcLr+n4ilITSeLCZzZV9mMMp/40Cp1GVCabKDBdJonOxGCKRIkNUP7+N2LWV7xQezHFv3rIeKfXbIzemGn51ojnWCOb/aDa+Tom/B6OIbP06daa01eWYwWn1z1t/6Kr5Pj96PfyXjD5AUvbFYxDt+9s3x+0Lifo/86vbpiwcrnhx/Qje9R3CRftcQnMT1ybU7OI/rLbvrHfjAelPz+SqnFzGZ6OlEVs6yjCJP3SWjc6IL5JNEpq4WE/IqJ4TI/nJDt2vZjfCP1cNDjsUxN2c3ydn+9vNH6PtkMllOK+p9y9B0dHWLUkltqpiUPPj0IVIEdldbxD6RpYVSaKlomx6tJNcvr4ghUh3OUJmmvt6lCqqSZLlhqjX7fUMmBEM/8OrXz6nXe+KsZB/ukR/P7+YsCvH2hRGCfFHx4KdPORkecvXZK85eXnC6azg6WjKZVwyd5ezZOftNzXQ15fCjExYnS7Y3O4TOiDGQGcPQJ9ifyUwik4fI0FvcNrl0hxhp1zVRSkyUuOhZHc3JV1Pqyy377S6JXhiQhOSZYR2qyBE+UPvAfrcGecWDHz5ETQrCvsPtG4L35FXO1ekaoSV6UoF19F1PGEn3+cGU4w8OGHYteXtFniVlt6osSOp/iqMPjpk9aCFGmvM1/uEUYRNEQmGQec7Nq6+whUqE7FHVKcoUd/XbFtd4vNG4aTGaITpMgCEEpPM4OyBMRjkp0bMK6j55hWidPCyWUwge30socnxmKE6OkF8lYvXVdsfMOtxgMeKITisyrdE6x6hs/CCOGB1BSsIoMiCUGLseKnUAfArciMAIDfPW3d4W6X65xZF+c42O97kQifBffHwP/WUHo6S4CCOZeaweeyWTIMIwQuSMQXqXHjeK6FwyV1USpUzqyAAihsRzcR5JCv7uqshKvAV1JcakSCeTWbSQkmhHSWJGbyAh8KNLfFQjv8OTFN1IiVNQEm9TUPjN2ra/VYvzr2F6QimEkAybBr2aES83qaofImHsnEYhUpdoJMrfwZpCxJOI8lIK/Gg0K0KqNkcBXoxS5TYFosHoJHhnEiwojhX+QEzox5GnkppcqeoixuJLVIowOIL1ZNMifd31tC/Pk/nkYo7vBsxigsjSvWRWc8KYBPmmJ7WQQc/K1Mlc10nFTslkXzDOl3OBLNeUVc717gbbD+n+0wrbDcjCQIzkecbs8T3qizVegomC2XzCMDha53BGgfNoqRBlkdQOjUJaj4ktykf2Tc3scE51MGPn9984Jd5xoHwriASdaQ4eH7F6eAB33J83x5iI6lsDUpEgZHWX1D3LCTuhCdZTKkUfEzwtSknvPWZSII3GW0ccHPNFEnFoRlXJrm4otSYMFi8lItP4tU1Jv48ILWHf4TJNVmbJQ04mSKUYoeJCqlQIuoVHjeuja3vMmJBPJgV29E3SSqGJeGuRUqQuRozkmabrLWVREJxPMuJKJShkiCiTeEyyMPQxQctjiPRdz/T+EnOYcREvXkPSvz3d7x7jdXmz9vp2r+47wgORgn+hFVEr2qst/cygS4WSikwnSGzfdrTbPShFU7cYY1BS0u0btBJEKdkNlrULaB8wRiP7dM8qIRBNQGSaqFM4FazHKQVCEuoeD/RKIrNk1B4zDT7tfZhRKKW3oBR6UqQCSW9RJmdo2nSWDBbZW6IUFIuKZX7AdW9o9i034Zqjw3fcvN81uW88VWvNZKre6py+4zfdrd/34/34//fxL06K3sQDf8tr4F8CkXuzW/SO3/NdbssR0EWG0ormasfZr1/QbJo7/4Grh2c0oiG6yEfbj9BNRCvJk8YxjMHP5Spj+fCA43nGX5/+GhMDTuZczj+F0ZdIF6laKKTAPjni5c+/5KZp2G9qnA/MbODDTU/f9hyUJfc/fpCqxC7QbRrqXU1wHl1kzFcz9us9As/BwwOO51PuE/B5SfvRQ9qRoPnBqzXT376iMJrhpiM8X+O14nRVsu37dBjPMuQIu/gollQybb5dP3Dx/AKbe57Jv2GxXzL94DGnq58go+Cq3xGbvwciu37L3776D8QQWZUr7n94grOOs/NrLq/WLOZTylmV5HoHy/lXZ+ADxWKSOBcjz2N+MCf6wPZmS9v1lEqmS6oE611N2NfMJyWTecXl+Q1yxKBvtjVq39J3PT56TvM5ogupy5D9BKRlURY80TlFdNQm53RYkbtD5vdLxPPfUDxY0b3YYOzP+eFf32N3Dtsrk6Sw2wEGjws98mzDCWnT10Ixezzn5utzlLxkdjxw8PiIQx2YXCec/uTQ0V29TFCS3SO+bCbk0zk/7HbYv/uSx3/6Q+biZ4gixzc7ulrjNw1u19EOlohA+4CTErSmzA2yH8hHyWdvLfZ6i2A0QwTwhoP4A4pM06mei/7vcV4wKw94uvwLbNvT6Zb5wQGuHXChYzP8Eu8k3bBFVpqwbajdFzhxAUpwND/gYPgRQgm+mJ5zJjap6jn6mNyaCiIVEsFPjkcFxxD55UVDPYQ3VtybCVKkc5b/56/+HUoqog5kHxwSzq4Qe5UkpH1IvjV+jMqlSAHfYFPQ3fdI77nI93yWP0+/VqmR5+OZ+JJ/e/0JRFiGKXGE28WQVL3QKSCJPnVePu0e8bg7RPjAwidTZO9TxySMn/mi/TXONRAFh8XHyFIRnOWs+UciCQLYW4sWeoShjTwnEqzqFlrlx3s/hGSYSd3C42PC5RaUQkaPq3vUKNpw+7pt94rN/mu0UvRuk7gYWrJpn7EXVygBjbu5I+LfW/6IIk4S/ytGYlUgrOPGf0kr9ncKmGKU7JVjJViOm62/5W/dbr8xgo/4fYMwiswrgh8DvzLD7xvk8Solsdua6AJu1yBvpeRHRT+daaKSSepbCqJNcE8lk+Gxd44QA7v1nigizjnMpKDvBxYPjxBCsL1cY52jud7RdQNegBl5LUpKNAIPPNoODFcb+n5gOq0oljO8c2RS4fc1g2t48kFHnv+Gths92+5u19sMP335zTy/OW949e9Ov3GyvD1a2/P3jvEkes16kcc/oPuTn2C3DV4tiRf16GmjU4dSSgIgc43vesLIaYlFxm7fkBXJpFZLQdt2ZEWO9Ekav253+LZDaZFgVpnGIxDeol7+iuziObaYEGcPCDLd/8In6Wbvk12CVBIVkmKclBCFpOsHVIgU46lqROocSykYbEJEhFG8IQwOFzxCGjyBNgS0kuQiiQe1TfIyypUiE4rq3hIjJe7lNX+hBqr1hr31PPNjwYLvbgbdNfK+pyj6zofi631pd7SmmVjqV9e0zT1UXBC8RyHveIWz+YysyllfbUaxD0PXdTgPpkimvP+xzMkB1zZkeUaOABcSx68fCKM5sdKKtnG02Y/xIdA7j9SSYB2lzimtpFhMWU0dT3hJ9IF+2zBsG/y+TYIMPgkYibIg1D0ohapygvN0m5qj+TMm8oo+thSbNW4+QxvNX2UZvkyl2P+l77m6LSS9/T/e3Ldv46h4dyfz1vfvx/vxr2n8YeBzd1+OW9st8/n3bfN849e98+dxrAhHSLivd7+g37e8+I9f40MkH31WmrphP91S6x1hiBj3AzTpkDiKqXKWLaZcS8nq8SFT6Zg/vyIXgT6WbMps9FqUd0Tr5mLH1Vfn1PsWoWXyIuh6/N6yaCwIxeFqxvzRASFEXvz8S/Y3OzKVMN3zo0UiygPeB9anN4SzG7IyY+gGzj44QP7gPiY3LL6+Yr4fENpRiVSZVhlcxUBW5BycrMinBe224eb5BXbo8S7S9gOTLGNSCBrVUhU33Fy8Ily/4n7xf2Z+fECDuZvf3ra83KVgNIrIxw9/wJN5xeGmZn+1Y3+9Y7+pCSEwm1Yo5xOp+WBGWeUIwFpHvU2qTmjFpMgQQxIF0MaQZ5J2GNh3PW3dJ+PSEMAP0EV6KTFFjtKCJgQ6N0CA1eFHtN1A5wceUo/+QIquWPDqJjB5nEjX2qhUYW1v0ESOPnrI/OmnECPdumb9/JLd1Ra37WDbE2OgcY7mYcRUOZNZxsMfSxB78rWn2AzYduBQ7KieCoKIfGYELzYN4WrHX/9ZSeELZv0e6w4Y+hVSDdTna0RbkRlNoR1dN9CLSJEXBOeQ3tNDgi0Fjxp9RaRWlMbQWo8Iirl+RCYEOm74ev2P9K2jrbd8vPi3FCIynQhooSpy9t0zrpoXhFxjRoNaNS2xvcXrLSI3HC8+ZiGf4Hctp3EPbFLFG5fgHEm5AD3JkZlmER2reUYI8Jur9jsWbFrnLjh+dfkMADPRPD14SDHRyK9buGDkNXAHX/JjciBE6oqo0c+oM5Zn+eXoIUTqpJjID+pHPGmPUjdk3HNCjHedIRFfC6AIITjqp0gxS4IPgEg6KYhbEQ9nacM1XX8NKI6rTzF6SgwDF81v8GFAGQOdI6ISuR5xZzdETJDAMCqPyDExiqRujJLytTcZJNnt2wKB8wQBLtQ04QLh4+jZk+a1ba9BrdMb2WFMYCQTtaJUR4gYUULgUaAcl/2Xd6acQpC8lbjVnUgBoEe8fnw0bkVKpIjgLHJapLfbt8gyI1qPXkxxTYepKvR8gr9Yw5CU/qKUCGNQ8wq9mtJeJAEU2h5hNDILCJc8iIIUZLlJssYuw4eIllBIQzEtRhGNiFeSuu0QMZJHUKQO89APuG70NXq1Jds3FEKg+j3lEJkup0QZ2TlPOTUcPvFIcYEUnt/5HBJg9xa7t28hut++y2H7HS8/OFxRfvyU6D0T68nut1x/9oreOqoyp2+65B81OKoso+5qml2DUEl5jxgZuoG8LDCj5HrsBvphSPeeVCgliLlOXb0QEb5Ht9ccVZ6X2xvi9H7qSJF8cYRzxBgS7wyVkh3n8DatwVwrVkVGJabIG8iAaC3OpS5oDBFjUofZj7L4mRxFT5REZhKlJKYy9JcdpcywPmAyw/6rS6wQnHx6zIftK1TbsY3hTvr9jWl/a37vktXxsW8+/p0doreulKCrWsysJ8ge8SLALoILDDJgGaXhm4a6bQkhJD5WCFRVydD12K6HCF8MFmU0Qilc2xF9QOcGjcBkisFHmn2LUJLpYkYI9/AxUM1LNjdb8irnzFmUC8hLxYOzNUfLLeW9BdXJArttEQhs3abO72CToXPbE0c+tMw0mZKoYU1urzBFhus925c3LB+teKQUpZYEIv95GLj61gx/1x0tvpUAvU+I3o9/jeNfnBTdpiVvdYnkt7a37x+/y9p7C6UniOI7bMdE8l04/ew5wWfJJM86uj6QVwWHDw4xPWyu9gjnUSYn+EC9rdFa09UdzE3yD8kUOjcIOyT1KR/wPjJ0Lc1NzfZyQ79rk+mrlBRaMfRDqgIbhclBj7Caoe5ZP7+k2TWUVZ4UsQbPzdl1ei8hUFLQbvapFd/bBIv62rG/2TI/mhNPrzFEZssZs+WUdttwdbkmuoCPjmbXkC8qDj46wW1bwlmN04osM3glEJlB5ZFsMeFwkAw3ji//4TM+/OkncDA6zo/B8O18386vyjTT4wXTo3mSk+0Gdhcbrl9eoZTEDo6rZxfMZxOur7aJTO8cUiYI0H5fMynLZEiYZxS5IsSAc4msegvrEcJAnlMVGf1g0VEitYEo6PshEYSBQYAdlZj8LZmkabn86oxHeQr0hHXEwmDXNT40iCpFseXBlGI14bgbGPY97XrP0A3EEJkfLZjcX6KlQfD13W3V7huayy3zI8G8muI6y+5yjRtyTJkhpaTQBf26pdndYLcOX/dpXYQkkytUIhxnSibOmvcj/MpTFAUC0GWeoFNSEDONGRxRSVRuQIBqZDKZbDvyMqn7DcGThYjMDPoWJlNkaB/gep/kk2NEVnkiia8b/LADs0+KZC4gswT7ERFcJHFF7i/J76WkPSsL6BK5OD3vzTLuGwv5Gz8XJDUvPSupPl6QNQfEl5tUCQViFAy5IQeETpyW9NjI91ESlErXMqbrJ7MEsZIh8X2ClKhMJ5PVGMekS959jug9PoY78+MwCjKEsaMqQkzmrC3J20VI8J5IIqX7kNZOmeXIIZIsD193iW7NXJVSuJCMX6WSoySyTIUUneBeQqZkxI8eOCHGZMDow9hlZYQ7JXJ/iAEdU0U6dagkWgjcMCDylLwGkYyF5ahSJz0pMbyD7qZ5IkK8Szo9QQpEIQjWJXjV4Qyx3RN7B9ahFtPEg9jWiCIj1i1xViHLErWYYE9vIAr84AkhEci77SmxKihPlgwvLvEjRDNTEiEi3gZcaxOsL9f4zmKMwklLe75mt60JwHRSkh0UXD87Z7aYMj1ZJThUluZKRvjocE3/4pp232K0Yrut2ZGSAB8CT3/0BF28RAj/3UfMbZz4xhO+RZH9jpekJ/ON+DLSna9pz6Hb7OkGy/FHD1h9/IDLz14mhTYlkaR7IFoS10sKlJYI+1oAI3hPlifYqNAKpZKqJDEQUOgiA+/RJkvXZ99y/OCQrduyBYbekmk1nkeJw+VDwA0Bo5MpuDYKFQXLqiCTiuAFUgnyTJPpmPafMfv3Ma1NnZm7pW4yQ9sPaCGwNj0uR8i2tQ61mHDvj54ieku2LIjX6YXvmuIoUp3zzUvyZoJ0+4W4w8d+T9n1jTMMIF9N8fuOLDfUWyjzjMF7rPVMFhO2mx3SJAW9W8GSpm5RSjGZVnSjd1HXW0yWii1CK7qmQ2vNEBKcWirFfDnD+ZD2nChodjXTScnQ2ySRX2QEF2jbgfPPX1Gerzn45AH5coK92aPLDGc9TmvywhDbnjAqeSajaIM2CYpHjORlxv6m5vrLCw7LJQXq3THVbeHonXf07TzGu1l+P96Pf43jD8Ipit9aQP90DeedBYtvju957F2L9nr6IS8nR8mFfNJC3+Gdx2jJ/HDO0Uf3kC8i8kxT9YeU0wneBfbrHVIpDk5WeKC52LH8T8+IwfG39ZwwWGwQ7L/8DO9S5dWEkHxJQoLh+BiZasNPgybaAPuB4CP1YDlzlrDIuHQd5rgaq/CSRT1waNNmdyvFCuC9J/YWpOSxheZ0h312jRGaLDMMTcf5vkVrxb0n97A3G+zgsFctp+s9J3/yEfOTJeFXr4gxVQU75/B9TyYzDup74CwqSLSLfPmfPmP2cMnP7v8x+bx8K6hdhI5H138HwDPv+Zs+KZ7dn2V8/EnBvQ88F19Gzr+Q1Ot9avkrMUJpkjCFt57MaKJ1VHlGON9RyASje1FI2ughBLwALVJ1cxgsEOnbjuNHx+imw7Utk/YVh7lKN5AWhD7cyRnXMcLpGX/69ILpqqKbSl5eaYp7C+qvX2AO/xfMfPLa1HMCOwY+71so4ROt+ZHZEK+/QoQaIXuEUlSLHvGjAXXiaedLvtouaDd7cgr+9I8eM1lNkXWGNT/Cbmr8tUSJZMyYC0FQChtCkimXCYeuKk3oBjywytKcu2g5b/8eZGBwDrEeuSbWcH/1x0gEeTbn4eIvCaVF5hXCSzKdoG5qrPqXYcFT8bPk2VOmaxniaK4IhDyQi1mSZgZ+2D/icXcAQ/INQUnyp0fs/Dnd8w0CydP8R+g64rzj//KRpg+RvDDYr39OtG92jr6xToWk+vkeBPjOcrNw+Acd4fMNR+ZTpNLkRhMHCzGkz1gIQm85Civ+65ufEJVMQgpEpNJMxWTk7JAgajHe/S1x9AORWnFHHVbyTniBMaETKkneBx+IQnJ//jNc1kFnkbpABAE+dW+DcyiRxEOIQ0qcxu3Jx4hmNHwWLZe7X+CDZwhD8gfynkl5yHT1STJTJSn8CaAwkyTPDMyKB+TZAuBOxhgpWDdfsG/PUhAmJZCMkG+637LrnyO0SpX7UThi0HW6Z8Y5SbC5OPLGUoLGmDwJJSE3yBDQUmAOZjS7FiEEqlT43ibVQ+sQZfJy6Z6fUX30iP6qxoWIdg41KxFKJylonYOShKZHZhmx7RMMS8kkv11pVicHXD27ABtG6PAOXWnW6z1BCmbTimJWIhCYSUHb9ujrLdanLsXsaI7ODa+OJpiTGUoI7tWO+cWW3c01ef6S1ZMVq3s3PJ5vkCJQqm+fUm8cJm99Gd/90LfHGwnR6gdLzFQwnG+5+uocXWQMTY+Ike2XZxz95ClZplMBLSaVQhsjQwxj4WA05x27qFme4V3ii/mh5eubn7NcTWAAkaVgWBiFqHLseo+yLt3L52s++ugTnr084OLsBnNcEBap8GSHZDKaFRmqvWa+PUcpxarIqfYCVlP+wd5nN8zpBZx6z9BbAKqqpG07tE6Q3mFwKK1SYqQVRkhWDw8hU4Svzjk63TGbVcyN4Tf9r3B+QJwH/n7YIog4wH5jKu9yeN7+97YbfDvZ/1TS+s2Lubg4oPzPDn8x534Q3PcDfRg4XWRYoxm6hFSYz6a0qqOpGzKtGUIyC2/bjuA90ypJqDvnyIscBOgYE9Su7Qm+ZzGfYq2jd5bgAsakx0yW4aNPSn2Dw/rArjzk7/hTYoQ/2XT8dw/XDK6mUTM2YZ5EIazHzCpC3SHCqN6Za6KPMDgwiQ80WVRszza8yhq6oyVRwDCkPezNuXwLkvjOKXufDL0f/7rHH06S+6219I1d63dJgP4AozMz1sx5/vklAkE1Ldmv93TtwPJxwYu//5p607DIV8wnJWII3GxrlNKcfHDCwaf3OfvVcybNgPvtGVIKXkmJySd451B5OgDsYGm6AecD03nFw6ePqJYTXG9prvd0u5baJe+Sosy5lJGz3R69KHFS0rY9eZWxQKJ2PXawCdLvUxXXe493ntnJknurGa9+/ZzVwxPabU2/7+jrdiRnwto6Ht5bEqzn5mLNmQs8+/lvKbTmsQ8IFUHEBNXSGlyk7EukTGo1eWZQPlC/2uBeRu5/dJ/VwyPMtEAaxbS7ZLL/PBHk7cB51xFjZJqXSDFBGrj3yROm9x7w6tfP2V0mqfGuG+j3A0We+F1RJNL1fDnloDC4wWEHR1NodKZo2w4RPFGA9R4jknSvD4Gb02uOntyDYeCw6Im2RwqBHVXqiClBdSHgguP6i8+49+c/QOqM4ASqyJg8WVB/+Vv8hUBPCvThDFVk9K7nvE4k7EdZxsTnKSgNiYwfwkDbn5Mf9WQLaIuMTS1xtuDxD58yUxWu7gjbii7XyLYiSIfJDVKHxLcYr6tzCW4BYIzBCUlW5YRuIIQUKGy6M3wYED4Z/gWgyJcIJXCtQwRFJRbEXBFCQAFWpu6RsA6aFhM0Sh+lQJTEm1FK3iUQwXpClgIafKCqDXNVpM6VkpjDOeXygOfbS+rBEjqPsQ61z9HCUFXJMFNPclxWEIJ9fdLGSF93o8dWlg7ZywFipOk7zvJz5NSgPi4RpzrxGnQK8uLgiMOAi8nUeGIFhVuO5PbUYYm3hqkxdZKUUqMQQUpyGPl3SohE8NfJW0vebkNKpkREiruqtpeSPMwpJwdEkvITjNXghLNLFWyVuCB+rKcKmTpPUYB0HvDs3eXYAYyJW+M9RhVM9REhJsGBGGNKpoS863qV2QzjqtEDbZQBF4LaXxLbM+6EEnwgSEnnNnifhBeAxKOyDjErk5BDSIUWbkUcRi6SEClRI4JcThKc0ChkmWCScd8gqgLrwPYONQzkh3Ns7xAmqaLZqw1hCCij0IsJYlqil5MkruADvu7wF5vETTMKXeZEC/tNncynT29wznFweJDWWIyI3JAtU2dqt94TRhW7W/7mbtcijEIj2J6twXmuQkRPcgwwPW84/vQhB5+syM0WcChxQxX36EyzN+P9+eYZ9I7z6LsB2d8/srkh0IBxVAcThrXDmKT8ZkPg6jcvk1eeMYBDGoPvBhDQdwNSK7QxECAGz2Aj88WUrm5BBnzVsa83yNxgZiXZ0RyZG7wL2F2b1niZJZGO8z3H6gMOH82wS8Gu2DB0A8V8Qp4b/ODI4o6j2RRdZLjzDaEfkENg0Cc8j5E6RrxPe6AcYa23KNauH1Bap85m58jLDBsC65eXVIdzjn78mI/KNQdHC0IG//jVOZ3tvpV8vvmNuP3iHRlPHO/b8Zt/+mJ8I97Iu5xZPyfuQRmNd54yRq4CyCJ1hwqdzFOHYUgy/DH1grVSaZ0ZzdAPVHlGO1hsP6TOnUpqe9podEz+TXWbOkzBB6TRKKPo+g4tFZOqwFpPc71hJwVtfm9UvHtF3j6nKAXBO3Y6+WF1F+uEHMiSsEz0PnVytQR9K2KSCinFvKQloFVInXP1jTv5nd399+P9eD/eHH8AoQXxzRTod33hd4/fN4kaTzJBxLU9ygWCj+z7IUEShOb6+SXBeU5OVggEbd2y3dWUVcG9Tx8yPVkSgcXDwySp2fR3pPN+GDBEuraHENGZYXW8YrKaMLu/Aim4/OwV1y+vcM5jtEIrlfw7xi7JpMzprWPoB7ROfkd28AQfyI1GiuTQ7lwyLdRFxu5qS9+mBKCYlxx+eJw27n1Hfb3n7ItTdIxcPb+kWk05/vQhXw4NzTZVmEqjCb3FC6jydHDdqp4ZpbDRM3iHCJAD+MDz3zzn4qtzVGFYnKx4ehixdZ+gGuJ1cMpIEBckuF0+zfngTz/i5uU1F1+fI5REy1vFMIGXCQrlnEfHRDieniyYTzTNvkFrnUxNhUpE7yLn4Mkx3a5huPNwssT/L3t/8mtblt/1op9RzXJVuzr1iRNFRhau0mnMtf1sBPe+xuMhgWgAQjK2RIsW/AvYfwAdWnSwRFpCoOwgPSSky/X1e7avbbBlO+2005kZxamLXa16VqN6jTHPiRNlpp1huOAYUmSevVe555prjt/v963K5BQWZKIWKUiFvxQj/0LQNZZmvScEh8rqRAvMDdWdq2zefUpztiHb7CkPZ5An2trzcy0KASpN42MA3w14PxAC5JOCYd3SNYmHPjxb0VuInU1ZFL1C+IDINb136b3VOapLRWo26gPwSUibFxlOCuwY/pkd1MStIrZgAtAMhLpA5Rl5lWOHQHQeP06V05tKdqoxBMS+S78bCxmcI2iJyhIdVKiEUMZco9oRBZASoQTCe6KImJMp5Y3Dl75bgv7pkt3lY3K9QBmD3ml80dJdCNS+Q8o4fv/StaDdNlw+PGd2OOXg1jEqT+eOmZboQqdMk0lB9toJ9u1nSBkJCGRuoE3W21FrQteBTFh0DBFpdGpCxrBJlMSFpKmJAhDyRR6Qtw71vIobKW5hzOaRI6qkRmc6EZLbnYAUDjzqep4LjZUQEBK9TyiJlAkrUlkG3r0wLEgueGJ8vUQnIzMIo1ODMJ5nUkikTt+l6F263D3PPRIQY0AI9QI5k1qDT7SeIFIIsggRo/SIKMlkZT42EcJ5VGYI4/sQo+14CDE1XRHUlRlqWmGfrVIo82KSNC3HC/x6R8yy1GRmGb5JxhDxuZ5ivUNVBdE75LRM1Kqmo9/syY5miE2TkDutcC4gosMUGXNVMEhomwZtNM22YbCW8nCKbfsUWq01Pjc4kQJJTV0keqpPVFthNL4d0jVSipTP4wL5oh4DXEcd0EjRiqRgatAfolS9rwN6vocIXrgjBp/Q3pdDLd+3132gsg/7gcEHbG/RWtH1FikkscoYrENJhQgeP1h817/QBKlME0KgbbqU5+MCQkKzb8mUJFpHtqiRu4Aqc8o7J6nZjxHvU3E+uJCK+TLDDxK3HdLbk4FFJVHzGgabjABuneAebMiKFF5qtSJGQ2gGYu1RWpFJsEohnKcfNTU+RGRw1GVB2yWdixCR3GjyMsf1lna5o5yWTF85RgbwfngJBhLvO2zvb0CfN60f3Ri9eMTzBiry0XXH+FpxbGwYMd3JtUNWj5eYCPXRjO3lFiUFxpjkiDpY2oslTiTUbj8MGKmSO9+IjkXAxYBUksm0YrfajnTEpDXqrEORjBa00sToQUuMNOmaFmC7S6ZPk3nN5eWao2mNKTIskWHXUUwKVJVBk5wFldHoqkBkhugsdr1PeYAqo+8dWqSBgskVZIph39NcbJlcXbxAs5/jbGm//tiD9tI9P2ucPlt/edenG94KfCR17s/S3Hwf62j7LreDRp+9xXL6OZyuU/heSJOULDOcX6xx1pMXGVdevcbRq1eJAi7uPmP1dIntLdWsIi9zmm2D7QaG3qKKnGAdWWYYa0t0mSG0ZHX/jIdvPaIqMg4XU/ZtR28tucqpj+bMtnvy+0t656mnFZPjCbv9Dr/pWHcDtTG4EMi0pnWOSVVgB0sIgWa1R0rJoz+5h9KKYlKRFRmTgwlKSzrvWb9+wr2+Z7i44AevHZFPJuyerTBlJDvMKKqS1bPLdCAc9Pcie9cTAhiv8NYnCqAPuOBpu565r7i8d8bq3YEHpqZa1KyPp0xemWHqgs5IvllnCCk56i446f4IZOT49nUW17+UbIZDalK7Xcf62ZJu06apaJklndfjSy4ryVYLZKYQ8wmyG4jes1pv2W8bqrpgfv0IoSSn77T86blE6SmFVLy2c+RSEeIARz1RCAZZ89bkJzm/qLg6zVFZ+2KTVYWhvrJge7omKEF/uqKalPzkPEdIwdRInlXJ/jyGhDzszjuyzR1uis+zfPuSIV8R7SV0lkv5xzwbUk6NVurFBDVIQSYEsiy4kv9A0oSQJv2u71PujfcI9NjcRPSipD/fcD3/MiKPqBCIgyVKiW8lrduSK0UQEboBtGbQDafLb6VmwboR3ZKI54U48UXaunSBKdep4xWkkGlKLQWKyPn2LfpiR37zEDU5h81bCGCW32S6OaJzJ6jcEN2YgO4DDBY1zXmse4LqMdMqWTF3A8OxpjdT1rOKpg5ks2Q0oHXgzmKLIGJ9z1nzbXbyIfl6ysJ8HpNpzuMl36jvpmI2S4WdUIob/oQ39zeIQnBvsuQd8wipFHeaK7zaHqdN3/uEhkFqTBCEGHjWvkUXVwjruVZ9gbw8BiVw1o0W/PqFNojwklZIGG7MvkIMDnlQ83j9+9gRfUkT9GTYF8fjnssZd45+KjXUYxMijWI2eY3Bp3whQiQQkCIVY4yIzmX7gE3/MDW0EYKSqDpjoo+5M/sJvHcoBGFscJ5Tl7yAM/cWrd8ih4iM4EedlZYyUXydf+G+6Zwnm5bk1w9pvv04mVX0jrhu4GT+wuGPErJRY4FOOUtydAAUdZlMXpQkrPcEKWGwBCFon61QISF9MgaUAILnc1LypSxjCJ7fDgOPfaDbt+giQ8TI0PTMrh2BD+y2e3wvkD7iQ8Q1PeXJLGU9dckJ7XmYaDktKY5nnEvJpZQIKVBIlvfPOKoNr0mBJOKHsTH6uM1IQHlSUl03rJ8tySYZmycXVLOaryyOuXO/AeBPrOWPrX3/Lhcjw/Yq+8cL9uuGujigtQ6h5WhvPqAieDlqm5RMzUhMyIXtRltyk2zxdabRMRAi2M6ijYQ26Sknt+bcXmxT4b4aePuZR1U5uQ/JpKO3+PYMLVsIHgZB0Va4ix7VW2JwqHaC3GxxhWSwCVkNvSUAb0rLF4RgkIr/2nc88B6lJEWesd+3oAT7vsdkGjXSAZNbaEOeGbRSYCRff/Z7hL4hxsAQhvchFB8quz/wi5ePrXj5Ph94yMd9jsBo4vACgqJ9umQYBkQ02MstgZHK7ANSp/NcjCiyEBEvIzFACJFMyZHmGHEuUE9rvPfUs5p92ydnRa0p5jM2+wYlJbODKavlhsliiusGhuCT9pdIoTOUFBxfPUz7YdAMzjJsG6rjKfPcUuoVTvXYeB199GPYdsA3f4Q8fIbwgUuxYOkUetTYhQhIKCYFu4sddt/x17McYspF/D+7jssQXiYhpn+NQ6P3fxSfNUafrb+861MxWvjE8dsHr15/Ed+18SqauT1TpSjCmu16zVqONBchEsyNYXo0Y3I0Y379AIDVvVPO7p8RQmQ6LTExMLQD7aZBAIN1FJMSmRnqmNPsW0IMrB+ecXm64tpr18jqIm3G43Sx7waKIufk5jGByPLZJZPMcFCW5HmOP99RtgNBKnyW4bxPQaWM2oTBkWUZWZ14/G5ISEOza+nXO9bPBpaPNEKAzgytkcTJlP2zS7bffsztH/8Cd26djEnlyWrryhdvYpuB4Dz7szVnD57R9X0S1ZYFjE5FVYxcLtfkeYbRhr6NPGnB7Vt228hZK5jMA+W0xN6syKYlU7VEskq6kXBAu9mjlCRG0MYwu1oyu3qAbXuWD87ZnK5Snk8Er5KNsXDghwGZpbySwph0/HvL03cec3zrhJs/cIf9+YbN5ZZ90xHXHhcDxbwgSsfgPEIZGo4QIaNwikVMYYjP4SCzqKkF7J+tiJmhCBHTtmSTAmzP5dkePauIRuI2Le1yy5xDvD2mPjxis/p6ojZpRTtscd6hdKLCMdX4OBB7R28DWIkzb2BMogVpAUGr5E5m0xTahaQpCL2l0Bm5OEyFZG/xxkOegZYJBRoGvDGQpU3V+4F9e4bYenRuRrpWRHuDCGP2jpKpePcRnR9TqCzpY7xB+IgoM+K8IEx7et0gXDPS6iLF05pslVPWV4hFwF9ukgmCFMQokVrR+oDDU5iIaxp874ga/DTDh4G+j4hlyrgpNeR0aC3oiHR+ib+u6N46Qx9+PrnDHWScxnVqPIo4ZmjB3M4SHSxCpy0XxY4IXJXzhHxkGutDQupixMrU1Cop6NyGpmiQOmIzgSkzhHVp+joWCs/RBCkSSiiUShRcc5Bc8ZTGR4HKFLpPE1fX2xe5NUEIBJrSHBJUovYRAmpeYUJJD2iRznXEmFHy/PuJwDPQhVUyiwCCE+THh1QbT50tiCKMOhKJG93pBBC1YrW9y340UHguEiemnBkBBKVGGmFEeI+5eUj/bEVwHlXmyYhi22KfLMkWNd3ZmmI2AecJ58vUqGmFlxJlHcpoUJHY9QxqwEwn0AxoETAnC6RRdA8vklOaS+fwUZVT+YzQDUxFQl7qWU3bdkQf2e8azKVJzZ4LLI4naK0QRrM5X7N7uqIqcxjF7WJeU8wqzMGEZrmjkZLqyhyVKYqDCf2F4bTZI1SBiGPWVnxpu3t5HxqHJjpXUETa0LK/2CEyaLsttTrm1phB89D78SHjxjYa07jWMPQZxeyQZtumoG6pcDrRKB1glEQh6K2HXKOtT7ojLTGFoR8seZ7Rtn1CDwZLkWlMZWA1kF2boQtDrVukCAybFdpW2NHxUGY65aeFHhV7gsno+4FwtiOrcpxwYC39kx2Z0Xib0FP6MQvPaKYRSufpBkcRkllAkWf0w4Ayikld0TRtMivxIYW3Fhl6pNNFHwghsOmWuG77vWzbLz4D8RJK9P2VCR9+dCQZoWS5QUTP4KEoc5SMWGtZHMwS+uXHLDxnqfKMg8MZ50/OyfOMsshZrbf0TXKpy4ocMyLHwXua7T5liBHZ7RqkkrTrPd556rpk1+zQdU6eG/p2IMSQ/t10rNoNbWw5EAIlPRoHU3DFIdbNCE0yKpJCEDvPtvdoqcF6opbJUTMmNN1kmm6543a2oJDJiCX7Ho/oZ5qiz9Zf9vUXgBTB9w35fB/fSyEEN3/4VYbiTfbZIa53hBDQhaGcVpgyI3jP9skyBZpuG+q6YnEyw/YWp5OIsVxMEUpwWOZY67C9TRkB/UCdZ9RVwa7puHhwxpXXrnHl5gmXTy9fiPjrgwm6ynj87YcoIcgyTbttaLZ7pJAMg6WoC6p5zfZyS1XkWO+ZVjkxQtd2WGvTpHQ0HRCAFZK8yF9clIdhYHexplUCNVI3uk1DuahBJSIBEZSWqHnSERWHEw7euMawbdk8PufywRlh8BhtkEZRlwW5lnS2p4+e+aTGBo/XEt8PrJ4NrM5WBCmY2RmD7wkkHUSM8PhP7mP34++UICsyFlcX1POa4zeuM7ky5+m3HzO0PW1UyDpnMi8p5jXbyw1SCEqjqeoSaTRPnl7w+N4T5pcTZidzrrx6lYvvPMKKiNISK+MYEJoKTCHAWk+QmuZiw+TaAVJLBJGoUjCtlJLu2Yo4OGSE7myTLIW1wq12dPsW2yddj1YSqSWqyoiNIm76RKWalZimJ/pIdEm/FQaXXNFGpyZ8wOQaGSNeArkGH1E+TcCjEinTpbfJAMAHhJZEAlZJtIjIUV9ktUoakn4YwzwjJoCLgtC5RCPzAbdsEwVrtHoXUkBdEIpIxI1ZNwFEpDypKYsFQ79DkIwHhosN9umSOlbo41eRGsy0Qk1LQtONiIEkaJDbJPz1rQUPsbU4YrKRbbukWbp+Qnv/HKs9682WrDbIg4TumLrAn0hC8ATnoTCILsG7QsoUMDoaRAxZ0k1FIMZUqEelCJlOaNu0wu+S6YMiuXv5kEJQ/eCQeY6YVkhjoLOJIkVqVKT3YO3oOscLc4fU2evUnIWIzjNUm4xBxGhwEcbrzvNAXGJEjM2WmpT4XYsUSdMlRNImiZHKJ5JtHcooQhPHYntsnIBoHUGPCJgPiRIoRqMInlMLA0ZIEAFpAyCTy6AxL5q853oCXRdgPe7ZClkXKFLj6X1ArveYawv0rWPc5QZFQq365YpsOkGGiGvalK90OCP0ELd74nySrtly1DiUGTrTBC0RRUYYLHGzJ5tLBgkTkyb0m8sNxbQkELn6ytWEimQGlWn6pkdWBfvLJU3bk2eG6mhK82wFRtG3PXldpOyZbZvCeZ2nvlWjtGbxxnXab7ydKLXxuasmn7g1RWBzsaHfd3jv0WNo6e5yS4gFwEir5EPaDGkkITq60y15luGMxsVAJKJCJGqF7S2mzNGZxo4B4kFEjFa4zqKUQBiFCSbRaYsMYzSRAVUXZNcPkGakl9qIOZoSz5JeTh9MiL0l9g5Rl7jBJbTOiuR02XaIPEthrj7gSIMEqRW99USVqL/RJHfHvDCo3Z7YpVBfT9IlNn2PKZNja2k0fYSmH6ikQPpANZtQHk3ZPf6EPfql4/3hT+BTWi9eJIKI1LeP6Na7RGMMAeE82+2eUGfJqdIlZ00R0new0poqM5jKIEWkyDT9rkETUUiciAhrmc4mieaY5+kc6zrqaU27bQiDRRVZooo2LdGkocVu14BPBg3BWqrSUHlDNquJatTfBpe0qtLRbffJgt0HggKMJjSesOuQ0xIh5EgZ9kQEpspwvWP9bIkoSnSdE1/yP3+ftOizHuiz9dl63/qUm6LvQp2LL938UV/GD/7uk+770l0+eHM+LZgcLpD54sVrhhCwTc/y3ikX90/ZrnZorTk4XqTAxDEDQ2SGtyaKaCRZiFx/fIEOKVfEFBkHR3O0kvRNn4JAfWD1bMWVO1dwTU+77xLdoMjYr3Z0TU89KRmcp55P6Lo+ISFVwdGtY3YXW4zRiDH40Nlk24sQaCHISoMX4GKk7y1ZligsVVEC0Hc9P4Jhs25pmpb5tKY+muKC4/ee/A6D68m15CduTTFKMMiCt6c/gheK4kTy+vHbnLzSc/7ujrNHRzTbHSwc9954AFJithXZXU1W5hyEQLW2eO8xxlA93qDPW+6vNty/c5vD169xxWYsrj3j8t4p59OMSwXEyMn9Z8xtYLKYEv7q63T/zx+g37V88eGS/skSd/YUYRSHWmGjQ78iUHaFDJpzaRDasGtamrst9awmn+VkM8PQtDg1JGqjlAQR6UNAaondd+S9Y/vwnGtvHHB92oD37H3OU1UjfKB9loIy8+MZftfhokIJiclzdAaud2z6e7z7aIle1PRhl6brvUW4QMw0CgHtgGt6nBRkUhKDQISIItGrWJQ83v4B7mKJGSI3b/807CIMHY93f4g3kWJSYDc74mBR3hOkRM5KTCy5Nv0yMgrEYF9oZ0pX80rx40lXMhbJOD8WMREzqyDTqRgPkU33lLuXv5IKyEwxefUqJnvGPLvFQXUHu9rz2+f/hSf9EjmLvJ3dR8RH0At+/OJzHOgD1LRMqGIYNTdGYSqFUhlXix/CmQHbtzzsfgcxN4gucrK+A3mJ1557z/4AJyL6wZ4hDuhpSXY44Zl9G7/v2b99yefnkrD15LuMa9MvIbTitNjzfxz+IdIHrm5r/vrZD6K0opTVqPmJhKZLlLEIjDkoznsOq89zfFgREeQU0HQE58ZCT+Gj5/H2j3B0MHhuTH+UIqaQ1oBABI+QKjW88ySUZ3RUiz4VvhJQiNQMP29GQ0AvaoZ3n42T9XQ/iMm4hEgYXfK888lCOyS9mixzYmc5b99lMzwe5RTvTdOjVjA2VZYmIUkIri9+lFzU6XmVTLoxEXi0/QM8A0JI2nunyYTDKMK+R1QZMcREg5MSczSlf3oxoplgipLgPMXVBXGfBPN+uUZNp8Q8h9YStUw5V2Mgr4sBITXm+gHDgzNW7V32XGK7nmV/hfzqG0yKjGa9Z3+54eiVK3TblvnxHG0SpffybJU0HFpRzmtsZ2n6geLqHLfrWT1bAmCmJbgUgDl3Ja/e3aKiQxVX6N/yDC7QtRai/+hNZKwQhYDpYsLm2TKdT6PA/h0tubffI4Ddx+hd8vkzrn8lcPqnDwmbV/DdFHKNIOk3O+dAKWyM4Dyl1rTSY+oc31kOjuZ471hu9lTzGu8DRqfgZJnnuCDf2w8juKZDmgqhA6K30A3oWYXoLaGzidq22afBggBlzGhIEvFSYASEfiAajTEGKSDUGX+4bnmWD9hg2eeaQgLOIWykKAztMBBIOiJrk113kWVoF7hx3nAQDEdryyqkxuvj9uyP+Qg++T6fcNtHvs5zBFA+oppuMD/ccvHWE5RS7E+X3Lx8HdVfA+fw4yBLSIUn5ezNrxoe9b9LebQiR/Mz/ZvMqhleR37VfJ02dJh8wv/LfZ4c8JOC3zqsCUrRNx1FWeBVGpxIqVJjIoAQcd5z0K95rX+bbBc5Wmie6dtsdjPiOjDsWnAK27yLj09H98YOoafgPbZPKL8YHWud9TjrUZFk5hMjD33DcG2OKg32gXjhRPfiIH7WEH22PlsfWp9SU/RCyvfpPN0nrPenLH9C4nKMuM7SbVu61Z7l40u6Jll0Kyk4PJjhgeAjnbPYUZPhQmRbZgQfKYVEa0Vh8heaBSFSQ2RD4Orr1zm/d4rKNKvTFU3ToU2yoZZKkpnkNJZ0SnXi/7Y9SinyKmd3sWWz3KIiyX2oyChrQ304ZXu+xjY9WQh0NoXJxRDo2h6lFW609zVaMSx3uKbj6vGc137sTXSVYcPAtlvTupbSpAunEBKEp9ESP9LqpNxTHURuzq5Sndzh6Z8+4pF7zBN/wTwvWOSa0ihcjATrUKMDTmgt9cmc0FsuL1vOkVxXDYsbE45uHHF27xRzMCWfF6xPl8guwNCxPF1y/o27DFemzE7mvHbrhNn1Y/ZnGx5/+xGhd5S5IiskIoPeDUymM3RRsb/c4gT0IU31zFFy71II7ABxcKng1smsoQ0Dh9OK9mJD8/ic/E2B0BIrTMqSKUwqNFWiM9W3jtjeO8OXBjOrCE3HYEFKS9stYblNXPpZlWhvz2mZdUHIDXHbomKA505wWoL1UEjErsWrFltZXNsQljukKvEChrhDznLCxLO/2ILrwWi0luAdtu+JeWqGotZkmSYu90QPZXZA1IqgZZp0xkCuSdSwSWrewr5HAU2h6aqBrMgors/xhSX4TXJue+aw71zS5j1NOVJYVDtmlEh6HLbtCTYJsYXRxEoTQqRfN2TKYYoaLQvEusUHUEaiqoKyuEk2mTLEPWenOc47us4TXMPu4RnTSUlQgvL6IepAM61yrDHUoqLuyoTo5A1P+zNMlXM1FBwMFbGPSBlAuWS04ZOOKI6aHw3IqsD4DLcnuZnZPulsspTxFHwgdgNt2GNlizaSkI0Nx4guyLrEeks0GlVkBPoUHuqTUQNjMxTG0GotEp0uFAaJIHZJeO+cQxQGUeSE0YxAjgMX4f2IMEbQkux4ij3bEENHK3qE8wn5kwLhAsSEckkiosoRukAGyNSE0hwQjEJH8NHhhEMw2ppHkBHk8RThAwhJsB6cR1bJZlganTKtdi0izxBNOxo5AFogjMHt9ihB0stMCtg7gvPJQXDfEruB6DxulYFSDKKnG5ZJ5yIOGfYdWZElFCNEhmZA54btxYYQIrYfQCtmixm50QghWZ0tCQJi78kXNf22QQwe2gFd5Qy7ju7xkmLq0MJjZEZobdJuOXh/VfjR6+jVq9im5+LhGT5Gjm4cg645fXD5ibubVD1C9WT1QOhBq4LOeap5jd21KA+y1CmeAIFRiXpKBJlrtpsdIQSGtqea1Wnf6Gxy4JThfa8dQ8Aud9g4EBuDNBlh26BnFebqgvbRBX69J27WCSXMDL6o0PMJUkpkTNoYYXSi0XUDospxmz1r57iYa9p+YKILhPPoPEOogJdQ1AWud+R1QVGXiQUqQGrJjemM4+M5+NT0v1+//xLd8ANLPP/f5yjcn3d9xOsJQNAhBGRTuPblY4iR2Q3D5OKQfHGD9f0zhqYnREExqei3HeVsQmY09/fnZFWPkRlX9oKjImO9W5PVDeVUc3Q85fqfGIpoWHcu0eucx48a5qquiZ3DiYBWAutS2O2kKqi6LQfNhnpWkU8L4mRCsw94F4nkIAI2tPj+Ervaovoef7Agr4sxiy05dobBjbTckVLrA956fK642O9YzI5e0JC/+4H7bH22/nKvTyWn6EM//jkQn+fyI/FR93vpJd7fBL1fnRmFxHtYn614cP8uj5YwdMn9xmSGsswxRWpumrYjIKhmFbODCUorpJY4JVnPDBZwyx1mP05tdApvjRHKwwlH85q+6YHI9mKNCFAUGX1vKacV1ZU5th3Ii4zgPNoo1pcbJKmR6bYN1nmmVUFvHXldooxic7mBCEM7YLSkbZKotV5MRqcbx3a5TWyRGMnKksXhhNuLmvpg8p7QHIEUCiU1SkhA4jrPbr9l314i65oicwQxWvoqTXXjgOuZoX/Y8ZQHLHc9ftswHSxFkSg/eaYJ/fPiTTGdlEyXBcsQOL/7DDubogvD4bVD7j29xOXHGKkIwMH1Yy6fXrDf7dm4novHF0wHya2jOYtXjnltWrC/2HJ29xnCSoppThh64r6ndaCNott3qDJD5pphP2BkQssEIpU8gVToRssuDsiDnCxMGPYr+h0UBxPiOMKUuUEohTQq2douKlRd4HcdoihQdU0VJJEeryVx8DgpkG2y0n0eqBq1hFyTqZrokk2y7ywBwVAbcpOQGi53cKgRswq5qIkNKJ2lrONICgJ2PgmtqwIi2G7AqBI79CAURaGxqy3BOYxJaEAAUImGSGdT0OOkSOLpfjQTOJygwyWT6phsXr/QwsQYGZ6uiA83KB8wSFSUqQB3zyleYyGtR/cx51E+gB/A9TjXIQto4yWiiYhFSbbSDMslulLIiSR6BxnQ9MjapIDSXFBHiE0Hg6W73KOnFeraAdWiZn7jVcrdTdzFFrOwTCYHhKZLA4zxuvD8fJdaEaVEWIcOgRDAKYmIEW0UIcKwaxKiY5IVuFfJslvqRGsL3qfnyBShD6DAaYUoFK5px5wiCXF03JQiCejHNyOkTE1OFGmafjLHnq1H0wUHwZMdHzFc7t7TUAiB9z6FtsZEkc2uHyb62+DSFc+BlBpG5CAKO7rhydGmPCbNGUDuE2rkA2Q5UmiUCwjvXzjtqSpHTQqGp2tEDGBTZpGaly8up7oqsesdxEBylhHJcCFXqKpEDZawa8EY3GaP1Bo9r4ltj55VuG2DX+6TDmwMDdZGE6yjcIapFjRnlwghqGcT+k2DKXMcAWRETwvctiP6QGt7ul2L956DkwW2s9imxxgDIgVHe5ds8NcPTvGvDegqoXVuRN/c803ku+xBQkiufuE29WKK7S3zm0ds7+/H298rPD+wLaXiO0TKumB96hEuMJ/X2BCYXVlgm56+twm9dI5+SGiOJBXK0ShCEJSLCU3TIoVAEzHKYApNJkzS8gG+c6nQ1hlBa9i1KK3xqz1qVpKdzHEh4rqOuN0QnUVNaqSS9M6RZRqFTEGyOqKKgrAf8J2HTIFKtzW7huA9GE2RZeyblqzKKecVrvdENNnxhPxgkhzZ1gPCgychq0KptK9H/5Flwft+/h6stv9sDZN4UUuEBNKOFM9EpzRHU6aLq/hQspjeBB/o1w2bxxccfe4Kzf1T1o9WiM+JlB/oA/lJTaYzdJcoyfnRlP3lJtHuB8c2pGt3KwVlnmiSbrA0+zbZZ3eBPM+oqgKCZ1HnXLtxAz1S4LyHGBw+enYXW5TR5EWOKTLM0Ry72qbhSIzpvxDSXuYDxmh8CDSrhsh47c4Ng4tYD0iFkOkIpnFKWv4l9DF1sp81Rv8t1927d3nttde+r+f41V/9Ve7evcs//sf/+MXPf+Nv/I3v+XX/+T//5/zCL/zC+27/hV/4BX7xF3/xxc//9J/+U/7lv/yX3/W9fOUrX+EP/uAP3vfevtt7+b/b+hTpcy9R5/6s362X96vv4XHv77He++ls+gabZ5FHDx/S+g6hDcYYcpVCLdumozeKrMiYXVlweP0QpRXdrmXzbIXtLUNvKfqBaZ6NIkqFVzJRoGJKiT+5c5W7X3+bdtuS5Rl1XTB0A10/ML+yoJpVnN8/o9s0yY1Ha7xPj1dG03VDCoubT2mbDqUV/a5NuStCMLSJ3tP7hEQ0bZc2pNFaWUpJMSlYXD9EiMjxo9/lZjFDbSruVV+gGwzdruXW7haTkxmTec3myZ57f/gOzkWU/hMQknWp+NUv3eDglSuYqiSSEw9K1FHOX/1GxfZig20cvfOJTy1TAOPz5m+/2XN47ZCbJmfR9Oz3G0T+FL54i4Pbx9x4fI795hNMZnhSSO6/cUR7UtKeLYnOQwz0Tc+T5Y520yBzxeHNY8LbT+Cxgq1mpnP+ptIIGwmzkv9dCTaDpe0j3wo1i/mELrRoKVMxEQdu1Q3BOiywPfo8xa2c5sF93r58QiGm+PicLjOGKO7TpK272CZdhA9UzQHX3/yxRGHavcXZ6bcZnKeSOYE0TY/OA5HYCoiB2DtknqUzssqIreXBs/9KmedICV3mEK1HTirCJE/6kq5BGE17uoGRaiEEmGC4Un0ZU2sGu+fh7vdAgnzk8PsOrRST+gpX6h9ChJgoNKOeQ0zzZPc+OIgBVRiGTcOkOGF27TV0ZnCX20Qp3XWI5UC0HqsVPxi+yJd2PWGwqayQKUR0ks0QNtFQg/NgFMV0yq3hK/hhILqBJ+/8OnGeEbyiG1ripKAJPW+d/QbOerJphsuTk1ldHHBdfREnPfJGQRBgpKBbbnFPdphtQeUWRO3JTubcGTIOnhW45Z7aq1EYnihbIjMjz75ncB4zuq5plVylXJ9QC6wdtT8RryWPdn/MIBtUYXCZQ/QCryIP1r+LGnxq/gqD6BRSGG4d/Di5NoSjPVrohEiJhChJUl2XQmQjUiS9VPvkCY275Nn2j0FEDu0PM7dHKT9IJic7NRZwz/U4clIy3D9H+sBB+Qaz8lZqLnIDbU90ntPuT2niOumarMf79HyPt19HbiVSam7f/GmUN8nwIDcIZxEhQJUlgfZgk/mCUohMoyflC0dkYTRojarKRCuWgjg4dF6A95jjBW61RYiIiCJ9H/Yd5vYxMjOIKse3Q8rO6SzCeYJNNKVb8iFXV/fZE/mOfp148nmWz1rc4MgKg/eBolIErbAEimnJfFayOVuz3zRksxLvE82427UYpZA2NbaTG0d49whixjYG/s+mwY0ZTS9K84/aY2Jk/7Th3v9+/32/3r31BD/4MUduzIUarc7fe57IlbOOQ9vx7I8fc6WdEEXFNGi+YyJ7H3C9RZVZQvadp5jkpMwqyJRk27Rks4SG53lGsC1fjn/KIoBGkx8l1kHfRd5pFnTrAWsjQqvUdMdAaHrcrsXMKtS8TnlV8ymh7SEviFKQaYVUGhGSllIZTa1vM8muYGXLI2lYX2woy3ykQgqGfkg2+kUGAvIyx/ue9XqP3DaYpytCjGy1YnqywHnP9Af/OhMRCc5y8Sf/P8LQvjjOz2uFl9GL7yL3+t7Wx8xLv3XR8O6y+9CLBH4fonrvFzEi5pH/dzxlftgTMkX48Tuc93tyrSgf/BaZlsyuDtTzOdvljsLlfOd8j7SCnRT0Bym0PCpB0GJsUiJYT9N0TO2KH7DfoZ6WvPrmlNcPB4QYuOwPuBdeZ7Pecb5d0skaGSW51xzOagqtyMwl8uxhQokyQxRpAChU0hTZwfGO/hyr/BjvHU4kyty0n5F/cc4VpZDR8+b2Dyh8iwuR33qwpXOB90+lP1ufrfevf/fv/h3/4l/8izSI+pj1R3/0R+9riP5HXZ9CU/TBK9FHXNq+1y/aR42S4of//aGnG4vcPmi6rWW2OKEWIgWt9gOrbYsncu316yxuHKJzgx8sqwfnXD6+TGiSFGkjAA7GKY+PiWdsRv704BxVmbN6coltB2aTChcDbdNTH0yoZxXtuuHpW4/RYwOT5YZ6XrM8XSGBrhuYzGpMmaEzwzAMDGPuRmZSXkWIUB9M8YOj7wZm04rBJjtXISMDCQHbXWy4+YWb1I8GRLdB60A37HjnT5/he4uSkvPHO/aLCaGxOJtTlDl0w+i6E/nW3Q0Pnrbp2Nw6RmaayWLKq1/8It2yYX+6Yrfcsd82DM7RdgNGK8osw+97hFYsZhN0Z9FCsXlywdXXrpJNCm69do1n33mCGBzWaC7We+rDKbeuLRjagW7bIr/zDHrP9mLD7MocHwLT4xnNckcmM4bgmF/LCfuWZrDEPGXVZLnB9Y7Tsx11WbBrerQucb1LlBQpGQZP00XqK3N8XjOcR5gl3QSQnNkyjd/uUhDirkeWerRF1qjOgDDEqMgXNZYkqjdjoyBH7YjMkxA/KJkobvsOoRWddJg8MshkM66CSIJmm3Jk5N5iB4saklYsKJmyemIEoSn1FIHEKc8Q9tDbpOnwHqsUWTElSoGq8jRpXjeJ1iUldrNFW4/oE60pvdGM/p0Ng/Oopsd7DwhMZvAkM4ciKHQPxCyhJlHgbEx5PEonhKzI0IuKfrkjdkNCIqWh7Taj61pE1QWiNCAiPu5RBoK1yBhTg6IjKmRkPmIbSZalDKDJoiTWh7htw3B3RS9W6DxDGsNC50StEToJ3kUAnSUk1g8dOjOp6B8RI+8DhFSMM9JPUSnfJZ0fW3rTIlqB71PDpADn94jSEAQ0/R7jJWUxYTI/Im4GRDlqZ0a6j1SS6DxSpYbaB49e1LjlLv0cHX3YIRc1tt8j5QleqdEsQaRw2bFANNcW2PX4WYdIbirKbJbqleThDApEpxDOgdKpmRqpez52yX7bKwIRIwWxdcgiJ272oBV6VuLOdwghiTISBehJkWikCISISCUQeUboUzabLLNkmvHGTYbTFX7bImYTxOAQVU60nrjeExY18sjgx8wsu26ITQ/WJTOLsqASHmcsxjpKEXj87BJlVELvxpwtbx2+7ZOOZ7eknE9QUlKWOc2+ozyeYXcdRW6opwn5jM7TnV+wHc6pvnQdH+EyeFyIYy/0SRuRINhAvxk++l6CF0G5H9rhokDbwMG0xpwc0j7L2e4927tPkDcPsEFhFhOCAOcDAxEvUjPkdx1ayWTfPur0irqEzqMv1+RTQyEyVJ2MFLrHF7Q+EoNO5/TgUAfThNpJgXDJAU7Pa9xaJ+MfKUaTj3EgsNsjhErXvCHFTahdhtAaYyS1Hq8ZSpFrxb7tMJMC4SOqd3RnG3xIGiOvJWFEZFf7jnXzFGMMWVOQH0woj2aJto0YkQjeQ4W+zyL8e22kOhfpPkidjADNB35Oro7KR6aVwiuPzjWxh/3pEr87ZbNa47TB2kg2m6QsQpLD4+AcRWagzumdw+16ZnVF2w10w8DhYsqJErxaV+SHEyaFp9AOu27p95q3Ls7YNl2qBfISH2EfIm7vOKkM2kXyukBohWsHhE4W4gHw7YDbD3R1QatqLCnXbPCe9WlP1e25eucKJpdMBkMVBqxPw5sXf/7393F8tv4c686dO2y3H+3S+Ou//uv8rb/1twD4V//qX/GzP/uzH3m/siy5e/fuX9RbZDabcXZ2xn/6T/+Jv/N3/s7H3u/f/Jt/8+L+m83mL+z9/EWvT999TqQIx/cYvd/DZev7+ia+9OAQwXtyJSDPubhYs2s68qrg6NYRV79wE9v0PPnmA9anK5x1FEVGXqTpfogglKDrBrJxI/XOo4Wg6TpUkeGJnD2+oCxz7BjkOjmusO3A6YMzFFAUOd1gmR/OUFqxvdygBDRjFsT55ZqqLGj7gWt3ruLO17jBEZRksI754Yy+6Wh2LcWkoA+RycmCYddi9x1ZrsmmFYevHKOnJepoQcw8q23HTvX0LpAXOYWUXKy2dO0lmUnue23bcXjlgGHf0fQ9dTkBJXn0J/dxg+f4jWvEmAwE8qszsuMJk33P7umK5nTFftsQQmC52zOrK5ZvP6E4mbG+2+H6Adf1bJ4tObxzhYNXTthdbFmertC1Zvnsku3pksPrR0SgyA2TxRTf2pRariWPv/OIw6sHbC93rM9HTvz1OWiNbboXga2+tXgpKOY1za4l+ADBYmKiI2ktkUpgt1sUR+QHJawiRD9m0qSgTF1m9DEme2KlEIPAlKOjj+3pNy2yEIhMMZ2VeDvmWZQZdD2SCENCY6gMfpuK0tgPmCIjtAMGYF4hXMB3A+6yw5VbtCqJZU5cpyJfagW9hc6ilUHngSiSq6AIYfwbU9L8c/tlOSsJzUDYdaNIH/pNg+wHxJDE+9Ik6k0YHNqHNDkeMzocyQY+GkUsc9SYc0Q3EKJjiJ6gBRlynEhDcBb3bD2+p6Sfw9mkdROjYHnf4Zv+BcUsxEj0EUhZMmG/xdcdQSqijfhdmybnMrkYSiUhMynzx9rkxEQkColSCpMlk1nf9am2UiohZaPOy6FS8yVS7lSIKU/Kk+iraIU0OVkOelokyqV1xE2bhix7iyIZZQgjCT5d24JSCFwyTIgjjTSmBsn7pHnUxqDynOF0hRIp4FgoQ3HlEPd0T6wEUqUg3+jTZxyIiEKj6pLu3mmqIWWybH/5GDIG0orxtV2IaKGQmXoR0hti0qqEvsMJiVeROHiESRNsYTShG4CUkRRG4waXHCoQCFRdJHts8ZxmKvG9xV5uU9Obm6T7GRwhpiY45IbhYoMbXBoMZBlx3RCcS3VwljK8ZIiYMZ+oVnAwzdnsGpwHUxbJln9wo9YqUBiDdw43WPrxOh06y+TqAZvHF+xXO3SZYcoMHyKmLrDepyHFy7vEJ/dEf75tJz5vRpOBQfH6deTsGuFeoKTE3jlh9WxJt2sTGigFZlYmijQBWWVYAXkxQQjB9HDObrdH+55iHLooH5LN+d1n+LMNYlqBksSmR0pBfuckXcP2Xco16y3hcpsaVR0wiyn95Y6wadM5HiJoQdi3kGloWtzQIrLktid0cvfTmaZpLXlm8N2ANiZZixuNlAKnFTpE2rEhM7kmuIDONLuzNcF5yoPywwftI471940SfdR6Gc77OO7eR3QDUQiCFPRdz7Bq0VlGfnJMMYmIqsTZQHV0xHK5R5gCXWSEJpJpDbnGheQs6K3DWYdzjkx6FmXBlVtHVJyNCHPEWsnubMfDpadRV8jyjBhDsvkenTOFFOxi4OBoDtueoR0IOsN16brohjQIjIXB55p+cIQYcD4hyCEG9i5yb98iQ+D6dMPNKznuOV3uY6iLz51rv/tA4bP1511CCCaTyUfeVpbvfXfyPP/Y+/1Fr7/39/4ev/RLv8RXv/rVj22KvPf823/7bwH4+3//7/Ov//W//m/5Fj/V9ak0RR9uff4bf4HGNyCUHAsMuDi9ZPCBm2/e5OCVK+hcc/b2E87vnSbjgyJPVIbBoTPN0Y0jysWEfFZy8SBdtIZVw2a1I5sWlHXOWzPN4AJFKXl9PRCsJysytuepKxbj1Kbr07Sx2eyJMVmuIgW50ZxXhvNplja51nA/DuiTeiw6BoTIubJqOQyRxbzi2wa2dU6wPbeHnqNZxfz6AfdPajZX50nD8mN/neZ8xXa1Y711iFcW5D5w5zLZYheZIR+tyEWEfFpy7Uu3mT26QN17llCxSc4f331Ku9lz5bVr9PMqFekxEk8quLNgsmq58c4F0Xk2Z2u2mx3bTUN5bcHRzWPOH5wRnePsnad4Hzh+9SrXf+AVimlFdrbi5HSf7JwvHo2IWGRAMFtMiSGwW+649uZN1k8uEQKqxYR22/BHDy6IIRCigBvJGvj41av0u47N+TpNmbXEbTpyGRMdSUiqsOGVs//CF7efBxPoFyuyqqdVE540U4igJkXSZgCL6hYn9ecRWnHZPODbj/6PZNrgQNZqpCq8d25fP7LMK//C/lpkGjcbePcudPuAMUkU7UNEdUOyTo4pgTwIgSoyou/prUVlimAd0Tkg4rwb7X9HZMWHlG800mVUXSKPpoSmJ9oUpCm1Sudk2xNsEvBj0meI9ejBE5VAZhk+eKTWqbgPgTitkWWeUI/xs/ndyduc5RuiVPzk8k2O3BQZQtIZCEEQgafDH+J8g9AKK1LYrDDJqEA+zzLRiiAkmS65Pf0xkomwQIoMSIGkgeS2KIl4F8bE5Ygabd6VScitGKlLwY5BuSFZCKfA3ZCKvJjctrRJAZ8uWpxMz//cyty2QwrWVTLRH0lNqTpOgZveJotzIUetWlUghvRZPLcnFjEk6tnoXBW9T/Q5GXFn63QVVIrSHPGF1/8mKI03uxcIUxybHO+T65WaTXCje2UcPFaJZLMOyUzDjvlEIiFdUSRE9Ob8hynyI1Rm8E2HNJrgLGfNt+iaNUEKvO8gBsx8SmyGpEkaUSqEoPOR33p3jQuRaa74yes1EYFSEjWbMqx3yDLDr3aEwROaDpEbICZr+MUEO7hkId4NhEiizjFqn2LKNVJFTogpTFYoyavdW9y292hC4OvuDmftjIOTRXJulIoQAi4I8BKtNSHCdFrTbRu2vUUJgcr0i+Yku3nI121ktoBsMSW+vUrnknivQfqo7QM+uTAXpGL5I8d8MfLN04bvnCeK2I9eE1z5Uc2w2vPNB1uoryJVop76bsDtkq35INK1OA1OJHtnyaYlWZlTRUEWc/KJITuZAQK/bVOgc59staVRYB3ucTKBiAjkKKKJuz6hjU6gb+S49T5FB0j5YhAiR4fCp6ffhPBt1MGEhps0LtHKxXhQiiKnbVosApVJOjukRr8XUBiiFBiZNLdCKwbryOd1agL9dze3+FTWx0Idn4CBjOhQfOnnKOD8SBELTQiaG5dfZLZ0CKX4/8Q7VHeugJIErZkdCLSLHNgOf75DtR0awepiy2wxpUvu+MztKX83+x1u3L5BdVhhYqI6X3Y1v/X0TR5vT+jHnMM4fp/SsY9pD4jQdwO/31YM4kvYpgMpcSIgFxqpkwZs33R4m9PZIVm5x4gUcmxuIrazBOv5r/o13pi/SvSOQf4KyYXkw8dHfBzV9LP1l2r9/M//PL/0S7/Ef/yP/5HVasVisfjQff7zf/7PPHnyhNlsxt/9u3/3L3lTFBP94oOThPc2j4/hwH3X533pIS///HFLJBoLRrHZ9wzAKz/yGotbxwTnefSNezx7cMqkKsmNpu17irrk6s1jTJmxX+/Z3n3K4c1jTl67hust33n3GXK0xxZa0kSY3zii7B2V39LuGoa2T5txkVFMy+Tm4zyby02ytB2LF6M1LoIoMphVNE0HhcEpSTdYJAqMwFrPiUqOUE3vMEezlGMjSM+9bzl7p8Pf+DyPvv2AqiqSbNIr5PyAQnfs9x1h8OTzCUWRs11ukvDWOrSSXDy+4OD2CcdvXENnmrN7p6w2Dfn1KbvNnvXvfpusyJgfzylmFcWixlQ5kzpncnWOkIL62pz4zQc06z3BBdpdy+tf+VzK+BjSdGy/3jM5mHD8uWvMrx1w/4/eRWvN0PUIqSgmJZtlygVBJmpJjJHrX7rNu7/zbXarHVJJusGlaZVKVr17a+H+GfWi5vDGMcunFwSjU8Mg05ScGFEC6swjmhVZXRCEJ8sShTG6kCiGVY6ZlbjWoqQmz2q8j0kDIQdCmSejAS9GvUhIYapSoGXEhCEJ3RFIKcjmGWamGMacmmh0Mj4YUZYIEAI6N8hMExtBXuV41yMzQ8gNSE+0YwaOkgxSEDOdQju1ol5MEEVyuwvZgCiylD3iPEJnMK0S8uE8sukIOoVGijzx0OM+CdijlOgY08Q300SZCqrnRf+gHXuVMpkCiRaWZRmC53oq8KFnEAMhRESe6Dp+3yYrYSmII6UshAC6QJkaE+WL72xEYKROFt9jAeX8ADGiR4toEQKehFh4axNSCASZCmWRmdTwh4ggNaHeuVT05QYJTEYhchyRlxAiuSzRRY4PyfY5hlSQSBVQ0aemRaTQVSULok85UjJGHBCz7EWivGy6hIAl8cmol0gZQlJIypOrtPdO0SLRI0fiZZoKj80XWpLVBf3jZUJURk1HmhoncXQyhEiFXACk9egyI6MgWMhUhRQKbzKG5QYXG4JUyVBBJzMOv00UHUban1AKURiabXLf1OM1L0bwg02OmUWeUPOqSHS6uoB9RywzBBG3bYhaEYNHek82q9HziuHJJSLKhBZpjegGVJkndLK3FGWGu1xhqpzMCIwwtPuOalJimyEV50phlHoxcNqvtshMJye6bqCaTwi9pVvtyQtPfqWgDZ5+u080sBcbyPdf4T3PeHmxHY20x8FHhlG17sOANBHXbeiGCj1NeU9NZ5G5wY3nczGtiNYlJ1GtiQiiCwzdQJElYxmTa1SdjrkXaYAgtw0iM4hJmTKm2gG0xExKwrZJf6vRad+SguF8A6NhgigUbBsUITXRg4NC4XYtLipa5ZFSYkyidkut2G52mNykbDMbyYQky0wK0FY5inTt8ENyJw0hUfh655n0H2fM/f2v71pJPNcsPb/jCznTe8XFyyDJ8xrGK0EfPcFDXFn84x5tNPf3a9RacPTaVfZPTum7gZPrxyityK4vcLuWTAVK59KAlmSqcbMy3LmWMT8AITp807F+9ymPmhnfDFNUlpNrjfAe6z1aK4bejmHVkbbpqMqC6BWXFnzIEDEFo0ct6dse2wWULrGdTcMjIrZPA1+tVdpbnUcaRS9yVg0UVZHOuZcPUkzHLfWLoxkMvBdW/Nn6S7d++qd/mjfeeIO3336bf//v/z3/5J/8kw/d56tf/SqQUKKiKP5bv8VPdX069LkIUbzfKvujJw+fHkz+HNp9kYI9OjmZScHmYsvrP/4m05M5zcWWZ995zOWzJVVZ4LynOqg5OVlAhItHF7TbBiUEbT/gBkdxUkEGk5OazdM16+UW6hxTFOxPl9jWsj7fI4Vgce2A+nCK6y39rqNpB4SSTE8WBAHBBdZnKwYREZmhPpiwUYJsWrM6XWJjylLJspRE7W1gcWVBcb5jvdzi255qXlEuavrHK2aTOmXw2IQkdJdbpidzimvH2G1Dc7l7YevbrTuuXTmk27WUswqjFNvllmFwXD4449rnb3BwbUpVaeZtx/3NEjFYJmWB6y2Pv3UfLRWTWcXRK1c4Plpw+egMQuTozlWufu463geqWU0k8uSdx7z+V95MOQmAjB4ZLJvLNc4LXvvxN+k2LQ++cZcYA1mVU3QFwxjEKFTk4sEZ2mhu/dCrPP7GfYT3tINjejChDZ68ygle06x2dG1PlhsObx6zfrZEVxkMSYD9/EIvlEhJ6yEkuqQQqFwTLoc0hW56zOEEf7YlBk8IFuccamJQlKmoLcx7BXJevJjgeSnpep+0LKNeRgC6VCgrkSHShpCK+zjqMpxHtAHCQNPv8bsNYnB4IwjOobTCxtSUeB1wzY7oepASLQVGSGQbUkipqRCFQLqAyDRIzxBBNn1qCofnxgKkpkNLsJbgXEJMRkoZUhJ7h0WACgRhGWKP8B7jItFagu/xIaPrBzQmPW+hiZMCJORVjo0Bd7kF5zAyJ6CQo/WTignJ8u2eqFLBJkeNw/PBQXAe71O4rJCSECQupom11mqkYUVs8CACOAdRIWxLVMl0QdcFsjBIqbEXKVvmOdVMCAFFjqgLzODw3jMMKcRV+JBQMiWJfUgNIoJQJUpMEAItNGKqRgQrNSrJ/tbhtUq5Yj4QSAghQiRaZpWlJql3L2y1GYuR8bTCS0F2Mmd4cEYMAmlycIkiaocWOSmgSW5Tqa4bkZSxcRLElEXTNQQ3pAJWZeAGTJS40CPzsYHcLFORPJ6vUUn0rILtSxoLOYbjuoicVPh+INgBqgJvAyomVECUecpCWjc8hxZ8BFY74qYZtVEBWebpb/YevEOK0bWvt6hJge8sOhfUZcEQPNZ5dG4wUo5C8pDsjCOYRYU2GhEjTkicAH1QM68L2vNTbNSEy55iMb5mDJ9I/4kf3K4+YhD33fYtQ2qe07HTOJWjTo45CIc86hx+bELpHVlmQElcP6CiQGmNmuQYIWheGO6khj6FbjEahfQIkwYPQicb9+g8wUiGrqOcp1yyaF26FpU5Mabhj9AqBSuHHpxLIb6jq1q/7wn1hH7v6LVFFoJ2NPZxIZApTZUnimM2Gjg0bQ9Z0rZURU7XpWtONanZLzfMpjWyyMgzPR6951Ss76Mx/aS+ViSTRPVcJIOCMRUsCJEs5SPIkLLC4vj79M7G2iUCMRCjxreO5vGa/eaC7TpSLSYU8ym7fuDy7ilhsKl+ePcppz1MDqecn63oTiqkkrR2wFpHNamYTgLl7asEIfCt5eLxhoerlm5yjCFL1yUtQUQKk7SA0caRWiuTs2iQtIOjdw4CdF1HXuR4UmA4UuC65LGox4bY5AbvPXY/oLUGna6z7XrP2cMzbr95nQ+e2e9rhl5qKsX387l9tv6HXz/3cz/HL/zCL/DVr371Q03RdrvlP/yH/wAkVGkYhv8O7/DTW5+qpuj9KQPv/fu5yugjUwhe/tVHbUyftF4aBD3njB++csLs2gF5XbJ9tuL+H75L26Ti2YfAlTtX6buep28/QSAwWnJyPMc6z3DhKQ8L/uvT38L6gWye8+WbX6Y53bE6X/MDa0uIyTyhvHFEUeW0+47Td5++EF5LkbQXm77jfm1QWiKuVOz2HXkuubZtuH6xZzqvKecH7M7XiKholx3Rt9SzCXXv2bYDmVZcXXbIzYDzgcPbV7n2+rVEVZpn6JuHrB9e8PjbDzlaN3gp2e27ZB5gHUNncb1lfjJnv205fOWQ7XpPUWlWZ2tuvjLj1voPwVrs1DCbNjz+1gN255oofwglJavtDvFsx+zZnqMf/RwP7p/hB8f2YssrP/Ja2oC1Yn71gPP7Zzz+5gNuf/k1pBAcbu8yb58QI3yrO2a3FkwPZ9QHUzanS04fpBBJrSRDNyTNlgs8+ON7XH39Ovu2RSNpug47WK68epXXnu7wMSLLnN/3ln3rsXefAgkplFK8KKJebMIR/OAo5vUL6pKsM2LvwHnsviebFuzaZ7xzdpoQvolGlQofkv0pQpBNqyT+lqnAP91PEHoCnedmvWHWWSgFt2d7nB6IPnIvP2DwGr/ckYI+DNH13Hv8a4i6AO8IE01sukQPcgGhJW2z552n/9+EjhGR3hKtR8eCVw7+KiiFMAYVFFJJ/GiZnHdD0iWR8kN8blAupByd8Tug8zxtfOPfJQD6ASkiv1d9hyfZE+Kh4Nr5ns+tG4QLrMPvsQ3Jlvu11/438tkx4ClOM+hauvM1b51o/FVNdnzEX9/8CDkZYqSSijJnKCMPzn+HICJmtAUPIaTwzxATvagfiKPz3aS8zsn0hxNlTUpUiAgJ2+Eh581bqXFUMhk9lBlC5chlQDrPUfEFZhynXJbcEElFafDJpUsQMRH8WHQLKZE+4EYtjzAG6y0Pz/+v1FCIjNvzn0AUVWokR2RKWpcaPKNTs/niuhYhRLSSZFcW2MttKtF00jrF+J6ehzGkV4otrhk4mn6Ow+wVwgSWw13u7v4vpKg47m4zMVdSKKsUiNEtO4aAixFlLY82v0/Tr0BIbh7+FYyeIPA8WP0X4qwk+tE9MEYiASFkQvgy877rc2j6JOQuK0I3YI4XhNNloipOJXGzT8iPT0hX9ONxKLLUgJZ5onFZl87TSbIh9t6BT81ksMmi2iymhAil0SytJauyRAVTkr5NaJEnopRkWpc0uy6J220yt/CdpRojE2wnMLsfJZ+VyZY4/EpqLNSH95qPHeF9YJt6348fsS8J4KfynC+Ozkxfn3yJP5xfpx3WPNs/w+MJWhOHAD6J33WREQaXTAhUap6tTfTm2WJK5gfi4MiuzccXEel4zWapwTxbJeRapIFH2GzRr9/Aa409WxFGep3wjGJZgSoMtk9UMFXm2E3DsOt4evQF7ptbBOfZd2HM2NFJ39IPYCTbXTMi2p5cKVRZ0DmLKfMUNJsbkOlarTLDmzvHpC7IVgPnPtJ3dswG++iN/XsamH7wofHFoSFGePWg4IvHSYfhwm18uAkCnkwMZwrsvuPk8Zqr2tAu9zy5PsXdPEioTozYbcv+dE00C5rLDZfnp+T1lExskq32dAoCmq6nKgv6tsdJ+M3YU+wC9c0Z7b6l2Xeo3GByg1GC7MY13tk+Be9YP2m5G29hpxFIluVCputPMRo6ifDcMltw4XLWoaaIgsZ6LAO4RECO41BGq6Tl1DK53Np+SJrF8e9SWUIhQ4jJWd/oZPn/va7P+qG/9Ovnfu7n+MVf/EV+8zd/k7fffps33njjxW1f+9rXaNuW1157jb/21/4av/Irv/Lf8Z1+/+vTN1p4eT1HZMX3+AX8BPrvh9d7s7+Xpxi6SK5uywfnvP37b+F9oMwzgg/U04qzB6fIEKmqgklVsO96pFIMTY/SknJaMbiedmgRRmDKjO3lBtdbTIgc3Thicjhl8/QyaWjGIluMrlZdP5BlWXL7KTNQgqG3mGmZnMW2PRMp6c/WiNYym9d0+5SZJIRkd76mXW4xJlm/tvuWqi65/cVbzK8dANDtOi4vL9kZRT4tKY7mrC636DLHEZlWBUEMSBrsYNFGY3tLiIHJosb1ln3T0W32mDggZIAQWJxkxGsTVj6w3EUIgeO6pul7Yu9onq4wxnB0/ZjTe0958q1HAJQHNUe3jjm6dczjbz1id75lejJDBovfbcjKnKNrC0x5AAiOXj2h3ewINoXcSS2ZXT+EGGm2DYurx+xXW669foPm2RIfPN55dmdr8rrAOk9z2aNOqsRtVxKlJF03kGcpQX4IqehUCIQP6EmBx6ZTbESShEyW3DIEvEykLKchioAMIOIohkck/v7oDhetI2waQp6BJaE0USSzAh8wuUSpDNc7jCzoLvqUJdQNCXVyHu8t7BOdJo45E1Ep5HpPzA1kiRZh8oww+GRrLAXCZEhVYvIsOT8NDitAZgrRpg0z6oT+oCRySJN6ntOetE6+ACONjMEhvEc4jwSc6ejnMtHVHltM50etnscRUCLSX2yIlx60wPkB3/ZE7+m1IWYKETLkLieLSaAflSROpohhg1OeED2u3WEWFeXxLFGGdi2xt/idR+VFEvAHickMQavRHCMSM01QBislVgqKWZX49b2Ffo/qLVIIzFRiZAoH9QiC9yglcP2AiBEfUxOGkEj3nJrp8CEkVEhKvO9xuzWd78jzCaHtMX3KKlPPtVBljjQKJVJ4LlnKQHqu1RJKgtaEzTq5zPlAdKkwFRGkEEglMPMat2xSblZUaFWkosc54kTiux1Rj3lMpNyrKEgaEq3QVYHvemwYiAxEodAqRxcTaJtkH15m+OUuGWTECFITiUnP9oICnS7CbrlD5Rpdl/TbBrf1qBAJvUX4EckcLAwRioxYZMSmQwoIvU3nVW6S2YH1SSdFcl/0bY+e1UQhCV2P86m5KYyhyEoG6ygmJe2+RSo5DrzS5HrfdGitqKsR6XCe7bZh6C02RobW4nYd5T5SHOWp6VcyUSNflhXFRN1MHfvHz+Y+aZtKP6Trfy4E9XNencwYVEEzbAhCkhc5zvtEBY3JXXToB4yQ2Biop9PEVlAKYxQiN6gQMXnaM4Qg0eMOFthVAz4k6tzoHhkHi5lOkJlhWO5SLEA7pHPHpSBjYsreEzGihEi5SbsWnxuaIGiCQqqMaCxiFOg3+zY1xlJQlDlSSFwMDBJU8CgEsncjpzNijMIpT55ruodrZmWOHEPGnzs0Il9CID7umH4v6yX0N4ak11IxksXEDghbSxSRfr3HX53S2IH90yXHTrA+W+N9YO0jCEN98zBlRh0UZJMZ4aJFmArnVPoeSIkQEqPUmHkFbdunGIE8oeadhL7r0hByPmWzbygzw9ErJ6gy0D3u2T0847QVtCdXUVIl2q4Uz8HAF0Y6trdA0g1WVcVqb9gHT2IXj3loKg2avffjdUzgfEBqmWJARip0mec0XZeMTfpkMnR4+4jjm8ekjvn95/1nJLnP1ket119/nZ/+6Z/mN37jN/jlX/7l9+UaPafO/aN/9I/+p0AUv/+m6M9wDF72pfvQ47/Xhmj85n7U3VSwGN9xce+M+3/8CCUldVnSdh1lWdDuGkyWEWISJaIlq24g7FoqmTbO/cUGcQhZnYTa+37LbtiSlRkxy9j3A9v7p9j1HkFEZobJfEIxKynnNe1yx+Z0RaclvumZHM/ofdIV7JY77N6y37TkY5r75dNLlBSYTKOkTvbDmcL7QLfvOThecPvLryGkoOktp+88gW2Hfv0YHR1n7zxBFQY1r3HeUyhNbQwhglWC5XKL0JJgJDEzxNwgR/tg6z27kVU8ROgDZDeOmE9ywoMFl6crtBIUWYYQsHq2xHtPNavQVcH5xQadaS7P1xR5zvR4jn73GRcPzsjrAhcl979zxsG1Q+wkQJk+6PpwyvzmEY++8xhjNI5I3/dsNy0616h5hd807Fe7lAjf9nQR+mbAh8jieE49Kbi73yKNYnY45+xyQ5ZnwICMydo3hIiyEjGZMAhFLwUIyd6mvzVKhaxKQmtx3pNPChRpAs3o7iasRxmFHyL6oE5aCCkxixq37RINhciw7vCzmjA4wqZLk93OEoRDFYaw7xP9a5dEsrQDUUv8agcHyTBB+vfCUrFJCE2IiLYfdUuJNqNMQhtkromZRgqRrMhDotE91waJkIp/pEQMqVDVPiSnM2OSZsQ5jE5UpEFKsqxkYhv8YMmcJtNlysDIIk5GPJJgFFFlSCOQlwIxpOyTSqbCK48gTMApAaUhMxU4T2Y0ZVZjvcX2A13bMzy9pDiYYqYl1dUFrhuw7UBWF9T6Cnl2ODrKaaQYaXv7gWG1Bx8IuxbfOGIXkApElcNgGdqePW3SH/UD3llkpxAhha+KGJOLoEwFW3iuAQOCbegEQEDKAi0EWheJ448E7wli1F55hw8dNkRUrlECfEhFjUFhrh0kl7DRZS76pNkA8N7ifE92MKIBFwMZOdqkLCwxIgGqLunXl4SJw/vkMBZEREr1Qr8UEOA8RmbEvAbkC12X9w6kRI1ZTtH7NIQhuVsxnkOFFrggyKUg+IAukmuhmhR052uUVsnlMAqCH1EOSFqidkg6F5eQOiEVUkRMIXEa7Pka11lMZqDIkznKGEEgqhw3OPJMM0XQCpEQTS3RuaHbpNDQKEUyphg823VCjJVSiCy55NHbtMNEyOc1emrQZZ1QrJiKTqnlexu3AELAu/67bDrvrVyl/yAykNF2aaizerrisjBk0/KF653KDX58DZNnKUsq1+QIvHNEIagyTb9tyaSi63qOZjX14MhziWgSlTTq0Qo8Jjt8tCJKQWwHGCwi16hZjd91SJHIYWF8jIxpqBGeD4CAKCXtcs9QTmgGi/OStm3ReXIv9N4zndY4H7AuIXteC6x16EyhTIotEL2nKnPadsCPjYlwAest1DldDOlaNQ6uXui7Pm6v/wBkJ0WyLRdAEBInzPvuFkeRZvSe0PQ05x2PL/dMjqZc3n+GyUtsO7ALHnFUkc0q3GWDzzUuRPww0D5dQmeZfu6QSMCu97T7lDGm5yXb0zOKPBsbiIhRCusD1npUpmn2HcIHohJokoHOdt9QGcXt1w4ojjLk9pLL+5dsBo/L65QzlCddphApOkRIQfTpfH5OvRVC0HcDw240tpEiXeMRSKlx1mOy5FaHj8kaHYEPHqUSW8RiR6c70IXGlBmHBzMyAB/54Lz6eV+fjnF8iVr6P36x+xexnjx5wq1btz729ocPH/43fDd/sevnf/7nP9QU3bt3j1/7tV97cfv/DOtTMFoY//+jvjMf+N1H0uc+5r4fe/snPMXJ+jvcae6R3XtIm9+hUzOGF4LwwNXrx1xcbrj2+Vs8e3DKH5YScfWQZrnlxxpQ1nFxviS+0XPy+RPq4ynnzVMeu3dxNkf5H6cfApNccWcnmS4m+BDYLDfsNntu1AX1yYzLpxdwvuMLmWHiJEM7jFN/w5VbV7HVjuX5Bq0lRgq8C/QjElBNq1SghYi1jqnRCCHYL3e8M8t4clDgTURam1AWpfCtZTqbsF9u+dzWYpZnLG4c8ZsHJbLQ6MIwdJb9cUnI4cq3knbg2ablt/Ue7x0hRMIFSC05qkp+8PXrdNsu8UOlZLAWHSPBe4a2p/yRO7y92dKsd8yWnqPHF9w4mlLPazYXG+7/4bu4N6+xvf3X+M75lv73Tjl+NV20ZydzysUEpZJgN5vk7EY6gzioeXe74fq2IR8cvVRkOmk+tJDEkJqzV2+9yVf6geWDC8Sy42yRASoVPUqhgqMqF5z5m+y3R5y3jt9+uB0nu5YQVwDcqg1fiBFtPV5rRJZQCVxqqkKMiMFhFhXBelRuiKOVspACv2tRdcGpucbFSjNcbImDRlY5cXB4YZOr26LCrduEIkwLcC4ZB2R6pCopQj9AbpKYWiXnLRFJttw6oTciRLzziDJPnPgQUD6J40MknRMhEmTi0esQQSRHNxVJCElMt0eVCpwAKYHee/7K+g5e3CYODlF6ZAFBCX5t9idcyBXKZNzYGqZW4HvPjfrHiFUgqkB2/rtYZUEEHoU/ACswec0d8VeQbY8InlvFjxNDZG0u+a1XHtB1HRO/59UnA7LKExJiHc1yTx8vuRy+SbSOqb7OSfnFlPcUPVfFm8+HoSAiYq45bb/FZnufaB1D1lDVEYfgafstrFyiypLr2Q9R+ilxNEjwTT8ilsnkI8jI0+7rODq0MLxy8hOEaJKJg0/hrmJErnRhsGrg7vl/QRCIWz82TlCJOTenP5boSmNoqRg/0+eZROvuEWfNn1JeuUH1bMIb859JTZknOfcpmRwK3RZC4Gz/Lc7tNxGAw4NJaKBQApoOlOZq/eX0HqRAoWHXpCFSaRDWE3r3glUqfcArST4pMUbyv762SJfXweGfdci6IAJ+1SBFyvQKEWzybEiNnlYw2LE4N+ncJJl6HNaWk0kLPvJ0W3IekjBcAWHbQm6S+UeX6J4/KSTKC1qp+JWu5yLXL/QMSkqavicvc7BJc2ZjQElBWeQ0lzu0ktSTinxWkV+ZQwhMr/4vOOcpj2aoKku0USlf0Eb79VMu/+TXv5tc5cX68Rvw06+kf/+O+yLfsG8Qnefr7/4q3xBPqIylLNKeUxxMqeuSwXls8KNLWMARUVHgnCdoxdAPWCmYlgV/UxkOMoPWgfMyJ7RDQpNHbV5QEtH2yaQlhGTcMzZAdrmFpscLidCJqjZIiekGYl0gVLLQ7vYdz8rb3Dv4Em3TYZHkVdKnOeepyoL9riGOSHuRaZpuQJcZth3Ig8ABQcJu3xGVBC1oraWe1WRG83jm2dw6ROUS94B0Phr1icf5g+uw1PzkrRkCWGXHvFX/cDIBCIn2OWwa2uWOftOgpOWyzHhsLbnNOKgHboV0znZNR5hmNLuWu5MMi6esK64821A93mJO92yLP8YdDuyWS76++yEOX/s8/tUDrux/i6Na4IXk2+Er5MWMrktxC9Z5lBBMFlNijKw3uxR0PZtwUjn+ivkTOB1Y3V9zefVL+BCwLjCtkxGOHMOlhUi2/YFA3/eJ8iZSAxSdBycgVy+alBATk6HrB6RRKciYUaMZ0vCFEEEKbHAoo5GkQYrtLbeebjmZT3DRchbAjsf7ZcHDi3/9TzD5/2x9Ousf/IN/wD/7Z/+Md955h9/4jd/gZ37mZ/jlX/5lYoz81E/9FJ/73Of+e7/FT2V9evS5P8vV7uUO54NN1SdNkb7Lei7sP7hSU5xr5HTCPM8o9y0xRIYhTXD3mz3VrCIqjw2BfFIinGU2n9DGlrcuVnTfanl98QX0VJMf5DSnFiMSPa9fNUwPpnRNS7du6AdLMSlRWqVcmyjIjKGalHSbhno24ejKAWjJ/OqCe48uQMQU2qoURZGl92ct3nnafUsIkfnhlIM7JwzdwMWDc5ZTzVAktEfEiLcWLVKx3GwbiBETkjtQd7mjOK4ZBLgYmJ4syI4mOOdRWjJ0kaEf6FSaeCcaiQAfU/5SlSUBqkq2rbNJyeVqmyh964ZLZ5m9eZXBe8Smw4dIt2k4vHFEs25otg1D59CTCf2zPdZZNg+X9P1At2s5up0yGSYHE3bLHT4EBufJhUDnGUpJqoMJh9ePePynD6jrgvW2RUvItOLpdx5x5dVr7J6u6HpLFHkKtYyRKjPUWlHRo+ZzPBIbBK3luaT2xQnlhUCV2UixCYStTbQ0H1GR5D4YI7FzBO2JmxaZ6USNlAK36wm9QxiFbS2yrgi+BaUR0xz6ROdJbkRjQ9Nb1MEEoSVxcITOwq5FLmri4JEuhfZKH/Ei8Jz1o7Lk0uadT5O+pn+RPROsQz1HYgVgRpMDKREi0b2iEFBqVNOmsbNWUOaJEiVSfkyMGhlkso8OyZY6Bo8TYGVCOkLb4WOGzEwyT7AOZzvErkcUEWoDfZ8yUbpAyHcJoZECGRXRWgiC/XJD0ALbRfzlnnCZigp8ILhA7z2ZVkggMxOiGEYdjhhRFIFWClGMU9c+UQADyblL1gXSKMqTAxgG+lVDLCKiyPH7Ht8NadNXMlEtlcILT+iSs11UCRErdElwSdQenxcdIlEPMQ5RCJAquaxZR2x6QjEdEZQ+ZVtJMZpdKMTo+BZFJJSKwXbkOwmTpAGQIwUIQE1Lwt4mzWIOwbkXVDIRGU1Ekl5TSIHRKf8Hk0w9opRIFOZgRrfeJhH3aFIQSdN9menxlElj4m6zT9qh3OAvt6nxzg2BhFSEzZ4YwGcZwjsYHDLPICYUUhJBCYrrC+pFSf/uM1Sl8b2GESkTWRr2ICXBD4gQ0DFSO4c0ChNA+Jh0G94npNSMNEogK3O6yw3VcY3WOrlsGc3k1SvE3rJ+5yl+cDTLHSrT2C5w+PmbuH3L/ukZizdvJqMIaT5y+3n+uw9uO0ZCqSPDtiWrNIqM9vSSxY1jNqtzdiGSK4Hbd7TP1timx2uF8x4tFURPPquSuYxJlN/JtE50ulyTOUdpDAyOYdsguzgedwPBI23KK5OjE2XUElXloGWyQhcgRExaVi0xAoJXmLqAbsBHcG2PPdCsGoeQhqLM2G9bJvMJ+3Uy6pFSJu3c+Jnr5zQ4o0GrNMxTMkUIxNFchEQLbDZ7ZlcXyEmJd6nIF/DC0nzsdD+8gb/8q5iYJZlKj1E+EqPCbjtWD88pqoJm09A2PWWVY0qDKHN6u6MfIrWPybzACcgUbdszDC5lcRkFJl0X88KQG83a9vhmj9Ielyl2lzsmJ1NmixIdG2SZ4doBr8YWQgjKuqBpOja70dBFSRCQx8j8+gF6uEv74CltL+h9JLqILnIG65L9dogv9pcQItvNDq01xahNe36MYq6Tg20AL8aw1pGaK11kGBxFXSQE2ij8rk/DPCXQQSZUS6XYihzJxTtPufrl19Hxg2c879sbn38DUmn3WXP0Uev69ev/U6FBn7Tm8zl/+2//bb72ta/x1a9+9UVTBElz9D/L+ovVFH3s+j6Yq59AfN3HyDpGwrRkWAtE19P6wHq5RRmNzg1CKpaPL1BKYSvB1cPr7JZbdps9OYJ8ajjOFqzOt7T39hy/fpVbr71OGTecvdVhygoQ7L2ndx4zq8h2LYtrhzx76zHNtsHkBlVIGtly9IUjDq+fQCtYPr7g2bcf0bUdmdaYMmd2skDnmnbdYM/X9L1FZ4aj2yf01mKKjCdvPaLftbR1xXrVMZ9NmGlNcXzA+umSMLrKCCnoCZhJSesjV1+7ymbbsltu6S+3bAZPqSSxzOibnnxaJAuoGFFSU5gCEBS6GA0LUnbOye0r1EcT/LcesW86dsst2y2sgsVoTak029WO8Hbg6hvXOThZsD5dsr77lPrKAdWsxA2GGAKTeQ3W0673EFNC9+Z8kwIhlSQvMrJpiVn1rFdbjo4mFNcPWZ+vKU/mFCLl32y3De/8wdvJxe5gwsHVAy7OV2gFebAInTa8ThmEDbQuvDh9PriCT1bNO+eRMdG/ZKaTgL8f8M+L4TagZ8lsITZ9yi0yitA7lJZJa2QUapEMHXCBsN4j6xLfDonrPTW41iKnClUV+NM1ciw4RYyIMiNsk0OVawZiNyQEI0SEdYS8xIaG2DlkZgCB7wdUkCCyhDjhcbHDO0chIkJkRCWwRqNDQGoNLoX7yUyPdL0UlimNJsSQslBGykuQkiLkTFSNGLVWwQdiNySDB5WQM+U0onG4bsAN6fOVRKxf45RBzCrk0BMHi6ehsAHvIPOjQ55L9r1ipAdpmTKZYoSAp7U7VFRElwJjXUw5PdJKAjD0LSFYRGHIXj1C53lqEB712FVLGDxDv8eYfKTOJWcnT3KtikYjpcJkE0Ro0SYHaRkA5y0S8ASUVEhVpWZ08Ogu0VNNnhGNAONQQ56cwfSI+GkN1qWifiwOtTRUixPCMqE51u3HYibDBAMS9LTEXdjRGMCglUEqhQ0dru8AgXMdjh2I9Fkm8MyjTQk+EkUgq2aETYsXJTakIZGH0fJ6dOnqBuxyRwTUrATn8b0ljoVwsB7RDUgfkoudVsg+GTLE3OD3XTJuUJHQD3gmtBvH0AUoFNXxnGa5TcVYmWHmVUJJpST0ligcg+iJXhC0IYw6leAcQz+kPDXr6IcBL1Lw8uZyg84NarQwd+s9m3tndH2PzDP0vErfReuwyx3rd58SpGB395T6lWM0kYVMzahQIHQkWJfs+ossUVhfWqVJTaguMjSQB1g+vsSqJVZFDg9mSCdYf+cx3bYlyufDAElQgNK0mwYtBJ7U3A7Opql+ZwnG4PuBbGaIWwij1bkQAnO8wG8b/HKbcrSqHHPlADOvCW1Pv+9R04qwbxFVTuxTHo46nKJnFXGI2N2AyqdEmSVzhBhp+2Qg1DUdSin6MZA5kwo7WLb7BiFB9Y4goJWJ1SCtIIiIjpLgPZkS5Cqh00qplN31gn/1gY37Y4aoUkgKncwSTIBuGeiWO542PefzY6ZXDzBVTrNt8INjcTilbXqiEYS2T26OCgYivUg2/kF4Qt+SycB226G0hqKg84GWmJomp8HmBBK1rt00FLXBTWZslgOhlfgoaPohaQ9jSFldSuCdT0yN3Y7rc8PB9ZKqlvSnHZudozUFwXmkMYjRMCb4sSEiIYab9RalJEYmjaP3MQ12pEYWBnxIukkgMwYXfArTjYHJ0YxyWhJ9xHYDclowND1RgB2HDKkxTSHDtQlkrsXj0/Xx5fWBz+VDzoyfrf9bLvO8kYbvyf3t5fu8/Njvtn7+53+er33ta3zta1/jZ3/2Z/n2t79NlmX8w3/4D/9sb/j/xuu/U1P051jfwxfz1/qO3+jTVOPzN15HPXRsLjYYkzItnHVMj6dMj2+hM03xzhP2f/yI49xw/fO3ePgn93GN4IfOf5inp5dkT3Nu/tSrdKsGvnGXIyyThefSRf4gj1AULILgjk+BlkNnUVohjUa+EeCnB7b5GnEhufLwOoTI5mJDNSnpmwEjBecPT5PjmIAsz+gHy+0feo3qaIofHKtHFxRZRht2CARXX7vGxb1TPrfsuTEIujbym/2WUBfUiwkPM4N1DmUyqostdtSR3Dlt4OEGWeW8dXPGUjmuX50Sn6Qsi4mZ8BO3fwbX2LH4CFhrIUbsYMlnFcWsomlTivqduuTGytK3W2ZVgTWarunZX2xpNnus80iheXrvlKrOqauC6ZU5trc064bd6TrRAi93RAHVoibPDGZaEqTgyY0ZZww8bXfMf+QG979hKbXiC6vkrialJJ/k7LZ78ixLRhi5Ieta9ONvMDmoGIoFv3p3kzjSH5OzEHqLjT1xpPIJko16lmlCZ1POTYi4wSW9yGoHWoNKjmMYRWhsapCkBBfwzY5odJruh0jYt6g8S2LYdZOaiJAm+2pS4J4s8UYRBvfCTtVZm95zCPiYGl6APu54sP0t2AmochRAOzDJrnJ98iMIH9i0D3kyfIvYDRxmt7ky/RJBqaSHhiS0VxLdW/zgks7Me2CkQo0CYB8hjgYiP7V5M9EvQkSHZJ6gxoI/RtA65/b8J5LjXRy4x38l+h7rBu7tfzehK63ClBl+uYEYeG0t8JlBZZry6gK/G/OT6hwzrVIp1Vn8vsX6DQ+b30bGZFUbwpgBpFXKK5rXxGkgO7qKLjIeP/59VADvAlfLH+R48Tq2s0lPNB5LNza7Qgj8WIwqIbiR/0hyqouWh+vfxYWeUBiUUWSzkqKa8+rB/wMhU2jowt0h9DahT9sWVRooMrCRMKTimm4Ak1Ci5zkgs+omB1d+kKE9ZaXu8s7q14k+cFK9ycHkc8iR3083oGYVJ7zBvL5OIPJk/fs0MjXMz1Z/kM63GMGHJAzPc+4c/jRZyJAm55XF/0J/+RRbN9zd/jYudi9oaUJJ7LbF7zqyeZ0obdYTrEtGI1ly1tMmIV/ROqLSuKEhyzOCtQSfnK1UmWHHUNXTp47Lcs6w9rAHp3bIIYW7EgPOB7Apr4gYOe//GBfAd5Z+/hV8nNI7T1HmL8QOIcRkVT2iGbE0xEyjtGbY93TvPoUI1WxCIyLKKOy+ozCa9bcfEnKDmpRsztbYwfFa3vO/ljVSgl5YijsdMUjsLqKL5AQJjAHNAhUjw74nqwuu7h1hO3C8D6xOZ0zyI47L23zr25ZhtU8uoEVG6AakTBP7MJ5zTgi00eRFTozQ7lqKuko+DTLZcSd0V+K7geygRhqFDTFpuWRqREPbM+xaRJkny3+tkS4he94HjKmQ05L+8SV6P+P27Muoec1223JXK1zXk2cZRioGm/avzAuc9zgZEwVXqeTeWeQoJdkPlhihLDP2bcfeDhil+Pw6UjvL4ByXn8vYPDgnuGE0shivv89FK/CRjdE0m/ETt34GfGD57ccsd2LMGxPITLN5dEnIVdI1+oB3yTQkhpCooeM1brkosUVBUWgmbsWR29PvOp5WEy4GsM7z6KDggXOYXMHuVdROEPT/n70/+7U1zc56wd/bfd3sVrfb6LNxpntnGhsD5XOsAxcIUagoqSRcSCCE/wju8BXi1le+K+ra8ikhuKGgpKo6HCg4Toxxl11k9Ltd3Wy/7u3qYnxr7YjIiMx0OjkyOF4pYjdrrj3nmvNr3jHG8/weRdIGP460647fGT+HPf0yu82eQQbvt7mMeiIaGq3xwXPvuOAvjL/HkTphfCdywX3W9+4QoyDWi6qQ+4gRGIIPkZwiYz+QUsIZ+ZnywVJshN6IjXAcxXNcOLpdSwwCHnKFpT5d4KylsJbx0OEi4jtdNoRdz2DFb2eUZlaWpBz4Wf2Uu5ePGHPGpo/66V58JFOshfpsSvTfwvpwoOp6vf6+j7++vr79/fHx8Q/8PH/9r/917t69y/Pnz/mH//AfAvA3/+bf/BP9G3/W15+6KLpl/P9gD5Z1+3DFrdPve3mTPq5p+KSH5ExEEacH16cL4rYn73vGMUiXNyXOty3Xz675sb/8E7z+s59j/cE5zckCjXD9Q4w0zYx7x/D46QX9Rcf2+YY0ZuZHFf2hJ2pwxw3jGOiGkeOHJ2yfXNPMK/aHntd+5g26lzqeNu/LzUDDsO9ZP72mbkraQ08KEZUrkbMpJWnwWvPKT71Gc7Igp8zlu8+5fP+co3vHlMuaMHi6p2uO7xzRv3nOZggsThYUFPjC4r1nebJkvz7Qdz3dOGKMoTYaC5PJWaRiCSWm/On908agk+LpH30gyGsF0UeK0rG52HD62h2aoxnr52tCTMwKx+JozrN3OlZnS3ZXe4Z9S+g9fvBoZxlDwOeMD4njoznzB8egFMWzDRfvPadqSvbbA0VdMF806Cim4OgDppKpx/mjC9pDz73PPWD35IrusOXVNx5QLxseffMRVVXSHjr6sWC+muHGHSl6Yo7ivUif7mTLGcKhJzVagu60hskUTM6YphDST++hG1GLCrOo8c83k5dDi9TLSDGknEGPXj7bmNDOoo4XpE48Q8oaVGnReaJ7TSZiPSuJ6wMsa8LoRRI3CHxDHXox2CqR9ylAWUUsDORAbkfp6BfiQ0takVUm5IC2SHGVMhopvLPWpMJhBim63JS3k7SeMNOJNI4o59BVSQgeE9MEJ1Av5Glay7Gr1XTugbWFeKWUJY0erRPmdCHUPKNRVSETtnWEozlFzOR5RTmrcCdzwijGcjurbsMPrVZELx6N4XIHPhJSRGfJ57jZ1OumxDUlFBbfjuhZQZy8KhpF8qCUhal7rSfpXVKTgT3JVCulTFYWHTM6QWw7mazsEl4pRqvxbstu9QEkJYWL0bimErneXBOu9+ikoC6FjLdvb03uCiG3KWNQThOvOpl+KYWqLbEbZLIwTXTHZ9eYeTn5BDQKg5nocZE8FXVZ8PKT9BBrUNmQYyDrAtUUKA8qKjR6inVTt76lDPTna+av3pVCHwRqkEWqScqoIJtOXTmZKhaWqpnht61MOPseNU1VynlNansICcqSrAxJyaRJW4ueG/Sixj+5wp4uCWPATrJCq6EPAzkminlN2LfYuqDvR1RINMuGsR8nnDUi3UsZZgY9LwktlAji385L+Xm0Znu5xShFUZV4H8iVJaTE5r3nKN3hljUORWEAo3DzF5JawYcLrEKulRLeTMyMj66orMVhaOoZOhv2z65IlZ4m0FHef2vI1wfmTY0fPIdhoJg7hnaYSIWZsR9oZhUqZEI/CuAkZRxZroezCrNs8OdbxvO1oOy1kYlFmuR0MYn00Ud0yrSHDnPoGa53NPURFBUpKnZj4BAi1mriIF1jVzrC4CmdI4N4n5jonYUVUqvWt4XSbt+Sc6YykxQyB6ya8n9yJoeE+dik7UZK95Gb+YeKIwXk1rN7dM3m4sDyZM6scoxtj6+86BeTeFuz1YxRAkpDlIlIypk8ekaV6FDY0opMrjSY5GBIlK5ivzuQtaKsC9p2wBVSXIcYpxyjLIQ5bdn1Hr2YsSgdYzsw+sTyeMF6s6MsS4iR+bxiUSYqpQnPLtnvIoeH98kowjhSFPp2n3QDU9AT+j+2HWVZSFGUZBKtAmifyEZLvh6akCNFVci1dgqK7q8PUJVYK82rqik5tD1GMz1OEybwEIDOkuurU5wCpD/l3nhzg7zVlf4p1D2frf/q68OI7K9//evf9/F//Md//Inf+/2WtZZf/dVf5Td+4zf4zne+A/z3A1i4WX/qougTa5QPd4C+V7Hz4ZPye8jiftAXcjMiBihSz+phjX/+jOXRiWR6VAVX6z3PLjesH19x+soZqwenHK52fOeb7xNT4uzeMd4HQogiU6kd7t4Kf71joxIjiVEp+nYABS/92Mvsfv8DjDUcfM/RTx6TThJD7hk2Qg2bdYHLd58TvGd2dERdVjx9ekEcI0Zr7n/uAaE00t1BDJTt4yuefOsDFvOayw/OKZuK1UmFShl/scMVljFENldbmrsztmR8Tlw/v2a+moOCG55WTpnQOLyPuNJgh8AsZWplaM2MbBK6XtA7zV6DGqOEgyqFI+N95HC1p1rU0qFMSTbsE/q5zxn74JjxrZ7r7Z48BlZ3VuyudnKzTEku1MNIMa85aPCzkq4byMuK5sEph0MvVCOkG6zI2NJRNiVEQRyXVUGoHM/WO15+6YTTn36V9/7gXbLLLMKOctNRhoNQ6KZsnk86BK3WNE5ufeU+YbUhWclLQmtUiCIrcpIjQSP+DF1J3oquHGkM5DFKFzglci++ojQVmqp0UiQVTgJkey+o4kFu3jFluucbnBVpQyBTZ+nOjSlLMRciNmd5fdMGNpWyAYkpYZMGX1BojWLKhSEJ5WpKlqeAPuwEW06JUYVkvBiNykKpyt3ITZAnKaLrijxvCLnHt1tyTIxWEa2GlJjlBq1E0nOLpFfc5s/ELCGr+mhG8fCE2I/4bUfuxBNkH5xJXlPvKU4XFLXDFQlqSz8k9qiJogXEDMbKpvRkKZuwOLKc2UmSIpNZhZz/2hpCkRhjQftcPHA+9Zi0J0yTDxUhR/E4CHIdhpBuTcVKK1JIZAI+RTKKpAQQwBjJBKGzGSd5UUDqA2O3leI4y3Qw9wKPKI8W+O2BuG9lOpMy5EwYR8YgExucwYQFzhRoU07Gepk+ugenjN9+Qqg6hiTUNadLCrtEK0GrRySYUumEqiq0MmifgIiblXSXz/BhS4wjKr+YViknOT92Von0Moj/CaWmHKksNEYlOTfZGLQxIrvJCasVYUIEJx/kmpAy7v6JSL26QfxR3mPHSHJGivzBS8NoQqCnKe8ojR5rLWeI/FmHwLjvcFVJVVqGfiRpcLMS3w4U1tLMKvb9iD1qUEOg3XeUTUVsR8IYKZRCr2aQMn3XgzjyUAUMJJ5s1hyd1RinMYebK4WEjuasmDWW+UlN6Ab6yz3zowUKGOm5Tmsurp6hXMHyuOHi2RWD96RZgyodoR3IeNyypjqeMXYeT6I+mpFSlgaQFWl3UrDd9cyqCqMUel6R0yAUSx+wtkQXFne6YFzvwQfioZNp6WEAp3EPT/HP1uQhMIweosKYBk0i6Zpra2Q6YcSYX1UVMQT6fiC0A/Ompm07CZpVCmMNxhj6caQwluXpkv3mQMyJpq6oUDIdtYbRavZjxOvM6Vnk9I0ZOXguN4nkIPjIZSt+PaXVC1vRhzbe3a7j/YtHDGPALSq2w8i267g2muQdWYnst7SWYbpHRx9JRqHHiFOKPok/rusGRh8om4BzGkxJ0DKJyzFgtEjXnNKEMTBOyog0TVvjBGDRpRMC6r5DKYU10J8/ZmkUDYHZssKVkVqN5ENPrxLbpGm7AaVkoq6Nub3+hBAJU6bZYdsRfKCuK7RSkm+karbnI4uHRxidmBcGmxW2MCir2F7uBDpkNSYjERNK/EZjJ01apTXXjy4YNweqqpQp8vSfKS348XvutxQ3F/WPfUafrT+T60tf+tLtBOdf/It/wT/+x//4ez7+JmzVOccv/dIv/Yme6+/9vb/Hb/zGbwBwdnbG3/gbf+OHes1/VtePQD53U8187Kz5JC3q95oCqU/5+qd933c9RN2+FAXc3XyLV7VhPr7L4uh/wM2PUbsDv9dazpV0m0xhOTzf8J3//Cbfuttw/PJ9rn3kZ9Yjm92Bozfu8c79Oe/90Xt0xyWmdhhKxnbg+P4J1bxi88EVRz4ypMTyF1bs/8qaPdds39/x9N88AyDVinotRsjVvWM++MN3aOqSse/pRi+QgS+9xHOnuX7vnNkfPqa53EvyuTUoLZk1i/dbVpOcCaVIVUEooBs9ti6Jw0hQcH2xxlgrvhgyWWveO6kIKWHGxI+d9/TbltOzxNXspwgpYd94yDeU5s2lY9XDK4MVFGmUoMl+31HOSoL3t9ScqpDN+qPoSV94yAfdnpNNz/2sGA8DZCiNYRgDj/2AX284vTPjeRoIJyV+EC1/U2aitjTWyoZxCphs6pLd9oCxhtB7lLO8e3dGSol3Li9Z3T/h+YM5qzryU0//F0rvBYmrFK5yMv34hHVn5vjFV+YQE91jkayZmAQ4QcYo8RQxdYRjNwq9S4tvCKUwTUkwnjSM0uVvSpl6hgRGE0ehy+nSEbqBrBTD6NETUpt2IIZA0JqqqbBOEzZ77KJBxyRegAmvnbzIQlAam5ECbvCUrHjlzlfQWXxRN6kTSutb/8qu/YDr3fsYZ7i7/DLH9jWZVmRkshRkoqb0hAJ3VjrHVcGT5/8b+/YZqin5zv2GvUnopPmr259Be0tUIh1hkqCJTkOjZg0u13gfiI+vsKsGWzlUSsQxwqxEF078SEpRpI7Pn3pMYXnzWvEv/7DlJn+KnIk3Ju/CgYJfepj5hfvjbe6JsuYj14g0DzzpVoQwJw+BZ+9/HdWOMBWTWomHSU05N3lCUCsyIUb5e2swhcGsHDqIZ8JozXjoZHqCFCIpRpE8AjmL1IcQCQgwIW5bASHMKlxVkNZ7iJ4A7Pwznm//COqC4/J1Xi/+ImYmHgW0ghAp37jH9dtPSTFyObzJ5fgWyhgelj/BffMTgmZ2VuANOd/CEMig/PT+NI733/8dht21TD3ylG8zXX9VTtR3jl5ckn0Uk7rWtwGzKmVSDkIlnEz4cfr3c8wQgxxPg5dr+loM+2m9xxzNiNuOse1Fgucj8XqPmdfEwaOtTBaJCRQUqxn/QzbYsmabNf8qR1pr2Hf9hLd2RB8xzhJGz+ZqhyosqfOYWnLAtDUM/UhVFYyHXshq3uOOZtJ8SZn2eo87rfhfPjdj8JfUxQlXv/vdN55f+AsVv/JLNUZrim8VcBXIKK7Pznlzt6Utd1TxJ9ifLLl+dEmsa5HzjZ6iKfFjIPlI8FGIYjHhDwOmsFTzWnwgGYqioEiSb5dTJExNBJ0TeQzkupg+ICmE1ZRhpI0lqUQ69AzvPEM5h7IWUxeU44oz82XSGfxhTPwHL0XqoGTi1Q8DvhtBK6p5zeijEB1zplIWaw0HP2KdJcREu5PJYFE4Yj/yyj5SdhIW+u07NebBknJu+L/+4jdZNj34iO8O6JDZecX/7fcNhyGR0wtJ8IfXdtfxR6eWcrWSHCSl2O5bkTGGhE+iJhgGT9Yyva5nNfu2AyOAo857KTJ9wPvAu2vIGLKfaIlDjyaz7wYWqzmmsFOgsbQRC+skhysn/BCxCP1ztphzfb2lKTI/6/+AZUrMzAIdNEZbwtUOlSL2eM74bC8SN6cJMVGUiptAIqUgxsTQD8QYZUo1XT796FmXDe3PvsJ7z9doZykKSw4JqzW6cMyWMw7bAzoqktEkq9hebHGFBRTrR5csH57w8CdfY/v0WhoxhUVbTd041Pvvf4+d1Ketz6qiP8tLKcWv/dqv8U/+yT/hd3/3d/ln/+yf8Q/+wT/4xMf+63/9r/mX//JfAvB3/s7fYbVa/Yme66tf/Srf+MY3yDkzm83+RJ6k/xbWj8hT9GFn3qd/6ftK5L7XefddfsBPk+3dsFIyWmXKZUnb9SyqQIpCn0kpMbQ9ZFg/ucLHRDVv6EZPoRS7tidrxdnnH/Dm4yu6tsfNSpKCoRup5zUxRJ699ZRZL+GofdtjS0PWaSrwxPsA4NuRYpQbzKM/fk9SwZsKnxJvfOULHD044dH0Wp585wlfQjGfN4z9wNgPKKCsSsos4bBKiz+kP/Q01QKPkOiO7h4TfKA99IQUCX6kdI5GaXSecjPiiEVRFI4n337M7l5Dtai5/uCSk9fvoZ0lj5F5IcGbqi4Zdy3z4wXDvr+ZPTH0I0dVgVaKYd9LIVFJOC2IVNEVlkIb9l1iN4ykQ4969zlDP3LoBoq6oKgKMaEjE5J66mYpoK7FKL/btezWe+ZHc1LOmMrRp0R6vpYco/YavKcoDW5WkFOivnvEED/h8ACUkslT3HUSyuoM2hlCO1AtZiItKuWmP17vUVWBdha/bSWVvbSYspBcj3mFKcWQbgpHOvTyJCmT+lFyhApH2LSolAhJZFnaWUxIRJQEB5eGvCxwd1boweP7kTzIBjSmgDXiNYqtIHAl9BOsK9BqytlJk3TKC8Ev9aPIQbTcOCNTVo5SIpHTmqQURnGbjcENunvfSabOsXhMaBzJD+QUpYs8ZEwWf4PWGns0ozie4693JJugtWgFdjWTojJn3KKmKCJhjITDgaQybTdiq8ghrpm9fEqmkoam4nYTkaeudcz5xXUiBvLoZZp2NGMaFYvG3xnyIQlIYV5Rf/4ew+Nr4q6DKPI/FCQtAb80BfN7x9Jt9YFy0cikrfekfiT6iB69eJBupkspwlQE5cHjlTx/1pqcp885Q2knaVzOcm7Na/JepjooRWocKkVSN2DnImE0ShNTojhdofSedCko+USWx8YAtUEXhYS4JpFXppQwhUPlSdqJmPxTiAIHKQx5iKSkbqeiGrCzGoxggZU18n5nSOMgE1GtUD6AlvBKvajJPqG80OaiURhtoR9Io5jwIwqTxVNnHtRon9DdKM1nhVwbbwiIKcuxc7mVEN19i14oTIw4o+jbEV84ko+Uk8n+6GTJ4AN2XhPNQFE4hm5AR2kk9MNIeTpn3HQ0U+GR9DRN8wFVOMJ0TPnakXIgaoWP+aMdckRyaiu5rsg0bURbjS4tp5+7z8nrdxg3DxnWljEm9KySfCJlpDh20shKvWdeSt7dvu3Z7Vvmx0u6fcdiOcf3I8VqQQzx1otjnPj2buVLCsFtW4OZV+Te4zcHqCvUokF1vUjIrRaM/ISFM8czUtuxWe84Pj0i5hGjYDj0zGcNMUYJ4zVafjalGYJIMo0SD2RVFFLoVQUqZqqyoH98wdHRgmw0izsr1MNjykah9dtoglyjmgLGyEi+jTL4tADXoimpljNCzvReJrJperitLDZI59MuasIgURLtvgMjQ+Xd9kDKiWEKrbbOUjrHZrNjuZzTD6PsAVBUU6h7mp7/xtuLgb6Xz3h5tCD4QEyB9dUWyJTOcbxsaGaSRVisloSLHSpEMpmwaQVKMk2hrTN47/FjuP0ch37EWGku5CyACTNd57puoDUeu6gFyqAUqjLiG/JBvI2zkrEdpcnRDuiY8TlPIfKwfnxFv+s4eeVMpJBDIKfExTvPp6bI91qfFUD/La5/9I/+Eb/1W7/Fm2++ya/92q/xO7/zO/zdv/t3+eIXv4jWmnfeeYff/u3f5jd+4zfIOXPnzh3+6T/9pz/Uc33pS1/6Eb/6PzvrRw5a+HDdc0Oe+WTU/YfGOj/I+pi87tN8TDfmQJALab2ccdCa7aZls+u4vG6xzjI7nhM6AQMYZzGFJVrDfDmjf/OCu6/exShFeHTFMiTUriMYg1WK8XpP2nYsrGZeldAPGGtwRUF/2YOC0Gvc4gyA9nFgOdGuQpBNQ3Ka13/iJRZnBeQ93dvnxPVA0Xk0BqsVm26kXoiXKITALifMrMRqhSotNmZ6pymMobOadt9JR9sa2SizpSg8pTIUB08eMyZlLCOmgWLe8GzVoArHuO1Rz7cU7UCtNZc6Y6widh26H9icrzm6d4y1Yug2s4qucoRFxagyNYKvTiHSjyOucJRnC/S8xp8rxuRRwO56jy0sx2crkai1I3Y/MCst63GkWx+olo0UZEbj5hUxJrbbA85ZjDGYMeBcomFP7AILPEWCVFjiGChPZujCYofISW0/Xk8zNyLpQymKWTV1qBXFrBTZIBAvA7YuxNQ9hevZRjDUYb0n9h6jNbowUIlULqcsun8Nfj9IMYDCNAVZgc0Z15Ryg1KCt2azg+NjlDbYskBNZvzZg2O664NsQr1ky+QQsbagMstp02np4kZka0r8JAZLyL1MJyZsa0aRQ2QYDhz8uUjpmhVFNOiUJNIiZZTKRG1QKaFSpsgVUTtUUKzW4KZUe5MkD0MVho3aE0iwXrO4nnP8xVcIQ4tuKsaxJawPuJnQl8ZdT47SPbWVIYZMtzkQMux1gk6jkuKluRjcxz7StZEUE0VpqGuNtoZVKVMe4yzbAba7j10VlGSoNE0m7vYQC8qjJSzmtDqBnvbjviPpPGGkO6w22GVB2CjCNqIOAl5gyKQACsNMLbGmxhhDSKBDIqspVygl8AGFFPU6Z5KzFHVJ8IHQtrdeszx4lHIUUSaDRd0Q001Io2fsd7j7p/i3N9QswMnmXFmDzhmjHRSONHr6YUNMQaZ9XtC72mcKNSM5h24H8jASXcSiKd0crS0pR1KjRPaZYDOIgd5qxbI0L3whN7tGK8hhXRXE4UBqOyHQTdcEQcBn1BhRQZpPKMXw6ErkfVOT6KYwSmPAVBrvE/5qT4h5AhpoQoy45GlmFTWRIWcBqZQFYz+wud5SHc1vTFr07UBVOIZDT0yJsqkZdhLe2+3FBzpfzLDWsLnaYqyhPJ6jkqc61CzuPWBMjnUjBUfyPaHfA7DbR959Sza6+cmIuYwok9iqAnN8nzR4xt/fwjZzbB2tUgw+UKBo24FZVTIMgWJeMYSIshrblCybkgycPjjFNaVIr2xCjQMUGV0X+HWLjQm/abEradhgjVzfpqyytG2J+xbf99jFnOwVjBrnHD44rueOQ9tzse+wVkJiU0qEVqbe4zDeTt2sMagM83nN0I9ErSAJ5dFYw6J0DMOIVorl/WPKZzuBtRjFw7MI9RaGDv/OOeqhI2XFs10mDjAExb25ZIclZbjiiJSQqdd003bHM2bKsL3e42rHwSiyz+TO45VnjBFXFqRNK17CWTV53mTTT2HJPqCMnqRxcNi1aK0Zx0AMCYXGGMkFKkuZyiXAFZYYEyfTBKuaV+wPVyTvcc4QGWnqkqPTCrsxjLsD9azCFI5x9Ohpamt9oCwLqAuIECcZt54yCV3hJjjEi+M9xihTv2mz1O86jFLYuhAAUM4M3SgerT7gIlMDJk+ePIvPSWSzRkuzYtcyfvMxq7srzh9dYArLfFFy2Wf6EPGI7+ijWyt1I0T5bP03thaLBf/m3/wb/vbf/tv83u/9Hr/5m7/Jb/7mb37iY9944w3++T//5zx8+PB/51f5Z3/96IqiDxUiH7cK3f5effhLP4SB6FZ7/AM+LEO5qPj9Dw7sUubqegcKXv7SKxy/fMbTP3qPrh0oGyEA2dKSxsDQe8pZxf7bj7n/7hXLyhFSImpDPa+xpmR7faBqSrpDSy4Lirpk2ATef/MROWfqO69x5+d+hTB4rh//AUWh2O0O3Hn1Lqt7x5TLhqJ4H5O/zv7ZmvmjYx5ezDkNkZQSa2exRjP0Iz5EunFk/fl7xLMF9UQWaved6JOHERs1PnnSJGlyJZj6m5RVpsmGzz/bUBhJuafKDDmxiwvG9quEduTBYs5rj3dU65HywRHvvXrGdnegvG452xwY2+HWEF2WjkfDwMV6Tbe0lM4yc5aEopnXjNct86MZ18c1T1JkVysyBZXTaGdQSrM4XpB94PjtS5ZZ4VOiu9uw2x1o95KuXjUV5byiXs7o+pF921HVJRpD7nf8+Pv/H6p5CWNENeLzQUExq0gxsXCKv3K/IbS9eIKmrn1OmXC1F6kX0jHHiPxSL+QYSFGM5aq0stl1crPVSmEWjXTZC0Pc93KDnpWYuiQnL9MEZyRPovfkYUTXpUxmfMA4mQTYsyVh2WCdlRt86UReYw1GK4qmIKZM7sbbQ97pOa8c/RIozX54zjsX/w5dGMIgm2KNUBZx8nOZyW+ilGLTvsc6vYNBcTf9FGX5qkjJQLxiMaKZkjlT4v7sy6SyBB95ZZcI2yyeK5SADErFv9ffZGs7imD465uvENqB/skFfrPHrhxUDn8jA0KmPj5k4qGH0WPbA4dt4N3lknR94P5PzPj7PxNQNvP4vY63f/ec7ByrfsvLcYd95SHLew9JSaE1/Kcn8O/eV9/VXPk//ljHz9zL5LNM/44mtpK79fzU0tlMHgNvnCWaIt4iqcngu55h9sukEoLaiJTNBAJKUL5I+GfKEkYp2HFp/KQkssWUskBNQiSGwLA5oIcRrCEXTjKLQmCZ77JY3hVPUs6oKIXE9fAu1/l9Zt2a+a7i9ZO/LNc18yLAF6aimsxF/00O46V04Cf8d86KN5Z/ieJoSTj0YAzGgknw8uoXcLokMPJB+YcAdCHxv767JaTMqjT8yhtHUtiRb4leZpqEjVdbTFlIBpLR6KpEBQ/LuUi7xgCFQZU1KUViYck+Yibq4k23XCuF6j1FFhliNuJRZAgoZ9GuFACO0oQbuRRgjaWoSlSWaXKwVgrrG5mVUvhpI2pKR1KBFAL9MJJG0E2BU4q4bpnXS37i8BcI/6Xj0XaHvn+Ps59+je78ba6/9R8B+OM/6vnjP+rIYZpyILK1+Rv3mPkv0T5bo775Jg+HS1anK36/PTCuKsYxCHQiI1CbLMG/oZOiIo+BclbR7XvG0bNYVrypryhKTzOzrLwl7s2UgTZSpSSTAAV22dB/cEH92l3iQjxkeaMJ/cBcL3h48ouUi4Y/OF/zr3Ti0A/EJAWFc5aUJDR0VstnNEYp1ppK4CDtIH7YhEigy7Jg33YUEzFvaDt8jDz4yudZZFAq8uPzf0cRrthfbCgPlvS4ZtSW3/o92A4wt5lf+4piVsI2lvw//C8TXHV7/img2PSs/u23eUkp2mx486wiXvop+DTinBM/TY44beh3rQBsgBwSIQTqphLPW2HxvSerLJlyKQqZVSu0csSUaNuOorDEnFks5/SHjl92jpcXC7TOfOf6G3i/w2SLcZqUNfFx4uaSYSppnKkpluBmmlgE6GPCFgVD22OnwOeIZIM5Z+U6jSGFNIXxZgkPN5rkM2Vd0ncDvh1xWtPMa9y8wjpDHCNxeyCSsWhyFn/n2I+YwlJqS3YyzYwhUtQlqrLopuBfbSSTCdTtlOzF+p4m8M/Wn/H1+uuv87WvfY3f+q3f4rd/+7f52te+xvn5OSklTk9P+cpXvsLf+lt/i7//9/++QEI+W9+1/vRF0cfPnQ8XRDfthunv8v8O59nHE5hN4UhGsd4cyDlzcu+Y0zfuEYfA9dMrxhA4ma9wpSMrzdWTK+4dzaiWNeOmFW2xNviYefXHXmZ/veP80YXINQ494+CpnAUlG6Tbm36Wmf/u+RZQdP3AyYMTjh6eUC4akZgMnqt3HnH99BpUgyuOcFXBZrNnGDyFM5wcL0kxstm1PGp76ArqWUW1arCzks3zNWOXWcxrXF1wfbkRb8TgMRNSNvlEsSixSuOsYbjc4chk79EzDT5DiGyeXtHUIu3YbiHHzHzZYMwaVziun17hJpqPKaxswrXGOsfu6TXBB3w38sbLd1FGcT4G+uipCsds0bA5tMQUScpQzCtBUCtN6SyFmgI5C4Oa8KO73YGrZ1fUVcl80bA7dIScyePIgomc1o7gNEVTsDhbYWclN3es8XovErYxYAqHv9q8IO41Jan3k+F3wjQbLf9NAbe6dKgseFqTk8iyQhTwQyleLzFDJ/IQZPjkjMAXpm5uGLwUWWPAFBY7l+cdu4G8brFHC8EBlZYUEvH6QHm6kA22UujaQVOQh0Cc5BiSyapRZYE1NThNbtdktITRIpuAG7KYSmmSosmxGVMgeU82IgdLOWPS5ElSCu2DdKOzIg4BnMUkLVOTugBriLtWpFUnCqUhZPGhhF2HnVcUesZw2FGerahOlnTbltyPGKMZDzIxMtaijSPtNvh2T0Ix3qsw90vyKPIepRX4EdNfYw5PSfst8e4JbtHIz6iQvJfJB/HiGiCIaGWmCaZ8RQo6KyGHpujQWshignmGoi7oO0Xng8iOUIxaJq9jzjilpuwZeW+Nk+PATPS+pEDFBCjy5BXAS/5SAnSM5E5yYLJVMllSYJUilUYmT2OmfO0O4XoHo4NaqFRkJcQoJd1cpqkTGqhFuplyxmpFjkhhYQ2hDRLWOnpituI5U8LC0810Y8xSmKWUJ9ViJraDoLaNBIHmwpH7ERVFHqicFM/GKvIQwRhQeiLpOdydI4bzDWnfC23PGvLoJxLhhL8/TLQ9BYX3jD5IhstKMrN8N0zUuIIgOiOGtid3mWJWUZuGPEay0ZRNRVmVEko9GelTTPhRYgaM1oSuR2cgwunn7rFUht3X3qa93jEuK4FIKDn3bvp76UZ+YMxH+3Fafqb6bEV9dkz+4Ipu28JxAXkK0d51KGeojGW3PlBM0mtltAQitz1l5TCFY9j3+FmkKC2xG0kxYAtH2ncyfbxR0CmFW80I+47hgwt5L42iPFkyrA/EZFBocoSkNOM03SuaktB7+kOH0oqmLvE5SvE+QTLaGxJd4VBWsPURydSZNxU+J8I40swbog9QKpHQKiBGXKmZnzRyjMZEJpOSIoRMsgqtMn69Z3+5I554umuZsOjSUqxm2Lrk7o+/TNz1pLYntV4mnyHjGok5yDExpoRv5Xg3WtDy5MysrOi6QT4vlSnLgrbvyV6OV9cIfrzddzSVwxhLVReEGBn3HUVKLBqH6wZ0aQWE4yaPXsoURsmENkbcrKI4XTJe7yY4kJJcsBxZuIpDhjh47BRdYJ0VpLySyb2aLll6ok3e7F2sNtJoOQzUi4qw72GCO7nKsXh4gnaG6vmW7cWWvh9YLGdstgdUJV7BkAUgNLS9QGMUxM4zqCzeTm5dhS/2Ti82UT/IVuuz9V95/cqv/MqnRol8r2WM4Vd/9Vf51V/91R/6uX/913+dX//1X/+hvvev/bW/9kO97j8r60dAn1Mv3oBPKpC+3/n1wzQmPjaN+qR/8vmE1gTFbJGpHl1yfO+Es596BWMNV++d0x16yrKgLAsWY+Ty6TMWdcnydMl3fufbFNZQFI62Hzk6W2FKx/b5BqPNpP/VKB+ITBe/bDlr7pBzprRz7LMt/q1nNDHTrGY8+PFXUVqJbO9ix/7ZY/p9oKpOMapCKUtWikUjXUZrDdcpUjiNO10wmzt2g+fy8QUr5zAJinFkKCy73YGl0TSzmvV6R9kYiCvarac2lhgvUTlgC8laGbYtTYzc1zs4qsjbZ5TzgdD2pFyhY8nJS2d0bz0jlQYT5edcnM7ZHwYurjdAZKEUvh3Y+MDyaIYNcHkY0T7TlUIv0lGM+KW1EjQbRCNv64KdyoIOLi1lkdEmwDjCNayakubhKU8utuicWc4q2DyhKgyzMJKtJWZPc7YknK641ho7Jo7rKQxyMhCHSceu6imM0cdbM3YePKoqQGvSKGQ4gNIkmoUijYF2LUnwubQUecSqhE6BYdCgHaapRNvdj8R2IGuF0SIP4oaQpjWpF4O9ayrM1Rr//AnBOdzxgnh9IKVICpngA2VdYKzGjwF1ukBd7SdYQKTzlxA1Y9wS+pZUOdxSNiJp12J0iclzVGlIsaPvNgAUbk5RNVNWTubgL283EzEItj6HaeqSpq7+EMlaM1vcJWsHg0e1g0jwtPjklDZoFenaC6wJJJsk86QuCesDKDh66ZRhc6C92NIczxmfXcNmA9GjZnOIonMPvYcsCOr52Zyzn54RdwfM84E2GorXXmFtFhy2Is1a9x+7jtz84fa6otF1wkSRIG5CZtPKhtcoKIHURfTMTXKxSNlfia9Nd6hYTwVPmnw4CqUyQ1qD1eRkKViQgwQ6ksWnFGKCkDGFhLBmLdJbaww5DLKJmnxgWSmyAZVBp4Q5mWMWmvbrH5D1GUrrifaWZaKk1C3eO6VMVZ9CLMj1SM9eAmxjog1rwiES+56oJQSXFOnDNTpbAp5sPiZvnn6fQsTvxLyeJ1hLntDoWU3FnLGQA2G9Q/kogaEo3KKhvbqWvKKqosiZEBO5H6CwoA05Tl3xeSW5RdZgqoJaK/xhIPk1vnL0sSenimgsGENRCWVx6AecMcR2vNn/Yo2h3YusqsyKcQiMBGbLGfW8Zmh7NFA0GsyOYf0uTz7YsmxLmqLg0B44u4rc2dZc9XvW3+c2FLotw/oZZPj852bMhi27i2vK4p5IovRErJyytKplI1PGwuKURunEGIJEA7Riur+Knny6YBgDs2Gkqh2p7UVW9WEwgVaUZyvayy06JszJgjxGkQOHkicxwnbPtdVC4KtKdustxlnKpqKZNwz9wHjoKLWiWTS0+46qqRm9F48iUGhLNoqu67FFgTOWo+6KKmw4ufeQYbjiMmaUSjQ2UXYAEz1RQUiaVWUpLdRWc/G+x280u1AQNxfkqMhG03cj8y8+JF4f2D3Zoo0BDbNFg78OJCPnrGtKum2LcxbblITJ+5edFPvaapSXqe7Qj+RCJpKuLijqAvYX3D+e0TJiQofxYJQVPLbK6EqDToRKJLjaIgWVVhSrmhSSyAzrguresUAzLrZyjsrIF5TGOsPJrOLxWhQJWimCj7iiIGZH5yW3bPSBTMYGPSkJEl0XSC4zhIwZvDTMYkYXlvXVDnW+YfngBG1FebCIUO0HwuAZsmUko61lPPRT7EDGZE1WmdNXzrjevjiOPrL9evG/T1j/7W5yP1ufrT/J+pF6ij61VlHf9ZtPe+T3Xz/Qt2X+13GY5B/wf6o8p81jzs4iz4tEFxPrx5dkBctlgx4DZ+9sOAVUm9imFjsNfFJMGKO5+/n7rN+/oOsH5vOGrus5u3/K4dBBiBAT/oOBn3v9qyijaS93PPvP3+Tl0ZMynP7cS4QxcPX2M3YXW8ZuwLoVtvgqIWSuDz0xiYa9qApmR3PKuuTJgyVXhUZrRakEJju2I2dvXeAGT71o+OOV5UBmt9mhtWZWV3T9yDi8gVaZrlCUswGVRoZtR3O6wOXMovd86el/kOycWcmgOoEGFKeM4xHn7z3HzkvWb5zyzr7j5M4RVVMx++I9Tt56ztnTLUrB9XHD+1qxfHjC1Rg4n1nCMMqUavRkrdluhKbnMgw54QfPbF6zfuOMR9c7AomfqDvmZcYkBU8zZhPYvHNN8fqxoFTjwM+rb1NcbSEKWnT10n3GxYx/+87mhfTn9ZV0uXMWY7nWtNuWwmjRlFsDQ4CDdEX94FHWUJ0tJK+pctxdDNybi7/o6X7BRVcDivv1hpXuyP7Ae+s5m52EUapZORU/MrWIY8TWxdQpneARVuP3PWkMVC/dEzITWUzwE13ILAtizkSt0TlTVA7fDqSZFArtfs17/j9iCzuFFwZ0jKRZJXS2wtHEUx4ufoZcFlyG9xjcN1A+clS/xtnyy6ScOW+/wdPd72MGj4pRkN95CsScckBUlokHSvOy/T9QL+/DOHlXcpaNekpoo1Am8/jwX6hDSXF3SbWq6B5dUBzNiIOnu95RH89JvWe43mPmDWkYiRdrOLuLaWqqkznN3QLygFKK1Tyz+DwoZlx3P8fj3QxlFN961POHz9uPXA4mzoG83hu9fshoqykeCPwjZ/jjP4S3rm+uRhkwQM0toCVE/vLZH9DsWlgPvDT7JZyuZHJgDMpo+nDgg+3XyEScmvHakQS5qikTK0yToZgy1mjcyYJhklGqbrgtavIEOoBMUhodBGJRvXqHzZM/IO86WCJFNpqoNcp7mfqgJsy64m7xRWFPNJkPhv/EYfOcpDNP9r8Pw+RfSglVOVL0vL/9XTHhG0PJg9ur5o2vI8coFMVJ7qWMFvAGcnyIVClKvtOUW6O0vj0nU9tjXUEcRtR8hmoHTOXES2UdpDgh45OExI4B8JiYsXdXVLOKi7f+AIYKrw0x/QSmOEIVhm7X4kcJam7bnjB6mCApopJSoCWfDC1T6Gpe0+1aBi+emXS4JJb/iSEnXr7/EuX4ea4uNjxQe07+w/+Xl/ev8/adOe9+n7vM4fG3aR+/CUBTVXypTJxfvct7859D3X9dNukhEVKAKAQ/r2X6GUgyrdRIMVKX+JR5Nyx5vi2ZYzkLiSrJFEGXAlq5Od6zj4zvn79QYWTJOQo+cqUavqlHxpgZS4s2iu7QUlROQqRjYrfZoRI4M0FmeoFgRDJ1WTKEII2dlFjUDT5YyUCLgZ/64I/4XO1ZlE/47b7jcYyg4D9MR9HtXThnCgN/9fMLKg2xzfzhNx5QrVaYpuTz+4FxAhqEPnD07MCwOZBipvcje53Zb5nomxOFcowiPQSGbsAiGH5rNCFFtrsWY8Vroyf5eU6ZMAwUWvGF/l3uvf0UNTXFlFY4ptgHo8lD4uJiZL9ocHWJqjImyvs/Dh6FIk0FaU6J/mKDO10yPF8LtGW6/heLBvfKXfbdyD7KNdKSCark62tH9lYmn66W42TyhQYEAqSjnOPDID6iHBL9MFA1FWGM7J6vuftjL3Hvyy/z0pMt6jvneJV5p7Q8SSPey4TNp0TuPc1iRtv2qA+f5x/ZMX3kf58Niz5bf27Xj6QoeiFZyy+6DZ84PvtwX+JDj/lTnICfNIzKNyf35JewpeXhz75OViJDWT+5oNu2FEVBVRbUpaNSmvOrDYdu4PWffJ3H3/yAylnGlDi6f0y5qFEp46yEpCqlKRc1xXVB24/MZzWXjy9ot4fJVN0zKzQha5YnC2Ync/pNy9XjK6zRLJaNbG6UYn/o6UdPVRQsjxbYwmKdJabEfnPgXEWKyaSJkWwClTMmZvARq0vxhkQJW01Zktyjn3T6JOysRPUJbzV2UYPRjOuWel4RrvcweGZG42MErVk+PCZGLBuxwQABAABJREFUQTbfe3BMt+/woyfmxLjvse2AKa2gYkMgJHj+rceYeUmzmBP6kcOmpXSOqCBqxfLuETkm2qeXhMGDgtFH8bB40YOHHFHWoSpHf4iEGPHtQJ6XLGc1+txjjSaazOLBEcXZknEUmUbO8t94viFdH2TTVTqsEzmCaSrCriMPkqOTkhS8cYzgE7H36JVAEz6Mi1Va3f5ZOYMtSzIlTs1k6pISOQhu2lSSMo8T6IN2kiuU2gFVWOpFLUjibUvx8A6F0YznW7LVqNIRh4CZFWijxc+SsxRqFtLSEkuZ1gjK2FA0DaETGaA2Gu8MpqwARRxGtMqYmEjOEpSSrCoFHDpy35OrEjxiTo6JFMXsr6xBKcmtMc5iQGR1pZOvpwSIUVtCZeXXGAPjrsMdNQKVaEcIiXF9wKAoj2byGW1bivtnpHEkXjwnVyVpUxLnL0lmzXT8yma+eCEHzPlDkqZPunlP16AsWU1ZSXhnagdR2KWSnMV7k6cNtFyCZDOjraFc1NANt5IWi2yyUw6oLFO/WxpcKRkkNyWWRoqnlDPOKNATnh1QVUHcHjBolMqoqpAQ0iTHUIqR8uV7oJ4yPL4EH+RniDKtUzEJwiGnSfbINNESCaSaZH0g4bQ4IxO4lMQD5yMBpImjRRKnSydX0Jv3MSWUloJbISrgjNAS4+RhimPAlFbocyFgjucCKOkHstHEmFHdiFvUE9AwTUV8JrWd5GmVTmAM4/SzpUzcdaSYmH35ZfTpgrBrydbgtJC3fAikEKmbSl5LTCRjiJ0njIHF0RyNovcjZlnD4PGdZ3O+JhcGt2pwXYAAIUZOzlbYbcbve3zO7PYHXnKWcl7yad23jzf+XkRDZ+y84OjVMykwJmKccgZXCclSxUw5K4iDvN44jJzcP2Vf7IljYOYqYs7YwqJyxl/0DEmjwuQRvDm+M8RhJAYhSzJhzo2W87I6brC5ZrNrZUIxespCpFvWSCbPYjWX6XVKdG0PzlBYUUD0QRofCbAI1Wx2NGPsRpJWNGdLlqssE1A5q8ifcCOWtDnxTrXPrhkPGVO8SgiJ/QeXANRVSbuTzXq3PlCvGtrnG/FYOggqkW6OYyUTra4bGMaRqioJWY7TrhswVlNUjr4bSCFSVQ5dFqTBU07Hvxk8hoRrSsw0nc5TZIKpasI4RSqkCKMUirZ20lgoLMWqwTYVafB0T68kVsAY+e9m83Fz70iJZVFQAId9R6k0T/YHUlwSs0x5c+9xzoIS7H8kiTxXgdVWAqRjolAanzLZS3CzD5Grd55TNAW6sBy9esblu+f0hxa7FI90TpnCiZdtt2uJccqu+wHWzcf5aYzfz9Zn67/X9SMpil6cZj/C0+fTZHXqo1//pGd84WWSwqgrjzi4ipwVh3XP46+/hw+R05Mls6ogxoRPiUM/Mjueyw1XQQjiK1jdPWI89GyudljFlJGg6TctDz53n/WzNbvrPXUtXTiToSod20OHmTfc/dwDlFKcv/0UP4zUqxnBS9epcJbj5UwSqoG+79HjlDWdMsY7ljrfkmbQmqYu2VtFWlXY0yWLsxm5GzjsWg472XQUEznNOkNppXNurWa2mpFTojqek0Jk2HWoeYU1Rt5UHzG+52j/hJASBz9yFWVTHIJldvQ67bZlNi+5TD3NbIY9m3P/eMb10ytiSuweXdH3o6RvG42pLGkIFMua9QeX2Lpg+/Sa0I70XU9dFgQQ2o41+BgZyopysWDuDGf9E3R7TbHzGAu2rpmfLNhYx/V+xKfM/VlBypmi7RkvB0wCrR1leU+0+GXGeI1qjhnHVqhtPoiBvC7IYyDuJcCwfnjCpYJrGRSx7iPbUaZK/Zh4PsWFXHSRVltYWI5Lgz30+PVBjMM+oowh7HvZXGslm8HCYGcVYb0nDR49q7BNQWzFq5GMIfeeGBN20ZC6gZQFIJHHIGQspUAp4q6FUQq8cLkj2RZtNGO+Zls8njTrLU06wpQSCNmlC9pDR99tMT6Cb4mTNwyYqHJOuqZeELI5BNr+nDi25JMVs6OHGFtiwsDSK+hkEtMtSzqlMCqQn18SuhFXFiy8dD+Hp9eYV+9gSifZIEpJyOV+S+p78m7L8IElnMwpjubsvOLxWmEq2I+Jq24kp8RuiB857283qjckl5x5sldYn3ANvLSC8npPdhaZtX5MivShDZ3KsHAj9gh0UlgseCmiNFKg5qSo9AlZQ2HmpJhgks4prUkxk+JAHzdoU2KKFU11Av04SccmDHA/io9Oa0I8MOgWdXzE+O4Vi3BEKjOWUiZQGvq0I6QeYqSyK1SQPBVTlEQvRMMqzFHuLoTAYdiAkm3NrDiDrEgp0vorMYbfBBR/+Ho7vY9q2jAb5wRVPEn4Ys7QSIio70UaZK4ONFGRukR2iewEXJLHAFc7IVbGRI6yhS5nJxR2LjJal24/xG64IkWRoJrVjNSPmJRYVULApCxo44xh1+GUZj1Ngfq2R6mCcRBEu6kLVEyU1qHnjrbrRe7sE8EoujZy97UvMnv5DvkbV1TFhqM80tSKxcM38Gcz/DCi+h9MmKCAsdB0tSa+tEA/LXFNOYVqKlLvxWtiNYfnG+bzRv5ea8ZhZHe5Fb+TE99TOmSUzZTujEZrkg3EuP3Ii8mDR9cllIl86G9hKeZoRqEDs+4ZSXnaznBIM7G4ZhiuduSU8V6uJTklKeSdYYxRps6DJ1tNWTqUjxw2e4r1gQdv3MdUjntHxxTjBYnEa1Vi7uV+qbVAIBKKJ+kuHovJmfefHVCHhubkmF1bkEKGeUk/ejY5kiYlRK8zY2FoG0fvPevBkwp3G95tZyX7rhfQQkyEmBiGkbquxOOqFEVRSICpGVmlHaYXr59MPGExUzS2wR3PSfteJLAxo4zCLhpsStQxE0ePqQtIWZpT5bRV6j3d9Z7cDreTY/wBHeReopUSIEeKmLSnGDeUtuJYNwwps1NRru1lge9H5rOGwzCgSBTOofpxyl9i8p4pzORJ1kYx+kz0Ea+CgI86yzs7z+svnVH+1MuUF2u2fSfZRxaGcaQoHH4YqZrq+27RXjSZ1If+/9n6bP35WT9iJPf3Mgh9gnTuBznjfhjP0cee92LxBVJ9wv7ZhmffkrTspqlYLhqRCuXMru0xxnD31bs8+fYjSbSOiQdfeEC1bLj8zlMOB8m8mJWOlDJX59eoqy333rjHyat3uH58Sb/rJPOhsBy/8YB7b9ynmFWEfqS93rOY14JHniYM/SA5R6vVjJyyoGudxQ+efvTcbwNdN5LIlDcoT1qevHrMRWGBhGt7GbFn8S7lnCcSzrSJMYrQj7hS0W9b5nMh/jR3VmQf6TYtttHoqmC2auB8y/zJ/48AbI8L3r27QGnFsFlx/WyJ1YZtadi/tGLctBzee8qsX0kQ4a7HNSUR8cbMlgvZqxrNo2+8D0bTHM9AKcYQWdxdMfQerTOutGgdsTHx7qJgNwTs4cAvbv+Aip6BhKsLVq++RI/id95aM8bMvND8T28coWOke9wTDoqsMs7Nean5WZR1AluYZBe76oJh+58xRzOqO0sAxvWBGBPj9YH8+IpvzRZ8/VKOH8UADC8OydvNSXd7aP6l15bcP56JNGbbCqJ79JiqIE3hiwqRbPhh8kGkzLg+UMwr6cSPAT14sheJiHaGHJ0Uild7dGFIYyT5QPRBTOFaoWNGOYcfPSYmDuqSNlyhleJo8QVeXv1lVDdwsf06j/rfFyP8FGKac0aFRCo0pnAYryAmkWoZmTqQM8/33wCl0J3jVfU/ocwSbRUvnXecHHoCmTe/uMQXE0Fs9ORcYzrPl95tcUVB9pH28RXzz91Ho2ifXmGbmrg8Ql1dgCsxxyuMk6nn+1vL//wNjbYg46yRFKPABT52PXjRwZeN9+881fxvwaGd5v/y4/Bjy4ao1ZQdpj86YlI3RZXMex7O9iyXgV71DHuDMRNcwgdBAhvHy0c/j0KIVjnfzr5vL1eeA893v0s+KGb+Ver6Z+WprCDPE6Cm5ovSmu3hA3Zn16yvzqmeWl5a/rz4jkqHinI+X+zf5DA+JqfM/cVXWZX3ZSI5FRwqZs7c51G1IQ4Db3f/kdHv0REezH8Km0tC9ry9/rekSrrRt+S9D68p1BcUKQq4IZDF8F+V2KaUzLNtCyFSt4k7rYFRsckj48M5GGnU6Bgxy0YQwWNPVorj6nWWxStC4ZuM8yh4En+HfbiQ6ZmRgiL6wBu8QxgOhF1mdL/ImCqyzvx+odhdbqkWtUx3p83mYXegmlX040A2Cm0U8TCgG5Em2+KY4F9j+5bm2JQcf+mPObUGXVfsascO2K0jbH+wO0wGdnPN+bEleU1RnhIPo0AjFFRMTYfCUs4rklHkJBLUbtNyfOcIPwbGfqQoCiGt9YH7y5/lpC4JVebdx/8vwr6TKT8in0MhG/BlI+9hL4HGZnzMF9Ijeu95Xj7gOn+B+axBZWj3LUM3CLqcTFVXuKUg5h3gQyBokVDa7HCVo87wRjbc33kqW3B0b8ClDXEM/I9aEfuR+mx1e0oFLP/z+PPs9IrkA9/+5mNyrVAxw1yTpmLGHM1IKeN7aWydHJVUBXRHBb1X5F4TvMdqTfSJvveUdUl76Mg5S5ZXKY2BsRPfVRcihbM8GN7lleEdqlmFTxnTB+rjOeakJvY1qiykKWEMSsmkf3z/gqyV4M5PF/h9R7o+TJRFRUqCnb+JOSBE8RQrBGoS021Rrm1GvfOH2CeXVO6Eh7NfIDmHouObVSbGhNGKvu9xEwSkbwfJVspG8uKmXCKVZVqjrREPoSvox5GidvT9wLPGESpDdVxTNAb71lPGQd6roixQWaSMSsnd7IXk+EZGlz92Of2sFPps/fldP/KcIln5Q5uO/LFff8D18W//YV7Fh1UhIfHkW4/YrneklFguG8J+z/kQ6bqBGBOn909k2hEiOWVWZyuWD0/44L+8zfXzNWVVoFISA6SRiY0PkUfffsQX/uKXeP3nvzAlY0+Sqw9tOHw3Enwgx0TX9YLsnS6wdiLLpCSj99oJIjSMXrKNYsRoTV0V+JgIOTEOnuSmsLd+IKaEtoZ+35FCpJzXEpqnIEQv1JtK/CrayceujGb20il2Vgql6jCQc2ZxuqSeVXQXW7oELmXsrEKHmuEiYpxmvzswv7NkHEZiShyeb0RT7YyYZucNMSb2uxal4OyVO8xXUjS06wM+Ckhi/XwjPgWrRMZGQIeEC5FZlImZrh3awNxpli+dSXc7pJuhgHi/DgPp0Ik5+HQuchJVYqsCYyy+G2UiGDNRjdhFSXE8fyGReiDhjLsQiduOqItbjXWG28yVm4nKrfJT8ZGbjFnNMKuGeBiJN595SvjeU8xK0r6TrImcsScL1K4nHwbUvMSVFamwQsyzMmVSgG5KzKIi+Sjdc6NF319avNaYbkT5IMhjZ7B1KaGUg5eMpRBEQpUzaqIeKWtIVjalOmd0iPJzWJlkaO/JxqDKQrxDY7g9LU07oOtE6AaRBcaIqwohaKkk6GZrhI5mjbxJbU+KMoHqrnfUqxnl2VImUYuacLLErubUdxymaEmI/EPYADKpeHFi88n37ZvKZpLzZCWS09B5Qh5FhhdF7vNhXf1Hpk5KzttiUYM3jN7io7xfTimhp4FQ2XLEKCBlfIy3JMOisAxxwrykhG4HlIto1HS8CiwBxQtJXGFxD47p3n1OwwMygvxOXmRDWskmOqTJe3aDIZ7gEHo6GJW16JTJxmCrkpBadJreSy2hrFlrKIUkl2MC9+IafWOQ9+2AsgZbSQhwSlO+UkrEXUseHfZ4AW2PHkdyTpOfQsGuJVtN7gZCCOjjJSpGVFmIHKj3SIKxklDU6VhNRqO1Fb9R6wVq0dQkJedA7vakviNYg2pKlFaUTUn0QosMPhKZJLchYq1h7EfmpyuUUuzWO7KVz7bbdVhn2fcteSnB09rp6Z7xcS7Xxw6xT/tahvbdc9zxq9SLhvFig5uVZDPJA8eALR3jYaCyhm6MInHMTJh16PsBrRRNUTBOPhM9Faj+fH1bFKnCkjcHmb4NXiTBzqJXDcW2JXWjAF2UwSnLoe/l57IaUxWQk2CeZzVFXYqsrh2x2qLsRKVUmRGonKWeLyjqSn7OEMkkxn2HnVU0p8sX8mIUw9WO/vqKeLdh9+hSwqZLK1l4CpKPmMJhk6JLEV1Y6gjj4G8nMylKY+hmSpqNwhhLYS2xKogxsljNpcgbBskIQjGvS9QYqOqSCovKCaelIFPIPS+FhPIBXTj89V4K8yFQnM6xpwt0IdCVeOjJlRP5cxK5oIQJaQhBEOHaTN5KkcKj5HrlL7fEkEhaCpk4CNa/qEvG7R4/XceNMcRBQBLWGVQhyPExeMaJ1GitQbsCp7VMiaJcw7tDJ4oBlTlsDzI1O5px8vCE66fXNE1F2/Ysz5asn18TQpwKo5vjVfZpnwnkPlufrRfrT10U/Slqlh9sfdr5+nFx9yc+5MU3xxjxPkzZDBW67Tg/9PQhUdUVD75wF200j7/9CKMV1dGMhz/9Gtfvn3N1vqYqLCkmOh85vrPCFo7D9oCbKZ43a57yASfVXdrzDnLmqIJXmkzqBg6zuzw/njO8dIx2HfOV4eilM7RaMuwsV++f0z55H324wlhLiKek6DCT6d1qTcqZ6+udbKiVwnuHyUpoQjO5+PkUqaqa8dCzWM7o24GoEm7mcF7wvLPjuRhMb4pWDcWyEe10U9JebsljIDx+ijWWOTPuXY2Eaw/aMLMF3a7n2M5phhq7nPFMGzZTcTGGIIhTMkllbOkgBnj6HgsXGA49KyMIYxM1u0NJGBSrpmTurmnMiDaGlR/JZUlVW06qUwotm/5FMWKKSG3hlWVBfxiw6x3jsCeXVvxUAmlG14H14T2KeUM3bjFZSHTtKvHclLD3NE5z1kw3wd4T1i2mtNypEuVMjrNHm8SjtUcpKIriNmAPbhWanO89PsoBeXfmKGclvh8JY8BksNYSxoiavBpKK/IUyqrqQl7vrELP5O/j6MXntG1RMaILhyoctCNDN4phfNqg59LJxvHG+B4iDB6TM/5wxaZ/B2Kk89vbzUYO3E5DU+nErzN4CdiMUxr7RC/ISqHnNaobyTmzb58yjltijmSTMFUNpeNhe0SylqxhNz4jjZ6yLFj93Buo3otcsu3pnq7JWuGcZTzfYmvNnZdrdKEocyu42spNReh0F5+0+h8pjr7HyjGhjHxOegpOzj7ySp2Zz+UceusaWv8J1xUfieset1owdwf8JhD2nm1vyTahh0STjqRzbDUxS5NEK40zmqw05XzJIr6GiYmiOgElG+PsDCqKVDUnTVYyJVm89ArOtOjNgapeSjc6ZYawIeaOnBJGVyzLh+iscKqSDu+Np8taMplD+4SgIhSGyhxR2gplFMo48TBNRMbY9jhrOGo82iVKFfnJVSAZjVMSAqytIW4O2NMFaZJdKSPSnuwjejknA+NuoL87kzythwtsGsVDU5XkUaM0qFlD8DvGXUs33+HyM8qioqssvjR0w0jbBuLBi4RoGHHHS4GMDAGTpHN+XJV0PejSTg2NCbkeE7PFjBAEca6UpiwL4pQ51u1a1KzAWStNmKmx0MWKNy9L0uORRQOvf2F2u8H/rtvLhzshH1vlmJl3CaMKmuc76uwotWGbpNCpjWX0HoWTgOs4ZdPkTMyJSKawFo1i9KISeKcshD6aAyMZteuoogQy20WDf74WemDbQ1OjVg2b959RLxcwjPhDxpc9emEggTGKmDPlrBLE+k2D7WpLWZeokDl5eELjA/un18zHjD70mMJx2Sf0GxXGabreU9tEOaswekVYy7913VXY0yNGlTGnJ4Te060P3CkL4tWBpqr4YByk6I2KpDQxiYyvrOSzaoOHIPCNpCUiIcWpgDaazXaP0oq6Kel2LfOUeLmuKLRh9FuGw/uUhWMRdhLK3ZQUsxJbFqR+II8BVzmGZ9eEkAjWYJVG14XENMREv83gCqJbkasgapKUqKtAcTKje7YmBZHkVa/cYbjckdtBJkfWijexqCibuwJsMg1vjTCMnrWyEvQ+qzm0PahE9JHKloSU0E7RdQPKKuq6YvBSGMUQmaXELGTG3hPmFesok8UQIvv9Ab1T5KdrHjw45ezsmN3FFrMfsP01q7bn7IsPWKHZ5oyfLnUfVuJ8j8P7s/XZ+nOzfsSTog+Pd/6U5dKHZXOf9E/9CU9cU1jqlZhFC6NRXUdQhpN7RyzvrhgHz/N3n1GVjr4fefgTr2CMYf3BlRB6rKUsHPWyoT30bNdCitNniucnj5j9VM0u7nj0B48hw0/dyfzyw0goPd9pfponq7+IefAzuNlj9PIDtqwZ93P8/oz0+gl33llTfefbaGPYXFccDivuvXpGc7IQY3o7iP8nS3ZEiANpGKmNwinFfF7jx4AfRoyR1HZlNaZ0tLuWYAJQ3EqiPsyRvwkVVUpRH80ZDz24knx5xbztWYwnYphNT0n+A0atOJl/nofFSyTv+U/zit9zBmeMZBUNA8paxs5LBoex3Nm9w/3xiSR6ay1Gd2PI6ucILCmTprRbmmZEO8Mdsyc7I7LAKJQqlSN33TmFtaSyYt8UdK3HPVyQYiR0I7ayxLYnGUsqOsLsXdJ2oL/eSEjeqmZvjvja4wMArx9V3JkVsgG93ssEyma+UPW89nnpRv8/v614upPQ0pti8sO2NTJ8+/JGSqf45deXlFNHOncjOSSS1RggW0PSspGJhx5jJbRPTPFCxlOVQ1eOtO9JWkmYZcz4Q4+PSbC7+54hJFLvcYWVCQ9SAKTRoyfi3cafs2+fkpJkuWhjbu9+CZmmGB8gapJzxJxJSnJztJMik7ZHz2vilE317PBN9DSiy8aQR42Omq/WX8RS4mPPW8/fJjcKe+aIvSd2HlM5mqZkbAfGXUd57xhzPMP5PafxghqHndVkZMObb93bSiYRIX8EgPFdl4Tbz0TdUqCUEWhEDAHjLH/pbKA8K8lW83//PTj4m8uJujXNq9LCOJI2W1zxNcoHBX7IvPWOYyDRjJpaf0WmIigJyJ3Cb3NMqJgpyoaHy69IrtVUuOQsxDe9bMj7TnxIxqCrgpPX36D9zmOO5guUtRNEIbHu3mcbHxPGkZcWP8e95ZelONEarDQidEZyjFLk/PAtevZgLK+d/TIz1+BDQGcxcqsghbmZFVibeTg/YIKHmeYLPymFdp8c33qkGS+3UpCsZqjC3spg8+Ch7xliQrU9ozOkhw2oOcPlhnI1F9x4zhAT4+VWOtKFTKo7e0EIV6hN5v3ljM28IM0yL10PVO20CW4HUtGhB2kqJCu+vJfPFthQ0lpNv93h64LSWQ6d0Of8FMWQiQwk7LKm3bWo2k1+sETSimRkF9ibBW+ffhWjFfOnb/LquENNmVWfcIR96rE330dOx0g2M+J8ifrOHreo+WMFvVEMBoq6QRmNqwv8poUM/RgwxuAHjyscXd9j0JhFxb/veqxXrGLPL1gDoya0A27KRtNNiToM0gLyAR0z8wd3iLsO01To670ANrSEsqYQGUZPtzngQ6ScVZR1IRJNQDvN5tk1x5+7R7lqePB0x72l+I0+eLjkg5lMmL4UHCooXNNw+IZlPI/EpPi9qzPKl16G0nLp9qijGTPn+Hyb8Nc92QUeHxcka4gpkbQAWpwx7Nue5CPKaYF4BJmKZA1l4XBlQbtvMVNMRgoRpTSvFY6/7BOzwnIVL1kP30R3GX3coE9OMI0g3P2uQwFh1xG6Aa8kJ0znjHKa+u4RqR85PLrkcPfL9GNBT4KFpbKOxijc+lukp9ekiyvc0RFqLrlWxfGcdgwyDZ1UIjk5Hq5+lrqs+GDf8v/utnIMp3QrH7SFkfwsZ/FjIJHIKjOfN+L79KNMQadr2Wo/8lpQxJh4M3fM7y6IKROiRDksVjNeOj9Q/f77VIuGl5YN2zbQP99TzkpecRVqM/JeyiIG/1j185E/TtfePEmKP5PUfbb+vKwfDX0ObjcUP9D6fj6h/Cm/f/Fkf3I1ntLceeMeftfRdyO2mWP6gegjT99+Kt2aSsy6s+MF5byGDCevnHHx/jnRR+p5zfmTC5yxnFqNamoebc4x9wzVqmG8+lDbefIK+HYgF5Fs5S8/Hi6bAbRidnfJ/cUbgGK5fZWQ7lIt6ulKNf3QOROGIOS85895vhfM6n57oGpKnFbYuqSpSgFHdL3Qu7TkJPS7ViRZWlFMfqqw7/BtLynrZcH8wTH1yQJjNDtbYHMity3Fy/dQiPTFtAOFz5TWEmOmcBqrRHpTOUfwsok3KZEOIhWsk8IOEQfo0YPVxNpSzGZEvSL0A83JHOvaW9kawLBpAZF95X4gnnRErxljR1jPZYJyAzKYAlR1UVIsamxdTJ2/ljils6d2kCyc2/dfio3u+ZbxcoerCjHV2+L2xqCNpiiKD31oHyoo1XcfznmSqunCUhzP8JtWfDwg8AxrUKs5fr0D59AzkQCl2AuxSxsUCl2XmONMmHxqVitUJe951BPW2WiRZA1ewA5xQCuIStQeUwlMQgIOs5mmKJMcKhlBLBMTahiBjEUJjvtGn2gtdKNMW0qLmlUix/IeFRIqJvRERkxlAa1AKdK+Z9j32EWNrgoI7paY5cqCcBgompIyeqpZg297VM5YJ4XwCy280P/SEMCZj9y8P9I7+dAfXhRPN3K4Of56j5tVH70ufOxfyikLPGDZkEcvH3CI6LqkmlWkPEKekusRH5+ZJmpJK3wS7T79SPRe5GwTOS6BFKDGoawlELAJ7NlSCvlNS04ZMxU5WcmmhBBuC3KV8q0/ICfxDSpr5HVP1xKyQhuDTUyZWXoKbxUJpC4dse0wLx1JGGttp+tMlmPfCfUqeylsUithUFLgMUm+kkgyowSRptGLxy1LPlfqR9lsp0w2inQYMMsZbi3hnWY1xyQpmrgJF86ZiMgvMYZwtcVUBcqJDEqfrnBHc1wqibuOpinZaUgq0xzP0Aja2ClNPwzorOj2HcujBV3XC7UzZiJCdTStmM/bXYe5uyKOgeF6T33viE9cnybZVNMXp6mxW9QcvTxn8+QKXU7SKwVlsrTrPWOKlNaQtWJ2PIeYmBUNOWbG0RNzph0GCmc47DvGdstQjFRK0T+9wrx6FxTY4zkhTtfGthesOwKZz4sGvWspnQWt2HX9Lf5dTz2DMHgKrSmPZzBEdEzUR7NbCWl9tsD1cQrvNRN4w5D7eAuP2b7znPb9nsVr9yjnIkscrwLh5SXt5ZZiyrla3j3i4vkaq0tGaXtIs8sZhmEkaTmBS23oe49KoAspFrs4kBDEvSscGahXc6zWVO1IlSXuoMgO1SJS5LMVikzqRvy2xZ0ssNO5H0OE9y8kjPXOCrua01+suXh0wc4HhllHsFOgqg+0g2dvFc5pFkVNWDvi6Cns5N/tRwyQnCX3cm9LPgplNI90mwOUlq73QivNGWMtpjAS3VBYyJbSGQbv6ccBnyImGYzWeB9Fuk+g7waO7x9zelyRaivNnOs9wQe6Q4crLM2sktDZlKhnFWr6XG1hiTl+8rH9iYd2/nSp8mfrs/Xf6foRhLf+V5TQffwf/6FOzsy8P+cod6xKaP7CG3zwzadsz7copdkfWoqyICO5GSln7n3hAZdvP8VZy8nrd2kvd2w3B7puBKVZHc0JIdAeelbHhh//8h1mqWNQAw8eyAs+LhqerE8I48jhYs5RIaGChe8phg6lNefXz9hf78TTEtcso7xeVdcMpvnIzzBpQnC1IDg/rxN3hgE/BhZ3S/q2JfSBtXcobbClQ6FkMmYjqla4pqScCDSH59doJV3Z3I+YHIidFAjNsuTknuHu6RnxkBmeJbSyBKvo6oLgDHnsuNq+RdIKF+DlyduQY3ohy0ImHzrDwgxUixpdWOl8KcUYE0pdEscdrjSYIhPWB8IoHqpMlnDHfU8eArop2LtjVEqEkEBpTOVu09iVlQA8VUgHPYcoUrKUoTCYmMkhMTOKzx1XpBCZ7Vu6jSBoTV1MsiUYbc3FLqOcpXGazx3LJ3Heena9bC5vBhnqo58UTw6BXRAN+4PG4pY1LmUoLOO2o28HZidz3MmSPMmDlDPkkOnOt1SnC3QpYYR2Vonfa9eCs+ghAELR0k2JiUmmW85AN4oMTk0m2rpEx0RSCgOoEEjOgkmC9R79hI8W6IKZ8K1M2Gt9qznnNseIIZBVkA7rTTGasxRUvSenCUecEjFEotVc6ohKA2bnebU/FSXcUUnbXZJGj50ZdnoFiyPW2vD0XIrW9y8Cvg+4qpieS99unj9R4zFVRh/1hGTevIb9YMnDnDeiY9kJpvtLR4H7cymWv34O7ZDJCq43mmDA1XMWtkPnRBoDZlFhIuRDQEVD8kjhZo3MmZL49WJO4CMhSaGZ1Ujrz9FJJtakgnzoyWGS81YZ9cFziiCfHSmiUsYYw7y5J1M/pSjcQo45rSUDSStyCBONULxCS3uXMi0xdYNWTt6CGNmMT8g6E5MX2WOcfF+lfG/ber5+bci2ElrjvpdzZ6Jz5VIofClmfE6YfkQvanJTobUmblqSVqxePaYadvSHA4GazmeULQT5PlHtyFmkoykzv+4wZPIQaFAEPVEPSyubuCgFaEhgG8Wmf0RpKtp+z/1wzCxrdGV4b99SVAVFUxFGjx8DriwwRjyZ0keTwhVgvD6wXDQM/YieV4QQ6ZoV3/hgzco07OsZsP+B7i9kxfshEJPIvPxsy7rr8Xd7rCsxXryRIQTsvMRNRUfoPf225cGJw1mZ3J40jqwh7nuy1tRxxMxglxa0JBosaqioXzpDhRHnnmP2HeOztRyDSvDsOmWaWY3qPXYp10atFFUp8Q19Nwg63CjKw8isHUkR6gjpfI8fPed1xflhYHZniTVwFCPV6ZxCKUxZkGOma+6xPdGs15mn9xzXg8fVjiGJb0gBT3VkXhn2RzVHQ6IePYHMurT4IHEI2mqS1fSD+NdWixmd9xRVQekc+0MHKRF8pgo77uy+Q1nXLAvHLmest/TDJXpR4+YVadeR2p40kQwJieHxJWbRQM40947g5C65qGmfX3O9s1zXp9iVI2QpH2OIGGvwo0dlw3vXnrO7S85+9mc43b2LjnuS7zlfe5LSci11gr+3RYGd4CwAQ4ziBc35Fnypk/igkhcJrdZqQvprCpOFSBiFQJdSYusUqVAcvOeDR3uGeYmxhkWCKijxJ20PuErC39XoKZqSh1/9HOfdM95dv03KCR/9ba3zqTXPTRPvs/XZ+nO2/iuBFuCjFc2HZXV8/+JGfcrvf8h1fHiXu61o/fuzX+Sln3mDk+s97bYVCcW+Z/Psmhgzxw9PyDHx/jc/oK4rquMZ9bJhu9mTvGcxq9BasW0HmuM5b3xxwc+757DtgEz+fCYMnuv+Hu/svyq+pqx4fYQcPebQY9QebTTXl+dszlsZkc/nHE/TiOEocz0e6LeddM2nIML6qMFV4lXJv/8uJ2WJLQ3uzkBeZDozcogzsi3org+M3uPKApdl46eNJgwenTPWWvy+n8hZmphlQ9Y+W+MGzb0vgJlbgnb05w05KA6FJhwbTFMyblvW8V3ImXmIfG6QC3BGzONJy0abkMiDxyxqlJ0RBk/sRynwCkcc36FQimIxJ7cQDgPDppXCB2hOFhAjxdEcVRU86YIEiNYFufSEXSeSwMmDo+cFqjCyOemF5GZK8fiEXU/YdqwaxxGZ9tFWfDQTgMJEmfCYyrHzBdePPSl45sdzfu6BfDa/+3h/WxTdHtIfOUYzb15JZ10rWD2ccTwvSZOJuDqaoa1m2PdUqwbdlIyXG9JB3iOjIZxvMcsaM5dJoa4KisnwPrz9VIoloxltxk56d434K5Sb/GI33iVnZJM5elQSoEI0hlyVEsA6+gkkEaefRTHVOcSqJMaICkES31GEKJ1OZa0QsICkFErJFESrhFdCUCxmM7qcuHh5jlewiDV/4fKn0FmjjhXv59/DzktyYTlHJl6PL3v+/dvDBCRQKI1kJSklG/QJCKE+fFe/+eWmGGSSw6VE1orffSKAA0bF/3lRYccIMfAXvxKxx5qQ4IONDLiyUjy+tMxSwjr4sQeRcmbJfbo1ytNoHA2xDcR+JHlPzKCsJlpNH6FclixqMYRv9495+vjrEBN2NOhUSl5RhuQM876leWY4a740fZ4yrcpaMeeUxfKOFPk53w4lyC9CgTNI4ZQUx9XnoHCS89R7MoEQA88P3yTaCFFM9KoucMdzor/CKk2H5d+8bxgjzLPnr1j5zHOcitAsqGXblOgUCeOIaSrJ5BqjTM8Kx9x57ro98XTgWWtos0Ht5RyNuxa9qMjbKfB6DMzfvmb2SJH7EZbHk3xVCWmLSfq4b8FadAxc92+RfGBctzwYv0ITLeWx5kmhSGS892ijaE7m5Ch5NM3ZEjMMaBSkjHaGZtkQJtCE70aKDH1zwuOT+7zbDiwWCXj/u8/vT9pFKvhG8Hxj+uOD00vU6cDF208hHlH5Y0YfyEYRhoBWCjvRyrSC+1VPYSWfaBzGaULr8VrhCy9wkvgKhdIErWiD5mRcMjstKfo12mnC5kCc3md394jh6UbgHVFTKLlf5ZTAJ9DIVK+Qe0u1PvBwBK00YbOhmJWEEHk39bRHNToFXn/zCfeMY6ktZR1RM0X3bMu3rk8Z64c0J0uezBT7mKnqAt8NqHYkG82ThaM5rhlV5IvPDrAf8aVhXSVsUsSpkWMQWaObZLw3oJVh9DJVygmjLHdVxxe6b+Fcg8bypOupVzOK04bCLvCbA7kdSV2PSpnQ9eiUqF+9izJaoDvXO1rAG8uhX3BZF4w11FUhE0wkhDnFRFWVKGBYPuTdjedy8PzV1ZrTRpHqmusrzdALFTMrySnTPtBdbEgJdiGQSk1ICWcs0SdiSoQQxSepIIfM0A8UhRNkv5ZrsrbiJ8pas58VtPOSXVXS76BsKlzleLVNmKeXZDLNosGHyGF7oKhLFssGUxjeevptNv36xY7sM+PQZ+uz9YnrR18U3Z5130sD91/tSb/rK2r6cs6ZrLKEU1rYXm7p1i3t5kCOkZgzi7MZZ6/f49EfvMO8qdkfOjZP15hpo1kWBUrBYduSydz9wgPmd3oykuWijEgCtNGC+Ny0pJQplw34QOhGmpUEq4LImNL0eBB5S7s54F3P5eOei/eeS7dpotTN7yz53Fe+QNlUvPTlVzl/+xlxDHDZMZQiewnjQNZQL2tKM2PYd6Qh3b42yeYRSccNwEEZQ86GeOgFz+oyaewxk9n9dhoy/apLR3Vn9eLdjwm/a2UTNkiX3yrRoidAVxJUm3yU8EY/EHYH7MkZbip68ALCYCJLpX2Hmwhbxf1jCRqMkTh48Vt0I7H3t4Z8BWQVbjuifpTPw1SOvOlI+15uBFYKw+H5DmLEFC+CKjHi03DLGhDzNiExPFvjzpa38ovbY+t7yT+nrylnbl9H2HdQWIplQ0oH2mdr5g9PqF46EwmR0aQpLyn2I2Hfoa1FlRZdleiqoPr8A8L6gOpGbJGITrr5KohxO95IOVIie9nYUkvhEbtRNoVao8nSxZzIZslaQeZOEyGVIR86XFkwMpGRQhQPy81kYsLAS5ipJiqFiQmjM2bRkAuwpSY3VoI90zRNsYZhf8Cvr/CNw50uMKWE5qYQX5xHN2p2pSaZmBiv5S2WjbrURZ/yQdwY5iddnS4EHmDKEkjkuMZft+SygOxu5YK2LjAaDEm8NM5glCI9GVBNLT6o2Snxm0+kIFEarQWoho8sz5Y4Z+mu9jJlWu9J+27KhcmkQ0ZbCzFR3l0RNi3EOSrJQZVyQmdkkjdR58SjgxDaJgKWyhmlbqZLSX4fo0jepvcGLWh3hRLfoJ6Kq8Ji6kLydKL/0HslBWUaZJJzi22fZHJ5Kp6LO0cUp0d07z4jpIzOCdUPjOcj0e0oXj5DP07o0clmXWnxdU3ZZWG/ZTjsUPOavOtIbYtvB6qzO4B83uQMo1D7VBYkeAZU4TCzCp0N+TDSDQPN2ZIuJrJPqMoRYiJPx3s6TeQx0q9bnDW0o6c4meN9wGmD9olmUZCcZWgHkRzp7vZkTnE6xj+pOJouAh+plZSiuX/MvVnJs98T2poaAmiJRjDOUGpNzFAuKsh7jFakEG+znHIx5UclmQqiIE4UtiEG0pMrjJpL6tYk90xTaGncD2ClKVCeLsn7HkKgHz3aJ/oYcIWT4yiD8gIP0Vp8iT6I9EvNHMkJ8KM5XhDWLd3mgJpAJWnwrI6XdHpG1/akoiSQ6ftR6H8TCMP7iC0dZlET3rqiBsaQUEGOw5gCGI3NimGIuNKy37XsdwcWR3OGMchnYBW1NZRBUdclGEMOgaJ0FKcLdGEZn68xIQtpbYK+mKaifvkMMhzeeUbsPMp7cJGN8VwNAyiF1YpxDNiJzqqT+Jn6aaJrjCEXEOLA+fNr6pcWVJ3FjwadZJpurCHmTL/tCIuILgqMghQFKDGOHo0ipoRzGqMt3geM0qjSYLRBK/HGmQw5ZuaLmQTSZjkfxxjROTMOI9vNni8enzA/W96GtV48uaReNJy8fCp7jw8dsh8+gGXg/j3nRZ+tz9afu/UjLIp+GCHdxyZIH/7t9zpHv+vbPv25M9LFe6zEKH+/f0rpn7F+5y1YvIKZVWy3B5ZnSx7++Cs8/qP3wEdWxxJyOnYj7U4mShfXG0iJ03slv/iLlnL+mGDha4fPYZzBGkdMnjR4tk8S+7eekH3ALRvq1Zzds2ueNy3xbs3swQn18Zov81xG5+2cb3x7z+WVJ2zOOfqxL7J5dMlwPKMvDdpodhmG6w1H94/h9TOu1lu6Q8d9Z0QaoxXZaA7DiBkFWKByFn2xQjbJnWeZHbauCVXBvsiMu1YIaasZWQv95vmupDA1u17x7iAekap0LDDf1WVqqkQz18RRs+8a2kETd73crK0Rz8MYUN2IripiTqjJqKoKg1Yik7GVYLFtXRBrJzjtphINOJHUe8Ztj1lWZB9xs1L8DZNEThdGipyUMSDhiT5iZyV4IRqRoX+6keeZpnBKK/FQTHKk2I2kwUuOTJr8DbsOU1juzx3FRDV7shvZDd9bo52njqfSQoy6OXar45kUL4OfpH/ildGFJZkRXVSSL7XrUYeBFBJmXgnK9mxJvtpLEesy2lUEH1GjTMVCErmjqQryroXBk53FrWb4fYcpHMkHdFPK16L4gm6ADxHxw2ktAZxFTLf4VqyZ5FsJ5SNKy1SImLk+vI0yBYw9YbgiHdUYGr7QvwRDoBgUSknhaXLBPD9EDRouEnt3RXG6YNmUfPmeFO0KiN2AcpbaRRZlIOdET0EbHKC4aD1XXfjuN16q5NvrgvxR8U3veR6luPtqVbBsNGPnbyV5SWne7ROFkYnZ1YXDKPE1zeY1uQ+kduTavYu3l/Trrci7YsJVM+7f/UlsXdCdb0k+kLWiX9as7z7ANQWzreXORYVF4UpL8fAe3bceUZbHZKWEnpYzOcUXEA4kk+VZvWHjetCKV+Jd5oPkljH9bMQoU7upmLkhd6XJ8akURMRzYgtLyorLvkGTOPjM544g+ESZEjzfSlirVpjSQTeKz8wUECPee1JIQMYtaplY9SN90DzvSlyh2B/Et6KskSKtEDJXDImwvkblgB5nJF0TjCcXlRRnajK9GEPae/SHM7UU0PUY6yjqC85SpKt6yvKEw64XIMfgxYNmNeWsJvWB9nxDXZXowuGMpi6cXCOchZTYrPc0s0o8M+lFwR1iEhw/yKb4ptn3Pe5P+0d7/H4kp8yDqmH99paqtFwbRWoKwhBo2wEzK0hZcUWDf7ZDa8XJLGEMjP2ImgpgPxWiQ0roLFj1ffRUz65ZLuW4tauG8fkackanRJyaHw+O5syWp+yvd7wfA0+Ugo1swutKwsaTLbioIoFMM0TmMUteUU4M+57lvEHHc5p6j+qf8466x3vxPnHZM7gFw24gkmlmFd3o8SpjrSN58R6llFg/uuLs3hEnr55xePec/z97f/JkyXreaWLPN/lwxphyuhNGggSBYpWVqhYytcx6kGmtrZb667TQRjKZ1jJVd5m6ySpVFYkCAQLgxZ3yZmZkDGfw6Ru1eD0ihzsAJMGWupifGXAzI0+cOOH+ufs7/N7nF0NiudwQtBJcdz8R5oTeH0ds41iisNVnmIVirR3bW08zac7qCWUqIei1jna2Vkgv95ROSHzUjjJMuNMN1ZMzKIXht89IaknZXpC0Jq42dIdJZveSzFCmlGV+01qU08SS74tf1hqR1LmaL8L7HPc1D862KHNFjoEcNWE8I8dM1DU/axwhF45GobImTpFF2zAFT+uc/KyYcLUjZunAhxRwnecDJQlq7zTHXp6lCZGo51xwbU1MiaatCT5w8YPHhH7i46u/oXtyAK247J/RqpoH773P+73h0diSgU9vp1m6freJ3yVE79a7dbf+gEnR7ymN+6bve+uPv/PlireSo6//wQX4TyFAkWDg/9h9ygOlcNsdfx0fcegy6wdbnvzJB3zxV7/FH0dOLjYYY9CVY9h1TMOEmyuz7//Jh3z3Txq+//B/QJH5Uj3mL/N/K9pgn3j5s0+IPvJEWR6VPbYWbDQoTp6c8Te3lo+vYZWX/NkHmn/2uKOkzNVvFhzO3idvMzdXe5ZDYHm64m9VYtwsJLCIiae3O05by/bxCf6nH3D526ecth3rxpFiQXuojVQZcyzkuwHyMZBRLNZLHhwMegDvDNOJdCLCcRSplIKI4+mlwmXHZVT8vydxMfyogX+l6teObYFcqMOBs3QDShFjy2hP0WdLtDGkSeCfpRTSpIS2Y5ZS5ZvpVFQWPWuytVIoowRPrUT7n/qJxQfnpNl5PHYTtnEoq8UHxIv/k6oW5GGeaVHAMFEQ+VnOCWU1zdmK8TgIpnnuTJQCqkigrBAMtDtbgTPkwZP6iTx4ppd73nt8yvvbWjxJQuYwpbdGXNS9vAmlyCExek+9aiRJvXuh0VQXa+Kux98c0Y3FrZcoJMC5i2JN5Qgv96TZ1LUsa2xbU52v8Qry5Z6ASIJKlBzOFlCNQ/lIbiqKD1gfJCkuQivSq4ZyGOT4z/Nq2WpsTKA12YqTem4cRVXYVChJjGOZZXoFhKbkA6py7IbfSPdJS+dO3UTUMfOTdIHW83yLBkLCYnmw+hMJVvw1N7tPUEpkT3+yMoKNdxbKgtCNXCwLH5zLXn45aF5MS1Dw8xf91ydF3J0T9UYh9GdBOplawQ8zbLRG1+7+GBTgb14OX6nNNFbxv/uhoVpbwnTgy0//vVTt4xVx9GAMJ9V7qFLwz3fkcRK/IKXoVoabnz6GfuSi0/x09WOMFk+vKq1ZnUrQpvoRxVxtTpJw5HlWSSnFp/Ulny+uyI1jfdmyLGeg1X23V89za8poSQyQubBCAWdRoWBikmsvF1JRXPaLOXHP/OhEZijSYWB4Jt1lPfut3SfBtXQgZz2iEB2zl32hNcdj4WZqsIcgXkJEOYZZrq9yB304OZfB/6LRRmPbhXTknCUUMFmoYEobue5TRvWDYNatw5SEXj5H+45cWlL/Hiqre38rZTVGafIU6I4D2ydnTFMgzl228TgIwAFwixpbO2xbc3h+Q7tq758dSs2AizvJwe9YBdh/crh/6Yen32PrM7kf6D46JdQi7dVKQQa9cDw7AGmNsppNueXsfA250HUD/XGcfboU0Uc2pxuBlRhNPx6Jw4Rb1mI4erIkXu1RnXgwJaNY7Qe+5wKDMeA9X1jN+myFaSp879FW8SJlvqwlEfwogu3FSiBMkVxphskzjB9zsexQzvA3+r9hF88xK8Vm/BuWKqOtZegnYpHOdSqFMgbpcjlDSonbz15it1vO/vgDzO2R6/MNx12HHz1aCYWuC5HlasFufySYHt38LcuTBfZFz4c3AyfnW1wxGGeoHm7Ry4Y8esLlLQxyj4z9BDFiljX1k1PQMH7yknQc8Q8/hLMnRK3ZHzshbWpDmFUbOSZiiaSYUCiaRf1qFg7xqYsZntU/4kVU3IwN63SFcwZ/G5jGx2TrGFY1f37swQgsAavRSvDsqWRoHKoImh+jKD5Tu4ohec615XvHRFCFFxvDoLWAcrLcuLTRkhDmLB5GSUnRrLZM3xkZFh11W9Fd7bkeA9dXn/OvNxs2J0tihufHIOTI37mb361365/e+keYKfqa7s/vs15/+dddrW+/3d9HkXdfGFGcfechp+URdtJs3z9n/8U14TiybGv6MeCnHuOseONozRgjH/7Rd3jwvUdoI3hnRbo3Prz65Rek+WFSrVsOX+7YjB7TSGXSj16MGJ1FryzjFJgud0y2w7QV7dmK/ZejSMGsZv/shoffecTFNPBx11GvBZ+aU+bm6RX75ze4TcPZe+e4cUKlSKUNZYpsz85w64bD1YHuao85q9EeTFOh2wYO4Y1DYhY1ZlGLMeMU0JUl7HqhfRn3leNeEMf7EiXRMEuHWy5RxtC0K0zf3MOs7ozwWDW4s5Ucg1II+4EcIukwUNpKJHxKAnLVOIw15FHkQ/X5WgAORom0LUugV0IkHAYxI1SK6dkNdtWgtMatF7NsR82BphXpT1uzOlnIfNW+l0qpVqhR/CDMdiFJybxZdC3dqunLa9IYCLsOt13e6zLLq8MyH88ydyjEMDgNHrusCNdHzKIWKdwMhACFWTYoF4n9CGuJ3hXqDhtH0Rr3YEu5PVJ8xF/eoh6fYZoKd7ISv4n9QO4mnFbQWoQ+JlI8ophmltGDNeK2PidYqale0ZBKmSv6EoDrSWaNRG6npAPBnOsFIVWpzQJ7sSF3I+HlATXLPAnxXrJmi/g7mdmYOM8AjNevRbTIGtPoOX78HFtXVA82s+wLig+UNstc1vx7hW7EttU8a1C+VSNf5nPydS8poyeOEVj8fkGCmhPmXEhTYPn+BcXKnF0VWjnnPqBSJs6fq9KK8dNL0uR5qB5hjaFsF5QCoRvJSmFR5EWD6sR8uRgtCYSej7fRcvzMHFDPAAKsJEMildNYZ2UOx8d7A1syqJTE96Uwe1DNv38u5CDdHFvLtZ67Sa5TwNW1gEycFdlRUai2Rk1BQAzaULwHLWhxXTv8rkMtGzGnbhwqJEzK2NMV2hjCi1uhOyrQ1ohHDEDKYmrpzD0l8q6DWaxGW4d1gpQvKRO7kaIVKmXGKdBuTukPPdVSAtk4RVxtGbuRlDJuWdM9v2W1XKCdZuhGke4CzlrsoqJqa1ZPzgjjl3L9a31vyvtNIoa37wGv9grYpmL7ozNuP30hcrICrrKUMVLV0ika9j3GOfFQUnDcdTQL6f5aJ/Iq6copun1H3Yg3jUH2j13WgKI6WxNe7uUazAXtRLIYdSFqkX/lEIk+k+YO9+SDdO6SyI2Pe8+ij9RtTVs5clPTbBZsT07R04hu6ns6HUqxeXKKvjyg24r1+yfolBkPPcM4kY1Q2FQuRAVOaW5/+4LGWaoHG443B6aYgEJSMI3ig9Z3g2DkjWK9WRGGiZO25vyjNSZE3OkKu2woUyAeeuLLndgWIHh6KOjtEvf4RJ4LT29It0dKSgw+cOh6Qsn3dgp39yqjNAlJ3nPOGGMYRy9yuhmtb7R4keUZLKRCBh/pu45SbRg1JK3wpVAvW0KIxCzyzTLPsxnEsFUpSWZUlq6Nz5G6dpiSGQ+BRVPTLlusKYzTNHcvZ0m40VTLmjRFbm/2hO2KetNy/v1HNJuWEjPdvsdpLQXELF5Vr7bm63Hau/To3Xq37tYf0Lz1zQvr9xPT/Z6Zzd8nAXp7SWzAf/SehVIUpdi1l6TacbW7QT8vLNqaKYj/QSlgEZxoN4w8+O4pj78/QfmY8TDx2/F71Kuam2oLjQShow9QWY79yHYJKQbMynA9JPa54sHCchsnJh9o25qnXcvtuGHz3hnV4w/YHY4cbo/4TcXoHOl8Qa1bTl9ofBZt/XK9xJyKJGF/faSbIrvFgsEpQh8IUSqMzk9sn/+cD3VhFRucAbusmXLhf/Qy35Giort8FSDdncFlBU8qS/aRJhV+fFKRc+HxqvDA7Yn9KLNSZ0uU0Vx2mb/+TLpTx+AZ4mthQvnq6ZMCvoPK8dH5Bhcj/voogaAzmAnsHCgrI0FzuD1CmoOjxqFi4KIacNuWqe95cbD4wcvAu9GYEEUmtGooPhCHUarZg4dlQ5xnjnSRSrE+WXGTCs/7CC8EjYwSTfyjlWN7tia9uBHK1hgwi5ofbyN/dCododuxZkr2/iCWmEjHkYURvLVyIsFLt0Lns0uRPbi2liHjukLnxMXKo1QhBrj2C0rMTAU+DppMhQ0TH355TfvBBaqW4MKdLPG3vRi9DtNsKApUltwnGD2mrSXAHMTAsOSCNVpQt/M5yaMXMmAuYhQ7S190SJQkCau+Cw4LlNuO0I2YRycs/vh9/LMb8uDRiKYfBbZt2OVPib0APooVuWNRSmSAY2Aab8hTIAfxV4rdSB49bv7dlLUch8jT4CgKJjSpn0jdyEVd8ZMHC9CKZwf/tV2j1xOmf/4YzlogJkLveFHWRCBmwZG/sUdfWzFnfnHZY7XCac0PLtaUFzumkPg0aUqXaIYDavwZufc407KtP0BZy7Jz/HB4RDuj6V90v0TVa5bbRzTphNRPqCBkQDVHakbJDIuZuz/JBzb7wAerhvD5Lc2MNi8py7wLkKt50Pvu3wpkDSYrLlY/xBdJMpQ12JNTKnvC+PF/lm6rg8N6Hquak1sNFGco/YRpa+LdTJiWxEQZLcnZ3ClNqWCdxTaVSGbHieqjR2itmT7+kvDFFfX3HtM+OiUO0kkTgATS0S4iZc2jdJdzQTpgMiQHqcDCYhY1+dBhfSA3NakYnNaMoxjThpJpG7nGx2HCGE2aAtU8m9b3A+1miWochULqPabKdE9vBF/92Uua81fKh7c5XL/X42huGF/88CUfXExMO4//j4YXXwSMUoSUcXXANBWLvceaSF0ZFsuKlAJjNwp9zHuRsSKdgRgiOSaqpsKYWY46fyDdVtSPTvHPrlGLhugT4cLwvPZcXe3YEXmv0lgUaVDk4yuYQE5ZYDOLhnG7JimFqiyVsbIPSqE+WaKUxv31U862iuZixdnDnuoikHPg9qpg95FVgZfbmmPOlDTTIJXspXHwmJjJLw/oE5HAkQppitSbFqM1/c1R9qhbM9w8wpTC5gfnbMIV/dNrqpMl/uYohaCDZ3s7oXJhrBXjgwXVgxNUbSk+Mn72ktBPmFRI1rILkXHyLDYL9ld7rHMorcQMe7aviCFiZ4Pzu3uHsQZrDMFHfM7c+pqFtjw9QNX+gLJR9MfEmCzKKpLKBC9dc2ctIUWapqHrepbLBSSZ7SpGlAl15bCLith5TM5UWlM5Q3uYeFQEyHCjYVhomkWDvjzw3naFWTd8qHtOrn+J7Sxj6XjpRhTwL/SGNRlDxWdXRz71iVxgivmbdu28v+8kx++SpXfrn976R6LP/Z1ci353l+jb/u3v8INKgZ8F/+pbxt8AYIrle/k7ZNfix4DzgVVbM44TPiQefO8xj/5oi4p/Tk4R7AlX6V9QbqBrLX13IE2R1cWW416M8aLLqCcK7TJdp/jsoBgbw+5YpIpPYd9c8Cwt2bJlVW2I3625+tVIqCxaKw5+pDnfsHmw5Tgb7vlpwmTL+mxDu12Sc2F/2zHtJ3ICs7b03cQqK75fvmSTPE1c0H54gbKGMST+fZgIaa4QjV89xA+WjvcuKkxlWYbEd1VEOcU29mzDgFk5oVC5EVD88hL+zW/nb1YBxes+QF9zEgCU+Ow8WDlWmxalFNP1gYIhhEQKA2qc0JUjTwGzbCRoAlRboXzhwSZi1Y6hUlyyQRlDfbHG7wdSzGgnKGuzaoTmFgWZW1LG1A57vkJbc//Rbq9GfnE5vP0xcWbJ+VmD0mekmyMlROIh8/3NgbMNmFXDZ92K/SiV9hIS/nZAbxzKSXCq55kKM0eQcQz4bsTf9LjGyb/FiY3ZUW9qxlC4vEmotmHKil9eDeQM523Nd9ea6dmNyEfaCuUM9YM15WxFfLknvNxhnIN59ql0k8wuLSp0nk1oSxHynhEjXaUlCFZKiZY+JFQIIt1xdlaozhanWqNToigZIi+fvSTdHGg+eoiqK+k8XB/Q6wUlZ7pNTx49ZQqUmAmHgWnfUY7QbBZCDNRCXYpzQJ/6kfC5x910jPuOZtXSna7QyxptDWEa0FpzUjwPz9eoyjDFzFUf78/b20sB/+whfP+kkBN8vF9yGWrCGIglUe6kXl+zYoZfX40UYOU03ztrcBcbBp/41Sd7IVc6zXubK0I4sMgbVnyASpl1rvlp+RAzGW6Hz3g+/gozamL/Q9rNn0nQOXfitJGZraIVKkSStRhkluu8XlLddExfdNSPzKuxqbvfzwj9roR0jy5Xs+Rm03xHPIgArMVsznBVQ9SfUDpPtInjSgokJSfZH1qkbbpxpN6j1EwCrBvUKFI4t2qkYDGb18bdUeY5Ji8Y7sqimwqzWZJuj/iPn8nXUGLgPJtokjJ58kK7Q0hyZRILhKSk44zRxMMokr71gny1Qw0TNA5bIM0D8XEMDCFBUeJDdOylYx0Tm0cnTLteunwPtwxXBzSK1XaFqSxmUWHaimn32asb2N83NlRw9tEV7/3wKJj/6X3eXzf0z2+5fnpF2A1sTzc8tjU5J+psyG1NNybxVJuTxHbRYIyhO/YYY4gxEqZAs7K4RfNaB0thT5f4l7cUHzApMx73+PPAoUDsAye5sDIWf8yUgxYK6RiJOdHWNTerluerap4rVDBO1KpQPWpIu5fkmHGfX2OfGcqvIDz6mOY9sRO4mH7A6gipcbycgsweDhOR2Ww4RHLORAW+H1GnNTFIwD8NE3HwGGepaosuFjTY/H1WZxvcQsP+Wu7pNx1h16NSprod2O4LKhbKqSFuFuTRky930pX2EZMLqYiEdLNsiVoTxsAbdgNacPN1Uwv+f74WS5opqrMEvJRCpQ1HVrzwUrwobkmKiagiZQnNQiTzhkL2CW2kaBpimNUekRgzKUXWqyU+RpIqNMbQbpacbTRnjcxVlZd7Fr7QthV/UyJ9gcP1ge9m2F4eCENgVT7G3X7O8mzFNNRcx4gGniwWfGAsmcBf9D3PU7qXCMMdnuZd4vNuvVuvrz9QUvQNmck36Q3e+GL56pe+6aV/8DVLpKxm88E5NRXr907ZP72mHz22rfnoJ49YXWxQukcpCyEwXu+4/vxv5WHycEP4zhnH6wOqsqwvtrCDxdJitMc6hw5SOffDhNGKWIpQmEKWm24Rw0NTW9rTlXQ2FByOg1TMKstyuxAvjW4iK8XLpy9ZbZfUi4bldolrK463R9GBpwyhUM/zEtXDrVTk3vi9C6+4xq99tUiXo8Qs5DIzO4xrjW0a3LJIB2EeoL7/dv1mXembrGS++kWRi5l1S1M7UjfKGMgUUasWu5Z5Kox6Yx+4tcM1I2WupIr3EYTek6OgTKvt8h7P/e2b6FVV+Os+ZskFf7XHLBvsgy3xtiN3A/hI7iP50OO9Zrotr4KoeSYmH0diQSQ9WosMo4iMol425BixdYXvJ8o8axCPI7gGs2yIQyAz0wqRg1qdr4l7g785YssK28pMjDYa93CLPVnhX+5IxxGlCqxqSoY0eIFJaIV2ImsqFPEnspZSiSyJlMQ7Jou0gxk4cRcsGBSpqtCTR5dC1pp8nOj/+jNK7Wgen1B/cCFI8buNsF3cb4w2icN8f3kLOWOXNdX5So7XrHVPYZ5BGQMUkSGWZzfYzRK7rGU2pjWCOR48zrZvntFv2n/MHjCvzXeZ2n3r9ng7Li7z9ymrUfnV3lHO4E5r2Xv5hMrXAgeZk86iNcZZVC+SP91PZD2gs8zvpFIkmWGmvjm57nKSZMaerwm//LUkpkWmBbWWa7AsaqlMe0ns9N2uVsh5nOd57kxeVWWxVUX8mpZ+CgmcEcRwypjNgnh1nANFTUHeSzpU4rtSKNjKibTnMBAoKFXwz29kPnPV0J6vmT67FIlsZSmDl0QImQ/EGuiHefA9CaHP2Xuprvw6gtpvtguKkdkru6jE5HUQCWgMAVMZci4M04SqDLGXAst00wlZkULsJ+loWc1021FCQLc16+88eHUw/qHPnvnWc7/XGsfqowc0FxvGfY91BruoiYPn5uMvMevC+v0N/a5nGiaq2Xx1GieZt7wDUFBIKZGngG5eSZx17bCna9Jh9vVJCQ0sVi3H4AUcRBSwTISoIkMI1MaSUuLoA8E1GBQWTVUJ9fT49OdMn3/O9mSDco8YUqbWiu5yjzVaDKU7z/KDJ4z9SBgHkipUs1QzlIwrs1G0j3gRQOMHL9511rDZrBj7kSkkVitBpi9cxcmHD1Bc468PqCEISp0iM5HW4B4syUPAnFrMdkm8Orzy+2prKVJaR9GCNNfOkEOmqRzGWsZplsihKKqIn9AdiXM+f6UUoo8sjQVryR5CiCRtMMwdzpSpmoppCjjrCCHQzMXV1aKl66QABlKYa5tGZHF36YlW+DEQkmI4jsSbA+16QYqJvhvR25p22VBSolKQg8fVDn89cbqsWZyvhCT5LXvx9ylXv+sQvVv/lNcfICn6h2jbvhqM/kOXeHmor7znnW74jTW/JpfEZfMCowxOKf7oX9eoaNDOUfSaUhRB1XwcPuT53/wWsgyx6k1Fc7oU/5m2pvOB6+fX1HXF/hCxmy14OOiCrT3DOFG3NSVGjBOogF3UdLuO5tmOVUicrBo+jYF+3WAay/EwCHJ0nrtRFPqbI99fLXG3I+H5kcOjNc1mgdOwfPqXVGVg4Qt1o6jXC0rt+NnzXhzBTeG//V6ZsZ+al8PijUOSQ6IqacZ/imTjbg6hGxRP9wvpDhSD7Sxm2bCo4F88eeuglsLn+4mXc+X+bafTu9Nz3g48WcmDoeTMNN1i1gvybk2JmtjBX4SB8a3zt3DwvR9YTEk01vEoVbBoOGL4/zgjgevN9NUT/kYQ+OZ77savSq8KyOxT9MTBYxc12UsVdKc3DL3MVnRdQLdLocelRO4m0q7DNDXOKPIwibFsLqi2ghlYUK9aClCfrcDAF7uErS2p17Ok0OBK4KcnFapybJrCk2VHcQGvKr58NhBe3GKX0g3TlUNVhvrJGSUmpqdXlG5CNY60EiiFGgPFB/Smvf+zzMcZMSBMCmMNZZhEo29F1lUQOVNJCe1nvyI1jwUZGRqOo8d/dkV4saP64ILq0YkAE3jt0GuF2y7YbheQC9PL3SzDEmBGuiPfhQRGYc5W5F1PCYlw6Fk1D1jWj4hjYNIdw7QDrXhvYVlVy6+9xu/WLy4HfjEZVFOxDxMxB0qBMeY3tob6hrdQgE+Fv3reCwgk5vuuojOJ9888agNh7Hn2+W9IxwONWbNqPiQraOszLjY/pfhAU9azUakTSiKFYjT7/inDtENpJTh+H6genWCnDY+qP4aTQlWWZK0wCm71lwyjGByfnf4I7SWJTjO1LZH5xfILvMuYkLjYJdYcKF3Fz8eemCKuaD7ACXhjRlmbtib5ACFJN9G8RrEsMuuVpkA2BhUFvmBO1/h9LwmVNdj1Qro8MZG7EXex4fRMs94a/NMrXn4Jx1ioTlf4qwNm3cq8hdE4a6RL1FayF1KWDsaY8YcB1VSoQw8hUp/W6K5nGifqZUPKhaqypJgYu4Fqs2T0Mq+ksmDXs4KYE3ZR40OkXhfa02dMu0+xy3/4o7EU+Hf/ruNXv5J5kJvPfkEYX4FqMKCL5gfVH9G2a+yyYph2HH62IxpQ54aU032hK6V0H7C62lEYOI0vWC0vuBnhz7+Q+v/aNTypZ+mW7ykvfkMq0B4zeXEiaP2lwX6kmUZPv7RcmQWNhmFTwxhYrJeSyJWCbhyf9lv08k9Z1QvqvqE1Fh8iLzff55PjhFOaD3TN/pNLqtMl5Mxi2dAfB1QpmFpoh580ikYbjjmSQ6StK/r5uZhzpmkqfIzEGNkaz08eDVR+oBoPhOe34AN60aDmGaJwUnN471zmS8mkXY+/2uMuNpKcT4FF8x6uvsA4w/UwQo5UzpKVoLENEH0g5oytHJCkG3mHvUcknkd7yospYZKhnyKLZct+d0R7RdawXS3p+gFjDX7ymGb2nTKKoR+lwBELZk5Ocp7nIY2mMlZmkmPiizFwrKDeLGmOIw+aCl1llp1n0TjBytvC023N6ZMzzK8+4WRVSdd/kKSoAP/Be36lIwXYlztJ3Nfd1f7LWONy4P/xf/o//8/38/7twJLF737hu/W/qPWPaN7KP/5195Xg9q2I+/dcqWQ+230CpVAbxZ88PKOqFSU3DOMThque69sjv1w4wur75Bnj2h17tsNAf3VDW1dYowlGbrTHLtBnPWNJBWs79JMYwSnpToXe45xlCgHbe9adp9yO6KXQcOzFGltZur0QetpVS5hlV+HzHSvn2G4X7EPk9uUtOgW+P33OZjziGkezWlFfbJmA396MTLFw1sL/4Y+h0tAdAh9rI1haIPSj+DrUjUgFYn7lu1Qy3jVcDoKR1kqRDwm1j1Srlh+c3cnQXh38g0+vkqK3TlVBgulN5TlrZjS1U5QnBuUyw/NEGsGXwmf9yK68cqMpwKZGXOsbh/KGE1VBUoQh8XE/8e2g7L/DKtJZUK3GrFtJEtYtZQz0OAajSdMENVKZ7UYZOG8r8iBdK6Yss1FKobcteRISHDGRZqkUPpC05tauKPuE0gpzUssMx77jOwuHNrDeGC6WPSwLx2C4udhSTgQ3ngZPHoP4KWmNdpbmwwekfU8+jhQf772YymzcqI1IlZRVmCJzG6Zy0h1qKkmAY8SgZCZIiZSrVBa6kZgyKhdyEUKWdZYYInooDL95hv/sJeZ0hT1fYzet4Lvvyq8UMIr60YnIOmKSruC8so+EmyPKF9RcTUeB0iuW9n3S5Jkuf8mkd+iHW04ax0klwcxddxP9qvJZgP/+44kXR4fSAG8nzW91hHj7ViJ/i7nw8c2sO70LNpTC6sLFWmaqDl3m+Skcdy+Y/MC2/Uh8gkzNWf0dVKtROeMnT1UKRSvMPGjvy57r4bfSgVEKyLjccf6Z4rT9SGQ9uYA15BA48JKb2y9QxrCe3sf5VqSQep7XUZlPFi/pKo+LGX0zUrBMg+I/hRGfCiuleVKKEAsHQfAXqwFLGiaoZghDYYYfZNzZmnSUjimItI5SqDYLIRiWQhom9GZBiZpy6MkxUa8SZ3VFsEdui6FkQwlifhkOo3SFSiYRCDFjrUMZR57pLUpr0nHCtE66i4eOcp4wRgt5EUUpmWkKLFYLopdhd3IhHEe2F1uGXUcyGr2oiMeRpq1RDOjqKdpkTL15ayP8fjq6txtvv/zlJPusAHRfebFRho8238EmjbGW+FkkXCV8ClRrg7Lz76OgamrCFMTnroBKnm1z5KRe0HnNb65lOz5eOZ6gRPNZMjz/hPV3HhFGxR4pxKgp0qhCjoo4WHaq4TB3JZfW4n0g50zlHGkKvCgnlMU5rat4Xx0xY0TpwqV7SG81OhUu+kz2nn7XwcZSKLjKMkXpYMZS6FcCCyrFUHlPW1WsVguO3cAQE5W1GK1wWvHwgy0f2V/AUBi+vJb7SiV+YtX5hnhzhI/OOTiYbvYoIO577MkSu1kw7EdSzGw2D1htfkDtLM+6z7nVgvkfponRB6HDzdI4ub1ZKiCVGRBRWcYp8kWniLm677AP/YS2hhgitXXsj71AaWLGOYvVGo8Q4sigjRi7hingKkcMkaLEDiJRcEqTS+SoCtOyom4d58PERYHFZsl39Ypu3wOJ4XzB8GiN2rZU0zl69+UbW6sAv4qvnr1KvXbP5fW5oTfvbW+/h3oHYni3/omtf9yk6BuXeu2/f8dO0zdK8tS9ZKZQvqYF/Dt+1hylv05mSqPn+V/+FuNqlDOkmCmVZehHUkxkq9n3I0EVovdszjYcd0cC0K5aufFoxWqzou8HqBwhCtln6iZsZbEoVNOSj56SkYq8gvXZmjhFSuMwc8VqHCeMs5w9PmM5XtO/PDBOgXhWkw3YmGi1YfFwi7GG5tGJSMeSDFbey4lKEbrTPhCOg8y8OKGiFa0kwB69EH0aR1JQeo9ZtxhnRcYBFB/JUySk/t7vx7SVgBC0fvP4qm+7/cqxVkZjF4K7lg6V/trvUXfnq2SUsfLabz+7/4Alv1cBUjeS76RxtQM7+xc1AgAw84C5coa7/VZCouRMiZnUjaTeS4fFGjGW7IXoVFLCNEZkGIgpZ9gd0VqQrsNOpDYLYyjLCDlRtFT2ldFCY6KQBy8zRZsluqmker9uMdslNkTC5Z6UEsQsqsLGoZ2m+CydokqkZLkbZ8JZEl8jCjlLkG5jkpmFRshkJJkDynPSpKyVoeUsnycN14Sn1wLOqKR7YM83M3nPyF5RELtJKspRugJm2VI/2FJCov/0hVDxlg26nyhhuPdXCrcHOQ6bFltZdIE4+82Y1lGtF/fzVUqpWUby1n66P9vf9vVvp9zNP0CS31pMX+uTJStzhg4iRcu5kDQw6/6dNWI0mRWurtBJkNnqLiFKGX2yIFztKW6ea7Aa5cVgU9/5PllDSeLPZUq5J2vpWQKkUppnOsBu2hmSUO7TU5CkRs/3CtNUYqRrtUixUpaOoVbiHZYF5V58RMdEsbJ3S0xU751TYmb48hr2RyYfJOErUD05ozoZKHk28y2Z6nRF8oEcJUgUolwiDz3WWcpuB5sLlLFCv1MKJpEYu7uKfi7UbS3zNlGKJWmKDPuOkgVuUgzYjSMqMNsFJcnsVLVpIUnl/ubpFWcfXLwpvVRv7YZvlYV/w5PmW7bN+PJAfy0ZjZ9n/xZVy1gOKG1o6pqcC9M0YZ2R5Gn0TDHiCUxXB6i2b/wwZcXsWjkZ/K+3SxptsIMFJajpNAWs0qKImLL4BCXY+UizXWKMkPf6lweMs3TDNBdA5HLKKEJKZIN03ZJ4+kw+koOmnwaUgmpRUXKhdo4pRVxTSYHAGqaY8AeRNOaS8RSWzrF9ckZ7DuWmEPYd4TCgU0a3RiTJOWPWLXnXM73cEV2FGkaUUdjTFf76SLrdoZYLlj98gjtUHC53GCfWA1kV8p1hsRJ/P2M0ldJ4ElMS/EwphaEXXyxjNCkU2rZh9BNpBl7UtZME0lpAZo4yEGNisVwwpSAy26JIMQk9sAiCO6mCM4acMqEkUkhi1hoCfT9yYTQKQ3u24sXfPiP4wGLZcPbhOfpU5MnavC2Nf2vrfWUzv9qd37SVX6VC7xKid+uf1vr/UVJ0d8n9ocLYV7jUggyRv30tq/vXffVnKm3ZfPfP0K7GAL/0nsOX18SDp1QGt6kZKOSFI4Uo7vZKPDGUiTw2PUYpKj9S20BTV+A0t3lB53uUUSzXC/blKP4jep6DOHGUBHkMHJY1/RgplWFaVPS3R7Zna6JP6NqSfSLuB3CGkBVPT2pKragby4PdX7PUkcW65k9/7HBxoKjMjYFUFM5o/sWTFakUKlV4ehUgGmIfiWPArUW/zSDBu2krMYkrEHc92hrcqib2njKrwU1dQUiYVS0u6t0k8pZeoAHKGp6owvZcPDS+MuAxK9mmDF8cCinUlD7BoVBSIdmCqqA4w0+2K+7xGPPbmBB4fnBUuYIIcSuJyJQ1//Jk9Yo++rX39Lf23jc+GQph17MaJ3Rb3xs9llSgCAXKbheYRf2V780poVLiwuxxlXTdXpgNUx8FZ71oICXScSB2ghUvIZGmIDMuuaArR+omdONoF7V0p3aBT40kXyFADhMYg15UKBS6qdF1RepGwl4kXne/36YNbL+vUWbD1fPI7fNZz64qku+gmwTKMM88YTTayiyU9YGkCsoZvFWCf/dBZo5Q98mQzCPN9FerQWmRvCCzWbnzhD7gv7yhKNDzHFXRmuTFY+pOKuTWS+xmidLIUH8rSZSvei6nXwo+PlmeLP8MXTTH2xcc9I561YhHSkg0viKkglk1Mj+Si1zDdx2rb3nmf32NtLy5X77hNlbbxHcfB+JKM15dcfni50ze05Q1m+oDqfyvpKNDiHSHL3jx8jnKaqbp9t5r53TzXdrFI2Ci1ScUFGmKaApomcMpiOmkVlo6PUU+54vpV+ThQDQQtyNZg0NhtyKNckbJfSEX7DxLkQ6DYNw3LflmhiaEiKkcymjp4kTpTOZupIyephhWN0K287YlnqzAIkbKVUXqJ4L2tO8/IF0fuewSN2GixJbJGPSywYyeqR8lp9QyuM8woLIj+Qk9dKjlRoJLI55mJWfxgcmRD6//iinBdYarR/+Cw2GkaipSyWwenOIaR399YBylS0AQCah1huQ9ldW0j9b4Y83qwZbh+nf0ml8TJbx++r+1rj6fF6UVZz85p1pYhhdHfvHLa0yzwW2WTPtOkgtdSNMCaypyEnmXMS1GZU6GG2pnodQ8G7bsnlt2pw331BwF9mRF3nVgNTkBpbCsIg9ffkE3Bc4/+A79Ysn17Z5TG1g34iUUxyDgiqbnUBYcxyhSVmfIXnHoBvKJ/B65JEJShNhQNRUfu0RoFcZYmlXLNE7EGKW4h0izfZF5z+k40iwbhuMgl2Eu1M6yrRM/NJ9wuhrQz/eE3a3Mn6UsmPfKgipkMqZxhC+uISaMHygl4z54iDIyb0mWa+QXw8Tl9Y5uGGk6hc5aUNinIhNOMd2bfofZ487WFXEKpJyxs2z9SdXLLF8+opaGZtGQyXyy07i6RkXJFsdB7qt149gfjrja4SpLTIlKz10+FOPk0U7fm9yqIkXJEMQnqV22TLsDVAZbW37wRJE+/5xKV/zi+TW3l7Lz/t3xmr+e5Nxf5lf79uvGCN74t9+9vd+td+uf3PoDCKf5e15Bf8+E6HUN1dtfvm9AvfmB7uaJ3vhqufs/qTS2D76DcS3Xv3nGi2cj2pxR6sJkxY9IGUVjDH70NKuWMkykEKg0nDk/e/x0WAp60oSU2R0jKSX648BqvcQoTX3SMo2BpqmIPuFjYuEcY6Mw722pKkfpJ5wz9P3EYtFw2B1xbUUZC7ZASYV9ZTBVQ9Lw4+6aiyU02wWntqOqIhnDrc+UWDBW88FKbvrT1YGrY8GuW7CFaiumgKEf0c7ianeP2iUV1OEo3aP2AkZPdFYCo1TuvSqUUvcPFYUi9ZI4rZRilRJuvUAvagms7hzrEbnC1Gd6HylRoZRFzw/AmCY4duAMD1atdBXuPG1KoeDoleL2xYBdVKhGiXdMN/JBW8trsrQOlVFg1CtpVoE0TCINdE4IdPpVlFNCIo+eeBiI0ygEOa0wRoJ3QoIpUowmKoSapPW9fK7kfB/wV+1LFkvB5j67zcQgw8Z2Hpp2pyvsXUclRLKPqJjRVqNXLawUsRtRpYhUIxYuXyRsYwkhoaqIIuKsmX195PiaZYMOEozoWR65XPScLXpKSvSrhn3fCo64rcgvblFzl0AjprM6ZdHUtxVq1aB2PYRE1Th0bSmLinIcYcYrF2O4oxvpe3PeNF9qsjcMkJVgaIkJkM5sHkehzmVmVLNB+US+6SDNNK65izsag1rUpNrxcPMjNvE9iIm+v8HaRH/biYSusqjKMu16qpwxa9F/i5eJ+l050dev1+WfX/fPpYiEsbKcNBka2K8c14tCOWbS5YTVVvZc7chGo3aJUQ3s+09RixpOFuRjhUsFpzZs8yOKnQ1TcxZMthKfq1IypjZCiUuZMgWohKjV+xf4eEtShqyXQogzBruS42A1fLitZ2NlkcT640BKmWbZ4K8O2DBLGhtH7iawFdnP1MIZHmH7zHIo6AyHlx3hO6coa6gfnrwySVWQDgNp17GbLRFMtSDnKDCGgpDy5i4Y2kHdUrKfgRs9eiHM8FLknpZTII8JU1dcqCvCMGCL49J7tDNUbc3YT4z9yHjoyTlTLxoqrYlJCl4xF5HuGkf37IbT725w6wXD9eGby3Z/74jxrrCjWL23xNRw88WXHBeaRVsRcmRaWIFwTAkzWPRU8DFx7CfqZc1qW/G4qamMxqia7rZiCprj0kF5hRI1TSXy1/0R6lpw+zGzGW9YK013/ZJ+aVluV6jjwNKM+BxwK0NzXtPve/Zekc1Srl0neywahVpkxtDjFjWud/RTJpbMFzlQb2oosKJgnaFeN4R+whnD7e6IKuCNp21rxsGTUqK2ApMwwMXjNT9wn2HGL/A3O/SiYXj6UopEy4rmvXO6bqQ62xKu5TrPOkPKuPfOsScrxk8v0UoTmgY1TPzml5/zSfMhRWseXnrOciH0nnrtMLXMzeYZ5FG0dF3vTLxtVrjKEnzkrEkolUklo0xiUVvcYsnzYPFjJIeEKYa6rYTeqbX4cBlNKQWnLa42+JjIPs1zYUU6TTGRg3SR0tx5bxc1rhkFyFRgXXlOHwTQkV/cXNPNRtT93c6ag6BXIdJd3PN1qhn+sHXpd+vd+i9k/YE6Rd8kQPk7rt8hS/j7vqd4YXxNZ+C1n1VS5vqTLzk+uyFXjqP3EhyqQlUKlbKkKdAuGo63R9EDlzIPYopJX+wGIUVpzZTEkdo5Q4iR46GTzxIzrnbkmMk+sjxfM+57nLPEKDSh5XZBCInjvuN46JgmocxUJ0v6XYfNhbZyVIuadmHZvv8+rZvQquBWE1ZHwiAB9ngzyFB0TGL0aDRmOXc2UhF/EB8xWShceiHIY5wlHkeSFw8YVWSGwVojwa+RoNYfB4y1MmfgIzBL6GaaVhqEHJYHT1CK7IPQzpQi+SCfrbLiyt4KrSv5cC+j0QXC8xtCZSnGiFms0bizNZmCqSzptiMcRozVaGsJgxcZWkhCU8uFFCPVhcwJ5DFQRi/mplqjajvn0ZI4pcmjrSF3I8Za7MlK5nBSJg8SpOGMzFb5gN6uyKMX/50kVLB789L1AlMlCR5Zovt5Nsoo0nEk7QfcxRq9atCA8ZG470Um1U8oJ8agfteLCeZs4hlHjwbCfsIuGvpPX2AqS/P47D75U3emg/d8cSRJtBa9qKke1Exf3tBfHzCbBeW2w7S1+NKAnPdUSMdR5GC1E8lTP4kxrrUYp8mzQW/Js0t6ZcW4NCRUyRI8z3I6MRPN8l+tZd+AVP7nxElZK6hmrV89t+Wgim9NgXR7xFQO20JlZQYvhMAYRqrVAlVLAl6UIo4TqrYwexspa75RK/96nPAVBdVrf3nT/PDNNVOwJSnPGXDoylKdWtrmBH3lxBOmFPLkST4QfaCUjOpGfIhYY8Q0tZLE9L6wYzRazZ4qqogcL2ZSiOgpQS1SOa0KFJHroRTKWbQBsxHwwb1/DGWe4ZF5ijh4zKqhzJAGShFvI6XuJcaEiD1bk2+7+72sW0c+juRxIt4eqR5sKUbjzjf4p1eo2pF8IFiL0wr7YIN/dgMKGXoPs4RwUZEIUtSoljBGlFGUaSSPB8zqVD6zUpTgyXWDHr1AaBpHk53sB2NIJeMqSw4RP3hcZUn7gWQMZaa+hdFTbxfUFxvS2AtC/vkNYL/1SfZNj6g39ut8uO53mnqlaKAU8hip65p8tsEfEjYXnFIkZzCnNWmMoixQ0J4uKUYTpgA2M3hPS8JYg960kqTO50t+lELXFcVaog+Eqz3Nhw+pztcMNx1RQZ8T58s13ThRYsJpg7aG1WZJHD25y0zHTmZiaovKhapyoCZCSlRKzR1tS5xl4crKTM0wBqYUqazCNhV5ErPaEAJTP+HWhqauiPPcS2M0J++dUW8V5Sbg9x1mURNvD9ANQtXbLqAU3PmGYd8Tp4A1Gu0L1cMt7mzN+OmlqCpSFqNapTj4iK/ENyiGiDKGxekS7TLZZJxyBB9FLmiE0GiMFppiXcm1Zw3GGJTPhPn+FVNG58zYjQyHCVfLda3QLFcLum6gtpaCQhdF4ywRMQpeVjWJQtf19N2AdRbnHJvtkn6Y8MN0T4p0i0qKiTD/966w+Namm8cH3r413RWl3rxvfcNGfpckvVv/xNc/OCm606uW1/7/H339XX/MGzeH+f+04eT7/xJdtUy3PZc/+4KhD1SLmkxB58Jq1YrWN0TqTc3x9ohSsG4MJ9WB22OHy4h/kI+C+pxf37aenzyRJGbIFbdTwzQGbG1xzhJKklmRfc9i3WJ/+5L2OOEWNbdjoGxamrZmfXng4XLFsBv54MTQuIrKKA71U8yJRrcVv3l6YPITVoFRC1orwY0/iKRtOPZY53Ba4c5WlJTxuw7tLHkKhNue2iTeywf0qBnrBTfmDLOo0NUJ2moZvraGNAZUSNBYTFtTIVKvnAuqUqjaynxJSBhnMa3csdMYKHNr/24gW8/yBhUz8baXKrCSPRXmJM6sGkpTMR0GYi9zR8tFhX9+OweKCmM0Ip5TYtDqowyHN5VgfqPMDsTro3S3ACYxTsw+ChFuNusjZpFBIIPfyhjS6Mn9iN0u5ZgdB2grsjVkH/GXO4xW1EtJbLJWVKsGvWr5N/s94y5SUHS+SCckJn567qhWLXH0DE+vMZsFtq2gstSPTkijF62/D5TDQLVd0F0d0SXjnBFCudHU7YIyBtyiYXp5S3hxQ/PRY9zpcjZ2nOVeWvHzS/h/dXIxjHHEp0BJhveV4dwp1IMNufciC035/uIxzs6SrSjzYk0l3bCQKFOEIr+zAkl4gkg+hbA3++/czRzNXjkFqcre+fNIXVMhg3XI62b/EJiFrwXUbPzKPEeyu/w1fXNJjpnnJz2XrsItLQ9xLH2RWaP9kYgcr//qw4xtC8pa/p+fFK6Hr0+MvnF9y0xRmTTjb2s0hach8T8FT0mKqBND6CgUHtrEH28DyUemFztSSpQQeVH3PF3VaOAH+T0+rD6EfmLJkjhNKDMbppYCKskxn7u05/UPWW/OUL3nl+sX9NUzyIljU0CvpaOpRaKk21oMIo0FI2hgpTVl7fhkrThcWJbbNY+fD/OxlqJFPg4C77CS4Fa7kdWXIyhFKInLrSK3Fq8yKsR7mrE5WaF2HfkwoOoKfIDtArddkq8PgttuKqoG0vUBFZIklM5QkiXXC748K/iY0W7i8djRuIVIO41FNw6tNH4K5FQw1pFTpl0u2V/u2V5sKbXDj16uL5dJWWroORemfQ/aMCmNrRPD1QFuO+rtxTec5G/eJF+px6vC//YjxePV/I/fXVNaQ86Kn91+yNUXgdyd4w+ZbCyTVnLd9Z5xnLBtDZWhypr3dp4UJlZLxar/WyYiF4sK7TT12ZpjyK+KHyCzoj6gmgo9BaZDx0Ud+fAHmukKLvsD+pg4/upjil4xVltWTc2z0fLLn91iKkefLHUj8rI8elFJLBuRijsphDypBh7aQIqZF3pLfbql33Ucnt5I4SxVaKO42Xc0q4bKVtR1jZ88OQTaVcNJo/jT5inttsP6CFl85OKuI/UjxchMbdiLcXa47cgZtDOSTJyvsCcr6uuKtf0pNIa/GSZ+3SYChZu8wE+B1dmaeNmJUWtKhBBRjRQvnDEYo4VApzUpRqy1uH3DuJ8IsfD8vEFXKw7TIJLiqDGHTA6F09MNU4qkUsgpc9h3c0IsVFVVOaYYOXM1D/eexsJz7xlby2pZy+zWMNH1I+8vF6wD1AGOG8/H02f89vnH1PFIHcVH78VdAequmPd21Ya7hLz8fg2hr9vX7xKkd+uf4PqDdIr+Z02I/q5L8cbD4vV/qE/fQ+mGF3/9K2mVLxuiUSQfMVqzWLeMx4FpTNxc3tIuG1JITMcD3zuJNGslLupFsTkXUpxWGldZul3H1N3w/vmKpzeZfda0TUVMGRMiVWUZx4ApipQy9eDZTgl8z7VTxLXM6pwkhf7ilq3VPLGaD56csnj/jM+HFwzhhhzgPxx69lPCasXttMRHCNcjKSSyUrSrJVlJEOCPIyoX0ugpUyTHTOkGSHtWjZeOiDojqxUlipdEmgJqDnqVMzKQXSAOE2ZGhWub4U77zWyIl5IM5qYkMABn52A6igwtJ9IwoTZLGCeSjyKfA3n4tvV9omnbSnDN3YhKMmReUpY5n1YkG3mcxKPJSDfLVE7oV6XMunR5ENq5m1dSBqvRbS00uHneSzuhYalGhv6Vn4lXNx3mfI1eNmICO3ioHTZl7KqRqvfjE+nUaEUu8PEN3Ax3sXQQ8z+j+emixlbSPcpnK+J+kMq5s+i2Eu+ORpIk3TjC7ZFmURFjxk8R11ao0WOd+KyonGkuTsghErqROEy4ZYPdiIGq0obLDn5+Oe9+lYBEKYVHD09QtztAkeefR87odUva95IoUkgojJIheJVnWZ5WpFKwMc+yQfksDF5mpu4lj3OV0szeVlmqrJlXpojaGLBzd6Lk+4KLQrovavbbyUqhZ0z4NNwwjrd4rdhtWo4PlqAVJ6PmfNWiUbjHYlxcfOT99cSmAb1s+J+s5fqOzvL73Ee+Nl16FXKUpIi3YrZ6TJFf9IGUFMoUQIhudqsZmz3TYUdeJIwz+H3PjfLcnrfUzlKGByy7c7SLKB/EH+qOvKb0fQePmFC1pUkr6qzITeGy/iuu3EGOYasFYrFqKL343OjKYnMl3w/SSawdWSuu+o6h0XBSk744kiePXtRyLguYB0sxSB0nSgm0faJMgXxa07UKtWxIxx7bjdz3R7Sifu+c4bfPUFY6QaGbcIMnF8j9RB4CuXFCPQxROnwZAS5UDd0q0BuN1RUPb2pKVuLH5CpKKpTWYlIWcAKQciIPHmM0Yz+QAbOomPoJlTPWWFRtCUG61uSCPwzYRmHuZJ/f9Di7Uxb8jq1S5v3y4RZ+eDaTzX7gyEtD8IW/+L95Xv62YFYnUGUpLhjQy5p4GHBZgU8cjz3p0PPebWS5qDl3Faq7QpvM8vQBdnMiYJdQXnWKciHeHO47jCWLkbUrnm0b4P2a9Fy6FK4MvKAizTYG3VDYT4ZcjHiI5SJyMaVoFy0xRMIY2LSODCzwWAdmU9ONjuZ8w+2LW9rNAj/JJGjwkc3DLYvVgu72IM+GnLFKsTpZ8/D9lofPfk5dJOCPXiSVqrJUp2uGL19Kd+/Qk4sioogpUVeW+lS6Wt2nl7R8wHbzHiElpkXhpQE/qyzamQS6WDQMNwN2YaVINwPaqtqx3CyZRs9xdwTAKI26yTjvaBYrvkiabiiMg8E4g01i7mrmhCpNYmVhjCHN8nDm56Vb1JQpsrCWi+SZbg80VuFWy/v46e4+568PfOfiDFM7fn39Jc9vn33bVrxf92oY9aofpO4TpK+5d32TBviNjfwt//5uvVv/Ba4/vE/RP0QC94eUzcH9Rf/GJ7yrrMzSnO7ZjQACmhrTOmprGHoPKXO8OTL0I7pxNE1FGLxUIauKdm3w1wGrDUkVbq92nFxsWSxaht3A+mSNGyfG0aNMTVUZTIGmrYk5S+JlpaOyf7nj0fkafbzCtTVGKUqINMsKvRtxqrCqDGcfXrD84EIGz4fXfkX16n+UQjpOUqVdt0Jpiok4BaEzjR5nLfWZSMliN+Gfe6IfCd2IenCGXbek20wcPFpL9cw4g415luIIYU0x47mbijhMop2OMvOg7h/GFrdoCbsjIQRBkh57zKJGNxUpBJyRIDVrdW8Qmn18ZQ6bxcwSo2cilgyr4hO5RPzNAduI/C51I3EcsYgBpJr13OXQi259tYBK3cu1qC3xMKCMxjTS9cIZqEQuaRYyoI8X3488CUlIaY2trEgSlVQD7XYpkrVXmD/Zcl9L3iuzZEmha0f9wOHWLdOLW/K+lyT2KN0ps2goWpNvDtSVg3WLn4J45BwGmAJFK6pli60rDELzi8NEGibxMFq1X/ksd3/X1lC9d8bw+ZUQ5yZJ3spNJ5QuQHcjekYvl1lOVVICV8m5yQFQZAWuromDdBH0LLERNZdI6SRxnc1MZwlXnmV0d90QM8+epbmzpHklsSsgCbeWZEGVgs3cU8gKoErB73rqzYKsIM0VaL8f8KNH3XSU9ACU4e31Wmzx9o3j69ccjIqCRQAsdwB5MTt9Q+GCWTja98/EmFYLKWy9UFzGjpSLSIpSFimh1qS7411AxYjRFTkK9Y9lJdLNUtCq3DfCldJy3Cm4zZLYCc7cLhuhm8wrKzCIvDYejoJsrywM8z6/038ZTZ6NfAsaFecgLgu1LWslHkBNTdz34tG1XcnhqZ0Q6cYgJrxDx/FvnwmoRd+dW00pioxGW8QLSSvxDQ5BfiljhTZZZA9aN5u7Xh9Qm4XMqwyeVCBOAaymqh0pZVKEmIMkPTkTupFqpmmWlPEpoY8D7YWhOVlSwltm1N989r/ymjsF093+SV66zgWF0gZlCuNhpF2fEua9a60hzZTLu/sSubBaLwkho2wvCUlXaGvLuhXJbx4DdvGa95Gau+WNIfeT7Ast9814HOBErit30lIHCdibqCmLmn4KGFOJ4WsxVJVjPI5UjaNylUiQrcEZjbaKGCOHY89Cw2LRMB4GymxIG6eIq2ReU2tFSBHXOurOEPY9beVYnq4xtaMMk9wbciF2I+PTK+zJkrzrmK72It0rs42Fz6iSaYxm+YMncj17eS6FVOiHiSFndjGwDxFbW5TRjP2EtQIsMFrBlMAXWEBVORateB8tKkesnKg/QqQpBqs0Ril0W8HgqVBgNa11UCuK1RwOw73KIaWEMQZrDGGm7oVuxDrL1E9sHp8QtgtUbbipFX0vcJvtxQZjDdVuFGn479h4d5Rcube8/sL5Hvj7BlTvEp936926X3+QTtHbOuq3vvqHXa+9ZSnfjsh9G82tlGb7w3+FbVaoDB/uCtOzjsVlx+cKfIhQCz5UO0uk0G6XWGOYfGDsJyYfKIuaj4clybX44YaLqkMZSxwinT9Stw376z1VW0POnDSJjRvRMbNeggqz5rm3lMEwHidO6y9YPrjCHyf+yFekSzDWsLaG+onFbRf8+XDF8T+LBG0It+QS0Ar+m+8kVpXINdbhBUYlOK35cmyJ1qBt4f3FAVslEoanx5XgxVPBbjTmZEPyNc8erDFtxbSX2SZSxqdMLoUQI6uV+MyUEFGpiKlizjLfYg1JyzFOFNQkD2sZIBX52EShtQbb1OQ5SNZtTfQR6+xcIRYZiLKGPAZJjpQEvNlL8J/8bFCnJaEoRhK1PEW01lSbFWqSIB0346HbhjJM0I2C09Ya01ZgNP5wg9muBC5QGbBWkooUSQO4ZSPzFseB6mwNo5duVBR6HEoAANPNERcidtVKx2mm/oX8un4TrCp8b7WnsUhQPEv60lrzRXtBjoV4HJmu95SrHbqpsJsl5uGpzDsphTUKkzIhJqqTFTpK1y3OWHOtwLQNaQr4qyPltuNhUSyrgm1rSZLmBHRTG4zV2HVDeHpDiRldWS7qH9LWDykx8lz/NUHtUQXUekHcC0ZXx4SKSRIdrbG5SCdQKSH2hQRBfJfuvUC0liRpTqJUkWOQS5k7QDL4rABXOVIuEO+kKQll7SupnjHgHErBj/37VPsnpJzp978h1j3T5MFaqlVD8YmrfsGLj3eoxYqPas93339AMYr/+LSji3OyoF7dvX7vOo1S3OTM/3XoUcBY3g5T5L0uu8D/8MkeCvzorPAvlwN6bWivEvpLKbo8WGpKZUWmmtRM7ssyKzQnflop+d2Bl7f/mWm6Ba35Ce+j2u9JWFQK1bJF3ywINzcoZ3HjB/z3n/45U5iojOafP2zEvHLXix/VoqKi4TE/xmwVvgq86P9KIB4KkS4aw2gULx5r8qSJrZWOyxTmGSOD//ySZtHcQxbssiUGIVoWJFmMSqFDQG8X6GVNuNxTYiYXkfWVDIQJnSLKamDuBhUt4IbKYo2hGE0aPUFr3KpFZQgpUDWCsjbGUGKmWbSo1qKUopqlh9PVgbZy2GWDKnuWq5bF+xecfHLkv2oXUOBXMfCXMfy+O4GzPz2jvRBc8meftPQvW9qLDV/8cklvFbGbOHmx43w60g+elw9X4AwFxeE4knOhLopsNJlCrAyfPVhy/vCEHI782KwxKaAOEw9SoUqRhYb/6qON7LPbA0x3ptly7zQZws2RsNW49YJt7WmeGOISFp/c8Ksvj1TGcFY9YHV2SimeT27BNmsS8iyKMbI7dIQ64yeRsX4+tXBoabLhdj9S5UvsukG7hHMWP/X8WP0tahxY/lbx0enI6sdrcjF89sJSnZxgSqZqK8JxoPvyBluLN1JJ8nyQ50IhhRkX7wz12RqmwLNjzfP2RxAiwVtKycQUeTl5Vusl0+QFVW8NbVPzPHv0kxU6AznhRov2midfepoQefwnHxKeSTfU1TUFRdU6SoGPbid8N+HqChstZkoMMfHbk0ok9/P1qJVQ7YKP2BlABAjFVSku//YZ4+hJD7fkJ2ts42gOI0+eH1lul/h24D9c/hwU9P5Nb6tvbFh/29e/aX1F7/ktr3mXOL1b/0TWHyAp+vp62iz24A96Nb0RW37D+7795bf+Xq0vUGaJTplV71kk6Cbx93EPTti/uKU5WdJdHzDA5EfsdsVqs5TK6G2HW7Rc7gOlwMI0bNpEHwNFydDz2A2kGS0MBZUnGgfWKqbumkfvP6BdtoSPJ6YrT8FiwxFrr6mWinqVMYsa0yiqVT23gTzPPn3Ji+7Nh7PV8GRVeNBm0mEkZY9eOOJ0JHWOOBVspVieBKraMIUkw9AJTOUwxrL8UAJDn2G43gtkIItkzTkrSYqW7goasBUqClghKanyJopIcjIiQ3OW2IuDfPGRkjKVUZTei8RrGDF1hakrGayf/XxSKVitBVGtFLmfSCnjaklgtLNkI1Qf1cz+REoIelorVGUYSpROmSqYwv1sUNGKvO9kTsIaUjeiKyeD54jcz2zWxDkZM00DpRD7CZzFLmrS9UGS5rYihZnCV83SwlyIV0f8ywNKK+onp5w11Z24Wz5ryhiV2baZyko37a6jFrIEnhiN3SykA3dzJB16QpKBZt1UmLbCoIhGo3Y9eZjQ6wV6Ps7xOGCWDSlGilZ0w0SFQk8TJylgtxuUn2g+uHg1SwVUJ0vi5U4IYCja6oQVpxSTucoGXxlJAHNBPTiBQy/ndk6C7rqDeUoYbWSuSymKKuK1ZcRXqZQi57IAIZCMQecsf8+JmAvFClCBmGS2CKHGSTdoltExdxTm4shmcJzaE3JOfBEsxzRhHmxlvmnudkylYrgV0loTJ9pppHqwxaT9/Tl6XbZ3fwuZf8a3FWI88OlrhokgHZiiXiW+Y8wMR9m3H20LJ6eaEiMrXTjfrKlXLVtzAi9lX9//vLnLVtRcDLJGjEtDZoo7+vgSpTQfpR/RDGuRp6ZMdXFBvh4p/hRdNahyxnUXOXhP6wy5SJchvtxTtgJiSDcDK/cEowyD7UT+WBnpoPYeYiYaTWcKaltJ8rpZ4q/35JywiwqMYfryivqDhzJbogUFnjqhdrqmhVBIRWEBd7IiHgZyGEmjFF2ECPYanEDPAaae6YptRQmRPHdrjXNzQhWxVcv6YnOvCLBa0+87tCqokIlToFSG5nxNmALBB1yjOV4dcGdr6inyHSOPx5c5/d4KCAXUJzXtRc3ukxc8/9RxfBlZvq94Vp2yj5Hdb/b8uDjqkqkKPFOFKQSZ2dKakiPDOFEKmNqyOF+TUuZgNdk6NBY1RgHtvEy4IaMazaOVgFCmwZCCQlUCWsnGiOy1ePzzW7TWuGWD0wlONV1c0JG5vt4zmSVa11htOFuvuTGO8TAQmppsNIvVAtt4lPZUy5oqNdwMBWUWVNuKMAYBmvhAfxw4WTtO+2vaMLBYVPzJR1BVtxwve/zphxRuoUjBaXp6BcZgVzUxJpknTRnGIEljguX7pwKVsIa47wnjht32AVMcySeObt+TSiFohR5GrDb4w4CuDMdDh1aGZBV1W2OVkqJhyFQYtpXGqZaLDz+gv9rjFiKTNpXleLnn9DiSMdTaULmKQuJ6DKiYWTcNQ5TnTtM2TDHMcvGCMgqDFqsOn8BoFquW6xlDbxY12/WC9uUVS+fwDFz2L17dfNRbG+x37MC/s+Hq7/PSP7SK5916t/7/dP2Dk6Ly+p++cuH8joTo6x40b3/L11Qq7kOWO333PHCv1NtveJeayd9LKnLTVhNOa5KPHJ5dY50hhMhwc8CuG1RlqJcNi2WDHwPdsYejupfCxBCoGocrsDEKo8TLJ+Usxuc5y407zXpsYNz1uLYilcKLLy55770LdNvQnjvG/UDVLqnaLaapcKvmDUO2+2Ds9UN1F7gpSFNg2h8l8Fi18wxCQR01aJnPiMcRRkWpWrKPaC0PzOQjOQnUIA9CNFO1wxqp5iujxJdn/tk5SucIHwWwoBV2RpiiC1hQ/STYXhRp35NTptosKUZJ8lM5mrqmTF66BTGJ1McZlIYQAilGjNIkq5mimD+WKcjn0YoSEMf2mFCVI+YEY8CXgnUWXeZqOtJd0EYM9Vgt0FYTZ++VohV6WUuHMKZ5oN2TjaaMHtc4coHUTzKj5MVnIx1F8qHnbotyYtZZYqJ0IyrD8MnLuQIten9lNVkr2vOVeMyQUcaQC4RuIrn6nosACKjiwQnBWfpnV9iqgm5EOyOyPqOxJzJDE2+OVBcbcsrEfS/miMbgVg2rszXj1QFlK/I0Ea532LMT+k8vac7XmM1CpG5tTfXohBCvyT7NIAS59goKQoZGujTVUgAYcdeRbg6oWYYkXkVZZG+Vk47dbCBcZhpc0SKpI6f7JAeUkOoKQoFiDsRnI9d7+poS9HkGCSLnWRI5vrJ/dJzlZkox7Xu0URilyTEQL19IInZ7A+cPBBc8y/nIr2Rl3xRXfGNn+mvnFplJdzMvQsk9qMz3roJ0A0ouuKVjVW3QzqBHgQXkWfrEbDKq7rH3ZVZfiuSoKI2eRYZihCswBOssdrtkeLFDaaC1MEPKNErkd1qTfSTcHNFna6HE7Q6kLPNOBfFL0quG3E0i+ZtnFrICW8k8X7g5yDELkawddl3jn99gtyvcdikHQysY5TpiDFhrKauG5vEp+fqAVtI5LDESfUAbg64azHILwxVsW/n8Rs0EQ+T6XzRihusMFJklbB+ckENiGnradUvKmRAj0+2RzdkGjKZetdKNQOAvqmSqkyVuUWPrTCbMe//r15v21Eo6mgrIMF0diUNk/eQcxsJwuWd82vLi+TVWQX+YWJ1swChsLKTKEDSgNItqIdLqXKicZfSBuqlwSUzB41XEpkQ4DKQo3QcQyXG4PUoxwmrBs8ckXZHakscAvmPKheZ7j6XAlAqmrVk8qqmWDZv6Avv4I3zvKXGFHQ35dMnx+oirLFSGtoXGB1I3slyeEJ2ixMh6WZMrC4Nn+eSUpBWVTqz7Lct6TVVpwv4pRRfMaoH2RuSih4Hx80tIRWieFysa15IGT7jay/06FSmSTAIpqd4/Z5oCLGvxn1IKVxmaZQMrGCdPU1X4bkRbAfdYbbCVIxmB8/hxlh23lngMhJg4fnnD6r1Ttt95+Ma5rVcNvpsgF2ztOD695vr5NWa7JPiIKgVnFDGKx5rRckXGmAQGgRbT1sOBkjKubdBW0PIW2L+45bublu2TE273t6/uQb9z3UVD6v5b5Nb1d0iMfs+E/916t/4prD/8TNG3fvUfc3316aWQweSfPPwz0lXkeNNxcxP44ulzTrZrhmwxtaNWr7xZaB3aiGZ4HCa01iw2M0Xu0OOcZtEETt/7DLuo8C8H+v2SjMI6MXeNpVBpjTYKO1fK/eAZB08Td2xMT/XskrCfICpOH6/5NHqeHhX0Aa7D3S/ATx8uebB0APzZo6VIsZQinH2XrGvSYeDj6cin8+9qg8M0NUVFVP0FhJ5SOT4PD9BJEbtMzop46F7NX8zJg3JClMszeUwZTZyiyONyQWslVfyScdbeB20+CvhA3ZHegGItqWRY1OhZ9pSOI6au0SWTlUipjILUj+imliFTH8m5oBPUVUWOiSpC8YGcRWmtUfhuwA8jlIKxlma7Bm2IwaN9oJsmNrXAGtLoyTUy/1NEdqe8+L7kycsDJSXpUtyK6Z/pZCbGzAmq6LvF1FTNXQdSnucENHkKlG5CnHe4R4GXYZJ9aTUlyAzGWAqfuRXaKHwu/Pknt0QlksIx7kHBWmn+93WDRRFcy+V3HuOv9xSfSGMQX5nKQYyopsKerEjjhLYWW1mG44BJI9FoqlWD0YLKDWvpIE1ToNWK6fOXqGVD/egE3dSSIKHwn77kxfHnXPXSSTtrP8JWf0opmcvx5/heABZlkAF+UzSPFn+GUY6kM0/7v0LVSrDSWZI/VyoeL/8ZxlimcODp/i9JKqOtnRMGJQlSynIco8yVpbkzpJECSL6T4GktyZjW4CMvj79h13+OypkxdhSbULrFNjVlSihbYU4voF2TyZRhAHUmEs27e8ZdV++1AOFNycpbN5nytX98Y320TPx3P5Bu0a+v4N98LECPX76EF0egGM5T5P31gFs2xNsO55aClK8tuheS48vhN3TTJSVlHp3+hLacQco8Wf6Y3PyAnDKOVpLEUlCnjQBVYuTp8T+hNxuq4zn/+oOWGB1Jw7MfbvC7Dv+85rs3GTPcMj275d8++gVoTUXh4iCZVD6OktgWxDy2tijnUIjPVkRj2ha6jpgz6y6x+fkV7feq+yJONhsuwzU9gXw4Un/0WM5pzjJ/4mRoPReEMGgMH44bYp8pLwoVc3HDGSogo8hz0p1zoBgBcHQ3+3t7hOgDWUFVV4Aia2jPV6QhsOwDHwwCjFg3FSd6BV8MXF+P/F/6HoBjeSWrfH39c1fxx/Pe/euHf8TnqwcUH7n95TXNpqE7Dvyq1LgLTegn+qu9QFGK4te28Lf7W5brJd/1hXIY6SYvgJW2IpfCr1tFyIWVgv86ZCpjMTFyS6F+cEI5DlwuFNUjkQj7L6+Ik7/3Xgs+gLPSO/CRQ7F8XM7R3mCUwV1sRP6sLKY2mNpx3nsWX/wWUPz4YaA8FLXDFxvD7ZVQ5po+4KzCLmpWh0tilPu7GfNs/Kr40Uc1tkRSyNzcanLS+G7k132Nion2/Q3JQNx1TC92hJlsqLUUDjKzvUEpUFVSkDkODJ9fsvjRB8TbHt9NxDYxlIJRmsPlXsx4Y0Jbw9hHTOMwc+FJO8Vqu2I49kIgTFnMpL3gurM2HF7ssMua9nwt+zWJlNdWjmrVABCnSHuxprrai53G4xXZWZyC791O6OMssa9lnrUeEz+KmXR7BTGJpK7SNJses/41yhnO6iMfXWu2N2fsxuPX7rf7m4z6yh/fvFd9S3bzhnfRO0ncu/VufWX9gXyK/h7rD1ideKN6+5W5Jli7NV9++hQ/BKo/dbSbBX038PJq4r0HJ5jjwHpd4UPAOkdRSrwrmorj5R5/7ElFKt2LVUtdj9i2p31oMUXBUWG1kQFVa/CDGHjaylGy0Gm0M7jK8sNH71FdfwrKs/zgzl8i0z+buBrelN4A+PSqer2pDWkKxH7isBvZTxOjj1yH+UbnJ+pW03aFzWZJ62U+JxXFsYMSRKcNiBljlKCBknFtDVox3vREH7C1E/BASFKZVwpXywMmxYRSYObjbmGe7TCkKcpDLSWMMkQfUMyzIqtWEq85+ClJAuBqUQsyN0QxAbWaYgTXPAwyi1WlRDf2mLpiUTcif9qsGW/3hJzQvSR/wXswltY4mR0yGr1uxRg0RIb9EVVZnBNfE62U6NdHj62dUMoGj9ssxHcpSBerTBI4a2uEcod4v5jGMQ53g+6KnDLKWarzJWHXi/+KM+KzsW5Ih4F4deDF4Fk8OiVWji86zZTKLLML4qtkDBU1ToEqYM5qmvYB2QemF7dQIHejeGpoQ6mjSJ/2g9DEBi/zFoeBOHrMqqUQMViMAp8L066jmul03Zc3NGcrdFOJB9QUGb+8QacCQfHg9Ic0aksxoALkfn8/FH6n+W8X59hSEYtIrFLw0jnTWoh1xtI252jEfNRYi85RBsNnwlrRCj1L9MpMutNAShFcdT84zh1kQWt0nCEYsaNXEshKQUKLvE8vMOuKeHuk1BV2u6JqK/m5lRFJltEQyhuWTm+suwjk9fvW7xlUtI3moxNQGm4GMRMuwHEqHOecuTkR/H+c0ffaGHIq6BDBWpQ1hO5In3coo0gLDZN0oatqg4qJqOdO9Zw0mrM16eoAOdHHHa6ylGhY64RuDalx/Hph2X/Zo5ximSt4uiN6z5WRAH6tLBfOiLRt7qgpa2C7kGp0ZSRZChG3XOCHCeucSLSqmqVqcINIhkTHVrP47mN88fjffE51Il3TPEyULL5eafAzTEUC16ovOFYQ5D2Us+jZ6w0KlTGkpkblTKkqMVa2NVVTE6fAMAMHLLBcSad8enlgfbHl4YcP+ego15yx17jxKSlEQh/4IsbXW/NfiUI3SvGeNpQCv7wJDGNm9fCUse+Yesh2ia8MyhaSE/KfKoVpirBpqZRm7yPv9Yk6w/pkPUNxIt0wMUZNVRS2JM5XK1oUxWgORhP7ETV6wvmaHD3Tx88pRqMriztZgtHi8aOkO6+AiCafnsk81/Oe2q3Qrcgf87FHNQ57mGh6kSi2JyMOKdD5ZkN1UUExUCQxpmQe1ppSMtkDWWEWBqPhobqitoloNMfmhJC0nLOlAF/6lOHYEZ7fSpdF3lD2+b5DlUKOGffwhLib7Rq8p/nuI/IY6J7dULQWf6GFka6x1zM5sFBbi1YCMTBKcXK6pjsO7G4PNEaIpvW6wYZCUzvW2ZJf7mlWrTwLgTAGfvPv/4Y8RBZnS97/yXfkGegMqRTOPnrA098+5/SDCyIQrg+cYNC5kJTQVo2GTVVzegjcXO5ZnW/wk3ggOleoFj0oxYMnhgc5Y/yOKvnfeXspf8D46c03/kd633fr3fpfyPpHTIq+uaL6e19wb2tpf88gpLx2ZSukOp9CxCjFcT/wvX/+fQiJB7+6JF8dOd4c6ewC0ziqtsKXTA6Jcd+LuV9b01pDGIO4TRtD8pmc4ezDR7iDYZgCPkTBRxtDDFGqn0qTYsIYRXuyRGep8rcXW5nTmaVxWt1bsrx5CGbqVBwD/tDTHQaOh4Hd2YZJ15gMWit8iPK5QuDwrKe/dTzubmkbQ1FzxcvPkhilYB4+JWZKLoTBE8ZEmAK2sSQtPiB5TKQIKiXGMInkIES0taRhksqnVmiEYmbaSig/bY0yGhdrqQQn0fGHbkIjSOFSCiXJHAyVlYHru6rvbL63XrSCBAdW6w1OaQ79kbZpRe6yaHHLhuC9zD8tG272ex4+fCjyHK3AR8I4oa2jaWesMIUSssxC5SIP7FIYd0es0lSrVh48URI3UzuKE7reXUBerGYYBnSZJYRaQVWRcyHMRCFVzZS+fsL3k0gb25o8eLovXsJ2Jd4sKJRV3Bk83s3R5JKJuZCzFblQ7ag/fCD7PEbi7ZF4uSdMnnQcsZsFWSmW26XIG2878hhJRQwQ9aalDH6WpGTC4HHrFqsV8fYoXkybJfV7pyhnGJ9eY3wSPx1bBDX7mqRVlfkBrRCZoDGootHWgfegDapy8qKi58DyFY0uK41W6T7IUrmQjfgrhVxojSRQJSVyyVhrBbaQBH+rc76fscFYrNEko4hNJQlCN+K/eClGoicrwagbQ8RjGwdKi4mwktGXPHeiQL9Jn7v7y+tffOt6ffVXOSB3XDs1TKRjxm7a+xep+b3uZoaUNdhlRYyJ6nRF064ZLnekIB0OvajQZoNlonSjGCKXhELJLFt5VRzSBUrtUI0ldj1Jy/3FttJ5lfk66cbkkIi3HZUGZQzTvoPWoTIobSCDrh3x5jhLwwp6u6Ao0HUlHYm5cMC+k26uklNNTExX16QpYB9sMI3MR6raQgjQzF1pH0nHkdA2LJuK6tEJ5cub2Xw5QZEZwqIUZt0ARYwyDwdB8kd5nZ4lS3Vjsauakgo+Z5TSxH5icbpGKRhHTymF7vrA7ranL4bFkzMh6RWFMhZUkuR8BoiUO78sNcsXEfnj/uqITpm9uiF/9IDjF9e0p2u626N0OYs8D1LMqBowGuMEQFMKMIZ7dHjXj2gjyZNbNrQrMdFWSZFTwp0tGKc9jJ5SopwDZ5le7pmMwliFzQmzqEhBurNSnJPELQNpiuTKklJmerHDrltUzsRuQi1q4i4xXQ5kZzDrCLagm4pS8isJaBGyYckz+MJK0Ud0mZqcZvPd1y+HedPrypInTzmO+Oe38s95fm8thabUjeimAiJ2UeOf3UrR5aOH6PWS7uPnmLpmOAxEEsN+pJrnX3MpmNoyeUlom1WN0oapH1k5x1gy3kexx8gFNAIASYnte+dU5yv2L/fYoWJ/ect4c+T0ZEM8TPztX/wND7//mJMnZ7jGYus1TzYN+4dLklYc9h3LdY3OhdsYWa6X9N3I4qRhfLEn5oTKiZQiYSy42lItG7aPTlheRsrzHYnCayLer67fMdf4u9YbRLrX7uOv/jvjqd4lR+/WP9H1B0yK/g5Zy+96m69bX3nrb79q3yjqaoVrBKd5+usXnHvQTrNdLwmrhHqxkzmW1jHO3jvWWQ6XO5wxNE0tD/vKcnvV0biW8uJPCF3F8qMnfNRm+vHI3t8STzyjM4zDyDQFckosSscT1XOqJ/LLHuOEgPT6je2Pzlu+s21e/Zo5E/sJbc+4Tkv2/ZGbocaXNdVFTSiGkgq6coRpRs0CMYn/Q9cN9Lseq1uUVsSQcFp06gwTZfR4FG7TMnpPXJzx6+1PhBqmFamb8Mcgum1ETmg0xBZyPc/StIVQpCOWvJi6qhFc7XCIbEPNSQfGUBaaXBL/G1vxIIjHytPnf0FoBkrMTDcdunFYI/NbelELUhqk26AVZfQsXI2tKnJK5NqSYsJai3aO0Q+cP7hA+UjsvWBpQ6Juznm4/im5FPr0ksvhF1AG7Ax0YO6gaQ3KaeK+l89fyaxQKhlnNDlk4lyJ//KiYtiuyFPk8WdHlkdJhIWgJ4dNWan4q5mQpwGV7oL7TLna868aizvfSNBQi3u58oFns3zsqAz/4ye3Iil6bbufLxz/4skJ1dlGYAzXB/yLHXpVY9aCBy85o4aAri25HyRAbSrcZolxjtSPxCBwg8oZwuVOOmWPTjGblipuiddHnvY/wwwC3QillyHu+XdRyqKxlJggB5R1fLD+X4lsLs8qd6VQRaEzQsFWSDcwBLAzHj3fyQ4zxlpW7pxH7R+BMezDc666X4tMkYJaNoJkT4k7+INGkuvsjCSHMZNi4tnasV85bFPx/tPAOkTcusUsKgnKc+Zfv7ciZUnE/vzzA2N6W5zyd9PoPzaa/65pUblgD3t03b5xyyrlldSlFPjkduTLK5nx+V9/VPhhP1JiEhTwoxNSjJzzI9a7h6iVZXf9K67H/4yyhkfNn9K6E7ltAGjQF0v+bfh33Kyf4YAHY6J2ggj+iy8OTKlgWsvmFBg9+WLFrxKk761YsuC/vvljzGaJzx23+WeklOW+1TrMukXNUtI8RglE525hVbKcRwV75Tmea2gjrvbYkwrTyEyHW67kHvTxlzITZAwmZfzLHfV7Z6AU8XJHCQkqh1pWVKcrgbuMQTq/FJFaVtVcWFKwu+Gn7t8xdpqOmt8++FccbnqmfpJOmQIaS+UsRmn8fuRwtWfx6IRddcYXi39F8REVbvlJf4sfPPvTlvGHT0Ar3itf8iR9CcCN/oD/+2fSibn2CmKcyXGyV7QzMvdTFapGElJdC7I/jgG7WcAGfpsK5vGapArjYZiliIFS10LSiZ4v+v/E3og3mfITVJbqfEO4PpBiYrvSvNfsqC42DPrIJ5eCuF8tM4/tDfWjM24mx5e7mvp8xZiluOH3PSqJF13qRi6d5fB+jXKWlz7BMyBlHj7Yc7E6gNI8vW3pvSH7IMWNSrDXWQtsRYUkSR/5jSJCHgWyk0dPOvTU750Tdp2AYiormP7ZDoFccOdrYj+R5jked75h+OIK7AN2Vw9JrcObGURUpPCnrML3nqYRCWIBnhw8jyLEqeP2wZqnRmYev9Mn6sGz2CzgMOAenRCnyNSNjP3IcOjRM2reNRW5wIu/+ZIcJh5//xqlAlkXbn95ZEqZdS78adOgpsDt0POkOaPUBasM+XRPW09UTcXyRKErw8tj5PYvew7VwPOQ+fkoz6Bhvjmot2Oef8QE5RWp9+8Bani33q3/gtYfmD731no9b/l68es/yrqfD6BAUWit2ZyuuTxewm7g6mefgIL2n30PU8QjYrNZ0kmpmOk4oELGKU0YPdf9SIhJhl2NoRjHNGlUcfidQifLar1l9XhDeegpKZFGTzKaftexTDuqz/8Grq+lO6M08EqqAwiJSBWUMcR+JB4H9BA46siV7zlMAajQtiIUg5kpRb4bBXZgnHRZcgFr0SkwTJ7FZDAxEfsJYw2568gpYE/WpABhHLHWEqfMTjvGMRJTohSNWWwYppH1dsVxd8S5CqPFh0HXhu62o90usJUlmkix0nWKObJ0MrxvUhbFRc7kIaGLJWqDMzVpKGhTkaYDtnGo1kklUwRW6DLPJwkuAZWlk6KjVChLSJQYBXJgDYrAqWlIR0/xgbhsMXUFaUJjaVhRNEQlOGmjNebuQZzynLQoQXzbijJ6yAIPcHUjHayYJPiqDLmxdCWRyUTvSUNAVW7GSksVvvSeYg0qSSdFOUhaTFCNMaiccUZhhlF+H9VRPT5Br5v7iuE0Jm5H6Yy8bszXWBn11s6gTleYZcP05TUlZPzVDrNeoGsr4IIZCGGANHim44CpHXazEBhCNxJjlpmWXQ8xUX1wgX3/nHS+Jtx0TLse5SMl5Dn6nv2+ikjdaCoUDhUiFYtZNilwkqKVmLUWefiWIujabEVGqcts/Dp3BIrWGFNT16coFGO4maVTBpWy4J+VQi8bUjdSQiZbiw5RgAQyLIdqa2IdGVcOlYUEl8aAutyjH5+gjSYDTQi4TUtMRSAjc5L8ZrX79yv6KMApxQOtURrsBxeoanr1gvltyms3gDEWhpApUWYf81DLflGK1E8yG3QMuOUZthSu0oRPB0rWxOoOUS+ABWUM9nTF1eVzDlWPSYUHzXyr15r9lBhjxiporw6QMvp0Sf/0hrKsqCbDNi6x5oRBKa4Oo+x5Z6gebMlz0KtnQ8rSeVIjs13aOkHd50zRmlQKSkF/u0dPI/Z8gztdAYrq4Ql51wng42KLf7HHlwJPr2m/85D60Ykk2kbLMbg5CgZeId5NbU0+jlJwsIakNaZkmmmHVWBPLzDAertifbEhZ4GwRB8wWpN9wsdEu2wppTAOiZd9pIwR9yJQX0fWJ1uGYrh6PpFS4r11YHsm0r5ru+Cm/v+y9yextmXpXS/6G+UsVrmrU8WJItMZmU5X6TTFtTGGdy9YPOlJSCBBA9ADhAR2E2GB6ILcoEUDLNGgsARGQuI2XuPBQwn3msIYEhcY25lOZ2SUpz67WOUsRvkaY50dJyIjwmk7TVoiRuOcvddae621155zzO/7/pWhOmsIm67sJRLGUPZQkVJxffMRn4sDY/SRGD1VZQj7ATWt6WIqehqjkNOK/dM1jAHRe7IKVAtD7Dv69boENrcV+mhWmoyhULGUEjStoJpK3KrH7RJKSaT3tEeaeqnpO0u+CLh1R+wdutYoI5HzCpUyuIBqLCFTEMH5BGkKZTtt7iNHV/ST/TFZTZF1VahzISFlLkYwlDwhIbvicuodsWuJQ8Kv98WMJmX00ZwwOMK2K06Cs4awH0i7AVVp4mZAzhr6BxeFglxpXDeUa1PT0j2yhKTpI+RJJsuCmmUJtdbIDHF0DP2IdjARmlxbtkYxPz2iu9oyN5J6iLTW4CdNYQsMnumswcwagvOFlikl0iryUPLDVo+vuP3JPQKHyAm/XxFiMR2qVcRaQX3LkmRXgnUBbmlSKseNPAyBNjsIl5Gwj4wCdu+rX57fcd5TLj3TAP8miqj8vr3r/Slc7/3+Ocz7mcHNx03Sx+t/kfVNQoo+DLX5nVTyve+1nhUa5A88fet5Q4oFUXDOMzmaIoBxdLiUGEZPnlRUkxrhPP1mS11Z9KQmxkRY74pNtdEMg0PmoqnpHl/htMFOmtL7KQrc0JfpqV1OCO88we26Qqu7XJHGEXf7JtXRtNB1BkdKudhcp1yso2cNDx9dsUsrXLVACIm1pgQ7Ujar2hiy1vgYUVK8S2VSkniwrhY+EceA7h3jbotqKkgBF8EsplBZ+qs92ziyF64YKaSMaW3JMkqZzeUGNzgAeheopzUCwWI5p+t7cojouuLq/AojBNOTGZvLLbOjKWMswa9ZKWLMkBMbEpdDQEtBHzKjz0SZUSkjZLHPjrlw66UsCEN0HqNKWKow6t28pJDIYWRQ5feXsUyPpdHFAU3J0qhUGppikpAQaDtBWX3QACmEiyRR0tRVjKAUyaiSFXPguqfRw+CKMYApbnjZxzIZjfmaTiYae6D8Fe2UoCAgoXNQlQu4OCBCKRTNjD9olhCwe+MRzfEctZgUHYIALcV1xkt67rQS+UBbA7AavZwSVntEkuRuRC4miHlD8oG468ljIApBMqYEZsaIaix1bYtTYF/yXkTIDK8/Qh/PUNOa+s4R9nhakKVtT4wJLQu9KMVYmqF5BU4RZUa4RE7lMy32eoncVMiQryeg6UC9yRRxNaJQMEUS1w1BIpUBwOGMl0CqTHHXy4VqIs8W5IttmVY7j6pM+Vy1Ku5eSlEliD7huoFJkESKDbDQClFpwj6Vz6O2CKURquhVSPEjd7H34+PPM1L8s/uVQhd3aWL88Gcqx1hxdUTmgjzERLjyJK0QBuzEkJ6uy3GcRKGumkJdiocnV5Oa7AM6gDYKlRNqYos1fSrmJkoIVM7F9e2QYzN24/XvkHIoe1nKxfWx1ujjKXn0hMsd5s5xCXy92JIGj7IKoSUhZ5QQVLdP6N98WJBCnUsemVbEp2vyusOeLZCTGllZ4q4ndSMiJyoh8CGzf+Mx1ckMtWhx986JfWn8ZAyok1mhAR6szrOPxZY7FRfNetbSr3Yl64s9qarBH1BNBH0/YhYtOoNQgstHK6oXjui6DidSaZ5EcViMGtSkKqiUFGSf8D7jVjt28RK/X5SMtZTxvjhTCquYzhbElIq5jtGM3YD3RfvWNjXBB4zWhFA0h8PVDms0iVzy7dqKuNkjA8RVj9YKvEdVuiDZ277sS0qVfbCypFw0oe4qosSkNKZa4ENCDQGhWoQfSX3R2TyjDatJjQolmy6udojFBGklcdchFtOi+VlOkZTMnLjPuNXmEK5dmmU5bQghFAQ0Blzn0NOKFByu69HLI7KSxcjGBfy2Q8xb7M0jpNHgA/hQXFx7RzKSuB+K7lAqUorE3qMnNeuHW8ziRbRWKBHRUtIYy2azQ+mDw1zOhTILSJXZXeyopzXjekt1e0LsFHHbcXR3Sb/aY2YFcfLO03Ujy8WEMHj2/UDV1GQtCDGy3XWcLRZEnzFWve+MFwTKR+IFZC2f26vFYTgsKWaugvRs53ie0fbsIvAhbpZ8SH3zUetD96/rsk186AM/boY+Xv+rrW+upuj5E/m3yHn97a4PI7xMjmdl6uoDL33mRTxlgjk7mUPOJD+QXcBdbTGLCc2yLeFrRjOsdiijOT47AinYr/fknEpTc/kQN/wqsbHMxRHyXpkMpYPVdRg9Yt+jJwcqzWJK2EvwEXe1L8nVSiKih7rGdw75ye/ky1+7IE8n2OmsFJKyIF5KayazlnHfk1LGVBbfDQzeo1WZRGlZLlZKCmJKVKrmzunvR99tScLzzvqL5NbSBcN/27+CV4ox5tJ8pERwgURBUmazCV03YG1Gpoy1Bl0ZvA/kFAm9Z0yJhbVYpcokMWWapsY5jxDyUIzAuO9pZg1fjIn5omW/74j1Z9iNW47rKUaVIrupNZ8ZfhnLDkQJ9UyxFMg5FCeu5HwRFs8axn2HSqArW4JCVS7hrL07mC1AH654/eo/4r2nEx5roD6YOchDsyGlpJ7URF8KU+Uj2ShS58hKkYeSTcWBxndr4zkJAYxG9bFk0WiFrA3t3RNCNxL2A2HdI5BF45Tenf5jVEHvnC8FcUjoSY0KgX61R247dF0xOZnxv39iQc6wGgM/d39X0I0xc/tR0Vv1jeRqqdCzpkzvB4eoLX61w9bHSGvQx7MSgukC46YjI8ipFMghRsS0RqWEWXf4GAm9Q7srtFHFXrsySKvfRQu6giDIlMku8HD/86W5mTUMT5+U3CSlkDnjU2ISjrg7+76iUzEaZEGJCvWqnKlNfcZZ9e0IrRn6p7x59Z9KDpYbynn1LKMoxnJs9SXMVs1bUn8QKIdI3vfIoxkKwe37e85qje9GlI8kqbBBFhSvtWQt0ULgVnvMjYrj7/jDtLohB8fFr/w0yQ0fSet9713lu0cx8s/3pYgUQ0ZclvbpWabmM01ReYp3901ZGy67N3hj9yV8PyJNoUklF6gnFe61JwifOJ28yunkM5QZSHNNH0sxok9m+FXP928/S86RnCPrswcA6JT4wZdmIAv64n7tEXLRkLoLXjPFTGaMe97c/1eq7TF+vQVyOY+A8cEl+miGaqsSXtyNkBOyMohQ0JHUDYSnq9Lwjh52PdE49I1jUj9Qv90xe31L/dIN1icLVuGSPLpr5z8lC7IcVnvQxYRBQKFXuUDqXUGlrCkN0a5HV7ogsrIUn/XRlP060S5mhCgYHp7zQ0hu3DzivLH8+0M22FBn3nr5iHOd2Hp/yJoRzG9YOOpJdWT0A0otSIPnAbd4562Go0/fQf7KU77TJ7Lb8XaK7JcNLrhCsTUOIQV+9AUdShnbWJRWZFcs5Ecf6Dcj8xtzTFuRXaCuLCElXLfj8+orpKs1i3mDGbtiN98U2/6wHxCAPtB799vElzezYjYxBiCRnWMrBW/WZ6Q3MqkqjAFbW9SkKc6QQFzt0Cfz0lQ7j6rLwITKkp0v2k8fEU0ZYCijSENXNF61RSjJsO15bZIYK43W0L8jaVIie4FXkaz7g8Nnwf2xh4iFpsIfGiVSAsUhbLXoNotOSWAmRYcVXWBTt7x1NmPwgdGHosnyjmpS4XpfBpZSEkwJOo6dp11MmSxbPn/jHL/+WarjFjXxVPVjZmeC0X0b+8s9D7/6gP3Vlst75yglsZUlpkhja3RIzCcN+8uB7eUnmZ7NcHEk8zOAY5sz/6LrCpuvg7gTHzlQCc+Hen8D5dJ7R88f/QNfT9L5Bl7g/Rqjj/uhj9f/gut3zJL7m4oSfcRLZH5j0WGKkWpSs7x1xOX9C/a7Yn27ebxidrZAGU0tDONBjF0tWvrLxDh4hm1XCr/KsFltcaPHGk1IidF7GpFh3KGVZX+/ozmdAxAPVsXaaszUEHsIo8OjMEdLRElhJAlB6jtEioi6xk5rLvYjSddUB+G1NuowFRUoKRm64TrHJI6OGEsWglLPckrAWI1OmdB12GWLqhfoqiXJkXAJfrVjKyZcqgqExrSGpqlYna9ZHs3wPhB8QApoZjUpV8TOYSuD6z3VosFvS7F4fLakHx31tMZozTCMtE2NTxHnAv12j1KKZtYSYsBn2FxtaJYTxl1i0FM2zRxcpMTcCPwYkTmSvMdqg21tETy7cLAST6AVbrsn5FS0Q4fcFSUlPgUgE/ri7iOUous31MYWy18OtC2rr92ZhKC4mOWMtKpQ+1w4OAQK8uAPoZnq2t1NK1WS5/NYgv6WDe3tI4SSqNpQHU+JJyPuckdYdYWSFw4T3phJOSJVoaGhCgKYtUbGSAgJEQLpYsPkZnlOF989GUTKqK7ksyj77MaCHqRY9DyyrYjdgF5MUJOqXOhqQ91W+Ccrwqoj7hWpsSWfymjUtIb9iJhYUsjI6YQscmk2YiJtCzqYXKGqkYtBQZ/3EBMaUJ9clCDYweEHT86RMRgwEgLkWI5/JYBnboVtg4rQyBYhNKGqcKstIklSYZxe54GpDEkVpCDtB8S0Rk5r8rYvGVkpE+0AWqNCQgWwAYJUJRhSKmQ3FpQw50K9Mgq/G3FaoI6nYPyB6vrcHvT+veY93x70U4eJ8WUqx1UR+4l3Z0YHGuRBasUze9yci/Ys6UTUjjHskFITukBzNGX/zjvFvl4pBAprZoVeBtdGA0kKxKwhPLximltyiqAy/WxKFCXvaHrQtQz3tzAE7J2W/cNLeLEufhgpEm3Chy3jdgVGIRqLf7xCLSeYGwukNbjVnuQ85myBOZkxvPEErSXRRWLsCy01Q64LpTJt9whR6E125xCP1ojTM+qXbzB+7WGxlG9r7NmynJch0b/zBGIxPRA5kU2htWZVHAh1WzH2DuFKiCshlpyemFFOcXHvnMmtE26+cMYr2w6z2TLOpsicuXhwjtUGP6lw3UCaWOIuEQaPsFUZKplMRhLHgMqw3nm0neHbJTZdUoVIDAHZKKQUSE9x3BSCpARtXeFzoqpqdlc77KRGSZCpUEqjyOWaMqlRraXfj4TeUWuF2q85mQsMA9Kq6wBgNa0J6x2qslQv38Cfr4kxkUZFdbbEnW+gH0EpUBIXSmRA7PtCKxMCs5ygtcJdbMrelhI0FlLGnW9QbaE0xtWesO0Qr1rMzNBf7egfr5DTJbvLDbNJQxw8wUfcrMZpQUQwDhnhioOctJF+v8LM6mKg4AS5H8vxESIixELTOtC/S2OXSEWRCjGiZy3j5Q7fO8LE8Gi9xUiNksWURVmDiJmqAp8TaSiB0lVti9PomLHzFuV72jYjRY9oBIgesiA5x+ZRz+5qx8npkq4fWK+2WGPo9w43eGZNcb+0VqPrOZmanJ+1HSVMenXIWgNKmvMH1iwHav+z/eS93Lj37CYfvj64c8nXL/Db6Gje3xx9vD5e/wutby5S9NvRDf0mphPP+LTv58k+/zRSmdJIIFACNJGXvv0Ofj+wfnyF1hKlNEjB8u4pcjWitKSpK5QxrHYjVkg6VygPs+MZ28st03mLQJC6oYT0kRmiwA8RW0n8/fW1sYOgBElKkUmdL6iRMeS6xg/FqjoogZoskSEQtyOJjGwTxpbJrJTF6QcBfvRAxlh7qKvENec3hsg4Oia2QkvJVCmsEBgyEYFTktA7ovJsx4Roa1w2GGuoZ1Oc82yutuhKMw6OBAgt2e96mqMJ8TAxFBms1UQXiFpQT6oSlup8yXNoNSIEdrsOpVVxifIBazTGatzeow+OZNEFprMJcCjigTFElFY4aWCfqSYtSgiij9haEw3XDSE+glTYMZKamjEnxq5n2bSFmnKgjogEjdJMrUBXttDNrCZJgdKKMLhCvesjoTaEMWBtsdsWsZAc/LYvfPAQScO7x10OibjuQEjUojREURwCb0WhtmUtMbcWxKsrpJWQJTGk4pwmBLHSpdk7IGUi52LmoCRpNxZHot5Rn85BGYw6aHKkwOmiFRpTwsXi7pasLsjJwSTDP12jZg1ZlrDEcp4JxK0jzNkCGQ4OYIPDx4ydtUil0CkRXSghuwc6ZtVWhHsX5ZhUiuQj8ao0Q4X1kYmDQ8xbxKRCHk2QCdyjS/IYiUOPRJHcgFaGJCBFR5aq/E2NIqoMrie4vpzPB4cJow1ZKdIwgJDIlBBIhLKkLmIW0xKwOLpyTK125MUUaQ3BRxTFSY3G4mJCCRAxYtTBBTKmghZvekhbbC2oKHTLLCh6l4MIOh9SbT9qIFPuy9d71vX2dnAYPPRCReslC2VLCIGpFVDDaotCUM9a4qMrGHxppnMm5EgKY2nslSnHWUqoSclSkS4QZCqGfzOLbjTgSVoQDnVcf7UtxiKHv5nOTWnEY0JMKtJY0G5x1BJGR4jFGS8dnMjCpkNNG5pXbhEfrpFBEEXJmopAUBKTDtrJCGI7gFEQAa0Jmz3jW4n07bexr9zC3XuKOp6RXShhm5WhvnNCtpr9w1XRGfpwCG4t9KO06UqodsqIsaDHShZNmjU1x0Lh3ACVZdSabCzb/UDvHaa22FmDtBqfCy1JGYHrA4qKrIv4XyRFcrHkZUlBezIvDpRaYpXG54TU0A1j+WAPKIfSiugCVWXJSmJri/QRUZew6RASy9NF2VdjcT08OmnZXkbSbo9JoH1At5YcErqtUIsJsesxWlK/fFpovFISRo9pLWraYDO4J1eQEno5RUhJ2BTtVjYKBl+Crn3P8GSFWUxwbzzGTOuC4AyesB/JaUV2oeT2IXDrjjx4quMj9g93VNYSdwMxQ/YBZaY0JzOM1lR7ifUZt+lIu7HodfYOpkUrR+8hZvywLcG7dVVcC1MqpjwhImJCxgSykMZ6n1n3kb3JtMu2UBCnDVIIwuhhDFifSFqWrL6cqWpL3O7pQ6RNRUentSVLgSEiRaHJ9hcb6tmCLIpezbY1phsPERSB/W5AxAneB0SIDLsBO20+sk754E0BnjnzlYFJfl8D8yGw0WEv+YbAnOduzO/76gPd5z5e3/L1kz/5k/zFv/gXv+72qqpYLBYcHR3x3d/93fze3/t7+ZN/8k/y6quvfuTzvfLKK7z11lvf8Ov/k3/yT/gLf+EvvOe2j7q2TadTXnzxRf7QH/pD/OiP/iif+9znvuHX+t2+volGCx92mv42xg0f8qPPTuyv/6O9e+IvX/39qPaY7DwvXXyVkydfISWB/t7P8vYbax6//QglAuFp4vjuGd8lLbsHG9KQeeflI6pJzW61Q4qSz9NvOlw3lkL+dMbRzSN2Fxu23rKe/H5aa6ieZXEAS5+5sykUiuNJxd1FRXKBr1rFL6REsvHggFUxbjo+4d7gKL6FTgkVSs6QtYZhGBmHkuKtD9k+biihsgJR0BxVrGgXtuVz6ZSJMKQYeKtu8C7Tb3v+v6ojVA0oy2r++6nqitF5hNCkEDG2NEiuH0rOjpa47QGRSkVvIawu1siIostRskzSDwVFipH9ek8gY5piSuF6BykTQrlPasVsMWG36xm6gTCGwpPXimG9xUwqvFR8UXyGbB2nVcv/U2nmjSWLyL3u53Fhi6CgK8ZaktLonDAxUclDkOF+X/QF1hY9USx5UTkmhNU0N5YMVzvGbV80SHCYbGeM1ojtwLAdyM5jTGlQhSzFse/GEmZbFfqOkKUhal44JoXIf3uw4cqXJu+FH7qDaRX+tXd4UWemp0eF+uISYQyIwSN6D9NCn0lKgpKYQ66SmDWofXm98eElVW35f7ywRFrDqvf8s/u7UmTvIV6Vg+9OLfnuo4rQjeQsis5BSb52OfDVi/7rzqfvvjnh7qwpdLgsGHYDVaUZ1gN1W0M+WNpnCFc7shSoypaGphuLSYUQ5JxQQNoOsBtIlSY1FWhFdWOBtpZ31v+DtNpjguWl2feTlaIfL3mw+gWIkd14ztc2/+4QKBzL9FhKlvoWp82nEdawkl/jfP8aAsGieplZ/TJaCi53b5IWAf/Ul0LLVrDeo1JxcRtj5NFLR+wmReT+woOe094XNKnS5VjtRr53WnH1+gXGdXznokEZSZcz/2fXMeb8EaYLH3wReYYQfd29h/on58zn78AP3MlIJbjaSC4vWvwTU6hS/QjDIcspJXxMPNl/iSe7L6OE5IXZ56j0ESiFXk5Iu4GQI/9x8WvsVM/0lTN+eLqjSZ7eRf7jrVfY7x3DmeZTqiVteiqX+ORrm0KJsgp1NiWs14zLhvufmhO2PbM7J3xm+i46lUaPubVkZm8wz58kHSd26RFPN18mCYGtDKn3ZAlJymukI6dUmsoQiduO8c1HVC/dpHrlFn61JXlfNIhSkg5otZZgmor4dCAZTcwUup4psQKkhAiH4yUVHWUzU/xv7Wt0l1se7eGf2e/ixp0bdFGBNKSU2O86jDXIBPM88PLcYY4q1iHwq/0cmTW+D0RfHBybgwX49msPOTmd415/imgt2mosCtNYxmEkATrBkBPSh6JBqTSxcyQXDiHQB+OHnCBmhvWal9/+Ob7rtAEcrSnUalJhBKhUobsdnxCPUK8ouDHy5pNDKPPgMbVluNwynm9RlYYUi5tlpRGXmvRsKBcc4/mW4CNZatymJ49jGfQZA1UFORE7Vz5TAW+8mTGyJnuNCwG7nJJCKpTi0YOUfOKpJz98Uow+lEZOK2QGtLoemhCK2UmSsoR6C5B12UsA6junDI+vrvPeJJFsJJdhyi8vvos1e4I0+G7ENAa36Yu2UMBdoVhc7GiqCmHLXi72kftS8Oizt1idzYnhu7CTkk/3B/kvvMBDQJDcq1xeNSxO52wutqUpqizeeWJM1Ac7eZ8SE2vKOfn+PeAbpMG9N1fxg/aRfC1Beq9eUTz39bMXfB53ev7RH/ZmfoM3+X7e3cdUum/pGseRJ0+e8OTJE77yla/wL//lv+Rv/s2/yR/9o3+Un/iJn/gNm6PfqbXb7fjyl7/Ml7/8Zf7hP/yH/J2/83f4a3/tr31L3ss3e/0O0Od+i03Q+4cl11981Al8IPTn928fgDQMm0B8uiFsLwjbC9Rsgjkx3P3uV9CV5t5X7pH2A6/911+jaWsmSpH6UJLHJxXaasYDNUBYzex0hj1slNuLDcYW7nXMcOU8Mspy0YyJJgniGIvAXUCsJFlYRgerMRJ8QnQ91VIybDzT/YY69hghYfA0JHL0TKylsubajnnoR/Sz3CUpqasyJW6MpZEavZZUWREOhcWgBE5KrirFZt9js6UbBSZn2vmMuOmxWoPKuG1PCpFm1uIGTzttMFKyXu9obixI2bO52BQjBqtpT+eMw1gswYVgiImUImZysEnVEmM1zbSh73pMZRn7kW7fl0YLcF3P0fEZw35gcbqkH4ZS/Mgl3XrPVVIEWyOcJJEJLhAE2IMlrxQUPrpWCKmQQyRVBim4RqmSDxAiaI0LnraaMzxZF3qZEiBU0RBJiVlMiKOH3pNCKDQY50GK4sCVwVpT3AUHXw47q2nuHKObMp0cM+z3DqEEo4CsIExqIpk4ePSsxdYWtx1w96+IPh4c9QpKpHIurmhRkHzE3pjjzrclA8RH7NUGe2OJUpItXCOJxMLX9/agWYqRmESZaEqBj4nef30KRjhQ8oRSxbjCB3zOVNOmWJJrde3GlkaPXE5QTUUePe7xFfgKXEDEcs4KQXn83pGHcvznnSEYjTqeIdsWJec08iZx3RPGXZme+kiMQ0E/hCjhrYXPhdASrduDdbomh1BsnKWh0S2QkQPEOJBqgxgDohsLcpUzatagUPQ50aVQrN/lUBwNB0eQAl0bMqJokzY9w3bFZAZWSOQ1KpTf1RG9byiT31fgCPERDdGz/e0Q+lQrWFYgtaDvi327XkwYL7ew2iNiLDlKB4F+TCNSKkKmOG8pRZYCPWuIq45MZpCOnRqwC4HKEeVGjFIEI9hdrIkS5HJCeOscckb7gx16bQsdrXPIowWuHwgyI+4ew1ocHMgceSy20uF8j/BLjJSIIEmi6PtE58ghIStdbJ8lxdxBQB4d0pQgzBQi470n6KMZ5mRODhG/2uPfeXKgocliUpMzQpf8KENB98SkGITEZ9ktqSCsxhoIkUY4lApsUyJrzcW+I1mNUBrpAilE0hiYTFtM9BgJdSVYuYjLgjREwiFbzcqCWHe7dXEtvXVa6J8+IoJCLmtSiNTWsO8HnBuxbcXoI8O+Z340RU9rZCrRCU1TIYXA1hX7iw31rGGyctido6pKQK1sLN29J0gJsj1D20xlK6pFw5A8/ZOBkKCe1OSQSLsRlYBQUC1/uUUtJ+SQEM+MaQ6ulxz2YLFewTjCpCU3Nao6DL9CRDTFBtx3sSDQ0yn1YlJQ7VTCdbv7F6TdSL7qEJVCkghDh9/bYp7w7DwRsujQcr6mvsoQEbpY/ed+xD1dFRr04bjgkH0XkQx2gjhtkDkz1ZrNwyvauirOlykxmdW8/Jk56/sXzG8s0E2hCw8TzeZsyjgG9HyOOzQcIoMcB5AKpcrwc3Yyp9/23Py2W1zev8BflhypDEglqQ6ar3wwIfrtrmcN0ruMt+fQ5Sw+kgX3bnWU33/Du89/3TR9wBN9VHn1XDOUMx/SvH28fifWv/pX/4of+qEfAoqGdrVacf/+ff7Lf/kv/NN/+k/5xV/8Rb7whS/w+c9/nn/+z/85f/yP//EPfa4/+Af/IP/6X//r3/A167r+0Pv+7J/9s/yDf/APrr+PMXLv3j1++qd/mr/9t/82jx8/5sd+7Mf4ru/6Lv7YH/tjv4nf9Hfn+t2RU/TecciHfXN46LPTWzz3s8+KOouUEj961o9XJD8yPF7z5pv32Q1rTj/9YtlAc+bWp+8yP5twce8pbj8wbS0WQTd0SN3S7wbCcCiG24osoZrU7J9s6PcDy9MFLoZD4R2JMeF9oVhoKfFa08vMzntk0JheYKyls4I+J5pZS78fGC43GGPoXWaoa/YxMnaeTKCqDGJ0BZ2Ih8ySXBzVGlOTU6KSha8vXCalgEuZnciktqILNUP0yGpG3ztmR0u2qy1alsBKYaZIWyZ/7bwmDZ50ELaq2tCvOqr5hFZp1BAAwWLSEGOiais8EEIkD0UQjhD4GLGiUPWqutBGht0h8+cApPmxBGi2bY075N0kHxlzIWGH3UhWhYKYY2YTIuSITJ5uExDTimQNadwjU0ZPa8RBdB0pBhNKCNLo8NFjTYU0FqMs2tRIFMENpVjPGXtw70oHIw6pVbEYHxN9jNS6QowRpSRRJHIKIEqTlHMmK1HQLlEIDlYJ6kojpMCOYFMgPd1hsYjNiKpa3MNLUjeQBaVAGT2isYX+JkRpPoxChEjaDSUYd/SMJPIusRof4+dzqgLUIWWhYJEpr10r6B0y5xI4+1EX8MNU0PtI6ApSSEzkSUWsimbIWAshMrz1hOwi9nSOvbGgunuKX3Wk/UDuHXE/kqIvhZA8ZDOlDPuRrCN9zthbS4SEMDOoRVW0JatcHONk0X9Jdci5iu8WVF66YhBgSp5TdK6cnwcr6pwzcT+i5i1SaegGMrkw/RZT/GaHTmB8KWhEKugmMSHaqtAjK00YO8SwQaT+OYrugTr3dR9jfs9/7+5Mh3JEPJvhinfpMs/9aJEsCVxI7IaEtAqXil25bivck22hAjUV7HbFjUvrkg11eEsheIIeyQnq1pIeXJbHKYlUCjVt8KsVFk3Wulg9P1phjUF5g4iqaLVysZSnrQ90KFVc6lxEHU9pZg1624HIhM4Xx7AYCU8uSeqUhCQlj1QKqQSxj6UcE6LQ2gqejM+ZNCluoLEyYCXeBcTDK+QYMTeWsJiQtj2pH4khlt5xTIcCOEIuOhgxqYvb3mpfGvFJhVCCPBZHzDR62jvHHGvHcYYulecbnSC7wNgNJXrBGJyMZJERQpLHYtutBOwHx+x4hsgCJxKisYxXey7efsKrr97GPdliZWkqo5FIrZk1ln7X0633iKpQdWXKTGvD+umGttUF8dcRJQ2LSlDlwPJoih62iFSuc3HTYScTgpYMu4Hm5gTRtKSqwl8M0B9cFgX43iNjukZh8hhJRpHPN2WYYE1BZ+ZtQehFoTamk5Nr3aSqdAk3jhFlJIqIbDVmOSmPSZm03eJcCQsXVUX7wsm7l/+cS5jsfiTuB4wt14Vne4GgRAKYxYSw7TBGEwHVWHI/kNZ7sEUrJOzBmCblEoYuAp5cwpYbMG2FE1BVhvligh49od9z9PISVVUkXwxdmrZm5wobIrvispd84PzqCqM6hJR0XcfT13a0RzPaSY2pDOGQh0Usx52oDCc3lmzXe64uN+hphT2qMMIcgrczSR00fjkT3QfEsL4PeXlPX3L9zfON0UfIgw4zlQ/vm57Ffjx7kuerp2cw9XPv5bkBzrXl94ei4h+v36nVNA3T6fT6+/l8zksvvcQP/MAP8Ff/6l/ln/2zf8Zf+St/hf1+z5/5M3+Gn/mZn/lQ+ppS6j3P9VtZWuuve47FYsF3fud38v3f//18//d/PyEE/u7f/bsfN0VliedO4XfblQ/S+/xm1zPm7TVB73DWfvBGIFh86vsIacaTX7/P7sGA1BGU4L9+8vuw1tBYxav3tpycacxEc3TjbY5vDIiYufFkTTjf8fYbj/jSzT9KGjOVKXzxurGYaX1AFiRSS/b7nsmiZXIy5+FrD1BI2nnN0I0kJdgsah47R31zyq9erjlqp8SY6LYjtq0LUqIlIsEwjLyuXuSheJnmqGHoAnVucBvPbDll7AbWFxtsZWmnDdJnnA8gJY3WfNt6xHYOZzX/+kjgRURLQz/5PoIJJB+hsnTbwr8XSqCVQFkDuSeMHufLBUcaVYJQx4I0TX3iM9tA3gaGXc84eBYnc7YW3qgFCEE/OPTBrnwxnzKMjmE/UNUW141oo2imDYMPNMYw5kTyRQg7OZ6RfcmA0tOK7dMNWhcL7DgUbcK/8R5TG7S09O330iCZScnnzC+BH8lS4vc9YvB4H4haUxmFULpkVkhJJRbcmX0eKSQ7/4SH6UtFa1ZXxTyAjBuHgwaomCkoq6lC4Mi+zNGtVxEucL7/Ndb9PchFa5RcII+ZMDjMwZb99704L43yuuf2f69Ru4xQ34466DW4tLyz+SJx3JJMU6iJshQl+kCFzCmRhmIcweCQlSUbjVUCRo/2iWa344eOJ5hZw7zy3JntEcDWJZ7uqpI50o3FaKEbv+6Mee5EAwSqsfhdX5pv4HW3Y19b1LLlEw92TKWh/dQd9l99wPjwktiNNK/cwN5YkMeW7ANh0xHWPXlfwkflgW6UvWBQmTdvKKLaM7GRcP/fIkJCtZb6sy8xvvOUvO0OtvKCibnJDfsZpBC801zwb+a/RBawjDtO1xmMKcVjLhNvYiQHDz6iTubEnMrXVlO9eIr76shLb20QtcX5iD70itKUsEihFVoL3OrnOPvMjP5qR7eWVIvJh3xu70OGnv3zDLl+vl96tmE9Dx9JcV1z/PxD+OXHEqng1aXglamClLh9+l1M7R2MEJzHX2AzPkLkzK3JZ5lMb5N94MHlL/Bg+0uY0wWf3J+gjAbvS0jwzIIxvL0/wrpITplbX37E4iuX1DfOuMt3II++HZ973rn8L1Bp1KQivP0UsWgxT/e8egl1fczyfMfLyzXJB7ZS8frZgjx4NqtHbPODgjAt6uIkqNS13X0cxmIVf7WHRrNaajZKo5OAiYEYEQKOLj3tkyvkvZ7Vp48Rn7iJe7yCVaGIqkmNOpri7j0txa0ANt3BKjuSlES5iJjXpGf3+4TMcLRU/MDwFfr9wMOt4UuTzxWjhsqgKkPvHcfHNbbOuPUekQxJFkReUqzzfQR71LJ7vMJWmsu25qsvzAlTzeZiiz5Y3AeRCvKbEtoo9tuemy+c8r8jeaGq8Tckv/bG/0VIe+ZyjnvUF/F+zhhRzhlhFGiFnTaFbrbrqWtL92jH6ydLZKgYn65gmmA3ELc98clj8tkNmLboxhBWe+xyjpo2jPeeliFMWyNTxCzbgkRZTRx8CVFNuSCPIYLV3K43HM8jUknsspwf5GKegAChMl97PbDb9tQ3j8ptUtLcOiqUOBcQWpb/cy7NiCznk0jFqCXPW9S0Ie/6gzFEGcgUW3QBqjQjcTUyigEfE1pI9t0OM7HUdYUVgnHdIeVjprMnJAGbt2a47gxpNPMbC86Op4Rhx+Ubjxm3PVIp/uvJpwkn34N0kRdWGZ0Hdg8uWJwt2F1s6Pc9tbWIQwxHZQ31csLi9hH78w259/iY+Z7qe5jeWBDqwP1X3ySphFs77v37+x+BJr23tnn3luf2E/Hsluc7qa/ns12/wgd1R9c/8t738b5RzfWt19KEr6Pqfbx+t6w/9+f+HFVV8af/9J9mv9/zYz/2Y3zhC1/4lryX3/N7fg/f933fxxe/+EX+23/7b9+S9/DNXt8UpOj9DdBvuh36yLPuvVtFzocTV/DeAgMAxdWDNZPZgs3VhklV8mKGCEiLirDf7bGbgfkrp5j5iNKucNaTR9clfG18skI3E5pZi7AK21akmBjWXaGfqHJbcUSCk7MF4yFMMgyOo5tLmuWEECLdbiA1lo0rNC5tDJU1bHcd7WKCMYb1kxWT4wW79ZakaoIccBG2m5Ex5OLqNp2CEAwIJIIxQhw8e+F5IRXh/ZM3n3CpbhBbg9925JSZLqecPz3nxktzOr+nXUyJLlDPGlzvEDEX8witkJManSHtBppZy7RtqHcjVTrQ9nzCKMWkMqzGgDcZnUDOGrIsIYXaKMIulERxMvXRBHpPJGOKqpuUMjEK5LQmjL4gVFLgN12hgfhA7Mp0tlvvSVqyGRzWGEZhCEIgh8gwDOhKFPpKzKRcLpimtkUgfHDiI5dwUS0rpFAoYRCDJ6RY9AcpYZuapmlw3YgV4ppyp5REG4PWNQSPTOKaSoYoE32EYLjcY9q6NDY+EB8+JZ9vUPVt6uYUtEFqQxpH8tiRRwfGHoTzEHPGAMRIigKlJbl3ZJVxwaN9QFaW0DsUojhdJdAxUiuFYWRWF+c5fzhfkgsoKUhNjd8NZCwftgTFatcYTe5HopAEk/E+4DZ7wt4zrta03/4C00/foXvtIeFqR+cD9Ss3EJWGrFG1Rc8awm4o01WK7ihuOvI44g9hruNqh7u/Q1UG5IxkFNUnbxEut/QPLsF5spXYego+EI2mlx4hcqFyCQrtRhSTkWv73nTg2Veayfe8QliXcMgsBH7XYaTEHs/JTzeE4JGAiMWVDR9JwhO6HSk76nnLxH44reBDt6v3jYjer6P+IGDch0xQEmLG+UP2k1LIKBBRYWLJ8MqHJ9NSo4QlH1wLo/PYo4rxyRXzG3dxb+5LeGhjiwV8FHhPOdfuXWIT2Mqi9hKtLCkUQxl1PCNe7QpiuRuROSMnTaHSRoeODmEkY62RaSw5RTkWu+iJJA19QVGNLpqf2iDaingwKskCZIrklIiVKUYJAtCSjESOgdxvGOtAtjfRR1OEkoSrXck1UvL6AwxKkZ3HzlpibUrwcgglDNRo4nZAtoVCpbRkOhE0tiJUlrkw9CojK0Xwidh7ohOoqWC/H6hnU0zWDPu+uDmmzDg46AvyUZ3M8J1j6Ea6+5d0KWLnLf2mo1pO2O86UJLJfFKs51OiUpLaB6bWcDI19A70doPJGXmgAqvalObD+RIaOm0QAtTFlnF3Sf3CCalpiEMgoaiWDcN+JOx20G3I8hbNcoKqDH7dlWb/gNAIIUAr9NEM3daEbcew3pNDKu5tWhY64eAhgbGCdtGgjEJU6hAnAGhFGN0BKQffR9KjK1RboQ/HG2RUVXRMelKhDrlyWQjSti/HGBTKcD8WpDlGQl2hkIX+fDwjpVwc6rTE7RzT+ZScCvpbkNDidpjGwJj3RDuwfXDJsLtDbm7guoGGBSokdg8umU5qdExkJUl1xbaDdjplP5xTHWzBzbYnGMHNT9xkd7VjupwyvvMU21YYWRDP3cWW/eCYzlqWt5bs3l4hTxWQ0JUiVofQ1nyoX8T7TvjrzeK9xc+7JlK8C/C876HvAZQ+7Ome+/oZLe8DA1yfe45nlvjve9A1xffj9btn/ak/9af44R/+Yb7whS/wb//tv+WXfumXvmVmBy+//DJf/OIX6bruW/L63+z1zXWf+0bW1w86Pvh+3j9H4bC3vLfIEKZCyvJrDLuR/nLPKAp9YHSeGArty7ZVEfZLCbOWq4s1YhaxVpISoCNCBW5//6d44egTXNzfsL3YIBdN0cxoxbgbSkjf4A4UMMnsxuIQ0JkJu5Hpclo2/hipZw2JTN4DKdEsWmTM9N1A6B2DlKijYretdcn3gZIVtLrYlEBNFxi6ESUkzjlM1uhpgwGC73C9w1dtcUOa1EwWE7ax5F3klOlWO5q2IoTA8uYRvncIn9ifb8Bq3OhIKdE2BuUjk6MZdm4xi8LJF28VjcY4OnRr6bqR4WLDfm7x0kDIZF0217qty0Uu5aJLSrEgUN1ALUFGGFJAtRVxDLjdgJ03hba0d6AlurHFeUoXGqQ6UCjmpwtcPzKpp/S7nl4mVl2mCdAsWiZkEgGIRDcc6uOMCBHVVAghcKFDGkOkaIX0wRZbG03uRnJjS4J7KDkiOeeSx9JoRrdHinLJ0qIuQa8iIJoyCY2XO8bGYI9nuPMrxvMtUjfkSVsoQjERQ09WAqYW0jG4fREiA6jy98+5iKuTj7jgEFGglMbImgdPzlk2E6KFqqrLudJ7/K5DnVl89JAFkZIXlUMEJZGquDMlH2gOCes+5ndzMp4//VyAqkJXmmqScTkixog0CnxkvH9J8/IN2k+/wPDmY8LVjv2X71HdOaa6tYRmhpASURncxZZwsS2ImhTY20eF7hcjVmlCWxGdJzxeUddTcAo7WyC+rSI8uATncMMGKA51UgL5oCWh0A6zzARZgj2jLH9LBod/ssKezjA3F2iR6X79Ho1IMJ0QdgOoYrMvhEDVRRAuXBHqT28sS+jrgT4lcjrQmT583POB25r4+nve40L33Kq1oK7K11Zk0hBI3UiKEZM55BBZNLYcM0IhnC8NXYxgD1bxg8Mz4mOPStDMJhhfOjGhZDHG2Aaq4xPYBrrUoZRlFCOuVphZhXtyhdACkUtj1t48KjS9wRMXDUIK4l6isyX5BMLCoirFdD4YkMR40IQVauwzd0UhD05xOUMCxkjKGdUYpJHFiTEm0uhxbz/BnC3RR1PiakfqR1h36CzIoiD2KcnrcGOUYnQetesxR7PSmOfMuO2uG2ZtNKbSnJ5McJuB/WpHqhVeCfADwmsaYejGiHEjR1LBUcUYA4hIGkek1YRYWAiXbz4h9o5oFEZL4oHqJYRA1xYfe2YnBqNApUgm0111qJyoJjWSErBbjkVASsLVFmLCLio0nvGdC3AJezbHLCew3xKfbjCLKb4fr13b5OltsKb8jXNGVRa33hMGVwJep01xsZs2hF2P341kBHEMhG5EAqY1VLXEHE1olwbdBg5jBqLzxN6RhSaERA6OMFb43heb9JQOFNN8iE5IxN0AQ3dtve/Gw2MOwa8yRnIQ5folBDllJKAQxfa/d0gp0MIytYlxWCOrCj2pS7juWFAo1RiynvL4wVtY1RKUobEGUVnMomXfjXij6DYdzjtkUvSDIBvNdr3jVEsymXrSsPcBrOHkU3dYbHqUUbSLCf2DK56cPyjD0lkDSuKtQqeM3/b0MdK/s6M+nSBHQYUlS4gpQp0LhTAJdHi37Cr9iiCkgE/uGsEhP5vnHfaL54qeb6hFee5BOfP1P5QpVNEPezbxIV9/vH7XrL/0l/7SNUL0hS984VvWFL399tsA3L1791vy+t/s9U1qip6HdX/n1nsmGwey7fyVz9HeeIUYI+/89zcRMYNMRWA/OpJSmMqyvtpirOa1VvGW8ggjmKqem588xebEJ2cXNN4xaEUt5sTH2yLozSV8NIZEPW/o13smdWkyslWcv/mYetFStzXrqxLclmJk7EYyUNUV+/MtAPWsYXtZROXLkzm79Z7BOZx3bNeQQ6LbdBzfOGJndrRNRbfryUqyOV8zPy2hmWM3ooxmsZyz33W82VrqFxaM+yn9vkdYjUylKVBaUVvD9HhOSiUHxWjFuHeYyqCaosNymx6VBWZaU58lzOR/EHc97qzm9epVVo/Kx97MThi6EWck9RhIMuG0xGhFZS2+L1lGORWUQRtNNW/wnSOTSwaOi5gEtjbEGIto1UiqumQhydqUieV+RFrF7GzB7mJLFjBse2bzCV0/8Avz34cKkbv1nP/XpCV3Dhc2PNx8kRyKJkdKQRo8O3nBVzf/N6oyGK2KI9ZQQlpFbRCmNEhCCrIPhcIhQQXJun+dq/E1UIIT+Qo3j3+ILAQPrv47W3GOqgyx9wwP14xXHcl7hK6IKXFv999hfyiIU9GDERIx+RISm4s+RmhFEqCgBBxKwRgCj1YXvHL6CY5n34dMO946/xpJvcWL0xcRUhL74oi46Wq6WCgsOQuEKsVpDKE4RAnBy43k02dzhJb86uOOr10O7zm/VFMhjC5J6znx4h7ymAgXW6RWmFtL/NMN/mqLOZ7RfuoO/mpH//YThnvnhM2e+uWbRUzeVNgTyIuWsOlxT9bwZMur44S47nAK3vjEhCQEp13LH7j6DAywH1acN69j757SPVrxtdV/QubMpTAws9dFRDYafOBy+xor/VZB9ihNZSKjDrbDNJZb0z32TsfYOB5NZuwuC3UnmmL9S22I+wHhQ9E0IbA35sSrLfUnO6pGkRzwC0D4kM3pIyfCfDiF5fDP5+8I/vAnIPvI46vAapwUW+JDILMQgrPmU5zYVw6uXBoo2Sg5Z/S8xa12nJ+9w6O3fhW/3nLrytPMW8x+i4y5TOLfWfHy6Q/SvnCL1Tv3+fcnX8LrQ6E6WaJPJzhmhWaLoG0bPqtLOGwXLF/bzMpeNsx5uTlFnVRcya/yJL1WctQmDXE3FJSiNsSD+yQCcqULVdGFgvK5cN0IxBB5OtPIViBsTUqRNDjGd54gm7vosyXZR87uDeh9IJK5NxvJ04YsZUFbQyQrSbzcQsrI2iBNCRzVk5o8BuKuZyo937v/IsF7fB1xqz1jPzJfvshL/ee5uALdaH7o5ox+tedCO96ud3gGLoXgnSuKnfe8IXSOcRipDnpETHHZCyHCMDK5+TZNs8Nkwfnbe8ZQUN6sPTqD0LJogg4un7l3EBK60XzqRof0K/rZlntnryAWM6yM3G0viPMNfhJ4/VFT6IfzRXENXbSotsLM20JldQG1K1l79vYJ7tEV4WqL630xlDmYyNhpjaoMd25nTmeeFLfE9Z6oa5ASaQV+vScPgTceGrbDIXg6B/QBiU/bHqFUMXZIGXe+Qyn4ZHVJYdEKXvdLkjjoiLSivnOCsJrujcfkwYPMiGnDuO5QT9dIq5GNZcGW3zf+HE7Aw3TG49PvY/P4ilobsArdWN7YL3h7+QeQKXM6jryw6pi/cMyjieHNfs9WBYYazHJC6hyOSNo52kWL70dmRuFS5GunNfJkxlUj+TZnEK4YVGz3Pbau6HPkjeOW3UzRAp+z0N6aMeTM/M0j8ttlfHJ7/iJSSK7CBU8+e59MZpFPeOXpp1G6DKee9Tr3N/f4lSf//XqLeA9CdP2FeG5jyddV1zWyJPJ7f+Y9e1F+l9Yr3ttkvWe97+ZnXlYfN0a/+9YP/uAPXn/9sz/7s9+S9/CLv/iL/PzP/zwAP/zDP/wteQ/f7PVNaop+iw3RB41Xv5H+6tn9OSOkQijD6u0LtND0SjKbTdivd9jKoKxh2BfBdT869jkzjRaFwsaEzwmtZSkipSwTs4nk9Dte4uKrD+gvtiglSFIQXWBmLEElumHEGE13uWV6MkcbfW3fqRvLuEvMby5ZPbi4DjKtm4p8lImH4M9EoV9N5hNyTEymDdoonC/FTHKlAhNCMJlN8L1DHSatKUSCymQF29UeWVvq4xmqsaAVm8fF1aydNMXprBsZ1h2Tkxn7i11pri53NKelyPGbgbq2ZQrq9uBW7B5fIfINgvMko0hSsN31YEt+h5KCeMg5ySkRfKAfRubHc4ZhJCeBUrJcAGQojlq1ZdjvDlPejBQlFT3Hov/w+x49q6+vAVIp+tWeWik651Ba0fUDUkm8tEST6bsEIlE1LWm1Lfz1VLjvToBLgcdXF2QfuDk/Zj6ZIkyx4c0hQYiE0SGkRM8nZGuQFCvk7BM5e5L3RA95Uux85eG9E1Kx0a51sQbeDQV1UJJsJEkDWoCLZJlJOSArCbm8BgIwqujkciInuNitabShspa96/nq43tM7XehMUybGasuEIcRYQ0pZ3I3MORMc+v43cmfAHFtQlAQozQG1OhRpi6Upeeop8/CE5VVaATj4BG9Q0/qItS/2uHPN1QvHOPPN2TAHs0wJzP0vGV45ynjwyv68T7Nq7fRsxZZWagysq6Qs5q07kkxIXPG7Tu8kuScSFoh0aXYHwXu/iViVmMWLbIx+IeXhKyIHJBiKYoN8EEc7pJH5BIAmaVE5oSIEX+xRS1apMioSpE3O5Lb4ahRtYVQ0Au7bBlTJm8LlSuOHr8bEGTiOMKkQajS8HwgIvRMNCQ+iBAjDpTf925x719Gl0MoDgGd1DUtMHuHEKkEbiqDsYWimQ5aKjiEmC7agoBNNO5rW0jF9ctYXXKocsafb8n7EXtjTlqNSKGIOuFFKOYEzqGsIqpiPU9ry0S8PwRkthUpy5KTtOoRHnTbIrQhdxHRWtyDS8zpnHCxhVoXG+4ci9tYpZExE0Oi8HRz0VyIQocSKRNFhhxQbYN0nugc4WoHWpWGYduTA8U9cNoQKG5zYlKRdwM6ppIl1juE1cXZUUvcti/IoijBpWm9wRqFcAEz0UxnlqpPaJ9YTloyGTk6NJk8OtqFwc4b9mtBtcu4/QBuxAuFsZoEDJe7QkNVEjc6hK5pK40KZb9HxoIwjRGzaK+vYal3RTuTc9HfSIE0Ejl0iG6PaQ15DDB6wm5DCpeYRUO2irgbSgaZ9khrqG8dMa72BaVrq5LrdLBCH955Ws7ziy1BqkJt0wLTVOjFpDhW5ozMCUIgdANR5EKPjgm7nNLduyANAqIujn8HFzqZy0DCXW5Lu54Ogj0lsEcTjIzktSNR3CBFSqhpjdCyDCRUsfQ34YAyGXUItJYIaxC7gcYK/L6nrg60vcGja4mqC+PB+0xuLNWkgnXEhYGQE6s3HtPLjCNjm6oY40wq6kpDm6grAzETQsLOG+ysYT96hn4khoRtKpRS3J29wureBXrRwkSTNsVwJ7hAaitwkYuvnbN86YzZjSWre+eISjJZzogk6lnN5rUrnrz2iOObxzSLFmUKYqakeq8G8UCd+0j3uffQ657TH31YDSWeodS/QYeTDzS+j3rxj9e3fN29e5e6rhmGgYcPH37gY2KM7Ha73/C5PsqMIYTwnueIMXL//n3+w3/4D/ytv/W3CCFw69Yt/vpf/+u/+V/id+H6n0Ofe76S+KDz7OtO4Pzuv/nrpxqNFBTiAVghiCGyfbohjr5wlykUndHLok2IielyVja5nGmmLSkH3BZWX9tgP3GD5DQpJuI20MotRjYsPnPKxaZie/+C/WpA6ineaPb9wGwxRYlygKAku4stdV3R73vcti8XhJOE1bpYf2pdXHOkYOgdl/sBXRnC3mFnxcLane8QOSPrGmMN682eRMZoyfJswfp8TVWX3J1u3RGlwBqNnShsY9k8XdNv9py+cErT1gglcYOj3/XUy5baaPrVHjmpUDljKUV9tgqlZSk6tUQIhaiWJOFwu0w836ABbxV9imiXUdoypFQCW6Umxcxmu8NU5npSaoTEp0jYOkI3otuKtrJ0qWdyPMFOFeMqIqKgnbfYwTOGxOpiD/MGGoOd1HRXO2KmaJTmDUNXEusXJ/NyUVrtiEMpLKqmIu8K0iGzopYNk3rCVDZc9VdUxpB8xiSFyKo0LALERBOyZ9VvIGUmdYM4hCYmIOpCHxOZw2Q6omyL5aB58B2pPkz/ZLGbTTGhdLmwR1fQJ6FlaQ5zha51ES2r4qQVR88YPfPqCKkVVmvunr3Cau/pRWIxmRAH2AXHZrthPp2TcsIEeR2+Ko1GG4GMDjXTjJvA4Euhbw/0KgA9eqphKL/TVsHClitsY/FPNygpCL3D7UfMyawURiHhHq+oXjzFX+3oVnvqF06QlaH5xC3UYsL49lN2X76H/sxtzOkcKSTGJ4yZwKwtmSv9SNz31OOuCNmDY5QjKjkSrjQjV9tiEHG2xNw9RW3XVENEWoMYHNl7BAaI1856QkikEMSYCgL0ZEU8mhLmCrtYEPU5w+Mrqjt3EW1NvNqRvWP/tYcwbYoro6AgHIOjmlfstxvkVOCShPwBblKHfe3DZznXE5z33J+BRhefAYDWQA6x2KH3Bn85Ir0tVCUpqKQipKEYcKSMERVKqLK3TGvidkN154QxRUYiGIG1poTVHl7QP7osf2OtiJcd2arrWirHhL1zXLQ7KWMyNDePsU82VFXZa4VW15TL/vKKHUeIQeArie0aZDI4cXDsi5GsLc5I2AdMbVFSktYdpETyERUzSZawV3GwVRZCgE/E2CO1xBzNcZsO21boaUOaeYRPhHzQlUwq4uCwZ4tCv9oNZWgjRHF0rCx52yOUoJmUPbha1gxK4h5eFl3KtCFrjdIG0SZqAylkktuhRWJ2bFiPa2RToUQZtAUfSNMG6SLGWhTFKU4pxVwnqCKWgXq1w8wEdVtRnyjMaihOlUqRekfsRwgRe+cE1VpUtyetdgiZ6PuInS8IG0fVNISdg8s9eSHKQCQURkQzb7GnBn++oX/rKZARR8WAJe17oOitog+IEIijJJuC1CgojpG9Q9aWvBnptxvMrKG5e1oc4ELER4HbjAy7QF+19KmUDmoIBxfEQj2NYySeb0q8WEqo4xnVnQnaj+QmUMkp3fpgjhMy4Z1zUj+W656UJfg2RIJSRVslQFiNrg2hc5hcULrgA4sbS7LgoP88RCpUBr/tyVaTZhXbwRFTZDK1GCFxCLoYmSwmBBfKdXR0UBm8Kbbxznlchs2TNfWtGXm/YXP/EnF2xo6E6AfU2VEJdo2R0Sd0iOz3AwhB7BzBea62HWknkFrQXWT8GKlEg5OSy03HXIC73FHPG2QlmNhSmPrkceGDjHGeH7k8kxG8D1p6vtZ634b0dU3OB9Ziz7An8Z6n/Xh98Hr48OFH0sbu3bv3O/r6y+WSR48ecXV19YH3/6f/9J+YzWa/4fO8P07i+fVTP/VT/NRP/dQH3met5Ud+5Ef4G3/jb/DKK698Q+/5d/v6Hcgp+k3c/ew8zu/ntpYzWuQP/vHfYyzfa4to/Be04lc3Hd2uxxwe3O16hNEokfExFT2Q8/gY0UrR7fsylby6y+6BZNp8mu5rF+B64mrHD01+BmUNXaP4zz+wJPIOwiZ8+L1koah8oJnWbNZ7pjcWxBjx2562qRh2HZPa4nKm7wfSGAgpIWc11Aa/G1ATi9905NFjdaFtxVimqf3oqKMtk8aUsdOalBN9P2Aqg60sUYG0mnY5Yft4RTtvSS4iXCi6HjiIYjPS6mKOsJxy/rVHmLYiCaiOp8hdyS2J1pBagRaiUDnyAr/9XvqnD7g5nXBnWDOOjosm8c7EMJk19N4jlGR5ssDnxL4fS3MwOPbrHdEFshJoa2HvmS1n7J0npcSNT605+rYdbjvw6NGSxekrtLeO+MSjLVyNPN047h1NUTeXdFc7TEiEmIg5IedtEZXXNX03EGNiwQE56x1UmdSN7HyPElNeWnwHsq7Yi6eM4ZdRWjMxZ9xpv7vQDlJxUpLWsM4PGK7+B/dXjzFZ4odiVrGYFMpZfFZQpgxCcrL8To6dRwt4OPwPdv78GqHJRrHb9SxvH0Ff8nJQ4lCwGW7Pfx+tqIuNe04QI84W0wclBLUx4AN3l4ovXb7DL6pHTPKa5giqjSaGyMX6itPjk9JQDw72PfXRjLl13KjOSQyc15aHY02g0CmR5Xf+1MLyiarof8LgcKs9djlBCoGsNHGMiGldDCkutqijCdlAXO8Z3nxC9cIJKIl7cIk+nqIXE+zxFFUZNr9+jy/1V+Azixdv8OqDERnLRTlLEFIyP13yPeME9+iS8PAJb6VzZIhlw5ASJSR5DKQHF+hbR5xOZsxevyoW3JliwR5TcayiaMBiKoYJSspSoPnI/ktvcU+/jF6c0utIHy+xIWFmmnQ4fnRtKV130YwpLSHBsB550yxo6zmjkMS84vmBzfvrhWd1SP4AEv8H7WOfPY78sU8d8lpEJvcR7wNTbjNbfichbvFjwLY1DI6n219jPT5AKcXtyffQVDeL9a+SZBdRRxO+VgfWn5wjUuZTq3StpXHna+K6Q09mhMstdjlH7FbX+T7CakRTEZ9sqF3ik48dk6lDvPmET/3gMUIKulTx9nYOKfMoPeXnTjegFC+f3OX75A+hasvT/BUu+l8HKbg8rXlyUhG7irMHe26Hkj0joBTSMR0azWLXTAJhBOhir5/GQAw77J1jpC7IxvmtihQi+YBeM/pCE13vqV88JXYj4+PVIYg4Q0qQocqeT91NiNGxffLrvNWfXAfA5t2AmDcMrHh79TNU05qoyrnitz3+13focSROGsziMyDvoiuLolipdzHwaaHx99bMzxacXX4JnR8j+khlawQWLrsSnXCwu4+jJw6evB+Q1iBrAyny0nJLdUvSbUdevz8lXYIVNbc7R7rak4ceeaqLdmwIZMowQ5qCGkVR9iY7eMJqV3ShqVBK0UX7KlMZ1mQpEaMvx3Iu15RsAs3Nk8NwrLjuCSF456HgyVc9WS5544WWrtVIIfi2ex1NVvhtT+KATD87powm70fG+x3ZCsR0ijmeI0VP6h1VYxkuN+VnfABbGtlcWdToSTESQtGXVYsJcjtgjGb/dM2u2nF854TROfzgiYd9KwP94Hg8rTmfloHA94zwR2ctMWd+vjG8FosOqVvtSo2R4O1lzeSs7IfjxYbKGCoFRnwJK64Q6Ypfb/4PNncXRBeopGQcHd5H3t4lVBcIo8dMavr9QPd0zVdmZag3xgCX30l/USyyV2cWBJySeElJru5dkhR8z63PM7+x5O3Nm3z5yS9/ROH0/l3nud3moIUt4dfPhkXvecQ39HzXdLv/OcqIj9dvcX2Q5ux/5nLO8e/+3b/jc5/7HD/yIz/yLXkP3+z1zUWKPpBb8huv9yY8X9/6Hor+80sJsJRgq92TNeedK5PQGIsv+2LC6nJDNWkIw4jSCikl4gD3D84zm7YoKeiHkegyJVFQUs1nhZaXIjplhEgcffKMOFzRv9PT9YWWsnqyQh9N0M9E9C6wGhxNU+FdRM1rRILu8PpNZUguHtzrJNYYjo5mdM7Tzlq61Y4kBEJrjDWkQ4q2T/lQzJY0+5QTZInKGd1Yjl4+Q2vN5uElk2lLNzpMWxE6R46J9nRGVVlWT1dURxNcN5J3Hns6g0OT1XcOexA4I0pDlZLENi3DVUf2gcW85WocEEIw9o4UCy1lHBxYhRoDuIAPCceAshphDUYp9LxleuuI8d45Sklmtxf47glus+fsM9+Bbk6QstA4mhdOaM4WrGt4crlFJvAukJXETCq8cwgEu/WO6SGPRnaOdHCKS8DVds3rm8eI0FDLb2e8cIS44rXV6yzaGRPtMTc/QQakjzzYnDOkQNN27NyKo2bK6AYqpQkxEUJASIOIqQijm+JqKJMAU5Viojscq2MgSQExMVMSLrYlVJMDfUPAdrPmnf4Rn/7EZ6mFwjvHerNmdMUNzcdIP/QEIbhlj3nh5BZv9yWQcwzFW04ohQ8lVDLHRBYZbUwZLjyjwLiApOilTC5DhjQ4zHJaNELTmtyNqErh1x1hdOickU1FCH1xpZpUxMETrvYlc8hqgvP07zxFNZbq5pKw2pNCxB7PUJOK9rN3UWZguNqyXe3p9ob2eI5sbEFwDgWXri36lVukG0ekbqR/4zHxYAmOEGT5rKDfoG4tqW4dER5eFdqYVCB5twDLCfVsC0mRiMRoQdx3XPzcl5m8+grZl2l27gdG50hjmY6rtiooUS76l+iKMYCe1iij8WMkVYpn7P3fsEZ43wXquq44NEvPzJykEFhTUBhSxo8l30mtB2LokNMJJu5JzxDwHMkakhYlUDdEspakzYB9+RiEJPQjSVJc9SbVNTofHq/Km3Ae0YCZNKj9Gq0UnoiYFOQsxUiGQrsrzDaUEgglEO7QEMZIiqm4ABIJfY85OSqoREiEoVDX0uDJpiVRogwYA/GwRxNLAywOjVASh6Y9g9iVAQtaFYOJBG7d43cd9oBckBIpZpSErFXZc7sRPW1oalvQyHVXDAysxuqAMmv0fIa8cqXpShEJRARiOyBTKoioFVTzCXE/ABZJgx41WSmuckaEUNw6KfREMXosguXxnNlsQp0TdmqQugbnCyKpCmtBLqblOJACaTVqeQK9I/YOO7WYWpPHnmZWA7kwCc6OCO+sYQiYaY2eSPRRS7UHfVkal7TalwYoOrKt6R9cQDcUChqANQXBlsX4QjqPaCvE0QQtZUHhfMAcaYQaCq3xYN7pLjb09yKICmLGaIVRAro9PH0KQ0bWDTTNYS8qGi8OmkdihCRJu54siylGtAo3OEQq54s5mZNiJImMXk4QF7tnpwVx1xMbW86XtqLtNFVlGPcD4+iIIbI4XRBCYPt0jakN3nv2nUNVmqOXb8JmYL6YsH7rEZ0uDoYpJKqmwsxrhCg0vfWTK6q2KhELFEaA3+7L/zHiEfT9gIdibBIiw+CwqTBCYk5IJTBGI0j0g8OliJEWP3iMMXhZhqDbfsT1AWs19bxhf75HZIls5LssmWcbyG+mqDogSM+DR9/wTx82q8NOxcfOcx+9bt++/TuOBn3UWq/XABwfH3/g/X/4D/9hfvqnf/q39Rp//s//eX7yJ3/yPbd1XcdXvvIV/vE//sf8xE/8BD/6oz/Kr/zKr/D3//7f/2291u+G9U3JKSrrNygVvpFz6xucSPSm4aqd8ui1B3xp+ybuhW9juZyx2+xRqhTqSitMZRh9QEqFlpJkDI0xbF3ADWUzNVrj9+8KzrOAy1TyKYJVzINjWgmW336LN1ctcnWBbWqGwdOOEV1FxBjoXaBVCu0iwmiaEEjdhkkODJuEriqklgSjCBGOThfoyhB3PcPlDhkSk6q6NiiQQlBNa7L3BUXoBsQQ0Y29thU21rB7eMWuH2kmNfHg/DPsetIhfLGqDI9//T5KK8SyxdYWawzBReqpYT5ccGRh10e65vTwhwpEv0VPE/V+ZCkG4n5gOlXMTyu61RadFXq0xUXKKERtsdOD49yzRq8fMdagTGY5S2i1Zt4qwoMHVIuB6UvHXO4nDF4CmeQD/aMVfT8SzlqsUCSdMUeTMsEbR6RU1HWFS+BHTztt2exWOGUYUybJwMnxCfZ4zrjN9Hh0Y1A0VOOCXYhMZg2/dvkOy/mSEBzT0yXKjUQ3kGOFsQ2XwxXZb2htxaI9IqcWUxuUqSFlzKEZDqEUkbqeoZxHiEhKHTEUi3Yda+IQkbompUDaZeIgSNHx8O13aOv20IgmlnXDqttBTMUePHqi9ygFR82UN68e8erxCebGi8UOd+zL8RICURT7ZaQo6e/ZEvA4ilBfK4latEQXSkBnzqVorA0Mjvp4Rtj3ZB9L6Oxywni5LefIzQVutb/WuGUfin11COw3HeZoSniyJmx67I0FetZwfPeY7umK8Nojwjtr9vcukCczxCfPinZISCpftDZyUiEqg358hew81pRML2kOAnQfSBeOfGxRpzPik1Ux0lAKTYWyNVIInNsTsy81J5BCQCpDujonvv2YmAQ5RuKmI+SSLSXIRU8hRUHGYkFX0jM3MDJh9GDN9QalBZy0pfcJCS6ecyJ9fpvLBTYqzV0+aADku4/ps+TRrrxGNQzMjERVkqQCw7glDz2ooo8xQpOlppGLA6X4oMESxaJfHk3JMdFsBCpNETFRTW1p8rY9cdMVlDJEYuXZd5cM45a5q/BCo5tjLp7cL+5wEkRjDuimIo0lmDhkRacFWSq8kQWFAcbouDJ7kupY07M3IESxkk+xUOJyzkQf0VKSVUETEAKpKE5khwI2DREZYawVSRcqnXy6JiCoj6bobgt4hFXsh8MHOrqiPXyyYloZmro0Smmx5KIv+hNMQE1GciwDljyMaK0I2y1qIpDzFjNrcOdrgi+IYwyFHizbiurmktiPLIzlrq4Jwwh5AJnIKrEQsHyhQuqITGXQF7YdtYXmyCKtobui2MJPG6YnhdqmagHTmtT16DHQE/DnO2QV0CuFns/QPjGKhLQCMauQNQVdNAJVKdKmI46hNBUhgIzEfkQqgSCStSmudilxUEuCVaSQSN1IjgkfI83JHHJXUKwYkZMprvNsH+1JoSHEiMkJff8Buip61ohj3O8QuxXy7DapbgBBFBKRMiplvKoJRtM92ZGXpRmWMWHmLW70pM0en1Mx31CG8CyzKJdspCwshIQ9muK2HYuThpNuTxp7Wl1z5QT7TYdVktoWXazvHU1tkZOK3cWO8wdXpG9TZc/ZdTSTBmkNzdGUcXDY1rB9vCLsRtIQsK0FBOutIGwl62DxsQwnQeD7kZMXTgndwNBfMuwPjfyYaWctWkIzaVmtd4XOO3qqaU3yCRdCCbWtBZerjhQSR7kiT2uu9gNpUWGnRwBEPxDHHp7T+HwUOvD1I5trG4br+z9QU/R+qt3Hzgq/69fbb7/NMJTa9c6dO/9TX7ttWz7/+c/z9/7e32OxWPDjP/7j/MRP/AR/4k/8Cf7IH/kj/1Pfyzd7fXPpcx90Hl1zSj7k/t/C+vUbn+Tt00/w+pNfJzYZf5gWaVlOZSUFShf6ktbF2ahQ5yQ+BNCSqASKknORR3/9u/Q58392e7oYWQT4y5dbKiUYwowvnXw7l1ee7cMrlDWk3ZqkNnTbjpfnE0SI+ODRlWHWP+Hl/tfpNx3pxqd4fSeJObM6bnk4s7Q3FgwXW/LoEbo4rMVuZEgJZRRu2xOTI4aAmdVQVez7HcvllNXbT5mczWkO4uNpVSGlZN+PVFKRxkgUJcdh3A201hT6ScwHi2bJtDZU+0f8sfxvqEXmgVzwH47+FEIJ3PqSp7/0f+H3IwtjePGyR4iSf3P5wgvoScf8yREvjK+ijeZruz2rk9K4qErDxQZ1KExFythJxe+zv8pJ/bPEC2iOJjR2Clc9/0Z8lofP6G+rjvx0w2bfs0kOcTZn6Ad0W9Gvu6I/8YnZ0Yxx15My+MFRVYYYQFtN1BlZWZok2ZmeX833mdopRimujl4h54xvp9QW3hofcrScYe0OrTWz3Rl3qxe43K65e3aX7fgGbWU5Wn6G1t3A1BUIWXQdSNLgyFohjeLm9Dt5Np176/xnCXpNGAM3lp9jtw08PH/MzfkRpq5Z2ITzgdZUjENfeOnBs1WaF05vIFJm5zr2Q4dEcCVG7qdLbh2dIZop6cXvZdvv2F4+YBGLS2KJfC0n2NZZ1uMx/lIVNy7vUVqTB4+qLbEbkVVx+JOqIriIUBE1aUjOk1MmulDsxZ+scLseezYn7Qb85a5QLAFcQlWauB/Rs4bUjQyvPcScLXhpmCGsIc5Occ1jwmrPcL7i9RPQL5ywOFrwbfcG4JBQLyX1Z+6i9MCN8GmEMaRhRKmS8bLq3uLRoy9RvXSTuO7ABxJw2r7M8ezTxBi52P8aq/7NUkwJScoJIQXKVAznT1GnN5C2JghBtBo9bdEplQwlawpK01ZlipwTWRaKnpQa7961nZtV8P/+HFQanu7hH/8i+PTePS6n4mT4bFwrBO9O7Q9FzZefwlfOgQT/27Hg//i0RkjJ1jzl/nhB3jlkWxG8Q289L02/m0X9uWI1n4sDX+h71KxGVEVz8XvOX6FiBiJxcfyIIEbcoxUxZmSOhBB5IL7E8PYlehD8ID+IMjVuNeX/5+/jZUbEiD5aFBRRTei+OkFkWJ1YXv/eGTlGthdNaY6F4JG95KdPf4XcDIzxgiQmRdx/EOALq4uNdyzU0JxzcdUbPcnq4u51cKkQMRNj4t6timFaiuFPPhyL8cjpnBd2j6njSPCJr6VjnFDInMtAYHCkJ+e8/B0KbSSXA/x/fg1chFtT+K5j0LWlevkGah9gP6CXS0AgBkeUkpwoiFk3kI1GPcsGayrMcsrR268xj19FH4JM9aJFGEHcD6R+KO56pGt76pdfrWlEjzCBN2TD5mEHMfKCeEo19+QYC+p0q1hbf+18RrKvIMfA2X6PHiLdfsuD25acErOblmXsiA8uETdvQfCk3pFdJO53YCsElCDbyiBCRE8bZFuhd0NBbqQiRSBHqEyhBO9HfDWQ2wQalNU83tU8/KpnXM9KIG+3JZzf50wp5I1biNmc1M4Qekm6fEp8+Bb6k58iSnug0SWi0rx+36DmLUnOSfdX2LsnpMqWv7cqDWn28dpSHlVQYNc55CHUNg8jqrVoKTj1F/yAvmD1+Ip3Ji+xO/puckq4MdAup+zXu5LxZDXTxYTXfvkdYtuy7SPq8ZbvqS3d+SX9977ERU74TV/OUReQSqAAPwaEVPxK/iTD7CV669BRUU8MXivC6FG1oZo3rI9mPPy1dwBo6gqhFUfHTWEWiGI2ZIRi2A3FalwK+tEjFi2r0wlCCZ7MG/rdyGK5xM5qTl7+BFJJtm//Kps3/8dh2zg0Rh9BaRMf8NV7b31fEfYhz5N5pi36yId9vL6F6z//5/98/fUf+AN/4Fv2Pv7yX/7L/PiP/zgA/+Jf/IuPm6L3nJ+/FfrcN3i2XW8IB/tP51PR6kiBUYrpYsZ2tcVaQ8zFGUxbjXMepcrUKsaE1opKSoKP12YEV/fOcexp6rLh+FgcxUIMMCZko5GU/Jijb7vD8qUbCCXZvPWU4cmaMSbk4GimLaurniRgsWjJa8d82ZI/cYPjfg5a4RvJycsn2GWLmTc0NxcIYPvOOdvLbXF8ShpbW4ZdT2MMw3YoYtxpjTCK6Z1j5qdztk8LdCqUZBwDtq2YTBr22452OSVSXNiUUrTTht1uwMwMofdMz+bITSaNPXbZcPbSGZPpgiSeBcdFlBFIDZO7RwgpmGpHf7lhdmNBG1rSG8XxSLhIc7Zg9/AS01qqyiKVxARNGD3V3WOUhPkLS+LoqY+mB+1FKu5jMZA6x9XbT5C7gaatmZ3MuOhGspHEwTGbNux3PePocQ8vaWctPkUeP73izrTBNIaYErKt6O/veHT1lIuYWL70AhEYcuDGyU2Cc0SR2fuBIRSb8K3rqYPmxCyJ+4zVlm53ASJgjxbEDI82lzRdw/FyibSy0AfnLTJlko/E/VjoYVoV5CwUjru2lrPjI5yPbMNA7gKjd0x1hRo6zGGKKzPs9huutCYJQT8O1Nqw7/eshzVjPXBBpq1btBBc7LaEcUDVRZgsJw3yQAs5ABRgLRwytjhYk+f9AEqiT2YlsFFItNGkzjE+Wl0XaWpWEwWY+YTsPP5yQ5YKe3NB3I8lr0TJA5IT8f2IvV0gfH//HPfWY8zdU+yNJe1nX2R4+wnj+ZoUIv0bD9H3LnGhoTqZl1yjg6i6+exL6Htz8tW+FG+5ODPJDAyOeLHB3jrCvf0UQijhpSmj8qEBEQKhilOdlKrQ6oxlc/WUaVWjP/0JNk/XGKtpbi0RQ6B/eEmKCZ8zNRW2MSXXRUn8fihN9+jLZD0VSokSIENEoiAXCuOzcxGKruxdLv/zfxR4FjqdM4RMgaeVIvmAELKct25E1pboPGZqYRhJmYNtfHEUzDkhM+iTGSFlRCphygZBqnShOl5d4p+sUIcJcSKDlcgQSEIjkChrwcV3JdxKItsa/8451WRSqMWU95sPYvocCjIh5MH23grc5VhYyKIUUznnYh7hIhiNDIV+m4Uq+q1YqEYiHIqwg0ufECAbW0J5M8Tgae6ekZxHhkAmEeuK3CvCEDGCQqkTgrwfCBcBc2sJQMyClA+ZZbpkGsnKUL1yUiyrn25Iu75QiU/nyLYiPl2VTyvlYgJgVAmfpYRRD9seXWnwEXYdYT8Ukxolyd6RD3ljZtYgjcJYS84lxDjnjKgtmIH0LFhYCobzNUpbQsy4JyvUGEgjRD9irETlRLQKVZnyubfVwRHzWUOZwA3I6QxZW3RKB5op6NM5yQfsrSX+fIPf7AvS/MzcImeS8/j9wHA1IO5qlNHEXULNJ7DpC92vsrA4QbQzUBZcRoSE1BZ14wVcCjCdkjY96pA7hJR4H/BXO+pbx4TRE843h7+PIM4nuKst5hD6ak7mhMstMWaskcjRk60i5UzYdKhpAwdNz9HpjE00PMoZtEZMKtx+hJAxc8PZKzfprnbMby5ZTqdcPrrkxiduIhLc+MRNvpQj+6sdkpIr6F3RVxljGINnHAaGxmKmFWGb0BlMbRAZtNG40bO92DA9nlHNW8b9ADnjnC9hv91YzgUh8M4jJNR1xX4s1GzvCmIURWbfFWOFkBLrexcs/IL5raOChL5vPR9N8nzz8m4G2jdj+vx8Q/RNnGh/vL5p6x/9o390/fW30g779u3b11+/9dZb37L38c1av+2m6Bvqad7DKfmA2567Y2IEx00mx0wQCh/V9SNSTETnWfQj+eIpL0jNVgo6BONQgs+klATnygWKTF1b6rpivdq+q5eRJXsox0QfIjo43rq/4tXPv4ITcKcecTFSR08cA9kKCCMTc8nhkozUivZTEvfKEi4mhTNvDfPQgBRodty+8SoIwfl0gjx+EZTkyAZ0HSCuybkiZsHDX3ydNHqWs4bQBUJlSbo4aQ3dgLSa2e0TchqZmYSdT9i8/pR6O9Ii8eueSguag2B3uPCk4FloTWstIYKdtwzdSGsl9e4xJ8HRviAZNze5mhhGabgpz8lINnnFBSWV3mnFY1uK7f5kTntSkYXCGkm9vyBvnnL27S/xoC2Tv/TkMWcnxWp1262p5i0TuWe9dzwMNciKsyhoDJAFbYTJGFm/fY66uWTnzmFiCTHhnEPpkn2kkajagBS43rFabTm6sWRxMsfkgPBPis1yFGRvmZpjmFZsjaFSmvP9GqtLqGRlDC6UC2AIiVPdsh9Het8RtuU4SsIzn1akfsS7K7oRrlYDo7/D6cltrDFwsP3VtgTqIiiOaa4idQZTWYiSJDLHswVvnO+YNxOs0ggreXt3iRQCHyN1XZOnil++egs3OhaTGclBYyvWeeB2fYTRGj1kQuiZZovHghzwgqJNeY5ELq1GVEXUXarCRFQCIRRZS2Ln0FqRQ0BPqqJnOQS75pBIqw5Ra9zgMUahTxbgAsF5RGsxk4q46YlDMdzIg8M/WSOlQB7PGGrF4D3ince0tqK6fczkbMYk7IhdQG87zq+uaGtJe7qkcqWpyCYjXp3S/dI5dJHazMgxoUxLW52Rtwkx0eizBf5iW6zXtUbFRKUnNPYYEHh6XHbQe4RU2HaOOj2murnk5HheqKwpUd+eodqK7s0nZTq96bChoT09wc4aOnVBDhEl4HZdBN1tJbm/Aq0kq/EAEMnneHHX6Pjhhuvp7ofvli5Jdt3B4thWVIsK0VjSuifuR4ILhCqUzydGxrgj9IEcAmJRk1Nfwi4Pr6dnLbVZMD64z4Q5+aBdSrUAZNGLHfZD0VjSviOZEqqajUZaRewG5MkShuf6OSkIm640NFA0WoeCOQ9j+T3TwTwBro+90Gj2uoj9F2aG3WeEnRJVxKftAT0q4Z0CQb0aiLrYr+sk6N94BAL2TaGCJgI5gm0qyIm4GxF1MWjYPtjjTUvvBEtpiEIwU4rOS5SEIZQhgWoq5MtnuMcrsgvkGJGtxXzqDv7JujQPUqKMoLKBuL1C1A1VY0nrPX7w139vVVtSiBAjjc5oA/ZWgxKuNIIuoGdTNKk0d02FqQtFCiVR3YioNGZa47uIrBXEgmDYOycsbyf8rkM8fgS3E7SmDKQIRXezXpVmUxanS5VT0XrmTD1uy9+462iOLRwtGJ6sIETqF86AzHD/HCF6mkrQP1kxuXWMUBI1rbDLKcP5llzVYOsSZJwz2ShEKlb4KZTz1z9aIWZtQUlzQkhoVSCGgDoPIA1+tS97zaQuGsdpi120+IsNOUT08Yx0uT3ofDQcAloJibDtMWdzwnZApcSyEdydRMaxZ9xKXDBEJEobnnz1Ia4fWbQNX/3q/dKo9h6fItOTGQ8uVuSjhn4MLI4avJYYo7FjyXYbR8/k9hH7TUddW7zzhfIpwI6Rpndcvv4YczA98v1I349EAd2mY/SBJHLJ1wueybQlHs6N3nmMFnSjQ///2fuvH8u2PL8T+yy37XHhMtLcvKY8q4vNaYIeI43DUAQFAgIISHqQgAYI8J/hKx8lUABBQBy+iAIESANqABHUDMUZNrvJNmWuTZ/hjt12OT2sHZF5XXWRXezmsO4C7s2IOCdOnLPNWuv3+7oi6b2GzuKmJm5qstxSbN5MI3e7pfiGTvdLoeF84ddFfPuhbwqi/9DGP/pH/4h/8k/+CQB/7a/9NX7t130AbBIAAQAASURBVH7tT+y9vK2p+nnW3v9zGb9co4V/W4ToK57/vZPIXz3vcP3AVp9wZeeJ8tQNSXTfwplz5L3HlxX/VEb+1XaPUQpjFN6nBO4woULOB26uNqAlWZ4RpUhZP1pymDaCkYzXJ38GNx5Rloq/UfbIMBKFoazalBvhtrwj/l8UJxW2H5GTCPhpq/h/7PWtK/Dd5/q+1nwnT/qTXan56XGB7QYe+5f8cPMxyS3rPfrtKeXrAyBYZRWHzvFZabki4gV4Lakzg216vv9YUIRr8pixebXluJhjO8u+65mfLRivO57UOXmRoSN897KlNI6+Gbj8nqGcl8SbC/7X5p9yXh9x5TT/l+cVLsCj+Zb/45/5b9FK8gnwUWKz8Nx7/pt2Ek08bQnT9X+sM36YpwX4Z67gab8kW5acv/4Z34/71EE/n6bTveB/erHn2RYI8L/7EXzvJJ3+sycb3Cc7joBPHs3Zf3BMd+hRwVPWJeMhWZeP0RMDKCk5eXjC9mpLBKq6RGxfosb/J0Ir6uJ9Pjj7y7xqDswMbP0ly6ok14Y8yznKK3Z9SyYUOi+5Fwoe7StsyMiVoS8NymikdLShRQyWnXxK8D1WO37n2Ut+YH+dhyf3qYoS3zhCJ9BGJ4rKouZh9Ruc+0DXttgxIDNwE1qQK81m2PM7XODLpHupV3OMHhmDxRQKLWY0xvDJxTO8jfzg9B3+l9n7HIaOp89e83B5go81Oz/gYwrrvUVR71bOENFFPqXWk/Qn1hOFQNoI0adw38IkTdTxDHM8Y7jaEfd90ib0DqUkrrNwsYNMoxcVPkSG0WHKLFHp+hGRG9S8wt/sGV5c89EPj+FhTTWref9fvab5/SfkD475tZNjxutLtruGj9+fI/yek2LO92y64Nrxhs5ucPca1E8GHoofgYBZcZ9ZeR984Gb/ETcri8x1omdNGSnL4j2WxbuICK+a38WNz4laE0OgqGdkxwuUUZhZyf6T14gqQ6xqopbJKZF0bO4XP6JaPIRS8knz/wEcBZ7/7fc8eanYofg//RYMdjIeEJ+rR98IpG83NLdz3dc4BEXn2Q4FH16k8ycAVQVEbrA3h4SqTJbFQqV55/X+pzTdS6hyZvqDhAINdrJ9j2SnK06bmnlUxBUpo0cK4irnifufCIARMmm6igxuNsn5jUS7jdYj6wJZZIS9e0OZhETXunUMjSmHipjyZQCiEgiVjruIiUZ4VcLVtxeIquDPHb7Ne9sTCHDh/4AtByTpM/phQGcZ9190k2g9hR3HXIOWPLPHyJBQNaQkWA8SsmWF37X4xZwnGwGHhKL8BgJyQ9zDj/9NhpkVqMogSiDTCOeTyN+mbBzf9MR+RK3qVNwpyTJvuZ9d46TnemO46mqESCGszjqUDwmBUhKc5+x45OhUoaobODisknchvHpZ0z+9ZHyxpXq8ILqQjFDOlghtUCFHFokOJ3JDbAbiqwsenbTo0wJbDGTnp4wXG3zsESoh6YSAKkukUngxIZb9wOpRyfvvjMShQZ0YQt+gFhVj5Rkvt2SVRAqwx/tkn328oHu2Z3y9RswWCCkoHhzhuxHbjcgY8ROqp0NMbnpZQs20j8QsFfaEMFHRAu+tGvJ5BquC3/0J9F3Avd6i8hR2rmcFw9UOXef4psdUFXmmcTf7dA3ViRIYuzEF5F7tMCdzqHJOLl5z7K9xITB05+y7R+l60z0HIzBK8zqTiPM5XdcnPWr0KOGQJ3N0pqhWyVxJqeR4eX7VIrctelbw2aHHW4/KDdooXDcifeSDzcDc7znq4cevNxSrmqzKud61FHXB1dV2Qu4jeZ1TzyucD3TdmNwtp+s9rzOci4ztQFZkEGBxPKdc1Z+bI77OQe6LBcsXrWC+rqD5krbo7X7NNzXQf9DjH/yDf8Df/tt/G0hFyN/5O3/nT/T9vG2u8Jf+0l/6E3wnv5zxx5NT9Pb42hvudleR+MNGCtz6QMzrREHITeoqVQkNMLlBOY/0jmGwiEIiCBijmS1mNPsWaTS+G1gsatabfUrdlpIgQAtJXeS0/ZByaAbPxe8/paoV7593VHVyT0vBpKRMod7ih2FKvQ934Wohhs83gafk6L7p2b1e05hT4oOILnPkoIjdtMmIKWn99J0z2pc3SOfRPsDoMYsiWU/PcsbGYjOFd2KazJgcfZKGJSsydG7o9h2hHYmDo6gLyiwjtANCS8gU5YMVUrec3LuHKQVyF/A+ThSTiCQi3nKtebsP9SWKJBFTGUyVoUuDnhfoWc5qdo4eJ472pBOIE1UoFY6CEAJEwXjoufjJU4J+TAQOVzu6XBEyRbSOXEhMaRKlxXlCO7K4t2Rok4bscLNnsZwRXEDkCmMEOtdoF5mbgiwXnNbHbIcGJRX77Zp1t6fQhnlW0o4DFkedF+z7LonsgZnKueo6um7PYup86CJnLjLGsSLXGfvDjiIKlBD0MdAfHFlfYTKTcolCQAqJ9wOHZuBqt0YJwfqwIwrBoWvxChZlyaHZI7XhcnvD6CyPH7zDcVnRB0edFSyrOYddy2Fosc7RdQ0n8xX50Qmt3rDZbMjr8m5HHgaLzDOEIoVatgNutHfoQLgVMU95Som6lihgel4S64Lx9QZ8CpM0R3VyrB5s0hTVOWaWJ9tsMV07zhMOPXJeIvs+6esOA8OmAyXJTpf4dYO73JK9d498VYHqCC7Q/PgptjrGTBuBSEQtK7LHc1hP723aYIMgRoG73KJPFrARqLuOhEjWvNPzb7utuiySDmzfTaGeBtf26LbHljnDeo+ZFTQ3O4xXyNEj9gNMTY2oUkaRCB6V58gx4kaPHTyqyL/E3v9KPOiLTaCpiBWQjr+SqEJh2wHpI1FL3LYFo9N5m5c4MxW/WqUcLCA7TsHP0fmktYqJvhZ8oP/49Z27V5xoOHpR458NiU4pkoudKvM3jm4xBSG7Q485WyJzg3x7lRBMNL+JqhgjelHiDymYN4Zwh5oordJ7C2+OiPQeUeawno6Vlim8uPeEpk+HKdOpKNPp9fEeofJUNK1bgtGoQmNDSHk/gyMIkXJ2mh65rPGHjqhU0s5Zj8hzPBK/6YhXe7LCoGYlsk6UZLoeWRdkZY672ePWB/JHp4R+JM8EyjVks5xDXpPZBVGIhJJummQlPwZS186DtcRdh8gUal7SP78mas240QxuICpJaAd8OyaTEa3QSjHuB8arLbhIbAdEAFXkhL4h9iMsy7QOXe0mlDqF9wolCSenSK0RRPK6IHQ9MUay0yUqb9JxjilkWwgwixLfpXmhPJ5jX68JmwP9hLwK7+ifXGDlMmmeMoURGdjk8hknN0spScWjlgQCKE2MKegX57jd/Afv0ZlGCY/JNaNIRjnl8SzpHnctqswwR7PU0FlUqKrA7g6p0BtdQoxdMnkZnlyQ3T9G1RkiM0jnicFQeYP3AecCKtOMBJTzqVA3ikPXszxbsr/aAoLZfE59ukj5fZmhPRxSLALJwEQbhY7gQ6SczHXsaGn3LbkU5JlhbAdsCJg84+T8iOA82/5AHlJu3tBb8lKiRULwTZkxOocdLCbTKEh7DSmSK66S3Dy55Pz7j75iEvk6wPmrDBS+brMVP/fP1z38zfiTGV3X3YWlhhDYbrc8f/6cf/7P/zl//+//fX7rt34LgLqu+Yf/8B/yox/96Gtf6xcNbzXGkOf5Vz72xfDW2/d46z739/7e3wPg7OyMv/W3/tYv9Bn/Qx5/9KLoj4LcfsXNZ72gocQfBoao8b1FaoXKNGGwuG4klD3hyGK7AX85cnyyYBjcBClL9ruGLDdoLQlaMViLKbKkSxAi2cJKQW8daEWWGdxlS13lOD+wOS9pCgHSE1sDMaBF4DQE/JA6itFFsipHjQOPROoomrwkDOmQzkvDTaV51cJPfu9nPH9ZcProjFbv6UxJPiuJskBIQfX+GSrT2JsDwXnybU/pAvPCoIDttqU+XdCsLb3yLLSmKwvGd46ILuA+epWMGUaHlIK8MAz7A6p7xrLS5I9Oedle4qSkXkSe9BrVWNbddAoEDF7w8TZRA14d+LliToB9iHzqPELAVbtlWKdE5V1/QN8ZV7x5jWURyFSiZkl1zHbI2D27YEfOoAVtO2DOj6DvU3o70CtQucF2Q0o5R7C/3tPsGhanK8Z+xA4jODD5Y0yVM3ZzruXAzo20g6Olp/M9KgpmWcHxfMnF9oYxePSUOfRZfwVRINxI5ga2siHTAT2fI3TiswsiY/B89/QR95bnjN6hpMYqyeX6klwoCinQ3tP1LVIK9n2LzQRFWTA/WRJEpB8HRm8xXUZlNHVe8mpzjbSWB4tj9nbg5uaKZV6yWhwRneXqsOHICZbljNWspvc7dDYwjC1CKxZFBUriDh3Ruan7PKDnFbouCFrCvsdPgYBSxClHSmI3DaEZ0Kdz9KxEz0vsrqV4cET/9BpGj+8t+mSG26Wi4hAcfgShFPnpjBAirhkoNx0qBFSRMzc5vvNEH9keGqTRVI9PKNYd3U9fIN4/5ezBPdqPXpI1AxfXr6jmjynriqL3iZL0aE7XHXBXOzJdUej5HZIS2p6wqJDHM2Lnp+t42kRrBUbDkFCkkBrb2FeXhOAp3n+ALjJEM2Bfru+c9rI8Q3tB69a4mwFVLBAku30hI72sCS6jt4H7co8+LvAGnu3g7VjXr5wOv0Qhjp9/TEAIk15IxmSKkSX0cWz6FOoqN+wxSdcTkltbdv8YZQuMLpD7FpUrhJT45zcIHwmT7vLg1kRvKUxGMVZofYpRaUPOpLnxb7296DzmeM7gI5/59Mgh+ISCOY92kapPxYg2GU3TpY8hJdF55C1l8PacxJD0X1KyUz2vjAUp2EjHoQmImcYODpVlDLnA5RoKgwlQrgOmzJL1uw0In9zRTK6TzilEYj8m2pZRaYNZpPv7tuCLISaDjQgoSXe9JTt0qKpIhXyRYV+v8c6TnS2RZYbbNbj1gfFMY++fY4UgaAPXkThY4qEjW5TJma8biaPD1AX5/QqTD8gypx0VvcsIQ8BZT3Z+mppq/Rb78hrz8OSOBjXsOmwHofVkZytcFugvd4iyIBBQPqc8XlEpi8817cWO4OaoXCe0zweEVvhDl2zDjWbYD2y8xbYj1SqnXs1SkRrBzCviYBm9Yt8ASiCGEVHmCG3oD5Zh3KYGntaoKrkZSp2CzmM3JjOTCNKkNTqSCu0iCBgdQinaVjKMHr0UxNzgdz35rEgRCl0K3nXtgN822INKZj2A1oaZzBP6sarpj2b4doDNlqKU0G3wRY3LdApu1yP1oic4z71SE2TEC4/vd4naDIhKoQeLcnuQgtkwUOxa+pfXnB7PaNSe1UqCGlBFJK8Nm25EGc38dMn6+TXWesTxnL2W+BDJMoGLMLbDnQ3+clkz6zx211EVGTvrkCIF5vbdiDQKHQU6M4xDj8wU0aZGTv9yjWxH8rMV1v1iFcrULvoFAZ83GqRfhBr3jaboj3f89b/+13/u40II/upf/av83b/7d/nOd77zc5/7i4a3fpXt9u34eeGtt+Odd97hH//jf/y11uD/cxp//EjRHzIONuPZOMP5FIYmtSe2PdqkFHBT56wPT9jmL/Ah4PRDCj0nquTuctg11PNqClYTBJsWR5NrCCAzRYbB95aclPINIuULHXrmj4/5pw/3zL99im0tn/23W8IIp5Xk//C+ROvkPqZzAwLu1/C//1OBKAKZUvSfVMQAT48Uv/0XTuB/cY/Tj3LO/385F//iQ66d50ZJ6oXg+JFjftqQz0ryR8foRUm83PHuriPuHeO6T5am1lEZy88wtFXNi5cR7i3p3l0hIrzrA/bZNcv7R2wfn6ALQx4H/jK/Ta0HDu4p/92/hNbCTYT/hkiMSQNxK4q+7uD/OuXFxc8VRF9dHX3sHZ/4yZHr+Yfw/CMArtMrfOn5/5sfwJ8+jYQg+Mnz9/hXHy1obx7yySrjSoM+XiCdRQnJ8mxOd+gYvCNaj0LQdgM6M9g+CZm311tkppBCMCuPcOE/I1bHXF6/5v99+C0WiwUuBMLgkEbRDD0ueNrdFbOswhGoswKynE/Unv1hz9xt+J4YIeagptR5HxKaIiRZB0VpUvexrpBRkHnPO0enhAivdmsOm2tyk5NnBifgo2yH1A3rZocLnn2zZ17WYBTXzY5u6MlNhvWO3dhR5xVH1ZwnFy+QQnEyXxEBGwKjtzy7+pSd+/0U8DqvOV/cT6GygiTmHR2qzBJScLFGqYQqmEWFynUShY8OWeboWUH/5CptbtoR9d37CJMc0Mg0xXtnqTCyLjnVLUrErODFkWDIE/IQo0VmmuI793j/ty8QVzuUEDz6eEcUYJ3jww9mBCko+i3f85ri8RnDZ5fcf7lBH83YdD2fPCqh33L/vOaDJh3zLm5oH440rz9i6e5zVv8wuTdNVtHucov4tkaMSfNGCOlqlSo5WCmFH5OleTAaZTUyCvCB8WqHngIi4+WGmGcEwCnJy8O/JlqPEUvUqsb1IzEzfLauMK4E1/NXz3fcfzfnOkT+z/9K3LpTf/34YiH0hSGEQJLsyaMPuNHh+5Hy8Sn+Zk/sRtbDp6wPH01BnxFzbwURzusfkB1yXHXGbSBxGB1SJcqb8wOvdr+DlQOzds959n3MKhmTqDptjIWUSKUIMvWc1aJCaMWNdfzTriVGqIbII1LxNus8j58kl6/h/ciHw5hysGKYnP/SBpDOTkGSSXAuM82H+jl/sNqDkMhZTpzNEMBw8GR1jdAGbzQiU+hDzwd7QQapMTJps6IQ+AASjwgJMQn7Lk1XdUAWSbgfugFZF2hj0FIwbA/EkN5P1CkE1fcj6miW3qfzND/+jOzRGdnRHFnl7LqB7acJScP1hKYnaIUAdJ0jMoM+EdhXG8g0aiVR0310uZmxlTWi0Ay7NZn1eBExZUEc20T52zWYByf4tscPBnP/GFEXXKqeeLRKodi7ArHOKbaO764aEAGMRrhAGEeoMigz+m1LbiSQ3t/6RUdzltCe6rNXfOvbHplpQtMjywy7bbgO8HS7QGRZ+lvbaY2L6g6dlSGQzaqEYDZ9cmyLkSAVaEV1b4mQktD0KK05+v1r8jGZQ7w4XjBKgfixJVvVlI9mtC+uEaua7HwFPlA9PGG83CC6kehcok0HyZktEqL1YIF9WCCXmsUicNZvCU3PVgteuQIRApILfPOUrMh4N694GCJOBiKe2A6EEPF9vLO09s1IbAVybThvByqqpKVzDlZwOPSM7RFEDSJR+MduROaaZ8uc0TuCCyks2nvyzCC0wg6WuZScP9+QGU0Iit8pwcaIzCM6CHSZcq6C8+z3DfWqxvYWZx0PbeTBbuSdneNJ57h8ew6ZGihfmj9uS6K7+uWXV8R8oyn6kxtZlrFcLjk+PuZHP/oRf/7P/3n+5t/8m39oMfTH8b5OTk7403/6T/M3/sbf4Dd/8zf/o9ATwS+jKPqj3C9v87NuvwwRv082zGquCSHge0tAgBQcLneEEMhjTrGs0C6HPuCtZb6asV/vk/10P5BlGWNwjN3IcjXn0DVIlSc3OqAoMsZJwDmMlnJRcfX0kvhn3mikU55gmnDkZL9MBNumXAKpVaJ4KQlDmj582+My6Dc5+dGMYlExf+eIy2cXaB8ICPp9x9M/+IwYoZyV1Kua5dmK/LhmdjpDRcG4a2nXB4RR9JuGIRq60VIsa1bv3YPpc5RnC46WNUEKVG5wSiKiSJvb2y5tFHfH+ZbG9va4pcgJeEsg/ubcfFVp9PmuVPyKn735/u5UO8f+swuaXqW/6QOFlMlSVkKYaHGDc4hMEXpLXRWU85pIxLpAfTTDh+QEVlUFYn1A5hpyg21HThdHtMHS9i1VVmDH5DK37RukkJRZRpEXjM5y1WyxznL/5Ixln3F4/TOKKpkmRB+Q07/WOqKEXgoW8xnFrGToRmzbo02O0YpHJqGK7dDz6cULmrGnVxYhDS6kQNY6r7g5bMlMsq1txwGhHNZb7s2PKLRm2zUQQGsBMVBVNf2649XVaxA9wghOT8/IJnvjOF2TwaUNopISnRlCZtBljtu3dC+uUGUOmUZqhe9GzLwkhoiqC4LztJ9cUL5/742mpMwov3WP7qNXBCnQSqYN3b0FwzDA6CYtiWd8eo0YXSpuc43dpuyUKJPjF0Ylu+PrPbYcKN6/j329Znx2jTgu0vHuLc2PnxKq42SxLASizMjePSN+ltzVolEprDVEAmCv98jjd3G79s7yWsaQNrATMoEUKR9ntYC6ZPuz58R9SyxydEw3RAwRVKICTtmaKQxTS7JZeUcpdYOlrAynj88S5SwGQN3dPP+u06GQIl3vPulohNHQW3Ce/HxF6G063ipRkbxW6EzRfPQc+/gHyKvujtIWdGoWxNEmXQ5J7yLrgmAtcqLdKqPRi5rQDElbpJMRAVFM1tLpBo5AmPrFvunx+y4Vk3HSqmUadi7NR0ImR0YSkhjCmJiCkwNojOmVgveoUidjCZXcv5wdMNkRwafn6Th55uU6IVSRScAfE1qv0+ZeIPCZQGlBHByub5ID5KKkOFkkDZQOSJNRLGe4foRFxa0DoIgRf7VDHc3SPRICbtehy4Iw2inEddJ1+ICclUiXPofbtogqB5fQTb/vCEMGOqbN/A24bUQUhtAl9zm/bfB1i44Rv28w947AebR1yKZBnJ+kYm3TYO4fMVxtUbMKs6xRQzOhf4D3yDpH1yVjM+D2LVmm0GWWjAqKLOl9AJSkfHRK9GtihGHbUs6r6ZoV6OUMZz2hH5FSEjKDs+naiTFRSG3Toerk2KoKQ3QJgjV1gdt36XfD5K7nAkwhrnG6vqNzuF2D8gEdAmxaqAsiKchYLmt0XSQjjxCx1x3eQXa2pNseCKcakWlkmVEcHzNc74i7ZHLBxFpAKUII9JsD0jqKs2XKpRIwHvpE967zhBqNLr1PoyjnJc56/GARzqOqHLWYocfAbDI+cu3AbFHSNQNRCWJIdO2hGxMlbnBoC270yFITiOSZYT2MKbIA0MZQGI2V0PUjeaYoZyVjbwkx4F0gCs3i0XHKSuq+sKDe/fM1+qJfcAK6Q4m+Yg92iw2BuJv3vqHU/fsdv/mbv8lv/uZv/tJe79NPP/0jv8Zt8+BXbfzJI0VfOO55BsfHknG7JpQzupEU6ucDWmvyKk82pEKgiozzUKIHic0zPtkdqJYVSMnMzBmHEWMKxkPP/tAilaTOMvrRYuqCw75DhUhmNJtM0ThLNq9Z9TnVJi2m31GGGD0LAaIrGQ8eoSP5UUGMkcMQeLIFU2f4NjI6R1CCHsnJT2+Yv2cwnSdf1pw9POOzP/iUew/vMfYjKgR8CPhu4NCP7F7e3NFwsirn6PwI3jkiO5ljhOB9JWjanmZ74MiDHFLIoIk3KJmccYZNmkddGPmZCuQIOjfRRm7HH0KNu3vOLzC+msWcisi3/0TnNLsB/CC5ZsdulhN9JJ8/IJqCrhsIUhBUQJaJNtE1HU7Aftegc5NExc4nmpFONrnrfctjLRnygaazNOMN79cn7GzLMzvQy5F26JFCYKTkZHVCbQrWw4FhHDFR8VAsOFVLXLSUs3cxQVOYZKPrvE2bLz+kzChyhBAcdi0iBMp5nYw4pEz5FU2HMobvPniXl5srno7PWPcbpFIsyxkoxbGS9HZMm+8io8pytocdN4ctRhuqrEDmBe/de4jzFiUCjg3HtWC2WLFr5mgfQSeqkskzYjeiVDK+MHNHGdtka5wZ2ipHjTYVTqPFzCp8N97dflGCOZkTB0v/9BK9qpFKUcmBbK5Y/toJVx9vcW2yHa+vW/JlCYXBbxoYHFjHzlmEHVEi5+TBMXK9J7Q9C5fyX4SFXa0gWNR+S/HDBxAizYuLqQ6P2H7k5fY19Q/fpZCKsvNk949pDweex5tEzyoEi+GcCOSjuSPZB0HKBiFtEIQPKCnImVPkC+RRzc32FaosCEqxuv8B8qrFDiN93CXBufWoTEMQCT3TKjncjRY3epSPhLKk13OkhsNuyprhy9a5v+iIMZIpz6oG3410VuGNBq2Re8Xs9AHmdEa7e43d3CCFQjuP2zREG9g+/5hM1KiqoKzuoXSB2LVAiiYIMtF85KwkTucdIYkEWrPFHa5o+x0LB7bpkzti/VY35K3Rv7hO6ItSKQOqzhl9IFib9CpSgJTJSVik/nWYNF6EiMgz8LemESlLJkTwfZ/MGVxAxkh+CFRMwcgyWb8nXZkALRE2IExqBEy7aqL0KTBKS0TvCP2OvhnQswp3c0AdzzBHMySghxG3ScWTD0lrYzKTbMy3DcEHmicXmCJPyNtt5kwIqHtH2BfX6MGTmxzcSDcMhOAgN7RWM75qcYeBZutAFrirDYVXiA8vKE4XKK0xp0fYXYvvcsbrkThWzMQO+/xTVF3jbyKq83Do6Fdj0ofWmpu9h8Fi0cQip7/eoXNDniVzCzn0zGYeqUeskTSHDrc5cPTQ4O2AqnNUmSXnwghufQAqotHkrqMwlqgcbTS4MZ0rWeS4wRH7HarMyeYVqi5ACLrXa1w/Uu0tWkrEoWUoJNYFqHOicDChkcIo/KFNph8C7JNL5P1jVKYwRXZ3vsd9Ryg0h4NFDS29jNh9CopOlVakuLfCEBGjTEHMIaGUSAH9gB0dsrccfbBC257xRcuhHRhuUr6c0epOT5lpRaYVotDJdj8zWBc4k3tinvSXfvR46wki4FqLqlJxVR+dAYIwq/jZtklOdTHiz5c827b4KqOqK1o7oo26o6yLQuOtS8YLNjAKMMrAfsf9VaDsL8hcwwSOvlljBV9wn/vCfPIL0uKmJ3/uS3H3r/jS49+Mb8avwvj3VxR9ESL4ec95a9TG8v594FxzsXE8bRTD9SEFl0tJdTTDH7oENQ+WH+YZSibax3+3mPGpEuy3DVIknr9wqauYFQYidM4RZeo0y1wjfKQZHYdFRpZp4r7jP3/1DvNxjgk972XPkDrRxPzznCgEqnTIey1CCdZd4P/2iZhay4Hb1s73d5r/1UEjr7ds6zkXS7j3rQeE3tHsmkTJSY1dhsHeOeXledrkuW7g5Ucv+GS9ZjiuWZ0u+bNZSfbxa8qm42E5S/qjWUZZfISQDTjP5qMdjUs0ov/7WyfgbVaw4A0Y9OXxR2h3v3Viv1h3XXcFT01ODJHhryhuDheoMme8vE9oE/3JDJ7RefKFJltUeBdAjiAkSqVFU5IW02gTlSZH4IXlig958uFrPnl+xXeX/ylz4JGc8XFx4N5sRe9Gcm1QES4PGwZvKUzOI1/zbbdkuHY8WP0AU0lsSAnvY3AYk5HnOe1hT7COKqsZ2o6u7Sjykg5BtJagBEVe4BC8vL5gUZQo4GS+ZLvvGMYBa3KsHdg0Ox6dniOA5+uriXIkODs6u0O1qqJg2+2x3mPqAh8/5HXfcJ6fYMNIJksCETU5Zskpr4cQqVTP45MBu7tmOx6xbUpCBDEmrZc7dKkbbD1SitTFLwzZvWU6e5NJwfLwlKUS6OM5XhyzedEyXO540Gvi1UDoLbow+N4xth0ffjDDGokePcXHryhPF9T3j3n/xRrfjwyF4afv1pMOISLaNeX3HyG+9z3ET57DoaPLBZ+VEu323D895b3Og5Lsvpvxs/XHiBj5nrzHr8u/kO65EBn3DSLLUD4SFUk3OA6JTqcUZ7PvMsvuIbKK8USw89fkWc754kcU1jMGzyeHf04sR8SuSyhZiIR+ZNy2RKPQRhGCxznH0Hmek3ja294R4poo4p1A72v2Kl9zp6SxUD3vrSI+H3l+ZWhcgSBS21PO3HeJp5FPh/8BWzZ3wbr4QMwFm9kFFBm2tbxvjqhFSRiTOxvOTzFIEuYlYTMmBzspiAYuht+nuf6MMFreETXj9QFdZsh31Off4PR1HN2EQE+6ocwQeptQyimT5ZZyypRTc/c6UqaN5MWOEEloi035Qj54mDKPpFQ8fL5ntrcgJCLXxFwmQ48JPQztMFn0p88ovAehk+uZNgmhHJO1sjwz2Ksdbtfh1gfM2QJzskRmJhX6REJvGV9eEydNlCpzhL51dUwoewyBMIz49Z7sg/scbz2LQwQhuL4n2SmHb3pePelBloQhbbpFjKiy4OhJQ9Z6lM0oHtcIMaKrks0/G4hOg855/IOC7KwkdI7tZ4q47vFK8LJ2xHag7QbaOEfNC8KuIz+fYxbJWMKt9xAiZRF4XO4RQHN0n5ccE0ZHf/kcNx/QzqfrJ0TwHmddQnmc42Q+8uAdA0rw8WcjW2eIwRP23WSYkMwkZJnh22TmEPuRzBhOdwO6HZFKcvnnHzBsdrjBopcz4ssbRG2gt+naU5KIJ+SacLXFXazJ3zlL2rp1QxwsLpdcFYLo+nQKroaEYBZp7kpIZwk3qRCKQ9JRxW5An63w13u8FByZltNjizOBjz/0hGyWrtmQzFNElqXXlaC0QSLw3UhR5/xg/Ay/7hLVUwjINFEKrO+wLzqkKvjWvf8CVdZsibxaVjT9yM36gD+dMy4ynHWU3qFzjRs8YwhkiwJjNO22Ja9TYLQUgrrKqa+ueGf3KZnNeDIMn2Oy363hX5pk3qzwP78geivZ6AuLtJi+/4Yu9834VR6/hKJIvGlj/DLupTvObHITyk8SzWE49NhuoHWB6nQOCMarPepR6jbGboRcsr/ZUxY5XT+ghSQvMtphxHeWui5omx5VGMTgKI1mlBHlfOJDIyirArtrefnJa2ZF5L7aQ3AUqxn9usH2A/OH5d2kJFTqioa7NsubYyEzc/exYoSXP3nK5YuLpM+QkqOzI24u11SLmgfv3+eT3/0kOfKUBXbqclcqGUK8+vQVH+0tx0EipeTD/+EPGAbL6mzGd/+cwxTAXUd2EjXf/fG3ju3POexvjxhjmoTFG9rdLwIwffHPffH5QkmyRcXqXs3h6XVCOMSM+emC5mqHVobdrkHsktNadTTjcLml1JK26RgHS7EoUxeQFNwrMhASNusNwzBwGDrmeYWIkVxqtNLMtKbIc4IPnFRzDnbAeYd1lpt2z3fOHqGEYiSAEEiluVxfMq/n7NoDuUwOYduugU5gjKHtDxzWHbO6RiLom4ZMGWKMbPuOQ99wGTbkJuO9h49ZbzcQBEfzBa0dUFFwNFuyKGteXb5ivduwquZkxvDi+oJZVXO8WLHb7xiuL1hVM67WN5zPV6AEMoLUSVhu9x3SKJx3yaXQecrzI9q+QnYK145IBCLTyc44RKL36GWN37e4TZPoOqcLVJ0jjSI/OSbcXDC+XkO+ILt/hJpXDJ9dENqR7OFxour0Fnvh02aHyY0xRIYXa2SdUzw6QbV9Kl6MRESZ3sNg6T56Sfmdh8z+1GOanzwjNqmYsRc7RpElfRegj+doUtimkJIIKK1x1iKRCa1RGqJM+gKl32zItUIYA6T8D63TBsgPjohEaYUSApcZpBxQVU5okiulagbkLE/XhEx3SehHYq7fXOdKIsK/Q1N10hlF5wk+phDfXMMdtUUgXWC82FG8f0ZWZog+oebu0Cc8NkRsYVJgptbIwSLGFpQkTJQ1IVIWEUbjxpRHpCLIRZXc4WJEzwoiiWYolPzKOSOGCDagtAaV6HMq08nRb9JEpWkjIuc19GPaZEnxxunQaLzziaI52XjHEHDWYrI8hQHf9pje8jqP1iUsLiR7ZLvvUjE05b7gI8JHYqZwu4QouN6mrnoI6GWFXzfEXY8zKuXhLOp0jLVCnCrGzQG/PhCtS2h0blC5QRAwyzJlfpUGfe9omvdj0vaQ5klVJQtzGyP21Q2yLtLnsw5ZZKiyIF8UyDpD6A61rBGdJTvVDC8bsO6ugFJ1hsy6hMD5gCirdD6dRxiFnlUpHLQbEEWGNCrRE28pfkWGPluiRAmHpOUydUF+IrEXm3RcDokWqAoDjUAIiZLTwZ/s/WOIKYtI+JSLpBJVdJxo3TFEhA8ERqLzqShRAlxAHc/xF9tJ3yahHfBGJW0vAlUXZI9Okqvl5Ra73hNGR+xsChkWgWgMalkifCQ7mWOvdoTa4McOVeYpVDcY8rMlw+t1OpfTmlWdLhKFdLAwA1nmqNwRd5Y42lSwSkHsB8KhJSBwRqO0TI3TMWnD9PkKrCcMlmAdsfcoLdEnM6QsKZY1wYJyESVTbEQ1K5FKMlvV9E1H344UKkeoRGtXMukQ8zxLqE8mUVEw3BqsyK+ix709dXweDbolr4uJyP7ztmLii9/E21f4it/6hj73zfgVG79cpOiLcMS/w7hp4XdepRcolGOVddiFo88y9o3G9WOaOAFiZHfznEwssK7F62NijAw2WV7vtw2jz8iKnG7boFUK7fMubXzDpFuJQoBMCfXOej7c7MnnJZtxgJ8ekCLy4Dce8jQImm3g/mnNd/oRKSHayA9N6r7sQ+CJc8lxSwV+36XOvPSe7mrH5ZPXQEKMfDcyTN23oR/RVY5UkuATVSNYiyBSDoG57Tguc3KZunpYyETEKMH+as8n/3LDu7/+EFVqfnC8xUWPVOC2OomKY8AceYSE0cNPrvkcne5Lp+ptrP7fklf6lc+OkcsmbTRAwPyUVV2zXJxi1QOCLbCblp8eOpiXyCwjWodShnG06NxgB4vzgWLKclDecbx/zsxI5lWO8I79bkdEcW0GYlUishKlLPuhpZCG+2pJ8J7D0DHzELzEBMHjxQkqMwQpGYcRrTRacGfHbUtNEy29txyGA1oqFBpEQGaKjbMMLm0MtVSQRZ7eXKCkYBSRwTuutxvcOFIYQze0U/EQqYuKpmsxWcbN+prVbEmUklU5Zzmb8/LqgoVM+S09guPVMUIpNtttcnqJiXKlsuTUqJRi7CNXO0UuDR0asygRIeLW+2RrqxSRgOtTcGtWZYyvN9h2wG0a1FFN8eiExuf44wcM13sOn90QFgv0vKL6wTvY9YHh9Yb1cYF+75T4aMby6QV+tGAd25lCBEl2XLI57DBnS9T3zjjd7PDdiLOStU4d+vYnz8k/uEf1nYfY33tKfdGkTev1C8K7j5B5Rm4j9xdHtB/f0I9rPs0LopQcyyWrISc4j1MKOVl3z/LjpKsBrD2wMS8JLsOYOUbPCQhClwT7hDChswlFCVWOdgHnPb7pUXWieoYYULkmOp/CI+tiuqb5SoD16zYn8a3/xZCOwUWj+dcXkuAhJ7DKO2IhMPtUbXkXEnXooJFGJVdOn6hjM47IokY4iQkJ/Y4SmuE1fmzx0bN/d8FYQKgER/aKDI3IFoQmUR/VyZLSrhD1CXImqLIelSkk8N4qT4wlk+h1yeU76a+EUcQ+5RZFSA2Zqcgatk1q0ohJazQr8duW4BxSa6JI9t4xBHAOmRfEkOhau1nGOCFNCxuTM5eS7JcZ8l6JjUnw7nVExch8b8G5NF0pmVzKjESWeWqenczZiPS4Do5lOyR0JNPIeYXINMWsJN4/JlhHaPpkE72oyIWlLmNCjlSGrCzRDZRVQMekK6sKg84NMQT2lUZ98CBRs6ZNuhCCfOYxQ0hoSC8YXw4gC2RpiPGQAjPjEcNTn7imNoALCJ2OQwxT5e3T+qURZJ+uwWi8HXG1BimwUnBYPUBGRR8y3L7Drg/UtUdVBQCDU/TVGW57oNtOCpLc0HnD5auEBLksRy80YUhzGyEmd0uZtL7iw4/h6AR5fIzUim7hsTE15ob1jmAkQok3xWumiTYQMoUIgbBvEa8TtdM2PdmiRlZFet5m0k5lnnHXYsqcMKQCse8CN1FjYqATJYRI2DboIks23jd7whSCGqxn/bxDmzmqXOKPHHG3TTrDWYl3HtoelEqFW54MMmSmcbdmJYNDGskiLRoQYDvmBBuQ1tEcniCjYoiBh1oyWIfQkhAlRua0heCZLxBC4oNFK5VeWwqa6djqPFl1e+s5fnSC7A6308rby+jnAlvvGpd35dHbRVL8Cu3RFzod0wT1uZ9+VSfzm4Lom/ErNH45RdEfBiF8Uc/yc8Zn2/QfwF9+ZPmvHjZgAhdNRWcNcso8UFWGyjTbwxOs9UTn6YY/xeLkUbIIti51axCMTU8xT+hCqTVRK4IA1w4omyY+OYW3dd5zc39BlJKMnKP+P8E5x00z4ycPPmAoDxTtBvHkFVILsoPlvy5qBPCxczx1HhS89IGXvgci72YjyxeX6MLw7T/3feanS7Yvbrj48AWzENk0LSFGjk9XvHp+gZLJwME6T32158FiRr87UNUFuYz4GLAqx+QSg6DZZHz4LxXf+Yvf4r/64FMy0aOMov1xQRglzvXM3x/RlWLdw0frFHP0BtX6uq7UL4oNfXm8aUCl3/9k3fHxdeJB/zmx4l5xj/7mQHf5ItngzkqeZRmHCKEdMVLifcCH2zydlK0zWkcYRhbS8eviU1QMzKuTxKs3GUrDVT1iZwOj90ilcHagEhkne0WZ1Six4GAbTJExUzk7O6DKFd3NDqklMUQ673EiUpmcy7zjwrQM48ghNhil6cchbW5CpMhynPB476jyChWgO1Z0tscoQ60KtNKIDKIQOO84WxzjpoXrar9Ba83Z8oh+HOjHnveOzpnN5hipMX1DfvaAmdTJHW13zSwroB/xfcq38M6jZgVRSdrBMYiS2EkQI9okDr7INLG3adPhA0orfDckW+VllRARH/HdSPvkkpcnC8xiBvkcTi39kwtMO2BOFik8sc75ULQMw575tx/w7S4SPn5Nf/B89L0lI+nvmgf3iN2IOez4kTXYpzf0RxX7ZUboEjLU//QF+YMjjh6ecfZ7N4kKI6Btn1H9qcfU3lNLyaBnPD1c8T+eN0gp+LXuA47Gd1AyEqxDCglCsjDvMK/eBx94ufuX7JqP8C7nnfP/lGV1PxkqbBuEdPghUb9utSWlUUkXA6lLP5k1SC/ABsJUjAiZEMU/bHwJdLktiKZcLJTkZ1vFhwcgCv6Lx/CX76eIgaHOsS8F9nKHPMsRZdp8u11HsA49eM55TFmeJi3N6FJQq4hcbH+fzu1AC15+/4fsb7aoM03xs99jdm9F7AxxGIlKIr3invoeYq7Jji2zxW8jFRyXGVEsiRE2Q8fvNemcRjF1vKuC2O4hI23cIWUbFVminIlECxKAXlS4i236XqTPLQJTPpIn6qQbjJnh6lQQj3OUFJTPOrKmIxJ5db8knBe4agqLjQbtAt8PAmmT+YowCW2TZUY8dIjjGV3T8fxRRRRQdZ7F0wNiVjK6gWg69KxIaFduEnJY5pjjxEhYmT334lWi+gFSlmAiw8Vl+pkPzMhQoU4aqcUDdr78/EUQIkz6UbdrGF8J3LaBIjm+qcnYov9EQ4zJ3MGl1xazlAPlrq+JsxlqXmPXe3TvOLmyCOXpVKBfpcbaIAzPDjNiOxDdiNs2qLogMmA3B+K+Ya9PeR1nxCEjGo8+kvj1nq2Zs2kD0WlUXWBmye47WofdHJIRgZQYJQnf+g4hhFQgediu1JSdl5DY7P4x7nKDOV0y+FR8yypPJinBIyKM+5YwBvJ5Segtbp/o56rMicOITVLIpB2bjEd2W0m7uIdoZdKwCVCnS0SI2KkQF0qiVzPEaNn3GfvPIipL6GD5XkH/yWvCoU/3uE00TjkrE70vNzB6snmVmi3rA9njE+6HVyg/EPOCoZ8xjqmov+x+DIMjZpJvj4KoFbF3xABxL2jKY9blf0JQKhUrUjKMI1IIqnlJZgyjTTlM3geywiAnR82vX32/uDaLL3z1+TU9fs3P4Xb5f6tQ+mZ8M36Fxy+hKPolUuem14u3d7AQaWGzDqxO7khFnRx8RoeuckQ7QEzIkHSpC973Hd45tJRomZxyhICu6RGZwbtAcI55niGFYHAeD0QpkHlG5z25Um+oHLMSlxu8ddQnC/onl4zrA3EcUSaj3zlMmRML/QU4mrtj886vv89D927KRxGwfHjC8sExw6Hj1ccvKRcV+fceJfvofYPSirP379NuG/YXW4wQdPuWURsQif6xbzuUktRVWlDamx1h5VC1/lzvSOcGqYavPNpvT63i7nx+jrycNkH/9qfx89/GiX4zva5teg6v15RHc8Lo6LoBfZSDAuE9WV0wdAM+eMK0gc+KgmHfEZwnywT5yZz5vRrfDXz26jkxBo4XJxxm8+TyM6ux1jGbz9AHTyEL5lmJ955ZVXHoGuZljdUC3/YYpdh1Ld3Qo7XBKM1+3HMz7mnrhBxIIZJJgoAQPDIKBm+xznJUL9JzlKIqCowx7LoDxhRoJZEqo20OzGcLRu8wxvB6c41SivOT+zy7eI6OiQKzbfbshnYKfN0wO+xYHZ1xsd8QgsMLnTq3h8S3F1KmTUdUSRcxaYzMokLmBt8OxF3a4IsiQ/qQNjhpd590INPvSJIuZHy1JnQD2ckCYRTFoxPi6OieXKAWFXJeUnzrnP6z13QfvQJKym/fh/WBaLuEVvqAfbVBH03OUpcHzKNTdpc3qO+cIWcFfn0ghEj/estYWvLHpwyfXSG8J2xb2k9fU3/rAQLIHp4g+kPSEEzX561FNz6hDlGnJkcIk3ugSi6MMoREs5qyc2IErEcAPiYarZqV+EM/BYbKFJ56G1A50YqCC8ToQICLlujjWxq9icDytSLoNIL16T0ZlbJ1JrrM1PxFFyZREAeJWNWpc+4883dOAWiGpANxMTVJsBbG1B+WWqd7zSgkCnFUM1zvsIdkoyylwNw/orvYpnwfJYjtCDUpjHVZvbn33xrj1Q7yiS42/ReVJAwWkafzIMscPS/x7UCIMQX8xphMFUzKmptg0vT7IRDciJIKbZKeMjo/FaMTOjH9xUgkuInG5JIeDh8R8wKReWg7RGHS810gbjtklSEDuK5HhDy5hhkJxuA2LaI0+F2D7wZ8O6CVRJ8uEJDCfp3DzkesSJ06oRL1U9gJ7crzlIkFOOtQo8XTQJkDArc9EJqOMDraV5bKyaTq8IEYA8Ja4pjWOakVclETugFVZmmqjBHXtIlG9u5DhJ0cH/cdYoL7Y4ipIA4RHz1CK+Jg0asZtulRKhV70vb47QFdl+j5HP/RAXe1TblERYY5WyKKPJ27dkiGE1mGGB2myNDzCkSH7wakEqhljTt0U8B5otGhJaIqCN2A3xwIvWX49BU+RkRvk8Z3VqKiwrcdIk/5R3aKuUgFf5vooblGZwo/WJzzyEOXgnGtIxYZwY+oMkPNq7trNLu3gtNlcg3sR4SWqFyjisk4Z9cSmh49r4iZTjrLKmUL0adgZ3yAAPZqh66LRC3tB9RxifYS3zrGyx1eZ4gs5WnJeZE0lqMjklwyQ0yhryJGFILQW6rJyY4QcTEw9j3Rp2afLgwqCnbXO3jDvH/rVvxC4fOF+/PzlLr4pee/TbG7m4u+fqp68zKf/9PfjG/Gf9Tjj8d97ms5JF//fIHg5QH+xQsBUbPIIydLRxg72l7TB0lohuSAYx3RRZSU7C439NZR1gVt26GNRo6JN66rHKtE6sqNgkMzICe7XlR6TqYVfTsQnSPkGZcnNUzZCV5k7K52FIsjXoSBmEHYtPzsdcssB/HeMe+t0mKYuYaqvwEip3nLg+VnAPhW4Q9JxDwUEr0SfPs3Si7bC7bOwbcEeUy0rY3Y0r9uiT7QjRZnLTpL4vqz+hXzs/S10oq8KijVAVyPkBrnI787WkabNg7mRURmgta+RZ0Tb/jHnz8dU4v3rY3eF5/xJarQ9HC+PMPMjoHIvcM1y25HjPBqfsYuq4mjp5nNEWZGN1peXG7I6oJQahrrCAh0mWG9R5WGYWfJZAq8m69KjtwLcu9YSsPswYpws2F/s+eyV2Smos5mCCT75sByKLkfK/wh8GB2xoko0EKxtyNGZZzmcy6aNUMt2bmO1iab9b1qqfOKEAdGPJvQcrk+cG95zGHoiUIwuJFcp41LlRdYaxltcvbadA0xRhbljCorqfISF1yiOlULvLfsmj3GZJwvjjFtpNo6/uzifWIIZCqFUg52ZJaVtMazNzk+Bk7KGX9w8Rmny+PUrY/TBotUwKvMII0idAMiN9PamPj7rhsIzZBoOFPhIELaALhdn77ODeaoxh16/GixV4nulp0uUj6OEJQPT+hfrQFY3WSUqsC/3jK8vkLeP8acL8jmNe2L6+RSFiLuao8VMnHv54bZ2ZL5j18l7cOiZmxGYjui1cDVvSP44Tn5Zy3n/QK/g2ysGMseYTT3z95lvk8b1KOhShSlCESRmhgh0oxX9OGAEIJM1hzJEuY1Wha4kFAaFUkohRIJXRhiooQ1/URJ8pi6TiGoQJSgM43WKhkZ+IiWgscyIQgml6xqi9SSnVP85Ea8YZ/e0lSmvx1DmHKEErUqxmmzEiNP1pF/rkAqxZFuKbLXuLCh3e8Qx+nOm80eIDtL5zte7l8g/QsKpZktZ0Qr8NYSdCRGxdhbFhctZteilSS/f5Q21j4kZElIBj/ycfWKqDQnxys+8B5pNErmHJXvEwaH31moJVEIzLCHrAPvCb1FLEyi1I0OOS8Zb/aTH1+aS6JR+H4kTiibFIIoBME6bN+jTLqXolaokKhB0aUsnv15TaMgek/Ikp28DHC0GdGzHNkEbqSH4wytJIurLhmyaIU+XTA8uybLFEebgSgFhZAIH4ijR1ifwo4XSVtmY8S9WqdCNwaMkhyiR2Ul5nie6GBa44MDk86RyBK6M3ZjQv82jnz9kqgko+8JdY6QAvtgThMkYzNQXR7QMhWK2b2IPsmJUrKzCpdpQjsk7VWucSaDShG6EdWNVE5jcoO0HtxIjIHybM7SXqcmQzVnfbm50zL5EHCbhi6TbOoTJJr96x67TuY8dRGoFxZZCJAjsQqIGvZ9RteGZCG+OSCNJj9boooMv2/xh47q4NBIUJKmSEi4XlTY0eJ3LdFahI9oo+C2eJliASCZmYhSJjfRmAxeKAwaAUqCd0nD5n1yUCTd93bfITON6EbUrAQh2PSO69a9tSpponWsXGDBgKpLbrxhryPReh7UJdUsIe4yN4k+EZJDZ+hHhARR5+gqx11tkJnGbw7oecmDomTsPSFYrrcS4QWqyom5RoTUWBhvDrjOkjPygb5gjB43BNQocBOtOgjL0DjC8pQLP8dohdEZvP0x/tCRVvHPr8lv0ezuHn27NPqal/l5f+Kb8c34FRi/HKMF4Jdx19x2Om5f8dNN+i8G+M/fG/nP3ouEwfLykDHuTdI/zEvqkwXt1Y7gkoA4zzOKIqFAth1ZLGt2bUeWmbQhGVI3xyxKZDtSr2bsbnYEpfAToiGkpB1GnhaKmOWJ0hAjalYQhOC3N4KszOFYEGpHVeaImwN/5egh5WrGvHvN/U1LtI682lLMXwORsc0ZtimXZSM12zIJV18fDnx003/pmPzZ7/0F7hXnjE2Pm6gLWaH54f0Ny9keIVJX1XbrZCs7JWpb4L8fBvaTAy9PvmAZ/DaaJb7sN3MbBHfbRfriWX7bW+OOJiegOHnE7N1fgwg//Ohf8e7FNWZe8j8+/B6fzO/jrvc8u9ojZwI1z2jlgt5a7JDOS52VRB/p7YjINEpK+j4lp7vDgQ/aDzmSnsXZA+JVz3C142K9oXzn19j2LZsYOLZJF1TIjMf9nGbskXZkI5IuaFXNUVmOa1vWYuDDcYOUkkPsqfMSUUie9VfURUkQEWsFlS6QQiKFJGrJ2eKUm5sbhDZkMiGEMcLF9hotFSdHJ8nxjUg/9EitKE2R8l0QFCZju98yL2q+E0/Qg8R3AR8FimQGsKrP2Gy2aK8RRYWXklfbax4f32dWVqnh3o3JOck5qDJ8jGiftAepC++QwUx2xiT0BIF7tU1vWEnMqkLVOX7XEbuRIQSye0v0vMRe71NuSD8SyyxtipQkv7fEvlxz/BmYVU0o54yZo39yiQye7FuPCYWm+/giHRsXYHSEdY+fldTzmm8rjbveMT59hZpV0Ea2xvEkdJh3TnhUnHP+0QOEFOxeXTC8m2gx79z7DvVaEfY2WU4TEBOK50kbp7V9ybZ/ikTwzslfpC4foFdzxn5MjmxtTxxtcjvzPmWWhEjctZPRQEzhoVNmU/CB7HRONi9pr3bIKZcm15If3iuSzqzf8f17HdJ5PnMFP7ksJiSLqQhJFCqUTPoFkRoP4lYvMlHSPjxIfrZPSMqfuXfB4/wCrwY0GRkpZPTB4z8N1tIXPT+9/mfsh9eUQZPtMmIUmMKgKo3aCVCK+1cDbm9RRYZ6J0tzHBE3pGJ9KCMfzZ/gjOTdk4e8t44QIpmqOJ/9kGF9Q4XhvSb1S/b9S15kl3eGHcjkzCmlROSpQLrtZkspUKs6UbcAZRRRS4RPn9E7S746Bq0SJdX5aY6JBCO5KBRB5XgfkEYhQ0Raz/nGUqwdw2D58HsLbGUwvae+6sAH8ndO8Ls2UTg7y/3nPjUKvEMUOSIGhFCEZsALgXAeXRjINEF4QBCEYE9F0xeoV+n8BOfSe7UOoSJRJnRGZBWhtzwYDfP1johnXEqGTCO0YqcVqsoZLweqNsdIjawzinc2iPwGZjUXP+4YDkNyW9MS4XpUblDIlEmE5ORZR3E2xx32BCmRCORhx6NHFiEsBwnbmOO7kTA4ICKVZHfZs78SCA34MdH27h8z81ec+S41s7xPxasQeH3EWFUILcGlQGB7ucWczJH3j8li5PQP1uhNTxgtw32DDZHxcpsCgZVELqp0nfc2UQG1mizOSaidEsT9AVHkqOUsFXW9JbYjruspzo8QRHQEu2+JgyVM8QIxBERu0nu6t+L1wfK7F81bq1Uav/Gg5vQorbnPtgee7NP1NReS+TxDzSeq42S9H0NA1EWiJXeT9ixGwj5lS6lccdpdEbxjsJGNPGfcd5SPTrA3+0RPDskpMc81IXR8YH+WPpeUQGRoBtxkmiFzyaWEpj4nAKt6Ca9e3L1/cbvw3i3C8c3CK94kBP5hvWfxuf+/XSz9nPHlfug345vxH/X45dHn/n3+iiBRV6YMjNvdul7NkjXrwlCeLlDbjKPFgta6yUlHYuqSQ9Nhco33ngxBURfsdg0x0wQlabrhjlNuR4dAMIQAIlLmhn60+CjIRdKbjMNIVmQpV8cFgpY0g2UmBL4dics3qdlCKyBtoGwz4AfJuAsMh56RmljPJupMfOvAvKlEhEjIVrlMTklCgBARU2Z3eQUxxlQM8eXsgs+D6G/XQm9OQpychr5yUo1fXGI+//tfPpUJmfLW0V/vuP7wBUWeEd79DcQy5Zq4q12i4gDBB6wP6DojKEnbD8iYNoquGUAK6lmJ84FmfU2mFMX5HKEk/cWGl5cXfLJbszj5DlEIRufQUmGdAxmxwbHMK14e1szLmuNyTpWXjH3Ltt0hTdrkLes5UkqiVox2RBuTbLS9Y7CWs+URzTik3BrAubTZOJ2vuNzfIKWkd5bKFBR5jvfpGkQIrB8RXtD1HZ0dWM4WBAGLakbf9wx2QAmD0YY6KxmcZWYKmq5BSIkfHJkxzMqKShm0SRQhMSE+3iXbau8COcDoGUeL8slVURYZdMn0Q0kJnUVMGxTvA37TIusctSxTflZhcPsOlRvyd0/hxZo4WKR0DC/XZKsaczQjf/eM4eWa5mpHfr6i+PZ97MWG5sUNzb8JiHeOKd47ZXh6nexsYyDue/qfPif/9oOUv7WoyM5WNH/wGepoDt5CjAzPrjAPH6AuyiR6P/SM6z35yTI5aT04ov/oJUEmrVmcglqls0nrM4XYBkgaIJcco6QLxH5Ejy5tyMMU4KkVUcjkFuZDcp3SOlkH60TBzWblJHaPhEyjwqRF0KlTni1qfL/DZzJtUW41AdNcEHxynRQiObExaa7g9vs3N+wtaoRI94gqzN2GMsYUtBrLDENgMavJ6mNEM+Kdx1qH8544pG68jBGV5XCciuMQUhC12zSJPmc0yqTPikpde2kUfrSIzOPdiL3YIqQgOE+Mk0PjrEgaNSHvHAGFSAHSYmoshSlEV+aG+HJ9F5Sr6wK3bfHOJsRS6YQeKQk+3lEjVZ6lgNaQmADEVKyhRCpe9kOi1cVIHCyMHjnRElWZ46/2d80As5zhti3ReWRVToc/bSalVtAMqXivEw1QFYY4WMZDjxKRWGTpfokg+6SRYeiJUoD1UGcoLbD7nsz7yQWuIrRDOl7LGnexJjuao3tH7Bzj5oB+eU32cJYCduc5wabjLIYRKUWiJ/oJRdEGESPD5Tbl8kzXnlAp9BcgdgMh5kjn8PuO7PG9RPvbtrjpfakiSyHBWiVHwTJDFZrQR3w/4l2ge90zqBOqb93HW0///JrMB4ZnV2QPjlHzEnP/iGxmGW/2qJkkmCkAWYiEYA8u3VNKQp4hYiQE8N6n7DQpoSyg6ROtXUrErEAvCtSgU5FqEhLsd226lhZJ6yPLHGUUbn1ATU56bzhhfG7lE+K2DPjCanVLvw0BPzhUmSUN1Whx3UhwA/hI6AbcukFV6b7V85J4pPBDQD4XKQxWpuxEd+hSAzMz6DKbGh8CnZs0V4dIvqzpdy0AvrcIGzj51jGmzFHXn94tpV9X6Ai4y3b73Nr7pdX464oecXeIPict/uIh+moqyTfjm/Ef7fiTD299a3zxBj4uNffqtAE8yfvk/OID89whfOrOhWzE9Q352YJvt1e86hpuLjes+yXLckUMII8rvJCMziI8WNdAppAI9PEM343oEHEh4gWUhWE3JPqCb/vE+wfGENBaEYeI9xGy5PSUzYvUsVaK17Xh8NEzVkvB1fxd+l3L8QAnz0cu/+AptAa7FgRR0+4ic71ELyuWDHx7CQjBLld0WXItuux37K8Sn/2WZy8k3BxaMnU7qSfBqQiRP/sgUuU/p/vzVkGjsoLq/NsgJCZEjht7J1y9nWALvecofwEx8rqJ/OQq/f4yP+Le7ByEoDGSfZYW5JVcoH7nCf22ZXQZ6+wdZJ4jX48sNq/Yvbghn+UMWmCdJyqRMmBioia1h47lyQLvI67piMGRv/gJcxl5RwuqSlOer+g/esXWLPgoXmPnZ1y2W6qiZi4UVSPIZEHpI5eywYuWvWiZhYrr/RZCoMhy8qxglmvqwvLk5jWL2WLKW5FY22N0xqHZoZSmHXuMyahkyabZ0bQNhckZ3UhdVLR9h/WWWVkxuBHlUpBvWZRIJIfuQJkVHM+WtGOPc5bOe8Z+oJkd42RASMtu3FPkOWiFtuCdY1kvaH2BcJ5uTOLpeZUoln7SVsiYNthSCKL3KJs0MfI20HVRohpBaAcCcQr/I20gc43dtGRnc5R1sOvBqJRiv2spHp8wvlpj14dkOXy5w29bivfOKN49w+9a+hfX2Os95fv3qO8tkNlA/+kFuip4oAvsy2vwgavTKevr9QUPrCM7W6Lqguq773B4coWuNCdXAyJCvPgxuzMYbi65kTteDgdmx6cEDjDz7LoPqfN71OYobSBCAK2JQjAr7qOZI0LAjluufIPZLJip+8jGorQmGo0S4KNglb1PHQZc19OGl3gVUcsqdY+tJ1/Vd5QuZXTaOMZUcIgpXHQYPS86KO6v2AVFJM1XyV96sqRWqSi6u8d8IAp4byV4f8VkviAme2PFLJeoloTUSYFrB/zg2JinIGHcrRGVIKfE+hT6zNUWOS8xdYHKDbLKiINDA8P6gNRJpxEOlpOj7yODYNRwvn5JqA3LbeCqrbAvr6nfKSi6Dt/09Gbkk/xVQvR9izHJ4l5ohRAy6eykQOTmzuqbyeLbT2gbAmatZz62+HXDpWgZjU45WzI1Ee4swW/d7Wyi3EUpEi2OpOFaLzQIhy8LolHgHE5Jru6V6FmBOcnoryKx0Ahl0Mc5TliiMJjjAqcd+eBZHlwqakh6JukC8eqAlWAeHaOsJ4SQmhG7NhU4RierZz2FcUoBhxFXKvYuYItEybQxECZ9jxKSWOQML2+4vu6pHt3D1yXNWCHWBm4O9I0lCIWuC4KA2PYorZlvHVFKTJ5c07A+IRqAyAxORl5dj4jC0LXhjRNfCIwvrlKBmRnMrEjnfrDELIWHtqrkYuMQg0uZQnXNeLPDlhoVFXZ9QC9r6ocndM+uUNZiX90g9BlNrRmKnHiacyRu8YrIroBh3xD2HeQZejKDEUZD0ydkt8hTo0BJYpVyuaJNTQt36FNDoOnQ5ysEyQwm9pZqrqjliF6AkAFrIv76Kd9bLTh6L1HTW5vR2rS9OSr0nVPbg3lGZdL1VSuBa/vkADm6ROU8dJOBSI5Z1OhZmWibfcYmgGgH9CZDFBn2qkFIg1rNKdVAnFBXeks2yzhejKjyDaXCNgM+2JSHJDX6YUH0Hh8k837NQ/+vUYPC+5Z/MSaKx1Pv31q2452TYfxSMfTvWLW8xfj42pf4Ymf1m/HN+I94/MkURb/gPXxSGX54r4IQOKZLGx+tqG1DoVOqt6xzBtdQzQz9USDbvOBRZrmxc0Cz2zf8dt9SvXNGtJ7DMDJb1GgPQ9dhiWkRDKnI8cGz7XqEltRFTucd9CO5UIwShA+p66mSI5UwGuECtrOEKuPHTYPIJa/I+N0bQYwFZ8887x0sMi5T+vuclLWzaZE3C65/75piVrJSiUazXeaEszmrb93n4qf/jP7mKUCyBQ7hbmJEilQoqYQgGSn43jKJOe8OcEw879uv37SYItIULN77dVCKevR8+3VDGD3KyJSxFCOr4iXfXj0DAf/6Nfz0Oi18R9UJ3z/7NQiRF5mAVcG4PuB+61POek++nHHzKqKL98nmFeJZT+Uaai35MAbm75/RdgODdXSHLlmuGkV1umC3a5MeQQpmVcH7m1cU3Z7ZrGB2/x5+29JuWj6r5myq09Sp9p6l1lRS805TsZotaPPIT+QVm2bPo+URshdsugP3ZysAqiznoCPdOFBmBUppnOvZT5ogrTPKvCTXhrqoAejGHiUlowtIY9i2B5bzBZk2eJfQh1U1Z/CWfhhSfo4QaG1SMSJSl3TXtRTGUNQ1PwvXHJVzqqxgqAU3w55nzRXfH47JhKLMc4ZDpHMDP331Gd9++B4q1/jREXXaSPrJFOQWOfSvXiPvncC8mrJcQBUZ1vqUwyNSCK4oM6JMxZPdtqhcE0h0F3e1RxYGC+SPz9CrOnX3Nw2xt3Q/fUH26Bg1K6m++4jx6SXtT56jPjij/LUHxNcb4ieXHL0YyDPDYXfgo+8s8EqQr1tWH7/CLGtEkaFXNRXAkyvuWYdoR5Adr3wPpeDCD1zUOTeuIdYaGV7TlK8RvaTOTojOTmFhkphnzPMHzEnzxfPdv2R3eIGQFdWjY8xY4a1LG3DvMWXOnHcRMeJDyzO/JooBXKISBZU0RMOhTxt8H1BZsu71+56xb8mlxGnJOr+P7jJuWsctQoxI96lUqXnxBn1NugkR4b0l/JcfCGJIj4QhIHPF87Xn0mpiNHeaJJVrri5+hioyBrnBbwb0okKvKigzqlWVijEgWo8/9EQXkGWGmsJJx0OHNDmLxfcoybB0NK8/gy4wu7S83Eb6C8nZccb5tkFE2MaG350/AeAoK3h/Ddn9I8TzIRWIegp8vc0WmtBnWeXEQ5+MEWLkWBiOPtvh24F13aIeHqepSUtin8KahYBxMg+4DYO9YwwpBYXmlbSIskDUOaG3xAheS14fZ+SP02sOp8nBLmYaISLxfpnCWY8NsaiYb0eWbbKMjplGGp2KssETR58cypRElRn+OhkHCCUJo0OVKc9KCJLjmBtRJqc/M3TtQPQO0VmiVrjLHdaFVOSVhsO9itY3oCV+rAlDgfQBlUmMUshco2QBdYF2kdVhRAwB6SJM2U56NU/zC4KeyKU8JXiFOsoQuzY5Ph4tkMsUmCx1Wu61VoSmw93siUqxt4Z9J4nrSHhxgAhmtUDUGpNnCQWcMqfK+ytCN+LXB4YPX3BzPEcdzVGZ4cGVx/SBKKF9kOHKPCGCTY/KDOP1Dh18uh6GZKEufEi5UNajtELWOSI3yX1vsAR8ogjnGQHwIVAtc+4bi6r6dOyzAKcV9vKa78SIWVZcxmNeryN+GBEHiwvpvTwsFfdIVvth22O1SnrjWZHsvp/fpOItgpoV5GcL1KTNvLrMiGSI6ylPTCxRVX53yQstkUFhzleozQ0PzwxS+mSfn2tCGQguJvQrRCA5SIYYeXjikPL3sfuW33Fz/r+D/CJvhNtF/A4M+xwa9u9etYgvfvMNKvTN+BUe/0Fpir5ueBdQ8wxEclALU5CanBVEIK8KQjsg8jpZMKvALM842EDbdFSPVwgtWR7NiUS6Q089L9jHJHj2ArwkpdIriSg03gWcIH0vJC4EpNHEZkyW3kaiXSTkGj/lgsjCIPpEv9F1ylvwzpOXINotw2gRVYawHutSsvVhfUAbjQoRqmSvrIxie7GhXFafOw5CCZRSnz84k/4hxvS4lAkpiCFReOLb6fLwBiuf2Hq2HQguEq8PXH58jckNoRnuuszo1zQP11TnSxBv65IirhnYfnbBVXAcHq3SwjZY6sWc4mRB+/qGrhuxbZeS1mcl/WDxdUm73qMmOkVe5JR5xtCPhAjGaKpZxX57wFpHriSzuqB+dEq+mtG/uOYnr5+gv/sOPgTKIifThnbsOSmO0VqTKcNNu0XMBVVZIpAcho5oNNuxRXjFKito+5aqNAwIur5FC0mV5TRjj7OWMXqMzLja3SCl4qReUJosObSF1Pnu+x4lBHVZU+YFfdeynC9Z5BXb9kCmdLJ77zvavmO5WCG1pspytNJcbq4pleHF+pJ3Tu+TZ5LRCVZyRtd3FFIzeMfL3Q0/ePQtysUMF5JbnLztHk6BiW4KIub8DJmZFO44K9L5lgJ9Midajz5f4rt+cm2LyHmRsl2EQJUm6ZNuDsTBMV7t8aMnO52Tv3eGmxX4l2vcYOk/eo0sDOZkjnlwjDx0HD67ZHxckj08QhqD/+gnWOfRR3XSi8RkaoIPdJ++pvreoxTqezRDCsHho1dpg+wC9npP9vAYJV2irj67wj9KG5Hs3or4aZzoXBIICFKxx9Q8CCEQYsSFgO4G5Kwk7vwUNJqaDNH5lPN06JFCoIsMVHIfk1WOjDBc7RGZRgJyElMH75KQvGsZs4IsJLqMvKXGkbRUMpcTWgSQkN5ErQuTVXME1PR8nyhH1kExubFNKIs0GjtYlJQ451EhkJ8tGS+2SV8mBSYzQKS72qOEQKpESZM60QyFkphFSb9rUZlBIaDOwVpCmUPwKUPtap8shK1PXXs5ueqpRMeMbWoEFUKgFhVCpyKTqUET/YRiyOTg59aTY2AUyMJMdtGWGDw6L1KhM7pJz5nms2xREKdrEq0mB8uQ6Iq3x01KMAoOfeqg+4AoDGJW0n/4AoRIuUpKErpJYCmn70NMOVMCGCzCBVw3YlazOzpxbEdkZfBdCieVQqSNvE5ZPSn4SCEFhAlBugsYlgJZmkTLm+bcOLiki8k1sTTpGJU5WZGoYMH7CQ0ckUJO4bETCmod6BxRFcSmw15uEiIkBOK9U/Qqx24apNbI4zmx6REq0SSJETs4xJAoa2pZIYuc2PWp0Mw0erVI1ODO0vcjRYiJ0tYl4wEgmRtUOZQ5se1xhx7XDkgf6K4DYrFIobXOo8oMhCCbIgCq8xX2cpuuwzJZtjNY3GBBp7UlND1ydJjTZaKwbQ5Jy7OswaZrk5Co7jifGn4CZJGRPTymf35Nf7UnVDNAE124C5N2h55hk6z8RUy0VKkTQjlumkSdKw0hmTTi9z1dM6BXVVoPVzP8rk1arSnDKDQ9csoXClM+opqX5KtzhNzgXt2gjmeEEBNlMUyUWQnCKFSmUDLRT103OcTeag1v6bcTnfaWkp+e8vOIdb/g+Dq63FeNbwqlb8avyPglIkW/YIvh3+Lmqo3lvGoYux2lF0QvCf3I3he0roaDYmE65quacX0geEtxb0H/4gajbyi3Vzx+ICjuL2nDgbLIedoovHUc9i0ueDIh0ErRjRYBaOe4t4gIFfE+8HIHGIMQiWeP1snxa7JG1ZlOXUSXglWNgKgkQ5t0EDHT7PMMcVQw9AovIlmRg1EMMqaOc0guYDIXjLuOul7wflCE331GPD8m++CMMIysbjpmsxJi5GqWYaXADymxO44OETz/RlTU3Hb3BfPeo4VgdbFnvD7gibzOFcNgqdUC9d9/SCYFsRlxxtAdOnymudhtCVKyijvYtBzvK8JswXdVspedH1qunz5FAystyV7vGQeLywzPjWBcbxCnc7yAfkjCXZMZkDn5+ZLtdk+7PSTevpa0Y3L4kzIVdjevb1KxqARFnlHfm1MezQi9ZXtxxeAdu3bHyeIodUGVorMDn1694DvzH9KPA9u+4UY1FHnOxbBDlnO6oSVIxamv0EoTxogUkkPfYqMn0xnHq2OyoaNtGk5nS6IQZDpjGHt6O3C137CoZlhn0Uom+/csS3oP71lUM3btnnYYqLOcgxso84LV8ojoHDmSqDP2bYOUkkIbxkmPZK4HlNS8V55TYKh0TjceGPCcH51SFgUegQK8tWkDrtImMWiFGh0igs5zfD8kXvu0mMYI+mhGaPq0BRdpkyZLk+hDhUFEcNcNalmiT+eMV1tUiFwox9jtKeaSB/dXZLOS8OKaMGnwuo9TcZQ9OqH67kPszQG/PbB4dEb93QfYn73CDw5ZzwjdwKAlFw9nRDdSbzc8XCxTx3ZZUTw8on1yiSHRXMbXG/QPzxE+uZ31Hz2Hs/vIeUnrL7nYjilY0yf9ShQZS39CZlYJuZu/T2GOkDHSjVe0u5fISYsUQiDIkptlQRtbskxTtA5TGFw/pq66ADE6smWF74bJGCGF5kqjkaKehPapiAk+cFTAf/k4UeCuesFvv0g/V1JAKskSXVgJIkkvEn3SIaFV0mFMyAKToDxan6zUrZ+ofAmFTBvMiC4zIpFx0xAODT5IlFH4TFHUBdEFvPcM13v0sqbbrXm9/n1MVxAMKcxaCw4fvya0A3pecnh9kXRIfUMjO+5vA8JB6WrOynNm5Sn64jVLGwkSRtPgnh6YPW/YV4qm1mkj7dJ1QmnYeDjcrxjbA63W5Fqnoj4mVzpCQj11ZvC7bqL0CgipKEFMBiMxIgqTRPzTflBHeChy5Ec3NC8ars+rdLhvj5UQxFKngh8YcsHLdxeIzlIcRhaNB6WILrlMMljEokBJiTUjh1pwyAVBClZOULXTNtSlIjyKhP4FnwxNwkT9Q8LNSc6YSaQUHN+MyMEhBYgxMF4dkg5qUU4W8oB3SegvJZsSQqWRY6KWem2RhQaZ46REz2vOj35AXEZ2Fy/Z7T6GCO76MNHSI+08Y7fQCCGodjsWVoCMRGtR85rxk9eIIkt5ZzEw3jRIJMKFFLI7sQ6iapLLXGEQuUqFZZGxm43s2w3CaZoRxPEcM83ZkLROvh+hzAn7PjX5yixZe19tp8gGQehHws0+PbZIkQvj00vyx2eI0wWdVVyIOd3TDcXRLKFIe8+i0sweHLP7+OWETnr660MqGn1Akgoh75OOzQGqKpO+zkdyUqC2nBxqg5aIzuIudjh2RClS8TgrEGKizQpB7MakR4Xkytf2yLM5L73BXWpmqznH1UgYLENQXO/0G+3e1LAotaN2LUIIZuuGv6KOUErxxDs+8+5u4xR/bt3zy+G4xVtt8jeF0DfjV3D88dHnvu4G+zm1VBY6jvH4akA4CEPqhLX6Hpf7RGEQ1UhdxGSHee2QpmT18Jjuao0re/IoiOaEkNUEMfDh68hoYxJPC8F8NeewawjAIkuiyBOzRytorePGVox4zLIi3CRzBj0r7mxYgxD4XYcMkZAphhAo6jx9JK3QhWEXAl1lcLXGh4ASEjuM1OcLumFMGTZGYQeHPKk5DnAqNdZ5rspTroNAG8E7q8jpYpYm36OMm13L7tUFrhsoipx+HPk3V6fYFylDpTye0b685PR0yeIa8jijcZ7npaI6r3DbnsXVnsW8ROQ5dnSJhlIarqqcajVnuz6wbWdgZxgq3hN7nO3xY8Ou6fFSoKLgzKfff7kqeFJI7BhwqYlKLAp8jPiQqBVHAozWDM4hRpfEqT5lyNh+YLaao4xNYlwvmb9/jzL32EPH62cvuHr5krqscFKhTUY7dmghuVev0DkQBOv2gFQiFUxGY7TmamxBRToTiT1Iqe4uvaN6wbrdY4eBzXZ9d02GGPAuMPiUpt4Fz7Kec7VdUypDnlXECEf1kkPfpMJpHJBCMCtrtJRcrDcU2iCkwgPbbk8lDJlU2Jj0TUop3snnHF1C07QUC8/ejeRZxnp/g8k1mZBJ8yQFBDBVTgwxFeWHHjO5dwG4bkSXeaLZ7bqEAN1SPXJz93vD6y2xyDDHM2IXEVqhYsRvO8gU+aLGtUPa4M41DA3zzYHV6RHl++fJrnffYzJN2LaMn7zGLwr0X3yEkNB99Io4QvGtc7rPXiWb4NzglOf6VBFjRt+1nG002ckcgPxsiW1H/OUW5UPalLUD6rzGXe8Im5aRLdnZkk4e6LsbvAQ5FVFSF5S6JFfHCCmZyXvMOAEBL/Y/42Be4fZJmC2kJIwZP9MV3YlAWc/31yNxkEknaB0i12RHMwZrE8VpKlqkmfJgjCZKkRArB7rIWBjPewuP1JGfbhS//ZxkMhBBiPi5/Uva9N9uemKi4VRZQo1C0tWE0SW0RkoInqzM8c7h21tEYcomGlxyg1NqcrRLyKtvR3zoU/EWwbcD2YM5m08/IV8dJ1RNQ7ms6K52hBjI5iWDa+mGj3HNDpFpzvycuLHM9BHnq++QMaPoJfenzVp7duDik9+nvh4IMaNdZMlxL0IgUYf2vcOf5vSHHkLSEMUp3PTOoGZCMG+1REoKgk/dcpVleDsQ5WQUMLiUjyMk0nruWYX98XOK4FmflQSdDDSQMtks2+m4ChgKzWWMiCJjJWF5aHFtf6fRE5kmWI/I0nrTHVdcH2UEGSkuLVWMYBRu1yUr/H6ckIDJeII3lOf10tCVGpFrZtuR0ia0ABdSsec8bt28QQgzhSgzPIKN9EmvpVLIeBgg6tsQXFgdzZldLVJx5nq2Y0IXgxRoqQgx0hWKy/MKKeAsUxytXXJbU/rOECGMjrBr0zE3ihj8G2rjlPEVXTIMiU2P7RKtLoTIVgnINQhLjAbWh2TlnZl0XEIgu3dE8J7WB2QQ+GaPNG2y1R4scfDTPekmVDmhWEJLxudXUOU0LuNgLX7IEAeLXmS4ZkS8Y5gdK8yypnl6gW3KSe8Godlj9/t0bc2XyLpGMRXhkwsiE82YCZVRVU5wAUnENy3stsTZDCuOqB6f4NYHgrPQW4RzyGVNnFdw6Gg/vWJY1mCOaa4iqyIgiwx3gItLgaxz0HIyvFAss455ZejXB04GwwOlyXJDGJiKore3TD+v+PkFXeXSU7/8AzH5/8a3f/pNdfTN+NUZf+Si6A157he8cb6WbfflFogymjD0iJioaVJKVJljbzqiLxOk7ve4wZIdzxEHg+89Zl5QS4nMDgxXewqjaIjIEDFGUZd5WiBHz2HfMsY0GW63B/LaUMxLorNIC2OuCFoxjJbgHPmsII6TS02IdIcuLYAqUTdyD2M7YOYFs4fHjE1PlNAfkk5J6jxlp+SatkldP3ygPF+xrJMuRzzfcVg3FLOS3fWeg4wsjheoerIOFQJ/GNg9v0EahY7JCU9lhn7XMvQpLVtrxbhv2Y+eB5MWShpJlmv8JHpGSXoiKobk6GM0B++xQqIzjfOeQGS42GL3HUop1KzksE2ZNvWiplkfkt1wjEm8K8ALsN6D0RitmM0rdus9o/e0uwadpY15WeT4EPERqkVF13QcrneYMiMXkeW3z1H9M9x6g3Oepx9/yq458PDkIQcE3jsG5yhMgfWOZbVENpIYA9Za8pnGeGjGjqbvWBU1je2Z52fJBUhrtPJc7W849B2r2ZxMKIZxRAvBLC9BafbtASklwzgQQuK/j95znKVryXpHnhUMdqRUGS54qrzAB8+j0/t0XUcbeuzQczRbsO86lmVNGywKwRh9oliFwFE1hyhY1DP2XcP58Slb94qmPfz/2fuvJcvS9EwTe3615FbuHjp1VQHVABo9jVbkNIWNWdN4QJrRjBfAW+B9zQ3MCWkkzWjTappooIFCAaVSRGQoV1su9SsefMs9MhNZhQJQxLCBXLBEVEa62L59iU+87/NSu0LM+TELbjfLRtNUBXEYyUZjjJGMmaoQ6efNUbYt5wuKh2spro2Yie1ZS9z1Ih1b1VLYhShhhIeeMAX0ukG3JSkGdAb/Zk9/01F++BB7vsAsazlvawc+EXZHpp+9Ii5LqqZmenUJbUXx/gUgwZvqruicJU/j60uKs4UUuSrTPD3j9tChxoCJmXh7Qv/gDA4dWSn8y2vcg7X4D/pRSH9WCunsI3lRzBKrhEqQc5Im+DSIvOfmKNkkALOfIeuZGpkySov1TiV5r92yJvUjfgiEwRN2J5HIWgFSaPfOT5NjRBVzQGw/AbWE5n5D+QrMjdJsENASsplnQpWQ2BLKORgmTCNAgXwcMYXk/pjSkYzGrRv8vgcfcXVFHgPKZtnAME/pd1uyNhQfPZX7Q1thVy2ukRydmBLurKV/fYs9W9C+d07Ome7nr6UpyRIamrVC0WPONeMXV+9kbBrssia8OEpopVICw/FR4ASIxyv6gTRPorWxUnha8VZlLd4hrCGPItlShWRGqZzlGlFKgCIwXwsCp1A5y+80Q/SJNC9cKBxMEl2QUChhKpDupG/zxD/dTchHL08jJZ+rjRJvWTeiVDsjuWeMulHk4yg/W87yfYLcW1XpwGhpYtT83xXv8NRFIRsvo1BWkaYEVhG7URD5x1HOjcKgQp5R0bINVNbinpwL3GIKjF9cEdwRbS2x6ySAuClgUUEW36yeN+8qZVRdEj/dCTlvWc9U1znN5o4cZzNoQxonkeoqRZqpgiCNkHLye0sadErE0yTFfhaf1d17XH74SH43RpHHQG0t+dChLpb4ToJzTVWA1oLcHr3IIlMmd15+GXVJPvaE68M9eVU5S8wZd7FGKcnBqh9tKJLCFBX+cg8h4dYbvLHoQiA2GoW5k2Fmef4pwJVWzp9uADL2rCEOkveUjCYfjxLqPgbKJ2ey4fWReOzJx540BsyqxZ0vmXYdtrCoYSTsT9hFBbrCrlshYsZE2HfouiQpua8Uq4aNXuLfujuF+1focL/OJujr7dA3q6qvB7x+81N/+Xbo12qyvju+O/4eHL+hTdGv0RB985r6S9fYt1x0es5AGT27g+IYK8glfZJJH0azO5UMrz2VqWnrxGrpQQWuvEU9PcOWjk/TW7plQzd6dPMRKmqST3TdgKsKsLPOPWeCioz9iM6RYlGRDwoTM7o02AdLCfxLgnhNgxS0upJcDm0NoRtxdUEKkePtAd15QiGYWVMZTJaHGFbzQBvqywNF5YjWcrU90t8cwSnsphQpS6EprOH61TU7U7L55CnTvmO329H1A7YpMNZIoas04+BJsy8ia00ymu0w8OKsEqJ5XfKo7CAlnAHeZqZhIixKbs4qqqpgFwOZxNRPeLfkx+m3UBGKWGK1onAGpTLl5DncHtg5xbguKJslJ6vo+4EcI7awclPWGh0iReHwHobTQO5H6qYko7DWknTkeOoJk0frzL9If8wHn6yoVreMt3uSUvyXP/xj/OYDlueOvVKUVU3SmuGwpS1rmuWK49jz0zhgFpZoDMokXFlgp4HCOWxZUnhL5QqiURQnzdlOYcKC8vEznneX3PYHQowsqpa3u1uMUsScWS1WLKqGF29fYoyhbSpSylTWcDY41Bh5v3zMp/EWnyJ937HqpaB71G5IZyU3/R6L4oflY/CZyjp2pwNNURNOnsrVaGMYpxE1jTxYbahNZHs90bhSHk4JcrrzbWRUykKjGgJmWRNDEHyxFikPRkvxcH2k3/WU751jVhJ46B6uQEHsPfn2iHq4pnxyxvR6Kw/8biTcHokXhrSwKJ+4elhxMwW4vqRYPKT68Az9wZIHr06kmyOLB0s+6E74Lw6oeEBFCNcHtA98+LhlutxBiPc+t0Tmy4WiiCfOHj3g/FbydIpVQ971qG4EFP72hD1boF4eiacRf7ml++icm4XIej4Mj3k4LMlWEwrPq8s/QaHYtB9T0r5reCopnM/dRxTlkmQVv7C36NwDEIeRVFVYbSXEcwrkECmbkrDr0Frjlo0UvsZQnC+IUyAcZqlXTHQ+8yLUMHlUofg//lBB1nx5UPzR6/zO46cVKsHPt4rhJ3Ib/OFG8XEpPqfNMlKVA0M8sA0Z7xq4a6IQMp5rW8mq0gqzqIjDRNFWTHMDk6KcF6Z0oBVu1UCIjIceVbl5o6QxKRP6CWLCGXNfhOlFjTtbMF7tyQcZUo1ux8vr/0y4PUnjqDX20YpiPOOB+gGp9XR2T8onrNGs957FYcJOlpscORS8w5DflW5GSyM5U/1ykGbnyS6grk9EBddPF+IpJWO0IY/hHvudtSItK77E4B9XhLmxzSHO/iZFdpY8zJRNFDpEshIi4LipeDlfV82YWV/32BjRVUvY7bBa094OvHcASstj/4DzzQUMnt30kiHcCuKcjFk2Qi0LSRqg0vHgemLaSSNbOjcH5yqBN1SWoOHyvCBq2QI/+GzEKEUO0gyqSRqEYDXFxYrwdkfsBnJToouGt8OPxb9FT/aSvbVoHrDhMRhFXHi+TG9AKZq44snqsTQhpcWUBTlLppM0q5pb/yWjOaF8ZF2+T12fk2aqoMirErfxC6bQSXNx58OKCUKGOG+eTiN51zGuSl60G2KGwhg+RhE/eyvXpTHkTvy6iKrvfpuXfSI72QCZVUvYneT8UIo0eWI3kq92XO8jQ5Wxm5axbHBGpJtMgXgYgBazbADJbbpvqOcm0DSFSEz7EbtsIQTisUe3NbopmLSCtp3VLfIeaK1ZDxltWtRFjd0ciV6CZbmwxNsDKSte7hrUUZOaUuAK8wZYzZ6x7gTPu4pyWUNVEs+lNOt3HjX9eiXWr3P8ytbmu4bou+O74zfTFP2Nrte7T1L8CgmdmJJzzvSD4TpUkj1RjmglFKChXHHcH6l9w4erI+taKFS7zjIlhTtfkM41u9sbfKWIOtO0LcOhRxtNEsczKUbJ4BhHpnJCntceGzVlYSVp3VqiFTmBLaxMqWMi3J4orSUWWW5qWsEYMLWhO/QUprqn94RhAhRxnGi7yAeuQKF5/vyGLkzYpuKgI1EZdOmYvKfQiqIpSV3CH3sOL67ZxoFQGmKMtE2Bs5poNafjgK4sapzIWzHjB5W4amU7VNnED9yITomyqjgpcEoxGs1l61ivW25v9oDhsDsRdIHffA8NGBRuxmavYscHROLkiZslb5cFVVvSHXts6TCmhMEzzmQh1VQUlaLrBpEQavFKJGsYBzEEl01JJtPkyD97uOXZYoffBT6tHvH6v7xkHEb6xxv6KbBul9Tasu0PLOuGY3+iGzvO2w1pUdA2Fa8vX5ODZPM8XJ/z9rCFmPDB83a44WK55sPVI/qhZ5t73p56Yo60VSOFIoq2qu99DjolSutYLVZ0/QlrJFw2xMhyMuhTgn6iPi/pk6csKz4KK4wzlNbxh9sv6fNEiolP4gIXFevFgjbDptjw5vCWpil5fvuGh8szHiw3OGWI+SivQc9T2SwP9ZySSIaakjx4dIY0eozVhH6gLJ3IPCePVhqqgtxPDM+vcE/OcGuZELtlQzzdEsdIvtzBozXF0w3Dlzcib8RI0KmXDdNuU0Ca/TO7Lc4l6sdnXDiD2yyI3cDDuiFaT1IJPx7ksXpzYt2NpMKSb0fIiaw0/cLx6v2a3B9R5pxzMkorFs8uOB2/JFkjHprTSG4KVOHIasK/vGH6bz/hRvfkkPgoPWWzfUAG3qSfsTt9BlpTN0+orGRbpdOEeVximpJV/YyquiCmgFUn8niQAUNMMHhSke99QtPtieKsxcxNpi6t3C/uNjxWYRclZJEXjT4S+oqcS9ZV4p8/mVBaUbyGP3qtvj7C1YoX14GXO4PSmk2l+cFDOQcbRmqXCJvI/ssT2AazrKSQdpZMnCWvhcgpc8YtKvy+R1cFcX8kjgHWLdko8YJ5keNEH/Cjx60bXFWQDgNhexLHU4j3gbL147W8zNLRf3ZJ7AbSIrPNLwnH69kYrqjsE9ZTzVnxAUknavcFihNRK5o+cr71mHTiuJJ7m7EFKUyypclZKHFphjrP8JgcAqtDxt2MZKXYPZVoBIUSaVear4U894qrhstDR7wo5fWnJMG8d4+YeWtFuqPlqXs8/aTg+kwAAHnnOdsK/CENE7pyhONAefJUPqCc5axdcta+h6ozY9wzxFuU1gIUOQ5SrM8yaxMiq1MSWmQ3ofqJ7Cx3SkqlFLoq2K4dk4HCai4qR+omOSeDbJJTiORCNigCr9Cw6wgbxd7Ov79FJUV/BhcKVuV7aK25Dlfk/JocE46Ws/Yj2dSWgkRPlYTG3r2ezt8ypAMYTVs9ZlU+FYmok0Yj58z++EpkfSDDgySgizSM82YpkceJ4arjtHV89qRmSpm2MHzvvCG9uJZfxySVvy4kl0jnRNaOmCJEaWr980vSpsOsW5Q2pEMnwI5+IvXQOUtfFnB1RFeeECPubIlpK3RbYSZ/n0uUvTzvow/ESbxqed6g62UtsA2QPD0vzzlrFR7xFptWrjWTYHFK6AS6TLQfJ2kcQ49Siug9p2Pi1W5D9hGzzrKJNxp8lOZJKfptYKhqctCYSmEWsjEdB/21oPR35VOe1W7v8Nzf1rz8On/zl49v7Jd+hcXhu+O74+/bof/qD/nVx1/rWslf+eev/KD5UApTl5IZkjPEKA9sEJpWU2LKgnB7eic7uSMKAdoZqosVyydnuJBIQW7c0zhhjGHsRwl57D2NtjilMYVMVEXWlRlSZDwM9G935JSo2gq/65luO1whMqWkRW427To0AkyIo6fYNGDkQVkuKoLKZDKlMTz4nQ9Y//Yz1j94wvr7T2gvVozjxBQCASg3Lesn57i6YJwCp9PA9c9fk4GzDx+wOF+yuFiijBCWYky0F0uqVUNQ0PUjuikkW0krAUFYIaH5aSL4QEgJHxLGiPbaNoLzzjkRVaZayPsegTAFxmFiilEe9DNieJwCE5n+0OGUFOspRHTpKAt5sGUjm7QcIovNQqbCSeh3GkWaAteXW8LgKZ2hOhcggF3WYhzvxENwXq94tDzHp8jVcUuhLReLDVprSltyGnsGP/L25pLCOSY/MU0jl4ctTlv2/Qmc5WyxprLFjFiOHE9HpmFkGicWlWQNZSSE9tR3vL695uqwZT8OWGupXAlK8Xp7xegnVOFYNAsuVmcUZcEwTox+4uQH4jAyzYS6Q39CAUlB7QrGvudisaHre86WG3JOfHzxlPNmSVPI726KEbSRYm3edvAVGYsunUg6ojxkc8pktORuTR77cC25JCGiZh+S//IGfyUae0pLcbYUgMBJNkM5Rqpn59izFoySDQ0IBjzOqGkr2wR/faD7s+eEXSchhYsau6iFGlcXFI83s4xNtquEiFnVKGMwc9Go5mZk+PytvP7ZS1C9fw5Wiu6ck9C1HiwBoR/GbkS1FYkssibkpaUQ5+ZJoWO8l0vlKIWyXbeCeU4ZNZ/LOs9bN60J4yRFXj+KPOY0kroJZQ3hOBKGCY1IkdIU0NYJcpuE27TYRSVBjbOEjPnjpJLhnSZmvt3pr0hj7szUd0ZuIVJaCaDenjClkxyVusQtKpTR+Mu9/NxTwB8H/KHHFg63aLHrFlNI+Kw2Ejg9Hgc0SoY4KTHsO4pHa7l/KoXdtO+2WfPrtG1J+exMmsJmlnehZq+LQAbU3CBpPftdykIw0vPfo/W9Kd2UpRTgma/JKecbP8oKlUuBNPVK3u973Pj8HLgvGq2W9/3Q3zdXzBunPG8W1CyXympuwIwWA75Crqm71xnj7HGSsNw7ebCeoQJp9ALbUfqegEYWj1AevNDqZoCOcnKOZx9Q1qLvQBl315FSUMjGTutZZggSsIwiT15UXj5AyrizJfHQcZfXhDGkQ0+a6YJ5kiZCIiMEOS0UVcQ/o95t5FKSTKMU5yaY+TpBNjXBB7KRoVBMUvCr+TzWWqFCwgAqiTALEH9SFqhBJnG8vWI47AR1zVdmAU0p742eUfUgTdX8tZSPEjqd5pD0mIi3R/rnV0xfXhF3Em6tSyv5ZCESdyeRrKYkYam7E9ObG4Y3N4TtaQalKKl8fECRqc4XlI/X2IWoKbIP+O0RvzsRDkfizZ58kC2ydQadRPbm9yfi5Oez9V3Nogu5PnXp0IsK5gFWDpF46NCFRZeWeOrlHjaTdOPuRL49EW6P+EP3jdbkm6I4vvJf1PwKvr2w+lXWhjz/39ePb2mcvlsWfXf8Azl+s6CFr15bf9VF9G1yuvy1/8FPb+A4r44/OYt8/DTjd3uwI2ZRodrMbVdwq7UYvs8VuVJgDT+9HXl5FFP6+05zXll6VZOT5vbQozIUhaUfB4aZfHbygaAyn51KdHLYoiBYCbhUvcdWjhQTp+0Rl6SQy4cDv/t+Sc6wve24KUr6Y09hDSkkmosl3e7E1A1M+45y1ZD7idhPPH9xyZsoD+g41gynAd0UFKWjXbekmNg+v2Q8jSzahqsWtjGhbGbSiv7QU+oafxrJIWJXNbYsUClhmxJ/knySdtUIctxaPJrP945xamjqhvhehT+OJCIxGYZ9L0VRhmAUUzeI5M8omqaWLUUIdHXB5y6TtePoA1M3opylXi+Ib2/p+ommLWnKku2px8ckeNnSYUuHGieSkgDXOHk2TcX76QseuMT6/IKrq0S/eUx8PlDfPKSul/wj932q9IAvtle8t3zE0/UZL/dX9AfPqaylQA+yRdoe94x+oi1rFmVLUpmr3Q2gcGhSjKi24O2441MuMRtDGiL/zDxlmZZ0xZIhBjo/iIyqukBrQ7/rsLakMCu+HLfcAqex57K/JtOwMZphHCiLEmstz9UONwc8fqDPWWNYmJZxofj5tKPRBb7PnNVLLJo+prlwm3h1/BkomMIg2v+YqNySs/ITtDZ045bt6eek0UuxUljSaYDZZ5JzJu071LLBPdng3+64o5SlwRPf7knHQbKG1g3m2JOCIRxn+ePZkvLZObouePDlkbNVRTxOvGoV0YHWmcdvBqwXWtjnywnbnNM8PefJ5YiuC+wjQUabTct47Hn9qCIaRZUVD4+SRbLUa/7l7gdgLfHyGv/ggDtforTCnS0FcaxEaiQhm0YyYo4DzU/e8MlHDxi+7FjVMyY3J/Iok3WdpOHI1qByEsz36xvsxZrLy59hRshK89uX76Pb95j2Rz67+AkDE3VR8XuHD2lMRXBw3X2BnomROSVSkiDXNEkzWq4dj363RBlNf6X58t+JN6XrDZ9fVwCU0fN//uGci4ZsKFLK/Gxn+NHlV26id42hVmQ0SgvmP3eJcBp59sxQGY8/9FzuS447T7o+4C6WdC9vyFpRFAZbt+jRi+HcaJGeBYGG5CmKB+jQg9KoMw0piV+ydF+R6cltuVwp3v9Xa45fTMRXBcl/n8zIKd3S2UvivuPYvKbrXpGBrTqgFwvSrmNdvcez5RK7arkxz0Ef0Gge7DOLmx2mLLl+VHOan0jaB1Qp8tQUopz/zIX2HIB797gxMfP0WjYqdj3y6RSlyUHNPj1pRKUZS++M5PMGOIOEcc+fkuamCafJPrOvDdtHJVMV2PSJs6BJwL57Ts8RgCFsxa+RM2+KxPBBK79DJ8OfnCSkVzUV+ZDQtiLPTR8hEo2CoAhaGsuo4MsPlxKo6iOPLsW3dNdw+uNIqBxvH4kyIZu5MXuwvG+OcYY3que5+gkxZ066l61YzrxdHvmP+mfkGFkfPZvJkg4d68XHNOqMrOaGcUyoyvKT6iVhc7rPPMtJgCDNYcSMnpzn0rxwZB/us/F81/HlA03UFfa84r9rKnQA7TRWgZ+bQoVchzlmYvbz0EcaV2M0USmSES9ZsWzmRmNuLK2TYanWqMbIPeDYi3TRaJTV9wOleJCtJM5i1i22KSXCwgfSqSdOAinSKFRdYupKhjhtJZmEVksTU1iZ0U4D7uGIqyxJG748LcgKnEk8bjpMW2K8ha2VzZDSpMs9rBupH3YnzMVKGuZGvlfTbzlrFUW54lUxN7PfkNYovnJt3pdTXy+q8lc++pcdfzMgw3fHd8ff3+M3Alr46jWTvzbt+5YP/rW/Klyd5J8MrOOBf3Jm0Q8N6aRJ0wlD4MhSaFYHkdCkIaHbiqsh8sVe1uKfbCc2jWVV1Dx/uOF4HTgME9FHYvBCkXKGqBTaaN7uIzUapSOmLST/xUC9qFAoxmGiUIrxNLBYadZ6lHyfSfPidiQYRew94Ahf3pAV6IR4lIAUEp7MjYb6YsHuzRa7jUwp0iwXVG2NnwJ+34lvxUdCDGwttOuGyQdsTNRlwTSbggGmg+SsTMcB6wyVAp+R6fY4cdwdUW6NNy3H7sAhA4XGrsUwbp1hd7UjO800SYq71gpj7P2k11mDOmUmK/kk+1OHMpY8ejwQJwlRbNqK4AOpAm0N3WlgWcx5PacBPwXMjOsttMYo+LDuefhAUbotp6Omv0pc//gVljVtfcGH5yv6vuPj4oKPV8/Yjh3sRozO2HPDyQ+0TYsPnhgCdVGz7w6MwVNpi1MigeyGjm08sCgqjnngSvfyOxo9D3XLOB4J3rOpatpYyRbNGiyGfUwMw4gPI2oFj1ZnKK0pJ8ftbifSOx+pqpLgPWZVkJRhGAfCfqAZNTYn/nh4QVPXfLB8RKMa+mmkNJambtjttxymju34c2xVyqKkKDC2wOSGVf0+1lhUttx2Pyd1I9pp0iiNg3YG9p6kvYSaXu/R6wXF0zPGV7cSpLmsyFMk7oS2VTzeENsCa0TWGN5sSceRdNZSPN7woHT0n74lF4bbxwuO04TKivYUqPpANJo3FwXTfkdTax6lEo2AAxIS8tl94dmdlYScqA8TF0rQ4lW0fDg+glFx6D0v/uJn6H/8EXZVg4Li2QX59RsyCk3G3xww5wvyMFFdd7jFgO8zJQFWCu1FrpSVQhsDhRWprBf5Utj1FM8u6LgmhBGTFR/vf4vF+cec9C0/OvuSU4Y+G6r+ES0VVIar06dMfhAPIcg2OUSKtpylLIH1h5UY50NAOUMcPKfBMy0li+diY/jhppN73B0qPcExwI/ecu/pAGYqnWxSZLOR0M4QjwO1MqyrQLfdc+lX8vcpYStH89453fUR308Uy5pwkul4cb6gWFQS9qwV03DC9iP5dKR87yHT9iRSymEibk94PWc2zbIiVys2HxlsVoydgy8fo5cQvOW4/xJVObrbS9SiJB57Bp3BrIijpzRLVtV7mGaBCzcoDmQUbR/Z9BJauj8rhXIGJMDMm5wcEsrOtFFzt5lRYIxg2HOmvRko6xLXJ/Rs8L+7FtIwCYQjpXu5HXOvJCqkPHuLFMqYeVuoUFHgBmFVcWs98byivJ3YXI4oaxjigb4T5HOes29yCJweNZwetiTvZcME902WTpBNKedmJbCZbArZvuQMpZWmBjg8KESqfdvx6O0w+6I0TAGVM8kZdheyJVVG329Bc1lAsKjCoEZPDm/IpRN4wXze3fgt24WFEOkPR9QR8jhRF+c0xUaa5rtzkMxluefYetnkGHlPtdZ8v0yYQTaAxIDSQsxj8KAVPngODwomp2mXjh9YRwkEq3gx0xWTn1HreoaTaCXch9l3kzNoMsYYck5CoJzinM2n768j+VgBlOhlja5lA4WzpG7kLs+POfMpXu3kd4dsHe+b4TzHG2gJ7Q0+Sth1jOgQScM0wyoKbGHI/Vv0akm0Jdt9TbaWykYeVSeUEsqnVom8bLCrmnhzhJwEspSRgODS4hYVcQq064bzcofRJypbz+fofE9Q+Svt0V3b8w252/3xy/7+r3/810Cgi9OCt//5//p3+P3+I1R/Z9/uu+Pv6Phby+e+efxahJRfJqP7pb2UTM/8oSeGiG5L7NkC7vTaTSkPmNnQekfS+ZYXR7lpaJcNZ6uWujBCP7ujGlmNNpqickwhMOVE7CZyzhRlQT6OjPtOkKROKGspJbwPTJOn7waoHTEE9l2PMpqqFgzylCKH2wNTP5JipGgrcmE4Hk4EHxj6AZzGOMvx5sDx7ZY8E+OUNZL14WZ9sdH4bgAFrnQUbSnyGq3xxwGnNHHw8sAJQnsLIWK0ZupHxm7Ezg9/O9/882ygHUNAK0Hg6lmelVNCaYWfPK6WhPNkND5EAIw1xCghmdMUsFZMz82y4fZaQmtRsL3ayeuoHFVTMvYjpTUstKZe1SyenslrP/XYRc3w+RspGhS8uH3L7rgnG80wjfzi9XNiFCnkplnS2IJVJdu1nDJnzZIYA4UrhF7oLA9WZ5TG4rQh5MA4jQx+op8GJu9ZNS2rxYKyrFBa8Xp/K2RCpem7ju1+h7GW0pVcLDc4pbk+bIkh8Hh9xu8+/ZjGFQxhoh97qrKiLWvqpmWYJpyTPJlhHETLruDPX39OPw4sq4bWFOSceHTxkGfnD2nqhfyelJZ0926U898acowzYEODT6jCSTEHsiXxEXUaBcigNdP1juFmT/nBA9ymId2eQEOeC/rpxTXp+TXjp29Ib3dUjzYorRleXNP/xZfkmKg/eSSSpTmINSuEahVFGidSL43/8ob+56/u5TjVozVxCthHK9lEOIty9p5MxVxUomUaDND97KVkmqAwbSWbLCc/r06Ip6EpicYwvd2iFwKOSAqyNeSETNCBbAwKMLOhnJSZ3u4xi0qkLM6iUfg3W+yqwTgrU/1C/kxa0NwMnjz/ozPSLM+6fnKmv9wTei8ZRmPAzrRHpcEfx/uJdZrEZ5fupL45z9jqPOPW8zt1Xf7K5oI5l2yYiIMUuNXFSihvlcM2FTkl3LKmPhe5Y0qJ8tEaCse466RZsIbUe8q2AqWIuz3pdsu4PYEzlI/WEki57xkv9/TX+3tUtt/3jFcHxsmTC0csHC7n2cCOhHmOXrKwnCWfRrQxIpOyswQ0pXsvFsbeE/hSmAvxeXMQRi+F7ugFy6zUfUDm3YZHzfQ4pRDfphG5tZrlcWTknCkdaf6d3Uvp7t5gLxtGrdQ9IU4ZRZpzr7D6PhPKxCyytvlcV1maIZ2yeLGigBViirPkcy7Yc5LXeddwaUUu7H2DereV0/GdjDCOXsANszxW38EkQpyBB9yHIKc7aEBGBlmlkCDz/DOomNDWzjJp9ZXQYNBlca/SUFoLCVAhW5hZBqeshpAgpPtcHtJMegR5j3ImD7PsdH68G60wSt1/He4IfCBfS83NjDUorVClk+y6WcJ3J+dUs/QyhUzWBoy5Jz6qWcZLkHt/9ol4fcS/3TO+2RFuT6QxEFMmgUgVg4StxnnLnrUmlwXBSJgrWbD1/uZA6kfC1V6ek9Zg1i26LsWX1I2YpiDcHJieXzG92RL2HXHwhENP3PWE2yNm1VCcLSR8tnQy4KlLAeEoSMeecOzRpUW3Je7R+n7bxvzz35dWd838L+1T5i30r9sQqa/8w7cvhr6DLXx3/EM5/taboq9NEH4T1803v8b85Q92zcsA+SpysU6sW9EnX6wCq3wiLxS3LzO7YHHnS/rQAXJz/tO3Jwoj2vSP3/sZH5xbJn2iC3uiD3Q+cLv4gKjM/QOZCggjRVJEDRHDy1OBn9fWfcxko/DK8WfPe5RKmFLzg7YnFIF9XXCDYnu75+FFyQcbS/CRt4eRY1HR9wNts8LvRhbrlpAzupRNSjiNxBQlc3AKWGfn90Uz5ohrSk5vdkxasV5smE4zOnmWClgreUi5KThd7tBaUdQlZSPY6sVmSb89YZTCFJboJ2ISSEChNQtteLDtUEqz14nbTUNG4X24N2mvxsjqak+zWXDr4EXOc5GXcM4xeE9RlxRNRYyRx4tIy4hRmuHVnniMhH7id598yqMPLc3TM45Xge55T/XhQ06fv6E/dZS24L3NU1b1iNaa2giqdOt7/nj/BrVQvP/wgr6PNHWFnTzd0PF0/YDD0LEsarTS5NHzj8wZ+7EUSWFVcXnacbFe8o/iQ05dz9KU7IYDxlr6KnNoFW/8DY9iwyo5alfw2vbsywmVYZ88JY5T3/En6ktaV1OWjkWzhKkTfDeZm+0VbVHwuDhjvX7GVbdjbc9ROdO7E3H6BTdd4OgHmqZFpxqdFM/O/gCdFJM/8vb4Y2KM+Lzn+c1/RFtD1JHcOHSeJ+cZfIo4jFC3omwWdC2Srjh6pi+vSHVB+f4Dwu1hzmxJ4qMLkcuV5Vgr8rTn/daijhKU2f35C8yyprhY8t6NZ3h+iVKKqyfiX0MhEqCYiGR+YTxFPLJ4eM6zK/HZpMOJj3ee1J8Yybz8aEHOmWYMqNv/hCkLdnR89kGDQrHa7/iweIDSiurDR7C7RqXMfun4NCTMbz1men4lfqWmoDhaLpjlMQrx+k2Bm+5n7NLnoBWrxfuclx+SYuSmeAOPLPnyIFI7H8mnkQ9CYnN1QrmRPzr7CRiLI3OWJmzpJJfIGqZDj2tLxquDgDh05uf/ww6MIuw9wy2kKYLTlOcLKfBGT26yFJ6zBEhpze8+UTxcyb3u5U7x3//o3b0wJ0WOivcazUIl1KrmNjcc9/LfJzsSe48uFX7bYdcNxVJgC93VnnrTUj9Y0r3Z4vsJWzmKZc10u+c9e0teHUhh4sv8TLYdKWMKR7aGYfKoKZBjortKfPr/6Dg+j5RBcWETVmtUUxF3gXQK7Dclt2cGzleExhEnyZ35tL7ksj6hneFm2MvWyxgePfo9HmSNrWrOgyXu5lv+3AzauqCpO4yzxCLg3/xYfJtD5MnqH6OzQVvFXv8XiBN6CHx4ikxvT5jkePb0n0DIhDDxdvsj/OkoviBr5jBdTfL+vvAEoLCUfZCtTCWhuckHlIJl8ZT3ludSzIYkzXzO3E5fcJouwZk5S0oa3jt0eAYIQs3TShoIToLNVqN4jBTSjOXRoxY1ahjl+jRy/09kGf59BRaRZk+LVkp6HAX1EHn44ij3iH6UZ5oxnC4qrhbzJkzNniwFefRgZPPwi/IVw1kPKfOBfcAH4QPi5LlebjmEy3uFe07iQ0Vr1AyBePWsZSoMygeeXU7YMaCN472XByKJYmkwn7zbXoTtaR7kyCYSJ4HKefCYwklTmO/Xee+CcFMSFHjIAkqa32d5QiLDkCxbtRQT8TiK0EELGj0ZCdAF2TSZ0qHqAuMsRT03iEEkdf4wkHpp8OP1XhoZZ4lAGiam2vFleojSmZAngZoMe8YHCz7vask6UnKuwZzJdxoIw4ghk2d67GJjOLMHzCLgwggUmMLx/qrkv/1ABqufb0deHqb5Vv/V1uWbRdO3FVHfNiT+eo119+/ql338d8d3xz+A4+/GU/TLJhp/1XX3lc+bkqWzNVllVhzJfiT1E6VWVIVDLy3XrmS3A1dqYtL3D7nrTqQJWsHvTNesSwvLTK40qIL9q45llbkJfjYIC5TAlhKAWBSOw7bH6JJsJbvHG9mE+HEih4KYM5tS0cY92iiCtVwOiZAzi1LT9HsoLfuU8cWCZO8qnsw4TIQQWJlW/Eh1gfeSjTAee8rCyQQ9Z8q6xBrDcZYTXL26ZrlZ0Cwahn4gpUQMkZASVikhzi0XkKFalsR9J3lJd5ugmDgdO4qmxFYlu/2JZ6sFqy5ItsayZOdEjpJzZuwmlNEUKdOeRjZ1zS5lqqYgKhhGz3LV0g0jk/eYwlIWFTUHLqYth6B4EBqqoqI4X/F7H37Ourlmev0l158qWJwTjj2/+MlP6aeBR4sHrMPI7elAHya+9/AZDxZrOpf5RerxYeImHGhdwb4/iaeoXmC0oSgKYobtacf3moec09KUJb0aGP3EfuiorOO3F4/Z5xM+J3bTkRgjXRvY2pExT6ynAqckp+e633FaSqbJom2IfWZ32mNrS58TJjvZ1CR4sD5j2+2prePx+oI2iEeiLSpWQPaREbgOt3jfc5oGsm5QpqLQDe9X/xQdFIOqZIJLJuvEcXiNqQr8PHlVzso0d93AzZ5kJQNDzxsMxkDcdaJhNwp/eyTuO3RVYJYVKiZS70k+0rcVx5VM7/vPjyxDAp0xVUE+yaa0bEraZU04DbyoFLmZSV93GyOtOK5L8vHI6bOBB6GmXi+wnWVTVvjDhGsLXl/M09Y+cLi9QXeJY6M5tQ3KWcztwPDZW6qPHqKrGp1q0s2RqTJM2aAbQ/7oDL89YoApOvIp3stVSQL76MftfZG6Lj+kbZ/CNHF18znmqSMtagm0DYq871iXispWjP3Ij8+vGI2mVIZllMI4dgGTinkjkElaGtKYM/svvAAv1Nz0kHEzdjeOgRBGYuPRdg4sRTYaGxU4Wxsg8/xW8eOX78hUycvGbfEw0zqNKQv6VNCPQMrEHNBWCuXYT6jCYtuS5vEa/XaPPw7gE66p8MOELSzF+QJXwjLv0bZgigk3KdmcKcVw6qifnaMv96ToiaeRsE8MtydSJ+b20Y7gHKOKjN0oP+N6wW5jpKkaJag3H3u25cChCFLQuwDZkCtHw2PWnWDolwlUQLJsYpbi7KjIxUqax1az/PLH+GlCeXhSblBBo2zm4BMxJ/LtkbOqZNhNFNryeNdi65ru9ppQ1vQvtnOTEGfLkYa6kLwYpWS+7rLgmjOoLAGuRLlfO7tgUTySxkdn0izfOnHDabqSgjwlkX5xZ/sQ2IaKiThvJSCLtK4oyKejwAW0ks1LTKRjL68nz0h4ref3RciIWtaA949RpZR45ozBhMzyMElkxAzrQAdGlclNOwfjxnsvD0pDFNnzvui5crL9eW+8YOHPyY3BqU6aLjdLFhEvXFazPDskjgvH1DjUZEhXE9podMy0h1Gk1yrMmVZIRs/2JNellZ+NEKUZQULRtZa8uRTTOzDGDB7JOQk1L6T5c+SNSCGis2z3ktEYRIp4V+brLOcWIaHMLK/sPOk43jl1ZFNYOvSqQi9rklYCubCGtD0KAbRyaGdJ3cSNt9hVA9pizrVslo4Tu6xgP6GbEttWhGOPqQrsusGuG4iJ6fZILgusmliaAWMgHE/4G4dpS+ocebosUEpJHXNfOv36Tcs7kd03tke/dNP0XUP03fEP9/gNyOd+yQX0bfK4r37KL7vufom07v6vjMjcKBxUpRCzguA17boFEFTpX/qe6t1Nj3caZGUN7ZNzyrbE3MkWsqTWkzNOawk1bEt0VaCtoWormlUrcrHBk51hygmVM34K3FztpIHoRwyKeIelTklCS2eJjFGKECLBB4jviqs7I3AKkbooCD5gnEj9yqoUQtrDtUxSjaE/9lKIWYMfJi7f3LDYtBAiT589YNFWGK1QQd5FqzUxJ5HApMQwTjhnxTfgHF0/4lVmGCd0Ydltj4yjJ2vFOHnCFEg5E1JmGEasE7qdnqUpCZH1Td2IIhP7Ae0D2ZScLVsW65bibCEPWa3RzlKeLVl+7xnH45HDz1/irOPyuGXMQjd6uDrj6dkD6qrCWMswDILxtZbb7sDt6UDKmYt2jQJu97fklNgdhBgYY+Rqf8s4DvN0MvN0eUZpHF1/oi1rjNY0VQ05EccJnTJ+8qiQKV2BQpFmLXgOkcvbK/bdkX4aWZUtTVlTKYtD3t99d5Rir2rxo+fF1Suev/mSoe/w3rMoKy7qFqc0PZGqqjHOYmPGKC1Fx3z6am3u39+J2YSfshCNBk+aAmZV4dqKpGbJj4LkA0ElcIY8BRgC1idMlol0v5UtiX26gba497AopcRsnLMobfpJtilak/tJoA3W4JzIRZVSsxREPB8aJQXZEJh+8Zbhi0vsopaJ7Fk7v95GcjpSRoV0n5fDXehjSvg3W8YX1zIQeLASydIsJYk3R8y6nT1fFq3foZ2l6BQKIkqhm0JkT/PvPpUOHTP+5oi9WJImL4jklMm9xy0bQVrPsimdM3GYCNsj4dAJxASwzmLR9/4VU4rMS/mAigk7e0RUSFLIzhu9ODehsRuJ/YQ/DcQp4G9PIhFzhhwT0QcpYKMUi6p0xBBFftdPDG9F9pZDQheWMEyMl3uR+BaW+umG5vFGpEbeY9QsuVLgljXLjx9SPHtAToZwPDLuT+R54BJPI1llzBwASpJ7XPlwLV7AObRWzdlPIjXMkKO8RqNIwyQej6Ykjp5gFDiLLgtyXYhpfW4epUDPBGdgXZPOFuRStiR5LniZC1RdWAFqkAlR/EAJmG5PqKYU0IiSj80xkqeAKixmKQHY2Zn78ywOXnKFvgKVYCbq3TUAWul7qWNGtljy3TMZoZoS0pwdhsj7ZlBAuiOmzhsNJaenfD0fZJgwy6gkEFbP2xCDQs49Vbr7xj6HOGf7iNQr3TVuKMkrOw7oUgrpXFiyUUQvTWCO4qfJd9LNu+atLKTZmOXHycsgMSXJ7Unzz6V8vJcmqpyFLDhDFvKsJLjflAFFu5g9qXdDgPl5rhVm3cwSOYkWICOeJK2lEVRyrigrm289b/Pk9yA/K0aBE+9Q8rNsTwtYRZtZvqjmpmC+L9w9X3MUP9Nd6HOMcX4/FJxG0tURPUWs0kL/LAvUshGpX5RWI6UEc1aSMlIzqEpyCtOhk3Pv0DO9uEKFdA+Q0M7Mwb6GdHvEtBV200qNsahJMREOPaEb5+Ln7r375p9/9fHLGqhvLdG+KaXLmRA84zj+2t/vu+O747/m4ze0KZrv8vMfXzt+E5tYBV9sB647gQqUJuKUAhz/+n3LJ+0kevMpYDYLwu2RH5aO37pYfs3jlDP85KpnDOkrrzNjneN7nyxxx4nBB8qqxHsv6Flj5KYXYJwmlNLkoHn79g3rByuSDwwxYesCMyb+UXFBKtZcmZqfxSNkuB0Nh7GkdSv2/ch+v6XaNPeIbGcMwSC5I/MkdxhHnLIcu4561aC0YXu5o6gLKZjmh1O1qJi8ZDalceLh6z2NNjzdB9ZhIqeBzZNzfCE/sN2s6K6PlKsllTUM40R/vqEzhn83TqzOlpzGiU8fNJSFY7KK0otv6KlSfLI7oY3m8cWKw+hZLBpSoXltNSlEHg6R5dVbCqOpy7fk/iVlU7JQjnZZYTBMRcKgcUvHrlpyDKUE0v7sLeUYOfiBp+sHPFqe0YXAH6YvWdVnnKaRf+wLJj+RteLZg6ek7Dntj3yfC1KIPK0e4qeRy+MNz/trfO0oV0sW5YZud6LIiSfLc/bDiSlF+jBxvj7HGINNFjOOTNPIA12zGhq2HZQoPt++4unmgt82D7naHrCm5rnKnGzgrF1xPjqqYKi0ZVm1nOLA7c2BbhqxRvC+t+EVjVNYXeNzQR8kWDPqSOVKtLX3xYRK4lMIKVLYBR+s/6VI1MJdcKUY0O+Aqv14xc3157gHK7rG8EZ78JHFduRiH6Sockb8AEqKFu0TlRNy47TvqJ6c8WgYObs+oRTslo7rhxVRzwhfZHKOs6goRV4sNBYpzJgbFhs1zz7bS2Cva/lo8c/RvSK8jNxuXuMenRGOA+/9f15iL5ZwLYGXuq7AIHSx2ReoUsa/vKGoHd//8ILjdSDueykkc8a8Ec9f3nX4+GOe50/RWtP7vdDDQiTmjJ6kGEkpCwWqrXi0/D0SgaJ9gDkl8uQxxvGs/H3cuuZo9/zI/QnBJIbJ88WHLdpYUozY2cfQBMO/GH9ITpByz+Xpx6RJMmi0DxCloMpBPERHV/Dp1qGteCLuiuUUIvqgSZPjBw8dP3gkkq7LW8PtTkq5dTX7KJRiujmggsgSlR6wiwrTlCgyfj8wvrzl448V9UVBipkXtzWntyfiMDHqE9X5kpxlcl89WmMWDb87aJSF8bTjTXFOGAMmI1P10smGeN3g1i1xP/Hq9X9CxZIQBwnftEnQyDrh6oLliz1nXSKeBobfe8orL9k2QWmqx2visecvzt7ymX11t1KR92Ld8Pg2sPBA8rxYJ/yMUR7agpSW6KrgZfiZFLYx4B/UhFTgEvx2jth1Q3cY+B/P/oKkwDHx8OZA8fSM7RdveP1hA9bQZsPDv7iC0nJqDJePJLtrcfI8fNWhCsvmGNBf7Mk5ocPP+SJ+CUpxs3bsVxVZwypsqfcJQYHMj8PCSlOWpKF4/Hak7gMoxYsnFVMxgwCMvm867oZLOiTe/+KI6rxkxAV1f64Yq0l9mOEGEZUy5XHiyZdyXegpopuGaDSn2nB5UZNTpvKZjz8/olHcrhy35yLLulla+scVcatYDYlPPhMIxph/ypfxU1JKLL4Y+Z4J5Cny5llLN8MJHzW/w6ZogES8+jO8GVAh81H9TyhsjR86PnW3xOlEUpnLC4N2lqwUjnOm2yN2NDwpfx+zcEz+wOv+z8neo3ImhoRGyfmhEBy7vvODQfayB0pthWoKOAxyLSnkWQ1zCHBGJSHKMc2Bv0aTBo92Eb2q70OiM9wHC/tDj9aCRY8xYlcNqXASLnv3cqxC7Y5Mc4PvVg1m1RBLRzp0Anppynvfbrjcoxt57/WyIsWE3x5hIVvG/VhwM67wuxNVNDwu5F7QdOl+qPs3Kam+2RypX/Iv6u5nixHvvRBiY/wbfMfvju+O//qO30BT9I0u6Js61bv//etexd8mu8twmhKnKf2lD//9Rwq9trN/wqIC6LpgNXqYxrloED9RzPAnb45sh/kCz5JhUTaK31k11K1kHEQf7rMzYhIZUuEMVoTJlPMEOfpIjpkpR3IIGKVZeoNzJbenEe8F72nqmu1pQuWC3emIj4F1VdAdetq64jQMFIVjHEaSl4T1lGTKvHRLSmvwo8dPE3038PDJOWGe+Ppxoiod4TRQasWHVU2dod4PfP9hy7A9sjiO6MJincX4yGCthMvGjDIWX2YuU8aERJwGyW8yii54rCsojBTRG+f4YdsQY6IGVo82GKU4y5naysPkQsGDrCFpmibRPqtxtWQ23D1o6pUUvCkMHLYSjnjz+RtUP1Fbx3q1wafA/tBxfTgQFu9zq3raZYMNjhwS/XHH1XbkMBxZuxaGiU/OH5PGzIKKqr6gKSr+wl5xtr5gvO3Yba/46NF7hEJzdbWnUJpF3XB72PJosWHsB267A86V7E8nnDE8dkv64LlYbuj8xKpe8Ftty+AnQqnZFZ6TH1kGxyIXHI8d3ZgJ3rPUjoUyXB/2qBzp1Q21dbw53rBpxAg/5URp7GySzzLBjklkRikLZc4YanMhE2qC+FGsRYUkORnWQA7km58wnQbGJy3TP31K7EaKwyUmQzz2IhdqK/CRFGQSHedsH0MmXe5ZrBqCdYTJc70oOFRKghJjlN9fiIK5NVaIW0EgHCrKNgql0AraLuIy2MHTXqxRxjL2B4bLV5S//YT6wRo+ewtvxPuQlCL1o0xjU4Y8+zXULBn62WsqYyhXK7rLEyZkyQE6HLCbmtRHsjrR0UEIUDiUn0mYlZNpuuNeHgvQmDUpJuzYEouRPMjUvs5L8ljQWEuhtJjmm5IjoGLGlAI2Cd2AGjTVsEJPkT4GYj8RhxFtJrLWsm3cHvFZsnBGpTma2VC+blEI4tvUhbx3dctZOfCgGsWf5x2lrSFnwQXHjG0lxDrPk3FTF5i2lO3PusGtG/Loqe0lCys4fWMU7qwl3mZCkq2cKqwUaaPHNo7NQib0nVKwFw8GUdDL2lryFCgvlmAMLDPj1DNc31JsWtp6yXQaOLYl1dMWfyNT9uq6xxiDHwK5cBijZVZvRNZ1M92gyvkRoWevTRlYKU/qRzSZawNjJaZ6nAYKqBy744EUI8SAXa3IMeLGyHRzpNi0nI4dV8WOCWhSYLM9UTw5I7Ulh0KhK4PBCYRh8OSnSw4LjULhIpL/kzJlyDRHL01LOHAyJ9CKG11y7QSt7Yyn0u82S6REngK6rcj7HnKmOk00BxlgmUfyQ8ddhztbEK72shlJmZwjCkW9G3FBnkHMkIacIgkJEGbOLcpaNhttF2dkPSQ9YpuS4BTH1kkU0vXAagJCoKv0PMTMTIXBlwrWJavDkfbgZYBg9hyC4M31lFnUjjwlrtIs2fWJyq5oWZFzZDkphnFAZ0374AyraqwtyVk2KtF7epcxpZ63N5bqe4+JP91RFw9wzqHTDE+Yr1HjhGwqMtNZLviVzYl44BLsT+h1c79RIkFS6Z5oxwwqycMkj34F2or0MftI2J1w64bQTdLwGIFOpGMvGHUfRbJ8c5Ig32HGhltDnPOxiBEPhNe3FOfLOeS5EIlwku9LaVHOCHxhWaPrAr2qSdkLVXNZ098GDrSkyVEpRzVmUBkbfv3t0Lcd9/K5b9ZoXx1mK8k7ijEyjLKlMlphjftbfe/vju+O/1qO36Cn6Btrom9eeH+TjdE3N0/fsonKiLY5dSOq3MApYZc1UYmBdHy9w521UnQg05I7zWBWsxQPaTCe/eA93nz2mtPkBcMZo4SipkQsNK625CEQjkcW1uJjBKsp2gKTFfUUsCaRe0Eka5VpNy1aw/mjNXGaKLVmebFkPHZY5CFiCwlOTSGgU2Y4daiY6LZHSme5OXT4GCmtxWmFm7wQn1CivQ6JsikwMdNWBSUKQ8YaxdmqROVIDpCGkWgtRVPcB9wqMmXlqBSsCilCvQ/UTiQLyggCFqVonGE1y+xiTDircUrjcsLGID6GWrM6W2LbEsuRPNwyXO4k6NUYoa6FKOn1g5cGFEWVYFSwGzsmf+Jqe0MIkXW74sXU8d76goWruSiX/GK3o7CO1iQm5zBaUxkrD7MQiQbe7K7RtaOpK37+5ecUfeK3FxtyCOxub3m4WLFYLFjWLf0wcRwGks5orXl2/oBn4ZyX+2uy1jxetNRFRT+NxODvQ327aaRdtazbFfGtp58kn8r7iaaQVPnGlpw3C/qx483xU0BR1RV99JRlRaUkvDBNcaZCCXb4DvihjRQJvRfNu5tDXNMsByIbkSWRpFgNkewT/vMrzIMlxbML0uGSU+cpksLuezIZ3VbodQv9RB6kAM39CMPERMKtW+zTM1R3kq1kypCk4NJKiRxUK1Rd3BO38JFstBQBORGzwlQFU444NRdhPjL84jXND9+nev+C8cU1ui2hsMRdJ5InpebgTO5DJ3PMjD97Q/WDJ5SLhrg/Seim1YQpohcVaphlfHPIpGCVIwZHzGI2xxlSiuRuIOckUsndCe2kcQKI4wSlwVvQRYENAbImKARxXohXL1UFxXJNPiTxe2RFGgPGzeei0WSD/E6SBHlGnTBRk+5CG42BppSsoNJRLBLTtGc6nylrmTkXKRO7AXJC61IkjSERQ8DNkrC7e6xCcM9u1aB0kG5Ma7SF+mzB8eUN3u+INjGmE7qcQ1LnbBpynPePGVMK4TMMo8AAosM4eWyYpsCOFdWDJbpwaGcom5J0HOfmWHxVui4EY2wT1cM1CRhuT7SP1xx3HVFDaUX+pZwTKfG+Iw+BKUQ4b+9lYth3OG1jDCrFe7raHSwhHyfMk1a2NhGsUegoEsa47SguVigmIZINE+bJhvD8SmSLuZTSMSShM/oosJLSvQv+zO+CSlFCqbvDp8t5K9I0NXrUqobTKHLKlKEwxCA46YSgwBk9dtUQ9939xoyZiJqNyMXiLLFTSQpWV5WQwgwimJspNRe+Oc/DCzsPV8THpLQhpvFehnYH1dBa8n+wM02RWdqnxO+TQxT/aR9RhZHGy2uR4GaR5GWVZ9CDNB8xRozNJD8Sxh5FlmbmTl44H3bdolYTxEgAEgl1Jw/8ispDFG9zATCTGpk9RyBkSe7kcM7Ke4AMdLLK9xTAHEQarwHt4z1ZLxdW5PXdKPjyCNnIa1YxibxuDjyOo8edL/CHHhUCaEvc9VirsZUl1AWnfU9RWsplTTwNqBAlR27yQjFc1eQp4q/36FVDuV4Qrl6hS4dZVKStZCNZ15L2omx5V0L9zaQ3f0lG921fZvYOh+Dn54+mLAuRN353fHf8Azh+g03RL5lifJuk7qsf/te5vr/l61z1NZ/uLWF7xCuPrhtSiJimhFVLuDlILsCqRrcV/+K9BSFnYsr8T88PDBF0CDz90Y9YWMN7WfHzR+9xe3viNIzomFgtGkLu+cfmP/LgB+cMPbzc1vSHnpgz5WiJo6epCnZlTQ4Bu+34NxbyEcJNQAGnYaSsSsyo3slFwnxTnx+Cd/kaUyc3YJnSCi6WKOji4mBIRuFjorJGzMClI/nAshDkMUpxnQtS9IJMtuKfSlmhohId/pwR0Txck6zmD449GdBGfmkpZTSZ4CdQCjsEXjJP0DIQhHhnyPyLtkYZjZ08upsI+0QY99hGCQY3JuI4yOfdBRlmQWUrQDnRl7vCUWgl0rFp4vPdNVPzmNe7K96khPF/Rp3gi9u3xOXv4Mmcr854FB9ytb3hol6SU6K0Dh8y3w9nfFRuOAxbjFUsy4Yx3PLq9FMeP/yIV69GPlr8LqW1LHAsWwNDoLUF39s8YusHrg87hmkiBM/SVcSc2LiS31EP8dtIFyZeXf8pG5e5aFc8e/TfUOslvc58dvnvSfFEU1TUteHT2zc8XV9gi2Ke2mlyloIq63kKOr8/d6btSMJpe38NxBTl40Zp4pQxmChehawUT4YNv737LbiOvF5sefG/LJne7li92HOxD+TR88ZGdm3APG6o33tA6if861tSiMTCoq3l4rNbzubNRNhP0HshYzlLjpGo4OUHC0IjCN27TJFQaD7//hqjZer+qfqJeILGwMODhsEzfnlN9cEDycO5PmLXjWC1wygNlrN0K/h5JcjlZ8M5/6h7Hz1WnB7vuez+GGImVE4gFEaJbyRnspZwTeZt6gP7fdrFY1JM7PwLro4/IefEiw+XDCrhXMG/3P2A1muiVfzHs59zshNaW/5Z/0MqXZB2/b3Xyh89l/HPCTnA4ZaXbkueIs42fPz4f4NKmY4Db8Y/F9J/u2Q89rOUKpNiRifZOimdBXwRAm7dctr35FXBwbfotuS4G8GesFXJk42nDkeKeuT1oWYfwc7If2bU8zdvqPn+HivGfmU07eMNfteRhsjzyxYKg25F3mPqgqKATy5O5FGkiWamePXe8roXKl1beB5tevIjOAwnLocWpRSr10d+oKRptyPopYQqb7aelYZ2Y/H7nuPnN7S3ie5VR1IKpzUX5W+xbB+Rc+bH67/gzdmRrBW+NPL7NFKgk8HOnh6UlutmvlasrXh/9Tsszx5zsXjBe4d56BUTxXLAseD0Xsuf3/6PkBKdU/ykydh//SHLLyL/3e33UFkx9K852J/DFO99Z/HlBIWTARwzMCFKkS33NSlbn7wdeXA5SIH52ZHi8YbwtufqrOBVLaGfYyHXBiHy9E/f0jzcMN10PH/WECwErfjs/UbM/GO4f1S6MfL+5SSDqsoA0tCMreMX74uPqt2PPL4ccWtBed9hsPcLy/DJUhqyQppLbTRnlz0XrwZ0UaAOnjRvpd4+KDltSlKI/P7pIx5Na5RWPImWcCNDnGWo7xsYoyTKIaXMy/1/RqM43rwlJqG/pRkdfn+Kzn+mpeaL5/9B/kVnYhbkeWLGn+c5f3dugFK+858hm42cuMOfzz0ZKcR50xnRdUHup/ttJPPGW3o4yaOim8h38RcZVFsKtMRo4nTnk4JYaJSP+EOHaSrSccDc+cxiQk0J5RNFKRlQ/jhgSnvvq0v9JF6tw4DZiAc69RO5VZTnK7kGrTwT7fmCP9t6vuh6AA53DfDf9vi22uu+TsvEEOT9VmrerOuvN6jfHd8df4+P3yx97pcdf93r6Vc1TN9osqZo6JNj6hVh6KieVpjCzlMkMQCnQ08aPSlEVusWtCKkJEhMkILteKTSClcUrB9vaJ5eEE4jxhppTLZv+Z3OUCx6xrOK2DjCQQAPpiqAYkaBylZleVazmM3jvk/gE8kbYpzu1/nZR3QlE1CdMvFuCukjtMhKPoMptMik5o+xTqaqmgxhZPIRbUp0oaAbcU1JngLDVjIuTF3Mk+ZR1vVFMQ/cMva8JJiOsO9Yzt/DlBIqiBYzftaIeZkskpJpIg4TWUl2RqMUnI6kXqha2lnUwkG5xs1FWwyB3HvC/kSeEjEkyZ2ZSXldmGhdic+Z7rgles8QPVkplnVL0yw5dXsmvyeEicpGTFlzHEfGsefz6y9xynDDkdIVLJsFu+Oe4eaAz4k4ei7W55TaYuuSl/tbtl94jH3EfhowKVGVFcumxeYMZcl2e4sGvnf+hBA8aE1ZFHTTgMWw1poX+2vOXM1QF4zjJacpoOOEUxkVM42JHKYj29OOIQaeXjxiXbfSpIpKDHnmqFkRkgWqgEzvc8qMYcKiKaybze6Sx6My9yCBDHgfcIWjtQ1nfkFWiit/ZHe9Q69LVNyQ0oE4TaTKMRQG5SdOn7/CblrUwxZ8xN8cyDnwaNdRRY0NoNsGz0Q+TOR+wFhL0shUN+h5ii1Si6wUQ23vt11JdeSUKXTmgQZtLeHmyKDAnC3Qgxcq4tkC11agxS8UK0fvRLoXc0XlN6RgiKc9qrRooNi0gBj6TVsRtydpknImOEeePNa01HEBheF6+Cl93hFzZucUx0pj8Uw60RYlWSW2ZU9XTrgRLoYKZxuKxYa0PYFSTL7neBxJKhKnyHG6kk1o1izqC5lW+4SZomzADr2Y5Z2Tn8tHchYMuilmGWKSrCmnFLGwHKdZiqWcFFIpUzaJRfbQH0jHjHIr0ujJvRTotimFascctZISfhjwh5HpYEiIhDUO03wbVXQUEDV5O5vWp0BdZt57EtBOkUMmxyBTc2NRPaRuxLaZRo0op/CTZNsEHyido5y9cKquULUgpLWPuLrAngLDbkQbR/r8hgZQTlOsGjZ9wzKuQMG0aDgoAT0kH1DOCUAjSyMiBa0mZi9DF61lMxgMVXNBmRZkd0YTZ6lUTnjtcKFm0g22LJj6gWgUx+hxlWa9WXD+coHKsIsVOx8xpSPeHKh+8JTp9a2c57OcWCklw4uU0DlDKb8r14nnVWtF7iPKb2nOF7x0nq4yM4iE+61MPSSKF1uKB4sZly3bjaGaIRPWQU6yybAaXvVz6Oj8HFEQtaKrLUorjE/AKCCE+Xokg7eKyTBv8aSZUEqkgtVNj71weD/7VrRmtIpTocQT45c0nMk9MGY0ijR6gSCQSUnkviklUsoM5kjuR7ppS8pR9Bk53UvgvnrYi4bjF29k44w0aneNT05RMpJ8lGHMnJmXg0BTZFChyWPAntV4Pch9cW5uyKIYiVrgLykImdPcZfDd/T8F8TCIN/cOVrEoSSeRnqOV+I/uaospkKZAnAcd5Iw5a2VzeBolv62wZK3xp1Gyo5pSJMv9KOj1JDJpVVjiMJJaRRg8IXvKRw9BwTFPvE5f9/PctUbzLuyXlFB3u8xvXQe9+/tv1FopJuJ90/lOaqy+WnR9d3x3/D0+/m6aor/N8c1N07dcmxqFXdQkH+iv95RnS6zTaMDWxb0+OJ4Gpuu9NBtOguxMihIup8Xketckaa0olhUgpK/yfIErVygiOcjNwixrzKz1j6eBME4oFLYpRdqkhIBlZpmebVtBriahSpl1I6GEKROOgtOGTHWxxBRWCEAzIam6kyndJZfHREwJs2qozfyAGjzZCIUnBfFHECKhG9BNJc1gP2FD5O526m+PJIQ4ZN1cNG1Pc9p7ngk5Gva9EL/uCl0Ee5ySJIFTFdQPN/dUHaUVeRR5R9r3Qs8KadZYJ2Kem8kMOmeaYFFTorDi85mS0MvOc+bxw/d5PQ5M00ilLaumIOuBz49C+dM5k3KgKitQCe9HLuol5WLFfprkvShrjFbE5DmMB6aYOB1PPFoptLFop1lUDZHMbhrwYYDSoVLiZjyBgoWp8DnRuEoKWWt4v3wCZHx1QT8mYswMMeN05pQ8Y8qUylDVNatCQkJTyug0E6a0uT/NlRGggeB7xVdmrKPVFT4EUorz1I6ZXBhIWjwHPkd8SpRJQUjY2hJzJiuNSop01REue9QYscuG6CTQVCUlErJrSVm3j9bYixXhei80qT4RFKjTiFk2qIuVZGysW9L2iM5z4GQIEpoapJlW8wbzzieRYkLFTFYGleXn9lcHstGYZ2eE59ek2xPq4gK3ssTjnEA/Y3UzmWQgFooIxMLM/oDMlAQ4kQqLXjUSgmi0vKa6ABIhBVRIpLnpiDlDVtikhRCpMkElgkn3ktqsFMYayqoQs7FTGKUhiEwzOZG2MedEafS9tzH1CaZECmIYR8u1Y1BYa8hJwxilqJqvsTRF8IGgFDgjjWohTbxSijhF9LqVc75ypF5gGjlEsjWEOGO8sxSTUzxS1hntLHZRkbMT8lVd3EsS9RyW63fSTI63R/RZMYdkIttla8khEpJCWZEIEiO6cDI4mQyhk8ZMG43JCbtpSDGDNWRnMXPYagwR1zjKVSkN5nGEkHCLGhM0xih8EPKZsQYfI64oRCI9L8NUzkRj0FnujxSFNCdzNxgLjQ+TUBetIS0rbD+hOoQyOEW0Mtj8ThKU3x5xZ4/JzyMojcpglJXSMmT89YHiyRn+5S1u2QriPjEHuGbSFNCbRqIL+mnOwZk37v1EmgLu2Qrd96AEOU3O0gDMm7U8ePR7KxgG2YCpuXi9k+tpySLKSa4FNRPguLfIyjlNEgJozCLzRSkh2c2AITV/rEpzsZuyhDwrkZsJxERIk2n2oeiZmAqZnALZGZRRxCjy56wkvPtuw6ByBiuBvYE8B7hmUgj3j/D7/shZzKoh7TtpWvJMmissuRuhtnMwr3iAlNIiTZ3JedJEJcJxjh0IUVQWepY2KgRMk2YCpBYokDFaGoAsvXaOEaWMCEcnj6Ikt6WAXdQccuvD/PqAKWAKh7ZWPGlJzcOILGHrSpFOE0rJ5ttf7rCrFlsVqNIRbk+opriX9jH/LBozNyZ34b+zquSv0Zj8tcNW5+7w3RZubobumu/83abou+MfxvE/X1P061xjX51i/JL7wWYXeTJI7sXboqIrNMPNgQ/PB5ZmQpUFpjWyCq81X2xburd7UPAHKpFXDlsXbGvD0c5o6Td/Jhpx7uRtiugnfh5KkQ2hmUIP1mArSeDWhcFMlTxQrHiEwuglp0MrmW4qmd4qo3FtSxo8nAa8l3wGqzXKGXSaQx6ngFnKRBwr2FpSkmYiJawxhLdbYjcSSBRNJYV1YakerkFrwjCROpEk6SQFkiqt5MBUheidTwNqxvTmkNCLijR5NJJHoktHuDmgrUG1FWn06EGm125RYVIWk72P+LdbQTcXIqlKg5eJdyXhoHfYV0UmHwdyYYkKirpGmSB+JluCDUwx8P7mEe/1C6bLjqfFY7rpDUwQU+a3pjNi1qSrnm76BUOAYegpteONtYRUcL78fW4Oe56c1dx2f0GLZlmc8S8++T+hlWEyjiJKszIomSYuqgVeZQpj0TMxyM4ylWznZsYYgjXo+fdpB0seA+MwQA0+ibRHWcPN4cR5XaK9+H4MhvfP/hWOYtbKM3eZs1xOy/TTmDl/KGXxqMQkhaqSTJLb4sh/3nwGZB72Lb/r/neknHGqEGRxP/E9/4TH2wuMj3zefMlPly+AzEWyPNkrptsDbzcFh7UTeUjvsesGpTVvPl7zdhSfzgeXI8Wxx9Yldt1i2orifMEnb28IbztijHzxYSuJ8BnJ9bjzKSiRZBa55uP1f4MNsLUd/2nzM5KB9VnFs3ROeHFD8fMrfjCdk6ZE3ArpkJjo2sD/7fGAipF28Gw6QcS+9T3795YEU5GPPa5ZopRsUFI/YYzhuXqBMW9lm3Y2oeyC5BO/73/IeVwTuoEfNZ/SL4TydEoiV1FKBhM5T6Q88cXtf0DlQDagCoWOCeta3lv8AbYsyH1AGYMymrp5wPfafwPAYXjLm92fYoDWPeDR8ncgZQ7TK64GkWiF7Ofsm3kTMnr8cZR7XyFF4+vBcjOWYvR2Tnq3nGcvRSB0I2GYyEpTrSrcWUvpkkTS3AgePYTZF1ZYXKH4aL1H5URqJEMorxLD/sRnu6dkYDdG/vByIGfF0wX873/QS1jnOBK9hKu+HSL/z59v0aXl984i//qp+GeuTgW3YSFenbkoNcuaR5uJpTlBTHwxWY6TJoXA5fQTrv0vCDHx4DhwphMhRKzVpCnIsCVljDOEFHn+XkNg9mrMNM5TGfl/L3+MDpnw8CBDnHXDaqf457eP0Uqx8Q3/5vr3Cf07zHBOiVY9RBkpzBfVEz5ya7Qx7NIrrt78hOp7jzlrP2az+T659DTHX3B2eAVWc+ngL9ZQ/O6HXPzJaxZvj3crYGlob468vyjxtz1xCnz58ZLRiczzi48WqARoSIsSgpfnjjb31EfgvnhWM+CkVIrvf3a8f1bKZiXTN5ZPv79CLyrCOBv8U2a5m3j0tv/aVlqlLFk/SFO0qT5mXTwDo9kWz7lVW7lBpbsBR+Lt4Uf0cSvhsMMkjXNKhNjdyzjjnVfHaH7xQY2uKnRSnKdEBQwh8e+fHwgpsygM/3TdELcn8UXODZjK0tyR5wynGElKiT/nXj/HPf6cmDB1STz0pJzgfpyi7rdQCml+8iznu/OCvXrW0FVKNo5KgRc56/s/22KT+L/yFEhWoj0E0hQpqpb3Nv8KNUGwE69OfyzRAP10HyJtK5FKq0I2XWmKAmypC6IXgI2Z4z4AXo+G/9fnO4CZlCtfR32tEPpG2/MraqRvHl8T4al3fyn9151c7ivF1zf9Xd8d3x1/j4+/fVP0q6Ruf5vjKxfrX/r6X7n4TcwUXh4c5UXLpCMqRdpFYNGae+JZcoY0RWle1hK8WDPAOJL7gUPM0tw0Jbrq5sZGfArJB3I3Ms5kH6UUpi0Zdx08XIv5VAkyNR0HuYFUDsZA6mf5mU+EnLApA5Z4cyQOEnBHBhWjkJ7qQqabM90m7jqCDyLhQ6Z349Ve/DiFRZeW4uycqqmEduNEcnG39tZVAZuWHBNhd5LprjVSRDiDWVSzXC4J4rmYG69ZkhKGiTRM6LoUCtDtEWVnY7NW2Idr/NWeeH0gMYfnOQtGJomSK5JQhwG1rIkz/ccaIw8OK9P1u2W/zpkIOOs47G8YQ+S86Pje4hGXhyt+ev2G7589wCXNby8e8/z2GpstJyZOcaIpDZXVTGHAB8/QnXhYL3F54tBdoYuaolhRssBqQ5sVx9ATlWIae3xOrOoFrizugxm1lyZO1SWjEviBMZo8epKSZsVPExSWxi2omprCNZgUqUPBw82FTH5TkHwObXCppDDNvRZez1lP3emEVoqQAm/8NYuqodJOsMh3ORtJiGKTiuxtR8qJlWswuqWeyVRhEh9bTYELkgVkioaplnM/v+zQNwOLiyXbdUUIPUYb8nEgzgCFKSYojQAxBo+KiuysNIYhYApLXVb4/UgcouS0aDFwpzuJUBKztshcDKVdYrXGGc3UFngi5nKL0hVmVZNuDpgvbqiebBjKQpr800RInhsj2ywzTuT5ugpKcxhH2cwamLwnIptesyylII89mWFu0GRTovvAamxYnBwxKXo9si8EDa7mHJSMFIraGmxRws2A7zt5Tc4IvABDVa6Fhmdkq5ymgFEGV21IIeLMUc5uo9GmpCrWKKXo8w49KrIx8v1ShpikECydSIZyhsETxx2nmDjN+TvGCsBAL2rsqhHIwflStstGJvX+5gjaQ1aMlxBNiWlLkQjN22Y7dago0+/YTyQfcNoxRAPG0BN5vT2SYmbhLHWZUAUSHKzl+piy4jAJMS0aaGsput0Ayos0WDKoZCtRmExlAikFiqrAJJH3pirhfQcxUU5BvGxZYwtL8JlivWC8OkgmXWFk02AMUYvXUmuNLg07fQIHU9ETJo85HCC2JB6higKTDYupIudizuGSjX7hHdOMajbaoq1s6HR/CWTC7ZFi9ZjSV7BcUfUvKLuAbkvUumCwiv7yloeP1uTrd5uklEVep1/esniwZjjciifIOtCaqbKzrEyhbg6YRU049IK9n8mpOWfJ8EH8M8xemLILci7Oz6acMmOhGRsnSgU9Py5jwvhIPc5+na8Ev8Yo2HqTE4VrqO1qXroVd/X4vYIi54yPHcO0g2kupEO6z1DTWqGcFciEk/ywoVSYSmOiIgUvz+MM+zHi5wgC86gR7HpMkMVbi5+3V6h3eUzzJirN/iGlIFsjvq7JyzN13ZBvT9II3UnS76IOlEJloR/mGYqhtWaa37MEGGeIfSafN4R0g5kle8SvwGzmvCGlNYVZYErD5A9kH1AaAVSMQa63kAhTJA9eQo3J2EYR5k4kTh6oUYUMQKc+sx8FNvFrl1V/DXXbLwtwVUo2dHLOyLTua83nd8d3xz+A4/8/5XPql/zvbzkCMM0TtATz1saSbGAiQBBZEkVBLhQ61phRChBbWMJpwDgrNKhhEsKMVvd4YZURatSs3c4x4OoavWoolCJ1I7mTBytBpCw6ZfIB0WxPEaxFNQU6zgngWW6opi7BC20sKrBWSUG7O8kDRQtkoSgl/C5NouG2m4VIqGrRKKcooYHkBMXXf6XqTsZhFO5ief+GahMkIM9H0TiHKAZbJQ9yc76Qh1XO5DGIcdUUhHES+lFT4BY1sRskGXxVSxE3o5lVIZKbPEwiD7QaPfoZG6WF2rNqIEZMlDR6PeurnbOEEHlvcYY1JSttKYuSl2HEGsfVcOT7m2e0heOD5Tl5OvBGVxRRUxQFu6FnGgYeLp/xyfoJOiRO+sBZs+Q4dCw0qOwJ40jOicJoppRoNDzfXuOHI482F0xkGEecsShXUI0RHwKmLJk8hOBptEEriL7n9nDNqlxCmDB5gBS5vb2mrqWs0LNHKJNJORJTmOUJszTKGJwRbHEZNIWz8rB3BmG9irTEWXdvgCciD/k4exSUSJQygNVEnck5EXIUup7SpDvKWEiMtwfKH15gr+eg4ZzJxx6chX6aJVIio4k+CqktVihnmbbHe5/NXYFx57FQdwGydx4oLcbpQESVhmzN7IuSgnZ8cYM7X+DOl/jtifB2T/F0QzBz1ogKM4lP3q98551JihJL9hDQ5Bixzt7TFbUxc+Ukk+4UIgx+bhwHQnIkk0Viq95NSyW4lvutVwxCSszzwEFHkU1ppcjTSFKGaBSYNG9cI3kOGCYEtBaZnb6bxloBSMjPNv8/xbtib5YzaSXyxpzv8qsyCsGRx8Gj9gPjlzdyTVmN27TYTYtZVtizJYWN+D6gbwzdzQF9FACAqQvswqIfN+joRRK0qJlujoRbj7YSlGqMoqwLfD/BOEGuAIVtKzl354JRmkSRLKlKPBe2LVEUcxinJ54GofRVE2qpBNPvLLl05ClSbGqYBGuuyhrXlITTyNRN8nMtaw6XexzIhF0prDHEjGxgjRFq2BAwpRVAhJrx/ymh6oJIIvhJtgRzYUyMKDsDTJTcc6OCdF4LjfEYxGvRjyQ7a76miNZGJHZdxDxuBZaTIF0eqT58IpLQGaufYpwzlQRmofP8u0wJpSGi7rc2avDYO89Smkl283mgUWgM2lhyitKIz9eymbfOeh603CHbdRKZnp6lUDkJlv2O1KiybKJV5n5zIhuVNEt8NVElPBIxke7WCsaI5Iw5pNbcEe0SxlhyVBRFDXEveRgRGcZ924PcGckny/OGPUZRFGiRhpumJJ0Gec3z4AXkmaxSJg9elBRzYK5uylnSNlMJ755tag4Knv9emoD5vZ+bJ10VZBR2lsDBfB8go8YAdYEa5JrJWpH8SA6amDxRa7SBeBpBa5Fsh3ngqRWJgNKKOARSThRrGWiEfoDzAoxFHTUOuU8kIL7bFf7VBdFf5/hLjZS6XwhJLyTn3VezHr87vjv+vh9/+6bol10vf9sN0lcv2F/xNf79OPKHk4Su/eO44LEy5Jz4Hz413AyJ+znX3Nz8wcOJRWFJRvMfLgdOY8Qmz7/+cEUVghQaVh4yaSZtpRixdUkeJlIw6FIyO8I4yet0BttUQoKap6fMOvOwPRL3Hekkk+poDWoQqo1uKoiO3E/YqiAPk2inFfcTsRgjas5nUqVDNaUUdT6IV8doCVabBOGrngo+9utvpcAbUpSJXrg+CPI2JEmkn4uWlLOQ7pY1tqmIUyAPE2bVoEvHqph40p4gZ7ZTxduu+co3yYIYtoY0TISboxiQrbn3B+R+mh9gI6kq0Em2Hroq7pG6efSoQnI16rYlh8ib8U9w3tA0geaY2bRLDqnnxfE/iRxhHIgkTFGQrWHRtCRlyPR8sf23HMYOFLztrimNwx8+5/r0hpwzo59Y1A2DlyyMGANdcHy67XHWYjMc+xNN0/LkwSNSaXGqxBaOVCtOVjxU1dmKZ/33iDFzOf4MNWbGYaS0CZJC36GDrSWrxIvd/yTFtSp4/+xfSer7XWORM50e+berPyNq8Xvp1qIKx+ZY8q+2PyClzANW/JvL38fHwNI2FGbO65ohIzlnPi/e8uP2BQoY9TuqUI5JfoZpYvOnb9isatLtiS8vHPvWgA988Kqn7U9kq3n5uGGqLbou+fDnW4qUCFOgfHaOvz1JcWfMvR5dzrmAchZ8QlvNqQr83y/+RE6XUia/KUlRp60hXB2k2bHSPG73B96812KerRn2p1l2CbcXJYeloOE/6p/yz28eQ8786eIFn9eXYl6eDdNazUbzuzvBTEIMOfNvNz+jyII/7+wkzaSSDZFRIr4xWolvJwfxg2mFsTUfnf8vUAEGf+Kz3b9HmXn6Pvv+lI/3BUZVXfDJ+f8WAM38/VOSQnl+XQnxE1hmmWQIKGuhtFLwzdSulMWfodEie8tZtmRzoGU4DMR+Yryy/PS2pFyLL0ltNBaDTjIJ97cnutPAT2KNrhZS/NQF2S+x68gPLoSWN5iKwmwYdx2bOkDyc+edpNGws9xpRu4rA0qleylQngJJZR4/hnOTSOGAJpCiwRSWH99O/PhljzKa/8MngQ8fJjGhM6HtSD7PfHbdElxNTonCGrnXacVHX5zEZ+KMEDfnjSvMhfIo/qGYEno68ln6d2ilaPw579W/Dxm6cMvr45+QnGGVH/PIfh+qgi/1G/64/RHKepbDgUe9I2vJWGJutM+a77GuPyTnxIexIBwlRNykgE0l+ocV/s0ObTQhBt7s/4hxe8I93vDB82tpZuaNapyJm1opspPnj2LeVua5KVJQ6pZPNv8rFJqd7fh3m78AMnXn+eDVwNyyyDWoFcuD572XnfjWJsnfyxkODxsuz+Q5cf624/xmFApaIddLnrORUAJ1+S/Lz/jRTH5/0h2pp7vIgBkTrjVffNjSW7AY/tf736UJBWN94vLH/z0oGWipxTvJ4lcf9LqwuLbC3xxReqbMcTcEkA9T8xBBPkEkdjnme2orGXl2D16ek714fJnlgnoOhNZKfJ33Yc4h8d7LjqSlq9SrQDr0VKkhTjPUIyW5jygljdH8ykMY+fz238EostqE+C3xClNaUsr4YcJYC0kUIZkZHJES/uaEWdfcdpnRtOjCcN5l/i8CpuOPpok/9NPdIxalflVh9Tcsur6iylGKeYgkf/4lmd13x3fH3/Pjf75N0d/k+v2WFXGXM92sj/Z3zUhMbI+eW3/39WVbohVQVZjKQMr0MdNFcNag6gJjK8z8TfI8icxBpmU5ZSlQ9ExXc4a6rSTU0s70rXuDCDAb5k1Tkh+uCbcnpt0R+lFkPKUj7k5zflKWKdgc/pe9h7YiojGFk4DMQiRpxEQeJvyxF79SypJHojSqkamsfPv55whRYAqHQQrhppS8kzT/92FCVQ7qAu0jefKEXUccPLpyUDppaEKENGBdL34mXZBDnKetmTxMxNETZy/HHZ5ZWSmws4/vAvNKh3ZOCr0QyCGQnBUzbsrEUXTqefKQM9YqUuPQwfBbH3zCMI44rfEI1WuKPTjN0U80tkEHj6sqQooc+z1dGKirhkerCzKJm9OeyY1CRDOOwMTJH4hknDFQKs4ebGhWSwywHieKzQLn3PwgjvjhRB4907x1uDN6m7ZEPWxQSlHmmtIvid0gnohhIvuZSJhPxJxxWkiBWPEPWUCFRC7gaAYCEQioaFDe4uxawjhRkDUbFsQUSEGaHmfMfYOplWLCc9S9THSzvs8jkcYJMbHvB/JhxJWWYlGjraBzzRQphiDFoKkYrMLEgL5YkvpAebbAlI7JDTBnDeUYgNkMrSDlhFFapJkmc3KR1NayxRnE8BxnyaRCZKZCxRID+mBABTF2Zy++kqgVuZTzy+mKNtaolCiCwFVw5t6EPVs1SHc0Si2vJYVEbyZGo+//jtnvZkon21crUrU431906VCjJyfQscAYSxEDwZ9IQTY4OWdSYPYWimzQxRWFbb9+/zKKNG+CU5ACiSy5Y9QOXdRSEHeTvA4NJqpZVhdmdLsU1Dkm0ly8aWcgykbs2I+crjrMuqFoK1xdYuYQ5eQjqRsZdh6rC3AGPQKuxKiA7bcoMsk4GpWpNzVlPMr5Pw+ZMnPmW0IyoPKdf+OukM0yWCosRWmoCg3KkKPkRSkFQ8wcUdIEFIqqBJLk+Li2ICuF6x3Ry72kfrhivNxDjNTOzbKpQNkWhMlTNDVp8MQY5P1tC+JxIMVA0OMM/KiJyJZkSoE+deiiJgwncivrwklFjvFIcIqq0dIMOysNg7PonHFVI81hTChTkrWEXUYd0JPCqgbbyjPEmYRivo9OnrqpiMeRjAyiUpLrHjLTJCeKyRJnkFIWFZhSOJNxusZoh7UZXztyjriUZ7WAeHHy/KeZImWYc81grnoz0SjBghszQ1dkIKUraabIat7JiiRvYCQ7JVAble4lfdpIVpDWilBogtOQDYVtqFJJsooiACngrJAP5dl0t4adr4dZcq5yJs5bFT0/D1JO6BjnNe7dH1matjuwgVIkPTc+k4A68tzkvPu8+U8lGxGV3+1eXJjP65QwQyBlhcsCtsDe3U/yu4FTklDj2A9QZ0IYACMDi9rBzQGcFYnr6AX7PUMTZCglm7BExlhNmDSnU6DAUmbFet7WVUrfvfy5rlC/omaaH0J/3eNrn6LelUxf/bLfHd8d/0CO/981RX/dC+mbm6G/wYWYx5H+xRbtLKYbsVFoSDEJUco6Ma6KxjhhUsbEgBoj/voAURLBbdOQp/guoNIa8Q1ZeTilUTY1urDiCdKCaM0+orLkAeWcyFnkC0pr3MMVZtXg9yfxKCFTo3i5Q5UFxfkashRloe9QTrDC5Cx4UYBJmo48TDKcbSv8MIlUJwPbkyCJ6+L+xhv6SQAHKaPXDfZiCQZCN80BgxNEg16XmJTxr3pyGNEnRT5bwmkkaIVb1qiqIpmBMAx4AtPVXrZbc7hnjrN8LjPTieR9SSGirKXPiTrkOVAPMaT6SHZa6EBzk2XmZirOORN59BKImyHVBU4QTCKNSoISPgw9U/SUSrObekpXoFLGFQXWKvpxYOEqklE8XF9QL1smA6p2VG3DxhhM6UQTbwyERDh05MFTu4JwdWQ4jVLwzXp8Y4r5uS5SHGIi7QPTm05kZ0YRKoVuCsz5AjsHsWYfyf3EeL1nHEe6cU8zm1nj3eR4Gu+R1hQFLmi0B+dFxuJLg40R6xVJzZlSSeFVRjvNmCeRw5k8m5aZZSTvCo1o5N91NOisyEHh9z35vCTFIOexEmT63fWYfGB621Gfb2Tz2U+kqz05RvR7Fdk5lBcioTIGTSYpwBmCDxAyJp5m03Ge5TqSjQFS2EU/SaOiW/En+CCT6zz7fe5vFxmfPKGQaa8xhpJCaGFEkp4/0EiGisAds3h7ojSnWSlyjrOhXd5vlWZpYkpMOmAqiw+ZMcyesFkWmBVz4SVULW0NWpdzbomQCMW0AdPUo62db2+ZPGWiH+VeEEXClK2RiXQ3EQ4yJNFaz9dylgHMPK0OMWAQqRR6JvTNU+9wBwcpHcon4qFncBbTlJhGGiBlDdROmswxkHuZRitr+P+y9+extqVnfT/4eac17OEMd67ZVWUb29jEzJBAAyE00GqpA0lDI8BAAIWEBJADiAhi8A9kE8QYZKIQJAcLY0LiplE60GAcDLEJJjF2PIFxzfMdz7CHNbxT//G8e59b5apylW3A+aVe6eree84e1l57Dc/zfCcbB8Ksx17YJa6CWII7cbXz64CeVKCErgUKaxSNSagElZX9EVeDBGnTFEtm2T5VadkPBUarq8y0kWaVCkYnlsmVKfVszEK1RRoEKkV18x5hDEQ0fj0w2ZlT7TSyX1EMOWMmZWijhRqbQyKPHp3BWEM0MsxKvuidlh3RzhkJ6JRIWa7/TimquhIr5UVPNpFcZ7Iz2yIXq0kqkUw5RpUGpQnHHUknchKXxOAUQWn84YrZ+TOwPiTnTGgM7M8IFw8gJ8YQyJWVId2YZVCnBbExWuisYseNDOwQLVsu1DKQYFKl1dZ1TWU5D03joFhGm5CBYm2tJCIipkgMI1RinoCSYxAfpDEBUpQYAAn61ZisSVmhxyQ+CVGuXzEpTKUwxhLSQMoZv+4fN6jcCvqzBLCncp3RSgYEWeXt9oVCp9NakJ9UUPFNGrttKnHMVIK6bZuesg8KXFQoyxS9kTQSqlDHstakzpNsca9VjqQp7npBAne1BuT1dOHc6qIvSimJprCtiesR1VbUZ+b4q0u5T4eI220JR51cs2MmDYFqp2G8ekRcrYmDgWpni/4+nr320Sh0n4AO5vre6rmG6Ln1v9n65HCfeybDjSd9zOPP3AvtktvVNcLg2T2qGVYWrRRXThm8tTLXfOgyXZkk/41xJOVEzhEe9YwpUdmWC+YlaBzaqa2zjh87Hrj0TkiiAdrQGrSzcqOJiUna5WzzYrSzrMJFHjt8n1BMdEmYn7fUZ3dJMUkWzLQRA4PKMos3scsFslVc1H/GcryILYUjfiRXVlAiH9BtLUXNGKhUMYNQAvErlFD1QOxDvVDrqCzpygKvFeOqh4S4xrWVaBFmLdkH6gv7xIMVcdXhLx9i9+ekwxVJaw4ORq6tM/0ikPMBoNExo+pKxN0RobOgCFboLKboS3LRRWCtWNBG0VrRVlI3pigN5uhL4ZvlXhczua7wIWCNwa4HublMG/IYGHsJnN2dzfFJiqD9yqELz92mTGUdpp2Jxfakotqfo7RimhJJaXHuWnb4qwtcTKxiwMUs7numWLw6g6qc5GMUetP56acwrc7LRLrQSDJZCrAyivyv8w9w5NZoFbn93iW1NphJhd2fMdk5z3BtycOH78J1gnx0fiSpjJ00jKcdOmVmqeELli+FkFjZNW/d/VNUZTgb9/msg+ejx0jlpAhEwYP2Mu+e3iMaGiXFuzblhp1k0njlwpRr52QS/GndndzSnQajuDa/h1V9VJqDTpATLda1UKh3Q2B44BJ5vQvzFjNvSYs1uRsx04pcO6GzUCgfY9hOWlMZSNCPUlMaTV9rPnyb5IepmWgH0mpATRpBEHZaWHTozdTcSGNAStzVPsr9zUUAXtjdzP/16svBav5nezcP1Fe21sgiHE6FgiJcfV3J9SEByonDmSoW+EopQq34g/0Pbouo8fQEUmKWW553ZNFZkSiib62o7Q437Xwmm/T3YijIqrvCvVf/UOitpcJJKUGWibYqDVj2USyQFaUgEvOWrIolsj45xvRGD1Ia7WQ02EJpSptCE7HppgRUdiN+0Qmyq6QBMm2F2WnRs4a4GtC1o1/DXfkU2k7JY9yK7YdU8+HLGjNvmbeBG9tjckp8yhnNrbtKAqxnFQyJ2HtOzWC3HRmXHS5OwVp5j8rK9Stn/vYNgS+8IM5cb7kbfvtYo7Li770wcutZhTKK22/0pCzDlzyNovnJirsfqYnOklLgFncR5xTROO4d50SEBmZqh5s1+OOuoOiJcX2NB8e3E7QiDgPZaGJlOeovszj4Q6wxjDnwKZcD1bRhdtMOK38VHwKhNLFZqULPlGP4sasfYDU8AsAN05cynd9I9oGLi/ezHq6QUuKeGy2reo7B8MXm5ezUDf1iydvPf5jlWUveyzCOhJypqpYvSZ/H5CigRhkYSEFf/uTSBKcs194CIGitmXnFC+9bSb8REzEKkqMSpCGg2ordaz2zI0G2dNHf5QxXjj7ENX03OcPxOY3abUkhcuOja3YWoimyQYYwpnXc3L4clyZyH33kXYzxGLTion8nF3MuDnQJE6QZiZ3ce06WnA85JmEYZCEApnLfUEoc4cRau5zLwgGWfb/RE2sldvReroEZthbeKCXMhEIPz2VooLISpCuJrb9FXE21FSOV1AVumH8GlZuTc+DBwz/Bh5VsR0GPUMg9wZotcpa6sWigBqG+Vha3N2VcdtAH0nLA7U2FSrk/BWuY6Y5z51c0p6bEaxXxyqZh236Ej6NPeYpnPl3z88T/fwwA1HPrufW/4vrkNFp44on6DE/IauqYnppLxsklxzCC0oq1UwxkaQ48hJXcYJqcC1UHSCVtm4gNBquEKqc86KxJUW1pSfjiWqMUOXp8J6hL0+xQT1tUUqxHKRJALtjRR9JxT+w99YV96nN78rt+xB+t0WuZ7GZt0UqKpLjssPNWKEkjckGvndDmFt12EpobydNRxfFG6j+hOKjKSm5KFE1LPO5QWcT4KWdsEncjZTRpEFQqkKSBGD2piO7dmR365UCKQBa3JKMVZtZssyVyBhWTiIazlwlbGWypmJkkQU1STpjei7Wvs9vvOg8BFQKqrlCtJKkrByllXDkWuiwBpaof8FqzzIG9eoJBsU6Sc9S6Rm7SY4DKYOetIF2mZCyNkuOUx0Bcj6yHEZcBrVn7Ea01xjgIQcaeWexYNwVoVpCtRZsaaydoo/EpoY3CZIhO6CsYCM4SC7c8hkjygbjoCFcWgh6dmlGd3SEcrwkHK+raksdI36+w7JGcQQ2aNjgMml551mog+8RObDAKfEqoGOXzZfBEOjViNjSyLHVI3iAaShFqt0VLFBZXSVOilZFjKIOyFq19scUtX5NS6FmD8olx2RGuHGFO7+BuPUu0vSA+WqO1JoYg1DldZvgxY43eFmDosi9jYnRCt1ODF/pbpdFZpuAMXpzFAHQWauYgQudkE32ZNuteM8kNRIXVrlhcCzKGkmN8I0I3qhQ1bBhFUjjmmERHSEZp6FzYnmebojREUzJQ5LiNm21TGmcngjcZOec1oNGEPMAgr21U0UBohUK0VbnQmlAycDFGaEzZXzctLpQzrRQ6JcAWXVbahgGr8jobO2BtLDln4qaIVkp0F+W7jL0nZXBGkxpHXgsiO46gl4FIxtaVoItak11LVoa0EafEhLMJZzLMLTlINpk1mug9FrCtxrSOcLAs58VkO8mfNFpCMWvLOESOjhKmccQhyme3BqvLwac1ycrARAU5DmrjUClQVQpNgKQgRBIa40R35nYm2CsLspUMoYFEYITOi8lCXQrmShOCZxx6DLD/whuodif0jxwI9bg4wSnY6idjoVL1aWTIAyZlGbIFKeKjinjtCSninSPUhpQU8cBjd0/jenElHZedUCSbCgCDxY4WU9eYNG6bZ8mRUcSctjou8fOW4zqljMoSlqudOQmZLdfYFBLZaKzSW1fNkDO5cuLk58UVUBCvybYZsUnhfNrqTBIZfMRMK+pqTgqeKkAs1ulRCQ1WY9HGiCOkgnHVkWJAFHsnK67F6GjjsMrmelVMIrZOclt9oASw69INSqBr0egpQW02zbwqaM4GZaWcrwm2YUmqssSUyaYEpCsxArF9Q13PSMkXZKxo6IrGL+aMKlrHjclDHgP1DacYLh9hUmZ49BB3bgfbVPi1J4WELSwTM6moTs+o4jFmjCg/YqtJQcyeTTLR060nTqCfpK16IlPniT97bj23/jdZn4Cm6OM8gz7a0572ZH38yd1HRd9MoJmSbm1Qe3JxnZ3K1A6hJ3XiloNS+HEUTcPxkjR60mJB0D1jc43UzEQUnRH3rnElVDNbhNjWELqRzSWanElmpF8fiagyR6bVRCaiVhF0pF/2jJePUZWlPj2XosjIjSuEgWEacSqTVZYb+gbytyJwT/1IXnbE1bD9XRwH1KqXC/V1WUObTAR0JqNPOM0pFnoIRfhvsNOGtOxIi04suIM4IlFbcsj4DP6By6huwLa1ZBCNQRCTUQqnFBKucSK2FrEHtbXEI9HeKGMw84akNfgkhW2hcRkjtCHtNOiqfLWl4TpYoAahJlE7JoM4kAVnqScNzakdoW4l2I11sQvPGOfQ53ZRTUVedVLEJYSisRpJg99ODCvAFic3ZyqG6MlaY021tUwHKeBTECQnZxEiq0Jr8dFjUBhXEcOADx6rDE0yjMHKUM4afBAjj5AS+mhFd21BVTnqm09Tn54zXDzAnZ7JDbUTK3aTEoMNWDRBRepgixg7sxwWKGsINgudcAwEgujAipuVydIkJ6OJlSPFiLai51HAaCJ9HIg5481J8RCMIlamDAsgGi0Ur9tmVHUjlK8rC8LlY1SIVLMKnC4Nd3lO0dZRmnZAvvsSgrgVkxf0Q27ZCmWsaGQypN6Ls5az4mJVCs4NVSilBCkzEuiMiN2jOblwbGzCc5lCS3O10cPkbQaLsYZkTKHniHGIQmGK5XNKgjSllFipAWsMQxwJpb4zFjojhV0O0JiqZHNJI4gxpFK8mZLjJRcYto6Um2vJBgXIldlm8GgMWlmyM6X4FndIH3pBLbTeZixKhJFQfVIpZDfOXqk4j22+5zR4/KOH6FmDPbsDCvzhCn24JMdMbCv03hRNxhqFygFNQX6N6CkxUijKNQeYVNhyfcsaEoZka1TrUJVBJYkE2G6rlw5TN+4EMQxjyaApAyqliF6OqzBGjEqMo8c6QdI04jan2wpTgjRN8ujKUu+39IsRncGRid2IL8eC9lG+46xw2RG1xegs2THOUp/agV6Rj1YQIqt+Ibb8uYYoDoc1Bp/shtEmuhNbGn2tMa4EfiuDBVLy+LEjKo/2CbvsZRijJdS2joYwrhiTRRmok9AXjdFiDlDuO9koUBqMwdq2UHsVupJjWJlM0H7LUjOqHFvKoJECX6dEdeEc2RrGgyNYr8UkJWVMFEt1fBC0P8lwgeLql5HrX7IaU0+wsZfjPAtlUFUOV9XE9VqMfLw4mWKf0BQtOjTS4KS0oaOpLV12O5Qp8MbG/ltmC6UZ8eKYqJzZ5gJqawuSqwsjQQxmRAtWbMwzQi9HnGybvbnca3MmKo9PPSl6uQYYQa60lrwknXmcqygbxK6Whjxled1w+Zj6/B5uf0pc9oLqa71lVihjicvIkDy61izL5/ZPKJDUdmc88V/PdD0JWnTd/n1uPbf+d18fd1N0PQL7CV3PHiPmd++G/3LvBo7vIQvE/jVn4M4dIMH6rgnhIBBj4NKFmuA0PieZ6lpHCpmHx/eTu1zME6SYjeuOGCWrxRbzAx1HQRy0RlUN69VF7huPwBl23Dludp9BPZuxSBe5uPgg9aRmWGX8Y4cAuJ1JKYoyV/t7ODaPoXzEq4CS3DkpqjLofZnWMsnQe/TuVG7AB0tiSHQx4sZAMhrrrBRihaqkK4XSDsZASkl49WMonOok7nUruVArpaRgBnTvSUrss7UHp/XGWRU3b8gJUjfAakB5D4MjaY3Zn1Kd35eCa9nBrJVibBjJwRdNS8ae2aE5uytGENcWcqMotrVpXGE2E/hCV9Q+oHen0FYYo8WNL2d04fy7wsHOKUuTt+4J/Yhxlnh5KdoIHzbAgYhci22qVDJyHFXacmp6O2faO+VxOW8nxBeXH+SwexBSpvcjsyqjs6JWVvI+vOfho3cz+EMUis+Kn4WyM5TO/MFN76GrxlLwyuTThMQddy/Idz+GO7NDfXaPvB7YueUsL3j0Gqn3jM2at935XoLKzPuGLzt8OVYbLuoD3rL/HrmxpiT7QylBP7VQpk4fe84fBlI/culMw+WzDVaLZgqtSTHywekD/MXsYRIQKshBCveHb2jRFxrQGm8QJNMY7pkZlPZUIXHLYoUbPPq44/mpJvUdA3DXnhRKqtA+ZZJaGp6MDAOKlfxWO7zV9ZRiG7ai7KyF9oItjlhD3E7PtTFkIn8xeYh7WqEw+Qqhy5amY4OcyESj/LwIsZUuFJ0ydd7kg2yc62ISRCQpJOTXeX7/7AdKQ5WI5+aFzqP5c/1ecs6cGeZ8/tGLpPmoLaUfkUGCUqRxLE6Eio31bYoius5lsp1VCZ1sHTElzrYvZteel31XjvWUMw8dv4vV+pI0bbDVNmhrCbns+zIh33Bx1EYLSSkuUyYuemI/Up3dpTo1xx8sUUaaQLXqmewZbplcQ1VGUMhRTCnIgPeCUhT0Ig9eLJFNAqO4snRc606TrgVuPB/ZM+LAmVIS45miSSSX3LKQ0VPJSrrvaM5ARYpZUCAfiF3PHaeOqfblem8tpKS3g448BJzL3H56iVaZrtJ86G4N7YS8HrBGo9YDXoHSMpiaujNcmH0aOSVW6wdZljDS3eYWdm67meGhq1w7vpuHjt4BMXF658Xs79yB8oFT7nZONXeiUsLZSkxilCuUYEE7bn2kIyJ0tSu8h8vXhAp6wzUvQ4SouG3/ZVTURJf4o90PMOhAmxq+9PjTcNkUp0aIPghoEmWA1banuePMnTI0KNoqlTPLcIlHl+8T7ZtWopUNidPNzZye37nV7hjVkF3FRf4nC/0gyRouHHjOH0dSZTFjGVeoclxuzpXakpwjHY+cnXwadgJJJR48+GN8XqNri3VVoZtD9F5Cc+ePd0iNq6FY9CPbCcXmv1DHijV4LqfwBrHa0MpU+RwohWoq1FoCybdDuo32RxXzhIImJdhmgykr2sp0uCICfhh56PhdpenUhDySakdsHHVlSRePMOpkqKNQW3OH1HvZplGQeUXGH66obtjHLzpSiGSynD9A6lry0S2EI/hzq3n7egVkPFtw7LqS6Mn+xV9iMfbc+ste/+7f/Tu+5Vu+Zfv/X/zFX+Tbv/3bn/Lxb3vb2/iSL/kSAN7ylrfwd/7O33nKx/6P//E/eNOb3sRb3/pWHn74YY6Pjzl9+jR33HEHX/EVX8E3fdM3ccsttzzt9v3Ij/wIr371qz/i51prdnZ2uOOOO/jiL/5ivuM7voMXvOAFT/ta11u8W2t5+OGHOXfu3NM+5zd/8zf5u3/3727//0Vf9EW87W1ve9rnfKzr426KnjHAezLcevz6GJqfp1pjlD/b5G+Vt9Mnq8tlaz3gH7iCPX+K1Hu6yyvicXeyKZWFRkJRs0J4wUTUzGK1K85VURziTAVJLpg6K5g4mDjiuifHgFIWNSRwmtWyw7UVVinCGOgeuMw4bWhvOoWeVGS7xK+WVDs1qYuC7ceIXgsFJ145kuKhrbHn9+SCrxWdNQyXj9FKNDyVM1QX9tDzltSPdA9eFlraxnAiZpISpEWFiK0d5vyemDZcPiIcLKUgi5Fsxamq2rhjWSN6jpjwR2usE4c4lRLWik1tmtYSNnv5WG6azqLWktlAEHe7iELvz9A7LWnwooHyhXKiNaq26JTQbbUtVHVMgpZlsT0exwDLgdppsf9WSibQWvRLm7yMOAbiYSeOblFsyVHiJCU0Cwq9Sm3pD8SESgqDlTBaVVzbMhAEqUAhhg8hFhFuPgkrTZ4YehQa46HVDp8jyjmi8RJ+Gsvn2pwAMRMeOySfmpNzxFaW2a3nGC8fEfqBLvVynNmWWtVkn7CtZTRBPntrYeyQKbGTZrroNvRqQJfPrDdiYyvGB6ZyhMqKmYKPxCTFQnCQdyrJ0lr24nhmDSpmybUC+sGTV4M04CHhsiKEjM0JsqBo2Sjpoks1o8wmXb40mtaUhHmhlGUr+zmrjcmEQfWeTOHte/lcuq2k6N6iLZlkYdTX5booBblkkJhCmdnQ1nJpoIs+yZRCTKmSZbTR8LA1OZYCt4SW9tkDCW0VCiOFVs4oBEkc8YLaKCU6jkLb294QlJiQKKuL1iVDDIK+bae35fGdh8pgphOsmsp5kovDmMw1BBEKm3Bpynkgx3XKMu1PRqGSaMRkW7M0mQWVTinjdieCTk4qkm9Iy160XL1H+YxzCl1psveoppKctiAUNIWg1Cl6QW7mjRipxMg4RPoI2lWgBnGls0IHzOV8Um6TeyMNbSoumX6Y0vUDqfO4vQmYiojHOEXVWmII6EooxGEoxi7OgAqoccDtNAStqU/PxPwiZ/wYUD5SGTF5SSHiqgrTTrEp06eW/tpF3LTGtQ12aGA6Rw+OMHh0jmhioS1bKi1Dmk3+EeNI7gfiqif1PVhLZbU0M8aQld8W/7XSxQZbUUWLNRWZSGciowoYvDS8KpNSxOQSaIp8zzGJ0Y01dTlW5XvXKPKoxElRKfEGKN95VAZlGgnRThE9KrL3EkI8lmNXO6yzYniD2NErlDRmApkSasd00jCMHhcMShuMKnbeRuIZFAZ00dNlpPm9HqLIxUwhy/9zzJI5uDEacBbG0gSqcu7kTZNWXqVk/ZnGEXzATmrUUM6HjdaTEiitCupbhghZs22McgiMSajsadExBIn7cJQGa1LTtG5Lyc3F3nKDRJWPIC6sZTCVtTSRKqSt1brvvVyTKlvo+2CqBoDgRzpOhnTbk/oTvZ6qdHuusfprXz/2Yz/GN33TN1FV1cf8GkdHR3zHd3wHv/Zrv/YRv3v00Ud59NFHecc73sFrXvMafuAHfoB/8S/+xeMalmeyUkocHh7yp3/6p/zpn/4pr3vd6/iFX/gF/sE/+AfP6PkhBH71V3+V7/me73nax/3yL//ys9quj2d9cmqKrl8fZfrRKoWDkj2SikW2wemMtkKJAcUYNXE14o+WNDfvkayif+QqWUF1Zi7ZPkZj563c1ChOXWXSnDduVUPAr6SJiutBhMNKoRpHtTORwrUyxE4RXEKpkf7Sw+jDa/hxRjXfkbR0MqaD9HCHmdXU8z3yUYf2FuM92Sb0zkSykXxg7AYRTHcDKkbMrGW4tiB1IzYEAgqrQKVIKIGpprLYphI77jGSlZZgRaCqnZgaOEu4fEReD8T1IMVWsY3VzhGLlgArbnKqOPjpEAnLTkImrZYAxlpuFjomQYhGKQbjGAVtyxldVXSrjmb0hOOe/soRJiMaiZxJZJzTpLYRqptP6Gkl5hZHK9GgVA7tA3GMDGvg0mPo2RzT1DJJ1iJETl7IB9V0QioULm2NFMCq3AwL3U4rtvQLrMHHAZ86cc5SGpUgeI82YjcrA02hYWQtWqKUMxi1pYFBJjAyhjVRRchp6+iktMLHIPQULdPfFCLdck12GnuwZLaGyflzED21WhH7gIojq7wm6kynhZaYUyKuB+HeK8iDuLel0RN1aYBzxvaZybQma01UmaQTUQEhoLLCNBXGB0gZM6lROxPisiN3g9Bs1oMULtZsc0wGK3bWahyp3Yy42+DXPWbaEKNoG9jQpGLeIhlqc25vND9lkCGWz0VXsBGkFeezTdOSi3B8qzVQSjJ9Ns2UUdTRYkom0GACAbG/bXOFDaKJ6dUoDnXXNSzSqBU3yQ2NTSF28Rkp9lSh8WxG1XAyjUYE3MnA2gyiSxpLAZxl+3UJqdTGwKZRzxt7Y/nMG7OH7CWTJ48RHwdG20GKONMIckLGJoszU7AKH9ayDdfvWyXFowEoWVIx51LYSp5PSpLx44/WMjWv7NYq3GnQuxWqURyukjTCzkqDvEo0k4qJkYGCMmKaoDbNpjXEfsQ6RbXsMG0l1LlWnMJylrBMtGLawv5Uo2LCBI/aqYhDQK1HXAA9taAC2mhcI45iwXuMtaQxlGPB0cVMzGIBv6HoMXhqEwkK6jMThiERa8dwsJRrWyWona6iUKFWEXXcEY7WpGlice0KkBgrJL7AGqJOjH6Fdk62I8jxU9UTaVSNEd2hbtAYfLdGKxlKKWOwReS/Wc5ZtA5gA6MNGKSQVinRx46URpSGYq5N0COTUBHJ1F4CZzfHYVaKCCfooFaobDB1Q64sCkeynjEOaFNtOH/S4BYXUNWPxJUYnFBosClE8IEAWCNOjD5mzKk5w3rAWoNad1TVVIYFqw6tTrRYJmdiP2AUTJwmJGgUEuxbmi4tHDpBHhWCvhSER29sthGEN4VIqh12WkucwawRjeeyR+tYaLO5DD0yMYrbXtLI91Dqi6zlfMlGY6sGGzJ5TYF3BYAzxcVPjVEynThBeXPOJ7onoyUfy0esNaQYMVa0fePhSvZtyrgLe3QpwyjuiK5cA7t8ckzAhiK3Ico91XT5ufV/pvXAAw/wb/7Nv+Gf/tN/+jE9/+LFi3zZl30Z73uf5AJ+/ud/Pt/5nd/J53/+57O3t8djjz3G7/3e7/HTP/3T3H///fzwD/8wf/7nf86v/MqvbDV9T7U+8IEPcOuttwIwjiN33XUXb3rTm/j5n/95hmHg27/923nZy17GZ3/2Zz/t6+zs7HB8fMwb3vCGp22Krl27xn/+z//5cc/5y1yf2Kboiefr9f9/JufwE5sf9YS/n2R9flXzYudIY+DB7oiVGlFJcevsmNk0Ud90mkvpLHcdOvLouf1zF9Qmsrz3MUw/Qe3vSu5QI1O+/tLhVlitK3GM23TPqrLo2qFnDWHVU5/ZlSl3yuJ8U6ZgWiuGvODewz8S7c24JlYVoJio85w79SKZThYdgfDPgb2EaSoeSe9moS+LoYK1xG7A1pbYjyhnGfuxJGYrTOPESjoJWpGNhn7EjEJ9y4CZNVBZ3KwFH4iHggalfpRJ57TBHy1Fe4QieSk8klZEJ81TN3TMqgaTcnHrMph6JvSADc1hkCKHQTQ5cfQizraGFAImCre9sWImMB4sJBizNAohBZKx1K4l+ciYMvWpaTGVSGLMoDV+CILiWSNmGWfPoOtaboCtBNFqpFA2/SAufE7QP7VBrEKCTnjjWctn3RaqBBbhPparB7aIwyYM9cL8JZzbe6Hw1ZU0Bxu3MaUl9DAlEb9rpXj44F2AuIMN+5Pt9x1SQGuDz54Qg5h5OM19d8yI1jBjypccvBS7rBiaAe0/wPjYNZbhIm+9TdwFoxHBtdEalJhdkBLJGRkGBGmEhYqSeV53gTNHL0A5w3t3HuQe9zDkjK0qwjBKPpSXfaxjJi971GrY6kbUGAsyUSg0ZO6/fV5MBhR6apjccRPD1WPGh69tnZ0Yg9DoGqFwZnUdhJ5yyeoophCl5snOkHsvIahaPX5QqkTQLbbdmycUW90y/X3x8hZuG86SM/yPvQ/zSHOIUvCZx8/nbL9D0vCOvQ9y4NaEcrwrxOZ3G0paRNiaYgesih1w2kyf1UmZotUWZdJGc1Wt+N3996AVtG7g5qPiGAcFiS3HiWbb3KmC6igKKlWa51y0X0f+Hq4uPoSKmZumf4NZdY4YIjfuvlxsoXPigcN30o0HYscOxXVMaG3pOt2W0WZLKSLKsaqyAg3VvJXtW/ZM6sjtO0uq0zMeWFt+8b1GdGWlOVW25VN3PP/3lxkZqliDzlkm6EqQQeMs52cj++tD9GyKbVqMLq+ji/FDzvzfXiCpCGntseNIzhO0M9y2v0adNSg1En0Jqc4ZFfVJ0V/OvyFk3v7wij4p9qvEi89Igd02cIc7QmVYx4r7/BSmNZVVpCtLslIswiVWx28XG2vttyHYR91DLI4u4QdPDkGy5YbA1eVdXA5/Ic1P5YCMColzs5cxMWcxteP87qeRW7G4fujwvzPWvbgxDoHRB8k+KtbSyUYeOv4T0cFUhucfB9IYiHHFA/GPZBjW1jKgA1o750uqzxPUc0xiZuBM0Z9BDpEEJGtJo2evvYEbZy8ltxWH3f3cdeVtWGPYr+/g3PT5og1qKojV1pxB1Y40eLRSxFDcT7Wgi8lo0tGa0LS4ven2HojP3DT/TEHumoF70h/g7BU5LnLGLztmVvNFt+8CMDx2QHy0BJSWM2pDkcvl+KTQ/1IZGohhCqTawm4LdbUduAQfBLEDfAg4bU5KC6MJBUnW5O3xkzPSSAM37n86LkzQIfDA8Z/Q5TXaKXzOmIMVoVwPbbHQF3OLTCiDh5whHKxEp6pkwJOtJgVB4zFiAHOA5l13H8p2Z7a6r/gkdU4uENTjB/mbRomPrJGeWIM9t/6XWXfeeSd33303r33ta/m2b/s22rZ9Vs/POfMN3/AN24boVa96FT/yIz/yOBTo1KlTvOQlL+Fbv/Vb+Zqv+Rp+67d+ize96U285CUv4Yd+6Iee9vUnkwmz2Wz7/8/5nM/hcz7nc7j55pv53u/9XlJK/PRP/zRvetObnvZ1vvqrv5o3vOENvPvd7+YDH/gAn/qpn/qkj/u1X/s1xnHkRS96EadPn+Yd73jHM90VH9N6+pbwma6C2P+lrad5faegVoqmtuzccprJ+V3as3PaeY3ue+JDlxiuLRkWA1kbUvR0lw9Iw4A7v4OZNuKWc7QmHXfQe3I3is31smd46CrdPY+xvv8S6/su4i8fkUaPaSv8qiMUbY4qKedojd2douc1+lSDnhjydILe2UFNKnTl0MqiMBhlMVr+b5JFK4c2DoXG7U5lGjl6Ujdg9mY0N57GzFrczpR6byqhrbOWOG1IbU2ettDWRG0Y0ax7z5BATRvc+T3s7hSzPyNmJQXuvIXdiRRiPkKKgqbUDiYi+NU+0u7OOHXujCAmSKGVgpgsDH3PweIIhgCDhyEwKrmBxHKzCf2AzWJfrmcT7KTCaSUTQzK2cpimoppPaW1FDJGgFJML++iSoaKKtawaA270OKOpXaE0YMhrSa/PYxSNQAYVM8lamNRC6xkCaTWQRim0sUbCccskMqOK+YMU/iF6QvTEMJKjJ5fskpwUKpV0+6xI3oujUpIMI63EuEEbQ8qBmDwp+W3zR5leasApDdoQQiBpRXJ22+zobNBDJh8MDPddwu22uHO7jCrQp5EUBRFUhbooxbkuxgqluHYG5i15b4rZ38HNd7C2gSERCkUsh4g2BuUcqiCmudAaNWIqoq3ZTkG1EXc5rZRYvTtD1OCHwOryEdUN+9hzO1tbbuH/F+F0zidZYYotQpM2uT/lfNeZk8+1QYDUhtJW8ntg67iWQRwHlRRMLmtqHLVyoIQ6mmLGJI3LFpfNFgHeCLXFaUs2WSOUNFM0TEqprXB6c0lSZT9s0J/ttD0myIloEt4kKJTAmAs9tEy9MwWdLO8Vg1jrZ1MCGze0IuT94zDQ5YCaSQHOBnXSFq0sVlk0kuezdaODkrNCMXwoNMWcCTFuIwOEwiMh1Zu8rs3O0FahlVyER23oI/Q+MSrDkDSxoHRaSQOWei9T/II6xsMV4fIhtrHYqRNXwdLs5jKgyCFhSdQ60UwryXWrpCmxTqNTROeEMwpDojC6hBKbktgoG6Ehjj4yjhG/MZwRWBetMsaKAQPF9MO0NebMnGpvgp032ImBRpFqhT07x+5OCMsVw9WrZBKuMuKcN3gUCaszKY4EP5B0ZlASUu2cxaGwEUwAk+Rak2NkGEd83lC7kiB2Shi1USVi9qgUsD5JpIAxKJ1QJuPXK1ARpeW4ckFjo8Fpi1UKs9F1Icec1kqcFAGDximLWoyYzpPCyKgTSRfjAmMEtZPLmlyPjMZMG9S0gaYi1I48baSZS1nywcZAvraUfLlFJwO3ADkqMBW2bnCzHdDC2vBrGeo4rXBaYVaDDJaU2lrS64LiaK23zp8K5BpLCUkmF0p3MepJibDq0asRNwZx4MsbwwlNMkXjqJU0LyGWgaQha0VVOZg0mKahms/RVU0uTnQ5JdFiupLflGU4mArtGmsEsSwoXShur6kY3GyMIShDDzuTusOnjA+ZMWVG5M+2KVKKJwDSPH7CfF0ndH2N9IQB0lMOldWT/P7JHvtMh9rPrU/IetWrXgUIxe11r3vds37+L//yL/N7v/d7AHzLt3wLr371q5+SFjedTnnzm9/Mi170IgBe/epXc/fdd39M2/1d3/VdTCYTgGfUuNx000387b/9twF4wxve8JSP2/zuG7/xGz+m7Xq265OLPrcZuz6LE3CZM1ejZBPgFNPagYZ2/xR17xgeOWB46BpdWtJXhivTI9ow4HZnNO0pxi4zXDmmPzoSepM1hNoWtx3FNDVoarnZDx3jlQXp2hIzrdFOHLJSP+JZY9qatB5AQXVqjp21cG4PFUYqK0XeRJ8iH2WGwyXBRxFqpkxQWSZLS4NzARixuzMmO5b+/jWVDrjdKew6UufFbrxy25t7Dom46gmLTi6+o0ePAVU7uqM1tVa4aU0u+pARaC+cEoTmYEEubkBqUqGBxfEClGIym5VCFrLWxT2tQvkRcqKeTHBTofmNIaCco+97GqVkkmYNlaskRNGPJXNDaB61sZi2Eo1ULTdZKZDkhhauLshHK3TltrkVuRRDrAeMdcRlV6Z9CaWsFPiVLcW1VJ7xuNtSVrItvPi0KczVdlKXrWKohOZgQsKM8l5a1ThdCQVNCUUwF33G5sDtrCfSE7LHxwHJxCmFZbkZ1j5B9mhn6TeUlASNmmBsIiqDGyJaZWzwLPQKHWFkxUBiPFzS7084dcMtxMMV6Xgt9u1RE5RmqQcUGRctdZSJ8mTpmboJMSYCmWPXEXXEJy9FQ9GCKBAB+2a/BcmDSTFtdTQZpGku2y5sMgkWzaVwyMWqeGdvzvqgE2czK450pqCPuSTWq+uRoc2ktBRkG3OGjVX1Bl3a6gVNmecUgwylC5WuXEI66zlGgiKjlsZHa03nPEdxDRpiYVYpo7cNa4qbcMbSsJWLktWGGRMpxsbIqhKb5JgK2puENteMgvjkpKhsC1ozCSNVVY7fOBLSgLabQqkgeQooTpSjyWQnx42NGVMc11LONPNWUKpQUKyNi5cWZ7ZY9p8CrGow1tFaTT8uRFuyQadTEs0JMrzQRlNPFNWpKSkO5FWgdZm21dJYG41VmTMTSDEzRFj4op/Rso/0tCEtBVlMo5yHALlxuHpXrK8HD06DK8XqpskcAwtVMUb57vemCquKEmR7P8jl+FAYJ3lS+IipHXEMUtSrxNmZYlSWHZs4PhyYtg5jFPWklu85CLUtVZC7cRuAaxsnE/1uxDqLm0/IMYOxVGdPEXqJWNAhEZBhgQwUhGoYl14s+es1fT4sRjG1WFLnTA4WXU2x1pKXh+i2BqVJwaMD0tjZEwMSNtk8ecsdRVXi8JmBGCMjndANlUHrtlBNI2NciVOa00ybPbIJGOMYwpJsFCEn0RP1I9iRIa1QQZPHHuOsuHOSMUGMFoQSqXG7M5KXzDiVM9GODGGBioo0IllD1lLpCUkpImJywZl9fBowHeR+QKGp7IS4HtEr0R8qJHA8U0Jb0dvBidai51NWFxdIaUq0T8RryzJkyNL4lHNy49JgbYvW0uin2OMqSsBqRVRIlEIrTcpEa5T29HFFbhPsNOjeE6ymsjOIEFQkpY6chZKb6nItVwrbSZOrjROadeGtjuPyOhpgpj09K57gSujORkNleHzDc/0k+Alo+dOtZzqgfvzLf/yv99z6hKy/+Tf/Jl/5lV/Jb//2b/Mv/+W/5Du+4zseh8x8tPWTP/mTgCA6m38/3Wqahp/5mZ/hK7/yKwkh8LM/+7P8/M///LPebuccz3/+83nve9/LpUuXntFzXvGKV/B7v/d7vPGNb+S1r33tR1D3/uIv/oJ3vvOdKKX4hm/4Bn7rt37rWW/Xs12fXE1Rvu7vjza9KOuPx4F35gGA/8fZgRedEWGpNprcOprbz1G5ihhEIHsln0M3GqtabuxfhBstg1pwV3oHIwNJZe65dUJQmama8KUHfwOnK3p/zENH/w28CITDohfko5XGJA5BUJz9GccPXGY8WNKck2L/1MRz016PMpprQ+IS14huYLy2IK5HUjfihxFrDFjD83aX7E8ymGOq83uk/Yb+6qO4XEPjUI3mzz4Y6IPDzBtxp6sd2hmqUzMR2bsZcdUTj9cyQcxiGpGOVijvCdayevgK05vOUF04hQ+RcLyGpkLPW6ajID+6H/FebowMPdlo0jiiUyQ3FckUrrdzmJQxSuGspe8HTCthekorgveErsfVreQtpSy2vWfmjJePyGMQG9jKEkkYn4ijF5oNGTWpC99d7JfRmhTCtuEAmforIA9BtCKpGC6UqemqW1EZQYacdYDaFtJJZQ53ay5eaMU97HLP/NEenRTnp3dybnqn6C6UIiVxyTOlOYjAn07v5qI7QGvNbcs10wHIkSGKDskZy60PrEArvMrc/bwZoTYYW3PL7ktpcsUY1uQP/xE+jaTdlj+47f3EclKkc3OMMZwKM/4vd9+BdY6jgwN2dA0p81B9lT8+fTfRWm44PsVnHN8hyEBMklPlFB9qHuad7o/JBIKK5CjFcdQKNQQJaM0lTHTTdGg5+YRFuKGa5BNqS9pQl+R3aTkQHjvkUxcGf6RYXuu565aJmEuUc1vpE9Ro03ag2NLw5ANvimG1zWcRJClLI7hpypwVVHdT7CONwgfnD/Eh85jQwHQq2V+Zd+3cA5PiUFYQnPIJ5dgpWphYbKvF/jjTZssXXnsxlapYmZ631e9jJKA40RQ0Q+DWexbkmJg1Z7l159Nk96SMPm3QKI6Gh7l49F4xnPCxoGjyuVWh0R2ebbl8uiIrxY2PdZy6NpCRbWq0IlxdwFTs7K1222aVQt8pWBq3nv4cGjsjEbn36n8l0InEqDRim+lhjolmZrlz7xAdrqJqh5mLk6FyBr07QSnFLWcN376fCX3gLw40v/HnpZ3OQpGkcajWEQ5X2J2JfB4f5U8tgnLVVlLcllBkrJFzXyl++88CH76cMJXh6z8tc8u0xCckCdREl9cbrzMqNiXYsyCZ86nlm18eySkwYrn/4DxppWmrxB3tseiYBsV4bbnVkWqjCN2AqSwJcDut0HsPV6SYCMuOGKJk1xTLZ2saoasVEwq6QRrUnLk83sWV/sOQMjfvfiatOY0yhhvaT2UYBtx+zWPz/8mwPkBXFcmW4OBiq568lwbFFeQGyN2ASggKXDKIglrzwME7hErXnuXmnc9CoVgP13i0fy85RFpzhjv2v4DkI0f9Q9y3fqcYCigkWiEEDscHOQ6PgLPkGAotUmNK+rA2GnwkZLHUVqMnGrmuPLR47xbVzEmQ2txrbt/9m0zqOWPK3H3bDK8d+qaa8398F2rZYVTFLfPPZVwcs2j3eWD4b8QUiunISQ2wsdLHFapyQWuNEcQmkLeW2Cgl1MpCZ9Oledyf3MHp6e2knLnUvZ/j8VGCKd9j7eS40uBqR1r2PLJ8nzSFxpCIjFZhsuHmyadjzYSQRu4/eAchD6Ta8me3TlDzhrrzvPBDRyifsG7G8079LUDTxSMePPzjLQXbzhrcpIZlsS1vNk58H8l524LtG0rh9pFPfOxH62qeg3r+V1o/9mM/xm//9m9z5coVfu7nfo4f/MEffEbP+9CHPsQHPvABAP7e3/t7nDp16hk978u//Mu59dZbeeCBB3jzm9/8MTVFUOIxgL29vWf0+K/+6q/mH//jf8zDDz/MW9/6Vr7sy77scb/foERf/MVfvNUx/WWvj58+91c5RXgSGl3MEJAAy/XVY8JqjTEyFfbDKFOl1pGdoTm7g5lPyNYyPHqEv7QkHI8k41DO0ExqJnWFUaCGDrVe44ZInRQWI1M9pSQ3xUdUjIRFh190aKMYD5asLx6KqPPwmP79d9E9cIX+0WuMVw4ZHr2KXyyJwaNqQ33zPpMXnmfy4huYvehGmuefo7lxF50CLNe42qKi5Pe0+xNsZVA5EY+WJwXGhtYzesJ6YOwGmVquxF7XnpqjpzXxaCW2p0FCahujqSa17J/i/rW5IYVFB/szfAwyWW0rwiA5Tur++2GxxJzaQTnD5Pwe7U6L8R4dxaChGweMtZIWnxNxGLFK07QtaqfF3niK6o7zVOd3GR+6QjpakVe9BCf2AzpmsQlHiYPRkEiHHfF4IPa+2PKKW13eCOJLUezHkUQm96PQI2KUPIqUqJTBKI1VhQKREiGGLS0jxYTPQitLWlFrS6WEmrIpN1NWaG2HvtKUAAEAAElEQVREExYjYxBaXNYQVSZkaS5yEdZXrsIWTnuKARUSJrHNN5Li1KK0xRgntLEMDEE0VioRstCqxhzFyXsdMEvPTjUDZVDlc6mQsDGB0phs5HWNQ7lKMre0IsRAUCWwMEPuhfKYCxooyEUu+UzFIU6rLb0FhTjCFTrWxmENym03Z8ZLxxAi7dldqt2pHFf2JEOHsr83xdT1VK3tCa7V44LvtTqhnsSC6kgYbWRjob2xsk4hElJkjJ6oYqEPlfNEiQA/m7x1s8obytF1BZnW0kTpDUqawSmDDeBSQXeKtiOXgpCS6WJR4BMGS6UszjhUVChl0FmofDGIli4pCBv0qzT1yQhtKaSIHz3By+fJPjLef1lMUcaAzhTb4rylf6aN5k+rEtyqyZFCX9Qnk7jyHLSShsJojMq4aYWbN9Rn57jdVtz1MjAGoVKmiOl66IetS99GZC5Ir7hlUgKdyRm304rLli2OhOpkGJFT3k7QY1Z4NN5nUozkjZ24PuHvqEpy1TbvaSp7Qs3UYmBhyOjgMSmREsQgkQubhj+V7QzrgWHZk0LEzidQdJB+2W/RO390jNubMLmwj9mdUJ3bQxeNZnaG5TjSq4w5PUftTjBthW6Lg+mO0M7MVLLd6vmM6d4eZjojO4vbn2HP7dDedhZ32xnsjfuwN0HtTWHelGYkiPOj1pjKoZsKXVAybTQDgYQ0gRtnNYwihpGEoLNGW7SxYA3JQEpBHARbR541pFlFajXJQXKCxMSNI6BSxG6QAZWVfB5ikpBlHyAGskpkEtkqbOtQuhgiOCNGF7UVqu6kxU6mhK44FiZIhx3aWKHHFcc6yneZlQS0il193Nrxu2L6szXIAHkfrbdUxJQS3gehcGaFSnLdztbgvScYhW4r4molQ7JiLW9mDaY12KnDTh2ustTGYHOGUPzrrJPzlowPUVxPZzXsTIg7DckooWVbR1YGrU1xHJRjqjm7w/biUxCgJ6M35ev7nXzyT/W4BucTwG27/tL7HCr0SbE+4zM+g6/6qq8C4Kd+6qc4Ojp6Rs97+9vfvv33F33RFz3j91NK8YVf+IWA0PbuueeeZ7G1ssZx3D7vpS996TN6znQ65au/+quBj6TQ5Zz5lV/5FUAQpb+q9YlHip54vj6bk+xjOrdlCqK0QrVThqzwo0YFhT/O0CoYE2lMRKWEYnawJi9Hut1jRhvQRHINqTL0KuO0xcx2aVLNet3jx4FAT/IB1TpSzoSYMIPHtbUUI53ojNbdQOMseXcH+pEQM+uFp9uR7I71+ohBKdSkop056tbCBLHzBoiO9sYbsOMxZn9WslBAtTVjMiSlCaNFNwblM+Hakl5nfJJgxTZrvJKsBlJmeOwQlmtwDk+mthZv5QakQyJcPmIooZ9ChYrowonWu1NyN2JiFGef+S7ULW7SkH3A7kwx01roeE6DtlhtmDRVQc98EcSKDalWCpYdYz/Kd71pbrTGnZ5hcsKvBlbLNclHWmMxyhT6iBRBKkN21dbUQW0yZ5QmZTCmomaKmVhSCgzj8VY0b9PG9eyE+mbURuQOLmYmXQKVsH0oXG6FDx29P0SjsKYlZ7E/92lNF3qs1rTesJMnctPWAyl1hUaVT5zJtCYg1KddP2GMilY5xriAoIl5lKwOJYVo1QUwCuNqKjUFn5jFVtzNYiIirmjKGgk2dZaUEqPyXKtWkiWzaT40rOK60JFUoSFKk5O1FoV72Y+ERFK5IHpp22yIhXCxluVkO3O5m6qiCUgxcbg8Flvbs1O0GUWjMAZpqILQg5TWW9rb5lJRUzHLLTnDkEfWut82QPIYVcweJG+rbIg0UGU/b/PFUt7q/XJMRY9wcrGZjQ2VrcRlLRbUhMyRWZNIGKWZjQ3GWOpoGOISPyZ8iuyNE5JqiGPElsBRozpQS1ROpBwY45EgPDEKyhg1g19u+78NBVBpTTYK3TbE1cDEO3bHCVppqommD0uhQiZQJfQ15DXr4QCdLNZOsbZGG8kYIypizgzhmGwiOYdi51wc9gp1MeeEmbZoo8hxZAiWfGqHHAOmG6G2jMpw7SiBMTQK9nIgO8N8t+Gm/Yx2mf1WjsH+YEk1azCzRtD0rPG5hqQI66FYeQv6szGUaFqDToGUMns2ctOORStwOaCtKw56YiKTuhFbOWnAeg+tXDPDGLjiLVlJE3u2lRDYvBL0OQ2RwXesJoJojxbMvBWkrhvJPhKNxzpLZVqhiyqFqS3V7AZiP2KaCjdrpcimLg6KmWo+IXhPVTni4IWGHCJxHDC7LYPuMOMhatagUmYwEWMcfddDk7D9UMJEM7qxQqFKuUQVDKJZM2IZ7oNQ6vR1zWVVVUIjrBSjWhKWA0M8EmqZUQxDx7o+KgY9vbAJzu0QAJ0zdWUJR2viapDzWCmoxRClMhO0a1CVYmRNdkhzWTv0GKCYDNmUBfEDCXFWYnMOcm2px5IDNETyjedI6xVrk+kevibfo9HkSYXqUslwQ1wMOSkhNtrBrX09MrgIgK0c2mp0tFS6IQyj9NFGhlshBdZ6gbYWvx4IMTKZTDCTWgLCN1EQUHSTBlVCrqMyxK7HuQpvelJIhFhiKJJQT5ujgTwmKmPJ61HQyxzpwhFKabqwICYxWDD7U1bWQh9YjU9mqcD2Uz9eR7TF1D+G9RTP2+zc5xqhj3k9+uij3HzzzU/5+4ceeuhjfu3/4//4P/jN3/xNDg4O+Mmf/El+9Ed/9KM+5/pm5qmMC55qXf/4e++9lzvuuONZPf/nfu7nWK/XAPyTf/JPnvHzXvGKV/CGN7yB3/iN32C1WjGdTgH4gz/4A+6//34mkwl//+///We1LR/P+viboieiuE9Ecz+RqO1HosuPe6Or7iwfvtTLBbJ2LK8CMdFMNdYZ0vFaLGfXwpd+6PBdVJWFHLjvhXv0KqGqmudf8ejeo93Ao+E95NWIMoqkMi6KwFWNqdhcK6LRYlvdjVTGkIYgk9KmwvQj6+S4d7kDQyTGSNYRsx6Zjpe54VRET2v0BvWxtkyNduRjlUmsv3zEfRdb1m7GcC0ShmE76b3/jjnr2mBi4gV3HVGPGRad6KCsEYpRbcmDID9VSfQOMYp9tlLYWUt7+3nRF4WI6j1qEI3QGDw6CQc9T2qS02SdUF3P4r4Fdkzb191w4vtxRDcW1zbkbhQanTOoxhG6gdSPjDFSWSNuSz4SjtZCDdlABCltbbJFEC8ZFjgNQzkICr0ppoytLHW7w43tZ1K5mtXqEg9174Qcilj/hGK3mWJfT8naORrZPRpELBvzdhp7uL6Xg9W9KKU4P38Ze9VNYDRXln/B8fgoGXih+mw+3d6JJ/HQ8E461pgs9LQhB0BRGckJUsryeQcvRJsWnQP3Hf0RwXdFU5OJSmFD5s77ViSVabXiljOfTdYGkiBSylqxz84nomOlFQnFo9U1HrNXhZtfXJu2k8jM9nNt/q9yPgkuLRQVBVsEgizmE2ZDZdk2SeX5GxpW0T6ElPhQm5necYbx8jFmtiMW7UOQP03RMZXv4Hqy/Gk/5/MXL0YleLC6zJ/sfphNgaDKJFgmqJlN+OpGQ5PLtuQNJS5nkpdCyxaHwQ2yaJThs47v5HSYS0GnFYTImDy/f+Z9rHSPy4YvXLyEKtXENPDAtbcT04ij4Qv1FwoSpyAfg7KG9foqD6qLZKXwecF9B3+EclYoikH0gyc5SaUpCrGYKci0O9eW29fn2ct3YJTiPdN7+PDeI2StuP3yyFkr14pjf40rD90NznLz/LOZmbNSzGc5b5TWPHL8nuJ2CDlvTiopYDcFIT7AekTNZtzvG/yHOua37PHC/Q5N5krU/Lt3B7KBO8/D/+sFBpPgtt3MP/gs0fKJI58SKhKITmRac7B2XFxP5JhYOahsKW7ZUutuHo/Zm4jV8d+5LaFc0blFU+hTuWRWZWxdCWIA6HmzpXgO2vLv/8yw9DAj8e0vz7QOdF2JY9i0JnvL3dcgDx5lreiknFhMbxwSsymGIkaT/IZGZrBtLahYlgwfQhQHutETY6KetaKVdBbV1uhiHoAzHIz3cJAixFpMaHxAp4pkBlwQ1GXoRuIYaPdnKGdIWYJ3c4tYtns5Rjb0XVU7lBMkM4aIQtOz5P71nxCNQlmw0wloRd933JffjcOSJwlbz/HrgeWy5/SNpxjuu0wq5CxdO3kPJMz49M6nsD+9lZQzjx6/m2P/GCYjGs5JLWilTEXkGLB2m9+jlEL5RJ0jt11c0MeOqOH+5++RJ2fpm8TND66EHt3WpGRRg1yriJtrSpacO8rxch06naPkbrliZ09I7NQ3cmH+YqIPJQhWBjRX4od58Oi/kawm5oSbNdidE1dZbfX2uqBUMezIQBB+gNqZonLmvuN3oYdNxICgj5bM8y97wEssgrNgDJ6eBxZ/Ivqwcq0004pVU/POe4+vK2M21LbHk+O2IdbbHz2DQuqJ9dETXvZJSXTPdnD93PorWy996Uv52q/9Wt70pjfxcz/3c3z3d383Z86cedrnXLt2bfvv/f39Z/V+1z/+6tWrT/m49XrNcrkEBB26++67+dVf/dUt5e77v//7Hxe0+tHWl3zJl3DLLbfw4IMP8uY3v3mLCm2Qo6/6qq96Vpqqj3d9YpGipzrBngnt9anWs0KaNPXZHdIYWF9dSiGSEDRiCPiDlVCFtARcjt1AHHpiv2I4zoxWY6taaCyFEqO0kiujVUJBCoFoNSYHdFsRjCb2Hpsz5swOWI3OMFw+hMMjyAnOniaHXAS0GYwU55oozdbhinTlGOUs5uxcHLbKlJ8sVAC7P8N0NelyTxwjSinMpEYDbVPB1ElIpBWTCJQhBi+hdM7iGjE7yN0Iiw47n4gAOI6SNbHucVeOyWPA3XQKpzXjvRcJ657stIh2jczu8rJnHAZc06BCoIuBZd9xfvcUuQGMpkajAviDpaA6bcW4XOEWiugDxmhqraQhcpaYMjiLmTW0udCWlCYuOnIIMr3TMoVVnZciNpYbmTOYLUUmUtmqBKye2FFnpKHSZeqaUpJCORcxdym+dBL+mspsTRgA0BRKjxSVIpiVG54p4l4SWGUgi3ucKrO9xtWEGLcuaVprDAZjLMM4iusfeUvz2li5qpyFamdLeocxMK1ISkuxt9FMKbZ5HGK5nLZT0pgytoiS0aLLMGoTXijUtQ0FTFhKxcmN0nDkEkpbmnNdcjs2A8YNbZGiLdlQGbW2ZK1QtWX94BXqC/vELFMkfCy6MLXtiTYlgNhqK1Sxvd5sg1BkBPXdhOymlCU0uDRq6vrHbgrvlCGlYiCB0PWUKkZ6RugwQRyttNIkNEYLPSkW8wSnxGkwp0SMEetAG4sOalsApjHJNmfJADJak1U+0WgotaUP6g3yJYwclMrokNDdKMizF11eHIWKGZU8J42BcREwWuEmNfXzz+EvL8RNbYOSbXpftbEPL1biTqhGurLEYSQeLYhHK9HIGM147Rg9jKQYGPKAr6Dan5C1YvARYywpK2motCL6iKbQDjOo2m61QsOwJqx7xqyI0YExZCMicq0V/niNbest+pt7D1ZjFVvaZgqRUCzZdevIWgZdm+2VRl3eXztDRKjUEUghiOMXSYxsupFcUEndNsR+LK59Gt1W20yvnBKxkwGKre0WnUQJcpGKPkoacDG1CEkGOzEk0LLdKRTr+pAws5pwtIaUMI3BxkDMkWpay3Vp8Ji6ggzj4Uq2p3ZCO2wcMQjqssm2IWehjCVx4LNG9gtlX9R7U4ajtaBVPpKdGGH4HCViKwpls57UjOuB1FYle0gYAsqJ86FuK6EUJoXyQQYHQUk+XUqixZrU8p17aSxVEOc9FWVeshl8GK2xSa4bXsn/V48dkGLCIsNEQezkfQTJViW/C2wxNBJ3xEiuHbo2+G6Qzx2jbEctVMmsxJCCnNBjwGSN0hk7EYTLThtMZcVmPAriHCn6tXLfVVphK0u/jluqpyITLWBBj+IW6KwjrgZUyoTaUBWNoBhElAuCVbjZhMkN+/RDJOXuuprlpMjZzHqU2qBC13c5z6B4+igPe8pfPdmw+UkaqufWR64bbrjh40KDPtp69atfza//+q+zWCz4iZ/4CX7iJ37iL+29nmlw61MhUDs7O/zGb/zG1lHumS6tNV//9V/Pj//4j/OGN7yBV7ziFXRdx3/8j/8R+KulzsEnsil6psjQUzVIz/C8f7pV28jEZvrFErynnU3QPkBK9BePIIOzu9SuElh/BoyeHA/Jy2NoDGoTBonC7U5J655otehEUiZbQZ1yEHRDjYqZ2iE7S1XVmMmaemfCalxAMxF0pFYY53E37xG7kXjlmNyPtLdNcecrwtWFTEdr0TZlHwiHK8ysRVUWU4qA2fmWrBSNHlmvIY6RYDVNF7GD5HfkiSVOHD4kghfakE6J5mApWqe6QrWV6FliwtQVWSWc0YQrhyStceOM2Z4jPW+H4bHM4Zi5eukKZ2e7WG2wdSU33RTFstRWnD2zT7da42JCF71VDF7oIFoc+ioQmlDlZCJbWaKPpGNBSbIXLZTORVOgiiVyTGRjhIZXpn85FcTHGOLgZTKpFOM4sOoul2yZNU11SgrkgnYAxDgwpAW52Oumog2RTKKiyVBC28n5RGuljGHIa7pwAGSsbZjqM+W+59Baptvzeh8FOGuLUB+UBZ9E39Lamj4c4ehZhzVDCjKBVYpuJsJ5jWF/FJ2DnZ8i7kwEdfMR+hHrhZK10dngI9EH0ZI4I7oJ2OZ3bgT9omNRpfkplCrNtmFT5Qmajf6CraGC2mhQKM1QeY8tMlMQJK0UjAF/uBIbdVXE2ka+y5PTvUyDrzv1B+W54o4gJI5df5JpVKbkuZwfm/eMUebcbD8TW+tbKDsgqi2C0g5F04W4iGUlxgxDd40xjGQDO11N5Swma47qjmUeCf1aKDDIdF72tdtuu0Ksr1dTS0Zjg2EvzcgKYu4JWQpjrWucmaKdIsSBrEtmGJlw3OFSxk89q+GqaP+84ny1j1aaRkXSsKBKmXHVY7SmOjNnHEZUPCSFsBWrZyWhy7qusE1FxRQVMvFgzbEZiwGIlkyx9Zrcd+QgVMXx8pJr1ZRpNSVGzR17CqrMuTqgyiAiZo3PDSpLscuoSF3A2oxtHFZXHK40yWdBE1JGOyVUqVooyMYZhmRZ5walBWUIR0KzC+viZKg1akjoyqA8TJqMVif5UcSERnPzDqxXnjpHQj1j4T1h3KCdmtSP6GlzYr8fIqqW66pfCtU1rCR8NCmwE4NNAwZDwNGPQBlsqGJR7xAb51Rc6ULvJVTYiuYujAHlA3ZnUsxAEBe3EmqdFPiUcaWD0H2HSlFYAz6SRi/GM7o08VafNPZaKHRpFNtzcfrL+OO1OKA6I/lPWkKZh+NOBhtGdDtayUBOT6utUUEu57AGgg8MaYUzDZGBGErhH6NYkk9qaWKcJa8HaCoJ9PURKk2XjzG+g1qLDgy5frfrQPYZFx2L1SUqNGPsoB+2KFAqTXGlHJXbEfRlQ4P10vCmDNoKelc1FXnZU7spBsnqG9Ma71dyjXIRZSuqaUNuNo5+iJkESFj15jhGBh05JkKIgiJZLQG0SkmI+iDmQdW8hZCZ5hmgiFYR1Uos4kEGEc6QnGG9M6UbE0f9Eyhz24vfieGMOGyeGM185BOe7OdPsT5WJOi5LuiTYr3gBS/gFa94Ba9//et53etexytf+UouXLjwlI+/Hu05PDx8Vu91cHCw/fczNWi4fh0fH/Pd3/3dvPWtb+XcuXPP6rnf+I3fyI//+I/z+7//+zz00EP84R/+IYvFghtuuIEv/dIvfdbb8vGsvxr3uSc7f6+vhJ7uBHwWJ/W5yZrnzQPBDNzra5YJTFvR3XcJKkcYI887+5k0egbGknKCwRPbYz7I78I4wPERsW8kVydEQnG2ylHE9BhT8goyY/JUy8htfhduuA1dDVj3Dqou46c95saJUL7WK/TeBDVNqLmG3UwawOwVzQbg1wPOGdJixMwa7N5MUJJ+FGtvpThbHXHuhkzfH3BXN6WjQefM+YdWuJLzcvctLUMlBWgExpSxIfP8Dx9BzEXPEcVFLme81pgUsdMa2gqjFfaxR7n1TI250HA0b1m8e0GjDGHwaJMwTY1taowCrMEbYNljQ8IQIUTJaQBsFuthFTM4g2lrlDGkQQJoUxTqilJKUKBCXUgocegCyTwaR1zlyo2ihF9m5HWRqTtWEcOaB4/+BICGObfsfS5KaRIC+MUMq/ExHlm9B+0sdm8qOhcjtL/YjdSzBl074qLDH3ckH8RYYTVwbXkXh929pJy5eefTOd98arGAlcYppcz5yYs5O5ObuN42Y/k6VCpy77X/imcs1LdCzTGa+26eEIxiFls+tf9sVN2WQExg0RFHjysNgK4tDEVwr+W2qjNiQCEbI+5YRvZtLmgPWm8RHtE8ySS83IvLTVmCSCkalJzZogKbbKG4DTc9+ZnavodQHqc3n2blY7Hq3uT8SJEneSOc6FxQXLML/nD3/VAQF8naUYKeZiRINhlylLR6Nla+m3NUiS5uA5lIcKLZmomcv9gzXxc6435CWUje89j6/az7QzSGz1BfQFPN6PLIW06/lxU9VZt5wZWIjmp7SUobh7yC/PS14f4b53giZ7o5Lzt+KTFm+nCZh5fvJsfEbnOGG3c/HZTiqLuPx47fT4oypVZGE3rPIt3HcbyHDNwYX8JL4svQ1vBYfA/Hdk28shD62/6EOHqumvuIMaB1JrYekx0qiNA8xoAeImenfwPtDaNZ8aezd7IOHYpEDiO5jTLapkEZS5sr7GVHO23YPVvxjZ/pZXpdGk2lFetoeWi1I99TP+L7EaMnnJ17zk96csgYrdBBUlw3qJUgQ4LcxBB5MDqcabBtxbjoUNnJMCIYMYUox5FqHNooXnBmQV2VwlaJ+6CLnv/ni2WE3y3hrosVyk1JKRP7XoKIVwPeR9y0wThDWPbkIaB3Wuh9aXIEndRKUS8PeN4NAeUMF48d667GNhVZoA8ZNlWG5CNJidbGNBW6nGe6dqIzWvVyvikIqx4zrTFFUplQQitOGTNvSUbL52lraCriohM6dQqojcNpbYWinLNkbxmNiZE8ZKgMKWb8fQ+R9nZpbzhNUopmd4JxBn+4JsaErR3Rl2mJUpicxSzAWSII1bwfuZoe5Eg9TDABphm03Q4ccpRsKRrJMaKysl+AECOPHL1bGg+Q645ROO244+FOPnuGS/kAv+7JTYXTGuOMhHlT7K3NDrec/ny5Rk0aGZ8se3yMqMrhnJVrXFuRJl7QbyfW4YfHH+Yw3C/RAo2jPn1Cv9HObF0zN9bnuQyNVHEzDD6gldpqNtOmXrnueiXW8DU3tZ+J0TVjWnP/8r/Jtam2mFlNvT/lKCnecd/xFsV+XG3zuFXOL7W5wqiP+N1TPPHJH/ZsG5snq7U2n/lZvtRz6xO3XvWqV/HGN76R9XrNa17zGv7Vv/pXT/nY22+/ffvvD37wg3zu537uM36fD37wg0/6Ok9c9957L8973vMAODo64n3vex8/9mM/xu/8zu/w/ve/n6//+q/nd3/3d58x8gTwkpe8hM/8zM/kXe96F2984xv5/d//fQC+/uu/Xlx+/wrXx+8+92zXM9lPpTh76uc++dmupKIjrQe0M2Ld6gO5clIUKyka8yjaGh2Lm4yx24m7Wi0FPSoUI0JE5ZPcCLMJb0MKLrdeoMJIQugV9bRGOUN1YY/6/J7kf9x+Drs3I6eEqS1mp8WemRO7AVLG7U9RjSsFuFCLcrnYKx9F0FpSz+OqJyehcKQQQGVCiIw549cd/aMPEA6v4q9eJl58BHP1MurogDT0QjFRitzWshdTBlfE7mNxe8tIVspDVwjHa8LBAr0amdiKnBOjgjh4VmMvTnw5o5cipHe7U/S8hTM7sD8ntTUpK5J14Ax6WkueyuBJXSAPUb6fJLbWeSN2LdknSmmhoAAOBWPc0m3EvaiEZSZxq8uF909KhOLsZYwV5zQ2RX+WpstH0qKje/SA7p6LdHc9yvDYAXn09A9fobv3McLgaW48hbvlDOqGPdoX3YQ7NeP67BQRg2uGGOQ2VqhCdqMN0xIuqK1DWYs1FqXFPSml4rCVwVS2FE9KDBPaCppawmuvLeFwBSXENpcgW0b5vNlIEYZWJTywnCpaCyXvOt3Oxt6aMi01G/pcOea2hgalyaFodCCXYFtBNTZC+e3rySO2iJ3WGm0NprLYtio6jbhNbd+Ipjf23NIEnbj4JXVyJ84giE9BoCivn1LeGknkTKFECWUwl+NCdoMq4cplNxSUi2LcEcdACGJqkYtOKkehb6acJIBxs8+0wlgj4bxWgmzTphlTimQU2hiqphZCTnmtFKKE3tZOkDo2crhMLo2baSpM0VCwaSKUwmrR8WzQr5AyfgxCh0yJMIyiddGK5twuZm+ydQIjZSnS1mvU4gi1OiL5NRkvrmW60PrqGlyFqmuIAfpeAmCNxk4qbC0DCV07lLPi1Hi4FlfKYp6QMyc5OkrOY1VbaQi6gXDcMR6shM5WGuemrSXvp3yJcdkTl4M0GPMWPanRTSWuk2MkFWMESgORYxK68xgkr6cgy37RE0cZZmA1am+C22khinZRN45wvCYdrnGVLXkyeksrzWRBJbqR3HlxvLsO7UzFPEMpRdVW1JMaU1uoLbEfGa8tWC+WYjix7MlB8pRUyujGoeetHO+1k6Z9DLjKiWnHpinYmZA1gvqNcq3PSgk1WGvspMG6koE0EfYDOWPPn0E7K8HiITIcrQmLfnsuNfszcbKzFpzGb9DYEKlq0Zuayopl9aymOT1jcsM+s9vP0952hurGfdy5HapbTmF3W/T5HXLriN7LIGUM0ugbVbRsolNKPkhQtzFYxEXS1pamrahOzVA7E/KkwkwaaW7aCjOfoIwl+0BEEWuHRmOjXMdVU53Q/aY1tA5VW3nvlNA7DdXeRI7FcjxLAHcqf0tzqYoL4+YeYjfH+QZlt0JpVzmjnaHPxRQiSK6SUEQ1dlozu+Mc8zvPMblhH9NUW1T+qXsUdd3f6gk/u/7n6gk//zhXfpI/T/aY59Zf63re857Ht37rtwLwi7/4i09L1/uCL/iC7b/f9ra3PeP3yDnzh3/4hwBcuHCBO++88xk9b3d3ly/4gi/gt37rt/jyL/9ygG3u0LNdG5rcv/7X/3obPvtXTZ2Dv66comd7Xn/E45/qBaTQMk3FNCMTdqOJlwLjmMh1zaK/QktNjpqkNDlEUhokLK5uULN90sXiPjRtSMVBzRWbUF07KQ6vLkljz3j6NMd2l1R11OEId7Si2mkxzhD7kY2jT1z3UvhCmYQmTFNtww+reUueSLMVu1EsRrMEIlKyF9AKM28x6xFrdmnNhHC8xvsOP0SUsSRtGC8+uO1v1GSHen6WmZth6ikhJ8ZwSEZR7c8wZ3ZYP3gJM22ozu3hj9aESyuWg8MMlosPXibQUhfee64dqrJMzBQVMyFFzE67bTa7gwU6ZXSxEte5OEFVrQSIrgdM0fugFdqXtPHN16o4oUyVfaecOG6pkEpEkSrW2KrogNgW+ShJYtc5A4Hj/jGMNvggmTIpZfp4tG0gklH0tdjA2n6gOhKLVktLtVaYLpHciFc9ozXY87vY/Rn+6oIhHnO8fkS+3xgZcEUv0tKoKVZr1vEArwLEjNVzamnvaKvTaDVBKeijJ6ZEW9dcSLt4rzGDQvcDOmu8SVysl5gsjmEbG+O8EegD19SKVFzFrg85fdwqzY3KbBulzX4XlpFMj7dD0VKobvQwCrb6Jcrjs+I6jt7mNDzRKamQmC08YfDUXWLZytQnq+teI0tDlXMWak+UUMSM5JGIfmXTr8tn1taIS2JKW+OCjUZqcyzogiZsAmkViqbaZ1rJz3vW+G6UwUL00jTlTBcPGNMKT2DqBnT2UoSlLMe5SizHy5DLdFkpQkxEF7jQ7aK0YtIb+uESOSZW40Gh3ybGfsnKXpbBQ1yiAFuQuxSzoACIU58ymsia4/ESRkFkLGir2GbHEInFBUxXDtVYfD/ix4CbNvjDFfiemGGpr6AVjGnNtE/YJFTU8sWj+hHhua6ZzPfZv31KM080qZcmYChUrlUvNCllQSmGxZq20swauZ5plVgzQbeG0IsYP/SjnKMxbSfPGUHx0xAK+oAYPgD29ByAsFiTRo9paxkcxcQqOEJ2qE5oohQrcGIiDp7oqkIJjqjK4tcrcqGQKWMY4ogxmjx43Okd0Zv1XvQxRouOzGiybbh62FPttMS6hiGTQkAbTVj2os8qRg+xF8OFHCO2raWhKCjitM3EscNMW7rBEDLopiINnmba0IfAfCr05RwyfVSMxZiGGDGzZqtxQWvCMGIqR3e8Yjqr2ZmDOdMSh8TxqPEhMNltqetE1OK6OnSU4Ymm3p2QYsLgsWHNbH+K1oI4m2lNigO60fgQuRoqFkmOxxuqxMxlcqs5PlD4IMHceZQwalNZ2J0wHK5QhysmqcNoYRbgDGZ3iprNWC4hLAaiVid0wNqJtgcZbOSim0o6shouklIgR4SfCmRGVITsDSRBmHTtyvaXvK5dTd1MpZGxZksdZnONNNKIG+cgFHaCl+t0LhTIjaY4xYS1DuqKaHo5Rqwhkkk5ssoHmLCEaebMfotrDRIUUi6uIXK7dY+7JndXjgm7E64UPWBmc8/7iAv24/73RDDnmTrSPRF3evrHblw6n8OHPlnWD/3QD/H617+evu/50R/9Ub7u677uSR/34he/mBe/+MX82Z/9GW9+85v52Z/92WdkuPCWt7yF+++/H5B8o2e7tNb80i/9Ei984Qvpuo5XvepVfO3Xfi3OuY/+5LK+7uu+ju/93u/dbsfLX/5yXvaylz3rbfl41ydfeOsThyGbK8D1A5SnmV6I3WzinDsmTyQjoN+vGC/1oOHi+s/kJhwiSWlUTMQcCXuQz14gWIc+XEvBbi3u9A7+2mK7aWGxlgnd3hRWPbmKPGbuJwfFmXnF+RtOkbzoe/zxmnBtITa6IaLaSrjlPqAre5Kx4xPjoqPZm0KGcdkTfKCZtxhr8ONINWmkeHEGe3pOvDygz+9TT8QZyTAyKgW7p1DdNUEgTAXnbyabGefPfzoNFYNfcv/Bf5WCOGfCpQOqWYudNvTXlvhrC6Jy3HfcUO+fJl3Yw9ZLETxPGwJS6KpukH0yjKSrx/gQcVrTlIlrdpKCLrTFQCoW10lrshPEztQ1upqi20pQNGtIIIYR/UgquSPheA2+FFSxTEmNOCTp4qyWjUIrydhJScwPfAo8NLwXU4oJXQpPNnqhlFjsOh65bU7OmdOPLTm38qAUO80NnJu9iGw0D68+SMwHkMQFUM9bzKThsUf+Ah2TmFuAFGMpc2Hvc9DT02SruTQ8xKjXxD5yq3452iuytty483L64IkhcLVbcGG+jzWGO47E1tqUYzmT6U3Pn+z8GaJIgo2hAZmThkSLOQGwRUg2wasbqlwq6MkGmbm+6REeffl3zie5VZsGdaNf2uYV5e1rb6yulRKDicIpIxys0Ps73HT/Aj1Gun7knhfs4K87nTe22TohYYtKbsrbJsjH68wDyuUhi2lGKiYC4swl+0bnQsXL8nhBp6ToMJXj7OSFnLN7qJx44OiP6YaDk8+B5J09fPie7RDi/LUyICmNSwgRcs+DV/87OSexiM6iM2qrfT7f/i2MNqyGyzx4/E4ymbhtIBXL4QpdOCiW5KWpTGlLUYkhbnUpWMO1/DCH6SLaGfS+pa72UCVPRytFtBo3rcVyedlJPooPjLF8/64ip8jF/kPkcSCt19x4nMhDL/suCyKiYkTN91BnzrK3t88Lbx0wZrW1oN5QxjDm5HgBXFWxMw/cPF9j3MjVoeW+q1OwWlCWEKWJymwzjLQx6GlDDhKyvUGP1aQSY4QxSNbaehAqpDUixreGh5czTKpRVpDItJLg7hwTqR/FTGUmjpWERCzUNVVEaAawO60MwwptTltDWnREZ7aNzjo2LPwZ1LVNSHGPbirGgxUohZtackiMRY8UUxZzBi8aH4zG5MwZd8zOjSNhWHP3eoegmi1lmpxpKsON1VXmc0tMmruPalTTkmJiXKxI/SgDnCA5WDkKxXi+P2PSZG6uLpJTotM1q3wa4ywmLri5WpIUXEs1B6upOIPmzHi8JsXEhfnIhXMe13bCqvCRnHrcXKjaKUb+04cT73msgwxf81LFbTsJ33nyqdOsvCAguh8JazE80JVjesM+5oZdntdcwiyXwghwmeZsxueRvzA7RJ+wriGXxl8V9C2GSEKQVqMVnp4HF38qeXObgGZnJXvOB9y8FUOHQaFpsLraUgIpLnOpxC1sc7Fgqw0rFy2ME6ZIiGKWMfaSs6cRBD9GQYu1Ats4YudRzjKsezSRS+v3glLYlefF05GqrjHOUE0kTytkxW3tzrZuSSGSz53mHgP/3767DhHPpcR58mLnyTCkJ1uPb5o+slg6KamevND62K2/n1t/WevGG2/kH/2jf8TP/MzP8PrXv/5paXH/7J/9M77t276N1WrF93//9/Nv/+2/fdrXHoaBV77ylQAYY/ie7/mej2kbb775Zr77u7+bH//xH+fee+/lDW94wxbheibr7NmzfMVXfAX/6T/9J+CvByWCv6ym6ImNzCfqNT/q6+VSYGToR0gONXdU53dodzXhcMVw2Mk0XAkNRjdWLlIzQ2pqqkLBqc/ugioi7L7HJCmq1LInDEEcgqYVOmZSiqis8KueuBgwtSOnJGYJ05b+yjFVzgRnJMSwBM1tdBFpDFsDAW0NzSmh1g2rgbp15EWH90kaMeRCrZ1QeiIwuf084WjN+Mg1UtOQb7pdzNecg6oix0ylQUeZpFujSJUl+oBtK+ykIa56xkWH7TqoHEPI5Eeu0d58Br8ayCnh18OWOohWLPtOsoS0Rlu5gGcrzdCWFn20QuWMBVJBfHRtafZmQvligwydUKnsRpi/oTQUA4bUS5K9spv9KDSJ0Huh71VWPjN5aw1bRnAyJcyZtBqIqx5/sMQv1jKN914MGzIEVVzEjAVjUWRcgGSyfK+DJy96Yuex1pK1BMNSJoveB+qz+9idHbEyVxX0S7Ca4BzDGOn6Aas0CoW1hqpq0Vp465lcMj7y1ikq5bSlrKGuu3luXMfI5AK+bQ0H8oYbe+J6VlokoTqVE2pTLKoiJE656KPK/tqEXW4aC7V9LZmgKhDaDkUfZMpUNovTYn/5CDNtsDbQdQNpu4lqy7HXiN29LhS+LTKliq4J0JVoADd0PWO05JlsULHSCElPV9z2QnEb3DSFvZessXJY5JCIKQpNLkZcW4FHmrxCpdJs0DfJJNHObrVUaE0o5hZGa3HvSrmgXGr7faUUsdaKuUmh/22mw9oYki76LqtLg68l8b6SY5+CMqEUdlKXoNSEv3IkRizzCRlE85KS0HOVxiAIphrFGCKNHtX1sj2zqaDeZUKulRK9X21x+xVWIrfQtVDlQJoapVShyxlscVAzjS4uhuVYqp1QfsOJ7i/GRPZBLNXbmjx6KAL6uOxlu2cNcdlLPkw3FCvtKNS1ss8opjOh9xgd8VcX6Gkt1+aNo13KhBylya8MzbSWI1YpYmVF39bWECLdo1ew+ztbO3G0hiEQU8I0TpzktEapLA5tzgqKEKJokgr6r3PGlN/peSvnmdI0pxV1E7A+0s52Uam+biIAKkUm8xHrEiop/JVAMBpnLc3OrFBaIY+imdlQuwUt1NTTHcmZ8g5ztaGdNUyMo6rlXqiOoJo3OG23TTcKsgZjhP65cXtT5QRX5bjcNA1yzstQZPP4zXXGNpXcy4qFuT9eY09NqXYmuN1K3PqMlu9XWWztaC/sEvqRWJkyfDQSb9GNaCOImDaaPAQiHlVpclTiWGgU4zphrENXBuvs1tAABRi1pZ9vDHm2bYFSIirVcm6nYrmevJyTYsJhcG1N6r38DrY5Ubn35Equb3qMVE0ljqfl/qJqzfJwRdMJK8TeVGqLIOyA0I3CHkmZan+6zco7uTY/WYHzxMbloxdV6kn+p57y90//0+fWJ8/65//8n/OLv/iLrFYrXvOa1zzl477lW76FX/mVX+Ftb3sbv/RLv8Stt97KD/3QDz2pxme9XvO1X/u1fOADHwDgh3/4h3n+85//MW/j933f9/G6172OxWLBa1/7Wr75m7/5WWmCXv/613P58mUAbrvtto95Oz6e9Qlsij4KhPNUq0yst5Obj+Nl195xsFLgdpnNEzaLxed8BvVUkXcn5POO8eqC7mhghcUoReUsOyOEg47Z/pymrkiLDu8DzhjqQS6eyln0uT2hbKx6Ys7gxDI15szQBy5fiTSnJtRTS3vLmeKYo1itFWlImKqFqMirAT2ZgocULU1thTJhxDVItxXxcMVAptqdorRi2WlSJXqgnRsy64cfob7hNGttJYxPZearQDAN2mqiz+gcqRMc9o9SeUg6YPZaVPTYtpGQ18ELfW7Vk1EYNPMIjW2Il5fCsy4Bd1bLDY4xMLNSoOl5S+4G+R4byRJRPqK1IZQMJ1VZtHPMpjVm3oqJwdGK1HviepRcpyiWq7pYUtM47KzFnJqhtcaemknB23vS6ImHS9J6wE5OaDrbHKKiz9loSzbWvWZSo5qK5nnnaXIiq8Q5HfBXjtmLE043u1LQklmGxwghMMQVy/USYy2Vc1SuFhqN71FITlXwHpM93liuXbmfIfUkrajyjGrS0h2ucDGiMbRKikEfAznBar5isD0hb1CTVFAvOf7XzhdL7VIYCjcN4zPTdUChGJ1imJSCvWh1ts3g9adQZquFUIoiMD6hgSlgQ6vT6sSI4Zzfo04WRsXF5ohRhROjhtJU5VQCUrWCXKy9U2K5V6NSxWJYc528iW0Qq0I+70YjVhqiKkB97MUCejbluO+lB9Ripbux5t48xxhd3O4KkKWKjTqCgmmtuTpdE8fLoBUdIxuTBNNWYsfbe5ZzR1QZox2To0GOJRA9iFVkZcAHklIF8ZVzI6SR4/4RlNb04zEgyNJm3whaZclW7LEnU03rAnpSs+4yiw5sZbfTc1c78hgI3Uh1ak6rRiq1IpvM0XrEP/Awaj5j93SFU5Fky3WqfG/3rixjFATx+WcsVhmUbqVxsYZoDHcdKEJINLXhjp1E9h5tAx+U+xKtgVtqjyZz3GceWsuxa61itx5lO03mKE5QSbHuNPF4zWZGrRGnt9QN6HmLWvSkbiCtssQXNOLeZiaV0GIV0HtMKWCVUkzpMVZ+l2KUwNIhshwddn8KKHHtHDwpBGaVmKXkmMgxoAmi9/IBNRXKnTYRfdoS2x26ozX1pCW5mpW30gQV5zvdCoqQvATMKsDttIwHK0I/ii4QRXt6jq4spq05CJm1Fy2NP1I0SwXKMa2h1eJCd8+1TC9JA9xx1qFdIkdFuzdjeXWN7yPdqkX5RNXWMkwyGh1HmsVl6iqAqfjzILfwISouD9Jot9bQGzEWWLeOIxrIsD9R3DBNkGCMjg/3mtzDWW3YGTNxNbI4qzgoqOlhd90tWck1VZnM5ZXnai8/Ojt1okOqrWhFB89wZcGBhcpZVDLM3IhWGaUT83ogZU3QkWWoCRuLc6Nwu62YN1gt+36nJY6B7CPBDYL8hUjV1pjGYRSYaYOpXEGPotQT1zXxMqgpNGulwEpTXy5zcj2N4sCpK9GoZR9PGr+QtiYwqXYSd1GLXtR3A1Whu1ZndqgbzTCMUFXUOzVh9NjakbWiu3RE8om4P+FRpyFFHosnTdEzWTlzcmHj5Lt5NtS459b/uuvs2bN813d9F6997Wu5++67n/JxWmve9KY38aVf+qV88IMf5FWvehW/8zu/w3d+53fyeZ/3eezu7nLx4kXe+ta38lM/9VPcd999gNDXfvAHf/Dj2sZTp07xPd/zPfzoj/4od999N2984xufFeJz+vRpTp8+/XFtw8e7Pv6maHtGXte5PPEMvR45ehIU6aO6VDzDM/5K11Jri796zPOfp5jpAD5wrlrIG7ca5sBpS3cp8xcPZXwQFON5nUU7SzUYODUjrUfJXcgZNW/RlRXjA6PFgrR1WF0L93nZywXbtlwMMzgwnIqJW+Yd2UeWfsKj6xlh0ZEfkXyjeOBRttDnnOHWGzX7eYGJEjaIUkzO7uC7kfXlQ6andriSZqzWFUorbt855HTyuPaQuw9kJ1V7M2477EQQnANmUmN3JgxXDjmu7xFRbGWpqj1BqUpB6I9X5MMVVCKKrpYD5zpL02qOHrtEd74iNhI8mss+0ZWTG5CzxCC259kaGL3YwTaV0Jt25uIat9GrxMT6gw+KaDrGk8Jca8mbyEDJ/1ExMSx7zNWFPM5eF4yrKBoSTby6kOK8CNMBdOWkKSrFqCqC2rEcrxv7bVtZzk1rdO3Yj2c4t/9ClFJc6u7iw9f+mBgj06rFKI3PiSYrySdxGpqZNBnrAVOoaFWKXH3sPRxcq8BY7rjwxUzMnKQiFkWvRrS1LLoVRmt67Xn3zr2s6XFGXPBSFFqR3qA+UChz8rcCkoKmj9zykGT/HO9WPDSVabfKGRLilLU5PwsyIS+xyRLSW6oZIJNVrbaoUC5Ih1aaT13cwik/JxvF77v3MdqliJfVhsq3ydaQJmqDzvQ+8NinnGe8usDnYlKxoe6Vxu36m7tcDzRKwWQ1cvOjPe7UjIsPHLE815AQqpkutrxKl2IhFSZ8mfiKYHr7gqVRVvz57OGtDuV20zELCmqDmdb4y8ckZ3j0xgm9FcTyBX3EFgtekcUIkmWLpklykDKRDM7zyOq9J2gqoCe1iLZrKbYximZ/jqkt83TI6XAIecnB7j5pvicaJx8I3YA2GtdWggiHyNwccG5HC9p09hSp+hRyiNww7Zg4mUDrYusfleZ335O4vFbUOvN5twdOzYzsZWtARRYDvPlDmVUfOT1R/K0bM3WludQH3vgB8GPill34ppfK865Gzf/7wzLJ/5S9wNd82hpS5rCveeBSLd9HaRyyUYKid5L/YytBUXwxBcnlHI6hhDMj+zIOASqHmzfSpIbADfvH1NafGHOkkRjg7qOG4Jpt4KqZN0xU4vl7Bxjtrzv2C4qxHlCxBKAqUJMa9iHsJlArDofA0VEj9X9dbKCLJsWvM2Y5QAa/6EhWQ+Nw2eLO7GAn9abK5sMXFzx8PJ7cmLIMrL7p5StunmYimv/fh+GxpeSAfsYFmDg5R2M/yvCpblk8ehOqndOcPYf3gdF7Tp3TnP3gW3AHiYM+8v9ZFc0cEVg8yU0zABK0+BkXMp97o/z8j+5LvOUuBVbzt+qGz60qAN714YF3j9dt+/bVyj6zhg9d67nnoEcBX3T7LqeLp3jsx/JhDQ9e1NjGoVXi+fM1lZZQ3huqQxKZ0Wi6dUsKSYZVmwFLrYSGHCN+1cs9xIgmLAMqytAsx4TdnUojU1xL1SboO4neFCPH7QY1j76YXRALK8GRS9Mjt528HXCgSuiq1SX6gHItLBlKZJpJzbgcqCcV1ayhO17jmxuw1jHXhtPTQ/prxwyXIro5Q3NmwgMp8lvdeov2P/67erp1Yu7zZL/7hLdFT7woP7c+Kdb3fd/38Qu/8AscHR097eMuXLjA29/+dv7hP/yH/If/8B94xzvewTve8Y4nfWzTNPzAD/wAr3rVqz56Lf4M1itf+Up+/ud/nsPDQ17zmtfwDd/wDTLo/l9k/fVrij6W7+BJTtjtj7TCnZqTx6tQS8GSvN9qLzZanvrMDq3aRY+c8NYBf/lIrJQbJwYHlcUEoYLE47UgHkqjZ604thmZaKVHDyFJUCqjJ3RrwvIYnMF3I74Ta2btDIxBAvuSUOZMkrBSPW/oLx7SlBBYxkA9a8TiOkSwihxkajkuOhqt0U2FntaoIO5Lg4/oURCysB4hiyucnU8KrU32VC6J8uHqMYSEvfEUqq4YNXDQoQehDJgbT0MzolaDuPZlCWhM3pcC1BT6H4ISWAkIVW21dQLjaEn0AY9ChyJWp6AiRss0MEqAZsqSkYMSDYdBivwNpx4vAtaN/TIxisFAzjK5t7YYWcQtUrSxjzZZCmeVckGkFNEP5EUH0wY9O4+pK2KIBJVpmxY/jEUfYAgxEJIEcsasaIxFhaKFikkCNqM4Gvl1h6pq4rqn1xI62Qdx7auso61bKmtZprWEtJYASosU/GwavKJFeRztTSlUPskd2tgdbxqRzXmx0fsIBaagTNedK5t5Yy45MlvXOopJAfIUYZUodDbyWCUNlIZtflFSm5lH3mYk5ZjI3UhYiP0xSpCDLXVMbZ8kNBXYNrKqBOTatiLGCKm4++mNtoXt5z95v3jy+bcbXkIvy3tJIGRBt7Q0xtX+jPHy0dZAIsYEjejD8EGOJVumyGQJHE6Fr1hb1FBsIXIWzZ91ZFcKdWsYy7lZN4761FyK+CSI59itmZ7fx1GhB0ExlNZUsxbjZEiRUiZGj9p3mEpJSOnhiB+FtpdiBJux81aGNqUp3urDNrSzTfjyhvaYShNpDDkV+3WjN8FWxWAhorLeyMSEDqTlGNhQptKgwTSSbUU557QmBSlolRNnxTh4ue4oMLNGmtOcBbkpEKKEzDrJv0lyVGQt26WUPnHnsxmTJuRstscQSkI6pXkS2tkG+VRaU+1YiHLNpmiXslK4vSlpDOigMcbg1z39ODI7vStht6Mg5WZngl9J8KatLGbeYCa1UO4+4k5UTsN88u9c6GlPfktT+MtHxJXGTqd0lxa4vTnK1Bw9do0H73qYW1/2PKCmPr2DIcnw6Lrb4JO98vU1bVj2jMeZatbI/nRs0ehnUgxtUPcyA2GT9xN7j1+Jw56u3HXntjS7ypVmXElDbIwmrmRguQlY1saQstDYQj9irMFNW0HgC/3Gr3qx4K4dKPC9Jx+usbNadEHWkIJ8p9qeZC9t9ILKFsRWcUIbzAXlRiieWguKYxpXaKMKvYmHitLAjUGOIessYQgkBeurC9H2KQmb3ez5Zn9GVVu6biLXqfzELuOZ4j3qKR/zl6IBeq4Z+qRc+/v7vPKVr+SHf/iHn9Fjf/3Xf53//t//O7/6q7/Kf/kv/4WHHnqIxWLBqVOnuPPOO/mKr/gKvvmbv5lbbrnlE7aNe3t7vPKVr+RVr3oVH/rQh/j3//7fP6UxxCfj+vibor8O3PZJTtgMzCrP6SYRu4HuODDmCNqgbA21E9HqujzYGiZpxaQ2BB9YxAlh2ZdUb7MtIPNqEP1KZcldBGfRjaRY66YiDyPh2hJdW9SsIfeeNAZ8YzlijrIVY1uRlwkdkrxOzvgkSdqmcaAUR5dXMGpCmLDuhf5GTJANNC2rK8cs/YrVUmgcV2ee2bzGGPv/Z+9PniXL8vtO7HOmO7n7G2PIiBwrs6owFQErAiDUJJsUh1Zr0drIZCZt1IaFFvonAMPfIdNCpt5oI1m3SU2ZiWQ3KQEUmw1QIEGiUEPOkTG+eINPdziTFr/j/l5kRmZlTaDUiAMr5Hvx3K9fv/eec37Dd2B8siRns69u6iiJk/Ke3Dm01tSPVtS3DmUB77Sc49NLgb8czzHGUD1Z4y5G1BC4jAHTazg9JV2tCEU9T7sK6qIGV6BLphK5aRqHbirBsjtL//C5YP+ngNEKFwJqMRNSfCwiF4UIL1LSEvaj5frn0gpY6DsobcgaluEhyY8ka3BKS5dKFUUzSvKzh81dV+ytNfjJo3KicnM6fYx2lu20ZDs9F7iXj6QOCWaNIcRInzxd0gSrCYXEb9HYbaDzh1jTgYJL9YSAl2tiFKoTKMjF9jNUrqhqJ5LBxnA2bFkeOLq6Y0gTQSeU0gKb2ynLKb3fB0VqHoQ4RIGsCWTu4qRGK822kcBsZ8SYrsvk152hHSQkXwdBeZeE7uTQd2OXRGVIOvPQPWdperIGbyIqFf5RFpU4rfR1ElYKEAokyCbjTudMlxtJim4GYIX7tfMjsjHRXo0YxBjz4s0F09Mr+q50wZDChwQwiuN0wLGfkWJiCJcMaS1kd+Q7amvozAnOiPHx1j/DTz3Kit+YO+kIBTaK1WgFJ30i5oBKiqOTd6mCIqbAVf8Q5bQE6eVaaquhs7iqErn+DASRmddtJYHXJmIrKzQtH0Fr/HagD5rZnTdZacN2FFlm6yThmh4+J1jD4o1bOGuo0NRdA0yYynJ0bHAzCewepJapz6g+8+2TzKzRL3TjklL8+QV067JWBkk6Y8r82mkixEwVRoxqSNuRVll+47Yi9JGjSpJO4ywHjeI33zSkELnbZVIQgQtdlNh2CY7AmARemSoryc8UiGRiP5JShZs1smY7j0tjOZ8BfaBQOpHUyI7PYk0uyp8Vf/Fc0Q8RrONpPxFTkeQoz5RRidUgz15j4JdPMypFNlPmh5eGnEAyRsgUvyGTyVmjoi1rU8ICmwdnuHmDyqCdJXkxvNXzBtvVnI+R5dW0y7z2+9LG7xRPXtysfnCueN5LT2frX7KD5UxaD/gA7Z0Frx31rB894uKq5/bbNSd3B3xY8r0knfnlTb7MS/bD3XzZ/W5mNdp5xqstt9uO796TTFf1kT8bpDt0dgPSdWvmmFdFDTFnnp315Ji51bX71cWME/1yI0mG0aSpoCvK/lXNnEjXa0vwidVQkZwlTprjw0xOIrvi/SCGxhhWU4UfJpyOnHZFAW7yxCZiDhwxjcI9yjC1huUmXPOhtJZuslKkLJyiNAYxtM6iZrlHIJe1EaUwRpNU3hdkdspzaEUaI7q22Loi+0BdhE5AOori36cJY6A7naOMpg+RP30sdyCNmclP5ATPv+Ke/fjxlxdsXadfv4Au1KvxhfG7v/u7/O7v/u7Xeu3v//7v8/u///tf+9i//du/zW//9m//lGcm4w/+4A/4gz/4g6/9+t/7vd/j937v9176t5cq437N8Yd/+Ic/9Xu/7vgP3yn6uuOrymFlnDQDry8ywU18HOZsUsv0+ELM3aaAPTgg+4g56NAx8U79kApPsoYfPAGyRi9aki9EXxSqlWA2k0n9hOlq0uil0gnkdcDeOZTFeJjEZFBr+ph4cGExLIjbAWUyRMj9KEaBRktyUbwkroJjOSh0N4fLInc6TOILM3pyrMRxvvB1znvN+dOAqnshpjpLCgGnQTc11axBWYNZtFg0t55uMI96ApnnrscPI1pp7EFD7EfUEFm8f4XVik1InH3jCHU0J217lLO4O0fi/m0NtPW1T01KMEyC2V9uiY/O92psCrBTInvxDQKwwwRtXXyR2MPnJI4u/B8rAbqKCZ0Vt9pvU+mWoAKb6YwUJlwS09NMgXupApko6nQg1UqlxUcm5VIdnAK1XnB3/h0whmX6iGE8A0q3onQtKEH63DVM4yTVyhSJlZynM5qTxTeY1/dJMbI6+yPGfCGV7phQlUZZzeXwPj4lzKTJtWVabjmftjx9/R6jSnRVjTYGZxxJq2tl65zI+do4df/ol9JwTomhNjy8373Q+RH1shIUI52VXbcg7Uq8+1cX/4wMOce9WMEuwNx1b1JOfK/7TKqvqMJH0iijxCi2cInkfu5kvneQNc32o2e079ymffOU6ckVefTSbdydRWavJDfvI288GVBjYPOtW3y6UETdStdWIQmXLxXdDG8MJ/zK+DZpCjztv8fz9RPpBqSMaWvQgde7u8zr11CV4dPLK9Z+BSpKoGRE4EAfNPsg4H60hKtIYxtev/0bON2Q8sRw9s8IYdirG5KRqnNSMIlHi+5KASYVKFTtcFZU9WzjCJMXgRNnCe6QT89HtDHE0RPOnws8x8o9M8D47IrUTyLNf3tXdYdbauS0TWRr+S/+LXxwFnGV5c5vwLxR5BTJIQOWkDL/9P0ba6eSTtVBlfnf/pairRQgIi6+DyxaxX/2S4oUDP1qwNZzSJnbLvKfvacgUhS5Mq6tiEsRJiDvkltIU4S6VPhzhiJkoYvBZ5o82hhOZhMHZismpQqm0iXQxuy9YxQKZS0hK/7Zx4qzfrdtbW6s/qWCcONZOnKR9440tTOs+sw/el8TPr8f5+tCwesHjr9xt0NbQ/QBE5z446QsYiGlE7ebHw+uen70vL8xOXfH5Hpty9dz6V98ypeONEVU7ajuHqKrmqoxvHn4Z9BNRFPx/uUJMf+IVYz8N8NWvLi+/HAvOx3xnGprVIZ34sA3v90C8N9+FPjHl+ELx3j7qOHtIxGv8OuBhyxIY+BeZXjjTk3ygXC1JWtNmAKhGPXGEJidLuSZaA3aWnKciGgermeErNFp4tt3LrEGEbBRsl6vtnC11oSU6WzkteZKBCwODeNqS1JKeEVNRfaeK3fI2bkUYUwtcLiUEjhHCvIsqeJDZbTsEbbAucPopUPvg2wbSpGDQIjDGMRMtuQEal+UUpDEcyykiCZTn86pFq2su0W9cDXCf/MBpKzK+0auW5dyhyQ4zLvHjxeV4r5OIvLTJiw//n3qJT+9Gq/GX4Xxl5MU3SxX3fz9Zzle/uI/7Qp22hrC5YZolPg8bKe9f4nuatJmJI8DdAPmsCJHha4tGnvdYegnorOYJH4c5nDOzlsneS8V35TEPC5E4tBj2lr4RWQx2HOGuB0KXEP8KeIYCFlI4WndY48XxOUGe7IgnK8IZ1foyqHvHmKO59jdJlz4PNEL8dQ0VYG0KAnSKntd3b9RiVdKoYJs6mxHxgdPmU41urb4YSQPg3Ae1r7I4QoEgphJyy32YCb8oCDQpDx58sUKnBMY2XILU7iWgTbiz0QSuALFDyX5gNIavx7QPmKcJhlL6qdC/Bf/oVw7VJAESu2gPwUCp1IWmCASZIiCoKiLhRCpbYWy19VeVbo9IAFmUnpv0KhLsqDqirgVY18oXYjJ7xWQyFnU+FKgqVt05TBaY5sKPW9QUcGUqLXBT9J10UqJ+3xboUyFn0ZU7RiyxzYVi0rzQRqx8466aqWaudt4C4doT/SF/T1N5ZrI37QovJWtVBec+16wQO/INjcqM4LfeaFRo3cV1vL5WWtUSiQlyaZWilgS4J2EvCpwPa2swNxCgZztkpbCVxJYXsKeCPY/XGykGyfNNAlCdnAuY/bmsVpraCsR4Ji0KGHtpv1OwtsaMezNkGIJEJ14j+h5g7GibKVQqNoKz60yqNahq0rEAoy5Ts6NFrnoWSOFje2IdbU42vsIJmN8JG1GdONQlRblsR2HRiuB76REWg2SxAGpn5hGj5s3opBeOtFZK6ZnS8y8ERPJMaC7Cl0Z4hBQTU3abpnOLzBdhz09IKuA70eSj5I4lARJW4Oxin0TLoufFcbAlMv11S/IsYu+sHAnbnYFTSkopBBJIVI5J0WZXIoMtSWrhCLjnMhZo7VIk3sxI05Wo7IhbSdSiLK+LFrxMfIFmjR4uVfO4A7mcl4IcV7WceGFhUFk611TkbURuFy+8QCXkUunZdctUFB4TLJsC1RyN8duTqsy71XpLNaWql7INYxpf+12/lHl1K5rC1wfi+tDv/ja/Tleb12f38KUVthFi1EtKel9gCyS0Fyf+41jfeEa7L7/589h9/ryJl1ZposB09Zy/750yPwNy564GdklnSoaSR6KNPa0GWG1EaPariX6KPLoTpJ9349YFQX1oFWR5DaEyZNIVEW8Z3WxRs8OcY3DJHCuwKuHCWpHfSCSiGEKwg9TiugDdTeXPaZ0d5wTlVAVU5n3ZQ83xcQ5lf1IibqlKnzN7HSxMSidIx/FA8losfAoXMUdLFXHjOtqmtPF5+68+vxVZAfZvb4b13dwvzzfeKv6WgnPzafpJxmvEp1X49X4svHzT4p+1sTnZe9/GRbgJW/zV5YpaeJmICdDjmJId9B5bAootylB84ieWbbda6yfXZHbhoTee7GQMqprxBujn0SAwAfyJGRfO2+J5ytUV0slXhfeghFicB4mGANZa+zJQtTdjufCx/El/vCB2A9Ud46ItcDzUoiyOfcj+fka7jk6r7D78qYGXYGFrdNEo/a8m93lmW2LtLGCzUzw+0nDqoO46pmOHC6OpF0hN0MeJ/SiZTUN5DETZpVUaDOkJxfiF2LEuBZnYRjJuSfHSNa6OKlLZ0WCVjH1i4W7oJ2RzwCBKU3FdNKY4skiFdkQA8ZUEsQOft8luRofYHxFJsn/xYQyjuP2LTQKHyeW4ydSqVepdIgUGsfxwbskHwQON03oxqCN5TI/JI4T3g1UXYfSijEuOR8+wufM4C+kAkrioHmNyh2SMlx0a67cFpWh5zF1tQWXiUPATNJFQitUVxG1RodISIlZVXHi72FcxRAnztoto0EI50aTjKKm4q3lMQbNpAOftGck9WKgk0t3Z5co7tTfdjaueyXHncCEuq5A7jozcJ077zZsbQpktPB9dt2lLE+ddJp21WnJwtghhpTR14FXISrnLDDA5v4J9cmc1Q8fkTeFwF26BfuhlXDz0Ixd5vy+prp9yPT4gpNnQuhWRfo4e1GTUy4KSX864zwlbFcx6gF3a0HMCeMk4c4xsgxP8WlLHjJTWKOsGIcqbVBNhsFz547BOaken6+k+5m04XJ6gMYSt1tCYzC2Q0XPYVsU0frE+dqCs/g0YLta1Bh9QDsx8czWoNuaWAxGbVsxrHqYIu6oY3p6hjtaoOuO7YMnIvuuNfiAPTzEnCzIGq56Q2zmwqnyGTYJVTludwZ7V2M0NO0IJuOaiu/ez6wngAJHzQofM392pvBJMQX47x8K2R/KMxMVnY1853Yx+VUlaXW2wHM1ysCF1/zFJxGlE0YZahPRCtom0eoBfCJZL8Uam0l4lJX1QKlA1B7TVHw2Gn7w8MY6nqQLqq0mZwsB3nMjszDgx8BfO5gxnDbEDP/mCYy7BkfhjdUWfv2u5HtawR8/FEjucrqxbeQXE5XdWE+RH+46P19jXA7X3ZWv2u5+7FYYE1SKpBUfXQxsg6axmXcOM8Yo8jBy2vSkrDDqRcL9C9vkS3hBN7fOpxv4lw8gJ8XJBN/s/BeSotszx1EjxcFZjExnKzG/7WqCF3hwynnPtRvXA3q9ERi4tQLbbSpSylhjhK+jFNVBix8TJ+1AahT1omLWzEUO2zqePJzQ1Sk6Gk7shhwiFYVHmjNDn1g9DejDGSlaUnSomNl4u4cTN2rk8EBDzMQQMAvL5NdUXSP8vJS4vMyMwcgaVYpnGThoJhothrfrPGOKClO7vedg9p48BpJRaJ+gMugMUWs+OBeD5JtJyhDSdaK8S7w/d79+dlL7T9spejVejVfjy8ZfLnzux83fr8IDfI3X+OeO8coSR02uJogjOSZO7vdUmyusBz2bkSupLv/wsznjNCOvMtlEWfzGIPCVKRQDbRFBSKse+gl1PBeMPBkuN6SUsPdOoLIC90L8W3BiUJi2Qg5l69BtJdK/26IU1TVM5yvs4QyMYVIaaxW0GjVvIGXmm0TbX39pgZvB6BTRqBcWVpUyh8uI9ZmkFdtGEbYDaMXzKuGbIKIEqpHOSYzk5YacE6NShNsNuZ8ElLYdJDmsHPp4sTeajNsBpiDEaWNEznQqHYSdt40qnQOQLoNxRe60JHBaQYI0TkV5LhFjlKp8SiQvssopCFb8vH9fEkpnyUqqy1bX3Jn/MtY4xnHJZnxIipGQMtqaIhXccqf5NqqWgCHVEaM1V/4JH63+NU4p1CCV8mw16/CcS39OsgadkkhwK8u8ucfp4puonHly8D6ftU+kq5LOIT9HKcU3lgOztSQQ+riju3vM9rPnRKepXIfShpP6HbJpWVhw7s+ZEM3bHCM6KlyyfKd/hzo7lmrDp81zdvCK3QTaVRv3CU35715N7uYUySIskUvSrriR9FA4XKrAjXZdOXhhM98V5XOpnu6DrB1/SGUR09DqxY6EEuiTbhzTxUbMe62WRAYksC88JFUqsUophtbwWWuoX2s5mTve+N5z6QqtphsBWSLhSwL6hIvFEmtrsoq4rkWHSOwn8bFSkbX/jCsQMnat0UmhUcIN3I40xzPuHK6w4xqP5yodE60hW8WyeSRw0MpTqw5dO5yJvHN0gSazerzmonfknGiO5tjDTjqiqy2hmKnaxu29bagdYTviaoue1fQfPsBfXJGiQs8zar7AHUn3Uxst3ZVaRB6WQ2bVl/sXswiwTIGTsedW4zDGUvsIjULHxH/0mnTgKBDJFCIDlh9cwtgnhgj/7Udyg1MQSFCMitva8+1ZpO4q6bpYkR7nRiD5ZKX4xx8Ib+MbJ4a/fleem05P3F306J2IAqI+Z4q/0m4TyG1CVYF/+SPLv3vCnv8nHUOFNrLYGWV557tHdE1kWvX8lt5gZ5Hoav7iYaYfkQJOgS01Bv7e25laZy4mzf/uTzJTvNF05XOB6Y2F9WqM/NmTzf6FX1nf2x3wxvqbS0f1x43da3ZvTVOAmSP4zPee9SxHmFXwd96SwpUmcbteC/xN3UBFfMlxv2w8WMKnS8gRfutA8969L26m9w8q3jtuRGGviKPsuJ+kxDT4vWBRihFVCmqC1BTlhspqslEop6GyuGLOrVXi7rwvXJ2BOEi3aQqGM39I3CZmVeSt+Tmm02SjiSkz9BOjsnw2HqDPFDEkVNWIobIC1wo37GhhuF0vMUoXD66ROAWMla6n94FeHzCwmxNZ1ijgtZNMl3tigo9WLb6yMndK5zuVzmqKItRglIjqjBP82fOBqL/srrzs/ux84naKnT/JyFz3kV4lRK/Gq/HzHj9zUnQdhJWfvmqe3txlfpKO0o99zfVWt4NkZLJ0XqIoB1lroB/J65GUE9S1JCuIypXpGuHrWFmMza0D4uVGKv7rAbXqpfwI5EF4AToKfM5frDGLtjiqR9TRnHx2heoacu6haqSyFpN4GymIKWLbSiAmk8cuOrr7x+TzFWbeipeHD6SpIm8TataUAFqI7XhFduVCxkQavVSuLgfyeiRXltFHhvVagoamlta/D6RhRFsrkLo37kiAqzW5n6CtxJk9UxzjB9JqI0mcFcnouJhJAjgF4V9NXngcZHBO7kUM7GAIeZwAUZDKQV63UwHLRQbaWLOXRDVAQsQGFFL1yylJYL8L6tWOI4N0LbQpQVgqMKZ9ZL/v4GmtydYSPRK07bDsJdhehYG6aXFaSyVRi5iAtkbk2XempmVjTFnMcFUsxpqHM7LTdK+fMj48J11sUUZRH80IjSEnS6Mck45y7laLD0bpBKlUxCtSRNkiI6uufWiVks10r/CluIarlQhLjiWJStZqH0DtzC9TaRHpnQSuKfC0zD5JUuk6WFIIfE4bgbrJwXLpFF37QO0LBdqyUxZMg2d8vpYkugQWylkRIlCqKNoVDxEQsY0y33PO4Az2sMPUjvD4Eh/lHjIXfzHnDMbaAmkNhBCxgNESrCsUuqvEDLXwfKwrVeJ+EhVIo0k+MDy7ouvkcbKHM5RrXgx4dYU/X5Eu16gDhzrVIj732jFtdSidZs3+3mhj0LNWigRIgu9mDUop+sEzPV+Kf0rVYO/U2KNFqUxHgX9OsSibFUPYUSSmwyDnTYKcE2HwqItLfEqErmGwmq49kG5pET+IwyRcN8EaQrb7dTUVaX5AVCBDRM2vjWQBgf8iam3ownOLOyGTInvvoyQ9NSgvXXKUCBSgC9RwVzH3AZT8rpSS66akUy+S/4lsriFku1HNG1JtJYnYBbSVkuPuJglyTG1ubBqlOHBzt9jNlS+OPX6JvcDJy8aX4eU+9xlfcvTrF2X2PDFVoIuFarIftnY8+eixrOMntwH90uO/DFzx0nNQFNjntYnz7nPTGPBXW8J2JPooioHl+VPbHr1colIiNg2pFUuK6AQauXv2Q0rMjucCYx8H4ughBxFcKGbKKWVM2U/TGIrip2IMkc1moO0qqrpFKUWrFMFX0Msav1P7TCAcIlPmyBQwndkLf6QglgthEHiGqy2ql3UwezERJybxBXQGrStZS0eHtQIZ3xUzjLMEH0g5UxXoag4is6+N7Ot5By/8ig7QzubgC8/C51/3QsJ0M1hSP/a9r8ar8Wr89ONnToryS376iQ+wL539tGchb/xB8JyFgFJw/Noc64V3c4VntUqo9gBta8G9rzwxC25YlWo9PqJyKcJebYj9JJLQRqMPOnFBV4ipqJkTV1uwoho1PbvCNBUsOqmiDRN5mDAHM+GLpCyQupjIm63E8kcLgaOUhdJ1NXHywmko1fPl1YbNGNCuyGw/vYCU2G4r8nEn4g4pF2w0XCSDUhM5acImSsCbMmrdkwFzNEOdHojj/CSQwLwZBHt9MJPAe7UlhSQBWEKC3xRhV2GPo1T7jN53Gvb3IYnB3t58tMC7Fs1r1GpGqhVX2wfEtEEZzVH3BpVuUVpxMT4gxv6av6A1MUXZQJHAMhuLUpnoBy42PxJ+f0qcdu9i2oZhc8WV/4wEBO15PrxPzJlGdxw2r5eOikI7h7GWGLx0OLLi4OBAglktJqAhiqx3H894bjO2qqnHNXfXw943wx40hL7HVY6cI3bR8jQMrPKIujfj3e0dZrklNC2T27I9e4JXiZSmPURtp+GfVOR8+z42wNYG8kkSHkFRc4Pi8UMuvjwFQlcSRbVLBtS16/y++5N2sMKSXO2Oc2PzFb6SvqZs7M5PcYNorPeY+mSEr0ZKJVgWTo1WSqTrgcoajp+PhPMBnzMXdzvpXKmSYBbvmVwUB5spcho06tGG2zZzd7YlToHju4pxNVK1FT5MtAeddCZjT0yJpANLUzMkUDFTzTvh3GhFWPVMF2uBh9VOnttO+EJxDChl+Df9jNgnXFtzVP6Wb6xP/nJDOFthugrsjLNepKFDVnv4qDTiEqGfyJPHWCvrikLERtYDpnHYWY1xpsjKC29kVkU6dYVuLaveMCpR2wvrQXzHKEmAMTAr8uBFpAUraolJwbnviP0MbTUnzYCaBlGbqxxJJZxR/I/uJ8ZRTDLjJMmMtkYCX2Axt1SGUtGX+3NtXirP4mmT+Zv3ItZZjueRO7XAaS8n+N5jQGVsK12uFxb2DMlTihuJp5siZ62UqDbqjEqK37idOO40KidmJHJIYow5Cb+IItO9Kwrtqv5jhD/6FKxW9F7W8s93iV7cs75q0ylFgJclRy8eiH0Xtzw0n/+zBn7jbuawffHzjCoeRSmVV7EXKznrW7ZBjh0OHdPzNeO2JqUvSNfJt/mSr7M7l/sL+PYphCFwmBzP8xGqV9yZef7u257Ye+x6YFgbwrpHbXtUjCg/YSdZr3BWClCUdavrsPN2n4jsYGq35hPOBYL3WKvIUyYax796oplipnWK37qvIE+oMHKn3ZJTpl1UHFgR9piC4nLjULZhnJQUpspWo60mbEZmM2jtQN3VPB8SHzypik9ZIkVJlG41htuLhkymqRV3raAg/mLbcLaRwtxTn3FKinZvLTacVgOJyPOVZRgTtpI9WefMECKztpJiWdyJL/wE8c+NZ3L3lFzfu10h66X9zGt49MsP+4XE+CcOqb7wXL8ar8ZfrfGXD5/bVcG+zuR72Ub0FS/+vpdNPfvI3wqOW1ajjOFytGRlRAZ6o4UfRE0KIyolzKJlPN8wrHtZ3AGnRG5XhShJzhTEm6X4l+QpkH3GHtaEBJt1z8IK8TzHRDaSLGUniUfwce/RkI8W5GEsQY4ifvZcyMqLDn0wI6578lYSj+1xRbwYgQHQqDcPJAnyAVM78JEwDhLQ1I6LaQM5SIsB8UoREzqBCaSNBFnGGrIPogJWO/FdGiYxrY2JPE3QiGyumjwoTYoSDBMC2SnUbE683LDjogBEL1XcXIJyVRTVFvYu8+ouWiumvCFse8iwcPfo7CnaKNbTM3zurwORIOo+PmWBSsSETgK/CjnybPUDstFUuuObR38P03YM6SmX/aekFBj1lrP4A7SzeHebA/MmoDDWirJQjFLpay3r5KltURTzQaq3xYNkSEtG1sRksL3nvrJYIwFvDp608RgUPsOzszOufvkel/dnOGX49fN3OfYz4ibwsP1z+u1jQmNR7SF6URG3I2HwQvoncj5+hJ4CU63J+UCSkHy9iyryDUjb9XzaBWR7A1UhEwmfJe1u0Y3jFMJ9yiUUy5ldWCY8OekA7Ju/pTOmyn1WSqG1KXjBdN29KkaIdt6gnaFpG+4/DlB1rNdblpUVblLKgC4dI71P/mZtw2uPB/LFlru3NKfukrwwuKqCI4OuNQoNWjxNog9F8jmSLhKT13u+QFgLP8SveulGmaLSOAWRiM4ZO2tRbcWffhi4GgLOKP7BuzCryrOeMtkH0tUGM2+o7h2RjeHpBun8jh6SmDTnlKEQw7XR5DjtjXRTSjhnwQuEk2JuHHvpoh4sFPfmEOOEShVPJgujF/NQo8FqcgbvI37yzA5nqH4ixgxtSx56Ul2zNkeMmwZjNQduxAFZZVIIsralzO/c3XWHIilmtBaRC+8T1lq0VeQk6okodd2Z0dJNIsNpo/iHvyTqmaYO0jnXmk8eKf5fj6vSgdx5I12PFCNkJcmdesmSrhQqJ75zMPHuHQulMx59pK4qEqokn/nF9xRe2xgVf/R5lbfdM7+Hjn4+KH0xaXvhh5ftU7sJ8ULCVOaWevGtN0/hu/cUbx4iCdALXTMlicaYSFMmZ0vKirO+pfFlTaIjdjNWPcSpl+TkS07vC6daPv/eAv7u25lp6TnbtjwdRHHwdrPmXXWO9xue5Jrz84QdeunUa8jOFviyIzpHshWq8HRMY6WYkgVS5zcjttIc6SW1SuiFJClhyPR94A8/svTZcFxnfv1WEAn+wwajtrjKol0mZ3ke+23mybbDVk4EO2biiScWA6AbR9uMvHULTJ348IHmn3+iICdSyOQgUuu/fqeFZo5Ccceccag3mEXNH11ovn9VLtAawKCT4pvHE7e7RH/Vs2peI2gne1rIgg5JmX7Zo7XCtDVKFY+vr7gPu2fqOqHJN5+y8jj9+CN8VRdK7Y/4sm7S10yRXiVEr8Zf8fEfVpL759oD3lXqBNaRRy9clTFg5g0xBkxdk4vqkWoqdJVIheiusyi4pWHCnR5g2wpiRNeVbOTGEDcD4flazEoLntneWqCtZnG8EGPCKZCerwhDwOaEHj160YrZ251D4tMr4rJHH7SEfqC5e4Kta4ZPn5LXg1S3jSQAOWR0V2PvnZImgc+klEjDKPLXZ5eS1Oji07MeZF9ui7t6KJCWEgynGIUfkUpwY42YEDqLP7sUQv26JxsrwTQQxoAKEjhJFyiJJKmrQOX98ZWR7opKiVy4IrpyYtC3w2UnhNszTQLjMXbvCZRyJIZAihI0pizdL+sMtRX8OjGQjNl3LFDChVCNKeaOoGqR/XXzGUYJ7MeHQHJ5371KBb5njCikTTnRuiKa4QygMG1FSoGQM9pZtNZoFK6IaxhrBCE4iQQ2zuBQLMhsFg220dCHouSnsV2LigikzWmoDXE7okLCGiNS5zFLV8gZISzbHUeoTJQYSbuuhBIj1H2v52ZgVrpAKpdEJeY9H6S8SuIwJRDFXdVX7zhhWhT6pEm4k9ZWxVR3B3lSZA04jZl1osZoNLZ22EVDfSI8NLUeiZNH50x194j63oF0Ugo3JRUxDlM7dOMwqwltJvHOaiO2asQA1Gi0EX+sXbKCkYqxsobkLGaq0YPM23DVo5y5hsAYTXXQ4Q5n15Hkzjx4F2Bn9hBOIoTNiL/ciLpizphWMz5fC9fN6JJIBKpK/IiUkzljO5E9TiEQhyDd0pSIo3QCTO0EjlpbUuPkudxsSV0RzSg+SKp2JDLDeiD5SDVvsNaQxsB0saFupRMerIW6wR7MsF0FWhO2I0H3GDWJgpYTqE+aJoFsNu7axDVGlDXUdVeUBTMqJlJIjNueuqqI5JLYuX0BBKWgstIZrh1KKUyjMXVZkvX1Ei+PZ75WErzR4fzCSm41bt6iq92bM2ZXSs+ZMExEnyFZgQ031T5P+TFbxJ7v9lWvefGH/Lm/fe69+fO/fIVu2K6YkTJhnLBNhaqcQIpzmfspFgEbMfKNBd4opsEGleR5LoJ0153gci9Tkq6f0tcQu93SkH0krCfoPa47gjHjNyOrx8/ozBI7DOTlSLYL1K0jQkC6sUqkpY1RUFU0s4YUoyijFqGhUIqGWQmn1g8BowJ6DGIN0VSkXjp6cfL4lMhB4WayV+njuXRVkTmZYsJGTbxI6Cx7dvACO85ZJPFNW1EfOWy7uf6mOe8hfwqBgGtjGDajwO7ajFu02K5+aVKuShKvlaKdt+Szsh6OIrmvFNRNRb/uMa27kV3ffBC+TmDz4vu+Xkp18127933+877sOD/XYOvVeDX+Bzv+/8enaDc+3x++8ctv3IW7M0WaFLWPxEGgK2kM5O2IP7vi7lsNxmZwE2ejJc9q1FzI2U1CVNKMGM8pZwnbnowmPrsibSfZkFJCWajuHDKtB4xRmFlDeHrFdLbEmCJVqzSqcZhFi7/a7iWNcQY7awiXG/mc2lG/eZvpfCV/n4J0s0Isql8JQir45oCqKk7u/hpVewBGcbF6n2lYSaW6cjBO6EJs1rsAKyTG8yV68mAzatGi25q02sLo0X63MRcpY2cIMcMkwW7ecWlSKo7hBrwkiyrnIrOswAifJ2pNmrxUERNcDg/Y+kvhVISVxP8po2NEO1AZTuu3mdwoYhVGiPs7w7w4TUTnuRw+IqSINZaj5j2ssdiqLZwipAth5NpnUzDotWNMW54M3yekRB/WeJCOmTOCdbcG4yzr7Yam68RRXRd5by8ePsSEqUXtKIWANQafJbkkZMy8otWK4yc9R8ctOMdWPWKyGjtr0KbCukPQivuDZtqU6zl4VBS+z9N7HckHIhS+kDzzKgvnhgK32wc8BQ64g1XsAj5JkgonqswZXUxPBeqm9/LWu/dlSpdIAUqMTPXNfy/cpZPziUprdOt47STSHFqirvh/f6boewWXI6sHI6BooHRoDG2OfHf7XKSWs+FsU5NCoqnhtF4TVwHXe44PwM0zjcsYW5Fzxo8TNrPnXZAzaQhFqMFgaotpHHmbCFdbSZKNmBSbtsI2Fe5otifkk4r4wOjJKL513DDOAvF8Rf7sOQMwTR5dO5F2rq0k1D4QSZDAOUcVMrmf0LWjnhlOO1EmnILmbC3vDT6iG4Ht4UU2OAbxG9OFxxVCKCayEHNFqiQAbodzTttMbhVrD6tBobXm1mFkVvfEOvDpkAm2pT6Zy73KWTpQ84xyoggW+lFkrX0USfCSWypr9kIFuyA7x7BPWoJ2PF82ZBSNSxzrEa0V/aS5GJv9M2SjkOkPq8h/+i0JSjexZjXtMpuXLeKZTy5HLgeR2f/uPbjdScJ03F0/35T7nqbI02XFFCp8P/I37yWm40Rs4V88kKXqK0e+rrTfoHbwgk73y871C3/aJdHq+u/7ztWLYgt//R6c1onkA35oeRiKjHp1IM3/3aFSYtxOfKODacoQJsaH54RiJrorVmhj+JaNqEaua/ZRkm8v3epslAhjOFFPAyRZCZFFUDxadWgzx2TFcf+Ycd1zUkXM1Vo644sOfCfCAuV/RmuR0K8s2Qj/0yDdHF3gqKTErXpLXUmBZjV1LAFZaME/FwPdd+diAN7UmqfbQF4G4fZVDm1F9TT4QJgCqmmpFg1xM6KKuINKmYve89naY1tNrCKvL+QavjOP/P37Yg+xzS2bVJN85BsnmdvNABkOZwY324U9N+/tdaKvK0eOYhB798jT9z1JR87WDVGJaE3TlufafT6E+nHJx4vJ08uToZc/j+9Zy5tGIMo/jJHHN8zJX41X49X4+YyfQ1L0pVnKl7+8QH6+TmXvSw/7kn/79in86m3IQfOj9yeGO7cIyy2qqTC1RZ0uOHJPaTrQh3OutobQJwgRu+iIz65EZaerydaQ1wOx9+I7UpSjchS53+q1I3JKWKOI65Hw6Eogbc7JWusMdtFgDsVbIW57pgceBk+uLGbWki43TGeXxJ2urI9SnR+LbnflyJtRjBijGJUmFLmPtItjWn0LcuD55Z8Txg0GiFq6P2m5lePGiKoc5nhB9fqtPSE1LtfkVS9B8axBzRvi5RWqqtBVRdz0qKYlW+la7ToFulQ006YvLqfih6JAOhmFOK1jLNAr6S6sx6dknorvzQ04i0JJ4pFhYW6DSihjyc6JeEAlikZ5mogmcvnoM1Ty2KbldPYNtHKi0GWddC8UTDlR5UxqK5EtV4q83LJd/ZBcTP5cW0nA4Yx4DlWGDMzdonBrIBTYkNbCowlJkgLtDDu8mpu3ct9GT1wPuOM5t3wiPxdTztBd4atUjDQ1ddsIzt0rzGxRiMk945MrfK354f2amCuRct5FbuWzlDVF0EA6bmrX+SlzIRX1N10mTiKjs9qLMZAlmd17PxXvlh2USSslRpVG75MkXbpG0lrSZKs4zYaZl1jol9VIGz3DoPinH8ByfHF6zpzGffMIqxWNjbxnLkFF+lHz/lCTomIWJt6pltLlrUE1CtKEMU44TjnjmpoUJQAMQQKf7CN11wBS8SZ30pVxRsyLK4c7LqpzN9aSHBP+ci3QxSmAj9yeNSgFU40k3Vpjiwz4NE04o1GVxVTFvwlF7keBDQJpmLBzxYlaYRc1z888PhziKrdPfJSzxOwJ/QRG40OUe9jW2MMOO8uEKWJNTWUb1t//gMXqQ07fPUJ1c0Ku2FYNOiXmpuf2iUNVjqFesAn1vuMXB4+qLVHBcrlhcXqAzVLg0J20cfLO28yofSshpyxcDOk9FghmzfNRYFbz7DluR8gwRsPTVZHuV4q8TaQEx67nt08nUIqnW8fTwUr1PkSSgqqpXkhOztcj50UQ51sHil+6VThMIbE9W6OUopp3wrPJ8ORKMQWDiopfO+lp71l6LdLiPzYp2mFMrxuDN7U0vubIL/6sbjTOPv9n4NsLz7sz6WZ9tO54PlmxOJh8kXFmz8NMg+cNo6FRYCpBAYRILCI3GnBO885xDUlk10M/gjeohXQrUxAYp24ttrZFxEHJvLCa8yGRcmb+9BlvdmugJ14N5NpiTw4Ig2GcFCZCPRMYJLkkROVcQbrnCgOVlQLZNPHaHUPjInGM/MWTOeul33OMwuixdct7RyL4E6aJJ0/AHS7I3qOw6KDEkyg7UtCoHqyTNZjiG4TVbLXhw21AbXuOSlcyh8htPXDnLpim4ulQ8fjCkLLhlr7gTieoibptSwzy5TdeWSn4KKW41SbiLDP1kYtRkZDn3SiDmzdM+qt8nr78Cfrqx+7lf33dGH6zknl+NQyvkqJX49X4BYyfU6foJwCi/jSY1a+1ce2wCRT4mSduehEicKYQxYFZTZi2qLMV0baYeUU8W5ILvMQcdIS1EDHtYYdaj6ICljIqBVmfjzpMV+OfXuELtEUbLcpatRXZbQ120UqQ0Y/YriEPEih7JYs4xbiRouJEkeBVXb0PNtLFmnixITx6AH4C69DGwZ23yQcG1Qk0z1SOUJTdQrnI7qCDyRNyJm0G4kUg11aI2bMORk9KURIdNHRzSKmINyQYRxSa5D0iMCbmqSmna7W+AtHSij0Mydwg+KeqQsUoAXWQMzNAKt2ObEyRPHZQV6T1eg/ZCtO4f6+qrCjI1TVJCY9kF2xSIE8ZhVaKxjmi1uRhQrUVIXisRPioyuyr266pRS65VPHNTrCiOJPv4ChYQ/LSJdKl+iqBtiJuB8xBi/IOXYQ0BH8eyK3GVJVIgmcksS7fLY0evPDV3EEnZp7nqz3JJykKRUFd87PIkEuSUnhb4glUxBUKZOQ6Acj75GY3RXISZa+cdgIP16avymiMyXsjzZxSgfAJPFDXFts47GqN8RnXOUztIRflwRvz8HrKSjVdguDyN62L741DZTBOCZylwKlySMX4N4tSZAlkBZKWqOuKjGKMvSSBzhJ9z7QZILfSuYyJvN6ia1GfyzHih4m8HYlDUdQqnVhtzd5zq5q35BBFgKWRhKYKch0yknAxBcJ2IHz4Ce7+XfRC5k1OWaTFczHdDJJcASLoMEXhkFQWZQTiNr9zSFiu2fzwI9b1kurtN4sh5oC99xrNa5q4eYQ1A2EY8esgcNdNT5wkQcPNSEFEOJIPQMaPnmk7cnT7AFt4jjs955QpPkCZNIopcyoS9JksME5E4EQlifpzLvMsJOlGsPs94qcyr43C1nqvoBd6Q+gtMSS0M8QQmIrRs62k4+o3A9N6QGtYnveMbVtMaWV+ksQoNsVE9Amta1LOdEczclgTxwyt+9obxU0D1P1+sZsbfJVE8uffeN1lUDc7TaVrlDOkfmC8HOijx24n+pVlsxGDXFMSHq1K99ZHrHPCMwtR0A3DSBpGTFsRXUWc1dS2cI8AW7h5wzjQuJqcMuNqwAwDqq3Jd45wTgRBcuFLjldb0nLDgVmR81bk+I9mMh+0wXQVrWmkA+usqHNqTQhimZBjQtVWCm1OlNnEyFzOxa8HEqIG52oRJ0hjxrQ1FPW5ECJmd6XHQN5OZBeLuVRRLSxwQD96BAWtsYsa4yyWCaXGG7cmE3v5XTuZd2G5JY9SkLS1JkVP1VTFhPfHV2ONLZwtBdZokjZop2HMqMZiuwZd1EOvb/yPG18Eu/0045UU96vxavzixs8hKfoJs5yvO59fjLG+1vjjh/D+ubzp3U3D4cUKM29YLwzxuBXz1QR6M6BeO0UtA3EUVSXbVmAN04NzYj/i7h7hH1+JL09MxEEctPXRHN1WTE+u8FcblFZUJzPcnUNM15BjlErgOBG2g0jSpow9mJG0xvuINaKIFUPAtrVIERfZ07gZsG2NMgpzOMcczdAnc8ytI8LZFWw3oOApj2j9BnpHv7pEI5AXqf5rwY9v1wKDyBD9iGoczdGCuO6ZHl2gMgTvqY7ntO/eY/zoCf5shbYaU1fEqfCHlC586YIZT1BNLbcWb6G0YzM84XL9gGwUVmmR0C7BlZomolKYAv9Ay8aoknQrng8fsg6PySs46d6jOTkm9FueDx/g1xeQ4Pbhr2Bzg1IZnRJu3hG3nierf4cyVjpLJTjWynD74DuEGNHaMIXCIZgNnG0/BMAYIZDr2pVgWwJKkgRvAp9I6JDQxkpCYCVJiL1AKHd8G20l2JOq++66j/ic6eYNu7qgkM6l62b07rPF/yorcF1DMwXuPZ9IKZMUPD2tRMZ61+lJAvkTFN0N0riRDtIOJ7dLSFWRzU4luSo4OIGiGEMuqnbHl575WBSzTIF0aEUcPa6ryU5z53CiUxo1wcxO1I1FV5anVxaUI6H4u/c3otinDWd+Qcqa2mRen28wJHSO5CBdUQvcn63ICaxJe77T017zrz4TifD7C8V3b0v5XxUhCFMCfF05qh2EJWeqWYMLNbkv0t6jKHRF3zMtt8TVFl25a+haSbKMs8LhsQbdVoTB42qH6uoCd0UUJpPAFAFUzJi6Ir/1OuZgJm73KTN4+GQ1w02OCUPTOsJ6wE8SNNYHLWbekivDtB25fa/lSD9ns3lEd6gxi1vYxqE80gnoaprZMZ1xIu1+Naed1+jaMto5D7eBFBLzpufoUJGz4uGqYtgELNBUDtV7UpNR1hbRE8WTVU3w4j2jlXz3zXZL19XSlSNyp96gyFiteONwK8+kNjwaDvDDRGiO8bdfF6+zmMFqLq+uWOfIkzHS1g1XfSL3orAZhkBKER8CTXXBXHliDLy5sNxqZ2jncM2CJ71Ge7neKWdUiNw1HmcT2mleO51QyoIaON8smJ5MuJOaf/iNiUSm9/DPP1b4lxXRXxBn+ByEruw5WeVrNNyePP+ShOhzv791WHNrJslZjom47vHGENWCxxuB3/poMBZ0lk6dSpl+M0ihIiRMCtx1VzgtXLunfUNeLMizrnBxAoREVSBrtc3cOk74rWLaDjy8sKhxwCRPer5h7AemW0fURzMyYMeO2/4d7IFiNn+Cqt/HKM3lZWZdH+PPIsF1Yp6dMrcPEzU9CsXzTcVmnahuHeyhtMQCLVYKsuLRZYXFyP0OBXpbCoZZIRxDZJlSi1b4fJtxD03NZS3OIP5GeO7OtlhneZ4b/uTpSM4j62nnd1UKbz4SY2LlK5abGgX0XhcgQyJcOPKmwTcVf+o9j5IYQD9e37jx+0dE8YefFKGVGw+G0YbvzD31AYQ4cqEqSrb2kgftFzEyPwyei7JOPow/ri369Y/7l/cdXo1X4//3x38YTtGP22N+yvHhJXxYDve2cxzqTF4FNidFGQohP+OsBKOxBjT6sBOVsfcfk6eAPZ5JtXgzSLcmSvBgjmZCwH++Io4Be9TRvHW7dIaUOGmPE3HVkzc97t4pTAE1a8jDJBXwLIaoYd2XavaA9wGbMmbeShJkjXS3SpXfLDrsQUe8c0RabgmPzhnzimlckbIj9yuiNnjnsGjyxQZdfJFUkk1L3zqUKtthR3XnABUj/sEZafJM51fMfuVNzGHH8OAJ+Wgu1d0gHYlUIFyqSN8aYNGdcli9WUzsBlbVY+F+DAPWWrLShBgwiEBZDoHsBGrhh3GvwLTWT9kMGaUNh/YeuTvE1BXb7TP6/BwVMrfqv0aSb4aylhwm0Jmz5QfYqhJvJC1ysE13wtvNr5AjBK2grrA5s5mecdF/RNZSTTSNKBplBTFqrDHorpZkQQlcRBkt8LHS4UoxMfQ91jlskqTGthW67OhZQa4M1jRURcGNID5MOy6HeOpIgKe0IR92cg2nQHf7ALcamM7XTCHw9HZ9LXSQIWuRRN/xQfaTKQnkg12wdRPSs+sw7SB4O07ODjdkFIukOVqN1KcijhDGScxWPeTgMbXlvcVEux0leJtVpDCQlePM38Zni06RXzmK5M2GqAzvx064d9ue+vwC5zTNyVw+NyWczRzbcT8vVUkYLzaJf/0Z0gm6A7/5mpbCBAJbTEoEJlI/ia9PSoR+lKAq1timIfUTaSyS51EMTE1VyXXwSdTfSpVXCOqFT+MjthLIkVYib559ICDdMxXlf7oR1TW6mljWhmQUacpcmRYVBcIWQk8owi4CS4PZ7QP8eiD6QKth3j+lO8yoeYubN5Bh8+SSMS6YtZVUzavSwVFFQU8pNlNFnBQ5RA7NFQeVVOqfh0OidRgn3VXVCtl8B1mOU+R8aQjJMo0TVVOjoibrhnGQwHvmDLeqDUYrDIlDtwXgstc8Wx6ickuq5zyZND/64AMWswWHR4dMuub0+Bbff/8DlqunmGXNwWQYhp5+GHjj3uvM5yfk4Yrl+hHPL89ZLpe8dvsOR7dvE8OCsysY11tUP5KrCqMypwuD0YmUEgsnktwxwJOrBaurgDq/4lffGpnfWbAKmj/8lJckRTcxbi/+656Ht+cb3ciWcv5C2Lh3PdolVgpuzRzvHNXEYSKsPfqoIdSKaRsZEeEIZYBxkg5oTPT9RIyJymnUMGL8wOm8xzYanwxPqkP0bIZxRvzFyv5l6gZlDVWTuXWYyHPN5fPIw7UmdS2JBjWL2BDJ255h06Oc5eDgmJP5WyijqBaZPH5ANoaVqni2ctTzhcAqtSKpTJPWApdUivXkGNu6wPAUqRQTsyrn5CyXoyaMGWeddM+KbQNa7b3wohfPOSYvaAGjRGjEx+J/JYWplDN1rXjtlsJUiqvziQ8vbqx75cLvfLiUVgzecL6tRUAnJ4wtcMKhIg41ca34YIh8L3x5QpHJfP/5iw9KBmqT+Z3fSBwoj0+K81UQoaB9MJO/8J4XH7UfX+W9dtN6+Wsex8TjmPav/nHH+3rjVUL0arwaN8cvLCm6ntwvVxh66bg5z3/GuaqswR7P5WeHCBoUrkQYJrTSxH5EzRbotmL43mfk0QuMrnJMTy5Fejplove4gxnmcIZ/dEGaPOZ4xuxb94tsLaRJOkTTqicuN1RFjSl6j7K1QGa0Qo2+mNnt+BqRqq2FaNpIpTGOnrjcotNSOC+HcyG8zmrMTKSOw9WWlKJwmJwoVTVNTTaa4ckF8dkWhQS4CqgrS26r/WfUb90hnK/Q40gcAnEzEs6WKOvQU5RNrfBICEHI2ymjclE3yhlt7B7DnrwnOIvtWulaTB5rLSEEgV0YIyap2x4fPFZLRVEVSFmaJmKMpPVWNt1JPjMX1TelFDlBmjxJi8CDacUckyBcrrx7cJoKPaWisCbdAFM3GFpiShgrXkSC0ROoVHa2fIYIbEAWY8IpCPQvRmJKDNlzdfYcnTXHiwM6Zti6wmolELbSEZv6kaqtRQFtintVozwV/lgWyN8uuFJOEmF30KIRhSZdOWKM+4RLGVEAxBqBFd6AKaI0ilTmToEV7i5AQjxgsrpOhpQEKiIEkqmyoTrq8JtBeCnGiBTv6DGVFR6WU/jJFwPWJNDDUZH6gFLlHJ0hj9L1zNrimkqS8UpDzHg/YYrsvUAN2XfCcrz2bJJLJGGCLryhguFEOYsysRibyv1NIRKHiWktcuA5OOJ2JOWwT45A4HfKGYHt5CwQvtph24o4emzjxFi4XB/bVigfyrMPKQa8T6SccFWFygINCldbUeOzRiCxKIHr7XhojaU57AjLHoYtVmX8hcKcdigXsbMGU0kHYPZax3bTlu/kCWmQAkoWEY40lG5lygJ9bCtSHuQZKuT4kKJATlXYJ4ZhmoilCxV9QiXEF80ajDGli6nJKV4H/UhXMY0BsmaMHuUTm+UVT2NgcXDA48dPuVqvePdb7/Hxhx8SY+CdN9/iaDpmfJq4XF0xD4ExTNhpYMpbDrqad995lxwT3azj0WcPsUozb2c0h3N85YhJVPGuLs+4ddyIdLjORf1Tun520aI2mfHqAhU9cXEI2X1uA9lXCF74t+tfXwxhX5BN3qHkbuxNN9+mynMcVj0Tsq7v7wNIYSDnfdKtY8LMasarnjgF6tM5NnjSZKDqCIdgGo21Fe12QciS0CorCTBWvHTS6PFjYGKD+N4qqq7GzVvpVvcThIDOWVTirCE6h28ajFJMW5FQVxncrKaKIkqia1nzVEYMf2MiO3NtZK0QWezy3UzlilKhzEdrLMoWWfyytqYpYmsn8OFJrCQyoCqDCtLh3tsF2ALZMxY7d5g63Lj4Lw6lilBKKj5VZU/NyP4vogkimMP6q/g3Xx1sKFTh9EqBgr7ApGN64VVf/4hf/jlf/xxfJTOvxqvxixg//6Qow1xr/nZdY1FcpcQfTaNIDO/GjT3nhf/eOMaN7vhPNf+vDjRnrXy99aMz4uSp7x/zMLaodSRdRkIJ2MZPn+O3I0ye9v6J4JE3g3RISpDrThaMj84lcPYSSAiEIXLLrRgvLxmS43l3SPX2HUmQtr0s1kNRVFNgKtkQUAjO2hny4IkXK9LkiduJcLUpjuPi66EriznsqO+doovqUPXGaZEFziWIZ59MNrcPuPi3menxcypyUcvTog5H+U61o/vO28R/+wGsBoaPn0gXoKlQPpIIwllR18R9UgAUeZq4zI/w4xalNENYEX0UhaL5DPpJ0F5+ElnwusZVFdFPEnBFkdQ21nJr/kvUZk4cB5bDA66GD8laM4UtYZrA1OQUMVbhkS5bCgFyEi5SztT1nNeOfo0QElknHp79CRglCm5GJJujFdf09TTg5i1dhjRGtFZYZ0Wlz11X/jIIXlyLHG6IGaxhsThgCoHgA9WskYQuRMIgwbnWirAZUDER8oipLNM04YPnG3egm5s9zA1gTIp/8qFijIpZo/mH74KZB/opEwfNeDUSfERNsXi4Fif6nBkqzdNb9T65ErW9WOSqi0+MUmAkSEhe5MNzzhwvPUdZY7Xldbvi5GQkpQ2qyehOodpaOk5RYdpMrRKqslitiFPAzuVzj/MZR7XAsj577ojBFnl2QZeEAB9ftFijsSbx+imijFbmuDbXXQxtb6rqURJHaYspo8XEt8AHI6By2gdgyhoOm4HOehQCMY1t2t9XlaUKnTOkINV64yy4hLIBY6VLkuMgBQhjmAbPZ8sWbR3aGcbVVooBGUigY5b5ksHVTpKh7Si8w9pRNwJHs60TsY+cOTjRnFagmxr8iE9QH8/3hPS4GVAsJCB1lrU5pB9r0hTYeumyhRh5rdrQtgIb+uNnNRfbGu0Mf/3WxNtNLIUQJZygkuz7cSJGgz95m2GCMG14rf8zDpsWZWserztSzHhj+PhSFBjrKnGn68EoBuNYn7xNTpnL5Va+m7X8zd/5HS4vLvjR93/ArQpmYc3hcmJcfYh1LbeOoZ9GjFLcOr3FnUYzqw2ZkVU8ZDNo7t+7v0/oMlDNW1EOrCz+4B0ebUb8ZpQiTEzEFBgZsXUF8xnn1sA2MF4lfsUl1KyinjvuHYhNwRQNT7cdGUVtIne67ec2nhvtV6Vf+NtqqrgchdF/WE0c1COkzPnacn6Zma56FsuJ3B5I99LLOqms5o3TSOsSSV3x5GHGqxpplAQRxNlOeKMxhwtUZXlm57isMBjuHQ5oo9ierzGVwx06tLXCQ/IeqzJGCe/RZOlu5pTJRlPPalIsRbYyh0YuOYt/XvzerjD2mDzBEMweahZ7j06lWNLV2Lrw8zbsBWbuzHoqJrJW/D8fTFyM6lpsRyn2xK2cqSz8g7cyrRlFFCLkwh0qCqY5swqGf/pBJmbFYRX4B9+0uNpxMST+L9+ToupqRyHK8NYR/I3X5buyzjzYHApkLhh22McDO3DUSSHrR33NJ4OsuY9/AtiZUfD3vwEHTSb1gVk5b+M0bxz1hM0lUzdDf4Go9rLx0ycxXw5w+9mgb6+Ac6/Gq/HF8QvpFFUovm0d2gfOrOVfTOMXX/SydUR9yb/ffP2XvqZM8UJAHxvNdqbJCXyK5OWWPiYGBco67OwQtKb/4WeoSWRy9fGcrBX+fCUiAla6B+50wfT8iulqhW0aVFvTvHUHpRRWJxZqS1UNGG15vpSOkVl04sGAkgoZUikUWE+BYQ8T4fEWP06oYcJ2LWm1RRf3+B1vJY9BpL4bCUTTukc1Dnv7kLydCMNEBtzhDHc0QzeOxTfuspw84XwJMRIvNzTffkPOZac2Nm+Z/7V3mR6cMX72TKBpwu5H50J21XJdd7yUGALZaGzYcDkuJTHLoJMYQdanC8KjC1JO4i0EpGkk5ExMkYzGWktSwu1o7TENB6g6cbb6FI+ogiljwEgAkGMiK1HqGqdRLIqURpkiRW0ds+YeVjlWccnjy+8zjRJ0qDGRa0ucFLNFy7x1LFcruuMjVErYpsJ0dfkeWYQmioJZiAGjNClG+r5nu94w+hGtDfdev0eOmcuLC6qqwjqLGiSYdsZJQjuFPbxqvVxyHh7DcUfTNhwcHWK1YRMUj64ymwmODhzzCpo20wXNZWqIxzXTcgtWOnQpCrE5LHuW+46qwFSUUmAyOUd0K0ENgO4qdO2EvB3lWT80E3dWAfrE6ZHipIE4hGvcfxv2SXfcXokKVXJiAFyeyziMzF0Wk9265ul2Rr8JwpXWGlEWzCwHS3Uyp1aBFJ+LK/z5mpwzzWGHaatrWEyS500pCtSvVKGzdJFSzhK0IRC7nKV7aJ1lvjBslxtyiBhjMDOLNYaUPCio2po4RoG0hUhzS+ZnjgG/WuE3PaZ22KpGV4agM49Xmb4f0JMmxkhjJflxbcM0TJgSP5vKobQmFsnvrBTVUQtBukraWVLfUzk4OTH47YbcapS2wkcLaS9xnNei3OivNlz5WLqBWialBVNb5keawyqQteHBv898cJYwJvM79zQHlZcmYSzV+vJ2kZjXhPkxzy7WVK7hTmWZVYGQNY8pfBg0K9VBzLQpcNJEyImgNProLuN25LA7ZfXpp7xx/w2stUSVeeedd1jEFZd/8QEbv6SpGw7nUDUNoRf+oglPqNWahe6p2oZxhFHVBWIo60W/2eKswxqDqSvOn/SMSzGdrtqWVLpvYZjQfqA6ntGzINsEKvO6FlGNzkfezZdUWjGYCmUasjEczi3vzKMQ5XO+IfutSpe1FEbKM3m2Vjw4k7bQ7SZwy6wgJh6ZuaxTRw1tJ0lpzkWZTStc1dKZFXM7gjU8RYmn9nLLrHbSsbS6SKQLvGzrFcmDWnvu3O2pW0dzkCAPwEQ3m5V5oVDakLaOvOoxpiKOAT8WU++YCD6IsqY12HkDGjbxOaY1TMsBBoetbRGzkG6iKv4/prIosyYHgbUZK3LcefLU9YbjI022hquPE5/1CnWj7LmTcwfonKh8H1SQF25/vZOPaKfIIeG3kce9widFVonDxuOqxEUP//5ZWRJ2N0Qpjhr41VORmT/LjseDiKtkBWSBxDYucbKIpJj4754OfH8y5d5+MQ3YczA/9zel4JsncHsGJLf3MNNJ9vzQZbZsUNRfOObXG58PZF6eonz+X68FQdT+KD9dZ+rVeDVejc+PXwx8TpXprl+suH3Za7/095fN2q883A24Q/k19SPpcoN2BnvYCfRkXkPI9B8+xV9JYG9nHe50QXh8KTyiQug2XSVGq4/PcHVFCIH29VNRlisEWT131CcLxl4U7FQnvIbp8YVwl0a/h4KptqI6mjM8X4rcNqCQv+VZxnS1cCSKH5Cy0n3QShGfXhEGCcrT1ZbwdFk8XzLWGOKDM/raUb9+SvvmbQ7/2js8+aN/h50yfrtFtdW+aqxKMG1mDc2372MXLdv3H4lDvdFkpYhJ4B5aS0UvpCQk2ZSJO36Kl65NShk/bJnNKqpbC9JWHNGzgjiNAoOqhQSbQhC57SwS36kEISqL/w/I902AtmIkm51s9HXdMIatdAl20BJjiShM4XWtp4H2cCb8sIMOtKKuLXrekpdbUgJdGWK0IlHsTJF4DntvHqU1VVORQ+T55RUpZ05vnwoUzxiU0kzjhDKGy+WKrm54ePaYg27OnZNbtG0jlf+YeHJ1wcFsRvCRzz55wOQnbt++zXvffI+cpbOi7I18v8AWhdMEzelCeEQxEVZbVONwRx3eZOrbFdEH6b5EUVKjsrhbC2xT7ZOlFCPuZL7H7LtxjQ5T6bIMwsmaNVAI3XE9YHb+NcXvKfm49/mJg8fNGkwUXta48eScqFqHH3x5vqRjVc1b0nYiVyXhMQJD0U4glH4jvAVJcq0kukq8TwQ6JM/fXk2vBDEa9upYKYlUfnvQkUNiWvW0p7OyDkggprTGtlq6R1Y+O46+nK9APN28va72l2p2lQ3bzZYQA7UVuN00eKwzGBQYSf5yymQrEMecoZTxMcbgl4X31wfhEC66fScvR5FL1kkgUjlEpouV3LsCJ9S1RTeVcEt2pp5FCZECa9o1II3R0lHR0mEjpvL9NDnCgwcP6HGc3D6kzR0GzzSICmYugWHMCVc7YhhYXl4y5cDQ1NRVxXq54tNHj6hdRUqRq01PzJGT4xOOkuX0vW9S+gaY2glMj4xz4gVmncU6h+saLBUEEffYmXa2MzGRjVMAHwTW7CO2sahppD6Yy6OlYNxObJ8tJZGvRXwjqIRuHHZhC7QyMGx6hssltm0JGfy0QjVWoIaDx1lLnLwkBHUlxQMF42agv3IMK7lfqQoCmXaafhgxaoZtHbapSKMXL6G2QKWVePqEEGGKqO6AuE1SsKgsWIM2SpTbpgCNQMfSMGG0wjXV/p6qAnXLIIF/eY8yWpIgr1ExoVLGdpX4+xTY2ni5wT9fC5zMKFKBhiYFSWXx8VLia5RCgBAJPuDdCLPr7i1KgSty1bUWuPKN/Vbt/9+LiVHO19t2LomJruS5VlYhTwf7zrG2JdhPRRp+d9zybPp+ZPO8p6oc2tSYSmSxQz+Ri1mzbRxZBUlQVeGF/RRZQNmZhC+aItrJ+pSKXUMqEuW7K/DVCoZfNb7+e67lP34GKM2r8Wq8Gi8dv5CkaJ0S/7deOC0j+UXo3G78pPP48x2iL3SMXn7AcLmFnHFHc1Rl0N2cdL4mbEaUFx8FZS318QL/fEneDpIMWUuutZiqfnaGaRtSTJgKDr5xyv35lSRcruaT5YG4zG894WJDvNiQhkmSjyDeKsYYQg6oYZLORIZcNjfB+gT8s0tMVYl5YsrEnEXSV0DjxCD/nnJAVMSEQ2IzIpOtNCokhh89FIO5917j4NYh2497prNz4tUGfVugBqSMHgPHl8Kx8bMjnnxL03/wiLQZSCHIgq81qq6ER1WuqQSY0jWi8A9y4cjkQQKDlIsoQkqYuiFnwV9rIGpNTCKp/WT4IToZMIaT+btY5cgx8Hj7PWIaJMiwkjHsoINaabSpuL34NZxr0MaRlcaTmIxGV4Jf1wmGcaQ7XqAaRy5dmzdOHSfDB3Cw4JnJ/MvHImrxzdnEb75eYB1KVI1QistnV/Rji5oLyb/f9nRdRw4SJKeqYvT3qdwbXKx6jhYexUDtKnTWHB0dop2lqn+FZw8/5cHZIy5jxVApFkcd/7Nv9ihn8Bn+rz8QqPq8SvzHb68wCi76zP/jfamY3p7BP3hbeApTjLydt0BEndbkKZBCFN8mvYJt5PtLx588TCKzXEx4tTU86wN2PaIrS6M8VWWueU9RQ7T8j7+huNfCuO75Zz+CM28xJvOffANOFiJIkRBzZLPrDO0C9EqELCgiBaZxmDpTzRtUijij8dsJv+wZsuVcneB7Tybwv/jGUCBBlh89nJFSYqZ67p4kXFfjR48pss25dJB23kvWWlSlcc7uuUR7zydbOgK18M/+8Q8ST1eKup3xn35LsZjXpJhEDrvA4nZwoKauUaph7CfGMPCtu5n5oiaQeDIuSKuBtoHXFhvi6DGNuN2nYSSGiH69wraO2jqcFdGIH54r/vihrF1vHFS80Yg582otst2mKOKJaiPcano6K1Dcxl4njX/vncz2tYy2ipMqkSMlifUobTBGCO4o2A4DHz/4hDtvfhOnGz67OiD7kbCdOD4XaNp5Cqy+9S1U5VjoDcedJ04jXF0RPvm/U683zLZXHB+f0C4/pK1bmoOatr2AaUC/5qXjGuVZ8/2I7nQRj4k0zlBZcWcNm4H1eaI7mnMcz5l3Agd+uplx+eCKlDLVyQK3aBi2E/O7B5JAR8/rzQX1SUUYE58tO7Z9oO+n0vHNrKeKT+IBkEla0ywcwQcRvOlEsCJOAqFVRjPVCx49FwnruZs4SpeYrsYtWmrVsT1fcb6yjOOCrGEymqo1qCJZjVakELjlr5hVEaM1F1tH4DZh9AzZ4OYW3YqJLkE4oSfmHG28KA4etgS1pZp3PNospIBDy5u3JoxVTMnwcNURx4jyPfcWPdpqWgNvHq1IGZRfYUJNmDzO1aQqkOLEJtUs9RF6XguXDiRpVoqwHckhcusgclBP+O1I1yKFg2ni1K24tZAu3R+fWc4+lZD8rH/ZrluKH8AY4b/6viDmbvzphX17DEYSNXhB0O21heJ/+Ws7WAWCkggRv0k86E+w3tDYyNuHKwBS40n9BJVlVttScIgohC+lrBh1fz5peVn3CGQd/kc/hNqKzcQvzRxqvREj9bL2hK4i5l0w8vUSos93er50fLFF9Lk/75Kwr/qsVynTq/Fq/CTj558UKZjIfBjD13v9T1LsuPmar+gY3ey2h4sNqnLQiCdKOFvhz5ZUd4/gci0E45zRs5r48Ew+xlpUZWneukW4WIsx4/GCdLFi9itv4TrLollDBdsEnz1WxD4zfnK5957QWhcncQ+xQGhQhBDEj6afpJpW4EyixmaIwyQJQ0wCVZomktZlw5CFNMSItU48hlAlAMnYyhF9FNGD1QZQ1HdPGB89J20D67/4iKOjXxPujFZYa5kFIU6bWlPfO8HdOWT47DnjkwvCk3OMUvitkO/FQE8EEFTKRT5VkVLxe9GGsNzQvXMP8+iccbnEGIuxVva14satzS6gTWz7M0kejeN29y1qe4gi8Wz4EaRhH+wqrUkpCFdGW6xyeDXnuL2F0YaQE1NOaJVp25q8HVGzmsXJHN044YsAVVfh0kTXVpg68GwKPFonSJk3ZomDOqNcLj45kri++cYdnq1rMdxMkTBOvP/0Mdv1hhQz777+Fnm6hfE1c5do3GdUKqILvn/mWnyMrPvM4vBNfunwTT757FM+ebzmne6Y9w4m2oOaZTT81z+EwStOu8zMTrgc2RjDk7XkNZWBeXXdFTgFcoA8beUZ6SzgIYgk9SfLie3T3QYsSUKahC9mmwqGhMJAf2NKZYNWht9RoBxUB3MepsBHFxFN4m+9BbdKJzVNAQ2E4q+ibC0891JFVUp8WIyVey+eJoE0iaeOO2gZtprnjwJ23nFypHizE1GUy63jw2c1efAYrYiDp1q0uCLFnVOW+Zsk8eovN9RdsxfqAPbCDCgEyhaTdIkqx4ON5pMrRbVO/J23FEcHjtxP+FVP6Cd01zL2AykbDBo/TgSVSXiasKVlxugNl2eJyjhal1nYAVVptA5MOWIag23Ed6zgDiHL/FtO8MMLJNv1icM7LaiK3AR0gZLFZS8kd6eompHDygvJW+1UCDNvLBTMkGKK1iIKobVU3bUilm6eAq6WV8wWb/La/XuolFn2mhgMwyryzSlhtcFjuDy8jekaHEuWT/8/XJ6dkXPmqNnw3uu3MG6BNka6iToBA6gBasghMm4GrDNC2sdzcHpcRFmK4bBP4nXT1jRNQoVEVwUqv6FbHPBs5bG3D7HWiG+TyrQHDf3zNfVBSzOr6PoNbn1FwBCeD2L266OYKWcIm5HHzzXVUYebOXStca5Ga1EuVCVS18WTJnlHr8TbpnEDrhIYb94Kqb6dt0StuBylmBWmgK1F4GTXjVVGM59rjtxEVonzOOdqo7F1i6kLhNpHYpGR7oeR+3c8XStdQpM3MIdpc8nTc0BbuoUjBSls9OuR86uKvg+0OvPGiSGVDu1pDoTtRMoZ5wLJZdAj+sjAoUP5hrWXTqjSijR4WVRyFq+geUNtInM9ENsoqtujrPXzFmwrSppPPs68f3EjAfiyvbtsax9e3Fhb0vWzC9fdm5xS+Z90M7OCRmfeO8jXPLIpEIhcNQ2PphqLpWkm5npJiomkAubYkYPHVUb2phAlsbTX4hdfd2Tgkyv52WrFXeewk8cmgV2mfiJVNcJw/LJj7HpN15/9tTtJXxrjXAdNX3Wsr8N0+h/SON1c8H/+3/9v/tI+77c2F3Dw2l/a570afznjFyvJ/fnOzlf9/ef2gTckjEPEr9bUd45RGvz5WmA8WjE9uSBH6eJgFL6fCtdGkbWmfuc28WrL9PQKPWsIm5H6jVu40wPIoVRBhbOUfGT48Cn0EyEmVEoYIHvhMmilCCmjKF4n/UD0AqshZ/zkJVEYJ1E6y6Lss1tQc5LEKWPIOaGDJ0xeyOBIVVQZI9XgnCQoefKc2fi2+EG0jXAh1hPr7z9g/ktvoKzZ8dsBIfBnAGOo37xN8/otxmeXbL/3CWk7iIR3FMUuk8S/J+RUOl5yHG0M/moLlSXkCLoYs5ZKtcoRW1Wk4EXuWJuiGCTV1kyB+xTSlSswlqwFvpCS8LxyDPQxcL/qUMYwlY3WZg1ZoUOGow7VVQIxKsGzbizKGlqnOFyA9xNMO1NUSUIxel89zUaSibqraZTg1v00EQ28cXqXx/kpl8srfvjRjzg6fYPadWS0kP+N2SfGSmkcwoFSnSUNnpODYy7WV6zXK9ShYtoM5KpDIUICSglKPyld5Hiv8eM586IhuzVSBX1hJhToyY3K624DVWRsU+0D5d1Qn/thd1+zEl8lO3PoGLCmuMxrgVmmDKH4yvjRY61BW0uaAlXjyBnGVU81N5LwZwTaWLuiDmhoj2b4fmK6HBkngbv6sSFHJwIPXYup47V3ULnnKV0vIilKVzqNfi+wEbYjuR8ZtiPWGawVT6fc1JBrjFUCxUTJvTKa7vRAYJ9JUbc1q7MNSovpcYeiWhyTqoGowWuYnyzIKGLcErXGFVnvxjYvXN2ck0DlBEwq3d4yy+O0S/iVcDsmL4IVOohi15TIUyA66eBabYrypWbvHWrFm8X7iKtkHvkpEr0ov7m6wrmat2+9QV1XxHEAZ7BVza1ZR/tEOtEHbcv8cMEwTvhxgJC4d/c1jLXYthGZd1MeLHWjGp2F5+EnkWjOSqGbik43hNGDD9iuIWxHUQFsG7TR1IdynarZnM5JYcc0NWpK+Cg+NzYlbO2wjWO43KJ1pnrrLnp1hXI1Lne4bs7mo4fFW02Rn51hJ49/VhO6Dr2YYY5mtLfF0JdyJ7ACN0yUjmIU2KudtwCYqcDaci7CIMJ/ylNgDAJR08Ug3DYOnXKRixfuky3J17AdoZ/Ee6yywl00mqqtqBrFtL1+FvrtyOQD9aKR5zUk6YC2FbZ3tFnTWo3Bi3UCYtatW+lw7mwddllHzqCfJhgSefT4JPBIJoHeijpjFlNgxKzbFGXVjNgRhBBFtKTsaV9cOW5WOPP+x5zZK7VJQr97ed4Lx+wLKGMkDJndQx1jlMRNIYU8bal1hZnKVyvd4BQibtFJMUQrQj8RRo/tKkzt9pC8n2XUsxnd4ZxxtWF4coFyivpgBhfLn/nYLx8/rmL81X0g9apP9Gq8Gj/x+NmTopfMW7Xf6r/m+LnN2xdOgrDcklC8cT8zOwjE48zH38+s+0Aay0YQI3a+ID2XFnwm07x+gnKW4bMz4UXljG4c7s4hYTPwTCv+6GPhyyxqxTcPK/TRrKiORfI0MYbCT0EqkSaXVr5SxTE+y+a9SyhyJsaIBVLxuIl7vpAlxVw8JDQJ8VBJSXyItFLkLBCinMFo6e4Mj57Tvn2X5t17jJ88I/cT4cEZW2vovnmfZYJ/sd0KWb3PjBtE5ni/4RmO33mTb+aR4cNH2DHghw04gbgZJZyXKYm5XUpCKI/rAZMVOIfWiqQ0pwe/zMycYOqKZ1f/nlU+F4hijLuIisfLP8PYWgJSE/admgfnf4y1FdpYbs+/g4rQp0Rbi79U0hMPLv4UZTI4Rf3miSQmRc5aOcOsg3tHA2kKeFvzcX9CGCZqtvyvvt3jnOOgFqPUHCL/5jH8m3MLKuNTwKcNZPiP3sj85mvCk/jm/QNQh4QUqeorPv30+9RVDWnJ8fECrQ1PrmZMyWLmFr/corYTunE0TcX6yZrz51d8fHQPHRMhZX7rdkVKELXi//Rv1qA1o08FogFPN/Bf/NmNJ71Ms3eO4e++lcHfcIa/MSsy8Bt3Et85kA7lv75U/PmzL992M/BPPoA/+lR+frqRIERXFtMa0ImY4R992rAcRJHtl09aXBZp7UQJukqiUXc12khCZGtHLEEkRtMYz9uzC/JCYQ00zZwcIqedZrYQ3l3vDR+vj8lXUrXf8ZtUZYXrkRI51aQiUmBrh64s0Ufu1CuauSTZprKM65643vAP7mVy02Cs4WSGJMZWOsdh8ihbobWmnrViNmzUvktTtw2urqhnljpuJAlWmUrXTP2IMQqXNclHtt7yZNuC1sztxJ1mSyZzb+b422/WKK2os0Ai41C4CoUnpowmRfnszbZnUQtPZSdhrpQITShnCTnz35kF25M52WhOt7ewxpFsZPKey6sr7r1xyt9ozyE8YvQ98zsyxzQw5SXr1Rq3OCV9kGiMZeE8RweHaKd5PFj+yfeuq/y78d6hdA8V8IOl4189ku+U91l15ru3Ar92ImHav3yk+dG6Rhn4nTd6vnE0kDP80SeRhyuNUoYhDMQIOQT+p+8ETo7yXnrZHhrCZsX4ZMJVmuwH4lphDg5xixmRLWYxYxoneH6JvTxn2l7w6fyYkD3z4ZD0qEHXInKRB4VxhmlMwgFzlkE7Pjz3xU9oJ3aB3PuDjhQSxg6M656qq2Xd247kKaJnBlVpDIr7ZsL7TAyJT33FdoB21jD6gDGK5CMfPKloGgtmRhw8KiWCb6kP56LAN29IcYkyFqMLbzUH8fOZAqatiEPJEnZ8OStcwrV3PN1KsmDzlvfubPd+QORMXPVc0HE5NSJvbUUowla2KD/KavDPPtF8dJ7I2fObb1f87bck2Xm0mTMGgyJzf7GhMgKZpXQxY8h8+NThvSlJlpKCl068sVhDjExJ8+CyEy+lKqLVBu0sfify4KzI5Beo7KJOvGc3ZA02etLkcfNWYM+AX/fkIDL3trkpgvDiaveTpAwxZ/77zwTOXCvF329PqDP4S1nTvmz8dPyi63f/ZP/+U77u6yBwXuVWr8ZfkfEL6RTt7e5+nFTlywpMP8ehnMVYRT1tmNcd24cX+PMJ3R0wXV4Rs6JuK6lUTeIxUd05pLpzxObffbQ/rxwizTu3CVcbmvu38GPgk5VUyG918K1bhu7t2/TDRDhbkowRkn2BfhHFtyQjVch9cqRLGQ5FzFlEBZQSoYP9rVHS/dGCgSclrDEobQBRqBOuTLpR6VcYY1l//xOae6fUt49Yf/AIGyMxBMaPnpBGT/zGfT4LQXI0Bfgv3gN3UNO+eUp164j1n3yf6CemaaSuW0CSMG0MMUuApmrL5snFXjEsRakEtu6AeXWbpBTaNmgvnCQpAMq18WzwaStPj7WAQmvDaLaMaYPKFbfMAcZU1JWBqiKkRIieUS9xC8H/74KFjJKN01pII23qwWaWXrHe1MTkOO5a3j7MqAKvSIVgvUyajy52nasIxQMok1lUUpmcH9rC93DAluNfPSyVUcHzX51d8nw9UnW38MsVtXM4I/d9fnDAG6/dR6H46KMz6q6hdTVHMwU6swmZj594ghI+zi5PHQJ8fHljupR/n9dy38UssSiglXuYkQrtQnnePlZoY/hhz4+dok82Nz7n5rwqHIyw9Tw4V5yPCgd861hhiy9LGoPAeGonjvYGVJagNvSTYPsLBE/HwKzZnamYoMYpYGyiCsLN2Gwty9WMFJKINFSNGKJuosCXtCJnBUoU83RQWOUAxxTXNM2uswKurahmDW8rSYJTFt5RiqKIpYzGaI0vFXhdCc8kh4RtLNXCMjs5wBmIPjJjQFcF05g0zbwtBYqMMoo4KDbeoayhrkBVosZZ5cghEYOWeTmMwpfT8lmqCC2onAgksi6y71CUARNhEq5Q8hMZzdVixrOmIcZEZM7mfM3R4RHdQUfTvsYqTUxP/hg1rvnwg/d54603qaqKaZpoq4a7bxzQj5H6YkO2Bm0ypqtQSjFs5NlL1/kBOcOhlftt2op10ny83D03ard88e3bFXYmBPWL5Ph4KQqDv3k/0FmBUp6tNR9fFQMAFSDL49zODcdzmXt+uSVnjz4yxNERholx45mGivjREwmMu45pM8J8Ls9EUxPjwKaCvD1Hb9Y8D0fUtw8xHWKKHANxCgJtSz1h1jBaDdmQIvhVvy8WTTlLFztn0uTxw0RaDZgQCcDIGu8MtqmoVMDZTJgmauUIrkCzazEA9iFytfT0W5hyonEOFSAEh6kF4hpj3CtPJvGJEG+q0OOj8FZFyAdUMULNQEiBYYDzsxFi5taxwYULnJHkIceEOjRsNxqVCwzVGLQTI+WUsghCoHjWZz58njBW8x/HgdcdKK0ZN56+PAv33Ehti8dVymQyQcO6qYm1dLN3Agw2ed5ciHDPZshsJocymtZlpimUe92jKwOuwEGddKD15JnV8vxHP2HnLbqSNVJbg1u00iU3+sVF8vPr2BfSoi8PRHKGi14gua1StLOaudKsx/RzQLzcPI+ftLsjr39R4OEnPMbXOf+/ali8V+Ov7PgFwufyy399WUn6F/DJKYNetDTv3iM3l/QPLxieXVG9/Q7jgytyCNiqhqYhBXHZtsdzmnfuMHzwhLQZMZWoPdnTBWEzivGp/uKnJSRIqb/9OrqyTJ89RxuN8oE8jqSYxUxRqT0hnZzFskEpgb+VoM4YQwryWm0sJMHHZz+hqlpgZkpep0nEIEpRuUiR5hKpKKVh8oRVjzue09w7wX/4iBQmNDB89JBx9OjuZK84JbA1+YKfF8cwBy3VvVPhPAUxzGPH51BQWTEa9c+XzL/zDS6fXNAYWzw7tEBTtChM5ZxI3pOUQAOpG3IIBTKmxXskQzAWqzWpsZJYRgkIsgaVMyEJh8I0FbP5ETQin00IYBWmcqQpkIKXLkVji9EsKGfQQ0JNgZ0iX5bcVWA/CoG9KAo8sUDPyrXSzoj6U7PzxigwRyMdEFdVHN+5xeFoSbbCaS0dkmWPSgldW+68cZ8HDz7lw48+5ttvvYc3E3MybduSxgmdJWA2ih3XmJsT6SaCZf9j6XQlL3K0aTQwJDFq1JpslTjJl2T8xZjgxXuu9gFFfmGexqLbEHyEAEZX4lGFiCxkBUZr6YLGtIfGoJOQv3d+RIUQr4zeG1MqJUl29pH++QpdWXJlybrCzuq9gEMKsSRHovQVNj1pGAmXS8zBAt9Hpu0gVfNbCRUz02qQgoGzkIUYv+uMaiOwNZSShC6IpxMx4wcvBsQ5QzcT0QgjJqeMQYwdKyvPpyrPUEiEYZLrlQVOmXwk5InUwbQdmdaBFCzaIBy9osCXfABjmKKIEmijqIzj8PAQlbYFaqr2Pl3T6CUBc4ZkFc5Zhn6F0XDv7l2ZYyFgYmJWV8yrFldpfuu3fpscI1M/cnx0Ip9fulRpChjrMJUm+IQik7JI5MsSIw+ELgp9ujGimIzC6nwNvcxlzij5r64dxoDOkRwSeVJAkYK2ek/IjzfiOknCZV2rDmfCywmBaC261XTHh9T1AcPGg0/onNB1RTBROqzGgbeoriaHCbX26IcPmayh604x1jAue4FqTVFgoZdbqkWDWzT0Z6IEmLYTYTvJMzlvUEZRHc6ku9gH0hAwTcW4GhmiZ/bmqXT8t5N0E5RCFUXLrJSIzhQ4qDUaG9XeCNVqBTEVuKIUj9LlllSLwItCYytLfTBDqSww0pjEKLrAx5RWJK8xlSnGz2tc5QTJoRUxBTmvAttEqcJL7aXrr9XecymPCU0p8CUxQU5JTGRjLJLcCXwvxujaCXQ4JrlvcQoYrTB1JYk8FHW5hFIGW2kyGoOoScYxYBuHqYpSX/Fa2gnFaGPwmx7d1mTn9uALeShNWV9U6Vh9YZX8kt+/OL6YXkj6EbNo5sWveOXXHTfX9a/bWVL7T1P7d/7EYwcheOE8Xh6ivWoUvRp/VcbPOSkqU+dmcPWTFz1+/Gu+xvi3j9c4LUFWWtzlaHab+NYbTB9dkldbbDfDdq142Cy3qCJNPT08JzxbSrVdAZXFHs3pP3yMPZ7BvZMXzvFyiPzzD64AuNVZfv2911C1Zfz4GSYlUpGENQlRatsZA2YJgpIWuJtsQpoYQ8HTKZHAzlLNzyEwxEh7cCTQhxTFcC9LIpOVQieBwUR17Uo/fvQYe/ge3Ru3WT46J/cDMclSbh485rv3EvPvvFscwOU7nW8Df/p4/WKMnEEdzsioIvKQMFrgEOJtI4tzGiamh8/p3n2N2aOOk8VdMrAMj7m4+oQI+PGKbC0WGPEE73FVLZLlQNaae4ffJXmHawyP458zbFfk7Pl0/SfgLDhD287RrWM9XPDtN6RSmxVYY/YwEq2VwJA0UAiyIYZShS/8DR32PkU5yn347n3Fe6e7JOgabrHQol6layddupKA5hTxk8fVal9KV0DbNqw3EWs1b5jnmMUIdcWD7SFBW95+9xucnJ7isuby4opPP37AG2++zuGi5n/91zI5TeiGffV157WRs8hvxygJ0MxCWMv1Ww6Os3BEiomTcMF//ssB0zjeXzv+D38m92z5Euuwl861m4kREqz+l99HOC8+8z/5tuFgIaTthbmQJAjNx1fCs6l05vXFUpImJRLsL9RFvRQAVG0JvRDbbaOxi5ZGFzPKnFFBEbYTeT2KVLlS9Mvt/v3VUccbb7cs3olM5xc82ESWyxljUvxgrTg4nct1CxFXOdJQ+HuAipE3bg0sjmvx8cpi7BqTGMraIjJinZWEs8/kWURbhe4qwsVGvGLaep/cZcB2tSRhWyOBcIbLi8SUZuTYMk3S9Y2TF/7aLkHMRireSgLHKQWauuXxsuZJko7m/YOemfXkDA+a73ClF9Rtw69v/z2LuGYcR/R4ge8nuqbFaiPSzWNCM5XrLDLStkWSDi9CFE1Vc/ciU42Zy2Xk/+jF3HNWWf7OO/MXkvGcoSbwg8dyH07txH/+K1u0NfzpM8Mff5b3Gf1uOflbb8F37xnAcGiEM6KU4j95J/F33takDP/1D+HRqqAOirqXAlmXK0U0lv/yA1gOUqnvp56cMp2K/M9/FSqV8Mrx0ZOO8XxDvsp848EWUkJnDXUrwi8xocaANlogk0CyGnzEr3pM6yAl3EGHOZ3L62PCn69F4txo0hS5ffBt6u4IrGF1/qc83zxhVs9FkW5qSFoRkpV1w4e9eplra6qmkhnmxNtMt5V0UScvnncVYA10NU5lvnG0FEEdU/Gjp+2em6SKafPMeu4vxFz3cJ5pu7UcV4mZqULx588t/+JDCcF//e6W37g/AYqL3vHD9QKl4bXFyKKayDHyq7da7jRS5Nr0ih+uA0HBdtlj5xptDT94ZFF5hsmJt057nMnYyvLurS0pZqaoeDQco62m6jqq+YAis8jwy4uiNKqgNm0xWpZET1Hym8wejhu2UuD44arij/5C3YgLPh8gZK72a91LOkAvTUauV6gvvkMx5sx/1W8xStbD8fN40q89cvlktT+Tm7SDLzsDgN+uKr5pRZL/j6aBj8NNsYefLoX5sne9Sohejb9K42dPir7ujPk5zqwvM1u7OdZjAmSj3gRNYyv8+Ybx6ZWoDc0KxAXxw5l94y5KKcYHZ3sYQSQze+cO47MrqdoddF/4HiFlLofSVi+O19Wbt8khMbz/UApcKRJTxCi9V4hKOUtnCBF2AEhFhtsoRYyi7qaMLsJ0Fh0n7LwhXKxIShOCx5bqLkqRjEGnBDkRS5oSLlaEqzXu1gH1e/dIf9aTfCAkWX7dw8e4ec38V96WjRfwcbdYX5ffcoiowaNiEFggEGPAWpHD3kmqaqUYn1zQVI76+E06/RrKBy5Xn9GHq2IOu1Ogg1nXkrwXnlIWv6aYoTYLrJsBkbQO6JjwKXIVLjk4PcYcVMQ6kogcthULt8XUIgmNiiJEkQzWOVLH3j1daY1zhrgN0jXaddiiCFtoa4X7UWVmRjbg/R4pEnqkIRYfk9KVQarLVSNBcEYCtRwicQxoW6EUNE2mmzWEpFADpWuWmc1mxJQ4rW9z5/4dgXi5zP1Th3VyzJQSfpxwVSUY+2Ei9gPBZXINpMzFxZbTe3dIuWZ1KepYp07xWhtojls+HAyP1rx8LubP96Fu/Lu62VFSPNtkcrRU2nD7SHFcRaKRYCtOgexq0lVEVw2oyKxTTGPP8uKS27dOr3FXsShOKTEaVcYQY0BNCl2VpCIL5CqtxTRYVxqtNONqi3UOuhqtNX61QR1Bu4i09w5YLxaEs4S9XJGso58MVe0I25714yXp4lLOo67Ibc1rC+lo6UI4T6lU8bUSifcY9yabYfSE8zXZKsyixXRV8eOSjs0wDqJCdrCQrlaUrp0AMQ2bHkATpwQEeTZ9hEK+jynBJAElQI2oNfpoUFr4FcFvwcHkPZtuznnoqCbD6yHSDRd0Wbxe3WGN0h6UR+uJxP+XvT8Nti3Nynrx39vNZjW7Of3JviuroZIq4NJcRCiSzvAqIH9EwALFixIGCmGEiuEXAz9K2ITXCGwIoABR63IRRAukE4QSqAKBApJqMiv70zd779XM5u3+H8Zca+9zzj5d5smqQnJEntxr7zX7Od93juYZzxMJSq5t8oHl7pzx0Q1SSEKGYg06KTaqGqIi+8TZRsbViYlmux5eGUlIFUIr9Nu7XoLJI+OO+x/WaKP42Pke32RhJ2wUfh4x1rDhDJMB7psB30WsMWyoKFU8ZyjIJJ9ExwctMLiMYPGUzEznF7DbSdVzJfyaSsV4qqm0ZrEMFBubA4I5YRYK3XsMGbYmuEqcSlVaVIxob4jRSx/ouCTuNfhZK0gAq7GVI8WMNsKE2O8tyVozuf8Io/ooVXuEsGjZc2Py+AhLbwTuWQqRhLKK3HmCD1K5VdIflr0wY2I0elRIcJwzelINEMxM9IHCCdx05BJYaHxk2WuU0qg8ELL4hC4H3ayc0DpSEtC1IYWhGgnMezjfWlKIvPWkolJSWboSDF1ykCCETqBrVjMdl4QAkcTuhTkhRnThKGKidFaeWVNinAMLSnf0iznRW6rpCFMZKmU5HzQ5a3l2So8iYZyhUkmSeyGS8wA/90G0sxjEkYFmZ452UiEupiOWc83Z2cGZ63C7Wb718MBj9WQe7l9k4NLAonj9lu7eVvC3G4/sVjniqdacHDTjarWCeL8Ku65a9Ia9YX/c7Z5Viq4hV7ibgXanc8mBTFAeqiy3XG51DCsHfnfO4mMvS6WjLCU7WTnysqN64BjliU2WH3lFXmJWNFjKk9tSWdhZivbL9pSYhkr+IbvM5HUZ3z14nJwSzcfPQrKiJRQDcYABWCWQgxT1+hiVkkx/HBpKUxZoHjCIOFrM9oTm/CV0WeGsaDEE36OSsL3JqSvElxBK3N3f/Thbn/1mRg8cJ16dEV66iIoCuSMrFs+8BMYw/hMPrKFMOgSBZLSK9sJV+hcvEC5eJVmDCl4ckxhIxqKNSDXqAc4D0Jy5zLEHnqAhUDkNJHTOYC3aiPNnJzVhNsfYAlWWJCe0x6qwApFzmtB3YDW6qqitxsWA2xxJg3SMIoDohqZgM+T7rBENp5BIUeBwoQ1DgBkhW7QCrzK6cCz7JdYZVEjS85PlKmYtTk1se+y4ggyxj2QjjHbKOrnZWgu8anjmfB+lRyUkys0RyWsIIvq4enZsaQlDUz2dxxiNLiy+jcJkVWhRldfCWkbKFGVBztC3nTRW50zb9RKMxEjlStq9BT5kcSxCwIwtblLLCzYLK+IKpphuN0bVTX8ZRF0l4M8xYwYtKbQiZkVRF8QErrQk5yic4YgtiSBZ8JQwZOn/Snk95pZdjy2lgrFqyo5NT2ggeE9ROJRTVBuVVI5CAmeY3H+SGC7QXl6SY2KxTISuQlc1thDYV3Nhj3T5KvnqVYGjOgd1jR7XmNIQ5x3RGmwly+suosjy3UDOEvtAUQ4OizOERtLQ2hqBJGWFq6WnwXdyf/ulwP2y0UQlQYIxhqzTEKgrVF0MfUSKOGwvNr2wniko6lKgiVF0dbrQcXV3RsyZaFuWez16MsI4KF1JJtMuGoqVAGxeFZU1ti7JMRJaz2hLArfgI0kbtHXkbAladhwVA3xTIKU5Jfzuch0QuMKKNtuyI44rovHE3qCqAm01VSXQVKMSZlURGWBQAukCZZ041WgJskJGBY3NGpMQAoBKE+Mg5qs1CYPOohsGeUi2gFGZuOxgWojOk4JiXKDSmK505D6iKocpLYpMbHsZl1GSCCkkSD3l1pjU9HQ7C7QxuLKkvbzE7y2l50YpMEYSG0B7ZY+qmOJGFleO8XrQuzPCqhl9lF6xgZ1UK+RFMogpK62IORF8QscMA2um0gpURpcFGEhErFXERSewzGGM5BgxdUFqveh2aTDGrVkaldYok9f9gNYqrIrkoQUxA8Qk/YsReSZixA8ipaHpMG5Mjonx9hgzKgUiroUyPe422HElrnyErLSwjyrpz9MDYYiQomhZBkFJqCz7U4M34tte5CxQwuZaOHQvzJOxrqQ3qSqJWa9I7W4xcd2q3rL65jDg2CeiPqIOfNpHI9zJnhPQxyTX89VGNW8EQ2/YG3aDveag6OBgvu6LO7ebgVmv397grB4g1jp8ufXn/Qkxeake2KoaaK8zqfVC0froScLVOc1LF9HakGLGbFYUx6YsX7yEMpp2Y8QHzy4ES7yiBb5ul5eWgV98dgeA05OCtz92CjOtWX74JaH/ni1IXYtJmWydwB1IqCw9ApkBHkWGLJlUlcWpV9pI9rAuyYWlWy6oR2PJYmqBgRgB9UuFaYBnZK0xnWf+O8+y8dlvpn7ifnZ3l+i9xcBYJ47y3kdfJFzcEejPsuUzszh5xRVFd7WiOrFF3JmhfERVJXSeZB16RQAx9DnknMnBo63j8uU/JOWPDM5PS0Sw8yfGb2M6OgllQV8vxRGMkXPhD2lji1GZl3Z+E20tymla1VJvTnCFONfCMrQKQgYWLnOgTyVErDU03vLyxYlUwJT0qqAVI+N5YnuHlDPPXM781MccSikemJS89fQUkmjs5LU+hqXcmqCd4ekLS16+Bnsm8Id3nhpxpNCk3pNyIbBHrbhve45RDWZisSoLPbjWPFRfJdUQg2TPTVUw63v+44cyXcgcGSse3wan5F5KEChkD82VBWVh0RqmRze5+PwFcTKnimxgWva89aTsX7R/5Qn9rFPw1mMykN7/SuZD59XB05Af14zFwwfkfkJCCCpMofBdj7X7PSePb+7hQ6TF8SMfUvRJk7rBQVeKk5uOr3mrZMRF1F6gouNyJI3jZgh2Q8SOSioKylmFtoajE89mukqwPTG/BTd9J/2sYa/5KM82gIZoCvRY1s+dp289vunAe1RZoIoCVVXEzU3cqOLlZY3RAiN7tFzgTMbVlofZkzt8XPrnGHoabC+BeCCRuoCKiZevznhlucl0soF1AjVSIaKSpfd75MpRj0cCMVzpuKVM7kWsNedMbDxNsyAXJUYbfAyUVYXKcHLaMHUdIUVms12qrSkqZR5tfo+3nTiCypkytWsGvdHGZAiI8nDdJagnJvq2F2rvUYlCs/SGH/uYwQ+KvKlfAjApDV/02JZso+npLs9oL1zFbk2x1tCd30HvztBlQdYjtDP084bYez7jmONNGxkSTEqF1oO20iDqqpTi7Kxid64H4WGp2IYu8FnVp/H59Ra60mzZDxK6PVKEc/kEfS8Q288+FfG99JaBBNsFgaLcIfWewhge29whhkQ/0ry0K3NBBqEp32uEtKLzQjk/VwSlh4JUwtRStdmcPMx9W+9kObvEFfsce/FltLPSE+k0/axhR7/A0p9FY+iTnP8K9pWA+XLOw5tLjh0Rim0U+C4Iu1ppMcbQtYHndyZQyH5X/1JZ8Py8JIVA5TIPTvegsGivZa4vRSR7VYHVRmO0WbPHZSAFQSgIqVDk7cc0j24KLfm4kHnCd54Nf4lxaSiO1jidCTNhNrSFIy0TaMXDxz0jK6ylLy83WUQJzJRSRC8Q5jPNERRbuKR4MM8oomgQxaYnaSv9Rc5iDKDVQCueWXaKF3e30GXBXoDffGVv/R4/zNq1HOLNqjqHweMOLJ7vPBD5RNjhIL4b7QNdx+8O12WeD40MD2xnn4ThIB7gIDHDQQlYRd7vBXzD3rA/Zvaag6Jrg6GblIjydYvc6UZvVtVG3XXZV1mDLYVFKQ+N9WZSMXrTaXLK7D39IsaIrk5SiurB4/RX58RZA5XDndpm9ooERTezkDKzXlJgW5W8pNyJLaabYxSwfPoFmpcv0M6uUun9QEjlvCaiU0qJ9hH7nA5aDe0kWYKl6sgWsxdeluzakAnOUWhjVRYY3lq8JEFSirQ7Z/mRlxi//RGmTz7K/Lc+Slp20kyeoTCaMG8pjm1x9DMfxkzqdaCx0u3xO3O6Vy7KZddaqjHDNSOJ7lJWkAsr9MImEhYzltFTlxXWWmJMOFNTFhs0OcO4JPuAs6Cz0Chro4kugI7Y7TFFI2KDMSWMMuTOi/6QGvDYSioOKkWBJcYkVKxW0+NIvaTJdSkaRDa2ONPRdg0+jrmwI+e4UZQsF4NeRhsIew1mXKKKkhw0Whl2WsXF+fAmXYkB5sTePFGVCLTOSJVHZzA0VEVC6SAkEMO9skqqBNkAOlM4SxdhEaFNUMZVRXTVg8ZAnhApnCV4yeo2uwuqacVoVNH7nvHGFBUTOBlIwQe0E5hQlSN1JVnb+oaRr675cVemtcBbhmRD9pF+OccojTEjLi0cvTJASe4iOUQKK9AsUw3ZbGfBGlxG4GYhSi+YkmNSQVjt/LJDFQHdzalKSwyOcCXh7AifChZBg9XY0pK7gGo9PkSi0eAcxakThNZjnMaOKkwtOkheG3zKWK2IIdHO9hhPxpRDrVabQjLZWqqemILYdEIN7jQYxcn77qOZHxVYZh/I2hHwpBDYWcyZ2g3J6itF6nsJVFKSykfrJfDIMCpr6YlzFhcFkquMRseeogyEbslkOkLnTOEco9qhWA5EFatq8fqxEfKNJAmTdraUvqq6ohpX0riOnPPlxtIP7GbkOCQZFGMDufUk7+lDpDi+hbGGfq9BxygEBnWFcQZlhIpdOYuOibKEvuvQQRNasIWwrqUBCtd3Jct5Ii78Pq1d1pyqJtTFBpDwF+ZEs4t2jlm3pOkV2hnYW1I6g8kldlyiVMZpISvISRgjbc44o0nO0jUtShn6WYMpHdWooFv2ouujQJcOkhApoBXF1phea0ZHtqjLDYJtMTh0FuffOQvGCMwxB7yOkEQwNK/GbIaUEpvjCVvTjKKhLB2hDygjAUTqOtzGGJ972kVLzJ7CSRLEVQWERGcLYhfBJ0Jaoo0iNYHU1xCkVqAGQoLYyTnE3g/DUyjrJYckcLVRyoxdHgTGI/PLC1RhsKUjz5foLpFLR3IGk0V/LNsCbRSWgEntmggoR42rS6nw+iBiu94KpM9pch9hkDtQhUUrI4yKixasQheSQEg5E3JJLMckrVl4z+VG3/Ca3w90bm83lQfJ1y7zibPrnaGbhz63OqpFzixu08u02vK1wrGHbf36K6AOiUPfKCu9YX887PUVb/0k2kHIBynjL+5JQ7ySSVJXjupNp1HO0jxzFlqPKgoAqgeEiak/t0MG3KgkOblUqxaLW1lGhP7C8JJf0YXWb3qA/tIucQYy8RwgKEgJtEYzVIbUAKfTakgYJkII9LtzqgdPsDxzgZwCylUiwqkFR66GzyhNTNInYZ0FpenPXkHXJaPH76N+/H6aj74sTb9D9lRbi65LzNZkoKI+MHXmTPZBXroZjLGkHLDGopyVitVAZ62rEnxAhYRJio1qAqOCVFnB4ptM4wSSkYwwTtnKkZcJo+WehcJQjitsNTQdG4VGockklfF7c+zGWG400HWBHDyL2YyidEyUIgUJBrQTMo009Oac3T1LdJc5cew4WmkUUeCMIRL2lhAz3VLgQWVwGB0Jyw5bZXLXo3ovUJOyQBWG1IgwZRrodq1hINWAvm2pRhIs9EmzwkMWpcMMjE+hD9LTFDKlM6ScKbQi+hU8UQIjU1poMqYuyIsWpzXV9nTt2EzGG/StQLxcchhrUGVJ60VoOKXh9ScFSorh5ga4PZTumuc7rwtJfYQ+ARjcMDiU1YyqCt/1RO8ptCF1ktJNWXplioGGeUUwgFL0vcdYy97eAoMmdT2l02hrBZLlparZ7TUkBzlAVBk1HqoyOWFrGcNpKeKNJHGUAUxhKLTCbY1QA2QJo4V6OGuyD6ioyEsoQ0Fegg9CNZ3CoCPm7EANnNHTihE1MclYTsGgW0NqA3SB3vdY6zB1ybG6JGWhdtZaC6xKK2CAYmmBYqUQhcRklfW3Fu0cGUUMmZ3dGVFlihBRdYWKGVWK02sYKOVhra+m1tkWqY7klCjHFTlmunlDCpF6e4qpC0qrUKusz8AYxqIjz4RJ0KdAOSmJnUchDrWui6HXSpxeWzm0S/vVG62F6dFogXUBpiroZ0t81xPmJWGupHpSOorNEbZyFJNNrBqjVUb1E/ANofH0Owu8N4QQqcYjsodMIoQGSosuRHRXJaH8t1YT2254JjJJG1RhKSpD8tIDFnPGZLCTSmB8WhM7jzWK0VZFMTIoE1BjDbNMaETkNtpIbCA2PW5aYZzA13IexmpIMhdkDTmRY6AspSrtxiWml3vNAOMzKKppTdtkQhLYrs5CahiCzFHkREqiMxSiaNbFgSFuRbU9RJxDZUiCMzMkLPSgHYbRNPNOYMRNh3aGsirRzuGO1nRtx/z8LqPNMaPNKU5N0L2MLbsxoTQFy9lSKmzWkpY9adagCivv2WVPLiyxb8k1RJWIKQhbnZQiWdBTWoNNilQW8p6KltRJEB/z4WqHdxvE3Nug507qSrda5mAgdPhyN6tu3Wyr116lAyWwa36//hju1t6oGr1hfzzsHgRFd+BN3WVV57Ywujuwz7hvwrGR4LL13oJud0ECwcCHSP3oSey0pr80ozt3FeUKQsoU22PKE1ssPnJGggytcEcn9PrOdrxK3pyb9/z8x3cgw4ObJZ92YiSHbx3FdEOYnvK6VjQohMu/1SQXs+j8GKUwSuHJNOcvMXriQcqNKd3eDBsjaqA81sOaShvJQGeBapGkRwkU3YsXMVVJ/eAJUJnmo69AHjDnVoRX25cuUT98/JroLzY9YWeOcoWwcWmhzjbjEaouB22aXhymoeH8xORPsPnAY2AN5y//LnN/Cas1vzV+lr56hTzSPHjJM+oz9IpgO1xRwagkLZckBb4PhJwwWWELw2Pbc4zJ9F3i+d2CBLQRfueKwpoRZ154hS//P+/Hh8Bit6XtR9iyoA2evRcvMl/M2dyc0m6/nTPJoaLni4+30n+QEgRx7sy0xlWlQGmMEcaylHh8YnjUlZK5rwq5e6Gg1ICPJKt59EhHZTzZB4rSQE6ECO99WrHTa6rK8pc+XTHRUiUwRuB/G2P4lncqUoLUdqRlhyrHA124LKvrgrBsycbgY0T1gdh52nmLKZ2w7KlB0b6w/O7ZzK++qKRasKKMJvMOU/JNoxIU/ErX8lG/xqFw8xfqtS9fHzP/4fclLi1U4hufhImTQM9WQghRoPiGP9GI0K/SqAxKe5QBpaFrO4qqJHeSHd/rDH94ZkTfBY6MFY8c85jek4KjXQot/hXG7CyKgdL4LNZeBaQxPCwbycJbI9dWSVBcKoUq5G9JS+O90oqmWVIXNfePnqS0g75JH4BM2wZevPrrhFIqWe28YTKuKWrDo0fmaAOth2cuV6SQ0V3E+7kEXFZT2GoIQJP0lBQWEHiTcoMAq5IKTg6RGPJA4CFZf6014ehD+MkxUkzsffRpyguBvuu479NrypFeQ0IF9iuwQ5mHpG/HGOnziyESO48rHbYq6WZLUhewo4LU9myODN/yDiGRUEMlXQFh2VHqDp2h7T3GGtzYMo8lL7UlMUZyhGw0blySc0v0fkiyGJTOA9x1CLKQ66ELi+0j3c4S0kj6CI3CNx2hD7y482skn9FO89jRGZPNEaYOuLaiu9LjlOWB8WdR2BEx97zif5du0aCp+PjuJqn1WBN57NgCV5X4BsojkjTIPtLPe1Rd4CorCZkkyYZqY8Ryd8F0uceJNMNNKszsLP3sg5imwyhN9DKv5j7CkOdQQyU/9B43iKkqrXlgumBaC6tfUQh9OQoRIx3468OyIzQd2We63QI1GtN6j9aKoKAqHHm4po1WfDwcIYQgOm3eS09JjNi6QCUR+Y5Nj6kLQudJQ0+kdo7sRVz18qLg7GwbVxac2OjZtMI2uve8wl8pGI03qeJR9NywPKv57WXHx8MSBdSjkgdsSU4T9LESV2qUKzh6tqXoV3pvDh0VsVd0c8MyRnTl0Mekgm+Tg/MnUc5xOcNPNksikHPEp531++9Tz+6sPnVn398q6LlxGzfOxgKLOzzoeyOIecPesFdjn7hK0SowuhcA3ut9tkPmzspqxoNWQrfsiLMGuzUmNZ7y1Bbu2JTcBZpnz0mFxmi01dQPHKM/v0tcCEWo3agpjm3QDxnUO4HZKoSqc9kLI8xq3RQi2RqKcU28OpfmfITZSa2orQf9CglupDrCkM3UShObFrTCHdskLJYYpQg5YxRkrciIqJ04XAKdUDnv03AraJ49g5lU1A+ewvee9MqOZH2VQE/6M1chJaqHT0jFKCbmH35BeohKi9ZKml/HFbkqsFVBmLcowIZEAnyI6NEEEx3JZ4jSKJ+dwReZmWnBOZq0pFDDMY8LzNYEbTR9uyTmjDWKsqhIbS/9JzZRjx22ALWnpDei84yPHiPnxMn7H+L8mVc4euwIZy+e57lLc05vHefClUvYouDY0WNsnTpOs7ekqA25T0zc0LBcFhLslFaCjXlHMgqdIU0yZlzjXM+ls5c5/eBp0eJoPRjJ3GatcHWBcz1OJbB6cEgTqqqY58yOV9Tr4ojcWz9r0KXF1iUbLpNCZNk1TE5urWE42lnisiPnhG87ylEtukdtjykd042RVAYGqOPqYe1T5moLSl038GxicyxhtLvDl+rBYbZyuvdaqVDWVmCbWisYHPGshHHt1FYlkLKBMl7mAekFs1oT+zA0/yeWix5Pgaoc9YZmst3T78xRMckz7qMwq3eZVFgUiW65h+8CMSbsUJEwgI5SIbPTWvo/YmJ35ypdDGxtbGK0lQpWCtjKSBADQDncT09wNT60KGMophv4DMonlnszdE4kKtrLis5H6qoS+GflCK0XQc0oMDRvoCgsboC7xqHaKOx7ku03WmGrEl0JW2HqA11KvPDKGeqqYks5bCwZVRP6dg8XLXqoYCvUWm9MDWW81f0KTYeyBt8HXOlAK8qNEUwRshKlUCmyYYBaoZzBt5Fur2E0kqdDKyF78G2PVZFCZ5TTJCs9mLa068dOF26oegVSUEPQgQSCSLUjtP26cqGjFVhyTKQ+iGBpDujSAgE/X0o10mhyb9CFwYzGuMkmNjiMcqhsiI2wRTbzoW9Mr4JjhSpFnqEcV5K4Wp1UFKxyihF6j7aG0faEkVaUYY7pWmLTkMnybFFhypGMs5QpRoX0Hmm1hrvlgT2OnNEqUlYakGBo3asRIkkrslGUW2OK2tF5yHONX7aUdYExBmM0adFAVWBLh99rWGrQyhLnHp0zTdtRVSW+6XGFles0aN0ZZzFu1V+U1xDevg2kYotoLW3XUHYd1aSirsfYooCgsMpCyKQMrc8sg3Cahl6R05B9yQPiQUNhHIVPAxGaRIvOOsgOayAq0Y5TRmFCplA1eAgxsttKxVrs1j0yh9u+U3CtkOknzm5Vm7n9uvvHfDfHfrfnei/crzfsDfvf2T458Lnrq733MmBabTaBTkDINGeuCHtYSDAqKB8+Ts6weOYMuenJRnRIitPbZKOkcjSIpNb3HcFqjfa3prxcT4jXBGoHSmQ5YyYVri5YXr0ivS/DglYbgfVlCPnAhRh+iLikIRtD3zbEtqc4vkXz0gVxLJQipkH122ghHlDqGppsUKQ8qG+HRPvCRUbjiumj97HsM/HKnBiTaB0pTTy/pOsvUT10jO7SHvSW4tQpqWqZYT8KYueJuwuM98TO47U0+6uqZNm3jJ1AM6zVlNqRrMFNKmwh/QXVlsL1GT0usZWjb3uM1tRHt4QtzgfpubIGXRpUWRFyxkcR54xLj5nUxKbjynyPSkUuXL3CxYuXWfaGvVni1InTnDh6gvGJLbQV1jqjFX7RockUGyU5ZRFlTJkUPXnZYn3EHtmUewCkKzuo0nDk/hOkZQ9VxlSOEBNuqAgZlVAajLX0bSdwq0Ic1lGhmCRFqTN+2UqQaTRuUgnTYBTB0G7RUmyMWAZIfcR7jysLYlAUVUldOlIX8H0v4pllQUTRhYywT+w/lX7oEckp47S07og6vGU5NOjGG7IKhw/ClehwoaJUO6ymDQM6iDSM5aGZPgmVb0rQJk1ioNztgwRHGcocMIWI/q54B7R1jEYDW17q8MuOZAwUmiLKcfdLTzAa1QWhWx7omEdVAaX0s5EEkuZj4MUXXsQqQxt6Yt/y0Kn7SbMWXZVMqlqqKXUia2Ha0rmUSonW2BToU4+JGW1rYtcTU4+uHTlHYlIYa7FZBGANEdVGYctSBmUNgcTOpT22tcJWFTkPlO45YXJE1yVs1gidX0ZFoSJuuwWXL57h/OUF09EY50rGWyNC78nG4Y0jhCGpAuQEpYniGJMxAw29HqQCtBEB4VUvU84Z7RwpBHGUmyBBVpdo9npSVMR5LzTdVmOrgmyhbz251Iw2KsraitBrXaCdxRWZRCD6jDWWdrFgb2eX6cZUgsFZI2xkpaUn4wqFi4pCCUmLGdWDgGzEGLDTEdqX9F1DKjQhaRIauoBvl5hiTJd6fO+pKkfuPdZBjj3WSfYha+TeGOmVijHiykKaNgd9Iq1AIfOCKi2lcdRmIkQfK1Y6rXAbFZONqVQDkV6rrBIB6c2MJGF2c5bko/TohF4Et0snfZiAHqrrSiv6vSWmdGgyk+2K4DVuVBC6oUI8KslRrkk0Cj2QtZiRaHuNVkF0iCLvUMm87C/uUJ84gm88GCNzQ8r4pkFPjpMaQx8z3hjUeEyPossKP7yvDrIJxfX7THR5lkPfahczfUioDE1K8v4aCH+ueTEO2+hiImVFiJkmS/DYHd71c808drsqyg3z1F3ZjfPfqwmsbr707R2bVxPEvbp13rA37A27ld2joOgW+LiD6ZNbVHbuene3+frolcB9M4itZ5kV+sFjLF++zOTRk2hraJ+/SNhZgjUYpbBHJrjjG7TPXZCqidaMT23xYFeiz3rKlPaZuV7NYSlFDon+yi6p92SlpUdmaLxG6aF3RBEyA8WzBEbrQEtJdjLMllQntrDjWt5dTStZ6XxA4FApVEpC2ZvzQIIwZKnJqL0Fiw+/xOjN91M+coK9ZYfxwkxVqSn3bX8OunCk81IVUEel+hS1CBbaPMSxZUa7PNBiJ37fPc+zk/MorTh94RztlZcGCuEeVWhizhw/t2QbKKqCalTiJqX0z4SIGfqp7JDRTkmy6SCitB+/NCb3nuAjXeoZndjGKMmGXzp7js2tLdr2Ph46dZoyRh4oGyYbE1QWbRFdCIwnJwms7jtVcHoyk8zv0EdFzvgLe5L135BGYKUUqe15/qXEstgmho7U9ujCYZ3lwaMNZV4Se09l9rPRSmlhSleZr3+7HgR3gasNfuYpNoXVTsFan6QalVztNT/yO5GAIUU1UO867p9m/sLbVsFBi5mIsuuzV+C/fnSoDhxofPOJoa9E8TkPweeeEurbX3ux44fP9cCdiw9mMjon/sKTmpMTRdtHfvQPDFeboSI5BEWx67FDM/lOk/gPHylovAgzrnh3j9mer3+zwLR6VfLCpbEICBtDYTOLnTm+bAi2w1aO7WnkSLkDRnM+aC4saim3FQbnBI6mBvpuKseJ6dugG/PK2TN8fLYkTR0bWxu8fZqxyzmqMHLMpQUDRfU/MbFDKUf0X0K2IwyBh7f28HmGKUZ89HKiW/b4ouSjVzZFIDlLX4e1ltJEHtncA6PY6wzPXa1Yzjt88EzHIwyr3kHIVrNdBx44FlG24/ISLixr+kVH0Z+hyJc5WRY8UNS87WjH5njK2FrKhytQip96ruDZ32IQ8pVnSivF1z+pOV2IY7q+rUa0cIyzQp4SowgQOzOIi0b6kHhhsQ3O0e4smF0NbB3fEArrukBnw/L8HNVbtJtw9GTBm08uWE1QOS3IIXFxJ/OHl0ekGDm1FTl5ZMxITVixkxkrQrZaa2qteWSsSKpf9zCiZQ5KPsgro+p48dIRdi7PyUrhvQQ2KWdemH2AwjmM1TiXyGh0AY/UlylGhTCuock9FA7edHRPYIo5S//KMOZSEkgjQ6VeGY1OCZUteiwJkzzACk+lzPG8O/RtDjplIXKu22Bn6Siqkgc2l4zVktB7+q5h6QXe6HpPMRDYxM4PfXYSvBqjsU7zlqKTuSm3fPzShKBlXs05EWMeElxZIIpeqrMqQUpRhGF7jwpSWTaFZdY7Xjhfoqxh0y45MclU2xu8dM7zS88L7FSr1XYhxw5Sf8PYb4eHLKP4+baRnjcgNqxffDre3umOy/VkIoLmSF3oTlR29kOLw4KM1+LuHwZV+9QIH27KnveGvWFv2Oti9ygougOn6uA89mogsDdLZt+wa9mRThkTM3HZM37sNOnUFLs5xoxL+kt7tK9cRk0q8rxDjQuq+47QX9wj7izQWmOPTqgfPIa9IPo65la0c4cd/lDoWWfuc6a/tEfftKKBogVnn1AYbQYIgjTZm4FzXK2IF2LEaBFI1cbRnrtMff8x3Ilt4uUZOUdwhQRGw3pqoMm2Q2CUcxadIKdWbSWE3SXz33+R0Z+4jzguUbMWO6rAjLGTDUIUrZ+chTZZp4jNmqgsSScK4/ApoLNkoYNV5PGIvtCErsdXGr9pKeuCyowBuLy3w9GtCXZUoZT0lITOC8RjoHNdseqlIPCqECL9skHPNd4Y9KiQTHRZ0jZLVMo4RMSwazpOH7uPqCy2qjg53hAK5BAgROKgiYNRBJXpuw53BLSVAGwFaVPbFQpBgikjBBZ57Ki3LYurAVUXpHlL37RUG2MMicJk2ix6NntXd5lsba4hkZCp7b5g5aIQvZjYdiJYqSVjba2Rc0cxD0qCGrXfJ9JELfebTLU5XtOm9iEx8xJUC0W5GhzjQRkecFqzMdLilGtY3A27All604xmUsGkgEJr9HpgD31wfZCAVils6bApM/eKLg7uzNAEPtYGXVuU7wlNwmcNXiBvygiEqbCGYkOITpRWpKX0g2iNOPeFEdiYVoQobpXXmbBccPnlj5D9JilF6tGUOCl465s+jeryMyjbkLVCjUuWrRBrJBMw2pMagWnmQYOlXczYOlETsuHqlStMx1soa4TaOoMZ4JU5Z+kdij1aaazWqKzYqEZDP5/AW5XRIhisoKgdzgWy78FrmkXm4sULTNNl3nSqYDKZ4JwjGI02ifpIJQ51yrRZBDhzlmc2pYyzQhqRQlo7+ckHaf4fEg1qpWdgYKVtYCpHngfmV5boqiIGhRuNSdqJYK4rWe4uCQFsUWAmNeiIiQuhiWfQEvIRxwRciakUuu7ReilEKcMYjCGhtSJqha4KdBbYbooRVzohirBKxKkXDVplshmjJmPivEUXA5lDVQjDYEhDv1SimNbQNezuXmJTTeX595p5s2RrPKWYjkQg1we0Fjp5YC3ejFHSU5XtQGuuBOY49JbGKMxtRgv1PigRZLUaF4cqnDNCDmEiPreEHLh06SoWzfHjJ7DeobBCvmONkIF0gZS89FnZQbtJYme5Vl1ElQ41VERzzhTHNgmLlnx1TiaTxiW5jxRVgbIRMzDopZhJpsDPO0aFxx4vBybPTBtu9lJNh/xtfx5oWQ33fCCaOZgYvcXLPLwaOMgf9ZDgzo4+H/i/rLWC0918jcwf/avzhr1hn0r22oOi281x1xeRrofOXb+t67+7md92U39OdtjkzCxl8qigPFISTMKNLd28oXn2HO7olLDs0dZQ3XeUHBP92R3IkJ2mfOg4WWvmOaASLDPkW1XErjOjwBmBVDij8Bf3WH7kJaxSJGNRqEHjZ6gerPtApM9jRcetciLFSExSvVJa01y4wqaPuO0J/vyOZD6HLLvKoGIkakOhS1QSRrfgGxEBVYqkkP4cNGqRUHuR8XSDthecexsDbQpYbaEymJQJnbAjESMKcVRjzqiQyS7TxpZcOGhaqsrAdEypMv1yRlGKzgXAifFJyYTOlqSccXUpkJ2U5biG6yAN5Bnf9TRtS1UVOG3kWhmNtSU6RMCijGRsT28fo65rVCW06q50mOglv+mMQLS0iObqwgoFuMvMswLP0IslLHxFbSjUvnpDTkkgdvUYZgKtchsjwu4Sf2GXmZ9jj5e4yRRNZPPINlJalB4htGbeDAK7ClxZDn05mVknDfcKy3SoGhmdmLqMzwqlJJutgMoqlsmglEH51TMDbVCs1GNXYp0ApVWUVticckrMvPR19HcN2xcR2RQze0uotaLrIimbA+M4r8UsF6Ity7yXIJcsTFhjI9duUmm0UYDFqIJ+VxM6T+EMY5tRGsrK4EYCZev7zLLNUvWYltgIymqyNoSksEnTh8DHn3sOnaBOp5kUls3phCcffAyzNcJq6fHpc2C0tUkOkcXOLr7ryCc3QCVUzISwJBkLuUeXIzoP3gc2q6n0WwBFqYlLjwqB5DQ4QzEy1KOKnBNLHxiNrSQ/BkY+UzhQwgInBBsdoZdG+RB7gu+ZFJaHJic4dtwNwaDGlx39osX7gDMlSkGlM9NSyu/LXp5rFCwCLKIhh8zYJrIP9DEQbIVKFuVBt0uquiD7IL0n1hBixNlMDh0acJVBJY8dFfg+UFQOg2jZtFdmzHZadqdCXqMGXTAzKYnWkdpE7iGEzHw2BJko3Kik61rq2mHtwEaXBticFirrlYaStppsFH3TilBxUmSnsYVcF1MV+GVL6KQPSBnp01IxsnXsJOPJiG7Z8MxHPsJsPuPxBx5hy1UsZ0vqIxNKNzBuDgyEKmVCSCRTEIPMO0Zn+r7HOqkGm2qfdl6ZgeQCCVK0luBYhUzsIkFnptOjGGs4euQ0fdOymM1Zzq7ShZ6TjzyI1o5kFSkIYiC2ET0uwCi6pdBzB+dAZVQIWCk9S+XOCXzVOdCTCp+hD4psNNkqeg9mXOLbIcmUJamxGqoOxUTtw+H8a4Zv3On6f3Qd+EOrNnfuEtzWDoMH3i7guTdX841OozfsDVvZvakU3WpM3aMJY213MAlJib8V5ing68YNj2wo/LzlD35zB+UqERu8NMNsj7FbI5YfO0vygq0fP3ICOy6Z+8RPLxeEKM2mN/Ze3Gz/cHJS8JmnJ3LIvWfxWx+HthOVbwZo3MAIp9UqgyxMczFKIKOUWit2i2OR0cYItrzpMJsCOcqAHjDeKSVwDqccD29/PlaXhNjywpX3E2NHGpwK2h6nRtx/4gtwZkSXZzwz+SDGOio/wviEtkmodlPGOUvo2zUsL62wOaVjl1c4s/s0LmaK5HnoMmSnqOqK6eljQuPt5eoZpWi7lrqqJHOOUDMLXM7RXd6lPrIhekcpE7xnNB0TvNBW4wyx83LNnMWMBnhL0zPe3kQ7Q+g9JmWKfskjR+YD45Oi6VpKY1HGkEKk3Bjxe2ciP/6bdghKtfTC6MznP6j4k6ekcqUQ4cvkA7nzInrrI25U4o5MiMueC0vDlcslprA8cmRJXfYkLzClnDMxJf7j74vAb+UUf/kdmmpiWPbww79vWHrYqOCvvBOKnJjayP/9ToW2VvYdxaE5s8j82/+lB3IO1jTsUQ4UGDRpENjcO05mvvABgU594IzmX/2m3DZ/TeXz+gzEjdmKjAQ5SSn+vw8ryeBnQydswINArPQSNEHxg78Lyy6TtcIP12+7gr/8DoPRwrqoAbRmp4380isLYh95dBr42ieNbEpDCqLd8/QFxX97RgKwz74v8PmnGhbLBVf7DXbzBmfOnWV3b5fLVy4zHU146/3neeLEgnJU83KzwexSOQSWEbs9ZbFcMnruKo9TQLbUyqIIhOB5Ye+DxKKW89abGG9or85RVipgLnseq66ix0BlMZMKZRXSUyZB0fYYNvwCZaTRPw70z7YsSDmzt7vH2FZgLL7rqNKch4qWjeObTDan5BSlq0EpXCU02ItLe9SbYzLwFY+VZG2IMfFjHzG8uAsxZn78aYFDWQPf9HY4Vjsymn//e5rdPlHpxF/5dCfVkYENLoRIQeSR6VWMsWvtqKwUy0XmxdkGXRcIPkgF0Gh2W82snRJCop5UaKcxyYI2ooUUMy/sZZJX2KKknFQUXYVfdmxcucDRuqesS4pSgsyVMDFaYYZkkkFjRo7cKZJVuHokGkRAaHti08l8GKOQQ5AoigrOTGgy5DRhtBOwTUtzdoOL5RaJLaqLPU+c6tCFEb01mWBZdI6zzSZ91+OWl3loMhd2ays04gxizsoZNJLI6buemCPFBcXozJyNrU2snZDNBu0BVp4Ux3S7Dt92XLh0kTPLwGhzLBC/YgKdwAXZEVbLft7QJ6H+LjZGWGeJQ/CptMK3niK2PP5Eop1dItgxL+kNstbsXmno0jHyfDUfRIJCpBOiSDB8mnM8PC4B+EDX81v+IGROXQPBhX0o5orEY3+euLN+xP2Z5H8z9/te+zd3ZSswoSTXcmYQSM5rSY/rbVWNujbYOvyO7GMAPjnEFW/YG/bJsHtHtHAns93tJpCDvtn127td5eg684DPQwJVgeo6Fh9+EXvkPtzpU3QvXgKjKe8/QndpRtxtQCmKkxsUJzfXu2pTJqxgaXe2a0Cc/8IoUudZ/uGLpHm7bnBe9ffkoQ9DKTVkTRNCEpRIyq41i5IWOE4KHmMlYxtnDeboFE3G1SNiUaAKB70n+EBhHaassRTC1qU1uqjAWZo+oEclrpxiRxNyUGRlKJaRFHtCMuhtReyD9PgYgePpUUkxrUl9JISAdxpXFiwuLTDJ41VGTwqsgbIs5LsLO+gIOENIicoaMolFWlIXpcBIUoIokB+3MSbMGrIz9N7jnMM5Sw4RSktuvbyzUyIuO1IocU76j5RWJLKor/cepcAZUJVm98ouOzs7jEYj6rKkKitxzgtDE5X0pwyaLjlkQlIoa6S3wUolSithMwSNKcx+BtZpoi0wrsSHIJC6Gsl2Z8n25Qi9cfQWlEroQiodKivaCE2AIgyPvVa08yVlXWL1EBiJ8BauhcZnYtqHTq18l5VAI4OeSY7CKjYutcDpgKU/7Dm+9dO9GnIrHZ0OvS8su+o1SCvYZsb3gdYblj6v+4xAcgC1k8rpan8pytjqYyai6IfePbNi0UtybD4m2iwQy671WJXZ2pyw3HNcePkc/bKhxvK2x9/C5mjMA9sdo7GH5MF3JGVRhSZri0+RydYGG1uZnefO8PCjD6PzQmCTOUMBEYGDUVj8TkPwSaonCrKPmEJhJwXZKJSFrl1w9dJllNFsbW3h256maTl27AhaW3RlhU1SG3LObG0LNC6GSOo8I2vZvv+ksKUBSa9EeyXQdOOKYjpCWwkCtBoCdatRMZKizCNdFKfIDqxhKLDO0abMss9gFcF7fNdjBwgXPhB7T1EZch/QnVSMtVFUGxPi5UQIcRCAzSSjwFqyUhRjJ1TnA9lLu9eglaIYSbBjpmOBkGpNaAKpT9S1oy6lkBo7jzJago6UiD6IvlVO2MJhGCjHB7ppW9ei0eNFwDl0PRSW8VSgpCZC3huEYLPi5In76duOZeoJQ08lORCanjQLaKspN8fCFqgnRGUwVU2RKrANReFwhWj7qBXENwhjX4wRnwNFVbGxsUndSzVcKdYItPXYyZaNjW2aPOehYyUXyxF9n0g+oWPEd37dY6oxoAzGCALADQxyxhqpGM4bVIZ6olGdVOa7mDFVIQQV0xEhyoGYwpIbL85tSnRX59hTR0QTaXB1rbpxDjjceT7MXr2z/EkLkA7GcndR6Xl9AoPrQXOwEuW40/1JklXWW20ppcxKtupGSN5tAtdVULWG770REL1hf3zs9Wefu10Smtt8f7Pl72Iyy17hZx3VsWOMN+5jMfP0uwvsEPx0L12SF1lhKE9vY3xGa7BhcEpucRgHzWhFZcWZqZ3DdJb26TOkK0JXLexwZk3FbU0hGUetCKlHE0gxkJU4hFkpgbkZQxqgc7YqIURY9jT9VXogntzG54ytS6rWoBcdpRV4WywMyhW4zaPiHJJRRU/0iWQCwfaktqc3S4GPOSOq6XmJMprgDNknTFFgSkeXWygh0GOMJQfPZFLQBAskmr6lProFOdNdnZN8wFgnfQNkdF2wOTLk4LHOoJwmDCxwi2Uk9FHEPn3AACZnwrzFFAZdWNplS1EV0hhsjVBiVwXaOcH/h4wnYbVAq9psefYPnmFzc5Njpx+kqEu6+VyghCFSWMuWE+pmeVgGMdWsuNxklHaUXuG0IUaPyonSCMzHjApSF3BW0SMN7KEP0pcwLsgxMwuakDLJCKRPKVDGsOsht7AM+49xyrDTQmkUydUo32OrYiD+EJYx8ZPlaSwMbFT7EDrJCktTNkjWcFzq/T6S1Xi4BgZybU/QYQN2rQqvJPCUISFwuv1tCzwvxUzsejaLitIoYszstLJczHClkd6XfRYATRNheyQu2JFpCXjpE0GRoggYGwWbuqeJLaGL9HECSREWgaP1BsdGWwLRdBq8aP4sW81OO+eVkPGlYzSeYJ2lb1tsMWaPjrh1jEU1YWJbVCtkIklBCkmEKLXGNx318U2cTqgQMUbYElOOKO3YPbPLolniExTHtmntmFh6cGNmqiKHvKZiLi2MnSRB+qalW3bUoxHBFvJMeKhtpi5WvWjAwD6p9BCcG828B59F2DkqgSIqYFqC1QqjMtYMTlJObLhMxFMp0TyzdSm9SL1HDYyQxhr0liV0gbkXMduUDBsnx4zbXqpLwzEppYQgpLCkBL7LhFlDURhcXRL7QN/Ocaok5YSxFUo5tLVcvbLHSBcUVSmQLgVh0RJ6TzQi/lyNa/YuX6GsLS0Gbxz9csHUd5SVoyg17WVPTonN7SmzIH2TJmZ2o7Abrp/3QoLC1HSEGDHO01UddSUU4+3uEg0sLpxn9vIF6d8petybyzVhwWrEtEtPRmjBY5Oox5sYZbgaYLl6pvPB8XOt5emYVi/pri6GYBJCF8gGXF0RvZd1C4srLG5cSbJIC2wZHdHCsCAoAFNiSktKBbQDYUQIWC1w6+QjOUZUyqQmECpL5xVzH1kOPZTtmqP8WlvVIWA/8fJa7eA25dP+XPQJIxXIN/n8SbGDULl8IKy51m4XQGq1jxSAvJ471kLbd3JNV8X+e3Wz37A37I+gvfag6Fbj5+4q63e/3B1a+0KN12PRkqgMsVsyesv9KKNZfOTMPgNRaQmX5zxsDSYr9lISnaBVNmeAFNzs8I6NHJ/74AQyjPw2W2eOcsydZHfjRc7Nf18gIgJkR2nNZv0ox0aPoXLm3PLD7OZzqE6ajmNVYLQh7s0xToIKbQ0qJigLUudpz82gLnnp0Q06p7Da8a7Lb6caaVzhRFQxZ6yteXT78wltR8otz+y8Hz12+Mrz3O7/JM8a0bbIiWQNWXe85H+LrKBZekauIHsIKULOFIUjhIAxormUNVRHp2ANk0KEK/2sIZUJPRkNTeiZqi5QSnHfRsO06DFVQTeX5Yy1vO9/vszRU49QlkYoqHMidF76jmrprxgfmQoddgY3rcmhkGlfKVRCsv0hkS10tuIjlzVq+zPYU4bZnkIvDKMeHj7Zk0PizUfg8c/R65d+zgL5+cDZzL/5TVAG3rLteHTiwDvu3+44Uc+JQ7+RLgWW8pGLjjaOKCqHK0uWuzPKrQ3+09OKc0vJ6q9Y3bsIP/p7Q0Y5C0McSvpvfvB3ZAAcrSu++dMdmYxvOwkE1wQcCpXhwc3M1745CHzOC52yLexQXZHKkbV6IFrIpJClf8EeDJLUdT8Pg9WtnBbW+iyrHiU5Hr0mk1BKsb1V85ffKQKVu53i+39b0aPYaeH7f1ftB0RZrvcDG5lv+bRI6j31tMYkQ2x75r7izHxC8pFjk8CfOflh2qalmj7MM1e3IIrWkRkP29RynbNWPNe/jZde8GjruPrwKdrpiNFkRA6RZbvERod7suDi+XNUzvBX9AfZzLvyHIUEUZEdECPl8U2cgcc2dtFdJ4mDKA323V7g8u8ZNrYeoqsqfvSjzXD5iwOXdLh2Ct5+HP6vJxLnz5xlazTFGYMtCz7wUuaXX5Dz+OLHNf/nAyIw69ueoi6GTL/MPyll/tvHNR+7LJv3Saq6rjD8+bcoTo1EANbkREZRqMzXP97TNh0YzXQyXt9XY0WIeVVxzDGxkwve83uZEDUn6p53v3MXQsQ4ST0rNeSks/TLzcKIF2cGVTtcVZD6QCRxciuzXV/ClQVpx5B2StplR/DHSWFEcA7f93Rti9YaVxRCYW+Ertv4Eck6fmvZcCF1WJ35pjd3THJD7BO7Fys2N4/TnfP8t+ViCEqEje16O24Mf35Z4dsWM0osqyVFYSmnI4IP+EVL9JlkHMY6ylNjbB0kyEiSjIi+Z2dZcq4bkYzitC/hjGz/V5uWP+jbG3d8iBkFX6XHTGcdoZO+VgrLWBWcOzUh2mvfME5HHtvchRQIpiPZjtR0xHKDj1/dQhUFKYnwL1YzcZ4T+ZzQ+28c5yU9JrWenXlkGY5i9yqeWbb8wXIBHM78thrPN7cbs5h3HtS8thf8/46MbNempfYDxBu/z/tz8aFbuT6oufNrJOy1//tc0z9K9oM/+IN8y7d8y6HfGWPY3Nzk0z7t0/hzf+7P8df/+l9nc3Pzjrb7kz/5k3z1V381AFVVce7cuTted2Xnz5/nh3/4h/m5n/s5PvzhD3Px4kUAjh49ypNPPskXf/EX843f+I3cf//9N6z7rne9i1/+5V/m4Ycf5vnnn7/pPs6dO8eXfumX8gd/8AcAfM/3fA9/5+/8nbs6zntlnxydotdih43322R7cgKUliABKI5ukFNm+ew50SlSilw5UuEoNsfoxdA0u56l7izXohVYrfFX57RnelDb6KJEU6NSTWiliRmlSVqBc+jxGB8iXa6I8yTwOsAw0MMWhdCGDxC2WBsR8gTcdCRU1ssWX2pUqdForBbHIqksvTopoZLBFJbYZcqjG8SuAaWJKqJHFoPCVwV+scTYEmXAp0j0PdEZEglVWdEo2hijg2DT7bgWp8pq4qwVZfoYsVVJdg7fdBitwAzitNZgnMEWhth2+LZhVFecPXeG7e0t6rKE0uHbHkLCjkRIMy67/fvpDM3ektGolGx1TJJBL63ABqxAlJZ7C+pxLWx+RvqFfBdIRhNjwtUFKkXKYj/0zSEJniRE2kYIGkLWhD5i6wpVRIwREV3jHGqg255ubaCCMDu5acXIajKaANeSGgwPkT/EcRMYmXzu40A2kQK7V3Y5euIIutDD2zGzkgUqLJASWmek/SgO1O4SHCgtPUZKaZTJA7nBQYfidiXc6w9dkfXw4lVqIKdI5NV29X4VC6NpQkKhSD6inaGPDFC7VRQqFcTYznBaY0gEL4Ge0MdrlNPs7V7m9HTM9NRJrsZNuq4Y+rUCJmVUJQKafdeSnQJKptMjLK8sePnp8/TbYwpnKa2wIXYzjw8z7HSKtpEQkwTTaujJSkluglGQklRYfY9WWXQ4tWK5WDDb7bH2CKN6yl6K9HEdkx56WX0C33uOHzsu1QwrfVIJRZ9k4ZiQ6pBWlANL4+qL6D0xZnpf0IUhG5wyZqAkdzpTGgidF/KE0onIqFNoLFprws5CqmClRduBbj5EtDWEEPFNpO00URtiBqMGodaVAPRAZ+0bYQPsdgNZHSH5QD8I0gYDalywefwIWikWe4p22VIVBWY0WjtuZVFTFvW1F0mYZ3CmJKZMGP4pwNUl01FBCuCuTMhe06+WuQm1fM4ZnzNGacrRCD2O2BPH6Zolzd4uJoNxBdWpKWU1QVtNMQqQZuQUpZdQS8Daq0yvFOPRGLWX13pPIQtke+2y5+tu/QGvNymFc45pWV1znOlgRWYIOJXRogPW96RlI0mpSYGalix7Qzfv0aVorMU+kOeRrugojpdSBSSTOk9YduhRiaorUlbE9fHeyq57eK9tLDpk6evrQLffej6w5N045Lda9l7A8l6vPprbAePuFLJ2b/PLmRgTOYO1+i62/oZ9IizGyJUrV/iVX/kVfuVXfoV/8S/+BT/90z/N29/+9tuu+573vGf9uW1b3vve9/LX/tpfu6P9ppT4R//oH/E93/M9LJfLG75/+eWXefnll/npn/5p/sE/+Ad867d+K//0n/5T6ro+ZGs3t1deeYWnnnqKj370oyil+H/+n/+Hb//2b7+rbdxLe32DojutIin2Xxp3O6PdLiACdnOmTNLor7yhAPrLM9JLV3DaCPOX04xPH6Wsa67MelTKzNPqBbd6GcgGLYpNLbCipCEMmb1JUVKaCf7SLqYvUSO9FmS1x6ZYvUF/foktRgPdakkoHNYYRl1FMhswFZiUtVaYnQSaT1AKHyMWKKpaegGWHTF0FMtASJrSZFJa0CdNagBnsVkyt5rMXugoHOSkMFkRdhbozRG5LkApRpMakzK990KZnQ3TrYrpxK3JCvTQ8GtsTY6RFBpitqRgiCGQu35QrgerAkr3wpqXIBtNObKELtIqhc+GNjtim1n0iuNHN4dsdCCPNaashAWqUJBFmHAHaZjP0zG0c1LOlCOh50VJ5SClDDExrkpRss8I40bMRJ3QIdG2EJ0hKM1yT5yPkYOxBmUUdak4dUQa/rfqTKUj1mji3gyOaEbbm+z2im4IYnY8LL1k6C8tobaatKoCHfaMHvaMX4NzV6RGHFlaRd8IdXfpNCfG0i8yLuDCQmGsQ+mC3OYbsoQjm6l1whjNuIBjVcRYw6yH5lCv6LAM8bWDVSFQDW0U2yNQKVKXGpUTGbN/akqhlMAKVzC7VYXJKtiu5dU/KTVNuUmTErPdnk0T0YDve5plS10WjEcTNso4sJ11uGDxg9BvuVmTsjjzz374o7z5bW8l6MiFC6+wuzMjbG3Tdo7gAykBuxpjDd4orlza5eRjR+hoB+c2k6xGawtWE/tAMqCzYidbtFOYqqDcbSEVbG4d4dLRKZdSYicNJb/rBM0KA1uD/1vnjhwiblSTUxwYzPJ+kIhUDM/uClxqWsHIDlWZ3uMbYSXbdEc4MZKA6moj1O3RB3LSBB+YX95jvDkWHTQj7HdFVRC7HrTDlG4NhZPqmqangKJAVYnj054QE9sjQ5eMVIqMxelI7L0wy11p6buend5ibKbAEFpPLgzT8QTjei41DQB9dvjKsQAJOO/QEhAOPIWXG0hZkRO0MZNios352kD0OlNKEYDLKYlea0hUqSIXBcYmXNfTNg0+eeLuHDuqwWa8lp6nlBIhJspxRXYjEiNmPqN8pBuYcNq8P3hlBF3Xh3rd8Xmr8MN7Iw09SlmmG5IP+N0FsfW4zRGYzJVLO0LhPq2hLEVst/WifTccd1VrqqpgtFkTLGBr2jYJ/HZUEAvHbMjQtOGu6Sevv6q3/PZuAqO73/O1ax22r9caGL1eFZNbbffOAqHXWmU75Fpl1pXfa/g13rBPir3vfe/jT/2pP7X+fbFY8Nxzz/F93/d9/MAP/AAvv/wyX/mVX8nTTz9NVVU33c7ly5f5r//1v17zt/e85z13FBR1XcfXfu3X8l/+y38B4IEHHuDbv/3b+ZIv+RIeeOABrLWcOXOGX/7lX+bf/bt/xwc+8AH+1b/6V3zXd30XjzzyyB2f6wsvvMBTTz3Fxz/+cbTW/Ot//a/51m/91jte//WwexAU3a7M/jrZHe4yAz/XNiik+vJ1F+GYMfi9TGc3ycsWvTnGVhVlU7Bcen50saAZyBVi3i9kr3ydI0bzF+qRMKmVigvHLSkm6rzFifatTM1JzCRjrehuGK/xVxfUj55gmu/nWPkEqvMoYyUtnBJHq0c5On0CjMakTG57cmHRhdyiNgRIWVTRlcY4g95SxPkCdfX9NHGGcp7z6gOQESw5iuzEcTIJcooQM2Z7BJNS9D62RpKN7ALdvEFbw2hUiSOoDMe2NA9N50LFXRfSGK1l/zkL+9KVbsKluTRARx/WkK3j1YIjmy26dGStuHLxClvbRzjXHeXsnqGdL4mppC4rzs4Tn3N/ZlLN0YOeS86tVMusVHmapPm5/9Uz94qJy/y1z8i4HOjmO4Q+rNmsYkpDUCmihNEHISsYaH93FpqPnR9j90peCYr/dXaOtvDZ98GXPCz3+TPvUzx5LMh1zguJ262HVIjoJYr//gI8fXH1nC3WLxwF6zdPvJnvcbtgvlcsPzrGAbWyODtDoTg5yvzVz5BKxcevKn7wQ1lgoVngalIlWxWUMp9zf+ZLHpHr91mn4R0npQLxc8/BB18+cKDX2MEMxf7hXr+kNZmve7tiu5A+Op0lGF3nNrJEo0IoIX1Eq56qE1P4y+/IGA0v7mR+4HcgZc3jWwX/v4daIRMwBqs1zbJhcyp9X8oZtlzgyHQm7IQpEvMO5XhEvLTBQw98Onqu+eCjF3n57ecoyoJq7xTLlyKozP17nvGyx4fIucePMT46pVv2qGOGHAZtGNR+XxGgfaJR8Itbp/EbBVWAL/i9q0yLiiso/t9mQRgci0S+5mJl4OFN+Nq3ATnT7HXYYkTOidBHXDnQpUe9Zg38jRcTv/mKRhnNn34CPus05BAxhUMXjnJjxJfJBSZrzY9+KPP8zkBOgRBiTI9vDn0GUuFQSFVPOSfja4BgSiUxEbPhYxdqUtbUZeZbPnMXYmDZKp45J2KskzLw+Amh9d+bZ17uTtCrhN5b8mAIgwBphU0Wusxv9olfX5Ga5Z6cbxQFvRNbwbtCgh97et9py2nJyou7nfjn1ZT4DwNcTC2BKwCah43jK+ttSqDI8GYSqlGoBvpcrLXLrDWkK4pn+55f73ZkOwfG8P4wv3ZgH1aHzQoubWuW8wUpZ2IKqNISQ8BeKSRr33ui1vQ7S5xRvJCOiMbRXPSd7KQixYSdNOgQ2agdjx+ZY6eZRa75yAsVyYjIs5k4jLW8sNfzO2fl2A8rquWhxHXTnpIDbHS3cs5fL5/6ZvCx6/d3Y4B0i6rP6+C+vJoq072obh12HHAHwZZC0BQrBMDBbQwvkzdgdZ84q+uayWSy/n0ymXDy5Ek+7/M+j42NDf7ZP/tnPPfcc/zET/wEX//1X3/T7fz7f//v6XuZc7/qq76Kn/zJn+T9738/zzzzDE888cQtj+Fv/+2/vQ6IvvEbv5Hv+77vu6ECdPz4cd7xjnfwHd/xHfzET/wE3/Zt33ZX5/nss8/y1FNP8eKLL2KM4Qd+4Af4pm/6prvaxuthN3I23rW9yhlFHfh3/d/upWWIWTTjwmqSyFBMayaPnGD61oeYPHCUamssU23OBCQ7GYdjWvkWqw8KsEpJRLns8Od3WPz+C+z9wUt0L17FGIdyTvbnDHpSYiYVy2fPonaXmC5K83UUkUisQReF6GEYC2jseITSluwzuiwZ1SNKDCZraAO5i5JwrUrUuCaNSsiiy5QrA1ahrcI6BcGTcsAdnaCOjkiVpQmePC2F2UlrbOWopjVua0J5ZMr42BZVXRGWHbnvyT5gYkTFQL83J7Ydue1RbQ+9xy87kg9EsvQU+IiZVLitEbaw2MJw7Pg2ZlCrT1GCRmsLfBcotcM3LVqDKSzaaqFUN0ocVSPOfEJYrmJMhK5Dh0Bdl0wmFUVhUSpjnUE7jasc2upBEwXM8DdnNKoqifOO0HoCGp8QiI4WEVcdI6UBpzLGKHIMEKXHYPXiGLRtCWkd2+7/LcrPmyB6bv/YiocNSWHLUvrdvCfHhDPSL6JyxsdM7xM+ZhKa3mf6LuBjJqDISosAZO/RCkqnsULodYcmg/Jw1iKF0WAFnYhxlhQi0QdiN5ShtDj3q34YafuQcaZiHM4jEZKS6zY0zOecme/N0Eoxm8/XWk8+C+xRGwUWIgHlpAqiUdhB8LgYFzzw5IOU05IcIttbG0JWgDBDTquS5WzJYrZk6/i2VE6MEuxb54mtJ/deaKszqNqxLDVpVFJvbDAaT9HKkNMwt+RMXKVcDwREINfaaQhdM7AJamIY1DkHdsc8VIu0NWStBY4VslQDkujiKKPXy1ijsSpj1dDblfNaKFgbgaiuIVireWugo0ohEH2Q71MidIHY9ix2G+a7C7p5Q9yboZqWuFwSOo/vAvOdPbqdGd3uHF047OaEyfY2J+4/zWQ6oa5rCmfRCI1/OjA+Qpb5NCLz8Gp+vZN/By3mg9sc5uo7HGSr7fmc97eRkHGWh3lda4wS/TitLdYWMp9nDUOFKmX5F4bKYmQ/074eGdf1nh48wpwzzfkduitz/OUZcdGSWi89pMtuYM4USK8DEe8e1cQ+0FzeY++VS7SXZyhjcEcmFNsTquMb2IloWKXOExOooqCYjLCFE/2woaI2tEgdYndyHT8JCdBD7NbguWt/u6VDf8vTybdb4JA18nU/9z/feg/XLn+rde7e9vdyU+CjUjcGRLwREH2q2cEqzwc/+MFbLruCzj355JP8k3/yT9Z//6Ef+qFbrvcrv/IrfO/3fi8AX/IlX8KP/MiP3BYS99Vf/dX81m/9FkeOHLnlciv7yEc+whd+4Rfy4osvYq3lR3/0Rz8lAiL4o9BTdD3M7vrP16fiBqfkiNaUSF7pcor4YblLKd34Ej3w5m1yvkbPW7YnAdCxAQK0bQx9Kcxwey/PSUpTMqFwYxLCriXUr5ncecK8xW2PyMuWzi9p1Ay9VRGWM4xX6NKh7EBPqxWqdOjSEvca9MjRt0vi0JCbvFR80l7AjCtyCGQHSRscinnfkHNm49gmwXuatmXj5CZllXEARcWiVWxsT6Q3IGeyj2gNpfagE7jIcq8TYcQjI8JGQZw1+DZST2vspMZ76DoR/mvajnJwTDGG3Hu5ZsmT2n6gGdboQhToSx3pcotxir7vUYWiK3rKQpielFaiBzKIc55biPPiI5wYZSYqMDYJZw1KZ/qQuexLUpeHClNGGygcHB9p0SXyYf87q5iMRJ9l2vacrsWh3yySBKop0/celUFbgxvIC1JM7IbMcnheagf3T+Xz5QbawD2zQOZcjFgllYqydcTgB/Yx8Wp2Zon7JkYIFUq3fvZT0BL550TdJ/zMoXTJblTMh2rEvOPWY2iAyB3+3f7Hc3NoHEJykCFnKyxlKaE7xWJwIhmgGTmvKlvixMeYqUvLfZNMypljlQREyho2Nifs7VmOHDmCVkuyFo2cnCzdIqGMIxZjFmR2Z4q+TYQoN2e28FAXlEXNhm9g9yKuadk4coLKFGhrKfsleVRSb4xwfkp2S2LTYn2W6mJGIr7CoI3FqgpazbLtOBcCNmZ20rXuSz744fosdMqYgZJbwXqOQCnGNnG6BtgnNMg5k5Tm5b28Xkeum14HOqEPbNaGBzIYIxwQkAlNvxY19U0nyQ9rBhY7O2hnZfZ2PclHEhayVJJjC9lYcukwaMqsaVNktHmUS3YBWtGkkt0+kwk0XcLHG2s1s3x7iFYeKmuvhvHq1axzvbPZZzib4h27fQfP6Yb9q4MfBif0kEpETpm+6dFuEO4mo+tyHdhapTBO2OfiTJ57omRcctujxxXt1Rk5Z6rjm6I/pDJNLkmNZ+fSktocp7QlbZe4OsAVF4c1Mh48/Du6nrdf5vUiQrgT+Nj1FZfXdgR3Vhm7do19Qm249THvh0H73x94cu72YA89luvC8evcqdvt441g6FPNHn744fXnw/p8Vvb000/zm78pooTf9E3fxOOPP86f/JN/kve///388A//MN/93d990/H+j//xPwZkPvje7/3eO55nH3jggTta7vd///f50i/9Us6fP09RFLz3ve/lq77qq+5o3U+EvX5B0c2CmesTIK913B2yvgK+sCh52AqV6o8tl5yJkZjhv7XNbZM/17w6xBNhQxu+ph4JU9tWzcUTTljills8ot4u8CyfyDGCj2STwcvL1kwqQkxUj58m9pGzzR8QrvYko3Bak1tIBmwEFTO6HpHbiBpJRllbRVaJbtlilWSLvQqopdCAm60Ro1CjJoqNGOm6nuQU1WRKt5eotyoemFxkXDtCTjx7ccrBKVGVjnGdeGS8R+o9sxm8yBa2LmmC4ZmzjtBojmxE7nMzdEzsdCNeWY4xeoujkzmPjBtyFvYlNfQeqZzJaWC20pocE7qwnExzjlUiVKu0FsHZ09KjtIL+kRNoSx8yP/Y07LTSH/Otn6UYG0OKktXFKJqs+NGPKrpB6JMB+nT/JPBXPtOIoJ2C2HtSiExKx9jtEsueN08r/pRSkEQ8MfpIu7fAFI5qc8LOxStsHdtGl44UIv/zRfjtC/IAffVb4E8/Lo/Tf/wDxTNX7vyxvanjMPw6y5n/rxkmvSWwA2DXz24KkceOGL7lszQKLUKnKa0rOspIYNm+7Og+vgEKPth1/PpQTs83G5/X/36zwAkJVP/Th8WX3n+YFAq7ZqZDZdKq3JoGaM5QwchZoRWcGCXe/fbBMfURPPL8JE2GQbBSoF7aWeZnAvnSFtY5PtB1fKDv5ABzDwzn96ElKz3brzAFx9o5yhl+upzyoQjOZDqVGVcFO+d3aGc1ZmfMbCeyXVusc/LM+oTrKxoPv/BrF9a9I88cmCTScN6Sghku17Dvg9dLGzNArqQ6FPpAxn7iiwAAUbtJREFUDBHnLJ/5gOMdpxOh7UkpUIxLUoj83POGX/ydoQ0nZ2EgVEM102gUhm94Ozy8IVldUiIsvdBID6yaKWWKeqgiDIQFfm9J3yae39nC+yTPd07YqsBgWb7kKJxQ35/2gcW8Z6+p+KF2RU8dyHn30MdnZddPswfhT/uPl3rN74C76YO4fn9nU+S9t3AubtjX7bZ94DdJTNy4nNaa8tgmYWeGLi1uUuO2RizP76L6IFIDscc4Q3Fsk9j29Jd2SSHBuAKj0Vrjlx1lTCijWXaKj14qCIvItD7Og3ODXgY+Ejz/o2nuSd3hkCngU87k2K4PYu5O9+dmW73zpe80gDrYw7M68n144F3Rad9iLzf/7W7WfMM+FezFF19cf75VELKqEmmt+Ut/6S8B8M3f/M28//3v5/nnn+d//I//wRd90RfdsN5iseBnfuZnAHjXu97Fm970pnt5+Pz2b/82X/7lX86lS5eoqor/9J/+E3/6T//pe7qP12r3Nii6buZd4bFf04vvdm/cm3yvM+iQyPZahOCtGnJvfgCDAxuEklpl6d+Yv3iRYlmjxopsLYq4D0saIC+6LlDRiSaREba3FAJxb0HWCvPYSYw17F68ipuMJMjZrCWL7iNqELMEiEboGbUzOGeGaoohdp6icuKQWkOtxQHNZI6dPIFRkboqIUUUGe0MWRkp0ucMTUd24njaUUG8uqRrWlxZ4ectWYkTHlJPpGHhexbLwGweGU8nZCvBoJuO5Bj0QO/dB3RZQozrY0WBLq1UYQYHOXYBoy0YN1RzItoVa4xXQmAzCXGiFRnnRI1+dYtizKSsGCr+ZGOE8EGvmNekemGcMOilHFFJmNqU0SLIqBUqwvjopiyTsgjD5nyA0U0TBlxcjhAaP5yXu/FhPKxacMNTdeAP15nAXIZnL6trFsrGgEpolYkhoAI0yyVGaVxZChsZClc5uizrr6Az98yy3Jd1lSilNWV3inLNchygG2sdDQmMjLMYq9BkYowUzpB8JKSIdpaUpEE8xSTPidZr3a6yGuGNVMZufk55+E/hrOHE/UfJSvHQ44+gqy361gusMESsyui5pqhqjp66FiawzpLlBAfgkIdfRnXIp33TWkmf0rBNrRW2XNFtJ4wCM4ieppgwQ0UtJkWKea0RFXsvxCdZHDCtWQs1pl7Gmu88BqQHaVyt52J8pJ8vSSnhM6jK4U2gHtfU1mCdo/CZcubW2GpdaIojR5jFeCj06rBrsYKS7eulyP9v7zDeeVZ+Za+1MXwV317Dp6P2P9+93W6QZdyogIXBDEybunGCuQX6PlCVjn7eUEwrdLSkpkONKoFzTh3RGlyC2PaYuiQse7rdJaZyFKMKNfesOuhfK6XCjed166vyiYZbXdvDc9i+bzIJ3+G297dy785rHaSpW80kn8yw5OC9vrdgvjfs1du//bf/dv35y77syw5dJsbIj/zIjwACf7vvvvsA+Lqv+zq+8zu/k7Ztec973nNoUPRrv/ZrhCCQly/8wi+8p8f+wQ9+kK/4iq/g6tWrjMdj/vN//s889dRT93Qf98JeN6KFlBIxChuXtXb/XXd95vlO3oG3motvUi+/mEXwMsdIt/KUD27rLi2EwFUfGI8rok74vU6cQhXoxi12IkGMb3vJ9sVEMa3Jy13anQv4tEParCkqjWt2qUcKe2qDcstASlQnSumH0YpmsSBiBYY2KmnaDlc4imkNK2je0NAeo/RwaCzKWWInNLl95xkd2xhocj07OWALjalKyUKlRF45WTHhe5it9HRygUEPPdoZN6lBQTEp0a6nLixJOYJ1YDxVrSk2xuvtkgUKdX4vsoygrebERDPOAk270BqaKJj5U+NMORZmu7MLRdeCVpr7xhlHQivNgxuK7SrjNLwyA5eFyfj+DXEcnVY8sqXwGfoAZ+Zyn9sIz++ATolKw4kVda2yzDtF6B11k6iKJOQJWRz2ECL9ssMVlnpcc3mZmSXpKSgMPHZUk3rP2GlmuwvqSY2I2tyNHXjF3uz5VweWuq6yo7Kii5rndzJKOVlOl/L9UDDJQGhYQ5v2XktEdItjTH3AFpb7NsCahFKaFEBbRYjwyh7ElCXoZPDVYkL4zCXQJyf6tiMEaJPCh0BWGcuCqiioS3F+tbUslOL8+pzSTQ5u/2+XUqKMkaxgNr9CHGjvSWDJ6JQ54zv2DoGArazJmXgDUO7OMjY5KMJME1pL9i2BDls6IUZIWapKQwA0xHKkoWp6bOR4ZCuj0Oum54GwXwJ+oMiR2ArNoYgzW5y1dFcj8aoInPZh+Om9sBjWNbYaMYsV0UpPnTw3HhsyPsYb/LULKd7B9HltMLSyO3fy7q0jeHfwvHtdC7nO6V1vXqq4OiZJFhlNt7sgpyxwXQXd3oL66AYEkRtQxopMhNbE1mOmjnq7ojY9dB2jyrCsAm6rAh14eajUXk63o6C4m7MRaNjdh62vr91JsPJqA5p7FwjdWL268SrmdQhycLxcu+SNAcpBEe7rAXL7+zr4t4NkFTdC6g72xn1K3ehPQTt79uwtKzYvv/zyXW+zaRrm8/n69+VyyXPPPcf3f//3833f930AfP3Xfz2f8zmfc+j6P//zP8+ZMyKgdrBPZ2tri6/8yq/kve99Lz/2Yz/Gv/yX/5LRaHTNus8999z681vf+ta7Pvab2eXLl/nSL/1S9vb2mE6nvO997+MLvuAL7tn276Xdg6DokAGUJQuaszTHH2r3crAdnDWyZPl+te+u+fr6Q727jQvt9sVtw+XFEldIRaI8OqWbNbwSfhc1N2A0yiliDriRgZTxu7vEtkMrhb+4x+am59TGnjTInopgdsmtR29aIJP6yCuMuLKU5nRjDfVkJI3mgEqZ2HaoNFR5ct5vqm57ch+IRks1xggd8oVLV3klRabjMZublUyEMZIO4E4W88Bz/Zhu2aKiJoRAaTR5qETZjRHoiJuMUFpRbsFWGHqg1CqnvK+zkXzgf12w/K+LUh36829RvP2EwH9++WPw0ctS9Xn3k/DQNJGV5qefgTMzaUr/v9+ROT5RWDJf+SZhAWui5l//RmC3SWxNLX/tbT2jyjDWir/4Nk2KiQtLxQ/8nuirXFrAv/tdKSU8Ok584zs1yhqWvuS5HYtvK04VcDJdpbAjUueF4nfWMDoyFQ0krfntV+DXXwGy4s+8KfPU6Z7lcoktHMV0Y63bcld2p8//oWl4Wf/MXPHvfn//9XnjyxL2aUNedT7g1ocXZauFSnzNWzIbNpG1MJSpHNntFf/6NxI+5IFEYDjSAUKnjbzSoxfK82Us+filEltYNsuON5+Yo+KSrEWk1FrDR0Pg55vbn9NqWvi1vtufHp75TQ67+P/tjt39O7wu66GViQtL80xNt1RE03Lk09kXv1WKrumEZMUO9NxKo7Uh9p5P32r4P06VaKPWVbeYswRUQTRyBHYqPUOx6Wj7hpASz//qkm6euO+++6jHWzhXMFIKYw1qIRDN31gsaPPhrtSrO//XMrG/uqDk+qrUtUdz5yiFg+u/tteTuu64DtloAjMqiYPmmcoC8c3OoPaWAmMspfq/IsXIQSqn9JFcFYymlgfjOYqtETkmlv0OlC1nzRY/PqDEX/2YPzz0uddVoHsXhuYD/7+5vZrj3wffHRYQqvUyt6IKXwUg8lmtlz2o7bT67fojvH5/B9fY//ba7d1qC9emKG5c48Zx9EZk9Im0P/Nn/sxNv3vsscf4m3/zb/Id3/EdN11mBZ0bj8d8zdd8zTXfffM3fzPvfe97mc1m/PiP/zjvfve7r/n+ypX9HoCtra1XcfSH28Eg7xu+4Rs+ZQMiuBdB0WGz2oA/MCtMx8pju/Pk6rW/302Sb/icD3qJ92BMm8IyOrFJuDzDX9jDbI1AK8ppTfaBVb5auUFo1WiBD2mwfoCSpYTqLmHqguLYFFsXZB9JK60SK4EUhcUkR64LySSu3ut9IAwQpQwC0QNUkoksW03fdAKvKyyp98Q+cPzEcbkFUYQxc0i4wmGUIvVBmrCrktD1uLKQbfeebBS2cGsGMVBSURkCMukVkn9ove6XyDHhqgLlIK/0aXLa16oBCcgYNDoy5BBJfSb2UkDIWZG6IPj5FeNbEIE55Sw5ZExdkpKHPqBLJ9BDo4dGf9mmsobYejji0KVc59j1kA3luCalJa4qSCGIowrYUSlU6AcyuyuygNj2oibfesqyXLM6rfE219vriDu4vm5xR7u+kzFxWHR16DJ5rTmzIgIwpfSyKK2F+UzLmFA5rashK5p1UiKGQIoS9Cql8V2HygW5jyQbSTFglKbve9ykXgcaB0Eth57CQSzUcLh5mH/UIRdhv3C9coBuZ7daQt0A6Zrt7DG7tMOxx0akHLEDA51VimpUCeQ0JaJPkAK2lmdL+wBpgHamhHIWek9ctBAiWSuCzvRNy6JZUk3GFFXFqBjx6BOn6fYi48lEjlZdlxfOrDVKrrl2N3y6Vy7rG+7VypQVAWllDaYqCVfnGGvQOeODZ3z6CLH1pL0ldlKTFu1w74U5UFlJhOnKoQZ5hJWQbE5J+viu3eN1v19XzdzPj3FwNFy7/qdajWjfbkh8HuZHcGMV5k7sIDTvZmsd9o26yfd3ErbcyVG9YZ98O3369KuqBr1ae+GFF/jZn/1ZnnrqKd7xjnfc8P3e3h4/8RM/AcDXfM3XMB6Pr/n+K77iKzh58iTnz5/nPe95zw1B0etl29vbTKdTXnzxRf7Nv/k3PPHEE/zdv/t3PyH7vlt7/YgWbhX8HFbVfS3bv13F+FXuxxl4ZFOhVaa0g+Pe9ZitkTjfGaxKTLb1IPCXaaOSACBnYQrTmlxoXC3BxagyjLY7lDW0LSyuBswgnpqaiMLhgxIHJkh/ANbglx2uLjBKiSO07ITRN2VUXeB9IEZpvrYgbEXWYLKw2q0aL7TWaGvolq0cW4jUxzcxFkZTBwpi15N8hhwoNkqyDwTfovqW2Mvbc7dTXFhI5eXoCI6PD7w0jfSYnKgibz4iVJ8bpRpe2nCqTPiiR+XM8ipc8BpXVdw/iUxrjdFQaumByMbw3NVMHxIhwSPbmj4kRk52Y42l8YmXLst1aTw8sSkZ1dj24nwXidOVInYiCmqxbE0zxI5K9dKQHgVuaYwZWO32mcFOjOFPbEVSHxjHlr29Jb7rcdZS1KWIgkbDXQ2ne+ElfiI9zUP2pZTi0SMKq6E0YHUmLHtUXfLxS0KzvQxKeoFWvPZD4Bn6zJVdpLfMWJSS6uSsEUinMprcD2xoNvPKS+e4/9QTBO+ITeJGsuZr7fZoqcMXuDeZ8GudR2UTuurZOXeWE+VDWCfJDmPs4MwOz99Q2e3nLaYsRN+pLQk7Hh8jrYpEE0WfJigWew17ixlbR46wtX2cclNzQWu6mGGp6LCkykEIh/q07Q2QwNfTrnPCDw0+r82r37EdVib9BNs+ccqB/69P4cZz0dYIlLft8bsLbF1KIguwW1OSD6IDt7fEZTBVgW+lT6gYl7itCf3Cc3UWKI2BbPBug9gr2i7yuJXeuHlKnL8NhG4flnmw6pBvuGNc8/Pw87o189zBSsnNtvDqbL3FP6JFjqlSnBiSyLspcWmVbDpknNxNYLcaSYclOm4dJr9hnyz77//9v/Oud71r/XtKiStXrvDrv/7rfPd3fzc/8zM/w6/+6q/yUz/1U9csB/De976XZhDM/uZv/uYbtm2t5Ru+4Rv45//8n/OLv/iLvPLKK9x///3r7w9Sau/s7Nyzc9rY2OAXfuEX+MIv/ELOnDnD3/t7f4+qqvhbf+tv3bN93Cv71KLkvr7a9FrWB15rZmvs4GvemtGLJaEY8fTzc7LWAl0ZGu+LIvDQprAX7bWWF3YLVOkEGpMke6etHfRvMtlLpi8uGq7Ebc5eqlGjcu0UqeH9lFIg5YTRGt92dDlw5cIuJ7aPkHySKk+M5NJJr4VW6KJAZ+kzQilS64ltL04oGZshGU3ukghBVg43rtDWULvAIxsLyJl2tpBm+NLhCkGRK6WkigOgNc/uaX76Wbm2X/CQ4qlHJEOpBnYsyHz2g4b/Q06G5AOhEQz95x6NfN52QhnLxy6NOLOosdHxpx7cYTxaNegrUWvvEz/1h5mrTWZk4a+8taFInnpSo72hj4mlKvnxj4lGz8mp4q9+usYqSMEJjXnKQm7RJ1ThqFXHQ9MolYo+EINCK4UpB3KHLPC/FbnCp2153lqLlksClBrRKiWkFN5jigJ9HaHHHdvNHtHM+rpfsyw3Wf5O9rOymyUUVt/d7G153WerM//Xm2C7kL6Y7AOmcMyawE/8oWIZJThOeSBcUUOFMGf6aHh5IdpgKSWWiwUpasb1BFvaQVDQYp3l/JWLnNh6DHX+GM0Fhe97GNz5w9yyW53+jTS1Ny5561lDHQqVuXFP+/sw48SJt1rC0THFZhygxcMyav/HKgjPGrL3pC7TPu9oXzYsfOClkWe3TIScqJ+/ysNbJ3ng1BPoxpAbAUn+7HLBubVicHuLY7yTh+jVz53XQ9pWPQz7Wz7oah908u4+urkXDHa3M7lit7hu66+ufYntO7DXmlKK+tgG/dU5rrBS+YlCtpFjwlQlaXdBLgv6GDHDLnIfMJXD1gV9r/nYmZJyL1McmdLPNdlHimT4ykqCoo+EwPva5rAjOPTjwT++ulfwa6ux/u9g+cD/V3azJ3v13D9oLF9RVcQ+8CGd+KUD8P/Dx+tNKuRc/wRev/StZrY37FPRtNYcO3aMP/tn/yxPPfUU73znO/nYxz7Gt3zLt/DMM8/sI7LYh85tbGywsbGxpuU+aE8++SQgwdYP//AP8/f//t9ff/foo4+uP3/4wx++p+fx+OOP8wu/8At80Rd9ERcuXOA7v/M7qarqGu2lTwV77UHROkGjDp0MrlnuE5HNu2Yf92aYp96zvHAJ4gmKaU1qvcDjQJyYVbY3JVDsB0Rq9boXWlylB6FWo6EqiDsBNRqTUsJYs9YgyTGirZYMegZnNL5JbEwn9MtWyCsqYRjLK8HGQXOInEVfJWURAQSy1TijMRmB5lUFtnL77G2Is5pTIniPKyzaWmH/CgFduBUnMFkJRG2VBhUxTvmQfBjWE4dVGw1hgHOEiM6QU8YqRbKG6AOpCzRdQ22FapwsTHarqpdCoyxgMphMtTlhYhPzKzO0H66lFRheXmnAKPZhd1oqZ/lAoLrqw1BGRGtzynL9jF7DwfRwfDln4tBrVGyOCZ2n73qqjRGucLKeOiySuNZuGc8cMi5u+NPN3qj5uu/u5JG/lU98M/jJzRYcmPmUVmuopBKKQBHwdQathOWNLOQawiqHwDaVpg+BedNwZEM0V9QBOGnIiY0j29R+g37v8LqCHM0qUNmfaA7m7vc5yPMAo7s+sz/kuFendbPTVqtt5/WeblZz2t9QJvjAZDTi6oWL2HAMM6nIITOfz7h46RLTyZRxVdMslmQf2L14CbQiXphw8VzPiQfuY3xsRH1sgu97Htp+mEmnBjKUQ+BDXP+HA9dlOKaDVMCrc5K/vD7u0Z0FsJ+artn6ObkJ//fhRA75mqt7/bkpoymPTomtF004rVFWYKep92tIqqsKwryR+RXIztBenRE6j60LWEGEgRATtXVDoH1n1/ITxxb3qXlv77XdrIpzy7NX8gwZa1DrpMbh9+ZW9+uPxxX+42uj0Yh3v/vd/MN/+A95/vnn+Y3f+A0+//M/H4Bnn32WX/3VXwUERve5n/u5t93ee97znmuCos/7vM/DWksIgV/+5V++58f/lre8hV/4hV/gXe96F5cvX+bbvu3bKMvy0KrWJ8vuWaXoVZE23qtA6V7PBKvs7TBR2UlNXsL5hSZcbagcvGkjghIWtKtLR+48rbL7FLQxClOcEnX3lT5Llyw7y4I0OJObZYsZtHpWej6LRuHR6/do33s0CussIfZYZ8WhrAti64W9yhiBiwEoRewGrRIlv1/MZqC41mgPeH/NKW+Wkcc2Na5wAxd0xlbF/iVRCuPc+tocreHJYwL7OV4kYo80AuewDgxX/SOh69FSYiGlSKtG+KDQzlFslpSLSOw8F15eMtosUFpzZAIh9WRlOFlWjI1AD61qSSEy3pqwvDqnX7boseGt24LhKo3i6av7r4184AUDkBNMNTy0Jdd6p9e8PBMn/mgZuX9DgvumVTR9Qeg8pdZsbNf084auaSnqkmpcs+gMIUlwGVLg1uS3dxe53OzFut7U9enA68fR0Dx/W9atW1WN7sSGvrKc86CNlHFW8bZjmS5J3wNaSeVvqBiRFLVKHK06lFL4UlOYE/gQ0KFjUiacc7Qh8kw3QRlNnEmvBQgL2g0O5iH50WuWWF+HfMCnPXjh1I2J/hvsEMf2mu8Ouz6QvCbtVeQrLSN1gjAvmV9uiE1PUNBfVeRUs5grJpuncWOH7z0xRroNwwOPldSjERcKxYUmAw7vE2W49nlLCEveDQdw/WeVD/nu3k6jdyr4d/2dupMa1qsP3g4Ey/nwY7wR4HWdqYNHebvS7eGZhZzh7LxnrzuQlIoK+shJLe+L2HREa5D8k8KNKiIKU1piH8kZnMpMRh6aJdo6KA3RBlRZ8+FzMlbOxMidXdVPDXutikJ/1Pa7st2UeDpIEvNcutV75HC77XPLtTXwW53n650cecNem50+fXr9+YUXXlgHRT/0Qz9019v68Ic/zAc+8IE1k91kMuHLv/zLed/73scv/dIv8cwzz/DEE0/cmwMf7O1vfzs/93M/x1NPPcXOzg5/9a/+Vcqy5C/+xb94T/fzau2TA587OEffacb6Xtlh76nr/3YwWyyeJV2G3zq3wCvNA1uaLz6aMBqWreWZV0qUG6MGKNvKEc9pcMC0ONraWRZBMbsiFNTHRwseOtKjogQPGQkyXolTdlIpfUlKkZDqT/YRWwgkjAEWprQSsobWY6pC+pCcJqUIMeI2RkRt+L2X5vQhrc9LXXfi92/A590HShtCJz0NoIghoAeoXggRoyXb/1CRefDhjFaiSZT9AJnRQASVs/TzxEQxElgAKRHayOU8Yrcx6EoqLXYsFOY7/hhXdiOusExGM4qUUTny5qkm6IJSJfpLuyzmczZPbjOa1mDGhN7zlW+1KDznF/D9HzLIqR58yAYATIa3HnM8ekLS6y/swn/+qCz1Oafh/k0NKbKz0Jzbq9BuygNHe2JzldB56ukIV4n6/OW25soO6NLRxsytgqLbw7ZuYbda7abj6LpX2k2e8cN3l2+eaV6fxvAEGbn/oISoIme093z54xprDP28YdEucdrirFuTkJAzumjIMbHwjnk7xWGZuMipeodyVPGxWcVPfHh1DJHb9RHd6oz2D/76czo8w3/tBbuTSejmy6Slwb9Uk1rL5QsXcVVic+skygdy33N69ABFN9CptwKDU8jkbDUwkbnh41db/vC6ZMad2kFH51bt4p9Yu8ts+r2y2wzD20Mj7/Yorx37GXj6wo2CsU4rvuTomIpMsoa8aNFaoaIQ9Zi6wE5r/KU9cs6MRoaHthcYZ7ClRlsFFHzsasvPtOrVzjafAnavgri7vV8Hg91Xt/87XfN6qvhXYuSV5jCY453bjex3hwU3+4HTJzsQfMNenR0kdphMJoD4Xqug6Mknn+RDH/rQLbdx4cIF7rvvPmKMvOc977mG3vu7vuu7eN/73kfOmb/xN/4GP/uzP3tHSa5XXnmF6XTKxsbGbZf9jM/4DH7mZ36GL/uyL2M2m/Hud7+bsiz56q/+6tuu+3rbq2yEOGif5CF1PXzoZnbQH7qVj3TIeqZyFEcmmFpoUpVS5LYndZ4MmI0RWSvisiPOGlIImHGFLix6VIIzaGdRRhG7ILu3RtiGUALbcgZlDMpoTFWsBU9ziNSjWvarNdpZgcuECCEyFILoUqDtO8xGjdaaqi4pj0xxkxpT7Me+B33ifPD/USBuOQTI0lPTz5fkzgvxQheEsrr3EvTFiFpBBHMmhEiKkWY25/yFcywWizVRhAi3arLWlMN1Uc5y9qWXOX/mDL3v1xUtbQ1954VFbwUpBHTM5D5gV4x/QDZCruCqYj82WAu6qmvPVh141Id9qYHVLh/Q70ne082WLHcXErDVBX3TE0Kk3hxjy2INocmtJ/VBWKHuyA554F7N8LlTH/31GJrrhIE8O8kHISBJcV3p1EYTWk8MkaZpKLSlLIo1I6MpHMoa8gBPTL0XyFBKXLpyica3wnK4hiW++hPJB1yD/397Zxoj2VUf+t+5W1V1V2/T07N4xvZgvEAcEEJPz4AdYxYTRuAYCA5LYiIgRCROwgdnwfliJSIJUhwUkwiJCFlxIggKxiLYsS0sno1JbEWAgfdi7AhsZvDYY0/P9ExvtdztvA+3qrqWe2/dW1u36f/Pck9V3bPdc8/yX849J/5melxs0a+6/VrWQSYdp1Bkcf8+5ubnsWyb4lSJ2YV5nEKkELXOiW3/X28JUD1OoK5S65RyJitD/e5rNPc+StIVu/SYoBrvt8XHT1aH4tpRtraZZxWFUgrDsbDmpikuzeEszqIaS5edhTJYBsZ8iel9CxT3zFBcKOOUi5iO2dgJtJlnlrsaDh3zaXjin61OrMV+FqOsHsvov8588rX9tP6XWLyO+I371Ml3mzGpTCGT+tDg/UsYN2tray3lxzCMljLzyCOPcOzYMQA++MEP9k1n3759vOUtbwHgy1/+Mq7rtq5dffXV/PZv/zYQnXl04403UqslvZ8ace+99/La1762Y0vvflxxxRXcd999TE9P4/s+73vf+7jvvvsyxx8Xoz2nqB+D9LO8xp74FQu9Kx7iwnRR9+Hxk5EFzwtNXnMwEpbmi0Zrm2rtN97HCUK0aWAUoiVmVlBjphhtf60co7G8yCDAi96ZCDxKhTB6D8lQrdPrTcfm9LmA42uRQrF/yqYQhNEwZajoRHOjMYD7PpiK2aLHvO3hapenVy08ZeI4JpfPBDhWjU1XoyKzFLahODzrYCiFQcCsVUW7PjOGh66bBKZqHMAaEvgB9UCxGZZQhsLBp2jWsLRqvTCPpwlqJuGmw+bmBidDhTt3iClVYu/ZgLLrYdkWzh6Fst1I+H1xFX81pLDmMr84Q3BqHWWa7DnoYBUUgdZMlQsYjoHtaJZ8jVetYNoGTrmEMkICN+T0qglGtAugYRgoU7FZhwtmIi9a8xkHvo+yjOiFxFCzUFCc2YwUQW/D5bARRve8GnDieUUYKKb3zlHCx69X8VyXtVIZy3dQYbSNeVhxqWx42HML8ZssdBrnsrXhfKtwkukXLs44oNsvZ+tsgReysmFBYGA6JnNFF0NpDNPEKUU7Gzp2kTW3QGNPRAzTRFdCQqJdEHUQUm+8U3z27ApOqFkwz4dVRbDef5e5NPrbQbuvtYm9MdG2lqgkx41zQK+GIT9seniaLwH5XnwmKZxr7CIWt1RmcCGmn1dkUF4KS7bGtRyhk6zPJtSan63Wsc2u8EYBCsB600towmod2whZqdC1HBRObUbf0s5v6mGgx6WTXrHKFDeiM3J6b42L0+sd6e2f7T03fYlZzKk9KSUanPZ8uhXYaJmxkc/rRG/Z2xaRk6Rs7vQeuhvpPrxVa83Zs2d57LHH+NSnPtVSfj784Q+zf/9+YGuDBaVUJqUI4Nd//df5xje+wcrKCvfee2/HmUa33347zz77LPfffz9f/OIXeeSRR/jd3/1d3vrWt3L48GFM0+TkyZN8+9vf5ktf+hKPPvroQPd61VVX8fWvf513vvOdVKtVfvVXf5V77723pbBtBztr97lBGJUgGUPVg288HX3eW4KPvTZSkEDjrgZ4dR/f1YRu5P2JvA7ReSxThZDzypt4roehFGgi63dJRxscBAGYJtqNBMWWGVhrjq/W+cELAcpQXFGwOG/KQQeaUKnooFAVeYq0ZeB5dcr2WZb2TOGaFg/+X4+VmseUDb90WDPjaNZtI9pUTYOlNa+ct7EA23M5Mr2GDvzGMjwHTbQdtef7WLbJalXz47MGfhhQNiu8fMnDsZ3GltWwubrJ2rGQUn0fUzPnMXvpJZy78ALqWlN78kk49gxurc7UBRWqhRXmFheZ9crMqxmsvXtRShEScubMMvbcKQ4sLWKYJkpFO6oYJhxc8NCzIYQeuu6DMnBRnFwvERpWdDq80fD6aM3ls5HCFh0qq9HaprkJBUZ0f88cr+NtRMu3fmG+iGmaaC/guRWNKtgc3Kixv7CBUTBZthY45c+gKhDWPbzVAEIba6EceeHi2ljSb3HtddIzU5zknjnqVuTA9XlxbYaa52AQUFqsUJwyMa3o4GGvUkMri2VvHq8SdmzLHbhe5PUEQqWBkNnFBRatKeonQhQaz/eB4ZaUZJX2Ok8+ai4v2frbnWJ/4WqL5TDgm/Vqx+/5ZNBewXGcvhut284ha2mI3SXup1C8FMStbDUZL3KOnkDDEzHL6pLpfgZb33WCW7G5/Xa34qBV7xPr925Ju2clzcMWn0a22uyNr2nvrfFepbTU8z3FPP00TtHJ6tTvyC/pwPtY0seh+FL03lX6jprCJEk7vLXJe97zHv7+7/8egEqlwl133QXAlVdeyQUXXJApn3e/+918/OMfp1qtcuedd3YoRcVikXvuuYdbb72Vz3zmMzz77LPccsst3HLLLbFpOY7D7/zO73DgwIFMebfz5je/mbvvvpvrr7+eWq3Gr/zKr3D//fdz9dVX505rFIzn8NZRaCTt81XPqJExjSzeohzlUYrGS+VgFmyCtQp2qYxRUYQqsmMFQQBhQwNRCqdUwNusgY62ww49H6tgExKtXTRLjW2gm+8foaONDoxoeZdRsDFLTpRn88DTxk52OgxxTAjCMNqFjkgpC90Q3wsI6oqa6+IFFkHdJHA1XuDjrUfL9GwjaLnqgyDEcSxM20K7PoVSEbSmOG1TqpXwPI/5omJuQWNaVss6WJ6bYd52cE8WgWhrcIgURMu2mZ6bYXp2hsL+CnsWZjEMg+rKFEFot6rWNE2W9u2jsL+IVj61zc3Ig0Y0iduWjdVYPogVeYZM04w2gjBtvI0afqWO2XxnSil8z0c5VnQ4bKgjxdRQjTOJNJ7r4RRsjFIR04q2QteF6CBEz/UwtMaaLmDYFkbVRAXgb9Twzm2iDXAWytEyx+YyvYQ2FTW5pkVVDWdAH8ecpftN3/EFbvXwMESrhqfUC/BrQfRcQh0tB0U1dpuLtpdXlgG2gYEm0JpKtcLUzDSl6TIoMKqRgjSKm4336PTe3Vbobu9L7/VWpJ5ke8TM1u9bKpbqCh1fliwlHp8As7UEKBKUjLYrcYLT5DxCw+TU+/5EM7Vstvgt+j+dSYmWvV6arTbavbNgZ0S6I5K63XgK/bxQvdPtsDUUl2KvQaM3Tv5ct4wiA9RL7hhb8ZpzRv9UdM+nLckrTcmJG89FIdqpKKWYmpri8OHDXHHFFfzGb/wG1157bev63Xffzfr6OpBt6VyTmZkZrrvuOv71X/+V+++/n+XlZZaWllrXTdPkU5/6FL/3e7/HP//zP/ONb3yDp556ijNnzqC1Zu/evbzqVa/irW99Kx/84AcHUoiavP3tb+crX/kK733ve6lUKrzjHe/gwQcf5HWve93AaQ6K0kkmpYz86Z/+aSOlURSnQZJ0kMfCnXRXuZSirYFp2ob/fQhMBWVH86olTe3UOaphgeOb0YFXyo48PjrQFAshe8oBaE1BuZRL0UGuhNGSOaWh4ttUQwcdagLXb5ypE/KjZXh+PVof/ot7GwejKlCGQRhE234bSuF7AYYBS2UXxzFwvZAHflJgo65wTM3RS+oUlM+mZ3L/0y+j7hnYXo1XGM/jVjc5vH8Pc/uWsS2Twux0lL7rR6KCbYKG1TOa06fKaD+gYPss7bWwbJvlMOB4EIAGf8MkWIv06809e6jOz6PRlE+fobS2BoC14GGWIqXFW7EJa71LzuwlF8MOQWsuBUw3Wm53enkZ0zSZnplmz8uKGDpEY3LGnSb0Q/zQ4IXlECPQqHpUj5UgwCzYWI6JrtQIN2uErgd+iG6cCB9qsOccFhZMbMdEhZqwYKEKFqVSAcMAZRqsbhqsnfYINmucCmDNMHDKU9GGAQ2On6uzXu9a6tUhR7dNUoPNzr1pDxIvMVCcxTVJAG/87gVcuWQzM+1QsEwWixUgahNGY1ttHWo8N4jsBMrCe8Gg6taZmZ0lVArHsdlUiv/xo/fzbE9T3ozayakw5H96NhboFATyTObtd9q+oKahtrbC9YpQaYPJKMmiFmVTnZTWvDwMsYOAQsHBtqONUzwd8oTnkbRdg95qsF0Cbx7b93gY7a5Y+axrmuahE6rn136pNr1uo2Fcz2H86lx/5aW9LOQoT7rnaCvN4e5vEG/KYG02/xYI3WUbxw5yf/mXfzmytEbN4cOHCU6+wHcPHOwfeET8rxdOYh480LHxgfDSZ2TnFI2FNKFulGN4BsfWpgcPHYs+nzejuHwfFPfOUl8Ho2YQbNYJ/QDV2J3NDWxe2CxAEDLvaGanAnQQoL0AzMhjse46vLheaEyaBZQRvSy7VNbsnYmKdUF5lbnpyNtBY6cvHWoCP0AVQfsBKjTwqpowhItnpnFnbEwV4lg+htJYnsnFey6lWgVv9TR71k8SuhbFszWmLiqjnOjcoaDuYhjR2UcAlc1NdN1ifjUA06BozBGcirxiP3Vd/k9LCWjbGezkyej/bl5o/9IukrU9yMbYYmFwaGqaRTPyCh0o7cP3fcJNj431ZeyiougUWHTWMEomnuGw6pbRWhF6Adr1KYUWodYEFRetDXAKGI5D6DW2qNVgOhYLezRH9rkoKzqsNtp8AV7cVLywEZ1J5a1WUIbCnJ/m1JrH8XUfVavmmnAyhU1aDZMWtj18b6ZxmkBvoAS3RXeUzqU3YDgWxfkZHCNabvXiRrF1UTc24fDdTZasn7G4uEBtzcf2D4NRwK43PIV1TcX3+e9qhdbCGN0sVrqls//+Wr2DhOr4V/UGj/k5Kf+sEdsFlOGFlWzxlA65PNSotQ0s02RpaZFSaYqq1vzY9/ESbGGtXRJ7hPjRDvRJw3f8OyHtZRsVedJSsWXK+o7G6BSibsYxCY6T8Z2A1e4hiX7Z+rvF4PXVTDd//81lhW3FUa28VNuv/WIkfxcEIRs7852iJKGw+/csQkyagJlp3EiyQikM28QqmegX/UgZskw00cGfYRCA5+MFPqEZRu9XhKAsAxVEux9VKxWqlQCnUIgObTMV2g+jXetMhV9zUbZJqH0Uje23fU0YBKgwjIR+HeCYFvXNKhXX5dymyfT8PkzDINAhvldns6I5c/o0ZmGO2cV52FQ4xSLWdAGz6BOGPu5mlZpbx3JsLAzqnktgwOyeJeqrU72VNbYxt2twV5Eb1zRNlGUztbQXZQW49Tr1ap3ArVOtb0bvtRg2hm2iTRUtrwP8ugeNQ3GVESk8RsGJhG6lmJp2ccobW8I40ZKwoOrirgRQ9zCKNr4FVsnBqoFh5DhHYtJzk278aQpinU02JwnberOVtmFFmyz4nsep50/h+z779x2gUt2k7nnMz01x3vkX4FgGM1MWldVCtLy0PVnVmYXOoBBlu6F4hSg+pAKVtFPdcA+xfTv2uG1zt34bXWMxDJOibWK6RXw/wPN8isXOZYnJlu/xN9qedqWbH7fXE5WkkOWLP3ga/elqPz2bKUzCo5dnyUa+kPEeknTPSTZFZXvaVdS08+c97kWygiDEMzqlaLBxMp2sylGetLo/D8BaHR4+pjEU2KZB2Ynew6GxTCJ0fUIdoqxoSda5VQ+vaoCh2PQNjIV9vHj6FOsrBmtnQw7sn+O8PesslM6BCjEtK3pnyfQxw3r0fpGKznYxLasxVAaYjoUVBIR+gDVVwPPqsHg+ZykyU3A4+d8neP74M1x8+eVcemgZN3yR2soZjD2r7Jmbx54KCep1qrUqa4HBE6uz6LChhFizKEMR1jR+vd5T1S+Gg+8K1knvwwiBxz2XKb/rmgf2zxrKIUUUxWjvBF9zvh955Xx81qcNtAJL++xb9FEK3FBxZl2BbYKCoHk6vOUR2i5hEFKpm6xVTELPZ8MFTIuw7BCe3aTkwZ590zhuW010e2KaDLogNW+7HOeMGWPg7J6iQw0/OVPDsRT4AQc2NeXCFDO+zY99B21NseYZrJ+MXpvTPnj1ele6ivUwbMtvOwWB/ItjooKnCWvxXob+6eaN00mo4EnDpDA3g+f5mKaB6br4gNux3XhexrDMaqgF3KPkpSuCjmKJ3mBekNGSxRSSdnX8vqhB4k4mjiAIwzM5T1E/4bGfkad9Hh/EIz0Q8eLMhgv/8Wz0eWlK8UsXltCbNcKah9YhpmWiw2hpm2lbhLrMctXCLji45f0s+2VWzTJ7lvZRqtVYPuPinnkc68Ay5aky+84/jFIuqhh5naLd6kIINWG1Tr3q4tddjKKNUy7h+z4vnllmfukALnvxCnP4hQLF8CRH5sqc+59z7Hvdj1Cmj32+g1MoYVg+vlfFtB1mphdY3zT4zo8hDLsfSwAqiKmFJqMXkkLg/yUdUnlCd+4NoGHBMHn1tImNieco6sVoy/Da5lkc/ywzU2UqVYvTbpmg5mKEGq1AGwo/qOEZdQxTUfEcTrtlQkPhWT71Wg3DsTg8s8CeqoHa0BS8trzb/22n3aPSLOwoZsbuNh/Xf1RMxEFl7D79TGt45mx0fkFBwVXzh5hRBpVqyHObUNVx7wO5rU+DvtydlUFS7/feQLsvqfO9pOav7fSm0y14juvuQw3/12ucPaFU1LHbzqIYXMwbs7g2hrE9q7A/7J1NXp1XKKW7qmsSZej2do4/17Q8snmgBvO9TGKcisuTtnEoOff+5eo39Gd9T2rH2C0EYcyMXinaKSaO/NJQzuRVKx+lFPZ0MXqhvO6hLZMg1AShT9EsopWmNFXCsEysuTL7ywdZCvZjrRehYOG7LnusUyw5irrrcurFFynYDnXXZf/BA5iODSo6v8CvutTXK+gwwNcuRsnCLhbYd+AAnh9tb6yAzfUNijPTmJbJufXTBD6U56ZxigU810Upi9JMueF1Sa6G7tVYGStnoFF0a4hPnwKbgkBzyVO3G9C0LUwFM1N7mS6GkZciMNFWdF6UUXCify0T5SjMcsD6+jrVwOLMxiql6SlKU1OUZssYhoF9LkDVgsarSDpdP2zef8cPcdcyVMbWLfWvzzzppxkokuT6LM+z+SgyhB39MNHeDpKsLf0rKdsL4N0hk97PScqjX6jhNYMdv8VuUrtKve008XDUC4468xo6/VZynW1weHF7dFpk0qGpSdfaSzAuuk0Qzd9GnWfaVg2T6UlJ41f6aNWPfiHSDUDR32RfuCD8/DEZT1HSmJ1nPN+hvXKzHvDDF6LT8pyNKkdKBirUOKaFB4Q6jHbYtg1834dzy9j1OlpDuV5jthBCURGwxKo+CCWoGOtQCHn+xHNsnlzjgj0OXs2lsrGBY9iYJZuwskgpKGGsOri+T32zikYxt/FTyov7KDoOdhgS6BDDU6w/5aOWTM75VWb3LmI4Nita813XJUSz4dLa4lV3yP0KrdIekqJnLX6adyFlks3+iDs3Tq7qkEfqNQwg9BSbJw1QYBkhP3aKoDSub7Bai94FMmp+I25AwYSnzjnAIrXAYtOwoQbUPJobQhRd3Vo293wQs2wwj0ySxTs6jIwz7MqrpPL1KasPPObWsRX4GrxMNzFMp9YthZ2Gd6zbYzNMC4snXoRIeg8iLs9s4tVoxL5hFaMspci/T1Zb4rkZ0Lel+o9L/fIaJOeO+lPtz2OrIL2K9QDWvLaoutEpsi6l6/se1fArOfvm3yS5d8X17tGSfBbTVinSzSWD9TXd9lex9Tz6N9XumJ2lzOb7yeI53aGClyCMidGdUzSKdAb1Roxi4M5oEd8yhkeDV9UPeXolWkJ0YNrh0rkCgRcJ3VbjoFCtQ0I/wHRsdL0CtU00mtB9HmWusbC4wLHVX+Qnp/ZQKBVZscCYDSks/CJKP8HK8rNoNAWrgFWw0fWAU/9zjv0HFvFMgxefXcZSBso0OTzlMb22Fh0Ap8Gr1bGUSbhRxJhZYKZYQJ9TeArWgpDvVqL3DHos6qp9EkoX+Hr3/hnWYpsvbp3mUqHG7l61KImtQb3ZWNzoHCkUpmm05dP8t20XvazF6tf+02a4ca5JGIVcHVe+OMcLjYMnE5Y8jstroTrKE79t8iTIv1nB1qKcXgG5eyCa4L0M4HTYKd6o1HKMpJ+le6i2Qmx5gFohNF1KSnJ7STIaJbcGRW/SanR9To2/Bebdejo5zvB9pr1n5jPT9eafZSTqVjy6D6ntTqHde9PssGnqYnwZ0ku2NZIOaPAQhJcwQytFvu9jWVZ67x9Fr4obpwaYxPuSJP93ZRXr6WgcLhpueNHWzrYJpsLwIDQUft3DNA2UaaCDgNLUFAtzNk7Bwdy0CMKAerVGYcHGmTKZnZ1jD0vMul50xpFShHUPN6wCfqskMwvzOIUChmlG4doKW5opU7i4FJ0b01ZfWidXXX8rY9L1tlqJezYKlB7XENucIJJnca3B8yKlxzDswV9MHnQpW0bFu6fuOsLnmLDzLE1KUHZ2LnEdtb/2ORqlPS2PAdJt9knVEGcb37M0zyThd+D7a2ujuVLI2razxh/H2D5m2kXNjrpT0dWh2lzfRtG95CpbXv3fs+oWynWbzWz4PpQ3/35xksT97PWx9bf39/4x88VJSy2tAyQbLLOZhLKUbIcvvxWEMTG0UhQEQaQU5SVp8uu3vKi71++wfqscC9f3mJ+y2FuuooOQDcPmnFcEU1G2XRamferVGlVX8/zGDGbVZMpe5g2XbBDUPVYKF7Pqz+O+UKdaqDI3E233feqMyeq65twmTFnF6LBV4AeOzXoQQPvSrq56UX5kxW8/nqSObvhFuh9CnMA5QEWnCvdDEiuE9SmjAss0oih5FaJBhL7uastajal5TKDBjziLUb7nkewNyvbWw+g9SXEPOT7v7t9aviLV2VUuAi6ybCzb4keex7NxSzZT0x8QvfVPj1Cf2iYbFpauPpWpppOqbswKUZzHYTC1Ns1O351D/zKkLePKUiWt2M210Ak5d4XuKVeScoCGMAhRhsIwhmt7g/TE/u/AND931u0kDjfNS3uZ4svTe61/abf8O1naS96RVBB+3hlaKXKc6BDG1qA9yMyStw9OcoVM22yUJUvDNLHnptHBKmW1iVWyQBmc8xW+51Mo+SyUPZgxOXmuwKlKicrqJodnTrFY8FiunCKszWPa+7EDk7rvsrz5Anv3LrFy2uSZlQ0qvscvHbgQA4Wv4Wnf53THFtlpk2GylyeLZSozsVkN8uASGlSa7JlwGwqFZVutb53J9ZkkdY6wtE14ebw1eWl/ZINY1rurNqnvxtX1JKz4PfmMYs+2uIYyivTaK7H9c++Clx50pBg1OVQo8uqCA8ALQZCqFKWVPE9v6wzbJUJmfdZd4eJtWgl9Z8JeoTxNuP1A4a34w7fEXKise+dlcTMmK0NbgnjMMNCwqBmWkRI/r1dmdKSbRUaRW3r95CWLMpz1ene4dvNR9D3NPCMIQpOhlSKlopfaOxSiTBFTfs9iMRx0VIpLr186SUJiwsxami0zYxkow6NSqeIGNlgmhVKBwqyDVaqABmdmClsVcZSmHqxRqWzi2A7VjSq+dlk+vcy+g5rZfUtUKjWY3cucM8XhmRnsswpdD9uyT5vmswp/8WJMZ/qjEkj7kaMx5fLipJehUxzsX2+ZlmuMS4lIUgwHVY6SvvcL3/Zzkrg1sGLdj4x127s+flxSeJKlP6UtqWRlaetD/vpL6s39haO8ImT20FvvKmw3vfeYPCVFm800yz68IDlOL8Xw43OWcsXv0dY0A4z6/vK3/35j+PCbIoxfnWivx6x12u0R6zbZCIKQzgiUohjxYngTSvLvg8ynozAId6fV/Rk4W/P5r2fXALCNkJJVBqZxA5Na4AM+zpmAohndSD1wqTeswK919mFWXdxqldnN0yjjcfbZJieq0/zwOECZTc8i0AZUavx3XWOG0VC5FoYxxWxOUtmc7sl0uyMyRhmaHA97BGa7OGGtYxrq8Bj2Tjp9y9ceYYTCfmI+uaINv0tZ+9+ede4aUGNaoz6A7hz3LVsjSusHuuNTdj9Cuz03Cv+k77UORz4V9DsjLGs+GUKqrjBZvZBp8mdMvI4y7AT9KAPNdzxG0Ya3RuaG90WNR8jeev9nNJ6bLOkMpmyM8/2VUaY7fu9g76lT2SeC9nqUJXCCMBhDK0Vdq1syBEoJ1x42ycQxCoVrECUpw7hU80Ke89yuXxXRcaRuTCJbu51dWihiO3PY5hwzMxrfq2FYJt855/K03yyoTzq97vh+dqXueLFJ5t0cYWSCTo5883opY4W1PtbEvIpKmnLfpJ+wmVWBaiUXq5akFmrYCbRfSxvVS9nD0P8es3gH09LIqSi3QrYvWoo4E4aciTF0DMcAlgPV9Xk7+vWOYqvcaZb7bFb9jk47lioZ6SPLlFs+snoMB7Vp9t1uPDanlHFsXA+qIw8VU5JsI/To/HKT84YJwk5jMucUDcuwnp4sylq3TDRy+icctu2CYNqTfDQpg/046mPsdT1GJiFpdAujTTLkm3976Ekw/vyjFjx+oWV8DFLuPHEyhG2sgdY0vAJZ23l3tb8E+vVIWkpCIlnf/tn60hxU2pdJbf0eZ+bIhkp8tWiYKXVUQvP4hO5ej38/O2w25Wky41jn3zz1FIULw4B6Y6dbx3EGKker5TU8jTtjyasgjJ/xS95xfSltlBqduSNfuhPq80kD3Q89l2f83nNeTiUsjWuSNJinVXHvpJbl5kcscG7nGDts3v2qLa+sOsrlnf3KMKp7z5tmX6E5g/CXkvfoFraM5iH0LglK7j9pj2pL0ZvwqSGT6p+TdWeMjLSt/+NJ6uS93sJ2hah/mv0LEbdEL74rZV/GNkkvQr682ufG7KNCe01ur4Fl+M6gdcPAGoSk70IYT0e9KfEaCbuL8SpFo5rs8ni/O74kLFFIE2qzrKLR7R/7uei7E4qsL7rrHYuVMGQlNm5vui0Xu9ats026w/WvsiR3RDPn7glywKU3eZXTnUg/BX4cikZSuO7Ze5B04tIcNH4eb0KfgmTKvm86cTcT1486LfNxJek1PsR/i88jTviNI65c7b9vPaDJdJ3s4k/HGDFoH9gmhWinDEPdqk/cmDuSsvZ0gcE7/U4XkDu3yulvSugcKbIrQ+NQm5pPXA/R503TpFhwogPcBz2Lr6tEgrBbGI1SlGV8zWquyRu2Gb5ncs2QSJoC1Ney3QyWz+Xe3MloK+EhKk0NZmbtX+YhJZWe5NusVXFLFkeQZV/yVlVc2catHGWl2WxGNd9NRIHttcUOlERfmg86zgrSHS69L+QT/vIaJfKkOG7B5KWz7LB9e+z+KsM4XLCD5pCsSA+uZKTHayn1Kq4tJxvbtpNhluYl12b29j25PtdJ7wqSfBNW9x2aptknvHiABCGO8XqKdmJ/66cAZUoi34DSa0MeRcUkaRejIEcJMwVMCJRbFhtQeIuTjcehwEyive80w19r7s6j4I+7onbiwJOVzrKPd2eu+DyTSB3HBrDPDCSYNXWiDEPBJFS9Xi+DCJr5GY3yGm/6yJtm9vBZbbdZwsUqcprMnh5pcYIwGkajFI2qR7YbebPm08/a3U73tfaxOMeEHrsrWUo+4xmwBvMSjSTZJKNn3LW47wM/h26BMUfdxq1KSsq7v1F1soxT/20nrg/FeY9in5FqBY8t4qDNdUAv3GiVibQHkKUBDc6w9zDKekhMZcDkByqXaleI0uNvh3KSJ8esW9UPomxNRpkeFe3+mWSP2qjp3dRisPhN4so+eKmbDX08vHTaRnZeCAMOP39ionkemmhuwiSYzDtF4+h/cVb/wUwyw5cjs+A46qzHULHjLnc/AT9H3SUK33F5pf3W/fuklJBJEHe//e4p7XqfZzOW6hqgf422b+wUD9ggTKBME3wvKIMutG10Hg2cQZFpu5Q2heW93f6O29FNzPkUtq1C5TuMdDzs3N3zxpu+wZYDKujqu7qjbQxoNRaElzDDK0WjNuIkKRlJead9z5JGv3wbv3Xs4NMeVsaKiIxtoGNjijzPLyt5FKFJkSaDZJFPRj035umzMZ6agbr8oM9gJz7PlxA7RX8Y3TQxSCrpuXduqDG5Govb0GMUalGkOE5iQIm8UePcrjmvsrWzSN7mIX2Dl0aI1rtzWe+tv+BkAkedAnOmia/g3lqVzTCp/e90g48gjJ7xeIrG/35rPpLKkba0KyZOa3fL2Dlgpw7MYyhZngS76jPTAJ/BMDXOk+A7M2JnPdY8CtYolcyuNHdatQxOVgtMZ4xh7r3dSt4UgMbZjrMs8xk329tWBrGIDZtjd57xHbdzmZseetlb/I6J4/O15Gu77UL/cK0w/lgJRXfvTG77k9jiPjn19A1e+rVG3fY3LffekUoBi6bJHtPEBUwxMAlCB8MrRQP59jOmMcQynlGjVNswFjtqqY5/Osq+zQPPwMN+muDd/b1fJj11kBAxY2HVMOtosnoe+/3eL70s17PJTvEMsmw0S1uMW3/TUoZGIdLsJPLfx+jOMGkKlKpDGB6P56Lpn9VkEgjzjF+JbautnrrHzFEq7kOi2v6On862k/cdmn5PrvvsufaUxmOrTPaCJJcyriT5+lRWj8Zgasl20/DApbxT1BqiU1OBuHfWfKXwAI/oSI8sfXAHdFNBmAjj8RQNoiiNY5IczhTVmYaOuZaUX/9F3fFx+957/mlt5BNhnoR02rKQhIQyV1uCsNWedJYl0br7Q9pEnlLmhOJlup5Gd7GS+klc8ePyyGBoSHsEfUWJ0RvddyDD9ab2c8aU6vyt+/MwxAunGZc75XmGiWF7leqs6UdtcNT+yPY3JkYvEqePIO0dN+m+tnyH3ak1Y+TzysRV+vhVgX5ljL++c1WUdJottbNlddd0Us1399H2p55Uj5m7ptrKo5mWD9xTq2A2Wlr70rmkMuXMVRBe0ox3o4U8xI0aWWTqJIFT915rTbTd662zaA55BO2+ieUPNkDgBgMsx8hj4IsbN1t10zY95BlfkwyJucmpyMQESp/q+mQ9SNFye9y6fktryxmVs8lazifBeGzk8Tn1O8x5KySqPXxcnKztLb2da9XdZXf+sx1XG2yqHdmf02jp3xLTVap8DHdmzygYj3KbNe/Re7XjDzVv78P5PV6a9mWTTQ9fp0dQt/1Nmlu27HuRjKPaGlszfY1mNWw+k7QypWYlCD+37BylCAbrge3KSYIy1B40dcCKM+90/zausX1Mo8/IFKI0siiHg9xf1vmlW2HVXRcy5Z2koaRp5vFknozzKOOTIEnB7f6eVp87chYdzH3V/b5HfJgo/S1HXnMpXG9azZJs2YF123W2hJm28AMZNdrLosa3e1caaa+Yj6xR5zaaqJ6/o6T3ybff6zi3I8jGcFt/D2ZY2G4Dy2RyTvYBqYQa6K1r1fU9Poe0NtSKGWf0Vc0w2WpEdf3782UkE4RkJqMUDTob5JVl+oXN2q/TlnqkpbG1xmG05Y6jlccYrOBpnpqshuvWP0Na6/rJUM3rGeqwlVTG+tbolPy3Mu5sHgPcZ5Z7zMJQCm2XR2+Cc2BHDXY9T9U1wWcRLePFkPw3lPzeQvqv8eeVpLsFVVdi+dpRmt9hpwmkYxinmsmmNI18GxgkLVvoF79zU+5+IV6qjNbL1jmxdL5bN1wOo1uG2j4sjsd72ZtnnFFhMONOI0HRawQhA+NXirL04STD1Kg6cv+5LMbLkDHdOAUqT5nz1E+sYpKQ2aDjZ944fcKPZBLJshSt42v8pD1QSVIj9QrzLX9AY3e8zORR1JJqNYeQOHA5+irinYXQsb+nkKiHJKhD3R4s1X5BpIDtoruF5n4aWUzjQ5QniZYhBN2jkOe7i7j7V4lj03ayZctLK1O7Aj/KsneP0YP6JsZgHExJsb+dNK2WciyxpX0TFp2rP/S+rxRvGIh70267vZqCsF3srOVzcQw71uXwbGROK6eQPjS6qxKypD+KMsSlkSPd0U1P3ZNDv3w77bXddsfORS1bf1OyTvdQtCvUamviSvc0xU2b3YuskvLMIJy1lSFOtNvKpf3uO/NL16v6LfRofmt3n+agJ3hCfv2dOW303nl3TbY7quLEs+6d4RLrd1CdrLtx7hzZeWhyDUkjNs4MQnyfHzyjZnp9x5z0RCK620i3caCdDG1o24TgkbfxHgtZxDj6ke74pxOVpU5jPOTdIRpzv26bV7KS9XykTNdFSxJ2CUprLc1dEARBEARBeMlx+PBhnnvuuYnne+jQIU6cODHxfIXxYWx3AQRBEARBEARBELYTUYoEQRAEQRAEQdjViFIkCIIgCIIgCMKuRpQiQRAEQRAEQRB2NaIUCYIgCIIgCIKwqxGlSBAEQRAEQRCEXY0oRYIgCIIgCIIg7GpEKRIEQRAEQRAEYVcjSpEgCIIgCIIgCLsaUYoEQRAEQRAEQRgbDz/8MEoplFIcO3Zsu4sTiyhFgiAIgiAIgiDsakQpEgRBEARBEARhVyNKkSAIgiAIgiAIuxpRigRBEARBEARhGwmCgH/6p3/iHe94BwcPHsRxHBYXF7nmmmv4h3/4B3zf74nT/Z7O+vo6t956K5dffjnT09McOHCAd73rXXzve9/riPetb32Ld73rXRw6dIhiscill17Kn/3Zn1Gr1WLL1p3PysoKn/zkJ7nsssuYmppicXGRt7/97dx3332x8ZVSvOlNb2p9f9nLXtZKrz3dRx55pPX9gQceSK2vSqXC7OwsSin++I//uF/1ZkMLgiAIgiAIwkuQQ4cOaWDi/x86dGhk9/Dss8/q1772tan5XXHFFXp5ebkj3kMPPdS6/h//8R/64osvjo1bLBb1N7/5Ta211n/1V3+llVKx4a699lodBEFP+drzeeihh/QFF1yQWM4//MM/7ImfpT5/+tOfaq21vvTSSzWgb7jhhtQ6u/POO1txn3zyyQFrvhPxFAmCIAiCIAjCNrC2tsab3/xmHn/8cfbu3cvf/M3f8MQTT7CyssLTTz/N7bffztzcHP/1X//Fr/3arxGGYWw6H/rQh1hdXeXzn/88x48fZ3l5ma9+9ascOHCAWq3Gxz72Me666y5uueUWbrjhBh577DHOnDnDk08+yYc//GEAHnzwQe64447U8n7kIx9hZWWF2267jWeeeYZTp05x33338ZrXvAaA2267jS984QsdcdbX1zu8SE888QTr6+sd/1944YUAfPSjHwXg61//OisrK4nlaJbzDW94A694xStSy5yZkahWgiAIgiAIgjBhtstTZBiGPnToUOL/WfnEJz6hAX3w4EF97Nix2DDf//73daFQ0IC+6667Wr+3e3DK5bJ+6qmneuI++OCDrTCWZemPf/zjsXm84Q1v0IB+/etf33OtPR+llH7ooYd6wqytrelf+IVf0IBeXFzU1Wo1MY2mVyiOF154Qdu2rQH92c9+NjbM008/3fJ2feELX0hMKy/iKRIEQRAEQRCECbO5udnyqvz5n/95y1vSzWte8xo+8IEPAPDFL34xNszv//7vc9lll/X8/pa3vIW9e/cC4DgOn/70p2Pjv//97wfge9/7Xuz7S03e+973cs011/T8PjMz00r7zJkz/Nu//VtiGmns37+f6667DiDRa/WP//iPaK0pl8u8733vGyifOEQpEgRBEARBEIQcHDx4kBMnTiT+n4XHHnuMzc1NAK655ho2NjYS/3/1q18NwHe+853YtI4ePRr7u1KKiy66CIDXve51zM3NxYa7+OKLAXBdN3XZ2nve857Ea0ePHqVUKgHwn//5n4nh+vFbv/VbAPzgBz/g+9//fse1MAy58847Abjhhhsol8sD59ONNbKUBEEQBEEQBEHIxFNPPdX6fMkll2SKs7y8HPv7eeedlxinqahkCQNQrVYTw73yla9MvGZZFpdeeik//OEPOXbsWGK4fvzyL/8y559/Ps8++yx33HEHf/d3f9e69s1vfpOf/exnQPR+0ygRT5EgCIIgCIIgTJjV1dXccer1euzvpmn2jZslDIDWOvFaP89M8/r6+nqmvOIwDKO1+cOXvvSljntuLqm77LLLuOqqqwbOIzbfkaYmCIIgCIIgCEJf2hWMtbU1tNaZ/t9ONjY2Ml2fmZkZKp+PfOQjGIbByspK6/2kc+fO8bWvfQ2gpTSNElGKBEEQBEEQBGHCNN/1AXj66ae3sSTZefLJJxOv+b7Pj3/8YwCOHDkyVD4XXngh1157LbDlHfqXf/kXarUalmXxm7/5m0OlH4coRYIgCIIgCIIwYd74xjdSKBQA+PKXv7zNpcnG3XffnXjt/vvvp1KpAHDllVd2XLNtu/U5CIJMeTU3XHjwwQc5ceJESzk6evQoBw4cyFXuLIhSJAiCIAiCIAgTZnZ2lo997GMA/O3f/i0PPfRQavharcbx48cnUbREvvrVr/Lwww/3/L6xscEnP/lJABYXF7n++us7rje3BQd4/vnnM+V1/fXXs7S0RBiG/NEf/RHf/e53gdFvsNBElCJBEARBEARB2Ab+4i/+gle+8pXU63Xe9ra3cdNNN/Htb3+bU6dOcfbsWX7yk5/wta99jZtuuonzzz+fr3zlK9ta3gsvvJDrrruOz3zmMxw/fpzTp0/zwAMPcPXVV/OjH/0IgE9/+tMUi8WOeBdffDHz8/MA/PVf/zXPPPMMruvi+37iuUi2bfOhD30I2PKk7d+/n3e+851juTdRigRBEARBEARhG5idneWhhx7ijW98I77v87nPfY6rr76a/fv3s2fPHi655BLe/e5387nPfY7Tp0/jOM62lveOO+5gYWGBm2++mSNHjrC0tMTRo0db5wndfPPNrWVv7ZimySc+8QkA7rnnHl7+8pdTKBSwbRvbthO38O5O68Ybb8SyxnOikChFgiAIgiAIgrBN7N+/n4cffph7772XD3zgAxw5coRSqYRt2+zbt4+rrrqKP/mTP+HRRx/lD/7gD7a1rEeOHOHxxx/n5ptv5pJLLqFYLLKwsMDb3vY2/v3f/53bbrstMe6tt97K5z//ea688krm5+cxjP5qyCte8YqOrbc/+tGPjuQ+4lB6u/f2EwRBEARBEIQBOHz4MM8999zE8z106BAnTpyYeL7bwcMPP8yb3vQmAH76058OvbNcXo4ePcoDDzzA61//eh599NGx5SOeIkEQBEEQBEEQdhzPPfccDz74IDBeLxGIUiQIgiAIgiAIwg7ks5/9LEEQMDc3x/vf//6x5jWeN5UEQRAEQRAEQRAGoFqtcs8993D77bcDcNNNNzE9PT3WPEUpEgRBEARBEARh2zl27Bgve9nLOn676KKLuOWWW8aetyyfEwRBEARBEARhR3Hw4EFuvPFGvvWtb1Eul8een3iKBEEQBEEQBEGI5ZprrmFSm1UfOXJkYnl1I54iQRAEQRAEQRB2NaIUCYIgCIIgCIKwqxGlSBAEQRAEQRCEXY0oRYIgCIIgCIIg7GpEKRIEQRAEQRAEYVcjSpEgCIIgCIIgCLsaUYoEQRAEQRAEQdjViFIkCIIgCIIgCMKuRpQiQRAEQRAEQRB2NaIUCYIgCIIgCIKwqxGlSBAEQRAEQRCEXY0oRYIgCIIgCIIg7Gqs7S6AIAiCIAiCIAzCgQMHdlW+wvhQWmu93YUQBEEQBEEQBEHYLmT5nCAIgiAIgiAIuxpRigRBEARBEARB2NWIUiQIgiAIgiAIwq5GlCJBEARBEARBEHY1ohQJgiAIgiAIgrCrEaVIEARBEARBEIRdjShFgiAIgiAIgiDsakQpEgRBEARBEARhVyNKkSAIgiAIgiAIuxpRigRBEARBEARB2NWIUiQIgiAIgiAIwq5GlCJBEARBEARBEHY1ohQJgiAIgiAIgrCrEaVIEARBEARBEIRdzf8HKHN2Pjoqg/UAAAAASUVORK5CYII=","text/plain":[""]},"metadata":{},"output_type":"display_data"}],"source":["# Visualization of whole-slide image patch-level prediction\n","# first set up a label to color mapping\n","label_color_dict = {}\n","label_color_dict[0] = (\"empty\", (0, 0, 0))\n","colors = cm.get_cmap(\"Set1\").colors\n","for class_name, label in label_dict.items():\n"," label_color_dict[label + 1] = (class_name, 255 * np.array(colors[label]))\n","\n","pred_map = predictor.merge_predictions(\n"," wsi_path,\n"," wsi_output[0],\n"," resolution=overview_resolution,\n"," units=overview_unit,\n",")\n","overlay = overlay_prediction_mask(\n"," wsi_overview,\n"," pred_map,\n"," alpha=0.5,\n"," label_info=label_color_dict,\n"," return_ax=True,\n",")\n","plt.show()"]},{"cell_type":"markdown","metadata":{"id":"8D-rITa4SANs"},"source":["## Feature extraction with a pathology-specific model\n","\n","In this section, we will show how to extract features from a pretrained pytorch model that exists outside TIAToolbox, using the WSI inference engines provided by tiatoolbox. To illustrate this we will use HistoEncoder, a computational-pathology specific model that has been trained in a self-supervised fashion to extract features from histology images. The model has been made available here:\n","\n","'HistoEncoder: Foundation models for digital pathology' (https://github.com/jopo666/HistoEncoder) by Pohjonen, Joona and team at the University of Helsinki.\n","\n","We will plot a umap reduction into 3D (rgb) of the feature map to visualize how the features capture the differences between some of the above mentioned tissue types."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"VpInLNBLSANt"},"outputs":[],"source":["# Import some extra modules\n","import histoencoder.functional as F\n","import torch.nn as nn\n","\n","from tiatoolbox.models.engine.semantic_segmentor import DeepFeatureExtractor, IOSegmentorConfig\n","from tiatoolbox.models.models_abc import ModelABC\n","import umap"]},{"cell_type":"markdown","metadata":{"id":"D8BFVjGESANt"},"source":["TIAToolbox defines a ModelABC which is a class inheriting PyTorch [nn.Module](https://pytorch.org/docs/stable/generated/torch.nn.Module.html) and specifies how a model should look in order to be used in the TIAToolbox inference engines. The histoencoder model doesn't follow this structure, so we need to wrap it in a class whose output and methods are those that the TIAToolbox engine expects."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"Af9QuM7PSANt"},"outputs":[],"source":["class HistoEncWrapper(ModelABC):\n"," \"\"\"Wrapper for HistoEnc model that conforms to tiatoolbox ModelABC interface.\"\"\"\n","\n"," def __init__(self: HistoEncWrapper, encoder) -> None:\n"," super().__init__()\n"," self.feat_extract = encoder\n","\n"," def forward(self: HistoEncWrapper, imgs: torch.Tensor) -> torch.Tensor:\n"," \"\"\"Pass input data through the model.\n","\n"," Args:\n"," imgs (torch.Tensor):\n"," Model input.\n","\n"," \"\"\"\n"," out = F.extract_features(self.feat_extract, imgs, num_blocks=2, avg_pool=True)\n"," return out\n","\n"," @staticmethod\n"," def infer_batch(\n"," model: nn.Module,\n"," batch_data: torch.Tensor,\n"," *,\n"," on_gpu: bool,\n"," ) -> list[np.ndarray]:\n"," \"\"\"Run inference on an input batch.\n","\n"," Contains logic for forward operation as well as i/o aggregation.\n","\n"," Args:\n"," model (nn.Module):\n"," PyTorch defined model.\n"," batch_data (torch.Tensor):\n"," A batch of data generated by\n"," `torch.utils.data.DataLoader`.\n"," on_gpu (bool):\n"," Whether to run inference on a GPU.\n","\n"," \"\"\"\n"," img_patches_device = batch_data.to('cuda') if on_gpu else batch_data\n"," model.eval()\n"," # Do not compute the gradient (not training)\n"," with torch.inference_mode():\n"," output = model(img_patches_device)\n"," return [output.cpu().numpy()]"]},{"cell_type":"markdown","metadata":{"id":"_XQpoea5SANt"},"source":["Now that we have our wrapper, we will create our feature extraction model and instantiate a [DeepFeatureExtractor](https://tia-toolbox.readthedocs.io/en/v1.4.1/_autosummary/tiatoolbox.models.engine.semantic_segmentor.DeepFeatureExtractor.html) to allow us to use this model over a WSI. We will use the same WSI as above, but this time we will extract features from the patches of the WSI using the HistoEncoder model, rather than predicting some label for each patch."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"VtSHvExqSANt"},"outputs":[],"source":["# create the model\n","encoder = F.create_encoder(\"prostate_medium\")\n","model = HistoEncWrapper(encoder)\n","\n","# set the pre-processing function\n","norm=transforms.Normalize(mean=[0.662, 0.446, 0.605],std=[0.169, 0.190, 0.155])\n","trans = [\n"," transforms.ToTensor(),\n"," norm,\n","]\n","model.preproc_func = transforms.Compose(trans)\n","\n","wsi_ioconfig = IOSegmentorConfig(\n"," input_resolutions=[{\"units\": \"mpp\", \"resolution\": 0.5}],\n"," patch_input_shape=[224, 224],\n"," output_resolutions=[{\"units\": \"mpp\", \"resolution\": 0.5}],\n"," patch_output_shape=[224, 224],\n"," stride_shape=[224, 224],\n",")"]},{"cell_type":"markdown","metadata":{"id":"p6LrLhviSANt"},"source":["When we create the `DeepFeatureExtractor`, we will pass the `auto_generate_mask=True` argument. This will automatically create a mask of the tissue region using otsu thresholding, so that the extractor processes only those patches containing tissue."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"KoTLy4k0SANt","outputId":"936b14d4-8d83-42e3-dfcc-ab637fc23c03"},"outputs":[{"name":"stderr","output_type":"stream","text":["|2023-11-12|17:50:30.207| [WARNING] Read: Scale > 1.This means that the desired resolution is higher than the WSI baseline (maximum encoded resolution). Interpolation of read regions may occur.\n","Process Batch: 100%|##########################| 630/630 [02:23<00:00, 4.39it/s]\n"]},{"name":"stdout","output_type":"stream","text":["|2023-11-12|17:52:54.487| [INFO] Finish: 0\n","|2023-11-12|17:52:54.487| [INFO] --Input: tmp/sample_wsi.svs\n","|2023-11-12|17:52:54.488| [INFO] --Output: /home/u2271662/tia/projects/tiatoolbox/code/tutorials/intermediate_source/tmp/wsi_features/0\n"]}],"source":["# create the feature extractor and run it on the WSI\n","extractor = DeepFeatureExtractor(model=model, auto_generate_mask=True, batch_size=32, num_loader_workers=4, num_postproc_workers=4)\n","with suppress_console_output():\n"," out = extractor.predict(imgs=[wsi_path], mode=\"wsi\", ioconfig=wsi_ioconfig, save_dir=global_save_dir / \"wsi_features\",)"]},{"cell_type":"markdown","metadata":{"id":"CMJKi5JkSANt"},"source":["These features could be used to train a downstream model, but here in order to get some intuition for what the features represent, we will use a UMAP reduction to visualize the features in RGB space. The points labeled in a similar color should have similar features, so we can check if the features naturally separate out into the different tissue regions when we overlay the UMAP reduction on the WSI thumbnail. We will plot it along with the patch-level prediction map from above to see how the features compare to the patch-level predictions in the following cells."]},{"cell_type":"code","execution_count":null,"metadata":{"id":"eNIpM0dJSANt","outputId":"d5dcd269-704d-486f-92da-5639ff642994"},"outputs":[{"data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAA0UAAAJvCAYAAAC0x3pRAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy88F64QAAAACXBIWXMAABibAAAYmwFJdYOUAAEAAElEQVR4nOz9ebBtS17fB34ycw17PPO585vq1UgVxSwoIyQUwkZWh4S6UMuN2kIOWQYcRBiHFBJ4EKFuEw4TxlKIwFZpsKzQgDosMLSMkdzIAtwGFEAVGKjpVb3pzsMZ97jGzP5jzXuvfc4+9973Xr26+X3v3L33WrlyWpm//H1/mflLYYwxWFhYWFhYWFhYWFhYPKOQ73QGLCwsLCwsLCwsLCws3klYUmRhYWFhYWFhYWFh8UzDkiILCwsLCwsLCwsLi2calhRZWFhYWFhYWFhYWDzTsKTIwsLCwsLCwsLCwuKZhiVFFhYWFhYWFhYWFhbPNCwpsrCwsLCwsLCwsLB4pmFJkYWFhYWFhYWFhYXFMw1LiiwsLCwsLCwsLCwsnmlYUmRhYWFhYWFhYWFh8UzDkiILCwsLCwsLCwsLi2calhRZWFhYWFhYWFhYWDzTsKTIwsLCwsLCwsLCwuKZhiVFFhYWFhYWFhYWFhbPNJx3OgMWFhYWFhYWFhYWj4Ov//qv5/79+297uleuXOE3f/M33/Z0Ld46WFJkYWFhYWFhYWHxrsT9+/e5e/cum5ubb1uap6enb1taFm8fLCmysLCwsLCwsLB412Jzc5Mf/dEffdvS+8Ef/MG3LS2Ltw92T5GFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFhYfFMw5IiCwsLCwsLCwsLC4tnGpYUWVhYWFhYWFhYWFg807CkyMLCwsLCwsLCwsLimYYlRRYWFhYWFhYWFhYWzzQsKbKwsLCwsLCwsLCweKZhSZGFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFhYfFMw5IiCwsLCwsLCwsLC4tnGpYUWVhYWFhYWFhYWFg807CkyMLCwsLCwsLCwsLimYYlRRYWFhYWFhYWFhYWzzQsKbKwsLCwsLCwsLCweKZhSZGFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFh8Q7g7//9v48QAiEEv/RLv7R0/xOf+ER5/2/9rb+1Vpz/yX/yn5TP/It/8S/K69/6rd9aXhdC8D/9T//TuXEdHBzgeV7juS9XWFJkYWFhYWFhYWFh8SWI7/3e7+Vbv/VbAfjLf/kvc/v27TPD/9Zv/RY/9mM/BsCf/bN/lj/yR/7IyrD/4B/8g3PT/8mf/EniOF4/w+9iWFJkYWFhYWFhYWFh8SUIIQR/9+/+XXq9HqPRiO/93u9dGTZJEv7cn/tzJEnC1atX+et//a+3htvY2ADg53/+5zk8PDwz/YI4Fc98OcOSIgsLCwsLCwsLC4svUbz88sv8yI/8CJARmX/4D/9ha7gf/dEf5bd/+7cB+O/+u/+O7e3t1nBf+ZVfyQc+8AHiOOaf/JN/sjLdz3zmM3zyk59ESsl3fud3Plkh3gWwpMjCwsLCwsLCwsLiSxg/8AM/wDd90zcB8B//x/8xDx48aNz/3Oc+x3/xX/wXAPypP/Wn+BN/4k+cGd+f+TN/BmAlwYJqlugP/+E/zLVr1x436+8aWFJkYWFhYWFhYWFh8SUMKSV/7+/9PXzf5+joiO///u8v72mt+ff//X+fMAzZ29vjJ37iJ86N78/8mT+DEIJf//Vf5/Of//zSfa01//gf/2MAvvu7v/vpFeRLGJYUWVhYWFhYWFhYWHyJ40Mf+hA//MM/DMBP//RP89M//dMA/MRP/AS/+qu/CsCP//iPs7+/f25czz//PH/wD/5BoN3hwr/6V/+K27dvMxgM+PjHP/60ivAlDUuKLCwsLCwsLCwsLN4F+Mt/+S/zNV/zNQB8//d/P5/85Cf5T//T/xSAP/7H/zjf9V3ftXZcxQzQP/pH/whjTONeQZS+8zu/k16v9zSy/iUPS4osLCwsLCwsLCwsLoB79+5x48aNlX9vFRzH4e/9vb+H4zg8ePCAb/7mb2Y6nbK1tcXf/Jt/80Jx/ck/+Sfp9XrcvHmTX/7lXy6vT6fT8gyjZ2XpHFhSZGFhYWFhYWFhYfGuwVd/9VfzQz/0QwCEYQjAf/Pf/DcXdoYwHA5Lhwz1JXQ//dM/zXQ65bnnnuMP/aE/9HQy/S6AJUUWFhYWFhYWFhYWF8DVq1e5ffv2yr+3Gn/lr/wVdnd3AfjoRz/Kn/tzf+6x4ilmgn7qp36K+XwOVATp3/13/12EEE8ht+8OWFJkYWFhYWFhYWFh8S6C53kMBgOAlecRrYNv+7Zv4+rVq4zHY37mZ36G27dv84u/+ItA5bb7WYElRRYWFhYWFhYWFhbPIJRS/Ok//aeB7Myif/SP/hFaa77+67+eD33oQ+9w7t5eWFJkYWFhYWFhYWFh8YyiWEL3C7/wC3ziE59oXHuWYEmRhYWFhYWFhYWFxTOKj370o3zVV30VaZry5ptv4rruhVx7f7nAkiILCwsLCwsLCwuLZxj1maF/+9/+t9nb23sHc/POwHmnM2BhYWFhYWFhYWFh8c7hP/wP/0P+6B/9owDs7++/w7l5Z2BJkYWFhYWFhYWFhcU7jM985jN0Op0zw+zs7PD+97//qafd7Xb54Ac/+NTjfTfBkiILCwsLCwsLCwuLdxjf//3ff26Y7/iO7+Bnf/Zn3/rMPIOwe4osLCwsLCwsLCwsLJ5pCGOMeaczYWFhYWFhYWFhYXFR3Lhxg+l0yo/+6I++bWn+4A/+IP1+n9u3b79taVq89bAzRRYWFhYWFhYWFhYWzzQsKbKwsLCwsLCwsLCweKZhSZGFhYWFhYWFhYWFxTMNS4osLCwsLCwsLCwsLJ5pWFJkYWFhYWFhYWFhYfFMw5IiCwsLCwsLCwsLC4tnGpYUWVhYWFhYWFhYWFg803CeNIJ/+e/8O+X3NE1RykEqhZISpRwcR+E6DlJKPM9DSYE2httC8HNxhJQSx3FQjkJKiRAShEAIQXGCkhDZZ/1EJSGK3wYQC9eaEEIAZuleFIUopVDKWXpW5IkaYzDGlL/r+cl/ld/e4zh8R7cLwOfihH8ezFbUmlhxnTLNVddFXjeN6yyEz39GUYgxht1uj+/u9+kAJ8bwj6dTolrA4mlxTr5a08qfq18v4slez/nHYGXFEWV4rTVRFOL7nfJePZfFT2M0xoCUBbc37AnBHzeCzUGfe1rzP86m6FrO6h+U7SfD17gef6jTWSrdYg0sfmuvteyq1mneprMHsnZmCMMQz/NqeV+Mqa2m29JbTn31k/XQjUrAxClGgFBysYEvPFHvS9mzWmc1LKUsq3S5j9Ta2lptQjT6gVl4V9WNpYJV4cvnTS2OZlhRq4fifll/rcnVZIHJ5QOm/N6IwVRPZe22EDImlytZpqpgBlNWVT2zWdgqrYW8muqzkdP8er0uijyuKmORRvGMNqZ6e+WzReGz7NXL0ZRdVZ4aVS9E4369/HmAst8XQbM6r9pR8Q7Kf3OxIETxXWR9S4hmGevhyN+/oJaeQEhZZKMpE0WVXiGHhaAas/IyzaazMslOp4OjFBr4H+dT7qa6TCvr+3XZVh/N6uUuvgNCriGlF/IrZF6OBdm1qk+V6cl66IX+2P5c9oyp2pkxS39FnNX4Xh9rq2euC8H/rd+v1XkW/nNJwr8IAyjGnbL9r8qTKD+/3e+w8fAh165d4+fCgC/E8ep6yN+pELJs/6YoW6NvZ/lrto8qWiGqfD6vFB/v9pBiOR0ArbM0VC5L6/pHU6SKsi9JIZZzX9Odsj5Rhc/iKjOLTjVCiqqtlx/1MsGVH/7h1vq1sPhywhOTom6nkwvyajAqBos0TZHCwXVdXDcjRtPJBN/v4PgOSiu0MWQSIv8rB79Kh0hTvaA8QjVUV2EbypfWzOcB3V43F0oLg4IxuK5XCeSWshUCvAiTpilCiGZehKkpi3l+k6TM29LgIaA2GtRVskqBqD3THBSr7+ucueu6XqNkwXxOuKAcNcp7xgB5FhafM4161hlZdtyaUDeYujq6MChJKfH9TiM0lOohwmS/TD6AgKwGYQFKqTLeQjHM2lb+rhrjZ5VbbXTWHhdKU6XdyPAZOkXeI0TWdoVoKucAjuOitSZNdeMZrVOMIR8U25SRWhq18biow8XPpq5sagQmq6M4ilCOgnmY5aDjN5Te5rstyEBNcT4zzUojrtddqZYvVmC9SDVStKhM1eNv7QZFGouEo1aKMukFgmwWv9fDLbCqhkK2UJTlC01FacUDteCVQlaPr5RJZW8ogleKX2U4acq8KidUylFJOmSDKGSPC1QR94Jszz4lQi4vNhCilkaNdIj8i5SqlXcbrZFKVek1ni/yV39pNX61NA4AxiDKsWWxAmrPLFdO3jdTXNddzmgL0iRBOdlw2h9uLJcN6CtJL0mXs1EL05bNpR54LivKDIpV3TTrbLnhr0uz8rBmMUcGRKbQA0gp2vtlGQeNPlbRyVp/MjBQin6vl3c9Q5okOK5LL47pqqLdVflp9s4MWqcZyc3bUtf36XY6dDodekrRT5IqXwtVUbaOVSS+XicsvhuB0TobnWp9ZKAUw7xMWbDqWWMMURgShiHdXhepFtSzVotvVXBRJ0ctekdmvGzDUqHyKPKBUkBrh7Ww+DLEE5OiTsOyXln4jNHoNEUpieu5OPmsUWdvD2OgYzTbxiCkRCqFTjUyJxx1m4g2miCK6Xa7y/2yraMW16Rk2OsicwV5MXxhfWnIwZb4MyVSIKUg1TrLr8ysYYsPdREkScLo9BS1MWQoRM3ySyWYcgWrSXIoryMygRqEIb1er6WIWb6b5KlFZuYWon4u3Dy/g5+m9MMAJ6clhfJYkcP8elE/xhBFEY7rIHMFbdEqXRAVU+SDqsxaa7ROUbXBK9UajMneTWkdblfsoyjCcVTNAlmlq/JkjAkRhaIuFUm3y2gUM00TzHxes47XFeKmYo+BmeNw5BVW3hZLfm3QbtxbUvTrqCz2ZUSrlHUBs9kcpSSe5y8o2wVBWIy/Mkg0UjWmvGQa17P2HAlBnKddbztiOl5+qMxfpSCs7DMLl0tlViyQkTIRsdSNC6XeEYIuohyTCyuyLGbekJWCjqgpwBWZWsrTgsW1sPLXlaKi7rQxzIzB5NbYgZRZX1GKWUtZFNA1ZCQzTwsgBQJASIkrBIXEFNIgnDyvqYBUVPkrSYuk+SJbSE7JbFioh3YsKmSNOM7AUpiF3zqfBWkjSkA5O7oqLZNopCNrHDSXhcbkpKoud5cLVRgYjDGlYSS7tdw/inCrypamKbPZlM3Nrfb8LsiUghC1xVWk1ReSDXkGET4DWmvSJMH1vPUeWGZ6K35X3zNip1rCL4QtyWnzupHV9+YEXV3yitojYkEfF2QDSTZGDlRBZvI6dVQuF6CvDUmSZPqCrIWhuWrBCLKxIR8DZarYv3SJIAgwUYgP2UxLEUaA0ZnxKNUpGHBcJ5st0iYrQ21mi9xQURjoinZbNC1ZG1eNMQTAw/EYN5cRFWESSAnj8YQgDBnOBw3dxWhDmiakaUWqjckIaBjFOEqhlKKcTc7zoVNNMfNUkqZc6FfGpvq4VY05SRyjtUZKgVCKS61twsLiywtPTIp831+6Vsym9Pv9LBHHyZep5R1XG54Tiv+H4+C4bkNxqgvPUhfo9xELgrocks4bY2ryu2H1NrU4coW9vkxOCAjCEG3A891MEXPdJhlZSFsCOkno+D7XkpQ/WZCIgjEsKs01QZSRB1MKySTV4DjI0rJYPauNLgW346jGsoMyxoXv43lQfv/DJptFK95dkzQUSnyFJIlRSiEQJGlCEueDc2PGpDkEmpxA1jJRKjmj0QlhGLG3u9e0lNXiKd5FHMfZoLSk4jcV4JrBkpNptmxRAX+0bskTLFjem3CShHma0lTUMyWzYbUu7pRNVtYs7tWSGiEkxuhqOU4to4XiW17NleDtre1GGoZqYK2HrR4XpSW0UY+w0GOqiwLBr0QR/2cctdaDaAZeSHc51rP06eYzNaWoRNu17Ln3uQ7/Zqdbth2dpqRpglebRSws+kmSLYMRMuvLYZgReZXPPCgpc8urIU1SUp3S6XSrNmoMSRDhdLw8V4ZZkvC/zANmAnpC8n/v93HihJmj+OezGdEC6drT8B2Oi99vLsF8I0n4+fkcgPcrxR/udBBC4O3FdK5n/TJ86BPeW1PhbUVh4qgpn2fxnMVG0hCNhiSJcRx3NVkq5Fn9Ur6c1Vma1c/gum5OattkOSUhKq/l4ZI4QiBwPJeVhTI1BXPhvSwvLWx5fOEZ13XZ3Nyq7plC6a2U3FK5XEhN6ywP9WVTAN/muRjjNlp8JStFeWFx5rGcQckJUbGksTBaFYaOyhhQPZwp6/WwC7mtKfaT8YRut4OUkiRNa+NRYSDL+lv5jG7Wic7fP2VuDEmSZu9cSuoKeJFbY6rZ6+y6Ic1nWFwpeb02bhRcTGvN180DptMpvu+j8iW/ruNU1pOl92rQ2hBoze/FMVEUsec4XMmXMGttIJfVOtUNAlIYqLQ2uW6Tl1dXJKgoQ5amri2DU2U7EHkffTVNUUohparVZ0Zw4jgmThJ8zyvfYzaOZO85TXW5iiCvFtI0xXGcyrBZEwMFSar3uUpXWDFSiKxNpkmK0RrlKIRUWFg8C3hiUmR0WiqzTdtRNihLIUnTBJkvtciEY67IxAndciaktqekZuWG9kGi3VKf318S/DpThvNw1SBXBlhQ7AuRbkjimFQbvJwEGGOYTqf0er1coaoGx7a0tc5mwBanyYuBSrSXlCSOq6Uboqbw5ErtfD4njuM8HyLbF1UKysoaV1jaQkT5XWJQSYLjqHIZVSF8MwUzodPp5Mq8IBaZYgKCcDJGCMHO1mb1rkW1z6lQ0I025eBRL18cxxzfu03X9bi2u40QMldcZWkRBoE2Wb21Lh8URfuq6rTUzPMRt1ofXVjes3/Osog3iYrJB/Om1b9ZnOx96TQhTTJlvcpjMXDqvB7O0lAhCgNczy+fT/OBsxz5HgNF7TR7RwZZzGJSNfuGwsfCkFkjie2D6ZlUrBGu3kXOIqlJ/r6K/u54Hg5emYM0TdEmm3H0HQejNXEcgwDP9/LyZLMtZX8TEhyI5hHaaJTJ2tF8Ps9mvYu61gbluMQyItQaJ7/seJliH5pMwcr6f0acU0eVpApApylSKVIgzNtKlCtBmRHIgDJ5PVRKVVlTuggHaRznVvFqqShNcZVZxbPIKORSXcZR+24awSqjStmXjUGnSS3yRV5RKeCmUAjzCMMgWVJOG++1fssYglmAALyuX5IErXVpYCjyEMVRrryaMv5S/huTG4t0npV8Nj1f0iWkbIZvFGXFOJK/q0K5T5IEJyfZ9aWdOtdC67OZi0s/i3JkxLGiRUW6Ih8XjTb14lHMMJAbvlKd5UMphcqVam10i9Ewe0YvkKKKrDVDF/L3OE8vjpPc6OaU9QnUCEw1y1Au5SzrIpMlQuThBWX8VV1nBKogg02ymcVTvLvqOqXBSSmJL0DEEdE8QaeaoNHkltte0abc3EiL1sSTaV6mKnxRVpmPt0m5xC4ncguxFwS1NnSgivFGJ5RDd2EgEtky6VonyOORed5qe9qERDlO2TdlbmCrWlD2LlS57LQ201zmq/0PUZSxPuZVy891TgozAmd9clk8G3hiUnQyGpUSouysNUt2MQtUduj8e4JgioHTEZ4Q9PNOGhmYag1C5GQijztXaATQkwK/rhBTjZMHB4dsbm4Qui6x1kRxTDdN6fs+URwTOi7SdWuG1Pq6+izNLcdB5tfnsxlxkjAcDsr0vY5P2us1BZAQeEIwyJd5RcZwFIZ4jkNPKTomWxMtpCBNUjrdLqEQzNIEhMSNYzZzJw1TowlzITgQEq+akqgNriZXuKtZAq01EwF6YYAUxtDXKVEU0en1mQAdDA6CAfngrxQjneJoQ18KBiZTCrXJpt7LDdfGVINlYX3UmjiOkFKtsbzD8LXDIUJIPN/PLGVaZ4K4Rfmvq+CQ7YGJ4wjf76CUypTZbrckfIZsHblONc6K/QAlcVnQ45sDfrUkJonjfEazmb80SZhNp/SHwzytrB3ofO9ZoQTo1KDq68MXimmMWYq/XP5TzrQUyvP5BKmyFNf7SJMcdYVg+yzr30XJWKH8LSxhK7NRJi3QJi0J91nol+kLjE5Jc4tzYZ2XQiCLpWoGyGeis+wsKEU1RRWg1+1lSmaaYAy4rpNZh8OUwpiTAL04xmhNB8MkSUikIBQCdzbLc1YpfEpKZqkmm6wyZbrTIIAwyGZKlMMkjgFwOzHT8ZQoiIgOHZJZtyRCOtWMH52C6NPf3md6PGJ2MsXpeeg4IZ6GYAyq49LZ1MSzMY7nIkJFp99HuQ4MyWapgXDik60GqpTl3E6UL82JEcEEx1E4nk+sOplCvaC4ldZrneLocJlUdcB4Bqkkeq4x8/wNikqRLjhBYRQqm0get9a6XBpVyL1iLEiTtKlk58qyLuOukaI8PqVUvuSyam+F3Cot+IUMXSA0dWidzSK3kZ56Q68s9oaCCGEKombK2ZtihqhYlozIliBm7a/oR5TErKlc15JcaOe1Cm/eExX5qBMj0bheKe9KCTBpbYZEIkX2/rJuKItIa2Np9mOkNchqKaRShVMJcrKUEUWlslmIcqzP21O9/utjrCCbEVRKIZUs331R9vIZKRv6gyzagwBHOWW9V23SlPVe6CyFMUsIkPnStCRJEIgs7eId5KSydFZQ6D1QawtV8yvImVQKQTXzVziq0WlajrNCCBzHadRX3SBQ9BulqlnWZrsQ1fsVVDpLo+HkhDsnQbLYIlC2pcXwFhZfvnhiUvTiiy9SidQFCAjnAZ1etzHwCCm5mab80nyOAZ5PEv7oYIDrunwmifmlIPMsA/X+WAm4P+B3+CrPywYVkXmzS5MYpRw2t7ZwPY//JQp5M06QAr7D87kkBLHW/GyacJhboArhWymaGTn7rl6PTi54+oNBqbQmcYyQglPf539OEhZtuy9Kyb+lFK7rcktr/r+5UPmw4/CHOp1yXbjMLS+/HUX8epRtxP+DvR57OaH4zSDgc7l16t+Ukvd4Hq7joLXOptZ9Py+7LC15xhgiE/NzUcSpbuasLwR/0nXpdHtMMPzTICQyhl0p+VP9Pg7wIE35qXmAEYIbyuGPdXyElJRqcy6EZT7tXy4NIRPqnufnM2fVdk5DpTSo2oxLp9Mt61tKiRGFtaqpVFBLu0CaJnS7vTKuYqbRGE3hmSnLXzZohcEcz/epz0gsK8z5eJHHuZh+Qa4Wn5NKMdhobqo2udWXIr7Ssld7tmmmJp3Osmv95v4x0/hmiv8XlDBKxa74XioWdSVhQSH8iNZ8pLYPYnGJUbFUo3gflZJZpd+0iuefKbX0i3JXs8BQLMd0VsRTKZMSeED2zsMwcwShpMqUhMLibpp5L/hgpnzqJrEzRV1RWrULq7jK9y8EYYiSmcdMDXxlMVtgNDejKFOapOKjSVLujymWwEjg9dosQoEoSfgYebvE8MU8L97AIfECppMxYgv8F/ooVxGM5iRxgnmP5uZvPY8+3uHkHkRTD6/fQScpxEnWp1LJy1/7OYZbRxgNJ//vCb10SHdvQO/f6WAGKUkoeeUXP0o0r82E5e+rcG7gpnOeP/0k0qTMRYdbe18H0qlmXhaWpvWDR1w7/UxZxiJa96MO3rd4CCmIfj0i/NdxLb3mu6obyooZlLqRpyQOCESuhBftqB6mlN6iUNCrPZFKyUzJFNmMbRm/IJM7iHwVQ9Xvq9mdqu0IIUqlMZO5TWWz2OdWGIxKQ6AQZdmz9FXDmCRktrSzkH06XxatVDYr6DSMKTVLf/F7oewF+Vr0JlbOUphaf16oS533R1mQApXto0kL5bwwOORp1ldA1OspNvCT0zEnSYI2mjQ1uI4qZznry83qMxcmJ+tKKRynUv7r47MxmiRJy/abkbdsNkVQOHtoyqy2JYNF20NQLkWH7B0V+/gEmW4RRxGkWftMNbiOws2Xluoa4a0vkytntgq5XL0eyMcioZv5IifEha6ji2XZqa7yl+9xrpbP5W0sJ1Il0V14J0uoxECjXgzLy7UL/L9ar1pYfHnhiUlRr9cvv1e2sgxaazrdHmEYkiQJvX6fJI4yqzgQkymWrufhuG4m2IxB1waORQgh0LkAmgdzHMfJLb0uUkq6vR4GSKOIJBcY0nEyt+CAnk6JyQa3QqgUgygYgnxJjpAShMyV+SwfjutmziMchzhJSGv5EwJSIXB9PxfOmphc+crDSCmRtZmUFEiLPUT53giVL7eJ8zSV7+M6mSMKAC9X0LNBq2b9F6BclzgMl/Y6ePng5TgOpAmxyWayYp3mimNWwkQIUmNIMEvT5U2Pe2DQJZkoBkvyOtRkS8qyNdNpZv12SzNguWG1dJ4AmAWGWdKqvChJEpfu26MwyL1U1bzOlWGL5Vm5Ah7HJHFcEjmtqz0+dWtcPY5iyUox05PqYildc6BNcou/Uqp6tlD0i+yXVshaey6sk1lVEt5/gAG8S/s03CPUyUVZzmw5hzGmsp6npubxyZRKenM2sdqkbky+rC+3tNbrvEi92KtTf/eFRbZOYIqnWgdeUyhUUB+mKwUozRUUWcaLaS6fLUhmsYlY5/2z/p4KRb1SUMiVyzRXQqmWogF1uVIuAZIyUwYp4s3zmmW4XApqTOXHMsxd3hfW/UIZKp6pl7eov1JpMaBnDmmcMA/n2e9Q4OEShDOS3PFMYjQGQWIAoVC+j9ERQuQKmuchlEA5At9xCTwPJppux6PTdTk+PSUNJeHxnCgQbF3ZydqfNiRhzGw8Y3N/SMd32GcXRcpUdJnt74OWTI6nSCnY2N8kjVPCWQCJphOM2N/cprfRq6zeQuC+7ND5gI9yFPE4ITqKSuW9aPFFe6qTIJ07Xyk9hQmJlPneytzgoUpCkynCWXQLBKEgKlD282LDfEF86kpwY1lSscSuMCTk7U5rnS2jTrP9FW3OIoTIVgAkaYrMlzMnuRdSo7M27SiF47nlrEUURdnMQ56+kzsS0KkmzYlRtq+r0U1XoxaokT1TXSjab86PyjZuBI3lauUSK4r2nfWBmmhdaN+mkQ6hm7XbOCYVGqmyZWHGQJKkpGTL54oliuWSNSkhd75kagKpkiECbQoZmJGYYvGbqHnsLPMlDMZU+zwrYxHoIq8SjMgJX73i8jRNMf5Kme2tcRSJqGWsUdk141P+r2hcMxV5bUjc/IliTXPGtCtZlfeZcodxXT616EkNmEVDYz2dKq9FmJRltOliFhZfjnhiUlT08DRNcyLRtEgD2SCSkwHHzT59KbmSX9t2nHLGoyME+2p5WU+1xlzQy9Po9Qcrc7UpJZfy6WmvptBv1860qenc2dIIIeg5DkoWI0aliOYFwugUB9jFoEUh1DVCKLpxROJkSzXcNGUnX6vcTVPSJC6iKGP0k4TtNMVg8JQkTbIlWX4UMYzCfM8EHIYBQkC33Bieebmb557VOrkb5UhrnDCkW+Q1z7YrBEG3hwbmxuDOZ2AMSsDRPEAaw0iACgIwhkRKDqadUhmvK6jF8pdsM2lz/X6Vpqh5MqpctVbKq8nrrNq8WyjvRXtaFMKZO3SZGw9zIlVTjot81F5tnpNcWa6SL1Eo5uW+oVqd1WdAktzZhRSyUgyaEaFLQrZoCS1ysZx2+WyhGNy+W9Mrmkszy4I10iyW4hSDa1Uf5XKJhfKIslZq8dWtz0W9CVEqibpGPFgMkysbRRpSioZjiULhEUKQkp2ThRA4wCaZVVJLOKVIolomW5QpUxpV/u5VmTaFtb5RR7mFO9VIMgu1lCpTaJUsz/8QJYmpylJYvgvCWZ1XU7XJYsa7uFfOoAnwfcXuTuFVKo9LZzLCcRQ6TjGmw+QI5odj5tEUJ3GRySkS2OjuEk0DhElg4BMGIdcuvcz+/lfxRvoFpsdTrr33Bo/evI+TGmJt2Hpul233lG46ZAMHPZwx2N9h731XiOScyUiy63Y47uwxiR2eu3SdO5+9yUbHZx5Ap7OFChRMEoLEZ/PSgJ7X5/ql69z6zC36qUcURlz98FUevnoPfWoYdHx00mM699l7+UXSJCEJE6Tn4HU7pGON2++g3BS1lRsOkgCXFMd1CB3FLNXMg6CcLSmJQK4Q+76PlNkexyiKEFLi5cc6VPKGtq5VktaiTUcRhFFQktbCqFHs3TAAaXNpnBDg+T6ekBiVGYuMzJYFKtFUviEjuUYKUiPzpWJgCiW92DcjBLJGqnVuADMmk32q6HO5g5Ys3mVZuBbqSnPtd/l1kdiYRmio9/mCUOlWy9WSXp8ASJmdPZiTynLPC+RE08mXZ1ZjSPFui2VrpmEpK+pQ4roydzBUGUCMyepq2ThTLY8vyZcQNedHlMbRJeTXHcdtaErFWLdc+PZ0F64uPVa0t2KWqzLArIia5fyWy7VXospvXQepxkxT9pnl1QWWEFk8O3hiUhRFYbksrBilhJT5koBig36OQuk0sIXhOwpFI4qYRNn69EsY/i81gVwov4Uw0VpjplOOalPfQKUT5orsR4APQ2YRmU55lCf8tWUecuXVGERuDUtzpwiHJycZCSsH0cIinSmcWhu+0Zgy/TQfLNIk4Y3CfSfwjTVF9FWKcaYS9D3g6001Df5qfn0f2M2fTeQJ93O31lKqUjylaUIwnwOCbq+bk4uUr5Squak4r8S75iBLR0m+gUopv1ObEfj63OuPAN6oWQozBXuZ7BbnMBTX6kK5aRum8VlkqiBYRcgz18rX2lChpDcGhlypLcmIFIVmVD5XRF04cCis+oub/Qtlv9IJ8k3DJiVbkVXbrJpDlU4lBMYIUFUYma9vLwbkRQLSKENN2S7dzS6sTy/KVreu1me76ktVy+UgWdbKpRGFNT7jFtVSm8UlQ1nVNQfJYvaqSreuaOb7evKXnaZpuQ/oWGt+ZT4jMdkhu/9X18OVkgcCfjkISmJZZhZT9kOZW5nrs0G5tCmbS+GVUcjaUpzcGUqaZoqHU9u0DCy3JWNKEl3Wj8ncyGuTzXpJpTA6W8YjhcB1sziv7gi++7u3s30XOmvY4wfHnDw6Zdj1mB+NePTwBjffeJloNiMcJ3RPuowfndIf9tl/8Qo3P/0GR7tDZs/tcvzwiA86Xa5f85DCQSBxXQ+jBZisjMooXv3fr+M4LzD0PUYy4r1f+yEebfZ49Gt3ufmZDfb2tpiczLj0/CWSaYSONcIzJIlm/8Vr3H3lNnudHrd7X83dwDA5iXjhckowCtjudYiQCCNIo5Q4StC9HicMES/+QZz969z63dcxqUYLw0vH70X+uiKcRxnp2Mss+5emr3EpvItyHP6POOJ3o4g4igmjiMLjmECgVDYTo3KiUCwzQ6cInZZ9+CyNsd42CiUvTBLCIKDY31POfJRtuzZbSeZV1RMCmS9jNoWgSgWYsJQdVWtdJbCW+1LRXgsZlLXnFOKasaQWeZOANRbKrq+vrqvfnlWMtmfF4s+sP2pM2X+KvTLFjHm2rFHRYvuskinCLt7LCUTZNwEhNNW00tlkZRVxKGTCkqyrh28OYBfHIpEq879exPUxqXn9nLYHjTG1Xs56XzornnOSsLD4ssETk6JXvvDF7Iyh3DKapmll9c+ltqkJ92KTaXm93jlZVpxLolNYpXNrHqWFyJSKJFTLyUxN2SmGr/ra5boQLASE1ukSAYDip2jmKf9E5ANdroyN83sN4WpK231ewGpJlaglIuqf5WVReZzKCV+xqdN1s9cXRWFeegFpMYjXnheQ5BekyRXZ/N0IIXKF3tS8vWXPqFyZLazo5eZ40SQGZb7bri1+ijKnFTER1WbjUvGvEYCKEIhGAymU70L5kVKUZ5VIleW19Pwmyqov6yQ7L4mGFbNe79U6c9ky3jbJVtFmGuvVKc7r0mX6FUkr/ilHqnIZYhAEJEmC67rl/oR6LyksfYWeVoyWOk/bcZxSoYzjuGo7QuAoJ1/nn7aUuVauOkxtZo6q7t3cOUSSJJnXt/zw2ygIkFLiOi4ImZEdrUmNJkpTEgOJlKW72iRNCeJ8j15NaSzq0xiDTKv9JEVbc/IlOZC9yzSFJE0hqZZlpbnBxphsX2Ca70eoar94b7qcsSsO0C3aQTFjAZlDBpGmpElCEGZnaBkpSbUmjAWpSRES7r15D5OkyKNTTschcm+LODWMT6bMTkMcIzFG0e0OOI1O2drbw8QCkyi0UQjpoo0ijg1pnJLGmbcqneZOSTDoJM5mKFKJRjJF093aoLs1RAiB53bxnQ46kURxCkoSzyMwhliTOa5QCq0NsesRhTGO0SjPRzoOQkpiKbOZ3FSjk2wfY5KkBGGM3+8TjkOCUYjvOHgbXbxOj4PX7/Po5kN6gw7DS1sM9zfpdLs42s3flSEFpOfgO6rqWqZaPqfzdwqU+5mWyFDNut1sr9WX4o7jeSAlURTl71kT64r8FrLPyVctKKWyZcDGVLL+TBZyjlK7qFznj4ja/fp+q9XRLZOmtdASthhHGyPORZX+pfDmrJur31n5hKnVc0H/mlKpPtOBKIxE1X6eJ8GZBGOduinkfO0lV/oPjTuLqPbyrJr1EQhR05vWZCrnpdsItyJdC4tnBU9Mig4PD8s10pkCL0qlf0FfbELUld3q99L3/LfJ3Y5WnlEgO54gUxAEghOyw9EyoZI9Wij2UCnyhcCpL5epW4YKJbkiA4sKf/ZccS97LvMAU/ckVCrlRfoUMw6Z4F/c1Fkq+OUsRy3/OdmqzwJk+yBqQq9W0UX9F2kUXt6kKjY2F0pu5na6UKKL+imIbbnnonbifbUuveXFimKOiIaArcb62mhekMvGO8/ul7NIovl8+ZwxjXtFW9JKl+Uu2mQ9lBE1pwQ1nlXEWVdMirKjF88FWVBgavWvlMJxVXkIsTGCRBuSNKnNaoryoOLsjI2qbQCEUhAag4xjZFpsKq7KUFkM85Ln8SmlcJREQrnsRudKrRHZ8j8lwRiZKXxak6Rpua6/Vv3VO6n9ZX1PVBux8/oxUqBzRyBJkhAkGqMTOp3mGDsy2RkuBkMM3DPZgacHWpf7+IoDC01h+c2JVtHvGwRdiGabd7NZhWzWoXr3xvMyYqUUteZWkvvcslGSx30pkbkhI/I2QFau0YXIrOAjcUIfgwk1G3oDISX9JObOp0L6mz0Gg/fyxm9+AZlsEGuD7u0SHU3w0l0cocBoBv0Og40B3UEPv+uThvlS2iTFSQ2zWNPrOehUE80zw0ccRghgriDouMw6LvgeQhuCMGL/vdcQAqJZwOTghERrpkGI3/HpDbvcv3uAoxSTWcBgd4PZaFou6eo4ktE8YXt/kO83M4RBmM3QpZokJ67FLInyHU4fnqIxzOKYa5euMDkac/uzN9nod3FjzfTNRxy/8QD3mkH6Pl7XJxEpRkcgqv1qTaW3MmydtSzI0C6CVsGpLdMu9swVjhGK2Uyx0AXe2r0UlRrfJk9K1EUYLd+fLAtn67xtaZ+HBcK2vByLprxZit80bq3MnlgQV2cVRFQfj/VKV9ZDXc8RtSBnELQ6BzW1sq4iiqV+UqVV12nWR5E/006qaxVzoWi/RNDTDt99//1vW3r/T/0Udp9YfMnhid/qB9733lxxz35XMw3VspZs2VCh+NWWEWUPLIWp4qk+6+cWCEFDSSr2pPzzMOCLuQU8zU9yLgbBuoad5gfTqcLjUH7ugTHZ/pF6fshK05AfovGl3T12Q4AtoLR+1/Y6VQMHpYKOAVHuh1lcW163pC2YolgeiBYH3WIZh+s4uJ5bkbn8XpwkRGGEoToNu4r3vJGURtr1/CyEqIRvyXDaN8QXZ1PIkiTmnpqMrpHwOglbKG8j1eX2ZYwh1Wmp8BdtVAqJVLXlbxRtUTcOUSQnHcJoRJrUEisZTJW/gstoUc7sUeQ3D29U4dyg8LJWK1+NDRZ9QQiBSA3k519U+4qaagOFM7DqxWScoFFH1SAMGcHCkMVdHy3LWZ2qr2AM2hEYo3LSVIMUeL0OIJgD/0u+lMnIzIvgypmqM1Bv50IIhFKNk+AvAiEz9/d/vN9nU0hS6XLz0jeSKL+snCSKmekpn7v8fxJEM3pxn63/fYutOGIeav6P347xfY/3fuyDnN59jtufv4lUiuNre0yPxxjlgM7O2+n1u9x/9V62l8Z3mY/maK25HGrc2ydsHc3ZcXskQUQaxtnhpvmm9zs9h9OOw2S3y/CuojsNUY7DxqUtjIZoEjCfBDiug05THOXguA5RFIMR+F2frUtb3H3tHt2OTxCEJCZbGrhxaZMkiEAbtE7o9DrEs5BgGtDr+gRBhNf18XodHnzxHkpK4jRlsDPk5u+9TpomWVqpZhaEpHHCzeMt7vtD+p1tJv4bmHBCOevfeKGVPBOFBnumhna+ItyGwgNoGbQSP01dsdZ/l+JeECoNvfkMgrPQI88ITLMMbYp5m3K7Ji6mUF8Ai/lZJ4+NMGfn68I8wNRjFCCaL7m1HkT7z+ViNAtXXza+OAY1omxrU7VhddEYUBiJzpKRS8Rp4V6TiBbGtRUGBwNCrDfOW1h8OeGJSdHm1g7FpnmRaYYoWdtsSlu3WhwW2hXmBkzlQhdDtaE7J0VJkpCGIXF5uF8WR5zqJeWtGvgESqr8rASJMAaVz6qkWmdOj0RRiix8oSuWHrLyc0CElOXyn2Jgb+iwhSJcEMIFpxQCqnRNtUZ6aUOvEAgDoqjfuuIvyNbfm8q5QLOGC8GaWf1d182WbIncg09BSIRAOQ5u7dqq/SVlAct8tAvZevilJXK1uMszHKSkSYrq6WXJKAV19Xcdq259VnDhTlmXqw6qq4x02ftrC2XKv7x9NBQYsRSWkmTWmm0tbLkU8RyU6RZ7Joqr5YyaoPAYWDc+tOZNNI0AjVptdVqRE/giDqnae7WAutejxjbqNTWdZSW6vZ+0Zv6sJLLKwwiDDmPCKCFMBMfRAf2rlxFScnjrEbc/exN/x+HBe+5iXMPOi3vMTueYFBKl0ClMJgEPvnifjUtbJIlGpIYgiIjjFJ1oPN9lPplxcnBMMA/RRuN2vVKOekqiw5g0Tuht9BjdP0YKgSMV4TRAyfxwYyU5vH/IRm7MufHB6/j9DsHJlEev34fcgQFC4Pou0nXKuoqizL9lHES4HT83CCVs728x2B1y/7O3s+WjUtLpdZidTEnSFEdKxtM5199/g2A0Yz4L6PgenV4Hx3FIg5jBoJ/NdscpqRGgXE4eneJ0XLztAcar1XnjFRRSuZAH2dVVr21lm1mrw5izfq4VX4MvFWNKW8NfuFYnTSvb7eJzC+K2FsX5pKOe/4sQqIvqwyvy0TCa1K9Xwi7/OGefVBnNsm5wZrZqhFcUsk+0k4dGdtrSWiBUWfz1B0pNY/ndFoSmPq7l/xY0SphCR2kZ+9YyGolaeVvSNy2yfzEGke+lXiM1C4svNzwxKboroVJN80HNaERaH+TOx3q6SyUchDGYfJ2/EJm1OXVdvJpFRNRHD8HSILq4/AYhqo3iUJGppcF3cWlge45NTSG9CM5T7s9TIIulZyZfelTMqghRnU7dVqbqM6sXd8Xhp28ViuVn9d+tWFE96yjWS+SqjLM2a/WEMG2azNK98kIjaEmm1mwzFbE6I8yippGT9uW22TRUXHSZSWO2sy3/eT4uvHylpcpK2raqiRgD2oAUhd0CEFyWMjuDrPGsYO5uoIVCacOdeyfo+8fgdbglb7Iz0wz2Nnj1U1/AMRCogOPjEVuXhyRRTJqAK10SIOp7zKOY24cnfOX13WwZpzaYRBPMAmS/w0kaE0tDV2s8Jem4PlLJzIObUmhjSGZzfM+jO+hy6/fu4fkuOklRCLTr4Ich0ktxhECmmuHOBvsvXsZow4Mv3OHR3UN2dzezGWwh0EmKkALHdYijmCROSHJnCJC550+2+/gfuMaD4zFH9w/L5ZHKdUjjLK3RaMxwe4ON3Q3ufv42jucQxjFXntsnDiJGQYSzPSAVhtgVxI6PTjXu3BCOprhdjw13g/3kMgIYhaeEadg6VpwpO9s0NrF8r+pPrU0J0WZ4as4rrDTZmWLWYTHytiwvNDlT/hZlPtsy2bA3Fffari1muF4XT0O7PYt4tdR7GfyMvm7qhpR6Dawglo+7X+jtVe5XGWjMyl/r5m2d5YHt9V2MKMvktE4Y107LwuLLGE9Miv4/UUgpxepyfcWa4VUDXd1xQYGGYF1TKKrHXDrTKjpXWunXU6Afd3nCmRbQNRRKUSqCivVqw1RWzmcJa9Rl+8ySaVVKSgVmqSmt4Slq0eJ8buAWTWRlpGe9WLPYdc9J+3wskbBaLp4s5iqeKrF2K3QWcMEIYgzf7Ps8XzsQ06Sa+TjgzvaHSHqbHLzxgFeOfDrbLxGFEcJoTg9HeP0OaEOv1+U0mWR7l6Ikc4ThCtIUZL/Do/0es3mIGs/4SpOdbZZEcX6WFZxIOHnPJZSjiG4fcunRGIA0SrNzr/LZ6kCD23Wzw0fjzMtdHGee/KQ2XJnG+ElW9DBKuf7RGyjP4eiNhxw9OGbQ63B6OskKKbMzdIQUeL6HjlM0mmAyB5MtoU1dxWuXB9wdnRLePeLlOKHneyRkh1WeHo+RUhKnhqvvv8740Smj4zGu56CkZPvaDoc3H3HiCY43XTwlibTJ3Ewbw9VTST9JSOKUF/df5sWtlwH4rXu/wd3xnXNe8nmNoHiZLHWL2g7HFapqnYyJpTui+tmSfnEQcJ7WIllZkcXF9FemYXLyVM9IPY22rl8bdltl+pnK82NALPRrU/u40HhS0Mx2UnFWVK37zhp6RB63aAZoXT4m2tpCBlOv3IWHFsR9S1uo2Ec7yS5q0eQGuqZx98xl62Lh+2KRWu1TJs+nWBnGwuJZxBOTokUF6HyFrrgvlq6sjp+6yKjk+tLGwIv37PqG/fNtShe3OS0KnyJNoCnAFiyHK5M/K53i6bMsei33ssPt1lGgmxlpbPrM1361WT7reweWlkzQrI9q6czq8Mt5aYu/eqbKZ62OzmmjzZnA1e+90ezM01P8z8biKPiYUZiW728h1k9iqVOUlxeXWGXXq5fV3Li8HJsgI0dxEIGB1z/1CtOTGbev9LnytR8lCmKQkiCISOMEz1VE0wCTanzHoec5RFohEcRBRDgJ6LgDZrM5XsfFkQLHy85gieYRfsfDJNmBs51uh5NUM5vO2b2yQ6ffxT8NCKKYYBrgeNmh1iLfo7PR7xDNAhylMEIglKbw2yJ0tidxPgu4/MIVBnubzI8m3P3cTUS+3831HJI4c/BhhM5nrfLjE7QmmYfoNCWNYtyex/x0QpimbArJVq+DFoJgHnLv5v1ytmnr0jbdjT53PnMT31HEccLulV0QgvHhCNdzEcYQxRohM6+XJk44HU/Z3eihE82jNx7g+C6blzZZbVnnTHHbJldXP1OpuatU0mZLadgomkFasniuTSIPU6j9KzteazwChGk8W5Yml01msQpSg1CVml0nbo20Fi04C/E0KWI7RP2z0vvXwtLKjbJkbW3ibDnXcHJQCfzaUyueXyn7lh0olAksEa7ldrVkF1pRJ2eNRRcxqjb3PVdk6qzwlXxs9qVWGWth8Yzgyd1nLMn1atahPhTVpebikobsTnVmA1Qkp7mnZ2GUKb7VLCnrC5LaMh5TJlhLQ5RhmlFehBjVFfXquZVLuErat4jl9K6mKW4c4w4G3EoSwqJMnCHMTG2QLKxyhhWEst0M2ba4qz6+1t2iNuItiFP5ilvelSH3DteS9TrpqZOxWp0ueaxbWEZZEvjac+eMVsv5oKjflufEct1Uka3PmBp7FdbBynjPaKdrDNhrozSVX+QZ2rWuNeNoku5mHAK4rBQbufOQubtJojzQhlkKn33lHvPxjCvvu87daQftdgnibL+i2/E4EhrHd3B7HToJhNM5ylEYCTpJ6He7XAr3iIOEyWyOs3eNuYFYpGxOArpKMYs1SRiXTkqCacBwe8jB4TEboznR+C7dZIbhiEFXosNjwiDCkZI4ivE8l/7eJke3DpjOAzY2B4RhRBTF9IZ9xocj0iBCCsHO8/sYrXnw6l2OSDE9j/3Lu8T3DjN34nFCb5AdxhzMw+xQ5TT3QKk103mIowQbUmIQ6PmMKMncU3uOQnrZ8jkhBdc+eIPZyYRwHmYH46LYffEyp/eOmU/m9IY+vWmMjhNc1yGOE4QjeeGlq+x7Pvdeu8v4aIySgs39TXov9bg6uA7A8fyQIA2ykWClXCre8XJ7axpQ1pHTBcloZwyt3SoPusgnmj9rLvQbkSwr6ab2XEnnSwMTjVbeLl1qoYpuqIoStRiAFofQah3fUqzNb6bxtcxqKQ1N87mzZF0LIWsq4rV6W1cetK1MeRxHAfX3e9HnVv0uX0/9PWQJtZHuxfZYeos7ryxtxtY1UOhe5f5hS4YsnmE8HZ+Ci8KyZnVoBih+LXe6xVmfcpNtY4Yl/8wHjCf1nlPT01sGgTynC4RmXSxNfS+M4XXyUE+vea8QozU30hgUgt/v+Vzp9sDz+MnZlLDcX7Uqn2b5p1gkfMt5aZapFk/OTtqXIBTMpyAjDda8lJXGUoEGoVrOe8MZQSNvzTCL95bcN7eWsMrzqmoRtc+Swi4R5/bnalXSUOCLa2X7PjuqZTzeWHhRHrIaj9sPV76EBa2kVrA2y2y9J4l83cpXux5f4bgg4O72BzgRWzz4/G1ujuYkpkPc05i9l9Bf9wK3v3ibjuvi+h6y3+HW8RHeVh8fiXjzEB3FhJOAzf1tpkdj5Fyye3gV33WZovm9SzPcbZ9Banjf4RwhBZPQkMwj4jjBdxXzecBg2GdXOuyeRAgl2b+cIDYfMp1MePjGMUn8Av1uh3kQ0t3oI4UgCCJcx8m8zhlDd6NPPI+QjiLRKf3NPt6gw/j+CScPTzi+OuTEaMK9Hpt3D9j2PeZJSmejTzgNSOIEz3VI08LlPkgJMtG8ONa4vksYw2gyxet49LeGJGFCkiS89DXvRbkOt3/vTYQ2hGHM7rU9hIBHbz7A91zcIKUXppCkOComMobnv+IF7n7hDl8cT7NtXrkjEz2P6dzv87Vf8w0IIfiNO79GML1fvvILN6eySSzL23pTqkI1e0tdAjUPCKjuLnKnM80gC6Tf5HJxlYwuJf6SgtxEfc9ieb/WlxZjN3lGF/XqTB4tGhcWKc7CtyWhsbBHcFEXWIFqqfHy2NEgCqa6vnaraBCj9R6pw+QKxuJrWnLQUAtwIUNWYyBYN/zZjzTG2BX5WPReusQ7V6lsFx6QLCzevXg6pKjRaR5zw3pdAJrGj5Z4i2GqIg+rM9bMzJITBrFOj39CtbFUepuDdTsxqpPG1WVzfA9XKZIFI9LisrWlTJQ/TSP8WdahtiUn1Vki7c+c1QbalILmeUK1b8UrFLkKsML5RWM/zwo0Z5vEku4NC7X0OINqbQBr1m3tXdbHr8ViP0FTu8jYVR/Ez3vuomRrnTRX2ANaAlQvoa6qLfRqah2geSfVTB6ecvPmQ4JxgOe6GMAVgpu/8zovfd376W31ITF0t/qMjicoNzunLIoiPNcldVIObj7k6vuuc3jnEa7rZh7WMBzPZpCfr+Q7EiViojhBAA/evI8xBs91MmIui/OkBNoY7t95yM7OnI7jEvs+SSpzpVgw3BoSnM6IowhHCmbTgMFmn43LW7z+yS8g8nO4Lr/vOvE04MErtzOS7iqIM0+dGztD4oMR2hi8rs/0aIzRmiRJ6fY6dAddppNZfsAxuCI7BPv6B55ndDyi1+8yenCMjmL2X7hMf2fIvc/cYno6xXcURhu2ru5w8PoDkijGVRLhuegwQhlDGKdce/8NHrx2j9l4Rqoz9/6+6yKVJDUQTAKC8ZzuRi97X9qUnjWfBFWLaWp3JY1YUBCzZ1aRlXo858vLeh6Wlq0thVlBqKj2NNVy3frEEgErry5+q9AgerVrzb5+wV5/YVl5hmS5qMBpi2rd/NSNLqJOMM6LYJ29oosCab0sFW10yRnUysAXQN2IV+gkdSViiQ1aVmTx7OBL5vSprE8umLFaTRjLAv2ihheoj4lPSHhWoWHtq5vw6ht4zz+Fu3mvGJqzOHScgOs0wp3n4lU0mMaaqNeVOSeNIqHHunc+sSnGr4tyiIxI1Z5b58GzLHONkbR+fbXHwVYVYNlQ+pYY5tosmdX7rBJ+znHopSlSKW5pzdTo2nN5CZofQOZ/8mXHxRWQAK8mCUltf4+hhUCf+xLPqonl2tzqbjPwhmBAui6PZiEPPn+bO8FtZHcH6TrMo5gkSTCApyS3P/MmL33te3F8l3Aa8OALt7nUdTCzmDiI6PZ83EGXaBqQRAndYY8wCnjYfcD2/ibuRNMfBRjA73RwHReUIkwDti9t4wjJ0cNjlJTM5wETnZJ0XYwU9JItTo/GOJ5L98aLHJ74TOYBWrlEacR8PKPrKhwNhoTdFy4xP56QJCnKkQw3+7gdn1u/8zrj0TRzBpGkKKWYnIzLYwKyg2slx/cPUa7DuOcx2BryyvEpoutky+kSTX8a4mmH8YNjusMeJ/ePiGYhwpVsX9vl9hfu8urxCW7fJUk121f3uBOFHD48ZFtJUArd9zkWKQZ44folTh4cc3xwipACVylcz2WwvYExMB+N6Wz4PHx0m+uXXuD5jsNe5APwRpowu6ibwpqYLaTqovSsmrKoP7JGxIsE4jxylMtYUfWBKt2q4Zvav2XMNXZiamNGFc+KNPPnHseWswrNBXhmKeJq3L44ixENZbsuRNuMcFn6q5dUVnXdjHHF3qBGqKpcbQa3pSfEgvxvZLT4WHjvZ0bYfqEwAq72wlpnN8vZWCLPZxojz8rsW6QjWVh8CeLJSdGFNbhVIrt57bxNgqYUS+cpTgtXFonXBXAxRfwMz3WLvy46pghBOptDr9ecdTgn5ZpGkP88m5BVyTUFZ6F0VCStRmbOrN7HF67nr55oqcQl3pK3mDrzWhjQ13WJ3fbK6rNnQpylMJ0R1+PoF2s8t6xnFBqkKVmmAL7KdXlOCBzX5X+OIiZJ/TQh0/YBZILkD3Z8BghmGG4lCQnL4VrzXH+3Zy67bZSIwqhQ3Ls+fI4Xt14mTRKC0ym3fM14dxtzcEpnNiJye0RxjCMkUZIgux1m4xnjgxGdfoc3PvkKcRizdQS9fpc0TRkHE3Yv7+J1fe598Q6u44BvuLn/OofbXS5fv8yHP7VJNI3Rsym620UqSRTGpIkmTSK00XQ8l2A8Ixp43Nzu0tvs494yvDcaEoWao3DI3V2HdAJCCmIdo7Z8rk8k8mjG3nOX6O9t8Nq//mx2WLaBwd4mD1+9y/h4RMf3SLVBxxrTkSRpduaRNobBxoBoGhBMQxzf4f7QJSJCb/oo1yUMI/b6QzZvHZeHZJ/cfURnY8DetT26O0OObj7ijQcH3N3rkULmjOLSgKM7j9ga+GzOUjY2B7yeBNza8HB7Xfw4onc8zhR1Y/A7PpuXtnAch4O7B7iuixwkJBsJQXfM1w4c+mEHA/xUMGOWLwm+GFb33qZ6XyMhC8/UjW5tsYlGyEUTXT2SyolPk0JV59IU96qxLFPuBdRmf5rb6FdCnEOamkGp9596qVbNXtXRtoSMpUstXuGo3kN9QqYakc7OdEUiF3PV/uQqGZ3l8yw95Gw9pRS3F5DVdT63TAfFUnHaTgoypjZm5/2qlezUv4tWntkIXJVa1C9bWDxzePJ1CmugGgBqnVyw1OvMeUKxhkU7oOAxNgi2BD8rB80UV4drcyTxdJDnwIBQ+VlDjYQuok2fF7bNrF8fjDJl2uR/5a3aY5WeK/K/xdgNi+kIWsbZQm/PzHgUB5q21nGDvwmq5QemjOixt8CY/JDgNG1tJ0WemksBsz9TKAGLvE2IgkFVWReNjzUzd5HA5E4pmvsBiq/dThdHvU2TyCtf5DKWq6+p2hptSOOYm5/6Arc++UXCwwkSiRGSCIUE+p6L52TL4zo9H4Hg+O4RNz/9Bo7vEYQRWmvCeUC332X70g5HD46Ic290URBmZ/5Adki1q4jmIbPZvNz3kxQHEGNAKqIoJko1fq9Dmkup6fEYYWAeZ57pRocnzEcTIJvVQSmCOGE8nuF6Dpffd537n34zIzauAimYT+aMHp0ghSQMI0yq2dzbLHmu1/WzWSApOLx7QMd3swNZhUA4CuE6hEFIf9iju9EnSVI8z2U6nhKGMR3PQzmK259+g7uv36XjOgx8DyUFrjGc3n2Echx2n7vE9fc/RxiEmRc9JYnDkOnJhG63A8bgOA6XX7oCwINbD0i1xvcclJAobTh47T6jR6dP1pZKIXF2kPq3uhyqjz+VhFlsnKIWclWY6rJpXGgLVh+3KstGw05Qj5D6eLqU3FIpz4OgfeRs1kYzlfYqbitfi5GqIAWmGezcg7cXheMaqZ8ZXUPG1l7WgpDOlmtf1Epl8hhXC7d1xF7bWFgfy7IqO7/kjWB5wqL+V2vHZ7RoC4tnAk/d+xzkQts0LTGZkF/QikXb86ssNKuSf/Lu2xyA1ovvrFw+Le8tq9IwwBeV4lGaoBPDfO010BXOz+Py/crGWo32xenXpZHzjFgaTsrKvUFrZ5nz2sZiU8qsarW8iyK95v60VbbMxbSNITsMVxukEI3MZ2XJFYbcereOU7aGgwio1e1FB+KngzeShGmep5GuZolaunkDKfDpOMZHEGPKWaInRsOOkrW1S1JxLT+PLHA3mck+85Mpp58/JHjfPsHJjL7nEsxCpqdTPEB6HuN5RJovB4zThPFownB7g9loCrnbbMdziS9tcjoLSIYeLw6HTI5HOI5ia2eTKAhBZgeijk7GqLGDE/aQSuK4DiJJcVwHV0nGJxP2ru1xxbtMmhOmQc/BCIiTBCOg2+8y3BoQTWfIUKMAEWqmYYLnOWx5c67e6BEcfoY3jk4x29ucSoFG8WA6RfqSKx2f9GTM1t4W4TQmHIe4rgOOII1TYpkw6rkcAI7XYTCLkZFGAkEYszNURHeOkEIgpWQSRnB1hzse7A18Tg9P2Rn2kT2fR1rjKQVhwmaYgEhJT0KSvW16W330/SnzOKHju8S+4lBIHiUuO9Jh9OiUk6MRrqMY9LtobTh5OEcfp3gdny+exPhf8RxCSZLoDUhnF2srldvJ5u+yKS0YdfLfovZvI7raM3V52dYPmveXZ+ALOlOFbs9b23P1uazK9U72qx57M556Xs9bEbAYz7oEpZZqYzyo8nbRhRlnypkym8t111Tkq1gW3XuvmlVZdEJQe6AlG1V6S6rL6ky3Blj0otjc87zinS2283ORv/0LjLXWLbfFs4q3zhycab60DQANmMUvb38nfJwUW8vUYADnJLZgKWtHOwkwwKei6MzkGxfXHfPOHJHy4cWQuc1e3KAsKB1JnImFIp2xLLqZ+gqp3vTy155c/YdZuCra3ploKiLZrYxIqdxz1vmZXqwjSu9TZz5VI1QXoUXnkZbFsMWXuppmMPxeHEMctzwkEGa1zTQBfjUML5DjFcitxkLWyWGt4Rp4Xjl8S8cHA3fEDr/3OjgjjXQUaZygXAeZpMT5LMt8NMVxHaJ0jhIye3U6e7+9zR7BaEaYakTuiu3ewGPkgbm2xY1JgjKAkowenaCNIXQCkjTBGE0chzhCgJQ4UiGUwBWgtUZrjes6KNdhcjLBGMN0MifqSnrDPlcu99mZJBzdfYSazHg+d54SpwlBnNLpCfavwcb+Q974jVcYDz/MaOjX2oZhc3PI5M1Deh0fv+PRuXmf66lme2+L0/vHdBzFNIq5s9VncGOPnb1NXvrXr5GczBBAGCXo0T16QuB3fCajKRvX9vn8psvxySkf6eyilEKlmjCKMX2fMEp5cXuLrVcf0HEcxtM5ExSX33+dl/YGjMdj5tM5p45k5kLU38I/njM9HtFRAt9zmc9DgijG7/iIVBCREj/3fh5u3EA4kmj8EKLpBa0m9WVnq3x7Fv8uEozzFMHVhGYR55ltLqpwNh15F/Ko7fiFdjL2pOaVRVnYJBoFmaDqr3XZdY5RqJlOE0uvvvW15O+wJZ2KQxXHNZx/ZMc6SZblXzmGN5dHNkeBIvgyabw41hk4i8wtEsnsX0t6LCyaeMtcclcK1xkdb0GQrNU9W6T8unTqS8r6sdZo9fj5bN0vtK6pbuUzgnIza4PNLM52rEi/Fn+dxDRF9jrWyrZ7TzD0r2hPdWR6lkApRd3mXOoEovm5Tjpl3OICRr8zsK4CtGSHoFGi9mdMc0no01C2GhkqIhc1a24bEa6ZaKePTjk4SIiSfbrDHvPxnCROSbVhHCXZ7E+iSXSKJiMqnu9w+cWraK3Z2N9iejQmjmI6gy6z0RQhBPPJDOE5nD46xt3ZI8UQTOdoY9jc2yQQHsPhgCgN0TMIkwQTG8Ioorc1ZBpkBoud3S2crs/91+8xHk3odTs4Qw8pJcqRnD485tHBlDAIGXR8jBBExpBqk800nU7wvRM8J0vbdR2iKGF7b5PJeIZONJPJjK0o5vrODuFohk41GxsDkihBSkmYpAwGXZ770Auw2WV29wh3NKEvJInRbO5sEMyCbB/WPABgOpoyFQ6qUIKFQGvNOEmZphopDGEQIKVEhBFDz+Hk6JTZb80Jnttl+9oO6tEp89EEx3WQUtBzHTquydZrJwlB4c5bCkg189Gc00enpGnK9a94vnrZi/rckubc0o5yr2aVoixaAi/PIqwK00y4jYws4ux7lcpcO9OtJDtVQc6T/sv3259YJ6amsWiZWNVRJwQGGtsyW52plE4tmsao9rDnZLXlkSzuFjqzaKQTtfwvPHMeWarGtRrPWMzE8o+F9leFWZXahQ5svUBdnU/4V7V7C4tnC2/NTFEpPdrE6VPobksa2YIwX6GxnZfyhXNXT+csE9M6YerhVt5eP3+NcOdosBcZixpusc9IoHWz7qJ+2zJuLd6rx9ianxoxuwi5KEhO8WwTTQtyKxZuZhxxVeIXow/VbJFpLk8s8t5SzqdGUM7K18L3p0aMziSSWUobnU0u9bI9KT0peeXmIya3HaZujwTY3OwzOh4zPRqjXMVsMqM/6OEMPQ4fHoGUdHwPhKTT79LbHTI/mTI+HGGMQTmK7Ss7xEnK3o1tHhycMJ/Mubdv6P6Br2B8+4jtccjutV3SniB46RJxGhPem6HkJsHpjMlkRuAIhKs4FZIH0Zy9OMTZHaCmM7Qx6NSglGB2MqY/T5DG4Hsuk47Lg9wpw42tPsnDExxHcTfocfNAofvvZe4McYSkv7vBMEhIJxPcROBp0GlKnM/wTSazzOOc60AKG7ubDAY9JgcTbn3uDiJNSUTmpttxFGEQ0el6KGVItSYYz9jFY7A5YBhq3hx6nBiDM+iyO4lJw5CuiDBxggbmzoTZ7oSplIyTB4weuXhArzNA6G3COCFMNaP8cNpB18eYCK/j8fDWA9IowXEU3Y7Pwa2HCCX44JYk8TwM8JkkLpd0NhtdiwW8mK2ohWgzzC0riee15IK0VOGeV4qrSmGA15OEh1q3crT2uBbz1OxR7c81rQfNYWVVasunGi0fVtuwYrZ4hWtRmBvMIDeWrajCatxq1nXdG2iZdi3uVm+ZlCKhJsPbGErTlfWTOpmt0+pz9z+V4atEW0nJW+X5tiU3TbfyVf7euv3PFhbvTjw9UtSw+ouGHK3Zh2phLogzHnisGZF14lnvofXDrDultTKax3iwqOxVBqK2W+fU3yqvPevI+MVzoipeYhYGiSK+BVuuyXPcklbbWLU0ZopMHTFUDnqX1ANTJdM422gxjUViYpqEpe6FqbAOtlVt67K/8mLTE5UwZIcLvi00aDUeKwfrdPx6mOIlAFv+Nh/Y+xAAx7ce8Tt3RnQ6z4OBOIyQXnYg6em9I/ZeuMTo8ITZdE7fy2aGpicT4iAkjlOCWYARcOezNzOnGdoQzUL6W31EEOO4LkIKlOvwWzfvMby8xY2PPsfg8w+5/8otRmHIcfIeNt/zEgnHPNgM0H2Xw/sJjgHfkcx7DtJRiP0Buylc1YL5LICtHq5KSBFoUhKgN+gxHvqMvR6dfofB1hbDjSHH9w6441/itN/NzhdKNR1XIZXkfdtbqFRycv8Id9BFG8P4dILyXUyq6fV7WXoCiBOc33oTHp6wny+7lVLi+x5HD49xpSBJUrQ2SGPoK8UggWEqmN06YHJ1i8nxiMue4qNOh4PTAE9pHCmQQpJsphxffUCSphhH0hGSXjhlpt5DEG2AUuzfuERy8iYIiKMYI8DreAy3BoSTkCRNmQYhnW6X/rDP3puPePF6B+E5vJkmTHXdelKo2eLcNnXu0u1CMa9r54UhokFS6mpu9u9LjsPX5cRtZgyPtK5l52xhv3pxX1ORbjeM1XLWanyszebUO2p5Nl327zIpW85umyGuKmNdyRaVjKpysALLRLRYHp2V6SzJUntpYjkfa8PkZTtr0CqWC4vaezmXEDUlY+uS8reNDFENaC0tru09Wlg863jq3ufa1eXlv0W0e7t5wow8SV9f93lT+zsvzDppXhRPU5615XNl/E9XKV8iPuWF2hr+uuJiFv9WxGsqFcVA6QihuGCqkWE5L6Z5bZ1ZqCZpqlk7V2fx3PhKh0hlHM2YnrSZNxN8gsgunNgZYRYahE5S7v7eG4SjGSe3D4mSBB0nuEKQRDHhPMDxHVxtOL5zyJWXrqExjE/GHN8/ZOtKdk6REoKHb94njWIQ4ErJoN9FCsGjmw95dPcRD16/C6nGaE0cxSTTkJPXH3Lrs28yOZkQRQnz0ZwHr9zm+P4hD2894OjeAY6SKCnwpaLnZqRoOppy/+Z97t6+z8nRiJNHx8hUZ7NGJivXyfGI0WjCPAxBCR7dfIBwJBubQ4zWIECTkYggThg/PCZNU45uPQQEvWGPyWiC67skUYzveXR8D6M1xhgO7h3y8O4BsyAgW61m2NzdZDKZgdFoAZvbGyglcX0PgSCJEk4eHHN4/5DZeIZyFJPTCdKRDLeGRHFCnCTMtcGVCtfJyJo0Aq0NM8fHaJhHMa7vZtLdGJTIHFKYRHN0+xF71/fxfA/IvAdGUYyQgigIefDq3XYjQm75Pl9G1z3FNUV14Zmy3u7qB2U2SVBdxW8qvUmUNNpqe3ZWdypjDFqnjbDF4ro272VNGlLl1zTyWCtTrWwrc7cgb88aqds835X7dQpzU7mSoOnbzrS536zJ4db7UHpJq36bM3jF+QN30yvpGriwTGx7b8t70d5pKlK18HfWwGZh8aWEt8Hv7jrm4cecBYHlPt2qVC1kYR0Z8LTCrJsH0RJmnbTarreZhNrunRVu8dqS7LzA+6rNAq0aiKqlEU3L7IIZd8n+erY9lpUyX9RurNgetVCGc6Nc8cjyMpAnQVs2F1/vRZJbCvtW6QkrI1gtHzb8Ta5t3AAD0Z0Z0+MJw70tJqcT0lQThBEqTfCU5PThKcp1mM5noFPEaMq1993g1udvodOUwzuPuPaB53jjd15FasPR3UNczyUNIibzACkErqPw+z2uhQYdx+g05UFHoZOU0fGYPSFQvoerJNObB8iOy0AKtsMEZQwdpZFSAhGe43AynxKnI/w4pascNgZ9HjiGIM0ONw19hwdbkkRrgq6TeX47nuA9mjDt9FAGhvOE/nGA7/s8SGJiV3F6OOLB/JQBgu0r24wenhBHMa7jsDEc0On4HD46BglSSNI0RQqBoyRRmjK9vEXYczgeG/bnmq3uALfjEcxDel0fo8BBYQxsOIrr4wglJSI2pGFCMJ0zdyV3fIGvFP3YZ+vuZRJtCFzJsScJjEEnQ4Tj0N8cMHnzADdJwHEIo8xJxXQ8424QcrcrSB2fzVFAGsfMJwFXv+obSYIpb0Qp2zJlZ6ePMYbXT14lSsM1G2p7Ky36iFgjXPvIlF15LUmYSglRyv3amUq1eaxG+CrVKvU01aQ6xVHk+xVXp7cKbfMAbakX5VwVW7tntop0Ud9XWE6crLJGtSS0FH1eFzWhVZC41XJ93XFnMYZ2gtdW20vLlYv4WgxbOne/n4Wrn5smyocbKSwk93QpyUJsovFhYWGxBt4GUrRGl1xXOV+l0L/dvX4VETsrfB2PIwUX01zHbduTkLYLx2HyLOUZNVmES0tA1uPIeZjzlZri+6psFhblYi9UFUFNQVjQWUpfEiviXMVDnwpReMJX+q6w+ZmlLy2/BQN/yMvb7yeazLkzfp0wiYlnIXGUIAHf9zECgnCOnMyQSiEdRW+zz+jolN5mn71re4weHjOfzBkfjnjuK17g5u+8TjIPMAhSrRluDphNZghHobXhxU6fcB4wn0cc9RzmswDPgFSK7Z0NTh8e81yiSCcxUgpElOBKCSIFZdBpipAJPa0xiUYISbeXkSmpwPFc0jTFubyJc2UbHUZ0tSE9OCWYBWztbbE1HDK6e8h2anCmCUPlc6xTuv0ebreLmY9AZmeVRfMQKSW9jo9yHWbjGYnW7O7vMD4eZ1Z8R6GUQhjDLZkSzsf0t7psT0JUfq/b9TNvdEaztbXBZDpjfDzi8sYAYzQ6TTGpJgoj9MDj0dDFCNiZ+Dz3cJue6zJ3DPFOh0RrjFQoV9EddhmdjLjiOhhjOJ3NUUoSRRGH0yn3fYFxFPI05fqwz+hgxG/eT0l1ShRGdLs+L37VFXrbfe6MbxElYU0+nD8rUH0/O8w6LvTruJWm3EpTqjmaSgFv2pIWZ32qFKQUgFwiJOuKyeYM1nloNz2uM2Mimv+0xFGbwVszdZOPYeWsX00Q141WF8P6zzSXKhbDwvLzC3a5ZhyLdVe+jqYhr73q6nM1zRZ08ZKf9Q4vqqDUcZH2ZWHx7sfTWz73NPtMffw4D2bF31lxiRXXV4VZFceT4kniaBvI6vlsqQNR7Gx9yppzeTBpPcFaXspBxdRe0eK7MvVZoiKAwIhmXPVSF4+f6STXUFuaQXFOKo3T6+pWvcesmwtwx9V4psadljm/WnsorLWTRydEswATJfRdh/tfvIsxho7vAgYH2Oy4dFyXnu/h5zMejutyePMhfq9Db6NPt9fh6NZDkiDm6geeI9EGR0qMMSRRzOWXrnLlAzd47iteoLvVZ7CzgRGSQBtwFMJRpEmC0Rq312E6nZFGCSLRdJVkliQcTudMw5hZknI6CwhSjVESpORoFnDr8JjRdIZJUpTMnEEc3Tng8NZDDm49YHI6IU4S+tsD0iDi9GREr9vBYDg8PMGkmYtv1/fQBgabA+ajKb7nIZVkNJlxdHxKEEd0Oh6nByegNXv7O1y6ts9wc5A7ZtMYbUiSFAy4notOUnR+lpKnHOI4QScprpIYnXUiCZwenSLIzjfycrfoGsHejUvsXNkhMZp5olFKkaaawcYAk6aEcYzjOJh8xqrneXR8nyAISaOEKE7Y2tkiDiMOHhwyn86Zjab42hCFMdPjCWmcNJvMuYSoamnVnykNNYb64jqWOv/6S7qrxVFtQ8ZZqyCklDiOk88wNlNvExarDDJvDxalL7VlaIsLDtdEuX659tyKMapYpnd+HtcZ4JefeixbpWguEWws9TNFLs7LRyULTR6JWByblnK7kIfacFb+nT0yromL1aPFk+HVV1/lB3/wB/l9v+/3sb29jeu67O/v8+EPf5g/8kf+CH/lr/wVfvmXf5k0TfmlX/qlsv897t8bb7wBsDIuKSXD4ZAPfOAD/Nk/+2f5pV/6pXe0ft4OPN2ZorMky+K99QxbGS5isr9I/GdhHVNdq+VnDdEqVnxfF6uIzzlpNXJ2ngHoAgai0reNWC5YScRaont8G1R9oUIewQrnA0tzES2zFEX6NxyH9zsOJox5QwleS57aEaQV7PgC1K3KpmGJ3fA3eGHrPQCoueDozYdsX98lihKkA0Jr5h2HW67A73YYjOZsIvAGXWbjGa6SxHGCweA5DndfvUN/o0+SZLMcd1+5xQsffZnOZp9kNEdJSTALCU5n7L3nCspR9JKU+fEUt99ha6fLdDJnfjBCGJieTNi9cYlJnpbwHG52FdPUIZmH7E8i0jhhb3cr2x+jFA/mcya7PQSCyemY/q0Dtjc3SFJNqsfZsrmOQ7jdZ2N/k77fZfLmG+hU40rJLEnZ3hiQxCmz+yN0kuJFKdr1mE3mREHMcKOPu+kxncyIozgL4zrsXdvHCBgfj5lN50gDVycxUZq5Lj/Y6iJ2OkwPTtnM9/N4votOEoa9LvNAIoFUp4SO5KCniFIYDvp8dDDk/oMxbpzSudZj89oOL0vQdx/QdRxmacKu9Nn2O9yONHMT0vFcXKWIohjlKKQQ+I6CBIJxgJOkdHsdhIHUAF2fay9c5vjeEQ/v3Mf9BsWly/uY1HD4mSN0pNsbGIt9v1K+V5GV834/PnIDD+t3/7pXvGVJ1RbuyXHxIysWSrTG6oVq1qzYF9Rm3FtWFjKy0C7fF2NYdOZThFuRWi0VSmcR5w3jS8u8ga4QfIPrIQ3MBfxGFKGLiFoSXibcphF31lxFKSlh2X9ceymeDHZu6J3Bj//4j/OX/tJfIlo4g/Lg4ICDgwM+85nP8L/+r/8rP/IjP8Jv/MZvvC15MsYwmUx45ZVXeOWVV/gH/+Af8D3f8z184hOfuJD7+HcTnsJM0YJV5iJk56K4yCzHeWHXievCpqPHsjU9xjNrJNVq4MlMV4XltzXOCxahFKBndZClUat+2ZQjW2l1rJnbqn/r16sBqSJdjz/9VRR7T0q+ynX5iqMRV+yQUOFxZxeLGbr69GCpTDQX/hTNp+v2eGHrJW70niN+I2B2OiNNNMPdDabzACkFYd/jsO8xv7LJzHcwwNblbZ7/yEtoIfBdB0l2ts6g3yGZh0hjkI6i0+1w7wu32X/+MrHRKCUzN9TzkGgWoo1GuQq356GThOSzt0l+5w3cO0conbmsPj04YTjoESSZS+qjvsvRhsd84APgSEF30KXT8YmiGN1x6XzNy3S/8f1ces913uv3uYLiKy7t8VVXLvPebg9/FuL3fLau75JMA0bHI1zP5WQ8xZWSzkafQZSyO43YD1KcMGE6mpLEKZ7nMtwagoE4jBFCMtwc4Hgup4en3HvtLsePjknCCKENz0mPj+7tcUN5nPRcvhjOuS810nPZ2t3KHEBEMVEUM57PmQYBRghiV3G/q4if32Pr/dcwr9xlbxrRmYacPjjC8Ryu7G/xkvLZD1Iuz1O6D07ZOpzy0Q+/l+GgR5Sk9Id9hsN+5lghjBgHEUopdJri97psbG2gk5Th9gabe1s8eO0ehDHdbodxcEr3aofNlzaRznnDV1161OXJRQaR6ls101RcK5wKLM05LTz1OLKk6h31uYi3Qyq1zcgsls/QNHYVzhWgPnt0Fs4rTXa/SQPaZj5WvEux/LM9tfytFmV+XFkHeAI+6vl8je/zfsd98ndVyEzqbfj8WM8qQv3dLrbbemu1o9/bi5/8yZ/kB37gB4iiiOeee44f+7Ef45Of/CQPHjzg3r17/Oqv/io/9mM/xu///b+/fOZbvuVbGI/HrX+f+MQnynA///M/vzLcCy+8sJSXT3ziE+X909NTfvd3f5e/8Tf+BltbWwD87b/9t/nrf/2vv+V18k7hKc4UtUwHmIXbFzFArXO/bdrhceO8yHOPO86tncDqWyK/Xq3Hrlm3zomuiEDIhcy3PVNwD1P7viLYuTDFx7J1bdkiunDF1AiXaXxk2Xp8LlTG0fwu8J6/ClEITzhRVKdvT0La3nE8blsXIIoTNE0RUV3Za75QgQANJ3cOGD08ZTaa0/Vdbn/mJv1BB4QgTVKMlkghiMOQ4e4G0fF97n7xNns3LnHtvdd589Ov03UdeiYlztuw77pMpjNEvg/n6M4B+89d4tHNh/Q8l9HJiM/92mfwOx57N/bpbQ+YHU8Y7mwwH8/Yu7bPnS/exsUg5iEGQZKmzOMYTRdPOTgqQRhDr+PjuA5zglwJAekq/GGXjfdc5cbmFm7XZXIw4uD1+4SzALXZ4fjhEVEQETyasKMkcRQjtGHr0hZRGBFGMZ1el16vw8nxKZ7nIoWLkJLRyYTJaILjKBzfxen6nJxmS84EWZ9PtQGj8Toece49DhTBbM6m4zLYyA5hdfIN/7PZDM93ufbcVTav7zDpuJgtj2gecetTr3J9HuB7Hp4SHNw/ZO/+MYe3HxEEYebYQQiSOObWF24z3BzQ63UBQafbYXwyxlWSIE7o7Q5I5iHKdeh0fU4eHiOA+WRGOAsQwDROCecTzMuG26/c5sUPvXR++8tl5PIwtHhYaSVLmrMXy3b5amt+/u3MvrE483QRLId+Sqf8nZFiUTLTknxLWRrnANWercW1Mo2iz6+YQVlcjLd6XqRl9mxNC/aiQ4XmzRXzJYXtd2EFRBVnM+yqc/guhJYZOLNQgcsqV3v+i/PvilmnxSJYMvTO4D/7z/4zAF588UU+9alPsb293bh/5coVPvaxj/EX/+Jf5NOf/jT7+/sopRgMBq3x+b5ffu92uyvDrXq2Hv4jH/kIH/nIR/jYxz7GN37jN2KM4cd+7Mf4C3/hL1ykiO8aPAVSZFb1v4vpguuEayNb5z37JLroYv4ftzznPbeGJBLAN3geu0o1rmvgV8OQsVm9jKQ1X6tHmQvjqXDEtYjueZX4eC+7yP8bSco/N3MADtI16/OceBe/vavQYJ882UtuEKMmBt6Ql3ffj0CgT2Pu/M5rhLGm5zo4QUxHOoxPpmitkUIgOyf4m8dEWrP3/FfjTvcYH4/53INH9DauM76+xcbhFKEdXASu6zALQuZxjIhj9vZ3mJ1MGAx79Ic94nlI13WZhiHb+wMufeAVLr1ngysfCHnt1xTDnQ2Up3jhK1/i8NYjgvEM3/foOC4SwdWTgChJ0Upwb6eL57ukQ4+NmctMT5HS5fThCbv9DkYb3J7H8e0D7r16B08pEIIrwmEYCIKTI3oAQhCFEdsbg8x73sEJIndOoFQ2QxKHEdvbGxwcnCCVxPNdhJAkYYzWhq29LU4PT3CUIo5jdKLpdH38QZd7r99FScGL05TNnU2U5zB78ABPKUIluN13cfwefTcbIl77jc8zMxrd99FJwkaUohyFkQIpHRwnZfzohLvTKaf7A7b3t5H3j+lPAtI4JZjNmU0zBwunx6coQDqK51NBdH+EdBQjV/EonCI2PN7r9QgfHeM5ilkQsrmzRXJ4xM5rO3Dgstu5yvj5K8SASWNGr/82Oolb23D9jDHROLOlKWzWdjiw8O2tJSu1jmfACFPrjs08sHCtPbbz8/q4Th+K9NvtiG3pGowRLcTootbTtvDnDXSsIZZbGVuTqZkqopmBXwjnSAShMegi6BM2jbPqv406r4flHmAJ0TuDL3zhC+Xenv/gP/gPlgjRIj784Q+/Dblaxjd8wzfwbd/2bfzCL/wC9+7d47XXXuM973nPO5KXtxJP/ZwioH3+tm3W+6K6YtszF5MB66Mu+ETL76eJNcogBDzvOHzIcRt/H3QcOgvnbSzl+dzI6+FrQ1dx7W3R6ZcZb7EMo5zyz5fPlYsoRK7wiMryddFXY2qfRzrls3HMZ+OYR42zQyweq83XK9cs3qiGes/xub7xHNcGNzB3I3pS0VWSjk4J48zdda/XwfEcpO8g5Qx/eIz0HjA5uE00D4nCiKjr8sXjE5Kr20SuwgiBxhCEEYnWCClRUjIfz9jZ3cIT2RlF2YyMxhESoxOufzTBHb7K/vvGKA86wx4SQXejz9X3Xkc5DkJIpJMZKDaDhCsotqTDqOfwQMFxmtAddBhuDEiimEd3HnF86xHKy87zOX1wjO+6REnK5u4WV3a3eE+vz26Q0ksNcRTjOdmBtIeHJxhhkI7EaM18NkdISZqkSM/JPOAJgTHQ63VwHcXxwyPGxyOMNqRJ1pZdR7F9eYfT/JwjTyp2E9iex8Sv3UdoQ7/fJUpSjn1JtLfBg/mch7cfMpsFuIlmMArYDlK2EJBqdrY32dgYZM4atGEuYb7d46FIOU0T0jglTVPmQYRUkjhJSOKEVBu01mymho1ZwmAcQs8j3Ohw1HUwPReAeRCxsbvJ6fEpjlTIRx0+uPsR5E0XI/foXXqJ7v4LCKmWmumSRGnRUJuzSI9/Ut7iEqSnAbOgDheb+p9GvOuW9OJlWT5wtg0r9xOtvNoeMqvvi+Wy7aylx8lFsXSyQAy8kiR8Lol5PU1yG9BTUhYWzuJbuUSxJnNXlrB9kqsRxbvUjPeuxKNHj8rvw+HwHczJ+fjQhz5Ufn/48OE7mJO3Dk+XFK0iQ+fJhbpRp222aRFnxbluHE8C0/LXlo+2fD2hacZoTXQ6Qpeb8VYIxrPydWa6FxeH5xYjT7O+Jnx19hanilbZHSm3qNRVhbeKI6+LVa/9XYmcbF6oSZzV9soAtV+1QXx+PEafTHCTmIFOEDpBScVcG4J5QGoMJtVIrYmimNQYTg5O8QVs7WwglUJrzdH9AwyGIIrRqSbOl5Bt9Hts72yytb+N03G5f+sBBw8OwRiE62DI9h0Ntof4vS5xEBHNQ8YPT0hTTTSac/DKHeI4IYxjhJR0Oj5CKQwQRXF2MKnWRGEMqUFHCXGS4jqKB28+4PjNR8TTkP5Gdu6OchR+z0c4CgQoKUEbHClItGYexyAE0nGIw5jhxoC9S7ukaQoimylOjWF7f5thv8fp8YgkSRHGsL27yc7+Nt1u4SUOTo/GTCczfNchiBOmszlHB6eYJAGdkkQJQoDnudlSRQNhfgCrkgIjBXEYk0YJaao5PR4xHU8xGEYHJ6ANo9MxBw8OSZOETrfD1eevsLk9JNYpfq+DIyVBGDIPQsazbGZWp5okiJiGMV7PJ5gF6DSlu9EjmM7RcUKK4YWPvMjo4ITbn7/F0e1HjB6dNNpbc35ANDpffV6l2QDr5GNVw12tSje8j7G6v5c7OFYcUrrqqVUpLl5ZR9JcdGfSusN3zZS1Mt1FMrZ4KOvTRZbzwqBW1LlZbChnojnIl/lffH1vbUHKnLTJzgYhbOw/Wp41XNwVtgrv6jHrXYj6zNC//Jf/8h3MyfnQulpBU+wx+nLDU1g+t2Iq4bxedRZxeRJSszhrbhaurfq+TpwXzctjzuq3ZiEvRxoG3Prff5lr/8Y3093dWR1/S14WfLatCtby4EUGkhXZWbH5Z+lqwziavaTVB75Wz6yamGxTd0T+cHl9rY1J602ZLTevXDF7mie4vm0olMqmxXoJrW267ZmFgMVhkDnDPb1zSGIEp2GSb+cSQEychsz7HqcbXYQQTKVGGMOw10P0E+7O30QrgXIV22nKdDYjOt4gTQcIA56jCJMUKSU71y+RBCFH94+YRTGulBiluLPpcxRqul/5Im9+JiI62MPEsH1tn+npHY7uHWYuobXBUYowikmSlHEcc7DXRwCzWCOSFMdRnI7GjEPJyWjMUAkGpxEYmEzu86kXLuFd22Q+GbM9jpiPZ0SzgPHxmCSJcV03tzJnrF85ihhDEscomTmQECZz5xwGIUopwnlIf6NHHMVMpnMUBgVEQcRsHtIb9LI9UPN5NtOlJEJHuI5DmqQIBI7vE8XZErRer0uYpkig5ypSBFNPcceDtCtwgogXEkkYhjhK4ShJagyDMOUDJiNqZhYyMZnzCucD11GbHUTP59I4Qtw9QrkOxw+OGZ2M0VozPJzREYYrw02IQtydDUxqCCZzpONw9eVrHN4+ZHx4yvbQR/FpDh8l7Dz3fpDNmd2i/rL2JRaaYnP2pXhCLNxr4mk4N657UVuXwFwk/jZUfa55qOzTmsFY4AO1ohmzILtr3f9inu5M7QypNjLY8sRivhaunTlTUj8aogi78MrK/J9FhtY5S/AiWIrK5P+b0kFRMe60n9ghIHeIcRHPYWfuvbJ4Ynzwgx/k+vXr3Llzh3/2z/4Z3/u938tf+At/gQ984APvdNaW8LnPfQ6Afr/Piy+++M5m5i3C03G0UHehuWbnydXd/Ecbk1n4etbM0GLY8xJe/L7OTM9bhSXh1F6I4siC2cEjjh/dp3frJp3tLSjOt2ifUGmfCzyjTpvRLAS46HRMPQYh1iQfNJpSq+wWC0PhEl8ph4bl110f2BY205aHCJo28nixUaGaAHkXDyiFInAuJ8rrumLAK0KubkDBaMajmw+zs3gGXXq+h9Px0KkmjRPi5/d4OB0TBRGpq9jtdhls9Tk5OCF1NKnWJPOM+GiV4nk9tjt+ZSnO34OOE5I4PxTUc+lv9Dk+GXOiwH/vdeLL25w8DPHiIUYb/KHipa97H+FkzvRowsmdQ8LpnE7HQ2qDcSWBJ4m1zvqiEPgGOkIwOh2jHIWnJExDkiQl7nm8cXyCN/PYcRW+Ixkfn2IQSJEd5hmEEcYYfM/DGJjN5niehysVnWGP+XSO4zu4jsPkZIJQktlowsb+Jt1+h+lsjhGSk+MxYRRny9biBJ2mKKXYvbSDQDCfz0mSFNdzUQaiOGF8MsLp+iipiOcBrtEkqUGjSaXDtO/R73VxDk7hcEqqnOz8IWMgSdGzOcNhj/F4hhQS5bnEQcTnP/sahxuZA4qvkD7v295isL/JznP7BNOAyfEYQXYuhtfxCIVLHCfc/uItpJJcev4Sh3cPiKcBW/0uOolxelMEExL9ECFa9gCa1dS81fjzNuCpEpKVWFXCt6GMZyTx+C581zNINdNqptmU9evF1TZcLbWlReLXlolz01mDYC09RM1pQvONi3qg+pWMka+ZrdpRCXbaaCXu3bvHjRs3Vt6/ffv2uXEIIfiv/+v/mj/9p/80kHl3+9t/+29z48YNvuEbvoGv+7qv41u+5Vv42Mc+huu6Ty3vF8Wv//qv87/9b/8bAH/+z/95Op3OO5aXtxJP95wiOKMDiYY4apsOfqKpiPNIUzFjtB4HOTuOxesXieDMZxYKI5qJGcDd2uLK13w9/qXLaG3Q8owitBCidWaLzsXFx6jssZrHnuZ6+bo1s0pCLGo1S6NUi8W3lORnoxlVbR284cnr50sd5/WZRbSaV0vT7eMpWws2lOBwjO84zJOQcB4RRQlOGKM8B1c5RPOw3BsjDAw3B8wmc8IoJtUanb/QVKcYY3CEINUaoRycjsd8PAOtCY/HTOYhqda4qOzsHmBzf5vhe68DEM9DCBO8fgfIltR1twZ0N/t4nsubv/saUkiMAJMkqDBEuS6xlESpxnEUnlJs9joEeZ5Hsxme54GSGKMxQYDSGqENHdcFmV0P4oSNzSH9zT6djR7Th6c8enSc7b/Z2QDfITiOka5DFERobTCk9DyP+VG2bE0DynUIw2yJba/XxfVcjg6O8Ts+ve0ByekMd9jHGXQI5xGjRyeYvB6Hwz53ophwHuIjCHWKnw/GBgjCiDSKEAi6vo9WsHtph9GDY6YyQBtwpEQ5mTc5YcDzDMqRJGnCnXsn6Nfv4/k+Qgk2tzZQriKcR7iuS5pqEq0J5yEGGO5scnDvEKM1270OxAnCSRFRwvb1rWyZ36qmW/6zcG1Fkzy7JV+046wfUzPt0szwxOm05fXpleLsSFYp+Y8jXx+HULWTjcWDxhcfyoe3FYSo0Ftah8C3k0CUpK8xei1lpxb0QnlrPYzd4i3Dd33Xd+F5Hj/wAz/AnTt3gIxQ3b59m5/5mZ8BYG9vj+/7vu/jh37oh+j3+29ZXsIwZDKZAFkfunnzJv/qX/0rfviHfxhjDN/6rd/Kf/lf/pdvWfrvNJ6YFJ2tHzd7UlMYrtnLLtIZl1lXZSTRZtkV9bppripg3ZLe9ty5EdTvNaYwannJEjAY/n9hmClQH8ynVeMQE8OoWOd5ZvGqjFbuU5t5q82XsMwA1yjKKpRFrEaNgiKvG51ZKfoXxqJ8pudLBWfl+XHieip0bW0ytEYGWjNUBFytJSw+FgcRHc+DJCGOYoJUcyIM9z2DKw2dh0e8EGdLyBw55BKXOJ3O6Y2nOFIioCRGjlL00x5RmmbnBAGuFPi+R5ykTGdzHEdxZ+ASdhzCRDF5dES60SH0Pb7wG6+igpit6/tEX/8SdD1Uqtn+4iMm94+z2RUlCeOYjuPw/CjG6TqEScw0zJbJdRF0XRfXdbkVzvn8hsPe9gbPX7/MV7zxkCQICRV8bstDC4GnJIk29Ic7bO9u4zwccXjzIePRJNtvlBr8zT6nh6cEUQRSMNwekIR5fYURQRhxZ6uD6XfY3BrSe/UBMozp+JkL7jRNGU1n3J+OGby4jx7P6b9yF52mbG1vcnTvANdxcOOUK/em7CQJeA639gckaYrju7iei+g4bPn7yNceEiUxg+EwW8IXx9mMF9DpdcDA6XiaNYHNMb3dKcYYNqMdvNMhWmuCeVSSn3sDDzpDvK5LGGnmWtPd2uC20cQDh52NAdw7ZlMIOkZy6c3rxA8drnzgGkfJMSnpUhPNbCRn9ZrcTFQYbFbMnj/JDM8qirM0i93I01n5OC+9Qoqvlj6PQ7iax8i2jO3mLPJSjXM1U9b66Z4Z9wrUGkNDIomWJnGeYF16eXk5yo2tj08cnuQQTJMbAZtjep4VU+kORTrZzFYZohlX7dm2g28tlnH16tW1ZoPWwXd+53fyx/7YH+Pnfu7n+Lmf+zl+5Vd+hS984QsluT84OOBHfuRH+Jmf+Rl+8Rd/kf39/aeS7iK+7/u+j+/7vu9rvffX/tpf4z/6j/4j1IIX5C8nPDEpKpTVdtuJaf95vtxcH6tGmoWkS0K0mMaK8Et5elycU6Zm8qvr0Bh4mKbN50QtdCnoVhek7eiFugtVUwv7NNE2HK6FVtewopxBW5nLNdbsizPe+3lNYjnmNvIvFr41Q5+XRhsWz6Y4D09MoharsdF+REvkpvVXe301wwolGU+mCEfRubTN0HNBGuTAIdEGDif0T2a4UtLb3CG4H3D1xvOk3YQkSghnATrVGG0wUYrb8cATDHwXz3cx84w8zOchwhg8IZk4gmOTggSlJPe+eIdhr4McTXHihPj2I8bPbzF86TLTe8eMfvc1TBiTGI1vYKvfy1yEBzPCNHOSoKJsKZ8xMDKCjpQI3yXxXdSNfWS/w/Vej4fHE9juMfHy/TdocCSpK5klCeHDE0ajcba0zXdJopjpbE44nmMkONJBOQ6X33cd1/c4uXfI4e0D5h1B98o2DydzrqUJnfxNpElaeqw6EYZ5GDB6eMj7o4Td7Q2OHhxmHuFMyvh4hEgS+lLCoEfQkwhjSBAYrfFSELFmNBpx9coVdq7s4vY79I7HpAa0NqQ6I6T7V/aJ5iF3k9vM0kN6nofjbOBIieu59LodojghThN032ckNU4a4nRdjN9nlO9r6m4MeBQn7LrZuUwxEB0Zdm7ssplsZedhLbaqvJktK8FN61nZzM/oVudJlLNcXdd2epShH4eUXOSJs/L71iyjy+XyOTLq7L1ElVxfuv8YWW49R2qlQGyOKSuOIVqK8+x2Uad/54xZa2PdFCnJz9JBvKZ6PUuzaaYijuvTcIunBc/z+PjHP87HP/5xAEajEb/2a7/GP/2n/5R/+A//IVEU8elPf5rv+Z7vKWeQ3k781b/6V/mmb/omPvaxj73tab9deCrL5x6vu68R/nFI0qrnHkcLvUhaj/143YYF1eCyEHCpDi6672W1iry28vyYZRVt7wHA1H3RceZ7Lgaj3DCWu6c9O5N1K1q7eD/DumfKf1bmqH62/Zn5WHnnAjCmnAlZtOStfOTCaXCW+fqciFeVt91OXl8PD7D53D6O5wKCg1sPeXT7IacdhyjpYpREGTBa0xv2mc3mhPOQ6M0HdDZ7oMmWtvV8tq7uYlKN1/czF9bGcPzqfe7duUOcpEiZachCyewgV2lQSpGmGqEkwTxzXNBXDsJ1OLl/jPZdksmcTUchtaHrudn+oDQlihN6no8rs307G1tD5rOAOIyIjSFJU4SrcJQgiWK0n5KmGg1I5eAPfXrDHsFkTjALmExnzBKBnyR0fA/pKqIgJoxjelGatX2dzayNUs18FtAddEmjhDiOMR2P05MxcRBhEPR6HYJZiNfzUVOFERBHMaObD3C1YXd3i9nRKUmc4DgOMj8fqeMoEimRjgM6ASGI44iN4QC/1yWaHKPimNFowvSzb3Dt/TfYurzNdDpHSBBG8cJXvszw0haPvniPLTNgpk6ZhjHj2RxvFuB52VlHrqtwOh16XZ+042CiONvP5XkQRiAgSTWu45CkCXMctDE4vuL6e66inWo/UUOWmVWybYGQQ1NTXMB5Pc2sFWqdjvV00CYZL+bYYP14qwSK2YqzTEnNPCwP05V59UJpr4F6Wquk9Sr76plXzpDDTaKdfRHmSdy+t+WkZuxdZXhtOWR31e+2VN+WvWgWrdjY2ODbv/3b+fZv/3a+53u+hz/wB/4AYRjysz/7s9y6dYvnnnvuqaf5P/wP/wP/3r/37wEQBAGvvvoqf+tv/S1+4id+gtFoxMc//nF+93d/l729vaee9pcC3jrvc48b1bqom3Tq6Z+XlXXI0aL0eVy+1zYlsG4Zzwn3ODW+uLa6ntDibp7ldJ42m6ziLVNeo44EnLM6rj4A1AyXj5/BhehXmBDfagiRc+X1zgG5MJ7YKChaf52pAtT6lvIcojDi8PWHBPOAvuvQwWFwHKINdIWk3+kQa430XUScEAdReQ6OOpIYIXCUwsQpJzcOSfYzxwKjXz1BaY9uzyeJYkwKQmuSJEE5Dq4RPH8a0csbliMkjsz2DEXTOTc/8waOUpz2FaIruPTcZY7uHyHiBM84XDkJ6Hseju9y6b3XcDoehzcfMj+ZEAcRW1rwVTND8uojOoMZxnUZbg55kDs56O9u0tsacPrwhJPjUw4eHHIpjHCV4I6jOOz77O5cIuh4HDw8ItWGOE3Z3Bjgeg46TgiShHjTI1ISE8cokTlOOA1ipBTI6YxuxycNAq7dG6FclXny0zGT6YyO6+XEQ+G7TvZetCY9POVlJUl1ysagjzdJObx5B09JpkrhuQ5ur8O9L9yhvzng0IXTSxuEkxnHHcG157Yw1zfYEy/Qi8YE4zk7zpz+IGQ6mnJn8yaT/og0Thk+vMb2rJeRVSXxvGz5oXAkUkr8foco1XgbPpef3+OD6g6d8f9JYDRKx2UzXmpk5xg4TF1pbA9x5t13RmW8WIddTTeeDsqx5Uwlex31eh0q8gRoXTtX5V8stZXH128MJpfZxRhLLscfkxi1vnLz1Mak5bHVkqEvJfy+3/f7+PN//s/z3/63/y0An/rUp94SUlRHp9Phwx/+MD/+4z/O5cuX+c//8/+c+/fv80M/9EP83b/7d9/StN8pPCVHC3XBcQbrWOpw5/TktfvkUyRmF8FTS7Ye0UKE7XP41OeYHntGrTWJFoIpFj6fVlULMGcynPooYMqp/frz5yZxEdejC65Ym606t26adkX/aVdNG4R8Ooc3tkde+/5Y7Wmxptp+1YM3VTSdpJzceoQrBF6vSxDFxPOADc/DcR3iNGUcRqQzjeM5CARSCNIkQSlFb6PP1o19dl64xPxowunOMfK6YXI0xt/w0CcCbQx+p4MhJE41SkoEgiCKcYIEESUkWmfOEKRCYIgShZQCnWoi18FIh2DgIy9tcfLomG0jcB0HpRTGkfjDLo7vcvWDzxFNA1799c+TzENcIegrRXx4SrjRx/dcdBQQTAMO7x5kBEQbpOOg3ISO52S8xHcJfMmx0aTTGaEn0YlGdTvMOw7DG5dIk5TRrQdEccLW7hbjkzHxPMR1FR1PIYxBKJXNxM0DbmxuMJnMiaOIeZqiZOY9z3UdojQtveBJnRHE7X4f381I6+mjE3ppSm/QY2I0m5e2iGYRsaMYHY9xdgdMJUylYXLrDurGDhuXtkF49Lqb9Lbguc2Q3Wl2htTW5S0eOfc4uXvEjTevc7X7HG7HxXFdlOcglawd4gzmoxopJYqUwaNXcaMAgy6NOg2RnM8Qn+sOv7GHM/tnlf75NLrfRbrXE4r2Gt4qybFGpeRBsgO4q5w0DXFnlfQplF40v69sEovMoDndc2GY2r9FhOYJ9YZlO+vqWc7HjbuJd8IKaNGGD3/4w+X32Wz2tqb9Qz/0Q/zUT/0Uv/3bv83f//t/n7/0l/7Sl6Tb8CfFUzi81dDsNKbQHN86mMUfC4Nac7KjHWLhe9vvRTKwKnxb3Bd9pg2r6tA0b1fZFQvVcZFMnhF28RU/xdF1acxZlPi10cuIhQBrt7PFAjTvVYf7NUM3W3WxYdWsrLl37dBhWFXoC9TvBdHYmGwQnuL617yMM+wQaY2Sgo2NAdpoTifTbJlax2dr2Kfre9mGf9fFCJHtYUlSklnIzd96lbufv8XJrUNGt47Qk4jOoIfjukRJwjw/VyclW9qGAcdRdDyXXsen73s4QtJxFI4QuIZsD5KS9ByJBxy8do/R4SlSQJSmKK0xcUI4nvHGp77I6MExAE7HRbkKqSSDnSFhkiCMIY0Sjk/G2VK+NGVyPCKKIuIkwghNEsdEOltil+oUKQxhMCeOo+zcoI6PEoIwCJlPZpn3NSlQnsPkeIROM29s/X4PR0jSVBPHMZPxhK3tDQyQxnHmQZzMQcX+ld18aaHGGEOiDZsbQ3q9Dh3fJQkjjo9HpFqTGsPx4TGDwZBgEpBEMXEU43kue9f32NnbpNNxiZOY13/r88RhAGiMSTE6RWuNxoCCbs9j59I2l67vs31tm43Lm3S3erh9F+nKbIRSEqMkKAlKoDGkJiUxJv9bYVIqNsFfAO0zy3mPF1Uaj9VNmrFdKPy6V996LJZ0tTfT4qDaht1ryaolWr6vTvnxZexZA3pL0DWCXRSGnBg+yUCx8KwQF2tNWR2uel+rsvY4yovFW4Fbt26V369du/a2pq2U4r/6r/4rANI05Ud+5Efe1vTfLjx9l9xrY4VkWNd4dE40F7J8P4nCv5bVpxlItHyrf7/o5LqpWd+asZnGv8Xq4DL22ibLZhWIRpYaGzWfpuZfKCCmIB1kG6ZbWUb9HJxa/p5wgGlrbudDVP8KLqx4fcnhiWeJFiyr5xnmF4Kehqf86q1fBgNbL2yxeavP9GDMbDrHkJEAz3XQQBBFnA58HvRdpOxwaZrgHow4PR5zcjTCUZJ+r0vvs13mn87OBnp1E8wLOyRxzGw8QwKO30F0ffQ8wFMqa3tCoJSi43soKZjPQ54/zPPgewTxLJt9cBV39vu5U4EYne8tcl2H8HTC65/6Ahv7W1x68QrF+VzdzT6q43F3POXRwEMqn60o5YNHIaezOd4lRbqZopVB7sXEiSEWgj1PsaUknuPw5txjFDtoDMONPoeHJxw8PEIgslkvbdjc3yKchYwPT4jjBNeV7D93lcnBiPl4xmwyJ02yo3HTRBOnKZcv76GUIokStDb4vsfGsE9iDIeHIzqTzCIphMAoidQax3HpdFyOD45I4pjOYMjW1gazziGdvQdscALTSaYUy5DwUHL6xgiAY23ItgEZPnYo+WpPMD2d8ZsEvJJ8oWEpEVKy/cF/A7e3hdEpR5/91yTBBDB4yQyBydrF29gHi3abySsu2FcuntaXFpZzdJaDCVMYr/LZvidN2TzG4aMZmoLtzNmiKtiXNIr6KH8veQ9qe1eFWc/iSwWvvvoq//1//9/zF//iX2R3d3dluJs3b/J3/s7fAbK9Rt/0Td/0dmWxxLd/+7fzzd/8zfzKr/wK/+Sf/BP+6l/9q7z88stvez7eSjyFmaJ3Mc4wgDQuL07JXCCeZgTVr8JiU80/1Kw45Yi7IkOtaeVUKs9Lm+G/mROz8GTzd/2/t8RQtKpOG4ZDQdvhtvV6Q6xjEF5IpKVilu2fq2PKNKFVNXx2LtYL9Q5ubV31rp/aTKEpX1jxzhKdMApHjKIRcx2QxClu18fN95S4rpPt74liokQzSVOCjkvY8QhNCsbQ63ToeB5CKqIkRc8EvajHFhuEYcrD0YjDecBUQugpxmnCZDbH87O9NEZrPN/LiE2UMAsikJLLm0M2HAcVxPTilE2p2N8YsnVtH+04SOXiSoWSMlM2ZLYfKTge8+ZvfYFgMkMaeHTrIZdeusr++64z7zocxTHzMGaYaPoaulrjixhfJLgdQdIF3QVtIjoipSMSXClAScIwQgkJxhCGEXEYsX1pG6kUJwcnJHGMECI7cDVOcTyHKI4QUtDb7nPjK17AcRTGGLY2N+hu9jk5PMnOTwI2Bj2MEJwen+K7DvM4c/SQYrJZM9/DcRRKOUhHMA1m9HsdpFLMJyOmp/cIkyNcP8TpRGh9ik5GxNMTkukJs/kpo/CUcTjCmYYMRjG7sfz/s/dnMZIm2WEu+JnZv/oee+6ZVZVdXdXdbFFsiZJ4RVLQcgeDGQnQQIQg6IWvowc+6FWABEgQCAF6EaAXPUigqIEIEBrceeFA0uDqkvcKvBQpspu9VHdtuWdEZKy+/5st8/B7RLh7uHt4REZWNdV5Clnh7r8tx+w3O3Y2OwedDelmHbppd/S8QzfrkkhH4ksST9Ar+vRGdQ+N4cBYjkZWteuCeZag8d9PtsmpFeQSMtkibf31wxnWr2dpWdzH5El2Btfk1TXWYNno1ccx63B9AzBvsgVXPk/FPMFSTAuJiztYdLa9FZe+eEiShF/91V/l9u3b/O2//bf5t//23/KDH/yAg4MDjo6O+M53vsM/+2f/jG9961scHBwA8I/+0T8iDMMvBd9//I//MVBai/7pP/2nXwoObxK+eEvRRZroC5n/BeXH219UZt7z6VPvCwd3/jReEo8rHRJfJgWcsihcqPlz5f8mxummJmgB437iz17KeBcfGAvnc/w1XZIZWrbUdTMvVzKqTc/v6e+L6rweJlIKWjebtJ/ukxuNdTBIC8IoJG5WqQiJrQWYZszBq0MK62i2mgShjwwDhv0h1pZR2Xzn0FmBVw0QFAghUUqNovgJFJD0B4TKw1eKPMmwtryzIpXCWkORZHhSYqQFqegPhgRKIM0KG1trDJ/vkWhDVQoKa0EIoiikKDTe6J6OkJJCwKd/8CPkgy0272yy/3gHmzusB3HoY5TlJNy8AxgJQM45cl1grcXoAjQ4a+m1u0SqFGzCOCJPMrITIW+Y01hvsbUZ0P34JbvPXoG2bLxzg7V7m+w9fYW2BhX4NFbqHO0ckg4TjHOsr62graXb6SGVJPR9nDZoa5GewhqL8iVGSQqjOWy3iePKKVMscAyHCcKTBFbgnGB4NKQumwSIieVU8reSQguMk0jp4Y3UdE5anABrLDrJgASBRViBkt7Uuizd6a4PRuvTjZjv02igZxbqkhy5M6uWWEh+JkBcWOI6YXq/zd7T1xGd7qy/WXA9gsh4ConlwZ0GF3RXIdwzm5yk09Pn11w2YqZUPQOXi40+Jx1fala/AHHwLVwSwjAkCAKyLOM3f/M3+c3f/M25ZT3P4x/8g3/A3//7f/8LxHAS/vJf/sv84i/+Ir/zO7/Dv/t3/45/+A//IQ8ePPjS8LlueDNC0bK77tICyClXe3UY73MBXZx4dEn8Tt0Glq5zyaJzmr5cEJpxXMcbnZ6YaellMQ6Xgln89qjdWYHy5nU5x3DGuQV22s6cjOQL+jjf4xel6b0euLxANPV9lvLhqtMwFYFpvJlK0eZbTeiuH/LJZ322/ftUmlXW72zy4uNnKASqLVl/6VgHGpUKAksySDgIIHtvg8PdA1wcYqxForCNR4RxHyklg6N3CMMtvMAj7ScIKUv3qzTFt6Vl0lpDURRIJbHGkuUFUpQuarHnUQxSan/4OWEcUaQ5SpXR0ZzR4ARJkhJXY3RWoJRg6El21ipY6yj6PcyzIStbq9hGzkf9IUIbqt6AFiCNw/kK4yyB7yODAOscWZqz4Q3YGIUZD49yxBCMdvQf1hgai7WOe4cJYW64e/82P0gGHK7HYCxfGRiKQcajP/6cz2o+g60qVeVT6SakSYoBanGM9D329w5RUjDIcoq4vI+0utoizXI8Kak2ahz0ujyJHK9WA969eYMjIak3PPpohJIYbajur7J5uEn0IuZnvxqzUs0ndRgOuvG7/GAQUt9s8q4nuZHmHO0c8nLzMQOvR9YZon/7uxTdMlpew4+or6xRX2tSW6kRVSNyW/AHL3+XXOdciz/bGJ0Y//4na8+f36BvThibDrI9iUUpMJ4kO319FC5b/eRMeZMels45JkNfX1Th3IfZFcXs8Z5N47zUwNcJb0WpNwlf+cpX2N/f5z/9p//E7/zO7/Dtb3+bzz77jOPjY4QQtFot3n//fX7hF36BX/7lX+YrX/nKl40y/+Sf/BN+4Rd+Aa01v/qrv8q/+lf/6stG6drg+oSiy6nJrqGTBe3PspBfliBemQ5cRiAqOxonaDOFsWsi5uNH5IlINCEQnQgSXyL9G08qN3k+iFOcRyXO1f0yjXyzsHqd5XdeWP0C4bRLMVvweU2UxNjfaS8T4QyBSVjfqiDWb3L8uU86SIlqMet3Nzl6tocPyMKihCDv9DGubKXjWzptiawEJP0CSxlEIFaa0M9Q0sNTDuMsd96/g1CS7l6bopcQFxLXS7DG4vkezbUqQRzihWVOoqSX0D3skBUFnpBUjEMOUjzKxK+p1hgHDosnJcP+EK01nvIoagGJJylGQoUwlv7uEYUqIx14vgQhCYRAel55P0aVyU195ZXR96KCPM9JhinCOaQ1qEKgtCld5ppVPN+j4hlWKjHHHz3nKIbcV7S21lhJLIOnezghKKoKE3gMtGHQH6KtIYpCVm+tU6Q5K6tNhv0hMi8w2lKtVhAITKFZ2Vyl2+5jpeNF75ioWsNbbZD2E3pYciVQEqSGSEUEOiLfK3ArlmZDTDB9zjmeveqTVRuEMmJ40OPV4x0O9g55mb4kbyQIoah1+0TDCN/zCEVEspfS3xkgPcWth7dZf2d9jIZ+Qbvfjf9155jZZY/DNwfLzsd1Mrzz3T/EjCKXtU4tSpA7//kksTo7X5bpcMH9pZMQ3nAuOeqlYAa6k2fgspa35d7j1d70W4HoTUOj0eCXfumX+KVf+qVrae+Xf/mXT3MNLQN/6S/9pUut45//+Z9/vXX/Ywxv1n1u1pyJOZ+ny8/jfa9jf85q4yKt95U47jmNzjZgzC63bH+XnJfFy1nMnf7rhnOWoZMxn7sJO6kPm31Z9LzNaxaIc4fJZUCAcGP5dS82l8zbBhdZvsYdRV43jOuFcNFau9Cqepkkf/PFPQskJ+G6axFbf+o+T//gE5599IQHP/UutbUGJtforODo+T4mycCVAQM8GzA8bFMNAwIceWGoeAI/N/jKYD1FiCTpJzz6bz+ktdGiubWCX69wq94kyg1CCJI0RwUezlpwII1lZavF2vu3KYYZeZbjkpx0kJD2UjJj8KKQKAqQnqJ/3MNZi5GSIPRJtEFrA0qRFBpfCZS2+FKBdKAEnrDEkYezjsQUWOewwmKcReQaKSVxFOEcJMNhOVNKlaG2pSNJBsTNKmsb6/j9jH57HyoRxpRCUyoi0kKDr5BKEQeK9LBDjiWqxGy+d5tQKuJWDZNr8ic7ODfEUwqtNbkQxHFElhVYa9A650a1xua9O0SbDbb/cIcYRyhKNzshSuGvIEd4Dq3t6SZ3UuGQ6KJAG0OqEw5+8Iruqw5SCioVj1iFWFMQRTFrrSa1Rp1qNSZNc4JqSJ4WFFnB3uNdwkZAeBK2G8gXqKUW5Gh9PZiphHMjK8kZnEYIFV+Mjv9iuB6BZHHrs4nLZdu7qPzp8/GXPLUQFvNx5/FcKrPSVRfUzGNozIIuxr0azqc6mOUMcdbG5Bkuxp6c1H8Lb+EtnIfrE4rGd+C1CxeXgGk+ehk4b0K5EpxVnZb8Lmhw0Zwsg8sE/V9+AOcEn9P+zxCaKRzNw/fKTLubyFckTpo+GcoUEpPWNDf3oHMzPs0rcVmYnutpCxyAO5OcZsCky8n5ZTt9ml8Z1dkwq71lf5sy8UzaOZfRTM+HF9rw/xoOAAgrmvr7mxyIAvPHT/H++HOqqw2CVpXWnXVW7m6w/9k2x7uHiMKw1s+pak3g6dL1zToCAeHRbZR3hxyJNYrQt1hbkB/toj9+hTaGF4gyN4/v8flqTKbK+yzKU8TVmLhweL7HcfuIyFf8uWaDtXubfP7xUx750NhoIUbht3XWpL13TKUWYwpNlhekeY4Qo5xGAoywCG+X6sounoC+1TyvRAjn0IWmowtUGHLT3qRlWmAsTgrCMMBiyTYzpLVIpbjvZaWroEjpPu5hugYnJbVWnWG7gxOCH4YwXA0JA5/qehMnBcNOn883a2ze2kCvNbn77BjbSUmHKXmW06pWMc7iEOR5gfIsehSMYRWPh401th7c5enuId9JBvTTIQ/7Db7ivkZjvcV+7SWPW5/inONr1U2gCsBh7R260RaD4z7f1r/PcfRD5IbDv+WVeaICj41HN3m/28APA4QUhHGEkRBUQvpHPbq9AVIIWmtNkoM2v7RWQVqPgXP8v4cDsjlLb6ljZwkF2amr8rRS57TIGLGaPl/Gys7JiDTd3RtnYd8kk3xOafKmeYAT4fvSmuwphN6I9DzZ20wUx+ZnUm5aJNDMx/WS3MhbeAs/0XC9lqLL7LZZhPEiGnQVGjWLClz0/TVo4QT/PjvpxQy4rDhzvs3JuvOlvOk+FuUsuNQLvaw5ZLqgOD9NpcLvAmJ/BQp/9UOhtBKNa/Vmtz0uvc22uX1x0afmwLxpnfcex5+56QN6ejOPsXFTa2BcCyrc5G8AGkfPltyrwREpSfP920gD7r99Tp4WDB7vcvR4l8pqnbW7ZcJWqSTGGKy2GG0IwoDhcY/dz7cx1iPXlmqrhud7JL0hfi2m6PRRhSkFDudwUqKtJSs8EgOeENi0YJAXiONumQ/JGOpIHn38ijgMOC5y2msR7Zc51rkyNLYU1Oo1+lnG2tYaVU+hC0Nn74giy8vcRVJiMTiRIqUkwmJMilSKwHPUhKDn8tJSJAQGixxNaxSE6Mjg8gLrK5Rw+LIM/V1kBYEXoHyPYW+Ic45qvcqgN8B6knC1UQoWxz2cLENsH/eHpL0h/tMjpHVorQmCMgpfFIXEgY82lk6/j7SWKApJs5y8n6LSguxVG6E8snQIIbQqLQIdMsiG5Os50jm8ug89hzOOfj+nW2g++84TDtbb9EQHJSS1KMb3JRZLXYbYDgx7GVprKlVLVI3oHfc4bHeIwxAnKHMwpRmhtkRKgijna66mZBnafuHWFKPALWOL+FyRBTictrLcQfPjoNO/rNB0YuEoTWLLSqM/OXDhdIjJUrOO0nO/jbn7zSfvb1/EW3gLi+CLiT43zVSN7+aLtEavu4enNXVXhSXwuNgysbitUx56GVxnqg/PT+a8qb7IoLcQrpGuLlLGlQLRFIM93b0bZ8uXHdFVRz7fKnVdfZ2fDjHGYFwN8wuX1Bwt9sWn8LwHY4248yWnuxZTBU63rDPYPAFg9VYTtRKh2z2U8hBeQLp3zMuDbmnhCX3W39ukeWcVIaAwFtVcpXK7UQo81qF8DzkSHoSUmEJjCkOR5uisIOkOSLOcejMkDhTOOIpeHzdIcMYRyhCDQBiDAPI0Iw48GkLghEBKhR1ZLm27h3OW42KPSqtOZa3B5v0bDI/7DHoD8jQl8gRm6BhKRxz5ZZ4kB8I5hJKnkdisdggpEErhrEUCoR+Qa4MSokxci0NYUMov3duMweTgxyFe4KELTaVeIdeabOeQJEkRQlARkrTdZVhYsjQjGAmGqR4QRwH1tZhARRzuHmIdhNWIoBrTz3OohmglSfOCivQQSDaaDWxq6B/3yANDqH3iWky10YReQp5mDPMB2ztPcYFF24KiKNBCQBai0wyMo7LfJurHRI0KWZIyHCTElbgMCe77CCnwq4J21uGdB7foux0IfTIHbjBjibsF7l+XNMWcKgTGicG4EWTChDT+/MeTIS2HPz0Jr2fOmdB1zggeMN375WBxHTc+/z+GcHauMXUAjisvZ50EYzb5WY4ES0Sim68jdnN6fQtv4ScLrlcoWsAbnft+WUFlHo1e1kIxj96/SVP+rDYXWsguF7duPpwdGrP0+fMFiNdgvWcZpy5o5sS9YZE1aNYdgNN6o46uS+798YDJMZ0Yp14HljXWnS84xnxMrVsxM0HLJRgcNwev0/ctSI+2efWHvwUONjyPn7sh6JhDds0qL+0WULq7eUqRGYvVjwm8JyDgo/0BLzrpGfMwwxI5jjUAERA5pBAEBfhK8PNfryPznOPnXTpHD8lSTZ4U5X0jKWnWavyUAVs4hoMhzhikLHMIlYHQUrJewaNOn1qjSq1VI67FJP2EYMdxe6dCqguSW12Gd46JfA/h+dg8JzcW60rLF1KgPFH2O4qEh6dwzuJ5Cu0cDou9USCERSIQQx87CsSglKK20kAXmuNOH18IwiDknb0+Li9Qnk91Yw0hHDvdHV68+5iVWkwuutzZfsgwSRn6ku2bDbQxJCJm80ad7WQAvuSr+0MUkq1uTuqgP0hoiVVa7RXe+emHtLp9cM/JekO+W/weO3dqJK2cYTGk4vmEYUhc/3OolQ2C0Of9DWhoUJFPMczYf77PwfY+Ra7xfA/tch7dfsLquyu8uC3Y1j4rWyvo3KL/1z4Uk6tLTC+Aa6D701r6eckzT9Qa4lzNL4cFnd6lYuz/079eHZatf5V+FuzkL+sQmBk29TyUBsSzc2+y9Oy6s8/JaanITSRhn9PS6Nn8+XsrGr2Fn3S4HqFoniC0SDCZ18YyQs+iZ/MEkTdliZrZ2dXrXspaNAKxsMK0CHQB0Z5TZilR7ZJzecL8TvYzqbUcPwimfcTHcfqTKhBNv7npef5CArzMfG+zN815jfuMygv3sDg3qImexg9+a7E2K0uIgDCM2Hx3Hb96Dz96QN5LyyAFgYfwFGH8FCF2ANA2Jzf58utihnbZOUEgK0Q1n/jhBtHOOraQhLWY3kGXgxd7DLo9/DCgvtLAJClhNWbj3ZvotCAbpiTdAcYTWGNoH7YZdAdEcUh1tUG91cIepFS8GC0SnK9InMPPC+QoSl2e5ghf4vkKay3WgfIkOssxxiAcCF+WqCuJFhYjHZ4T5Zw4gbEOpyTZMKXf7YMA6fvUVxuI7Q4Sydpqk2FvQK/bx3iGQuQUysNKi/LL5LTCU3SzjEIXKE9xcNwl3d5jK3eseQGuyOkcd3BSlrmaUsParQ1Wb9xADB6RJxmPv/0p6mfWMKpgqAdEYcD6jVU23r+LM+9i81UEjqo/xOwco4cZw24Zae7dbz7EOkeeZrgQan+xQuHndA87NDaaZL7AOjnfmDnv+zJ060J5f6TOmpSUxvj0KabZgVsgqL8pcBcP5EuA18PpdH6/yENgrLs3fPVorMsx2jvP5HPBGl30bFyN+hbewk8qfPHJW18X5glPs77P29+zFXpvCKYQuaivZc+HMeuSO/1hWa39mb+3m6ozrVl3V52jpYxOs1wErtLZ9cIXaXWa3Y84PWjHrUSzDJzXChMNj72Dy3R20sYFr3DmeT63jiDH0R0txr4tyGUBTQWAxoKwWK1RwgKMwnTPNmDOXJonAvqEcCQYFqUg4lD4GzHWKPAk9eYK8Z0avb02w91Duke76MKQpxn6RwXK90AInDZIP6Aa+uSDFE9bzCChP0hRg4Ia4EuJspK4CFBSINEYkxMIgecpTJ5jrYfyFJ5SGF1ao4q8wCCIfK8M8DCyUllrKSQ45fBwVBykIicdHOJhsQRE9Qr94x4tJVndWuG4OyDvDYiiEL8qeZl6eHGILz2SXlJapKRPaCw+ElOUd5oCBK4w+GFEc2OV/b0Dao0G1lrW7mxw+6feGb0jRU5A5gLSwpIVGk8q7t5Z4+7PvIvyPPp7kOWag8e7JH/8FHfY4+4H9+h3Bxy9PAAhqK3U8SKfjXfX2WpWyAWEaYDwAkxqMKldvPBmLcJlyc2cdV2u2xFrPndznghN43btL95iNCtk9ZdvHXidvt3Eny8NFvqBn31wuJnKwMVNn/cfObV8usknV7O7fbmWy7fwFn6c4PWFotexwiyyKs2zAs2iAPPOl9fY47PPtgvY0ZmBFS5BrWeMbaLHmbRreVNa2da05WjZ2leEpYSjsyILdVmjkE+zj4H5CVmXhR+fI+FEDXmC0eSh+MbO/6WMgfNMsScfzzThY+hPLuITDfklVK2fFJpHul9OzfAz3OGjGcjZ00aNdRMM6jgKJymLT1z7zwlHo4q5dfzXZ92xFfZ/TAntjnqg+Is/V8flmiKP6HcfUqSazkGHwVEXlxWIQcrdEUPsqzJCXeT7Zf+hT24MD/rr3Dl8AAg+bb7kcfCCKo6670NmKfIcRIC2Fq0NOi+w1hKEYSkAulKh4bAIKXDOcr86RDoIheOo8oJUarRVDA6/TjJMKLKM7fc22Q882v02X/PKMNmNeJWvPP2Q1eM6nvLodgeEShEauEtEfzBEeAoviPACD7/lU32/wuGLV+RFTpYVbN3d4ubX7wOQdoZ891HG6q1vsvugRb+5Q5Y/p1Wv8td+cYt3b+Tgcj553OOj/+051Z0jPCkJm3XyzoDNe5u4TJMNMyrVmG6nx6tPn/P/+PCAOC4Y4vg3//uAQV6+E6vdcsqly2z4BWUXhvkeD1N3srbGmOQ3BZcJoX1hqWvQwpyJgifKiquMfQ7zfp0EccKKvcCUdxkr3zgtv+IrnztfSwhYF8+5GCv71nnuLfxkw/W5z51j4mdJMG7s2xWTU17njp1vSBnRsVnWl2uARdYuN7voFwbTY56lGeXN4LXUq53R+YnIsIwcPd3PrDpfttIRppfI2QY7cS1cZu+c1wm/Bix46cuzOTMaOMffjFob5zJdmb8oP01Nb8p/Yw2MM4FzXT1PadTZ7J6ETT9nJHMCnEObceKmzzVnnENKh6oovDjCq65hLazeWSftJ7z8+DmDgy7SOoyxWOvIC7Da4vsegRQEnkfgBVT8eMRECwrn8Jwj8D1QClsUJINh6UJnyghrYRjiR0EZ2MFanHBYOyJezqGswQ98tNFoYQiEASmxzuKMBhzDNMUNHSLwkNKCMyjPo1qt43shncMOVoCTkkY1xjpLpRIiRiHPXWHIck3n5QHDbg8/DKk2qmy+fxuhJCYr2Pv4GQe7h0jpQSUmXmugjwy1zRZxLSKQGmscx4+2OXzSI6rEpFmGM5YkyYhbdZJewiBJKZzBU4qbd2+QHT+iGQYUVmALhy3Gds241O3E2QtbCpancGLq27mdOc5knwhHJ4K6WEZyuxqcie1ugnKMP5v+NleQujThOD+ua9JVjrXPeYWGcyOZc2xMCxOgLmz92t7MZMLY6zk9nRsnWm6mcHQmrL+pE/stvIX/8eDa3OcEZVSnM2Gi/HW6FNOHBnOKLuhpBlc8s9R4+RPaMbevmdzxDDXzQlPGgmeXgXln5cL2p1j9mfiKqSPwTH939rObqFc+PTtW3bQRYxznC3G8brgSGz4a9XnR6GIR44s7WM7YKya1kmOWsoswWgrbcQvOQnX4GS6LGx8r6Gb9PqWMdSN2bYpvPYkgNWmZmS/Ojr/PiXc7xhwvUuafa/KEmVgwiQ6wSBJVRUpB1nEcfvyIbJDhtIFmhej2KuHmCvtPdpHWkiYZkSjvvdiR0CWlokAwHGQoXxEEAU1Rx9OGWiEQMgTryJwuo655HtY5fN9H+Yosy1FSUhSloKOURGuL04bI9wHQUuBLQWgFDSS5dmgLdpgR+D5GWwptENqQpTn1jRbZUR9ZCZE4fKnoDRN8ZymGKcJT2ELjrMNIQS4hk4712ze4eecGfhySHvfZ/fQ5veGQLFTsdLpUV+sMBgkq8AjrMUMt6OQSkxv2nu2jCw9pDE4bCm2o1Wpk3YRGq87qrXXqaw1UoPA8S0808QlIcDj6M17QVffs8nVOKehlu5mj4Z9FRk+o02WTI8/sckFvV7ERzKIa04lDx/teto/ZAppYmHto3pNTweiSZ5TDTWRguCg9xCye5jwtugQC0/i4GYL0+ERPNXvqgn2JPr/Q4/stvIUfQ7g2oWj6bsrUwxLErB/nwNzzbInTZ0KD5Bbv9DnmhbkH3WWVe7PG/kYozwI1/rn+xt7WBbmUxp3Slmay3zRlFdNkXpzyvm5qwsUU1ufZ42U1wuNz8OYFpIkZd9P7a7zMa3ZyOpR5czJLczw9x5fD5kzQfp0RnNQfX3DnN5sb62lWTqUJYUqM1ATj9OOCtZyqCh+1/jzWOF789+9x58UBQeDTNpoXVUXdhax97TbpgxVeffaScLvNe6lDG4sxBicEUeDRQbG/3cZXkrsba3y1cQuXFfhCQjXmKB/wiTym5+cIBFaUQpUtSkEJKSF1yFEc7zDwy7DcEgprMQKUgEgpbnZypIgY9nNW723ihwFFVKGTHeIKjbOW6kqNwX6HqBFjjcVYi3I+qxsrmGGGjHyKfkqeZLQrPruxpD/0aL6zxe4PXxBWI/Z++IzOcZeoFnOwVuEzaREUxM4RCkV1pcH3DkK+fwDtlwe0X6XUvCb4HiEQxjFSCI72j8nyHOl7DIZD1m+uM7SW/8X7GQLZoNaKSPmPQHr2Yk6XhZj8bYl3ellwMz4thBPLwQxU5uvCLoP0HAXBBCyjTrm4z4t0d9PPrS2tnNMCxriL11Wpwiyh5bJWIoQY3eNcPgrsuR7OnU9zyl12QYqzNXNu/maR6REjdOk5eAtv4ScY/uQFWpgFF/BwV2tSMHHLfRke7ipq+2VOxVn1LxrnDHzPk/nzhaYVaksfUGOFxdgPc5nL1+CHT5X/C60W84PgunlVFsAJUz01qjcGZ7eIxj9djPf1iWszWprT+CwRafrjidZ+ERtw9mycNVq00MUETmc1zqtoxMQ8Lup91KxbMI8T2lmBFWV+Iq0tGEuzVacocnJnaR926f/hkEq9wq0P71O7vUn8/RckRz2kH1BbbXD86ohgcwWNQEmBdeA7hfYF0oLvBCtRxFajRZoc4bQto8EFHirwGPYGxI0K2miUp7DaYq2l0qriBz55J0d7Ai/wcbko8xyFAZXVOhv3tiiSnMPeEDyJkB5Ro0Jnr02R5VTXGniuFEyUp+gedfEQZJ0+WZaT5zkdHXBQCIwt6O53qCM4evqK3jAhCAOsdWR5gWhEGGPI84KVrRpho4Jx4Ixl98krAlfD9z2yLAMH6TChKDRFnhHHEb7n0T3sgoM7X3+A9R1JARFq/juaeLUjonGZ8+LyfOvC/Xe6dJZQHl18F+R8BrPlLTEn+Mwr/3oH6SzcrS2FawEoT031PalaOXWFPQ1H/fo4LV1djGNwAQU6R+7erAByubclZhyWb+EtvIVFcP15isY+LjT0LLNHFzK9c35fdODNUi6fVx6Pvs+wMM06aH+cac1Sczw5ySeixOQ0zbYiTBgaJootkW3p+rj3uQ2PCxMnMJ3Re/wWwPQoz6H4xnA+D+7079R8CyYSxE+jcyn0Zpz6Fb+KL/3LIzrd5mgCrbP08y4OUEKwJiQCsEKRe9X5OM3rS0CmU1KdjPVfvphxF5lJFmtG83Ne7jSbNo80nPwgsEh/gPQF1aYgPooxAuJKzO1myPGrwzJXUJbTPupyU3o8uLsJdzd5+YPHaF1QXatTpBlSSZTnYYWkXWiUFJggwDiBkYoIxbu3b9HrDrDA4KhHpRYzsH2U7xFVI5x1EECe5BhtqNaqBMpDCokucgotyH1FkmVI4Rh+9xE2zcmyHFMYJAKbFgy6A9IkI+8O8epVXGHKaHe+R1IYhACpJGEYUq9XyZMjqvUKnoOsl6AF+IFPpVWjvt7k6dOXxHFIMkxYjVf4yofvEeQRuZS0DzscbRfc8UJsDkVWRu9LkwThSovYYJjSqkRordFpaS1rKAlKEeWGVujhpIfF0c3Mgn3gEMrHqzQAUA5CUzLq0mp8nSAALX20F+EAz+R4prRCGSUwqnz5ibak2o6tj8UEQox9uh7l/Xk3teVrnsBse9XrBUQ43wuUFgspyrHPcl8+ocViqs44NbwKnNLLOUM5uZ9zJffBcyiN8gUt1ebl+lssGp9/KmZ8Wh7eClJv4ScTXlsoKv11OWe/nfh6Wco9T+BYtE9nnUfLqKUv+u0yMAvfKzbzZnjvKxB93OQ8Tr3LuWb7ZdG5klmKqZNzEqfpxiabnQxHPm1RYNH3y1wceINC81muikXmjMvBid/9V9e+xs36LYw2dPc7DDt9fN+jvtkiH6TUN1oIKciTHKtNGQEtChh2hviRT1AJkVIipQAhGBZD/uuz/w1tNA0h+VuVKj6Q+nWer/0MCDk1OMHMZIVje//R0af86OAHpxagk1m5WA5f8mVMGo1mNXTKZAkvI1r7IUIK3vmf4O7mV3Ha8uQPP+Wn4i2KoM7jTpvntxvoJCdLcl58/wl3vvGA+uYK2SDlzjfe4cUPn+JJHyUV+8bx6OUxcRxSDQuwDmUst9diGl1HtHkbI+HIHiDaPgN6pL0EU2isdQgpMLlBIhl2B+AgG6REvsNKnyfNgH4KQhd8rZeijCVNc5qNGoP+gCIpaFQqFN2kDOygNdJXKBTGWqQnqUQh/d6QOArwGjViEtJhSlJ4xMYQGUcQBqzf3yLtDvECj263T6NV5/3qbd7dbgLwuObz7IePyY6/gbUFgXAUQLPZIE9SpKfIs4IkSRnmBaHn40nF93/n21jn8Hyf+OE63/xGFSlCEm35Xx+1KcwMpdboB7+6wvo3/wpCCOq54Z3jHAHU0lfcbH8fgE50k72VDwFo9Z+z0fkUBHSais4oFPz3Xg347HDMZe/CzSguRQ8uw6TPKztO4WaXmdJicD0kZSaTLgRKzbDqsdgqMx5C5Wq4zGl4spOJMsskFp/b1GlAGGbG+LjM0TCpqpxX6/UOmdn4vBWI3sJPJlyLpWimrHLRzl8k+Mz6POu3q0gPlxHQZg3sspauK+B7/QLRfGTPUBrXHY47MSxh9VkWLpq7OfMzLowsPKQusR6+CBe464KTYZ26kIymwI0/fB044R9d+caLQc7eox26R13Wb29QX6szPB5w8Hyf3mGfzXdusP3RM2ymUUqxenedw6d7aG3Kuyexz8a9LeqrdaQqE4ueXFpWgAQ6Lw958fwxKg4JqzFBFFBpVVGBx+HTPdJ2n6AWs3JnHWddmaBVCoSUI00sY+to/Mt5S+a5BTePvzjlYOYIm6ea3zE7oiitRUJIokZMVI9x2lFbqdE9arN+a4P1UHLYCOnlmjBUCMqEpL2jLsI60mFKtVFj0O6R43BG43kKlCIpNIoy0IHMDVI50ldthFTUZYAx0FQeSb+PthYZ+qVm3EEYBTjnsGV4OkLPx+YG4yA3FoUg1xahNQ7IswKEoFqL6e63wZMkScagN2BttUVYjekeduj1B3SznEoUUW/U2BmmGGOwxpJQ3v0xhSZzjs7uEdmgFG6UV05xpdVAOEGR5Dz/7AXDJCGMYvyOochTPClBuFFOJstwmOAHPtI5rBBkScpKJSZ0BhPFtHeO0A9zooqctIDM0ticUDshOTG7CjeyYiBxuaHf7jGo1qApkFIgXblmcZx+FmKWreMiuOqheBmYTdlmBS2Yh8KJwfXHgy0eE4kWTPJCfGds/4lj+Y3fuZnE7jp7O1FankV6X9T6G9TUvYW38D8IXItQNK3H+dK23GU6/rGhHUtKaa+Fy5nYM33Bfdqd7Hr6vgSnfhXhclHRsbKzq8yahcvCErWvbe2cdymZwOKKg2gJSU2W3E/uVdAyBMAlhu2nT6lvtqg2qww7fXY+OibPCpy2yJpleNAlORpgrcFZR5EXRJWwtB6N7gwcvzigu9+hdafJSriKwdDCgSvAOUyhGXb7mKM+MvDI0wI/9Hn4s1/FCzz6u0fQDOhGXfr7Hfzcw7cRXhzg3/VpeS2Ur0CemS+LIEMHZdjsvJejE31+5ubwyWcuKKPZPhWMJrX70y6ZVluGB2kZ7CCTpcVNCqSS5EmGzjWtzYj37xl2TYfwwOGpEN3PEEHAwGheHBxzY3ONupK8/PQFTgpC32fj7hYvP31JNQ6wGPZjRSolMvBpFJrQgULSqChsryA3hoPcIaMI5XsUucYaAziiwAfr8KTC5AXWSlaadeRhikThCUGRF5SygiDLCqQUOGMxhcGa0n0uzwukgEalgh8GpMOUTr9HpAqULohqZWCGaiUi15r2zhFZluGvVNnwQxqNOpUogFRz9OKAQbuHDSXJYEiSJFSlorXSoNKsYpylt9/BDzysgCLLCaLSEplkBZkSMEhwgSXWgiBzGO1Or4JKqWiGrTG3yvKBHzSJhzmd/S4vnu5RHCbUV+vc3VQcpSGPP3nJof8EVVtj671bBIXgyccZnu/R6Wni2hbKU1T8gLU4BwGBHqJMBsChtSQzNuYJCktZLl4XTpbxTFo1rak7++vEUifC66J1QRl3Kpyd1VrQIGWjy4bfXoZkXqegNKlImYHPAqvUhYKOK+9qSSm52Cdz9vO3ItJbeAtn8NpC0fhGnrm5xmnBZXffOD1/HYvNvPKXFn7EaYSq2U8nm53Z9txJeg24xNjOH5HjVqHzVqPTWtNR6i75LgVzFLfTeM2YxNPs3UvAGS8y7qE+T3v6Jqxy1wlTg54Q9q6A+dia+FOBz58OArDwqvkBnfgmAKYwDO8P6O23KY6HZRhn5RGEkk7Wx+aG9rN9MBZfSvzIp0gLusMMJSSeEPS7A7JhhlCK7kGHO3fvs/XOFjEpav+/g9XU1husNDd4+clLajgakcfeUZf+UZfGRpPeWoPD6jG7zY+xlQL/eYX7vfdZ3Vih97zD6lGLxlqT6lqdxo1VpKfYv71Ne/0QIQS7v/+K7pMeJwToVJiZFnTGmOWzBTE2UePBVsb17aMFrQeal7+zDUAravHwzgc468iTAptphsc93vkg4C/+zA85WNnh2fdiXu485Gj3kOLuOjtrK1RW6sR+wINmFSUknf02x4cdHI5Ko8Kg0yfwPX4vSUgbMVGR8VeikPu+T95LEC8+pVFNKNKMLLxHYkNyo8uErw4CvxR6rDM458iNQfkBxliKvCDwFNY6rNbUGlWS/hDrDI1qnWF/iO8r0jTDd6CdRXl+ec9nkNBLUqrG8FVtyIdDWqqO9RS1Zo2jg2OGSUKtUsEfFKx2Uh7c2KSRGZL2gN7LQ7Rvsb6Psw7ledT8iGqzhhMgPY+733wXU2j67T7dg06Jp7U4UQaO8EKfm/dWuNl7hNfJ6VmHsOU7i72Yn739cyipJvZL2k14+p+/R9hPWIsilBS0n+1x8Bze/emfJv6//Cwuf8TB13bQNzP2Pg44Pthk7cYqnf0Bt6o3WLu7yZ2m406zbHOz/UOaw3Id/FaS8KmezGk1uQ1PmP4lrTeXAvFaQtekZ8DF4stVOrowsawb+zvakxdRu3LMP47s/eI5upRL9gwQQpQC0bleT07y80zB5Im/CH587IVv4S18UfAlRp+bYyFZdg9e5IFw2XJL4TBHIDphVr8I7R+MqRovJqjTgs7455Nfxs+gxW0sAzMmYYlD7dzcLTCgLdSsTSvlRkzwZMnpkb8BuIbzZJ449zpha8fbkE6g84Kjp6940e2ClHihjx/6VGoV9nfaDNMcJwTWWKSSdPfaOByeECgnyPOijCglBLkucIBEEAU+SZYjrOTFR0/p7LX5+k/f5mRi4lrM5upNkl7C7uMd6rUKSgh2fvQCpRRWSZLDDt1KmyTPuGlDbn/lNrufvuTw1RHNWoXui0OOnx9QWTvg1of3EHcoLTYjoeeULZiQbaYE7NFeEo7zUvnM9zf68VxSzrO/JwlWPd+j3+4h1TpepCh0TpEJPOXRjCO2+wmHaZ/j/WPq1ToblSqNrRYA2TDDFJatd29y8OQVeZpjlIcRgiI36HQA6y38RgxtR3rUI6hGtKoxEoUVFu2Vc6GwhIEHUuAKCZ7CFJZup8vDehWTZKXQ5HtUKjH9wRBPeYRxSOe4CzjCSBD4CmstKMmwKADwfA9jDGme4ocRSimqjRgVB1igEoZ4vkeR5YRxQHW1Ac7RebHP4cEh9vYKAkfke+TFkEFusXvQ7nTRxrB1a5P7f/ohzRur3B7pZpy1OFveZZW+gjxFdMQErTgllQKctnSPuoRxSFQJefb9p6TdAY0oLEOa+x6RlCRZzvbn27z/5z5gY/UmdqtMiJsNM7wgQA9zvMDn4MUBq7c3Rmtt9L4Lc2l90TiL+noBDRb1MUvNdb6v82LQfAv1onaWwegiGKfrSwXs+TJgWq8y8WFOhXlPLhLmTk2Mi8ud5B0UJ3XE+LO38BbewjJwjXmKLkuf3Pyvsxoa0xrNLbMI5pVfpp2r9rksvK41bNbzE95tQadnx6U7KzmzT8FE0YU4uUmmfeLDEtrBJeZYiAvuOY2p808Yj/mXjN/QcXEta8VNfJrk5edbwBY0M/ru6NcUe82A/c8P+OzjATK4g/J9hllOqgviepXNe5v09rtkvSEi8LHa4CuF8j10llMYg7EOlByd245AKRKtKdKcQEqSokA6GB71ePajbW7cX0XgKIIA5bW5+/U6Th9zuJ0SxRG94y7bP3rG6u11Bsc5gyTBV4rWxgppd8j+9j4mKkiiAT0DgVK0sza7331BY7VJuBafxm44Yeucc5fQJJ/M9OVfoFGGQaOHyTXDoIfoSpSS9HuC50cbDOOIbn4MzpLnOX4l4FYQYQpN59E2z4XP3a8/IKrFrG2uYLMCU48Q99bZ/v4jpI6paYfIC/rasZ8cIKshkWriVXxMXuBcjjUFOkvJnEVKwUYc0xTrOGvJck0vik6FxqKb4QqNEhBGEcNBgi40lSggSzIc5X2maq1a5kYyZbQ1qRQSUFgK51jZWGc4SMjTlPU7m3SPOlSaNaqVmKNXhzg3YOPOKn7YIesr9p69wlpH0Eup5Kp0uZMewgn6vT7CQRQEoC1HT/fRhaafJqzeWCOshsS1mGI1x0mLtJonxwXSaDIka9VNNILIixEIDl4ccLR9iLOGh996H6ylGocMhhlJURCEAbHnIWLHodijHWwgfKj1Gzjn6B/28CMfAdRaBVF1SOPmMVm/Sm8fnnzvMTvtF3ztYZ24UUXLfWDMUjSX9E3RyjcA5+neLGTGie94Xq/zZacFuQutPq8FS2jTLgETcVtep905jgvj6SzKYsscZsv1t2xBMfPz8p1NWpj+ZFmJ0qLN//KD/+cX2l/M1hfW31v4YuDaAi1cuvAyltvLdDSz/IioL+J9L7IsLTO4RWO5SNi7zOxN1L8cVRe4yYPgvFV9npGnPBxfWyl4hQYWyj3LtTduE5tueHmG5MfjcDjTCyz57uea/gTP7lbovFvnk+PPubW2wlp/1DgW6/mgLbufvsTkGislQpaRzQrPQZYDDmssQgp85ZUafCFQzhIqVd498RSxHyCAtCjY2+nx3bUHrN/dQMoBnvxjvJrjnZ+pkBdN2rttqmFI/6jL6u0NKnGIJyXaFQjh6B10MNbSa/V49WCfzDicdQSexyDPiZ8EvLP+Pq1ba1+AavT8BirCnO13n5ENM7ZXn3Nj7w6VOOTlbsjv/f4HeHGAzZ9TGb7Al4qKNlQGgigMUdU6nU6PnY+fcfeb7xFWI4QnOW5GPI8E+/11Nl62uTk0SOfYLzQDIQjaKe9tvUslUKjI8nz/98D0CJVAWlfmMxp6fNP+PLiQfprxudFkRkNhwJZCDr5HnqQ4BNWVGoFSdA7aKM+j2WogRu5yUkC9UcM5x7A3pCg09Vadmx/e47v/5fcQQnK8vU9WFGzcv0nn1RHWWAJvj9W7GZ5ss/vYI00KlCf5alSj3e4iRRnAoDCa2PPomZwkzSgOj8m1JgwCDvcOGRz2GCYJhGD/7xkbH26Chec/7KNTTexX+PkHfwZfBlhtcIWlvXOE0Ro9SNl7ssvqzVV2PtvGOYfRmsQYVBhyVG/z/PYzohs+t7nHzc/vAbC9/4Lj9AgpFbcedrj3zW1ufc3y7A/v8dFvDxkc9XC1e3xnWGG9tUYSFJAPZi+VcRg7nr4ImG01Yuy3M5FnHmU8oaeTqQLGLBQXwHTuuNca+wU6rTMhaEYvV43ceWp1PuMrzucqukxzr//2Z1qaxOz5vbC3GbzA67r4vYW38CcJrinQwgUwT8CZdmNZhkpeRWi5zJ6eh8NSSp8lIrXNEkBex4r1WjDjVJllIRovs+iAHytzruVljTKXtMpdeLl23GLmpptedmFcKNlOPb+eQ+SyeoH5pcXEnxMo8gKjDShF7vmookCZAi+o4JxFF7rMK+IctTBCZAnJiAuwozwcnu+RZwXGaALPwyoPqQSRUghdkGUZYRxTq1bo9wc8+8FT8jTn5sMGnlei6IU+7/3Zr/Lkjz7n8OU+ceCz+2ib+HaF2PM4zgZYbSgGGSBQnqRvDMKVcRakLOc8y3Oe/vFnVFZrE+O8zJ208+/v8u/TCz2kL1F+GcI67/Q5NjnxSo21VoObd2+y+2IXlxrCMABlGRQ5lTgiywuOXuzTurGK1YZ8kBKuxNx8/w61xFHTkGc5WhUUxuBGwRCE8HBSoZSHFKoUVj0xikQnEKKMrHYyJOlAa0OuDeurTQb9Idpa1tZWSPOMhAKhymhuwzTDFppCF6jAJwpDEFBtVJGewo8CDj9/SbvfI4orJEWB7/nYXJMMEoy2rL2zQlANSI/7HDxNUd4G2hRIT6CLYpS/powu6JSgXo0oCk0vy9FJjqS0ukVKkSAosgI9zDh8tkfcrHESXt8ay/6TPaIgwvMUUgo6+0c4JWkEIQef7+CHAdI6jINaHBMpgXZQ2DKC3tHzA+yBJsoqNG+vIqQgHSa4IMDzFdWVKlIKhu0+x6/a3Li5DsaSFYZ+uw+xO3PxvYrUMzqDXldomG1dngWTdH4ZRv2kzHVbuiZDiJ99mBtyXIwH7J4SdMaFlykQCNyJT+2MAYx7I0xmgxLTkzp7DG6OsPIGYJY3xCwqNl1ntrVLnC90khzvLbyFnwD4Eu8UjWCcb1tGUJgHM/j3cyqcK2qGloUJgeiSzP10dxejusSAxnAoz4fpOuekhJkNXHbaZgqGsyxyMxseI9dLDPFyB891EPbXjVz3BcLJ3JwgOyYZhkmE/8SjultBFXGpNReSPKpSjUKyLMNIxcn9oSQvCKRHri2erxBOIp1D5wWVKMLzYtQomaYxhn5/iDMONQqhjBCl0CTh5Y+eMUwrbP4Fhx/7qMIR2TbvfKuJyQ/oHBqkdUgXE4b32Ko4qvFdoliipCRIQla6q1hr0VEKfolDcQThoIr5SOPnwdg8XDxVG9VNfOWDc1SzQ4QzEy9ZA0+1xsyeaMYLK0/R3FpFfCrJCs1gv02DBr4TGAfDWy38QHD0dIfQGHShSYYJhRAo3+do+4Csl1BozcFxh+7NJqsPNql94w62k1J0E9RRn+yoh7WOg6QgLwz4gkGh0aIMt621QVUipBfgrAHPx+X5iMcpI9IJqfHDgOK4g+95RLWI/k6/jDxnHS702XUFeOB5HvXccnzUQWuNtZa1jRXy3pC9nQOqUQUlFRJBo1Glf9wrLYjO0rx5D2M0+5+1aasc0xwwHPa50bzFStLAAcZY+v0BuZRYqxGU0fwcjl63jzaGQZrTbNTxqz7H7QMOnxyy9qe2uFkJMb4lPUh4tb2NFIqsKLCtKrsmp1qtMZCWXFuCIqWWW2CUN8fz0UWBn/k0jppkg4Kj/Tav2CaoRYRxgNEWJw3JUUTef8De55LPPkvo10L2PcgPe7QaVXoHHVoPV08X3VFyQKaz84bFmcq9E3o82759ebisWHW1Hq+K5zzd44ndaRmL+Kxw3Zc5E8SZ6Yfpfbw4jPkF7hVjH69DNJoU0Kb6ng6CNAcdce7XSWFvkYLxixLw3sJb+LLhyxGKrsLHLmtNmSdVXERfr6LNW6LeTIvJgjYWoTmtB7o8Y37JGpcR7Ja19C3T0Czh+JqkkPm6tOVhca3l2rzmYV3c2YlSdPSO/KcB4jPD/eNbWOWhRUEoHQPj8KXEWciNxlceQkiMtWTO4SuJpxTaWJx0SATWWowG4RxFVuD7HtUohDgiLzQuL0oUjCGoVSlyzcFRh+8+e8ZX/sKHrGJ5J/kYT8HDn63wg//dkvRS2i80+8M71Js1+l2PzapjdaXJ4aHjRqeG8j1ebW6T1A+RUrLSWaW5t0KraGFvj/wB51o23WheyuhNH258g3rQRFrN/YPfx9fDieID5/h1M8DM1ZiOrSwBYTXCVx6V1TrsH1PfblNdcRR3V9l/d51iq4avBMXnuzhj8DxFNSzv8SAl2TDFCkGSZuT9hCLJOaiGqJWY9DhkqzCoQYrRlmf9FE8KYimoBBanLF6lgpSAttg0B2GQGIRSCAS11SrJq0PCKARrEVJiteHVzh5xvUraGRDFEaZV5QUpKEk8yGmaAm0NKvDQgwSba/SYVcMh8IXkYO8IFfg452i06oStdzl60WH3eZvjuy/prz1BGsPLnRryKMLzPRxQa9Rx1jLoD2k2YuLQI9eGyJNIL8T3FFmWkwwSvH2fW+E9Htx+SGW9SpHkPPr0E2QEzZU6R2nGf3Mp8v4GeSWi0KbMO3TUYyspIy3meYEpSoG9klRYP1rHl4r2UZeO7BJ9tsPK3XWUKq1+L78XEMXvY63jD3/wEdndFV4Wmi0lqGQ5Qgiipx4//c1vIZXk91/+Lnv61RmDPZlga8yiNIfcvgZNfXN3fd4knM3EhDXnwmonotRlehKnnyb7X672+Bl8rtbpD9clFo01Ot3pnKNsAoWRhf/s2fkxnxN8xMSft/AWfiLgfCzHK4CjJO4nWr3lKrCYI7zo+UUwbXma9Wz8n2M5vC7Z/5WaGsdh7PMZesseFGNtXNT+IiFy2UGMz+NFsMy7d0uUvQwIMfav/H7235JNXBMqJ8O7wEh3fZ2d9Djq8PjpHsODTnnvQgiEFFipkEKQFgVZnuOsAykojCEOA/zAL5nDvMDlORiDkgJjLcY5DIJMa7K8oLAWYx2hpwj9MvFqVmiyoy7KWSLfZ9AZ8OyPP8dqc4paWI14789+gBd4ZUJCpTjYO2L3+SuyvKC+2mCt1UQ4MEWZPLYQAucsvqcAsGZKVTtrLYlJAuEsFEnGsN0fPRanTILOipJ5dSe7b9bLGf+tFBStc4TViCAI0NZxsH/I8c4hRZoTNitsfHCXex++QxCV966SLEepMnx2luUESiKUJBmm9F+1scagU42KfIyzRHFIpV7BSYmTktyBzcu7Qtkgw4U+rhqhtQXnsIUGB0VRkPSH5bssNFlWUFjDMMuw2lFkOcZYgjBACCi0ptaoUWvWsKM8TFmW44Bhf0jnqEMURQipcAJyaxChh3ZlVMLVu5voJOfVZy/IRgKgtY5avcowSYh8Dz/wEVKSJClFklALfCJPEXuKehxSjQIqvoewFs9ZNm6tcfeD+zz45ntUGlUAdh/vkvVTwtDnYO+IYXfA+uYqazfXCeKwvF9F6aJnjCXNMqQUpMOUvChoNet4vo+xlko1xjnL0c4haWdIpRLhjGXQHWC1JekMsboci+eVFtU0SUmTjKPtQ452jk7XgkDA6fpZsEWZwdYL98budLiptfz6vSw6/5dvfdxd7WyXLj5YLkPDZ2F2nTMsxBk21yWYToxvdHZNPJsSaE54svL5F6J6ewtv4X8IuLY7RTPDUU9rMGZpNJalGcsoXKb7ukz7M2GGVDFLNXSx8ni555cQJq4l/PdlrWl/AiASgvc8DwEMreORKaNACXeiKZtaSJc0GF33FM1t7zqlr4lmSzeJpDsgNnWEL5FKMTAWPwzxAGcdmdY4IU9OV6x1KAeDNCOIQmIl8IVgYB1CSrJRaG5rLDkgUShhCWoxzpbBFwLfJ8tzfAFCW250N+gfZBz3BpgbNxBC4hnFzahL+DDijz7aZhB6KN8nMhk7z3aQSpL5ik4oMM4Rmzq1vRyBIKPArB3TbkiaKxGBF+KAvUHBMLfn5jVau4PyIzCO5997Ch2NCiThn94gCEvlc32Q8/R7HxPfXOXW5jqFAG01u71tHHbiZSnjWDnOEFLgCngVSFzkcWwLYm0QOPrdPjvff8zN9+8SeR6VB2tU77RwP3hO8nIfowQm11R9nzQraOmQtJ0R5o7Bi0PiRpXmVota4NM+2EUqSVKLwBMYrVnzb9NwCaIa0T54CdLgKQVKYq1EKgi8fQbWELY8EpFxlGYksWF96ysYK3jV6bEiBXmaMkwT1gLHRu5QUtNePUJYS0yV4ChEW4sX+sRhiDUF/X4fXLkmMJpGq05tvcHeJy8ZDBLCSoSwDikElVaNxBTEUcCw0FSiiLTIybICYyzHr4ZYyvxFThuklAgpCCsR1nOsvd+luamJq5bj56vYwlAJfDwpqcYRg3aH4WfbVFtVYiGoOci0xjNlrqNaJSaOI/K84LDXo2LK6HxqFGq72ajS6/Z59WSHKA7JpCRPc/IkJ09zasbhJaUSYLNWRfYSkiQjCHxefvqC1maLjeomkRfRO+ohBNRW6gDs9ncobD5ju07eDVmW3lzGqD+r7iId4mIaOU5PF4kAc022M5+f6+602PT8XN5CtCxmF8H12YCWf3uXec+lnORGyr+38BbewjJwre5zF269eVTkdSj6ErAU37vQf+Ga3Z2WFayuYq1Z1OcF5val6y+C63iH022c4nsxEjUh+CthhAJeFgVPjC5ZVzE++FntX2VS5sB1ekxcG0wiJKVEKsnAOOKiQPk+2jiCIKA/TAjjCJ1rjNHl3SFrUA4sjjTLcM5QhDFSSiwlk2kMIAQeYIoC7WCII88LKpUIkxuqccwgSTB9wf3iPXpJwuClYf9nV1m9vU6UHbLV/mO2mo7aV6v8wbYjOerjSfAqMVLAfgDblQjhKW4NCrb2YnzlsX3jBdsbL+iEe/yid5cPb9XAwf/5osewmGJAhaB+9+sEjXXIDXz2x0g0xgp+v3aP8OYKnoPbH7/ipUiQe5Kmt8rN9++Quoz9wSv0SeS20boJcsOt7TJCW9F1/H7NYzvpE4WCe32HUop6vcqzvODZ9z5nrxpTbVRp3Fjl1tfv0EgLesddhKewviKQEr3X4b0wxAz66EIjXvVZz6G+3qTneXiBx+cBpLGHj8fPiPdYRyACSTc5xIkhXuBRyFL4lTKntrJL4RKcc7yqOzwhOe5YMvUNFB4ZBfWdHr1hivIUD7RgtZsziHs8vf0CazS35F38wwBnLLVqTL1VZ5AMYCjwPUVqDLbQrNxeJznqsf9ij7BRwRQanRe4kcues5resHTPS7KElbVVDrQmzXLiWoVKo0Jci0veTpV5tJobLVAFH/ylHxI391GqRne3SWO9yZPn+wx1QZEXFFnO7YFDtlOiSsgwSbjdalI4C0IQN6rUV+vsP9rBOYvRBmEduXXkSUY9joiCgHSQlIEdtCaMQ4I4oN/u0RwWbHRyet0BaZaT5wU4hy8FOjU8+d5j7n/9Pn4z4PPtzxgc9Xh38yGVlRqdrE2RnReKyuV0ZtEV57funDqMPBOWFxKWZpXd+a/jdoo5jV/ZTWIhqXecusqV3cxQdM2osgDT5WFsTBdbxJbrzY2sYReVOhvv2edJ570TPkWc/rJci8v3/Rbewk8CvL773EjFJE5dkjgvQcyyiFzkPjWjj2VxOaURo3/j3kMz+56LjztfZHp8i3B1C8q9Lrxpq870u5zV/9LzeJ1IXaL0gsuh5w41ceb2MLvWuKPdBXhMe8AsV+yNw4mLK0C9VUd5HkJ5ZNahjMUYgy/Ke0JpkuErRV2VyUaLvCAtyrtBse8TCEAKpFLgKF25KnEZbU1rnBA4KUjTDAHl3SIBwyTB8xRKKQZJSsX38aTgsz/6hM4oMSyU76J1Z50PfvGb3Pv6A4JazHAwZDhMUVLSjAKctUgESpQCXhQGeFIyTHMOXx7MVypMrVMzct8rsoI8zegedoAyktnR9iFCSZQQdHaOeP69J1gzCsLgyuhuk805dFaUocytJRsOcQ7iWoU4Djk6PAat8aVEpxn7L/Y4fnFA3k/Zev8OjbXWKU6elIRBwCDPqVQiwijA9z2iRkw2SLDW4nsezfUVPL/MoyOVAgQKCKohFnBZUWLol3fBhB0JsWUmVAprcA5MponqFRr1GkoKwkpIGAaIUbAM6cDmBda50rWRUlDxK2XeozzJ8KTE6jLQQxyFhJWQvce7JcNeGGxhRhENy+9mFLChXq9SrVWQvuTBhw948MEDKs0qDhh2h/TafTq7R/T22gyO+uSDlOPtQ/ae7GGKMvxF68YKtx7epsgLdF4QBj6NZo17X73HV372Q6IopNftEQUBQkq0Nvi1mEIbBGWC4jRJkUqWbplF6QZar1ZKPLXBD3zyYYZJS8HucK90kxMOWq0Gd965jaUMtnG8c8Tn33lEkRdlctdc8+h7j+cLQzNhucPv7Ph9favAYjLuWModa+lzYP74Jp6c8hlX6fCaDqaxJsZd5C6DyTScnSfzJMAZQsnJNYXTYc3r8aIDfN6T8WdvBaK38JMFX1yghUV769L77iITyyXgIgvN63Z3Ea1eYMC4sK83Ze2Z1fYizd8imnyV13NZ5dRYPwmObxc5EuhYuwC1+RrOs2A+I42ccKOD6OQwPOmUifFN9jUpUE8YIsUJMz0Hu+tSzrnJD7eUx01V3rtpxwEvKwolIBjmtIAizzGeQCiJK0AbTSANqQhLC5AsdSh+nuD80kqQW4sUgjwrRgqI0vKQZjlxFKIBH8jTvIxypg1CSSpxSCcvGOQFoR9QGMP2py9Y/7MPOK7eQwAHwPPhM+yapX5/haAI2P3hU9rFHm3rUW1VMXXHcSVnmCZUsoiNwSZZURCuqsm5mDGfK4mhqjRHj/d51umiYkV1rUXYqOGAzn6b7MUeXqaRlRhnobPXxqC5e/M+KIEnMlaCp0gJIhIcrYUMjwraGDZ6GVpb7t/YYKtSZXjUhb0EJyS5MVQNrGcW/dkORyt1inqVyge3yF4G9A46OGeIpcNzjk5/QC2OsdbS3+sSxGV0vSIr8HaOaUlHIARx3SOQirzQmEITxAEit/gICDyU8Mv1Zx1YyWp7A5cZQuvxMu2ivJCNVpVGs85gMCSuVEYCRgBCsXl8A6cEhojhep0kKzCNkCLLOawG+E7THK251tY6nd1jkmGKbtWwK3UO9g8RuWX9MKMl++zhc9gI6AhNpZ8jDtoEvs/q5hq9gw7aGJRSOOe4/e5NWg8OcOITooqP2u0AOf3hK3a9F7BRo3Iz4Bd/cZOiP8SLGhw+WSesVjC+Ye3/usFHv/tdUjFkXW7RbXep7MXkusD3PIoo51Vll7Wb6/iHgmxXEijFoS5oV3xwHsfC4CvHoBZw1IjBOdZur3F3rUnVQnevg7WW3FgqcUieZPQPe1SaVdLjPiYr6O61+dDz0TbAAD8qCtITJlec/Dm/YL8Unf21ukichxN3wfHoamd58catI+MiwixXgvkwfkdp3txeAfELe7s2OHX9Pu2i/N9YEIrL9Hoy0/PgrRj0Fn6S4fWFonlKhdcRghYJCBMCipv8bRHhnmWtmn6+gOmfzlY9FxYJCIueX/TsuuCqfSxb74J3e+UM6BcJWKMmB9bxf2TZpZo+XUYTaImJsZSCzAwELhCYJ3NHuOlOZiBzEbZLwLk2ysl74Hn8hSDAaMP/p9vjqLVFZh23HaT9DF9KTF5gDXhKYZxjaCVGWJy1FNYSewqhFFYIgsCnP0yIKhFWF2hn8XwPLDhRXug32qDiCJMX6CRBCEFeaOJKTKNRK4MyaE0UBvQPuzx/2aN49yEA270XfLT/38E5mq0mm39uk9pXmwTf/hSv3aWQimylQbuaMkhTPuh/lc3DBwwGQ0L/eHaI2TGSsTEsaNkMdTTkBxWfLPYxJqXyYo/KzRaDoy516bF5f5Mizei1+1ht6Gy3WXFr3P/pdwloszX8Q+KaR7a1zn+5USFtSI53D7nVL/Clx5YfIaVAp2UgBekc0vfY8APeEdDZO+SV6PNJkbKiLM2HW/SaId3DDnc7GXVb3p/KCw3OMuj0GfQgUBJTFKwUmlojhkLj1yVaAFLihgZVD3BWl9Yu51Cj9Sg9hSp8NvZvYXNYUYrdwDLo9VnxPaIoIBumGG2IwpB+b0BD1Wm93CQIPNqVgCerClH1OPQsg2GGqYfcVAqnJcpBGAfsfvYCBKSNmD3P0q56vJ9A61WPm6LC47VNnhqPIA54p7DUrCNNcw5eHaCkpFavkmY59796j9V7K2z91CdovYtJDd5nKXk3pfMy40crljQPuHGjxof3+vjKkbRDPvtdR6W1gl01tL9yTCUOOfj2Hqsv1rHW0TvskuQF1WpMVhvyqrVNvjpg1bZYPbpBkmXkKxX2qgopJUma4UWKXs9yVPMIlORpt83Wgy1auSUb3SkKAE9KVOCT9hOqjQqvtMaPQ7J+ws/WwM8sshHz1GhSO6VScW5EKibX78wcOLMJ2JVh/Kg6S+Vz4uZ1/Szz+TNhttAzt+cllW9fxPF6vSAm/ox/mVCyzRKgR4LUSK030cikiLickPknb+7ewlu4GlxL9LkvHmaYw193115Q/7WJwjVZ8L9wmLbAi6l/cJ6GurF/U88mE+Et0d94m68F5+04E5aaiTGKiRQ/p7ahC5iO02kRJxpPcf7BFCrnWlzk8TCj6ARMr7EZhymAyTWDdh+sxVqDsw4pJQ6BNQ4lQI2irxnloa0lDPxyPMqj8AJySncjZy021/ieV95T8j0MDiEkUgiUlGjrCEcuU3EYUq3Go7slmiDwiXwfB8SViGffe0TSnQyH7cbmsbrV4uFf/Cnuvnvn1K0r8jyUp8gKPXLtEkhvylK0YP/pvMA4N4poV1D0EtLOEJMZ1u5sMuj06Rx3qDQrRNUIqSTHO4fsfvoSz1dUWhUGBz26r9qAQ/ke6SABKYgqEdJXuJHLmhd45TqyjiIt89dUm/UyYAHQ3T9m+5Pn+GHAxt0t/EpU3r8xFt/3CKMIozWh71M4h/Q84lqFPNdYY8iMQY/KKwEuyfGCci6CKCjfuTYYAUWhKfICX0j6SQZSkKUZ+zsH6MJQqcQMhglFUWC1ZtgbUAl88lwjpShDdjNyjXSWMAxwnsQKUJ6HTnPyrMDzPbIkpdPrE/ge2cgdsHF7nXe+/pAHX3+HzdubNJt1BILVVh3pbCksNyp88HNfZ+v921gcxhhW72xw66t3WX/3Bqt3NojqFWorZZ3koEMxyDBJUeZV2lyhSHJMUQZqWLmzUd6XM6Xr3sHhMb7n4XteeSdICpIso7BlNMMiL0jSDOlcGexhlMw4rIQ469AjN8eDR7uk/RQv9BgOE3ShiSsRzjmsNihflS6Ltozqlyc5+49fnQk0szb0lGvUNBk5ezB6Mr6+l40EuwAu0iMuA9MR7s73IU7LXRmWrHq5OKM/jjBJxBY6e8+h/VeFP8mz9hbewmXg9S1FS2ppJmCW1WeJfs51Nav+zDZnIDmLN581lstSg6vMx58EWHYelh77OWnpenCYO//ifLGR0DYnPcOFXZY8y5g1YmHFcQlxXEN39cXizn1ZoDF2jmHQ4rB+g8QNcPo5N4cG6xyxBacNRkoSIdDW4EuJJwRpXqCU4sZKlTzNUFLRHWaIOMSlOYFSSF+RF2V+onyY4pyjEvgUeYH0FA6BBrzAx1pHNQ5J05w0yVHWEMURySCh1qyQJhn7z/a49/UHNEKPDzYq4ByJdhz+4AgBRBsxd7/1FYSSvHj0EgFUgxAlJOkwweG40WrR6pUhqP1i1hw7lNjFE11c/hnrw5AojPFrFT7udTh6vEu1WSPZPUAowZ2v3aHSaBNEMfuPBhy+ith/8oq1zYjGjZ/hINumaCvWtkthKE8sGMeg26f33LFvNV7oU2m12DpoI6WgUljaaR8hBL7JibOUahCSVh2HL/ZwAtaCiPXbmxztHpKnGV7g4wcBRZrhSUWhNeSC0Fd4UjAwOzgKZFHgpMV0BwRrqwgcNs3xlM8Hw1ts5oY8c+xXI4wVZEHI2o01DvaPcNbR6/RorbZQStJYa2Ct5Wj3iGrgYwpNmGnuJYZBosnzAuFgfavF08MuO806NT+gg6bdCvGjEKkPuJMdojxFpfBZ/+rP8epJh+1Xn9KVMfV6g06jg7vV50AbaAnWb2/Q+maDe3af2OwgmpaVWgWV5EgpOdYNTLUOwmNrcJ9qkiNSw5NhDRUokh7s1yIO97vUErhxXKB8QRDVOBwMqQUhKo5QUlK4MiAItrTE6ErK0cYug1qCxNE8dMRxyKGwPP7+I5prLVrrK7QPjrCFZvfpLtXjAZv3t/CfvWKQJIRRyGCrj7mdkdaGFF5Os7lGWIv5KN2k3XTc3XiP7OUPwZ63bk/rlMatNZPUZIZV6TTS5sVOd/MtBoufXRf8yRZU3hwsO/fnyy3nJDizxP+o/MtbeAtLwvXcKZoWMOapmF6T9o3lW5yBw3y91lL7fNzqMUPyKn9288c23sZl4EsiQFd2Y5sHk/b82eOa/v2SQvF1w8XeJot90Kf5kAt6O2ny9Ai7VhhH5ry0BAKScIXD+rukYojHMd7REF8phBSowAdACgGFpXAObxShTnmKhoSgHuIQJLkmB7SxxBKyQuP7PnZknQiUhx1FZjPaUGDAlP+CMMDJ0UV7B8o6iiQjDv3S5SoM2PnsBa0bqzRXBasbFcDx+DjlyQ/KS+2rH6xQvRFz6+v36R606XcHNGpVPFEyi82VOjcaPq3OPs65SaFobA0quYuwAqUfs5neJ3+6R31zlVsPtthvdzG5Jgx8th7e5Nl3f4jv/RFf+fNf4e43qnjRJtuf7vLoOy+Rf/5r6Op9jp9/Tit9TPP2CvHaBj/8xJIXhtwUvGpFWGtpdXu8ZyWeExjr0LLMEXXXi1kZJnhas+cpisjHCUH3uENVC4KwjAoojQFjiSMf6xyBV94tctYifUU3fUZiu5iiwKN0YfMaMaYPOtf4xvJBdpuOM3SM4dmNOu3hkGyYEiYprbUWxV4b5xztThc5Stab5qXlxauE2F6fIM2RT/cJhKDWqtG6sULeHvDCCV5VfPqhjwp9DhNFGPt8Q1niF08pkoK1m3+BLLvN8YHihrTEwx4NkXP4oMuO26ZWq3Drg3vU7zXpymNWDl+wqstEtea5wYt8rBMc9FrkRgI+N/RdLB4Z8N2nEhF4yMAjrWeIn74PcsiNzlNsntOor5DXJOkwp1GJcVkODnJRIB3UqjF5MmRvvccgy2geWe4kMYHTuGZEIh3He0cji59Fje7pKV8RRAFSSpSUOGfprLbhoebVwUuiqILyJIfPD/lBrUq+9T69rXfJX30OxWyXXzdSdpzIOCcBLk529nzD8gz6fgWG93J3VRadKRcLZ9OluVSN64bF+F5uNNdVf9kal2j5rRD0Ft7CBLyZQAvTFO2cuf+K7TGLoXTnC03VnRBmlqG257jdMeP+l0+tx2DeMXQxyZ15YL4uzLOUTH/+oojwrGUyt8B1dLJsjSnLkjv/7MruJLMEoikIqhFb792m9/wQZyzaaFKtkVBaeSSYIMKYkuFTgHYOaSEcCU9e4JH1HVYwCriQY53DF5JKo8rxQRtnHZ4ncUKSao01Gul5mFGeGiVFWd+V4aqNLMM5V6OI3Uc75P2cW+/NE14FfhSw+c5NOt/+hIPjDrJT5d3aOu98630kz6GYnouze2GnLpFSUF1tECc1KnnMoJ9QbdXoJOV9GumF4CDrJmS2w8sfPeX2hx9QXa0T1zp0Dzq8/OEzbn9wj9UHN6jWjhFAbbPFez97h5fff0JblGHLq60aK1qwkpTzKpUkOe4xyFKkVGzdWOH4+R5WCHIAY0u3rVyX8y8FvSTFV4og8olG7opFXiCEQheGUBhkKBFaoAIPEYeIwCvDTTOSREcCry00fiVktVlh7+kOeZJRbdZYub+FHGyXQjECXWjSQYqQZRS9NWMRAhpbq1RW6+T9lP6rY/rtHtY5jC1zIwkpUSNhuZ8MubneorZeJx3GvPh0Fz8OMNage4ai0MSNCnc27nDj/bt4leCcJVVnRRk4YuytDtoDomqdnc9ecPiyR4Llk5UQbR2NzRart9aJ6jFe6CNTiYp8lB9z9+u3ePLdR2RFQZpmFMYgAvCEJIpCtHGkaVGuUyERUmILiys0Kg4Bged5hHGI5ylW/Zwb92+cWmia9RqFtdx5eBu1JTl+eURFCNJeQp7k6LiBF0YItST9cEy5744fRMu5TDg3+7T4cbQCXarWDDr6Rupcvcrc7heXWW4WXvv9zeLP3gpKb+EnFK5XKHoNQnOp9pftYJlic+jJhXRh0cOLKi9Spl0KFtowLtPM68NlrITL9ncZq9Ksfqb5hmub39eAsTXsRozONK9zJvi/zkYqw2/f8TweeuWdHbOSsn97B50XHCU7BM5HuzJfjC8E1jm01gycRBYFnVrAUJX5bVRW0HCCUAsKIUuXr8AjLwzGWfQoCp2MPFYf3kLGAQcv93BSEkiJUYoChy8lOIdUEmcdKhwJWUoSNKocdxOiOCQfpLw8aGN/NsILPDrGwnYfEAz3hux/ex8QbMU17r7zkM72AdGW5MH9kMrqPp/sHTFIUwAOrDkRiSZehLa3yPKQ/pFl5c5t9j/bR1pL9gefsOIplKd41hQMfcH+Sp314/d49cTSurVGVK+y9e4tku6A9qtjWjfXqK/7o7tMFilSVm8eEwaKj/7oBXcHd7C9I2TueDXIkJ5iGCqSekxlfQU/jigaMb1I0j1oE4YBxjmyMOJVkqGzgpsEqLbFAo2Kz1oU4AQoAoTvYZ2hcwwmyfB8D20snrWYJMfzFFKD8H3QFmc0Skp6Rx2itRa+UtzINfbRHq21Jg//3Ie0nx9w+GKfQXeIFwW881NbhNUjhIxJfMmO6/Fy+wlHHc0grSMiwcCLkFKRpRkiy9F5QRCF5EkN12pw8CKlfdjFUAVrOIr3SN/rsPW1NbKmh7AB7Y+7/KkgoKUkAojrBiscSMXvvhAMchBCshLdpdA5Bz88Zv/5PtaWe+l+HtHvDZGdjOTjHeLNFcIPbvB87X0QjkAbmptH3Hp3yIvDI7brOUpKTFzgBHTaPRq1CkpJ0rTAOgvW4YcK3/PQWY4QkiLLcVjqa01qa7XSqhb4+B/c4fNnu4TVCG/HoxHUsalDF32M1ASe4mZqWQljmn3NsXXosf2/rL7qMrRpESVZ3k3rIl3iskSaC1q6IsziP+aR0ZnKo+UOqXG11fyw3IsCU7yunel8a/N6WqryhcrDt/AWfnLgeoSiRZah66CDr0s/xBh5EtNeXvOpwEwZb5HFaZbybhFBvgwxWkj53On/l2bjLxLMriK4XKb8m7S0XcbLYBqfeeNZ+K6u95A7bfMqzY6NQwjBDeXxM34Zce5RI+OTjQOM1qSVBLTAEwIVBgyHaZkXx/NHQo6jG3kkFR8hFb3jDD3M8AqLNhalDXmhURYKbUCAH3jc/OpddJIReB7VVp1kkJIbi/IVxlnEyNXI4ghCnzzNS7esmkcQBVhrUZ7Cd4J9ndEepNy8dZtBJx29L0d6mJIdle5GN7eqvL/ewD1sjIbfATo8M32ejhK2jtuSx/eHdZsMDqHdbrF1q4IxFnBs5BYSjVaSH/qC9mCA3VqleZQyPGqTDFqEdUVtvcHGvS0Onu/z8qMnfOXP34HQUQbqyFBim/qG4+vfWuPxd8DmDp0XZSAE6WEbFV76DtIENxggjiSVVg3/zjppf0iWZBxJSevOOt2DDo12yka1QmEMtyoRjUjheR5agMlzhFL0A48iLy/3y9BDKokepEhPYIzBWYMQEAYBKkvRacbhqwPqnsdqP0Eah312QMcIqq0q8TffAecIKhE23yPpf7+8Q6NT/jjKKayFxg2MuoG2FgUI6+gNhwgpCeIQoS1FVsHZdQ72d/F8D+UrnDYMmz1u/LXbhDcqHPzXHQY7A6QQbMQV7ngeQkLwviV3OSLw+c4rOBiAJwU/f+8G+0+36e+FKOkQzoIx1A/7VEfufkpKikd7dDoJu3/tpwgbFer6mI3oE268Z0lrBU90l8JatACty0AVvX5CICW1KMJLfQSOXGu08dDOIDCEUYjONTuPtgl6BbnwWL25Dt+4jah5vNo5hGeOpx/vE0QhTVeQpRm+VNzxW2xWKqhhuYcWUwIx497jMgLI2d2j+Qz6WYsXwSyPhEnyufhQmfC2EMu4b198rjkcYtyncHYTZ2Vn4nl52r2cC/Si59d5ZkzO5ZXvgb0ViN7CW3jD0eeuwjBf58YUjCW1Kxt3p51MdnZtxpvLwGXN/RfQuNcWiMZhnJNc1uI2z4vjMgLWrL6W8zW42hkzs94MJBbOwdU6nhfNTpz7cAk4ySZ6qs8sQXlq5DrmSDoDBr0hXp4SCdBZGTDBOot2FuNAjvoWSiGxoAty6xgkGcIakkGCVJLCWezIKpXmOUlnQLxaJ+sO8AtLvRojpcQ4SyWO8DxFOszIsgJjLGEQID2FBaJqiPIUeV4QKI88zel3ephcnx/mjDmbVgqfLKfy2XikpnKOrLEUmaYoitMocXGzxsY7N6muNTDaYLXhePsAk2uElAyGAz79zg/Ze7yNKTSbD2+z+c4NTFpw/PLwFAE3iv4lhKC63uCdP/s+G1+5xertdTZurqGsI+kNyUbBKOwoOt3wuEd3/xgHNNdbWAft/WMaq3WElEgJoSrzQHmhjzEGYSxRJUblhtiVRF048KMAISSmM4DClPPg+yAFnpLlxEiJ55UBG0yuiaIQ4cBKgR6kRLWY4UGPo893+Pz3PuLzP/qEpz94zO7OAVleEAcBQkmMcNjCEPllhLs4jkrBC0me5rTWm2WSXCFQvofTlqLQPPjmQxq31kCOGP/ToCUl4bbWkfZL1z2p5MSmsMaSdRN0luOc4+b7dwnCoAyJ7fsUhabd6xP4imSQ0Ns+whQGk5dj9SKf9Ye3WL9/A9/zCDwPXyqkp+h0unTTFCklzUYNay3WGIQUBNUIL/DBWSIhaNWrVMIQieBwe59Pf+8jiiTn5nu3iaIQ5SgTtgpR7gVjqTarBJVwctueXJo9t7bd6X/Lw8Vi0FlJwbyErOP9npygp7+PHaMnedfGcXTu7LQda3Dy7wVwVnx2hcsy/td1nl8Ux+7M9XPegbY83stG8LtMa1M/vYW38BZGcL2BFpb9fRwuYTk4T7ov3s0nF1VnWQLGAzZcmi7MEwDGObHx35Zp78rE6Ro1UtN4LLKMTXdzESoLn7/WBCyHyzLWu+mKs9C6aLovBbPfz8LZmPdKz4X3FTzTmv/f6PfKseT2tiTtFhRDgwojEt8jywoqtZi006PieRgpkdayOjBkwz4BDlG40nXIGApLeW9ESpSSZchooFKNITe0P9+lutog6QzwIp9BPyFNU6xvqVd9vMAj7Q2RUiJEaWnyAg8V+AglKHKNyTRR3WfnYI/9Z3t8RTX5ZhgD8NRoPtGloLTdzRjm5txUHA7LiGiL3lWRFSgjKArNTsWj9/4Nbj28zXrucMMc/f3HWD1EWouUgubGCsPjY3afbdN/1WF9a5O4UWXl5hrSV+ztJQw/fA+/FhFzxLvB91CRD7Igqu5z/8+sowIP6fkcPco56m/Q+ANB0kk5MoZkpYYuCla1oH4wpNjpsuJ7CAqqKai0oHACbS0v+xl93caTkhu1AIwh9D1crst5lYKgEqLbA3Cw3f8YKRREMS+jlNT36IYgB3eRXkAx7FGrVfCsQxelNStVkooDYx1pu89AVOiv/wwO0J4kzH0KLRBdeC83+NJDJob9vT7VSkQYhfR6farVmPptw+eHH9O/k1GJIzq9Pjfv3yAPfI7++x4AWTvnJElysJURxpClBf/ngSBphzghuVX/gFv1kOFhn/azI1q3NoirMevv3SoFV68M8hEGPoXWNKsVDA6vsIQfvaBZgMwTtg8ibn7jPr4b8o3YsTM8pOM0BysVCm2J+hXqBy2UABn5RFGIJxXZoOBumiOFhFEQinzQwzU6bAcdgkpEkW2Sd/qkg4QH+PQ6WblHcssw19TjiLX+YzY7hxTOomy+cL9/mTzrbHFpDkaj/TaL6T7V05zIvOcsG2czMJ7M9QyPC2CJSXotZ+grHU/zrFuLnl4Nxm8XLzfOGcRxoTfEW3gLPxlwfclbp/fhm9j5M+BC5nGi5MwHc2HaOWChBWHmOEfYLWLGXxNmJqg8h8OiBmYUf513NosRXWotzNCSvqm1s2y7YurvNFzHGj8V2ictO0sxAYKJ+T6tO7beDpxl3xpw8LWBx50jD2sEx0HEccfiS0ulEhHFEWl/WLp2IcgKTQtBYUrhByVPXdtwpbVCawOuDJrgKUUcBpi0gNCju18y7NKLqFQj2u1jcgtZoIkDr0wmiiiTwhpDNihDeUul8KVimGb4nkKnOYPDLs2NBh86gRf4ZLhToaidaNqpmZiXEwZs7rYYlUl7CaJjkRLakWKw2WA/kGymBVHgsX5vC/noMVpreu0uw4Gj0WiQ2pwiK/Ms9Y579I974EmGA8tRtkJ9bY0Vq9n8ICRoxjhtGTx+hqwdo8IyLPnNb0iCz6vw3gd0d4/5g2cv6RuDEIJYG25bibESlzk8Jak7SR/BsCioNmsct/sY7fA9xUoloOL7FF7JTBZaIzyJDHxsmuMCj262jfAVymvwRA0ZRh7dxKG5hXIOL/AZ7PcILRhnyYYpmbbU15vkw5RskCLiOi/CiKhaoUgybF/j+R7V4ZAbCKSz2FRDZnFpn1oDmtJjbaXJR/t/zIvqNvWNKm2RoG5I6j/X4uA7R3Sf9iaWtRQCr6kRUUG85vHo2x47A1BC8hfv3yKyEc/2PyfJ+wQ31qhtrSCUon1wiBEO4yzdQUpaFISeRxCHhBL8bkrl+RG1W6scDlY53g5ZvR2xPniOH1R50jnmOPDwlEQWjpXjNSLfp+GqDPMUoyxbrTrD7oA0T3CA7ymktRxs9div7eOHPtKtIIxAKkXQTlgbFDhrQQhyIVBKsBkNaQz7FDiU0+V6XbDr33zY6kV9T/5deIxNPxxX1EyfDSdBT05o30w+/erjvqQ6cEb9Mbe0S5zdF9HwM5Fv/NPrvHt3iXHOac2d/o83zrS9hbfwYwxffvLWcSZ8CYZcTHw+cxE4/++spBCl7kngEMKd5rpjRlvnezmBOVRxvK1zMpS7FDG9EkxxfjMcFs7DRTjNamLWuxkfr7ho/q7Q51Iw09/k9en6RdagRdampft2p3PnRlHBztw8L8BthjZAiNkueYLJ34WU+IGHLyXSOYo0Z9gdoEaR4fKiKN+nEGhTBlGwI1SLvMCaMumnHSW4bLbqVJtVtLUMhwm72/u0u316g4RsmBHHEVEUUhQ5npJkWU5jYwW8MkJZ6HtkwxSba6JKSKAUke/jKUWjWaff7tPZPaZ/2Dsd9OloZiSZEoLSSjT+nhxjDJooI68FHkVWgJDkvYT27hHPv/+YtJ+Wv+OwODKtcbnG5AUOiFSA53ls3NliZX2lTFqLAOc4ePoKqw1BvYJTCmccfhyy+s2HNO6uYxAUaUGe5KTtAclBl8bNNd75mfdRkUIXBXmakWYZWZqh04ykP2SgNfFqAz/0SftDrDV0+300pTuMNgaTFVjrMICKAkxWoJsVrFJllD9PoQIPJwXSlUKG0QaHI6pEeKFPgqXQhnyQ0jvuogtNa2sFbUZ3yBBI62hUK6UrZJYhpKDX6bG3f4gVjvXNFVTgkaYZ9ZU6e4926PQGREGAw6ECjxtfuY0XB+fenRwFHrGje2jixP95DDo7R5hMY63BCxTDo17pnmYdJiswWUGuNdZa4jBAUoY9R0AyTBl2+viRz/CohzUG6UnCekQQBXhhmVxXOKiFYZl4tihYW18hjHz6gyGVRpXWWpNAeehC40lJokv3xGocsfHgBu/+mfdZvbWGH4dlEmQHxjnW1lo8+OmHhI3K+Q08A+aRsqXo/BsB8Rq0erqpM83FdLqL6060urz74Vm514mcd9HxcVb2OsYpxsjc2cu5cLTnur2Og/MtXAV+7dd+7fT8FkLwN/7G31iq3t/8m39zot6v/dqvTTz/5V/+5bl8wUV4/PZv//bccr/1W7/F3/k7f4eHDx9SrVaJooi7d+/yrW99i7/7d/8u//Jf/ks+//zzpfr8cYM35z53oXBz3kR+Dma5cY09XFx7huWBab51HIez1k6up57ynSfM1LL04py2bKruNdKd2caVS3RwbVas2fO9TLUvBcYXwrUIODPqznu4wPvkUjCG202p+NN+Ga74JEeQlJM6j92h5fdflFp54wIwGiU8nBD4viIIPbSnyLMcYy0i8BBFUVqHcGhTRuGygAVwjlwb8m6fJM2QShJHIXYU+jfJc1x/wPqNdRq1GkftYwqjiaOIzn6bIPTRWYEQMMwKhoOE+moD3UkQUuAXDb4hb7Fz8IrsheNHZpUb4S02ojb/N7kNCD7WBZ/p83eOZs63EPxsELAhFYXUqEaFl3GBKTTqoxf86Xdu8PR7j/m9/R7NW+sMjnvcHhqcNgROYAuLkhKlFPVWi5V7G+SDDG0M3eMufiWks99mcNBFSIX/hxHWWB4lfb7rlai0wjUanRpHT18x6EmkGCIrETcbMWtffUgxTBk82sVPCobtPozCl1erMcebNbo36xRpTvNwgDzqM8xyEDWQAlVYVhsfEOuM5nqdnnqGa8QU+93S9TEvkAX8Wf1VbOrRtvBfVUCW5/gofN/Dk5Jmo4otDLkQCDPAF5/TamxjB4Kbuw8IKznhpqR994BhkuK9BFihEvjo5pD2jT71u+sUSc7nj37A0Y0BYRoSfbJJ4Hvc/1rIhqsgng/oDg1dSin2f7oLN2vly0oTxUu/hnWQ2yFQWgOddbS3D3Au5+v/c5f19xy9ds63X25ymEe8Gkii+ClpkRISs9pukA0LKnFEmuaIKqM7YobGSgO/Yrn705LjxwWD7/mI/ffJ+ynHnQHKUzQbNYbVDjsbT0BK0jTjeZZRq1ep+FXY8+kbg7R3WF/5GhsPb6HCDUzhsxqH3ImrhFtrJP2E46063maTA1/yv378ES4trU19e0GkhSkadHL3aNLp7Jrzzl2Ez2WJ1Vid+Xhe7whmqYcuAjfxeWxOLzHmcaHqi7K9zHKdeyve/MmF//gf/yP7+/tsbGzMLXN4eMhv/dZvfYFYQbfb5Zd+6Zf4z//5P5979uLFC168eMEf/dEf8e///b/n61//Ot///ve/UPyuA15fKLrizrtqHpar12OC0Z2+a+Smyo4br67ErF620rUJB5cwtY33exWh7RrLCbGEkDwTXnPiZlUff3/zLGbTC2bJvi52rbhckyeF61LwVa/czoePt0mTjJtfvY/yzgSjwyzjRT/H4Xjv1h1IDclRHyEEXugTt6rsfL5NlhUEniIfpgjKiFwAyPJyvu/7eALyQpcX/RHUalWSNEV65SV6Y0orUjrMyKzBFppqEOFRJrY8iTwnAOEc8Sj/jAOSQUJhDC0ZcbffoqIFz3s9HieGYU3w4UbEfa8M5b1vzeRELJhdAdxVHveUwnk+n+eGMA5xQCPTNFNN1BmyXVXs7x8gHHxYOERSurX5UUBUiej1umze2SBqVlGBR6WXMOgOyEeMauflAbbSovhcIwQMtOAHyRAH3AhbVD5JydMYZy3WbnP08oBas0ZrcwVPGyq5JWrWaW6soDyJFIKin/B095ADVYYz/6lKiOp4+KGPzgtMoFDaUlVrVD1BvdmiP9hGYbG+R9Lrle6JBm7ZDUwCFedQwqGwhFFA0m8ThQHtXp8o9EfGtRzpH7F2x+E9LwhSie1lDMIBenOb+mrEirfGhljHaMOz7BEvkqe8WxO4imPnxQ5J07AxuEH9sMGt25u8u6bweuU9Ir+wo3cjuN+E99fKe0RPey06WYh1YGxy+g7zQUr3qEtUgcbWIa3bmmDdYzgI2Hma0w4da+sJgbJkwwRx7JCU0Q6llHhRgFWCrNsurTyxoHFHMjxMWF2v8PT/OyTwA+o0URK0MbRFj+PaIUopEj/FNQR93WFT3mQ9vkG1Vaf1Z96jv1XHGkv7eZuDF3skvSG2r7kZxazc3aB9d41e6IGz7NkyN9NFtHGmC9gpnz6uAvvxZ4EvcvN+3RHMs/Bcxu4z7TFyKhhd8ZiZrS8WkwWu6ey/tIVrfHGNfBdf10r2Fl4fGo0G3W6X3/iN3+BXfuVX5pb7jd/4DYqiOC3/RcC4QPRX/+pf5e/9vb/Hhx9+yNbWFp1Oh+9973v8l//yX/gP/+E/fCH4vAl4M8lbF8E8vmUJ5vwytOOM1syLq7O479Mkj8vSr+k2FlnPvizryEnfs/0xSrgWWrjcAM9bC8dmeM7PC/GbZf1ZNNZJZOb3eVEfy8BICJ+9BM77hIuJpxc07expOYFg5e4WQimEPFv7VhucPVnTgqhR5f7PP+DlD55w9GiXwVGPrDfE8zykc0SehwY8Y3BKkWmD0RqEoMhzfN/HOofyPWq+T1IU+J5PEAc4Y5HBiSMgWGNIi1FdY9CDpMz9IgRKCLSzBJT4+oFHkmblWIIyIWk1DKgGIUWng9GGnR+9JI4OaN1ZH5uj83N4dsDPmEsBQkl0pkuXs9yghGJ1c42P0h6eUkgBTkBciRgMhrSatdM7fM44dFrmq3HWIlWZoNX3fbpHXUxWLd+LkGcd4ki7A9QwwvPLO0vpIKFz1CPpDEg6g1GEM4ngEK0N1VaNra/c4WD7EJoBKgrwpcT1y3w3RZ4jRIArNNI6zOjel1cJsccafIGMfGxhStc568rIazLAWUNRFDRvbVBFoFQZPU8pWQoMXulK5qyldned3sERaSdF+T7SObr9AfSHyKFPdNRhkGa0G4MyOa/n0XnyqgxzPrp31qxV2Hh4E+EdzF7XoxdVJs1VOHtCH0aaCFcKRSBKK+NIWHemdInOhim+VHhCkGuDRZb5s/wyDLyQAmcdYRwx9MqIdCbX2KIM9NFtdxFmExOI0joYhaTGMEzy0sXUlWG5w0qI1gZrHRv3brB2f4snSrL/aJfjF/tYbUv3xyQlHTpebB9xfNjhKB9S/6kHeL6c6cI9H8TUtzfPsC7OszP282UUQmK6tTNiusyI5gqIb+w8vVrDl38/8w7ly7TgZujqlhBwTrs+b2mabOetkPRFwd/6W3+Lf/Nv/g2//uu/vlAo+vVf/3WgFFT+9b/+128cr9/+7d8+FYh+5Vd+hX/xL/7FxPOVlRUePHjAX//rf51//s//Ob/7u7/7xnF6E3ANQtEl2LdLENBzTU/0d3FDM0tcZA0Zc7NZmvtdZkzTzPabhFnM/Sw8pp+/qYPlxGXi3N2n0aOxAANXQeXazsTLWn7mLo/5UueiZqef1YXgL0URakGlTtPnk69UAYiHNV7ubU75DzucsTigu9dmh2fc+LkVlKc4er7Pwe4etmVRLYPY1/hBBZ0X/P/Z+7MY27K0vhf9jW42q4k+dps728oqqgoKKDBgrrHKrmsu1wf5CGPZl+baSMhYsi0/gNyIB0t+sGwj+QlZlgWyLGMk8wD3+li4fI9dcM7RAQ7gchmoysrKrGx2H3tHu7rZje4+jBWxY8eObjeZWUB+qZ2x1lxjjjHmmHN+42v/nxKCxgecn3thbPpbFnkCXsgMgVRwtXWeWYjkWao901mPyQ1aa6qqxijFbGdK1XUprG6uqGW9gmA9JtPsuG3uXL1P+0LNICwhXxcgBKNJxRu3wHuPUwngITpHlJJm1hyzsoeu+/DDdMgb/JttyxcFCCRXcke0HqUV7+ZQDTXiGy7zyh80FCOLE5HdKyvcsxbfl7x0dYV7r9/EKsmX6OgWMtz2BLG5Az6Qh8hLIxgsDeH+hP+lbYFINccuFoBd7nPzYo+2aVne3OIFU7B6ZY2u7ZjuThBKUgxKikFBiLB0ZZW8XyCMRkYgRMqLizh9Dz/sED4QvEOhiCFwr34daJjMrmBdhaBAaYU0CfZcaoX2Ct+lZ0MpST4oQUpuXxrinENNA5cmLbnRbF+fQFgnW3qZ7BsmjJa/xKipyXqSxaKgDYGN6h6jSxNa52hUTaEkujAIIDeaUimefwE+shDordzh7d1t7k9TGOde/cBbEpwnRonJDbfyj7HFCkR45fIMUTv27u7y+/fH1CslFy72mbTNPP/IE32qzZR5zdIbl8iloDMZbw/zgyLJeqlgtNRDNi0LMdI0DfVoBiIl1zqbkPuMMeyJyP31HqPxjLxdZPn1jIVhn/FkxmBYUtct+uqLjD/1PDdubzP7H3cwoxkXiWz0NKHQ6MxwP1eovkEYxe6te6xJuPqJ5/i+/8cCg0zgXORz/3nEZHwohO44g+ET7BsPhX895nnPnMSDnp9WqXtoOQ5N9bz9nnc53xdvSeShu/SkK7TP88Uj67G/AT8Y7+D748gJH6gl948X/eiP/ij/5t/8G77whS/wla98hY9//OOPtHn99df53d/9XaSU/OiP/uj7ohT9l//yXw4+//2///dPbauU4nu+53ve6ym9J/SMPUWniLVnKQbn5gLnMeef1P4EemTa8ZAgFR8Sqs7s9hlM55nSYSZ4evTCwZ8nnuL+bnOc5y1x/0eOH9fFqQcfeY6OYfzHnXuSQvy09+NYc/fTb/5GCF7UGhPn/e0/hnNQBtc5BqXhzuU+UYDeXaCarKeaPgLaacPk/h6T7RGDlQWIBSNnEW7KhWuXub+xxe5sD2LkIy+8ymx7h66xKUxMa2pryZRKtWFiqkPUeU/wHt+mi9ZaIYkJPa5ySCEo+gUOQTOZkWUGlWl0ZzFKM233GDiP1BrXdBTDEpVpRBtxFy3V0pQ4FvTzIZoEyLAzrkErTJE8N761ZJkiM/lD63W8p23fNL1/kyIbPgELSCT9UYWvO0IITIj4pqaX51wqCrqN3aRkDA21dTz/8hWmm1OCtTS2ZZxL9rRg8859nu+Sl0YrQTlpWFtehM7xjnMHz8LB4zIoWPyOV9l64zb2/ph6NKOa1rz4qVdYe/4iwXtMv8DkBmU0RBjf3cFbB4OCweKA0HaUl/uIqSUTGj3NcU0qaDqSY8q+Z7x7g2AE7M0wq0OiVkTrk6Lby6Gz6bORSCVp645dGQlGUmQapT0xBLa2ahSai90i+XNDygvvMLo+5v50Rj7VLAz6hNyzp3aT0isERTEgOE8+7LFW5gyvrXHVaoY7HYgdJm3F3Un3yDMffKSrO7JewYxl9lgnOs+F7Yb67S2accVotcANMm61FbO6wrYOZQqa8QzfWVxriTsZRV4gcs1sxbBy9QLbdzYJMRIyiW6hFzxKCKbbY0DQNC0my4ha0TYtvlRsiohe7CO3AmonwEyzXlwg7AFdTnHpCm/d2eL2mzd5aWZZD+A6x3iYM4spXM9mmloJpNFI57h7fYN6MuF//ja4tJ5jbSTLDoVpHX5cD+9B8RC7OwdfOVxbaJ8jPYGofeLRx2abx2oyJ8/nOC+HOPL3vHSc7+PBlE7r7TT16Sl4/JEFPH5+j9nviRvnccLLkSFOuh3zeX4YSvf+0rVr1/jMZz7Dr/3ar/Fv/+2/5Z/8k3/ySJt9L9Gf+TN/hueee+59mdfm5ubB5+Fw+L6M+UHQexs+d6xAeoIX5hzC+8O85EijU/jsuZn4H4V3/0l0wMc7/fQTjn5/jDWNJ51/5qSOaXTem37Wnni4zbkX50h1j3i+EwUPrHv7Q4YY2bu/w2ApIY+lzSwVwKzGNbu3A8VCSXu9xv5+RzNr5uFRkvHWiABMt8YUvYKlT69xd/sm4oX44DUTInkMtMY6j5SStkv1YmwICJeskAFAJCv6/mS9D/SKAiEFXWcRUpJpTWMtSinaueDd15rcaISQdLajAW7JVAABAABJREFULLLkkcozmvGMweqAbnGB2eYEHYsU1tZ5PJEgBSZTuNaSac1sUlG+2GeYLx94GY/WPDlQiA7TgU7+4F6YMiMqh0QQQmC8NaK8tMr6C5eYRsH29ghhPbkx9Psloy/dQvqAloquaRjd36WpW6KRCBcRWqEi1NOawfPLiJk4UGYPq0bDi8sgJH70JjE0hOBoJhW2apm2DfXeDKU0MlNIJCJGMqMPwr983VFeKpGdITYdUYARkhA9Qil611aor2+SX1qivr1JJhZQRUZwNd2kRl3UuGiJIoWJ1VsjZrtTXGfRRiNyjTYhIfRJiXOOnTtbrDy/xuKLl2jrFtc5oohUVY2zjr4xVN5SmIwyz7HTlmx5wPLFpRS+tlEfIBimEMRD78r8/VBG09YNulcSiVTbEzZev0X9tfsszHO6hBREITEmI3TpufVTz2xvSlSSwXDAWixoRhOcDyytLmF6OcwVNmU0zbSCEBmsLeHaMd4Gqqol6y2jc0PwKRxShMhwdYF+4xk2gbppULkhRsHqcxcY1ZaN67chBLxzGGVYWOlzCwchIETE+sDS2hKddTS7I/Iio6oaNm/cZ3XYI0hzugf/KelBAOJRT/3JStLZQvB+i7lH9rx88QRZ//it+70Txc8F8jRveXovT0iHRJ5H9ZBnedXPoK8/CjLRH0L6q3/1r/Jrv/Zr/OIv/iL/+B//44dAk2KM/OIv/uJBu/eLlpeXDz7/1//6X/mBH/iB923s95OeWinaZ44P/v9AsDvseDn55XqUqx7HwI/77SS2ljbe+WdxBs8+UZk6g9sf8/OThiu8p3TKJvRUdFYnT+UNPO95++LvkWdt/6fDysxZnsrDdFRnf9IFi48Gdp04noBSCL63KMiEQCjBzrohhEA3vMQs/0Yg5XfEGLn35h1uN3d4Z/pVohL4KpDFHDWQLE6XWNlcZ1AUjOqWGGA2mfHxnYzF/+NtPjld4H/Ujp39S7Seolfi6pYoBN55vPcUWYZUkqa1KCURUrK/2jGkULhAJFqHNgrvA23TYnJDFJGusyAF46alnxmyLCOEQNbLsU1HO6vBesq6pPiNBZYGBb3FRbx3DJYGjOoG7zyhEUQBuTFU3hGurLDTGyMQVDsSukMuykPKz0PIUYdo/6spM6yoECLQW36XWdahV1/ka9sv0//2l5m8u8G1t++xcnGIfOc+ddXQWUtuNN2kZvP6PYSCjeeWaccVQiu892gleX5lldWrnwUB3WiT8bu/BzHS7t5l+0ufhxBRviOKEm0MG+/exbYd+UKPXr+k61Jony4Ubl6cVgDTvQmZFCxv5lxkCdd2DIMii54KWBh+gpcuvcJ47wZ7+jZdntHeuM/g8iqjWUNMlXfRQjDQmlf3Kib3bmK8x7+4llZRSt7oOzyGgc9Y3RixfXuL1a11XuRjXNHPM1JvUpZ3mW6NqEeOLBfkwyX8C2vMPrKGyg3TW1Pu/J8bANzvAsalELFp5w9C2r5hrWS9nxSDJrzIGyNBz5WEGyPU22+x3lp2lgpuBU/RK1i4uooZFLS7E978319kGD9B56Ha6zBZxsK1i9yfddx/15JFwadUTntrD7ZmTF5cJ3iP6yyDpQWkEOxcF3zlf/0IN77gmaqWd698hSzPkJMh39i+xIrKaaLGak2RZdwTgfriIssXhzRfvcmL44oYAkOhWLq6zNbdLZo8Ivs5ZVFwpXKYN+/hYqQuJTWgleD/93sVXx4FVl+4ROXk/ImNBwK72Nc2zgmle5TOg0L26H51zEZ9nm3w6ADn4rWnz++4Y+fipQ+1f/j6DquH7+c+fbL482zCCY8d7ajtGU6+j8d5iE5r/yG95/SDP/iD/K2/9be4efMmv/7rv85nP/vZg99+/dd/nRs3btDv9/nBH/xB7t69+77M6bOf/Sw/8zM/A8Bf/+t/na2tLf7yX/7LLC4uvi/jv1/01ErRcRaXg2PHMtQTYqEOvZgxnnD8pLf0kXCD40c7F53luT61w68zhWifHnc3eVo6zzgnrfP5dzwOLJVfp3RYUTtxnvHBxqiAK0pTILAKNjJBkJpY9qn9EjGm0LlbX36X7etTeh+7wKB/n6bp6JSlGzZIKZhWhsusI7uG4ANRCpz39GpP3Gop392jXCjnCkTEO0/bWHIhsSGSZQl5rG5blFIopYiQQuWcI880Rgi6EAhA2zmE80ghEYCPFilgMCzprKPuLLUQqBAZFAVyjkwXfSAzmq7yyFlGHkqGgyET9mibDq1SnZpMCDogirRSTfAUeRIknT5hB3/osAAx9yAdEdhiBCElUYzQxpING3buVnRhiL60RPbVO+TjmtHWHsRICKlgqnUBbx2D5QX2rEWUJgncQhC8I1y/z/OffhVpNMHZg6l42+D3GiDy3LVr9GNJvTPFO0cEjDJIo8E6rPOIziKVYjSZEddKMCC0RneCEglWYWTCV0NJ+r1V+vkqnRoT2xtk64u0b28QpzV5bhBCpNwZJcE5BjYQbaA0mrpXYEOgrmpikWpWra4so3cqonVsvr7BtU+9TKn7rLwAWjnixVWC9QgpEEqxs1bQDYt0b+pAtZmQ42qOE54jC7l6oBS1QyZ1xs2vbbNzZ4tSCMpMsaEFNitZ/4bn0UUC8pjWO0zu9di9VRK1otq7jSpzdC9n2llmmSIf9FnShvv39iitZyZlqlEkFSYz7GxsIqRk90ZBvbvCPX+dycsjemVJXimWomBJKmZFxvYoxcnTK4irC9zcHbHSdix1Dq00F59bZzaeUdctplfSKwum0xndTs3VwQJBCm7GFi0kkchOI6mvT/HrEncMIvdxICFn0bmUnKP00B59SogGHLP3PTBKPfSzOEnQfzCfxzEgPiki2tH2T1cI9tkbPJ8E7vtkOmWT31/2ZzLOh3SY7t69e2r42q1bt56o38FgwA/8wA/w7/7dv+MXfuEXHlKK9kPn/uJf/Iv0+/0n6v9J6Hu/93v5vu/7Pv7zf/7PbG9v8xM/8RP8zb/5N/mmb/omvu3bvo3v+I7v4DOf+Qyvvvrq+zan94KevnjrWZb0k6z178WY5xnjOK/BcUz/uMKrp/Sd4r6f/ALj/pjPmp50nc5L4ph/p83l8NhHtdej/07r56z5PO5vjzvOGY3j0WeM9LLt/3twSkJgkwA+MNkZE2JMoU0ieUh8iEy3x2y9u8Hm23epd6dorbGTGikEs7ZFiQR13XlPphQIQSVUqk/jHCFAcIEgJM4GkAKhQEjBbGd8oBxACosTSqKVhhjJTbKdaK2IRGZtR+cDuVIYAX0tGRY5WkkSZFvEOp9QyISg3yuxztEETxcjTd2ipaQ/6BGFoPMeOVeAjNZorWnqlqrtUvK9ksSY8qq01tSjKUKBVGJuSH9wY1M9SMFJXqKD7wLacYOd1jjnEEIhkDSzFtdaegs9ysUBOjPU4xmlMQghKbOMgEASExy5ELjWEqTAhsilF6+QlwW7m3vs3to64SFKx1RmeP6bX0EXGUorykGfrMiYjWfgI1opQFD2SyKgIygp0UYTfMDVbULO8wEbPFXwqEzhrU1Igd6hexl6bUi7O0n3J4C0HhEjeZkjpKQ37CO1RucZ2hiKXoHUEqMU/ZUBC+tLEGHz5n223tk4eLgFAiElssggy4hSgkiFcZvRDClTnpVW8+Kp8/daIlIR2Pl98p2nGtWICNXmmJ07W0glE1KhTXDutu3Y29ihnVQIJQkuIee1TZsK0DqPrVvctGFybxcRIr1BjxgCrnOI+bjRB4QUVNOK4ANFWSCNwRQ5RhtylSGiwNqA84Fqb4b3ga5tUUqiEUx2x9i2I3hPZgzrl9eoJhV7u2Py3BCFoJrOcNaSZRpTGvbGI4gBQUBJsK0j7/cAiQLUfE0O1vUxCi4efrgfRfM88nX+76Bo6OPwuBP5ZyqN/qDXk8LTDnuHxMOHH5c3P0M6u7Dr6Yt01vlnIJE/XhTDWXTaOh4XRXH4tzg3SH+oOH1d0H5o3C//8i9TVRUAVVXxy7/8yw/9/n7Sr/zKr/C3//bfRs/Lfzjn+OIXv8jP//zP8xM/8RN89KMf5du//dv5j//xP77vc3tW9L5BcsdDG+mZL/5xitRZjGW//RNN7hm02TeDHiQRHLnOE4x2h404T8MQ96GCj6X3YrM5q8+jjP70PfJ8fRw9dl46j+fvqa1o+x2Ih77tkwa+ryxZEBIbI/+pqZnFSC7gfypKus0Rk70x02+7hh8a2lzy1gs9Rtsjdr70Ngv/vUJHya4SbK32yVcL4iAyntXEEFE6wV0rIVFKImMEKYm2I/jAsMgZ9S5x78J3IJdfQH1K8PzSLtOdMUwiappgi0MIhBjxgJGCoYDWOUIIWOtREpRQWMC7QFbmWBmIIRKlJFMSMfeMKSVprCPLDUVuwNv5Ky3wMaK0IkqB7SxZZqjqhnrW4JwjhqSYeSJSKdqqJheCIASiX/PyZxLQwq3/S8L902/0vkIlDr+SMcFXy9wQfMRPP0rdBMZyhRd34LmNKXm/4E6e0VqHjbC8ukSMkc3JlF4RCTFQTWYIIeiaDgRs3t7EdZYYI5P7e6y+eOGRJ+Tw96xfsHRllbtv30b4wO7mLnmW0SsLRtMZUim6aUNR5NyZ1bRBMxz0EDaQzwuy3tRj2kHgvmtZm73N9MtfJExmPH9tSn+Y0/UiX50IHJFcS2SZETtL6z1vrZXYCD5GikGJ8gFxv+GVWaDamXJBlRT9kpnRRGvZ3thm+YV15BznIobARrfA7f5HUJnmcn6HbxOvEfuRhT+5iPzOVRDw27894/d+L3mNvt1kvGo0IKjFy9y/Hbn52nWufcLjmg6pFHdXepgrK+giQ27v4nZHjHdGmDyj3p3SWMvWUoZZzimE4rmdGhkjg/oO/dGErMi4HBTRO7x15AGe35jQ1g2h7bDzHDCxvsjvtFPcUobavcDy64Z+ptkKit8pGvq1YLG2rGiVQDAkyODprGVxYciazqlnSSHSCEKMXNirWfSexcUh7mN7fE3fZnc4QWlBpiVSai6sfRdL68/hdgX/z2xM2ZvRRfhPTT1HKzwfzR3mh57tw4xSHNP4yKty3qHO2IcftT0c0/AkHnvc3nhofu9FqNs5fGgPTeY909cew/B64k2YyxuPlCU4dtKPceUfepbOpMuXLz+xN+gs+uxnP8vVq1e5ffs2v/Irv8KP/uiP8iu/8itMp1OuXr3Kn/2zf/Y9Gfc0KsuSn/3Zn+Uf/IN/wC/90i/x+c9/nt/+7d9me3v7oM0XvvAF/sJf+Av8vb/39/hn/+yfve9zfFp6ek/ROS08MZ5uizm7A45nICd5fU6yhnDM8VNJnHne4fylh8af//bQHhePnHN0rCekA4XoPF2cdM+epQfprPH3xzt87L22FJ52fc/kuh9cwNHuBLAmJZeUYl0q1PygRLAuFdf6Pb7p4y+iV3q0mWDStbz51eu89Qdv4vZGDARIKVnMM9ygZFrm3JnOsJ3DSIXznhAC+VyJGbtACJHO+ZQD4zxb96b0X3yZvVYjBj3y5Zy2rpCZRkpF8I5iHjrXX+jTE4FZlMysT/uj93jrkUJgjEappICFEPAhEEJIQrxL0MazWYPzAdcmZLosK/DOoWPEzL1gzjqYI3UJBEiBF9A2LQKRCm7mCd65jQmeWyiH7jnKFYEuHoTXnHpnDj1fB+aZOZKfDYG2zQh+wPiupRckcntGPwgGSwNe/OZX+eRnvoUXv/MbeP7bX6Uc9HAIPJHV5y4mMUMIhsMh0XmkUQfrEfdDo05xPC8/t0YuFc7bBPrgPLu7I9q2JcZA07VILbnyylWUVPiQDCAhxpSrIhwjbamEpd26x3jjJlbMKLRjMFQsLWfkZYYSArVQJnCGGCFEZkRmAmolCD6gMk1oLNmspR9gkGUEH5FGkxnFlW+4hlSKZlQlnh4i3hSM4oCpXCAfDnj5pSFrfSi6MRcvSK5cNgwG6uC6F6XkklRclJJus+PWa7uErsfOrV2GF5eSt8xbtuuaLlcMlhdQ2iCFZPfOJjfevM5kb8REBLrCMA2ewnry2uE39+hZz3pZUrhAV7XJOxUiedPRD5EiQG+hT14W5MsDxt4zth0TJ+nVPXrdkKFZoDWKza6h8g5tDCjNeFZjraPf76OUYvf+DjubuxRaI0QyFBQBnh8usGoytib3uF3foSlmRD1F6RmXny8ZXriEt31C12NVaC5KxQU15wunUTzmo9jfT/Y9FucQfA944dMxvvisNo2j3Txht+eVMsRDnx94lp9k2MPnHzvQM9pTH57bozM90fP3UNPjLLMPGjxitP6AvHcfUtrvf/iHfxh4EDK3//dHfuRHHgJfeL/p6tWr/ORP/iS/+qu/ytbWFm+//TY///M/z3d913cdtPmZn/kZ/sN/+A8f2ByflJ79qp7AVYRI4RIHbU479xTOlDwq4ohP+inf3Ie62o8vODrG8XPa34zEvEBAjCKZyePBjw938MBU/XDu1LOY++FjR71Uz0rhOUsxPYnOe4uOsxiedKufBcM+osS+VxQBF8GGVABSaYHRAmMEUSryhQFRKNpJy/TmDtu/fwM96ujrgpiV7LjI1AX2rKeuGiaTGSLEA9hsFyICiYsKITRaSZy1aKXQOoWm2VlLr1fQNS34gIyp1lC9N0OQ8AoyPAMZCU1HJTQdAqEkymikUkitsT6AT5DNXWcTAphPitN0MsNax3gyJcZIkWUoo7HW40JAC0AIGucJEkLwKKUQPgFIqEwjtCKfo9wpqVJtnn4v5a0IQXSBapK8DrF1GARakP7x6D+5H4p0SDFJAn1CGTNKsR/yF2NgNp4y3ZtQTytcjNz46nWmkxnSKEyZ0VvskylNdJ7p5i7BB1YvrdFb6BFtmk8mJJPtEXaaPBgP08MPW9bLyQYl0QYikUlTY4lkZYEPkdwYQtNx7+07KV+pbojWEWOkVAqEpG0sPanoSUU0Ci0FAYH3EVdbulFCXFP9AucsgYCPCVDD5FkKvWzalGsEWOuQuWG8M2Lz1r0ExS4lRb8kuABSglA4B+2kAZcAHJTRoA3F0hDXRnau7+DbgARMJsiy9DwFoRhvT7n+++8QYkQaxd7WiN2726xeW0cgaEdTqq0ReZkzXBrguw7fdgzzjEIpEKCNpqu7OR9KiihGU64v4axLoYhK4mPEd5bgA1pK6smMsl+SLw4gRprW0uv3UJkBKcmGfVaurDPol0QpWLiwQn9lgagkIUTarmM6nWHnOV8xJKS5Is+4cu0SQiu2tveYNU2qfaQ1jQ/IKLnzzgZf/e0v89bvvMZsd8Rs2mKjwAv5gJWeK3ph3++atqoHj9njMLNT2h7ltacZHM9Dx+2fz3RzehY+nSedy1kheM+aHrbyxENzOAiBO+d0HnpsziNPfEjvG+2HyH3+85/nd3/3d/n85z//0PGz6AAtFui6R8sgHKXDbQ6fexa99NJL/PiP/zi/9Vu/xU/+5E8eHP/Zn/3Zc/fx9ULvT/ic4EAoedp+9l/+h/s6Z8fnerGPuoXiAwS7Y5W9hzs+VDdz/n1utYtHrXfi6RjN44Y/PE6fZ9FJ1qjT2j8OYz2r3Um/n+UJPMk7dly7Z7y/eeA/1hUKgcngf/5/LdMfSnyrufe/f5T7r2/S7E54YamgDIFMvMz4jZa27ZhMW1JJmUjROp6/M8J5j1qPXHcpJM01C5j2FaoQWXQ5IXQpR6fQeCUxMXkC2mnDcGnI6k7D2mRM74092t5ztJXE5Bkz67AoorXECINeSd20tK0FIcjLPAn+maHpLComWOQQI1pLlBB465DaEEnodMIHpBQMF5fIixwPCC1xraMsC5o6FXbNtMbNWmzdIaREyJT7lPcLxqMpIsbkmfKRsl9AhFdmlktdpL88OEHogv+tbbixX4h2/3hIuSXKpKKwIgZKnadcIdfS2pZ7N+4x+sRVvvb7FW+8e4vvcYH1yytoH/j4yFF3DdoaJt94DZVpdl+/zkf2WpS2MFcYX3h7G7tk2TrqIubB4yilBKMwRUaMUC/1EB+5TFjssbZT49+8iyFyLa94+WKBChN6TR8RDEZIXq56LATDwGh2VY6Xjigkt6tl7rwbcbszQkz5YL6ruTv7Aq71zGRGyD6BkQm8gqpFri/R5YavXejjXSCva65Yy2BxSNd1TLcnLF5aQuXrNO0S99+5y+7tPT7yiSnlQo/NnQk///kUSvEJL3hpZ0aTd3zrZ1b51F9fAwTjL1/jS1/Q3Lz1No1U5DqhLLa+oxpXLFxY5pUuUu1WZFVktjCkbTqEkrw8aonTlkBklCcPpessCOhlhkYKbr+wQvv8Eq7puN/MCFmPvi/5SCdSXp33KOtYvrSG1SoprUrRLQ94IzgGmWH40kUGWtJOZuxkkv9Gi8Wilnv0ZMp3yvOcpZWC7Z29VKNJKVYurdJMK7a2dhFKstTv0/Rg1lku2MsMbA8pBTsL19mZ/h7vvFnwX9f/FAsr6+hc0vzB/wZdfT6mcjSK6mAvOoen6FmQYI6Sd8q83k894RnQU8RqIE5iQCfQieUDHm+EQ70dVgr3+Y149H7syyL7wSXHhd0f3kv/kN3DP0r0jd/4jXzrt34rX/ziF/mhH/ohQgh8+tOf5pOf/OS5zl9aWjr4vLe3x4ULF05uDOzu7h58PgzB/Tj0T//pP+Vf/+t/zd7eHl/4wheeqI8Pkp69p+iw8HsOz88j5z7JeE9DR6MNHo+vnfzbvvnuMFc5tA4PT/spuM6zVDbeazr8HDzOvJ/EmPgk57yHFrEIjGJkJwZGRJZWFGtrmqUFwbuvb/DOVzfxrSGPJdoZYquZbnT4sSTrcgqT4ZwnWktuA0tCI5xHSIlWikE5QPgeQiwSQ4YPgcZaZBSYLIMYsM4xm8xYfeEixkXyxjPwgum9HXAeHZOnIjOaXlmQaYWzDje3gGdakRmFlIKqbhks9OcADQKlVcphUpKOiBNinijvsNalhPwoaJsWrTVSSFzd4aXAaIULga5zuODJyzyFnimJzvTcwu9RUpHlGZGIax1t1cLelHLSUOzOWHSBFSlZFoIVIVmRklUpyY4YZPa9zcWwTJ4nUj0o6xytDYDAt55mXGNzjVgdUhPYub1FCBERQbWWMkguri6jjWbz5j18ZyldZH3QJ7eePpIyCjIfDj1YDx6y/SmFEFISv9bpWGG4dW+L119/l+tfu5VCCQWUmaLMIrn0aJEgrkMIZA5WZE4/apqmQ8RIEIJq3LH75hbVbouP4DuH0IqOms5P6Npx8pB1Fi1kKm7qA0JKnNHEwkBh6C8M6S0P8M5z72u36KqW6f0Z1U6gKJaRQWM6S9yZUO+0bG46Njcd7UyysrBGbgvq2zsUsmF5ELCd5+3X79OIEpWX+ODxAp776DWe/8aXIEZU6yijQM5quqpGZwYtJLmLDBDkLqBReOuTjUxAlIIgJeW1C9RSUBGpZKTWEpYGlMM+S5dWsE3Ks/PWMt7YYTKaMlxbolgewrCkyTS184zv7yFDoChzahFRawu0QuBD8pT1+yV11aBJRo/VlUWC9+xs7VEazUKRo7TExYSyuGD6FKJEeYOLFb1hpHUjfv+rd7gzjYzzAfGUrPwDljYvpnw0bOtBjvwzYmJPKwyf21PxR8UVcZ5rON+inATecOhuP9SXOL7RCUOfPc+DsT9UiD5w2vcKvfXWWw99Pw+98sorB5+/8pWvnNn+tddeAxKg0QsvvPA40zwgYwwf/ehHAQ4AIv4w0VMrRQ8sHedkaqc1PVfIwDnbHTvweY4dHeysXs+r7e0j8jysFT0IgIgHm925ujt+iPPR00QriCP/ztPmPd3vDg1yVnjm/m+Rh9s90fxOX8Tjwji0BC0FWgqcF9SV5d3//g7btzbp5RneWTanY7a7lt22QswFH5MZbPAYKegZjdEaZQzeRwqZk2EgQBAOKR0ei1Rp/NXnL9CMpqmYpE6haGnWEld7/MyhpKJxjnHrUp2ieThR3XWIuRJUdy2d99RdqlkkRSrYqubzwScLfAwJNU0BK6uLFJnGzGsYSZVyn0SIlFqBD0TAek+WGaxzVHszUElREjKhjOEDUsqkkPlAPWrZvT1l8509Fp+/zOC5NdoQuPfGu2ze2mB3c4ednTFtiLRAiA/uiZYaLQ2ZybBty+7uDuiAznOU0WgiwgXqvSloyd6dHVavrIOUNLP6AAACo+chj9DtTWmnFdEFBoMeRit6wx5lkbNze4t22qKlxkidwgGPPDfeeUbbY7quTdDczhM6i3AeYkSXGUFJhJFY2+FEQGrwKtAJhzWS3GiClGghkSEkYXw8JcqACC55+QYlssxQeUk+GKKkpmc00TqUVggSPLvUEokgI8F3N03DdHNEOSjRCz3INDv3dgjAeHOPtefXWLrUI8QWQcAog1EZQhqCNGTDAabsM75XM9u1jO+OCaT8sECgv7bA1U9cY/HyCqY0xBiZNg0iN6gip51WDId9tE/KyHBtmagkeE9ukqcnhoibK/XaKHSuEzKfS0rTcH2ZYn2B8d4UH5LiFyNMtkYMFgasvXiRwcVFli6tIqRk79Z92vEsKf1KsbS6xPLFFXq9gp4QKOcZ7Y6xbUuZaYSSTOqGzXvb9IuMQZkRlWCYlVwaLHPFlFwoegyygn5WoNB4L8lNQdNWbL17k3pvBEIhlEHocwRxHCSszncRIRBPHYn2GCc/Fv88vt+TsnHe82C0E+f8eBtWypV+XMvb/qfjxjpvX0fPPbSSER4K/z/umTjjEr/u6i3+MaYf/uEfPkB701of5Bmdh77ne77n4PNZ+T1d1/G5z30OgE9/+tNPDPcdY+T27dsAXLly5Yn6+CDpGYTPPVwmbj+8TcCDuhTHhZ3xAC3lvTdGnDRKfCSi7cxuDp26f/CkGgYHiHtzaKBH6yYc7uoc4XRPyqc+SP52eNmfZdjbiYOc95yno/PIA4eLGCsh+JPXhgyMImjB/3W35Mab19l9q2Z3UFDKDLKIHnwJhMN0Oas7z6cwuUhKaEfQxPQ8Oe8ZzPrkX34JhKBZrNm8/CWUkvRGK3QbQ1YuLM+ViohSAnuAAAk+PEeQF9ibLtLMRhAtXgj6ZUmoLTZGMm3o5rkrRmmWVhaZ1Q2usxRFTnABqTWttTTWkucGScoDyoqM6ALeBWIMICQmk0gizjm8kBglCT4QBJRG02lFsJ64r2DNi9giJcTkoQkhsPn2Kv/tl5YoF/uMsj1utTegp/jOH7jMpd4uSy+s8hv/LfDGmzOAOZpXBCH4povfwkq5irOW1+wXePe5twgBTP7dLJcr7Ny8R9NZ+iFSDkqEkVR7UxbXlui27hJ8wGrJG6sl177to9y/fp8X705Y2qrwzjPTad6z0RRrHbt7Y1a6Fb77W78HnWk2pnd47f6XHjJ+VLvTOUR2wXB1Ce5tkTctmda0V1Z5MxMoGcn611H5DplQbBnIlgy+sXzT5FWe0+uIpiF4Dwh0L+dSuMNwrUQuDXnnbo6bOEQdeHntu3FVwBeOK0FTx8jGpOYLi31s3ZHbwOXNGblSzCYtSkq8c9TDDPmnPsZv3dtFDwzrQhBD5OJHG77pf/oqzazl1lcGXL3xZwFBLuD6vre8itjfsyijaGvL1Y8Fog8QIsVSj92NHfbu7OBaiw+BvRfXeMd7XNvxka0Zq61gsttye7XP7vKQHRquvrvHN2w3bN+d4GLEIOgQzDZH9ItUeDh4T4iR3VnFm5dW2JyMcK3hm7M+PgS882TDHlLJhKDoA85a+oMSnRvG2yO0EEx2EvrdlTZwZdrRdhaBoBMCKyS76z12i+S5Uio950Vm+ORuj3I7MtkbITEsmgzTy5mJFW42DZ23LF94i4Z3ufF2wXMvfB+9xRWCa9j6g18j2O5UJhMhKUJHgXZOiqA7uic/sjWKYz8eO/Bj0eMz5DPPOGlbfz9Dvt6jfeZspeT4HejMwMkPdZ0/dHThwgW++tWv0nUdWZaxvr5+7nM/+clP8t3f/d385m/+Jv/qX/0rfvzHf/zE0Lt/9I/+EZubmwD8jb/xNx75/ed+7udYXFzkL/2lv3QqyMO//Jf/8kAp+t7v/d5zz/XrhZ5B8daTvx3QMcpE3AcmOOPUc0/gOIXlKRhA4qvHakHHtD1+oPPWmRBH/p5J51E0Tvvtcbz851HUHml7ijb8rMY9qdHj3POz1u5EweGUTWsfkv0gZOvBk1RqST9TeAmv3xnx1usbuEagypxJMBBqJBUCh/KWlRgIXpDnOS74gzo9eI/1ASlANpphrwc4dBkBRyDlEy1fXGFvYyfl52gNRHSRIaQgYnBdYLrdIYRGSoGIgqzIGU1rmAOjmCLHCpE8CFJQ9HJGdYPzHuc8w15BPWsojCaG5PVRUiK0YjSaICMEAirLUELiRaq1w9wjpSPEzGCdnwNGBOSsweRZCivTmq7tsHNvhunlZDFDmRUW1y+wOa4ZhwTxpi4ssHxN07UttsgZhfDwXYqQ64LS9Ni8fotN7uGyDoGkmk5ZGayztLyI2Wpw3uLalOvU1i2DIocYk9CbGTopaIh4rehrQ2U9EajbDt12qDkghes6JltjjNMUvR6Zyh/CXwnOs3N3m+H6ItXOlNloihES5Tw9kzFqWiZC0isMtqvoDRxZ9LSZpAmWmo5Z6OjmyIGlFKnw7aAgc4JMOMqVknySE2yLHdXEhQwtBTK09L0jyzRtnuHaDmYNurOslQXVpKZvMi6+cpnNd+5ilgbcHk+5f3eby0WBs57p9pj7b+8iVcZwzVAUAu0MSicPo5VzpciD6wyujdz4vbcRQD7oJWQ5o9m7u4OdNZhcg5C0MaPyDlMYVN0RRjOUC3QC9LBEFDmlMmQuIusuKech0lnL/Tv3GTjHyrV1tNYordC9nFnXwaAgGIUpcrI8S7Dv3uNdoN6dMr23g4iR1VcuY1vHZHuE845iOMCUOeGd+7jOI6SmmdUgBcN+j5VXrqCWS5q9GfW04d6deywKmNSC2bhmd2zxrkYpycLCgEovspANmEpPuVJQNRXVbMzujR3UR5YpBn0QZwRyzPlSMj4eMcwdZU8nseSzvOrHu3HO38fh8c8dTveAv54q5J/Cn5/VXM7u6llrGeft74S9Lx7JLXoy3eqptvAP6dnTyy+//MTn/ot/8S/4ru/6Lqqq4nu+53v4u3/37/L93//9XL16la7r+PKXv8zP/dzP8Uu/9EsA/Ok//af5a3/trz3Sz1e/+lX++T//51y7do0f+qEf4jOf+Qwf//jHWVpaoqoqvvzlL/MLv/AL/Lt/9+8AGA6H/PRP//QTz/uDomfgKTr+rTnXu/S+vXDxbGF7Lss+yBs945wPgmk8S8XxWfS7T4/ojvF4y+VZ1svz0sH1nDDxM673sauTn3d94qHL5+G47CgiXkmcElRVw72bm9hWQDQ01hKsp3UzlhfAxwAxYGXylIybGqQjywzKSGIDIkacDwx7yaIdfMQ4RRSCpnP0s0B5scfWvc3Un9Eo4fHK4bVHRqjHs7myI/HzULbgPGVRYK3F+4Cbe4qc90xGU/pLA/Iyx7YWpdQ8yT3irAeZILp7ZUFXNenSpcRoRdumUDvnPdpAmRuquiXYlE/SL3OsdwgX6OqWcrFPM5rSW1rGTxu00SAEqy9cpJrMuHRtGaUCuY70evOQNC8YLF9gujtFupaekBx+6AQpXridNdx8/TriZejlBbPOE1vHzs0NVhaGDIc9mtGMdlrTL3OacY2en++dR2vFxWvrKOcJnUealCPl516JqqpYXl+h3bQomSDLN2/c59onX3zwgMypnTXo/fWXgmaWiooqKZl1HdYZjCxSWKI0aC/JAgQJ1npan8IDRYgILTD9Aq8Cwmh0ryDYlhhCit3MDWEyIynOAucatMnxUlLmGbQt9XhK4TytFHQxsv7yZXSeium6UcXknmb58hrszrAA/YK69sz2Iv1lg8DQjCvufvUmQiuKYY/BUh+TG/Jhj7uv36SrOwRQ1x2dCxQXFyjXFqirBolASkFbtfSX+6lI8b0ZIZeoTCNdIJMC6T1ZkSOlpLOWmBm01oTpFGKkms5YCevoCKHpyKWk3p4w2dimFJKYaaZ1gw+BdlKx/fZt7KSBGJJHclRjpzWGlKc0XB4yHc+wIdApSdd2cyh7wc54zM5b0K0vABHfdigXUC7QNpbQtHTWYlQkRMfedI/72xG9skDZMxA1WpUopdje3KTrAs9/8wtInR2ExwX3KHLUgXI9f8T3n/TDNev2edCxgAjn5GkH9LhdPOGQjxO8ARyrpJ1LmTpn1+e9jKM62mn6pHhkk3oGllxOM9Y90vDR3z/0Iv2RpG/5lm/hV3/1V/krf+WvsL29zU//9E+fqKz8uT/35/j3//7fo9SjxQEWFhYAuHnzJj/zMz/Dz/zMz5w45rVr1/ilX/qlJ85L+iDpfSve+lh03At7+LezGPW5X+6HGdLhbo/lm8fxrWM9Jccce9bK0+kc9xmP8aSmtQfC6Nlx1/NgsydUdM6kQ90eW8/hvdwQBEQpuP7CANNT3P7iFvc2XiS0Og3rUo0eo1SCuQ4eITPeXuvhg0BlDWrxTYoyw4wy1t+8QqY0/dLgvWcynrKUL6D+IKNtO6rFCbvftcHmn1ynGBZ0/6nBWcfo0jb3Xr6J+Khg7d5Ftn7zXhLmQ/LudDHiYyCKiAuBwbCXYI3bDq0Vs6YljgUoCaSEc2s9w8U+2/d2KIucrMioxjNCiAlQQUqGywO27+9hvZ97qVLhzAhIKQjWYTtLkWdUtkaFgO0sIoJUCqEUg15J03XcfvM2H7sUeHn3NkLAy98uUd+yRld3/Ma/nfL533yJCy98go/ff4M/0d966Da4zjJSkhmKXq/Pytcuk2lJaz2DQY+uawn3K7JeD58Z3KTm5Z2G9e2Goge7IXl/2+0xrxaGvdfu0C9LZK9HmHsIh0VB1JKmbhgsDmiqVIx29+42y1fXsN4eep0ie3e2me1NwEWkEEQpIUQW+j3GVUMMKbywc5bL7RqrYpG+SspvbS1Da1mKfbRSSC0hM0iTIbTE9HLEuCZan9ZbehrX8e7kt7FVR9EKVsK3EGKBGfbIJMSuxWvDGz3BzJRMS8nF6ymkQsSIMYZmPMPniq8sGjYWDf3dNdb+v8+xfGmZ6W6Htw3KGOpJxWxUMb0/ojcocT7l95giw7WW4bDHrYWMvaWczaWccdvDh4iUAoxm/doFRAT97jZN3dDr97i2OeVCf8ba1DO1Hlt3uAgbL6wg+zl33u5QRrN69QJMG17ZmGCE5OJSjWsdO9stYXXIuy8ssXd3h2nQKOvpOseg87wwaqnqhvx+xYoSFAiu54qteB9BpO4ptktBf7iEEIKm7ainM56rWy68fhtkgux+VUlM2yEFTJUk04qF3tuURYt1AXZfoddKRJlxw3+ETgSEbxHDP6DC0javsv4tn4Go8V3F1u99nuDtySzmII6OY3jZ+yztPo0i9Uwn8fSDP9i+58rlKX2eR5k7zS751F6nZy1jfOgl+iNDn/3sZ3n77bf5uZ/7OT73uc/xpS99iZ2dHbIs49KlS3znd34nP/IjP8Kf//N//sQ+/uE//If80A/9EJ/73Of4jd/4Db785S9z8+ZNZrMZRVFw4cIFPvWpT/H93//9/PAP/zC9Xu99vMJnR0+vFD2usHoc53hcl/6hc88U109l0PGU3044tn/a45iPPmgLzFnGqDPn9yTcMT786RxjPDMe/AGu9yOQqIfIKQESOiK5LFKYUIAQPc45tAIpJGWWEXxGKyJOQKkFQXVY1zIUQ3r9EhkFVZOE5lxKbOexTUALjUbQf36RUASWn1+l/+qAm69dx/qWaTuhaie03SLdqEIoQZEVtM5ioqBrLZnWBB+o64beoMdymVPXLaK1CCERMVmjc62RRlFPG7QxxBjoWktEYExSnGIMdI1NNcqEREtDXVdopRLC3DxZXM1zk4RIIXzOeooyB+fxPtB5j5KC2awhywt0aAHITUY+zNibVsgqcPOrG/QXLpJvzegP54nnAtq64d5r11Grn0YNNC//iY/xxm9+maZqyIIgto71lUW27m1RN01CmROC0mhcpsmURCiJzjW2arE7U1TXEYWCfokNniIz6f67SMDTdi49E0axcGU11VmKSQGOc3O20hrfeoSStK0lLzIyk0IklwYls8U+dW6I3pKpjIGQKCGxWtLVllzmSTHzAp0b7DQQZEAIgR6WhNEeALLIqMZ7BOeZTkYp16wWZKXAWks7remCR+UG23Z0WY7LPHdv3KPcbdBS0TQd450RRivIM3Y396DM6PYk9VjSXzTYuuPOV29hyiJ5dkh1oqxzdE1Hb7FPUzfEGPHeYwnY0Yze5RVa51IuVvBoKZFKsndnmyUlUV6Rlzn1aIYKAWEdeVYchKtOq4bli0uQG7TRRB+pp1OWfKRXGmLVUm+OKLVGLg7YdJ5p22Il4B2DtRXKvRl6p6IvVAIDkRLrPCaTxBiRmUmKUGcJtqOr2gRFnxtC3SBDYj2ZSPlJgognEgUUecbySkm5aJBCEW+W7I2mDNQCXW2QRYYIgaWFnElTsbNxl2IgMGUvefpO5TnHc6BHvz0lPd028AyGP7+H/3w5OY+3Nucd+2jPx8/7tLv2DOlw5MZRq+95ZLEP6X2hH/uxH+PHfuzHnujcj3zkI+cC6FpYWOCnfuqn+Kmf+qknGgfg1Vdf5dVXX+Xv/J2/88R9fL3Te1sSNx769/VGh+YlOEFfeq+8CUeZ0Wn9imPanGaGOs8cn+Z+RN7X+/qQs0ocOXjS+KfNTZzw74loPtDBn8P/pW57QjAQgr6QyBpuf+EGTMFIjfAgW4e0Dmk9WXwADa2lQMiOnvFoHci0JjcGqSTeOpqmTRDFxqCUpHUuob5JSa41yyuLGBcRIrDyDeuoRUnTWagF7b0a2qSMSe8S8EGMCQ5ba1SZJcEXwXhviu0smTFkRtM2bSpWSUTECCFBfWcmwXcTAlpJfEghd7azuK5DZYqVa+ssXlpGF4YQIkoIWueRYl4vKET0PDm+ntVk/QIlZQJqIBW+jRLyYYlXAq8EXRRUVrK1XVNbh3cebx15LwnM9aSi84K7t0YMn7vKu196B9fZJMjGiDQa3ctpmxYfI2WvBARKSYoyx3YW7xxSK4QA11q6qmE/Mm8/1ynG5F2btg0ueIySOCkIPcOrf/obWfvoGp3qyIr0PAyEQFnP5u37KCMJRF74xItceeUqg8UBPoLKDCvrS2g8uQQRPSIE6rZjNKuIShFiTGhq8zUyZY53AWLEo2iCoK4cwXnyfoHIksIgEQdFHrUxSBERvsPgmd96TJEhy/TMaZkKoKo82dFia8ljxI6m6Ah6fjwrMiDljbnWUU9rvAs0TYdznvH2mM5bLI6gkuJ5//oGd968xdKVNXSeoVXy3oze2aC6t5MKB+uUp+bmBVpD8EQEvrNIo4hNh4nQNxmyc4xv3cfujBFCsHh5FVPmtBJ8mVN3FtdZgnUURQ4ITG7omharFDbTZGWOk5JJl7wzqlew/PwFVq6uk2Warm6JSrCytszC4sI8ny7Qtpa6szSdo+lS6KIK6R5NJhZbC3ynWL2yTGY81WwPRUvTToixQSrJYNBnWlVsvfUuggahDnkXj+FrDw4fF6pwiJ6K1x1DYn+k92eD/yAR0R5n7EfvwpPM+8k00AMsvPggvPIgYvckw+8HbbT9kD6kryN6ek/R0Wql7zWdGBoQH/pz8JN4wNAeDZJ79JQT6aQQvkNM5cACfNw8D0/zNO/aUdfXs/Q0PVEU3GOedMpcDxef278j8dBvDx3Z/3O0vyd9zM5jODyz/cM3I8b9x//4SUngzxcl61JSTzs23ryG/mpOtztDRsu0bgneU5YFbWsxLvK1C4KgDUpbirXXMAKUUnREggtooLWprkznPEpr5DycTYmkVF2Khm+42yG3Ruwud9z61Jix3UL8ruCVtz/OxXCRYlBQT2oUEbIkXEshaNuOi1dXCY2lqRu0EDR18sqoLFW4VgK00alukhMoLWlahxJg3dzrpXXyjASBD7B4aZmlyyvkvZysyNl46y69PKOxlizPMEWG3RmTK4kDVIS8yLC7E+ppTWsdCxeXUJ2lWjTcLlP/m65g552Cm1/L6UaBPjDeHlGsFYSJ543ffo3xtT9Bs/AtvPDJV+Ctu+zd22VxfQnbdrjO8cI3vcL96xuMdkYQI6uX1pjujoFANUl1FpRKeT/jzRG27bh49Qq7t7dwc0XMGI31njLPicBEC75UaAYrC2QfkfTWr+Od5+r9lv/3bp8IbLSB35p1ZEpjegV33rx9UFR2cXmIs45ydp9XswqjFMUcsr8WEebKr5/nNSEFQqYCvSEEgocb4wXqLiBva8wqGKNo5nliSkpcbkBKpJCIZsZ3XRWMZtu0Wc6NOnkLjdEJDTAKUOn+ax8YOvhYJ9jecygEer8IrhRIo5mOJsmjCGRFTlOlXKneQp+uN0UuS5yo8LIgzsC2LdVeqhe0c3ODF/ZaliaOqurwoUVpRVc1GK0T2IXWVLOGO+/cQSB4pbOsXd9lbeLoZqn4aZYZfASk4J23b/POWklvdYF8UNJVNYTA6oUVtu9sMb67BTKyu2iIwBU0z7eRvG6ZCUF/2KOb1ljrwAeqtmW4OEQrxbSqyNqO6FwqTBxIxgsUznlEhF5RUjUv4e5rBkt91q7e47kXN9je3oNBj0GRwCm0EBDAh442/BZmYYKJEiH8OT36Ry1HR35+JvQwc35EYTguMuG9Eg/O0APPd+J56WiB1PdilP17KA4+HScCHBfO96hYsT/bQ2efdS8+9Bh9SH/M6Rl5io57g0SSGI9YIsTB//df1kNtzvp3pP+jgQLHv8jikP3kSLjccQL3AWcRj83R9i2vx/Z3nJXvGAXu5M7P0ea4cY/SY1qGBA9j8D1yT87jMTrkSdn/8lB1h8j56j2cl1Gfdo3n9XI98vvhrSmZ4YQ4ZqAj5+UIshAJe1OkEzz/6kt4C7514FMNnmYyQ1hP23Z0PoUOISDOaw5F4VKYjpKYzFDkqZZLr1emELMYMfPESCEEw+UhRgiUi4gY8NqTLRcIBKGOTO6MGV+/R4zQxkDWy+kt9MmNITjPbFJhCpO8LvPE87zIyTKTEts7S68siEJCCBilyXND01m8T8ANIQRiSLDEppdgiN/5b28wvruTvCvykIKsJLO9KUIkxa5zHpNpwqxB6ATOIIksrC0yq6YJ+Y5AkOAitF7QIXFz79Nkc0SMKR/phU++RNcF9jZn7O1ULF5a5f7NewlaOwZCTErCcHmBpq4J3tNfHSbvT4jYuiXPsnT3heDGV6+jZKrRJI3COcfmzXtp7nPAhNVLa8yaFi9hNJkx2hvjhIUiIlSgEKmga+wsL3zjy6AkeZGxfGkZYxS2s2zd30UpQYYntjU6eFTw2H5GMAqhZcrRilA5lxQXQGhF1s+J3hOEQvZKnI00G7vIwlBcXCTTCpEbgg9gHaFL4Y2uqVFKoLTAhcDC6iKhdYgQ8QRUrhNsdYgJFGJ3ipjXptrnxXv393CtRQAm02RaMZlMIYJkXvg21widPJVKK3oLfYSQVOMZJk9Q2iJGfN0gIxghMcaknCQp8M5BhF6ZY7Qiyw2ZUhgh6OUZmRDkKtW0Wrq0kjx8MWAGJaPRhN3tPSZbuxRFjreO2HUo26LLElXmKK1wUuDaNoUyCsHevW02b92j2h0jlWChVxKsZXd7l65pKcsCYwyLgx79siBGWF1bYnV1MaE/GsVwaZnpzLJ1Z5fxzQ2Wri5y8bkVTAGTdsqkmbC1N2J3Mk38UDgQLilE56B9zvq0dO56eWfRe+2FeN89HCdVVYJnEToRH9pjHv/yjhbzFUdlq/NN4kOF6EP6Y03vIdDC8W9W3PflCjizStFp1vt4CvsXhw0i5xS0j1qcTkr4f9Z03PjHWWsen0P+4aaTvGj7dNLtOc0Ld5aF7NRHcV+dP6L1HvOMDoVknj5EVyq2JxVj6XntD75EtrrO0iuL7HxtN+XZKImMoAChFEYp6rYlL0qM6NNZiw4q1QWIgraRENJARa+gmtWUSkIQTAIoIVGDklk3AsB1nrwLDLXBSokCdG64c/8uTdsgM8XSeg9X1QxWelS7FVtbI/rDPv1+SWcdrnPz9UmFWQHatpsL0AkcojcoEQKKsgRgNp4RgBgiIUTGt7aJPnDnzds4m+CjXQhIKcgyw2h3nJQKI1CloOwbZuM9imIIWpNryejeLtFBnisy5VEK1LxaZZYZOtuQ5wXtrGVWG3q6R++5HpfWL7L92jZf+52vsHJ5DV9Zrn/pXbRU6EKzdfMeLkSyLEuvfYiEGAk+IDqP7CuacUVmUkFQKSJCCkyeoWYVMQS0EPT7PaZVw9a9HVYvrnA3tGRKc/e/v0M13ePap17GR7DKYr3l1jtb3MpKZGGYxYCuGva6lryX0zUdvsiwzQzV0yjn6cqMWdshlaJtWoiRQmpaEaiFo21rqsmMfEkSgWBTTlO0DiEEdlyhi4x8UBIAk+cEDAaVvIyhI9cG2yVkQyL4GOmMTEYMrdBa0zqPntRMJxUxRMq+xgwNGMiHGdZ7+v0SKQUygAuByjmEUbR1TRYkeIFzgi5aytUVptsjYt3SbuxQuoAwLqHoRYiUdDrl6Vgt6ZTEZprgHAKwncUKEAsls8mUcqGPazq6zlFeWWG0sUssMmzw5JnGWYtQSanc2dgmk5IgNUUvp91pkMHjrMMJwEiElmgfkUi6SU0vzzBzBDpi8uSuri7SjO7im8QpMq1S3Srn0pxtR95O6OcBRSDLJKbMGKwvstgEAo667pJiKyU6yyjNIsHmp9YEOcKkjvC905jhSV2cbS0601ty3L71ON6i0/SO035/H+n4qTzdxE4s7fEYbQ+f1BfiQMCbxpi8pid1eqaY9KGm9CH98aD3DJL7facjTPeZz+ooUz+vl+Sk8897zkl01gZxnM/9CejMKZ/FXB9RNk/oI57y+7Ogp3og5srPQ8mqAo6xpkrgz5UFV5QiCPjCp1fYsDlv/rf71NVXkOoNekWfda5Qks8LY/oE9WttUjpERlsLxPTj2CiRCJASR8TXjs51aJ08NvuFXGs/915JwVgXfPGt6yDg5VHJJ2aO0a0R3K8QGSxcWOZrb3yNtqow5Hz8YsNwfIe8X/CaXGb33YaslzMaTbE+4J2jMBLbOqy1lMMeXdtRDsqU+K4k486SG3NQz2hxdYF61tJUNcYHtEw5Op11aClRucHXLf1Bj7ZpabuOYZGz15uw/dItRIysLa2xfrvAWYuRObZqWVgYsJS3vLgyRihBXSg26KGMRmcZrvKIKPjiDcEr3/ppdKYxQnKhzrj5pbfZvb2FlJLxdDvlTSmJ1AkQINokDO9t7BDmiG2u7pjYEYFwYNCJQGgctu5QUqX6N0KQDXqsLg6ZtB3sTPlUpvG+YRPFjn6ZpbVvYBfF9QsN050JX1u7w81hngy582ff9pdSaJsrmF1bory/xxWl6ARMqwozB58A0ErROMvNfMpItwx6BWISKKXE1S26yHAugBBEJecgGcnjOB3NiEaQrRUoVbC5scPspqPoF8hM4ZRl9/4OQUa+dmkAWlIOeuR5RjfPK1NKJQ/Sqka9HMF42klFnmmUlsTWkfUysigYDQ03hUMoBVJAE+m6DqkiZmeMKTKuboxZjh22s2y+fJvNQYVG4etvoZlqZGYgQtO0yAXD1cmM9TzHCs/bKznT5ZzGDvjITgJyCL2cd64usNHMmKkCkxtC3eG9R0mV0P6UJDhH4xx2b4yIkQ6oVoa81u8QUvCxtTVe3hizvbGNbRvy3BOVpK1bnHOYzLB4scAqRZGbZDDINNNpxVsDzbSfMxz2+M7iLfKtO+SLPRZevIzp55jW8n9rMibVNtv3N1PBYgJmucfN5/4UvrpK11XE8DZza8ipJA4xu0cDrI7ha4+I9eJEBNADe+Y56++dMMTxdNz+eJIQf1yf76EYcjzy3NEN+Ek3rvdG0xPA9xYFV1UK6/2VtmHTn/78nHqrvk7EvA/pQ3qv6f2H5BaPfHj8U4G4z5gPC6bieN567k6ffGpPd95p9DTeov3zvw4sayfSSfM77iYe9aYdVkrPuzedtq+dctKBHHDw3J08TY0gA6bjmulkyp2Ne6m45jCnWOojOoFzjhgzpBCIGMmUopOCKATaaJpWAAYpJJW1EB2ZMQiSp0bHB6JPnFv0fQj0eyUqN7hq/muISB9ZWF6gV3qyCyvs3t6iRFOHiO8ctq7pD3MgUq4MEbc9Xd0ihCD6hIzWH/bZmm4hlST6gBSCECJFv6RtOqT3tDi6KiWLm3nYW64krrPkvZIsM1jriVLgfaAsC5x1TKc1vV5BrjXWOawKLC0OsHVgb3eC1umas8zQhED0HiljinAVSWiZjaZkwSJiQGU5s1HNjddv8cI3vZxQ5AY9EAKtJT4mNLDOe/qLfV76lo+we3ebja/dJi8y2llNcJbhpRXq3SkxeAQRk2sUkQBM9yZJkRKSnslovGM2q5BZTpFlmH6ePAV1R9Yz7O7VLN7YYe3yGpO9mo237hNI9YZ6g968P4nuF/imoxgU7N7bpiRSWYcVEaRA+Ygk4pwDpQg+MO4qssGAwjuKXobpa0Jr8VVH9IHoAkiJyDXRegIRLSXWOmKW4aYdWikGgwHOWjCC4eKApmmZtB1aa8qyx/DSCjFEmlmNaANZkaUQPC1ACaxtuX/rPkZr7KwFJektlKxcu4AtNVv3t6mnFeWwnxSHuZAWgicvMoyUqMYRAS8DTqb8NGdbglB0TYtSCl0YlPUsDnoURY6WEqEDGIWNAWUUXiSjxXR3iospT0u4mPLvrEAqmXKcyhzfSQrpENbhhGT92gXKxT57t7bo6oamapjujHBVnULkFoeMx1MKqXAa+oM+eZGzuryIMoqdnRHOpnpW69cuMFgq6fULVsoZgxcyZKYP7CvT3TG9pQGrr1xm8fIKwaUwRfpDJuuXsGhilI+1p6VgxngOtn+SZ+JwqMJhNeucCtHRTfg8kz+r/WkK03tOj17zBwn68CjFR74JRNqHhEAqdSRPYn5fD+9/4kFwzHFK4GMpwh/Sh/SHmD7QOkUnKjAnCqsPx9tG4CjQw6MheY+hJh0NWzs6/lnfn8Z49KwMRidtKO8XT3scJfNpFb7j+npSxXH/3HN7/h6EzglgQUjMXCmvYmAzwLjt8FNJ3pUs52usfNM6C5eWoIWL8QrTd8Zs37ifkrJDIBMKU+eUOkMC07qjyAoCEuccwbWUykCZ0UoBRqLKkm4yIzMFTCPFoESXmixmaSkGhrZQxKygvLCEGfa4/+49jNIpd8kHqqahG6aFM0WPqMbUowolBYVOAuZ0e8zK+gqTnTGdtTjrMUWGzg0+RFRMCoPRCqkVupegpX3bMR7VIAS2cwQf0EYhEHOPTUWW6RRO5zyiA1PlSKmh0ZjMIKXCOofoBJPZjGnbY7NKi90qTa4KBmHIqN5jGAVLF5a59+5ddu/uMFwasvzcWkKhc46FXsng4jLVrKbeHFHvTNjd2OHCS5epRjPqnQnOCBqhWFwe4KdjcA4hJWUA2cupuo6QZ7TWo6OknkxACAZS03pPf6nPC3/io4yrhq3f/DIuRi4tLXL5wjL13V1u/I+3UUphSo0K0FUtWZ7jOktTNQxKjXQNtq7RhaMKSTHVShHmYAraaESIqMzg2kDjHML0yTINUhBDpB3PkDEilMQ3HaHS6EGJKXKyfg83sdRuAgSabkJthiAUNQGhFR7IsoQmF3zKJQo2hVIKKajrhoWFAe2swY4t070psQ10XWA6q5FSUtUNpixwl5coVwY0kxmTnTF5v0DlGa5pE4Jh5xArBjdtEc6ijWCY51gdmE0rgvBkhaGQBVJLnG1hYOkyQeM9XiSACyklSj9IUnedJThPb3FAb9hjdyPVrpJKURQ5Xd1iQ0jQ4UqltSlyqp0Jk/GUKGD37hZ51VD0S4YLA6RSuOCxIjJcXyYoyYyAvrAISpBnks07mxgEsbGE+x1x0bGXd3Tz3K3gp+BdUh59iQiB/qVVpGxQSmCFwtUjnDT4ruYQhM/prCzub4mPzwjj0U8x8bnTMmnO6Oh9o/dyiztvvw8kEHHo2Fn+urOEjuPGeTiA8dFwxrQ3jUKg8J5Ayr188Kt4ODvgkAccQCFYkgKJwAO7Z0DCf0gf0h8l+gCVosePUj3XGfGQpDo/64npOKH9LA/GaXSc0H2035MUq5NC9Z50NziOBx/Ll0+78LPOfcy5HD7/uHmdds5J63e03/P2eQodLPmhcT9TFDwvU57B57qOO94jC813TD/BC70BvnTcHr5N3VRsvr6BvC6Z3pnRdR1KSpAKOrj05gtEYNUY8lzT7k0JPiSobCXZ9DPeXO/jlUJmKSndG8eqg0vWMx3PwMEL//fn02ULeEuIlIh/p2Rwo4UQEVJipKTxjp0yUl7UgMB6w/KFZdp9KOXYEH0CgbDbI0LnkEbTKxPrcDHQNS39XoHJDHSW1jkK02P73h6L64tcfGWJZmdKW3tgDsVtLbazyBix1mGdp5dn9GYDLr27jtQ6Jd4XOa61SCVQMZ372o7iP91MF/eRtRVeXn2F9dFlfn/6Rbzw7N7dASHwznPz9Zvs3N2hmTX0ej36q4tM7m6z+PwFsiJjtjnizleuUw5LLn/0Oe68eZsvSctMCN4Z7/DxK45CRTIp+WS1QNd5JiLnczEw84Ewa3h+Kljt9VJCv/dUe1O+8tq7vDnQVBf7rErNZ1ZXMZsV7/7eu4gItmqIpiT6FAbZHw7QpaTba1mWHYOwQzZMyiPG0DqHDR7fBYr90LWYwuiUUvgQ2J7OGOSKhH8RUFIgI4RMp9wv5+l2Jqhhia875ECx2XyRemOXjVbwpfXvQeYJfKCMEL3He0+vLGjalmY0S/dMyuQNUwmmfO/6mPAW9PUCvXbKxI5YGPTJMgNCsH17Ey4vUi4OmJV7NKMZgUhWpto8znmkhnsXbpI/P8JE0BJiEAilCCvvopwjz3Je7F5CWQWLnttXb9FJi21B7HyKrmqxncM2KR9KaonS6dqFlNjWEoUgLzOi93TeY63FzJUzR6Sd1dhb99FKsnhplegDzZu3iRF6vZLgAtPxjNBatpdKvkSNaxyyU2iTxlq7dgHx3CKje7tc2dhjZXcKQvB/XuxRyUUg0L+yC2KCKASf2LhIe6Pi0ssrXPzIHVQfgmvZ+oNfo52Hxe7D0p+PQR1oRufgZYdF6mPc3wfM7us05GA+pfcrBfhRerAuj+Sb7rtgHjr6IDv1Sek8KmoE/mvbHLT08WEF7bAs9WA+6VhPCv5S2acQgt0Y+PezGSeXDf6QPqQ/WvSBeopOpGfNe88S2M9iqI+j9DwunSd87CTvy0khBUfDzM4zh1N/fMwLO6+CdOgaHhrlLI/bk2yAj3vOKV6jg00kPghRkQJkCPi6IxQKB8gIRIFRBt84vvpbr9HoGrqIeLtANRoEFEonRC0gulTsUhpJPU3WdilSWJ0PkTLLUt8CvO1wbUrydzFQasW07djb3GNBDBFzFLsQAS3JVgbs/s42ymjMYo+9yYhCZuxNxlwWywcX17Ydk9GUoswZLg4SDHGItJ0lzpHlHNCTit6wj6862s5hrcO5hCjWTlvKIme0OaKtWkRjIQSUEKm2zrytVAla2pEQzcoyJ3poqoacBOSADxglCfvCnpDYuYwYg0AGyWyvIi8LtDa0VU1voc/CypB71zdwdUemBEtX1/AhYJ1n883bDFaGDC8sMdsacee1G+SDktH2CL/eQ8kEqKBECrmy1uKloMySguJjRKiEdrba76EQWAnrVy6ydfMek3u7uN4Kw7VF+iQF9O3feR3XOco8RxlNFAnq2/lIPa3mUOYKX1f0M42Qktp7FCClIEaIAoIUBwhhQpCE/gBG61TAtZqCn5eMLDO0lthZi3ceslQDKFqP3ZsiBiVSwUIvp9/LmdmAlIq2S6F3SEFdNaAk1WRGlAIZ07OISCh8IURc41i4tMTihSWqvRnPf/PLmHl43ebbd9ltOlguD2DdXWuJcyjzGAPReTIlyEREhICKkmg00np0pmhUesaNFGRaEYCs0Ezbmn0Q1a272wy1Zjqe0c80Ya4YKKVophW+69BSossMIQWddZRljnApf2zWpFBBYkAozXB9kWZcEbQCLKPdUTIoCFBSIZQi6+WYSCqwOg9hvXdjA50Zil5BvwwUrae1DqLEA8gE8qDyBJ9oa4fzkTtvbxDaG1z95EVinhODJ+5nxz8GC06G/3iukKeHt4oj/qhHGPJpe8GzCnU4QucxRn6gCtFJdLLqc/wq7qulj3qW9gs9n3Q/9++bOBgz/Q2nhcMdbHBHjyUFUwuR/n1ga/shfUgfDH19KkUn0jnim56QJ3vvEUI8ivRzksfhWRvODl/a0cs8zatxHoXquLk+TpjbCdN83HNPpZgqvz9WoMZ7tf5PQjEJp4OVIVQVRAhxjuBlPdXOBLEnUEoRLQwWcoqlHl3TId3c6zJ/BvM8xzmbvocwT2hPuUohwMCTaqIoSaclWklUlHjXUhjD/XsTlraWKAblwa3v6pad1+6h6qSIdbMWiaC2LRt7FS+U6+n5ryW9hR7TzRFta5nNakJIOSg6NyysDFNBTh/Y3R2RZQmmWUlBb6HPaHucUPe6jl5RUNcpx6iydg7RrXEhEIHh0oCFlQV2bm8iVbLqE8LBbh61xseYvBNGEUIk7+XIeY7R4Ru2fHGZ4fIQrTVvfeENXOu4/LHnmI0rynLGhZeXWby6QgyBzXc6Ju/eY2+qmHhDWOyhgapumMSAEQ5DxGiJKjyN6AjW07UtMcgEIqAmBAJZ35CHDCUloe2opjOQgsHqkOevrOGrlswL7s8q4rCksB7VeWIU6OgZmEghIl1saFVLiBEVO0BQhZR/JQToLMOH5BnqnCMrckJIIApKSWKXoNx93WF3J+giQ2qZCutKgwiRIATGGESu0VJgq4Ywa2i9h9Bh4gipBQRB16T+yyJnMq3QSAzQl4p6UoOHqRa4psGbQAx7JGzDGhc8OtdIU4OeUKyMEY2gbAdYBNZH4qyjHJYE3aIzh4qRxa6j7OWQCfApDygIQXQBVzuC0njR0EqPlYGu6xA+gFQUecZu3ZIXhgtLPXqZYdw5bt3dIVOCPAQGZYGUMtV6msN7Z1Kxk6WCyKtX1jFKEaxna2ML++YtfNexogRNaYhIjI+sLQ6ILtAUCi9lMj4QkTGF78lMMRlNsVtj3NQRnUdLwVCmvChdamwYgM8I1jH2EXqGTMGNbUf15oS1jy2iB2sJ/jx67HTvKRnUSXQMEz1y6Hxb3RktzuKvp0VRnEQfuMB+nk31aIvT2zyOF+nwfTms0B4d46zQvaP31wP3vCcTMA4f4s59SH+86BkoRe+Ruea83p3zMk5xMleOMeDnSb9ZJs/X737fZ4V5HaazPD5PK+SfditO29nOHDce8+nIgadUKh6ygp3mGXo0IuHhc06aw1nK40let4cOPRwv/hAanUj/O9jURBKQ6r0J090Ra8+tc+XLLyB8RGeaeKVD5QHVCtx1gfeCnslBJBCCCGTGIKWg7SzeOYLWFFHy0m6HJGILw5tLEheTQFZZS2EMvb0+l7/8PP3V4b7ZmLuvXae5WWJVQMRAcD4VmkRwXXWsPN/DaM2l6wZdZCnHSe8rY2k9XOeYhQqtEnJXwLC7PcJkBh9jgmAWCYKZKGialhACJtOYPDsEYSyZOotpFbPRDOcDWkiUFHgfycoc7xsg1f6RUmLyjNF4yvKVFTrfHFr0BDShM5MSipVk7bl1brx2He8CUkte/cyI5z61g7dv4NqOF/9kn82vbfAf/teXuR00CsFgoU81qVBrBS/pbRYyRRst75rr2NCSFYZvnq0hEEjdMVh6ExVa8Bld7xWkUNAKmhsN5UKPl7/hRaRW1ELwtfub/LYOqMWMtS7y0jgVjR3IluXcEnPYCHe5bzYpQsR0q0y7pYSoJ1O+WZgjC6ZHS+KsIyuypJBqRdO6VLdIQr7Qo6u7BB+uJK61BFLIpLeOGAKuapMXou1Selyo6PV+n1Aa6pkiTj9OZjIkkeXVxQSM4SJXbm5RFAWTQcYbVxbwnWO1nWHM76PVKlpqCJrx/RHPfXqTy5+8TTuZsfjFK3Q7F9jdrJjudVSzhoUmsv3KXZrVCcYHnrsxZa3tYRb7KC0JNjJ+e4fy4jLtVoWtK954KdD0NF4InHcUStHZiA2BsiiQmebl9ZwM6JwhbIyRxlAo+MRSH60l02lFKxWDLGNTKf6XuiIrckxmcJ1jb3uPIMB3HZkxzFYL9rxjMOhzufJMb2xSz2q0EKzHw7wxeWeGK4u0VTM3aKQ8rrpqWL4/5pLW2JnjHfESlZEsLgwZPW/Y2dpLgBD+W9ExZ/H+kMvf9BLKaHw75f5//xzBnz+I6QEOUfLoncbi5yaIY4Tpw2zw5B4e4YsnD/Jw54ePn8S3n5lY8bhWzMfflA+PcNKank3H+ZDECdN4EPx4du7S+UesYuT/U1cH3z/MKPqQ/jjRB+wpejxJet9JfBwU8tl08jlCSJQ6X7jBock8mymc51KehK8e3WzOo1yeax/Yd7yfMvHHme/TemieZOwnHm9f0ji+E+9SQvzhNs46hEvhQhevXmR0dwepJG1s6awlNxlaCPKymNdOiWRZCo9jHqJUzgtXNiEgtJ4//xEHGKmwIUAMqHkdIhEitu4Q890s+Ei9W5GVJcFVSGlSHpMQSCFoqoa2bdHGEAX0lwcprMt2KQnehaRwSI1QMgnnCDKTEzqf6rhECC4pc0oKrAs01pHNBU0BlMYQJWRFhmm6FOjuAyYzlMt9xltjhksDmrrFh4BUmuB8CumrWzzQXxhgZfKkCAHeBnbvbrN8ZZXZzmQOzW2QQtDOGkJnyXoZOm9BBGKQdLOGbJBhJcgoEFLSu7qKvSfptveQMRKCx0dPCJ4gkuEkCIFWilYEkCksSyGIrSMV+gGtM6688hxbb28wGc9SnstCQXZhAICtZngfDpTI6D0hBHQm6YkUHteEQBYjMQSsDwkFkIiSau6BjETrEUrQHw7SXEXEzvNOovMpHwhBLzeEqiU6D3jIsxSm18sTamHbkReKNghi8EgvUNpgY0xQ8Ptog0oSG0t/cUA7qQmdRPRzVJGRyZxqd0Jvscd0LAhuyHhrnAr0xjSu6yyusYTGYoxGZxoZIypGjPcIoHdlldwlNMbYJcS/3voipjQwLJFCUCz2cc6CTblNUQpkmePHEKUgVxqDJNMKpE+hqAK01ijroImYmNr1Bz02qwTfbduO3apJtalIIayZMSw9dwHBPNxPwOY7N7hYNywUOS5Exk1LWWTJyxkjwfv0zPpA27YI6bDOoYwi1xopJDqmmliDq2sUvYJ6d5Le/apFSoGWkq17e2TDe1x49TkQT1pj/Txhb4kOmXMOjhz+ftrW8ERIbOfhwfHoh8cf57BS93hnP51ysa+mHM3jOWkWT6PUPBj72YVOfKgIfUh/XOmplaLH9hOdl7+d+PtxMc+n9H9OPqGUevDlhHPOjAA4LDMfN6eTOjvLg8QZbY8b4z1y4ImjHYoTPj9ep4kiZ+/fT7o/PvE6pAnFQxv0UccVwOa89gnBI5Yy+irDt5aNzVv4iWPCFlmtESW0tiYEj4seukAuelRtqjlUNS0mz1gY9hAh1ZQBkJ3FaIW1nuADznuyPKP0UPgInSMulNQIfAs7TYvOFZmPGB9ouw6JJO8VVNOKflGwPFxgd2+HhYlncGPMykUDosJfKFHXBHYDStmnqRokSdmJIdI6BzGQ5RnEgGs9RVkw2hujtMLPQ5+0SMJpV3cUeUbbtHjryU2C9PYhMh7PKAcF9WhGpjUIgbUeTVIyTWawzhNVCj3MexlKy4N1b6c1t956F2KkHs24+cYtyl6JQLB1/T62dUl4DhFldIJrdgHVGnIfyScNeZaxGJJS0zjISgPSI/w8NE0qtNDsFlMakTHLwXYDAhEXFNOQER1EL/HesfOlt7Ghode39JYyGt1g3QwRoJUtO9oRZEArSRkSSmDpFI1eoI6Wvi7JvcTBAVNRSh4AZMSYakEFF2iqBh88MUZUiETviJ1DBvAxeYR0kcG0JrpAND6th/VJuQ0B5SILl5eJWYcNCXLch0DddSxmPUyVoLDlrGX91ReoJxWT+1v0gRgiRmfsdENC02PXeppeRtu1bHYlsVrD1n2c6yGrilJBfq1EG023NyPvGnInKC8uIe7MaGtHudRPYXFGo5XEj2sIkf5LF1m/2CfbGeO7GX7WARBCS8/u4bxkUBmsMcgmYjtHGWZgJdJGalUm5S5K8nIlPaeAmucZ9Rf6+M4x2dojNgHbWbZu3SeGQF4W2LZjaBR2WLIbAlnryYwixEh/0CNTCuEDupcRFxIgQ11tEWKHwLC0dInB+ipRCJyKdF2g2brPNGzRhZaikOg9hfKQKcHW7TdZfl5hcsnjIAkcFpDPi6B90rcHdDzjPSvf5UnpYQXiyft+trN6vJHPNB4+kxEefHtaxWqfnnVmwIf0If1hoqdWio5DNHmP5PEH/Z0VCvVEnT7cb2JoD67kEYXomPNOnMJJCyKO/PSswuiOG5v9e3TcRM4/7rFr8Dj76GOHPR469qy9SueiQ8LFKR7K32jb1FIInvvOqzy3XlKNZ4w39ti9s80oSi7tXUHHLKGAWZcs8QiiczSdQ4gELBB9YDquQMJwIXlOZnWDkpJenhLnEeAnDc/NJMI7Jrni7ZUCFyPeS+6HltFixsXGc9UFhmuL7N7ZITeaCARSDlcEnn9zwrf+HxtcfFHyP74lsnGt4G51m+HeAnlbopUikoRlGSOZkoSY6hQJBP1+jnUeESHPM+q6pShy6lmN8wFrPUJA0SuYTmYE51no9xJwg7UJ4th6TG7oWpuABYxO3izSuredp780pLfYh9mD92U2mlG6nBtfepcXP/liAm1oWkAw3dpLG7wUD/KQRPo+WFngY7pgZeKQ0XFt1HH7nW1s3WB6AWEUBJvq/BBxyvO7S28kHmcWcLufwrce7wPXQ0zw2FLSLFus9/T6gmzlbWIIRCGQRLTS+AXB3fm6L3WLLLQXCFJgwgJr1QJ4TykkNUl5ISYPCCJ5xqSSuJDWWsRIM8/ZIiR0NCMKoq2AgPCemGlkbjAx4mcNISTLQ0dAZQrTK4jWUXuf1lRADEnhraqOrOp4cacmzzK61rF5/R5ZkZP7mpd7HbbpaMwC/8N9khV9ge65jna5YWtjm252jYWNb+LO6zf56NaE71zICOUCX7pwi1vZBizUvHCv5tJeD7+5hQ+BWGZJ8ZMClSVPoVooidMGN6m5/LWO9arFNg5hDEoIut0pyK8QpURMHPfn+UJCSoo8oIxGaMWmD/jakeslXlj6U+gyA+eQWXonJjtjbNMyXBqyoJfYvrkBPoGM1OMpSgjslRV2+iXV7oTFG1tca6ATMBtNqOcFintBg/MM+yX93g4xbJEVBWZ4jba1jDf30NOKMjeYpuLeK6+zuq6JXnF14yXUFKzquL7+FuPRBpdeucaB2/ccFI/wqmehsJwkaJ8c2vWMxjvad3z0q9hv9z7uDfvjHlUgDitzDysph48/ellnKTJHZavjRt8/cno449kb8KNL/qGa9CH98aFnFj53nFPjWHro3Tql5ZMqCI/T/gSF6MFP8dimp/ZznnkcO9YZ9MSetZManzHq46z/s1LmTjr/ab1Rj7FZnrihHFyjmJcoevCEPNiM5keSrsNoc8TNr1xHAro/wJMETkmkyDIEAhUEDsi1ovWBGCJZpsmNxjnPeG+KKTIUgsJoZlVDXmRoJQlBIKVA6RyRCVxIHiSkpG4dtmpBJqjti69cYXx/j67uUmhZZ/EhkJs5LPJkmtDygCgivZUBjoizXUI5UwotFUIrnHMplCk3mDKjHldYa5FCYFuL94GszFIelA8oJSjynBgCIqQw1UCCjZZAZjSutXStRWcaco13Pgnw1s1D/WBhfTH9PntwQ7qqoS9LnPPsbY/RRYar24QiBijJQSI8iCQgSglIhhdX2L2V4JKVSqGHfo4oaK09QLtTQuCJ6bQo6JqW2Fq8AyUkIYYUZhfmHjJUUjoBlEAbg46QC5FyuWJSLosYCCrlhLU2eQpFiOzh559TCGEkJu/O/JqNMSk3iAgyKaeZlAzXFoj3784L9gZ0ryDMBWQhkpIBEF0geI+ch3mJfolWkhgdIaYx1RxAIHqfkPW8Jx+W2KajHlcsX12iEVN8jAnEY3uGjZELL1xEi0i7POTO2xvMJg07d3cZrC7ibXpuRGOhq1FaUlxapnljEwQ4IegXCRkOF/BNR/SeGEEWGbFzScEZSHzn6BqLyA16WBKrNhkuVgbEEAjTGj8PwYvW4a1DG0XUAmcdQYDtEgJedJ6ua0BIFpYWiBJ2723jvUdJw2B1kXKxj2st5dKA6APtrEn1kRCUeYbzAS9SmGfbdsQQWVldTFDrWQAhmU0a9jZrvPdcuXoh1YKyHVuDm2x3Y6IVXAiB5eEAtSC5Kd5ib2uPhaWFY/gQJ/PdR/a144Ta98ICdwwdZxA7T/t45O8xdKKR8hR6evH+eG/M/r5xFOEtHrPO5x0/GX7io8cOK71HjJ4P1K6T6Emv/n23Rn5IH9IHQs8wpyg+HZ8917mnCPMPS6Zn93XSO35O78ZDoXLn5RfH9BlPE/gfdx2PzvPI92Nd+U+zQ5zgATs4fFzf592bn8S79AzodIvd8b8dXdX9771hSb8eIDpB0ZVUwUDUBB8IIZBpgwpQRI9G4KXExwgxUlUNZZGlBP4YUSqhwuVlRjVr6HzAaEWM4Jynt9hn1UBXW2Kh2HWOam8GKxlS7lH04cJLC9x5bRNEAkoQSIiRyVLGjfWM7EKOCIGFiaW3sMimaVBZhgL6y0Omu1OMFCxcWWV3Y4fOOibTirZuWF1bxuQZ1aQiy036azSVbRAxIfG1dYJEFpnBd44QAoOFPt1cQTMieUa8cyiRlADrPVlucHWTvEQIembApcHlpOD5VMDUtx3jzRE602it0FHQOUuwltlmj9EwB6C/OsWUDqFEUspEUib3YuBW25AXCqPGCO2ISXcCAkZkXGgXUEhaFDezEWWpUF1ktVsgRIUAvBCgQKLQVUQCVkbIemQkb08XIlaACzmV7bAxJiXKB5CpSGuMkTDPbdJKIefeIu/nnied1se7gKjHrK8sMBxE2IoEoxC5AevAJwUozL1TwXpkjOjMYApD7BUJgrduWCsN/brBZ5GGPVwBxktm/T4qMzRKEqNCLZbc6xp0yKlDpOqgKHJ8Y7n/9l3KhR4rF5eRk5r+9pgra0tk3Zimq1Ctxbg9FguPMuA2tjDDkq5z0Fhsa2EO2x4am8ICiwzfOWQ/T6GjzmEiSeNVgqzMMReXCK3DWUc7axCFoX9xiWxYYuuOye3tJEdqhZEGZTTWerwUzNoGrTSyc/ibmxAjhRI0CNavXqC3OkQIQVcndMB6PKOpaoYLPe5NWvoiYtuGUkiM1gQbkAImkxltrwdB4qyncjuMTce1Fy8xlBkFmqqDPL9MnOXgInW/ZDLMWX5pmYVihdFkj9GdbS71e0QfcSGyNbPnF1E/CCP/0/Luc17ck1yWOPzhieR8ccI3cexSnz+U7dGzBRwgsj4SGneo6UWlGIg0/oZ3VMduvE9OTxuO9yF9SH+Y6OsXkvv9fA+fYKyHWNhxDPa8m9G5rX1fx3Ss5+uUXedxNqP33EB1zhslSB6TeGRKBxa7Q31EsI3FzTqe33sJsSnIMsNrKwVTGYkueQKUlGQIPhKnZFKkXBclESJ5F6xP4Am+s4gYaWcteS+nV+RUTfLgIEm5EdsTPv2JF9jZnHG/rRmv9hlv7CKWJFq+CcDq1Utsfs1g6w60ptSK3a5l44U+/3/2/iTWsm296wV/o5rVqnYZdZz6Vr6usI3fQ2nx7MdLnpBAljEWSslYpgEdJHopWjRo0YImNBDY+NqysmGJtAQiSYHJ5FHkMxjb+PoW554y6l2valajysZYsWPHjr0jdhTn3Gs7vnvj7LXWnHPMMeda8xvjG//v+/8XXx1w9KNr3Ly15I1PF3jnWXQCnacgbHG4QGlFU7eoeYMETJUmqTHPQSSqY0FECkkEimFJ1/YEHyg3Rth7B0ipqOsWax2jYYVQCtdZjJKpjsQlxCUSqcYDQt2ke6Ik1aQCAVeGV7k8uMLBrV1ut58idEw1Ss4z2hxzdGcPIRObHVLy/v+n5PDWNYSE9/6XbzIpZ3jrscsWUxj6pucD4flks2JQarLh+wQ/RymVECcnKHTB/3zwJfKQMVMNe+P/hteR7Tjip3Y3yAEvk54UITCtAwc7SyDiywnN5RvEmFKtuhhwRHrn6cIq1UsIoky1Q1GkgM35FMAgBKFNtNWWVTqglPgVScNg/1O2t6+gPp3j246waCHTCKOIMt1fVRV4lzSP0s9ZIJQkBg8hoH3k3YVgcb9hsTigyO/Sx8Cy2OTrG38GtKLpenSUiEygZEWYWkQwOO/IioSChRCo5w3LecP/en2b77epbmd/cYsHB98kCkHlSr5gM4Tw6K0NdJnR39pHlgkNanemCKNQeWJfjM4jtUromVKICN4opHWEzqaFhBAxo4pimCjb+65HZJr2aJnqyQpDdWUD1/b4ex6pNXmuiPMFo0GFtYGJEPyprQn9ouU7h0fU6wXEQDetCTGyd/tB0uCqW6pRxXy9ZDrMMFIyuevYVjnD8QCUZLY/xXc932y2qE1J7zrc8HfYuOm5t9Hx3uGYTZcTB0N+Z/EOlXuT1lk+GVr2h5pJcCs01dMcTPnRG5tkWjHvPP/2wyP8meBPPPZDj2fMnb869cJ1KOcsiB1/9qIRy1nj3mcxBrziNl9+iD67hdPaQ2fZj2QZX9YpBfT/Wdd85P2Fz/oqxGRf22v742QvSmtzhr1Inps49+0z7TQqdLKNZ7X1tIDjLEd8Tnvx9Itn9f9kn5/nek8ed1bwdfpenAddPK3di/bhacc8T3sn7fTK4osOWKf7d6G2PpvB4Oj+AR99/SNs0yNJk1gZI4VSGGPI83yly5MopTOlGJQ5WiaRUh/88cT3YfJX21mWi4beeSaTQRI/FSKRMUTBcn/G+ltXiCvhvfpwwfz+EawGPlPkbNy8hNYKIxUBgfUpIJnuHaQga3VHpJRIo2iaLolrhkhRZIQQmR7M0yDdWqo8YzIe0HUd0/0pJs/S5HUVpAQXGI4rmr1pEpkNgbpp8d6jy4zD/SMIkSrPEZmhs5bgPKPJgGZRE5ynrVuuvnedfFAc39/gAlmRM1wbHafaiRgJLpAPS1wMdNaSGUO/aJjd26eeLjm6t8/OB3e4+61PmR/OV6iL4sHH98lzgwse51IKotSpiD6uqKyDj3iXWM/yLCOTkkwIcutRIZJLRR4iqncI7/FEmhiopaAFDqNnHlL6nEaitUJImeqDAK0UEHHWHksEhJjQsiigjyGxwIek3eRX6W9bW2sURYY0GrQCo5IuUWshRrzzdMs6pfdphchMEnyVElUYMAqEINYd2miGg5LMe3LryH1AkVIdizxPaYQk1rro0+9KKIXJDLrMyQcFmdaJ9nvZErqesGyRvUtMddsTsu0xalLilMA6j65ypBJkpcE7T1+3BO8T850QRK1SjRcktrlck11eI18bpmOlRA8LbNPRHSxAQFZmx5/7ziYx26ZDITCjEtv1RC0YjgYEF6iXDdWoQsq0KGEyjVKSnU8fsH/rAYe3HiCVpBgNuPrFN9h46yqX3ruR0ulCYFDk9M7RNB1SK8YbY4TWeB9wbUeMMKlKjFYsZktc3YFNk1dhDF3XY6RCSclivuDBnQfMD+YE6/HO43v3bF/1RO2QIJ46Jq7+9/Adp7ae/Cye5UCfd9w66/VF9n+yO0/an+B5/JNJMSIJCD+nieeeeL221/bH214dUnRGjuvTLC0KnXiszwpwHmt/9Z9X+fy+bHraWdufBx163u0nx7IX6ftZaQ1P2/aCKQbHa5AXSY27WGOP9+tF2nkFJo51ieLJDx+9Xq3UltMB7ScLNmebGJnhY6BtOtxQ0dpErTyoe5QQ5AHylb6O7R29S/TVMQYyIcmlwsaQghSZWPCigK53mMzQ947MKHoFD7qOy+9dIZvNmSwaopRM7xxycF2hMoOpFdvvXWH64JB+uiTGQB8SwUO7TIKse7VletQBMLn5BrEbcu/bt+lsCo6qKqeuW9q2o1ulepVFxrDM8XmOC4G27SjKIqERUtDWXUr1EwJrHUWeMdma0C4ahEjis8u+x3aWPDdoY+gWLTozBOtQZcald67y8AsPznN4Z4/7H95DG00xLLHWM9wYsndnDyUl29e2Obi/z7LtGGYZRzsH+PuBN37EM1gfM94yfDyqOJwGjBRsFQGrA1EGjBij1ACCQC4kIUIuNY3dxQdYNh6tBMqB7RvulPuIFTrmhScYWJSWOtsG62l1Qe1TzVAMEZSkX63mxpX+UBLpTNTXUkpcSFTcRpvj51CZFCT3fYdWGiUE46riCzdgVPTYuubufIkWEiHAjIf4tkdnErQidhaURAmZhE/DiuLbBzApsBFa4UIk9o54NCfrG264HXopOPIOX2mG60PCwYKNuSV0PXqwTpVdIojIXLU8iAesr2c07YJ5E8hdIIqG6sYmtnfkdKxtVcSNkv19i+8d+XiAKg35KDEHogTEhKqqKid0LpFeGIkmBewMC8gUAoFvO/SggBDRVY7rEw128IFyc0QE7KIhH5YIraCzYD1jrfmC1oTxkOZozh8uOqTzLHT6DvJRRTEoyYqMYlIlltIVsle0loEpeHC0w7opqKJiUTfcb2vyyYj86jo6g2Y6oxyWCHUJKT2+s9yNh+zGGSLkHPUDghSMRgPWDyOLeoGysDG+wuzoACEi+28LhmsZyyYFisfO9WmZBuKRL35sh7hCCI63n+9IzxxqnjUOnvP5RfSMLqR5dLofL3r8H2E7eYV3vQPSAsriReRKPktE7nO0ckPwf/t/DD638/3fb/zx/539SbTPMH3u5Iz6aTPbp1hcTRpOpSa99OLGealqTwt2nrb/s4KH06jTs27Bs5yUOOP1RdGh8+xZgdZZX+c5QcqZp74omvYygerTgq9z7sdFu/XoBp3fUCTp3qzf32ZzuUXQjuyLBbe+/glt3SYKZxfQRnHtqGWQ5G7oQmDWO4QUaZWdiLMBJRKRAgGMTlTSUkFZ5DRNSzUs8bOaECJNqbg7Muy2DVeub/Lm/+/9xLilF3yjHLB2dcLm/YyNRnPlC9f59Hc/QK4WGYQQhN7hneeDg4b5nQUCwZ++OmYj2+T+h/fwrseHgPMrKm5Wejk+0LQ9qd7FJ9HXzDBaGzI/mOG8x2iFiJG6TfUik7URWki6ticS8YD1HmM0440xrnccThcUoqDve25+8XpiWFvd5Lvv32bno/soYxB4gnWMLq1x8/vfYrgx4vYffEJXd2xc3uDw/gHdqi4pCMFwe41qUuP7kAgsyozMe94YdETt6HpLJa6hhGaxaBG3DCYolLTs8NsgHLEwiG4AApay578Mv42QApFp5FqF14rl3ZabxdupiH/149Jap3vtPFqAjYmYQQqJX7GLRUEKXKRIOlURpFIYo5O+VdsRvCe6QFkWvPGlm1yv/pB103D/4B6yK5HVmNA7siqDEBJ7XQTbWaTRuLrFTEoIEddZ0BI9rlakAzbVHRUGlWeU1vLe7n/FScn+JOODSYnOMjZNy9vzOdF5xuEm14ttgtH8Hnscjj5kbWtCeH+f/d05qirQmyPGG1uE6ZIrm4Gt8RIpIMaSw2mPKUxCtazHK4nUOqX15Sbdo1xj5w0qU8hcE2wi8UBKQmcRVZ6IIQggBcro45XzbFisSDs8elAgegV1JHaOzSLn/1pVuGXLN4qMf6sFmoiNMNmcMLq0lvqGOEZMvUsU6OLTPfIP7vNu79hcKwgxInPD3bWcb3uLDpFLl6+wPSyYTxdMH2zQ5BnIwH8e/C4yq/FC4+MP09eeMBry5byiPmpp5g3xcEwVR3Sq5fb/ZhjeGNDNeuLvw8lUufOyGER8chExscWtVlae8H/iiX0fIhLi4ebnQX9O+d+nBisvuAD32HmedY6XsBdZh/y87Pes5ff6iwv7PmF/xIOh1/baXqW9uqBIPPJqT86Zz37qHvOD53icM+lEv1c81MVn1GfbRQeCp+33Ig7taUHaeQjSiwRZD9t/nv1eMo5+kT5c+Os7qx8nkKOHA7KUgsO9Qy5d2+be+3fo6pYACCmRRFzfpxS1h+dfac88vN9GKfAeVRiaugUhUlqOFBRZkQZ/IfHWU5U5y7pFk9CGftagt9bQK10VKQRH9w+YXNk4XjkeXVmnGBQsjxYoqXDeIb3H28cHVqEkOtOM1ga0jcEtO3rrGI0qqlX6nu8cs4MpQikyoxmsDckHBbPdKXXdoZVES5EmudJhlMI1PabM8T5gjCEzaZJrcsPycEHdtKhMI4gEIRhtTx4F3D6y3JujVsGF8x7nA4MQQMD61Q3uf+cus6M5ei7JBwXReYaTIZ2I7HzwHUaXKoRKZA/OSoosoS6tDxR5hpQKqVMqk1GK6CLCexQekQl8n1L8ghKE4LECRm9sYyYD9ncOOLy7S94XdN7jQ9Ja8s7T9zbRaq/Y9NIEdUWTHyM+huPJqhSCIGKa4CtJCCtxXqWQKybAd7/6DkWVE3qHbWpkZymzEV4rpNH4ZYttOpQQiNwghjkIUIMspQYCwgW8T2KvMtMUa0P00RKMpriyTtdb+p0pmVbkXU/pc9y8RgnB2lffpLu7j5wFonWoEBkONRMpCQdzBBGzNWFwZZ120XD48QMGG6MkuRMCLgRiZxFCEdqedlFjJoNHtUQ+4Joe1QkwGlXliBDxTZ8CRilQucEL0JnGW5+C8261cu7TqoNYQSJydV9kZZBe4+cNi6bjoSC4iJFgLTHPECGyOJzRLGqKYUUxLHlIi25XrHj9rQds1y11iNw7nIGAgRTItYK1tRHWOXZu7bB1fYtrV27SLVtmu1OkhMZaxoVEScVh3+M83L9zn+9fu8TWzcv43rJze4e+78nznKwyL+i8ztpBXMjpxdV/X5h2+/Q486zPxSMf+sR+z3OuV2zxOLi8yE04PWievvCHwejz1vI8ZdITH7b4qoPCl53gvLbX9kfPXjFSlGbY8bH3cJ7HeqYfe9mJ8atCJ86asJ+XyvWsfS6SAvYs1OdVDwAvE9R91ud4Ve2eE1g++toeD2xO28Nx8VnhfSSymMzx7/Z8+/7XuWaGbGyOEFpjCSydI7pIjqDzHkcSj5RAXmRIBHlu6HRKp9NypUtDSrvr2o48M0glaNqeTKXaFBUiW7UlcxCKgvrNbeZ3dqjFkOktQX1zjegiSt5DZrD+pwt2//AebZzjyh7nE23x8R0RMLl2yKXtSJQtX/9/z8lkiROS4COLwzltm1IAB6MBWZWnIMl5Du7u03QdZZGRq1QjFVb1T4o02SWEFXICbdczngyTSOzqeoaDgsX+Dl+4mnMp7mG7IXW2xvJgjm06qkFFvWzorUsitqMqdVslgdp22ZLnGYvZguGgIsTA9S/f5O6H36SvYeP6Bt1cYIyirVsW8RBKRyeSaKqJEjLHWHikhtA3KCOJtkdnORuHm7Qx4nNJ+d6E5bRl//09bPCM9YQsZoSYUuC6VZ1JlmeIGLHWEUNKm2OVUie1QkSJVEn81vtE8620pu9tEm+NMTH1WcfmQDDKW8LhAXMfmM08Poygi9iuRlQ5hIDwATEsVjTXgBLIzCAyjegdbtmSb48TEucDoQ8p0Fh9l6r3ZGWOWh+yNcwIZarBGgqFrCPZ5hi3bGmKA3SZIf2c7YVH5hmXb1xh1KYgphhX1PszhBQsXIayGf2ipdc5AgNKUGR6hVxC6FNgQ4jpXrQWMywSBXkkIXPmkfZUDCTR2sLgXdIAUyKwMQhIYXFBsOd80j3KSpTWRBwiM+jM0HY9uu1QeY6PkbK1jKLAuo6u7tndPURKwaB1FJ0DsdLdMhnLpmXb5BQh0lqH250ipoq1MierCupv3KZRknJY8t7lDfJxyYcHb9O0CybVgEaXhMwyPdjn3lrL+mCIWc/oP00aXhvrAy4f1oh5TbsM1HGbfFziouPe4s65Lu9hsH1yYfHx9LKzo5Mz0aOzHN+LojsvgwqdZfHky6f78Rex59N5Eue8ftq2Z6/yPgpQz2o3ffaQo+6cEeyZ53htr+21vYKg6Elm/Gc/eC/0aJ6HJJ16f3ZM8gwv/DQU5o+THzkr9fCsVMCTn7/oYtFFF9We1rfTbT1vX56jzxfaVXAsLH8CIHq8BQFHl/aY5QfUasaPFN/PeFkkQdb7U5adIwiBEtCvIq1ICrr6roeYGKekVsgV6YIQMjFlhTSlafueIs/QWuOsI5OK0Fsm3qKkZypmTL90hf16jvUGf7jF3nfWuX5phpIfpG5+qWCZzbkTbpGjUEHSdf3xlQjg0hfv8+Z7R2Tr9/ngvwxp9nLyXNM27XHtk1cStwzUyxofHk7AIplOherWJzIA6zx5luFJWkBd3SIkxBCpBmUKyFa1Ej4EZrMlg1jzA5st+fxbTKvrzMWIO9/8FLlCV8rxgCIElouGfFDQzht0bkAIhsMKKQVGStqmI9MSKSTj8f/Ct/7zB/jWoqRlPFoJd1ZHdHqBjaAAIyRKObblAuF6tElBCSEgrGR89yrSByZXx+x9eoRuA9vqClIp+rpH6oTAOe/S9xgCfdejlEpaO6TaKAlgEqEDIaKExEWPUAKiwPapFsk5h3OprmYwKHnnhiaf3qLfOeJ2Z3G+JDcaZIseFDjnEEaDCogIMs+gW7W1bBExMb1Z25P1LqXRRRIaU+Uwb1KQUWWoKkOWGXmWsaYTPbbfn9OHpAGUf2WTtprS7M/w0zlfWBtiTE5YOFwIyNKglGSwPSE4z9yVTHcdMWikUUijEEoSpCOutIxCCBBiQri0QjpPaHrUqESphK6G3hFkJHYeG1MNkZBJzJhMkmnBlXyGlNB6zW4wBJeEhEPdEYkE61IQ6hxBCmQICSWbtVxvAtY5xBtX+DiDo7t7rLvI1TYFP7fHOQebFX0t0EcdW21CBrcixMbhDmsuX9pESINSmmZnyfLDXYorG2z/0J/i7t4RD+5ME3qVS0bbE+6sfZPm8pDmsGPDX6Gg4PobV/jSt/4AGSy7Bz1TvszG5iVc6bi/uJdSBi9qKz8biSvE+dSG57EXRXKeZ2x4+rrqE/bdryd68j6eFF59GJI+/3B6sSPO2+vFpjLf7Xv52l7b528vzT4XYzxmrYJHE6pHodKT3ix9+mqWiuKpfw97EUkO/+Ek7ZWcKDX9dDvp8QSnb8iT75/WxlnHX7SNi9p5bZzV/tlf5/eGnf1DeA676A0VT8ZC4mQHkg23xnRNS7NsIAT6ELAx0jpH3XY0Nq02qxVaMlixaBlj8DEmhCAE+lWtzWh9RF4YpICm6WibFbNX8AQiuTF0zifyhLrB1h3ZqEIBMgR2P7qHbbpH3ZaC6z/4DmZY0AVH6zxd2x7fynRN6X7kmWE4GeCBZdeDFJTGUOVZIokQ4EPEaIVZBXNZngKguu3RAvJMEQRIJemdO243U4p20VAvanxv6TuHXDHjbVzdfMQ4F+HBd+7QL1Ifl4uaerpYkTho+lnDzof3+eZ/+kNs21MOCmxvwQdGkyHWevY/uEdeZHzlz3yVa1+4zqjMEC4kpI3E/pZHgbIeJQRKJRFWVulrs7bFishRcMxshzSGB4dTpPNpYi8l3qdJPSFpDCmVqKRDSDNQkxu0TjpEkUiQSZMHREqjfCgkKyRKa6RWkOSbCD5QlAXvfvktdBC0O0d00yXWOoJ1ROeQ4xJZGERrkZ1FaUV0Hr9o0EYjlERWOdiQhITjquBeSUSmcW0KjFNNkUEWGWpcocoMt2hoDxc45wmDHHN5jNkaEazDzmp8a6lGFXqQAykdLR+VKVCVEoQgnwzQZQYuHDPgxRgTtftq0cEuGqIUuLgaJUJAxHicPheaDmJMZAuAzDRRpICOFXGFlImAQZqk8yWMWjHVpfq5sBobpPVJN6xPhCMiksRevedwOmc+XzLdOcS1lqIsmNctewdHzOaLpB22NiQfJKr4IFKwVpU5wyLn8mRMLiRCaboQqNaHrG+vc7BzyM4HdxlMBmxc2UwphD5AH7BNCxFmhzNCCFx99xoq03TLhsXelHbeEENgeTBPpB0XsJNsc8+HerygrVZ5To7xT/T0ou72DH9+3PJncCmPs/O9yPFPzm0eirrG4z1O27Mv5KL9Om+fZ9ZzvY5/XttrA161eCvPmI++COpw4WNeIvh5ztWox475rOy8lbLzEPmztl8kVe+sz0+29Vle52eBPn1GJoR4LPhPH3IMGa3mtYgIo4MJ3WHNxs42fZ/xoLf0ztG5VBiuWLHIxUjoLUVukFKilFxRcatEQhAjCEkIkcO9KQBGa3Ih6K1jMqzo65aogZhQBr/q4vJwTjmqqGdLJIlN7P77PTffvo5UgmpRc9kteLvW2HsW2pq3316wx4h5ao7p7cCu9xzc8vgGNrbWWMxr2rYj+MSUFlfIlhAS7zxCCvI8AwG+d2il8D6SjSt0FLjeYpQirwqW9w+QShJ4lBhitKRdibkO3nyDw1FHjJE79zv27+yRGc2iMHTlkNl0xrqHyntuf+sWi8pgq4zMaJCC3lpuvH0NKSU7e0e00yWz//EB41HF2HomVYbWCkuk22tpWeB90orSWUSjuJS/hVLQRs9yrWPqe7JqxHiwzt7+nCgDnjSpDzEkjaYQEVpgtMaGQIxxFQgF2rrFZIYQIiGAVokpzq/Y5oJPVOwxRrSSq/0iVWYYjSVvXF/DhCnt3fvQLldBBYwvrYELiYSgT2lhSIHMNKGzaeKtFajUD5zHtj0UOVFJovVIIsJIdJUT+sR6KGYtYfXcSa2gSCmAIUToE1W0LDKklmTjkhgCQklUpiliw2jUpXTJ1XOiSpgtJb0QoNWqVkphSsXQLygm4JrA4TLgy/w4RU7kiYlwTS7RY4HQIS18xUhvA1M1SJTjIRLbngB0wbFXlkgt6Fqwyw43ayhLOPS3UiDSKcblNaRUlDZws/X0ncVFWExS/V7TNMzvp2A8qzJqNcE5z5HtWdzfZ21rjfK9G/im5/D+HtvxgDjfw7aR+WSdOleg0/qjygLtCJo4YnF7l/VL64zWR8yO5oQo2DraZuvgEm4fDJpyMqSuHbfsBsGVLEo4GN0hkzDcuAl34uOBw1N9pHjsVTxe+Dg9iX8V9vg0/MQay9Pt7FSPM1qPnKkO/iJj+WOHX/TqH6/hedTt84+/aNsnkaWrSnNdqVQ/aS1ZmUSoP/GOnRWD5ek+PDcq9L260PnaXtt3wV4+KPqeWWF43BW8NIx+XvBx+pTnbbuoPW+awFmDxnlBzUXPfVYbZ9nTsPmT2y9y/vP2fVY/zuvz8xx3QXv4i0qipGKV3nWqsdVoH5xHroRXRztr+N+3bDaX2MNhQyoMl0KSyUjrU2CQUqkSLbK3jug82mjaPqENaoUiOO+JQN/3Sb+FiNSag6MZk/GQurMYrakGBXXTYZTCNx1qY4zSKrUdAwd3PfvZmLXrWwxnHzKe7fOeKxgcVcS7+7z9e/t075TcW13awUeBbDewPMo42qkJQZPlGdtXt/Btj4+R6eGMIs/I84y6bimqghgizbKFGDExYpVCa5W0YiIMqoLZ3nSFniTh1azMU6A0W+K8o5wMMVeusbtCkt6/9Q2qLGNZt5gvXuXw0pB7X+8ZCUN/f4YS4Mcl03FB03eYxlJGwcF0QXQBKZJHuDwq2SgNstBEUhCilSTc7+h8h4OEbNgaFSTbl/40xXCNBY67aoei1JAbDvenxE2Plgq/KsWKIZElmDwV/YeQdIVCCFgf077BQ//o5+pDmthIuaL0JiL8KiFqxe5XGcONd28wnH+K/OTbWB9o+57l4ZzNK5uUZYY/WpBdXidCCsB6BzppLSmjCbnBLjtkZ9NcUgryqiSEgC4ygpKEpicsO6xaoMocozVOyRRsjTMIkX5eo3OD1BKZaUSdgp6oZEpN8wE5UEl7KuvZNi3CQLA+ITZBsmhK9GCN4NxK88giq5y1rGFtGHGio/Zr1E4QOpuQIJeC8EubgVwl5jkBSKOwXlAfCXqXyDbUuMI2Hd5F7uwlNAopEBnERUuzPGJ/eQfZe3I/pjKXCVoy6APXlx6L4IFSfHR5kIgVOkuMkXJYMa0bjnKFjBEF5MDRzgF1kbNxeYP8jS8y3vlt5Kd77O/tc0sM6TYnBOuZjAYEIYhCYne3Ca1j7/YOXdMhpMT1jtH9McNuzPqepxqU1NMlUUBdvYlZz5gzZ3/7v7Nxc4NgDoh/EC82ZjzhHx8fIV8sveoce1pDFx1znhoQPeXAi/r51fh58et+ck9x7paHnz8Mbs6bPDyqAjq7D4KbSvETeUHMYkJ2lSIS6dvIjvPfQ/Ov1/ba/njYK0CKnmMm/CIPsHjy5UlBuoeTVuBJ7brjfU5B1xcJZp7lvD/r1ZWHQc/pfpx33lfpHMXpN5/BxX6eq1MvCSCmDMyIiOKxAfBks0qrR6db0eU6H0HBsmmJPqZ94opdDoEPAWxiGtNaIXQKgpRcrfyFkOpIROqEkqn2QgFN0+K8gzjA5GnCqjJNWDZYH/BRYntLVhb0folAoKLj/vt3KYYlw/WEfhVlwWg0RG9p6sMlj/RPHl1dVubkuaKpI03T0fdJFHS8Meby9UtIo1KdiU8oges6CJFcpn57rfCto+s6yiJn2XW4FdKkpEQAXW9xvSMEj8kNb/3gOwmZiNDNm5TOJgW51hxOa8r3LpMPSkQb2dhaI/aWuswRCnIlURrGkyF9b8mlSMEhEb0S1JSZJliPkArX96AkRmqE98S2R2aGbG0E4yqlJUowRUYbPXt3dpAi9d26FJAGG6jKIt2ftieKR78DsdINevg70Von+muZoFgBqX5GJzay4FO6WAyRUVlw/c0rFEqlWqDeITtLLiJRKzIl8W2PHFf00yX55iilSPmAHOQEn9jltFLIwiTigt6llDQBKs+wh4sUHJU52cYoBdSDgmh9EoPtHbowtNOa3gWykUFoSegcZlIRfSBYl2p/Mg2kvgu3ohzXGl936FFBP29RxZjQ+uPFBiEgWAeFIvgePSqRvcHPWsxkkJAmAVIn1j6kQKuEBsbVOYIPSBLyBDHpCWmFXN1rmSfKb2U02bjCjCtmn+wQpWIWHLmV6Xnygd5ZQqnJckM1qggusJgtWL+6CQJs1zN/cAg+oETEOI/vOh58fJeNq1uUGwPG8gom0+yXgawq2d89TAKxZYHTqX5PiIIQA7rIyYuMue04XCzI8wptDOVogO8sqjCE3tF3lunygPJLI4aX1ugOu8cd0UUzAT4ve95Ft5P7vfLx4dRNio+f7mlHiTP3FGe8Or3H01o/PyQ96zghBEKpUx+e1/bzhrivNCR+ba/tj7S9AqKFF8jAvWhqGI9lKJ04TzwRAZ08+9kP97k9vCjS8zSf8bK+5Fnoy0X2P30d58UxL4RsPdnQE81f4Hs8t7nTY8OJe33mZZz88CK+/EUQosdUZ+OJurRHobUAvqQNW2pV8HGsGyLIfGCnblkua3wIaKHQSiJjJApB7/0qLSoVSCutkFYeByJFnpFpTQCUkizqBiHThFlJRZ4lxGZZt9iuR5clUUvcCvVAgBQwP5gx3hjTL2syrViUkTutY/c7t/jB719nPbtJbGfYeItBCRvbm3y6uobV/49vgwtpKaLUgt4HfITFdInUEhEivXWYIkvoCDDKDTEEugiud7jeUeQmoSa9Q2tNbjRdb5FKUhhN13Z4Ce/+2JcYbAwhRmY7Ux58cI8+UxyOcmwuGY0qtmcds505g7wg9B6dGcysYbQA5xy5yUEKssIwHx/gKofte8SgxMREBT5ZtuRdgODp6zkRizMKVWZUG2NUWdDEO3glsT6QqTFHy+44vS0SCTHSdolifbGocauUFqWTaxWRVY1LSoVLZBnQO5fqySTpezMaRUKbYggUyrC5PWEiWtT+LbwURN9STAa4gzm+6ynHA6KSiZVNCFRmEiV7bpCDgpBOdFxLZIYFzYMj9LBEEBOCIoAg4WHgsOpDvz9HD3JU1EQlcXVP11rkKiiJK1QGRErLCxGdGWIMCfnJTfonPVIKumqd+4cBRMFyHvC2w3vP5jhQVYmRsCwFUmqEllzaiIyMJIqG3d1IyFa1ZT5g6zoF1HmW6pAEXB53IDWu8+wuMrx1mHGVECoSGgWppq0cTCjDNmW1zqL1HFU9INBKcMUbpk3gKHqWRwv6RcNwY8za1hqCiMoMOtNIBAe3d0AJtICRyahaS/PN2yy2IxtvfB/lxpQb9iPsXsdmrahnNdg549GYtSbiRWS5bJmvVRR5Traxgbl1SG5MWjwpMqy1MFR8qj8BFbCTiMlTnZQqFFvfvwkBysZz83aDAA5D4BvWPsX1PZlu8JkTFDx0mhddY3uO4OizYJx72OHP6q48HEmehiIB3Pae/6Nrn9jjvvenjjwrme8CJuDMNMTX9tr+hNpLB0VnPn4XnnyfN5s+K0fs2c08cjQvMP9/3snzRYKTl7WXaecit+6i7Z9a8XvhRbznPPCzBJOeqnx+rBj/qDD5sb6sxqz3jOZL2uB6y9GDQzZvbIMQ3CoLDq9u0LtUc+F7S7eiGE4F4KkRo1ZsWQ+1ala0y/OmxWhNWeSUZU5R5CyaNk2+k/4pbduhswyhUwpe0/TkVY5aISEhBIL32LolSokLkVpFZgNN9I7sGzN+4MYV+voGzu0x2hRcefca2J6TgzJiNZGscmYtBCRGRTIiLkZcn1Kggg+EzkIMGG1onF/p6qT6KWst5WjM8mjBYDIg9EljKIaAHuQ0iwYXPJtvXWG4NQYB7bTm9jduoQE7ynkwyrBWsb0+ZPJgxpXaMRAOnRmmsyXae37sh94jhsDtb34KRYYmMptMsZs1OM9Hq2BUS8k77ZzB0hGFQAwU2WCAUgKdZ6gyxxOZuztYEZEmw/uKAkUDCCnpV7pOwQe0WKF8K2IFYzRd369+L2lbJCKlTJTRakW24FeirWG1PUQ2RkNGowFCK/zRPcL0Proq2LyxSXswo48RvTbEVDnKB3ABUZikK6UTS2FYoTf4gDAgtMDNO0AQ+zRhljLVEhECvnMED/laBTGlpaEkpsxxTU+9N6PcGhHrLgXBR0uElpjtSaodGyS9JJUbHC6lkqpUR9MvW6bNkEM7IvYrUgjryMcVa+Ml6yOLWtVG+WWPGhSMmDMYRAhwpEvmTU+uUj1FPhngmg5VpiBcCsGmahP9ubPshLUVMpR+v1FLJCkVDyWxh5bRrGQi36CtGm6ZGQjBJZFzZTxko1DUPvAdEj35/GhO2J+mNM+qIF+ReDRtx8bmBLtsGC87rquMXmZ0ewHx7jsEecRmv4ObHqEQ+GiYTVv8g13wBxSFJAj4eunY3z/EzmeMVs/UtS/ewHlPoXJcBUcbe8QMBpMhqDylpwKDmyV5lbN56PjxnYAEPnSWb9iXEPP8rOysRawXQZPOtGcdfPZi6flhz+N+//y1y0cB2ROXd84Y/FjWyqnPT6NSd73n7mqh5fHg7/TZxPEer2b6sWrpokHsa3ttf0zsFesUnWNnIRknAyBxeseH208cKJ745NSrs5/cMz+9iNc43exZDX0WCyynkZMX2f88R/a0QO5p+7wKu8h5zvoqn7bfs871cGXyrPOfdcjDlArx8D+nG3zU7sn9pZTkRfbY/uPtNerpksXOUdKeScwKyBMDmxIC6x1CJaHQaljRtx1KSZz1zBdLfJFTlgXDVYGttY4IrK9NsN6jvUXEQDEq6bqe0fqQndkcpRTR9jSLGpNl+K7DKE0Iqf6jPprz8YMZi7bn8qjk6pc204T+nLlU3/bkZSowtzagVOq/Dg4V08RUS0EIkhhDYqCrchbTJUIJ1rbXEi3zxoiqzJndP0IZTYyRerrEhcDw0oQr710DIWimSz78r++TGY1OiqeYIqPvlmijEAGUUuTG0IeIRnD9izeJMbJz6wHBeUDgIgghwSZq8ERIIZAIxIrxLN8co3KDyRJKgZaIuKotUhLqDlc7ipEhCk3T9yz7PpEqkAIh55OmkDYa75NQKyGhREImJjvnPHL1gwzBY7QhBn/MOjgeD9nYGiOsp581dJIUnPeOrXfX6faOaI9qIoJsWKCKDOoeMkXvPEVu6JddYpOTKbAXIaKrfMXE5xEqMdwdM+BJUGtD3GEKGnVnIVMQBX7WINfSL7YY5NBaYu/wuQeZiBds26c0MmmQmcbWXSLciOBFTxxEdK6hjshc4+qOYF1KzxMCM8hRKqFjIJBFQpuij8eL2NnGEH20KirPNKp4yC4qjuv4tJJEH5BFRugdcpCBSIx++EBwjhgC0Xq62RSHJUpJIC0gZMYcB6lOSYySqL6jqxvK0QBl0rV1TUs9X6JiSnvtpUAYTalgvjNlcnWDajJAasXo0hixeYl2ryaGgCkzTJGDjxwcFNRdj3UeNTGYTLFoGtY3N7j63g3MsCDWPTrPGF4pWN/cpA89g8kAHwLBBaY7B8QIw7UR4/jI/zwx0T9ztn7W6+8hi4+/fFovH9NdOl7Q4uyjHpt2PPvaLxJqnTu0nLPWezrweTF7cgH5oVLRyaDryWt8znSO1wHRa/sTZp9NUHShif1zrGnEk7PVpzS32uWFnuPngOuf2caL2KtEmV4mgDvra3nV4+bngbI9swvPPlF8KHx4zm/i67bnrk8IUBzl0CU63S0fiCs2todriHme453HOod1lojAmJSuJGRMn68m0qNBxWK2JBJxMTCbL5mMBpSZoTCaIs9Tah0S6wQyCvpFmyZLRYZetNzMND5EjmLHdABaCN6UkktR4AnsFYaPfMNUdbz71R9mtlUSgdZ/AO4QInx42HJ/kfRrKDaw05QCl+cZzbKljx4lZFojfSg6GsGsyB26tmM4qjBFhikzlodznPXYeUsIAdc4rHcQazauNbz1w+v0xSG3zDUWs0g9yCn9av1TSup5TSTyyd1djqRif2Q4qBQ+BJZOsPPBLdYclGXOjc0RG6MSISVXQ6BbbCKBw+YTnF8QfSBHoiYlMtP43qIyTVYaLo078lITouPBLCMogagMk3LBoHXoOOd2zOlPCLAapZBCJmY2nxjVlBIILclsizm6lxAqo9NvSkkuDQ1XtxWDtRGLfI0jv8F0b8qi7dAhEtpAXLSsbQzp7u/iOo9fWoSWSBewuzOkAGUGFGWOrzukkYkavLMQIrEwiS7cOtS4QgtBdEkTKtFvC5qDBTEKzCBDlRmiSal1oswI1hM7i5/XmPUhMTcIUkAaWosMEbTCxT4FxmVGXFFmzxaCfhnJtsYc9YGoAiLTbG0IBnmPUJJS+kTUsNLsEiohXfuLDGdKIDJiyXDk0YVB44lRE43h338cqS1kMvATNyPaOUSEG5sCVXU4L3gwNYSYEDqMoJvW2FmPWpdEKcl7Tb6f4QXMOseHzYwoBK0UvCVESnPsaqIUSCEwZZYEX7XmqNDMC4VVikUJfXTcamu+9MNv0U8qBHC5HbOxdpXgAx8etcy2MqQQXLuqkbXl8M4BfW1wteat8QZXtjfoXIPvBdNLY4JRaGDj3lWmOwcwEOyM7lFNKqSQNE3P7u1dTCeJYQji7IT2h6jI4/W3n7GzPWs+Hk+9P21nfHbxXj701c+YJ5y30PaCE4fH1nrPOuVqBe1ZY86zA7Cz0K5nHXuBAf2Ja/8eDZRf22v7HOzzQYrgnOfsZKrbxfJhz/ZnJ5UYXtLO8x8v2vDLTPYvguycRkXO6+d56MvzDgZPu56nL+c9u18X6dOL3s9nXOdZc4RnDWIfe8/H3h/DRnF1zI/UDe3tlvpgDhGscxRCJpa2zOB9Togr9iwh8SKhCdalCWJzNE8ojFQ46wkxUrcdZZ5h255WWuquR2mFkgJnbRI0XV3fMAry2iZBykJSywSzbiH4Ea2pbc9vVznf0VBnkU9rw3p+Na38z+4iOCQCd2epVkYIwfdf26Rtl7StZTQqybTC+hTkRaUSGhMDvXMEIPhUzO98oGs64n5ErwgPTJZ0W4KPeB8oRoK3f7hAmftMQ8/vfhCZPjjgkhJsdJ5ASjtUWqCNZGo99+dLYmXIM8GisRRrBcO5ZIxGSsmkyrhUmES73K4l1ETA7fktagKqzJDrhuA9qjCYcYkxClMatjd7DC39rGenHhGXFpFp/K2PUpBSDTFXb3A4q491poIUBBewwRPySOgdVVUkdMxLhoVCj4bHekZSK7bymmuDGVHM+LRXfDRVLBY1UQhsZykGBVEKxhsj3Lwm1i3Re7JJhSwzlJaJvGPFrCeNXpE3pPQ3oRURcHWX7kOm8fMGpEy6RcOSmOvECkikmFTgAmidKMLrDpxHjUqyzWGqz+ksobXY2RKkJMxryDQyz5DjMqE2ucEvO/rRiI4R/sDB0oKuEVpSqY61rEUpldIIPas6JU9wCTFaiA2WtUYqwZuDfYZjcG2D0gYhUjf/+73AUScYKPjT2x4pAjrXbGeeyJI2wN26QpY5BKh3pzT3DjHZOiE3BOuRXsJMY53FR+hDoHVJp2rkA11v8aQU0rzI2BgMUFpSjAfcGRmciuQx0jQ9SzdkcTRn+eEtLr9zjcnVdTacZBAlQkvuN569JiCJvP1WzziTjG+MuNK8A7JifjSjb5dUkwmH04aPMsW863BHS348Znz5za+yX+9xO/uYZjanGhhWGre43h0HljzN1X3e6VDn+euz+vF59euCwdizG/juBw9PjlFnYUMnZ1ji5K6v7bW9tlP22QdFz3jwHk4kz97ydP/1WLzyIg/48/i255nUX7TN5+3HRdPpnndwedF796JO9azrfZUO+kJI5QXbeY7jBYIYIve/eRs5E/gQyYwhNwYhBEtrVwX3SThTSImIKxphociMRuUZvbWoLE3Yzap+oHeeKk9dCs4TQ8RZh84zhFJoIbC9w1lPZlQiM5AgpSDaHh8CsagQRpFhkMGnlCEqpg8OuB8kl794PV20OP11CMqNEe52miT3TU/fp6L7Ks/QRUbbdGiTriECWmXpmusGoqBQiYrYe0/X9iAlWaZBS97+UzfR2Ue43vLgo9ssG0NW5IjWYV2PkpJMK6J3uOBREYSSFFV+rIEzHBQMuoDqBVIpVIBoXfoKQ9pHSkE0Gkye6mWMxhtFNqkSwmE9IlP4toflgqgzMApZSXznUo3UqCIEQVFkXNmYJMHOkJCs3ibqZhETY5/ONDLTZLJB3WkSiu1DYsEQKe0qCpJobV0TuxRIahcIWWJXK4qcdn9Gd7REdBYzyNFSgPXIEBMj1YrcIDiPKjNiiImIIDMgEl18WDHMIQTohJKoYZEQpcYSQkJFU811hN6C82RX17HTGnqHPVgcM8wF5wkkSnJBCurFCgXzswZ0qq0SAmRmiEYjjcL1lii6xN5ndPqt6YSqqswQdQAhkVYhokqU6blB6JC2x0TrHpw7vnahBNLopA+7EokVrFLydCKJcNbhZg1BCMQq1TWrCmQAL1IKrFQKu2hZLBsGK/HhzevbAPSdpVk07HzygM2rmyitiUONyg2htZjCEKVAac3h3hG9dSyO5rw5rpkUJ5b+BAghV4sDCqJk9/4S53q8tQzX1ymHA5Z94PIXrjGyFnuwwP7uHQiJeEVphTYamReUKuKsZ1zm+COX7ulTXNdxitXD/F/x4mQCTyU4OJlf/LBHr8ovf9ft0YWcVZd0+rPE0/P5RCCP3+IVuyN/xG/3a3ttn6N9fkjRmZYe14vz18VH2FI8EQx97yzcPGmfRZ9Oe7mLnuNVB2oPA6PTX594Djd8XvvP+/lz2JmDeXx8jzM3nbwn8fG/P2JytoXk8N4B+9Oa1pU4a3lrc8y4yLDe862dI/rerhjixPGglZsk5jmfJzFOY/SxiKiRkvGwSjUyziO1ShO7hzTePiQB0VXhftu0GKMJLiCImGpBsX6Y6ImXE6y9jDaad1vPplJIKZiqwNHdXYL33HzrDS4NLgPw4eF3mPczIK2U9yHgnKfMNLleFcbHiA6ByXiAlBLXWXSVM9s9QueGvMjxvcfJVR2LS3o1MQZsCLzxQ+8gNwd8pyxZ1jN2pvd5NyZ2s8wGZKYQUnE0neMmeWpD7THenBJi5M1+i2tiHRFgurXkgTxExkg27fELuWJGS2KlelThK0dZlPRdjyoNxSilzyEEMjf4ruf2TJGNLuG7AGWJcC0iUwQB/XTJ4Po2wu0QpyCMop8u6a1jvL2GynQKxmpQIUd4hYg21fIQIYpjkoWlNdzxY+yy5ZCCPgSs9eTtEXGxpFCK3Hd0yxm+6fGZTuKNPiRdrEzjnTsOPlgFf6F3KQAUKQD3PiCqHGk0oUk1P2iJXbSphkpKVIjYeY0IEVWkFDE1LNNPPMYUMMZItI4QIqrIkTEilWI4gvWyxgw8s1riqwEhREZ5z1ppCdYTegtGoycZpU4PUQRC3SHzDKVVErFtHdEFtgc5I5lqoP7T7cjCghKan3xHMJKQZ4o//w70TkCI7MwysnKEInB5UBNX9VMqN/hgqY/g4+xLdIVEioxbUiCcoy8kOwNNN+u4VBVsOM+QEqkkznmC88xLw3J7Dak2kfcOOXhwgDmcs/g0kpUZynvm6xVepNTJ61ZQ7ixwd4+Y3yzY+tIXCD7yRtVwfZjIR67Wd6iWHb0P3Pmhjns7OxgR+fIXDqHvWDOGhWzJq5KpP0JlAl0YcpOzcXWTznaEmNLhBpMK3ICv15poPfF6RWy+fb4DPOmen2tx6/Gdzw2n4qM9Tv550Zn5w+XRM8/3spkcL2XxzDvwtEXe784k5ezKIvEyC5uv7bX9MbXvclB0QXtWSsBF7GnoxFnbLurDXoVTuUgbp/tz0VS1p9205/HTZ8Jzz9r5nGMves9OByGnX5+0M4Ozs5t9yBT02GArHt8jBd3P+MWd2PyGUrzh4Rvv3yGWY6ZlifWaoYbNUY6znltFwbLtiaxEO0PEC4FbUTpHQCJY31rHtj2LZUPnOsbjAUYJQmvRmWHZ9QlpCkmU0nmPUpK8ygmtJcpIIJLnGSbvKUeHCKUoQoVYpP5ey3M2rSUvCj4wjr3es9w9Qgq49uU3kEZxd36beTcDEZFSsPXmNve+cYv5skVKgZES4QOuFykVSSu6ZQvLBgBnHUIn3RoRwDuPVILOOvSw4N0f+iLlqGQuJF//FJoDwSjf5q060NYdkpTKJUhF/XmuaesWVc2R+h6Z1lwVI77SJUa/3ytq7pYHKAFN17FoAtImXR49LMkGFg0EoBpVxxTUkDRw+sMlobO4vELUEu8DJg+4zuEWDd3RIgUdMcBsd0WgIKkGGZUAJRbE2iVEZNGhKKAB1/aEzmJGKb3MHi0IUmAR1Jmhnzvm0ZGVEKSiW07Jmz2yLEMEIARUlZNvjhLNtpKoKrG9SZMCTTUoiD4mAeAyw02XeOsSLXYEcpPEVXODEYKYB3xvkSbpIkkJqsyJvcM1HWZQJga7WQN1j0+SUWRbYxACA/hpDUJQlD3rpiHfLLC9Y+pBSEGhLRsDSwwB33uQEWkCtkuIKasALK6K4/tlm5DPQlL4JYX2oA3fvut4YA1Gwv98QzI0oAR8eTOloDovef9gQN1q4mLOlnEoRSJHmDW4RU+zEOxuvUFjA9Z5aNsVE2QkrpXIjYpl59n2kSxPCN5QSg73Ztw6dNxb5kzWJ3zf1Q3KzjPdPyLXhqr3IAVz06I3Bpi1EW9oB3f3yQcla+MbzPc1t775Cc2i4b0f/SKT9RHj3QfI+ZTFwZQHVzyzDc+lqxNGV3agXbK3u6S1b1DqdTauK27+wBdY7C1Y+iXNZkvTJuQxyzOOdqfU046Cr5CNC4J2Z7ur45nwI9/4fMPX6YHlgke/ZMAinjj3Gd35rgRHT/bpibsiTr14ynrh04VcH7V/9pnP6t2zxGHP78tre21/Uu0VirfC8z9hL5LnFR9/+d1+qM8LFl5FsPS0ts4671mvOWO/89o6beddw9PyxJ+2/Tw7L/h5FXbOICRWJ45p8f54RRw4oUt0qomTEwnxKENEHPdZoMsctz6hd4YhgkG/JDuokVlFZUxatUfQhKRVlArlM7z3QKQsM+aHM7z3ZJlBKEM5KmnnDT4mXRyxQpl8jISQdI2SHk7ql4ugM4UUEQ8Eo5E+IoVMk9GH6UJBgXWY1echRA7v7dM3PVe/+ubjFwtsv3mZ0caYvY/us9yd4UJAep/S85Si6y1FkdF2PXmeEYMniohdsdMRBdJkXH7nChs3ttAmITTNtObw7h5FVTLcmqD3auSyIcZIb3uKIk8oSO8wD78nF9C5RPqIth4lwEBCL6RMSEFrQSuyjSF971B1h8wN+aRKuk9VhsoN0fmUIuZSrZGPETdtQArqnRm2t0gfkhSVVomowDlElRgBRe8QmU7BS26ws4YYQiIp6B2qSOdxs1QvJFcpUK61+GVLO6/pZY4pBJ0QlFJR+ojqU32WHhRkVU4E8vUB/f4MIwXROmRh8HVHbxfIzKCGBWHREhD0jcU0qfZMGpX61Dqy9SE+WPSwJPQWEwNISbQuCZ2WWUJ2hEjU3Dqx9VHoVeQuUIXBNz3ESDYZUKyJlIqlQa+os+3hEXGiQUqE0Uit6Ns+pTJmmtBaRJUj0qODysxqgUCAUelZckloVzgBcUXIEMD1KcUUHxLrnFJ0tSWvcqKbExCE6DHDAfWDGeghnfW0naMaVeme4xlvTGgXDUEKVJUjFo7R2pByXEGMXH7rCsNcooPl3od3eTBt+P71CcvpnK7vME5iQ6DLAovdHp0ZLIZoHaMi4/DWLsOtMUe7R0gt2b21w2h9ACQdoo3r2wzXSg5nU6pRyWDNoZ2mcxJ3x3L3/TsU1lDeWqPISrrWsjxaIDJBMSwTy2RMtPDWWoIPxDI+4fZOPMYvb485wPO2n7CLjNHn+On4mB8Wpzd+1+w8Ou9zb/EF7v2rYMODx4f/89p8DRC9ttd2tr0C8dZH9tn7qM/RCz5vQPCq7CIDzel94hmfvwpo/FXB68+6lxc57mQQfFbw9UI/DYEQq/z6E+d6JN6a7Pr4DS4Pr57KoxOsLT+l7I8QES5LhYiRjWubSLeL+/ge0Uc+ufJ9fKArijJQ94lhzodACD6RI/hA6PuUDicEziY0xWiNdR7bdvTOMxiUqNxQt32a0CPAe0xmsL1lMCxTvUphCLlHb0R8dPjc4UjB153qgKla4ESiiJYRhPcsC0sbIkpJ3qqvsdYI5Md3eHPtKjevvImUgje7XYbtXSKC4VffZW9nwv1v3abvHSEKhkWG6Ho668iNwflAiJErb2/i+m8iREAMSj71PbdUw8F0ny9tfR8iJpQmRHBNRx8Ey4MZWkkGRrE5zFesX1OORp8ipETrFmNyVBDUi1vcm94FIchsx1uZRUUolg5hNHo96fnEZdKxEYOc4APZoEAoSegsvu7xyxZZ5Xgh8E1PN6uT+Ov6gEoPmd/ZJ64m827epmDWR/KR5tp6T+iXdHVgz24QOoswCnu0JDiPWTHSySpnkG0yidfwzjELd3lw7w+JEcq4j1gu2VAS3y3IVGLV85kmyw2WiGx6GiXJygJW9NNSK1Rm8N6n9LhFi687RG6Is5oYI2GQY4xOxfg+0M+aRM+daUyRwbDEtT2u6dGZRhmN71oIEec8USc6ajMsIMaEEKkhotDgAkuX8clReoDq1uF8l36jRhF7R1SJ1lsIgck03vrjRznaxIQXY8Q3XULAGpsm+86jlOJ//5KksREcjE169tQq9dP1HlC0s5pIYoK75zYQQeAWsNZ/gcHgOvddpHeB0caE+nB2jMoOAmw9mFOOSvbnR/y+kjR3p2zdUwz3F4llb5AzMorN3FCJyP79PbaubfPhcsktPD4EJlIxmvUQe7resT4esn55k92P7tGsfgdSCFxnCcD/t+/ougYpBV/5VPP2oWM4P8SZhuJSwaVrE35CO6yTzPeX/P7020ShCXnkzYMvMN4Y091u6duetUvr3D36lLs3P2VyeYI2hvi7j3u6ePrF8QJPPP74XETmtMWTL+NDT/rkdnGBfU/aGX78EdrxeC8/Tzur3xeqxDpvzH7h8erZ9nTtpTPsM+zLa3ttfxTtlaTPnbGmfsqZnWUPCwBf4ol8Hv/4qn3pQ//8vO1eBP05aS+y6nbWvqf7+7z9eB57Wp/Pu1/iKdvPCwKfpw9P3fHkoHfqFxlhlI+5MrhGPV3S1S1KKwZrQ270+4z94nj/pm7ZvL7NtpZsFZaP/vBjPsHjjeGo6xlOhly6so63nr27e0nPRQpYCX76GAgxEPpAiD1SKdbXR7jGspjOKQclRWbogkupa4B3DhciocrBJyFOUXl8ngRCVZkK4aOCA1lzpJZpdV2l9CVdKFxmISYa5iFXuG4q6r5n95MlYSLZfucKa919iv6IiORw+CaTKxuMtiYs92csDhdIKWnnNcuDOWGlkVOOR2y8sUFRDAHHvHXsfriPC5G1fI0vbX0FEJg8Y7g+om86nHMMypy+6ZFERgoypVhklmF2sNLgkUQfITp87OmygMwMufeovRalJSHPmLUdA+twy6RjZKoclSV2OrdoU52PDwmFGuSgFX7R0s8a8o0B5eYYIQW+7RlsDminXdLkKTOUUYncoPVUboEuFU1muPvhHD2skJmma6aYcUmUEpzHLzu6aYvKSrAeXRukX0F8fYvr56hBTpVpXFGgBYmoY5CzmC1ReYYMAWESyiLLjBiT/g9dxB0tUIMCtaqTEidqeR6iOnpQgPOIKk/U07tT9KhERIMEdFUQQ0Bqha87Yoi0yw5vPXJYInrHQyY/nWW4eklbe/o8TxpETaB3DfmoRGYGoUBoSWgtwXf4FfJDiIhcE13A1Q3Z2jARMkQQRhGcQ2UGIQU3i54oHdEEhFVg8qQ5FCRSa7xN1OgiglCaaSPpFg3+KPJmNYJYYAiI6FkczSgzTWs95WSAmzas+0geYKEU94YZLpfUteXG+oTx9hqLwxnmaEEIS7xRVKMB40trXLv6BtZ2NIuWzXszyvqQru/pXWDzxja6MKxf32K5l4Kw0eaYd3/0iyAlnzrH1FkyIfgz+z3rooJpYDarcesGkxvW/BShBKbosWPPtIehGXB1dp31bB2Rp5Q4IQXVuxV3vvAxptA0O83ZPvSsSbo4f5fns4sd/SJpXE+b5H/Wa5QP236lccNnHIRcODB6DRe9ttf2hH1mNUUXee6f3ze8Ivd02pN+N5zDRUegs5ARTh37MoHTWXZWv552vudBgl5m5H3a1/+i2yKPaRGJE8NJJB4fe/TgkG//9jfJicg8I0jB4PqC0WSViBcCXd2hjERnBRs3thhf2WRj+8fozRjvPXe/8SnTvSmpDqOgXjbH9RSRSDWqKFY0zjGCyRJd8qJzICRKSFABg0ZlkfCQAa4q6ZqOosxRHqJIOknOe0RIAp5eJhpjE0EJQUCAFIQQkoiqD7Qh/fMhUGpNJhUH9w749HDO2miXK1uJ5jkhbKC0YnR5ndGltdUNiwQX0qAsBFIrhFqlQ5HIIY7vrxC43vHgO/d5UDfYSZbSo/qAbztCCBQqp1QaSUR4v2KaiygVCUIkWu1KEOc1YbYkCEG2PkSUGfVsSVUWaCTaxcT05QPtwSJRmSuZUI8m1XgFmTR2VG4YXVtLyEWbdKfqj+8gBiUiM8Supz1ckG+OUIVBuA7hE1ohlKS4vJaIJeoOfKSf1njn8b1LQqqyhJFDQqLPHpZ4H4CIMqlWSJU5skxBiu89wXqGwxKGBbFzSAFxFVxE6wgrRjs1KPCLFjkuQclEFe48SitCDIkEQgjCvEFvjFC5pl/1y/eWrMyxRwvkiq46Wo9b/ZUCgnX0nUNaB3kKLtW4TNfmUkCuC4NvInL1mw7WIVWGHhRJF0kGQmchN0idtJCyMgMEaqCOf0eEuCLlEKhM42JEuMRk53uH1IroQwps3cP7mYKvelrjli1ZLBLrogR8RDpPlmmCEMwXS2zfo1xKMV3sz9GTHGUEUhnEsqdtOvzOAYujOcPNMde/8iYmMwglMbnhaJgxzgdMpODKZIzOcvZu7TCZVKxfWcfkhnJcEULganaNm9/3Jsqk7+KhrzleqVoJzV56+yq1XbLYX4CPaGOo1gpiISl14Mb1mwy+WbH70X3qeU21NqAYlpibhmJQnL9QJx66spP/5Xj6/OIu+RlHnhi7Xpzn7riJxzl8BIh48eHuRYbchyc6Tj88J8XvmSjb54rIPOd9fo0Wfdftl3/5l/nrf/2vH7//S3/pL/Gbv/mbzzzuZ37mZ/gX/+JfHL//pV/6JX7xF3/x+P0v/uIv8s//+T8HnsyAeVY/fuu3fouf/MmffOr+//E//kd+4zd+g3//7/89d+7c4fDwkKqquHbtGj/2Yz/GT//0T/MX/+JfJM/zZ577e8VeSVD0uJ9aTRKfedQfwafwPMTivIDh9P4PR5/zgoWTxz/r9jxtiewi53haP8/qx6tElE6POs+L+F0kxfD0+c54mwbUR6Pqe8bwQ9o81laM0AvJH3z7NtEFRqOCOqRjj0bvINdLhIDy9v+A4BM7GCnQUkaitERIgRaa0daEvU92KI1Jwq2Dit5a9Eq3ZjFbsjxagEwTdm10Sn+KkSLPUAJsWDHB2T6lp13fTqKphwuCC6mIvlZwX4HzDLfWyIaGKGGupjR5jQScDygBTogk7GkM0ns+yZYEPUc5z/ow4+p4Hesc798v+WCmWb+xjfEaodOX+DDAWV00KpOnvg+D9V8BEdAy8pXBEQf3Dihsye29T7GzGjPoMMP7SCXRQnFnLaXAzaTglpHIENFtzTu3lqv0uYfBmUXNGmzn0VWBHBaYUUWMkTc3v48Rqe/77XdYLvcJS0DpVHeRa2KRoaocu2gZXl1HBE9/f4et7YjOJNlkyEcfWdRkTD8PXBl9lXJzQNssOAofp6AHzQeHQ+RUQJbRL5b4pidYByFiFy3luuDSjxt8BDdfcPfu18nXBzSLI7RIaW5mXGG9p1obICOoUYVftiymM7IyozSGK6OeYrAkRNiZZrjeoXLNJXlIVUC/O+O+HOJUEm/VkwGeSDYsuJQdUo1zApKPj0jpgplGj1JQ9hA1SzpBltB7ut6iPIgQ8DqlqBkEIUZYdmRrA2JrERLszixpDRlFMa6AyFGT0YaM2Ci2h46RtmiVpdS1lV7Tf/wUPj469RgLwf/2jmA7Cymlb4Xwxcxw57DABoUInhvrLZpUu+XnDXJjDbts8dMloW7oq8hO+3u4tudIlujyi9gQsdYyGZaEEFnEwL2raykNse54a3dBvaxplOQPS4E2gTe/dI2NomTv0wfcrmvUl64zyEfM95aEKlGva6O49M4V1q5ucKm/zbD+Q2IN/6nveFAEKCK7uzsJ6UTyzvp7ZCqnn9fsaM1yWBKN5O5HJU5Dsztj7f0H4AOizPlT65eYH85ZfGvO19//H/RNT1f07Kh7yFqwYda4/MYlskHJibWc9Hf1JopHjvBROl189Px+lvYKJt4iXcSjD44Xsi5u5wdGp1cfxZP7ntP/CwV7n8N05/Fv9zn69Box+p6zf/2v/zW7u7tsb2+fu8/+/j7/8l/+y8+xV4/sk08+4W/+zb/Jv/k3/+aJbdPplOl0yje+8Q2+9rWvce3aNf7hP/yH/NW/+le/Cz19fnvpoOh0+tuFn/0XeiBfkWd5WSdwUQd/3oBzkfO/Skd10UDr87SzUvvO2/60z04e/9xLhvGx9yMf0R/cYePGFuUkFUP3bc+3Pt0l1JqtYYHKC7RNE8YP3z9ATr5IPixYW1tjUPhHtzpG2kXLx3c/YtpppBCEPq24112HYaU5IiVZblBakeUTuqZLtSHeI1apZUqlWqMIyFWhvo0RJVJK2PzuPr335FLSBU+uFXEJIihMr9E+Im2kNUuaPGIRSCI+gpKJkjmGQFnkuN6zK1oMsGYyhgFimXGrWmfpIrNbHeLOdyjWhgw2huSDgrzKj/VRgGMiiOgjIUS8LWjnDe28pXvQMgwlzAOeJqU8CUeVz5Ex4KWkqZIipZCrhMYQ2fCW7V4gogdvE7qhJLLKodLYECiEwC07hBBkuqAsNsmiZYpAyogsylTwbxQxpJlj8IF8bYBdtIS2J6ocvXiAKQRSO4KaECKUw5JRvo1pNRmGafcBsZQEH9k/svgYkT4RLOgVYhFjxMXIaL1i/F5ONq44+MBy/9v3OFom3SRtNGZQQIiUo5RWZ7bGhN4dB8NyUICS5NQUqsP3nnZukcUYrKccB4p2jhItZryJlykYjyRGOeE9eTMny1r0ZIQaZIQu0q/S7XzdISO4WZ1S8ZTEC4+wAeF9Qv2UJIhE0CFCxC874qBAj0v6gwVmY5COW7ZgUn2dC5LZokcQWavSPZeZRip5/Lg+WMJ3Dh93UVLA/8WBGOiEaq7qjoQxLBqJMwUSTwgt3lqEALMxxMXIcmeGny2Qw4pya8h85wHOeWo1IpLY7jIpoHN03tG4wL22QWnFVojckBq1ts5sc8BHA0U9r9nbmTG4N8VZx9LArfc/RaqkrSRX/l3KgvWvvp1os+s5A3dABBb1kl0fVg9G+qOE5Evb30fWGr79u59yYBQ3v3iT0Rsb3JuW9FKg4hrsWdysZrw94cH/+SmzwzlRCLxLqbGmkCyHM4KILGdzlr+/4Es//uXHXGV84s1Z7vACSMeL2HlZDs886ERfHvPr4sntZ5zqPHv6dnHi1fl347kSHb5L4+3LInKv7btr4/GY2WzGr//6r/O3//bfPne/X//1X8dae7z/52X//b//d/7CX/gLPHjwAIA//+f/PD//8z/Pj//4j7O9vc18PufDDz/kX/2rf8Uv/dIvcffuXf7xP/7Hf3KCope274XViosiD6fRjZODzVn9l2d8eBZ6dNa5ntaf81ClZw1Aj3Imzr+Wk/0UTznmae2/jL0M+nRBO5mCIRCPgA4lGV1ax1QFEZgdzLj1Bx9zlxuItXdBa8g0ldEIKeg6y51v3uLNH3qbh/kpD7vhfeST3/+AeVmxDAXeepRcTVS1xnY90WhChK7rU4eEwPuQhBmFJC8zuialkokQUFqRD0q8tVjryJRKKWs+pDS5GLEhvWcVJOEEBIhRYIQk2oAEglLHgYsFSiERHgbKoLpIlmXYTuL7iIxQKoX3DpSgtY7mcMZ87zD9LLSimgxW16bIy5y+7mhmibI5hgA+oIVAxJgEOVckEzJCFiJZSJNFF9PfICPRB1yMGK3IpULaFHyQG0SZoZTCthZjA3kI0DeI3KCMQpYS1y4RVUa0BqmGFFtjhEpinnZW462nny7JRxWepMWTVwZV5mSlJJY5Skqatsf3ARt7fAzIUiC0TmxuncO3fRI/zTRRSKz1eCko10eUg5xiU0Do6WcN3VFPvj5IdN9lhs4N/dESoRK9uZ6UyFzj5g34QFYaZKYTUuIXdIsl3bxFhk2kSC7GL1tCsBTXNtBNCYtACEnzBwEoidaGsOhwZQmyAAOx7VPwqSWxd8hhkVjhrEt040bhhACXKN+1BrxIqYxS4L1HA2pUHKeyyTLHz5ZIo0ErkAKhFSG4lH4oJSezOM4DjUNkRT/+SBzWuwi9I/geXaX0u9C4VFuUGer7s/SbGg2orqzRPDgi9CGlqPr0/YZg0UYRTUpHlSrStx31whKmLeVBiwDaoxH9u5e49MYltjc3uDrv2fnwLkp6hsOcxJQeiCHireNw75DDu2O237sGShJ9QhoSy2M4vtbjISME9j55QNt15Crn8P4+sTIcdAsa71lbH/Gld69ij5Y8eP8ORwczBsOKvMzJpcQ6z4E4wiiDj44QEtU5MaHYJ/BawgV84nNN9p/HzvXL55FFnxpEnjj+yWDoyU9ftT26O9/L4cZFe/hYzdFZ84/vpcXTP4H2V/7KX+Gf/bN/xq/8yq88NSj6lV/5FQB+7ud+jn/6T//p59K3/f19fvqnf5oHDx6Q5zlf+9rX+Lmf+7nH9tnY2ODNN9/kp37qp/i7f/fv8vf+3t/jd37ndz6X/r0K++4FRa8cvTjR4Fme8rsZfD3PNT5vutqzEJeLBirPSrm7yDEv811+zo74IcL5jtb8eJalCU51hemNtzmKkfen3+Ab6gPsFw3jWcZVU7Kc1UgXKKqc0miC88z2Zuzf3uPmOILzRCnZWfsid+7VHAw1eb5G33mCMahV9BVCotN++FVJmQQ9AYoiT2KZCPIyp122SJ/2lTFNppSSKCFwMdItO6pxxdHulM6uJkVSgtLETMHUQZsReseN4WV+cHKd4D27eceOapFCcMkNuCRKpA8op9FBUtee2ThyUNUYAZ8ObtPGVAPlVxPd6D1xxWS35wNRpdQqEUCWEXlJ4mNECUnsE3ISpCBzqTaImCaWm7Hkzx5+HzKkwPChOK0PgUxKpBSoIDBbkI0qhFa43uHbDh8txbBCxsA83ubI7hBiZKd5H2NKQq/oTYuuSrz1NHcPidanCX1uKK+s0x4tUVLikhotn3TrlCbHfdwztF9gKDSiUkQUZBoRYSt8H8F6lnnPt9a+jScQlCD4gC4zLq2P2djtca3lwR8cUN9PAqV9K4gxoEIkLDtc3SMLjXcekxse1mOZtQGydxACdm+G2BrDigAhX6vYOpoxGVcoo8lVBlYgM8W1MMVnAh/hLkN6L/HW8aldwy1aDBU+CPq6JV/VoIQ+6RnZuluxwPV4rRIJiE3isFFEylixUX0VUxYs6x0W2YOE4kD63lrL+sCxZo6Qgxy9QqGE0fzBVPOvPpKctv36jGczwv/rO5CrhDr+8KUhWd9htOTaZYeMixS04WlaixwOaO8vE6IVImpcECMsavhw/MP0HmQQXL47QyDwQ8v83T1MCBRrkvlsgfOecTWgaDdT7VvvUB88QH+4i89y7jQd1lncwNC0PZnRKKXwwSGF4Git5H9kkTe3Ku5dG0OoycucH/hDyY8fprq1f9e27IYACLwN1IcLqmHB/hd2+bT/gLwvONr3NHWLUTfB/E8APNg54N61MZNLGxRCcmO/ZjFbUGQlb374DoOqYLqseesrb1L9p4q3C8dPVFMAPvWO/9x1z3Sv4jFn/tkPkk/vz8XP/6I9fb4g8CXvx6tYLLzgOR6hfqdP/L0czr22k/bzP//z/PIv/zL/7b/9N77xjW/wla985Yl9vvnNb/Lbv/3bSCn5+Z//+c8tKPo7f+fvcOvWLQD+yT/5J08ERKdtPB7zD/7BP+DrX//659G9V2LfRaRo9cC+7LMaT7x40bZe5LhX5WtedInurGNOrvo8K5h5ns8veswfoRWmh+QKlRBcU4r7n+5wyzrED7xDVuQ8CODe3UBJydrhDcazdYZbE7q6ZbozJRpFnhtUkbHzyQPC9wXQiUXOZiPU5U0Wt2pE58m0xnqPIqEqkogIns6HlBYkZNJjkeBWq/IQ6ZsOJQXjm9v0R0uapieGiFCS4WRAXXf0i5bJ5TVGG2N2bu3SdanWKGUHCvo+YhwgDQNr2OjLJBwqW1qxwMfIph+yZguM1igt8NYxNoI9d8A8cyghOMhqgmwwMa08RwFOpWcuywyC9LkPHi0kcbWanXisJSKD1ie2Pb+qYSKGNJD7AZvTTYL3ZD7Q+UDUisyYRDkeAkFEikmZ6qqaHtH1mGjwGeQyX13zAVlZoTKNnbe07SEi04lMwkvsssM6Tz4sKAdDENDtzYlETJXjrcXVHZ0sE8plJVtXL5GpErtoUZnGW0doPDofMby5TrUW0BsNRI9cQSDKKOzcwk6XWNAsLHc8utKo3KAzndL3nCcqmSjHtU5Io/W41mKbDqkUse6xrU21OxOF0orx9pgsn1MaB9GhsgyygtD2iLYnL7JEwuAdMRoi0HpDINLPPEKEhKZJkRjmXLrfwqiEMkiJNIp2WiOkJMRIJiPhcEF1qYA4Iqt6yPZQuUmpdCERP2R5YKQlQVhUjATl0JViuRe4NSVd4wVc9c4y/ZUC3ts0DJE4ITDigFwloeAY47Huk697umkivciqnPZwgZeKWbHJvLaUXc+leo5RipYlB8u7ZEpCVJg8oGIgs+l3pJ1nYAxjaciKxIjXEpFIrrx1jeGbm+SjkmA9i3sH3P3gNr1W2HHJUXDc2tvBDOZcuTbkC7lmM1gwkkw8wkWEEmze2Kb3PR/ybfbFAbJTmMKgM48QM4L33P7mJ+l5mwzY9w7TWqq9aUKDOxiJIfSSdVXQfKfjcHnE8GbBlXWBlJJ5DBd0y/HUu/T+s0rF+l5N8TqXue05ApsnMLD4au9nXP33LBr0427Gh5n7T57vCZToycZf23fRbt68yU/+5E/y7/7dv+NXfuVX+Pt//+8/sc9DlOinfuqnuHHjxufSr3v37vG1r30NgJ/4iZ/gr/21v3bhY7/61a9+Vt165fbk0t33tD3M5zrHTqZ5ndpNPOPQV2rxxD9O9OcifbjoPs86/1mvz+rfs/49z3270H4XgaM+2xy6SFyhMcfJLPjeMd+f853f/QAQvPOD7/GFH/0K7/zge6xvTqhnNSpTXH73Kps3tuhdCmh8Z+kWLe3icRrcclzx7v/0FfKtEdOmpXMeF2G2qNk/WtBaT/ABtUJFijxDq6QbE0mIS9f01MuGwweHWO+JBPQqqMrLHKUV82XD7ic77H/8gBgjSqoVCqLZur5Blhl6HxNdt5II0mTcWYeXaeIUiQQZ8SQR0rxIaV0pPQ+cc3gh6IXAKYkDRBRkQpIrg+g89IHoIjpIRB8IdWL2yjzIPhADGBfQHrTUKVVOKoJSWCnxISBDxMZIMBqhNTLXyFJjCk0mIrJuELM5mW2pTKQQlrzv6OsmseuJSD9rqHdm9IuW8tKEamOIkgKESAX7SuKWHXa6xPeW0PQoBGaQMdock1UFelRSbE8Y3NykmFQE5wkh0NYNtusJMlJdWSMrk2iulmCUwBCR1iFTdIitO1Z6uuhRkX5nIf1uZK6RhUk1KS7gu4SkLecNi90Zy90p3jr66RIPiYktU4nGPYIsDNYHRKZxdQqWu0WH0BpdFQhjEvufEEiT6nhs7xAR/KIhSkEUItVYFRlRSuQwpY1GH4guEGRKLY1S0HvQoyEiWkRX45Y19f0pwSU9qsTWZ+mXLTFGRATXOcRwQFAqTex5PCA67SbPMyEA56DpjxczovUIkUhMIB5rMOlxSXCR/mAJUhHaJKgataKJcFC3HLYdnQ1Mm55u2RMaS2xd0jyKkc57Zk3NfDrnaOeI2cGMtatbfOEnvp9LX75BuT5cpQVKumV7rBs2WBvSzRtCHxhvTggu0EyXLA9n2D4x5ClACZBasPHeZYrNIVobYhB4F1BRMClKhuMB9WzG/oNdynGBjQHX98QYGQ0HSCnpnUOr9OworTg6mlH3PUdHc7xQeCkJFyBREE95d57Fp31zn9dY+xLnOP9Q8dhVXeT3eVajZ7f/Yh1+UrbkWSueYiVA/lwnObvZ783Y9Y+9/cIv/AIAv/Zrv0YIjyfAxhj5tV/7tcf2+zzsN3/zN+n7HoC/8Tf+xud23s/bPjuk6JlIysssSZzguBOPVkYebX110+yndOFi9jCweBFk6SLHPE97nweMf6FOPG7PKTf3XG2fafH0G8H2m5e4rwSHUjPbn7I+WifbLTh6cED3oKVfdAw2htz78C55nlGNK9pFQ5YbuqalPlzCVXXcdjOrsW3P5NIa+bDg4NYernMoKRFGoJUixEhrLRKwVqC1RqyQojzLcNahREZmFG+ulZgVFbDveiKCQwruLSzeBbxLNUtSgtQZvvfUR0tGw7Si/TAE7AUEIkEk5xoCfHN4h8bUZELyp5Zvc11vE6yjKDK07YhC8ba/TtOn2gVNImgISnGvnzBf9Cjv+d+znFKm9DfXOzKtEC4gQ8CHSIipnikfDxB5RmctXdNRYciFwuJpvWe0NkJqzWx6i6OdP0QFy2R4ne3yraQn5AHn8Nqw133CvNtBB40TqTZLxAiZQhLo7+1jqgKzNsA3Lf0SlNFYF5B1j4uBaqXZI0Igr3L6wyVCCqTOWdYztCoRheD+/u/g+hYlCm6oHyNsrlFdi/yv1xZEGVjcqfngP8woL28Sm576wRQRI2ZYEHqXAhvr6VqL0iqRDuQpAAydxRQZwyKj3ZsTtUJrRd87jFpp8AhBdB7f9tzeUbhsjMo0QgjcrqNfBKqtMdIZQu+wUeOaFpVniBjJBznROoRSqEhC0eo+oXzOE9s+BRvDAq1TIEPTo33Au8jMTbHL/5DqhyYDkAE7rSEGeuvJc43ODEKmtMn/sSj5bx+mZ3Len/P4nfrsSRcVuT5acGkjBT2ZAZ3lhM4RvSfPDd5FYoioTFEMxmz077E5sbTasDxwLNuaXgo+3C6xvUaoglLcxHUd9d6Mt5cWLaGOgm9MDIPhGlpJiKDKjPWbl9gZlewCIXps7egXLcsHRxzc20MVGdtHLT/QRub3jmi+OmE53+H273/EJ/tHFCYyGTh+3GxTLVKK7fvv3OPW6AD3piP8ly8jljfIROALh19na6S48nbGf81/h3vft8OoXOPNj68jnKQscoaTId55lk3N/be3OJwv07M8GuOB/Afe5N9uFUglme7fgQ8uks9/OjR6ui+9kKd90fHmosfFh38eITMvi8iclX1+8lwX6c/5537RtJDHjz3d/tOu+bnvx8kVi9f2XbOf/dmf5W/9rb/FrVu3+K3f+i3+3J/7c8fbfuu3fotPP/2UwWDAz/7sz3Lv3r3PpU//4T/8h+PXf/bP/tnP5ZzfDXsFQdFn/BSdGC1P+8rHBtITG195T54VnLxoKt3T9n/aRbyobz0rQPsecH5nAfyf9RlPDqAAWZ7xzg/epCjfQRuN8IL2oOXwG1MUkr5Nq9SLvRnFzW3G22PaecNgbcBytqBe1HSLlKrFFhze22ft8gbV2pBi3vDgg3uICEalWpyHqWVGSIxWWOdQIrHdZUbT9i4FEUoxGuRMBjlKKaJzoHUqso859xYWt6q92by2QZCCvXsHKC2ZzmriQ4YsKYjep4vVCpMZlOyRUlCbnjpvmftAE3u6rkdIgQshpb7FiHKagTB4EY+FY1sX6bsc5w2l1kzQlCEyqAocljIzLHpL11mECBiR7rxrBKJXFF4SY4ZBIIFWSkSeJWig79GhwS0+pm9bRsONRBe96Ik6x3uN1woz0KjoCDKAAC2yRC1tHd2sRZQlURvqgwW+Sdflg8dkJrGuaU0/q1OBvlZpkSUEhI2EOiBMQItIZ3t6v8CGhkxHRAj005qYWcbGIXBI7ZkUA+K8xy7blJYmQHZuJdKbVvUDAvpVfVW1EiJtOqIr0YMCM8zRrUwCrKv6LZRMukBKEvqebqnp+9Q/KcALiVM50hv8XgdKoCqZ6ssEYJKmEVJCnui3o/UE54jWEzONGZa4wyVx0SaxViWRawPcrCEzirbtCFWk2z1EqQJIiFff9GiTaNJFBkGArnLqqeT+4uJZvZyxXQC58pR5CnyApGEUA77uIILtO5SpMOOS0AVkZ9DFENs7crtAR0GtJGpc0LcdwToWe54oDLkdwLKlMpIlFl8JGiMpygKjFWpUsQievVs71NMFxJhQmrolagW5xnU9m5Mhee8JIVIfLLj94AMOZwtc8FRZhqVnIAXbUuGV4FtZS1cEKBQ3fvj72TiMiLbh7buHbGxl0DmO6l38xFOLhs0YEb0j1xkhRKQUdM7hhyVrG0PapufO/V0GwwEP6h7rxoksJateylOeb5+hj37OMel7KRXvrNS2k+PMhYVVX+jcJ2/cS5wjnpggfA/MD/4k2nA45Gd+5mf41V/9Vb72ta89FhQ9TJ37y3/5LzMYDD63Pn300UcAFEXBW2+99bmd9/O2VxAUPQVCf4oJxCMxqed+fuOZwdFL+5qLBhvn+Z6zRvSnvX5eJOhFZhVP2/68Du+8/p7TzkMNoGdB+Q9/B+Jh5Pu8XYqrlULx+OfnNXXMNhdTHYx9iDiKiCIgCTRHDdP7h7TTmhgi480xk+01YoyMN8ZMHxzStx0iJhaxEDy3P7zPG19+i7Zu2f/kAb7puf7Db1NuD7j+AzfZ+XCHxf78GNqUQqKVou16rHPoEFBaJ6FNqSh1hnWOdtFg10tEiEif2LR6H6i7HhMjwmj6vmexbBiOKjKt6K0jL3JUkaUUKimQKmKUJkrIpERHmV6j6R34KAgr0VekTjTTMRFDoARaSSopiFGxPhrQ9I5v3/O4AJ33tAR6a6l96lcfDAHocYyKDLzH2phSiaSnUAopUrDmYiJdKIclou/RoUdhUYMRQg/o60iYFChjiFKQGYkYFLRhgGwyiBEtwOsknit9JDhHsECbBE9lYTAkLR1hfaKO9iHpPNUdwSj0oCAfDVepdUnYVuUGU1WoNsNFR1CSgEfYnn7RMP34iGq7whQV+Sjg5jV6fUB0jnbRgrWJ+tynAFi4lA7Rzx1KSeQgRxSG6Dyh7cGltLgYIqEwZLnBe4/QEpVr7P4hwo6RWUQXiS1OCdBlYq4LnSXEiBQxEcDliq6xyEyDjtBaVG5SClgkMcaFAJ0Flyb2EcAHFKTgLEZ0ZjCbQ1SZ00x7iu0xoenJhgWh7tBVQXBLzFqRAiR5sUzgZ7mVGJOIrVil/Nl5i5s3+M6RbwxBg8o0IOjrDhcCIVhCiHSdRVc5UgkWy5bx1gS7bPBHU6SITCQMlST6SFYWKKORXctyscAjkLs6BXnBp5TbIiNKiCogjSJHUHvL+ltb6ZnGs//hXY7CEhsSeltlGVIqfGd5OOTOdxfsHViyoqJQMJ6U6LFme3CZLLQ0zuG7gFKaXGcobWh9y8Z4QDYsWC5qTJ5hux5lSmJvGRc589mCrm/JBwapRyCezj13kUzsMxR7nn3QZ2ZPHzQF4nh2cFaAcvFzvDjS9LCH+nghV+Be4p48G7U7OwB75rEnL/OCY+dre9zu3bv31Jqe27dvv3Dbv/ALv8Cv/uqv8hu/8Rv8o3/0j6iqirqu+Y3f+I3j7Z+nHRwcALC2tva5nvfztleYPvdqYIeTTu242ZU9kfV0avvTWn1m3+KJv+di6E9p/mQbL2pnXdPp/pzVl4ue90W+omd5yAu1F0+1c6pBccZnz2rxNNolTnf0Yq79A+e4v0xV3V+yn/Kj5SHeef7rHyy5307QRuN6y/qNLXRu2LqxzXL3CDtv0CIxx9m2Z/nFEXLN8GBS8vHvfEoeFIc7h8yyKYN3h4Q3Aze33iAcBKIPHO0cMd09wluPkDIhSBEUgjzP6JqeoCRCKaI2fLBfp8BGClAa39uk+6IkudFUg4Ku7dlvjiCAFhJCZL0yXK4MUUmic6hVnch6mzEShkxKGjshulQYP9ADMiPxMfC2HVPbgjLTfHP9Y3bjlP2m46e6H+TNfoMQ4aN1y3f2p7Sh47c2P0Aoy0BqqiKja3uO6gZVSsZGk3eGH7VfpjAG4z1ylVInvKXslmQrggWpPMoIhuoab4h1wliDKbBSQ5klimUlV/fe4XsLRqXr9jHRNq+Y7jAKlQkoTCJCWAXCsQQKg/eB2CWx2MQLprg5+hFEyIgbEpMN6KwneMl29WOIsSC0Dbf738MYAXfhevwx7MYIL5bUu/9n+uX5jnJrgh5V2KZD9B6xYteTmVnpGnnaWU2uFd5H9CrtEO8RJgPArOjfQ90BJWZYEoLjRu6RgwXFpsD3DmcdsXPc89vYEBEici0/oKg85BkfuwFNFxCAGuT43qKDJgqBLgyis/i6xzZ9upcAzuPnLXpcgvMI6+mXPQKDyHwiV5AC4QOxd/iuh1Ico/pn2UVd5Ul3/Ml+xUyT0KF5S7A59dRRTiaU441UjzbwiVxj1vCRCTTzJTWRb18akI8rlrMlsYflbEnZOW7s92wWGW1I9PTWOmJZMLq0Tn04Q/q0UNIJWC8dl+UShGBP3aYdJgHk4f+fvT+L0WxL77rB35r29A4x53zmU3WqXLarbJcpG1z4ayxQy4AE6gaEbcASsrhCXFjc+KrhEq65QL5AAvXXoAYL9DWf/blx+zMe8ITLQ02nqs6Uc2aM77SnNfXFeiMzIjIiMzJPnlOFyUeKzIj33Xvttae11vP8/8//KQosgaGUuB8ccMd69r9+k72bu0grKI1hVFWsrI4YXl5H31LJ4Q2CjbcvEhYgXM8XLv8BebTIDFb/akQNNM1M88pvvk7XaboYeXstpzWCe5VA0XGgLflKzpVv3mVza43QWgTQWMX9uIse7dEhGQzKJ15n8cgdefwEeDol6yGJ7aNdVJ/S8rF5LZ7Y8ul78mH7LxCsSclfKZMwzLYP/O9tsxTc/OiQoudi8ch9fUGl+7baj/3Yj3H16lVu3brFL/zCL/BTP/VT/MIv/ALz+ZyrV6/yF/7CX/h2d/FPpT1Hp+jkoPr4Nykuo/Mnm3j086eJNZ71/Tnsacapp5nxH+e8fRRj4+OQq8Pvn3WQe1Lbj2x+ZHUk0k6n+5xPvhCP+IZi6RhFEPLR/hyLnsX4KFoV01ZdjHRLD6v1lswuaGYN/bSBPOUWBCUZro8QAoILxFlNO2sIAiaTmnwZ6S+3CmyAdtFSiYreOr7+lW/xyVfeohxVVKsDsjIHYOOlLZppzTd+922aRYOQkirPyE1Su8qKjN5agg9Y6+g7hQsBISUxRjIpCYApMjIEWghUZnAx4kJSnIpCkBcZuUoXy0tJ8EnlLlOKIgq8j1RBEoNChIgRIqm1SYkKkJsSrSVID66lyMDUkYOdOShFgyeTErRmJlvKkURmElEqMpdTLjzz6YK5sAThyKUk1yrVGCKmHKseotWoIgOVEsSdgyAVejhM550bEIKgZEJNfCTPUr0Z4RWSpEKWBDRI0sxCYAEXI3HWopa1kbplgVHdO7wAMrNc+AfoIzIWKJFEB2hsQqB8ZCUbJXXBXDEZKHrbYXqFdiP6e5IWsLOOKCK27ZFGYcocVRrwEaVFQi+cR2Wa0HTI3EBM9Z1cZyk3x8TcYJuO6JMYB2WGKsG3PTKXNPtTFKCrDBN7lAwI2yKNQnmBrDKEc5QZ5JnA9x2xVtB4RJUjM53qNLmAHpW4pgMX6KY13jpia0GQrqdzqMPiqTES2oRCqcykPKxMJ5RuWBBcKjh8niTvs+I8J4eVGKF3gkXdU+9OMaOKvBogncQPB9RNINhAsJ6+7vAx0nWOyaKhyww1gYP9KStrIwa9oZnV5EaxqlNeVa41EcHubMZ017KjHUVR0IkkkVHkBhV7chmRREZZxOskkx+EJ6sy1jbHeNMSVcSPAuU4p5QlpswoN1cYXd3AFAZ5f59l0TDkXJLVksxkDOpbVKJLx6tKxFAQhWJr9SLb1xcICb0UMMjpFMz2p9joWV9f56qyzCcLVoqC2PVkUjIVgcV8j4tvXkLM7BPvxXnv02l2FI05BXQ4t31YR+Sho/aUdsp8eOZ89BTznxIw6ixGSVotTxzm0bP9qJ2lM3OLluPlI+/skwKxLwyAy5cvfyg06HEmpeQnfuIn+Of//J/zr//1v+anfuqnHlDnfvInfxIpP16dtPX1dQAODg4+1uN+3Pacruo5+VTPZPGUn+Uhlwvtox+fvf/pfz73Lh7r21Pa0f0Ez9bOk87vWc79kZXKM7QBLDlqz7rno5+JQyrcg18e2KHCXNpOpCjd0fDzKRaFwAtN34OzaVFNhCyTVLlEekt3MGVvZ0a7aMmrApUpBlsrjNfHqChQQlCMKnY7y0CC7gXX//v7hDqgpUOLHi16VHQMRxkvvXkRJQUhBnqf6udY72i7HqHToroYV5QbIzYvrTNYFkntY0Qvc0yEkTRdT7csoCkAIyXZMg9BitSvTElc8MSQxBYaEWiix8WIDyCkQkhJoVWiahkFIeKFADQmKygweB8JnaVrO2xnGZQ5WQQVQfmA7Xpk7VB9xDjJSOZkpqDISpTWRKWwWhGNRgmBVBqxtoHe3ITcJDk3LQgqHdsKgVs6h3Xf0zlPNBIvBEIoeiuIwuD7iPMS23p6L7BtQKIRKiMbDEAZpNHk44piXKLGJUWZM1gd0Ld9ygfTEqLD+57gevxA4iqJKwRqUKCKjKgl/c4MuztHZIqgQaiEeOVVRjkqGa2PGG6M0YWBzqGMQg0LMIpiUCS6l5BIJVFaYq0jhJjU8IxCBY9WkA9z3KIlyFTbRuQ5YryCQ2JdIAgFWQZKE7IMRMoXUoOcaAyuD/R9IAiBVwJZGNz+Am00ftERWgudS+p31idRjhAQy2cphEg7qfE+4OYtoU0qebrKEv1OCLAeN6uhbkAr2iBoXPIxj75uzzY0Rebv3Wb6x9+EridfGRAF6HGVFP4WHWJZH8tOFoTlS55VJdpolA9Ia5nd38PkGasXE8JppWAWA67vWDQtZVGwupbycJqmRSyRPDdvkG2PaBpC2+IXDXHRpXy0ELlwcYPx1gpx0cOsY/3KJpc/8zIvff51XvrBN9h69SKF1hgb8VJgtWD73i63vnED3/QML67RC0UnND2KPghsEOzeOeDee3fQItUrOwziVJnh4soQLSRGSZTREGHvYMqk65k3Ld469u7vI8M5HNQHKP3jtzuqNieOuUDxQ6+Zk0Nwyt0/b8PxaJ+O9u0Me8rg3rFtz7l+CEBrLXXX4yLkQpALyM64H+c51chRxdTTOnZaW6dHZeORz0+9Xmcsu17Yx2uHFLlf+ZVf4fd+7/f4lV/5lWOfP8mMMQ9+P1SOe5wd3ebovgCvvfYaAG3b8sEHH5zr+P8j2nMUWngO9qwhpu9k+6ijLGed/2Ew6jTU6ttky3n9+bb3NE2eDGXG43TNWXmJDza+i1t7NzgYbKNzQ123vFbu8dr+7+MmC3baNYbjDczaJjcWHXtdz+UrV7nSHlAcdEzuHRB2NnExZ+YlVz54he69nsvqMp96+Q/IRwvwgvqbFdEKLueSO4ViOg9Y72lJSM3WyxcQWjLbndEsGnbv7bJ1cZPFwRwbA1mW0Xmf1MS0WhaDjWgl0cKkfBQgSEGQgtj0mMxQZRnOe+6qmvuqIRCR+xlyoSi04tW1CqUELkS8D6gIse158841YrhMFIL377aIfoFXkv/L5oDcR4TJ+fUso48W1cL33rxGEXOk0kQB1npMFKgiJ9MK37vk1EoBiqU4gqdjwu35HyMEjNdfYaP8NK7t6OY1yhiqqiD2Do1CS8l6+RojeenBs6AOEQ0AKeidwywL48oStus/ppFTQgiIELBNR/Ae0fvkeGjFu81vEaNAbQy5fnUVMSrQveQH332FSpiUm6MkUiiabsqN3V9HxIgNAZEBvUuqcpmCHmSRIXONm9TI3KDXUtHVYm3A9L37NPcneCAoSR4ja2bOeP2AbG3Idjdk+06iVm73GZNFyaLXtPfA9CMKV6DKHLfI6HoHNAip8FLwXp1DTHkn3qf8ITdvUy0srVCDHJzHrFT0d/YJPiCcB6VACnznkIXBLwu4Kp2QRlySj5ZaoHJDFWasD3aRmeIbe4H/8I2Ehnb+0Xc1aXI/5o098VKH3uHqHrW5xugT11JekTTJiest8fCc6h5hNI0QfL3S1F4wznPevHVAnmkaAl/bPWDr1cuIl7a4OaqYHcwIwSMRjDZWCVIgD2ZcvrqFvLHD6u19tFJUxR7j4V3K0YDXDehiE1Pm6GFB1uWIu5bxrmWw8PjeIX8I4oVFUpP8bYW7GWjrlnd/+CIHecF77jbXG0WhLOO9fX5HbRGcJcael39/xuorI+7+yT7eGaTvqb0j5CVoSdZ7PrHfszmxlHHGvPMMBiV3p3NgWSdsrNi8skm5MqCp2ycMieeDBI4Wdz2ODn34Af2RNg4P9Yzz1VmoywO0JD7qIJx+Hk+BX52Yaw9C4P+t0ocbfc/frgZI4Jb3/NKSSvdoA+e3o8jPIW3xaK+PtvjwLM641ycYLh91jaoXdn777u/+br7v+76PL33pS/ztv/23CSHw/d///eeu+3M0/+fg4IALFy48dvv9/f0Hv6+trR377otf/OIDKfBf+7Vf+9hzmj4u+wiLt54YJZ56BXtWm0cbO6O9k0y+05o4y562n4871oe1D9v283CCvk0+bxJpeEi/O519ePakdVK04RH23LLA6dFLFIRm1kTu3JkhlKatWzKjWV0fIOoZe+/eQFwcMihUSrLODAWSfFAgJzC9vsPdP36PuLnKoFqhs45SlOAENGBER6ZqXO9RNjK5NUVUQ1761OeIecn+nT3uvX+X4D2myrj73t0UvQ+BLDPMJnOEhEIZRisD3FIiO9qAVgopJSIkYQTv/DL/SIGUuEOaU1gWTJVgZUAg8M4hHeAjrQ9oJRmUBU3T4awnF4rSaboeyiLDKE8tLb3zKOcoM02m04/FIZRmkK2SdQLhQGmNzBNah1JgPQKQSwcmEhG5obcW6zuaZkpQAmZTxrFDWYtWEmM02gZ8ZnCKJFmuFSYbIjOd8oPapRJapgldD9Kjo8D1FqEkNix5l94RXUSuDdERhLL4LuUi2dBRXFwhv1AiNgyd7wHBytV13E6LXThEaZBRIF0g+BaUJGaCAOilip3vE+0stpa+szjnyXKDMg9V5YoLK7T3JyiVCqk6rQiqxZQ+qdx1EbM5wh3UOBfAghqtEMoFi2kHgyHKp4KynY8Uqzmxtdj9BX3vUYOMENWDYwbrMVVOXNY7Ermh7+ySguaIRpOPS7JxhVASPciZX98htD1yXJINCqx1qCwVevVNh1SC0WqVgOCFYtJy7L099upJcfiCn/LOngIkC4lZGyMzgfceowyISOwdoXPIKme+N0MrtawBpeiVwCGYHEwZHczoXcBmim6jYH5vn6zIMeOKYZmxc3cHHwJr60NMmVNbS28t3/OFT/PSQZucQXWLvBgilHwwmIjDQcWmYERlYdCDEBo9kkzdAf20p/lyDbclNnjaH97izr097nU11dYKtjbcm85o2hajFEIGFl96n08O3qSLGo2g6y3DtXUkEaU1eZ6BnVNEwbgs6G2D1IrVjRVsl6TeL/25y+x97/3H+p4PxsFjSM+Tdni4tP7w+NBjO3Xiz6ejlp0lWX0qV47Hu4JPttPnoBBhtvR8hiJStT2myKkO62w95Tml3pxz8RJBiLOQo1M++04PLP9Pbn/37/5dvvSlL/HOO+88+Pu89sYbbzz4/Wtf+9oTnaKvfvWrAGiteeWVV45991f/6l/lH/7Df4i1lp//+Z//U+sUPRf63MOh8iTn6+wJ8Glb/9ANnRV5elp4+KxtzxqvPi7o+XwBv2dvE045l4/u5FJuwlnEjg/nYR/S6iKgEVQi/egYufWNm9i2x4U02WV5RrW1wnvv3ODG3W2mswVt0xER1L7DbGSEPOKVorUCKzN6H+itA0BJgbWO3RvbNDYy72DegxMZXhW8+yc32L21g+0s1z79Mq98z6tc/uTVVMR1yT8KMVKVBUWVo7OkRjZfNPTOYX1gvmiY1y3T2YLJdI71nhBjqhcTAiFCPkhyz10Eu0RlTJQYrdGFwkpLryyIlIzfNB0qwsq4Is8MWiuyPOUsEdI2hVIUxqTovVIYMjKZU2UDjFSoJR1PKJmkoJVMSMRSDS9KmQp/KoXre3SWColKo1AIpLM4enrt8UbQAS43+EzjEASlcELgM82i6emtR+QZVik8gqgVfYwEpVBFnlT0uohyEuk0IdPEpse2faIICoghosuMam2IFII8eqpMknlHt7NDd/8OvqtBgBzkiW43zImVIV8bUl1cJdsYo8ocaVRCrbzHNx06N5hhQQwprwQpKFYHmGGBXApjROchpvo4xIiSERUcMliy1ZLQOXCO8UubaBGwizkyUwizjG/5gBkWZOtDylc2USsDyBTCpPuQZLkTciiMgqWaW+gsoTSoPIKwyPU1KMvkRPrUXzOucDGickM7bwlNchYJEbM2QBQm3esz31tOHTIeOwRL8IsW0dlUOykEgk8/MtMIJSlXh4SFR4oMvMLa9IxFLSmHirKCLEvqhLPpgoOdfaa3tml3p2jrMT5S3z8gLDoMgm53zu637tDOGoSSyLLEmRInc4LIiMEQosEGTdNDbQWdMnQmp9U5ZOndjT7QO0fnLMNLq3Szhvsf3CPLNNmgoJdgBWiTHOU8M3Qzx/zWDO0NLgRyrdnf3kMrSVmmelpqWFKuDeklLLzjxs27NNby6ve8xif+zKeSguNDbvHjR8klrTj9PLwT8QkT48eJITyLetzDs3iIaAlYXhdOnMBToEEnlzhHXUoBpRRUUlAcHoclVVkKapb5q+LZUZjDO3IUpTuezfXwuE+cmc94SZ8XAvjCno/9xE/8BFqn8V1rzU/8xE+ce98vfvGLD37/T//pPz12277v+cVf/EUAvv/7v/8Rue8rV67wUz/1UwD8xm/8Bv/m3/ybc/fjK1/5yrm3/Xbbc0GKzvIRHo8QLyO2T3z3TrZyjkX4h3mfn3bf54HgnOZ8nOcYZ/kGH4MT9kAy4QlsmA9xAI6dyLGDPO0FObrFUnRhmWD6ptb8L0UBMXKv9fzW3T2MVHS9pawKrnzqJb48fo/3vssQvvsKl25LLh10RCd4u/oGq59bo7mywL57lcX9ETe3PyCqDOccuTG45YJSZBn/9stpAaVlwRcufz/ZSsa7d/+IfqdmPr/J3W/d5rXPvo5EcP2rH6C1wntPpgzWejIhqaqCycGMoswhgFyq1oUQiBHMUgfWOU9vHW3dsjNJCy6lFa63yBDYKBWfGa8SnOZLG+9y6/I2eWZ4af4mg2aV6ANGKbrOpf6rtCCVSvHaxuBwLUymJUVREJzjzx98JjmyzmOCBCOJsBRBSPtHoxA+FVj13hMEKC0RDqIL+CWdKWpJ43Z5d++/YrUkiEuY4tNE16U8J5+2cy7VHCKmHDLbWlSueXVrxGqu0TIhCEla2nBx9XP4riMPgZv1l6jVIi0IfUjqcFKQjQuElCjr+PPX38EUkiA07+7eZ7ozRWQ5xcUh0ijkIMlP40Oiek0bohIIKZHaIKocs1IlwYx5S31/gq4yqgurSJXulR4WzKYLdGaS0xMDelAQrGNTzVgR24RNxa7MmThNd+uA19/UaDxds8utfaBaIdcKN2vxraVYHyZhBq0RIWLrJOqgBkWq1SQFtD1RSmJn6bXg9mfXaL78x8jsCnr8BWKEgZ9x+fovo/KM4AO6yBBGEic1ZlTgO4veLIihQ+XmuS+mpFIMX7tIYSTeeULvktKaICnn5QbhBJvFD6AGQ3YWLe+sr7KzfYAvPO996l2UjISuINt/iyAkZe+5dm8KPuBjJMsMYrpH+GCPl7ZWaCYdzfu7vCMk1bDEvbTK/qU3kUqytrNgZXtGsI6bheRGcKAl65c2uPjGFXRu+OLK11gVU7qmY3/ToDbXcMOSO9fv0ncd5doK+zdm1I1KyodCEbwnL3Iuf+NlrvISw40VvmG/hqkUG3nObDQgasV+2/LlocINS2KmWEQLKwbVWTa3J7y8tYrjRO7AcjJ+ZE4+BqaLR3Y5y56CVPZ0djqQ89T2WBTrBHnlfFjQ6bS7Y/2NMJKC/3s1wAB7IfALTY0HtkPgf409wvX4eHpW0KOdPC0UeDp15CHa99BNOqudo58cK4Xxwr5j7cKFC7z99tv0fU+WZWxtbZ1738985jP82T/7Z/mt3/ot/uW//Jf8/b//98+k3v2Tf/JP2N7eBuAf/IN/cOo2/+yf/TN++Zd/mVu3bvEzP/MzFEXB3/gbf+PM48/nc/7pP/2n/N7v/R6/+qu/eu5+fzvtOdPn4im/8ZiQIU83wj5pzfu478/a50ltndz2wzhNTzvgHw66571GRwfpo+Pis9qxEfS0gx2F6c/yzE4JW52DBfCImlA80pkz9j8XfnRiYtMCKgR917P93k2i28RL0EqxfnWD0daYWxbE1gglwN9TsDJgd3+CWpdkaxleO3Z3puy8u41TGQJBrhUCaLsOISAvchoHCwtaCpzMUORElRNjj+8ckcj7f/guUghc70FFhEgLw0XdsHltk2p1wP7eFOs8RZZx7Xte4f0/eg/h09TmQ0T1Dq1VotcRWTQd03mN1ppBkaOVREZBqTKClBgNUqc6Q13bEp1HCYHJDfO6TTV2nEcbjZQy1QlSCmISQui7nhBBR4kWgohKCIpLSSXBaAgBQnKGghQIG1I+kU8FYhGSUC9A9kSWuVDepx8hEXlkujNjPpmnfBijyYoMBMwnSVLdu1RwNEwjl0pNLEZIKfHe0XWWLDNIk+OR9N5jG4EPkbzIiL1HaPAhsNiZgo/QLAjjCVZ4+j4wvTsgqgwzUEgtExVMCvrdGb536fmzjuADUcmkdrd8zkKIqDKjWB/SHyxo7uxTXl5DCNBlRl7kBJmcPIxGaIlEEeoeJQJ+1sB4E5Fr8mubSLlPuZJTDDNuvWNp+5pibYCd1sgoaW7tInOD1JpoFMFbYtOjc5NQrEVSt/Mh4l0g3xoRosdXJWF1BdclJ88IhxrkuMkC1TmiTshJVmbpHZUCkWsQPdKcozDR09jylRdSoDNFtzeHEFMBWylwLqB8oNlbsKYyZNQMyyHT+wepTpOMRO0JBFrpsM4jtUBKSaYVRZFTjSoWkwWeiOssW2sr7BzUBK2IzrPYn3K3b7izkyOk4NLMcmVhkUKwv1pg10pyk3H71oR5E7n06ZfwUjHeXEUg6T+TUe9Ktr96nV2mqNWSruux1hJbz7DIqQZDZnWNUZosGIbFiNFohaIs2JvNqUKO7S3TRQ1Scn++YLg2ZjQsGV1aZ297P6lGWodfvnOnOUAAx4frZ4vofWSL6A/tEB1iKOejpz2c2h6/7QMq9hOivwKohMAA9ZEgXohQx7AMIB5Bqs4438dO94dtnHIeh+dy2OdHz+n4DHn++/iRucEv7Jz2+uuvP/O+/+Jf/At+6Id+iLqu+eIXv8g//sf/mL/yV/4KV69epe97vvKVr/DzP//z/Lt/9+8A+PN//s/z9/7e3zu1rc3NTf7jf/yP/PiP/zjb29v8zb/5N/lLf+kv8Xf+zt/hC1/4AhsbG8znc959911+6Zd+iX/1r/4V9+/f50d/9Eefuf8ftz0Xp+hwEDpmH47h9Kg9zYB5nnf4w/bvnL7Ac3PUnuacTv7+EdixCOOpfTvywRP6cqpk9oldH7nMR5TlHh7xyTfz5LMahMKqgsY69vemCAPWe0bjASsX15IaVx2p1gd0+wuMzjjYWWDrnsHGCDMocL3j/ju3qbxCZgaUorOOpuvxxjO6usLK66vE94+HKRcHc0LvyTND7zyZSgIEfQwYrVBSUpQZizrJSavCsHd3D+89o2yA9Z7ZzhQlJTFErLMQJT5Ggo70zlEagx5kFIOCrrXkmSH0jqgUkUQfNE6RyZwuBDJpKIREZ5rQ9BQqLQ6DkEldLkSUVkQEMiZ6IFLSWpccmZBqNwmAzCCWKE2MMTlBCJQUREEqlGk0waf8JzkaErsWqUtcSMIHKNBFhlcZ1lraeYMpMi6/tMVoc8x8+yA5oeMKWycFudHFVbp7u3S9QxhFnmmM1umih0iZ50gpKPwKoo+YIsPGRVox9g7vA/P7E5QItCUUhcGJgByUqGFFPq5ACKSAdntKP2/BJ6pOkrEORJmKwgLIGJNP31q8UUm8oOmZvn8fAJ1psrVBcqwWHd6D9RKkgmEG1uPbCXXraAggBAuVIYoxIDDrATkH1/bp3nQOVRWoMkt5SrVDKIGve0RI1EkZoXdhKWsfkdGje8jH62SbG7j9BcVLV8hmSWxBTCB0FpkVCEDFiOuSWIadd3RVCiR44FQlsSPv88Nodjzx28N3NFci5ZyJlHsWbUgL+pgEKfrWYgpDsJ7QWtpxUqCbWEumFW1vEVrjnUFFj3QarRXV6pj+7h6ud8zbnuneFL2k4WmtmU4WNDHijKKvG0SMVCJjRSq8khjd0auWLMtQlcIMSoISVGXBYrLDjT+cMHkDFuMCRjm+7JhO9ziYLwgDQ3QGj8Y0no3xGutvXmGyv2A6X9D3NuUwFQZTZrz6PW/w3h9+k8Y7ohBIICsL+rYjWMfk3h7DsmCkDUUQ2GnHB3/wLdQbGnFZoo1CefUgqf/YNV4i8fGEcyTgCIPjaSatj8ZOCgo8rgdHp6HHzgUnHrhzOwdPmK8jMAsBGQKL0+azcx/m9A3PLm5+eG0ede6OiyY8jTt7/Gq+sP9x7XOf+xz/+T//Z/7W3/pb7O7u8nM/93P83M/93Knb/sW/+Bf5t//236KW4kSn2ec//3l+53d+h5/5mZ/hV37lV/jlX/5lfvmXf/nM7V955RX+0T/6Rx/6PD4ue070uWdcgT/Nu3YW4nIWknHaCPo0jtBHMQ6chuQ8zT6nfcdjvn9e9qT2H3cu5+ibWCafPn4nceSb0xs96SjF+DBy+HDiOo5AzYstPtj8HLvdNpPBByipGJYFF1+/RLU6oF90yC8rLpTXECHgF46ua8kyw/DVNepuxuTePnIvshIG1FIjQ6TpeqQS3Hr9Jpuf2+TmGxn2joXuYX+VVsQYcT6gRUrQb51PtLglda7rHcpoNq9uMlwdcvfdu0uHSeCC4ODeAW3TIZWkqAoGo5KyyvE2MJ+k/KeqMsymNVpKZp2lLHNYynMjNRd2riCaDaIUjFYGBC3pnSfXCg5Ro8zgvE9FR6VESwHycLUVMUYhrEeIVC/Ih/RdiDEl9KuUU+SsRbqUTxRjRPqQ7kmREYSgYIMr6ocRSjLLLB+UC/SgxE0kynhWh1XKE3KebtHSd5bRxgq26fEhMFgfonPDRBt2ru+hBwWvrJUMY0RLkeh6TQdScq38HuRYEUXkRvOb9M0B0Xn0qERKgZKSO3EFO0uL0myzROUGqRXRBdr7E5rdWZIyjxBjwLY2hYYPF5YyyVpzeL4kECpfqfDTJtVdAlTnkJkmast+W9IcjI6/V8UGv/vOPre6/XSNRXyQc/f944zNiyWLuwfoTBMBVWWExqbaQVKA9WSDpAonTaIUxi6ilvV4RBv5DOtQjZF7gVe3NqDxHOw1XN9fIIzG9w4tJSY3xHlL31vKjRGz1vF+M4ROslO3wOLRV/dINP3sd/yh/cCVERuVJjqP35niioeqf+20wfWOfJRyZ2rn+aUYaIOjtTahm0Jgg6SZfRqtJCIICIIsM2y9eZWr45rQ26Tm2DuapmGiJV+2c/yKYt1WXLQe1/WU04aXa4tSEvd6jf/Rni62tO9FmqlCFRnDtZsU4/t0i5b/z//3M1y782dQuUaVX+dgZZdbG9BNP0nYX0cAn7OwYTRlHfn/bR8kBCxTDMcDBmsjBILVlza5NKt5++vvoYHBqGJ6MEPEwCA3lB62buwn+XAhOGgTbS5rc16WL7N6aY3bk1vc4Al1VA69psOF/Dnmpucd8zyfPfmoz0w8+bBzaYQZkf9XvUhUXiE4Ir543B35kPP1aepwh4GGZ16Lndr+C4zoT4v92I/9GO+++y4///M/zy/+4i/y5S9/mb29PbIs49KlS3zhC1/gJ3/yJ/nxH//xc7X32muv8V/+y3/hN37jN/j3//7f82u/9mvcunWL/f19qqri6tWr/OAP/iB//a//df7yX/7Lj8h7fyfbc3CKzngJH4w0J8JUTztiPc0+T2OHXTv51p+3n+dFeZ5H3z/KUelxThdP+I6jvGQ4mVx07Lujv51s81yT8JEbE08/3ulNxQf7pF2OOkwQkXip2NuZk1UV2bBgvDaiWhsiBOzf2cG3nqKqqGdzXO8QSjFeG5INC27f/YCsyAna0gqN8x4jNUYpem/xOKoLA4Lyj5y4VKmmTBQJOXG9RecZupApz8UJWuu4/OYVLrx+iVtfv4EQgjzPWTQdeWaW6lgqLZSlpF+00DuQEiUlIYaUo3N4ZYTAeU+WVwQJfW+RQhP6nhgCrgwEpZKMtZboJXUuhpRXFJ1HG5X67Dx+WVBWLp0lodN3wju8czTOoX1AlQXKebx3qJhynmRuyAAbIyqCkQKkRuU65S8R8FESe48PIqmDzVu6ec10Z8psd5Yofnsz8lGJlOqBQpizHucCMkb6zia1OKnwMdBmmswHpBeI3hKHOUiJ1ArhAs3+nHKZexO9Bq2QIiEX0Uec7YmNpd2dEVwgWykwVQ5aJSqOS0IAQkpcZ3Hzhhgiru7IVgd472kOFgwurNDtz4nW4ZxHOIOucmKI+MMaMwKCTc9cyDNs07Lkl4JYvgJFTr83xy4apKzwMTlhznmk0Qgl0EpBZxFlhm/6tA52Fh8kvXdor5EuIo3ByIK46LH7U4Ttkcv7FUJgNCyIPqBXKvr95QIwN3gkIib1vUeG0FNIBGfFuA5NS4EOgX7eII0ihocOOD6gM43ODf1kgQBsppnOkpMspUrX00eiE3QetJaE6Njb2cd6GNyZMhwPKMcD8t4RgmcqlrWEfHK4Y5+kyC9srjO8sEq1PmLy6gF3V2+w+85tJrWAuE4WBbkU1O2czGh27s+obs4Yv7xJt7dP17Q4JZDCoLNqWXy5Z3rzHmZl8GAIdtZiBnmqbbX8cHhhheyDItFfY4EUMMxzlHXsHdRUBzNGq8OkrigEWiukkOx+sMv65kaqVXTGNU4qevGUKe98E87HsVg+vvB/hC8Aj/3+DHvEQeeJ89zj2nkwrUWW2Vwng3wfjz3qLJ3TpTkDOTsrh+mFPX/76Z/+aX76p3/6mfZ98803H6xnHmfj8Zif/dmf5Wd/9mef6Tin2Y/8yI/wIz/yI8+tve8Ee345Rac6Ex/RyPCs7+eHfa+fNTx2dL/vtLHlOd2is4ffNOIeRXiODroPBnDBuV5sOCWN9sEkd5xe8IBad9i5+HD7o23Y1tLsz8mHqQr96OLKA6c+BggyMK/nmFzQ2Ui2XHSKVlCKISZkHLR7dBGIgWAtPkSqPMf4jIEYYboMYlqCxBBwvWV6Y58QA0mKYBlZtI62SXSyQZERbWSwMaKrO3Zv7qClwnmP0pqu68l1wcbFNfa2D7BtT09ksD5OdX+aHqM1xaDAdZZm3hIBr2Ra+EmBEJIYAiuZpg8eoyRFpjEuEBpLXNLjYoyoQ8chJKpYUJKoBKGz5EvHLBxKWQmBDJECgTAGCcvk+CRPbDKNXCJIudEEaxPCoST4pG5nhCL3kmgTKOWzSHlpSGUHlFWJVhLvEzozu7NH9IF2Z4rKNH3bMxiWKCXRWibFPaDuO6SROCOR+we4zqK9IXqN7Q1GZwgj0FKilaS1NUkFTuAagbeevunISQ6SEAKRabLVQUKCpEjXSIEpBUiBXVh2v34f4QNohVGS0Flc3aNHJaK1S8cz5R0Et3QthECJgI6WaHtWishmlR7kaS/oXbrWUkvsooW2JVZFui6zJvXHKELT411LdAGVKXzb4bVCVhV+0aGkxE1r2kGBqTL6SUNd7BB8xPbz5PhmiqIsH4IJS7TM9w5GJW2XUMLOPSp1f9KGGRRHZ55TgiRaBLqdVIxV+ICocmRuEMDg4gouREII9E2fjrcsfBxjxDlLkefkg1TTCimSQIM2RCHo6jkLb5nu7mP2BNoHMq2RmWQymbGxtc5IFxSyIRsPWH31IvmwSF3N5+x96w4HBzOkWgMvGAwrvHP0XU9WKJA9kzvXGV4ymFLhakPXdWnciGB7S7HiwfXE7j5ZOSDzDt9bhlsaIVpihNp6GAi23tjkW3f3MSGyMaxorcV4gXI+0VdDQiZElVOsjtjd3sZHR591eOOWL97xi5yGxENkfXnRH2MnF9ynb31eXCE+QJKVfMKk+JiH6XBOeZIzdBqycigU9Fym45Pzy0k7zZf7EPZ4itzjDnzK14eB4Sdu+MJe2P8c9hHWKTpiz+JMPO17eNbA87hjP+6zk/s9D+fhWQMvZ53DRxWNetKq5vDwRybaYw7IMfj9NED/oV5OXEa9n47tvJyYT8zBkbjkyp8Sh44sFwdHPlva/GCOkJKD+wcM3BDzyWtIKenqFiHBDXtYj2RFgbmlkHOFGRZc3LnKVrjMvW/cwjeJ5hb6JA0dEHgfeW3nLV791idRmeR6f4OOHiEF9965zeL6dLkYM7Rdl+qQGJ3QoMzQOUdW5gxWBtx++ybVsCS6gO0dUkBRlVSjisneNNGhQqTIDe28oaxytJasXlyjbTraeUNW5ogQqecNN5VELXMprmSSly+NCG2fipK6gA0RHwNKaFRMye1EkCZRmsTycioXkUoTDhfL8pC9DlJplJTYrl/S9VJekY+pPpH2nsaT8lmEXCreyUQx05rSwZt+ldBGdk3P7ssOIQUXxYjNRYZGoIxGaQlLhyy4kOo8GU30IR3Xe+gdtndcNzP8WDMYFbD7ZVSZajSti+9ic2WEESL1ocygbfj69LfwtocQCb3D27TIDD45iVFAvz0lND3DlzYRUtBv7zG4IHnlBzJUkbGYlky+pbBSEonowmCdx01q8gtjzGqVaHdxmZO0aBMyJ2CrqlkdzEFK3ry0RBAR/Ievwjf3HtbLKTbG9J0FIVINn5BqUolhkZ53n/Ka/KQGSAIMi46waJMwhBQ09w7oCkM2LHlv9zeSGl8MZOMCZRQqT0WBYwwoJclLgzKKu33kD+5M0mu2VAEkRDis63PCvvgyfO5ifJh0fuxVjYQAH9zrWeQGGVJ7Qilc26ONWYpQpHOy+3P6JjLZmyKyKokrxEjvHd3uJIkprAww4wFmUCAzhe8c0/05s/0pxaLn6r0Z3nt6FxisDRkMK8o3LlPnmlYppoeIt5LYzuJ6SxQRLZfUx9wwqzuUTOIjevABHdfx3U3MMKOZLvA+0HkPXU+WCT71F2+zUU1YTO/w27/2FoKMgGfz2l2M2qFzgd+5MaHzgVwX/IVLb3HzazfYWAGjFbieXhfsihYRYPDSFntvXebd9+/SF5E3fnDKjdfeYXpjBtcfOj8nh7+TzLkPZ+LRX0+b8+JTTH+PnYc+jFPzFPueteGJQNsjn520DzFfHw0gni4M8QxX4gn9eaFK98L+Z7Tn5xR9p78/z0DZeqp2T2vvSYPgsyJPH7Wdc/AW8DBR9wFL7Qk7x8N9TkYun7zfIXpz6kdHag8dOmOPi2k+7EFkfjADBJtXNrjy6ZdxvaPen7F7exelJEoKtIQYPT4KjNKsXlhDBMH8zpSD63upen0IoFJtmpUq0Zja2rJ/Y4+t1y5wpJ4efWuXqmupjlE1rFhMF8QQMEZTtx1SCjYubCCEYH4wR0qR6gfJpPJWNy2LpkUbTTUoqBctzgfsvKEcV2RL2pGQgmxQUBYZWW5o5g3BR1zTozKNGqV6BLLIEH1ST5PysLAqD2hxIURCjHjS4lcG0EoSRVJNc8EjkGRSPHgk3BJRwnqUUUsEKKm+dTqplXkhiFKQi5Tz0zmH8YIsS+IIbqlaF4MnuoiLHdJr2ranWKq2CSUxmUEKQZLTE4TUUaL1S8lsiywki66D6Fi5MKbMPEppRtMVinyFKAR2Z4aIiojCSMli0ZMVGTIkp1vnhtikYrDEiKpyfNMz/2Cb8vIawVra23t093NUWRDkZbx1KLGM6vcOqSXBOuysRZlUOLRfpHpBD+L4MTlGfrYgWx8dqyonD5HV5WpWSoEqc3zvyHJNrHtEYThUbfTO45Qkk6lWVNyf4wKJ8qckyoeUItZ5bD1J8t2jMjk2ziNdQI0TlTD2jugCZnWA0JJQ+weR/wdxkhDhjFxdJcBEj1g+/4i0fSTV1uoXLbYWCFUS5fL+kYqX+rZH5BozKFjc3AUbaH0gBI+3CW3TShOIOAmLRU1b15g8pxwNKNYGKKlQVc4oW6ectoxb2N/dRxcZEbC9w1mH0BKlZMrJEgLfW/beu8vefEqRZcQ8R3pDX3e0dcv6pQoVIIueetEwuX2fKz/wCcr1EereTnIYvUfLDJlFBpdH+KLFWUtvJSZT6EItMeOIjy4FO1Tg4uuXyJTh5ts3CM4jhWCwtcLq5ioXX72EWxvwlQ/uUtcNl97YZPO1hiADQYQj+M1DZTYejI2njbuPTkxPvUB+XLOkOmUf1h4NfZ2OGp3+2VPYSQAsnrg+pzlHJ/d/Dvaw5tJxey7Oy8cVcH1hL+w73D4epOgoTPtxOQAf9iU/LRDzrAPFhz3nx0WqDu0jH8QeEg6O1jc4utAnwlDKB1W7ncrx0hCBXolUIBPw7Zzg7bHWBbAqJYZEMdsL4Vii6sNzPXGiD5Cho/pER3c6MoEt+22UpDISiORFZCFnHIh9tl69SFbm1NMFk+0Jk50DyrKgWCnwbUNdWwZSMtooGIwDrm+58/ZNvAs465BCoLRCa41Uis5aTGa4995dVi+vMsxTQVMtNRtXN7i1fStNaELQ1UkswToPUpJlBhc86y9vMdudQoiMtsY00+aBCICQErMUNfDWs7I6RCjJZG/Kzs0dVjbHaK2wdc/W6xdpDxZIoygzg1gKHIQQkxx4DKhBgQ0NIToEUKiKuBRISDkyKY9ISIEICR0MApwW1L1jnxkCyIRhw5WJ8hYDCzshA5QqyFWFEIKma5P6nBKoGHChow+eXkjISnRMi+pAQqyklpg2OboS6HpPkIrGemzbo42mVH0qUBp8EgYIic4WIylHKlpKL4gmQ0dJqSPGt+RFSbY+oL/b0IeA8HOariErJEwDRaYT8hdDylUhkq2W2IMa0UcyXxJNhWs65h9sI6RAro9p44Du9j4iq1N+CyCCwjBEZhJr53S2wy/peXGpDOe0pu/Sdd6sInpYptyz3iGUTEVXTzzmssrR0zrdr0wn0YYIsbFIoA0lAgVag1oQbIsQEqUV0nmiUumZOKxFNMhBCqSWqEGG0oqw6JIzXGZIGdGuRg8GZG049ioKBJzs45G+Tnu432uIUBmJcI5Q9+jCIHNFXS8Xt0om5IyHSoVOCKL31HcnNPcsolgjuA6d5wSp2dhYTWhd3bF3bxdjPbmUmNjjm47F3vRh8VclwUWmk4QUGSEZSUVzZ4fr9/cQgwJdZmitUErRL1paO6daWaPICxadoms75vMFo3VDFC1RRDKpsZnB9pZgPXbWLIsXtwRmNE3g7v1AdHCw08O8J+skr33yFVrex7WWfkn3RAgCkZmdUVyreGntFRYHSZZ+OBqwmWkObu8xn+2Q7e9z6coGFy4O6adTICblQU4gckeGxbNUP89vR12sb1907yM/8rG1y7fvPB8nH34eGfJH7JTNJbCu5HdcrPaFvbCPw56DU/RhvIUPaU+DtJzlJJ3mWIgzvj9Puye/O8sZPNb+kQOeRdv7ThihznBqjw7GnzUZn88yAG4Vr3HXrzFYGfLBUHNfRLIq4+Abv0W7d+tYGxL4S3nOJa2xwL9dLNgL4VxdevT5O+xPPPLJQ0rf1sDwZ64Nic6zv9Lz3vdHsloiZKD7RsOtr32QFh5R0NQNG9Uqdk/Sdxadv0+5bgndfeb715gdzBFCYJQixIgGlBB0XZ+C+DHirGO+PeHPvDZGoAHNwY7BOofQGiUkXknKsqCe1ilKDQzWhyituPn1G4Tec3B7HymT4yRkko4OIaC1RstErVos+6O1oqs7svURg5WKbplj0s27VMNIJonf0FuEKEArfGe5N/sai/4eusi5Wn6WSl8ghJDEA4QgiOQI++ARHqwE0XqEivzuyuAfsVcAAQAASURBVDepZYeykr+0+1lWTUXd1dyc/z4KT14PeGntz2J0hl6qslVFjhMzdrs/xDrHgR7g1j7F+MJqEiSY1PRNx4Yt+ES9gjSKSRv4oOsTCmaS5HCsOy6OMlZVypMiBDJj6HuLkoIQQSjFtW5AdJKiUAzWW0TYQVcVKMNk2xP7jjuLP6SdN6hMIzNB1qd7K4SglgLf9LSLJG89yEZczX+AGARtVfPB/m8jYmSxI/jW/1bTLSz51pxgJMJFSta4Mvw8WkoOwrtsN18n1h0IQV5keGF5LyjeeT/R0Yo34dKVLKFLmSa6cGxBKyBRKuctRklQoAYFoe4J3oOWCJ3TqrdQsYS2pzB/lOTFjSbMG+Ky3eADGEXQEqOTaIUZl4jlucsiA5mCIsPM8tJqQ1QtC2uOvowcMlXPemF/8zr81o305w9erbgQHIQyBS20gpjqTwmTpiepJMF5UBLvEkrVTTua7i1cnxO0pGsjZI7FdM76tS2UVpT39nhtapG9wxiDjhEbI/OuQ0uVnFch0EaxsrJBsI7V+zV9b9k2cN05mAm01hij0VIwMq9g5y8zX4hUPLaAochTXldvkTE58nGZx+PaHoFIiNPoHYzWBCT/5ctfgL5kMZ3z0t0p37M14KWVVf7b+xNa1wBwOPp1vuV3bv3mw2sYInjBBSt5fbehfec2b6wN+ezaiDW94Prbgf/tjxJNMj7gy51AfR47n3wnTDYP7fyx1I++30cVTR/066zlz3NcGh2XxDilX8utnnStzmZQxAdRjUoK/m9lRf6IKuwLe2F/+u1DO0XnFoF83uPV+VD/87Xz+FHk6fc5bb/H8owPVznn2P48x/pITDxMsj6SP3Ty7ksSa8b1jrs37lB9zzXaacvdWxPuabj05lUenOgJECe6gNIpMvoIMPTU7I2HbZwAs4CICBE7rblx+zb3Xh1z5Y2rxGnk7rdusdiZ0vWW9fVV2rYl9B5vHZkAYxSSjhg9tusxmU6rlxhTLSGl6LqOfJTTLjryIieXkvnenMuvRWRiXGGXCe6HfRRCYPKMNz9/jVtv38C2PZfevEI7b2jmLUarlCMjQEiJ957gQ0KmlKTrHa7pKDODJyYBAtsyXB8lHE1ANijopjXZ6gA7WSABLQQqplyh4DyUhiA1LR5rVJJ01gqWNDmpZKJ0eYFQghyB0GnKziuDdZYMhZSCuukQ3qOCRxqROF8ASlJlGUIlhbw2BOr5HI1DrY+Ztx16XqO0wpRZWmyiKESOUpJp2+F7jywMpiqQOqFmhQLtLHFJLYtLylqwnhAjRkpEiCnHKEsCDFIZTK5xSGSIqBjp8Yjg6DpH5lO9KGU0ru0pjKZ1HkekjBFlPXqU4WxEIDGDgugceE/oPZKMfr9DyCSmoaVCRZFkvIVMjk7vCKGBwiSaX5T4eGRNFSMogTtYILRCmZJDfmIUEL1PC+UQ6ZoW40J6V5WE1tL3PcGL9Ny0jphB7wNFmUGMhKZHKFIelVGJLuk90SiI4O2yKK51CB9Q44rQNkgRk/jBsXErLD2is19YfxgoItXu9T5CSMViVSURSiVannX41ib0qsoIPuCtx04bQmsRWmG9ZLI/J6wm6tu8ntJOa1ZWhlRZhgkLOuvpeptQTKWSSEaMDIoSnRvm85r9vSmrRU7XdczqhrrKECY5jviAi5EQBH2XEGEX/APFx4UU5EJifAoczJuGLDdkeZZQNykwWrHoaopMozPNbLennzgIAWkMw41xKkobk4z9MVQiQuBIgEgcjnAwvjCiql4hHxTo0iAQSB+TWl98goP6XOw540OnzIEfuatz2kRx5qZPrpf0wJ7Y3pMXEo8vxnq0X0d+iY9v9xjV8JjTvMwAjgK1DN+F3iFz/cR+vrAX9qfFPh763HnsNObT40yc9sczegdPS+v7qMaHx3X/WU/tMYVRn6Gx9P+p7aXvnCqYywHvfOWbZG9eI0b45pe+wYERmKtrbOY5MzOkK9Yf7CmEQBIplrLVIsJqodMCC0GIQ45ddCEQMVDYGRDxEbaD51Fc6WGorkCwsSxIti5zmkXG/VuWgwNLvpJTzitkkNjVnvn9KZkumO1PUYXB1Q2VUQilyMyQqhowLDa5O3PgI0aAXyq0dV3HYF3y2g9c5pu/+zbtPKBURjOpaWaacrwCUbKYtoQlmuGWPW2mC7Iq560/+110XQubEPpIdlGQL7KUh7Sc9ASpWKZSiq53RCJaK3xMdLPgAxJoFi3VoGA+acDPGW+t0NYdhVZkKgkFGAliqeaV+ZzSDwlCoIVJQnIh5WcoKVI+Q4wYrfARlErS0TIKttyI0ipymVOZDG0MMUryfg0fHYUeLRdtISnXhQje47qAyTcgBLQrGARN2Em5UqPNFbAtucyobaCoCrKNjMX9Kd3eDB88McL6lXXWLq+yCEkAwasAKiC1wjiN7EJ6F7RMi2IbqVvIRhXWKrp2j76b0zUN3llkjIgQiFqnnBIfsEva4mhoEKMKuz3F99DEKSFGrF9AZyF4lDBoSrwMhODwZQDv8bGn7vZQOqePCaUxZYbwAdtZlFYI/5DqGSOE1oL36NUhEB9EqyMkFEcrqAOu6QhCoMYlft4S6g4RAqIoUW6OwKFMixhkhHsT/N4MaXR6n8XyPmqFyCSF8cjcoYyn7gIy04hME9oeN10gNzOEPv7GpcCyeDAanD1KHH9HVaZTLtCwTPTBrkc0EZlp2oMFpsrAR/q65aAxtHNH1CVzremALjd0PlCEmAQjeovfn1IE6MsMbyRKKUyWkMPgXMobtB3C90QpsBqiCIxWhvSFQauUS1eVBUrrFAxYXu+sSEi4mB/gZvvM5zVZtsBkglnXE4FBWZCVOWZQoKsCs0RzH4xfIr2/xaDkrcurXFjR6H6KeDCKHR3vTrmQgAV2jESsVekDnwRQdkMaN1PxrMc08EQ7eRefdqJ8CjvKqngme4q+PetyYXmIx6JDT2XP8VoeO6fHOU/HMK5H+iFIMb473pMBoe2QKp305vPr7Qt7Yd+x9pzoc/AdgbM+rWPzuC6fp60nnfJzhM+f1Z7aIToRBjuaP/TgiyPndLL1veIyX5qtcH9Y8NbLn6Ce1Agp+aTK6O7M2fraHV4avIzafB1TGA4TrUWMDHd/H/oZUgg+f2WINQLQdO77iBTHjuNnB7yy/btUleYgBP7XxYL+xMU+RIsEcFEp/lpVIYGp3OD//ANNcyAx8SLVbxrcVyPq/6qYfGGXu/oGq7c3Wbu5QbSerfUBl8clUQqy/NNkVcVqsc4H/puUYh8vJUZreuvw3nPpjYay+hqvfmbG13+nJAZN38PNb67wyve8klCDeJ1DGe7eubS/99z62nVe//wnMBuG6594hyACcgjtf+jwPpJnhirXLOY1A6NwZok0xCSoQIwYpWisQ2eGZtbQ1x1rF1eZ3J/Qd5ZiULCiJZulBgEZpJpEQXJx+Ba+SIncTmmMkakWUkjOtQueYFLdHuE8IUSkVuig+MLBW8ilXHnMkwpaDBmvb/wwnhS9NkrjSUVMU5FDhc7GvDz4czjriBEyDN4H+t4jO8FF1pl2nttKklm4+83bdIvkVGqjsM4z35vxlZ0ZbduxdmGV8lVFa1qElLwWx6xlGRKQ1iOUxHcd37wekSsZUgj6g9+i357iVXq+hYQsz3BSJInspaqeloK46Aky5eD02nKj/gN80+O7nihA+EA5WOOltT8DQjB329xXbxOlYDHZZT79bTKXI2LEd57OKPLcYIRIdaZMAUI8iPLL0kDQeO9RStLNW2Is0+IaQWwtMQSEVpiuT2ITgxxCSEiQjGTqbWIMaBXwM0le5IhMIXxEVRnRBYRKDkquPa+v1ygZaem4MbqInXcILRFFRuws0XtCDKij6g8ciaSfskY9Pe6VkCoAa1Oh4KQ4t0RTtaLcHNPszvFR8M3s0xwMJV3wWB0oBxWLgxksGhbWURWGwmRJ9p7AuysKm5V46yjynGq0hgLms4bFfLG8pwplFBMlkQi0GmO0YtR2tF1P6PqUVwQYIQmZYfXVC1y6c5PR/GtMun3+ZNdzoCqk1mglybQmHw9SjltnE71VJPESbx3CeSQG27Z8av0+m9bT7oEO/Smj6qMmgP0Q+fd1fcqXDyeek+P/2fLNj27z8B49yZ6Ds/Ss8+SDUxUP/35ceyd9gUNH7Dzd/zbM50+Fw5314p3S6rFf4/HP6xj5j02dvpIgmpoIfPb8PXlhL+x/WPvQTtFzo9M+aTA7AlI8usk5jnQezPtx3z0rNe/bYsc7+1RT1in0hUe/jKd/vfwwK3KuvfUSMUT6eYNwkYVt8dZx/U8+SPkoSvCJz7/F4mDOhZcvIpRYcoHigyOliFxSnxImRVeDD+xc32b7m++yMtinfHmdB7D/E66EJMXX7793j36+yajImdQt3gZCnyK0w82UBB9joBoNiNaiRaJPZUuZZ2U0trH085Z8Y4VmVtO0HTo3aKkoRwVCWMabY4YbJc2BwEjJdHvK9a/fYrw+4mBnilaSECNKKRCQZ4b5/hzb9MhKEkUEGRldXEVd0ezd3CPGSNP1DMuCaljgM830YIHrPUQweUYIAZMZinHFYrJgsDZg5eIa3iXKXV93SQIMEAFiYbDWYWKi3SkE6FSANiFOEaTALZ0+tMRZj/FpIR4hiS+IJPMdXaoXIzKD7Wyq3RMjzjmIfrl9ory5mIrX1ouWXKkk+b18BnKdrndQAmk0Umm237+XhBVyk5QBXSoG23WWGFIB2Wp1CJnDZKkfVVHBJCXWB8B1PS4E6mmD7lqMD1D3RCORIsXqdZGhDp0+69FbY2LTowREo7GzBgUIJQlNT/AOmZn0kEkJgwIGBToKxELSHyzSonhJQfTeL6l9jtj2hLgUl/MBVIrwP6CrIgjOJRRHylQzZxlIiEC/NyfkkpgZovfY/TmxzFK9Jx8QIaJzie+WKnxZUiF00yYdTwpElYGWiS5TmPTT9ahhQdhNog8yN/jOpgKztImeFZYcvqNDxDnHvRhjqqeUJWqfVBLbOwgRpZMEt9SK7qCmmcxRJscJRxs0+WhIvzfBOcfq1lpCSa1Dlzlt1xN9TNRKJZG9w4sk+jGbLui7Htc7xmvjpYNs6dqO6DxVniVxhxDJjUYJwaLrkcv+1l2LDwF1U7KxqCEEjFYoGbHOMV4ZIFqHNknsQiyj7A9qdyGwLhCcp7OOjQsrZEWLsPVxCtTJQewkcCQSBfC0S/2o4MzR757sJIlTO3HWZ4dHfIYk/+dhJ0/12zDnPsvS4KOyY9S4M74/DwHwKGj3HRDufmEv7GOz54AUPX4x+tT2hJHlpBrm+Rtd7nh0/9OQ5FMPesbvz8ueByp1ctMji6rz7JAJuKSSZHIbI/eWIgdPO9DntFxdS0NqEx23dpPak1nW36mqEl0lZbU779xm99YOtu659umXaMyY6UHLvQ/uovVl8gtjZrsL3vmjrzJYXWc4HnCwO2Hv7h6Z8Ox4jZgq4saYvFhJ+UzRMXITIGJ9ZL9xRMBLQ52vs39nj71JZG08wCvBWAqs8wxXBqhOU02H5PsVpsuILhVJbUPPwhRYEZgwQ8SWlWIVl3l85zBG0zuPCBGJoJ4oilGi/K1dHjHf20FpgRaSbm/O7rylGpTYOkXCBQIpwOQGN0vCApnPqe81BOEJVvDGW6/iPezf3kVJhdcpYr23fYCUkiJLSfBoiWtS3kMMAW8dw7URIQTmBwvG6yPaaY0cFcs8l0iQgszF5JAUktg7jJS45bPkhUCEw7o8AlygtQ4fPEaQ6gKVOfQWKZL8s1g+PFKAFyBFUrGLMaIgIRtS0lpHrxX7KslzV71jXaY8Jy8eTt+2s3gD9cGCGCIuWFbWR3TOk48qSpOEJWzvcL0liIzeKJSS2F5QLhe6deyxyhJIfRcHdXJQyhxt9IPhQJQZIgSMD5gyQ41KXGfxXcoDEdYnZ0JnDEeXkwBCiCDAh4ARBXXch97TNHNKuU5cLvyVlKkosHGIEoKP0DuiTPlaAwUXR6lQ6cJ6vrUXiL1AZIcLbEGmNBdGSS7bxIAoMkLTIvMMMo3RipAb3KJNAg/5KqKQ6EzSiRneWrJxhd+dgXOEBuRKhR4UCJ1QI70xou9JiJ8PSGcZDiOubhkMkhADwCiDN9bSfZp0sL1Ig0qMD/MQN0pYPQ724ltLseiwscAvnWeRabJBQbAOGSJ6lLHfFnQmo592tEPwJAd7sDJksnuAFILxxgrNvMH3lrXGYXuLsJF6YNA65ffUiyY5MUqhM2ibluFogDaGsiqgXSCmd5C1IBuuEtQQISKXxyW5ClgBk0Wkbh3zyZwDK8CPaHRGr6aAJy9ytFCICGaQI6RAD3LYTucsY0z5dAEGQvHJN65yb/ce+97Tx4g7dXg+schdXtSTNVkfAB/xECE6DwzyNM7P8T6dts9HSLD7aOyRzj59WdfvpPM9u98nz+o7qdcv7IV959h3Tk7R4yEKHqyyjnlFJ7Y7bUR+ACmf47An7WkdoKNd+jCOzod0vB6oCy2jk4/tyvL6rEvFXysTveyG9/zCEjI/44I+uNTHLq+AlfoO1+wu3jq+sr+Cn+dkmUZpRTvv2ds9IJtrXvnu17j+lQ+QQnLvvTsICdv5mOm2Z3+hUL+v2XxpRLV6Cdt+wL3r99gWKaKstKb3gvtbn+WDSUfoMgY/+ml0lVP5Gd89/W1kDOzWlv/63oQItGbErY3PMRdzFnGX0aCkmdX4GBlXOYuDORd3rlDuDdl9dw/hIcrk5NzVDRNpiVLwvvyAWMGlay+x+plN5B/3tHWHJkWB+xC5+a2SavMttNEMVluI95foRkZmDIu6RYqEfgilUEtqmfOpls9sZ8rK6hq3f/M2PnjG+QqfeOnTXP7EFfbv7xNdYLFoE60L8D7gieBTNDzPMjIt6ZoOpST13oz5zhTbW6bbE7T3qLUKaRQ6RpTzKKlSnRrAO48NjqAkUiukgF6AXgpKtL2lzAwBTd9Z8twkZ0mrdA5KEpZOA5FU5NI6fIypvo1MdY2s8HgiszLjt0c5zgUu9pb/pU35N0hJNBLnQ5KiFoLNly9wcO8At2iYHczRWrOYLBhvraTipTGyf/cAe/llbt1tiCKypXqGMkk73xv2HLiarm4YhZ5SkHJyck02rnA+4PYXYB36wgoq0+AC0XrcosW7AC4JXIQQMM5wufpe0Ok8xbLY6NTu8sHt30BkihEbXK2+H3GIHsik4DeVd9hrv45etqWW6msvZYI3Lo4BwR/eWfBf3284NlRH+MLLJZ/YzPGzBrufctuEUgQb8LikVte7VFMJxcXh91DICrTn+vy/ISqJWR1g6xZZ98iVAWFa40clQUX6tofgibJC5oboAlUVuFLs4WJHrjIIGUIbXl+H15Ypgr93C37pWxBjGh0Oc4y+7zL88EtHhhEfqO/PubtY4c6OQ0hJ11kKtRSfCAGzUqGHFdezT3Gv9djV5Ewbn4roRiEoq5Lp3hSjVQps+MjLB5bJ9gELAourq4iVjGo0SLXAZjXNfEGV53R9T123lHnGYG3ItZHg0tu/x8G9fe60F5ld/EGkMazlliuDnr5puVOW3DEVXW95ny2sHCOGkkb8Mbncw+QGEQAl0VXyArNxhdEawbImWVZwcdKzVa7xMpr/c9GwsPXpw754igX6M9C7Tmv5WeKO4qldiedr56EFLjd8/El/lOdw7P48Z/fxQcz3dJTo+NHEsf9e2At7YQ/to3OKjg7Ox3gBTxpyHzeqx4fO0bN6Didpeqf5Yh9msDgrQPeE03qedvTQcalk9MhAGU/8GkkRcClPdPtReetH9jv6WUwKWPXBgtl9h28HxPEKs1mNs5Yiyyirgnbegk+KbVIIbnztOkhJmWdpIbVUWGumDWZQJOoXKQqPT7kk2aBADXPe+dZNbn/pm1z5xDXyMYjlY3ISKUsLNcHO7V0mUiKERGjxQMVNLWWIL7x8iXvfuo0LMS2YBiVWWdqup9ocsD/bwTlPPasZVoNUdNNbXEjJ0/2iY7ozY+3yekIZckO0AWsts3lguDIg+EA1Kuk6i6u7pEg1W1CVBcWwfHCBj17erMi48omrvP9H7yaBBWsxQtF5h/dQlTmZ1ixrp1JUBdWwpGktfdsjlpSbfFBitKaQqThltA7pU22faF1Kes8zZAg452hCwC5lwuWSppTplFeklw5RbDuiUklFbCmJDekmSEu6ZxFEptICflnjyOQ54/UhRZURpWDsI+LOBE9SMRTWp9o71jG7P6faHHHh1Qvc+dZtVjZXaBcdzaKhW6JuSiS04WBaU2wMqXdnxKUYhACiFGAUOjN4JYhGpcK0QqCMSovaCChBOFigNsfY3Rl2e0IfYurzYR6cTOiWMRqiIEpJ8EmpTQqdFNxaD5VAFVmqNeQDymSEGOldwEuBDhE9KpHOQ+/wdXfsJV7WRX34PC9pePiAmzSEuodS0NYdmZTUTUcpBToEVDREleTXiyqnFw46hbeWflpjNsY4t4/sLGZY4JWEYCmKHILH944YI8E63LzHuoa8THlY0S7rG8W4pIkd5hcdReUfDqqCmAI1kXRsJUErikrRtxalRDrZuCxSaRTdrKGZTnFmjK07dJHhfCB6n5zsGFFGMT+Y4dqe1dGAlYvrDIzmzt6EQGQ+mdG2LaurK4xWh+RlxmwviWMI75keTKnnNeWwYW3WUJQ5uSrYm8xYHQ9pY1KfE21NjDnVcEARA711tEYzP5gRc0GmFVoprLCo3GCGBSDIVwZok4IOXQj4umHNOtY+sYlYOuvxGORz3glIIMTxAfh4DtH5EJ9HF9FPnghP3+djxomOTEtPn3vDh+/qY5Yhp0pfH5tzj/c4Hvn3SefyZAfw0ftw6rYveHEv7IU9Yh+z0MJJHtqRfU9H48/Rzjn3eZYB8GlO7XkiTh/CDifXeHLEPaV/Wmk2yq1E+9qe8kff3Gfz1Ys0G0Oo6wdEgqPNPNpmRFcr6HKMkJKAYjptuXFzSpOVhLIiBhiPhwglaGY1q5fXmdw9SGpmy0Kl1nmsc7S9RSvJyoUV5rtzTG7Iq4x+0VJlhiigaS1b1zZwwbN6cZ3NRQ2rBjPdZX5zj3y9R2tJ0T3ssQo9w/Y+wzyy2FDcvtuliUkpRlWBlKDLBeOLlsG6YTrpabczhFKAxs8cmSzIJpYts8naYp16v2YxXdBaRxiVWAHWe8Yo9m7vsnZ5DSkFWW5obZuECpxnNlmQFxlGSUqtmAhBV7eMV0fkw4JybYCQgkvDy/gYqEwqeIoQbL20hVKSu+/epZu3IFnmwcQkfuA9WZkjlaRuO7pFnxSdlaTKFJcurROnNaUUqfCrD8QEMqU6MDEiiiTV3PR7zFyDtY4y26AsBilfQwpsjPgQ6TqHW8qC+7bDRRINSgjUsg7M+jAjorB1h5EqJe8qiYrLPK4VxUvFLUSm2ZCSTM1wix6/MOh6HeUDlRCs5Ro3rRmsCl76VEGMLaONAbs3BbZLjp8UgkvXNtmf1eSjkkGWYWJMKJgUDIJZ5ilprNK4HgqjyauLqFpgRgVtsYeokhRzDJH6YIEjqe+1LpDnmmiTDHZwLXuT6witU0BBCRSKVs6SxDVgZWCSW3zbU2YlurfJWfSR2FmCVsRZA3nqG0t5dBEiVXRcHWdJUr2LaJ+e6S3tWckCjayZZxJrHSo3NG2X0IhBgS6XznWXivu6zkEO3aQmZAl9c32P2RgTO5tiTiESjCQIiIsWUZh0Xi7QxEhTjfA6RwdLacIDClewHmVgrRC8OXZordhtBduLlG/SOsWkTTLbg2L5XmaG5m6DYADOIxHkGyNkZhBK0k4b+kWPk1DPG7yPdK4hzw3OefSS7pscrci8buhnDWs6x5Sa+8ESdxrWygLbOaYILqxcYrUUbLYN83nNfNIyVGvYumM6mXHdjMjyjIUr0JMZQ5VhnEMKjQsrBCuwmSOrCgadYw1DWFujzlapzYJ+Kf0tltL11cIxcpKAoVMaxgW99ZhrEfkpxUJPCco/oEWec5Q/Mi4//cR26Ag9vpjGOSaQM7f/mOzDzqtPs/9pDtBjCShnwVGPuEpnNn8eO3lnxLFFywso6IW9sKe1jyyn6Hzv43P0Fk5FpjgbuTm633nnlyegSg8Gtuc14j2DPeSSn+HEHIHvS13xfZc/z97729y+d5Ov2hHj/RVGW2Midx50/UmdNyuXKS99F+Wows4tt97f4f64YlF3qNKQS8mibhMCYRRt3dLWLQIIIdB0PZkxFMZgQ8DkhtHqiL1bu+hcI5dy10YpOudwzqIzzcGtXfbv7fPS977MymAPu2hYGwm29gJaBFx4yNDP7Zwr+3+CAEavbhHHV9m9sUPb9NimZ7QxQqr3eePP1bjecv2rB3ywc4G27zGTDFpFNioZ3dO8+rnPs/9be0zfn5BlaRq6oSOzTKCLitf2OtS8w3cOtaRLKSkIIVIWGW3TYYG2bsmMYjAs2d+z1IuGrdcuUo6SxO7nLn/+kUsvpGTj6ibDtRHv/PdvMBhUuM7SdRatE7WQTNF1jq61eOtZ31yhbzoub63wcmWQZoAAeusIUmKUTEIIIeCcT4ISWrFfX+fe7AZKay4XP4jJVlFS0PV2mZeheX/WM91vcETyQUFfd+hBjpKSPDPQdAxLg7OOTCmCPFRVS8VAu3nDejnjR9/8Q7JxyttxL1l0bph8uaT74zG51qxExXi9wnrPZHEDvblL31ise5lqZYt779/DZBrnAgf39rmYZ8R3dli/tsk4erzzKCm46DI2owERuakLejEjdJ6L629RhZKYaW7lf0jIHQiRBBWqjG7icCFCDPQxogSowmB9z7b7KkFogk3XjyUlL68y6B19Hnl3sKA1ljUXeF2MESEk6ekQCVqihEiIVpYocO32lKwwvL5e8gmTEvY3dz2DhQegHNXosWU+m3PjYMxuL3FNj1YaVWlwHlVk2MkC4Za5XdYRbFq0V5tj+rZHoXDzFl1mD4oBoxKSp8cVfUfKnSoN/SJwL64RDjwjWfOKnuMtqMygtCJax2um5/XPZKhM8F8/EPzqeyRK48Jwfa/ALlpeuWgZOZ8QRSTRB8qNIa7rQQh8b5P0u1EE6+h9S8SwurXKbG+aajWREOGsyBI1t+1QUqGGBb9/b5dyUNAWktdud+TTDjZWead07N/e4dVLhlenf4jtOmaNYbof2BSO+5sbfKVcx/ae9YXlM7WDW/vEEJlmGV3fs5cLFi9l6LZjfHOPwbRlY3OdO2+U5GsbeCWYLSY0ezO63RmvLiTDmeWiHjFVc/Z6y3B1SPlDFfe3bhNdxL3tiC1HReM4Mvgef/8fOxKfbsebPI5RnLZ4P88n57KnmffOw6o4q72nnV+fw3z8VMISIgUrY0yBq7M3O197j2JMx/c7Wqj8vP17/PV44WC9sP957OPJKToPXH2Ww/Kk/c463vN8h09r66NGox83STwRwVpGo5ZIztkOYaSd1tz8+g2IMBiUFLlOUtnn7p9Aaf2Q8gWYIqMYlPStxS4j4ZnWdF0HQrB3e3dZrl2gjUYpiXNJ5UwpyWhrzHRvRoxQjiom91MytdASgiDXBt875vMa5wPb79xGvuRxIrD6+mXkN7ZhKet7/CKmCyEkrF/dYveDbYiRvunwfUU+KIAFUkkGa0N0mbH5xmWc80y/cQNdGNavbOJDpNmdU+qk8KVVEhFQRuO7HqMVdtawd2uPzVe2yAcF3bxFaY1SiaIXYqSocnyfFOFG4wGz2YLFZJGuYabJyhykoF905FWecmaIFMOSvMp564c+Tb2/4OY3biX2o1ZM5g3MFkRgMKwIWtEsWozR5CEinccpiRLgIhgAKQlFyh0yhzloIeCdo1zWjtGZfpCjdEjRczEds/MeYmQxXTBcG2GqnG7RMZ/VFEIkSpYXeOvRQiCrDDtvoU8L2+AD5foIRMTPG7JBjlCSam0IWUIFpJaEziJkkq1u/QGDi2v4Wiba41KW0juH6yy27vA+IKTgpU9eplDQz1oQ0PeWvNBYEXFKoH3ADHKkzfB9T8girulxs4Z+2kDTk/ulIIVJ+S69AN90ZEYhc4PUin7RgBRkIeKdp3EhxeNLQbNosCQFP9tbBlXBwFTMaw3LYqVuUmOGBTIEZFkQpSTuL4i5RmaG6JLMeVgqtIU+Kdc55/EuUdeGF1dY3NoHwPep2KpAJREJ5xG5IlsfEgVkVY7rLLH3ROfJRiX9tEYiwHkw6ZqHuiN0dqmMJ5O6oE3KfGJJCTzM+VJlhjCKB0u3GFPxXOtwdYdrO1xtEaWhPVigs1XoE4J0SLcLLtLsLQhdz2JvTl9ZKCLzgyk6V8SQnDelNdIH6oM5Os+wCUwlr4oHjruSgvGgohMiSaLXDdPtOeNrG0yu30ci8FIRywFRKUyRUUqJ6Wc0vkV6z8pwwPrVLbJRidKRd0LP5P4+4xgJIXL/3g7+Yosde4os0UCn0xmDewfEchUB5CsDLlx7A9kuWHv9Mio3aRAVh/Tmk+PqGcPt4zY6w87a9+xF+LcJbThtvj9JLjlppwU0nzQRP4eJWhw95pkUugdkCoAHDtFxh+rc2VBn9OM4k0M8oaVHjvYERs7zYhq+sBf2P4p9BwktfEh73AB1XmfsCVG6x0awnmTniAKee9+nMnFsf60El4cZUkCuMrr9GhlBGUXrHKvDEqnkWS0drlsYZkNWy3VihOkkMr25y2BtyOzGPtw6oJs1lLnB1R1CRCwOrTVd07KyvkKeGfbu76OzDNcn5SnrI9W4ZP3yBje/dh1IBUnbuk2JyiEmmpRNCfXRB6o8QzvB9E5LuTkguJyvWQsxcBDCg8s2j5GvWgtAsVpz6VMH1Iua3fc72sk6870Zt78hWLmygjKKi69kZEIRg+X6l3dQUqaFTO5pxAJGnr5xlDEtNi9qQ+0j3kEuBcoY7rx7h3q6YPXCKrOdGcEH2q4nr3JsZ9m8ssntd++gCwM2CRTE3nPjazcQywWoUBJ8RBpJvWiQSlFVBcP1IUJIVi8l9MZHsI2lyAwxJnlgpSSllqwNMgqlkTGy4wN5XjAcZMhZgwTqZpvGzTF5xnD1Mirm+LYnKAkBlJRpgRnSgCFCxAsIAtq6Sw6JlmijiEok9bVM43vLbFqzXw9TjZzes2kUwgUyo3E+/d/ueeT7GyAgNAo5nhCsx+/k+BCwvUMZnRCLGBkUa7j5HGEqyvEKrspQS8lwJQR5lbOYLMjLnHpSs339PsPXtvDBo5BkUhJ6T8kG49EI7QKz6V3aLMe3LbaeYvuaxbxFh3S+kURBRAhC25MLAUYTl85aXLRkAnRhiHVPphU1gWbekhvP5eGYECJGW6zbZqEKwtAhyZBKQYzoZd6R1JI4b1GjEh9CynGKEbc3J5KjypyF8/heUPuKPkqstaxe3Ux9JNEhw1L0QXjPPO5QXdwgygBTidLLcaEl3esQ0qKtSLLiewuDyjUuN1BDdIGgJd2kJqsyvMiZRUnsIlkIjKoIWrJbw63dNEiECJ+9FAk9rGuPq5NU/GJm6aaO6DOiTk5UCJGoUn4NUrDnRyykZpqPaDEQoW86ZCeS41kWCClo65boAxtNcgDrbo4cV+zudohcUK9PaMM+1mrWJteQmUZ2HerKy+RrY9qDe0zW9lDDIYtMocuMtmlZXXN85pMDynFFIwbsNZ5G1ays5HxuVPD+fEa+AJSkazu273pkPiJWBfiW2i6Y7h5wdyTxW2tEwPqAyVdY3G5ANIAg+kiwy2Krj7EnLU4f1JM7Zz7SYVHvk4jH0UXzId/go5VPWJ7ZuamDT27qIzNx5h9P3Pw0KXSxdGGeV8cFR92Ys1DAp4nmfowUlxf2wr5D7OPJKXrW8e7ZQicfXdtPa2fNZE9z7NMu67nGqSNRviOUuVxJvu/KABUjk9sNN6/fw3uPjIHBsErJ63SPHOx4wC6yUV3gey58lsX+jP/29gf0/gA/bQjX97D3psgQUAKGmWHhLEor0IpROUJrxWR3ilqqkikpiURCjKxdXme6PcF3jswY2kXLeH1M3/Qpz0FKBlVBV3cIKdFKMW067IFgrEpmu5LfalvCMl/l8DLshsD/0bYAfHq4z9/8Ybj2Wcev/z93effXRyil+OBLkn6+STEsGK/t4to/wWSal956lTtKkw1z6n6P1csbKA9qLmj2LZHI1qwDpYg+onKBLwwqROb7c7pZS1HmCAmrl9Ypq5x6WtMsGqSUaaISgqIs6KYNhTE0vkMhyI3BlIooBV3TIYXEL/MpDran1PtzqrJAiv5BHSGtFINRhSky1nPFa6McGeHmrOXepGUoNddyw1ArYtNzYG8x6W4ie8llJKPhNaSUaZFepwWUWRZoFTo5bjEzy3o7gSgFK1srTLYnLG7uUqxUbFzbZDaZozLDu3cO0GVOESMrRYruSykxUtBbS6gHHPz6NfIyoxjuEuWv4nuL3ROJsqbTYjkvUg2mSl9Cx1VUB7Nphh4Y1q5uIISg3p8jfYQQMblm89ULXNoaEq0FBFGCMSmaf1W+lWoDWcutxe8yn84wMZJtrRC9ohCSaBLCEHzAu5AKnQaTEMKl2IQkyYcnVCRAZoiLBpNr1LDgwuWLrDcreBeY+rvcmv8JolOM87WUmySSqIAqSmSukVol+lhuUKtVeoBDILb7qZ5RlbPbZMxbQzPvl0EFic40yiiEkQif8mxUVYDzHKgPWLj7uKanuT9BD3KKjRHZIMcdKFSWJ5THe5w03F6MEPMl5UelGkV5YfARFrtz2kwzXSTEcH1gqUyHNJp39wX/+9uRGAI/+prkr30SfB+5O5Pc3RYE69mdS6xeIS8M+PR8ubZPo1WVE3rPu+ElDgYXMGuGrOnQMRKLnPneFFVmOOdpZw3eOSpjuDSx5H1gFj2/X9d4KQjGcffqTQKOsh3wvfcukTmFFRmL6Uu4eJFF5phc+QZtNcEsJshsQJ4FLmzCZ/7cBmuvXeL3/uCAP/4/pmns8BWfVhVXLs/4yrcWlOO3yKSiLS5x0OR0i4ga1bi4zcJavjHdZ/7mBmZYcvdXb9LstMdhhnOuOx9s9px9h9MdHvGY7571iOenmh3dLRIfoMDnO9I5cZeTXz/ntf+pQgsPDn0Su3v+i5FT/bezGCdH/z5J136BEb2w/8nsdEjgqeyQlvQx2Ed9KHHk5+jxznPck9uehVh9bGOMONKPyIPyphGiD+y9c5f3/ugdDvanFFWByHNe+d7XGW6On4SoH4tv7dzcwftA7wOLuqNte0LwKKMJWtM4lwohRqiUopm3TPZmKckBgV7m2ggEWinqecNsL6EqSqpEGQsR733KQxGCclCkoqRVkeShi5xqUHD5jSuPRkofwxAxVc61T1wjhESzkiHSzhrKUcV8e0K/aFOE3nmK9QFZmehGrrX0TYfJDEpKpFSJArW8MM46wpJSlC8Xk8Ugx7tAsz/H1n2iV00ahIC+61FKMhyWqbaJkggpKItDkYBIkRvW1sdkuUEgKHJDnhtwgXpWE3zKNdGZSeIUuUE5jwnJoYlKJkloo2nqjtC7VGtHSWRmMIMCUSypT0v+e3QelRtknuiUSThApCKigpSAL0BrlYrOdpa1C6v41hJ9IC8zvCDJV3tPFCxlyCVRpHyy6FN9H2UUwXq6pmN294DF/UlSvBMQQ0y5WUYhtUr9Uok2181aJje2KauC4fqIrTcuU6wO0t+b42VRT0/oHBIICOTyXQhCEHKDjBHfO4r14YPX1jY9KElwIRVY9SE9C9Oa0NtEIYPkJKmkLieWNZyi84TMoCPo3LC4s5+ohkIQlnQy21l8a8nGZUIvICnQ5SblzCzbSz/pWqu1EXZ3SrQpV84vWmLbp9pHJgk9AAijE2oXY1Lbi4BNOVJuVqOB0Fhc06d74XwSVMh0kkFfKjzGztE1PaHtl8p5Hq0E1caQuMw/izHR9HyzzI9aFu6VSiVBi96CdUSXhCn8okWvDxM1MgI+JKW2QUGxuYLUmnpnSh8j2mimOwfM5zWLec1iviAqkXLfrEMLQa40PoRUjLfrmB5McX0S3ejbjmpQsTIasjIcMFwZUpQ5hkRJPSwybPKMxntcUeGJNH2HdZZsWKRrARzj4sZIuTJg88oW/WzBWuhonaV1Dk9EC0luMmwIzBc1kw/uLwutniirel4Gw/Lvx25+qEh4qh2fjARnI0rixDL4yMxxbjurhtHpthw0nzQ3PsXc+cTNnmUOXqK1553XxdHzeopjftglzuHdO5U5fvZOxx2ij3Wd8sJe2HeWfefS574dZNZnHY0+akftGY4hheTq+BpKHr/FmRI0+5677+/i/BbloMLGCCHw/pff49XPvX6yJMqZnZrvzdi+sc3KhQLZ7eM7h+x6PJJFbxFSUghBnhn2jcBrqIeGcefRQtJ7h4gCqVJ7i7phVa5TDQqES7QpvMcImXKEfMpzsZ3DO08xyIltRztryMcVRVXglhS5xwUn9/c8v/s7KXcntBcYrkkWkwVFltHVLULAZDsw3LiKqTaY7h7g5nuUWyuIrmHx3gK36wjTgAykPBAlaecNQgpMkeOcA6OQqwInHVJGqpBhe8fe3T2cdZhME73HtpZRVRCESHLPUkCeIaSgs57MZLi6pas78kFJCIGdu/sYrdga5Sn3aqWCGMmUSgtaQPmAFnBn0ZOtDmk7TzuZs3JxjXpWszosEFoykltQJ4nsHVVzW1wnikDpc1bkZUKh0FmF79LCVgmQPtLjGW6tMNmfJ/TKaLquZ+XyGtP7BywOFuSDAt87slFJJCRUUsmULyMlQim6g5THpXODm2uk+DQyg9COgOToCSnwywKyvXPUDkIMLEJM9ZFay4FNPzHCtYsLVvtbCDSy+ATBlwiVRCUQAuFSLpdaonTCe2JUyEGBrTuECzjvUx6TEPgYmL+yim8sorWszJJTYwEhBcFaZNCs5JeRZYZtZrTs0naOIGsO5u8SrKf2BxQCZGZQy+cxOE9dFuzvt0dfL47/EXl9lDHYzKldjRUZYdESc5OUBQcF3bxByqTwWFQFg8wQuj7VsDqo6UOEtkeZlKNkJzUxRLwPZJFUMNUowrwlLqWxdWEgCmJviTNHLAx6ZUA+KoldcpakTPXDovPgBUIk8QQhQGj9wEmOQaDGVZLytp7gPWPdk4kWuZJRx4zdD/aSquJYsHd7h7LMU60spejqhkFtyZaveDNviCFQDUr2tcSXmrgyYjjYxkWHtA0buzUr4wE4hf/MNWzn2Xv7BnpnQl93OJlogd55FkIiSQ7WvjN84yCjUoZprln9RJKzr23kW3uJ+lZcuYY56Jn3lpFy+DBDIAi+ZVgUtCrSND3NZEH0gWIzI19NcuaX77ZkfSBEeNvZhM2fMucdrlUf+GSRh7mip4zJsKTSHUrQH6NTPb2dhRQ8jlr3tOhCJEI8C7MSRzd8uD0nHLv4DMdezhHH5NAf28aSbnhI9XvS3HwC9XqqTj2FPQ6VOi8S+afCphb+H//9YzweMP74DvfCPh77eJ2iD+vofFgH6ZzHf/ph6Yx2zxqMnofDd8aAfNh3JTSf3PwuCl0QfaBfdCwO5lTDKtUQWnQUgzItUgGEREmJzsxSBOEx/SZF+e+9eyfJSrsFZZ+cCWEyVDZIdYVCSAhImfOBidzUAREFb/aRwnt8iMQYKAtD01my3FCNSm5/4xZEcN5jrEDkGr2UKY7eM5/XjAYl87bD+4gnsnZl40HdmCdd27v3LL/4S2lldW28yuWLl5lsTxBZhl5G2y++9Vluff06PozpF7dQvI+Ra4RFjhIXcXcEMXqilAwHJfW0QWmNdQ5RdzgJoevIVzSyTPkdphbkgEWAlCzmDRqB0iqJAghwIRCkwJQ5XdPTdJbeeYSEvu3wMTIcVYgYqbTkE9fWIQSM0aiQaEuSlL8QYuTuoufG7gI96wg+MN4Y463DCFKOjlasmZcY51dwreW/jd7m1nhCcIEvqk+xUY9QRhODJFW09USW4gYxLtG0hI7p3KCMRknJ2qV12kVHVmRgPUGA1JogUq0plRlEF5JCWt3Sdz0uRBQVVnwWnRm0SXlLQkpC22OqHKk1c9twr01RfqElJs8wVU49NExHGcE6Pr34Mp8e3kIaDfmbLO5qQojYRYvwqS5QlCIhKM4jIsTOIpSgnzQpsh9ieqZiRF1YYe/VFWKZIQ4a1r+2T1ZkhGmDa5JqWm5GbA2/CyMlM3+fW/O7SUaaA7b9HN87yv8/e3/2a0mS5/eBH9t8O9vdb2wZkUtlVlb1VuxlpCYpaUYDzFACRtADAYKYIUGAfCQI8IWCSL6R0JvmX9CQGkgEBhKGoAANBWEaEIfFZquryarq7qrKyj2WG3HXs7u7rfNgJyJjj8jMyOoqdf6QGffec/y4m/txN7Of/b7LpQllHOaK0rrPXKym4KQN/NHx+rmPfHFtyLVfOqD7+B6m7wjrHm109hOarfEx4WwW49BGIUtNnK+QRhMLieocdI5UCkRlSDGx/OQEWeoMX4uRcnuIGtb4tkc3ZTbhDREKTWh7ZIiEtWW9XDPcn2RPJhJJZhEVQoQo872lJLHPnB+3WJPCAESusAmjaVvLGzcSY9UitOW9my3eRbyRuK5HFTVBgO8dWgcKpbg07aG1tG3H/qCmHtSsL1o+uDSirUBLS6o/ZNAo5KLnnVOJWXcsleH2O5rZck1qDPXdOQgY7zWcKoWWieAjRmuGZcndFfzuJ4ItV5JSZOubBqkl05/O+fjjOaTEt/Y0k0tDjj64zUgFRgMwSnJHR4KSlJUmtW7D0UxUlwrqrYayMPz2dy8Yz3JSfTME+hif2Wc9Oa99wSz3CcPuL1oaeVZC9JJ4v5eMlzJcfeTXzfab5O9zT/rTU35Pue/MFgzPPvfntvW5CcjLzSqebryannvkBz6C93O1h/lZL3tt/rQkTl/H1/GC+PmtFD1YInvKa0/b9mnxBZOPn4vK8cvA9Z544cmO0656Pvn+h8zPMib+8sEu6+Vm8iUFRhl2Lu0ijEQalZXn1rxwhalbdfizwLAwdL7DCKi8haRZ99mPRghwPjBftbitMsOtEpSVpFw7hEyZa0SGxW3vbXHy8TF9ZxkOagQCbz1tSBgtETEyqiuUUizWHVJJdvYmTK7tsv/a/st7Hj4UAlCFxsdAbx2lDfTLjhgjWimS2JDnN4aXUtZ0bZ/hXwkUKatzeU9RFvRdQBmTzR6VyomhUAgSvu2RXlEVBh9TlqwGTF2QbOa8RCUggg+e7cvb2E/uZR+ikBiMh/lrk+KB+EGRQJNhW/gMh+tjhKagakr87B51U7I4nSO1xNmK4fYQucw+VMH5THInJ7ps4FCmMBnW5TTReYTQCC2JDsTGzFMWOiv3AQN4oGpXDqvMC9twn0IEUxqIgZjAJZDOI6QgOU9pNMJ5khS5wqAz4V34jbKZ0ahBlcFHQlBOGlRqs2x0aRBAt1jTyQqxXWHKiqYao8VJfjLyJcWuuyxmoQTeZ+EPETfKaTEhhEQ2FWmRYZNCCOLmPaUzRNItW7YORow7g7CBtDNkdfOU0FpiymIBQUgQ2RzYlFlpUFYFZquhHDekdU/CE+ctZmuQE7fWPUR+f/IeffB7oTF7E9ynx0SfoNDZANkFhMw+WEZmMQkSyJ0RSgh87wjLDlkYYmszTFJLqq1BhgkCBkGYrRGDMgt9QPa/KjUykWGLwzpPumMi9A7ZlMhCoWQWBRGKB2WN5GPmGQoQpkGEPNwk6/Au5MRaZ/VBrTMs1PaO6CKp3MA0jcL2Fuezma8ZVKwX6wdwsRSz+qNzjsH+mLqB07NI9OQ2p0iKIGTCLTvOj04pO4eIkdlqRSh6Utsyrms6HF4KhoMBs7bNnDnrid5npF+X8OtsghxjyqqJo1yhrQcNfZG/Q1MUBG2zlUCIVNujPJTFSPQRdHqiOvGseJmtPqva5Lvl4Tvoq+GrvGCfX3ax7zlj/mdrgffLPF/iWJs9CQRJgFDqkXN77vThaS8+3pbP0bb02G8vkk1/sj1fIFlLz3jvC68Kfx1fxy9+/GyToj/pB+3x6srj7fmqS81PO+4rON5nykP3d/jZAe799A6nR2doIdFKcnR6wVmtqV/bYeYje1d3CW9eIrqO9b0POT87Y+VWT21XOSkYXh2QEph7Gi0kMkR0lMQLg0OjrEGLDDURKq/EdzEyXEuUzd17GRVKKSRgVIbGpIHi4mJB2kykpRQP0OwxRhQS63x2jE9ZHnmwga0VwTK++ICyKhCuRbzkhIMNRHxysMV4MqRfWxZty2WjmL5/jPOexcWcy28a+i6rafW7LWf9J8Qy4NptjJ5wnmB3UGVulBAMa81BXSIKxSf1Ma3s0QLiXiRGgRGKrbMdlM6chZGCQZm5RHc7T987ZILVxZLRqKFbW7QRHL5+yPJkxm6lqZRiKEB0lmQ0NgTOWkesC/reMmwqyiQ5X3b4skBqyXhvzu7bU8YHW6gPDMGWSMEDdbNIlqtuDhsKKZEzgSx0ntD5iKg2fkMm/4wmy4trrRlf3mExX9MuW85unmLXPeP9MabU7DYGBBRaUVfFg8miVBLlPFZJ5KCi957eepY2UHhyNUWA0A5lNKe3T3IlrG6QdcnZ7bMsMqAUyijKNKEZlGijGTQ52Q3W003X+K4i+IDUCkpNDAkZcoVIRGDjiaNlvqdTSiSRkzRVa6SWmEGJ73vaW8dEN0AJSKVm9vYO7axl3FUb8QWJ8AGREqVWdAJ0YzCDOickEeKyQ5SaJJ/HBXkyBAJZF5uktCBsrmXSGRZYNWVuQ50rcCQQSiJjgmFFWvcZBHSxAi1BSryWBBdQAjAaOahACMK8pRgZJlxQbA1wdKgyglasXGQpwF2sCOMAReZeXd02/Nm9NXrcsBsDp3aIqAvW3Wc8LJFXSyhHNdOFZdoqSl9y02/zibOsQ8SrJmeyG5Pc3YMd2tmKI2EpL29lntrZCl2VbF+Z8O+97tADRQie29N3OPv0lFJpfuoik8mYVA+Z3ZsSY6SLAf+ta8S7Z6zKc9bO07kFWsp8bxeSoR8y/GSL3bTPUs5YDReklCi3DOM3B/lah4LpD85IQH/uKNcJLyXqACIeMx5yXZS8M5wQ77XYFOgXmZP2o6KjGifq/QlmmRiGSNGUm65bkHxk9sGMGL7oAPFlB9tnzfpfYr9fpskvmVi8umTvs1Ty8VDALxlDs1H3/KGz9E9rz4tgdI9s9KJ3v+B5pcf/eMlq0YvQLF/H1/GnLH7+KkXPWyZ92t/Pi8+z7avoBF62g3nFHU4eRx/uBHOJLcVIO1shUqLecA/WJGZ7A05MhqXV3zjADwvsYsHJ2Y9I6RnYuQTldsnuL2fp5PQD6IVHSkFcK1KriSKRlKbdkCUKlblAEti2kR2fEzMfA3YjYOCdoywMpi4JG+JzUxikC5RCoKVEbXgyZgO/IiVMoTMXSgmc67jk7qBcJoN/3gusy1wtO/30mO0ru6QYqbYHzD68S/QhixfsjLPU9RXL3E3pu57+vEHLArRmNHeYzlNPhrx2aUxjFDEF/riYMlMLCiHxlyNJSWSQTObbma+iJG8cbFGEQKcV9+4t0FJgXUD0DikESoDRivnROeO64I1xlR/cjfIZKXG+6vnBzVOacYMsDIWf0a97nI2I0COlpD6c8fq/01JUUxbzS6RbO1n5L+YkQEAm6OMQPmYpahcyGd95kiBD6QTIjRhEYTRWSk6PpwTnsV1OUoQQmKpAxMRBpTf+Polmd5SFKpYdqrOEEFFaooQkhsQ8Jm5drPF2lmFz3oOSDEYNi6Vl7/IuSUraWTbZHW6PcK1luVxjrKdcdOzfOGBQbyqAqx47XxPiNlprbO+yt1BKmLCBzJQaZom4tqSxR5QGEXIlQADYQFiucdNVFoxA0t89R4bAUsCnr49gtyDYmjjlQbULoxAhUNUlMYFdtBSlIVmLnDQZwvfwcyyeyQx4JGRZYA638edLgKzEOCgppESN6gd9gdHZNwslIUakUviQjWxlBGy+/4RWKC0xk2E2ez1fIKoClKSuJQesMUVEXJaEbglaUSbD/MyhqgJZ5n2kGLk6hivfLpEycXRquNcOcXdWxHVEDTYJoABdF/TLjjOrUeUeyx+f8ZN0naN6iyAEZVXiF2u2D7bpO0uIkfHOmIsQcCFSlYbXtyZcvn6A0gEj/wDZORIlW1vf4YM//gmLFPlgt+KuL0itILDCOc/lt6/hv30DObuEOnqPPXOH6fmULuSq6aAqGMldqh837JlLME6sh0sQguawodzxiELTfm/B/PaC8e4Evw6kRaTUCldYpvWSt968zLu+ZvThBUJJ5m+N6MYFuiy49Q4EH5Ea2mgpSsPu69v5vgFCF5h/soCNgMojXfED/szTbpavejb7FZYR/oQm4s9SrJMC/kxRsCclfYKfek//sKrpK24Fm1a8qF0vjj/p1eev4+v4xY2fv6To8Xi8r3gVfJzH9/3zEl+0UvXISrN45PXh9ojlbImLkSQETkT6EIgpsn24QzGo+FwXc7NpO28JNtEKgdH5NnLB4zd4dqMzdEyobBzZWgcxwgbO4pxja9TgW0tKEJctjZQorYkhT8TrwmA33BiZMrfEe48mMSg1ejJAFIqdSwNEd/QYVnwzeD/v1MRmwBGCyaVtTKHZvrHP9HjK8Ud3Cb0jpoTrE3WdeT/19hAxdeAc0hhCn40pQWWoWIjIBHKjiKUioASBXNHrY56QJpWhhCEEvM0TdWezqhhSUhrQJpPxoxDoQhOBMiVkiFklDOgF9CFge4s2hq5zVEpxfnSOc57BeEBMieHWgHpYowqHMgrdVCStgUQKWf45Q5LkAxWxAiBGoswTteSzl42PCZVARSi0xllP7DzlsGTnUvZ8Cj5mPkpMGIoHX8N6tqK4b2AbZK7q+XxvipQhT8OdEbbts4FvzN/97HzBcHtA39pc+VQSoxXDrQGtFKzWWeo4uVyNkJvJpduoF2olCUQaU+B79wAS57XGa7InVO+wF0vK3TFdd45AImNEIDJ3rbcE5/Fe4Pqw+W5y8oTcKMv5gFGKaBRpHhBaIgFrPVWZIYkIkHWJIGHX/cbsdHPbPvmoPTENFUJQXN4ldo7k8gRdCkFaddnotsrcroz5SohaIZuS2Dmk2AhNaEFMWU5dkDCBrNBXGlK/SQyLrAioJyV+vkZtDZClIVhHsvcTHEG0jug8agMHvc/PiAGidXmfkDlQWwNIiRCzmp+sDOt7U2xrSbsFwmuqIkt/C61YL9dcunEJKSW+tTSDmsVihfCR07vHjAcVo/0mw/mCQ5qCZnfMtV95k08/uE0fPH3XoUsDRjPeG3Pw7mtIo6h3x9S7N/Dr26gQWazWLPueynm0Vrnf0RtOWZFNe4MPqKpgdTzl/L1jLo2voUJWL+y7noX3uH3PleuXGO6OKW1PqT2q0NTjAXGQ4cLNzpgEuHWP0gpTFnjnaU9nFE2FMcVzOq6H7pUNlSSJh++TLz44Pn8i/nM42X6pKs3z4jnnu4Hvh2UHdfFg2y+SFn4mhnAf6Pjoce+/9uhI/lVDV76Or+PreDx+/pKiL93JveQxftb7f/i152F8X0mkBz+qUU1RGWzdkYpsxOklmMJQVIL5J9+HGAm2fW6V6MHPjVzz9HjKJE0o65K6LLi4mOOlfHBqEuhs9ifSkCFTKSESjLYGXFwsaJ2nLA3eerTM8tySmPkbhWblQxZ/kBIRRRZe2EvI5PEjSXvtgmZnSD+C9MeZGP+iePzST7sLfnzyh5BgOBmyOJlx+72b+N6RXOYrIPe588GMgzevsOMK9k7uIHzkmC1mKaFlTmgW85b9K/vcPFtiCkWhBGE7oWIipMjEbuOQlEKTYva/KYXk3qwlCIGSgms7A5QNWQpYZq6H0gpCyBAoF7i36IlK4SXMpgtkErTWZ5U2YD5dIqVEScXWpW18nyWKp/cm3PrBNrFzNKcFAxJKCHCO1PforTGvr/e4Mt1Fx8TEVUgpiVJwuviQYCP4yLi6gRIF0XsORyWdVcjtBqTA9Y660tTDGhkSwjqUlJSDCrvqES7iN/wXuUkYEpB0lvc2OlJdKpAtuKLHHntCSkgh6Zc9trMAeB8QCObHM0SMKJH5KFWhs+DHYU2YNARtEaFArLLC3Eoes2gvUBt4nDQau/QMB68x2X4D7xyreJ55TN6TQk4+k43s3uvwvc+T4NaSZDasvXxmUUZRizUX6SOkMNgwQ1Ym+w81JaNSk5Y9MQRi2yOmKyaXanaHLbLy3LNPdsWPT75uznpmXYAE3zaGw3rC+uN7zLZL7CbxE1qhCoMaVrhFS9wklbHPsuKiLtClIczXeZGiMplntOxI3iPgQSKAC/TAXd0g1AB3r0ekhKpGWJETOSEl0fnsq6QVuERs+1whLiYZgihBGIUwWdwi2rCBNgbMbECtdgmXND9qK5IQuRJVFRAT4+0ResPNM3WBKbMENypxvHWHs7ufsOtGNM0Fdr1m++3rlIfHpCuS3V/f41uzBc46TFkx/2iBriPL2z98cGV3C8evDwYs3Ihb857vVZkvNCexFJGikqzVNu2ZxveOHaVJH59w/JMVu2GX2Dvm7ZJmULO1O2F0aYd3vvVt4jaIhaCIlqQSPsL4tKCe3XfB+GygO6yvkUKifW9JuSzxIbJ1bZdP4y0CT1aKXhwvmranx7b4nPyVF+3/Gci7F1Y+HuqcHzeVfe5x0ktu/1h8SymGZxeU+3v8YfBM42fjXyIbIH/PWWoNwTu6hyUAX+JYzz7fJ8epZyezP4eJ6NfxdfxvOH7+kqL78Xhy9KIK0cskFC+TmLyKeFHC85Ucd9NRp4cuWYws703pnCUdOMrRhjfhBSIlqoFm+fGPNpCzTTyrX76/LLnZQCpJ05RsXdnFdRY5zUTVGLKHTGstCdBKYa1HKomPEW0M61WHkpJCG0KKlIOS+bIjxciwrmg7i1vmFf48eVaMqgKTPHE74lJA78HF7gnqHcWsWzM7vWB7a/TQ9X16lSjx6Fe/sHMW/ZxE4o3JmxRtwe6lXY4+vENVlSAS7bwgxOt06122mjE3Ys3F7VNmew3CRPCevu0ZG81itsT7QFEXaBLrzhKaiPKJcZhQ6wGFUDgkhICXgntdVnErjeJbjaYqNSIqpMzKXnWR/w4psWwdP75YU+3VOB84XWfS+mR/wnDUcPzpMcEHhMnnf37njGbUYFvH3Z8KFvdqSjPm2rhkdFgge48YDYirjpjgqt1BnSt0itAucUVCyIq1v8cqzhE+MSguQVSUWrGnIIwrEjl5S8MSZ11Wc/MB3TSUW4MsnhAT0nr6jYBCYTTCaAQJlxLGaHTpkbuJSpYsZyCOwWyku21vM79MSibbI9SGCxNDylLsKWV/HyWJE0O/JSGVxNu5GhZj5Gj+MevVPczmTtBKYqVmd+fPM57s413P9OxfIIclaRZA52qJdIHtW5vKldEkKVEIVIgcXjjMSJFkz3n/EcorRG+zv5PICUFynqBzcuhXPVFJ9OyCvX2HqmqaruZZa8P3b+O7C8fdRVZNfLeCcecxq4Q7MIS2JRWa5Dy6HBDafiMeAf50htAaOoscVohRg0wJNosPosjqc/SZ98OwRrpAImExHF9o9LCiW2ZBFNnLrF4X+rxI0jrkjiL5CEYiyoLoAmHlUEWT+wejs2+RC8SYqMYNSUqa+S6j4RWckQyVI8wWFGyEIWLg/OiU4daQ7esHSCFozxZ0q45yqJnvnOH8kiUaZRVdckzOj3jtzdEDb639lABFP11y8aPb+FWif6hf2NWab9QNMGT7as1P7W0Wy5ZQRla1or91l73XLyH7Ldyq4/yPblK8v+ZKdQ3nHCEFLr1xmeHBNqo0DPbH4IHjz4RLbEp46yhXikFpHvhJ3e9T78MmU0wE7RGFxJ95RHw5G8EHXfNDXd/DA93TpuSPuxG9Ulz6M8a358l7P9JkPuujn3ukR47z+ZOHt4uC1+qG1Fk+KRTTh3Z8v27zR/ctHh450v3qzv1tn37sp4slPEc++0vGF0kMn7YPeJWcra/j6/jFii+dFP3CFnh/Xhv9rEWlF1bQnv5NiJA2ktuZfxI36lZlXVGOapYPdvoCqNlDjRBCMNoZoeuCwf6Y2z/4CCUEISUmkwFnF4vMIVECYzQ2baBzgCRLaAsJfW+pBiVRSqqqgJSwLlBUBW6xZudgm9V8TUyJ1nnqFLI8tRas5muadwYolaWim8mA1fkcV70k7OSJM8tQIJESwXv2r+7TzVaMD7e599Fdyk0VRpeGndf2md85Qwio6hK3jlRGgheUZUFdAiEnbxGyVLZRKKEpyCIUVWlwXmZlLRdRCfQGPhacR5ArG2WZeTlJChyCOK7ZPtgmxMjxH35CTImtw22arQF33rv9IBElRgiBoCTRBkII7FzZARdRISLrgmZnRHe+JLUWn0BvJG6j8/gUkeslcTGHS1eJPhBVhj7azlIXNW1vKREZUhYD5n6yYDRKKVJpCAJW8zW6LLJ4htFI6/He4ZXcSOAKxMYcNBaRGBPaSJqtAb2Y5QpHjBgpkIUhkRjsDgm9o1/3GQ6nJGWhGY/KXAlxAXu+JCaIUuSkIGT1L6XkRoY7IUTCDPM94zqHNgJhHVQiewBt7ocHGCWVn5Ni452EUVnRLgSEMujKZChbL0jWI/dGCCUJ3qPGNaF3hBgpr+6ikibae1n0INWPPWUvfhRlk8U5ElBc2iItOxhUxBCzgp7JXDxZl8T73631pMWapBVyUCKq7IElAOECMSXEoOS+UaWqCwSC0PvsfyWy0MN9yG4IgZAShEjoLHprSPQeQV7QEAEUIhv1AqFz6FGVleNCxLUdvoZuvsamiJSS2ekUUxhiCGgpMzwxJtSgRFcF490x89MzbGEpS02MkbZ1WO9JJ1O275wzfuPwQV/1YJonBEl8BoG6f6HTZrtyq+HG9Xf5+Pd/wvJiTVkYzo7OOLt5gimyJcClleNyVdC3PWVTcuVbN9BNlflzSrCeLulWHYvTGRfH03xvxISzuQq3fWmb67/6JvOTWX6ORg2mNBR1SfAes/EnS/cFFr4YVuszaPBTbx3xtM1fSTxvYn7/vcd9dV6ulc+PR1O8l5jYb95afPQJ7dk56c/91lP2lq/MZ/t79EjiC125V5dsPAGrfQX7/joZ+jr+tMeXTorSIx3IF4kXpFVf5hl9XjX65zUpela7Xqa96dHNUkjEFAkuUc9rpDMMpOR1l9jdKtlzBZf3f5WUEq1b8eHF+w8GgKcduz3vOP7eMQmoZw0pJFZnS2xrs4FlStg2S9FqpehD2KjI5UmHVjLDiWIi2kQiUlQF09MZk+0Rs/MFRZUnYUYb2kWL1BLfO4qypLURdZ59bkqtuPTjmsvldYRO/MHlU477FeVlw97BHklK3NJx8ZOLR07lia//odNdL9YsVy1FYXDeUgyyYln0EZscxx/dpRiU1KOa63/mG6STKednUwSCrbJCC48KAVLCxYSIEZ3AKYmuSi6dN2xRE5Hc7XuCSMhCo5zH+UAbIjenLY3RlFpDTMS2JWz2V+8OmVzfQ6567v74CGsdBzcOsb3j7odHqA18SqvsObVYrdm6tJ1Xq53j6tU1ZvoT0toyGn6H/qymna+ymIPK/J5ZuIPtLhC9YzKXGCpETOyNvsFWDd2iQ6uaQPZUkkoRQngwbSjqEm0SMn0fjyWmkluz17HdHCUF9daQuOwR1nGlKHDBUZTFRsAhINYrwqdHmElDnRraYU23aIkhQEh4YLw9ZHY8p6wLkhAEIZBS8uYbLa+9cROpj9B3BvjuW5ASi/mCbvlDRExsDS5h4hVSbxFVgbIeTElZDxEhPbA+wQXKSUN7PCMoiTKK6HKVihAQhUI3ZeaaAMl7kg0bKeuUE4OyIIWs1qbUhuN0PEMO6yzYIMkKdCGyrwXfuTQAAXcWluPlkyvUT4SU6GGNCIF4HxLV9iBllo1uXeZKKYlMiViZXM1tCsykyUa4Z3OwHjGooHMZquojstSgN9yvzmXIm1a52hMiIiWKvTFutqZLJXdWNcl51KIiWIfUioWXeJuFMmLvQAiKrQFmWJFSwp4v+DQesF61SCGYOUeKiboqSDERXaAYFBASZ+/fYXSwTQwB5zy97emxSJ1ofX4NQHnF1k+3GfU72PWC7cM5QiQWS8en6eHJeL5jl0PNH30rV5jnBjyOq7/8Ovf+lynm5jlFaTIfrXc45xnaQL/u2b28x+E3X0NIyXq65J68xbpacHp8QvyppFrXFMZwtzH0hUJoye7C0n18RDMa8PEffYR3jigE070h42v7zO6d8zqaYV1Rjkpu1K+ztmuUkoz2sidU5zs+OH+P+Cyo83OSoWfFF58IP7pi92L/os8SjGelE+mhfT4PFPK8Fn+e85m8/RaTt7/BryvDN7UkCvie7ZnHyGdp0MPn93DS9wWv2y/sSvLX8XX8bz/+BOBzX9FKxNMqLF9Bx/MqV9VeZTxxqgnsqqPvLCkm1EqjvQEtOBTwxvYE7SSuuIKUgkW15MOL9x/bR3pkf27hmM6zOWRTDKkGJcuLOSEEFAqhsnSplALnsgpZ19q8MqgkZV0yn63QRb7txpMh62UHMbGcrTLkKkS0UXQkpBR0bc/WpW2WZwsigoFvsK2lMoorpxOuT/fwW4LffX3IzVSiRMeVA0M9GdKddUzfu3jkNJ56rTbhOktwgXLQIBKs5kuaasjO1T1mR+f41vLxH3zA3o0Ddq7t8fYbl+l2J6yOpyzPFhR1tVkVdijEg+Qw1SU6whVrGFNhE5yqgE+RqCC2PYNRgxeCJTBf9Gjj8SGwbi0GKHdGXD3Y5mJtuffBEYuLBVfeuYa3jvNbpwwGFe26x1nHeGtISAktJc14wNFPb+VrsDhmr/oATCTYq3h1uFmVjoSQUD6y7E9YdrdRPlKP3qWIDSQYlJeIWlHVmdzfbyS1I4mQEmVZQGlQpUHIHsFHyLBCqzFrcQNXFMzuXdC4iFGKWshsHKwUCYg+oIzGrB3q3i38sgB9meHO21RNyep8Qb+2aClYXiwxw4rVbEVZF5nHNKw5vLzkcHw7+0yt/zz24jJx2bJe/AHT/i7eB17b/22G5T5Ge0RT4n1A+4h3EqNyYi+MJrk1pinxgwoxX+OlRFe5KgRZMEFXBlUVhM6SdJb5pneoQYUc1pl3tOqg0PiTOTQFcntAMWoyLDQJYmtJApr1kje3dhBK0rr44qRocxPryYC4PieVkjRdIptseKoKjRAZIpeMRhUaZut8bkZil22ufEpJWFvkJMuDU+QkTShFWPfE3uVDxSyDL5TArztkaZC9I4bIuoNY5mRIWIlqxuAFdrFERA+FRiIQdUE5qnOFqHN00xW3JpJlXbKYLrIqoO0QxqCaAlMY+rbH2pxQrT65m4UrUmLd9VS1ojSCuijyMycEI1lzyA3q2YTj9xfU6ynNpEJ24ZG56P2JbVsrPrleE0Pk3od36Zct9bDm7V96g3JZsbxY4PoOhKAeVAyu7FBPBowv7eCt58P/9ccspgvuXPmE9mDOOlpeH7xDEytCiNjdERcyC09M1p4madqLJcF7todDbAzcrAyzvifWBfaiZ3qxwm5UC5VWpJjQneTqL91gHVd8dPH+05OiBwPT02vhrz4e3+fz05H7KcbzqkmPQtNe4qgvscj5vOPp0QD74W3efO0SojBE4EfOMSfy8Gj/1ITvieTmJWcHr3Be8vM6H/k6vo5f1HhF8Ln02CuPxysi1LyoB/gZrL78vHZATxsbpnfOmS1XlErhXSApT/Bw45dfJ6XE7T/+FF1q9l7bf+La3RctiJuJq0A8tI2gaEq26h1ufv8jio3SlRTQx0hhDG3bUahsiqqUypOnRUthDLXJZPC2s3Trjqou2NoZMzvLCRYpYa3FdhZTaJpxw8WdM5JSmahNyqvFvWN1OqPY2qIZD4gi0YyGtKs19WTw8hduc16j3TF74gC37JBSsnt1H+8D48Mtzm6e5NV/Kbn4+Jj53XNGh9uM98ZsXT9AlIa7P72Vz9kHSmMoVCaZ58pWQVIKokSrrLRWbhTlYllQVgVp1SJColvnSViuxEhSVXDw1mVcazn79ISLexdcevMyIQRuv3cbIyVGZOPXiMT2Du8DW7sTmq0Bymjsumd6dMHVb2R4V0gC5z1Sa7RKRJEhYlKKbEDqI0KXhHofQshS6DEnqkFJjBRoo+nWPdIoBGDKgrDuYZAoKoOIBcFCCDGbAktBu2opt8fEEPG9p6xycqRKTUKgdFa/s4sWWTvsusseOlpRT2rsqs8aAMsO6/3G+FOxfWWH4O/CphoQ2iwukUQ2iqXL1UzbWXywlEJkVbqyIKpAURhib/P90DtE3+EWLcW4xi5bQucISlJpidQKP18jekca1ohSgcuTbjFuMkRVyszZISuTidJk9bdB9qLJgggVSpQkJUnHATtdUuyMnnmrfuZH9tnTLuuCYjCmXS4zp0iALDQuBHSIyCJf9+QDbr5C1yXF1g6hc3SzFaEymEnzAF4XYiRGEMsWuUkaZZXhiHJj2it8INksgJF85sR46xAI7KIlLTMcT8kMrcwcGgHLjjQoAQidzdDGEFgv11RVkblwQqCMpp+3SJEhpdookhC03hO8R3YOHwJ1UTAaGgZ7E4SU6FIzGu9S39lCuszHWV0saCbVk8/8Q79GHzm/c5bNfQvDarZiaVve+M4v4bssiy+kACmQSkFKnLx3m5OjU2ZnU5RUxJhY9xYpBJPRkHARSETq0rAzaViczwkxsrU9oV/3FNowGTbcW62y+I33jLZGmFVE9A7nE+26oxlUjKqao0/vMtwdoQ/KZxu/3q9yfgXxMnyVlz20eGS0elZy9Ori+TA6gdqZIMr7yomfferhytBTgX5PfA0vavWrTWGeSA4/7/zn0VWCz+LrKtbX8ac4XgF87vEn6BU8UY/v4uty84sjPfpNpBDpZqtcrahK7oxLfCFptOGK88w/usvibI4ymsnhNno4ZOebf5ZIovKJ/VnP3fdvc3b3nGvvXGP78g7n7RmfTj/O+4+JGAO9tdhhxUWhKIxilCRM1yil8MEjZVayCjFXE4zIctWrdU/X28xDiYnTO2d58iQFy/kagUBLGE4aiqpk/9Iup8cXtKuOuiwIzvPJRcvpD2+yr+HwW1fQO5rFesl0fZFhS0+7TM+5hKum4Oxwh9OP73G5GjCwEdk7hjsjdq/vsTpdIGL2VwrrxPH7dzn54IiqKZGlYWt/i+gjs7vnJKNZ9Z5vLl5DuMSoKKmokDKT1V/fbjIszkfeny3p5vm7ClJkSFiMOenoLeWo4d77d1jP10Qf2HttnyTg1h9/itlIT3shEGVBsYE3KSWJItEv28yjKQ3jy38GWVpC55BibyOZnq+/9YGiUkzMa9RqDzGAZXfO+eIuQkh2Jt9EiQE+JcQmOSImlM7mrUIIRMyTcFUoiq3/A4lImFmujBqkUlx+6xDXWuphTXSe0ntEjMQ+IoTIFY4twZV3VV7BbQOn7x9hF2vUesZ2bQmTLKxQDioCiZOLPTrzJv2qh29XuBsN/Rz6D32u+oTEaPwNtDnM3kTFBBMiISXmZ++zbhJCSg74BjoZ4qpDbPyJ+tM59dVdyu0hat4SYoLKZK4OEO9XUoYlxaghzdYQYubkkHKS5SM+ZSNIszNCaJn5IhqWrqBbjKA0tAb8dIlqSq6NCsZVPsYnFz3HK5fNZDfCIwB/4CzveY8QcKVKGClQusiJisj3WOocosqJqhASM6zxrUUuWlyIKKMwEYTJMuEIj9SK9nSGubRNXHboQZkT5BgJGxnzFBMiBmRZ0LdrimGFNIrudJ6viwuIKns9idJsxCkksipJIdHNx8xvNdgwoaj2MTKry8WUSEVBv+4YjhqG28M8aS00obOEozN25h1i2TFZO8R1TTUZMLq2R4qJclxjQok4guA9O3tbXFfb6FPPOCb+z0WF6y16IKivBRAJiSd+74LbP77F6nDARzcMpirYH6241n2Xi9MzRu/sU7y+Reg987v7HP+k4eZPPuG4ucf6+gqpFbtih8HNIT4EpjsNq53MHZzPF9jlghAjZ1s1fSVZz9d8e2tIaTSXD3cZqZzwzW6d8FH9PmoMygkOjq9SCMXSrzi9cRcx8uxduUz6JD29I3vmfPuz6suLp+1P5+N8NVyTP6Elxs1h/8BZfiokDApS3z1Y4L2vQvfwOSsh+PNFSSMFNsH/r+8eMnJ92WTnKzzf+014FNzx4LcnkroviQD8Or6O/63GVwOfe9rqw5eNp8HjHn7vaYnUs7b/eYrnAac/RzzeJ6aU/VPSBvZyr5KZVC0kRx/dRcTI5GCL5emcex8esffrb1HvvU4Chp1ncPs24p5i4reINyMHNy4BPEiKhBTYpUUoxVLCtDEUWjLoE0pKlBL03qOExHlPMx4ghcgcj3UPwGTUYAYlZ0fnKCkZDCq6rqdznrIqEALqyZCyLuh0rlZFJYla4XrLysJqveTi9z7g0t5Vru++wXt3f4wX/qXkuR+/gr0SLCY1xa/cwKwc03/9U2LvaLaGXP+VN7Gd5fzWCd28pZ+3m1XmAELSz1uCtujC4FNCVwVi1TO5qNieNAxDgZK5ChJEYrs2xBhZ9Z5KSharFp8ScVOFKwYV/bpnLBPdsmUdIkVdsHNtj2pY88kPPqQqC8q6yB44o5q7N48ZTIb43jHYHnLlm9dYnS0YbA3YurJLVWucjdlkNyQqtVkJVRJtctWqKXapQkQaySf2DvN0D4Wktq9RxoJgc7KhksjiATHRO0dVFsSY8N6RVh39vKGcNLjesdeEXDXwAa9zlSkVBXGdcvUpJcSqQwJmlDCHnsGhZj2NzG9dUA8kIxw3dl3mrsWEEC1CSEazMbcuJtkQVkXSYY3ZNnR3NeJCgJYM/Db11h6pc0QtUdETS8l0cYxNHcJFJoN90nAPU2UYoEgS0Vq60zlm3BABofJEV6gs5Z3oUFoR5YZ3kxKsWjhfIMcNSUnMoMgGsbXJ/JxlVoVLnSU1JWvf4BcWtTNADbMwwpDIZJL9w87WnntLBwhEVkwB4FYIsJFr3tmpMbM5bNVooxBSPJAMD7M1oi4RVa6yKiACWklkXZAWLZDl0EW5gQDWZfYFWrW58qRVrk4UGlkY/LrH7I6Qhd5UmCBaj7ee4eEWq3tTdAjoUUOUIieaWiG1or9YsjyqadsdbIz0q0RkhWyyka13Ga43P53SzrJhqthU1hCCS2j6haX0kWPrOD86I1WG9d0LqkFFrYZcaq9SVUPKYc14JhApV6C2jSFqzbo9Z2Q66nEDbWDxiaM8DRyP4CNg68o2hxVMPvoplFOGWxa2Zvje0c0LLm6v6a0lHlrcwQrrPW+G15ncVljv+GQgWFaKSwd7VKs1RYzUw5oQItOuJ04aQgdn8yVeC5SL7Awa1hdz7OECX3nCOjFxu3ibaGXL+esnmImgHg9APLtSlDa3iLj/92Z8EaSHhpoXgdxe9WD5FYK8vkRTb4VASh5ihjk87/oo4E2l2VaKNkV+1wr6Bxf8JeNnsrj72bV+uB73xDfw8zof+jq+jj/h+Nlwil6UsDweL1OF/qLH/nmOL9HW+2K+DxaARFZ+W8eO4EOWe00B6yPD3RGXbhzie8v5rdPscH/rBHZfo523nP7wE1YfnFCXhuGgYtX2XNw+hf2H25po52ukztA4valuiBDRUuB9xNyf0Gz8a0a7o2xWSXqgPhVax872mNW6Y7Vs6bueZlBx7ds3WE4X2FXHR3/wPl1ncSEybsqM09MaH7KPkG17Tt4/4rXffIutgy3i1bQx7/Rf4DqygRBFDt+6kuGDG8PNoim59PZVUohc3Dnj7o9v4YHQ9rkKoQtcZymMZr1s0Uqhjcqr9invN8SE2qz2922foYla0fUOmyLKGCZbQ9pVi+ssKUZ0U1FsOA3ze1Nc5xgNa1RV4NY9wQVObp/mVeqzKU1TM9odoYxicTZn63I2pnWthTrDRGTKSmL3ldO0ybA/lMwJj/VIBDIkEAkrQG0MgFWhiZvqRxIpJzvKUwwqhMscI2k963tTtBDopkJszDCNyBCkkHJVKTqP72zel1II51EB5kcXxPUQt5KIQUm1PUBonwU7jMjVCiUxTYnpisxJUoqw8eMpK0OnBCSBVBnKFswGJlcaEAnhHHKgMH2k0prQO2gMwUdQCpEcTJc4m803BVnBER+Jgsyfcx45DwQBqSxydURnnlTSimQkdIG46qAqiDGipURu4IRJ5GcpLTpUXaCairBqia1FVkWGRD24OZ/sGAVk492qgBhIdrMYkhKu0OjOIoxCV4awaAFQLhIEYPI+w7oHEnLUIKVgOKpJvUONG9QwJysoSWr7rFRXFgijCbM1JqXMPZQCbRT9xQphFHED5RIxJ+AxRuKiJfWOdr5m2lXZsDREeiMRPitUppQIffY38zHm/SiBCoLQWVazlsm4wc56Vm1H73vMcsxquaJfrPGi5/TkJle+9TaqNKRNgvAw9LCeDIihxbU9OpXYdcdwb8ypElR1wXBrhOgWpJAYHYxptoe4YU05rDn645Zb7x8RQ6QxJbGukc7RnXQMigmVUVw63GUlAipYtrZHWOtYrztEgt56tFKcnV8wCInxeMjaWdrzaX62jMan7O1VVxWjasQiSG7FSFFnGOALh4mnztVfLil5KkzsS8er2d8rS60eWkEUCJA8kjI+7WhpAz9PtXz02go+yzxfUbM+dzyBo3v87a/LQV/H1/Gy8eWToqc9yV/FM/gEWf4xjPMvSmXoVUfK/yTAIPgPqpKBECRhuOeGrM9bnM8mqX2Cre2S3ywuKOwUpyq6Nw85+uAud35yC3tpxK2f3MTfOWfXJ2SVZWgrozn68C7fbEb8J3WWDnZJcDqs0euOFDO8x8X8/8AYVjJgu55CClKMyBjozuaY0lBqhQsxK4rFhBXZYHJrZ0RSYwY7I9bTJXd+ehukpDCaojSoBG3bs9xAzQZNTe88USk+Oooc/XDO+No+J9/7AIgEG58QWXhqiPzPuA/cOO+49+ER56dzzuct9aBCvpsovmGQUtJ8WDFJe4z2xvCNy5zdPsP1HlLCdZaqLlBa0LfZm+W8TxyvF2gEpjRoIai05rVtSWkMbW+Zz1ckrWiqGu88F3cvkEaxtTthejYnuUCQgvn5gsFkwPJ0TlFlWNJi2eJDQApB02S1vKossKuOs4/uMSmPeGP4I2II1FvfRLjrSOvyxF2A7R0q5om8KQ3S5cRIxsTe4G22B6/jvOfISIJeI0PitTRBOT6TopYCoSS+s5mkr+WmGrGRhE6JuO5J1mO9RzclrnPIGAkbJTOAqinxqy3Se7+R972K7K4Dphgw2u3wl9/PyVqhH0DJJudHVJwg9gTaXcAPlqhSM1/f4nh1kxAi+/IGKk5QRhFcyL5BrWNr/G3MzoCicpSioScnr4fjXwHvUKPE3bN/gyeBC6hxTSTLpscENJnfocsC4Tw2JcywJlmPCJFCSmRdEmwgusxvEi4QO0foLKIpkUplXtmyQ8aIbErUsCYsOyKWN3YqDkc5kf3pacvp+tFEP6WEX7ZgNKG1mPGA6HxulyDD2HpLDAEzyp5B/n6fkWLuQ4cVWE+0jlQW6EKTQiCECIsWlIRhxWik2dUzkgtYPHfOOlSTq0qhz95UMUVsZxnUJX66wiuFNhleKQvF4vYp0+2r3PQDUgK9O0bMl/jW0mwSMC0kRPLfITK+c4FaLbG95XatWRwMWQwik/1tvFvQz9f0MZB8oqwcq99YcPz6EXHd84NbGdL4cOybxP9pbwwpcYbku++W1JNdJkXgL3Qn+J+csjuqqDcLD7fakh/dKjFNyfFPF0ghkTLRrnZZnR+gjeZIFMihZLQ1oteC+vIBftXjeouIkbIoWLcdWikmwwHDpsNPlyAlZ4djTuZzdncvcXg3gbdoobBrz0U7p9M9RmvqwWPcqOd0Z18FWONnEs+ppnyRc3kmF+rJzOaxIzz6Ga8k/9/kMV2WoO9eamB5tB2kryg9+YrnOvnK/GmZUH0df9rjZ1MpelbC8qwO8CUSnEe6l59JSfqzI/88RXroGgrgutZsCUkQmuWgzBUTAcTEYGfItXcPGb33ISY4ejPEdobVuiOqmlt/9Anz5YqDpkb1PWbjx4EPIAT9nXPe3Y6UVcHNVc9iVJPunJEEhJSNCoPzWAtKCZCSrncMhzUpJFSRjQu1AV1kZTlPnkQ7axFrGO+MESGhgKIsqQcVwfncxpRno8OmxnmPUoLkYe4jC0oWn8w4KBWrOyt4WJ3pJSGKRUhs28jW1QPipT26VUtRldzc+oj19hIhBEUhmf7oHovTOVHAYGuIX/eIQhNJ+GUHAXRVkmLibLrEOk+KkaquEAK2m4qro8w76WLEDCq89QTnqQY1PgS2Lu1wfuuURCL5QL01YL1oWc1XWUjBeVwMeO+RQjIaDYgxD19RwOpiRRwnDg4D29URMUZ8OCTyWvaZ2Xi/SK0yN2jjd4NRpN4RvaeSw0zeH2ju6HOWsUO4gO0Cw6rCaJWTmi4byEoE0UeSDxitscGDlFhrUTGhExQx4C7miDJfH6MUxIBP2UNLMUBMBwQf0IVm1ARYR5KPhJFmebJChUAxqtBGoRczVFzmCs3G7DJM1ywW95ivAyklJtUBVRgBCZEycR8pmVT7KDUgjBJyZSlSou8DhdlDy4CsFXL5I6QJuHWH6HRW3LsvWS0ka2tppEcXOpvMCgiLdb7pQiSlmMUJKpNX8KWAzoJRyBCz9VFdICYDQtsRe4e8b6g6WzHeGjAZZR+lWzMLaaNKt6kaCZH9d7Jwgyb1lriRwRaAqgqSD1lGeyM2kVqLLHSe3O8OSYuWECMIgW6KjWiKQKYApSaVedvSJAa0iEpgmxFqe0TacNb6W8eE6YxkDPpgD1llmF1iAzENgf6sp28t7U6BlQ0+RPxyRYoB31mCNmitiEJgvWV+ZpFScM1FWPYU3nM8LrjnLXJUoUiMxwNiiHRS4qNDFpLwhmA5nuOk4+PgiD4+Ml7YkB5UkBbWcvdwnBXqzk749ukpKSWU64iDEiVg3iVOqiHuuKfa2uWNXx7TrTuiEdxbrhBSMBwP6GXPue0YGkGjFT5F+taiK0NB/p7uHp+hEPgQaKqSi4sZJ/WYZVMQnePNi4qxGtBMhoi9yMViRdgIgdyHeL0IhfXI9P5LlVdeNeztJfb3isfyl01Dnr3VJiUQgk+Dhyi+xHTg+ef/M59ZPIyve1YD0s/bjOfr+Dq+2vjySdHzEp6H//4Fj4c5O6+0k/iS1ycXOTLX4X7FAyFYTpeEBsq6YLFcE5zn4PJOVjMjPRAcVYXBKMW064ixoalryiCwYc2b37zG8QdHdMuWvb0xo2ZFDCdZQnh7iOhBhUhVabTayBUvLdZ5iigpjaaNkd76TXIT8DHgfURIkRXo1h2DytClhHWei+MLAHau7rF9eYf1bEUUsHd5B997pFHUg4rFbEXfW2KMqELR+UBVFdhF+5Bh4wuur3jo58OXD4HUitX5grm7wOxpuj6ra60vFgz8kLbvaBcd5aJjsD9m98YBR+/fRlQGbzts51ECYswTMKTEx0iKkePTC2ZDQzUoCUrSrvvMz1AZMnTw+iEnn54QQuZCJCVYz1ZZlWsDqQuAERKlNfWwJqU8+dQqV9ZiiNRlgRQS13uKqiDYiKo0xCyUkSSYQhNCTmTEBlsPoEW+jzrriBKSTJvJd/6uU0yEEHMiGPOkLcWELDKcsnMWozWFkll9rdCEGHE2ZFG2mDYcqvxEhXi/spjNLpESOovSCpkS7nSBPZ5vki6H0hqtNKEPhGWfExAlME2ZEwafoVjCZ/hhqUq0y2p1Hui1QHgo1h1qUBG9z5A3k7krqSpIts9JYQqZQxRj9t2xjhRKzAaW50JASUNatVAWqLokTpf4pJGdRtUFMcRcYaoUyYUHalexs/k2DQHvAqw6kg/ZmDWBPZmjxjVqUD541nN2tcGnbUjh+IgoC8JshRxUWB8xAkJr0YOSNF2RQkQOKmJpiNZljpBWCKOxMVGUOifWqw5pNHHZIXaGJOsxdUmKkRizyl40AfpE2ijxRaUy5FApmoNJfqRsQMWcFEYtac/mOCGYXSxw2wcEa3NirhRKawajhmpriBmUuHWP7yyLkwusXVIpiUARlcpS5j5QG0OUmbdYCImXksHhNsWw5uG17YcFKrh/DUV+XlazHj/sOV+0XNsqUEqxODpDDSvKYRYGUY0mdJ5b3/8A+UPD7t0DVGGIr+2wu7/DcrpAC0kxGtC1PfWmH+oXLbPzGdY7Xn/9Gs5bxk3FbLlgsWohZL7WoKxIIpJiQGhJ5zxy2dK5rLanlSDEhO8cDJ6yZp/S/Y7rs5ce3eApycHL15IelvD5k4VifZ761zNG6s89L3msevQFx+uv+rqlzb+v/DgPMvCvU6Ov409HvBr4HDw9OXrWc/TsKvXT9/34Zx9fqXnays0zO6+nZW0veuC/tF3bVx4CQZSC7//amKrWnN8JdOY2y/Gc85sXXJ+WfKNNFBcd/2y9JkZPFTSXJgOEgEmS6NszyqYG69i9tEOzNcD2GfajmxJxSTItBkgtmS0809tn1MOG/a5nOO0Bge4jEknnI40B2VT0naXvLSSB3pC2tVQkH1FK0XcOAexf3uX87gVCwPnROc32gMtvXiK6gAK8FMxnS3yM7L+2j5CCvu1ZTle8u+hJq4BYXaD+jzvopsDOLSf/9uS5ELrBpYadd3dIJLaWE9I0bSouiWYy4PYPP2L5TxfY0lFWBd+8fs61b3TENwM/ev+Aadsw2BpSDiquvH2Nex8eZRljQZZF1gq3sgyGDUJJut4iUuLHp3NGcczF8RSkpreealixe2WXk0+OqaKnHFZYF3C9Q2iZDU7bnmZQ59Vm74lB4F3IfjtKETfo+KoukFoytVdZnY5RCfbGe+zWGyluJRExgvVImVexkUBIJJl5OOH+YOgj12JN0gNSiFRoiqpAlZr1NFfQfIzcnnY45ymqkkOT0CqT/qXaSDIrmb8zJDJGtM5E/ZQvNwKB81n6+QGEa76CqiSd7sL3fz2LBWiFByKCtHbEpcWnrIS3WgqkgG75Kd4f00wGjK7uwHn24ZHLFrSk7CNozTp41HzJ6uL7+MITlWFn8qvEUFHIXO1k7bIpq1ao0mCtx2wSXmEUsjJErRDLfAn9us/Gp0WWPyfEbLIK4APResS6z+INhc5wukVL89o+i+MpcdnBLJt24jyp0Nje8VatuWpy9TesOpJRiJgYqwyTi+s+84tiRKSI2h2D9eADapilxVVvH3B8fGghRqIQFE1FtJ44XaGVJG5MaGvpOZwsISWsl3x8XBE6j686YtA4oKwKzKAhDRuKjQ9Td+8if/ciJ7l3VhPujN+kVxJ9cIUBBaEs6BZ5wcZohbUO1XaYUYnZVDP3XrvEllWsP7mXfayUwjQVulDY2dssZaQQnhR/gFYR01Tc+e5dgg2klBMiKR/rtQcafnWMiJHxh5I3vv8GQiuK48Dvv6fx1rE38tTR49qe8so++9025//6mO7C45OnKgrmJ1NO14aqNPyaUrxWGJLK3DNah7OR71+0tDFxePOc1dsXnLQnyMaizrfY37tKURrS8ZytGEFH7h58RFCOUTXixtlbhGVgul5y5YPr7IYDdr5xwCfp0w0cKz9WL9Lh/uJj1pcb7Z6Ern3Z0fPJzz9bKvwZx3rmWPAF2/aiJOlpZb0Xlfq+kob8bHfzdXwdv6jx6uFzz0pSeOj1h/OQL/IQPq9TeeH+Hu/8fl7TnM8biSgEF1sGMzT40T5h3WFtj512jC9gEiG4wO2QKzaj4Bkez2h7y/ZoiOh6vF0yGg3ypNh5+s6yfbidUQOlpq9kFmg4n2IXUNYlwnoGcVNqkZKYAlpkRSozqPA6J0Ag6DdS084HYggPJsSDQc16tsZtfE2UECxO5ggXWE6X7B3uMJsuWS1bInDy6QkpZNGIsinZb2oWF0sSjs63jA8mSPUcJPTmDVVp6oPMk2rvLfnxv/xDtDHYtie6QLQWmTQ7jOinLcX+nHp8jNSSrf1r6HRA6C2rO2esesfqPHNamsmA8cEkiyB8dJfkPCAZHW5T1SXTu2csjy4Y7E/oLlbsXNlh+/Iud35yk262olcK5RNa61y5CIlu1UECoxV9Z2nbHm0UKgp0ypBDaz3eeExh8upyGtD3BUJIBq4mWI8uFGEjVJA2kEeFyBWZPldnQowIYyiAGCKFMAQLMUmSzNfVVCWmtEgcwQUWiw4XI9p6Dg+GyMSGUwRSSXzvYHNfBQRIkT2MigIlBWpT/YgyV5eidUijcSSUrxHzITplBIsCnHOgNYGEEiA86NKQRCJxQoqJalhnE9JlTmDKqkABIiVWIVAajV239KPA2s0pgkRHTzICJyVh3UFKGf7WO6J1aCURRiNcQAuB6z1KKURVkDqLHjek1hJ99ncSIWzuf7LAglE5CdUyV3hCRFcF/XTJar6m0Zq6LkAIZN1ATATvGZaCerFCKAUpoiYj9KAi2oC9WJJCJIXs6aRcYHUyz89n2yOUwAzr7J20SYRNXZCUhNYiUswZXesQozqLoyhJvH3C4FsbI1fRMGs1tg1UhaGoNNqnfMxCZUEHrehPZ4TOoQqDjwm3WLMQB5wPDsAojFeQPHVTMdwaEjrL+mJJ23V0fc/F6TQn+CGyc22fetxQ7W2xWK6ZLleMhyWmGFJXh6zO57iwpq88ewcD6t0Jpz88ItqszMem4vlIR6AFbBVIKdhyE/bfu0J/vuLo+z+laHaYXNunv/iET3/nuxz88luoRcne4DL+smOWzgDBarHi4LVD0rhECcGBKbicQCidBVK8w/WWce8RQH90hv7mGlkukHZNYbazkIzLPkjbZUnbOdb1ksnlAVLBxfszpFM0pkS7knG/RbWuEZ+D2C/u93VPfOTz7OPzj5GfDfWPJi3PXIJ8eEx/ygLrsz73aisjrwoH8tCJPG0A+goSj+ddh2ee1ePt+Doh+jq+jiym9KXiPsj5Ra/x2GubyfArPe5XHGmjtPSked7nJV0+Jb7Q+WyADQ/t8L4YlDKaejzE9h6ByFyeQue8JVMqIEbO755lM88Y2d7bolCZY7KerVjPVnjnKJuCy28eYkoDQtKvLMujKUGQ4VwpMaorCqkgRgotGVZlrkaESPABMyix3udkKMZs+CqzKWIzrOk6y2K+oqgKmmGFi5kHYNeWEBKnx1Pa1qKUolCKwmiapmQ5XXFx55zF2QwpwPqAX2SlJ4FA5bn3M290ASxP5yxP51wcndNfLFiezVlOF/TrFjbXTlU5yZCbT7k+QEhMP75H98EtitpgasPVX7rOO3/u21z/zptsXdll98YB7/y5X+L1f+dd3vx33+XSW5c3Ro4gCoNznqvffo3tw21u/tHH0HZU4wZhMmk7bZTEsk9NxGhFu+4yl0jmtgklKasSUmJyuMV4b4xrO3ShievslRNjpO962nVP4LPHTxQKo3T2n0Gg6myumYR4MKNSSmQVsJDNZEPvcNaxni4xTZmrPTHCBr6miwJpDM6oXOGSmYCPSBR1RTNsaOpiY55q8N5nqW1yFShu7pEYIl4kyv0xg9f2QGej12Dd5lnkAexPImh7S4qeatJQFpoqRNxszeLogo36OF6pjXw2uN6RQkJLCYUmIUlG461FhuyhJOsKtEZojagMcmuQKw/rDqEl5bCmcJ52vs7+PGrzcElBmC8zJFFI1LiGEImzda46xURa9bCBEIpSo8qCusqGqd5HhNHIqiBZT5q3JB8xB1tE63KVKUTCfE1ctoiUkEZlXt+6o9hA2ELvEEoh5EYRL8aMuusscdMeKTMXLJus5ntNFBkmiVb4s0W+D10gOc9wf4KqilzF3CgWJiWxnaM7X2aTWimJvSe1Ftc6xLAmKkHfW9rlmvnFnNXFAgGYQUWzNWQ8GeF6R4yJ2WyJS7l/uv3BLbp1R7tqSSniU8Rvvh/rHNPVmt39bS7/2luoYrPO93Ay9PisMEEMEEOuCksBIkX23rwMUjD7+C4n79+ingwxTfGgb44xEVNOUGPKFbZyUFNvj9BaUjcFw4MxZmdAszeiacoskQ60wdMtVmwf7LA1HmOtY7VuCSHivcc7jxYSJRXBRc6PLlBCZB6i0hSDgr3r+w9ESR50Xo90/E/2bZ/98lXPeB8d0PMl+8z29KU+/viunnGqn69Vn/e8X8V1Ek/8KdPmPnsE4viiY71MW77w6vDX8XMef/tv/+0HnNHf/u3ffuH2H3/88Wcc04f+N8awu7vLm2++yV/4C3+Bv/f3/h7/4l/8i5dqw1/7a3/twX7+tMSrrRS9CPL78PufBx788Ge/9LP+WSLxYAHxwaCZG/b4ylb+5aEO/4kb5PPdMC+1avOSexIPnUgKiaPvHiGUQEvDdy79JulDqD85xgXH/N6U/W8M+b/9X3eRyrM4EvzO/32FFgqRMuxqOGzo+0zIDs4zSSt+WX5AfX7EuhpzbL7F3Y8+pbeew3eucfbRXZQPxJSwG7K2FBs/oc0kSymJt56qKXEuy4O3bY9SksGozupUGzPQsi5YrlrGW0OiD8ynC4zWSCkxUtJ1lqrK/jxoRZqv6bselQTReqQ37P/xNa5UN2j0kj//1k8pSs1Rp/nn7z95mZv5iGvvvcYnP/yQIjUMDhsG22MGo5rTmydcHJ0hgOnJlO1LO9Racv69E8rhkJWIjK7vU4+uUwxrdO9IPtIuWqQUlE02tVRGUama+fGU4w+PGGyPuHHjAF1obGtp52s+/tGnBBtoxoPMMwmJ1cUSoQT1oGa9XGNKgyo125d2qMY1Qgj6Rcf0zhnOOnbePGTr0g6LexfE3tHePSfqXJUTAlyp+eTmCVfffY0dLdkZVXny4jLo7r6UtIjpQZVHyE1lKGSvIaUUoi5yBURmbocyGiMV375eZR5UhEGhSFpi1wuOpv8GaQQEzeu7v4kuDAkD0mJ7C22Pamp0kWFbQpDll7tjzi5+ilpXHFx+m2G4QrCOEBPJOnRdZi6TFAQXWPqbHF+cMB7tsbD3Mqxv0RJHiSBBSoHtHDpElIByI0MupeKw+DahTAgip+c/JrSWUJTsDH8ZmSS6b7m7+LfElBOZVGiUFPiUJaeNgqBknpSHgBhUKDsgLlvUMCchclQRFy2qyhyjFEQ2io25z0k+UFQGB/Q2oIpAmmYiv5Qi76PKiVKcr2F3jB7VbJ861HKNbBrumAWuLjIvq9BE53EBZEyIEJCTJnOelm0WjRiUqEGJ7DVu3lLsTejP5giliKuOVGlEqaEwqKhBJMykQRYat2xJncevOkRp8vMnJWkjtz8Ql2jYJ+5K7sQC5z0xBFSpqErDarnKZsxVQdVU6NLkxRKt0UYTUiKse1xnOVm0xBi57iXbas2WrPnxcsnOtQOuX3mT0bWaYqzwbXhhr3nv2PP/+MdnAByEJf+79Zyb//KPWHYG/c1/B7Mz5vK3AlevJVTZ0VpLe7Ti0x99iBaS4XDA9njArKkeeK+d3PkeprJwq+XoxjbnROy45/3JkK5tqKqab90d0r43ZxBLQg9aa3Z2t5hezHDBk0Lixq23UHcgRah0zd61fbb3B7weP8Ksf8CF97mq95SxYPPfk0NJ4jGI3bMGm8878Xl8EH8yGXhsgH1BPeMpW7yCuf0j1arnIlTEZnbwKrg5n31+Vwj+vXvnlK9d5lgJfqfrNls8/xgvV7d61nmJx7d4+XjsJnpV9bOv4+XDe89/89/8Nw/+/t3f/V3ee+893nnnnS+0r/Pzc87Pz/noo4/45//8n/Nf/Bf/Bd/61rf4L//L/5L/6D/6j15l03/h42ejPve0eJmn7PMmTi954JxI3N+9eAySLXjir/sJkXjy/T/5eCiBS4lumo1RCxkpRxWHgyssuiVFbTh6/zbbr93g6hWDNJKjeYvRBVFKpJTYVcey7YgJhlXB4nzJ4ZUttusLsDOcbohqhF9XyEow2BrQbg9ZdRcsup5KZw6JCwEbIi4ESq2xztNUDbbNhPjh7oSLsxkiCtrO0gjBet3hrEMuJd0GFjYY1kx2x2R/GMFysc7QsT5zlEyZDV6l0XTWgpBUVU25LPEfWYavl7yxV9Atl7h6xNO+O+01+/Vltn9tD9v2FHVBCAFdGK5vj9h7bZ9+3VOPGurtIdz9PsmWSDGkWzrunt3k2jvX0FVB6CyffP9D2taCyEnR3rU9ti5vozYGqa//+ttIIZjeu2B6dE47W2YydVEQU2S9zF4yRWVIKWGdIynJ/o1Ddq7tootM0F9PVxx/fMR6vma0M+byt1+jqEtWp3POPz0hacXKuryyPxmymi0pBgXBaGiqXClMWSxBkCstYcPLQQqSFFkyPSWi2FQMfECS0IWhXbWZ8C5z1U9qKH1A1TVJCrzzGKCPAeumJCkpaIgxoYhEH5BK5QpXWSDzU4kPAZEgKYkTnlVaIOYzajlisHMJM2oynybmCmRvM/dKG4X3a9bhArWC6C0uRupBhRFgfKTDoYXIUDgBad1jZFbdM6FGaYXoOkI/pw1LQmoox0OKoiGZlrRS4C1qVGOXXT4X7xF1gUmJZDTOeYySJOsJVUksDFiHllm1LkmJny5z9abMZqhyI3wQYkLrnHS2q4522dGMa0LnSNajhjVu3uYFhK1BlmpftOgW6qomTNeUlwfYk3NCazM0MCaSzJatqq6IPuJti5oMiG2PaCpEoXHHM1RlQCt0U2Vp9Y2cuipNXggKoIcVGJVlv3uPaQrsuoXeoWJExkQaZUlxY2qaYpdegHYeLSIxRfr5Op/nhgO3alu6VctgMsz9WIzZ7FXlxZrReEC36jFGs1VXuFlL1HNWZaK7d874xgQzqDJ+8ol4uNyQO33bJ27fckDC6EhTCd749j47Ypu7l66hSkPdtBQ7EkFAkLmP2W8s4rxHCEPoLHJSQe9RV7dQxTnzHx9z/Mlt7mwP8UnAcJsgSsrxiP7ODHfGRslPs7M9ycqAKWGKInPsXKLvLCjJ1lv7HL77GkWyDE7XKOtZx8DzMoXHCy5PjhI8k2N5f4HtM0+np336yf0/M915ygT98Q3yhFs8+PmsvX/ReGbi8dTs8f4nHi5TPZxtfLG2FEJy483rSCXwPjz70A9FeuS3lzjuF2zeE/nyM9vxdfws43/8H/9Hjo+PH3ntH//jf8w//If/8KU+/5//5/85f/fv/l0gzwsXiwUnJyf8/u//Pv/0n/5T/of/4X/gRz/6Ef/xf/wf8/f//t/nH/yDf/DKz+EXNV5tUvSih/LL9G9P++zT+s2Xeoo/68YfHUTyCpF66LW4gZ1kea+XkHl+rIHpvvbry37kC8WTJ52Hm8hwf8hoq2ExXVM3Nccf3MWHXM25uDOl1FcQwpA2Xh4hJcrC0K86nPV88zcvk9o5kIntotBELTFNxXK2YnE2RwsoVVZs661HaEVrHaSEc54YA946hJJoo0gktJJIJVFa0bYZ1lVvZGeVAImgW1uisGilqKoCpfNnTFTYzeCidFa9k1UBm8n4crZEForL17dxvacaNLB89iqmJFKUClM0ICTTT+/Rni1wzlOOaoSSjIcVSivK0YDm9cvMji7YOdxmPVNoAcl6+o3Cl0iREMC3lrvvH3F265SiLmgmDWa2ZHE6p1v1OB8IPjLcGmcC/wY6NBw1tPMVXecY7o658vYVqmFNipF2tmZ654zZvQtSShx+4wrDnRFSay5unnD2yclmRT5SNiWv/fKNfLy7HcWg5PI3rxFDRDUldrHOZqhaQIoYmQghgBTImDlqUmTxgyiy31SsNxLeQmCkBKNwbY8pTBaCgPwdFgbhAqosEIUBckIlpMA5j7eeelhlyJrMfkcpRETXk8oCU5doUeEX2Rg4CoGKidRZlN9weJQCEYmthcpgxhVyCsREsTOiDwm/WfRQKSE6nyGblaFddVlRT4H3ARsT0QW87XAxq/4ZH0giYVdrTJ0hYn7tMrTMehg3BOsQKSIKjZCZO0WCpCXS+wwtbMoNh0iQQhZmCNMVQmXjVDXYeBuZLC5R7U3wKdJdrHFKUh9uYVMCF5B1QVz3YB2+c6RVRzeD8rVLiFENrsNsNejJgPbDe2jnSbvjDBeLiRQTsXeonSFomc2XVz3JutxjdD5DCUOAugRp8Z3LQis6c9Dios0mrlJm3mBhsrpg7zKKywWSD3TdCtM4glH01tI5j3UeIwS4hJEFLkZUWRCtZblY5YUTrSgGFRKBEoJkItd/7RsMd8fIlLh4/4i7J+eY13eYLVZMb50yuezQDaSY/Zke9NQPz/g2GNqUcj/3cLdZThrqakI1qhBSYMqClHLCHEOGI1//pTdZHE+zCpyUHB2dIBuNKjS2EMjxgPLN1wl2zrRfkHygUZrSaDpnscGjjaEuDJOtEe26Z7FcMZmMsN5TVgXlZMDW1R2KQYVpCpJIxBQIJBJpI37yeGefPjvPh39/ybHi873/WbwqPs+TCVHe+1cej0wAHm3Fs1Oiz599JBJeClSC8JLX9wud/efNYMRTjvMsCObX8TONf/SP/hEAe3t7vPPOO3z3u9/lv/6v/2v+wT/4By8FZSuKguFw+ODv0WjElStX+LVf+zX++l//63zve9/jL/7Fv8jHH3/MP/yH/5AbN27wN/7G3/jKzucXKV59pehVVnc+zz6+yJJGyjLDD3OEKin4v1Q1lRC0puK7b/4mXmp8t+T8j/8FKYZHjyfEpuj+eLn6Ibxf2rz6VfUwT8LJESJg1B9Sl4o3fqXnh/8yEZzn1seO/9fvfJN6d8CtH77HKMxpNpLWxIgpDJffvsqPf/A+TSpZ6TGf7v0WiMRFVfHJsOaj7SK7wZ854thw0CsOZx3BuexST0JFiXeeQV1mxbHOYZTCt45p5ygKTQopVyJipCoMPgaiT9SDirKuWK1ajJCYyuTJdErYZct4PHggKpD6SCKhpMw+RkCMgYEL+JXA3tsiSEHnAtA9caEG3QnXT36Pbt1zbEekt38doxWz2YooJadnCyDRni24+qtvcDa8wbS5SjtaMbj3U/7dvYiS5xRbv0Y33ONKKfnj9++yOJth00Zu2ApEYZjeOc9mlHsT9MYksxo1SKPRpWZ5vsC2ltndKd4H9m7sc+mtywgpaKcrTj66x/x8gQSUUey/eYkQI/c+vkc3W2dhApk9UHRpuP6rb1CNGo4/uotpCnZe26ceNixOZ8wGFT5J2nnLa1s/YW94TGwtgl/H+n0oMj8FHx5UuaLzedKaElEKVIyoILJcc58rWkkIoss3pDCSomzQq5Lge5Amr4LrgqKpCAikd1AYgnWopiKwWbEOiSJBZTSSLF0chERq0F4RU0KnBBt5cO8ifedILtBNV5g33iGoa7iY8GqX4EvSxYJWK8q1hRBZdH/E3E4ROnOq+rbDpkijAypKrBHcXfw+UincscWLSJASZQOyKlBFVirL6n1krlBpECFlERGlqKosGJCsf9DfoCRye5j9v8jwK3wkyiz9HTe+YEkLlrM1qtSUB5MMJTuZIlJOVrGWYDTzb45ZCo+IgStvACdnmL3Ip3KP5ScXyKbELdqsnte7bKbrAjIm3LzNcMCYiNaj6o0hrVZ0vSeo3DypFanNRrv2bIEa1WglSTGfmxAiS46HSL/q8KuO27uaW4VEkrjXWerB/c8kuq6jtw5dFpixQSrJlVlPdd4jhEDNPWVZUO6NWfy7NzipCy6M5MbpGiUlWkm8zWIOTVnyW793waBIpAhO1ySVO8ZoAwjQI0n9RosQiaOl4J/+RHBfryBDGSPG3uPKcoqpC7p6ix+5/z3dbMXHP7hN1/4xi9mc8faY0c6Y0FqkDyymMyZbY37S73DTK6SAZbBUtiU6z3wtEERCipxMCuYlbA+HvBsN57fvsbuzxfZowHK9Zn4+ZbFcY63l+m++xe/d/le4aBEkCr8GEgF4AiD48CTpsQnTk+CGZ9cpEiAemvM/PVl5lfEnIPD9cE7zVJwh3G9XrhflhVLxYFT//G0+DZF/sl4hAJtejuX08Jzk89I5fn4k1L+OLxLn5+f8s3/2zwD4y3/5L/Od73yH7373u3z66af8zu/8Dv/hf/gffulj/MZv/Ab/8//8P/Prv/7rzOdz/s7f+Tv8pb/0lxiNRl9637/o8bOHzz1tCYbHXnve9i96/YWHfyyDeAxLIIFdKamlYKU1xWALIfWmZ3ryYOKBPxBP73Dvj0o/8zp0QrJGCEUzUYwnA2bnHUmX/PgHM67/xj6hOKC1Z5RKk5Sk9YHDNy6x+8Yhv9KUfPyDDzi9N2fv+gFKSTqlmVnL1DmkEmgtKSpD168JUlJIgScRNolmjNmYNdrMJYhGI5oyr8AncDFQRE3fdmiT4WKm1Fx59zXKUUM7W9GuOwQi+6oIGA5rVl3HarFiPBxAKQgh0IwaVGGo64KLO2csl2u8DWANkUR8fIl1M+qp6CncEt+uGI23mJMNL9GKvu3xKVJIxeJiyU9+90ccvH7IwfVD1M4Abv4h6fgMqwROHdLsX+fam5eYlyWffniXsvd0rcXHSLvKctWX3riUDx8T3bpndnoX27nM7wgB73KlbfvSNodvHJJi4viDI6Z3pxveV8L7QFEXHL1/B9c7yo2oRdh4/4z3J1x+5xrVqMK1Fj0o2N0fM9gecvzxEacfHyN/9U2qUY0cVOgmgJwSlYOUBRzoA13wFMaA8wghkT5S1EVePd9IaiPzvS11NjYNZENYsam8oHLVAB8QJlGVBUpvqnoxkmQ2gPWA2UDPkJKkJTplLpmSecKdFdDyBJ37YgzWk4wmhZhNbWMiLDv8rEeYCa4y+FVEGIFynpBAFIYQA61b0XZTZIpUwwZZSsqUcpmhMMje0cYpUsosbKE1KEWwDrTKFRcloct/Q+YFSZkrmi5GEDoLIChJWluoiyxAYiSRTfXGqCwX7gMkiMsOrSTD8YBWtKymK6RWFJMBfr4GF3KCU5ksT14o4nyNIFIUJcVOSfQtwpfQWcLdC0JV4G1HsVHIi+s+W1LJXP1NHVn+e9wQN1VYYRQ+ZrNYoSSkRDkoScMKqTV+uiSJTTXFBUJv8SESOgvjmgvvOWo7jNF4oxkOaho1YDFbUhsFbsNFbHvKwlD3gYPhEJSg3h7SXN4Bo5iWir5U2BCZ3zxjPc2y/MGHDGutK4pPljS1QhcaZJb9930WfBBKIkWgUhZlJH1Qm8Ww3BVEH3CdpWhKSm0R3tH7CUc3PTf/7S2cdRB7BJL52YIzf4EpDIwLmtEwexatPedLgUsR2ydsLyEVlFVB09TMF0tWCqIUnPUd83VLVZaMJIjVkkGKJKPoq4L91y+RRGLpFljfvRjf9CL4UwIh0oNNnwffytvfX8BLj02wP/vtAcQOPv+s/XPHz4LVIj6bG4j7idD91z87+hdphQfO4tN4YM9tzheeM3zuROhVLmR/HV86/sk/+SdYm/3r/spf+Su8++67/M2/+Tdp25Z/9I/+0StJigDeeust/rP/7D/j7/29v8fFxQX/1X/1X/G3/tbfeiX7/kWOL68+93g8PXf46kPwUsd+WochhEBLjZYGLTRRKLqV4+L2BYvbZ7hFiwwRLdVmO41UBqkNQukHe30g2LU50v0B6bFfXm08pUp0/3UfEz5EopTsvLGPFx5pYDVd8vHvv8fF7VNCSriUVZWuvH2Jq9+6gpSJ+dkMKSS33rtJcD1CRrrFiovbpxliqBWD7RHbNw6IweOEp8PjJVjrKJVi0NQMtkf0G3EFZ7PfS9mUFE3JoCnpu56YACkYbg958zfeZuvKLkpJlMlAxiQSW1d3ufFn3uTwm1d481fe4LVvvoZqCq59+zqX3rrMaHuI7Xrufnw382REVmazKWFTThY2X8uD65P3LYhSM7tY43y2Ei02q+VlU1EUWbZYSIld9xy/f4ePf/89FqczzNYQUZR0sw7vI/2y5eLmCdF6XvvVN7jxZ97inT/7LlffvcZgq6EqJd3FjNXJBce3TrIKXYj4lLLvjlYMtwd84zuv89q3roAQHL9/h+md8weqd0VVUFQFy8Wa6CM7l3ZoBllCOdWGa995kxu//g2qUTawnJ/NGe1OsKuOex/c4fj9I4RP3PzDT+gWHaY0lIMBto0EJ0lpozSjFSrk+yJpRRIghxViA50rNknQ/YQnpUSQWXLdb0xSQ4wEH5FCkVAImbkp0TlCb7OMthIQc2UlklXuQteT5mtwEY3CVDXFRrY7OU9q+zwRL0yGX5F5GhqJUgYlNS5tvtuY7/8Yc3VNKIlWma9CZ5FREBx0rSckiegCftmSNqanSglEzCITImb1PaF1TqjrAqREbw0gRkJrESHiT+eIzmZ58JRIrSOtekRtEEoQ73OEqgJhHUkI5LhBNdUGppvQRqOMYjDMpq1htkLIRHN1G7OVPY/k1gA1aQhnC/zZDL03wXeeGCFGkWGSW8OsQFdmiGxsLVHr7E/UWkKIEFJWzIsR1/Yk7wkhomLKCZ6WhEWL1Ao1akApYtuTbMDNVrh1TxACjAZjsNqwbAMxSZSQSJGf5fl0jhnVbF/aQcRESBElBUXYQANLw0XbcrpYofcnpFJnmKyUXHx8j1v/5gP6VcfSWlRhKJRkeT7j/JO7KKMJLhvw2pRoO8tq2WJXHa53dPOWxaJnetHiHqLlRCCWBj0ZkApDkrn/j0jO75wyny0YD2pu3LjMjTeucuVwh0sHO0y2x+yMh1RComJCKINRkuX5nNB5Rs0gGxS3HdPTC4y1+N5SaENdZFn4/e0JQRecezjqAnFvm2t/5g0GByNCDDwwZX1evOxYmx7kOS8xCr38WPWVrPU9ck7pKa+95GfFM/5/ieOkRxLCR5PDl437lSYe+vmiT9zfTvCZethLxReZcz3epJ/5wu3X8bS4D5179913+a3f+i1GoxH/6X/6nwLw3//3/z2r1eqVHeuv//W//uD3/+l/+p9e2X5/keNnXyl6GnT4eQ/jsx7251WVnnj50aL3g44m5fe01PzW1d+m0hXExB99esL5R8d01qPvvkeSgmZrwHcuf4fB7pi+VHy8VZIE2PkZFz/+l0+R6X5Kwx6McfdXpJ48iUeHwZdZIXv6cV1M/ItP5whAV4ZLf27EanjO2dFNYv8rXBzPmBjD9s4E4SNVbbn65h2kvEvwA6QaAPD6N8cMh3+EkAIlhwgO2L+8x/m9cwBCiEx3L+jrOxSlZnx2SPzAoMoSUxYcf3qS5XNTojElfdexXrfsHOzQtj1CKYaDiv0bB2xd3iGGyMnH97j70zs453AuGyUu7k3RVcH8dJYd7OsCqRWf/vhmNqUU4oE0tJCC4XDIaYz8L+sVkVyJSE+5XMtyn0/3f5nj9TFlPaQmQ/q6zjLaGecKjw9s70yYns8QCdbLjo//7QfMdodcefPPES9FFhct8x/9FD+f40NkuD1i8NolqoMddq7tsXt5i0v3/g3aTcEUfDz4Fl3UpELzwVaJTYlBcvz7d/4tJTPsvOTfXhwwvTfLktFC4LzDtZ6yNBRFwXhvjLeZQ7UYGOSf/SZH+xPaznN5YbHrHqkkxx8eURhD21qkVLnqUGhOb56gjeSwfIdx+SYu9AhXIEOW1y6qgkDmyQQBoXPZd8hopJb4kL2nREqIGPF99vCRIQ/uUkkEJVcnv41IEV1XyFRmdbkNwVzGhCw0VYwYIXDkJF0ATbHHm7v/PqIuCG2Gd6aY0FVBt26Jvc0KaxtY2vbgLXbFGyituKUsbSMpYqJfOpzwyKJAJyAmjNZc2f1NbNtCVdKezTDFhLqM3J7+ryThoHMUw4q47olaZf+mBLKzWdd+bXMSIQQ4jy6LfFNpiZ4MCOs+L0qkiIqgEhs1P7KUdl0itkekziILjW97UogEkSuxpMTlLUc9yWpVmp5qZ0jQLTd7yXrVYyYNYblGlCX27pRbaoJQQ2Ln6M5WeaIPWVRCSPSgzPywVTaPlSkr+Ym6RCCQSuWE9f53Gz0pQtQiq9S1GhUC/fGaqBXJWdRwkCF/IXCS9vnp8DoWMM0QbTNPbTVfYaTk9NO7jCZDhuMB8+ki+zRpSZDwQS3oR4pm3NCNDKpWyEnB/HzO7T/+GCklP6xrVnsVIkS+ZSVa1nB7RnWjoJCKVUr8v7s1fUwMdOI/KbIf0Xk0/H8+GGT4mfiMc3QnBP6f6yUAB4NL/PLerwKCvg8oeYQpCxoR+ebBkBQjfzhU/MHFnBgD153jzdszpNH0G6jw7nnPqJHE9Zqzs1k2j1WSQklMUVI0kdVixaCs6GUWrhgNtrh2uE05Lvn9o39N90lHImGjfUHf/+rjwZrRZnx65vD7VVaHHumjxVNee8nPfq5J/n0Y/NPf+TLx8s34Ekd6KhTwSXjN54L/fYlq1dfxxeLHP/4xv/d7vwfkKtH9+Kt/9a/y3/63/y3L5ZL/7r/77/irf/WvvpLjHR4e8tZbb/HBBx/wr/7Vv3ol+/xFjz859blXFU95aJ+sBn9WHnha7iIQNKahoODs47vM7ixxoiJITxkz1MmfLLh3smD3imX0y6+hq2Emf/drXqb3eMLZW9xfjXsKBvwp7X7auw/v6mmLPmuXh36tPb4JHPzGFdbfu8X8PYcpKgC8C1RVwbVfOkQVP0WIBCarVA22h+y9sYuQp0CibMbMP5oyGA4IMdKvO+qmQo8NvgxEAkWyNLLChYiKER8DUkkmoyE+BDrnqYuCi9MpW/tbQOLqt69TDCpC77j5h59QVSVSKZqywG0gSu2yx09XCCEJBITN6lfaKMqyeIBQNHrDNykLopJMY3zuKl2UCqsa6sNDYky4ztJOV8QQ6VZdVg2TiXaxRqvsOZJLW4nZSUe3PuLaL73O6b1jQh8wMWFSxJ2eszyfcrKzx1v/3q+glaBUniJ5ooBqUKJ0jVcCtZ0V27RtKY8sxlvOjk44vRAIobAuEGJWApNSEHykqAra6TJD5mLg6q++zfmlLXrAiwxnamcrTj6+S7QRu+jRKT/wUmeI2nq24vDGAWc3F+z/8g2E7glrS1j2GKXy6n/vICakllkwwXtkimAjaeOTJGU2XJWQhTRsrqwkKbDWU5pBrjAFQRIZnnYfdZogG5e2PSFFEJKiLLPhaWHAKbSXKBGIwZHalj4lTFVhQ8iCHkIidcKUDcl5dBBoIt2q3QggSGLvMu/F2mww7D0i5tX91guqwTZ1NUAQUVWBiwHpAnG6Rk4ahPWo0sAqJ0gCSDFmX6XeUWhDDBHd1Aijc4UKcjVKSlLbkaqCZHvUqMr7DzF7l9Tlpsqcpaxlo0m9R4SIahy19kSjqbdLCBZdgR4UJJcIqx6zv4UPkb61iKM55toewQeKG4fEzhLWPSBwwaJkTiioDCrFDCc0kuhytU/YkEUsQiRZCwOJKQ3JyCzBvupJfU6iCBGaGqkkujTYaU8PrEz2JBMrS1lXuGVPoRRaa5ILXNw9zwIKAjCKTiRSb5nP1wyHDVtvXyMMyyxGcjZnfvMY5xyDrRGrUiFEiY7/f/b+7FezLT3rBX+jm83Xrz76HXvvzJ2d005wpo8xlnwOOnAKoZJLwlQJQ0H9A1xwzQWXlpBBiGvL2AmohBAgkApxVIdjwC4wGNvpdLa7j3b16+tnN7q6GF+0OyIydpO4Yb+hiFjrm92Y45tzjPcd7/M+T+TV125S5pr1vWNCd44oU13hPATamGCmXjrKQYmIilnlcA9W4jdDqYsw21Bc95B0ukcMkbd+91uc3z0lK3LyTJMRCcD5csUseGzbsr1qMXWksRYQjC7t0RMSt6wYbo9Z+6S1tn95j7PDM2LdsnN5h939CeVkwGh/kqCgm3Hdho7KVjSufvGY/xHsQf3UR1tie2qjeEbNy2OEQi8+xYPq2xfv/LL7fbL99HIBwyN2vuetzD5q+aNa4x9GEPmiRdPnff7YMR/rYfjUfhj2IEskhOCv/tW/+vDzP/tn/yyXL1/m8PCQX/3VX/3EgiKAz372s7zzzjtcXFzQdR1Zln1i5/6jaH84gqIPM168xBj47E1PRg4CQb4ZxzWCbtVw8va9VKMgEt10VmbECNWiol7VSO85u3vKeVUz+9IVevtjVASjzGZpLSI2ZbA+xqSn8kTDn527/8G39IMmkGd8IMDIRN+spIaQBABvfuXzrG97ghcIFxgfTLj06iWyXkcMCkTEO2iWFVJI5hdLti8bEvORJDOG5WyJdZ6e2NT6BEFoIc8ytNAIrchMEjtVWjMa9qiqBu8DZVkmLRspWZzPeeWLr5D1C4J13Pn2bZbnS2zRJVpsrchyQ240RZkhlSKEkNjmMo33Adt2eBfw3kFM/R5DpK0aBnH0WLwaH3lC8bFOilDNV7zzjXe48tplJgdbXNw+QUuF6DyZSM59jJGizJnPl1y6uofKU71LPiwRWvHqVz/L6nyBrTsikXbV4DpLO10xvXfOcKePixItNV6mtp8dnjK+vouOMTFaBY81AoQklIaiMdSVTVpAQiCNplfm+M7RNF0SRZWS61+4gd4Zsdjce7eoufvtW9TTJbrIEUokx7yzWB/Y394h6+Wc3D7BO89qVeNjRBpDyKFZVIQuUmhF1Iogkh6R9y6t6scIQqKEwDtHpxQaCdYlqFZMzHVIiY6RKHVi5BOSEFMZEs6nWpt+kWo/tCaqhG+JnUvsZ0oiRWIga2MkOk+9WCDajmw4JGYaHQNeBVoBomnJpEKTYG46SkQQiK7DW4/ONcEIcA1CKZSMWOcoNnpFfrkkKmg7h1SRYBTCeVg3qZZo2RC1xLYO7TxmWCb2ts1NiY0eFzESG0vrPMWgRHSOsBHFRUBXtakuSFpCqxOt/LBETPrIpiOsG8gNZBpfLaljS365JAhNCA43rRHlCNGGTd8plBCQm0TE0M8R/TLV9IkkzKq0wiFQVZfo2NdtYhnMDSiFDI4uBJRMtWmqcyBB9Quq2RxtJGvvIO8TAe9TXaDqZeheD+8Ftl7iMhAeysZCqRKxRgSdJ8Y1HyPrZYWP6d2NrUdJCT6yOxlRlDmLt+5RjAcszmb4zrKuW0ajAUZrqvWSqq65vLuFGEi8d8Qs4qKmjo6OSFEmcodSK6yQtFrghEB6+VDEN7hHNR5PLGlFWBxPOb13mmr7dicMhgUuQhsC81XFeDSgso5l67iS9ajaDqUVs9WaytrEXipICzghUIz6yNMphU4Mkze/8jouOjwJYvrArE804U8EBJ+kLx2flwt57gFPqFE83kdP7cazZrHHoWBPmni49XlhiHjyii+wT66D4mal5uk2fZyw60O5Nj8w2NqcMbJZVP3wrfkh5vf+h7TDw0OuXbv23O1379596XOFEPjH//gfA/AzP/Mz3Lhx4+E2pRR/5a/8FX7xF3+RX/u1X+P27dtPbP84NplMHv48nU45ODj4RM77R9X+cARFL7LnvftPj1QvGCMen2AeKIJrAT9b9hhLiXVwp3OYfs7w+h7KaC7unFJPV2SDkv3XLxF94P6b93BVQ7hYUfz691F5xnh/xBs3/zRZL0eKKUa9CcC9Rcc3DldPNTc+WrKDR+KxHy6p/cz7expxYKThf7r+0xS6wCnB+/M+nRCo2vLFxbfoqgqTaapqyXuzFUpLXJeKwJ3tCF7hOsfdk4K7n/8pEIK2dujsGLusCM5RVQ0xwvBswMH6s+R5jg8KbwLOp+yGUopqVWF9YPfyNtWyplrVKCmRStDfHQFw9NZ9ludLtFKpJqnI6fULhID5dIWUAqUD1bohyw3d1OKcJ/hA0dswZmUanRl64x69ySDp7Dx8AB7v3ycfloujC1bTFWd3z5gcbOHqBiUiSkDdtgwnI4TRrB/oJFUNmhxbNUijEOM+UkuKXk5oO5p1y3q6ot4o1t/7zm10YTiZTLj6xhWU1jhpGG0rRN2x/XvnIASDa33+81dHNNWKrB1x6e1r3P/uPXCJytqFSNsmBz96hy5K9l6/zNbVHWIXeOOk4vzOGSdv3kW7AFJSGk3nO7rOMhyWCOupqpqm7bCdZXGxRB9M+O3vHTLcHeNaS9tF5rfu85VX9hn2spQRUIpQ17g2wefyfoZsLVFtWOo2MDKfa3RMNNdaCfAgrEMouWExkwjnk9aOS9TXyujEvhaBGJIwqk1Bu1QCvwkK0Ypev0/nPVmZM28ajouWqV4iheCVfJuiEjjrubwyXFY5toGzxTe5Wx+RSUnoFVA1+BjRUuCVQjnwQtCdLNFGYTIQxiRYXp7+DzFiejnOOcQD4oQIxFS3FzuP0OohbTxaonzAVh2ZEohRmeLyCMpIvBrSdJa8S2QA/mKFyA1qa4B1PtXuWMfxokSpEnmco6tUO9acgjkoEbJGtDbBGononRHej2hO5hQ38odPfHAejCIrcpzzRDbMgUISXUCIFIDqPEPGiG0dEJBaU3eStxfDpAOlFGY30m1ggUoIlJB06yHri33W1QG60XxmsaauG+bjiDsYUvT61Ms1trX0Rj1s3bJuEj21fgC1NILJ/Sm9dYd1niw3DENIixFFTqxqmm7K21e/T7bV4HoD3pqckY966DcM3/y1Nb51DEaSv/pXdjAmcnR3wX86GZGP+0QluRF2iEAzbbj/n46ecOYFaeHDW8e9793iIpNMD0bMtkvu5hm/FR1117Fa1Ly2DEgpKMdb1Is1Uggudvp8R3hM1uNrOzu44zl6Q7Gucs2Vz92gW7ep9il4fufov7LsFk+MQzFC69pnD/Ivg6R+kT0LO/xSx7ykPfDVnxF2PQ7aejTPvcyM9wfgwj+jnz8Q0omnnY4nFztTVz8Z4DyZWXtOICie7r1nh2NxM599GuD88bJ/9+/+3cMg6nHo3AP7a3/tr/GLv/iLxBj5R//oH/G3/tbf+kSu+zLP5v9I9gfPPvdh93k6AviI47wA+kIwEILFssGGFt96zm+dIJRifHmLeetolzVndcelL1zj+o++ysm7hyxOZvSVQvrI/NYZblqxe/OA3RsZmZYIIFPPuUHxYNh8HBzwcR7EZ6+oCQSFKshihoiCYJO+kJaKyzcvc/it9wmNxW+EW6MLIHKSfxQxmaatWowy1F4jtWJ+PKNZVgTryI3BGJ1WOr3AWIOQGt85jNHEjdinUpKmdhitWU3X5L0cqVqc8/TKEpVrFiczTm6dIkWCYfV6BW3bsZivUHJD+xsFrd0EOSGiEAil2Lm+x9bVnaRroiSIRLFLhIVffKBfHvXZxmKkXTTkWUa7bujqDo9IjFMqMaktlmt6ZZnuO8swgwIpJauqxYdANthAEWOkqTouDi+ISPavXaKpaqYnU3wMNEXGe989oussvbKgN+lRzVZ0nWM0HtD1Isf9C8zI0NqOrVXD/s1LnN89o141+BDp9QuCCdTrgCcy3EvZsOg80/dPUkBkNIPtEavZimpVI1X6jperBpMZqtmarrUMhj36wx6r6ZpmVeOBdrFGa01xaZs2BMpNvZAUApVpgvXkSiG7DStZjCjrN5mhxBIXQ6DbrJ6jZGKKi6k2KUByxIuktyM7l6B11qHL/KGuV6dlGpyUJKqY9IDqFqOT4KlzDhcjnYzUeDKlqbuO2JsQVg2y8ehSE4mEYGldk4gWYtK9EbMlTklCvyTapDOklQUcQZdI78EFsCB6OVrKRAARwWwylYSIiGBioBOCuu0ovEYDuswI1tHGSD4apkfOeoSW4EPSTdrUU4WNppcEfGuRmcGMesQYWHeOdtVgoqNp1ojM0HWRfNlgCoNSCrdqEEUifRDDApNp3PkSdXkLWRhUv0haQ7kgKEkIgWxvjCoymtM5+IAIaTIIIu2jjAIfCDYQgsJ5mWB3iwpvfXr3W0vwAdd1NHPHvAVhoMgE/dGAWiY4ajqfoakbqnWdmPxyQ24M7apm+2Cb4DzlrEW6hlJIhPVoEtFDoSSjnQkyExzJNzn1DbN1x9ldzcGPvQ6ZYBUDLgYkgsFQEZsKLSwrHLXrUELjOkdWZKh8o0QXnxwLhBCszucszxcMtgasRz2i0axjwLaOqm4YKE0PyXS+RPVTlmh/Z4sLDeO9LXZev8xeXjI9+v0Ndbimqzqu/tirD8eeQKD1LY1rHhuHnhy7n7A/IBiTeHxqEQI2tX5PTDmbnx8l35+cj/4ouO4PA5EX1FC91HmeJvN5wX7PdT6fmwV6cs5KH4mHh/zgyz4j2vsUHvex7fLlyx8qG/QiewCdK8uSn/u5n/vA9i9/+ct85Stf4Rvf+AZf//rXP7GgaD6fP/x5e3v7EznnH2X7+EHR4y/Wx17JesY5nh6AP449XlD0+CQkBba2RB8xUmGrltO3DumPStazjlwrzt45Yv9zV7n6+ev41lEvK5z3ZJmmXtbc/v33CW2PK28kVi4lPIVOnGE+RGyIT7ZBPGOQerphH8huPGOF6indg0ylFeJQeU6+f4/VyYqQa6afv8zg6ja6yJlc3UFFuPvdW9R1orwWQmC9p1fkKKNoVivKXsHkYML6YoUaFLSLOmV/tKIcD5hc2k5O8doSFh25knQbqFlWZHSdRevE9uW8x4VAcI5ok3aIyhRSSuanc4QUaKPp9YoEZfIhffU+kJc5Td2mlVwf8DowubzF9o09TG6YHc84vXcGNlHrdm2HdY78agH5B3tYKyh06kYdHPWioiwyPJEQPElnU+BjxMjE1LVYrJhMBmzfPCAQmd47Y+vqmIPXdmjXC6pFx+p0wepkjlIKbwPHd4439RYZWWZoVi39IlItksjrwWevII1icmmHGCP3795i8Lkx9WxJqXt0ocXoyMGPXsG55Bxf3D2nvmjJy4zLX7iOzjXNoubo7fvMT6ZIKTFZgul4n9jpFmdzhEzByaXXLiOV5NY336OuW5rDM7SQxBi5893bKBfYvraL7Bxyd0i0HrGppdKFIkqXiB+kwIeQ6tk2ekxCQAwRoRX0S2yI6E0BUQyBGAIugtaK2FlcaKB1ACiZQdOBUSDSs4CzoDfMb0YjQg9pPVJEnEjwVDZwvqhEWkINDtsz5Ej8BsooYgryo4C4rmHYI+QmERysKuJ4gMo0ssiSdpZ1iCLH6Y1T17pUzzXuITevbiJ3gM4lvR8VIz2VdIBCrvFd0gPqjXup70Ylfl6nALHtUKMe4jHYXQRC0xF8QGaG7ugCNRlgcsP6+IJgzQaSmrJY64slg2EPsz1ADktc51CtTdo9Kgns+ukKeWmLbGtAPF8mbSIi1kNsk/isVJJoEw1JcAFRGIwQiNykvs4zYkhkCTKSRF6bLgUgWYYwinbtsLlGFSotiIgk3qtdh+scIjYQI53z9PopaBNKIUJg59oeg/0JQsBgbdk72EFnZqNBpDG9HC8svmk5fu8u218a45YNUiYorykyCIKeFAQh6QmB6DwiJFhzWEbWJ3PKfk4MXYJEohj0N2Ozj9T1oxG0mlcoqdidjGhzw8nhCda2GA1lnqGCZbZs6GUm1TkVBVmvQElL07Qcv32Pq/1RIoPJDD0FsVmjfUtD0hiKhA8S8zy9tiWe8/MLDvmk7XG1iYcBEY9Po4lk5eHMtAmIHkDf/nD43E+34vElyfikb/HgXl56tfzJ/R7Xz+Vlz/MsN2Dz2csnB1/GQfoBkLxP7Q/Ulssl//Jf/ksAvva1r/Hmm28+c7+f+qmf4hvf+AZvvvkmv/mbv8lP/uRPfuxrf//73wdgb28vyWz8D26fbA+8zFv8Mu/fswKjZ/3+oUbdBzCJR4c9vgi2OFswunqZ5fEM71JGYnG+oG07jC6o5mvON4HRlS9e59bvvENwntH2mIvTKQY4enuN7fY5eOMqO+WUP/vamyDg1rzlm0dP0Sg+pzA1xk0LxVM5pMf3f7jC+WQHaKH5iat/Cnfeceut97jwZ2hjCJ1j9Du34HfeJ9vfIn7hOuOr25TjHqfvHTE7vGBdNQ8x1cTk3O7d2EeeLLl5tKB3bQex6FhoiXCSsswJzlPN1/SqNgVi1pFlmrZ1+FWN0Rq9ocQe744YH2xRLytmR1OUVmxf2QHAdg5CpDcoaauWal2jtSbEwHBrQLWoiCEw3p/gYuDy61cwhWF1vuT+9+8iI8zOF/T7BcWgZHoxpxiWDHfGsOID9toEfvZzEL3nvffn/OdO4oTk8muX6Y37HNy8xPL2Gc26xsWIFIJer0AVJlElFwb9ygHavE1ZnEGzJvhrFMMR1dkCrQ1r16KzVHC/d32fLNOslzWCyHY/CdouzmZUqxrfWQbbY7aGO+zfvQwCqm7Bm1d/F6Kn2B2hywwzLFEzw+fe/2LKwsTI4ffuMTuaAmAyQ123KK8JrSWEyOx8QXCpnsYUBtt0rC6WRJFqwHxn8SqkTNl8Rb41oNgacOf33uWVQcawzBFEWh9QyKQDA9iqRWxILZRSeOcxOmVQggvJ4d84HVIngVU6l9oNtHbBveZ3CU1LyYjL/a+kR895aC2yyFiFU6bxfWSIiPWQvd4XWHeWKRXToWPWdlQhYDeU2ff1mnPTkgnJZ8WEYZtU5J0EZxTOegygF2ukdTRao0WC8dHLcEajVUzZD5vqmoRIpBWqXzzwmwjOE1ubMoMCimwTQBgNnUVJidmf4M4XxFVN3NQsRbmh7peSuKGpV0oShSa0DpEbbGOxTUu+jongYthDZhkuRvSqTtkbo8lHPURmiJ3DjPv4o2kiGFESURhsBFt3qHWDGfdw3mNnFaFuMVrhq4ZMTch2R7jpmjBfplqiPLXVeIXMdBJm1ZLoPX4TyAijCG0k1B2RjAsj+N64T9YvsK3Fx0C0gbYRKKkJuUYIQe4C4/0tyu1BqmWKJAHctqOZrtCZpps3NLMVg+0R/f0JaMF33f+P4/Yu1dWW+cmKyaDHommYOEcMgVJo/lLZJ5MegUf+lyNUJpjUBde+cxOEYbAjGY7fITYea+d84f81wRSG997r+Of/YrpxZBM0EGCw7ti9f8aNXklRVqyn36RpO/BXQVwnINgZDQhSUDUtcWRw3lFNa+7enbLdBkZ7E97oHbE/nGFOp/yrpuJoI/5tvX2mT/oEP9hzfNYP68J+pOnyGQd+8PjHAp8HqaKHjfuDyxE9cEPiZuHiwWfw7PjjwQ+bZNjHNPEc2aZH8/UT25/+bh9m2h4teD59vqeDrY/e08847ocdaX9qz7R/9s/+GVVVAfAf/+N/5Gtf+9oPPOZXf/VXP3ZQdHh4yHvvvQekgOtT+8NUU/Si9/pjv6TxhecIIa1kd8s6QcZygxLgW8g3wpAmz7g4uqAYlUyu7XL5javc+f33WU4XbO1vMT+Zol3g9NaUGDRXvmDIiwTn0vIpqNyzgiF4KpP1ggY/KkZ67Lzph1h5zt48Ig8KS6TXL6mqjWq9C7Qnc5pru/S3hizP5pzcOkJJxbCfCBCs9xiZIDblZICUiRGryDTj3RHZcgER5rMl4XxOphXbQqAQyZkyGu89eWaQQLdh/VrN12SZQZUZr/34Z9CZQUrJ+myJlknLZLVINTtZlqG0TM6nDwy3h5hezqXPXCH4wPx0xp3fP6GuWrRWGKMoNwxevrXsXdnj8uevUev6mUGRktAz4IInNwIfIsFb0DJRVvdyapF0d7xzDMcDWuvReUZTNZx//zYiRG78WKRbL9GZwNUNIfaSNlTTIiHVikRolxWyyOiPSqplRegsZa5ZHc4ISnB47wJtTpOAp5RMLm0xen2I2SpwTY1zNd46Vucrpt+co84zBpMhh+/cxzaWrf0J/WGP++8doo3GGE3jOqQSRJfquoKLjLZKTm8d0zYdWZknZr9MI2IiHIgx0tsa0NsaIJViOV9zaTxIorpaEaUkErGAMAk+ZiIpS6MkNVBsICjapMyRCCnIkFoRfYDOgQBPxNkG31TkvQGqzImdI2z0a2RnabuKSi8pCk1f9lACWu+Zm8Csq+lrTScVziahWGsCwVnIDJV1bGU5befoiVT/E2MkKzOCT0xiuszIAkn7qPPoMie0Dhsdea5RLvWfNIJoUvZH5BkqS9kQAFY1yECQAgUEBCwrRD9PdOZFhhyWdPM66RYFjzAGkWnwSdtIGZ1qxlqLbC2hl6fs16JGdB6vFVmRIZoOaT1qZEBrnHXgPGZ3hMkzovNEo5EhovsZMusRQkzEFiHilcAoie4XtMsqsdJ1lrCsiJCILzZjj7IOH0j6RTGAFMSqRhYZDqBNjHYOiEZShzS+nM+W9HoFEtg62KJtOqqmSedXCml0CixtqicLPnDnd95iOV0SzmuGbdLnye6dsTdbcelPvkp+MGJ9WrFyLQhYNS2Z0oxfu4zMDaKLFEKQb84nA8goyLRh99IBXRUock8mNuOxUejY0evnFMWTHmoxLEEIMqWQLiCtZ+fGmMtXb7A4ucBzQFvvcn58DvNzjqzAhoDs7yOMZOvyDqOLFnWxZu+1y+yZll57Tggdznd0m6Do+QHPU178c+y5m58ZaH14ezhXbeahH3SOD5dzePkcyIc/y2P1S08ED49D+h5r7QPq1geZmZfKEr0I1vLBfWN8cN505R989+LRfy/15X2CGZ9PA6I/EHsAnfsw9k//6T/l7//9v0+ePwMO85L2y7/8yw9//nN/7s995PP8cbKPHxR91GDmecf9UF7KR4FIoQqEkBjAq4LWR9SkZKK3Obu/xDuXGJOkeDgoGZkmU2cUd++cku2PGexPGO6NWZ0vqBcVe68ccH40pes67t4/w4bAq18QmF6GUAKdyk4SrbBtX/pWn0BUPBq/6W8CEYg4ldqqhGR5OKVrLEIr9vYnqfZltiQblEyub3F2dIbJPPiK+d374CPDUY9l0yCEwJDwzlJK7LpBaEV/b4g0iuH2gEsDzfxwStNZ1sFR15ZORNYiIGLEO0c+7iVNHMAJgdYSXGR1OkcYxfJ0zuhgQq9fcHHvjN7WkOpsiY8RoSQiBqzzGK1YzdaYXsbnvnyTZlXzzu++g206iixDkYrwtRQ0XYfRmtY7vvilS5SlwDbdU524meCDIHSC0EqUyjckDobh7ohIpFnVdHWH0gZNpK5afIhUyxrfOjKjadYNrY8IJMpoepMhzSrBggY7A+Zni4dxbVu3NKuacDIjxEjZL5lWa7I8w7UOoRQmMwSgWTfMDqes7IL+/7qFFTl2VaHGhnLcw7ySU729YnW+TJnKcZ+d63uc3T5BK4VWgugjZZnTth0xBoiS/riP7xzBBQaFoWo6hFJ0dYsQAh8ThbRtOowx9PdGOOtSpjTPkA+KgF0gaInSm0ADUuAsBX6xppOCzGgsLTEEvE/1SNGDaB05WaKyN4rMG6LqkxWJsjtICU2TSDi0RjoDy4AXimJvBxNzSucocEhT4KTASPBSkEmJQGAyjQKsrXFaQvTInkZeWESvSKQNSkBuyDINmSFMV+neNoX9WabTfgi8TA62BITS+LZDGk1oOtSgpMizRLKxOyT4RAUtZYFrOnyICBfwqwb6BWFZpWGoyJCmSKyGdYcPgdimgNBVDcp75GSAGBSEeUUmBcoHsp1hgpDOK0Rm8KsWS0CWGUhSrVZTEzKN2h7gqg4zKPDzCmN0gi7mGr3VR+iU3dOZwVUN+bgHoz52viQj6UihdHKKm47epQkxNyl7tKrxkwEygFs1RBUwhSaKyO7WELQmeI9rOgZbQ9yJo/WOtmo4u3VEXmRJo0okopXlxYLCKAaDkmEeEd7jheD86ILRxR75QZ9xsUVOSxMr+mWOGpaorMCtHZ0NLIOnDQG0wNVpYlutOmpbQ5FR2zX9oUNlEqxgtnDEkaB2T05E44MtTt+6x7Lr2Lp+wOnROdV37zHIDimGfbau7yOXQ/z9U2qdkZmIbVu6ZQ2FZLQ1pMwysqzj6J37XPtswIUUhPtnrmQ9Y6B/6uPnIq2fZZ/QSn+67oeHwD3IuH0A6fDwvPG5nz8r4/EInPfguEf7PLtLnvfps9Mz4jmLlJ+cPfaFPMQjfogLiif74Nm9+uiznhDozeZ1jPhPg5w/9Pbee+/x67/+6wD8jb/xN/gH/+AfvHD/f/7P/zk/93M/x3Q65V//63/NX/pLf+kjXfedd97h7/ydvwPAzs4Of/2v//WPdJ4/bvaHJ1P0IvvI+f8nTSL5k1d+gmE+ghh57+45p+8cMtwbs/e5a4jBnOndMxSCZlnTdZYoEjPV0lne3MqwPnBydML/fP0KOzf2WJ4vaKoaeS4pX7/EtxZzQgycVR3hd/tc/dINzN6A/VcSPfbq7vdZvP97H2kcfjAtSAH/l7Lk0qZw/WhX4XNJcIJ3/ssKbRTKaLau7fLWb30PJQTb1/fYf+0S+5/Zosi/RXQdubxNUb5B7ZIWTQiBPM8QxE1B/grbdJzfO+WVr7yOOJvzaowMxhPePp/xbilYLVaclIpDU0IIKK0RSqKHJQJBVBKhFZcvatTFmlGZJ8Y2H8mHJa6x5GWqP4oxYq1je2dEVXd0VcNo1CcbJ+au2fGUaD15nvZXSpEpRVN3qXg9l1y52uNz7bcRp4HMO57k80m97peai98WaJ0j8wl5HjD9knJQAoKszHE+MNzuMTudURYZKAEhsF4kRkLTy/nWyYzlbIUAvjx5FTuv6E0GzC+WZBsyAKMNZZlTVw3KJE0fqSW5zqlXNYPJkLCqkELQ1S1aawbDHqGF6l94Xvn8F/BDy7vNt4lUDHfGZOOC1fmKQb9k95V9qsWa1WyNjBEhFW3XkWeGLDPYLtUWmUyznq7IM5PqQ6SkazvyXp62LSoyrXHrlmqxZrw3od8lSKW0Di9FqlvZ0GT7jS8RBMg29XOeZ7jO0UrPvdl/ouuqBD3bEG8Y0ePVrZ9CIjBOcHX8U4lsQAg6QEiBzDRCa5p1RSm2eWX8pynyDFqDHGjyXs4Vq9j3Q9ractbvOB95QojkmUELCSFwdvY9nLHE+Rq5lzJf0TqiVkSjEZ0lNDYFeS7VuImqQ2caJ6AJoGVymhIdfUR2DpWpVJSWKULbkZWGUHfYsyVdiAgiwUUwitDZBMELgcwndj0VY6IcXzdEKUBIXNshtMROK7TRtM7j52v6V3cIszXKR+QyERSo/QlRCtrjWSIXQdHcO0eXGbFuIc8IF8sECdQShiWyl+PWDeXuEDddESKIwsDFMmW4yhxXpSCWuiMUBmk0XomUQfMBdzrHbI9S/ZH1D0lNog/Y8MilnV8sKPolupdTrWuaw1TX5f0mmM4U66alazp6gxJ3eIEuc7xR+LrFug7fdujM0B8PaGcVVw5f5fLWK7SrNbdeeZM4AZEZ7v/GMa5KNWnvPeb9ud9yIASuqZDFf0RIyeUrGT/+M32Ujpws+/yb7zhGVUZ9/mRSPu8XlJMB99sWe33CrIiUx4Iw3WK6CJyerfjMV68z3p0QOk9fCMajEftEVBswt6a0UiOMZnxpm19r3+OsWoEA+2AQ/zA+8XP2feGU+Ak5+R9ruv0A6cBjGbDnwsue9al45vYPBlHPz5a8jObRE/f6IiKEp8/zxH0+/a2Ix3Z7Khh8iizhBzcsvqD5jzb8z8bwapYTgH9VV9z3jh/8QLyYHv1T++Ha17/+9YfPx8///M//wP3/wl/4C4xGIxaLBV//+tc/UlD0O7/zO/zcz/0ci0Uio/q7f/fv0u/3P/R5/jia/KGeXfByA3R87O/zjv84I3SEBzpCSii00LiV5ey9U5TMOLp1zv1vvU/Rz7nxldcISmCtS3osEcoyZ2dvGy8EItPML5bM7p1TjvuUwxIZIt26oWtTAXIxGVAMelTTmnvfvk89axHSIFWWCt4/oomNiwaQCcgQiKajmS7QUtCeL6nmayKCwd6Y1fmS6CMqM4wPtgBQWiHwCBlQOmGulVYYrTBKM9waIjNDr1/gqo6u7rAbh6k3KJndOiEvDNvXduiP+/QHPYKUOBEJmYYiY3RtDzXqYx84zs6RCxLTWWeZzlaoTd+a3LA4XXDls1cZ744ZDFMxe6+fJ0KD+Yqj2yccv3uI2QQa0SdI2HBQEmOkqWsyo8mMYrA9QEaHih4ZU93Gwwll8zdGyLICpQzaGMqtAauLBdOjCyASmi4xuE367F/fp21tynpYh/cR21ouf+EGxWSA25BotK2lGBYQI8F5OutI6p0RZST713fJyxxTZPRHPXqDEqUkq/ka11p8CJS9HIjMp0vmFwtCHZjfnuJqh/UeO13h1w2Dgwk+eIp+AS4wP5pRFBlFL6eziaa8N+qRF0k/qzcsWc/XeOvTMxoCbdshBAzHfcb7WynjoQT1Ys27v/MW1WLNlS+9wnpdE2Qi4sgynUgPNs+glIlEI2pFRKA29NWxbXFtA7ZDRUf0FlyL7BpoWkLdIuoO2QakNHidgZaYEGhJNOhRQLAW5wU2CKgt3axCtI5CKYoAwzynl2UYH8k3tN6uapEIhBJU8zlhuyQ6hxwUmL0xsp9glmp7AGWGzDRq1EO5+BAmlgg/MrSATOsN855JWTfrUi2NT/oyQZBIJ0gU7jqCLFMGUGeStrOpf5xH5IZoUvYlVG06R0x0613VpOAxkoJZ61jfO6dTkgponcMuKta3T4ghkpEgv05LhJQ4F4gkkhNRZBCSZpWdrfGtJdYd7nxJcAHXdMSNgG9w6Z6DFLhllejQM43M8/T8+pDqxLzHtx0h4RAxk366Hx8QKmlWuc5RFAVlluGaDqk15TjtZ8oMnRu8D0RAK0mzWFMt10nvSySqe0nkyutXOXjlEkrAxbuH3Pr336Y+WtLbGjO4uku+PUjPmg0P/7Yx0oZA3TrqLtJ6aFykbRuC8Pjo0LnAFIoYA0EoqlWHdU9OLFJJbvzYawQtuX/vhMo6hDJc3t5hd7SFbR3BBz7z0z/ClR97jb3PXyffG2N6BTHPkdtjrn35Jte+8ho7rx5gBXRA9wDB/bz58EP4o8+bLp/c6SNMmJ9QVkGINF6IJ86ZWiw2f9InTy9XfVKNe9a+jzI2HyC5+Mj2Ufs4PvXBs8/zbHDei6E53e376M6Si5d37uJLO2qf2idtMUa+/vWvA/D666+/VI1QURT8xb/4FwH4t//233JycvKBfbquY7VaPfx7eHjIN7/5TX75l3+Zn/3Zn+VrX/sa7733HkII/vbf/tufZokes4+dKXrkIsEfSkBqfOI/IFE2H3/vDr0sQzmPK3Mu7l9wdu+c8f6Y/dev0C5q6CwmMyitkEbRd5KmtfSl4uT9Y3qjHpODrRSIxIizqZB8NV2yPxigM0O3qLj49h2iEQz2RnghiBtK2NalAvaXv5UP9m9WZAx3dmid4OLuMT6MEN4z3Blx/v5xgiIZmdi8YqLcrVUflKcthnTHHX2TERDUzjI9npL3C2rvESpio+faK5dwraVZ1ogYOXz7HtmfeA3tOqRWSOdRYVMvEALLszmT/S3yMmdxdAExEEVA6cCgzFgtYX66YL5Ys311h/XhlOntE7IyZzjpI5yn84Ht3TFN1dK2lvvv3Of1r3yGrF/QLBu2JgMWixVda9GAt5bezh7lzojFQhKcpcs0W5UAKbFElpvJsIuRixgggPUd169tU8aGYT+9DtU8FTyafkGIqY+FSNAyFyM4SdYvKF3JwAywnWNxf4r3feplk+ovYiQKQVbkhBA4O5zS1C1SKWbnqe4CBNE79q7tEYHl6Yw8Mwglk1MjJat5hT2xtLFhsjumO7ecvHfE5TeuMb93kVYaN1m+IAVZmaXvOUSqRcpAlb2C+dmc4B15WTDaGXF87/Shg3L03hFFL8fVnigE0TmadY0QgqZucUWBKjMkgqAVMsTEWgaJulqmWhUvBKVWxK5DxQKVZdA5hDFEQKkeMjdED3EDF1Q+IJqWkGXYmNi5dNttJupAlA1tW+NVhrHFQ3ggOgUX2nVoGlQXiVKC0ZhmjWoatNFIHwhCYLYGROuQMbG8IQT5pS1C02HXDbgukSOsGkII6NwQfEiEFdahrEX5tOYcvUdIknaT9UghEK1N7Gwx0m2elWhbpNTJ7QkbFj4lkEImraPE741SBjlbEdebgM558o1obp4ZTOeI4xxXNbQhUHQeVBKWjT6xQYamA60SQkcpopLp+Vo3uMYiMk2sW0IXCFLiO0fsLGbTNm90qn2MEd906KIgGxRJpNU75KQPxmwgsRBWLbFzSAG2apjZOUpJiixlxHNjaJqWLE+/L85naKMJXQKRxSJDD0qqiwXjsmB8aZvdvGQSBUf3TqmXNUZCZx0GSfXNd7kcX8G8ms4XbMCUI8AjRGTEChE8sRAImWHrDtl/oF8GfelYBYMOkqBgWC/IDDSLjr1eWiefZI7Mr8kL+MJP3GC1mtNMV7CytFbQekd/lDPYVmSFI14qaH0gu1ISXEjC0kYnWnMc1lp8cM+Fhn0UU8BYJtmHKCRWlURScN6p5AbLEMk2bKcyOExIcG0vwW+kIpwwWJlv+rIhdO0n6Be/IB32MGEUH4YpL3fZx7Iuz+zPZ8Pj0m8fzDY9nct54ogPodXygBfpMcTgB6//+PkeLtB+SHupJgnCjavMNvWb9iV799Nw6A/OfuM3foN3330XgL/8l//ySx/38z//8/zDf/gPcc7xT/7JP+Fv/s2/+cT2X/iFX+AXfuEXXniOL33pS/y9v/f3Pq0leso+EfjcY6jZze8PVoI2/z43Xf50iv1DXeSZMdizB8xHOwYfaJsGu04QI9+29IucMs+ompaL+xcopdh9ZZ+7371FlmfkJsGKvri0LFcVg15BvW5YHE3JenkqGA6R6AO7r+1z+NY9lhdLro/6NOua/GyJ+U9vc+Vz1xjtS/TrEwC+e1Lx/bP6JW7+ORYjMQpc/CKLi8DxUSQvCoIU5L2cZt0gY6StWhYnU5RSyJ0+7+/9BEEK/I9M0fe/xWpdk2UZtuvo5Tkz73h/p0RIRb8WfHbcZ3E65/Dte2wfbDM/mTFa1ZzfP3tI1xuFoDfqk+eG+fGM43fvM5gM8CGgpcBtWXzuQVhyYVgdVohakPcLiu0B1apOwYSPyNwg6w4hBOWwpByVVFXL8btH7F/f597371C1LVXdMuiXRK+QQjK5us0yg99+HWYnc964dIW//HtJu+S2d/zrpiYCd7znn1SJDfAL9h5/ppjCpchcFJwyRhhFv8zp1g3VYo3zYeMEgwwiCY8Cn9/9Im/sfIHD799hvZzhtQcfiD4xzs3O5qyWVaIwz3SCUZlUNO+DB2dRRrN9Y5d7370LpMJ+H1J9i5Dpd3c/cunwGpO9CTIznMdztq/tMt6bsD5fspyusM6jlWTn6i7Toynr2YqsTHC22ekca5NI6NaVHYpBwbZ1nNw/Y3YyY7gzRAqJWzeJct0YTJaxnq3oTwYoKQguoDbvnbeO2EWESuxzQStyJYjWI0Mg6IJXt34yZVqNRmiJ9CkIFS7ihEgscyT2saglSsokCNp1CCHJM8Nxfcp09V0iMM6usF9+gShM0k0yGu8D2ek9evIeKkSigK5uUSGiBYhBiV815Hsj8B5/tgClkEWCcIbWIsscuawJzuEWFR6BjJEQu/ROK5XovBsLg5JQt6AkPjOJiluKFOCESJACgifUiXmQukblaahygA6BqFJfBCkQtUOMFFhHXNRItYHmieTYeuexRsOmTirPMrJN7VeMIFwKSAGElAglaWJErhpkv0CLFKTJDQuiEJJIghoqH+h8RDRtgrNGEsxuVSe9sJAypjIminAzGaaMsQ+JjjzEdE2RAmIVAkFAf9xnvapxTYcLnrpqCC69g6Ux9A92WJ3NCaWmWlS4ztJ1Fplp3hWB5XSOywK9N/aIzpMBbxxXqDawvHNB8a8yrv3ITWKmqD7/ZTopKWj42fhvKPAQU5YwuE3w5DxCes685D/c7+OFZKta8b8tD8ldRhQC/UWNLjL8/ILu9n8FBOJqyfxrA2594110rXDn19m6conh8Iwi+z2MyXnzYs3b549pDX1gtoEQ/YsDoh/ktz61fSwl/49eDyMErRlyZ/vHCRGWSvDOVmK1HNvIzVliBB00J1yafRuA9UBysZWm/KPiFW733gABy1u/z/L2t1/QiI9oH7gv8dRPz+uZF3fKx3Xin03AIPhgqPRs+wAU7mXtWcFQ5Kkg7ClPavMOP6tLngUL/A+2RWxqlj98PdGHxHZ+ah/bHidYeBno3AP7M3/mz3D58mUODw/51V/91Q8ERY+bUorRaMR4POaNN97gq1/9Kn/+z/95fvqnf/pjtf2Pq33soOhZ2YuXK8/8EG/ss8aq5xz+gWE2Lak9zGd562iXnmxQUFcdWumHMKCyyJFScn73DCklO1d2mR1NOW27hImPERUC2jm0ECzPl9y4scf2lR3O7p5RzdZk5VW2r+5i3zmmqtdMdkYs5mui9Rx+5zYqRravPIAYvHwXPPtmxQaOJ+jWFmEMqsyRMaRAzXmiVhADd75zCykEk89do9sfgJEUkyE3/6fPc/q9u8ynSwbDPtHHBIlTiU0ud46L++fsv7IHIWA7x+s//gYnLjz8DjxptTk6Tz7qs3Nlh9nZnPWqTtowIaCVQCqBj6kwX2YaU2hW5wv6r19m99UDLu6e4Zeexln6vQKTGy4OLyjKnKAE5bhHtayQUkKE0XiIiAHvIN/uUQx63L9/i1l1RlWvuPOtt/nx8z6DnfGGlOLRo2Pjw1wEMvoN3CMAiYGqPl+yvliSj3qs5hWutYz3R9SLCp1plJIIkQQtq7MVyhi2D7Y5vnuKloKiX1BWLW3VYH1yhstRH9e6DTywZL1hxuuqLhExhEAMkJc50mjWqypBIKKivz0gOtC5YrA9QhmNbTqmZzMgafEoKZkdT9FK4iHRPWtF5zvyPAOZ+lBshHW10bg21ZOtVyt8CGztTlgt1wx2hvQnQzKjifM6OcLWoxGgNZ214ANL58A7lMnwkERZG0shFLqXpWxKCBAcQpJoqENACknMNbFLNWXCOkJhWFQ1RoqUfdISbQOdFHijCF1iW6MsE/GBBGU0qnHIXo70IQVZRiNDEmQ1wxJ7NkcoiewXROsIbUcMhm5RY3ZHoBVBSFRuUE2XaoGkSqKjhUnBkQ6odQOtJRQZIVqiUQ+fK5EbXNMRfMQoCc4SBz1C5/GtQ/VyvEgMdcQIVYcXKfh16/aRPyIArfBNh3SCqDU6N4lJ0PrE3iclItMEIZHWE6NPmSityLTCbZjqKLL0rmzY/+jlKVASpCA3pOcGIuWlbXCeuEqaQlECPuCkTG0OIJY1oXOJobE02FlFFAIXAvmwRGqZasykoN8rCDHSrhpkrolKoiP4LkFBYxPRUjIYDRARqtM5pycX9MqcrJ9q+oqiQDpPLQXbUnB674TxZMhod4mVYMUWLQGdOcxQYDaBcRLV9Yk5UEp8Z8kHfXwUG50gQdnLiK1NwWtncU2LcCNETIGVxCNV5MaP3aQ3HnB1dhMhJX5ZIfUcQSDEgI/+g+Py89BbH9jv5Zzwp00j0BG6zlMdL2iWDTMRWNyYUJ8vEUVBLPuoIpHRqJBqZFQUm0A5QV+F3LANPs5b/Qn4xA9kJZ7O1zyVjnnuJdNnL+qbl2tkfKINzznmmZd5UUc8+eV+4LDHvJ+n2LWff9zjp3hsPyEeBV/P85aebunHI1b4NCD6722/9Eu/xC/90i996OOklNy/f/+Jz27evPkJQkOT/cqv/Aq/8iu/8ome8w+7/dEgWnjcPsJ3PsgGKKmRCJZ3L4iLyM5rl7jze+8SA/iqwXuPkYneedAvmd4/R21YlPAxOSBSoFRyRmwIZJtVnK1ru8yPZ8Smo37vhCuvX2J+ZwpVzXpVM5oMmJ4vwDruf/8CfGB8dYvhMHBFJ4ri+dyzXj+C0r1wIIxw/kDcNCZBzHLS5/qXbmIyjdQ6DcRCEEOgqVr6vQKhJWdv3+PudIpXgnGes1/2uPxjrzI4nHJx55TWJQd9mJV0LtBXkaLfkRUt+Y7h8K0FNA1zIrazm5Xi5FSu5yuc8ygpCSGijaJrO0IIrNtAoSQ+RIyQxHFJS2Rr0OP89injq9uYYcnseEbbdHStZWd3gtbpe9NCElqL3dTCEAJ13TAaD0Ao9FXD8fltOpbIxpJHSRlEKq7n6cW4R5NlHSPHIfW7dy2FXXDlUoGOE05uz1m+f4TUGq0VzgZ2vnCD06MLqkxRRIjeU9ctZVGwWqzZ2p+gMk21rKmrNgU6MWB6Oc2yRilJiDFRc28gLtPDC/au7HB672xDixxTBmlnTCBp2chMYTuLGmUs5IyRmJAdZFzZv0Y9XzG7c0ZpI9V0SbV09Lf22Lq8w/mtE/rDXhLntQ4fAs1FxfRsjrcOKQWL6QKtFB5YLWvyYUlXt3jZsFieoqwjN0OEVkS/gW5lBgGUShJVom1/kOkzmSGGSGgtMbRJqHMDLQshIkIgZInq3jlPXNSEGBDrBoPAxgSrM5AySgK8afBlh/UB2zWENtGEoxOES7QJLEIISB+QWhIbS1QSNeghBLh1A4sKtTcmrhtkBLxPcEURCasaoRR6a0hoLEoIQmcRgI2ATpA1KZKDp7VKwqutTeQiucHbFKA4RIKXhZCozJ3HAyEkQVSCJQpBWDXgU1ZQsOlHrdD9IkHibBof5KBI9XRaJciidYkmXEuUD4QAwgd822GVwmWGQqsUHMYU/CTSE4lREmc9KgbINN46jPPoUZ/YWLrDM2TTgVTIGPGzNbHpEBG8DzgpsBcrpE76Q4TIeGfMYrpA+Ig0KtXeiDRg2y59D5V3uPMpSkgKpdFSU/nIumk5P59jyoxoFEIrsrqjrwKt88RRj/l0RZdpiht7vPmdd1nWLfN3+gQpGJeC5U8VhKIgisiqWxKQxKZj7JPGWZCKkeqwraUMLbZqyUzS1WJgcI1lfX+JCoq8XxCio5mmFfcgA0uXCpJVCTYKaBytCy8cp59nMT5AMzwdKDzDRKoN2ZESCQyUYWqGrE9mnJ+fczo6Z1VZmkLh1gVnh+eIICi9YP+Lr9B5z/LemrxXUM07pBxh+jmLo4ozcUR/MkDIHD3YephBedAk16wJrv2Qd5cCmuculcbHMzXPhhV+GKjhIza7Z53nZWzzDX6AGOLhBZ67GPs0cOXBJ+n2RDot8TmIlueEe2JTFygee7Ke85i8KM/2vL791D61T+3F9kMMij7kdPHxF4ae0wrBly99ha1iG9c57t1/l2pRsWU91770SmLhqlvW50ts1VEt1zRdcoiicxR5hnWO7Z0x0mi6tmM9X1H0CiYHW+T9AtfYNGHZwPj9C64PhrjtCWfLjnpVYzJDkRvs2uG6bd77VmBvsceP/t92+N++fATA//5vF/zWf3sk8PqspP7j2/6PJsE2lJD8qRCo7s24+849tvYmdK3l1R97LVElO1IWrCxw3qNi5ObxalPnMOdYKeaDkr3XL/PKT7zBxe1T2lXDZG3RRQZxSt+8SXMC9vLnePdgyNvLBds3D1DzOdFHdi/tIJTEu8DifE5rO5QQiVEOQEpuVYZTaxBGIUqJGGmCFLw+bShDJNSW0d6Y8f4EQVJKDy6gjeb8ZEo1b9BaMRr1kVphEFSLNd26ZfKlHc6/dsK7v/MdJlpi0Cit6Y1LemHwAhSH4D3veL9ODFZfcXf4mfYMgMH2TVTvOm/95rfplwW2c6znFe0w4+LgGm6vx415y7CGzGjqddIS6uqOg1cvMT2apSyAdYmQYjxgPV0l9rwiT7TUWhBiYH2+pHd1hyuvXWZ2MsM2HdUiUXYPRj2CEAz3J5SjHu24wV3ueD9+l3IyfHhLozdabtxNbZge5WSjGwgpE8QzNyxmK+p1zdu//SY6MygpGO2MaduWalmhywJnHb1Rj51XD8jKjNP6e8ym30WsO67t/BT9bBtdJLY1bXSq15ACFSCqVGuEkikokGCkxtUt0aUAgM0qvosR13QURiUq7g0VtiQ5BcpoQoy4EFK2xijmq3t03SlapQDDhnRtoSVKSbxPdU7CR3y1JvYKVG6IVZeEqXKdWNP6BfFBtsVs6n06l4IQ65PorA8Im/ah6YhKoSHRxcsUaEtpEntdphLczCYIqTJJOFe7RLNN3JAxx1S3E4AgPaJzKXDTaeFAxpgcKJGEXUPTpSxPYxFlltjefDpnlAJVmhSESkUIFvp5CtiajryfMmlJjFlgrUcHiNESnEeFFLi6kGqa8BF3MsfNk7grAcSiTrTgQuKNTpmUlERBSknMk5ZY6xyml7O8WBB9oNvoXakskUtopdCZYbVYEXND0S8ZTIZopeimS0IDxbBEtQ7nAzakDNZnZw0DOjqtef9gwCIHuzYc25p5HhF5zmdOlkjryI3h+9e+Qn9vTO1qfuP2v8d6y1Zu+L/vzhDO0RsY/vT4ArtckQ8KYm5QmcaXAvGj2/i6I9uvCN86Qu+OsYuc2//HRXJe4x0eOLmIuMlipLwyAjYL+o/G6echseLjuYsnilCebxH6UvAXyx45gkXW51+o1ziVc9RliYtghjmttdj752ip6CYl37Oed07OEhFN8Tn6ecFg3XHtG5bB1oAT22F+1HDx1n2U1njxWXZeOSCfDNhI6jB98zepjt57ztj5bEvxwAaZ8YyJ68lbfjJ7/9Gm+Sermp/Rmg9c4SFt+LOuGR8LKgRPzBUv487Ex/55cOjzPKEHLXoIx9scIMQTDXnqVp7sqee7TeID+z7TPkpU/6l9an+M7eMHRc947/7g37P4GOOlQJCgTrM757TLBu8DzWyNzjWn90+59MZ1rv/J17F1h60aqkVFPV3RLBvaukUKwWK6RBvN5PIW+69dQmiFkILpnTOyIqM37OFmS1SMVBdLdm7sszqeYduOxcVmlVEKrAtkRnN694L5fc+1r2za+RyqmGcPpkn3Io29aY9iUKaV3NbRrRuadcPBa5e5/e33EUJQbA1Yns1RmWF3ays5ccDsZEqzbqhna4a7Yw4+f22zcJZqpKItwM1olzUBuPLl1zi/d8r86AKMJDqbrj/uJ/w+cH50jvWO8c4EQmS5WBGcow6BMipcTPUKWZlTjHo00zV63VCMSm5/872k72IUW3sTxvtjRle2WE1XzI4uiCQNHtt0mCzD+eRw6p4hKh7SkSMl9nyNazNUmUSixIPuEk9OKg+elfRfeMgK5pxDImiaLkH+BLSNpX9zL/V/iBy+fT8V28u0LuesJ1iHNoq27SjK5Gzf/u5tskwz3OqzmleU/ZL9Vw+YHU5ZzpasLxbkhSbLFL3xhNnZAp0bmqajbVqG+0mg02pLMSqwbZvqFYSgWddky7Siq4xk69oOzhdEYOuVPc5vnyZxUOvpD3sPRUxXixTcD3ZGNKsWk2esZmt2hUAXWVqxTCRlaCWTPs8Gqhd8QMmNexgjUipC9LjO4jefp6ySRMiUxUBKhE6ZheAcTbURuVUJoqVkcjyEUnQ2aSoF55E+kG+yICJLNUqhcUQhIYqU7bWOqFKwp3KDA4TzqEGZCBPWTcoIhfjICQkBETbiiibBaOO6TZ8ZRWgs0YYUmGQ6sa2VOdL6xHQXAmoTrAgh8CEADnc2J27ESYUU+BhRvRztQ4L0dBapU/bMdw4ihA1DnVQRIRLtOVIgAojNtURuCNUqBZgRfKExGwitubqNO1kgrMc6hypyQtMREEiTCq9FDImcIQaESP0erAPvCa1PZBFFhujliM4TOwtFnoK3/oCwStThomkRuU5wRh+IwaP7GXbdQUjkG70yZ1VbXIwURc7u/jbL+YrgAu10Re1TpleVGZmLDK/sEdqOs4tFela1gShQQqQMaZnEcK0QTA52kCGybyXrWUWIkWbV0duVxCjxAXxIRCfDqzvYiwURKPoZJh8hmwiDBM9lO4dJj3zSI4oMd9SlxQrvCUE+Ni48Gfk83xHnwQ6bweWx3x9fu386IHrB6UQERdLKqo6nXOgZOiuwztF5R66SkLKWClVo2hgJjaWVjihAZxn5qI9oPB7L6mJNjWN664RoNwydWnL2vXuMr+0yvL7LUxHBY/fwYnvkDoiHA258rD/iS8aCL14lfbpJz4e6PcojPQmkezgNxBeEDo9v+AGwpBeFZS868vFtL5QxeirwflEfimf89OIGfPSQ9FP71P642Q8lU/TEJPKy9vQk8pGvnAbzxwcNIVYQBNXx+4Sg8SHS1Q361RFSSbpxzdF0ztmtY/JhyWBvzPizO2yjcLctp+8e0awaRIycvHvE9O5ZwuX7SGMtba4BgTGKfoh0VQtElFZEUi10FIJer2TVtJhMQwhUU1iejBKzWdUA62fd1HPvNJ0cml5N8WpBca5Y3FtQ6pyjN+/x2tfeYHg0YnWxoGs69j97ldvffp9m3aCNYnRpmxs/+irlKMGrfOcS9KVqyAY9YojMVw5fjBi+ep3Y5eTzQ1672kOQsbxYMrszZ33vDsFfxZQZ1idKaKE1vWGJ0opqVSGV3mTaWsZ9jdYRSUdDxlJEEJGxUgz2JrSLiiignq+ZHk030CTNYGtIf9ijmVepsH4A3jmiEFSnc66+fhV//5zhWY3QijIbcl7so7WmcS1XuxQ4VDFyEcKTK7vAKgTuek+wHucc7aohL1NwEUj6QqvDKTuvHaSMQd1xducUQURJlQJj54kxEXqEENjan5D3cu68dS8xAYZInhuqxYp6OUJnOunkDArmq45iUDI/mqGMIoZIMSw4eOMK5bhPJFIfz1jn5zSzJdmwRJU5F/fPyWVO7tL3GGKL9VMAemPB3o/s4K1jfmI4v3OKjJHVQjLa32fr6g6Hb95LgY0PRKmolzXDvRGFdsQ8MbYZLYghIpQgZul5F+nxSwH9JiCOIgVJMYJzKTCQJJpypTJi09HFmFjLmi5B34ymJwXekwIn58gBlxuyrI+vakCitE41RZki0wKkTLU3mUYVJgUZmUYbg1hWSeh0uoQYkaMekUTwEK2HIkNt9RM7nnUIKYmdTxC/1uJjxEEKEqRIArSdpYMNnFOgtEwQRO+Rwx7hbEHY1D5JmaBqMWw8HSWIVXq/Hiw4CCmhtQkKpyQyPoIWhRAQIX0fYVWjhzl6UOBma6RMsL7oHK1R5L2cWFuyK1vU6wbZ2vQeEskRiRUvJOf3Adwt+oAc9xCrBqkVft3AMFG8C8SD1YOUseoXULXEuk6ZsTLHR3DLCkJEupCovr0ntIkqPCiFyA3tYk2fJIiMUTjrqOerVOujJUXnkRsyCXv/nLJNAaNdnrCoKjzg6x1CVtDLDdIolPVorTF5jhAVW3sTRgcSIeYo1VHuFuio0Tpwd12j8kliF3+vxfQyzLrlspLJs2zB3wsgBPVUcG4L6OBsnWCQUsrnrvJvlzDaiMnHEPHWpUUhq6nsi4KeZzugAjiQKtX9IGjMiCgEpZSc9XvI1nJsl5TDglVjyZSibj1O+QTzlkkTLjaW3Ggqa1GZptfLUSJigbmMBOuwhaFd1+lZyAyicxR5ztFb9whKMr62gy5HZJP9D7TTrmdE1z3zHp683cdqeh57tp937z/ok0/O4qMFsoefPLqqeHLXj+ySPPO4l4n1ntOuJz99cTj48hYfO9un9ql9ah8/KHoc+/oHbptX+8GSS/LQ0PIdYtVi/PvE8HlELMnHBfMvXxC/5vn93/0vLJoZ3XZSlVcLRdYatvrb/InyT3Pza28wvXvG+a2TVHzcOYQAXeR4I7m1m/RpttEUh0t6wx7eepqqIY+BICT9rRFaK2prIULXdJy/e5k3/89LCCGYHVtgumn/k7fzotsNInJ8/R75OGMhpojDDMiplhWzO2dcfuMad771PtWqwt52jHfH2KpFxMji3jmzu2fowpAPS4SWjHbH5P2Crmo4ffM+3zs+5XB/i/F6ix+5Jvia+D5uaqlmKwb7Y/gMfGc25vcXa/z5jLBZDScEFhfLFGz55JD1+wW1c1xRFbtFwAnBO+2Q+kev47aH5G+fsrp7RtEv8M6TD0qGkwGrxZr1bJ1ooGPk/N4pWZ5RZKmA2+QmFdn3MvRkyLX3G6LwcGObX3/lJwlCsnVyh79o14gYecs5/j/1B1n/3vKOd+oE//mMc+z1C1rrUErhCZggGB4vOHj7lNHemKbqCCE5/hroj3qcn8xSkBMjWikuTmZsXdpKtMchUM8sVhuyXsnyYkm7qjG5oas7mrrFZBlCCNp1g+qXrM9XzI+mHFzfIxv2mM/PWG9VlDtDdG4AQW/cZ18N2Pm9BcEHTG4J7n7KRkiR6I1zw81SE14PuNZyO15ltX3AyTuH+C7VydStxQuHtwlOeNBfE0dzdBHx0SZYaZmjIkQpcBsnMDqPUCoRByAeQszCps5Hab2BfnUI68ikwIWIyBR5WWDbDpRCOU/KtaRifRGArkukDCKmQFFLIoKAQGmFDhHvAiGkonkpBL7rUibPOqJS6TyNBSnTs6lSvUlzZMm2BuA8ISbtIZEbhPUokUSbfYzICM46QmeRSqbn0KgUUGlFNAq/qmHVpJV5ozbw1LDJfEmoUxATc52geUVGMAq78kjrkSZpBcUQkrMWAhQbSvMYcfMKc3Unfa41IoIIEddZnFaEszl5jLSdxShFhqBrXQpOYANfTN8LccNuJxPJhhKSmBnkoGR565giMyiV9MWyYT8J0ZYRdzYjiIA52MEuKmSepazZhtRla2+L4Dz1uqZbN/TGfYbbI6pNXSE2Mtoaofe2qaYL1m1HFzwqSJo7J9xcWbJZhWs7DnbOMHtLfBAcuANCLOiWLZ1taNoEz23zjN1Lu1z68lV6/e8gpEWUkqs/uo9XAruy/L//91v4NkEV/X+dI4Tg+hj+n18MKBPxx4HqP9WA4C1r+Tf1g+yxAsKD2PCZM81Xr8BPXkvTjW/thlFR8C/flXzvQj13enqeZQL+QlkyFAInM97f/irT+wtsF/jXMVK3FrF9leBDoipXCi0lTdPiQyArUraxtZai18O3DXQROejhI1woON4uyEQaR7PcbEhXHN2yoRYdSivsbA1Xdxhe/xLDa1/8AATw7Fu/Rjs7ev6NPNVpQvCDEi0/JHtGVU18fOszEX4v3P4HbY/iyk8qlPnDeJef2qf2B2c/FPjcR7aXXD15KYup3FNsXvp6tsJ0LT0laW2kWtVUy+Qkr87ntN5jMk1ZFklrpLOcHZ7z1pvfZf/KJfZfu8TW1R2aRU27rLGdxa5bquAhBPLgCDHpxAwPJkxvn9DUHb3gaNHMpovUkpAU4GWmKSf91M741KTxYccpkdZ7xtd2UFuC5tzRK3Luv32Pa1Jw/Ys3WJ4tmB9PqZapxklqRZ4Zlqs1XdeB9eRKcXG6pLU2QbU6R2YMIgrWpwtmqxVLc0y+1Ud2jqNvvU9/3Kd36YCbr38mUX8fT5neOUNplepsfHK4pZYsZstUZO89bedQxkCI0HlsY9m9tgv3p3SrhqzIaZYVymgGoz5KSXr9ktA5Sm0SGQMJcjU82GJwYw8bLbe/8Q6j6RIdJNlozWq8xlrPaFMULZ6eKJ8KQMNjH0spkQ9op0PAk2Byi+Mpo90R3nkyY8iLnK5zzM6XlGWemL5EEjCcHEyYn8yQSlG4jkyQmMOAtkr0zlkvp60tSmuEkhSDAtF12LZLdR8+cHr7lOH2kPLmhLZ6F9PPk55Mv8T0csLSMT+a0tUtu1d2QMnknMeIyVRaSY4KKQVd3RK05/bvv4+tO3oa2hAo+wW7r19i68rOY49hJHpP1KnnurolizHpThmdHEEf8DFRUiul8M6nzMtG9HPQzxGNoIkJ5hasS4FPnmrMQrsJHDbfpxCb2p06ZXWiEPjWgUjnjxt4mBCRYBSSmHR3iiy9XxsmPi1lqv/ZUGY775I4KQLZy1PdYNUS5mvM/oSoFLG1hLSWkl7KmIIDHyKmXyQYoA8IJDLLUkbHGNxisWEyTNAt1ctTdmVDX431BARxVSMHRWK0sw6sS9dynkhEhtQHQSY4nlQyZYzqLpFb5IbYpexolBKtBB0RtW6QUpEbjQgQO4fJTMp4WZuY05RE+YgMAYoS0Xbpu3MeKRXxZEHWK4mb4AzncOsaJYpEBDHuE5oG31n0JoCEiHACb12ir3cu0XWLxHBnuw7dy+nma3b3t8mH5QMdbfSGsc+7lFlTIQkjb22PQEI+6lHuTmjtZUIc4ttUZ+V9Cj6yYZmypSaRmYgHUAORMFpxk7FEyUREsdFuQkS6qiFai4xDog1J2ymm4ejhkCDlJqMnnolXEgLqao2tWnp5kQh5YkBE8yEG7wdjUCSxpKb3zi9rTk/usF57Whtor40IGybBurO03uEWFqElrrMEwASTmOWEoO0sclMH06wb5nOPl0Dn6U1GzBYrlFFgYxrnCoMTkMfEqLm4fUpXdwQi/a0h5c4w1bU9zlT32Lj5rL55KOLzABb2QnzY8077/At9GP2np+t2XmZ+/aGECi+Axm2+rue2RTzdqI/sdz3Zp58SMnxqn9oj+6PHPvcD7BEl4aPRI4Qhq5M5WXaJni+onWR6/wLxPc/WF/YYrMfEdc3u1phRNkpMUSUE6yiznOndVENT9gvKcR9lNAJBMeoxkBC7Cqc1y1VHO+kxyyT3z+YY72hVhlIKNsXkzienrQAulhXu0gShxEPhvYf2Icep4AO6yCgGGjtd0XaWrMy5//b9pBg/KBhtj5P2zirB00QIlEWOD+HhXJVtnC1CIJOCPpEdF1OfCMEFI+y5ICt2iFvbnDYd66XAjzr6oz5KK1zdMRz2QQiObx8TrWMYBcJ6vLXMZcD6NAEPbGDXBGRj6YY52z/9BaZ3znB3z1FeMhz0MEaR9wryMuf+0QVda8m1pqmSiGumFOMmsl43vHrpCvpoiZ3WtCcwPX2HvVcO2Lm6zbrZTfh8WfFqZ5/oO9d0mH7x8LNto5nfnSGlwPmA957caHyM9Cd9gBRQlDmdD/RyTd20ZJlicTanrTsEMD+dIRBoJWnJ6KR4KJgZQ+Tg2g7L2Zrx7ojzwwvWyzVaK0oJNSTHdgMR9ELQk4obgxFu5fASuiLgW8vFouN0JMmubnM6KvAhkvUzTJdhqozl+YKia9keKYpBgQwKqQVFkSGcxSNQCOIgct6dI7rINeXpM8Z3zUOiBNE5mrggCI8IqSZF+UDdeMbFDkST3o8IuZQ4pbDWPxS3fCj+iaCzDpY1eWZSFmeTdSAGvJC0KomMqtwQdIKRmVGqXaNzkCWWRbGhHqax2A1hg9kQPiATLFQPe2gfaFuX6NibDqEESkiklNijKWpriCgMWkp8a5EdSV8pgmgteljiTheJVW5nSFL/dPi2g41Oz2qcg/MY4Sllqmd84BtKkr/uqg4zSpTqxOSURpFqRoKIKfvkPApBLvsYmSd4XdDIfp760gckAaJAFwYfw8NshYok/aVMYY+mSSi16Qi5QW28wug2tSRSPKKVjgItk+MrvMdaT1bkiWFPCLLtMfXbS8KqIjoQuST4iBTpOO8DSqd9Y2PJc0PYeMRKSpp1Q7OsaNsO6xx5njMqEsGHEIJgLZlJCx7LypP1RqzerJiev4MLBW3dkhcZW1d2GV7exrYd2ahH8JF6naNNztFbx9yeHZNt9ciygt6lHgDae3bbGiki45HmdLxFt6zIG085XVGM+88OfKRknAUOhun5P6/g/GGSWSCFSn6/dSBkWnSR4rFalA8xhgvJyXCXldKcHB5yXFV4ZWhlQEZo6paoJa5uEzGHkklDa/NsPfCcpUhyCoaUIRRKYjf6X/1+j9ZahFF0q5ooBdu7E3Smqedr8l7Oar7GLyqMVgTraGYV4fYJw0mf4cEWk2KbOEg3JsWClNuFs8rhwgaO9aCW6PG+fNjG562kflB353kT4csGRPFhIPboVM8jmvthWQFcVilz6GVGk40AgZWCtYwE6yFCtVjTm/QppUJXHTrTuNJi8wRV7JYddmUfO/PLQkoetyf7/lPo3Kf2qT1pnwB87sE/P8QU7Ic49eMteTDAWneTrhli25r+oM9YdDQzh/lvJVvVDn9C/RTvv/8u+q7m0qUdok8wnovZkraxDIe9JDK4bqhXifUtyw0RwSqTZPt9qjoVH598do9ZIZjnks+FVI9Q1Q1FUeBjQEmJIq0ef+/wDD82HLxxlUX+HKaFl+ygB4O/J2J9QCmFylMmxltHNa+olzVaSax1xNaytTNOJBKLNU3TYXoFnUuTe90msU9tA5erFb0sY9plfOfgT5IPShbnC6plRSQyqAf0T+bJGfCB0f6E2Z0zxvsTtq/ucnHvlOtW0l952tbxTsy4ZyU9l/HnlOFS1WGU4v+r1sQbe5i9m9zYHbO6dUJ1vmC9dPSHPVYXS7RSOOnpvE/1KFqSBXjlbkWIgaB2WX72p7nze+9THVXcUGu2xRTjJLcnn0fnGYP2lJ/1Veq3EJnfP4fOM97eevj0XEjFN2JEaslw0qccJo2k3qTH1tVdIEG8bIg0VUss0vPgXFp5h5jEcqV8WF+TFRlCSYIPeBfQkg0RSBId7Q1KVrM11qUsmNGCojDUVarTMlKiThbctGt807HMBfcnJeSG6TZ883+5jABkpmnXDcJE+ncL8u+VLC8iV+KCr35GkxUZ0iqC84TOYaXEes/lm1e53d3h8PweArh20eOg7hMXGn0p4nKPI3A+/31aXRMQKVvjA0LljLKfQkSZ2iDAdV0K1rOUUdAx4qREkmi5+6NhIrVwqSYibBw4EyG2Duk8XiZq7WxYIrb6uHmVMkaAcEnI1Hmf6vc6m2CUGwpsaTTBWnS/TIKrjcUIyCJ0MeKkIMaQtL18aoNYWmIQOEESeL1YP8xQhKYjbqjG/GwNO0O8kIi6RWhNR+DW5ZRV6a8cN2+tiFKmjEPcUGNvsojeJx0dFUDETWZNilT3FEIKRDrLpH+VSX6doBQX69t0/YJuViGzDR228xitcXUFncNrRRCCclTS3r8guECsWqwSiNamDAopSOkECX4YQHiLGvSIUiFWNcH7FEA1Fuc8vrWoIsPsjDHbI7rTRaLPjhENZAhm6zVFr8T7VIszX64SFXuT4LRV2z6s0ZnsblGMeujcEOo2EVMcLfDek5UGnX+e+7cdddOgtSbPddKvQnB+/4z7799HKMUbf+pLDPcniOzLvP/bb3P3Iuc43sMfnpJrxc0ffZ3R9T0mXcP/evw+ish5r+T/3LlGQLB7WPET9xeJ2MK7D8whCPjcTuTPvZ6esf9wC/79+49qZpSQFHmODBsx4xAQ6jl4ux9gTil+65WvIE3JyfQdmvmaxnqiUKi6SeO7TxlAoxWrtkUqhZQJsqwynQJ076lby3DYT9+zSzVYVVWjhNiMT9DPczqSqK+tKoiR5bpGKEk+LMFHfJAUuWZ+vmB9sWR1uuBPHVxn/8obQCRT30TKBR74tXdmzNtn6Da90JJb/vww6Xm03S9nD+ixH7y3/90twpZS/F/LHirCOtvm3u6fIEY4nC/4vcWCxXzNsN+jCzUmDti3koPWwsoRvhppfiRF4ae/d8b0exuI/Ut0wAOf4Mn+e/LATwOiT+1Te9I+wUzRk4HRC8OkFy1wfNz08MbJfAhJgFTf01iUkPjFiqws2Nvb4vjkgjvfvsX1H7mZdDYulqzXNTpGVNdQrzv2Lu/irMM3Hf1hn2LUI4RA11iadRLc7JwjywxbB1v0tgaEEFBGEdaWGEFrzXgyIJ/0iTFSTVecnUwRfc3J+8cMdkYfO6RURiO8IB/36NyUSa8gNJbgQ6LMNor5xRLbdpSDktH2iHLcp56tUIs1tfMsm5aD0YDzqk4rpFsjkILVxYLWOoQwTE+mjIVgMOrj6o6qs8ynS+qqZVtA11jyYcnklT2kUoy3BjjnWH/vkKGUqA0EKgiSqKmIhOjxqwbnHLN4ymBrgNKKq5+9Bp+N1IuKk9snLI+mbO9tkTctbdXSNA07r19JzuFmtTQISbuoUZlJK9RKMj26wHUOGzzjy9tcGzuIkWa6ROeGrMhQ/Y0M52O8qJNre4wv7zDaHW30I9hMMqnG5OzWCXlZ0LUO5wJZlhFiRG8opQG61tIf9lBGsX1lh2ZV4xqL2dLkuaGtO1aLikgKtA9u7BE6y3rdUFcti+mSsl/Q3xsjOpcILHZHnL1zn7q22GWffH8Lt3FeY+fIlEQIQVZkrKZL7EViHDu4eRnBKTEk6vSmzSm1xobAzrVdtq7vcfvsDg8cFe8cd79zi+3dLYZawgYK5mMkdg4hIrJX4KRAuQABlHM4B0EInJBIncglknYPJH4EhdxkT8VGRycgcEqShRRk4dO9iEzh24ioWmS+qSlqbNI7ihFZ5hgh8TFAbohVCz5s2AE7ZGbwrUUQE2tdCESZxC+xniA3GRqlkt7PgwBgMsBPV8SmQ+oEQ/TzKgVKMT0//mJFGJXEACZTyJiyTl4mUeBE7+2gzMEl/aEYE2zuQe1REOB8qpJ6AJ+KeYbc6Gt5sXkmfcCeLxG7muBSTaMIEYTEtpagNTok8WGkSCQIbZcYAjeosgTFi4mKPAayXmqXkRvEGRIlUtujDwnaKGIKluySdl2R9Qqi85idIc10DYMCXwtyrRhvjai7jrIsyPsFq/kKGaHXL7g4naZ6L+sZbY8oekWiMm8tMUTsqiEIQW9YYjKTxuoY6RfD9DuCrWEPrRWHt44Yb41Yzte0i4rhwYR6tubs+IJ+z7A3GLB2FYu2ZX08ZXRtN7EoapWeg8fgcDJLrIOP29NjsZSC0HYovYHfPbajENDOVxT9HlLGFNh+EKzwaEn+hQN9Cg58a5OGF9DrFdgYqK1FivRed52jKHJ0Z2nbjvVyTZFnBG0S/Nd5XAi01jGaDJlPF/R6OXmW0dUteT9l3aquIxuUzM5nuM4lwp2YFta61uLWLSHpZDMa9llXDSY3NOcrzm6fY3oZezc3sLRn3NcH3O9nBibiA/8+ufV5TsBLh0U8yEDF+MGv5AP2SadOHkwnm4vV795itrpMcJGL2Qq530dpTdV25FlGNa+Yd4FdL6mXNWIhn5yXntnOp/F3j2XHPk0FfWqf2oeyHxp87r//usxm7e6pCwvA1R0K6Hyg7JUsmg4jHKNBj9lixel7R4wPJsxO5zRVw6pq2J8M0NpTDkpO754CUK1rFvMVw60B40tb7BZ7zBW8e3GB7RyroynycMb2tV2GN/aZuxO6tsNkmtlqSeY6DnbGjPfHzKfLtFLvoJ2vKYbblHuvJCjX+gLfvjwTnWvHqKZPdb6m5yTaaPI8gxA5W89YLpcUXywZvTFEBkl8y+HqDjfuc6eqaAtF2R8x9JHGOsrMUDcdF2ezTRAjyTNDZwP9VUdYH9OMevS3B5TOs6oaqqrh+NYxPkT0hWZ8MKGzDqkE+5+5wn5Wkt29IJzM2BKK0HSoaFkMHUWuCHQYJ8lma5RsWFuwIZINSuzukNHe6zTvHnHx1iFbkwF2ueTSoOVSv8ZXC+7GhhAD7aKFswlCSPZvHDC9f04IML9YglbMvvUe3URhdjPWs1RzcfVzr+G1YmpXLJo5AMt2xqrIIROs16uHfb1VKPqZwncV0a5xlGkF1wZQiTo5GEXWy/GtJXhJU7WM90ZoKVmcLcjLjH5/wMnd00R6AZjcYJuO9aJCdI6yzNjem+BjyrTE1tGGwNntU0Y3dvEqcH7nHn4APdmnz4DYQDev8J2HcYJrmm1Jc7Bm58Y+del4+25AOoe93mdydYBA0JMClWecNEfULhWdP1hh3Lm8i8wMetLHNalGaJjt4rNtIGkJlTGg8wylDaHtsEJiScX8QgrIM9SmlkhojQJkDNBaYoy00lM3Z1ghyNouvcox0tkpomsQAhoJjW2RuyXmxFOuWnyMULcpyyIg2x+noK2xlHqMViWiU6AlshOoXs6yO6dpViitUWWGrDtE0yWnI9PIMgW2SEFsHIPyMiKKVAfmAlIrXN9ynM1onaUYG/qHDX7WIkrFaGmJIVA2if1NCkHcwOTo5dB0qdbDBbwUyM21Qowk2d5IYXOM3E5BSXQs7DHRe2wzI4z1JqgBQkSoVL+TZYkiW6pEJhGWdYIYGoNUqb7GSZkEUtsONtpMSPGwTiooBTaxmKlBDwEEJYh1i/Qh1Vata2IEtT1EKZFor5Vja30PX2bMnGbeeqy1rOarDYNbgpQF7ynHA9aLNe2qQkQYTAZU8zXWOYQR1MHRQyFyRZf38ERUhK3dLbphwfJixWpUsAyena2O8YFFiFPur+8yH14w2u3RqYhBI5oGiozZ3TPK4YBpcxUJTDtYrJap7SufYJ1SMpSSz2nD08CvfROQWcA1lv2e4Uf2kpe504Ou7ViuVng9wDUalGDHSd7Q6vFp6SnHVFDl23iRpt+ZIul8aY1Asrx/wWq2ImpFY+2GydIjM5kY/pzj/HxGXhiiD+zubFGtK4SWSKlRLuOSA9V45MmCfRGRtWPRWVY61apppbDW4ZZretoQNxBJ23REATHaDfw11Syt646YK7rOcm+2QtctpjLUY4XWPbLtAXpnRM+mrFV7cZ+wybw97Ij4A3z7j2kfBIb98E0JOBhkSAFeaOZ6J8HPH2+GlNzRhtBa7iF5/9YxJs9YGklrfaplJOm3FWWOi5b7zmKNwJ60HKwPUm2rWz47FnrsYg8ft4flW+LJrZEXsgB+ap/a/+j2sYOiD5EfevKgj7LtB500ghDxA00ILmnyDHZGXPrcVY7fvM/54TmZTquE1aJi75UDtFZ01qONZm0DSkiaVc14d8T0eEqZ52SZYTFdsV5UaK1QN3a58eWbnN85Q96bcuWihsMFze6Ai9d2ca1luVihVUHTWmYn53yxSKxqoq0TTv3OGTd+/DNsX36dGCKzN3+T6vidx6CJz7EIRIld3iD6CW5ZsTx9E+8Dh0dn9PKMUa/HxXrOcftNel1OT/S51r4OrcdnitUXrnL43n3GSPbXgfPFAgQMhwMika7psN6z3SsJbctnNgUSp27NfW9RSqOMot8vU+EugnpZUZ8t6Zzn/rJmtDfhxmjE7muX02r1vXOGTQcELgZrFpnCA/0Q2M1KYtPQSkFrJKGb89ayZnD1gMGfuEHvYsX6YonpKb56qaY//w6zEPjt9QobI7rWXDubMd7fZnY6J8szjIm0G9YtLQ1Lm/Of35cMtvfSavn4OiYzvDd7h2/PN6xK7W3g9ge6/E9eHjApcmTpcN4j1RWKXsF6vsYTk/ZJhGZRJXa0zCSnYrrGaM2Vm5do1jV3vn+HoszpDXrY1qYagRhZTldoKVmuaop5hXOOEBOVcq+XI/WA9epVzg4FmR1x+WKX0XvJgY4xEGrL6mDB/d57RO9pBw36ZwzNwZrffWfFme8QQcD0vQRNeVBj8sQ7EyEmcozt63tEBPnukPZ+S/SRnd7nEJlBaYVwPmHlpMRLgXcNKlN0m5oG4QJee4R1SVDUJ6gYQiKFByHp2nPuT/8bVmsym7IwcUPxLUgwtmVPcW8/Q6jI7qU+V99z6dpiAzcT0B1OkzhwppgUNxkV15Io7AOGzCCo69/ClBm+7nCLKsH8egVCCYQLqExvMgOW6AW74y+Sq4JAciakEFSm47e3v0EXLf0847XjpGGVrS3Xm8RGGJ1PJBkyyQNIrWHdIDJDDC7RVvukMSTCg5Xs5NQMs8vsDD6LCIHD+e9z3n4n9TEgTwtUP8cv6lQXKAQyM8RlRRQykSY8cH60guAJKtVA6hARSuJCTDVaszVmMkg03NYTpYdeQYwO6gQJVYMBIJJGVAeqzBFSEs7m6Rq9ki25pJgeYlvNLX2Vc/kqvm7pNvCuxXyJkJJyMqDzjhA9sYtsbU9SFr9twWiOcslkbxs7HtBVLYt1TRcDhda8Wy8xsaXtWtoCciX50qWGsv8u57fP+E6c4j8j8MM+quuIQpJrzcXtEzrncP3L/NbRjzC6vMu6aDm88+snDSuUAAEAAElEQVREAbnWRJODFFyWistlydMTiFEtwdbYdcPrvcAXvpg/HJeDL5nsbXO0yLloSxTwBZHz1Txt76oW23T0t5PQcgiBiOTu7o9QuYzl8YzfbNfEQcn42g6u8ly8d4wuc1rnEnQxRjKTqPudtcgARWYSecYGqqiETFIKecZEaW6sGzIlkCJlRkPtuC0CjAd0XQq0iiyjc5bluqIc9tLxUmGJZL2CQKTsFQghsG2HQBDXLRfDjK6niFLyzpFGiQE7co/+9W2KwhC94+S3/w2hXj5/7trYo4TGy5MmPN/SuPXEaZ7jjjzXU/lBGZaHA2XaaLTkxy8PyJSgUT1+f/xTeKkT/b1MMgbV6Zx/fuuY6CPrfg8zTm5XVJKuaTbZ600mPtccOcvxQFGMC0Ib0beuMNjq49sFxPupTuzpW3xeIu6JWxMv5V89/l08rvT0qX1q/yPYJ5cp+mFWLz59zufmvZ8+aANhqjuiEOx/9gqr0znn90/TCk2IhBgTqw7QG/ZYLdZIKcmKDK8ls/M5e9f2yPIMbx06MwwHJV2Xipqn986ZjzJ2b+7T2x5R/s5t6mVFV7fMTqZJO0JKEJAXGaptmJ3O2drfYlgOEG3FalVx9L07XPux19DFY8xFTw/wT9zuY/oCmx/yUY+9Vy8RpitmbcdiXaGVYlyWvFM1ZANN8Jain9O/MmbtA82yJWy0S2xnyXKD7Rz1uk4iqIDODFZAkSdBT+s9Mi9QSuKDxzUJ2lGvfaq9ABCS3AhChPndM+60ZxT7W2xd3mF1NMXbjYDlhiVKSEkrJaZLAYIHQuVxCNpasVxbtnfHfPZHXiEuG3o5mPP5w6H7wb/FsKRnB8xP5kTADFLAsqnfJ1MbkcyYMohd3XH01j0uf/baplsfK/Z9gLl4/Hna/C61ouxnVHOLD5E809iNQy+VBClo2o4sy1KfxMjZ0ZSrr1+mWlQoKWirFlFEpFF0bZcyHhvoS3/cp16nGrBoHbW1mGHBlc9cZ308Yzjs0795GaUkMtfIXNMtatbzNfYgku8MaVc14+u76CJLGYQNFOvBJPoArvPkO/QgFEnsYW1dkw97CCnpX9nGdsd4pZEPgpyYWPqCFLRNRzQaESOFlEkUVKUaGpQkE4Lw4Pn4/7P3X0+WJfmdJ/ZxddTVITJSl2yFbmAgieEuzXa5S5rR+Mfwj+Eb/xE+7NL4tja7M8Rg0INuoLurukSq0HHVka744CciM6uyCt1Ac2yXSDeryoi498a94ee4+098BekaCyHQSqEyMwoSSBhs6tSMcmBCy2Q8GhMHLDYDojCIJhBCTBLbt10pH4llUvFTOqnO3SUcISAGhx/qtCZ9UoQTuwYWk+SrtO/QRzO6VzfIwiQBAARBSYxRhN7hbmXKgFB3iVM1KsIRk+CCyjRqcHfeQHfdJ+uQ42vVuP+omLo9UcikDEdKvlyIaQ323MEW2bewmibooTFjcuWJvSPGAEqC1qn7ROIOSSmTj1RMsE+Z6SQ7HgNxWxOEIGYGZS0iBuK8hEYhlSDUPWJaoIxCzipEnmOBcjXFnq2T1LpRqDxxnEymMTonCqikwGhFMSmxI5+SziOjwFrHer0DRi7OKJARrGdoepptTZTpeocQiEIw9AMuBA6PD5gflLB/wcU/POP87JL9A4XINX7tKTJDpgXLxYy66Ris4+z8muy3L1lc7Jj/8XFyJH5jLYchqRsKlZQPvUuGvMF5ZO/AJtn5ftcipMCUyaDI9Zarq2usrpDA1c01pSuZVKv0u0fRDsbCRuJUCW6+eMXV2YDOM7zxhAiXv3rB8vER5bSk64ekIKiSKfLQOyRJ3XA2m1APQ9rHpKStG7LMUEiJRJDHyLTIU4KvJK7pCSFSqPRZYgwpMbrzaht5Rj6wD5bZao4SAlnkWOswRmObIW0L4/1mcoMRkn4YhR06y+UvnnH0s6eI74gq/qnQ4PsC8MSP+UYyEONbXY+3g35xd0Z+1+d4KzG6i1/eyIri+P03EqE3P+vdL4jp3nVNT13vUVnaB9uXN3TtQLOu05kGyFzg2gEfAqpIJsUQkSR473wxZVs3dCGdx/W2ppwU319vjm9mc7cf/Z8XjL1PgN6Pf83jX5wUfXudjgvqXcYEv48e5u/+hndvJ954/EOtmI5qQMvZDH08JwyOZ7/4in6wxDEgNEazPFoSfRjx94kE3uwaTJmzLRTb3Z5yljPZdjjvcb1nNpswDI7cO+Jnp9TPr5kezDn5wQPqyx2DHYgkud2F0ph9hzGaKckjYnu9ZfLJCYUK2Lpls37G/Lzh3o8eIXXH9x4h8TUUIRJoL79G7i6TV86h4KM/rXj1mzVnrwTWWoqqIPbHdLuSarZif7Lk6rqhHyy6aTnxDgZP76GaVkn9apShtt2AtY66Hyi0IoaAEoJZgIAiWMtOSmotWMwneB/oB0vb92TGYIoEC3OdRWcGqSWLeyuGfYcXsAk5rg3JbNVYah/IcBTG4Enwoqy4wsxK8pnjMgjMsURUGWqf5Jnvbi8EQSvUHz9l/fOvqIyh33VJ3KB3zCYVUUm2my3TSUW1mNB1A7buOf31cw6fSP7EZG/cZqli1ucCaxIsqYgppBdSsnp0yPpiT5FnTOYT1us9ZuQydXWLyXOIkazMUzI5pEQw+GSQOVmU5Jlhc7MjIm6bARS5Ic8NRx+f4Jue089fUEjNg48f0O9TolTNp9yc3SACFJOCy+s1EsFkOaN91rJ6cg+lFbvNlpuz6/R33PS/xwITfBU8OyWQ1mIuv0bkE4a84dh7fLtDB0GVnRAbsN5TVRUqzwnB460nFBnCp8BWG42NlufyFCTIwVPuhxS0uT3O+ZS1Wo8oDDQ92kyZ6MNk3msUplEIBGbY4OszzKQguABjMlqoJYWZI4QkSMu6+TrdV3FBbiqQgml+ggkTQozU+owQElzP71uUVnijkH1KHJz3vCgviVKjheHJcJggiV7wpD4kEKDvyGYhJQ9vBGHKaZbTx0SflOJQEnxkoKELNwlWdisT7ZJkdorTI13csW6/JviACpJF+UGyDrCXuJBgcUIlmfUgJdkkT6au4tbDCaKPdwlw9P4u+VJGM4RAHiNy5H7FMkP0Lr2u7dCZxhfJWyo0PWpaoJdTQm4QzjOcb2A1Q2SJmySkRk1KqFtyISmqnCEGhq6nKAq6fUu5mtJc75gvppipYn2dihark0Ns27Pb1UQlabqeruvZNx3ltIQQUDcNE5ksBJ5ZS9t2uOcNz087Ztmc4BWLm4iTJGhYnmO9p1OO3bIhzzSayPbghkbtGPxwd6/LmcT8kcHtEidPKonQGrEbiNc9spLsFobN6hBCZC56YmjQJznxHPoLR3+pYSLARAqVcXH1NQ+OJFobro4mrFcz1gcF0/0SZRW2GbiwkQsFUgaClPTBY5Rm++IKZTTOOWwITIqcvrEYJRFKoyOvPYqc4yOpKLXGmMA+XKIAbSTZyZIIWGeJBQilqIaBJ6Wnc45ehYSqCJHaS3bWoaMAJRj2bRLq8YGubumEoNAal8kk2S4E/a4FqYhGIo1hf7Oj2j0n/KcXPPijJ5QzSShyQoQX29Fa4HvGNwPxdzdqbguBY9lKfI9Aw1hoIEI+P0ZPFt+53UUfkgmzVok/GAJ+cAglk70CvK6JjUUO3w3Ul1uiNOxeaNqLDbt6R1P8IzZAKDL2k4y27VmerJB7nWCtQIiBPDPjWg9oo5NlQG/xKtB1iV+rc8O2bpj6FbvrLcX0kMmDH4CAYXOObbbfmptvTAJ3xb1/5nifIL0f/9rGH65TdLsDfV+/Gr778X/x27+uDEngz7OMD5Rmc7bmVeGpg8cPlkAky5JMtnMOKRRd3dHsGvbbOslTK8ViUrAPnqt7UzpgiuDDTWSxnLG52hBikvvNh8APeoFvO+xFzbPccPDokIPHRzycGtavrpGnG55se0yesThectM52qbj6vQKmwuQAp1fEsUpumqR5g3YwZvT9WYV7LagHyPbr/9zgoYpgfp4yeSBpJiCtzOubzqyoDDux2zOPWKYsc07Wt9j+p4fbloyJJumhUk1SpqnqrrJM/IixzY9282O2gdmZU4gMus9VZ0+56tK449nlKtZIphvGpT32MGinOLgyTFP85JSG2zTJ/6M90xmE77WBadti5GST2cOpePokWLJlcZ6i8y/IARHeyV4frzg4IePcF4Qfhv4pkWiVYKrpyvqYLn67TmfhnAna91Yi7ACKSTWeW4uN2it0SZ56zxRhr/Ikyy3HyxSKfaXG/oPFzT3ynFeXh/D+awinziijzjr0JmmmJZE55JHi3WUkyL5qoSIHj1mgnUURcZsOaWrU7Lc95aoJHmRcfzpA4pZydD0nH32HJMZpvdW3FyuefWb55wcHzA/WVHOJ8kHSmvuP72PLjPc4Ki/qpn/YsXkYEZ903J2cfF7HIyve29/e8sJ8Bbx1c+BhOL6b5/OMbEhrDsehwUmFnipiP2Az0zqdvgAAlSMhCiIUdDGhr9dfI7zlio6PtjuQQiMT348t4ZdsbNEISnEnPvTn40VT8EndeqYXA1fcCHOcbsOtLqr6C7KRyzLD5FC8HL/c3bxlFh7Hs//glzPgcjB7FNECFgCzzc1nU8wMCmAzhKswyPQqwl9t+Xnky8YlKAUBSeXc4w0FE7zZ7uPAHBux9fhEgqDaNP+EiNkxYwH5U+JOnVBhEvdgG33nNP2kqBESlpE8n8SIRBjksPfNS/Yi5egJPfLn/Ag/1G6p8Qv2AyvGOoOJcSd+txdFf22uO09RDGq3qXPIyKQa9wuwTpxydi2d6kDl1kHRhO9xe9aQmZQauxyu4BrOqTLEWWOCIH980uM95jFhGgk0UvkvGLYtQRjQUGWGbo2qXUOTU/wgfXVBqWTSptWivX5NT5GbPTkQnL46IgQIvblBX03kBvDT2cLhlfXRGnZ3KuoR9+ounnIvFxSZAM/qgec8zRt8oaaLabc9Ne0y+SPtLnacProeerULC1xmyZLHkqK/1MOIRVvgo+YwiDPBMPfbgnO87me8h/9Amk0f/Y48uNFi8s14VwQzhWLRrE2Go+jzDKOP5nh1NdYafj14x/xSpRURzOefvUx6qXg+a9+w9mHU24KT2dt4lO5gPMDwWgQgmEUAdns9mipMJlhsA4hFV3Xk2WGZYD/Y5kx04Zdd87L+udoCV25pJv/gNZ7ap9gwyEEfBZZKYXOBYRA6xzOOV7KCdcNo0myom47sjLHNIFMaXoRiaWhKPPUoZSSkBv8iIBwvWU6zfiZv8B++ZyH01eUx3OQUwYfOd/bN6S63yg4vbEnfVOMO0UTr2FctwXP+OaT3vjyLR+i2ybO+G958iGThz8CIv2mwXcWPXqa+Wbg8utzbDeQT0uOP77P9nTN9vIanSdT8+WT42Sw/tU5wXkm8wl1uyXIJa1TnH/V47oKfGS+2VNNK4au40qBCwHbWQQCSxgtHjwyCMqyYGgbul2bPBKrkqZtiSH9HXYUiAmD5WpT8/Djhyx/8BQkrH/z77+RFH17vFnYez/ej/fjdxt/gKTo263ld3379nP/BeM7wcDpwTdrR946rn/9kq+ef85ezQgxUJQFQzcwm1ZY58aqfWRoe4iRSZ4lHkqm0TYyIJC5xraOGCP79Z6DkwOkELRNh1YV7a5ObfFRbvnii1PWFzdcPpxz+PCQykHcXjD0luvTa2bLKX1vkwQwGut9MsT0nuh/B0nT752DdEDks5LH/+Zj4t+94KZuYJlR5Bl10yK6DhUjziXVtBgDk6okeE+9rYmkQ1QIeQcHyzJDBNrBkeUGZx2DtUm5zSTPle3pNRJBNwwEKe74MvvzDef9DQdP7ycCqBTk04Ihevq2H3kXAukDRoOLSfDhdjsXJCiXj5H+eo/dtcS8wF7vMJPqW3MjhODwyT1On13Rtj1GO4Qc4VQxHbZt3VCVReLsEMlUmRS9hCD6QHu9Q2XmNayGsRs5nrrBeYgRYxTZJGN3vaOYVqmz1vUpmRxs6g4JgTGa2cEMlGQYpZGvT29GDghkRca9D+5xS9Fdv7ji6tkZwsPywyOiEDz7hy+RytB1A/1Zem27ayiLnMlyytEn9xE6dQdvzm6oVtM3bgq+vSa/tXS/E6s5Fh3HAEVJJscLWC4wuwqxE8iuxyqFCgGtJNnIXYmjZDNCEG1SXhOZTMlMSJCqMEJ3YqaJI4SQGJFZ8hGKo1pYiDHRlxAjbEuPsKbkrSOlTNydmEQm4uDwgPfpHo8hAQajSjAjkRtiK+6k5KMU4EIShBhc+rmUCAnCx2SAiyZIkcQXRvjOcL1HLUvoLEqKBHPzIUHmXDKfjeNcCJGgeJq0P4lRiVExJklSJGiikozTQAgxkfBFkhCXSiEzDTbtX7cCC2F8jygTnFDeym1JgcxUqlI3Pbowae5ixLpAHpO0OkYiosbfzl83IKwlVjmu7akeHiK1TmbMSiYemxDIziZoVhQYmWB3kYjSOnWWR1hjURXUu5rc5BBh6HuUTIbCcfAUVY4ucrrNHkFS7Tx8fIw8TUIn3jnauiPkmkgyf40RVicrbGc5e3XBtEzwvoNHR+y+3jArcjbXW/ZtR5SCQilcN0BM/Mc3YVPRJe+w6AN90xP6AT9YWMzI5iXdrqXfDcRp8q6yXc8wWDCK3luESF0GESIxy8jKPCkrhphsEGJk+/UlKEldt3QiwakiqaA1qUo2uzpB2UZVRiGSMELb9mRaM3Q9SkBpNItSk8d0LVRVEBuS9PlguQqWtk8dsaoqsO2Azg2NtQlSOl7DTOfowRCUpBNitDlQSe0werzRlPMJ0Xraiw1mUiRD5bGQVAlJ11taGan3LQfzCe3pDcoostXk3efUO7YZ8QZ4Lm058Rbhe3d9vivAf+1N+Mbl5E1oHAmCfLnj7PPTVAGJIEYfs91mTzUtGTpLe76lWdcoKfEu0FzvMcagMs3+7IaoFLZzGKOIWmPbnqbtqao88a6cwBPpRrguWlDvG6ppSbfd4wjpTFCGYbDJmsFohsGSZxlSCAbnENFTliWegDCa4XzL5RdnrJ4cMjua/x6hlPiuttv78X68H+8Yf2D1uTfxt/z/ZiF+52bwBpYW0EuH32+ZPQzcVwU3vSHEwJcE/KLATQzZeqDINN57ijJLHj6DRWeaoe3puoGPHh6QVTnX52cUoyrb+jJxWeTYXi9mJcYYvHW03UAgyRn3u5az377iwwfH7E56hq5HbhoWWnF0suLKDUQCIUKxm5B9ppgspmy7BtiNlbLvmMy3wNXpnxAiX96MBFvpeLTc8ul/NeXquWP9oqGzgbLMESoFaSdHKx6uZOIGGcW6SkFGcMkXx/uAbgeyiz1t3aYkIM+YLqb0dcswWAqpMEKgtUwKOYC3KTha3luyvdrStT0X3tN9+ZIHP3nCYbnkw8MZth+Ifc/Ls2uGricrBcJZjFI4Jem8x+ikjCaFwDiPtJ7u1TWzjx5yNezYYmG54C8e/jgFg0YRu69BwMMflSAfsD/f0rc9WW4YeouSkmI2Sd0gnfx6qsWE89DwbEgQs+yjFSILRJshP57TFxLb9BzuNzyoNMO+ow8D84cHbL6+ZLpMqlogCCGw29VM5pNEUu4GhBRU84rdxQZESjqNlqAk09WU5aNDhm3D9ekNTdujpcL7yOrBAU3TU1/vECS+Q+c8qrNE65LMrnWovk/+OAdzjv/4Pht3w5frz7lqL/mdTsVvJNpCwP3pQ0pdsb3c0J3UZIcZAnixd5zXFi0Ujz+8jzjvGZ5fIpXEaIWNjufVFVYGYu+YXbUYIen6PQe2Q2hBZhWHxUdILUGljlTUChs7tpwi/cjpGJXLIiJxb7QiC0tW1cepsaRGDpdWGDklGgWdZ1beJxOGYBRGlhBGJbhACrgEzOUJZTlHRNL7WAdENs0z3LqmOJ5xsOlxISBwfFmdoaIcDTETN82Gjs1xjsejD3JWNz06M3iZ7gMQd4m0Uoo8zjiuPib6QGfXtO7q7gKIGJGjmSw+IIykdlcEZ0GA1hOOJ58SgW33ChssCvC7FhlCSgidv+MIzidPEE5ArqnjGb7r0h7nA5hI7jyl1ikwH5NTSUQoQVYaRNSEXVLck0VGaDpEkaNKA71DmQzXWbz3qDxHSEFW5WgE1geKWUWzqUEpuqHDaI02mnJS0Tct3gUOHh7irMP2A3XbYb8+pe97nI9keUa/7/hss0GqwOr+IScP5uy2DZubDZtFwSAFebDs2j1xVRLqjp99/ISbL0/pakf2fMa8ypiLnpfVOQiSHPx4v683nv/539UgImoPx8UJKtMUMmP1Q09uFKYryMoC21vsq0toLeJgzubFc65vrpgtV+hihZSGaBSthAcPDogRHlxYJtIgty1qU1NfbogiJeqYdJ0nVUnTdASV9K9tDMmw2DpUSGIHXTcwuKSY+sQ6Mik5xLIbThmqCUPXc3LwI/oQufYeP65lpRR9b5HittAlkpy9SN49Q4xMteNhlXiPSereUyDZm4ohCuqrLSpGpNG4pqfIDMMosNJ7jy4zZK64LB6x6WridqA6v+bk4QSRF4Qv3t577gQBxOtCU3wzm7ndgN444N6EzX1r6xrX15u/YlUesixWuHag+8c1wy//gWA9+UTjZ5OkhrjvUblmni/xIaSOaG8Z+sSfEkoSbEjc06ZHFRldN+DqFlNl2K5HEHmuEuTbq8CgAjoMiKrAjl3y3jlym8yYY4Qiy7DW021rTJUhIxAi+32Dzg1lkaWOsxSIILDtgCeyW+8pDiZM3yx2/ZNjTDbHFtt74bn34/34/vGHSYper7rf8bnj+H0X6O/8FhFzNBD9JeX9hqei4NguEUryQkYureXaBz6MEdX1aK0IPtIPlq632JsdUkoOj5YclCUXn70i7hvUtKKs8lSxNnrsPES8D7i2J4ZAZjTVakZQ8Fw4vA98fXZF0BEx0RyHElMm4vtKVryq98TgmV3NOV6vOH7wgBu7h+9LiL5jPkKEf7xMRm+ZEjyafUlRSh5+kqHEY579/QvsbmA2m9DULbOgkccLul3Lxb7hHxcmBUfW3f19HyxnfBySv1BdN7hh4ObyBqU1s/kEHwJDCAw+oEJECUFZZHSD5fzZBT6kKv1lJrmUghfPz/i3qxXhs1N2TcvywSEP7h/Ttz1rc0HfDsgYUR5UblBGopRCeItQCuE97fmG/fGS4U8esX1+RXd+yZ99+JdMTo6hdHx58z8RCUQ9Y/jBv2Ezm/D8F18lOE6ZsTyYcfnqEqEURVVS72rKecULv+MXfYL7HNybcPTTg7vOE0AMBR/cNNwf9lxfnLFVn6aKv0qiCs567DCgdCL6h1EwoWu6VMn+4pRu11BMioRN15LVySpVhIH11Zb1zY7pYoIUgiKviEIk3xwpU/A/wkT7rkePnQUhYLaa3QUWrWj4x+tfvn2TvKs6K954xjvW1tPFhxxXJ7zcPuPv7X/k3k/uoY3mi//XM7qbnkxp/vpJZPVghat7bNMns+Bg+Xn8FV205CLwSdfhe4ewjnu71NHJ5IyT+Y9RRuOriPSJFFj3Z+x98lK6rRYHm9Qjb+WjJ2rFbH6YRAZiTB3N3EA/EJoeEQNzcwL6ZOy4BKJNhrq3yk1CSQ7yD9If6j1RKyggesu+O8N1Ne5sw/0qw25bBiX45Ydf4pRAjiaiUctkOjpP0MpJG1hed0QRUaRuEVISc42wqRZe6AWFXhBC4Kb5kqa/SKIRPgUvUUAchQWkD+z7U3buOQJ4uPxzFtOnaY71wGbf4X1ADamlFG6V+3RaMwflx+SiIsjIV/vL1FkKETINRUaIQzKJ9R5R5Yi6I2WNAtumfZHFhNAPhMGCj/QvL4ky8ZQwEr1c0O/apJ7o/J2YhdCCdlsjY8QNqaPsmgElJNcX15gqx1Q5Nxc3RO8pJyVtl0RfDh/dY3N+Q28d280Wn0um946Jiyld07G52WK05lwKrHeErqc8rHDWgYw8fnnF9mZH6AXL58fcf3jMWXvKyw8uIESMlgiSyMDlled/+B8TDOmkOOGns4+QSnLwwSmH/12az/A8EIdIOZ+grwTyZY+qaxYTgfqjApMFQgd1L1FlxsTnSKDrB+5/tuFxCOSzCb/NA9YluG0mS7bep/02RgKR3b7BBk+yNw5E59FKsdskrmKeZxTAvzUZU60JtuGl/QyxUUzMAR8f/R/oY+Tm1XOetWukVGN3M4mZWDde/xjHfTmiM8NEOLKYFBGlkMQ87eNDr2kaj9QKVeXkRU7fdLTBI41CKIWSKlkPtIGz2ScwF+Qikk3/hqtuy9GTJ/h3mdmOm9I3pV7eNd71jHep1b353b3pfT6afMTz3/6Wgwhiqui7gUELLvcJQpoJAdbTOosmCQpt1nuGwSZofabJipyhTQqsXookMhRAOoV1yf/tYpGTZRl11+F0St/yXCC9R2qDF4HOO7RRNPtkeF5VJVlVYkMS0UBJQkyFVu/StXHepr9r1zBdTunrDjskj7bvnaj3ic/78X78s8cf3qfo+yA6YxeCsXX/L0qQvvONx46RC3SbhrzIyIVB6IwgBb7vklqVD2iZAtfdtknwKiVZHszJqpzl/RVZkXH2m5fs647ppMRZi6gKHv3oMeWiGnk9qeviesv+csvlF6esr7fsK4M+yDEChhiIPoyKWoGLr87wPnA+NbiJRimF0RojNfmigrG4f1cde/tPe8d8fXOTFG/9VEjB6sMTTDnl1T98zXazJzOGdtfgBkskIqc55WpKVDJVbpueq/Nr5PmGYp9khm+TwOm0JFiHUZIwejIsTlZoo9merxHWUeUZAXDeJ8d3Keito286rjdnzKzHt5b180t2WmFmBfOfLLAhY3exQfiQbk4fUN6nQzAklTqnBM2mRmYTyntLZL1Ocupna8J85LW9AU6fnyy51w3sLjZoLWl2DdEnONXQ9qn7UOXQvJ47Mc7bmy2UECPDCD+Z3luirzOcCymglxLnHSEGtIDpcpbUsnrH/GieyMuZSt2U3FDNK4ppmQjLwDA4tpcbYkgdBT84lg8P2F1uCSNXLpIC5oBM1VYl6UZBi5vrLYej5Pm718U7bhfx+p/vCk2CD9TbhvJh9Y7fnV4sjCKblYgYUT5idy7Bfwivyfo+JIPhUT5bhDAG5DF1i2J4PfPOI6YlsfN4HxBKIN2tKhuEkKreY5k5fT3YlDwLwJNgayESvHyNyBGpG8M4j8mokkSsFyRlrVvFlhHS5bVDjvydqEYxhJCuRvAQJcgASogEyxn5T2FwxCoZw8beIoscP1iE9wkiJ5LkedAKencHvRVK4UdFPu99mguR/ujbgDaIiHc+cXO8Typkb1ybaD3IBI8TWkFMPDakTIa7kWQwfL0jSInWMqmuKTniuUbVO+uQVYGsCtpnW3Iivh+QRQaDh8FhRYcLYVTJc+giQzioimQ62rU9SkqGukcbnQRthEhrRgm8gMOHx+jc4J+dUUwKtB4ljWOCFQopqLc1+00NInkyRSEopxXTTLNb70BJfB8I1tK2KQlrncPGwPnpJbusIwK5UqgiI9K9fePHiO0de7+HEKiOe7pNkxLgMH4eJdCFIZclAijmE6KIXJxfELIVhEDsLXqaYdseZRSqMGircdsaeU+wvLeiXtcErcZExTP0CWKrMo3tB6qyoKlbJAmCLLsBFzw+ePp+oJrOyKXElxk6ZngRE09lhKou8qR4aa3FmETwdyF1/wH0CDO9VWgUgDGG/b4e4ZkSEQUagSyz1LW0gWaoMWWWzm8hiPWAKXPC4OiJZD5QFDl12yByx2K++ta+8nbPOr6GxX1PC+PbHaL4ja/FndDSa8hcZPPsks3Vllxriiytp7525JMFXWuTwAEgfeJ/6jwjKoFWEm9BC5l+o5EUZcb19QYhk3F523RIJbG9I8szqvmE3lpkBkoleGcQEd/25FVB1ydT4+gTXC4K2NcNQkmsc2iVlFitcyiZErjZrMK6gG0HTJGBj9h2YHe5eQsy+MZEfXvcTfj3BWbfvjLpJ+/5SO/Hv77xh0mKfo91I94VWP3Bh+D0+h7FRlFKgVUK77rkkO4cq97SNR196yiV5t6Te0wOZ5gyI5+WxBDZvrzi5W9Padue+bxK3aEgOP70AZOD6d0OnIjMkXxakE9y9hcb6nVN1jsedRlKgBsx5cF75jbgbDqgyiZyP6ZDflGWHN4/QGrFyfQBpanugr7bUv4tLwEhuJlm2G9W4EJg/+o3RDfgQ+Q3V0nAIDLg469BK/yPDbJ9yvXVDjrLcecQMeJvHGZXk08K8vsr9o+OMEaTXeyTbwkRZ5OynDGJPO69RwrBQmrU8xuUUmR1h1ISJxy7QtHHSDUtmR4vaK62XJ7fcC4jV8LjFzkqN8wnFevrLf43NZN7UybHT1Cfn+K2gVxJfiKfgutBBD6rTlHR0+8aKCp0kRGeHvBL+SX5/SVD0yNP55SHc3SAg/pLAA4PISwlMQSu1oJXxQGbiw22H7j3w0fozIxJURp+mDHsHhFj5LE85URcEn3g0A2gBFmZsyxf8LOfHlM/qnlxcUhWHbK73JBPC8pFib+2dPuaex/cp/z4hBfxC84/f8mjHz1hiC3CB8RMceKecPnZBSLCZJLw/6v7B9TXO5p9g0AweI8Qkjx3TMpLtFE8+fF9pnLAFIKNgF+tP4cacrvj32ZJRe+V93w18tTelVsDTB5OKFZJYvg2uEDA4e6Ko/2ezfq3zFVOcT0QI7x0YwITA+78t7isILYDMj/CX7fgA8c3A71tMTLjXvYRWii8sGyGZ2A9Xo2iFTEiHHdFg0GlTpjwAZFl6BGCQkySzV4rpPOEMVk4N2vO9RqpJPeHA478nJEclswsc0NsEyTS+5FnI0TiFOkERxQ+IFwYBQnS49H7JDdeD8TSYAbHyUVHIOKU4PqwQEUQLnKwsWjnya3hsPgEbTRtDv8weQZCYFrLwTomWXJXMC8fQkg8KqkSh8rHJJ+NSv9Zl5KxJHueOtO74RS7qZG5IddzCqagAtf7r4nSjddY3Knzbodn7AeDC57B9ZAlc9YYAnRDki+X3HG2vBQon7yMIgK1mOH7pIwnfMC2HeZwwXBxg8iSOh2tRY/wRUFkHrZ8OHzBcObYrB7yIpQp6MsUXqbrnFcleZmxu9kipOT65QU6y7AxYq82NOs9/WBZHcyZHi3p13s21xtknjrsQz8wn0+pmxa6PomXRMizjMnDCSdOc/r5c4L2bI5umE0KvE4KbnmmyRYV0EGEgwPFH/9xMmBWrWPSfgXW0aiWn18kk9xX15a4DAihuJzM+DlpjX44iyxiZNl0bINOfKwQ2MsZ9c2abDHFzp/SXyvOfvUFZ/Ul4cF9ttETtLzz7jJG03X9yH1L3cJyWlLXLU3T4kNMBSkiPlqu288pe4EoAS1TJ2+qeFF0tL3la90SXTIDFpAKE0JgtEFnOilkxlRYCD51zMLI74shdahCBB9jglb70ZQ6BLQXNE1LMa/AKOohQbsQCaonjcY4w8HmPrNfGaqbkr9SBWQDFvg7a3Hx++Fw//S45Xi+Fmu4TYjuEqMQ2V1uqTKDX0342lv0qmTwFm8dvu3pFORKg49kUhG9T5YU1uKMSrDGrqePA1WlxkKPQBlFOSnZ7fbJzNmnTm1R5rR1m9ReY2TfNAmuPn7Irk1n42w5x9Y1Mk/+WBJQWpPlGd0wUE5LjNGEsZhaFEnFdPCOSilefXnGXy0iq3GP/8w5LkP4rql6a7xOhb45999MiN7x4v+Vj9qu+H/87f/9v+D7/d+Y/Bd7t/fjv9T4w3eKvjm+EYl9qyL0XdWNbz72O0Lnbl/y6uKYYn2E0ZJ2cDTdNc4n8uoSmEwrDn7yiMnhDF0Yhnag39SsX1zR3Oxp254QAnmeJRM961BaMdQd4WCWgjIpkEqlTlFn2by6ptk2zA9mzCNcv7xOsCetknCD1tjoyBcF06M5j4uMcpECeyFHtSgfWIUFkz5Ph6GStNsm4Zq7IfF8jOLiyRz5YEV5ML3z1iB4mouv8G7AR/jNVffGxCWlOFVOOfnf/V+ZodD7ng/P9gkqsW1ZfnXGzdkOoQ3bg4quHThczVgETd92WOepsoy26TFG04bApMgoOofadmgpEobd9QQXqBcZYp6zvdkluEKRYaTkpUtzEGOETHEpA26eMwyS/AqyveNn4oBwswEp+aS8R+EDVnu+nFyhREAOnqbZMZ1NYJXxq8Wal1/9IwfmkMevPsSsM44mgafh1wgC3gXOPnvO/U8fUS3vEx58TDYtEEpy9NH9b2GtbV3x8m9TQvonH3p+ll+mgFO/vhHvLS4Q4hKxVKjFB8wfnbC72LA+vUIYzcGH99jebFI38vyay49O2Tw8Jz9M19Rozf6iYRHvsRshm846posp3b5he71N3SGZ4FDlrOThD6esDjuEhEV1yQfzDQj4xYXg1yM95WfG8L/PCwTwN3ZISdEYbN0tkngbVAimj6YsPpq/XmghQaEO/9MVR3XP/MPIpRDYi5YQQbvxAI4Bd/45VkhAEWWO7AIqRg5f7rFxIM80x4tP0SpjCHu2/hVeSrRLnyfExBVCCoIQCRIYYvL/qQJhDBoQgqgU0oc701KE4CLb8A9VSj7yaDiyyWyUEIlEQjukbpIUyOBfB04hED3gUks2eJ/EB5KMQ8KijpK/DA5C5PCsRRDpjeRmmeGlIB8cJ69qpA+U+SHH8x8glOK83PHL6u+IMTIfety6QS4mzIcV8+JBCkRjHN9HokiNJk9MwXIEocQo5e3x1rG1L6m1QlrFo+mfUxVJFauxN9ThJn3emIwgfQhct1+lzjxjMconU9nscJq8ntTYcdRqTA4j3gUIARkjdt8gjCG0PTovEsSv6YnWEwJIJLIyyCofVfBg1l8z8Re0XUd/5ZGzH47Np1Flr8gY2h7vHDHCpCyw2tEPA0opFvcO2F9vKYyi3TVJYMUleJEbBooiJaOb681ImI9M51Pm91fI3KCdZ/jlKd55rBy4undGP8kp8oxikKye3kNPirs1fHCg+W/+2xnEyM2rK2Ksaa/3/PoC/uMvJiiTeIgHYcf0eMlFPuFcgppIZsOaQ1Mzmc/YblMXCSFolcFXFdIp9v6IUM3Z3S/5XEO32+EyoOvTfWaSWWpQEhNhuZyx3uwSP6vI2NctxegXVJY5uRjY7D+nNgIjM/zoiRYNnOYtN0NDM5eY2kCf/Iek1giZ9t/gU6CdjEVD6vgIUFIR2jEx8qmLqyyEwSOVQkmBtZG+Tx0w29sUzOeGIte4CJ3zhL4nyzMOXxygTiPmq8hfPiwwuaSOgV9ay52Jwl0Fhu/tfLyZ8Nx+99bT3/laweJwQdd7Pouel9OMYlYgzAS3bXCkLk6xzFBeEl2g33WJWwSYPKPteuxg8dbS7lsCkTw37LcNEZKNACnRv75aY4zB+UDbtBydHBJiYL9rQEBRZPTtkNYnkSDTPqOUpAsROwwJWeEcm4sNUkkmiwnOBfp+SDxhREI2+MhjF/mTPBWy1iF8d1L0epLentR/4tH/baVD78f78Ycb//Kk6H9lONbbzdN2Fo2mbQY6a5ksJxTzClNmFLOSfFLgB8f27Ib2pmZ7s0+yykqipGCaZ/Q2wU68czifiJhXX5xx/ewyVYuWU0xh2F9uCT7imo5qXnHyk8cIIZifLJI87yTh528hLmI0m/TW0W4b7PkmKVEh6OuO7fUuVXOFQGea4AN926fKsUyH4GW01KdXVNMSU2Wsnt5jcjAqscVxFu7a5rcZ6e0siQQZmxTk84BEYKqcy6/PkqGcgGHXooVgfjRnimb/+Y5usEyqgqIsKKucvh3Yb3ZJuldI8swwOIdUCqElZZmxU5LeOs5fXrJYzlgeLbi+3CRnex9QzpMfzcEoVK/TQeMC28stS2MSZ0cKglAEEmQo9o783pLrvzllHy6Y/uQRk48Ome0bdp+t2ZxvMGWPzAf2esP0YJqCPqXY3+wJRVJtO/jwPjrT30iI0oFr24GrV6ep6l9t4DGE4N/qdKbrOUIVYzIPnR3OmR0vkuJU29PfNEwOZlg7oIB7Hz7A9wOZ0TgpMGWGIUcYRehSoGp7hxdJZSyflFSrCYvjJZOjGdrUCZ4RAiE4+m2TgqJQpM8y4uxiiHcqS99aHN9RYAiDxa5r+ovNmDgkQm9W5CgtcYi3A5A3vhQkI1MRTfLcURIR5N3TAgliGF0gBItQFVJIRK4RPuAkKJcCNikF0cek3KUkIqTgSYw8iCgEqW6ezE+jkim4I6G/CH40Zw0jp4KUXBiFHFzqjMSkIChvlajGn0XvCb29UyIUJOVDYdT4++KdzPUdrHH8TCEmuWIxJnkIgY9hTApSoifnRUqEpEgS2O3rare/vY9CSIa4IXJryBrd+DeRRFyETMp8QSZ2jAyROOodx9GwVoQRPjeqbBEjosqQeuSBhNQpEghEmaO2DUGQuFIi/X3aKGJvUUKgsyzBQKcVrmlBS+SsIJtXybgyRELTQ6bRFFQ6xw0OaRTVfEKz2adrq5MPT4zxTmQhKQsG+ibxJpQUlPNJqpA3Fong4P5h2guVJPYDeI/1ARsCV6dXuN5Cbykvaso8Y2UqTqXEhYCX8OiPPmDx0X269cA3hxAJUuh6i9SafGLIuzIVpPqevukpB8dQt0Qi0+MVDInvJlUSooj7dJ8IIdDa0F5u2X72kuLA4PcdThsG7xJ0UCcxGSUgUxpnHc57Yp+k+5XRDG1HnhkmVepKECOV0QTnIM+ISmJCQFZ5Ujj0kX3dEmTiiQUJUhn06ImjM423ySpBa5WEcXy6r1xv73x/GL16ohSEwaOFIAiSmp4U+MFRSEXd9egqZ/ABIxXRRwYcond0veOozEFE2qstam5gRDbcIRa/sYd8a8S3t5n4jU3ndYH1dV8jvn6Q+QfHdOcbvHMor7CbBr2sEDpJ1Vc6p9025LOKwXZ47xECJpMJ/TAQQ4JwBwSTxYS+7XGDJQiBkpI8N1gXmC2meO/Zb/YQPEZomrqhnJR03TDygwJFkSWRjTurhoDSisrnoCTKKIZOMITxWghYHC3S+/aOyawiKMjnJba/wEeP0prfJ/i6Vfm77dS9YQH/frwf7wf/JTpFt+Obwdj3rcN/5hr9I2M4VjL5fVQTtgMcHh1TzCt0YQjO4wfHUPfcPLtke76m7y0mMwlXPwZxznnsKJeblfkdD0SIJLfbxsDlQUW5rMh8YFlmRODBjx5RLqo7NZ35w8ORnELysukG+l2bIHY3e3yIyTBQJPJ2CEnGs1lW7FRyWv8gKxDrGhEji9mE/bZOJOrVjBgd9XbP0amDFxsO/vxj6uUn9FVPNi9ToCcgOMv++S+JwRNsz+aLv0XIJE995JM8cG1Kbp6seNW3HIjIvedX7BvLrJySz0qmqxn2co0gBWGLJ0dsX1yxWW9x1rGYTeicwxcOPU3v22MBlar/3rO52Sb5WKOphEboSG8d+8styihMlVNOc2zdcTHRNFpTVBkTuacQAaMSZE9khqbuWN4/QOw61n/3JVPb8SePj+gfFBzMM7LCMPSef/+1RPU9B1rxx58+QgDrCLOjxbc4MkeV4UdywKxmyDLnWW3BD+y+LHk2/2OCdexXW+xyIALbL3f06wTN+nj5FY9nl0Tg//MSbroExfrxgxuW+Vfog4Jnc0UtUwIqdQo2bRgYXjY8+OQhX/3yM7qPd2T3Ihk5/yb8gNWDA6Jy3HRf4u0F2gtW8kO67Z7eXvNyXo2B3Ir/enqM1IoVgqGzeBc5NpL//uEcoSV1f8G+P8fWPQcHH1DlRwDczBquLi8ZTtf4pkMCQUluYo9ZZcQY+dWmYxsSvKezqSrpgf/QD+QjNOcvnhzBqxo5eA7LH+LxhEzxy8MzCB4VBcf7j9FCoPIqQTgibETDr6fnmMFSajgWPwPrqXP4+fwrxOA49HMetQcp0FcyQXaQPGgXZF6BkhwPs1GMIXVghLy9vvE1p0+KlGRJgYwBfOLo/Kp8SW88wTt2WuNDiQyRo7VDWQfDgFAaAeRk/Jv6g4S495HV1CIiaFUk4YeY/MsebloCAVMPKTGxno4dV92vCDGyH9Z30tk+Jgl8eSvOYPSdD5Ef1cJETLLgUikiIiV8Uo0JVLom0iiQScEuDi7tRVKkQowbA+hNm/hV4i6lJ3YDYexY3KqDRZHu0TD6hoUwwSOYPDhAbWv8psFf7RhuasgMtu1QQiap7DJDtoJMG6RR7De7O+WzvCxo26SEVncds+mELM/Yrrfs6wYtweSG6fEyyXMbDRH6XYMuMmRu8G2H8Cnpa5s2JRRD4rJ1H58w++QB3ek597I5swdLzEzT33zJ5d/f4Fp3dxZdXjn+x/8hCS2oSjN9smTfbtkMybw6EKmWM/JxzXZ1S7Wc3iWyMtNjoSDt3bYeUJwg1ILd+QvWJ/dZr/cME401KpnlypTw+5AgoPXQAoIsz2iaFmUUru4gRnx0dPuGpwPkg2VlPKbMyVeTVPhwPhULhEhw5lFB1YeYIKJSoqSkbVqiD0wmFVGN0NCRK+dtMvcFkHfrQxKVJIz7dXCevu4wmSGEQBcj0qiU9MpUuFBKEYOnqkrOZ44bJZI/1zPF4WHF6of3+Wv/W0J0dDHyN8Pwumv0T4xvQn/vRGLiu4FeUlyTZZrZ0RnzF5HV9CkiwFfXNXFZUU5K8IGyGPlb4rXPVzt6a9W7mr8qCwoE2nrMtKJe75KH05jYZ3kyBnfOE3PFTfgK5QViX7AYPkBNJ/ixEJMX2V3AleUZ+/0Vm/plKnhoRbTJ1yiodC+JRkOTYL5N3VCrx6zFClEZfq2WiJOHKKO4efEb2F7+0/M3ivQkA1rSXvk7zv/78X78axn/8qTo91lV76pS/wE7TR9rzQ9Mqpx8PZ1iphO6XcvZb17QbhrskFzLBSBH35pi9Nzxo8jB9GDG9GCGykwiymYpOBG3EUSEOhMMh1Uyb+09D6/bkTMqqC+3vPrVM6IQ6DxjcZyC7+3pDc3NLmGGZOIPxBGzDTA4n0xEA7zyA7sy5+jhAdJJ5lozDA6vJNJohFG03tMMA5P5lAf1DnPTYH75inZm2DvBweyI+cOjZLQ3tNQvf514Es5Sv/w1ALmULKtJqoZNVvCzvwYFp1+e86dkmG2HfHlDf2/JZDFJUAAJQ9OhMkW+qAjPUkdLxkiZZ7TFwDCxZHmG6AWh8SyXU6RUtPuWbhiSt4fWnHx0nxih3dTsrne0N3tEppjMJ/gPJlxZix8GMrmnFJHMSPpRwlzuOvpWUU1yjucPaD67QF20HD+5h5hdA7Bzjp+L1H14GgOfdo52XbPNIB6kKvntIRF9YJFLDj89QWhFv4ehHugHx/leMT95jMo0p4vn1MUOISUvNz27Zz1CwEfLV9yfpibAZQNfrUHLyH//Z3BSeHbXe2aHP8a6BFvRmSaWGcV8ydSt0Fbz6fFPeP7TL5BTReUKfnD1gNgHttdXBPcFOIffaMzkL5nIFU0x54vTU7yDo0nJn64+ASJaCHyWOpwnQvBIVegq59I3XIWIryT39Zz7xz8AIfib/HMu96epkyAT+V/EyE66hI8Hvvxy4Kpxd2s1kpKiv7ep6l5G+Kv7SzIy3MsbDqYf4aWg1QOfZX+DE56FmPHj+U+RluQRNHoSdarni+w5aM8Dc8gP7ceQSfb6lN9UvwVl+aA54XFYpXU4QuikEhzZOUd+TrztYsnweqMZg1VBKjoIF3BjciF8vAsSPPD15IqNaRJPZqKIQaCj4OB6g4pJ2EDIpMKYYfiwewi3nbCZRlqXIHo+EGJShDvae3zTJQEFkSTzu/oaN2nxmzp1mmIkCEFAoEMgulGeuB8SXHBMRG87nYIRatgPiFIgQ0xE+LsMJwWiUcc7YRdJ2na8c8R9hxo5YWHsZkXrCc4RZeq44Twi04ShS8mT1pAp/L4hRyFcEsBACaJzRJP2yvLoiP50g28HzMEUnEZrkzypmgFHSHChpmW2mNJsa6JWdH2PszZ1i6TEZJqubjn/7UsQILMES+sHR9/2WJF4UM57Sp2hJ8UogiPI5xV8+pArrQiTRxwUH6Fyg93fcPPrvyOp670+c9Zrz7/7n2sAZk+mPDyeEsqKsxcvsU0/djYDbd2hMkMxKfHDay+5WxEMgSD2FjMt6P2K3ZeC/OiPqFXktL0im+WEfYcC8lFIwrY9MjMERq+sMXn34zxMJyXb7Y5cSk46y0wbdNOS3SsQzoNMXK7oPWiVhCWsJ4SIVip1HUlFvjzPR6VGkDYZ93rHHUc1jPdQJhV9cImL6jxSpCQoKoGKSQxEFwakQNmAdJFBOHqdDGZlkDSDpT2o0Ah0hNZ9zAvrEf6AP8lfooJlEwP/yVp8jAnW+46C6dshgXjHz16Pb/Y7pNig1MDig4GP3ZQoDFcvrygPCpwQVLOKelvT7WvyKk/zICVlkWGHgaLKMa7kwwiP8pyu6cgHR57lIDVh8GRao6RASIVTiq7reO5fEQTkccoH5Q8xeY7PPNLo5L8GiFyjlGRfBF7al8RCIcY4o9u3iT/2RlPe9Q6rAl/KFWuWEAO/dSV7dczieMnu6tXbSdE7mj93PxICqd6cyfdp0fvxfrw5/st1im7H77IG/4WJUvSBV//5S66bIuHxAaWT6hA+4qwligSrUFXO8ZNjDj68hykMCPnGe6fS0RtfJhjP6OSd1K1eH7JXX5xx+tlLRq44wQeuX6SDXMvkDu8GhxAyyYD3lmKSYwdH9JZASpa0UgmGIwSmMJRZxrQdGPqBYlay3dTEkPPgowcs7q845Dn11xesz27wZknTNLT/0LK/3LJ4dEixyP7JOQvWoXLNyY8fs912XPzyBQcHC+pdnZSxbEraCIGszNNBSoIrLacVUQq8tYiJoswElmS+KJVivWtRMkGeZKaTkhZw8fU5B4+OmD8Ylf6eneN9pN00OKORhUGJNG/eD/TO4UdFOBkjw+UWpiVZbqie3iOO0KbQJtPFqPO7+yn0ls35Dt9Zln/8CS8Hx+7ZBc1NTd9bvPMsVhvy7CV5mXH9smboDmCEZnXXe6aPDvB1y+6rM8p7qwRtuj1uYiT4iPcRP0SiF4QIwaXAqVgmCJ+3FtFbBqtp+56D5RHDvsWuPbv9Fe3JFu0MhZYJqrN3tF+es958jcwVRXFMMJ5ORgbfI9shdQX2DVoPeK2JWiJzRa4Ebt8wXHusS5LUuIDvLFZ07J9d4nxgf3yFX0T0yYJoU+cyELGfbYhF6ly8tb7e/Oo2/wAQguLpEV2E4dV1yhBjUg0MWbqH4vhc5Twul0StUoX2TXPTGEGNQXvv7lTjogClJd4mjpSwSSRkpP+kAHU0aUXe9kCSOp2UKdlQIiUIYjRrjXArgHXHQ0pNKAHuVtyE5EuEGJMY7gRWlJZjF0oix89PSNwbvayI/UBwHhch04LQDXAwTdBRwR207lbmm+DvuEwiJiNWNT7uBen6hAh5IHqPRyaVuru9L0ko4wNRjWbFQiBsSo7kCPWLEbRMnJNYGmSeuEMR7jhlocjQswIRIq7tyKTE7xv6zxuiAvPgGL9tEGWGXFbJ1NO5dE03DfmiQO093WAxRUZpEjdRjgqXUSROZlnkTA/mDPuGelMzP1pyM7hUdCoy9tsarwSVVFSTCh8DXQj0LjA9mDM9WaKrfPSV8Qybhv3pNdurLZPVlEd/+cN/cv97c0gpOXh4yM3La/p9Q1fXSKXYXe/IjCaf5K+frFKy6p1LXTut8HuLyir6iy17lfg59a7BR/AeZEyctmxR4p0nM4ln1ezb1EnXKiXQ1hIQCWI4WGRMSIUg0u8QPiUrMSQYojN+hGaP5sdKkRlD3w9JiKLIaLshqRCOq0OOoh6R8R4UJCn2wVNoQ+yT+XAIkazMknJaBDuqcMaRC6t1MnONPjBoSRwsxZj8oSTdpub0F1/x8dMeVSR1O+BtlPc7DvzXlq7fCAri6+/ehte9OQSqyjCzkvNfXaY9wwVs3WG1IliPkpK+t0ymFVp6uroll5LYWIyApVRUPkHkVJ4lbtW49rWUSUBJCGQIKF0irQY8Js/IqhwRSKIkWiWOYKaRISKdR2YqQU0F9H1HWSiqeQVSoguDbQec9yivKLWiFIaJKXAi0lvLzcWayWryvQjEb0zmuN+9nufgPdY5jDEJmv9+vB//yscfNin6XZKZ3zfh+Z1X/OvnNzc7fFNiVEkfJF5EjFF3fJBMFpTzksW9JeVyQtSSs2mOkyQPEJvUrWI38LD1ZJnG9xapFEPT03QD2WeObt/RWM/XQ8DkhlYK6o/vUe8bvPMcPjjCVIapiyz2A/XVLqHppGRztSEvclb3DwDom579eo8dBrIswXTafUuYaWyXultfRUvIM8JhxeTJEdOP7iEE2D/9gHaWcfHVGdX5ltw5eudQ5zv6X71i+fSIPzr4CVIJnBScTg1RwNz2iMsvIAZcveHm1/+eQKTQjtmkpG46VoeLdGhKKLSiH1LSaZuB2dGce0/vsbvaIQNE6xCbCE4SA1RDzQ8XS/re3gVrvfesK0MrIj56zr84pZyWyJGHEr1LB2YIxKZPRpKZQkpNsD0HL/dUIkIQhMljXFWSHZR0r75AhIBvekI30O87xPyQnx7+Mc564uma7QLONud0f7tmx9/iQ6ApDPXRjHxVsWkG5pdH4APDkBFGDHxmron1Nco/wO/P6eOOerPn0/4hs+kjUIKX6oLPby6YHi/5kw/3/HTTYnLNFEdz1bI+2/Jk+gknW42SU3YSuqFkUebM1g2FNFihOP7VDLGqmN0/pn55g6pdSmisIxAIIsk3+94lRTESB8TPI5fVM+zFhkKtmJePoRvY2UvW9SuyOKGYLln4TxAmcq0Hfmv+AQxc9FvcZkCI1P3RI1xmc1Lh5zkyzxhe7aF1by+0Nxay9Y7/9+d/Q6Y0Okj+cnoPvW5hNHmMt4kEiVzsY0SFSNSKKXP+cvcJIgSqWKSig/Mc+Ql/6T8CKahcCQiCC7zK17zILiFGHtojHvarMS+97Q5xJ5QggM+rU9a6RgCf1g9YiGlKnHwYuz+Kn7ZPGbDE6Lmsf4OPA3E0XBSjgWwwIs1BCMkMdky0Yki8nyTPH+7kvd3NHnNvSXhxlSCJt6pbSiIkFOogXaeRA3Ib4O3sGc1wQfSexeQpE3OA0pqr3Rfs4zUIwU37FbvhHKkU1u0RirETMCZULuDfgEjd8QikJMnbh9RDGz93aHpUmSeoT4y4PEOROFwi14R9wG7rBLciIqoCNS2wdZdcdbYtoemQRhHzjBAiK3fJH8Ut9b7havaIM7tAjfvwMO4pygb6rse9vEgFo0xzeXaFCIHZakE5KbBNTxNS8jA5mifYz/kaqxXr6y1t01FOS1zbM2wb5hc7dDcwDwH1cs1qsUCtJBfjHLw2xX59CAmgv+45+w/J4LU8KqgWFUKAc2HMk0VKEPybh5JAGMXhIlCqATOXXFU33MQbNrsLdPURejB0QMw12ifuoRcS39kEo+scNqTOQ1Fk7OqWYlYBqaBQSMkPjjLmShGVos4MeEtUozS2UmijkZnGj1Aw7z0BsLc81BASxDDEsbsxFumsTXAqKSiyjOPeMPEZbdeyvu2wItIZODi8TYmXkgIvI8LIxG2LES1kMoTtLEWR48KtqIMkU4o+Wv72kWbyYErbe/zf1UT3Jvzttp/x7UP/9SO3z3/3827Hi91APaS/N7/Q5HJKnhlW9w+4uFnj2g4CzFczgg80TZdESLQmG1o2XqKI/OdCkctIqSR/GgJlarPciZ/IUdI8KkkuCo6Wf0KWKUTXcbX/RTrHTDIIV0rhG1ARrPMENSQunknJaxgcsoTQ9ngivrfkRRIyiRGeqj3TfYLefl3co9ET3GD5aFVQ6ikR+PyqZdP7d87Ju2Z1sJa66chzx3RSfWv+f9/w6/14P/63Pv4ASdEbfd43fwb8TkvqzeTozTgr8s9ekd2uIxpJcXLAajGhWExQmXpb+e7uI0b6ZuClCmz2DduLLf2uTZ2G3vLTjWWiDYO1GK0YhkRy1pkhGyzEyDYkwrc9nLF7ch+/Krl8ecnVZg0bONgNPN4lwmWWmXGDj7R1y/Wra6pZOVa5IyTxJwTQbGtePF+z7xzeeXb3KrpcMfSO+1omSWFgM5H4Hz7A9T3lL1+iBocLSWnPxZ7QeeY/fMLyo3sMRrE/rvACym4HV1+OnjeR5uxzPJGyPOajv/5zzn79gpuLNSGkpE8vJqgsKae9+vVzZqsZ9z95yIMfSYZ9x6t/fM5+vcP0ieBbdj1T33B/WmIjNPuBtu8ZigXlowPWlxsiga4f6K1DaYlEoZEYpeitA+8ZnMXIdLgutxZjB4zI2D5cMgRFbDVHR3Ni2+Gu9+nAtA5x0zPpDM3asb4W/MoohuwkQQgyTVXmDIXmepbgIMd9xUw8RBUS7xKMwWhNVlxQHg5k1RWTexWzsqLdNDzoDnkqj9mv1/x6HrlcVKyLjP/GNxyWkX6zpsxnyGqK1jnl2SGuNcTCEJRh32zJ6tSIaW1NmRkW9RFQoDYR23fYCGpSQJuhYqBwHr9OPlPGenofEM7R7W7wRSBMLfsXG6rpkiAFnd+z86cYV2K6igPzMcYGnvMbvlAv0tK1EeFH/oEA0Tlwnmsia9sx/fETnBavl/k7Cho+BH5x9gUAk6zgv/qznyF/ew3bsTLdt8igESROkCR1VEKMZF7zqX9I6HqCAIQDIZlQMuuTUlgg+RUF79mYhi/KU4hQxZKH/ihBxm73jFszI1KX5CLb8LW5QCB42B4wD9MktjBy+ESMPGpXYxfL42/+EeeTrw1jt0aKN9zgQ+IA6bGDJVWCMEkh8COMVoyJhriXEoHgUscakRS9glJk2ZxF8WRUsAyIsYNqY0vbnSOEpMgOWBUfEKVg25wjuAIhaNwVEk3wkRA8iKQgJ02qzodISkiFgCIbvYxUgmZBSuBiquJHQYK4GY0MgeAA6ygeH+HXNcEnkQXXb1DGEO1A9vAAQVIOzI4WhDpJY/sQMVISjKEa1pQCer+nHmZkk+MEX4sCpTVucEwOZ6wvrsnKIjUyYyRmCiMlzc2WdlvT2HQPDc6xuVgn36O2J6tybD+wu9lyc3FDiJEiwCdDpMpLhAus65bjIeC7eHes3N2+I3Tsdgy1Zfjt5g4ZcPJX96hWM7bna5pNjSozpoczTG7euPPjSNq3TI8VQvXs2nO6Z6eIXUvTVQzlCUprfEimqd6lzzDPczb7mpgbirygazq6zT55GxnFfr1nupwju54Hq5LKB2wuaYPGjT47IoKXSeBielJx+upqhE2mtpTROokEAdgkLBIRDF1PUaW1JaUgJJUPpsHwcMjZRMksN4iuH++PlFhpBG3XJ9EFJcEGqklO3w9YXOoaKYUKSTxF5xozBJxWqGXO85OW8kmJrR3x56+3k9fX5e1DX7z5hLfG9wcHN63jpkkJ/k8fHzGLSaC8vd7jiKjM4ENgu6sRIZJNStoh8YsHlVEZicwMP29aooVDrfgkCrIsI4jUOcYI8BEKgw4B+sixeYhSii7bcLr+n4ilITSeLCZzZV9mMMp/40Cp1GVCabKDBdJonOxGCKRIkNUP7+N2LWV7xQezHFv3rIeKfXbIzemGn51ojnWCOb/aDa+Tom/B6OIbP06daa01eWYwWn1z1t/6Kr5Pj96PfyXjD5AUvbFYxDt+9s3x+0Lifo/86vbpiwcrnhx/Qje9R3CRftcQnMT1ybU7OI/rLbvrHfjAelPz+SqnFzGZ6OlEVs6yjCJP3SWjc6IL5JNEpq4WE/IqJ4TI/nJDt2vZjfCP1cNDjsUxN2c3ydn+9vNH6PtkMllOK+p9y9B0dHWLUkltqpiUPPj0IVIEdldbxD6RpYVSaKlomx6tJNcvr4ghUh3OUJmmvt6lCqqSZLlhqjX7fUMmBEM/8OrXz6nXe+KsZB/ukR/P7+YsCvH2hRGCfFHx4KdPORkecvXZK85eXnC6azg6WjKZVwyd5ezZOftNzXQ15fCjExYnS7Y3O4TOiDGQGcPQJ9ifyUwik4fI0FvcNrl0hxhp1zVRSkyUuOhZHc3JV1Pqyy377S6JXhiQhOSZYR2qyBE+UPvAfrcGecWDHz5ETQrCvsPtG4L35FXO1ekaoSV6UoF19F1PGEn3+cGU4w8OGHYteXtFniVlt6osSOp/iqMPjpk9aCFGmvM1/uEUYRNEQmGQec7Nq6+whUqE7FHVKcoUd/XbFtd4vNG4aTGaITpMgCEEpPM4OyBMRjkp0bMK6j55hWidPCyWUwge30socnxmKE6OkF8lYvXVdsfMOtxgMeKITisyrdE6x6hs/CCOGB1BSsIoMiCUGLseKnUAfArciMAIDfPW3d4W6X65xZF+c42O97kQifBffHwP/WUHo6S4CCOZeaweeyWTIMIwQuSMQXqXHjeK6FwyV1USpUzqyAAihsRzcR5JCv7uqshKvAV1JcakSCeTWbSQkmhHSWJGbyAh8KNLfFQjv8OTFN1IiVNQEm9TUPjN2ra/VYvzr2F6QimEkAybBr2aES83qaofImHsnEYhUpdoJMrfwZpCxJOI8lIK/Gg0K0KqNkcBXoxS5TYFosHoJHhnEiwojhX+QEzox5GnkppcqeoixuJLVIowOIL1ZNMifd31tC/Pk/nkYo7vBsxigsjSvWRWc8KYBPmmJ7WQQc/K1Mlc10nFTslkXzDOl3OBLNeUVc717gbbD+n+0wrbDcjCQIzkecbs8T3qizVegomC2XzCMDha53BGgfNoqRBlkdQOjUJaj4ktykf2Tc3scE51MGPn9984Jd5xoHwriASdaQ4eH7F6eAB33J83x5iI6lsDUpEgZHWX1D3LCTuhCdZTKkUfEzwtSknvPWZSII3GW0ccHPNFEnFoRlXJrm4otSYMFi8lItP4tU1Jv48ILWHf4TJNVmbJQ04mSKUYoeJCqlQIuoVHjeuja3vMmJBPJgV29E3SSqGJeGuRUqQuRozkmabrLWVREJxPMuJKJShkiCiTeEyyMPQxQctjiPRdz/T+EnOYcREvXkPSvz3d7x7jdXmz9vp2r+47wgORgn+hFVEr2qst/cygS4WSikwnSGzfdrTbPShFU7cYY1BS0u0btBJEKdkNlrULaB8wRiP7dM8qIRBNQGSaqFM4FazHKQVCEuoeD/RKIrNk1B4zDT7tfZhRKKW3oBR6UqQCSW9RJmdo2nSWDBbZW6IUFIuKZX7AdW9o9i034Zqjw3fcvN81uW88VWvNZKre6py+4zfdrd/34/34//fxL06K3sQDf8tr4F8CkXuzW/SO3/NdbssR0EWG0ormasfZr1/QbJo7/4Grh2c0oiG6yEfbj9BNRCvJk8YxjMHP5Spj+fCA43nGX5/+GhMDTuZczj+F0ZdIF6laKKTAPjni5c+/5KZp2G9qnA/MbODDTU/f9hyUJfc/fpCqxC7QbRrqXU1wHl1kzFcz9us9As/BwwOO51PuE/B5SfvRQ9qRoPnBqzXT376iMJrhpiM8X+O14nRVsu37dBjPMuQIu/gollQybb5dP3Dx/AKbe57Jv2GxXzL94DGnq58go+Cq3xGbvwciu37L3776D8QQWZUr7n94grOOs/NrLq/WLOZTylmV5HoHy/lXZ+ADxWKSOBcjz2N+MCf6wPZmS9v1lEqmS6oE611N2NfMJyWTecXl+Q1yxKBvtjVq39J3PT56TvM5ogupy5D9BKRlURY80TlFdNQm53RYkbtD5vdLxPPfUDxY0b3YYOzP+eFf32N3Dtsrk6Sw2wEGjws98mzDCWnT10Ixezzn5utzlLxkdjxw8PiIQx2YXCec/uTQ0V29TFCS3SO+bCbk0zk/7HbYv/uSx3/6Q+biZ4gixzc7ulrjNw1u19EOlohA+4CTErSmzA2yH8hHyWdvLfZ6i2A0QwTwhoP4A4pM06mei/7vcV4wKw94uvwLbNvT6Zb5wQGuHXChYzP8Eu8k3bBFVpqwbajdFzhxAUpwND/gYPgRQgm+mJ5zJjap6jn6mNyaCiIVEsFPjkcFxxD55UVDPYQ3VtybCVKkc5b/56/+HUoqog5kHxwSzq4Qe5UkpH1IvjV+jMqlSAHfYFPQ3fdI77nI93yWP0+/VqmR5+OZ+JJ/e/0JRFiGKXGE28WQVL3QKSCJPnVePu0e8bg7RPjAwidTZO9TxySMn/mi/TXONRAFh8XHyFIRnOWs+UciCQLYW4sWeoShjTwnEqzqFlrlx3s/hGSYSd3C42PC5RaUQkaPq3vUKNpw+7pt94rN/mu0UvRuk7gYWrJpn7EXVygBjbu5I+LfW/6IIk4S/ytGYlUgrOPGf0kr9ncKmGKU7JVjJViOm62/5W/dbr8xgo/4fYMwiswrgh8DvzLD7xvk8Solsdua6AJu1yBvpeRHRT+daaKSSepbCqJNcE8lk+Gxd44QA7v1nigizjnMpKDvBxYPjxBCsL1cY52jud7RdQNegBl5LUpKNAIPPNoODFcb+n5gOq0oljO8c2RS4fc1g2t48kFHnv+Gths92+5u19sMP335zTy/OW949e9Ov3GyvD1a2/P3jvEkes16kcc/oPuTn2C3DV4tiRf16GmjU4dSSgIgc43vesLIaYlFxm7fkBXJpFZLQdt2ZEWO9Ekav253+LZDaZFgVpnGIxDeol7+iuziObaYEGcPCDLd/8In6Wbvk12CVBIVkmKclBCFpOsHVIgU46lqROocSykYbEJEhFG8IQwOFzxCGjyBNgS0kuQiiQe1TfIyypUiE4rq3hIjJe7lNX+hBqr1hr31PPNjwYLvbgbdNfK+pyj6zofi631pd7SmmVjqV9e0zT1UXBC8RyHveIWz+YysyllfbUaxD0PXdTgPpkimvP+xzMkB1zZkeUaOABcSx68fCKM5sdKKtnG02Y/xIdA7j9SSYB2lzimtpFhMWU0dT3hJ9IF+2zBsG/y+TYIMPgkYibIg1D0ohapygvN0m5qj+TMm8oo+thSbNW4+QxvNX2UZvkyl2P+l77m6LSS9/T/e3Ldv46h4dyfz1vfvx/vxr2n8YeBzd1+OW9st8/n3bfN849e98+dxrAhHSLivd7+g37e8+I9f40MkH31WmrphP91S6x1hiBj3AzTpkDiKqXKWLaZcS8nq8SFT6Zg/vyIXgT6WbMps9FqUd0Tr5mLH1Vfn1PsWoWXyIuh6/N6yaCwIxeFqxvzRASFEXvz8S/Y3OzKVMN3zo0UiygPeB9anN4SzG7IyY+gGzj44QP7gPiY3LL6+Yr4fENpRiVSZVhlcxUBW5BycrMinBe224eb5BXbo8S7S9gOTLGNSCBrVUhU33Fy8Ily/4n7xf2Z+fECDuZvf3ra83KVgNIrIxw9/wJN5xeGmZn+1Y3+9Y7+pCSEwm1Yo5xOp+WBGWeUIwFpHvU2qTmjFpMgQQxIF0MaQZ5J2GNh3PW3dJ+PSEMAP0EV6KTFFjtKCJgQ6N0CA1eFHtN1A5wceUo/+QIquWPDqJjB5nEjX2qhUYW1v0ESOPnrI/OmnECPdumb9/JLd1Ra37WDbE2OgcY7mYcRUOZNZxsMfSxB78rWn2AzYduBQ7KieCoKIfGYELzYN4WrHX/9ZSeELZv0e6w4Y+hVSDdTna0RbkRlNoR1dN9CLSJEXBOeQ3tNDgi0Fjxp9RaRWlMbQWo8Iirl+RCYEOm74ev2P9K2jrbd8vPi3FCIynQhooSpy9t0zrpoXhFxjRoNaNS2xvcXrLSI3HC8+ZiGf4Hctp3EPbFLFG5fgHEm5AD3JkZlmER2reUYI8Jur9jsWbFrnLjh+dfkMADPRPD14SDHRyK9buGDkNXAHX/JjciBE6oqo0c+oM5Zn+eXoIUTqpJjID+pHPGmPUjdk3HNCjHedIRFfC6AIITjqp0gxS4IPgEg6KYhbEQ9nacM1XX8NKI6rTzF6SgwDF81v8GFAGQOdI6ISuR5xZzdETJDAMCqPyDExiqRujJLytTcZJNnt2wKB8wQBLtQ04QLh4+jZk+a1ba9BrdMb2WFMYCQTtaJUR4gYUULgUaAcl/2Xd6acQpC8lbjVnUgBoEe8fnw0bkVKpIjgLHJapLfbt8gyI1qPXkxxTYepKvR8gr9Yw5CU/qKUCGNQ8wq9mtJeJAEU2h5hNDILCJc8iIIUZLlJssYuw4eIllBIQzEtRhGNiFeSuu0QMZJHUKQO89APuG70NXq1Jds3FEKg+j3lEJkup0QZ2TlPOTUcPvFIcYEUnt/5HBJg9xa7t28hut++y2H7HS8/OFxRfvyU6D0T68nut1x/9oreOqoyp2+65B81OKoso+5qml2DUEl5jxgZuoG8LDCj5HrsBvphSPeeVCgliLlOXb0QEb5Ht9ccVZ6X2xvi9H7qSJF8cYRzxBgS7wyVkh3n8DatwVwrVkVGJabIG8iAaC3OpS5oDBFjUofZj7L4mRxFT5REZhKlJKYy9JcdpcywPmAyw/6rS6wQnHx6zIftK1TbsY3hTvr9jWl/a37vktXxsW8+/p0doreulKCrWsysJ8ge8SLALoILDDJgGaXhm4a6bQkhJD5WCFRVydD12K6HCF8MFmU0Qilc2xF9QOcGjcBkisFHmn2LUJLpYkYI9/AxUM1LNjdb8irnzFmUC8hLxYOzNUfLLeW9BdXJArttEQhs3abO72CToXPbE0c+tMw0mZKoYU1urzBFhus925c3LB+teKQUpZYEIv95GLj61gx/1x0tvpUAvU+I3o9/jeNfnBTdpiVvdYnkt7a37x+/y9p7C6UniOI7bMdE8l04/ew5wWfJJM86uj6QVwWHDw4xPWyu9gjnUSYn+EC9rdFa09UdzE3yD8kUOjcIOyT1KR/wPjJ0Lc1NzfZyQ79rk+mrlBRaMfRDqgIbhclBj7Caoe5ZP7+k2TWUVZ4UsQbPzdl1ei8hUFLQbvapFd/bBIv62rG/2TI/mhNPrzFEZssZs+WUdttwdbkmuoCPjmbXkC8qDj46wW1bwlmN04osM3glEJlB5ZFsMeFwkAw3ji//4TM+/OkncDA6zo/B8O18386vyjTT4wXTo3mSk+0Gdhcbrl9eoZTEDo6rZxfMZxOur7aJTO8cUiYI0H5fMynLZEiYZxS5IsSAc4msegvrEcJAnlMVGf1g0VEitYEo6PshEYSBQYAdlZj8LZmkabn86oxHeQr0hHXEwmDXNT40iCpFseXBlGI14bgbGPY97XrP0A3EEJkfLZjcX6KlQfD13W3V7huayy3zI8G8muI6y+5yjRtyTJkhpaTQBf26pdndYLcOX/dpXYQkkytUIhxnSibOmvcj/MpTFAUC0GWeoFNSEDONGRxRSVRuQIBqZDKZbDvyMqn7DcGThYjMDPoWJlNkaB/gep/kk2NEVnkiia8b/LADs0+KZC4gswT7ERFcJHFF7i/J76WkPSsL6BK5OD3vzTLuGwv5Gz8XJDUvPSupPl6QNQfEl5tUCQViFAy5IQeETpyW9NjI91ESlErXMqbrJ7MEsZIh8X2ClKhMJ5PVGMekS959jug9PoY78+MwCjKEsaMqQkzmrC3J20VI8J5IIqX7kNZOmeXIIZIsD193iW7NXJVSuJCMX6WSoySyTIUUneBeQqZkxI8eOCHGZMDow9hlZYQ7JXJ/iAEdU0U6dagkWgjcMCDylLwGkYyF5ahSJz0pMbyD7qZ5IkK8Szo9QQpEIQjWJXjV4Qyx3RN7B9ahFtPEg9jWiCIj1i1xViHLErWYYE9vIAr84AkhEci77SmxKihPlgwvLvEjRDNTEiEi3gZcaxOsL9f4zmKMwklLe75mt60JwHRSkh0UXD87Z7aYMj1ZJThUluZKRvjocE3/4pp232K0Yrut2ZGSAB8CT3/0BF28RAj/3UfMbZz4xhO+RZH9jpekJ/ON+DLSna9pz6Hb7OkGy/FHD1h9/IDLz14mhTYlkaR7IFoS10sKlJYI+1oAI3hPlifYqNAKpZKqJDEQUOgiA+/RJkvXZ99y/OCQrduyBYbekmk1nkeJw+VDwA0Bo5MpuDYKFQXLqiCTiuAFUgnyTJPpmPafMfv3Ma1NnZm7pW4yQ9sPaCGwNj0uR8i2tQ61mHDvj54ieku2LIjX6YXvmuIoUp3zzUvyZoJ0+4W4w8d+T9n1jTMMIF9N8fuOLDfUWyjzjMF7rPVMFhO2mx3SJAW9W8GSpm5RSjGZVnSjd1HXW0yWii1CK7qmQ2vNEBKcWirFfDnD+ZD2nChodjXTScnQ2ySRX2QEF2jbgfPPX1Gerzn45AH5coK92aPLDGc9TmvywhDbnjAqeSajaIM2CYpHjORlxv6m5vrLCw7LJQXq3THVbeHonXf07TzGu1l+P96Pf43jD8Ipit9aQP90DeedBYtvju957F2L9nr6IS8nR8mFfNJC3+Gdx2jJ/HDO0Uf3kC8i8kxT9YeU0wneBfbrHVIpDk5WeKC52LH8T8+IwfG39ZwwWGwQ7L/8DO9S5dWEkHxJQoLh+BiZasNPgybaAPuB4CP1YDlzlrDIuHQd5rgaq/CSRT1waNNmdyvFCuC9J/YWpOSxheZ0h312jRGaLDMMTcf5vkVrxb0n97A3G+zgsFctp+s9J3/yEfOTJeFXr4gxVQU75/B9TyYzDup74CwqSLSLfPmfPmP2cMnP7v8x+bx8K6hdhI5H138HwDPv+Zs+KZ7dn2V8/EnBvQ88F19Gzr+Q1Ot9avkrMUJpkjCFt57MaKJ1VHlGON9RyASje1FI2ughBLwALVJ1cxgsEOnbjuNHx+imw7Utk/YVh7lKN5AWhD7cyRnXMcLpGX/69ILpqqKbSl5eaYp7C+qvX2AO/xfMfPLa1HMCOwY+71so4ROt+ZHZEK+/QoQaIXuEUlSLHvGjAXXiaedLvtouaDd7cgr+9I8eM1lNkXWGNT/Cbmr8tUSJZMyYC0FQChtCkimXCYeuKk3oBjywytKcu2g5b/8eZGBwDrEeuSbWcH/1x0gEeTbn4eIvCaVF5hXCSzKdoG5qrPqXYcFT8bPk2VOmaxniaK4IhDyQi1mSZgZ+2D/icXcAQ/INQUnyp0fs/Dnd8w0CydP8R+g64rzj//KRpg+RvDDYr39OtG92jr6xToWk+vkeBPjOcrNw+Acd4fMNR+ZTpNLkRhMHCzGkz1gIQm85Civ+65ufEJVMQgpEpNJMxWTk7JAgajHe/S1x9AORWnFHHVbyTniBMaETKkneBx+IQnJ//jNc1kFnkbpABAE+dW+DcyiRxEOIQ0qcxu3Jx4hmNHwWLZe7X+CDZwhD8gfynkl5yHT1STJTJSn8CaAwkyTPDMyKB+TZAuBOxhgpWDdfsG/PUhAmJZCMkG+637LrnyO0SpX7UThi0HW6Z8Y5SbC5OPLGUoLGmDwJJSE3yBDQUmAOZjS7FiEEqlT43ibVQ+sQZfJy6Z6fUX30iP6qxoWIdg41KxFKJylonYOShKZHZhmx7RMMS8kkv11pVicHXD27ABtG6PAOXWnW6z1BCmbTimJWIhCYSUHb9ujrLdanLsXsaI7ODa+OJpiTGUoI7tWO+cWW3c01ef6S1ZMVq3s3PJ5vkCJQqm+fUm8cJm99Gd/90LfHGwnR6gdLzFQwnG+5+uocXWQMTY+Ike2XZxz95ClZplMBLSaVQhsjQwxj4WA05x27qFme4V3ii/mh5eubn7NcTWAAkaVgWBiFqHLseo+yLt3L52s++ugTnr084OLsBnNcEBap8GSHZDKaFRmqvWa+PUcpxarIqfYCVlP+wd5nN8zpBZx6z9BbAKqqpG07tE6Q3mFwKK1SYqQVRkhWDw8hU4Svzjk63TGbVcyN4Tf9r3B+QJwH/n7YIog4wH5jKu9yeN7+97YbfDvZ/1TS+s2Lubg4oPzPDn8x534Q3PcDfRg4XWRYoxm6hFSYz6a0qqOpGzKtGUIyC2/bjuA90ypJqDvnyIscBOgYE9Su7Qm+ZzGfYq2jd5bgAsakx0yW4aNPSn2Dw/rArjzk7/hTYoQ/2XT8dw/XDK6mUTM2YZ5EIazHzCpC3SHCqN6Za6KPMDgwiQ80WVRszza8yhq6oyVRwDCkPezNuXwLkvjOKXufDL0f/7rHH06S+6219I1d63dJgP4AozMz1sx5/vklAkE1Ldmv93TtwPJxwYu//5p607DIV8wnJWII3GxrlNKcfHDCwaf3OfvVcybNgPvtGVIKXkmJySd451B5OgDsYGm6AecD03nFw6ePqJYTXG9prvd0u5baJe+Sosy5lJGz3R69KHFS0rY9eZWxQKJ2PXawCdLvUxXXe493ntnJknurGa9+/ZzVwxPabU2/7+jrdiRnwto6Ht5bEqzn5mLNmQs8+/lvKbTmsQ8IFUHEBNXSGlyk7EukTGo1eWZQPlC/2uBeRu5/dJ/VwyPMtEAaxbS7ZLL/PBHk7cB51xFjZJqXSDFBGrj3yROm9x7w6tfP2V0mqfGuG+j3A0We+F1RJNL1fDnloDC4wWEHR1NodKZo2w4RPFGA9R4jknSvD4Gb02uOntyDYeCw6Im2RwqBHVXqiClBdSHgguP6i8+49+c/QOqM4ASqyJg8WVB/+Vv8hUBPCvThDFVk9K7nvE4k7EdZxsTnKSgNiYwfwkDbn5Mf9WQLaIuMTS1xtuDxD58yUxWu7gjbii7XyLYiSIfJDVKHxLcYr6tzCW4BYIzBCUlW5YRuIIQUKGy6M3wYED4Z/gWgyJcIJXCtQwRFJRbEXBFCQAFWpu6RsA6aFhM0Sh+lQJTEm1FK3iUQwXpClgIafKCqDXNVpM6VkpjDOeXygOfbS+rBEjqPsQ61z9HCUFXJMFNPclxWEIJ9fdLGSF93o8dWlg7ZywFipOk7zvJz5NSgPi4RpzrxGnQK8uLgiMOAi8nUeGIFhVuO5PbUYYm3hqkxdZKUUqMQQUpyGPl3SohE8NfJW0vebkNKpkREiruqtpeSPMwpJwdEkvITjNXghLNLFWyVuCB+rKcKmTpPUYB0HvDs3eXYAYyJW+M9RhVM9REhJsGBGGNKpoS863qV2QzjqtEDbZQBF4LaXxLbM+6EEnwgSEnnNnifhBeAxKOyDjErk5BDSIUWbkUcRi6SEClRI4JcThKc0ChkmWCScd8gqgLrwPYONQzkh3Ns7xAmqaLZqw1hCCij0IsJYlqil5MkruADvu7wF5vETTMKXeZEC/tNncynT29wznFweJDWWIyI3JAtU2dqt94TRhW7W/7mbtcijEIj2J6twXmuQkRPcgwwPW84/vQhB5+syM0WcChxQxX36EyzN+P9+eYZ9I7z6LsB2d8/srkh0IBxVAcThrXDmKT8ZkPg6jcvk1eeMYBDGoPvBhDQdwNSK7QxECAGz2Aj88WUrm5BBnzVsa83yNxgZiXZ0RyZG7wL2F2b1niZJZGO8z3H6gMOH82wS8Gu2DB0A8V8Qp4b/ODI4o6j2RRdZLjzDaEfkENg0Cc8j5E6RrxPe6AcYa23KNauH1Bap85m58jLDBsC65eXVIdzjn78mI/KNQdHC0IG//jVOZ3tvpV8vvmNuP3iHRlPHO/b8Zt/+mJ8I97Iu5xZPyfuQRmNd54yRq4CyCJ1hwqdzFOHYUgy/DH1grVSaZ0ZzdAPVHlGO1hsP6TOnUpqe9podEz+TXWbOkzBB6TRKKPo+g4tFZOqwFpPc71hJwVtfm9UvHtF3j6nKAXBO3Y6+WF1F+uEHMiSsEz0PnVytQR9K2KSCinFvKQloFVInXP1jTv5nd399+P9eD/eHH8AoQXxzRTod33hd4/fN4kaTzJBxLU9ygWCj+z7IUEShOb6+SXBeU5OVggEbd2y3dWUVcG9Tx8yPVkSgcXDwySp2fR3pPN+GDBEuraHENGZYXW8YrKaMLu/Aim4/OwV1y+vcM5jtEIrlfw7xi7JpMzprWPoB7ROfkd28AQfyI1GiuTQ7lwyLdRFxu5qS9+mBKCYlxx+eJw27n1Hfb3n7ItTdIxcPb+kWk05/vQhXw4NzTZVmEqjCb3FC6jydHDdqp4ZpbDRM3iHCJAD+MDz3zzn4qtzVGFYnKx4ehixdZ+gGuJ1cMpIEBckuF0+zfngTz/i5uU1F1+fI5REy1vFMIGXCQrlnEfHRDieniyYTzTNvkFrnUxNhUpE7yLn4Mkx3a5huPNwssT/L3t/8mtblt/1op9RzXJVuzr1iRNFRhau0mnMtf1sBPe+xuMhgWgAQjK2RIsW/AvYfwAdWnSwRFpCoOwgPSSky/X1e7avbbBlO+2005kZxamLXa16VqN6jTHPiRNlpp1huOAYUmSevVe555prjt/v963K5BQWZKIWKUiFvxQj/0LQNZZmvScEh8rqRAvMDdWdq2zefUpztiHb7CkPZ5An2trzcy0KASpN42MA3w14PxAC5JOCYd3SNYmHPjxb0VuInU1ZFL1C+IDINb136b3VOapLRWo26gPwSUibFxlOCuwY/pkd1MStIrZgAtAMhLpA5Rl5lWOHQHQeP06V05tKdqoxBMS+S78bCxmcI2iJyhIdVKiEUMZco9oRBZASoQTCe6KImJMp5Y3Dl75bgv7pkt3lY3K9QBmD3ml80dJdCNS+Q8o4fv/StaDdNlw+PGd2OOXg1jEqT+eOmZboQqdMk0lB9toJ9u1nSBkJCGRuoE3W21FrQteBTFh0DBFpdGpCxrBJlMSFpKmJAhDyRR6Qtw71vIobKW5hzOaRI6qkRmc6EZLbnYAUDjzqep4LjZUQEBK9TyiJlAkrUlkG3r0wLEgueGJ8vUQnIzMIo1ODMJ5nUkikTt+l6F263D3PPRIQY0AI9QI5k1qDT7SeIFIIsggRo/SIKMlkZT42EcJ5VGYI4/sQo+14CDE1XRHUlRlqWmGfrVIo82KSNC3HC/x6R8yy1GRmGb5JxhDxuZ5ivUNVBdE75LRM1Kqmo9/syY5miE2TkDutcC4gosMUGXNVMEhomwZtNM22YbCW8nCKbfsUWq01Pjc4kQJJTV0keqpPVFthNL4d0jVSipTP4wL5oh4DXEcd0EjRiqRgatAfolS9rwN6vocIXrgjBp/Q3pdDLd+3132gsg/7gcEHbG/RWtH1FikkscoYrENJhQgeP1h817/QBKlME0KgbbqU5+MCQkKzb8mUJFpHtqiRu4Aqc8o7J6nZjxHvU3E+uJCK+TLDDxK3HdLbk4FFJVHzGgabjABuneAebMiKFF5qtSJGQ2gGYu1RWpFJsEohnKcfNTU+RGRw1GVB2yWdixCR3GjyMsf1lna5o5yWTF85RgbwfngJBhLvO2zvb0CfN60f3Ri9eMTzBiry0XXH+FpxbGwYMd3JtUNWj5eYCPXRjO3lFiUFxpjkiDpY2oslTiTUbj8MGKmSO9+IjkXAxYBUksm0YrfajnTEpDXqrEORjBa00sToQUuMNOmaFmC7S6ZPk3nN5eWao2mNKTIskWHXUUwKVJVBk5wFldHoqkBkhugsdr1PeYAqo+8dWqSBgskVZIph39NcbJlcXbxAs5/jbGm//tiD9tI9P2ucPlt/edenG94KfCR17s/S3Hwf62j7LreDRp+9xXL6OZyuU/heSJOULDOcX6xx1pMXGVdevcbRq1eJAi7uPmP1dIntLdWsIi9zmm2D7QaG3qKKnGAdWWYYa0t0mSG0ZHX/jIdvPaIqMg4XU/ZtR28tucqpj+bMtnvy+0t656mnFZPjCbv9Dr/pWHcDtTG4EMi0pnWOSVVgB0sIgWa1R0rJoz+5h9KKYlKRFRmTgwlKSzrvWb9+wr2+Z7i44AevHZFPJuyerTBlJDvMKKqS1bPLdCAc9Pcie9cTAhiv8NYnCqAPuOBpu565r7i8d8bq3YEHpqZa1KyPp0xemWHqgs5IvllnCCk56i446f4IZOT49nUW17+UbIZDalK7Xcf62ZJu06apaJklndfjSy4ryVYLZKYQ8wmyG4jes1pv2W8bqrpgfv0IoSSn77T86blE6SmFVLy2c+RSEeIARz1RCAZZ89bkJzm/qLg6zVFZ+2KTVYWhvrJge7omKEF/uqKalPzkPEdIwdRInlXJ/jyGhDzszjuyzR1uis+zfPuSIV8R7SV0lkv5xzwbUk6NVurFBDVIQSYEsiy4kv9A0oSQJv2u71PujfcI9NjcRPSipD/fcD3/MiKPqBCIgyVKiW8lrduSK0UQEboBtGbQDafLb6VmwboR3ZKI54U48UXaunSBKdep4xWkkGlKLQWKyPn2LfpiR37zEDU5h81bCGCW32S6OaJzJ6jcEN2YgO4DDBY1zXmse4LqMdMqWTF3A8OxpjdT1rOKpg5ks2Q0oHXgzmKLIGJ9z1nzbXbyIfl6ysJ8HpNpzuMl36jvpmI2S4WdUIob/oQ39zeIQnBvsuQd8wipFHeaK7zaHqdN3/uEhkFqTBCEGHjWvkUXVwjruVZ9gbw8BiVw1o0W/PqFNojwklZIGG7MvkIMDnlQ83j9+9gRfUkT9GTYF8fjnssZd45+KjXUYxMijWI2eY3Bp3whQiQQkCIVY4yIzmX7gE3/MDW0EYKSqDpjoo+5M/sJvHcoBGFscJ5Tl7yAM/cWrd8ih4iM4EedlZYyUXydf+G+6Zwnm5bk1w9pvv04mVX0jrhu4GT+wuGPErJRY4FOOUtydAAUdZlMXpQkrPcEKWGwBCFon61QISF9MgaUAILnc1LypSxjCJ7fDgOPfaDbt+giQ8TI0PTMrh2BD+y2e3wvkD7iQ8Q1PeXJLGU9dckJ7XmYaDktKY5nnEvJpZQIKVBIlvfPOKoNr0mBJOKHsTH6uM1IQHlSUl03rJ8tySYZmycXVLOaryyOuXO/AeBPrOWPrX3/Lhcjw/Yq+8cL9uuGujigtQ6h5WhvPqAieDlqm5RMzUhMyIXtRltyk2zxdabRMRAi2M6ijYQ26Sknt+bcXmxT4b4aePuZR1U5uQ/JpKO3+PYMLVsIHgZB0Va4ix7VW2JwqHaC3GxxhWSwCVkNvSUAb0rLF4RgkIr/2nc88B6lJEWesd+3oAT7vsdkGjXSAZNbaEOeGbRSYCRff/Z7hL4hxsAQhvchFB8quz/wi5ePrXj5Ph94yMd9jsBo4vACgqJ9umQYBkQ02MstgZHK7ANSp/NcjCiyEBEvIzFACJFMyZHmGHEuUE9rvPfUs5p92ydnRa0p5jM2+wYlJbODKavlhsliiusGhuCT9pdIoTOUFBxfPUz7YdAMzjJsG6rjKfPcUuoVTvXYeB199GPYdsA3f4Q8fIbwgUuxYOkUetTYhQhIKCYFu4sddt/x17McYspF/D+7jssQXiYhpn+NQ6P3fxSfNUafrb+861MxWvjE8dsHr15/Ed+18SqauT1TpSjCmu16zVqONBchEsyNYXo0Y3I0Y379AIDVvVPO7p8RQmQ6LTExMLQD7aZBAIN1FJMSmRnqmNPsW0IMrB+ecXm64tpr18jqIm3G43Sx7waKIufk5jGByPLZJZPMcFCW5HmOP99RtgNBKnyW4bxPQaWM2oTBkWUZWZ14/G5ISEOza+nXO9bPBpaPNEKAzgytkcTJlP2zS7bffsztH/8Cd26djEnlyWrryhdvYpuB4Dz7szVnD57R9X0S1ZYFjE5FVYxcLtfkeYbRhr6NPGnB7Vt228hZK5jMA+W0xN6syKYlU7VEskq6kXBAu9mjlCRG0MYwu1oyu3qAbXuWD87ZnK5Snk8Er5KNsXDghwGZpbySwph0/HvL03cec3zrhJs/cIf9+YbN5ZZ90xHXHhcDxbwgSsfgPEIZGo4QIaNwikVMYYjP4SCzqKkF7J+tiJmhCBHTtmSTAmzP5dkePauIRuI2Le1yy5xDvD2mPjxis/p6ojZpRTtscd6hdKLCMdX4OBB7R28DWIkzb2BMogVpAUGr5E5m0xTahaQpCL2l0Bm5OEyFZG/xxkOegZYJBRoGvDGQpU3V+4F9e4bYenRuRrpWRHuDCGP2jpKpePcRnR9TqCzpY7xB+IgoM+K8IEx7et0gXDPS6iLF05pslVPWV4hFwF9ukgmCFMQokVrR+oDDU5iIaxp874ga/DTDh4G+j4hlyrgpNeR0aC3oiHR+ib+u6N46Qx9+PrnDHWScxnVqPIo4ZmjB3M4SHSxCpy0XxY4IXJXzhHxkGutDQupixMrU1Cop6NyGpmiQOmIzgSkzhHVp+joWCs/RBCkSSiiUShRcc5Bc8ZTGR4HKFLpPE1fX2xe5NUEIBJrSHBJUovYRAmpeYUJJD2iRznXEmFHy/PuJwDPQhVUyiwCCE+THh1QbT50tiCKMOhKJG93pBBC1YrW9y340UHguEiemnBkBBKVGGmFEeI+5eUj/bEVwHlXmyYhi22KfLMkWNd3ZmmI2AecJ58vUqGmFlxJlHcpoUJHY9QxqwEwn0AxoETAnC6RRdA8vklOaS+fwUZVT+YzQDUxFQl7qWU3bdkQf2e8azKVJzZ4LLI4naK0QRrM5X7N7uqIqcxjF7WJeU8wqzMGEZrmjkZLqyhyVKYqDCf2F4bTZI1SBiGPWVnxpu3t5HxqHJjpXUETa0LK/2CEyaLsttTrm1phB89D78SHjxjYa07jWMPQZxeyQZtumoG6pcDrRKB1glEQh6K2HXKOtT7ojLTGFoR8seZ7Rtn1CDwZLkWlMZWA1kF2boQtDrVukCAybFdpW2NHxUGY65aeFHhV7gsno+4FwtiOrcpxwYC39kx2Z0Xib0FP6MQvPaKYRSufpBkcRkllAkWf0w4Ayikld0TRtMivxIYW3Fhl6pNNFHwghsOmWuG77vWzbLz4D8RJK9P2VCR9+dCQZoWS5QUTP4KEoc5SMWGtZHMwS+uXHLDxnqfKMg8MZ50/OyfOMsshZrbf0TXKpy4ocMyLHwXua7T5liBHZ7RqkkrTrPd556rpk1+zQdU6eG/p2IMSQ/t10rNoNbWw5EAIlPRoHU3DFIdbNCE0yKpJCEDvPtvdoqcF6opbJUTMmNN1kmm6543a2oJDJiCX7Ho/oZ5qiz9Zf9vUXgBTB9w35fB/fSyEEN3/4VYbiTfbZIa53hBDQhaGcVpgyI3jP9skyBZpuG+q6YnEyw/YWp5OIsVxMEUpwWOZY67C9TRkB/UCdZ9RVwa7puHhwxpXXrnHl5gmXTy9fiPjrgwm6ynj87YcoIcgyTbttaLZ7pJAMg6WoC6p5zfZyS1XkWO+ZVjkxQtd2WGvTpHQ0HRCAFZK8yF9clIdhYHexplUCNVI3uk1DuahBJSIBEZSWqHnSERWHEw7euMawbdk8PufywRlh8BhtkEZRlwW5lnS2p4+e+aTGBo/XEt8PrJ4NrM5WBCmY2RmD7wkkHUSM8PhP7mP34++UICsyFlcX1POa4zeuM7ky5+m3HzO0PW1UyDpnMi8p5jXbyw1SCEqjqeoSaTRPnl7w+N4T5pcTZidzrrx6lYvvPMKKiNISK+MYEJoKTCHAWk+QmuZiw+TaAVJLBJGoUjCtlJLu2Yo4OGSE7myTLIW1wq12dPsW2yddj1YSqSWqyoiNIm76RKWalZimJ/pIdEm/FQaXXNFGpyZ8wOQaGSNeArkGH1E+TcCjEinTpbfJAMAHhJZEAlZJtIjIUV9ktUoakn4YwzwjJoCLgtC5RCPzAbdsEwVrtHoXUkBdEIpIxI1ZNwFEpDypKYsFQ79DkIwHhosN9umSOlbo41eRGsy0Qk1LQtONiIEkaJDbJPz1rQUPsbU4YrKRbbukWbp+Qnv/HKs9682WrDbIg4TumLrAn0hC8ATnoTCILsG7QsoUMDoaRAxZ0k1FIMZUqEelCJlOaNu0wu+S6YMiuXv5kEJQ/eCQeY6YVkhjoLOJIkVqVKT3YO3oOscLc4fU2evUnIWIzjNUm4xBxGhwEcbrzvNAXGJEjM2WmpT4XYsUSdMlRNImiZHKJ5JtHcooQhPHYntsnIBoHUGPCJgPiRIoRqMInlMLA0ZIEAFpAyCTy6AxL5q853oCXRdgPe7ZClkXKFLj6X1ArveYawv0rWPc5QZFQq365YpsOkGGiGvalK90OCP0ELd74nySrtly1DiUGTrTBC0RRUYYLHGzJ5tLBgkTkyb0m8sNxbQkELn6ytWEimQGlWn6pkdWBfvLJU3bk2eG6mhK82wFRtG3PXldpOyZbZvCeZ2nvlWjtGbxxnXab7ydKLXxuasmn7g1RWBzsaHfd3jv0WNo6e5yS4gFwEir5EPaDGkkITq60y15luGMxsVAJKJCJGqF7S2mzNGZxo4B4kFEjFa4zqKUQBiFCSbRaYsMYzSRAVUXZNcPkGakl9qIOZoSz5JeTh9MiL0l9g5Rl7jBJbTOiuR02XaIPEthrj7gSIMEqRW99USVqL/RJHfHvDCo3Z7YpVBfT9IlNn2PKZNja2k0fYSmH6ikQPpANZtQHk3ZPf6EPfql4/3hT+BTWi9eJIKI1LeP6Na7RGMMAeE82+2eUGfJqdIlZ00R0new0poqM5jKIEWkyDT9rkETUUiciAhrmc4mieaY5+kc6zrqaU27bQiDRRVZooo2LdGkocVu14BPBg3BWqrSUHlDNquJatTfBpe0qtLRbffJgt0HggKMJjSesOuQ0xIh5EgZ9kQEpspwvWP9bIkoSnSdE1/yP3+ftOizHuiz9dl63/qUm6LvQp2LL938UV/GD/7uk+770l0+eHM+LZgcLpD54sVrhhCwTc/y3ikX90/ZrnZorTk4XqTAxDEDQ2SGtyaKaCRZiFx/fIEOKVfEFBkHR3O0kvRNn4JAfWD1bMWVO1dwTU+77xLdoMjYr3Z0TU89KRmcp55P6Lo+ISFVwdGtY3YXW4zRiDH40Nlk24sQaCHISoMX4GKk7y1ZligsVVEC0Hc9P4Jhs25pmpb5tKY+muKC4/ee/A6D68m15CduTTFKMMiCt6c/gheK4kTy+vHbnLzSc/7ujrNHRzTbHSwc9954AFJithXZXU1W5hyEQLW2eO8xxlA93qDPW+6vNty/c5vD169xxWYsrj3j8t4p59OMSwXEyMn9Z8xtYLKYEv7q63T/zx+g37V88eGS/skSd/YUYRSHWmGjQ78iUHaFDJpzaRDasGtamrst9awmn+VkM8PQtDg1JGqjlAQR6UNAaondd+S9Y/vwnGtvHHB92oD37H3OU1UjfKB9loIy8+MZftfhokIJiclzdAaud2z6e7z7aIle1PRhl6brvUW4QMw0CgHtgGt6nBRkUhKDQISIItGrWJQ83v4B7mKJGSI3b/807CIMHY93f4g3kWJSYDc74mBR3hOkRM5KTCy5Nv0yMgrEYF9oZ0pX80rx40lXMhbJOD8WMREzqyDTqRgPkU33lLuXv5IKyEwxefUqJnvGPLvFQXUHu9rz2+f/hSf9EjmLvJ3dR8RH0At+/OJzHOgD1LRMqGIYNTdGYSqFUhlXix/CmQHbtzzsfgcxN4gucrK+A3mJ1557z/4AJyL6wZ4hDuhpSXY44Zl9G7/v2b99yefnkrD15LuMa9MvIbTitNjzfxz+IdIHrm5r/vrZD6K0opTVqPmJhKZLlLEIjDkoznsOq89zfFgREeQU0HQE58ZCT+Gj5/H2j3B0MHhuTH+UIqaQ1oBABI+QKjW88ySUZ3RUiz4VvhJQiNQMP29GQ0AvaoZ3n42T9XQ/iMm4hEgYXfK888lCOyS9mixzYmc5b99lMzwe5RTvTdOjVjA2VZYmIUkIri9+lFzU6XmVTLoxEXi0/QM8A0JI2nunyYTDKMK+R1QZMcREg5MSczSlf3oxoplgipLgPMXVBXGfBPN+uUZNp8Q8h9YStUw5V2Mgr4sBITXm+gHDgzNW7V32XGK7nmV/hfzqG0yKjGa9Z3+54eiVK3TblvnxHG0SpffybJU0HFpRzmtsZ2n6geLqHLfrWT1bAmCmJbgUgDl3Ja/e3aKiQxVX6N/yDC7QtRai/+hNZKwQhYDpYsLm2TKdT6PA/h0tubffI4Ddx+hd8vkzrn8lcPqnDwmbV/DdFHKNIOk3O+dAKWyM4Dyl1rTSY+oc31kOjuZ471hu9lTzGu8DRqfgZJnnuCDf2w8juKZDmgqhA6K30A3oWYXoLaGzidq22afBggBlzGhIEvFSYASEfiAajTEGKSDUGX+4bnmWD9hg2eeaQgLOIWykKAztMBBIOiJrk113kWVoF7hx3nAQDEdryyqkxuvj9uyP+Qg++T6fcNtHvs5zBFA+oppuMD/ccvHWE5RS7E+X3Lx8HdVfA+fw4yBLSIUn5ezNrxoe9b9LebQiR/Mz/ZvMqhleR37VfJ02dJh8wv/LfZ4c8JOC3zqsCUrRNx1FWeBVGpxIqVJjIoAQcd5z0K95rX+bbBc5Wmie6dtsdjPiOjDsWnAK27yLj09H98YOoafgPbZPKL8YHWud9TjrUZFk5hMjD33DcG2OKg32gXjhRPfiIH7WEH22PlsfWp9SU/RCyvfpPN0nrPenLH9C4nKMuM7SbVu61Z7l40u6Jll0Kyk4PJjhgeAjnbPYUZPhQmRbZgQfKYVEa0Vh8heaBSFSQ2RD4Orr1zm/d4rKNKvTFU3ToU2yoZZKkpnkNJZ0SnXi/7Y9SinyKmd3sWWz3KIiyX2oyChrQ304ZXu+xjY9WQh0NoXJxRDo2h6lFW609zVaMSx3uKbj6vGc137sTXSVYcPAtlvTupbSpAunEBKEp9ESP9LqpNxTHURuzq5Sndzh6Z8+4pF7zBN/wTwvWOSa0ihcjATrUKMDTmgt9cmc0FsuL1vOkVxXDYsbE45uHHF27xRzMCWfF6xPl8guwNCxPF1y/o27DFemzE7mvHbrhNn1Y/ZnGx5/+xGhd5S5IiskIoPeDUymM3RRsb/c4gT0IU31zFFy71II7ABxcKng1smsoQ0Dh9OK9mJD8/ic/E2B0BIrTMqSKUwqNFWiM9W3jtjeO8OXBjOrCE3HYEFKS9stYblNXPpZlWhvz2mZdUHIDXHbomKA505wWoL1UEjErsWrFltZXNsQljukKvEChrhDznLCxLO/2ILrwWi0luAdtu+JeWqGotZkmSYu90QPZXZA1IqgZZp0xkCuSdSwSWrewr5HAU2h6aqBrMgors/xhSX4TXJue+aw71zS5j1NOVJYVDtmlEh6HLbtCTYJsYXRxEoTQqRfN2TKYYoaLQvEusUHUEaiqoKyuEk2mTLEPWenOc47us4TXMPu4RnTSUlQgvL6IepAM61yrDHUoqLuyoTo5A1P+zNMlXM1FBwMFbGPSBlAuWS04ZOOKI6aHw3IqsD4DLcnuZnZPulsspTxFHwgdgNt2GNlizaSkI0Nx4guyLrEeks0GlVkBPoUHuqTUQNjMxTG0GotEp0uFAaJIHZJeO+cQxQGUeSE0YxAjgMX4f2IMEbQkux4ij3bEENHK3qE8wn5kwLhAsSEckkiosoRukAGyNSE0hwQjEJH8NHhhEMw2ppHkBHk8RThAwhJsB6cR1bJZlganTKtdi0izxBNOxo5AFogjMHt9ihB0stMCtg7gvPJQXDfEruB6DxulYFSDKKnG5ZJ5yIOGfYdWZElFCNEhmZA54btxYYQIrYfQCtmixm50QghWZ0tCQJi78kXNf22QQwe2gFd5Qy7ju7xkmLq0MJjZEZobdJuOXh/VfjR6+jVq9im5+LhGT5Gjm4cg645fXD5ibubVD1C9WT1QOhBq4LOeap5jd21KA+y1CmeAIFRiXpKBJlrtpsdIQSGtqea1Wnf6Gxy4JThfa8dQ8Aud9g4EBuDNBlh26BnFebqgvbRBX69J27WCSXMDL6o0PMJUkpkTNoYYXSi0XUDospxmz1r57iYa9p+YKILhPPoPEOogJdQ1AWud+R1QVGXiQUqQGrJjemM4+M5+NT0v1+//xLd8ANLPP/f5yjcn3d9xOsJQNAhBGRTuPblY4iR2Q3D5OKQfHGD9f0zhqYnREExqei3HeVsQmY09/fnZFWPkRlX9oKjImO9W5PVDeVUc3Q85fqfGIpoWHcu0eucx48a5qquiZ3DiYBWAutS2O2kKqi6LQfNhnpWkU8L4mRCsw94F4nkIAI2tPj+Ervaovoef7Agr4sxiy05dobBjbTckVLrA956fK642O9YzI5e0JC/+4H7bH22/nKvTyWn6EM//jkQn+fyI/FR93vpJd7fBL1fnRmFxHtYn614cP8uj5YwdMn9xmSGsswxRWpumrYjIKhmFbODCUorpJY4JVnPDBZwyx1mP05tdApvjRHKwwlH85q+6YHI9mKNCFAUGX1vKacV1ZU5th3Ii4zgPNoo1pcbJKmR6bYN1nmmVUFvHXldooxic7mBCEM7YLSkbZKotV5MRqcbx3a5TWyRGMnKksXhhNuLmvpg8p7QHIEUCiU1SkhA4jrPbr9l314i65oicwQxWvoqTXXjgOuZoX/Y8ZQHLHc9ftswHSxFkSg/eaYJ/fPiTTGdlEyXBcsQOL/7DDubogvD4bVD7j29xOXHGKkIwMH1Yy6fXrDf7dm4novHF0wHya2jOYtXjnltWrC/2HJ29xnCSoppThh64r6ndaCNott3qDJD5pphP2BkQssEIpU8gVToRssuDsiDnCxMGPYr+h0UBxPiOMKUuUEohTQq2douKlRd4HcdoihQdU0VJJEeryVx8DgpkG2y0n0eqBq1hFyTqZrokk2y7ywBwVAbcpOQGi53cKgRswq5qIkNKJ2lrONICgJ2PgmtqwIi2G7AqBI79CAURaGxqy3BOYxJaEAAUImGSGdT0OOkSOLpfjQTOJygwyWT6phsXr/QwsQYGZ6uiA83KB8wSFSUqQB3zyleYyGtR/cx51E+gB/A9TjXIQto4yWiiYhFSbbSDMslulLIiSR6BxnQ9MjapIDSXFBHiE0Hg6W73KOnFeraAdWiZn7jVcrdTdzFFrOwTCYHhKZLA4zxuvD8fJdaEaVEWIcOgRDAKYmIEW0UIcKwaxKiY5IVuFfJslvqRGsL3qfnyBShD6DAaYUoFK5px5wiCXF03JQiCejHNyOkTE1OFGmafjLHnq1H0wUHwZMdHzFc7t7TUAiB9z6FtsZEkc2uHyb62+DSFc+BlBpG5CAKO7rhydGmPCbNGUDuE2rkA2Q5UmiUCwjvXzjtqSpHTQqGp2tEDGBTZpGaly8up7oqsesdxEBylhHJcCFXqKpEDZawa8EY3GaP1Bo9r4ltj55VuG2DX+6TDmwMDdZGE6yjcIapFjRnlwghqGcT+k2DKXMcAWRETwvctiP6QGt7ul2L956DkwW2s9imxxgDIgVHe5ds8NcPTvGvDegqoXVuRN/c803ku+xBQkiufuE29WKK7S3zm0ds7+/H298rPD+wLaXiO0TKumB96hEuMJ/X2BCYXVlgm56+twm9dI5+SGiOJBXK0ShCEJSLCU3TIoVAEzHKYApNJkzS8gG+c6nQ1hlBa9i1KK3xqz1qVpKdzHEh4rqOuN0QnUVNaqSS9M6RZRqFTEGyOqKKgrAf8J2HTIFKtzW7huA9GE2RZeyblqzKKecVrvdENNnxhPxgkhzZ1gPCgychq0KptK9H/5Flwft+/h6stv9sDZN4UUuEBNKOFM9EpzRHU6aLq/hQspjeBB/o1w2bxxccfe4Kzf1T1o9WiM+JlB/oA/lJTaYzdJcoyfnRlP3lJtHuB8c2pGt3KwVlnmiSbrA0+zbZZ3eBPM+oqgKCZ1HnXLtxAz1S4LyHGBw+enYXW5TR5EWOKTLM0Ry72qbhSIzpvxDSXuYDxmh8CDSrhsh47c4Ng4tYD0iFkOkIpnFKWv4l9DF1sp81Rv8t1927d3nttde+r+f41V/9Ve7evcs//sf/+MXPf+Nv/I3v+XX/+T//5/zCL/zC+27/hV/4BX7xF3/xxc//9J/+U/7lv/yX3/W9fOUrX+EP/uAP3vfevtt7+b/b+hTpcy9R5/6s362X96vv4XHv77He++ls+gabZ5FHDx/S+g6hDcYYcpVCLdumozeKrMiYXVlweP0QpRXdrmXzbIXtLUNvKfqBaZ6NIkqFVzJRoGJKiT+5c5W7X3+bdtuS5Rl1XTB0A10/ML+yoJpVnN8/o9s0yY1Ha7xPj1dG03VDCoubT2mbDqUV/a5NuStCMLSJ3tP7hEQ0bZc2pNFaWUpJMSlYXD9EiMjxo9/lZjFDbSruVV+gGwzdruXW7haTkxmTec3myZ57f/gOzkWU/hMQknWp+NUv3eDglSuYqiSSEw9K1FHOX/1GxfZig20cvfOJTy1TAOPz5m+/2XN47ZCbJmfR9Oz3G0T+FL54i4Pbx9x4fI795hNMZnhSSO6/cUR7UtKeLYnOQwz0Tc+T5Y520yBzxeHNY8LbT+Cxgq1mpnP+ptIIGwmzkv9dCTaDpe0j3wo1i/mELrRoKVMxEQdu1Q3BOiywPfo8xa2c5sF93r58QiGm+PicLjOGKO7TpK272CZdhA9UzQHX3/yxRGHavcXZ6bcZnKeSOYE0TY/OA5HYCoiB2DtknqUzssqIreXBs/9KmedICV3mEK1HTirCJE/6kq5BGE17uoGRaiEEmGC4Un0ZU2sGu+fh7vdAgnzk8PsOrRST+gpX6h9ChJgoNKOeQ0zzZPc+OIgBVRiGTcOkOGF27TV0ZnCX20Qp3XWI5UC0HqsVPxi+yJd2PWGwqayQKUR0ks0QNtFQg/NgFMV0yq3hK/hhILqBJ+/8OnGeEbyiG1ripKAJPW+d/QbOerJphsuTk1ldHHBdfREnPfJGQRBgpKBbbnFPdphtQeUWRO3JTubcGTIOnhW45Z7aq1EYnihbIjMjz75ncB4zuq5plVylXJ9QC6wdtT8RryWPdn/MIBtUYXCZQ/QCryIP1r+LGnxq/gqD6BRSGG4d/Di5NoSjPVrohEiJhChJUl2XQmQjUiS9VPvkCY275Nn2j0FEDu0PM7dHKT9IJic7NRZwz/U4clIy3D9H+sBB+Qaz8lZqLnIDbU90ntPuT2niOumarMf79HyPt19HbiVSam7f/GmUN8nwIDcIZxEhQJUlgfZgk/mCUohMoyflC0dkYTRojarKRCuWgjg4dF6A95jjBW61RYiIiCJ9H/Yd5vYxMjOIKse3Q8rO6SzCeYJNNKVb8iFXV/fZE/mOfp148nmWz1rc4MgKg/eBolIErbAEimnJfFayOVuz3zRksxLvE82427UYpZA2NbaTG0d49whixjYG/s+mwY0ZTS9K84/aY2Jk/7Th3v9+/32/3r31BD/4MUduzIUarc7fe57IlbOOQ9vx7I8fc6WdEEXFNGi+YyJ7H3C9RZVZQvadp5jkpMwqyJRk27Rks4SG53lGsC1fjn/KIoBGkx8l1kHfRd5pFnTrAWsjQqvUdMdAaHrcrsXMKtS8TnlV8ymh7SEviFKQaYVUGhGSllIZTa1vM8muYGXLI2lYX2woy3ykQgqGfkg2+kUGAvIyx/ue9XqP3DaYpytCjGy1YnqywHnP9Af/OhMRCc5y8Sf/P8LQvjjOz2uFl9GL7yL3+t7Wx8xLv3XR8O6y+9CLBH4fonrvFzEi5pH/dzxlftgTMkX48Tuc93tyrSgf/BaZlsyuDtTzOdvljsLlfOd8j7SCnRT0Bym0PCpB0GJsUiJYT9N0TO2KH7DfoZ6WvPrmlNcPB4QYuOwPuBdeZ7Pecb5d0skaGSW51xzOagqtyMwl8uxhQokyQxRpAChU0hTZwfGO/hyr/BjvHU4kyty0n5F/cc4VpZDR8+b2Dyh8iwuR33qwpXOB90+lP1ufrfevf/fv/h3/4l/8izSI+pj1R3/0R+9riP5HXZ9CU/TBK9FHXNq+1y/aR42S4of//aGnG4vcPmi6rWW2OKEWIgWt9gOrbYsncu316yxuHKJzgx8sqwfnXD6+TGiSFGkjAA7GKY+PiWdsRv704BxVmbN6coltB2aTChcDbdNTH0yoZxXtuuHpW4/RYwOT5YZ6XrM8XSGBrhuYzGpMmaEzwzAMDGPuRmZSXkWIUB9M8YOj7wZm04rBJjtXISMDCQHbXWy4+YWb1I8GRLdB60A37HjnT5/he4uSkvPHO/aLCaGxOJtTlDl0w+i6E/nW3Q0Pnrbp2Nw6RmaayWLKq1/8It2yYX+6Yrfcsd82DM7RdgNGK8osw+97hFYsZhN0Z9FCsXlywdXXrpJNCm69do1n33mCGBzWaC7We+rDKbeuLRjagW7bIr/zDHrP9mLD7MocHwLT4xnNckcmM4bgmF/LCfuWZrDEPGXVZLnB9Y7Tsx11WbBrerQucb1LlBQpGQZP00XqK3N8XjOcR5gl3QSQnNkyjd/uUhDirkeWerRF1qjOgDDEqMgXNZYkqjdjoyBH7YjMkxA/KJkobvsOoRWddJg8MshkM66CSIJmm3Jk5N5iB4saklYsKJmyemIEoSn1FIHEKc8Q9tDbpOnwHqsUWTElSoGq8jRpXjeJ1iUldrNFW4/oE60pvdGM/p0Ng/Oopsd7DwhMZvAkM4ciKHQPxCyhJlHgbEx5PEonhKzI0IuKfrkjdkNCIqWh7Taj61pE1QWiNCAiPu5RBoK1yBhTg6IjKmRkPmIbSZalDKDJoiTWh7htw3B3RS9W6DxDGsNC50StEToJ3kUAnSUk1g8dOjOp6B8RI+8DhFSMM9JPUSnfJZ0fW3rTIlqB71PDpADn94jSEAQ0/R7jJWUxYTI/Im4GRDlqZ0a6j1SS6DxSpYbaB49e1LjlLv0cHX3YIRc1tt8j5QleqdEsQaRw2bFANNcW2PX4WYdIbirKbJbqleThDApEpxDOgdKpmRqpez52yX7bKwIRIwWxdcgiJ272oBV6VuLOdwghiTISBehJkWikCISISCUQeUboUzabLLNkmvHGTYbTFX7bImYTxOAQVU60nrjeExY18sjgx8wsu26ITQ/WJTOLsqASHmcsxjpKEXj87BJlVELvxpwtbx2+7ZOOZ7eknE9QUlKWOc2+ozyeYXcdRW6opwn5jM7TnV+wHc6pvnQdH+EyeFyIYy/0SRuRINhAvxk++l6CF0G5H9rhokDbwMG0xpwc0j7L2e4927tPkDcPsEFhFhOCAOcDAxEvUjPkdx1ayWTfPur0irqEzqMv1+RTQyEyVJ2MFLrHF7Q+EoNO5/TgUAfThNpJgXDJAU7Pa9xaJ+MfKUaTj3EgsNsjhErXvCHFTahdhtAaYyS1Hq8ZSpFrxb7tMJMC4SOqd3RnG3xIGiOvJWFEZFf7jnXzFGMMWVOQH0woj2aJto0YkQjeQ4W+zyL8e22kOhfpPkidjADNB35Oro7KR6aVwiuPzjWxh/3pEr87ZbNa47TB2kg2m6QsQpLD4+AcRWagzumdw+16ZnVF2w10w8DhYsqJErxaV+SHEyaFp9AOu27p95q3Ls7YNl2qBfISH2EfIm7vOKkM2kXyukBohWsHhE4W4gHw7YDbD3R1QatqLCnXbPCe9WlP1e25eucKJpdMBkMVBqxPw5sXf/7393F8tv4c686dO2y3H+3S+Ou//uv8rb/1twD4V//qX/GzP/uzH3m/siy5e/fuX9RbZDabcXZ2xn/6T/+Jv/N3/s7H3u/f/Jt/8+L+m83mL+z9/EWvT999TqQIx/cYvd/DZev7+ia+9OAQwXtyJSDPubhYs2s68qrg6NYRV79wE9v0PPnmA9anK5x1FEVGXqTpfogglKDrBrJxI/XOo4Wg6TpUkeGJnD2+oCxz7BjkOjmusO3A6YMzFFAUOd1gmR/OUFqxvdygBDRjFsT55ZqqLGj7gWt3ruLO17jBEZRksI754Yy+6Wh2LcWkoA+RycmCYddi9x1ZrsmmFYevHKOnJepoQcw8q23HTvX0LpAXOYWUXKy2dO0lmUnue23bcXjlgGHf0fQ9dTkBJXn0J/dxg+f4jWvEmAwE8qszsuMJk33P7umK5nTFftsQQmC52zOrK5ZvP6E4mbG+2+H6Adf1bJ4tObxzhYNXTthdbFmertC1Zvnsku3pksPrR0SgyA2TxRTf2pRariWPv/OIw6sHbC93rM9HTvz1OWiNbboXga2+tXgpKOY1za4l+ADBYmKiI2ktkUpgt1sUR+QHJawiRD9m0qSgTF1m9DEme2KlEIPAlKOjj+3pNy2yEIhMMZ2VeDvmWZQZdD2SCENCY6gMfpuK0tgPmCIjtAMGYF4hXMB3A+6yw5VbtCqJZU5cpyJfagW9hc6ilUHngSiSq6AIYfwbU9L8c/tlOSsJzUDYdaNIH/pNg+wHxJDE+9Ik6k0YHNqHNDkeMzocyQY+GkUsc9SYc0Q3EKJjiJ6gBRlynEhDcBb3bD2+p6Sfw9mkdROjYHnf4Zv+BcUsxEj0EUhZMmG/xdcdQSqijfhdmybnMrkYSiUhMynzx9rkxEQkColSCpMlk1nf9am2UiohZaPOy6FS8yVS7lSIKU/Kk+iraIU0OVkOelokyqV1xE2bhix7iyIZZQgjCT5d24JSCFwyTIgjjTSmBsn7pHnUxqDynOF0hRIp4FgoQ3HlEPd0T6wEUqUg3+jTZxyIiEKj6pLu3mmqIWWybH/5GDIG0orxtV2IaKGQmXoR0hti0qqEvsMJiVeROHiESRNsYTShG4CUkRRG4waXHCoQCFRdJHts8ZxmKvG9xV5uU9Obm6T7GRwhpiY45IbhYoMbXBoMZBlx3RCcS3VwljK8ZIiYMZ+oVnAwzdnsGpwHUxbJln9wo9YqUBiDdw43WPrxOh06y+TqAZvHF+xXO3SZYcoMHyKmLrDepyHFy7vEJ/dEf75tJz5vRpOBQfH6deTsGuFeoKTE3jlh9WxJt2sTGigFZlYmijQBWWVYAXkxQQjB9HDObrdH+55iHLooH5LN+d1n+LMNYlqBksSmR0pBfuckXcP2Xco16y3hcpsaVR0wiyn95Y6wadM5HiJoQdi3kGloWtzQIrLktid0cvfTmaZpLXlm8N2ANiZZixuNlAKnFTpE2rEhM7kmuIDONLuzNcF5yoPywwftI471940SfdR6Gc77OO7eR3QDUQiCFPRdz7Bq0VlGfnJMMYmIqsTZQHV0xHK5R5gCXWSEJpJpDbnGheQs6K3DWYdzjkx6FmXBlVtHVJyNCHPEWsnubMfDpadRV8jyjBhDsvkenTOFFOxi4OBoDtueoR0IOsN16brohjQIjIXB55p+cIQYcD4hyCEG9i5yb98iQ+D6dMPNKznuOV3uY6iLz51rv/tA4bP1511CCCaTyUfeVpbvfXfyPP/Y+/1Fr7/39/4ev/RLv8RXv/rVj22KvPf823/7bwH4+3//7/Ov//W//m/5Fj/V9ak0RR9uff4bf4HGNyCUHAsMuDi9ZPCBm2/e5OCVK+hcc/b2E87vnSbjgyJPVIbBoTPN0Y0jysWEfFZy8SBdtIZVw2a1I5sWlHXOWzPN4AJFKXl9PRCsJysytuepKxbj1Kbr07Sx2eyJMVmuIgW50ZxXhvNplja51nA/DuiTeiw6BoTIubJqOQyRxbzi2wa2dU6wPbeHnqNZxfz6AfdPajZX50nD8mN/neZ8xXa1Y711iFcW5D5w5zLZYheZIR+tyEWEfFpy7Uu3mT26QN17llCxSc4f331Ku9lz5bVr9PMqFekxEk8quLNgsmq58c4F0Xk2Z2u2mx3bTUN5bcHRzWPOH5wRnePsnad4Hzh+9SrXf+AVimlFdrbi5HSf7JwvHo2IWGRAMFtMiSGwW+649uZN1k8uEQKqxYR22/BHDy6IIRCigBvJGvj41av0u47N+TpNmbXEbTpyGRMdSUiqsOGVs//CF7efBxPoFyuyqqdVE540U4igJkXSZgCL6hYn9ecRWnHZPODbj/6PZNrgQNZqpCq8d25fP7LMK//C/lpkGjcbePcudPuAMUkU7UNEdUOyTo4pgTwIgSoyou/prUVlimAd0Tkg4rwb7X9HZMWHlG800mVUXSKPpoSmJ9oUpCm1Sudk2xNsEvBj0meI9ejBE5VAZhk+eKTWqbgPgTitkWWeUI/xs/ndyduc5RuiVPzk8k2O3BQZQtIZCEEQgafDH+J8g9AKK1LYrDDJqEA+zzLRiiAkmS65Pf0xkomwQIoMSIGkgeS2KIl4F8bE5Ygabd6VScitGKlLwY5BuSFZCKfA3ZCKvJjctrRJAZ8uWpxMz//cyty2QwrWVTLRH0lNqTpOgZveJotzIUetWlUghvRZPLcnFjEk6tnoXBW9T/Q5GXFn63QVVIrSHPGF1/8mKI03uxcIUxybHO+T65WaTXCje2UcPFaJZLMOyUzDjvlEIiFdUSRE9Ob8hynyI1Rm8E2HNJrgLGfNt+iaNUEKvO8gBsx8SmyGpEkaUSqEoPOR33p3jQuRaa74yes1EYFSEjWbMqx3yDLDr3aEwROaDpEbICZr+MUEO7hkId4NhEiizjFqn2LKNVJFTogpTFYoyavdW9y292hC4OvuDmftjIOTRXJulIoQAi4I8BKtNSHCdFrTbRu2vUUJgcr0i+Yku3nI121ktoBsMSW+vUrnknivQfqo7QM+uTAXpGL5I8d8MfLN04bvnCeK2I9eE1z5Uc2w2vPNB1uoryJVop76bsDtkq35INK1OA1OJHtnyaYlWZlTRUEWc/KJITuZAQK/bVOgc59staVRYB3ucTKBiAjkKKKJuz6hjU6gb+S49T5FB0j5YhAiR4fCp6ffhPBt1MGEhps0LtHKxXhQiiKnbVosApVJOjukRr8XUBiiFBiZNLdCKwbryOd1agL9dze3+FTWx0Idn4CBjOhQfOnnKOD8SBELTQiaG5dfZLZ0CKX4/8Q7VHeugJIErZkdCLSLHNgOf75DtR0awepiy2wxpUvu+MztKX83+x1u3L5BdVhhYqI6X3Y1v/X0TR5vT+jHnMM4fp/SsY9pD4jQdwO/31YM4kvYpgMpcSIgFxqpkwZs33R4m9PZIVm5x4gUcmxuIrazBOv5r/o13pi/SvSOQf4KyYXkw8dHfBzV9LP1l2r9/M//PL/0S7/Ef/yP/5HVasVisfjQff7zf/7PPHnyhNlsxt/9u3/3L3lTFBP94oOThPc2j4/hwH3X533pIS///HFLJBoLRrHZ9wzAKz/yGotbxwTnefSNezx7cMqkKsmNpu17irrk6s1jTJmxX+/Z3n3K4c1jTl67hust33n3GXK0xxZa0kSY3zii7B2V39LuGoa2T5txkVFMy+Tm4zyby02ytB2LF6M1LoIoMphVNE0HhcEpSTdYJAqMwFrPiUqOUE3vMEezlGMjSM+9bzl7p8Pf+DyPvv2AqiqSbNIr5PyAQnfs9x1h8OTzCUWRs11ukvDWOrSSXDy+4OD2CcdvXENnmrN7p6w2Dfn1KbvNnvXvfpusyJgfzylmFcWixlQ5kzpncnWOkIL62pz4zQc06z3BBdpdy+tf+VzK+BjSdGy/3jM5mHD8uWvMrx1w/4/eRWvN0PUIqSgmJZtlygVBJmpJjJHrX7rNu7/zbXarHVJJusGlaZVKVr17a+H+GfWi5vDGMcunFwSjU8Mg05ScGFEC6swjmhVZXRCEJ8sShTG6kCiGVY6ZlbjWoqQmz2q8j0kDIQdCmSejAS9GvUhIYapSoGXEhCEJ3RFIKcjmGWamGMacmmh0Mj4YUZYIEAI6N8hMExtBXuV41yMzQ8gNSE+0YwaOkgxSEDOdQju1ol5MEEVyuwvZgCiylD3iPEJnMK0S8uE8sukIOoVGijzx0OM+CdijlOgY08Q300SZCqrnRf+gHXuVMpkCiRaWZRmC53oq8KFnEAMhRESe6Dp+3yYrYSmII6UshAC6QJkaE+WL72xEYKROFt9jAeX8ADGiR4toEQKehFh4axNSCASZCmWRmdTwh4ggNaHeuVT05QYJTEYhchyRlxAiuSzRRY4PyfY5hlSQSBVQ0aemRaTQVSULok85UjJGHBCz7EWivGy6hIAl8cmol0gZQlJIypOrtPdO0SLRI0fiZZoKj80XWpLVBf3jZUJURk1HmhoncXQyhEiFXACk9egyI6MgWMhUhRQKbzKG5QYXG4JUyVBBJzMOv00UHUban1AKURiabXLf1OM1L0bwg02OmUWeUPOqSHS6uoB9RywzBBG3bYhaEYNHek82q9HziuHJJSLKhBZpjegGVJkndLK3FGWGu1xhqpzMCIwwtPuOalJimyEV50phlHoxcNqvtshMJye6bqCaTwi9pVvtyQtPfqWgDZ5+u080sBcbyPdf4T3PeHmxHY20x8FHhlG17sOANBHXbeiGCj1NeU9NZ5G5wY3nczGtiNYlJ1GtiQiiCwzdQJElYxmTa1SdjrkXaYAgtw0iM4hJmTKm2gG0xExKwrZJf6vRad+SguF8A6NhgigUbBsUITXRg4NC4XYtLipa5ZFSYkyidkut2G52mNykbDMbyYQky0wK0FY5inTt8ENyJw0hUfh655n0H2fM/f2v71pJPNcsPb/jCznTe8XFyyDJ8xrGK0EfPcFDXFn84x5tNPf3a9RacPTaVfZPTum7gZPrxyityK4vcLuWTAVK59KAlmSqcbMy3LmWMT8AITp807F+9ymPmhnfDFNUlpNrjfAe6z1aK4bejmHVkbbpqMqC6BWXFnzIEDEFo0ct6dse2wWULrGdTcMjIrZPA1+tVdpbnUcaRS9yVg0UVZHOuZcPUkzHLfWLoxkMvBdW/Nn6S7d++qd/mjfeeIO3336bf//v/z3/5J/8kw/d56tf/SqQUKKiKP5bv8VPdX069LkIUbzfKvujJw+fHkz+HNp9kYI9OjmZScHmYsvrP/4m05M5zcWWZ995zOWzJVVZ4LynOqg5OVlAhItHF7TbBiUEbT/gBkdxUkEGk5OazdM16+UW6hxTFOxPl9jWsj7fI4Vgce2A+nCK6y39rqNpB4SSTE8WBAHBBdZnKwYREZmhPpiwUYJsWrM6XWJjylLJspRE7W1gcWVBcb5jvdzi255qXlEuavrHK2aTOmXw2IQkdJdbpidzimvH2G1Dc7l7YevbrTuuXTmk27WUswqjFNvllmFwXD4449rnb3BwbUpVaeZtx/3NEjFYJmWB6y2Pv3UfLRWTWcXRK1c4Plpw+egMQuTozlWufu463geqWU0k8uSdx7z+V95MOQmAjB4ZLJvLNc4LXvvxN+k2LQ++cZcYA1mVU3QFwxjEKFTk4sEZ2mhu/dCrPP7GfYT3tINjejChDZ68ygle06x2dG1PlhsObx6zfrZEVxkMSYD9/EIvlEhJ6yEkuqQQqFwTLoc0hW56zOEEf7YlBk8IFuccamJQlKmoLcx7BXJevJjgeSnpep+0LKNeRgC6VCgrkSHShpCK+zjqMpxHtAHCQNPv8bsNYnB4IwjOobTCxtSUeB1wzY7oepASLQVGSGQbUkipqRCFQLqAyDRIzxBBNn1qCofnxgKkpkNLsJbgXEJMRkoZUhJ7h0WACgRhGWKP8B7jItFagu/xIaPrBzQmPW+hiZMCJORVjo0Bd7kF5zAyJ6CQo/WTignJ8u2eqFLBJkeNw/PBQXAe71O4rJCSECQupom11mqkYUVs8CACOAdRIWxLVMl0QdcFsjBIqbEXKVvmOdVMCAFFjqgLzODw3jMMKcRV+JBQMiWJfUgNIoJQJUpMEAItNGKqRgQrNSrJ/tbhtUq5Yj4QSAghQiRaZpWlJql3L2y1GYuR8bTCS0F2Mmd4cEYMAmlycIkiaocWOSmgSW5Tqa4bkZSxcRLElEXTNQQ3pAJWZeAGTJS40CPzsYHcLFORPJ6vUUn0rILtSxoLOYbjuoicVPh+INgBqgJvAyomVECUecpCWjc8hxZ8BFY74qYZtVEBWebpb/YevEOK0bWvt6hJge8sOhfUZcEQPNZ5dG4wUo5C8pDsjCOYRYU2GhEjTkicAH1QM68L2vNTbNSEy55iMb5mDJ9I/4kf3K4+YhD33fYtQ2qe07HTOJWjTo45CIc86hx+bELpHVlmQElcP6CiQGmNmuQYIWheGO6khj6FbjEahfQIkwYPQicb9+g8wUiGrqOcp1yyaF26FpU5Mabhj9AqBSuHHpxLIb6jq1q/7wn1hH7v6LVFFoJ2NPZxIZApTZUnimM2Gjg0bQ9Z0rZURU7XpWtONanZLzfMpjWyyMgzPR6951Ss76Mx/aS+ViSTRPVcJIOCMRUsCJEs5SPIkLLC4vj79M7G2iUCMRCjxreO5vGa/eaC7TpSLSYU8ym7fuDy7ilhsKl+ePcppz1MDqecn63oTiqkkrR2wFpHNamYTgLl7asEIfCt5eLxhoerlm5yjCFL1yUtQUQKk7SA0caRWiuTs2iQtIOjdw4CdF1HXuR4UmA4UuC65LGox4bY5AbvPXY/oLUGna6z7XrP2cMzbr95nQ+e2e9rhl5qKsX387l9tv6HXz/3cz/HL/zCL/DVr371Q03RdrvlP/yH/wAkVGkYhv8O7/DTW5+qpuj9KQPv/fu5yugjUwhe/tVHbUyftF4aBD3njB++csLs2gF5XbJ9tuL+H75L26Ti2YfAlTtX6buep28/QSAwWnJyPMc6z3DhKQ8L/uvT38L6gWye8+WbX6Y53bE6X/MDa0uIyTyhvHFEUeW0+47Td5++EF5LkbQXm77jfm1QWiKuVOz2HXkuubZtuH6xZzqvKecH7M7XiKholx3Rt9SzCXXv2bYDmVZcXXbIzYDzgcPbV7n2+rVEVZpn6JuHrB9e8PjbDzlaN3gp2e27ZB5gHUNncb1lfjJnv205fOWQ7XpPUWlWZ2tuvjLj1voPwVrs1DCbNjz+1gN255oofwglJavtDvFsx+zZnqMf/RwP7p/hB8f2YssrP/Ja2oC1Yn71gPP7Zzz+5gNuf/k1pBAcbu8yb58QI3yrO2a3FkwPZ9QHUzanS04fpBBJrSRDNyTNlgs8+ON7XH39Ovu2RSNpug47WK68epXXnu7wMSLLnN/3ln3rsXefAgkplFK8KKJebMIR/OAo5vUL6pKsM2LvwHnsviebFuzaZ7xzdpoQvolGlQofkv0pQpBNqyT+lqnAP91PEHoCnedmvWHWWSgFt2d7nB6IPnIvP2DwGr/ckYI+DNH13Hv8a4i6AO8IE01sukQPcgGhJW2z552n/9+EjhGR3hKtR8eCVw7+KiiFMAYVFFJJ/GiZnHdD0iWR8kN8blAupByd8Tug8zxtfOPfJQD6ASkiv1d9hyfZE+Kh4Nr5ns+tG4QLrMPvsQ3Jlvu11/438tkx4ClOM+hauvM1b51o/FVNdnzEX9/8CDkZYqSSijJnKCMPzn+HICJmtAUPIaTwzxATvagfiKPz3aS8zsn0hxNlTUpUiAgJ2+Eh581bqXFUMhk9lBlC5chlQDrPUfEFZhynXJbcEElFafDJpUsQMRH8WHQLKZE+4EYtjzAG6y0Pz/+v1FCIjNvzn0AUVWokR2RKWpcaPKNTs/niuhYhRLSSZFcW2MttKtF00jrF+J6ehzGkV4otrhk4mn6Ow+wVwgSWw13u7v4vpKg47m4zMVdSKKsUiNEtO4aAixFlLY82v0/Tr0BIbh7+FYyeIPA8WP0X4qwk+tE9MEYiASFkQvgy877rc2j6JOQuK0I3YI4XhNNloipOJXGzT8iPT0hX9ONxKLLUgJZ5onFZl87TSbIh9t6BT81ksMmi2iymhAil0SytJauyRAVTkr5NaJEnopRkWpc0uy6J220yt/CdpRojE2wnMLsfJZ+VyZY4/EpqLNSH95qPHeF9YJt6348fsS8J4KfynC+Ozkxfn3yJP5xfpx3WPNs/w+MJWhOHAD6J33WREQaXTAhUap6tTfTm2WJK5gfi4MiuzccXEel4zWapwTxbJeRapIFH2GzRr9/Aa409WxFGep3wjGJZgSoMtk9UMFXm2E3DsOt4evQF7ptbBOfZd2HM2NFJ39IPYCTbXTMi2p5cKVRZ0DmLKfMUNJsbkOlarTLDmzvHpC7IVgPnPtJ3dswG++iN/XsamH7wofHFoSFGePWg4IvHSYfhwm18uAkCnkwMZwrsvuPk8Zqr2tAu9zy5PsXdPEioTozYbcv+dE00C5rLDZfnp+T1lExskq32dAoCmq6nKgv6tsdJ+M3YU+wC9c0Z7b6l2Xeo3GByg1GC7MY13tk+Be9YP2m5G29hpxFIluVCputPMRo6ifDcMltw4XLWoaaIgsZ6LAO4RECO41BGq6Tl1DK53Np+SJrF8e9SWUIhQ4jJWd/oZPn/va7P+qG/9Ovnfu7n+MVf/EV+8zd/k7fffps33njjxW1f+9rXaNuW1157jb/21/4av/Irv/Lf8Z1+/+vTN1p4eT1HZMX3+AX8BPrvh9d7s7+Xpxi6SK5uywfnvP37b+F9oMwzgg/U04qzB6fIEKmqgklVsO96pFIMTY/SknJaMbiedmgRRmDKjO3lBtdbTIgc3Thicjhl8/QyaWjGIluMrlZdP5BlWXL7KTNQgqG3mGmZnMW2PRMp6c/WiNYym9d0+5SZJIRkd76mXW4xJlm/tvuWqi65/cVbzK8dANDtOi4vL9kZRT4tKY7mrC636DLHEZlWBUEMSBrsYNFGY3tLiIHJosb1ln3T0W32mDggZIAQWJxkxGsTVj6w3EUIgeO6pul7Yu9onq4wxnB0/ZjTe0958q1HAJQHNUe3jjm6dczjbz1id75lejJDBovfbcjKnKNrC0x5AAiOXj2h3ewINoXcSS2ZXT+EGGm2DYurx+xXW669foPm2RIfPN55dmdr8rrAOk9z2aNOqsRtVxKlJF03kGcpQX4IqehUCIQP6EmBx6ZTbESShEyW3DIEvEykLKchioAMIOIohkck/v7oDhetI2waQp6BJaE0USSzAh8wuUSpDNc7jCzoLvqUJdQNCXVyHu8t7BOdJo45E1Ep5HpPzA1kiRZh8oww+GRrLAXCZEhVYvIsOT8NDitAZgrRpg0z6oT+oCRySJN6ntOetE6+ACONjMEhvEc4jwSc6ejnMtHVHltM50etnscRUCLSX2yIlx60wPkB3/ZE7+m1IWYKETLkLieLSaAflSROpohhg1OeED2u3WEWFeXxLFGGdi2xt/idR+VFEvAHickMQavRHCMSM01QBislVgqKWZX49b2Ffo/qLVIIzFRiZAoH9QiC9yglcP2AiBEfUxOGkEj3nJrp8CEkVEhKvO9xuzWd78jzCaHtMX3KKlPPtVBljjQKJVJ4LlnKQHqu1RJKgtaEzTq5zPlAdKkwFRGkEEglMPMat2xSblZUaFWkosc54kTiux1Rj3lMpNyrKEgaEq3QVYHvemwYiAxEodAqRxcTaJtkH15m+OUuGWTECFITiUnP9oICnS7CbrlD5Rpdl/TbBrf1qBAJvUX4EckcLAwRioxYZMSmQwoIvU3nVW6S2YH1SSdFcl/0bY+e1UQhCV2P86m5KYyhyEoG6ygmJe2+RSo5DrzS5HrfdGitqKsR6XCe7bZh6C02RobW4nYd5T5SHOWp6VcyUSNflhXFRN1MHfvHz+Y+aZtKP6Trfy4E9XNencwYVEEzbAhCkhc5zvtEBY3JXXToB4yQ2Biop9PEVlAKYxQiN6gQMXnaM4Qg0eMOFthVAz4k6tzoHhkHi5lOkJlhWO5SLEA7pHPHpSBjYsreEzGihEi5SbsWnxuaIGiCQqqMaCxiFOg3+zY1xlJQlDlSSFwMDBJU8CgEsncjpzNijMIpT55ruodrZmWOHEPGnzs0Il9CID7umH4v6yX0N4ak11IxksXEDghbSxSRfr3HX53S2IH90yXHTrA+W+N9YO0jCEN98zBlRh0UZJMZ4aJFmArnVPoeSIkQEqPUmHkFbdunGIE8oeadhL7r0hByPmWzbygzw9ErJ6gy0D3u2T0847QVtCdXUVIl2q4Uz8HAF0Y6trdA0g1WVcVqb9gHT2IXj3loKg2avffjdUzgfEBqmWJARip0mec0XZeMTfpkMnR4+4jjm8ekjvn95/1nJLnP1ket119/nZ/+6Z/mN37jN/jlX/7l9+UaPafO/aN/9I/+p0AUv/+m6M9wDF72pfvQ47/Xhmj85n7U3VSwGN9xce+M+3/8CCUldVnSdh1lWdDuGkyWEWISJaIlq24g7FoqmTbO/cUGcQhZnYTa+37LbtiSlRkxy9j3A9v7p9j1HkFEZobJfEIxKynnNe1yx+Z0RaclvumZHM/ofdIV7JY77N6y37TkY5r75dNLlBSYTKOkTvbDmcL7QLfvOThecPvLryGkoOktp+88gW2Hfv0YHR1n7zxBFQY1r3HeUyhNbQwhglWC5XKL0JJgJDEzxNwgR/tg6z27kVU8ROgDZDeOmE9ywoMFl6crtBIUWYYQsHq2xHtPNavQVcH5xQadaS7P1xR5zvR4jn73GRcPzsjrAhcl979zxsG1Q+wkQJk+6PpwyvzmEY++8xhjNI5I3/dsNy0616h5hd807Fe7lAjf9nQR+mbAh8jieE49Kbi73yKNYnY45+xyQ5ZnwICMydo3hIiyEjGZMAhFLwUIyd6mvzVKhaxKQmtx3pNPChRpAs3o7iasRxmFHyL6oE5aCCkxixq37RINhciw7vCzmjA4wqZLk93OEoRDFYaw7xP9a5dEsrQDUUv8agcHyTBB+vfCUrFJCE2IiLYfdUuJNqNMQhtkromZRgqRrMhDotE91waJkIp/pEQMqVDVPiSnM2OSZsQ5jE5UpEFKsqxkYhv8YMmcJtNlysDIIk5GPJJgFFFlSCOQlwIxpOyTSqbCK48gTMApAaUhMxU4T2Y0ZVZjvcX2A13bMzy9pDiYYqYl1dUFrhuw7UBWF9T6Cnl2ODrKaaQYaXv7gWG1Bx8IuxbfOGIXkApElcNgGdqePW3SH/UD3llkpxAhha+KGJOLoEwFW3iuAQOCbegEQEDKAi0EWheJ448E7wli1F55hw8dNkRUrlECfEhFjUFhrh0kl7DRZS76pNkA8N7ifE92MKIBFwMZOdqkLCwxIgGqLunXl4SJw/vkMBZEREr1Qr8UEOA8RmbEvAbkC12X9w6kRI1ZTtH7NIQhuVsxnkOFFrggyKUg+IAukmuhmhR052uUVsnlMAqCH1EOSFqidkg6F5eQOiEVUkRMIXEa7Pka11lMZqDIkznKGEEgqhw3OPJMM0XQCpEQTS3RuaHbpNDQKEUyphg823VCjJVSiCy55NHbtMNEyOc1emrQZZ1QrJiKTqnlexu3AELAu/67bDrvrVyl/yAykNF2aaizerrisjBk0/KF653KDX58DZNnKUsq1+QIvHNEIagyTb9tyaSi63qOZjX14MhziWgSlTTq0Qo8Jjt8tCJKQWwHGCwi16hZjd91SJHIYWF8jIxpqBGeD4CAKCXtcs9QTmgGi/OStm3ReXIv9N4zndY4H7AuIXteC6x16EyhTIotEL2nKnPadsCPjYlwAest1DldDOlaNQ6uXui7Pm6v/wBkJ0WyLRdAEBInzPvuFkeRZvSe0PQ05x2PL/dMjqZc3n+GyUtsO7ALHnFUkc0q3GWDzzUuRPww0D5dQmeZfu6QSMCu97T7lDGm5yXb0zOKPBsbiIhRCusD1npUpmn2HcIHohJokoHOdt9QGcXt1w4ojjLk9pLL+5dsBo/L65QzlCddphApOkRIQfTpfH5OvRVC0HcDw240tpEiXeMRSKlx1mOy5FaHj8kaHYEPHqUSW8RiR6c70IXGlBmHBzMyAB/54Lz6eV+fjnF8iVr6P36x+xexnjx5wq1btz729ocPH/43fDd/sevnf/7nP9QU3bt3j1/7tV97cfv/DOtTMFoY//+jvjMf+N1H0uc+5r4fe/snPMXJ+jvcae6R3XtIm9+hUzOGF4LwwNXrx1xcbrj2+Vs8e3DKH5YScfWQZrnlxxpQ1nFxviS+0XPy+RPq4ynnzVMeu3dxNkf5H6cfApNccWcnmS4m+BDYLDfsNntu1AX1yYzLpxdwvuMLmWHiJEM7jFN/w5VbV7HVjuX5Bq0lRgq8C/QjElBNq1SghYi1jqnRCCHYL3e8M8t4clDgTURam1AWpfCtZTqbsF9u+dzWYpZnLG4c8ZsHJbLQ6MIwdJb9cUnI4cq3knbg2ablt/Ue7x0hRMIFSC05qkp+8PXrdNsu8UOlZLAWHSPBe4a2p/yRO7y92dKsd8yWnqPHF9w4mlLPazYXG+7/4bu4N6+xvf3X+M75lv73Tjl+NV20ZydzysUEpZJgN5vk7EY6gzioeXe74fq2IR8cvVRkOmk+tJDEkJqzV2+9yVf6geWDC8Sy42yRASoVPUqhgqMqF5z5m+y3R5y3jt9+uB0nu5YQVwDcqg1fiBFtPV5rRJZQCVxqqkKMiMFhFhXBelRuiKOVspACv2tRdcGpucbFSjNcbImDRlY5cXB4YZOr26LCrduEIkwLcC4ZB2R6pCopQj9AbpKYWiXnLRFJttw6oTciRLzziDJPnPgQUD6J40MknRMhEmTi0esQQSRHNxVJCElMt0eVCpwAKYHee/7K+g5e3CYODlF6ZAFBCX5t9idcyBXKZNzYGqZW4HvPjfrHiFUgqkB2/rtYZUEEHoU/ACswec0d8VeQbY8InlvFjxNDZG0u+a1XHtB1HRO/59UnA7LKExJiHc1yTx8vuRy+SbSOqb7OSfnFlPcUPVfFm8+HoSAiYq45bb/FZnufaB1D1lDVEYfgafstrFyiypLr2Q9R+ilxNEjwTT8ilsnkI8jI0+7rODq0MLxy8hOEaJKJg0/hrmJErnRhsGrg7vl/QRCIWz82TlCJOTenP5boSmNoqRg/0+eZROvuEWfNn1JeuUH1bMIb859JTZknOfcpmRwK3RZC4Gz/Lc7tNxGAw4NJaKBQApoOlOZq/eX0HqRAoWHXpCFSaRDWE3r3glUqfcArST4pMUbyv762SJfXweGfdci6IAJ+1SBFyvQKEWzybEiNnlYw2LE4N+ncJJl6HNaWk0kLPvJ0W3IekjBcAWHbQm6S+UeX6J4/KSTKC1qp+JWu5yLXL/QMSkqavicvc7BJc2ZjQElBWeQ0lzu0ktSTinxWkV+ZQwhMr/4vOOcpj2aoKku0USlf0Eb79VMu/+TXv5tc5cX68Rvw06+kf/+O+yLfsG8Qnefr7/4q3xBPqIylLNKeUxxMqeuSwXls8KNLWMARUVHgnCdoxdAPWCmYlgV/UxkOMoPWgfMyJ7RDQpNHbV5QEtH2yaQlhGTcMzZAdrmFpscLidCJqjZIiekGYl0gVLLQ7vYdz8rb3Dv4Em3TYZHkVdKnOeepyoL9riGOSHuRaZpuQJcZth3Ig8ABQcJu3xGVBC1oraWe1WRG83jm2dw6ROUS94B0Phr1icf5g+uw1PzkrRkCWGXHvFX/cDIBCIn2OWwa2uWOftOgpOWyzHhsLbnNOKgHboV0znZNR5hmNLuWu5MMi6esK64821A93mJO92yLP8YdDuyWS76++yEOX/s8/tUDrux/i6Na4IXk2+Er5MWMrktxC9Z5lBBMFlNijKw3uxR0PZtwUjn+ivkTOB1Y3V9zefVL+BCwLjCtkxGOHMOlhUi2/YFA3/eJ8iZSAxSdBycgVy+alBATk6HrB6RRKciYUaMZ0vCFEEEKbHAoo5GkQYrtLbeebjmZT3DRchbAjsf7ZcHDi3/9TzD5/2x9Ousf/IN/wD/7Z/+Md955h9/4jd/gZ37mZ/jlX/5lYoz81E/9FJ/73Of+e7/FT2V9evS5P8vV7uUO54NN1SdNkb7Lei7sP7hSU5xr5HTCPM8o9y0xRIYhTXD3mz3VrCIqjw2BfFIinGU2n9DGlrcuVnTfanl98QX0VJMf5DSnFiMSPa9fNUwPpnRNS7du6AdLMSlRWqVcmyjIjKGalHSbhno24ejKAWjJ/OqCe48uQMQU2qoURZGl92ct3nnafUsIkfnhlIM7JwzdwMWDc5ZTzVAktEfEiLcWLVKx3GwbiBETkjtQd7mjOK4ZBLgYmJ4syI4mOOdRWjJ0kaEf6FSaeCcaiQAfU/5SlSUBqkq2rbNJyeVqmyh964ZLZ5m9eZXBe8Smw4dIt2k4vHFEs25otg1D59CTCf2zPdZZNg+X9P1At2s5up0yGSYHE3bLHT4EBufJhUDnGUpJqoMJh9ePePynD6jrgvW2RUvItOLpdx5x5dVr7J6u6HpLFHkKtYyRKjPUWlHRo+ZzPBIbBK3luaT2xQnlhUCV2UixCYStTbQ0H1GR5D4YI7FzBO2JmxaZ6USNlAK36wm9QxiFbS2yrgi+BaUR0xz6ROdJbkRjQ9Nb1MEEoSVxcITOwq5FLmri4JEuhfZKH/Ei8Jz1o7Lk0uadT5O+pn+RPROsQz1HYgVgRpMDKREi0b2iEFBqVNOmsbNWUOaJEiVSfkyMGhlkso8OyZY6Bo8TYGVCOkLb4WOGzEwyT7AOZzvErkcUEWoDfZ8yUbpAyHcJoZECGRXRWgiC/XJD0ALbRfzlnnCZigp8ILhA7z2ZVkggMxOiGEYdjhhRFIFWClGMU9c+UQADyblL1gXSKMqTAxgG+lVDLCKiyPH7Ht8NadNXMlEtlcILT+iSs11UCRErdElwSdQenxcdIlEPMQ5RCJAquaxZR2x6QjEdEZQ+ZVtJMZpdKMTo+BZFJJSKwXbkOwmTpAGQIwUIQE1Lwt4mzWIOwbkXVDIRGU1Ekl5TSIHRKf8Hk0w9opRIFOZgRrfeJhH3aFIQSdN9menxlElj4m6zT9qh3OAvt6nxzg2BhFSEzZ4YwGcZwjsYHDLPICYUUhJBCYrrC+pFSf/uM1Sl8b2GESkTWRr2ICXBD4gQ0DFSO4c0ChNA+Jh0G94npNSMNEogK3O6yw3VcY3WOrlsGc3k1SvE3rJ+5yl+cDTLHSrT2C5w+PmbuH3L/ukZizdvJqMIaT5y+3n+uw9uO0ZCqSPDtiWrNIqM9vSSxY1jNqtzdiGSK4Hbd7TP1timx2uF8x4tFURPPquSuYxJlN/JtE50ulyTOUdpDAyOYdsguzgedwPBI23KK5OjE2XUElXloGWyQhcgRExaVi0xAoJXmLqAbsBHcG2PPdCsGoeQhqLM2G9bJvMJ+3Uy6pFSJu3c+Jnr5zQ4o0GrNMxTMkUIxNFchEQLbDZ7ZlcXyEmJd6nIF/DC0nzsdD+8gb/8q5iYJZlKj1E+EqPCbjtWD88pqoJm09A2PWWVY0qDKHN6u6MfIrWPybzACcgUbdszDC5lcRkFJl0X88KQG83a9vhmj9Ielyl2lzsmJ1NmixIdG2SZ4doBr8YWQgjKuqBpOja70dBFSRCQx8j8+gF6uEv74CltL+h9JLqILnIG65L9dogv9pcQItvNDq01xahNe36MYq6Tg20AL8aw1pGaK11kGBxFXSQE2ij8rk/DPCXQQSZUS6XYihzJxTtPufrl19Hxg2c879sbn38DUmn3WXP0Uev69ev/U6FBn7Tm8zl/+2//bb72ta/x1a9+9UVTBElz9D/L+ovVFH3s+j6Yq59AfN3HyDpGwrRkWAtE19P6wHq5RRmNzg1CKpaPL1BKYSvB1cPr7JZbdps9OYJ8ajjOFqzOt7T39hy/fpVbr71OGTecvdVhygoQ7L2ndx4zq8h2LYtrhzx76zHNtsHkBlVIGtly9IUjDq+fQCtYPr7g2bcf0bUdmdaYMmd2skDnmnbdYM/X9L1FZ4aj2yf01mKKjCdvPaLftbR1xXrVMZ9NmGlNcXzA+umSMLrKCCnoCZhJSesjV1+7ymbbsltu6S+3bAZPqSSxzOibnnxaJAuoGFFSU5gCEBS6GA0LUnbOye0r1EcT/LcesW86dsst2y2sgsVoTak029WO8Hbg6hvXOThZsD5dsr77lPrKAdWsxA2GGAKTeQ3W0673EFNC9+Z8kwIhlSQvMrJpiVn1rFdbjo4mFNcPWZ+vKU/mFCLl32y3De/8wdvJxe5gwsHVAy7OV2gFebAInTa8ThmEDbQuvDh9PriCT1bNO+eRMdG/ZKaTgL8f8M+L4TagZ8lsITZ9yi0yitA7lJZJa2QUapEMHXCBsN4j6xLfDonrPTW41iKnClUV+NM1ciw4RYyIMiNsk0OVawZiNyQEI0SEdYS8xIaG2DlkZgCB7wdUkCCyhDjhcbHDO0chIkJkRCWwRqNDQGoNLoX7yUyPdL0UlimNJsSQslBGykuQkiLkTFSNGLVWwQdiNySDB5WQM+U0onG4bsAN6fOVRKxf45RBzCrk0BMHi6ehsAHvIPOjQ55L9r1ipAdpmTKZYoSAp7U7VFRElwJjXUw5PdJKAjD0LSFYRGHIXj1C53lqEB712FVLGDxDv8eYfKTOJWcnT3KtikYjpcJkE0Ro0SYHaRkA5y0S8ASUVEhVpWZ08Ogu0VNNnhGNAONQQ56cwfSI+GkN1qWifiwOtTRUixPCMqE51u3HYibDBAMS9LTEXdjRGMCglUEqhQ0dru8AgXMdjh2I9Fkm8MyjTQk+EkUgq2aETYsXJTakIZGH0fJ6dOnqBuxyRwTUrATn8b0ljoVwsB7RDUgfkoudVsg+GTLE3OD3XTJuUJHQD3gmtBvH0AUoFNXxnGa5TcVYmWHmVUJJpST0ligcg+iJXhC0IYw6leAcQz+kPDXr6IcBL1Lw8uZyg84NarQwd+s9m3tndH2PzDP0vErfReuwyx3rd58SpGB395T6lWM0kYVMzahQIHQkWJfs+ossUVhfWqVJTaguMjSQB1g+vsSqJVZFDg9mSCdYf+cx3bYlyufDAElQgNK0mwYtBJ7U3A7Opql+ZwnG4PuBbGaIWwij1bkQAnO8wG8b/HKbcrSqHHPlADOvCW1Pv+9R04qwbxFVTuxTHo46nKJnFXGI2N2AyqdEmSVzhBhp+2Qg1DUdSin6MZA5kwo7WLb7BiFB9Y4goJWJ1SCtIIiIjpLgPZkS5Cqh00qplN31gn/1gY37Y4aoUkgKncwSTIBuGeiWO542PefzY6ZXDzBVTrNt8INjcTilbXqiEYS2T26OCgYivUg2/kF4Qt+SycB226G0hqKg84GWmJomp8HmBBK1rt00FLXBTWZslgOhlfgoaPohaQ9jSFldSuCdT0yN3Y7rc8PB9ZKqlvSnHZudozUFwXmkMYjRMCb4sSEiIYab9RalJEYmjaP3MQ12pEYWBnxIukkgMwYXfArTjYHJ0YxyWhJ9xHYDclowND1RgB2HDKkxTSHDtQlkrsXj0/Xx5fWBz+VDzoyfrf9bLvO8kYbvyf3t5fu8/Njvtn7+53+er33ta3zta1/jZ3/2Z/n2t79NlmX8w3/4D/9sb/j/xuu/U1P051jfwxfz1/qO3+jTVOPzN15HPXRsLjYYkzItnHVMj6dMj2+hM03xzhP2f/yI49xw/fO3ePgn93GN4IfOf5inp5dkT3Nu/tSrdKsGvnGXIyyThefSRf4gj1AULILgjk+BlkNnUVohjUa+EeCnB7b5GnEhufLwOoTI5mJDNSnpmwEjBecPT5PjmIAsz+gHy+0feo3qaIofHKtHFxRZRht2CARXX7vGxb1TPrfsuTEIujbym/2WUBfUiwkPM4N1DmUyqostdtSR3Dlt4OEGWeW8dXPGUjmuX50Sn6Qsi4mZ8BO3fwbX2LH4CFhrIUbsYMlnFcWsomlTivqduuTGytK3W2ZVgTWarunZX2xpNnus80iheXrvlKrOqauC6ZU5trc064bd6TrRAi93RAHVoibPDGZaEqTgyY0ZZww8bXfMf+QG979hKbXiC6vkrialJJ/k7LZ78ixLRhi5Ieta9ONvMDmoGIoFv3p3kzjSH5OzEHqLjT1xpPIJko16lmlCZ1POTYi4wSW9yGoHWoNKjmMYRWhsapCkBBfwzY5odJruh0jYt6g8S2LYdZOaiJAm+2pS4J4s8UYRBvfCTtVZm95zCPiYGl6APu54sP0t2AmochRAOzDJrnJ98iMIH9i0D3kyfIvYDRxmt7ky/RJBqaSHhiS0VxLdW/zgks7Me2CkQo0CYB8hjgYiP7V5M9EvQkSHZJ6gxoI/RtA65/b8J5LjXRy4x38l+h7rBu7tfzehK63ClBl+uYEYeG0t8JlBZZry6gK/G/OT6hwzrVIp1Vn8vsX6DQ+b30bGZFUbwpgBpFXKK5rXxGkgO7qKLjIeP/59VADvAlfLH+R48Tq2s0lPNB5LNza7Qgj8WIwqIbiR/0hyqouWh+vfxYWeUBiUUWSzkqKa8+rB/wMhU2jowt0h9DahT9sWVRooMrCRMKTimm4Ak1Ci5zkgs+omB1d+kKE9ZaXu8s7q14k+cFK9ycHkc8iR3083oGYVJ7zBvL5OIPJk/fs0MjXMz1Z/kM63GMGHJAzPc+4c/jRZyJAm55XF/0J/+RRbN9zd/jYudi9oaUJJ7LbF7zqyeZ0obdYTrEtGI1ly1tMmIV/ROqLSuKEhyzOCtQSfnK1UmWHHUNXTp47Lcs6w9rAHp3bIIYW7EgPOB7Apr4gYOe//GBfAd5Z+/hV8nNI7T1HmL8QOIcRkVT2iGbE0xEyjtGbY93TvPoUI1WxCIyLKKOy+ozCa9bcfEnKDmpRsztbYwfFa3vO/ljVSgl5YijsdMUjsLqKL5AQJjAHNAhUjw74nqwuu7h1hO3C8D6xOZ0zyI47L23zr25ZhtU8uoEVG6AakTBP7MJ5zTgi00eRFTozQ7lqKuko+DTLZcSd0V+K7geygRhqFDTFpuWRqREPbM+xaRJkny3+tkS4he94HjKmQ05L+8SV6P+P27Muoec1223JXK1zXk2cZRioGm/avzAuc9zgZEwVXqeTeWeQoJdkPlhihLDP2bcfeDhil+Pw6UjvL4ByXn8vYPDgnuGE0shivv89FK/CRjdE0m/ETt34GfGD57ccsd2LMGxPITLN5dEnIVdI1+oB3yTQkhpCooeM1brkosUVBUWgmbsWR29PvOp5WEy4GsM7z6KDggXOYXMHuVdROEPT/n70/+7U1zc56wd/bfd3sVrfb6LNxpntnGhsD5XOsAxcIUagoqSRcSCCE/wju8BXi1le+K+ra8ikhuKGgpKo6HCg4Toxxl11k9Ltd3Wy/7u3qYnxr7YjIiMx0OjkyOF4pYjdrrj3nmvNr3jHG8/weRdIGP460647fGT+HPf0yu82eQQbvt7mMeiIaGq3xwXPvuOAvjL/HkTphfCdywX3W9+4QoyDWi6qQ+4gRGIIPkZwiYz+QUsIZ+ZnywVJshN6IjXAcxXNcOLpdSwwCHnKFpT5d4KylsJbx0OEi4jtdNoRdz2DFb2eUZlaWpBz4Wf2Uu5ePGHPGpo/66V58JFOshfpsSvTfwvpwoOp6vf6+j7++vr79/fHx8Q/8PH/9r/917t69y/Pnz/mH//AfAvA3/+bf/BP9G3/W15+6KLpl/P9gD5Z1+3DFrdPve3mTPq5p+KSH5ExEEacH16cL4rYn73vGMUiXNyXOty3Xz675sb/8E7z+s59j/cE5zckCjXD9Q4w0zYx7x/D46QX9Rcf2+YY0ZuZHFf2hJ2pwxw3jGOiGkeOHJ2yfXNPMK/aHntd+5g26lzqeNu/LzUDDsO9ZP72mbkraQ08KEZUrkbMpJWnwWvPKT71Gc7Igp8zlu8+5fP+co3vHlMuaMHi6p2uO7xzRv3nOZggsThYUFPjC4r1nebJkvz7Qdz3dOGKMoTYaC5PJWaRiCSWm/On908agk+LpH30gyGsF0UeK0rG52HD62h2aoxnr52tCTMwKx+JozrN3OlZnS3ZXe4Z9S+g9fvBoZxlDwOeMD4njoznzB8egFMWzDRfvPadqSvbbA0VdMF806Cim4OgDppKpx/mjC9pDz73PPWD35IrusOXVNx5QLxseffMRVVXSHjr6sWC+muHGHSl6Yo7ivUif7mTLGcKhJzVagu60hskUTM6YphDST++hG1GLCrOo8c83k5dDi9TLSDGknEGPXj7bmNDOoo4XpE48Q8oaVGnReaJ7TSZiPSuJ6wMsa8LoRRI3CHxDHXox2CqR9ylAWUUsDORAbkfp6BfiQ0takVUm5IC2SHGVMhopvLPWpMJhBim63JS3k7SeMNOJNI4o59BVSQgeE9MEJ1Av5Glay7Gr1XTugbWFeKWUJY0erRPmdCHUPKNRVSETtnWEozlFzOR5RTmrcCdzwijGcjurbsMPrVZELx6N4XIHPhJSRGfJ57jZ1OumxDUlFBbfjuhZQZy8KhpF8qCUhal7rSfpXVKTgT3JVCulTFYWHTM6QWw7mazsEl4pRqvxbstu9QEkJYWL0bimErneXBOu9+ikoC6FjLdvb03uCiG3KWNQThOvOpl+KYWqLbEbZLIwTXTHZ9eYeTn5BDQKg5nocZE8FXVZ8PKT9BBrUNmQYyDrAtUUKA8qKjR6inVTt76lDPTna+av3pVCHwRqkEWqScqoIJtOXTmZKhaWqpnht61MOPseNU1VynlNansICcqSrAxJyaRJW4ueG/Sixj+5wp4uCWPATrJCq6EPAzkminlN2LfYuqDvR1RINMuGsR8nnDUi3UsZZgY9LwktlAji385L+Xm0Znu5xShFUZV4H8iVJaTE5r3nKN3hljUORWEAo3DzF5JawYcLrEKulRLeTMyMj66orMVhaOoZOhv2z65IlZ4m0FHef2vI1wfmTY0fPIdhoJg7hnaYSIWZsR9oZhUqZEI/CuAkZRxZroezCrNs8OdbxvO1oOy1kYlFmuR0MYn00Ud0yrSHDnPoGa53NPURFBUpKnZj4BAi1mriIF1jVzrC4CmdI4N4n5jonYUVUqvWt4XSbt+Sc6YykxQyB6ya8n9yJoeE+dik7UZK95Gb+YeKIwXk1rN7dM3m4sDyZM6scoxtj6+86BeTeFuz1YxRAkpDlIlIypk8ekaV6FDY0opMrjSY5GBIlK5ivzuQtaKsC9p2wBVSXIcYpxyjLIQ5bdn1Hr2YsSgdYzsw+sTyeMF6s6MsS4iR+bxiUSYqpQnPLtnvIoeH98kowjhSFPp2n3QDU9AT+j+2HWVZSFGUZBKtAmifyEZLvh6akCNFVci1dgqK7q8PUJVYK82rqik5tD1GMz1OEybwEIDOkuurU5wCpD/l3nhzg7zVlf4p1D2frf/q68OI7K9//evf9/F//Md//Inf+/2WtZZf/dVf5Td+4zf4zne+A/z3A1i4WX/qougTa5QPd4C+V7Hz4ZPye8jiftAXcjMiBihSz+phjX/+jOXRiWR6VAVX6z3PLjesH19x+soZqwenHK52fOeb7xNT4uzeMd4HQogiU6kd7t4Kf71joxIjiVEp+nYABS/92Mvsfv8DjDUcfM/RTx6TThJD7hk2Qg2bdYHLd58TvGd2dERdVjx9ekEcI0Zr7n/uAaE00t1BDJTt4yuefOsDFvOayw/OKZuK1UmFShl/scMVljFENldbmrsztmR8Tlw/v2a+moOCG55WTpnQOLyPuNJgh8AsZWplaM2MbBK6XtA7zV6DGqOEgyqFI+N95HC1p1rU0qFMSTbsE/q5zxn74JjxrZ7r7Z48BlZ3VuyudnKzTEku1MNIMa85aPCzkq4byMuK5sEph0MvVCOkG6zI2NJRNiVEQRyXVUGoHM/WO15+6YTTn36V9/7gXbLLLMKOctNRhoNQ6KZsnk86BK3WNE5ufeU+YbUhWclLQmtUiCIrcpIjQSP+DF1J3oquHGkM5DFKFzglci++ojQVmqp0UiQVTgJkey+o4kFu3jFluucbnBVpQyBTZ+nOjSlLMRciNmd5fdMGNpWyAYkpYZMGX1BojWLKhSEJ5WpKlqeAPuwEW06JUYVkvBiNykKpyt3ITZAnKaLrijxvCLnHt1tyTIxWEa2GlJjlBq1E0nOLpFfc5s/ELCGr+mhG8fCE2I/4bUfuxBNkH5xJXlPvKU4XFLXDFQlqSz8k9qiJogXEDMbKpvRkKZuwOLKc2UmSIpNZhZz/2hpCkRhjQftcPHA+9Zi0J0yTDxUhR/E4CHIdhpBuTcVKK1JIZAI+RTKKpAQQwBjJBKGzGSd5UUDqA2O3leI4y3Qw9wKPKI8W+O2BuG9lOpMy5EwYR8YgExucwYQFzhRoU07Gepk+ugenjN9+Qqg6hiTUNadLCrtEK0GrRySYUumEqiq0MmifgIiblXSXz/BhS4wjKr+YViknOT92Von0Moj/CaWmHKksNEYlOTfZGLQxIrvJCasVYUIEJx/kmpAy7v6JSL26QfxR3mPHSHJGivzBS8NoQqCnKe8ojR5rLWeI/FmHwLjvcFVJVVqGfiRpcLMS3w4U1tLMKvb9iD1qUEOg3XeUTUVsR8IYKZRCr2aQMn3XgzjyUAUMJJ5s1hyd1RinMYebK4WEjuasmDWW+UlN6Ab6yz3zowUKGOm5Tmsurp6hXMHyuOHi2RWD96RZgyodoR3IeNyypjqeMXYeT6I+mpFSlgaQFWl3UrDd9cyqCqMUel6R0yAUSx+wtkQXFne6YFzvwQfioZNp6WEAp3EPT/HP1uQhMIweosKYBk0i6Zpra2Q6YcSYX1UVMQT6fiC0A/Ompm07CZpVCmMNxhj6caQwluXpkv3mQMyJpq6oUDIdtYbRavZjxOvM6Vnk9I0ZOXguN4nkIPjIZSt+PaXVC1vRhzbe3a7j/YtHDGPALSq2w8i267g2muQdWYnst7SWYbpHRx9JRqHHiFOKPok/rusGRh8om4BzGkxJ0DKJyzFgtEjXnNKEMTBOyog0TVvjBGDRpRMC6r5DKYU10J8/ZmkUDYHZssKVkVqN5ENPrxLbpGm7AaVkoq6Nub3+hBAJU6bZYdsRfKCuK7RSkm+karbnI4uHRxidmBcGmxW2MCir2F7uBDpkNSYjERNK/EZjJ01apTXXjy4YNweqqpQp8vSfKS348XvutxQ3F/WPfUafrT+T60tf+tLtBOdf/It/wT/+x//4ez7+JmzVOccv/dIv/Yme6+/9vb/Hb/zGbwBwdnbG3/gbf+OHes1/VtePQD53U8187Kz5JC3q95oCqU/5+qd933c9RN2+FAXc3XyLV7VhPr7L4uh/wM2PUbsDv9dazpV0m0xhOTzf8J3//Cbfuttw/PJ9rn3kZ9Yjm92Bozfu8c79Oe/90Xt0xyWmdhhKxnbg+P4J1bxi88EVRz4ypMTyF1bs/8qaPdds39/x9N88AyDVinotRsjVvWM++MN3aOqSse/pRi+QgS+9xHOnuX7vnNkfPqa53EvyuTUoLZk1i/dbVpOcCaVIVUEooBs9ti6Jw0hQcH2xxlgrvhgyWWveO6kIKWHGxI+d9/TbltOzxNXspwgpYd94yDeU5s2lY9XDK4MVFGmUoMl+31HOSoL3t9ScqpDN+qPoSV94yAfdnpNNz/2sGA8DZCiNYRgDj/2AX284vTPjeRoIJyV+EC1/U2aitjTWyoZxCphs6pLd9oCxhtB7lLO8e3dGSol3Li9Z3T/h+YM5qzryU0//F0rvBYmrFK5yMv34hHVn5vjFV+YQE91jkayZmAQ4QcYo8RQxdYRjNwq9S4tvCKUwTUkwnjSM0uVvSpl6hgRGE0ehy+nSEbqBrBTD6NETUpt2IIZA0JqqqbBOEzZ77KJBxyRegAmvnbzIQlAam5ECbvCUrHjlzlfQWXxRN6kTSutb/8qu/YDr3fsYZ7i7/DLH9jWZVmRkshRkoqb0hAJ3VjrHVcGT5/8b+/YZqin5zv2GvUnopPmr259Be0tUIh1hkqCJTkOjZg0u13gfiI+vsKsGWzlUSsQxwqxEF078SEpRpI7Pn3pMYXnzWvEv/7DlJn+KnIk3Ju/CgYJfepj5hfvjbe6JsuYj14g0DzzpVoQwJw+BZ+9/HdWOMBWTWomHSU05N3lCUCsyIUb5e2swhcGsHDqIZ8JozXjoZHqCFCIpRpE8AjmL1IcQCQgwIW5bASHMKlxVkNZ7iJ4A7Pwznm//COqC4/J1Xi/+ImYmHgW0ghAp37jH9dtPSTFyObzJ5fgWyhgelj/BffMTgmZ2VuANOd/CEMig/PT+NI733/8dht21TD3ylG8zXX9VTtR3jl5ckn0Uk7rWtwGzKmVSDkIlnEz4cfr3c8wQgxxPg5dr+loM+2m9xxzNiNuOse1Fgucj8XqPmdfEwaOtTBaJCRQUqxn/QzbYsmabNf8qR1pr2Hf9hLd2RB8xzhJGz+ZqhyosqfOYWnLAtDUM/UhVFYyHXshq3uOOZtJ8SZn2eo87rfhfPjdj8JfUxQlXv/vdN55f+AsVv/JLNUZrim8VcBXIKK7Pznlzt6Utd1TxJ9ifLLl+dEmsa5HzjZ6iKfFjIPlI8FGIYjHhDwOmsFTzWnwgGYqioEiSb5dTJExNBJ0TeQzkupg+ICmE1ZRhpI0lqUQ69AzvPEM5h7IWUxeU44oz82XSGfxhTPwHL0XqoGTi1Q8DvhtBK6p5zeijEB1zplIWaw0HP2KdJcREu5PJYFE4Yj/yyj5SdhIW+u07NebBknJu+L/+4jdZNj34iO8O6JDZecX/7fcNhyGR0wtJ8IfXdtfxR6eWcrWSHCSl2O5bkTGGhE+iJhgGT9Yyva5nNfu2AyOAo857KTJ9wPvAu2vIGLKfaIlDjyaz7wYWqzmmsFOgsbQRC+skhysn/BCxCP1ztphzfb2lKTI/6/+AZUrMzAIdNEZbwtUOlSL2eM74bC8SN6cJMVGUiptAIqUgxsTQD8QYZUo1XT796FmXDe3PvsJ7z9doZykKSw4JqzW6cMyWMw7bAzoqktEkq9hebHGFBRTrR5csH57w8CdfY/v0WhoxhUVbTd041Pvvf4+d1Ketz6qiP8tLKcWv/dqv8U/+yT/hd3/3d/ln/+yf8Q/+wT/4xMf+63/9r/mX//JfAvB3/s7fYbVa/Yme66tf/Srf+MY3yDkzm83+RJ6k/xbWj8hT9GFn3qd/6ftK5L7XefddfsBPk+3dsFIyWmXKZUnb9SyqQIpCn0kpMbQ9ZFg/ucLHRDVv6EZPoRS7tidrxdnnH/Dm4yu6tsfNSpKCoRup5zUxRJ699ZRZL+GofdtjS0PWaSrwxPsA4NuRYpQbzKM/fk9SwZsKnxJvfOULHD044dH0Wp585wlfQjGfN4z9wNgPKKCsSsos4bBKiz+kP/Q01QKPkOiO7h4TfKA99IQUCX6kdI5GaXSecjPiiEVRFI4n337M7l5Dtai5/uCSk9fvoZ0lj5F5IcGbqi4Zdy3z4wXDvr+ZPTH0I0dVgVaKYd9LIVFJOC2IVNEVlkIb9l1iN4ykQ4969zlDP3LoBoq6oKgKMaEjE5J66mYpoK7FKL/btezWe+ZHc1LOmMrRp0R6vpYco/YavKcoDW5WkFOivnvEED/h8ACUkslT3HUSyuoM2hlCO1AtZiItKuWmP17vUVWBdha/bSWVvbSYspBcj3mFKcWQbgpHOvTyJCmT+lFyhApH2LSolAhJZFnaWUxIRJQEB5eGvCxwd1boweP7kTzIBjSmgDXiNYqtIHAl9BOsK9BqytlJk3TKC8Ev9aPIQbTcOCNTVo5SIpHTmqQURnGbjcENunvfSabOsXhMaBzJD+QUpYs8ZEwWf4PWGns0ozie4693JJugtWgFdjWTojJn3KKmKCJhjITDgaQybTdiq8ghrpm9fEqmkoam4nYTkaeudcz5xXUiBvLoZZp2NGMaFYvG3xnyIQlIYV5Rf/4ew+Nr4q6DKPI/FCQtAb80BfN7x9Jt9YFy0cikrfekfiT6iB69eJBupkspwlQE5cHjlTx/1pqcp885Q2knaVzOcm7Na/JepjooRWocKkVSN2DnImE0ShNTojhdofSedCko+USWx8YAtUEXhYS4JpFXppQwhUPlSdqJmPxTiAIHKQx5iKSkbqeiGrCzGoxggZU18n5nSOMgE1GtUD6AlvBKvajJPqG80OaiURhtoR9Io5jwIwqTxVNnHtRon9DdKM1nhVwbbwiIKcuxc7mVEN19i14oTIw4o+jbEV84ko+Uk8n+6GTJ4AN2XhPNQFE4hm5AR2kk9MNIeTpn3HQ0U+GR9DRN8wFVOMJ0TPnakXIgaoWP+aMdckRyaiu5rsg0bURbjS4tp5+7z8nrdxg3DxnWljEm9KySfCJlpDh20shKvWdeSt7dvu3Z7Vvmx0u6fcdiOcf3I8VqQQzx1otjnPj2buVLCsFtW4OZV+Te4zcHqCvUokF1vUjIrRaM/ISFM8czUtuxWe84Pj0i5hGjYDj0zGcNMUYJ4zVafjalGYJIMo0SD2RVFFLoVQUqZqqyoH98wdHRgmw0izsr1MNjykah9dtoglyjmgLGyEi+jTL4tADXoimpljNCzvReJrJperitLDZI59MuasIgURLtvgMjQ+Xd9kDKiWEKrbbOUjrHZrNjuZzTD6PsAVBUU6h7mp7/xtuLgb6Xz3h5tCD4QEyB9dUWyJTOcbxsaGaSRVisloSLHSpEMpmwaQVKMk2hrTN47/FjuP0ch37EWGku5CyACTNd57puoDUeu6gFyqAUqjLiG/JBvI2zkrEdpcnRDuiY8TlPIfKwfnxFv+s4eeVMpJBDIKfExTvPp6bI91qfFUD/La5/9I/+Eb/1W7/Fm2++ya/92q/xO7/zO/zdv/t3+eIXv4jWmnfeeYff/u3f5jd+4zfIOXPnzh3+6T/9pz/Uc33pS1/6Eb/6PzvrRw5a+HDdc0Oe+WTU/YfGOj/I+pi87tN8TDfmQJALab2ccdCa7aZls+u4vG6xzjI7nhM6AQMYZzGFJVrDfDmjf/OCu6/exShFeHTFMiTUriMYg1WK8XpP2nYsrGZeldAPGGtwRUF/2YOC0Gvc4gyA9nFgOdGuQpBNQ3Ka13/iJRZnBeQ93dvnxPVA0Xk0BqsVm26kXoiXKITALifMrMRqhSotNmZ6pymMobOadt9JR9sa2SizpSg8pTIUB08eMyZlLCOmgWLe8GzVoArHuO1Rz7cU7UCtNZc6Y6widh26H9icrzm6d4y1Yug2s4qucoRFxagyNYKvTiHSjyOucJRnC/S8xp8rxuRRwO56jy0sx2crkai1I3Y/MCst63GkWx+olo0UZEbj5hUxJrbbA85ZjDGYMeBcomFP7AILPEWCVFjiGChPZujCYofISW0/Xk8zNyLpQymKWTV1qBXFrBTZIBAvA7YuxNQ9hevZRjDUYb0n9h6jNbowUIlULqcsun8Nfj9IMYDCNAVZgc0Z15Ryg1KCt2azg+NjlDbYskBNZvzZg2O664NsQr1ky+QQsbagMstp02np4kZka0r8JAZLyL1MJyZsa0aRQ2QYDhz8uUjpmhVFNOiUJNIiZZTKRG1QKaFSpsgVUTtUUKzW4KZUe5MkD0MVho3aE0iwXrO4nnP8xVcIQ4tuKsaxJawPuJnQl8ZdT47SPbWVIYZMtzkQMux1gk6jkuKluRjcxz7StZEUE0VpqGuNtoZVKVMe4yzbAba7j10VlGSoNE0m7vYQC8qjJSzmtDqBnvbjviPpPGGkO6w22GVB2CjCNqIOAl5gyKQACsNMLbGmxhhDSKBDIqspVygl8AGFFPU6Z5KzFHVJ8IHQtrdeszx4lHIUUSaDRd0Q001Io2fsd7j7p/i3N9QswMnmXFmDzhmjHRSONHr6YUNMQaZ9XtC72mcKNSM5h24H8jASXcSiKd0crS0pR1KjRPaZYDOIgd5qxbI0L3whN7tGK8hhXRXE4UBqOyHQTdcEQcBn1BhRQZpPKMXw6ErkfVOT6KYwSmPAVBrvE/5qT4h5AhpoQoy45GlmFTWRIWcBqZQFYz+wud5SHc1vTFr07UBVOIZDT0yJsqkZdhLe2+3FBzpfzLDWsLnaYqyhPJ6jkqc61CzuPWBMjnUjBUfyPaHfA7DbR959Sza6+cmIuYwok9iqAnN8nzR4xt/fwjZzbB2tUgw+UKBo24FZVTIMgWJeMYSIshrblCybkgycPjjFNaVIr2xCjQMUGV0X+HWLjQm/abEradhgjVzfpqyytG2J+xbf99jFnOwVjBrnHD44rueOQ9tzse+wVkJiU0qEVqbe4zDeTt2sMagM83nN0I9ErSAJ5dFYw6J0DMOIVorl/WPKZzuBtRjFw7MI9RaGDv/OOeqhI2XFs10mDjAExb25ZIclZbjiiJSQqdd003bHM2bKsL3e42rHwSiyz+TO45VnjBFXFqRNK17CWTV53mTTT2HJPqCMnqRxcNi1aK0Zx0AMCYXGGMkFKkuZyiXAFZYYEyfTBKuaV+wPVyTvcc4QGWnqkqPTCrsxjLsD9azCFI5x9Ohpamt9oCwLqAuIECcZt54yCV3hJjjEi+M9xihTv2mz1O86jFLYuhAAUM4M3SgerT7gIlMDJk+ePIvPSWSzRkuzYtcyfvMxq7srzh9dYArLfFFy2Wf6EPGI7+ijWyt1I0T5bP03thaLBf/m3/wb/vbf/tv83u/9Hr/5m7/Jb/7mb37iY9944w3++T//5zx8+PB/51f5Z3/96IqiDxUiH7cK3f5effhLP4SB6FZ7/AM+LEO5qPj9Dw7sUubqegcKXv7SKxy/fMbTP3qPrh0oGyEA2dKSxsDQe8pZxf7bj7n/7hXLyhFSImpDPa+xpmR7faBqSrpDSy4Lirpk2ATef/MROWfqO69x5+d+hTB4rh//AUWh2O0O3Hn1Lqt7x5TLhqJ4H5O/zv7ZmvmjYx5ezDkNkZQSa2exRjP0Iz5EunFk/fl7xLMF9UQWaved6JOHERs1PnnSJGlyJZj6m5RVpsmGzz/bUBhJuafKDDmxiwvG9quEduTBYs5rj3dU65HywRHvvXrGdnegvG452xwY2+HWEF2WjkfDwMV6Tbe0lM4yc5aEopnXjNct86MZ18c1T1JkVysyBZXTaGdQSrM4XpB94PjtS5ZZ4VOiu9uw2x1o95KuXjUV5byiXs7o+pF921HVJRpD7nf8+Pv/H6p5CWNENeLzQUExq0gxsXCKv3K/IbS9eIKmrn1OmXC1F6kX0jHHiPxSL+QYSFGM5aq0stl1crPVSmEWjXTZC0Pc93KDnpWYuiQnL9MEZyRPovfkYUTXpUxmfMA4mQTYsyVh2WCdlRt86UReYw1GK4qmIKZM7sbbQ97pOa8c/RIozX54zjsX/w5dGMIgm2KNUBZx8nOZyW+ilGLTvsc6vYNBcTf9FGX5qkjJQLxiMaKZkjlT4v7sy6SyBB95ZZcI2yyeK5SADErFv9ffZGs7imD465uvENqB/skFfrPHrhxUDn8jA0KmPj5k4qGH0WPbA4dt4N3lknR94P5PzPj7PxNQNvP4vY63f/ec7ByrfsvLcYd95SHLew9JSaE1/Kcn8O/eV9/VXPk//ljHz9zL5LNM/44mtpK79fzU0tlMHgNvnCWaIt4iqcngu55h9sukEoLaiJTNBAJKUL5I+GfKEkYp2HFp/KQkssWUskBNQiSGwLA5oIcRrCEXTjKLQmCZ77JY3hVPUs6oKIXE9fAu1/l9Zt2a+a7i9ZO/LNc18yLAF6aimsxF/00O46V04Cf8d86KN5Z/ieJoSTj0YAzGgknw8uoXcLokMPJB+YcAdCHxv767JaTMqjT8yhtHUtiRb4leZpqEjVdbTFlIBpLR6KpEBQ/LuUi7xgCFQZU1KUViYck+Yibq4k23XCuF6j1FFhliNuJRZAgoZ9GuFACO0oQbuRRgjaWoSlSWaXKwVgrrG5mVUvhpI2pKR1KBFAL9MJJG0E2BU4q4bpnXS37i8BcI/6Xj0XaHvn+Ps59+je78ba6/9R8B+OM/6vnjP+rIYZpyILK1+Rv3mPkv0T5bo775Jg+HS1anK36/PTCuKsYxCHQiI1CbLMG/oZOiIo+BclbR7XvG0bNYVrypryhKTzOzrLwl7s2UgTZSpSSTAAV22dB/cEH92l3iQjxkeaMJ/cBcL3h48ouUi4Y/OF/zr3Ti0A/EJAWFc5aUJDR0VstnNEYp1ppK4CDtIH7YhEigy7Jg33YUEzFvaDt8jDz4yudZZFAq8uPzf0cRrthfbCgPlvS4ZtSW3/o92A4wt5lf+4piVsI2lvw//C8TXHV7/img2PSs/u23eUkp2mx486wiXvop+DTinBM/TY44beh3rQBsgBwSIQTqphLPW2HxvSerLJlyKQqZVSu0csSUaNuOorDEnFks5/SHjl92jpcXC7TOfOf6G3i/w2SLcZqUNfFx4uaSYSppnKkpluBmmlgE6GPCFgVD22OnwOeIZIM5Z+U6jSGFNIXxZgkPN5rkM2Vd0ncDvh1xWtPMa9y8wjpDHCNxeyCSsWhyFn/n2I+YwlJqS3YyzYwhUtQlqrLopuBfbSSTCdTtlOzF+p4m8M/Wn/H1+uuv87WvfY3f+q3f4rd/+7f52te+xvn5OSklTk9P+cpXvsLf+lt/i7//9/++QEI+W9+1/vRF0cfPnQ8XRDfthunv8v8O59nHE5hN4UhGsd4cyDlzcu+Y0zfuEYfA9dMrxhA4ma9wpSMrzdWTK+4dzaiWNeOmFW2xNviYefXHXmZ/veP80YXINQ494+CpnAUlG6Tbm36Wmf/u+RZQdP3AyYMTjh6eUC4akZgMnqt3HnH99BpUgyuOcFXBZrNnGDyFM5wcL0kxstm1PGp76ArqWUW1arCzks3zNWOXWcxrXF1wfbkRb8TgMRNSNvlEsSixSuOsYbjc4chk79EzDT5DiGyeXtHUIu3YbiHHzHzZYMwaVziun17hJpqPKaxswrXGOsfu6TXBB3w38sbLd1FGcT4G+uipCsds0bA5tMQUScpQzCtBUCtN6SyFmgI5C4Oa8KO73YGrZ1fUVcl80bA7dIScyePIgomc1o7gNEVTsDhbYWclN3es8XovErYxYAqHv9q8IO41Jan3k+F3wjQbLf9NAbe6dKgseFqTk8iyQhTwQyleLzFDJ/IQZPjkjMAXpm5uGLwUWWPAFBY7l+cdu4G8brFHC8EBlZYUEvH6QHm6kA22UujaQVOQh0Cc5BiSyapRZYE1NThNbtdktITRIpuAG7KYSmmSosmxGVMgeU82IgdLOWPS5ElSCu2DdKOzIg4BnMUkLVOTugBriLtWpFUnCqUhZPGhhF2HnVcUesZw2FGerahOlnTbltyPGKMZDzIxMtaijSPtNvh2T0Ix3qsw90vyKPIepRX4EdNfYw5PSfst8e4JbtHIz6iQvJfJB/HiGiCIaGWmCaZ8RQo6KyGHpujQWshignmGoi7oO0Xng8iOUIxaJq9jzjilpuwZeW+Nk+PATPS+pEDFBCjy5BXAS/5SAnSM5E5yYLJVMllSYJUilUYmT2OmfO0O4XoHo4NaqFRkJcQoJd1cpqkTGqhFuplyxmpFjkhhYQ2hDRLWOnpituI5U8LC0810Y8xSmKWUJ9ViJraDoLaNBIHmwpH7ERVFHqicFM/GKvIQwRhQeiLpOdydI4bzDWnfC23PGvLoJxLhhL8/TLQ9BYX3jD5IhstKMrN8N0zUuIIgOiOGtid3mWJWUZuGPEay0ZRNRVmVEko9GelTTPhRYgaM1oSuR2cgwunn7rFUht3X3qa93jEuK4FIKDn3bvp76UZ+YMxH+3Fafqb6bEV9dkz+4Ipu28JxAXkK0d51KGeojGW3PlBM0mtltAQitz1l5TCFY9j3+FmkKC2xG0kxYAtH2ncyfbxR0CmFW80I+47hgwt5L42iPFkyrA/EZFBocoSkNOM03SuaktB7+kOH0oqmLvE5SvE+QTLaGxJd4VBWsPURydSZNxU+J8I40swbog9QKpHQKiBGXKmZnzRyjMZEJpOSIoRMsgqtMn69Z3+5I554umuZsOjSUqxm2Lrk7o+/TNz1pLYntV4mnyHjGok5yDExpoRv5Xg3WtDy5MysrOi6QT4vlSnLgrbvyV6OV9cIfrzddzSVwxhLVReEGBn3HUVKLBqH6wZ0aQWE4yaPXsoURsmENkbcrKI4XTJe7yY4kJJcsBxZuIpDhjh47BRdYJ0VpLySyb2aLll6ok3e7F2sNtJoOQzUi4qw72GCO7nKsXh4gnaG6vmW7cWWvh9YLGdstgdUJV7BkAUgNLS9QGMUxM4zqCzeTm5dhS/2Ti82UT/IVuuz9V95/cqv/MqnRol8r2WM4Vd/9Vf51V/91R/6uX/913+dX//1X/+hvvev/bW/9kO97j8r60dAn1Mv3oBPKpC+3/n1wzQmPjaN+qR/8vmE1gTFbJGpHl1yfO+Es596BWMNV++d0x16yrKgLAsWY+Ty6TMWdcnydMl3fufbFNZQFI62Hzk6W2FKx/b5BqPNpP/VKB+ITBe/bDlr7pBzprRz7LMt/q1nNDHTrGY8+PFXUVqJbO9ix/7ZY/p9oKpOMapCKUtWikUjXUZrDdcpUjiNO10wmzt2g+fy8QUr5zAJinFkKCy73YGl0TSzmvV6R9kYiCvarac2lhgvUTlgC8laGbYtTYzc1zs4qsjbZ5TzgdD2pFyhY8nJS2d0bz0jlQYT5edcnM7ZHwYurjdAZKEUvh3Y+MDyaIYNcHkY0T7TlUIv0lGM+KW1EjQbRCNv64KdyoIOLi1lkdEmwDjCNayakubhKU8utuicWc4q2DyhKgyzMJKtJWZPc7YknK641ho7Jo7rKQxyMhCHSceu6imM0cdbM3YePKoqQGvSKGQ4gNIkmoUijYF2LUnwubQUecSqhE6BYdCgHaapRNvdj8R2IGuF0SIP4oaQpjWpF4O9ayrM1Rr//AnBOdzxgnh9IKVICpngA2VdYKzGjwF1ukBd7SdYQKTzlxA1Y9wS+pZUOdxSNiJp12J0iclzVGlIsaPvNgAUbk5RNVNWTubgL283EzEItj6HaeqSpq7+EMlaM1vcJWsHg0e1g0jwtPjklDZoFenaC6wJJJsk86QuCesDKDh66ZRhc6C92NIczxmfXcNmA9GjZnOIonMPvYcsCOr52Zyzn54RdwfM84E2GorXXmFtFhy2Is1a9x+7jtz84fa6otF1wkSRIG5CZtPKhtcoKIHURfTMTXKxSNlfia9Nd6hYTwVPmnw4CqUyQ1qD1eRkKViQgwQ6ksWnFGKCkDGFhLBmLdJbaww5DLKJmnxgWSmyAZVBp4Q5mWMWmvbrH5D1GUrrifaWZaKk1C3eO6VMVZ9CLMj1SM9eAmxjog1rwiES+56oJQSXFOnDNTpbAp5sPiZvnn6fQsTvxLyeJ1hLntDoWU3FnLGQA2G9Q/kogaEo3KKhvbqWvKKqosiZEBO5H6CwoA05Tl3xeSW5RdZgqoJaK/xhIPk1vnL0sSenimgsGENRCWVx6AecMcR2vNn/Yo2h3YusqsyKcQiMBGbLGfW8Zmh7NFA0GsyOYf0uTz7YsmxLmqLg0B44u4rc2dZc9XvW3+c2FLotw/oZZPj852bMhi27i2vK4p5IovRErJyytKplI1PGwuKURunEGIJEA7Riur+Knny6YBgDs2Gkqh2p7UVW9WEwgVaUZyvayy06JszJgjxGkQOHkicxwnbPtdVC4KtKdustxlnKpqKZNwz9wHjoKLWiWTS0+46qqRm9F48iUGhLNoqu67FFgTOWo+6KKmw4ufeQYbjiMmaUSjQ2UXYAEz1RQUiaVWUpLdRWc/G+x280u1AQNxfkqMhG03cj8y8+JF4f2D3Zoo0BDbNFg78OJCPnrGtKum2LcxbblITJ+5edFPvaapSXqe7Qj+RCJpKuLijqAvYX3D+e0TJiQofxYJQVPLbK6EqDToRKJLjaIgWVVhSrmhSSyAzrguresUAzLrZyjsrIF5TGOsPJrOLxWhQJWimCj7iiIGZH5yW3bPSBTMYGPSkJEl0XSC4zhIwZvDTMYkYXlvXVDnW+YfngBG1FebCIUO0HwuAZsmUko61lPPRT7EDGZE1WmdNXzrjevjiOPrL9evG/T1j/7W5yP1ufrT/J+pF6ij61VlHf9ZtPe+T3Xz/Qt2X+13GY5B/wf6o8p81jzs4iz4tEFxPrx5dkBctlgx4DZ+9sOAVUm9imFjsNfFJMGKO5+/n7rN+/oOsH5vOGrus5u3/K4dBBiBAT/oOBn3v9qyijaS93PPvP3+Tl0ZMynP7cS4QxcPX2M3YXW8ZuwLoVtvgqIWSuDz0xiYa9qApmR3PKuuTJgyVXhUZrRakEJju2I2dvXeAGT71o+OOV5UBmt9mhtWZWV3T9yDi8gVaZrlCUswGVRoZtR3O6wOXMovd86el/kOycWcmgOoEGFKeM4xHn7z3HzkvWb5zyzr7j5M4RVVMx++I9Tt56ztnTLUrB9XHD+1qxfHjC1Rg4n1nCMMqUavRkrdluhKbnMgw54QfPbF6zfuOMR9c7AomfqDvmZcYkBU8zZhPYvHNN8fqxoFTjwM+rb1NcbSEKWnT10n3GxYx/+87mhfTn9ZV0uXMWY7nWtNuWwmjRlFsDQ4CDdEX94FHWUJ0tJK+pctxdDNybi7/o6X7BRVcDivv1hpXuyP7Ae+s5m52EUapZORU/MrWIY8TWxdQpneARVuP3PWkMVC/dEzITWUzwE13ILAtizkSt0TlTVA7fDqSZFArtfs17/j9iCzuFFwZ0jKRZJXS2wtHEUx4ufoZcFlyG9xjcN1A+clS/xtnyy6ScOW+/wdPd72MGj4pRkN95CsScckBUlokHSvOy/T9QL+/DOHlXcpaNekpoo1Am8/jwX6hDSXF3SbWq6B5dUBzNiIOnu95RH89JvWe43mPmDWkYiRdrOLuLaWqqkznN3QLygFKK1Tyz+DwoZlx3P8fj3QxlFN961POHz9uPXA4mzoG83hu9fshoqykeCPwjZ/jjP4S3rm+uRhkwQM0toCVE/vLZH9DsWlgPvDT7JZyuZHJgDMpo+nDgg+3XyEScmvHakQS5qikTK0yToZgy1mjcyYJhklGqbrgtavIEOoBMUhodBGJRvXqHzZM/IO86WCJFNpqoNcp7mfqgJsy64m7xRWFPNJkPhv/EYfOcpDNP9r8Pw+RfSglVOVL0vL/9XTHhG0PJg9ur5o2vI8coFMVJ7qWMFvAGcnyIVClKvtOUW6O0vj0nU9tjXUEcRtR8hmoHTOXES2UdpDgh45OExI4B8JiYsXdXVLOKi7f+AIYKrw0x/QSmOEIVhm7X4kcJam7bnjB6mCApopJSoCWfDC1T6Gpe0+1aBi+emXS4JJb/iSEnXr7/EuX4ea4uNjxQe07+w/+Xl/ev8/adOe9+n7vM4fG3aR+/CUBTVXypTJxfvct7859D3X9dNukhEVKAKAQ/r2X6GUgyrdRIMVKX+JR5Nyx5vi2ZYzkLiSrJFEGXAlq5Od6zj4zvn79QYWTJOQo+cqUavqlHxpgZS4s2iu7QUlROQqRjYrfZoRI4M0FmeoFgRDJ1WTKEII2dlFjUDT5YyUCLgZ/64I/4XO1ZlE/47b7jcYyg4D9MR9HtXThnCgN/9fMLKg2xzfzhNx5QrVaYpuTz+4FxAhqEPnD07MCwOZBipvcje53Zb5nomxOFcowiPQSGbsAiGH5rNCFFtrsWY8Vroyf5eU6ZMAwUWvGF/l3uvf0UNTXFlFY4ptgHo8lD4uJiZL9ocHWJqjImyvs/Dh6FIk0FaU6J/mKDO10yPF8LtGW6/heLBvfKXfbdyD7KNdKSCark62tH9lYmn66W42TyhQYEAqSjnOPDID6iHBL9MFA1FWGM7J6vuftjL3Hvyy/z0pMt6jvneJV5p7Q8SSPey4TNp0TuPc1iRtv2qA+f5x/ZMX3kf58Niz5bf27Xj6QoeiFZyy+6DZ84PvtwX+JDj/lTnICfNIzKNyf35JewpeXhz75OViJDWT+5oNu2FEVBVRbUpaNSmvOrDYdu4PWffJ3H3/yAylnGlDi6f0y5qFEp46yEpCqlKRc1xXVB24/MZzWXjy9ot4fJVN0zKzQha5YnC2Ync/pNy9XjK6zRLJaNbG6UYn/o6UdPVRQsjxbYwmKdJabEfnPgXEWKyaSJkWwClTMmZvARq0vxhkQJW01Zktyjn3T6JOysRPUJbzV2UYPRjOuWel4RrvcweGZG42MErVk+PCZGLBuxwQABAABJREFUQTbfe3BMt+/woyfmxLjvse2AKa2gYkMgJHj+rceYeUmzmBP6kcOmpXSOqCBqxfLuETkm2qeXhMGDgtFH8bB40YOHHFHWoSpHf4iEGPHtQJ6XLGc1+txjjSaazOLBEcXZknEUmUbO8t94viFdH2TTVTqsEzmCaSrCriMPkqOTkhS8cYzgE7H36JVAEz6Mi1Va3f5ZOYMtSzIlTs1k6pISOQhu2lSSMo8T6IN2kiuU2gFVWOpFLUjibUvx8A6F0YznW7LVqNIRh4CZFWijxc+SsxRqFtLSEkuZ1gjK2FA0DaETGaA2Gu8MpqwARRxGtMqYmEjOEpSSrCoFHDpy35OrEjxiTo6JFMXsr6xBKcmtMc5iQGR1pZOvpwSIUVtCZeXXGAPjrsMdNQKVaEcIiXF9wKAoj2byGW1bivtnpHEkXjwnVyVpUxLnL0lmzXT8yma+eCEHzPlDkqZPunlP16AsWU1ZSXhnagdR2KWSnMV7k6cNtFyCZDOjraFc1NANt5IWi2yyUw6oLFO/WxpcKRkkNyWWRoqnlDPOKNATnh1QVUHcHjBolMqoqpAQ0iTHUIqR8uV7oJ4yPL4EH+RniDKtUzEJwiGnSfbINNESCaSaZH0g4bQ4IxO4lMQD5yMBpImjRRKnSydX0Jv3MSWUloJbISrgjNAS4+RhimPAlFbocyFgjucCKOkHstHEmFHdiFvUE9AwTUV8JrWd5GmVTmAM4/SzpUzcdaSYmH35ZfTpgrBrydbgtJC3fAikEKmbSl5LTCRjiJ0njIHF0RyNovcjZlnD4PGdZ3O+JhcGt2pwXYAAIUZOzlbYbcbve3zO7PYHXnKWcl7yad23jzf+XkRDZ+y84OjVMykwJmKccgZXCclSxUw5K4iDvN44jJzcP2Vf7IljYOYqYs7YwqJyxl/0DEmjwuQRvDm+M8RhJAYhSzJhzo2W87I6brC5ZrNrZUIxespCpFvWSCbPYjWX6XVKdG0PzlBYUUD0QRofCbAI1Wx2NGPsRpJWNGdLlqssE1A5q8ifcCOWtDnxTrXPrhkPGVO8SgiJ/QeXANRVSbuTzXq3PlCvGtrnG/FYOggqkW6OYyUTra4bGMaRqioJWY7TrhswVlNUjr4bSCFSVQ5dFqTBU07Hvxk8hoRrSsw0nc5TZIKpasI4RSqkCKMUirZ20lgoLMWqwTYVafB0T68kVsAY+e9m83Fz70iJZVFQAId9R6k0T/YHUlwSs0x5c+9xzoIS7H8kiTxXgdVWAqRjolAanzLZS3CzD5Grd55TNAW6sBy9esblu+f0hxa7FI90TpnCiZdtt2uJccqu+wHWzcf5aYzfz9Zn67/X9SMpil6cZj/C0+fTZHXqo1//pGd84WWSwqgrjzi4ipwVh3XP46+/hw+R05Mls6ogxoRPiUM/Mjueyw1XQQjiK1jdPWI89GyudljFlJGg6TctDz53n/WzNbvrPXUtXTiToSod20OHmTfc/dwDlFKcv/0UP4zUqxnBS9epcJbj5UwSqoG+79HjlDWdMsY7ljrfkmbQmqYu2VtFWlXY0yWLsxm5GzjsWg472XQUEznNOkNppXNurWa2mpFTojqek0Jk2HWoeYU1Rt5UHzG+52j/hJASBz9yFWVTHIJldvQ67bZlNi+5TD3NbIY9m3P/eMb10ytiSuweXdH3o6RvG42pLGkIFMua9QeX2Lpg+/Sa0I70XU9dFgQQ2o41+BgZyopysWDuDGf9E3R7TbHzGAu2rpmfLNhYx/V+xKfM/VlBypmi7RkvB0wCrR1leU+0+GXGeI1qjhnHVqhtPoiBvC7IYyDuJcCwfnjCpYJrGRSx7iPbUaZK/Zh4PsWFXHSRVltYWI5Lgz30+PVBjMM+oowh7HvZXGslm8HCYGcVYb0nDR49q7BNQWzFq5GMIfeeGBN20ZC6gZQFIJHHIGQspUAp4q6FUQq8cLkj2RZtNGO+Zls8njTrLU06wpQSCNmlC9pDR99tMT6Cb4mTNwyYqHJOuqZeELI5BNr+nDi25JMVs6OHGFtiwsDSK+hkEtMtSzqlMCqQn18SuhFXFiy8dD+Hp9eYV+9gSifZIEpJyOV+S+p78m7L8IElnMwpjubsvOLxWmEq2I+Jq24kp8RuiB857283qjckl5x5sldYn3ANvLSC8npPdhaZtX5MivShDZ3KsHAj9gh0UlgseCmiNFKg5qSo9AlZQ2HmpJhgks4prUkxk+JAHzdoU2KKFU11Av04SccmDHA/io9Oa0I8MOgWdXzE+O4Vi3BEKjOWUiZQGvq0I6QeYqSyK1SQPBVTlEQvRMMqzFHuLoTAYdiAkm3NrDiDrEgp0vorMYbfBBR/+Ho7vY9q2jAb5wRVPEn4Ys7QSIio70UaZK4ONFGRukR2iewEXJLHAFc7IVbGRI6yhS5nJxR2LjJal24/xG64IkWRoJrVjNSPmJRYVULApCxo44xh1+GUZj1Ngfq2R6mCcRBEu6kLVEyU1qHnjrbrRe7sE8EoujZy97UvMnv5DvkbV1TFhqM80tSKxcM38Gcz/DCi+h9MmKCAsdB0tSa+tEA/LXFNOYVqKlLvxWtiNYfnG+bzRv5ea8ZhZHe5Fb+TE99TOmSUzZTujEZrkg3EuP3Ii8mDR9cllIl86G9hKeZoRqEDs+4ZSXnaznBIM7G4ZhiuduSU8V6uJTklKeSdYYxRps6DJ1tNWTqUjxw2e4r1gQdv3MdUjntHxxTjBYnEa1Vi7uV+qbVAIBKKJ+kuHovJmfefHVCHhubkmF1bkEKGeUk/ejY5kiYlRK8zY2FoG0fvPevBkwp3G95tZyX7rhfQQkyEmBiGkbquxOOqFEVRSICpGVmlHaYXr59MPGExUzS2wR3PSfteJLAxo4zCLhpsStQxE0ePqQtIWZpT5bRV6j3d9Z7cDreTY/wBHeReopUSIEeKmLSnGDeUtuJYNwwps1NRru1lge9H5rOGwzCgSBTOofpxyl9i8p4pzORJ1kYx+kz0Ea+CgI86yzs7z+svnVH+1MuUF2u2fSfZRxaGcaQoHH4YqZrq+27RXjSZ1If+/9n6bP35WT9iJPf3Mgh9gnTuBznjfhjP0cee92LxBVJ9wv7ZhmffkrTspqlYLhqRCuXMru0xxnD31bs8+fYjSbSOiQdfeEC1bLj8zlMOB8m8mJWOlDJX59eoqy333rjHyat3uH58Sb/rJPOhsBy/8YB7b9ynmFWEfqS93rOY14JHniYM/SA5R6vVjJyyoGudxQ+efvTcbwNdN5LIlDcoT1qevHrMRWGBhGt7GbFn8S7lnCcSzrSJMYrQj7hS0W9b5nMh/jR3VmQf6TYtttHoqmC2auB8y/zJ/48AbI8L3r27QGnFsFlx/WyJ1YZtadi/tGLctBzee8qsX0kQ4a7HNSUR8cbMlgvZqxrNo2+8D0bTHM9AKcYQWdxdMfQerTOutGgdsTHx7qJgNwTs4cAvbv+Aip6BhKsLVq++RI/id95aM8bMvND8T28coWOke9wTDoqsMs7Nean5WZR1AluYZBe76oJh+58xRzOqO0sAxvWBGBPj9YH8+IpvzRZ8/VKOH8UADC8OydvNSXd7aP6l15bcP56JNGbbCqJ79JiqIE3hiwqRbPhh8kGkzLg+UMwr6cSPAT14sheJiHaGHJ0Uild7dGFIYyT5QPRBTOFaoWNGOYcfPSYmDuqSNlyhleJo8QVeXv1lVDdwsf06j/rfFyP8FGKac0aFRCo0pnAYryAmkWoZmTqQM8/33wCl0J3jVfU/ocwSbRUvnXecHHoCmTe/uMQXE0Fs9ORcYzrPl95tcUVB9pH28RXzz91Ho2ifXmGbmrg8Ql1dgCsxxyuMk6nn+1vL//wNjbYg46yRFKPABT52PXjRwZeN9+881fxvwaGd5v/y4/Bjy4ao1ZQdpj86YlI3RZXMex7O9iyXgV71DHuDMRNcwgdBAhvHy0c/j0KIVjnfzr5vL1eeA893v0s+KGb+Ver6Z+WprCDPE6Cm5ovSmu3hA3Zn16yvzqmeWl5a/rz4jkqHinI+X+zf5DA+JqfM/cVXWZX3ZSI5FRwqZs7c51G1IQ4Db3f/kdHv0REezH8Km0tC9ry9/rekSrrRt+S9D68p1BcUKQq4IZDF8F+V2KaUzLNtCyFSt4k7rYFRsckj48M5GGnU6Bgxy0YQwWNPVorj6nWWxStC4ZuM8yh4En+HfbiQ6ZmRgiL6wBu8QxgOhF1mdL/ImCqyzvx+odhdbqkWtUx3p83mYXegmlX040A2Cm0U8TCgG5Em2+KY4F9j+5bm2JQcf+mPObUGXVfsascO2K0jbH+wO0wGdnPN+bEleU1RnhIPo0AjFFRMTYfCUs4rklHkJBLUbtNyfOcIPwbGfqQoCiGt9YH7y5/lpC4JVebdx/8vwr6TKT8in0MhG/BlI+9hL4HGZnzMF9Ijeu95Xj7gOn+B+axBZWj3LUM3CLqcTFVXuKUg5h3gQyBokVDa7HCVo87wRjbc33kqW3B0b8ClDXEM/I9aEfuR+mx1e0oFLP/z+PPs9IrkA9/+5mNyrVAxw1yTpmLGHM1IKeN7aWydHJVUBXRHBb1X5F4TvMdqTfSJvveUdUl76Mg5S5ZXKY2BsRPfVRcihbM8GN7lleEdqlmFTxnTB+rjOeakJvY1qiykKWEMSsmkf3z/gqyV4M5PF/h9R7o+TJRFRUqCnb+JOSBE8RQrBGoS021Rrm1GvfOH2CeXVO6Eh7NfIDmHouObVSbGhNGKvu9xEwSkbwfJVspG8uKmXCKVZVqjrREPoSvox5GidvT9wLPGESpDdVxTNAb71lPGQd6roixQWaSMSsnd7IXk+EZGlz92Of2sFPps/fldP/KcIln5Q5uO/LFff8D18W//YV7Fh1UhIfHkW4/YrneklFguG8J+z/kQ6bqBGBOn909k2hEiOWVWZyuWD0/44L+8zfXzNWVVoFISA6SRiY0PkUfffsQX/uKXeP3nvzAlY0+Sqw9tOHw3Enwgx0TX9YLsnS6wdiLLpCSj99oJIjSMXrKNYsRoTV0V+JgIOTEOnuSmsLd+IKaEtoZ+35FCpJzXEpqnIEQv1JtK/CrayceujGb20il2Vgql6jCQc2ZxuqSeVXQXW7oELmXsrEKHmuEiYpxmvzswv7NkHEZiShyeb0RT7YyYZucNMSb2uxal4OyVO8xXUjS06wM+Ckhi/XwjPgWrRMZGQIeEC5FZlImZrh3awNxpli+dSXc7pJuhgHi/DgPp0Ik5+HQuchJVYqsCYyy+G2UiGDNRjdhFSXE8fyGReiDhjLsQiduOqItbjXWG28yVm4nKrfJT8ZGbjFnNMKuGeBiJN595SvjeU8xK0r6TrImcsScL1K4nHwbUvMSVFamwQsyzMmVSgG5KzKIi+Sjdc6NF319avNaYbkT5IMhjZ7B1KaGUg5eMpRBEQpUzaqIeKWtIVjalOmd0iPJzWJlkaO/JxqDKQrxDY7g9LU07oOtE6AaRBcaIqwohaKkk6GZrhI5mjbxJbU+KMoHqrnfUqxnl2VImUYuacLLErubUdxymaEmI/EPYADKpeHFi88n37ZvKZpLzZCWS09B5Qh5FhhdF7vNhXf1Hpk5KzttiUYM3jN7io7xfTimhp4FQ2XLEKCBlfIy3JMOisAxxwrykhG4HlIto1HS8CiwBxQtJXGFxD47p3n1OwwMygvxOXmRDWskmOqTJe3aDIZ7gEHo6GJW16JTJxmCrkpBadJreSy2hrFlrKIUkl2MC9+IafWOQ9+2AsgZbSQhwSlO+UkrEXUseHfZ4AW2PHkdyTpOfQsGuJVtN7gZCCOjjJSpGVFmIHKj3SIKxklDU6VhNRqO1Fb9R6wVq0dQkJedA7vakviNYg2pKlFaUTUn0QosMPhKZJLchYq1h7EfmpyuUUuzWO7KVz7bbdVhn2fcteSnB09rp6Z7xcS7Xxw6xT/tahvbdc9zxq9SLhvFig5uVZDPJA8eALR3jYaCyhm6MInHMTJh16PsBrRRNUTBOPhM9Faj+fH1bFKnCkjcHmb4NXiTBzqJXDcW2JXWjAF2UwSnLoe/l57IaUxWQk2CeZzVFXYqsrh2x2qLsRKVUmRGonKWeLyjqSn7OEMkkxn2HnVU0p8sX8mIUw9WO/vqKeLdh9+hSwqZLK1l4CpKPmMJhk6JLEV1Y6gjj4G8nMylKY+hmSpqNwhhLYS2xKogxsljNpcgbBskIQjGvS9QYqOqSCovKCaelIFPIPS+FhPIBXTj89V4K8yFQnM6xpwt0IdCVeOjJlRP5cxK5oIQJaQhBEOHaTN5KkcKj5HrlL7fEkEhaCpk4CNa/qEvG7R4/XceNMcRBQBLWGVQhyPExeMaJ1GitQbsCp7VMiaJcw7tDJ4oBlTlsDzI1O5px8vCE66fXNE1F2/Ysz5asn18TQpwKo5vjVfZpnwnkPlufrRfrT10U/Slqlh9sfdr5+nFx9yc+5MU3xxjxPkzZDBW67Tg/9PQhUdUVD75wF200j7/9CKMV1dGMhz/9Gtfvn3N1vqYqLCkmOh85vrPCFo7D9oCbKZ43a57yASfVXdrzDnLmqIJXmkzqBg6zuzw/njO8dIx2HfOV4eilM7RaMuwsV++f0z55H324wlhLiKek6DCT6d1qTcqZ6+udbKiVwnuHyUpoQjO5+PkUqaqa8dCzWM7o24GoEm7mcF7wvLPjuRhMb4pWDcWyEe10U9JebsljIDx+ijWWOTPuXY2Eaw/aMLMF3a7n2M5phhq7nPFMGzZTcTGGIIhTMkllbOkgBnj6HgsXGA49KyMIYxM1u0NJGBSrpmTurmnMiDaGlR/JZUlVW06qUwotm/5FMWKKSG3hlWVBfxiw6x3jsCeXVvxUAmlG14H14T2KeUM3bjFZSHTtKvHclLD3NE5z1kw3wd4T1i2mtNypEuVMjrNHm8SjtUcpKIriNmAPbhWanO89PsoBeXfmKGclvh8JY8BksNYSxoiavBpKK/IUyqrqQl7vrELP5O/j6MXntG1RMaILhyoctCNDN4phfNqg59LJxvHG+B4iDB6TM/5wxaZ/B2Kk89vbzUYO3E5DU+nErzN4CdiMUxr7RC/ISqHnNaobyTmzb58yjltijmSTMFUNpeNhe0SylqxhNz4jjZ6yLFj93Buo3otcsu3pnq7JWuGcZTzfYmvNnZdrdKEocyu42spNReh0F5+0+h8pjr7HyjGhjHxOegpOzj7ySp2Zz+UceusaWv8J1xUfieset1owdwf8JhD2nm1vyTahh0STjqRzbDUxS5NEK40zmqw05XzJIr6GiYmiOgElG+PsDCqKVDUnTVYyJVm89ArOtOjNgapeSjc6ZYawIeaOnBJGVyzLh+iscKqSDu+Np8taMplD+4SgIhSGyhxR2gplFMo48TBNRMbY9jhrOGo82iVKFfnJVSAZjVMSAqytIW4O2NMFaZJdKSPSnuwjejknA+NuoL87kzythwtsGsVDU5XkUaM0qFlD8DvGXUs33+HyM8qioqssvjR0w0jbBuLBi4RoGHHHS4GMDAGTpHN+XJV0PejSTg2NCbkeE7PFjBAEca6UpiwL4pQ51u1a1KzAWStNmKmx0MWKNy9L0uORRQOvf2F2u8H/rtvLhzshH1vlmJl3CaMKmuc76uwotWGbpNCpjWX0HoWTgOs4ZdPkTMyJSKawFo1i9KISeKcshD6aAyMZteuoogQy20WDf74WemDbQ1OjVg2b959RLxcwjPhDxpc9emEggTGKmDPlrBLE+k2D7WpLWZeokDl5eELjA/un18zHjD70mMJx2Sf0GxXGabreU9tEOaswekVYy7913VXY0yNGlTGnJ4Te060P3CkL4tWBpqr4YByk6I2KpDQxiYyvrOSzaoOHIPCNpCUiIcWpgDaazXaP0oq6Kel2LfOUeLmuKLRh9FuGw/uUhWMRdhLK3ZQUsxJbFqR+II8BVzmGZ9eEkAjWYJVG14XENMREv83gCqJbkasgapKUqKtAcTKje7YmBZHkVa/cYbjckdtBJkfWijexqCibuwJsMg1vjTCMnrWyEvQ+qzm0PahE9JHKloSU0E7RdQPKKuq6YvBSGMUQmaXELGTG3hPmFesok8UQIvv9Ab1T5KdrHjw45ezsmN3FFrMfsP01q7bn7IsPWKHZ5oyfLnUfVuJ8j8P7s/XZ+nOzfsSTog+Pd/6U5dKHZXOf9E/9CU9cU1jqlZhFC6NRXUdQhpN7RyzvrhgHz/N3n1GVjr4fefgTr2CMYf3BlRB6rKUsHPWyoT30bNdCitNniucnj5j9VM0u7nj0B48hw0/dyfzyw0goPd9pfponq7+IefAzuNlj9PIDtqwZ93P8/oz0+gl33llTfefbaGPYXFccDivuvXpGc7IQY3o7iP8nS3ZEiANpGKmNwinFfF7jx4AfRoyR1HZlNaZ0tLuWYAJQ3EqiPsyRvwkVVUpRH80ZDz24knx5xbztWYwnYphNT0n+A0atOJl/nofFSyTv+U/zit9zBmeMZBUNA8paxs5LBoex3Nm9w/3xiSR6ay1Gd2PI6ucILCmTprRbmmZEO8Mdsyc7I7LAKJQqlSN33TmFtaSyYt8UdK3HPVyQYiR0I7ayxLYnGUsqOsLsXdJ2oL/eSEjeqmZvjvja4wMArx9V3JkVsgG93ssEyma+UPW89nnpRv8/v614upPQ0pti8sO2NTJ8+/JGSqf45deXlFNHOncjOSSS1RggW0PSspGJhx5jJbRPTPFCxlOVQ1eOtO9JWkmYZcz4Q4+PSbC7+54hJFLvcYWVCQ9SAKTRoyfi3cafs2+fkpJkuWhjbu9+CZmmGB8gapJzxJxJSnJztJMik7ZHz2vilE317PBN9DSiy8aQR42Omq/WX8RS4mPPW8/fJjcKe+aIvSd2HlM5mqZkbAfGXUd57xhzPMP5PafxghqHndVkZMObb93bSiYRIX8EgPFdl4Tbz0TdUqCUEWhEDAHjLH/pbKA8K8lW83//PTj4m8uJujXNq9LCOJI2W1zxNcoHBX7IvPWOYyDRjJpaf0WmIigJyJ3Cb3NMqJgpyoaHy69IrtVUuOQsxDe9bMj7TnxIxqCrgpPX36D9zmOO5guUtRNEIbHu3mcbHxPGkZcWP8e95ZelONEarDQidEZyjFLk/PAtevZgLK+d/TIz1+BDQGcxcqsghbmZFVibeTg/YIKHmeYLPymFdp8c33qkGS+3UpCsZqjC3spg8+Ch7xliQrU9ozOkhw2oOcPlhnI1F9x4zhAT4+VWOtKFTKo7e0EIV6hN5v3ljM28IM0yL10PVO20CW4HUtGhB2kqJCu+vJfPFthQ0lpNv93h64LSWQ6d0Of8FMWQiQwk7LKm3bWo2k1+sETSimRkF9ibBW+ffhWjFfOnb/LquENNmVWfcIR96rE330dOx0g2M+J8ifrOHreo+WMFvVEMBoq6QRmNqwv8poUM/RgwxuAHjyscXd9j0JhFxb/veqxXrGLPL1gDoya0A27KRtNNiToM0gLyAR0z8wd3iLsO01To670ANrSEsqYQGUZPtzngQ6ScVZR1IRJNQDvN5tk1x5+7R7lqePB0x72l+I0+eLjkg5lMmL4UHCooXNNw+IZlPI/EpPi9qzPKl16G0nLp9qijGTPn+Hyb8Nc92QUeHxcka4gpkbQAWpwx7Nue5CPKaYF4BJmKZA1l4XBlQbtvMVNMRgoRpTSvFY6/7BOzwnIVL1kP30R3GX3coE9OMI0g3P2uQwFh1xG6Aa8kJ0znjHKa+u4RqR85PLrkcPfL9GNBT4KFpbKOxijc+lukp9ekiyvc0RFqLrlWxfGcdgwyDZ1UIjk5Hq5+lrqs+GDf8v/utnIMp3QrH7SFkfwsZ/FjIJHIKjOfN+L79KNMQadr2Wo/8lpQxJh4M3fM7y6IKROiRDksVjNeOj9Q/f77VIuGl5YN2zbQP99TzkpecRVqM/JeyiIG/1j185E/TtfePEmKP5PUfbb+vKwfDX0ObjcUP9D6fj6h/Cm/f/Fkf3I1ntLceeMeftfRdyO2mWP6gegjT99+Kt2aSsy6s+MF5byGDCevnHHx/jnRR+p5zfmTC5yxnFqNamoebc4x9wzVqmG8+lDbefIK+HYgF5Fs5S8/Hi6bAbRidnfJ/cUbgGK5fZWQ7lIt6ulKNf3QOROGIOS85895vhfM6n57oGpKnFbYuqSpSgFHdL3Qu7TkJPS7ViRZWlFMfqqw7/BtLynrZcH8wTH1yQJjNDtbYHMity3Fy/dQiPTFtAOFz5TWEmOmcBqrRHpTOUfwsok3KZEOIhWsk8IOEQfo0YPVxNpSzGZEvSL0A83JHOvaW9kawLBpAZF95X4gnnRErxljR1jPZYJyAzKYAlR1UVIsamxdTJ2/ljils6d2kCyc2/dfio3u+ZbxcoerCjHV2+L2xqCNpiiKD31oHyoo1XcfznmSqunCUhzP8JtWfDwg8AxrUKs5fr0D59AzkQCl2AuxSxsUCl2XmONMmHxqVitUJe951BPW2WiRZA1ewA5xQCuIStQeUwlMQgIOs5mmKJMcKhlBLBMTahiBjEUJjvtGn2gtdKNMW0qLmlUix/IeFRIqJvRERkxlAa1AKdK+Z9j32EWNrgoI7paY5cqCcBgompIyeqpZg297VM5YJ4XwCy280P/SEMCZj9y8P9I7+dAfXhRPN3K4Of56j5tVH70ufOxfyikLPGDZkEcvH3CI6LqkmlWkPEKekusRH5+ZJmpJK3wS7T79SPRe5GwTOS6BFKDGoawlELAJ7NlSCvlNS04ZMxU5WcmmhBBuC3KV8q0/ICfxDSpr5HVP1xKyQhuDTUyZWXoKbxUJpC4dse0wLx1JGGttp+tMlmPfCfUqeylsUithUFLgMUm+kkgyowSRptGLxy1LPlfqR9lsp0w2inQYMMsZbi3hnWY1xyQpmrgJF86ZiMgvMYZwtcVUBcqJDEqfrnBHc1wqibuOpinZaUgq0xzP0Aja2ClNPwzorOj2HcujBV3XC7UzZiJCdTStmM/bXYe5uyKOgeF6T33viE9cnybZVNMXp6mxW9QcvTxn8+QKXU7SKwVlsrTrPWOKlNaQtWJ2PIeYmBUNOWbG0RNzph0GCmc47DvGdstQjFRK0T+9wrx6FxTY4zkhTtfGthesOwKZz4sGvWspnQWt2HX9Lf5dTz2DMHgKrSmPZzBEdEzUR7NbCWl9tsD1cQrvNRN4w5D7eAuP2b7znPb9nsVr9yjnIkscrwLh5SXt5ZZiyrla3j3i4vkaq0tGaXtIs8sZhmEkaTmBS23oe49KoAspFrs4kBDEvSscGahXc6zWVO1IlSXuoMgO1SJS5LMVikzqRvy2xZ0ssNO5H0OE9y8kjPXOCrua01+suXh0wc4HhllHsFOgqg+0g2dvFc5pFkVNWDvi6Cns5N/tRwyQnCX3cm9LPgplNI90mwOUlq73QivNGWMtpjAS3VBYyJbSGQbv6ccBnyImGYzWeB9Fuk+g7waO7x9zelyRaivNnOs9wQe6Q4crLM2sktDZlKhnFWr6XG1hiTl+8rH9iYd2/nSp8mfrs/Xf6foRhLf+V5TQffwf/6FOzsy8P+cod6xKaP7CG3zwzadsz7copdkfWoqyICO5GSln7n3hAZdvP8VZy8nrd2kvd2w3B7puBKVZHc0JIdAeelbHhh//8h1mqWNQAw8eyAs+LhqerE8I48jhYs5RIaGChe8phg6lNefXz9hf78TTEtcso7xeVdcMpvnIzzBpQnC1IDg/rxN3hgE/BhZ3S/q2JfSBtXcobbClQ6FkMmYjqla4pqScCDSH59doJV3Z3I+YHIidFAjNsuTknuHu6RnxkBmeJbSyBKvo6oLgDHnsuNq+RdIKF+DlyduQY3ohy0ImHzrDwgxUixpdWOl8KcUYE0pdEscdrjSYIhPWB8IoHqpMlnDHfU8eArop2LtjVEqEkEBpTOVu09iVlQA8VUgHPYcoUrKUoTCYmMkhMTOKzx1XpBCZ7Vu6jSBoTV1MsiUYbc3FLqOcpXGazx3LJ3Heena9bC5vBhnqo58UTw6BXRAN+4PG4pY1LmUoLOO2o28HZidz3MmSPMmDlDPkkOnOt1SnC3QpYYR2Vonfa9eCs+ghAELR0k2JiUmmW85AN4oMTk0m2rpEx0RSCgOoEEjOgkmC9R79hI8W6IKZ8K1M2Gt9qznnNseIIZBVkA7rTTGasxRUvSenCUecEjFEotVc6ohKA2bnebU/FSXcUUnbXZJGj50ZdnoFiyPW2vD0XIrW9y8Cvg+4qpieS99unj9R4zFVRh/1hGTevIb9YMnDnDeiY9kJpvtLR4H7cymWv34O7ZDJCq43mmDA1XMWtkPnRBoDZlFhIuRDQEVD8kjhZo3MmZL49WJO4CMhSaGZ1Ujrz9FJJtakgnzoyWGS81YZ9cFziiCfHSmiUsYYw7y5J1M/pSjcQo45rSUDSStyCBONULxCS3uXMi0xdYNWTt6CGNmMT8g6E5MX2WOcfF+lfG/ber5+bci2ElrjvpdzZ6Jz5VIofClmfE6YfkQvanJTobUmblqSVqxePaYadvSHA4GazmeULQT5PlHtyFmkoykzv+4wZPIQaFAEPVEPSyubuCgFaEhgG8Wmf0RpKtp+z/1wzCxrdGV4b99SVAVFUxFGjx8DriwwRjyZ0keTwhVgvD6wXDQM/YieV4QQ6ZoV3/hgzco07OsZsP+B7i9kxfshEJPIvPxsy7rr8Xd7rCsxXryRIQTsvMRNRUfoPf225cGJw1mZ3J40jqwh7nuy1tRxxMxglxa0JBosaqioXzpDhRHnnmP2HeOztRyDSvDsOmWaWY3qPXYp10atFFUp8Q19Nwg63CjKw8isHUkR6gjpfI8fPed1xflhYHZniTVwFCPV6ZxCKUxZkGOma+6xPdGs15mn9xzXg8fVjiGJb0gBT3VkXhn2RzVHQ6IePYHMurT4IHEI2mqS1fSD+NdWixmd9xRVQekc+0MHKRF8pgo77uy+Q1nXLAvHLmest/TDJXpR4+YVadeR2p40kQwJieHxJWbRQM40947g5C65qGmfX3O9s1zXp9iVI2QpH2OIGGvwo0dlw3vXnrO7S85+9mc43b2LjnuS7zlfe5LSci11gr+3RYGd4CwAQ4ziBc35Fnypk/igkhcJrdZqQvprCpOFSBiFQJdSYusUqVAcvOeDR3uGeYmxhkWCKijxJ20PuErC39XoKZqSh1/9HOfdM95dv03KCR/9ba3zqTXPTRPvs/XZ+nO2/iuBFuCjFc2HZXV8/+JGfcrvf8h1fHiXu61o/fuzX+Sln3mDk+s97bYVCcW+Z/Psmhgzxw9PyDHx/jc/oK4rquMZ9bJhu9mTvGcxq9BasW0HmuM5b3xxwc+757DtgEz+fCYMnuv+Hu/svyq+pqx4fYQcPebQY9QebTTXl+dszlsZkc/nHE/TiOEocz0e6LeddM2nIML6qMFV4lXJv/8uJ2WJLQ3uzkBeZDozcogzsi3org+M3uPKApdl46eNJgwenTPWWvy+n8hZmphlQ9Y+W+MGzb0vgJlbgnb05w05KA6FJhwbTFMyblvW8V3ImXmIfG6QC3BGzONJy0abkMiDxyxqlJ0RBk/sRynwCkcc36FQimIxJ7cQDgPDppXCB2hOFhAjxdEcVRU86YIEiNYFufSEXSeSwMmDo+cFqjCyOemF5GZK8fiEXU/YdqwaxxGZ9tFWfDQTgMJEmfCYyrHzBdePPSl45sdzfu6BfDa/+3h/WxTdHtIfOUYzb15JZ10rWD2ccTwvSZOJuDqaoa1m2PdUqwbdlIyXG9JB3iOjIZxvMcsaM5dJoa4KisnwPrz9VIoloxltxk56d434K5Sb/GI33iVnZJM5elQSoEI0hlyVEsA6+gkkEaefRTHVOcSqJMaICkES31GEKJ1OZa0QsICkFErJFESrhFdCUCxmM7qcuHh5jlewiDV/4fKn0FmjjhXv59/DzktyYTlHJl6PL3v+/dvDBCRQKI1kJSklG/QJCKE+fFe/+eWmGGSSw6VE1orffSKAA0bF/3lRYccIMfAXvxKxx5qQ4IONDLiyUjy+tMxSwjr4sQeRcmbJfbo1ytNoHA2xDcR+JHlPzKCsJlpNH6FclixqMYRv9495+vjrEBN2NOhUSl5RhuQM876leWY4a740fZ4yrcpaMeeUxfKOFPk53w4lyC9CgTNI4ZQUx9XnoHCS89R7MoEQA88P3yTaCFFM9KoucMdzor/CKk2H5d+8bxgjzLPnr1j5zHOcitAsqGXblOgUCeOIaSrJ5BqjTM8Kx9x57ro98XTgWWtos0Ht5RyNuxa9qMjbKfB6DMzfvmb2SJH7EZbHk3xVCWmLSfq4b8FadAxc92+RfGBctzwYv0ITLeWx5kmhSGS892ijaE7m5Ch5NM3ZEjMMaBSkjHaGZtkQJtCE70aKDH1zwuOT+7zbDiwWCXj/u8/vT9pFKvhG8Hxj+uOD00vU6cDF208hHlH5Y0YfyEYRhoBWCjvRyrSC+1VPYSWfaBzGaULr8VrhCy9wkvgKhdIErWiD5mRcMjstKfo12mnC5kCc3md394jh6UbgHVFTKLlf5ZTAJ9DIVK+Qe0u1PvBwBK00YbOhmJWEEHk39bRHNToFXn/zCfeMY6ktZR1RM0X3bMu3rk8Z64c0J0uezBT7mKnqAt8NqHYkG82ThaM5rhlV5IvPDrAf8aVhXSVsUsSpkWMQWaObZLw3oJVh9DJVygmjLHdVxxe6b+Fcg8bypOupVzOK04bCLvCbA7kdSV2PSpnQ9eiUqF+9izJaoDvXO1rAG8uhX3BZF4w11FUhE0wkhDnFRFWVKGBYPuTdjedy8PzV1ZrTRpHqmusrzdALFTMrySnTPtBdbEgJdiGQSk1ICWcs0SdiSoQQxSepIIfM0A8UhRNkv5ZrsrbiJ8pas58VtPOSXVXS76BsKlzleLVNmKeXZDLNosGHyGF7oKhLFssGUxjeevptNv36xY7sM+PQZ+uz9YnrR18U3Z5130sD91/tSb/rK2r6cs6ZrLKEU1rYXm7p1i3t5kCOkZgzi7MZZ6/f49EfvMO8qdkfOjZP15hpo1kWBUrBYduSydz9wgPmd3oykuWijEgCtNGC+Ny0pJQplw34QOhGmpUEq4LImNL0eBB5S7s54F3P5eOei/eeS7dpotTN7yz53Fe+QNlUvPTlVzl/+xlxDHDZMZQiewnjQNZQL2tKM2PYd6Qh3b42yeYRSccNwEEZQ86GeOgFz+oyaewxk9n9dhoy/apLR3Vn9eLdjwm/a2UTNkiX3yrRoidAVxJUm3yU8EY/EHYH7MkZbip68ALCYCJLpX2Hmwhbxf1jCRqMkTh48Vt0I7H3t4Z8BWQVbjuifpTPw1SOvOlI+15uBFYKw+H5DmLEFC+CKjHi03DLGhDzNiExPFvjzpa38ovbY+t7yT+nrylnbl9H2HdQWIplQ0oH2mdr5g9PqF46EwmR0aQpLyn2I2Hfoa1FlRZdleiqoPr8A8L6gOpGbJGITrr5KohxO95IOVIie9nYUkvhEbtRNoVao8nSxZzIZslaQeZOEyGVIR86XFkwMpGRQhQPy81kYsLAS5ipJiqFiQmjM2bRkAuwpSY3VoI90zRNsYZhf8Cvr/CNw50uMKWE5qYQX5xHN2p2pSaZmBiv5S2WjbrURZ/yQdwY5iddnS4EHmDKEkjkuMZft+SygOxu5YK2LjAaDEm8NM5glCI9GVBNLT6o2Snxm0+kIFEarQWoho8sz5Y4Z+mu9jJlWu9J+27KhcmkQ0ZbCzFR3l0RNi3EOSrJQZVyQmdkkjdR58SjgxDaJgKWyhmlbqZLSX4fo0jepvcGLWh3hRLfoJ6Kq8Ji6kLydKL/0HslBWUaZJJzi22fZHJ5Kp6LO0cUp0d07z4jpIzOCdUPjOcj0e0oXj5DP07o0clmXWnxdU3ZZWG/ZTjsUPOavOtIbYtvB6qzO4B83uQMo1D7VBYkeAZU4TCzCp0N+TDSDQPN2ZIuJrJPqMoRYiJPx3s6TeQx0q9bnDW0o6c4meN9wGmD9olmUZCcZWgHkRzp7vZkTnE6xj+pOJouAh+plZSiuX/MvVnJs98T2poaAmiJRjDOUGpNzFAuKsh7jFakEG+znHIx5UclmQqiIE4UtiEG0pMrjJpL6tYk90xTaGncD2ClKVCeLsn7HkKgHz3aJ/oYcIWT4yiD8gIP0Vp8iT6I9EvNHMkJ8KM5XhDWLd3mgJpAJWnwrI6XdHpG1/akoiSQ6ftR6H8TCMP7iC0dZlET3rqiBsaQUEGOw5gCGI3NimGIuNKy37XsdwcWR3OGMchnYBW1NZRBUdclGEMOgaJ0FKcLdGEZn68xIQtpbYK+mKaifvkMMhzeeUbsPMp7cJGN8VwNAyiF1YpxDNiJzqqT+Jn6aaJrjCEXEOLA+fNr6pcWVJ3FjwadZJpurCHmTL/tCIuILgqMghQFKDGOHo0ipoRzGqMt3geM0qjSYLRBK/HGmQw5ZuaLmQTSZjkfxxjROTMOI9vNni8enzA/W96GtV48uaReNJy8fCp7jw8dsh8+gGXg/j3nRZ+tz9afu/UjLIp+GCHdxyZIH/7t9zpHv+vbPv25M9LFe6zEKH+/f0rpn7F+5y1YvIKZVWy3B5ZnSx7++Cs8/qP3wEdWxxJyOnYj7U4mShfXG0iJ03slv/iLlnL+mGDha4fPYZzBGkdMnjR4tk8S+7eekH3ALRvq1Zzds2ueNy3xbs3swQn18Zov81xG5+2cb3x7z+WVJ2zOOfqxL7J5dMlwPKMvDdpodhmG6w1H94/h9TOu1lu6Q8d9Z0QaoxXZaA7DiBkFWKByFn2xQjbJnWeZHbauCVXBvsiMu1YIaasZWQv95vmupDA1u17x7iAekap0LDDf1WVqqkQz18RRs+8a2kETd73crK0Rz8MYUN2IripiTqjJqKoKg1Yik7GVYLFtXRBrJzjtphINOJHUe8Ztj1lWZB9xs1L8DZNEThdGipyUMSDhiT5iZyV4IRqRoX+6keeZpnBKK/FQTHKk2I2kwUuOTJr8DbsOU1juzx3FRDV7shvZDd9bo52njqfSQoy6OXar45kUL4OfpH/ildGFJZkRXVSSL7XrUYeBFBJmXgnK9mxJvtpLEesy2lUEH1GjTMVCErmjqQryroXBk53FrWb4fYcpHMkHdFPK16L4gm6ADxHxw2ktAZxFTLf4VqyZ5FsJ5SNKy1SImLk+vI0yBYw9YbgiHdUYGr7QvwRDoBgUSknhaXLBPD9EDRouEnt3RXG6YNmUfPmeFO0KiN2AcpbaRRZlIOdET0EbHKC4aD1XXfjuN16q5NvrgvxR8U3veR6luPtqVbBsNGPnbyV5SWne7ROFkYnZ1YXDKPE1zeY1uQ+kduTavYu3l/Trrci7YsJVM+7f/UlsXdCdb0k+kLWiX9as7z7ANQWzreXORYVF4UpL8fAe3bceUZbHZKWEnpYzOcUXEA4kk+VZvWHjetCKV+Jd5oPkljH9bMQoU7upmLkhd6XJ8akURMRzYgtLyorLvkGTOPjM544g+ESZEjzfSlirVpjSQTeKz8wUECPee1JIQMYtaplY9SN90DzvSlyh2B/Et6KskSKtEDJXDImwvkblgB5nJF0TjCcXlRRnajK9GEPae/SHM7UU0PUY6yjqC85SpKt6yvKEw64XIMfgxYNmNeWsJvWB9nxDXZXowuGMpi6cXCOchZTYrPc0s0o8M+lFwR1iEhw/yKb4ptn3Pe5P+0d7/H4kp8yDqmH99paqtFwbRWoKwhBo2wEzK0hZcUWDf7ZDa8XJLGEMjP2ImgpgPxWiQ0roLFj1ffRUz65ZLuW4tauG8fkackanRJyaHw+O5syWp+yvd7wfA0+Ugo1swutKwsaTLbioIoFMM0TmMUteUU4M+57lvEHHc5p6j+qf8466x3vxPnHZM7gFw24gkmlmFd3o8SpjrSN58R6llFg/uuLs3hEnr55xePec/z97f/JkyXreaWLPN/lwxphyuhNGggSBYpWVqhYytcx6kGmtrZb667TQRjKZ1jJVd5m6ySpVFYkCAQLgxZ3yZmZkDGfw6Ru1eD0ihzsAJMGWupifGXAzI0+cOOH+ufs7/N7nF0NiudwQtBJcdz8R5oTeH0ds41iisNVnmIVirR3bW08zac7qCWUqIei1jna2Vkgv95ROSHzUjjJMuNMN1ZMzKIXht89IaknZXpC0Jq42dIdJZveSzFCmlGV+01qU08SS74tf1hqR1LmaL8L7HPc1D862KHNFjoEcNWE8I8dM1DU/axwhF45GobImTpFF2zAFT+uc/KyYcLUjZunAhxRwnecDJQlq7zTHXp6lCZGo51xwbU1MiaatCT5w8YPHhH7i46u/oXtyAK247J/RqpoH773P+73h0diSgU9vp1m6freJ3yVE79a7dbf+gEnR7ymN+6bve+uPv/PlireSo6//wQX4TyFAkWDg/9h9ygOlcNsdfx0fcegy6wdbnvzJB3zxV7/FH0dOLjYYY9CVY9h1TMOEmyuz7//Jh3z3Txq+//B/QJH5Uj3mL/N/K9pgn3j5s0+IPvJEWR6VPbYWbDQoTp6c8Te3lo+vYZWX/NkHmn/2uKOkzNVvFhzO3idvMzdXe5ZDYHm64m9VYtwsJLCIiae3O05by/bxCf6nH3D526ecth3rxpFiQXuojVQZcyzkuwHyMZBRLNZLHhwMegDvDNOJdCLCcRSplIKI4+mlwmXHZVT8vydxMfyogX+l6teObYFcqMOBs3QDShFjy2hP0WdLtDGkSeCfpRTSpIS2Y5ZS5ZvpVFQWPWuytVIoowRPrUT7n/qJxQfnpNl5PHYTtnEoq8UHxIv/k6oW5GGeaVHAMFEQ+VnOCWU1zdmK8TgIpnnuTJQCqkigrBAMtDtbgTPkwZP6iTx4ppd73nt8yvvbWjxJQuYwpbdGXNS9vAmlyCExek+9aiRJvXuh0VQXa+Kux98c0Y3FrZcoJMC5i2JN5Qgv96TZ1LUsa2xbU52v8Qry5Z6ASIJKlBzOFlCNQ/lIbiqKD1gfJCkuQivSq4ZyGOT4z/Nq2WpsTKA12YqTem4cRVXYVChJjGOZZXoFhKbkA6py7IbfSPdJS+dO3UTUMfOTdIHW83yLBkLCYnmw+hMJVvw1N7tPUEpkT3+yMoKNdxbKgtCNXCwLH5zLXn45aF5MS1Dw8xf91ydF3J0T9UYh9GdBOplawQ8zbLRG1+7+GBTgb14OX6nNNFbxv/uhoVpbwnTgy0//vVTt4xVx9GAMJ9V7qFLwz3fkcRK/IKXoVoabnz6GfuSi0/x09WOMFk+vKq1ZnUrQpvoRxVxtTpJw5HlWSSnFp/Ulny+uyI1jfdmyLGeg1X23V89za8poSQyQubBCAWdRoWBikmsvF1JRXPaLOXHP/OhEZijSYWB4Jt1lPfut3SfBtXQgZz2iEB2zl32hNcdj4WZqsIcgXkJEOYZZrq9yB304OZfB/6LRRmPbhXTknCUUMFmoYEobue5TRvWDYNatw5SEXj5H+45cWlL/Hiqre38rZTVGafIU6I4D2ydnTFMgzl228TgIwAFwixpbO2xbc3h+Q7tq758dSs2AizvJwe9YBdh/crh/6Yen32PrM7kf6D46JdQi7dVKQQa9cDw7AGmNsppNueXsfA250HUD/XGcfboU0Uc2pxuBlRhNPx6Jw4Rb1mI4erIkXu1RnXgwJaNY7Qe+5wKDMeA9X1jN+myFaSp879FW8SJlvqwlEfwogu3FSiBMkVxphskzjB9zsexQzvA3+r9hF88xK8Vm/BuWKqOtZegnYpHOdSqFMgbpcjlDSonbz15it1vO/vgDzO2R6/MNx12HHz1aCYWuC5HlasFufySYHt38LcuTBfZFz4c3AyfnW1wxGGeoHm7Ry4Y8esLlLQxyj4z9BDFiljX1k1PQMH7yknQc8Q8/hLMnRK3ZHzshbWpDmFUbOSZiiaSYUCiaRf1qFg7xqYsZntU/4kVU3IwN63SFcwZ/G5jGx2TrGFY1f37swQgsAavRSvDsqWRoHKoImh+jKD5Tu4ohec615XvHRFCFFxvDoLWAcrLcuLTRkhDmLB5GSUnRrLZM3xkZFh11W9Fd7bkeA9dXn/OvNxs2J0tihufHIOTI37mb361365/e+keYKfqa7s/vs15/+dddrW+/3d9HkXdfGFGcfechp+URdtJs3z9n/8U14TiybGv6MeCnHuOseONozRgjH/7Rd3jwvUdoI3hnRbo3Prz65Rek+WFSrVsOX+7YjB7TSGXSj16MGJ1FryzjFJgud0y2w7QV7dmK/ZejSMGsZv/shoffecTFNPBx11GvBZ+aU+bm6RX75ze4TcPZe+e4cUKlSKUNZYpsz85w64bD1YHuao85q9EeTFOh2wYO4Y1DYhY1ZlGLMeMU0JUl7HqhfRn3leNeEMf7EiXRMEuHWy5RxtC0K0zf3MOs7ozwWDW4s5Ucg1II+4EcIukwUNpKJHxKAnLVOIw15FHkQ/X5WgAORom0LUugV0IkHAYxI1SK6dkNdtWgtMatF7NsR82BphXpT1uzOlnIfNW+l0qpVqhR/CDMdiFJybxZdC3dqunLa9IYCLsOt13e6zLLq8MyH88ydyjEMDgNHrusCNdHzKIWKdwMhACFWTYoF4n9CGuJ3hXqDhtH0Rr3YEu5PVJ8xF/eoh6fYZoKd7ISv4n9QO4mnFbQWoQ+JlI8ophmltGDNeK2PidYqale0ZBKmSv6EoDrSWaNRG6npAPBnOsFIVWpzQJ7sSF3I+HlATXLPAnxXrJmi/g7mdmYOM8AjNevRbTIGtPoOX78HFtXVA82s+wLig+UNstc1vx7hW7EttU8a1C+VSNf5nPydS8poyeOEVj8fkGCmhPmXEhTYPn+BcXKnF0VWjnnPqBSJs6fq9KK8dNL0uR5qB5hjaFsF5QCoRvJSmFR5EWD6sR8uRgtCYSej7fRcvzMHFDPAAKsJEMildNYZ2UOx8d7A1syqJTE96Uwe1DNv38u5CDdHFvLtZ67Sa5TwNW1gEycFdlRUai2Rk1BQAzaULwHLWhxXTv8rkMtGzGnbhwqJEzK2NMV2hjCi1uhOyrQ1ohHDEDKYmrpzD0l8q6DWaxGW4d1gpQvKRO7kaIVKmXGKdBuTukPPdVSAtk4RVxtGbuRlDJuWdM9v2W1XKCdZuhGke4CzlrsoqJqa1ZPzgjjl3L9a31vyvtNIoa37wGv9grYpmL7ozNuP30hcrICrrKUMVLV0ika9j3GOfFQUnDcdTQL6f5aJ/Iq6copun1H3Yg3jUH2j13WgKI6WxNe7uUazAXtRLIYdSFqkX/lEIk+k+YO9+SDdO6SyI2Pe8+ij9RtTVs5clPTbBZsT07R04hu6ns6HUqxeXKKvjyg24r1+yfolBkPPcM4kY1Q2FQuRAVOaW5/+4LGWaoHG443B6aYgEJSMI3ig9Z3g2DkjWK9WRGGiZO25vyjNSZE3OkKu2woUyAeeuLLndgWIHh6KOjtEvf4RJ4LT29It0dKSgw+cOh6Qsn3dgp39yqjNAlJ3nPOGGMYRy9yuhmtb7R4keUZLKRCBh/pu45SbRg1JK3wpVAvW0KIxCzyzTLPsxnEsFUpSWZUlq6Nz5G6dpiSGQ+BRVPTLlusKYzTNHcvZ0m40VTLmjRFbm/2hO2KetNy/v1HNJuWEjPdvsdpLQXELF5Vr7bm63Hau/To3Xq37tYf0Lz1zQvr9xPT/Z6Zzd8nAXp7SWzAf/SehVIUpdi1l6TacbW7QT8vLNqaKYj/QSlgEZxoN4w8+O4pj78/QfmY8TDx2/F71Kuam2oLjQShow9QWY79yHYJKQbMynA9JPa54sHCchsnJh9o25qnXcvtuGHz3hnV4w/YHY4cbo/4TcXoHOl8Qa1bTl9ofBZt/XK9xJyKJGF/faSbIrvFgsEpQh8IUSqMzk9sn/+cD3VhFRucAbusmXLhf/Qy35Giort8FSDdncFlBU8qS/aRJhV+fFKRc+HxqvDA7Yn9KLNSZ0uU0Vx2mb/+TLpTx+AZ4mthQvnq6ZMCvoPK8dH5Bhcj/voogaAzmAnsHCgrI0FzuD1CmoOjxqFi4KIacNuWqe95cbD4wcvAu9GYEEUmtGooPhCHUarZg4dlQ5xnjnSRSrE+WXGTCs/7CC8EjYwSTfyjlWN7tia9uBHK1hgwi5ofbyN/dCododuxZkr2/iCWmEjHkYURvLVyIsFLt0Lns0uRPbi2liHjukLnxMXKo1QhBrj2C0rMTAU+DppMhQ0TH355TfvBBaqW4MKdLPG3vRi9DtNsKApUltwnGD2mrSXAHMTAsOSCNVpQt/M5yaMXMmAuYhQ7S190SJQkCau+Cw4LlNuO0I2YRycs/vh9/LMb8uDRiKYfBbZt2OVPib0APooVuWNRSmSAY2Aab8hTIAfxV4rdSB49bv7dlLUch8jT4CgKJjSpn0jdyEVd8ZMHC9CKZwf/tV2j1xOmf/4YzlogJkLveFHWRCBmwZG/sUdfWzFnfnHZY7XCac0PLtaUFzumkPg0aUqXaIYDavwZufc407KtP0BZy7Jz/HB4RDuj6V90v0TVa5bbRzTphNRPqCBkQDVHakbJDIuZuz/JBzb7wAerhvD5Lc2MNi8py7wLkKt50Pvu3wpkDSYrLlY/xBdJMpQ12JNTKnvC+PF/lm6rg8N6Hquak1sNFGco/YRpa+LdTJiWxEQZLcnZ3ClNqWCdxTaVSGbHieqjR2itmT7+kvDFFfX3HtM+OiUO0kkTgATS0S4iZc2jdJdzQTpgMiQHqcDCYhY1+dBhfSA3NakYnNaMoxjThpJpG7nGx2HCGE2aAtU8m9b3A+1miWochULqPabKdE9vBF/92Uua81fKh7c5XL/X42huGF/88CUfXExMO4//j4YXXwSMUoSUcXXANBWLvceaSF0ZFsuKlAJjNwp9zHuRsSKdgRgiOSaqpsKYWY46fyDdVtSPTvHPrlGLhugT4cLwvPZcXe3YEXmv0lgUaVDk4yuYQE5ZYDOLhnG7JimFqiyVsbIPSqE+WaKUxv31U862iuZixdnDnuoikHPg9qpg95FVgZfbmmPOlDTTIJXspXHwmJjJLw/oE5HAkQppitSbFqM1/c1R9qhbM9w8wpTC5gfnbMIV/dNrqpMl/uYohaCDZ3s7oXJhrBXjgwXVgxNUbSk+Mn72ktBPmFRI1rILkXHyLDYL9ld7rHMorcQMe7aviCFiZ4Pzu3uHsQZrDMFHfM7c+pqFtjw9QNX+gLJR9MfEmCzKKpLKBC9dc2ctIUWapqHrepbLBSSZ7SpGlAl15bCLith5TM5UWlM5Q3uYeFQEyHCjYVhomkWDvjzw3naFWTd8qHtOrn+J7Sxj6XjpRhTwL/SGNRlDxWdXRz71iVxgivmbdu28v+8kx++SpXfrn976R6LP/Z1ci353l+jb/u3v8INKgZ8F/+pbxt8AYIrle/k7ZNfix4DzgVVbM44TPiQefO8xj/5oi4p/Tk4R7AlX6V9QbqBrLX13IE2R1cWW416M8aLLqCcK7TJdp/jsoBgbw+5YpIpPYd9c8Cwt2bJlVW2I3625+tVIqCxaKw5+pDnfsHmw5Tgb7vlpwmTL+mxDu12Sc2F/2zHtJ3ICs7b03cQqK75fvmSTPE1c0H54gbKGMST+fZgIaa4QjV89xA+WjvcuKkxlWYbEd1VEOcU29mzDgFk5oVC5EVD88hL+zW/nb1YBxes+QF9zEgCU+Ow8WDlWmxalFNP1gYIhhEQKA2qc0JUjTwGzbCRoAlRboXzhwSZi1Y6hUlyyQRlDfbHG7wdSzGgnKGuzaoTmFgWZW1LG1A57vkJbc//Rbq9GfnE5vP0xcWbJ+VmD0mekmyMlROIh8/3NgbMNmFXDZ92K/SiV9hIS/nZAbxzKSXCq55kKM0eQcQz4bsTf9LjGyb/FiY3ZUW9qxlC4vEmotmHKil9eDeQM523Nd9ea6dmNyEfaCuUM9YM15WxFfLknvNxhnIN59ql0k8wuLSp0nk1oSxHynhEjXaUlCFZKiZY+JFQIIt1xdlaozhanWqNToigZIi+fvSTdHGg+eoiqK+k8XB/Q6wUlZ7pNTx49ZQqUmAmHgWnfUY7QbBZCDNRCXYpzQJ/6kfC5x910jPuOZtXSna7QyxptDWEa0FpzUjwPz9eoyjDFzFUf78/b20sB/+whfP+kkBN8vF9yGWrCGIglUe6kXl+zYoZfX40UYOU03ztrcBcbBp/41Sd7IVc6zXubK0I4sMgbVnyASpl1rvlp+RAzGW6Hz3g+/gozamL/Q9rNn0nQOXfitJGZraIVKkSStRhkluu8XlLddExfdNSPzKuxqbvfzwj9roR0jy5Xs+Rm03xHPIgArMVsznBVQ9SfUDpPtInjSgokJSfZH1qkbbpxpN6j1EwCrBvUKFI4t2qkYDGb18bdUeY5Ji8Y7sqimwqzWZJuj/iPn8nXUGLgPJtokjJ58kK7Q0hyZRILhKSk44zRxMMokr71gny1Qw0TNA5bIM0D8XEMDCFBUeJDdOylYx0Tm0cnTLteunwPtwxXBzSK1XaFqSxmUWHaimn32asb2N83NlRw9tEV7/3wKJj/6X3eXzf0z2+5fnpF2A1sTzc8tjU5J+psyG1NNybxVJuTxHbRYIyhO/YYY4gxEqZAs7K4RfNaB0thT5f4l7cUHzApMx73+PPAoUDsAye5sDIWf8yUgxYK6RiJOdHWNTerluerap4rVDBO1KpQPWpIu5fkmHGfX2OfGcqvIDz6mOY9sRO4mH7A6gipcbycgsweDhOR2Ww4RHLORAW+H1GnNTFIwD8NE3HwGGepaosuFjTY/H1WZxvcQsP+Wu7pNx1h16NSprod2O4LKhbKqSFuFuTRky930pX2EZMLqYiEdLNsiVoTxsAbdgNacPN1Uwv+f74WS5opqrMEvJRCpQ1HVrzwUrwobkmKiagiZQnNQiTzhkL2CW2kaBpimNUekRgzKUXWqyU+RpIqNMbQbpacbTRnjcxVlZd7Fr7QthV/UyJ9gcP1ge9m2F4eCENgVT7G3X7O8mzFNNRcx4gGniwWfGAsmcBf9D3PU7qXCMMdnuZd4vNuvVuvrz9QUvQNmck36Q3e+GL56pe+6aV/8DVLpKxm88E5NRXr907ZP72mHz22rfnoJ49YXWxQukcpCyEwXu+4/vxv5WHycEP4zhnH6wOqsqwvtrCDxdJitMc6hw5SOffDhNGKWIpQmEKWm24Rw0NTW9rTlXQ2FByOg1TMKstyuxAvjW4iK8XLpy9ZbZfUi4bldolrK463R9GBpwyhUM/zEtXDrVTk3vi9C6+4xq99tUiXo8Qs5DIzO4xrjW0a3LJIB2EeoL7/dv1mXembrGS++kWRi5l1S1M7UjfKGMgUUasWu5Z5Kox6Yx+4tcM1I2WupIr3EYTek6OgTKvt8h7P/e2b6FVV+Os+ZskFf7XHLBvsgy3xtiN3A/hI7iP50OO9Zrotr4KoeSYmH0diQSQ9WosMo4iMol425BixdYXvJ8o8axCPI7gGs2yIQyAz0wqRg1qdr4l7g785YssK28pMjDYa93CLPVnhX+5IxxGlCqxqSoY0eIFJaIV2ImsqFPEnspZSiSyJlMQ7Jou0gxk4cRcsGBSpqtCTR5dC1pp8nOj/+jNK7Wgen1B/cCFI8buNsF3cb4w2icN8f3kLOWOXNdX5So7XrHVPYZ5BGQMUkSGWZzfYzRK7rGU2pjWCOR48zrZvntFv2n/MHjCvzXeZ2n3r9ng7Li7z9ymrUfnV3lHO4E5r2Xv5hMrXAgeZk86iNcZZVC+SP91PZD2gs8zvpFIkmWGmvjm57nKSZMaerwm//LUkpkWmBbWWa7AsaqlMe0ns9N2uVsh5nOd57kxeVWWxVUX8mpZ+CgmcEcRwypjNgnh1nANFTUHeSzpU4rtSKNjKibTnMBAoKFXwz29kPnPV0J6vmT67FIlsZSmDl0QImQ/EGuiHefA9CaHP2Xuprvw6gtpvtguKkdkru6jE5HUQCWgMAVMZci4M04SqDLGXAst00wlZkULsJ+loWc1021FCQLc16+88eHUw/qHPnvnWc7/XGsfqowc0FxvGfY91BruoiYPn5uMvMevC+v0N/a5nGiaq2Xx1GieZt7wDUFBIKZGngG5eSZx17bCna9Jh9vVJCQ0sVi3H4AUcRBSwTISoIkMI1MaSUuLoA8E1GBQWTVUJ9fT49OdMn3/O9mSDco8YUqbWiu5yjzVaDKU7z/KDJ4z9SBgHkipUs1QzlIwrs1G0j3gRQOMHL9511rDZrBj7kSkkVitBpi9cxcmHD1Bc468PqCEISp0iM5HW4B4syUPAnFrMdkm8Orzy+2prKVJaR9GCNNfOkEOmqRzGWsZplsihKKqIn9AdiXM+f6UUoo8sjQVryR5CiCRtMMwdzpSpmoppCjjrCCHQzMXV1aKl66QABlKYa5tGZHF36YlW+DEQkmI4jsSbA+16QYqJvhvR25p22VBSolKQg8fVDn89cbqsWZyvhCT5LXvx9ylXv+sQvVv/lNcfICn6h2jbvhqM/kOXeHmor7znnW74jTW/JpfEZfMCowxOKf7oX9eoaNDOUfSaUhRB1XwcPuT53/wWsgyx6k1Fc7oU/5m2pvOB6+fX1HXF/hCxmy14OOiCrT3DOFG3NSVGjBOogF3UdLuO5tmOVUicrBo+jYF+3WAay/EwCHJ0nrtRFPqbI99fLXG3I+H5kcOjNc1mgdOwfPqXVGVg4Qt1o6jXC0rt+NnzXhzBTeG//V6ZsZ+al8PijUOSQ6IqacZ/imTjbg6hGxRP9wvpDhSD7Sxm2bCo4F88eeuglsLn+4mXc+X+bafTu9Nz3g48WcmDoeTMNN1i1gvybk2JmtjBX4SB8a3zt3DwvR9YTEk01vEoVbBoOGL4/zgjgevN9NUT/kYQ+OZ77savSq8KyOxT9MTBYxc12UsVdKc3DL3MVnRdQLdLocelRO4m0q7DNDXOKPIwibFsLqi2ghlYUK9aClCfrcDAF7uErS2p17Ok0OBK4KcnFapybJrCk2VHcQGvKr58NhBe3GKX0g3TlUNVhvrJGSUmpqdXlG5CNY60EiiFGgPFB/Smvf+zzMcZMSBMCmMNZZhEo29F1lUQOVNJCe1nvyI1jwUZGRqOo8d/dkV4saP64ILq0YkAE3jt0GuF2y7YbheQC9PL3SzDEmBGuiPfhQRGYc5W5F1PCYlw6Fk1D1jWj4hjYNIdw7QDrXhvYVlVy6+9xu/WLy4HfjEZVFOxDxMxB0qBMeY3tob6hrdQgE+Fv3reCwgk5vuuojOJ9888agNh7Hn2+W9IxwONWbNqPiQraOszLjY/pfhAU9azUakTSiKFYjT7/inDtENpJTh+H6genWCnDY+qP4aTQlWWZK0wCm71lwyjGByfnf4I7SWJTjO1LZH5xfILvMuYkLjYJdYcKF3Fz8eemCKuaD7ACXhjRlmbtib5ACFJN9G8RrEsMuuVpkA2BhUFvmBO1/h9LwmVNdj1Qro8MZG7EXex4fRMs94a/NMrXn4Jx1ioTlf4qwNm3cq8hdE4a6RL1FayF1KWDsaY8YcB1VSoQw8hUp/W6K5nGifqZUPKhaqypJgYu4Fqs2T0Mq+ksmDXs4KYE3ZR40OkXhfa02dMu0+xy3/4o7EU+Hf/ruNXv5J5kJvPfkEYX4FqMKCL5gfVH9G2a+yyYph2HH62IxpQ54aU032hK6V0H7C62lEYOI0vWC0vuBnhz7+Q+v/aNTypZ+mW7ykvfkMq0B4zeXEiaP2lwX6kmUZPv7RcmQWNhmFTwxhYrJeSyJWCbhyf9lv08k9Z1QvqvqE1Fh8iLzff55PjhFOaD3TN/pNLqtMl5Mxi2dAfB1QpmFpoh580ikYbjjmSQ6StK/r5uZhzpmkqfIzEGNkaz08eDVR+oBoPhOe34AN60aDmGaJwUnN471zmS8mkXY+/2uMuNpKcT4FF8x6uvsA4w/UwQo5UzpKVoLENEH0g5oytHJCkG3mHvUcknkd7yospYZKhnyKLZct+d0R7RdawXS3p+gFjDX7ymGb2nTKKoR+lwBELZk5Ocp7nIY2mMlZmkmPiizFwrKDeLGmOIw+aCl1llp1n0TjBytvC023N6ZMzzK8+4WRVSdd/kKSoAP/Be36lIwXYlztJ3Nfd1f7LWONy4P/xf/o//8/38/7twJLF737hu/W/qPWPaN7KP/5195Xg9q2I+/dcqWQ+230CpVAbxZ88PKOqFSU3DOMThque69sjv1w4wur75Bnj2h17tsNAf3VDW1dYowlGbrTHLtBnPWNJBWs79JMYwSnpToXe45xlCgHbe9adp9yO6KXQcOzFGltZur0QetpVS5hlV+HzHSvn2G4X7EPk9uUtOgW+P33OZjziGkezWlFfbJmA396MTLFw1sL/4Y+h0tAdAh9rI1haIPSj+DrUjUgFYn7lu1Qy3jVcDoKR1kqRDwm1j1Srlh+c3cnQXh38g0+vkqK3TlVBgulN5TlrZjS1U5QnBuUyw/NEGsGXwmf9yK68cqMpwKZGXOsbh/KGE1VBUoQh8XE/8e2g7L/DKtJZUK3GrFtJEtYtZQz0OAajSdMENVKZ7UYZOG8r8iBdK6Yss1FKobcteRISHDGRZqkUPpC05tauKPuE0gpzUssMx77jOwuHNrDeGC6WPSwLx2C4udhSTgQ3ngZPHoP4KWmNdpbmwwekfU8+jhQf772YymzcqI1IlZRVmCJzG6Zy0h1qKkmAY8SgZCZIiZSrVBa6kZgyKhdyEUKWdZYYInooDL95hv/sJeZ0hT1fYzet4Lvvyq8UMIr60YnIOmKSruC8so+EmyPKF9RcTUeB0iuW9n3S5Jkuf8mkd+iHW04ax0klwcxddxP9qvJZgP/+44kXR4fSAG8nzW91hHj7ViJ/i7nw8c2sO70LNpTC6sLFWmaqDl3m+Skcdy+Y/MC2/Uh8gkzNWf0dVKtROeMnT1UKRSvMPGjvy57r4bfSgVEKyLjccf6Z4rT9SGQ9uYA15BA48JKb2y9QxrCe3sf5VqSQep7XUZlPFi/pKo+LGX0zUrBMg+I/hRGfCiuleVKKEAsHQfAXqwFLGiaoZghDYYYfZNzZmnSUjimItI5SqDYLIRiWQhom9GZBiZpy6MkxUa8SZ3VFsEdui6FkQwlifhkOo3SFSiYRCDFjrUMZR57pLUpr0nHCtE66i4eOcp4wRgt5EUUpmWkKLFYLopdhd3IhHEe2F1uGXUcyGr2oiMeRpq1RDOjqKdpkTL15ayP8fjq6txtvv/zlJPusAHRfebFRho8238EmjbGW+FkkXCV8ClRrg7Lz76OgamrCFMTnroBKnm1z5KRe0HnNb65lOz5eOZ6gRPNZMjz/hPV3HhFGxR4pxKgp0qhCjoo4WHaq4TB3JZfW4n0g50zlHGkKvCgnlMU5rat4Xx0xY0TpwqV7SG81OhUu+kz2nn7XwcZSKLjKMkXpYMZS6FcCCyrFUHlPW1WsVguO3cAQE5W1GK1wWvHwgy0f2V/AUBi+vJb7SiV+YtX5hnhzhI/OOTiYbvYoIO577MkSu1kw7EdSzGw2D1htfkDtLM+6z7nVgvkfponRB6HDzdI4ub1ZKiCVGRBRWcYp8kWniLm677AP/YS2hhgitXXsj71AaWLGOYvVGo8Q4sigjRi7hingKkcMkaLEDiJRcEqTS+SoCtOyom4d58PERYHFZsl39Ypu3wOJ4XzB8GiN2rZU0zl69+UbW6sAv4qvnr1KvXbP5fW5oTfvbW+/h3oHYni3/omtf9yk6BuXeu2/f8dO0zdK8tS9ZKZQvqYF/Dt+1hylv05mSqPn+V/+FuNqlDOkmCmVZehHUkxkq9n3I0EVovdszjYcd0cC0K5aufFoxWqzou8HqBwhCtln6iZsZbEoVNOSj56SkYq8gvXZmjhFSuMwc8VqHCeMs5w9PmM5XtO/PDBOgXhWkw3YmGi1YfFwi7GG5tGJSMeSDFbey4lKEbrTPhCOg8y8OKGiFa0kwB69EH0aR1JQeo9ZtxhnRcYBFB/JUySk/t7vx7SVgBC0fvP4qm+7/cqxVkZjF4K7lg6V/trvUXfnq2SUsfLabz+7/4Alv1cBUjeS76RxtQM7+xc1AgAw84C5coa7/VZCouRMiZnUjaTeS4fFGjGW7IXoVFLCNEZkGIgpZ9gd0VqQrsNOpDYLYyjLCDlRtFT2ldFCY6KQBy8zRZsluqmker9uMdslNkTC5Z6UEsQsqsLGoZ2m+CydokqkZLkbZ8JZEl8jCjlLkG5jkpmFRshkJJkDynPSpKyVoeUsnycN14Sn1wLOqKR7YM83M3nPyF5RELtJKspRugJm2VI/2FJCov/0hVDxlg26nyhhuPdXCrcHOQ6bFltZdIE4+82Y1lGtF/fzVUqpWUby1n66P9vf9vVvp9zNP0CS31pMX+uTJStzhg4iRcu5kDQw6/6dNWI0mRWurtBJkNnqLiFKGX2yIFztKW6ea7Aa5cVgU9/5PllDSeLPZUq5J2vpWQKkUppnOsBu2hmSUO7TU5CkRs/3CtNUYqRrtUixUpaOoVbiHZYF5V58RMdEsbJ3S0xU751TYmb48hr2RyYfJOErUD05ozoZKHk28y2Z6nRF8oEcJUgUolwiDz3WWcpuB5sLlLFCv1MKJpEYu7uKfi7UbS3zNlGKJWmKDPuOkgVuUgzYjSMqMNsFJcnsVLVpIUnl/ubpFWcfXLwpvVRv7YZvlYV/w5PmW7bN+PJAfy0ZjZ9n/xZVy1gOKG1o6pqcC9M0YZ2R5Gn0TDHiCUxXB6i2b/wwZcXsWjkZ/K+3SxptsIMFJajpNAWs0qKImLL4BCXY+UizXWKMkPf6lweMs3TDNBdA5HLKKEJKZIN03ZJ4+kw+koOmnwaUgmpRUXKhdo4pRVxTSYHAGqaY8AeRNOaS8RSWzrF9ckZ7DuWmEPYd4TCgU0a3RiTJOWPWLXnXM73cEV2FGkaUUdjTFf76SLrdoZYLlj98gjtUHC53GCfWA1kV8p1hsRJ/P2M0ldJ4ElMS/EwphaEXXyxjNCkU2rZh9BNpBl7UtZME0lpAZo4yEGNisVwwpSAy26JIMQk9sAiCO6mCM4acMqEkUkhi1hoCfT9yYTQKQ3u24sXfPiP4wGLZcPbhOfpU5MnavC2Nf2vrfWUzv9qd37SVX6VC7xKid+uf1vr/UVJ0d8n9ocLYV7jUggyRv30tq/vXffVnKm3ZfPfP0K7GAL/0nsOX18SDp1QGt6kZKOSFI4Uo7vZKPDGUiTw2PUYpKj9S20BTV+A0t3lB53uUUSzXC/blKP4jep6DOHGUBHkMHJY1/RgplWFaVPS3R7Zna6JP6NqSfSLuB3CGkBVPT2pKragby4PdX7PUkcW65k9/7HBxoKjMjYFUFM5o/sWTFakUKlV4ehUgGmIfiWPArUW/zSDBu2krMYkrEHc92hrcqib2njKrwU1dQUiYVS0u6t0k8pZeoAHKGp6owvZcPDS+MuAxK9mmDF8cCinUlD7BoVBSIdmCqqA4w0+2K+7xGPPbmBB4fnBUuYIIcSuJyJQ1//Jk9Yo++rX39Lf23jc+GQph17MaJ3Rb3xs9llSgCAXKbheYRf2V780poVLiwuxxlXTdXpgNUx8FZ71oICXScSB2ghUvIZGmIDMuuaArR+omdONoF7V0p3aBT40kXyFADhMYg15UKBS6qdF1RepGwl4kXne/36YNbL+vUWbD1fPI7fNZz64qku+gmwTKMM88YTTayiyU9YGkCsoZvFWCf/dBZo5Q98mQzCPN9FerQWmRvCCzWbnzhD7gv7yhKNDzHFXRmuTFY+pOKuTWS+xmidLIUH8rSZSvei6nXwo+PlmeLP8MXTTH2xcc9I561YhHSkg0viKkglk1Mj+Si1zDdx2rb3nmf32NtLy5X77hNlbbxHcfB+JKM15dcfni50ze05Q1m+oDqfyvpKNDiHSHL3jx8jnKaqbp9t5r53TzXdrFI2Ci1ScUFGmKaApomcMpiOmkVlo6PUU+54vpV+ThQDQQtyNZg0NhtyKNckbJfSEX7DxLkQ6DYNw3LflmhiaEiKkcymjp4kTpTOZupIyephhWN0K287YlnqzAIkbKVUXqJ4L2tO8/IF0fuewSN2GixJbJGPSywYyeqR8lp9QyuM8woLIj+Qk9dKjlRoJLI55mJWfxgcmRD6//iinBdYarR/+Cw2GkaipSyWwenOIaR399YBylS0AQCah1huQ9ldW0j9b4Y83qwZbh+nf0ml8TJbx++r+1rj6fF6UVZz85p1pYhhdHfvHLa0yzwW2WTPtOkgtdSNMCaypyEnmXMS1GZU6GG2pnodQ8G7bsnlt2pw331BwF9mRF3nVgNTkBpbCsIg9ffkE3Bc4/+A79Ysn17Z5TG1g34iUUxyDgiqbnUBYcxyhSVmfIXnHoBvKJ/B65JEJShNhQNRUfu0RoFcZYmlXLNE7EGKW4h0izfZF5z+k40iwbhuMgl2Eu1M6yrRM/NJ9wuhrQz/eE3a3Mn6UsmPfKgipkMqZxhC+uISaMHygl4z54iDIyb0mWa+QXw8Tl9Y5uGGk6hc5aUNinIhNOMd2bfofZ487WFXEKpJyxs2z9SdXLLF8+opaGZtGQyXyy07i6RkXJFsdB7qt149gfjrja4SpLTIlKz10+FOPk0U7fm9yqIkXJEMQnqV22TLsDVAZbW37wRJE+/5xKV/zi+TW3l7Lz/t3xmr+e5Nxf5lf79uvGCN74t9+9vd+td+uf3PoDCKf5e15Bf8+E6HUN1dtfvm9AvfmB7uaJ3vhqufs/qTS2D76DcS3Xv3nGi2cj2pxR6sJkxY9IGUVjDH70NKuWMkykEKg0nDk/e/x0WAp60oSU2R0jKSX648BqvcQoTX3SMo2BpqmIPuFjYuEcY6Mw722pKkfpJ5wz9P3EYtFw2B1xbUUZC7ZASYV9ZTBVQ9Lw4+6aiyU02wWntqOqIhnDrc+UWDBW88FKbvrT1YGrY8GuW7CFaiumgKEf0c7ianeP2iUV1OEo3aP2AkZPdFYCo1TuvSqUUvcPFYUi9ZI4rZRilRJuvUAvagms7hzrEbnC1Gd6HylRoZRFzw/AmCY4duAMD1atdBXuPG1KoeDoleL2xYBdVKhGiXdMN/JBW8trsrQOlVFg1CtpVoE0TCINdE4IdPpVlFNCIo+eeBiI0ygEOa0wRoJ3QoIpUowmKoSapPW9fK7kfB/wV+1LFkvB5j67zcQgw8Z2Hpp2pyvsXUclRLKPqJjRVqNXLawUsRtRpYhUIxYuXyRsYwkhoaqIIuKsmX195PiaZYMOEozoWR65XPScLXpKSvSrhn3fCo64rcgvblFzl0AjprM6ZdHUtxVq1aB2PYRE1Th0bSmLinIcYcYrF2O4oxvpe3PeNF9qsjcMkJVgaIkJkM5sHkehzmVmVLNB+US+6SDNNK65izsag1rUpNrxcPMjNvE9iIm+v8HaRH/biYSusqjKMu16qpwxa9F/i5eJ+l050dev1+WfX/fPpYiEsbKcNBka2K8c14tCOWbS5YTVVvZc7chGo3aJUQ3s+09RixpOFuRjhUsFpzZs8yOKnQ1TcxZMthKfq1IypjZCiUuZMgWohKjV+xf4eEtShqyXQogzBruS42A1fLitZ2NlkcT640BKmWbZ4K8O2DBLGhtH7iawFdnP1MIZHmH7zHIo6AyHlx3hO6coa6gfnrwySVWQDgNp17GbLRFMtSDnKDCGgpDy5i4Y2kHdUrKfgRs9eiHM8FLknpZTII8JU1dcqCvCMGCL49J7tDNUbc3YT4z9yHjoyTlTLxoqrYlJCl4xF5HuGkf37IbT725w6wXD9eGby3Z/74jxrrCjWL23xNRw88WXHBeaRVsRcmRaWIFwTAkzWPRU8DFx7CfqZc1qW/G4qamMxqia7rZiCprj0kF5hRI1TSXy1/0R6lpw+zGzGW9YK013/ZJ+aVluV6jjwNKM+BxwK0NzXtPve/Zekc1Srl0neywahVpkxtDjFjWud/RTJpbMFzlQb2oosKJgnaFeN4R+whnD7e6IKuCNp21rxsGTUqK2ApMwwMXjNT9wn2HGL/A3O/SiYXj6UopEy4rmvXO6bqQ62xKu5TrPOkPKuPfOsScrxk8v0UoTmgY1TPzml5/zSfMhRWseXnrOciH0nnrtMLXMzeYZ5FG0dF3vTLxtVrjKEnzkrEkolUklo0xiUVvcYsnzYPFjJIeEKYa6rYTeqbX4cBlNKQWnLa42+JjIPs1zYUU6TTGRg3SR0tx5bxc1rhkFyFRgXXlOHwTQkV/cXNPNRtT93c6ag6BXIdJd3PN1qhn+sHXpd+vd+i9k/YE6Rd8kQPk7rt8hS/j7vqd4YXxNZ+C1n1VS5vqTLzk+uyFXjqP3EhyqQlUKlbKkKdAuGo63R9EDlzIPYopJX+wGIUVpzZTEkdo5Q4iR46GTzxIzrnbkmMk+sjxfM+57nLPEKDSh5XZBCInjvuN46JgmocxUJ0v6XYfNhbZyVIuadmHZvv8+rZvQquBWE1ZHwiAB9ngzyFB0TGL0aDRmOXc2UhF/EB8xWShceiHIY5wlHkeSFw8YVWSGwVojwa+RoNYfB4y1MmfgIzBL6GaaVhqEHJYHT1CK7IPQzpQi+SCfrbLiyt4KrSv5cC+j0QXC8xtCZSnGiFms0bizNZmCqSzptiMcRozVaGsJgxcZWkhCU8uFFCPVhcwJ5DFQRi/mplqjajvn0ZI4pcmjrSF3I8Za7MlK5nBSJg8SpOGMzFb5gN6uyKMX/50kVLB789L1AlMlCR5Zovt5Nsoo0nEk7QfcxRq9atCA8ZG470Um1U8oJ8agfteLCeZs4hlHjwbCfsIuGvpPX2AqS/P47D75U3emg/d8cSRJtBa9qKke1Exf3tBfHzCbBeW2w7S1+NKAnPdUSMdR5GC1E8lTP4kxrrUYp8mzQW/Js0t6ZcW4NCRUyRI8z3I6MRPN8l+tZd+AVP7nxElZK6hmrV89t+Wgim9NgXR7xFQO20JlZQYvhMAYRqrVAlVLAl6UIo4TqrYwexspa75RK/96nPAVBdVrf3nT/PDNNVOwJSnPGXDoylKdWtrmBH3lxBOmFPLkST4QfaCUjOpGfIhYY8Q0tZLE9L6wYzRazZ4qqogcL2ZSiOgpQS1SOa0KFJHroRTKWbQBsxHwwb1/DGWe4ZF5ijh4zKqhzJAGShFvI6XuJcaEiD1bk2+7+72sW0c+juRxIt4eqR5sKUbjzjf4p1eo2pF8IFiL0wr7YIN/dgMKGXoPs4RwUZEIUtSoljBGlFGUaSSPB8zqVD6zUpTgyXWDHr1AaBpHk53sB2NIJeMqSw4RP3hcZUn7gWQMZaa+hdFTbxfUFxvS2AtC/vkNYL/1SfZNj6g39ut8uO53mnqlaKAU8hip65p8tsEfEjYXnFIkZzCnNWmMoixQ0J4uKUYTpgA2M3hPS8JYg960kqTO50t+lELXFcVaog+Eqz3Nhw+pztcMNx1RQZ8T58s13ThRYsJpg7aG1WZJHD25y0zHTmZiaovKhapyoCZCSlRKzR1tS5xl4crKTM0wBqYUqazCNhV5ErPaEAJTP+HWhqauiPPcS2M0J++dUW8V5Sbg9x1mURNvD9ANQtXbLqAU3PmGYd8Tp4A1Gu0L1cMt7mzN+OmlqCpSFqNapTj4iK/ENyiGiDKGxekS7TLZZJxyBB9FLmiE0GiMFppiXcm1Zw3GGJTPhPn+FVNG58zYjQyHCVfLda3QLFcLum6gtpaCQhdF4ywRMQpeVjWJQtf19N2AdRbnHJvtkn6Y8MN0T4p0i0qKiTD/966w+Namm8cH3r413RWl3rxvfcNGfpckvVv/xNc/OCm606uW1/7/H339XX/MGzeH+f+04eT7/xJdtUy3PZc/+4KhD1SLmkxB58Jq1YrWN0TqTc3x9ohSsG4MJ9WB22OHy4h/kI+C+pxf37aenzyRJGbIFbdTwzQGbG1xzhJKklmRfc9i3WJ/+5L2OOEWNbdjoGxamrZmfXng4XLFsBv54MTQuIrKKA71U8yJRrcVv3l6YPITVoFRC1orwY0/iKRtOPZY53Ba4c5WlJTxuw7tLHkKhNue2iTeywf0qBnrBTfmDLOo0NUJ2moZvraGNAZUSNBYTFtTIVKvnAuqUqjaynxJSBhnMa3csdMYKHNr/24gW8/yBhUz8baXKrCSPRXmJM6sGkpTMR0GYi9zR8tFhX9+OweKCmM0Ip5TYtDqowyHN5VgfqPMDsTro3S3ACYxTsw+ChFuNusjZpFBIIPfyhjS6Mn9iN0u5ZgdB2grsjVkH/GXO4xW1EtJbLJWVKsGvWr5N/s94y5SUHS+SCckJn567qhWLXH0DE+vMZsFtq2gstSPTkijF62/D5TDQLVd0F0d0SXjnBFCudHU7YIyBtyiYXp5S3hxQ/PRY9zpcjZ2nOVeWvHzS/h/dXIxjHHEp0BJhveV4dwp1IMNufciC035/uIxzs6SrSjzYk0l3bCQKFOEIr+zAkl4gkg+hbA3++/czRzNXjkFqcre+fNIXVMhg3XI62b/EJiFrwXUbPzKPEeyu/w1fXNJjpnnJz2XrsItLQ9xLH2RWaP9kYgcr//qw4xtC8pa/p+fFK6Hr0+MvnF9y0xRmTTjb2s0hach8T8FT0mKqBND6CgUHtrEH28DyUemFztSSpQQeVH3PF3VaOAH+T0+rD6EfmLJkjhNKDMbppYCKskxn7u05/UPWW/OUL3nl+sX9NUzyIljU0CvpaOpRaKk21oMIo0FI2hgpTVl7fhkrThcWJbbNY+fD/OxlqJFPg4C77CS4Fa7kdWXIyhFKInLrSK3Fq8yKsR7mrE5WaF2HfkwoOoKfIDtArddkq8PgttuKqoG0vUBFZIklM5QkiXXC748K/iY0W7i8djRuIVIO41FNw6tNH4K5FQw1pFTpl0u2V/u2V5sKbXDj16uL5dJWWroORemfQ/aMCmNrRPD1QFuO+rtxTec5G/eJF+px6vC//YjxePV/I/fXVNaQ86Kn91+yNUXgdyd4w+ZbCyTVnLd9Z5xnLBtDZWhypr3dp4UJlZLxar/WyYiF4sK7TT12ZpjyK+KHyCzoj6gmgo9BaZDx0Ud+fAHmukKLvsD+pg4/upjil4xVltWTc2z0fLLn91iKkefLHUj8rI8elFJLBuRijsphDypBh7aQIqZF3pLfbql33Ucnt5I4SxVaKO42Xc0q4bKVtR1jZ88OQTaVcNJo/jT5inttsP6CFl85OKuI/UjxchMbdiLcXa47cgZtDOSTJyvsCcr6uuKtf0pNIa/GSZ+3SYChZu8wE+B1dmaeNmJUWtKhBBRjRQvnDEYo4VApzUpRqy1uH3DuJ8IsfD8vEFXKw7TIJLiqDGHTA6F09MNU4qkUsgpc9h3c0IsVFVVOaYYOXM1D/eexsJz7xlby2pZy+zWMNH1I+8vF6wD1AGOG8/H02f89vnH1PFIHcVH78VdAequmPd21Ya7hLz8fg2hr9vX7xKkd+uf4PqDdIr+Z02I/q5L8cbD4vV/qE/fQ+mGF3/9K2mVLxuiUSQfMVqzWLeMx4FpTNxc3tIuG1JITMcD3zuJNGslLupFsTkXUpxWGldZul3H1N3w/vmKpzeZfda0TUVMGRMiVWUZx4ApipQy9eDZTgl8z7VTxLXM6pwkhf7ilq3VPLGaD56csnj/jM+HFwzhhhzgPxx69lPCasXttMRHCNcjKSSyUrSrJVlJEOCPIyoX0ugpUyTHTOkGSHtWjZeOiDojqxUlipdEmgJqDnqVMzKQXSAOE2ZGhWub4U77zWyIl5IM5qYkMABn52A6igwtJ9IwoTZLGCeSjyKfA3n4tvV9omnbSnDN3YhKMmReUpY5n1YkG3mcxKPJSDfLVE7oV6XMunR5ENq5m1dSBqvRbS00uHneSzuhYalGhv6Vn4lXNx3mfI1eNmICO3ioHTZl7KqRqvfjE+nUaEUu8PEN3Ax3sXQQ8z+j+emixlbSPcpnK+J+kMq5s+i2Eu+ORpIk3TjC7ZFmURFjxk8R11ao0WOd+KyonGkuTsghErqROEy4ZYPdiIGq0obLDn5+Oe9+lYBEKYVHD09QtztAkeefR87odUva95IoUkgojJIheJVnWZ5WpFKwMc+yQfksDF5mpu4lj3OV0szeVlmqrJlXpojaGLBzd6Lk+4KLQrovavbbyUqhZ0z4NNwwjrd4rdhtWo4PlqAVJ6PmfNWiUbjHYlxcfOT99cSmAb1s+J+s5fqOzvL73Ee+Nl16FXKUpIi3YrZ6TJFf9IGUFMoUQIhudqsZmz3TYUdeJIwz+H3PjfLcnrfUzlKGByy7c7SLKB/EH+qOvKb0fQePmFC1pUkr6qzITeGy/iuu3EGOYasFYrFqKL343OjKYnMl3w/SSawdWSuu+o6h0XBSk744kiePXtRyLguYB0sxSB0nSgm0faJMgXxa07UKtWxIxx7bjdz3R7Sifu+c4bfPUFY6QaGbcIMnF8j9RB4CuXFCPQxROnwZAS5UDd0q0BuN1RUPb2pKVuLH5CpKKpTWYlIWcAKQciIPHmM0Yz+QAbOomPoJlTPWWFRtCUG61uSCPwzYRmHuZJ/f9Di7Uxb8jq1S5v3y4RZ+eDaTzX7gyEtD8IW/+L95Xv62YFYnUGUpLhjQy5p4GHBZgU8cjz3p0PPebWS5qDl3Faq7QpvM8vQBdnMiYJdQXnWKciHeHO47jCWLkbUrnm0b4P2a9Fy6FK4MvKAizTYG3VDYT4ZcjHiI5SJyMaVoFy0xRMIY2LSODCzwWAdmU9ONjuZ8w+2LW9rNAj/JJGjwkc3DLYvVgu72IM+GnLFKsTpZ8/D9lofPfk5dJOCPXiSVqrJUp2uGL19Kd+/Qk4sioogpUVeW+lS6Wt2nl7R8wHbzHiElpkXhpQE/qyzamQS6WDQMNwN2YaVINwPaqtqx3CyZRs9xdwTAKI26yTjvaBYrvkiabiiMg8E4g01i7mrmhCpNYmVhjCHN8nDm56Vb1JQpsrCWi+SZbg80VuFWy/v46e4+568PfOfiDFM7fn39Jc9vn33bVrxf92oY9aofpO4TpK+5d32TBviNjfwt//5uvVv/Ba4/vE/RP0QC94eUzcH9Rf/GJ7yrrMzSnO7ZjQACmhrTOmprGHoPKXO8OTL0I7pxNE1FGLxUIauKdm3w1wGrDUkVbq92nFxsWSxaht3A+mSNGyfG0aNMTVUZTIGmrYk5S+JlpaOyf7nj0fkafbzCtTVGKUqINMsKvRtxqrCqDGcfXrD84EIGz4fXfkX16n+UQjpOUqVdt0Jpiok4BaEzjR5nLfWZSMliN+Gfe6IfCd2IenCGXbek20wcPFpL9cw4g415luIIYU0x47mbijhMop2OMvOg7h/GFrdoCbsjIQRBkh57zKJGNxUpBJyRIDVrdW8Qmn18ZQ6bxcwSo2cilgyr4hO5RPzNAduI/C51I3EcsYgBpJr13OXQi259tYBK3cu1qC3xMKCMxjTS9cIZqEQuaRYyoI8X3488CUlIaY2trEgSlVQD7XYpkrVXmD/Zcl9L3iuzZEmha0f9wOHWLdOLW/K+lyT2KN0ps2goWpNvDtSVg3WLn4J45BwGmAJFK6pli60rDELzi8NEGibxMFq1X/ksd3/X1lC9d8bw+ZUQ5yZJ3spNJ5QuQHcjekYvl1lOVVICV8m5yQFQZAWuromDdBH0LLERNZdI6SRxnc1MZwlXnmV0d90QM8+epbmzpHklsSsgCbeWZEGVgs3cU8gKoErB73rqzYKsIM0VaL8f8KNH3XSU9ACU4e31Wmzx9o3j69ccjIqCRQAsdwB5MTt9Q+GCWTja98/EmFYLKWy9UFzGjpSLSIpSFimh1qS7411AxYjRFTkK9Y9lJdLNUtCq3DfCldJy3Cm4zZLYCc7cLhuhm8wrKzCIvDYejoJsrywM8z6/038ZTZ6NfAsaFecgLgu1LWslHkBNTdz34tG1XcnhqZ0Q6cYgJrxDx/FvnwmoRd+dW00pioxGW8QLSSvxDQ5BfiljhTZZZA9aN5u7Xh9Qm4XMqwyeVCBOAaymqh0pZVKEmIMkPTkTupFqpmmWlPEpoY8D7YWhOVlSwltm1N989r/ymjsF093+SV66zgWF0gZlCuNhpF2fEua9a60hzZTLu/sSubBaLwkho2wvCUlXaGvLuhXJbx4DdvGa95Gau+WNIfeT7Ast9814HOBErit30lIHCdibqCmLmn4KGFOJ4WsxVJVjPI5UjaNylUiQrcEZjbaKGCOHY89Cw2LRMB4GymxIG6eIq2ReU2tFSBHXOurOEPY9beVYnq4xtaMMk9wbciF2I+PTK+zJkrzrmK72It0rs42Fz6iSaYxm+YMncj17eS6FVOiHiSFndjGwDxFbW5TRjP2EtQIsMFrBlMAXWEBVORateB8tKkesnKg/QqQpBqs0Ril0W8HgqVBgNa11UCuK1RwOw73KIaWEMQZrDGGm7oVuxDrL1E9sHp8QtgtUbbipFX0vcJvtxQZjDdVuFGn479h4d5Rcube8/sL5Hvj7BlTvEp936926X3+QTtHbOuq3vvqHXa+9ZSnfjsh9G82tlGb7w3+FbVaoDB/uCtOzjsVlx+cKfIhQCz5UO0uk0G6XWGOYfGDsJyYfKIuaj4clybX44YaLqkMZSxwinT9Stw376z1VW0POnDSJjRvRMbNeggqz5rm3lMEwHidO6y9YPrjCHyf+yFekSzDWsLaG+onFbRf8+XDF8T+LBG0It+QS0Ar+m+8kVpXINdbhBUYlOK35cmyJ1qBt4f3FAVslEoanx5XgxVPBbjTmZEPyNc8erDFtxbSX2SZSxqdMLoUQI6uV+MyUEFGpiKlizjLfYg1JyzFOFNQkD2sZIBX52EShtQbb1OQ5SNZtTfQR6+xcIRYZiLKGPAZJjpQEvNlL8J/8bFCnJaEoRhK1PEW01lSbFWqSIB0346HbhjJM0I2C09Ya01ZgNP5wg9muBC5QGbBWkooUSQO4ZSPzFseB6mwNo5duVBR6HEoAANPNERcidtVKx2mm/oX8un4TrCp8b7WnsUhQPEv60lrzRXtBjoV4HJmu95SrHbqpsJsl5uGpzDsphTUKkzIhJqqTFTpK1y3OWHOtwLQNaQr4qyPltuNhUSyrgm1rSZLmBHRTG4zV2HVDeHpDiRldWS7qH9LWDykx8lz/NUHtUQXUekHcC0ZXx4SKSRIdrbG5SCdQKSH2hQRBfJfuvUC0liRpTqJUkWOQS5k7QDL4rABXOVIuEO+kKQll7SupnjHgHErBj/37VPsnpJzp978h1j3T5MFaqlVD8YmrfsGLj3eoxYqPas93339AMYr/+LSji3OyoF7dvX7vOo1S3OTM/3XoUcBY3g5T5L0uu8D/8MkeCvzorPAvlwN6bWivEvpLKbo8WGpKZUWmmtRM7ssyKzQnflop+d2Bl7f/mWm6Ba35Ce+j2u9JWFQK1bJF3ywINzcoZ3HjB/z3n/45U5iojOafP2zEvHLXix/VoqKi4TE/xmwVvgq86P9KIB4KkS4aw2gULx5r8qSJrZWOyxTmGSOD//ySZtHcQxbssiUGIVoWJFmMSqFDQG8X6GVNuNxTYiYXkfWVDIQJnSLKamDuBhUt4IbKYo2hGE0aPUFr3KpFZQgpUDWCsjbGUGKmWbSo1qKUopqlh9PVgbZy2GWDKnuWq5bF+xecfHLkv2oXUOBXMfCXMfy+O4GzPz2jvRBc8meftPQvW9qLDV/8cklvFbGbOHmx43w60g+elw9X4AwFxeE4knOhLopsNJlCrAyfPVhy/vCEHI782KwxKaAOEw9SoUqRhYb/6qON7LPbA0x3ptly7zQZws2RsNW49YJt7WmeGOISFp/c8Ksvj1TGcFY9YHV2SimeT27BNmsS8iyKMbI7dIQ64yeRsX4+tXBoabLhdj9S5UvsukG7hHMWP/X8WP0tahxY/lbx0enI6sdrcjF89sJSnZxgSqZqK8JxoPvyBluLN1JJ8nyQ50IhhRkX7wz12RqmwLNjzfP2RxAiwVtKycQUeTl5Vusl0+QFVW8NbVPzPHv0kxU6AznhRov2midfepoQefwnHxKeSTfU1TUFRdU6SoGPbid8N+HqChstZkoMMfHbk0ok9/P1qJVQ7YKP2BlABAjFVSku//YZ4+hJD7fkJ2ts42gOI0+eH1lul/h24D9c/hwU9P5Nb6tvbFh/29e/aX1F7/ktr3mXOL1b/0TWHyAp+vp62iz24A96Nb0RW37D+7795bf+Xq0vUGaJTplV71kk6Cbx93EPTti/uKU5WdJdHzDA5EfsdsVqs5TK6G2HW7Rc7gOlwMI0bNpEHwNFydDz2A2kGS0MBZUnGgfWKqbumkfvP6BdtoSPJ6YrT8FiwxFrr6mWinqVMYsa0yiqVT23gTzPPn3Ji+7Nh7PV8GRVeNBm0mEkZY9eOOJ0JHWOOBVspVieBKraMIUkw9AJTOUwxrL8UAJDn2G43gtkIItkzTkrSYqW7goasBUqClghKanyJopIcjIiQ3OW2IuDfPGRkjKVUZTei8RrGDF1hakrGayf/XxSKVitBVGtFLmfSCnjaklgtLNkI1Qf1cz+REoIelorVGUYSpROmSqYwv1sUNGKvO9kTsIaUjeiKyeD54jcz2zWxDkZM00DpRD7CZzFLmrS9UGS5rYihZnCV83SwlyIV0f8ywNKK+onp5w11Z24Wz5ryhiV2baZyko37a6jFrIEnhiN3SykA3dzJB16QpKBZt1UmLbCoIhGo3Y9eZjQ6wV6Ps7xOGCWDSlGilZ0w0SFQk8TJylgtxuUn2g+uHg1SwVUJ0vi5U4IYCja6oQVpxSTucoGXxlJAHNBPTiBQy/ndk6C7rqDeUoYbWSuSymKKuK1ZcRXqZQi57IAIZCMQecsf8+JmAvFClCBmGS2CKHGSTdoltExdxTm4shmcJzaE3JOfBEsxzRhHmxlvmnudkylYrgV0loTJ9pppHqwxaT9/Tl6XbZ3fwuZf8a3FWI88OlrhokgHZiiXiW+Y8wMR9m3H20LJ6eaEiMrXTjfrKlXLVtzAi9lX9//vLnLVtRcDLJGjEtDZoo7+vgSpTQfpR/RDGuRp6ZMdXFBvh4p/hRdNahyxnUXOXhP6wy5SJchvtxTtgJiSDcDK/cEowyD7UT+WBnpoPYeYiYaTWcKaltJ8rpZ4q/35JywiwqMYfryivqDhzJbogUFnjqhdrqmhVBIRWEBd7IiHgZyGEmjFF2ECPYanEDPAaae6YptRQmRPHdrjXNzQhWxVcv6YnOvCLBa0+87tCqokIlToFSG5nxNmALBB1yjOV4dcGdr6inyHSOPx5c5/d4KCAXUJzXtRc3ukxc8/9RxfBlZvq94Vp2yj5Hdb/b8uDjqkqkKPFOFKQSZ2dKakiPDOFEKmNqyOF+TUuZgNdk6NBY1RgHtvEy4IaMazaOVgFCmwZCCQlUCWsnGiOy1ePzzW7TWuGWD0wlONV1c0JG5vt4zmSVa11htOFuvuTGO8TAQmppsNIvVAtt4lPZUy5oqNdwMBWUWVNuKMAYBmvhAfxw4WTtO+2vaMLBYVPzJR1BVtxwve/zphxRuoUjBaXp6BcZgVzUxJpknTRnGIEljguX7pwKVsIa47wnjht32AVMcySeObt+TSiFohR5GrDb4w4CuDMdDh1aGZBV1W2OVkqJhyFQYtpXGqZaLDz+gv9rjFiKTNpXleLnn9DiSMdTaULmKQuJ6DKiYWTcNQ5TnTtM2TDHMcvGCMgqDFqsOn8BoFquW6xlDbxY12/WC9uUVS+fwDFz2L17dfNRbG+x37MC/s+Hq7/PSP7SK5916t/7/dP2Dk6Ly+p++cuH8joTo6x40b3/L11Qq7kOWO333PHCv1NtveJeayd9LKnLTVhNOa5KPHJ5dY50hhMhwc8CuG1RlqJcNi2WDHwPdsYejupfCxBCoGocrsDEKo8TLJ+Usxuc5y407zXpsYNz1uLYilcKLLy55770LdNvQnjvG/UDVLqnaLaapcKvmDUO2+2Ds9UN1F7gpSFNg2h8l8Fi18wxCQR01aJnPiMcRRkWpWrKPaC0PzOQjOQnUIA9CNFO1wxqp5iujxJdn/tk5SucIHwWwoBV2RpiiC1hQ/STYXhRp35NTptosKUZJ8lM5mrqmTF66BTGJ1McZlIYQAilGjNIkq5mimD+WKcjn0YoSEMf2mFCVI+YEY8CXgnUWXeZqOtJd0EYM9Vgt0FYTZ++VohV6WUuHMKZ5oN2TjaaMHtc4coHUTzKj5MVnIx1F8qHnbotyYtZZYqJ0IyrD8MnLuQIten9lNVkr2vOVeMyQUcaQC4RuIrn6nosACKjiwQnBWfpnV9iqgm5EOyOyPqOxJzJDE2+OVBcbcsrEfS/miMbgVg2rszXj1QFlK/I0Ea532LMT+k8vac7XmM1CpG5tTfXohBCvyT7NIAS59goKQoZGujTVUgAYcdeRbg6oWYYkXkVZZG+Vk47dbCBcZhpc0SKpI6f7JAeUkOoKQoFiDsRnI9d7+poS9HkGCSLnWRI5vrJ/dJzlZkox7Xu0URilyTEQL19IInZ7A+cPBBc8y/nIr2Rl3xRXfGNn+mvnFplJdzMvQsk9qMz3roJ0A0ouuKVjVW3QzqBHgQXkWfrEbDKq7rH3ZVZfiuSoKI2eRYZihCswBOssdrtkeLFDaaC1MEPKNErkd1qTfSTcHNFna6HE7Q6kLPNOBfFL0quG3E0i+ZtnFrICW8k8X7g5yDELkawddl3jn99gtyvcdikHQysY5TpiDFhrKauG5vEp+fqAVtI5LDESfUAbg64azHILwxVsW/n8Rs0EQ+T6XzRihusMFJklbB+ckENiGnradUvKmRAj0+2RzdkGjKZetdKNQOAvqmSqkyVuUWPrTCbMe//r15v21Eo6mgrIMF0diUNk/eQcxsJwuWd82vLi+TVWQX+YWJ1swChsLKTKEDSgNItqIdLqXKicZfSBuqlwSUzB41XEpkQ4DKQo3QcQyXG4PUoxwmrBs8ckXZHakscAvmPKheZ7j6XAlAqmrVk8qqmWDZv6Avv4I3zvKXGFHQ35dMnx+oirLFSGtoXGB1I3slyeEJ2ixMh6WZMrC4Nn+eSUpBWVTqz7Lct6TVVpwv4pRRfMaoH2RuSih4Hx80tIRWieFysa15IGT7jay/06FSmSTAIpqd4/Z5oCLGvxn1IKVxmaZQMrGCdPU1X4bkRbAfdYbbCVIxmB8/hxlh23lngMhJg4fnnD6r1Ttt95+Ma5rVcNvpsgF2ztOD695vr5NWa7JPiIKgVnFDGKx5rRckXGmAQGgRbT1sOBkjKubdBW0PIW2L+45bublu2TE273t6/uQb9z3UVD6v5b5Nb1d0iMfs+E/916t/4prD/8TNG3fvUfc3316aWQweSfPPwz0lXkeNNxcxP44ulzTrZrhmwxtaNWr7xZaB3aiGZ4HCa01iw2M0Xu0OOcZtEETt/7DLuo8C8H+v2SjMI6MXeNpVBpjTYKO1fK/eAZB08Td2xMT/XskrCfICpOH6/5NHqeHhX0Aa7D3S/ATx8uebB0APzZo6VIsZQinH2XrGvSYeDj6cin8+9qg8M0NUVFVP0FhJ5SOT4PD9BJEbtMzop46F7NX8zJg3JClMszeUwZTZyiyONyQWslVfyScdbeB20+CvhA3ZHegGItqWRY1OhZ9pSOI6au0SWTlUipjILUj+imliFTH8m5oBPUVUWOiSpC8YGcRWmtUfhuwA8jlIKxlma7Bm2IwaN9oJsmNrXAGtLoyTUy/1NEdqe8+L7kycsDJSXpUtyK6Z/pZCbGzAmq6LvF1FTNXQdSnucENHkKlG5CnHe4R4GXYZJ9aTUlyAzGWAqfuRXaKHwu/Pknt0QlksIx7kHBWmn+93WDRRFcy+V3HuOv9xSfSGMQX5nKQYyopsKerEjjhLYWW1mG44BJI9FoqlWD0YLKDWvpIE1ToNWK6fOXqGVD/egE3dSSIKHwn77kxfHnXPXSSTtrP8JWf0opmcvx5/heABZlkAF+UzSPFn+GUY6kM0/7v0LVSrDSWZI/VyoeL/8ZxlimcODp/i9JKqOtnRMGJQlSynIco8yVpbkzpJECSL6T4GktyZjW4CMvj79h13+OypkxdhSbULrFNjVlSihbYU4voF2TyZRhAHUmEs27e8ZdV++1AOFNycpbN5nytX98Y320TPx3P5Bu0a+v4N98LECPX76EF0egGM5T5P31gFs2xNsO55aClK8tuheS48vhN3TTJSVlHp3+hLacQco8Wf6Y3PyAnDKOVpLEUlCnjQBVYuTp8T+hNxuq4zn/+oOWGB1Jw7MfbvC7Dv+85rs3GTPcMj275d8++gVoTUXh4iCZVD6OktgWxDy2tijnUIjPVkRj2ha6jpgz6y6x+fkV7feq+yJONhsuwzU9gXw4Un/0WM5pzjJ/4mRoPReEMGgMH44bYp8pLwoVc3HDGSogo8hz0p1zoBgBcHQ3+3t7hOgDWUFVV4Aia2jPV6QhsOwDHwwCjFg3FSd6BV8MXF+P/F/6HoBjeSWrfH39c1fxx/Pe/euHf8TnqwcUH7n95TXNpqE7Dvyq1LgLTegn+qu9QFGK4te28Lf7W5brJd/1hXIY6SYvgJW2IpfCr1tFyIWVgv86ZCpjMTFyS6F+cEI5DlwuFNUjkQj7L6+Ik7/3Xgs+gLPSO/CRQ7F8XM7R3mCUwV1sRP6sLKY2mNpx3nsWX/wWUPz4YaA8FLXDFxvD7ZVQ5po+4KzCLmpWh0tilPu7GfNs/Kr40Uc1tkRSyNzcanLS+G7k132Nion2/Q3JQNx1TC92hJlsqLUUDjKzvUEpUFVSkDkODJ9fsvjRB8TbHt9NxDYxlIJRmsPlXsx4Y0Jbw9hHTOMwc+FJO8Vqu2I49kIgTFnMpL3gurM2HF7ssMua9nwt+zWJlNdWjmrVABCnSHuxprrai53G4xXZWZyC791O6OMssa9lnrUeEz+KmXR7BTGJpK7SNJses/41yhnO6iMfXWu2N2fsxuPX7rf7m4z6yh/fvFd9S3bzhnfRO0ncu/VufWX9gXyK/h7rD1ideKN6+5W5Jli7NV9++hQ/BKo/dbSbBX038PJq4r0HJ5jjwHpd4UPAOkdRSrwrmorj5R5/7ElFKt2LVUtdj9i2p31oMUXBUWG1kQFVa/CDGHjaylGy0Gm0M7jK8sNH71FdfwrKs/zgzl8i0z+buBrelN4A+PSqer2pDWkKxH7isBvZTxOjj1yH+UbnJ+pW03aFzWZJ62U+JxXFsYMSRKcNiBljlKCBknFtDVox3vREH7C1E/BASFKZVwpXywMmxYRSYObjbmGe7TCkKcpDLSWMMkQfUMyzIqtWEq85+ClJAuBqUQsyN0QxAbWaYgTXPAwyi1WlRDf2mLpiUTcif9qsGW/3hJzQvSR/wXswltY4mR0yGr1uxRg0RIb9EVVZnBNfE62U6NdHj62dUMoGj9ssxHcpSBerTBI4a2uEcod4v5jGMQ53g+6KnDLKWarzJWHXi/+KM+KzsW5Ih4F4deDF4Fk8OiVWji86zZTKLLML4qtkDBU1ToEqYM5qmvYB2QemF7dQIHejeGpoQ6mjSJ/2g9DEBi/zFoeBOHrMqqUQMViMAp8L066jmul03Zc3NGcrdFOJB9QUGb+8QacCQfHg9Ic0aksxoALkfn8/FH6n+W8X59hSEYtIrFLw0jnTWoh1xtI252jEfNRYi85RBsNnwlrRCj1L9MpMutNAShFcdT84zh1kQWt0nCEYsaNXEshKQUKLvE8vMOuKeHuk1BV2u6JqK/m5lRFJltEQyhuWTm+suwjk9fvW7xlUtI3moxNQGm4GMRMuwHEqHOecuTkR/H+c0ffaGHIq6BDBWpQ1hO5In3coo0gLDZN0oatqg4qJqOdO9Zw0mrM16eoAOdHHHa6ylGhY64RuDalx/Hph2X/Zo5ximSt4uiN6z5WRAH6tLBfOiLRt7qgpa2C7kGp0ZSRZChG3XOCHCeucSLSqmqVqcINIhkTHVrP47mN88fjffE51Il3TPEyULL5eafAzTEUC16ovOFYQ5D2Us+jZ6w0KlTGkpkblTKkqMVa2NVVTE6fAMAMHLLBcSad8enlgfbHl4YcP+ego15yx17jxKSlEQh/4IsbXW/NfiUI3SvGeNpQCv7wJDGNm9fCUse+Yesh2ia8MyhaSE/KfKoVpirBpqZRm7yPv9Yk6w/pkPUNxIt0wMUZNVRS2JM5XK1oUxWgORhP7ETV6wvmaHD3Tx88pRqMriztZgtHi8aOkO6+AiCafnsk81/Oe2q3Qrcgf87FHNQ57mGh6kSi2JyMOKdD5ZkN1UUExUCQxpmQe1ppSMtkDWWEWBqPhobqitoloNMfmhJC0nLOlAF/6lOHYEZ7fSpdF3lD2+b5DlUKOGffwhLib7Rq8p/nuI/IY6J7dULQWf6GFka6x1zM5sFBbi1YCMTBKcXK6pjsO7G4PNEaIpvW6wYZCUzvW2ZJf7mlWrTwLgTAGfvPv/4Y8RBZnS97/yXfkGegMqRTOPnrA098+5/SDCyIQrg+cYNC5kJTQVo2GTVVzegjcXO5ZnW/wk3ggOleoFj0oxYMnhgc5Y/yOKvnfeXspf8D46c03/kd633fr3fpfyPpHTIq+uaL6e19wb2tpf88gpLx2ZSukOp9CxCjFcT/wvX/+fQiJB7+6JF8dOd4c6ewC0ziqtsKXTA6Jcd+LuV9b01pDGIO4TRtD8pmc4ezDR7iDYZgCPkTBRxtDDFGqn0qTYsIYRXuyRGep8rcXW5nTmaVxWt1bsrx5CGbqVBwD/tDTHQaOh4Hd2YZJ15gMWit8iPK5QuDwrKe/dTzubmkbQ1FzxcvPkhilYB4+JWZKLoTBE8ZEmAK2sSQtPiB5TKQIKiXGMInkIES0taRhksqnVmiEYmbaSig/bY0yGhdrqQQn0fGHbkIjSOFSCiXJHAyVlYHru6rvbL63XrSCBAdW6w1OaQ79kbZpRe6yaHHLhuC9zD8tG272ex4+fCjyHK3AR8I4oa2jaWesMIUSssxC5SIP7FIYd0es0lSrVh48URI3UzuKE7reXUBerGYYBnSZJYRaQVWRcyHMRCFVzZS+fsL3k0gb25o8eLovXsJ2Jd4sKJRV3Bk83s3R5JKJuZCzFblQ7ag/fCD7PEbi7ZF4uSdMnnQcsZsFWSmW26XIG2878hhJRQwQ9aalDH6WpGTC4HHrFqsV8fYoXkybJfV7pyhnGJ9eY3wSPx1bBDX7mqRVlfkBrRCZoDGootHWgfegDapy8qKi58DyFY0uK41W6T7IUrmQjfgrhVxojSRQJSVyyVhrBbaQBH+rc76fscFYrNEko4hNJQlCN+K/eClGoicrwagbQ8RjGwdKi4mwktGXPHeiQL9Jn7v7y+tffOt6ffVXOSB3XDs1TKRjxm7a+xep+b3uZoaUNdhlRYyJ6nRF064ZLnekIB0OvajQZoNlonSjGCKXhELJLFt5VRzSBUrtUI0ldj1Jy/3FttJ5lfk66cbkkIi3HZUGZQzTvoPWoTIobSCDrh3x5jhLwwp6u6Ao0HUlHYm5cMC+k26uklNNTExX16QpYB9sMI3MR6raQgjQzF1pH0nHkdA2LJuK6tEJ5cub2Xw5QZEZwqIUZt0ARYwyDwdB8kd5nZ4lS3Vjsauakgo+Z5TSxH5icbpGKRhHTymF7vrA7ranL4bFkzMh6RWFMhZUkuR8BoiUO78sNcsXEfnj/uqITpm9uiF/9IDjF9e0p2u626N0OYs8D1LMqBowGuMEQFMKMIZ7dHjXj2gjyZNbNrQrMdFWSZFTwp0tGKc9jJ5SopwDZ5le7pmMwliFzQmzqEhBurNSnJPELQNpiuTKklJmerHDrltUzsRuQi1q4i4xXQ5kZzDrCLagm4pS8isJaBGyYckz+MJK0Ud0mZqcZvPd1y+HedPrypInTzmO+Oe38s95fm8thabUjeimAiJ2UeOf3UrR5aOH6PWS7uPnmLpmOAxEEsN+pJrnX3MpmNoyeUlom1WN0oapH1k5x1gy3kexx8gFNAIASYnte+dU5yv2L/fYoWJ/ect4c+T0ZEM8TPztX/wND7//mJMnZ7jGYus1TzYN+4dLklYc9h3LdY3OhdsYWa6X9N3I4qRhfLEn5oTKiZQiYSy42lItG7aPTlheRsrzHYnCayLer67fMdf4u9YbRLrX7uOv/jvjqd4lR+/WP9H1B0yK/g5Zy+96m69bX3nrb79q3yjqaoVrBKd5+usXnHvQTrNdLwmrhHqxkzmW1jHO3jvWWQ6XO5wxNE0tD/vKcnvV0biW8uJPCF3F8qMnfNRm+vHI3t8STzyjM4zDyDQFckosSscT1XOqJ/LLHuOEgPT6je2Pzlu+s21e/Zo5E/sJbc+4Tkv2/ZGbocaXNdVFTSiGkgq6coRpRs0CMYn/Q9cN9Lseq1uUVsSQcFp06gwTZfR4FG7TMnpPXJzx6+1PhBqmFamb8Mcgum1ETmg0xBZyPc/StIVQpCOWvJi6qhFc7XCIbEPNSQfGUBaaXBL/G1vxIIjHytPnf0FoBkrMTDcdunFYI/NbelELUhqk26AVZfQsXI2tKnJK5NqSYsJai3aO0Q+cP7hA+UjsvWBpQ6Juznm4/im5FPr0ksvhF1AG7Ax0YO6gaQ3KaeK+l89fyaxQKhlnNDlk4lyJ//KiYtiuyFPk8WdHlkdJhIWgJ4dNWan4q5mQpwGV7oL7TLna868aizvfSNBQi3u58oFns3zsqAz/4ye3Iil6bbufLxz/4skJ1dlGYAzXB/yLHXpVY9aCBy85o4aAri25HyRAbSrcZolxjtSPxCBwg8oZwuVOOmWPTjGblipuiddHnvY/wwwC3QillyHu+XdRyqKxlJggB5R1fLD+X4lsLs8qd6VQRaEzQsFWSDcwBLAzHj3fyQ4zxlpW7pxH7R+BMezDc666X4tMkYJaNoJkT4k7+INGkuvsjCSHMZNi4tnasV85bFPx/tPAOkTcusUsKgnKc+Zfv7ciZUnE/vzzA2N6W5zyd9PoPzaa/65pUblgD3t03b5xyyrlldSlFPjkduTLK5nx+V9/VPhhP1JiEhTwoxNSjJzzI9a7h6iVZXf9K67H/4yyhkfNn9K6E7ltAGjQF0v+bfh33Kyf4YAHY6J2ggj+iy8OTKlgWsvmFBg9+WLFrxKk761YsuC/vvljzGaJzx23+WeklOW+1TrMukXNUtI8RglE525hVbKcRwV75Tmea2gjrvbYkwrTyEyHW67kHvTxlzITZAwmZfzLHfV7Z6AU8XJHCQkqh1pWVKcrgbuMQTq/FJFaVtVcWFKwu+Gn7t8xdpqOmt8++FccbnqmfpJOmQIaS+UsRmn8fuRwtWfx6IRddcYXi39F8REVbvlJf4sfPPvTlvGHT0Ar3itf8iR9CcCN/oD/+2fSibn2CmKcyXGyV7QzMvdTFapGElJdC7I/jgG7WcAGfpsK5vGapArjYZiliIFS10LSiZ4v+v/E3og3mfITVJbqfEO4PpBiYrvSvNfsqC42DPrIJ5eCuF8tM4/tDfWjM24mx5e7mvp8xZiluOH3PSqJF13qRi6d5fB+jXKWlz7BMyBlHj7Yc7E6gNI8vW3pvSH7IMWNSrDXWQtsRYUkSR/5jSJCHgWyk0dPOvTU750Tdp2AYiormP7ZDoFccOdrYj+R5jked75h+OIK7AN2Vw9JrcObGURUpPCnrML3nqYRCWIBnhw8jyLEqeP2wZqnRmYev9Mn6sGz2CzgMOAenRCnyNSNjP3IcOjRM2reNRW5wIu/+ZIcJh5//xqlAlkXbn95ZEqZdS78adOgpsDt0POkOaPUBasM+XRPW09UTcXyRKErw8tj5PYvew7VwPOQ+fkoz6Bhvjmot2Oef8QE5RWp9+8Bani33q3/gtYfmD731no9b/l68es/yrqfD6BAUWit2ZyuuTxewm7g6mefgIL2n30PU8QjYrNZ0kmpmOk4oELGKU0YPdf9SIhJhl2NoRjHNGlUcfidQifLar1l9XhDeegpKZFGTzKaftexTDuqz/8Grq+lO6M08EqqAwiJSBWUMcR+JB4H9BA46siV7zlMAajQtiIUg5kpRb4bBXZgnHRZcgFr0SkwTJ7FZDAxEfsJYw2568gpYE/WpABhHLHWEqfMTjvGMRJTohSNWWwYppH1dsVxd8S5CqPFh0HXhu62o90usJUlmkix0nWKObJ0MrxvUhbFRc7kIaGLJWqDMzVpKGhTkaYDtnGo1kklUwRW6DLPJwkuAZWlk6KjVChLSJQYBXJgDYrAqWlIR0/xgbhsMXUFaUJjaVhRNEQlOGmjNebuQZzynLQoQXzbijJ6yAIPcHUjHayYJPiqDLmxdCWRyUTvSUNAVW7GSksVvvSeYg0qSSdFOUhaTFCNMaiccUZhhlF+H9VRPT5Br5v7iuE0Jm5H6Yy8bszXWBn11s6gTleYZcP05TUlZPzVDrNeoGsr4IIZCGGANHim44CpHXazEBhCNxJjlpmWXQ8xUX1wgX3/nHS+Jtx0TLse5SMl5Dn6nv2+ikjdaCoUDhUiFYtZNilwkqKVmLUWefiWIujabEVGqcts/Dp3BIrWGFNT16coFGO4maVTBpWy4J+VQi8bUjdSQiZbiw5RgAQyLIdqa2IdGVcOlYUEl8aAutyjH5+gjSYDTQi4TUtMRSAjc5L8ZrX79yv6KMApxQOtURrsBxeoanr1gvltyms3gDEWhpApUWYf81DLflGK1E8yG3QMuOUZthSu0oRPB0rWxOoOUS+ABWUM9nTF1eVzDlWPSYUHzXyr15r9lBhjxiporw6QMvp0Sf/0hrKsqCbDNi6x5oRBKa4Oo+x5Z6gebMlz0KtnQ8rSeVIjs13aOkHd50zRmlQKSkF/u0dPI/Z8gztdAYrq4Ql51wng42KLf7HHlwJPr2m/85D60Ykk2kbLMbg5CgZeId5NbU0+jlJwsIakNaZkmmmHVWBPLzDAertifbEhZ4GwRB8wWpN9wsdEu2wppTAOiZd9pIwR9yJQX0fWJ1uGYrh6PpFS4r11YHsm0r5ru+Cm/v+y9yextmXpXS/6G+UsVrmrU8WJItMZmU5X6TTFtTGGdy9YPOlJSCBBA9ADhAR2E2GB6ILcoEUDLNGgsARGQuI2XuPBQwn3msIYEhcY25lOZ2SUpz67WOUsRvkaY50dJyIjwmk7TVoiRuOcvddae621155zzO/7/pWhOmsIm67sJRLGUPZQkVJxffMRn4sDY/SRGD1VZQj7ATWt6WIqehqjkNOK/dM1jAHRe7IKVAtD7Dv69boENrcV+mhWmoyhULGUEjStoJpK3KrH7RJKSaT3tEeaeqnpO0u+CLh1R+wdutYoI5HzCpUyuIBqLCFTEMH5BGkKZTtt7iNHV/ST/TFZTZF1VahzISFlLkYwlDwhIbvicuodsWuJQ8Kv98WMJmX00ZwwOMK2K06Cs4awH0i7AVVp4mZAzhr6BxeFglxpXDeUa1PT0j2yhKTpI+RJJsuCmmUJtdbIDHF0DP2IdjARmlxbtkYxPz2iu9oyN5J6iLTW4CdNYQsMnumswcwagvOFlikl0iryUPLDVo+vuP3JPQKHyAm/XxFiMR2qVcRaQX3LkmRXgnUBbmlSKseNPAyBNjsIl5Gwj4wCdu+rX57fcd5TLj3TAP8miqj8vr3r/Slc7/3+Ocz7mcHNx03Sx+t/kfVNQoo+DLX5nVTyve+1nhUa5A88fet5Q4oFUXDOMzmaIoBxdLiUGEZPnlRUkxrhPP1mS11Z9KQmxkRY74pNtdEMg0PmoqnpHl/htMFOmtL7KQrc0JfpqV1OCO88we26Qqu7XJHGEXf7JtXRtNB1BkdKudhcp1yso2cNDx9dsUsrXLVACIm1pgQ7Ujar2hiy1vgYUVK8S2VSkniwrhY+EceA7h3jbotqKkgBF8EsplBZ+qs92ziyF64YKaSMaW3JMkqZzeUGNzgAeheopzUCwWI5p+t7cojouuLq/AojBNOTGZvLLbOjKWMswa9ZKWLMkBMbEpdDQEtBHzKjz0SZUSkjZLHPjrlw66UsCEN0HqNKWKow6t28pJDIYWRQ5feXsUyPpdHFAU3J0qhUGppikpAQaDtBWX3QACmEiyRR0tRVjKAUyaiSFXPguqfRw+CKMYApbnjZxzIZjfmaTiYae6D8Fe2UoCAgoXNQlQu4OCBCKRTNjD9olhCwe+MRzfEctZgUHYIALcV1xkt67rQS+UBbA7AavZwSVntEkuRuRC4miHlD8oG468ljIApBMqYEZsaIaix1bYtTYF/yXkTIDK8/Qh/PUNOa+s4R9nhakKVtT4wJLQu9KMVYmqF5BU4RZUa4RE7lMy32eoncVMiQryeg6UC9yRRxNaJQMEUS1w1BIpUBwOGMl0CqTHHXy4VqIs8W5IttmVY7j6pM+Vy1Ku5eSlEliD7huoFJkESKDbDQClFpwj6Vz6O2CKURquhVSPEjd7H34+PPM1L8s/uVQhd3aWL88Gcqx1hxdUTmgjzERLjyJK0QBuzEkJ6uy3GcRKGumkJdiocnV5Oa7AM6gDYKlRNqYos1fSrmJkoIVM7F9e2QYzN24/XvkHIoe1nKxfWx1ujjKXn0hMsd5s5xCXy92JIGj7IKoSUhZ5QQVLdP6N98WJBCnUsemVbEp2vyusOeLZCTGllZ4q4ndSMiJyoh8CGzf+Mx1ckMtWhx986JfWn8ZAyok1mhAR6szrOPxZY7FRfNetbSr3Yl64s9qarBH1BNBH0/YhYtOoNQgstHK6oXjui6DidSaZ5EcViMGtSkKqiUFGSf8D7jVjt28RK/X5SMtZTxvjhTCquYzhbElIq5jtGM3YD3RfvWNjXBB4zWhFA0h8PVDms0iVzy7dqKuNkjA8RVj9YKvEdVuiDZ277sS0qVfbCypFw0oe4qosSkNKZa4ENCDQGhWoQfSX3R2TyjDatJjQolmy6udojFBGklcdchFtOi+VlOkZTMnLjPuNXmEK5dmmU5bQghFAQ0Blzn0NOKFByu69HLI7KSxcjGBfy2Q8xb7M0jpNHgA/hQXFx7RzKSuB+K7lAqUorE3qMnNeuHW8ziRbRWKBHRUtIYy2azQ+mDw1zOhTILSJXZXeyopzXjekt1e0LsFHHbcXR3Sb/aY2YFcfLO03Ujy8WEMHj2/UDV1GQtCDGy3XWcLRZEnzFWve+MFwTKR+IFZC2f26vFYTgsKWaugvRs53ie0fbsIvAhbpZ8SH3zUetD96/rsk186AM/boY+Xv+rrW+upuj5E/m3yHn97a4PI7xMjmdl6uoDL33mRTxlgjk7mUPOJD+QXcBdbTGLCc2yLeFrRjOsdiijOT47AinYr/fknEpTc/kQN/wqsbHMxRHyXpkMpYPVdRg9Yt+jJwcqzWJK2EvwEXe1L8nVSiKih7rGdw75ye/ky1+7IE8n2OmsFJKyIF5KayazlnHfk1LGVBbfDQzeo1WZRGlZLlZKCmJKVKrmzunvR99tScLzzvqL5NbSBcN/27+CV4ox5tJ8pERwgURBUmazCV03YG1Gpoy1Bl0ZvA/kFAm9Z0yJhbVYpcokMWWapsY5jxDyUIzAuO9pZg1fjIn5omW/74j1Z9iNW47rKUaVIrupNZ8ZfhnLDkQJ9UyxFMg5FCeu5HwRFs8axn2HSqArW4JCVS7hrL07mC1AH654/eo/4r2nEx5roD6YOchDsyGlpJ7URF8KU+Uj2ShS58hKkYeSTcWBxndr4zkJAYxG9bFk0WiFrA3t3RNCNxL2A2HdI5BF45Tenf5jVEHvnC8FcUjoSY0KgX61R247dF0xOZnxv39iQc6wGgM/d39X0I0xc/tR0Vv1jeRqqdCzpkzvB4eoLX61w9bHSGvQx7MSgukC46YjI8ipFMghRsS0RqWEWXf4GAm9Q7srtFHFXrsySKvfRQu6giDIlMku8HD/86W5mTUMT5+U3CSlkDnjU2ISjrg7+76iUzEaZEGJCvWqnKlNfcZZ9e0IrRn6p7x59Z9KDpYbynn1LKMoxnJs9SXMVs1bUn8QKIdI3vfIoxkKwe37e85qje9GlI8kqbBBFhSvtWQt0ULgVnvMjYrj7/jDtLohB8fFr/w0yQ0fSet9713lu0cx8s/3pYgUQ0ZclvbpWabmM01ReYp3901ZGy67N3hj9yV8PyJNoUklF6gnFe61JwifOJ28yunkM5QZSHNNH0sxok9m+FXP928/S86RnCPrswcA6JT4wZdmIAv64n7tEXLRkLoLXjPFTGaMe97c/1eq7TF+vQVyOY+A8cEl+miGaqsSXtyNkBOyMohQ0JHUDYSnq9Lwjh52PdE49I1jUj9Qv90xe31L/dIN1icLVuGSPLpr5z8lC7IcVnvQxYRBQKFXuUDqXUGlrCkN0a5HV7ogsrIUn/XRlP060S5mhCgYHp7zQ0hu3DzivLH8+0M22FBn3nr5iHOd2Hp/yJoRzG9YOOpJdWT0A0otSIPnAbd4562Go0/fQf7KU77TJ7Lb8XaK7JcNLrhCsTUOIQV+9AUdShnbWJRWZFcs5Ecf6Dcj8xtzTFuRXaCuLCElXLfj8+orpKs1i3mDGbtiN98U2/6wHxCAPtB799vElzezYjYxBiCRnWMrBW/WZ6Q3MqkqjAFbW9SkKc6QQFzt0Cfz0lQ7j6rLwITKkp0v2k8fEU0ZYCijSENXNF61RSjJsO15bZIYK43W0L8jaVIie4FXkaz7g8Nnwf2xh4iFpsIfGiVSAsUhbLXoNotOSWAmRYcVXWBTt7x1NmPwgdGHosnyjmpS4XpfBpZSEkwJOo6dp11MmSxbPn/jHL/+WarjFjXxVPVjZmeC0X0b+8s9D7/6gP3Vlst75yglsZUlpkhja3RIzCcN+8uB7eUnmZ7NcHEk8zOAY5sz/6LrCpuvg7gTHzlQCc+Hen8D5dJ7R88f/QNfT9L5Bl7g/Rqjj/uhj9f/gut3zJL7m4oSfcRLZH5j0WGKkWpSs7x1xOX9C/a7Yn27ebxidrZAGU0tDONBjF0tWvrLxDh4hm1XCr/KsFltcaPHGk1IidF7GpFh3KGVZX+/ozmdAxAPVsXaaszUEHsIo8OjMEdLRElhJAlB6jtEioi6xk5rLvYjSddUB+G1NuowFRUoKRm64TrHJI6OGEsWglLPckrAWI1OmdB12GWLqhfoqiXJkXAJfrVjKyZcqgqExrSGpqlYna9ZHs3wPhB8QApoZjUpV8TOYSuD6z3VosFvS7F4fLakHx31tMZozTCMtE2NTxHnAv12j1KKZtYSYsBn2FxtaJYTxl1i0FM2zRxcpMTcCPwYkTmSvMdqg21tETy7cLAST6AVbrsn5FS0Q4fcFSUlPgUgE/ri7iOUous31MYWy18OtC2rr92ZhKC4mOWMtKpQ+1w4OAQK8uAPoZnq2t1NK1WS5/NYgv6WDe3tI4SSqNpQHU+JJyPuckdYdYWSFw4T3phJOSJVoaGhCgKYtUbGSAgJEQLpYsPkZnlOF989GUTKqK7ksyj77MaCHqRY9DyyrYjdgF5MUJOqXOhqQ91W+Ccrwqoj7hWpsSWfymjUtIb9iJhYUsjI6YQscmk2YiJtCzqYXKGqkYtBQZ/3EBMaUJ9clCDYweEHT86RMRgwEgLkWI5/JYBnboVtg4rQyBYhNKGqcKstIklSYZxe54GpDEkVpCDtB8S0Rk5r8rYvGVkpE+0AWqNCQgWwAYJUJRhSKmQ3FpQw50K9Mgq/G3FaoI6nYPyB6vrcHvT+veY93x70U4eJ8WUqx1UR+4l3Z0YHGuRBasUze9yci/Ys6UTUjjHskFITukBzNGX/zjvFvl4pBAprZoVeBtdGA0kKxKwhPLximltyiqAy/WxKFCXvaHrQtQz3tzAE7J2W/cNLeLEufhgpEm3Chy3jdgVGIRqLf7xCLSeYGwukNbjVnuQ85myBOZkxvPEErSXRRWLsCy01Q64LpTJt9whR6E125xCP1ojTM+qXbzB+7WGxlG9r7NmynJch0b/zBGIxPRA5kU2htWZVHAh1WzH2DuFKiCshlpyemFFOcXHvnMmtE26+cMYr2w6z2TLOpsicuXhwjtUGP6lw3UCaWOIuEQaPsFUZKplMRhLHgMqw3nm0neHbJTZdUoVIDAHZKKQUSE9x3BSCpARtXeFzoqpqdlc77KRGSZCpUEqjyOWaMqlRraXfj4TeUWuF2q85mQsMA9Kq6wBgNa0J6x2qslQv38Cfr4kxkUZFdbbEnW+gH0EpUBIXSmRA7PtCKxMCs5ygtcJdbMrelhI0FlLGnW9QbaE0xtWesO0Qr1rMzNBf7egfr5DTJbvLDbNJQxw8wUfcrMZpQUQwDhnhioOctJF+v8LM6mKg4AS5H8vxESIixELTOtC/S2OXSEWRCjGiZy3j5Q7fO8LE8Gi9xUiNksWURVmDiJmqAp8TaSiB0lVti9PomLHzFuV72jYjRY9oBIgesiA5x+ZRz+5qx8npkq4fWK+2WGPo9w43eGZNcb+0VqPrOZmanJ+1HSVMenXIWgNKmvMH1iwHav+z/eS93Lj37CYfvj64c8nXL/Db6Gje3xx9vD5e/wutby5S9NvRDf0mphPP+LTv58k+/zRSmdJIIFACNJGXvv0Ofj+wfnyF1hKlNEjB8u4pcjWitKSpK5QxrHYjVkg6VygPs+MZ28st03mLQJC6oYT0kRmiwA8RW0n8/fW1sYOgBElKkUmdL6iRMeS6xg/FqjoogZoskSEQtyOJjGwTxpbJrJTF6QcBfvRAxlh7qKvENec3hsg4Oia2QkvJVCmsEBgyEYFTktA7ovJsx4Roa1w2GGuoZ1Oc82yutuhKMw6OBAgt2e96mqMJ8TAxFBms1UQXiFpQT6oSlup8yXNoNSIEdrsOpVVxifIBazTGatzeow+OZNEFprMJcCjigTFElFY4aWCfqSYtSgiij9haEw3XDSE+glTYMZKamjEnxq5n2bSFmnKgjogEjdJMrUBXttDNrCZJgdKKMLhCvesjoTaEMWBtsdsWsZAc/LYvfPAQScO7x10OibjuQEjUojREURwCb0WhtmUtMbcWxKsrpJWQJTGk4pwmBLHSpdk7IGUi52LmoCRpNxZHot5Rn85BGYw6aHKkwOmiFRpTwsXi7pasLsjJwSTDP12jZg1ZlrDEcp4JxK0jzNkCGQ4OYIPDx4ydtUil0CkRXSghuwc6ZtVWhHsX5ZhUiuQj8ao0Q4X1kYmDQ8xbxKRCHk2QCdyjS/IYiUOPRJHcgFaGJCBFR5aq/E2NIqoMrie4vpzPB4cJow1ZKdIwgJDIlBBIhLKkLmIW0xKwOLpyTK125MUUaQ3BRxTFSY3G4mJCCRAxYtTBBTKmghZvekhbbC2oKHTLLCh6l4MIOh9SbT9qIFPuy9d71vX2dnAYPPRCReslC2VLCIGpFVDDaotCUM9a4qMrGHxppnMm5EgKY2nslSnHWUqoSclSkS4QZCqGfzOLbjTgSVoQDnVcf7UtxiKHv5nOTWnEY0JMKtJY0G5x1BJGR4jFGS8dnMjCpkNNG5pXbhEfrpFBEEXJmopAUBKTDtrJCGI7gFEQAa0Jmz3jW4n07bexr9zC3XuKOp6RXShhm5WhvnNCtpr9w1XRGfpwCG4t9KO06UqodsqIsaDHShZNmjU1x0Lh3ACVZdSabCzb/UDvHaa22FmDtBqfCy1JGYHrA4qKrIv4XyRFcrHkZUlBezIvDpRaYpXG54TU0A1j+WAPKIfSiugCVWXJSmJri/QRUZew6RASy9NF2VdjcT08OmnZXkbSbo9JoH1At5YcErqtUIsJsesxWlK/fFpovFISRo9pLWraYDO4J1eQEno5RUhJ2BTtVjYKBl+Crn3P8GSFWUxwbzzGTOuC4AyesB/JaUV2oeT2IXDrjjx4quMj9g93VNYSdwMxQ/YBZaY0JzOM1lR7ifUZt+lIu7HodfYOpkUrR+8hZvywLcG7dVVcC1MqpjwhImJCxgSykMZ6n1n3kb3JtMu2UBCnDVIIwuhhDFifSFqWrL6cqWpL3O7pQ6RNRUentSVLgSEiRaHJ9hcb6tmCLIpezbY1phsPERSB/W5AxAneB0SIDLsBO20+sk754E0BnjnzlYFJfl8D8yGw0WEv+YbAnOduzO/76gPd5z5e3/L1kz/5k/zFv/gXv+72qqpYLBYcHR3x3d/93fze3/t7+ZN/8k/y6quvfuTzvfLKK7z11lvf8Ov/k3/yT/gLf+EvvOe2j7q2TadTXnzxRf7QH/pD/OiP/iif+9znvuHX+t2+volGCx92mv42xg0f8qPPTuyv/6O9e+IvX/39qPaY7DwvXXyVkydfISWB/t7P8vYbax6//QglAuFp4vjuGd8lLbsHG9KQeeflI6pJzW61Q4qSz9NvOlw3lkL+dMbRzSN2Fxu23rKe/H5aa6ieZXEAS5+5sykUiuNJxd1FRXKBr1rFL6REsvHggFUxbjo+4d7gKL6FTgkVSs6QtYZhGBmHkuKtD9k+biihsgJR0BxVrGgXtuVz6ZSJMKQYeKtu8C7Tb3v+v6ojVA0oy2r++6nqitF5hNCkEDG2NEiuH0rOjpa47QGRSkVvIawu1siIostRskzSDwVFipH9ek8gY5piSuF6BykTQrlPasVsMWG36xm6gTCGwpPXimG9xUwqvFR8UXyGbB2nVcv/U2nmjSWLyL3u53Fhi6CgK8ZaktLonDAxUclDkOF+X/QF1hY9USx5UTkmhNU0N5YMVzvGbV80SHCYbGeM1ojtwLAdyM5jTGlQhSzFse/GEmZbFfqOkKUhal44JoXIf3uw4cqXJu+FH7qDaRX+tXd4UWemp0eF+uISYQyIwSN6D9NCn0lKgpKYQ66SmDWofXm98eElVW35f7ywRFrDqvf8s/u7UmTvIV6Vg+9OLfnuo4rQjeQsis5BSb52OfDVi/7rzqfvvjnh7qwpdLgsGHYDVaUZ1gN1W0M+WNpnCFc7shSoypaGphuLSYUQ5JxQQNoOsBtIlSY1FWhFdWOBtpZ31v+DtNpjguWl2feTlaIfL3mw+gWIkd14ztc2/+4QKBzL9FhKlvoWp82nEdawkl/jfP8aAsGieplZ/TJaCi53b5IWAf/Ul0LLVrDeo1JxcRtj5NFLR+wmReT+woOe094XNKnS5VjtRr53WnH1+gXGdXznokEZSZcz/2fXMeb8EaYLH3wReYYQfd29h/on58zn78AP3MlIJbjaSC4vWvwTU6hS/QjDIcspJXxMPNl/iSe7L6OE5IXZ56j0ESiFXk5Iu4GQI/9x8WvsVM/0lTN+eLqjSZ7eRf7jrVfY7x3DmeZTqiVteiqX+ORrm0KJsgp1NiWs14zLhvufmhO2PbM7J3xm+i46lUaPubVkZm8wz58kHSd26RFPN18mCYGtDKn3ZAlJymukI6dUmsoQiduO8c1HVC/dpHrlFn61JXlfNIhSkg5otZZgmor4dCAZTcwUup4psQKkhAiH4yUVHWUzU/xv7Wt0l1se7eGf2e/ixp0bdFGBNKSU2O86jDXIBPM88PLcYY4q1iHwq/0cmTW+D0RfHBybgwX49msPOTmd415/imgt2mosCtNYxmEkATrBkBPSh6JBqTSxcyQXDiHQB+OHnCBmhvWal9/+Ob7rtAEcrSnUalJhBKhUobsdnxCPUK8ouDHy5pNDKPPgMbVluNwynm9RlYYUi5tlpRGXmvRsKBcc4/mW4CNZatymJ49jGfQZA1UFORE7Vz5TAW+8mTGyJnuNCwG7nJJCKpTi0YOUfOKpJz98Uow+lEZOK2QGtLoemhCK2UmSsoR6C5B12UsA6junDI+vrvPeJJFsJJdhyi8vvos1e4I0+G7ENAa36Yu2UMBdoVhc7GiqCmHLXi72kftS8Oizt1idzYnhu7CTkk/3B/kvvMBDQJDcq1xeNSxO52wutqUpqizeeWJM1Ac7eZ8SE2vKOfn+PeAbpMG9N1fxg/aRfC1Beq9eUTz39bMXfB53ev7RH/ZmfoM3+X7e3cdUum/pGseRJ0+e8OTJE77yla/wL//lv+Rv/s2/yR/9o3+Un/iJn/gNm6PfqbXb7fjyl7/Ml7/8Zf7hP/yH/J2/83f4a3/tr31L3ss3e/0O0Od+i03Q+4cl11981Al8IPTn928fgDQMm0B8uiFsLwjbC9Rsgjkx3P3uV9CV5t5X7pH2A6/911+jaWsmSpH6UJLHJxXaasYDNUBYzex0hj1slNuLDcYW7nXMcOU8Mspy0YyJJgniGIvAXUCsJFlYRgerMRJ8QnQ91VIybDzT/YY69hghYfA0JHL0TKylsubajnnoR/Sz3CUpqasyJW6MpZEavZZUWREOhcWgBE5KrirFZt9js6UbBSZn2vmMuOmxWoPKuG1PCpFm1uIGTzttMFKyXu9obixI2bO52BQjBqtpT+eMw1gswYVgiImUImZysEnVEmM1zbSh73pMZRn7kW7fl0YLcF3P0fEZw35gcbqkH4ZS/Mgl3XrPVVIEWyOcJJEJLhAE2IMlrxQUPrpWCKmQQyRVBim4RqmSDxAiaI0LnraaMzxZF3qZEiBU0RBJiVlMiKOH3pNCKDQY50GK4sCVwVpT3AUHXw47q2nuHKObMp0cM+z3DqEEo4CsIExqIpk4ePSsxdYWtx1w96+IPh4c9QpKpHIurmhRkHzE3pjjzrclA8RH7NUGe2OJUpItXCOJxMLX9/agWYqRmESZaEqBj4nef30KRjhQ8oRSxbjCB3zOVNOmWJJrde3GlkaPXE5QTUUePe7xFfgKXEDEcs4KQXn83pGHcvznnSEYjTqeIdsWJec08iZx3RPGXZme+kiMQ0E/hCjhrYXPhdASrduDdbomh1BsnKWh0S2QkQPEOJBqgxgDohsLcpUzatagUPQ50aVQrN/lUBwNB0eQAl0bMqJokzY9w3bFZAZWSOQ1KpTf1RG9byiT31fgCPERDdGz/e0Q+lQrWFYgtaDvi327XkwYL7ew2iNiLDlKB4F+TCNSKkKmOG8pRZYCPWuIq45MZpCOnRqwC4HKEeVGjFIEI9hdrIkS5HJCeOscckb7gx16bQsdrXPIowWuHwgyI+4ew1ocHMgceSy20uF8j/BLjJSIIEmi6PtE58ghIStdbJ8lxdxBQB4d0pQgzBQi470n6KMZ5mRODhG/2uPfeXKgocliUpMzQpf8KENB98SkGITEZ9ktqSCsxhoIkUY4lApsUyJrzcW+I1mNUBrpAilE0hiYTFtM9BgJdSVYuYjLgjREwiFbzcqCWHe7dXEtvXVa6J8+IoJCLmtSiNTWsO8HnBuxbcXoI8O+Z340RU9rZCrRCU1TIYXA1hX7iw31rGGyctido6pKQK1sLN29J0gJsj1D20xlK6pFw5A8/ZOBkKCe1OSQSLsRlYBQUC1/uUUtJ+SQEM+MaQ6ulxz2YLFewTjCpCU3Nao6DL9CRDTFBtx3sSDQ0yn1YlJQ7VTCdbv7F6TdSL7qEJVCkghDh9/bYp7w7DwRsujQcr6mvsoQEbpY/ed+xD1dFRr04bjgkH0XkQx2gjhtkDkz1ZrNwyvauirOlykxmdW8/Jk56/sXzG8s0E2hCw8TzeZsyjgG9HyOOzQcIoMcB5AKpcrwc3Yyp9/23Py2W1zev8BflhypDEglqQ6ar3wwIfrtrmcN0ruMt+fQ5Sw+kgX3bnWU33/Du89/3TR9wBN9VHn1XDOUMx/SvH28fifWv/pX/4of+qEfAoqGdrVacf/+ff7Lf/kv/NN/+k/5xV/8Rb7whS/w+c9/nn/+z/85f/yP//EPfa4/+Af/IP/6X//r3/A167r+0Pv+7J/9s/yDf/APrr+PMXLv3j1++qd/mr/9t/82jx8/5sd+7Mf4ru/6Lv7YH/tjv4nf9Hfn+t2RU/TecciHfXN46LPTWzz3s8+KOouUEj961o9XJD8yPF7z5pv32Q1rTj/9YtlAc+bWp+8yP5twce8pbj8wbS0WQTd0SN3S7wbCcCiG24osoZrU7J9s6PcDy9MFLoZD4R2JMeF9oVhoKfFa08vMzntk0JheYKyls4I+J5pZS78fGC43GGPoXWaoa/YxMnaeTKCqDGJ0BZ2Ih8ySXBzVGlOTU6KSha8vXCalgEuZnciktqILNUP0yGpG3ztmR0u2qy1alsBKYaZIWyZ/7bwmDZ50ELaq2tCvOqr5hFZp1BAAwWLSEGOiais8EEIkD0UQjhD4GLGiUPWqutBGht0h8+cApPmxBGi2bY075N0kHxlzIWGH3UhWhYKYY2YTIuSITJ5uExDTimQNadwjU0ZPa8RBdB0pBhNKCNLo8NFjTYU0FqMs2tRIFMENpVjPGXtw70oHIw6pVbEYHxN9jNS6QowRpSRRJHIKIEqTlHMmK1HQLlEIDlYJ6kojpMCOYFMgPd1hsYjNiKpa3MNLUjeQBaVAGT2isYX+JkRpPoxChEjaDSUYd/SMJPIusRof4+dzqgLUIWWhYJEpr10r6B0y5xI4+1EX8MNU0PtI6ApSSEzkSUWsimbIWAshMrz1hOwi9nSOvbGgunuKX3Wk/UDuHXE/kqIvhZA8ZDOlDPuRrCN9zthbS4SEMDOoRVW0JatcHONk0X9Jdci5iu8WVF66YhBgSp5TdK6cnwcr6pwzcT+i5i1SaegGMrkw/RZT/GaHTmB8KWhEKugmMSHaqtAjK00YO8SwQaT+OYrugTr3dR9jfs9/7+5Mh3JEPJvhinfpMs/9aJEsCVxI7IaEtAqXil25bivck22hAjUV7HbFjUvrkg11eEsheIIeyQnq1pIeXJbHKYlUCjVt8KsVFk3Wulg9P1phjUF5g4iqaLVysZSnrQ90KFVc6lxEHU9pZg1624HIhM4Xx7AYCU8uSeqUhCQlj1QKqQSxj6UcE6LQ2gqejM+ZNCluoLEyYCXeBcTDK+QYMTeWsJiQtj2pH4khlt5xTIcCOEIuOhgxqYvb3mpfGvFJhVCCPBZHzDR62jvHHGvHcYYulecbnSC7wNgNJXrBGJyMZJERQpLHYtutBOwHx+x4hsgCJxKisYxXey7efsKrr97GPdliZWkqo5FIrZk1ln7X0633iKpQdWXKTGvD+umGttUF8dcRJQ2LSlDlwPJoih62iFSuc3HTYScTgpYMu4Hm5gTRtKSqwl8M0B9cFgX43iNjukZh8hhJRpHPN2WYYE1BZ+ZtQehFoTamk5Nr3aSqdAk3jhFlJIqIbDVmOSmPSZm03eJcCQsXVUX7wsm7l/+cS5jsfiTuB4wt14Vne4GgRAKYxYSw7TBGEwHVWHI/kNZ7sEUrJOzBmCblEoYuAp5cwpYbMG2FE1BVhvligh49od9z9PISVVUkXwxdmrZm5wobIrvispd84PzqCqM6hJR0XcfT13a0RzPaSY2pDOGQh0Usx52oDCc3lmzXe64uN+hphT2qMMIcgrczSR00fjkT3QfEsL4PeXlPX3L9zfON0UfIgw4zlQ/vm57Ffjx7kuerp2cw9XPv5bkBzrXl94ei4h+v36nVNA3T6fT6+/l8zksvvcQP/MAP8Ff/6l/ln/2zf8Zf+St/hf1+z5/5M3+Gn/mZn/lQ+ppS6j3P9VtZWuuve47FYsF3fud38v3f//18//d/PyEE/u7f/bsfN0VliedO4XfblQ/S+/xm1zPm7TVB73DWfvBGIFh86vsIacaTX7/P7sGA1BGU4L9+8vuw1tBYxav3tpycacxEc3TjbY5vDIiYufFkTTjf8fYbj/jSzT9KGjOVKXzxurGYaX1AFiRSS/b7nsmiZXIy5+FrD1BI2nnN0I0kJdgsah47R31zyq9erjlqp8SY6LYjtq0LUqIlIsEwjLyuXuSheJnmqGHoAnVucBvPbDll7AbWFxtsZWmnDdJnnA8gJY3WfNt6xHYOZzX/+kjgRURLQz/5PoIJJB+hsnTbwr8XSqCVQFkDuSeMHufLBUcaVYJQx4I0TX3iM9tA3gaGXc84eBYnc7YW3qgFCEE/OPTBrnwxnzKMjmE/UNUW141oo2imDYMPNMYw5kTyRQg7OZ6RfcmA0tOK7dMNWhcL7DgUbcK/8R5TG7S09O330iCZScnnzC+BH8lS4vc9YvB4H4haUxmFULpkVkhJJRbcmX0eKSQ7/4SH6UtFa1ZXxTyAjBuHgwaomCkoq6lC4Mi+zNGtVxEucL7/Ndb9PchFa5RcII+ZMDjMwZb99704L43yuuf2f69Ru4xQ34466DW4tLyz+SJx3JJMU6iJshQl+kCFzCmRhmIcweCQlSUbjVUCRo/2iWa344eOJ5hZw7zy3JntEcDWJZ7uqpI50o3FaKEbv+6Mee5EAwSqsfhdX5pv4HW3Y19b1LLlEw92TKWh/dQd9l99wPjwktiNNK/cwN5YkMeW7ANh0xHWPXlfwkflgW6UvWBQmTdvKKLaM7GRcP/fIkJCtZb6sy8xvvOUvO0OtvKCibnJDfsZpBC801zwb+a/RBawjDtO1xmMKcVjLhNvYiQHDz6iTubEnMrXVlO9eIr76shLb20QtcX5iD70itKUsEihFVoL3OrnOPvMjP5qR7eWVIvJh3xu70OGnv3zDLl+vl96tmE9Dx9JcV1z/PxD+OXHEqng1aXglamClLh9+l1M7R2MEJzHX2AzPkLkzK3JZ5lMb5N94MHlL/Bg+0uY0wWf3J+gjAbvS0jwzIIxvL0/wrpITplbX37E4iuX1DfOuMt3II++HZ973rn8L1Bp1KQivP0UsWgxT/e8egl1fczyfMfLyzXJB7ZS8frZgjx4NqtHbPODgjAt6uIkqNS13X0cxmIVf7WHRrNaajZKo5OAiYEYEQKOLj3tkyvkvZ7Vp48Rn7iJe7yCVaGIqkmNOpri7j0txa0ANt3BKjuSlES5iJjXpGf3+4TMcLRU/MDwFfr9wMOt4UuTzxWjhsqgKkPvHcfHNbbOuPUekQxJFkReUqzzfQR71LJ7vMJWmsu25qsvzAlTzeZiiz5Y3AeRCvKbEtoo9tuemy+c8r8jeaGq8Tckv/bG/0VIe+ZyjnvUF/F+zhhRzhlhFGiFnTaFbrbrqWtL92jH6ydLZKgYn65gmmA3ELc98clj8tkNmLboxhBWe+xyjpo2jPeeliFMWyNTxCzbgkRZTRx8CVFNuSCPIYLV3K43HM8jUknsspwf5GKegAChMl97PbDb9tQ3j8ptUtLcOiqUOBcQWpb/cy7NiCznk0jFqCXPW9S0Ie/6gzFEGcgUW3QBqjQjcTUyigEfE1pI9t0OM7HUdYUVgnHdIeVjprMnJAGbt2a47gxpNPMbC86Op4Rhx+Ubjxm3PVIp/uvJpwkn34N0kRdWGZ0Hdg8uWJwt2F1s6Pc9tbWIQwxHZQ31csLi9hH78w259/iY+Z7qe5jeWBDqwP1X3ySphFs77v37+x+BJr23tnn3luf2E/Hsluc7qa/ns12/wgd1R9c/8t738b5RzfWt19KEr6Pqfbx+t6w/9+f+HFVV8af/9J9mv9/zYz/2Y3zhC1/4lryX3/N7fg/f933fxxe/+EX+23/7b9+S9/DNXt8UpOj9DdBvuh36yLPuvVtFzocTV/DeAgMAxdWDNZPZgs3VhklV8mKGCEiLirDf7bGbgfkrp5j5iNKucNaTR9clfG18skI3E5pZi7AK21akmBjWXaGfqHJbcUSCk7MF4yFMMgyOo5tLmuWEECLdbiA1lo0rNC5tDJU1bHcd7WKCMYb1kxWT4wW79ZakaoIccBG2m5Ex5OLqNp2CEAwIJIIxQhw8e+F5IRXh/ZM3n3CpbhBbg9925JSZLqecPz3nxktzOr+nXUyJLlDPGlzvEDEX8witkJManSHtBppZy7RtqHcjVTrQ9nzCKMWkMqzGgDcZnUDOGrIsIYXaKMIulERxMvXRBHpPJGOKqpuUMjEK5LQmjL4gVFLgN12hgfhA7Mp0tlvvSVqyGRzWGEZhCEIgh8gwDOhKFPpKzKRcLpimtkUgfHDiI5dwUS0rpFAoYRCDJ6RY9AcpYZuapmlw3YgV4ppyp5REG4PWNQSPTOKaSoYoE32EYLjcY9q6NDY+EB8+JZ9vUPVt6uYUtEFqQxpH8tiRRwfGHoTzEHPGAMRIigKlJbl3ZJVxwaN9QFaW0DsUojhdJdAxUiuFYWRWF+c5fzhfkgsoKUhNjd8NZCwftgTFatcYTe5HopAEk/E+4DZ7wt4zrta03/4C00/foXvtIeFqR+cD9Ss3EJWGrFG1Rc8awm4o01WK7ihuOvI44g9hruNqh7u/Q1UG5IxkFNUnbxEut/QPLsF5spXYego+EI2mlx4hcqFyCQrtRhSTkWv73nTg2Veayfe8QliXcMgsBH7XYaTEHs/JTzeE4JGAiMWVDR9JwhO6HSk76nnLxH44reBDt6v3jYjer6P+IGDch0xQEmLG+UP2k1LIKBBRYWLJ8MqHJ9NSo4QlH1wLo/PYo4rxyRXzG3dxb+5LeGhjiwV8FHhPOdfuXWIT2Mqi9hKtLCkUQxl1PCNe7QpiuRuROSMnTaHSRoeODmEkY62RaSw5RTkWu+iJJA19QVGNLpqf2iDaingwKskCZIrklIiVKUYJAtCSjESOgdxvGOtAtjfRR1OEkoSrXck1UvL6AwxKkZ3HzlpibUrwcgglDNRo4nZAtoVCpbRkOhE0tiJUlrkw9CojK0Xwidh7ohOoqWC/H6hnU0zWDPu+uDmmzDg46AvyUZ3M8J1j6Ea6+5d0KWLnLf2mo1pO2O86UJLJfFKs51OiUpLaB6bWcDI19A70doPJGXmgAqvalObD+RIaOm0QAtTFlnF3Sf3CCalpiEMgoaiWDcN+JOx20G3I8hbNcoKqDH7dlWb/gNAIIUAr9NEM3daEbcew3pNDKu5tWhY64eAhgbGCdtGgjEJU6hAnAGhFGN0BKQffR9KjK1RboQ/HG2RUVXRMelKhDrlyWQjSti/HGBTKcD8WpDlGQl2hkIX+fDwjpVwc6rTE7RzT+ZScCvpbkNDidpjGwJj3RDuwfXDJsLtDbm7guoGGBSokdg8umU5qdExkJUl1xbaDdjplP5xTHWzBzbYnGMHNT9xkd7VjupwyvvMU21YYWRDP3cWW/eCYzlqWt5bs3l4hTxWQ0JUiVofQ1nyoX8T7TvjrzeK9xc+7JlK8C/C876HvAZQ+7Ome+/oZLe8DA1yfe45nlvjve9A1xffj9btn/ak/9af44R/+Yb7whS/wb//tv+WXfumXvmVmBy+//DJf/OIX6bruW/L63+z1zXWf+0bW1w86Pvh+3j9H4bC3vLfIEKZCyvJrDLuR/nLPKAp9YHSeGArty7ZVEfZLCbOWq4s1YhaxVpISoCNCBW5//6d44egTXNzfsL3YIBdN0cxoxbgbSkjf4A4UMMnsxuIQ0JkJu5Hpclo2/hipZw2JTN4DKdEsWmTM9N1A6B2DlKijYretdcn3gZIVtLrYlEBNFxi6ESUkzjlM1uhpgwGC73C9w1dtcUOa1EwWE7ax5F3klOlWO5q2IoTA8uYRvncIn9ifb8Bq3OhIKdE2BuUjk6MZdm4xi8LJF28VjcY4OnRr6bqR4WLDfm7x0kDIZF0217qty0Uu5aJLSrEgUN1ALUFGGFJAtRVxDLjdgJ03hba0d6AlurHFeUoXGqQ6UCjmpwtcPzKpp/S7nl4mVl2mCdAsWiZkEgGIRDcc6uOMCBHVVAghcKFDGkOkaIX0wRZbG03uRnJjS4J7KDkiOeeSx9JoRrdHinLJ0qIuQa8iIJoyCY2XO8bGYI9nuPMrxvMtUjfkSVsoQjERQ09WAqYW0jG4fREiA6jy98+5iKuTj7jgEFGglMbImgdPzlk2E6KFqqrLudJ7/K5DnVl89JAFkZIXlUMEJZGquDMlH2gOCes+5ndzMp4//VyAqkJXmmqScTkixog0CnxkvH9J8/IN2k+/wPDmY8LVjv2X71HdOaa6tYRmhpASURncxZZwsS2ImhTY20eF7hcjVmlCWxGdJzxeUddTcAo7WyC+rSI8uATncMMGKA51UgL5oCWh0A6zzARZgj2jLH9LBod/ssKezjA3F2iR6X79Ho1IMJ0QdgOoYrMvhEDVRRAuXBHqT28sS+jrgT4lcjrQmT583POB25r4+nve40L33Kq1oK7K11Zk0hBI3UiKEZM55BBZNLYcM0IhnC8NXYxgD1bxg8Mz4mOPStDMJhhfOjGhZDHG2Aaq4xPYBrrUoZRlFCOuVphZhXtyhdACkUtj1t48KjS9wRMXDUIK4l6isyX5BMLCoirFdD4YkMR40IQVauwzd0UhD05xOUMCxkjKGdUYpJHFiTEm0uhxbz/BnC3RR1PiakfqR1h36CzIoiD2KcnrcGOUYnQetesxR7PSmOfMuO2uG2ZtNKbSnJ5McJuB/WpHqhVeCfADwmsaYejGiHEjR1LBUcUYA4hIGkek1YRYWAiXbz4h9o5oFEZL4oHqJYRA1xYfe2YnBqNApUgm0111qJyoJjWSErBbjkVASsLVFmLCLio0nvGdC3AJezbHLCew3xKfbjCLKb4fr13b5OltsKb8jXNGVRa33hMGVwJep01xsZs2hF2P341kBHEMhG5EAqY1VLXEHE1olwbdBg5jBqLzxN6RhSaERA6OMFb43heb9JQOFNN8iE5IxN0AQ3dtve/Gw2MOwa8yRnIQ5folBDllJKAQxfa/d0gp0MIytYlxWCOrCj2pS7juWFAo1RiynvL4wVtY1RKUobEGUVnMomXfjXij6DYdzjtkUvSDIBvNdr3jVEsymXrSsPcBrOHkU3dYbHqUUbSLCf2DK56cPyjD0lkDSuKtQqeM3/b0MdK/s6M+nSBHQYUlS4gpQp0LhTAJdHi37Cr9iiCkgE/uGsEhP5vnHfaL54qeb6hFee5BOfP1P5QpVNEPezbxIV9/vH7XrL/0l/7SNUL0hS984VvWFL399tsA3L1791vy+t/s9U1qip6HdX/n1nsmGwey7fyVz9HeeIUYI+/89zcRMYNMRWA/OpJSmMqyvtpirOa1VvGW8ggjmKqem588xebEJ2cXNN4xaEUt5sTH2yLozSV8NIZEPW/o13smdWkyslWcv/mYetFStzXrqxLclmJk7EYyUNUV+/MtAPWsYXtZROXLkzm79Z7BOZx3bNeQQ6LbdBzfOGJndrRNRbfryUqyOV8zPy2hmWM3ooxmsZyz33W82VrqFxaM+yn9vkdYjUylKVBaUVvD9HhOSiUHxWjFuHeYyqCaosNymx6VBWZaU58lzOR/EHc97qzm9epVVo/Kx97MThi6EWck9RhIMuG0xGhFZS2+L1lGORWUQRtNNW/wnSOTSwaOi5gEtjbEGIto1UiqumQhydqUieV+RFrF7GzB7mJLFjBse2bzCV0/8Avz34cKkbv1nP/XpCV3Dhc2PNx8kRyKJkdKQRo8O3nBVzf/N6oyGK2KI9ZQQlpFbRCmNEhCCrIPhcIhQQXJun+dq/E1UIIT+Qo3j3+ILAQPrv47W3GOqgyx9wwP14xXHcl7hK6IKXFv999hfyiIU9GDERIx+RISm4s+RmhFEqCgBBxKwRgCj1YXvHL6CY5n34dMO946/xpJvcWL0xcRUhL74oi46Wq6WCgsOQuEKsVpDKE4RAnBy43k02dzhJb86uOOr10O7zm/VFMhjC5J6znx4h7ymAgXW6RWmFtL/NMN/mqLOZ7RfuoO/mpH//YThnvnhM2e+uWbRUzeVNgTyIuWsOlxT9bwZMur44S47nAK3vjEhCQEp13LH7j6DAywH1acN69j757SPVrxtdV/QubMpTAws9dFRDYafOBy+xor/VZB9ihNZSKjDrbDNJZb0z32TsfYOB5NZuwuC3UnmmL9S22I+wHhQ9E0IbA35sSrLfUnO6pGkRzwC0D4kM3pIyfCfDiF5fDP5+8I/vAnIPvI46vAapwUW+JDILMQgrPmU5zYVw6uXBoo2Sg5Z/S8xa12nJ+9w6O3fhW/3nLrytPMW8x+i4y5TOLfWfHy6Q/SvnCL1Tv3+fcnX8LrQ6E6WaJPJzhmhWaLoG0bPqtLOGwXLF/bzMpeNsx5uTlFnVRcya/yJL1WctQmDXE3FJSiNsSD+yQCcqULVdGFgvK5cN0IxBB5OtPIViBsTUqRNDjGd54gm7vosyXZR87uDeh9IJK5NxvJ04YsZUFbQyQrSbzcQsrI2iBNCRzVk5o8BuKuZyo937v/IsF7fB1xqz1jPzJfvshL/ee5uALdaH7o5ox+tedCO96ud3gGLoXgnSuKnfe8IXSOcRipDnpETHHZCyHCMDK5+TZNs8Nkwfnbe8ZQUN6sPTqD0LJogg4un7l3EBK60XzqRof0K/rZlntnryAWM6yM3G0viPMNfhJ4/VFT6IfzRXENXbSotsLM20JldQG1K1l79vYJ7tEV4WqL630xlDmYyNhpjaoMd25nTmeeFLfE9Z6oa5ASaQV+vScPgTceGrbDIXg6B/QBiU/bHqFUMXZIGXe+Qyn4ZHVJYdEKXvdLkjjoiLSivnOCsJrujcfkwYPMiGnDuO5QT9dIq5GNZcGW3zf+HE7Aw3TG49PvY/P4ilobsArdWN7YL3h7+QeQKXM6jryw6pi/cMyjieHNfs9WBYYazHJC6hyOSNo52kWL70dmRuFS5GunNfJkxlUj+TZnEK4YVGz3Pbau6HPkjeOW3UzRAp+z0N6aMeTM/M0j8ttlfHJ7/iJSSK7CBU8+e59MZpFPeOXpp1G6DKee9Tr3N/f4lSf//XqLeA9CdP2FeG5jyddV1zWyJPJ7f+Y9e1F+l9Yr3ttkvWe97+ZnXlYfN0a/+9YP/uAPXn/9sz/7s9+S9/CLv/iL/PzP/zwAP/zDP/wteQ/f7PVNaop+iw3RB41Xv5H+6tn9OSOkQijD6u0LtND0SjKbTdivd9jKoKxh2BfBdT869jkzjRaFwsaEzwmtZSkipSwTs4nk9Dte4uKrD+gvtiglSFIQXWBmLEElumHEGE13uWV6MkcbfW3fqRvLuEvMby5ZPbi4DjKtm4p8lImH4M9EoV9N5hNyTEymDdoonC/FTHKlAhNCMJlN8L1DHSatKUSCymQF29UeWVvq4xmqsaAVm8fF1aydNMXprBsZ1h2Tkxn7i11pri53NKelyPGbgbq2ZQrq9uBW7B5fIfINgvMko0hSsN31YEt+h5KCeMg5ySkRfKAfRubHc4ZhJCeBUrJcAGQojlq1ZdjvDlPejBQlFT3Hov/w+x49q6+vAVIp+tWeWik651Ba0fUDUkm8tEST6bsEIlE1LWm1Lfz1VLjvToBLgcdXF2QfuDk/Zj6ZIkyx4c0hQYiE0SGkRM8nZGuQFCvk7BM5e5L3RA95Uux85eG9E1Kx0a51sQbeDQV1UJJsJEkDWoCLZJlJOSArCbm8BgIwqujkciInuNitabShspa96/nq43tM7XehMUybGasuEIcRYQ0pZ3I3MORMc+v43cmfAHFtQlAQozQG1OhRpi6Upeeop8/CE5VVaATj4BG9Q0/qItS/2uHPN1QvHOPPN2TAHs0wJzP0vGV45ynjwyv68T7Nq7fRsxZZWagysq6Qs5q07kkxIXPG7Tu8kuScSFoh0aXYHwXu/iViVmMWLbIx+IeXhKyIHJBiKYoN8EEc7pJH5BIAmaVE5oSIEX+xRS1apMioSpE3O5Lb4ahRtYVQ0Au7bBlTJm8LlSuOHr8bEGTiOMKkQajS8HwgIvRMNCQ+iBAjDpTf925x719Gl0MoDgGd1DUtMHuHEKkEbiqDsYWimQ5aKjiEmC7agoBNNO5rW0jF9ctYXXKocsafb8n7EXtjTlqNSKGIOuFFKOYEzqGsIqpiPU9ry0S8PwRkthUpy5KTtOoRHnTbIrQhdxHRWtyDS8zpnHCxhVoXG+4ci9tYpZExE0Oi8HRz0VyIQocSKRNFhhxQbYN0nugc4WoHWpWGYduTA8U9cNoQKG5zYlKRdwM6ppIl1juE1cXZUUvcti/IoijBpWm9wRqFcAEz0UxnlqpPaJ9YTloyGTk6NJk8OtqFwc4b9mtBtcu4/QBuxAuFsZoEDJe7QkNVEjc6hK5pK40KZb9HxoIwjRGzaK+vYal3RTuTc9HfSIE0Ejl0iG6PaQ15DDB6wm5DCpeYRUO2irgbSgaZ9khrqG8dMa72BaVrq5LrdLBCH955Ws7ziy1BqkJt0wLTVOjFpDhW5ozMCUIgdANR5EKPjgm7nNLduyANAqIujn8HFzqZy0DCXW5Lu54Ogj0lsEcTjIzktSNR3CBFSqhpjdCyDCRUsfQ34YAyGXUItJYIaxC7gcYK/L6nrg60vcGja4mqC+PB+0xuLNWkgnXEhYGQE6s3HtPLjCNjm6oY40wq6kpDm6grAzETQsLOG+ysYT96hn4khoRtKpRS3J29wureBXrRwkSTNsVwJ7hAaitwkYuvnbN86YzZjSWre+eISjJZzogk6lnN5rUrnrz2iOObxzSLFmUKYqakeq8G8UCd+0j3uffQ657TH31YDSWeodS/QYeTDzS+j3rxj9e3fN29e5e6rhmGgYcPH37gY2KM7Ha73/C5PsqMIYTwnueIMXL//n3+w3/4D/ytv/W3CCFw69Yt/vpf/+u/+V/id+H6n0Ofe76S+KDz7OtO4Pzuv/nrpxqNFBTiAVghiCGyfbohjr5wlykUndHLok2IielyVja5nGmmLSkH3BZWX9tgP3GD5DQpJuI20MotRjYsPnPKxaZie/+C/WpA6ineaPb9wGwxRYlygKAku4stdV3R73vcti8XhJOE1bpYf2pdXHOkYOgdl/sBXRnC3mFnxcLane8QOSPrGmMN682eRMZoyfJswfp8TVWX3J1u3RGlwBqNnShsY9k8XdNv9py+cErT1gglcYOj3/XUy5baaPrVHjmpUDljKUV9tgqlZSk6tUQIhaiWJOFwu0w836ABbxV9imiXUdoypFQCW6Umxcxmu8NU5npSaoTEp0jYOkI3otuKtrJ0qWdyPMFOFeMqIqKgnbfYwTOGxOpiD/MGGoOd1HRXO2KmaJTmDUNXEusXJ/NyUVrtiEMpLKqmIu8K0iGzopYNk3rCVDZc9VdUxpB8xiSFyKo0LALERBOyZ9VvIGUmdYM4hCYmIOpCHxOZw2Q6omyL5aB58B2pPkz/ZLGbTTGhdLmwR1fQJ6FlaQ5zha51ES2r4qQVR88YPfPqCKkVVmvunr3Cau/pRWIxmRAH2AXHZrthPp2TcsIEeR2+Ko1GG4GMDjXTjJvA4Euhbw/0KgA9eqphKL/TVsHClitsY/FPNygpCL3D7UfMyawURiHhHq+oXjzFX+3oVnvqF06QlaH5xC3UYsL49lN2X76H/sxtzOkcKSTGJ4yZwKwtmSv9SNz31OOuCNmDY5QjKjkSrjQjV9tiEHG2xNw9RW3XVENEWoMYHNl7BAaI1856QkikEMSYCgL0ZEU8mhLmCrtYEPU5w+Mrqjt3EW1NvNqRvWP/tYcwbYoro6AgHIOjmlfstxvkVOCShPwBblKHfe3DZznXE5z33J+BRhefAYDWQA6x2KH3Bn85Ir0tVCUpqKQipKEYcKSMERVKqLK3TGvidkN154QxRUYiGIG1poTVHl7QP7osf2OtiJcd2arrWirHhL1zXLQ7KWMyNDePsU82VFXZa4VW15TL/vKKHUeIQeArie0aZDI4cXDsi5GsLc5I2AdMbVFSktYdpETyERUzSZawV3GwVRZCgE/E2CO1xBzNcZsO21boaUOaeYRPhHzQlUwq4uCwZ4tCv9oNZWgjRHF0rCx52yOUoJmUPbha1gxK4h5eFl3KtCFrjdIG0SZqAylkktuhRWJ2bFiPa2RToUQZtAUfSNMG6SLGWhTFKU4pxVwnqCKWgXq1w8wEdVtRnyjMaihOlUqRekfsRwgRe+cE1VpUtyetdgiZ6PuInS8IG0fVNISdg8s9eSHKQCQURkQzb7GnBn++oX/rKZARR8WAJe17oOitog+IEIijJJuC1CgojpG9Q9aWvBnptxvMrKG5e1oc4ELER4HbjAy7QF+19KmUDmoIBxfEQj2NYySeb0q8WEqo4xnVnQnaj+QmUMkp3fpgjhMy4Z1zUj+W656UJfg2RIJSRVslQFiNrg2hc5hcULrgA4sbS7LgoP88RCpUBr/tyVaTZhXbwRFTZDK1GCFxCLoYmSwmBBfKdXR0UBm8Kbbxznlchs2TNfWtGXm/YXP/EnF2xo6E6AfU2VEJdo2R0Sd0iOz3AwhB7BzBea62HWknkFrQXWT8GKlEg5OSy03HXIC73FHPG2QlmNhSmPrkceGDjHGeH7k8kxG8D1p6vtZ634b0dU3OB9Ziz7An8Z6n/Xh98Hr48OFH0sbu3bv3O/r6y+WSR48ecXV19YH3/6f/9J+YzWa/4fO8P07i+fVTP/VT/NRP/dQH3met5Ud+5Ef4G3/jb/DKK698Q+/5d/v6Hcgp+k3c/ew8zu/ntpYzWuQP/vHfYyzfa4to/Be04lc3Hd2uxxwe3O16hNEokfExFT2Q8/gY0UrR7fsylby6y+6BZNp8mu5rF+B64mrHD01+BmUNXaP4zz+wJPIOwiZ8+L1koah8oJnWbNZ7pjcWxBjx2562qRh2HZPa4nKm7wfSGAgpIWc11Aa/G1ATi9905NFjdaFtxVimqf3oqKMtk8aUsdOalBN9P2Aqg60sUYG0mnY5Yft4RTtvSS4iXCi6HjiIYjPS6mKOsJxy/rVHmLYiCaiOp8hdyS2J1pBagRaiUDnyAr/9XvqnD7g5nXBnWDOOjosm8c7EMJk19N4jlGR5ssDnxL4fS3MwOPbrHdEFshJoa2HvmS1n7J0npcSNT605+rYdbjvw6NGSxekrtLeO+MSjLVyNPN047h1NUTeXdFc7TEiEmIg5IedtEZXXNX03EGNiwQE56x1UmdSN7HyPElNeWnwHsq7Yi6eM4ZdRWjMxZ9xpv7vQDlJxUpLWsM4PGK7+B/dXjzFZ4odiVrGYFMpZfFZQpgxCcrL8To6dRwt4OPwPdv78GqHJRrHb9SxvH0Ff8nJQ4lCwGW7Pfx+tqIuNe04QI84W0wclBLUx4AN3l4ovXb7DL6pHTPKa5giqjSaGyMX6itPjk9JQDw72PfXRjLl13KjOSQyc15aHY02g0CmR5Xf+1MLyiarof8LgcKs9djlBCoGsNHGMiGldDCkutqijCdlAXO8Z3nxC9cIJKIl7cIk+nqIXE+zxFFUZNr9+jy/1V+Azixdv8OqDERnLRTlLEFIyP13yPeME9+iS8PAJb6VzZIhlw5ASJSR5DKQHF+hbR5xOZsxevyoW3JliwR5TcayiaMBiKoYJSspSoPnI/ktvcU+/jF6c0utIHy+xIWFmmnQ4fnRtKV130YwpLSHBsB550yxo6zmjkMS84vmBzfvrhWd1SP4AEv8H7WOfPY78sU8d8lpEJvcR7wNTbjNbfichbvFjwLY1DI6n219jPT5AKcXtyffQVDeL9a+SZBdRRxO+VgfWn5wjUuZTq3StpXHna+K6Q09mhMstdjlH7FbX+T7CakRTEZ9sqF3ik48dk6lDvPmET/3gMUIKulTx9nYOKfMoPeXnTjegFC+f3OX75A+hasvT/BUu+l8HKbg8rXlyUhG7irMHe26Hkj0joBTSMR0azWLXTAJhBOhir5/GQAw77J1jpC7IxvmtihQi+YBeM/pCE13vqV88JXYj4+PVIYg4Q0qQocqeT91NiNGxffLrvNWfXAfA5t2AmDcMrHh79TNU05qoyrnitz3+13focSROGsziMyDvoiuLolipdzHwaaHx99bMzxacXX4JnR8j+khlawQWLrsSnXCwu4+jJw6evB+Q1iBrAyny0nJLdUvSbUdevz8lXYIVNbc7R7rak4ceeaqLdmwIZMowQ5qCGkVR9iY7eMJqV3ShqVBK0UX7KlMZ1mQpEaMvx3Iu15RsAs3Nk8NwrLjuCSF456HgyVc9WS5544WWrtVIIfi2ex1NVvhtT+KATD87powm70fG+x3ZCsR0ijmeI0VP6h1VYxkuN+VnfABbGtlcWdToSTESQtGXVYsJcjtgjGb/dM2u2nF854TROfzgiYd9KwP94Hg8rTmfloHA94zwR2ctMWd+vjG8FosOqVvtSo2R4O1lzeSs7IfjxYbKGCoFRnwJK64Q6Ypfb/4PNncXRBeopGQcHd5H3t4lVBcIo8dMavr9QPd0zVdmZag3xgCX30l/USyyV2cWBJySeElJru5dkhR8z63PM7+x5O3Nm3z5yS9/ROH0/l3nud3moIUt4dfPhkXvecQ39HzXdLv/OcqIj9dvcX2Q5ux/5nLO8e/+3b/jc5/7HD/yIz/yLXkP3+z1zUWKPpBb8huv9yY8X9/6Hor+80sJsJRgq92TNeedK5PQGIsv+2LC6nJDNWkIw4jSCikl4gD3D84zm7YoKeiHkegyJVFQUs1nhZaXIjplhEgcffKMOFzRv9PT9YWWsnqyQh9N0M9E9C6wGhxNU+FdRM1rRILu8PpNZUguHtzrJNYYjo5mdM7Tzlq61Y4kBEJrjDWkQ4q2T/lQzJY0+5QTZInKGd1Yjl4+Q2vN5uElk2lLNzpMWxE6R46J9nRGVVlWT1dURxNcN5J3Hns6g0OT1XcOexA4I0pDlZLENi3DVUf2gcW85WocEEIw9o4UCy1lHBxYhRoDuIAPCceAshphDUYp9LxleuuI8d45Sklmtxf47glus+fsM9+Bbk6QstA4mhdOaM4WrGt4crlFJvAukJXETCq8cwgEu/WO6SGPRnaOdHCKS8DVds3rm8eI0FDLb2e8cIS44rXV6yzaGRPtMTc/QQakjzzYnDOkQNN27NyKo2bK6AYqpQkxEUJASIOIqQijm+JqKJMAU5Viojscq2MgSQExMVMSLrYlVJMDfUPAdrPmnf4Rn/7EZ6mFwjvHerNmdMUNzcdIP/QEIbhlj3nh5BZv9yWQcwzFW04ohQ8lVDLHRBYZbUwZLjyjwLiApOilTC5DhjQ4zHJaNELTmtyNqErh1x1hdOickU1FCH1xpZpUxMETrvYlc8hqgvP07zxFNZbq5pKw2pNCxB7PUJOK9rN3UWZguNqyXe3p9ob2eI5sbEFwDgWXri36lVukG0ekbqR/4zHxYAmOEGT5rKDfoG4tqW4dER5eFdqYVCB5twDLCfVsC0mRiMRoQdx3XPzcl5m8+grZl2l27gdG50hjmY6rtiooUS76l+iKMYCe1iij8WMkVYpn7P3fsEZ43wXquq44NEvPzJykEFhTUBhSxo8l30mtB2LokNMJJu5JzxDwHMkakhYlUDdEspakzYB9+RiEJPQjSVJc9SbVNTofHq/Km3Ae0YCZNKj9Gq0UnoiYFOQsxUiGQrsrzDaUEgglEO7QEMZIiqm4ABIJfY85OSqoREiEoVDX0uDJpiVRogwYA/GwRxNLAywOjVASh6Y9g9iVAQtaFYOJBG7d43cd9oBckBIpZpSErFXZc7sRPW1oalvQyHVXDAysxuqAMmv0fIa8cqXpShEJRARiOyBTKoioFVTzCXE/ABZJgx41WSmuckaEUNw6KfREMXosguXxnNlsQp0TdmqQugbnCyKpCmtBLqblOJACaTVqeQK9I/YOO7WYWpPHnmZWA7kwCc6OCO+sYQiYaY2eSPRRS7UHfVkal7TalwYoOrKt6R9cQDcUChqANQXBlsX4QjqPaCvE0QQtZUHhfMAcaYQaCq3xYN7pLjb09yKICmLGaIVRAro9PH0KQ0bWDTTNYS8qGi8OmkdihCRJu54siylGtAo3OEQq54s5mZNiJImMXk4QF7tnpwVx1xMbW86XtqLtNFVlGPcD4+iIIbI4XRBCYPt0jakN3nv2nUNVmqOXb8JmYL6YsH7rEZ0uDoYpJKqmwsxrhCg0vfWTK6q2KhELFEaA3+7L/zHiEfT9gIdibBIiw+CwqTBCYk5IJTBGI0j0g8OliJEWP3iMMXhZhqDbfsT1AWs19bxhf75HZIls5LssmWcbyG+mqDogSM+DR9/wTx82q8NOxcfOcx+9bt++/TuOBn3UWq/XABwfH3/g/X/4D/9hfvqnf/q39Rp//s//eX7yJ3/yPbd1XcdXvvIV/vE//sf8xE/8BD/6oz/Kr/zKr/D3//7f/2291u+G9U3JKSrrNygVvpFz6xucSPSm4aqd8ui1B3xp+ybuhW9juZyx2+xRqhTqSitMZRh9QEqFlpJkDI0xbF3ADWUzNVrj9+8KzrOAy1TyKYJVzINjWgmW336LN1ctcnWBbWqGwdOOEV1FxBjoXaBVCu0iwmiaEEjdhkkODJuEriqklgSjCBGOThfoyhB3PcPlDhkSk6q6NiiQQlBNa7L3BUXoBsQQ0Y29thU21rB7eMWuH2kmNfHg/DPsetIhfLGqDI9//T5KK8SyxdYWawzBReqpYT5ccGRh10e65vTwhwpEv0VPE/V+ZCkG4n5gOlXMTyu61RadFXq0xUXKKERtsdOD49yzRq8fMdagTGY5S2i1Zt4qwoMHVIuB6UvHXO4nDF4CmeQD/aMVfT8SzlqsUCSdMUeTMsEbR6RU1HWFS+BHTztt2exWOGUYUybJwMnxCfZ4zrjN9Hh0Y1A0VOOCXYhMZg2/dvkOy/mSEBzT0yXKjUQ3kGOFsQ2XwxXZb2htxaI9IqcWUxuUqSFlzKEZDqEUkbqeoZxHiEhKHTEUi3Yda+IQkbompUDaZeIgSNHx8O13aOv20IgmlnXDqttBTMUePHqi9ygFR82UN68e8erxCebGi8UOd+zL8RICURT7ZaQo6e/ZEvA4ilBfK4latEQXSkBnzqVorA0Mjvp4Rtj3ZB9L6Oxywni5LefIzQVutb/WuGUfin11COw3HeZoSniyJmx67I0FetZwfPeY7umK8Nojwjtr9vcukCczxCfPinZISCpftDZyUiEqg358hew81pRML2kOAnQfSBeOfGxRpzPik1Ux0lAKTYWyNVIInNsTsy81J5BCQCpDujonvv2YmAQ5RuKmI+SSLSXIRU8hRUHGYkFX0jM3MDJh9GDN9QalBZy0pfcJCS6ecyJ9fpvLBTYqzV0+aADku4/ps+TRrrxGNQzMjERVkqQCw7glDz2ooo8xQpOlppGLA6X4oMESxaJfHk3JMdFsBCpNETFRTW1p8rY9cdMVlDJEYuXZd5cM45a5q/BCo5tjLp7cL+5wEkRjDuimIo0lmDhkRacFWSq8kQWFAcbouDJ7kupY07M3IESxkk+xUOJyzkQf0VKSVUETEAKpKE5khwI2DREZYawVSRcqnXy6JiCoj6bobgt4hFXsh8MHOrqiPXyyYloZmro0Smmx5KIv+hNMQE1GciwDljyMaK0I2y1qIpDzFjNrcOdrgi+IYwyFHizbiurmktiPLIzlrq4Jwwh5AJnIKrEQsHyhQuqITGXQF7YdtYXmyCKtobui2MJPG6YnhdqmagHTmtT16DHQE/DnO2QV0CuFns/QPjGKhLQCMauQNQVdNAJVKdKmI46hNBUhgIzEfkQqgSCStSmudilxUEuCVaSQSN1IjgkfI83JHHJXUKwYkZMprvNsH+1JoSHEiMkJff8Buip61ohj3O8QuxXy7DapbgBBFBKRMiplvKoJRtM92ZGXpRmWMWHmLW70pM0en1Mx31CG8CyzKJdspCwshIQ9muK2HYuThpNuTxp7Wl1z5QT7TYdVktoWXazvHU1tkZOK3cWO8wdXpG9TZc/ZdTSTBmkNzdGUcXDY1rB9vCLsRtIQsK0FBOutIGwl62DxsQwnQeD7kZMXTgndwNBfMuwPjfyYaWctWkIzaVmtd4XOO3qqaU3yCRdCCbWtBZerjhQSR7kiT2uu9gNpUWGnRwBEPxDHHp7T+HwUOvD1I5trG4br+z9QU/R+qt3Hzgq/69fbb7/NMJTa9c6dO/9TX7ttWz7/+c/z9/7e32OxWPDjP/7j/MRP/AR/4k/8Cf7IH/kj/1Pfyzd7fXPpcx90Hl1zSj7k/t/C+vUbn+Tt00/w+pNfJzYZf5gWaVlOZSUFShf6ktbF2ahQ5yQ+BNCSqASKknORR3/9u/Q58392e7oYWQT4y5dbKiUYwowvnXw7l1ee7cMrlDWk3ZqkNnTbjpfnE0SI+ODRlWHWP+Hl/tfpNx3pxqd4fSeJObM6bnk4s7Q3FgwXW/LoEbo4rMVuZEgJZRRu2xOTI4aAmdVQVez7HcvllNXbT5mczWkO4uNpVSGlZN+PVFKRxkgUJcdh3A201hT6ScwHi2bJtDZU+0f8sfxvqEXmgVzwH47+FEIJ3PqSp7/0f+H3IwtjePGyR4iSf3P5wgvoScf8yREvjK+ijeZruz2rk9K4qErDxQZ1KExFythJxe+zv8pJ/bPEC2iOJjR2Clc9/0Z8lofP6G+rjvx0w2bfs0kOcTZn6Ad0W9Gvu6I/8YnZ0Yxx15My+MFRVYYYQFtN1BlZWZok2ZmeX833mdopRimujl4h54xvp9QW3hofcrScYe0OrTWz3Rl3qxe43K65e3aX7fgGbWU5Wn6G1t3A1BUIWXQdSNLgyFohjeLm9Dt5Np176/xnCXpNGAM3lp9jtw08PH/MzfkRpq5Z2ITzgdZUjENfeOnBs1WaF05vIFJm5zr2Q4dEcCVG7qdLbh2dIZop6cXvZdvv2F4+YBGLS2KJfC0n2NZZ1uMx/lIVNy7vUVqTB4+qLbEbkVVx+JOqIriIUBE1aUjOk1MmulDsxZ+scLseezYn7Qb85a5QLAFcQlWauB/Rs4bUjQyvPcScLXhpmCGsIc5Occ1jwmrPcL7i9RPQL5ywOFrwbfcG4JBQLyX1Z+6i9MCN8GmEMaRhRKmS8bLq3uLRoy9RvXSTuO7ABxJw2r7M8ezTxBi52P8aq/7NUkwJScoJIQXKVAznT1GnN5C2JghBtBo9bdEplQwlawpK01ZlipwTWRaKnpQa7961nZtV8P/+HFQanu7hH/8i+PTePS6n4mT4bFwrBO9O7Q9FzZefwlfOgQT/27Hg//i0RkjJ1jzl/nhB3jlkWxG8Q289L02/m0X9uWI1n4sDX+h71KxGVEVz8XvOX6FiBiJxcfyIIEbcoxUxZmSOhBB5IL7E8PYlehD8ID+IMjVuNeX/5+/jZUbEiD5aFBRRTei+OkFkWJ1YXv/eGTlGthdNaY6F4JG95KdPf4XcDIzxgiQmRdx/EOALq4uNdyzU0JxzcdUbPcnq4u51cKkQMRNj4t6timFaiuFPPhyL8cjpnBd2j6njSPCJr6VjnFDInMtAYHCkJ+e8/B0KbSSXA/x/fg1chFtT+K5j0LWlevkGah9gP6CXS0AgBkeUkpwoiFk3kI1GPcsGayrMcsrR268xj19FH4JM9aJFGEHcD6R+KO56pGt76pdfrWlEjzCBN2TD5mEHMfKCeEo19+QYC+p0q1hbf+18RrKvIMfA2X6PHiLdfsuD25acErOblmXsiA8uETdvQfCk3pFdJO53YCsElCDbyiBCRE8bZFuhd0NBbqQiRSBHqEyhBO9HfDWQ2wQalNU83tU8/KpnXM9KIG+3JZzf50wp5I1biNmc1M4Qekm6fEp8+Bb6k58iSnug0SWi0rx+36DmLUnOSfdX2LsnpMqWv7cqDWn28dpSHlVQYNc55CHUNg8jqrVoKTj1F/yAvmD1+Ip3Ji+xO/puckq4MdAup+zXu5LxZDXTxYTXfvkdYtuy7SPq8ZbvqS3d+SX9977ERU74TV/OUReQSqAAPwaEVPxK/iTD7CV669BRUU8MXivC6FG1oZo3rI9mPPy1dwBo6gqhFUfHTWEWiGI2ZIRi2A3FalwK+tEjFi2r0wlCCZ7MG/rdyGK5xM5qTl7+BFJJtm//Kps3/8dh2zg0Rh9BaRMf8NV7b31fEfYhz5N5pi36yId9vL6F6z//5/98/fUf+AN/4Fv2Pv7yX/7L/PiP/zgA/+Jf/IuPm6L3nJ+/FfrcN3i2XW8IB/tP51PR6kiBUYrpYsZ2tcVaQ8zFGUxbjXMepcrUKsaE1opKSoKP12YEV/fOcexp6rLh+FgcxUIMMCZko5GU/Jijb7vD8qUbCCXZvPWU4cmaMSbk4GimLaurniRgsWjJa8d82ZI/cYPjfg5a4RvJycsn2GWLmTc0NxcIYPvOOdvLbXF8ShpbW4ZdT2MMw3YoYtxpjTCK6Z1j5qdztk8LdCqUZBwDtq2YTBr22452OSVSXNiUUrTTht1uwMwMofdMz+bITSaNPXbZcPbSGZPpgiSeBcdFlBFIDZO7RwgpmGpHf7lhdmNBG1rSG8XxSLhIc7Zg9/AS01qqyiKVxARNGD3V3WOUhPkLS+LoqY+mB+1FKu5jMZA6x9XbT5C7gaatmZ3MuOhGspHEwTGbNux3PePocQ8vaWctPkUeP73izrTBNIaYErKt6O/veHT1lIuYWL70AhEYcuDGyU2Cc0SR2fuBIRSb8K3rqYPmxCyJ+4zVlm53ASJgjxbEDI82lzRdw/FyibSy0AfnLTJlko/E/VjoYVoV5CwUjru2lrPjI5yPbMNA7gKjd0x1hRo6zGGKKzPs9huutCYJQT8O1Nqw7/eshzVjPXBBpq1btBBc7LaEcUDVRZgsJw3yQAs5ABRgLRwytjhYk+f9AEqiT2YlsFFItNGkzjE+Wl0XaWpWEwWY+YTsPP5yQ5YKe3NB3I8lr0TJA5IT8f2IvV0gfH//HPfWY8zdU+yNJe1nX2R4+wnj+ZoUIv0bD9H3LnGhoTqZl1yjg6i6+exL6Htz8tW+FG+5ODPJDAyOeLHB3jrCvf0UQijhpSmj8qEBEQKhilOdlKrQ6oxlc/WUaVWjP/0JNk/XGKtpbi0RQ6B/eEmKCZ8zNRW2MSXXRUn8fihN9+jLZD0VSokSIENEoiAXCuOzcxGKruxdLv/zfxR4FjqdM4RMgaeVIvmAELKct25E1pboPGZqYRhJmYNtfHEUzDkhM+iTGSFlRCphygZBqnShOl5d4p+sUIcJcSKDlcgQSEIjkChrwcV3JdxKItsa/8451WRSqMWU95sPYvocCjIh5MH23grc5VhYyKIUUznnYh7hIhiNDIV+m4Uq+q1YqEYiHIqwg0ufECAbW0J5M8Tgae6ekZxHhkAmEeuK3CvCEDGCQqkTgrwfCBcBc2sJQMyClA+ZZbpkGsnKUL1yUiyrn25Iu75QiU/nyLYiPl2VTyvlYgJgVAmfpYRRD9seXWnwEXYdYT8Ukxolyd6RD3ljZtYgjcJYS84lxDjnjKgtmIH0LFhYCobzNUpbQsy4JyvUGEgjRD9irETlRLQKVZnyubfVwRHzWUOZwA3I6QxZW3RKB5op6NM5yQfsrSX+fIPf7AvS/MzcImeS8/j9wHA1IO5qlNHEXULNJ7DpC92vsrA4QbQzUBZcRoSE1BZ14wVcCjCdkjY96pA7hJR4H/BXO+pbx4TRE843h7+PIM4nuKst5hD6ak7mhMstMWaskcjRk60i5UzYdKhpAwdNz9HpjE00PMoZtEZMKtx+hJAxc8PZKzfprnbMby5ZTqdcPrrkxiduIhLc+MRNvpQj+6sdkpIr6F3RVxljGINnHAaGxmKmFWGb0BlMbRAZtNG40bO92DA9nlHNW8b9ADnjnC9hv91YzgUh8M4jJNR1xX4s1GzvCmIURWbfFWOFkBLrexcs/IL5raOChL5vPR9N8nzz8m4G2jdj+vx8Q/RNnGh/vL5p6x/9o390/fW30g779u3b11+/9dZb37L38c1av+2m6Bvqad7DKfmA2567Y2IEx00mx0wQCh/V9SNSTETnWfQj+eIpL0jNVgo6BONQgs+klATnygWKTF1b6rpivdq+q5eRJXsox0QfIjo43rq/4tXPv4ITcKcecTFSR08cA9kKCCMTc8nhkozUivZTEvfKEi4mhTNvDfPQgBRodty+8SoIwfl0gjx+EZTkyAZ0HSCuybkiZsHDX3ydNHqWs4bQBUJlSbo4aQ3dgLSa2e0TchqZmYSdT9i8/pR6O9Ii8eueSguag2B3uPCk4FloTWstIYKdtwzdSGsl9e4xJ8HRviAZNze5mhhGabgpz8lINnnFBSWV3mnFY1uK7f5kTntSkYXCGkm9vyBvnnL27S/xoC2Tv/TkMWcnxWp1262p5i0TuWe9dzwMNciKsyhoDJAFbYTJGFm/fY66uWTnzmFiCTHhnEPpkn2kkajagBS43rFabTm6sWRxMsfkgPBPis1yFGRvmZpjmFZsjaFSmvP9GqtLqGRlDC6UC2AIiVPdsh9Het8RtuU4SsIzn1akfsS7K7oRrlYDo7/D6cltrDFwsP3VtgTqIiiOaa4idQZTWYiSJDLHswVvnO+YNxOs0ggreXt3iRQCHyN1XZOnil++egs3OhaTGclBYyvWeeB2fYTRGj1kQuiZZovHghzwgqJNeY5ELq1GVEXUXarCRFQCIRRZS2Ln0FqRQ0BPqqJnOQS75pBIqw5Ra9zgMUahTxbgAsF5RGsxk4q46YlDMdzIg8M/WSOlQB7PGGrF4D3ince0tqK6fczkbMYk7IhdQG87zq+uaGtJe7qkcqWpyCYjXp3S/dI5dJHazMgxoUxLW52Rtwkx0eizBf5iW6zXtUbFRKUnNPYYEHh6XHbQe4RU2HaOOj2murnk5HheqKwpUd+eodqK7s0nZTq96bChoT09wc4aOnVBDhEl4HZdBN1tJbm/Aq0kq/EAEMnneHHX6Pjhhuvp7ofvli5Jdt3B4thWVIsK0VjSuifuR4ILhCqUzydGxrgj9IEcAmJRk1Nfwi4Pr6dnLbVZMD64z4Q5+aBdSrUAZNGLHfZD0VjSviOZEqqajUZaRewG5MkShuf6OSkIm640NFA0WoeCOQ9j+T3TwTwBro+90Gj2uoj9F2aG3WeEnRJVxKftAT0q4Z0CQb0aiLrYr+sk6N94BAL2TaGCJgI5gm0qyIm4GxF1MWjYPtjjTUvvBEtpiEIwU4rOS5SEIZQhgWoq5MtnuMcrsgvkGJGtxXzqDv7JujQPUqKMoLKBuL1C1A1VY0nrPX7w139vVVtSiBAjjc5oA/ZWgxKuNIIuoGdTNKk0d02FqQtFCiVR3YioNGZa47uIrBXEgmDYOycsbyf8rkM8fgS3E7SmDKQIRXezXpVmUxanS5VT0XrmTD1uy9+462iOLRwtGJ6sIETqF86AzHD/HCF6mkrQP1kxuXWMUBI1rbDLKcP5llzVYOsSZJwz2ShEKlb4KZTz1z9aIWZtQUlzQkhoVSCGgDoPIA1+tS97zaQuGsdpi120+IsNOUT08Yx0uT3ofDQcAloJibDtMWdzwnZApcSyEdydRMaxZ9xKXDBEJEobnnz1Ia4fWbQNX/3q/dKo9h6fItOTGQ8uVuSjhn4MLI4avJYYo7FjyXYbR8/k9hH7TUddW7zzhfIpwI6Rpndcvv4YczA98v1I349EAd2mY/SBJHLJ1wueybQlHs6N3nmMFnSjQ///2fuvH8u2PL8T+yy37XHhMtLcvKY8q4vNaYIeI43DUAQFAgIISHqQgAYI8J/hKx8lUABBQBy+iAIESANqABHUDMUZNrvJNmWuTZ/hjt12OT2sHZF5XXWRXezmsO4C7s2IOCdOnLPNWuv3+7oi6b2GzuKmJm5qstxSbN5MI3e7pfiGTvdLoeF84ddFfPuhbwqi/9DGP/pH/4h/8k/+CQB/7a/9NX7t130AbBIAAQAASURBVH7tT+y9vK2p+nnW3v9zGb9co4V/W4ToK57/vZPIXz3vcP3AVp9wZeeJ8tQNSXTfwplz5L3HlxX/VEb+1XaPUQpjFN6nBO4woULOB26uNqAlWZ4RpUhZP1pymDaCkYzXJ38GNx5Rloq/UfbIMBKFoazalBvhtrwj/l8UJxW2H5GTCPhpq/h/7PWtK/Dd5/q+1nwnT/qTXan56XGB7QYe+5f8cPMxyS3rPfrtKeXrAyBYZRWHzvFZabki4gV4Lakzg216vv9YUIRr8pixebXluJhjO8u+65mfLRivO57UOXmRoSN897KlNI6+Gbj8nqGcl8SbC/7X5p9yXh9x5TT/l+cVLsCj+Zb/45/5b9FK8gnwUWKz8Nx7/pt2Ek08bQnT9X+sM36YpwX4Z67gab8kW5acv/4Z34/71EE/n6bTveB/erHn2RYI8L/7EXzvJJ3+sycb3Cc7joBPHs3Zf3BMd+hRwVPWJeMhWZeP0RMDKCk5eXjC9mpLBKq6RGxfosb/J0Ir6uJ9Pjj7y7xqDswMbP0ly6ok14Y8yznKK3Z9SyYUOi+5Fwoe7StsyMiVoS8NymikdLShRQyWnXxK8D1WO37n2Ut+YH+dhyf3qYoS3zhCJ9BGJ4rKouZh9Ruc+0DXttgxIDNwE1qQK81m2PM7XODLpHupV3OMHhmDxRQKLWY0xvDJxTO8jfzg9B3+l9n7HIaOp89e83B5go81Oz/gYwrrvUVR71bOENFFPqXWk/Qn1hOFQNoI0adw38IkTdTxDHM8Y7jaEfd90ib0DqUkrrNwsYNMoxcVPkSG0WHKLFHp+hGRG9S8wt/sGV5c89EPj+FhTTWref9fvab5/SfkD475tZNjxutLtruGj9+fI/yek2LO92y64Nrxhs5ucPca1E8GHoofgYBZcZ9ZeR984Gb/ETcri8x1omdNGSnL4j2WxbuICK+a38WNz4laE0OgqGdkxwuUUZhZyf6T14gqQ6xqopbJKZF0bO4XP6JaPIRS8knz/wEcBZ7/7fc8eanYofg//RYMdjIeEJ+rR98IpG83NLdz3dc4BEXn2Q4FH16k8ycAVQVEbrA3h4SqTJbFQqV55/X+pzTdS6hyZvqDhAINdrJ9j2SnK06bmnlUxBUpo0cK4irnifufCIARMmm6igxuNsn5jUS7jdYj6wJZZIS9e0OZhETXunUMjSmHipjyZQCiEgiVjruIiUZ4VcLVtxeIquDPHb7Ne9sTCHDh/4AtByTpM/phQGcZ9190k2g9hR3HXIOWPLPHyJBQNaQkWA8SsmWF37X4xZwnGwGHhKL8BgJyQ9zDj/9NhpkVqMogSiDTCOeTyN+mbBzf9MR+RK3qVNwpyTJvuZ9d46TnemO46mqESCGszjqUDwmBUhKc5+x45OhUoaobODisknchvHpZ0z+9ZHyxpXq8ILqQjFDOlghtUCFHFokOJ3JDbAbiqwsenbTo0wJbDGTnp4wXG3zsESoh6YSAKkukUngxIZb9wOpRyfvvjMShQZ0YQt+gFhVj5Rkvt2SVRAqwx/tkn328oHu2Z3y9RswWCCkoHhzhuxHbjcgY8ROqp0NMbnpZQs20j8QsFfaEMFHRAu+tGvJ5BquC3/0J9F3Avd6i8hR2rmcFw9UOXef4psdUFXmmcTf7dA3ViRIYuzEF5F7tMCdzqHJOLl5z7K9xITB05+y7R+l60z0HIzBK8zqTiPM5XdcnPWr0KOGQJ3N0pqhWyVxJqeR4eX7VIrctelbw2aHHW4/KDdooXDcifeSDzcDc7znq4cevNxSrmqzKud61FHXB1dV2Qu4jeZ1TzyucD3TdmNwtp+s9rzOci4ztQFZkEGBxPKdc1Z+bI77OQe6LBcsXrWC+rqD5krbo7X7NNzXQf9DjH/yDf8Df/tt/G0hFyN/5O3/nT/T9vG2u8Jf+0l/6E3wnv5zxx5NT9Pb42hvudleR+MNGCtz6QMzrREHITeoqVQkNMLlBOY/0jmGwiEIiCBijmS1mNPsWaTS+G1gsatabfUrdlpIgQAtJXeS0/ZByaAbPxe8/paoV7593VHVyT0vBpKRMod7ih2FKvQ934Wohhs83gafk6L7p2b1e05hT4oOILnPkoIjdtMmIKWn99J0z2pc3SOfRPsDoMYsiWU/PcsbGYjOFd2KazJgcfZKGJSsydG7o9h2hHYmDo6gLyiwjtANCS8gU5YMVUrec3LuHKQVyF/A+ThSTiCQi3nKtebsP9SWKJBFTGUyVoUuDnhfoWc5qdo4eJ472pBOIE1UoFY6CEAJEwXjoufjJU4J+TAQOVzu6XBEyRbSOXEhMaRKlxXlCO7K4t2Rok4bscLNnsZwRXEDkCmMEOtdoF5mbgiwXnNbHbIcGJRX77Zp1t6fQhnlW0o4DFkedF+z7LonsgZnKueo6um7PYup86CJnLjLGsSLXGfvDjiIKlBD0MdAfHFlfYTKTcolCQAqJ9wOHZuBqt0YJwfqwIwrBoWvxChZlyaHZI7XhcnvD6CyPH7zDcVnRB0edFSyrOYddy2Fosc7RdQ0n8xX50Qmt3rDZbMjr8m5HHgaLzDOEIoVatgNutHfoQLgVMU95Som6lihgel4S64Lx9QZ8CpM0R3VyrB5s0hTVOWaWJ9tsMV07zhMOPXJeIvs+6esOA8OmAyXJTpf4dYO73JK9d498VYHqCC7Q/PgptjrGTBuBSEQtK7LHc1hP723aYIMgRoG73KJPFrARqLuOhEjWvNPzb7utuiySDmzfTaGeBtf26LbHljnDeo+ZFTQ3O4xXyNEj9gNMTY2oUkaRCB6V58gx4kaPHTyqyL/E3v9KPOiLTaCpiBWQjr+SqEJh2wHpI1FL3LYFo9N5m5c4MxW/WqUcLCA7TsHP0fmktYqJvhZ8oP/49Z27V5xoOHpR458NiU4pkoudKvM3jm4xBSG7Q485WyJzg3x7lRBMNL+JqhgjelHiDymYN4Zwh5oordJ7C2+OiPQeUeawno6Vlim8uPeEpk+HKdOpKNPp9fEeofJUNK1bgtGoQmNDSHk/gyMIkXJ2mh65rPGHjqhU0s5Zj8hzPBK/6YhXe7LCoGYlsk6UZLoeWRdkZY672ePWB/JHp4R+JM8EyjVks5xDXpPZBVGIhJJummQlPwZS186DtcRdh8gUal7SP78mas240QxuICpJaAd8OyaTEa3QSjHuB8arLbhIbAdEAFXkhL4h9iMsy7QOXe0mlDqF9wolCSenSK0RRPK6IHQ9MUay0yUqb9JxjilkWwgwixLfpXmhPJ5jX68JmwP9hLwK7+ifXGDlMmmeMoURGdjk8hknN0spScWjlgQCKE2MKegX57jd/Afv0ZlGCY/JNaNIRjnl8SzpHnctqswwR7PU0FlUqKrA7g6p0BtdQoxdMnkZnlyQ3T9G1RkiM0jnicFQeYP3AecCKtOMBJTzqVA3ikPXszxbsr/aAoLZfE59ukj5fZmhPRxSLALJwEQbhY7gQ6SczHXsaGn3LbkU5JlhbAdsCJg84+T8iOA82/5AHlJu3tBb8lKiRULwTZkxOocdLCbTKEh7DSmSK66S3Dy55Pz7j75iEvk6wPmrDBS+brMVP/fP1z38zfiTGV3X3YWlhhDYbrc8f/6cf/7P/zl//+//fX7rt34LgLqu+Yf/8B/yox/96Gtf6xcNbzXGkOf5Vz72xfDW2/d46z739/7e3wPg7OyMv/W3/tYv9Bn/Qx5/9KLoj4LcfsXNZ72gocQfBoao8b1FaoXKNGGwuG4klD3hyGK7AX85cnyyYBjcBClL9ruGLDdoLQlaMViLKbKkSxAi2cJKQW8daEWWGdxlS13lOD+wOS9pCgHSE1sDMaBF4DQE/JA6itFFsipHjQOPROoomrwkDOmQzkvDTaV51cJPfu9nPH9ZcProjFbv6UxJPiuJskBIQfX+GSrT2JsDwXnybU/pAvPCoIDttqU+XdCsLb3yLLSmKwvGd46ILuA+epWMGUaHlIK8MAz7A6p7xrLS5I9Oedle4qSkXkSe9BrVWNbddAoEDF7w8TZRA14d+LliToB9iHzqPELAVbtlWKdE5V1/QN8ZV7x5jWURyFSiZkl1zHbI2D27YEfOoAVtO2DOj6DvU3o70CtQucF2Q0o5R7C/3tPsGhanK8Z+xA4jODD5Y0yVM3ZzruXAzo20g6Olp/M9KgpmWcHxfMnF9oYxePSUOfRZfwVRINxI5ga2siHTAT2fI3TiswsiY/B89/QR95bnjN6hpMYqyeX6klwoCinQ3tP1LVIK9n2LzQRFWTA/WRJEpB8HRm8xXUZlNHVe8mpzjbSWB4tj9nbg5uaKZV6yWhwRneXqsOHICZbljNWspvc7dDYwjC1CKxZFBUriDh3Ruan7PKDnFbouCFrCvsdPgYBSxClHSmI3DaEZ0Kdz9KxEz0vsrqV4cET/9BpGj+8t+mSG26Wi4hAcfgShFPnpjBAirhkoNx0qBFSRMzc5vvNEH9keGqTRVI9PKNYd3U9fIN4/5ezBPdqPXpI1AxfXr6jmjynriqL3iZL0aE7XHXBXOzJdUej5HZIS2p6wqJDHM2Lnp+t42kRrBUbDkFCkkBrb2FeXhOAp3n+ALjJEM2Bfru+c9rI8Q3tB69a4mwFVLBAku30hI72sCS6jt4H7co8+LvAGnu3g7VjXr5wOv0Qhjp9/TEAIk15IxmSKkSX0cWz6FOoqN+wxSdcTkltbdv8YZQuMLpD7FpUrhJT45zcIHwmT7vLg1kRvKUxGMVZofYpRaUPOpLnxb7296DzmeM7gI5/59Mgh+ISCOY92kapPxYg2GU3TpY8hJdF55C1l8PacxJD0X1KyUz2vjAUp2EjHoQmImcYODpVlDLnA5RoKgwlQrgOmzJL1uw0In9zRTK6TzilEYj8m2pZRaYNZpPv7tuCLISaDjQgoSXe9JTt0qKpIhXyRYV+v8c6TnS2RZYbbNbj1gfFMY++fY4UgaAPXkThY4qEjW5TJma8biaPD1AX5/QqTD8gypx0VvcsIQ8BZT3Z+mppq/Rb78hrz8OSOBjXsOmwHofVkZytcFugvd4iyIBBQPqc8XlEpi8817cWO4OaoXCe0zweEVvhDl2zDjWbYD2y8xbYj1SqnXs1SkRrBzCviYBm9Yt8ASiCGEVHmCG3oD5Zh3KYGntaoKrkZSp2CzmM3JjOTCNKkNTqSCu0iCBgdQinaVjKMHr0UxNzgdz35rEgRCl0K3nXtgN822INKZj2A1oaZzBP6sarpj2b4doDNlqKU0G3wRY3LdApu1yP1oic4z71SE2TEC4/vd4naDIhKoQeLcnuQgtkwUOxa+pfXnB7PaNSe1UqCGlBFJK8Nm25EGc38dMn6+TXWesTxnL2W+BDJMoGLMLbDnQ3+clkz6zx211EVGTvrkCIF5vbdiDQKHQU6M4xDj8wU0aZGTv9yjWxH8rMV1v1iFcrULvoFAZ83GqRfhBr3jaboj3f89b/+13/u40II/upf/av83b/7d/nOd77zc5/7i4a3fpXt9u34eeGtt+Odd97hH//jf/y11uD/cxp//EjRHzIONuPZOMP5FIYmtSe2PdqkFHBT56wPT9jmL/Ah4PRDCj0nquTuctg11PNqClYTBJsWR5NrCCAzRYbB95aclPINIuULHXrmj4/5pw/3zL99im0tn/23W8IIp5Xk//C+ROvkPqZzAwLu1/C//1OBKAKZUvSfVMQAT48Uv/0XTuB/cY/Tj3LO/385F//iQ66d50ZJ6oXg+JFjftqQz0ryR8foRUm83PHuriPuHeO6T5am1lEZy88wtFXNi5cR7i3p3l0hIrzrA/bZNcv7R2wfn6ALQx4H/jK/Ta0HDu4p/92/hNbCTYT/hkiMSQNxK4q+7uD/OuXFxc8VRF9dHX3sHZ/4yZHr+Yfw/CMArtMrfOn5/5sfwJ8+jYQg+Mnz9/hXHy1obx7yySrjSoM+XiCdRQnJ8mxOd+gYvCNaj0LQdgM6M9g+CZm311tkppBCMCuPcOE/I1bHXF6/5v99+C0WiwUuBMLgkEbRDD0ueNrdFbOswhGoswKynE/Unv1hz9xt+J4YIeagptR5HxKaIiRZB0VpUvexrpBRkHnPO0enhAivdmsOm2tyk5NnBifgo2yH1A3rZocLnn2zZ17WYBTXzY5u6MlNhvWO3dhR5xVH1ZwnFy+QQnEyXxEBGwKjtzy7+pSd+/0U8DqvOV/cT6GygiTmHR2qzBJScLFGqYQqmEWFynUShY8OWeboWUH/5CptbtoR9d37CJMc0Mg0xXtnqTCyLjnVLUrErODFkWDIE/IQo0VmmuI793j/ty8QVzuUEDz6eEcUYJ3jww9mBCko+i3f85ri8RnDZ5fcf7lBH83YdD2fPCqh33L/vOaDJh3zLm5oH440rz9i6e5zVv8wuTdNVtHucov4tkaMSfNGCOlqlSo5WCmFH5OleTAaZTUyCvCB8WqHngIi4+WGmGcEwCnJy8O/JlqPEUvUqsb1IzEzfLauMK4E1/NXz3fcfzfnOkT+z/9K3LpTf/34YiH0hSGEQJLsyaMPuNHh+5Hy8Sn+Zk/sRtbDp6wPH01BnxFzbwURzusfkB1yXHXGbSBxGB1SJcqb8wOvdr+DlQOzds959n3MKhmTqDptjIWUSKUIMvWc1aJCaMWNdfzTriVGqIbII1LxNus8j58kl6/h/ciHw5hysGKYnP/SBpDOTkGSSXAuM82H+jl/sNqDkMhZTpzNEMBw8GR1jdAGbzQiU+hDzwd7QQapMTJps6IQ+AASjwgJMQn7Lk1XdUAWSbgfugFZF2hj0FIwbA/EkN5P1CkE1fcj6miW3qfzND/+jOzRGdnRHFnl7LqB7acJScP1hKYnaIUAdJ0jMoM+EdhXG8g0aiVR0310uZmxlTWi0Ay7NZn1eBExZUEc20T52zWYByf4tscPBnP/GFEXXKqeeLRKodi7ArHOKbaO764aEAGMRrhAGEeoMigz+m1LbiSQ3t/6RUdzltCe6rNXfOvbHplpQtMjywy7bbgO8HS7QGRZ+lvbaY2L6g6dlSGQzaqEYDZ9cmyLkSAVaEV1b4mQktD0KK05+v1r8jGZQ7w4XjBKgfixJVvVlI9mtC+uEaua7HwFPlA9PGG83CC6kehcok0HyZktEqL1YIF9WCCXmsUicNZvCU3PVgteuQIRApILfPOUrMh4N694GCJOBiKe2A6EEPF9vLO09s1IbAVybThvByqqpKVzDlZwOPSM7RFEDSJR+MduROaaZ8uc0TuCCyks2nvyzCC0wg6WuZScP9+QGU0Iit8pwcaIzCM6CHSZcq6C8+z3DfWqxvYWZx0PbeTBbuSdneNJ57h8ew6ZGihfmj9uS6K7+uWXV8R8oyn6kxtZlrFcLjk+PuZHP/oRf/7P/3n+5t/8m39oMfTH8b5OTk7403/6T/M3/sbf4Dd/8zf/o9ATwS+jKPqj3C9v87NuvwwRv082zGquCSHge0tAgBQcLneEEMhjTrGs0C6HPuCtZb6asV/vk/10P5BlGWNwjN3IcjXn0DVIlSc3OqAoMsZJwDmMlnJRcfX0kvhn3mikU55gmnDkZL9MBNumXAKpVaJ4KQlDmj582+My6Dc5+dGMYlExf+eIy2cXaB8ICPp9x9M/+IwYoZyV1Kua5dmK/LhmdjpDRcG4a2nXB4RR9JuGIRq60VIsa1bv3YPpc5RnC46WNUEKVG5wSiKiSJvb2y5tFHfH+ZbG9va4pcgJeEsg/ubcfFVp9PmuVPyKn735/u5UO8f+swuaXqW/6QOFlMlSVkKYaHGDc4hMEXpLXRWU85pIxLpAfTTDh+QEVlUFYn1A5hpyg21HThdHtMHS9i1VVmDH5DK37RukkJRZRpEXjM5y1WyxznL/5Ixln3F4/TOKKpkmRB+Q07/WOqKEXgoW8xnFrGToRmzbo02O0YpHJqGK7dDz6cULmrGnVxYhDS6kQNY6r7g5bMlMsq1txwGhHNZb7s2PKLRm2zUQQGsBMVBVNf2649XVaxA9wghOT8/IJnvjOF2TwaUNopISnRlCZtBljtu3dC+uUGUOmUZqhe9GzLwkhoiqC4LztJ9cUL5/742mpMwov3WP7qNXBCnQSqYN3b0FwzDA6CYtiWd8eo0YXSpuc43dpuyUKJPjF0Ylu+PrPbYcKN6/j329Znx2jTgu0vHuLc2PnxKq42SxLASizMjePSN+ltzVolEprDVEAmCv98jjd3G79s7yWsaQNrATMoEUKR9ntYC6ZPuz58R9SyxydEw3RAwRVKICTtmaKQxTS7JZeUcpdYOlrAynj88S5SwGQN3dPP+u06GQIl3vPulohNHQW3Ce/HxF6G063ipRkbxW6EzRfPQc+/gHyKvujtIWdGoWxNEmXQ5J7yLrgmAtcqLdKqPRi5rQDElbpJMRAVFM1tLpBo5AmPrFvunx+y4Vk3HSqmUadi7NR0ImR0YSkhjCmJiCkwNojOmVgveoUidjCZXcv5wdMNkRwafn6Th55uU6IVSRScAfE1qv0+ZeIPCZQGlBHByub5ID5KKkOFkkDZQOSJNRLGe4foRFxa0DoIgRf7VDHc3SPRICbtehy4Iw2inEddJ1+ICclUiXPofbtogqB5fQTb/vCEMGOqbN/A24bUQUhtAl9zm/bfB1i44Rv28w947AebR1yKZBnJ+kYm3TYO4fMVxtUbMKs6xRQzOhf4D3yDpH1yVjM+D2LVmm0GWWjAqKLOl9AJSkfHRK9GtihGHbUs6r6ZoV6OUMZz2hH5FSEjKDs+naiTFRSG3Toerk2KoKQ3QJgjV1gdt36XfD5K7nAkwhrnG6vqNzuF2D8gEdAmxaqAsiKchYLmt0XSQjjxCx1x3eQXa2pNseCKcakWlkmVEcHzNc74i7ZHLBxFpAKUII9JsD0jqKs2XKpRIwHvpE967zhBqNLr1PoyjnJc56/GARzqOqHLWYocfAbDI+cu3AbFHSNQNRCWJIdO2hGxMlbnBoC270yFITiOSZYT2MKbIA0MZQGI2V0PUjeaYoZyVjbwkx4F0gCs3i0XHKSuq+sKDe/fM1+qJfcAK6Q4m+Yg92iw2BuJv3vqHU/fsdv/mbv8lv/uZv/tJe79NPP/0jv8Zt8+BXbfzJI0VfOO55BsfHknG7JpQzupEU6ucDWmvyKk82pEKgiozzUKIHic0zPtkdqJYVSMnMzBmHEWMKxkPP/tAilaTOMvrRYuqCw75DhUhmNJtM0ThLNq9Z9TnVJi2m31GGGD0LAaIrGQ8eoSP5UUGMkcMQeLIFU2f4NjI6R1CCHsnJT2+Yv2cwnSdf1pw9POOzP/iUew/vMfYjKgR8CPhu4NCP7F7e3NFwsirn6PwI3jkiO5ljhOB9JWjanmZ74MiDHFLIoIk3KJmccYZNmkddGPmZCuQIOjfRRm7HH0KNu3vOLzC+msWcisi3/0TnNLsB/CC5ZsdulhN9JJ8/IJqCrhsIUhBUQJaJNtE1HU7Aftegc5NExc4nmpFONrnrfctjLRnygaazNOMN79cn7GzLMzvQy5F26JFCYKTkZHVCbQrWw4FhHDFR8VAsOFVLXLSUs3cxQVOYZKPrvE2bLz+kzChyhBAcdi0iBMp5nYw4pEz5FU2HMobvPniXl5srno7PWPcbpFIsyxkoxbGS9HZMm+8io8pytocdN4ctRhuqrEDmBe/de4jzFiUCjg3HtWC2WLFr5mgfQSeqkskzYjeiVDK+MHNHGdtka5wZ2ipHjTYVTqPFzCp8N97dflGCOZkTB0v/9BK9qpFKUcmBbK5Y/toJVx9vcW2yHa+vW/JlCYXBbxoYHFjHzlmEHVEi5+TBMXK9J7Q9C5fyX4SFXa0gWNR+S/HDBxAizYuLqQ6P2H7k5fY19Q/fpZCKsvNk949pDweex5tEzyoEi+GcCOSjuSPZB0HKBiFtEIQPKCnImVPkC+RRzc32FaosCEqxuv8B8qrFDiN93CXBufWoTEMQCT3TKjncjRY3epSPhLKk13OkhsNuyprhy9a5v+iIMZIpz6oG3410VuGNBq2Re8Xs9AHmdEa7e43d3CCFQjuP2zREG9g+/5hM1KiqoKzuoXSB2LVAiiYIMtF85KwkTucdIYkEWrPFHa5o+x0LB7bpkzti/VY35K3Rv7hO6ItSKQOqzhl9IFib9CpSgJTJSVik/nWYNF6EiMgz8LemESlLJkTwfZ/MGVxAxkh+CFRMwcgyWb8nXZkALRE2IExqBEy7aqL0KTBKS0TvCP2OvhnQswp3c0AdzzBHMySghxG3ScWTD0lrYzKTbMy3DcEHmicXmCJPyNtt5kwIqHtH2BfX6MGTmxzcSDcMhOAgN7RWM75qcYeBZutAFrirDYVXiA8vKE4XKK0xp0fYXYvvcsbrkThWzMQO+/xTVF3jbyKq83Do6Fdj0ofWmpu9h8Fi0cQip7/eoXNDniVzCzn0zGYeqUeskTSHDrc5cPTQ4O2AqnNUmSXnwghufQAqotHkrqMwlqgcbTS4MZ0rWeS4wRH7HarMyeYVqi5ACLrXa1w/Uu0tWkrEoWUoJNYFqHOicDChkcIo/KFNph8C7JNL5P1jVKYwRXZ3vsd9Ryg0h4NFDS29jNh9CopOlVakuLfCEBGjTEHMIaGUSAH9gB0dsrccfbBC257xRcuhHRhuUr6c0epOT5lpRaYVotDJdj8zWBc4k3tinvSXfvR46wki4FqLqlJxVR+dAYIwq/jZtklOdTHiz5c827b4KqOqK1o7oo26o6yLQuOtS8YLNjAKMMrAfsf9VaDsL8hcwwSOvlljBV9wn/vCfPIL0uKmJ3/uS3H3r/jS49+Mb8avwvj3VxR9ESL4ec95a9TG8v594FxzsXE8bRTD9SEFl0tJdTTDH7oENQ+WH+YZSibax3+3mPGpEuy3DVIknr9wqauYFQYidM4RZeo0y1wjfKQZHYdFRpZp4r7jP3/1DvNxjgk972XPkDrRxPzznCgEqnTIey1CCdZd4P/2iZhay4Hb1s73d5r/1UEjr7ds6zkXS7j3rQeE3tHsmkTJSY1dhsHeOeXledrkuW7g5Ucv+GS9ZjiuWZ0u+bNZSfbxa8qm42E5S/qjWUZZfISQDTjP5qMdjUs0ov/7WyfgbVaw4A0Y9OXxR2h3v3Viv1h3XXcFT01ODJHhryhuDheoMme8vE9oE/3JDJ7RefKFJltUeBdAjiAkSqVFU5IW02gTlSZH4IXlig958uFrPnl+xXeX/ylz4JGc8XFx4N5sRe9Gcm1QES4PGwZvKUzOI1/zbbdkuHY8WP0AU0lsSAnvY3AYk5HnOe1hT7COKqsZ2o6u7Sjykg5BtJagBEVe4BC8vL5gUZQo4GS+ZLvvGMYBa3KsHdg0Ox6dniOA5+uriXIkODs6u0O1qqJg2+2x3mPqAh8/5HXfcJ6fYMNIJksCETU5Zskpr4cQqVTP45MBu7tmOx6xbUpCBDEmrZc7dKkbbD1SitTFLwzZvWU6e5NJwfLwlKUS6OM5XhyzedEyXO540Gvi1UDoLbow+N4xth0ffjDDGokePcXHryhPF9T3j3n/xRrfjwyF4afv1pMOISLaNeX3HyG+9z3ET57DoaPLBZ+VEu323D895b3Og5Lsvpvxs/XHiBj5nrzHr8u/kO65EBn3DSLLUD4SFUk3OA6JTqcUZ7PvMsvuIbKK8USw89fkWc754kcU1jMGzyeHf04sR8SuSyhZiIR+ZNy2RKPQRhGCxznH0Hmek3ja294R4poo4p1A72v2Kl9zp6SxUD3vrSI+H3l+ZWhcgSBS21PO3HeJp5FPh/8BWzZ3wbr4QMwFm9kFFBm2tbxvjqhFSRiTOxvOTzFIEuYlYTMmBzspiAYuht+nuf6MMFreETXj9QFdZsh31Off4PR1HN2EQE+6ocwQeptQyimT5ZZyypRTc/c6UqaN5MWOEEloi035Qj54mDKPpFQ8fL5ntrcgJCLXxFwmQ48JPQztMFn0p88ovAehk+uZNgmhHJO1sjwz2Ksdbtfh1gfM2QJzskRmJhX6REJvGV9eEydNlCpzhL51dUwoewyBMIz49Z7sg/scbz2LQwQhuL4n2SmHb3pePelBloQhbbpFjKiy4OhJQ9Z6lM0oHtcIMaKrks0/G4hOg855/IOC7KwkdI7tZ4q47vFK8LJ2xHag7QbaOEfNC8KuIz+fYxbJWMKt9xAiZRF4XO4RQHN0n5ccE0ZHf/kcNx/QzqfrJ0TwHmddQnmc42Q+8uAdA0rw8WcjW2eIwRP23WSYkMwkZJnh22TmEPuRzBhOdwO6HZFKcvnnHzBsdrjBopcz4ssbRG2gt+naU5KIJ+SacLXFXazJ3zlL2rp1QxwsLpdcFYLo+nQKroaEYBZp7kpIZwk3qRCKQ9JRxW5An63w13u8FByZltNjizOBjz/0hGyWrtmQzFNElqXXlaC0QSLw3UhR5/xg/Ay/7hLVUwjINFEKrO+wLzqkKvjWvf8CVdZsibxaVjT9yM36gD+dMy4ynHWU3qFzjRs8YwhkiwJjNO22Ja9TYLQUgrrKqa+ueGf3KZnNeDIMn2Oy363hX5pk3qzwP78geivZ6AuLtJi+/4Yu9834VR6/hKJIvGlj/DLupTvObHITyk8SzWE49NhuoHWB6nQOCMarPepR6jbGboRcsr/ZUxY5XT+ghSQvMtphxHeWui5omx5VGMTgKI1mlBHlfOJDIyirArtrefnJa2ZF5L7aQ3AUqxn9usH2A/OH5d2kJFTqioa7NsubYyEzc/exYoSXP3nK5YuLpM+QkqOzI24u11SLmgfv3+eT3/0kOfKUBXbqclcqGUK8+vQVH+0tx0EipeTD/+EPGAbL6mzGd/+cwxTAXUd2EjXf/fG3ju3POexvjxhjmoTFG9rdLwIwffHPffH5QkmyRcXqXs3h6XVCOMSM+emC5mqHVobdrkHsktNadTTjcLml1JK26RgHS7EoUxeQFNwrMhASNusNwzBwGDrmeYWIkVxqtNLMtKbIc4IPnFRzDnbAeYd1lpt2z3fOHqGEYiSAEEiluVxfMq/n7NoDuUwOYduugU5gjKHtDxzWHbO6RiLom4ZMGWKMbPuOQ99wGTbkJuO9h49ZbzcQBEfzBa0dUFFwNFuyKGteXb5ivduwquZkxvDi+oJZVXO8WLHb7xiuL1hVM67WN5zPV6AEMoLUSVhu9x3SKJx3yaXQecrzI9q+QnYK145IBCLTyc44RKL36GWN37e4TZPoOqcLVJ0jjSI/OSbcXDC+XkO+ILt/hJpXDJ9dENqR7OFxour0Fnvh02aHyY0xRIYXa2SdUzw6QbV9Kl6MRESZ3sNg6T56Sfmdh8z+1GOanzwjNqmYsRc7RpElfRegj+doUtimkJIIKK1x1iKRCa1RGqJM+gKl32zItUIYA6T8D63TBsgPjohEaYUSApcZpBxQVU5okiulagbkLE/XhEx3SehHYq7fXOdKIsK/Q1N10hlF5wk+phDfXMMdtUUgXWC82FG8f0ZWZog+oebu0Cc8NkRsYVJgptbIwSLGFpQkTJQ1IVIWEUbjxpRHpCLIRZXc4WJEzwoiiWYolPzKOSOGCDagtAaV6HMq08nRb9JEpWkjIuc19GPaZEnxxunQaLzziaI52XjHEHDWYrI8hQHf9pje8jqP1iUsLiR7ZLvvUjE05b7gI8JHYqZwu4QouN6mrnoI6GWFXzfEXY8zKuXhLOp0jLVCnCrGzQG/PhCtS2h0blC5QRAwyzJlfpUGfe9omvdj0vaQ5klVJQtzGyP21Q2yLtLnsw5ZZKiyIF8UyDpD6A61rBGdJTvVDC8bsO6ugFJ1hsy6hMD5gCirdD6dRxiFnlUpHLQbEEWGNCrRE28pfkWGPluiRAmHpOUydUF+IrEXm3RcDokWqAoDjUAIiZLTwZ/s/WOIKYtI+JSLpBJVdJxo3TFEhA8ERqLzqShRAlxAHc/xF9tJ3yahHfBGJW0vAlUXZI9Okqvl5Ra73hNGR+xsChkWgWgMalkifCQ7mWOvdoTa4McOVeYpVDcY8rMlw+t1OpfTmlWdLhKFdLAwA1nmqNwRd5Y42lSwSkHsB8KhJSBwRqO0TI3TMWnD9PkKrCcMlmAdsfcoLdEnM6QsKZY1wYJyESVTbEQ1K5FKMlvV9E1H344UKkeoRGtXMukQ8zxLqE8mUVEw3BqsyK+ix709dXweDbolr4uJyP7ztmLii9/E21f4it/6hj73zfgVG79cpOiLcMS/w7hp4XdepRcolGOVddiFo88y9o3G9WOaOAFiZHfznEwssK7F62NijAw2WV7vtw2jz8iKnG7boFUK7fMubXzDpFuJQoBMCfXOej7c7MnnJZtxgJ8ekCLy4Dce8jQImm3g/mnNd/oRKSHayA9N6r7sQ+CJc8lxSwV+36XOvPSe7mrH5ZPXQEKMfDcyTN23oR/RVY5UkuATVSNYiyBSDoG57Tguc3KZunpYyETEKMH+as8n/3LDu7/+EFVqfnC8xUWPVOC2OomKY8AceYSE0cNPrvkcne5Lp+ptrP7fklf6lc+OkcsmbTRAwPyUVV2zXJxi1QOCLbCblp8eOpiXyCwjWodShnG06NxgB4vzgWLKclDecbx/zsxI5lWO8I79bkdEcW0GYlUishKlLPuhpZCG+2pJ8J7D0DHzELzEBMHjxQkqMwQpGYcRrTRacGfHbUtNEy29txyGA1oqFBpEQGaKjbMMLm0MtVSQRZ7eXKCkYBSRwTuutxvcOFIYQze0U/EQqYuKpmsxWcbN+prVbEmUklU5Zzmb8/LqgoVM+S09guPVMUIpNtttcnqJiXKlsuTUqJRi7CNXO0UuDR0asygRIeLW+2RrqxSRgOtTcGtWZYyvN9h2wG0a1FFN8eiExuf44wcM13sOn90QFgv0vKL6wTvY9YHh9Yb1cYF+75T4aMby6QV+tGAd25lCBEl2XLI57DBnS9T3zjjd7PDdiLOStU4d+vYnz8k/uEf1nYfY33tKfdGkTev1C8K7j5B5Rm4j9xdHtB/f0I9rPs0LopQcyyWrISc4j1MKOVl3z/LjpKsBrD2wMS8JLsOYOUbPCQhClwT7hDChswlFCVWOdgHnPb7pUXWieoYYULkmOp/CI+tiuqb5SoD16zYn8a3/xZCOwUWj+dcXkuAhJ7DKO2IhMPtUbXkXEnXooJFGJVdOn6hjM47IokY4iQkJ/Y4SmuE1fmzx0bN/d8FYQKgER/aKDI3IFoQmUR/VyZLSrhD1CXImqLIelSkk8N4qT4wlk+h1yeU76a+EUcQ+5RZFSA2Zqcgatk1q0ohJazQr8duW4BxSa6JI9t4xBHAOmRfEkOhau1nGOCFNCxuTM5eS7JcZ8l6JjUnw7nVExch8b8G5NF0pmVzKjESWeWqenczZiPS4Do5lOyR0JNPIeYXINMWsJN4/JlhHaPpkE72oyIWlLmNCjlSGrCzRDZRVQMekK6sKg84NMQT2lUZ98CBRs6ZNuhCCfOYxQ0hoSC8YXw4gC2RpiPGQAjPjEcNTn7imNoALCJ2OQwxT5e3T+qURZJ+uwWi8HXG1BimwUnBYPUBGRR8y3L7Drg/UtUdVBQCDU/TVGW57oNtOCpLc0HnD5auEBLksRy80YUhzGyEmd0uZtL7iw4/h6AR5fIzUim7hsTE15ob1jmAkQok3xWumiTYQMoUIgbBvEa8TtdM2PdmiRlZFet5m0k5lnnHXYsqcMKQCse8CN1FjYqATJYRI2DboIks23jd7whSCGqxn/bxDmzmqXOKPHHG3TTrDWYl3HtoelEqFW54MMmSmcbdmJYNDGskiLRoQYDvmBBuQ1tEcniCjYoiBh1oyWIfQkhAlRua0heCZLxBC4oNFK5VeWwqa6djqPFl1e+s5fnSC7A6308rby+jnAlvvGpd35dHbRVL8Cu3RFzod0wT1uZ9+VSfzm4Lom/ErNH45RdEfBiF8Uc/yc8Zn2/QfwF9+ZPmvHjZgAhdNRWcNcso8UFWGyjTbwxOs9UTn6YY/xeLkUbIIti51axCMTU8xT+hCqTVRK4IA1w4omyY+OYW3dd5zc39BlJKMnKP+P8E5x00z4ycPPmAoDxTtBvHkFVILsoPlvy5qBPCxczx1HhS89IGXvgci72YjyxeX6MLw7T/3feanS7Yvbrj48AWzENk0LSFGjk9XvHp+gZLJwME6T32158FiRr87UNUFuYz4GLAqx+QSg6DZZHz4LxXf+Yvf4r/64FMy0aOMov1xQRglzvXM3x/RlWLdw0frFHP0BtX6uq7UL4oNfXm8aUCl3/9k3fHxdeJB/zmx4l5xj/7mQHf5ItngzkqeZRmHCKEdMVLifcCH2zydlK0zWkcYRhbS8eviU1QMzKuTxKs3GUrDVT1iZwOj90ilcHagEhkne0WZ1Six4GAbTJExUzk7O6DKFd3NDqklMUQ673EiUpmcy7zjwrQM48ghNhil6cchbW5CpMhynPB476jyChWgO1Z0tscoQ60KtNKIDKIQOO84WxzjpoXrar9Ba83Z8oh+HOjHnveOzpnN5hipMX1DfvaAmdTJHW13zSwroB/xfcq38M6jZgVRSdrBMYiS2EkQI9okDr7INLG3adPhA0orfDckW+VllRARH/HdSPvkkpcnC8xiBvkcTi39kwtMO2BOFik8sc75ULQMw575tx/w7S4SPn5Nf/B89L0lI+nvmgf3iN2IOez4kTXYpzf0RxX7ZUboEjLU//QF+YMjjh6ecfZ7N4kKI6Btn1H9qcfU3lNLyaBnPD1c8T+eN0gp+LXuA47Gd1AyEqxDCglCsjDvMK/eBx94ufuX7JqP8C7nnfP/lGV1PxkqbBuEdPghUb9utSWlUUkXA6lLP5k1SC/ABsJUjAiZEMU/bHwJdLktiKZcLJTkZ1vFhwcgCv6Lx/CX76eIgaHOsS8F9nKHPMsRZdp8u11HsA49eM55TFmeJi3N6FJQq4hcbH+fzu1AC15+/4fsb7aoM03xs99jdm9F7AxxGIlKIr3invoeYq7Jji2zxW8jFRyXGVEsiRE2Q8fvNemcRjF1vKuC2O4hI23cIWUbFVminIlECxKAXlS4i236XqTPLQJTPpIn6qQbjJnh6lQQj3OUFJTPOrKmIxJ5db8knBe4agqLjQbtAt8PAmmT+YowCW2TZUY8dIjjGV3T8fxRRRRQdZ7F0wNiVjK6gWg69KxIaFduEnJY5pjjxEhYmT334lWi+gFSlmAiw8Vl+pkPzMhQoU4aqcUDdr78/EUQIkz6UbdrGF8J3LaBIjm+qcnYov9EQ4zJ3MGl1xazlAPlrq+JsxlqXmPXe3TvOLmyCOXpVKBfpcbaIAzPDjNiOxDdiNs2qLogMmA3B+K+Ya9PeR1nxCEjGo8+kvj1nq2Zs2kD0WlUXWBmye47WofdHJIRgZQYJQnf+g4hhFQgediu1JSdl5DY7P4x7nKDOV0y+FR8yypPJinBIyKM+5YwBvJ5Segtbp/o56rMicOITVLIpB2bjEd2W0m7uIdoZdKwCVCnS0SI2KkQF0qiVzPEaNn3GfvPIipL6GD5XkH/yWvCoU/3uE00TjkrE70vNzB6snmVmi3rA9njE+6HVyg/EPOCoZ8xjqmov+x+DIMjZpJvj4KoFbF3xABxL2jKY9blf0JQKhUrUjKMI1IIqnlJZgyjTTlM3geywiAnR82vX32/uDaLL3z1+TU9fs3P4Xb5f6tQ+mZ8M36Fxy+hKPolUuem14u3d7AQaWGzDqxO7khFnRx8RoeuckQ7QEzIkHSpC973Hd45tJRomZxyhICu6RGZwbtAcI55niGFYHAeD0QpkHlG5z25Um+oHLMSlxu8ddQnC/onl4zrA3EcUSaj3zlMmRML/QU4mrtj886vv89D927KRxGwfHjC8sExw6Hj1ccvKRcV+fceJfvofYPSirP379NuG/YXW4wQdPuWURsQif6xbzuUktRVWlDamx1h5VC1/lzvSOcGqYavPNpvT63i7nx+jrycNkH/9qfx89/GiX4zva5teg6v15RHc8Lo6LoBfZSDAuE9WV0wdAM+eMK0gc+KgmHfEZwnywT5yZz5vRrfDXz26jkxBo4XJxxm8+TyM6ux1jGbz9AHTyEL5lmJ955ZVXHoGuZljdUC3/YYpdh1Ld3Qo7XBKM1+3HMz7mnrhBxIIZJJgoAQPDIKBm+xznJUL9JzlKIqCowx7LoDxhRoJZEqo20OzGcLRu8wxvB6c41SivOT+zy7eI6OiQKzbfbshnYKfN0wO+xYHZ1xsd8QgsMLnTq3h8S3F1KmTUdUSRcxaYzMokLmBt8OxF3a4IsiQ/qQNjhpd590INPvSJIuZHy1JnQD2ckCYRTFoxPi6OieXKAWFXJeUnzrnP6z13QfvQJKym/fh/WBaLuEVvqAfbVBH03OUpcHzKNTdpc3qO+cIWcFfn0ghEj/estYWvLHpwyfXSG8J2xb2k9fU3/rAQLIHp4g+kPSEEzX561FNz6hDlGnJkcIk3ugSi6MMoREs5qyc2IErEcAPiYarZqV+EM/BYbKFJ56G1A50YqCC8ToQICLlujjWxq9icDytSLoNIL16T0ZlbJ1JrrM1PxFFyZREAeJWNWpc+4883dOAWiGpANxMTVJsBbG1B+WWqd7zSgkCnFUM1zvsIdkoyylwNw/orvYpnwfJYjtCDUpjHVZvbn33xrj1Q7yiS42/ReVJAwWkafzIMscPS/x7UCIMQX8xphMFUzKmptg0vT7IRDciJIKbZKeMjo/FaMTOjH9xUgkuInG5JIeDh8R8wKReWg7RGHS810gbjtklSEDuK5HhDy5hhkJxuA2LaI0+F2D7wZ8O6CVRJ8uEJDCfp3DzkesSJ06oRL1U9gJ7crzlIkFOOtQo8XTQJkDArc9EJqOMDraV5bKyaTq8IEYA8Ja4pjWOakVclETugFVZmmqjBHXtIlG9u5DhJ0cH/cdYoL7Y4ipIA4RHz1CK+Jg0asZtulRKhV70vb47QFdl+j5HP/RAXe1TblERYY5WyKKPJ27dkiGE1mGGB2myNDzCkSH7wakEqhljTt0U8B5otGhJaIqCN2A3xwIvWX49BU+RkRvk8Z3VqKiwrcdIk/5R3aKuUgFf5vooblGZwo/WJzzyEOXgnGtIxYZwY+oMkPNq7trNLu3gtNlcg3sR4SWqFyjisk4Z9cSmh49r4iZTjrLKmUL0adgZ3yAAPZqh66LRC3tB9RxifYS3zrGyx1eZ4gs5WnJeZE0lqMjklwyQ0yhryJGFILQW6rJyY4QcTEw9j3Rp2afLgwqCnbXO3jDvH/rVvxC4fOF+/PzlLr4pee/TbG7m4u+fqp68zKf/9PfjG/Gf9Tjj8d97ms5JF//fIHg5QH+xQsBUbPIIydLRxg72l7TB0lohuSAYx3RRZSU7C439NZR1gVt26GNRo6JN66rHKtE6sqNgkMzICe7XlR6TqYVfTsQnSPkGZcnNUzZCV5k7K52FIsjXoSBmEHYtPzsdcssB/HeMe+t0mKYuYaqvwEip3nLg+VnAPhW4Q9JxDwUEr0SfPs3Si7bC7bOwbcEeUy0rY3Y0r9uiT7QjRZnLTpL4vqz+hXzs/S10oq8KijVAVyPkBrnI787WkabNg7mRURmgta+RZ0Tb/jHnz8dU4v3rY3eF5/xJarQ9HC+PMPMjoHIvcM1y25HjPBqfsYuq4mjp5nNEWZGN1peXG7I6oJQahrrCAh0mWG9R5WGYWfJZAq8m69KjtwLcu9YSsPswYpws2F/s+eyV2Smos5mCCT75sByKLkfK/wh8GB2xoko0EKxtyNGZZzmcy6aNUMt2bmO1iab9b1qqfOKEAdGPJvQcrk+cG95zGHoiUIwuJFcp41LlRdYaxltcvbadA0xRhbljCorqfISF1yiOlULvLfsmj3GZJwvjjFtpNo6/uzifWIIZCqFUg52ZJaVtMazNzk+Bk7KGX9w8Rmny+PUrY/TBotUwKvMII0idAMiN9PamPj7rhsIzZBoOFPhIELaALhdn77ODeaoxh16/GixV4nulp0uUj6OEJQPT+hfrQFY3WSUqsC/3jK8vkLeP8acL8jmNe2L6+RSFiLuao8VMnHv54bZ2ZL5j18l7cOiZmxGYjui1cDVvSP44Tn5Zy3n/QK/g2ysGMseYTT3z95lvk8b1KOhShSlCESRmhgh0oxX9OGAEIJM1hzJEuY1Wha4kFAaFUkohRIJXRhiooQ1/URJ8pi6TiGoQJSgM43WKhkZ+IiWgscyIQgml6xqi9SSnVP85Ea8YZ/e0lSmvx1DmHKEErUqxmmzEiNP1pF/rkAqxZFuKbLXuLCh3e8Qx+nOm80eIDtL5zte7l8g/QsKpZktZ0Qr8NYSdCRGxdhbFhctZteilSS/f5Q21j4kZElIBj/ycfWKqDQnxys+8B5pNErmHJXvEwaH31moJVEIzLCHrAPvCb1FLEyi1I0OOS8Zb/aTH1+aS6JR+H4kTiibFIIoBME6bN+jTLqXolaokKhB0aUsnv15TaMgek/Ikp28DHC0GdGzHNkEbqSH4wytJIurLhmyaIU+XTA8uybLFEebgSgFhZAIH4ijR1ifwo4XSVtmY8S9WqdCNwaMkhyiR2Ul5nie6GBa44MDk86RyBK6M3ZjQv82jnz9kqgko+8JdY6QAvtgThMkYzNQXR7QMhWK2b2IPsmJUrKzCpdpQjsk7VWucSaDShG6EdWNVE5jcoO0HtxIjIHybM7SXqcmQzVnfbm50zL5EHCbhi6TbOoTJJr96x67TuY8dRGoFxZZCJAjsQqIGvZ9RteGZCG+OSCNJj9boooMv2/xh47q4NBIUJKmSEi4XlTY0eJ3LdFahI9oo+C2eJliASCZmYhSJjfRmAxeKAwaAUqCd0nD5n1yUCTd93bfITON6EbUrAQh2PSO69a9tSpponWsXGDBgKpLbrxhryPReh7UJdUsIe4yN4k+EZJDZ+hHhARR5+gqx11tkJnGbw7oecmDomTsPSFYrrcS4QWqyom5RoTUWBhvDrjOkjPygb5gjB43BNQocBOtOgjL0DjC8pQLP8dohdEZvP0x/tCRVvHPr8lv0ezuHn27NPqal/l5f+Kb8c34FRi/HKMF4Jdx19x2Om5f8dNN+i8G+M/fG/nP3ouEwfLykDHuTdI/zEvqkwXt1Y7gkoA4zzOKIqFAth1ZLGt2bUeWmbQhGVI3xyxKZDtSr2bsbnYEpfAToiGkpB1GnhaKmOWJ0hAjalYQhOC3N4KszOFYEGpHVeaImwN/5egh5WrGvHvN/U1LtI682lLMXwORsc0ZtimXZSM12zIJV18fDnx003/pmPzZ7/0F7hXnjE2Pm6gLWaH54f0Ny9keIVJX1XbrZCs7JWpb4L8fBvaTAy9PvmAZ/DaaJb7sN3MbBHfbRfriWX7bW+OOJiegOHnE7N1fgwg//Ohf8e7FNWZe8j8+/B6fzO/jrvc8u9ojZwI1z2jlgt5a7JDOS52VRB/p7YjINEpK+j4lp7vDgQ/aDzmSnsXZA+JVz3C142K9oXzn19j2LZsYOLZJF1TIjMf9nGbskXZkI5IuaFXNUVmOa1vWYuDDcYOUkkPsqfMSUUie9VfURUkQEWsFlS6QQiKFJGrJ2eKUm5sbhDZkMiGEMcLF9hotFSdHJ8nxjUg/9EitKE2R8l0QFCZju98yL2q+E0/Qg8R3AR8FimQGsKrP2Gy2aK8RRYWXklfbax4f32dWVqnh3o3JOck5qDJ8jGiftAepC++QwUx2xiT0BIF7tU1vWEnMqkLVOX7XEbuRIQSye0v0vMRe71NuSD8SyyxtipQkv7fEvlxz/BmYVU0o54yZo39yiQye7FuPCYWm+/giHRsXYHSEdY+fldTzmm8rjbveMT59hZpV0Ea2xvEkdJh3TnhUnHP+0QOEFOxeXTC8m2gx79z7DvVaEfY2WU4TEBOK50kbp7V9ybZ/ikTwzslfpC4foFdzxn5MjmxtTxxtcjvzPmWWhEjctZPRQEzhoVNmU/CB7HRONi9pr3bIKZcm15If3iuSzqzf8f17HdJ5PnMFP7ksJiSLqQhJFCqUTPoFkRoP4lYvMlHSPjxIfrZPSMqfuXfB4/wCrwY0GRkpZPTB4z8N1tIXPT+9/mfsh9eUQZPtMmIUmMKgKo3aCVCK+1cDbm9RRYZ6J0tzHBE3pGJ9KCMfzZ/gjOTdk4e8t44QIpmqOJ/9kGF9Q4XhvSb1S/b9S15kl3eGHcjkzCmlROSpQLrtZkspUKs6UbcAZRRRS4RPn9E7S746Bq0SJdX5aY6JBCO5KBRB5XgfkEYhQ0Raz/nGUqwdw2D58HsLbGUwvae+6sAH8ndO8Ls2UTg7y/3nPjUKvEMUOSIGhFCEZsALgXAeXRjINEF4QBCEYE9F0xeoV+n8BOfSe7UOoSJRJnRGZBWhtzwYDfP1johnXEqGTCO0YqcVqsoZLweqNsdIjawzinc2iPwGZjUXP+4YDkNyW9MS4XpUblDIlEmE5ORZR3E2xx32BCmRCORhx6NHFiEsBwnbmOO7kTA4ICKVZHfZs78SCA34MdH27h8z81ec+S41s7xPxasQeH3EWFUILcGlQGB7ucWczJH3j8li5PQP1uhNTxgtw32DDZHxcpsCgZVELqp0nfc2UQG1mizOSaidEsT9AVHkqOUsFXW9JbYjruspzo8QRHQEu2+JgyVM8QIxBERu0nu6t+L1wfK7F81bq1Uav/Gg5vQorbnPtgee7NP1NReS+TxDzSeq42S9H0NA1EWiJXeT9ixGwj5lS6lccdpdEbxjsJGNPGfcd5SPTrA3+0RPDskpMc81IXR8YH+WPpeUQGRoBtxkmiFzyaWEpj4nAKt6Ca9e3L1/cbvw3i3C8c3CK94kBP5hvWfxuf+/XSz9nPHlfug345vxH/X45dHn/n3+iiBRV6YMjNvdul7NkjXrwlCeLlDbjKPFgta6yUlHYuqSQ9Nhco33ngxBURfsdg0x0wQlabrhjlNuR4dAMIQAIlLmhn60+CjIRdKbjMNIVmQpV8cFgpY0g2UmBL4dics3qdlCKyBtoGwz4AfJuAsMh56RmljPJupMfOvAvKlEhEjIVrlMTklCgBARU2Z3eQUxxlQM8eXsgs+D6G/XQm9OQpychr5yUo1fXGI+//tfPpUJmfLW0V/vuP7wBUWeEd79DcQy5Zq4q12i4gDBB6wP6DojKEnbD8iYNoquGUAK6lmJ84FmfU2mFMX5HKEk/cWGl5cXfLJbszj5DlEIRufQUmGdAxmxwbHMK14e1szLmuNyTpWXjH3Ltt0hTdrkLes5UkqiVox2RBuTbLS9Y7CWs+URzTik3BrAubTZOJ2vuNzfIKWkd5bKFBR5jvfpGkQIrB8RXtD1HZ0dWM4WBAGLakbf9wx2QAmD0YY6KxmcZWYKmq5BSIkfHJkxzMqKShm0SRQhMSE+3iXbau8COcDoGUeL8slVURYZdMn0Q0kJnUVMGxTvA37TIusctSxTflZhcPsOlRvyd0/hxZo4WKR0DC/XZKsaczQjf/eM4eWa5mpHfr6i+PZ97MWG5sUNzb8JiHeOKd47ZXh6nexsYyDue/qfPif/9oOUv7WoyM5WNH/wGepoDt5CjAzPrjAPH6AuyiR6P/SM6z35yTI5aT04ov/oJUEmrVmcglqls0nrM4XYBkgaIJcco6QLxH5Ejy5tyMMU4KkVUcjkFuZDcp3SOlkH60TBzWblJHaPhEyjwqRF0KlTni1qfL/DZzJtUW41AdNcEHxynRQiObExaa7g9vs3N+wtaoRI94gqzN2GMsYUtBrLDENgMavJ6mNEM+Kdx1qH8544pG68jBGV5XCciuMQUhC12zSJPmc0yqTPikpde2kUfrSIzOPdiL3YIqQgOE+Mk0PjrEgaNSHvHAGFSAHSYmoshSlEV+aG+HJ9F5Sr6wK3bfHOJsRS6YQeKQk+3lEjVZ6lgNaQmADEVKyhRCpe9kOi1cVIHCyMHjnRElWZ46/2d80As5zhti3ReWRVToc/bSalVtAMqXivEw1QFYY4WMZDjxKRWGTpfokg+6SRYeiJUoD1UGcoLbD7nsz7yQWuIrRDOl7LGnexJjuao3tH7Bzj5oB+eU32cJYCduc5wabjLIYRKUWiJ/oJRdEGESPD5Tbl8kzXnlAp9BcgdgMh5kjn8PuO7PG9RPvbtrjpfakiSyHBWiVHwTJDFZrQR3w/4l2ge90zqBOqb93HW0///JrMB4ZnV2QPjlHzEnP/iGxmGW/2qJkkmCkAWYiEYA8u3VNKQp4hYiQE8N6n7DQpoSyg6ROtXUrErEAvCtSgU5FqEhLsd226lhZJ6yPLHGUUbn1ATU56bzhhfG7lE+K2DPjCanVLvw0BPzhUmSUN1Whx3UhwA/hI6AbcukFV6b7V85J4pPBDQD4XKQxWpuxEd+hSAzMz6DKbGh8CnZs0V4dIvqzpdy0AvrcIGzj51jGmzFHXn94tpV9X6Ai4y3b73Nr7pdX464oecXeIPict/uIh+moqyTfjm/Ef7fiTD299a3zxBj4uNffqtAE8yfvk/OID89whfOrOhWzE9Q352YJvt1e86hpuLjes+yXLckUMII8rvJCMziI8WNdAppAI9PEM343oEHEh4gWUhWE3JPqCb/vE+wfGENBaEYeI9xGy5PSUzYvUsVaK17Xh8NEzVkvB1fxd+l3L8QAnz0cu/+AptAa7FgRR0+4ic71ELyuWDHx7CQjBLld0WXItuux37K8Sn/2WZy8k3BxaMnU7qSfBqQiRP/sgUuU/p/vzVkGjsoLq/NsgJCZEjht7J1y9nWALvecofwEx8rqJ/OQq/f4yP+Le7ByEoDGSfZYW5JVcoH7nCf22ZXQZ6+wdZJ4jX48sNq/Yvbghn+UMWmCdJyqRMmBioia1h47lyQLvI67piMGRv/gJcxl5RwuqSlOer+g/esXWLPgoXmPnZ1y2W6qiZi4UVSPIZEHpI5eywYuWvWiZhYrr/RZCoMhy8qxglmvqwvLk5jWL2WLKW5FY22N0xqHZoZSmHXuMyahkyabZ0bQNhckZ3UhdVLR9h/WWWVkxuBHlUpBvWZRIJIfuQJkVHM+WtGOPc5bOe8Z+oJkd42RASMtu3FPkOWiFtuCdY1kvaH2BcJ5uTOLpeZUoln7SVsiYNthSCKL3KJs0MfI20HVRohpBaAcCcQr/I20gc43dtGRnc5R1sOvBqJRiv2spHp8wvlpj14dkOXy5w29bivfOKN49w+9a+hfX2Os95fv3qO8tkNlA/+kFuip4oAvsy2vwgavTKevr9QUPrCM7W6Lqguq773B4coWuNCdXAyJCvPgxuzMYbi65kTteDgdmx6cEDjDz7LoPqfN71OYobSBCAK2JQjAr7qOZI0LAjluufIPZLJip+8jGorQmGo0S4KNglb1PHQZc19OGl3gVUcsqdY+tJ1/Vd5QuZXTaOMZUcIgpXHQYPS86KO6v2AVFJM1XyV96sqRWqSi6u8d8IAp4byV4f8VkviAme2PFLJeoloTUSYFrB/zg2JinIGHcrRGVIKfE+hT6zNUWOS8xdYHKDbLKiINDA8P6gNRJpxEOlpOj7yODYNRwvn5JqA3LbeCqrbAvr6nfKSi6Dt/09Gbkk/xVQvR9izHJ4l5ohRAy6eykQOTmzuqbyeLbT2gbAmatZz62+HXDpWgZjU45WzI1Ee4swW/d7Wyi3EUpEi2OpOFaLzQIhy8LolHgHE5Jru6V6FmBOcnoryKx0Ahl0Mc5TliiMJjjAqcd+eBZHlwqakh6JukC8eqAlWAeHaOsJ4SQmhG7NhU4RierZz2FcUoBhxFXKvYuYItEybQxECZ9jxKSWOQML2+4vu6pHt3D1yXNWCHWBm4O9I0lCIWuC4KA2PYorZlvHVFKTJ5c07A+IRqAyAxORl5dj4jC0LXhjRNfCIwvrlKBmRnMrEjnfrDELIWHtqrkYuMQg0uZQnXNeLPDlhoVFXZ9QC9r6ocndM+uUNZiX90g9BlNrRmKnHiacyRu8YrIroBh3xD2HeQZejKDEUZD0ydkt8hTo0BJYpVyuaJNTQt36FNDoOnQ5ysEyQwm9pZqrqjliF6AkAFrIv76Kd9bLTh6L1HTW5vR2rS9OSr0nVPbg3lGZdL1VSuBa/vkADm6ROU8dJOBSI5Z1OhZmWibfcYmgGgH9CZDFBn2qkFIg1rNKdVAnFBXeks2yzhejKjyDaXCNgM+2JSHJDX6YUH0Hh8k837NQ/+vUYPC+5Z/MSaKx1Pv31q2452TYfxSMfTvWLW8xfj42pf4Ymf1m/HN+I94/MkURb/gPXxSGX54r4IQOKZLGx+tqG1DoVOqt6xzBtdQzQz9USDbvOBRZrmxc0Cz2zf8dt9SvXNGtJ7DMDJb1GgPQ9dhiWkRDKnI8cGz7XqEltRFTucd9CO5UIwShA+p66mSI5UwGuECtrOEKuPHTYPIJa/I+N0bQYwFZ8887x0sMi5T+vuclLWzaZE3C65/75piVrJSiUazXeaEszmrb93n4qf/jP7mKUCyBQ7hbmJEilQoqYQgGSn43jKJOe8OcEw879uv37SYItIULN77dVCKevR8+3VDGD3KyJSxFCOr4iXfXj0DAf/6Nfz0Oi18R9UJ3z/7NQiRF5mAVcG4PuB+61POek++nHHzKqKL98nmFeJZT+Uaai35MAbm75/RdgODdXSHLlmuGkV1umC3a5MeQQpmVcH7m1cU3Z7ZrGB2/x5+29JuWj6r5myq09Sp9p6l1lRS805TsZotaPPIT+QVm2bPo+URshdsugP3ZysAqiznoCPdOFBmBUppnOvZT5ogrTPKvCTXhrqoAejGHiUlowtIY9i2B5bzBZk2eJfQh1U1Z/CWfhhSfo4QaG1SMSJSl3TXtRTGUNQ1PwvXHJVzqqxgqAU3w55nzRXfH47JhKLMc4ZDpHMDP331Gd9++B4q1/jREXXaSPrJFOQWOfSvXiPvncC8mrJcQBUZ1vqUwyNSCK4oM6JMxZPdtqhcE0h0F3e1RxYGC+SPz9CrOnX3Nw2xt3Q/fUH26Bg1K6m++4jx6SXtT56jPjij/LUHxNcb4ieXHL0YyDPDYXfgo+8s8EqQr1tWH7/CLGtEkaFXNRXAkyvuWYdoR5Adr3wPpeDCD1zUOTeuIdYaGV7TlK8RvaTOTojOTmFhkphnzPMHzEnzxfPdv2R3eIGQFdWjY8xY4a1LG3DvMWXOnHcRMeJDyzO/JooBXKISBZU0RMOhTxt8H1BZsu71+56xb8mlxGnJOr+P7jJuWsctQoxI96lUqXnxBn1NugkR4b0l/JcfCGJIj4QhIHPF87Xn0mpiNHeaJJVrri5+hioyBrnBbwb0okKvKigzqlWVijEgWo8/9EQXkGWGmsJJx0OHNDmLxfcoybB0NK8/gy4wu7S83Eb6C8nZccb5tkFE2MaG350/AeAoK3h/Ddn9I8TzIRWIegp8vc0WmtBnWeXEQ5+MEWLkWBiOPtvh24F13aIeHqepSUtin8KahYBxMg+4DYO9YwwpBYXmlbSIskDUOaG3xAheS14fZ+SP02sOp8nBLmYaISLxfpnCWY8NsaiYb0eWbbKMjplGGp2KssETR58cypRElRn+OhkHCCUJo0OVKc9KCJLjmBtRJqc/M3TtQPQO0VmiVrjLHdaFVOSVhsO9itY3oCV+rAlDgfQBlUmMUshco2QBdYF2kdVhRAwB6SJM2U56NU/zC4KeyKU8JXiFOsoQuzY5Ph4tkMsUmCx1Wu61VoSmw93siUqxt4Z9J4nrSHhxgAhmtUDUGpNnCQWcMqfK+ytCN+LXB4YPX3BzPEcdzVGZ4cGVx/SBKKF9kOHKPCGCTY/KDOP1Dh18uh6GZKEufEi5UNajtELWOSI3yX1vsAR8ogjnGQHwIVAtc+4bi6r6dOyzAKcV9vKa78SIWVZcxmNeryN+GBEHiwvpvTwsFfdIVvth22O1SnrjWZHsvp/fpOItgpoV5GcL1KTNvLrMiGSI6ylPTCxRVX53yQstkUFhzleozQ0PzwxS+mSfn2tCGQguJvQrRCA5SIYYeXjikPL3sfuW33Fz/r+D/CJvhNtF/A4M+xwa9u9etYgvfvMNKvTN+BUe/0Fpir5ueBdQ8wxEclALU5CanBVEIK8KQjsg8jpZMKvALM842EDbdFSPVwgtWR7NiUS6Q089L9jHJHj2ArwkpdIriSg03gWcIH0vJC4EpNHEZkyW3kaiXSTkGj/lgsjCIPpEv9F1ylvwzpOXINotw2gRVYawHutSsvVhfUAbjQoRqmSvrIxie7GhXFafOw5CCZRSnz84k/4hxvS4lAkpiCFReOLb6fLwBiuf2Hq2HQguEq8PXH58jckNoRnuuszo1zQP11TnSxBv65IirhnYfnbBVXAcHq3SwjZY6sWc4mRB+/qGrhuxbZeS1mcl/WDxdUm73qMmOkVe5JR5xtCPhAjGaKpZxX57wFpHriSzuqB+dEq+mtG/uOYnr5+gv/sOPgTKIifThnbsOSmO0VqTKcNNu0XMBVVZIpAcho5oNNuxRXjFKito+5aqNAwIur5FC0mV5TRjj7OWMXqMzLja3SCl4qReUJosObSF1Pnu+x4lBHVZU+YFfdeynC9Z5BXb9kCmdLJ77zvavmO5WCG1pspytNJcbq4pleHF+pJ3Tu+TZ5LRCVZyRtd3FFIzeMfL3Q0/ePQtysUMF5JbnLztHk6BiW4KIub8DJmZFO44K9L5lgJ9Midajz5f4rt+cm2LyHmRsl2EQJUm6ZNuDsTBMV7t8aMnO52Tv3eGmxX4l2vcYOk/eo0sDOZkjnlwjDx0HD67ZHxckj08QhqD/+gnWOfRR3XSi8RkaoIPdJ++pvreoxTqezRDCsHho1dpg+wC9npP9vAYJV2irj67wj9KG5Hs3or4aZzoXBIICFKxx9Q8CCEQYsSFgO4G5Kwk7vwUNJqaDNH5lPN06JFCoIsMVHIfk1WOjDBc7RGZRgJyElMH75KQvGsZs4IsJLqMvKXGkbRUMpcTWgSQkN5ErQuTVXME1PR8nyhH1kExubFNKIs0GjtYlJQ451EhkJ8tGS+2SV8mBSYzQKS72qOEQKpESZM60QyFkphFSb9rUZlBIaDOwVpCmUPwKUPtap8shK1PXXs5ueqpRMeMbWoEFUKgFhVCpyKTqUET/YRiyOTg59aTY2AUyMJMdtGWGDw6L1KhM7pJz5nms2xREKdrEq0mB8uQ6Iq3x01KMAoOfeqg+4AoDGJW0n/4AoRIuUpKErpJYCmn70NMOVMCGCzCBVw3YlazOzpxbEdkZfBdCieVQqSNvE5ZPSn4SCEFhAlBugsYlgJZmkTLm+bcOLiki8k1sTTpGJU5WZGoYMH7CQ0ckUJO4bETCmod6BxRFcSmw15uEiIkBOK9U/Qqx24apNbI4zmx6REq0SSJETs4xJAoa2pZIYuc2PWp0Mw0erVI1ODO0vcjRYiJ0tYl4wEgmRtUOZQ5se1xhx7XDkgf6K4DYrFIobXOo8oMhCCbIgCq8xX2cpuuwzJZtjNY3GBBp7UlND1ydJjTZaKwbQ5Jy7OswaZrk5Co7jifGn4CZJGRPTymf35Nf7UnVDNAE124C5N2h55hk6z8RUy0VKkTQjlumkSdKw0hmTTi9z1dM6BXVVoPVzP8rk1arSnDKDQ9csoXClM+opqX5KtzhNzgXt2gjmeEEBNlMUyUWQnCKFSmUDLRT103OcTeag1v6bcTnfaWkp+e8vOIdb/g+Dq63FeNbwqlb8avyPglIkW/YIvh3+Lmqo3lvGoYux2lF0QvCf3I3he0roaDYmE65quacX0geEtxb0H/4gajbyi3Vzx+ICjuL2nDgbLIedoovHUc9i0ueDIh0ErRjRYBaOe4t4gIFfE+8HIHGIMQiWeP1snxa7JG1ZlOXUSXglWNgKgkQ5t0EDHT7PMMcVQw9AovIlmRg1EMMqaOc0guYDIXjLuOul7wflCE331GPD8m++CMMIysbjpmsxJi5GqWYaXADymxO44OETz/RlTU3Hb3BfPeo4VgdbFnvD7gibzOFcNgqdUC9d9/SCYFsRlxxtAdOnymudhtCVKyijvYtBzvK8JswXdVspedH1qunz5FAystyV7vGQeLywzPjWBcbxCnc7yAfkjCXZMZkDn5+ZLtdk+7PSTevpa0Y3L4kzIVdjevb1KxqARFnlHfm1MezQi9ZXtxxeAdu3bHyeIodUGVorMDn1694DvzH9KPA9u+4UY1FHnOxbBDlnO6oSVIxamv0EoTxogUkkPfYqMn0xnHq2OyoaNtGk5nS6IQZDpjGHt6O3C137CoZlhn0Uom+/csS3oP71lUM3btnnYYqLOcgxso84LV8ojoHDmSqDP2bYOUkkIbxkmPZK4HlNS8V55TYKh0TjceGPCcH51SFgUegQK8tWkDrtImMWiFGh0igs5zfD8kXvu0mMYI+mhGaPq0BRdpkyZLk+hDhUFEcNcNalmiT+eMV1tUiFwox9jtKeaSB/dXZLOS8OKaMGnwuo9TcZQ9OqH67kPszQG/PbB4dEb93QfYn73CDw5ZzwjdwKAlFw9nRDdSbzc8XCxTx3ZZUTw8on1yiSHRXMbXG/QPzxE+uZ31Hz2Hs/vIeUnrL7nYjilY0yf9ShQZS39CZlYJuZu/T2GOkDHSjVe0u5fISYsUQiDIkptlQRtbskxTtA5TGFw/pq66ADE6smWF74bJGCGF5kqjkaKehPapiAk+cFTAf/k4UeCuesFvv0g/V1JAKskSXVgJIkkvEn3SIaFV0mFMyAKToDxan6zUrZ+ofAmFTBvMiC4zIpFx0xAODT5IlFH4TFHUBdEFvPcM13v0sqbbrXm9/n1MVxAMKcxaCw4fvya0A3pecnh9kXRIfUMjO+5vA8JB6WrOynNm5Sn64jVLGwkSRtPgnh6YPW/YV4qm1mkj7dJ1QmnYeDjcrxjbA63W5Fqnoj4mVzpCQj11ZvC7bqL0CgipKEFMBiMxIgqTRPzTflBHeChy5Ec3NC8ars+rdLhvj5UQxFKngh8YcsHLdxeIzlIcRhaNB6WILrlMMljEokBJiTUjh1pwyAVBClZOULXTNtSlIjyKhP4FnwxNwkT9Q8LNSc6YSaQUHN+MyMEhBYgxMF4dkg5qUU4W8oB3SegvJZsSQqWRY6KWem2RhQaZ46REz2vOj35AXEZ2Fy/Z7T6GCO76MNHSI+08Y7fQCCGodjsWVoCMRGtR85rxk9eIIkt5ZzEw3jRIJMKFFLI7sQ6iapLLXGEQuUqFZZGxm43s2w3CaZoRxPEcM83ZkLROvh+hzAn7PjX5yixZe19tp8gGQehHws0+PbZIkQvj00vyx2eI0wWdVVyIOd3TDcXRLKFIe8+i0sweHLP7+OWETnr660MqGn1Akgoh75OOzQGqKpO+zkdyUqC2nBxqg5aIzuIudjh2RClS8TgrEGKizQpB7MakR4Xkytf2yLM5L73BXWpmqznH1UgYLENQXO/0G+3e1LAotaN2LUIIZuuGv6KOUErxxDs+8+5u4xR/bt3zy+G4xVtt8jeF0DfjV3D88dHnvu4G+zm1VBY6jvH4akA4CEPqhLX6Hpf7RGEQ1UhdxGSHee2QpmT18Jjuao0re/IoiOaEkNUEMfDh68hoYxJPC8F8NeewawjAIkuiyBOzRytorePGVox4zLIi3CRzBj0r7mxYgxD4XYcMkZAphhAo6jx9JK3QhWEXAl1lcLXGh4ASEjuM1OcLumFMGTZGYQeHPKk5DnAqNdZ5rspTroNAG8E7q8jpYpYm36OMm13L7tUFrhsoipx+HPk3V6fYFylDpTye0b685PR0yeIa8jijcZ7npaI6r3DbnsXVnsW8ROQ5dnSJhlIarqqcajVnuz6wbWdgZxgq3hN7nO3xY8Ou6fFSoKLgzKfff7kqeFJI7BhwqYlKLAp8jPiQqBVHAozWDM4hRpfEqT5lyNh+YLaao4xNYlwvmb9/jzL32EPH62cvuHr5krqscFKhTUY7dmghuVev0DkQBOv2gFQiFUxGY7TmamxBRToTiT1Iqe4uvaN6wbrdY4eBzXZ9d02GGPAuMPiUpt4Fz7Kec7VdUypDnlXECEf1kkPfpMJpHJBCMCtrtJRcrDcU2iCkwgPbbk8lDJlU2Jj0TUop3snnHF1C07QUC8/ejeRZxnp/g8k1mZBJ8yQFBDBVTgwxFeWHHjO5dwG4bkSXeaLZ7bqEAN1SPXJz93vD6y2xyDDHM2IXEVqhYsRvO8gU+aLGtUPa4M41DA3zzYHV6RHl++fJrnffYzJN2LaMn7zGLwr0X3yEkNB99Io4QvGtc7rPXiWb4NzglOf6VBFjRt+1nG002ckcgPxsiW1H/OUW5UPalLUD6rzGXe8Im5aRLdnZkk4e6LsbvAQ5FVFSF5S6JFfHCCmZyXvMOAEBL/Y/42Be4fZJmC2kJIwZP9MV3YlAWc/31yNxkEknaB0i12RHMwZrE8VpKlqkmfJgjCZKkRArB7rIWBjPewuP1JGfbhS//ZxkMhBBiPi5/Uva9N9uemKi4VRZQo1C0tWE0SW0RkoInqzM8c7h21tEYcomGlxyg1NqcrRLyKtvR3zoU/EWwbcD2YM5m08/IV8dJ1RNQ7ms6K52hBjI5iWDa+mGj3HNDpFpzvycuLHM9BHnq++QMaPoJfenzVp7duDik9+nvh4IMaNdZMlxL0IgUYf2vcOf5vSHHkLSEMUp3PTOoGZCMG+1REoKgk/dcpVleDsQ5WQUMLiUjyMk0nruWYX98XOK4FmflQSdDDSQMtks2+m4ChgKzWWMiCJjJWF5aHFtf6fRE5kmWI/I0nrTHVdcH2UEGSkuLVWMYBRu1yUr/H6ckIDJeII3lOf10tCVGpFrZtuR0ia0ABdSsec8bt28QQgzhSgzPIKN9EmvpVLIeBgg6tsQXFgdzZldLVJx5nq2Y0IXgxRoqQgx0hWKy/MKKeAsUxytXXJbU/rOECGMjrBr0zE3ihj8G2rjlPEVXTIMiU2P7RKtLoTIVgnINQhLjAbWh2TlnZl0XEIgu3dE8J7WB2QQ+GaPNG2y1R4scfDTPekmVDmhWEJLxudXUOU0LuNgLX7IEAeLXmS4ZkS8Y5gdK8yypnl6gW3KSe8Godlj9/t0bc2XyLpGMRXhkwsiE82YCZVRVU5wAUnENy3stsTZDCuOqB6f4NYHgrPQW4RzyGVNnFdw6Gg/vWJY1mCOaa4iqyIgiwx3gItLgaxz0HIyvFAss455ZejXB04GwwOlyXJDGJiKore3TD+v+PkFXeXSU7/8AzH5/8a3f/pNdfTN+NUZf+Si6A157he8cb6WbfflFogymjD0iJioaVJKVJljbzqiLxOk7ve4wZIdzxEHg+89Zl5QS4nMDgxXewqjaIjIEDFGUZd5WiBHz2HfMsY0GW63B/LaUMxLorNIC2OuCFoxjJbgHPmsII6TS02IdIcuLYAqUTdyD2M7YOYFs4fHjE1PlNAfkk5J6jxlp+SatkldP3ygPF+xrJMuRzzfcVg3FLOS3fWeg4wsjheoerIOFQJ/GNg9v0EahY7JCU9lhn7XMvQpLVtrxbhv2Y+eB5MWShpJlmv8JHpGSXoiKobk6GM0B++xQqIzjfOeQGS42GL3HUop1KzksE2ZNvWiplkfkt1wjEm8K8ALsN6D0RitmM0rdus9o/e0uwadpY15WeT4EPERqkVF13QcrneYMiMXkeW3z1H9M9x6g3Oepx9/yq458PDkIQcE3jsG5yhMgfWOZbVENpIYA9Za8pnGeGjGjqbvWBU1je2Z52fJBUhrtPJc7W849B2r2ZxMKIZxRAvBLC9BafbtASklwzgQQuK/j95znKVryXpHnhUMdqRUGS54qrzAB8+j0/t0XUcbeuzQczRbsO86lmVNGywKwRh9oliFwFE1hyhY1DP2XcP58Slb94qmPfz/2fuvJcvS9EwTe3615FbuHjp1VQHVABo9jVbkNIWNWdN4QJrRjBfAW+B9zQ3MCWkkzWjTappooIFCAaVSRGQoV1su9SsefMs9MhNZhQJQxLCBXLBEVEa62L59iU+87/NSu0LM+TELbjfLRtNUBXEYyUZjjJGMmaoQ6efNUbYt5wuKh2spro2Yie1ZS9z1Ih1b1VLYhShhhIeeMAX0ukG3JSkGdAb/Zk9/01F++BB7vsAsazlvawc+EXZHpp+9Ii5LqqZmenUJbUXx/gUgwZvqruicJU/j60uKs4UUuSrTPD3j9tChxoCJmXh7Qv/gDA4dWSn8y2vcg7X4D/pRSH9WCunsI3lRzBKrhEqQc5Im+DSIvOfmKNkkALOfIeuZGpkySov1TiV5r92yJvUjfgiEwRN2J5HIWgFSaPfOT5NjRBVzQGw/AbWE5n5D+QrMjdJsENASsplnQpWQ2BLKORgmTCNAgXwcMYXk/pjSkYzGrRv8vgcfcXVFHgPKZtnAME/pd1uyNhQfPZX7Q1thVy2ukRydmBLurKV/fYs9W9C+d07Ome7nr6UpyRIamrVC0WPONeMXV+9kbBrssia8OEpopVICw/FR4ASIxyv6gTRPorWxUnha8VZlLd4hrCGPItlShWRGqZzlGlFKgCIwXwsCp1A5y+80Q/SJNC9cKBxMEl2QUChhKpDupG/zxD/dTchHL08jJZ+rjRJvWTeiVDsjuWeMulHk4yg/W87yfYLcW1XpwGhpYtT83xXv8NRFIRsvo1BWkaYEVhG7URD5x1HOjcKgQp5R0bINVNbinpwL3GIKjF9cEdwRbS2x6ySAuClgUUEW36yeN+8qZVRdEj/dCTlvWc9U1znN5o4cZzNoQxonkeoqRZqpgiCNkHLye0sadErE0yTFfhaf1d17XH74SH43RpHHQG0t+dChLpb4ToJzTVWA1oLcHr3IIlMmd15+GXVJPvaE68M9eVU5S8wZd7FGKcnBqh9tKJLCFBX+cg8h4dYbvLHoQiA2GoW5k2Fmef4pwJVWzp9uADL2rCEOkveUjCYfjxLqPgbKJ2ey4fWReOzJx540BsyqxZ0vmXYdtrCoYSTsT9hFBbrCrlshYsZE2HfouiQpua8Uq4aNXuLfujuF+1focL/OJujr7dA3q6qvB7x+81N/+Xbo12qyvju+O/4eHL+hTdGv0RB985r6S9fYt1x0es5AGT27g+IYK8glfZJJH0azO5UMrz2VqWnrxGrpQQWuvEU9PcOWjk/TW7plQzd6dPMRKmqST3TdgKsKsLPOPWeCioz9iM6RYlGRDwoTM7o02AdLCfxLgnhNgxS0upJcDm0NoRtxdUEKkePtAd15QiGYWVMZTJaHGFbzQBvqywNF5YjWcrU90t8cwSnsphQpS6EprOH61TU7U7L55CnTvmO329H1A7YpMNZIoas04+BJsy8ia00ymu0w8OKsEqJ5XfKo7CAlnAHeZqZhIixKbs4qqqpgFwOZxNRPeLfkx+m3UBGKWGK1onAGpTLl5DncHtg5xbguKJslJ6vo+4EcI7awclPWGh0iReHwHobTQO5H6qYko7DWknTkeOoJk0frzL9If8wHn6yoVreMt3uSUvyXP/xj/OYDlueOvVKUVU3SmuGwpS1rmuWK49jz0zhgFpZoDMokXFlgp4HCOWxZUnhL5QqiURQnzdlOYcKC8vEznneX3PYHQowsqpa3u1uMUsScWS1WLKqGF29fYoyhbSpSylTWcDY41Bh5v3zMp/EWnyJ937HqpaB71G5IZyU3/R6L4oflY/CZyjp2pwNNURNOnsrVaGMYpxE1jTxYbahNZHs90bhSHk4JcrrzbWRUykKjGgJmWRNDEHyxFikPRkvxcH2k3/WU751jVhJ46B6uQEHsPfn2iHq4pnxyxvR6Kw/8biTcHokXhrSwKJ+4elhxMwW4vqRYPKT68Az9wZIHr06kmyOLB0s+6E74Lw6oeEBFCNcHtA98+LhlutxBiPc+t0Tmy4WiiCfOHj3g/FbydIpVQ971qG4EFP72hD1boF4eiacRf7ml++icm4XIej4Mj3k4LMlWEwrPq8s/QaHYtB9T0r5reCopnM/dRxTlkmQVv7C36NwDEIeRVFVYbSXEcwrkECmbkrDr0Frjlo0UvsZQnC+IUyAcZqlXTHQ+8yLUMHlUofg//lBB1nx5UPzR6/zO46cVKsHPt4rhJ3Ib/OFG8XEpPqfNMlKVA0M8sA0Z7xq4a6IQMp5rW8mq0gqzqIjDRNFWTHMDk6KcF6Z0oBVu1UCIjIceVbl5o6QxKRP6CWLCGXNfhOlFjTtbMF7tyQcZUo1ux8vr/0y4PUnjqDX20YpiPOOB+gGp9XR2T8onrNGs957FYcJOlpscORS8w5DflW5GSyM5U/1ykGbnyS6grk9EBddPF+IpJWO0IY/hHvudtSItK77E4B9XhLmxzSHO/iZFdpY8zJRNFDpEshIi4LipeDlfV82YWV/32BjRVUvY7bBa094OvHcASstj/4DzzQUMnt30kiHcCuKcjFk2Qi0LSRqg0vHgemLaSSNbOjcH5yqBN1SWoOHyvCBq2QI/+GzEKEUO0gyqSRqEYDXFxYrwdkfsBnJToouGt8OPxb9FT/aSvbVoHrDhMRhFXHi+TG9AKZq44snqsTQhpcWUBTlLppM0q5pb/yWjOaF8ZF2+T12fk2aqoMirErfxC6bQSXNx58OKCUKGOG+eTiN51zGuSl60G2KGwhg+RhE/eyvXpTHkTvy6iKrvfpuXfSI72QCZVUvYneT8UIo0eWI3kq92XO8jQ5Wxm5axbHBGpJtMgXgYgBazbADJbbpvqOcm0DSFSEz7EbtsIQTisUe3NbopmLSCtp3VLfIeaK1ZDxltWtRFjd0ciV6CZbmwxNsDKSte7hrUUZOaUuAK8wZYzZ6x7gTPu4pyWUNVEs+lNOt3HjX9eiXWr3P8ytbmu4bou+O74zfTFP2Nrte7T1L8CgmdmJJzzvSD4TpUkj1RjmglFKChXHHcH6l9w4erI+taKFS7zjIlhTtfkM41u9sbfKWIOtO0LcOhRxtNEsczKUbJ4BhHpnJCntceGzVlYSVp3VqiFTmBLaxMqWMi3J4orSUWWW5qWsEYMLWhO/QUprqn94RhAhRxnGi7yAeuQKF5/vyGLkzYpuKgI1EZdOmYvKfQiqIpSV3CH3sOL67ZxoFQGmKMtE2Bs5poNafjgK4sapzIWzHjB5W4amU7VNnED9yITomyqjgpcEoxGs1l61ivW25v9oDhsDsRdIHffA8NGBRuxmavYscHROLkiZslb5cFVVvSHXts6TCmhMEzzmQh1VQUlaLrBpEQavFKJGsYBzEEl01JJtPkyD97uOXZYoffBT6tHvH6v7xkHEb6xxv6KbBul9Tasu0PLOuGY3+iGzvO2w1pUdA2Fa8vX5ODZPM8XJ/z9rCFmPDB83a44WK55sPVI/qhZ5t73p56Yo60VSOFIoq2qu99DjolSutYLVZ0/QlrJFw2xMhyMuhTgn6iPi/pk6csKz4KK4wzlNbxh9sv6fNEiolP4gIXFevFgjbDptjw5vCWpil5fvuGh8szHiw3OGWI+SivQc9T2SwP9ZySSIaakjx4dIY0eozVhH6gLJ3IPCePVhqqgtxPDM+vcE/OcGuZELtlQzzdEsdIvtzBozXF0w3Dlzcib8RI0KmXDdNuU0Ca/TO7Lc4l6sdnXDiD2yyI3cDDuiFaT1IJPx7ksXpzYt2NpMKSb0fIiaw0/cLx6v2a3B9R5pxzMkorFs8uOB2/JFkjHprTSG4KVOHIasK/vGH6bz/hRvfkkPgoPWWzfUAG3qSfsTt9BlpTN0+orGRbpdOEeVximpJV/YyquiCmgFUn8niQAUNMMHhSke99QtPtieKsxcxNpi6t3C/uNjxWYRclZJEXjT4S+oqcS9ZV4p8/mVBaUbyGP3qtvj7C1YoX14GXO4PSmk2l+cFDOQcbRmqXCJvI/ssT2AazrKSQdpZMnCWvhcgpc8YtKvy+R1cFcX8kjgHWLdko8YJ5keNEH/Cjx60bXFWQDgNhexLHU4j3gbL147W8zNLRf3ZJ7AbSIrPNLwnH69kYrqjsE9ZTzVnxAUknavcFihNRK5o+cr71mHTiuJJ7m7EFKUyypclZKHFphjrP8JgcAqtDxt2MZKXYPZVoBIUSaVear4U894qrhstDR7wo5fWnJMG8d4+YeWtFuqPlqXs8/aTg+kwAAHnnOdsK/CENE7pyhONAefJUPqCc5axdcta+h6ozY9wzxFuU1gIUOQ5SrM8yaxMiq1MSWmQ3ofqJ7Cx3SkqlFLoq2K4dk4HCai4qR+omOSeDbJJTiORCNigCr9Cw6wgbxd7Ov79FJUV/BhcKVuV7aK25Dlfk/JocE46Ws/Yj2dSWgkRPlYTG3r2ezt8ypAMYTVs9ZlU+FYmok0Yj58z++EpkfSDDgySgizSM82YpkceJ4arjtHV89qRmSpm2MHzvvCG9uJZfxySVvy4kl0jnRNaOmCJEaWr980vSpsOsW5Q2pEMnwI5+IvXQOUtfFnB1RFeeECPubIlpK3RbYSZ/n0uUvTzvow/ESbxqed6g62UtsA2QPD0vzzlrFR7xFptWrjWTYHFK6AS6TLQfJ2kcQ49Siug9p2Pi1W5D9hGzzrKJNxp8lOZJKfptYKhqctCYSmEWsjEdB/21oPR35VOe1W7v8Nzf1rz8On/zl49v7Jd+hcXhu+O74+/bof/qD/nVx1/rWslf+eev/KD5UApTl5IZkjPEKA9sEJpWU2LKgnB7eic7uSMKAdoZqosVyydnuJBIQW7c0zhhjGHsRwl57D2NtjilMYVMVEXWlRlSZDwM9G935JSo2gq/65luO1whMqWkRW427To0AkyIo6fYNGDkQVkuKoLKZDKlMTz4nQ9Y//Yz1j94wvr7T2gvVozjxBQCASg3Lesn57i6YJwCp9PA9c9fk4GzDx+wOF+yuFiijBCWYky0F0uqVUNQ0PUjuikkW0krAUFYIaH5aSL4QEgJHxLGiPbaNoLzzjkRVaZayPsegTAFxmFiilEe9DNieJwCE5n+0OGUFOspRHTpKAt5sGUjm7QcIovNQqbCSeh3GkWaAteXW8LgKZ2hOhcggF3WYhzvxENwXq94tDzHp8jVcUuhLReLDVprSltyGnsGP/L25pLCOSY/MU0jl4ctTlv2/Qmc5WyxprLFjFiOHE9HpmFkGicWlWQNZSSE9tR3vL695uqwZT8OWGupXAlK8Xp7xegnVOFYNAsuVmcUZcEwTox+4uQH4jAyzYS6Q39CAUlB7QrGvudisaHre86WG3JOfHzxlPNmSVPI726KEbSRYm3edvAVGYsunUg6ojxkc8pktORuTR77cC25JCGiZh+S//IGfyUae0pLcbYUgMBJNkM5Rqpn59izFoySDQ0IBjzOqGkr2wR/faD7s+eEXSchhYsau6iFGlcXFI83s4xNtquEiFnVKGMwc9Go5mZk+PytvP7ZS1C9fw5Wiu6ck9C1HiwBoR/GbkS1FYkssibkpaUQ5+ZJoWO8l0vlKIWyXbeCeU4ZNZ/LOs9bN60J4yRFXj+KPOY0kroJZQ3hOBKGCY1IkdIU0NYJcpuE27TYRSVBjbOEjPnjpJLhnSZmvt3pr0hj7szUd0ZuIVJaCaDenjClkxyVusQtKpTR+Mu9/NxTwB8H/KHHFg63aLHrFlNI+Kw2Ejg9Hgc0SoY4KTHsO4pHa7l/KoXdtO+2WfPrtG1J+exMmsJmlnehZq+LQAbU3CBpPftdykIw0vPfo/W9Kd2UpRTgma/JKecbP8oKlUuBNPVK3u973Pj8HLgvGq2W9/3Q3zdXzBunPG8W1CyXympuwIwWA75Crqm71xnj7HGSsNw7ebCeoQJp9ALbUfqegEYWj1AevNDqZoCOcnKOZx9Q1qLvQBl315FSUMjGTutZZggSsIwiT15UXj5AyrizJfHQcZfXhDGkQ0+a6YJ5kiZCIiMEOS0UVcQ/o95t5FKSTKMU5yaY+TpBNjXBB7KRoVBMUvCr+TzWWqFCwgAqiTALEH9SFqhBJnG8vWI47AR1zVdmAU0p742eUfUgTdX8tZSPEjqd5pD0mIi3R/rnV0xfXhF3Em6tSyv5ZCESdyeRrKYkYam7E9ObG4Y3N4TtaQalKKl8fECRqc4XlI/X2IWoKbIP+O0RvzsRDkfizZ58kC2ydQadRPbm9yfi5Oez9V3Nogu5PnXp0IsK5gFWDpF46NCFRZeWeOrlHjaTdOPuRL49EW6P+EP3jdbkm6I4vvJf1PwKvr2w+lXWhjz/39ePb2mcvlsWfXf8Azl+s6CFr15bf9VF9G1yuvy1/8FPb+A4r44/OYt8/DTjd3uwI2ZRodrMbVdwq7UYvs8VuVJgDT+9HXl5FFP6+05zXll6VZOT5vbQozIUhaUfB4aZfHbygaAyn51KdHLYoiBYCbhUvcdWjhQTp+0Rl6SQy4cDv/t+Sc6wve24KUr6Y09hDSkkmosl3e7E1A1M+45y1ZD7idhPPH9xyZsoD+g41gynAd0UFKWjXbekmNg+v2Q8jSzahqsWtjGhbGbSiv7QU+oafxrJIWJXNbYsUClhmxJ/knySdtUIctxaPJrP945xamjqhvhehT+OJCIxGYZ9L0VRhmAUUzeI5M8omqaWLUUIdHXB5y6TtePoA1M3opylXi+Ib2/p+ommLWnKku2px8ckeNnSYUuHGieSkgDXOHk2TcX76QseuMT6/IKrq0S/eUx8PlDfPKSul/wj932q9IAvtle8t3zE0/UZL/dX9AfPqaylQA+yRdoe94x+oi1rFmVLUpmr3Q2gcGhSjKi24O2441MuMRtDGiL/zDxlmZZ0xZIhBjo/iIyqukBrQ7/rsLakMCu+HLfcAqex57K/JtOwMZphHCiLEmstz9UONwc8fqDPWWNYmJZxofj5tKPRBb7PnNVLLJo+prlwm3h1/BkomMIg2v+YqNySs/ITtDZ045bt6eek0UuxUljSaYDZZ5JzJu071LLBPdng3+64o5SlwRPf7knHQbKG1g3m2JOCIRxn+ePZkvLZObouePDlkbNVRTxOvGoV0YHWmcdvBqwXWtjnywnbnNM8PefJ5YiuC+wjQUabTct47Hn9qCIaRZUVD4+SRbLUa/7l7gdgLfHyGv/ggDtforTCnS0FcaxEaiQhm0YyYo4DzU/e8MlHDxi+7FjVMyY3J/Iok3WdpOHI1qByEsz36xvsxZrLy59hRshK89uX76Pb95j2Rz67+AkDE3VR8XuHD2lMRXBw3X2BnomROSVSkiDXNEkzWq4dj363RBlNf6X58t+JN6XrDZ9fVwCU0fN//uGci4ZsKFLK/Gxn+NHlV26id42hVmQ0SgvmP3eJcBp59sxQGY8/9FzuS447T7o+4C6WdC9vyFpRFAZbt+jRi+HcaJGeBYGG5CmKB+jQg9KoMw0piV+ydF+R6cltuVwp3v9Xa45fTMRXBcl/n8zIKd3S2UvivuPYvKbrXpGBrTqgFwvSrmNdvcez5RK7arkxz0Ef0Gge7DOLmx2mLLl+VHOan0jaB1Qp8tQUopz/zIX2HIB797gxMfP0WjYqdj3y6RSlyUHNPj1pRKUZS++M5PMGOIOEcc+fkuamCafJPrOvDdtHJVMV2PSJs6BJwL57Ts8RgCFsxa+RM2+KxPBBK79DJ8OfnCSkVzUV+ZDQtiLPTR8hEo2CoAhaGsuo4MsPlxKo6iOPLsW3dNdw+uNIqBxvH4kyIZu5MXuwvG+OcYY3que5+gkxZ066l61YzrxdHvmP+mfkGFkfPZvJkg4d68XHNOqMrOaGcUyoyvKT6iVhc7rPPMtJgCDNYcSMnpzn0rxwZB/us/F81/HlA03UFfa84r9rKnQA7TRWgZ+bQoVchzlmYvbz0EcaV2M0USmSES9ZsWzmRmNuLK2TYanWqMbIPeDYi3TRaJTV9wOleJCtJM5i1i22KSXCwgfSqSdOAinSKFRdYupKhjhtJZmEVksTU1iZ0U4D7uGIqyxJG748LcgKnEk8bjpMW2K8ha2VzZDSpMs9rBupH3YnzMVKGuZGvlfTbzlrFUW54lUxN7PfkNYovnJt3pdTXy+q8lc++pcdfzMgw3fHd8ff3+M3Alr46jWTvzbt+5YP/rW/Klyd5J8MrOOBf3Jm0Q8N6aRJ0wlD4MhSaFYHkdCkIaHbiqsh8sVe1uKfbCc2jWVV1Dx/uOF4HTgME9FHYvBCkXKGqBTaaN7uIzUapSOmLST/xUC9qFAoxmGiUIrxNLBYadZ6lHyfSfPidiQYRew94Ahf3pAV6IR4lIAUEp7MjYb6YsHuzRa7jUwp0iwXVG2NnwJ+34lvxUdCDGwttOuGyQdsTNRlwTSbggGmg+SsTMcB6wyVAp+R6fY4cdwdUW6NNy3H7sAhA4XGrsUwbp1hd7UjO800SYq71gpj7P2k11mDOmUmK/kk+1OHMpY8ejwQJwlRbNqK4AOpAm0N3WlgWcx5PacBPwXMjOsttMYo+LDuefhAUbotp6Omv0pc//gVljVtfcGH5yv6vuPj4oKPV8/Yjh3sRozO2HPDyQ+0TYsPnhgCdVGz7w6MwVNpi1MigeyGjm08sCgqjnngSvfyOxo9D3XLOB4J3rOpatpYyRbNGiyGfUwMw4gPI2oFj1ZnKK0pJ8ftbifSOx+pqpLgPWZVkJRhGAfCfqAZNTYn/nh4QVPXfLB8RKMa+mmkNJambtjttxymju34c2xVyqKkKDC2wOSGVf0+1lhUttx2Pyd1I9pp0iiNg3YG9p6kvYSaXu/R6wXF0zPGV7cSpLmsyFMk7oS2VTzeENsCa0TWGN5sSceRdNZSPN7woHT0n74lF4bbxwuO04TKivYUqPpANJo3FwXTfkdTax6lEo2AAxIS8tl94dmdlYScqA8TF0rQ4lW0fDg+glFx6D0v/uJn6H/8EXZVg4Li2QX59RsyCk3G3xww5wvyMFFdd7jFgO8zJQFWCu1FrpSVQhsDhRWprBf5Utj1FM8u6LgmhBGTFR/vf4vF+cec9C0/OvuSU4Y+G6r+ES0VVIar06dMfhAPIcg2OUSKtpylLIH1h5UY50NAOUMcPKfBMy0li+diY/jhppN73B0qPcExwI/ecu/pAGYqnWxSZLOR0M4QjwO1MqyrQLfdc+lX8vcpYStH89453fUR308Uy5pwkul4cb6gWFQS9qwV03DC9iP5dKR87yHT9iRSymEibk94PWc2zbIiVys2HxlsVoydgy8fo5cQvOW4/xJVObrbS9SiJB57Bp3BrIijpzRLVtV7mGaBCzcoDmQUbR/Z9BJauj8rhXIGJMDMm5wcEsrOtFFzt5lRYIxg2HOmvRko6xLXJ/Rs8L+7FtIwCYQjpXu5HXOvJCqkPHuLFMqYeVuoUFHgBmFVcWs98byivJ3YXI4oaxjigb4T5HOes29yCJweNZwetiTvZcME902WTpBNKedmJbCZbArZvuQMpZWmBjg8KESqfdvx6O0w+6I0TAGVM8kZdheyJVVG329Bc1lAsKjCoEZPDm/IpRN4wXze3fgt24WFEOkPR9QR8jhRF+c0xUaa5rtzkMxluefYetnkGHlPtdZ8v0yYQTaAxIDSQsxj8KAVPngODwomp2mXjh9YRwkEq3gx0xWTn1HreoaTaCXch9l3kzNoMsYYck5CoJzinM2n768j+VgBlOhlja5lA4WzpG7kLs+POfMpXu3kd4dsHe+b4TzHG2gJ7Q0+Sth1jOgQScM0wyoKbGHI/Vv0akm0Jdt9TbaWykYeVSeUEsqnVom8bLCrmnhzhJwEspSRgODS4hYVcQq064bzcofRJypbz+fofE9Q+Svt0V3b8w252/3xy/7+r3/810Cgi9OCt//5//p3+P3+I1R/Z9/uu+Pv6Phby+e+efxahJRfJqP7pb2UTM/8oSeGiG5L7NkC7vTaTSkPmNnQekfS+ZYXR7lpaJcNZ6uWujBCP7ujGlmNNpqickwhMOVE7CZyzhRlQT6OjPtOkKROKGspJbwPTJOn7waoHTEE9l2PMpqqFgzylCKH2wNTP5JipGgrcmE4Hk4EHxj6AZzGOMvx5sDx7ZY8E+OUNZL14WZ9sdH4bgAFrnQUbSnyGq3xxwGnNHHw8sAJQnsLIWK0ZupHxm7Ezg9/O9/882ygHUNAK0Hg6lmelVNCaYWfPK6WhPNkND5EAIw1xCghmdMUsFZMz82y4fZaQmtRsL3ayeuoHFVTMvYjpTUstKZe1SyenslrP/XYRc3w+RspGhS8uH3L7rgnG80wjfzi9XNiFCnkplnS2IJVJdu1nDJnzZIYA4UrhF7oLA9WZ5TG4rQh5MA4jQx+op8GJu9ZNS2rxYKyrFBa8Xp/K2RCpem7ju1+h7GW0pVcLDc4pbk+bIkh8Hh9xu8+/ZjGFQxhoh97qrKiLWvqpmWYJpyTPJlhHETLruDPX39OPw4sq4bWFOSceHTxkGfnD2nqhfyelJZ0926U898acowzYEODT6jCSTEHsiXxEXUaBcigNdP1juFmT/nBA9ymId2eQEOeC/rpxTXp+TXjp29Ib3dUjzYorRleXNP/xZfkmKg/eSSSpTmINSuEahVFGidSL43/8ob+56/u5TjVozVxCthHK9lEOIty9p5MxVxUomUaDND97KVkmqAwbSWbLCc/r06Ip6EpicYwvd2iFwKOSAqyNeSETNCBbAwKMLOhnJSZ3u4xi0qkLM6iUfg3W+yqwTgrU/1C/kxa0NwMnjz/ozPSLM+6fnKmv9wTei8ZRmPAzrRHpcEfx/uJdZrEZ5fupL45z9jqPOPW8zt1Xf7K5oI5l2yYiIMUuNXFSihvlcM2FTkl3LKmPhe5Y0qJ8tEaCse466RZsIbUe8q2AqWIuz3pdsu4PYEzlI/WEki57xkv9/TX+3tUtt/3jFcHxsmTC0csHC7n2cCOhHmOXrKwnCWfRrQxIpOyswQ0pXsvFsbeE/hSmAvxeXMQRi+F7ugFy6zUfUDm3YZHzfQ4pRDfphG5tZrlcWTknCkdaf6d3Uvp7t5gLxtGrdQ9IU4ZRZpzr7D6PhPKxCyytvlcV1maIZ2yeLGigBViirPkcy7Yc5LXeddwaUUu7H2DereV0/GdjDCOXsANszxW38EkQpyBB9yHIKc7aEBGBlmlkCDz/DOomNDWzjJp9ZXQYNBlca/SUFoLCVAhW5hZBqeshpAgpPtcHtJMegR5j3ImD7PsdH68G60wSt1/He4IfCBfS83NjDUorVClk+y6WcJ3J+dUs/QyhUzWBoy5Jz6qWcZLkHt/9ol4fcS/3TO+2RFuT6QxEFMmgUgVg4StxnnLnrUmlwXBSJgrWbD1/uZA6kfC1V6ek9Zg1i26LsWX1I2YpiDcHJieXzG92RL2HXHwhENP3PWE2yNm1VCcLSR8tnQy4KlLAeEoSMeecOzRpUW3Je7R+n7bxvzz35dWd838L+1T5i30r9sQqa/8w7cvhr6DLXx3/EM5/taboq9NEH4T1803v8b85Q92zcsA+SpysU6sW9EnX6wCq3wiLxS3LzO7YHHnS/rQAXJz/tO3Jwoj2vSP3/sZH5xbJn2iC3uiD3Q+cLv4gKjM/QOZCggjRVJEDRHDy1OBn9fWfcxko/DK8WfPe5RKmFLzg7YnFIF9XXCDYnu75+FFyQcbS/CRt4eRY1HR9wNts8LvRhbrlpAzupRNSjiNxBQlc3AKWGfn90Uz5ohrSk5vdkxasV5smE4zOnmWClgreUi5KThd7tBaUdQlZSPY6sVmSb89YZTCFJboJ2ISSEChNQtteLDtUEqz14nbTUNG4X24N2mvxsjqak+zWXDr4EXOc5GXcM4xeE9RlxRNRYyRx4tIy4hRmuHVnniMhH7id598yqMPLc3TM45Xge55T/XhQ06fv6E/dZS24L3NU1b1iNaa2giqdOt7/nj/BrVQvP/wgr6PNHWFnTzd0PF0/YDD0LEsarTS5NHzj8wZ+7EUSWFVcXnacbFe8o/iQ05dz9KU7IYDxlr6KnNoFW/8DY9iwyo5alfw2vbsywmVYZ88JY5T3/En6ktaV1OWjkWzhKkTfDeZm+0VbVHwuDhjvX7GVbdjbc9ROdO7E3H6BTdd4OgHmqZFpxqdFM/O/gCdFJM/8vb4Y2KM+Lzn+c1/RFtD1JHcOHSeJ+cZfIo4jFC3omwWdC2Srjh6pi+vSHVB+f4Dwu1hzmxJ4qMLkcuV5Vgr8rTn/daijhKU2f35C8yyprhY8t6NZ3h+iVKKqyfiX0MhEqCYiGR+YTxFPLJ4eM6zK/HZpMOJj3ee1J8Yybz8aEHOmWYMqNv/hCkLdnR89kGDQrHa7/iweIDSiurDR7C7RqXMfun4NCTMbz1men4lfqWmoDhaLpjlMQrx+k2Bm+5n7NLnoBWrxfuclx+SYuSmeAOPLPnyIFI7H8mnkQ9CYnN1QrmRPzr7CRiLI3OWJmzpJJfIGqZDj2tLxquDgDh05uf/ww6MIuw9wy2kKYLTlOcLKfBGT26yFJ6zBEhpze8+UTxcyb3u5U7x3//o3b0wJ0WOivcazUIl1KrmNjcc9/LfJzsSe48uFX7bYdcNxVJgC93VnnrTUj9Y0r3Z4vsJWzmKZc10u+c9e0teHUhh4sv8TLYdKWMKR7aGYfKoKZBjortKfPr/6Dg+j5RBcWETVmtUUxF3gXQK7Dclt2cGzleExhEnyZ35tL7ksj6hneFm2MvWyxgePfo9HmSNrWrOgyXu5lv+3AzauqCpO4yzxCLg3/xYfJtD5MnqH6OzQVvFXv8XiBN6CHx4ikxvT5jkePb0n0DIhDDxdvsj/OkoviBr5jBdTfL+vvAEoLCUfZCtTCWhuckHlIJl8ZT3ludSzIYkzXzO3E5fcJouwZk5S0oa3jt0eAYIQs3TShoIToLNVqN4jBTSjOXRoxY1ahjl+jRy/09kGf59BRaRZk+LVkp6HAX1EHn44ij3iH6UZ5oxnC4qrhbzJkzNniwFefRgZPPwi/IVw1kPKfOBfcAH4QPi5LlebjmEy3uFe07iQ0Vr1AyBePWsZSoMygeeXU7YMaCN472XByKJYmkwn7zbXoTtaR7kyCYSJ4HKefCYwklTmO/Xee+CcFMSFHjIAkqa32d5QiLDkCxbtRQT8TiK0EELGj0ZCdAF2TSZ0qHqAuMsRT03iEEkdf4wkHpp8OP1XhoZZ4lAGiam2vFleojSmZAngZoMe8YHCz7vask6UnKuwZzJdxoIw4ghk2d67GJjOLMHzCLgwggUmMLx/qrkv/1ABqufb0deHqb5Vv/V1uWbRdO3FVHfNiT+eo119+/ql338d8d3xz+A4+/GU/TLJhp/1XX3lc+bkqWzNVllVhzJfiT1E6VWVIVDLy3XrmS3A1dqYtL3D7nrTqQJWsHvTNesSwvLTK40qIL9q45llbkJfjYIC5TAlhKAWBSOw7bH6JJsJbvHG9mE+HEih4KYM5tS0cY92iiCtVwOiZAzi1LT9HsoLfuU8cWCZO8qnsw4TIQQWJlW/Eh1gfeSjTAee8rCyQQ9Z8q6xBrDcZYTXL26ZrlZ0Cwahn4gpUQMkZASVikhzi0XkKFalsR9J3lJd5ugmDgdO4qmxFYlu/2JZ6sFqy5ItsayZOdEjpJzZuwmlNEUKdOeRjZ1zS5lqqYgKhhGz3LV0g0jk/eYwlIWFTUHLqYth6B4EBqqoqI4X/F7H37Ourlmev0l158qWJwTjj2/+MlP6aeBR4sHrMPI7elAHya+9/AZDxZrOpf5RerxYeImHGhdwb4/iaeoXmC0oSgKYobtacf3moec09KUJb0aGP3EfuiorOO3F4/Z5xM+J3bTkRgjXRvY2pExT6ynAqckp+e633FaSqbJom2IfWZ32mNrS58TJjvZ1CR4sD5j2+2prePx+oI2iEeiLSpWQPaREbgOt3jfc5oGsm5QpqLQDe9X/xQdFIOqZIJLJuvEcXiNqQr8PHlVzso0d93AzZ5kJQNDzxsMxkDcdaJhNwp/eyTuO3RVYJYVKiZS70k+0rcVx5VM7/vPjyxDAp0xVUE+yaa0bEraZU04DbyoFLmZSV93GyOtOK5L8vHI6bOBB6GmXi+wnWVTVvjDhGsLXl/M09Y+cLi9QXeJY6M5tQ3KWcztwPDZW6qPHqKrGp1q0s2RqTJM2aAbQ/7oDL89YoApOvIp3stVSQL76MftfZG6Lj+kbZ/CNHF18znmqSMtagm0DYq871iXispWjP3Ij8+vGI2mVIZllMI4dgGTinkjkElaGtKYM/svvAAv1Nz0kHEzdjeOgRBGYuPRdg4sRTYaGxU4Wxsg8/xW8eOX78hUycvGbfEw0zqNKQv6VNCPQMrEHNBWCuXYT6jCYtuS5vEa/XaPPw7gE66p8MOELSzF+QJXwjLv0bZgigk3KdmcKcVw6qifnaMv96ToiaeRsE8MtydSJ+b20Y7gHKOKjN0oP+N6wW5jpKkaJag3H3u25cChCFLQuwDZkCtHw2PWnWDolwlUQLJsYpbi7KjIxUqax1az/PLH+GlCeXhSblBBo2zm4BMxJ/LtkbOqZNhNFNryeNdi65ru9ppQ1vQvtnOTEGfLkYa6kLwYpWS+7rLgmjOoLAGuRLlfO7tgUTySxkdn0izfOnHDabqSgjwlkX5xZ/sQ2IaKiThvJSCLtK4oyKejwAW0ks1LTKRjL68nz0h4ref3RciIWtaA949RpZR45ozBhMzyMElkxAzrQAdGlclNOwfjxnsvD0pDFNnzvui5crL9eW+8YOHPyY3BqU6aLjdLFhEvXFazPDskjgvH1DjUZEhXE9podMy0h1Gk1yrMmVZIRs/2JNellZ+NEKUZQULRtZa8uRTTOzDGDB7JOQk1L6T5c+SNSCGis2z3ktEYRIp4V+brLOcWIaHMLK/sPOk43jl1ZFNYOvSqQi9rklYCubCGtD0KAbRyaGdJ3cSNt9hVA9pizrVslo4Tu6xgP6GbEttWhGOPqQrsusGuG4iJ6fZILgusmliaAWMgHE/4G4dpS+ocebosUEpJHXNfOv36Tcs7kd03tke/dNP0XUP03fEP9/gNyOd+yQX0bfK4r37KL7vufom07v6vjMjcKBxUpRCzguA17boFEFTpX/qe6t1Nj3caZGUN7ZNzyrbE3MkWsqTWkzNOawk1bEt0VaCtoWormlUrcrHBk51hygmVM34K3FztpIHoRwyKeIelTklCS2eJjFGKECLBB4jviqs7I3AKkbooCD5gnEj9yqoUQtrDtUxSjaE/9lKIWYMfJi7f3LDYtBAiT589YNFWGK1QQd5FqzUxJ5HApMQwTjhnxTfgHF0/4lVmGCd0Ydltj4yjJ2vFOHnCFEg5E1JmGEasE7qdnqUpCZH1Td2IIhP7Ae0D2ZScLVsW65bibCEPWa3RzlKeLVl+7xnH45HDz1/irOPyuGXMQjd6uDrj6dkD6qrCWMswDILxtZbb7sDt6UDKmYt2jQJu97fklNgdhBgYY+Rqf8s4DvN0MvN0eUZpHF1/oi1rjNY0VQ05EccJnTJ+8qiQKV2BQpFmLXgOkcvbK/bdkX4aWZUtTVlTKYtD3t99d5Rir2rxo+fF1Suev/mSoe/w3rMoKy7qFqc0PZGqqjHOYmPGKC1Fx3z6am3u39+J2YSfshCNBk+aAmZV4dqKpGbJj4LkA0ElcIY8BRgC1idMlol0v5UtiX26gba497AopcRsnLMobfpJtilak/tJoA3W4JzIRZVSsxREPB8aJQXZEJh+8Zbhi0vsopaJ7Fk7v95GcjpSRoV0n5fDXehjSvg3W8YX1zIQeLASydIsJYk3R8y6nT1fFq3foZ2l6BQKIkqhm0JkT/PvPpUOHTP+5oi9WJImL4jklMm9xy0bQVrPsimdM3GYCNsj4dAJxASwzmLR9/4VU4rMS/mAigk7e0RUSFLIzhu9ODehsRuJ/YQ/DcQp4G9PIhFzhhwT0QcpYKMUi6p0xBBFftdPDG9F9pZDQheWMEyMl3uR+BaW+umG5vFGpEbeY9QsuVLgljXLjx9SPHtAToZwPDLuT+R54BJPI1llzBwASpJ7XPlwLV7AObRWzdlPIjXMkKO8RqNIwyQej6Ykjp5gFDiLLgtyXYhpfW4epUDPBGdgXZPOFuRStiR5LniZC1RdWAFqkAlR/EAJmG5PqKYU0IiSj80xkqeAKixmKQHY2Zn78ywOXnKFvgKVYCbq3TUAWul7qWNGtljy3TMZoZoS0pwdhsj7ZlBAuiOmzhsNJaenfD0fZJgwy6gkEFbP2xCDQs49Vbr7xj6HOGf7iNQr3TVuKMkrOw7oUgrpXFiyUUQvTWCO4qfJd9LNu+atLKTZmOXHycsgMSXJ7Unzz6V8vJcmqpyFLDhDFvKsJLjflAFFu5g9qXdDgPl5rhVm3cwSOYkWICOeJK2lEVRyrigrm289b/Pk9yA/K0aBE+9Q8rNsTwtYRZtZvqjmpmC+L9w9X3MUP9Nd6HOMcX4/FJxG0tURPUWs0kL/LAvUshGpX5RWI6UEc1aSMlIzqEpyCtOhk3Pv0DO9uEKFdA+Q0M7Mwb6GdHvEtBV200qNsahJMREOPaEb5+Ln7r375p9/9fHLGqhvLdG+KaXLmRA84zj+2t/vu+O747/m4ze0KZrv8vMfXzt+E5tYBV9sB647gQqUJuKUAhz/+n3LJ+0kevMpYDYLwu2RH5aO37pYfs3jlDP85KpnDOkrrzNjneN7nyxxx4nBB8qqxHsv6Flj5KYXYJwmlNLkoHn79g3rByuSDwwxYesCMyb+UXFBKtZcmZqfxSNkuB0Nh7GkdSv2/ch+v6XaNPeIbGcMwSC5I/MkdxhHnLIcu4561aC0YXu5o6gLKZjmh1O1qJi8ZDalceLh6z2NNjzdB9ZhIqeBzZNzfCE/sN2s6K6PlKsllTUM40R/vqEzhn83TqzOlpzGiU8fNJSFY7KK0otv6KlSfLI7oY3m8cWKw+hZLBpSoXltNSlEHg6R5dVbCqOpy7fk/iVlU7JQjnZZYTBMRcKgcUvHrlpyDKUE0v7sLeUYOfiBp+sHPFqe0YXAH6YvWdVnnKaRf+wLJj+RteLZg6ek7Dntj3yfC1KIPK0e4qeRy+MNz/trfO0oV0sW5YZud6LIiSfLc/bDiSlF+jBxvj7HGINNFjOOTNPIA12zGhq2HZQoPt++4unmgt82D7naHrCm5rnKnGzgrF1xPjqqYKi0ZVm1nOLA7c2BbhqxRvC+t+EVjVNYXeNzQR8kWDPqSOVKtLX3xYRK4lMIKVLYBR+s/6VI1MJdcKUY0O+Aqv14xc3157gHK7rG8EZ78JHFduRiH6Sockb8AEqKFu0TlRNy47TvqJ6c8WgYObs+oRTslo7rhxVRzwhfZHKOs6goRV4sNBYpzJgbFhs1zz7bS2Cva/lo8c/RvSK8jNxuXuMenRGOA+/9f15iL5ZwLYGXuq7AIHSx2ReoUsa/vKGoHd//8ILjdSDueykkc8a8Ec9f3nX4+GOe50/RWtP7vdDDQiTmjJ6kGEkpCwWqrXi0/D0SgaJ9gDkl8uQxxvGs/H3cuuZo9/zI/QnBJIbJ88WHLdpYUozY2cfQBMO/GH9ITpByz+Xpx6RJMmi0DxCloMpBPERHV/Dp1qGteCLuiuUUIvqgSZPjBw8dP3gkkq7LW8PtTkq5dTX7KJRiujmggsgSlR6wiwrTlCgyfj8wvrzl448V9UVBipkXtzWntyfiMDHqE9X5kpxlcl89WmMWDb87aJSF8bTjTXFOGAMmI1P10smGeN3g1i1xP/Hq9X9CxZIQBwnftEnQyDrh6oLliz1nXSKeBobfe8orL9k2QWmqx2visecvzt7ymX11t1KR92Ld8Pg2sPBA8rxYJ/yMUR7agpSW6KrgZfiZFLYx4B/UhFTgEvx2jth1Q3cY+B/P/oKkwDHx8OZA8fSM7RdveP1hA9bQZsPDv7iC0nJqDJePJLtrcfI8fNWhCsvmGNBf7Mk5ocPP+SJ+CUpxs3bsVxVZwypsqfcJQYHMj8PCSlOWpKF4/Hak7gMoxYsnFVMxgwCMvm867oZLOiTe/+KI6rxkxAV1f64Yq0l9mOEGEZUy5XHiyZdyXegpopuGaDSn2nB5UZNTpvKZjz8/olHcrhy35yLLulla+scVcatYDYlPPhMIxph/ypfxU1JKLL4Y+Z4J5Cny5llLN8MJHzW/w6ZogES8+jO8GVAh81H9TyhsjR86PnW3xOlEUpnLC4N2lqwUjnOm2yN2NDwpfx+zcEz+wOv+z8neo3ImhoRGyfmhEBy7vvODQfayB0pthWoKOAxyLSnkWQ1zCHBGJSHKMc2Bv0aTBo92Eb2q70OiM9wHC/tDj9aCRY8xYlcNqXASLnv3cqxC7Y5Mc4PvVg1m1RBLRzp0Anppynvfbrjcoxt57/WyIsWE3x5hIVvG/VhwM67wuxNVNDwu5F7QdOl+qPs3Kam+2RypX/Iv6u5nixHvvRBiY/wbfMfvju+O//qO30BT9I0u6Js61bv//etexd8mu8twmhKnKf2lD//9Rwq9trN/wqIC6LpgNXqYxrloED9RzPAnb45sh/kCz5JhUTaK31k11K1kHEQf7rMzYhIZUuEMVoTJlPMEOfpIjpkpR3IIGKVZeoNzJbenEe8F72nqmu1pQuWC3emIj4F1VdAdetq64jQMFIVjHEaSl4T1lGTKvHRLSmvwo8dPE3038PDJOWGe+Ppxoiod4TRQasWHVU2dod4PfP9hy7A9sjiO6MJincX4yGCthMvGjDIWX2YuU8aERJwGyW8yii54rCsojBTRG+f4YdsQY6IGVo82GKU4y5naysPkQsGDrCFpmibRPqtxtWQ23D1o6pUUvCkMHLYSjnjz+RtUP1Fbx3q1wafA/tBxfTgQFu9zq3raZYMNjhwS/XHH1XbkMBxZuxaGiU/OH5PGzIKKqr6gKSr+wl5xtr5gvO3Yba/46NF7hEJzdbWnUJpF3XB72PJosWHsB267A86V7E8nnDE8dkv64LlYbuj8xKpe8Ftty+AnQqnZFZ6TH1kGxyIXHI8d3ZgJ3rPUjoUyXB/2qBzp1Q21dbw53rBpxAg/5URp7GySzzLBjklkRikLZc4YanMhE2qC+FGsRYUkORnWQA7km58wnQbGJy3TP31K7EaKwyUmQzz2IhdqK/CRFGQSHedsH0MmXe5ZrBqCdYTJc70oOFRKghJjlN9fiIK5NVaIW0EgHCrKNgql0AraLuIy2MHTXqxRxjL2B4bLV5S//YT6wRo+ewtvxPuQlCL1o0xjU4Y8+zXULBn62WsqYyhXK7rLEyZkyQE6HLCbmtRHsjrR0UEIUDiUn0mYlZNpuuNeHgvQmDUpJuzYEouRPMjUvs5L8ljQWEuhtJjmm5IjoGLGlAI2Cd2AGjTVsEJPkT4GYj8RhxFtJrLWsm3cHvFZsnBGpTma2VC+blEI4tvUhbx3dctZOfCgGsWf5x2lrSFnwQXHjG0lxDrPk3FTF5i2lO3PusGtG/Loqe0lCys4fWMU7qwl3mZCkq2cKqwUaaPHNo7NQib0nVKwFw8GUdDL2lryFCgvlmAMLDPj1DNc31JsWtp6yXQaOLYl1dMWfyNT9uq6xxiDHwK5cBijZVZvRNZ1M92gyvkRoWevTRlYKU/qRzSZawNjJaZ6nAYKqBy744EUI8SAXa3IMeLGyHRzpNi0nI4dV8WOCWhSYLM9UTw5I7Ulh0KhK4PBCYRh8OSnSw4LjULhIpL/kzJlyDRHL01LOHAyJ9CKG11y7QSt7Yyn0u82S6REngK6rcj7HnKmOk00BxlgmUfyQ8ddhztbEK72shlJmZwjCkW9G3FBnkHMkIacIgkJEGbOLcpaNhttF2dkPSQ9YpuS4BTH1kkU0vXAagJCoKv0PMTMTIXBlwrWJavDkfbgZYBg9hyC4M31lFnUjjwlrtIs2fWJyq5oWZFzZDkphnFAZ0374AyraqwtyVk2KtF7epcxpZ63N5bqe4+JP91RFw9wzqHTDE+Yr1HjhGwqMtNZLviVzYl44BLsT+h1c79RIkFS6Z5oxwwqycMkj34F2or0MftI2J1w64bQTdLwGIFOpGMvGHUfRbJ8c5Ig32HGhltDnPOxiBEPhNe3FOfLOeS5EIlwku9LaVHOCHxhWaPrAr2qSdkLVXNZ098GDrSkyVEpRzVmUBkbfv3t0Lcd9/K5b9ZoXx1mK8k7ijEyjLKlMlphjftbfe/vju+O/1qO36Cn6Btrom9eeH+TjdE3N0/fsonKiLY5dSOq3MApYZc1UYmBdHy9w521UnQg05I7zWBWsxQPaTCe/eA93nz2mtPkBcMZo4SipkQsNK625CEQjkcW1uJjBKsp2gKTFfUUsCaRe0Eka5VpNy1aw/mjNXGaKLVmebFkPHZY5CFiCwlOTSGgU2Y4daiY6LZHSme5OXT4GCmtxWmFm7wQn1CivQ6JsikwMdNWBSUKQ8YaxdmqROVIDpCGkWgtRVPcB9wqMmXlqBSsCilCvQ/UTiQLyggCFqVonGE1y+xiTDircUrjcsLGID6GWrM6W2LbEsuRPNwyXO4k6NUYoa6FKOn1g5cGFEWVYFSwGzsmf+Jqe0MIkXW74sXU8d76goWruSiX/GK3o7CO1iQm5zBaUxkrD7MQiQbe7K7RtaOpK37+5ecUfeK3FxtyCOxub3m4WLFYLFjWLf0wcRwGks5orXl2/oBn4ZyX+2uy1jxetNRFRT+NxODvQ327aaRdtazbFfGtp58kn8r7iaaQVPnGlpw3C/qx483xU0BR1RV99JRlRaUkvDBNcaZCCXb4DvihjRQJvRfNu5tDXNMsByIbkSWRpFgNkewT/vMrzIMlxbML0uGSU+cpksLuezIZ3VbodQv9RB6kAM39CMPERMKtW+zTM1R3kq1kypCk4NJKiRxUK1Rd3BO38JFstBQBORGzwlQFU444NRdhPjL84jXND9+nev+C8cU1ui2hsMRdJ5InpebgTO5DJ3PMjD97Q/WDJ5SLhrg/Seim1YQpohcVaphlfHPIpGCVIwZHzGI2xxlSiuRuIOckUsndCe2kcQKI4wSlwVvQRYENAbImKARxXohXL1UFxXJNPiTxe2RFGgPGzeei0WSD/E6SBHlGnTBRk+5CG42BppSsoNJRLBLTtGc6nylrmTkXKRO7AXJC61IkjSERQ8DNkrC7e6xCcM9u1aB0kG5Ma7SF+mzB8eUN3u+INjGmE7qcQ1LnbBpynPePGVMK4TMMo8AAosM4eWyYpsCOFdWDJbpwaGcom5J0HOfmWHxVui4EY2wT1cM1CRhuT7SP1xx3HVFDaUX+pZwTKfG+Iw+BKUQ4b+9lYth3OG1jDCrFe7raHSwhHyfMk1a2NhGsUegoEsa47SguVigmIZINE+bJhvD8SmSLuZTSMSShM/oosJLSvQv+zO+CSlFCqbvDp8t5K9I0NXrUqobTKHLKlKEwxCA46YSgwBk9dtUQ9939xoyZiJqNyMXiLLFTSQpWV5WQwgwimJspNRe+Oc/DCzsPV8THpLQhpvFehnYH1dBa8n+wM02RWdqnxO+TQxT/aR9RhZHGy2uR4GaR5GWVZ9CDNB8xRozNJD8Sxh5FlmbmTl44H3bdolYTxEgAEgl1Jw/8ispDFG9zATCTGpk9RyBkSe7kcM7Ke4AMdLLK9xTAHEQarwHt4z1ZLxdW5PXdKPjyCNnIa1YxibxuDjyOo8edL/CHHhUCaEvc9VirsZUl1AWnfU9RWsplTTwNqBAlR27yQjFc1eQp4q/36FVDuV4Qrl6hS4dZVKStZCNZ15L2omx5V0L9zaQ3f0lG921fZvYOh+Dn54+mLAuRN353fHf8Azh+g03RL5lifJuk7qsf/te5vr/l61z1NZ/uLWF7xCuPrhtSiJimhFVLuDlILsCqRrcV/+K9BSFnYsr8T88PDBF0CDz90Y9YWMN7WfHzR+9xe3viNIzomFgtGkLu+cfmP/LgB+cMPbzc1vSHnpgz5WiJo6epCnZlTQ4Bu+34NxbyEcJNQAGnYaSsSsyo3slFwnxTnx+Cd/kaUyc3YJnSCi6WKOji4mBIRuFjorJGzMClI/nAshDkMUpxnQtS9IJMtuKfSlmhohId/pwR0Txck6zmD449GdBGfmkpZTSZ4CdQCjsEXjJP0DIQhHhnyPyLtkYZjZ08upsI+0QY99hGCQY3JuI4yOfdBRlmQWUrQDnRl7vCUWgl0rFp4vPdNVPzmNe7K96khPF/Rp3gi9u3xOXv4Mmcr854FB9ytb3hol6SU6K0Dh8y3w9nfFRuOAxbjFUsy4Yx3PLq9FMeP/yIV69GPlr8LqW1LHAsWwNDoLUF39s8YusHrg87hmkiBM/SVcSc2LiS31EP8dtIFyZeXf8pG5e5aFc8e/TfUOslvc58dvnvSfFEU1TUteHT2zc8XV9gi2Ke2mlyloIq63kKOr8/d6btSMJpe38NxBTl40Zp4pQxmChehawUT4YNv737LbiOvF5sefG/LJne7li92HOxD+TR88ZGdm3APG6o33tA6if861tSiMTCoq3l4rNbzubNRNhP0HshYzlLjpGo4OUHC0IjCN27TJFQaD7//hqjZer+qfqJeILGwMODhsEzfnlN9cEDycO5PmLXjWC1wygNlrN0K/h5JcjlZ8M5/6h7Hz1WnB7vuez+GGImVE4gFEaJbyRnspZwTeZt6gP7fdrFY1JM7PwLro4/IefEiw+XDCrhXMG/3P2A1muiVfzHs59zshNaW/5Z/0MqXZB2/b3Xyh89l/HPCTnA4ZaXbkueIs42fPz4f4NKmY4Db8Y/F9J/u2Q89rOUKpNiRifZOimdBXwRAm7dctr35FXBwbfotuS4G8GesFXJk42nDkeKeuT1oWYfwc7If2bU8zdvqPn+HivGfmU07eMNfteRhsjzyxYKg25F3mPqgqKATy5O5FGkiWamePXe8roXKl1beB5tevIjOAwnLocWpRSr10d+oKRptyPopYQqb7aelYZ2Y/H7nuPnN7S3ie5VR1IKpzUX5W+xbB+Rc+bH67/gzdmRrBW+NPL7NFKgk8HOnh6UlutmvlasrXh/9Tsszx5zsXjBe4d56BUTxXLAseD0Xsuf3/6PkBKdU/ykydh//SHLLyL/3e33UFkx9K852J/DFO99Z/HlBIWTARwzMCFKkS33NSlbn7wdeXA5SIH52ZHi8YbwtufqrOBVLaGfYyHXBiHy9E/f0jzcMN10PH/WECwErfjs/UbM/GO4f1S6MfL+5SSDqsoA0tCMreMX74uPqt2PPL4ccWtBed9hsPcLy/DJUhqyQppLbTRnlz0XrwZ0UaAOnjRvpd4+KDltSlKI/P7pIx5Na5RWPImWcCNDnGWo7xsYoyTKIaXMy/1/RqM43rwlJqG/pRkdfn+Kzn+mpeaL5/9B/kVnYhbkeWLGn+c5f3dugFK+858hm42cuMOfzz0ZKcR50xnRdUHup/ttJPPGW3o4yaOim8h38RcZVFsKtMRo4nTnk4JYaJSP+EOHaSrSccDc+cxiQk0J5RNFKRlQ/jhgSnvvq0v9JF6tw4DZiAc69RO5VZTnK7kGrTwT7fmCP9t6vuh6AA53DfDf9vi22uu+TsvEEOT9VmrerOuvN6jfHd8df4+P3yx97pcdf93r6Vc1TN9osqZo6JNj6hVh6KieVpjCzlMkMQCnQ08aPSlEVusWtCKkJEhMkILteKTSClcUrB9vaJ5eEE4jxhppTLZv+Z3OUCx6xrOK2DjCQQAPpiqAYkaBylZleVazmM3jvk/gE8kbYpzu1/nZR3QlE1CdMvFuCukjtMhKPoMptMik5o+xTqaqmgxhZPIRbUp0oaAbcU1JngLDVjIuTF3Mk+ZR1vVFMQ/cMva8JJiOsO9Yzt/DlBIqiBYzftaIeZkskpJpIg4TWUl2RqMUnI6kXqha2lnUwkG5xs1FWwyB3HvC/kSeEjEkyZ2ZSXldmGhdic+Z7rgles8QPVkplnVL0yw5dXsmvyeEicpGTFlzHEfGsefz6y9xynDDkdIVLJsFu+Oe4eaAz4k4ei7W55TaYuuSl/tbtl94jH3EfhowKVGVFcumxeYMZcl2e4sGvnf+hBA8aE1ZFHTTgMWw1poX+2vOXM1QF4zjJacpoOOEUxkVM42JHKYj29OOIQaeXjxiXbfSpIpKDHnmqFkRkgWqgEzvc8qMYcKiKaybze6Sx6My9yCBDHgfcIWjtQ1nfkFWiit/ZHe9Q69LVNyQ0oE4TaTKMRQG5SdOn7/CblrUwxZ8xN8cyDnwaNdRRY0NoNsGz0Q+TOR+wFhL0shUN+h5ii1Si6wUQ23vt11JdeSUKXTmgQZtLeHmyKDAnC3Qgxcq4tkC11agxS8UK0fvRLoXc0XlN6RgiKc9qrRooNi0gBj6TVsRtydpknImOEeePNa01HEBheF6+Cl93hFzZucUx0pj8Uw60RYlWSW2ZU9XTrgRLoYKZxuKxYa0PYFSTL7neBxJKhKnyHG6kk1o1izqC5lW+4SZomzADr2Y5Z2Tn8tHchYMuilmGWKSrCmnFLGwHKdZiqWcFFIpUzaJRfbQH0jHjHIr0ujJvRTotimFascctZISfhjwh5HpYEiIhDUO03wbVXQUEDV5O5vWp0BdZt57EtBOkUMmxyBTc2NRPaRuxLaZRo0op/CTZNsEHyido5y9cKquULUgpLWPuLrAngLDbkQbR/r8hgZQTlOsGjZ9wzKuQMG0aDgoAT0kH1DOCUAjSyMiBa0mZi9DF61lMxgMVXNBmRZkd0YTZ6lUTnjtcKFm0g22LJj6gWgUx+hxlWa9WXD+coHKsIsVOx8xpSPeHKh+8JTp9a2c57OcWCklw4uU0DlDKb8r14nnVWtF7iPKb2nOF7x0nq4yM4iE+61MPSSKF1uKB4sZly3bjaGaIRPWQU6yybAaXvVz6Oj8HFEQtaKrLUorjE/AKCCE+Xokg7eKyTBv8aSZUEqkgtVNj71weD/7VrRmtIpTocQT45c0nMk9MGY0ijR6gSCQSUnkviklUsoM5kjuR7ppS8pR9Bk53UvgvnrYi4bjF29k44w0aneNT05RMpJ8lGHMnJmXg0BTZFChyWPAntV4Pch9cW5uyKIYiVrgLykImdPcZfDd/T8F8TCIN/cOVrEoSSeRnqOV+I/uaospkKZAnAcd5Iw5a2VzeBolv62wZK3xp1Gyo5pSJMv9KOj1JDJpVVjiMJJaRRg8IXvKRw9BwTFPvE5f9/PctUbzLuyXlFB3u8xvXQe9+/tv1FopJuJ90/lOaqy+WnR9d3x3/D0+/m6aor/N8c1N07dcmxqFXdQkH+iv95RnS6zTaMDWxb0+OJ4Gpuu9NBtOguxMihIup8Xketckaa0olhUgpK/yfIErVygiOcjNwixrzKz1j6eBME4oFLYpRdqkhIBlZpmebVtBriahSpl1I6GEKROOgtOGTHWxxBRWCEAzIam6kyndJZfHREwJs2qozfyAGjzZCIUnBfFHECKhG9BNJc1gP2FD5O526m+PJIQ4ZN1cNG1Pc9p7ngk5Gva9EL/uCl0Ee5ySJIFTFdQPN/dUHaUVeRR5R9r3Qs8KadZYJ2Kem8kMOmeaYFFTorDi85mS0MvOc+bxw/d5PQ5M00ilLaumIOuBz49C+dM5k3KgKitQCe9HLuol5WLFfprkvShrjFbE5DmMB6aYOB1PPFoptLFop1lUDZHMbhrwYYDSoVLiZjyBgoWp8DnRuEoKWWt4v3wCZHx1QT8mYswMMeN05pQ8Y8qUylDVNatCQkJTyug0E6a0uT/NlRGggeB7xVdmrKPVFT4EUorz1I6ZXBhIWjwHPkd8SpRJQUjY2hJzJiuNSop01REue9QYscuG6CTQVCUlErJrSVm3j9bYixXhei80qT4RFKjTiFk2qIuVZGysW9L2iM5z4GQIEpoapJlW8wbzzieRYkLFTFYGleXn9lcHstGYZ2eE59ek2xPq4gK3ssTjnEA/Y3UzmWQgFooIxMLM/oDMlAQ4kQqLXjUSgmi0vKa6ABIhBVRIpLnpiDlDVtikhRCpMkElgkn3ktqsFMYayqoQs7FTGKUhiEwzOZG2MedEafS9tzH1CaZECmIYR8u1Y1BYa8hJwxilqJqvsTRF8IGgFDgjjWohTbxSijhF9LqVc75ypF5gGjlEsjWEOGO8sxSTUzxS1hntLHZRkbMT8lVd3EsS9RyW63fSTI63R/RZMYdkIttla8khEpJCWZEIEiO6cDI4mQyhk8ZMG43JCbtpSDGDNWRnMXPYagwR1zjKVSkN5nGEkHCLGhM0xih8EPKZsQYfI64oRCI9L8NUzkRj0FnujxSFNCdzNxgLjQ+TUBetIS0rbD+hOoQyOEW0Mtj8ThKU3x5xZ4/JzyMojcpglJXSMmT89YHiyRn+5S1u2QriPjEHuGbSFNCbRqIL+mnOwZk37v1EmgLu2Qrd96AEOU3O0gDMm7U8ePR7KxgG2YCpuXi9k+tpySLKSa4FNRPguLfIyjlNEgJozCLzRSkh2c2AITV/rEpzsZuyhDwrkZsJxERIk2n2oeiZmAqZnALZGZRRxCjy56wkvPtuw6ByBiuBvYE8B7hmUgj3j/D7/shZzKoh7TtpWvJMmissuRuhtnMwr3iAlNIiTZ3JedJEJcJxjh0IUVQWepY2KgRMk2YCpBYokDFaGoAsvXaOEaWMCEcnj6Ikt6WAXdQccuvD/PqAKWAKh7ZWPGlJzcOILGHrSpFOE0rJ5ttf7rCrFlsVqNIRbk+opriX9jH/LBozNyZ34b+zquSv0Zj8tcNW5+7w3RZubobumu/83abou+MfxvE/X1P061xjX51i/JL7wWYXeTJI7sXboqIrNMPNgQ/PB5ZmQpUFpjWyCq81X2xburd7UPAHKpFXDlsXbGvD0c5o6Td/Jhpx7uRtiugnfh5KkQ2hmUIP1mArSeDWhcFMlTxQrHiEwuglp0MrmW4qmd4qo3FtSxo8nAa8l3wGqzXKGXSaQx6ngFnKRBwr2FpSkmYiJawxhLdbYjcSSBRNJYV1YakerkFrwjCROpEk6SQFkiqt5MBUheidTwNqxvTmkNCLijR5NJJHoktHuDmgrUG1FWn06EGm125RYVIWk72P+LdbQTcXIqlKg5eJdyXhoHfYV0UmHwdyYYkKirpGmSB+JluCDUwx8P7mEe/1C6bLjqfFY7rpDUwQU+a3pjNi1qSrnm76BUOAYegpteONtYRUcL78fW4Oe56c1dx2f0GLZlmc8S8++T+hlWEyjiJKszIomSYuqgVeZQpj0TMxyM4ylWznZsYYgjXo+fdpB0seA+MwQA0+ibRHWcPN4cR5XaK9+H4MhvfP/hWOYtbKM3eZs1xOy/TTmDl/KGXxqMQkhaqSTJLb4sh/3nwGZB72Lb/r/neknHGqEGRxP/E9/4TH2wuMj3zefMlPly+AzEWyPNkrptsDbzcFh7UTeUjvsesGpTVvPl7zdhSfzgeXI8Wxx9Yldt1i2orifMEnb28IbztijHzxYSuJ8BnJ9bjzKSiRZBa55uP1f4MNsLUd/2nzM5KB9VnFs3ROeHFD8fMrfjCdk6ZE3ArpkJjo2sD/7fGAipF28Gw6QcS+9T3795YEU5GPPa5ZopRsUFI/YYzhuXqBMW9lm3Y2oeyC5BO/73/IeVwTuoEfNZ/SL4TydEoiV1FKBhM5T6Q88cXtf0DlQDagCoWOCeta3lv8AbYsyH1AGYMymrp5wPfafwPAYXjLm92fYoDWPeDR8ncgZQ7TK64GkWiF7Ofsm3kTMnr8cZR7XyFF4+vBcjOWYvR2Tnq3nGcvRSB0I2GYyEpTrSrcWUvpkkTS3AgePYTZF1ZYXKH4aL1H5URqJEMorxLD/sRnu6dkYDdG/vByIGfF0wX873/QS1jnOBK9hKu+HSL/z59v0aXl984i//qp+GeuTgW3YSFenbkoNcuaR5uJpTlBTHwxWY6TJoXA5fQTrv0vCDHx4DhwphMhRKzVpCnIsCVljDOEFHn+XkNg9mrMNM5TGfl/L3+MDpnw8CBDnHXDaqf457eP0Uqx8Q3/5vr3Cf07zHBOiVY9RBkpzBfVEz5ya7Qx7NIrrt78hOp7jzlrP2az+T659DTHX3B2eAVWc+ngL9ZQ/O6HXPzJaxZvj3crYGlob468vyjxtz1xCnz58ZLRiczzi48WqARoSIsSgpfnjjb31EfgvnhWM+CkVIrvf3a8f1bKZiXTN5ZPv79CLyrCOBv8U2a5m3j0tv/aVlqlLFk/SFO0qT5mXTwDo9kWz7lVW7lBpbsBR+Lt4Uf0cSvhsMMkjXNKhNjdyzjjnVfHaH7xQY2uKnRSnKdEBQwh8e+fHwgpsygM/3TdELcn8UXODZjK0tyR5wynGElKiT/nXj/HPf6cmDB1STz0pJzgfpyi7rdQCml+8iznu/OCvXrW0FVKNo5KgRc56/s/22KT+L/yFEhWoj0E0hQpqpb3Nv8KNUGwE69OfyzRAP10HyJtK5FKq0I2XWmKAmypC6IXgI2Z4z4AXo+G/9fnO4CZlCtfR32tEPpG2/MraqRvHl8T4al3fyn9151c7ivF1zf9Xd8d3x1/j4+/fVP0q6Ruf5vjKxfrX/r6X7n4TcwUXh4c5UXLpCMqRdpFYNGae+JZcoY0RWle1hK8WDPAOJL7gUPM0tw0Jbrq5sZGfArJB3I3Ms5kH6UUpi0Zdx08XIv5VAkyNR0HuYFUDsZA6mf5mU+EnLApA5Z4cyQOEnBHBhWjkJ7qQqabM90m7jqCDyLhQ6Z349Ve/DiFRZeW4uycqqmEduNEcnG39tZVAZuWHBNhd5LprjVSRDiDWVSzXC4J4rmYG69ZkhKGiTRM6LoUCtDtEWVnY7NW2Idr/NWeeH0gMYfnOQtGJomSK5JQhwG1rIkz/ccaIw8OK9P1u2W/zpkIOOs47G8YQ+S86Pje4hGXhyt+ev2G7589wCXNby8e8/z2GpstJyZOcaIpDZXVTGHAB8/QnXhYL3F54tBdoYuaolhRssBqQ5sVx9ATlWIae3xOrOoFrizugxm1lyZO1SWjEviBMZo8epKSZsVPExSWxi2omprCNZgUqUPBw82FTH5TkHwObXCppDDNvRZez1lP3emEVoqQAm/8NYuqodJOsMh3ORtJiGKTiuxtR8qJlWswuqWeyVRhEh9bTYELkgVkioaplnM/v+zQNwOLiyXbdUUIPUYb8nEgzgCFKSYojQAxBo+KiuysNIYhYApLXVb4/UgcouS0aDFwpzuJUBKztshcDKVdYrXGGc3UFngi5nKL0hVmVZNuDpgvbqiebBjKQpr800RInhsj2ywzTuT5ugpKcxhH2cwamLwnIptesyylII89mWFu0GRTovvAamxYnBwxKXo9si8EDa7mHJSMFIraGmxRws2A7zt5Tc4IvABDVa6Fhmdkq5ymgFEGV21IIeLMUc5uo9GmpCrWKKXo8w49KrIx8v1ShpikECydSIZyhsETxx2nmDjN+TvGCsBAL2rsqhHIwflStstGJvX+5gjaQ1aMlxBNiWlLkQjN22Y7dago0+/YTyQfcNoxRAPG0BN5vT2SYmbhLHWZUAUSHKzl+piy4jAJMS0aaGsput0Ayos0WDKoZCtRmExlAikFiqrAJJH3pirhfQcxUU5BvGxZYwtL8JlivWC8OkgmXWFk02AMUYvXUmuNLg07fQIHU9ETJo85HCC2JB6higKTDYupIudizuGSjX7hHdOMajbaoq1s6HR/CWTC7ZFi9ZjSV7BcUfUvKLuAbkvUumCwiv7yloeP1uTrd5uklEVep1/esniwZjjciifIOtCaqbKzrEyhbg6YRU049IK9n8mpOWfJ8EH8M8xemLILci7Oz6acMmOhGRsnSgU9Py5jwvhIPc5+na8Ev8Yo2HqTE4VrqO1qXroVd/X4vYIi54yPHcO0g2kupEO6z1DTWqGcFciEk/ywoVSYSmOiIgUvz+MM+zHi5wgC86gR7HpMkMVbi5+3V6h3eUzzJirN/iGlIFsjvq7JyzN13ZBvT9II3UnS76IOlEJloR/mGYqhtWaa37MEGGeIfSafN4R0g5kle8SvwGzmvCGlNYVZYErD5A9kH1AaAVSMQa63kAhTJA9eQo3J2EYR5k4kTh6oUYUMQKc+sx8FNvFrl1V/DXXbLwtwVUo2dHLOyLTua83nd8d3xz+A4/8/5XPql/zvbzkCMM0TtATz1saSbGAiQBBZEkVBLhQ61phRChBbWMJpwDgrNKhhEsKMVvd4YZURatSs3c4x4OoavWoolCJ1I7mTBytBpCw6ZfIB0WxPEaxFNQU6zgngWW6opi7BC20sKrBWSUG7O8kDRQtkoSgl/C5NouG2m4VIqGrRKKcooYHkBMXXf6XqTsZhFO5ief+GahMkIM9H0TiHKAZbJQ9yc76Qh1XO5DGIcdUUhHES+lFT4BY1sRskGXxVSxE3o5lVIZKbPEwiD7QaPfoZG6WF2rNqIEZMlDR6PeurnbOEEHlvcYY1JSttKYuSl2HEGsfVcOT7m2e0heOD5Tl5OvBGVxRRUxQFu6FnGgYeLp/xyfoJOiRO+sBZs+Q4dCw0qOwJ40jOicJoppRoNDzfXuOHI482F0xkGEecsShXUI0RHwKmLJk8hOBptEEriL7n9nDNqlxCmDB5gBS5vb2mrqWs0LNHKJNJORJTmOUJszTKGJwRbHEZNIWz8rB3BmG9irTEWXdvgCciD/k4exSUSJQygNVEnck5EXIUup7SpDvKWEiMtwfKH15gr+eg4ZzJxx6chX6aJVIio4k+CqktVihnmbbHe5/NXYFx57FQdwGydx4oLcbpQESVhmzN7IuSgnZ8cYM7X+DOl/jtifB2T/F0QzBz1ogKM4lP3q98551JihJL9hDQ5Bixzt7TFbUxc+Ukk+4UIgx+bhwHQnIkk0Viq95NSyW4lvutVwxCSszzwEFHkU1ppcjTSFKGaBSYNG9cI3kOGCYEtBaZnb6bxloBSMjPNv8/xbtib5YzaSXyxpzv8qsyCsGRx8Gj9gPjlzdyTVmN27TYTYtZVtizJYWN+D6gbwzdzQF9FACAqQvswqIfN+joRRK0qJlujoRbj7YSlGqMoqwLfD/BOEGuAIVtKzl354JRmkSRLKlKPBe2LVEUcxinJ54GofRVE2qpBNPvLLl05ClSbGqYBGuuyhrXlITTyNRN8nMtaw6XexzIhF0prDHEjGxgjRFq2BAwpRVAhJrx/ymh6oJIIvhJtgRzYUyMKDsDTJTcc6OCdF4LjfEYxGvRjyQ7a76miNZGJHZdxDxuBZaTIF0eqT58IpLQGaufYpwzlQRmofP8u0wJpSGi7rc2avDYO89Smkl283mgUWgM2lhyitKIz9eymbfOeh603CHbdRKZnp6lUDkJlv2O1KiybKJV5n5zIhuVNEt8NVElPBIxke7WCsaI5Iw5pNbcEe0SxlhyVBRFDXEveRgRGcZ924PcGckny/OGPUZRFGiRhpumJJ0Gec3z4AXkmaxSJg9elBRzYK5uylnSNlMJ755tag4Knv9emoD5vZ+bJ10VZBR2lsDBfB8go8YAdYEa5JrJWpH8SA6amDxRa7SBeBpBa5Fsh3ngqRWJgNKKOARSThRrGWiEfoDzAoxFHTUOuU8kIL7bFf7VBdFf5/hLjZS6XwhJLyTn3VezHr87vjv+vh9/+6bol10vf9sN0lcv2F/xNf79OPKHk4Su/eO44LEy5Jz4Hz413AyJ+znX3Nz8wcOJRWFJRvMfLgdOY8Qmz7/+cEUVghQaVh4yaSZtpRixdUkeJlIw6FIyO8I4yet0BttUQoKap6fMOvOwPRL3Hekkk+poDWoQqo1uKoiO3E/YqiAPk2inFfcTsRgjas5nUqVDNaUUdT6IV8doCVabBOGrngo+9utvpcAbUpSJXrg+CPI2JEmkn4uWlLOQ7pY1tqmIUyAPE2bVoEvHqph40p4gZ7ZTxduu+co3yYIYtoY0TISboxiQrbn3B+R+mh9gI6kq0Em2Hroq7pG6efSoQnI16rYlh8ib8U9w3tA0geaY2bRLDqnnxfE/iRxhHIgkTFGQrWHRtCRlyPR8sf23HMYOFLztrimNwx8+5/r0hpwzo59Y1A2DlyyMGANdcHy67XHWYjMc+xNN0/LkwSNSaXGqxBaOVCtOVjxU1dmKZ/33iDFzOf4MNWbGYaS0CZJC36GDrSWrxIvd/yTFtSp4/+xfSer7XWORM50e+berPyNq8Xvp1qIKx+ZY8q+2PyClzANW/JvL38fHwNI2FGbO65ohIzlnPi/e8uP2BQoY9TuqUI5JfoZpYvOnb9isatLtiS8vHPvWgA988Kqn7U9kq3n5uGGqLbou+fDnW4qUCFOgfHaOvz1JcWfMvR5dzrmAchZ8QlvNqQr83y/+RE6XUia/KUlRp60hXB2k2bHSPG73B96812KerRn2p1l2CbcXJYeloOE/6p/yz28eQ8786eIFn9eXYl6eDdNazUbzuzvBTEIMOfNvNz+jyII/7+wkzaSSDZFRIr4xWolvJwfxg2mFsTUfnf8vUAEGf+Kz3b9HmXn6Pvv+lI/3BUZVXfDJ+f8WAM38/VOSQnl+XQnxE1hmmWQIKGuhtFLwzdSulMWfodEie8tZtmRzoGU4DMR+Yryy/PS2pFyLL0ltNBaDTjIJ97cnutPAT2KNrhZS/NQF2S+x68gPLoSWN5iKwmwYdx2bOkDyc+edpNGws9xpRu4rA0qleylQngJJZR4/hnOTSOGAJpCiwRSWH99O/PhljzKa/8MngQ8fJjGhM6HtSD7PfHbdElxNTonCGrnXacVHX5zEZ+KMEDfnjSvMhfIo/qGYEno68ln6d2ilaPw579W/Dxm6cMvr45+QnGGVH/PIfh+qgi/1G/64/RHKepbDgUe9I2vJWGJutM+a77GuPyTnxIexIBwlRNykgE0l+ocV/s0ObTQhBt7s/4hxe8I93vDB82tpZuaNapyJm1opspPnj2LeVua5KVJQ6pZPNv8rFJqd7fh3m78AMnXn+eDVwNyyyDWoFcuD572XnfjWJsnfyxkODxsuz+Q5cf624/xmFApaIddLnrORUAJ1+S/Lz/jRTH5/0h2pp7vIgBkTrjVffNjSW7AY/tf736UJBWN94vLH/z0oGWipxTvJ4lcf9LqwuLbC3xxReqbMcTcEkA9T8xBBPkEkdjnme2orGXl2D16ek714fJnlgnoOhNZKfJ33Yc4h8d7LjqSlq9SrQDr0VKkhTjPUIyW5jygljdH8ykMY+fz238EostqE+C3xClNaUsr4YcJYC0kUIZkZHJES/uaEWdfcdpnRtOjCcN5l/i8CpuOPpok/9NPdIxalflVh9Tcsur6iylGKeYgkf/4lmd13x3fH3/Pjf75N0d/k+v2WFXGXM92sj/Z3zUhMbI+eW3/39WVbohVQVZjKQMr0MdNFcNag6gJjK8z8TfI8icxBpmU5ZSlQ9ExXc4a6rSTU0s70rXuDCDAb5k1Tkh+uCbcnpt0R+lFkPKUj7k5zflKWKdgc/pe9h7YiojGFk4DMQiRpxEQeJvyxF79SypJHojSqkamsfPv55whRYAqHQQrhppS8kzT/92FCVQ7qAu0jefKEXUccPLpyUDppaEKENGBdL34mXZBDnKetmTxMxNETZy/HHZ5ZWSmws4/vAvNKh3ZOCr0QyCGQnBUzbsrEUXTqefKQM9YqUuPQwfBbH3zCMI44rfEI1WuKPTjN0U80tkEHj6sqQooc+z1dGKirhkerCzKJm9OeyY1CRDOOwMTJH4hknDFQKs4ebGhWSwywHieKzQLn3PwgjvjhRB4907x1uDN6m7ZEPWxQSlHmmtIvid0gnohhIvuZSJhPxJxxWkiBWPEPWUCFRC7gaAYCEQioaFDe4uxawjhRkDUbFsQUSEGaHmfMfYOplWLCc9S9THSzvs8jkcYJMbHvB/JhxJWWYlGjraBzzRQphiDFoKkYrMLEgL5YkvpAebbAlI7JDTBnDeUYgNkMrSDlhFFapJkmc3KR1NayxRnE8BxnyaRCZKZCxRID+mBABTF2Zy++kqgVuZTzy+mKNtaolCiCwFVw5t6EPVs1SHc0Si2vJYVEbyZGo+//jtnvZkon21crUrU431906VCjJyfQscAYSxEDwZ9IQTY4OWdSYPYWimzQxRWFbb9+/zKKNG+CU5ACiSy5Y9QOXdRSEHeTvA4NJqpZVhdmdLsU1Dkm0ly8aWcgykbs2I+crjrMuqFoK1xdYuYQ5eQjqRsZdh6rC3AGPQKuxKiA7bcoMsk4GpWpNzVlPMr5Pw+ZMnPmW0IyoPKdf+OukM0yWCosRWmoCg3KkKPkRSkFQ8wcUdIEFIqqBJLk+Li2ICuF6x3Ry72kfrhivNxDjNTOzbKpQNkWhMlTNDVp8MQY5P1tC+JxIMVA0OMM/KiJyJZkSoE+deiiJgwncivrwklFjvFIcIqq0dIMOysNg7PonHFVI81hTChTkrWEXUYd0JPCqgbbyjPEmYRivo9OnrqpiMeRjAyiUpLrHjLTJCeKyRJnkFIWFZhSOJNxusZoh7UZXztyjriUZ7WAeHHy/KeZImWYc81grnoz0SjBghszQ1dkIKUraabIat7JiiRvYCQ7JVAble4lfdpIVpDWilBogtOQDYVtqFJJsooiACngrJAP5dl0t4adr4dZcq5yJs5bFT0/D1JO6BjnNe7dH1matjuwgVIkPTc+k4A68tzkvPu8+U8lGxGV3+1eXJjP65QwQyBlhcsCtsDe3U/yu4FTklDj2A9QZ0IYACMDi9rBzQGcFYnr6AX7PUMTZCglm7BExlhNmDSnU6DAUmbFet7WVUrfvfy5rlC/omaaH0J/3eNrn6LelUxf/bLfHd8d/0CO/981RX/dC+mbm6G/wYWYx5H+xRbtLKYbsVFoSDEJUco6Ma6KxjhhUsbEgBoj/voAURLBbdOQp/guoNIa8Q1ZeTilUTY1urDiCdKCaM0+orLkAeWcyFnkC0pr3MMVZtXg9yfxKCFTo3i5Q5UFxfkashRloe9QTrDC5Cx4UYBJmo48TDKcbSv8MIlUJwPbkyCJ6+L+xhv6SQAHKaPXDfZiCQZCN80BgxNEg16XmJTxr3pyGNEnRT5bwmkkaIVb1qiqIpmBMAx4AtPVXrZbc7hnjrN8LjPTieR9SSGirKXPiTrkOVAPMaT6SHZa6EBzk2XmZirOORN59BKImyHVBU4QTCKNSoISPgw9U/SUSrObekpXoFLGFQXWKvpxYOEqklE8XF9QL1smA6p2VG3DxhhM6UQTbwyERDh05MFTu4JwdWQ4jVLwzXp8Y4r5uS5SHGIi7QPTm05kZ0YRKoVuCsz5AjsHsWYfyf3EeL1nHEe6cU8zm1nj3eR4Gu+R1hQFLmi0B+dFxuJLg40R6xVJzZlSSeFVRjvNmCeRw5k8m5aZZSTvCo1o5N91NOisyEHh9z35vCTFIOexEmT63fWYfGB621Gfb2Tz2U+kqz05RvR7Fdk5lBcioTIGTSYpwBmCDxAyJp5m03Ge5TqSjQFS2EU/SaOiW/En+CCT6zz7fe5vFxmfPKGQaa8xhpJCaGFEkp4/0EiGisAds3h7ojSnWSlyjrOhXd5vlWZpYkpMOmAqiw+ZMcyesFkWmBVz4SVULW0NWpdzbomQCMW0AdPUo62db2+ZPGWiH+VeEEXClK2RiXQ3EQ4yJNFaz9dylgHMPK0OMWAQqRR6JvTNU+9wBwcpHcon4qFncBbTlJhGGiBlDdROmswxkHuZRitr+P+y9+extqVnfT/4eac17OEMd67ZVWUb29jEzJBAAyE00GqpA0lDI8BAAIWEBJADiAhi8A9kE8QYZKIQJAcLY0LiplE60GAcDLEJJjF2PIFxzfMdz7CHNbxT//G8e59b5apylW3A+aVe6eree84e1l57Dc/zfCcbB8Ksx17YJa6CWII7cbXz64CeVKCErgUKaxSNSagElZX9EVeDBGnTFEtm2T5VadkPBUarq8y0kWaVCkYnlsmVKfVszEK1RRoEKkV18x5hDEQ0fj0w2ZlT7TSyX1EMOWMmZWijhRqbQyKPHp3BWEM0MsxKvuidlh3RzhkJ6JRIWa7/TimquhIr5UVPNpFcZ7Iz2yIXq0kqkUw5RpUGpQnHHUknchKXxOAUQWn84YrZ+TOwPiTnTGgM7M8IFw8gJ8YQyJWVId2YZVCnBbExWuisYseNDOwQLVsu1DKQYFKl1dZ1TWU5D03joFhGm5CBYm2tJCIipkgMI1RinoCSYxAfpDEBUpQYAAn61ZisSVmhxyQ+CVGuXzEpTKUwxhLSQMoZv+4fN6jcCvqzBLCncp3RSgYEWeXt9oVCp9NakJ9UUPFNGrttKnHMVIK6bZuesg8KXFQoyxS9kTQSqlDHstakzpNsca9VjqQp7npBAne1BuT1dOHc6qIvSimJprCtiesR1VbUZ+b4q0u5T4eI220JR51cs2MmDYFqp2G8ekRcrYmDgWpni/4+nr320Sh0n4AO5vre6rmG6Ln1v9n65HCfeybDjSd9zOPP3AvtktvVNcLg2T2qGVYWrRRXThm8tTLXfOgyXZkk/41xJOVEzhEe9YwpUdmWC+YlaBzaqa2zjh87Hrj0TkiiAdrQGrSzcqOJiUna5WzzYrSzrMJFHjt8n1BMdEmYn7fUZ3dJMUkWzLQRA4PKMos3scsFslVc1H/GcryILYUjfiRXVlAiH9BtLUXNGKhUMYNQAvErlFD1QOxDvVDrqCzpygKvFeOqh4S4xrWVaBFmLdkH6gv7xIMVcdXhLx9i9+ekwxVJaw4ORq6tM/0ikPMBoNExo+pKxN0RobOgCFboLKboS3LRRWCtWNBG0VrRVlI3pigN5uhL4ZvlXhczua7wIWCNwa4HublMG/IYGHsJnN2dzfFJiqD9yqELz92mTGUdpp2Jxfakotqfo7RimhJJaXHuWnb4qwtcTKxiwMUs7numWLw6g6qc5GMUetP56acwrc7LRLrQSDJZCrAyivyv8w9w5NZoFbn93iW1NphJhd2fMdk5z3BtycOH78J1gnx0fiSpjJ00jKcdOmVmqeELli+FkFjZNW/d/VNUZTgb9/msg+ejx0jlpAhEwYP2Mu+e3iMaGiXFuzblhp1k0njlwpRr52QS/GndndzSnQajuDa/h1V9VJqDTpATLda1UKh3Q2B44BJ5vQvzFjNvSYs1uRsx04pcO6GzUCgfY9hOWlMZSNCPUlMaTV9rPnyb5IepmWgH0mpATRpBEHZaWHTozdTcSGNAStzVPsr9zUUAXtjdzP/16svBav5nezcP1Fe21sgiHE6FgiJcfV3J9SEByonDmSoW+EopQq34g/0Pbouo8fQEUmKWW553ZNFZkSiib62o7Q437Xwmm/T3YijIqrvCvVf/UOitpcJJKUGWibYqDVj2USyQFaUgEvOWrIolsj45xvRGD1Ia7WQ02EJpSptCE7HppgRUdiN+0Qmyq6QBMm2F2WnRs4a4GtC1o1/DXfkU2k7JY9yK7YdU8+HLGjNvmbeBG9tjckp8yhnNrbtKAqxnFQyJ2HtOzWC3HRmXHS5OwVp5j8rK9Stn/vYNgS+8IM5cb7kbfvtYo7Li770wcutZhTKK22/0pCzDlzyNovnJirsfqYnOklLgFncR5xTROO4d50SEBmZqh5s1+OOuoOiJcX2NB8e3E7QiDgPZaGJlOeovszj4Q6wxjDnwKZcD1bRhdtMOK38VHwKhNLFZqULPlGP4sasfYDU8AsAN05cynd9I9oGLi/ezHq6QUuKeGy2reo7B8MXm5ezUDf1iydvPf5jlWUveyzCOhJypqpYvSZ/H5CigRhkYSEFf/uTSBKcs194CIGitmXnFC+9bSb8REzEKkqMSpCGg2ordaz2zI0G2dNHf5QxXjj7ENX03OcPxOY3abUkhcuOja3YWoimyQYYwpnXc3L4clyZyH33kXYzxGLTion8nF3MuDnQJE6QZiZ3ce06WnA85JmEYZCEApnLfUEoc4cRau5zLwgGWfb/RE2sldvReroEZthbeKCXMhEIPz2VooLISpCuJrb9FXE21FSOV1AVumH8GlZuTc+DBwz/Bh5VsR0GPUMg9wZotcpa6sWigBqG+Vha3N2VcdtAH0nLA7U2FSrk/BWuY6Y5z51c0p6bEaxXxyqZh236Ej6NPeYpnPl3z88T/fwwA1HPrufW/4vrkNFp44on6DE/IauqYnppLxsklxzCC0oq1UwxkaQ48hJXcYJqcC1UHSCVtm4gNBquEKqc86KxJUW1pSfjiWqMUOXp8J6hL0+xQT1tUUqxHKRJALtjRR9JxT+w99YV96nN78rt+xB+t0WuZ7GZt0UqKpLjssPNWKEkjckGvndDmFt12EpobydNRxfFG6j+hOKjKSm5KFE1LPO5QWcT4KWdsEncjZTRpEFQqkKSBGD2piO7dmR365UCKQBa3JKMVZtZssyVyBhWTiIazlwlbGWypmJkkQU1STpjei7Wvs9vvOg8BFQKqrlCtJKkrByllXDkWuiwBpaof8FqzzIG9eoJBsU6Sc9S6Rm7SY4DKYOetIF2mZCyNkuOUx0Bcj6yHEZcBrVn7Ea01xjgIQcaeWexYNwVoVpCtRZsaaydoo/EpoY3CZIhO6CsYCM4SC7c8hkjygbjoCFcWgh6dmlGd3SEcrwkHK+raksdI36+w7JGcQQ2aNjgMml551mog+8RObDAKfEqoGOXzZfBEOjViNjSyLHVI3iAaShFqt0VLFBZXSVOilZFjKIOyFq19scUtX5NS6FmD8olx2RGuHGFO7+BuPUu0vSA+WqO1JoYg1DldZvgxY43eFmDosi9jYnRCt1ODF/pbpdFZpuAMXpzFAHQWauYgQudkE32ZNuteM8kNRIXVrlhcCzKGkmN8I0I3qhQ1bBhFUjjmmERHSEZp6FzYnmebojREUzJQ5LiNm21TGmcngjcZOec1oNGEPMAgr21U0UBohUK0VbnQmlAycDFGaEzZXzctLpQzrRQ6JcAWXVbahgGr8jobO2BtLDln4qaIVkp0F+W7jL0nZXBGkxpHXgsiO46gl4FIxtaVoItak11LVoa0EafEhLMJZzLMLTlINpk1mug9FrCtxrSOcLAs58VkO8mfNFpCMWvLOESOjhKmccQhyme3BqvLwac1ycrARAU5DmrjUClQVQpNgKQgRBIa40R35nYm2CsLspUMoYFEYITOi8lCXQrmShOCZxx6DLD/whuodif0jxwI9bg4wSnY6idjoVL1aWTIAyZlGbIFKeKjinjtCSninSPUhpQU8cBjd0/jenElHZedUCSbCgCDxY4WU9eYNG6bZ8mRUcSctjou8fOW4zqljMoSlqudOQmZLdfYFBLZaKzSW1fNkDO5cuLk58UVUBCvybYZsUnhfNrqTBIZfMRMK+pqTgqeKkAs1ulRCQ1WY9HGiCOkgnHVkWJAFHsnK67F6GjjsMrmelVMIrZOclt9oASw69INSqBr0egpQW02zbwqaM4GZaWcrwm2YUmqssSUyaYEpCsxArF9Q13PSMkXZKxo6IrGL+aMKlrHjclDHgP1DacYLh9hUmZ49BB3bgfbVPi1J4WELSwTM6moTs+o4jFmjCg/YqtJQcyeTTLR060nTqCfpK16IlPniT97bj23/jdZn4Cm6OM8gz7a0572ZH38yd1HRd9MoJmSbm1Qe3JxnZ3K1A6hJ3XiloNS+HEUTcPxkjR60mJB0D1jc43UzEQUnRH3rnElVDNbhNjWELqRzSWanElmpF8fiagyR6bVRCaiVhF0pF/2jJePUZWlPj2XosjIjSuEgWEacSqTVZYb+gbytyJwT/1IXnbE1bD9XRwH1KqXC/V1WUObTAR0JqNPOM0pFnoIRfhvsNOGtOxIi04suIM4IlFbcsj4DP6By6huwLa1ZBCNQRCTUQqnFBKucSK2FrEHtbXEI9HeKGMw84akNfgkhW2hcRkjtCHtNOiqfLWl4TpYoAahJlE7JoM4kAVnqScNzakdoW4l2I11sQvPGOfQ53ZRTUVedVLEJYSisRpJg99ODCvAFic3ZyqG6MlaY021tUwHKeBTECQnZxEiq0Jr8dFjUBhXEcOADx6rDE0yjMHKUM4afBAjj5AS+mhFd21BVTnqm09Tn54zXDzAnZ7JDbUTK3aTEoMNWDRBRepgixg7sxwWKGsINgudcAwEgujAipuVydIkJ6OJlSPFiLai51HAaCJ9HIg5481J8RCMIlamDAsgGi0Ur9tmVHUjlK8rC8LlY1SIVLMKnC4Nd3lO0dZRmnZAvvsSgrgVkxf0Q27ZCmWsaGQypN6Ls5az4mJVCs4NVSilBCkzEuiMiN2jOblwbGzCc5lCS3O10cPkbQaLsYZkTKHniHGIQmGK5XNKgjSllFipAWsMQxwJpb4zFjojhV0O0JiqZHNJI4gxpFK8mZLjJRcYto6Um2vJBgXIldlm8GgMWlmyM6X4FndIH3pBLbTeZixKhJFQfVIpZDfOXqk4j22+5zR4/KOH6FmDPbsDCvzhCn24JMdMbCv03hRNxhqFygFNQX6N6CkxUijKNQeYVNhyfcsaEoZka1TrUJVBJYkE2G6rlw5TN+4EMQxjyaApAyqliF6OqzBGjEqMo8c6QdI04jan2wpTgjRN8ujKUu+39IsRncGRid2IL8eC9lG+46xw2RG1xegs2THOUp/agV6Rj1YQIqt+Ibb8uYYoDoc1Bp/shtEmuhNbGn2tMa4EfiuDBVLy+LEjKo/2CbvsZRijJdS2joYwrhiTRRmok9AXjdFiDlDuO9koUBqMwdq2UHsVupJjWJlM0H7LUjOqHFvKoJECX6dEdeEc2RrGgyNYr8UkJWVMFEt1fBC0P8lwgeLql5HrX7IaU0+wsZfjPAtlUFUOV9XE9VqMfLw4mWKf0BQtOjTS4KS0oaOpLV12O5Qp8MbG/ltmC6UZ8eKYqJzZ5gJqawuSqwsjQQxmRAtWbMwzQi9HnGybvbnca3MmKo9PPSl6uQYYQa60lrwknXmcqygbxK6Whjxled1w+Zj6/B5uf0pc9oLqa71lVihjicvIkDy61izL5/ZPKJDUdmc88V/PdD0JWnTd/n1uPbf+d18fd1N0PQL7CV3PHiPmd++G/3LvBo7vIQvE/jVn4M4dIMH6rgnhIBBj4NKFmuA0PieZ6lpHCpmHx/eTu1zME6SYjeuOGCWrxRbzAx1HQRy0RlUN69VF7huPwBl23Dludp9BPZuxSBe5uPgg9aRmWGX8Y4cAuJ1JKYoyV/t7ODaPoXzEq4CS3DkpqjLofZnWMsnQe/TuVG7AB0tiSHQx4sZAMhrrrBRihaqkK4XSDsZASkl49WMonOok7nUruVArpaRgBnTvSUrss7UHp/XGWRU3b8gJUjfAakB5D4MjaY3Zn1Kd35eCa9nBrJVibBjJwRdNS8ae2aE5uytGENcWcqMotrVpXGE2E/hCV9Q+oHen0FYYo8WNL2d04fy7wsHOKUuTt+4J/Yhxlnh5KdoIHzbAgYhci22qVDJyHFXacmp6O2faO+VxOW8nxBeXH+SwexBSpvcjsyqjs6JWVvI+vOfho3cz+EMUis+Kn4WyM5TO/MFN76GrxlLwyuTThMQddy/Idz+GO7NDfXaPvB7YueUsL3j0Gqn3jM2at935XoLKzPuGLzt8OVYbLuoD3rL/HrmxpiT7QylBP7VQpk4fe84fBlI/culMw+WzDVaLZgqtSTHywekD/MXsYRIQKshBCveHb2jRFxrQGm8QJNMY7pkZlPZUIXHLYoUbPPq44/mpJvUdA3DXnhRKqtA+ZZJaGp6MDAOKlfxWO7zV9ZRiG7ai7KyF9oItjlhD3E7PtTFkIn8xeYh7WqEw+Qqhy5amY4OcyESj/LwIsZUuFJ0ydd7kg2yc62ISRCQpJOTXeX7/7AdKQ5WI5+aFzqP5c/1ecs6cGeZ8/tGLpPmoLaUfkUGCUqRxLE6Eio31bYoius5lsp1VCZ1sHTElzrYvZteel31XjvWUMw8dv4vV+pI0bbDVNmhrCbns+zIh33Bx1EYLSSkuUyYuemI/Up3dpTo1xx8sUUaaQLXqmewZbplcQ1VGUMhRTCnIgPeCUhT0Ig9eLJFNAqO4snRc606TrgVuPB/ZM+LAmVIS45miSSSX3LKQ0VPJSrrvaM5ARYpZUCAfiF3PHaeOqfblem8tpKS3g448BJzL3H56iVaZrtJ86G4N7YS8HrBGo9YDXoHSMpiaujNcmH0aOSVW6wdZljDS3eYWdm67meGhq1w7vpuHjt4BMXF658Xs79yB8oFT7nZONXeiUsLZSkxilCuUYEE7bn2kIyJ0tSu8h8vXhAp6wzUvQ4SouG3/ZVTURJf4o90PMOhAmxq+9PjTcNkUp0aIPghoEmWA1banuePMnTI0KNoqlTPLcIlHl+8T7ZtWopUNidPNzZye37nV7hjVkF3FRf4nC/0gyRouHHjOH0dSZTFjGVeoclxuzpXakpwjHY+cnXwadgJJJR48+GN8XqNri3VVoZtD9F5Cc+ePd0iNq6FY9CPbCcXmv1DHijV4LqfwBrHa0MpU+RwohWoq1FoCybdDuo32RxXzhIImJdhmgykr2sp0uCICfhh56PhdpenUhDySakdsHHVlSRePMOpkqKNQW3OH1HvZplGQeUXGH66obtjHLzpSiGSynD9A6lry0S2EI/hzq3n7egVkPFtw7LqS6Mn+xV9iMfbc+ste/+7f/Tu+5Vu+Zfv/X/zFX+Tbv/3bn/Lxb3vb2/iSL/kSAN7ylrfwd/7O33nKx/6P//E/eNOb3sRb3/pWHn74YY6Pjzl9+jR33HEHX/EVX8E3fdM3ccsttzzt9v3Ij/wIr371qz/i51prdnZ2uOOOO/jiL/5ivuM7voMXvOAFT/ta11u8W2t5+OGHOXfu3NM+5zd/8zf5u3/3727//0Vf9EW87W1ve9rnfKzr426KnjHAezLcevz6GJqfp1pjlD/b5G+Vt9Mnq8tlaz3gH7iCPX+K1Hu6yyvicXeyKZWFRkJRs0J4wUTUzGK1K85VURziTAVJLpg6K5g4mDjiuifHgFIWNSRwmtWyw7UVVinCGOgeuMw4bWhvOoWeVGS7xK+WVDs1qYuC7ceIXgsFJ145kuKhrbHn9+SCrxWdNQyXj9FKNDyVM1QX9tDzltSPdA9eFlraxnAiZpISpEWFiK0d5vyemDZcPiIcLKUgi5Fsxamq2rhjWSN6jpjwR2usE4c4lRLWik1tmtYSNnv5WG6azqLWktlAEHe7iELvz9A7LWnwooHyhXKiNaq26JTQbbUtVHVMgpZlsT0exwDLgdppsf9WSibQWvRLm7yMOAbiYSeOblFsyVHiJCU0Cwq9Sm3pD8SESgqDlTBaVVzbMhAEqUAhhg8hFhFuPgkrTZ4YehQa46HVDp8jyjmi8RJ+Gsvn2pwAMRMeOySfmpNzxFaW2a3nGC8fEfqBLvVynNmWWtVkn7CtZTRBPntrYeyQKbGTZrroNvRqQJfPrDdiYyvGB6ZyhMqKmYKPxCTFQnCQdyrJ0lr24nhmDSpmybUC+sGTV4M04CHhsiKEjM0JsqBo2Sjpoks1o8wmXb40mtaUhHmhlGUr+zmrjcmEQfWeTOHte/lcuq2k6N6iLZlkYdTX5booBblkkJhCmdnQ1nJpoIs+yZRCTKmSZbTR8LA1OZYCt4SW9tkDCW0VCiOFVs4oBEkc8YLaKCU6jkLb294QlJiQKKuL1iVDDIK+bae35fGdh8pgphOsmsp5kovDmMw1BBEKm3Bpynkgx3XKMu1PRqGSaMRkW7M0mQWVTinjdieCTk4qkm9Iy160XL1H+YxzCl1psveoppKctiAUNIWg1Cl6QW7mjRipxMg4RPoI2lWgBnGls0IHzOV8Um6TeyMNbSoumX6Y0vUDqfO4vQmYiojHOEXVWmII6EooxGEoxi7OgAqoccDtNAStqU/PxPwiZ/wYUD5SGTF5SSHiqgrTTrEp06eW/tpF3LTGtQ12aGA6Rw+OMHh0jmhioS1bKi1Dmk3+EeNI7gfiqif1PVhLZbU0M8aQld8W/7XSxQZbUUWLNRWZSGciowoYvDS8KpNSxOQSaIp8zzGJ0Y01dTlW5XvXKPKoxElRKfEGKN95VAZlGgnRThE9KrL3EkI8lmNXO6yzYniD2NErlDRmApkSasd00jCMHhcMShuMKnbeRuIZFAZ00dNlpPm9HqLIxUwhy/9zzJI5uDEacBbG0gSqcu7kTZNWXqVk/ZnGEXzATmrUUM6HjdaTEiitCupbhghZs22McgiMSajsadExBIn7cJQGa1LTtG5Lyc3F3nKDRJWPIC6sZTCVtTSRKqSt1brvvVyTKlvo+2CqBoDgRzpOhnTbk/oTvZ6qdHuusfprXz/2Yz/GN33TN1FV1cf8GkdHR3zHd3wHv/Zrv/YRv3v00Ud59NFHecc73sFrXvMafuAHfoB/8S/+xeMalmeyUkocHh7yp3/6p/zpn/4pr3vd6/iFX/gF/sE/+AfP6PkhBH71V3+V7/me73nax/3yL//ys9quj2d9cmqKrl8fZfrRKoWDkj2SikW2wemMtkKJAcUYNXE14o+WNDfvkayif+QqWUF1Zi7ZPkZj563c1ChOXWXSnDduVUPAr6SJiutBhMNKoRpHtTORwrUyxE4RXEKpkf7Sw+jDa/hxRjXfkbR0MqaD9HCHmdXU8z3yUYf2FuM92Sb0zkSykXxg7AYRTHcDKkbMrGW4tiB1IzYEAgqrQKVIKIGpprLYphI77jGSlZZgRaCqnZgaOEu4fEReD8T1IMVWsY3VzhGLlgArbnKqOPjpEAnLTkImrZYAxlpuFjomQYhGKQbjGAVtyxldVXSrjmb0hOOe/soRJiMaiZxJZJzTpLYRqptP6Gkl5hZHK9GgVA7tA3GMDGvg0mPo2RzT1DJJ1iJETl7IB9V0QioULm2NFMCq3AwL3U4rtvQLrMHHAZ86cc5SGpUgeI82YjcrA02hYWQtWqKUMxi1pYFBJjAyhjVRRchp6+iktMLHIPQULdPfFCLdck12GnuwZLaGyflzED21WhH7gIojq7wm6kynhZaYUyKuB+HeK8iDuLel0RN1aYBzxvaZybQma01UmaQTUQEhoLLCNBXGB0gZM6lROxPisiN3g9Bs1oMULtZsc0wGK3bWahyp3Yy42+DXPWbaEKNoG9jQpGLeIhlqc25vND9lkCGWz0VXsBGkFeezTdOSi3B8qzVQSjJ9Ns2UUdTRYkom0GACAbG/bXOFDaKJ6dUoDnXXNSzSqBU3yQ2NTSF28Rkp9lSh8WxG1XAyjUYE3MnA2gyiSxpLAZxl+3UJqdTGwKZRzxt7Y/nMG7OH7CWTJ48RHwdG20GKONMIckLGJoszU7AKH9ayDdfvWyXFowEoWVIx51LYSp5PSpLx44/WMjWv7NYq3GnQuxWqURyukjTCzkqDvEo0k4qJkYGCMmKaoDbNpjXEfsQ6RbXsMG0l1LlWnMJylrBMtGLawv5Uo2LCBI/aqYhDQK1HXAA9taAC2mhcI45iwXuMtaQxlGPB0cVMzGIBv6HoMXhqEwkK6jMThiERa8dwsJRrWyWona6iUKFWEXXcEY7WpGlice0KkBgrJL7AGqJOjH6Fdk62I8jxU9UTaVSNEd2hbtAYfLdGKxlKKWOwReS/Wc5ZtA5gA6MNGKSQVinRx46URpSGYq5N0COTUBHJ1F4CZzfHYVaKCCfooFaobDB1Q64sCkeynjEOaFNtOH/S4BYXUNWPxJUYnFBosClE8IEAWCNOjD5mzKk5w3rAWoNad1TVVIYFqw6tTrRYJmdiP2AUTJwmJGgUEuxbmi4tHDpBHhWCvhSER29sthGEN4VIqh12WkucwawRjeeyR+tYaLO5DD0yMYrbXtLI91Dqi6zlfMlGY6sGGzJ5TYF3BYAzxcVPjVEynThBeXPOJ7onoyUfy0esNaQYMVa0fePhSvZtyrgLe3QpwyjuiK5cA7t8ckzAhiK3Ico91XT5ufV/pvXAAw/wb/7Nv+Gf/tN/+jE9/+LFi3zZl30Z73uf5AJ+/ud/Pt/5nd/J53/+57O3t8djjz3G7/3e7/HTP/3T3H///fzwD/8wf/7nf86v/MqvbDV9T7U+8IEPcOuttwIwjiN33XUXb3rTm/j5n/95hmHg27/923nZy17GZ3/2Zz/t6+zs7HB8fMwb3vCGp22Krl27xn/+z//5cc/5y1yf2Kboiefr9f9/JufwE5sf9YS/n2R9flXzYudIY+DB7oiVGlFJcevsmNk0Ud90mkvpLHcdOvLouf1zF9Qmsrz3MUw/Qe3vSu5QI1O+/tLhVlitK3GM23TPqrLo2qFnDWHVU5/ZlSl3yuJ8U6ZgWiuGvODewz8S7c24JlYVoJio85w79SKZThYdgfDPgb2EaSoeSe9moS+LoYK1xG7A1pbYjyhnGfuxJGYrTOPESjoJWpGNhn7EjEJ9y4CZNVBZ3KwFH4iHggalfpRJ57TBHy1Fe4QieSk8klZEJ81TN3TMqgaTcnHrMph6JvSADc1hkCKHQTQ5cfQizraGFAImCre9sWImMB4sJBizNAohBZKx1K4l+ciYMvWpaTGVSGLMoDV+CILiWSNmGWfPoOtaboCtBNFqpFA2/SAufE7QP7VBrEKCTnjjWctn3RaqBBbhPparB7aIwyYM9cL8JZzbe6Hw1ZU0Bxu3MaUl9DAlEb9rpXj44F2AuIMN+5Pt9x1SQGuDz54Qg5h5OM19d8yI1jBjypccvBS7rBiaAe0/wPjYNZbhIm+9TdwFoxHBtdEalJhdkBLJGRkGBGmEhYqSeV53gTNHL0A5w3t3HuQe9zDkjK0qwjBKPpSXfaxjJi971GrY6kbUGAsyUSg0ZO6/fV5MBhR6apjccRPD1WPGh69tnZ0Yg9DoGqFwZnUdhJ5yyeoophCl5snOkHsvIahaPX5QqkTQLbbdmycUW90y/X3x8hZuG86SM/yPvQ/zSHOIUvCZx8/nbL9D0vCOvQ9y4NaEcrwrxOZ3G0paRNiaYgesih1w2kyf1UmZotUWZdJGc1Wt+N3996AVtG7g5qPiGAcFiS3HiWbb3KmC6igKKlWa51y0X0f+Hq4uPoSKmZumf4NZdY4YIjfuvlxsoXPigcN30o0HYscOxXVMaG3pOt2W0WZLKSLKsaqyAg3VvJXtW/ZM6sjtO0uq0zMeWFt+8b1GdGWlOVW25VN3PP/3lxkZqliDzlkm6EqQQeMs52cj++tD9GyKbVqMLq+ji/FDzvzfXiCpCGntseNIzhO0M9y2v0adNSg1En0Jqc4ZFfVJ0V/OvyFk3v7wij4p9qvEi89Igd02cIc7QmVYx4r7/BSmNZVVpCtLslIswiVWx28XG2vttyHYR91DLI4u4QdPDkGy5YbA1eVdXA5/Ic1P5YCMColzs5cxMWcxteP87qeRW7G4fujwvzPWvbgxDoHRB8k+KtbSyUYeOv4T0cFUhucfB9IYiHHFA/GPZBjW1jKgA1o750uqzxPUc0xiZuBM0Z9BDpEEJGtJo2evvYEbZy8ltxWH3f3cdeVtWGPYr+/g3PT5og1qKojV1pxB1Y40eLRSxFDcT7Wgi8lo0tGa0LS4ven2HojP3DT/TEHumoF70h/g7BU5LnLGLztmVvNFt+8CMDx2QHy0BJSWM2pDkcvl+KTQ/1IZGohhCqTawm4LdbUduAQfBLEDfAg4bU5KC6MJBUnW5O3xkzPSSAM37n86LkzQIfDA8Z/Q5TXaKXzOmIMVoVwPbbHQF3OLTCiDh5whHKxEp6pkwJOtJgVB4zFiAHOA5l13H8p2Z7a6r/gkdU4uENTjB/mbRomPrJGeWIM9t/6XWXfeeSd33303r33ta/m2b/s22rZ9Vs/POfMN3/AN24boVa96FT/yIz/yOBTo1KlTvOQlL+Fbv/Vb+Zqv+Rp+67d+ize96U285CUv4Yd+6Iee9vUnkwmz2Wz7/8/5nM/hcz7nc7j55pv53u/9XlJK/PRP/zRvetObnvZ1vvqrv5o3vOENvPvd7+YDH/gAn/qpn/qkj/u1X/s1xnHkRS96EadPn+Yd73jHM90VH9N6+pbwma6C2P+lrad5faegVoqmtuzccprJ+V3as3PaeY3ue+JDlxiuLRkWA1kbUvR0lw9Iw4A7v4OZNuKWc7QmHXfQe3I3is31smd46CrdPY+xvv8S6/su4i8fkUaPaSv8qiMUbY4qKedojd2douc1+lSDnhjydILe2UFNKnTl0MqiMBhlMVr+b5JFK4c2DoXG7U5lGjl6Ujdg9mY0N57GzFrczpR6byqhrbOWOG1IbU2ettDWRG0Y0ax7z5BATRvc+T3s7hSzPyNmJQXuvIXdiRRiPkKKgqbUDiYi+NU+0u7OOHXujCAmSKGVgpgsDH3PweIIhgCDhyEwKrmBxHKzCf2AzWJfrmcT7KTCaSUTQzK2cpimoppPaW1FDJGgFJML++iSoaKKtawaA270OKOpXaE0YMhrSa/PYxSNQAYVM8lamNRC6xkCaTWQRim0sUbCccskMqOK+YMU/iF6QvTEMJKjJ5fskpwUKpV0+6xI3oujUpIMI63EuEEbQ8qBmDwp+W3zR5leasApDdoQQiBpRXJ22+zobNBDJh8MDPddwu22uHO7jCrQp5EUBRFUhbooxbkuxgqluHYG5i15b4rZ38HNd7C2gSERCkUsh4g2BuUcqiCmudAaNWIqoq3ZTkG1EXc5rZRYvTtD1OCHwOryEdUN+9hzO1tbbuH/F+F0zidZYYotQpM2uT/lfNeZk8+1QYDUhtJW8ntg67iWQRwHlRRMLmtqHLVyoIQ6mmLGJI3LFpfNFgHeCLXFaUs2WSOUNFM0TEqprXB6c0lSZT9s0J/ttD0myIloEt4kKJTAmAs9tEy9MwWdLO8Vg1jrZ1MCGze0IuT94zDQ5YCaSQHOBnXSFq0sVlk0kuezdaODkrNCMXwoNMWcCTFuIwOEwiMh1Zu8rs3O0FahlVyER23oI/Q+MSrDkDSxoHRaSQOWei9T/II6xsMV4fIhtrHYqRNXwdLs5jKgyCFhSdQ60UwryXWrpCmxTqNTROeEMwpDojC6hBKbktgoG6Ehjj4yjhG/MZwRWBetMsaKAQPF9MO0NebMnGpvgp032ImBRpFqhT07x+5OCMsVw9WrZBKuMuKcN3gUCaszKY4EP5B0ZlASUu2cxaGwEUwAk+Rak2NkGEd83lC7kiB2Shi1USVi9qgUsD5JpIAxKJ1QJuPXK1ARpeW4ckFjo8Fpi1UKs9F1Icec1kqcFAGDximLWoyYzpPCyKgTSRfjAmMEtZPLmlyPjMZMG9S0gaYi1I48baSZS1nywcZAvraUfLlFJwO3ADkqMBW2bnCzHdDC2vBrGeo4rXBaYVaDDJaU2lrS64LiaK23zp8K5BpLCUkmF0p3MepJibDq0asRNwZx4MsbwwlNMkXjqJU0LyGWgaQha0VVOZg0mKahms/RVU0uTnQ5JdFiupLflGU4mArtGmsEsSwoXShur6kY3GyMIShDDzuTusOnjA+ZMWVG5M+2KVKKJwDSPH7CfF0ndH2N9IQB0lMOldWT/P7JHvtMh9rPrU/IetWrXgUIxe11r3vds37+L//yL/N7v/d7AHzLt3wLr371q5+SFjedTnnzm9/Mi170IgBe/epXc/fdd39M2/1d3/VdTCYTgGfUuNx000387b/9twF4wxve8JSP2/zuG7/xGz+m7Xq265OLPrcZuz6LE3CZM1ejZBPgFNPagYZ2/xR17xgeOWB46BpdWtJXhivTI9ow4HZnNO0pxi4zXDmmPzoSepM1hNoWtx3FNDVoarnZDx3jlQXp2hIzrdFOHLJSP+JZY9qatB5AQXVqjp21cG4PFUYqK0XeRJ8iH2WGwyXBRxFqpkxQWSZLS4NzARixuzMmO5b+/jWVDrjdKew6UufFbrxy25t7Dom46gmLTi6+o0ePAVU7uqM1tVa4aU0u+pARaC+cEoTmYEEubkBqUqGBxfEClGIym5VCFrLWxT2tQvkRcqKeTHBTofmNIaCco+97GqVkkmYNlaskRNGPJXNDaB61sZi2Eo1ULTdZKZDkhhauLshHK3TltrkVuRRDrAeMdcRlV6Z9CaWsFPiVLcW1VJ7xuNtSVrItvPi0KczVdlKXrWKohOZgQsKM8l5a1ThdCQVNCUUwF33G5sDtrCfSE7LHxwHJxCmFZbkZ1j5B9mhn6TeUlASNmmBsIiqDGyJaZWzwLPQKHWFkxUBiPFzS7084dcMtxMMV6Xgt9u1RE5RmqQcUGRctdZSJ8mTpmboJMSYCmWPXEXXEJy9FQ9GCKBAB+2a/BcmDSTFtdTQZpGku2y5sMgkWzaVwyMWqeGdvzvqgE2czK450pqCPuSTWq+uRoc2ktBRkG3OGjVX1Bl3a6gVNmecUgwylC5WuXEI66zlGgiKjlsZHa03nPEdxDRpiYVYpo7cNa4qbcMbSsJWLktWGGRMpxsbIqhKb5JgK2puENteMgvjkpKhsC1ozCSNVVY7fOBLSgLabQqkgeQooTpSjyWQnx42NGVMc11LONPNWUKpQUKyNi5cWZ7ZY9p8CrGow1tFaTT8uRFuyQadTEs0JMrzQRlNPFNWpKSkO5FWgdZm21dJYG41VmTMTSDEzRFj4op/Rso/0tCEtBVlMo5yHALlxuHpXrK8HD06DK8XqpskcAwtVMUb57vemCquKEmR7P8jl+FAYJ3lS+IipHXEMUtSrxNmZYlSWHZs4PhyYtg5jFPWklu85CLUtVZC7cRuAaxsnE/1uxDqLm0/IMYOxVGdPEXqJWNAhEZBhgQwUhGoYl14s+es1fT4sRjG1WFLnTA4WXU2x1pKXh+i2BqVJwaMD0tjZEwMSNtk8ecsdRVXi8JmBGCMjndANlUHrtlBNI2NciVOa00ybPbIJGOMYwpJsFCEn0RP1I9iRIa1QQZPHHuOsuHOSMUGMFoQSqXG7M5KXzDiVM9GODGGBioo0IllD1lLpCUkpImJywZl9fBowHeR+QKGp7IS4HtEr0R8qJHA8U0Jb0dvBidai51NWFxdIaUq0T8RryzJkyNL4lHNy49JgbYvW0uin2OMqSsBqRVRIlEIrTcpEa5T29HFFbhPsNOjeE6ymsjOIEFQkpY6chZKb6nItVwrbSZOrjROadeGtjuPyOhpgpj09K57gSujORkNleHzDc/0k+Alo+dOtZzqgfvzLf/yv99z6hKy/+Tf/Jl/5lV/Jb//2b/Mv/+W/5Du+4zseh8x8tPWTP/mTgCA6m38/3Wqahp/5mZ/hK7/yKwkh8LM/+7P8/M///LPebuccz3/+83nve9/LpUuXntFzXvGKV/B7v/d7vPGNb+S1r33tR1D3/uIv/oJ3vvOdKKX4hm/4Bn7rt37rWW/Xs12fXE1Rvu7vjza9KOuPx4F35gGA/8fZgRedEWGpNprcOprbz1G5ihhEIHsln0M3GqtabuxfhBstg1pwV3oHIwNJZe65dUJQmama8KUHfwOnK3p/zENH/w28CITDohfko5XGJA5BUJz9GccPXGY8WNKck2L/1MRz016PMpprQ+IS14huYLy2IK5HUjfihxFrDFjD83aX7E8ymGOq83uk/Yb+6qO4XEPjUI3mzz4Y6IPDzBtxp6sd2hmqUzMR2bsZcdUTj9cyQcxiGpGOVijvCdayevgK05vOUF04hQ+RcLyGpkLPW6ajID+6H/FebowMPdlo0jiiUyQ3FckUrrdzmJQxSuGspe8HTCthekorgveErsfVreQtpSy2vWfmjJePyGMQG9jKEkkYn4ijF5oNGTWpC99d7JfRmhTCtuEAmforIA9BtCKpGC6UqemqW1EZQYacdYDaFtJJZQ53ay5eaMU97HLP/NEenRTnp3dybnqn6C6UIiVxyTOlOYjAn07v5qI7QGvNbcs10wHIkSGKDskZy60PrEArvMrc/bwZoTYYW3PL7ktpcsUY1uQP/xE+jaTdlj+47f3EclKkc3OMMZwKM/4vd9+BdY6jgwN2dA0p81B9lT8+fTfRWm44PsVnHN8hyEBMklPlFB9qHuad7o/JBIKK5CjFcdQKNQQJaM0lTHTTdGg5+YRFuKGa5BNqS9pQl+R3aTkQHjvkUxcGf6RYXuu565aJmEuUc1vpE9Ro03ag2NLw5ANvimG1zWcRJClLI7hpypwVVHdT7CONwgfnD/Eh85jQwHQq2V+Zd+3cA5PiUFYQnPIJ5dgpWphYbKvF/jjTZssXXnsxlapYmZ631e9jJKA40RQ0Q+DWexbkmJg1Z7l159Nk96SMPm3QKI6Gh7l49F4xnPCxoGjyuVWh0R2ebbl8uiIrxY2PdZy6NpCRbWq0IlxdwFTs7K1222aVQt8pWBq3nv4cGjsjEbn36n8l0InEqDRim+lhjolmZrlz7xAdrqJqh5mLk6FyBr07QSnFLWcN376fCX3gLw40v/HnpZ3OQpGkcajWEQ5X2J2JfB4f5U8tgnLVVlLcllBkrJFzXyl++88CH76cMJXh6z8tc8u0xCckCdREl9cbrzMqNiXYsyCZ86nlm18eySkwYrn/4DxppWmrxB3tseiYBsV4bbnVkWqjCN2AqSwJcDut0HsPV6SYCMuOGKJk1xTLZ2saoasVEwq6QRrUnLk83sWV/sOQMjfvfiatOY0yhhvaT2UYBtx+zWPz/8mwPkBXFcmW4OBiq568lwbFFeQGyN2ASggKXDKIglrzwME7hErXnuXmnc9CoVgP13i0fy85RFpzhjv2v4DkI0f9Q9y3fqcYCigkWiEEDscHOQ6PgLPkGAotUmNK+rA2GnwkZLHUVqMnGrmuPLR47xbVzEmQ2txrbt/9m0zqOWPK3H3bDK8d+qaa8398F2rZYVTFLfPPZVwcs2j3eWD4b8QUiunISQ2wsdLHFapyQWuNEcQmkLeW2Cgl1MpCZ9Oledyf3MHp6e2knLnUvZ/j8VGCKd9j7eS40uBqR1r2PLJ8nzSFxpCIjFZhsuHmyadjzYSQRu4/eAchD6Ta8me3TlDzhrrzvPBDRyifsG7G8079LUDTxSMePPzjLQXbzhrcpIZlsS1vNk58H8l524LtG0rh9pFPfOxH62qeg3r+V1o/9mM/xm//9m9z5coVfu7nfo4f/MEffEbP+9CHPsQHPvABAP7e3/t7nDp16hk978u//Mu59dZbeeCBB3jzm9/8MTVFUOIxgL29vWf0+K/+6q/mH//jf8zDDz/MW9/6Vr7sy77scb/foERf/MVfvNUx/WWvj58+91c5RXgSGl3MEJAAy/XVY8JqjTEyFfbDKFOl1pGdoTm7g5lPyNYyPHqEv7QkHI8k41DO0ExqJnWFUaCGDrVe44ZInRQWI1M9pSQ3xUdUjIRFh190aKMYD5asLx6KqPPwmP79d9E9cIX+0WuMVw4ZHr2KXyyJwaNqQ33zPpMXnmfy4huYvehGmuefo7lxF50CLNe42qKi5Pe0+xNsZVA5EY+WJwXGhtYzesJ6YOwGmVquxF7XnpqjpzXxaCW2p0FCahujqSa17J/i/rW5IYVFB/szfAwyWW0rwiA5Tur++2GxxJzaQTnD5Pwe7U6L8R4dxaChGweMtZIWnxNxGLFK07QtaqfF3niK6o7zVOd3GR+6QjpakVe9BCf2AzpmsQlHiYPRkEiHHfF4IPa+2PKKW13eCOJLUezHkUQm96PQI2KUPIqUqJTBKI1VhQKREiGGLS0jxYTPQitLWlFrS6WEmrIpN1NWaG2HvtKUAAEAAElEQVREExYjYxBaXNYQVSZkaS5yEdZXrsIWTnuKARUSJrHNN5Li1KK0xRgntLEMDEE0VioRstCqxhzFyXsdMEvPTjUDZVDlc6mQsDGB0phs5HWNQ7lKMre0IsRAUCWwMEPuhfKYCxooyEUu+UzFIU6rLb0FhTjCFTrWxmENym03Z8ZLxxAi7dldqt2pHFf2JEOHsr83xdT1VK3tCa7V44LvtTqhnsSC6kgYbWRjob2xsk4hElJkjJ6oYqEPlfNEiQA/m7x1s8obytF1BZnW0kTpDUqawSmDDeBSQXeKtiOXgpCS6WJR4BMGS6UszjhUVChl0FmofDGIli4pCBv0qzT1yQhtKaSIHz3By+fJPjLef1lMUcaAzhTb4rylf6aN5k+rEtyqyZFCX9Qnk7jyHLSShsJojMq4aYWbN9Rn57jdVtz1MjAGoVKmiOl66IetS99GZC5Ir7hlUgKdyRm304rLli2OhOpkGJFT3k7QY1Z4NN5nUozkjZ24PuHvqEpy1TbvaSp7Qs3UYmBhyOjgMSmREsQgkQubhj+V7QzrgWHZk0LEzidQdJB+2W/RO390jNubMLmwj9mdUJ3bQxeNZnaG5TjSq4w5PUftTjBthW6Lg+mO0M7MVLLd6vmM6d4eZjojO4vbn2HP7dDedhZ32xnsjfuwN0HtTWHelGYkiPOj1pjKoZsKXVAybTQDgYQ0gRtnNYwihpGEoLNGW7SxYA3JQEpBHARbR541pFlFajXJQXKCxMSNI6BSxG6QAZWVfB5ikpBlHyAGskpkEtkqbOtQuhgiOCNGF7UVqu6kxU6mhK44FiZIhx3aWKHHFcc6yneZlQS0il193Nrxu2L6szXIAHkfrbdUxJQS3gehcGaFSnLdztbgvScYhW4r4molQ7JiLW9mDaY12KnDTh2ustTGYHOGUPzrrJPzlowPUVxPZzXsTIg7DckooWVbR1YGrU1xHJRjqjm7w/biUxCgJ6M35ev7nXzyT/W4BucTwG27/tL7HCr0SbE+4zM+g6/6qq8C4Kd+6qc4Ojp6Rs97+9vfvv33F33RFz3j91NK8YVf+IWA0PbuueeeZ7G1ssZx3D7vpS996TN6znQ65au/+quBj6TQ5Zz5lV/5FUAQpb+q9YlHip54vj6bk+xjOrdlCqK0QrVThqzwo0YFhT/O0CoYE2lMRKWEYnawJi9Hut1jRhvQRHINqTL0KuO0xcx2aVLNet3jx4FAT/IB1TpSzoSYMIPHtbUUI53ojNbdQOMseXcH+pEQM+uFp9uR7I71+ohBKdSkop056tbCBLHzBoiO9sYbsOMxZn9WslBAtTVjMiSlCaNFNwblM+Hakl5nfJJgxTZrvJKsBlJmeOwQlmtwDk+mthZv5QakQyJcPmIooZ9ChYrowonWu1NyN2JiFGef+S7ULW7SkH3A7kwx01roeE6DtlhtmDRVQc98EcSKDalWCpYdYz/Kd71pbrTGnZ5hcsKvBlbLNclHWmMxyhT6iBRBKkN21dbUQW0yZ5QmZTCmomaKmVhSCgzj8VY0b9PG9eyE+mbURuQOLmYmXQKVsH0oXG6FDx29P0SjsKYlZ7E/92lNF3qs1rTesJMnctPWAyl1hUaVT5zJtCYg1KddP2GMilY5xriAoIl5lKwOJYVo1QUwCuNqKjUFn5jFVtzNYiIirmjKGgk2dZaUEqPyXKtWkiWzaT40rOK60JFUoSFKk5O1FoV72Y+ERFK5IHpp22yIhXCxluVkO3O5m6qiCUgxcbg8Flvbs1O0GUWjMAZpqILQg5TWW9rb5lJRUzHLLTnDkEfWut82QPIYVcweJG+rbIg0UGU/b/PFUt7q/XJMRY9wcrGZjQ2VrcRlLRbUhMyRWZNIGKWZjQ3GWOpoGOISPyZ8iuyNE5JqiGPElsBRozpQS1ROpBwY45EgPDEKyhg1g19u+78NBVBpTTYK3TbE1cDEO3bHCVppqommD0uhQiZQJfQ15DXr4QCdLNZOsbZGG8kYIypizgzhmGwiOYdi51wc9gp1MeeEmbZoo8hxZAiWfGqHHAOmG6G2jMpw7SiBMTQK9nIgO8N8t+Gm/Yx2mf1WjsH+YEk1azCzRtD0rPG5hqQI66FYeQv6szGUaFqDToGUMns2ctOORStwOaCtKw56YiKTuhFbOWnAeg+tXDPDGLjiLVlJE3u2lRDYvBL0OQ2RwXesJoJojxbMvBWkrhvJPhKNxzpLZVqhiyqFqS3V7AZiP2KaCjdrpcimLg6KmWo+IXhPVTni4IWGHCJxHDC7LYPuMOMhatagUmYwEWMcfddDk7D9UMJEM7qxQqFKuUQVDKJZM2IZ7oNQ6vR1zWVVVUIjrBSjWhKWA0M8EmqZUQxDx7o+KgY9vbAJzu0QAJ0zdWUJR2viapDzWCmoxRClMhO0a1CVYmRNdkhzWTv0GKCYDNmUBfEDCXFWYnMOcm2px5IDNETyjedI6xVrk+kevibfo9HkSYXqUslwQ1wMOSkhNtrBrX09MrgIgK0c2mp0tFS6IQyj9NFGhlshBdZ6gbYWvx4IMTKZTDCTWgLCN1EQUHSTBlVCrqMyxK7HuQpvelJIhFhiKJJQT5ujgTwmKmPJ61HQyxzpwhFKabqwICYxWDD7U1bWQh9YjU9mqcD2Uz9eR7TF1D+G9RTP2+zc5xqhj3k9+uij3HzzzU/5+4ceeuhjfu3/4//4P/jN3/xNDg4O+Mmf/El+9Ed/9KM+5/pm5qmMC55qXf/4e++9lzvuuONZPf/nfu7nWK/XAPyTf/JPnvHzXvGKV/CGN7yB3/iN32C1WjGdTgH4gz/4A+6//34mkwl//+///We1LR/P+viboieiuE9Ecz+RqO1HosuPe6Or7iwfvtTLBbJ2LK8CMdFMNdYZ0vFaLGfXwpd+6PBdVJWFHLjvhXv0KqGqmudf8ejeo93Ao+E95NWIMoqkMi6KwFWNqdhcK6LRYlvdjVTGkIYgk9KmwvQj6+S4d7kDQyTGSNYRsx6Zjpe54VRET2v0BvWxtkyNduRjlUmsv3zEfRdb1m7GcC0ShmE76b3/jjnr2mBi4gV3HVGPGRad6KCsEYpRbcmDID9VSfQOMYp9tlLYWUt7+3nRF4WI6j1qEI3QGDw6CQc9T2qS02SdUF3P4r4Fdkzb191w4vtxRDcW1zbkbhQanTOoxhG6gdSPjDFSWSNuSz4SjtZCDdlABCltbbJFEC8ZFjgNQzkICr0ppoytLHW7w43tZ1K5mtXqEg9174Qcilj/hGK3mWJfT8naORrZPRpELBvzdhp7uL6Xg9W9KKU4P38Ze9VNYDRXln/B8fgoGXih+mw+3d6JJ/HQ8E461pgs9LQhB0BRGckJUsryeQcvRJsWnQP3Hf0RwXdFU5OJSmFD5s77ViSVabXiljOfTdYGkiBSylqxz84nomOlFQnFo9U1HrNXhZtfXJu2k8jM9nNt/q9yPgkuLRQVBVsEgizmE2ZDZdk2SeX5GxpW0T6ElPhQm5necYbx8jFmtiMW7UOQP03RMZXv4Hqy/Gk/5/MXL0YleLC6zJ/sfphNgaDKJFgmqJlN+OpGQ5PLtuQNJS5nkpdCyxaHwQ2yaJThs47v5HSYS0GnFYTImDy/f+Z9rHSPy4YvXLyEKtXENPDAtbcT04ij4Qv1FwoSpyAfg7KG9foqD6qLZKXwecF9B3+EclYoikH0gyc5SaUpCrGYKci0O9eW29fn2ct3YJTiPdN7+PDeI2StuP3yyFkr14pjf40rD90NznLz/LOZmbNSzGc5b5TWPHL8nuJ2CDlvTiopYDcFIT7AekTNZtzvG/yHOua37PHC/Q5N5krU/Lt3B7KBO8/D/+sFBpPgtt3MP/gs0fKJI58SKhKITmRac7B2XFxP5JhYOahsKW7ZUutuHo/Zm4jV8d+5LaFc0blFU+hTuWRWZWxdCWIA6HmzpXgO2vLv/8yw9DAj8e0vz7QOdF2JY9i0JnvL3dcgDx5lreiknFhMbxwSsymGIkaT/IZGZrBtLahYlgwfQhQHutETY6KetaKVdBbV1uhiHoAzHIz3cJAixFpMaHxAp4pkBlwQ1GXoRuIYaPdnKGdIWYJ3c4tYtns5Rjb0XVU7lBMkM4aIQtOz5P71nxCNQlmw0wloRd933JffjcOSJwlbz/HrgeWy5/SNpxjuu0wq5CxdO3kPJMz49M6nsD+9lZQzjx6/m2P/GCYjGs5JLWilTEXkGLB2m9+jlEL5RJ0jt11c0MeOqOH+5++RJ2fpm8TND66EHt3WpGRRg1yriJtrSpacO8rxch06naPkbrliZ09I7NQ3cmH+YqIPJQhWBjRX4od58Oi/kawm5oSbNdidE1dZbfX2uqBUMezIQBB+gNqZonLmvuN3oYdNxICgj5bM8y97wEssgrNgDJ6eBxZ/Ivqwcq0004pVU/POe4+vK2M21LbHk+O2IdbbHz2DQuqJ9dETXvZJSXTPdnD93PorWy996Uv52q/9Wt70pjfxcz/3c3z3d383Z86cedrnXLt2bfvv/f39Z/V+1z/+6tWrT/m49XrNcrkEBB26++67+dVf/dUt5e77v//7Hxe0+tHWl3zJl3DLLbfw4IMP8uY3v3mLCm2Qo6/6qq96Vpqqj3d9YpGipzrBngnt9anWs0KaNPXZHdIYWF9dSiGSEDRiCPiDlVCFtARcjt1AHHpiv2I4zoxWY6taaCyFEqO0kiujVUJBCoFoNSYHdFsRjCb2Hpsz5swOWI3OMFw+hMMjyAnOniaHXAS0GYwU55oozdbhinTlGOUs5uxcHLbKlJ8sVAC7P8N0NelyTxwjSinMpEYDbVPB1ElIpBWTCJQhBi+hdM7iGjE7yN0Iiw47n4gAOI6SNbHucVeOyWPA3XQKpzXjvRcJ657stIh2jczu8rJnHAZc06BCoIuBZd9xfvcUuQGMpkajAviDpaA6bcW4XOEWiugDxmhqraQhcpaYMjiLmTW0udCWlCYuOnIIMr3TMoVVnZciNpYbmTOYLUUmUtmqBKye2FFnpKHSZeqaUpJCORcxdym+dBL+mspsTRgA0BRKjxSVIpiVG54p4l4SWGUgi3ucKrO9xtWEGLcuaVprDAZjLMM4iusfeUvz2li5qpyFamdLeocxMK1ISkuxt9FMKbZ5HGK5nLZT0pgytoiS0aLLMGoTXijUtQ0FTFhKxcmN0nDkEkpbmnNdcjs2A8YNbZGiLdlQGbW2ZK1QtWX94BXqC/vELFMkfCy6MLXtiTYlgNhqK1Sxvd5sg1BkBPXdhOymlCU0uDRq6vrHbgrvlCGlYiCB0PWUKkZ6RugwQRyttNIkNEYLPSkW8wSnxGkwp0SMEetAG4sOalsApjHJNmfJADJak1U+0WgotaUP6g3yJYwclMrokNDdKMizF11eHIWKGZU8J42BcREwWuEmNfXzz+EvL8RNbYOSbXpftbEPL1biTqhGurLEYSQeLYhHK9HIGM147Rg9jKQYGPKAr6Dan5C1YvARYywpK2motCL6iKbQDjOo2m61QsOwJqx7xqyI0YExZCMicq0V/niNbest+pt7D1ZjFVvaZgqRUCzZdevIWgZdm+2VRl3eXztDRKjUEUghiOMXSYxsupFcUEndNsR+LK59Gt1W20yvnBKxkwGKre0WnUQJcpGKPkoacDG1CEkGOzEk0LLdKRTr+pAws5pwtIaUMI3BxkDMkWpay3Vp8Ji6ggzj4Uq2p3ZCO2wcMQjqssm2IWehjCVx4LNG9gtlX9R7U4ajtaBVPpKdGGH4HCViKwpls57UjOuB1FYle0gYAsqJ86FuK6EUJoXyQQYHQUk+XUqixZrU8p17aSxVEOc9FWVeshl8GK2xSa4bXsn/V48dkGLCIsNEQezkfQTJViW/C2wxNBJ3xEiuHbo2+G6Qzx2jbEctVMmsxJCCnNBjwGSN0hk7EYTLThtMZcVmPAriHCn6tXLfVVphK0u/jluqpyITLWBBj+IW6KwjrgZUyoTaUBWNoBhElAuCVbjZhMkN+/RDJOXuuprlpMjZzHqU2qBC13c5z6B4+igPe8pfPdmw+UkaqufWR64bbrjh40KDPtp69atfza//+q+zWCz4iZ/4CX7iJ37iL+29nmlw61MhUDs7O/zGb/zG1lHumS6tNV//9V/Pj//4j/OGN7yBV7ziFXRdx3/8j/8R+KulzsEnsil6psjQUzVIz/C8f7pV28jEZvrFErynnU3QPkBK9BePIIOzu9SuElh/BoyeHA/Jy2NoDGoTBonC7U5J655otehEUiZbQZ1yEHRDjYqZ2iE7S1XVmMmaemfCalxAMxF0pFYY53E37xG7kXjlmNyPtLdNcecrwtWFTEdr0TZlHwiHK8ysRVUWU4qA2fmWrBSNHlmvIY6RYDVNF7GD5HfkiSVOHD4kghfakE6J5mApWqe6QrWV6FliwtQVWSWc0YQrhyStceOM2Z4jPW+H4bHM4Zi5eukKZ2e7WG2wdSU33RTFstRWnD2zT7da42JCF71VDF7oIFoc+ioQmlDlZCJbWaKPpGNBSbIXLZTORVOgiiVyTGRjhIZXpn85FcTHGOLgZTKpFOM4sOoul2yZNU11SgrkgnYAxDgwpAW52Oumog2RTKKiyVBC28n5RGuljGHIa7pwAGSsbZjqM+W+59Baptvzeh8FOGuLUB+UBZ9E39Lamj4c4ehZhzVDCjKBVYpuJsJ5jWF/FJ2DnZ8i7kwEdfMR+hHrhZK10dngI9EH0ZI4I7oJ2OZ3bgT9omNRpfkplCrNtmFT5Qmajf6CraGC2mhQKM1QeY8tMlMQJK0UjAF/uBIbdVXE2ka+y5PTvUyDrzv1B+W54o4gJI5df5JpVKbkuZwfm/eMUebcbD8TW+tbKDsgqi2C0g5F04W4iGUlxgxDd40xjGQDO11N5Swma47qjmUeCf1aKDDIdF72tdtuu0Ksr1dTS0Zjg2EvzcgKYu4JWQpjrWucmaKdIsSBrEtmGJlw3OFSxk89q+GqaP+84ny1j1aaRkXSsKBKmXHVY7SmOjNnHEZUPCSFsBWrZyWhy7qusE1FxRQVMvFgzbEZiwGIlkyx9Zrcd+QgVMXx8pJr1ZRpNSVGzR17CqrMuTqgyiAiZo3PDSpLscuoSF3A2oxtHFZXHK40yWdBE1JGOyVUqVooyMYZhmRZ5walBWUIR0KzC+viZKg1akjoyqA8TJqMVif5UcSERnPzDqxXnjpHQj1j4T1h3KCdmtSP6GlzYr8fIqqW66pfCtU1rCR8NCmwE4NNAwZDwNGPQBlsqGJR7xAb51Rc6ULvJVTYiuYujAHlA3ZnUsxAEBe3EmqdFPiUcaWD0H2HSlFYAz6SRi/GM7o08VafNPZaKHRpFNtzcfrL+OO1OKA6I/lPWkKZh+NOBhtGdDtayUBOT6utUUEu57AGgg8MaYUzDZGBGErhH6NYkk9qaWKcJa8HaCoJ9PURKk2XjzG+g1qLDgy5frfrQPYZFx2L1SUqNGPsoB+2KFAqTXGlHJXbEfRlQ4P10vCmDNoKelc1FXnZU7spBsnqG9Ma71dyjXIRZSuqaUNuNo5+iJkESFj15jhGBh05JkKIgiJZLQG0SkmI+iDmQdW8hZCZ5hmgiFYR1Uos4kEGEc6QnGG9M6UbE0f9Eyhz24vfieGMOGyeGM185BOe7OdPsT5WJOi5LuiTYr3gBS/gFa94Ba9//et53etexytf+UouXLjwlI+/Hu05PDx8Vu91cHCw/fczNWi4fh0fH/Pd3/3dvPWtb+XcuXPP6rnf+I3fyI//+I/z+7//+zz00EP84R/+IYvFghtuuIEv/dIvfdbb8vGsvxr3uSc7f6+vhJ7uBHwWJ/W5yZrnzQPBDNzra5YJTFvR3XcJKkcYI887+5k0egbGknKCwRPbYz7I78I4wPERsW8kVydEQnG2ylHE9BhT8goyY/JUy8htfhduuA1dDVj3Dqou46c95saJUL7WK/TeBDVNqLmG3UwawOwVzQbg1wPOGdJixMwa7N5MUJJ+FGtvpThbHXHuhkzfH3BXN6WjQefM+YdWuJLzcvctLUMlBWgExpSxIfP8Dx9BzEXPEcVFLme81pgUsdMa2gqjFfaxR7n1TI250HA0b1m8e0GjDGHwaJMwTY1taowCrMEbYNljQ8IQIUTJaQBsFuthFTM4g2lrlDGkQQJoUxTqilJKUKBCXUgocegCyTwaR1zlyo2ihF9m5HWRqTtWEcOaB4/+BICGObfsfS5KaRIC+MUMq/ExHlm9B+0sdm8qOhcjtL/YjdSzBl074qLDH3ckH8RYYTVwbXkXh929pJy5eefTOd98arGAlcYppcz5yYs5O5ObuN42Y/k6VCpy77X/imcs1LdCzTGa+26eEIxiFls+tf9sVN2WQExg0RFHjysNgK4tDEVwr+W2qjNiQCEbI+5YRvZtLmgPWm8RHtE8ySS83IvLTVmCSCkalJzZogKbbKG4DTc9+ZnavodQHqc3n2blY7Hq3uT8SJEneSOc6FxQXLML/nD3/VAQF8naUYKeZiRINhlylLR6Nla+m3NUiS5uA5lIcKLZmomcv9gzXxc6435CWUje89j6/az7QzSGz1BfQFPN6PLIW06/lxU9VZt5wZWIjmp7SUobh7yC/PS14f4b53giZ7o5Lzt+KTFm+nCZh5fvJsfEbnOGG3c/HZTiqLuPx47fT4oypVZGE3rPIt3HcbyHDNwYX8JL4svQ1vBYfA/Hdk28shD62/6EOHqumvuIMaB1JrYekx0qiNA8xoAeImenfwPtDaNZ8aezd7IOHYpEDiO5jTLapkEZS5sr7GVHO23YPVvxjZ/pZXpdGk2lFetoeWi1I99TP+L7EaMnnJ17zk96csgYrdBBUlw3qJUgQ4LcxBB5MDqcabBtxbjoUNnJMCIYMYUox5FqHNooXnBmQV2VwlaJ+6CLnv/ni2WE3y3hrosVyk1JKRP7XoKIVwPeR9y0wThDWPbkIaB3Wuh9aXIEndRKUS8PeN4NAeUMF48d667GNhVZoA8ZNlWG5CNJidbGNBW6nGe6dqIzWvVyvikIqx4zrTFFUplQQitOGTNvSUbL52lraCriohM6dQqojcNpbYWinLNkbxmNiZE8ZKgMKWb8fQ+R9nZpbzhNUopmd4JxBn+4JsaErR3Rl2mJUpicxSzAWSII1bwfuZoe5Eg9TDABphm03Q4ccpRsKRrJMaKysl+AECOPHL1bGg+Q645ROO244+FOPnuGS/kAv+7JTYXTGuOMhHlT7K3NDrec/ny5Rk0aGZ8se3yMqMrhnJVrXFuRJl7QbyfW4YfHH+Yw3C/RAo2jPn1Cv9HObF0zN9bnuQyNVHEzDD6gldpqNtOmXrnueiXW8DU3tZ+J0TVjWnP/8r/Jtam2mFlNvT/lKCnecd/xFsV+XG3zuFXOL7W5wqiP+N1TPPHJH/ZsG5snq7U2n/lZvtRz6xO3XvWqV/HGN76R9XrNa17zGv7Vv/pXT/nY22+/ffvvD37wg3zu537uM36fD37wg0/6Ok9c9957L8973vMAODo64n3vex8/9mM/xu/8zu/w/ve/n6//+q/nd3/3d58x8gTwkpe8hM/8zM/kXe96F2984xv5/d//fQC+/uu/Xlx+/wrXx+8+92zXM9lPpTh76uc++dmupKIjrQe0M2Ld6gO5clIUKyka8yjaGh2Lm4yx24m7Wi0FPSoUI0JE5ZPcCLMJb0MKLrdeoMJIQugV9bRGOUN1YY/6/J7kf9x+Drs3I6eEqS1mp8WemRO7AVLG7U9RjSsFuFCLcrnYKx9F0FpSz+OqJyehcKQQQGVCiIw549cd/aMPEA6v4q9eJl58BHP1MurogDT0QjFRitzWshdTBlfE7mNxe8tIVspDVwjHa8LBAr0amdiKnBOjgjh4VmMvTnw5o5cipHe7U/S8hTM7sD8ntTUpK5J14Ax6WkueyuBJXSAPUb6fJLbWeSN2LdknSmmhoAAOBWPc0m3EvaiEZSZxq8uF909KhOLsZYwV5zQ2RX+WpstH0qKje/SA7p6LdHc9yvDYAXn09A9fobv3McLgaW48hbvlDOqGPdoX3YQ7NeP67BQRg2uGGOQ2VqhCdqMN0xIuqK1DWYs1FqXFPSml4rCVwVS2FE9KDBPaCppawmuvLeFwBSXENpcgW0b5vNlIEYZWJTywnCpaCyXvOt3Oxt6aMi01G/pcOea2hgalyaFodCCXYFtBNTZC+e3rySO2iJ3WGm0NprLYtio6jbhNbd+Ipjf23NIEnbj4JXVyJ84giE9BoCivn1LeGknkTKFECWUwl+NCdoMq4cplNxSUi2LcEcdACGJqkYtOKkehb6acJIBxs8+0wlgj4bxWgmzTphlTimQU2hiqphZCTnmtFKKE3tZOkDo2crhMLo2baSpM0VCwaSKUwmrR8WzQr5AyfgxCh0yJMIyiddGK5twuZm+ydQIjZSnS1mvU4gi1OiL5NRkvrmW60PrqGlyFqmuIAfpeAmCNxk4qbC0DCV07lLPi1Hi4FlfKYp6QMyc5OkrOY1VbaQi6gXDcMR6shM5WGuemrSXvp3yJcdkTl4M0GPMWPanRTSWuk2MkFWMESgORYxK68xgkr6cgy37RE0cZZmA1am+C22khinZRN45wvCYdrnGVLXkyeksrzWRBJbqR3HlxvLsO7UzFPEMpRdVW1JMaU1uoLbEfGa8tWC+WYjix7MlB8pRUyujGoeetHO+1k6Z9DLjKiWnHpinYmZA1gvqNcq3PSgk1WGvspMG6koE0EfYDOWPPn0E7K8HiITIcrQmLfnsuNfszcbKzFpzGb9DYEKlq0Zuayopl9aymOT1jcsM+s9vP0952hurGfdy5HapbTmF3W/T5HXLriN7LIGUM0ugbVbRsolNKPkhQtzFYxEXS1pamrahOzVA7E/KkwkwaaW7aCjOfoIwl+0BEEWuHRmOjXMdVU53Q/aY1tA5VW3nvlNA7DdXeRI7FcjxLAHcqf0tzqYoL4+YeYjfH+QZlt0JpVzmjnaHPxRQiSK6SUEQ1dlozu+Mc8zvPMblhH9NUW1T+qXsUdd3f6gk/u/7n6gk//zhXfpI/T/aY59Zf63re857Ht37rtwLwi7/4i09L1/uCL/iC7b/f9ra3PeP3yDnzh3/4hwBcuHCBO++88xk9b3d3ly/4gi/gt37rt/jyL/9ygG3u0LNdG5rcv/7X/3obPvtXTZ2Dv66comd7Xn/E45/qBaTQMk3FNCMTdqOJlwLjmMh1zaK/QktNjpqkNDlEUhokLK5uULN90sXiPjRtSMVBzRWbUF07KQ6vLkljz3j6NMd2l1R11OEId7Si2mkxzhD7kY2jT1z3UvhCmYQmTFNtww+reUueSLMVu1EsRrMEIlKyF9AKM28x6xFrdmnNhHC8xvsOP0SUsSRtGC8+uO1v1GSHen6WmZth6ikhJ8ZwSEZR7c8wZ3ZYP3gJM22ozu3hj9aESyuWg8MMlosPXibQUhfee64dqrJMzBQVMyFFzE67bTa7gwU6ZXSxEte5OEFVrQSIrgdM0fugFdqXtPHN16o4oUyVfaecOG6pkEpEkSrW2KrogNgW+ShJYtc5A4Hj/jGMNvggmTIpZfp4tG0gklH0tdjA2n6gOhKLVktLtVaYLpHciFc9ozXY87vY/Rn+6oIhHnO8fkS+3xgZcEUv0tKoKVZr1vEArwLEjNVzamnvaKvTaDVBKeijJ6ZEW9dcSLt4rzGDQvcDOmu8SVysl5gsjmEbG+O8EegD19SKVFzFrg85fdwqzY3KbBulzX4XlpFMj7dD0VKobvQwCrb6Jcrjs+I6jt7mNDzRKamQmC08YfDUXWLZytQnq+teI0tDlXMWak+UUMSM5JGIfmXTr8tn1taIS2JKW+OCjUZqcyzogiZsAmkViqbaZ1rJz3vW+G6UwUL00jTlTBcPGNMKT2DqBnT2UoSlLMe5SizHy5DLdFkpQkxEF7jQ7aK0YtIb+uESOSZW40Gh3ybGfsnKXpbBQ1yiAFuQuxSzoACIU58ymsia4/ESRkFkLGir2GbHEInFBUxXDtVYfD/ix4CbNvjDFfiemGGpr6AVjGnNtE/YJFTU8sWj+hHhua6ZzPfZv31KM080qZcmYChUrlUvNCllQSmGxZq20swauZ5plVgzQbeG0IsYP/SjnKMxbSfPGUHx0xAK+oAYPgD29ByAsFiTRo9paxkcxcQqOEJ2qE5oohQrcGIiDp7oqkIJjqjK4tcrcqGQKWMY4ogxmjx43Okd0Zv1XvQxRouOzGiybbh62FPttMS6hiGTQkAbTVj2os8qRg+xF8OFHCO2raWhKCjitM3EscNMW7rBEDLopiINnmba0IfAfCr05RwyfVSMxZiGGDGzZqtxQWvCMGIqR3e8Yjqr2ZmDOdMSh8TxqPEhMNltqetE1OK6OnSU4Ymm3p2QYsLgsWHNbH+K1oI4m2lNigO60fgQuRoqFkmOxxuqxMxlcqs5PlD4IMHceZQwalNZ2J0wHK5QhysmqcNoYRbgDGZ3iprNWC4hLAaiVid0wNqJtgcZbOSim0o6shouklIgR4SfCmRGVITsDSRBmHTtyvaXvK5dTd1MpZGxZksdZnONNNKIG+cgFHaCl+t0LhTIjaY4xYS1DuqKaHo5Rqwhkkk5ssoHmLCEaebMfotrDRIUUi6uIXK7dY+7JndXjgm7E64UPWBmc8/7iAv24/73RDDnmTrSPRF3evrHblw6n8OHPlnWD/3QD/H617+evu/50R/9Ub7u677uSR/34he/mBe/+MX82Z/9GW9+85v52Z/92WdkuPCWt7yF+++/H5B8o2e7tNb80i/9Ei984Qvpuo5XvepVfO3Xfi3OuY/+5LK+7uu+ju/93u/dbsfLX/5yXvaylz3rbfl41ydfeOsThyGbK8D1A5SnmV6I3WzinDsmTyQjoN+vGC/1oOHi+s/kJhwiSWlUTMQcCXuQz14gWIc+XEvBbi3u9A7+2mK7aWGxlgnd3hRWPbmKPGbuJwfFmXnF+RtOkbzoe/zxmnBtITa6IaLaSrjlPqAre5Kx4xPjoqPZm0KGcdkTfKCZtxhr8ONINWmkeHEGe3pOvDygz+9TT8QZyTAyKgW7p1DdNUEgTAXnbyabGefPfzoNFYNfcv/Bf5WCOGfCpQOqWYudNvTXlvhrC6Jy3HfcUO+fJl3Yw9ZLETxPGwJS6KpukH0yjKSrx/gQcVrTlIlrdpKCLrTFQCoW10lrshPEztQ1upqi20pQNGtIIIYR/UgquSPheA2+FFSxTEmNOCTp4qyWjUIrydhJScwPfAo8NLwXU4oJXQpPNnqhlFjsOh65bU7OmdOPLTm38qAUO80NnJu9iGw0D68+SMwHkMQFUM9bzKThsUf+Ah2TmFuAFGMpc2Hvc9DT02SruTQ8xKjXxD5yq3452iuytty483L64IkhcLVbcGG+jzWGO47E1tqUYzmT6U3Pn+z8GaJIgo2hAZmThkSLOQGwRUg2wasbqlwq6MkGmbm+6REeffl3zie5VZsGdaNf2uYV5e1rb6yulRKDicIpIxys0Ps73HT/Aj1Gun7knhfs4K87nTe22TohYYtKbsrbJsjH68wDyuUhi2lGKiYC4swl+0bnQsXL8nhBp6ToMJXj7OSFnLN7qJx44OiP6YaDk8+B5J09fPie7RDi/LUyICmNSwgRcs+DV/87OSexiM6iM2qrfT7f/i2MNqyGyzx4/E4ymbhtIBXL4QpdOCiW5KWpTGlLUYkhbnUpWMO1/DCH6SLaGfS+pa72UCVPRytFtBo3rcVyedlJPooPjLF8/64ip8jF/kPkcSCt19x4nMhDL/suCyKiYkTN91BnzrK3t88Lbx0wZrW1oN5QxjDm5HgBXFWxMw/cPF9j3MjVoeW+q1OwWlCWEKWJymwzjLQx6GlDDhKyvUGP1aQSY4QxSNbaehAqpDUixreGh5czTKpRVpDItJLg7hwTqR/FTGUmjpWERCzUNVVEaAawO60MwwptTltDWnREZ7aNzjo2LPwZ1LVNSHGPbirGgxUohZtackiMRY8UUxZzBi8aH4zG5MwZd8zOjSNhWHP3eoegmi1lmpxpKsON1VXmc0tMmruPalTTkmJiXKxI/SgDnCA5WDkKxXi+P2PSZG6uLpJTotM1q3wa4ywmLri5WpIUXEs1B6upOIPmzHi8JsXEhfnIhXMe13bCqvCRnHrcXKjaKUb+04cT73msgwxf81LFbTsJ33nyqdOsvCAguh8JazE80JVjesM+5oZdntdcwiyXwghwmeZsxueRvzA7RJ+wriGXxl8V9C2GSEKQVqMVnp4HF38qeXObgGZnJXvOB9y8FUOHQaFpsLraUgIpLnOpxC1sc7Fgqw0rFy2ME6ZIiGKWMfaSs6cRBD9GQYu1Ats4YudRzjKsezSRS+v3glLYlefF05GqrjHOUE0kTytkxW3tzrZuSSGSz53mHgP/3767DhHPpcR58mLnyTCkJ1uPb5o+slg6KamevND62K2/n1t/WevGG2/kH/2jf8TP/MzP8PrXv/5paXH/7J/9M77t276N1WrF93//9/Nv/+2/fdrXHoaBV77ylQAYY/ie7/mej2kbb775Zr77u7+bH//xH+fee+/lDW94wxbheibr7NmzfMVXfAX/6T/9J+CvByWCv6ym6ImNzCfqNT/q6+VSYGToR0gONXdU53dodzXhcMVw2Mk0XAkNRjdWLlIzQ2pqqkLBqc/ugioi7L7HJCmq1LInDEEcgqYVOmZSiqis8KueuBgwtSOnJGYJ05b+yjFVzgRnJMSwBM1tdBFpDFsDAW0NzSmh1g2rgbp15EWH90kaMeRCrZ1QeiIwuf084WjN+Mg1UtOQb7pdzNecg6oix0ylQUeZpFujSJUl+oBtK+ykIa56xkWH7TqoHEPI5Eeu0d58Br8ayCnh18OWOohWLPtOsoS0Rlu5gGcrzdCWFn20QuWMBVJBfHRtafZmQvligwydUKnsRpi/oTQUA4bUS5K9spv9KDSJ0Huh71VWPjN5aw1bRnAyJcyZtBqIqx5/sMQv1jKN914MGzIEVVzEjAVjUWRcgGSyfK+DJy96Yuex1pK1BMNSJoveB+qz+9idHbEyVxX0S7Ca4BzDGOn6Aas0CoW1hqpq0Vp465lcMj7y1ikq5bSlrKGuu3luXMfI5AK+bQ0H8oYbe+J6VlokoTqVE2pTLKoiJE656KPK/tqEXW4aC7V9LZmgKhDaDkUfZMpUNovTYn/5CDNtsDbQdQNpu4lqy7HXiN29LhS+LTKliq4J0JVoADd0PWO05JlsULHSCElPV9z2QnEb3DSFvZessXJY5JCIKQpNLkZcW4FHmrxCpdJs0DfJJNHObrVUaE0o5hZGa3HvSrmgXGr7faUUsdaKuUmh/22mw9oYki76LqtLg68l8b6SY5+CMqEUdlKXoNSEv3IkRizzCRlE85KS0HOVxiAIphrFGCKNHtX1sj2zqaDeZUKulRK9X21x+xVWIrfQtVDlQJoapVShyxlscVAzjS4uhuVYqp1QfsOJ7i/GRPZBLNXbmjx6KAL6uOxlu2cNcdlLPkw3FCvtKNS1ss8opjOh9xgd8VcX6Gkt1+aNo13KhBylya8MzbSWI1YpYmVF39bWECLdo1ew+ztbO3G0hiEQU8I0TpzktEapLA5tzgqKEKJokgr6r3PGlN/peSvnmdI0pxV1E7A+0s52Uam+biIAKkUm8xHrEiop/JVAMBpnLc3OrFBaIY+imdlQuwUt1NTTHcmZ8g5ztaGdNUyMo6rlXqiOoJo3OG23TTcKsgZjhP65cXtT5QRX5bjcNA1yzstQZPP4zXXGNpXcy4qFuT9eY09NqXYmuN1K3PqMlu9XWWztaC/sEvqRWJkyfDQSb9GNaCOImDaaPAQiHlVpclTiWGgU4zphrENXBuvs1tAABRi1pZ9vDHm2bYFSIirVcm6nYrmevJyTYsJhcG1N6r38DrY5Ubn35Equb3qMVE0ljqfl/qJqzfJwRdMJK8TeVGqLIOyA0I3CHkmZan+6zco7uTY/WYHzxMbloxdV6kn+p57y90//0+fWJ8/65//8n/OLv/iLrFYrXvOa1zzl477lW76FX/mVX+Ftb3sbv/RLv8Stt97KD/3QDz2pxme9XvO1X/u1fOADHwDgh3/4h3n+85//MW/j933f9/G6172OxWLBa1/7Wr75m7/5WWmCXv/613P58mUAbrvtto95Oz6e9Qlsij4KhPNUq0yst5Obj+Nl195xsFLgdpnNEzaLxed8BvVUkXcn5POO8eqC7mhghcUoReUsOyOEg47Z/pymrkiLDu8DzhjqQS6eyln0uT2hbKx6Ys7gxDI15szQBy5fiTSnJtRTS3vLmeKYo1itFWlImKqFqMirAT2ZgocULU1thTJhxDVItxXxcMVAptqdorRi2WlSJXqgnRsy64cfob7hNGttJYxPZearQDAN2mqiz+gcqRMc9o9SeUg6YPZaVPTYtpGQ18ELfW7Vk1EYNPMIjW2Il5fCsy4Bd1bLDY4xMLNSoOl5S+4G+R4byRJRPqK1IZQMJ1VZtHPMpjVm3oqJwdGK1HviepRcpyiWq7pYUtM47KzFnJqhtcaemknB23vS6ImHS9J6wE5OaDrbHKKiz9loSzbWvWZSo5qK5nnnaXIiq8Q5HfBXjtmLE043u1LQklmGxwghMMQVy/USYy2Vc1SuFhqN71FITlXwHpM93liuXbmfIfUkrajyjGrS0h2ucDGiMbRKikEfAznBar5isD0hb1CTVFAvOf7XzhdL7VIYCjcN4zPTdUChGJ1imJSCvWh1ts3g9adQZquFUIoiMD6hgSlgQ6vT6sSI4Zzfo04WRsXF5ohRhROjhtJU5VQCUrWCXKy9U2K5V6NSxWJYc528iW0Qq0I+70YjVhqiKkB97MUCejbluO+lB9Ripbux5t48xxhd3O4KkKWKjTqCgmmtuTpdE8fLoBUdIxuTBNNWYsfbe5ZzR1QZox2To0GOJRA9iFVkZcAHklIF8ZVzI6SR4/4RlNb04zEgyNJm3whaZclW7LEnU03rAnpSs+4yiw5sZbfTc1c78hgI3Uh1ak6rRiq1IpvM0XrEP/Awaj5j93SFU5Fky3WqfG/3rixjFATx+WcsVhmUbqVxsYZoDHcdKEJINLXhjp1E9h5tAx+U+xKtgVtqjyZz3GceWsuxa61itx5lO03mKE5QSbHuNPF4zWZGrRGnt9QN6HmLWvSkbiCtssQXNOLeZiaV0GIV0HtMKWCVUkzpMVZ+l2KUwNIhshwddn8KKHHtHDwpBGaVmKXkmMgxoAmi9/IBNRXKnTYRfdoS2x26ozX1pCW5mpW30gQV5zvdCoqQvATMKsDttIwHK0I/ii4QRXt6jq4spq05CJm1Fy2NP1I0SwXKMa2h1eJCd8+1TC9JA9xx1qFdIkdFuzdjeXWN7yPdqkX5RNXWMkwyGh1HmsVl6iqAqfjzILfwISouD9Jot9bQGzEWWLeOIxrIsD9R3DBNkGCMjg/3mtzDWW3YGTNxNbI4qzgoqOlhd90tWck1VZnM5ZXnai8/Ojt1okOqrWhFB89wZcGBhcpZVDLM3IhWGaUT83ogZU3QkWWoCRuLc6Nwu62YN1gt+36nJY6B7CPBDYL8hUjV1pjGYRSYaYOpXEGPotQT1zXxMqgpNGulwEpTXy5zcj2N4sCpK9GoZR9PGr+QtiYwqXYSd1GLXtR3A1Whu1ZndqgbzTCMUFXUOzVh9NjakbWiu3RE8om4P+FRpyFFHosnTdEzWTlzcmHj5Lt5NtS459b/uuvs2bN813d9F6997Wu5++67n/JxWmve9KY38aVf+qV88IMf5FWvehW/8zu/w3d+53fyeZ/3eezu7nLx4kXe+ta38lM/9VPcd999gNDXfvAHf/Dj2sZTp07xPd/zPfzoj/4od999N2984xufFeJz+vRpTp8+/XFtw8e7Pv6maHtGXte5PPEMvR45ehIU6aO6VDzDM/5K11Jri796zPOfp5jpAD5wrlrIG7ca5sBpS3cp8xcPZXwQFON5nUU7SzUYODUjrUfJXcgZNW/RlRXjA6PFgrR1WF0L93nZywXbtlwMMzgwnIqJW+Yd2UeWfsKj6xlh0ZEfkXyjeOBRttDnnOHWGzX7eYGJEjaIUkzO7uC7kfXlQ6andriSZqzWFUorbt855HTyuPaQuw9kJ1V7M2477EQQnANmUmN3JgxXDjmu7xFRbGWpqj1BqUpB6I9X5MMVVCKKrpYD5zpL02qOHrtEd74iNhI8mss+0ZWTG5CzxCC259kaGL3YwTaV0Jt25uIat9GrxMT6gw+KaDrGk8Jca8mbyEDJ/1ExMSx7zNWFPM5eF4yrKBoSTby6kOK8CNMBdOWkKSrFqCqC2rEcrxv7bVtZzk1rdO3Yj2c4t/9ClFJc6u7iw9f+mBgj06rFKI3PiSYrySdxGpqZNBnrAVOoaFWKXH3sPRxcq8BY7rjwxUzMnKQiFkWvRrS1LLoVRmt67Xn3zr2s6XFGXPBSFFqR3qA+UChz8rcCkoKmj9zykGT/HO9WPDSVabfKGRLilLU5PwsyIS+xyRLSW6oZIJNVrbaoUC5Ih1aaT13cwik/JxvF77v3MdqliJfVhsq3ydaQJmqDzvQ+8NinnGe8usDnYlKxoe6Vxu36m7tcDzRKwWQ1cvOjPe7UjIsPHLE815AQqpkutrxKl2IhFSZ8mfiKYHr7gqVRVvz57OGtDuV20zELCmqDmdb4y8ckZ3j0xgm9FcTyBX3EFgtekcUIkmWLpklykDKRDM7zyOq9J2gqoCe1iLZrKbYximZ/jqkt83TI6XAIecnB7j5pvicaJx8I3YA2GtdWggiHyNwccG5HC9p09hSp+hRyiNww7Zg4mUDrYusfleZ335O4vFbUOvN5twdOzYzsZWtARRYDvPlDmVUfOT1R/K0bM3WludQH3vgB8GPill34ppfK865Gzf/7wzLJ/5S9wNd82hpS5rCveeBSLd9HaRyyUYKid5L/YytBUXwxBcnlHI6hhDMj+zIOASqHmzfSpIbADfvH1NafGHOkkRjg7qOG4Jpt4KqZN0xU4vl7Bxjtrzv2C4qxHlCxBKAqUJMa9iHsJlArDofA0VEj9X9dbKCLJsWvM2Y5QAa/6EhWQ+Nw2eLO7GAn9abK5sMXFzx8PJ7cmLIMrL7p5StunmYimv/fh+GxpeSAfsYFmDg5R2M/yvCpblk8ehOqndOcPYf3gdF7Tp3TnP3gW3AHiYM+8v9ZFc0cEVg8yU0zABK0+BkXMp97o/z8j+5LvOUuBVbzt+qGz60qAN714YF3j9dt+/bVyj6zhg9d67nnoEcBX3T7LqeLp3jsx/JhDQ9e1NjGoVXi+fM1lZZQ3huqQxKZ0Wi6dUsKSYZVmwFLrYSGHCN+1cs9xIgmLAMqytAsx4TdnUojU1xL1SboO4neFCPH7QY1j76YXRALK8GRS9Mjt528HXCgSuiq1SX6gHItLBlKZJpJzbgcqCcV1ayhO17jmxuw1jHXhtPTQ/prxwyXIro5Q3NmwgMp8lvdeov2P/67erp1Yu7zZL/7hLdFT7woP7c+Kdb3fd/38Qu/8AscHR097eMuXLjA29/+dv7hP/yH/If/8B94xzvewTve8Y4nfWzTNPzAD/wAr3rVqz56Lf4M1itf+Up+/ud/nsPDQ17zmtfwDd/wDTLo/l9k/fVrij6W7+BJTtjtj7TCnZqTx6tQS8GSvN9qLzZanvrMDq3aRY+c8NYBf/lIrJQbJwYHlcUEoYLE47UgHkqjZ604thmZaKVHDyFJUCqjJ3RrwvIYnMF3I74Ta2btDIxBAvuSUOZMkrBSPW/oLx7SlBBYxkA9a8TiOkSwihxkajkuOhqt0U2FntaoIO5Lg4/oURCysB4hiyucnU8KrU32VC6J8uHqMYSEvfEUqq4YNXDQoQehDJgbT0MzolaDuPZlCWhM3pcC1BT6H4ISWAkIVW21dQLjaEn0AY9ChyJWp6AiRss0MEqAZsqSkYMSDYdBivwNpx4vAtaN/TIxisFAzjK5t7YYWcQtUrSxjzZZCmeVckGkFNEP5EUH0wY9O4+pK2KIBJVpmxY/jEUfYAgxEJIEcsasaIxFhaKFikkCNqM4Gvl1h6pq4rqn1xI62Qdx7auso61bKmtZprWEtJYASosU/GwavKJFeRztTSlUPskd2tgdbxqRzXmx0fsIBaagTNedK5t5Yy45MlvXOopJAfIUYZUodDbyWCUNlIZtflFSm5lH3mYk5ZjI3UhYiP0xSpCDLXVMbZ8kNBXYNrKqBOTatiLGCKm4++mNtoXt5z95v3jy+bcbXkIvy3tJIGRBt7Q0xtX+jPHy0dZAIsYEjejD8EGOJVumyGQJHE6Fr1hb1FBsIXIWzZ91ZFcKdWsYy7lZN4761FyK+CSI59itmZ7fx1GhB0ExlNZUsxbjZEiRUiZGj9p3mEpJSOnhiB+FtpdiBJux81aGNqUp3urDNrSzTfjyhvaYShNpDDkV+3WjN8FWxWAhorLeyMSEDqTlGNhQptKgwTSSbUU557QmBSlolRNnxTh4ue4oMLNGmtOcBbkpEKKEzDrJv0lyVGQt26WUPnHnsxmTJuRstscQSkI6pXkS2tkG+VRaU+1YiHLNpmiXslK4vSlpDOigMcbg1z39ODI7vStht6Mg5WZngl9J8KatLGbeYCa1UO4+4k5UTsN88u9c6GlPfktT+MtHxJXGTqd0lxa4vTnK1Bw9do0H73qYW1/2PKCmPr2DIcnw6Lrb4JO98vU1bVj2jMeZatbI/nRs0ehnUgxtUPcyA2GT9xN7j1+Jw56u3HXntjS7ypVmXElDbIwmrmRguQlY1saQstDYQj9irMFNW0HgC/3Gr3qx4K4dKPC9Jx+usbNadEHWkIJ8p9qeZC9t9ILKFsRWcUIbzAXlRiieWguKYxpXaKMKvYmHitLAjUGOIessYQgkBeurC9H2KQmb3ez5Zn9GVVu6biLXqfzELuOZ4j3qKR/zl6IBeq4Z+qRc+/v7vPKVr+SHf/iHn9Fjf/3Xf53//t//O7/6q7/Kf/kv/4WHHnqIxWLBqVOnuPPOO/mKr/gKvvmbv5lbbrnlE7aNe3t7vPKVr+RVr3oVH/rQh/j3//7fP6UxxCfj+vibor8O3PZJTtgMzCrP6SYRu4HuODDmCNqgbA21E9HqujzYGiZpxaQ2BB9YxAlh2ZdUb7MtIPNqEP1KZcldBGfRjaRY66YiDyPh2hJdW9SsIfeeNAZ8YzlijrIVY1uRlwkdkrxOzvgkSdqmcaAUR5dXMGpCmLDuhf5GTJANNC2rK8cs/YrVUmgcV2ee2bzGGPv/Z+9PniXL8vtO7HOmO7n7G2PIiBwrs6owFQErAiDUJJsUh1Zr0drIZCZt1IaFFvonAMPfIdNCpt5oI1m3SU2ZiWQ3KQEUmw1QIEGiUEPOkTG+eINPdziTFr/j/l5kRmZlTaDUiAMr5Hvx3K9fv/eec37Dd2B8siRns69u6iiJk/Ke3Dm01tSPVtS3DmUB77Sc49NLgb8czzHGUD1Z4y5G1BC4jAHTazg9JV2tCEU9T7sK6qIGV6BLphK5aRqHbirBsjtL//C5YP+ngNEKFwJqMRNSfCwiF4UIL1LSEvaj5frn0gpY6DsobcgaluEhyY8ka3BKS5dKFUUzSvKzh81dV+ytNfjJo3KicnM6fYx2lu20ZDs9F7iXj6QOCWaNIcRInzxd0gSrCYXEb9HYbaDzh1jTgYJL9YSAl2tiFKoTKMjF9jNUrqhqJ5LBxnA2bFkeOLq6Y0gTQSeU0gKb2ynLKb3fB0VqHoQ4RIGsCWTu4qRGK822kcBsZ8SYrsvk152hHSQkXwdBeZeE7uTQd2OXRGVIOvPQPWdperIGbyIqFf5RFpU4rfR1ElYKEAokyCbjTudMlxtJim4GYIX7tfMjsjHRXo0YxBjz4s0F09Mr+q50wZDChwQwiuN0wLGfkWJiCJcMaS1kd+Q7amvozAnOiPHx1j/DTz3Kit+YO+kIBTaK1WgFJ30i5oBKiqOTd6mCIqbAVf8Q5bQE6eVaaquhs7iqErn+DASRmddtJYHXJmIrKzQtH0Fr/HagD5rZnTdZacN2FFlm6yThmh4+J1jD4o1bOGuo0NRdA0yYynJ0bHAzCewepJapz6g+8+2TzKzRL3TjklL8+QV067JWBkk6Y8r82mkixEwVRoxqSNuRVll+47Yi9JGjSpJO4ywHjeI33zSkELnbZVIQgQtdlNh2CY7AmARemSoryc8UiGRiP5JShZs1smY7j0tjOZ8BfaBQOpHUyI7PYk0uyp8Vf/Fc0Q8RrONpPxFTkeQoz5RRidUgz15j4JdPMypFNlPmh5eGnEAyRsgUvyGTyVmjoi1rU8ICmwdnuHmDyqCdJXkxvNXzBtvVnI+R5dW0y7z2+9LG7xRPXtysfnCueN5LT2frX7KD5UxaD/gA7Z0Frx31rB894uKq5/bbNSd3B3xY8r0knfnlTb7MS/bD3XzZ/W5mNdp5xqstt9uO796TTFf1kT8bpDt0dgPSdWvmmFdFDTFnnp315Ji51bX71cWME/1yI0mG0aSpoCvK/lXNnEjXa0vwidVQkZwlTprjw0xOIrvi/SCGxhhWU4UfJpyOnHZFAW7yxCZiDhwxjcI9yjC1huUmXPOhtJZuslKkLJyiNAYxtM6iZrlHIJe1EaUwRpNU3hdkdspzaEUaI7q22Loi+0BdhE5AOori36cJY6A7naOMpg+RP30sdyCNmclP5ATPv+Ke/fjxlxdsXadfv4Au1KvxhfG7v/u7/O7v/u7Xeu3v//7v8/u///tf+9i//du/zW//9m//lGcm4w/+4A/4gz/4g6/9+t/7vd/j937v9176t5cq437N8Yd/+Ic/9Xu/7vgP3yn6uuOrymFlnDQDry8ywU18HOZsUsv0+ELM3aaAPTgg+4g56NAx8U79kApPsoYfPAGyRi9aki9EXxSqlWA2k0n9hOlq0uil0gnkdcDeOZTFeJjEZFBr+ph4cGExLIjbAWUyRMj9KEaBRktyUbwkroJjOSh0N4fLInc6TOILM3pyrMRxvvB1znvN+dOAqnshpjpLCgGnQTc11axBWYNZtFg0t55uMI96ApnnrscPI1pp7EFD7EfUEFm8f4XVik1InH3jCHU0J217lLO4O0fi/m0NtPW1T01KMEyC2V9uiY/O92psCrBTInvxDQKwwwRtXXyR2MPnJI4u/B8rAbqKCZ0Vt9pvU+mWoAKb6YwUJlwS09NMgXupApko6nQg1UqlxUcm5VIdnAK1XnB3/h0whmX6iGE8A0q3onQtKEH63DVM4yTVyhSJlZynM5qTxTeY1/dJMbI6+yPGfCGV7phQlUZZzeXwPj4lzKTJtWVabjmftjx9/R6jSnRVjTYGZxxJq2tl65zI+do4df/ol9JwTomhNjy8373Q+RH1shIUI52VXbcg7Uq8+1cX/4wMOce9WMEuwNx1b1JOfK/7TKqvqMJH0iijxCi2cInkfu5kvneQNc32o2e079ymffOU6ckVefTSbdydRWavJDfvI288GVBjYPOtW3y6UETdStdWIQmXLxXdDG8MJ/zK+DZpCjztv8fz9RPpBqSMaWvQgde7u8zr11CV4dPLK9Z+BSpKoGRE4EAfNPsg4H60hKtIYxtev/0bON2Q8sRw9s8IYdirG5KRqnNSMIlHi+5KASYVKFTtcFZU9WzjCJMXgRNnCe6QT89HtDHE0RPOnws8x8o9M8D47IrUTyLNf3tXdYdbauS0TWRr+S/+LXxwFnGV5c5vwLxR5BTJIQOWkDL/9P0ba6eSTtVBlfnf/pairRQgIi6+DyxaxX/2S4oUDP1qwNZzSJnbLvKfvacgUhS5Mq6tiEsRJiDvkltIU4S6VPhzhiJkoYvBZ5o82hhOZhMHZismpQqm0iXQxuy9YxQKZS0hK/7Zx4qzfrdtbW6s/qWCcONZOnKR9440tTOs+sw/el8TPr8f5+tCwesHjr9xt0NbQ/QBE5z446QsYiGlE7ebHw+uen70vL8xOXfH5Hpty9dz6V98ypeONEVU7ajuHqKrmqoxvHn4Z9BNRFPx/uUJMf+IVYz8N8NWvLi+/HAvOx3xnGprVIZ34sA3v90C8N9+FPjHl+ELx3j7qOHtIxGv8OuBhyxIY+BeZXjjTk3ygXC1JWtNmAKhGPXGEJidLuSZaA3aWnKciGgermeErNFp4tt3LrEGEbBRsl6vtnC11oSU6WzkteZKBCwODeNqS1JKeEVNRfaeK3fI2bkUYUwtcLiUEjhHCvIsqeJDZbTsEbbAucPopUPvg2wbSpGDQIjDGMRMtuQEal+UUpDEcyykiCZTn86pFq2su0W9cDXCf/MBpKzK+0auW5dyhyQ4zLvHjxeV4r5OIvLTJiw//n3qJT+9Gq/GX4Xxl5MU3SxX3fz9Zzle/uI/7Qp22hrC5YZolPg8bKe9f4nuatJmJI8DdAPmsCJHha4tGnvdYegnorOYJH4c5nDOzlsneS8V35TEPC5E4tBj2lr4RWQx2HOGuB0KXEP8KeIYCFlI4WndY48XxOUGe7IgnK8IZ1foyqHvHmKO59jdJlz4PNEL8dQ0VYG0KAnSKntd3b9RiVdKoYJs6mxHxgdPmU41urb4YSQPg3Ae1r7I4QoEgphJyy32YCb8oCDQpDx58sUKnBMY2XILU7iWgTbiz0QSuALFDyX5gNIavx7QPmKcJhlL6qdC/Bf/oVw7VJAESu2gPwUCp1IWmCASZIiCoKiLhRCpbYWy19VeVbo9IAFmUnpv0KhLsqDqirgVY18oXYjJ7xWQyFnU+FKgqVt05TBaY5sKPW9QUcGUqLXBT9J10UqJ+3xboUyFn0ZU7RiyxzYVi0rzQRqx8466aqWaudt4C4doT/SF/T1N5ZrI37QovJWtVBec+16wQO/INjcqM4LfeaFRo3cV1vL5WWtUSiQlyaZWilgS4J2EvCpwPa2swNxCgZztkpbCVxJYXsKeCPY/XGykGyfNNAlCdnAuY/bmsVpraCsR4Ji0KGHtpv1OwtsaMezNkGIJEJ14j+h5g7GibKVQqNoKz60yqNahq0rEAoy5Ts6NFrnoWSOFje2IdbU42vsIJmN8JG1GdONQlRblsR2HRiuB76REWg2SxAGpn5hGj5s3opBeOtFZK6ZnS8y8ERPJMaC7Cl0Z4hBQTU3abpnOLzBdhz09IKuA70eSj5I4lARJW4Oxin0TLoufFcbAlMv11S/IsYu+sHAnbnYFTSkopBBJIVI5J0WZXIoMtSWrhCLjnMhZo7VIk3sxI05Wo7IhbSdSiLK+LFrxMfIFmjR4uVfO4A7mcl4IcV7WceGFhUFk611TkbURuFy+8QCXkUunZdctUFB4TLJsC1RyN8duTqsy71XpLNaWql7INYxpf+12/lHl1K5rC1wfi+tDv/ja/Tleb12f38KUVthFi1EtKel9gCyS0Fyf+41jfeEa7L7/589h9/ryJl1ZposB09Zy/750yPwNy564GdklnSoaSR6KNPa0GWG1EaPariX6KPLoTpJ9349YFQX1oFWR5DaEyZNIVEW8Z3WxRs8OcY3DJHCuwKuHCWpHfSCSiGEKwg9TiugDdTeXPaZ0d5wTlVAVU5n3ZQ83xcQ5lf1IibqlKnzN7HSxMSidIx/FA8losfAoXMUdLFXHjOtqmtPF5+68+vxVZAfZvb4b13dwvzzfeKv6WgnPzafpJxmvEp1X49X4svHzT4p+1sTnZe9/GRbgJW/zV5YpaeJmICdDjmJId9B5bAootylB84ieWbbda6yfXZHbhoTee7GQMqprxBujn0SAwAfyJGRfO2+J5ytUV0slXhfeghFicB4mGANZa+zJQtTdjufCx/El/vCB2A9Ud46ItcDzUoiyOfcj+fka7jk6r7D78qYGXYGFrdNEo/a8m93lmW2LtLGCzUzw+0nDqoO46pmOHC6OpF0hN0MeJ/SiZTUN5DETZpVUaDOkJxfiF2LEuBZnYRjJuSfHSNa6OKlLZ0WCVjH1i4W7oJ2RzwCBKU3FdNKY4skiFdkQA8ZUEsQOft8luRofYHxFJsn/xYQyjuP2LTQKHyeW4ydSqVepdIgUGsfxwbskHwQON03oxqCN5TI/JI4T3g1UXYfSijEuOR8+wufM4C+kAkrioHmNyh2SMlx0a67cFpWh5zF1tQWXiUPATNJFQitUVxG1RodISIlZVXHi72FcxRAnztoto0EI50aTjKKm4q3lMQbNpAOftGck9WKgk0t3Z5co7tTfdjaueyXHncCEuq5A7jozcJ077zZsbQpktPB9dt2lLE+ddJp21WnJwtghhpTR14FXISrnLDDA5v4J9cmc1Q8fkTeFwF26BfuhlXDz0Ixd5vy+prp9yPT4gpNnQuhWRfo4e1GTUy4KSX864zwlbFcx6gF3a0HMCeMk4c4xsgxP8WlLHjJTWKOsGIcqbVBNhsFz547BOaken6+k+5m04XJ6gMYSt1tCYzC2Q0XPYVsU0frE+dqCs/g0YLta1Bh9QDsx8czWoNuaWAxGbVsxrHqYIu6oY3p6hjtaoOuO7YMnIvuuNfiAPTzEnCzIGq56Q2zmwqnyGTYJVTludwZ7V2M0NO0IJuOaiu/ez6wngAJHzQofM392pvBJMQX47x8K2R/KMxMVnY1853Yx+VUlaXW2wHM1ysCF1/zFJxGlE0YZahPRCtom0eoBfCJZL8Uam0l4lJX1QKlA1B7TVHw2Gn7w8MY6nqQLqq0mZwsB3nMjszDgx8BfO5gxnDbEDP/mCYy7BkfhjdUWfv2u5HtawR8/FEjucrqxbeQXE5XdWE+RH+46P19jXA7X3ZWv2u5+7FYYE1SKpBUfXQxsg6axmXcOM8Yo8jBy2vSkrDDqRcL9C9vkS3hBN7fOpxv4lw8gJ8XJBN/s/BeSotszx1EjxcFZjExnKzG/7WqCF3hwynnPtRvXA3q9ERi4tQLbbSpSylhjhK+jFNVBix8TJ+1AahT1omLWzEUO2zqePJzQ1Sk6Gk7shhwiFYVHmjNDn1g9DejDGSlaUnSomNl4u4cTN2rk8EBDzMQQMAvL5NdUXSP8vJS4vMyMwcgaVYpnGThoJhothrfrPGOKClO7vedg9p48BpJRaJ+gMugMUWs+OBeD5JtJyhDSdaK8S7w/d79+dlL7T9spejVejVfjy8ZfLnzux83fr8IDfI3X+OeO8coSR02uJogjOSZO7vdUmyusBz2bkSupLv/wsznjNCOvMtlEWfzGIPCVKRQDbRFBSKse+gl1PBeMPBkuN6SUsPdOoLIC90L8W3BiUJi2Qg5l69BtJdK/26IU1TVM5yvs4QyMYVIaaxW0GjVvIGXmm0TbX39pgZvB6BTRqBcWVpUyh8uI9ZmkFdtGEbYDaMXzKuGbIKIEqpHOSYzk5YacE6NShNsNuZ8ElLYdJDmsHPp4sTeajNsBpiDEaWNEznQqHYSdt40qnQOQLoNxRe60JHBaQYI0TkV5LhFjlKp8SiQvssopCFb8vH9fEkpnyUqqy1bX3Jn/MtY4xnHJZnxIipGQMtqaIhXccqf5NqqWgCHVEaM1V/4JH63+NU4p1CCV8mw16/CcS39OsgadkkhwK8u8ucfp4puonHly8D6ftU+kq5LOIT9HKcU3lgOztSQQ+riju3vM9rPnRKepXIfShpP6HbJpWVhw7s+ZEM3bHCM6KlyyfKd/hzo7lmrDp81zdvCK3QTaVRv3CU35715N7uYUySIskUvSrriR9FA4XKrAjXZdOXhhM98V5XOpnu6DrB1/SGUR09DqxY6EEuiTbhzTxUbMe62WRAYksC88JFUqsUophtbwWWuoX2s5mTve+N5z6QqtphsBWSLhSwL6hIvFEmtrsoq4rkWHSOwn8bFSkbX/jCsQMnat0UmhUcIN3I40xzPuHK6w4xqP5yodE60hW8WyeSRw0MpTqw5dO5yJvHN0gSazerzmonfknGiO5tjDTjqiqy2hmKnaxu29bagdYTviaoue1fQfPsBfXJGiQs8zar7AHUn3Uxst3ZVaRB6WQ2bVl/sXswiwTIGTsedW4zDGUvsIjULHxH/0mnTgKBDJFCIDlh9cwtgnhgj/7Udyg1MQSFCMitva8+1ZpO4q6bpYkR7nRiD5ZKX4xx8Ib+MbJ4a/fleem05P3F306J2IAqI+Z4q/0m4TyG1CVYF/+SPLv3vCnv8nHUOFNrLYGWV557tHdE1kWvX8lt5gZ5Hoav7iYaYfkQJOgS01Bv7e25laZy4mzf/uTzJTvNF05XOB6Y2F9WqM/NmTzf6FX1nf2x3wxvqbS0f1x43da3ZvTVOAmSP4zPee9SxHmFXwd96SwpUmcbteC/xN3UBFfMlxv2w8WMKnS8gRfutA8969L26m9w8q3jtuRGGviKPsuJ+kxDT4vWBRihFVCmqC1BTlhspqslEop6GyuGLOrVXi7rwvXJ2BOEi3aQqGM39I3CZmVeSt+Tmm02SjiSkz9BOjsnw2HqDPFDEkVNWIobIC1wo37GhhuF0vMUoXD66ROAWMla6n94FeHzCwmxNZ1ijgtZNMl3tigo9WLb6yMndK5zuVzmqKItRglIjqjBP82fOBqL/srrzs/ux84naKnT/JyFz3kV4lRK/Gq/HzHj9zUnQdhJWfvmqe3txlfpKO0o99zfVWt4NkZLJ0XqIoB1lroB/J65GUE9S1JCuIypXpGuHrWFmMza0D4uVGKv7rAbXqpfwI5EF4AToKfM5frDGLtjiqR9TRnHx2heoacu6haqSyFpN4GymIKWLbSiAmk8cuOrr7x+TzFWbeipeHD6SpIm8TataUAFqI7XhFduVCxkQavVSuLgfyeiRXltFHhvVagoamlta/D6RhRFsrkLo37kiAqzW5n6CtxJk9UxzjB9JqI0mcFcnouJhJAjgF4V9NXngcZHBO7kUM7GAIeZwAUZDKQV63UwHLRQbaWLOXRDVAQsQGFFL1yylJYL8L6tWOI4N0LbQpQVgqMKZ9ZL/v4GmtydYSPRK07bDsJdhehYG6aXFaSyVRi5iAtkbk2XempmVjTFnMcFUsxpqHM7LTdK+fMj48J11sUUZRH80IjSEnS6Mck45y7laLD0bpBKlUxCtSRNkiI6uufWiVks10r/CluIarlQhLjiWJStZqH0DtzC9TaRHpnQSuKfC0zD5JUuk6WFIIfE4bgbrJwXLpFF37QO0LBdqyUxZMg2d8vpYkugQWylkRIlCqKNoVDxEQsY0y33PO4Az2sMPUjvD4Eh/lHjIXfzHnDMbaAmkNhBCxgNESrCsUuqvEDLXwfKwrVeJ+EhVIo0k+MDy7ouvkcbKHM5RrXgx4dYU/X5Eu16gDhzrVIj732jFtdSidZs3+3mhj0LNWigRIgu9mDUop+sEzPV+Kf0rVYO/U2KNFqUxHgX9OsSibFUPYUSSmwyDnTYKcE2HwqItLfEqErmGwmq49kG5pET+IwyRcN8EaQrb7dTUVaX5AVCBDRM2vjWQBgf8iam3ownOLOyGTInvvoyQ9NSgvXXKUCBSgC9RwVzH3AZT8rpSS66akUy+S/4lsriFku1HNG1JtJYnYBbSVkuPuJglyTG1ubBqlOHBzt9jNlS+OPX6JvcDJy8aX4eU+9xlfcvTrF2X2PDFVoIuFarIftnY8+eixrOMntwH90uO/DFzx0nNQFNjntYnz7nPTGPBXW8J2JPooioHl+VPbHr1colIiNg2pFUuK6AQauXv2Q0rMjucCYx8H4ughBxFcKGbKKWVM2U/TGIrip2IMkc1moO0qqrpFKUWrFMFX0Msav1P7TCAcIlPmyBQwndkLf6QglgthEHiGqy2ql3UwezERJybxBXQGrStZS0eHtQIZ3xUzjLMEH0g5UxXoag4is6+N7Ot5By/8ig7QzubgC8/C51/3QsJ0M1hSP/a9r8ar8Wr89ONnToryS376iQ+wL539tGchb/xB8JyFgFJw/Noc64V3c4VntUqo9gBta8G9rzwxC25YlWo9PqJyKcJebYj9JJLQRqMPOnFBV4ipqJkTV1uwoho1PbvCNBUsOqmiDRN5mDAHM+GLpCyQupjIm63E8kcLgaOUhdJ1NXHywmko1fPl1YbNGNCuyGw/vYCU2G4r8nEn4g4pF2w0XCSDUhM5acImSsCbMmrdkwFzNEOdHojj/CSQwLwZBHt9MJPAe7UlhSQBWEKC3xRhV2GPo1T7jN53Gvb3IYnB3t58tMC7Fs1r1GpGqhVX2wfEtEEZzVH3BpVuUVpxMT4gxv6av6A1MUXZQJHAMhuLUpnoBy42PxJ+f0qcdu9i2oZhc8WV/4wEBO15PrxPzJlGdxw2r5eOikI7h7GWGLx0OLLi4OBAglktJqAhiqx3H894bjO2qqnHNXfXw943wx40hL7HVY6cI3bR8jQMrPKIujfj3e0dZrklNC2T27I9e4JXiZSmPURtp+GfVOR8+z42wNYG8kkSHkFRc4Pi8UMuvjwFQlcSRbVLBtS16/y++5N2sMKSXO2Oc2PzFb6SvqZs7M5PcYNorPeY+mSEr0ZKJVgWTo1WSqTrgcoajp+PhPMBnzMXdzvpXKmSYBbvmVwUB5spcho06tGG2zZzd7YlToHju4pxNVK1FT5MtAeddCZjT0yJpANLUzMkUDFTzTvh3GhFWPVMF2uBh9VOnttO+EJxDChl+Df9jNgnXFtzVP6Wb6xP/nJDOFthugrsjLNepKFDVnv4qDTiEqGfyJPHWCvrikLERtYDpnHYWY1xpsjKC29kVkU6dYVuLaveMCpR2wvrQXzHKEmAMTAr8uBFpAUraolJwbnviP0MbTUnzYCaBlGbqxxJJZxR/I/uJ8ZRTDLjJMmMtkYCX2Axt1SGUtGX+3NtXirP4mmT+Zv3ItZZjueRO7XAaS8n+N5jQGVsK12uFxb2DMlTihuJp5siZ62UqDbqjEqK37idOO40KidmJHJIYow5Cb+IItO9Kwrtqv5jhD/6FKxW9F7W8s93iV7cs75q0ylFgJclRy8eiH0Xtzw0n/+zBn7jbuawffHzjCoeRSmVV7EXKznrW7ZBjh0OHdPzNeO2JqUvSNfJt/mSr7M7l/sL+PYphCFwmBzP8xGqV9yZef7u257Ye+x6YFgbwrpHbXtUjCg/YSdZr3BWClCUdavrsPN2n4jsYGq35hPOBYL3WKvIUyYax796oplipnWK37qvIE+oMHKn3ZJTpl1UHFgR9piC4nLjULZhnJQUpspWo60mbEZmM2jtQN3VPB8SHzypik9ZIkVJlG41htuLhkymqRV3raAg/mLbcLaRwtxTn3FKinZvLTacVgOJyPOVZRgTtpI9WefMECKztpJiWdyJL/wE8c+NZ3L3lFzfu10h66X9zGt49MsP+4XE+CcOqb7wXL8ar8ZfrfGXD5/bVcG+zuR72Ub0FS/+vpdNPfvI3wqOW1ajjOFytGRlRAZ6o4UfRE0KIyolzKJlPN8wrHtZ3AGnRG5XhShJzhTEm6X4l+QpkH3GHtaEBJt1z8IK8TzHRDaSLGUniUfwce/RkI8W5GEsQY4ifvZcyMqLDn0wI6578lYSj+1xRbwYgQHQqDcPJAnyAVM78JEwDhLQ1I6LaQM5SIsB8UoREzqBCaSNBFnGGrIPogJWO/FdGiYxrY2JPE3QiGyumjwoTYoSDBMC2SnUbE683LDjogBEL1XcXIJyVRTVFvYu8+ouWiumvCFse8iwcPfo7CnaKNbTM3zurwORIOo+PmWBSsSETgK/CjnybPUDstFUuuObR38P03YM6SmX/aekFBj1lrP4A7SzeHebA/MmoDDWirJQjFLpay3r5KltURTzQaq3xYNkSEtG1sRksL3nvrJYIwFvDp608RgUPsOzszOufvkel/dnOGX49fN3OfYz4ibwsP1z+u1jQmNR7SF6URG3I2HwQvoncj5+hJ4CU63J+UCSkHy9iyryDUjb9XzaBWR7A1UhEwmfJe1u0Y3jFMJ9yiUUy5ldWCY8OekA7Ju/pTOmyn1WSqG1KXjBdN29KkaIdt6gnaFpG+4/DlB1rNdblpUVblLKgC4dI71P/mZtw2uPB/LFlru3NKfukrwwuKqCI4OuNQoNWjxNog9F8jmSLhKT13u+QFgLP8SveulGmaLSOAWRiM4ZO2tRbcWffhi4GgLOKP7BuzCryrOeMtkH0tUGM2+o7h2RjeHpBun8jh6SmDTnlKEQw7XR5DjtjXRTSjhnwQuEk2JuHHvpoh4sFPfmEOOEShVPJgujF/NQo8FqcgbvI37yzA5nqH4ixgxtSx56Ul2zNkeMmwZjNQduxAFZZVIIsralzO/c3XWHIilmtBaRC+8T1lq0VeQk6okodd2Z0dJNIsNpo/iHvyTqmaYO0jnXmk8eKf5fj6vSgdx5I12PFCNkJcmdesmSrhQqJ75zMPHuHQulMx59pK4qEqokn/nF9xRe2xgVf/R5lbfdM7+Hjn4+KH0xaXvhh5ftU7sJ8ULCVOaWevGtN0/hu/cUbx4iCdALXTMlicaYSFMmZ0vKirO+pfFlTaIjdjNWPcSpl+TkS07vC6daPv/eAv7u25lp6TnbtjwdRHHwdrPmXXWO9xue5Jrz84QdeunUa8jOFviyIzpHshWq8HRMY6WYkgVS5zcjttIc6SW1SuiFJClhyPR94A8/svTZcFxnfv1WEAn+wwajtrjKol0mZ3ke+23mybbDVk4EO2biiScWA6AbR9uMvHULTJ348IHmn3+iICdSyOQgUuu/fqeFZo5Ccceccag3mEXNH11ovn9VLtAawKCT4pvHE7e7RH/Vs2peI2gne1rIgg5JmX7Zo7XCtDVKFY+vr7gPu2fqOqHJN5+y8jj9+CN8VRdK7Y/4sm7S10yRXiVEr8Zf8fEfVpL759oD3lXqBNaRRy9clTFg5g0xBkxdk4vqkWoqdJVIheiusyi4pWHCnR5g2wpiRNeVbOTGEDcD4flazEoLntneWqCtZnG8EGPCKZCerwhDwOaEHj160YrZ251D4tMr4rJHH7SEfqC5e4Kta4ZPn5LXg1S3jSQAOWR0V2PvnZImgc+klEjDKPLXZ5eS1Oji07MeZF9ui7t6KJCWEgynGIUfkUpwY42YEDqLP7sUQv26JxsrwTQQxoAKEjhJFyiJJKmrQOX98ZWR7opKiVy4IrpyYtC3w2UnhNszTQLjMXbvCZRyJIZAihI0pizdL+sMtRX8OjGQjNl3LFDChVCNKeaOoGqR/XXzGUYJ7MeHQHJ5371KBb5njCikTTnRuiKa4QygMG1FSoGQM9pZtNZoFK6IaxhrBCE4iQQ2zuBQLMhsFg220dCHouSnsV2LigikzWmoDXE7okLCGiNS5zFLV8gZISzbHUeoTJQYSbuuhBIj1H2v52ZgVrpAKpdEJeY9H6S8SuIwJRDFXdVX7zhhWhT6pEm4k9ZWxVR3B3lSZA04jZl1osZoNLZ22EVDfSI8NLUeiZNH50x194j63oF0Ugo3JRUxDlM7dOMwqwltJvHOaiO2asQA1Gi0EX+sXbKCkYqxsobkLGaq0YPM23DVo5y5hsAYTXXQ4Q5n15Hkzjx4F2Bn9hBOIoTNiL/ciLpizphWMz5fC9fN6JJIBKpK/IiUkzljO5E9TiEQhyDd0pSIo3QCTO0EjlpbUuPkudxsSV0RzSg+SKp2JDLDeiD5SDVvsNaQxsB0saFupRMerIW6wR7MsF0FWhO2I0H3GDWJgpYTqE+aJoFsNu7axDVGlDXUdVeUBTMqJlJIjNueuqqI5JLYuX0BBKWgstIZrh1KKUyjMXVZkvX1Ei+PZ75WErzR4fzCSm41bt6iq92bM2ZXSs+ZMExEnyFZgQ031T5P+TFbxJ7v9lWvefGH/Lm/fe69+fO/fIVu2K6YkTJhnLBNhaqcQIpzmfspFgEbMfKNBd4opsEGleR5LoJ0153gci9Tkq6f0tcQu93SkH0krCfoPa47gjHjNyOrx8/ozBI7DOTlSLYL1K0jQkC6sUqkpY1RUFU0s4YUoyijFqGhUIqGWQmn1g8BowJ6DGIN0VSkXjp6cfL4lMhB4WayV+njuXRVkTmZYsJGTbxI6Cx7dvACO85ZJPFNW1EfOWy7uf6mOe8hfwqBgGtjGDajwO7ajFu02K5+aVKuShKvlaKdt+Szsh6OIrmvFNRNRb/uMa27kV3ffBC+TmDz4vu+Xkp18127933+877sOD/XYOvVeDX+Bzv+/8enaDc+3x++8ctv3IW7M0WaFLWPxEGgK2kM5O2IP7vi7lsNxmZwE2ejJc9q1FzI2U1CVNKMGM8pZwnbnowmPrsibSfZkFJCWajuHDKtB4xRmFlDeHrFdLbEmCJVqzSqcZhFi7/a7iWNcQY7awiXG/mc2lG/eZvpfCV/n4J0s0Isql8JQir45oCqKk7u/hpVewBGcbF6n2lYSaW6cjBO6EJs1rsAKyTG8yV68mAzatGi25q02sLo0X63MRcpY2cIMcMkwW7ecWlSKo7hBrwkiyrnIrOswAifJ2pNmrxUERNcDg/Y+kvhVISVxP8po2NEO1AZTuu3mdwoYhVGiPs7w7w4TUTnuRw+IqSINZaj5j2ssdiqLZwipAth5NpnUzDotWNMW54M3yekRB/WeJCOmTOCdbcG4yzr7Yam68RRXRd5by8ePsSEqUXtKIWANQafJbkkZMy8otWK4yc9R8ctOMdWPWKyGjtr0KbCukPQivuDZtqU6zl4VBS+z9N7HckHIhS+kDzzKgvnhgK32wc8BQ64g1XsAj5JkgonqswZXUxPBeqm9/LWu/dlSpdIAUqMTPXNfy/cpZPziUprdOt47STSHFqirvh/f6boewWXI6sHI6BooHRoDG2OfHf7XKSWs+FsU5NCoqnhtF4TVwHXe44PwM0zjcsYW5Fzxo8TNrPnXZAzaQhFqMFgaotpHHmbCFdbSZKNmBSbtsI2Fe5otifkk4r4wOjJKL513DDOAvF8Rf7sOQMwTR5dO5F2rq0k1D4QSZDAOUcVMrmf0LWjnhlOO1EmnILmbC3vDT6iG4Ht4UU2OAbxG9OFxxVCKCayEHNFqiQAbodzTttMbhVrD6tBobXm1mFkVvfEOvDpkAm2pT6Zy73KWTpQ84xyoggW+lFkrX0USfCSWypr9kIFuyA7x7BPWoJ2PF82ZBSNSxzrEa0V/aS5GJv9M2SjkOkPq8h/+i0JSjexZjXtMpuXLeKZTy5HLgeR2f/uPbjdScJ03F0/35T7nqbI02XFFCp8P/I37yWm40Rs4V88kKXqK0e+rrTfoHbwgk73y871C3/aJdHq+u/7ztWLYgt//R6c1onkA35oeRiKjHp1IM3/3aFSYtxOfKODacoQJsaH54RiJrorVmhj+JaNqEaua/ZRkm8v3epslAhjOFFPAyRZCZFFUDxadWgzx2TFcf+Ycd1zUkXM1Vo644sOfCfCAuV/RmuR0K8s2Qj/0yDdHF3gqKTErXpLXUmBZjV1LAFZaME/FwPdd+diAN7UmqfbQF4G4fZVDm1F9TT4QJgCqmmpFg1xM6KKuINKmYve89naY1tNrCKvL+QavjOP/P37Yg+xzS2bVJN85BsnmdvNABkOZwY324U9N+/tdaKvK0eOYhB798jT9z1JR87WDVGJaE3TlufafT6E+nHJx4vJ08uToZc/j+9Zy5tGIMo/jJHHN8zJX41X49X4+YyfQ1L0pVnKl7+8QH6+TmXvSw/7kn/79in86m3IQfOj9yeGO7cIyy2qqTC1RZ0uOHJPaTrQh3OutobQJwgRu+iIz65EZaerydaQ1wOx9+I7UpSjchS53+q1I3JKWKOI65Hw6Eogbc7JWusMdtFgDsVbIW57pgceBk+uLGbWki43TGeXxJ2urI9SnR+LbnflyJtRjBijGJUmFLmPtItjWn0LcuD55Z8Txg0GiFq6P2m5lePGiKoc5nhB9fqtPSE1LtfkVS9B8axBzRvi5RWqqtBVRdz0qKYlW+la7ToFulQ006YvLqfih6JAOhmFOK1jLNAr6S6sx6dknorvzQ04i0JJ4pFhYW6DSihjyc6JeEAlikZ5mogmcvnoM1Ty2KbldPYNtHKi0GWddC8UTDlR5UxqK5EtV4q83LJd/ZBcTP5cW0nA4Yx4DlWGDMzdonBrIBTYkNbCowlJkgLtDDu8mpu3ct9GT1wPuOM5t3wiPxdTztBd4atUjDQ1ddsIzt0rzGxRiMk945MrfK354f2amCuRct5FbuWzlDVF0EA6bmrX+SlzIRX1N10mTiKjs9qLMZAlmd17PxXvlh2USSslRpVG75MkXbpG0lrSZKs4zYaZl1jol9VIGz3DoPinH8ByfHF6zpzGffMIqxWNjbxnLkFF+lHz/lCTomIWJt6pltLlrUE1CtKEMU44TjnjmpoUJQAMQQKf7CN11wBS8SZ30pVxRsyLK4c7LqpzN9aSHBP+ci3QxSmAj9yeNSgFU40k3Vpjiwz4NE04o1GVxVTFvwlF7keBDQJpmLBzxYlaYRc1z888PhziKrdPfJSzxOwJ/QRG40OUe9jW2MMOO8uEKWJNTWUb1t//gMXqQ07fPUJ1c0Ku2FYNOiXmpuf2iUNVjqFesAn1vuMXB4+qLVHBcrlhcXqAzVLg0J20cfLO28yofSshpyxcDOk9FghmzfNRYFbz7DluR8gwRsPTVZHuV4q8TaQEx67nt08nUIqnW8fTwUr1PkSSgqqpXkhOztcj50UQ51sHil+6VThMIbE9W6OUopp3wrPJ8ORKMQWDiopfO+lp71l6LdLiPzYp2mFMrxuDN7U0vubIL/6sbjTOPv9n4NsLz7sz6WZ9tO54PlmxOJh8kXFmz8NMg+cNo6FRYCpBAYRILCI3GnBO885xDUlk10M/gjeohXQrUxAYp24ttrZFxEHJvLCa8yGRcmb+9BlvdmugJ14N5NpiTw4Ig2GcFCZCPRMYJLkkROVcQbrnCgOVlQLZNPHaHUPjInGM/MWTOeul33OMwuixdct7RyL4E6aJJ0/AHS7I3qOw6KDEkyg7UtCoHqyTNZjiG4TVbLXhw21AbXuOSlcyh8htPXDnLpim4ulQ8fjCkLLhlr7gTieoibptSwzy5TdeWSn4KKW41SbiLDP1kYtRkZDn3SiDmzdM+qt8nr78Cfrqx+7lf33dGH6zknl+NQyvkqJX49X4BYyfU6foJwCi/jSY1a+1ce2wCRT4mSduehEicKYQxYFZTZi2qLMV0baYeUU8W5ILvMQcdIS1EDHtYYdaj6ICljIqBVmfjzpMV+OfXuELtEUbLcpatRXZbQ120UqQ0Y/YriEPEih7JYs4xbiRouJEkeBVXb0PNtLFmnixITx6AH4C69DGwZ23yQcG1Qk0z1SOUJTdQrnI7qCDyRNyJm0G4kUg11aI2bMORk9KURIdNHRzSKmINyQYRxSa5D0iMCbmqSmna7W+AtHSij0Mydwg+KeqQsUoAXWQMzNAKt2ObEyRPHZQV6T1eg/ZCtO4f6+qrCjI1TVJCY9kF2xSIE8ZhVaKxjmi1uRhQrUVIXisRPioyuyr266pRS65VPHNTrCiOJPv4ChYQ/LSJdKl+iqBtiJuB8xBi/IOXYQ0BH8eyK3GVJVIgmcksS7fLY0evPDV3EEnZp7nqz3JJykKRUFd87PIkEuSUnhb4glUxBUKZOQ6Acj75GY3RXISZa+cdgIP16avymiMyXsjzZxSgfAJPFDXFts47GqN8RnXOUztIRflwRvz8HrKSjVdguDyN62L741DZTBOCZylwKlySMX4N4tSZAlkBZKWqOuKjGKMvSSBzhJ9z7QZILfSuYyJvN6ia1GfyzHih4m8HYlDUdQqnVhtzd5zq5q35BBFgKWRhKYKch0yknAxBcJ2IHz4Ce7+XfRC5k1OWaTFczHdDJJcASLoMEXhkFQWZQTiNr9zSFiu2fzwI9b1kurtN4sh5oC99xrNa5q4eYQ1A2EY8esgcNdNT5wkQcPNSEFEOJIPQMaPnmk7cnT7AFt4jjs955QpPkCZNIopcyoS9JksME5E4EQlifpzLvMsJOlGsPs94qcyr43C1nqvoBd6Q+gtMSS0M8QQmIrRs62k4+o3A9N6QGtYnveMbVtMaWV+ksQoNsVE9Amta1LOdEczclgTxwyt+9obxU0D1P1+sZsbfJVE8uffeN1lUDc7TaVrlDOkfmC8HOijx24n+pVlsxGDXFMSHq1K99ZHrHPCMwtR0A3DSBpGTFsRXUWc1dS2cI8AW7h5wzjQuJqcMuNqwAwDqq3Jd45wTgRBcuFLjldb0nLDgVmR81bk+I9mMh+0wXQVrWmkA+usqHNqTQhimZBjQtVWCm1OlNnEyFzOxa8HEqIG52oRJ0hjxrQ1FPW5ECJmd6XHQN5OZBeLuVRRLSxwQD96BAWtsYsa4yyWCaXGG7cmE3v5XTuZd2G5JY9SkLS1JkVP1VTFhPfHV2ONLZwtBdZokjZop2HMqMZiuwZd1EOvb/yPG18Eu/0045UU96vxavzixs8hKfoJs5yvO59fjLG+1vjjh/D+ubzp3U3D4cUKM29YLwzxuBXz1QR6M6BeO0UtA3EUVSXbVmAN04NzYj/i7h7hH1+JL09MxEEctPXRHN1WTE+u8FcblFZUJzPcnUNM15BjlErgOBG2g0jSpow9mJG0xvuINaKIFUPAtrVIERfZ07gZsG2NMgpzOMcczdAnc8ytI8LZFWw3oOApj2j9BnpHv7pEI5AXqf5rwY9v1wKDyBD9iGoczdGCuO6ZHl2gMgTvqY7ntO/eY/zoCf5shbYaU1fEqfCHlC586YIZT1BNLbcWb6G0YzM84XL9gGwUVmmR0C7BlZomolKYAv9Ay8aoknQrng8fsg6PySs46d6jOTkm9FueDx/g1xeQ4Pbhr2Bzg1IZnRJu3hG3nierf4cyVjpLJTjWynD74DuEGNHaMIXCIZgNnG0/BMAYIZDr2pVgWwJKkgRvAp9I6JDQxkpCYCVJiL1AKHd8G20l2JOq++66j/ic6eYNu7qgkM6l62b07rPF/yorcF1DMwXuPZ9IKZMUPD2tRMZ61+lJAvkTFN0N0riRDtIOJ7dLSFWRzU4luSo4OIGiGEMuqnbHl575WBSzTIF0aEUcPa6ryU5z53CiUxo1wcxO1I1FV5anVxaUI6H4u/c3otinDWd+Qcqa2mRen28wJHSO5CBdUQvcn63ICaxJe77T017zrz4TifD7C8V3b0v5XxUhCFMCfF05qh2EJWeqWYMLNbkv0t6jKHRF3zMtt8TVFl25a+haSbKMs8LhsQbdVoTB42qH6uoCd0UUJpPAFAFUzJi6Ir/1OuZgJm73KTN4+GQ1w02OCUPTOsJ6wE8SNNYHLWbekivDtB25fa/lSD9ns3lEd6gxi1vYxqE80gnoaprZMZ1xIu1+Naed1+jaMto5D7eBFBLzpufoUJGz4uGqYtgELNBUDtV7UpNR1hbRE8WTVU3w4j2jlXz3zXZL19XSlSNyp96gyFiteONwK8+kNjwaDvDDRGiO8bdfF6+zmMFqLq+uWOfIkzHS1g1XfSL3orAZhkBKER8CTXXBXHliDLy5sNxqZ2jncM2CJ71Ge7neKWdUiNw1HmcT2mleO51QyoIaON8smJ5MuJOaf/iNiUSm9/DPP1b4lxXRXxBn+ByEruw5WeVrNNyePP+ShOhzv791WHNrJslZjom47vHGENWCxxuB3/poMBZ0lk6dSpl+M0ihIiRMCtx1VzgtXLunfUNeLMizrnBxAoREVSBrtc3cOk74rWLaDjy8sKhxwCRPer5h7AemW0fURzMyYMeO2/4d7IFiNn+Cqt/HKM3lZWZdH+PPIsF1Yp6dMrcPEzU9CsXzTcVmnahuHeyhtMQCLVYKsuLRZYXFyP0OBXpbCoZZIRxDZJlSi1b4fJtxD03NZS3OIP5GeO7OtlhneZ4b/uTpSM4j62nnd1UKbz4SY2LlK5abGgX0XhcgQyJcOPKmwTcVf+o9j5IYQD9e37jx+0dE8YefFKGVGw+G0YbvzD31AYQ4cqEqSrb2kgftFzEyPwyei7JOPow/ri369Y/7l/cdXo1X4//3x38YTtGP22N+yvHhJXxYDve2cxzqTF4FNidFGQohP+OsBKOxBjT6sBOVsfcfk6eAPZ5JtXgzSLcmSvBgjmZCwH++Io4Be9TRvHW7dIaUOGmPE3HVkzc97t4pTAE1a8jDJBXwLIaoYd2XavaA9wGbMmbeShJkjXS3SpXfLDrsQUe8c0RabgmPzhnzimlckbIj9yuiNnjnsGjyxQZdfJFUkk1L3zqUKtthR3XnABUj/sEZafJM51fMfuVNzGHH8OAJ+Wgu1d0gHYlUIFyqSN8aYNGdcli9WUzsBlbVY+F+DAPWWrLShBgwiEBZDoHsBGrhh3GvwLTWT9kMGaUNh/YeuTvE1BXb7TP6/BwVMrfqv0aSb4aylhwm0Jmz5QfYqhJvJC1ysE13wtvNr5AjBK2grrA5s5mecdF/RNZSTTSNKBplBTFqrDHorpZkQQlcRBkt8LHS4UoxMfQ91jlskqTGthW67OhZQa4M1jRURcGNID5MOy6HeOpIgKe0IR92cg2nQHf7ALcamM7XTCHw9HZ9LXSQIWuRRN/xQfaTKQnkg12wdRPSs+sw7SB4O07ODjdkFIukOVqN1KcijhDGScxWPeTgMbXlvcVEux0leJtVpDCQlePM38Zni06RXzmK5M2GqAzvx064d9ue+vwC5zTNyVw+NyWczRzbcT8vVUkYLzaJf/0Z0gm6A7/5mpbCBAJbTEoEJlI/ia9PSoR+lKAq1timIfUTaSyS51EMTE1VyXXwSdTfSpVXCOqFT+MjthLIkVYib559ICDdMxXlf7oR1TW6mljWhmQUacpcmRYVBcIWQk8owi4CS4PZ7QP8eiD6QKth3j+lO8yoeYubN5Bh8+SSMS6YtZVUzavSwVFFQU8pNlNFnBQ5RA7NFQeVVOqfh0OidRgn3VXVCtl8B1mOU+R8aQjJMo0TVVOjoibrhnGQwHvmDLeqDUYrDIlDtwXgstc8Wx6ickuq5zyZND/64AMWswWHR4dMuub0+Bbff/8DlqunmGXNwWQYhp5+GHjj3uvM5yfk4Yrl+hHPL89ZLpe8dvsOR7dvE8OCsysY11tUP5KrCqMypwuD0YmUEgsnktwxwJOrBaurgDq/4lffGpnfWbAKmj/8lJckRTcxbi/+656Ht+cb3ciWcv5C2Lh3PdolVgpuzRzvHNXEYSKsPfqoIdSKaRsZEeEIZYBxkg5oTPT9RIyJymnUMGL8wOm8xzYanwxPqkP0bIZxRvzFyv5l6gZlDVWTuXWYyHPN5fPIw7UmdS2JBjWL2BDJ255h06Oc5eDgmJP5WyijqBaZPH5ANoaVqni2ctTzhcAqtSKpTJPWApdUivXkGNu6wPAUqRQTsyrn5CyXoyaMGWeddM+KbQNa7b3wohfPOSYvaAGjRGjEx+J/JYWplDN1rXjtlsJUiqvziQ8vbqx75cLvfLiUVgzecL6tRUAnJ4wtcMKhIg41ca34YIh8L3x5QpHJfP/5iw9KBmqT+Z3fSBwoj0+K81UQoaB9MJO/8J4XH7UfX+W9dtN6+Wsex8TjmPav/nHH+3rjVUL0arwaN8cvLCm6ntwvVxh66bg5z3/GuaqswR7P5WeHCBoUrkQYJrTSxH5EzRbotmL43mfk0QuMrnJMTy5Fejplove4gxnmcIZ/dEGaPOZ4xuxb94tsLaRJOkTTqicuN1RFjSl6j7K1QGa0Qo2+mNnt+BqRqq2FaNpIpTGOnrjcotNSOC+HcyG8zmrMTKSOw9WWlKJwmJwoVTVNTTaa4ckF8dkWhQS4CqgrS26r/WfUb90hnK/Q40gcAnEzEs6WKOvQU5RNrfBICEHI2ymjclE3yhlt7B7DnrwnOIvtWulaTB5rLSEEgV0YIyap2x4fPFZLRVEVSFmaJmKMpPVWNt1JPjMX1TelFDlBmjxJi8CDacUckyBcrrx7cJoKPaWisCbdAFM3GFpiShgrXkSC0ROoVHa2fIYIbEAWY8IpCPQvRmJKDNlzdfYcnTXHiwM6Zti6wmolELbSEZv6kaqtRQFtintVozwV/lgWyN8uuFJOEmF30KIRhSZdOWKM+4RLGVEAxBqBFd6AKaI0ilTmToEV7i5AQjxgsrpOhpQEKiIEkqmyoTrq8JtBeCnGiBTv6DGVFR6WU/jJFwPWJNDDUZH6gFLlHJ0hj9L1zNrimkqS8UpDzHg/YYrsvUAN2XfCcrz2bJJLJGGCLryhguFEOYsysRibyv1NIRKHiWktcuA5OOJ2JOWwT45A4HfKGYHt5CwQvtph24o4emzjxFi4XB/bVigfyrMPKQa8T6SccFWFygINCldbUeOzRiCxKIHr7XhojaU57AjLHoYtVmX8hcKcdigXsbMGU0kHYPZax3bTlu/kCWmQAkoWEY40lG5lygJ9bCtSHuQZKuT4kKJATlXYJ4ZhmoilCxV9QiXEF80ajDGli6nJKV4H/UhXMY0BsmaMHuUTm+UVT2NgcXDA48dPuVqvePdb7/Hxhx8SY+CdN9/iaDpmfJq4XF0xD4ExTNhpYMpbDrqad995lxwT3azj0WcPsUozb2c0h3N85YhJVPGuLs+4ddyIdLjORf1Tun520aI2mfHqAhU9cXEI2X1uA9lXCF74t+tfXwxhX5BN3qHkbuxNN9+mynMcVj0Tsq7v7wNIYSDnfdKtY8LMasarnjgF6tM5NnjSZKDqCIdgGo21Fe12QciS0CorCTBWvHTS6PFjYGKD+N4qqq7GzVvpVvcThIDOWVTirCE6h28ajFJMW5FQVxncrKaKIkqia1nzVEYMf2MiO3NtZK0QWezy3UzlilKhzEdrLMoWWfyytqYpYmsn8OFJrCQyoCqDCtLh3tsF2ALZMxY7d5g63Lj4Lw6lilBKKj5VZU/NyP4vogkimMP6q/g3Xx1sKFTh9EqBgr7ApGN64VVf/4hf/jlf/xxfJTOvxqvxixg//6Qow1xr/nZdY1FcpcQfTaNIDO/GjT3nhf/eOMaN7vhPNf+vDjRnrXy99aMz4uSp7x/zMLaodSRdRkIJ2MZPn+O3I0ye9v6J4JE3g3RISpDrThaMj84lcPYSSAiEIXLLrRgvLxmS43l3SPX2HUmQtr0s1kNRVFNgKtkQUAjO2hny4IkXK9LkiduJcLUpjuPi66EriznsqO+doovqUPXGaZEFziWIZ59MNrcPuPi3menxcypyUcvTog5H+U61o/vO28R/+wGsBoaPn0gXoKlQPpIIwllR18R9UgAUeZq4zI/w4xalNENYEX0UhaL5DPpJ0F5+ElnwusZVFdFPEnBFkdQ21nJr/kvUZk4cB5bDA66GD8laM4UtYZrA1OQUMVbhkS5bCgFyEi5SztT1nNeOfo0QElknHp79CRglCm5GJJujFdf09TTg5i1dhjRGtFZYZ0Wlz11X/jIIXlyLHG6IGaxhsThgCoHgA9WskYQuRMIgwbnWirAZUDER8oipLNM04YPnG3egm5s9zA1gTIp/8qFijIpZo/mH74KZB/opEwfNeDUSfERNsXi4Fif6nBkqzdNb9T65ErW9WOSqi0+MUmAkSEhe5MNzzhwvPUdZY7Xldbvi5GQkpQ2qyehOodpaOk5RYdpMrRKqslitiFPAzuVzj/MZR7XAsj577ojBFnl2QZeEAB9ftFijsSbx+imijFbmuDbXXQxtb6rqURJHaYspo8XEt8AHI6By2gdgyhoOm4HOehQCMY1t2t9XlaUKnTOkINV64yy4hLIBY6VLkuMgBQhjmAbPZ8sWbR3aGcbVVooBGUigY5b5ksHVTpKh7Si8w9pRNwJHs60TsY+cOTjRnFagmxr8iE9QH8/3hPS4GVAsJCB1lrU5pB9r0hTYeumyhRh5rdrQtgIb+uNnNRfbGu0Mf/3WxNtNLIUQJZygkuz7cSJGgz95m2GCMG14rf8zDpsWZWserztSzHhj+PhSFBjrKnGn68EoBuNYn7xNTpnL5Va+m7X8zd/5HS4vLvjR93/ArQpmYc3hcmJcfYh1LbeOoZ9GjFLcOr3FnUYzqw2ZkVU8ZDNo7t+7v0/oMlDNW1EOrCz+4B0ebUb8ZpQiTEzEFBgZsXUF8xnn1sA2MF4lfsUl1KyinjvuHYhNwRQNT7cdGUVtIne67ec2nhvtV6Vf+NtqqrgchdF/WE0c1COkzPnacn6Zma56FsuJ3B5I99LLOqms5o3TSOsSSV3x5GHGqxpplAQRxNlOeKMxhwtUZXlm57isMBjuHQ5oo9ierzGVwx06tLXCQ/IeqzJGCe/RZOlu5pTJRlPPalIsRbYyh0YuOYt/XvzerjD2mDzBEMweahZ7j06lWNLV2Lrw8zbsBWbuzHoqJrJW/D8fTFyM6lpsRyn2xK2cqSz8g7cyrRlFFCLkwh0qCqY5swqGf/pBJmbFYRX4B9+0uNpxMST+L9+ToupqRyHK8NYR/I3X5buyzjzYHApkLhh22McDO3DUSSHrR33NJ4OsuY9/AtiZUfD3vwEHTSb1gVk5b+M0bxz1hM0lUzdDf4Go9rLx0ycxXw5w+9mgb6+Ac6/Gq/HF8QvpFFUovm0d2gfOrOVfTOMXX/SydUR9yb/ffP2XvqZM8UJAHxvNdqbJCXyK5OWWPiYGBco67OwQtKb/4WeoSWRy9fGcrBX+fCUiAla6B+50wfT8iulqhW0aVFvTvHUHpRRWJxZqS1UNGG15vpSOkVl04sGAkgoZUikUWE+BYQ8T4fEWP06oYcJ2LWm1RRf3+B1vJY9BpL4bCUTTukc1Dnv7kLydCMNEBtzhDHc0QzeOxTfuspw84XwJMRIvNzTffkPOZac2Nm+Z/7V3mR6cMX72TKBpwu5H50J21XJdd7yUGALZaGzYcDkuJTHLoJMYQdanC8KjC1JO4i0EpGkk5ExMkYzGWktSwu1o7TENB6g6cbb6FI+ogiljwEgAkGMiK1HqGqdRLIqURpkiRW0ds+YeVjlWccnjy+8zjRJ0qDGRa0ucFLNFy7x1LFcruuMjVErYpsJ0dfkeWYQmioJZiAGjNClG+r5nu94w+hGtDfdev0eOmcuLC6qqwjqLGiSYdsZJQjuFPbxqvVxyHh7DcUfTNhwcHWK1YRMUj64ymwmODhzzCpo20wXNZWqIxzXTcgtWOnQpCrE5LHuW+46qwFSUUmAyOUd0K0ENgO4qdO2EvB3lWT80E3dWAfrE6ZHipIE4hGvcfxv2SXfcXokKVXJiAFyeyziMzF0Wk9265ul2Rr8JwpXWGlEWzCwHS3Uyp1aBFJ+LK/z5mpwzzWGHaatrWEyS500pCtSvVKGzdJFSzhK0IRC7nKV7aJ1lvjBslxtyiBhjMDOLNYaUPCio2po4RoG0hUhzS+ZnjgG/WuE3PaZ22KpGV4agM49Xmb4f0JMmxkhjJflxbcM0TJgSP5vKobQmFsnvrBTVUQtBukraWVLfUzk4OTH47YbcapS2wkcLaS9xnNei3OivNlz5WLqBWialBVNb5keawyqQteHBv898cJYwJvM79zQHlZcmYSzV+vJ2kZjXhPkxzy7WVK7hTmWZVYGQNY8pfBg0K9VBzLQpcNJEyImgNProLuN25LA7ZfXpp7xx/w2stUSVeeedd1jEFZd/8QEbv6SpGw7nUDUNoRf+oglPqNWahe6p2oZxhFHVBWIo60W/2eKswxqDqSvOn/SMSzGdrtqWVLpvYZjQfqA6ntGzINsEKvO6FlGNzkfezZdUWjGYCmUasjEczi3vzKMQ5XO+IfutSpe1FEbKM3m2Vjw4k7bQ7SZwy6wgJh6ZuaxTRw1tJ0lpzkWZTStc1dKZFXM7gjU8RYmn9nLLrHbSsbS6SKQLvGzrFcmDWnvu3O2pW0dzkCAPwEQ3m5V5oVDakLaOvOoxpiKOAT8WU++YCD6IsqY12HkDGjbxOaY1TMsBBoetbRGzkG6iKv4/prIosyYHgbUZK3LcefLU9YbjI022hquPE5/1CnWj7LmTcwfonKh8H1SQF25/vZOPaKfIIeG3kce9widFVonDxuOqxEUP//5ZWRJ2N0Qpjhr41VORmT/LjseDiKtkBWSBxDYucbKIpJj4754OfH8y5d5+MQ3YczA/9zel4JsncHsGJLf3MNNJ9vzQZbZsUNRfOObXG58PZF6eonz+X68FQdT+KD9dZ+rVeDVejc+PXwx8TpXprl+suH3Za7/095fN2q883A24Q/k19SPpcoN2BnvYCfRkXkPI9B8+xV9JYG9nHe50QXh8KTyiQug2XSVGq4/PcHVFCIH29VNRlisEWT131CcLxl4U7FQnvIbp8YVwl0a/h4KptqI6mjM8X4rcNqCQv+VZxnS1cCSKH5Cy0n3QShGfXhEGCcrT1ZbwdFk8XzLWGOKDM/raUb9+SvvmbQ7/2js8+aN/h50yfrtFtdW+aqxKMG1mDc2372MXLdv3H4lDvdFkpYhJ4B5aS0UvpCQk2ZSJO36Kl65NShk/bJnNKqpbC9JWHNGzgjiNAoOqhQSbQhC57SwS36kEISqL/w/I902AtmIkm51s9HXdMIatdAl20BJjiShM4XWtp4H2cCb8sIMOtKKuLXrekpdbUgJdGWK0IlHsTJF4DntvHqU1VVORQ+T55RUpZ05vnwoUzxiU0kzjhDKGy+WKrm54ePaYg27OnZNbtG0jlf+YeHJ1wcFsRvCRzz55wOQnbt++zXvffI+cpbOi7I18v8AWhdMEzelCeEQxEVZbVONwRx3eZOrbFdEH6b5EUVKjsrhbC2xT7ZOlFCPuZL7H7LtxjQ5T6bIMwsmaNVAI3XE9YHb+NcXvKfm49/mJg8fNGkwUXta48eScqFqHH3x5vqRjVc1b0nYiVyXhMQJD0U4glH4jvAVJcq0kukq8TwQ6JM/fXk2vBDEa9upYKYlUfnvQkUNiWvW0p7OyDkggprTGtlq6R1Y+O46+nK9APN28va72l2p2lQ3bzZYQA7UVuN00eKwzGBQYSf5yymQrEMecoZTxMcbgl4X31wfhEC66fScvR5FL1kkgUjlEpouV3LsCJ9S1RTeVcEt2pp5FCZECa9o1II3R0lHR0mEjpvL9NDnCgwcP6HGc3D6kzR0GzzSICmYugWHMCVc7YhhYXl4y5cDQ1NRVxXq54tNHj6hdRUqRq01PzJGT4xOOkuX0vW9S+gaY2glMj4xz4gVmncU6h+saLBUEEffYmXa2MzGRjVMAHwTW7CO2sahppD6Yy6OlYNxObJ8tJZGvRXwjqIRuHHZhC7QyMGx6hssltm0JGfy0QjVWoIaDx1lLnLwkBHUlxQMF42agv3IMK7lfqQoCmXaafhgxaoZtHbapSKMXL6G2QKWVePqEEGGKqO6AuE1SsKgsWIM2SpTbpgCNQMfSMGG0wjXV/p6qAnXLIIF/eY8yWpIgr1ExoVLGdpX4+xTY2ni5wT9fC5zMKFKBhiYFSWXx8VLia5RCgBAJPuDdCLPr7i1KgSty1bUWuPKN/Vbt/9+LiVHO19t2LomJruS5VlYhTwf7zrG2JdhPRRp+d9zybPp+ZPO8p6oc2tSYSmSxQz+Ri1mzbRxZBUlQVeGF/RRZQNmZhC+aItrJ+pSKXUMqEuW7K/DVCoZfNb7+e67lP34GKM2r8Wq8Gi8dv5CkaJ0S/7deOC0j+UXo3G78pPP48x2iL3SMXn7AcLmFnHFHc1Rl0N2cdL4mbEaUFx8FZS318QL/fEneDpIMWUuutZiqfnaGaRtSTJgKDr5xyv35lSRcruaT5YG4zG894WJDvNiQhkmSjyDeKsYYQg6oYZLORIZcNjfB+gT8s0tMVYl5YsrEnEXSV0DjxCD/nnJAVMSEQ2IzIpOtNCokhh89FIO5917j4NYh2497prNz4tUGfVugBqSMHgPHl8Kx8bMjnnxL03/wiLQZSCHIgq81qq6ER1WuqQSY0jWi8A9y4cjkQQKDlIsoQkqYuiFnwV9rIGpNTCKp/WT4IToZMIaT+btY5cgx8Hj7PWIaJMiwkjHsoINaabSpuL34NZxr0MaRlcaTmIxGV4Jf1wmGcaQ7XqAaRy5dmzdOHSfDB3Cw4JnJ/MvHImrxzdnEb75eYB1KVI1QistnV/Rji5oLyb/f9nRdRw4SJKeqYvT3qdwbXKx6jhYexUDtKnTWHB0dop2lqn+FZw8/5cHZIy5jxVApFkcd/7Nv9ihn8Bn+rz8QqPq8SvzHb68wCi76zP/jfamY3p7BP3hbeApTjLydt0BEndbkKZBCFN8mvYJt5PtLx588TCKzXEx4tTU86wN2PaIrS6M8VWWueU9RQ7T8j7+huNfCuO75Zz+CM28xJvOffANOFiJIkRBzZLPrDO0C9EqELCgiBaZxmDpTzRtUijij8dsJv+wZsuVcneB7Tybwv/jGUCBBlh89nJFSYqZ67p4kXFfjR48pss25dJB23kvWWlSlcc7uuUR7zydbOgK18M/+8Q8ST1eKup3xn35LsZjXpJhEDrvA4nZwoKauUaph7CfGMPCtu5n5oiaQeDIuSKuBtoHXFhvi6DGNuN2nYSSGiH69wraO2jqcFdGIH54r/vihrF1vHFS80Yg582otst2mKOKJaiPcano6K1Dcxl4njX/vncz2tYy2ipMqkSMlifUobTBGCO4o2A4DHz/4hDtvfhOnGz67OiD7kbCdOD4XaNp5Cqy+9S1U5VjoDcedJ04jXF0RPvm/U683zLZXHB+f0C4/pK1bmoOatr2AaUC/5qXjGuVZ8/2I7nQRj4k0zlBZcWcNm4H1eaI7mnMcz5l3Agd+uplx+eCKlDLVyQK3aBi2E/O7B5JAR8/rzQX1SUUYE58tO7Z9oO+n0vHNrKeKT+IBkEla0ywcwQcRvOlEsCJOAqFVRjPVCx49FwnruZs4SpeYrsYtWmrVsT1fcb6yjOOCrGEymqo1qCJZjVakELjlr5hVEaM1F1tH4DZh9AzZ4OYW3YqJLkE4oSfmHG28KA4etgS1pZp3PNospIBDy5u3JoxVTMnwcNURx4jyPfcWPdpqWgNvHq1IGZRfYUJNmDzO1aQqkOLEJtUs9RF6XguXDiRpVoqwHckhcusgclBP+O1I1yKFg2ni1K24tZAu3R+fWc4+lZD8rH/ZrluKH8AY4b/6viDmbvzphX17DEYSNXhB0O21heJ/+Ws7WAWCkggRv0k86E+w3tDYyNuHKwBS40n9BJVlVttScIgohC+lrBh1fz5peVn3CGQd/kc/hNqKzcQvzRxqvREj9bL2hK4i5l0w8vUSos93er50fLFF9Lk/75Kwr/qsVynTq/Fq/CTj558UKZjIfBjD13v9T1LsuPmar+gY3ey2h4sNqnLQiCdKOFvhz5ZUd4/gci0E45zRs5r48Ew+xlpUZWneukW4WIsx4/GCdLFi9itv4TrLollDBdsEnz1WxD4zfnK5957QWhcncQ+xQGhQhBDEj6afpJpW4EyixmaIwyQJQ0wCVZomktZlw5CFNMSItU48hlAlAMnYyhF9FNGD1QZQ1HdPGB89J20D67/4iKOjXxPujFZYa5kFIU6bWlPfO8HdOWT47DnjkwvCk3OMUvitkO/FQE8EEFTKRT5VkVLxe9GGsNzQvXMP8+iccbnEGIuxVva14satzS6gTWz7M0kejeN29y1qe4gi8Wz4EaRhH+wqrUkpCFdGW6xyeDXnuL2F0YaQE1NOaJVp25q8HVGzmsXJHN044YsAVVfh0kTXVpg68GwKPFonSJk3ZomDOqNcLj45kri++cYdnq1rMdxMkTBOvP/0Mdv1hhQz777+Fnm6hfE1c5do3GdUKqILvn/mWnyMrPvM4vBNfunwTT757FM+ebzmne6Y9w4m2oOaZTT81z+EwStOu8zMTrgc2RjDk7XkNZWBeXXdFTgFcoA8beUZ6SzgIYgk9SfLie3T3QYsSUKahC9mmwqGhMJAf2NKZYNWht9RoBxUB3MepsBHFxFN4m+9BbdKJzVNAQ2E4q+ibC0891JFVUp8WIyVey+eJoE0iaeOO2gZtprnjwJ23nFypHizE1GUy63jw2c1efAYrYiDp1q0uCLFnVOW+Zsk8eovN9RdsxfqAPbCDCgEyhaTdIkqx4ON5pMrRbVO/J23FEcHjtxP+FVP6Cd01zL2AykbDBo/TgSVSXiasKVlxugNl2eJyjhal1nYAVVptA5MOWIag23Ed6zgDiHL/FtO8MMLJNv1icM7LaiK3AR0gZLFZS8kd6eompHDygvJW+1UCDNvLBTMkGKK1iIKobVU3bUilm6eAq6WV8wWb/La/XuolFn2mhgMwyryzSlhtcFjuDy8jekaHEuWT/8/XJ6dkXPmqNnw3uu3MG6BNka6iToBA6gBasghMm4GrDNC2sdzcHpcRFmK4bBP4nXT1jRNQoVEVwUqv6FbHPBs5bG3D7HWiG+TyrQHDf3zNfVBSzOr6PoNbn1FwBCeD2L266OYKWcIm5HHzzXVUYebOXStca5Ga1EuVCVS18WTJnlHr8TbpnEDrhIYb94Kqb6dt0StuBylmBWmgK1F4GTXjVVGM59rjtxEVonzOOdqo7F1i6kLhNpHYpGR7oeR+3c8XStdQpM3MIdpc8nTc0BbuoUjBSls9OuR86uKvg+0OvPGiSGVDu1pDoTtRMoZ5wLJZdAj+sjAoUP5hrWXTqjSijR4WVRyFq+geUNtInM9ENsoqtujrPXzFmwrSppPPs68f3EjAfiyvbtsax9e3Fhb0vWzC9fdm5xS+Z90M7OCRmfeO8jXPLIpEIhcNQ2PphqLpWkm5npJiomkAubYkYPHVUb2phAlsbTX4hdfd2Tgkyv52WrFXeewk8cmgV2mfiJVNcJw/LJj7HpN15/9tTtJXxrjXAdNX3Wsr8N0+h/SON1c8H/+3/9v/tI+77c2F3Dw2l/a570afznjFyvJ/fnOzlf9/ef2gTckjEPEr9bUd45RGvz5WmA8WjE9uSBH6eJgFL6fCtdGkbWmfuc28WrL9PQKPWsIm5H6jVu40wPIoVRBhbOUfGT48Cn0EyEmVEoYIHvhMmilCCmjKF4n/UD0AqshZ/zkJVEYJ1E6y6Lss1tQc5LEKWPIOaGDJ0xeyOBIVVQZI9XgnCQoefKc2fi2+EG0jXAh1hPr7z9g/ktvoKzZ8dsBIfBnAGOo37xN8/otxmeXbL/3CWk7iIR3FMUuk8S/J+RUOl5yHG0M/moLlSXkCLoYs5ZKtcoRW1Wk4EXuWJuiGCTV1kyB+xTSlSswlqwFvpCS8LxyDPQxcL/qUMYwlY3WZg1ZoUOGow7VVQIxKsGzbizKGlqnOFyA9xNMO1NUSUIxel89zUaSibqraZTg1v00EQ28cXqXx/kpl8srfvjRjzg6fYPadWS0kP+N2SfGSmkcwoFSnSUNnpODYy7WV6zXK9ShYtoM5KpDIUICSglKPyld5Hiv8eM586IhuzVSBX1hJhToyY3K624DVWRsU+0D5d1Qn/thd1+zEl8lO3PoGLCmuMxrgVmmDKH4yvjRY61BW0uaAlXjyBnGVU81N5LwZwTaWLuiDmhoj2b4fmK6HBkngbv6sSFHJwIPXYup47V3ULnnKV0vIilKVzqNfi+wEbYjuR8ZtiPWGawVT6fc1JBrjFUCxUTJvTKa7vRAYJ9JUbc1q7MNSovpcYeiWhyTqoGowWuYnyzIKGLcErXGFVnvxjYvXN2ck0DlBEwq3d4yy+O0S/iVcDsmL4IVOohi15TIUyA66eBabYrypWbvHWrFm8X7iKtkHvkpEr0ov7m6wrmat2+9QV1XxHEAZ7BVza1ZR/tEOtEHbcv8cMEwTvhxgJC4d/c1jLXYthGZd1MeLHWjGp2F5+EnkWjOSqGbik43hNGDD9iuIWxHUQFsG7TR1IdynarZnM5JYcc0NWpK+Cg+NzYlbO2wjWO43KJ1pnrrLnp1hXI1Lne4bs7mo4fFW02Rn51hJ49/VhO6Dr2YYY5mtLfF0JdyJ7ACN0yUjmIU2KudtwCYqcDaci7CIMJ/ylNgDAJR08Ug3DYOnXKRixfuky3J17AdoZ/Ee6yywl00mqqtqBrFtL1+FvrtyOQD9aKR5zUk6YC2FbZ3tFnTWo3Bi3UCYtatW+lw7mwddllHzqCfJhgSefT4JPBIJoHeijpjFlNgxKzbFGXVjNgRhBBFtKTsaV9cOW5WOPP+x5zZK7VJQr97ed4Lx+wLKGMkDJndQx1jlMRNIYU8bal1hZnKVyvd4BQibtFJMUQrQj8RRo/tKkzt9pC8n2XUsxnd4ZxxtWF4coFyivpgBhfLn/nYLx8/rmL81X0g9apP9Gq8Gj/x+NmTopfMW7Xf6r/m+LnN2xdOgrDcklC8cT8zOwjE48zH38+s+0Aay0YQI3a+ID2XFnwm07x+gnKW4bMz4UXljG4c7s4hYTPwTCv+6GPhyyxqxTcPK/TRrKiORfI0MYbCT0EqkSaXVr5SxTE+y+a9SyhyJsaIBVLxuIl7vpAlxVw8JDQJ8VBJSXyItFLkLBCinMFo6e4Mj57Tvn2X5t17jJ88I/cT4cEZW2vovnmfZYJ/sd0KWb3PjBtE5ni/4RmO33mTb+aR4cNH2DHghw04gbgZJZyXKYm5XUpCKI/rAZMVOIfWiqQ0pwe/zMycYOqKZ1f/nlU+F4hijLuIisfLP8PYWgJSE/admgfnf4y1FdpYbs+/g4rQp0Rbi79U0hMPLv4UZTI4Rf3miSQmRc5aOcOsg3tHA2kKeFvzcX9CGCZqtvyvvt3jnOOgFqPUHCL/5jH8m3MLKuNTwKcNZPiP3sj85mvCk/jm/QNQh4QUqeorPv30+9RVDWnJ8fECrQ1PrmZMyWLmFr/corYTunE0TcX6yZrz51d8fHQPHRMhZX7rdkVKELXi//Rv1qA1o08FogFPN/Bf/NmNJ71Ms3eO4e++lcHfcIa/MSsy8Bt3Et85kA7lv75U/PmzL992M/BPPoA/+lR+frqRIERXFtMa0ImY4R992rAcRJHtl09aXBZp7UQJukqiUXc12khCZGtHLEEkRtMYz9uzC/JCYQ00zZwcIqedZrYQ3l3vDR+vj8lXUrXf8ZtUZYXrkRI51aQiUmBrh64s0Ufu1CuauSTZprKM65643vAP7mVy02Cs4WSGJMZWOsdh8ihbobWmnrViNmzUvktTtw2urqhnljpuJAlWmUrXTP2IMQqXNclHtt7yZNuC1sztxJ1mSyZzb+b422/WKK2os0Ai41C4CoUnpowmRfnszbZnUQtPZSdhrpQITShnCTnz35kF25M52WhOt7ewxpFsZPKey6sr7r1xyt9ozyE8YvQ98zsyxzQw5SXr1Rq3OCV9kGiMZeE8RweHaKd5PFj+yfeuq/y78d6hdA8V8IOl4189ku+U91l15ru3Ar92ImHav3yk+dG6Rhn4nTd6vnE0kDP80SeRhyuNUoYhDMQIOQT+p+8ETo7yXnrZHhrCZsX4ZMJVmuwH4lphDg5xixmRLWYxYxoneH6JvTxn2l7w6fyYkD3z4ZD0qEHXInKRB4VxhmlMwgFzlkE7Pjz3xU9oJ3aB3PuDjhQSxg6M656qq2Xd247kKaJnBlVpDIr7ZsL7TAyJT33FdoB21jD6gDGK5CMfPKloGgtmRhw8KiWCb6kP56LAN29IcYkyFqMLbzUH8fOZAqatiEPJEnZ8OStcwrV3PN1KsmDzlvfubPd+QORMXPVc0HE5NSJvbUUowla2KD/KavDPPtF8dJ7I2fObb1f87bck2Xm0mTMGgyJzf7GhMgKZpXQxY8h8+NThvSlJlpKCl068sVhDjExJ8+CyEy+lKqLVBu0sfify4KzI5Beo7KJOvGc3ZA02etLkcfNWYM+AX/fkIDL3trkpgvDiaveTpAwxZ/77zwTOXCvF329PqDP4S1nTvmz8dPyi63f/ZP/+U77u6yBwXuVWr8ZfkfEL6RTt7e5+nFTlywpMP8ehnMVYRT1tmNcd24cX+PMJ3R0wXV4Rs6JuK6lUTeIxUd05pLpzxObffbQ/rxwizTu3CVcbmvu38GPgk5VUyG918K1bhu7t2/TDRDhbkowRkn2BfhHFtyQjVch9cqRLGQ5FzFlEBZQSoYP9rVHS/dGCgSclrDEobQBRqBOuTLpR6VcYY1l//xOae6fUt49Yf/AIGyMxBMaPnpBGT/zGfT4LQXI0Bfgv3gN3UNO+eUp164j1n3yf6CemaaSuW0CSMG0MMUuApmrL5snFXjEsRakEtu6AeXWbpBTaNmgvnCQpAMq18WzwaStPj7WAQmvDaLaMaYPKFbfMAcZU1JWBqiKkRIieUS9xC8H/74KFjJKN01pII23qwWaWXrHe1MTkOO5a3j7MqAKvSIVgvUyajy52nasIxQMok1lUUpmcH9rC93DAluNfPSyVUcHzX51d8nw9UnW38MsVtXM4I/d9fnDAG6/dR6H46KMz6q6hdTVHMwU6swmZj594ghI+zi5PHQJ8fHljupR/n9dy38UssSiglXuYkQrtQnnePlZoY/hhz4+dok82Nz7n5rwqHIyw9Tw4V5yPCgd861hhiy9LGoPAeGonjvYGVJagNvSTYPsLBE/HwKzZnamYoMYpYGyiCsLN2Gwty9WMFJKINFSNGKJuosCXtCJnBUoU83RQWOUAxxTXNM2uswKurahmDW8rSYJTFt5RiqKIpYzGaI0vFXhdCc8kh4RtLNXCMjs5wBmIPjJjQFcF05g0zbwtBYqMMoo4KDbeoayhrkBVosZZ5cghEYOWeTmMwpfT8lmqCC2onAgksi6y71CUARNhEq5Q8hMZzdVixrOmIcZEZM7mfM3R4RHdQUfTvsYqTUxP/hg1rvnwg/d54603qaqKaZpoq4a7bxzQj5H6YkO2Bm0ypqtQSjFs5NlL1/kBOcOhlftt2op10ny83D03ard88e3bFXYmBPWL5Ph4KQqDv3k/0FmBUp6tNR9fFQMAFSDL49zODcdzmXt+uSVnjz4yxNERholx45mGivjREwmMu45pM8J8Ls9EUxPjwKaCvD1Hb9Y8D0fUtw8xHWKKHANxCgJtSz1h1jBaDdmQIvhVvy8WTTlLFztn0uTxw0RaDZgQCcDIGu8MtqmoVMDZTJgmauUIrkCzazEA9iFytfT0W5hyonEOFSAEh6kF4hpj3CtPJvGJEG+q0OOj8FZFyAdUMULNQEiBYYDzsxFi5taxwYULnJHkIceEOjRsNxqVCwzVGLQTI+WUsghCoHjWZz58njBW8x/HgdcdKK0ZN56+PAv33Ehti8dVymQyQcO6qYm1dLN3Agw2ed5ciHDPZshsJocymtZlpimUe92jKwOuwEGddKD15JnV8vxHP2HnLbqSNVJbg1u00iU3+sVF8vPr2BfSoi8PRHKGi14gua1StLOaudKsx/RzQLzcPI+ftLsjr39R4OEnPMbXOf+/ali8V+Ov7PgFwufyy399WUn6F/DJKYNetDTv3iM3l/QPLxieXVG9/Q7jgytyCNiqhqYhBXHZtsdzmnfuMHzwhLQZMZWoPdnTBWEzivGp/uKnJSRIqb/9OrqyTJ89RxuN8oE8jqSYxUxRqT0hnZzFskEpgb+VoM4YQwryWm0sJMHHZz+hqlpgZkpep0nEIEpRuUiR5hKpKKVh8oRVjzue09w7wX/4iBQmNDB89JBx9OjuZK84JbA1+YKfF8cwBy3VvVPhPAUxzGPH51BQWTEa9c+XzL/zDS6fXNAYWzw7tEBTtChM5ZxI3pOUQAOpG3IIBTKmxXskQzAWqzWpsZJYRgkIsgaVMyEJh8I0FbP5ETQin00IYBWmcqQpkIKXLkVji9EsKGfQQ0JNgZ0iX5bcVWA/CoG9KAo8sUDPyrXSzoj6U7PzxigwRyMdEFdVHN+5xeFoSbbCaS0dkmWPSgldW+68cZ8HDz7lw48+5ttvvYc3E3MybduSxgmdJWA2ih3XmJsT6SaCZf9j6XQlL3K0aTQwJDFq1JpslTjJl2T8xZjgxXuu9gFFfmGexqLbEHyEAEZX4lGFiCxkBUZr6YLGtIfGoJOQv3d+RIUQr4zeG1MqJUl29pH++QpdWXJlybrCzuq9gEMKsSRHovQVNj1pGAmXS8zBAt9Hpu0gVfNbCRUz02qQgoGzkIUYv+uMaiOwNZSShC6IpxMx4wcvBsQ5QzcT0QgjJqeMQYwdKyvPpyrPUEiEYZLrlQVOmXwk5InUwbQdmdaBFCzaIBy9osCXfABjmKKIEmijqIzj8PAQlbYFaqr2Pl3T6CUBc4ZkFc5Zhn6F0XDv7l2ZYyFgYmJWV8yrFldpfuu3fpscI1M/cnx0Ip9fulRpChjrMJUm+IQik7JI5MsSIw+ELgp9ujGimIzC6nwNvcxlzij5r64dxoDOkRwSeVJAkYK2ek/IjzfiOknCZV2rDmfCywmBaC261XTHh9T1AcPGg0/onNB1RTBROqzGgbeoriaHCbX26IcPmayh604x1jAue4FqTVFgoZdbqkWDWzT0Z6IEmLYTYTvJMzlvUEZRHc6ku9gH0hAwTcW4GhmiZ/bmqXT8t5N0E5RCFUXLrJSIzhQ4qDUaG9XeCNVqBTEVuKIUj9LlllSLwItCYytLfTBDqSww0pjEKLrAx5RWJK8xlSnGz2tc5QTJoRUxBTmvAttEqcJL7aXrr9XecymPCU0p8CUxQU5JTGRjLJLcCXwvxujaCXQ4JrlvcQoYrTB1JYk8FHW5hFIGW2kyGoOoScYxYBuHqYpSX/Fa2gnFaGPwmx7d1mTn9uALeShNWV9U6Vh9YZX8kt+/OL6YXkj6EbNo5sWveOXXHTfX9a/bWVL7T1P7d/7EYwcheOE8Xh6ivWoUvRp/VcbPOSkqU+dmcPWTFz1+/Gu+xvi3j9c4LUFWWtzlaHab+NYbTB9dkldbbDfDdq142Cy3qCJNPT08JzxbSrVdAZXFHs3pP3yMPZ7BvZMXzvFyiPzzD64AuNVZfv2911C1Zfz4GSYlUpGENQlRatsZA2YJgpIWuJtsQpoYQ8HTKZHAzlLNzyEwxEh7cCTQhxTFcC9LIpOVQieBwUR17Uo/fvQYe/ge3Ru3WT46J/cDMclSbh485rv3EvPvvFscwOU7nW8Df/p4/WKMnEEdzsioIvKQMFrgEOJtI4tzGiamh8/p3n2N2aOOk8VdMrAMj7m4+oQI+PGKbC0WGPEE73FVLZLlQNaae4ffJXmHawyP458zbFfk7Pl0/SfgLDhD287RrWM9XPDtN6RSmxVYY/YwEq2VwJA0UAiyIYZShS/8DR32PkU5yn347n3Fe6e7JOgabrHQol6layddupKA5hTxk8fVal9KV0DbNqw3EWs1b5jnmMUIdcWD7SFBW95+9xucnJ7isuby4opPP37AG2++zuGi5n/91zI5TeiGffV157WRs8hvxygJ0MxCWMv1Ww6Os3BEiomTcMF//ssB0zjeXzv+D38m92z5Euuwl861m4kREqz+l99HOC8+8z/5tuFgIaTthbmQJAjNx1fCs6l05vXFUpImJRLsL9RFvRQAVG0JvRDbbaOxi5ZGFzPKnFFBEbYTeT2KVLlS9Mvt/v3VUccbb7cs3olM5xc82ESWyxljUvxgrTg4nct1CxFXOdJQ+HuAipE3bg0sjmvx8cpi7BqTGMraIjJinZWEs8/kWURbhe4qwsVGvGLaep/cZcB2tSRhWyOBcIbLi8SUZuTYMk3S9Y2TF/7aLkHMRireSgLHKQWauuXxsuZJko7m/YOemfXkDA+a73ClF9Rtw69v/z2LuGYcR/R4ge8nuqbFaiPSzWNCM5XrLDLStkWSDi9CFE1Vc/ciU42Zy2Xk/+jF3HNWWf7OO/MXkvGcoSbwg8dyH07txH/+K1u0NfzpM8Mff5b3Gf1uOflbb8F37xnAcGiEM6KU4j95J/F33takDP/1D+HRqqAOirqXAlmXK0U0lv/yA1gOUqnvp56cMp2K/M9/FSqV8Mrx0ZOO8XxDvsp848EWUkJnDXUrwi8xocaANlogk0CyGnzEr3pM6yAl3EGHOZ3L62PCn69F4txo0hS5ffBt6u4IrGF1/qc83zxhVs9FkW5qSFoRkpV1w4e9eplra6qmkhnmxNtMt5V0UScvnncVYA10NU5lvnG0FEEdU/Gjp+2em6SKafPMeu4vxFz3cJ5pu7UcV4mZqULx588t/+JDCcF//e6W37g/AYqL3vHD9QKl4bXFyKKayDHyq7da7jRS5Nr0ih+uA0HBdtlj5xptDT94ZFF5hsmJt057nMnYyvLurS0pZqaoeDQco62m6jqq+YAis8jwy4uiNKqgNm0xWpZET1Hym8wejhu2UuD44arij/5C3YgLPh8gZK72a91LOkAvTUauV6gvvkMx5sx/1W8xStbD8fN40q89cvlktT+Tm7SDLzsDgN+uKr5pRZL/j6aBj8NNsYefLoX5sne9Sohejb9K42dPir7ujPk5zqwvM1u7OdZjAmSj3gRNYyv8+Ybx6ZWoDc0KxAXxw5l94y5KKcYHZ3sYQSQze+cO47MrqdoddF/4HiFlLofSVi+O19Wbt8khMbz/UApcKRJTxCi9V4hKOUtnCBF2AEhFhtsoRYyi7qaMLsJ0Fh0n7LwhXKxIShOCx5bqLkqRjEGnBDkRS5oSLlaEqzXu1gH1e/dIf9aTfCAkWX7dw8e4ec38V96WjRfwcbdYX5ffcoiowaNiEFggEGPAWpHD3kmqaqUYn1zQVI76+E06/RrKBy5Xn9GHq2IOu1Ogg1nXkrwXnlIWv6aYoTYLrJsBkbQO6JjwKXIVLjk4PcYcVMQ6kogcthULt8XUIgmNiiJEkQzWOVLH3j1daY1zhrgN0jXaddiiCFtoa4X7UWVmRjbg/R4pEnqkIRYfk9KVQarLVSNBcEYCtRwicQxoW6EUNE2mmzWEpFADpWuWmc1mxJQ4rW9z5/4dgXi5zP1Th3VyzJQSfpxwVSUY+2Ei9gPBZXINpMzFxZbTe3dIuWZ1KepYp07xWhtojls+HAyP1rx8LubP96Fu/Lu62VFSPNtkcrRU2nD7SHFcRaKRYCtOgexq0lVEVw2oyKxTTGPP8uKS27dOr3FXsShOKTEaVcYQY0BNCl2VpCIL5CqtxTRYVxqtNONqi3UOuhqtNX61QR1Bu4i09w5YLxaEs4S9XJGso58MVe0I25714yXp4lLOo67Ibc1rC+lo6UI4T6lU8bUSifcY9yabYfSE8zXZKsyixXRV8eOSjs0wDqJCdrCQrlaUrp0AMQ2bHkATpwQEeTZ9hEK+jynBJAElQI2oNfpoUFr4FcFvwcHkPZtuznnoqCbD6yHSDRd0Wbxe3WGN0h6UR+uJxP+XvT8Nti3Nynrx39vNZjW7Of3JviuroZIq4NJcRCiSzvAqIH9EwALFixIGCmGEiuEXAz9K2ITXCGwIoABR63IRRAukE4QSqAKBApJqMiv70zd779XM5u3+H8Zca+9zzj5d5smqQnJEntxr7zX7Od93juYZzxMJSq5t8oHl7pzx0Q1SSEKGYg06KTaqGqIi+8TZRsbViYlmux5eGUlIFUIr9Nu7XoLJI+OO+x/WaKP42Pke32RhJ2wUfh4x1rDhDJMB7psB30WsMWyoKFU8ZyjIJJ9ExwctMLiMYPGUzEznF7DbSdVzJfyaSsV4qqm0ZrEMFBubA4I5YRYK3XsMGbYmuEqcSlVaVIxob4jRSx/ouCTuNfhZK0gAq7GVI8WMNsKE2O8tyVozuf8Io/ooVXuEsGjZc2Py+AhLbwTuWQqRhLKK3HmCD1K5VdIflr0wY2I0elRIcJwzelINEMxM9IHCCdx05BJYaHxk2WuU0qg8ELL4hC4H3ayc0DpSEtC1IYWhGgnMezjfWlKIvPWkolJSWboSDF1ykCCETqBrVjMdl4QAkcTuhTkhRnThKGKidFaeWVNinAMLSnf0iznRW6rpCFMZKmU5HzQ5a3l2So8iYZyhUkmSeyGS8wA/90G0sxjEkYFmZ452UiEupiOWc83Z2cGZ63C7Wb718MBj9WQe7l9k4NLAonj9lu7eVvC3G4/sVjniqdacHDTjarWCeL8Ku65a9Ia9YX/c7Z5Viq4hV7ibgXanc8mBTFAeqiy3XG51DCsHfnfO4mMvS6WjLCU7WTnysqN64BjliU2WH3lFXmJWNFjKk9tSWdhZivbL9pSYhkr+IbvM5HUZ3z14nJwSzcfPQrKiJRQDcYABWCWQgxT1+hiVkkx/HBpKUxZoHjCIOFrM9oTm/CV0WeGsaDEE36OSsL3JqSvElxBK3N3f/Thbn/1mRg8cJ16dEV66iIoCuSMrFs+8BMYw/hMPrKFMOgSBZLSK9sJV+hcvEC5eJVmDCl4ckxhIxqKNSDXqAc4D0Jy5zLEHnqAhUDkNJHTOYC3aiPNnJzVhNsfYAlWWJCe0x6qwApFzmtB3YDW6qqitxsWA2xxJg3SMIoDohqZgM+T7rBENp5BIUeBwoQ1DgBkhW7QCrzK6cCz7JdYZVEjS85PlKmYtTk1se+y4ggyxj2QjjHbKOrnZWgu8anjmfB+lRyUkys0RyWsIIvq4enZsaQlDUz2dxxiNLiy+jcJkVWhRldfCWkbKFGVBztC3nTRW50zb9RKMxEjlStq9BT5kcSxCwIwtblLLCzYLK+IKpphuN0bVTX8ZRF0l4M8xYwYtKbQiZkVRF8QErrQk5yic4YgtiSBZ8JQwZOn/Snk95pZdjy2lgrFqyo5NT2ggeE9ROJRTVBuVVI5CAmeY3H+SGC7QXl6SY2KxTISuQlc1thDYV3Nhj3T5KvnqVYGjOgd1jR7XmNIQ5x3RGmwly+suosjy3UDOEvtAUQ4OizOERtLQ2hqBJGWFq6WnwXdyf/ulwP2y0UQlQYIxhqzTEKgrVF0MfUSKOGwvNr2wniko6lKgiVF0dbrQcXV3RsyZaFuWez16MsI4KF1JJtMuGoqVAGxeFZU1ti7JMRJaz2hLArfgI0kbtHXkbAladhwVA3xTIKU5Jfzuch0QuMKKNtuyI44rovHE3qCqAm01VSXQVKMSZlURGWBQAukCZZ041WgJskJGBY3NGpMQAoBKE+Mg5qs1CYPOohsGeUi2gFGZuOxgWojOk4JiXKDSmK505D6iKocpLYpMbHsZl1GSCCkkSD3l1pjU9HQ7C7QxuLKkvbzE7y2l50YpMEYSG0B7ZY+qmOJGFleO8XrQuzPCqhl9lF6xgZ1UK+RFMogpK62IORF8QscMA2um0gpURpcFGEhErFXERSewzGGM5BgxdUFqveh2aTDGrVkaldYok9f9gNYqrIrkoQUxA8Qk/YsReSZixA8ipaHpMG5Mjonx9hgzKgUiroUyPe422HElrnyErLSwjyrpz9MDYYiQomhZBkFJqCz7U4M34tte5CxQwuZaOHQvzJOxrqQ3qSqJWa9I7W4xcd2q3rL65jDg2CeiPqIOfNpHI9zJnhPQxyTX89VGNW8EQ2/YG3aDveag6OBgvu6LO7ebgVmv397grB4g1jp8ufXn/Qkxeake2KoaaK8zqfVC0froScLVOc1LF9HakGLGbFYUx6YsX7yEMpp2Y8QHzy4ES7yiBb5ul5eWgV98dgeA05OCtz92CjOtWX74JaH/ni1IXYtJmWydwB1IqCw9ApkBHkWGLJlUlcWpV9pI9rAuyYWlWy6oR2PJYmqBgRgB9UuFaYBnZK0xnWf+O8+y8dlvpn7ifnZ3l+i9xcBYJ47y3kdfJFzcEejPsuUzszh5xRVFd7WiOrFF3JmhfERVJXSeZB16RQAx9DnknMnBo63j8uU/JOWPDM5PS0Sw8yfGb2M6OgllQV8vxRGMkXPhD2lji1GZl3Z+E20tymla1VJvTnCFONfCMrQKQgYWLnOgTyVErDU03vLyxYlUwJT0qqAVI+N5YnuHlDPPXM781MccSikemJS89fQUkmjs5LU+hqXcmqCd4ekLS16+Bnsm8Id3nhpxpNCk3pNyIbBHrbhve45RDWZisSoLPbjWPFRfJdUQg2TPTVUw63v+44cyXcgcGSse3wan5F5KEChkD82VBWVh0RqmRze5+PwFcTKnimxgWva89aTsX7R/5Qn9rFPw1mMykN7/SuZD59XB05Af14zFwwfkfkJCCCpMofBdj7X7PSePb+7hQ6TF8SMfUvRJk7rBQVeKk5uOr3mrZMRF1F6gouNyJI3jZgh2Q8SOSioKylmFtoajE89mukqwPTG/BTd9J/2sYa/5KM82gIZoCvRY1s+dp289vunAe1RZoIoCVVXEzU3cqOLlZY3RAiN7tFzgTMbVlofZkzt8XPrnGHoabC+BeCCRuoCKiZevznhlucl0soF1AjVSIaKSpfd75MpRj0cCMVzpuKVM7kWsNedMbDxNsyAXJUYbfAyUVYXKcHLaMHUdIUVms12qrSkqZR5tfo+3nTiCypkytWsGvdHGZAiI8nDdJagnJvq2F2rvUYlCs/SGH/uYwQ+KvKlfAjApDV/02JZso+npLs9oL1zFbk2x1tCd30HvztBlQdYjtDP084bYez7jmONNGxkSTEqF1oO20iDqqpTi7Kxid64H4WGp2IYu8FnVp/H59Ra60mzZDxK6PVKEc/kEfS8Q288+FfG99JaBBNsFgaLcIfWewhge29whhkQ/0ry0K3NBBqEp32uEtKLzQjk/VwSlh4JUwtRStdmcPMx9W+9kObvEFfsce/FltLPSE+k0/axhR7/A0p9FY+iTnP8K9pWA+XLOw5tLjh0Rim0U+C4Iu1ppMcbQtYHndyZQyH5X/1JZ8Py8JIVA5TIPTvegsGivZa4vRSR7VYHVRmO0WbPHZSAFQSgIqVDk7cc0j24KLfm4kHnCd54Nf4lxaSiO1jidCTNhNrSFIy0TaMXDxz0jK6ylLy83WUQJzJRSRC8Q5jPNERRbuKR4MM8oomgQxaYnaSv9Rc5iDKDVQCueWXaKF3e30GXBXoDffGVv/R4/zNq1HOLNqjqHweMOLJ7vPBD5RNjhIL4b7QNdx+8O12WeD40MD2xnn4ThIB7gIDHDQQlYRd7vBXzD3rA/Zvaag6Jrg6GblIjydYvc6UZvVtVG3XXZV1mDLYVFKQ+N9WZSMXrTaXLK7D39IsaIrk5SiurB4/RX58RZA5XDndpm9ooERTezkDKzXlJgW5W8pNyJLaabYxSwfPoFmpcv0M6uUun9QEjlvCaiU0qJ9hH7nA5aDe0kWYKl6sgWsxdeluzakAnOUWhjVRYY3lq8JEFSirQ7Z/mRlxi//RGmTz7K/Lc+Slp20kyeoTCaMG8pjm1x9DMfxkzqdaCx0u3xO3O6Vy7KZddaqjHDNSOJ7lJWkAsr9MImEhYzltFTlxXWWmJMOFNTFhs0OcO4JPuAs6Cz0Chro4kugI7Y7TFFI2KDMSWMMuTOi/6QGvDYSioOKkWBJcYkVKxW0+NIvaTJdSkaRDa2ONPRdg0+jrmwI+e4UZQsF4NeRhsIew1mXKKKkhw0Whl2WsXF+fAmXYkB5sTePFGVCLTOSJVHZzA0VEVC6SAkEMO9skqqBNkAOlM4SxdhEaFNUMZVRXTVg8ZAnhApnCV4yeo2uwuqacVoVNH7nvHGFBUTOBlIwQe0E5hQlSN1JVnb+oaRr675cVemtcBbhmRD9pF+OccojTEjLi0cvTJASe4iOUQKK9AsUw3ZbGfBGlxG4GYhSi+YkmNSQVjt/LJDFQHdzalKSwyOcCXh7AifChZBg9XY0pK7gGo9PkSi0eAcxakThNZjnMaOKkwtOkheG3zKWK2IIdHO9hhPxpRDrVabQjLZWqqemILYdEIN7jQYxcn77qOZHxVYZh/I2hHwpBDYWcyZ2g3J6itF6nsJVFKSykfrJfDIMCpr6YlzFhcFkquMRseeogyEbslkOkLnTOEco9qhWA5EFatq8fqxEfKNJAmTdraUvqq6ohpX0riOnPPlxtIP7GbkOCQZFGMDufUk7+lDpDi+hbGGfq9BxygEBnWFcQZlhIpdOYuOibKEvuvQQRNasIWwrqUBCtd3Jct5Ii78Pq1d1pyqJtTFBpDwF+ZEs4t2jlm3pOkV2hnYW1I6g8kldlyiVMZpISvISRgjbc44o0nO0jUtShn6WYMpHdWooFv2ouujQJcOkhApoBXF1phea0ZHtqjLDYJtMTh0FuffOQvGCMwxB7yOkEQwNK/GbIaUEpvjCVvTjKKhLB2hDygjAUTqOtzGGJ972kVLzJ7CSRLEVQWERGcLYhfBJ0Jaoo0iNYHU1xCkVqAGQoLYyTnE3g/DUyjrJYckcLVRyoxdHgTGI/PLC1RhsKUjz5foLpFLR3IGk0V/LNsCbRSWgEntmggoR42rS6nw+iBiu94KpM9pch9hkDtQhUUrI4yKixasQheSQEg5E3JJLMckrVl4z+VG3/Ca3w90bm83lQfJ1y7zibPrnaGbhz63OqpFzixu08u02vK1wrGHbf36K6AOiUPfKCu9YX887PUVb/0k2kHIBynjL+5JQ7ySSVJXjupNp1HO0jxzFlqPKgoAqgeEiak/t0MG3KgkOblUqxaLW1lGhP7C8JJf0YXWb3qA/tIucQYy8RwgKEgJtEYzVIbUAKfTakgYJkII9LtzqgdPsDxzgZwCylUiwqkFR66GzyhNTNInYZ0FpenPXkHXJaPH76N+/H6aj74sTb9D9lRbi65LzNZkoKI+MHXmTPZBXroZjLGkHLDGopyVitVAZ62rEnxAhYRJio1qAqOCVFnB4ptM4wSSkYwwTtnKkZcJo+WehcJQjitsNTQdG4VGockklfF7c+zGWG400HWBHDyL2YyidEyUIgUJBrQTMo009Oac3T1LdJc5cew4WmkUUeCMIRL2lhAz3VLgQWVwGB0Jyw5bZXLXo3ovUJOyQBWG1IgwZRrodq1hINWAvm2pRhIs9EmzwkMWpcMMjE+hD9LTFDKlM6ScKbQi+hU8UQIjU1poMqYuyIsWpzXV9nTt2EzGG/StQLxcchhrUGVJ60VoOKXh9ScFSorh5ga4PZTumuc7rwtJfYQ+ARjcMDiU1YyqCt/1RO8ptCF1ktJNWXplioGGeUUwgFL0vcdYy97eAoMmdT2l02hrBZLlparZ7TUkBzlAVBk1HqoyOWFrGcNpKeKNJHGUAUxhKLTCbY1QA2QJo4V6OGuyD6ioyEsoQ0Fegg9CNZ3CoCPm7EANnNHTihE1MclYTsGgW0NqA3SB3vdY6zB1ybG6JGWhdtZaC6xKK2CAYmmBYqUQhcRklfW3Fu0cGUUMmZ3dGVFlihBRdYWKGVWK02sYKOVhra+m1tkWqY7klCjHFTlmunlDCpF6e4qpC0qrUKusz8AYxqIjz4RJ0KdAOSmJnUchDrWui6HXSpxeWzm0S/vVG62F6dFogXUBpiroZ0t81xPmJWGupHpSOorNEbZyFJNNrBqjVUb1E/ANofH0Owu8N4QQqcYjsodMIoQGSosuRHRXJaH8t1YT2254JjJJG1RhKSpD8tIDFnPGZLCTSmB8WhM7jzWK0VZFMTIoE1BjDbNMaETkNtpIbCA2PW5aYZzA13IexmpIMhdkDTmRY6AspSrtxiWml3vNAOMzKKppTdtkQhLYrs5CahiCzFHkREqiMxSiaNbFgSFuRbU9RJxDZUiCMzMkLPSgHYbRNPNOYMRNh3aGsirRzuGO1nRtx/z8LqPNMaPNKU5N0L2MLbsxoTQFy9lSKmzWkpY9adagCivv2WVPLiyxb8k1RJWIKQhbnZQiWdBTWoNNilQW8p6KltRJEB/z4WqHdxvE3Nug507qSrda5mAgdPhyN6tu3Wyr116lAyWwa36//hju1t6oGr1hfzzsHgRFd+BN3WVV57Ywujuwz7hvwrGR4LL13oJud0ECwcCHSP3oSey0pr80ozt3FeUKQsoU22PKE1ssPnJGggytcEcn9PrOdrxK3pyb9/z8x3cgw4ObJZ92YiSHbx3FdEOYnvK6VjQohMu/1SQXs+j8GKUwSuHJNOcvMXriQcqNKd3eDBsjaqA81sOaShvJQGeBapGkRwkU3YsXMVVJ/eAJUJnmo69AHjDnVoRX25cuUT98/JroLzY9YWeOcoWwcWmhzjbjEaouB22aXhymoeH8xORPsPnAY2AN5y//LnN/Cas1vzV+lr56hTzSPHjJM+oz9IpgO1xRwagkLZckBb4PhJwwWWELw2Pbc4zJ9F3i+d2CBLQRfueKwpoRZ154hS//P+/Hh8Bit6XtR9iyoA2evRcvMl/M2dyc0m6/nTPJoaLni4+30n+QEgRx7sy0xlWlQGmMEcaylHh8YnjUlZK5rwq5e6Gg1ICPJKt59EhHZTzZB4rSQE6ECO99WrHTa6rK8pc+XTHRUiUwRuB/G2P4lncqUoLUdqRlhyrHA124LKvrgrBsycbgY0T1gdh52nmLKZ2w7KlB0b6w/O7ZzK++qKRasKKMJvMOU/JNoxIU/ErX8lG/xqFw8xfqtS9fHzP/4fclLi1U4hufhImTQM9WQghRoPiGP9GI0K/SqAxKe5QBpaFrO4qqJHeSHd/rDH94ZkTfBY6MFY8c85jek4KjXQot/hXG7CyKgdL4LNZeBaQxPCwbycJbI9dWSVBcKoUq5G9JS+O90oqmWVIXNfePnqS0g75JH4BM2wZevPrrhFIqWe28YTKuKWrDo0fmaAOth2cuV6SQ0V3E+7kEXFZT2GoIQJP0lBQWEHiTcoMAq5IKTg6RGPJA4CFZf6014ehD+MkxUkzsffRpyguBvuu479NrypFeQ0IF9iuwQ5mHpG/HGOnziyESO48rHbYq6WZLUhewo4LU9myODN/yDiGRUEMlXQFh2VHqDp2h7T3GGtzYMo8lL7UlMUZyhGw0blySc0v0fkiyGJTOA9x1CLKQ66ELi+0j3c4S0kj6CI3CNx2hD7y482skn9FO89jRGZPNEaYOuLaiu9LjlOWB8WdR2BEx97zif5du0aCp+PjuJqn1WBN57NgCV5X4BsojkjTIPtLPe1Rd4CorCZkkyYZqY8Ryd8F0uceJNMNNKszsLP3sg5imwyhN9DKv5j7CkOdQQyU/9B43iKkqrXlgumBaC6tfUQh9OQoRIx3468OyIzQd2We63QI1GtN6j9aKoKAqHHm4po1WfDwcIYQgOm3eS09JjNi6QCUR+Y5Nj6kLQudJQ0+kdo7sRVz18qLg7GwbVxac2OjZtMI2uve8wl8pGI03qeJR9NywPKv57WXHx8MSBdSjkgdsSU4T9LESV2qUKzh6tqXoV3pvDh0VsVd0c8MyRnTl0Mekgm+Tg/MnUc5xOcNPNksikHPEp531++9Tz+6sPnVn398q6LlxGzfOxgKLOzzoeyOIecPesFdjn7hK0SowuhcA3ut9tkPmzspqxoNWQrfsiLMGuzUmNZ7y1Bbu2JTcBZpnz0mFxmi01dQPHKM/v0tcCEWo3agpjm3QDxnUO4HZKoSqc9kLI8xq3RQi2RqKcU28OpfmfITZSa2orQf9CglupDrCkM3UShObFrTCHdskLJYYpQg5YxRkrciIqJ04XAKdUDnv03AraJ49g5lU1A+ewvee9MqOZH2VQE/6M1chJaqHT0jFKCbmH35BeohKi9ZKml/HFbkqsFVBmLcowIZEAnyI6NEEEx3JZ4jSKJ+dwReZmWnBOZq0pFDDMY8LzNYEbTR9uyTmjDWKsqhIbS/9JzZRjx22ALWnpDei84yPHiPnxMn7H+L8mVc4euwIZy+e57lLc05vHefClUvYouDY0WNsnTpOs7ekqA25T0zc0LBcFhLslFaCjXlHMgqdIU0yZlzjXM+ls5c5/eBp0eJoPRjJ3GatcHWBcz1OJbB6cEgTqqqY58yOV9Tr4ojcWz9r0KXF1iUbLpNCZNk1TE5urWE42lnisiPnhG87ylEtukdtjykd042RVAYGqOPqYe1T5moLSl038GxicyxhtLvDl+rBYbZyuvdaqVDWVmCbWisYHPGshHHt1FYlkLKBMl7mAekFs1oT+zA0/yeWix5Pgaoc9YZmst3T78xRMckz7qMwq3eZVFgUiW65h+8CMSbsUJEwgI5SIbPTWvo/YmJ35ypdDGxtbGK0lQpWCtjKSBADQDncT09wNT60KGMophv4DMonlnszdE4kKtrLis5H6qoS+GflCK0XQc0oMDRvoCgsboC7xqHaKOx7ku03WmGrEl0JW2HqA11KvPDKGeqqYks5bCwZVRP6dg8XLXqoYCvUWm9MDWW81f0KTYeyBt8HXOlAK8qNEUwRshKlUCmyYYBaoZzBt5Fur2E0kqdDKyF78G2PVZFCZ5TTJCs9mLa068dOF26oegVSUEPQgQSCSLUjtP26cqGjFVhyTKQ+iGBpDujSAgE/X0o10mhyb9CFwYzGuMkmNjiMcqhsiI2wRTbzoW9Mr4JjhSpFnqEcV5K4Wp1UFKxyihF6j7aG0faEkVaUYY7pWmLTkMnybFFhypGMs5QpRoX0Hmm1hrvlgT2OnNEqUlYakGBo3asRIkkrslGUW2OK2tF5yHONX7aUdYExBmM0adFAVWBLh99rWGrQyhLnHp0zTdtRVSW+6XGFles0aN0ZZzFu1V+U1xDevg2kYotoLW3XUHYd1aSirsfYooCgsMpCyKQMrc8sg3Cahl6R05B9yQPiQUNhHIVPAxGaRIvOOsgOayAq0Y5TRmFCplA1eAgxsttKxVrs1j0yh9u+U3CtkOknzm5Vm7n9uvvHfDfHfrfnei/crzfsDfvf2T458Lnrq733MmBabTaBTkDINGeuCHtYSDAqKB8+Ts6weOYMuenJRnRIitPbZKOkcjSIpNb3HcFqjfa3prxcT4jXBGoHSmQ5YyYVri5YXr0ivS/DglYbgfVlCPnAhRh+iLikIRtD3zbEtqc4vkXz0gVxLJQipkH122ghHlDqGppsUKQ8qG+HRPvCRUbjiumj97HsM/HKnBiTaB0pTTy/pOsvUT10jO7SHvSW4tQpqWqZYT8KYueJuwuM98TO47U0+6uqZNm3jJ1AM6zVlNqRrMFNKmwh/QXVlsL1GT0usZWjb3uM1tRHt4QtzgfpubIGXRpUWRFyxkcR54xLj5nUxKbjynyPSkUuXL3CxYuXWfaGvVni1InTnDh6gvGJLbQV1jqjFX7RockUGyU5ZRFlTJkUPXnZYn3EHtmUewCkKzuo0nDk/hOkZQ9VxlSOEBNuqAgZlVAajLX0bSdwq0Ic1lGhmCRFqTN+2UqQaTRuUgnTYBTB0G7RUmyMWAZIfcR7jysLYlAUVUldOlIX8H0v4pllQUTRhYywT+w/lX7oEckp47S07og6vGU5NOjGG7IKhw/ClehwoaJUO6ymDQM6iDSM5aGZPgmVb0rQJk1ioNztgwRHGcocMIWI/q54B7R1jEYDW17q8MuOZAwUmiLKcfdLTzAa1QWhWx7omEdVAaX0s5EEkuZj4MUXXsQqQxt6Yt/y0Kn7SbMWXZVMqlqqKXUia2Ha0rmUSonW2BToU4+JGW1rYtcTU4+uHTlHYlIYa7FZBGANEdVGYctSBmUNgcTOpT22tcJWFTkPlO45YXJE1yVs1gidX0ZFoSJuuwWXL57h/OUF09EY50rGWyNC78nG4Y0jhCGpAuQEpYniGJMxAw29HqQCtBEB4VUvU84Z7RwpBHGUmyBBVpdo9npSVMR5LzTdVmOrgmyhbz251Iw2KsraitBrXaCdxRWZRCD6jDWWdrFgb2eX6cZUgsFZI2xkpaUn4wqFi4pCCUmLGdWDgGzEGLDTEdqX9F1DKjQhaRIauoBvl5hiTJd6fO+pKkfuPdZBjj3WSfYha+TeGOmVijHiykKaNgd9Iq1AIfOCKi2lcdRmIkQfK1Y6rXAbFZONqVQDkV6rrBIB6c2MJGF2c5bko/TohF4Et0snfZiAHqrrSiv6vSWmdGgyk+2K4DVuVBC6oUI8KslRrkk0Cj2QtZiRaHuNVkF0iCLvUMm87C/uUJ84gm88GCNzQ8r4pkFPjpMaQx8z3hjUeEyPossKP7yvDrIJxfX7THR5lkPfahczfUioDE1K8v4aCH+ueTEO2+hiImVFiJkmS/DYHd71c808drsqyg3z1F3ZjfPfqwmsbr707R2bVxPEvbp13rA37A27ld2joOgW+LiD6ZNbVHbuene3+frolcB9M4itZ5kV+sFjLF++zOTRk2hraJ+/SNhZgjUYpbBHJrjjG7TPXZCqidaMT23xYFeiz3rKlPaZuV7NYSlFDon+yi6p92SlpUdmaLxG6aF3RBEyA8WzBEbrQEtJdjLMllQntrDjWt5dTStZ6XxA4FApVEpC2ZvzQIIwZKnJqL0Fiw+/xOjN91M+coK9ZYfxwkxVqSn3bX8OunCk81IVUEel+hS1CBbaPMSxZUa7PNBiJ37fPc+zk/MorTh94RztlZcGCuEeVWhizhw/t2QbKKqCalTiJqX0z4SIGfqp7JDRTkmy6SCitB+/NCb3nuAjXeoZndjGKMmGXzp7js2tLdr2Ph46dZoyRh4oGyYbE1QWbRFdCIwnJwms7jtVcHoyk8zv0EdFzvgLe5L135BGYKUUqe15/qXEstgmho7U9ujCYZ3lwaMNZV4Se09l9rPRSmlhSleZr3+7HgR3gasNfuYpNoXVTsFan6QalVztNT/yO5GAIUU1UO867p9m/sLbVsFBi5mIsuuzV+C/fnSoDhxofPOJoa9E8TkPweeeEurbX3ux44fP9cCdiw9mMjon/sKTmpMTRdtHfvQPDFeboSI5BEWx67FDM/lOk/gPHylovAgzrnh3j9mer3+zwLR6VfLCpbEICBtDYTOLnTm+bAi2w1aO7WnkSLkDRnM+aC4saim3FQbnBI6mBvpuKseJ6dugG/PK2TN8fLYkTR0bWxu8fZqxyzmqMHLMpQUDRfU/MbFDKUf0X0K2IwyBh7f28HmGKUZ89HKiW/b4ouSjVzZFIDlLX4e1ltJEHtncA6PY6wzPXa1Yzjt88EzHIwyr3kHIVrNdBx44FlG24/ISLixr+kVH0Z+hyJc5WRY8UNS87WjH5njK2FrKhytQip96ruDZ32IQ8pVnSivF1z+pOV2IY7q+rUa0cIyzQp4SowgQOzOIi0b6kHhhsQ3O0e4smF0NbB3fEArrukBnw/L8HNVbtJtw9GTBm08uWE1QOS3IIXFxJ/OHl0ekGDm1FTl5ZMxITVixkxkrQrZaa2qteWSsSKpf9zCiZQ5KPsgro+p48dIRdi7PyUrhvQQ2KWdemH2AwjmM1TiXyGh0AY/UlylGhTCuock9FA7edHRPYIo5S//KMOZSEkgjQ6VeGY1OCZUteiwJkzzACk+lzPG8O/RtDjplIXKu22Bn6Siqkgc2l4zVktB7+q5h6QXe6HpPMRDYxM4PfXYSvBqjsU7zlqKTuSm3fPzShKBlXs05EWMeElxZIIpeqrMqQUpRhGF7jwpSWTaFZdY7Xjhfoqxh0y45MclU2xu8dM7zS88L7FSr1XYhxw5Sf8PYb4eHLKP4+baRnjcgNqxffDre3umOy/VkIoLmSF3oTlR29kOLw4KM1+LuHwZV+9QIH27KnveGvWFv2Oti9ygougOn6uA89mogsDdLZt+wa9mRThkTM3HZM37sNOnUFLs5xoxL+kt7tK9cRk0q8rxDjQuq+47QX9wj7izQWmOPTqgfPIa9IPo65la0c4cd/lDoWWfuc6a/tEfftKKBogVnn1AYbQYIgjTZm4FzXK2IF2LEaBFI1cbRnrtMff8x3Ilt4uUZOUdwhQRGw3pqoMm2Q2CUcxadIKdWbSWE3SXz33+R0Z+4jzguUbMWO6rAjLGTDUIUrZ+chTZZp4jNmqgsSScK4/ApoLNkoYNV5PGIvtCErsdXGr9pKeuCyowBuLy3w9GtCXZUoZT0lITOC8RjoHNdseqlIPCqECL9skHPNd4Y9KiQTHRZ0jZLVMo4RMSwazpOH7uPqCy2qjg53hAK5BAgROKgiYNRBJXpuw53BLSVAGwFaVPbFQpBgikjBBZ57Ki3LYurAVUXpHlL37RUG2MMicJk2ix6NntXd5lsba4hkZCp7b5g5aIQvZjYdiJYqSVjba2Rc0cxD0qCGrXfJ9JELfebTLU5XtOm9iEx8xJUC0W5GhzjQRkecFqzMdLilGtY3A27All604xmUsGkgEJr9HpgD31wfZCAVils6bApM/eKLg7uzNAEPtYGXVuU7wlNwmcNXiBvygiEqbCGYkOITpRWpKX0g2iNOPeFEdiYVoQobpXXmbBccPnlj5D9JilF6tGUOCl465s+jeryMyjbkLVCjUuWrRBrJBMw2pMagWnmQYOlXczYOlETsuHqlStMx1soa4TaOoMZ4JU5Z+kdij1aaazWqKzYqEZDP5/AW5XRIhisoKgdzgWy78FrmkXm4sULTNNl3nSqYDKZ4JwjGI02ifpIJQ51yrRZBDhzlmc2pYyzQhqRQlo7+ckHaf4fEg1qpWdgYKVtYCpHngfmV5boqiIGhRuNSdqJYK4rWe4uCQFsUWAmNeiIiQuhiWfQEvIRxwRciakUuu7ReilEKcMYjCGhtSJqha4KdBbYbooRVzohirBKxKkXDVplshmjJmPivEUXA5lDVQjDYEhDv1SimNbQNezuXmJTTeX595p5s2RrPKWYjkQg1we0Fjp5YC3ejFHSU5XtQGuuBOY49JbGKMxtRgv1PigRZLUaF4cqnDNCDmEiPreEHLh06SoWzfHjJ7DeobBCvmONkIF0gZS89FnZQbtJYme5Vl1ElQ41VERzzhTHNgmLlnx1TiaTxiW5jxRVgbIRMzDopZhJpsDPO0aFxx4vBybPTBtu9lJNh/xtfx5oWQ33fCCaOZgYvcXLPLwaOMgf9ZDgzo4+H/i/rLWC0918jcwf/avzhr1hn0r22oOi281x1xeRrofOXb+t67+7md92U39OdtjkzCxl8qigPFISTMKNLd28oXn2HO7olLDs0dZQ3XeUHBP92R3IkJ2mfOg4WWvmOaASLDPkW1XErjOjwBmBVDij8Bf3WH7kJaxSJGNRqEHjZ6gerPtApM9jRcetciLFSExSvVJa01y4wqaPuO0J/vyOZD6HLLvKoGIkakOhS1QSRrfgGxEBVYqkkP4cNGqRUHuR8XSDthecexsDbQpYbaEymJQJnbAjESMKcVRjzqiQyS7TxpZcOGhaqsrAdEypMv1yRlGKzgXAifFJyYTOlqSccXUpkJ2U5biG6yAN5Bnf9TRtS1UVOG3kWhmNtSU6RMCijGRsT28fo65rVCW06q50mOglv+mMQLS0iObqwgoFuMvMswLP0IslLHxFbSjUvnpDTkkgdvUYZgKtchsjwu4Sf2GXmZ9jj5e4yRRNZPPINlJalB4htGbeDAK7ClxZDn05mVknDfcKy3SoGhmdmLqMzwqlJJutgMoqlsmglEH51TMDbVCs1GNXYp0ApVWUVticckrMvPR19HcN2xcR2RQze0uotaLrIimbA+M4r8UsF6Ity7yXIJcsTFhjI9duUmm0UYDFqIJ+VxM6T+EMY5tRGsrK4EYCZev7zLLNUvWYltgIymqyNoSksEnTh8DHn3sOnaBOp5kUls3phCcffAyzNcJq6fHpc2C0tUkOkcXOLr7ryCc3QCVUzISwJBkLuUeXIzoP3gc2q6n0WwBFqYlLjwqB5DQ4QzEy1KOKnBNLHxiNrSQ/BkY+UzhQwgInBBsdoZdG+RB7gu+ZFJaHJic4dtwNwaDGlx39osX7gDMlSkGlM9NSyu/LXp5rFCwCLKIhh8zYJrIP9DEQbIVKFuVBt0uquiD7IL0n1hBixNlMDh0acJVBJY8dFfg+UFQOg2jZtFdmzHZadqdCXqMGXTAzKYnWkdpE7iGEzHw2BJko3Kik61rq2mHtwEaXBticFirrlYaStppsFH3TilBxUmSnsYVcF1MV+GVL6KQPSBnp01IxsnXsJOPJiG7Z8MxHPsJsPuPxBx5hy1UsZ0vqIxNKNzBuDgyEKmVCSCRTEIPMO0Zn+r7HOqkGm2qfdl6ZgeQCCVK0luBYhUzsIkFnptOjGGs4euQ0fdOymM1Zzq7ShZ6TjzyI1o5kFSkIYiC2ET0uwCi6pdBzB+dAZVQIWCk9S+XOCXzVOdCTCp+hD4psNNkqeg9mXOLbIcmUJamxGqoOxUTtw+H8a4Zv3On6f3Qd+EOrNnfuEtzWDoMH3i7guTdX841OozfsDVvZvakU3WpM3aMJY213MAlJib8V5ing68YNj2wo/LzlD35zB+UqERu8NMNsj7FbI5YfO0vygq0fP3ICOy6Z+8RPLxeEKM2mN/Ze3Gz/cHJS8JmnJ3LIvWfxWx+HthOVbwZo3MAIp9UqgyxMczFKIKOUWit2i2OR0cYItrzpMJsCOcqAHjDeKSVwDqccD29/PlaXhNjywpX3E2NHGpwK2h6nRtx/4gtwZkSXZzwz+SDGOio/wviEtkmodlPGOUvo2zUsL62wOaVjl1c4s/s0LmaK5HnoMmSnqOqK6eljQuPt5eoZpWi7lrqqJHOOUDMLXM7RXd6lPrIhekcpE7xnNB0TvNBW4wyx83LNnMWMBnhL0zPe3kQ7Q+g9JmWKfskjR+YD45Oi6VpKY1HGkEKk3Bjxe2ciP/6bdghKtfTC6MznP6j4k6ekcqUQ4cvkA7nzInrrI25U4o5MiMueC0vDlcslprA8cmRJXfYkLzClnDMxJf7j74vAb+UUf/kdmmpiWPbww79vWHrYqOCvvBOKnJjayP/9ToW2VvYdxaE5s8j82/+lB3IO1jTsUQ4UGDRpENjcO05mvvABgU594IzmX/2m3DZ/TeXz+gzEjdmKjAQ5SSn+vw8ryeBnQydswINArPQSNEHxg78Lyy6TtcIP12+7gr/8DoPRwrqoAbRmp4380isLYh95dBr42ieNbEpDCqLd8/QFxX97RgKwz74v8PmnGhbLBVf7DXbzBmfOnWV3b5fLVy4zHU146/3neeLEgnJU83KzwexSOQSWEbs9ZbFcMnruKo9TQLbUyqIIhOB5Ye+DxKKW89abGG9or85RVipgLnseq66ix0BlMZMKZRXSUyZB0fYYNvwCZaTRPw70z7YsSDmzt7vH2FZgLL7rqNKch4qWjeObTDan5BSlq0EpXCU02ItLe9SbYzLwFY+VZG2IMfFjHzG8uAsxZn78aYFDWQPf9HY4Vjsymn//e5rdPlHpxF/5dCfVkYENLoRIQeSR6VWMsWvtqKwUy0XmxdkGXRcIPkgF0Gh2W82snRJCop5UaKcxyYI2ooUUMy/sZZJX2KKknFQUXYVfdmxcucDRuqesS4pSgsyVMDFaYYZkkkFjRo7cKZJVuHokGkRAaHti08l8GKOQQ5AoigrOTGgy5DRhtBOwTUtzdoOL5RaJLaqLPU+c6tCFEb01mWBZdI6zzSZ91+OWl3loMhd2ays04gxizsoZNJLI6buemCPFBcXozJyNrU2snZDNBu0BVp4Ux3S7Dt92XLh0kTPLwGhzLBC/YgKdwAXZEVbLft7QJ6H+LjZGWGeJQ/CptMK3niK2PP5Eop1dItgxL+kNstbsXmno0jHyfDUfRIJCpBOiSDB8mnM8PC4B+EDX81v+IGROXQPBhX0o5orEY3+euLN+xP2Z5H8z9/te+zd3ZSswoSTXcmYQSM5rSY/rbVWNujbYOvyO7GMAPjnEFW/YG/bJsHtHtHAns93tJpCDvtn127td5eg684DPQwJVgeo6Fh9+EXvkPtzpU3QvXgKjKe8/QndpRtxtQCmKkxsUJzfXu2pTJqxgaXe2a0Cc/8IoUudZ/uGLpHm7bnBe9ffkoQ9DKTVkTRNCEpRIyq41i5IWOE4KHmMlYxtnDeboFE3G1SNiUaAKB70n+EBhHaassRTC1qU1uqjAWZo+oEclrpxiRxNyUGRlKJaRFHtCMuhtReyD9PgYgePpUUkxrUl9JISAdxpXFiwuLTDJ41VGTwqsgbIs5LsLO+gIOENIicoaMolFWlIXpcBIUoIokB+3MSbMGrIz9N7jnMM5Sw4RSktuvbyzUyIuO1IocU76j5RWJLKor/cepcAZUJVm98ouOzs7jEYj6rKkKitxzgtDE5X0pwyaLjlkQlIoa6S3wUolSithMwSNKcx+BtZpoi0wrsSHIJC6Gsl2Z8n25Qi9cfQWlEroQiodKivaCE2AIgyPvVa08yVlXWL1EBiJ8BauhcZnYtqHTq18l5VAI4OeSY7CKjYutcDpgKU/7Dm+9dO9GnIrHZ0OvS8su+o1SCvYZsb3gdYblj6v+4xAcgC1k8rpan8pytjqYyai6IfePbNi0UtybD4m2iwQy671WJXZ2pyw3HNcePkc/bKhxvK2x9/C5mjMA9sdo7GH5MF3JGVRhSZri0+RydYGG1uZnefO8PCjD6PzQmCTOUMBEYGDUVj8TkPwSaonCrKPmEJhJwXZKJSFrl1w9dJllNFsbW3h256maTl27AhaW3RlhU1SG3LObG0LNC6GSOo8I2vZvv+ksKUBSa9EeyXQdOOKYjpCWwkCtBoCdatRMZKizCNdFKfIDqxhKLDO0abMss9gFcF7fNdjBwgXPhB7T1EZch/QnVSMtVFUGxPi5UQIcRCAzSSjwFqyUhRjJ1TnA9lLu9eglaIYSbBjpmOBkGpNaAKpT9S1oy6lkBo7jzJago6UiD6IvlVO2MJhGCjHB7ppW9ei0eNFwDl0PRSW8VSgpCZC3huEYLPi5In76duOZeoJQ08lORCanjQLaKspN8fCFqgnRGUwVU2RKrANReFwhWj7qBXENwhjX4wRnwNFVbGxsUndSzVcKdYItPXYyZaNjW2aPOehYyUXyxF9n0g+oWPEd37dY6oxoAzGCALADQxyxhqpGM4bVIZ6olGdVOa7mDFVIQQV0xEhyoGYwpIbL85tSnRX59hTR0QTaXB1rbpxDjjceT7MXr2z/EkLkA7GcndR6Xl9AoPrQXOwEuW40/1JklXWW20ppcxKtupGSN5tAtdVULWG770REL1hf3zs9Wefu10Smtt8f7Pl72Iyy17hZx3VsWOMN+5jMfP0uwvsEPx0L12SF1lhKE9vY3xGa7BhcEpucRgHzWhFZcWZqZ3DdJb26TOkK0JXLexwZk3FbU0hGUetCKlHE0gxkJU4hFkpgbkZQxqgc7YqIURY9jT9VXogntzG54ytS6rWoBcdpRV4WywMyhW4zaPiHJJRRU/0iWQCwfaktqc3S4GPOSOq6XmJMprgDNknTFFgSkeXWygh0GOMJQfPZFLQBAskmr6lProFOdNdnZN8wFgnfQNkdF2wOTLk4LHOoJwmDCxwi2Uk9FHEPn3AACZnwrzFFAZdWNplS1EV0hhsjVBiVwXaOcH/h4wnYbVAq9psefYPnmFzc5Njpx+kqEu6+VyghCFSWMuWE+pmeVgGMdWsuNxklHaUXuG0IUaPyonSCMzHjApSF3BW0SMN7KEP0pcwLsgxMwuakDLJCKRPKVDGsOsht7AM+49xyrDTQmkUydUo32OrYiD+EJYx8ZPlaSwMbFT7EDrJCktTNkjWcFzq/T6S1Xi4BgZybU/QYQN2rQqvJPCUISFwuv1tCzwvxUzsejaLitIoYszstLJczHClkd6XfRYATRNheyQu2JFpCXjpE0GRoggYGwWbuqeJLaGL9HECSREWgaP1BsdGWwLRdBq8aP4sW81OO+eVkPGlYzSeYJ2lb1tsMWaPjrh1jEU1YWJbVCtkIklBCkmEKLXGNx318U2cTqgQMUbYElOOKO3YPbPLolniExTHtmntmFh6cGNmqiKHvKZiLi2MnSRB+qalW3bUoxHBFvJMeKhtpi5WvWjAwD6p9BCcG828B59F2DkqgSIqYFqC1QqjMtYMTlJObLhMxFMp0TyzdSm9SL1HDYyQxhr0liV0gbkXMduUDBsnx4zbXqpLwzEppYQgpLCkBL7LhFlDURhcXRL7QN/Ocaok5YSxFUo5tLVcvbLHSBcUVSmQLgVh0RJ6TzQi/lyNa/YuX6GsLS0Gbxz9csHUd5SVoyg17WVPTonN7SmzIH2TJmZ2o7Abrp/3QoLC1HSEGDHO01UddSUU4+3uEg0sLpxn9vIF6d8petybyzVhwWrEtEtPRmjBY5Oox5sYZbgaYLl6pvPB8XOt5emYVi/pri6GYBJCF8gGXF0RvZd1C4srLG5cSbJIC2wZHdHCsCAoAFNiSktKBbQDYUQIWC1w6+QjOUZUyqQmECpL5xVzH1kOPZTtmqP8WlvVIWA/8fJa7eA25dP+XPQJIxXIN/n8SbGDULl8IKy51m4XQGq1jxSAvJ471kLbd3JNV8X+e3Wz37A37I+gvfag6Fbj5+4q63e/3B1a+0KN12PRkqgMsVsyesv9KKNZfOTMPgNRaQmX5zxsDSYr9lISnaBVNmeAFNzs8I6NHJ/74AQyjPw2W2eOcsydZHfjRc7Nf18gIgJkR2nNZv0ox0aPoXLm3PLD7OZzqE6ajmNVYLQh7s0xToIKbQ0qJigLUudpz82gLnnp0Q06p7Da8a7Lb6caaVzhRFQxZ6yteXT78wltR8otz+y8Hz12+Mrz3O7/JM8a0bbIiWQNWXe85H+LrKBZekauIHsIKULOFIUjhIAxormUNVRHp2ANk0KEK/2sIZUJPRkNTeiZqi5QSnHfRsO06DFVQTeX5Yy1vO9/vszRU49QlkYoqHMidF76jmrprxgfmQoddgY3rcmhkGlfKVRCsv0hkS10tuIjlzVq+zPYU4bZnkIvDKMeHj7Zk0PizUfg8c/R65d+zgL5+cDZzL/5TVAG3rLteHTiwDvu3+44Uc+JQ7+RLgWW8pGLjjaOKCqHK0uWuzPKrQ3+09OKc0vJ6q9Y3bsIP/p7Q0Y5C0McSvpvfvB3ZAAcrSu++dMdmYxvOwkE1wQcCpXhwc3M1745CHzOC52yLexQXZHKkbV6IFrIpJClf8EeDJLUdT8Pg9WtnBbW+iyrHiU5Hr0mk1BKsb1V85ffKQKVu53i+39b0aPYaeH7f1ftB0RZrvcDG5lv+bRI6j31tMYkQ2x75r7izHxC8pFjk8CfOflh2qalmj7MM1e3IIrWkRkP29RynbNWPNe/jZde8GjruPrwKdrpiNFkRA6RZbvERod7suDi+XNUzvBX9AfZzLvyHIUEUZEdECPl8U2cgcc2dtFdJ4mDKA323V7g8u8ZNrYeoqsqfvSjzXD5iwOXdLh2Ct5+HP6vJxLnz5xlazTFGYMtCz7wUuaXX5Dz+OLHNf/nAyIw69ueoi6GTL/MPyll/tvHNR+7LJv3Saq6rjD8+bcoTo1EANbkREZRqMzXP97TNh0YzXQyXt9XY0WIeVVxzDGxkwve83uZEDUn6p53v3MXQsQ4ST0rNeSks/TLzcKIF2cGVTtcVZD6QCRxciuzXV/ClQVpx5B2StplR/DHSWFEcA7f93Rti9YaVxRCYW+Ertv4Eck6fmvZcCF1WJ35pjd3THJD7BO7Fys2N4/TnfP8t+ViCEqEje16O24Mf35Z4dsWM0osqyVFYSmnI4IP+EVL9JlkHMY6ylNjbB0kyEiSjIi+Z2dZcq4bkYzitC/hjGz/V5uWP+jbG3d8iBkFX6XHTGcdoZO+VgrLWBWcOzUh2mvfME5HHtvchRQIpiPZjtR0xHKDj1/dQhUFKYnwL1YzcZ4T+ZzQ+28c5yU9JrWenXlkGY5i9yqeWbb8wXIBHM78thrPN7cbs5h3HtS8thf8/46MbNempfYDxBu/z/tz8aFbuT6oufNrJOy1//tc0z9K9oM/+IN8y7d8y6HfGWPY3Nzk0z7t0/hzf+7P8df/+l9nc3Pzjrb7kz/5k3z1V381AFVVce7cuTted2Xnz5/nh3/4h/m5n/s5PvzhD3Px4kUAjh49ypNPPskXf/EX843f+I3cf//9N6z7rne9i1/+5V/m4Ycf5vnnn7/pPs6dO8eXfumX8gd/8AcAfM/3fA9/5+/8nbs6zntlnxydotdih43322R7cgKUliABKI5ukFNm+ew50SlSilw5UuEoNsfoxdA0u56l7izXohVYrfFX57RnelDb6KJEU6NSTWiliRmlSVqBc+jxGB8iXa6I8yTwOsAw0MMWhdCGDxC2WBsR8gTcdCRU1ssWX2pUqdForBbHIqksvTopoZLBFJbYZcqjG8SuAaWJKqJHFoPCVwV+scTYEmXAp0j0PdEZEglVWdEo2hijg2DT7bgWp8pq4qwVZfoYsVVJdg7fdBitwAzitNZgnMEWhth2+LZhVFecPXeG7e0t6rKE0uHbHkLCjkRIMy67/fvpDM3ektGolGx1TJJBL63ABqxAlJZ7C+pxLWx+RvqFfBdIRhNjwtUFKkXKYj/0zSEJniRE2kYIGkLWhD5i6wpVRIwREV3jHGqg255ubaCCMDu5acXIajKaANeSGgwPkT/EcRMYmXzu40A2kQK7V3Y5euIIutDD2zGzkgUqLJASWmek/SgO1O4SHCgtPUZKaZTJA7nBQYfidiXc6w9dkfXw4lVqIKdI5NV29X4VC6NpQkKhSD6inaGPDFC7VRQqFcTYznBaY0gEL4Ge0MdrlNPs7V7m9HTM9NRJrsZNuq4Y+rUCJmVUJQKafdeSnQJKptMjLK8sePnp8/TbYwpnKa2wIXYzjw8z7HSKtpEQkwTTaujJSkluglGQklRYfY9WWXQ4tWK5WDDb7bH2CKN6yl6K9HEdkx56WX0C33uOHzsu1QwrfVIJRZ9k4ZiQ6pBWlANL4+qL6D0xZnpf0IUhG5wyZqAkdzpTGgidF/KE0onIqFNoLFprws5CqmClRduBbj5EtDWEEPFNpO00URtiBqMGodaVAPRAZ+0bYQPsdgNZHSH5QD8I0gYDalywefwIWikWe4p22VIVBWY0WjtuZVFTFvW1F0mYZ3CmJKZMGP4pwNUl01FBCuCuTMhe06+WuQm1fM4ZnzNGacrRCD2O2BPH6Zolzd4uJoNxBdWpKWU1QVtNMQqQZuQUpZdQS8Daq0yvFOPRGLWX13pPIQtke+2y5+tu/QGvNymFc45pWV1znOlgRWYIOJXRogPW96RlI0mpSYGalix7Qzfv0aVorMU+kOeRrugojpdSBSSTOk9YduhRiaorUlbE9fHeyq57eK9tLDpk6evrQLffej6w5N045Lda9l7A8l6vPprbAePuFLJ2b/PLmRgTOYO1+i62/oZ9IizGyJUrV/iVX/kVfuVXfoV/8S/+BT/90z/N29/+9tuu+573vGf9uW1b3vve9/LX/tpfu6P9ppT4R//oH/E93/M9LJfLG75/+eWXefnll/npn/5p/sE/+Ad867d+K//0n/5T6ro+ZGs3t1deeYWnnnqKj370oyil+H/+n/+Hb//2b7+rbdxLe32DojutIin2Xxp3O6PdLiACdnOmTNLor7yhAPrLM9JLV3DaCPOX04xPH6Wsa67MelTKzNPqBbd6GcgGLYpNLbCipCEMmb1JUVKaCf7SLqYvUSO9FmS1x6ZYvUF/foktRgPdakkoHNYYRl1FMhswFZiUtVaYnQSaT1AKHyMWKKpaegGWHTF0FMtASJrSZFJa0CdNagBnsVkyt5rMXugoHOSkMFkRdhbozRG5LkApRpMakzK990KZnQ3TrYrpxK3JCvTQ8GtsTY6RFBpitqRgiCGQu35QrgerAkr3wpqXIBtNObKELtIqhc+GNjtim1n0iuNHN4dsdCCPNaashAWqUJBFmHAHaZjP0zG0c1LOlCOh50VJ5SClDDExrkpRss8I40bMRJ3QIdG2EJ0hKM1yT5yPkYOxBmUUdak4dUQa/rfqTKUj1mji3gyOaEbbm+z2im4IYnY8LL1k6C8tobaatKoCHfaMHvaMX4NzV6RGHFlaRd8IdXfpNCfG0i8yLuDCQmGsQ+mC3OYbsoQjm6l1whjNuIBjVcRYw6yH5lCv6LAM8bWDVSFQDW0U2yNQKVKXGpUTGbN/akqhlMAKVzC7VYXJKtiu5dU/KTVNuUmTErPdnk0T0YDve5plS10WjEcTNso4sJ11uGDxg9BvuVmTsjjzz374o7z5bW8l6MiFC6+wuzMjbG3Tdo7gAykBuxpjDd4orlza5eRjR+hoB+c2k6xGawtWE/tAMqCzYidbtFOYqqDcbSEVbG4d4dLRKZdSYicNJb/rBM0KA1uD/1vnjhwiblSTUxwYzPJ+kIhUDM/uClxqWsHIDlWZ3uMbYSXbdEc4MZKA6moj1O3RB3LSBB+YX95jvDkWHTQj7HdFVRC7HrTDlG4NhZPqmqangKJAVYnj054QE9sjQ5eMVIqMxelI7L0wy11p6buend5ibKbAEFpPLgzT8QTjei41DQB9dvjKsQAJOO/QEhAOPIWXG0hZkRO0MZNios352kD0OlNKEYDLKYlea0hUqSIXBcYmXNfTNg0+eeLuHDuqwWa8lp6nlBIhJspxRXYjEiNmPqN8pBuYcNq8P3hlBF3Xh3rd8Xmr8MN7Iw09SlmmG5IP+N0FsfW4zRGYzJVLO0LhPq2hLEVst/WifTccd1VrqqpgtFkTLGBr2jYJ/HZUEAvHbMjQtOGu6Sevv6q3/PZuAqO73/O1ax22r9caGL1eFZNbbffOAqHXWmU75Fpl1pXfa/g13rBPir3vfe/jT/2pP7X+fbFY8Nxzz/F93/d9/MAP/AAvv/wyX/mVX8nTTz9NVVU33c7ly5f5r//1v17zt/e85z13FBR1XcfXfu3X8l/+y38B4IEHHuDbv/3b+ZIv+RIeeOABrLWcOXOGX/7lX+bf/bt/xwc+8AH+1b/6V3zXd30XjzzyyB2f6wsvvMBTTz3Fxz/+cbTW/Ot//a/51m/91jte//WwexAU3a7M/jrZHe4yAz/XNiik+vJ1F+GYMfi9TGc3ycsWvTnGVhVlU7Bcen50saAZyBVi3i9kr3ydI0bzF+qRMKmVigvHLSkm6rzFifatTM1JzCRjrehuGK/xVxfUj55gmu/nWPkEqvMoYyUtnBJHq0c5On0CjMakTG57cmHRhdyiNgRIWVTRlcY4g95SxPkCdfX9NHGGcp7z6gOQESw5iuzEcTIJcooQM2Z7BJNS9D62RpKN7ALdvEFbw2hUiSOoDMe2NA9N50LFXRfSGK1l/zkL+9KVbsKluTRARx/WkK3j1YIjmy26dGStuHLxClvbRzjXHeXsnqGdL4mppC4rzs4Tn3N/ZlLN0YOeS86tVMusVHmapPm5/9Uz94qJy/y1z8i4HOjmO4Q+rNmsYkpDUCmihNEHISsYaH93FpqPnR9j90peCYr/dXaOtvDZ98GXPCz3+TPvUzx5LMh1zguJ262HVIjoJYr//gI8fXH1nC3WLxwF6zdPvJnvcbtgvlcsPzrGAbWyODtDoTg5yvzVz5BKxcevKn7wQ1lgoVngalIlWxWUMp9zf+ZLHpHr91mn4R0npQLxc8/BB18+cKDX2MEMxf7hXr+kNZmve7tiu5A+Op0lGF3nNrJEo0IoIX1Eq56qE1P4y+/IGA0v7mR+4HcgZc3jWwX/v4daIRMwBqs1zbJhcyp9X8oZtlzgyHQm7IQpEvMO5XhEvLTBQw98Onqu+eCjF3n57ecoyoJq7xTLlyKozP17nvGyx4fIucePMT46pVv2qGOGHAZtGNR+XxGgfaJR8Itbp/EbBVWAL/i9q0yLiiso/t9mQRgci0S+5mJl4OFN+Nq3ATnT7HXYYkTOidBHXDnQpUe9Zg38jRcTv/mKRhnNn34CPus05BAxhUMXjnJjxJfJBSZrzY9+KPP8zkBOgRBiTI9vDn0GUuFQSFVPOSfja4BgSiUxEbPhYxdqUtbUZeZbPnMXYmDZKp45J2KskzLw+Amh9d+bZ17uTtCrhN5b8mAIgwBphU0Wusxv9olfX5Ga5Z6cbxQFvRNbwbtCgh97et9py2nJyou7nfjn1ZT4DwNcTC2BKwCah43jK+ttSqDI8GYSqlGoBvpcrLXLrDWkK4pn+55f73ZkOwfG8P4wv3ZgH1aHzQoubWuW8wUpZ2IKqNISQ8BeKSRr33ui1vQ7S5xRvJCOiMbRXPSd7KQixYSdNOgQ2agdjx+ZY6eZRa75yAsVyYjIs5k4jLW8sNfzO2fl2A8rquWhxHXTnpIDbHS3cs5fL5/6ZvCx6/d3Y4B0i6rP6+C+vJoq072obh12HHAHwZZC0BQrBMDBbQwvkzdgdZ84q+uayWSy/n0ymXDy5Ek+7/M+j42NDf7ZP/tnPPfcc/zET/wEX//1X3/T7fz7f//v6XuZc7/qq76Kn/zJn+T9738/zzzzDE888cQtj+Fv/+2/vQ6IvvEbv5Hv+77vu6ECdPz4cd7xjnfwHd/xHfzET/wE3/Zt33ZX5/nss8/y1FNP8eKLL2KM4Qd+4Af4pm/6prvaxuthN3I23rW9yhlFHfh3/d/upWWIWTTjwmqSyFBMayaPnGD61oeYPHCUamssU23OBCQ7GYdjWvkWqw8KsEpJRLns8Od3WPz+C+z9wUt0L17FGIdyTvbnDHpSYiYVy2fPonaXmC5K83UUkUisQReF6GEYC2jseITSluwzuiwZ1SNKDCZraAO5i5JwrUrUuCaNSsiiy5QrA1ahrcI6BcGTcsAdnaCOjkiVpQmePC2F2UlrbOWopjVua0J5ZMr42BZVXRGWHbnvyT5gYkTFQL83J7Ydue1RbQ+9xy87kg9EsvQU+IiZVLitEbaw2MJw7Pg2ZlCrT1GCRmsLfBcotcM3LVqDKSzaaqFUN0ocVSPOfEJYrmJMhK5Dh0Bdl0wmFUVhUSpjnUE7jasc2upBEwXM8DdnNKoqifOO0HoCGp8QiI4WEVcdI6UBpzLGKHIMEKXHYPXiGLRtCWkd2+7/LcrPmyB6bv/YiocNSWHLUvrdvCfHhDPSL6JyxsdM7xM+ZhKa3mf6LuBjJqDISosAZO/RCkqnsULodYcmg/Jw1iKF0WAFnYhxlhQi0QdiN5ShtDj3q34YafuQcaZiHM4jEZKS6zY0zOecme/N0Eoxm8/XWk8+C+xRGwUWIgHlpAqiUdhB8LgYFzzw5IOU05IcIttbG0JWgDBDTquS5WzJYrZk6/i2VE6MEuxb54mtJ/deaKszqNqxLDVpVFJvbDAaT9HKkNMwt+RMXKVcDwREINfaaQhdM7AJamIY1DkHdsc8VIu0NWStBY4VslQDkujiKKPXy1ijsSpj1dDblfNaKFgbgaiuIVireWugo0ohEH2Q71MidIHY9ix2G+a7C7p5Q9yboZqWuFwSOo/vAvOdPbqdGd3uHF047OaEyfY2J+4/zWQ6oa5rCmfRCI1/OjA+Qpb5NCLz8Gp+vZN/By3mg9sc5uo7HGSr7fmc97eRkHGWh3lda4wS/TitLdYWMp9nDUOFKmX5F4bKYmQ/074eGdf1nh48wpwzzfkduitz/OUZcdGSWi89pMtuYM4USK8DEe8e1cQ+0FzeY++VS7SXZyhjcEcmFNsTquMb2IloWKXOExOooqCYjLCFE/2woaI2tEgdYndyHT8JCdBD7NbguWt/u6VDf8vTybdb4JA18nU/9z/feg/XLn+rde7e9vdyU+CjUjcGRLwREH2q2cEqzwc/+MFbLruCzj355JP8k3/yT9Z//6Ef+qFbrvcrv/IrfO/3fi8AX/IlX8KP/MiP3BYS99Vf/dX81m/9FkeOHLnlciv7yEc+whd+4Rfy4osvYq3lR3/0Rz8lAiL4o9BTdD3M7vrP16fiBqfkiNaUSF7pcor4YblLKd34Ej3w5m1yvkbPW7YnAdCxAQK0bQx9Kcxwey/PSUpTMqFwYxLCriXUr5ncecK8xW2PyMuWzi9p1Ay9VRGWM4xX6NKh7EBPqxWqdOjSEvca9MjRt0vi0JCbvFR80l7AjCtyCGQHSRscinnfkHNm49gmwXuatmXj5CZllXEARcWiVWxsT6Q3IGeyj2gNpfagE7jIcq8TYcQjI8JGQZw1+DZST2vspMZ76DoR/mvajnJwTDGG3Hu5ZsmT2n6gGdboQhToSx3pcotxir7vUYWiK3rKQpielFaiBzKIc55biPPiI5wYZSYqMDYJZw1KZ/qQuexLUpeHClNGGygcHB9p0SXyYf87q5iMRJ9l2vacrsWh3yySBKop0/celUFbgxvIC1JM7IbMcnheagf3T+Xz5QbawD2zQOZcjFgllYqydcTgB/Yx8Wp2Zon7JkYIFUq3fvZT0BL550TdJ/zMoXTJblTMh2rEvOPWY2iAyB3+3f7Hc3NoHEJykCFnKyxlKaE7xWJwIhmgGTmvKlvixMeYqUvLfZNMypljlQREyho2Nifs7VmOHDmCVkuyFo2cnCzdIqGMIxZjFmR2Z4q+TYQoN2e28FAXlEXNhm9g9yKuadk4coLKFGhrKfsleVRSb4xwfkp2S2LTYn2W6mJGIr7CoI3FqgpazbLtOBcCNmZ20rXuSz744fosdMqYgZJbwXqOQCnGNnG6BtgnNMg5k5Tm5b28Xkeum14HOqEPbNaGBzIYIxwQkAlNvxY19U0nyQ9rBhY7O2hnZfZ2PclHEhayVJJjC9lYcukwaMqsaVNktHmUS3YBWtGkkt0+kwk0XcLHG2s1s3x7iFYeKmuvhvHq1axzvbPZZzib4h27fQfP6Yb9q4MfBif0kEpETpm+6dFuEO4mo+tyHdhapTBO2OfiTJ57omRcctujxxXt1Rk5Z6rjm6I/pDJNLkmNZ+fSktocp7QlbZe4OsAVF4c1Mh48/Du6nrdf5vUiQrgT+Nj1FZfXdgR3Vhm7do19Qm249THvh0H73x94cu72YA89luvC8evcqdvt441g6FPNHn744fXnw/p8Vvb000/zm78pooTf9E3fxOOPP86f/JN/kve///388A//MN/93d990/H+j//xPwZkPvje7/3eO55nH3jggTta7vd///f50i/9Us6fP09RFLz3ve/lq77qq+5o3U+EvX5B0c2CmesTIK913B2yvgK+sCh52AqV6o8tl5yJkZjhv7XNbZM/17w6xBNhQxu+ph4JU9tWzcUTTljills8ot4u8CyfyDGCj2STwcvL1kwqQkxUj58m9pGzzR8QrvYko3Bak1tIBmwEFTO6HpHbiBpJRllbRVaJbtlilWSLvQqopdCAm60Ro1CjJoqNGOm6nuQU1WRKt5eotyoemFxkXDtCTjx7ccrBKVGVjnGdeGS8R+o9sxm8yBa2LmmC4ZmzjtBojmxE7nMzdEzsdCNeWY4xeoujkzmPjBtyFvYlNfQeqZzJaWC20pocE7qwnExzjlUiVKu0FsHZ09KjtIL+kRNoSx8yP/Y07LTSH/Otn6UYG0OKktXFKJqs+NGPKrpB6JMB+nT/JPBXPtOIoJ2C2HtSiExKx9jtEsueN08r/pRSkEQ8MfpIu7fAFI5qc8LOxStsHdtGl44UIv/zRfjtC/IAffVb4E8/Lo/Tf/wDxTNX7vyxvanjMPw6y5n/rxkmvSWwA2DXz24KkceOGL7lszQKLUKnKa0rOspIYNm+7Og+vgEKPth1/PpQTs83G5/X/36zwAkJVP/Th8WX3n+YFAq7ZqZDZdKq3JoGaM5QwchZoRWcGCXe/fbBMfURPPL8JE2GQbBSoF7aWeZnAvnSFtY5PtB1fKDv5ABzDwzn96ElKz3brzAFx9o5yhl+upzyoQjOZDqVGVcFO+d3aGc1ZmfMbCeyXVusc/LM+oTrKxoPv/BrF9a9I88cmCTScN6Sghku17Dvg9dLGzNArqQ6FPpAxn7iiwAAUbtJREFUDBHnLJ/5gOMdpxOh7UkpUIxLUoj83POGX/ydoQ0nZ2EgVEM102gUhm94Ozy8IVldUiIsvdBID6yaKWWKeqgiDIQFfm9J3yae39nC+yTPd07YqsBgWb7kKJxQ35/2gcW8Z6+p+KF2RU8dyHn30MdnZddPswfhT/uPl3rN74C76YO4fn9nU+S9t3AubtjX7bZ94DdJTNy4nNaa8tgmYWeGLi1uUuO2RizP76L6IFIDscc4Q3Fsk9j29Jd2SSHBuAKj0Vrjlx1lTCijWXaKj14qCIvItD7Og3ODXgY+Ejz/o2nuSd3hkCngU87k2K4PYu5O9+dmW73zpe80gDrYw7M68n144F3Rad9iLzf/7W7WfMM+FezFF19cf75VELKqEmmt+Ut/6S8B8M3f/M28//3v5/nnn+d//I//wRd90RfdsN5iseBnfuZnAHjXu97Fm970pnt5+Pz2b/82X/7lX86lS5eoqor/9J/+E3/6T//pe7qP12r3Nii6buZd4bFf04vvdm/cm3yvM+iQyPZahOCtGnJvfgCDAxuEklpl6d+Yv3iRYlmjxopsLYq4D0saIC+6LlDRiSaREba3FAJxb0HWCvPYSYw17F68ipuMJMjZrCWL7iNqELMEiEboGbUzOGeGaoohdp6icuKQWkOtxQHNZI6dPIFRkboqIUUUGe0MWRkp0ucMTUd24njaUUG8uqRrWlxZ4ectWYkTHlJPpGHhexbLwGweGU8nZCvBoJuO5Bj0QO/dB3RZQozrY0WBLq1UYQYHOXYBoy0YN1RzItoVa4xXQmAzCXGiFRnnRI1+dYtizKSsGCr+ZGOE8EGvmNekemGcMOilHFFJmNqU0SLIqBUqwvjopiyTsgjD5nyA0U0TBlxcjhAaP5yXu/FhPKxacMNTdeAP15nAXIZnL6trFsrGgEpolYkhoAI0yyVGaVxZChsZClc5uizrr6Az98yy3Jd1lSilNWV3inLNchygG2sdDQmMjLMYq9BkYowUzpB8JKSIdpaUpEE8xSTPidZr3a6yGuGNVMZufk55+E/hrOHE/UfJSvHQ44+gqy361gusMESsyui5pqhqjp66FiawzpLlBAfgkIdfRnXIp33TWkmf0rBNrRW2XNFtJ4wCM4ieppgwQ0UtJkWKea0RFXsvxCdZHDCtWQs1pl7Gmu88BqQHaVyt52J8pJ8vSSnhM6jK4U2gHtfU1mCdo/CZcubW2GpdaIojR5jFeCj06rBrsYKS7eulyP9v7zDeeVZ+Za+1MXwV317Dp6P2P9+93W6QZdyogIXBDEybunGCuQX6PlCVjn7eUEwrdLSkpkONKoFzTh3RGlyC2PaYuiQse7rdJaZyFKMKNfesOuhfK6XCjed166vyiYZbXdvDc9i+bzIJ3+G297dy785rHaSpW80kn8yw5OC9vrdgvjfs1du//bf/dv35y77syw5dJsbIj/zIjwACf7vvvvsA+Lqv+zq+8zu/k7Ztec973nNoUPRrv/ZrhCCQly/8wi+8p8f+wQ9+kK/4iq/g6tWrjMdj/vN//s889dRT93Qf98JeN6KFlBIxChuXtXb/XXd95vlO3oG3motvUi+/mEXwMsdIt/KUD27rLi2EwFUfGI8rok74vU6cQhXoxi12IkGMb3vJ9sVEMa3Jy13anQv4tEParCkqjWt2qUcKe2qDcstASlQnSumH0YpmsSBiBYY2KmnaDlc4imkNK2je0NAeo/RwaCzKWWInNLl95xkd2xhocj07OWALjalKyUKlRF45WTHhe5it9HRygUEPPdoZN6lBQTEp0a6nLixJOYJ1YDxVrSk2xuvtkgUKdX4vsoygrebERDPOAk270BqaKJj5U+NMORZmu7MLRdeCVpr7xhlHQivNgxuK7SrjNLwyA5eFyfj+DXEcnVY8sqXwGfoAZ+Zyn9sIz++ATolKw4kVda2yzDtF6B11k6iKJOQJWRz2ECL9ssMVlnpcc3mZmSXpKSgMPHZUk3rP2GlmuwvqSY2I2tyNHXjF3uz5VweWuq6yo7Kii5rndzJKOVlOl/L9UDDJQGhYQ5v2XktEdItjTH3AFpb7NsCahFKaFEBbRYjwyh7ElCXoZPDVYkL4zCXQJyf6tiMEaJPCh0BWGcuCqiioS3F+tbUslOL8+pzSTQ5u/2+XUqKMkaxgNr9CHGjvSWDJ6JQ54zv2DoGArazJmXgDUO7OMjY5KMJME1pL9i2BDls6IUZIWapKQwA0xHKkoWp6bOR4ZCuj0Oum54GwXwJ+oMiR2ArNoYgzW5y1dFcj8aoInPZh+Om9sBjWNbYaMYsV0UpPnTw3HhsyPsYb/LULKd7B9HltMLSyO3fy7q0jeHfwvHtdC7nO6V1vXqq4OiZJFhlNt7sgpyxwXQXd3oL66AYEkRtQxopMhNbE1mOmjnq7ojY9dB2jyrCsAm6rAh14eajUXk63o6C4m7MRaNjdh62vr91JsPJqA5p7FwjdWL268SrmdQhycLxcu+SNAcpBEe7rAXL7+zr4t4NkFTdC6g72xn1K3ehPQTt79uwtKzYvv/zyXW+zaRrm8/n69+VyyXPPPcf3f//3833f930AfP3Xfz2f8zmfc+j6P//zP8+ZMyKgdrBPZ2tri6/8yq/kve99Lz/2Yz/Gv/yX/5LRaHTNus8999z681vf+ta7Pvab2eXLl/nSL/1S9vb2mE6nvO997+MLvuAL7tn276Xdg6DokAGUJQuaszTHH2r3crAdnDWyZPl+te+u+fr6Q727jQvt9sVtw+XFEldIRaI8OqWbNbwSfhc1N2A0yiliDriRgZTxu7vEtkMrhb+4x+am59TGnjTInopgdsmtR29aIJP6yCuMuLKU5nRjDfVkJI3mgEqZ2HaoNFR5ct5vqm57ch+IRks1xggd8oVLV3klRabjMZublUyEMZIO4E4W88Bz/Zhu2aKiJoRAaTR5qETZjRHoiJuMUFpRbsFWGHqg1CqnvK+zkXzgf12w/K+LUh36829RvP2EwH9++WPw0ctS9Xn3k/DQNJGV5qefgTMzaUr/v9+ROT5RWDJf+SZhAWui5l//RmC3SWxNLX/tbT2jyjDWir/4Nk2KiQtLxQ/8nuirXFrAv/tdKSU8Ok584zs1yhqWvuS5HYtvK04VcDJdpbAjUueF4nfWMDoyFQ0krfntV+DXXwGy4s+8KfPU6Z7lcoktHMV0Y63bcld2p8//oWl4Wf/MXPHvfn//9XnjyxL2aUNedT7g1ocXZauFSnzNWzIbNpG1MJSpHNntFf/6NxI+5IFEYDjSAUKnjbzSoxfK82Us+filEltYNsuON5+Yo+KSrEWk1FrDR0Pg55vbn9NqWvi1vtufHp75TQ67+P/tjt39O7wu66GViQtL80xNt1RE03Lk09kXv1WKrumEZMUO9NxKo7Uh9p5P32r4P06VaKPWVbeYswRUQTRyBHYqPUOx6Wj7hpASz//qkm6euO+++6jHWzhXMFIKYw1qIRDN31gsaPPhrtSrO//XMrG/uqDk+qrUtUdz5yiFg+u/tteTuu64DtloAjMqiYPmmcoC8c3OoPaWAmMspfq/IsXIQSqn9JFcFYymlgfjOYqtETkmlv0OlC1nzRY/PqDEX/2YPzz0uddVoHsXhuYD/7+5vZrj3wffHRYQqvUyt6IKXwUg8lmtlz2o7bT67fojvH5/B9fY//ba7d1qC9emKG5c48Zx9EZk9Im0P/Nn/sxNv3vsscf4m3/zb/Id3/EdN11mBZ0bj8d8zdd8zTXfffM3fzPvfe97mc1m/PiP/zjvfve7r/n+ypX9HoCtra1XcfSH28Eg7xu+4Rs+ZQMiuBdB0WGz2oA/MCtMx8pju/Pk6rW/302Sb/icD3qJ92BMm8IyOrFJuDzDX9jDbI1AK8ppTfaBVb5auUFo1WiBD2mwfoCSpYTqLmHqguLYFFsXZB9JK60SK4EUhcUkR64LySSu3ut9IAwQpQwC0QNUkoksW03fdAKvKyyp98Q+cPzEcbkFUYQxc0i4wmGUIvVBmrCrktD1uLKQbfeebBS2cGsGMVBSURkCMukVkn9ove6XyDHhqgLlIK/0aXLa16oBCcgYNDoy5BBJfSb2UkDIWZG6IPj5FeNbEIE55Sw5ZExdkpKHPqBLJ9BDo4dGf9mmsobYejji0KVc59j1kA3luCalJa4qSCGIowrYUSlU6AcyuyuygNj2oibfesqyXLM6rfE219vriDu4vm5xR7u+kzFxWHR16DJ5rTmzIgIwpfSyKK2F+UzLmFA5rashK5p1UiKGQIoS9Cql8V2HygW5jyQbSTFglKbve9ykXgcaB0Eth57CQSzUcLh5mH/UIRdhv3C9coBuZ7daQt0A6Zrt7DG7tMOxx0akHLEDA51VimpUCeQ0JaJPkAK2lmdL+wBpgHamhHIWek9ctBAiWSuCzvRNy6JZUk3GFFXFqBjx6BOn6fYi48lEjlZdlxfOrDVKrrl2N3y6Vy7rG+7VypQVAWllDaYqCVfnGGvQOeODZ3z6CLH1pL0ldlKTFu1w74U5UFlJhOnKoQZ5hJWQbE5J+viu3eN1v19XzdzPj3FwNFy7/qdajWjfbkh8HuZHcGMV5k7sIDTvZmsd9o26yfd3ErbcyVG9YZ98O3369KuqBr1ae+GFF/jZn/1ZnnrqKd7xjnfc8P3e3h4/8RM/AcDXfM3XMB6Pr/n+K77iKzh58iTnz5/nPe95zw1B0etl29vbTKdTXnzxRf7Nv/k3PPHEE/zdv/t3PyH7vlt7/YgWbhX8HFbVfS3bv13F+FXuxxl4ZFOhVaa0g+Pe9ZitkTjfGaxKTLb1IPCXaaOSACBnYQrTmlxoXC3BxagyjLY7lDW0LSyuBswgnpqaiMLhgxIHJkh/ANbglx2uLjBKiSO07ITRN2VUXeB9IEZpvrYgbEXWYLKw2q0aL7TWaGvolq0cW4jUxzcxFkZTBwpi15N8hhwoNkqyDwTfovqW2Mvbc7dTXFhI5eXoCI6PD7w0jfSYnKgibz4iVJ8bpRpe2nCqTPiiR+XM8ipc8BpXVdw/iUxrjdFQaumByMbw3NVMHxIhwSPbmj4kRk52Y42l8YmXLst1aTw8sSkZ1dj24nwXidOVInYiCmqxbE0zxI5K9dKQHgVuaYwZWO32mcFOjOFPbEVSHxjHlr29Jb7rcdZS1KWIgkbDXQ2ne+ElfiI9zUP2pZTi0SMKq6E0YHUmLHtUXfLxS0KzvQxKeoFWvPZD4Bn6zJVdpLfMWJSS6uSsEUinMprcD2xoNvPKS+e4/9QTBO+ITeJGsuZr7fZoqcMXuDeZ8GudR2UTuurZOXeWE+VDWCfJDmPs4MwOz99Q2e3nLaYsRN+pLQk7Hh8jrYpEE0WfJigWew17ixlbR46wtX2cclNzQWu6mGGp6LCkykEIh/q07Q2QwNfTrnPCDw0+r82r37EdVib9BNs+ccqB/69P4cZz0dYIlLft8bsLbF1KIguwW1OSD6IDt7fEZTBVgW+lT6gYl7itCf3Cc3UWKI2BbPBug9gr2i7yuJXeuHlKnL8NhG4flnmw6pBvuGNc8/Pw87o189zBSsnNtvDqbL3FP6JFjqlSnBiSyLspcWmVbDpknNxNYLcaSYclOm4dJr9hnyz77//9v/Oud71r/XtKiStXrvDrv/7rfPd3fzc/8zM/w6/+6q/yUz/1U9csB/De976XZhDM/uZv/uYbtm2t5Ru+4Rv45//8n/OLv/iLvPLKK9x///3r7w9Sau/s7Nyzc9rY2OAXfuEX+MIv/ELOnDnD3/t7f4+qqvhbf+tv3bN93Cv71KLkvr7a9FrWB15rZmvs4GvemtGLJaEY8fTzc7LWAl0ZGu+LIvDQprAX7bWWF3YLVOkEGpMke6etHfRvMtlLpi8uGq7Ebc5eqlGjcu0UqeH9lFIg5YTRGt92dDlw5cIuJ7aPkHySKk+M5NJJr4VW6KJAZ+kzQilS64ltL04oGZshGU3ukghBVg43rtDWULvAIxsLyJl2tpBm+NLhCkGRK6WkigOgNc/uaX76Wbm2X/CQ4qlHJEOpBnYsyHz2g4b/Q06G5AOhEQz95x6NfN52QhnLxy6NOLOosdHxpx7cYTxaNegrUWvvEz/1h5mrTWZk4a+8taFInnpSo72hj4mlKvnxj4lGz8mp4q9+usYqSMEJjXnKQm7RJ1ThqFXHQ9MolYo+EINCK4UpB3KHLPC/FbnCp2153lqLlksClBrRKiWkFN5jigJ9HaHHHdvNHtHM+rpfsyw3Wf5O9rOymyUUVt/d7G153WerM//Xm2C7kL6Y7AOmcMyawE/8oWIZJThOeSBcUUOFMGf6aHh5IdpgKSWWiwUpasb1BFvaQVDQYp3l/JWLnNh6DHX+GM0Fhe97GNz5w9yyW53+jTS1Ny5561lDHQqVuXFP+/sw48SJt1rC0THFZhygxcMyav/HKgjPGrL3pC7TPu9oXzYsfOClkWe3TIScqJ+/ysNbJ3ng1BPoxpAbAUn+7HLBubVicHuLY7yTh+jVz53XQ9pWPQz7Wz7oah908u4+urkXDHa3M7lit7hu66+ufYntO7DXmlKK+tgG/dU5rrBS+YlCtpFjwlQlaXdBLgv6GDHDLnIfMJXD1gV9r/nYmZJyL1McmdLPNdlHimT4ykqCoo+EwPva5rAjOPTjwT++ulfwa6ux/u9g+cD/V3azJ3v13D9oLF9RVcQ+8CGd+KUD8P/Dx+tNKuRc/wRev/StZrY37FPRtNYcO3aMP/tn/yxPPfUU73znO/nYxz7Gt3zLt/DMM8/sI7LYh85tbGywsbGxpuU+aE8++SQgwdYP//AP8/f//t9ff/foo4+uP3/4wx++p+fx+OOP8wu/8At80Rd9ERcuXOA7v/M7qarqGu2lTwV77UHROkGjDp0MrlnuE5HNu2Yf92aYp96zvHAJ4gmKaU1qvcDjQJyYVbY3JVDsB0Rq9boXWlylB6FWo6EqiDsBNRqTUsJYs9YgyTGirZYMegZnNL5JbEwn9MtWyCsqYRjLK8HGQXOInEVfJWURAQSy1TijMRmB5lUFtnL77G2Is5pTIniPKyzaWmH/CgFduBUnMFkJRG2VBhUxTvmQfBjWE4dVGw1hgHOEiM6QU8YqRbKG6AOpCzRdQ22FapwsTHarqpdCoyxgMphMtTlhYhPzKzO0H66lFRheXmnAKPZhd1oqZ/lAoLrqw1BGRGtzynL9jF7DwfRwfDln4tBrVGyOCZ2n73qqjRGucLKeOiySuNZuGc8cMi5u+NPN3qj5uu/u5JG/lU98M/jJzRYcmPmUVmuopBKKQBHwdQathOWNLOQawiqHwDaVpg+BedNwZEM0V9QBOGnIiY0j29R+g37v8LqCHM0qUNmfaA7m7vc5yPMAo7s+sz/kuFendbPTVqtt5/WeblZz2t9QJvjAZDTi6oWL2HAMM6nIITOfz7h46RLTyZRxVdMslmQf2L14CbQiXphw8VzPiQfuY3xsRH1sgu97Htp+mEmnBjKUQ+BDXP+HA9dlOKaDVMCrc5K/vD7u0Z0FsJ+artn6ObkJ//fhRA75mqt7/bkpoymPTomtF004rVFWYKep92tIqqsKwryR+RXIztBenRE6j60LWEGEgRATtXVDoH1n1/ITxxb3qXlv77XdrIpzy7NX8gwZa1DrpMbh9+ZW9+uPxxX+42uj0Yh3v/vd/MN/+A95/vnn+Y3f+A0+//M/H4Bnn32WX/3VXwUERve5n/u5t93ee97znmuCos/7vM/DWksIgV/+5V++58f/lre8hV/4hV/gXe96F5cvX+bbvu3bKMvy0KrWJ8vuWaXoVZE23qtA6V7PBKvs7TBR2UlNXsL5hSZcbagcvGkjghIWtKtLR+48rbL7FLQxClOcEnX3lT5Llyw7y4I0OJObZYsZtHpWej6LRuHR6/do33s0CussIfZYZ8WhrAti64W9yhiBiwEoRewGrRIlv1/MZqC41mgPeH/NKW+Wkcc2Na5wAxd0xlbF/iVRCuPc+tocreHJYwL7OV4kYo80AuewDgxX/SOh69FSYiGlSKtG+KDQzlFslpSLSOw8F15eMtosUFpzZAIh9WRlOFlWjI1AD61qSSEy3pqwvDqnX7boseGt24LhKo3i6av7r4184AUDkBNMNTy0Jdd6p9e8PBMn/mgZuX9DgvumVTR9Qeg8pdZsbNf084auaSnqkmpcs+gMIUlwGVLg1uS3dxe53OzFut7U9enA68fR0Dx/W9atW1WN7sSGvrKc86CNlHFW8bZjmS5J3wNaSeVvqBiRFLVKHK06lFL4UlOYE/gQ0KFjUiacc7Qh8kw3QRlNnEmvBQgL2g0O5iH50WuWWF+HfMCnPXjh1I2J/hvsEMf2mu8Ouz6QvCbtVeQrLSN1gjAvmV9uiE1PUNBfVeRUs5grJpuncWOH7z0xRroNwwOPldSjERcKxYUmAw7vE2W49nlLCEveDQdw/WeVD/nu3k6jdyr4d/2dupMa1qsP3g4Ey/nwY7wR4HWdqYNHebvS7eGZhZzh7LxnrzuQlIoK+shJLe+L2HREa5D8k8KNKiIKU1piH8kZnMpMRh6aJdo6KA3RBlRZ8+FzMlbOxMidXdVPDXutikJ/1Pa7st2UeDpIEvNcutV75HC77XPLtTXwW53n650cecNem50+fXr9+YUXXlgHRT/0Qz9019v68Ic/zAc+8IE1k91kMuHLv/zLed/73scv/dIv8cwzz/DEE0/cmwMf7O1vfzs/93M/x1NPPcXOzg5/9a/+Vcqy5C/+xb94T/fzau2TA587OEffacb6Xtlh76nr/3YwWyyeJV2G3zq3wCvNA1uaLz6aMBqWreWZV0qUG6MGKNvKEc9pcMC0ONraWRZBMbsiFNTHRwseOtKjogQPGQkyXolTdlIpfUlKkZDqT/YRWwgkjAEWprQSsobWY6pC+pCcJqUIMeI2RkRt+L2X5vQhrc9LXXfi92/A590HShtCJz0NoIghoAeoXggRoyXb/1CRefDhjFaiSZT9AJnRQASVs/TzxEQxElgAKRHayOU8Yrcx6EoqLXYsFOY7/hhXdiOusExGM4qUUTny5qkm6IJSJfpLuyzmczZPbjOa1mDGhN7zlW+1KDznF/D9HzLIqR58yAYATIa3HnM8ekLS6y/swn/+qCz1Oafh/k0NKbKz0Jzbq9BuygNHe2JzldB56ukIV4n6/OW25soO6NLRxsytgqLbw7ZuYbda7abj6LpX2k2e8cN3l2+eaV6fxvAEGbn/oISoIme093z54xprDP28YdEucdrirFuTkJAzumjIMbHwjnk7xWGZuMipeodyVPGxWcVPfHh1DJHb9RHd6oz2D/76czo8w3/tBbuTSejmy6Slwb9Uk1rL5QsXcVVic+skygdy33N69ABFN9CptwKDU8jkbDUwkbnh41db/vC6ZMad2kFH51bt4p9Yu8ts+r2y2wzD20Mj7/Yorx37GXj6wo2CsU4rvuTomIpMsoa8aNFaoaIQ9Zi6wE5r/KU9cs6MRoaHthcYZ7ClRlsFFHzsasvPtOrVzjafAnavgri7vV8Hg91Xt/87XfN6qvhXYuSV5jCY453bjex3hwU3+4HTJzsQfMNenR0kdphMJoD4Xqug6Mknn+RDH/rQLbdx4cIF7rvvPmKMvOc977mG3vu7vuu7eN/73kfOmb/xN/4GP/uzP3tHSa5XXnmF6XTKxsbGbZf9jM/4DH7mZ36GL/uyL2M2m/Hud7+bsiz56q/+6tuu+3rbq2yEOGif5CF1PXzoZnbQH7qVj3TIeqZyFEcmmFpoUpVS5LYndZ4MmI0RWSvisiPOGlIImHGFLix6VIIzaGdRRhG7ILu3RtiGUALbcgZlDMpoTFWsBU9ziNSjWvarNdpZgcuECCEyFILoUqDtO8xGjdaaqi4pj0xxkxpT7Me+B33ifPD/USBuOQTI0lPTz5fkzgvxQheEsrr3EvTFiFpBBHMmhEiKkWY25/yFcywWizVRhAi3arLWlMN1Uc5y9qWXOX/mDL3v1xUtbQ1954VFbwUpBHTM5D5gV4x/QDZCruCqYj82WAu6qmvPVh141Id9qYHVLh/Q70ne082WLHcXErDVBX3TE0Kk3hxjy2INocmtJ/VBWKHuyA554F7N8LlTH/31GJrrhIE8O8kHISBJcV3p1EYTWk8MkaZpKLSlLIo1I6MpHMoa8gBPTL0XyFBKXLpyica3wnK4hiW++hPJB1yD/397Zxoj2VUf+t+5W1V1V2/T07N4xvZgvEAcEEJPz4AdYxYTRuAYCA5LYiIgRCROwgdnwfliJSIJUhwUkwiJCFlxIggKxiLYsS0sno1JbEWAgfdi7AhsZvDYY0/P9ExvtdztvA+3qrqWe2/dW1u36f/Pck9V3bPdc8/yX849J/5melxs0a+6/VrWQSYdp1Bkcf8+5ubnsWyb4lSJ2YV5nEKkELXOiW3/X28JUD1OoK5S65RyJitD/e5rNPc+StIVu/SYoBrvt8XHT1aH4tpRtraZZxWFUgrDsbDmpikuzeEszqIaS5edhTJYBsZ8iel9CxT3zFBcKOOUi5iO2dgJtJlnlrsaDh3zaXjin61OrMV+FqOsHsvov8588rX9tP6XWLyO+I371Ml3mzGpTCGT+tDg/UsYN2tray3lxzCMljLzyCOPcOzYMQA++MEP9k1n3759vOUtbwHgy1/+Mq7rtq5dffXV/PZv/zYQnXl04403UqslvZ8ace+99/La1762Y0vvflxxxRXcd999TE9P4/s+73vf+7jvvvsyxx8Xoz2nqB+D9LO8xp74FQu9Kx7iwnRR9+Hxk5EFzwtNXnMwEpbmi0Zrm2rtN97HCUK0aWAUoiVmVlBjphhtf60co7G8yCDAi96ZCDxKhTB6D8lQrdPrTcfm9LmA42uRQrF/yqYQhNEwZajoRHOjMYD7PpiK2aLHvO3hapenVy08ZeI4JpfPBDhWjU1XoyKzFLahODzrYCiFQcCsVUW7PjOGh66bBKZqHMAaEvgB9UCxGZZQhsLBp2jWsLRqvTCPpwlqJuGmw+bmBidDhTt3iClVYu/ZgLLrYdkWzh6Fst1I+H1xFX81pLDmMr84Q3BqHWWa7DnoYBUUgdZMlQsYjoHtaJZ8jVetYNoGTrmEMkICN+T0qglGtAugYRgoU7FZhwtmIi9a8xkHvo+yjOiFxFCzUFCc2YwUQW/D5bARRve8GnDieUUYKKb3zlHCx69X8VyXtVIZy3dQYbSNeVhxqWx42HML8ZssdBrnsrXhfKtwkukXLs44oNsvZ+tsgReysmFBYGA6JnNFF0NpDNPEKUU7Gzp2kTW3QGNPRAzTRFdCQqJdEHUQUm+8U3z27ApOqFkwz4dVRbDef5e5NPrbQbuvtYm9MdG2lqgkx41zQK+GIT9seniaLwH5XnwmKZxr7CIWt1RmcCGmn1dkUF4KS7bGtRyhk6zPJtSan63Wsc2u8EYBCsB600towmod2whZqdC1HBRObUbf0s5v6mGgx6WTXrHKFDeiM3J6b42L0+sd6e2f7T03fYlZzKk9KSUanPZ8uhXYaJmxkc/rRG/Z2xaRk6Rs7vQeuhvpPrxVa83Zs2d57LHH+NSnPtVSfj784Q+zf/9+YGuDBaVUJqUI4Nd//df5xje+wcrKCvfee2/HmUa33347zz77LPfffz9f/OIXeeSRR/jd3/1d3vrWt3L48GFM0+TkyZN8+9vf5ktf+hKPPvroQPd61VVX8fWvf513vvOdVKtVfvVXf5V77723pbBtBztr97lBGJUgGUPVg288HX3eW4KPvTZSkEDjrgZ4dR/f1YRu5P2JvA7ReSxThZDzypt4roehFGgi63dJRxscBAGYJtqNBMWWGVhrjq/W+cELAcpQXFGwOG/KQQeaUKnooFAVeYq0ZeB5dcr2WZb2TOGaFg/+X4+VmseUDb90WDPjaNZtI9pUTYOlNa+ct7EA23M5Mr2GDvzGMjwHTbQdtef7WLbJalXz47MGfhhQNiu8fMnDsZ3GltWwubrJ2rGQUn0fUzPnMXvpJZy78ALqWlN78kk49gxurc7UBRWqhRXmFheZ9crMqxmsvXtRShEScubMMvbcKQ4sLWKYJkpFO6oYJhxc8NCzIYQeuu6DMnBRnFwvERpWdDq80fD6aM3ls5HCFh0qq9HaprkJBUZ0f88cr+NtRMu3fmG+iGmaaC/guRWNKtgc3Kixv7CBUTBZthY45c+gKhDWPbzVAEIba6EceeHi2ljSb3HtddIzU5zknjnqVuTA9XlxbYaa52AQUFqsUJwyMa3o4GGvUkMri2VvHq8SdmzLHbhe5PUEQqWBkNnFBRatKeonQhQaz/eB4ZaUZJX2Ok8+ai4v2frbnWJ/4WqL5TDgm/Vqx+/5ZNBewXGcvhut284ha2mI3SXup1C8FMStbDUZL3KOnkDDEzHL6pLpfgZb33WCW7G5/Xa34qBV7xPr925Ju2clzcMWn0a22uyNr2nvrfFepbTU8z3FPP00TtHJ6tTvyC/pwPtY0seh+FL03lX6jprCJEk7vLXJe97zHv7+7/8egEqlwl133QXAlVdeyQUXXJApn3e/+918/OMfp1qtcuedd3YoRcVikXvuuYdbb72Vz3zmMzz77LPccsst3HLLLbFpOY7D7/zO73DgwIFMebfz5je/mbvvvpvrr7+eWq3Gr/zKr3D//fdz9dVX505rFIzn8NZRaCTt81XPqJExjSzeohzlUYrGS+VgFmyCtQp2qYxRUYQqsmMFQQBhQwNRCqdUwNusgY62ww49H6tgExKtXTRLjW2gm+8foaONDoxoeZdRsDFLTpRn88DTxk52OgxxTAjCMNqFjkgpC90Q3wsI6oqa6+IFFkHdJHA1XuDjrUfL9GwjaLnqgyDEcSxM20K7PoVSEbSmOG1TqpXwPI/5omJuQWNaVss6WJ6bYd52cE8WgWhrcIgURMu2mZ6bYXp2hsL+CnsWZjEMg+rKFEFot6rWNE2W9u2jsL+IVj61zc3Ig0Y0iduWjdVYPogVeYZM04w2gjBtvI0afqWO2XxnSil8z0c5VnQ4bKgjxdRQjTOJNJ7r4RRsjFIR04q2QteF6CBEz/UwtMaaLmDYFkbVRAXgb9Twzm2iDXAWytEyx+YyvYQ2FTW5pkVVDWdAH8ecpftN3/EFbvXwMESrhqfUC/BrQfRcQh0tB0U1dpuLtpdXlgG2gYEm0JpKtcLUzDSl6TIoMKqRgjSKm4336PTe3Vbobu9L7/VWpJ5ke8TM1u9bKpbqCh1fliwlHp8As7UEKBKUjLYrcYLT5DxCw+TU+/5EM7Vstvgt+j+dSYmWvV6arTbavbNgZ0S6I5K63XgK/bxQvdPtsDUUl2KvQaM3Tv5ct4wiA9RL7hhb8ZpzRv9UdM+nLckrTcmJG89FIdqpKKWYmpri8OHDXHHFFfzGb/wG1157bev63Xffzfr6OpBt6VyTmZkZrrvuOv71X/+V+++/n+XlZZaWllrXTdPkU5/6FL/3e7/HP//zP/ONb3yDp556ijNnzqC1Zu/evbzqVa/irW99Kx/84AcHUoiavP3tb+crX/kK733ve6lUKrzjHe/gwQcf5HWve93AaQ6K0kkmpYz86Z/+aSOlURSnQZJ0kMfCnXRXuZSirYFp2ob/fQhMBWVH86olTe3UOaphgeOb0YFXyo48PjrQFAshe8oBaE1BuZRL0UGuhNGSOaWh4ttUQwcdagLXb5ypE/KjZXh+PVof/ot7GwejKlCGQRhE234bSuF7AYYBS2UXxzFwvZAHflJgo65wTM3RS+oUlM+mZ3L/0y+j7hnYXo1XGM/jVjc5vH8Pc/uWsS2Twux0lL7rR6KCbYKG1TOa06fKaD+gYPss7bWwbJvlMOB4EIAGf8MkWIv06809e6jOz6PRlE+fobS2BoC14GGWIqXFW7EJa71LzuwlF8MOQWsuBUw3Wm53enkZ0zSZnplmz8uKGDpEY3LGnSb0Q/zQ4IXlECPQqHpUj5UgwCzYWI6JrtQIN2uErgd+iG6cCB9qsOccFhZMbMdEhZqwYKEKFqVSAcMAZRqsbhqsnfYINmucCmDNMHDKU9GGAQ2On6uzXu9a6tUhR7dNUoPNzr1pDxIvMVCcxTVJAG/87gVcuWQzM+1QsEwWixUgahNGY1ttHWo8N4jsBMrCe8Gg6taZmZ0lVArHsdlUiv/xo/fzbE9T3ozayakw5H96NhboFATyTObtd9q+oKahtrbC9YpQaYPJKMmiFmVTnZTWvDwMsYOAQsHBtqONUzwd8oTnkbRdg95qsF0Cbx7b93gY7a5Y+axrmuahE6rn136pNr1uo2Fcz2H86lx/5aW9LOQoT7rnaCvN4e5vEG/KYG02/xYI3WUbxw5yf/mXfzmytEbN4cOHCU6+wHcPHOwfeET8rxdOYh480LHxgfDSZ2TnFI2FNKFulGN4BsfWpgcPHYs+nzejuHwfFPfOUl8Ho2YQbNYJ/QDV2J3NDWxe2CxAEDLvaGanAnQQoL0AzMhjse46vLheaEyaBZQRvSy7VNbsnYmKdUF5lbnpyNtBY6cvHWoCP0AVQfsBKjTwqpowhItnpnFnbEwV4lg+htJYnsnFey6lWgVv9TR71k8SuhbFszWmLiqjnOjcoaDuYhjR2UcAlc1NdN1ifjUA06BozBGcirxiP3Vd/k9LCWjbGezkyej/bl5o/9IukrU9yMbYYmFwaGqaRTPyCh0o7cP3fcJNj431ZeyiougUWHTWMEomnuGw6pbRWhF6Adr1KYUWodYEFRetDXAKGI5D6DW2qNVgOhYLezRH9rkoKzqsNtp8AV7cVLywEZ1J5a1WUIbCnJ/m1JrH8XUfVavmmnAyhU1aDZMWtj18b6ZxmkBvoAS3RXeUzqU3YDgWxfkZHCNabvXiRrF1UTc24fDdTZasn7G4uEBtzcf2D4NRwK43PIV1TcX3+e9qhdbCGN0sVrqls//+Wr2DhOr4V/UGj/k5Kf+sEdsFlOGFlWzxlA65PNSotQ0s02RpaZFSaYqq1vzY9/ESbGGtXRJ7hPjRDvRJw3f8OyHtZRsVedJSsWXK+o7G6BSibsYxCY6T8Z2A1e4hiX7Z+rvF4PXVTDd//81lhW3FUa28VNuv/WIkfxcEIRs7852iJKGw+/csQkyagJlp3EiyQikM28QqmegX/UgZskw00cGfYRCA5+MFPqEZRu9XhKAsAxVEux9VKxWqlQCnUIgObTMV2g+jXetMhV9zUbZJqH0Uje23fU0YBKgwjIR+HeCYFvXNKhXX5dymyfT8PkzDINAhvldns6I5c/o0ZmGO2cV52FQ4xSLWdAGz6BOGPu5mlZpbx3JsLAzqnktgwOyeJeqrU72VNbYxt2twV5Eb1zRNlGUztbQXZQW49Tr1ap3ArVOtb0bvtRg2hm2iTRUtrwP8ugeNQ3GVESk8RsGJhG6lmJp2ccobW8I40ZKwoOrirgRQ9zCKNr4FVsnBqoFh5DhHYtJzk278aQpinU02JwnberOVtmFFmyz4nsep50/h+z779x2gUt2k7nnMz01x3vkX4FgGM1MWldVCtLy0PVnVmYXOoBBlu6F4hSg+pAKVtFPdcA+xfTv2uG1zt34bXWMxDJOibWK6RXw/wPN8isXOZYnJlu/xN9qedqWbH7fXE5WkkOWLP3ga/elqPz2bKUzCo5dnyUa+kPEeknTPSTZFZXvaVdS08+c97kWygiDEMzqlaLBxMp2sylGetLo/D8BaHR4+pjEU2KZB2Ynew6GxTCJ0fUIdoqxoSda5VQ+vaoCh2PQNjIV9vHj6FOsrBmtnQw7sn+O8PesslM6BCjEtK3pnyfQxw3r0fpGKznYxLasxVAaYjoUVBIR+gDVVwPPqsHg+ZykyU3A4+d8neP74M1x8+eVcemgZN3yR2soZjD2r7Jmbx54KCep1qrUqa4HBE6uz6LChhFizKEMR1jR+vd5T1S+Gg+8K1knvwwiBxz2XKb/rmgf2zxrKIUUUxWjvBF9zvh955Xx81qcNtAJL++xb9FEK3FBxZl2BbYKCoHk6vOUR2i5hEFKpm6xVTELPZ8MFTIuw7BCe3aTkwZ590zhuW010e2KaDLogNW+7HOeMGWPg7J6iQw0/OVPDsRT4AQc2NeXCFDO+zY99B21NseYZrJ+MXpvTPnj1ele6ivUwbMtvOwWB/ItjooKnCWvxXob+6eaN00mo4EnDpDA3g+f5mKaB6br4gNux3XhexrDMaqgF3KPkpSuCjmKJ3mBekNGSxRSSdnX8vqhB4k4mjiAIwzM5T1E/4bGfkad9Hh/EIz0Q8eLMhgv/8Wz0eWlK8UsXltCbNcKah9YhpmWiw2hpm2lbhLrMctXCLji45f0s+2VWzTJ7lvZRqtVYPuPinnkc68Ay5aky+84/jFIuqhh5naLd6kIINWG1Tr3q4tddjKKNUy7h+z4vnllmfukALnvxCnP4hQLF8CRH5sqc+59z7Hvdj1Cmj32+g1MoYVg+vlfFtB1mphdY3zT4zo8hDLsfSwAqiKmFJqMXkkLg/yUdUnlCd+4NoGHBMHn1tImNieco6sVoy/Da5lkc/ywzU2UqVYvTbpmg5mKEGq1AGwo/qOEZdQxTUfEcTrtlQkPhWT71Wg3DsTg8s8CeqoHa0BS8trzb/22n3aPSLOwoZsbuNh/Xf1RMxEFl7D79TGt45mx0fkFBwVXzh5hRBpVqyHObUNVx7wO5rU+DvtydlUFS7/feQLsvqfO9pOav7fSm0y14juvuQw3/12ucPaFU1LHbzqIYXMwbs7g2hrE9q7A/7J1NXp1XKKW7qmsSZej2do4/17Q8snmgBvO9TGKcisuTtnEoOff+5eo39Gd9T2rH2C0EYcyMXinaKSaO/NJQzuRVKx+lFPZ0MXqhvO6hLZMg1AShT9EsopWmNFXCsEysuTL7ywdZCvZjrRehYOG7LnusUyw5irrrcurFFynYDnXXZf/BA5iODSo6v8CvutTXK+gwwNcuRsnCLhbYd+AAnh9tb6yAzfUNijPTmJbJufXTBD6U56ZxigU810Upi9JMueF1Sa6G7tVYGStnoFF0a4hPnwKbgkBzyVO3G9C0LUwFM1N7mS6GkZciMNFWdF6UUXCify0T5SjMcsD6+jrVwOLMxiql6SlKU1OUZssYhoF9LkDVgsarSDpdP2zef8cPcdcyVMbWLfWvzzzppxkokuT6LM+z+SgyhB39MNHeDpKsLf0rKdsL4N0hk97PScqjX6jhNYMdv8VuUrtKve008XDUC4468xo6/VZynW1weHF7dFpk0qGpSdfaSzAuuk0Qzd9GnWfaVg2T6UlJ41f6aNWPfiHSDUDR32RfuCD8/DEZT1HSmJ1nPN+hvXKzHvDDF6LT8pyNKkdKBirUOKaFB4Q6jHbYtg1834dzy9j1OlpDuV5jthBCURGwxKo+CCWoGOtQCHn+xHNsnlzjgj0OXs2lsrGBY9iYJZuwskgpKGGsOri+T32zikYxt/FTyov7KDoOdhgS6BDDU6w/5aOWTM75VWb3LmI4Nita813XJUSz4dLa4lV3yP0KrdIekqJnLX6adyFlks3+iDs3Tq7qkEfqNQwg9BSbJw1QYBkhP3aKoDSub7Bai94FMmp+I25AwYSnzjnAIrXAYtOwoQbUPJobQhRd3Vo293wQs2wwj0ySxTs6jIwz7MqrpPL1KasPPObWsRX4GrxMNzFMp9YthZ2Gd6zbYzNMC4snXoRIeg8iLs9s4tVoxL5hFaMspci/T1Zb4rkZ0Lel+o9L/fIaJOeO+lPtz2OrIL2K9QDWvLaoutEpsi6l6/se1fArOfvm3yS5d8X17tGSfBbTVinSzSWD9TXd9lex9Tz6N9XumJ2lzOb7yeI53aGClyCMidGdUzSKdAb1Roxi4M5oEd8yhkeDV9UPeXolWkJ0YNrh0rkCgRcJ3VbjoFCtQ0I/wHRsdL0CtU00mtB9HmWusbC4wLHVX+Qnp/ZQKBVZscCYDSks/CJKP8HK8rNoNAWrgFWw0fWAU/9zjv0HFvFMgxefXcZSBso0OTzlMb22Fh0Ap8Gr1bGUSbhRxJhZYKZYQJ9TeArWgpDvVqL3DHos6qp9EkoX+Hr3/hnWYpsvbp3mUqHG7l61KImtQb3ZWNzoHCkUpmm05dP8t20XvazF6tf+02a4ca5JGIVcHVe+OMcLjYMnE5Y8jstroTrKE79t8iTIv1nB1qKcXgG5eyCa4L0M4HTYKd6o1HKMpJ+le6i2Qmx5gFohNF1KSnJ7STIaJbcGRW/SanR9To2/Bebdejo5zvB9pr1n5jPT9eafZSTqVjy6D6ntTqHde9PssGnqYnwZ0ku2NZIOaPAQhJcwQytFvu9jWVZ67x9Fr4obpwaYxPuSJP93ZRXr6WgcLhpueNHWzrYJpsLwIDQUft3DNA2UaaCDgNLUFAtzNk7Bwdy0CMKAerVGYcHGmTKZnZ1jD0vMul50xpFShHUPN6wCfqskMwvzOIUChmlG4doKW5opU7i4FJ0b01ZfWidXXX8rY9L1tlqJezYKlB7XENucIJJnca3B8yKlxzDswV9MHnQpW0bFu6fuOsLnmLDzLE1KUHZ2LnEdtb/2ORqlPS2PAdJt9knVEGcb37M0zyThd+D7a2ujuVLI2razxh/H2D5m2kXNjrpT0dWh2lzfRtG95CpbXv3fs+oWynWbzWz4PpQ3/35xksT97PWx9bf39/4x88VJSy2tAyQbLLOZhLKUbIcvvxWEMTG0UhQEQaQU5SVp8uu3vKi71++wfqscC9f3mJ+y2FuuooOQDcPmnFcEU1G2XRamferVGlVX8/zGDGbVZMpe5g2XbBDUPVYKF7Pqz+O+UKdaqDI3E233feqMyeq65twmTFnF6LBV4AeOzXoQQPvSrq56UX5kxW8/nqSObvhFuh9CnMA5QEWnCvdDEiuE9SmjAss0oih5FaJBhL7uastajal5TKDBjziLUb7nkewNyvbWw+g9SXEPOT7v7t9aviLV2VUuAi6ybCzb4keex7NxSzZT0x8QvfVPj1Cf2iYbFpauPpWpppOqbswKUZzHYTC1Ns1O351D/zKkLePKUiWt2M210Ak5d4XuKVeScoCGMAhRhsIwhmt7g/TE/u/AND931u0kDjfNS3uZ4svTe61/abf8O1naS96RVBB+3hlaKXKc6BDG1qA9yMyStw9OcoVM22yUJUvDNLHnptHBKmW1iVWyQBmc8xW+51Mo+SyUPZgxOXmuwKlKicrqJodnTrFY8FiunCKszWPa+7EDk7rvsrz5Anv3LrFy2uSZlQ0qvscvHbgQA4Wv4Wnf53THFtlpk2GylyeLZSozsVkN8uASGlSa7JlwGwqFZVutb53J9ZkkdY6wtE14ebw1eWl/ZINY1rurNqnvxtX1JKz4PfmMYs+2uIYyivTaK7H9c++Clx50pBg1OVQo8uqCA8ALQZCqFKWVPE9v6wzbJUJmfdZd4eJtWgl9Z8JeoTxNuP1A4a34w7fEXKise+dlcTMmK0NbgnjMMNCwqBmWkRI/r1dmdKSbRUaRW3r95CWLMpz1ene4dvNR9D3NPCMIQpOhlSKlopfaOxSiTBFTfs9iMRx0VIpLr186SUJiwsxami0zYxkow6NSqeIGNlgmhVKBwqyDVaqABmdmClsVcZSmHqxRqWzi2A7VjSq+dlk+vcy+g5rZfUtUKjWY3cucM8XhmRnsswpdD9uyT5vmswp/8WJMZ/qjEkj7kaMx5fLipJehUxzsX2+ZlmuMS4lIUgwHVY6SvvcL3/Zzkrg1sGLdj4x127s+flxSeJKlP6UtqWRlaetD/vpL6s39haO8ImT20FvvKmw3vfeYPCVFm800yz68IDlOL8Xw43OWcsXv0dY0A4z6/vK3/35j+PCbIoxfnWivx6x12u0R6zbZCIKQzgiUohjxYngTSvLvg8ynozAId6fV/Rk4W/P5r2fXALCNkJJVBqZxA5Na4AM+zpmAohndSD1wqTeswK919mFWXdxqldnN0yjjcfbZJieq0/zwOECZTc8i0AZUavx3XWOG0VC5FoYxxWxOUtmc7sl0uyMyRhmaHA97BGa7OGGtYxrq8Bj2Tjp9y9ceYYTCfmI+uaINv0tZ+9+ede4aUGNaoz6A7hz3LVsjSusHuuNTdj9Cuz03Cv+k77UORz4V9DsjLGs+GUKqrjBZvZBp8mdMvI4y7AT9KAPNdzxG0Ya3RuaG90WNR8jeev9nNJ6bLOkMpmyM8/2VUaY7fu9g76lT2SeC9nqUJXCCMBhDK0Vdq1syBEoJ1x42ycQxCoVrECUpw7hU80Ke89yuXxXRcaRuTCJbu51dWihiO3PY5hwzMxrfq2FYJt855/K03yyoTzq97vh+dqXueLFJ5t0cYWSCTo5883opY4W1PtbEvIpKmnLfpJ+wmVWBaiUXq5akFmrYCbRfSxvVS9nD0P8es3gH09LIqSi3QrYvWoo4E4aciTF0DMcAlgPV9Xk7+vWOYqvcaZb7bFb9jk47lioZ6SPLlFs+snoMB7Vp9t1uPDanlHFsXA+qIw8VU5JsI/To/HKT84YJwk5jMucUDcuwnp4sylq3TDRy+icctu2CYNqTfDQpg/046mPsdT1GJiFpdAujTTLkm3976Ekw/vyjFjx+oWV8DFLuPHEyhG2sgdY0vAJZ23l3tb8E+vVIWkpCIlnf/tn60hxU2pdJbf0eZ+bIhkp8tWiYKXVUQvP4hO5ej38/O2w25Wky41jn3zz1FIULw4B6Y6dbx3EGKker5TU8jTtjyasgjJ/xS95xfSltlBqduSNfuhPq80kD3Q89l2f83nNeTiUsjWuSNJinVXHvpJbl5kcscG7nGDts3v2qLa+sOsrlnf3KMKp7z5tmX6E5g/CXkvfoFraM5iH0LglK7j9pj2pL0ZvwqSGT6p+TdWeMjLSt/+NJ6uS93sJ2hah/mv0LEbdEL74rZV/GNkkvQr682ufG7KNCe01ur4Fl+M6gdcPAGoSk70IYT0e9KfEaCbuL8SpFo5rs8ni/O74kLFFIE2qzrKLR7R/7uei7E4qsL7rrHYuVMGQlNm5vui0Xu9ats026w/WvsiR3RDPn7glywKU3eZXTnUg/BX4cikZSuO7Ze5B04tIcNH4eb0KfgmTKvm86cTcT1486LfNxJek1PsR/i88jTviNI65c7b9vPaDJdJ3s4k/HGDFoH9gmhWinDEPdqk/cmDuSsvZ0gcE7/U4XkDu3yulvSugcKbIrQ+NQm5pPXA/R503TpFhwogPcBz2Lr6tEgrBbGI1SlGV8zWquyRu2Gb5ncs2QSJoC1Ney3QyWz+Xe3MloK+EhKk0NZmbtX+YhJZWe5NusVXFLFkeQZV/yVlVc2catHGWl2WxGNd9NRIHttcUOlERfmg86zgrSHS69L+QT/vIaJfKkOG7B5KWz7LB9e+z+KsM4XLCD5pCsSA+uZKTHayn1Kq4tJxvbtpNhluYl12b29j25PtdJ7wqSfBNW9x2aptknvHiABCGO8XqKdmJ/66cAZUoi34DSa0MeRcUkaRejIEcJMwVMCJRbFhtQeIuTjcehwEyive80w19r7s6j4I+7onbiwJOVzrKPd2eu+DyTSB3HBrDPDCSYNXWiDEPBJFS9Xi+DCJr5GY3yGm/6yJtm9vBZbbdZwsUqcprMnh5pcYIwGkajFI2qR7YbebPm08/a3U73tfaxOMeEHrsrWUo+4xmwBvMSjSTZJKNn3LW47wM/h26BMUfdxq1KSsq7v1F1soxT/20nrg/FeY9in5FqBY8t4qDNdUAv3GiVibQHkKUBDc6w9zDKekhMZcDkByqXaleI0uNvh3KSJ8esW9UPomxNRpkeFe3+mWSP2qjp3dRisPhN4so+eKmbDX08vHTaRnZeCAMOP39ionkemmhuwiSYzDtF4+h/cVb/wUwyw5cjs+A46qzHULHjLnc/AT9H3SUK33F5pf3W/fuklJBJEHe//e4p7XqfZzOW6hqgf422b+wUD9ggTKBME3wvKIMutG10Hg2cQZFpu5Q2heW93f6O29FNzPkUtq1C5TuMdDzs3N3zxpu+wZYDKujqu7qjbQxoNRaElzDDK0WjNuIkKRlJead9z5JGv3wbv3Xs4NMeVsaKiIxtoGNjijzPLyt5FKFJkSaDZJFPRj035umzMZ6agbr8oM9gJz7PlxA7RX8Y3TQxSCrpuXduqDG5Govb0GMUalGkOE5iQIm8UePcrjmvsrWzSN7mIX2Dl0aI1rtzWe+tv+BkAkedAnOmia/g3lqVzTCp/e90g48gjJ7xeIrG/35rPpLKkba0KyZOa3fL2Dlgpw7MYyhZngS76jPTAJ/BMDXOk+A7M2JnPdY8CtYolcyuNHdatQxOVgtMZ4xh7r3dSt4UgMbZjrMs8xk329tWBrGIDZtjd57xHbdzmZseetlb/I6J4/O15Gu77UL/cK0w/lgJRXfvTG77k9jiPjn19A1e+rVG3fY3LffekUoBi6bJHtPEBUwxMAlCB8MrRQP59jOmMcQynlGjVNswFjtqqY5/Osq+zQPPwMN+muDd/b1fJj11kBAxY2HVMOtosnoe+/3eL70s17PJTvEMsmw0S1uMW3/TUoZGIdLsJPLfx+jOMGkKlKpDGB6P56Lpn9VkEgjzjF+JbautnrrHzFEq7kOi2v6On862k/cdmn5PrvvsufaUxmOrTPaCJJcyriT5+lRWj8Zgasl20/DApbxT1BqiU1OBuHfWfKXwAI/oSI8sfXAHdFNBmAjj8RQNoiiNY5IczhTVmYaOuZaUX/9F3fFx+957/mlt5BNhnoR02rKQhIQyV1uCsNWedJYl0br7Q9pEnlLmhOJlup5Gd7GS+klc8ePyyGBoSHsEfUWJ0RvddyDD9ab2c8aU6vyt+/MwxAunGZc75XmGiWF7leqs6UdtcNT+yPY3JkYvEqePIO0dN+m+tnyH3ak1Y+TzysRV+vhVgX5ljL++c1WUdJottbNlddd0Us1399H2p55Uj5m7ptrKo5mWD9xTq2A2Wlr70rmkMuXMVRBe0ox3o4U8xI0aWWTqJIFT915rTbTd662zaA55BO2+ieUPNkDgBgMsx8hj4IsbN1t10zY95BlfkwyJucmpyMQESp/q+mQ9SNFye9y6fktryxmVs8lazifBeGzk8Tn1O8x5KySqPXxcnKztLb2da9XdZXf+sx1XG2yqHdmf02jp3xLTVap8DHdmzygYj3KbNe/Re7XjDzVv78P5PV6a9mWTTQ9fp0dQt/1Nmlu27HuRjKPaGlszfY1mNWw+k7QypWYlCD+37BylCAbrge3KSYIy1B40dcCKM+90/zausX1Mo8/IFKI0siiHg9xf1vmlW2HVXRcy5Z2koaRp5vFknozzKOOTIEnB7f6eVp87chYdzH3V/b5HfJgo/S1HXnMpXG9azZJs2YF123W2hJm28AMZNdrLosa3e1caaa+Yj6xR5zaaqJ6/o6T3ybff6zi3I8jGcFt/D2ZY2G4Dy2RyTvYBqYQa6K1r1fU9Poe0NtSKGWf0Vc0w2WpEdf3782UkE4RkJqMUDTob5JVl+oXN2q/TlnqkpbG1xmG05Y6jlccYrOBpnpqshuvWP0Na6/rJUM3rGeqwlVTG+tbolPy3Mu5sHgPcZ5Z7zMJQCm2XR2+Cc2BHDXY9T9U1wWcRLePFkPw3lPzeQvqv8eeVpLsFVVdi+dpRmt9hpwmkYxinmsmmNI18GxgkLVvoF79zU+5+IV6qjNbL1jmxdL5bN1wOo1uG2j4sjsd72ZtnnFFhMONOI0HRawQhA+NXirL04STD1Kg6cv+5LMbLkDHdOAUqT5nz1E+sYpKQ2aDjZ944fcKPZBLJshSt42v8pD1QSVIj9QrzLX9AY3e8zORR1JJqNYeQOHA5+irinYXQsb+nkKiHJKhD3R4s1X5BpIDtoruF5n4aWUzjQ5QniZYhBN2jkOe7i7j7V4lj03ayZctLK1O7Aj/KsneP0YP6JsZgHExJsb+dNK2WciyxpX0TFp2rP/S+rxRvGIh70267vZqCsF3srOVzcQw71uXwbGROK6eQPjS6qxKypD+KMsSlkSPd0U1P3ZNDv3w77bXddsfORS1bf1OyTvdQtCvUamviSvc0xU2b3YuskvLMIJy1lSFOtNvKpf3uO/NL16v6LfRofmt3n+agJ3hCfv2dOW303nl3TbY7quLEs+6d4RLrd1CdrLtx7hzZeWhyDUkjNs4MQnyfHzyjZnp9x5z0RCK620i3caCdDG1o24TgkbfxHgtZxDj6ke74pxOVpU5jPOTdIRpzv26bV7KS9XykTNdFSxJ2CUprLc1dEARBEARBeMlx+PBhnnvuuYnne+jQIU6cODHxfIXxYWx3AQRBEARBEARBELYTUYoEQRAEQRAEQdjViFIkCIIgCIIgCMKuRpQiQRAEQRAEQRB2NaIUCYIgCIIgCIKwqxGlSBAEQRAEQRCEXY0oRYIgCIIgCIIg7GpEKRIEQRAEQRAEYVcjSpEgCIIgCIIgCLsaUYoEQRAEQRAEQRgbDz/8MEoplFIcO3Zsu4sTiyhFgiAIgiAIgiDsakQpEgRBEARBEARhVyNKkSAIgiAIgiAIuxpRigRBEARBEARhGwmCgH/6p3/iHe94BwcPHsRxHBYXF7nmmmv4h3/4B3zf74nT/Z7O+vo6t956K5dffjnT09McOHCAd73rXXzve9/riPetb32Ld73rXRw6dIhiscill17Kn/3Zn1Gr1WLL1p3PysoKn/zkJ7nsssuYmppicXGRt7/97dx3332x8ZVSvOlNb2p9f9nLXtZKrz3dRx55pPX9gQceSK2vSqXC7OwsSin++I//uF/1ZkMLgiAIgiAIwkuQQ4cOaWDi/x86dGhk9/Dss8/q1772tan5XXHFFXp5ebkj3kMPPdS6/h//8R/64osvjo1bLBb1N7/5Ta211n/1V3+llVKx4a699lodBEFP+drzeeihh/QFF1yQWM4//MM/7ImfpT5/+tOfaq21vvTSSzWgb7jhhtQ6u/POO1txn3zyyQFrvhPxFAmCIAiCIAjCNrC2tsab3/xmHn/8cfbu3cvf/M3f8MQTT7CyssLTTz/N7bffztzcHP/1X//Fr/3arxGGYWw6H/rQh1hdXeXzn/88x48fZ3l5ma9+9ascOHCAWq3Gxz72Me666y5uueUWbrjhBh577DHOnDnDk08+yYc//GEAHnzwQe64447U8n7kIx9hZWWF2267jWeeeYZTp05x33338ZrXvAaA2267jS984QsdcdbX1zu8SE888QTr6+sd/1944YUAfPSjHwXg61//OisrK4nlaJbzDW94A694xStSy5yZkahWgiAIgiAIgjBhtstTZBiGPnToUOL/WfnEJz6hAX3w4EF97Nix2DDf//73daFQ0IC+6667Wr+3e3DK5bJ+6qmneuI++OCDrTCWZemPf/zjsXm84Q1v0IB+/etf33OtPR+llH7ooYd6wqytrelf+IVf0IBeXFzU1Wo1MY2mVyiOF154Qdu2rQH92c9+NjbM008/3fJ2feELX0hMKy/iKRIEQRAEQRCECbO5udnyqvz5n/95y1vSzWte8xo+8IEPAPDFL34xNszv//7vc9lll/X8/pa3vIW9e/cC4DgOn/70p2Pjv//97wfge9/7Xuz7S03e+973cs011/T8PjMz00r7zJkz/Nu//VtiGmns37+f6667DiDRa/WP//iPaK0pl8u8733vGyifOEQpEgRBEARBEIQcHDx4kBMnTiT+n4XHHnuMzc1NAK655ho2NjYS/3/1q18NwHe+853YtI4ePRr7u1KKiy66CIDXve51zM3NxYa7+OKLAXBdN3XZ2nve857Ea0ePHqVUKgHwn//5n4nh+vFbv/VbAPzgBz/g+9//fse1MAy58847Abjhhhsol8sD59ONNbKUBEEQBEEQBEHIxFNPPdX6fMkll2SKs7y8HPv7eeedlxinqahkCQNQrVYTw73yla9MvGZZFpdeeik//OEPOXbsWGK4fvzyL/8y559/Ps8++yx33HEHf/d3f9e69s1vfpOf/exnQPR+0ygRT5EgCIIgCIIgTJjV1dXccer1euzvpmn2jZslDIDWOvFaP89M8/r6+nqmvOIwDKO1+cOXvvSljntuLqm77LLLuOqqqwbOIzbfkaYmCIIgCIIgCEJf2hWMtbU1tNaZ/t9ONjY2Ml2fmZkZKp+PfOQjGIbByspK6/2kc+fO8bWvfQ2gpTSNElGKBEEQBEEQBGHCNN/1AXj66ae3sSTZefLJJxOv+b7Pj3/8YwCOHDkyVD4XXngh1157LbDlHfqXf/kXarUalmXxm7/5m0OlH4coRYIgCIIgCIIwYd74xjdSKBQA+PKXv7zNpcnG3XffnXjt/vvvp1KpAHDllVd2XLNtu/U5CIJMeTU3XHjwwQc5ceJESzk6evQoBw4cyFXuLIhSJAiCIAiCIAgTZnZ2lo997GMA/O3f/i0PPfRQavharcbx48cnUbREvvrVr/Lwww/3/L6xscEnP/lJABYXF7n++us7rje3BQd4/vnnM+V1/fXXs7S0RBiG/NEf/RHf/e53gdFvsNBElCJBEARBEARB2Ab+4i/+gle+8pXU63Xe9ra3cdNNN/Htb3+bU6dOcfbsWX7yk5/wta99jZtuuonzzz+fr3zlK9ta3gsvvJDrrruOz3zmMxw/fpzTp0/zwAMPcPXVV/OjH/0IgE9/+tMUi8WOeBdffDHz8/MA/PVf/zXPPPMMruvi+37iuUi2bfOhD30I2PKk7d+/n3e+851juTdRigRBEARBEARhG5idneWhhx7ijW98I77v87nPfY6rr76a/fv3s2fPHi655BLe/e5387nPfY7Tp0/jOM62lveOO+5gYWGBm2++mSNHjrC0tMTRo0db5wndfPPNrWVv7ZimySc+8QkA7rnnHl7+8pdTKBSwbRvbthO38O5O68Ybb8SyxnOikChFgiAIgiAIgrBN7N+/n4cffph7772XD3zgAxw5coRSqYRt2+zbt4+rrrqKP/mTP+HRRx/lD/7gD7a1rEeOHOHxxx/n5ptv5pJLLqFYLLKwsMDb3vY2/v3f/53bbrstMe6tt97K5z//ea688krm5+cxjP5qyCte8YqOrbc/+tGPjuQ+4lB6u/f2EwRBEARBEIQBOHz4MM8999zE8z106BAnTpyYeL7bwcMPP8yb3vQmAH76058OvbNcXo4ePcoDDzzA61//eh599NGx5SOeIkEQBEEQBEEQdhzPPfccDz74IDBeLxGIUiQIgiAIgiAIwg7ks5/9LEEQMDc3x/vf//6x5jWeN5UEQRAEQRAEQRAGoFqtcs8993D77bcDcNNNNzE9PT3WPEUpEgRBEARBEARh2zl27Bgve9nLOn676KKLuOWWW8aetyyfEwRBEARBEARhR3Hw4EFuvPFGvvWtb1Eul8een3iKBEEQBEEQBEGI5ZprrmFSm1UfOXJkYnl1I54iQRAEQRAEQRB2NaIUCYIgCIIgCIKwqxGlSBAEQRAEQRCEXY0oRYIgCIIgCIIg7GpEKRIEQRAEQRAEYVcjSpEgCIIgCIIgCLsaUYoEQRAEQRAEQdjViFIkCIIgCIIgCMKuRpQiQRAEQRAEQRB2NaIUCYIgCIIgCIKwqxGlSBAEQRAEQRCEXY0oRYIgCIIgCIIg7Gqs7S6AIAiCIAiCIAzCgQMHdlW+wvhQWmu93YUQBEEQBEEQBEHYLmT5nCAIgiAIgiAIuxpRigRBEARBEARB2NWIUiQIgiAIgiAIwq5GlCJBEARBEARBEHY1ohQJgiAIgiAIgrCrEaVIEARBEARBEIRdjShFgiAIgiAIgiDsakQpEgRBEARBEARhVyNKkSAIgiAIgiAIuxpRigRBEARBEARB2NWIUiQIgiAIgiAIwq5GlCJBEARBEARBEHY1ohQJgiAIgiAIgrCrEaVIEARBEARBEIRdzf8HKHN2Pjoqg/UAAAAASUVORK5CYII=","text/plain":[""]},"metadata":{},"output_type":"display_data"},{"data":{"image/png":"iVBORw0KGgoAAAANSUhEUgAAAxcAAAKQCAYAAADt4ofoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy88F64QAAAACXBIWXMAABibAAAYmwFJdYOUAAEAAElEQVR4nOy9ebwlSVnn/Y2I3M5y99qru3qj6Ya2AVte2bVZtUUGZFFGEBhmYEB0QJR9ZFG0BfEzDIoD6CuLICLbKAoO0AMMOqwN3Q3dCDS91b7c/WyZGRHP+0fkOffcqlu3qrqrafHN3+dzq845mREZGRkZ8Sy/5wklIkKNGjVq1KhRo0aNGjVq3EXoe7oBNWrUqFGjRo0aNWrU+LeBWrmoUaNGjRo1atSoUaPGWUGtXNSoUaNGjRo1atSoUeOsoFYuatSoUaNGjRo1atSocVZQKxc1atSoUaNGjRo1atQ4K6iVixo1atSoUaNGjRo1apwV1MpFjRo1atSoUaNGjRo1zgpq5aJGjRo1atSoUaNGjRpnBbVyUaNGjRo1atSoUaNGjbOCWrmoUaNGjRo1atSoUaPGWUGtXNSoUaNGjRo1atSoUeOsoFYuatSoUaNGjRo1atSocVZQKxc1atSoUaNGjRo1atQ4K6iVixo1atSoUaNGjRo1apwV1MpFjRo1atSoUaNGjRo1zgpq5aLG3Y7nPOc5KKVQSp3W+e95z3tG53/+858/4fiVV145Oq6U4mMf+9gp6zx27BhJkqwrdzooy5Jt27aNyrzzne88rXKvf/3r111r+GeMYW5ujoc85CG89rWv5eDBg6dV348Chs/lOc95zj3dlDuN4Vi98sor7+mm3OP4xje+wS/90i9xzjnnrHt3brvtttMq//nPf35U5j3vec8pz7/ttttG57/+9a8/4fj4vPCjiPH7O92/0+3rf2346Ec/ymMe8xi2bNmCMQalFOeff/493awaNWr8kFArFzV+5PG+973vlOf81V/9FWVZnnHdn/rUpzh69OgZXWszeO9ZWFjgy1/+Mr/7u7/Lfe5zHz71qU/dpTprbI5xoW4jZbXGifjGN77Bwx72MP7mb/6G/fv336l350cB9dg4+/jTP/1TnvrUp3LNNdcwPz+P9/6ebtIJGBp/aoWnRo27B7VyUeNHFpOTkwB88pOfZH5+ftNzh0rBsMzp4r3vfe+67//3//5fvv/9759RHTfeeCOrq6usrq6ytLTEDTfcwG/+5m+itWZ5eZmnPe1p3HrrrWdUZ40adyfe8pa3MBgM2L59O9dccw1Hjx4djeHzzjvvnm7ejzxe9apXjfpzs78fxb7+vd/7PQAe8YhHcN1117G0tMTq6io33XTTPdyyGjVq/LBQKxc1fmRx+eWXc8kll1CWJR/84AdPet5NN93Etddei9aapzzlKadd/8LCAn//938PwL/7d/9uRMc4U+9Fs9mk3W7TbreZmpri8ssv5y1veQuvfe1rAeh2u/zRH/3RGdVZ4+7Be97zHkTk//dW7Ouvvx6Apz/96TzqUY9iy5YtozF8T9GSnvOc5yAiiMg9cv2ziSRJRv252d+PGgXs6NGjHDhwAICXvvSl3P/+92dqaop2u02z2byHW1ejRo0fFmrlosaPNH7lV34FgL/8y7886TlDZeDRj340u3btOu26P/jBD1IUBQCve93rePjDHz661tkQcF7xileQZRkAn/nMZ+5yfTVqnC30ej0Apqen79mG1PiRwnDcQD12atT4/zNq5aLGjzR+5Vd+BaUUX/3qV/nud797wnHvPR/4wAcAeNaznnVGdQ8pUfe973254oorRuVvv/32s2LZzrKMiy66CIB9+/adUdnxYNnbbruNpaUlfvu3f5vLL7+cycnJDTnky8vLXH311Tz0oQ9ly5YtpGnKrl27ePKTn8ynP/3pU15z//79/Oqv/irnn38+WZaxa9cunvKUp/DP//zPpyx7usHepxMAvLq6yh/+4R9y5ZVXsm3bNtI0Zffu3Tz0oQ/lDW94w7pxcP7553PBBReMvj/ykY88IWh2vJ9OJ6C7LEve8Y538KhHPYqtW7eSJAk7duzg53/+5/nQhz60qeJ5/P29973v5eEPfzgzMzM0m03uf//78+Y3v3mk1N4V3HHHHfzGb/wGl112GRMTEzSbTS6++GJe8IIX8C//8i8nnD8efzAMJH7DG96wrq82CrT+YeFUAd3D5/LIRz6SrVu3Escxs7OzXHLJJTzhCU/gbW97G8eOHRudf6ZjY4gz7dezieNjBW677TZe+MIXcv7555OmKdu3b+epT30q3/zmN09ZV57nvOMd7+Bnf/Zn2blz56j8Ax/4QF7+8pfzjW9847TbNXw24zEMx/fnRn153XXX8fznP5973/vetNttWq0W973vfXnpS1/K/v37T3q9wWDAJz/5SV74whdyv/vdj8nJSeI4Ztu2bTzmMY/hz/7szzZ8h4bz5hve8AYgzOXHP/Pxezh+nj0ZNovhOH7c7tu3j9/4jd/gkksuodVqbVj3oUOHeM1rXsNP/MRPMDMzQ5qm7Nmzh2c+85l89atfPWk7AL797W/z/Oc/n0svvZRWq0WWZZxzzjk88IEP5MUvfjHXXHPNpuVr1DgrkBo17mY8+9nPFkBOd7i9+93vHp3/uc997oTjP/3TPy2APOxhDxMRkSuvvFIAefWrX33CuZ/5zGcEkHa7Ld1uV17zmtecVltuuumm0XlXX321iIgsLS1JlmUCyHOe85xNy7/uda8blb/11ltPet7ll18ugDQajU3rOx6f+9znRvVfc801smfPntH3jfruC1/4gmzZsuWEc8b/nv/854u1dsPrfelLX5KpqakNyxlj5F3vetfouTz72c8+ofxmx8YxrPPd7373Se9769atm97HT//0T4/OP++88zY99/h+Go7V8TrGsX//frnf/e63aX2Pe9zjZGVlZdP7+/M//3N56lOfumkdzrlN+2ozfPjDHx6N1ZM9sz/5kz9ZV+bWW289ZV+97nWvO+02jI/Rkz3Pk11/o+uMzwvHY3V1VR784Aefsv0f/vCHR2XOdGyI3Ll+Pd37Ox0M55XzzjtPPv/5z5/0nUzTVD7zmc+ctJ4bbrhBLrzwwk3v/bzzzjvtdo0/m9PpS++9vPzlLxel1EnPb7fb8slPfnLD673kJS855fUe/OAHy+Li4rpy42PydO57/PzN5vHx57JZ33zlK1+R2dnZE645Xvff/M3fSKvV2rSNv/M7v7NhOz74wQ9KFEWblr3ssstOeh81apwt1J6LGj/yGHoU3v/+959gNR5Sop7ylKecEed36LXQWvPMZz4TgKmpKZ74xCcC8JGPfIRut3uX2l0UBTfffDMAu3fvvtP1PPvZz2Z1dZW3vvWt/OAHP+Do0aN84Qtf4MILLwSCdfBnfuZnOHbsGJdffjnvf//7ufXWW1lYWOD666/nJS95CUop3vWud/E7v/M7J9R/9OhRnvCEJ7C8vEyr1eIP//APueWWWzhy5Aif/OQnufzyy/m1X/u10b3cXfj617/Oz/7sz3L06FGmpqZ44xvfyLe+9S3m5+fZu3fvyJI5HrR/0003ceONN46+f/KTnzwhaPYRj3jEaV2/KAp+7ud+jhtuuAGtNS95yUtG1//qV7/KM57xDAA+/elPjz6fDL//+7/Pxz/+cV7xilfwrW99i4WFBa677jp+4Rd+YVTHn//5n59pFwEh6cDTn/50BoMBu3bt4t3vfjf79u3j0KFDfOQjH+He9743zjl+7dd+bV0a5/POO2/UJ3v27AFODDx+9atffafadHfjTW96E1/+8pcBeNGLXsRXv/pVDh48yPz8PN/+9rd597vfzROe8ASMMaMyZzo27my/3h1YXl7myU9+Mueddx4f+9jHOHjwIIcOHeK9730v09PT5HnOc5/7XKy1J5S97bbbuPLKK7nlllvIsoyXv/zlfP3rX+fYsWMcOHCAa665ht/6rd9i27Ztp92eZz7zmayurm7an+N9+apXvYo3v/nNQJi/v/CFL3DkyJHRnPKgBz2ITqfDU5/61HV1DjE1NcV//I//kb/+67/ma1/7Gnv37uXw4cNce+21vPa1r2VmZoYvf/nLvPCFL1xX7hGPeASrq6u86lWvAmDPnj0nPPO7M/B8uA79xV/8BXfccQeHDx/mU5/6FDMzM0Dos1/6pV+i2+3y8Ic/nI997GPs3bt3NMcM16LXvva1vPvd715X99LSEs973vOw1nKve92LD3zgA9x8880sLi6yb98+rrnmGl796ldz7rnn3m33V6PGCPe0dlPj3z7ubs/FysqKNJvNE87vdDojC9A111wjInJangvnnOzevVsAedSjHrXu2Cc/+clR+fe9730nreN0PBdXX3316JznP//5J61rI4xb1JIkkW9+85snPfcBD3iAAPLIRz5SBoPBhuf86Z/+6aiuAwcOrDv267/+6wKIUmpDa+jKyorc9773HbXn7vBceO/lsssuE0BmZ2flO9/5zknrKMty3fdxi/FG42kcm3ku3vrWt47q+e///b9vWH7YV4B84hOfOOn9AfL+97//hOPOudHzetCDHrRpW0+GH//xHxdAZmZmNhx7x44dkwsuuEAA2blzpxRFccI5Q6v+nbWwi6wfo+94xztkdXV1078bb7xxU8v+Zp6LK664QgD5hV/4hTNq45mMjbvar+PXetWrXnXK/uj1eidcY3xeecADHiCdTueEcz760Y+OzvnUpz51wvGrrrpq9K5/8YtfPOn9Hv8enQ5Opz+vvfbakcfiXe9614bnFEUhD3/4wwWQn//5nz/jdtxwww1ijBGllPzgBz844fhmnoZxnG3PxdzcnNxxxx0b1tHv92X79u0CyDOe8Qzx3m943stf/nIBZNu2bdLv90e//93f/d3oOtdff/2m91Wjxt2N2nNR40ceExMTPOlJTwLWZ3L66Ec/Srfb5dxzz+WRj3zkadf32c9+dsT3PT5O43GPexw7duwATkxTezrw3nPbbbfxhje8gd/+7d8GIE1TfuM3fuOM6xriuc99Lg94wAM2PPb5z3+e6667brQBYJqmG573ghe8gAsvvJCiKPjwhz88+t05N+rTJz3pSTzmMY85oezExAR/8Ad/cKfbfzr4zGc+M7Jg/sEf/AGXXnrpSc+NouhuacPQk/BjP/Zj/Pqv//qG57zpTW9idnYWgD/7sz87aV0PechDNvRuaK1HY+6b3/zmhpbnzXDttdeO+PavfvWrN+SAz83NcfXVVwNw8ODBUUa0uxMveMELmJiY2PTvsssuu9P1D/vpTBI2nAnOdr9effXVp+yPq666atM2velNb6LVap3w+5Oe9KRRMPXXvva1dce+973vjfbV+a3f+q1RkoqNcHe9R29729sQER72sIfxvOc9b8Nz4jjmjW98IxCs+UtLS2d0jcsvv5wrrrgCEeGzn/3sXW3yWcPLXvayk3oO/vqv/5rDhw/TbDZ5+9vfftLYote97nW0Wi2OHDmyLlZufK64u96DGjVOF7VyUePfBIYC2Uc+8hH6/T6wpmg885nPPKOUjkOlodlsnpC61hjDL//yLwPwuc99jr17956yvgsuuGDdDt0XXHABr3/967HW0mg0+Mu//MtNheVT4fGPf/xJjw0X1osuuoidO3fS6XQ2/Ot2u9z//vcH1gsk3/rWt1heXgbgyU9+8kmvc9VVV9FoNO70PZwKw/uI4/iUlKO7A4uLiyPl5mlPe9pJx1Oj0eAJT3gCAP/0T/900vo2ExwvueQSINCwFhcXz6idX/ziF0eff/EXf/Gk5z3pSU8iSZITyvyoYqhcv/vd7+YDH/jAWQmIH8e/tn5N0/SkBhOtNRdffDEQAoPHMS5onyq5wt2FYRse+9jHnnQ+6nQ63Pe+9wWCQebaa689oZ6FhQXe9KY3ceWVV7J9+/Z1u8grpUbz2EaJPu4pnM5c/ZCHPARjzEn7xXs/Wi/G5+r73e9+o3npP/yH/3C301Rr1NgMtXJR498EHvOYx7Bz505WV1f5+Mc/zr59+/jc5z4HrKWrPR2srKzw8Y9/HIBf+IVfoN1un3DOUJHx3vP+97//jNsaxzH3uc99ePGLX8y3vvUtnva0p51xHeMYxlZshGH2mptvvvmUltLhfY/vSD6exeQ+97nPSa8TRRH3vve979J9bIYf/OAHAFx88cX3SL78O+64YxTPMxR6ToahBX5hYYGVlZUNz9nMsjh+f+OpPU8Ht99+OwCtVmsUN7ER0jTlXve6F8CmWXDOFt797neP9qg42d9d2Ujy9a9/PZOTk/R6PZ75zGeyZcsWfu7nfo7f//3f58tf/vJdTh19tvv1da973Sn7Y7OMdMNsWCfDcAwdP36G79Eww9UPG51OZ+QVfv3rX7/pfDQe8zE+JwF8+ctf5tJLL+WVr3zlKF7jZLvID40j/xpwOnP1Nddcc8q5eqhsjffLRRddxIte9CIA/v7v/56LL76Yyy67jBe84AX81V/91Ql9WKPG3Ylauahxt2N8ETwdi+L4OZstoOMY9yj85V/+Je9///vx3vPABz5wU6H4eHz4wx8eeT4e8IAH8PWvf/2Ev7IsRwLG6VCjxnfo7vV6FEXBTTfdxFvf+tZRKtq7gs2E7TuzsA4Gg9HnTqcz+ryRojWOUx2/KxgK6RMTE3fbNTbD6urq6POp2jB+fLzcOMYDizfDmQrFw+udTj8NzzlZG3+UcMEFF/CNb3yDX/mVX6HZbLK6usqnPvUpXvOa1/CQhzyECy644E7RGIf419avd3b83NPv0Z0V9MfnpJWVFZ70pCdx9OhRtm7dytVXX82XvvQl9u/fP9oNfHV1lYc97GEAZ0wtvDtxd87VEChn73rXu0YGjptuuol3vvOdPOMZz2DXrl08/elP3zTFb40aZwt3D6myRo0xjG+mtLS0dMosJONUkGEWjdPBs571LP7oj/6Iz3zmM3znO98Z/XYmGBdAXvayl53y/O9+97t85Stf4UEPetBJzxnu0H1PYHjdK664YkNqwemWh/WKxkbY7Pjp0NI2EwKGGaDuKUF4XBg7k374YQtxw+udqo3j59xTgubZxkUXXcT73vc+/vzP/5yvfe1rfOlLX+Kaa67hs5/9LLfffjvPec5zmJ+f56UvfekZ1/1vpV/v6fdofD5529vedtLYpc3wkY98hMOHD6O15nOf+9xJY3XOxj2eLp32bCgww7558pOfzEc/+tE7VYdSiuc973k873nPY+/evXzpS1/ii1/8Ip/4xCe4/fbb+dCHPsSXvvQlrr/++nqTwxp3K2rPRY27HePW+aHQvxmGqQCjKOK888477evc73734/73vz/OOW6//XbiOObf//t/f9rlb7nllk158ifDXbGI3t0YuuFvvfVWvPdnXH48cHWzZ2et5fvf//5Jjw93Ih96hTbCgQMHTnpsSDX5/ve/f8ZUobOBPXv2jASNjVJjjuPb3/42ALOzs+vS4v4wMHxenU6HO+6446TnFUUxel4bBSf/KCNJEh72sIfxW7/1W3zqU5/iBz/4wWj8vPGNb8Q5d8Z1/lvp12E/9Hq9Td/XuwtTU1PMzc0BaxStM8V1110HhPn+ZIpFURR873vfu1P1j2M4b8Gdn7tOF8O5+s72y/E499xz+cVf/EX++I//mFtuuWWUbOCOO+44IY1tjRpnG7VyUeNux3h+87/927/d9NyiKEbZTK644ooNs6FshnFPxVVXXcWWLVtOu+z73ve+EY3g2muvPSUn+ud//ueBkOXjbAeQni38zM/8DBC8QaezC/fxuPzyy5mamgLYNHf/pz71qU2F/p07dwKbB1f+4z/+40mPPfaxjwXCLsx/9Vd/tWmbj8c4te7OCJYQPGg/9mM/BrCpVbHf74+yBG2Wiefuwvi79pGPfOSk5/3t3/7taMye7j4fP6rYs2cPz3/+84HwHhw5cmR07HTHxr+Vfh3P9nZPGUUe97jHAWE+uTPzZp7nwObP68Mf/vAJlKFxDJ/7qeaD4bwFJ5+7nHNnJSPVcK6+4YYbzvpeG1prXvGKV4y8I3f3TvI1atTKRY27HZdddhkPfehDAXjnO9+5qeX3DW94wyjw7D//5/98xtd64QtfyHe+8x2+853v8Bd/8RenXU5ERtmlLr30Uq644opTlhnGeCwuLvKJT3zijNv6w8BjH/tY7ne/+wHwq7/6q6fk2x4+fHgdLc0YM1LY/uf//J9cc801J5TpdDq88pWv3LTeIW3s+uuv5/rrr9/wuhtt4DfEox/96JFw/8pXvnJTq+vxFIXZ2dmR1+GuWBj/03/6T0BY/N/+9rdveM6rX/1q5ufnAUYC7Q8TV1xxBT/+4z8OhI36NrKyLywsjDYR27lz50hJ/lHGqYSloTXYGDNSluH0x8a/lX69+OKLRxmL3vKWt/ClL33ppOfeXbEKQ1ra3r17efGLX3xKj+rxz3Zo4f/Od76zoXdi//79vOIVr9i0zqHR6ejRo5ve5549e06ZevwP/uAPTitr4KnwzGc+k+3btyMiPOc5zzllDMatt946UrSG3zdT1g4ePDja+HXoPapR4+5CrVzU+KHg7W9/O2ma0uv1eMQjHsHVV1892pn40KFDXHPNNTz96U/n93//9wH4qZ/6KZ797Gef8XUajQaXXnopl1566RlNoF/84hdH2WqGSsOp8MQnPnFkCfrXSo1SSvHe976XZrPJrbfeygMe8ACuvvpqrr/+ehYWFjh27Bjf/va3ed/73scv/uIvct55553glv/t3/5ttmzZgojwxCc+kT/6oz/itttu49ixY/zjP/4jP/VTP8XNN9+86S7jT3va00Yc9Cc+8Yn83d/9HfPz8+zfv5/3v//9PPjBD15HQdjoPt7znveQpinz8/M86EEP4uqrr+bGG29kcXGR/fv38+lPf5pf//VfPyFlbqPRGNEn3v72t3PTTTeR5znWWqy1px00/YIXvGCUrve//Jf/wm/+5m9y4403srCwwLXXXsuznvUs3vrWtwLwhCc8YdO0k3cn/uRP/gRjDPPz8zzsYQ/jfe97HwcOHODw4cN87GMf46EPfejoGf/Jn/zJaSdN+NeM+973vjzmMY/hT//0T7n22ms5cuQIR48e5Rvf+AYvfelLede73gWEsTceVHsmY+Ns9mtRFJumYR3+3R0C/tvf/nZmZ2fJ85xHP/rRvOpVr+Kb3/wmCwsLHD58mP/zf/4Pr3rVq0YB0WcbD3zgA0c7vb/jHe/g4Q9/OB/60Ie47bbbWFpaYv/+/Xzxi1/kTW96Ez/xEz/BU5/61HXln/KUp2CMwVrL4x//eD7+8Y9z8OBB9u3bx3ve8x4e/OAHs7i4uCml9oEPfCAQvCBvfOMbOXLkyOiZH+/NeO5znwsE48qLXvQivve977G4uMi1117L85//fP7rf/2vZy0xx3ve8x6MMXzta1/j/ve/P3/8x3/MTTfdNPK4feMb3+Bd73oXj3/847n44ovXxZW8973vZc+ePbz4xS/mH/7hH0b9eeutt/KhD32IxzzmMYgIWutN0ynXqHFWcLdu0Vejxhg++9nPytzc3Lpdijf6e+xjHyvz8/Mnref4HbrPBCfbofu5z33u6Pebb775tOt7xjOeIYBEUSSHDx8e/X46O3TfFZzuzrFDfOUrX5E9e/acsu8Bue66604o/6UvfUmmpqY2PF9rLe985ztPuQv3+9//ftFab1jH7t271+3QfPwO3UP87//9v085hjbaXXt8l9zj/8Z3Et5sh24RkX379sn97ne/U47flZWVDcuf6v5EzvzZboS/+Zu/kSzLTtpGY4z88R//8UnLn+0duje73yHGd3c+0x26T2dcP+ABD5BDhw5tWu9mY0PkrvXr+P2d7t/x/Xa6O0uf6l28/vrr5fzzz9/02qe6xqnucbMdz7338sY3vlGMMafsgx//8R8/ofyb3/zmk56fZZl85CMfOWUfXHnllad1351OZ7Q7+0Z/L3nJS057h+7Twd///d/L7OzsKfvFGCMLCwujcuNrzmZl3v72t59WO2rUuCuoPRc1fmh49KMfzS233MJb3vIWHv3oR7N9+3biOKbVanHRRRfxy7/8y/zDP/wDn/70p0e7HP8w0Ov1RrtS/+RP/uQZWaGGG7pZa884FuCHiZ/8yZ/ku9/9Lu94xzu46qqr2LlzJ0mSkGUZe/bs4aqrruJNb3oTN99888g6P44HP/jB3HjjjbzwhS/kvPPOI0kSduzYwZOe9CQ+//nPnxYF6BnPeAaf+9znuOqqq5idnSVNUy666CJ+8zd/k+uuu+6U+0cAPPKRj+Tmm2/m937v93jwgx/MzMwMSZJwzjnn8NCHPpTf/d3fHe2kPY7nPOc5fPjDH+bRj340c3Nzp53K83js3r2br3/96/yP//E/uPLKK5mbmyOOY7Zv387P/dzP8cEPfpD/9b/+1z2eKehpT3sa3/3ud3nJS17Cfe5zH1qtFo1Gg3vd6148//nP51vf+ha/9mu/do+28Wzi2muv5c1vfjNXXXUV9773vZmcnBw9l8c97nH82Z/9GV/96lfZvn37CWXPZGz8W+nX+93vfnznO9/hbW97G4985CPZsmULcRyzY8cOHvjAB/LKV77ylPFxdwVKKV7zmtfw/e9/n5e97GVcccUVTE9PY4xhcnKSH/uxH+NZz3oWH/jABzbcjPBlL3sZn/jEJ3jUox7F5OQkaZpy/vnn89znPpevfe1rJ2x+uhH+7u/+jle/+tVcfvnltFqtk2aGarVafOELX+C//tf/yiWXXEKapszOzvLoRz+av/3bv+W//bf/dpf7YxyPf/zjueWWW/jDP/xDHvnIR7J161aiKKLZbHLRRRfxxCc+kbe97W3s3bt3XTbFl7zkJXz4wx/mBS94AQ984APZtWvXaH297LLLeNGLXsQNN9zAr/7qr57V9taosRGUyF3cXahGjRo1atSoUaNGjRo1qGMuatSoUaNGjRo1atSocZZQKxc1atSoUaNGjRo1atQ4K6iVixo1atSoUaNGjRo1apwV1MpFjRo1atSoUaNGjRo1zgpq5aJGjRo1atSoUaNGjRpnBbVyUaNGjRo1atSoUaNGjbOCWrmoUaNGjRo1atSoUaPGWUGtXNSoUaNGjRo1atSoUeOsoFYuatSoUaNGjRo1atSocVZQKxc1atSoUaNGjRo1atQ4K6iVixo1atSoUaNGjRo1apwV1MpFjRo1atSoUaNGjRo1zgqiu1rBV/7fP8SiERQZjhyD0UFr0Qq8ihAFDQ0Sp8RGYYymHPTpSoQ+5xImtmwjTWK892gTMTU1idYGYwxojVIapdTomiIAglJBNxIE7zxah/NEBBEBBQpFKBp+J3xk0OvR7+dMz0yj9bCeUeXVdQQRj7WWJElh2IThKVX9wzYcf8yWFmMMSivWCodP4kr6P/g6bvUYIoJuzZJeeAVR2ghnjLVjVE6xrp6NMLpHBC8yap9S4ZNUbQ3f1cZlhyeeULenN38IdfRmfHcBFae4bIp8+jy2bNuF0joUPL5s1U/DPjq+z9ZdboPrnoDju6Aq4314VnEcV5114jM5/p4B7MI+ikPfx3UXUGmbZOv5xDvvvUFjRr2Jc47ekTtg/jaktwxJAyUWrSDvdZAoJcla+EEXnTQRZ1FaI+UAlbZQKPygi0oaIA6lNb7so5IWiMfnfXScIuJRJkKKPioNx6QYoKIE8KBjpOiFY94hZY4y1WttYiTvorI2eIvYArRBa8AkSH8Fn7YweMSVoFR4hiZB+quobAJxFrE23LsxqCiCQQfSdigjDvECUYQyMTJYgbSNchbEgfcQxaBiJF+FpI2SEsSH9poEdAR5B4mbKF+GXnclKkrDO170kLiBtwVKG5QrUXGK8h5V9NBJk6LTxScJSgvEWRgjRQ+iLPSv0mBziBuh/nKAmDi0Q5nwPW6gELADRMco8aANyg7wcXhOuAJ0hIhCtEGVfXyUocSjXIlUcwk6QtsezjRR4lA+9CFaIzpGl11c1ET7EuUtIuC1xusI43pYnaHFAh4lgscgRESujzUZCgsISjxOGTyayPexKkPjQNaOoQyx5JTE6Oqt02JxROANsR9Qqhi0R1Q4ZokAHcqpGFXNDQZHKWF8xVJSEqHweCDCUkiEQhFTYsWgEByamJKCGAXEWBwGRHCiSCgZkGDwRDichD50oklVyUAijECsPL6yhzkUGSV9idAiRHgk9BYWTaYsfYkxeIzygMKjcMrQUCWD6lhYuQQrGj+sk5gIQSvQKhwTNBklOTFGCUoEjcdWtaSqpJCIqJpeDB6rQx+mUlKqmFiH+diIpVQxgiaWAqtjIvGjY1aH+Sv2Bc7EYUpVhkgsLsrCSHA53iRhPlCGyOXYKEMDxhWIiVFKEBNhygE+aaFFoW04BiA6Qhc9JGuhKTE2R0wUesQkmLyLz1phXnNlGLsqRkyCHqzis4nwLlZzh+gITIIadJBsAmyJkjAWiWN0FKEGK/isDaWr5gAPcQwmQvVXIZsAV4Tx5i3EaZgf+su4qIGmWkttgY9SlIlQg1XI2sjWc/Hn/thpLBg/HKxb19RYK8aWldNZ7kZVjMkfZ1LOe49WaqyC9VcXERjKTCIIMpIFxAtKK5RSeBHwQa7wS0dQ+7+L6iwiSQPlXVg/yhzXnELOuwyaUwBobaqbV4iX0bovx8k4w9Y554giQ3zou0SL+1FFj8Xcs2/fAS467zx0nCCTW5DzH4CgoOihb7se1VkEYwAd1pxBB1rTqJ0Xw9yukXw3lB+lzFG3XodaXQgXNmY0fsnaKFuG+wKs0vgoIir6kLXAWfDVGI6S0fiVrI13Ltybs+g4BgTfW8FHGUkcgyhwZRjbxkC/A2kzjPfhOpU0wpo16ELWRJwDFeQHhjJi3kUlzdAObaDoQ9oKa1jRD/WLoIxB8l54R7wEWWIoP5gIBj0ka1MU4IocFcVEM1tp3vcnaLXaZzDS1uMuKxdpFNGL2jR8QezDwrsSt5ktV0CEQ6UjKkuarRRjDHZmG2n/MJE2RK1tRFFBPP9dTNpETW3HLB3FLnnyeIpGGqH7i6i4gZ7ehVvaD7bAZrMMel3aaoCOM9T0LmRpP74cwOT2oGCsHAKToGfOhaX9UA6gvRWiBFk+gBKIm9uQO27F2T6qvQVvUlg6EAbKzLm45YOoso9pz+HiBrJ0ICg7M3tg9XB4uK1ZVDYBC3vDpDx7Lqo7j/SXGZCRTW1Frx4Kb87MuUhvAfor0Jgkbk1hlg8iePoqwt1yPW1jIZuEiTmY3xsWj5lzUHkHuguQTaAmtqIW9gbhbHo3lD3ozEPawk/twB25DS0emdpB3lshs11ImujpXcji3jCwJ3eGRaFzFOIMNb0b5vcitkBN7cDjkdUjEKeoqV2ohf0om9OY2IZPUlgtwCncxBz62M3Iyq1IeytEMWrpYBi0M+eilg9C2UPaW5AoQy0fCIvQ7B5k+RDkXWw2hW600csHEaWRmXNRK0cg70BrBhqTqMW94eWaORe1eixMHM1pfHMKvbAPgLK9Db9ylEgKaEwh7Rn0wt6gJM6cix4sI72l8JK1t6IX9iHew9ROYu+IbYlEJegI9y//jBKPTO9G2R6qM48kTfzkdszSPrR3ZBPb1wRVpfFbz8Mc+T4JDje5JSyuZR8Q7NwFREduRdkC15gFEZJigHjBbj2f6OitUA6w8SRKR6TFMbwrybecTzp/O6rsU8YZYjKSwVEwMYO5C4kX96LzPqVOcXFKOjiK14b+9Pk0lvdhih65aGzSptE9iqDoTO+huXqYqOiSO003maC1egxBsdzeTXNlnrjoUuRCP51gsnMEgKXmTlqdRZKiw0KxSC+ZZhcrILDY2EZWLpIVHfIoZzWeZqa/gEKYz7aSa0/iNOWgZBC1aZZLKISeTjFSkDjBUtAzTVp2FY2nowyRODLvsSrnWG6Yi3MiJXS1QjlPy3u8KVgqW7QGfYwWesqhRGjgcAxYpckEXYw4upSI0rTE4vCs0GSCHgZHH4cTmCAcW6bJBH1iHD1KStFMKocoYUlaTDAgxtPHk2OYJEfEs0yLtuqTAn0cA2KmKBBRdEg5T+ZpUdCjYFk12OVXEGC/mmJWLdOSAbkULNJkt1pFKTjCFFPSJWVAoRzHmGAX8yiEI0wxwYAGAyyeI0ywS5YwynNIz9DXCQ0FJRHOJ5zrj2LwHCUjw9LyOV55btdbaZg+hpiuNNniu0x4h1aKfdE2GiYnUtA3LRChKV0cEQUpu4pDxALLugHKMOmXsUpzLN7CFjtPLJpO1MLrjKlyHqcMC9lOZgdHiZ2il0xS6IzpwTG8Niw0tzE3WCBxOf10Ehs3mewdBWNYndxNq3uMuOiRpxNhjK4eBKVYbe+mMThGUvbJkzZFY5r26gGUUnRn9tDoLxINVrGNScrWFrKFOxAR+rPnknYXiforuKxFPrmdxvwdKIRiy7lEvRVMbwmftbHTu0iO3oLynmLLuZhBB7O6gGRNytlzSY7cCt7h5s5Flz306lFIm8i2CzGHvxfmgLk9UFr00kEkaeC334vo0PfAFsjsbhCPXjiAJBl2+72IDt0S5pm53SitUcf2Qpzid1+C2v99pKtgeicqa6KO3hrWud2Xog7dDF6Qya1B6T90S1COz70UdeQWcAXSmkI1plAHb0a8Qc69FDl8K5oIlUzAxBzqwM3gQc65BH10H1iDVhlsPQ/2fy8IA+feG44eDEp9msC282HvdwHw2y9Alo5A33D02AKT976c7PDtIOC3no9aXoB+D7RBdlyKuu1fwGtk9zmo7ir0utBMKXdegL79e+A0sns3qt+DfjfMw8k0cuN1UJbI1u0oa2HxGKQZautOOLIfygLmtgehcOEoJCmydSccOYTkOcxtCQaWY4chTnBzW9ELR1FFATNzoV+PHoYoQu/cjRw5hAwGqJnZUNfRQ2Ai9I7duGNHoNdDzcxAo4EcPhiMFTt2w8IxpNdBTc5Au40cOhCE/x27kcV5pNtBT06hJibx1TG9Yzd+eRHprKBaE6jpWdyh/SCC2bEL11nBryyjW23M9BzloQPgPW5mltha/MoSutlCz23BHtiPeEe0bScy6OGXFlGNJmbLNuyh/eAcZut2pChwi/OorIHZtgN3aD9Slpgt2/CmjS06aB2j91yCu+37UHiKLCHtDpD9B1FJgtm6A3vkABQFZnYrYjRu/ig6Toi278QdOYTPB5iZWYjicE9phmzZRn7oCNKPac5t48Kt98YevAPlFPHu7cjeW6HfQ09NQ3ML5cIqSmv0nnvhD+/F5xqdRRiv8f9yA6Aw23ciSwv4XhfdnoTmVsr5pXDsnAvwC0dCuSRCz+3E33ErAOqc85CVefLBIBjZ5nbj9t2COI/bNkfc7yA9UCKo7Xvw+29BnGBmdlAuHaVYcZR6wMS9zoeDe8F5mJhFDfpI1+PLErdlJ/rQXpQrcTMzKGfRKyWu26Xcuot04RCUJW5mCrxHr5RI3MfObcccPYCyJX6qhTIRenmARA6/7Rz0sQNB6fMNvIkxSz3EFBRzO0mOHUaXOa6dkOsIs7yEKE2RtPDf/xfu/4AH3mndQMnx6uMZ4tsf+GOc0pX1pMCZpLIRgRbB6WAbSnGotEkUO0ykMHiIsmAps8FiqwkW3KDVNYLnIl9FpS3EW1AmaG5JA7EO4/JKc7MobYIFN2sDAnkX4gztfbB8FF1IJwAPRR+JkqDh6TgIsdlkuEYxCBZfpSrtdzUI+95CmYfJQQXrLvkqKptEuwIpBqGMjoLGmK+Ecq4EWwIqWIWiBAYrqGwSZcugASP0ixKPoR25ynpjwzWHll+TBKUkm0DZIvSxc/g4A2OQ/kqwhFYWPOVKfJTSy0saukSlwXodrD45xM3gURmsInETbInRwYLr0xa+svxKnKFtsPyqso+kQbDQZQ/iLFg5lIGih0+a4ByRy4NFWkLfq6KLS1soLyg7CMoFKliH8w5diUgjTSQ21KUUXsXoooONm2ixKFcE5QKNVwlR2cXG4dnr6r6c0oiOiMoeZVR5EsRhy4ISRZK1iMoOhWmivQtjQzxORXhtiG2fQqcYcRT5gFhrJI7xWpMMj+FAQIujVDHeGxI3oFAxWjkEIRJHoWJEFIkvKHSMcYKgibwlV+H+UykoVLCQC4pYSnIVoZWQUGCJUJW1NpWCPgmIkGKxyoAoLIZUSvrV9RNlsaKDxVg0DSnpkaCRoPQQLFgOQ4MiHBMhUqENHo3F0JCCnoqJlSUiWG+c0jgMTQpWnCFREFceMasMVkU0fE5fJcR4FIIWoRM12ZvtxJokzAsmQuvQDj30LFbOuuBRG3M1DT+p4f8KbaKRJ27o0Rxaw/SwzOg/xfhPWmu0iYKVbVRvsDEO61xnclShfUOPlTYGU11/3H44nEbHbYOqKjjus2wt76W5ciAIuEkLVY1fAawXrNI0pMCmbbQL4xcIc4dOMHkHn02gfQHeobzHmxhvYqK8g0ta4X0QQXmLbW2hd87lSNIEgda+64k6R8GVeJPiBSLXxydNyqld9LZeTD7oMyE52eHvY7oLSNJk0NpCee7lJFk2dofhnuPbrw9Gku4qNsqI0wRVhPkhWMdiVN4Nlm6RcMwkobROUNU94TyqGEAUB4ukiYMVvDERPD9lHowWSkOUoHqr+GawnmPD/DCyPvZXkOZksILbMct6lKJ6y0hzChnOvyJhjo0SVHcZaVbzr3PBWxUlYb3oLSONUCfeo5xF4ix483or0JgIdQLKlkgS5mbVXwnWTl+EMVHmwRDkFeXKIsnkTJibtYFigKTNMOb6HXyckfd6xFkTU+bQrNa3QReSDHFSWfZ70AqeTZX3kMrrOezDgYpJoxht83A/mmC97K+GfiosFHlYS5SC6p58NoERCUK51uFaJoHuCrTG1jcFouKwdnZWUO2p0E9V/8pwDeus4LIGGo+uPBcSJYiOobOKtCZQZRnabi0kKZgYuqvQbFXPkqBApKF/6awijVbwliqNFDlkzUCd6HZQjWYYP1pDPkAarTB8e13IGoj1iDHQ76NaYX1j0IMkpSxyojSDQT/0vZfwOU7Wxk2vC+1WWKvzMH6BYNHudqDdDmOpGITxi4I4RrodaLXDfVb9K1qTe48Z9NGT0+GeyuDNVVEU+rG7Cq0JvC2DV1kEqY5JtxP6yVnE+TX5IYrWjtkS8T6UTRKU0VVfNCt5hKrvk9CmXjf0tXdhRi0LXJIiSqHzQRjnzoa5tCxDnwIM+kgcU+Y5hXXE3kMjQ9AYW6KSoedNo4ocSSpLe1mE5yGC1xqVF5RRjC0LpChQUUQURag4xhQ5ZRyD9xjvgndShFKEqCwoTERqDBGCF/CAKE3syqqcBEOsgCP8xa6kMDGRtSjvQcAajTeG1NsghIuEudc5Sh88AE2EXBt0xQ8xIjgTUVqLKgYMUDSzNDBVEEpRCIrEWXriUS6wbRIFfR/Wo4aCTumIjUFFhlg8A1GIgkwJBQrlPU4gVUKhDRA+lxLWM4+QIPSr9TVFKFFoCTpOpoSeDyyduJIRVjF8z8b85m+9jDuLu+y5iBRoE1zVxgc3soJAE1CCMTEoMNaBd2hxaBcED0yE8gK2xLoOcWwQRRAYdYT4IljSUeFlUMGdpFRwt3ubh2t5F+gINkdyA0jwVHhXufUMlDmCJrwc/bAIKFA6QpU5nk4QbsoeogyiDZQVXcIHuo+yfSAIsKg+2uZBfhaP63cCDSnJUMUgUClscCMq2w8Cs04RrdDlAFcE4Va7AggTvcaS9wbYvERLWLxAcDosxMbluEGOEY/2FiVCadLRsZI+WgF4lPcMMGit6UuB7fQqoU3Q3mF1FxCMzSllGSNCZAzaW3LdxSmIfIFTJiwuoojEUugOWiCWcCxQEYJi0PdLOFsyEWu8Cs/BiyLGktMBIJESrzSuoiEkWAZiyBWkWJwIvTwokhOJYUCnEraDAFb6QElJseSqB+JJlQegUCa8rJQUhPuNsHRWV+mWnunZGRrKU1CgBaKKcpKrKIwtKSkkJ9IK4y14sN5Vgm+BEKzWQypFxVcISgxgtAM8RjxGh7EWBHMdnkslxCsT3MyxU0QaqFz9xmtMZML9eh0m1opKY3xEYiq6hAOvY0DjVYRxmmaUgvYYNwg0HzQoVR1roABj80oAiwM9quzTMilKmyB0KBWoFmh0OWAyyVAEJR4IQoAyRLbPVNysxnaBAlyc4UVhyoippBHefxvG9tT0DrbuuQwaU0GhqPpmKOCvQVgTxcc/j7zq4bPS646t5x+w9kUpWH/m6PdhkXGK3kaUufUNOP7LiUrQqWD8IqZnUJEmjjVIjAxylNbEcTBqRNaRREGQk6JEvKNE4cs+FAOsJ7z/rsDaEh9nmChG+wLnBa01pqJMWXEsHT1MMrebbdu2Eh02aLGIOLQOq61WghDGZTS7Be8s0dJBjNEVjcqTJTHJ1PQ6eioEpSrSgvYlaEFHOqio4hBXVF0jgR7jyjDSbYlzLsy9hrAuuDJ0pwuUOaWjILw5FwRKfFAgvA0CrPdBoClzYDjWFJAEgcpZVFEdK8P4JcmgHB7rB0GxOiZKobyrhLlBqKMswshQOghWzkLRD1QJVyLOYZ0jTtIgzJUDlHOj62MMypfhnooBVDQ3XImoGIUmVhIUihF1r6gEUAEblJHUVL/bEqnaO3y3xAkoE4wvRVQJ3kWg9KFCW2xJFGmwEhQI5yAyiHdBMcv7iCO0UWtUHAcqoXehXl8dUwqJ0iB42hLyXnhG5SBcK5IgsDobaBjiw/WqV0VKB7ZE2yjQKW0RvMpe8L4Iz0tpRDxSlpUwCxCOhWdkR/3rfGX0ygehjAuCoHIWL9XnfBDuU4LBk7LA2UBRVYM+UhYE+VFVQncQrnU+QAZ9BMjzHFXklIMgb0RlidcGX40NUxbYfBCMKWURvO9KIUqjiwLb7wIQ2aAkeBUUOGNLym63KhcUYKcjBmVB7B3SD2NUlaGfXBQoa7Gz2OUVvAjaWUQEqyMcQuQspV5AC9W6LRRK4QVS8eEYQTAW7yl1oEcn4igIxh6NoAXyyoASe08hoLVCSRCae9XsFzyiCl3RqWJgUFlUUoRCwBYleVHSSmIG4Y2kFWmc0igBh5AoGPgwfDMFlYqDlSAYd51HvJAqKiOuxitFphU9F9b/pgn3mTuPE0+mFX3niUwUylVKh6BoGEWvEubTIDSRV5SvhtEMnEcPrydCHxCtaBpNzwVJMq3WkZ5zKBQqMvQq2TZSQZAfuNAvKULuJVCaFRhgUDEGxWhK5zGEPnZKUZYOpSAyCrEOFxkog9xQOBfWCaOxPrTFi+C0Iq/6QhtN6cOYdyIooylceJ9MZHBecB6cFyKjKV2QbSIT+qI7sOyb753GinZy3GXlYmBSnI5APEZT8X8VLemhga4oIvE0lcN6S08yWrZHhNDXCuUcSVHQ9w7VniWzHYw4+t6DCkKVKwWrYgwO5Q3OBqHQeI0vPJ6IhuthpKRnIgShaQssjr5q0PQ9Im/pRRqrDLGAx1ES0fRdYpfTM2B1ROTB4ymUIZIgyBcyACVMuBwHdFTFe1WOUgagFYkYnHMsL3WZbURkFPTEkauIvLNKo9HERxEaTyQeSw5o2hKEs1U0SkEMWCmxopigwCjoYIiU0BTLQEFfYjIVbLSlDjzdlvfkWujphFjCZNqz0IigJUKhhL7KaDNAi6ZPhFaKTEpW+gU9lbItgQhNbjK8VhgveCL6UUbL54jX2LiJAmKnERXRj1pkrh/44TrBlxalHTqKyE2L1PWIXIlLmhQOXLFCkmS4bIpGOSD2OaWPGFhH7HOceOZdzo7JFlkWY+ImPorJipUg2GaT6CIntgPSpIWPE+LeCihF0pxClTkm75IlTVycYBcPs3J0iV7U4LwtO0ncABc1oDGF6S6DeLLmNMqXmP4KzbgJjTamuwTicM2pYMvvrwT6QjaJ7iyhvKXZnkGsQ3dXkayBNCYwvYWwuDanEUB3l5A4QxpT6M5KsOa1pwGF6i6GmIDWFHSWg6AzMYXSBP5olCDtaVRvGfIBSXMCFSXVsRhpzwYrVt6H1hQSa1gJvFOZmEF1lilXl0im59BpM3BLtQmUu/4qDLroxkTgzK4sgNLoydlgtet20K0JVJbA0mJY+FotfK+DUSmq2YasiVs4htEGNTmNLgrorqIaoQ9leTHQO1ozJOkErCwHy1lrApaOIc6jZrcEy9zyIjSaqPYksjQfhMqZudCXS4uQNWByCpYWAt1sekuwei4vQJrB5HQ4VhahnAiytIBKUmRqBrW8iBQ5ano2CEmL8xAnyPQsamUpWBynZkAb/OIxiONw7uoK0u8H13sU4xeOoaIINTOHdFaQXg81OQVxjF+YRxmNnt2KdFaRXhc9OQVJil84FgS3yR3IsUOIElQ8gcpSyiJCGUM0M40f9Cm6XVTcgjSjXFxAG9DT0+jC4jsrxGmGT1NkdSVw9SemkLLE9bvorIFvtZCV1TAnt2fYsmUP3aNHcM0MWnOwvEpR9iGeIItj7MoKmAw/tSP0S1ki7Slc1KTUk6goRWZ24pcWkLLATM9iywK3tIhOGqjJ7bil5WDdzyZRsaEsDU5p4plZpLuC2BjdmKJwikOHPVFs2HneduYPLdFZdmzbNUmURBw87InTiB17trF4eInVRcuWXS2SLOHgEU8UR+w8bysLhxZYXhiwdVeLRjvhwJFjaKPZee4cywsdVhZLZrdmNCYyDh2dRynYdd5WVpf7LC6UTG9p0J5ucfD2EPO2Y88s/dU+CwsFUzMxE7MTHNo7j3OeHedMMejnzB8b0J42TM9Nc3j/It46tu+epVNYjh3LmZiOmNk6x6G985QFbD+njbWWo0f7tKcMs9vnYHUR7zU6aYIHTwkS4bNJ1KCLeI9SCQDiC5SP8M02qtsBMSgVYv+8FOANPW+g26GZRXgJHjWxGucFnzWJihysQuIYrSOQEm8VNsow+QBVBMumoFE2fPbaoHp9KC2uDPFdJg9xNTYWtOsT2RLnFD5K0HkQBV0So2yOLgucA28ioqIMwq/TKOeIygKbW2wUE5cDEE8PiytKMiwyyClUROIKNEI/tyjrSKTE9XoUKiKVAiNCt5cHAVBKShR9DM0QzUO/O0C8J8Ni0Qy0puEdBmGgg5KQSkEpiq7XNFWI2+mtBPmhpSwW6HhNQwmRtywVwQAxlRqshxUnNLWQauisrCKiaEchjmjVQVMJifJ0l8GimIiCoLdSQitSZFroWMJaHwfL+qrTREqRiGfQzbECkbOI91hjMEqRKijoU0g4DwV9D5ogDOc+COWZDu7gvvcogYZWFAIlQYBHhBwwClKg8EIuQqYCvWfgPVppmkZRohh4T0Or0L8ujIdUhXKF9zS0xgC9ysPRMganFVYpmnGMRdEpLNY7VrTCitCzjkxrYq3o2yD8NozGSVAoMqWIFRRKY6KIVhzhROgMCoz4YOV3ga2RaY1U31NjSI2i7wSfWxomGLP61hEryIym7wVLUFCUgoETIq0YeM3AC96HPlQoBlU/FU4oBUoRGlUsSq4NwU6jKKOIQoSUYNuyJsh1IoITWMaTahUUgjRCeSgIikuuIxIJ90IGSiuchGdnoygoQQKx1qDC806UxmlNQwSjwOgItCKulCtvIiIJXsJmZZw0zobYNKWJnCdW0DIRrjLSaGNotyc5d3rbXdIN7rJy8b3Vkg5CJJ4GjkJ5dpkeLZ2jlKDyXjCiaocQ4YsuXtswifVLNEKkCjIVk68sgRSAw2nYF28jxmAxDHxMK3JoHIU0AGiQIyqh7XpM2BUicaQSLNyJCy+GaEciECMsLC1xi5rj3J078WKIyz66sxoES7HMt3eyvHCMLdu247NpYjcgkhxrGmztHqBZuOBSa2xhpbUNTUmcTCAmJi5XKfo98sOHmW3mNJRhMm6zPHMhCwsLTMzNIc1ZjCvQtgtxi4mVA8SdQyiBmfY2enMXQL7KUq/kHLdEo3MErWA6amLzPg0x9L0h33kfkvZkCDb0iomj38ctHyFqTVPsvBQXpcECY1Kah25E95eRuBGClPorwbLTnAoWjN4y27Yk+KRNVHZQrkCaMzhHcOfHKTQm0YMVVJkHfi5Adx6Loa8bpBKR4JlpTAYBtb+E6Jg8ysikAXkXaUzjAT2I8Cimp+bw3WWMjZhoTuFUhO4Fvt+2PZOQd4ltjjSnKre4B6XoqogkMURGI1kbFadVIJRCGm2UCQFUZG0kaYB3tLM20p4mM6B64NMmVsVEcRasa0kG1kBUEKdNiDJUlAbPV5SBKlFlTCGKoleQOY0mwbuIfrfPhI6AELSsVIKgKJ2gURgMqAhRJgRWeR0sjUiYfbSqPGoGxIA3weDudTjXmcBWsAolCcprnA0WKWUVeA1OgdMgBrGGcuDoDlaYTiPiqIlIgjgN3uA9YAXlNWLBlcFKpW2go0mhoNSB02w19CMogvdR4gxlPTbvITpCeQM2DVamQQTWQ2mQKA5W2NKAaFgt4bvfCkpQkiImDtQF72Ffto6GQBxDXh1LM5QIkgcagooTJB8Ey2vaCFbPfBAsrXGKFINgVU1DYKvk/RADlKbBgmpLyLIQUDcIx0hSpCiClTrNEK2RQT8oAmkDKQsoCkgbKK2QwQCMRqUZYsvA086yYMYr8xBwnt4WPKPVMdE6nKcUKk2RfgSDOATj2xgpU3whqMigyhg1iIJl26ZI0QjBrb0sKJ95jKgMdCtcw3tU3kBcDLlF6QaoNNyf98iSR5a/S5oPGCwvgImQvgGXoYom+cAiXcJYuj3wonEW0jRYobse1y9wve9jkFH/ivdQFOgkpRvFqJ6HErwN5ALVc0ikwOXQL/CDnP7KKtft86wc62LiiPSOeYrVDkW3T/wDj3WOYnkVExmim3rYbh/bz8mmBvQHJZ0DR2lvmaL9A8tgcYnVw4sQHyKZmSA/uoi3gWIh3tNoNxj0b0e8EBkwcUQys4jWCtsbYBrLYCJ8b4CIoG5YAmux3T46TQItI8/x4lHZPHhH2e3jjYYkJvXVO9hYxFuL7+XoNEbiGAYDvPOQHkPh8f0cncTc+4IF9kxYtPd0dQflg8GoQNFB09KeCE+XZVCKllhKpejJMZrehmNqCdEhZsgqHQRqccTLnq4sB6usyym80FHztAykeLqygleGNoHGseI0ExEkeDp+GYeirRxeYMVDhidTnlWv8MowqcOxVVG04yCM91RYm1sqJCRY9T1icTSUpy+KEsOEDpbUVd/FeKGpPD2BXBQTKlhnV0WjxTNhhP5gQM/DhAnW3SXr0J5wzEPPw6SBWMGyAyXh3IGHVeeZiiDWiiULykt1TFguHNOxIjOGJSsoBdOxom89S6VnOtakRrNig1GziBSFC8cmIk3DKDri8aKgVJQCS9ZTRtBEsVR6rBe8aKzAYunII03TaJadw3pPSIcAy85jlcYqzbL3Fa0m0FkO5o69K5aJSNPxkAvMxRqtDYvekoqnpRU9FIXSTAd5kyXnyYxmwmh6AgNRTBuPRrGMIdWatg6/l0YzWXkhusaQGUMLIScIym1xiPP0jKGZhrm81Joiiom8xXlhUNGWtCuxaAoUceXJlTgKHiVxRHGCzhokeLTzpJEh8ZDYAodGa03iHYkIaZaBNmRljmjNZNZAFzmRd/isQZI1iPMBOoop0hQ1GKDKHJukiDYkRY6JIlyzRWQtsSsDBS9OSIrgHc7jBNvtEtsSWi0kitG9DojCNZtE4omKHGk0UXGK7nVCQPrEBNra4M1KEkgyVK+DeME1GmAtqS1QjSaSZPjVlWAAn55GeYddXsLHKS6K8asrII7G1u34ssR3OpgsI56cCnVai7Qm0EpwKytIFBNPzUCvE2hnE5Nhbu92UEkMzQlUrwPWYiamgkyxuoKK40BP7HWQMse0J0Fr7MoS1kugf/Y6RN4RT88gSuGXF0M80eTsyPN/Z3GXYy5uvOG6dfQGLZbZI9+h0T2KQnBRiveCsSGSXYuv3OYenzRQaIzth2BqqTjwRQ7TOxnsvA9+Yts6OsQ491ophdKG9NavhKwCNscnrWCHKXpVNpjK9eNLOqZJd+4iJu91PwDMLV8jXtwHeZdBPEF39jzc1guZmJhAa7NGAegskNxxHWYpBA26uXMpL3owKs5w3qG1xpYlZVGgbv8GE93DmLJLGbfwOy5heWI3k9OzgXYxrDPvEt/yVfTCXpxzuOmd+IsejGpNI0Wf5JavoOfvAASJm1jnYNBBt6ZwWy5ELvyJ4AredxPJsVvQnQUkbeO3XoC74CfCszh6K+bATcjyYZxOMDq4PcWVOJNi4ihwoYdxMpVbXpI2RWExtgg0L3yIhSkHIasBgsq7iInwPmSyicQGrjCMjlE9H8lDRhIFqKKHRwUlQEch207SQrzHD7qBRhcFS66q4jgUQtldIY5jShK0SVBFH0maqCqGBgjKBDocSwM1R4o8tDfNgkcg7+GTBq4cxlxIsNwrFdz8lUKiXBDcJGuAEcg79K2Q6gxcoJyQhrGm8iqGR4XsMzgb4k/w6KJfZXwRtDKVgLvWh8QpvqSKW8lRzWZQygdd3DC+R0eBlpCFviDvBmoIGlQU7j9rhYDLPARFEmmUMUGgTxth2BX9wGWPKi7toAtpKMcg0B6I0sBNHvSDN8aqYNWHQAeMTTi30QwKwJD2kGZVDE8PSRuBclIUgK+uv3ZMXMWnlnAMpaDfQ7IsKA4uUCjJmoFONugFPq4PrnGsRRpNQCH9SinxLixttkRljeCmH/SDsiJSjd8i8IGFSrmIgmA5FCSzLBzLBxW1QQclo8jxaaPis4e4KzGBH63yHJ+mOFtiKrqFGAMVj9gnaRBQy0DbkSgacYx9kuKdYAd9nHMho45RxN7jogTxgrbBKuxNoIyassBG1T254Fe3OmSkM2WJjWL0kNJSWbwAjC2x2oTgXu/QIvg4wVqHLgu8MURVpistjkJHIcmPtfRcyAcYRQacI1ch7iQVT1kRzITgoc6DTY7Ee1wVr+JEMM5y+7LnW3tLji0UaFPl/dEKm1tEeQYrPVwpGKOJmjFaKwadgijRFIMSsYJOIlozTQadAWUnx0lJNtmm6OSjDIXOe5JWk0GnW91TyHSjU0Nzuo0rPSbRuNLhyzC3mSSsLa7w6EQFqowNWXNMrMBoXO7QMSjRIeuKF3QS6neFQ0UKJcNlLBwb1hnFmp+6b4Nz5mKMgr4P1JGGCnQMpQW0CgHzvqJuaEVRccK9BOpI14XzmnEQYjXgBBIl9J2g0TS0qugfMrJgd12wujcigxOP8+EVzbSiZ4P1OzOqop5W9JBI07OBWpFVVM5Qr6dhFH1fcbiNAhSFp6KVKPouWHqTimaRO8F7aJhABzEGEh1oiWGGhlQLhVeYSAe6tVL0beCCZzoI2rEKtB2jFbloEEg1WKXQSgXWp4JSAvM9xVOiQ7yfCtbUES+dQDesgr2ICBx5rQO33VfBYKIUER6rQia0EBsYUmKKUkTisDpCCRhXxc7oMH8Yb3EmlDMV5cprU7EyLK56l7UrQ/82p+lO7w6xQUqq+C5NXGXTtKVFEKIoIkmSQDeTEHFmtB5lzBxmSxxm2tRVJkfvPc45jFaUNmQ1ytJ0dD4SsjV5HyhDkQmKjdIarUKWROcD1SiK4xNiz5TSaB2yQpXWIhKyeFK1EYE4SUYZOl2VWUkpFWJsVSjrquyKVZNQImEeMZo4ilFaBdnDOcoqpjWKTPCiaxXum5Apq9PtEsdRoJeWjqK0NJsNsizDGB3q8X7UX2Yse+gw++hQ5hxiJDWrkKlUoUZxhOMnqFEGUz/KYmqtDeebCO8dbkilGutP5wKt0Zi1TKky6sP1lOGKhTaSiYc/HK8aDEuF+3XVPUM8vK4MzxtmC1NMT09zZ3GXPRfnX3Tx+h+8J3LzqFiqgLc0CCW9RXzSxtsBcWVlFJMQpRmqTwgwrgJbS79E0mjRnNkaLNcnwfA5msYEqt+GQqPSJsWgj0bjVYzRQByBy2m2Z8l2nYvEaSjXnET324EaMzFDsuMc/PTWddcQEUoVkUZxCCQ3Vbq9KKXb69BstgN/PkmJkxQztwPtuyAlpjFBaRLiJGPIMR/BJIg2QUD2Dp1kQSgDVJQgOgrB094hURKyF+DxSTNMgIQX2bSmUcsZRClWR+g4ZZj2VeI0CL1xRpS2wQeOsCZwO3WUhQwDcQMlbhQoK3FKFDVC0GAaUnCKruJc4gyNB2/pWyGJkyBsDdN8SjhGFJRFiaqUnsOUaSKVd4EQ3O5tEOidxVAJsLoSgJ2FpIn4krgVvCIREd6kiLPBem0LVJhjsaLwWpOaOJSzeVh5hgGFURT4z2kTrYN1RokLFCMTh1SiSSNQl0wM3lblFMoVZK02MrAQ6dC2KA7xPFVbEBv4oLYIAX9KId6F4GvvieI0iGJREjjNJg5B8cojREF4rlJIqihGJRnifAh2dBYxIe2nMnGIf/ASAjZtiTeBmog2OGVQwkhB9jpCeYtSOow5CN4TpfFKB05yxQMOsU0G7YMAgrOBfrfaYXB0nuxeFxJ5HybEYTCsgC8KiAymtFhtwzHvwTlK2wmWpXKAHXKvEbQXnA1jywz6lKVFiQ+TtbP4PEcZQ1wUlHkZUrJ6j7KBRiEo4rKgzIsQXIcQOUc5KMJkXeTkhLgBZTSxc+TdfhCaXbD8IoJXithb+qtdRIR0mIjCB+5v6h0D3UeJEHuHqxZvqxSZd/R1j+C7EhwV/5VwrFvF/sQSaAQOhUXRwNGTLlqpEByoFEU/xylFE08PhRGFqVbkEvCKtWMq8JwVEoQ6rWgBPQZU4dBoAlfaMqwT4opnG2uF1UWgNnhHrhRRUF2JEQYS+O8NBQOheueFyDv6YlG6JINKoBU8ga7Rc8Gi39BQCCg8VqCpobCW1X6fwoakCFQCny/B+ZJerwM+COSJztCxZjAYIHlYgDUGjSYqNYO8i3MO60tiSSldgVYEQ4SzKBsxKHpkcXhHS2tD9pa2QZzGlp58ZQBOMHEEg6B8GGK8F6Qavr60WCfEjaRSQgxYcBWZSJAQcygOZ4U4jtEmTHVGB+nfSYhn8VoHjruqUj7rtaQERgdqhFFCQki/Hp5jsOoPnwtVWs9ECbEOyR+8QOwdkY7QBEpEqgwowSlF7EuSKplCJIIfxixpQ+wt7Sq5iZaQ7hKlEaOJyoLpOK04+CHZitIK0ToEl6fBgKJ81RcqxNrpoo9PMowEoUmhgsdMBaMFaVhvVJWO2psIp0AVA3TWqnjfEh6AiUJ7B/1A+SuLQB3zDp028VB5PUPyAKmMOzptBBpYHo65osB7CckOkiz0fTkI829FE1E2RzfaxFEUuPFxEjQwE9J8qrQVhK5iENYnKo9DPkxPupYKXKmQDlWGaU1dSAWutKmMOAky6KKyFuJLxJYopWlPzjF33r1DvEY1z2itiSITwlvKQDPTWhFVgeNDIXEoXQxTx67ZjSvBF8jzEKuzuroSDCHeE6dNoijCe09Zljgf4gsRsA5caYPiphSltRgTEScxWaOJ1kE4X5PHwrVEBFVYev0+/co7qLUhy1K0jkjSBBHQlYEkJOrQ1WP3o6QZw3hekaHADdqEWFKlAztFV6nXtdaY6nyq90qsI44TijKsY9rEZCYiTVNMFFXKmEcbw/i2BSP5DwkGGRkqauG4VMo7oipDiYyUgJGAPwalQgr4YT8MH43SKswTQ6M5IW5EK13J+pViMToaHO9wXOITtXZdpYZp/8fbsBZTqHUYU+NehTUFKlzs+Ni6O4O7rFy4b30DtWNXyNiwsgTNFtLYDgePgYdy+050r4Pp98hzodx6Ee2FA4hNYNd5SN7Hd3tIGqH3XIzc9l2Um6DUU8ixRWTxZlSWobftxB/cB2WJ2rItCIzzRyBJcdNzqO4ByCOkMYtrCv7wPnTawO65N2rfD7ADQbfa+K7F3/Z1VBTjt2yh7O5D+gm6keL7gtxxbUglt3M3/uhhpN9DT88wiGbx3cUwwW7bRvGdb2HyHDszg2638Ycqr8bWbfhejKwGC3vuYswPvhcW75278UuL+M4Kuj2BS7fhOgtAhN66DX/77eFYs41rbMMdmAev0edegKzMI90+igi1cwvFjdeN0sWpMsN3YySLMfEM9sbrEGcxW7ehywzXTVDOUG49B33odpQV9I5zsM7hegNUGiE7L4K9N6Odge2ziPP4fg+cEJ17b2TvzUiuUI0piAx+MYckQbZfjNv7faTQmMYEJAluvguRh3MuRB/eiwx02L+h0UQWbwcDas9F+EN3ID2FThIk24pfug2lQjmO7kd6weLsW9tQC3eAFmTnHpg/jHQdygh5Mk20sA9jIsod52KWj9HrliAFbnIr5sjtwdoyN0282kF1LZLnlJNbMcfuQAF262ygx3UHSK4pp7YSL+wD7+i1M8g7NG2Bj7t0smlay8dCIPhkA132ibpdXFTSm9xCa/kwyjv6jQjtS9J+Bx/FLGZTTCwuYLyj3wiZ1LJBB6cHrLTnaC8fRdmSQWZD4Fi+ilMdFhuzTPePoF1JN8qxKCaLDqUXDscTbHPzJDi6UZ8BhpmyS+k8x5I2WyQndiVd3aOnIuZ8HydwSDXZwoBULB3VZdVHbGeAAIdVk2mf06CkS4dlidnBAHGOO8Sw9egRWtrRXVlmkZRdBK/GQTKmVUnbl/RUh6Mk7JYBSoR9PmJKCZNY+qrHARtxblSggUM+oqk8k8rSd4pDPuZcE/jWRwYJGTCjS3JR7HMRe4wlUsLBfk6iYFY7ioFmvzWcayyxEo72DRqYU45C4A4XsSeyJAhHXAgg3GGg8PC9XDGjIAPmJeQz34qn8MIBL+wwhgxh0Q/oOc8WcTiEAxa2RoqmgiWBnsB2DaV13DEo2JFETCYxS05Yto6dkcID+waWucQwoRVL1rPihd1Zitaag9YziaelhFUnLFrPrjiI/PuLkqnIMKkVK9ZyrHSc20gR77ijmzOTJWxNE1at40hRcl4zxSjFgdzRMIrZKNAljpWe3Ungbh/1gd88YzQD8RyzwvYoWM/nRZFoz4zWFAKrSnFhEhIV5N6glaKtHYlX/EsPFo6s4qynOdEgcQmDYwVRYmicM0V+qIvNPe1t08zsnMKWHeJYs/OSGQ5+d4H+akFrJuLYqmcwiEALs7Nt+gsNin6ByXLirKS3nNCIMy7/fy7gu/+0l5XlnFbLcdGlO7nxn/YGWkg7ZzlPic0kzht2tmHVRzgUsSmZm7uA7qojThyLC3ux+RQq17QnBuT9mHRyFil6bNuRsP+WLr3ugB3nNrA+YWXVMT05yWU/dQE3fvkAZWm56P5bOPgvxzhwcJnEWK543MXc+r0VFg4sMDMDzhcsuxw90DTPvQ97DyxQFJY999lNmRfcfOth0ixm1713c/DWA+SDgnMu3o1vDti/7w6yRoPLL/t/mLY5EYKanqVwHr94FJ0kmNntuPnD2EEf1Z7CJCksLxBnDaLtuyiPHaborGCzNlGjRdRZCgr7tl3I8iKS99ETU6hGA3fsMEoboq07ccvz+H4PMzGFarZxxw6FTGtzO+gdPYj0VlCtSWhO4BcOB+VvZhtxvwODTvBUt6ZQy0dAFH56S4gb6XVQjRbN7TuRhcN4ZykaM6j+CqbokrQnybbuwh47EDxs0zuQvIfvLKKyJtKcpjy6H7wl234uZb9HuXgs0BQn5/CLhzAI8dxOjHhkdQHiDD8xx+DQHbgiR1rTxHFElK8SpRlmdifF0X24PCea3kqSJrjlYygTY+Z24RYP4YsBemIWHcW4xSOoKMbM7sQtHcYXfczELMQJfuEwykSYud245aNI3kO3Z1BpA78QUtHquZ3Iyjx+0EO3plBZC7twMCiU2/egGw3GZcNgka68ikoFT2iV7EMQjAoKp1SGnqEgqbQaZeAb1pNUHpB2qxW8V87SaGQjT0KaJAyimKLIR56SStpEG0MrTUjihCSJK4VEYJ2YSjhXadJUYYyiiCtFQSv8UBGt2mUqOtioqFYYrdcL+UMjsgn3JjCyrGsT5vpx9swQgiKKouClcG7UyqCEBAHfVwrLmuH3OKXgBBfA2BcZ/2Xc8l9dvXKKDZVBEUb7fKzpfcHbNiw46kl1fDbDtZrX7nStLWrs39A3w/1E1NqtDVs2ppPI+D2MdbfICU/1jHGXaVFLf/vXwUprDHZpETM1g7ZltYmIC+nMTAg6k2Yr5J6GwB2rUslJtxOCOV3FnS8CfQGlkF43pJJza6nkyEKqPul1Qx0+WGxl0IdmoOYwqPjdzoc0jv0eqlltQjYYoJJg+VVxhPR6ISXcMF1cVG1cFEfQ7UKrjXcWKYrwYhuDStKQw7rVCgqPDWnwvFa4OKnutxnS6rkQ4IQJ1gzfWanu1+GKMrhFkyRwx/u9IIRXfOqQqi8KG6n1uhV1xAat1bkqjZ9B9Xth/4nK9YqzOB0FF2ZZ4qKIXm+VKIlJtQ7eG61RgwEDgbIfMlo1I4NPEkrvQiBZHFfWUx34lXFlT7PBki6Vtcs4i41C9i/jLKUQNpPRmkQ8pYnCxlPe4ZXCq2HaN0sRxWjPKJWcqGDhTXxJD00kQlRRL7wCi16XEs5UVgNLCNBKxTIgpJ8b6udWVLAmi6WPwVQZRIxSWK2xKliT+2hiABEMUKBCVgocAwkBaxCuWRAmjAxHrjSmcpVHIuTBvEAm4VggiwT3eh7YWGQquOy1BPpCipBXqXgT5atUcsEqnChPzwWlJFVC4cMC4ggbVPZ8cPikOliq8SEzRkMJXR8oAxHBtezFU/oQVNixQqwg1sFI5yUErLVMdcyEYyKC9eHYRAQrpZDoYEFXhAA3L9CONB0ngb6gQmrYUgTroWVg1XpiEyY8owLtwyJMRJqeC1xqCFm0chfa06ooGBXDglirUR82o/A55NdRJHos64hWoX8RHCHYsS9hgc50eH7L3nCby0bWHGPMyGIYGUMcxyMrmlJri2KSxCPXe7CABXd+UZaVJVpXVjpTjdxqwtUarYYUBRmVjyqK1nAjK22G5zFamHW1EEtl6IqiiKIoAuVHa9rNBnlR4r0nMoY0TUMGO8XI1e+Hi4mqXO4EypD3gb4QR2YkyAwtlc451IGb0d2lQC1LsrBg2gLilH/+wRK3Lxd0u32mmpOYbkx/KafRznA21NtZ6jG9dYKi06fXL2lNNVk+tARFycKxVZrtjM5iSdH3NFoJk1t3sXRwhaKvaLQ1SsPqSp/ZHdNsu2AnS/uPcnTvKs0Jw9yeaW694VbajQSPwjQidNZk9fAhGrMQG0/febK0zbn3upDl+QG9hQVWDvdp65hSx5SSM7NzgsIZukeOMtnMKEvL6qBky+5ZFg/Oo3VCnGp0HFL4Jo2MiekmR24+gFYZipJ4tsn0zllu/9btTEwqZmYVC/0+/V6fbXt20mg36Cx2AE/UMDgUrXZKXuQkzYRed0B7SwwzOcv9JdqNFhfsuZDHPuLRtFpNlFL0en0WF5fwzmIig3cujDsgTlKyrMHkZJs4jnHeM+gPKMoSYzSNRhbSeCq9Rn9YbwBd+zKOakx77+l0OiwvL4+stdYFyodCSOIqVTDgJViWfTWmnfcopWg0W0xPTWJMGPNllXp2ZI2vqDFUc+26xongbLhvrc2IVjOkPqqqrUPhek3g8ljrAo1ZqWqTXl1t/Erw2FYWdIZW/5NKRrL2r4z322lYe9fJibKO4TK+4e1xRmfGN6Bd24SOEd1IVX1TMbxG7/Dx11ZjDSitDRkiK29YZbSusnet0XiGdCE99LpVf94PvQlrHTV+fEjxGbYJAmXR2uCtiOJo7TkP27aujSfrN0ZtGz2zYR+gWGd1H7ZlvJ7KOzLMKDZ+/dO12K/1zXFNHLuQUmBtoJgZE7wqYah6jis6zkobq2uDtgypUcdBr2ki6+sZagqjxoV2jb9dww1SR/cuQwWOe5YW5TodXJyEBTQfBCuCD5x0DSEHMoSUcGXY8TC4NUNshQA6z/GDfqB1eAHvcP2QBksXOb7brXaADG40F4e0sVFZ4qMo8PWFQA9ZXQ1yfFnidXiYXgVh2K4sh5u25SgdnCgV0retLIMMj4XfvQr5mIvFRTwQVdqvDbIbKVAuLIzoEkJIh2oVxM5RaoOIEFV8PquCoBF7T85CECx8CLoqTeXu9p68mkKiSigplEKkShcnCq2DcItQCbghd3GhFEZBcHGHclTHSqVACTbPKSDwVQnp6XLxUNogxESGgdY48aRK8MpgwtxNJJ6BClzzpKI7iIQUwakK9AkEMkJmBO+DUOcQeiEem6wSYp0CrwSvIPdhQs9C8UABEQEtwS0LIy07r7iXSityFyaWtHoncgn1KU0ltAZhEwLnVwgCbekFT+D8+rFysVFYF2b7qFJ+yupFddUxIWRpUEphq4nRm8DRVpXQ7ADrKsqHqiwWw5e7EkLxgjLVPg/Vi6gVIQ5EBebV0D3pVQiWG95nqhnx4z2BIoEOAliqgpBdMUiJESIVEgyGvSwYKXAJQlObQKUIxACcDrSIyFumKtqFGdvnAqWIxTFbxTOZamdWGfGKS7ZGMUpCak+EQC0DtC3ZHsWBeUEV71IdU7YIVIMq971Gqh1GVUglGoVAfZGQRlFV8wplyNuvfOCoBipdGj4Pg71FKrpaGcppqpzzBqa2cMW9HoCJojCWva94ySHGIE2TkZXQVbSB4IqvUl7DyOpnraMocqx1xHFElmVBiBtTGoaLnfgQwIxAFAVOc+DjBmFJqzGn95iw4yXsQj8s58VTlrZShCIGgwLn/Ui5GXKndVWHq+JW9Bh1wnuPG8Z2yBhvVwTrBOfCfGrKEpzDlUVFHcpD5ph+n9VOzqCfE7sE0/P0VgfkgxLx0D22TK9f0Jtfwq506ThFc6JBf7VPEhkGpSMVTVE4rNPotMGgU9LvOJRKUCrBuRLnNP2uY9Cz5H3BluEv71u81wxyEOWJI/DFgMIKCQYrnr71TM9NkOeeMne4XGFLGGQpRW4Dzz9rcuy2Y4hV5Lml0y8waRraVQqJ8ZTGEDtPp1uQthSxiShySIzHIahSsbLYI88d0cBjBoZurwiGBxTdpR7H9s7TbMXktiCbapNmCc4Kq4sdrPUkluBdLUvyqEDwNBpZxd+GJImZnJyg1+sFBRBFqiOMMRWXPK3oWcFQ0Ww1aVRKpq5okTJGpVkn0Bz3aQ3V3Kc17XYbpRVLi0uURTEcpGhdZanyZaXwGrwKMRve+6otbSbabUwUMYxBTJJkdMkThbb1bVFKE41iDRgp3CPxceyGAnUlXD/ELWhiidcLV0MlQmmUkqreTRQLxXAyDwa+sebJ8LfNlAw57oNa99/6Nm1YXNZ9Iyzr1VqxFpN6smuLGtJjFPGQViUysjporStDy8lFwzCPDAX741tftbJSiMbjTIfK2NCgsv7Gh4rFWGOP79yNsOENj5UdKiHDa1V9tW6MjSk26+s+7trjL8tJLjfU9IZfh0apTW9ErQ0CNVI4N36QG11+1Kxxl8RYAUGN+h11nNdkrB+Giu5Q0TlNPeukuMvKxe0ry3RFo72nHcHAKwY+7I5rtKbnV9FAQztyr8lF0agCXztBLqGlPLkoehZaRoiU0LFBUGubYAXuuZBXOELWhFgFTikKFAlgxDMg5KZOKgt5qQwxhHIAKFI8tkoBlmgVcjNLEBtTHaajXEJ9qVL0JaQITxE8wsAJsaY6Fh5OGppEjkJrSFBBaBVFUj3QQirrsgoZLKxzpJW1ZeCD5SdToS1OgtCsgIEEBaRRbbBTiCNVwWo8kCpQb5hmTkIAn1ZD4TukaCuBUgkxYWOzgQ8CR8OEfNNehSC2ThE41aJD/5biKL2QEPY0ycMKQ1qlkit8ENITHe6Xqt1BMFdE1SAbVG/3oJo3rdJEOnDa80ihlQn8WaUotSZCKAkb9InSOARRoLQhIXgk0ipwzlSCZVrl5Tfiw2JuTKXYQRytBdylWoOJiKqg1yyKQIdjLROBHno2hIm4EqKdZSoKm+1pazEKJK64yrYM8RdJErILOY+PIiKtUWWBiuNwbpUDnirmZyg0izFIUaKcRWWNKvg4Dx6pOK429KriP0SFOqtNhMTaKsYjDQJqUYTycRLiUsoiUAZQ+CLEMOg0Q/lAD/NRDKhRTv1QzlcbLaZoo8M9AcRhMz7tS8Qk5EWJG/QxxhA1msE9XQyQOA2etjJsNiYVd1mKfmhnHIc9abzHR3GlZFtM2kCZCDvoY4sieAertqg4RScpbtDH28rrKSEHPCYKCoYtAkk4ScI9pWFDTOI45Iq3JZKEfWGoNp80U9vImm3iOLj4O90uuR2E9iJ0e70QANhokCRJWIgJefjXLI3hH6kE96HLvd/Px7i5xy1oUBlFgnV3qFyMzlGaOArc4KBEBMXDF0G5sNah8hDYqXWwDq92upRFgdYKkzVG/OphnWuLh8LaoNx0VnocObRA1oiZmm0zf3iJsnBs3zWHUoqDe4/SaGXsbEywcLTLoG+ZnksoCsviEc30TMr2nTs5vLqA6udMzk2QNFJ6xwqWji2x65xJ8tUuRa6IphQmS1ld9lBomrFGE9FHmN02Sb7QpfSa7bu3om1JZz6scO2pGF86+n1P2lCcd+9Z/uXYApHxZFnE1h0tDt8ekyYRWuUkmaF0GhcpJhuG1cLRbCTc68d343oZ3kZMRILqD4gSw6Id0GxppuaazN8OKoKZ6YRObpmcm6TR8OSpxsQZXkrmGo7+QJiYabJlR4vO0XmMjlHWsW1HisQNFhNFK41ppoalBU3Wirno0l3cdv0hYh8zE6UsC0xu30F7qkHvwH6OHFxFGUM21WRi9yyRZLSbTS7cc0EQ1F3Y1yGKI1qmVXnG1sbN0LulVUjJOeSorwX0nii8nyisrJOSGD9RfKDjaK2ZaIfYhNVOl3wQQrK9d2HDMNaEVKV0CP5PUxrNjCSOg6WcINSK+LXLnUyAHG8DxwneVTNPSsCoFAkRj6qUguGp6wSyjcofr3md8FmdcPqmisUGZw/NzLKBknHqGoYGiLV/12o9yb49wz5cV2qtRl8Zt1Tl/TmuaBDWh8/gOAF97T81KiCVFjjqOq2IdDQ2Hx7fa8POPY2eUGrUhlN6HDZQFFS1Gd1QP1LHna84/sDGXoNhvaNnWBmzgs1PV4kGxmuvntxxbQ63o6DybAw9b2sOhaGXZk1BGGvaUK9Z36yhJj18R2So8LH2XI5TiEbXPNX7eArcZeViYbDKkg0UidwpBh66aGYj0FaYLxyRUkzFIYPEsvXMxSEbxEIRshZIrOk7YdkKonVIM1dtAKJ0yDn83U5JmQuJhmOlQwGzOuQ0XhTFtiQiM4b5Kufx1shQAsecZ1ZrGkazLMFqO6sh9555J8zFhkzDkgtUnK1x2JxlwUFbCS2t6WhN7oVpBNGKJRQNJ7Q09HVEqRSzlSVwxUQ0taIJ9I3BacOkBHdwx8Q0qtzFuTEhdzOC0RqXJMQSNsWJ4wSdJDQqoU6nDSLxJLYk0hFRZGgUObHRpFlIn5YURcj+kmVkeY5BKJstjEhIw5Zl+KyB7nVR3uKaExiliAa9kEmpNYEZdFHW4tuTITiyu4pOUmi1kdWVQFebnAqu6+5KCE7NmkR5n0g80p4EwK8shU0N21NExQCVF/hWGx1HsLwcNuibnUP1e8FD1ZogSjJUZzkELE5OQ78Dgz6mPRViO5YXq30CZkOWo0E/7MOQprjFBVCgp2ZDDE/F6zWNFm55AfEePT0LeY7rrKAaLXSzDcsLCIKemkOKAb67Euh4WRtWFoJ3YWoWbFUubSCNFn5pAS2Cnp4NAuvqMiptoCamcMvzuLxAtSeJjMGvLqHTBrSnkNXFYD2fmAmWw84yKknxzTZ+JRyLpmZRSuNWFkPygNYk9FeQvIBmO/gXOsuoOMa3p1HdFSQfhLRyRkNnCZSBiSmk1wk0wmYb4ow475KkGencNqTfwfU6+LTJwAl28UgwXrVnwgZjRQ/dnEI3W5h+CP4zU3Mh6LLsQ9qk7Jf0juxHiSeb3Y52JTLohN2g0waquxSsau3psGFWbyUkRcia4d4VxNPbSCOFyXvErTaqOUE+fwRb5LjGJN5aTH+VpD1BNDlDuXiMctDDN6co8gF+ZREfxUjWwvQ7QRFrTYaJsbcSlI7WJKrfQTmLnpgmimNMfwUdp8QzW4jjYPXVGtqtJnEUdlW1ZUk/txRFibOOycmJIBBt6MoPP6xzLQ8TKGhNZKKRArHGXagUDIRYm6oNunKhh+9Dr0aoMlzb2ia2tIHqonWgUGmNq1zwgpAk8cgCqqrFbUiFqlYalhZX+b9fuZ7lxQ5JGpM1UzqrXWzp2X/rMYwyrC51yZop+9spvSVHv2tJDltcL6G3kNOaENpbZ9ErFrPcpywiTJqRJVtZ7eYc/M4KiZnEeEcaz+B6Dl0MiBtNtE/oO0ekMpqNOaZnPceO9NFRhi6DAUJphVVgMoND0GkE2lN0B2GjqEGJ1SlWJziToLUiTjPKnsVECQ4hd5apmSniiTZ519BbWYKe4NEMSo+Ioj0dEoLYXGhmGd3CQNImnp5l6eABYtVAqZSGiSm0R0WapNFA6QgRjXXByxNFhn4eNkvDa+i3YGBRSQNlp1k5uA+xbZZXge1zlNE0B/et0r+lQ5o2wGkGtw5YuPUoTGVE507glmLKvEBHBqUcSkK/xElyglAlUlE+/JCuUo2zjSyzBKv3RiLexsKdjJRhUGRZgzTN8OLxTihtSZ7nlEVBlmWkaVopF/oEbv2QdnNWcJrVHC98n1DueAXieIwdH6fj3BUEWqI/vbrGT1mvE2xgdN/oYXPiPa+736EUWs014xZ3Ob7YiYrFqRSCkcdo3HJeXXMjNe2Er+OXrBSL8X7b2ItyfCOorPhjigVA5cEdeuCGJ4/T0dZwXGeMHVJjNyjDdlbxFsOTh45hXyW0WE9hW1M6gvwLSGjH8J7HH/jQ07HWperEPlCjgwgnUv5GfaiOew7qrr2fdznm4pv/75uwKuwMGkugAsWVBVkBhYSbTfBYNDrQ0tEEmtCQZuGUCZYOCDtem2DRjLzFm4g8m6IzvbvKEjCkFgwtNjqkTKsmsOHCHCba4EEZ/hZct4FKYIwOtIeKugCMAm/KssQ5T2T0yKrpJfCcIRzXWo3SeK3nGY4JHKMHNn48WJWsc0TGEFUBT8OHLozRIsZdXdWAdM6hlBq15XhL1LCsr/iQWoe+HXKrx1OriXUhlqWyVgTL1vg8FNrkvcd5H/iqlYDinRul4lXDzDvDbD/a0Gq3SON4TahSIF4YDHIGgz5+bMfIIX99yANem7yPt2QMZ/exF+x4bX1knRtq+dWdjC0Mw/sPf1X/DmkjshaMBcH1HkURkQnj3Ds/SuXmq3S26+ee0PYgiAavyqgPWLMcDDmeQ+sOlbUouJ3dmhA6fP6EiSiqOPomCoG5AjjvsGWwaIfxs/aeGK1J4pgojkZ9PerSIS3GuRF/dhhAOIxDWJts18ZxGMOWoihGtERrbcVllRHtYjiZrhnkgzs+jiPiOBrVP/4OjqwqY2Nfj/Gnh8/UOV+NZz+WTjBYRFX1fIf164pSMry3tec+emRjFqLh/55+v0+eF0RGk6QpzslYPcNnsvb/2mIhozZppUb9Pq5cjLi31Ry2xhmv+o3jZIjjGuzFrxtLw/qGbRu3Z47XOyz/ra9/j6/80w3sv/0w7ckmZRH2HyoGJTPTk8FYstChNdEMnhKj6K70SE2G5AkL+1dJEkNceQ8XjnUpi5IsbdDcsoUsMxy6ZR9RBINC2Lp9GtfxLK96mhMJed4B4zFpSiMz9LsFRQ5bztnC6kKPldU+SqdMzsS4Mmdlscf0tinmts5w5Lv7sVajY8/0+TvYd/sCkdZEfsDMVIP+wJHnq+jJnJ7rM7d7jrnZPei8ydHblrCry9iiBK8prWPLzimSLGbvzUdoNg19DFGzRdxMGRw9xlSk6RXBKdYvLFGSMrl9GuMtiwcWcFajtGV69xT5YMDysVUmWilRFLO0mDO3c5Iky5jfdwylDEVUMn3JbrpWWNl/hGTQZTozFKUnazi6xSo+1jSbKfe65Bx+8dd/nvbsxOhZrqUbHR8So4G7JqCMCRYnw2kJymMK9HCt2FCAJay5Q+/ECddiTTnfVPTYQBA+/n3dUFgeL3/cKePt3VC5GCs3duJJ23M2cFIPw0bYQL49TRv/ya9/Ksv/JjL12qS+SQvUuv/WKxej34LZ//hq1r6rsfNOfqmNrjv+VYYP8YQ6pJKNqix71XoUlKFx5ULG1oYTYy6ASllf65cx1Wddm4Z0VBFG6WbXD7ExD8O6de+4lo+1Y3xNWtem6jeRYR1VGRXiItdkixPLTk5OnvDb6eIuey6m57YFPnQUQZVaTeNRKigJRCkYjfRDTn1VBRyLs6g4DfsgDDqQhpSsQEjLlmZhwRx0UVkTM7uD5Lz7jnV4yJFsy7CBT7AQqiBERQZtDN4LRVGQD/IxgQBAYSsBPT5OQB/mJDaxxdlQpzERJopJ06RSWjxFYckHg6oXAod/pBGPjYDh9YZ5jodBmkMhvsTjxI7euqEQP9Jwq3PHuYvDdg4THUjlXh4KWiOhtXJhDheFUZaCkbAtay+AYl27xof5aNAPleYxoX/tXsPLKSLEcUqzkZHE0cjqGupRKB04w2VZUhQhDzYqZJUYCabDdis1UiJOGPhDd/pYfwyVubVWg1ImcPyPE5ZDf4aFrqyCcJMk7IwbMlowmmjWFNP19z0UHke8de9HykTQVYTx2WD0clf9rMeE+JFAWN1/WQbrZ5qEMaeqnULH6Qbjlpq1ALe1fhkJAJXwSaXIjCzvQvBImEBdGP143Mw8VHJHLm6RqlxEo7FWbnzcjE+Cxwvtx0+CAicoveNUjmHdw7EyTIsYRRsELZ4BhuNsLXh0uLCsjZ1Wq02rdVeX8JPhJAKYyNgfVd+vCZRqpJiu3b8AjHGuZezAaLEbfpZwjbSRkKQxSZrQaGZoE4KCEUgaCZE2DLoFjWbK4pGlkFO+m4Oz5MuK1uQk3WOLqF4/PBMSokjjrcX2+kzs3s6xvRrEAp4oElSqkdWCOE6wpSfONESa3soyZS6YKKM1ldJZWMVojzGBkijeEhmhPZmixIJY4igF7UOeDOWJTNhXIUkUndWSRqLpFDmTM01mt8+QGINxoLWAOOJYh/0sEBrtFK19iDHSnixJmNzaZmWpi8KTtRIGZYlSnjhSTG1t0ZhM6R/pEWmHNjpkx2om9JaWUFpoZBGDfkGcaObOmWH54BIKi9aGxGgmZ5p0Di6hXEG7lZIYofSCdT7s9aENxgv9hVV+8M83cd/H/DhJIx29x0OT5bj8W2keoy+jeXQTnK5wO3oLqnG0Vvf6GjZSLIZGo+O0Zdb/cFy71PHCqBpbz44veuI7evx5a0Lf2j2cjDp0QiXHKzObCd0b4SS3umnfn3C9Eys5aenTVIY2VSo2UO7WPY9Nyq4TqtfhBA2lOm3s+Z202jVPwqYYV4TX/wyo4JGR9UcqB0P4poZxEmpU2fgasWHHDmWq8asFnWl41fXt2Ugvq9odxLKN1rb1MuGw3lP1yNqVT9BM1jXgbHnjhrjLykU0tws/OYsuB9BbhayJmdqKWjmMURDN7sDnffzqIiptYqa3YecPhFzUM9vAlviVBVTaqI4dBFegp7eFzchWFlBJSrzzohMmrSgKVlzvPJEPCk2gCZhKaPMhZ3USMiMMMwR4L0SVZ6MoyzBwhgv2SNDTmEhhdMgYE8dRoB+EhOSkqSKOzGhTmZHnY8yiFOb5tUDK4W9DC/U6Hp4M+W+ybhgOhYr1f5wgXA6Fe2tt5VHwIwuuyHAwrtWslOL7+7/DgYV9tBsT3P9eP0GryuM9HGC+2s/AexcybTg3UpJUpQgJUmXeiEizhLRKVWeMqe6dURkgcC6jiHa7SZalrKNqHDdzr3/xxjT7DSwPJ0wko69qg8/rVwYXJIwN2nH8uevr0RvKtuP3cHxDTzbjHyfMV89KCNmWNrUMDWsYCewbC9xDhWaoJIxGzVCRGl5jOGBG/60xdP8/5v7rWZYkPewEfy5CpTry6qrqqq7WaBBogCBsOcMhZwmSs5wxW/W0Zjtm+76v+wft6xpn92FpSwyFUQAEQAAEwG6IRnd1VZe4ddWRKUO52IfMyIyIjMxzzr23GvyunZsh3D//3P3zT7j4Yv1KsDxLUeWr+LnWtmv7plbjxszjqoCuGaBds0IVUa4qp2NmqFPn153p2m8XONdyzkSFtxqXTaeoVaFO2+OmMutG/9qJ2wJR6792PZtG5tnLC370Jz/GGMs3v/MB03HOi6dnjA77vP/hY37yo08pi5L3v/WE0PXw04gSwdfeO+XHP3zO9fmce98fMXxwyItpxhdfXODm55RygJea3C44GpxQyJCygMcPenx0LXBeEdoZ2jqmV3OOFyUffvuAn/75FRhFHEimkylKRRjjefRA88VLS14W9ENBHFhEPMIT8v4TzY9/ChpBosHIkpkPUGHCUW/GKyFQQQAu58k7AZ9/KXDC894DzfnZGIMn0oLTZIDqP4FFn+/+xkP+w//rLxkv4OioR1iccz3tAfCNv3XM5x9Plx9eldALxszNAKMdw1FJQUAeBlhZ8OE3B4yjEZNFQRDMkYEgcwqtBd/87iGvPjsnECHD0LLIHPHRCdYpInGFCgKc8dw/Djl5d8Dnzy9wgeTDDw/49PmMEkEcCLQpmaYFRZrxYBDw6ctrnv/2H/O1Dx/z3b/1QW1laptPWky5ZUTUeXIrMtEedI1kK9TOrybCqgRrC7SWqCJhTzG3gfX47UTUFDht2dOZvFr93iWmOwy/6plvp6/f1ozKBp5bGvxr6NRztwDR+r01ihWxjbp28NO+euww7HeXv0S2a2NUpYPqEaG6bYBWxp3Q0jWrshv2WF2PVem26ly72Sfbq6RtHhFiFeQBqgmjTrtnnaFZ7GbyeBc0HZG9FK7Lvgtz3gxv7FyMfvk3163h8cuoA0IgHr6zPmzG6m3VQvrofhPJ4w83BO151wXLA26yVpFq9ne5j3G5FUQTr7brVGHxqq84+toWio2xX2N1UTfcqi0XYjWbrQnYXqoSrYvKuG8IYLrHwWb2d3uZ8DbiOQzDmiNRz1ejU8DTV5/z8Yuf8uz8Sw76BwRBwN//1X+4A+syr/N+tSVotS1opZwCrVsz+1VdPM2wa3654CCWIQerjwD9zcLSgWw/q2BjBK/v1knqy5aiI+8ux+RGijpmA5dkbBzQ14O6kGlid5v13q5sy5+qez3r/bje++XBuFtTsKOMW+UUaxKXkV2aQrNuwOxVQLctsVqlqdlLvtVuu+rTfrJWkgCIjcNTz9HpmXRzVp1GWxhkoIDlVsU//J0/4/NPv6QsDJ9/8oIo7HN1PuHweMif/9HPwEOeFXz+kzOUixFFwNXHlzz946fLL1hfe378e095/F1JMfNcfDFBx32ORwmXmUG6mLn0xCMFTvDxtUKGGrzCm/5yIsc6TF5wPg2W3+oRmnShuJp4erGmyHOevtKrA/AhUmmyzHIQRUgv+PQzuwpz7LELy1UqGQz6RGHIX//5lCAM8B6sUHz2okBGyxWTp5eWQSQJvCUzhkg/Zji4j/SCP/ztLxjPFxQ2wPmIi2mIxoKEj/7ymmiwjMjkhOc8T+iZHBUprucho16IU45g0OMyOkJGgqsvrzETx0hoUIKgF/LRX85QYrmt4otXJYOTA+LTA7J5yvmZJo408zzH9I4YT3KyxQIdSf7qPCfRklIIMgl9EdJzHuEUH7+8xn3+Ev/8gsl4zsHRgMfvNfXk2uX0NR5j/7zEzlnzup1eM4xqI7DNhZvx1h4LDZ6+vXtRmZxbg3qf4VzL3LDn1jbjBpHvwrFLdNflX/3ZDsdkbYi2PRzR8ex1oVV2h/26VXbVBbtl46ajuyaEGgXtqPutt3it0d1hW9iaxv2NdzcKNg6FAKrzDRVtVYpGqW3zqgWNcdLlCa8T3GQrdLyqESIEeL9xzjabNtpnJ2oSYTXR0OE776fhNeCNnQsV1FB4WH0UoTZbXsE24cv23R7F+2yPbQfSr/yZ+qj1rQEiEHJzDqNZ7O0adDObWm1rgeZWq1Z6qh1+AoTfbFFp1LWjTVZM19UE1TamnQ0kavtxOyRnnc55OiPNFyyy+fp+uw4bphNiGcZVdU/Xb9FZb6uNstp4W5VjUjfO69s3umjZ1GSraluCdnNxgxRfCUTnbnmoroZ7swf0Vou1W+Xepaz15UrZdrgejaQCtni95re2hPrudt9FR125dte+OZY3+z79Lcbe6txPe834JtJ8VxV2qt1bQ3O4NUtoTNR2UwW+1Vs1hJUSWhs7leJaZ9hH/xKPCtS694uyJM8Lri8nS54moFh40nmOFIIyMxTzfLmddChxWcnzj54hjEGGEZOrlLKwID2Xr2bkhccaSaBCFlZSWNDGk3kLgcELzaL0RKFafmMmSlBlSZYWzK5z8BJrFdZJylKA1ywyh1CaZNDDC8/kOiMrPc4tQ83Ki5w89xgj0FqQCokxgtJJxpc5xgi8XZ4zQinKwpMbgbWSCEvpPYvU0OvFJEcjJlc55SJnfHmJlQFCBpxfpYROYp3AWUc6N3jtcShK63EKJjODCsE7RekUHkHhFNdnU8bTBXlWMvQSS4CxAk/I9Dojz1ddLBXx0QGLScH07ArpFYu5AQLkoMerL6+YLUp6kWaeW3IJmfEoaQicW38/AqWZTlJktNxmNZ+lW5wg6hK2vgpZcVAXG9XlZks1bbF8h8zZxfcNd3iPxbsuvsNIXacTNVm25WTsNzR9671vP6nJbtH2SNZ17rAP98nJuuFXJ3Ff29/m+Q1wg1+0snNrlXvNcio+aMj8Trm1I7tobRtv8UiDd/CdtpWga2vThrZd0NCNzSGyuRI1mrpsinahHbbYhoYNEo9AVDtJGssva6+mRk2zITdYVld1B2NDdP2um8ZqV433Dexv16XYwBs7F1vL/X7TnHVoL2eJevuv87aMnfr7BmfU3222y6yT+vZFKwGi1t4tarcEq2eLoWqGk+/mwHqq2n03nm5YnuPY6vr6bGrb4va19FtCsvn80ekT+vGAUe+AQW/Ik/vvrj8qszY81/K26QR0U8t620a94H1z2vVVrS4l095kUjkga5raeGoG6cYIp4Gji/Bq7/B2nn15m7Q1D8Z1aWwaW87W52hqNd03yLed4u0cW7K2U8t0UfZVgNimgbbDsCf3vmR3UfZ3qml3v+3N4Xfd1FBVll0nnTvkR9u6qykPWG5JfPHsHGscD5/cI1vknD8fMzruc+/+MRfPp5SF4d7jQ5xROAODQczly2eMn19gnWPwRHL8+H0+/8kL4lguzyjMDEmkgYJeDEoHmFDy8CDEWEFqHVHgUb4kSBS9YYjI5xRCEuuAg75CS02WlWjlefi1EYvzC6zzxAkcH4dcThxSWE4O+/igh/AebRekFCBLRscRKhdcXll6scS7jOHAEx1E9PqS8EAxzwzGLb8ifu84ZHLpML7k6CDAzEtCqfjgew85eeeU559OefXyJREpToUU1hHGksiVlIXEYDk9VYSHCS8/gkCUKF1SiOX3ZLzKGAUJykpcmWGmOYHx9ALFUSxQBnJTUmQTAkp6ASxKy8N3Dnj8rfv89I8/Q1NwfBhwPTYMDga88/iAnz9/TmIcB/2AXgL5whF5QRyGDLzlcl6CcByf9OhHCU4ohHEcHPb44ufPiJKIew+OG2NqyWme+uxl24Brcta27OzkYWp6YS2PbzOp4vfcNfE3DaYWySu52nYXtpDuHLod1vROnSZA1FeAuoVnl+Ph7fLcnQr0xgiv2s/79V56gW9utVlFKmoooJqIb9Oys9235O3mRSNgxj7YZaRXPOVbDsYdnZS1DqweNPbMtcvdNvQ36boKXo2Ahj5uvm73WXOr6yqfF032Wv23NAeb9krVTRvt0aFH2upatN5v1a1WlxqNvlVSO6LTVvS4Ct2a1u02q7k/O+h5PXhj5+I2sN4vxzYTNQ6RVAZyYxWikRyoZuCbRmyXsbU101L3ILaebcNmZrpZjw2OJqduZmXbjH/XTttwrRfNZe4GHat2EGsG9I2860R+Y5JXz5XU6y8FW2MIRVgz9sVW3ZfZNwuFVTWXg6yrEbuDzFGlb0ynd7eBWKOu8Uhr3DYEZocg2alUWzTXWc43UIlGv262t7V4rVMxt3mg6Yg0ePquErpVSu1ESneVRbuMNxckax54HdJ36YabX25J89dvuSZOX8nq12maOzo4vvau20XcNgjrRfyn3/kRn378FOc9B6Mh5RRm45SkH5Ekffyshy8t9kLz4vMvmC4KzDDm/ItnmEBROkNWLMh6PcrBAGsKQl/inUJHId5DObeEhwc4oYkM2HFOnxiTzigHmutxxvDkgFEpeXqdEitQWiCjHk44skyS9HsIFQByOdN//4SX00u8VGSLjDwvyOYl/Rj6/R4LNItFjk40+lqBX36csHcyRA37XL24RJsMEcRgJMZBKByhENjCojLI5tBLRvSP7qGTiKsXT5mmJcNEo1SCFAHS5wib4owCrxicHDCflBjjiAKNDj2pkUgHzhqKeYl1y49KHkdwaQDnGIQhC+8QSpCaguEwYJJ7kIJ77z8EYylmGaEO8NYiVERy74R8VpL9fMzABIiJI1hYspkjDkLiEhZWUOQxhw8P+Obf+jof//nnnH3xihc/esbnf/FTTj98yOGDI37pV77J93/1W029WhlCa115M89u7XnfsosaVu621UI7fY2eVpq27dzGsH7eQFRpOF9THbXcNXq3J21uYZR3Ultp3ls2IiCURCi5rsN6TX5lkLdDh66h2hGwZYBuWzXrcttmkmimq2/rWT+tT761obK/aNllVTGVLq7aZUv230Vw+u3bLWZdEdR5yKaD/htlt785XZWkKwxvh2OxTtJOLpqJ6hZa3WaDXbbDGsnWk/ZoupWT37C7m3b123UpNvDGzkVj1mQ989u1rQE2ntbGyN01u9pcOmNvC1TldtK0TLD1/DbQNp6aA66j41uD+86F1R0CoBGEfAtdNcgllZit2vU2nujTV58yS2dM5hMmZ2f8df+HfOv9764V07Ifd1k3rb3uVaHrPm27Q+267qZrM+PQ/bx5L2pp9+FcUtnltC4jH63UgNikbUvuumi4ifYtoU+7/C6oM8BNvLVVMpXqWt7VXcDbOBSrlJVA3VXNHTZ/06m+CZrjfzfcAldnO78miK72ugu0+q6Ttjb+dt+0RlWNF5fNu/ydzzOefv6CTz56inOeUTJC2oDx+ZzRUQ+zuGR+nZPPMp6mY5Al9EJ6oz650uSmADyXc/DXKWUYUaQ5oU/Q0pLlgtJK5kVGX5XIIOLzVw6lQsoSjAwpFp6cnFlaUgYOhGJqQU8cceGxPsa4gI/+4hrjNMZKrsaOQlmcTEhNweW1RHqL0glOwXieIZOA508niCKnpwLS1OJkSCgHTMcl84WHMmSYKBbpMlT48xcZ1iqM1VxNwBeK/jBhclXy7PMXnL1KcS5klgf04xBjFSZbkIQH5CZHoDl7acjGC6zVWC+4WgiMVhQF+CJBe0FuBFopFhNJbktKY7DGYZwkN4rhoMfZtcVmltHpCfNMMX96xmJmSCLJyxR6B33mqef6L16ymAEiJC8L5lGCLVJcAcUiRw8iksOYIrX84f/6V5RpjrUCm1jsecaLi7/i0TeeEMcR3//Btzp47xZWQ5eMbyegJvc6h0dz0qK9ttDG1bbstrbXVM93GK3bp9vEttxqOBr1q02CLgrqrkRd6tO4r9K0jMxWmVujvNbWW7slWjnaNWzCxmHYVT609KXY8byVvtG2NeN4q5zqvFhll6zf7dZfN9K2Ku+u22G3YTMGtg+Ji0059Wf1NNUOhn1qwLf4tqsjOhyY9SO/4QnoduS66uQb5dTobRXV7oX2mKk7NVvj/y3q1DeL5ciykat/62c1Q3M7Q3vk386IaOy4WWduW913aZFW2k4yWobCjaR2egF3IqfxcaGas1GPoLMJF7tKVLW3byGr/dQZ0+MJg5hQhwQ64PTRE4aHJ5vBJ+pOSkf11tVcFrrMcgtl1oWv3gS+xUOIxmH6dl7R8ZGX7bM+3QVXZ2WkbA4wIXxDsNZJ3Szs7Bb668tOEirHaVOndrJl1vaIurE2nXRs+OSOHSOaVVxHKKtQrf6qasrOMz5fLVTy4LVWTfbBXZtKtC5uaoq2DPPNDJuhvFuIBsHymyu9fkychAShotePCEJF3Iso5ynzFxfY2YJQKfqxplzkhIHiwQcPibRGScnhvRFRqOiPErQEqT1JrLDWrMK0GlxZcvrkGOdKAi0wpqTfi+glIRJHojwDLTjqhYRaIoUFZ5DCEihIJ1MC7QkDAb7EmZJeL0BLRyBBrkLJHpz0GR70yBdzXJERakEvVngcUSCIewEKi6AkiRSB9nhnGR3E9IYJtsiJYgUSkkTTO+gRJ4rFxQRhS5JEIQVoaQkjhZIOIRyBgjCShLHG5hkIh/AWgSUJJVp4lIJAeoRwRKEgDCUPHh0SBQrrLL1hyMHpELXKe3x/wOHDA8p5yvjVJUp4BIZAS44fjcCU5NMZcSTBOw4OE4osJQ7lkqZQ8+D9+5i8IB1PKbJs+X0oJZbf2gFCrZmfXRPUzzyymWQSa+PqNeQyGznaDMiyDXVbpG6Qb0vP6qp+vRvnOjJiVYtKJt0gepe0+07Z1zS6NqOs+X6j05o703fR2Xy5cVCadW7KaFFL03ZFGhK8oQv8PqnQtnXvCF0Gfbd8FRux9bbgbeFaOyj7W2BtCnk62rNLI2/wbqGu2Wh3rki9gfduodmcYe2CTYjytbdSy1PTKX7D742zwjWd/jY1+VvYFrUaHA1n9PUEWsc4Ww/W5ouamBDVwKi83sq43Mzj7i6nytBM1tyvt9kC9NVD+4uTov5qbeFW5DcO5daaaGsJe329ac1377/HfwljhJA4D9/52vfWeT2VR7w5C7D5Zt22EAK2Vo9aG6j2tt/WFqw6zlpb1JWdoBpQ29g2eTZ5u2HbKF8viHioZmK6t7p1YBN1J040ntfLaZyf8Esltv9gcIvM1+XF2rDZ6h+aw6IuM7f21raa7W7K7M0GUtUVzfNGgul8zA9/9qekecoHjz7kG+98azsf27Z9m/hPvvyET57+jDAI+ZVv/YCDweEO6qsBURd8NcK2hMbmeTVUGl3pV8aD3/Dr2cU5f/nTvwYP3/rgG7z67JpXL644uTfia197wqd/9QppPd/52x/yxUfXZOmUlx+d0U9nGCtBCO6PYtKFQeUJz/9qzG/9X3+NP1OHpNOMX/mNb3J2rniVToic4oMnAc+eGYSUPDjWnI89i3HBycMTDkefMc1CUJJHpz0mecliAoVzfP3Q83kGWmgOe57IGQotmY/HHPYnXJcjnPckgeP+iebzM4GXig+fwEfPNZNFTnhZcO9xzESHOCMYiSkL02ceek4fDXh0Apcv5ghT8uCB4ctrhYs097/zkIOg5PMfC3QgOUjm9J58nVwnzM4nxMUrpBzggfvHGfM56LhPMIo5Cib8PNNEgeLD7434vU++wIWSUlk+vKe4KPoUi4I4mSJ8jC4lAY7jcEGujrn3IOKDb/SYnJV8+tMrIu14+Mhj799nMS9JsksEBh0mGJfz/V8dcZVK0osxg7DEBwETq5kXhnvHBeeTiEIJfvkH7zI5u6SYGDySg2HOZNFHyoDDYR+jChamxGZw2E/4/f/0R8wXC548esR3v/2t5tewbzPc6rqwla+dvTHs1o6EaMrLXQVvDYfmht6me7Kn4C68tUxLNVkX5Cx1RZfuWo/FZtm+9lSsFOB2/m2i3kQ874eaXtt+1A2vaYY1BX3btut+fhdoH+puv7s9IlqmYKeUvwV0OA2N+tWc0JUNdlvyNtcdzluN09bGwGv22NY4XaGqfzGcqtStcV6z4xqPXrODV/AWnIt9xvse2GfvdS0Trfm5FQyyJUOaTLs1KmqPtwUprY7YeSjobUEXWgG4jsdiySlrplkLv9aZFdgyArt2db+4ek5pSgIVEKqAjz79MY/vvbNM3+67tRxuDRGxabK1g9eyktcOUBc/tOjdtx/09fvidul3sU0bU90P3Y15+82m31o26F3rs4tn1vZ/XaHWm7ij/W4jy1rjq3q2vd929apzifcNhGarnAqTqK2uCeCP//oP+Pmzj5lnc66ml8RBwjsP3t04I2u6txVbVb3LySV/+uM/5vnZM+IoISsy/tFv/g9b2ywr1bBXx3Q4mfXy1r+i3sBitRrnMaXhD//0T/jyxXPA88mPnxLkPS5fTTi6d0B27YlUD+stP/7DZ0xeTbn4/IKehCKIUZEnLyzPzyyulHgXop3h3/8vP+b+tx+iDoc8/aRgdr7AXi3oq5AXr5ZUKK0Q/SPCMsUVElcYbO8Jyi7whePVZUF/OGIY5TiT8dGrAhGXBJGmKDUCiXMZB4cxMjrkMLJcXi4whLwaLz9smkSKn75YftAuTgJmZcbL52OCUcLooM/L5yWRKHGhZFwUzH6W47KMJBS8WsQYkRMfxdCP+MmfnKGVRgNTe8TJwyOuPx9zdXaBmUWEoUZ4x2TWw5QZSVTivePZNMJRomPNn/3xc+bGIKMIEcC0GFJOUsrcoKMDtHDgHHma4+wBdjGhdzDk1c9z5hdjlPUYU5KO3kVLz/XlNeeznKEIsd4ThAHXaZ/F2QVllhL0I+YlJMMeZTrlPO9D6Dg6OeLFixnjLyZ4J5fbsPJDwkghwwQfO8pUY9OMftLjX/7zf8uTX31MZnKursYcHBzw7pPHTUa7afhtOcJtVq4dDm8k2wRGuQnHvsI7D5mutgR3HVDd2D11y7Lp2GxFp1vLx7YW8606tF0cv54M+Oqgy2DqMpRbmrxj5X6dZp9xWLdjO4tdtaLw7Rf7wdfbruKVHfm6ztXW7m/Sj+vNeDUaq769+aORrHTCnnS+ww5pbdXf6++2637jBKev/bZ4dwed+4Z1cyFq4xJuFbsDQ83teW14Owe6u/njdnkEHT3VpZBFdzvUpN7SL6kz2050e6A+G+7Zu/6365Vv/Gwnu4GeTsdqi7bVffW+wwDbJa8EMJtPmGdz5ukcW5TMTxfLfJ19t2NnbhXuYl1+ZXY1cyyT1T5n3xoV7fquHZW1qoDG7EE9/wrfm/nYtSo1SbvtNlK2OqH+uOumchRrzuH20aztyFhduAUd+47b0Hp+l9XFTS/4ejd3p+0Uoh3juWbw74NuA37DyFWLTRdTrqZX5GXOMJnx6Rc/550H726V4dueSu31dD4hK3ImiwlpkXIyP8E515wJrqO7lc/UZqDWhEftGyGVQBd40iyjLEuuJ2PA0zPAzDKfpQghcKlmPi5xxhJEEVevplincLbAFDkpmrx0CKXwRmGdQKiA2XWG++yCsJ9w8ekli8uSwmjwBhcrsIK8sLx6MaF3cIDNS55+fE6UhFijsN4xmRQUJgMZobRERpqFTckyS6AVlIKyFMymhghYTHNKp1AoppOc0i4PUUsJYaSZLwp6PYXDcjUrsdpgRYB3Bi8U03FOXIJzGocgzywyidEHI86+GHN9neKJMcYzOOpxcbbg1ZfXBB5CHZPngBPowOOcwmcO6QRZDl5EGEIuX87IjcJLSVY4TJZiS4FUMaU1ZKVDiAALFIVD6YD51JBPS4K4R6Qkw5P7pEby/ONz5rOModTMSyiNJB7GXL2cMbtI8V4zKzx62CcvWUesCpOI+bykvBqjnMIYAI1QAVKHyDBmOj6ntAUgSGcZIip59eIVMtYshgums2mL924/zht8WbvYmd13cjW7BoZv/rdDrm0iEi0z1R0IELWzdl3+u18psc35hkpCdDgwdcUhavLXc4NBViHYrv1dI+7chKFx10rcdJFq/+0yyGuz452hXKm3bNtxrNq0+0Dz3WE3gp0qzHcHU9lA5R3uboN6up0OQmNbXUWRoN0Bdbt/n61Xs4QaDzbBQ9oTXjUbdu1k7apFx3Oxs2bL4tfV2N6YKHZcvw68uXPx2kzWMpz2tMcauiVZM8mO8wIdK77QHp5bBs8+wbxyPPbQdNfO2XkE+9YGLg2BvzuN4OHpEw4Hh3jnELOMJ/ffhZrgvi1UqxKVA9HlbVcCoRrSXmyC7G7C8TUruXxUnwfZrmdb7i51wusNiQ6fZ81HG117C9VR54cae+yMgFabIXkd2r1fzpgKIZZfpqfdXt3c3qS1pjA6Sagb85tnmy2Id4c3OSvRVebj03eYp3PyIuPk4JQf/NKv3Rnv/aP7HAwOeHz6hCgMeXTyGF8aUO2PLK6gk3e7BFldxonGo8pgqlacFrOUq/MJB8cDDoYjjuN7eO85ejCiOFNQSI7ujZCl5pPnn7G4nPH+t58w+uYjnv7sHJ2W9MXyHEMeKLQrUYFinlsOT/rM0pREK8w84+BAUV4vyIwhDByxknilGAwTsvkEm3q00AhZkAiDiyTWOkJpGI0ETgf4rERRYGyJFoLDniYqYKoNWjpODwXP5iWFt0SBJIkj5gtPFHm0NICnUIae8qjQgXWI2YShd2ilKIRCh9ALIMugLHMGgefRL73HPPUsPn/KIHY477DOMoodpFNCV9KLHLrMyISkd9hDuBRjPSKGRCviUpIXAptNkRQcDyKmqaEfOUJglnqMKYi1J0gCRJxg5iVgUEnM9HKGCgyjJCJ1in4iWLx6hVlk9IKA054iX1hyI9FuQeBKhqMAVMDp4z6TrOTpZ9cc9CRalhRakJUlh4caM83IrCdMFO9845hSBpw9vcKVJcNBgCcm0oJ+TyALiRGaYX/AowcPtvnuruA3hrYXNR29QxDXDePG86bwXOFtrx3UkVayv+58rJ7VP9q5Ncw2xp6vjLUOB2ZbelcCbe3J1MhYTfrUJxdXjkvbUNiSsFtOCO2m2YJ9mmVtKW3lW7WN3xXKvN5I3cZrC1V3mmpGqXvmsRvEZqJkRwE3k1AVv7YrmvbYNgusnIpGl92gW6u6VZjWh/l2U7ZHwu94tuNtfdv1ypZsHCZfZ7u7Xdals7fsozt26V3hqwlFK1bGQ8toanxHQNRER9Ww9cFdeY6VQdd2qW5ob1H7vw2+42rfo04cbee4i+MaaNtMvkvi7HBYOqqyGbrbBmsrYbNEAYeDI/7Br/8WX756Sr834GsPP6B7439TDXS1aJvMLWXUuPW1/t6kaY+nWwZY26r6zmS1vfDbgtyvn+/aMnOnoV2X51vL+tXgYC0sbzo0ubuc5faZvCjBe+IoQmnV4J9q21zXViXn/CoccQftK6i2Eb3RVq5fAPzat36D4+EJWZHy7v2v0U8Gd8aRxD3+wd/+h3z+/FOiMOL9Rx+sD9DuhLpw2jEpIVqvGlBr77OXV/zuv/kT5rOMXj8iVgPMlzEeTy88pUhnlBPB3JeEPmfyYkqoNH5uOD8/p8gdPRVx0DdMjUZ76GtFPhUY71BhwIAe169KytwgDiVJ0mOeFvSTHqGekltJ/2TA4aHk7OUVcTTCB4pQFFxcC6wBF1rm2RSZaMoiBz9DE+FLT2Ac0oNSCucc/YEgCAMCI4gjhZKSaWHxEoZJycXMgYU8zVE9QaAjyjznYSBZzCXKC6JIY/OUdAF4z7uPByRxj+d/+RnlLONolDDJBEIH2HxOcQ2R86jCoiiJk0PiKMQXM/LSI5xFhRqXXaF8D+Ec9w5DzjKw1mONJ0o8iIT5NCXQJYePHvD8yxkmy3n0IOHsIseUnkcPR8hRD1cqPv30Oc5c00tOiaQilCkkivnUUHjBwUBxNdMEKiLpJ1jjCUpPOTeMHinG1mEUuN7S6cksDI+HDO4l/Pg/PyMrLINIM9InTOYFWImeey6up+RuwTsngkhHbCL/1CTX6w7ZuvDr4N1dq8trm62liRtnGWrOQwVtc7huXwkhQIoaFmrydeNMbHCzftYFbeOv0k8V7nYEpWpVY9dB9PpKyFaZt7KxuxJ1tsYWCLrl8q6Z78qe7aJgs6hRL3NzpvUGU+eG84PNeuwyyrdMmE4dtmnnpq3Q8C72wtLUbOrfZpZ6n2w4pG6dbHGwaN23rrvMu8rmXT6vcbBvvtu7IiO6LredjK08axustrvkLYDwrzv1uILpfNpto1fOhWgzwLaz0GB0v0Gw6bzdAnJr8G9u2gm3391kKd8GdnXEFq/vKXTfaO0S7nUBtjbSux2lTVzwXY5Wa72kC01NoDREdp3u1bXD7RTmOwjY5Ie1517fG/96M/obvJUAqWY/us8E1K46fLXb0dC9ZNwWPlWf1A/vNvJv5d3Vd2CNoSgN3jnCMEDrbWO4fZZlvbonqvG4Emodfb+LNffGS78N3KSh3iYINhOOv4gyb+OFV8q69uo//Ycf8md/9Necvbji8GiEmyoW4xLvPVGgWFxNmVyk9EYRUS/h/LNzQiUJBgOIYq4vUg4Ch+8pJlmO96AMuExSlIqDUUjQH7GY5+AE0hUY5yiM4ugkIZ9PCAMY3DvCLmbMJ3NUMkAJS7oArUOyhcGKHCvAipBAeUrhCENFWnoehoKIgNnCk+cLorjH8GRIurAEavll7vncI7wlzzO8dwgZ0z+S+GPF+XRBvsg4KBWJkeSFRKkCiUAHMQjP8NEh1hR8+ckFvVgiZUBWLENyh9qisMggAZNRGoj6I2xpyIsFDotOBohygXDLELrOOKx0qDjCqBhRLFBW4g1Y5wlC0HHIfO4IZUkYxsynKSoIGR5FTLOU6PiExaszvPREUYgtHZG0OCGY5xItLYFV2NxgreD0fo/h/QOe/vQMZzLGQws9gZeakXeUC8sk8/RjjSoBa5Ei4KAPwmRMpzneGYhTgr5DaMU7X3/A//Q//0O+/cvvt87htQyGG2ZLKtOpaSO1rMrVdV1/bFYLNv+3EDeHQz04R1faDmG4sbX25F1RU/3flaZrZaP9vl6Pdj27zMQte6WNq+qTnTJon3OxX/9st31Lpq+3ee03+6HuXGzD2pao7LMu06x60eW8NHT6tuFez3Qb/V/pdbkKJ78X6jZGLfXGt/CbevntXt3VF3Xzqm6rbrOvaD9ooNysWqy4vMtZ2NUWorOE3eW1YNcKz3Aw3IdxL3w1KxeV0hRVxKGOgzY1Add2zqoZg10NtT107witRm6sALSdnF0Fr/u/KVh3ELl+UBVdfa1z7eXXG6BeRhcR7bQ7HIsWqZ24OslsOUZt3wY2fbQZsMuS9p0PaC7B1QdhV0V3x35er4DdKKzZ9NPKqahWPdtnV9aJO7pgLx0VhmqtvuswesddfT9n56REvf/E8kG7bQXLw7fh6l6q20aWXjaAaPdsh1bxK7rWbsiOlZ27wp2N/Tb/VMZNRUClrLpZaWNKCN8o8yvzcTp0knMOBEgpWUafaZYcBJooClBaEsUhRQpRBPOrKRefXSPw2FKgCAmiAK0ESgBFsZYlpXdoFFJ4pFJEWlOUBmcF/WGMTALy6YLSAtKRRArrBd4YpPBESYAOFX7uCLTE4SnmKc4t8RSlR+oSqSQOhxYe6x3OOkIdopVAW09ZFggcWgvCQDIzOZQFDkk6dwTKI4HDkwG5CxgdKV5NL0hnKYmWaAUhkOWOSAuyvESrgMFRjyBUTL68xHtPEimyzBJHAc5apPAcDBOmC493JXEyIAgl40kKwjAYRmTGgTNEWpHmJUJIDo4HjJ6ccn6eI2Yl5aIEJZBC4J2hzBbgAuKeJluk9IYxQRCSzadYWyJwKLlsC0yBR6KUoCxKonhAvx8yfzlnmISM5yVlli/D1j45JhAllGNmLqOwFikd/Wh5vkQLi1YQCMidxzvPYp4ihWRw2KeUHi8zUJLhwQC92sK3FVihrgRusMHq31dqmGFrvV5LWrtZ60LvqZ97WMvrnecX2wN7d7K6z7TO9RUMYrFWzNV9k46ubQu769fKu7vUjuRi6+2uLV9VdEeqleZaxqXJ4FvPmpUStXf77J/GRrgu42JHM9xmIuomp68L1rp3Z4L2ba0la3q4sT14K/NuK6qetrGNkLaD3kpeL8y3+KmdUWwR1oF3m8bKrt0ZVGeNomWM7ynutvDG37kAlsS0Gm4ZVnFvbdoZNrKvmiXZIQx97W+ZvkrTkHpL4SjoXP4TKyYQtY6rjP6djdoueJVra8Wk/beFZzWD3kVU456tum+Lmno9ahmqS9F009oisXq7NQhaDxtb1uqkruu4nxPX9K3/tuu2LqBTWGwatL787JzrdE4qFLcXUbeFDR31g9i7O/sW6OqXW/xVv+6oJwIdaLRWrdnKbWjEtr4jVMqpA2n959ZQ1XWrl3fJDN8aVr7FdvvG7Qb524n8sndstxLVhLVUculYwHpsvnx+xb/7F3/Cf/jtP+Hk9AhpYkIzJCThl3/wAen5nPJiwf1hyOjwGOUjhNV852+9g7MRxkSMIpCFQZYerOQkMLiFgIXgGx8e8+63n3D05B7HHzzi/XcEFgsaHjwMKX2KD2BR5tw/LknnyxWP++8sv9tgSoH1mm98PWJ02mMwCnhwrOkPNIXSpFJxHE1Y+IJMFgyHnliXeA/D/oBf/tUDRKTIsgVFfkUQzXEHUA48Dx9kWCxZNic9uyBaXHPkNSOvef/Y4uXyHEYceQaDnEuXMbYFHzwRoEGFoJRlEE2IRwFelpwM5hR5QZYXhKHme790QJnlIDwfPJIM+jG+NMRRQD9aEIYxh/eP+Y2/9z6DRCPGU8r5nEejbGmgSfjud0aoxEHfsXALHozmlHnOfDrlMMroaU+sFKGSvJdMCUuHLC0DlRP3LAudUUae4cEV89OU/N2SrHfF8+nnfK5ecn1S8Bs/uE9fJIS55DSUjDQkRtCzkq8fG2Ip6HlDKAsGw4DRwwf4IOG7331CLAfYuebFX7/k5z/8Cf/2t3+P3//3f8JkPGvyaWXHrMbKWte1JxR87deL6mJjvnblqd90Gpvbo26ttxp4PFfTS/7jf/n3/Ps//Tc8O3u6o6Ba3s5xX2m3Dh3dKrvr/bqtqksvNm1Wf7H+E/VsW2XVPLW9sNZwd1hirdJvGZC1ft+OfLQL2w55Lio8tyZrJ+7mvWhd7zR4ujHu2C7VBe3jFF2ORXNI3FGnizar12yZG2n0m7yixjPUdfbN9XyNqfYuJG/sWABvvi1qNp+tr+uGeTvqwtp7gk2YuX3W3z6qWj5E9V8j+kOdpnVn+aWxXZMPlVl4q3IbiW6wXOt4asyxnGCtDPVuL3MLR6dw3p7J7qp/J2m1Q9db9d9Be2M/nt/kbZTdgWbjMHbVgZX9VeuQGo3LfNv1fpO9//6mrvPNmmzT3dmx6+d3HU1iU8jO/lufdxDtVt+GrrZsb72qlUxFdDVUd9HfPHPRyt8uvVE27GLLTt77G4Ab6agLii6fd9tDqmHenS/Pcv7FP/s9vvz8HAEEMiKSPS5eTBkdRLz86y+xc0NpLMY5Hr7/mM9/+opeLDl+/x2e/vgpEkmSaPoHMc++nBAGjiCMSLMC5yT33jnm5FuPuLrI6SXw4qMX5IscJxT3v3bCq6evcLrH0XFEMZ7i05Rw0Oe977/H9bNrLl+mhNoxPO2RHEXMZwXxMGZcKF6+SkmUozAzynLOtLA8iWPCsed6agkDCJOQowcHnL+asUjHmFFIqTSBt4RWE+aWzGqGkUN6T2YEUixXPrwzhPEQU8zI44DUCZQUDLRG5iWFkQSyQMmA4cN7TM6uMWlOEobMM0kcGg4Oj5hNc9JFShAIhDfkNiSKHKawjI4OGL1zShxL8leXfPrROaEukToiszA6PqAwC+ZujtUJsTQEmWY+ztAqQFAyOhyiD0+YvXqJyzK0FBDGpH5B0XOkQhNpTz6wqNCRATEeLyQzBJH3DK5i4qnEOMFRALZ0zFKQ0mJdTig9WkU4abA6JB4dcPHlcyJtUNKgpCLpC6binHsf3uPek3u8/+G7/Nb/+PdaBkudTTeMLVbO7t5BUl3u2FTfPetcabWb56K99zhn+Vd/9C94+upzSlPy6OQx/+g3/ymDZHt7Rock68bbomtry1Nr+3YnNORYfYvUjtqtx3yNyroM3SEUfL2gLT21S+Z2HZBfuVV7BNtu/em3ruqr1o3Q3Otn3XQ2qVk+uf2qRFPXvs6qxm7MTS+j8wN5O3V964motcmu1cJuIppltPvjtgxeFc12uIQGuprdd1sYDv8Gt0Xt4t3GlpnVk/V1zcvfF0q50TdbzFsbfXts6rU3XxOeXc79Fuqu6xah3UO6uRdxm3y/sbi2im6Z6A0Z3T5s0+FYNB9sE1A1mdimewextUerOre/sO4379vhUFfijc0huyatzW05LUp2Wnx3mH33rGla03+Lgdq1/edmwrYPoNfHcRtd1yBvu3ptXqjaE78fdxs2QmUHrNmquth2cBvnA9pCsUKzWo1rhjnc9HpHhlWkpHphb6447gK3Kk20fmHTLnRth6gLvtqYaJ1TmU1T8qzk4tUYIaAfjphbx/RywaufPaOYZWgZkpcGpSSLzJMXHrzFP58gwj6z8QJjC5wOCfsDsCWL1IJIMM6Sl4Lry4KXn11CkeOsoygFzjtmM0P/3n0WmScznvmkJFKa9Crjix+/oH9yRHCwPFcxXyy4eHWFF4rhOyGmP6CkREqB63mwgvJyxizz9KxECE2al/hAMU89MkxIEsVUWkovkKGkGFvwCotiXhpCLRFagfAoFFpJguEAbUOMdWTzAiUkIrdERpIbgdAB8XBIWgj04IDegaSY5ZSzjCCKmUxLxhODkCG2NAgCSitACKxVTOeO4tkMXaTkswXGSrQKSXOQYcJ4XJKTo/ohWemxQJh5vI+WaSONj/pMrjOU7pGXJYX3JEGATPrM7ZxSK0IJmfR4BbkHYy14R6YUKIkuQS8KMhkxdeAKcCIkjDTZpMQrh7We3FnCvsShkaqH8wtwFmsd+SInOAiYjueUpeXo+GC5VayKdiaapkd9Y95aF++zN6vV9n3ypoWjsf2zNjTWR2J93TCDwhZkecrF+BznHMejY6bzydK5qOkwavKo8bwDmsZW7a5h93c7HhXdlWrbyMAuo7pRzPpiWc+qrstid5O715i55WxMl/EhVrvdqorsM9a7ZPZmpX4p1pqE1EWdqDNJLTpes10bOTued0Bd5t6gyBtBSLZ2iXS38Xbz7mKsyvkTNd4R28nuolzqyvWGHQhbUGvqGx3kX6B+fWPnoj5QK+HR3nqwy7zYW1fRHuTNd0uEHryohTPdR2CVbSNEutjds4P41qO27VQ98zuJqVkoFR1buLtZ4zYKYC2s99C9LXOaAtW36rIeQx0UrRm54WtsDWEkm5jabdVW/Yja4Fjj8rUXrwv1rmhVYn1GpHP9l+3nXV5fg3G2ad08aTtEvvH/TcO9vhK/u4zb4VhT1Mlo+7HdXFaNWypnqAPnZqx0SoRbQ9dIuzkW+jbcmsvqg6FmJO1EtCX4lhfpPGN8OWN01GN42Of09AghPIGXhEGfyctrXJ4RhYIoDAhKQZYv6PUkUU+TCINfXHN87z7SF0iX4YoZuIhHHxyRzzPOX04QQlBMLjh6MqCXSNJsQSg8UaKxXjIIDS9fvKRwMclRxL3TkHJekBWwOH9BKB1x/wA7mZCOXzGzhqA34IHLSOIhs9iTX13R6zum6YIET6gLDqKQsRSECN55MqCUAoshwVLYHIsiKBxHscB4gckMUeiQ3mJtiJCOWFuOHp1SohmOjpnbEvOTV1hKDhK5tNClIiQnvz7j8N13CEPN/OwCnxn6oz73H8ZMX45JIr/cjuZyjk4OGU8smDleOqIgQhZzXDrFuYI4jsAsODkYQSC5vJjQj5bGu1B94kBCmSPjkNIahqOQ2cULChdxetKDqMRaEBS8984xauZ5ebGgpyWRd5RWY4ygrx2FsYwLQaI8A+mIlEM5CPTS6I9PDlHeYPMSpTUKgc0LtAiIIwgf9ZGFYzrOsVYS6JDRYUxyMuLVp88prxbMZynzWcrx/UOiMFgZt23jauVm7LNLasZoXYrXxev2hCINw30zCpp7/9dnMhHEQcLR6IR37r+HMSXDZMTx6GR7TK0Gf8NArtepQzjUv/MA7UmQTUu0nzSthTb+zXc0mpONG2diu4zKweg+R7dp01YrdwqqtgFco8G309BypG4BjaIb3sN2ug6D7nW34TZho5Nvu+2n7t9s7RSpy2PPDQ1Rb8+NbmlsVRK0q90NNcd4nWePU3xXuAnN21jxuQu8tQPd9f7qrsINUYtaB9C2D912FbaETejpSsBsBtKSnm1EzS0+9ef7/ZQtXqwzxw7bvjKkhOwwWG+0LG/Pe7tdk20Cm3J4Zch3yLCmyNoWYDsbEWqzPRsnprrvMjlFLU3DsXgDH2PXgOrkxR2OSCWctl773Vm2cHaKRd95V5EmNkV352zx212aydcEbiWI39CV26xorBX/jnRvWM4+2LvVcmeeW9J0S3m0HHJ+3Qb1bGfPr/ndf/VnpPOc/iAmEMnyg3gX1zCbc/iNHotZgUEipCTPPV5F9BLHqxcTotGIcjLmILLLr3U/OkVkl1xeFRSl4/mnF/zSf/M+00Iyv5oTRIbzT1+iBkd4JA+P4CyVOOfJJxf0ggAKQT5e0Bs4xjagdJ77J8cMRn1evpqTzuccHoVMfZ+xcZylM8qPp4wXEukMJ0XOwoUkWjHQFtkHu4AcwVn6gqtUM1uUhD4liQOE7KO0YBBYLiea0Ct6fhlpbmEVDk0yyJhcjplOS4qh4uG7jxjIHvM05WgguVwopNeEiYZyQjrO8MMEygVO9wmHPcYXM6LQQa4oSsu9Q42SAWVREGlNEpScj5cfJTzsG5CKtHAk/Zgn7w34+SczNJ6EnDC+Ry4i8tmYB4cxZxfgvMVnc4I4oMgE1+MZ9xLHJI2Zz3MC6+k7jcoFxjoeFYJXhWaoNAcBXMqc3Gti4TgqDDMXop0gcCXZUFL0HcUsQ/QMpYmwQjI6GTEez1CTlKMHBwSZYXKdo1CYNGP2wiGJODn+kOsvMv7Xf/a7WO85OBry9//pb9DvJ2wmopacv1svb/TG2k7rfHrbgdHEW1+9WOsMIfi7v/zf8vGXP8NYw6PhYxSqiU60MDVnpdZGf7tI5yxZVoCAJI4QQjakcrc6brtSNU1YNzB3VrM5sbTPON693XeXReVvZdcKfOeRtIYz9BpbZrbLWVJ1e2v77uXdxkBuRs6qMlaORdOuaEyE36AIRA1No29FjSc2qLsRtJlsq6tfo/1rBsnNm87eojdzA7yFULSrMxeVYdGF7S3WpWEmi9YAqf2/l4i6I9sSWMtq3ME7rpnEt3FMmqsF24ZQVYetw2o3ce6N1q2o5euS0rWzDC2Kd/os67y3MM/aHllrFmHXF0Nvg7bBEzvPanRkqB5Vedp1bVnw+7pib9+3tsM03nXhqrXnbUfnXZ2LtwlbZa+d+iX4jpSNUMPt/F8FvG25tIWv3l+7HePf/zc/4od/9BHnL685OhnhFprxqwWT55eoMOT43ft8+lfPEBg8IZIAKSXC2yV/Bgk+n+OdxKNASh5//R6Xzy8Zj0t6EYg4ZPTolLMvLtB+aUz5cIAwCwSG0hmcE0SBRHpFajSh9lihwAuMgUAWxFHIIheEwjAfQaENJYoEh1YBaSkJnEFYRwwUaHqBxUhLLjXKO4rCoBBkRjCSll6cMMkdzhniXBEUntJokthjjCcrJGEokSonTmC2sIwGIUF8wNmLBc4voycNBzFXE0OSOKwzZIVHCQi1Ih4mLHKBW0wQCIQICUJNkmiKecbV1DLsC6zzlGYpF3VYYClZlJLjYUiEYnadLrtQWEbHh8wLQTa5ItQRCI11ECVQ4shKRagsPjeEUpOXnuMnfa7nMyaZI1YWXSgir/BeInslWWxZOEFfedTEowqBcRLZc8TvHTAzjnw8xc8tfakprMDbHO8EUiccHCTkkxnKGcocUDk6gt7hkMFRDxFneLlgfDXla996h7//v/s7fPcHH65Zfy31uuaM2tAQjRszsq6r2qK1PZn0VsyAtY3Y0p87BchK6wqBMYYsL7DW0YtDgjC8OejMnteV1r9LvfadG7hL6PVK120WY5qOQh3WR2TW6ry77C7nYq1Tt/q/aW21eePucJOjunl9UxjinedAWucpqwAf3jucc0ip2PBzl4tS201T3xIltin/avTZqqx2uMP15W3a/m4j8U3OXLxxtKjKR20IqPbfayPd/G1QLa8ELNvJt7Nt4kCIxj9fQ9cKuybaOHa83Bp4ovYr8O0oRzX6NzM/Nc9mR9uI3QS9BtQQdOLyeGfZtNYqYYegabf3raHhiNAe9dt0th83qa0JzyVBVazrW1niNyjQOt5dFN7NB6pybH9jY4tdRNU0NUdrzfv7meAWLvVbga5oajvs7I5WrDlqtb56I0HsYXMgb8UD9ZAfHV255WPfubz6xeYwoF8/Epu/liBTWhEEGiEEYRggpSCfLJYhT41Beresh7PEQYAO9DKkqTXgDdkiIwwVQkJ/GOONYXo55t57pwSBRmtBmeUUswWnT46RgUThsFlOIDzOOwb9mDDSeGdJhgkIODjqE8UhQniEhEBJcMtzAUot32sBgRTEgUK65cfyAjyxkgRKgRQIJRASrHMICaEURHgCKehHAaEApSRRoAiCZbjWuBfy8IMH3H//Pof3Dzg4HRJFGrwjDDUnT44JI73cOqYESrJsAzxKeJIopN+L0IHCYon7IWVWEEYKKSAKFUqAyQrKIiMINYPDZNlhziKEIwiWoX21EJR5xnw2Q2uB0ssQv1oLtFYMBwnOO/DLtun1YrwzZMUy9G4ShzhnUQqEd3hTopVEK4nSEis8hXfkxiCUxFiL9R4llgfZl/H6HXES4J3DmIIoXNY9L0s8Hik9ZVnibLnsHwHWGpQS9PoR8+sZrz59wcufv+D5J8+ZX8158dFTijRvOP1r8VMx7o7xIHbc3SSXKi1845kwWkX7xs/qerOZamlLiyqAUy39/hkEpRSBVkShXn5stPm6m7Ab4W5CpK5lt97dIfKRoHJC1kqjE9/GahJ7ye0K59r88Oy61DoFHfWpWzq3aZtb6u1a8nqZdd5Z64D1ff2v7VjUVKwQKLWUJ3WcjWhSHc7UjlaHVps0bdI76OQGwftz3d7Fva0D8ubu0dsJRbuCmw+T7MqzGQC7/m0ssW5zZaXma/+675dpu4nZ2AaVRedXf+3SmvWqjMLKbl4ebBUIv/pr12V3c+x8/na6u17KRkgIqTavbIdk77pfy7VuR28rz42jal8NV/3m3daA6zqW0cmHXYam3wjQhpJl6X76Rt+3HUsahv/+/mxWfqNEasqhdv/Fq0/53R/9W/74x39Ams4bvHtXuGuumxYy12Gi39TJfKt526K77rFt/6035b2R51UbPw0a216N5+WzC373t/+M3/vXP+TBOydIr4mDPtIJ3vvmPfIggF7COw8Sxs/GaKnpxzEPR5ZECBIPHxw6kkgziEJ6vZiT04I8sZihQ9oLvDeM7g2I+zGP7hnmFxMoSv72f/c+OoBQgZKC08EC50tGJwnf+dUHfO1XBjz8hiE6mvODH/SRZEiREqgpQWRwyuCU54Mo47h/hLg2DLKMoSwJZUkSwHf7Ofm8QMwKRt5x6D167GDs+LBviDEcUhK6FJdfoPIxkU352lGGEuCswWUzgvKaYj5lenHJQTQlsw7VT0gOYo6jFGEzBhE8GE6ZjsdIDJFyfPhOQLRyPj58CD3tiWxKXzsenRjyNGUxnxNxhg4gkIbF5TVHyYT+IODwuM8vfWvEMAmIpScUntN+hgGs9xwPSvqxIpag8Nw7nFGGBeGxIpBXBKIglhYtHY+OcwLl0NISlRMiaQi8BWt5fJgipEGIgg+eDHn/8QmDIsBNLQ8PC4RWeOF5MIp558EBwdigU3g8KhFOop1kGHpODzSBhrIsOR6llMYSJRH37x9gyxn5osAWnghLWEYo0yO9Xjqhv/Mv/5g/+Hf/hcm4JlcErIVZB9QN+Pqz9p+grnNXo8O3he4qTeu5WL/ZDK06OcsVqJru9LWRXtNFXeMdscQshCCKIuI4Qkq1JVM9NZpE/flu8fNGIuQrgoaTsm6gJdx5o8o6opjYfr4DVTXZcjuDt6n77goNvrktVAy9+q1Kds7zlz/7K37nP/8Of/nRXy7tjSrduoAmVzavmvSvnevq1UrP+731FVuXVQj5po1Z3e+zPl4X3g6+t/gRPUEjxmsbKh6t31c/e+qycQcq4bdip5p11xRRu5l+ick38rQ7ps0u+yvR/Wjvq50PdhPdaINdpL0O1IuuBpySy370O8rqtNv3NjjtAFNbTgc77NWtB6shXJ+paUeCqHmbbXlQL+NtNKFzHin2++e7wss2YEWYEHA5vuCP/ur3eXn1gl7UZ57N+fu/8lu/MC229eGtNp1d17dG3rzd+tDXHfK2MNEYyfWOrg/CTgVxB1hbWRvHovrZDJnVovpKiaeLgj/413/Bs8/PUVry4//8BWEQIp1i8uWEL1+UEEekZcpZGlIWKd4pBJIXlx6JQQrBdd4HJckzh8otWRAzM1OIJVNi5p+/wus+h6OAs5eaEMfk+QUvD0NO37nPFx+dMwgEVwuNZ467LimeaA7vOYbCMeiFXJyl3HvUozCe3ugYEcYUZwvM9ZiffmK59+SQXPe4mk7oH4GQFqUEX85CIlNSWs/kosSWnp6KSRLF5UXJMPaMFwvyzKCUB5ORZ5bn2TH9fsh4ajl/frWS6ZpQwWU+IBpqRK/PbJxz/dmYWHt6AYznEaECUBQm59NnBWm2/JDd1TwiDmZo4SiyDOdH9PoKYwxOnyDLBRhDFAv04AGjKKLMCj5/usDnBu1BWc+rPMLiEF6SuiEDIckXC1y+YKEjwpHCypKZUxz1IySOQFpeXThCLSgtzFIPQuGt5fTRiAKB5BypFT7qMzo44WRgScdXPH1pSEIwDiYLOLjyiLlFZ5arswQtBIlSOCMYz0qUjpBY5vOYQFq8VIyvFhSlRElBGAQsZiFCWoLegEcfnPDv/vkfU5icd77xhOl4zm/97//uRn7dckg0NwB3S9QGKrE9LgVVZMGaSVaNnX2yskNvNF7X5Elziy9rB6OWeG9Bm/y7tcbbN+r2w82664a+gNvL22Xi3eWtH3Y4H3s/8c3Wu33bwTrr3EpWRetb2xm34SG//einn37EX/z0L7i4vuD44BgQfO8b36vRVTHFtgNQTUnuKnp9tqMVCUq0ctVbfH/EyrcHu7j7TeEtOBfbA27v/vktbvcdWJrYPWKrASqPtZ2zJbK2hGHDuG0zace1b6fosoJvge9NoNPwvuXb2+NuKY2WjbnvCMPmptYfon558yDZX4MOp+IW0OnH+RWdjTByO0tsIRLrGbN1OLw3a/4lVI62h+vZFYt8wXh2RZovONA9pr/7Jwz/3q+x2TzbVbkmrjcy5Cuo2xBfAbzOd0q2kaz+63KEdtF+m2LXjkTrsd+x7tm1zct7Jtcz0kXO5asxCEEv7iF8zqufn2GKguSDd1k4ySz3yKxEuxAvPLmxSKmxTpPlBdrD6PSQWDnyfE6W5+RSU1qHRhL6kHxhsYXBu4C8XFb+i5++4vSDh6ATrhcZMtTk1hFIyTzL4NqT5hlCwXyhKFVIURYU44zJZEJeKCKlcU7z/NkcFfew5YKFFRilWFhHVkg0EcYuVxatcYQqxMuQNJ3ihKUoPfcfH6ECRXkxpchyrmeWxSIHGSF1glKS+aRACE//cEDy8IDZ3PDq+TV55ghkxMW4xDgYnYywc0tZWtKyJCtBSIUwOXPhSXNHGAREw4Q8g6yAPM3QOsR6idOatJSMz6eUpUGTEymBMRIdJ4RJyHhaLLetGcHZRcZ8YZAiwAiFDCIWi4wTBHMjWBSeSAtMDs4u5Ys3Fqsk0cEBRsecffEKYTWl8VydzZG9Q1R/iEoNi3yBKBWFtaQZnD+fEQ8PsAamc4fWEmMlSRKSlRakACRlDqGQ5KklCAVCxYSxJkszvFQMDgbIIOSLj54hgwVOWz764SccHI8oS0MYBssh4cX+cVFznJuDqK4pb5hFrQ2nxkTZylzociz8xiqr6XwaM1ab8LEdTkVH2d2ktQWnXz//RTsR0G1w16nYeXZjj7y+m7y9qd5t3b1Jv3V2cZ3Or53LxvO2bmqZER1Fds5EbpmdviPKV1fe1f319Irr6TWT2QQlFVeTK5oGY9MUuCtb+BVN0O7XHTZIu7+6ku2b162Vtc+B+6q4+y2uXMDGFah98wBuGNg3V22Dqkv6tLFtyhZUTvTGXe2ejK3czw4D4Yby2sK18djXhNPOat7OMr2tgOt0imr1mi4m5GXO8fAY5+Fqekkv7tGP+9t1aOHsJtWvE5isRMdB0xPxDQzNQek3RQpf3/G4VcLtB8A+58+3+vt1LOf1ByBpGvu3gRscAwGcHt5n2Btx7+ghSZjw4MF7hAePNpluIvetKJab8f2NQKf+rzvFq5d+T5599Wn510tcHeO6ln5DQlOGZGnOZDynP0wYjBKOTg9RWtJLQqZnKUVR0teC/PKK40enxOT4cUpfBRTWEUfg0ozR/RMuXswJlUC6lONHp4Qy4ouzZ0gPBIq+KYl1yDz3xNISxII0NQRxgilS7GLM6eMh0+dTosijDBQux880EZpSKQ4PhvR9j1c/v2IyueL0+BgjSoT0CJMxTBLK0uBLy72eZmxnxCSMAogGnsxZhJRgcuJQEvTg6Egz9h4vPP0k4v7jI3r3BkSfXSK9xRchKhiS5YJBLCjnKWVZILzjIPaEgSUzGWUxY9iDtCjwtuDB8ZDoUFMWJd6V6ECRRJosz+j3FDYrEIOYeycxUguKLEWTE0aew5M+40uDJCefjHHFUgn2Qgc4jNAcHcTEJ0MG5ymXlzMi7ZE+RwrB4TBAHipya/HeABbvJNY7vHPcOx0gk5gstQQyJHl0wDwXTJ+9JNEFYRgwyQzF7JJ+9Ah3FBGaAGktArcSjxnlxBGPDnjw+CHZxYRXF1MGvQFHA82zVzMcBmNKRj2NzxxhIEn6itFxn1fPxkSBJRoEhInm4tWEYU8itKCQyzMH05dXFFnJ9eWU45MDguhmU6A+lOpD7K5zEH5rrPrNWOoqsIF8t37a9XG/zsR1/NUkU+OMwe2cpK8MKvthl1HY2eA3OIh3JuB26Sqr7yYuWAcqabWflK3V/5tkdHXRxTP1d60oj3X0XSbCvZMHnByeoKTicHjA4weP1+ZKXSXcONFan5jakfjOk31tk2r78a3z1/F8ler9rXznoqsLG8s99d6sjMk71Grftpv2PMPtcm0y+R0M3063Ibxdfo2JGp6yWBuibyPM2w3Ercqtz+E03wP89PO/5kcf/xnOWQ6Hx1hnmczHKKH4O7/0v+G9B++z+ZDGCm/NkK4cpS2mXBWhk/CWFHd9U/TmPr4l8kY5O9XEqhJd9v62QPfUP/xYpa/Pkt2G125TkVFvxN/7W/9bPnv5c+Iw5htPvkOgg5sz3hE2AnN5dWv6X0uyvSVol1cfU40P2e3w4ro8b9Fx3cjWxFEZIQ0+aLSL4NWLC37v3/4XsjSnP+gh6FFkimKR4XoZn3w+Jg0D+qOYXuL59PwVcRhwMnKUlwUCgRSg5ALnjugNEyjGTK+mXF0WvPftB3zt3UN+9LNzgkBxoguc6JEVFqk9B0nJdFZSLHIeP0o4Px+jh4qD+6fY7Ck2iHCl4fr8ivH0glJ58vGEH/zmr/Dss5ccvKtIognZLKJ/dMj181cE9pqMAzwGIUqCVGC8ogwlpweOWRBgnCMI4agnMZHG+JJQGNJyQGlAyxG9XoiQCh1FvPudE5594bg8v2Dy7HIZKtT00Fozu37OopiS5o5B4vDWM82h1+9x/90Br16WLBY5vQgePxjy/MwhM8ug50nViCL1XE4yeuGc2VwQaEUvyUAFEEK6mJNEhtwmWOsIdEmaS4wX+CBE5VMuzxYgBIHIWBQBUb+PjCTu8ozU9Al8QBIYrssMFfY4fnjAd37zMR9/MSf28LUnfa6/nPH081d47zg+VFwUAQQBeTlhdjFmPJVMzq457udM0gQvHIMY5mJGNi6Z5QEnQ4s40ljtSeWCUDlyKwDJwaHi7IXBAA8eHjF98RxbghQC6TIm545QhuR5Rr+vmY+nqMMBrz4/43/5f/42UT/m4GjAP/jHf4f+qNc57NpDqktWiNrgqtRl3T/fP1O7Z7blViC6x26XVbn3frvArUiCvwjHolbeZuWm9f6Ok0V3jWx1l8hV0J60a71Y676aDfU67eibtHWn8es09c9bNK47cAJ88OR9tJScX19wenjCe4/e226xTdSVG0itLKV9pHY7GL61/Ca2Bl3HhFoHtFe9fkGsuynzTUPRzuaznXVs7nGsl7qHGVdJu45vNM0g0fhpJK59lfkNq3cDiCaf+VZT3Nz/29Bh+NRWhjdparg3dtWOpUy/jBLzz//j/4ePn35EWqQcDY8QCC6nlwx7I7793nf5J7/5P24PnF3TVQ0iO6zstiHXVf9O3L75+q7dt+Vc7BepXUdLOgVrgx+reZq24XkrM70T2k33VXDtG+G9SVH/1wCdnmLt2b5ViNvgXd938ejm2e/86z/lz//0Iy7Orjk+PqKcRYzPcybPLpjbEhsrrNAcBpZ0EDEVgsJZDiaWwcyTW0mioZgZoqjH6P4hJivIM8N0Yol7gvC9IS/OLvEIDgQMhCArJIE0lEVBXhi8Fwz7PWSQMJ44nrx3yPX8HOMLQOD9BTIcEx1FhFITDhJMYZhN5iSc4BdH5CZmdBhxcblgNp2DCOiHAqwgMwFxCMZZPI7CCmIykgDC/ohQweQyxVtPbiSn9wIO3+0xm6eriFcDJl+OuThPGSaCzCgKH9FLAgq1wOqM1GsGypNeF5SlZtiPGaqAbDInKxVJ6BBaY63GmBKlHAejHldTg5YFwgms13jv0dISaImTCVFomU4WeBlijCGUFmNyVDDg5EGPiy+vsXYZ7CLpKQajhHEKdjFBANYLnBcIkRL2NfNScu8k5rrIyEqDFYKhAKwgLRXJ8nMiCKUprScsC4bRgDSV+DIlCjW9fsR0nEGQQixZGIgCKL1HaUHhJLE1yNyTFwopHFiDElAYQajMMixtAcPDHvPZgjgOmM5LBgeg+wXjyTX9JCaXhne+/Zg0y3nv64/5jf/m+/zyr3975xCo5F1DJK4U9W5dvmNGZZ8g6tAbVXjnt7KNsgu2aNkU3g5I2m2i36zkNyr7Zp10I6mC/WdTbqBh+/m23bCxm8SdJoIbsM8e6KShnnA37LTpOhyLXWTd5IRuT36uXonqP249YbgPxBppjZybzqDUHM69dvTrbIVuwd9oKNoKtvQvyw4SdE0ENoLBLhO3nIl6jKfqr2m4LZ9VAZ22LFFPi8FE6481hVUkCrHj3TaOFpqqSFFzbMV2lteFRvaOQbOp1W4LfllHiVQKKeTyWioEAiUVqh4x6kZC2v3QQUznfas16+F4u9nh7tDu4hbuLfB1HtvQVe1TXEc1WeFco2709QbHVnf72u+OSrVnU74qd/hOeNdV8tsZ9xkHv+jpkS5Y092e3LjFQPQdfyzxbYc7rmQHDQWhlFyFuhQoJRFSYNIcu8joBYpICjQeTInwjkBJ4jAg0Gq5PcUDOAKtKPMCm5fki4wyy1FK4m1JOpkzOhrgvUeKjdFSWINzDiEFUgrKokB6z2CQoAUkSYi3BpwlUArnHADxMCGdpoAg6kXLj9wdDxF+WZ/Td085PBlhzNJAF0rg8Hhvcd4RJyFCLkOueudxpQHvGB0Nl+FVnWdyPWV+PkZKQZiE+NKQzVICLTHWEYSa3iAmGUT0+zG45YqvcA68JwwU3lkW8wXWWqRSKCVxZUlZFstrZ1EBIJehXf1qYiWKApI4whQ5i9mCbD5fjm9rUFJgrWHYi4kGMYvrGdYagmAZnjIKNN45FpMFEoiiEC0FWIuScok3L1iM52SLDI9DIHDeI8Uy/DDeEWnNwUGfKApRUhL3YkyxLD+KApw1WGvxxmFMibEGUy7pqPi5LjIDtfwYojEGFWiiQBKu+E1HS5qdcwghSAYJs+kcrRRZXnBwMiLpx5jS4K1bbk3pEOXtwdEw7NZWWss4ql/7PSFJ2zqyywDtmGFqqPu38desYcOduCkazw40O6u6XdbtBeY6re94dkO+rj0N+6ArNO2dodWP3tPcLn8XVK0ws3vLvEsR7WhmlR24qn7dphPtVYu36es2SBC3cAqWRsPeqtadoL8BeDvORV0oVLbYus8qq2xjde9zYtf5RDNPZ3k0B6jYSrQxChFNlC2btwZt92bboaku2+NkJzv4zeBYfyfgbXT4DbMB9URCSL793vcIVEASJbx7712OB0fEYYQUgu987btbHvRWGb79sLoVeypfhw5CW9L5rY0DX1MMNzW5X7oFvv5gF63VZQ1nWy82ct7GydxT6bcpv+6Efz1uOhzAfQ7TV03wHWBJ3lsYbKvs22Ju9X/lzKzgW7/0PtppBmGffi/h2997jJ/M6Sv4Xs9wYgzHaUbPSd4PJfGVozeB09iiMfQCS6Qdo36G14Z0NuaDJ4reAGSQobVhaC8xi5QkVMQqJVIOSYFwhgeHliRSxJHkwSEcHPcINcwvrjmWU4Qp0M5wIINldCQChkeH/OD730fYHqLoIbIFgSnp9wOiJOIRV8zGY4KeoJcY4sSQHCrCg4Bf+XaMiy2iX9IbOMIgpxAWHys+fE+i+oIyzhkMJOnVFfMxFGXI93/lFDUI8BHoqOThPUk8kqjQ8Stfixg4xSCD2FqOVQZlgc0zjuMxcSTQyuDsgm9+o8/oOMTLnNP+nCCUBMoSRIJf+t4BvVBh8pRhOCbQglAvv9vxjXcCerEGbznq5ySJQBQLymzGu8cZXqeoKEe5VxTzCcrlCFfwtZMS7wxKOB4OBVosnYxFmnNPz+hLRV/AUGVoUgKZIUXBsbjA53MCmzJMUgImyHiGD1KU+YKL6SW5yhj24IN3DzjsBwhfEM6fQTEnKOcIM8YV13g7pzRzHh0VRIEkwjCIPFoVxL0AZy0nRwZrS0aHPYppSqglC9EjuP+Qv/uPfoPrVxfMLq6YnF3x4P7RLrZvbendDPCdIm1tCO7QC3X5UbN/OqLWrsrZyPFK7+6zUZvfQtpCdiM0IoU25OCbh/18k9ChnZO1O3DVm/JmM7U7xS13AN0BdlvD9ZrtdyR22RB3lPFts05UE8wVGbX+rhuNrwtt3q7bOzto31qB8X4Z2rlByrZj3zhj/JXu3NkPb+HMRXOn/y6G3mdX3XQo3m96fIdDUKdmaShWqf0WUX79vCEzG/WpZ2phX8ec3Cvd1uV1zyzsGfZd9bqpcffChtG+PPucOIxxznIxPmf6yafkIuf4gxOenn3BO/e/tu6MdQ27xrJzy8ObLL1s38xRI7KZeVs9Vfk3QkfUsvra9V1q2jzE3yy9/bxbsFYOWcfjrggUO2Lg1UmvC4NtZ1ggqvM5rSJvV/V2QLsmDRWeTqUkQPhbzH91dd5d4LV4dw+eW+Bq1L2KELYL19YL0RD6vv16D4pnn5wT6Rhpc0Sp+fSHT9GlIcDx7HL5MS9fKmI8Z59ZXOEIo4A8UCSBpSjtMmITAVG8XM24nhlOHw7QM4uyOZdW4Y3BWMfMC0LtCKSgtJbrVNIfhMSjPlEU4U3AYnaNc3MKXxBLjw4lM5Mjg5Dh6RG90ZCf//yK0CZ4GeHpcf58TOlCysmYMwVJP2CSWc7mJb1+Ql6mmLzkR88dTniMVqTC4oKIRZERo/nLLxdM7YwylMxDhXCHzC9LpCz4SzWnd9Lj6svrZbjdwoEoUIHgJz9JUakjJiB0itzGRHhCpZjbAU5ZXOlR2jM2CmSJEwXXRcjjQOCcJZCSq4lgMAiZjUsuJgrB8qNzvWHMPA0QIiWQgsL2MOkCZwMC5RlbhdYFOgzJbAClQQuNkoKXY43wJUIIStWntAatFJEMKP0hgfNYoLAa53NK71AaZi4gKFK0BykVCzOjdxASesOi7BNqQVp4rq1BjhccPTggjg5RPCSKNJcvxpi5pMCRiJAiT7meerAFpZOMZxZvYXjaI5vPmS0ER/eGzK4LSmtIRweogz6H7z3gX/1//xBdXDKMAubnl/yH//e/5//0f/8/I2SHEbVSeXcauqLx03zeYWTdFW8n1HSIF+w/N7ADT0MfVELT1x80M7eskhuhfm5xt1l/e9iVvy3rt7u0de7xjmcsuqChxzujEu3G3VV+/RtU7Wiw7ZKrnx0Su5W6FjW0chp3GZbrcjv0xx5StvJCh/5Z4uyygTu/Mi6a3La/r1ozYneG/VvLbgNv7Fysu78r/Kyop2kZlVuYKmm0baBupe00VDZSYGc5fvNkHQ+7hm+zPaWGp7Ypv+4RdtehPWh3eKS1iy4HZyvhHgZp1GOPeemc5Xp6xfn4bLnkXha8ev5zCu0JDg+5PF5GJKqFH98Ca91qm0crNnojysZ22c0q7ZlRWvVPoy53YPD948jXOGQ/tNzP7XI690JuhOPe/aq+clK3sK581i6ndpfbUv3uia+94/p12reR/nWE1ttyLHZ1ZNsjrim65bisnIbdtHSFmu12LHY33NWrKddnU2bjFJzg6udXjGclpXHL6EvC47xkUUIhLVbElEZRkIFxZIUj1AFax3gZkBceWxrs5JrMCOJYkkrBzIFHEXnIS4GxAuM11oJZWFzoKI1n+mJMmnu0CrECjPfI3JG7nMOTPoWzXF1NWBgoLXgpGZweUZYlxVWJKS1zLSiFx6Kw1jGf5hihiYIAqSXW5hQWAg84SeElT8/mhIHEeI0MQ3Ij8VZTWMXzl3PGeUkQQ+EV0gmyyxRjS8ChC0ssJQ4ohCA1gswIZOEYhAohNFlmEaFilnkmc0fpIoTwjGeOvFhuC8tfzJFxD6cSTCkwpUGHERcvc+aLjMJIwjBBJ5DNLHnhGA17iFhgs5w8s0izdAadDxBeMZ17MhMsHYRCMjeezEjQGmXF6jukAoVFqhjrHKX1GCPJhMOzrJfFU7gcgcO7iHnuMB6cF1xOc5hfMeiHKOmIYwVJzOH9I8zckeYOPZ2TXqU4axBC4rEIJUAsv28xOOyTznPmsxKRaGTSx4cJP/mLLxn4lKNYspjPkTrg53/1Gek0pXeQ7PAk/I32VTWstuVjy2BvPWrc7hvjt5UfVfm7ZlbauEUrzU7Z8joCrFnhzbTnVwR7ZNs6yc54vXU0d3d/bqtfb8Qjmmdl9zq2laivy/3KgmhVc2PE16y0Vnvtar7lBNWOl/tgbdP4Zv69hl8t+w6nbxcpYuv/14O30Y9v9yN6O4zumwzObqYUe99uw27zytd8n3azd9MqWg82ETBugq7BuJndrzN6hzO2l2VucFQa2FtvBUilOD28xyydkhUp2nhenV0jYk3Pak4P7m1y7KinUjd8cGk1el97K0rDgXsDaDRXo8Vp8mlLanXNOtD1vkM41eSaWD+o9eceo7zxlfAbPc369dsQAbeELcF4R2gr8NeB/bMTa+Zt+2cC33DCOw2kGuNvObedhsmOsebh3uMDDk+HWOfpx5pXsylKwPAoIe5HhL2ERSEYDiSZDUgLSPoJ85fPEN6RFyUHUcTodMDV1YK0zBEClHAIL3CFJYgCIu/RUnMSC8LSsvAC5S1CQhgFRNIx6EEa5ARaMVCCw9M+F+cZXsCje/e4950D5pnl8KjHUV+TL5Yf/js6GvLowZDzFwuSGK7GM16dXVMaiKRASUFmPcPQYV2B8Z4UySAAXVhmAUhnEHiCJGSWlUTaUVqNdppeJJB5irAQa8mhcpTekXuPFJ7BUOKNY5bmaFVwPAgpVYAzJeViQRKF5IHn/mmf3mnMfDYlCD09AbKcI0NHIB2R1CSHmnJaspjmRIkgLVJcYUgiidYS50psbtGiIBwOuPewB9LSL0Os9QRaEYZ9zp6nJJFlNp4TaU+/PyAKHKXJKSWEwmKdYRj1yEtHHApGw5jrWU6RToh0hJMKISVJKBBILlKDVBYtS/I0R8uAnoLDOOA6K5hdTwhwLAB0hBjFHD24hwxDHjwZEkhFOsmZXKccjkJcYbma5CS9hEDCi6fXiMhzOIqQ93p8/vSCRMC9JEb7nDIISeKY46MDLl9e0Bu9s1/27fEw7vJ0p+Nw0xjfi6cagx1auC1/OxR/Z2Cmtqi90RxpK4SvAN5QjnZNbr2dw/Kvf/i7Xb6oRd+scFe23Faf12V3w9lYp9igaENtIrDRLC19ddePvVbb3xucWKf9BnSbj0FutFH30Kh9Df2NurAeKknAG+N7q86FvwU93XP6futJ130Dzc2wtu/E1kTG7rTdiSrevbU/uK7kpr5tR3XX7HXztn3fpmqfFhB1QgD4ze//txwOjsnLnHePH/OjaYg7HZKMTvm1b/36zbh3VL0903A72KWKGsOmXYXbY28dZup2e+kwRJfG6FYTtKSVoKlk2+U1C2ld1/BuC8HtGFRvxeHaAXt9qK6Eb8s5eE3wbiVndm118KstZtTXnpoqaoOs2bLViKn5kM3fm2hbpbv3+Ig8s+AE5TjldBTzNMuYzRY4M+fieoRxmnQqORoKTBoxmaaMVMksn2HKHHCcnMAXX1xhrEMHhsxojFNIHEk5pygiokDRUx6rkmV9pUT7jLRMcJlD6TGvHixIZcBCepIFZGUPncQ8eP8RiY6ZjK+ZZZoP3x/x8atzlAs5PBiSzyMEBUIF/PJvHPFv/+WUIi8YBB6vHKWTpGXB1wPBl1mfzHjCqCQYOC4zSHTIY1lydg49Qux0TKItgV5GpTpOMl6IECMERltGTnDtY6w1nPZKnl4Kkl6P06MRh98e8dnLjPRyyiCecWUFpVbIrx9R2gWLRCGEYKQXXM4ceaIBy5OjHmeXKdPrCaN4Tm4HLKPnQV/MQR0TDSISec3ltQarUMmQY53x6dMcFQU8etTns2fXzGyOtwKlJqjgPk5LAjGnKAsQMbmznCjDfCYxxiGtIRUl6cKjUPRcSiGPyErHow9OefFqQjFfrlS8H6eUgQcpuTdUBBpSp3Eu4jC0vCgCFoVlcXXNxWRGRowUnq/fj7nKQuaLkjwX6CTgVWYRwnMcZ1yFIOIQ9XDAxbMXCBUTB5pDlTNbOFASmRu+++vfpshNjZnbg6UaJN2DeJ/N1ImqPalTM/JuaX91DNhuo76Bz3fT2pAEW/FKO5DtJaqNvQvNG3ycb1+229pGO2FP0NrX1MU30tLlIN5CV29y3I6gLeO8fqikMtBEVdCbG9f1QgWicX8r2LPCVPn4GxX1Zh97XPtnb6POK3jjULTz+RzY18Gi46qd/ivy9LulSBMqm9D5ZdSMYEfUpK6Zi10d4Vv1W/Oq2K7q3s5sF7avjVojv0HjMu963GwnuD1dLbxi+2HDSG6+aUd+3mGJ+3buHUn30ldpkS6u292JjfqIzZmd7ZjVrbp2hK3dKYy3nAu/63Vn9rcF+7r4KxqRvxi4ifDaGOhM2hgjbeGxu3eqvvy93/5z/uKPPuX8xZggK5ifzUlTC8ZgZIyVEZlRhKpESYl1EgFoPcW5MVlhORkkyGTA5dUC5z2xVkgkCyPQ0gIKj0QqSSiXTkXqFMqXWBESxH2QkmmyYHpoyPohw9IyeJnANRTGc3oQc+/JIRcv55SzMd7l9AYB8eGQw9MjhOxx8TIjieB8PuV6PGZROJLIUwiDEZq+9ERlH20Us9xDuKCIDYXUjBQclzHMHNcLi7Nz4jAiHBwRRZIv8ytUH6al5wiPnUmUiwmUB2sZ9SJ82GNwKJjYBefTlLLMQUhwHhv2uP+gx9X5mIUVSGAYBwTA1czSx5CkEpdJBB4pLAfDhHkmscUE5yVR0kdqRT6fAI6s0Nw7TYiGPfLUkqc5aTmDnsTJGL+Y4pwmjnt4C84ucDhKH6FFicsBA0oGJIMSNQSDRruCcmFw1hPECQf3+5xfTrjMHYG0DKUhFG4Z4tYZjBB4GRNKTyY1xkPpFaHPUVIuv3PhDFooJH4ZplZ7dD9hYQTCGbI0RUsoRUBAgcWjkx62KBjZcw6DnCzPOTw54v479/mf/uf/gUffeER1eFWwLQu2thN3bYdmdQasNuGya+L3TvbMrqFXFbM+7Np0DrYk/T574CYabxCMt91OdGdjcEe5Nzl1lcK//crEXb+IUcv5Ns5t1HHUZ+13TWCuDz37Rv6upFVggrX71478tLaVfvGwq806z6JUedjonK1tU/51v622mZgDGL1BKNq3cOZiV4izajTUlG/tzS2RrzPcRs13ktBG1jnDvFrdqLb9bCzKHbgqlKJTUG2ZLHUpfVvYoqHlNFSot6oj2J4O9+s2bBLVAtG+2XNOoSKn9jX0PZg7uGA7xc2Ox82wYZkuKrZ5ciesG3aDcemr+I6+bJXV3py5p9+Xsw9ieeC4QePmcpePshNnK32TRetv27Mpfl3eTf7RzVC1U8vpumEMvH55uzLVCq2MoY4Jj22ne+M47iqkXZX1iGlEFvEURYmxHus9KlD0B31kLuiHER6YTjIE4IxFCgi1WoYGDRWD4yHpdIEQAmsdHoWSEg9Y53HOYYQgkAKNYNjrUboApzRpXuKtQwHCOqx15KUhsAIpFNPxGG0LslxQFjneZ1iTY4xndDhCBZ5ikTF7fs2YAqM8QioC5QmCkJmTBJTYIgcR4xDLr4Y7jxGOzEFhLAOlUNIjkQxGA0Q/IRCOvk6YuzlKaYQpCeUyvcAjvUNKgZOCYpYxSSdk3hFqBUpiS4txjnye4qwDv3S0ZKAYHvbxQzjuKbJPxhjvMUVJHEcEvYh8siAUy/YTgCnMOqSv8x5rljP4RZqxmKaICEajPs9fzgm8QwrIsxzrQGAIlMABUkm0WlopDglCIFbnISaTMQEh/V6f6KCPTkKEFCgpkViqrxfnRUkSaZIo4TozZEVJqUGrgAKP1ppQK5TXYEuK0qxW8wTWGYrZgkJoQiVWfCQoSoeSEMYh87JEeo8MQ7xNIYqYZgUPA8nwdNic+OgYVssZU9/9spZzY6KI/WPeL52Q2+jyrbj9XcKiy6i8Be5G/n3Ox1uacbmz8b6z3N1WlYAbYs9suY63cCxusOLuasveYGDUpXHN32jRUhkjTdncdUSm6WBu+LOtGppkidb9dgCj5p1oNpNvIb4rtM2L+nXNgWg7IvUdjFvvWiQLUU/zGjR2wFvbFrXNI10csxI59ZqJ3dzfZW6K1gHr2w7SrS8mNvp6dS6jeTT/Vni7xlp1xqIRteiNrKabi7814g5GbbgQrfpsYW3XY+1ktA22zf+3oWz9CZ0GGa3+uoNP0KC1hqoSE2sh2qVIbogucqsoDTue7nJ5dhLeaO/9DdDedLhfANbGj99q7T35bwbvPdZYYGlwyX0xDW/it7sQ4P2alyt2WY/vavz7DW+t5X4DNox2c/3rpWy8sm//yjv85Eef0zuI6J8m6CxlUoTEw5gH9xM+/skYM89IM8fRYUgqJEoKesKhwhG5DCnLBeH0mmB4SP+dY957/5jxNGcyy+kPYh49GPDRz5+jI803v/EOk2vFxXmOtgXi7CWfXlicg1NRMi8DkjJAOM/DIOUi7iMEHGnI8imZiHHScqpz5sEBc+cZjAQ6CPg8T3He8rVDwyeXoL1nFHuCIMDPBEpqvnFc8vnM4ZxhFAly5ZALRRRKTgcLzi8iZKzQ1jEaOOZJgLeGD0PLj547BqGmHzv6PXieWqxzvBOUXBmJDDURhsBNScJjvID3+yWfXFkCLGHhOBYZL10PYT33mZEWIYEOGJz0eD8W/OV/uUIgee8dzcuzFEQJ0vPkBGa5QGjF8f2Ypy/mhFoRaEFSnvEic6hewLffH/D5+RTnSlQAp+GcV9MeArgXlyy8oj+IcWXKaTjj+aKHdY5RaBmc9rnKPNnU0eOC0oaILOXbP3jA4CDis4+vWEwnHOgFk9LQHwR87wfvM7makH/5JXla0Cs8cxORSM1AamLjmEmN1pIPDiNeLQzGZRxHIUYLpuMpMgg5PYh5fjkjwHAy7BGGnudXM1Ce906GeC85uxgTaMk/+b/8Fv3DAZWxtUvctldwl0bJDmu8bai3RcBq8uE2mnbXl6rreMVtD1zvcRgqMfu69tX+b2L4G9O8FuyZtNnslqhZkVW2uvFZ+/914bVWLFpFbnC0rD/fQd0+cnf4tCuW21gnK+O8vs35plo0vnzdFWmxTqtvYtx1KHwvb9wyVFvDTRSiodvu9qX129tt++CtOBe7iFgO1K6R2t2Q27KoKyxs3be+PTM30nc4mJ2wkjQNJ3RNV8vHr9kYfoex1rUJo76xSDRf7KtI68HWCO0ofRd0F3QjhjtYnruSNgbDTeW/KaffVKEdg160nCa/I12zoBrat7BUfBOI1h7hejVvKnXfftXXanLPWmtVWw29Uhse8H7bqavy3ZrndxFYE42i7ji1RGZ9L+tORmuO9o3sqGnkVbqNgbWcXXv57Iqwp5ET6N8fEqgY9+WYqy9ecfbzDK0ksQw5jCXpwqG8xxQWF/VJkoSLl1NipckDh5vMmJ5dMnvxEtVTFEIhGTK+54iGJSoRXBcZMjwhm82ZfvmCMl8e9A6EIs9CwmuBlYLASa5cuFyRMIYrD0kvglKQxBG5TgikZJpbfvrROT0xQyqJ03A5DXlw0GNReIp0jjMCk1m0dpzhkX6CVnDyziPmE8XiakZYWl7mITIUeCtxKuZFClFkCRW8XPSIXI5yGuUl/t0Bvdzgs4yn1xZvUkzmsbFg7vtglx/G+/jV8hsTSRgSSLgoI3BQ2pIXQYRIx2RG484veJlKjFB4BT/7ck4AWAQqkFzOJHk+JQgCXqQW/DJoxXyxYFqADwTJQcKXlznXszlx1CfSjtwlDCKwTrIwHqUdZZqiXcaljrHSEIYxepgwmc2ZZYbSFszlgFjAYpHxF7//U+5/7RHlPKMXKgqliHXJyfsnMHKEieUAhcg1xZUjmpekZUqaGlIAFeAEvChAyOXH9Kbl8vN9xoKwngujCLzHec9iPGbmHHEYUS4WvHx+xbtPTvj2d97n7/zWr/Pk648b4T7r9kxDRovmGbDNlpTmQNo5xneM2J1Q+e03hanqQvgaKlD4Pc/+K4Q3Oci7adN9n99t80FrknYrRzcxdz8TcEsbxtdT3pSnOqpceaP1VxsLcRvDSg90kd/IUEvQ1Xhiv5qrJWugWH/+4Gavp9E3+4bMmuw6n7cP1d9Q3E3wFpyL3R0qatQ3xv9qZr/Z0HWTfYO66vIq/7bqb0GzoG3aGi7ljoGwztbMu6HBbz27HbQlX8uj7Uq2q5Bdae5oxG6dQlgvm92uZk2G3JbMdfzblO3SBLv67O3ATltyZ+paP92xfet7R98ubHi7bit/5XrwJukoQAiJ9A4vQUqxjJ2/yruWBm1h+ZZ8r42zXykQUSuXhgBer2+0n20pi4YErgpYv2tPJpy9GHN1NmE2WeCN5/LjS65fzPAeIhUghSIvPBfW4JA4AqTQ5MaxuMiQcQ+rDNkiw2YWIQW2tOhSUmIYT+a4l5bJ1RUoweIqJFAB15cpixxi1acwEuc9RkmUUeRA4UDIEJBYzyocrmdhIEcgLMvjDGiuL3PGeUFpNIEGLxQLZwmShMVigSodHs20sDhf4K0l7PfIRUh4dMCw6OHLgkVa4EqLcZJIJRQZXD6fEUWaIAmQySHTWYFREKaWqXeoIIQITJ5TlI6isEgZMS8FIIl0QjJMKNCcz+csnGZeSpyX6FLS78VYPPOiQJcSUyiUDHBu2ZXGeq7nBukt3gekhWcwiJBBTDotMU7hhKRAko8LvEuROiG3ksw4EiQ4DQgi4fDWUZYeJzTGBaA0hBHXiwVZmeODkCA5JMsdoU7Aw3SRUfz8krwUeDRGgikyik+fo4YCkVjkKCSKBkSHAaNCsZilRFpiSsv11RRXWgpncUW5dCpWg9NJgZYKoyVhoAk9xPHyw3qFtRgiTp+c8k//b/+Ed77xDmESbbZXtMbhekW5Iaq7JE3tvvLh26OnU2fdIIDriv+ukw81Wm606Np4dgrSGxXGHlK+ugmmmwu/bdlt87bLZvkK6r5LedVswG09KtaG9/KMD60jQKJ5tcXj207GbrfJr3CLZhax4xtTLdR+u6h2AVsvX0+f375v9qd8c0viLW2LajfDlu+1VZFdPtKN8kN0POuk4QbYM9jWjOg3c5Z1c2QvgTVu2j574dcOV5cff5MM3A21um+tFHWH0V0PkVZ73hwD+/VYfntui6ZV3CSsKUd2NNR6WN91huo14pWvD05ViO6C4rWWi5srZtVv3a1tHqe/OaRCu0lv02xb6W5ZFaXkrimHzeXrM3wTVReDr8vYspY2TkVtzNy8N3nX69a5JA8n90ec3D9AacVomDD92StGiSJQCljuq8d7hrFGhSGLzGNciXElAodJLUFo6UWSolzSFgWC3kGCiRK+/r0n+CAjjjTWe04fHlGMI+Y9TVAonCkIlAYkOoyYuTmJ7qGFQyhLlpfgBEJYvDNIo4lChxACLTSZ8Whh6OmADEscgpWe3mEfEUaMwj7j6RQtHFoJ4kBhTYAIA04f9oEeCM1gFDJ+ccnLL15ivUYLSxRELEyB9jmDsI+QjjJw9JzF5wtsWRBqRSg8NvY4B4duOca9s2gpkEWJKjzea0Iy0AqsIQg1iXY8vtfnOoeRNMy/mJDhOTwaIo0kvR6jlKAXeAIdUJYe6zyDniDPMsJQ8PjBgOssJSsKSuOIAkdmSyKVcBArikWODhzOCQJpEa5A6IjDYUzQiylKz2yeURYLIm0QQcR8MaWvQh4/GfLyy0t0IsnzOXEQMIw1RkrSHPJZih/nHD86Jow1vV6COAhRLmA+zxgME5z3XF9fk4QRrrDMLyZMJ3MevHsPGQUsiox+LyEIQ4SE8dWU49NDyqJkMpuShCHvf/guH3z/A4SQrcG0j/dvKTU8Dbnsobm61yqrFQ10L94GqbeYKGw4JxXsqoZvJv0bdAVuBbtXA+5Qg1XTde23F/UEt8J4i/Lqbb/LKKzMgtbkcHW/dTxxZatVQQR2T9TWVh/aOvkWuqhbC4hO87dNg+jK2gE7/dv/2pmxA96Cc7FjlP6iRui6HL8tQFq0VUKuCS3OqNMtNgOsWlDb2DG+5g23aapMULHtsdb9gNpzv6LX0+Hl36YNdwjM3eHblv+L1Qxye2ytDddbfHBnP6Erwiqjbtcac4OA+oDt6JvV9frL7V049wzk9S6iXTNW60PbVZ93zOD4Gp23hh2Dokuwtfikq3+bUcDrLnD9WTvlNiX7ZN5rzV/UmqcTyduQCbfu8vopjDpxuzJvv7wT+QJ+6dc+QGvF1fmEB0+OuXc44A/+fz8kHS84SqAwIXE/AGmx5Yx5EaOV4p0TzbSMmBcQak8/DHlxLXDOkQiDWSQIOeTsZxlRkPHluSYINI9OYtLC46UkHAyR6SvO8z7eO+7LHGViLsbLFYF7vYJneUQkNSdRQVFqrgqBKCyPjkrOFpLIwSgo8KJAyYRACh4eWD49m+NExijK0IOSsQGN491Y8sX1IYtLy/knEx58OMQKQVp6vv6NIc8+fwnCcXyaMLmeYH2fQEgO1BUfpx4Xa8Ke50xdc33UZ4LjW9LxiRHMCktRGu5JyzUaj+Obac5kkpAaRxQJjl0OakRZlNxXC7KLIVoneOUYjBzXs4gXkxnvDVJy4fBRAJHmICr47GJpXI+4IicgOjxg4R1DMaYkQUtB6KaoYEg4OsAXC3rqipk9xljPUKdEx4dMc4GPNQ+PPH/+8YJZXnIUl3hvSGczrPE8OShIJ1dIMrTLcVIQH/RIkoCHR4/5sx9bvLW8/Mklf/fvfR97GNDrJ3z49a/x8588Y7HIefzeKT/88Q85LybkYcA/+Mf/DZMv53z+F5/y6//41/jo+cd89MknmMDwne98j7/40ScUYY7sex68P2Dy8StKVfL4m0c1x6Li8qbjv32U4jaye0cSz2Z1pDVguuy8dsrGsy0y7iBQumdqtpPtkl2vK7x24nt92E1JtZq6HUVoScJGBu794GGrhLusvOx0fG6q/+u294q3RDVR1JFg1+rc5uMYt7e7Nmbnjkm9XabQPugYR6+7nXpt3722sn1zJf3GoWhn81n3i53eYycZbJpjX5aO1t9hcG3tDOzwJrdw1B2ULWHQ8lD3fa6xJojXBnDbELyV87UtAW87h1B9yO42vbuZIdg+y1J3LrrkY1cw2u2oBTVzt1Pe+EbX7mTJrsc7Xf0dUCN08/G6jr6teaKbg883lH+Xwjve7d7edJMLUKXqxlsv+W8EdlX7FkbJrfCurtufXGpyrNjKUt3tI6F7Ba36gOL+FQ/vPdfnU/71P/vPfPwXX1LOM+bPp/hSMCsg0g5kgidAKYnSEo8nLTW9aDmjjlAUhcG4FKTD+BAlS4hDCqnwHmIB2kHhI0Y9iRWCeZpTFJYBnsBJrOyDXeCdQAeaRWZJQo/wjtIG9EIwEvCOWe5IQoeUDkuEkobcKASS0ip6B5YszLiyjkR6gkVEYAJyI9EyByFQ/RH33jkin6ecffEMJyIef+2I87MJaS4JhEUNJDI0zI2gN4JPewtmByEBgHNo77lGcJgWhFoyFZ5QSoZngtFUMTOSgXKY1KGiPlpJ7DSnF8TkNiISKaUSLOzybElsC9x0yryQHCQC48AKhUTg8oxAKQofEbgFgVzyjLGOQHsOTw5JbUA5G2NKj7ESpUNGQ4mIBC+vFvSUQ6uYWVpSekkS58TkpE4QC4vUHlfkGAdBoBiNRlgdEYeS0sPkakJaWrRb8N/95gf8H/8f/weElg2Z+fmXT/mPf/QHfPrF5/SSHt94/wP+zge/QjzqMXULfv9P/hOffvkZcRRjU43yMdfjCffuHSAjw2Q+IQxDvv7e+/zT//4fo9Qy9PpyHqVjJLyNiYAK1R0MpbaabYiQbkW0H9ld61Hlue0szC8A3t6B8KZd8LbPA27maTqcm42pcUPm+s32xN5WV+xzfus4djnMW7zUkf4XAI2Qs/XoV53bz2EfgfvOudx26AzfIBStvDnJftjZna9ldG2y+uqf90sN75dTKdWXD6v3iE1Z7Rnm2qs1T9f/OoleR7Zp/7Uz7argylBd4RFsDhFt7lrEdeDYxxT7/pZpVm20NYjrdVuVsz7/UrV6s6x29dvttm84b/fR2uWp/duQBrUBtanM/oL2dGhdyOFrDky7aetMsp7dqPNRpd1qdO/tv12wI5OHOsLtqqwcvx3lbeyCVUMIVlr59trw7jK04uo7IO9m1jeD2hAVQqz+YB0SpHXdfLwZndXflnuyxlcr03u8d7iVfKrklF89r/7AL8OELhEtw5w6jww0Ukik1GitUKvQs8Y6CmOxzpMXxTIUq3EEShIFAaEO1pRlpcE5h5QStRJuRVFyfT1hNltg7bIs4xzGWrIsJ4xCdKjJi2Wo1f6gRxCFGGOXIU+NJSstQi6dnLy0GOswZvlMBgFhEiOjEANIqZBCIlhGJpFSEipNICTz8YLnP/2SxfUMZz1lUXD58pIn336XgwdHICTGWvK8xFoLbqkIy3IZZcw6h7EOpMApQWEtTgiMczjvkUIghVz2mVyG6RVCrMoyFKXBec/gcICUgrIwhKEmjCO89xi3jEo1Oj0g7Md4lsrQlIbeQZ8gCNbd3ev3CAc9itwgVn2olSIKA6SSzKZzBILcGGZZvgw5rCTCgwO0kngEWmuMNeRlgVYKrRTOOoq8pMwLrF2GpNVBQDbPcG7JQ/Uxsonjv5Rp3nlO3rvP4GS00YueFV/WdAHLMLvUebU2EP2Kr982rEXrDYKiLRbqovj/z9x/P0m2ZPmd2MfFVaFSVpZ+WvR098z0zPQOMAQWtovdxRq4pNGMZvyBfxh/p9GM5E8EzEBwQagBAQxGont7pnv6dT9Z9UqlzsgQV7rgD5GRcSPiRmRkVb3G+rNXecOvi+Pux8/5Hr/ux+d+s5BwrnOa/6/3wY1hlWx6o66Z7+fXLWoOP9xU3U0lfZcORqZErIFI12GjPp6Hwo3JrpXgnEKoPa+o43pA5hhmlnDTAXvD7pzqrlWh+brX9ZWu45XfhM301rxFicXn6diINQ2pSxIW57RY4sE6nGnaOiSuzjmIWlztz5zbtUXM3UTP0nPD+2XfCX4uXWPfLBLewPGr+fkGgq6F2HwJda8STf07T18zpavCvHyYCpWGdonF1GuCWPG3qclNhNSTzPvbm71/EwFb66IGL39rs00f5kdtuV8W39+o+69toFnhTdy1JvuGad+g35om9Qb0rKStSVmsGO96ldN+WqVzGhHGXKL5mT9vlMyWObbvdNh/2OPV0RE61LQLybgES0ESBnQjx6v+GOM9Wy3PuGoDjp29Lns7iidfj6kqQytKEWEbHURoodht5ZxGirzI6QpH7jVaSloW7vqMoyyiFQq2ggpbhlA6qqJgu1XQp4uyDl+dE0fg9h2hUOy1JMe5xUvJXiciGysuBpNzDrE+Z2z3ibua+/danIwtR6cVGsP7nZynFzFKSZLI4p3FyZhEQac6ogg7hDIktCOC4pJOt02vc0CvOOTXFxYloZcb3us5rPcEDh6mOU/jmJZ3JNax5RzPpcYbx30yRomgCCxJ5TjQhsPKErQ7HLic4VjgrGMrCnj3gWJ0kmG8IxYlaaVIooBWDG2ZcT4akaUZ93oVYmeHTqvLVlthfvVLzn1EGCne/7DHyashLhshhWU3LnCtOwhp0fYS5RztoIOpYEv2OXNdnLV0g4ookQwLh5Keey3HL04KAh2zHUu6WwnVoMKMx8S6YIBESkGgBSYdUGUlKkiobMXnX39JmqU8uHufTtSlo7YICfjg8fv8+b/7JWG7xf1H23TDfdrWEhjJ937nHX7982Nc1GWn3aG3F/L1F2coIXj34ft8/dlzLi+G3H98h8fv31ut99aFdfK4Potqc71R7q0BCutk0rUWW5FoNov9nBv7NzMW3iTc0GE3vudm+kW9X7nC1s3lfVc2RtOOhrkIai8a9cCcpK5dCndTxVf5PPPGcn3L0yJIXYLununpcL+Qf+1tBZvw1S14b7rw+10x63dtYLyxcdHUv+t+ry5lhaIXK3hvZUnLEmyRl8Qty5wj86qca9a/ATDfTl5vynmr01yDy3rElbC5NsxEUwl1o+Tt+LXYdK7NaufarepK8+q60OWLbdYgxfnKbhsa6fE0HRa+sa61J9VXVt8Y5tq/6EDAz/157TrWpb6Vjp4mrk+8DZpfz9ZAwjryqIP8+rHrRvVdNxA30O9zixgNVE9Va1UZhvklKnG0WjGlLOHLU4wtKEpBmsVYq9nZ30KHEbskDFNBpODwRYapDEkrod3uojSkpaLTaXESDTG+wEpLPwDjMlKvcM4gBwpFhZCa0ikqazF+coPzoFAISqTWEAp81MeVFVYKTifnvEEq0iKkLNooGRAoT1a1KKoMhopRW9AOtomrS2xlOK9iEgm5dxgDrXaHdGwpTUGa7NAOFGkliZItnn15RqVS9nZbFNvbbJWGywqqBHzkSZRHe8exlmhrJ56XlOBMRng5uRTuSRcCCtIgQFcGNwZfGcZ+gAwUbe2xFrZ3Ep786hBdlbRaEYUJSVoRW3fvEcuCk2fHCDmROUVnh/uf3uXF8yHHh2eEKkFoR6fb5vR4xOXJGcoH4AqivS2McgwGQ0IBwiukFyReMrYRW52AtHBU1tOSGuFLEi35+uUAYyCOE4aZICgdQkqCOOQis0SBxjhJqBRZZRgcnpP0HvHTn/+ML775inGW8sWXX+NGGlmGREGLv/g3X6Jkm6ryfPX5Mc5GyHSP0Id8+wtQ5Q5Vf0DfKE6+LEjzmFY35qd//JI4zBn0x+x9+QqpJA/fPZifDxvKS3/1z83gr7bwdm2aNynqBT0mFtLdIoipkn49YPKauK5JgFzp3hsqvlH01GXnJrTd4I90ybP2dxCWhm+xkSvaNL+92jffatBc23xddYxWs1nmtMEi7809MG+0rMIZghq4angp6vxcf1zXquksud0gbaDC3nLG5fDWLtFbChtZmdOHmdB5DUc+G9Y532uLBrOnBiwaGaiev+l5DR0bSIwlkN1c8kLsrTq5OdavMO1uKnrBUFssudlcnG/VyjaKSY+sPHtxJSzWwbvbhpVfHzYQ4I1ULAmY5VSzK99W0HRDvW++nrHGqN8g1OT0+gRN8XUS1mS/dZhTHIsqfbWGm20rW6SpZprMKYV5UCRE05clQf98yGiUcnbWRwhBO0oI7+3gvjmitCBVSNztMi4c46NLtDJUVjM8N0ilqWyELDV9W+GcpawkFRFZEnBRZqhAYZzFC0mpBKYUBIQEPsBaTyA1ut3CZY5xmQEahMRW4ERBICwVbuKatrpCGt6RjQSuMBirCJXHEmGd5HJkSZ+co7QirwRaRQxKBThyI7BOMSxyrIxIog7HaUUYBZO2VkAQUJVweJwhxob2fgeXGU59Rik1IzW5LdsFAXhBrhReg0VRBhEEHoQltwUpgFUY4TFSoKVElIoqA+sVF2NL4QLGlSEfOyIpcWGMKwVnRwMqG5AZj5Axl5ln/LeHnPVztiJJ7CbbosZGMLjMQUTklacVtchFyPlliveS3HjKwk/OUxhI4g74kNKWhHGM1ZrSGXzpyFyICELiuEdJwSi1DEuLdRbrQ2zpsAJsVfBgN+Gbn/6ag48fcnx6yuHJMUVRUIQVPg0Z9lNGF2OqUYvOFpSlJc8NRWo4fXmJFOC9oCoMpfE4W1KVBuM1OlAk4YBux4MSOGM5eXXBw3cOmDuYeLWIs3qhpDZdNhHFcwseK2b3BkbNraT+mwrJW62gNGW6beYVrVvX6AadtTEY/Q4Mi7mFzFV1+gbDZs6wqD/Xzm5svHXPM1sUnBz0bqrnmpg5IDj3sKwO1lTZeBb3+g4NMZd0dTE3ataNwusM7Y0uc28R3ti48E0/agQu7xVbJ6t8Q8pFCHn7Zl+XJa44+hpIivk0a+XdouXxugPf7Bd51e/1snbR67K/bt51PlGjdm5+3Uz/pq1sMreW8l0RIGqXMDWV3bhq0JSoacDeYC7ODMsFQTPlwdpWm5uMge9AXq8ONSt55o+g8Zj9Et2rLkO6HXeLpetkrmta7Ig3l5cbhInGWitpfP3d/HxecnNYb8taK2r52XvobXdotWLu3N1BKYVGEdzZJWhH5C/PGZ0Z2omge/cOZ0/OKUdmcnZBO6R3aGGwtsQ5ixIOicKNC8I7ATtKUhYlSlicdwihib2joxxKG4wD5yruPjigVDGRsgxOBuRpTmVAOInCUVlBEivanRZKa5wOSKKI4jLm/KTEVRlFmSLRBDog0pNtPlJLWpPT1xjrJxf1CUMSCMamxBUVsRAob5EqpKXBWodTgkQDwuAuU1CabQWZtxgH0jisF2gEp8bRthanNUYKIqlpRwGikpxaQ9s4Qm8nxoVwRApa0jBwDp+WBHg6MYQBxK0QURWMj09JXI7Wgu5WBx1pZOAZnV3Q0ZqWqEhCqEqDrzI0JZUrScKEuwddXChwXmNLR0WBKB3GV7S0Y3c7YjRMiZRnb6dDNjwlFJYyH1LmGVvtLTothSs8sXYMs5KkJfGZJTcVPoqJCTDZiM/+/Of8zj/+O2z3ttjb2mM4GrPd60IY4ktBNcxodSO62y2Gg4Lqos/oMmdwMiBQoJTGOo9VAb7IkEIQ4IklKOsYnvQxzlNejvj44/uMf/iYINCEYTivPH7jQVxPxNki0wyJ/kblbNO62EZyTCz8XXjVqCAXK9kgrADna9P7+sLWOnQxr03eKDQCmam1uUkfrW9c02W19a1h63LPHM/ME7ux0bxU3vr1s9kWr+bCpwjxmvdfh4bbZ3mjfE3hO/tyMQfb6/0zw2jz6cS0UxcaOD1HIRoys5h4Mazaye6b65pPUqNr+nuG1K/zbSIL5hu0lt5FAt6YSfzE9/Ok9KUrYK5Tz8HPTSrdiLDlttambWNPzCjdpO4FCbSB0G/80n7FCH5urGlIeFNYNprmZf88cXUIvImx11xlE9GLbNk8C6ZPi3XX58VaoTxN4RfqWzcONWPotcNK627a/762vW5Kk68psflxujayVjPk8vPKjplvfBSH/P1/+Pt8/sunSCl48PiAf/PP/hzRVhz87iPinx/y4tUJDsvf/d99n7/5D19w2c/oJJLQ57w8c0hgr2U4zRxCBVhrib/JcLpL5GBLpGQiYmQMkbD05AWnVQshFR2d8/yLzwnaO+w/2Obv/Y8f8PNfXGAqy3vvvM/l+YijozFaeD75eItffz3CVpbuVkgrijGBJRCeh3fgl79OycYVW62SLC8xZcjYWfbbKRemRxgEbLcFl0VGIUK8s9xPRly4fdLCsN9V6CTn5NLjleRxa8S33YBSOXCOA6UZSRAKfq8S/CKSaByxsbSM4VmY4Lzl+6Xgc6nxKkAnmm55yVMp0UJwV2UMVUiOYIDhzsgwFtu09nb48R/e42d//DUqdygp2I1LjgeTW863oxEjpzClxCG417F8fSGRStESFTruIbs7qO0Wj3Y83/R3GZ0Mid0JJQatFHhLi0v6PkJojfIF3mc4AJvxoGWJDvYQiaQ4OyUId8CCMgGtICczEleWoAsG4SWH1Zh/8e//Ne/c/4TsaIsqT+j07hFthZw+eYrLQx5+cMBXRzmHT08Ii5Qw1AidUGJpmQG57yKkppMk7PYihibCWcf77/Y4eqXIxjmBFvzJH/8HnqXP2DnY5re//wM+ev/DjefoOq80bzNcy0kPiMUTT/M6bOkujZrQacS4q8hfhfc3EZBN1azspu+4/xqKnzR7deNfd0xFk5BvtB9EbUFvvkObHHc2GglN+nyu0iuw5lcN2Ix7Z8kWeeeK2pu64xqe1iifOk4Qtf4UU+Nhfd8v2Dprw2JfNRlbv+nwxq5oh02uaOcw8k0ae/qztlJxTdwKwDtXpJg7Q7F2cWEFDp2uvM7V5ee3Kq0co1XGxcYLEE0NW4POGpFr7fzB1CPIijrmoWQd3E5B2aS0VcdVl6mfh6/zlNfy1SbInOF5nWp1HdP3U2G0ONaNda0qyzclWhAc9T1Sfnkg5/jmOuL25sH8Z9LXnYbTFZbptpx5fpqfE8tjKkTz9rPFMZptlxCrQbi/aSSZZ5TXCTcV7q85ZUWlN/T0BuLqWl8tZJpetLhu/v75f/wb/uYnX3D08pQ7B7tcfDHg9MsTPJ7eXo/te9sMhiV3Hu6Qji0nz05J+ynOlQjhqbxC+wrnNIGKqKxDYOnEIVXp6coSoxSFDLAeWoEEHdBPHVpaCOOJWhOKOFKEOiKvFEnkcULhnKM0sL0VopViMHTs3mkxPh/jBVg0+w86eA8vvzpHVTkqiom7MVkBra6kP8p4dZLRCjxCByg8w1LQCjJkbEk9JAryPYONCsaRZl8ohBacC0fgQQUhyjqO8MSlY+gUedImYrL6Hng4F4I7OBwl/bJAOsfWyNNNPWOh2TaO8DQkoINQgsgaVGVJy4CtrmA8yjFOErdbFDbDhoLLQvHwTkyM5vJVHycEgbJs73YwUYduR5COC6yHYT/FpAMEDiMSYlmB1lTWEUQxkRoj3SW5tbRwtA/ukexvc/7qgtMn3xBFASJoEWiQYYIMNcaAUH2q+BU2LPjgtz/BDu4gyy0Glxl3DrpoqTh+0ceOxqQGqryicJKOFlTWU3iNcAbvPFEYUHpJJ4Ig0ORGIHHEcgRFn/4wpdNRuL0c27EcPDrgo/c/4H/6H/5HgiBcPQeuWN3X5MiNYYPFn0lZtVlVE7az7NNV3RohdRr9pYvpaAABAABJREFUlVSsYdzrfOvorE/d1zAebgxvUuabysvG8budMN4A4zaHVdiokaRbWmur6pneP7E0lsvoZKI/l/XanE3CzTw+BxdWJmrS0DNqFrdOeedmXg1FPZ+fS704Nm/LuHgTV7Rv6cvFitm4sqPr8FbUQJFv2PO1YDLMlTkbGtGcupmEmkG7/EosFTDFTWI+4SKhrxUWWWtuAmxa9nQiiaZegKYJVS9/WqVgVZUbagVWy+XZl6c5u/7qbwPgqyUS9dRXgzEx+MQM0N1CcV3zW0OepUl5o0J4fbPg7QZRM5KhieDFvZz1ubc4Bksc02iUNWbYhNS3H2oypInHbiJl2eick+Qro2Yvmo6ML9fmrMdaiweMsbT2uoSnKXl/THoxohxnjDJDNRjSvnuH7t0d4l4bbIUzFZeXBaGOMbnHWEGcRERaMB6mVF7jRQhCUlqP82C9QVtwXiKlxLlJvMNhnSV1hqLSWGWxU7fUFk4uDcILDBHV5SV5WlJVBlSIHQ1p73YY9EfgSqLckg5TCispRgIbBkRxhHMlnW4bW5Yo69BBQFkVOCHxSiGFwAUa76HCEqNQV73nAKQkxBNKmEBiqLxHSYn1DgAnBFKqiUvdssJhsEKAkCAFSmuqtEJICdagnScINUJeLaHIyT0PpbHIQBO3J652XW5xCECitSRoxWSjglFeUZaG3DrywtCJQgSeUQluwnoTF8B5iQhKtHSTcVcKEQaTvs8NFhiNh4RtTRQmxO0EFYX0z4YYWxAkAsPEJa+1Hm/dxIWucVhjGBz3KdMUH0R4IScX4okJ5zsPgdYoKVFKYDOLR1EZR1WBVoLzi0tMdkHlwEno7ivyvMAai3N1F8o3zZ+FBGsR6GyerJsl15fHiGXA1qQL5uperLwuxjcFWmLF89swOv5LKIsVzb5WnavA/9uS0xv32206p4HR5qyJRj+eq0uquTNb2sq/gVW1CnndlGtdt8zxrLhKNQE+S/Nuibz/gl8spuGteIua27e3pmcXIcyk82ou4pgMbN3j05wwaax9RewK2bjEJ2L2Zgp9F+XJ4vMNw7oyeh3jbSyzGomfgsWJQL7Nmacp5p8/rLpIyZp+bi52RdziZL+lpF20jHyd/24xpVcpj6vfYkFIXadbrOINFcWMn96koJlhtbrfm2P83HNzuF3PbhAWGX3N9Fm5MMCql01nmepSx1+P6LWZVTfmF3I2ESiYYZ/FtP76ZVOZk/hPfvAux4fnbG13aXcSIhEjAs/g1QX6dIgJE4ysCK2jfPmCXCe0ei3e+XiPMnL0syHb29u8d/8xxy8GCCHodgK+/usnXJ6NCQOJVBXB1g5REuPSEUGnw3BYkPeHRNJyPrCYqiDCUFmJ0gFaegKVMwCkciRK47wid2O8h+3YMKKLcwY3OmWYX6IJiULJfnTJUR4jnERXFWXlCFQP6SyP5DmX3V06Xc3B3jblSPPVyxSRO95PC144BcbT1ZZWYiiTEA28nxu+CRUSOBCCfeP5tbYESvJ9PF97R1tIEme5J+AJkhLBfVcwDkN85HGFZSvJeNkL8M7zsZVYEs7yjMJVbHcr0nCfsqw4kDlD1SIIBK1AsivGjOXk/EsSZIzPSnKjyE3OVlRQGkU3lLS0JS0lvU6PTqC5uyX4/LAgqyo6CjpbWxyfF1RlyYfvb/PyuMJXk8sHx6bAOker1eJxT/FyOEaaMZHXyEwQ6ju0xC6f/Pgjfv6f+whKOi3N2eff4osxzhZEfsSYAKElUdiiowQXJkMhCKuCS6MxxjLOLHs7HVQQUWYFvhgQxYoQaEchbS0obImyincePp6cu6iz9yoAuphmHabZ5Msm80sDs4tOl8PcXLwW07OZfmt4telKRFPamxolFv7W89RFxuKB4Dld1BA2Ec617Ndfml7Dc85rw9UNM95Kz/imXpl+rfBL5wBXkbVsfizwja+nbeaqZTyxCdJbjL25k/wVIH47ZsMGFtMbhrfy5WJ+vojG+GlEo1/q68kl5nZf3FTZ5t0zE2orV1rEDKyuqG6WWKxmtJupWBfXQMAmJda69LYUrRbd82HVFp6l27hvVf/aCq9rm49ooFgs1LqxpdZU7XT2NmQWc3+uV8pmomRNhW+oH9aF7+Duq1nZK+JnRv+MB72fX2pYS9YGjLpSRPva34W5uGy7bNg59c8+NQUxZ4g00XODFTQFQFO67hzs8o//j/81g4sRnW7CH/9//wLV9my91+OiyBBjhxISGUm8F9g0ZVQVPCmOYSfHJpp7n7R45/d6/Pi/+QhrPTt32pT573NxMqa7HRHHAcNBMXm338Yax8V5SqsdEEeK01cDskFGohxH37xi0DeE0vL16RHPXp0zGoxx6RA7cngLgZRUWRtnKhwBVTX5SqalRHnD2IZEIUgDWivaBLiyJBSWw1Pw+gwftDBxGxXvsbPdwRc5w0yjRyMiqVE4+nc91jsSqTiRgpb3VAKc8FyEGi0FAYKXfnJTd6EVynj6ODQSqQLOOhGRVBR4ssDzVdtR+Emffj12dIaGcSRQynJpO6hIkxYZQrfYvrPD6VnJ+LRPVpRICVpLhIioyhxjw8kBe2mJg4rSOPIKkqCHDwSd/YTjswFVWaBQqKANxJhqQKRD+lmEUuC8wKoWXjmSuEvU6nB80ceUY8oipR1KzGWb3buPiMwuL55UBHGMDCrOnl9SFSVSWCSG3GY4N8RaRRYW9C8ynAhQgFWSdtJGK0FgLRfnJwgdEWlJ3NIYl+GFQAaW07MRu+/uoLzi4vRi5qFnhRExcSCwsIJal3G1r8uvG+oefhpdptZoq0/Dt34CZJ1ivcVC3k3vpnbE4l78ya8VRNzU0DW0L261aS5zhnluFW67bnhrJdagjBcFdBOYmwrja7U1u0pyCbnOg4yVZsF1/Y3xs3e36cJ6adMFsNvMpbU2/mvQ8zrh7R/ovho4sRjXlO4tVHWblPWxme/gBmaqeZWaMaOoJRWLL28RbrKgllNOf60Xm1Pi/PWFguvTLorjeYFWr3f+e87yxJkH1zOot0zBLGY2LcUMITdZpHMk13rgurkr2rowNLfbh7jaEqgfGqzz0e3B9HdoFdSq/W5qmZQ8E8q1f99CpRtlX5iL9Vm1yKHLHHuVdmoULW2vmHL0lWpfCS78YpY5SqbxM/HhieOQ+N4uZycXDAcpp6d9EBAd7JOdVpSXOf2iwlYVpZ3YziJwky0/ztAfXnJ8esonH35wXVuUBNx7vH1N1vb+TLRLrbn7oHf9+957+9c03vv+OwA463j+T/4tbjAgCFt0kgOqkeH8sI80jnHepvKTMwFehggbIuM2TsHAlng/ud07t2DxlE5TyMkN2toKbGH4+ptzVBRjgpgwbEEA3gnycQmdiKEsGeNIhUQJT6wkYyUonedUCPrOoxQMnUMKQWYcXkpwllyCl4IwjhhWhiJQYCXOOzJx1YcjhfdQSom3IHJPOcjxTqG6EarU5M5R5DktAqwTFKWgAiofYWRI1EoQUY7NxlS+xBOiCChzT39k6A8cmQmQUpK7kHRoyI0iihKeP+njraFwiooA3drGiIj+2FCmGVWZYT1klSfpdCi94vx4RAFUleTwySlRNabbgrwweBROaHQgUFrR2d+m093GWEEQamQQEcUxWW7QWC6OzhgOc/KqQmuDEA7jPKdpQe9+TOEM48Nj7t69Q54XJK1kmd+v5sHkdnSW5/oC4L9xxWsNGFxaeKvrp4XzAqurqaVrXqeaD6tkVxOdNwmperra8yrtLxpiJ1nfACyJxZ9NwHmhwqYCVvXVYt5bG2E3dGJ9Zade55K9M8V4S6CNhmRz26PFEtPOlbgUX08gmLkgn+KK5aSrx28lJqnpo9vb55vjy+8yvHXjYsmouMmanAY/92fhYaIdrkHEwkVki2BzMzqnxK3K9F0OzLyNPA/Mm1LODidde8JpDDWIPTXQbzmp56+muxklzm6RXEkJDfBzoc5lk2MGXZcTz43atU1yBQDXrICs6rbJdstVnrQ2C5tj6TmTaqHdb98MeN0Sb6JmaWx8zZT030VL1hIDK+qeP4Y0M3nnVquu363QoAtCTVA7Gzb1Znede16wi9njXDxAr9chSkL2D3YmXwJIiB51OD8ZsbUdc3nUp8gKUJL2gaR1zzI2OXu7O2xv9+b0nl+4KGyu3lr89dbihfZKJdna6rJ/sEOe5bRbbfReSJTEKGPJei2ka09cno6HZEVFZYcEYUhvpwXecnTY5+Bej879fU4Oh2hhSfspwkNaVsQYqqLEFSUyEHQOQsKtDirMsKNLelKgPLTcxM1t5DzOeXoCcsA6izaGOAhJtKQvBVvG4hREgDUW4SxBWSGkoOehch59JRd0IGhpgXeOLe+gcpRhifPQjiJiUYBJaUWWsPJsPdhlcDFG2AodeGQ7oh1YynGKr3Kkd0RaEQuH0J6ttsKOBM6USKnx1mOKglBq2hGMz05RAoTzxMJjfYUrh9jM4KqCVqgoS0sUCB5/+phKKjq9mKwMefI33xIi6CYBshjhKWkFAWEYs/V4BxOG7N/bRlrN8LIgaQWAwpYWHTt8kfLwg3vkucEUOUV6SWmG+EDx4J27qJ7l/PyMrb3exN1wFC7xzuK0WAvWb3O+YUNhMZnmi4mvwJmfzWdRr38qFurTYxXdi/PlJsNoGjYxSOaIqxW8qu1XZS7Lj3VhgeAm+t+mYL6pzQ1xvv50Ey2LKzMbEDRTBX6p75ZQV9O4XX0im+OhOYK+K1y4WdmbmQ03vZ2hyjfBPDeFNzcumhhnwdibkzkLCwmLzWqEngtcsmzJ3yChVvbdwgQXy6+aks6bJW82W9dA4TnC6uQsw5fVEmoKpBZT3bQasgzuF5Zf5sprQDELZUHNKGy6EGdB8i+3qN4XDZyzkZJaQd8Ne/FWfbKdj91US/qFp2m+9ZywXN+sJ75ro6RxHgMLnwKv/3xX4nd1mO/JuTdzzD9RHIvD2ZTv2lhlEWvUBd5shlx/umaeg/2VoBN1/r4qOIwD/sF/+/v87c+/Rgj4rR+8x8tvB5weDrhzt8f9xzt89vPneOv53o8ecjY44fjsjN3tbX7r44/n6RINXNAwENcrdlOZOkVlHv7of/M7tLsJRVHy4YePqQrHt0+OCIXg4cEeT77JsSjuP4j4i7/4Kz775RPKccZWGdDP22hZ4ocDKjHCjiVBEvCDTyK+OQoQBXRlSjYc0jcB1go66THPy4TcTgyKPSH4Csg9/FgqfikcyntaxvNRmfOTJEA4x/eV4AsvcQ6UgIcOfolDKMl7o4KvcRQeUJr7Zc5nVwe4H8uUs92QsdJ4BL9tC37pJF5I7lUnnPUDqo6klJaP2gkvR47CWvbiAnGww9mwZHh5yQOV48IdyrTAlENEZwuPpsw923LIQMQIGdJRGUWoGBSay2HOVpjSLzt4J4gkRNpxaSuqsuJ+V3Oag9ABn/z4fbYf3+fJV2cUpebDewlf/FlKEIQoYRGtC4hy4q0ef/8f/gO++GpMNi7odfaI45ij599y/qJPVPS5yBRbDw84+vVTksBT6oT2Toff+oP3OC5fYIXn7sNtfvD+J/zJv/pPfPL73+PjDz5ASDkBH6tu1VohcjYBLMvzbdH3TXOmKcvW1xIWybmW5NN9VGI2N5cMDt9AZbPtMiN8sSFNzyvWKGaPTYh3ARj5Wvx0gt8YGnRiU5ImQLA21KT6KjJupYI2MCxWU7AiQU0BLZJ0lXleZwkaFyLX9rNYSLL4+/ZhKo8X2ze7e6PRMnsjJTvdRvxd6+k3dkU7Gg3ZiKnfUsc0hjVl3ziHbqKrcbvO22zAauh4uxm4ANg3OdE0l3vWpkX4exNNy3J1OZ2okbYarb5+mOiPNfv934DL54yipely23G6OYiGX/9r8Um1GK6BRB3A87Z7ZCEs2WI1jl1hJ17zRW0MF/V64604C1/mxAIP1MVnE+hpxBGLSsnXam8q5Cbt5Tfp9WY+vSZ/+fbApfxTMp58+4I//fOf8OTpMyKpSV8IygtHmpZI68FHlE6jhaMyIaaCzGiSyCKEIreaOBSYlkHGnoGBTmQwdyyXgbv26BRLyVALdkvPUCmOlEB78MaihGIYag6EpHKOgfVgLVWaEjjPuBWzax1Wa7IrumNj0M4wigL2HAQ4tJgYkUlf0BprzgvYEo6w7OIyQZGVdHcV0Zbi+atLOtrRcpogjCnSElPm7Gx1yV1EIErGwwIhJA5FrB2VrcgqTSSqiU0pwKHpdS27DwK+/tU3RFqhdUwQBST729x95wBTefr9nCSSCCl5+dlTKi8Jw5RSHaK7gvvvPyQQDwndNpcXGTu7LfqHlzz/5gxnKwSOVqhpPzggPz2htCVpVhJFAWr3klKe0n2wzSeffswf/M7v8cG9d4m7yeQsRQ2Yz30pXxSwq4yO28jzlXlmvFi/52p218X09UqpXwPTDWBqftVgBV0LxN3UrlVT8MYp/N2uIq+u96rGJRk4pWYDw6KpQN/UqVdSalPlUO//G2VgvexFWSZmxsUSNU1sd0Ndc5cvvw7Dz1MxK6G5jE23czfe8dKYZYHmNePxX94V7SbGxJsKmxVgYm3BiwbyKkt+bVifYFEgLDvBvGEmrTQGbgvPVi+5LMGFOla+ervZTZDNhsUm08s3JXiLcnRuVaIRoNUJWaDrBlJuvp170gtT/femB6znxfKNazZvo5K3Ux4wE7ffoXnRhBKmY762TQs3fWyoNxeNgnVG9sLupNXl1RIty6g1gkpw7VBm3g3zHNqazycWyljcz+unRledmuUJc4XRsNZgncXjUXFAay+h20uIRzndbpuqkBy/GlKOxuSpBTTIyR0aTnis8+SlwwYOHXhA4bWksBWlnrRHS0ElJ+5Yq1DhKodQCqEVxjqstZQVDJ3HWEeuJMJahJCIcHL5XeU9znsqJnPYKTFxgwsYJcB6SgERkkBKrBcIKbBCUBUGmwNKE7ZjxsMBzjssUFqPqBxBO8E7A0JjraMsS5TSlKUjjAO6ewmmrNCVoNPVE4CrBJWB3pZldPKcoqrQUuKdY/fuLj4IKPMK5wTp+ZDz/oD9d+/itUZKhXUOBES9BJEEmKFFGIOtLMdPjzl72cc4RRSGSOFBQjbK0K0IlTtk6dBxQOksVnpMVVFkxeRixl5rNupzU2kG0BbZcYldVmEBsdpsXT1haqn9lPGvMtT3QdXTXM+HBoG/qp618bcQknWALlaDxeaqNky7shPX0LSm6EVfKMu0NAiqm2jwfmW1r3tue6J7pzp2WY5Nfvo5HT3dkTD9AjeLn/5dKOc2nyCmY72BvF8f1o/8rS42bi6gXtVV3HeOLoC3YFx4Jh6emqyqRntALL+93faOWcobDyfVcjSra7FQYkNhYj1dS59cF+jcPCynn+eL2vamqVeepsnQELWKkgnpbwoCbyux/VIqX38lGuJvEW4LbG81sZaImpqWsz38tyF6pe28EN7oq0UNiM7pyrckUZZmjag7B7gajZXuWZfDjQZqPeGi4PTLfTpXXk2TLhq7q/u4XsqydVknw9eTiOU019wi5kpcuQwxNVmXPpiJWh01D13+OhfMzhAtt2byvlZoDavNpRTTcZwPjx8+oJP8mm60TRIEfPDjD/jyb0YgW9x71MVZhfMBcXKXO7sBf/XvnzIepiTS4iR4GyHxbLkxWdkB5+hi2d/RHI4g0JIPOyHPhAdn6JSWew6kMshAsOU9T73HWUOUV+w6xyulUFLwoDL0gwghJ1uttl3Fc63wznG3LBlIgfYCLeA9qXjlHNo73osFo77DoYiE406ScVxIkJJ4nGFdxbaWtDRs65LzQtDb38JUF3Q6isGrIYFydNSYItpCBxD4IUiQXlGOUraikotMYpzHn4+AjEi0CHXM975/QNW7Q5k79u/EnH51xOB0iFaCg7ZjFHlUoin7ksBKdnsPaOsuH/zoPb74ZYbIDNmzM5St6ETb5EVGKywZpYpIaHbuJPQvT7EmoxhptlWI2Nml1e3iUsv7j9+dh5Si7sRjaoHW+Os2YYrh6mXdLisLM2hGTpPQrcfVsdkmSKpuz3AlyzZtcqPu8nOerjbxZLXWE+UbqYJauUv9Nu3bFfXOC7Ebg6jzTJ19ppXXjYAlOmsysdZ3YjHRVYLZ4zw2nP94MiOksXc3bVeNmDl5+xbDdKH3+tJg38yHizbRTdsK34R3Xie8hS8XtUGb49UGi3cu1MBH06tVcYtuW64RU6MJPgMcYi7DvCBlgfFXhgUNPNfGmhRbNWvmS1qgqzmbqD3N48I3YOqVWcXc09zoNFnADT+XR2Ih/5pZfe17aZUe26Bf632zFpRvjndvKKApfrNC6+py+d0mZWxQ16JgvoWC2CTMfQtYZGimAHZzWLH0fu5cjphPMKdM6klnjZyjzS83fT0b1M5nLBoLi8p5TpPNGHgm+OdQy7UCnOJ333CgfFKEnytnifZpFwux4CK/eZAneRr47Vp3rXDeWys3zwp8plFVQBAlnLx0yKBHdnzB1z89philDPol29sxgxeOxx/tcvpyiB1cYEREXk2MBmFigtIhhEaVkL9SKKWIhOfcG/Telb96BaWa3A0hraMMFUHmUEKgpKcKQiIlEd5TdDWtKCT3HiUhkwrhHRJPqjWTDxYeZz2jSCE9KCk4N4q2E8ROEgtHXlmUsBjjKStBNwwwmUEYw8BPDpfLIEC0OpRFhQ4U3U5IlTniWHFxMSCIEtJRTuECvDBcmgJr3MQVrfAUeYDzIfsPHqL27mMtlOmYpz89YowhraDXafHNl8fE3YA8z8A7RNlFmy5h1eHwlUUkCZeDUy5zS4cIHEgvGBcapTQQYEtPZycklAGdXovunZCCMWmeodsh41FGt9OtDfWiZGqYvU2W8VrZskICbKgvN6ujqdrVWGTmmGGexEW5cds6p+X56+rrs6sBNzRp+teQ07PSruppKuOattoYr9K1S7/9MgZbCgt4sAHgTba2NeC/af/XiWoCS4sZYNl1cp03r7b54cXyeM5tc2riULGyK99WWNoWN6VRXLWrofZbH8NpGOPvsk1vzVvU8gJ4bdI0fXtbSru6mX4hzbSrGyDEJpQu2QiLmEAsjG+jg4orZpvys3ev64d4np3neGGVMF1XzUKeG+Xi3HaszUys9aF27qGJ/rm4uU0qN8usaTp/JYBXpt/AqGj6vSpbrROne/Dni7lSBzWN1Dx0i/07UyLC396cmP/etwa6v/5gzpfR0N8zzvFzCrWJotciY+EQ5uK71UfGmlCEx4v57yoTXppPO6N7+kVgppDEcqIZnYsGx1KptXSNvDtvwSwlEQ2PV3NhuhVjbWiieRpV2wezOI7zdXqODs8ZDVIGF2OKrKLIQ8qh5vDJCQEVQkCeOvI8I9CeohxBGKF27jA4HZOWjkCFjE2AswZjwSWaqpSYdkyaFZy5EkpLESq88ngFY++QUiBUxLiCMR4fBjgkqZI478kB5Rwj7zGhxlnP2E+Ms9xY4igkN4ah83jpMN4TCIkcO0oCUicovURaTWU9ZWXY3btDkeUEXQFlSZpZKie4vKwIVYt0MLkdvVQhI2MQmcXpGK876DhEO0UUCUw2RIUWPEjnEVR0dnuMU/jlT56z/WCPi2d9ymwMkSJItqgKz0XpCMsxQilcbuhstRiPSowdkZ4qrIg4OU1xPiBSMXiNVwlCT25Bzyt4+eoMoQegLWmRM7TgREGeZVA5Pv/rX3Hv7sECILv6swjuVk3qeeHUENYYFrU6V+eoEXWrcLVa3UCTWHpgNvdWHWZfKhnm98eI2lxao3A2gkW3s6hEw9MsptYeP1P9U+PHezepUwqWZQXX247eCJA22KdzNF4rFNHspKJGz0wmzy8CLS2PiFq6OhZd4LfFnen183ZNbV7C6tPL+16rh2ZeB8WcsXMzwr3+0rEEXG+s8u1ggxXhrXiL8mLdxz6//LhG8MzDr4XWL1m6y4r6RjB9Q1g29OptWxY21/ZmU6WbyIW6Uoe5G0mv2+lZ6t+6EbQu3JxkQ+5awYirIHEjMFpZVcOLlbNZ3GyrXvubnlmRTUBpLRZcQ8viJarLLN50OG8ZwK541UznyqRifdc2kXE7fXVD2mlnTGeLX5/8dUN9Cs4pgBolzmGNQwcaBJjSIrVECjHZ7+8m7zxgqsnty1JKnHMYYwnCAICqskgpkOpqf74xBIGuVTgxpJyfvfMejLFIMXHr6q/fKYQQGGMRgslKsvdUlUFfgT9jLQBKqVm7mib4wn0uNf26pt8WmZcFZpkahbWyGzHVTM5tbXdptWPavYRut0WZJwyrCkVJICy9XpvzKkVhJm5gL4fIVovdgzY7D9/h8EWf/HyALTJagaLQiq3tmJNyQCIDVEuRW49yIJ1gVykKLBJPYgUiDtiJFa+cIcxKSueIpcA4R6gVSaCwhWFHClwrRI4yAq2Q3hMYQ+E9d7stRJVTGYuSEETQDiVOCGI8uhuR+oL7H93j4N4WoXQ8//IUGSikgjSr2NqJMRcFXlSE2z22ewGiLPBKoESAdBXdjobUQlniqsn2KiEVEoEwKb6MQFRECEJfUmUjQmEQ3uEAjSWMFJIKaye07t/bQW21aXUiYh9zcZLhq5xIeeIQKueQWIQEWxnK0qFsThQ4qspQDFKqouL9Hz3i9PgcYaBMK4w1SClQUi2M+rwcXZSd1k34VyuNx2OMRV/xva3xtvdX75SanG0xFu89WuvJO2vQWnPTwtFtMNG8d7Sbw9yh2AaAPUslZulYg4FWTVLP0lxeQVBD/c1pbsZhC/eX18bUWUtZTtwyR1EwxwPA3AJrY3NudYfU6rBYdnNps1RLX5Drq/y1wqaYX1wZgTNDgJpBcG1p3VD/ivA2ra7bFD1t8rwqnhW7CJO/Q4OiHt7cuJijeF4r1S8ZawwNIEcsPDWunglYtcx94/jexhSdRq6d1H55QEX9/bwgnvDuAhFT2b24J3yuqnnQtgxe17VhsdDlsVqZ9uaZ3hBWrKRey+tV0LsmzdcphBp/zfI28ZmYb+bVQNTUx/JKxqbhBoU1rxPq47q6UbPWz1HYpJeuyxJLsd9xaGj3bM1lLnKWvha1YpTmir6xJXOJJrkPn53yV//xM4q84tF7B3jnefn0hCgO+fiHD/ny199Q5iX337kL1vLtV88Jw5BPfvtDvvrlE7I05/7jA6Jkl6dfnRIEik9/9x5Pnz4nG+cc3N/l7/y9354YLsBlf8if/LufMRql3LmzzfbWDk++OEQpycc/eMizZ68YDTP27myx0+vy9a9fIqXkw+8/4vDFCYPLlO3dHnfubvHVr1+AgB/86AM++t7jhV6pt/sKWC0YzJN+a5K19TuAamBijufFtdypH3pch2ru3N0m2gPbH1FEht///Q/5j//850j9ik6g2OltYfw2zpRsc8ZZ0aa4LFDZiN1HhiSI2f/0MZ+8r/mLf/c1VVaxu9NiV7R4cpTS6SR8kDqOi4QWip3Ik7QUn5UOLxU/9oKf7Fe0peGD/QPE0Tk/Kwe0tebjU8HL5A6iqnBVxQ/2e/ypMRTG8IdbCb88H+MDTdCK+MQLfnpRoEPBQcfDQGCEAi348G6Ln38b4qIWncjSf5aT96FKc95/qPk8VeRphe8f4UqJcSEuVjxoV3xxAo6Kuz1LfukZZRIlKu50U86MAjzF+IyxFbS79ynKggdBxvFRiECxnXjaD7b45nkKHt7d13x5Mqaylvcf7HPv00/5+tkYk2p+7w8e8M/+73+Jd4J2pJHlkCKPkBJ21ZAzn4CUOANt1SMnIPMWf3pC3t8jDu6ws99Gb8X883/1r1BK8rs/+CHvPHpU0wHz41/njF9/9oTPfvEVQgg+/uQdjl6c078Ysb3T5e6jbT7/7Gvw8OH33uPk+JLz00t6Wx0evnPA5796gnOODz95zMCecnZxRqfd4Y9+9HfotrtLrLepUdEIDzfVXXW9V9eX9WX0OiRYMBJuU8cGy0JsRPiCPlyqS9QSrfvSKyR4x/WCp5+aURMZMS8fGsi4VrLL7r5nifz1nxU2V61N643M6d/ZsCzgirm8i9i0VtIVLpiiidf9+vCmzl1fN3fdUGwcID/rzo389ryl8PbuuVhGity8xHxzqO/pbjSK61bnCro8TPxeX8OgupnXEBbyzlsJs7rqNy7Ml3YtPep/Foj2C4+Lv1eE60m/quz1weOvt4K86SrDpP5VAqcBXTZQ6+caM139WC6rUebXSmkOq71WzNM0P15ri1xVxFWeeXNgxj0zsXebkZs3mxbbfn2Z2ya0LnbEIqK/bajlm1JZJ+PazfyCvXgTaY1ppvNjFb96+Omffc6TLw4ZDVJOD/sIBOcnQ3rbLb7+8huCCIaXY45fnWGLgvPjCzq9Nl999oQoDumfDjg7HuH8CZfnBa12xNOnz2j14OJ8SJbmHNzb4+PvTW60/tlPPufpNy85Pbng/M4evnzB6DInCDXffvuSuK04O7nk4nSbcmRJhwVKS549PSJuBZweX7J/d5vPfv4NeVZeeWFyPHrngKQVXfVh8xyd7S2e8a1flE1LXz1qvHTV4aIGjFYb6PPxHsGLV6/IqiFWF4gw4C//8qfEXUXUrgjaW2Q6IB2NuXN/i+EowGQDnNTkSvH06SWlHZOegivv8PCH7/Ltrw45Pbzgzgf36MR9fFZwLlq0dYAoBFXLc1oYtA4IlOR/UQVh5CBwHL14QvSgR7fQaK35LC1pVSVeS6yX/DwrkFrjvOdzpXGBwgrBZX/Ir9oKoQTOGJ5cCPatpzQO6xw/+3xEUQnGw2MuPzckhWWQSTqJ5ptXILUiT0vKIkabCqnAGcuzYYj1JR7JxcijrEUiaLcTjtOUIPboMGSQxRgtcFLiK8MXl5KtbYdHUSUJcncPdVxis5Kv+2OCwIMWhO884KjvKKqAIAr543/5FdkwQwhNYcFWIQJJGCiOUo+nwqsYEcScDEEFEaUpCYIHlMOAy35Ben7MYf9z9Jan1UlwHh7cu4fWwUqxgYfxOOUXP/ucp9+8AgEvnhwThRGnx332D7b45S8+o8hznPc8f3ZMGCUcH12wf7DDr375DWVVYozj6OIV0a7n9PKEOzv79Npd/u6P/k6zfd0oYZcmyPLPDeX5/IHnhfKaUetauTQr7vVdzV4vh72Oa6IlUmsRtTZKpQg8gESrCSycrDvU6hTLcKVebvNX6zUKpmErab2PVh9sF8wbFfP0zadbUf06B0RTY6O+7bbJlfFbDCvd0E7xkbid8bKq735ThgW8DW9R11aumDMmBCzdGjuf8TaV1J7FwouFemdv5hHNvAr1Mwa60rKrQc36yKmxPs+rmwyhmHu87Un/m2pYJU+n7b2x/3+TXLhQn198WPFF52YWWujVa400A2WzLSGblbhI61L8EvGzX2KB+qkgbdrq0kRN42/PSm8StYqXaZzGL+a5ydgQC383ClctnboGbOjmtT0/lS9rQllU5FlJVVnK0iI8ZMOM8fmAqhoSRBB2EswgRWpJVVZkWU6VVeTDjNHlmCBo4RH0jzOKdkhrD1CTLVRVZajK6rp/qrKiKCbgqMxLhA2pSoOzDi8lKIu1ljwrcWZCn6gEQkGee6y1ExegzlPm5cRAcJPtUglRc4/4Gh/Vv0Ss4Lnmfpx/vP7icaPXuJnaL02JsRZjDUVZYMsA6QS9B/ts79zH5T14UTDoZ7R2OiAFl5c5IlIIJJQC4z2nz04Q6g5eCLxUoCRhOyHtG5wH5QRWSgZFztgZjFaY0iCERXmL8w4XKoq8xGmBER4dReRji3OeygnsqCBjspI6HGR443EaSgdZXmIQFJVh24VYJM5Pvl5UzmGsQAqB8AKHwnpQYURapngvCCpPFEYY66iMI0srrAehA6RQOOvAggoCsjRHBpowUnipiOMWaVUxHqQI69A6IMsMCEXca5MNcpwDpCIvStodTRhqrJeYylJVjnRc0j8d4KRCSA3WoYWmtA4dhLSUQgSS3ApsVqEUFJVFqklZL785Ii8hjFN0cYrcstx75x7OWqxz6KlUrJ09qIP6sjQ47ymKiXGshQZXYo0jzyY8kucFADqMsL7AmkmctWYyN7zHWKCcbPsqyoKyKufZuS5zrvDGWnatuxh6nXCbrOvwvpgHh82idb0Avg1MunWYgyACrWdwcG7Rz9eMEr9O/TW8WWp0jZeWXBjOskDDAskS8VM5uNBnNdwwt6p/S5aon+er6+WmEbtt8ZtuI5vX6zW+vlHUN4/FHK23MLpfJ7y1A92LbZmMt1+wfJe3T1z7WZ8rozYb51bNaOgMPwc8ZjikLgZnb2exU4ac0jT7Xc+6ZAmvGpBVoGylYbQmLIJUz/UkmnOes6bARp65bt46ibimsFsYULMuXBQcy+Ox2UHu1wgrxqTxkpnFTaUsCJdNldWaCdsc3Ww4rUzW1J51tDUYA2tdHb7mWIjFpzmf9NN6p++bhfZNFRhjefLlM4qi5J33H2Jyx4tvTmh3Yz765CGH354Tas29+9ucPTkmP7xAacEP/84HDMYZ6SDD2Zz0fITUIa1uglNw9vwSKotu5fTuH3D+qxcUA0lQas6+uKS73SVrDdne6fLLv35CECje+/AhX3/7DS7S7O206QS7fPHXzxidDOiKhPEIvE0It0P2393mpbwA5/CXfYbHnsoqkntttu+0ePm0j1SC/bs7XF6UfPNZn/17bfbutnjy1REA7310j8txn5OzE3a2d7h/cH/5C8bSWNQjZsbBZL75eRe3c2Utys7pYdhJ/OP7D/ly9xukkgQ6YOvdXb757CVSCu4+aCHMLv2TAUV/xKN7Xc4vOggHW3dCBsdneB8QBJIOKVqBy0vagaXb8hRZRbCt0FVB5QJUYQhdxd17Wzx7lRMFioNUczIASs2OhySv+LY1ua37ExtwGEliWRFeGvSw4ttQogPFI6V5UVZIrdiONHed40hA5SzvJg7GDus8sZRs64yTIkAISScuKAo/2YsuKvY6JZXsEWuBFRkq9pTGkI0y7u5GjIMu1nvismTQL0lLCITl48fbnI4MRW4IbEpbCMoiJQoD9lqGUSGxAvz4km63Q+BTVAiR01iv2T64y737HSxbZKMzBi8O2ZMZg1BhjUf7gliCUZIggG1tGBhHmWdIaWmHIWlV4IDIQxBLthJBR2qi3V3OzICtqMO7jx4RBcE1SM+ynCffvEBKyXvvP+TspM/5aZ/9g13293c5fpmDgPc/2OXkKCMrYtrdmDt37/L061eA58HjO7x6eUYQQrsTce/BY55+fY41jnfubZFyjh1pWrLNu/fe4de/fIKpLO999ICsyHj16pitXpfHjx+s1Xuz0CAwl1Dha6LOpqquZZyfxdWKfq1171q5r03hTYtF18n8YsT63zdWuvx7tqZXc8fdANNW9dXEtpwBbNFgWFwnvCrTzy14L8u1TUMdL25iIr6tsPQ1aKPxXH3j/SK0/C7DWzEumr60XemvySGjGietswBpiL95Pa2pA2ufzFYAr/oh7ZnaXaj9NQhsMmneLNQNgXUfujas8VazYB0nrz49cPPbRYJW0H5jEfNtb5w4TU1YKndN/a8xkOIKwS0K7Flxa+heWegmCTYj9m1sh1sM9fFetWf12m/3XL6VBS4V8Vd/+td89fm3FHnJL37yJWQho35G0okIAkUgFUXleP6zJ5hBxla3zdZeh/7XF5wfnpOmJYHwCCeI9ttUJxWDl0O8dVSZ4TLvI3NFVBW4wmIKT1BZTDbm22cX/NNSEW11iFsR0V5FuFehVA69lPFpF1dJqpHhKM0oCSmAwbMzjjrHdB7uErdjhiNF9mLEWIacRRmvfn3KqD8mbIX0nw75q+gJrZ09tvcSgjijKHM88Dd/8yvYHjIcD+m2u/z4d36fDx6/P1mDqVvn9T5rdI/jr3jzeqUB/NX3i0VLv/HuHkEURvy3f+8fcHJ2QiuK+ebzl3wrD/HeT77eiBKvPSKGo6MhUbRDECeESURpLyidRzgQ7R3ssEKLALzj8uSIfJRz8O5dhs9KBicXpCXEgWV3fJdu6UnPxhQiQFw6lFLoUmA/qgi0R1WOMnJ0xBjTCdhOBNWRYtdJRtaQCmglAUaCrwwDX4H0RGFAWSlif3WYuagockEvTvAOsBYdW6zRWG+wuaRzp00xLsEqkBNz3XvPZVoSHUjSQU5VVhgkQgf0em2GuSLPPef9AlVqJKAQxFKSFZZACYz1FKOC06/PEFagFbTa2/gkJGnv4UyLwpacPT9ClAWVcJAaTO6BChOHhFFEnAQ4P0ZVl0gKwlhSVEMEinakiWKFqypy67GhZDtLyPOAH3/6O/zot3/7evoZY/n3f/yXHB2eIaXkr3/6a7AwHIzp9Nr4aht8D4Hg7CxmMHAcPh9w8TLn4rlFJ4Iwjjj+9pxvv/yStCgoB0Na8V202EYIy/lzT54a8kLQKgP+7N9+RpEXGGP5+V//CpE4hqMxnU6LH6UZ3/veR6ukxkymTIHs64i6RaG0WgUuPQvBhGeu8i17i2oqYG7Szt7M7ci4RUP8wo/bbqdqEsoNMON6kWphI7+fS0HDIi3MLtq7pfV0491es5OYy13/5sZkE4JtKu2mLxMb62APZV4SxuEt9PaKHRvTn4vd8B0ZGW9sXEzcB0+VFcxmGTWi55HCEvZY4v0ZwwlfPy56i86dWjd1mm7KvyKZv7KO13+lu2bpJTqWN13N+uP6tt1FcNhU18r6V3HH/JmDuu19Rd3qohpnzPy7DRdFFsJNDXt9Tl+d8yZKBXNbxabs95rXb9ZXaJqpW6bnNe2YtxMWGQPebClmkU8aVtdvDAvixFnLi2+PeP70FWVp6CU5Io8Ynqe0OjGVMQgB2SjHDkbEOuDixRnpyQBXVSitEU7hraWyDt/PGZVDyrQE7zHGUQjLs89e4OzkhujcOxyO8mRE506Pb37xDBtqtve3aX9QoLZzxsUITgLckWKUVhRCMc6u5rZWoDzHpwP6ecXuo3180CZTFuc1Z4djgtCR5540zZHSEbU052dnPP8sJe6ViBhkqOk+dogiZZgNyPOMF4cvef/R+wtLWlxhiam0rA3E9fhO1eOyYTv33Dj+M7kcBgEP790HD3/y7f/C+ekleVbgfIIXA0aZxWaO4VnB7r6hrARy6HFBd3JWwVpGw5xO4hBBC5KArBxReRiMMlyyhVAjBI40K/n2SZ+gs02W5rwYGwhhVFWUbYv3hjSSEEDuPcLC0OUQx1R7MaNLQ155Tpj0TQq4smQYONACjeAkV7QMpKWflFEGxARko4x2qFEqxHpFVjmsjRCZYDxyKDRRKKmMx4uQswLiy5I0M4SEOAKciBjmnpNRQV6WOBcQ6y55nqFEgHEhlfV0Wx2qYcEgz3GuIuq2SNOcvICdVpvBoMSQMrwsMZVAEDDILa4wGCuJWz3CdozVIYUTRL0uvYMIc9wn1Irh+ZDCGcrCoRy4qsIKgbESU5T8+I9+wO/+0e8ixGzB7fz8ksv+kOffHiKEIIkTlFAMh2O6wwpTeUaDiVeqr395xHCQY5yiGznGp2c4CpJOwt2PdugebFOd9UnHOS+enlCWMVVRcfnqKa22xWnB2bfn7D7eoyhKnPNs3UmQiWM4GtHtdnj+4pDvfbrCuGhGeTNmXhJBmwO8zfXxVGfUt6o2FXCzPpjM4IYvCjeRPad2NtdhHlYfk10ko3aJxbX6mHb14oLr9aLF/B6R+YJvJrKRtBVnyxbl3NsJr4d43jSEcbhMxtqwIPdvSjYX8fba9xa8RQnmDYcad21M500m1Lx1u2Kr3kK4YQQ2td78ChC+YX3NsQtT68ZZ/boDPk/59Hlz19kLqwobCecpaPFXv2ZmYcMRrNk738wz60RyM73zBuWsa9dPuGVXv36+uFsEUX9Y+GzbpEJ87d+14S3N/SVjefHvretdYfq/rlxvyCekpNtrs73TI0tzOq0WMo6osopWOyAdVOhII0VM78EOZCX9ZyeEOCyAt/jSIJVA4nBpjqkqBBAEkiAICSNNpAVpWoLyKAShVBR5jq8qsBZRQf/FMaIb8OD+Ft57tjtdilEC+yF37m8zPM04fnKGs452V1EJT6Qk7VijWzHF4SX9QUYLQZGVmKpCKcXDjx4hfcBXv3hJog2uzPHSouOQ7p0e2496WGfodXt0252Fvlr+6F8fm6Uov8inV48b8tdsS5Wn02uztdNBKUmvF2N9jLQVUSAY2YyQgmCrQ7erGZ4WeJOjNGx3E2xVkqcGkWckGOJYk2iF2o7Z6W7x6skZab9ECkt3K0DZiL4ZgnFoL9mWmlRa5NAQKEm800aNCqrK0DOW1Enu9lrkF8PJfRrOU/mKpHIE0qMMhFLSDj1bocAZT+AdaEUoKypRoaQgDgVFXhDJkqTVohU5MpsTxp79vYSXLwckgcdiCTBEyuNNSRIqxlmJcQYhHUnoKUsDpiDyJUp3iQNPux0RtyTp2IAp2e1G5M4ipEcpz/79bQrracWK08/PKMcFQQCBlATKUxkz6ctBiW51yE3B8PycrV3F3sN99u9uk49Lhpdj5BT8OsNwlHJwd5ff+68+5d7jO0glr2ezs452OyEIA3pbncmXIqWJwwhrLVs7LfI0wlWG46NTyrRgpxWTF5JeLJFVQFVWpJdjymHCo996SLSV0I5ihO9iSs3FYYEWkkQ4Kq0YnV+i3C47uz2qytBqR8RdhXWWrV6HXrezLCuuzkw2LQZNWNRfif25PQ2bqb/Xkf91cDJdob8JZzS8XlyaWk3vwhLiay6K3aats12UAlE7szp/Fqbm8kZQ+4rz3S2jzS+U3FxP3Q3t5mtgN3Xu9DD4JmXdUFPtUPniduZ5v5fTuHk6Nsevbz/INy+ifhj26n+//HP9oN0MGRd/zx04qlc/l0osP1+nW1Hn4oy+flzBqvO21UK+JaLmo6cyYQPgtu7t+hQraHidAsU8+GgaF3H133z9Tek2o2mBlRZKaUjtuRbodTNj9r+/et/QL1dtXyeUvPdrLm6bL6c5clUHbyAA3qKMuLEN1wlvTjL5bunn/quP2IwvXpfYSRkffvCYsl9SXVbcf7DLVhwy+OaIb//kl0QvX/Hyz3/Niz/7Fcc//RXDZ4e0d3oYC3f2E8q0pMoq4iQkCRV5VqGU5qN3dtFMbp0WWKT2WOfwxrO736IoKuIwZrud0DWG6sU5/rBP9jcXPPuzS6qXW0TlDh/+7j7+zjl+/5y//3/4gF47ohiNSYdj7kQh/ec53/zlKz7+5C4ylugAKlfgqyEORffOHp98b5enL15w2fKI3Yh7WzEVXYZZyOhvhxz/54zi2y3M8RbvPfhg1v9Tvr36fxLXwGc1ESjEbDLP/l03QuK6Lu/rIELw4aePqSqDtZbd/ZiDe1sIpbBScr+bUmanaDVkd9fyzuOYIPTEoeDdgwKzpyl3JbqnsP2SV088L7+ouNdSEOaEPcO9xxHvPhQoMWTvYch/83sP2Mq7BEcB8XnMR0cx7usY+yvN939eIXohri1RgeP70QD7zlOSP7jk793J6X54Ru93T2h/cs773oEAHWk+7SkiLXDKo2LJ415OkeVErYh37mq8q0BKZBTyyXsR/VFBpSQHWwKlHKX3ZJXh3SgniiMCoeipnMCXhNITB4L390sUGYHKaXFBFEl8oKm84Hd+d5+stFgh2GuH7O1HFNUQVMn3PtrBqpjSaEJbwfAS4TwayX4wxqoAGSZILbiznzAqSkZ5SeINo3PF4JVCuS4P330HL3dQyQF/9D/8V3Tu9kh2W2w/3CZ5lPCzZ7/gX/3JH/PFV9/wb//5f+af/j/+Az/9T5+zt30XM25TjVr88Ld/wPBUcvzEcvptxqffe8TotGTcr/j4TkzkHc5P7ra4v9PCi5BAJ6jM443CGkUQtfjhj96lrDxlbrl30COMLE7miNhzp7tDWW5RVTu89+730GaX4fOE4auQ9959jxmwuGJCf1vpsmHqt4KBF2ibs+hX64PpstN0bor5F6vp9LVJ7hverw0rUU5DuGrXtZGxMtn8s6jJnlsYb7c58lhfshNCXP8/R9Bct/umAuaDXy8dG2n5DjD9HGq5JbT7TQfhN0YZzWE4GgFcA4q50/n1igTUlVmThT6XbZUJD7PVgNrLaytOsPRuIesktfdIIddzTN0M3jQ05Jk/lCPWt+3W4XoJcb3gWVHPzXdFrKu5nndVZbO2L56fm6Va+PxbW0VdR9HMDe5UyUy5cN1lQvX8rJQATdNi2gZPzUXoooG70uZpoOlqIszcyb7OVKzPqQ0Ntk22+b2FIJae1lC4OPmnfekn+Z13/M//z3/Hk189Ix1nbHV6FEcpT/7qK6SwxEGIVIosK1GBpLQWHcXsHmwxPBtii5KytMRJgPAe6wRhqDBliReQZiWtZPL5OctKpIAoCChMRVVaWq3JAdcsr/DeEd3bxnYievf3eef79zCdPuNqSBAEcLaFvuzx5U+eYNMRYdSmKDxFkfPw07vEWwHPvj5G2ALnFEIFHLx/n3Gec9jvk8uQh9qSl4rKQKAU0uWoKkUlCR//3nv8/n/9CT/++5PtIfWbZPHzsraJH733c9tNJ6x3E+/MGxf1cfo3/+JP+eLXTxkOxmzvHGDcNl/97CXSlPhsyF4vRnZa9Pa3yCrFy2/7mPEY19YY7Rl6xTaeaBiQDj1lldPbKnn8SZdRZuglIYPDDKcDend6jC8FL786p6gC9u+FDHsFqbAo5wgelegHFac9wb1SUNxPKaIUpRVhCS53HLYyOhcR9vk+kekglKR7pmgfSo7Hjk4IaiRxhaCyHmxJHAhGuaSdCKxXVMZineDOTowrMy5GhkQ7kk6CTkKGgwKXjYmkoDCKQBpkbHG2IDeO3e0e46HjMvXcv7tF0O3QPzyDOGZvW5CPnjPKMgLh2f/we7T27jDoZ6TPD+kfX2IIiTVYNHllECpGiwItPaWTCG/RUtIJNSQttroBg+GQ/rhge79HEI3Y2pekWcHBo12qZExmU8IgQAzbhFWPs+NL9u/uUJWaPLUoJVFBwMmTI9LcQZFz96MPyYaG02cnbPVChtmQcSVox5MD5oH0WOepZM5HP37MIE3Z29smH7WpCsnJkxOQfWJ9SSosZBWdnU9p79yjqiytluLsyQuOj4Zs7yT84T/4mP/p//yHBKGe581FENvEwesE3irZ3TwNbhcWy15zq9/iAd6Z1rh6s8olak1eLq1ob0jz7ALf2zXyDSHkyjB3ud20F26sa8OBFMuppsMy1aivA/9uHzZlvM1Lg3mMvR7i+iud0Zyq2+2+Ni1v4UC3v/4j6mhwjVW6GL2KXeq+pZqw1/WwzP6pgc0pM87SX+tcP/nUNLsgZgUB15XXIOycwb2wRl9TuvU3S/dqNGPM5XATd7w2IF2s4nXLuGrTGuPmJttt0TxZpm0DGmYseGOdy+U3gP4VDDorf6Wltjp+DixPy73iotplFZuPxHJlN15aOU33XVsVtVCfj2L5RUOGWWfP8YefuGxNxxlFXlLKkrNvjzGVoReAdR7nLc4YvNREOmQ8Ljh5doItJ7cVT/bFT4w5azx5wdV8dhjjcNYjlMA7jxcCUxkUUHnIswKpFN55Aq2prEciuDi6oLMfEkeOoiwxxqCLDra0dO7ukp/C4DxFigilQs6P+jzce4BSGu8sTl65tc0N43GB8RKHZOAlWkDlJiMaeyisw49ynv3yGZ/+zqPa9KsZi0sas/Ys/OTwtxe1EfFz/64fybq1P0tb5CVZmlMWFUVhqExFUVq0B+nFxN3uuEBHOS7sELQTyrzkMi+QkaISgtyBcEAQEgcBeXnI4TdHJAc7lMahIo31irwwGBsQJR2ysmIwLikTTxFO2hUpj5QOYz3DQOJtSR5YpHBIrRAdSRRpOibCJiGjkQfniIzClZbKQVZYdKmpco9WGiUUeeVxUlGUhsp6dJIgrMc4SDODRxImCUhFOjZkpSGWkjBOsAVgoSgrrHeEcUT30V3Of/6MvHQMBxluWGKsI24FjC4vqcqSylriVozTmiwrGZ2PGJ6PUEGIsZqglZCNC1QQY5xECIV1Bq0CispjSoszFpc7MBHWe8rccHE8wLljDp8OcVKAMHQeBxQ2x1qDLiJsnmMqSzYu8ECeVuA9QWgY9FOc0mgHx98c09rbR4cxgzRFSIXzjqKwGF/hA0luLEJXDPojKuFJ0xJThuSppDQObwt0YqmoCIMQjyAdFxjjSM/GnL7qo4MQazzffvmSo29e8ejTx0scensNUJ8bb/h+VVjELNcAfrNq6vpxLQniKl1t0eu2sPX1vi2vlhlzEkWwmQf8axKarcXr+zRWFrSmDWLxcT7tolr8zWjJ766WjUpehdHfgsH41i7RE7VnFp9nKWbTf2EZ2684c+BrzDYrYY0nHr9iVfn6/eSfiVcHh1Bq6cDpWjU7be86IN3oZWVVECvTLK12+1pcsxRaQ9QNYQ6ErE62+VS4gpX1YZ7LLJbSblTJAp3NY3UTyq/9bmz3OqhVg7zO4WHyBeyGMOXJDbt5gzBf0s3cu5rPvqvgF37dDGAXlZGgP+hzeHxEp9PlvU8fcfL8jCIsufton9EXR0SBJIwUrd0Oo/MBkTTIbhsnFIWpUMKzvRMyHBvCQLG/FVOYikFq0UrQbmsu+hmdtkaHCu8sAodWiq3thPEoJ1aSdqzAOfojR6sV0dltcVlZ8mHG+Wev+PDBQ6TaQ4eKh7/9kOOvM+gItn/wPkc/P+TpV2e0w4DA56QXQwIdoE1JpXIGmaOtJcKkjJxHKQ3OEviSUk28hOwEcFk5Sgd5f8jw66d4/9vNhuJC1MXgnKPzQ3rtLe7s3OXZ168oK8O7790jbsXXiy7WOJ4+eUWel7zz7j3anWSjUX7/40e8fHmCDjR377VxfpfDz0+RuaEbg9YaKQPkcEiyH1K1HdtJm/tDx1eXKV0R0Ao9d5KAM2tQEvbbLc7TEeSa7fs9ZMtxMVbEnYhPvr/Niydjnv3qJe1WgNiXHJ4U4CV7g4DLnoQzy24s6cg2RyZES8FjF9FvV0ip2RcRW7bNE2HxQvAg8qR4SqloKc9OUnGYOwIF7aCg3dvh6CxHmIKHd9qc5wYfSlpBgYgdvpIIadiLLE+zDB1IuiHsdAIuc2jFEbv7PY7PM3Q7Ic4uSS+PqUionGQnluQ+oB16svMxrVhQmYC9+3f5rR894MmXI077lygzJkoShA7Q0tDylxgSvBPEyoE0WBkQJYptYXg5Nngg8II49Iy8YVtrHCEX6UQPBoWi7RPKsaOz1+Gd33rE4deGysZoZel1W1hTIqylm8DLIocwoRtrbHpJduYJJYSyYmQdrVDT1YrdMOB55nHC0/IChh5vAkxe8MGP3ufVi4zivE8xEERKk5ews9/jvY8fcNQX5GlJ/+gFW62QoNVFCkM3gZ//2a8YlZbH79+jsgWvTo7odTrcO7jLs6NnFKbg0cFj2kl7A/6tc/KalfvXWGCe+8J9FVZhk1qK2ksx//fG+qeQWVzhqVsQ3UDPTbnnLyTmSh8vtLdW2PQc4+xunfXtWP1WzPDiqsXsJUNis7IXw5LXp7esRjfZZbGMdUXt3TxZTchzXenf5ULj27vnYl24tjwmYG5xpWyCO+umA809Unux2imrWOrR5cNUV36Wpaj5TZ7RswnfbHaofJ6y1W9qNda45UYhdwOueOsw0s914Yw+sTiiGxZ2q/RNJdQs23WW9vX41wRSzRpeWu9aaEh9q930YkgBCClrBuvmVC/UtvTmzcJvznjYKMzNxZtpq/suv7js8//70/9Ef9CnFbcILyOkUwgjqIYl5ThHSkmpNAmAkKQqZEcplLNcWk8QaSrjUVJSWYupSkpjKY0BJEUpEM5hrCNUEEYBPnbEYUC728JUFipLUVVEQhAKyPMSdTJEGYvKK9wo5fN/Zem8u8/BO3cpeiX6/iUyHhLsSR6G73J+UTC6GLLdbnP6YkRrfx+fGRId4GMIwhZx1EWVQ4STaOUppMQrgReSERVhEJEXE29XR09POHt6xP779xq6esZbZ5dn/Ief/jsuR31aSZtgsEN6YTGl4atfP+O//8d/lygOAPirv/glX/zqKWVZ8sWvdvhH/9s/Ik6i+cFc2qsoqCqDDARIsN5DJWnFHarcUoqENPeTFfVeiLk8ojSWpBWxd3+LNBecDTN6DqwryVKP9wblBErvcPLKEEkDxjEclgQ6RxUVrR3NnXcTOomkyhIqKqqigGOFLiuEnXw5Ka2n2lcgJUM0QlZICXLkKAKJdlcXKlqPIMaXFgI52ZITaKwQqCAiCDTOWCKhaO91yc5zxoOMAot14LykyCuemYxcStCasbCEpmQ4LshSi1QtdBiTno3pDweUArQOJreEW8dWL2F0McQbR14GhEFE58490lSQHvUp0xKpI4yTWOFJum1iKkonMV4Rh47LwYjSTdqeRRojDUoprPfk/TGutAxsSrul6CU9dCsiJOTr//iC1sNt2jpiGAR42WY8rHj57AjPKZUPaLcjzqqMorQoCdYJrBKk+RjvPKGs0GGMRVF6xyDs0h8OCYOEotQMnmjG44osEGxvjxBaEYQBo9xQKgle0453KHVMScnlIGOYW+7vbTMqgdJzeDTk6TcveXWZ0d37NXInZ5iOaCUtwrYgr8aUpuTLrX3+uz/8R8RRvEIWNciet7Oqtr6MVWD4pspuWf+tv0I00LOqhLmLATdVNzW8MIFctRu9VwKp5gGbc2I7d59Sg25tQtsbhsZdAN+Bel19K8V8na9nCMyXvsnlfX6S4I1Z/jdjXACLau/61wIa3hywr62m9rPGIterBs0d3Gz4TrcQzA9S44Hk16B7+VrBNeWJ5ZWQ1eXeHObauNJb1XK5M1ttcW26ofbvzjBeUfeKl2LlT2CRO6Huvatuk0yF8Os7vrgyxK6/EYsbFM0m4VbfBJZoWRVem6xrS+yGdEtp5pXDi8NXXFz2eXV0SDtuUX3tcQNBmVcMn18wOB8j7ATQpqOcQEBWOaLM4D1Y68kKg3MQaEVZec7GFcILqsoRhCGjYYnwTG489gZb+ck+e28YvzhHSU9RTFbTKy8oSo+QFnc+RniHE4Jwe4u0dJw873N5mjI0HaJdz6gcwYnEHCvCnR3EyHByaZFhRHo4ptdOiNptkrbk8rIi9yFexaSVBxQ+aJNf4fnO1RYqh6BwFUdHY06/eXllXMwM3jnGFvD8+Bnng3OOzl/RjrqYFwOqgcZWhiBQHB+d8+DBPgh49vSQb58eUpUVWisOX53x3gcPZoXNrdvMJOu3T19xcT4gzwq860A1wOmYtBqhghb4krx00B8T9hyFrXBakF8agnYXPfb08wrhJRaFc4q0kLjS4UXC8WFGMS6wIiYKNLk9YzsNMAh03CEtBMMLi7OT+yxc6ClQHCUWKx2pBKSnao0JE8NQGQgUFWPGIsIKS5VFBEaQ+gBvHYYQ7yzGe0IXcjmyVFaipObJ0yFea0qrsLlAKI0II/IqoxKCAgteIiooswyHRlrLk1djeluCPPeMUohae2RWkVUKhSZLU4rKoyONN5C0E4Zjw8nPXnHx7TmjCpKwNeHHOOS8X+AqhZZQlIZhWiJ0giEkrwqsChFKkFk4GRboSuC8RgiNETl4yeXZiMHZEIOjjEKs1wwuExBdjp8PCEnQcUCeO47PchLvQMQoGTEsDJXT5BZCrTE6oqwMpbPEkWYwdpQiorSCdilRRpKOBVXg+Ownz2jf36YqofKSrLKU1jEYFlw+6zNIBaeHQ7QLGRaC87MxwhsKX1CMhpS//JaDjzroomKYD2glLYwe46WhNBVKao7ODnn3/nsLixszDHAtbWo6da39sfhylXybrrlNJ8w0bjH9TTLyN6Q7gVsJ+tn2WzG31rAxuaKOyTbMOWcviNq2HdGcaKMwXVxc0v711zPcOJV/3+X63fUW8wajyi9HL7Gjn8eIKw3EDW8If5Pw1oyLlZNSrI6fy3ybiuo1rlpuvq5jFj9zizaNW4cSZ6BvUsz0+PBNxK7oCV97t+FcWq5pIWOND/181EZhajStrHHtQoBf82u+qDqGvv7tZ9u75o2SK/C9qpPewlyYcxzR1PybpEed55o2kq7TUIIJzy2eU5n59luVaS05ryfvbi5zbdnr2tmUqZ5+lVCo5eu0W7TimFbSotvtUPYcIlCcfnvM4MUJLS2onEVHIc44AuEpnAPvUICW4IUnDBRSQeglk0VlRVtCgKdQAuElAYIkCZACfOGJQk1pKkKtwHriJACpCbMSh8caQyAlRWHxeYFqBwRKkY9Szp9kfHT/0cRtbKdNehGzcxDT7YU8//wlpirQUlCkKf0yQ+vgyp1rm7ireHE6hmqM1BGJlFjnyayhKxxJIKlKi8tzLp+ezJRJfbBqE62TdGjHLVpRi61uj7wTgQwp8pIgDOh0YqSSeDztdsz2TocsLQijkE43udZosyWWadGzgep0WmxtdZBS0umG+DIiSxyFMHR6HeJWm8OXF4DF5QVhrNnZ6aCTLpgApMQOh1ycVSgcQeCJY422hqGpUN6y1Q4Zlw7pC0IhaEWaUkjabQ02YvdAUo4y4l4H0yk5GRfEZvL1p104QiUIlKSbaeRWxJ5MGFzEyKHBV45YGBIkpdYkytNrtxjlfZQQxLFEC0+gPVpYvLMkSYCSEltU9NoJmZU451CBoBVHDEc5cSgJlSMtLbEG7yCRjgpLomEwTnGEJIFClCWVqZAqQAlHoGHn3jadRJMfDbBFRhhoQmFBeJQzVOMU7y1JEmKUoBPHEEWcnY+JhSXRAQedNoOsoiUn/TMuPMJXFGmG0hM+7EQBJtLs3N+l1UlAai5eXeDynM5OhAw1SjpaKkQ7w3a3yzD3aA+indC/HOOtJVAKawylk9i8QiUxO7GicI7tJCEeOXypcL7AVx6RZ2zt9SgvNMrlYC2hANUOcd5xlI3Z32oTBB6tIBCAc8RJQP/wnO17IdvvdjBU9DodSiEQgScrMqIgpLOwLWqmd1aHxXe+DtY2XVBa936t9fIW0t86/61Ng9dKPp91oT9X6pDVK4Ji6QvqqjIW6phTaOsbMQe86yS/8WJgvdgGa2Gl0bpmMNdih9qv6fbsNZ+c3pa58eauaGurAs47rl1RCmqAcrpasJB3EasL5lq25C7U111dLoZ1nTV1B7do5c4bJ3Nuy1ZaRILrU6GNVW4muupZ/WKSDedNY/56pF94ftMJUe/ChesvRUP5k6jZi+unGmP7WeRcRdO8iw5OX7s9N7DM3FxrcufXmG/+5Un/mH/55/8f/tmf/BP+9uufr57AgokxsbQfd8ar82/ekiS7RTF11tlIN9WDWPi/Ht9gw68KD+/dR6sAUzpM5fmDv/87VKOS9HhIW1gC4TB+4tHn7kEb4wVCKGQAOpocFkVIDu51McYhpGB/p027FVAZR1k5Hu7HSFMhnENLT5JoSmOprGV7v01eGiovkFHA1k4L5yf+y9979w6l8ZSVQxnDThCD7YDroY/g6OcXmLOI0LX49HcPqII+YrvgH/6fPkUFFY4xrQ50OwVDb7nIM3bDFEJF0A7pdRI62RkIiZeSOz01WbFDI1SAjkr+9uKQ//f//Md8+dWTFQMBjw/ehXGH4jihOIv40W//mGy0Rz6+Q6x3+U//4i/5v/1f/il//C//knsPH5HnexTFAa3WXX7xp0/5f/1f/5J/+U/+movz9MrL1GTQ60P70SfvUhmDcZa9OxH797ZIjSNz8PiOpHIB1gbEKiYbGE7PYg6/he//1gMgRLW6vPc77/PD3zogDEOUUOyoMwoL3kmwJYEc4gONiwJimXL2omB4ESCJ+eDjHpX1FMbxKDRIH6KqCFUEfJjGFMOI/ELzw68nZ0hG4zFeen5IlyKyVLHlo6Sg7I0Z3x0z3hqQcETegiy2hMEl0hT4qsSUGdvhkOE4JS0LdloFrQgEDmsr3t8xtHVIS2m6oiCSFrzHOEtXnnE5fEVWHLHbzthqKYSQWAH39wxRJwINnViwu7+NCTqcvBwTZqdY4UFKtMvZjkHGIaWxvNMu8VjwFVV6gRscksiKbiT4uFthqxRsTqQN9/Zy4p1Lou0Bj+5Aa79i6+OAuz/a5w//0e8hA41xjt/6rT0uj/poAe1I0rUDLl+dElnPJ++0cEnEGEElPFsqpywtTkh2VIrG0o4UiYZOdYEwgpaOuNM12FDgOiFBNyH2Q86PMoZnFQ8PdsFPvEpl45w/+L2HpP0MvODhjiQKII4mXt56sSYrWnixR/bKk1Tb2NM29jzhR4//HvlXWxRf7tIpH7K7tdcoo6ZifcLDTQLIL6/svs7qXVPRi3FisgDihW+Wm28ByE6d16wlctXK4MpcYo7EeWSzTu8t1rW2kvV5boJaq/IuYMzXAtO3acctw5KKnOLSJVRQd4t/JZM3/BIx7573uwlv4cuFuLaoanbGwuoujfx202GW5cPMV+W9rjnfaKTfMHs3qmZmQjXeqNlQztLiuFiddnPa/Jz/+dlCi2c+1l8D6Dk3qK89y+oofbnOWbxn5j52GjmlhytW8bU3GxLUZLSuInVdEP76LM1tV+u99/zVL/+Cp4dfk+YpeZlzZ+eAOzsHc+34LqbzxrrnpspXte0WaV93ajaFb1+8pCoNQgikkPzVv/0ZSkpMVjIYG7RQKDxKa749HNNuRShXUhRucru2d4Dn6Gh07UI1HVeT23+NI+iEnJ7m9CJNPzeUlSUvDc4ZrBGcvBog1MTb0WhckmUWGU1c0j5/cUmn3QKfU8kQk4fISJFIyUU5ZvjlBVuPNHnP8tmrLyEqkUry9KjP/Q/2efr5IVVpKHWPsB1SlBU/edJHhlCIEOdLUtVFW4fWiqMBtCZHD/DOc+wMxasjBtpSFhV3792h25mu1M7m1TffPKMaSXwWIZKYv/iPrxB0uHx1yr///Cfo+AIbQGYt2V+nCNnDi4rP//qc488+J97d5t67++hA8d/973/YCFJ+/etvUIFCSsHxcU6ZX4CanEf64qUniRymdPQNGLeHExH9s4J//U8+5+DhNq70pCnYzj67DyLS03NejHuEWpAXhpaOGBhJhSOWihf9mO225vL5EDPI+FqeI9ttdKT42+clNskwMsS3Q77MC5yXoDS/OBjSVh6pFePzMT+xh0gpkaHgF7Ej2Aa0gbHhq1FAEAIWjgcgB318Jdnb71IlITLLKa3j3ER0RzlFMTEwjocJceRJlGZUSAI8gZaEUjM0CqEm916Uuk3YbSOyERJ42ddEsUQajwvb+N4uZW4ZHw0wNiSKoawgswpURBAHeFcxoIMUBaHWRGGbcZ5jXUVlDH/zssQ5g5cBRZZhgwu8MkgEufcEcnL7+2V2AYdtZCBRgeRvfvaKUAiUVjjjyfKAbugYnPf5z2NNstumqCRRIHl+YXHCEyjJSabZigVWB8RScTYOMUVJohTPTyeHvivhaCUhRXGHfFwgTseInsV6CXjycc5//otneGOQwOHAgy3RgSSOWgwzh/AlOtCcn4959vNTZCtGVjF/+a+/wmQRw5OCs52Kk5eXHDzcWSlfpppmlZ5ZEmW3Bfk3ycKFhdW5c5z1vLeWp7XMVwWuL2LFWw+N5xhqr6egdmm9TSz367VXu7W0NNFwmwyLdKx4v6DkV64lv1a4LZCr5fKbGwgz7O2XFir/1xDe7pmLq5XX64ucpoZFU1jViWvGpb7X79ZhDVqcO1y0JulNiwhNIP62i+tvxiINE9cvxF/93rC4WZarpzm558W18JntLlvVYl/7d1b49N/p2/UrSvN0NY7Ia67yXJ+lqclkf73laVFY13MAwuO8Jy9zRumI0pRUpiTLU2xl0VpNSthEALzmStVG2V5P5r3dUK97keH9/HOW5eRFSVGUjNMUM7L4vp98hUCQVRacQOclDkGeTw5pl8YiAKk0zoKtKrQUlNYSB4rSXLkqHeVoW2FDTVk5dAjWOcqrcxpCCLSXeOOwucdLS+km5GkBzlmc80Q6InWevHREWpMkMZnJOX15SrvXQsUh2ThHSEEShES7PXp3C4rL0WTVV4GUAVESYYSlMuBRyFBjlMZ6UEic0CAEFkHpHf2LS0Q3xD64S5EVM+Piul8FWVaSZTlFWTEaZZRphRmXjIcFWIt0UBWGwcWIyvewrqQoDOOLc0zlOXl2gjMVj99bBmlTnsvzgvEoI89LtKqoioq8sJROMkorilGB8wJrJQYQMkDFmst+SjZIkUGCGabouIWVGt3bgtKSVwYvFKPKkvQS0n5BaaAlAwajkrISnF9kSFkhC0XcjvBaY4SYuPOtSqxzFFJQeIPWDiNKciyDUIF0ZFrivCcUkkpLKu8JA42XClNMlr9i6wl0RFE6SiswHionqbwjMJ6LqsD6gCgKKSuPCMTkr584ESDUOCyl83hbEYQhKoooy5AKCSrElCWigqp0yDjGRxFnX5xQZRVJJ8JUJVVlUV5gkLjKY4VmkFcILJVzBDoiCGOyqqCsLApJlLTwQhMnCgJHIQqiOKB7kKCUI6sK4laboqjIU0ehJIFKsEoxGleAwxUVaWYRXmGsp3+RYVVIPs7ptVpYNGXliaTEBRoRhuSjMcZN+kkbwEAqPGkxuX8jcAKtY9K0QpAixOTLBWFIURjS1EzcMluBcoKydGRFTmE91oIKPN1Q8vyrV2w/2EVrST72XBwOODu8oBVJRv/wexw82Gbh8qvlcI3qZwLqNlhtdm3FFEPML4rWil2eQPX0Yvnd2wi3WUudy9FIw6IeXxGuDZP5Ri0VucauuV7vXDd2b7DAtRKd3abvm/pzYyA3zxyCiQv067dL1uZ8D343avztrQ6+sXFxfdK/djGMvO6Q6d/a5H1N8DcrZh3j35C/Xv/CqsFsxb0hz9WL1bh8uVErGXdN++tHQZboXfV7Zbl+xa+ZeXD9xfc2grT2d3lIb/pkcPV+UXL7xXQL8avaOl1VubJxGseniaRF4hsl2CKDNBczDVJK3n/wAaUpMKZit7fH3b37OOvwWjXmX1nN9WqTb+bL62TLjV2rO1a8vI5ewQeN2Zq6StDQrytC0zxcePnOwwd89tmv6URtuq0Od35vj1e/OCY/6mJHQ8rKM84NcSDQkaY0oBF4JbHGYJ0gCQNaoSPNHa50BNpTSYVsRSRasVMOSa0CLel2QrKiQBERhgEylORpibOepBXghMeOSoQQ7N3fYXQ+wlSTy8K2EgHDASKH3XaLkUy4LDwXT074rT/6HkGoUEpy795dqlSzvdtBC8fpiwHfPjukKirCTKKSBK01W4HG24rzskArRRQ6AjxCaWIZ4ozB5gZSw9ZWj93d7cZufvedB3z2t1+RtnN6Wx12Hhzw4mkFtoc9H2H8iLIMoZJ8/0cHvHpeMB5aLs8Kup0AVcSUlynDJ8948qtHlMbz6N1dvLS8fPWSVpLw7nv3OXxxjpYhB/famHyLajyg0p7tMCVLDbHyBNLipeayTEHBvbaltJpxmZNf9Llz/y5CxrQfdPjww4Rf/ewZMvO0I0iCErWXMLgc0I4tYdBlmDmkq2i3BepOG1dWky9XnYhB7jnY7mLkBSfWo5Ti3fMW4+0c3dNsiZBW2eJI5hgB21KRG48RnjbQCzxn1mKcoxtCAKSFJ9Lw4GGLl889IxyJypFRSFEJgsCThCWoEK88Jh/hhaLSbUI38RylW13ibpuDnYSjVwbpMtqqgw5LjI4QETx+Z4vcG3w+ph142qSUDqw1tLQhkSVORwyqMXGg6OzsUArF7m5Ae6/H8eEI6S1bXc2oLDCVod3eQoSa84sTqrTgIDhgLDJG/SFhW6CkJtrzBGHAvXsHtCLFN3/7FfmgRBtQoUF6QS9soXa3UN0O598Okdk521v7WOvoRpKkE8HuNuWzFJ2OacmQyHtwBaK9RZkaRGXZaiuOgShSaFchpceh2d/b4t67W4yPB+SUKAflYIh1AuEsB+0WqYpJ84o4VJgSLo8u6SYxn/7wff56UNCOQobHZzz92y+wwtDpJtx7sH+7FeHbhBvO6L09uLaq/MWvBAvGzSq1xgbxqyudq2pJh6zQM+sj6uVvuBLWpJzWNL+eZv03lDU+nBZJW8Jmb8Jnk1rn8OPaC0LW17XWvXJjzW+PU9/cuIDVq7J+YeRXgsQbKvH1Ne3pv8tWcWPGJoKbUq1DZQsrqiuBVdPvTTIt0VRnppkxcLswb+EuGwAzNC5q3htW13KFHD3zjO9rc8mvvsStPnKLhtqip6ppaxft+pWGwqahaRwXh2XdoanFwkSNSg8/+uT3ubt7j6LMub//kCiMrutZ+el9cUvhXBDXhs+sD2YG2nRlQwDez/ZQXttKDc1uUoTN/b0i/23Cqq5cOY4LfGA9LvOQAwFY6RBIVBhQOoGWgslKPoSAMQapFVEUMchznPNoJej5ilJH+LLACEG626OSIVp4/LjCX2RUxiFUgnIOYywqVNjKIIxBOQNVSafdovQF2juKi0ukv7rluyhonx/TKf1kFZ8ebv8eWnrSYcbXP/uKO5/eQ2nB3kGLH/zwUy7Oxuze6fDn/+GnBPsVg8MzypMRo5GdeM+Rnt1OTGogFJKWEozN5LNJFEZkfsK8trR4N/ly1niAznmkVSin0E7jvKBMS06+PSH0JUJ38ELiTBdhIaBk9OoQaQrSQpJXknary2d/c8Tzwz9m95179PYi9NYpo9GAKIpI9C7Caqg0ogwo+xnVIAPjsMUYYQt6vS537+8zKCPOvjrFlBWpEmAcgYrQ3nJ2dI6RLaT0bG/1OHjnHi++PsXblCx1FE6gtWZcFuS+xOsYLSNUO8IKj9cCK0FpQZQoqrLEOTc5pG8tBB4RWryrEHGI6+ZYk+GtQ/Q6SNuGNEN6GKmSPJyccymsAxvgRcBwXNHtl7SSGI2kykuQHqkE3lRU3hDEEh1oKhly6RWlgRLJfvfeZOWdNuNcM876SKGwpUFHCi8FUdxCJpr+L18hvEergK0k5ng4QKOQ1qK8x1QV3lsciv4op7CC4XlO6/kpqrVFFCqeffEVIztGBRplDSoaoFqS1laH1KQUviJMQspRiq9SdJAQBAmEx3QfjbkvwfUt5WWB0QFRK+Lh47tY0ePiPKWr2jz78oIsTYnjmNI7Ls4HdJL25Esgkwv9lDdkZUbQ2kKjENIxFJZSQxKH/P+Z+68uy5IrzxP7mTjqSlehVSpkASgAVRAlugSqpwWbYro5w7U4i0MuPvAj8CPxA8zDTLOnZSmUQhW6BGQDyESKiIxwD1dXHmmKD9fFle4ekYHm7FjX4wgT27ap/d/HbJttFGmd4BtPcdxghwXSNkR4fDHh1r0MF8UEa2jfucfRBIbPjnmZT+lrhQwRRy9G3HsrELW6BF2iUvjDf/efeftgQHerzVd+/V2+/JV3Zn3iDWv6r7no6AYUWPFktEZ5vzL9z13WDejhTOFdtKQve4FaR+HCeLaQxdKccGMgeM3ktCC3dfP/60xu5/Fuqr+upQ2RbwoGb0zXw4XFLN8cFP7c4GLZZ/HS29VH1wlOLIs9LFwv2GY/T+WuKP9Xp7Mg8rX5zil+6zILS/cb8pzhsUUQNVt9FNbwIC4frCsPG1haAUQzfuZhzKox4IpWHrjm68cVrWNDxOVx4FLBnh/jLuUUzhfVvyrYOFfOLzrhpUDnx8D509cv3oZZvpcAG+7ferCS/gWtnRiulOxC3udfCYMIl7HOMr75Z/xVFLw4sFxktHK45CJTc8ldBbZfha2lrJ493Wc6LhgPpzjjOXk2JExgMihoKjeb37xkWlmqJuCdxwhP7cAYgbGeybSiCZ5GNjSNYxokNREVErxhPw+0HNRlw/BkgjcNpjJYYzHOEWtFXRmcddR5Q1U2JJHGWYcJHmc9SkvqokGqmYvXidG4MhBUTJrAyfAI/+KYrNvi5HhE2tK8d/sug9MxZV2Rl1NUP6HX28N9PKGe1FS24XDqiNIWLghOJg3l2bIv2ZbUWoEwlKZhPJ4yGIy4dWtnUfYh8OzTl+STkumoJHjJi2dHjI4C0yqQRRKsQrValBV88JOXeGMZHk3ABaKki4oTamuY5DAYHbG/n/PoKz2irSHj6SmRigjlEK26lEVNcDn1VDA8qTB+tu+glSbINGZkJYPcUYYIhWRsIhIC1kpI2jRlQ+08xdMhp0cF3b0u8dYWoYgYTyuMl7gQELKNcGC9pZMpRkcN7nSEUgKjFIxqcgvtDlghmMpALCWf7U5RqWMcNXijcVuCUWkJxlFOLVo6cj0TXiM19Vl/S5sE5xUozaQuefq8JO62EEIjoy5lUSAihRAJlcxojKBuYOpiTJwyLMHHGmygFc9cz1ZFQ2EUMmpTOEnjU0QIpFnC048HnI4avEwhijkeN9RG4FAEImzNDFCKmEp00UrNxq9IM6oqaEo6nRQbx4Q6R8QSYyxZPyXei2kqw/7J/mypGg6ftPAe3MkEOZCMRqfEsaamovugh95rkxcVjTV8tn9Kp6Moi5L2zhbRlmQystjKI0VEaQPNsMI1jthHdHVEWRsKn9KyCqE1AclhURFizbRs6DuBFgk+WCYTw4uXBZUVSJ3QiMD+wYDWdpft21scTBzHp4ZxA30Z03iPEjMX0T/+h+fE7Q6VV2jXYArDJ794we6dbTq91iW44LJ/IOZPq19Pl8P4OsXrdQe8pbSuUHQ3z5BvCCVdObWfG7DEQo7rl7xfo8gug4o1t+t4utoA9znoyolXXLXd5BXSeRVamsfndLuL0i8YDTc60V1J4upcZ6mtOj36fPRG9lxc7FifK/9yOwph0Si8rBuHub+XdKZCiWURLgtgTc9cUaCvKICYV6pXT8Vel+OCRi3gXIFe098uPU+ssBLODADLOzTm1/OL+dU/awtzke+K2WBNoVcs2pcK+XmdLCjSQiwUdTHDueRe57j45S9bG2hdc19eHreEk9ZltpjSfBXP1d/5qyUssfp8ORmxItj1zK9plwuiXdTvVxO5GOjDFaB+Kd+1GH9OcBd5rg5gm2jBReNyvtfF39g8F4XSaqWkWUqaJXS6bUzP4b3hqCjpRpLSeVQAFSusmbnvVN5DcMTRzIVrFCvwjlgprPeo4NDBkylFJGOSSNESCcYYhIJMJzjriNIILSMUAusDOpKIAEpLkjTGh5lffiFnXy/C2Vka3V6Luh0TOgmT2pNohQqKyeGAnVtbKK2I4tmwm2YJWmvanRZCgJYZ/a/f4qMffEo1ajDeYeuSLMsQWtLgQAa67QTvNF4oYjGzrmfp8mFhM+G22glZlpCkMd1uCiHCJIZIerJEY21FMZmQ+5rdW12Ma4hkYPvWFkQZLw9ypK+ROLSGepIzPfDcv5fR2BQ7brB5TdJuk8SadieafU0IA+KWpp5aet0WIY1op4rJyM7y1oLIW7JY4WTE1nbM+DTgcosOjiqviTHoVpfevR7hJUwnDZkSoCTWGbROUDQECRKDRBBFErTHIkhFgCxFiAolJLpRtGqF7cS0a4mNEsI0EFREHKCjIipv6AaYaoGyszXQUSpJSyAIFGBsRUwMCOJE4WuobEOcKaZ1gcYSa40SgWBrEhUT4VHSkyhJVVUE26CCpxNptPREUhBJaLVjypcnRCIQhCfTUJeGWAU84ExDrDLivTZCN9SVQZ3NESJY0lhSNg3VpEHFlm4SYyJNO27x8Iu7lDanGVfUjaXJGxCBVrtDMS3xzqGkojgpcJHGxZ6qKXBOEoxDSoWvGnxkCMYiveX+F+5jfnKAqWt0gEhYbFEivEUERyQDQYHAYcopUrXJCBQhYLyhn6XEdUOqJHU989gmvUc1Bm8bWqlg6i3BObb2OjRFymRQEQlHK0vInAEkcapREvrbGccaFCAjhVaCNNYUL4YE7xFSXk4Fy+vbz0egtWcMnL1fO8GzOs6vJLAcRqy+XyGxMlTObwMUFwrVFZm/CQyyUQe6IV1lYNs0V1zEmQ8obja/zEe9if63Lt519Cp8bExgze15McPl/uK1eilnuoLY/H4h7LxRdDnfS2vtwvPXUenm6Q26oj2jwJVLxAKLyjUL97OOMu+Mc9mJ7GYUfwXdQEgLiPyqABfXq1BnJeZZYc/5X/Vee/FmSUm87FDnbuQunbEuOncNczJc91vh57qyhaUX8317PtEwz8nrtcKLgXzJn/RFfS+Nm2GJnfnsA1xuhtrUxwQraa7LaMM4vzgZnUW5LP1c4hsaxOUGLRbEtuIocJn/OREtw8+b2HPEnEyXxR3myrIx/rpnUlwt5zWPXqnvBnj0+D6RSnCVxNbwrX/6VappTd1Y2jF0EoW1Dhkke7sJQUgsgl4rohULlJgBjLv3ezTWIYWkqwT9ekJyeIQ6OuJ2P6Kua7wzCBno9BLQAi88O4938J7Zpu00oreVEZSkDo7HD3eQPiCFoNNtce/JLZz0TPKc2y2DOH2BePkp4vSQu/0+9TTh4BcT7t27w9/+8O/5N3/07/nhz3/EV7/xBd57/xHvvf+Yf/Ivfo2o29B/J+LJV3d52A9Y12BNyZ2WIdKO4GuqquSWl3SC5t7WNt/8+pfpdLLFD3dnF4/fvodSCu9mp5D/5u8+xNscIUv6qqQVaYKLkF7z3ltdqrwi7aTcvZfQDD4B9uls13zpvR5Gt/FZj+LI4AcBV3ZI23d498FtJsU+Vp+y9xAePunhQo2nYS+uMaJL2WS00ow7bUFHKYR1vN0vsKGhdiVRZHj4UKFaAa8sj3tTplXF4fGAppjwq1/fJd3tYLVgNx0TCYl3jt2tNvfuOMpWg+/DvX6DjwOyrUgSxSNnsT7QOM+7+22k9zgcMfDNk12EyRBVwtdsSqoj/Jnb2LetxA8y/HHCHQwaT9EYjICdaMJgMGE6qbi7rYj7MSc4Rlje2bLYMkeYmvdalp6v2BWBLS342v0IYxq08PR1TRY5SAUhluzEJYIEUwaocrZSUNZS5QWxOSR4RVk6ouC4/+4OPovZenSXP/hn77J3t0O/r9nKAp1sSqtbIJMhLTHFdkr678R85Z//Kl/4tS9ilaSR8CvvfpHbX3hI7+Eu995/xFd+9bfQ/gFReMjX3v0G5F3MUZfU7fJo6wnSbROxw69981chncD2hHTP8uu/8YBWOyJ4y6OkRlSWelQgjedhT+LszAFDW0+QoSBWBVliuSdyQhFoxpYdHbAIpjrDJC2++IU9ItVFVDGqaoiEIJjA/k+f8+tf2KKbKLLgkPmIXlsgtcX6mif3UoyR+KCJkMRBokKCyQPm+ZBqUi0OO+umLrE6Jq0bN68dxpbdv35eBZ/5NRvnhp1rEr1yWj5zY3rN1H2ui20+AuDKyOuNa6+UzJJz9pvEXdJTNob5PPR543OmP13oA+FSm78Ac+KiOYoV5TFczOvnYa8kseG36d0boDd/QvcG/W693icWLbc3Qf/z4a4Kvw7krg1/DbQVYR0qWGRrma8NeYiLfJakMHcgzDwCPR9O1uiaS39XOFrIbfFiKdj/H+nya0i4si7XGl/WDOYLbW8NkFuQ2JKCfflwMwILZx163kYwH0MshF2TuphrAfMF8nP9Y4NiPov3OcxQ6xvRUitZRJmX8rrJCeBX0wrnZ+gw+DADKmsSf/rJPk3lkEKjRMT3/uOPLxy/jCqBEjM3rSJ4jo4alFY44GRSoYQgEjMQ9Oz5BCklOlKzcysmJcpY4kgxqCsEjlgKvHUMpyUWT6Tg8KNDgpvVm3CB0bg8c9ep+HR/hFQCITVV1WCHARFJrDV8/IsXJO0UVVsKq2DcJ8v65Kc13/2b79N7EBiMThlNxrS/1OZf/J9+FxD88Ic/Q+oanRr6O1s4n5D97JCqrjg0kghAQTWdEGnYyzT/7X/7T3jy3pO1NQjw6Uf7OOeQSqKU5G+/+wukaBDCMDARO3u7tH1FWUz57h/9nO7tDnUh+Oijz0i7cOtOxvZelzrcYo+ak5cTrAp8+P2X7Ly9R9ru8SzfR0QNqqU4GU1wkwFZW2GmJS/rLv2xofSenx8NUVFCv5VBI/gsD0RRAGs5fHmKCwHvBCbU/HysybRHSjg6mbJ/PMWKmN5Wi4o2qh4jrWdclJRKIdsBGyqeeokPliAltfB8IiDWCqEkH96e0pUSLRRIzffKAyLZxjvPj62l4y1KCpQLPB2nRLVCCMX+saAtA0rB9m6f06FAyUBjDR8cVIh+glUNqp1wojOSeERd5EziCKwlk5btKOblwJNJqOqGHEn/3i3GL0d4GTis22wlGls7KhshrSQWEKqSienNTohvHPGtLcq0y8nPX1AXY579tKGXapzUeFHjdUnta4SCZlvw+Fcf4GKodcWn+5+Rdtt0t7c4thNaWx3sdOYBKx84er17iAAffpiTxLs0dYVOdjiZOiLVQSL42SefMj7+DH0rQ7R2+MmPPmXrVo/8dMjHx4aOipAqop/FDKoaJQPeOiwZkXLE2qG8Y2A6tJUmBMnziaTVjXHaM5hW/OH/8nN67S6drMewKolSxWQ0pZ4K/vqPf8bO7V3yoyHGBI4GI5JWhpaKj/drtu4qghcUjWC71yeOUjBwdJxTDQuyfuvKwWndKchzKj2Lo/+lgrjWIszifH4dXbX5dv4bxo0XCF0xaG8cy69RhzaGf9N0rU51BS2VYW0dXKM7LvDwxulsJr/hWuZN7eJG7eBinr9SsViX6eeu2jcDLpaZ3MTVjRvM6vbty9KK5aCzUGv0kwuL8sLiuUVF6UxlZHNP3NAob6JtXQlmNqe3bCFYz1VYX+iL8IsoeDN9DoV1KZmVTnAtmF4DgjbEWy3GWb0JWPv97nyzdbgUbRCvMabMA6CFvxezx9pmeaXgF3X4s2q8ftK4+SS1ms3VtNomlw8Qvy72643DYgYsNlCRV5RFTVnUKKlw44bpMKcxnlxZtBCzteJBALOlUSEIJFB7N3NZ6QXBB5RWSOvwwuJ9mH3xALzzYB04j2rsBdCpK4N0AjwoBI2xWOepzew8jEgIXGMQEkCjshhjHE1tUbHClDVNbYl6bbz1eBXRWNj/5Dl0u1R1TVEUFFVxIeQir8jzkrpqmIxLdLtNtrNFeXBC7TxpnOIdCBtwwXD/rTvc+8qTS2muEWWRVxRFTVXO0qxywWhQ4oOkbhwHB0OS7hZCwGQyxeAwtaO7lZHual4+OyAfTmnf3UJ1unSIaY5zrA+8/OQlSmt8EmiCIX+ZI+oekdpGtVtMhznWK06GJUHGpEoQmgYTAloLglSzvSuz40gQUiJ1hAwQHORWgJBEUiOBqvHURzm9VkwSt2nykspB3Xhy5Ym0IiXgkdTGoWOBC4FSgQ8OFVumqaMQhqEr8EpTRgJbOVpqVmdGCgqhMB6aRiKEII1iirLEWMmkdCStNuNhTpTEjPIKrwImSCoHmQDrJQ4FaYrNLTgYT2oQlkDAB0FvZwunImyYfV3DS8om4AQXrl1FlKDjiEkxJQSP1jHp3T1O9oeUJqDjNvbskEclZm50K2PwMtDtd9l+pwOZoipypnkOQF4UBAdJEuGCo6prppSEKiafOKQUxFmMigQ6CEwIIAXWe2xliRJDdn+bypZMi5omr6hsTNzpUJ2MKBB4ranrhlhI6sZjPLOlWyrCOWZeuRwUFoQSRFFEg8JrBTIiHxmK0RitNUoHYqmRMmCCp2ocuvYgNCHMzn0RjcERiJzg9DCnaQJxBkEqpqc548bQlQHbmLmeMTdKLqsUZ4YPcTaHnDvCPNce5mfMzaPXpYlw6fEbttJcQzcKuyZRsfjqfI/hSsxlJXQ5v9dVL94EaFlWrBdkv2HG3WSEfYMgKqzN54oMlvSFa8Nfl85N2t/nbaf8Mr5cwBWVsU4JvPiz8H7eNrA+8XBlqPV5LlogLp4s95B1X0iuxB3r1L6wqPOupLVeSDet08AlZnodt7eXHJwNgReehxZle5NNQ+e0CVRclmn5YD8xF2YVoc4PzvOhV3D8xaa8c7PTZYiwdDDeylkkK+Bg/TF/a2mtfM+ker4fYhHXXlzOMbFYlivrLFw4ULiK3sw4OF+XYuW08cvaufnH8ivDnWXnvefg8IDGNNy5v0unl9Lfzuj2O+zc63OQ7lMMx9A0KCmg9kjh2eoqrNEY6+lEjkbEFC4i0oJ2FKhqS9M4WmlK3TgUEZGW9B7sMnh+Qmgs7VhgtCKKNFJL2lGEUCmlcUjf0AqzL1coSZJoJiODUhKdaLJOgjMW1UqR6WzZj3fQSTXdnTYnY0uUxrjjHCaB2Ge00y6P7p07AAg8fnKP589fkrUSWu0M7XvoCExxRH48pXECowMKwa1OzG/9X75NnCWXAlzTWB89ucvPfvQJebemv9Wm+/gWoQDbGNrKYGuLczUP3tmlPChpkERpzL27XaI+vPjJAUIYtt82iBYkkSfdvsfRhwPGU08zaPjSt9/l5XHC8GjAnYcd4tAFYeh2ugw+OMLZGCccnUyRtRKOhzVpqnj49m2mpWU8bmjJhrIqGU8t3Sxit20pc8HUWNJgUCqgVUrd1LRDRRNiVBoQzhBLQzuKacewpyW5gqnWJFVNR8ccOItC8CjfZtoa44Rg1yi69Dlpd8knp2w1HlMZGgEdb2lpx8vYEaUZv/KFOww+2ud0UOObnIdPtmhlMaPBhDRYam/ZjSR7rRbbwnKqPEo5+m1BObQ0oUECe/0I3+og0pTtluD0pEBZSxRDV1dkWUoDqMqSSknlBFkn5uGtmNwpku0eSV2QF0N6cQAFdTUl8hlRHIGV9LoZyf0e23d3uf1gh1F1jJCwt7NNGmcMkiFxHNPptBkcFVC22N3tIaNthG/QStBOLadHE2wD489OaGeaKGnT29ti+57ExBNGo5y9vT5R/x4vPxvT724xUQ0vj3PaUhMHh/IVxnoUgQzHTr9HZQS+qegqh/UJQTiSUIPTJCohSyXtHcGkDBhT0VIB4RpiHRNr+MKv3qMwEeNnHi2h3+twMrHcf3yb++/e59Ofj0hUQyeLCKakGE9ptzO22glJO2UtbbDGhBAu54aFeXs+8HWj7XKiV4XcYFWbe7zpK++6eJfajljZFC02eWB5ZeV66eXqRL347FUU3HX0eZTeFXvrDVHDGwQ6r2H5m9XVG1D2X5k+Z7l/OeACVpYKzTrpIrerVSvWvNnQAFY6x1p4t4m71csN4H0ZKK7W8bJ94vq8L0WzPHJwqezeMLVZtEtF71VoPp9FhfUq2V6V2BJ4EOfXqwPnujMa1sHFZd38EgNcwIlFJsLZ//NWi/WYZ/PDs868yMFlhJWmsnxzASLODpQM4WIwX62jpRZ1zeB7UU2v2khehVYA138lCoG/++E/8OEnv8A5RyftEGhAWoJoUEkgiEDWSejqFqa0EGqMs7jgmVQG5wM6StCdbUzhcTKQKkMIBvTs4DOlJKjZZt0QAirSFEXNzlafpqrBQ7CB0G/Rfvdt/LjGTkb4o5cEBKnSCCVxAqQQeCGRQs0ssGVDJmJUK8VUEyIniVptwihHxxGp2uL05yVBwt2tFGmji/q7d/82f/BPfpPByZDt3T4/+snPeTku2f5ChtQnlLYEAS0d8e3/+3/Hk9/44lyDODMDnLc9cWYzEZLgNXhFcAoXIqyICXGGbrdh2pDXliKvydIek0GNjGKC7+FKwG0RROCzf/gxe19+gFYR27s9JgePGYzHHD+DeiwQkaRzb4usnxCaI2Q2ZGs75sk77/J3/+4jbFVT2gbnNL3+HsI7Ri/2mboYJyOIBYluY11Dq93jwZMuP/neUwSSKE1Jo0A59qRKoUSFkYKo15odLictBRKpNbQ8rq2ogydqSdCzDbzCBcS0Rt6WREIg4xj8TGsUQqGFx6Ua4RyRVsjM4EtBLQsMBUmvjRk0RFJxevSUbLfPnV6LXqY4ORwzmtZEUwtSEJyjt9tl58E2rb1tTkeG7dtdbj/a5tMPBxw/PabwFVVtCFYSlABhsMJikTRYMpkQbKDIS9768l0SkXDyfMB0eEKW5ngEMnjKcp+dzgOevPeI97/5Np/al7w4PkYmDp15fGEJwSEU/M5v/Ab7T1/S2+nhyoTv/OzHhFGC131Gpw7bxBy/OMZMBuTGYVB0U8XoZUUdHFFcoO0uPgMfEnyaoVolQk2QSeDRl7Zp/raiaGYe0CLpQcQoBFpKytIgkmxWHwFECERa02tJTKaomkDjDFHqqQDZidm616cbCcajit5Om+1be4w/PEFJjQgxjh5RCu3dx3S2+8ApUoEzJelWQFQepw261SLppFzOIktgfM3cf36xyWr/ysPbqllsJcRaZtYp7MvXa2h+ZlkAE2Lp5RodZB0bK8qPuKosS/FuxOUNaSPQW0NX6HU3Xl72CoBgSf1YpXNd5FWKPN9Gbxrvunpcd/+G9Yg3Ci4Wlp0sMboOImyuq82K7lrUKVbVzLX8Lae41FEuLxYw/5X9+cp6WacAiuvctS1aARbYuijzVYBrSVH9nA1m/TeZDaBQzIHKdZnPVcBiGmI+lbV0iQE39/RNS3k2ApSrKJxXxWposXLB5o7MnAwFq3XEHNNr2+PanG/0+MrSXtUuzkHhhYcUsfq15MIytqYHXCfkDR3KWsuzF894+vwZ1lm6qkfIJZPJBB88g5+OMKeG6emUIsxO6jUmEEWScR6QMsI5x6iR+InBEJMJOB3lKGex1uN1QAtP01iEEpjnAxRgjedkmGOsw56dqp6HmG63ixQJrVhwsv8S5wJV2SCMwnuwgK0t49PpzIVt7ZiYkig2+Npjg2IytRQGhPGElsBOG5rGMjgY8+nHB9y6s30hjN2dLXZ3t5hMp5ycnDIYnRISz96vPaQpC0bTMbfv3KLsClbXQV3C4fM29/Tjl0wnFZNRSQiCT5+/5Gh/gup0OcmnxFZRNY7PPj1BzU5SQFjYfzEhaUdYWhAsxiv2P35G784OUqWIbh8bLATP3/7tj7nzxQjjLSIofCMZT6bUJuFkEGjfvcXoFy+JohSnE04GU0TweBmhotkp0ePgiJMOLu4xLSWfPne0dvc4fDFmmjuaJML4gMxiRjqlMCXWO+IkZiwC1dmZJ58qASIwlQGhFbkMTBD44HDbE9LMMc4cIa85jHOKccApR4FHC8lUgVCCxilKKSAIfvHRiI5IaEJEJDxToxg+P6Sz3SVqbUOSUA9KJhPHVMR09raQrZSpSPBZhKsrxuOaT//4I6rKkhcNkXBIqbFSIXzg1GvivMF4iXIxEy/xVtJYw8f7NePJCWXjaWvwLuB8TbCOO3fu86/+X/+Cd373qxycHvHT//yMcTEiNhHDD0/QkWBa5HTyNs+ePefL732RtJvyR//6J0xODeOBJbiauoDDzyZU0wqVpEjl8UHhVUTpBMYrGgc/+LsP6G17dK+F8JrjMGI6LQFoRJfWdp/icAoonIhBzFSM3FrEuKHVz/BeMXUJpZPIWlDiZ0sZVYRSiv1pA1IRXODjj47oqYDQEaZxTMvPEDom6fWZNI7TQQNJiw+//5yDz4YQPE4ocltgJ4baW5TXiO02cTtZHfeumVKX6eYOUddrPFfpKWunkKuy2zi/X+a9vDhLcFWc+Xfi+vkoLN28yrHm80rYq+goC2Fvlt+61Rfz/jmv9bK0DKJW+F3WRa+mFTe+18zFC3V3U51u3Rx7bR2+WXoz4GLOWnZO6+a9Of365koeq+Wf6WjXK6TLtBlNLqYV1lrxr66Fy1DX1P5ywTd14Dlkfn65OEysduYFIPQ5Gs35cp5Ny2/Ww42NL9fK/ab1tgoEF+W7Vr1akuM8RniV9nJ9G53xslLjYs2lWIxxztPasyQWX27m40YD1IbYN2vWN6LgHEK9puO5OeFJKYmjmE67Td00JCohNII4jmm3M5q2JfERJ1IgEcRitpY7SSPyoiJSEoJEKAiRwllPpCU6VkReU6tArDzBz5YzSS2QUsLZ14wgZoehKS9JYs3WvW16ux3G+8/ob7eYthJqa5EBVBKhXYUQkiiJkFqiIolSCc44pBBIJUnTCN1KUKclSgpa7ZRqOqXyjuH+MXE0d3r7XFuI4wilJK12RgiBtKXZubuFHqTs7O6SpenGuXx+uV+axSRpTJREtNoJo4HBVyWd2z2q3AOWSAqyRIM5269iG+qxJc26ZO2YUBqmZUGUSpIkJk01cdxlOjTUwyEur7EjR7SdkaYJQSrq1NButzBNjM56OOcxgwHeGLSUCOdoXEBqQZqmxM5TViWmaXA4zEjQ7WX0dtpksqGYFGgkVJbu3R66dgwKS08JRCuhxNOSguA9bampgyWTgrysSBKFFArdSNICyhh6MqFEgQ0EFJKAdgEVPO0AOlII7XHO4ZoSaw1pHKOEBQKplpi8xA4123tbkMT0OjFCJBAExajEDMaEoKgHFVVRUFQOLxWJVrTiaLa/ooReqsmbEmMsTmjaaURkPVXV0IolkQoEUxOpGBVJsjhiPC7JYs1X/vGv8/5/8w2EFKRJQqQ1aZKQpRkuNMSJxhhDrCOkFyStGAEkmabVSSgLQ6cTcfzxS1xp6LQ0tSmJY4F1AVfnSALJmUMELWPq8QmmNsjbW8g0otWe7U+IidnqbGMMGFNjAU/AAi444lRTlxURjlYaYYODWCKVROiA8Q7hHDJYpJ8BijSNCPmEsqjxRQ6nJZ1+l6TX4cG79zh6+pJpbQnOMng2JkljtIRIKrwpEQG63RZ7T24vzZdLGteK7eSKs4NuoOCtm9av11iumZ3m870CIFyaRmeRrp7H5uOwIBaxGuzqNObn2jWZBsLlEp9Xpqs05Ctog4Hw8vVVoOE8bmBFMBsAxkpO14HX+ffrKABijROBcM7KawnzMu1fIn1+V7RzdJV+M1vzN/udK1RhKc7y/TmJpR9L15voqrHh/OLSTeclf4vx5g4suybPpW66PtMbtYXLhjzfpebls04nfVNtRTAPLMLlw6VA4ob/1owyiwW5KePLjWA5ybN3lzU5V4JN+a3LX5yX7zrW5mp8Ls4Ke+uw6lJeK9fzOYcNC96uldsNeskVr9d+sVhJPSCUnCVznYVkw/vz0kmp+NbXvsHbj9/mvSfv8Du/9Ztsb+/OlvM4wW//s68zPclpGkdHWbajgHAO3xge3+1gncN4RysFbcfE5RhdTnnnQRtBQNoGdQYCrHFIG+jvtfEi4PGoWJJmGnzAGMtO6gnek/bb2JMxDx/fJXn4EHXvHnfeuY0QgiSSJGlEu5fQGIuxltsPdohjjZCzpStfem+b+OgA+fIF9zREukdjWlibUOZD/uOf/Qn/6c/+lP2XL88aXSBJEr7x9a/y7tuPee+dJ/yTb/8+X3j3Xd576x3eevSEL73/xY31cnR6xB/+5Z/w7//sPyGyBqkyrG3R1DFffrsNrkT5krcfJ0SMiNOczk7g3ScCI2q8bEjCBDM8gWAIwpPWU06PGopTxXYnZe9ej3Svy9aTOzyOupz+oqQ51Ox27nDvzg5QE3zJb/837yA6h7QejvjqP7/Pr3yjR7xzQrY34cu3a6hPceVLpD3mTv/srBIFT7YKTJFTjUZIU/DeW23iVoJ1jm37kp1uTGpqusHzjrTElcSNLN/MMqQCax1tHfGNTp9gPBrB1561iJTCC0jaMd80O9iywlvDV6wg9YKgJEILvpYqgldYK7i3Dd2WBCzeNrxzp42pJXUlePxgF1ladNKinlq2W5IPPp3w02cTDj99zounL/lsUPOysNyJp7SlRgP9xJKGgiwGieVhWtAWmsxJ+gnEvsBKS3uvw9udmkiUpGrKVhxoNRX9JOLrv/tV/uBf/aMLpwh7u3v0ez1CCDjv+L3f/B3eefQ27z55l9vt2yjf4t//f/+GP/x3/5nbD1oEXUA8Ies0dMSQEEqKfMA79wTb79yhEY6kG7PXc9RJ4MjmxK6mFfXxpoUfwhffe4K0MVSKr33jCboTiG8r9t7f4U7mZv0a6MgKkcSMKsvEOLpidAGEenaEKixJpclIeKvjZg4YCNxShr1OSreVkkSa3axmcDThs5+9IIyOuftwj87WNiEoHqc13jQob+krQZIGvGqIuoKv/86XFsbWMOtml4ra0jxw7UqITRaz83lArJ35rh5vz3i75HCRzj3Hbjp/4OLd2e9iY/pSWiHMO7VfSuA1KZwxuLDPcIVeTxG+XDD9evHFzW4ubpeB4ZWeluZCbWwTa7LaxMK69ytLysWGvP43RiIs79R8RZrm0+sDnaEvOEe3VwhnWZs+v76SlgNcX6SL5M915/mGtc7ssBrz7G4eUd4s7xVayS+sPt8khBVjzJph6XPV8AbILVYuNhmB1id5HvCaOr4A9nNWkWWO1gzDFyHE8qOL/M4rfA14ek0jyXxbuoGh5/J2eQHmDerronQLhpdF97HLYr74FLyc/g3yWxFJuLy4MfARa95ddLglKBfgow+f8Vff+XtefHZIf6uLPTBMnw549pOnbEcSlcQMS4sUAaQkeDezjClIEVT1TElxzhJjsQ50GqMkTCcFWRpRmYYkVlSVIYo0vnF4G0jTmNZbj+g+ukftApkWTI7HkKVUeUl1eMD4+VO6WY8si3BaUk5my0Niqei0MkbDnJ3722w9uMXzH3+KcQ6xs0t86xbD2tHta5L7I7aedJBS8uDuPf4P/+SfESezA9oWqvcmBxwKCN7zb//0P/Bs/znGNCT+Fiq/y8lhRbulGL08Zf8Xn7H75C5ZS+LrCbrXYmu3SzHVnDwdMjzNiTBkcYRIWmSx5OVnL5gWY7ROabVatPbuUBNx/+1bHH74I3w9IO62ePK1B6gsZzQeoLzEW0vaaTGeTMhkQtrtUFQVaZpgJwmTDyfUCOpRiZV7FFOQeLSWKOGpjSKRhtoGVNQCPN6V7GxFHJ+WtDNB02kzNA4tBdFtietZciXZCZ5cB4SWSB/Qt8b0Hlectgoe9O4z+JGlKSRWKdTQ0wpdjrxle1TTHHaoC0lRNuxmMe2qITeC7bYm2JLxaEgQggfv36eVxdQigrLis0ng9DSnctBWgThARUxbOLohIPGUNtBKQOAQaYatcnwNidSEoBGqoW4Kkl6PrZ0Wg8MDqmaKThKkaeiKin/6L/8R3/of/ylCXWovp8MBf/yX32H/5UuyLOXxg4f87td/m+I0xwbPX/z5j3n+7IgkiUAGkizixScHbG31GT53nOyPuf3wFmqrhw2Bjz58STcVOKA2HmMtWxJapmbawFY/ob2Vkm63Gb04pbUds/P2LscvB/R7bU5+MmDyMkcohXEeF2kGuUO4Eh8SJJpOv0fkHZGEQe7JWlAlAYfHC0lPedKmoDaQiEBVR8g4oywMUSyw1tO6dRtlSsp8gBYWJxU+TKA7RWp4+PYDvvWPv8kffPs3LoeXuXngfF6ZH6MEzJ2Ru14JvREtD5zXWqyunnwWXNVfgIdZ+I2K/VI5wrm/3bllrytx55ZvXx6SvCiJyxUOl8P4wlLi/y0pwOvmnmXa9O4q9fJcjK9ZZB/8GRBdmMhX8t7oTXJjc1l7JPNmw988zcmq2+luZv4a+vzLom6gHM4+68wCvcqyvMs05r8mrCZwbX9dl+aKPne1unpNagtw49o0rh1wbiCkBeX+UkF+bah4ZsVZtVQvy0UsXV7TI69T1JfFtWEcX1Fqr+kvG/NZKd6c/D4XCLukBYC6bjwQ14jugrelMAsD2Lp+MI9qFvvajfLbRBdeU9ZL+sb9bwVUzJRh4Myl6/y7wHRSUEwrirxCIPBDi/WAVOQezKTC20Bvr4cPMB6O0UKQqIjGOMrG0UJirCdISWMcmXI03uEDFKVBiIBpLKYxhBCQTuCNJ8QBawL5tKaqLC5RkKUYIfE6oq4MdWXQogYliEREUxu0mp2pMBkXWOOoxxVFJ6epDc57YhUxri2IiOFwTKyHhK5BxxF39m5R1TVxkmw0hC0Le7lKGmNomobheIT3Due3CaOSYtpQTT3VtMZ4mE5rklaKyFLyvEZqhXFdVL+HH9Z462gc2GkNnRgRZXR6MeNpTigtxeFk5pFrVCBFhQyWZlIwGY3RrmY6neLzBqkV06KkaWrM+JBpp08lAkkSI+w2otNC+MD23i3Gh4LBsEBJTRSnmKam8YFOr48raorSIwSkkaLKLc4LCiuYTitM1qI0lth5BIKSwEhKZKqYCg+1oZdYhromTxxD0VDiGOkIL6EtJV5C1QTGAYIL5I3ABE2UtTDNbNnONLdIbyhrj0g0o9MpIw/pzhbNpKCoIyZOoqIYKx1CSKoy4BHESqK9xFqL6iRI5amCwAVN3RiCBKElvvG0+j1CknL4YkRlm9nyPQfeOr78/mO+9i9/B6nkpVIoAtNiStMYpkVOYxomvSlCCLbubnF4NKRpDJNxQakVOpHkkylHnx1Rjw1K7pBsb1EhEcZzejzGRzFT2yCFYNA4EJLMOkAjtWBaGkxdkTpPkddUTUHIJHVjGI8rVLeNParx1iOjCKESQqjwxAgRg0goq0DlDK0kQScJDktdVdhY4UIgA6QJECRBSPLa46uG4AIyihFxQl4YaCzCC1xgtqlez87XkEpQe0OeF3MdiLPTrc8GmzWHcH0+43tg1eHMq9DmuPOK4rlSv3Zp7RI7s//WDMDMg4f1HMyvYlhRWMX53Zz175dNVxmuroqzKcyGdxfG4nDF4qOwGvX607DnHl11sNWGdBfSfk0D6IIldJmvN6QH/VK8RZ2DgXlFN8xpN/PbpK9cMyZWLm5Eyw5PX5k2ZneV4r2Oh1fIfx22WXk29+LC+fY62Pnqpb4ZpxtHn6U8l4DF+fUmBf8mNAdCLprSRhx3k453DeoR81lsGpmWNb2r8psLtjzAsOw2YInFi1CvX7ObAMlNE1yW1izNsPDupml573l5dIizjju3b2Mqw+HhCf1+h62dPodHhzSm4e79XbZ3ewgJrXZGtKc4/XTE5OUA6pJur8tkXCC9JdKSbiuhri0Ch9SgtSBJFHEK3jmElsSpBj87UE5ridKBum6InGZrq4PwAlM7Wu2UTi8ir0v8tMDZiFaWgdS0sgjRTykOQMnZ+vwk0fR2ujjj6GYxdeNw3pNkEVt3+0yHE2xek0iHiyQOQUdkWHNKZjpkWUYmYkKAp589Y2d768JqtHyi+nxDCIu3xHHM3s4ex4MTrLXstLs0cRdTDEi0IpyWtGLJVr9Ftx3jmgLZ7tLrt+l0ewxOHfnLU5g2aC8xRmILw15XUZiK0fSUfrRF1NaMHQRT0G2BdTFNHUhdxO37W3Q7KeX+KTuP70Msyac5onAEH3H4vERXgV4rpbIpbtKwfVtz6859BPsMDo6RVY5AEyEIxpDhESloJYm8QbViOmmML8bsdltMXKCyNbdrReEFXgp6IdDyCiEhQrB7lFB1pqh2m51S0R+D1pogYC/LsC5CaE02bkijwEvhqINFlmMS4QmxxtdTolCgpUBIiTY1WivamaAlNGLYYKnRAiLp6LZbFNrjqoZWcAQUXnkSKQneIE2gFUOaWPKqIVKBnX7E9r0ezz49xjQF/QSynZSpb0jrmG//j39A0m9dAIuTwSl5WdDr9Oi22/R7fdIk5vb2LSpXcTSZstXbottrs7W7QxxptncTPv3xR6RaIEzN7t02p8c1rXbC1u2MwfOXxEGSCUddlcRBIRF0pSNSmroOJJGgGyl0q02WZIRiiDaOTqdNt5vQvt2nOa5oqpqsJSkRjMoAxhITMEqSJZK2llTVFCkSbm136dmGo3GBCwKNo6cMNTHO1kTSI3WbWCj27macnOaQJiA8sTM0wVC7ikgqpFJs723x5L0nPHp0j/WIffNc8Urr2ecHyKuAxbox8iaGxQ1znWDVTfjnpfM01xqUFqz08/JcE+4NUAhzBs/rvjrcBGCcB1xOa90Et442qjqX+uzGdrPQRrgIvzacmPt/CVTcVFcTN5XJLwkP/lLAxbnAruJ5YwXcHMgtvF2veK0uWrp8tS7VsOZqPuVz/1HzocTa3K9sAGuBxDlg2ESLmvq6NvG5BpkNCHo2yKw3o16WOlwq/evw1zpUfFOcthx+Ib0FDuaezKSzvnOJC34vMtgAesSaq420jk9WAcrC581X6tRnFpTr5LRCYnF8mv+GfdN8xfpJ7OatbbEi/vaHf89Hn3yM955u1sUMApNJTpYl9O62GJVDnHPs7ezyB/+73+DwxSm9fpujZ1NODn5MaGVEWmDzEgE0teHWzjbTySnCe7RQKK3QjccGjxQWYyygiLXENY68biBE6EjhHPggSTstTNUQjGcyLVHHxwxGBU3jkJ2EcO8+dPokWcpOp82hEgRvyRKNFLODzHQsQUm0EmilyKcFtmho99rktaXfbzFJWtQm0NnuIAYF+WcefSdmIGv++M/+hKIqaGdtfue3f5s7e7fY2PnORBuWXsQ6InhPCIEklnjlEN7Q7rVxnYjRWFIOc+493OKDD46olUHFXXZ2Ukw1wjaOSEmMcSj0LINoiHHHxK0Jqi24+yu/jjgsaUaBCEfjWzhjGD4N/Kv/228yaca4wnBr6xYvDg8ggkdvP+HP/tcXnDx/js0bVJxRVQ2mianHCVI29O7u0N3toooTXj6f4iqDIkLpU0Id8AFEojllF73dJdtNsXlBUzuQEWU+xYoMEUXgZietB2fxwZEYSeEUsU5xY0t29w5MJ9jKoJFUlUX2EpyAlpNokVB50EKiYknwglanRxKlnL7I0U6DC9T1KZnr0NlKSKqaoXNI07AlLYk1ZDIiakPiYP/UoFWEzacUzRjd7ZHGEU/eusNP/ssMEHZ2thm/eEle1CgRaPUNY31ESDW3791j7wu3LxSuDz75Bd//8Q+oTUO33cGHgBCzQyLzJudPvvtn1E1Dp9XFhl0EbZhJlOHLI1SsaXUisk4f++IEM4XukzaZUpjSErzBGoMJgnaaEKezLytSK7wzlFYjBtBUhlv9LuXJiFjEyG6Ejlt4IqxzyCTCCEkVCbTS3Om32J9AqTwP7rTxTczhac2kHPJwr00kY4pJBdWASlsqZ3DOstWOUa2YtN/h3a8/5vbEsP9sRD2qceWU2pY4DXvbXX7vd3+Pva8+ZGtvh0eP7m7oQJu71tqR7Hwp0XUK5KvQ1arIL4fWpD8/tS5b1C/m1JvOWQuJvRaHi/PNTZT/EFj0uLvJILjE3zq6sNuKhbkc1uGt8zZxQ3rlup3Xc87X2Fxj+ryRzVlc8/7z0Zs9ofsGz9eV4ZWs/CsNdlm0l4r3ZvA5j/6WnbWt6xPz4Rdhx2qa4TU71VnjOUPqQoilz5WLCun6pF+/hWw06KxRuBdx9CIt1MYvCRGvAyYLdXGl5ejV5LPQhc/dyL7C2r5lgLLJDd358wUwd7bxbvZh6Oo8VwHvhnLepPhXyCiwZE3alO58QzgHM0JQNzXPnn/GJ88+xXlPV/Wg0AxPRnR6bfygwUcGYy1CCIyv+fLX3sX7wPf+04eMxyVGKMpJTdR4GuOQCo4PJuizU7ArE/BVg2k8MhIUE0OkJcYYBkOLRGDMzI9NUc8O42uM4+TlmLqqaCqL1JKqqhFaYsqGXEdQWHyo8UmCHZZoqZnmJemkREtFkdezeEIRSYGpDcZJPvvgBUkrxdSOl7WiSRSl9zRCYUTC8HBCYyWnw332aFM0Obs7u3z86Sfc2bt9gwq7pLqpefFyn+F4hHMePx7ANFCWNUkRcZxD4yXVqOR47HBpm/Gw4eMf7/Py0zHeWKomYInQaGzQ2Npi0hojG8gC9HcoBRipIcs4GjqUD1g0x4dTPvzec779P3wLxEwZ2X6wi7OOw4OKycCQjyO0ivjpz4Y4U1NaQVFaOhOo7GyDfJzdYu/9XcLzIUJVVHWKcyUemNJCJRljC1ZHiPYutqmAwMmWoLEVxoHUmkEwVDJAJKj2KjotgVUW3Us5sjXDJuAQPC0sAkXeGDKpmTaastYYFIfjitQ3GKfxUeB0ItHpFgHImzFKKcqywtUNtYnRMmBsYOpm+xRULNBSMDIZSjmqerZcSsoY4aGqDB89zek/ukuRNxwdjCgqw+zov8ALNybWDWlH03prixfHL3mv/Q4E+OjTj3lxeECe5/R6fYSQjKdjhBcUdU4caSZ5Tj+9jRvCeOjRkeflp7+gsZbGNfRv3eZkWGFkhq8EH/xiSNkEjJMIFJVqE4TG6pjTpkYXDTqOMEZQeY2cQjG2VHlBq+upRxU6Tjn4eJ/R2OKcIJCSG0OjY+rGc+pbkAZcEBwMajItIIqom4KPn02RKNy5Jy/hqa2l122hO9tkO1t4BPv7E5wNNM7TvbtLgyN2Y4zzPHrvEW9/+yu89db9WccQS16T5vYRrKU1j9ctH/ql0U10qrkibB6yrzFNnxmOzsfoq7/WvKKZ+/PIKcxpFzecsi+nmRvqQdfxJxa/SNwosavAz6vQsi38VcGwuCLAsj7xSwKynx9cvGIDWgs4V0zbN4Hy65D163BxblGee3zepi9a61UxL++W29VNmvgFiAiX97M0Xr3G31S7Xp/qFWnPCUIsBxRc3dBfLfsNAVZ64pW0AOCukdYyOFgd3c8Bx5p8Vq6WeV26n/+asjL3neU1PymeXZ57yVqIv8TeBsbWPt+MjWeJnbfRM/yzGnAFh18GUEqhlSLLMowxaKmJsoSjvOZ0MKX7Tpt2t0VV1yiliOPZ5mYhIE40WTth++4246agORoihUArSXu7jU4iDj46AOcQQiAFWGOQ8rKepZx5tpJaEqcxIXgCYJ3HeIuOIrSOsc6gtEJEElEJQvBEStI4C8HhRSBTGqMsaRyhpML5gPcBiUAogZKSuJXMlk11UurTCc4alPBESqC8JUoi6iJQFxXKV1QDiWxL0jghjZNFpC5AXPP1SGmFUopW2sJYQ4Qi8glFy6AltFoJ0+EEKRWRFuAswRlkpGgmUxAgRSAKIPBIEYi1JG1lTKczF8B7D3bJei2KskIlAlfWuLLCncl28OEznPl1VBwRQiBKIyIREY8sKpIkqcaXOc1kgowCWEU9KGgmOSZodm/3cCZCRh4FdDoZ+s4tiqok0pJKdKgbSZE7itMRPiiCjGj3M8oAvW6bQ1MTW4ePJKkPEAKpl3SdYoqiJWIMko6KqUyBbCxZUFRAJ1IUwRNjEVqhHbS0pBCSYAq0UBgzAzDdrkQSUFIQSYHe7eJLT23CbLkejrKuSVsxGk/SSUhbgnaaInXCYJxTlTUuePr39nDGUTQ1ITgkMzfJwgt6aYvW3V3SLCU525MTmC2Dy5KUpmnIkhQPSBTtTgupIUkSqromTWNMrEkSTxxLRp+VSCA4TxxJbMOZi2GFkAGsASQtLYl0zHFtiFVA2kAkARGQMiCjiKQTU4/HOGOItUZEiiSLqIcWjSNKFMP9I8gUadLCmxwpPJGA2hq8hFhpSmfJIjVzX9vM9plIJO2dDk3lePKrj7AuRqCYDnNGL44pxyV5HWgSQbzT0Lmd4ZUk62akabzYUdaOheFyLL2x/rjG4jbfGd+kFXjTYHwjy/S6iKvpBHE+pl8V9iqD3fXZrCQVXkVxX8prLo1VDpfm6evUyU1yE6zIfjPee8Nocw1Pl813SWY3aWvnkdfqKGvq4FXrcwO9UVe0r0xzSvUlzTWKFb1LsE5K6wHLUnpraZbWZl1rTQ1v1K7PrlYGgzN+z+MuoZOFT3/LxVt3Ha74nQVcWff3xhX6VQobb36ZtLFC1hbhYrneyjkm1wyc57+1QcNq2Ll7ERZrRKxU8hJ/YgYWVqr2zIpy8ezM7d9s3fXZ78ZA6erCznN3/uSi+GfWaAEcHh3xx3/+Hf7oO9/hs/0X/P2Pvs9/+JM/5Hvf/zv2Dw/44z//Dn/4nT/h2fPP+P5//jH//n/+E/7ur37Io1tPYBTBOOELT96lHXVIZYt7jx7ze7/9e7gjDccJW3qHg08G/Id//Vd89zs/4Cu/9RZvf/EeX/7Nd/jv/9//kre/8pjgLHhPXzuGz09QWtHtxOz1U9JIkkaKLz3sE5+5oE1amjiG4D2mbrh7b4uAJwjB9k6X27sdnLcE4O7btxBCoqSiHUt67QipNDJOuHWrC0KipQYpSToJpp4tIdl9sI1xfubyNI25/85dlNL4ILiXOcLBZ8QvPiYeHnM7VaRxD9soWk2KcIHJ/pDpwZC3HzxeAzjFYrtYqDvQUvONr3ydtx+/xTuP3+Yf/aOv0M4yJIpg4e17GdZBQHL3Vsrt7YxUBGxZcDueErzEeUGmHFksMGG2cfZXHj6BegvZ3GIv67Dba6OlRErJk92AVBqEItaCybNn5MdjOHMTfD7E3X3QZns3QoiG8fEx97Ix0gk6rRa3dtu0GCJDTTE4pTt9xssPP2Zy9JLxZ/tUT094/lHF6bHkW19/xHgKZSWRKuLtxwq/3WB6Db/WUlRVjZQC7QJfLB1OgMXzpZctdAykHiEaflPeRWqNt55fzQOp1KggwHm+mTbEQqCd5367YefRNrKX4lPF+w8VKIWONZkwaKFxJsG7iN/8/SdkvQhhC1Kfo7XEhYhRaZD1AUVTYmxFSo2px5RNQelK7rVLRFRgyyMSOSWKR/jWKT4b8ZZq8+677/KFd9/j3Sdv8+DOvYtaf/+d9/E+IJBs97d4sP0Ec5Lixhnf/NJv4Uc7hOE9OtEtHj95iHUJVS7Z0QkCgVIa5Rreent3pg0oyTv3Y2QIRAhSAQ9UQ1xBUgnuxJYokSACSjpudy0yVqhEcacjKCdTvGkQzvCF9zo4d8xk8Al3/SnaCuJc0ifl7axBOIu2jluixBY1VWmpasPOlsV4Q+MMezsZD95+j87td7Guxztv7fLisyGHhzmRb5gOp5QlTEaG5sWAz/5LzvhAE9Ph9HTIf/gPf85f/MXfUZblXC9ZGg3XAvY14/O5a+75IXyd4ewNz38X4/wCM/Pv555dNT+9Rs5XJn0eRKw+umGyG9+vH+OuS0MsvDufI6+Mew0vV+6h+GXSnMDDxd81+nLY0D6W6RXK/KaK+0vZc3ETusoD6GKLnRPolXrgzc0F6/NZk+JVy1/Oos5/Kl3ccjuPBK6hqypzPvoNLSuLO+mvz/4m6V9nrRHr3i3n/9qN9oZQ+pyXlaBiTjcTy8EXrpatFVfT1durNls6rrjbsPzpYrkUi6eKzq7Pd3IsyinMIi7eb6I1OHrt3ZkcG2P4q+99j+f7Lwgh8ItPPyZNIk4GA3a2tvj7H3wfZz3WOT764CmxTTk9HrK926fKDXHIwFo+/uELImLSuE0atfjBdz4gFhm+qPn0h4d8wiGH+yfcf2u2Zvr/+P/4LYKHFx8e8Mm79zl9PqAajHn2fEjayWgmFXUNwgVqZ1A4fnZQI1TABIduBMoHpIQ4VrzYH8wOTLOO6bTEaU0SKaJEc3o4PrM4C3SakTcCIRVNXvHJ0wHOWiIdYYzj9GSKjDVxEnF6MCJJYqampCorDj45on9vF6Rg/9MDtAr4siFEDUf+LlnaxpcVEyqyRiClYnI45uc/+4Df+J3fYLGziaW7pS4mAg/v3eP+3XsEH/j0gyNwIyIliSPFR5+MUEIiXODTX5ySxgm3b/UYH51wUqRIEdBSIXt7mDKHxtK/u8VHz6dg2vi64cVTy7bP0QJMUfLxgZlZmb1Hpim2FTM+GNC/v4PU6qLLDY4LxqOcOPG0MsH+QYSUFo9BdGOSrVvUkxLfFHw6cCjhwBvqBka2jXGaoDv85Q9KgtTYxuLTlOepI91S+LzgxwkkSlD4gBGBDxJBRAAp+fBuzl6qiCKFKD1/516SCo0Jkp9nktQEYiQ6CH5exaR4vHMcm5S7vQxVBfARPz/2xImmaSwjE9GNFa4M5GXB9//qE3Yf93HTCZOxxNSBICTdrM1oDE0xxiNx1mPCBBNABsdAwoO+YPwix0Q1XpekEbTjlDtffMT/8P/8vyITPfMaNUcff/oJSZRQq4bxsORkEJB1RmTb/N13XpIkO6i6JD9scVJPIWiqcclkbMiSCJ1qytLz/GAy6xMtxc9/MUYJiAAcnAwkmYW0gaHVKAoQgjhNGDQRaeYBx2kdCLYiaQzeGD764GMSUTC1YybuNh3dwkwDvSTlIAfRlAjnOcolvUQhQ0CaQGk7RGpMnKW0n7yFiHq4esThzwf87AdPqW2DDVBMQekWsUpJlKdA44xnfBL4+z/9gJPRPtMqp9fvEHzg9779rYVOczHUr5vn10056zrcFfRalvnlNMQmqHNTulnMzTPsNXPvplfnCv4VVv/XlcsNtYFZvZ7zMR9HLD/YlMBrsXfRtt4UJJl373utTrHUPje6sD0Lu+hhci7ehe//16c3AC7WaZIbIPzca7F4sZSSWJLWJTrbLOJ1WuwNlftVBq5+H+aVvXkO5itkSem8TuFey+ai6rgYZrn5hqVGtSnNDTxd9e68s9xMW36jNL/X5eZ+nhdbSVgKJOaerdbhzUmccbUWYYVrOvbc4HuJCed5uhwVLyUwDxSWQUO4+H9tduGqvrPA0uKDdRYyoCpLGmMYDEdAoN1pUVaCvMwRQuBsoCzL2YFeKlCUDfmkAATeQV0ZvPe4OEPYinxagmB2EF5jMLXB+YDznqOnh9iy4e6jW7MJQwkmJxOqaYVuZ4RxQTmt8UFiGoeKJLnzOBuQBAyOYD3WOiIhCEHgjMcoh2G2rtvUltw5qjBzwypqA0Cr08KWhiZ2OOPxiaIsHMEGmtrNTnauDEIIbGMxZUOSJcRRQlM1AMSJY3oypSwa0l6Ca2qaumE6LglJiQsRQUY4X1M7iQ2WyguKsrxsDQuHp1y2vPOh8rKlzf5KAUEKJqOKfFJTTBvKYUGRGywa72E6rimpQMdn+UfUTYBIkReGsjDorE0TNMPjCTZIfFAUjUcOCk4Pc8rxFO8kwggaLygqQ//RA2zRLLa2AONBRVUaJuOakLawoUZYRVM3uKYgagmifhcpAtV4DCrQ6iX0b/VpVIvToSVkCaVX5FZTuUCkgKLEtxKMVmhhkQrqALkQOAK5BieATiDIEhOl2KomiDbTEKgSQav0lN7SyBgvFCpIqlrQOEncSxgXntILvJNIB7Z0CBFhQkPZBKrJEJxBdca0XIfQbpGYQFlZSucJvkHLhCRLGOcVlTEEJQhCECQYBONJiUEgEkUcJYRuRPv2Nt0v3CVqJXN2gkuFc1pMGY3H5EWBmQqU6dMYx3AwRUlFHEvyaQOhpBg7Dp6OqIuSOK5JWnLmcMBpOqoiLwSNr2kmFY2TVNbTeEsWUoSMyWtHFkPa7VLnNaWZLaFrxg21k3hncY2B4ZSsl9JUhtG0JAhJ5RWmAuMEtdCUZYVB4wiUxpBogdYJ1gTKytMETZymNE5w9LOXHD6fIDC4lsCrs3NggscrSWNByllaXnrwkpPhKdXf7ZPdyvAhMJ5M5wfShbHsQq9YOD16g3p4Y2Bx2VM/N105+a4zcb0CArqIse5chKu5vzznYoO5TLx++Vdx3eXceKM0lxT88zl/UY9aNNStS2MtM1cxu1YVeE2QuQxmN2IEsfxgztC6Hjxcx8rrHBmxTG/4y8UmDXqJVvrtlRr2WYiblvZVpfJqnfAilznf2DfqyivA4MrLlbDr7OPLlurFd5dj5WuV8AInnYOby4QWzsO4Rtzz4/Xr8LJS7zfo8KsHAp2HX6d+z5+iso67uQxv2NkvsxWbeV5S2gXnk8S5zK44FOk1aMU985pJYU0kvPccDY4AuLV9i7KqGAyG9Ps9tvp9Hj18QAiBLJ2t+6aB7d4WcRwzOJrirGNnp091aAgNbG33yVoJo6MCUxm27/apT2uaMpAojR9Pme6PKWtDWwhccGztdKmOB+z225wMBtRNw97bu3S2O/RvdVFY1MGAEAQBSbeTUjc13inSTNNLU4yxNI2d7Ukg0BgDUtBOFMYG2u0ErQSEQFXURFFEq50glKYuazIsOlNUpqDjPaaXcnIqqUtDks7OSkDO9jzcf/8Bh784oLfVoXe7j1KSpN9mfKjYvrfFdDTBG0ciId3pMmkgSTTTQqMbx3a3S7vb5fFbjxebzIy9y8qZaxzralIA9x9v87N+QjFNcaMptCR57mbTbDmls9MlJBLVaCanOY0PKBcjbKCtHL07HWgKOsIwJVA0hm5LsrWdcfjJEWnkEa5CpR2mhUMFQ6YaTqY53eMRe7e2Ltjcu9ehv93iwRNHnCru3u5y9OmQ09NytjZfOOxUcue9e7Tf6jE6nTApAu0Uut0UhCWKJM3klKmrabcEt9sZyVbGUHjinS4qz3E6MAyeLWZfBcY20BB4r/cEV/+cIsR0BMgBjHstcmXpyxkQqLcV3UyTSstJaikby04rodWS5AMPvqHf0xTe44Knk2i0bSirgAyGduTYupXR6in0bkL82YDngwnWelIdIYUgVg2RcHjRYCNPS8bcaaf02inRTpc03aLzTptGerIs5eGDu5d1LMA0hsPjE9I04f7de7w8OEX6jCyKSMM2+IYsi9ja7lKMJc2oZvrsOeNBDd6z3YtIVIozNZhA0nFsdVNwgSzTDE5ylIbGOCJh0FKitabMKx7c66NSKPLZwZRxHAippAqGVIFIY0DS3+ritORllJBGilQagjJY6UlERKQsQUdMy4rgS4rcoOMe3XZEHHuCg9sPttHNlPzoECkVvURio4bKg1QJwlQkOqYWipb2CGnxWUJRWrI4pclPyK3l4f17PLh/h0tj3Wo/WWtICZcAfnMv20SXg/75rPO6lvqN4/SCXevy5pX3awaWvjAsCuPK6e6qrBYivim4dQ0gmKPlECvVuMY++znY2szEuTH682rsN+UvLF2vK+M61XFZJ/+cusfnBhc3qpv5djU/OV4sKbrCRCq4pj2uoua1FtjVoFfHuSryutHoCro492M+r5s07OUs54MtWDOuslkvKpYL0ZeGkuVB6XKourSULcda1LUXU1nm58q2OiePedFcpBaWZLAwqF4wsDnRK/NeY264SEEsTTCLJM7CrJTuhoPWcn9exh8Lq6TOboRYFNbVtb+akVi2hG1wNRJC4K++/5d89vKz2WFcrR3yYU1RlLRbLX7zW9/k0f0ZuOi3+vz7f/1HnP5iRMt12bm1w8lhMXPf2d7C2gnl8QB7esqTxw8YfzBhcjImT08ZFjCe1Ozu9WBaUxYRgZjBpyUyK0hubxG1Ej786Od8mn+KdY5e0iF4A87hyoo0lQwnBoKgrCu01AjhqBpHomeAwThHWyWzTeRaEytFt9vi+HCE1IpepwN4XONRUrJ3e5uj/QFSQKQF5vmnuAbqSLHdUoxlROUbnHO0+12GxRAhJXESgQvEUUQiJLY2VNMSHzxZO2Wyf3p2WF+YrcmvPE1t6Yg2u07w1vvv8sXf+RpP3np82YLDcu/dTPP7uJJMEwJ4AqqVkDo/8wDlA2VesnUnJp9M2b7fY2835dnTirKsSbGk/Q5SBsaDEbNdGz0aHzB1xOnzU6pmVh7lpninkBIiHfH3P/qQ2xg+PBrwtW98gS9/5W0Q0Oom/NP/86/wyQcnpMnMRen/8v/5Af50ivMNykhcljI+rQm64ij3jE4qpkdTdDbkNJdEWrG3bUm2E2oHVlf0o5imMiS9NlskHPoSh8d6uIXgVASMEuxtbzOQgspNSXd7xB94Bs5CpukOPVUImMIidES3NWHkZkqwcGPyk4TJoEKjuK1KbBzjXaCTKMZNOlMeVMR4dIiaCmQSsftOd2btLwuEd2y1Yl5MCkIk6GaSIh7jlCdJU97a3eX++w8oH+7xtX/6NUQi+ezFAa0s5a23Hl704aZu+JM//wtOTgdordjKbtMcZ4RCEne72LCFszVNo4hp8cEPP2FwMiWRNVvbJWPjcI0hFoKQ9mjqKTSKTrvL8f6YsrFoD7WT9DsduqmgmY6ZNpYkjdh7dJsXz6aYpkZ4x63bWxwc1bhGIiNF5/Y9xpMK52OqKKbs3SXLMjQ1Kq/wMuBNye3bWwyspi0EbaHZP2gIUpPjSLRl++4dmsIxfnmACxVJ2qFspjze6zNsEiZ5jbKeSDc0IcIjuf9km2djS1HUaAldvcWkbjh9OiUMzdXj46vQOoVho33q82lorwZIzhh7HSvea+j+m1zUbwr9eehS6/g88lzVppfn39eisPDfYjJhlstrA4ubq5lvOvLnxoG/tD0XG93L3ggoLKKLdVGW8cerSEIwp09e6zFIbGg1l6r2dcrdhXJ6riAsIMsrGsDZqxWFc4WXNfldOQKuprlwstuKnnwJJy7DLR/qtlrfrz7GrR74trqT4JyT8+UiS+VYuBHrq+4q/pYCrh0TltDGPL+rEuBSZpurYy2tpCTCmRVk/u1SKa6xoMyZUhaCLw+IAKPJiP2jfT7+7OOZciiOUTZmOBxza2+XZ599xm9961tA4D//5fcpRiUiKIpJzc9ffEw5bggh0EyeMnxxwuBwhLSWp3/zDFsFvPeIJIE4wwbN8UFOJCN8gMZ6pKrweY0rKkxV8aP/8l/YtXvUpqFfdmDfMTkeY4pmdnqzF1gXsEJQ2hpnIU0jxnmDsQ5rPbbx1L7GG4fzgfJghACaxjEajBEBvAsE53j24cHsoD0k+ajEWod1nkYImpEikgqCpMwrVBrT1AblA5/8wyfoAFXTUBVHSKURWYOzgaNPjlE6wtcFJhIcvZzQpB1q64nTjCIv+Ppvf4vbb91dantLwH/eqho2f8P89INjirxhOqpIUsWLY0vjNRZB4xsOXw4RWqGGEplske3GTJ+fUiJJuz1OTyaYxjFqUqQXqKjP/mcTRBxRO0VMRMkWsQXjNIXIqSYN+Ucv6O/1SbJ4Bi7O+Ov2U776rQcQ4N/8Tz+FNMGnKfWkoVEZphQMh6cgIckivG5RhYbQSAwSgeSZDUjvKAUQPMenU0yqqUc5o1YAGSgRpMHzsYYTGagk/Ew9pdP1TMSEKOkw6JWMT2rUTpePNKAF48qQBEnpNEYIjFa8rCImR0Mmjabfjjm1GmEMwQv2T2oCChM01nmOckP59AWd21sE6QnbGWoUkemUUikSZ2Ztse1IugmqHWj1t5Dv3+Mb/+zrCCVRkQIE/X6Xc3e+5/X74uCAo5MTPvn0GVmW8slojLZtppMG11jKfEzRaEJV8MnfPsfVFYEIqQ1HkxKnDO1OC9pdYhXjxxXjSWD/xZSiFNiqIjQZUSIQaRunPeO6pDGQtlKeHTjGA0PeaKIo4XgsGY0M3se4bJuybihyx3hs+GxoqFSbqhHY0tNndlK59YKhizFKY4RnWEuCVDQ2omoMSadHXAYmwwG28UQ6pTCObpoxCF3Gk5yi8rRUCj6goxQpAz99OqEIHodG1hU2WEAyPMn5mz/8B37t938VoVZ92FwYkK5zT7u+K659Jlbmh7mbi+kgrISdf/PaXzpgvefypQll/fy8GnGtce2KiX3jnHwlzY1gV8joRjK5aabz6uYN41yNwS7n1De2CVws/T9vmV6uwJUs1/CwUZ+Zo8+Hhy/oc4OLTYr5gtJ5rs2HpRAXbWlJwV+Q2+UyjvN3m/O64oVY//haK+DmbG9O5xbn87IsdJ5XOJhmmTGxJJu5V4vHQJ930Mu/K8ndsEEtQ4oZ+ApAWDugvY5hY95auymN8wHvuvSXod/aYxVfq3KvgKTLBdgQ5Dzra8e2866zNtDKrHajye/i9gzcrqu7SGkEgjiKEEKgvCRJEpSSxFFMpPVFv46iiFa3RTSakCYxTeUJrZnCffjxC0Rl6fTaiLqhMR6hHY0NaDXz4mRqjwwQC0kIjnpuQ5kzlt52l9PREXd1hPMenWhkKmeH5WlNCAatFMZZtJbADLxYZyAEtFZ4D0oJvJ+5qk2iGf9eCmxtCVLgjMNYh44UwTvwYIyl08uIk4iqbLB+tlcjVhItBb12duFiV0WK4GfW6Mm0BHm2eTyJcMaA9wgl0FqRtWMapQkSvIco0iglKfNypa7EeR2ddfiF9rxsgLiozEAUK6JYobQka8VoLYm0wDUWIQPCOtJ+G18ZCDWtdgetJVoGhHcUk5xEeLw3aDSxkjRVSaYlUZTg64pWK4GyxgaJCDNgVg2n7N3ZJor0RftebppJrEgyTe92n1oa6sKBNSg8CIGWoOIYmobGe5yzoDTOGJrCQNZCiUCSxiBB+9mG4FgJcgJtKZkSSIQkiEAsYlIShIM4QNxuEQ8qRGHIkhSlYeo9SkKkBAGPE8xcGbuGOIrptiNS4bFTQ+MsrSyiLA2tToqvarSSNHlFMJYoUqSthK37u2xtd7CNZfv+LvmkoH87RvcNg3xAr9envd1FpdGChVMKsaLoaq1RUhFpTRLH2FgT6YiyaGZug2PN6cGYejRBikCWKConcNbS2UrR2z2ydoqwCu0E+ADGIAQkqcKMa4KzdHodjNLEkUOJ2Wn3/Vtd8BZXFmfjgsRbizcNcRKjlSM/HeJR1JOcTq/P0fEILSXWWyIpqIMgTjU6UqgsAWOxpiGS0ITAVq81k+G0wDYNsVY4Z4h1ys6dPuNBSVNXxEqjtaCVaUZ5hZOOuNsiyVImhUE24Sxfh1aSkxfHNNOKpN9aMzae9Sc5Q3Er83HgesCxhq7cc7dMC51jQ6z5MJsmjjldAxb727khdSPwuXh4A3CzoOwuPn99SLTu6bK1b0O+8/QqRrww9//nxAOv5B72VWkO+IZwTau6iYzW5vFGxHBBn98VbZj7LT9bvVnbR9epaZdd40xxXcjoDdTczEfo+pQuXHueTYrnM+M8cwvI+jqAEi7+LgQ/15+Wi7b0C0u/i7yvynqNuC4lGW7E9zKJ81QCc2BxLo01yb2h2lri4/rRYqWUKxeXQrl06zpfV+v/Qbg8l2RTwa6yGglAhAt3rpuC/1cjITg4fsmf/vV3+LO/+XNOB6cXr9pZhwdbjxGnHTjt8Gvv/xpR0GivcLVju73Dn/7rv+ZP/vV36Xe7BNNGmm2wHb70a7+C8y2mp55b3Q4hN/hhQ+w1d/YyKhEhkjbbXY0XHoA00ewlBb4pUfWUTvBIAVIopNDsuS5hEhOVXR699xa7uzsoKaiLkt3bLZTWRFHEVj9jZ7czmyRDoL+bIpVEKkmnm9HppBjvMN7x8EGfBEeSSNrtmK2tFlkckWjFvcd7xJE+iwvtnYwgQWnJzt0OjXOzEVRLZCTQkSJOIh68exsfAkiBjDX9Wx2ED3Q6be483iUAPnh8VXGnq5ht1lC000CpC/7sr/6CH/z4h7w8PuTP/uYv+M5f/wWHJ0dn9XX+39Kn9rn2OJyM+Iu//Wv+9K//knTbE8WaKFLYouZBVlEpi00CnVSinUFLhWssv/XtdwkClAKqEc3RIWloCLZmV4+ZSCgUCHLa0tJptZFe8nC7phGBEEkePL7HdpbQjDzjpxN+5f0ny+xdXHz51/fQ8Zj29pQv/vZt9nYkBAcCHm7VbPUzQlMQi4ZbSUUviVHO8+33b5Hmmq1JzE4V8Uh5dCqRMXzBOoIHGSQ08KuFJ+BQEn47+RLZtKQ9LGiXJX/w1vukjw26e8I3e4pMCWIFOli+3Bb4VOEieHfPsZtqOgQyKfnSQ4V3ARVFtHVJJ9W0eintbocd6RDOMz0ccv/ODtt7GXHboRLLb/3+l9AdQ7YXePu9R9y+tUdMhHTw6O5D/vK73+WP/+xP+fjpJ5dzU4BiWvEXf/oD/uP/+tfkY0Nb3YHhXdzpLr/xG7+GKxOk6bCVtchMSTmYEinJnSynMRbvLN0kJbEKX+5gpz2++tX3kUoTnABb8ehhhlSO4BpuZznBWZQM2MmUviqRaPCS999JccIQlCVK4e6WRekIEcd0dYO1GmtbpK1tvvbODqlXRAbuRQZEjHEpyJQHbYkwEaHWdMlJkoCOAw7HnV5DXTqk10QuJ00V7dv92T6scEyiHFrU9HVNXYyog6V2li/fUoSyweY5HQEtAQqFaRxZKvjrH36PP/6rP+HjZ58sD4IzN7PLfery9Y1o1SXohohn+sR5nvN94pVoFXuuZnL2W1k+LJavw9z1pm3Tc65412QTzsbbN0LL2S/rXxeXN8hvbo6/Uo28QVLLxd+U35XvPqeINh5JMg+U5i06r8DL5oMZXp3ezCF6K/yswT9n4cLCMqDrcNIcwj7PZ1PfvbJPBxZ2LF0oesv5h6WyrBP0Eu8b+bmER3O3q2xxDmKuarWrcjo/+2chxPLD5SSWeJylerNVjBdfLMKq9ePiFasifRXFOSzfXYh3lsGqE875eGEx7mqCc2/PP4PPpX+G1M7dvq01Ei1rR5+bzstxReNdU6zXz2c1nbIq+e7ff5f9owOUVIynE/7F7/9ztNLUVc3+z0fosoMQgp9872N04ihPcqJG8h//pz/DFR4fPD/7/guU7lAPFS/2D/nZd57ipcSWDQ2WjARnBULC04lHJSlKKE6bQAieRCt08AzGFu0tibeMpiV6S6O1xjnHpIA928a6wOFPBshxSXAOYyzDgUELifOewagkBI9SglgrmmFBt5VwYiyTaYk6U6BdsHy8PyDSiuBnp1inQaAkeAEnL8doLQkhYFygyg1SSbJ2yvi0pLY1Jngs4IoGqSU6UuSTBis8Dk+kNcOTfHb4WTdl/+NDhJZ4Ak5IjktBlEVUZc1JNSa0C0Yf/gy2NH/7o7/HeosPgeF4yP/+H/9zkjiZtV+x1HbOqtd7z3f/7ns8P9jHGMPHP3uJNrvoSBKmFU9rgZcWlGQsIK2hNTsFgx/+3TOiOCFJNaOBRciGYAOJhGG0jfWCxkvqJiJrNNgS6S2fHEqQsy8LdYDapsRSUA9qfva3T/nClx+dsTjjNwgIPvDJR0/JOjV1UyLSFnpvD46PiZRgGnokpkJ4Q5bFWCvxpiFSkg9+VqJHHhE5hBMc3ZZkmcaXNb8QgdB4vBL4EPhpC0TwpJHmJ9Of0CpyMtmQyIYftX5I962IYn/MD/IDMn0LZTxKSX5kHCKJ8ELyvIhoxRLnBN1U8XykiKREtTJGwxoRHAmB3u0Opy9jUmko8pIff/cHPPzmA+LMk7YFP/rJP5C2PaG0HJ1+hlSSSCgir/k3//O/JQBxN+JkcEq302VvdxcI/PVf/ogPfvaM6aTg0w+P8WUPWe4Q6YTv/buXDJ4NSLe3Ge47Tg5yYjk7EXzst9jaihlOGqqmpqi6uMIjtiJ++qNTVJAIITEGnj0dEOkYQs3LXNKLKryDYjShKiJa/QStNT/9YIoPFi8Vtbd8dBAQSmLqhuelxvuUKOkhZIuf/GhAK0iUkBzXfXpS07iAMZoPPrIkXYMwkuNpSppJtIUsEjz7zKOCxLuA7NymfSthMLVMRiOSoGhrR+NhXFvKACjJ7m6P/TKCJicTEh8klQ2YxtHJEuo7ng+ff0RRlxwPTui2O+zt7K0fd9eoBau6wnq69qvAaoRXG9evmB5upBxvmpyX9YYNet2CPXFdmJtO+FeJc4OutPwuLFzd4PPENcbARW+NvwS6qlxXfS0SsH6dGxu+UlwjjwtxnJX33OvOVfm8Br2ZPRfi/M/5RLeewRACzrlZxlpxk5YYCGef+TdqxzewIIuVMOub0fqOt+wtaSXAKtNL78PGjriy2XrBHR5rnp01wTVjwYpF4ZrB5kKFXmbhbEmKWCrDvBIfxDLAmK+nc3kvpz0H8NbRRZ9YN0AvF+4yzkJRr2kP52UI82Bu/iyIZQAhLrH8Cgx7zX54eWKFWEzmQmZi7v5N0DKjlwsRp/mU2jQMRgMEgr3tXaq6otPqMJ0U1LVhcDIGQMeGfHRCSCVt2Wc6mpKf1sy8qjQM9j9jfFKRqYAUglpEOA8tFbDGUTQBM7XUqkWQ0ZkFxqO1wnnBpAkoE6CxVHVDEmskirpqcER4D4OTCUhB8JL6kxNOX5zibCDgsQSsAxoHwdMYhw4Bgmc4KbHWY6SjsRZnHJGMaIzDWoeQEhfAIzCVQWg1O4hNJQTnz5ae1FRlgzGWLImJpaJyDWVRz1zRGotxHrygzGuaenb+g7MOU1mqyuDKZmbh84Gy8aRCMS4s1gaUqwmmwuE5GZwgIkFRFxBgb3uXPM+Jo2SuYVxOmudDRF03FEXJ8ekJIQTaLkOMp+TjmmA9hZdMg0IKRctbNJLJYIoKYE4KROxo/Oxcj6AVQgTSbsYk2qKZGOrGkeoWtVOIoEjiDnld4hGgNPvPjlG2wYWZR66Tg9FCy79sgoLRcMLgdEw+LQm0INnGiBgbAqL05IVBqoTGSYrakVezpVTWW9LOFpVXDExBWVmMlQQBsZQYAtMQkCIgtGCoIJaBwxef0O+PaOKa07igUAUnEtwtiX4eqDJB7QUjJM45qspRe0ikIpSespFMK0kWw7QUKO/AahpjaEY1ggiimNpNsUAlHKenQ/IinwFUU+KdoZyWlJMCHWum+YSJn1DVNUEKokbT7/cZjUfc2t0DAqPBlJPjEVVZE5qEUEWMh5aysEwPxoxfjtCHDbcebWGcxASNM9BptxCtmARLORzgjCN4RVFB/osDFFMa4zGk5IWhqiGvZ4A8Lxy1LVBOEGRMIxJOjitQhipENF6QNxJTWXyIMbWhlcQYKYhUwslpzXA0xcmUibFo65FKgtCcjmuUDoh8BoajKGJaOpqzecc3AWslSZwgUsXJsGSYN2g02ltyF7B2tmQtylqotMW08jTTHOtnJ3zXpgIfiOKIbHcLuhNORwNqU9Pr9BhORkvgYo0B5prx/XK4PlcLlzW9NQks25FeZ4zfZItak96NV3MtqFiC9dbQNXws2DdeYUK8KugV9tGF4q7oWZsTvFGoq4S1Vom/IZ0zPi/jpTpcm+wKkAyXQODKsGcZbQp7EWoDkFnm7zXpDW7ovp6beb9Dq0b29T3t0oa8CdHNXS+zIhZa/kK8V+kIm8KKszwuPwUulUGE9Y2Jy757KYMlxTusKVqYi7BWJEuD4zpaiHepnFxsGlyRzSVfV0vsPMAGEHANLSru693DLj65yeg0V/eBs862mN66tM4V/wtAuVRH68e0V5gpwll5z9rnqoEoLPaNV5mEbjQnXAba6m/Ra3d5cOc+Uij63S2El+zvH9Lrten12+zu9JFC0N6O8fI2pyc5e7d6qI7m1E0YHpzSnB7SKSDCkyYxpRTEzqKVQscJugkM64JYS5JU0niPCYFYBrIIhk1A6ECSKYz1RBraUYQVHt9Ytu7tYDNDFmuiTsZ2p8PktOBUCaJUk3YSmmlNrBUiEkgNtvG0XEMlE0zToIIgSzW29vigiRNNO515/fEhIKRAurMWEUm67RZV1RBnMQGP0AKdKOI4QuLJWinTsprtHUgiXK1R7YQki8E7rHe0exmmMWgd0buzxfFnh4jgIWiiCHZudaiPcmwEsU/wTiCUoqVadPc6TKdTgvd02m2SJOXg4IB+v0eappwOBwQf2NneRorZCtc0idnZ3mZvvIcxhu2si096BDtBOcu0rBlPapARcRRoRYIiN9ze65B1IlSvy0gKiB0P3r/PZGrobaU86G3x0c+OefrhAd4XZJGmc/sWdjpG2AqVJBDHUBakLc00b4gQ7O22N9qA7j+8xf7zY6RU7N5q4cwWo/0J1ckQGQxJpKm9wTUVwQRiHdFuKZRtaHxN69YOO3Gfz9wBOm3jck9bSPJgEQR2HEgbaHRN13v6xxm9uM20nbLntvDxPRLZ0BST2YF5UQI9T+90dsL3RAZy4WmLAp3EICTt1HPnbgczlDTeEEeGWAeynYREWFKlKaqYSES896V30V14/gn0WltknR2KacFYTul1WiStiHa7RbfbxVnHwfOX1KYhEprd7R0OXh6Qtdrcf3SLw5djJqOKW7c7hKqHDBXNaAzlgHbLYUPB9vYttu62+eSnL1HBoeoh7e09RCbYTjscvTjBKQvlhCYfEMczhwuRKLl9u83piaPUlkxagq+RwZPEknbahp6eLUEc5QTl8FbQUg0+8ZQmEEWe3Z2MybAm2UrotyV2VFF6CTIQR4Z2pFCRIAkS52rq4BGRopMBWnMycUhTkWhB2u3hPITxEBcKYp+w3ZJQWxoLQQnudDNEr8V+XePyAmEsIYlwsUSVjm4aoba32L67Q2evRaNKiqKik3W4s3dndQ6dV0qWp9lNYONizltRfW8yEC/dXB9nVeURcw/Pvgp+XrenVwGL5VefUwl9lTMgNoY416WvC/dKiS7Rzarn+jxulMb6klwpo5V6WB927deZz9FUrqL/qid0y7ONdUKIxcM9LnrvjALnOuCsRpd0wg04QyylMB/4zZiAFwD9nEV7kya40kfDUinPBqZweXlpDlkp5CIaeyV/EkvAa171FvOBLqpkWaGfq6jlMolXlO8GhmfLws5zX/q4vKburwTY86BuCZ4G5mU4n+ZSnLm6vogvwtI5A/O0XgbranIVyizixhkQgpsuWfs8FOmIb//m7/Pxs09QUtJLt/l3//ZPKcuaTrdNVCt8YQnA3uOH7O8X2KFkahK2leLkvwwIxnO322VUDKlCYFoWRImkKKERkp2uZmgkPu4gY0m3JXk5djgPUQxWRgQBSRwTVyOqpkILQaoCZZQgdEw9tbz93l0+PTyh10pIOzG236KcFiRJjFSeuqlJCfSVpAoxVWMYA1mm8FUgjjQeaHfbFKcTGuvpxooib6iLmq29PsZbTF2jpKTBUNY1zjhc5UnaCdJL0JAkCaOTCcY5Ii3JkoTTyYQk9rTutyhH+axCvSdOY5rKIpUi66S43GCDmx1yRiBKErxzJFJTOYm0MD2a8ujRfUZHA6yxUHv+8I//iDzPydKU/vY2x8NTQgjcv3OXf/St30RKiZCSbruLbQzOedrtlHwgZ19nhGBLK567FJwkOMdUpNgQczKVvNONmIwcke4wOD7gUO0ju32adsaT3TbH8ZR+UEgE+JpqMsXkBY/utZjQpSoN3ljiTCPx1E3D5MURwXmEntvedzYG9be7NLUjBNBKkiYJSbdNfjyijaW0EUVjSFRAtQTOR0yD5/EdxQvtODLHGKmJI0tpKlCBnRBoIkFMwDtLpzuge9fTVYpu1aLcucuY/x9v//kkW5IldmI/V1eFTPV0iVddXT2tpkdggQEWNBrItSVp5PIb/0oaacZdYoAFOMAOBsDM9IjuaVHdXfppkSoyxFWu+OGmiIiMzJevqgb+LF/c69fF8ePqnON+zpmSpds8iEOeuqcsJsfcVgMmtxtUAsE07B2kHNWRIMCYgMxTvA1UbWB4J6X6XNA0nrQXSNqEdt4wn0/ZHkbaOiNoSZ7epjyusScNddLn3ft7/Obpx7hSkQ+3+MMffY8q1gyGA6qq5ujkz2lOLEfPj/nz/+0vqG2N1oat3vs0sz6+SVFimyTLeLR/yOTFMXvbkUnb4prAq2e/4+6HPyIfD5jvH7OV1BztH5P0BhS7BcN5yf7E42Jgt5/Shu4mQVSSfFRQvTqhRbGbzjkKE4RR6ESz++F3ePLKo0JE2QUqJAjrCaUnTwJ1081fe3JAMthFDfo0vib1gYlLyPMc44+ppaaVCemwYEvWvDyE2nreuzeiDODLCW3UpKJiXjuCDxSioRApzmuoBc5bajmkNxyQbQs+1/u8NA6RtoyC52SQUXnPdgNq0WOy3zBpD7n7VU16K0XlBVZmpCpheUC+jReKuCQZPF+yT/dtceWF+DeFN+RZJqCXGJ/zVwHnFh/EDVq0vm1fsdGc32I426C+CZG9EYxvUNglsusa9uKG1ZzrZYhvBNnbhw1CzOVvp5Qwm2mwt6vqkgz4ykTfLPzjMBfX9LFS6uLbFQNarD2JM0nvWewygXc26Ta6K/8apNmNmcNNjYwrUSs07mn8etuAK44ulziOzaJyvtZMF+trytn97XjZYqrYJFlYs1RzlY+Ipfd18K+F+Jy5uhzd8QDiHIar0MbK+h5XmLz1JWOFmTpftDe36drRtIEBWu/71ecN0C8Pqa8jhvmanEiv6PGjj34IwH/5z3/Hq1eHHBxO2B4O8YeO+WGJEPDLv/ySuoL951MGqeDZoqWuPUiJbWt8Aydlg9ZgW00IAh8c+1HSComQGZWzzKexkz5GQesNwQMiobGB9sQSnEMawzSC8AInI2XZ8tnTAxCB2XTB83lL/fyIICUIwfT1DBlh3ljKoCFpKcsWk2riQiCEZLFoqFtJpWxnJMd5JocLhBTYxmGtY17VNNahBbiqO+0IrUMaSVs2tC4QQqCe1STaoJQhRMnR8QJnA2FWcfJqTrCB4CNV2XQKHBEOnxxQLyoyo3HWU3s4WDiaKKlaD6JGioC1niAjn33+BVVdUs0qggskecLx5JjxaMzjl8+obduZ8xVwfDJhZ2ubtm158uwps/kc5z2PvzhAzsfMjit6/YSnJwLrNEIoaro77o1XxMbz5StLc3LC9oM7kPTZf1lSP11w3wYOjwW2jrhWkog+jYtU05rhoM9xKLB1w/FhSSLBTj0uCAKKLz89oF3UpMP80hryyW8eU1edp/IDVdM0h1R1oPYSYcZI4QlCko5SxHaPIipwnk/jMVJ7Gq04kR49KlgEBwI+JlIAlYionufprkXvOOok4Us3o8hSJkaRKMuB+5Jpe0IjSj7dzkl8xdwEKASfGEGjFAvneTHTDJxg4STMW37+uymV1JR4RJWQWkFV1+AsTQChFDEoPv/4FVk/oy4li4nnZ3/zO14/fkZrLYN8QLPw/P4//TFKK/6//+5PCSoQdWAyOeTkl1O88gxGAz597aHZYj7zaErKl/u8+vIYJQWvThwysTTR08w07ZdHeN3HYXi2iGR5oKFFJoqDWaCJHeN37BQhBEIUuJjy5MWck4WjDorDCImKVLRYlfFq7iiDwjeWUGZkUqJlQpCCwzLgRIL3llmyy7A/omzAA8d2gJcJdTTMbZ9CaZqkYNjP2J8mLNyC1gsevWyxvulMG5uEOuY4GwnRkBU7WNuZca6jZybG5L0+ZVD8+uiQo3HDvFCMRcZ+mlHHyMyDtCkpmlZrlJN8OZlRvD6kGPUZJAO+/PQ53/vRe6ws1utbubhi+d1Au1zlCPmtwrUSs6vCxSn/+aHLNzLbeEUQa78X1V9fxzdhRt4m75twdkOCfFkQ+bZ1fBNP3AKx+cBojY5Z1bO9INgu6ezGpd+lRt34ROtbkGp+c2tRbwqnUljggui7ibD7nEC8LL2NcGqs6Mw6QVz9+I3D2SC5Dq6bhKV7mGvE9pVgCjgzSdBVdZp6w4nB1+Gtl9eIi6Zc/XZRSwfH10HvWTsEZ+7mNpWyQuaf4yheiotrOa4I65nPa/8aIQpEFBcT+IbFCE4Z4a+NtKWrWf8tQux0oZLk1JNwYlCqU1KOPvDq86ecPNlHtg5lPdEHpIi0tqVqWlxwCCHIEo0AnLMIItY5EtmdQHo6BXApoUi7eqSSaCkJwZ8ztME5dKoxp3bpfdt2TsNubyOVRCWaJDNo3ZlZlVKSaUkUAqklAtGZdhWC6D3Oe6QUXZ1KdvlUlz5JDcZo2taSJIa0yMjylCQx3QopBWiFDR3s1jm0Vp1CrtLE4NFaYVLT9XfozNsqJQmcmjKNEZMlKK26vpWSJNEo3ZnzJASUEGRJ0lmnil1+KQSubFgcz1FSIRBokyBVZ45Ua40QAq00RJCyw4UxBqUUSspzU7TFICNJDbJz5oEiYq2l27g8SgkkEUJgfGeL4B0ywux150hQKrrTOzpzs1mWMNjuEayjms47JXohyHsZ0Qe07Pq2mdcrm1+MHSWmlMIkGiEF2sjOLLGWpJmm84gA2iiCt9SzivJoSjtfEKxDi05p2UgwWqIQ6AB5EKRRIEIksZAJhQkCXzuiCyRBIYRElY728T7isCRBERtH4jv8pRE0Ah0iRoCKnXlbESNKxM5UrZFIwCQKoiUGjzGK0e6w61NrmTzfx5ZVZwLUOoSPZKlBIajLmv5Wj/nxjAgooTBGY7KE7Xdu0R/3cI0jNB4lBSZRSCEoj6ZMXhyipKDopeT9nLyf0xsUjMc9tu6Mu9OyREEMED1t3aBkhFMjB0Z3hg8EoTN360/nMhEpAlopMqNQSrF1Z6sbU7EzTcxp+1Vi6I8KRjsDsjxBiW59N0YQnKeazAgxkKUaoyVSCiSdsrwWAV83JBKMhHK+QAXXbXsxEE+txBV5gtEKET1aCnzolLPzfkKzqGiahr42FEaTaUX0DhkiRojODK13BCJaCrLE4J1ndjzn+Mk+nXLWWbh6Qd8kUDyzKrWJlnv7JXeNdrmqoEtCs/WP65aqNiS5rp4LouqKjVesvV9RxnV1vG14S8bi2q35knDv6oTfiiftTXi86vsNwNr0bZViuwaQmzBp18H7NcM3Zi5WydGlyKu42HXgr8RL5Nz+9NUVnwqBT7mVb40I2yCy3jRx4nqiy2FTC25G5q4jscPHRggjnam1s7/LQKw8nuddr2KJsVkpl4u15xLcNya2l6fC1VPl3CQgm5mny2vEKSO2wh9dMR6vXXkuWKmVf7GzOnORchNc4gJvZ/WvdtflcJlr6h6X7v+dRb/VWvc11sXXh/v855/+F/7r3/0Vd+7tIGpF5gpSmfF7f/x9apGzf9zSEy1DGchcBbZix1TYtgXvGA8kShtMliF1QjEQqLyAtGBnKOn1Uoie1Cge3DGoOwV2R5H3Lb1CYhKPUJ5ev7PvP9wekhM7nwchIrXm975zB4lHR8f9796hlycE51jMS+6+s9UpAmvBeKtHf5hiVHcq9877e2jRKapKI0kyiT41HTvYzkBLkiIhyxJ2dgbQOkLruffhXdASYSRKCXZ2hijZXeG59WALFzxCC6KMbN/bAhkxvYTh7QE61WRZgkkNuq+JWiCM5PbDXXSi0alGicB7ezmJjKQa7ucjjBRoIYku8oMPfo/tfJsPPvgO//xP/jnttMEdl8gQ+ePf+wl3t25zf/cuH33wIcP+AACtNA/vv4+sMnRd8PDDOxTDIenWkCg1D5KSJEAuJH0qChkxPpJrw7Y4QsoGOzvg/e+M2b09xLlAW3v++L/b69qOpdANo54i76dILdlWB9i2QUXP3rjgwd1djNlC6hF3bvX4u7/5Df/xf/0pn3/ypLviejpPvv+j9xHRkyWSrS3NBx/tEa0jWMeDYQ0BUq1IgiO3Rzjb0DY1P+xFMI6sL+j3DO/agAqQIfjjMiClIIkRExJ+MumhgkAj+YNX26jKUQSNmjt+8mhAHlp6wvHjiSFDkSqBTAR/qBNUFCRCcyev8K7FFAqZKn5wr7MWlQvBTtYyzjVZKtGJ5rvv9tFGYTJDP4nceXeX6Dz1vOZ779wmLwqU1Nx77w6f//2n/Pt//Z/527/+BQ/ffQhVhrYD7t16l3fuf0AmtilfBz54MMJVc2SsccevyJIZKl3Q2EP6/oT5QhPEmB/+737MOw+3Aajrlg/vaZRO8DbQ6xvu7CQkMSC95/3thNR0ukMJlg8fjsiVwBDZSwSu6WPaHcbFFh893KZnEnQbuD+siTFQDFKKfsL3vz8A3yLx3O0tECLgmhJcw49/OGB4Z0hvt8f33jWkiQTbMD+Y8G6v88NRpJLv3TU8eP8WW8OcXEreHS6603QRkfYI4yt0tPRzw4/fT2hmJa6p+YFIuF8Ldl9LhhPJvyjh/anhwyPFuzHQTwWkngUN41SQ5Fu0PuP14wMe/+wr/vzf/4K//a+/604Xz+iHDYv28v53LsxcsQt/lvfrCPuuI5T+G4UlAdwb9/MVWmIDQxNP499KCHvDcFV5SwRNvBS3lu6KMja149LvRubqgiETp0LIKypYoqeu6dtzUiRySRfgkmRYXAgg1+pZSXjDftjYn98gfCvXosTS0yppxIaGnZK3N2jwVc0UK99OCTnOtC6WuY6bhiVqei1mtbbVmm9a7Pn1qPPsFy5u3nj6cDpYI3HtSGyluHNCO8R4mWM8R4m4FHcl4KeFC9Yn3jUQL6PpurgVIDbg8zxtXPlZ/SxW2n2pNLEaf1W46PkLG05xLYFY+b4R0Iv3pZM0sSnJG+BYN2XYrV/LsddP/85z8/WVLrezbmr+8m//iuevX6Kk5Dd/9wXG9VGNhlrzd3/zlKPXJVUpMD5jq55Rt2Abz4HJIXoUcDIDpEQqTRssje/TyxVTH7Eq6STkoZMiPhLg8ghCcNIYhpUHJci1YHZk6Q1yTGY4mcwZ3N1GCYlWis9/+5jRgzE+el789hH10YzeqE+9KHn85LBrm1bMywbnHK21KC15/vQAKQVN3aJbQEtsDCRKUc8tPgSk1gglqRcWhcAoyauvXneEqtGkaUqSpeRpQpSw//KYNEtonMYTONo/RhmBMpL9Z4doo2hsxTAvmM0qlFC41jJ5XaPl6aIvFS9enGAE+OA4CS1KCNqqoZmUvPr1C/7kj/6Yd//gA57vv+DZwTNmkyOOv3jNF5NP+Bf/479EKMmD7z7gTAcshMDTzw5IQgHO8uSTOcpkCJ1Qnsx5+tKTB0BJkuIWdTlFeA914FXdkCTQ2xry1cdPyLd2US9aQuv41c9fU/QkQka8SslHI9rGghU8fulJtKC1gcZKXr0Eb1NSHfnl717yxeFLenfGvHx5SFFk3L2/Bwgeff6UNNVU887M78nxlNhajAi8ODKAp7Y10ThmrUCoQGIkXyJJ+5pWeIKAxzGgoyQTkt/kEiUgKkk0kSd7FhMEMcCXt6YUJN21vVnJk+9FhtrgYuT5fYtRCULWiBj5RCsSo8AFXtseUgScAqEiH39RUZjOg/ekNgyFoLUNWll+9ZsSZQSmyBHjHvN5SzktufPeHr/77CW2suzcv8VsUfN6us90tmBma1wLRgxobcnhsxIpFHkyQojAp795TZINKectepxTH5SIaBluFYjtd/lg9xbH+yUns5T5YUnWz1kcHfHp88BgoLE2cHJYE2OKoYIYqGSPQd+yf3hCAA73awyBhMjRSUZCgo8JNENeP7VkStH4wHHbI0kkZpBTbOf85pevcFWFEpFJHFIoaJqGItMcMSQbGoKPTBYDhJxB2SKU5WllMKo7nzppM/q1Q7aeNAReTzPwLfOZJSpJT4ITEVeV/OK3LU4IhkZRS03/RKBUyi1lELXkB1VJZcEXfQ5yT4okEYGDaY8kRoQ01NHyV3/xG8zWgNvv3aKuWv7l//HHnO+q15l0h81b1tm9qJtIid8YvkEBV5Eq61K58611Tfk7rjbg61iA+kdTFl4hejbXL07pwbcrNhJc6E6Vl8q6Fn+rlV7Ad+n7tR+uCWs4jEt4/VbG2KYav91CvwXmQlx6u5IUF2zk7tdNuMXz2DOToZeMdl7i1t5MRr4J/tURucIkrRO7a9V07Vyv+6IVl5UZ4DrG4lyjf+kU4SqjuRc47mLkZi+FpzzYaZ03RdP6GnFJCX/569fheN+U52IMrFYX11KclrXcVeJiNEUu429FiX7l+8U1sFWBznVIWx87Zwz0ppovyryc5/rSV7G8AeeCzuPum446TuehAGbzGVVTc3TcEefFfAcx8SymJT7C00fHTMuID4K+DRy3EdcGAoHoHC5IhBBIOD3hCUQhCAhmkU7Xofb4EIlRsmgDdVC0srsepEOg9oHgBQvniC6i+znHL4+J/ZTGeVqlED4S5wvc64BtHTHxzI5nHLw6JjESZz0IiTYa33q8C3jXOedrvSV43+ktJCk2eoJzVK0jTRKCDUgPbWXRRlFWDWnoBogS4LynbSz1q5qyrDq+QCq8iwQfsU2glS3OepRoMUpBnuKsp20ceKjblhAiSgocYBuHzFJwkdIK2qDIfEugxeKxMjCdzxjsjsh7GSefnbCoK0JhsKVnNjtm+/Y2ab9zEHg2FtqmpVzU7L+eEEPEuh6w4Oj1HDuZsmgl3mu0ShFFARHqkwrbWjIpERocksXRlLRJECalLB0Hr0t0amhDpzSe39rj5MtDwoml8QaFpHGB44klKRIWZaQUnmAa5q+mpPOS0faA48Mpd+/vIYDjwylHBxMWs4oYK5p6xvS4xbaawSCnGBY0Bwvm7QKbabxIkCYlmIpFqKlNd63NA62AefD0Tq8DnRCJRcAmgTJvuutpIlLmgUpDM2gpRpJ2LDqm9xHYk0NOUomTEm8ttUtxNmBCgrWCae1QMsFOLTFE6jqSughIbNAgBQJL3dQYI9gdDnn+9Ih5aZnNLcGVtHVDIwRZPyXEwGy2wLw+xlmIKNqmPZ2ikvm0JM0S2iDwbaCNoLRmeP8Wi1lDELCoBa8/fsn0qOLo2RHVoiXIDJONaOuSySLQOMFs5oiNo7YSIRJq5yAIvJDYmDGft8xmnsZrMhwtijZIXnx1jB4LFo1gUUmijywqh3YLpFF4ldIES4yRxGQcTiy1FcxNCnWkalpiCMjG0SxC14ejPs28YVE6pJC4o5rjwwU2aoRJiD7SeEVAYkNkFgBhSNIEJwSV73DumoYiTyCqbo3BU1cR6yJCeYKWyNRgYqeX5AGhNEFEXh1N4KTEusDe3a2LhfFrEW5i5Qe4upz1NOtxy/FX5dsUrsoTLz2uJVknZm7e+CvNom5MfPr7BjjfPizpnMSV6E1JN8IrEKuMxTJcbxM2pT+vU2ykQ87TXCpjiW6J60lvIJT+OrB/e4cWwLfAXKwSPjeAbsPkiuJyvijOiMW41OjrZt2aovEKcEuj6tKE/mZs4HU5lwn/C6K3O3o6n5hXSUHeovIN6LucZpnJWQ5vYKpv5tthM9N1Vdw6YX99OFM4X55kF4zAMjvalX0midlE8F8F0PqnG5/VbAJ3ieF5m368ppalhfmcOYwXH6K4mCNCyqsXiQ0SufFwTL/osVVso7SiNxwR0gwvJGI2x01nGC8YZhlaJ6TBUnqLFoCMOAJSaVJxetlPJQRf46Un1QZ8JGIxAhohkcIzNgYXBQFJngVyG2hFhBgYjAt23tlmcTIlFdBLEtoAeaK5dW+LZJxTlS3jfkb18UsSo8hShS5SbOsx/YK2qdFaY2IgSRPyIqWtGhaLiqJIEZlGnCyoy4q8n2GrFiEVWW7wNoDP0IkmSNHd40aT9TMWiwXGaLRReCHoD3qIoxkmVRidUNctQksKrTF5hm0sMtUUiWYxr9CJIks0SZ7ijxb0C0XW08ynx6QxYjAkeYEXka3xiI9+/3v0724xnZbcurXHaDCmngcGOzk7os9Xv/mSB7//HiYzOOc5PjxhMOwx2h5w69YWrXUMtwqCzXnx66cQGnrS401CIJB4xeBWTmgtOIvCkSApeglWOopcYJsE0czY20mQac7Rl5FEWkZDxUkWGfQMYuFoQsSpeHptTVIUEuk9LRERPaFtyYxm7/bW+fC8c3+PF8+OkHLBzl7B6y8aekNJrAWKEtEE0hSircjSnEp40lhD1SJHgsO6ZZxopFGUPmKkpmgjbfDMVKA/FYwbRa/JwXqGrSS7N+JIe4pFZFCm+O0C37bkvYLFvsZHyyhKFJKFjrTWI0xA9jICgUzUDA14BGmI3VieNjQG7r27hc4aDvct/dtjdGzwxyfkqWY8LqDJeXm0j/OB8Q/eRRtJM4fRsI8xitZJ5nPLzm6GkgpEymCQwnaKbRKOnx2hfA2pQKcFw1HO8N6YT/7hBVAj6wW3tkYczzqTzc41hBDQWUIiLQhHUCBkYGfcw7aO+aRCmZatUcpUTVHGk5iItw7vAraskVIw2ruFahRu7kj7BT7VDPJA36TUJycIIdgZGYIRVLOKXurZGSnKylOeVIhmipYOszfi7jsjjr98hW5bHIJRTzIYDXj1oiIXLc6AUIqyqjDa0UsUMs+59d6IVgqOjirK0uJmJb4qMVkPrRSxbaiqBc6Db1pqq1H9Mb1EsJML5hoWXtKXKa3QzGqLXNRwMmM+XVA3DdvbI5TeTBat71mrPpHWBWDXrOPrUfHqJfuisivKvCJcXM+5yHhJaLYMxJV7xlq9S1uxWH9fPllYLnM5/3VMxpvCcplLtMCN6OLlfG9D7sVIvInlqOsAOKX1Vsq4lu5aR/JFWtGBtGpueBN+r4PxqjTfMoPxLZxcrJN36182vV2PgeVrj9cxupuEAFdDsZpjY94zAk1s+LYUccEorML0RmjOJcZLI22lrlW59HJJ5/3+NTv/wpLB24Urp9WbBup6upXXDTN8k3h+fTZe6pjLxPLFac/lHn6ba2E3wdNVxo/Px8g1hcTYOVKTUnLpbuVNwnJTlq7OnX+7io+MFxcIIaK1pmj7uINIEJ6979/hs0nFcRWwBzW9akHVCFTdkGeRWWmpG08/07i9lJOoMMYggkVNNWUbMSqhl3ii0NS2ZWtgmDhDU0d6acbDQZ8vDzrCZzfXxDxQzxuiCuw+3KJV4FJBmguiMWgfaRvHvQfvsD93KO3ojYa09T+gpaS1jsGgoKrmaOcZD3pY57B1S/COwd4OLx83BCGoGssgTzqlXqERRGIUeOtRvQwygV9EXNuydWeL2fEcoxRN22KUpgkOHSVpqmlnNcJHbNPS6/eo207qnPQSqnlNJFLkKU5G/GxBY1uGgwSRGXz0JP2c3czy4uAFACMz4r//f/wf+PhXn/Ljf/YjMD3+w7/5GwB29rapj7ZwU0lUfYrv9vjrX/2C3x09YWdri8VBzXy2IM1TRuMxrXV47xmPc3730xeU85J+YdhKap7XBhED1fQQH0aYpCAg6MkFZQvORvJ+jqAz3etjwqivOSolyIS9d7bwdkYINRjNeOj4chIJRlL7ilg6dP8ui2nNdiGYAlrD4mhCv19wNv939u5QVq+wIQOGDIeWV88qkl5BGo/ZX3TXrLQRWEoaOSDEyAPlOVCSEAU+BEZWcywldYAHreOLzBMUNNazvVA8HzhMptg6TqkGCciSkEq2Xm7zqAehVbyfvs8n4Tmh9USpuZOlfGwtTkgeDCSTKpAhCLGlkC3P5hKhJP2x4WgSKEZ98q0BbVnyOmTMZgHXeO688y6PvjrEWc3esM9Lo7CtQ5Mg3F1CmzE/TBimli++OsZHkNZQjAeczCReFPze92/zX//9b5mVAZ0nMPeURx5pJd/9Z2M+O1zQVCUxFUjXQEhYzBruDwLHbUpVB5pFxbCfsGg7fZ7xeMijLwNN3VD0+4yHBZ/VluBhtJfz+HWLE5qFb/CzQ8RwC4QklxWNyzCFZnG0IMwPsc6gjGZnW/HoZdM5y3WRtDri+QtLaFq2kgUzpxDSUc2njNKWI9EZXnj4nR1mJy3RO5xR3BoGnhxGEmXY7ktO6oZ2URKfR+6/1+NZY7EhoIUjnDrEnHpHFmbYuUMISaEd/kTQVBVTJRnuSSb9lDZCqjRZGLPwLSel5NOffcJ+fUS+O2B7Z8y/+lf/lCQ1rDshW95/rxJSr+81KxaErpHtXY443SOvI3KuIdTX/UZdZDjdHM43qGsIiusYjrX3lf1u6fdckHgt8X3Nt6vSrYH+hu38rcIK+XEuqNxcyHnaU6p/lc2M5zTfjcIaYSnW8Xle5DX9dhO67JvJ028cvh1TtDcQCq8Q9nFDlrjM/18z2pYYumXueSM5uInCE+twventLNNmQrL7sqlBbI67plMvTLtecKTnwzTG8+ZslDy8IXR42jAjxao3hVX2azNr903G5rIM5Q2JrotY+RLX8HXhKIbNY2C9hGuOfrq2Lo24s3G67Ofk+synjxde3s/zSbEyds42pzfdPrtSUfwGC7hYizg+nLD//IjZwQIlJT/7+0c0PufZs2PS1iEbgWwcrnGcVArvA95BEwWHUVJmhiQxmLkiJeICKBWZ192d6raNvJxJopFgUpSRfPm8xbmIlJpDvyDGksZHjIhMbCDRkphp5kFAa3FSI2zgk08PKbbG1BV8/jefM5s13RUKZzl+PcOFQDWvgUhbt1jryZTi0W+fgxKECJPpgvm86syFApPDkjTR1LUlSRSts5SLkqzIWUwrvAvUZYM2Ghkl3keE0rQLS/AB13ryQcpkOgchsU3L0b5Hi87T92JWESREH3E+crw/pbitsW1n+vbxp08RbYP3nsXC8OIXz/jee+/z0e9/nz/7t3/Dl589I0Z4/mQOMeXVowUnL2acWEHlJhx8ccIrc4CwkqP9CVs7I776/CW27TyPf/X5EbNJjQ0K6+CYMVGANikL1zI7bnBR0M8STmwBvuJof44SBtl4yhqcl/zmk4q8H2mDxqqUp1/t07iAC579JsXSEKQmUUNcMNS1Jx+MmIVDtDE03vP40yf87hef8aM/+h4q0Xz8y9fUtWA6BVfOeP35Ia0zRFcTkxQUlCGyNRgwiZaFCxRG82WiEcFSK8FJhEMJJd36+atCYIOnFJJhH77sL3CpxaTw5fs1o9wxp0b0BL8Sh9hFQQyBX7h9ahpmwpP4yC8bSys11jkeTSMiOhphSIzh0cIThMAHeP6qxbeQ9FLms4bP9j0ViroVDPIBhzNP00paC58+OsD6QGMdj7+YkhdjZhMNQfHsyZzZiaNpI7PjfZL8hEUN2zuWp59PqE8WOFMwmZWMkj4xCupF5C9/9prDkxmVlsycpK01jVcoAQdxh8GtlPmTE6bzhiA0jYXoBR//Zk7ey2lcDo3ni09PqFuBFIZjtgnymDIIpARrRlQ1LKYt2D6xbkmUw4wzjsqMNghynfP5c081b6mcxLSezx5VLOrO7HOUOda3zPenVEeeUEus13gh+fSTKdK1EDRt2/JoX4LUCKM58Y46BJog8Mdznh+X2AguCgohGSY9bFQoEThcJKfCAoVIcoyU+JjQNg2/qwVOWrxSUAYGaLwQTOuG2dGE0S8nFHe3ePidBzx+9IIPP3rveuHQ2ZK8TIQg1lUW3j5sklx+C+GM5hLEJVp3jRbYxI+cPa8RujeVh71NKy6h7k2E8nr8MmG4luZaM7Fr9Yi1ci7dJNm4z14W7J3LP6+qb0PdG8OVxMDb5vlvG74dU7RnDPE1n8Rask1ZLr6JpTRrFoTONPLPfzdX9macrmrGR7jGwsE6QX5Vuss1XPGBc7Nv6x/EKbF7vmBdUJOR9SznGNqIy9X1YB3zHQ7PGLOLMpZynuL5nFRfJlCvxcEVjN6mgbDcYW8zEc4ZI7jAzNvbOnhjlZHOdCab8H8p6aXCL8wlX85/Vd3ra8+6UZKL3GvIvGZsnvfh2kLZOV4DJWVnAlVK3KJGRIERkSzRpyZRO0DSxKCkIMTOlKOSAikEPgaU6CwphRgQItJaC0CWaPpZCgjqtukUrQX44GnaFuc6j8pFaijGfUxq2L6/S5YnOOfBdyYzbdmglIQYKY9nxBgQQpCmKZyafvWhU8yzwSMEmEQz2hmitOpMtmqFPz01IsTOFO4pTpRSDAb9TrlbdO8ueKz3pyZeBVqqU/O5CiklMUaqRYm3jhjDhdMpuerPJ5zNYym7sqVASkGwDnWKY3zg2adPsSGijDrvH6kEQnZFzQ6mTJ7sszieok6vwAkpOv9B4rQ/gXpadrowUrLzzh69XoZtLdZaNBHnHP1BDyI0tiWcmtMVAmzd0t/qo7Q8XXsjaWYItpMUH3z1ivpk3vkjUZLgO3OpSgpSo5EhUpUV5WJOlqUY3Zkm1lrz/IvnvPzyJTFGpOr6rDOlK/GtI1rfmfD1obuSJgRKCIrEkGmDEgIhZKdbRCRVChk7AkBIQe08WkoSpSi0QZ7WG2wkRIGMEqQgSdNT878KnSQdHsOFwMB7jzo1N6tCAHcGS1eekp2JYak7R3OLgxknzw47k7RKdRaipguayQwlBDiPrVvSPD09tQxI1Y0B37S0Zc1gq09apEgB3nWmbV3TsjiekfZSCJE0NV29UnT5ga1bW6Rp0kn+vSOEzuxy1ktRSnTWnfKEpq7RRiEFOGuRp7iXMXYmiGOnE2SMJE0NIUZMouiNep1U1jkAiiIluEBzsoAYSDNDPszQSiJE6AQpsfMHU4x6mESfWjIMzMuK4CzydCkK3tNUNTIGwqmUOM0MRS9DEHG+WxukFCRaYiSkWpJqSWZ0Ny8E2BAwiSbRisx0Ao/xeNBZbBMC27ZoBNFHtOrGR2IM/SIHoFxUNLOqO9HUcn2xXQmnW8/FMrtMHqyZiL/K6uE3Dm9Z5MUOJM4JnRXY3rRxxqXf9bTXbYxvAeelpBv3smsAvYqgPMt21d96mmuriSuc1cU4OMXp2inFCn6vw9O18K1IHy+3jTfHX4nGq3CxXt/XCN+cuXgTxbUpw3XcxjlRvZT+1HzXmRmvC5NZ12FmE5CXidBz4i92drpZKXsVljfxHucHA2scb1zvyPPS1oO44HLico2C1eXgYlm4MMG6Gn8O1vlassxIrePwLPYSkKdQLcOzAu0V6N/AjG0Mawh7m7BCda99+DYYwCUIL1iLJXxvAGedX1p+Xe335X5d+7fJFO+ZPsM5cyBY7rcVHLwBJQDOO371Dx/zF//xL3n1cp/bd26RJTmpyfnDHz0gLStG1YJe9NwZKk791FHkgdY2JEZ0JiMzSSoFBhialmgEcpCgC8Og1xIzheglvHu3QIjQ2asX8EG/IZGB4FsSWpK8QQ8W9O4o/uR//AOSYc7g/hY//pOP0HVF++oQOZ2zFRaIyRFmesw4EQx7CanWpGlCfydHG4XSgsHekGE/Q0pF2zqGw4zhqE+Rp4zGfYbD3qn/B8P4Vh9ipJenKK0I0Z/6n1Bs3xpijKYosu5++7jofFb4wO7dMUYr0jRld3cLoR1aKaQU3L27RRSgjKLo54y3e2QmoZ+m3HmwAzZQFBl5mvLwhx8gt/YQW7sMd0Yc+RNehyMeP3/Mg/dukWSaNDX84Cf3IBqCSzCqQB41qKaHPZB897vfIU92MfI+Im5zZ2uL2WuPL3MePtxj+/YO2w/uIKLk3qghRE8Mlr0t2NtOSWXE2ZaRnCIC5HnGzrZiazcjSQRSC/7Jn+wRnAVvyaIlEwHrFBHDFlNkUBgn0LZkmLX0hpLeyDCkhTTQu5Xx8I8f8vDH7/HV0XP+/ue/4IPvjkEbkl5Gkka2egGdS5zwvL/nGe4MGO/20Djub1myu5HBdzK+n3WK+4k25BF+GCBTAhUjD8uAcIHMQ9/n/GgypAgpecz4watb5EEzUAW9oscfHm9RGEe/gD/KbqHKQNZGqGt+nEiUXJANLN/ptxTGgVxQuzm/ty3wDgyG7QFkqSeIhiY0fGfUooxHyJZB39LPTpnhyYJ3BikxNChh2dmBnVsDsoGhLit25DHRRmgdwyyy09dIBLb1vDOqaTNL02uQRYtOHFWiaPOE99KG5qBmb2ub7UHCrXFA9VvIW374vYx6OkMoy2Cg2BlB3jdA4J07EWkg0rI1znlwP0XJQPCW++OK0U6PVHu08uxkJcKWyNiy15uRDdPuymJouLft0YlCGcF7Ww5sQy4DKjoe7kZ6/RQtAw/SmmGqGOSGJFE87JeY2NKTjtu9BtmP6K2I6geG6oC2nhLcnJGcU2QCpSKNbdk1U4R1GOfoK0uuO38dSkBuZnghyAc5770z5N79gr1RZG9L86Cekkws47mgaBt6wmGiJVPwcDRABgMzQYrmwYM7l4nOtddV2eANN5u3FaCdV7bhZdO+K1azbS4uEgkdTRXPaJ8NdW6C/SawcranfkPK9LoKrvp0FbNwqp9wfmX6hn/xjHbaUOQKPq7o14v9++o0l8rYyCBdRC41aXU4nJtGXitnmS95AxznfMy31H3fzrUosUrunIf1iGVEnbVkg/LyJbL+ioZeEHRn5N+qVakLmC7X8aZ+vqhXXEq8Ttqt5BOXU76prjf349mgOW1xPGvr+mpyhpGlkXWO4otOWhn0S5BcyO2Wv59zSldB9e2GZRDO2vlNndqsFnlRzwbF7zMUnn9ZYRJOx9U5jBd4vgThMoO5PISWhv/yknF5j7i4rnbeL4I1r+8bYF9+WNfFOP3061/8ll/8/NccH00Yj8e4k4hRKQL46//3X2Ff1xQOjI0clQ3BeySCeXnqaE1IbHTs1w4zTBEEWl3Q62fYoJFIZi5Fmc486ZOJxbYBo1KkggObIVUEPDKTiH6N0pHxeymfPH5ENu5B1eCNIQuRxXROtJaXZc2DH0pE2XD4xRPaRYmKhqAUi6nDEzBGEwRUTSDRBm0U+y+OMacSXwDfOpx1DPp9ykmNkQLvOolrW7WkRhNi5ODFMVmecDKrmC4qEi8RIaCF4GR/zmBnhFASYyRz3+Jbj1aKw8MZyO50QhnF4nCOVhIdAoevpggpSdMUIxWv56BGWyjreN2rsGnL05OXuF8L7ESRpIYYI19+fkJVStpW4aTg4GXNu7d69NKMr35d084T6mnGcDDi5//1M+4+/IjnnzzjN393xOjuXdo60FSOF+Rk/e5O/pOnJ4x3txHCYhTMXZ8scZg05Yvf7rN37x46UQgCn/zuhLYsgYg3GWUlaKNAmIxZu4UvK7TOmVmJ6gWSXEBsOEkDw92c0bu70IN/+7/+B7JxTp5l1OUBSbFNXDiePjmmcYKgI3mewL1bjKyjejmjVZFqFCFzpGP45KhFRtFd0ZOKJ85jG0cEnhcaEyM2CoJreVzUJE4RtebxeMp22O4crUnF53svSWKG1pIv3Ut645xJ3WKi4KuRxzQeHyOvfOdHUQVP4j2P55pUKTya41aR9cEQMLQ8twIhHWjFxElkE4h0Uvcj19JUc0wqaBDIukGlkv52zotPMwa7iioIZtOIql2nf6E9j4PGi4om8UyFoiw1Pk1oBPz97+Z425KMthnv3Obg+RNE1vXZz379HDeriULhtMbVAqEjQgaeH3p27gqCDJRVw7PHM3Si8K3l869Kth8USBGRIfDkyRQwpAbmccDe7QHtfo2vHQdNik4krm159BpoW1LdpzBw0AiiapEx8NKmuOA6x44q8HSRILwl04aFyRh+Z4RfOBInmD/zEBtkItHDLXoiUE4s0QVmdU4eAx5FaxWVa/FSkslIGwagW2Z1w+NnNdvbCu0CWzs5LxcjzHFLWqQkWlOKBhklWghczDGxop5a9j9+zeRgyt7d7fNVerMZ8uV1fHU137TCr0Rt2vTXN4CNm+sb9sGz8s+lmZvT38jS0BVMy7Xfblr+poKuavMlqd3NiluF7+vRD5tyvTXuYLUN4szTtriagLqmihjCil5p5IIeOX++Kfo3RS3Hf0MC75szF2fS+U2QnBFf65fEV6S4G7KttXCZexRrKTcRf2dvG4mwS/NOXIC5Kf0msC8BLC6niEvv5wNrY+bT8RivSLPe/niR61LapbhlJuKmA+6K6XSjLBs5y6+xyFz6ekUZKwvO5fwbWKVL6daJ+JVkm3B7KXz92bc6a9aQGFfn0zmTsy6VWXlYauU5Q7kZvqPDY44Ojjk5meLrQCwlk5cnSKVwtWcxq4keEqOoaoezEa0lJsvxrcUHsFqBTqikJgI+CKKHOgpsVATrEFHgosJVnSWk0ka8kfgY8SEQMFg1746WDTQyUB9MaOce7z1RtqgkJXqoqhYpFEfPDztdhmmNayxKic7MbAxEAU20DCqLSQzltMJ5TwiBpnXY1uFCwJ/qO9Tzmra1+BhpW4csDGXZ4KzvrnfZzv9G2zoUAuEDtvHE0KATg8lT6kVDPu5RNANePn6FUQphwFmPFIKmtizmNbjYXcfS8tRvh+Fof0rdaqYqwYdIsZXghGHRlBwcHBHnGeWku1pmTM7xsaD1itILwrzl9fNjkjzB2ZIXn55wfFixOF7gnGQysUST8+yLI1o5ZHrS0ARDW8Kw10MXKdPZlDaU1FbQG/Up5xbhHOnCspha0qGnaiKN07x4OmM6aWi8YGswplkcUQfF/n5FEzM8YK2k1+/RRkf0guAlRrf0tGReLrrrXbni+HjCTGuqeU7wOceHFSdHDVhQuWGxsBz/+jkiRpooGd7NqGXDTAbm0ylRdH5JyiiZRqgVHJ8dr5lIMAll8ByYhl7icEmDQ5AacEIxjy1ROezAUYUjtMvIa0lpoLSONjiUs5RGI4m084APkXljSYqc43mkKjvGUTUtVXA0QdJ4WEjFNHiElBS1YF4GGqeYzBzJwBEkCBGZTS1lOefkOKCJzFtN/brCOQlSkYqUNkjaOrJIBSZLsaGldpokJMxKhyXFNRKCZnZUkY5SGp2zaC0SQQgSpTKq1nN03KCjxuMJMSXUArOIBBKmVWTx1SHOa8DQzBxq6nDRsLAenEcKhbOeVBn2X5Xsv5iSGlCpJkrT2Xm1Fc4lmKKgchX1tKINlohCeUdAEQIIk2AI2ODxXjFMUw72F8x8RLct0gpqC0masGjBBZhVDulPHUxGBQi8gKg1Pkhs45FeonUP6wKzctFZ0UsU2qXI4QjlGpqgiHVDL1VEJNYJrG/xUWBd4Gh/yv6L41Pm4nSHWDcasnFlXd803pKgXU++Rtdce8X6EkH4BvPnS1vGCi9yXdrrYL1pWMkXr9jPvoW6riEpNvqB2sQXXgfHOtxv4vnERZ2X9vKz55Vy4kXCpbIjIOQZ1XLRQV3pX7NTrmvXNwzfzsnFm8K1NOtltMQ1baE3o+3y5N/4PcZLcSuE/fXFfo2wZAB1w2BZTbESydmRwzKPsvq45vtjbZDElTTrCS6/XhmuF4JcU95NKlibmet1bVrgNjBfm0t+E6vI+f34qyC7+I0bC1m3CLL28VK6C8jOtov1cXtNeTeZ7Mv+UdYyxRg5OZ5ijGbv9i5bW2OCDeze3sKdwPzFCVt7Y4oHBY+qz5nsT0kSjXV0d9yjR0mFSQSL2pMJUFoiQ6ANnlQIciFwCAwWrTtv0W2ImBDw1oJKGfYU0lqs97QCsIIEQZbn3H1wBz+Fem6pq5atokc2tRw+fo0yCpNrdKKJEZJUYX3EjBKyfkFbNsgIi7LB1g3jOyNi7Cw5JVrjQyRJNMUgx7WOOKvIMsNwVFDOayI1aWowqtcxGMGTZwnuFKdJqtEejJREJbn9wV0WxzPK4wV3P7yDl56jl4f085R4dm9bdE7nsiJFtI4owAtIjCExkkEvQxUJVdnSz1Pu3LvNl189I01SBr0eJhmQKQsE0iyDFp5hSURE64gRsL07otcvyHSB+/lT/HRCmiu2t3P6/YSXnz6iyCJFrpiFkkRrer0thuM+h9URsZmSmILb7wxZPJ+xmJTkhcHPHDu7Oa0LxDJSH70koWMMh33JTLaEKAnTI1LhMWlkbj25VIwejHj0+JBMRYSHMA8Ue0N2tkZEIoc6p8hTdkYDFmWGDS3v3n/Is18/pfaO8TghNZJyVnLSBORkQbYb0FlBLBtsWaOKHCMkWzFQpp0pXiUEPR9IfaCRgf5CMaokMRQgFGlUjMSYV3HCHb2NMwmzZop3kbHJcL0C5wM93xKjIlEOHQK94Gm9wEVBzztS5UgzBdqT+cDezpCnz6YY6UkUCAnRKPoisp0KDkSkXwhs4xgWPcq6YTQ2ZPkA60qagymjzBMIONMZRijdnDzrI1pHJj0myYiNZagDuvXYJLIzyBH9hNlJTRMiwwTSnYznByWaQNI6jEmovGdgQMfIzFtS7VEikmeeJPOMU0VwARc7BW6hIru7GSf7E3JhUbrT8XAa9t4Z0njLgbLc2sqZVw1BSogB6UvSkcEVwKSmSByL2qOyAhkdMXgWMVLoDoc+gygFYjbDVzUyavqpRKWRLEIQllg1aCPJpcWoSK671TEgaVpLkRswKRpHtagQ3tHb6SEXLYvFAdSKoYo8+OBDRsOG+aLh5OURvg0EpbAuIGRLDC1KKaSI7OwOb7DYblqaI+ur/TWJ3xgEEEIkiogUcrMQDHhL2+4bt9x/1PCN6aivUc/yFrhJ4LocbrS3skqXLNFo3dNVNyyWaAfBJZ2MSyTIavKVsEzvhRg4mU/Ikpw8za/F8XXi26apWdQLRoMxSiiuO6V72/CNdS6uB+OMJbsiU4Qz813d31Xux5d0Li4SLxW/9HJ2l/D0eYR/2pkAAQAASURBVOVvBYSLGt8Y1ptxVd0bGnqmLXEtplbwsKwNcbnMFbr7TDdjvXpxVuMVFo3ElS/XtmdjWVc1/QbhBpi5cTjH2tkd0ngB3uW0m+MinCv1X+B/c+OWTQuK5X5euai5qXWiYzTPlOnj5VQ35/uuMDC8Nt5DCPzlX/wd/+5P/5w//Z//A5ODGc3EEytJLBWpUJg8Yf/pa8Y7OTsf7KKHmkZailHaKSMLSZFIgo/E4AnOky4qVKvQVrMjoI4VQTYE4xibSFsLCIaehhgFaZoRgmSUOiQSKSRFTLjlcx7u3uWP/+DH/OQPv0/rLFFExnfHFIMcoxTBOcYPbtP0Rhx64PY2+kc5/iNF759vM3h/iEokeSaxrkVqRQidYnmxlRFi6BRUc8No3EcIQd1aRjt9bAyIRBO1ZDDuI42GCLs7YzSSVBuM1pjMEAkIJRjfH7OYlyyaiqefPGb+8hgVwbtAb5ARpAAtWZQ1ab9TGPZCsnt7xGB3QFWWNMF2V5L6OVEIdBlo2hZlND44bt26Rb1w1IvArVtDRFCIIBBBsTMYMD9yNJVk784Wve0ht79zD5lkyLris1++ZjaF4bDP9PkhTd2C1Oz2PYcvjzl8dYhJLEkmQAtaIkVPMBc5U6uQuSHsGOaJY9GTDHqOViiC1vTGGTuDQKZaZCjZKUpqGcFI5u2cZjKnP9iidZpbcov56wHP/8Fy/LkhpO9x1O7wajHi9nfvc8iCR6+e8uWTL5A9S9ODKovsjR2TUDGnoqFG4SmdYx4COzbgvMAGaIsMUzYEY6h8YFi2tEIQlaFFc8cqqjCljFP2ZhorS5yd0zQn3A8DSjGljTN2p5aQW/SOQG4FvvedHPMDiX+vZXurwdgE2SaENuGdoUBoSSAwHghcmlOJhFKk3FYaUfdI2oKxyWmixwvB4bRmrDR1ZVFCsbs3QI8NLg3MsaT9GXYQ8f1AsQPJMHLs58xMy5ZsOTmokc6QBkFiGrxylNLyvR8M8VnAJ47GnsBwQbPtqHc8g+2WWRKo80gYKsSuou1pZpkm37Uc9RrKXTgaNqR9TYOmspLdUXcSgPOdztBQUTYBkRa8/8NdDpoaN0qYGMdg23LkFxy6BdmoZJE2TMOENqu4YxxBFZi0x1hHjNeYoKCCW4UFJfF4Ml+iKhClIM4jW7HCSJDe0mNO6kt6JrA9MKgwoQ5QOkcviRTCYIJBWc04XUAyp233CeIQkziksdhQce+OADEjSUp6eoGMFXVTUtsSEedY0+BNjckCibwsBFxdd98m8orNcT36Ek1zylicGZ9YzrDp9Toy5JuEtxYqftvhTLz3LTRMXPG3kibeMB0rkWKZFltLeK3S/JXliivTWGf53/7+3/H/+9s/5d/+9f+Hx6++3FDwRbhqaL44eM6/+av/hT/7m3/Ln/3031K31Qpd803Dt+BE79uAZJktXI/vwgX3tel+OtfGrH9+83y4akG4UeYLMOLF4/n7tcCfSZ5XoVjmPFd/L2Tfl3yYi1NMrTfljZL/yw08k7F/21Yvul5f6s8NsEXoELJynHl5vFwF26bYdUnBedzyfI6n9RJPrUVdSCnEFbZg1yG6Llw3a+Jpe6/PHy/QcOmO7Wrew4NjHn/1jM8//QqtNU8/e0EqUhbHFalZcPJqwqtHL2mqhj97vE9qEqKW+LLFLgIIiQ+Rw0lNKiUiCJROOHSaurQkieEgQiTgiOgoeF2neC9pGw9pisMTnSAKz0GbEYOntgGhFKJJ+Zf/4p/xwQcP+V/+X/+Rum5pm5YnHz/BH05pG0uaJRyVguGHtylnFVP7CqUdo3e3SO7mTH57zOjBLpPHr6gXDfvPDk6l2ZKTw5LWObwPtK3n6OAYax1KKz7/5Dk6M9jaU81rFkdzIoI8y5jNG4p+j9nJAhEFVdnQVi3CBz7+i49JjMY6z/RkTmgtAkFrHUcHM5I8oarbzurRwhEah0wTjl5NkYmiKltyAZO5p027U4hPHn9F1s+pmoosyfj1Lz6jnHpihI9/vo+1OYiEpq44SAxluUA9O0GQo3RGVQe2373NV7+DtnHMF0edyVB5zLyGTGheVzlRCerao2NGlJIWwXzecHSk8QpsLZCyB8+nHFYtRZbwep4AASsEx5OGRSuRIhKC50mV46Qi7fehkTzZbxCJQYuE/QYULdNJ5He/fsnQpJw4QZEp/vxnzxFEmkyx8IIazdxF2sby8ybgpCAZ94mq5bUBX2SUVUM96JEiOBbQLmooMuau0234Mk/Q3lIZw9TUfDycEpOaGOCzHUvPDpjJGbk0/Ey9ZBYWIOEX5iW62Wama/TI8PezV5D1qDPBi/kW8YmgdoIwt9Q2w4aIDZHHx1DYlrnXFDLyu0mCSAxtqTgKILxhUQcyI3k6r9HKo1PD8/2GkE5ZWAeJ4lXZwyRQWYevAmiDS0BLyVdeIYWiaiOzxOBcwCpF1bT83aMZwSgaIi+rBVbWVDmkUfBFndAziqgTpjESS8E8dCdnn7WKvm+ZJ+BrwZFNqb1GIHk5k9wedSaIW69Y1JLaeSSan382Y+48CyExSjD3CpdAiJGnAlIVOW4adqTkd4sM6w31pGHqNUpEFl6Ah2ehwBFJigwrc1LvmJ50vm/2VWfBqXWRgyZSJJ6oFEIJ9ts+XnhClOiY0ExaXIhIWigiUdQED4N+hvaKmkiy1+eLl8ek45Tm2JJvDWnLFlG1CAQLBVLT6XiMUw7mc7bYvXb9vW5lvtixr96vzqKjiJek2ecfT7eBFcnzhm3hRvvypq3hkiT+LcLXkYZtKuON9Z7RNVdUcgk54vL3K8K5aG6Z4NrUF1eVsY6D8234jO4Sm/MvtfmSV3HB5Vv2a4zkk9ePeHH4nEcvv6BfDMjSnHduv39a1c074zdf/ZLn+0+YzCc82HuXr55/we+998OLut5Ag7wpfDumaK8JG/BzEd4otr5Mrl1mJtdizh7jFZm4CYO/lCGuZT5vz1Wih5uG5REGy9aezqTfIl4/VJZPRQRrA/UMYrF5vsT1l7h6ZrJayBn9unFluzBu9a2HZatYYolBW5ISXIf2m4pzrpRMnMFwIX/ocCou5VlhkK7qtGVQlofYUoI3WtpYO5XYPEJWx6xcUgBbN5VIjNSTOW3dIoVAK0XwnmpW4unwLk/TKSlpvKNxDogk2nRFhM5UpJCSAEA4N10L3RGuFALvHEIInPfYUzOwIXpSo9h9704HuTjTgep+ddqZH23blmSQMjs4wdeWGEJndpNAWmTsvnuLJE/R/YJUdFAIJWmtpWnt6bARnW4Gp7dUpUAZTZqmeAHBekKM1FVD3VjmJ3MW0wXeOozRCCGJglM8yQ42pbo/fXakDDF6pFLUVUPwDi0FPgKyc/omhEAYRTmriCESfEBIidKKJElOCQp5buFECBASnHXn/m7OeN+T18dU8+o8XTbI6Y87Z3MiBlQ8bZfz6MQQpUCnCVpKlJIkWnVX5l5POgZeCnzrIEamBydIAdY6nA9IOqeP01cnxOBPYejaZJ2jqhryJGU06CEjKEAlhtZ5WucRSuJbu7KBziczgg8dbmI4NVEqEEqS5il11dA6S9ZLacsaJSRGCIKA5lSfRvqIPF3DlOpMBjvvu/VTCoTvxprppd0F/ggiREKMKKUIIaLzFHFq5pjWEW2grmpiCJjTMRhiINWapuqcJUopsNZ2BgdCQCuFyTQmMeS9nLTIEXTXJaQQaKPRiUGos2tz4K2nqRpkZyG3UzbPDP2dAUmekvdzlNHoRJHkKVKq7mRNCLzzVNM5OtWI2J0odutxN9+FFPhT07Q6UedefbVWSGAxXZze4Y7oRKG1wmhJ9KFbISJIJTocS0mSJ127lULQGSwIp30fvEfRrRVplqASjQ8e7ywidr5rhFZk/YLh9gDvHCYxJL0UlWjqukYBPkYQEud8J0SWkspZlFZ450mMppdnGK0QUqGMJoSu3wWwtTVg+94ug7s7DPbG9O9s07+3g9KdqWakYO+j++y8t0dRZIxGfUbDPlvbQ3rjHqMHu0ij3kC4LK/Hl1fdjR/Xwzm5cnkvOUsghDg1Q71EuCyVfH5isQmmtyVPbkKTLsO5vv8ulx87WkScn+KvU+FiMzxfh0lZKWNzAcvm4K8u5oa3WN4apg3huna+gWQ5o4U6euhiP48hYFv7dnWdjjFYYrC+xfCt61ys845iQ9zlcD0JvbHglRSbpvTl3hEbY2/w9ZKTtU0KNBuAu7ZZ12Nk/Ub+Mh7PoAkxntvov6KSi7zxgtnYDNoVjMy65KQTt6wUcNWUXl2J1p31ifMv3zRcPTSu4KrexADAZVg3pT9LK9ZzbIbh8ii90KmJZ4h+Uzg/PVkq8JKTn4j3nt9++gknsyl3bt3m/YcPkKIjWN95cIe/+0+/ABOoTqYUp34BTGL44LsPOD6uOHxxhCsrhoXmZGoRIrIzTDhZRBACLSL3s4A76Pwt3Lk95LgsiZVFasFuH17oPtF79hLPsZO4tCNO7meOxzONi55CeVQh+fnHX3DrZMoH333A8/3nGC947713WPzqkMOdIVVV8ZN/+pC/+k9fUGjN7NiBdDCXaFL+2f/wPX72r3/B8NYWlRSEylILwCmGo4zJtKKXp2ztjahnC6TqfEuMdnJOJhWDYY9+L6OxFlggtKIYZJQnFTGGjsDtJ+AtLgr27m5RtoGkyNCZIeulnEwrEqW59+4ez14eII1gvDPklkl58vIELwN3b28RtaZ5cYhtKgZZJAgwEh4Uuxy6mvfvvsNoPKS4t8sv/vYLiPD9H+/y8784JpWWzNe8e3+HT74InbnSg1ckd/dIhzkqNXz0YcbhwSFJKtgqPGUZcFlCwPHRez3awT2aypLWh7w6mpP1MqRw3JElTwY9smHKeL+kySMlkdQYvjNr+GqeoPGIUJGZSOUSlFTcUTOetH10tGTSIlKFH+TkWc5o8ZKDOjIsNGE+Q5c9klvboAIfJfDTgwWFl/RVYHen4NGhw9YV7/YDT8cJ0gtG0TCyLcfWYkLknXnJl72UVAoGQnJnVvNpP6XynntTy1Eq0BYa63j/KOf51pSoFP9d+iM+rT+jr1OyWvDR/Dv8vf4EEw2/L+7yOKlp8RRJ5If1Nn+XLwha8W4aeCUgT6HoJdyl4VElwCje3U44Ook0dU1sAx/uCJ6FjGSc8f6e4MieQIwkOnB/e8DBrAKteef+gHkz5Mk/7COrwA9va758NUUKwb3xiP4H28j9ikRJdsoJvzr0ZHnCiIYklfhgMUrw4a7ksRSkqWDsIqkSNEKiReSDxPFYSJQMJFhGQvKYGickP+4bvvAR6QO7g4y7leBJ1Djr+fCOpM4NMoVsaOhpy5OJYtG2/JOtlKMjS54I+kayXQQ+ObaA4DsDyfNFIFeSRAa+uyv44gCkc+zkNWr7HmVMSWPDTr/hoNHEpiUVU+ZtjYoZvX7BB7cEv/pygZCwUwQsKbK3RaoCP95xPDqUhLqll9Y4JyiKATt3hnz3+w/4/OkJIk348Me3adqWp8+mKK35yR/e5+//65POxPTtbeStESQJxih+8ifv8+pknxgju3vbvPve3ZsTuutL7+UoVjbdmxD4Z8SlYOlUI55Gre6pb0UTbqr/a8pD35QmXn65AoA3lL8JocsCuhuFzfv3MsWz+fToawTBZWnuW+D43E/SCt273ODIO7fe5avd+yQmQUvNjz74A6RUJIlaqnDNytkGnP3w4e8zL6fsjm+zNdji4b0PV7romzIc3zpzsQmcJRL3Dfk2E6BwOrXiBR31pjkaNym1cjnuAq61Elc6Y61V4qp0bwhvIGgviMU1Uv8UxDOTd2dYWmEsrmS83gDeijTksorxWQKxkvbN7OLZ91VB/bcwgd/Ew63ZYjtvU1xKeQn8b6bG1GFp8yi/qsyNDPHZpAbOPadfteC+IfzyNx/zq99+zMl0ys72Dv/in/xTfvCjj9BG8cWnj8jGCWHiMFs9jp8cUAx7bN/fIb21zf3bBtPr0ysSJp/vI2eHoCTHswatOqdbiIifTBnbmqptKdsFvcTgy5pECV6kOaGfk6A4lJ2ExEZPv5/w4oXBaIlHUgvNIZ5f//oLnj7fh7wl2zI0deD46BDpHCZLGN4a8qu/+gxnu6tOMkkQIcfNPKko+OyXT0j7OdZ6HIK6rAk+kBqJq1rSRNMuanzjGQyHTI9nuBg4OpxhjMbkCXXT4pVEZAmJkkTr6RcJTasYjHvoU+do1JbDyQJTZDgRUSHQIkEp0iLj+ctDbLAkqcZIweF8QVSRICJH0zn9fkEgoo2mxXRMXwjMp458AX/08Ee8/6Pv8Gf/+u9IUkMIkaePp6SZprGW1CheH2tGu7c4fjXhcALhi9eI0RYqM3z6+QwnWzKliYM+w7sJsycneGv56tGc0d1jejvbZLt3qGe/QyQBLTxfFYHxhxmTeckrXyFFxClFjC1PQ46zligNNhqaEwUqZW5LJiEjlQEtJLPWogcJuw9vMRymHH9cYuYHNM7R2+lTfPc2rQ+cPHrJ354E8ph2pzpNZCYDtmrY3hrySExoi4baKBqj+Oy4RGiFDoHPU43yAaUTQoy86mdE58i0Yp9IrhRYi5KCL7JD+kpitOLz5DGmVYjWEkvH5+I5RmS0ruWr9glZ0cOYln5pePU+DKcFDYHnIUIuiLVDasWrKNBJg9OaIxTOO4yCUW54PI2k404xev9V2VnAChHlHMfz9vSkBF4/nRFdH39cM8g0L54fIGKJjLD/eMHERnxvQDrIeCV7JGLGbNFyIgOjcYowFo3jiVCE1KOHCXUTsdKQWkciBMdbKb3osN5TWcscOiJEwBMT0bXHO0/Qkv1S42XAC8/jKuPWFoREQ2J4OUsJmcRJ+OTYoYUnKwpGtwe8fvkSox0COBI9enlCvfA4GXk6ixglu9ONdEyeambHLeXihJnVIBx+tsDFiNYZWg/o9zTPjh0+SmIQRL1DlhnmNfS2ck5cZNDrrFdVRy1BdQSZax2//tkcXWiE1zz/tAINi9eRqC0/ffKYelpjtebFp3N6vRZlFPkgQ+uU/+n//q9oastw1Ds9KbhCoHRNODcxerGKv926vSLYEqvHEmt5V0yZrpM1V5Ba4vR678o2/t80rIp9b4TeqwnKm1Z3MwbsBji80HC8pm/j5chVpvCGcKyVcpFfoJTmf/+T/4FZdUKWFKQmXYLvQvC9Uddj6XlvfIv/0z//n6jqkkE+RJ46Zf22wjdmLq41k7YSrktzVQmbLx/dNPflhMvU203gelN5VzxfwXysmEF7W0r21D7yKrPUcVvn82DDZFoRGlxR7YUxs1WpyEWOdWr85jgTS/9v+noxh+MKrjaFm7A06yluanNbXDye/1x9kroBkrjKGq8KMK5G/jnPs76PXHeMe+3C1/13cHTIweEhs8UcrTWvXr3i3u07KK052D9iUVWdhFnA4J09moWlbh3Hr6csjhbUi5aJ91Sv51SVRQBKCXyA1gVCbZmVFS4E0sTQ+EA5r7DOo/KMoDKmTiAJOAlISSMk0xZwimg7k6xBRg5PSuafP6d9bw96DV52ugp+3iBeOKqyhdRwXFXYJCMIUKnBao0LcHw0pX48JZ60NHWLVgptDItyQTAa5wMIsK3n9dMD3KkpWpN0PiR82+ARNIsaeUrMkxikdcgYqOoWlSjKaYlJE1SW0LhAu6ipa0v0kSglVdXQVBapA1FEGmtpW0uhEqqyBiBPE6YnC6pFRb4zpmkcrTZ4Jek1nlRo9vZ2aCrLYl6x/2rS5ctTnO0hTMHc1VQHNUEarDN4FZg/nRJf1Jy8zplMGrwq8EWfo6MFOZJkZ4ydSKqZZ/b5EcXEc+ujbXrv3OPli2OClMwTzeT1ETYG+qbz1t5IMAjqScB7iUCgfecHpG7Be43WKZlW1KFjPP3MMvlynzw3+MOSHENUYG7vMG08T/ePcNYjGjDW4tBYIjp4FlZgnGQ+SFhQ0yp4XjeUIhBNio+RTAiC81SiEyJFZ2mVIipJSqRRkjoq5lmNNC0TeUIv62GjQeVw0izwxhGiYJZ5YhaJXiLLCYt+IAxHuHnNiZaoXor9bYtvFFUUHMwtOpHUbecUUgRN3UDlJCkJJ41DnDhMW9P6hqSCEA2LqkUU0FY1TWsZHDQIanw0zBcOVOd0UQkBacbr11MYS2yItDJnITNK57vrXDbSKo21EesCMnaOMa3oribWWTdH6mgRAWoh8bHzpG5VpJYS0VoMgkZJThqJLj1VqUFksIiEVxWVE+xPPCcVtLG7FqjayNwrQhDszxpmNtLKzgO3XzjwilkTUHlG2zZECwhNM2k5np3QtJIs0STZCNs46rKh0JqiKGidZDLxlFVD4wxKKl4d1xBLWq+ZHM3Ae4KP5KM+vb1b1Iuaeel58WqBCzVCRqQ2vPzqNUJ2prGTROKtILQRkaXMJ0eo9phkXFDvDDi4OyZNE9I0uSDav66k6cIO+M2zbCRa16X+p+FMUrYsHb/hacSNjddsIrSvS3fTcLYN/qMwNRsAug6+aw9Qlvtj+cTomgLXP8XlTzdH1CWh8lVpJAx7W5dJ2TM68RzXHVVydiVynR5LdELSTwgu3BjGm4b/Jgrdm0+2Lqkgb8x3XsPGZGJVov4tCMaXir4y+toWX8oXVwj/jTLyN8K9RDiu13+6mHU6RGd3vk8xI65y7rbEMJwqH10+tbiA7TpV6hV83ESSsuHEYKWwa8JVMNwoLB8tnlodOztxuHSraK3CZZbhTFdrdRysSmTg4iTjOrbsPMW3sNiu9FCE3e1ttrfGRBEZDgaEhePFo2fsPLjFzu42W1sjvAvs7W3ji8j0cM7JyyPK+TExSk6OJtC2hNLjJWRZio6BEDyI0PmBUApjUnwI5FrhtCDGgFHQ02CEpbGOPNEoAoGILEv6RtFGB0KRJzk2TPClYGs4QI/72FjTVC3DQYGyHYOT5ob53KOlB6mwVeisV7Utw2Gf8bsp9rhmdrLATSvqyZy8n5EXKQFJ6x3ltCYrElpBp2+hFcZoesOC1nny1FA2bTefBAgtSZXGR8hTQ8gSmsYy3B1QzmtSo1koSa8wKLq2O+8RRhHx5MKgU0MvSYkxkucpWimc9xSpoSgMsUhphCTTEmMEhohJDb1BTq+fs3drTIiBPM+pZwajWtIEfGiJIpAUml7PMCvnRO3xs5pxrkBpgnTE0NK+rrBZwYP7I+rXC8rjCl+X5GEIaeRAO3pE0hCpfKAR0EOgIwQf6EtJYaBOIy2BQnpUKgkyYGIkxUP0BKnpZZKGlvpkRixhd5SivMSZhHt7Q3777CV2VpJJSU9rRPCUSjBWkuAdTRrIaWjmFUkmmFpPv7L0peqUn33onBz6bjwN6fRXrBDY1pLGQBIDTfRs1xlZo9Dzgt3RHgM/QFYeJx07toBeSk9abN0yjBnaBXw145YqqJsEU1pEKsm2cmTi8UEwNALnLIUBJ6GIFq0crY5kIRBVBCmJHlSsGPWgRBDnMOplHFtDGT39HIrRkOAV0yfPSdKM0b1tbITB9pDnhzX7s5Zb4xyyHq/rGld3Hql7ETCRPNF4WqKMLGTDNgkKWKiGzApUFKAlEwMDBGWEeYCeEJ2DxxAxWrGbKJpjh9Cn3radI5OCpPAkfkHfSGJmEMKz288wFiY0yOM5A+mxpptLaRtBRmKU9GVDlkYa6WldwBDRwYHJuf9wTJZq5gczXr9YkAhHqC3WG7S0ZDEgiPigSFSA2BmVSIUlRocn4uYTvEjZuTXEzAMmttRVxHpHRKJCi48eSYK2AYHE4omtJxlJymmFP4n0E82gl9LUnZ7VcNg/dbZ5SsC/7ekFcOYR+o1pr1j3z4naDQLLi/3kBkTPsqGPm7ZjfXO/Sbo3pYnLZDpLm+c34eLWs1+1iV9RxQpNsorL1SLFucBuhdY8r+aa04wloeKZzse687xre/GMRFsTW4qr6hMXvytXvrqKL+WR8kLlWinFtx3+0RW64aq+fQMnuJLyqn9LFVxRVORsAMSr08Wlv+tC7MzDnZk7vbR+iKWES7+r8/XrTiZxXqE4/1sdMKuqx3BuFvWSedTVNsF6W5ZWsrg0qeLZPBTr2S+yXTPHN4e3p6xX0Lwxe1xJEM+ZmCW4Yzw19RdWssV49UAQmyrcpEUvQIj1Gi+Sn/2dm829soFviLsCSoC7d2/TyhLSlmBaFnrBX3761/zpf/pTSjenmbaEKhBbuH3vNpNXM149OqCa1TxtBZPhCH/3LoOHd2nv3GKxs43eGxJk57zKS0F+d5tma5vFYITYGnQEuYhoLbjTTNCvnjE6esXt+T5BR4IIkAh2hhY3MJS5pN9XJNJQLSzTwwUPb79D9bymPbCMB1uoxBA0vPjiGaO4wL94Tjx4CS9eEhtPvWiZHs354A8+oJIWn0fGH2wjhaCcN1Rly/atIa51JKmh188Y7XQKzz54RlsFRwcTmrJm5/YW417nT0BHuHV7TNVaXIxIo7n74BbBB6ppRZEo5vMFxIBRkl4voalrRIzsbQ/ZHowQLegoGe2NQQqsdWxtD069gYNwgUx3DgOt8+jQkiYJUnXKtXu3RjSNxbaed98fItWc3thx97tDfvxPbmO9R2rBv/i/fo9770/Iel+wu/eCH7zn2XnYZ+tBwr17hqAFdet4/PSAew8KYpbjkUy/esJX+19SFjWLseOOrfAuIh3cMwnGBbyHOghuZ55mFKh6DWLQ4PYq/D0H7woe3pUEKyiKjIcP71C0LaoO2JnlvfeHLLZzXuuIG2VsD1NMYdA9w92+w+6AHTbEYYPcrSnvBV4M57zTj7RSUbWenjJsW08rJTbR3GlbglFIY/AxMFjUlNYjkoRbrcUrSPKU1gtuzwYEI2mi497BFrX1BBRWK96f7WGVx0bLO+U2logoEmrp+VANKdWc6fELdsSC1jTIbWAseW+gcUgCEhUXyIFH7UgmpmTEPmn0pKHm3h3DNK84zGpOxgE17vNUjDnObhO2d0mLlADULnL7dka6myNzQb8n2bo1opzWLErL9+71kFqjgIESZCOoh1BvaT58APbhAcmHE7YfTrn7zgHiu68RPzzkJz9IEd/NMe8Zxu8kvJP20GlB0Ck/Kgro54REY/GkRU0zgKYnyEcTXuYHhPcci9sLbn9kqe/MKW/NuP2gwt4O+D2Lv+W4dTfQ3vaUtxzjHUflJCqmKFlwK/M4J0lMxnfeHVDs9ah9zcl0xoAJi8MJiXdsZS2eQGMttfeMBw7T75MP+rz7zojb93fpDfr0xyM+er9HNiwwRUKetpwcv6SsJzSx4v6WIEkGSJmQEbsTOwwxaG71O8V8KSNFrun1tqlcjxcHkcd//xn/8//zz/j3/+a/8Of/4ac4u6QYuyox2vy8Mbx5XzvVyV1S0GV1nRds2FPfcr+8KZn1NuVtKv86umqZDroJnfV1YXkTXFfBfmXmpXAV3Jvir3u/9C1ezWWupRfrERvDMv23Ie4NdXyb4VvQuViV4f6jlfEmTvSakr8VGCN45yjrBiUFeZ51zsUujcEzxuNUmn3OvIrTI4VlKbdYpU3PkpynWGZFVwnRs2OuiySRlaPSlfRnkpjNTbsanacZLikonbPU14flJFekXZFosKmnzm+gXgJ/vcj1fOtfN9Px4or3NXwtcV/ilONak3OsVnuJWdvUqs3frh6qS2nPHzdJfwS/++q3uGgp7ZxZlXP81TGz+QytNU9+/QpTZ5TTiok84eVnR1SLhhglr4MGk+JUhpeRYw+x8DghOJk2CO9pnUNGTWU1tVKERLJ/MqFoLW3TUkpBtaghRNoQeJntYX3AKoMj8kXIiVqxCI79uiVF0bqa+fGCn/7nXxBdS103PFo8Ih617H/1Et+0vHrqIUI7mSFyQ+MiIZFMj2f8zX/+OTE4yrpCtIHWddcnrPV88qtHneWoxtKeWp5Ji5QYAq9fHmO9x1vPi69eEHzsLCsNNE8f7yOlJITI0dGc8qTCu4B3gYOjOVEJrPc0jaWcV3jnMUpRLyxKys5Rlw28fnJAjIK6sbx8NcH7gAuRJkA5D1jVjYfDhePOD26RDwuqRc3jL193V8Ji5Nf/8ASjUwa3h/T3BhwvDDJNqRrHF48f0b+Tclg+I9vpsW8Mzjla5xC3donNjPKwQTvPL76sEUEREMyGAtH31MKR4PldniCEolWSZ87TSkGDwDjP3/pArjSVgtcuEjVUOuAI/HaSk2vJ7Kjmt9MneBTpsM/u3RGf1QF9b5fmxYRff/UcG2pqBYLAbxOFDo6FiqRpSqkjpYwoF/mZFyjn8Vpz6CLzVFMpgQJ+l6fdVS0pSLTiuda0UuB94MmgQPmWmkg2CHy1MydLA1Ws+Zn+BBMyJn5BguanxRe0bUvQgX/IH5N4zVw2FEmPn6pHtANBO2/5bbTIImNmHdp7fl0KvBedx/eoAEetFf0kY38u6YeItY4XM0+TaE5ax9bA8DcvSrwqaJTgyUuH6y1YLBxSaX73+DXvDDTzeUnVCkoKah9precvPz6g9QGL5CA2xEbSDFKUgF/uLih2IgtdMnGexZYhSEtoA38XFuiwhTOG2etAvd/g206e+NetRcfIlEgaFS2aUkJuBE9MRjbwzFXLdqF5oQRWB9q65b+8ekW/n1C5SE9qvpCWVkNjW35bF+RBUTlN1gS+LHskeYJODC+qiMdSI5gcnPDx64B2EYHioM4JQkGakPYVJ0pTLyqs953JZCmonaHVnnkdkUqhigyXedp6jgUSIo+PDa5xWNld7/Le4qRAK8GrMiXiQWsmU08dEoJJcdHxN795zO2TBIqEh999hyePX/HwOw9Wl9XlZfbbJsY2lvcmmuVqyfWVpyfX7ddXidDX6a54EX1Jlrqef5leWaNfrk58DZBXlL0xbKJRNhH9At7mhGp9tz0/iXgDPFcS99eYnT8/FYmnFqHOxKRXKB5vUDO+BDt8e07y3hS+FYVugTgH/OuFb3G2LnN6Yv0W/DXpr5pUS/E+BEDgfDh10CVP61lOvtTx62N2rfdXq4yXJu619ocuKVZcqmxTrlVY4lo5GyuCZTNuZ+vL5lzrPkjefhBfbvEFA3Zp8rzF2rmh2FOUidW4pZfV1qwCsc6SnItlNnbZJfHD5W83XJw2CUEuFXm23sVw/tulv3BGSYQYIkdP9pGmIC0yhJJorYhGowMQPEp0x6fh1DllqjUiE6RpQnm60CkpyNMU4y1N1RBcdzXhDMYoJUFIJAIRO/OVIXTmOavWYvAIOmItj+pivMXI9OUxvnVIrbtFNXSnUGfmNiWCxXROsbV16mwKpFF4H85N4MrTu6ZGa2TsiNBq0ZCmBokgMYa6anHOk6QpTd3irUcrifOnTqxCpHXthTUPKbvrT1XDmZneEAJtY3HWUTa22whid5fe1w0mNcTYmaINISCFpA0BkQikktSN495HDyinFTpPzomEM0da8fQ5hIiQkqyfMz2Y4qxDSI/SCpml2IWlKgO2dXgrGd7b4dXRCyIQXECH7jqY9w6hBEYponWgNTEIHFA2bWdeV3azXSqJDwGVGFTozPkG7wlCdCcv1iNFt50U/QLdL5BSIbRkfjSnnlcYE4i9iFDq1BhFRHrAe5xt8VKBEgRO2+cFcwRldEQpQXZjKHjXjUclEadKiJHOJC66M/mqtEJqiQuexjsyIqafEctTc7sxIELA0ZlvJUSCEnjrcLbFVgLvOxypU+/qERDeo4LEC4Vzjsx0Pl/wIJWkN+rj5x6EYnFSonYNJtVEwOQZBkF0Ab/Wp8456lmJaxwyAe89WutzwWYIp2Msdqadz5YbJTvzrxFQmelMGhcpST9FyBHudYfn7NaI9ukEYS0ydAS6AUwMRCfQsjNPG06/SX26jkhB4xxeSKSSpLnu5pWU6DRBGE3dlngp0EJS5Dk2Slxn4oAIeOexwTJfzIlREc7Mrie6M84gIyiDjwltXVIupoQgEELhvQcJPnTOMaPy3dqgbWfa2Dq0SnEhINMEpQVN6YhSkGUJ8yZi6HRX8jwjmoRUBpyP1DaAiCTA7GSBrOtuTIez0+wrhGtvIau8ZP3nUoL1xwvib7majYKsdZg2greU83yrubiSfonGuHpzv34bOyv3Qpp6Zd7N4bpKNxPTV4Z4litu7rtNZa0wQl3EWVuiOKPXrqB+3mI8rIdLtNw6TIK1vl1+OW/lRS9fA8eVY+gbwH9d+NatRa2E66ifS625uoXX08BLsuY1DvCt7Ra/Ad6zxV6I1Ttq1zLkG8teu9IVzz+skJAX82D1rv9VVVwf4mUknk6iC2Zm89w7pQPexKax0q7zxKelLmdeer6KfbqOuVptwNeYFYIbmZ47kxZc6PhtyrMGg7gCqnPkLvXtVbzI5UyrxgAuimGlN5bG//cffp/J9Jid8S79YkAztbjpM5ST/PAPf4/P/+YFRdqidIYxOUcyYZhk9OuG11phW4+OnnGMnGhFDJEHewNaEVgsGrTR7G3nvD6ZE33g1q0+zcsG4TKS1KCzhOmsIkYYSc+0rTCLY/p5wnav4AtnMImkjyKPkkkQtNHzR3/yI37997/BpAkPHt5n/quX5MOCYD27O30mRyVSOnxb40NH7DXzmn/yf/t9fvnTjxFG8eC9e1RfHHLQOIJzbO8UHB3OUUJgUnXq50FjjGR3d8DxtCL6wGg8QGQa6xw6NYzGOfsvJ5hEIxRkmeksUKWG/iBj0TpcnpH0M3aGfdrSoqVgZ7vPybQCYPveDk1VoUpFXuRkp167ExK0CNzeMrxuKmSM9AeS2Iv86svfcPfeHe49uM3TRzWu9ewMJU4NSDOJqzw//MktTo4bFrMFu4M9pvPHZDqlKFI+eHCf337+DG8te33JsU4YakniBQ+3Iy+PIBkYPvrBPX72+tfkHhIP34mBT4HMw60QcSHQeDBK8lFreZrmROfZU51TRUfAhMADs+Bw0CO4lq1hynt/9C4fP3vN68UJW08r5gNFNlLsKkM2VHxWlUQf+bHU/CqASiQDF+lXLVZkECU/XrR8knZXs/qtI4+Bl6LzQ/GwrnmWJuRKkrnAOAQeK4Ug8m7pWWznCK1I64TRfkJ929KPGT+ev8OXzXPqaOi5hI/kO/zcf0rwnu/u77A/bmh0TmYVP9Lv8fPiGW0MfEd6jk1G7VtSF/hubPitLIgSdoTDCkNrBIkMPBx6XgbDfF7ze+/v8lVzSKrAGMNHOvK46fQi+klgkAlOcsnctYy1p5lp0mLE3iAlTVNeVicwiPzkfo+f/nZGnkJ64ijGmsleQxYUvz/p8UkxZdzrcX94l0I0fC4eo0Pgj5oe/zA4IMY5dwc99vqCz8ZTVFR876DPb8WUQe7ZWqSMheGrhwodA/cP4MW2RPU143lkTMKLkaCe13y4kLwea0Qq6C8CuyeB3wZFLjW/N4AFmta3JNHy3nbg0esagWAnnRMTg/OBfqJ4uJUwkVu42nJn5FjElKefH2KbBe/0LUehj/WBxM+RIkdqQaIN23nDYWkIBAbaI2JNVdcILRmakoXP6SWRXDuikIioUKnmBx+OOWgUbe0oQk2oLLaNaBnZzRMqb6gPHe7Y8+Cd20vL7zX7xBWEuLi0Cd4g/5ns6rLYanMllxOtlHsh5FwS+y7VFZc3oLdmBDanFZcrWAExvsV+fUlY+zbhjJm7jmARVzyzhPMlPilyFT0SuWrTPzMv/3XN3K7cTGEdF+vs46aXG4brGMpvEL4Fa1EXvzcisoFLVNUN585mHCxNnjeV92bq+OqMopPgpqe2+m9SxmWcbI65TGSvEoyXGIqbztHzdHGJmj2bMatscVzH45pEZZ3pEDcekVdw+5eBXAprHXXGWV3i5L8uu72B0boGtHNB+jkel1tzGYZ1FvdioYo3YCiWC1ldXM51h876MK5+WQ63tm/xf/7v/y/Mqzmpyvn3/+bPUVWKSQxPPj4gUSnzV51n6ePMI/ICFQStyYm2JdhOqXLadjoBiTFMFhZtPe7UUlL79Bm9Xoq3jma/wmQJyjqyRGERpHna6QyUDcnsBUZKslZxnBiElgQREb2EulFEr2hby+efPyPJUkLVcLI/o2oaxKmzt8WiOznIsgTogwq0QmGrhq++eEbWz3GzSFXWZL2ic1imBSFIsizB1i0pAlc5og8EKTh6NUVriYrQLCpcI1FG0zQNrmkp0oSybCgyg289iVEE56lDxAwywqLG2UAzqUlkJ5Gf7M+ookMnivlkim89vX6ObSzOdtJmFwMm08zaKYkWuBBoM8Gn+18Q55Kn+8+ZP7mDFGOa+Yyf/fo57/w4x7aGp798zBefnxBVgkg1X331lH7PIkTnfflg8pjBIGCtxeoW2UaM1mhveX3sMUL+/5n7rybLki2/E/u52vKoiEhdWeqWuqr7djcajZ4GGsAMBhgQHKMZv8N8hnkjvwfN+MwXGg2cGYgBSJCwAQaCMIgWt/vKqrqVValCHrWFSz7siMgTESciI6vqNmaVZcU+e7tY2923+/ovX74WWkuW3uFtQhWKWgqehUAmJCFFbJ4jUkKnRJYS+3mOUUCEtQvDjpAcDqC/zDU+OFymONE9B09+yr6z5CrhHhaUCuYE5smz6CCIiJHwZ8niRcJKwTqThKRJIVEn+LwqSMGfBvqTrJAoAeqUl1wI7Cn8P1ISSUJLwYGUFN4TZQLhWO54qijQHr4Sz8miQIbBJOdXfDkc8HcdL6oFKmSIGMmE4knxKwrliXLNsZaYuEdVlcjO8QRDco5MKfbbnqIEWZbE4Hi2Bi0UiIR6tMNMw+GTF1Q68aLN0b0EpVkfR+aiZ71qMJlk0c6oFhnIgnmb096LxB1Fdt/w48U+cuwxRc7ed+8T760o6Kld5EvTMd3dZVlE5qtj7N4CbVrqGPl0/BMKL1h1RyyOTvDfyahnGXWZ82J/zfgIur5B15b27Yw6G84Ird5VTIRkWUmKPYlViix5yp2CpQ2MlcaKQK4jh0tB4Q3JJw69IaNHqUgl4OlCUsxqtNHIYkq9WLLuenCez14KUtbgrUd4Rc4cbM9OqZgjCGrYnXIyI/OgtGIyK5EyY0d5PIKyAJN6xLon+Y42ScBTZDk7d8eE0RjZQ6VgGSSy73DLlhPf0feOTBnwlsVSg1akAF/92ZyDJye89eH918sRG9P7GV0GA7cIQ7UBLK5LsI2FDW36NqE2cdEs6jphetvye/neNWxcf5j5VlLajXSuh/smQu+3JjBfVXZebeMNmeLy+PjWKG24O36TlzsblVvgUdr4+y0DjG/NW9RfhB3Xa7/127JwXUO+7ht5nVHb5Wo2ZWRxeuNS3YlXRmUX+Duv/5qX2kTVVyX/S+luftnbOBNOZ7aBgiuHurfzvXHvEgLfpinYDi/e4Ms8B1GvGwTpYhdcAF/iQjmvomV/vbF9+SzJeXW3oS2I+lU7DTevjJtLlGc5WZbz7KsXrNctR4dzpBAUoUNYhXURLzUOTdsPoCFTEHykiwkbIjpAipLeBrpFg1l1RB8RMuJiYLlagYDJaIQKsGo6Fs3pzl4UhBhIYTCj8dZjy5yVjTRGQ0zI6IZIwymRFmuefvECRRjONpwMLmKP90+oJxWpi8QwBI4TuwYrAxiDC4mvvniBJNH3DtYelxK2cyAEVrrBDaeLw3v0Dik03idaZ8mLjOACwSiEHky1bGeps4zeD7EAVoswfM8xkdY9lIMgGhK0rUU6Cz7Re0/rHChBMgLXO3RmWJysSTGR5wqvJSlBGzxNlxClwXmPKjTr0NOdtLTrRLtfMX9hWO6v8V7z0//0FaN7d9DFlGUb6JIHITCHBzTtCbKInKyXBDsEkCMBckprLSmv6PtAbwXCRco8EpcNJz7ik8SThrb0gSCHKO1aa6wAQmSVhujc1mhaHSFG2pgIStGuFblShCQ5ii3WenylkQheBo+M0EuBTQmhJK0eXNy6mFBasyIiQiKkSKsVK6GRJJKQOKVokqARibWSw2H304jRnZQkM5jLrU5tzJ2CVXB0NuCyhrx0MOuhXtE3DkaalW+I0iOMps0TUThGKifElkZ74umXtRIWeQfC8wJkZKElfZ7jVwO4FEoRdEYTI8kG+gS+l4g+0VvBk/0T/D1YhkBSEtdBcgKiQHSe2K/oe0AWeATtsWVWSlRtWCvPSsKT/ROkzhFaEmRCKQci0BaRkIGaghItTfB0saFSPWuzZBUbhOwQGJZ6CRNJUJG16jmxa1Iy6ElJ4yX53QmKkmUazPiMU0ifWJ+6VBYK1mqIIF4qgVLQG8U8CqzxzG0gSUEKGh0kKxeIxiCQiJDhG4c6bNAiIcsRfbCELtJ3kRQFsWvIfU8Shj4JXGFY9g6fPFM0Nkl8G3G2IS8Gl9hCCnIEAYXKMjgdf1pJhNa4oma5DswXPcfOkgtI1tL5iMJT5jnRS4SCzgcIiRAFi6Xlj//5j3n4nbtIdcnfzbZF6kyevHzGYdOK4rIJ822Vg5t0ZQk603zdIv2W9faCemybb9jb8Jiuelq8Ke95c72JcvTXSacMbVvh05kXzo2kA0tXAVu6cv/0Trq0cF8H0lLa7lDnOrav8Tx1KdVGObeUps7a41qw+2b06zWLuomucP6aV7+EpG8t8l1G4NtQ+qXkm/J4gleHrq910Px1ZosbaNvEsE1wvw2lQcgVZy+1Nf+5AdDVj2zTna3Y+Fg2cr5i7+u0wfXAZmj7Tc3/6+g2gGcbDN6CKs83KcSl+t9E+7Kl3POhssnY9jLT2a7Vue3nZV5f5b1pBE5nE8qyYGc2xWQaE3K6fYvrepQEgaGuKpxIGCkRUiAiFEaiEwSfyKUg5hrRJlw8jbuAJReKEActudaDzbeRg92284Eyz6mrnBACy9SRG0XMFKSAEILitC2iMlTBU2cZo52SvrNM8pJR0qyOloO72NQSwhAQLZIgeEKf0BJ2dkZoY1itG6ZlTdvAMwW5UWijhmBhJHSmKeQg3EshGNVjQvRAYjSpaN0QjXxcF9RFTtt05HnG7O6E+cEC5/1wZkJJdh7s8PKrA7SSVEbijSIlgReRzvcYo0BIpFSYGAezyhhOz4R4tI+MJiVWDruiO9Nd7t65w+HRMXd2xyzWFSZq7NEBIlmQEPuW+w8rui8P0FojlaEQOWNliFozrSeEArxPgweqLKe0JTFpVBHpj1tiH5ner5DWUnhHDIodqbAhYmPES0kVAhKBJzE+dXXtrCeSGOcZISaSgMJHtAApElIKCqBNgTZAngSRiFACqRUjH1AIlIAyRiICkSJGwK6P2CzjMEZUiOc7JvMQKX0EObhWNWKYq5QPoGAmIcSEICFDoAiB3AAiMrUFqtPcT7vUeowJAdUIorHM/ISYS6ZCEbBUaIST7Osld/uaVkRqlRP6jtoIdF7gQ0/Vt9ggyIwiJI/Q0FqL0JqaSKYDSiryzND+6iW2D9RKsVdktCrgscNZqGaJCjXj6YxcCHyeODxogJ69apf14gWFCOwYQ240Png64Zh2GXrtWaTA3p09/PqYsFoRx4kpY0bRoGNkJGuG3pBIBXtpgo0KuW6YVCMoS+ISfOoZB0leFOhujXKQywIzMRyEFbutwfeRPEsIHylFNric1Yn7ZcFKthg1nOUZjQ2FUPRry8QEfPK41iF8ZG+vZLxb8nK/Qy47nBKo03liUuToxiJnE6ZjzdoI1MsTjjpLbSSjsuCwD9QmEZNFRIgY7NKTq0BVFuQ6gRxcMAch0bYjrQc3w+NMUmcaoTW6DwhnEd5CUhiZyEyiNhknnUNEx/6nT3j+iy+5+51HGKPhihC3MXefCWJiYx28ACyGu+drgdi4n95gUb+8Q7JNwXdexVUBeFOQSK8KuFrHlvKu3jxVMl5GCpta8JuKfkMx4ZuFuL2+1G3nJ89jfl3xT38aK0Ju5rman213trZLOit2GEZxM9vZs0TTN+QmRyuzvcyz663g82vQmWxyphT+BvStuaL9FkXrW9HNWtt04b9X904FtNMPflu+V+5GT4W2dPH3Ztrt1xeYvL6Pz4s99Wd9pYotE4e4lHdbluvQ8U18nma+CJ4Tr0yntvB9/nMDHGzWLzZ/X6r3Qhmb/XQx3YVPd1sXXE58m2/hcjmX823yfe4r8OtUtK3uxKvO3mRoO5uv6rsp+dksvwXInFJZFczqMX7lsXPHR997n+gjzfGaftExEwnXB6JPzILDukGANlLxIFdEKWmFYGecU2Q5IAghcefOjOghU4bpaES0kcwYtDQ8frCDkdB1LahERBAQRCTvTsfIUIHNmTkNYUaMd3HqATujCl9b0ixw74f3GL87o353ShNbJns1Sgr6zqJiYlzkKDUcAH/7O/dxuYM6sfvBDnffvUt9d4aLidG0IPpBCBmPS2Z3xiQjCVpQPxjhBOSTCpQgyxUIgU+JelKQQqLvLVKKIeiWEHijePhwl7BqoXfkQLVTYkWk8T3VJKcoSzAaoRVVnSMjeO94+8NHZNoAkr73VDn4zCLrxIcfvos9kLgDRX8g+OCDB9g+4vrEW/cLdJ6xOFwRhGa36mFkcCYxyguaZkrb7bJaz3h892PW64qurbm/u4dWhhgFQWU8nARWJtGZxL3dghxISdD4wDvWY9PQV3tKMckFspT4TPKBFrhSQWWoRaTME34k8TPD/Ylncc+zvuvRe4FRqehzSV9K3osRlxlibpjmBW/FDJkULik+Wg2xI6xQBKUZtZ4uJlYxcXfZcAQspaID9lzECugEvG09KdMDaEHwIAZQkigFj0MkaEgKbBf4JN5B7eZ0XcNH4T2cFjDKEXXGx6v79K7FJsu7i12kCYDF0fLJ0YwuLfG5491xhvokoj6xiB9GPphZ+juK/o7k3q5mlNfIOLhffTDTnAhFUxQ8fLTHbFZRjAva4Pm4jkTp8PTkcs3KrXm2XNFUOR/8ZoH87SlfjhZ8efA5Lj+h+l6G+iTjnfGC+P4L5LvPGZsvmaUlYtqwtE/54MshNkgMFn0E99UeQUvWvuU33Qd0fkl0LSNjeGc6Q0xbuvyE357eIc5OkNMTtDrggf+SuPsT4p2f8F3/Epv+GF/9DMaf8xZrnHmBLV7yoV/TypfY/ku67kveEpLudKfzcQXtuh92kELkQd0jtQFpuFcnFs/nLF8u6LrArmnQeUm5O+P7f+Vdxh+/hytHtKbmvfemdDEjqApLB7IjN54oeiZ5Q3AC13qkdyx7Q+PG+Owe737yNmtdcmIH5xDztEbcKTDv7PDJ9+8RRiMYjZClobWOrgNrJY/ului9GeP7u6hM8sXJS/4f/7d/wj/4H/85Xz55fnFKvTDVvm5R2nh8ZrVwnThxG3rd+vfazOlaOeLW/Ij0Ck+cyi+3eZ9vsGrenPNrFnyz9LhxsQEehby8k7WlT2/Zvxc80G78PXsV5x3/yx/9M/7Jv/0f+cf/5n/g5fEzLoRh2KaAPru+9E+ciwhi6/Mr6S8oU78+iXT5FPQb0mq9unjjDcD4tekvC39vTJtRFdne0VfKvezp6Oz2K6MhcXay+bzMazphY0CeCfXi4qMh7+WmvxYYbOYSF7fFvg5tRbqb3IlT8JoupLuAE74Jqj3fd3uDMraMk6ttertyNjUQt6r3W1GaXAqKdJtyr9MkXZ6UzoZ52rz5ig5fHPHP/qd/wac/+RXaaDQ5Kip+/u9/gY8RP93DZwUxJaRKKAELnxgLUEisj6SYKBdLRm3DYt1TFJqUPNb2kGA8qkgJmtZiMkVeD5qWru3xEaTJ6DtHXhasx4/pZEm1O0H2LfQ9q2QopGPn4QEPPyzxRMZUcBx5/tkLmv0Twose5SXJR8TM0IzAZgqi54Pf/5DRbsV6vWYmR6Snji//5Ev6k8FsS4SAzgxJSlzw+JjYebTL8bMjjDGsFw3CgEBi8ox6UtPuz6kKw2LekNcFos45XjRkSmKkoMwNJ4dzZnWJyjTNssX7QF5kFOOK48MlWabQMRFcGEwLlUDmmq6zlJMC8TgnVJIYEo+/8y5lVrP/4og79+6wOJyxPBEcfrGPkpFEZNVLHr495vnyBD2uSCFR0KDtgpBlPH7/ATF6fPB4F8irHaIY8+Kwx3Rrmr6n94Hq/i6JOfNwjKsyqhgHD0pS4pSkCh6hYJEp6ghRCGRmWATPTEmEThyLSB0ZzOcSrJVgFBIpCVZaME1DRHed4EjCzEZAcaIkBQJ36n3vUMLIWnyCldFkp4u2EbDKMsa9BSlYCsilxCTIhGCuFVM/mMB1WiJTotABIzxLI9mj4/FfX6Dfc0TrMY0m8xnP1Ql3mhFOWpzxBJGY+BzpYZ997rkdmiISCoFPnvH6Eaa5xzO3ZrpSrH+i6PoSLwTjFciF5LiDsYz4YABDHyAfN2QPAvuuZyYk6UThlwEbIY+R6DStKKhMIt4LjB8WnHSO0ThSfWBYVJGqj4S4j7YL1kVkp8/QCo5MSx0MYlwiPRzHNTML5ePAcryiDBmp8+RkHIk59+QdrI/Ms4YiGGLUGGvYj0fcCxOSamjzNbkuyLMxeq14IY/ZWU2xTcm60JSjitxrZC/4crnPg/WI9skezSojWseYEeYg8HIVqLDIhSY5g3OBUniMTKysIhcdIqsp93ZIQjKqJdH2HC9hOkocHi9pekdIgpnqmQpL5wQx9mhZIIXG+YQUgxvflpydscEXkSADTetxYU0cSeJkxCSTZJ1G9JFVHyj6Hre2eKsoc4EqFdU4JxU5bvESzz42dLz7g/f4+Lvv89/+H/7GxfX+8jx7Jhdct55d0PJvnaJvT6+Rs68vXnBlt+Lr8LFZyYY49BdG33KdV3ZFXlf2G9V/O2H43HvXxvj55Vc/49/8+F/wqxefMR3t8Mnb3+O//t2/R/CDV8DNUn+dXTAejb923m/fLOrrdP43Ft6uVjoUeZ10tr2MV3k2J4Gzjr/0bEt9FzT4XAQFV5tkc3LiFdq9zGI6Q5LX6LJvGr/nOGjzHU7vneGGjVd99Q6nW4Nbivx26GuUvCXLxRa53MIbrZ9epTpbIDbf9+qZk0vA75Jt6beINzYZu0qvmz3EKVBKl5IkSDGeepsQQ7DAmAghImSA6GlPGrI8w687hJSDa8w0aLFD9Eih8HGIKxFOF9YkwEVOwe0AcqVUxJTonceowURKR4ltBzMeIQWZVPQ+DHyQiCmSkDSrjrfeu8P8V88JfSRJ8L2lWUTMOCfGSPIRqSTlpGb1rIMYSSmRKUVMljScwMBZRwhhcNXqI9EP7iR9iBSZxlpPv2gY702wPuGdZ324RMSE0mow0TIZLkZSgr7rB5eUG2DUFBly0RBCJM8zTJkNYF8Iuran6yx5Zsiqgnbdw7kb3ETwAakVPkRMHA6NIwdVUYwJlSukHsy3SIMpmu8dzYmj6yzjcU4SEvrBnEgbQ9v2gCCTHqEUznraZYOpDCHEwXTp1KtTcB7pAtLo4ZmPhBDIxzlWAkIS/OBiOykJSpFERKjhcHKSEn/q0tiFiDw1dUoiYRiiPQspBlerMQ3uhhlmkiiGLfKkJD4KejnsDPnB9ykWgTsdXwhBPBvbQpLEAGxCjAQpcKemgjEEQkpY7/Ei4YVGCfAhgIyEkNCVJp/WtPY5+Iiyib51MINohk/cBofINdYFMiUQSuEZxqkXkRA9IQaEGN5HjApSJXFzSw+MvcHZAGkArjEM7di0jryCpulRpaJdd5hUksRpe2gDSRJcJESBs4HDgwV6UqG0wvsh2nvykRQcQULSEpUXCBGRJqHzCozCHXWgJOTQr5Y42aBERGl9br7mQwAjiSSCGkzYUgK8JHgHzuGURfiE9AaRj5FCI3INSRMl2L4nNhaDRmqFujclt1MWy4YogAiizEnrBpPlqEyz7gJFXbGzm4NzLL9coIxBGI1d9ySp6BGsDk5YO4WbW6yIqGLYbZRSkKRCRIEUmsxkaJ2RSYnwjlXXQ0ysVy0hCZLwrFuHyiJlVrAMkdYlbBsYyYwUh/GalyWrFHHBQVS43oFQhBgIMdA7S7dqT93SnoGHyxP3q0l6c024ijFeL7xeObt6WYi/XN4Ws6bL6901T78ebVP+XubtQhUX40p/a5Lw63YEuH453U7ixp+3yfJNE25TgocYCadrXQj+NAzCaVTtdCX5a6vblOv+ouhbBBcX1KdvmO2akXdBSL+pWdKly0s7Cm/UnqeeATa/im35L3kGeGNvY2/6kW0eDrqlxv8KuNkqzIpX/09bXvXiZsarXDd9xTcKzTc8vIIF04Xbb/ZhvPJKvVnbhd9p8+03D+Rds4t1Hb/bJtgt97YB0EF4HQDO1dglX5+EfOXPa+/eDjt3Zkx2J0gpuDeb8b/83/8NWV5QiMTYCObrlpgie7OKl1HTRphWOSPbc3zYEkjcG+c4byEYitxgyoyT4xVawM5sRLvqKIxCa0k5zlmtW1KMPHzrDuu148X+CYWG3R3FF20iBcvDqaT8zg7dZ/sUSvIWJYtnlkqPePu7b7M2C6wNGCmpF5H2sMH7RJYUBIvwIGJiN8t58NZDYohMx2Pm5pjlumHdrZlNJxy+PEYoyWynpo4Vz754ie96Hj3aZXHcMCoy9vYmeCnYf36Mc45H7+zRrxy67ZlOKsyk4uTghKoueXR/yuFXR4zyDGkUSoHqFcW4YHZnzLPPX5AZye5shNaSFy9OSDGyuzNGz2bsH61BRsZkzG3k3tsP+d4PPuCrnz2nM4q6kNz9cJeU1tj1kt2i58RCmQtk6Hn/nub5iWB+sqKsPGVe0K8T/sTx8TtTvjqc00fPTK55cRTwJx1FoXjvruDP2kiQc+q+xZQZ1luUi7zvAi9GOV2M3BMSqyReRDIJ73eeX4wUUgke+mFHQiLJreeTtefPCsVEae73DnrHKtNoEt8NiR+fxp6YeEcfAkdJIaXgu+ueJ1VBTDA5PS/xTAgyKXnctnyV52QhUAdP3vXEskCKyDvW8jLPcdFTeM9MRJ6rCBHuzVuWE4kQmkeT+/xGcvwkOWIKfNzt8mXcJ7QNo07xmHf4s+wL4jryUfsWR9UJXjtGsuL73UN+kj8lKviIXY6Mpg0Lyt7xQbrLH9/vScHxnQPP4Ugg9qAImvcPO34aBDt7hvFqTRorljsGYQLf8ZHP6yHw6j0Szhu8k1QKHurALyeeei9w1yrCakVQPXkv+OF6l5+9+xV1GXhb7YD1NP5zyiznL09+yP96/G+RWWDvaIRsLEH25HnG75a/yZ/zS6JM3JV3GIkRv0ifodH8SP6APy8+J0XH/Thl1O7yqX1CMan5Yfguf3byc+oMZslwJ3uLn4rPMUbwgX+HL+ZPCdKzm/Xcn+3x72tPaAXvm8RxLtgpDdm6Z6fvaFrN5MGM9x9m7H8VqCrFqFSY/pCXywptDDUdPZEyq5jOat5+r+DLwyGey26Ws37ynKCGoLU7dcfcC0xd8nBW8/JpZP+ko5CCHdnztJeMiLxVZBxHh1tDWUg+nCperBMUip060bxYUgpDkpGZWnLUGkRn0URyE7AIZEx88MFjfvb5T1k1ax7ff8y93Xubs+zG1avrVx59tk3MsGkssn1NSxcXisTG2Udx8bnYuPf6VWH4/4bS8Y20wVc8x9yU9ZaBALYt0F9H/j3Nd4OOdbsY9zWq+lboNY3zzr33+OzZL4bzFtrwvXd/eAo0hp2LKyD0NbQh5f2F0bcILi4O+DcBqlfSbmryOdPcfztc3oYuAfBL98+Azi2+gusEzW3A5ybt9SYySK/07TdWn7ZPG5vAKV2jARnSifPK06ucvHYyem2Hbxkc177HNZ/EtnF2TVni0r0tuOq0rS52ypW1IW0+vYnn60hcbPxLZV5Bb9toy/NXHiOu9vRZ17re0zuHNgptNL/68RNUgug8wkf6Zwdgh0i4S+9Rswk6CWLv8ccr6m4IMCdDhjoFt72zWD94b8q1ol/3GClpQkBnir7rUUoiJMxPlpSjEUYJYgis+oRWgiQl+0+P2fvNh+THc4ztOFoJQhdZ4zkZOQSDOc54b4J6xzF/+UtEhCQTrXNkWY4RguZgzd/5r/46vbXIJPl/P/mXZHcrJt0OyAwOBjvso4MFdZFTquFQ9+HzY7QxhOAI1iKR1EqitCH2ARcGPXZUkvVqjZAQomdxuMQIOWirO0eUkJUZeZ1z/OIYrSQyCay1nKwcSSaEEoS8QlVTtKgpM8GyP2HycIe6nvL8s0OkdaTWEpYtnx88ZX4YyGuDNQodOxSabn5Cu8qQpuDedIfV8QEhGoiGvo38/Mdf0HYLtFGctDOkKKnqktAs+VIK9F5g7XrKiaQTHvRgurQscjKjiYAFWizkCuMiL2pBISJRK6KRiD4iWk8e4Ulh0FLRhMQ6SYLKCELQC8FPzOBiuPWRZz6QkMNItZ5nmSZ5T1KSCKzl4FJWOMehMWRS0AmJc5GgNUoIMiE5UhoTItIMHqnWGYBDK8m6lhRCMtoZsXt3zAt1iIgV9njBU7FC+4gUkJmMl+kEExUpMxz5ExQJaSSFzPnKHaCdImg4qdfE1RGqnFOayMEHmikFfVCs7kdUo9C5p1aS+b4iP/YEHXAPDJPv77BOlvFOzlx0FMsh6niPJDUG0UNRKFbvGO7eV7SZp3UdKhxgUqDSGUcfLqjTkmVsCFVGmOboxkGY87n8CXXhSCOLKixa1+SpZ2TGfKX2MU4jtcQlxyIdoWJABckX6lPqQtORMONEWyVyRmgr+Cp7xnQ6wqaeIsuY+68o6NEyMBdfMXYRZxLGNjw72EcnkEbzom/JdgT0iUjHwo2QPnKyWvDTXybU0pEc2GhxqkCrwfNTp2t2H5c03rAz09gQmZYeayO6KFmjCVFQmpy5d6xdQzjuULGgqjRTByn1nKw946rABgVaU0mNDYG8iTzvIlFDiIKldeRGMZIKIWDZQpIelGI0LjlZhkFDHOE//fyPEIWladd89vRT/ubv/pfszXZP5+ubFrDNhf5yuo28YvP5zXP/tYGkb+3eJ13ELRu8bQ32d2Wp/wYar+uyXub568p5N+T7zwYgrqNbNGORFfyt3/m7HK8OqYqauhgR0xAYVp+J7f+be7GL9GvzFvXGivlr0XB6JTsJseG5afgTw+CW8LVC+rdA5x4abpIur3yM1wiNlwDUq+Je7XmdVXcBpKbNdK+D+9eHfbv86+KGz0XNidhMsFnC6/DVNvV/OtWXbHjXuFLEG6Hxa3Qk6XzI3JDz5vrOwOTlOTaRkMiLfXjT+BOv8l25n275upcB6hvQ8eExq0XD8dECErTzFmkyTFkiidiTjmgjQYCvBZ2N9EhCsNB54mqIQr3wYQis5gJaS2LyeOcJ1iNKBnemCFKEvndY74DBc9FybYkJmj5i28RaC0JMsHa0X53gqgLXdAQbETbSfHlEPjYYE1nOVwQfSK0jCUVve0I0pCwjak0SkvnxiqosGY9G/PTHn7JcrFmuGvROhT22dL3HWU9KDaF3eB9JMQ7RoJXD9pYDn8iyDNc7hPTMFw2JwYTKeU/T9fTW01sHoidDsVq16Fxj6mxwOXu8xrY96tQjVRfcYGokBEVdYtGsFj0py1hbiwcKpTh4OWdNInU9J/vHfPmT5zj9mJWryDJDrgNCacYP76BEYP/JAtslKqEo79zn5GhO5xMxgV31GAP5tCbmOzhX4vuA1zlz5ehlJOSSRYggJU0EmWtWUuFIBCAqSFrTKQaTq5iQEqwEbSNBwQKBjdCdmg02KdHJhKwKFimxsB4ZI8oY5ilS5zlCStZArzUrQDhPpyRRK6RUNEqiTGIdE1IIOqWIDDE3OqXohCQ3GgUErWmUAONo5WA2EIxGFxnMKvZNixFrXq6e45Oj1wZTWVbGIUcFru1pdA9K0oWIMYKFbAmdI5SaRgdiCKxDi640K23BtthQ0vjBtMtlNSmHlRGEzuOEYK2g95Z6rIgGbGZoRWKhB5OwIBLKa5CGLkVergO6ktR3NJ13aGvBO1a5I1WG7s4S4da0tOxnJyST0447fPDM28/QU00jO4RMpOBZ6IY1lpfukFxpGnqSTCTnmMc5JitYyQblJGvVEnBEAkuxJqnIggYjNEuWKJUTiCzTCiElVgby3QobHPudpVeOk6KgP1lT+YBuehqtyFSOjJo2JJyN2M5SekHrFV4UVJMxImlQklRLrJa0rUesIiLZwczRB+ZHjpMWtFRkmaZPEqcC1keevVwx0hlCF1T1mOMjT1h5hJDI0tA5WEQGl7U24aMFqQgxsZ731KMcERNeVXS2QyI4bNYEKemT4/hkgXjuyCeRpmtQWvPy6AV7093zSXibwP+6+VywoSO8kOf6nFdW8m3a29tqci+vy9fpKrdoJlOCdOoK+nV049r+DXDKrenr7oK8Lv+23Ra2pL1eLHs92Eqglebu7P6rR0KSZdnruP726Bv20bdrFnVFC36xFS9sHW7cv/kdrgrIZ1tDwGsH+cWoBpth719xeE2113C2kePK41Ph6tWWywVN9Sv8cNZWN0iiYgsL4srFNb8v3bp2IF/Vrrxi9+J+BVdSbocuV/x938jYlp2Ey8L6DV2w/bUuivDbRuQ2Pq72Rjr1U301x5vMV6/KvaIy2pr2teWnyxev52Y8HVOUOdOdCdooVjHj3p07zOct3XyBc3YIbKY11nYUqib5wMhIKpEgE/RJEKVASMiEoiwNKWnaNmHk4O5VAPiAVhKSJMtLlFKYPKfvPZxGWJ4rmGhPUoqCiGkadmZj/HyOaSNGD8KeirB7d4qUgunumChL8iD46s9+RVlkyLAA7/AxoZ0hnh5229mbUI9LxtOa8WREGPWsnhwhgLIwSMA7Tz2tkUqiM83JwZzRqMS5QCChhSDLNXmZIbRCSzGcm5CCybii8KCFpHeeYpQzGpe0vYVMQTRkRuNOQVgAqnFJ8hHnHdoEIJBiYOfuhJ17uygJOkVMCBx+eYhbLTF7MFYCIQJaBIrKMJoV3L1XU2QZzz4/RLiWmALTSpK6RKESuzsjmpUlQzIaaQpn8BGiT5hMM84Ta+soESQX8BL2lCQVGW1vWflAnSRaJObAuA8EJVBK0sTAKABhiLtQuEAhJeSaamfMvdmI4/0li8M5I6Xw1hOipS4yis4jpQCtKRLIFBEpsYiJGiAOpzSU90ghydSwyzEKgZhAxEihDUpAISVrASMhiUIifY9JsFOUvP3+I+bK87Cc4dKCdqkhKHaritpIXoRD7qs91mlB5TIiktw5SpWTHOzamljlTETCRkveazKVgYQ7YkKTjxnZweXuLC+RXQI6dpyg6z11iKxlpO4F5ngNdWTXanxdYudL1skx8YnkBCEHYwN5kIysYNFZpq1EjWpMHRjLmtyDTJK1WTONE6AgpUSdhojpBs2BjUxTRWKIDzI2I0RMGGWQac697C5BW8QaqlhhpMGIDOxL9pjidUI7RZYVGKHJokIowW6c4aXHeIX0kkpUTPQuMSVmZc2yqMl3S1aLBpXAdJZoNLu5xBPRJpFKhZGSaRQsnUYJS1UKdJWBkJS1RhJOTRolwUooNPtPF3TLBaOYQBuKFEk4xiKyLjN0nkPb03aBvb0Zk48f0KwbjvYXdPM5sczIdQ62pdCGKMAJgRIeES2Ent0HU4JSzI8SXRQkH1GZJAYY5zl7s11MHYcdzaJmNpq9mlgva/o3Z+Z0KmWcKyIvTv4XrTEuyyPb5/RvFFNMXHO9yc/r8p3+vOA16QZB+deqWN9ssJvW1QSIxE0yy7W0IYOcH/y+KBKcpzs/13pT+afCgPeeGAOZybenubGA19TxJvRNwddr6FtzRbuNtn12F1yXXkp9QXbe9u/02RmwuFT01o45O5gszmt4NQSua9fznZL0qtLBhGgbvN8saHguxOAn+cxf8tn1lRe5fOs29AqhvEGmGwo7K+aa9rssqF9f6yA8nwOLK++V2PS5e7YNe/ZhXnDNxivHtK8FoZtg5HQiP3PVduahQ6RXLtyGCsWVF7tuOj/7Ky5w9YaUzvi6RpOz8eB2wIKL/XaFp9P2PeW3qgtm0zF23dEvO5JzHNc1z1GcSMPdu1O0NCiheG+UU+wfU+8fUS7W7NWGPg7bsTt7JVF4fOrxwTKbFsgkiClx98GMkCJSCmzwTCc1/eluwaQuh8BbbUNuBO8WDeLoK+T+r3hgD1ErgTtO6GzGo6KmSWMsU4TN+Ct/7Uf85u9+l9/4nU/4g//976GrHJ0ZlIsUUoNQaCExzQpnLTCcMSmqnEjA+p4f/fUfUI1LdK5RmUKXZtCU5xnf+72PkZmhnI3JyoxyXCCNQuaGH/7+96j3plg7vEdeZWglCTbw+IOHNL0lyUSWKcpMIxAEF9i5M0HqwT++0Zp792c0y5aT4wWlsZjaEjghsOSj739Mt6hp5jUf/+BHWPkWbXjMaOdjdkfDwV5rHbXuSAiCF3gv+K2/+phGBxapZ1JbzERipppUwm98/Jhyeo+TZz0zEUljsGWgM57HWcQqQVKSu1pSVxo1zrC15vuZweUJNVI80oIqQAwJJwU/sIbGC2xUjJ0k94JVkMxR/M6je6h37rMIiRc/+YLu6QEdgqWP3Jsv6ZUiCEmREqPe4YAmBt5pu0GTjyBPMOstUQq8lLy1WtILQRQCI+CedwStcFLwYYoE6RE6UGSCdyf71B89of74S/7eX9ujeH9BmHyOunvEhycKtMVUge/P9/BZgizRzY/5zvEeXWpxdLxvHxN1jo+SVBX8dvkbtCrgDLzb3cNoSKolVpa/REW68xXqzpe8L48Z7z0je+tz7PTP+dHkOdn3/5Tiw//EB9XPqOKfEcs/RX3ykv/6b92F7x8g33/KvXcPufvxFxQ/+gX1b3/O77Rf0rj/QBz/gju7Le88yshHB8T0Oe/8sqQVHVZGdtSMXVvjQ0vXz/md8DGNarGxpU45d9khVolWtfx2+IQmddi+RTWJe80OIRf00vKb/Ue0fkVInjIr+dC8h1Uepx2/pX+AE46QAtJHPozvYGOLV5aPeY8+WgIRoRM//Ogh6X2F+o2KH747Aj/sUrgYeT+PhCTo1z138wabEr1zxBiYcsCLz19w8NUh4zTHNQd4f0KzOuSeWbB6eUJctTzOLDF42tYzbyzYY+ZdJHSeuyNB9qhmvWf4eTMnl2tiVTF+5yE/+Msf8vbelKnIMB08Uh15nhNTAmFRquV4dchqteQ771VM7o4ZVYYsBarMoouebCfyww8+pj/qiYuEsYY7szsX5+Azd6TbpuErE/03pG3r1C30jGd5r/zeNKe6Sea6XP4byC3fSEq5zXJ7iwpSZHA2cPlg7G3L39QqXpf+gvzCtWPii+ef8Y/+9f+Tf/Cv/j7/4af/v2ul4ZvY+dZoS/9d4OcbDtlv0RXtNlX5ZS31Zfv9s/uvXLa+MV2vmr5d3msa+GwgpgtC36UMrwOSN6Hry3muK+uaMobAeK9Byaf83jSABVzZon0dnSW/chYmXUp0LV/XpLm2Pb8FiL2tHTc0E1uLf12bvIaldA64XlW8FQtcqu82GqrLn+35a230OyRShKODE/7Z//Av+OynX2AyzWGnmbewWDpmKZC9OIbGnq4Xw4zbdp6qUHTeYU819lINrmpDiNRVjkTRtYP5glYSpWC57siLjJgGb0QIwXRWY31gtW4Gm2gyGjvsMqhqhpw9YqVr7t0tWXz2JclZfBLMKsF/99//HT75nfdIJP7x/+V/5vM/+pyTp4e0tuNQNlgpUcEz1vB/+r/+n5nc2eHzX37Jv/r//js+/+UTJrMx7kVL93zJl3/2BXWVI4SgdZGqygcvWt5jracuc/JRSdP2w46DD2SZ5uhgjs4NeZXTdxapJJkQqJBYrTvGo3KI3K0EPgScC5jc0Kw67t7foWu7wZQqgdqrqO9NeL5YsjvbZe/x92nXg44nrwqCjfz8j75iVgs8sG4sEShzyeTuGKoJ9x+OOPaOz376Fc4FJpUi2JZVUtwpFXcnhvGs5IuffklSivzdR5xE4GROeD+nDw0OqASMMskLmZgkiFIOkcxFYuYFRNhPgSmSNgzgfC0lMx+xIfHSKO6OKzotaQ7mLBLUzoNWrLSiCJGQEprBhGoah6jfa63IvCfFhAqRtdFMQ8SlSGs0JsYhUrSUnEjBxDp8inTGkAmJEY5KJZaZZpcW+fYvCbMlk7rmwVvvY2zJV90Bj8s95s1zuqxDOU/tBaYoOKoX7K3G2GTpK8AIsrmkNiOeqSMeybt0OtAnR982jKxisjvieXzJvbRLmyw2Omy0jPsC3Ub29RE7qwqvPHpc0IaGyo4RpuZw1LHrR0Qxpn9pWTQL9lRFXileygXjxtCLY1QpsHuKh3oHsV5zpI+YpDGLrqGcTpirJffVfWIIvLQvmWYzgpKoaDjmhHtxBxc9J9mKymeQIAuGQ3HCPb+DD5Z11VGkfDi/kjL20yGPzENcchyHE3KZY6KgiBkH5oQ7fpcgPUtWGJVRuSl13OGlPWSn36HLP6DNJ3RHS+QvW/is4SDT3McQDiqaFx5nHaWAwieWa5gUARsVLghiEuSmoSwcTRCUeJTXpABJagoFXetYe8NspHHaE1OgaR0h83RlwhYVk0zCYU+WJD7A/b2a6aRmtY74xYKj5CirnMZD4RvkesFy1XF3d4rOc0Z7Yw5eLPDhAFEfIQrHWx+8jTKKLMs4Ojzi3t49/vBv/HU+/uSjS+vAxjy9bVfgklLy3FPj5Yl/qzp2y5PLgv3lNfW69eVKnsQ1dsM3yyPXrdvXFLMVEL3BWvet0GXRLW3sRFyX6A2L50LuxLnN3OnDGAP/4F/9fT57+kt62/Heow/4L3/7b3Nn595p3mvqFmclvqrlJi6/mbR0Mff/tlzRAq9/tbQl1dfEODdU9TrZ9ZUcdhXsnCU8AxXpTOPNq3uvErxeiN8cZJch1xk35yLhlmK2zSWXB9HVQXXG7839sV3Gvgj3xBY+rwjqtwEL5y94/sW86oJr2bztp3LdzJouRbfe4pJt2xe5aeZ3AZy8wad7od5X7vkuN8Mm+7cpXQhxboKW0vUjTwgI3hNjxPvhcLJ3At9BVuaE5QolJM4FEgkpIJ3GAIkM5yJiPBu4EQR03QBEFIow+KlFKon1DiEESgqii+dnDZzzGKPQShHSGTAe6lRCYmOiby0uFIg8x/fDWYSYEl/++Vd8/NvvkhhiRbjeoYqMzIBbr0BKEBLvHM26ZXJnh+A9IQRiHLT+0Q5nQ2JKgwnV6WfbNN3AY0wQE611hGWiaTqkGky4utO9XWPUaf6ITInkAqXWiDS4u5WA7ezguhVwzpPlBte7wfVrGFwDO+tI64YETB7skADnAgDKBl58+nIYF3I4CF1OBi9c1jl0UbBuOvo+x8dITINLWqkEfRoijvc20K0D5Shn99EdXhzOOXzyHF/UZDGgek/UgiQFmkgTAlGe9nNKpBTxCGyMJJ8IRuAj+NMxFkg0QtCKiC4y5r1ledwhQ4JcI9C4EIhC4xiiZ7sUScbgoyCEgBPD+FV6OBCfhCAyRGuOQhClHNwrC0lMiaAkMQkC0MeAkIkuDH27pKEMgayQjB9OSFpibSDEyGK9IqhENInoA7HI8SYSSIRy2AFywiKURmeKLvQknWjaFaHU9PR0tqOUJV27ItDTuhUuB19JQpQkF/EqEI0k1BKkwkuPKAzZzgSfDGG9oO/X2CaQyDAPZxTlGILFHZ/gK3VqBiXp4ppmtSLLBtfMgYiaGPrYE3XChp7QO6JOuGiJxoBWxACeQBRx2LEL/fC5SgGZwsmEiBLbd8hcooVGyQARej94g3PBknwAkSGVJBFxyRLl4JY3ho4s1vShJ6ZInzwueFwK+BSR1g9tGyKNdwgb6OOwdsYQiUISiESh8TGB0lTjmjLX2OUhQkiMMsQkCSERfIQkCEiUkDStJWpPIA5zqFbY4Gg6S5WVVGVOgaJpPQfPj1m/mJONp0z2piyXKxbrjiAVuZIIk5EV4HwgSc961dGsW7I84Z1j+mg0uMYOHmGhXba8XL/k6adP+ejjjy7Grbgw17+eUooIIU+v0wU547UFXRBethV+Ox4uFHZbafTWoGX7o21p/sJco17uqg1Qtf31t/dFgtMzJ2cK8WssEjaznv6NDC66nbf4eLomB79Rys0d8boU6TLPXwtlfHv98c3BxZnc8RoAfPl68/eva3ht/xbO/Dyl8wniKo/bJLx05ep8QkiA2BBYr1Sctty7Mtovj8Vr6brnV7Qb17Vw2gAIZ29xGizhJoXFlZf4mnjwOnh1M93mS9kOLM7rSVvf4s1BzW3Z2JIuXfq7HdSI7Tst19DgMWoLwDi9cefeLjt7UybTMVJJ3ntwj3/1r7/Az1dUpeZOpTlYSwKJca1Zri2JQUgZ7VTMo0RIyZ0CmuUaFyJVVZIZhfPQNT3FuEA1QxTTnb0ZVaH46skBPgaMMRgthuBzWrE7nXA8X9PbyG4RWBmwwSO6nt/6jXv8x/+4RgB1nvjiP/yE/3VvzP337/Hej97j4OUJpfPcuT/j5N/+W44Ol2ghaddz1sthF/Xtdx9RT2sm98cUec4H3/uYP/4nf8R0Z4wUgxMIFT1ZZrizO+b4aDkEv6tykhI0rsMYxduP77L/4pi2c1RVjilz2vWauiq5s1NxPO8xuaYoc6SIxHUkqzKKzNDZQLtqicGzuzvhYDWAt0kh6NBM6or7j3fZ3XnEz356AgmqsOZp11CXBdH3zHLLqhi0zHcU7DyqsYuOpl1QeUuVQVEY9pTj6dpiihwRLPdzybJOZI93+Ju//z5/+vSQzw8OGTWCt7zni0rhUuKdZFgbB2Wg6hIf2JyfVT0FkftW46LGOkjO85t95M+rHI9g1LZMy4ovuh6s52Nr+bLI0QhmMZBC4CBGhHM87C1P8wzlA3XXUQjByagiE4K3reepUYQQGMdEET1BaHSCt6zjoMjwwMR7ShL7WiKAB61lsdtC4ciPYOdlxuitD5g0E36g9vjp8c8YZ5GyhTt+hxfyBcLUfMR3eBmf4VcNY6H52D7gZ8VX4AQf+nc4CHNiJpjqEQ8WMz6bPme9XvHR6F3W9hiXWyZ6zMPlPX5pnhFFznt+j5P2EF8IJuWID/07/CR+Rr+yPBRj1iNNl68Y5TUfZR/z5/5zQiV50I2w3QkrGRlpyff1D/mz9Z+gleb98btI5fmVh1IU/CB+wC+KX1HInofuPgSHrBTGab4vfsCfx18SYsFdt4PsIrF0ZDLng+5tfpV9hfCRh2KPMmhEDrnO+Mi9z6/4gqAn7IVdxoz4VCUI8D35Mc/LfaJP7DHlTnafn7lforXkE/0xXy3mtAYmsWA33eGXhwlzIHhoE88RWOcplWKcFrjREInmIYp+ldHLSNe1zArPwTqnmGW886DmUHU8PbQs+zX3jONpMhR1yfvv7vLs0wOa1uNtw17taJNBZwYjPKWWuCDZEZL79xVPTiKjMudhVXP09JCj1QnlWPB7f/kRP/3ZCYdfHZHnjswIQm+IveOteyMOwgKfXlL6gofv3UXNcqqy4t233+HTX/ySQhvGozEjUWJbS1Zlt1QCbc72w2Quxa/VGv16umZ5PBVfBrpJCLmN8nAz7Zki6RV6enOZ4XXL/gU95am4v2luspn/mrLElqvrXk3AxpmTdAODV+9ppXnv4Xd4fvgUHz3Tesq93QfcKPldEupuNeauZ+EvlL7VnYs3sh/b6L3b5DsTCy+M0QRXt7a+Dm3uWrz6/xUkuKFZvg4lXhlq2zQcN3Bx8RDYRd6uCJ2vpeukW3F5s2bLsL3cK1d/nbH5qm8uOei9DQrapvW4UQ3wpvRqR+mMt+tLumEm+xqA4vqpYGMgXVfPNZPxJofDrsXGG56nvThenfPYziGlwBjF4qRF9ZYsJmTvaV04tUWGphuCkwkpyfOcxWhM1Bnee1wm0J0jCYeNAuFOuZGCrnPEENFaY62jWzRkUiGTwDc9osrJpCKGQN81aBFAJVZNjygHDV5YtbwMJXJWYl1gmRw/fbLi87//H3j/t95nUkWK+2NY98hZxd7OLqv9NSIGfBTYrgegsz2iSqhakY9yDg6OSM6jJIx3xjRHSzzgredg/wQpJd56tDkNAqgSQgSePdvH+0iWabLM0K1WZFKggqfvEuWoJK46MqPpup56WgPQt24I5heHHZrjWCCqDKUg5Ino14ynM7QsODixoDXtouHZ5/uMqpyjdSArBHOjWYcOYQTHuebws0+Ze0EWLCNdUlY1icSRtZgqQ4xzCp3xWdXhwhLRWLraEacOaT1ZlVhkGqEiMkEjPb7uSEVEqsTLUY/RASsja+HhaIrzEeHgM2NYd45OJ3anY46bFi8EtZQsdAY+4Qn0PqJQpBAxCBbGYFLCA1IrnBCkGMmMZpFrhHUgJEkKOiFQgEqJpZHoGIeD7lIQTSTLQYaAfbBmfGdJ0pa792oejP+QZg2rpw0/H+2T3WkRssVIgXyQU/iA0pJWHKAXPVJ5spQ4GXUoN0R8PxFLjMkQqUWjWchDdG+RIdBmS4gRKQRGKQ7UAZlQeBPp9kBkFcQVRmY8zxpUHJNSw1yBpEVGS5WNOSifINo1Hk8/kgjTkaVAgWc+O2AWR8z7Y4JaY6UEKcl0yWE4otQFNjmca4EhIGKpal6mFxRoeqVAB5hI5NKTq5wT9snTEHFdEGilRcaIXHv20zO0AKkFQkmWfolAYpRmXxyS6Ry6YVfv2B0j4xCrZJ8VqahwyeFVzstfrnErQVwnTk5AEZFpOOTv7ycKF+m9w7YZ5ojB440QzJuESJHV4YJfLAZXztYpTNB8lhxeR/rkeLZqUEQm0xHSC7LSsj46orcSZGKi8sExxLpn30kskr5PZMLDtCRKy/78BP/vLXU9Q8x2iIsTYhLEFMA7+rwjtfvofInKO3Yef8SiW2JXlh//mz9Gl2bY5Vwfsv8nP6P/S5+QVdmrCTfxam2+qse7NN1fVirerGr7xoLiJZ421+pvWvSVei4VeL4m3UJBdl2hQ/YbOHydXH/d9bdAb7rrkkgsm8Xg+twOARxdsKSokUoipbqS/uKYudkw6raH8rcw9muhbw1cvOnBlDelV42czkHF161x60e+Nd01SPIaufC81G0f06kG46IMum0i2YaVt9BWFHPDzsIV7JB4td2UOD94cVmoFaftcENjiyv/v4Gu20y5AvAuJ70OKHHx1bd2mdiedkvKVwWLS1fXpd9S2E1zYXrDcXsFBF6mLVFQeZUn+Mj+syOW8xXHB3OEEMyXx3Qu4RO0nSe0HmsHMyKpJCEGvE8cN462ivQCjMk5XpygG4v3EWc9LkS8HUyhvJNoqejafogc7QIiJlIImFHO+mQFJDJjWLUDH1JKvMlpmoBNOSddZP1ijTUZre2RDkIQHD2dE/QT7t5RGOXxLhCBECVVNcbaDh0HkwyAl/sHrNYNi9US6yz252uC9SzmDdENgnU8BVT+1PNc3ztc9AQVB9MnAZkygCSGRPfykHRmWmYdfVGS2Z6+tUP0awldb+nbHqWHxcJaT1IGPdJ4beh7hwo9wgiiUrx8sab1mpfPek5eHDHShtZHyEvMXsWzkwNiOXgGctGilMZpqMZTmjX0c4vJNK733H20SxOGaNwLKXBG4NuW9lkPOrFWkSQFySS8GjxfxdwjqsQqj6RCcYQleodNHp9qnIrMpaLINAc+YKY1ssx5umqwWtEpjfcenxtiiFgpBjOdGOm0wknJMg1jwCqJlBkhRjoEjfUYrZBS00kxCO9KsgK0ErQpQgz0UpK0QBqJy+Rgiz/zTHdhdG/ESN7n4EnD0VIQesd88oKpXrLSLXpH0qslTdmAlHR4UvSsheWlOyHpjqVuSS7Qdx6pchapJ8mIqHtWcYHbcTzPj1BaMA8rQNCZFiclKQ7epLx0LPwCHyNBL4lSEspIlMcI0bOUS2IM9AKcDsRcIKNHZYFlWBBl4MQdIkOkTS0ISQiCuVjQuRZPJE8lK7vGpwZVaxYsWdk1yAOyrGIVVsToEFqzqDva6DguFYXOWdg5iME8bM4SozXz2KCSYhXWg5AtBcfhBK0Na9mirWKp1sNUkmCRFqioOXEC4phju6I/CbQvc5p2hEBgwmD+uAiO2PVEkWgFQ0TwtSAPmj5IoshAFEQhadxgcueINFEyymvIc6KINCHy/KsTRk6Sx0hZFliRMGU1aI8DLFpHjBZnA4sqxypIUnG8doSY6KQhScPhEtrFGo8k1xl947BBoUTOSd/SuZakA05JDk+OWa2XVOOKPvZo5wkiolSiPX6BKbOrU+1NXhJvs+l+PtHfKvHt6SqW2V7+m1R5eQG75vcgC72m4GuUaGcPbxkv+JWiebPM0/vpdFvmsjy3zcPT2S6OuAYsXl/99jo2qWt79k9ecjjfxwfPbLTDwfFLCpcxmk0p6uoV/2dWFuJSE50qh8/w7C2Z+89C3xhcbCrT3yzjxvVNQvANGW/duK8p/OsA6wu7beeDd6O0bVHY3mDX4Vqezh9sbJUAW88HsOUZ5+Pz1ExIgLh41P7CRboJOF7jiG/zTMI2rLRVHr+iwrn48012bG4FJLaXeb6Ny1UomDa2B8TVrZ8rhX8r3/SlbhVnJZ9OpmcmUWdPXAjIU8E9RfDBUdclRZkx2RmhlOLk4ACdFERBlklSCmgt0CpDSYGPgr4PjApNVmbYTBFjojAaaQTBKfLC4DpLXgwLrdESHwJSCYoqp1+skVIitUArhVCSpmmZ7U1YdG6wBU+JeqRBSzRQiYBInsm05LjryWOilAk0dEcn1O8+oqor2nXPeFKx93CXxYsF9WjC2nfsP30BwGQypiwLRqOKUT3C388IynL8ZB8fApmUmEwzuzvFdxZthkPbSguySY7znr7rKcuK4CN905PlZji/0oHMBtCx+9Yezz97xmRaI4Xg5GQ5uK/NckKKCGA0LhCTkqYLSAMuJu6/fZd8Z8zenYr5OuflZ0fMCkUmwaVANPDg7RmN6li0PeWopO16hHfUMmOaIk5CdrrDUueG9uiYTmlqEZiMzSD0S0kdoYigFNQh4WxAG83aR8ZSIXzE57ATDX1nwSXayjCqMpQYY5uewgequiApyeFiTdb21EoiiBQ+MBw5hzYJKu/Ji4x5iGjrQAoIkSYljHcUWiMi5DEhU0RHQElGpwGiEoJCSYgBlRJaQukDyISwEe0ie6Hivbt7zLOW6TxivCQ4B8aQjmA6LZCzjL15RqwVeV4gIlTlCNU4yBR7Zpc2+cHtsgxkXqE6TSQycwVWBIpqFxs7RqGmyisiiR07onGCcAKhEkyrGdIlkILpKidVY4QwLPsV5TpRT2YkEdjVu3TO472l6RwTNRrOKKSO3XwHZETGxIIFtatRyhBJ1H0GRsIiEaRjL7sDEmLrmBQzeu8pdA0xsasnRCAGR0WFcAFtNSF27I3u0LVrpBaUskIIgXEKhOAOOzgVkUKRYVBJksecJCJ39B3a0KAC6GhQMUf7Ci8DdycTVuMRq14OQpDRmK6ji4lxTHRCkCkBMVGVkjwXxCgwErKywPaBrnMgAnu7NaYTSLtEyYARgSQlY63JFz3tcoFwsPeoYvfBPfrWEVoHYcWyC7Rdg64lfecxJqeqDFJJVJ9QyZMbQWpabB+QyqNURESP75eo3pBcQCPZmUwRfUQGAR1MRmOkUvjeY1TJx//t30HnelDEXHbJeiNdJ3tcFni/HWixVfd4m0yX03/LWOfGOm9D14GR63Cd2C6lDFk21/mNsxPiPMEGm68HD+elpe3p8jyjLmt2J3ewrqfICib1lHE1vcjzpgeyC3y8AqDnCtNfRz99S2DkWzD+O++SvzC6fPj3gpvR03/njZ8209wELy6MpAt5rxcT06uBkDh1p5rOn539O3O/e7WU63sxbZSRLjCUQKStZ4rT5auz19rg7+z+ZcR+/qG9wcC6vi2voa0A4fZj55uK6+lSu2wrTVxqk23bx7fj+FLeLe5vtzB49d+FEi+wvwGeBClF/ujHf8r/9D//Y/7h/+uf8pOf/4x/+s//Gf/wn/1T/viXf8pkbzwIzdbynftjzHJNvlqjmzW5CFg7RPHOR5oYh3EQQ2TXrtFf7VM8P+StSpMLiRGCDLizOx4OdIZAUQ0LrvUOay179yaEFEhSMBpleNdjraXte95+9x4xBkLwvHMvQxYeZxyhhEeywzlFDIrdXJOmFatJzSLLUG1Pu+zxLrL3YI9yVJLlhqwoeOvhWzz/6VNSStzZ26WoM4Lw2NTzoz/8Dbz3SC0Z1TlZndNax8H+CbrQNL3DVAXvfO897r/ziCQMQmbcf+suIiaCi+TGsJvnQ3wHB+998BbHT48IbhDWZWlwMRGT5M79HYRSBATWe2rdYVkTVMuHH9+neve7LMIurdjhw+89YB2g05p37muK3GA7T/CJH324R/QK38OP7u/wlp5SNxmFzfhoFCCHkAk+eJhTPtaktxL6keQ3RxpbSlKleEtK1G7EvQXubuQ3R4Lm/jH+8YJ3x4FZtkYVhwT5kr/kMng3Ih55dsuezHqSASrDb49KXsxXrJ1nFCN1iHQkrFZ8N4UBvWSGUQhkJwtsGlzYvrte45QgKkmdYKe3ICVBKb7rPFEN4LEgcT95RJYIKvCxiFBAyANGRx6aOdXdI3bfa/i773yAbiPxyJI7wYdFB48/Rz/6nN8WFbpIRLtGaMH31XdpViucjPwG34dc0a1XJAW/6T6kaRc44fmefZt8aghZj9eWH6w+HHbUlOHDxbuEF452GbBO8fvTP8Bpj1eBD8M7mEbjPPR94PfU9+jKhkYsue/vUMoKnwm6YPk9+z2YgjCeh3aHXb1LzDS9CPyu/j2a0OGC46F+yK7ewwtPT8/vT/4LWu1II81U7fLITlE4klvzB+lHRLtGB8uOq3gn3EEXkWh6fuv4Q1whcLmiFCUfmndJwuJiw+/p38JrDzqS65wPxHt46ehSy+/EHxKSw3mL9PBd8RE9Hpcnftt8RBCnMW9U4pNigs8Eaqfi9z56G7QmSk2D4JGNNDbSB8G7hSNETxcDaMUH9xJFkTOqS75zRzCdlIymI+4/fsBf/tFd3Ehia5jOInKU4TJFJ6F98QUvv3pBFyzf+dEDHj3epc41kzzjN3cNdR+QizV7fcvUB4RPROuZlQ1eClCanZ2Cu3slUko651FNgywEqMBsNmFkcoSKpGR5//7brPaPaRYrRrtjWtnzD/7RP+Qf/uN/xFfPnr5S1F2zMAg49WD/DSW27QLEtbRF17W9vOtFm+vXuTcR+b6poJouMXmZ59esmbehVyv1pczpcpqbgMVGo1zTPlJIfv8Hf8j33/0h33/vN/i97/8Bk3p2Hq5gs7QL4uyru5crveHhN6AtdX+tYr6pK9r1qSvaG8borYWxDWn+1a2bUl5Br5uCYLokTF/PxRWh9RJqPHcdd44SNzz+XMfgZV43y72Wn3Slva5rilf1binpukK28HdzmnSV9wtJrhn513X6G6Dra9v2Mi83vcu2Qq5ryI154cYPYkvd17/WDe23ja9r+D6zYDvbOTnfst3IcHB4wP/nX/4LfvXkC/J8CM6T5xlHx8fsTXZxLyPLwzXJRw5+/AK/jDSdIzcKGQQpJJSUCDVU3raOLFc474lx8OSjVEIpQd9ZyjInSYgxEmPCGIX3nuWqGQLcxQQxopVCZRKVaQ6PF4zrgrzM6P2g7c4evsWJnrASGTtGsOwixWiE85HMr1G54DhALSK73Zw7paa8N2OyV3P41QsOnhyhlWRcZvzVv/uX+Cv/xz/kybOv+Nf//t/x5OlXjEcj+p+1iHni03//C1RMSKDvHFIrQkoYrfAhUVY5IUbWbU9eGPLc0C8a8JHJqMC7wLrzp20k0Hqw1y/qnKa1hJjIMw1SILWkbXpGsxF9mWGlwFQZex//AD2+x/MXDXdmGS++PGb/xYIyzyhFwvSOVuS89/0HPHl6wMmyoywLSmcZK8F8GdHKMs89oVToPCOfRZhFjmRgJya8UXTBg5ZUxlHMEofjxKwBVzYk4ehwzLqIEo7jqWfqCsTUIAvDMnUUL2fw8h7PmsAEwYmDk5OGXitGdjjDMBeCMgQCYnA3mxJV30OCNs8oYyRJiUqRtVJMwuDlZ60kJSBlQjhHl2dMgicpaJSglAohEzpG5hL2kmX0cEV+T1DpjAwodMZzv+COHtNNVixZIPpAJWGaZxxWS+5zh56elhaAShcUMud5fMHddJfeWzoswihGpkY7wVP/nAf6Pn2QdN4RjWAUMnIMz+IBD/K79GJOiB1tt2Ki72BEzYt4xJ4f4yYBnzzzdsEsjKhHFfviiL0wwdEjgUZ1TNqaXBfsiyNmYYwTPVoqVmLFntwDJTkQR4xdRSsDWhjmac69VU1pJMfr58yqPaxMqKBZ5g17co8QPSdqTq1qWhfRsuIwHXHXTlA6sUgnFKLEt45MlBzJY+6Ju1gdWbAkkzmZNJQUvPAvuJ/u0vRrmsJhVIZsJ2R+hxdxzoNwh/mPp/SuRmVm2Kl6dsSztmOcwCHwQiBiZHySw3PFYauY5YHcAdKQlTllrcknBYerxJ09w1G2ZO3XnBwtmXlJsUw0TlMWoN0RvlsPyoCP3kF6yYtfHZIRiTon+Mh81aKMIMtyrCrQKpCiwbUO52B3aih0ZNE65gcvGD9oKEcdne/Z3dvBB0fQEeEh+IApCtZdy8PHD6l2aubzOWVZ8v677/G/+7t/bwgMeYYiLk/r1yrSLi48twrCdovHt8q7Xau2nbXbrNk3LZhb8m9aB7y+3MvC16tn17ImzhKIb9Zeb0gX3uuKSHnL/r2c+YIW8TZC1g1JXivcXKX/rK5oX/eKN77+FUHt8tuf/r5w6w1a6MJmRNoscSPJ6zv7uhQXAMalgi/LisCWmBkXS7/Ylpdngs10Z++yhbN06e8ZAn0NYLuObiOfX6z8hg9aXP45lH4FKIrX9fBr6jlLccXX6+sb4TYj6/LkeLM+4yIM3eyes7cXm7aFWwtLV3aUziars1J7Zwc3n35wbSeVJKXIar5kpGuiF7jeIaVEFxl21aHUYO6U4mAuIwRoLU+BTCKGMJhXne7OpTS4LA1xqM/6AEKipMAYSaY1eZaBEPjgST4ghUTERNt0CCkJCZyL+BhIMaKlJMlBuLcBArBa96gsIyWBERIfA1aC95HF0RIbImWd45aWBPgY2X24x2//N38ZBFjn8CHgfaDvLbaz0CS00fi2J6UBqYmUEDHiw+AOVnaCJIbo3SSIvccw8NS6cOaJF9Lg3lcJNbjDbC1aK4Id4mUIJRBRDO0cAjFFHJKduztEIWk7j/eBp5++YD7vEFJjI+RCYJNA5hm9DaxXHVEoWusppGSxtpzMW2a7BXuP73GwWrFuetREkk4F4TYlpIQoJDFBFImOQIgJKyVBJIJOWMDXBpErfNYSS0MaaaIB3ydkmdFlErygax3WQZCKKBVeRlyMOKUQMSGUwIeEl4Ko1fBtaIUPAhc8mVJEKfGn4ygIQRcjmRBIJfEkLAJSJAiBFSBTOg3KqMmrgtE00umWVniS1Ni+Re8UmHHFqp/TE6CWFIDVEe8cXWZJKmLTcC4oGGhChyfQxRYfI30eEBry5LHeEgi0scVHTZccKQiytce5gM97VmGJmCX66HA2EEQgZoGExLpAs17RxQ4xNbAKOOFwvmftVlAOZ0es86RS0rmhvl45Ao4gPT55Ot8ilKHrW4zWeBFBQ/QBl3pMEMQcutQRjYZMDeX4hiTBJotw4JQhCIvzntY2YD22sKQQEUoh5ODW1eUJHwMOP7jL9EOb+OBY0xAz6JMlpIimJqrhfFPTezyRLkT80QIzb9DOYwFHIiRoU8QISYgCIzWF1rgQ0VITXaK3Hc4K0ryhJ+c4Kvo7njYObmx1lqGTI4ZESJJiXKN0ZL3u8D4gg0BmhuActncIJFVd40LPsnd4IcjkwIMIgwOM9aqll5G29yAUzjm0s5SzCh89SgmCAOfd4DrbOiDhvKNZNTSrhhQjzjsSkYQ6tTy+ui5tLkFfW056o0Rfky5rS7+hHHtO30S43QYqOFszT+WHaxWNbwYsNk2j3kAHein/JV4uAKAtg2BTgbhR/9WEr35fdF38a6CvAUCuo2/lQPetNMybdG3LnArNF8bMaUvetMHy5ocvNmrcqpK/yNFmZ15w+bkJADaGRXo1WC4g1iv+3jYrYeuBsDfyCnBburFfTt9l48UHD1biPPDMq3faUsCFsi8j8AsX32AM3xYQbv9Ar95LVxkSV/yBXVPEVbe+rzQulwHilmLSJYCxVat0KgxfKm+Tv3t373H3zhA9VinFbDrli6++QAbBbHdCPZnypH+KUpKP/vb7/OSf/5SDL48wavDOswoeLSVVpQh+mMSqXJMVmsXKIgTUdUbvHFLmSCmox4r5cg0IqkmJRBKkpMg0wVuWJ2tcDNRVjUqB1HvquuDR3Zqnxw3eOu5VEkyGXVgKJdkVlpd4VC3Y6cBpyzqLZEKy6wUrXXHYRXaOG1wX6INmVGf8zt/+HbK6AODxg4f8uKoYj0cURc4nf/ABn/7LT9FKMtkZESKcHK+QWvFob8TJvKXFMapyUJIUAmWesTvOWS57VslSVjlKSezhCqkEo2lNnuesly1Fabj/wVv86se/QkrB3Ye7vDxZ0niPkQKTF6ide0wePuSDD+/y8yeRp58uSasln9wb8eUS0IJHFRwdgdzNqSrJvcKxUHowQavgODimjyve/fABD7874z9+8YSXX6x5SM5cDkL5WGre6eGz0XAS4kGjcBOHSC2V1zx6qvjynR7qjHfsHahbysxRiYx37Fv8TD6hMop3dioWqwxVv0CvJN87mPCfgmfue2bOEVIi5QojEncWloMqQwvJHiBS4CglVIy83ToORxkqeWYRZGqp7zt0UIyfahZ3WqraUx4UiDZjLjIMibejoB1VpFHB28ZQtpbnZYZWmr3nEj6Z0JWR2VowWVSoyZpsVPG9+iP23RNSSuyEMbMw48v8KaFzfCw/5Ll9ijeesst52OzwxZ1jEpJ35nc5kSd0qWMiS+419/i8OMH3jg/KxyxHS9zqKVVreD894ufylwSpeae9S9M40k7OOBvz3e4tPs2/ICB5tB7hlKJLLXmn+WH+XX5uPyVLird4gE+WJD2Fz/lAfcKn8ldor3mcvwMa2qMTprtjvsP7/OzwT1A+8SC/R+UkamzIRc67+Sc8iZ+jguRu2CPLCoQHHRRvpQ/5Uj0lE577s7fIloHn6RlG5Xw4+S4nYcFidcyd/AExRT73v0Ih+ch8zJPuC1zq2fUTZtU9Pg0vUEHwYfYeT44kdjlhtzDU2ZRPO0vfdNzvA8cCqggmwWOtOVgPttf3q0ivIkl5SpkYyRULVaKNYWQ6VtbhwoK4EEx1oO17Ri4wvWdIJlFFKERkYhuWMVJoxf1HE1zv6QkYDJOQsVoFZG7QZBytlpyEE0LnqVJOJz0jI5hmFX3omK+fk2UF78z20I8zkpaURlHUhqPlCWkUGeuaTveEGBjVU2Z3J9imJzaezGV8+otP6b3l0cOH7O7ubl9ibiWtvibBr0OafBOl49dUTm4r443lly3L6HmT/joB1zYeNhnYeHYl+velfBee3igwn2mDLye+WNBFCeCaNr0M7G6kTbnv26FfUxC9W9IWgRM2329TOL08wgZhfcvd86sNvfj5szdvu5u+qkQS4lzgvo7/zf9/3W/h1t/2TR8B6dX2yRYB9XLGCzsKIm3eHYbijSDx8kdyXbpL9DWy3JzwBph/DgK2Pbxoh7l5zPtio11/XOzCDHje7Ocz7Olf8QrTXWLr9PFpEa+C5l0eySmBloq/8Qd/jZf7+xijOTw+5NnLZ+zc30FoSTe3CBRKKA6/PEIC0XpMnZFISCWIKdI5j0zgvcMHCH3EBYuUkqaPjCY1svdoITC5pm96bAjMT1YkZUgICq0wMievhsBx4+kEG8HNB2878+OW5CMmM6yWHZP3a/aPOpQR2NHgYrJJa0b3c6wIpzsBgReMsWuwIfLnz9b0+2tUUfPg8dv4rD5tL4H1jiQG96rGKJbHC4zRaK1pO4fRijw3xJg4XnbEyOCtqG8oRKKLCRM8fWcAgUaipCQf1ehVBwJmd3cRStL1jnpvSnuyZNhhSqy8RcxKRG9xUjD9zg8pJ7s4qXixKGjm+7Trjvt7E5Y+Dgd2haDVGqc6pAJGGbIqoR0iXrcS2tITq5yjMOfTP/klR7Env5vRlB5tDEJEyiQ5KZeoKhBFwtcRU6wxeU8ZFO6xZrIjcKpDmCPKmaeUDVM0rXrJZGxYJ49MDZleUtg5E5/DuGLnVxLXAT5gpCQ3UMSEHwlyEZBGoPUQRE3KREYgVIlCe1RmyGNP9egZzciSB0WxF5DSESYw2SkIz76LVCVVZniwu0Of4Iv9Y1ZtC3UaoqC3FrczZmd3ysnTX+HkBM+cTFnqvGBpnyKbFlkGdGVYdwtUjCgjWbhDjMmQPlLlJV0RyUc5trfYukd1giw3aCvoJgblK5LoWbUtjgZBQKbAeurJ4uCO1UmHigGJJfOWdb5Edp6Ua2zuiUahMFSd5iAcI5MALXAmINXgjlX2kWfrLyH3BBytW2AmFWZUoBy0+ZxpWYLtMToRkkckyFROE47RNqFVQpcSRCBLkjwaAieMXYAskbuepCBDkaPZYcR/tfu3OKqP2BEz/mnzTzGAEZqFP0YlicoNsUusg0EyQwQ4Xo7gizGpaYgqp0mR0LQka2m1QFkQEcooiCcS04NMYF0iWUvmDKNcEIOA091WUQvKssN2AZM8opPsxcGtrLYROa3oFp5Mw3LhmT6YUe1NULVC3m0o80hd5Xx0/yEzvUuxN6Y9fMm/+9P/hDpxpEWLpsXtL+hjoIkKISOmWvPg4UPKByN6B6vDFlVqoneYvCCvM1Yv5ogCur6hUDmLg4hve5SQfPrpL/jZL36OrjWP3nmLv/mHf53d3b1bAIxbrua/LsF5m9D5dYTKi6LY1+fl8q7P5bI2xYl0uuJ+ixr2gY3XNPalLrvJBGqzr2/bLteKKJs6ym113SSD3SykXUh7ZXh+C2Pvm3uL4oY+vgGAXaSvtxG12X7X5RaI80PWbxJYeTP/hTrP6rpU2Ga6y6jyPM3XsgHc3C67oZ02NeDX0lVNvtj8qC88EucfxqZ3otfSpjrhvH8uCuSbb3Qta9+YtqkMbpdl281XAOBqjJBNCPtqY/UakHy59DecIFO6vo+1Ujx68ACAP/mzP2W+mNPYlsMXx4SXgsXzNUpJRCeYH6yIEdaNGzhOg/mT7QevPS4kVp1DKonzEaUGUyfrlzgXyDOD7iVtZ4kxEYQkxUBvPRKBDB7XOQAOjpb0MdLbgO2h0wlSoO8dQtbIlwsan5Au0SEHs5aYeGpbVJlYy0hAcBIEMkm8UAgfaPtIXSjaIHnyqyN+5/feBxIvD/ZZNatzV7TP/7SDw4T3Q4TvtulIEUymaZYdxIQPkWVSrITAukDnLaJxaG2wzuEOl3A8nC/TRnP48gTfWdq2p1t3SKPoektKieVCoaclHYmdBw8JVc3xkUMIz/5hi+ssDsPBOpAiWKVwnWPdOrTOaZ7PaZdrgo+0PmEirPE0UdAsG07aJfodRRpXrGPk2EikEfQxcRQcfpRwdSAIEPRo07Ese2KRc1K0YOIQIdYsqWViZVYIDat8jReSLg4mJyFXrIoWJMyPHd2oHCJYe0ci0RmBDxJ0PgBSJVmGhJcJaxQiaXqRyJXES4GoE9xRmJ2IEgovIqUy+DJg1ndhvAurnC5Efj5fYZcdC5HoVcuElj61JJlId0c0L56wyiKhfUkqF6zNnLVfs3BHKClYZx7hX0CWmLdHCK1YqZbkEmu5xltPyiQ2RaKOONEjJKx1h1SaffuCZQokEejFkhRaVmaNyiUr+YR1XA4RnAuPQrIQC7xrcEbiR4FgBLZ2CKU5cSe4quIlc1JwOBEJrkf5wLruCVXFS3WAFIqejrDqUTJnaRr60HO0eorpA52yyCiQRrF2S7rQsC+foTE0riHJhCAxdyfoqDhRR5gsY2lPiMEijGHJEukEL8JzxnLE1Ez40n7JPJ5w4PYRSXAsTkgelqohVoqQ9pkHR3SBk8MZYl2w6CSyTKwPjzleDW6mexRIQZ8E6ySwSdHaNLhwbkD3AuvFqSmiwqYhOrtftcjc40SimNZYL/AoiJE+5tgu0EuNUJB0zldPDtixEVE7xLhh1S9JKtDmgf/ir36CkIKf/GyNelaQ3AnZZIxrHWUqSE0LCaRUjCZjYh149mIfSYHQOTZL+OSYvzhGK42zLbQBFxyrkzWmMPhoIUmOV6vBfFQminHJV8+esbuzezqxb1PXncpLGwq7G9fUS9rxv3C6rv6tu+vX3L91HdcI6jfx8jqevia9Vr/5umPKl/m7zPvW7NepKK/KSWdFXJFNt8h3W6u5Uv+lWr6lsfatnLn4duiV+dBFHJIupHn15DY1f/vRN845EFs68xytXhUrvxamGCq6WsE1dMU92WaWS9D0gltVXn0wF7DBFiEaIUjxVXTziy+4PY7H5Sn0xrc4Req3AqzbMl+b5lVDbHMVl0inMSjOIopeNP4Sm+mugLHLpV1uuOH3Wb7ztr/mJTf74MJ9cZGfm8b2aDRiMp4QQmA2mtA1EbErCc5zsn9MchalJFqBCx6tFUZplBrOUKzWPWVh8METjSaeao6ywrBad2gt6e1QRpYNNvVRMLiYlVBmOSJ4hJRE4uCSVEJe52TRnUepVSJR1BnzpaM2AkEgE4Pf+0oMh8hD8kylJCmBE4GgNHmmULlCxoCyPeNJQUqRFGE8qinzklFdM6pqur3s3C+eP1oxP1nRtz2jUUF/CrDXTY/UcnBfyXD2xPsACoSH3CiEFHgfECnhO0umJMloRuOSJCVCCkKMCK2IKTGa1Hzw/bc46nIi4FYtx0/2ScGRiZyZUaz6iMQz3SkITcNopJE6kifHyvXUmSbhsG3LzkgjfGS3KvEZWBxBSKoIWR/wRHaipHUCeoFVUOqc2khEZZnZEhtXZFJh88huXlAphzCKHbM3tLuNrF2ibgQi5HiTmLSKcNIzSRVFUTDey1msGppMMkYSEMQYWROpXAKlOfGOqdZIYyi1ZK0Tj+/OGH2nYGVOGKmKQE9pMo78MTvFDkeH+RAnw3Y0vSX3gVwmagd5VOiQoZDcqSZkQeKbY6adps80hdohzyukFFSmRshjdtyEYCLaCISQww5CUfPCPudedZdWWbz1BO+osxEZBtd0zFLNapkwuoRSk7UWGRUhBu7XD2jiikIYnApUvSFvwWnNnewufQGyyFiuTxjpEaIXtO2CCQVu7VAyp8kcNYayGiNYs6NmFKxJNtHmObu7O7jegofiJKHLERkClRpGYoo4nQtqNSbgyVQBVjBhjOstQY2pixHBWUozAp0YM4VcE1eBIqupsxECRZSBMSNykTOTM3RQECVaFKAUd9QOK5sjUkbyDi2hqktiaKkai191jH0Crcm0IveBmAS1Eqcu2gPSKMoioUIkBE+VC05WPRKJCwnf9hTGYbKM6SjHRonOMpxPZDpDBcPR3FLIQPQGEzR2sWb5pOfR7+4QkmMyHjOZjNGZIiXY2Z0xGo8YrWtG9QjXOtLODuvVmsm4RmvF86+eIkJgfHeHfgFN0+PmgXb/mHW7oiwr9h5PGe3WfPXZV0P8Aw+5kQgxRKuPIRFkoMpLxqPRqwn4evHgW9e6fy0630G/pZLvTTT3vy7aJqx/7fy3CND3bdE2mf/y+Lgi2l6nSBZXdzPO7p8pgS+7U93Gz19An/3FxaF/zfvC8L7p2qQXQcY2jW/imja7Rd0XkPNlrfTgY3Yj5es6T3C+nXL6L21mSQzlXa7r2hfgpgcXB+bZwDkfoNsE7leOeS+/xcVaLgaxGdhOFzDF5tMrMFAkxJnp2q36YKAYrxe8t9L5a4qr/6606QYjF3g6g0ObwGHILM4LGUbnayHrsPoPLuaA4fDwFl4us/sG73vdK53Rd956n37fY19EjM95/zvv0jWO/V++pDQwr2qa+/fwezu88+gOEknnAuU4o/MB6wN9CNSTAusTwSd2dkYoBJnSjKuSx4/vIopBILz/9h7incf0j96i2dnjwaO9Iep2CMzGJUKA94EY4eHj+3QYvMyYaIkUEqUUfR/4II/Y8f+fuP960izJDjvBn6urPhkydWZVZcmuru6qbrQiGoIEd5ZiZs24NjbzNGb7Mu/7t+x/sGJsdm12jaSRY+TABjSqpdghQDQIEGhZIitVyE9e4XIfvhQhvsiMrMoGTmZEXOHX/fhxdYT7OQE3DOzGGtXUOJkIRvLBWGKvRJorjtGVxODKBvNeyb3jJXY24x/+T3/I/+v/8e/5/GcLPnrvG7x/913eefNtfvf/8Du4PBFHmvH7V9je6CMRNIuOjc0ezgUUgu2dMcON/rP+98adK+gnuG1uDrl2fQsXE84Hbl3dIImEV4okJf3dEWFzgNgecmV7i5TfxGx9g6S2ee+9XRbzlsdfHnCn6ih1gfCS2Dju7kRSFQmF4+aooR4sqLdrlqOaO28G2rcC9W3LaLQku6XgjiDuJt7rC8K1RLzieUN71OaCcGOC3Z7wrVkDvfvIwX3uqoyRXlCZh/TKQ37D3iD1Fuhxw1vZTQp9laWvWNSST+69h5tnJDvizfgWm+kt7HIL57b4m7u7qHd/Sf7On/PeWzO+8x3J5rcfsPHxIX/vu2Ou/+iQ3e/f49vfdXz8fsed397nxo+P+W++v8mV35qw+1t73PlG5K3RNiGzNGLJb/Z/wDwYFqmkUBXv9K+wPK6pa8d3UCAiKkbyZLjOiEYVxMGQ9483ODo84Hh5DC7woXkLJzxd6Phu8z4hRZyMEODD7i6drbGp5bviI4ILeCNQRc73iu9iRcJ6z/sHt5Ex4aQnmsgn9g1c5ghF4N3uGlopWmOxmeM31LfwwuFCx1vTqxQpJ20WdDLwSfshi+mEdrHg5mSLoaoIoqNxNR8/uE0MNcI33G522JAbeBx1Pef7x+8jsRjhuM0VbsorpOjQGyU/3vwbhAy8jOzmV7lubhJVwEvHD0e/Q0tH0IFRvsXt/lvELGKl5a9v/l0+qL7NN/RH/Pjq/4675h2SjrjQsiuu8k+P/gH/z73/G38S/5gttnDC40zke9l38SLiRMQozTezb9CFkjaUfG90A3cP2s8l4r7k3eOS9HCH8GCLD+oB2o4JszGqHXDLJFyR0yrFZrmigcfhk+PWVmBjOGCz6vHuzpC87mHvGepfBd7f3SbMMkRb8d6bVxn2K3KZkeucaxsFkop2IagftBz/55bjv5C0DwuG2Qb/9B/+G/7R//Qv2b8/wxQaLwJeeL77/U+I0tPamtRGlscLmq5FFobv/vAbyF6L2ex45/t3+MYP3mN8a4yuJNtyYxV/JQWKvGDcHxOFRmaKt6+/SWY0eW6QEa5fvXZqLTm3Jjy7fG79TmddrX5NiBfld4L3WKt5P7uGvMSC8DqZ8kvX/uuSKp2+PLvx+XzydH6tT0+5p0vU/yJ805n36/TnF+T/hLU4heMphuAyWty/JGHwa7uiXTxxRfuXDk8GycpH8FO7x0kiPxUWXqTNXp/v6fTP8zy/rWp99zyptX8uLp2QRF9G8ZfhehbHtffPhYC1+veLcBAn8X9a8fNoi9OJn+Z6+t0l8T+FYzqbUKyR9E+KoC8h5rpB97XhIq3C2VRrCHcyi2dpzkxVL8H51JBNZ2j0JIP/7x/8//jPf/IzjvaP2drepJsF9j8/YP7oiFqVNGTErGRTRfKDCXbR0HmHlJBnhvaJK1oQeBfQSqGNwDpL01jKXk6XEhFQWqF3tvEbG8ySpJcCvUf3CUfHoBRCa5yUtJ1nUGYkKYkkvAukakB25TqLoMgINHcCtnI4kag8KCGZiMSIVfRnGSOz4NmoFfmh5NgpyhQpOsfO5hCKgjfvbvN7f+tDbt5ebVH4/X/wz/n5n33KfDInzR3Hf/YQ11jKMiM6j0iC1nl6/ZKiV1AvGnKzituRFRmLWUOmBF4K6qZDIohakhUrF7T9QYkYlVj9JGpzGnH9g28yrRNXrlTMrOfLXzwmdo7SGDIBk0WkNA67JahjQCkJuaMYwmH0DGIijTVd8gghMSGRScFMwjaSZteRyoCPgR6RXFgOBoHtOcRyD1lZbAZXix5F6JjoI3azKzR9STSKlo4BO8gw5FF3yLBe9QeFppaOkdzGLnL2YseGyGn1z8mrhmVhGU8LtCo5ZEp/oen8nLIqqPuOHbVFSoGJnDOgh1eJIq84TpMVAxvgyM+oUo5NJSb22E9zdpodFr/aYP/Ag/WEpiW1llbBTiFJtyxdYSm1QdOiu5r9rOF6PqC6XrNw+5gsJ897mE6zX0y5GrewzZQm1ugiQ8WMQg54lPa5nl1j6Wra0JJIlDKjTJrH6THbcZtlLYhlgY+entbE5ZKD/JgbZgerLAmP1ZG+L8lVzmG1YNz2aWJHqi11qBmLAcpk7KV9hnUJdOgu0BaOQRiieyUH6ZBNs0Vsa4zQNKZlLLeIKbHfPGaj2sa7liIvmcUZm2ITUmLOlF6qCCaR6ZJjf8i22sE1DbM0oV9tcDve4e/0/2u0FEyLOb8/+Ud83v2SXBYgJJkoOLR7bJkrNDhmabVlSqqcMhvwyO2xK66zrMfMHMiQyH61S/7LTR7cX7JhW+ZLSRsM0TnynqA/EOzNHCPlOJpPyIscmWf0aouc1nTBMCgE2iuqXp8UIS80Ikb2HzUo0ZIqje4XdK1HSw9p5bhhNDK0x1PwjpAExA490EyOa+68c43htQxpIk3dMtzNUQPL0eyQ0XCEqzsUgvl8gQqSrm5ZNku2trfwYTUHBBnY2tlGCMHjB4+Z3Dti69oGWzd2uP/ZvVUgxZhofUfyYLRitDWmsTX9csSdq3f43b/zu1SD6oly8cQ68ezPU47hjIZIvIRdPbdAfIUF7axW/Jww8UQl/hU5wlPbp9cr3f/SGNtXgYu8b17oMldwQtm85v26Ol5GcLsIXshKndhx8aIt8V+x/L9SV7QXw6sOgFfseYJnxFz/1Su24IV9RZyaH9Yb08SzcbkW0bMZfyVG97kA85zXPj1xvTz/5xPaSX59ndB06quTxTzL4nwhT09wnED3UnUV627SuTdrELpEG6/NYn3fPPv0KcVPO/kSZxOsL+fEJJtOnjm5DIpnkXgmN6c1bX2mXz2hW9da2rrFWUe9bGmOW/bv7VHEiKwqgpA4H7Bp5QI1xkRKq79t53AhgE3EuPpxPqJ9IhFXFgkXyHslXVi5e21ai4yJpATJRbx94lHIB0JKIDUpRJwLBDzxmWVPUjeOoCVNCjgBTkuiFBADUWtIgSasIuomIUhGYhMonYFLOAnaBg6+PCQbD7C3xrSN5an9uGstzbLBdo4809RdS3JP/MqGhFGS4ANt2+Gtw7lAKhK+dVjrWS5arFHowhATKxe2CKIPq3MqIaBipG49WZmzef0aXiic7Th4PGdyNKNpw6rfNo5OSFyAvJfho6NLoOVqe9nCdViR8EoSfcAqEESMVgQpCSnQSYhErAgkI/BKQqYJOlBngWygCX2/OtAtA046RCnppKUNCSfA60AWLa6Z0XY1RkmSdETvcSKQeUsXBY1tEU2DLSYUVcApaLKAbJZYY2kHGmEKUpWRRKDtOoQWdMGijAEtiKmm8y3LsCBKQycsSIHtBCJI2tixDJ7WOxoXCM6jE2gJFjiOloFIBA1NdGSxw+lALDULHKlraI3FG0FyilDk2GipRQN5orUdIjryJHBuik0N0zQhSkEjWnyM5FlGnezK7XDb4ouSJtSEFDEyx6uWID21aonC06WWECJFURCFo3U1i9bjYiBkCes8nY4IWrxKdCFA3RAKSYclxxIzg/WeRTdD6URSCYvFaofvHE565nYOyZGAxi1pVYFWGhtaCPGJy9+Aix11WoBKWBGo4wKnPKbUSKFougU+OhrfEFRASUMQAYejiTVWRJpQI6UikwrvF3RdzVLXODGgZeX0wc8dbtHR1o7aaIJStE1CZQU+dRxNGqwwdMowGI+YzGvyTOARVGVFu1zNOe2io56uYugUmaAa9DBljtGaaVuzOFyijCGrDCYvsHXEeygGfXzTIhM0yxbhE0WvROYZTd1huwWzoznLhWTz3T7OOZq2wbUd7WSJD4EiK1YuuyUslku8D9i6w0ePloZyUJBIDHaHqMpw+PgABMhc085rOtuhhEIiePTlI2LyyA3JPJ9zcP+Q2+9X5yfydQrK58GLXoldeqpIvYz2/NQWmnVa8VPr0tfVwImXr8lr1smvUszr/G4dHdcKFpclz7p0J9v3FPP14qQvK/OkILeuCz0TnL7KgeOvCa9BuDjXc888vyx8HZH2RCs9vXyl7F5FA/5c8/Aqew5fGDhmzcTzojF4uX4inv1+3o+f4vA8wnd6luFJxvWime7pPtqL63CW/74UrOs6J3FJZ+l8Br+TtycEgWfCAeJ0kiTWygnPhafVN6csYs8SPhEvT3173kJxtkddpDg4q8k6p304c7uc1dz71X3yMuf2Wzd4eO8xs8mC67eukPcy7j34EqMNt+/e5LPPPycaz9bWiEmdMDrSE7BdJh4lQdM09LKMrUpy3Am0MBRFhm0dXRfQOpEZzbJZBUar+gVd3RC9IDeKKze3eHhvD6kkuQjUXUMmJFUvZzBcCR5RgDSKhfOr8xW5phr1OCwEUQiumJKZ0iyMJ7nEm0XO57HDx8RVZfBRkKSikpLNCPtK0qXESAfyXBCrhPaCGxj2gqVWS7r5jF4v40//5D69fs4b797hwYN9dFVwZXeTzX6fn/3hz/C1ZZjntM5TlJJKafIy52hRI7Rgq99nsmzINnI2iwqMQCpPcoEeGUJpSheQSmC1YnO0we6bV7h99yZfPFK01mPvP2JnZAgyUlY5VyrDw8mMQKBAcW2r4FO/RErPdttx3E94AqWP9FuYXzUg4NpE0OQRUUTGDYxmkocKoojcTBVdsSDmgY1swM2uz4P+jOA819UGqAlJ5PTMmLerN/ilfYxNgZtxk9ncETLDQPe44Tb5wh1hVWLXGRYzcCpiGs/bx9scbddYG7gRNpG9kofhIT3d463yNl+KL8lExo3eNVKIBCkoYsbb8i1+Mb2HFYZNW2FSgdcFpot84Lb4Qnvo4FqhiarE9Y+InefORPFlP4JoGbcF28vAoe7IouR2t8Hj8QKdJW6Pr9JfPuJBtJTDMTfnOxzqOa5t2CzGbFLxGZ+C0ryl3uJxd4T3kUFbsRVG3DePoDC84W9y2D4mlI6d4VW26qv80n9JVIkbcZf97gvIElvFDrv1gF+Je0SVuLW4QiMljiGDNnHVGj4V9wn9ird6b2Flh0qPGRQVVxd3eJjv09Jytd1FZBU+QUXBm/EaD+OKhtfVdXwRQUFByZvFXT5vf4UQcEVfw6AQGoqi4oa+w4PwJaJNbOtddBAoraAR3NDXuTf7lONmnx2xwzAfM5RjMplxJ3uLh/EhPgS25A6ajCQFOmneMHf5sjnCp5ytNCJvdhCHguQcd3Yr7v3HmoGGgY5kVSDOA8oLtgpPGGTUDUjbMBxBqQdoY9jZycmCYTINbF/pMZCBX/3xQ5plixYdy9kc0++xeW2H3qLl0dGMFEDUEVdLgpf4qMnpcAkGGwNKabAikpkM0XVcvdbjz/74Hm3bMe6NuL67S+NH5FnGoOzx85/+jLZpKWJBpXLojxBecO3adf7TH/4pOmk2NzZIPpHrjNHukFL1+PKzPWINrXUYmWGdpCgyNod9DjmmbhpCl9gcbmGbbr0WWZxkYp+uTM/X3Jfo99a8OqXxvDjtpRWPp1C7qND1SsMTa+ZJZewLlW+vCn/5vPGLebaz+8VfkMcq+QXr+hrG4KtU9cWC5l8B8XhN3qJOXn2dI9Trx8lXFVNX8CLvOidSnRZKXjKwzyW5RNudavwLqnNSbFn/7iJB7iVlP1Gci+d+TZ8x0s9LPJH3M8uAeC5zPJvLxPoJBogprg7qPpNmnkyiF5gJnzHWT9KepdFpnE9UW4gLm+n01qzTz56+Wff1c5nppNPZ54i/iOJCnD+Hcc7wInhG13Op13TxZwfsT6id2rrlD/7Rv+bg8RFZbvij4k+w1rFc1AzHffTVxLJbopUm1zlqAMQIVcBsaHrbFSEmlp2lFxOFXbDhHLJeImWPzORkCqTSBFYaZBs6kg+YPCd5iwiBTAoKIzn69D6x8wyKnMJ7yq6mCRGzjMhlS3IBHyIZkImEJSAJzG4P6EY5PkUmJqPtPEugkoJGR+RKtKNLctUeUiBjwiJRQqCkxJQKr7vVIfKYmG4oWl+wjIG/mN7n//5/+X2q3W36w4JqEBBlvoomXhoGd69wXSeSDcSjGe54Rld3hDzDOofsK1yCMMwwecI5R1eB2jargHeNRemCscuIRvPOD97nOOU82p+htGbRJlIuaJylCx3aCIxR5JsFe/M9wo0Oi2AWE51p8BIyJQkBTEwgBSoJ5HZCjwLeeqIEqROyAFmu3O2K5Ekp4bwnVBYzUsiYmNQQlhqqAlcMkSbijCdmQxaxT7KObjZjGXKgD2FOmmYs6paoEl1XU9uElxBVi7SRroqoJKHrCNGTaBAmoERg2R2DWQk6QSWaxRKLI5OGQ+8JbkzILLHcxi4Vbn5Anlc09MhSQKNxc0MaHJPUjEEQMBYYO0cpx0byGNmhZYdQirY0ZL0c/IJ6smB4rUDMFYTEsp6g+hnKCOJswUw6RGXQRcFyuSTZgE0R23natCC5DmEUjWpQSpB8RARYxCOE8UgNdnpEgUelRGo65h3InoFMUB8nEjfxaU7sNHbUILu9lQVkuUAIh8ocJiW6vAMlMf2KbHuEQxAbgTYlTglMLFkcTPGZAyJGS7IgaUWNiJLgIhSrYHrJeaQQONmSRU2mMlSA6CPSRcp8wKPiMZ92n7GUSwZmTEqJJCUJxZKG5CD4RMoElkDyAqE18zYQ202EKojLIe4X10mHHVpKWqcgHACKmAJu3rBRlJBA1UvSsqWqhmwM+3THM8pcE9uAm3a42KJUiT+uaZVn4/qIDbHJYJTYe/Q5B3v7HBxNuXF7l+N5Q+tW1gVCjowSkwIiLZFS0LYRT4PWBb3NAe1kRogVrrWElFgcLjEPE9/5uz9i0O/x2f0vuH/0EBpNSc7iwWTlXrqX44NnvD2mrmuOH00gBJpmhp+3aLFFVV1h8ugRQmeonkHj0CknosjKnEWzJGWSxXRGM6+JMaFOnGZ9vgycXnfWXZ1eQM6sEevg7Fr8MuHgoufpLHZrynmq9LtAeftCLflTjdxX3YX/dXTPL8jjIgHilawWL2BRz4Yp+LrwwgDKF5T/5OJkJhclfj10fgKvfVvUVyHmOmbuOVwmrzNpTgwYcY4RfQX749k80wXa5VdA7Wye59vzBXETTqR4IVXWmv5ehMYKi5Os9Dm81pjxTrvfTc+Y7GfJXlToiWZYCS/iwmZcpX8q1p8Us55kciLhWY9Ka8s9883pQs9KBE+Sv0TwXG/QOUGwE3vLzgUO5wkt183JJybjxw8OmBxN+fLTB5hMIxAYo1nOa5bXekifWPg5SilUVKikVmeiQsItVkHPfLfaJhVsh1SSJhhiKEkpELslKrYQJDGAUhD8aiuTdQ2ZEIgQcX4VXVvKlfepWWs5bjr88QKfYDwscY3FL9tVRG8iQUScc6hM8dh1tFmOUBofAlSSRVp5lJoni4VV5GCpAHBKEBMcp0QQEEQCJUhKsoiBIsJEgDSSVgg6p/js8wPS51O2rm2SjzpM4WiaDhEBH5jXLXmR0RUKL6GNAd80CCRCC5L3PJpOyY3GEVngkVFQXhuhY8Xm1g5//fvf48a7t5jVlj/4J3/C0eGK8dlbZoSsT+1gmRT13ONU4KA+RO8kyCW1SpAkVgmWJOoUaJVAS02S0BGxw8TSWJJZMYBSwKIEUUhcStTBrQSmgSDbkCwrD75jmgdaYRF5wvsv6RWBmahJYcKXM0vXSWzXEoyBaJjYBusc97sFSSRiIVHbBu8Dk3lLVwiOt4/RyWGFA7lyJTs3NU4nDuNs5UZYWqIFS8esZ6mXDfdbh3R96hhxLqJ0xTRLLFzNvmtQS8E8dLTNkiigqyLORubBoYuEU4Fj1yB0xyxfCReNlqAM09hC2mfZ1TTFHB0bFuMCkzLmpoYikp64l6WNHLsjVFWx9C2i88wI1HmHMhaXLIjANM1IjSBEqE2EGAk7Y+LCsZAtxAmxl+jySBCJWhVQT5mkiJfwqPuUUM5J+SoyvVjWLFRHFzv2NxLBe0JMuDaSkmIulwQfOG6+xAhBV9Q8au+BgmmcUMqKw+YQmTS1XPC4fYjWimmc0lnHkT3AYFh2M6J0KK2YNke0omU/7CGVYcGCMQuigEk4RkvDzE6RUbMUS/bCY1rvmYo5qY4ceIlMW8ySJdmEW9YcPkjEENlfOpSTTNpAmzwjOaCeOaLzlLlByghtZG/REoLCd5Fm0WIziE1HSp7D1BGahuhXgnQxsOjSYXoZXsCvfvmIYtjDzRusFxAVIHFR0qQnQs1sQZVnDLY2WCxaYkj88ucP6EIEJXAh0dva4I1bt0AI/vUf/luOZhO6riNkFVY5uuMFOHgUH9IfD+h8i84UEGm9pfMeu1CIaGnbRDZWyKLATRzOdixETTUGGy2d6+i0473vv49Up/3kpKe/LtD+ixMPn786sxi8jG05aVw/cXNud8UFQsgJW8qlGdeTcJrvu1j1d/bu165Tf1LIRUrmr3ww/RWsMmvLeCkD9xoosy6bF5X7GgUL+DVH6H7OBL9mrC8La4S2l5olLpPhusTpPEO91spxJs05yqy1CjwdIU/vEmftnc/ofIGV4By8RDOytsXOPkzPzRon5Y6zwtLq/5OJ62Uakgth3Renp+WTMU1Of3LSLnNCu3KqOc/XeO1RiWdC1mnB6myRq9fpzIdcRKQnz04HszkrqPeHFXme0RtUVL2C4CMSaBYN0gvy3JCyHnmWk1wkkzkxrCJktwvHlVu7aKNZHrTs/WqfZd1RVBmdXe21LwYF4/4I6WE2bfHdKjKtFgohJVpIRAz4JiKUxAVPEgkhJZmWbO9usrc/wXtPaTSmV5AAmxy9MqMRkAuJiRHpE1JJTPSYBF4kCueIRlFKSSclRRJoKahTokIQABmgTpAHMEIQpKTnIlasDjwrAUMjMZlhufS0jw/QSrOxOUBKSW9YITpPdIFevyJUOVdubHP48AgVIs2swadIcoF2XiOFWFlLkqDqV4x3NijLktu3rvPODz9ACkFUNSZTDIclJtNYY5C9Aucila9oRIdMiaIwICERsD5S+AQGlAAjJTpCGRLSCMZB0lmHTgKhJKXJqIqMJC0bNjFtanJt8LkidS1ZK7Ba0PMZSXv6WUFQkkEG/WixvmEgC5QzVCGjLQyVrsh9TjvvKJaBvOhTjvu00jPUJVFFfPIUCZxtKGJJ24sMuhJhPQ7PMPaIyVOWPY7tMflhpBiPQHXkJFpKit4mR2HBWFYEq+g8ZMtADALTCpyGUSvxhSJZj7GSEDy51iQjGJuCDtBZhk4ak5ekOlHHlnE1gq4jL4eoTmCynDIUeOPZFANa6RCziC5zdJ5TZmO8SmzkBV2syWSJ9IbMK/rlGB8C22JMrSOlFHT1EtMmynyMjY7NNKQziYFWtF1NmWWoucEFS98JmkyQfI4sc4pOkacBKMNYjXGxhcbSqkRf90mtoGnmjHSfrg4MehW1UgyyMUKuLBRVVxK1QHiFkNDXQ5ReucWtYoFrWnrjDYiJgRwRUyQYR5EqvAaTlSQLRZsT8PQoyVOO6uWYmBFlYCRGGLOK3SAkCJFRqD5JNmzEjIlP5N6iU4LoyFLAIBgVkjBdUmpJXhm892zt9DmaOISw5IMeXghSF8m0RBeC1kEvN+hBhjKKetEQkyc5S+fAaOiPRmxcHROvbZC6BC1MJx1GBFpr8WkVH6YoDNfe2OHeTx8x2N5kMdlHC/Ax8dYnb/HRb3/72Wzaq3qM+kOWqmZYDRBln9nxlOa4AQWDwYB20RIaj1YCrTKKkJCZIrSJPNMMN/qMtgfkvZyizIjZkqy/crV7ZfcKH338TUyR8Wzqf9HCf25RObu+rEn+KgvnMxZhLUNxIbww1UvYuEsFojvBKFwKo6/DZ7+CAPCXDi+0EpzQOn+d+oszf18Cr1vY+8tzRQusUD+P/lMafr18XzOsQ2o9+s9fP+NXn29sOqcIfzLg09kJ5YUEOFvoei2/uOAf6bnrtKf3L6rTypPukx2U4nmS0z/i9MfiwtJPlCx46qI1rbP+nMTlxHU6++4cPBEvzppcT9A1rXu/tvDzBaWzP+lpC55oR3E67drsXwZPzMY/+d/+nL//P/xT/snf/2d8+vN7/K//+F/wD/7Hf8Kvfv4Fw/6QMI/YaeDGzg4//dc/4/6fPODxTx5x9B8PufdvH7L8rOXj9z4mEFaHc8uMjd4I6z0uBH7rv/wBd79zl2t3r/LRb3/E3/o//Rdcf/cWvXGPnRtDHIEoA9UwZzCsCEIRkqC/WWKGFcXWkJ23rvLhX/sGxfaQYnvAJz/+Jr2NHspohFJce3OXTktqKdi+sUNeGEiB4C3fXCSKP3lI/odf8v5hJBeCIEEYzd0OLCuN840AZRJ0KRFS4ludxLKKPH01JgYRvBCETPOxkyySp0mBYQb9m4b5uxnTO4qq6/j5L2oe1T2qK7fYunaHZTdk2fb4zm99n873idk2b3zyMd/9u79Nde02G2+/w3/13/8fufqtbzO6+wEf/s5f4zd+969TH42Y71fsbN3mf/5nn/J//f/8Z/7wzw8Z3NhhUvQ5zio++s4uD+MD7ukvcZs1V7c97a6jGdW8bxI2BjCCyig+1BJ2Am7D8kHypL7Fb3bQs3w4k4QcbAYfdj3Ecobtjomp4Tfza5gNTaDl3emQQSiRrcC0id/0dwka2rbl9uEOerlFXW+xmFR8/PgG9byjnlqu7eWYeSAUguz6mN+98W1aGWhk5JrtkX0xpWk7XKb59vwuy7qmqVuucIWN+AZNO2ZZV/y14veY131qt83VjW9xw71PdzDGTkb8eP4B9jgQDhPVHtzY17hJi28c33s8gOiIwtPHcCuA7z0i9B7z3XmGGh2hNx8z3k28V11DjMHnHd+vr6GkIBuWFLLi2+JDOqvpnOH75keEAG0IEA0fx2/gZaBraj6u30URSbFFOcc3D+7iQ4a1im/Fb662HqmEnzf8IH1EkB1ROz5o7lBkfVoSQSo+efA+i+Ocph5yd36FqvY4P8d1M7715RsQr9PNdrh++C7lImPZdtS24wfpe7i+pEuW2/Im22oI2hGN4+PlN7C6w0rLlt1gN+yCTahc83vV3+Juusu7/i7fjb/Bj/Rv8kH1ER9sfcJ//fZ/z3uDj/hw67v88Nrv8dbwA5I0RCH5fu+3CL4jBst2tc0tcQebLC4LfNd8n1YElsJjRMld810WzQa13+R75mN8WB3Ujk3HWyLii4auavnoSsDKjqg7Qpjxxm6H3YB9taDMDrGTGWlZMx7k3Nm0qEXDVi/nzeuC/kaJ1JIQAld2YN50HM+WFMKxffM22zff5fY7H/Lj//338L6HbUu+8b13uPLBFuVVTXU156Nv7DDKJVsDw/d/6x0++eFdvvPb7/GtH77Nd9+/yeaw4nu/+U1+57/8Ifc+PeIf/o//nj/4xz/hav82/qBP3B+x23uDrd5N3KLPYHCTb77/MUcPDvHW09c9Bvot3OIOs/kNbl59i6x/jeGVt7j1zrtsj7eY70Vme4EP3/4Gbpqj7Ab9bId33n/vefwncX4lOLl2ClZJzuq0hHi6Tl6wPF1mGUGciHXw5Oe5du05F3ly+ebkms75Re+rwBpdbIqvmNnXYe1O1e/lGb2S49ST2X0d+lz0s66crwqXFLJeNxf9tV3RLpfLZ9cXW95eVsT5L14NXiQGXrbs0xpo0hPNsViX8mm+5588vTp1NmF9cec/XEOG1Xaj02mee9ddMwmdzPSksvxJJiu3ZZywOpzNZ52m42lG4vz7lykrTmxnOpf0skqVCwbH8557iX5zpoucpV068fuFSoULLT5P6PuCpKca75wVaPXo4ZeP+ef/9N9y77P79PoVMQXyImNyPGNzNCYuYHawwGSGT3/yS1zTUQqohjnT1KH7OTffvYnelpQ7GUfHR8haIrsc4moblQiSXBcc7h2ztTOmnTTU0yXTR0cs9+YUJqdpLXlhaKxfxYEQq3MDPjra1lFVOUiBDwGtNQhJEJJlu7JS5MbgnSekSKZA4Wnqmq3xADUYMj2YY0NAvrlFeHuLPRnZkIpl8AgpcEpQ+YRQkrlMjCIEKdEpMScyigqBZEJglCQ2Jbx3zEViR2qMlExFpEoCeZwjJ5FZEFwdFWz3e7RdZDAoIFjyTDI5rtna7hGjYzatKauMFAVZnnN8uGBzZ4gLkvmsoygMNs8xo4q9w5qdjYJl11LbgJbwePEQpxZ0lWEcoCWRlEQkMALKmJioxGaEbtNjywhCkEcoguCoSmx3mi6PWBUJzlMGTylhv++5Vm6svAI5i3eWftKYmNiXS7Z9Qb2R6GTAyUjlCqpUsWcsO7KHsw2ptfihYVQMMCnxaHnIdjGmVaCUYJkc5V6N1AWPpWNgNWl0QF46pqnhyuA2cVGy55aMYk5IiXIwZK4sm64gLSMT11A1kQBoDxM6xqEgpMBMe6qkCQqqouDAL7g6GNCpxxzbfXoiA+kY9iuO0iFXy5ssO8UiWvzcYujREwMOCsd2Kol6SsMCFQVZIRmO+zxoHrAbN3GxXkX2bj2ZKemVQx6HPXa7DRZ1xBlJ0op+z1BowR77bDxW2L4g9Q1d22BmUFRjHopDrqpdloucEA1OJXpLjVkK9v2CDWtoSwNFjjOJQVig1B7T4ZzdwTWcX5Blmnk3ZdRWKC+YlksGtiIWCdkFlqpmM25SyIJJd8jIjHnTvM1/ce3v4VoLPlJsDRFKnjusu9c+4p8/+l+4t/yMUlU42SJDZG4WbGQ7LFPHggVZMHgkmexxkI7YUddY2iGTxmI8aFGQt4YD2dDbkzSf9qlrjUiQLyCbBfbbyE4maIVi3nqkFAxrz2YXWTRQlhIjNc3SEnwgpkASkdoqetkqQrwNgSzPufLGNv1ezv1fHTDsa6qdzZXFs/X0NyAfeo4Pp2xuD3njzg5Xq4zN2zts3d5FZ5rgAlJJfOewdUdvs8+Xnx/xb//FT3nw+SHDjQrvHEoLlouW4UZJkp7p8Yz+sCKIKTEsOdw7Io8DRLzNstGMNks8Eikjy4UnNXO6yZSmcygtQTTkRaTaHPL2h3f4/m99k7vv3jipZXy+pItnq86zIKrP1pkT714ZvipHeFnm+Cuos9cHmuX0er/u+oK8Xk6b50iePJNwjr04xV+t499OnL84i9dFCHw9rfiLYQ3tL3T8cll4Cb3Pwl+xK9rzJyVend5rzIJr3p0+dnyy071MI7024zUpz7+/+IsXpT0zcp+cJ1j5JH6CiTiR7mwH8gGh5DNrwCrNc/zX4nRqJD1JK9JaBlyQnlgOnrLUz+2V4izuiGfT4NqTHudG8AUiZTrRT15Bm3C2yJfKwhcJLOnF5Z2l7FON0qleI57S4+zkeab/vhS5daiuOkZTt1hraZuOFFcMc9kv6NqOWjWkWtAsWo6Xx9jWkWlNkJJlSEQpqJcN+w8O2OgPiEtHZy0mZRRGsjiqUUqRiQyfAu2yZSqm+IVlcbwgCYFPidmiRgqFkorCCKJfCbjKKEQSOLc6hxEFOOsQwqGLHGEyhJQIIfDO07Z2dYBVCZxz+BDxUtB1HfO2A0CS6GIgakErwSPwEoICHUCmiAM6wEsgJbqUaMVKOG5iQhGJApIUWJGYy4QhsnwS/FL5hJGGEAKTgznd/SkBRTOuyEtJVRraxrJcKgSRpu4IISKQOJvoWke97IhJUy8tzgbiQFKLlqZxfLZ3SNO01DEhAXUlIEtNFwLzCFJIOgEqJYiRSKID5hqSiDR65b1NoVgicDnUEnzwLLwFLYlK4HuKzkTmOiC9p5OOhCOLEZsCVgbmmcVGT6MjXguMz1hgcSowjR0yB5ciwbeUqaCeL2hl4OD4CKsl2UaPxrWIfkkKAus8jQBhAl1Y0OnAsl7ik6DTkaWMBJ9w3YJFaNFdh3SSZWyJUq+27tlAlyWWyUKu6cxqq5dQgkaDt4Kj6SEpm2EHngRkGdQs8QUstcXHnPligceTpYxoPI2tqXua5C0L3ZFCZKQKZnFOGxrqrCV0HdPZPtIYhtowd1OcdtSVp4uCLou4pkHUGj9UWOlZ9iDIRN3MEJlGjPvMU4fXMFvOsAxpUyDEBFaDjVjpWIiElxInLBHIpEVkjjo2HC8OENLSJEFLRx5AGk0Ta6QSJBFRhaC1DW1YEp2jCw1LqWlkTfSBfFghtT6lXD45azWhwUZLGxpCisRsdT6m8TWaKU5CLWtsUqByuhhpYsOcGuszlslB2zHo54QK6lmLaMA2kjoNMEUGxy1eSIKEaYhAokOik0Brg+1WZ0p0VkJMqEJhpMTkAhcToonI0NHNZvgoMb2M/S8OeGwd3kkWey3F4zlJarrW0R868r7HpojwkTfevsr7v/sRwXlMpkGI1bwkBFmvIKtyEIKmsXSto2sdy0VHCI52umAxq2lnBb2dira1CClJukHlgSQT9cLRzSb41EMbRb1ssW3HsvbglmjhQWqCiyQc1lsWdUeuJd/8+K0TM/sZzuQJQ3tyBTj1Tqy9eQ5fV638OoSQS38invE6685SntBr/nqZc+DUidt0+s35tOe0jRffvwpc9tsLGf8zI/0rCHyXhksKfZeBry1cvEr5F9LkhZmsZ9kvYhQvpvsrtsZltekvSidOJ3i+NelFVhaB0JIXtu5LqyKe/V3rii6tBA/SyVKelnWWAX7OZa9jtM+jeFo4ee6baU3LXLJJTrr2E2cPRl9EozXts/ag29k3aT3l0+lfzzQIp1JctoudIXUi8eDeQ5aLhq3tMYNRn/HGADetiXPHYHcLJRQ717aIczi8t0/qOm5uD3BNS5sE/X5FpxzzZUOcOd64cpO0JRg3Y/pVjzTVPIp7aKO4dv0Kj3+xz8P9+7T7U8K8pa09mVZs9gua2tP6iPWePDdoJzFGs705oLEdUoCSgv6wz2Q2QybBaGOARTGZLihzQ6/ImS1bUkqMBwXTY0eZZWxd2QQU9WQJQrBhBQezDhMCRW7oVyV7HoJSbIuAVYGUAmUQXJUZDwLkETYjaL0SwKsk2HKJSZmjbUfPJUqln7l0vYnlqIRYRUatpK8jj7WnthOGUXMcJa5QbOuS4WaPdkNSasOd0YiHiwbbaTaKChE1dS+SOse1En528IjaewY+MupLDmVExMSWTxyKBBK2g6DoIvtiFR/keiuY5YGURbYaSSngsYhILbmVcuZYsJahlfQx3M8TQhpuyh5H9RTR04y85Jof8kDMSUGxa3Na2eFdYCw0YznmUZ7wAm6ONlk2AdKSATnjQ890nFEnz/bEUNuKVgmGTrFlS/ZzQaEzrqYclyRoTeYi1+6P2e8pXE9xNRuQxCa0E/QyMmozpqWnjIJxUOTO4EJLERM7XcHBRsQMBNfFGJkSe9kh6ajhprnOl/Ujej3Prc3rmGzAF/UXFKbgtt/myBygs8CuHyGWBVF5pE7c7t1l31lEC1fkJuHQIgeOWDveyW+xcDNcXLIZx1T7BQ8HCV2V3JQ3mIslJMFG6HNDbvOgO8a5nOt2SJe1xEoyEJrNpsc99QihMq5zlblt8K1n0ORcETf4PC4ImWInKbxt2VeJgTds1SMeKUvbWW6pK3ShJdnIuBzx1u5t7od7LObH3BrfBRFh+TmDbMSVuM1+ekSpCrbdBuVcsTHcIM963KneRVcF0qjTytczcK24zla+DSmhpaHKKx6GL5GtYldeReY5Kj1EusS1dJNHeU20GTuMkWEH4pRsuMGbvWt8/uVjsllklBRlb4uJHGIPZ+wMM6athygZFoL+IGN/GlAJdnJLMJJ50TFvDun5RIeBBGWCiCbPMravb/FOucX9LyfMDmfsbuS0TeDoaEGeC/K0ZNEpBAKxbGndkiYIMufZ3fgun332Oc2y5u3338Faz8MHBwwGFVev7yDlikI37mwxGBYMNwqqfsl4NOaP/pcHdD7Q2JbtnT5yOKbq5eze2ubx3hEyDqFqaYsRM1Fw8OUeYj7BihwhM3INuQJ0TmdbZAqEKIlRMnl4TL/MVi1zKjDU5UCQzvosecHi8RU4y7Md5msxpy9nfp6dwlzTUS9d9FOF4KX5nRPrejrLq6zevtC97K8TLsOsX/j+TP1+nYLFiyaYV4RfYxC98/AqvNd5/fnrLeOV4ZyJ7ARzfZlCT3Wui757Oik9Fw5Ob9VKz1+fncBepeInhJ6TsS/OCQviRFWfpD4XkefppxfJDuLp2D6jFTjTwCmtXI6uR1ecEG7S6d1ZJ+Gyz+B0vI6zmpUzz5JYk24dqq84IJ8aj/7Tf/xz/uwnf0HbdgwGfYINCKC3NeTm3RHLRQMOFntz7v3pZ0z3Vx6hTJaTpHoSKEnQkyW193RTz+Ef7/N3/89/ly5aNscb/Jvf/yNElBAlfhm4/2f3qPeXVP0cYSXBJWyICCJIhXyiZVes9u92nWVv74hAoOscWq+8qriuw2SG1nY0XcRZiwoOFSIgSULQtY7oIwkI1iNlQKSIEiCmc0aLBXPnKLVG71yjqAY4IxEpkXYtyIhQim7hUFLgpCQliU0Oi0cjEJkheI8xCh08MURMJvEx4YYJryxJrKIM28zgQiTEwEQJpiFQR08bHpMOoMk0Gnhkj+iUpk6Bx9MDkg3MEGRKsgwz/BiihBgidQx4sXKZG2JApZUGPgIYSEogUyL2IFWOpCOdSOi0OiyuvSS0c7yOpB6kMkOoHsIG3MLihaQ3EDSdQyaLTwZZaoIQhHmH6GXI3gZ4gx5sU5QOJyIq9RHNZDUIW4tdBDoTsCLQOU/wAj2ukEKj5RBtIsFb4lytgiwSMFbS1H2clyByZLtB1BJtNUWXKBeCJgm80QircQGCkKjxgGI0oixr6sWE5fKYXtng/CHFKMNszCmDI+WWLF/CLGGKjCzLwUlkNSTJBtcJTBZIwaJyTQgdRmQQBHFuaRcNNrXkWQYionOFWDpSXLnWNf0eUmuC9cTkCNETgyOgiapA5hl+JnHLgDOAzAm5RiRNtB6vIQZFQiOzCi80WEmwHpUXeOUIcmXhDa5FWofC422LEhmqLBDO4PoBcoGsSkLXkYxA5JpgA2HZonOBAvr5iB9f+W3masFoa4dr/Tsoefp45LrpJ1M5f/3q3+Zh8yWZzJmlCY+mDxGZISkFSkKbkFFgfSTKDGSPJPv4LhE9iCJnflwTYlqdn6pKKrPN3s/n0EmUVlS1wDYR3Xr8oiFHI7UkbWYcjZccLywjLYh7nrYRTwLZtSvTo+7h7y24fnXIYLPPYGvI9k7G41/9grn1VIUmkyW+ywgxkRuF9xGfAstZxx/9b/+B4nqG7Rw//+Izkq2Yz2uqKudbH7/He+/debKMRRABREIQOP7iiK5NSJ2htWL+sCWWOXERqR8uaWNC9zfYub7Foy04+OljjnzDrdGAgayIwjDKE04E9iYtJu8RO4dhRUuCQelsNRfLCxroMuvBRZDOJDq7Fr1o7XnBWnWRmPDMFfoznuRshunC24sKTieuLsXgfx1mTpy8eM5w/JUJFqdw+rr5XUazvYJnNT+tmT+faF2av2rLxWvA4Zy0dGIH0KnXX7+AE4Wchcu315qEL6HC6zb9PeN+vyJlzk4cz7K7KM8TgsRTzf2lFPVP6PKEi06RJxaIdYLM806QOEHRM6R93aQ8BS8yKF307Gt2zkTis19+wf0vHlLXDcPhAKJgNllQFDmz4wVGah7f26Od1rjaYZ2jqkqmyw7frLYbOe/J85zYeVyI3PvlI/b+9AGf/O3v8ejeY6Z7RxwfThFC8PDPH7GcNigkvo04H0koYhJ4DyIlbFgdog6hpbX+WZWlgpgSWivazmK9BylWsRO6sNompRTWd7gkkEqSVMBZjw+e470Jsspom4YIeB9QUhJDwGY5R1uK1kmCBbuRsCkwF4EgYGIkySUcgk4EEJGFjCSp+YVYWQ0aIkkrbPAsg6DIND8TkUxAnQJ4gRSeaQaZVCyEQEdoREJGkFIxTZ5MSObJYZxjkSIbUkKlWBAxEpZu5eVqIRPxiVCxECvvXXUKaAK1Wlnajogs5KrvL4uIziIz41FasRSJOoskEVgYTVZkNDqgQuRxc8gy2pXg3Y9keWJZgIyB47hYxSbQYHdzpNRM6BCVZCpntI2nqxsWfkKMnpnxBJ1xeBOapsWLSDAChKBGYHXkOFsQ68iyrqm9xkdY5GClZ7IRkBGctVi7Dwlm2lEGyX4RUVFQh4gPfiUIjg11Dn+u9sE6DttjUm6YiRlTPaWTGbNYo5AsXE1qGqQyHOsFCyyTbIGJhoVvoS/wzjIVLTIJpo8+R+sd5tIiwgS3Y1koy9y1IBxF0CyrjkwsOJKWWlhwiWWcIYVgwRylDI/CI2YhEFNkUQZILU30pOR56O5jC4c0ki48xsfILLeEOvFYPljVNQaCjEjjmIcWZOBIt4S48rIV5JKsF5ilDpHn/Gf/F6A8FgsqklrLIq+xomUu9ihkiZWWpZgzN3Peu/IJ6qn3oUtCoQre7L8NwE8O/5CJnzAPU7zzuOCZpzmZyTnQ4NqM2lhSMiytYKEFamk5DDmCyEI5FH0WdcvhUUAkge0seYSlhSauzlF4VjE3plnADgJdzzBrHFoY0BpMhnY5JkIbJMkFfvnpMSLNUMbw6NMZMS5wwKyxBJ+v5hspCd6jpCAkCUQ+u/clvZjhvac6qBGpz3ze0O9XjMcPee/9OwA8+OKIxbxlPq3xzrP/ywlJZEid0ThP/XhOVDVSwqJuUEoxurpFpysOo+D+4ZKoDI3sU5kc10WWAY7nNV6shJtc9ig0tK5jsL3Flz/fZ1AZNm5uP9cTcrk1a7XmvYJKVZxJ8iIW50VZpTPnDC4q63IPXwhizdWrwKkl95UYzzPM5FdlIl6jVv+FsK69TuB9/vWLmJGvwSd+Td7m12C5+Cot8JQJfT3lP9fJP4WnQze9nC+/6N26xj710YuyPd/4SZwPGrdKcibtCQ77+TEJcbHF4GXa9Scvngv2J2anUyr7JwLByeIuzVCfEg+e3Qv59PK8iePkxHN2vjxpZXgq37zy+F7XLS+6fhU4+90r9mEhBGWvpD/skUj0+hX1pGZxNGN45xoqV9ilpZ3XaCkohj3qumFjdwxBIL3gaO8YEsS4CryV93J6ox4/+Rd/zDd++yN6wz5Zv6LXr1ZxMaykFTM8iUGR4U1G3XZoQBlNkWnEZInSisauDi8KQIiElKuo3UYrfExkQmOMxltPWRXoIqNSkraNGClJCDKjKfRqEc+0Ju9VZG9dp140uMatznMARa5pYiSXENLK3axWGkeiSoqAQGiFBcoUiFEQtGKQJDZCrjRKJnIfGZicFDzaR5KCQktcimQRpBD0UiK3gagkMiaciFQoFImIpEBgQ6JKEZlp+kHSOU9PJCoBEokGPJGBT6v990ZiEEAgS4ogBAMlaYn0UkDFhHBQSInNM/pSY1XCR49Uin5ZUApN5xZUjce1jkoKghTkUVF0kU4rxsWAlCliAucsWQ1GaNo80SPHuQh1IFnIKoMOhthLjEPGsluiYkbQkX5W0i5ajIyMixzbJqgDMUoqlSOEIEbHyBg8FtlFlj6QoSlGFbJMjFRB5xyZlEx8w4bsoUvDsW/oiwwroD2oqbKcspFk/YKUBcqQk5TGeEWUib7sg9Z4H6myHqGzFD7DycBAVCxDZKAqVBOJTtAzJV5F+gvw4x69foE9rimTpu8NjagZqTFd3qBCS2wdRmdUoqSjZRAKBBkgiCKSS08eFcHOGYaKRgZ6oiT4QB4U2AyXwTCV2GjII9hcki0EppO0StH3GqclMnrqZUOeZeSZocsKBuUICo0UjoWbUaYMrQoCiY1yE19PyVOJQqGcJsegiuz0vPKKc1SlegzUAJcsI71B3S1BS7RTeF0iVUUSCwapwJNQeYZYemSUqGWgU5KtcUXtIxUeVWWYKJCdRQdBTzi8FKtYNiESZh39LGKNoiCRqVXbJgnSR0yKBGEY9TOEUGgE3kWIGt9GhNZsbQ4xg6tIXdJ1Hu37tJPHTBYNMgiqMqffK5kdTZkdHbFzfURR5PQHFZlSpLiygFe9jKJc/fSHJXWvoVcWtDbSLRqc70hSUxQaYiAvDJlR9EvNF58+RriOzSrDpISIjuQDrbcoIlIlfAgURkJ05LnBCMEf/dN/x/RnO/z4v/s9+ttDhHxJPKqT8Ey5d+7h6T5w8tVF8LI16ERfuuhg8OvQ8H8NtnYtnBoCa+r/0i1PX2EMnarDKSXnC8o6yf68QFe7Fq+zfMoavuUZ6/ck1tSLqHypbVSvxUJwHr62K9rzOKW1T9d/+bpqJDjZCs8chJ4q4vyB4lPfirPPvxoW61+cyPxZcS9SE4hzd2ddv34tJ1+ns7o4zbPLpxg8+ffUte3ZPJ7SO4kTf59eJ055Sno68C7EIT1Jls48vaDXvIwcZz9MZ35eC5yo47pyLyjrvW/exeWW0HNs3hqBcyzmcz77+aeMehVaG3ZvX+M7v/cb/PDv/JCrd29Qjfrceesquq/ZfHOLndtbDIcVQUhShF5puPf4If/v/+Ef8rOf/5zNKxuE5PHR8dt/74dc/9ZNxKZhRodSYJtA5xJVlTGZ1jTtamvW9Z0hhcrIteH2jR2MMXTe4wVsbowRIqNtItd3t7DvbTL7/lXab+4weHvM5JMxx5+M2Pr2dXrbG7ikWLSeLZVRH80QMXD12hZF1cMFQdMFfvjJFcSthvnGATuZo2clKebgJR+1Ei8SXiZ2dcZQKQIr68Y3rSTIRNRwqyjY1hnCKEjwUczpfMT6RO4iO0niQsQDn8wCySdEgC2buNklYgx0IfBJJ1daaNvRazve7gIIh6fjEyuIeHyylFpwJyScdDjt+XbIiZnCm9WWpze6gOhZbNVxdypQ2lFkjvEo5xO9RV5Blnm+eZwRj5f4xiG7wPcahR5a8p7l3QNFROAVhBD54GhIXbcsZzXvmitsXN0kpICdLXnvvqaJHZ0OXD8y9KiIKqdt4eOHAyyemEk+uvIm16otUl7gleGTbouukqTNnHd2rjCMkibULN2Sj/ZLWiVwWvH2rTe4M94lCUEQ8Nc33yNoCUZxoxpz04xxItER+J3iXUIuCUR2q11u6tssZUVb9vmt4kfETOJTYuhL3nFbpDjFdYf8dv5tbAq0zsK+5d3FVZq2xXnHh5Mr2GVNSp6cnG+J2wThEZXiE/chpAIfczQ9PtHfpu1qrPR8R32MKQtiphBK8b38bUI2IeVTvmWvoT2EGHF1y2/Eb2OJdJ3lY/MN+mpMSiWiGPAj/zbJQ5h3vDMfUUZDLAyhl/Nhu4t3nqQUbxzl9JcG6xSLo47vh+9gU8T5xK14h+1uiGwdsW74m8Xf4m3u8qZ/i0+2f8ibb3zrwqnrsvBB+U2ST0gn2FSb3Olu4Z0jGfiR/IioIkEF+nnOe+EKAY+Nlg++KHH3e9gvNzHTHm/MarxwdKHl9qAmr0pcEnQJxmKOs5FgI+90FvkYsi8k+Z7gDe+RXY5sMnZTR1YDM4U7sGy5GYtpzXxeM84lO3ffZvDmu2y8/y4/+FsfEPKM1Ct5872rCLdE6IBUiY8//A7tgwHzXxa8ceUdxsUOLCviImPn2gb/7N/9C/7Jv/h9FuGYbNQRyn18dsjf+G+/xeDmABdqMtGSQk3rlvjYsdNLiGLAvJMMCkOzv4fIDTHTXOm1uM5iu46eSgTtuEfiMNdsFh4XEzLLePTgMQezff71T/4T//jv/wF7e4dfocXWQyKd3sYLL1+/161tr8LjXIZHOFnWBVl8raV1Tcd/MTpnhLn0FcfOGsXxWtxe9v1lLEFn0pxzcb82n9WDi7aRXxpOEkfwam1+CfjarmgXy8XrweQkXFpD/hQusJasq9maPM8GK7scvG65nMvXOz0XnsQJt3eXzvMi68bJIG4nDScvHEhPE74g0VpSrTlsfu6zSwzss0aSv1J4iabpDJ5Ph94f/Kt/zi8/+xXzxZxxb0y71/GLn/yKFCOGkjffeZPFtGZje0Rwgf1f3qdzgWZec/P9m8ynS4osY7FfMztY0O8X2NziVUe53ePuh3extadZtKvI3lGgpOb4cIKftiy+qAl1RKaE856UEs6uXLXWTUN4cl5CGcgrRdNZNjZG1I0jJoGznvpGyeLNHnXfsIHCqoQuDYHE+IuajU9rjg9mVLkhRYsUER/Cap8yhrpzVEUGf/MGfjtjMl+QZlDSYyphpBSdC4gYaZWkMgKpEgsRGAmNk6BiotOCTVVAE5iwckU7tRadoNaCXkhIIViKSPFEAC6RLIxgI608WdUaCqFIWpDFyDGeUZRElehkpIiCwMp17DGBbQ++VHSVIcZEdIHMRxaZYCMKYtlSa4sUikHPUKTI1HRs+wKrEjZaREromCFqOBCOK0nT7SY66ehcxJAzMBWHheVK6hES+BCJmWRzPCJbWh6nJdvZiLpIuOBYLGuKRtMTPQ5zz5YqmU0fY/oKPzCMZB/ZSB53SzZVgS9X29imbU0x9cTOcawd/VaQpMAkSVPAbn9EkRumsWFkSiyBLEmOllPG5KiNAUduiVkGrGhQwTErPNtZH0vDLLdUKcNkln6uOWLGbhyAaVmkKbpTiLyPm0mO05RqZih3S5aihf0aE8eUbLEYRKpJJIxqQs/hm9XWwJ7MOcwW7HQ9umxO3U7RZU5V9ClDxl46ZNOOWGqPFYGUInopUQvJcX/J1iyn25SoQYa1LaUdkHcj9uWCLTGkXgZCFIRMMNQV4bBjSs3IGuqmRQpwqaVyDlNIjofQswVyuyYzjka0DF1B4QNLM2cox7yffcCP5O+QDSvKJ65m4QVT9ZpnZ+FfHfwBP138GcfuiA2zxbQ+YqEaClPidIWSA/baA3azK8wPoTWStLDEByPUZwWzXs6Wg/lPl1ivgYSpE1UyTOaBSlq6zmNDwihJXih8u6SLhr72RCeIKKRUhM5iYsC6DKPb1QlvJSgHFZu3tunvDjiadGxuFCymlhSgnjVw/AjfPSYoiY6J6++9j28S88mSzSsjikKzf3+Csg128IjiukRulAyrAdILjo8nDIcD3KSPChX3f/YAO1uwWC6JSKp+hot9tt+4RSwr2tmEn99/gByNUTIyWkRGbQSVU20WfOY9jxrHwEi2vKVvLa2HPHO07CFU4M57t3n/W+/wt/+r31lplsXLWupiC8KqrdNLFJKX6BWX0aBfJruvutaeYNFeG+f0Mv7ubEGvYvn5SvzEq9VsZf04i9iJ508D/a7B+3xJLyj77ONXsJz8FbuivYCxR5zmTF8zH36ynOe0OeOa9gQKT8O/n+43p1K/crm/HkicO6ydTtAwnegHFwoWq452LlDfmbRnqfE8pserjMI1Y/Hkg3WCwNObs1Gyz+W+bpSf7m/PcP4qE8JrF0rOqSFefP8E6qZmvpjTtA0mZSQE/e0B3nrcJHK8N8X7gFaSo71jFpMFWmt8iMynSw7u72OkZuvqFY73ZtSNxfQEkUi9rJlNF+ASi3mNUpLYRYw2TA9mDPp9hG5ZLhYoIZFKoJRaae+tJ0UIceUdKsRA23qsCxwdzUhJEtPK377qZ+RbAzqTcC6BStQqEVOiai3LpiMl8EAMAaKHlDBGElid42icY753hNMFIUVKU7JwEYtgFgJOAlIQ1Kp3SyKtXB3YjAiMEnQxsEyOpCS1jyAkXkkikETCKkGIkaVM+AhKSqwULGNYudLUkqWKeAFCRFwu6aLCJglqFWOjDQkZE52EWgnmUkC2Oo8hn2wd8xqciLQKkozMdMBoQW4SiIgnUNMQ246mJxFSoiYO0RtgdcGkcSTnmFURkSt0VNTJ4VVk5lpIchUDIySK1tAQWNZziqKkdZ5F7KhDh1A9go7UBESzxGYRYVaH2ZXIUVLhSsm0brEzRxCRNgWiVFBAJxNGPdmCBbQEjicT8iqnLiPJg7cdWmvmriU4h9aJuQmItoHSI3Sgy2Hml0TtWdBiceR2dZ6nzh0ZkTxLTO0UnSS5zpCbFaGF4AOddCzjEp+19JuKIBrqAMJEvG+w0uOEZZDABUsjHBMCMbRM44RMVGAFrV9SyyVKKtq6oy4CAH3dQwwlTWiZ9RTEQBtrkoxASRcX1HQoP8c7aIQgWZBLT9KS9on7Y5cSzjpsckgdabB0WkOySGpa0dH4BrU63ESnLMu0YBEWqCojH/dXB69PzijiieH3zEyzTjF9cpqpw5K5n9GGmpkyuDKxDA02eSKClAStckzaOUGVzGPAxw7ZVWTlgNo6OLKkCLWHmKAXBX7pCFHRIUEoPBCioMxyFIJ2YUlO0DMFsUvEEBEoyrKPzg1F3ifmHanK0FWOR7D/cMqyDsTGYttAPetwrUN1C7JcYFtLr1fSNo75foPODHbRcvjTQ6aLjpQc8toUQ0clt9BCg1sFkpRS4hca6SUqz8iqgiLG1aF1ofFZQcgK2tZzdLiArKAOCeUiZRB0DkRKiCQJKDoCRhpUoRExoRIELFIqyo0SlyLLZY33kSxXl1k4TrTa+QXxWcysl7Icr8CTvGjdu2jdetrpLmL5Ll3eSTcypzm3V4KXffIypvoiuEhoecJMPmNrXybwXaQZWFfGCdqePQMTQkA+cfG+LrtEIqWEvIQQe67MXyP8Gr1FXV6KO2U5SHAy4Npa7fWpcbhOhnvO9ApWTMXThjmtQP46nOUF9Tvd804hfJa3PpnmAg/YJ2CF9UnKXAxP6p+e0/V5UL+zFD3ZYc/XaV155+uxfpCtqvi0/KeyxBoG/IXdZL0WJr2MXC+Ap1PbOY8Yrx1eXLmnffKNW7dZ1kvarmNQDQiTgIiSsiwY90ZMHy6YH88Zbg44/HKPLFO4xjLslYy3xxzfP2L72gbX7uwy35+CD9x56yafffkrnEqMxj38kUWUirzK6WYLgoert3bZurLJwkz5i65GJBirEte2RCUwEnKjaTpHrjVSaWy0uAiZlgyqHtO6I8RIeezwe0s2BPR6OWW/ZPpwSkqJrVGffOA5GivypMkaxazwKCW5e+Mmsy7xq8M9Si/YKEbc9x4bYOwjUWgQjn5U9IXkWEIUkk0gCJA4eih2k+JRsmgtGNsEUYAR5Al2vOA4RTqZ2AgKouDQRCop2QiCw5AwStNrPRtaMxGCQko2IixUolCSa8KgteTztHJJuuNXDGUmE5teQidIMmAi7HaKeRaplWfLGlIbCDJQ6YLrdUmX5iSt2Gws2eMj9m7uIpVmex6YNh6XS0Y2o1A5pnBoZbiZbdLKCHLBrqkY+orHcYLznt25wReGrt+nahJbreGBrCm1ZsdmJBSYlr6VDNyAPT8lFHAFgXXQZp5hJ9l2Pb5kTi0T11xGFImoPcOo2Ww1h7mj0LBjc1QUROsYbRfs5mMO3BxdDrk2GhESPIpzROcZdznH1XL1XVdCBiIqjJfcEBtMmSGD4+r4ClVcBYnTXeJWcZvjzIJs2RQVpRrxUBiCW3Az7TJVGbmKbOUVsVZM9RI/F9wst5irJSoXbM4yqv6YR0aQq4LdxZiZm0MfNsUGpS55KI9JIrEbtlkuZ6QqMep6bPk+j90U7x1XmgG2K/HGcbUY0PeGL5dzApFrPseKiN6Q9LxiOw14mNc0vuOmKplP76G2JWU0XA9vMNH7TNyMq2qXvoaDeMgwH3FDvEmxPQT1gmCjL3507tmd6i6f1w9xlGzrDZIIOJlRYLia3eShnUOIbHUFOmwgYkP0hutbY+Z2gH84Z+QDVVXwqF0FtNwZRLokmVnBRqbAW6RLqBApu5rWQykkmfT0WRKkprOWKgskIjEvyAxsbBomUuJjh57MWSwall1ClxrdNsQ2oYyhPyjIYs3ERW7cvcJoUKEipM6T9g5YzI5oU0KmSL9JZIWmEiVXd68QWg8h0a8qxrvXOTqqyUcl2+Nb+M7x+PEeGsXGlRvMY8nx3ozOtYRCIlRAaxiJgGwDplBsGYEtJPPjhq1c8caVCrFQTOaWer4gzyR+GRFDGPX7pBAAc+nV4qWwTv54bWaANbBOo30Sj6+c7UVmlF8zt/sKkIAQPA8PviSRuL59E63Miu94xlhyBuVLWg6ePHup0PjknXzqKS6d5N7Onk1d6+z/cnDyMO1rVLa+liB6FxP1FTBNF92eZW7Xq5uf7ra7DM/5qvR7TvvnzOhFeobEOgb6RMM/a7+npq8n+YgTApY4I3A9K0uckEfEc9XVS7X/nCDbV2Wln+sZnotuz+GsvHe2NdK51GusFueIukYEvKCBnwkKl4hc+VywOK0h+CrwLNrq2nIvl/FH73+TzfEGy6Zha7TJv/yDf0+SkigEIgpC5+imNQsbiNGzqJcUmWF0fUzRKxlf22Lj2hb5qMAlD8ljKsi2MoLv2N9/TG/WR+kcN/Ec/WKfpGH0xi4iwe4PrnCgj1hMFswPl3TBEVQiCksVM5KILF2LEYraBaJQeKlpgyM9cf25GSD85BFOQr8qGecF1DWRRLXR4/H7OZMgGJmcvh4y7Wqs6xi+ma/c1e73sV1kd1igTQQFRcqJUiCtgxApUoaOcfXMJ+KT8bjS2HgoEkklkgiEEHE5SBcpUJAiQoJUkZ7JqbEYIblZbULd8ahp8M5DEFgDUiQa37EQnpArJk3HoJcTtCeZVR6ttyQNbfSoFHFElFLkpcBVnlY4ovRID9poFCCXDicCNos43UeVmraVCDRR9FczsvJIIxkMS2aDGmEUMkKIFikDPjpC4Um5RHiJDIIu1rhU41JkVPVQKoGEogTLgpSmxEKiwypehI+R0M3xypBMBK0QnSLaBCKhjEJJMFmGsIIiQcwdmAQWiDkRmO9NGKceYldglCLPNH7ekOUKOSool4GJCpACOmbQ5GRJkyXNYFEyKwPetgRnYJyRUgkJdCcQYo4KNXmZY4TChYioMnJXEusGpEIZgfGadLhECUOZG+peRNAhMkkuKnRmkEqSmQJBTYwRmUuUVwgjiTGsyhznyLhA2kiWZSvXxUahY45TVxF2hrcFaqFBBIJ3pJCBPkLEgCoLTCcRWiGUobiyRdg95NDtI4eJvOwRQkc+MOg5FGqAaaYoZRjvbqNzw0v3ip6ZXS7Wd4OjYsaARRIsGIOvaXVOkhmukfhli2trgtWU/R6I1fxeyhGTxxr2FanLiZ1ENKsSQpagLCFEjpY1N26V1F2kmy3I3AKcJpHTk5CFwNJKcmFQJtBVHXXX0XlHcwTzlBMSjKTDhUjUPVqV6GuPMYIgLYNMMV9Y8p4h36jQUiEFTB8f47sZrVwQhUJK6MuV+9owT9BppE8QBIujmth+zuF8Rj4skVs5utXoLlFVmtGVisW9SHSrLXJKC7SSZFogfCApQ1ZVlKOKK4czFl4ybgNlF5gliY9Q9YbUyymdCBw9WLnt7WY1eVVcuj1ful6sU6a+5JNnNoLLMD0XWSxOXr9m/v85n/NU+ft1FX5P8nqR1eBS2ST+7X/6l9w/+IKU4NrWDX77k99DihPHlF/VcvKyNOv0xuk0DyfSE95FJE4643mpG+N15Zx8/WuQ7V6T5eI1ijun8jttOnv2bg1xvkLWJ+DF1oBzxqinDb5OqX6hFPq8M4iTCU8UeXZAfaUB9qJJ4AXZPRvUJ0wCLxbOTsbHOF/8Rfg8nzxeguuzF8+jmr8QnqGSTuW7Vtg7gcDXt1ok0mrf0KUEm3UghODmtRsk4Fe/+IL5fMF0sqArHEcHh8gGvvzplyv3C5UkykQbHLUPyFkNSrKYN0yO5jRdhyHx5cFjFs0COTTU1iFJ1I9nzB4dEX1LVBF3/wBZKKQVhAqMKdDKUPQTs8mC2Dqmc0v0EZHAdQmXwCcPQiCVoW4tQgpc16GUIPqAi4LH8xbnPCDYu16wKBRLIxExcqw6fE9jo+AvJgdoo5kXgdJIfmVakjZ4Eim2iCSZq0CSirl1CCRtjFidUCJR69U2q0kRkDphM8FEJIJ/si1LCH6KpRCSZCQhafaDY99ZRlnOf3L16nxFkdEkaK1nGSETgkkFRiSCSqgSjmjYjxYtBFZCHhITEWmNQJjEUq+2xXyqLZmKLJUjDwErI9bkuORwfQXWMzMKGksYZMzVak5rjEVnGVOVSHniIJ9SYyFAHVukVBzHhhgDB3pJbS1JClrjEERmwqF1zpGcYwn44MHUEAMLFUmVZLJjaV3Cx8CXnUMAU+mAyH5WE8wq+vkjOmwMzOiok+Rx32O0oI0W+hU6OebR4qThL+SEgeozbxaEJ5HbZ95R9jJmWx2hjdTSoWSHt465cJQa/mQ4QQvFgsQDe4RattTZEqMVtf4Fxjqm7hhVGGyyTMQCWQh+Gh6SnMQGg84FXTGjzTTRBf4i+4Kib1iIGlEGjrMFczdBScOSBcTETNTQCnwmqIUnikgnW1RSzE2N7AuO0mc0qSMJ6OQAnRrmMSKj51Gc0xKJWpD0FJUWzL0lycBR32M9dMnzK/8lsmqZNgtEpvgzdYwgYJNHdg2traipSVbwefMrPuDjC2ej59rJy692P63vceRbpr7Fpz2CrjlyU7SDw+4Q1SSO4wyZ9zjO5xx3DjmQ/OlP5jDtMZ1GKEumTWTZipXLayqUS0wXgUwqvphYOiIBRXAVG8bQWYnzDtEZYlBkZY6rShZhTqcFVUrsR0UnFGhJF0BLWEZwXcBZhXwSY6cmMbee4c6IRdsxmXia/SXz2tIlj1eKJFcup5eFRxWKGDyPHz+GEFlM5ySXeHD4kIgnCzlSS+g0s+USFy37+48QjFgsHdMo6aJhFgKF0KSlpucSaeGJfs5iWiOCZj5z/Cwu6Q1zFl1ikEFWDrC2pmkc97884Bd/+hmf7IyfnZ95EazYg7Ntu2Y3QDrPY5yywK+xMJzzTHkRvFTZ9xpgjW74JG6vtB6/yKryNXGe1zP2Jo/47OGvgLTaRryYsDHYPIPCaw7K99LhnU5ffn325Xm/eY3WKfi1botab2G48J1Yl/6iqfQCzvnkXplLE/0rDLpXBfECjfqL5ZoVBU4KJTynysWdes0Iu6yF49SzdC6ndDb9yaB66UyiF6D0VFuxVsa74NMXwbMB8lTAEE8l/Bek/xpwqqspeSa38/R/uWVlhXxZ5ZgsW7lX7Fe4VuFsi/eevMjQmSF6S1HmDDYGVEWJbS3GB1JnMUqhpSDYSGEMqlexu7OFPCpws4Bwno1M04jA4cNDtq5tkG/3GY6HKCVRGwoTNIePjxgNBjz+80cc3jvEP9n32TOG1gVGVYH1niw3aKORKSBJdNYj4yp+hQAiCTfr0D5DKEEpDUFLEhCVplQKEHQp0kuKxiUyrbBE8ggygkFQRYgIpJCIFOkLiVBgk6eUEhsjWRIIn8gDyCjxBKokyJVZRewWkVEQuCCYI6mSILmADAKVIgOlkCIQ5Wo7lTYZA2PwlWFHZixSi2sXCB8oI2QuoVNkJDOCBInAAFoohkbig6daNCglIM9RT/pmHnOWPtBTBbVMlCKuhDUEPZ2zCIGezPAKlFakFOnpDBMkrfIMRUETHEqXBGspMkmGYZlacitAxZWmX0vEcQs+oSpP0SiW0ZIjMIWhpw3KZdSdXQlYPlJIjdCClZFC0SAYi5wgFSauzpjsXL2KO+xo54EhhpA8eu7RUiH2m5ULW2kReLJdqIYbyLSksoqoVoH/shpEVWCCoE2OKuUokUhdQyFzZOcYDgd00lLajKQNfd2DmaPIS4zWTKxjUFWgF4T5HC00Js/ohYwm6+ipAU07py8rZDKYpCmygiZYRrLPUkVE8qQYyZMiazVLs2RYjZjPj1AyJxar7Yl5nbPAkTee4AQ9qehCRAUolKa1jmGvZJkUJgmUkOh5i3ZQZDkD0cOHmiLPWLKkP9ogn4CVjr7uU6jyUlro07PK+k+eToGVLBiokjZ09EKONYG8k2ROkWlDJqA1jlHZxwpDT6yC+JFJiJ5cQ6kSM9uRgmRQ5eA6esOcQEEePdbO6fUyQvRURlFEwUIJxkXOtGvoXEcIHUVpGO/0eDRpVm6mc4NICR8jQoCWq3gzmQJBJJerPeQq14wHJeW4T6/KsZ0k6hprJDk5utS0JEbDiuy6ptjKaZ0lzwqUiHRtQ4wR7SQyK5BCUeY5iIw2d/R6JUoYlDC4cUXyQx67FtE5jBHkmaSMgpgCzbzBO0tmSgbViq6haykzQyY9ILFa4X2AlOjEat42KlvTSl8B0gXr1tN1bw1zeDL9KzPCL2PhzpT1VfK9mJe5BOe8lg18IZNzvogLIDer82i9ovfkPIMkM6/ajq/XHJBI69nkl8FTnutFPMjZR68B7a/tivbF8DLm9+ldOvfsWbJzUu4FLy5b9lkJbR1HnM7fns0jfV3iJ15ejbQygz0p8kTxF7iCPYng2ReXwvckM/60I57O7qyA8yzliwjy5PvV+XPx7OGZos6hQuL82YqX0e2EuXB1gP/ZyHqtBjbxtD5CPDlYf3bJF2fSi/WD+gxOV67uMMhKwtTiJh3f+61vYeuGFANFZtga9jFC0euV/PD3vkOIiZgEg1EfGSNBOVIWuVJtIOoM/xCGZszdd95EekHoIluD3op5Tob9nz/mzTevk4qOmHd8/KMPkHqlDaw2e/zOf/Nj8q0CTGI0LghYMh0xOvHmtRFSOJp6Sj8HYkSIhCkMt29sr7b6hcSdUDD4tGH0R1P0n054+zgjxEggcjtV9NCIBCYz/MBsIqSCJLgdMjaiQimBJ/GB1zjviTJxTRgKl/BxFWPiu2GIc4LkFVdDxo7UJJMQmeD7viIqQRCJXaF5A4NSEh8Cd6cds7RgIWtK6bk50IihxZUt3yLDqYBTgbHWfJQNycoMmUl+oykQpYJC0heK91KfoBRWaT6pR3QdNN6getf5oLiLNT0aVfBxu00MmpAk0cG78xyvIGWKj8UWhEggQEh8uD/GHUJ3LLh7vE0heySrEdHw3cUt/EwRu5Jvzq9TNiWpKRGp4kfuTVxM2Nbz/nKHzWyD4BV4we92b1FUG2g94v38NldiQSEgS5Hf6a6hgkM3LW/UBVd9TiEi0lt+fLyNFyvLzPggMLYWudsSt1p+ELfosgk2O+LaKOPNzQFiuyGOG767v83icU17aBkvct7Jt5FdjVSB31xeI1hPsJGhLXlL38GVI+qU8133XfIEPWW4ko/52N2m6hp6eP5ac5tsIMh7noEUfJjewEWDdYIPDt5AqBJrJVmq+KR9n1hoyDU/GPw1TDmAPEeXfX7Df0ToPL51fOPxDXJtUJVB+MAP64+Ji4w0zfjIXyWbOOgcsXV8+7HGL5ektuGNo4oeQ6Ic0C4EP3C3CDoQROCN9hqVzVFGESX8lvwRMTqIkSuLTb6xeIt3hh/wRu8dPtn64brp4NSUcuF0f2Iq+fnsZ/z+g/+Zf/7of+WNbBMnEkEIyjZj9z/M6B4cQIr87uB7oCSqKqgw3H10BfuLHu7zPt+vhvh5TRKRykS+vZvIM08MS67nB9SP91D1kqvjHu9tGMQUZKO5XjkaBIGMJiRGZo5MkAnJbpjD0R4Dv2RAx5tiSumm9PyUN5jQixMqf0AvzLg9WBJ7+7S9h7zxdp/NWwZfHeKzCR//5nXMtSV6d8pbb/e58cGYwRuC0fs9fvw3fkxqN0jLTW5efZt+9Sbzo6tMHw+4Ge4gF28SDt5ku3qbnd410rSPn5b86Ht3STZiJzXqeMYoBirVJzrJraHH5YqQC4oq0ZMdmZCUVcGHd/u4boaMCyrp2KoSIvN40eCOjnj3nbuY7HJnLsSJhTZdtL69QFF2cm0558r0RLqvAmvRuQwL9oIMXxwBfM2DdczvRVL2Zav5gnR5VvCd977P3Rvvcvfmu9yoK/7Dv/ln/JN/9w/593/2r7GuO43/GliR6BWIdGHS9Gz8XyREPrtN6Qxvlk7Qeg1cNKl8nfZ9mvXXd0W7PIPRa4Sva+L6qt//OsyBa8p46sHqZTLYyqx5EqFLSsQX1uP82Ynn26IuaMUzHfrZt+KE94STfy8CcfJSrH3+NJ90UYZry1hjLXj25GltX68m4WWwTlOQnti11wtWiUf39viDf/CvuP/pA3qDCt86Fo8m3PvFfYoyQ+YaLxI7N3cYX90lMzkPf/mAbjonCEsQkWpYEW1kvLlJ0oqtnQ3cxFMfNxx89oj5fM54YFj6iJOe/gea3Y+uYDKDWOTkXcXh/oTN7THdtGVxNOfxLx9Qz+pnAfMGVU7dtaSUMLmm6vexTVhFCs8MeV5Q1y31vAYhyHNDsJ7xzojp9zaZ96BuWypp6GUFB6FlLAxdkCip6UQij2BSZKYTVRBYr1baewmFECATMxkYCo0lUGSSVkR2lSaYxJEODKPCtRGCoJGJayojuMhD11KgiNFjBBzrxEgoyAXT2JEniVIKg8DqxG5StBKOoyN3iYCgQHKIZVvmOCGpVUILiUmBykcOTWDLK3yuaXVEWY9Okn6EPePZ0SVzHLNmiVErzzOZ0BzRspv1IFf4FEkSci0pK8NBWrIVS1obsY3DkyiVJs81R7Jj1/Tp+h0BS1SJ0q+09Xt+zlYs8F6ji5JZ19CPkp4PHIslQ2fowirScpNFBqpERMG+m7Nt+nSFILrAQlg2giTlLfN+xyiWdKGjQjHLOsZpgIjw/2fuP58sO7IDT/Dn8oonQ6aEKgBVQKEki82i6ianp9VMj+2ajdmYre2fsPt5/4L9f/bD7k53c4bdJLubTVGsYimIggYSqUI9ed8VrvbDi8iMiIyIzARAzh4g8t3r16/7ua6Ocj9nphsGssC7DNPlTEXDrihBeSazA0pTQllgdMnDxRHjlcSPBdOwxGLZzFdczxJTNWXkRnTJ0/VANYl2FjHFFnNdsZ3tMPeCo/0j0qJG9yRbL2+yL2dcE2OW9R6dbjFaIxpFIftMeiu2mj4VDY1viD5Q6ow8Gg6zGRvzEi8GdEtPNJLCD7FuzP1qzqiC2rcEAo5ET2ny0jDJPcNGEkbrSNK1a+gJjykqFhs1fVdirMf4QNXO2e2u8Ud7P+Ib3/9tertjpDneRHDaAMtpY+y5deMCOGgP+PP7/zv36rsUqmCicoIe8mC6R/HrO6SyJbzUoz8YkdDo1jDRFVvLDRYfvUBd56gQ8Xdr9L7jsINtlagqh5SG4D1lEtjWs2wko6EmGwxoqo6uqumcQ1jJqpb0pSMsGrSQBClQpkLnFY2PGLGObJ5SXEe3xyNJOAGZAL3tETagCsP1126SFYpZs6A0BWHhMFLTNg1Fr4fNLNPFjNFwRDfbRsYB9aqjGPToouajn9+hnkzIo2H39i6tUOzeKFBULBYrRlt9vMjQNueDn35MU1eE8YCF1MjgUCHQUxJtcgbJM7s/o+wPybTA9iPz6R5NF7BZwosFXq+tFsOs4P/x//y/M7q5eUWPPYanbqk99fhpOxfOuDj9WkjeiRlEPEl7v4wm/WuCr3w+4zlw//VvfsrPP/oZ+4t9tke7fPfVH/CD13/7q+NwDJc6l3kkUaxv0jFjdHa8nOV0OGWhemKHyHNanP4PdkX7FeEqRv4yieqyZxflex4cTso9JUw/czFfm0ByajV49PMMNqsLFpF05sGxh6TzFocnrEhXo/WknHKqla5qrCvkiCdrP9fyz9QJV7WJuDzPV4D1RL/iMNVFA+iC6OTHhQGC5aKirRuW8wrXeULTcXB3nxACQklcjLgY8CmxnFWk1ZTp4RwtAiaTeCLz+QKNJSToqpa5rHCTjgcfPKBdNohcMHMR5z2iiCxXK/JqgWoV2WpAswysqhqtJLEJrOoGFyMhJULTEVNi2bTEEFBWYvo504MZWV4yP1pAgv6wR7Vs1lHDM4NwgqbtcJMZ8yPJUhuiAKUNXnhamVikgNcSJyJJCmKCqvM0AtCaGKAmrs8TRwgpUAsQeIJOeAkdiWlyBGCRPK13xAgaxSoEYucQSbKUab216Hj7RS0SWgqUEDgjjgXoSEiSeejwft13C5swhUa0gZZErWCh5Tp2RvKI6CkEdDpRiYAiImJkESPCCAYxEoSgtZJp8HREliaSYktfW2QmSEHQiEAKgZUMxJDoSUXtHQvlkEiSS1QykERCKsmyq1goDz6QVEdrHCQYiR6VDyxlh/QR3yl8ckQiplkfQq+MI6aAEwFZGGImyZVA5xk0LbO6pQ4RrKQhoG1EZoFKtSAhiY5OKirZoaNBkFiqFq8SsUvolFjSYmJCLCqWoqFj7Q1IyQ431MxCh68aZnmLiA2GmiwFamqU0vgEDQ5ZSJTqE5KjDi1zUdNIy0x1JNVSSslBc8RCLVGxI8maWZghg6DPiFZEFs2K1LYkI5izJBBIqUcdI0u/dj8rnKApFClGkD1aE6jxICFITysjSQuUSDjlaW1iEQLBt0QT8VlCxpZGrVimGjQY0aGyRB0bRnVNnTWEeUXaHXNKm0K6YEFJaR15+qq1sHJL2thS+QVdaJmZAR2ChV8RrpWYoaXrO1yao0SBUo5Ft0TWOW3XMJkFpBDo2iNRrFJg6hMpCFy3duscu8BA5yQFk8lqHaE9KLA9lPFUq5Y6CEAxGg4hSkLrELphfPMas9mCUNdIPEkJtBSUZR9TGhrv6fcz5LbDmRaEIOhEHVqarj72mhOolyu6uqVdtYQQ6KKDCG5W0M7ccXBHw/xwwWxSk4LEdxH/yQEeRXXfkcKcLgRGmwN6N2+hssSq9iQ0s6pjLiKFUSi3diHdpYgVAmUyuiBYzlYMEKgswzUrovN0okVphTaKW996gXyjd3lnXUUTnpb9Ajr2SFF5/vl5jf6XEgROrP/nyvwatNvrYX+imT8jQT2+POVI54nn4oL7dErAuqptL7MOXZBex46Vq6nbFYt6zrJePInT1wTnBZbH4kF6hN7p/j5mQ06xro9xOrtd/Nnq+7rgH1+4OM/If9l3z8D5EXa67NPstDgvCH656p6jjKsKfbqHoVO4n6rv8UHqc5P+fEknjHV69OKVA+i8+ewiU+gziiKnkHjy8owcJC7J/DXAlzlffXrSPk3pc0ZuufD5k9LYk8LZ+p/9/UOqqmZzZ8xgNGA8HlGU2Vq4+PgBRZETXWC0PWTRNFy7tctw2OeTn39Klml6wpD1JbOuJi8HlDpn4+Y288mSzZ0RH7/3Lso7eqVhMMqZ+zXxLpUC1XFj+wZ5mZPHksWdFt96NjZGVAcL6PfIXjRs7o6ppgs+fe8zYuOwStIbD9f+4iVI7zFGkmcWJQRZrokxsbUxIi8zJkdT8jxjYHosFwHvPOPtjOQF+WRFZgW2Z+gaRxsCg37JikSKHUMhGEXJoUw4CUMvCVIywVMGwaayzJ1npaCfFFmp0dohXGAjKCoJNkGviVgl0YXESsHYCw5SR4yBkRMU2mKkoEiSzaCYiUBSll1lwHuU9xRRsZ1ylhq07NgNBusTSnqM1OxGzZIOYuSGKkl1hx0IRBvY9ZZaR7oU2IgS1UQkBiEF13RBqBOojLEq1ucRljUxJDZ2hkQE+WRJTxvyoDnSgahg02la4RG+ZjsZspliWho6nbhth3gi0bVsipzxcJdJqGhT4HolCakDkegHw/bmJvUQ6uS4lvp4t44TMd4cU8iMTx5+QlnCdhihpcd4w8BrtmPOgaywxrPdFWTKovyKstMM3IiKiGxhO5WkJhE0jIcb3MivMcGhO8nO5g7Le/eRWqCj5NZsQNFfoK1ko+tjegMmaokWmq3xbebzClG3XBts4NsCsyFoqkMGU0ksFbKv2GpySj3gThRkvYKduMFqUeGEY7PO6Q2G3EchleIaGzSigTBhR40ouy32m4ZoFdfKTapDSdNBr4oUFMwzR7KGG+WYVCoOM0cWHMWs5qhX4QvFTXOL1oGRmkHos1vnLPWMqhNs9Xd5pfcGdtRH6XUkeU5F3D3DEwpOHQq+nFO4VlxnbDcIyWOF5Ybd4F5aQqYY5duY1DGjpjQFO3GLqewInWBHG0R/g25/RllkjHqBWSvwnWRoApmIHLYtrvOY6GmWijYZcuEo/BJFhs41o82c+VJz994CLTo2+hlmY4SrW2LTEduGnZdvs7mVkxcwOewIMbFzq6TzgcO9FeOtnMH1wMFkhXOB3e0MHzpSXTLqlQx3LNPDCW3dYLxhVbU0B1O60NG3iZXvKDZH7GxkLD/ZQ9KyMc4pQmA2cTjXUXULBoUHD810xu0Xd1FbY/YtKNfRJMH2cBPhOnp4CmPQ1mBCgxSOfDyiji1bI0sQEGPECkOdajZeG7NxbZvvfectsiK7gnqcpgHpXMinSxRlpx+fuz/NaD4BlxL0S9Iue/8p7zw3k/pIYXmBsHSurCdynH/vnNwhLrKyXIrGY0vPYjXnaHbI5nCLQTl8lOf27ot8/vATjLb0bMmN3u6Z90/OZXxZONsGl8/x86mPd5xcpPl9hgIurP/rga9FuHhy7F6FaDqb5Xm+6QxHerqVnkVlfkWeR9LuSe5LzQDn8HhK2un3nuedR++dHjCnt0alizD8ynB2GqcrhvgFcFnGU99/pscumAtP7E88ZrzTE2bAfwC4YNvBxTWebvlzi9tzanFOhLl33/mAX/7923TOMez1CI0nuUgza9i/8wCVZ3TOkxuzPkw6HOHayIN37jC5f0SUksxqymGGKTR113Dz1g2iExAE0SWkFEQJKQUiawFKKwkBzD3BNbHNG997Cxsy/sP7f0YKEe8CchV5+PYXmDLj2rUNBls9br56ncm9A4wy9DbHPPz4Pr2iR9vWCBXJe4Zer8d0URGajrKnmc/nONciRSL/9RE6NMgUKewKR6TwHaWx3NiKPGgqypTYGLUcfHfASkli06EUJJnwIiGVJkqQRkAA5QNOxXWwIQ+kSBc8pZFct0M+qSuS8/R6OYhIpzpEFFhp8Aq0VkgvSUoQjMIHQR41hzlIEiYopAcIRLE+eD2TLQiJ8gGDRGhBTIlCaOaxA63ompaBgWTWVp5yIWgiJO8JaPqtQeDWh4qVos5AioCQcHNfcFh5EvBCpTlaznF1xVbZR79csG88MSYyZVnUHozGJ8NW6LM3OyBqgck03rQkaXBaY2cVKz0jWEmUGSIcC9RWcm13h0+6fQhgM4tQgVRH3GrFVn2AsfvEGCh6BtI2uA5JTpk2kEaR5TDubyNbUO0eohOMGDDpDokuEGqH7Q3Ro5xYFJSqz353CAhsljO8scn+/A46N9gDCZlEBEHeH6GMJYkFkcggGurFgr4RlKsGoTUz67E3S/ofeo4aQbIKO9jCLju6OEElQ7/YoSahdEBvbdFng7BcIowid33qGIlBEvKCfNYnCokwOWaRwfII2hVEwUaesRILdC9jPOqzCJ7QtvgmUnQNsT/DjgbI2QJTrKNTe79i5IbU0pFF1gKb2UBm9ljleAV5f2x8Pn9zJkumcv74+r/gzvIzMpVTq4aHs/8NI/ZQBy1mfAOxo9Zb6fJN7u8dEOmRxJBcamyR4VuHdZHU5cTGE3yEay2r2qFjot8kqj1BCAJHpKnnNL5ASkGeJCFaNJ5CJZKs8a5AlgpjLIcHjpZApiwbG9scMUeQyNQHabIsAAEAAElEQVQYV7fgKlKdo7sezdFDvI+kYhPqBRxNib5H8Q3JYToiKokWGW4mofE4b2iGGtfLsP0+B3tzZtUcW1r0RoFpHXEh0UJQ4FHZCg10zjHf22c4HJKiJ4SO3OY8nM3IheCFQYZKhhQkwyyjGUW8kUQlqFdzjqYzbK/ghbdeRN0YsKBC2AY7is9JDE6Y4pPePIFLBI3TPEt6Cjdw1ePL6NYzkduzBT83g/oEi3WKgxQXlHtW73p5sSfK+tPkWYhTr6SzVR9n3Js+4C9/+edUdUUv7/EH3/tjdjeuAYIbW7f4ox/8C/anewxMyW65da7Or358+WyvX9Sux50lIIWEOImJ8yzNfgUb/CzWjS8DX4tw8cxCxSNG8+yXnB+UT37jk/La80E6e3U8gZ90/XoyWc6P4gsClHwJi8XjxePpWvFH1RxnPGsqF2dDiFymWRBnpfILMzzB0qfnH2jPuDidndAXJFxY5z/AqL+wmtOqjxOVykWS4SW9dsbE9GyD42QafPTBJ3xx5x6rVc3I9onTyGx/Tj1bMVssyHJL5wNKaVKMFMZw5zdfUE8qlFEE5/EqMq0ctYVu1fBgb0YvjywmFSnA4WRJV3ukktSTOcpIUoKoBCkmXti4yasvfIP/+qd/S9c6VqsGM1vSLCtmhws4XDDbO8T0DTo3XHvxGs3Sce/j+6xmK1yhCXh8DLRdx2yxwju/Prj9MKKlxDuHloLFpKNrOxKJI92RZwaZItEkPprewcdIjInlm4mu06x6QKH4DS0SSUsCEkmutzc5BDPhMVrTEPB5RJKY0ZG04aftFCUEC50AhxeBhY5kQTAxDRpBJQMm06Ajk+TIhGCae7IkWAiPFhDyxFwLbIq8TYVKMFcBiSDhmAuPApbSYaVkrgIqF8zKyFR3aCFpCo/1ikYk5t5zoAOVcwgEX9gOpSRL51Ft4kHlcPtLhBDcWXpESsS2ZRkkBzFyFANJrOMFehWZuRatYKpqapXwwfNus0fuE3PdETvPQQ86sY5zIaQlS4qFaLH9gp9Vn5JSovEtsfMILZlngeBq7okPidoRisRR2aJSQxM0WmneiUfICFXXIJtDpLUsM0EoLL+OM5QzrKJnNlS01YzZsqFoVhwVFaXNmfoaqY7o8pqjaoUKDXLQcs1FVrbhIBwRSEzqCQpJO11S6ILaL5hmGbPlPlNVo8uS2a1AvXQsVh6jDK2pWIqOZd1Q+5a8LJhTo9yUh0yYiwXRJ1rh0Fqx0B7pKvbkPm3MSPWKxtXI2LCgQW8N+GDyKe1qjjTXSHlO8DBXHps6jjYPicWKGFp8aRCmY5rmgOc9+z6qdngTmLdH3FcPeK337atWlQvWlyduHsscQKl6fGv0bUjw/579v1jGI5pyiXxjyEx1zGjRQXF49D7SFcyFQ7lEaBYsALesWcxztFMs20g2LNhbLajNuoJumWOVokkKpQoWXgCSFBJ3jwIhVKycJEbwUZAWM6RWGC2Q+ZCH9ytmB0s+f/cAkxfo3NIsAkorphNHN3d8+tE+jQ94F5j+Zh/pGrzQ+NuSaXufqGc452kDVE2iXiWCicy0xG6O2NuvCAdHdEGRipzFrOZwpnBVQGBwIpJLsXYG4RN391vYrQlJsIwaoQsEAltmTDrYFILKOfAQncYLaLvEofcopVksW+4+vMt4R7AMM5pg+PzhHX7w5g/R+jGLdZWa8zH5EWe3vFxGTx5p/U9xMheRq2chR8/KyzxBih+/+FWUnV9ZgfmUrCeWBXEO3/MIf3z3Q/YmDzmY7bE92uXjex+yu3H90fPt8S7b490z73wpV7SXNtYFHXgu7yNLjjpWg5/o6p+Cwtpx5lqBemE7/gOwWF9ZuHhivD3xtU//knTmveeo/FxfXNZnF3f+86WJq7I8I3yFGIqnDRjHP1cP6sdi0kUD9ZLF6vSj8x17ujvTJXmeAmfj1j1NoHxsnxHi/IL7jwHpwrn+tHfS8e/TFpzTh/kzaynLAu88WZkTao9SiqaqKaxFSIlkfSj69lsvMT1a4GaJ/qBASMlq2WDLEoYCN52Sa0OWG4pezmpZ01UrhuMBR90UJSVSCXqlpWodIkVyLelvDBBCkOcZeZFjjKHsFdCL2NzgW4+UClxkPp+yMR4xezCjXTYYrTBakRlF3ULnPL08p7w9YH4wx7fdsaVEMdrZYH40xwLer4UdELjWkxuLFAKbWVznwEVC4/EqIWOilBaFJAVHT2iSkHR4iihIQmKQ6zMeAWRIZFrTV5ZF8GgPRkAWQFlFKwR5TOsgaUicgNyDT4lcK0ohgUQRoEoRoxQyBfRxBGKlFHmEOiV6UdBJSbne4ISIiVxKVkJia08XO4q+RAtJhqIQhkUKZGldRxAaYzQygg1i7WFHKvAtRipiiBDWAfqCC/h5w/xejb7dQxcWqxQFkkoqjNB0fr2VI1iD7DwyCcBhgiRF6OuMOnYYZbBRofCYLiL7GpUguBbVOWRmkT6gKr9mBJPGmUQpDURLYQV9UdAFiUqJNnXoNhHrliRadIIAZDpDI7Bo8o0xvptjqkRqO/KtHlYoSpEhVSBXGdbL9YFZv95PP+gNqU2HrSosGtUldJIorSlUSTuw5KuIbtdb5crhAOeP4LDDbmv6ssAlj3YCO4mIIlBKS2MipSwI3qOToG8LKtEwMn0W0iC9IqKQdYdtITOWodTMjmYUSiCkQbUOi2EhoG8Lll6iRYFLglwYbFEwqxYMyxF6tSJXlq6IGGXpl4P1+D+nePq6IBM5pSyp5JJBPqDqBLpuyKIk1oE8aGrjyZXCa432LSIElErkMmKUIFcSejnBeaSAzEiKTNFGMESMkEgjcC6AgsxqsJrNnqRuaoggZGL71jZHdx5gpCATgWa5pF2uz9OEicRowaKCVnRUODrvCUlQp5ZRLtbRu0PDuBco+gVStJS2h40a103Y3B5R531cCHSHc0K1oswtixRw0ZNigNCQZxmZtnR+iTEGFQVaC3r9jKKfU9VLmrbFaosVYS1I1TVtk9DhmCAoxaCf40JH6Bq0kbhlhzV9MpWR2Qyj9dqKyinadkL7nqCrJ7mOeY0nPA9yJQ26kjf5qmPqNMtyKa1/bkJ5Bk5UnM/KpJ/kPf/Oc3NX517IbEZuc4wy5DYnsxlPbPU6x/NcFlvkiaqO3eI/YSV4xLterqK/dLtZupi3fSJ/gie33v3Dw1e25ZzV9adzT8619HmjwJm8Zy/Pl3RpmacyXNVwKT12yXUhXIrbxc/TKUTTaTen51EUp//EmeQr4fR7F5R75UQUz0qonstR2pO4nb5+BuX+iWvYy9bAM+lnVAvp+Qhv4tKhsn58yVhIl7z2lPIew4kg+nRkH0VNTYlvvfk6fpWIjWTn+g67t7c5OpzgY2Br1MNLj+kpbn/rBi+/+RKdi2SDHm/9k2+ipUIhGI6GFDIjNpLc9vndf/4j8Imw8hx89ABZN2tCj+DWdp8utDR+RUgdm7sjtm/tAPDN77yKSOuYDbbI+Nb3XiE4hxKwMexjo0Q4mH5xyOaw92je94ucPM8IcR308JXXXkBLS6g9o8EAqzUpJjZvbfGt771OIiGVYGt7TFZmaAVKC164vYuMESkS1xvF+POW/l8f0H93ye+2A6JOSJ24KQw7Klv7yFeSH/s+nfOEELi+Uux0GiUUTef5YV3QKXAysS0ML5oegoTQkt9rRyQSRkrG0fACBd4HOh/48awkIFDGsBUU3+pyNOtx/Ht+RIoRGROjqHkz9kg+EGPgd6oeMiVkjPSzkh9WOal1BB/5LbdJjOtZYFH8oL4G+9ukBxu8+KDg6LN9lgczqqMlt2UfbRXGKm4Oxlit0ELQy3P+6IVvwwrcQcvrboMiz5EikVLkB8sRMSSiT7wpr9GXOUJphNL8/uIGSI1C83LcZJgsTiUWTcubX2QcHd2n6mbsdpZisaRLD2j1jD9cfRcpbyF5iZvhBW6rG8SFYHV3yY8+GbO8uyIcwc684Ma0R2oMrhb8eHqDduJhCuMHkp17guQ1utfj9+obLA8n+NTRi4ZX2yH5QGEy+PbyG4gOFJaRGvNm9m1KUZJFy++N/xk3l1u8Yl7hjcEb/Ivd/463rn2XN7fe5P9081+S9UfYfEjeWt54eB0SaCH4wep11qf+JWmV+MH964BD6si3Z7fRE4FsMkSr+L3sdVJM+JD4ptukzCV2GEndnN8JNwj9DWJvyDf9kJ7uEZuAKnN+a/8GIQrw8HJzmw2xjdUjXKv4Hfm7SGdQtWGctrjefxEh5dNpz7MsPcfLz0f1+/zJ4f+HP5v+b7ykX8ErQTSGkR3zRvZtki9IwfJH+g1k0YNoyBO8VWwTDxKsDD/Y0agQKbRAHi3Y3J+jDyzmwPJa6MjrSN9Lsgi3ttJa8YDg1oZHCY/VAqJje9ix6jwhwmuv9NgYFygVQAZ2zQFWV8Q0he4eq2qPkCYIVXGj19LkBe2gz60Xx4x3x2QbQ9ooMXcaqjsg6jHfePllrt+6Tb+/SX9ji3/2T1+jmVV0XcuW9hSpodfVFF3NDg8ptaXfK9jd7DHoCYSKJBl5/XYGsqa3CTd6kbyekxY1WeO5XtQskycMLMt2QZEHhEzITPK9795CZ0O0GdFXm2yJDdJhAbOC12++cXwA/QreXJwnpE8ZAOd5jKto0jPTrKfU+Ux09zKq/vQKHvPY4uz3XVzN47w8SWcvw+AJruN8xuNuePOl7/DS9W/w2u03eOn6N/jmC2+S4om68CxjGvw6mvuzCBZn4Cl9dnG8sWN5JF1wBvcCuJC/OnHL/zzj4StaM77GA90XcPjPI9A+IRFedH2uoHPvXD0Xjtmg59GAX4H/80SVfCRhX1beRVLsiRemM3Pigu9/Fjgu6pFp8JSq47TW4/EWKh7Vf2Z8xStwfwYUzoui58s5X9SZfn/Whe58IRe99ww4XzV0Twsm58fS8yyyJ6374a8/xQqLTo6jezPCyqGswuaGg2aJLTUq06hBxr07BwgkwTk++XiP1HRoozk4mtO6Fp004+0tfvVXH6CRzB9MyJJEtIFhWQCJh7MFXnYYI5AS3vznv8Xw2gYAn/zmM7RWaK1IPvD3f/5zlBBYa5gczelbg2F9/uD+3QMyoxFi7QmqzAsk6wBiDx9M0JnFN54qrRiOClYIDj/bW1sstCQkODg8wmpFEokYAvcf7oMEhaBrO65XOeG+57oyvNsckfUtTsI92ZCLjCxBDvxcL7EIklTMdSBlChXAtpF3hx09L/BSMtWRlBoyKSmF4u+KJUWStCnS2MSCFpMEhdL8rFyRIckC1Dox1YEsKYoo+JmYkaHIRKJV8LFusE6Sa82vNh3WrS0VIXa8tynIVA5J8AszIy3XnqNSkryzD7YZopXi/XAX0xNoJNvXNlktYWj6LPdnLGLDYHNEEwJ5UfBJO+eFmzd5+NlDPlwdkm1YisLSSxkfmIaSDBcdd+ySotDkMiOPll9kR+Rpvc//83yFcgEpJFpp/rq8u2aIVOSL3hE2NRjpybPEz+SCQfEKy9iyFyyyXiCmAdVI/jrukWHpnGMvdUQXkR6UT/xE7ZE5RasSs7iOhq2qiFSRn24couqAO6p4EDvuZSvUINAf9PnE32F3bum8p20a7nSf0EslRhlmZskf7f4rvBTs7LwAwPd630Yg+Kv5u+RuQCYdZhh4P9tDe4mSirf1xxSiwKgckxW8bT4liyCk5P3sC4pliWIdRf7v3R1yYyFGPskOyEKDVZ4sV/ziJUNhRngv+I1a0h9cw1Igg+TXN2ZkXtPpxOflhKyzaJ9jXMbPm7fp+QJixzKrmHRHbJe7T1ecnKFzl3AzAo66A34y+yvudV9QyIKftr9AmQwpLNO25kF1F9NlmKj4G7tPWmhMlhFlwbtfzNDLhHSK9+4JlG+JHahMsaiG9JXC1Q17oWAcwbeB3EDdDuiVjqpa8fBAIHWgqxc0NrJsLciI1Iq3f/mQ1DQoGQHPgZcIluR6HYTTGAmdQwTHb1YDfG7wSfAgaDazRMoVuTHcXyxhvmJ0PefuhyuMLugNR2Qm57/9xw9wkzn4QBslGZ4sBaRr0dktbl/fIsqM+cMZjQ+E5FAicX9R8eI3Iv2RJJXXmb4zY7XsyFLJ/UqTjAMLIbMsA4RmQSfgvY8CSuaEKOm6wNt/8TlOdWxeM3zy3gO++dprjwSMk+46o3c8RUfW2/4f07nHdPiEBziVeKm0wuX07svw/s/xzmkrwhnN+SV1X6jWvErO+qoq94sEinOQZwV//Fv/khgDUihCWAsQx6Elz4DU5wPnXgZXWz4e97e44htPdfgF52uedE97apvcuTIv7o5LuJ2v2OZf05mLryjinMBXnABXnUMQ4mSePuLgn8x3QdpT5+UzDNrnleofT9K18e9RuceS6+n9mU/geRXCT6Fix1UcX5+T9BJnt+udrkc8mXapQHhGGhRnvuv84yeQexo8q6Bz3rPG6Q8/Sb+kjU9X8sTWrqdG4T5dxeNyFrOKydGcumpQQtJMV7R1BykhtUDlGjvIaX3AL5fMpxXdsqbIDSZBs2pp2hadK0SmaXyg3Z/hFx3LyRJjJEsktW+RQhB0g8oFLgakMqjcPPqS+XTJfLpgtazXbll9oGk72m4dD8IBIQSquiEA4dgiGIWhPpqBFJTj9Xadg88P6FzAGkW9anDOsZxVVHVNPNb6lEWOKS04gcwMyXnqqsaHgM4y5l/s0bUde3cPOHhpk6DXkZGT86ykpFKJJBMuJSRifR5DCnzsWImEs2LNRChBq0GnRPSeuYy0x+49TRJURDSelBIrlfChRUlBJhRLGVHREYRgLhwVAiMUVimWBBJrq9BcBwSBHhpJoBIRXRqSCkzl2l1m2QQya6jxHLQdisR8FQBPtgG6MHjZcTifk1UKtz/Hdw4retQHE1arGnJNKwLT1ZLGQnQrlp1noRwxBmJKdASCSBA89SqwKuI6yKIFHxp8CojoSc6xsA4KRcodyiQ6GVmJjqVbsbIOYwO+CzQ01LFDRnBHSyZ1RY0mioSKrF21dhFSYhEDLZKYFObYrWkSCogslKMRiehbig1NUwcq4XDaUcuGVfAoGVmYQCta5n5GkrDwc6QQ7BTXKb61g1om/LJB93KEWBP7SVgyCRXLWEMBcSA5XM5QWpMrS1MqqtSw1x0gRE2lV4iYGJht/CCwCi1TmxO8YyEgiIjSjjbVVNFhdrZxmz0qJ+jqGjUsqGZTpquKtluShh0hawgEtLJ0NlK1FRFPko5kBV1X43VgFZcIsfvE2vB4TXq88JxfhS6CuZ/Rxoa5n1KLFbWEEDSz+ojUgYuBuXVoFNLXBCdpDNiuT4ieaZcgQi8kRCepu8jDtsXIxNJHJAoZEhKFR9IGUE0gZSWFKchKQYwOJ1qQgbbzNF7SVZ7QtSgZSMqQBEiTEYKn8okuebSPJKHJhyP6xTZHnaKrO2bTBbqniUGwCmntltjV7N07xOYl2SCxqlpSCBzut0zrQOsTPSkxQuFdoJ+XuFajRc7swZxm1SCsXDP0IiF7ObPJkqZuKQYb5NsCv5ywbCKqZ0gmZ7FoyaNAGgVG0TlPVXtiF0hCcNAtEXqFVx2t89x+9RYhxLPCxVOJwgUMzGWk5GLDO4gLthc9RZn5DwpPqeO5UThRlHJeUXoKvqK1Roq1MCGVJPnwuJ4zLNE5HuKSss704zMIeVd53DrZCpbOInI5XMiLXoLm01F7bvgahIun2WfOidnP9SWnevQZhYHLUTyZdOmMBuFCxv+8gv2r1H0aLhNaLpHUxemHFxiGzmS/QBq+uLyLYf3K6Rl0KibGuS44q355sr51t4tjZvv0ZEmc6dPjsp4qWPAUxj2lZ+vPSwu/vPp0Hv/0+PueBS4LjvPI3W1K3Hr5Onv3Dliaiq1rmzyc12SZoRgUjDd6kAGFZff6Jkd3lqQEZVmws91jevcApQTaaopcM7i9xejamMUXE8pxj9mopAgelME3HdZopBY0dMQU6fdLXv3eq4++5/YrN/j0N5/jmo7N65v0hOXwg3sgBYW1aCImGPqjPia31F1H23b0Mssqdoyujbj1+m26acfBp/sMBiXDfknVLCmKjP6wh9SKGAIhBLavbZGcY0lEacH2cIO5NcxXK3pFTjRQG4XRhpuyx8Jrgtb0g8R1ApFLhigyJ1jKQC1ho1PETDIDBsYw6CSL5FiGwI7I8EmhgmNgM0ZJUyWHComtqNFKInxLEQWbKqOWCRk7rnmNJxGFIneBEYrY08TWMe4khVmf8zDWsiUsXejwIrCZLD1dYL1EAwNpCW1EKBhajQbUTgBgK9tgKRbUAcTKo6aB2gjyzREDnaN3S3y7YLsYsHtzm3tyxUHt6dcgVQGxYhQNfWFYyI6GyIbIEKKDZsEWltIbJr1EFz3Xag0WfDuhX8HuYMxCNdQmcl33SSpjP+RsxSFDtcs8WuZRst1p6mnCoehJw2beY2kcC+nZzguki+yFBf2soAwZC9+ifceWN6S6QY4kfZtjG4PDkw02GC8k0QkOBJSNYceVDKxnkeZs6E10ZlGdwgjDhtogI0OO1JrUhoiQkhgT38iu84G6g9cdWyEnzueEpsTmlnEY4qNG6sRG26c0Yw7DHCngWrlLveeIfc3WymLDgL2upWsdm74gREfUGRtxQK+3w8P5Ejfq0Z9FmnlLW3jGMadcjZiFjk4mXty5CaJDmYqe6LPZGMpc0JqOcbbBbnH9eA04WROeXJNOYNIesfIVO/k1hBDsN/fJVclGts20m7D0C8Z6k74e0rcblKLglh6x1xyCb9mRGyQ2sEzJRUbR9pnWsAyKm9f7eGXpxBJTGrKmpSbSRhjahIgNCI0gMbQRFQ1KWjICihWESHQeEQP9zR5qu6SXJbq65YsHU2xmGGYCYqBqHFZEoMNrQW4tG+OSfGNAFSSb1wYMnYHfTJh1K0oTKFPAm5y+Vfh5Q2kti6ZDVRWbL91cr6yLFdsq0KgIzlFkmrGCpRT0jaKrjtBiSG4CQgmS8iQb0Erz2lsvIo2kWbWU/T5KeA7u7iNcxa5RHLaBgYgMCsWmaJkERehWCCMxJiO6hFYalSmCtgQSqXUYcwV79YgMiuP/L6Nh55iGC4nMqWzpGejSORL85OPTouwzcOqCtSvUC95/ljqeCc6h8UzM/fOUe4lSWJwcyP866rlCGftE+kVw6vkJP/JcnjQvKf+8xel02leBf4Q4F8/SK5etqunU1TGTdmpCXlbT+bY+Ye8eCxjPLhM8nSH/cnDmvcsG+EVNd6l08SUROVVNOtf2l65BFwgu58sT6fybJ3r/0wP4a7J4nUHk/HJ4zpPGSbbj3/OxPR7Buc5NnMt3QedfNMlPLGYXwrGg0i8LfONIIWKEoF4sMaVC9zR2o0BKxWKxQqLQG9t06ggvoHEJFHgCmVxHk/Y+UC8bRlsDukbQth0zKTAmEVMkxYjWGiUiIQVEpukNHwd7KvMMv1jByhGXLfhADAGJoigLpsuaKBS1i1AmagL5IEMbA4sWU1hijOx//nAd6U5phACTGaplxXK55IUXb3Pvs/s476mXLV0fzKhPVhQUtmSaarSyXH/jBrMvjljcX5JJRRkkM60IMWCSJKqIxxMzyQ6WQ9ERJOSZQSvJPKyITcOuGjITLZGECZFcWybRkWJiO1mmOJJWqKQxbUBqECKxEw0fUIMSxCjouUSSnmA0W85wPyZkSuRWkTURqRTCw1ZQ3M8VViZsgHIBstDreBUu4yCuAIghUL68YCLXo6tXlqzaHqqFvOiTvznmwXyPSecICQ6XD1kqx0HqeC32mbZzVqlhtzeiDsfjTCh60XAoWjrv0dHSWuiUpF01bE0D97cCqWcx3tCZDmU0PiYG04L9XqDrIiEVyNzQaFiENaN6r56ux0wlEQ2EXMCo5Pb1W3xY72Fdw2ZvA0uiXgVyaXi1f4t36yl2sUAdRQwClUmi8tzoSj7vJshk6JU9QrVCCI9PkZHepU0HxBgQUpDZnBgiXgSsE7iDOfbaxnovsVLrLZ9KMFBrYUoLh80Lwv0Ob2pUYRh7y35cEdsVroOxfoED0eCDJ1ta5qXC60gjBX1X0LQB58C0GZ0RtE1L40puqDGf+zmu9WzXAj9YIvSSaFrGLjBVE/KBZqQbQrWg0jW2c7yVfkxJjzQ2vHb9LXJdPl61rli/P5i9xy8O/g6XHEMzQsjI3M3QUjPOdzh0h3Sxo6+HVLmjDp4oOjZnim4xBetRbUtmEwfak2LkhniFqiuQq47oBujDBjqQmWEgPcuY1pp3odge9tnrDARPESoWTrNwEI3kRqqZHK2DZea2YVE3uKBZCEffOgqpEd7j2hmYBEGATBQq0NqC3s6IF77/MstOU+0tqVYJ+ck9xGGgdIGdsUQNclyQrILDeEBkKCHpph2hqkkxEJxna6Pgo70FEkEvM+jg6LqWoBW58UweHCKykrwUqK2WuW9QZc53f/8FetmYumrZub7Jf/73v+b+Zs7ycIqbtAx726yAIgVskaj2pkgtMDGQoiZ0HqU6Ri/0uH+4TwLqxfJJa/9punABD/MoLtVV8IhBfJIAPaHLfYoQcRnEGPFhHVBRafX0cp6hjqcf2H66tvbMF3/d6vbTCuWnfc/ThIBnqeuSci478H3m+aObp4gA5wWadNnDs3h8XY5zvkbh4hQXdRlulw6IZ5OOScf+ls5LgCe3l9S7nuDn6kjnfk8G1mV1X5B21UB/tFXygvdP2Oznkg6/an9f0vaP1qBLmufKss6VcfrmIl5+fX3aZ9azrYDpaSuJOOea9xLszltiLp1EV7b1FVLthdlOvvgi9eQaPnz7E6p5RTVf4ZuW6WxO3Tka52g7z87NbbrW8WBvzmSpmLWJzCru7k0YE/Ah0DhHFJDXLRFYBYXoEr7z6MzgG4/3Aec8y5TIS02XEuW4zycf3GFzZwMSfPiLj6imFfPDGUd39lg+nJFCJCR4sDdBGkNMkFygXlRrjV8I1E2LNZKmaXn46QP27q3PhrhVyzQ4lBWEENBasb93wHK5QgBLV5NnA1oRMSIwnx3SJY/oGT7/5C5x5Wma9Taq/TCjafskowgmIaxiHjzKwc+NI6ZIreCh6FApMRWeTgn+milWKhYy8EB0SOGZm4QLHT8RDi0lMxHQoUMoz0xFWiQ/YYFFMMcjZSRliZWALnrezRtkSCxUQCRHMIGKgImBt7O1K9ylSsjQcpApFngE8L5corRgIQJJSiaiolIBqRQfiQ5dKnxpqEi8mw5px4KYzHqCbvSpfY3ykr/Z+4RGBkQmuatrFJoKjwgNB2mJExEXPehA2c+omg4L/P12RAhom446VZgAU92ykRf8zB4hPdQy4OMhmVFM6fCu4i/TJ0inqWUgdYrUj1QqEedz/kv7Dr2NHsvY8sViDyMSM7/E6Yy/XX6O1iWrAuh1hOBYZpEg4L3tOWoVWDQNdgBtr2VJh+7gw/ZDtkTG0i85aPdBHLIIM5RQ3C/3aaXHxghScjrC73v1p6ziimVcohUcDg9YKM9SLPBli4qSpVpie4p3ynssuxXIyDvuDkL3OWwqEgPu+gO8ztfbE5VDi8RcJPTRnIddTTCC1ne4sgExZ25XCO/4YOsIVENXSj5fvk8hFHWak5zmrvqUf7v5v9B7cefsOnC8BF7mzeXD2XvcW92hcktG2RhkZOqOKFTJJ80nKGlZ+Dn9fMxKeA7ThCxmHISHGC1ZsuTAWKKBOTWZtvx0eoisbnI0cyi9oj5smK2AesVeG9Fe0GI4WrXMW+hiwmoF5Q6m0KAiWZHwdGSpIfiATzneB4JQaCVYRQ1Ksmo7dJRsDjOkkAwGGUFAphSdFHx+Z46wJcs60XYtR9N1AD+VFLPOUyTFMib8smZATuESPigeLBq6X3+O2h5jgfe+WNJ4iEJztHTkocNHSVCKeRrTLj2x60jZiiwFWuvYvL7F5/fv8T/+y28jgE/ef0hdtdgyp2xL9uaegg5pMpoUmS49xiiihFWl0AQQht5WH6dWeLm2pC2aFd77M9aLE+Y/cdoSfwVduTT5gjhX50nkZWT1JP0KGnfioCay9tIn5KmB+RX0gRcJGI/QPsPYXb5T4ZHXpX9Iz5FXsSTiguur8p7XlYtz91xwf55HO+1p6oLnXw4uUoR+vW369R/ofoYnVwhml8JaovvytoInGfnTjO3TJOpnxPgZ0RPny7kItfPFntJUnCamzwOn0btoLVqnP6O641RBT1sf1/U+fvhYm/+EWH5x1Rfx5YknMl89Ai8WCk6qfPoXn1r4nkg5ST+xboinIXTmmbGGLM9o65au6ciLnC4EBNAf9zB27dawma/QeoSWIMPaPapKAaUU1lqEkeRlTtHLSXVkuTddm+u1Ivi4lp+VRCmBMQqcoK2adTC94w8ymSEvcwSCZrpCS0XQ6yB8WZkTPdStY9gvcDrgRcKFACmyubuDF5F6ukIrBUiICSklSgqkEGipWM1rlFY451EJfOuoG8eo11tv20qQtIRVoGtabGHZ3NlgqQ1dG8AoVBIoJEpIMqmQSqK8IMSAZb1QKsAmSZICG6GRcn243RhMShRCEkioJLAJ8ggojU4dNgqSluRKswyBnjQEEWlSRMWIJFIKTSUChVCsiCghMQlSSPgYCFqQCY33EWsVirVXKuNBSIEVEh/XblBlTNhMkSXFSmsKYVm5FcJ7rDFoJLnRVNKz2evTCIeTEZ8iJmqsNCjXkqGBQHSJiEAEgU0Ki6K/OaQoLTEkJodHFEpjc02VPHkHTitESHgJIgh0kMgEudCEkMiVBeEwSUCUWCXJo8TXDlKNHmuKLMfdvUsKFUIYEhZz/RZaCkwUKKnQMWGSwOQamQIqONTCk28ZcmExucUET+4tqySwSZOkxCSLEQYqh90ozthATxg3qzSZtCihKFROPhygF83aYUJU2Cqi+pC14HKF9RJCQimD8RJlJLmDiKTp1h63REpoF1AioWOgDQFhBFokDGDLnFo5+tkQVIW00NKR5z30vEPlktL2GAxG2HEJ8vFqeKLUSd3acqnKJ6M6G2mwMqORDToqkBItDJnKkTKipaUWmkxkeAQ6aoyTgCGTlpVsyUVJ5yXSJ4xaa6SNUmRlhvXQVi0qpXUsGqHRMUBQFDmgJK4NJOdplxGdrw+J98YFpTDYTJNCRBLwwTNdRqxoqeuGhEAJ6JU5mZHIMmd8c0znPF27VnhoLTC5YTZtcfMlwTuUEGhtAMgzTeUdIq5ddCsiIq6F9VC3yKbDlAatBQQHSpBiJEaP0Ya8zICMcqg5uL9ApPWIEQmKXokx5tGSrK1CGUVWGDa2b6K+mDM7WqFQ9PV6jEkpsbkm1o4yt+TDEaNdzYODhxAio/GA26/dXu/ZP92Rl+il1sq9i5npSzXYpwn56euraM6TxP6JskUSCCnW7qvFep06ozh+XjjG76m8ihAncWyfwOkM+k+L/3Fh2ZfgxekKT6df8P4VfMlzwXne7ly/J9JjQeuE75Hiy9V1lSBzEUv7FQTHi+CrhxU8Dcfj8KJkWLfXSV8KjmWFi5jMKyt4fnjiEMwjBE6Q4vHEPP13nHF9e8nHnSnrWTBNJ6qL86lPXCdOGNbT/56q8Nm44kevnFeWnVmTRHp0wO1KuGiQXtE0j1879V+6oKEv+5YTQnA82Xzn+dlPfsmf/vu/4Bc/e4f7XzzkP/3JX/Jnf/KXPLi3x8//9tf86f/3L/j7v/kVwYdHzR1i4Jcf/IL/9JM/5e9/8zP2Dvf4Lz/7C/787/6cBwf3z+JwGpdH11e0y0VEI13QX6cyfvT+J/zHP/kL/uq//ISXv/0CMgM7MBi9dlFqpeXmK7f55//2D2nnHe2kIR3NcJM5Wa9EkHhho0+d9VmVY1Q54LU3X8Iog4iSG9tDqtkSIQWlVmwMLcpKlIJv3b6G8IIsKqoHC3xw/Oe/+W/815/8Fbuvr/d028wgjWZrY4yNGukk24MBec+QRKB1LRuDHs4FtFJc295iY3cDmSR+5Xjzt76Jc45AYndzzLAsIUqaVcfWzhb9QYk1hq1iQImBow6qwMvXb6ELjc4UO7ub3PzmbfLtPkkn/vD6S4gAKsCNVjPqFBmKJCQ/rkdEazBJ8qLPuN4oMiQqRP7AjZFSkUnNTVlw21t0TAQSP+6GqAgZkpum5OVUopIiJPjR3EITyL1g5BXfcPnxbgTJj5a99TY2KRkEybddjhKJoOC3wphSFthWY73mm67EhEj0nu/OC0wI5FoykJrvpDHGCIRIvOmGyMoh5g6xcLzVbSCqiFwGvln3kV3CRAE+8UN1jeQjIgq+xQY2CmRKqJT4UbeJSpBpxathzM6dFbceOrbmgX997S1MP6O3MeCNZsgLWzcxFCQn+cPuJtJGtPC8zpBsJhDR4lzih5MRXnRE13A9ZtyQY0w2Rg03+b10E19Hwsyz0fZ4YeNloijwusfv5S/hpnNUTGysNC+uesjWIILhx4ubCLOOSN6vDa/HHXITyWzgh923ud7u8HJ7i9d7b/Ba+QYmSlQS3Fhs8svq7/lP+/8rv5797JFzgJTgrfJVkm2RuSPLJL/dvkJmc2giP/ZvkQWLDjnW9vlR+000BdJnvHG0gw0CK0HLxI+nJZqWrIA3Q5+yyNFGoiX8uOmj9D7a7POGHLHZk5RljQxTfn/5BjJErDS8IF9mS10j8wVSWt7a+DGql6/XpPPkSCvkJXv0v7/127w4eIXXR2/w3c0fsTO4hcsltY78aPP3qXWkNYKx3uJF8zpxYQmN5Z/m/wydFeiYM459XtXfRuubRL/JH/SuI2uLnRvsfs2bhUYEgYyC728F+iJxTSeuF4qXBi15Lkg6cNsekFYzZD2jPdhnJ1/Rdp6A4KVbFjvIUYUh7+e8tL2OQ2NKTaE6ukYS2hJfG9749osgxki1ybfeuIkxmmZSsVysyNJDZC/he5GdwpPLRLuq0Urz6k6GlpJMa1Ro8V1DqFqyjSE/fGMTmxuEiBQ6YpUmihJHzpvf6pFvg8rmFD6QVY6xLHnllZf5wXfeetTWt17c4vVv3+D179zilTdu8H/5v/0Rb/3wBQrT4ts53lUEHLbU/JN/+iI3vj9GbVbM9u8xkIqb402+/9tv8Tu//8NHh7nPuj0/dox6hqFb07eLNcfnCOOaWB//nS7jAjJzni5fyN+cTUuktfc4rY4VRHAl7fuScMILnEH3DH9ytXvb58Lowszn+I5nVAQ+U36eMQ+cYuXSo9tnEni+ChwX37qGn7z3V/ynn/4Jv/nsbe48/Iw/++mf8pe/+Atmy+lXryZdGfzh6bCsls/3wumJ8Oj6atEpnct+wup/WWHjSrxOJ13keeE5yjtxe/tEOZepvi98fk4seqQJgEcbdZ8bxbNS/+Pqzi5iV83JZ4anfeOphDVWxxL8JQehf/Gzt/nFz97m8OCIzc0xzWp96FIg0EaT55ajwynbO5v81o+/y7e//y2EkPzm8/f42bs/ZX+6x3iwQdd2xBgJIXBj+wb/+g/+DUVWPhvuTzx+cvyeWIDEuZELgof39/jz//iXPLj3kP6gR+giSkrm0wWTzw6Z3p3T2xry0hsvkgJUk4q9zx/SdYGVHaE2N4izCiGhiR60ZbtQvHRrgK8bSIm7v/wMlWBZtfRLS0iRLgSMkhSZYVWvCAm0lRRvldz43q11NNnDhJpKDu8d0s1XTD88RPh1z8RcIHqSqm7IrYEsQ1lN13WMxn1e/OYtPv3Vx7hly/j6Nvc+uo9EYLSkl2cczRYMhz2atkPIdWTwwWYfYSR79/YpejmMLRu3N6ibFtFGdl7YZXI0QwdYfu8a9xYzYmnIvETnGTM6xl4irYTcsuwaNjCIEDnSgXHSdEJgtWIaO7bISCIyTY4e63MQ1mgmoWXXllTeM+0ajAcF5EKxFIGdZGmlZ648KgiUj/SM4Uh7doKhwTPxNSIJsmDpJcNCJbaloRI1jU24xlEaSx4jRzaymQwrPE5FUkpknSSvJVMd2FYFjfB4IiFFdISszJiKlm1ZsMIR5drKkKGxQnAoGrZSTlAR17Q4DTu1ZPfhik60bAw3ePCNIW6nZL5akU1ahBTcdwtuxpyq9BQDy7JZ0hc9Ug0T6xkGS9M6rDY0uWDXbqDbgrlM9L3A+xWprlhKz5h14KmlDvRtTkge5kvCrU3Khw1Bw9x4Sp2hiw5tPUdhwUawiM0lbb8hlwU3Hg75n47+AK0T5W+/zH+a/gfu1ncw0pI6T54VHFYPuT58kR+Vv8Mb135ASom/qX/GX9c/40HY45rcYVHVzGYzUkgUJseQccCU7TiiQ+FToOs6pJcUEQ4HLVurkm6a03lNUIIChaoDR7lnq1G4/D7YltjX9KSmpyOTbMqm3IQ8AIlVNWUURgxij7lcMAh9vjX4Lv/01X/7iIl8nl0IMa3HwcQf8e8n/4477R36sk/jHTSJhVqyXVzHRc3+9ICBKlAyUmrDUZgwilus4jUWUpIFSXi3IHuwwRd3p2zUDVKWHOxXCBL9GNk0gkDGoC+ZisCDyQLXdWQRxgkqryhNBKGJUUJKxOiQRlAFRZY6PC2RSFmWqCSJS0fjFP1ckIxFKA1IbJ5IdBxMGjQdqpcTjaJxEZMcyMiig53SkuPJnMP7hE8dhEDRH3DrrRf49KMD7s9XtD7Rl4LcKWonuXZtiGGJ0o57nz/EisiNIvLH/9d/znf/p99dnys4XsZP+ArvAlJJpBTEEJk+nHLngy/42U8/ZTqvGYx6OFbMJ4cs64buYMG3X3mZP/o//yEvfu/l4zLFozKfPHibTh3kv2ogPI1ZuPidx29doPG8jIZfJtt8jWzW2aK/An/1ZeGqNhDHPNuZjF8BnpFXuspD1NmkszzSlfVdlOVc2t++85e899nbzKsZo94G3gVWzYrMZLxw/SX+9e/+Wwb9wbN9xAXwNUToPu3n4MvCZTan0918eiD+AwzI80WmtYkwcUFcjAvm+0X9Ki6z8YnzNxdYVU4k34sO7Zw0zWVC2UXr0Zm0syWeLuVkIbwQEudyPgM8z9C4tNj1g0RiNl0wm85ZzKs1QXOJ5bwihog1mqzIqKoVEsH+g0PE99cFzhYz5tWMRbUgRUgxUdc1icTmaIvlavmkcPEU/B43R3pMRI6THo/csw2QSExnc1bVivlssRZy3PrgZFM39LaGxCDRNmOyN6VeNFT7c1ardu0SMToyF0EoIok2KWRM1J1nPqtwyxXV4Zzlcm3KDyFS1Q1IQYiRECTeO1KMNJ2jsJbZdI7ez7BFhj1SpININa/wy4561SI9SCHWZx06AVJQt249voPDh8Bmpnn46UP2v9gns5b64/u0TUdIicJonPM455jNl6y9eyWUUtRNS324ouu6NUF2MF0sSAJyYzk4mLCqa6wy7M1nLEuBk4GeEURfs9IgNAQZSSHSqUDqIjo3zEPAC3ACNIEGj4hrRm2uIzWRKBMmOCqVcM0SKSSVikhAxsQyBFYiEFJAZpqj5NFakBlJGxyLFEAkhIJ5iiAEfdbvOyNpjCRKzdRXiFKCTDDo0bUrFjHRuEClHIREL2kaJalTYK48gUAVOoSSlJmhk45KBFJqiCrRCA8IhgpWMbJMHUpKQgy0xhFFYtAE5qsF0sK8WXDUwHzZ4lNk0FOsZgtqEzhIHa3qmHUrYiFI3oGBig4hI5UOKAJd41HektuMlZW4FHFthZAdjQFci5SShfC0LhJFIoUGuhVtBsjEXDlWIqHECpMclWqQokFTU6UFRqzYHQ3RomTj2g4TXdPGlrmbIhBYnbHqKiq5YhFmzPzkkTJiEmdM4pRFXIKHtnXMzQpEJPYsya9YdDUIBTKjMYE2tWTSUKXIggahJKmw1EIQuvXBf3qwkhERHBSeNquQmQEUnepYZS1aVcTUEpTH5S3G58TaUfkKVGRpVzSLFcWot54D6dmFDCkkQkgmYUIVVszCnCY2NG2LQNOEhrRUJDKWuqZNHVZBjWRJRUw9GlcxUwq6iFoZOKyYV57YRGRoqaMlBI90HlkFlFXojQEOT5M0nQAVPDMPURi080hg5dbOIoRMxJDwSSKtweaaIMT6vEYQJJERkcxXLTE1eGEQCLI8IFREKIs2lgaou0RIAmGz9ZZMEVnERHSB6NPaBTYCkNB6JgcLFg5aDB0RH6AKEh8Vi1VChZYUVzQhoY3k9puv8J1/8ztIdSqGQXrcGdqo4xV8vYVs6/YWi7rDvr9Hs7+g258znz5k1c4RmWZje8Trf/htXvnhq0906KliT4F4RuHya+J1xAXX52nzRYrf54DnFRa+7Jc9hcV++vvp8fuPY3utLUFfq7DzJdvxInhs13i2HRRnvusSmC2nTBdHVM3a+UAMsFgtUVKxOdr+yrj/I3iLuhiefm7gfPpzdPpTmeuLyr24Ja8Mfneq7AuLTY8vL0LxRGh6wjJxurorGf10EUfL1dP8STk5PfHv0+A5J+DTNCYn+Jx8izglmKXTmAlu3rrGZx9/ju882zubkAQqSQ7uHXL9zVtIJakPl/hQ4feX3Pv0IbawXN+8wbAY08w9W/0NtFHMp0vapmVQDihsj/t3HzIc9in7JZPDOd4HtnfGeO853Jsw3BhQ9gsmRzNc59jZ3UKqi3cWnglIeIz9bDKnrhu2tzfp9/sMe0P6ox4ZgsX+nOXC0d8uePWtV5geLjBaMftsn9B2+LbjxtYGSuTEsUSkSA9F7TxBREa9gkGu8aZPN68YDgu62qOPz1cYKwkSutZhlcB1jrLI6ZmMZAW61mxubdB/qaRTDQRo4pKmzIguYpVEDnKcjpTbA0SIzKdLooHt7U1eeuNl7v3qU4SUGK2xen1404dEmRsg4bwnzzNsYUldoG47UhcZDvoAbGyOaHVAOUU2yOjnxTqCcYTSWIS3FHnOpF6xkRRCCCYpsKkyyqSYx8hKBq5pjVCGJAR9J+l3icoI5iSuk5NkwtDRFwbdBTojsCmyJQ0yJg6FJDOKQSeo6JgIwaiVqBhJSlBKzUhnBAICx3YwWKNRMqF9YlOWSG3YSw0bbn02weR9msYxwDIsBkBiWAtcUiz9mpHZLApUhMnhlPFAovs5rTcIoRld28R1HQ/u7TMscgJQSYcjsZUyooQYE5vJIKNhJRReRAaZZmQTqzGMh1vIos+kZ2jxjCrJ0nsOZMu2KinbnInqaJqO6xTQRmRPMm4U2hsWBmahpVg4NgvIgqdMCt0UVCGwlJIdVUCKSBx9L+kFSaUUy1qw4QxSJmSEMml6GLq8XruC9SW2XXIYPEVvwI4boyYNYdyxle3Q1302zCZaWnqmj4sdaRroq5Jr2c4jDu5Fc4v320/oQmRzmZGcJE+GECLjQ0sqLCk6dtIA3WRMVzUNlqHP8KFFdB3XZE7oSrqhwWWG8aGik5EkGjZkgQ2b1FEQXGI7DjCDwJGcsRlG2ChYhAovHVvNgLIYIOuHDH2PW/2XKIblesk+3uaZQoTjA7NXabDn3Yw6rNhWOwzVkJHeYCB7iGrtfvWwOWRL9lH5CKVzSlkwFpamqUjBsCN6OL2JmCVyAeU4Yx7WI3ijJ0l1IFYN0TlUbOnlhqN6xuCgZbiVsyoSTRsYEKmbllV0ZDowyC0igCfRyyUiMyw6gXArlPfYLEdJWDUVbR1osfRVpNAat9aQkStPlIEmBETnsToSY0IbSyEUXiS0lGgiJZ5Sw1HVkGWCIjcIpdjYHhC6iPcdR64ll4Ban9/CVcRuQRArdOHQ5Lz+u99EZeYsJRPn9EfnLnZvbTIcl1y/tYWWgvFIUq1KVD/jxkvX+eb3HwsWj0jeCW/wVQ/LPsvrj+ireOK7nrvMZ33nDL9yRYEX8WJfkpE/2SJ9pojL7p9SzdcpTDzXmcuL8j8lN5z+9ks0senx78k298fC01np8cbWTQ5nB1TNkkExJEVBv6gwxrAz3vnKcu0/vnAhTn6uwPzLWAKfWulVXPoFFZ2Mj+OOPOvl6Mm3nhzbF9vdTtt5ztti0qN6LlPhnxVJTgs+CU4dlzjrfvWMqJHO7/d8PgH7WSTiC9F+1oxXLMKCxGDYx60csYuENlDIjHvv3qU36rM12uAn//tPWB4ucM5TDkYc1g6EYHN3THeQEQ5z2jZj56VdjuafIKIizCz/8d/9V5aLFXmeMd7YZP/BhBgjG5tD/KphMVuS5ZbNmxvs7e0TQ2T3xg5//K9+D3Ws/bpMPIXEb975iF/83Tt4HxiN+sSFJC4krQ/ceu02n/z8PtN7MwZ2gN02xBhxXSITgqVLKGkIdUvziqbdckTr2ZrWxNmKIARlEbn24mvc+fQhPkQyo0kdtL5bB4MbWqZtgywM3/v97/HzP/kZbd2tDxtPMhbVgn4a8sJrN7nbfEFoA9WkwvYsrmpwRAojsYWhi4FXf/ga2UDxwfsfU2722f7mNnff/gxlDMWwh/ASV7Xrg9XGElxHEgqhNGWec1RNiTHQ74/w3pNCYjVdUQxL6rbGoMi0plEeEqjccGt7m/tpShKCMigauabcXiWuRctemBOUXAfaqhydDTgJ2yFjohuSEqgQ0UiiSPjoeVWWvCNqIolcazIk+8GRNGw7wyIPaMAiKaRmIlZ4IdgJms9NJLE+PNrrJCDwSrATFPflem92UJD7REOgFZ7rjWX/wQGtifR2dsnu1yyaBiEluyuJe+cA6VrGfUXmGz6bHKCtpj9aITYsYtlSpEB6acBHu5LkPEOZs6RFAF2I3KTH3DhCBJ1ZDr8xZFY4wk7Jt269zP7iDiEmhsrgUyLhqZLjdfrsxSPIYBAibpwhUk2VJ94y1/koLSiMYicfYuqWWV3TBrixEBz1AZEolEZ0kSPR0cXAC0vNgXX4GpSX5NYijMeFxE5T8n6+wMeEl4ZROSLFQ7pmRb8tUJlFaIUSioycGBIhOLbFFnfrz9FYkhOMN66vLbwCxmxSdwrvLVH22HKGB/EI5zzf6r3E5+1DRCnws5qdbsB+vsCFxMiNObQtEAkDTW9RM+EBKdeMRmOO/AzUnGQKbrmSj/IaYWFUjWgISAWuq3mx9wbT+ldELSh0D9l4UvCEAoYMn2A+kWIdqMs8GQX4BD5efMDPD/8OHz19MyTkAq+gFo5Xi1d4p/0UyiFGbiLbjDrMiKrjJfUS95Z3mbeOoRgw2HuR9u6EdtWx1cLewwjBkExioBwzHxE+sN3zzHqSiXIk7bguHN4KfPIUKjCrM7Qu6GJN45a41EMLgQ411QqEyCnzHj4dcn+xZJxZNvLEnRBpYiDPFTfGOQcLRQLGA0UMiapO5MawXQQe1pG2c/SbFa2HVlh6Cnas4MHKE0moFLEmJypNkoJxT3FnIklpbamMTUQJjas7tjZXzLIZ/V5OQcfWK+cio5/vl9M7BtYyEGUv54/+9Q/47KOHZJnh5devc+fOfeaLitu3dtnZ3TpbxmOq9tVZmQt5onMlX8YyfF3wTErCS+BCDeqXbJWr6r9sE8wJnAjxX2e7PCr6axIgz+N2Wgn/NMHsFEMp0jrWWBKnudfHhX/75e9R2B7Les7N7RfITM6H7/4KEwXf+s5v//+L5eL57T/PNLyeUfq8EJ3zL4mLcHxaocfMbnpsikunOumRblo8Uq+f1VefqfNxr59S0F/w5PFvOtcA4kzaYzHl4gB1Z8s4nfdkX+Ez9dhlk/VrEvzOBJB6ZI05O/lPn1v44J2PWVUNi+kSJRTvvnuX5bSiHPb41X/7NdP9GW3V0huWLKqW6W/ukFLi/v19pJUsDlt0rHln8RGtb4kx8kl9BxkERwczxhtDPvngAW3j8T4yHhaoFJnszxhu9Pnks8/xydO1a9enD+/vc/P29VO4nm62x430m19/xOef3qVe1Yz7Y0QjWBxUNKbhP/ztn+Gajq5zHNw9omk7XAzkuWVvtiI56ELgXmyZq5yVarADwf2DjlFYR5VuVjXv//JjOheplg1dG5A+4kJCxkjbtlShY3N3k7t397HDgqPDOUjBKjq66BBo2v0aEyXVbB2xtl00yOMFytU1Qlna2jGdzNDWUt4ekhJ88PbH2FEBApaLCt+tY25IKZkvKvRxUMXOeR48ODj25hKZTmYgBMEHOuGoj6YkBfViRVu3BAXLtsF3ng+uS1YDTaMCD7UnScFUeLTQ/K2akaSgjR0P/fpZRUQKwU+zOUYq5iJyT0S0VMx8i0fxt1lAJckCzx4tKSbmMtClxC9Mh5WKuQhoBFPRsVICHxM/DQsyoZjjMZllJhpmIiID/FLOyFJiIlu0UtyXkbnrEFrwYVpgkmLmOvKjI5pVRe3XW8Lu3V+xkwRp0nBwb0HbrsdECJ7KHpLlFhc849tbfL5T06U+HY4PwwSjNLVJmJh4lwmOQJCRBz0J0TGxDmLDw8P38TJRty2unRNNQ2UDhI7/1vsCYRx1Dp/VM0TUTHVLmSw/YY+MApdrZkqQXMNUOnrG8POdDhlgkRx36ikSwcxEcuAXww4dYZUlFhuGqUzMfCCTkr8zD7AmMo8dVhzR9CKz2JJj+UTd50f1m/SM4rDZZ9IesehmKKF5p/0VqoVKrxjkgQ8nv+EHZoSyml82H1LFjmloUAge2oppVxF05NfZHZSRzOISqUum+iFLm+g6z/vyHkrCXLYYP+fuaIUzgSDgAzPH5pJKLrCt593xPp1qcDJwZ5jIrGYZZ0jV5+fp73GyoQsO7TuyJVRZjSbnw+Y9XklvnmUAhIATweKSdfX92bvcPXZFW/ZGLKVnmmb0RMlf+1+jRMY81RixwKUZc9mQO8/fhI+JNSwzxVGXc//OEZP7EhU1vzzwmFYw7UBmimXb4Z3EOclHXqNCoMk0s+Q5nNa0SIyS3AklKlMsWsmN0RgjRog20bUtE6cgJdqUCK6jNusgmMskUSajN4oEB41r+PjAobVCSsW8k+Rp7VJb9zKm0aNtILhIUiW+rWm6DqkFd7pE6x1BSJI2hCjxRtI0js+nESc0UVpWXSR1Hu89PSuYKgelR2/Cy9/8Br7/JGETF12Lsw9GG32+99v9R/evvfbSky+fuv9SDOcpWniaql9k2TpzNvEyov5l6PVF7/wDMORPqxIuSbyIlXt2Dek/DpzXPp/D8Ymx8TXidTIeHruvfaxcPskhheTVW6+fQfSHP/oDCBGhL1d2PCt8ZW9RX7Y9zs3ZK8r/6ic6Tkq6PO2yGs7FykzrFHFMFE6+4cSbkRAnz47TTp6dXKfjqtLZ6zN/cKFw9Fh8OPnv7Man0xaP819z0RmK527T04vllzXxnv7GR2np+O9cRZe8oLTCWI0QgtV0yXJRMd4ZoaTEdx4pBNZoREw8/OQ+7bLG1R2u7tY+xwUYq1FKoo1CaYWSEmMMQgqM0SilMNagtUSeemYzg1KKFBLdql171VD6DJqnMT7t40vpdTlSKrRRaL3e1rM4XBCbdawFJSX1rGL/84cIIMsz+uMBxq4nuhICIyT4RC4VUkq0kkghiTFiy4zgPYqEkqDsOuK0looYI8ZoRlsjlFHsvrBLb1iSYkSItbvY1bQixYTNDDGsXeIJyTr68fEgUlKQQuTo8z0EoLVGa4VSknJQMtwdI5XGhwBCoKSkNBqRIjoGiiJDK7UO0KTW2n593AcJUEqS5RkpQWg927d2yIqM4ANWG/q9AolAxohKCS3Wh6uNUmRh7SZSCYVJAglrr0nGkql1NOyeNtgEGoFRGp0ENqzPVyi/9v4kExih0FKRS40SkjyzWCHXLoDT2v2tiWv3uhaJSKAD2MData3SICRGynXfIiikZpjlDE2GUYrYeJTSSCR5kWMHBXmRsTw6dpeZ1u2dW4vWinJQ4lvHcn9OVzu0kOTGosTaxSjxGAdtKPQxvghMkoQukFYdqQ3IJkLtSIsOITVIhU0SLTSltCgkQijWDnAFNq1d8mY+QeNh2WLk8bwREh0FyidETKiYkGG99ckqjUZi1boc5dO6zYXEJInWGpMUSmtUJ/DzFrzAYDBR0B4tEFqjhEYKiZIaIw3aWPLBgBQTWmqUUCwOZiQX0Ciy4738au6QUWDQ5ChEGymLHtJoMqGRUmGERkeJkRrdrtdU4yRWGYzQWKHR2mBVhpCKrOyhpCE3BVatXd4aJxERinKIPMZfS4POC7K8RCaB9AIt9MWL8Sk3lBeBEuvI5FKsXdBqoVGs05RL2LCunzpgkkIniZUa4SImCIy1WKNJLqzd6oaISJFEIHiP61r6gwJrFZmWSCCkAEqQZZrMaHKtMNEjCUi9Zlx81xJDxFhJ2cvIc7teq6RACsitJlOCzCpCjPSsprCGrVGffpkhYqBrG+plRVvXBO8JdUMMnnKzT7nRx5aWwaBYn+3oalZduy4fMEahBJgyW1+HgHlEfyNSrN0IpxiOPatBCIG8l6+dVzyiNyftf6Y7zjzjiWeXZnkqY3Oh98qzGc5cp9PpZ/5OPE+JCySjr8g1PROJf846HrXVuUYTZ36+HDwLKl+TQvRLwXlN8mXPL7s/A0/52Av5rIvuLxrf4msRLOBrdUX7ZGt86b58zLU/OXFOw2lm/cJZfp5rP5d8Li3FZ5zwzwLnGM7Hyaf/O79eHKeeWU3OWjQes6tnrRzn851Ok+K0SPIl4RRRTOnc0niq6e8+/IK/+Ls/569/+ddMZhN++tNf8ed//ld88MGnnJyzOdUY58a3eJz+yOLCmbZ647uvITNFMc4Z7Qz5vX/zz2DjBeLgJi++9BI6SVIAgqBAMv18j4cffMHk/S9wsxXt3ozusOIH33kTuYioReRbr71CoSxZUMgu8aN/8ia68eja8+rrt+kXBRma1CSu90c8fO8e1cMF/aLH/r19/uxP/is//etf0DXtE2Pr5PKN73wThSa3JbdeusHOzU26ekU1mfHKzS2slggFZZkx6Bdk/QxpFX/4r38L33mUENwwJS+0ihuf1ww/X/HmYESeWzIjyHPFq99+iW5Ro43mje++jFByvXdZSQbGkgmFVZp/8sffJyst4+tjjDVc29jABEmoPBrJ5HBJlJouJHavbZKsQOWanfEQbTRlkeMax2//4Lu8+spLvPrKS/z+f/djio0ho5dvsPniLreubZBnkiQC43GfrVGPwbhH2bO8/uYrJClJQrG1u0V/NEKYAlv0uPXCLUye4X3ixq0bbG9t0dc94izwO1u3cVWDkYpbPmfsNBkKMsPvTDI0gswlXnSGm15TSEEmBX9YD5E+UkbBrjNcaxQ2JIiJ3171EClQxMQ1LC/HnEJKtIA/zm8glaRAsoXmDTMilwqjJH8YNjBCkrnEKAi+2VgysT5f8WO/RWo9eROQs45vLNbjRwbJ9+IWIgoKNH1heIsROjNoa/nu999g8WCCVIKin/PCS7cYjEoyLXjl9nVC65FKoYPgrd41+mWJlZrv2WsMdMEgKyh7Jb8trqO1xkrLi3WfPCm0FMTO8buzIcZNKdOMN2LJtjUMrSPPA/+9f5VMRcYkXlsWXK/6DOQGhpI/li+itCY3lp25YMfbNQMbEz86LNBG0TOGm7LPLT0kKzJkbvhdv4vWhhzNcJbY3UvYqFFS8fv1LUT0FAnGrsdLsy2yZJBe8Hr9Ah/rT/gvh3/GQbvPq8M3eG34Bq8MX+ePb/4rbmcv8MboLW73X2Jr8zo/L3/JX67+klfsNUgG60pkpfne6lXoxoh2zPe+uImsI0UyZFLzW9PbyEpiKfhe/QrDtqRf9bGh5J/p71EKS9nA92Y36DtDaXuoLOdHszfQSVHInG9l32bke5S2j4zw+/H3EGmMTlvckq+xWexgy5IkIi/kr/I3e/+V/3zvT7m7/PzR4iBO/XuS9tniY/7zvT/l7/b+ipcG38BnEVEorme73DSvY9wuYZLxT90PET6ncANumOvc6sZkIWEE/EH7CuHzTex71yn2NLd8opQdOtS8tVkj+4piJLHWs1N22F5B1i95awA3KLnWZQw7yQvRMeo0m2rId64pNpNnJ9b0heP60LGsaqbTJWM1ZdS3jEvF1rDgVtFSek/RdbzZF9hCooqEyOH17Qgb4EeR7S3QG4Zp7pkax47qmB801FVko9RYBVYfCyxxji00RsFu31AYhc0NUkve2jHY2tPrIiPlKFWNMiuEaNhqNIXPePPVb/Hy7Ze4uXvjcZufY27TCZ0855ZdHDPGXzXY2EVuVlO6WOB4rKh8hjpP6Uof8wn8wzDVj4SE54CL+C4uSfs/QBD42g0aVymQn1b5U1jRpzl5TaesXxcWJp7x7yvA17At6vKP/Lo665ksHE+LDn5pgSccbrr4oBBPEXAuRObs9VmlwlUFnZMiEReY0p7Md2GR6eJ08UhiPZ/9cvPGI4HnjEvd4wpO3U4XU/7ql3/Fw4MH5FnBr3/xG0zoMZsvePDggKLIuH37xpmyr5IbL3p254t72J5BVZpyc8h+1aO83id2nrffeReCQCaJlYrVomY47OFSoG1blg+n7H94H3+4JK5adG4ILvH+X71PNV2ynC7Z6Pd557+8jahaHr53B/dwRm+jTzNbMbtzyDuzGdoqhBZ8/IuPufPx53iRGI0HeOf58R/+1oWWnTsf3qfISoJbcXh/yuzuPvPDCaNezmG9ohjm+HlYu24c9tBGUfQz3nv7M0IMgGK5rMkfSAZNSyYlRz1PIaEjUq9WHDw8WlsslOSzz/bJM0PTBmIItHVAaZAh8c5PfoPJzfp8w2zFwf4cosSQePDRAZ0P9DYGmLJksqxQx9rIhW/ReYZLASUkLAP/w7/67yElPv3wLmZQopc127e3ufuT99FTiDEyXy7p93KUMlSLFfPpiiwvSDExWzRkvZKYFClKJvMK13hkErgQaaYd7aRDR83bkwOUBiNh3wakhCQFmVD8umwolcYZwb4MaCKZhDzBz9WULCo6AvPUEVRAS0kvws/lFNl4ZKmY+BWHWqEUZF3gZ+xhk0L4wEp7qtRhBVgp+Xm2JE8KhcSlxBe6xoZAJhRvc0hYdZgMFInPzArtQEvBOxyuLR0SQoh8yAIj1x6/3v3Nh4S6AZFompa6achyS9d65m3NYNyndR35sOBuWGLTNklqvjArenmPaTen1BnvxQlFVNTB8YVZUFiwQlAmydv6A4rQIUxkb/sImTSFdPSl4Z3RZ4xkxsItmfVqoisxqqSH4GfdHgUS13ZMpMPKbB1MTCvev+EpoyEoz7JM+OTQCXJteGezwSzXHroqHVgYubbUJMWvzX1yl2hNIvU8D/MZ1isKafh78SuGhaFeeo4mS3688we8tfF9hJBoafhmeg1fCoRR/LvJ/8rd7guU0Pxt9SEqjcArsBm/YoGsS5SUvLe1YqgUWZFjOsuvzEOs0zgBH4kjcp+Tl4Ze6vHr9mMGRYZLkU/kPWwqoPZkpeHDa/fpiR5NbLgrvqC3maOSRlfwMz5CpyEhdOyZJf22QhlFaQf82cM/wWBoQsNBs8c/v/U/MM42HjMBac0UHNQP+buH/429+j49M6DOO1RmiAH2mFOtFGlRopeRv9MPUE4TY8NEzxBlIJOKIkl+cWdB/+gaswCzul4Hnlss0UrwbiVIqcb0SqS3/OZuhc4kvTJjkXYolzOU1BQEmlhQItAuMlnBEIdSAlXX3G1ztLSYPGNSR/q0WGHJUiCJHru9QOc8Hy4a0jCCNRgN78WA6gtyoZkoiUqJlBUsm5oPaoMRkJLg4ZHHxnCs3Ep0omRkFUnAsg7oTGMyTVYY7n+WKLpA4yJt45EykmcCLSJta/hXP/wn/Nb//Ef0yvKU6kqcIzbnJI0zS/lp8eMsmX+S1z7J8SSdvBAuFVieTah4cov0PzB8HVVcRuSfpfzzSspHl1ecCb2qvqsffX1w0j0X6cHPsVaXCRwnfOFVbnvERWP6Hxm+9gPdF/DmXxJON9slRsTTjffVwnWcgfP9zLn7R0csLlgzLhs7l8KFq9SptMuk+ueZfI8gPd5yd0bIOMXpX1Lu6TMRZzQ3p/LPFlPqpmaymKBXS8SyxISOqqopipyjoxm3bl3nvG3lIjzPPz2hv5OjGbPJnGVVEbGs6pyjqaCaLrDVClpH8J7WK1Zty3xRIZXg1mu32Pt8/3if/4Lm7U/obw3/f8z9Z69tSZrfif3CLL/t2cddf2/6zMrM8lVd1exmt8ghOUNoBgMCgwEEAQKkz6OX+gJ6M4IgQIMZuu4ZathsUuzq7vLpM2+a64/bZ7vlwunFOvfc467JqmRTT+Y+d++1YoVfEf/niYj/0/UbGzjcm2OtZTldMhiNqBYVi9mKZtXgbj8g+IDUCpkrVnWDUorp/pTFnSXJIMUaw/Tg8GkVz3R/zv7uYXdWozXMD5eoROOzbltKbQykETqLOTyckwSLsZbZ7grru47WGA+tozSOVniMsLQysKhrojhi/9EhpDE2tLTLFl8ZrPWUwSKloLKWLz+5w/blTWSAalURBFRlTWscSqvOE7UL7N4/INaS4BzeW3wI+FgThYjWe6x1fP7hl/zkv/wDBILD/TmzwyXLZYkInqiXsWpqXGuRAcqyOrLOCUIQuKMJMbKOqra0rSWKFIvpgtY0GGs53J0z2y+Z7s7IsoSHDx7SXssISuJ1t7+7ko5DX+O1R8pALQJBBLQ3HBpLRYtXmjh4VsF2zDx4FhhW1hBiiYwEFYbGG3SIWEnJMgIZPInQLLRH+oYgAgthUHi06LZmHIYW6RxawowWgSDxFidNR90Ze0IUOAwO4S09NMp7FjiCFgQcC9+iraXfgBCO1hi880ilmC8WSAR21zKYDGmaFt8qDkpJsx9IeynlrEJWS5bSYOiUp0ZY0OCUZEHDQlu0LxFJjYlqQiwh8kjXsgwWUy2Q3qEKjS0CoUiwtWLWtpRVSVAxWmga4QhpDL5h4T2NF4QooAPUwkEbIAQWwVM7B0oSJYHaeaamxUtPqSWVCARdolhSSk+sLTJtWCUrlnZFcClOxLTWUtg5h2bKjd6t47EgWhsQATvmEZWv2Gv3QAhsWKfEcVgvcCrFtZJDWRN8oI0CpW9Y2RoXItqsYHbk66Y1jkTD0ragHD5pafoGl3oaZxDKsEoND8uHJFmLFSuCBGsNK6lZiiVeG0pnqLzAK5BtxaqdYalwwSFsgnAK6w2DeMisnXbKhXi8Kt2B0cPmgJVdcthMqV1FKVuCEFS+wviMVRPYr+es4pimroiDYBUagrHEQrJUFaWraNtNtFcsncc7Sbs/Z+lAOo+wEc5JyqpF5QlGOaYHNWVPsJULinxAO6txAZbG0KKJVCCXDp0lSA06TqmMYFEGIq0YRjnzRQlaIRJBkmpCnqCsQyjHvqupnMWi8Dqi8h4pum2dznkqHxBRymIV8GULQdBQ00/BBIHzEqkFjRMQJJX16Fggqhb2lpRWUjmFC4HagfYCKwNOCHpZxtv/xQ/IjxWLE3PNGbr3p4LTZ8kJCPJUX3jPfvz0l6P5+Ryeep6ScuJWZyw90lj/U+PLrwn8LmIL/Z39Xpyrk/8cYPoiq/TTQp4m4zkXxUVRiyfPdlFf3MnO+1P5O2j7p8g3qFw8A5m+MNo+HUc48fdkmJOMS+e3+ry45v5YUTi7NHB+oDnzW/DkzMRjQ8e51YWvKUfjwEXK5vka6MSHgHxhb46nD4ddGPgpCYkTGklXZ+HCEXQyWqeX9RhGm2RZQjYsaBcRIazo93psba2fSOjsgfSLcnyU3xA4ODxESsHW1jqj0QjTwsbGgMWqh1nNsIf7ZMEj+wmLpcNYS6wkKuoslb1+zvzhlERHpHGEqVsWDw4QUjAY9EgjRR0CpmlJYk26OaJd1gjvMa4D0+robIGOE6I4YtDvs1wsKHdWuPGY8WjIbDbDOMvaeHzsoRVg+8o608Mpy3LFWn9EHAJ7XzxikCRo5xAe2taSDHqE1jAc9xltjhn1RqweTnHWkyjBMNF4a0jjCB2BtQ1JHNHPUoo8wpuCdDKi3V+w3FuwrB2J8sSxoHQQGsto3CdOunMkRZbili1xHOGBSEt6w4z9/RlJHJGPR6zKitA61jfHTMuKWCnGw5y+jJjuzyDA1uV1hmt9mqplbXOISBOEc9z94A5CSTKtqOuWPEsRQrE0BmssvV6OkBKlJOPJgOBS6qamtZbQGJzwqEsFmUxYaxVSpJTAwEh0lhL5ipHTZEJRt5aF9gwrh5IRIpb00SQ+psETgqfXdmdRmuDIGs8aKd56pnXJIMvRMubw0YIsjYnSGA9IBBOvUFqiQyBDkViBEQ6hUzaDRhmLxCMDaCuJkpS6J7kyXsfrmN1qgVs2xDXo4EBYRl7TWoiilDgoikyw9Z1XuPvoEfZRiWgceZHRNh1tcKwjIq3Jg2Iz6bOaBgY6ptcrqMsSEQUmovMAXSpH6y1jH2GFxrdLxiamH2kqlVI3LZvRkEQrHgZJgSIxCmc1TSJYT4aUOxKzsuS28zZugqeKNes+QggJsmbgIuIq0ArDMoJN01EAB99SNBBbiYkFeMdarVBBs4ejJxWJGmAUHESGNdkndSumXpKplM0oR0eBabNDj5yNZJM9s4sWmqEaU5mKlZvTiwp6ssc4WkcJhQojZk1MXc+5JHs0BoQV6BBIDxx9FMJZ1suUEPpk3tCEwMSnFJHmnp+zHY0JqmDV1hhn6HsLcwOpYkMPSYWnZkHjDetqhDKhYxdjhI/HrNqaytcMmpS+0Cz0jJEbkadrtNZS+ZJC9xjHa+xWj8h1QRH1WJoFtS2ZJJv0oj69tEdfD1lPExaqZuYWrIsRsyrBypphNEA3BVVoSFLNcBlTOIXWGVmQxFtDjMnZ2V2R1zUMEvy8JlUCpQNN6xDCodqKfqagDSS+pKdixr0EnQ3oF7Dan7K3aJEykBHwdoWKc0YDRU+lFIuG5WJF8I7JQHHQWmzbkLYarVOySUHelGhSDiqPWC6YjHtUIeCcI4sFuqoJNayNcnKtqeYG6yEyBlvP8Sgi6Sl0twXUeUkhBf1LI5pEMVoryGPgYIGzLQaLplud9jawsbFGb2t44TxzbsHhuduexNH/T12GuCjmF5NzUT5FYzn3U5wIema+/ibA5XNXXl4wjpPW93O3n4rGTz/+lFWLZ8bxtDy+AFx8EaXn2UjmbJInFItz6R+l9lzF46I8vajvlBeQr2Uhv1i+8ZWLc/k5VykX9dJnwfnzEYaLfonjPy8s5waV80m9WJaeFfyE0nBudeOCMajz6n3y4Scxn7SodM79njzzLDmZ9rNCnqTdfRz6lBfRo4geK31nO3caZ+i9K7g7nibSXH/nFX775S6Lw4jDZECR9U6EfgG1PXQK1H/427/izv27AGyNrtAsMnxlKfc1fvcui48fImYLithQKo8nkGhBGqeslhUqjuilGRiQVmDxbG9M+PL+DiEEUtUSXMBZx9rmCOkDe48OiHsZorUIYzDOIyXkScqiahiu9cnTgo1L1/j0vS+498EuH6y/z3uf/ZZsWLC9vcUf/cFPuwPfwORWjnkwhcLQuzTC131Qgr29GeujActVhdICiae/3kdEitYa3vzuKzy6fZ9Hd3aQ0pBmmrSVqEiSxYKD1hNnKcI4tAvoSLH/aJ9Llzd5YBRt3h241M0UX1cEJ8B2vh2CgnwtJ8408/kKgUDrhLpakOWCQT9mbW3MF18+YlWt8HUHtMtVzcJBm2n+7P/9bxHA+vY6rumc87nGcu2160zLmmHTYucltmzwGrwM5Ilmf7lAKsmgFxOcx7WOtlqxvT3h/gFIacm2Bjx8LWPqKmqheH28we2kQkrY0jmNkkwdmOB5o0l4bww4yyCOQQv2RYW1gqsl/CZa0ggHjUbYBJt6Khm4dsdz9/Nd+s6wkVqKLCEsDlBSc+XGOh9c9fhgiL0g8xE7saVRgVfEiA/NIcFaRNCsqYTdUBGE4JrNmKYOqbt3/HKScVAfIjLBpTbmLhVegkJyLRnwSbyktR6d5Xwulpjr66RWcuOOYP/BLnJekiU5pjFIKZFC8fai4JMvHuJ+c8irP36H98YSi6dWnlfVmPfsLkJLRjZjqgJCRJRoXmtzPhg/wqIYhBwiiw4B2RO8Ir7Fr/bu4kYpGRPqvSnGdCtml23K7aLEOE9sArJfE1jSSM0tN+K3RUktLaYRJHFMo2qCDrxxWPBRVGGigCRHGUPFgpBlXFvmfDheYqxEkDDKJbvuAFsEJmrCnfQ2ZdSwiJf8uv4lu4tdJHAlus5sdUjjKgrVw+cRKxkQON5Qm+w8eoAvLUY7LtkhD8wShGRU9Vn1HxLigEgll+d9dvUeXgQu+ZzDzCOMpPWWq9MxHxa7kKRcHm/yYPZrlK8Jac7VcJn32CeIwEiucegPaZ2nihxvuDG/XP4CoWHUXkaNUlqmzMOSG/p1bvvPMG2J94b/8OjfMDczIhmxlV/hfnkPFxyjdEybrahZgXK8lP2Iz8tPaEkY1JpUtVAYVm7K9/Qt/nb6Ac60xGFALm7yyB5SB8mr6Ra/3mup7y/pJRHCV9jW02QRr44EHz9YIKUiyyRpq3BVTENAhIqdRzU+yuj1Cy69NGJ1e8p0OiOPWypyVqsVUSG4ugZBO/JckgnL7YOGViqSPKJuFyw8RI3jcl/RMxGuCYgmY/hgBirDAbfWNDt1QrxyCOClWwW3aWgaw/r6gL2Fpl60+FYwECXWBxCSJIZoAmVdUbnAS+9cY+eTL4iqmlg10C+ZO0usNe/8F39AlMadf5EzU85JHPVcTMDTA7yITvIECzyZP5+G406t34ezV18AlIRvwIvDeYvk37E8qZ3fKQvPW7h5XqTnqvvi1nqWV7GTuO1cDBemf7rMp9HxWc3qa4LTFw37DbS5CM9Dps+R5Wp1IkfH0T75+sJnIZ6ijoYzQPxrAv5nydkcX9iP4Hgr0ekcngfXTw5jP17auCChExFddKjr+PYpJ3Inh5nHQ1N3TwhxnJezm8ceX3uyunPWj8azVy66NM6aDY4GSMG57VF3bu/xF//8fW5/8Igki6jjFBMEdz/fIwkV/+ifvsF/83/4CVKf5BE4mbtziXNweMif/cX/wief30YIQVpvEJkxB7tLhoOEnfe/ZP/eLlJJYtUitaduWibrI6plQ1sb+htDyv0FEslqVZHnKT5Y6tbgjliUtFIYZ9m+uc3ulwdIrUnyhGpRkiURxjqiWFHbQH+tjxcQpTGjS+vc+eQ+o80BjFa0foEepLz9zrf4o5/8lKuXrgDwz//d/8Sndz6hrEsGfg1/P+Lehw+oD5eE1lIbSxCwtj0GDbKXMN4cExqHKy1fvPcFmdYkSYpBIKXAmpY4i6ialoGOGFzbZnawYrF3iOuPqYlpEUwiTzh4gG0rpNaoWHHj7Zsc7s/IkoS7v/4S0xoApOoYqOqmpdfvIVRCW1sc4DAMRhmWwOaVDaJ+QtMaCIFi0EdHMQd7M8aTAaY11HWDsw7ZGvZv32NxuCBNEoSHqjb4EBgNe0RC0npPf1BQu8DhYYmxFvWtCctv9TkcCjbTHi54fNVgYslEJgQPe7QMncSpbkViGQwjF6F84EC09IlYuRoVPDMMW7qHM4Ed35A5yfrfzhjeaSiXJf1+QVBQVjWRUkzf7WNf6rGQhonKcLFgqi251GihES0chIYtEkIwzEJDJCV+2bA27DGPHRMX4ZVghgHrkU4hg2Lf16yrDOstK2kB6BmBqA1VX3CjN0H9uweE+wu89wgDrnTMFyvyLCWoQDYqKGcr1I8v4X64xVflPhu6oPUOIwMWT19oggociJKxiWFyiOg7mgTWlppCCGZZzZgBjb6Mb3Mq5enNYH5nxp6wrImYRduQZhGNt0wkxGnLQVqTW0UjJDIIFtqyEXIQgn3VkDtFKCWyEsx9w8grnDbMMkeChtiSJoJlYthCk/QXzNJD0hDRQ5GWgZmes5leQkrFIizACcZ6jdzmHLZTBtkah4njQCyRSEQzxM5iHlZT1k1G4wRTb/DO0UtrBkNLNW6ZmCFllbCoW4zzjOqITMZMVUW/1JhC02qweMaxJR1bHrUP2PBDjKgxosXpwCgMELXhsCgZhxGhqXFty6ot2ehvoLVg3+wwYEQcoqMzFxVDOUY4yaw9oNB9Gm+J4pjKl/TTHiZu2HcP6ckBszDAhoIlJRPRx5qaPTknWgpSqVCtZMaKdX0ZEW+zZw2pl5if9Qgfp0ynFf08UNUllexWcbQMaBzz1jOOEkLTY15qhHf0fc3AW1ZVYDJS6BwOZkuatkUGTy+OKYnIRMtkEBEVEe28xOiMpVfszWr60pKJwCJoHFAoSaFjykbg6znKW+KkWxlM8hQbFIsassiTDhLQkqY2CBxRP2FvaSmCIaoWKBW68Vk29G/2KINlMOjhlpp6t2J6ZxeV1CRrjkO3IktS/t4/+Xv8V//VPzw7vRzPbY8BoDi5cnF2deB3MGCejuBJwgFOzdkXgdMns6I4YzsNT0DJ10n7/2/lBX1uX2Dlf+GCXWTd/V1F8AQXPXdF4zlnQE7m54Sx+PH533DynOvvU/5TeX/BsAH6/f7Xi/+EfANsUYGLrdBHH8Gx4n1RyAuf4XTAs9V3ARR9sSyG0z9P3j+pYoVTn6ObZx469SIcF/UE7ezJXyfYmoQ4GeqMViqePH1WTjNGnBz8HtfG6QKIE891X86GO6v0ieO2evwRj/N04laXz3PZA7qDxEKAkAKlJaas2fvyEeWyIljPgw/vMn2wf6Zcz5IORHf/SlxjgY79SAjQSkJVd+3nPUJr0kh35yoOFtRVg4wU1aIEQKouNecdAUGkNVkco7VGSkFv1KOtTPdyyy5NIcTR9qaAtd3haKUV1aykOVyxd2+PYq2Pbwy27Ohu0yLtnj/xegkhkbKjn1VKIbUkH+RceuUKMlKkWQQh4FtHMezRLmuUFB11rVZH75DotgsFj/cOqSRRFhO8Z/zSZaRWLA/mYD06dMcLQgjYpu3yrSTBe4INBOtBCHTUrazIIyrlLIm7Ng8QnKMqG1rrUEqRZSlV1dDULUkvRUcdpa9U8rjNEXQ0u7KjoVVK0hv3uPrG9Y5RqJ9TDHvoSJEkEVIIojQGKTDO0bYd0FZS0u/nZFG3FUh5j/KBWHcMRd7YTlUWgkgqIgQyQHABfXRdRhH6iFo21lHHq+8CadxR08ZKEesuHyqJUbEmuG4bnM6Tjuo01git0GlMckSDKzyYxoHxqBNvhoCOVlUrgnFHyr9ExRFaSGgdWS+jPx4glCS0HhFplBBo0fWWWEhM2RJMIMmTrhxKkeUZIQSUkqhIExA0ywqpJO2iJlKSOEs6gG0d2oPwHSWsRiARJJFGBYUyAeECcRBo0w0FUZqgpELHEfiOhjjNUqQQeBeIhCC0Di86fnQZRwgliXVEksToJEZIhbMeZwPOeXQco4QgEQKpBCqJcJHGio5IW2uFtAFvHDoIpNJH9M5R5+k96ihl3dLgFzVSSOIoRgaBEkf0zKjjfftKdA4UsRwd/NY4BMJ6YqmJo5hIRgTriLMMWntcP0FIVO3AOCKpyYc91JHRQSDwB1U3HniB8ALpJdIFtNKkRbciG0mN1BEK3XmpjxKklxBAOXH8rBASpSK00vjaoFDEumPQ6tj9dEcH7DtyChlA1N3WSdF2TiCDDcQ6QiBJ0xQVayIpwXqwHuFAx5o0jQjWE2qDjhVZkaKVQB3Rbgsh0AKiOCLSqqN0BdI0QicRi9mcZlUBAQmE4GlcC1IQRYpyvsBWzdE41J090lrTWIsxLUmwxJEG66gWK5q67kgRtKaqa5qqpl3V1GXFclVSVRVN3dCsaqplyXKxoF6UXf/pJeS9jDSOcM5h65Z2fwmuey+EEuRrPeIiRQuBaRriNGbz1jZxnp6eax/PYycunvp9VrF45jz1AnIyXvGEcepZgPqYKeocJHiGKf7MHH4q7d9Hzsb7vDifl78zF792Fn+fMoUT2O53TNeHgH8Wu+hx8AsKfBaAhtPXT21xO4szH389y9h5Nt5ng+2ny++5WnFSfn/l4gULIeCYu/2F5NTLeNGtF+9dp8hfT2DqF/s8VgpOJ/lUpuqn5fcpL+S5OI7DHeX49LH/E+EvUmOeKDAgCKLTfMMLVfoFYU4qHhwpSeJJvQC0teEX//42/+5fvk9TtfTX+uisIISIsTnELfYZqopJDjc2FYON4XNz4ozn13/zOf/bv/oND79csD68jmtuoNQrfOeH7yKSHNUbEA/6fOv7r5JMNqEYMxmPCEGgZUyaJKyN+sSxpllW9HtZB2jiiDiO2dpeR0bdZDoe9knTmP64T7usWZ8MyPsF1jqKLCbLEuJYI6Xk6tYaWkJwBh087WqOr+cE03ApGnH9xi3efP0Nbly5xvbm1nG1vvvat7m+fZ3XbrzOW+++ydalLfJJj3yjz7vffwNfOVQQRBZ6OmE46iM9/PhPvkvcj8iGCXEquXprm7VrE3Si2RgWBBPoj0ZsXt8iU5JEStIo4noSiJVAi0Ce54z6I+p8Ez++wmi4xsGhRI2vU2xfZTweImNFlEZcu3qJKNJILYhjzdZrWzRv9SlfSXnprWukcYqrHba03Lx+mbByyAbefPMW2oFuLNI63n73JWgaIu947Z2XGW+OuPr6dSZXN3jp9RsIIYjzlNHmGvO1iL2bKbtjwfqNCe7769Tfn9D3ip6QDFwgrQ1/0AyRUpFIxZbP2BQxg7hTGv4ou0weawZJxDWZcUVkFECkJP+wuEGqYgY6Z9RqNhpFKgV5pPjelctIIUjymP6oYDjqEymJqVu+n1/ialWw8duGyV3Hxj5ki0DcSH7kJkRBkjnJKMS8mW4QuQjVSr4nt3FNoEgL1tc3+M7GLRIdkyUpP914mTxJGWcFwzTjzaoglhGRl3yrGZLIhFgl2Nrw3R99G/+9bey769z6g9dxNwaY725QXc3YfukKy1s9FrcKNm1Gc9DtlR+M+vykuEkkJZnSXLM9+iQUxPgg+eHiGnqZUDRDXlG3WK8npM0GMgz5k/w11NISHxquHQq2K8FEa3qR4h+wwSCPGaYRozKlmGlSUxDrPn8sXyEVOYVNuBSG3HIpAw3St/ywXUf2NEmmKJaeyTwibgW6hXcejOlHLVtRy6ZJea3cZqsZMK4yvn/3VQqTM1722VQbvKreoL/KyQ8U32pfB+9J0pQiLnhD3CJqIUbzk+RV4gbySpKR8HYzIROStbUB3z64SuYlWaOIa8ePDrbpG+g7wTv1OpnXpCKmNx7ww/glhnlMLuB7w3cZEjFymkGv4MfLb5GQkJLxWniZIX2ySqMs/Kj9HqHN0GLCzexbrOktsjBAiYTvxD9AaI+OBJeKy7xavM7rk3e41r/JT7b/FBE7dCq4lF1hklxG6x7ImD8M30ZYR+oVlxhzKWyRVZqUmD9sv4WwBWk7ZsMPuDm7RvyLTfzf9PhhnGF3VkRNIHeBrcQRqpI4knxnKyWymsxEjNKYN9YCsTskFSu+dRW8KxkMoZcrBnJJGiyJb5mEJRu9nIEMxEoyzCSLgxad9Xn39U2SVJPGgUgHtlNPTwtSGbg88myMJMO0RqkG7XbIRc12X/Pt1wbcem3AzVuSS9uK7bjE1A34wIiGGQtm0ZI6sVweK+IoJYpTfNUS1YG4TYhFxh/+ydvceHWbt3/6Om+98RJvvfMaP/j7P+Sl11/mnbde5+Jd6men5SfA/RSOfvLnGxdxIs1TGXtqks8AMX+X8qx0L9qtcU67Oxvg2UmdB+Rfs8Diwq8vVHfh5JfQGeM6w+cJJeUY2D/Nin0mvad9XkCeGKLPxHvi+9dSnr4JxeSM/P5nLv6OO/STlaSLl4RObvk5zwERjr+dkhcsw/Hi3cmKP9Ehzi2UhdNt9Ph6OPemPEfEk21QT54/W5rT8T3ueqcW5UQ4tULz1HI/M2viVJI//3e3+ehX91jMKm5/uENtY5AJeMvuTs1AW5wC27Tk268RJfGzYiYAv/n5F/zyZ7eZ7i0YTfocuAxTbxGalp/9xwX9XkJja8oS7j3w6P4YWsteOSUPEQJHrBKWq4q2aSh6OXGRsVw1qEjhfOBwtSJOYoyxndfjSxOqssZZy3RWsn5ti/nBAoMjjTqPtR7Y2T1gtD0m0or5asH65SFeO2ToLN7/7B//Y4abY3pFtz3kcV1e3bzK5ngT4wzlrObBe/8BlWvyYc7eh4/QQoGD4ODhF48QmWZja8KHv/mYwWafK9+6QpFlxFGOubdHW1XstZa010PHEfv3D1jsdp6obXDsG4EIjjxNEVqwn21gUKhEs9s6WFhkCPQnfeRaD7GYI4Tg3s4OQoFQEpVHlN8dUR048n7GVw+r7nC/E7jK8W//h78kOI+Qgr+4d4gzLYv5ivrRIR//+19jrEFHGjMv6Q0L2towuTnhi/fuoqOY4AKPRE396pBaGkILn2xkpKMJq+WKXR2R40mcIwuSD7KSQifUiWBRBVIZiAVkwfPbsE8mBT5LKC3Y1qGRJAbeV3MyF9FKQaMdVhkSKegFySfTPRLVrUas5iVBeKJYE8cRe5/vET9I6B0aisbwUHrAkPViPsmWCNc5K3TBc9dW5GkGreerpCZ1CZULOODTcp9gIev1+KDcIQqdZVoJweesUAakUHysVyQBZKTxDv7N/mfEr42xreWjONC0Q2a2YkjMJwpUtkFVVtzJYmTdsNhrGfQkH2Y1ygAh8EiuSKzCekcsE97PS1I/oC4DDxJHpnsob4jnOT978Bl+afDSsWcDKvYkWjBEczuv6bfdhCHHiqAKdGhJ2pj3wx4DoZFRATKwEiX9GGKheC/fwddA5DAjhRSKTMQMiNjr7bDRUyyHEXpZ4yPBYBWRyZRduUvP9HHSoxaBeTojVzliUfO5uI0e5VjTYmj5rPy0s1ZLzW+bO8ReIaMYbxxfRFPWJiPiJOaL4SMyC6Lo/Nl8Gj8gaz1eCR4OlqTZGO3n6CjmM+5QKIlKNJ8vP0CXJUpWpK7h48EdUjKssHxl75JlKUmRkdaaX7W30XpMaSq+KvfIlECQkCVjPgrvoaXESEep5vzx5j8m8jGJTPh3yz9DJxKsZZcHtF7gZYRoI35R/ZZCJCxCw8wtaGYVcaLp+YT31T5xGCJQLJohs19l6AcRuqz4xaoBL/FO0RpPveocy0lneP+LllTmxEEjXcSdh1M0hl4as19J0tSzsiUb6ynTB3NiJUi0wLcJ/nCBsYIohnmcIGRENbccXB+SDy37ywoXLFMXkcQajaNsHKGZ0jSWQRFz68oGVzYHXHn3JfS1Mb/4zWeIhw1ra30O9hLCr+6hY82ejJkVlgNWYBpuNynDECGkppEZqxUoWxNtxggv+Cf/7fcxxpIXnePN1hmSJDnlNO/8BuITE9AFhuLnwYPj7cxf5zTtqY0G4YnF+jjO7s6pa+IZW2yeJhcFfQKFvp68CHY4Gzzw9LMoXxP7fiNySsH4OuA1nJrPz+KuwJNyPr5yHP9FUPUJTP1azXnR1vczFy7+/vj30yry6N7zSHa+jnzjB7o7eXJUKZy+/A3EzFHMF79m57YOwQn/FRdYCF4ksXNxX3j7OGdPQH84c+fEF/E1G/C5b9fFcZ26evaA17GCHc5de1HZ31mw93BOuWxoWmid4XC/pj2icY2kw+IhFpSVvSCG8wnu78zZ35kxm5bUVrAUga++mlHPKy6txUxjwcHBikfW4IzH+m77TW4cy7KiNZbpzJFEEoTAes/BoynWOEwIpJGmXNUgwDpHmieISDF9NEUFgTWO2cECYz1eBJZVTVMbXPAIKanKhtWiIu5pGmcpmxbvPEmRMpqMyPP8wrqKo27V5N7tR6yWJYv5irY1tMYgE029qgirkriIKPdX3H7/S+KBZrg1pKrrI+eADYt52fHee03Qmvl0Bb6rymXd4qzDK0ubRJiqxaURVqaUXlJ7RX60ArXar2j/+hMKW2Gc7ZZaZaDoZcSy80tQlyvmiadVlmRZkziPMZ6De/s0raUpG0LwtG3L49W2w4MFdVMSgkMgaMoWHSmqqqGarZBC4b2jbR1eZ5QY2gSIJa0yeLsi5ALVttQ4ZraiEgaSCCEDlkArOkdhSyxtovGyQWtFCwTdLZGuQsClgrZtkCpQy0AoJDQNizjQtA39smTUdI7ASim7syze0VrH4axCxTE6S9ipl0wrzTL3NPWKKAeXQhU8ghaJZB5aRCyorQfpWa4qbGMQSrAwNZE2FMGhkEzrFWUrCCqwFBYpJb1UsQqBKoLdtsEtKvBLZBKxpmGRehoLM2OQSlLbFVY5fCSRucZEknnqaE3NSrYQAoM4oRKeyjtm1CANVrQgNaGck2UZSwxBVDRxRBt3LFMq7TyxL7THuhafa0QmabwlNA14qOKAkAZrDDIEDCAyhRGWhSiJlGWlPaqX4/sx1RJc3VBph9eSUi+ofI1pHKFJcC6nYUUbGWQciGmpo5ZZe4gSKStXIoeSqN+CMixXM2xjqNYLpn4BHmIjqSTMzAobDF51/UGGhrjXsFILVtQopQmpZGUMKMloNKSUDaum5VF7gCZQ67rr0anFmwVVUrMr9mmkppQWJLS2IWpgLpe4yFHHCZUBnwl2Vg9JY89KVcAU3AyBwdiWcbTOQbvLS8Ub3ZjX7rBb36elxSpBqxRzuaCJGlYuQskeq3pB29aIWLBSDVZ5jPdI61j5GvNggV7WTA8ldtrSab6eJsS0WhEiWDY1obZkJsYIQesVDw9qpJTUKqapPF44CqForOdgVuNFhPcSU1uCE6zweBGRighvNa1QtHOLXtTMWk/lBUIlOBmxbAM+eBAWbwGhSAd9Ri9f5o//T3+fqEj55d9+zGK+YrUsCQgqGyMGI2Z7c+SVHpVeYTQ0UcKyhLA0EGkaD1iQbYP85AGXb653hoFEgxRoJYlExEnUEM5My6cUiDPaxO+KwS+UC4C59918cjEOOJPyM3Dqc9P8vRSMF1WxLk7iFAb/JgzRF4H0k/de8CzE15Ejk/JTM3QOg4oX7EC/o4LxonLhitiTmxevLn2D8p9IufiddrO9mDxtaesZcnIF7bTV4vlLcee00ON7z+5sjzvkE7329J3TmTuTnecNCk+Rx4eHLqz736tBAlVZU5Uto7U+IDjcW5HkERuXh+zcmyGVZrJZMD907M/ntMslWSI6mlEEL719nW//8dtPT+FE/jYvDRlNBlgn2dzqs1spfDVjMs4Z9xKUb1kRSDUgBdYLvHf08gznE7yO2FzvM58ekvbHWGOR0pHEEbNlcwTyJdY5tHMUg24frzeevMhIMo11nsn2GLMs6RdxtxSqJHme4LVER5JhntNYQzHs48qWrasbRHF0XJ5jqsJjs0an5K5vT+gNemxsrZEXGb43ZNzv89Fff0SsFFprtFTgBDdeuoZxLVEcoVHYlWPjyoSwMcTUAYKkPVwxyBOCgKbICNZhVUCJQBRp1kcZi1oiTCCOAknc8cWTKAYyI1pK5OUJvrVcu7xBHCl27+/RG/f5sg6M4pgsxGSFYG0g8a1DK8m4XzA/Gr8mkyEEx3JVMdocsTicUdUN3jk2r20wWB/wyed3CV6ACYyuTViWNcpFiKBwNjCOU9L+iLpqaJqWSZFDU2OFYyRS0qhP4zytDvSVQNc1Mo1YEzFxFNMGy6JpWUNBEDgca0kKQONbSuEYGHkEMBx9BIP1NfJliTOWvEjRaYwNHlM24ARCKqyAre0NXFYTaBlEGZQCMUw4NBUTIqTr9q4nQpNag9OBOFcUC0ecRKSJJotT4kZga8vKSdZ1Tm0atBekcURPRkgfeGgrhrVAiZymMigHG+OCzes9dtoF6zKnbQyHszmz2ZLtbMjaSxt8tThgg4y6LVk5SSM8EzKUUngtGFcSFTKMLWmDZxLnZCFH2pLt8TrlvZK2hVJJxj7CG4sPjpHRKK8wyrL0jrVQEPdSDqgZOE0kUlrhOGwbxiuBKRIQlmErUSLHxSlTY+jXAVxEFFXkISapRiRxhVWWSTFm4CIam5GQkqwXaKVZuDmD8aijEbYV0RHFsI8EYiDIbjfkowE6jVFo4rbPylqCcoxNipUCqQuUVsRWI4LiwB0ycX1klFL6FUErxvEQIWKa+ZzJSoH09CYjQiQYS2jrFdEoY1NvYoJkYUuc9PRcTCIUrrFM9AjfJtSRpNKWSTKA5SHWVxQkaDdERS2VbkjrhKEYs18/IiVj4tdZjy+xdHPGfkLtAw5Hz+as+ZxybtD5gLVkQBwn7Jl9ipAR6RHlQiIbzaWtHuJ+hhFzXGrJewlZMeTu3QWFMFjfMNICnCfShkhHHC5bBjG0pgIkaRbTU4G4allZy7KekQRPkRUsQ02/yKgqg1MRRdJtM125AMIzziOUj5jvBZSw9OKIuqqJg8EKQSw9lbMUvYTBMKMVjnq5ZH1zRH+YU7UrxuOCxvSJVcrt6QFRDVEOj9KEgRCMM4V0Duc9XoMSFi9ArFZEq5KqKmmNYTgaAoHpbE6eZ6RJ+mQ+FiBCOD0Tnz1Y+PjyC8yOL7RicUGQY6ryCybti/DFM9ZczssFwZ7qX+FF5SnFPLdy87VWJC6wlH8d4Hsy7Amgd+4g9YusujxVcbkA/X9dzfNsFM9bYTiV/slb4nzZnvXc89J9Wr/7BhSNb0y5+KaVr5PxXdQBL7LAn79xctGKMw0SOLfseP7xZzfihXm4mFtacLLDH21PEmdSP7WN6uhQrXjy4j7ROZ5W20/uBM4qUifzcfGvp1368vYDfvaXv8EYx9pkgPA9DnaWSCW4fH2D+UrT2gRTS5Z3HnKwu0BKuH454dF0TlSkDLYL1i8Nn5bEKdm4NKGs72C8p3UZuphTD1p0T6JDQ7kX41eSIATjgeBeJQhI0iLlIL5EYz122KPI1nhw2DkVuzqJKHd2UDrgZcz6IOHB7j6EQPDgTMA7j3eBQS9nd9XgSkssNQF95EFacPnSBh999iVxpLszEjrHVAEVJfzxf/0n3eFrHg+0Z9aEj76uTYb88T/4EV/evkeep8RS8ef/j3/L6NKIZl5hR9s0tcMIWL96nfu3P2f6xQ6Xb15htDVg59GUw51D3v3ht/jsg3vgPEIEjEiYiYSsFzEWnvumW4VJ4+7g6KGXiCDZ7lnuFYLGBZpEMuq9zG69xLWOsVGILw9wJMx2KgaX1ngkVqzahtfX1zBfPCLJE9JBziBVLG7PkAhGhWa6aBDC49uWa1cvcfvuDk3VIOKUvZdyloMJNkiu5kM+dHNsSLmqCopC04gWgeLNTxwff/6QAri5uc691zRBSloJN0vNR1mFax2DJiEkMSJucZHipu/zGz0lSElmusPxUkLVtrwbbfBzeYBzgUGc4pxmjwWNFlzpDXjYzvBSkPVyhBBMH+7jnOfb33uNjz/4Au9AlC3jKzlTa2mE42Wb8zkOK0ArxYZMOGBOjeMNV/AhS3wTyPIe60HzgT2kmi74lh/xhWixwtN4w5ZNKdUCZx3XozXuuEOEcSiVcDVkfMwhNniSuysWg4BVLS5NeHWwxV8u94mGmkvFgP1ZSZCBZVvzqu/zt6rGC8m2KNjXDca2VJHm7egSvzULvPMMRYHujdk5aFitHDerjPdEjQ+eYilpQgOiocbw9kHM+8NdpPIUZYu367iRoHSOt5se7+VzAoEiZJhF4GHSMjfwI7XFL+WUgCdXOSreZbZ2SNsE3p1u81nzCOU0wyTmT+QfcW95h976hDc23+Vu+SUzO+NSdoW+HnB7+QlKaNaSCf96/19AEOg0IdtX7FxpUdrxKkN+oe4SohZUzDW2+cwuED5wbTniTnwXERmCbLmu1vj14AGEwNXhK3xR7WPVDNfv84p5iZ+v7hOPcib6Mnf4EqM0pfK8vLrCL+MPcW3LtrjMtD3AEqjakjfFVX6hP8VLz7pax6+Pmc+78r8WXufD6DfY2oGB/7j/vzBXc6RXbOfXqGxF6w0ZKSLWuGaXmpY3Fzf5G3GHICNG2TrSGB66hlYL3lq8xM8+c0gtyAYDolhQNgu89Lw6Uvz6w4fUVtLvOcat45GRKGKuZJa7jQPpUVJwTQjuLwWpg0nRcq+1tNaTRwlJe0DbCLQWbE0SHh5mtF6TjnPGuaQ59NSrhs2BYm+3xYeA1hEqdkxNRBblFOaQsipxQuKlo4oW/Pn/+mcATNbXMekMly9p4sDNqzf57XzGxtUJ9c4dlmNNaGv2dcQV1zIPGQGYDHo4O2NeNiyM5e5H77H7Lx+CEqxN1nDSM1vM0FHEj7/9A65sXzkx95yYex8rFeIMvjj+8+Io8mLeoyPnZictyRcBjYuMis9SEjgT7j+JFfxFwfkFVt8XAfTPiu5Fqv0pYZ4Ycl9wJeNksLOQ6OwcHs6HeaoILtzidpzms7DkMxSBLspwykXA11Yaz6ZzVin5PeUboKJd/v65eIacOywjxPn38AU78TeYqQv64kXVeEFeT4V9Tma/0bIc9eRT2vgFub6gGP/z/+sv+Oi9z1nMVqytrYPNONipKPoJxqRolXK4X6Kbkt0HU6pWkGYKofdJ0pKyallf6/Pf/J//ET/6029fPHaeeDn+13/1Kb/46/vsPFrSW9N8sPs5qziQpTH5/UAxlawqQZZ6GuWoQkAKKFJBlEimJjBUAd9C2XZLz7mZ4+d7mMYSxYIsCZ2ztrZlOB6ytj7m4ReP0ErROIVForQC09JLI1Zlg5KCJJeUdUUcR8gsxiqBV5K8SPmH/+zv84//67935AX68Vz1fEvAP/+//xkf/epTZnsz5nPLlII2ylAicG0dNkeau5/cZbw2YLA5Zv/RAdXBAh2l9Mcj7n9yn2I0oPSKgyZ0ZwgQJEXKsnaMBin7M0MdpcSxxg8a4nXJQkEfgU+gUd0hteGnU9LP9qnLhmQtY/btPoeDzgfI1QeCta9aprMVw15Gu1pSN3XnKyRJQHRsVmkSU5YWLyRSKewrPeqXc6axZWg1ZSphkBIiwbASpC3sm4pRiMh/MSV5UNE6B28Osd9f45GqSVYO189JhgWz+YJtnRDnEXu+ZD0uWFVN54VcOEatIoTAVFkKI/BKg5CUOjCoA144pjT0iCj+co/+XcvhbMGlG9tM7x/QmM6fhNaSJIupmhYxiNh7KaHcjIks6GFG3MvZbVdshQSpBVNh0AgyJ5Gt50C0TIhx2rNUHuFDx36F5JFdshEyTGVoVAAf6OuYWCh22yUTkWFwlN7gCYzyjCyJ2KnmjElYNQ1WB5yAXpxAErGvG9ZVTt02WA1WeMYqJool9+2MNZ9iCxCmoQ2GiZow2rrC/ekBayqjmq/AOkosowak9OzLmnHWw4dDhKmolKFnxhCGTBMYiBgnPRqYi5ZhKzHaseOXjJxCD3rIJrCKHWNv8elDDotDMhcxtIHCK5Z5zfX4Jt9vv8O3Jz8kuzQ+A+449Q795cH/xm/nv2av3WUghzxc7jDbEERJCg8VoRmwI5ds2j5GZsyaGqUUSbtHliwphxVbYUQjDCtVg7H0xBrYhB2mbPo1WtujagNOwjizqPoRy/WKtTDGxp56ucBIz7BO0Vqzm85YcyNMMJi2oREtG2pCHmXsmR1GYoSp9lER1KJmJDeIoogDt8cwGlOJBgKs/JJhtE1rArt+j77oU1UJQg2Yi4oNeuBqpnJOYWKa995CPLzG3MKaDJRfTtlbeSIVsDNHGhQ1CeuFI45aZqsa4R1BKVSsmFWevK3JVw5NihQgMo9OYWEEqS+JfI2wDuMceT5EqoJVK7j08hoozf7dA+qqIV1LWNmaw9bTkwErBLUNKCnptVNop7gAt964TIgO0GOB955s0ENEioP5lHF/QrN/GVPmNGXLnpvzOTMWw5zcOAYPA3mt8EGwIUpSXXE4X5EqSIclo9fG1G3DcG1IVEQczKcM+gNev/Ua/+iP/+G5sfdJ3xKnhuoTcOOYev3piPfEzH7B+YtwEgQ+T76OcnAGRjxtl8WF8gzr+PlkLlhdOBnPU0DqMYGOOAPQfxfEeQFoeMzkeWx4fazAna3EU0mfMDRflKfnNfHvsFpxrFxctML1vPjE+fo/55rgeYrY07rDs5SLI+n3/rNS0f4O8gwt67ylXRz9PU/Get7y8J8ubycvhxNXwjNVxpP3T3FWPRFxweeClM+nE84FuygXT/J81pZylJh4/DmRn1O5D6d8WpxkzfLW08xLXGNwrcU0BuccURJ1tJlSInxn2U2yuDvbcKpUJ38cXQnh2IgUAsweHYIPaCmwZY1vW4K1SAE60mgtUR3nKlpK8jRGC4lxAWsswjmk9+A9AXC+s9QJ2U1sQggGkwHLwyVtY47CPMmHVN0rInzAeUdVNeRp0tGmNp2vhiAExbiPitSZF/05A+pRkcURNaHSmv64h/ee4ANxpACBiiTDrRFN09Ksaua7h+TDAlMbpFYEQec7RIiOavaIJi+KI5CCZtUQpyneB/wRna81Fu88MnRvlQ8BGUD5QBJFBB8IPlDXDXh/bNlzxiIRHS0voWtrBMZ52tbSVC3WOoyxOGOxxqIRHdUogjRPSPO0azcEsZBI75ECFHSrR0ripMD7gG0Mpm6OKH4TXN2ij6pVanWkBCiUFCjfTeQy0qg0Rmh1dDg6IF3AW4/giFrYeQgd5a0UIAK0ZUdd6ZwnSiKQsqPblZLR1rjz0K7VEc2t7upMy64Zj/ZPS9FRj+okJoSAsx7rPME6fGvwxuGt62h6ZUfji/cIZzvDieraUcpOuZVKomPdURInMTKNyIY9irU+cd5RxSZFRjHqkfZS0iLt4hYCrMOsGsJRP3E+oKxHuK7fSxfAOggBV7eIIxQlQkAcUbDqIkUpRdTLiIcFKNkdni46mtzQOoJ14I8stoHO8aT3Rw4VDbgAzqOERNJR6WZrQ+TRFsCOPjUg05hk8ngyOzMYnhq+ntyTcYQeFIRVDc4RWofyHgnIxuIWNW7V0kxXeOcRHmSsOproxiJ8ICgJUiIrg3AdTW9HQa0wi5r2YInSumu7VdNREKcJUklkFhMVaUfJHEBIgYiO9vm7QGgdpmzxLqD7OSpNEFIdjasdpTa+639CqM4w4UM3XjmPr0wXl+3GMKkkzoG1DpUlCCWRUuKNo95bILIYL8G1Fq0lSIFzHtO24D2RVuAD3loW0wVN1ZDGmqzIu/HQe5RStKbzDeKcI9IS4z1F3ilSUgmQ3Vhj65am6Si4y8UKCCRxjI4UQQikkoQQiCNNqjQQcI096vcdDbFvbddHwpOpSAAq0hQbAwjduO3ck/fm8TnKOI46mlopu/MLQhB8oFnWx2Pu4/nkzLD7THmch2Pin8fo9XlykRIhOO+WIjzlc+G983P9k3hPIoqnAJczefn6QPkCZqKL4j9XseIJYDjJoPS7yNk6enzZebz1uLp9giGegaeeoMhngMVvyqj7WFk9q1wdyTEb6IWg9tnRnkLDX0chfRz+d22HryHf+JmLk3k+2YdPK1dP14QvqqNT1x73UXHm3rMNCify8fjvCTQuzr9tT9vfeHGbfJ239bH2efGTFyjoJ36L43fnon1XF9bdiQH25BfxuPjPWLh6bAV48+2X+fyDXXpZzNblCWYRcee9KbNqyiBqmJVbGBtIfclwWFHHNd4G3ri+RmNTGmPYur7B6+/cempa+/szPv7wS7SS3Hp1i9/8+hFJIjl8OOfW1Yh7hwbfWm6qhraqiYKAKmVjELOzrFECtvOU5eGSvGyIYsU4kTxcdQd9b4wzHsoBoSfJEslmZvmi8QzGGevrEz7YeUBYu0TQgiu55suFRcUxI+3RUtBkHhEst8YRDw+n6Eiw3uvh0ojBtQk33rjOO9999WRzcMLk9bQKhgBvfP81Pv/kKwpRoKxnb6+kqUr6uuCVzStUvkQjyZKM0bhPU00wZcNLN7c4jDJ83qc3yKE0PIwCSileNpalUogA/Swi6QUWriHRmm1neKgVifLkWrAuIz6nQbaWlzaGHAQLNyLEKvBqMeYTb1Gx5tUrBXv39lA9DTiujSZ8xCFKSTbbmEfliibxqFqwRcZXPYeKFW+N1rk/CJTVgkxqftAMef+zB3gfeGUyZlEZ1O6KeFDwxivXub24jfeB677g06UhVo5sPeUdvcX72YLlruWqKAhGsHIS0Tp+1Kzxa73PEMkll9C2gTpxxFLyHZPzK7kgC3BJZARrqXxDjODd7cvceXCPJI4RPjAaFti66WiHr21weCWhCQa/1zBSKXKQ4pctPx1c41dul3rl6XnJZkj5RJcoBD9kyPssGCYJ/SWM65Qv1BJnJd/vX+L+lw/ID1sGo4it0Rqf37mPFPDWW1e4t7NLdiDojzU3r13hvfc/RkrJG29d5zO3T240aZ7w482bvPf5hzjg1eFVPo9KWgEFCW+Kgr9xD1FEvBqGzFzFMgQKHfFtu8EvxZfE1vKSSZFJzmE0QzvHd1YjfhkfIKTmap1itMVJTyIj3q6v8+HoAFmMeSXdxLgCt9xDTGu+Ne3x29GSHMWmzRDCUw8hax3fW4759XAHp1rG7YRMjZFZIEHx4+gP+KT8FYWJKZKMV5JXkVG3rfDU1o8zr9DrxVt8MvuQfugz9gO21l7mr3d/gdgxvHVnxIebEX1rGMiMt+yAvy2+xDSWd+ZXOCjuoJykSPu85V/hl9FHuOB5e+8yd9WUOrZkc8874TJ/03uI9IpvyTeY6tuU0pFkA96tX+Jv1a9IopxXzS2WUc2qWpDImB/I7/Hz5q9IXcQr/VdofMXSzhG15Scbf8Ivq/+IUJob6lWsMFTVCi1j/qD4Q/66+WtSodmer1ECM1Ghk5zvz17n58kD+jbiklqnnJfU/YKYjB9c2uKvH0BfC8YpRFaw8grnHa+MKx7MewRvSYMhszWzOiKJU8Z+l/utRXnIs4KNXmAeW9rGMIkVTdojXrQ0y4pxEVOtMkRIuLGueXDoSKQnzyRqtscuU1zrmUjHo5mgSDJSGbi1VnB7Hqi9Z5jHRCrDLBwSxesvv8znDz9DSM31tUvsHpSkFSS9gje/c4uf/80BQXjeWe+x88Ud+o1AasVLuWdWOUKAUaLI+zVTs0BYxatbV5hnjrZuuLp9GTWMqZsaLTS3rt3il7/6FVVdc/PGDTyOr+7cochz3nj1DeIkPtXRnjUrXoxyzv56gvie5qvga8l5MNDN+SfcT1+47ebizH0tOafXv2AZnmCbo8y+aNm/BliWWhOsQ0WdbxwA5ywf3/2I2eKAzfE2ty69gpDPQloXpH9SzpT5wm1pz5FTqw/H5Ts6BXS2vBcoROca4Wl49/dRGn7f58/IN65cPEs5eAJwn97RTioiJ2H4WZaHk4pBCBele5HycDJPT8npSWPZU/3Gn+4NFxblKePP07rk6etPOuLJI9riRKTh+Klw4u9jUPsk1Lm8PavzhCNt2oUjh3Pd58EXc7J4gClLFjvw6c+/ZH+vQgXLPFZkLGm9onQrRlstyrSM8pTrP73MP/hHP6VuDP1hRpTEFyZflTX/9t/8DQ/u7xFFmuDuEydDXGvBedodSVY7nIPatER2D+mgF6XYA01uulgXbXdITraWLItYzgOpCyQy4bASMJogvCBKFQfTfVSUUS49732wgxhuYb1EpIodAWrkKK0jLmKUc5Q41jLNgT+klR6tFdlazp/+8Q9Qk5yXvvcqw/UT2zkuOGtxVgRdv35wd4ekn9I6S9JLiZsvjqx5S778sOTK69ep9paIPOXuB19RbI1xVcv9lSO9VOCygntLQz1QSJ3gnOVulZCtDIgYG2vmoxYZLFY69rQmiQSNFnhheRQCwncW7Y+jlvhWSh0MERGLvCBrWmzj+aqGfH0D6wRJoflktIfPhzilmA4KVl9JKu2IiChfu0TatsxmS94LjqwNZEqTV46d9++wuexWftq4JYkE6bKi1xdUWzGDSY+9u7ssex4pBVpK/LTkA71LMswogX3RkIUIAkQGPhVTEuvwwVGp7pxHohPSOnA7a8lbhbGOVeZx1qFMIPHw2d4+uVTdJBU6q3Yv0cSTPl+kFX4Uc9AaikzDWorXkAxyfrm4RxwpUgkqOB5FDZrOCd6ncYmuHU57RKTY95bIKWTZcvDlPpOPavThkvWRpHYLJliiLOar/+fPiJIYtarQ+ZIHf7OLXq5QseL2bkPz+oCQBCIv2f3sNpuVwzrHfH8HdbmPbyyhCnxCi6odKpHs9SwyCPCByAY+iXfInKBSit2kYmCXKOVInefTdEoeJCvh2I8bkjxGikCRZHx8eID/aom4NuHQSwgtaT8lj1I+j1dkjcIKT9tz2H5DqgyDNOF2fociCBpd4ocxbl2RSk1aSm6r26RtRBUkUkfM4yVrF42EZ/DATvmA1CWsrERoyX2zIFZD/OyQL/qWyGaoPEXXkvuDO+S6xkvHw+QrBmlKKVpCZfhU3SURMc5Zvir2SHRGnMVkNuHj5aeIWqDjwJ1wh0xrAhK58nxk3ycZdNvBdlafE1MggyMXmi/TTximBcvSMmcXKWNirejpHh8tfoO2CgNM2UHFMTKOSXzK+/X7xMmAuj5gtz5EXlpD1RmJyfgofUjaKloB04MDGjkmkgW6SvjFFwvyeJOm9ZgqcPioIjSSBMH+IifF0ViPIFDHfYIzBCeoTcyGbmi9JG7mrKIWn3hGGwWDyRq9/jr3P3vEsp7zaKpRMqOsHXceetKeJBYKv1rycOc+wjcQAtl4wtp+SW1qQlvxMEgUnRf4srEUEiKlEMHzcH+fOEmxbcve3gpRFcgSorrHpx8foiKNtZbdRy2b04ip9WRRoFWG2Bp0FINf4foloV4ShYj6ciDNclpr2NnbI29SXGWQOuP/8+f/BqU0jWn59JOPIRIsyxVFnrNcrfjpj39ybAx6Nr4KZ349mYmfOdi/qFz4+O9oZX/WvWcV8gVB5ovqAF+b1vRpIDJcHEwcnXN8LB9+9R6/+ewXHK6mTAYbKKW4sf3S8VjywpTB563iv7OcUipO2kzOYszn6T7HA+JzFMkXvfci939H+U/EFnVeztXZM+rmdNUdgeZnVMDF7XBeMTgBv5/14OkMXdiOj236ZzcbPSNTx6uC4UTnenoGAl2ZT+b5hML7pM+H04xUv1c/ObKECPk4zS62vYdz9h4uqKuWcmbZP6hojCCPM5BwsGqxwbE2iijtisY2JHHKylmSXkI+uICa9URGp9MFq2XFzqODzvO2UHinOZxWtFYhHKwaCEKzV7YUNmCdx9SGxnvcEcVuJAIhBFrnkd4TELQuUDUGHaW0DlYeVOPQjaU1nqqsu0PZJuCEpA6SyjpaDwFF4yBYMFJz0DgK23TtIOGwrPjywQ7fuvY6vWHvdGt+DQPJ3qN99nem1FWD7+Vkw4J6d0rVNGT0eHRvl8XhEuMc871DqhDQkWK2bMgWLUZpGu9ohWSGRytJkBEmQCslB8HTSsEiEmilsFohBVSi2xblvaER4HUgUwKwVMLjgiO0ndUbKdCNp5UxqwCtNSy9ZWFWuCYwbypUT1L6QPCO1XLGQnrIIW493llKb9g1lqaqEI9KLLCIBHEesVqU3VYsBfv39mirhrqcs18rqoHEi4Yosbh6SSUtlpbYtKwi1wGC1CCDo/EWlTgkhrlrWQSPkwIiqI0l0GJDzVwaai1olkuaw5baOZyzmOBwSjB7dMDhpI/xNXNX00pNnCYslWNuHXEIaAsr36J7CRbPtK1QUpFbgdawkBadSsysYmlbiCH5+CGDRxX1qqZdNQgVaNsGZx3BQxLHyEiCFiyWSw4eTRFCYIeOxUFDnYEvW3AOuVp29zZSplZwWC1pvKJ1LXXSsejUIRCnioWpEVHAa4vXLY5AQLNc7bPQlpoWoRU+SNrgcFojg6EMAe8EbWrwgJlPMbVHKs3cN6jKERIN2tMGi0haXNpyKEpq34B0xEEylw2xBt0aFnJGEkWUS0cqoM4sh+2UXbPDTfH6BZa607Jf7zFtD1iaBUYrpiZmP20wvYZ0pXBRxaxeEXSD0EvKbIXIBUHE2NQxp+y2rLmOwlUAg+EEoQKHZoHRDXUsmdFtGTNCoIJj1s6QuUct51jvAU2bKKRdUKYtO/VDZB3w2mNUA1Yho5RlXOKMIziDty0+otvO0njKqKL1NavgCTqh9ivaQR8fDpiGGWVYgeohZdz5gokSnGiZ1Y6VbGgqTbxXcThdkc5qbK0oW0GeFdSzFb1UUzcdWUKhMpxUzFYtznnGeYZZ1iS5It0aE8cBGSmaIDHTEq81yWSd+f2a4BQejTCGpnS0eKp7+wSgtp58kKMmIzITERqHkYpp66hQSAlr1iKUw0nJ4XJBmILTFd45WhUTmkBVGnYfzlm2ktIkIKC6v0s5N4Q4g+ARwRGUxLYGly8R0zk6U0R5xmGzxK3mVIuSTEUY0TKbz6lmS1zjSXs5xjkOHgSifkyLZbVaMhqOXmy8Dk/m32fLBQGOgeULJPTCcjqubjfGkcPfp20h+TrRnpTHcYbTl849+pzF+t9ZLsz7xQntzXbZn+8xXx2ipGJvtsuN7Ze6qn9a5p6l0IjT98W5PW4vKM+yvF+0MnX2mRdREs6Gf5aSIp4W5mssHT1D/s6Ui5MW9YsWBC7G4o9XH04fjH78wEWKyu9TLaeeFRxtGToN3k/n72uA+WdqohcFvtgHeKd0XDx6nOynJ1czziZ2VnE7Vb5To0MXy/r2gPWHc2bTksh7EuWwkSCPPV57cqWpnCSXDhUCUZJw7cYl1tdHqJN0eyczd0LG4z55kTJeGxBHGilyvC+Y7y9RpaeIFA3dIdu8yMh1zbxpkUlEJpPuLIHzJFIQa8GybIizBKk1qmlxIRCrQKICtm5IpCYSniSNwFmUhiLTtLWh8IEikjSuO0shnSGLFT5A5gQ9qQlxjBXdPt84jdmdzXkpdGcGzvXJF+iM61sTNi8fspqX9Ac5lC3VvCQf5Fx95Qr1osasD6j2F4xGA0Bw+cY2g1bh8gxTt8iFYwG0zpEJ6KuAVoFVaxnpjLn0RElGIhUyBGTwEAJDQAZNjSd4UCiiKGYaDBsiprWK1Hq01vSLmLQMuFgxVIpURcQqRUSSnozAeDyey3FG6zT9tjv/0Q+C2ApkbVlPErIC2n5gVTZI58mUIvRyEq2gtsRKk48S7Mqzng+Z6UBhJJNizGpVMcWw5jRFrNkTloGRRFLhTEsdK0YuItIJhID2oXP6JwWz4BkbiVcFyniKNmLQ75FtWA5dw0inoGB3PictErKlIzYSIzTrcU4cF4h6SWwlqRcoKZACrgzGVLUBE0idIGocSRQBLZs+wgA6dHvRi4Eiki2tlKQ6wuFIhwOcscRpwvrldR5+9QhMILSeyfqIfFhQRwoRJN5YtA30koRo3NV9nA2I04LFwZyx13gZ0QbLqm2YJDliZfBRzJZNcE7h84zKVIyNJEMixin9KEU7SeMDpW8ZWon0IIVj5BQ0HkNKaQOjxgAOI1qKRqMaidewjAXjVYoRJSLLGIQE3XhE8MS5pl/2iKhRRaDvczJrKdb7zPSCUVhjXW9048Pjk4DiCIudeYcm6TqTZB0lNINohIwiVIgR/Rw/rxCyAFrGVY5Qnl4r0VlK6hWZTvErwzYT6qaiICM4S1/2UE7j/Ir1qqAsIQ8GGywjmRI1hmgEl8QGPsSYssa2nkEour7GIWM9RJiWoAVNz5IvY7TI8dIxUoPuIHUaKEXJKIw645E8ZKzHDIWkJTALipEYY1uJWawYhBxFH+8i5qFiogqaJqNdNKwPesj1HovPltSVIU88znYIuFA1VtYUUYIeSKQ3DHsSLWN86XDLwLCfYFrLrbeuk29LVqsSHSsSmSNdgpCe4ZUxot5h/6BGKUisJYnAB0msPXVrWB9mXHr7JnlvgLq8yb2P75F60EvLvHbU3iGEo58oUBERnkE/R8R9TGvI4wKaAkLL2jgjrhP6ImX/qz3Mcsb2xohFY8gUxF51xhBrMCvPeDMi31pnsj6mWtYIHZHFPUbjztij45QiTQgmYBvH7r1dtBCkvYikyBn0+0zW1k9MdydQ14X75C/uk2dCnL/8NLDydeUUeDxhAr9oV8c3KUfFCv4pB5MfZ+8iyHHy2tdQdM5h5RBYVUu01qRxempV82SeJsN11gYTlFSMemMmvcmTQ/UXAfBnydn8njM0P2uL1BnusBNpf+2tVWfB7wuHfYp8DXzyu8p/lgPdL1KeTlk8cWxFPFEgTxkAHsuRVv3Md/7k53n5Ck+uiHBk0X/8ueC/Z8rZtI8+T453X6S4PDnKfrLkJ4+0C8SRG/gT4Y7dwp99khN57T4Xpn9mdAhBcOn6GlVp8V4w2howulRgCsUiDmwOJGXlMK0HJ7ka53znjZf50U/f5Q//8Luc1gKfVPLJZNIsod/v4ayjaQwvv77F0ghmVUvlA9lyB7XYI29mrMmKOhgMHq1gra/QviHYko1xglCeIAzOt/QLiWlLXFshqynRcko630dNd7mUK+yqIvKeq2mgmN0lmt0hWd7nVV2iD/eR+7tsuiVhTVGPJOWaZDJUqMSQjhWXXl9nL8y5v9rlX/6rP+PRo50nNRnCic+zu8cP//jbfOfHb/O9n7zNn/7Tv8f1t24w3Bqx8fIlXnnnFqvlitnOIbHSyBBom4b5/pw33rxG2QZUnqPimGEsCZHCRootu8Tdv0N8uENxuM/IQxMsRnheIqIVDlRH17oRJK2AVsBlF7PyYJE4qXnly5roF4+I/vYBNw6WLCeBctBQDixb/RzT05ie5lrcQw9SVC/B9lO+/QWMfrbP6K92ee39hvH7cwYfzNHvzdlMcqpqhbA1G1tD2rrFlDXNqvP5UNcNLngmIqco+kQ6wirJO/0NWtWCcqzLmMhpvA+UTc2raoJNFAbBiJSxkAjRIiPH621GhcNrwcAqBpXCt1C1jqs3N9n5Qc7sJyOan6zhvz3h8N0+8z+Y8KN/+gOiaz1sDukwY9wIvHN473iJPiaCoKA+LNkyKT5AKwWvhSF18FgX8EFyScQ4ZWiV4e3vvkZ0dGjchsBoMGC+v2Q1r7j1yg0OHx0y3Z2ymC0ZjwbdikbwXOuvQaTwAogk/avX+PJyzp2rPYY3bmBM50HehsBrco0Ki04kl9sUTAAXaJXgFbfJSjqsDGzTQ1SGuq5oB4qbzZA2UVitGck+GT1s0Kxc4OVyQC0FNggKn5FlHpMvqPozbjjHsveAJn1IEqZsuoCXK4yb8sZ+jpOHKLGk7x1baoIPjqaA17M3qHSDcQ1tU5NM9ZN358iwdNFw/cbobd6dfJ9vT77Hjyc/4VvRFqlZkKYt3+1t490D1GCJSufcsiNMu6BeHXB9uka9KCGKMCHwcnUZkwlsP+KWuArCEdoSE1a81Y4IxRKRr7ih1pCRBimpcbzqX6YOhlYFtuRlZJJhpaDNBS/xOoeuoUSwPriFVAmNtyxCxQ1eY0FN6Tt2qjjuY6RgLhpe0W9QmorWGnpVSr8aI8hpguaVvUvUQuNDSmEH9D/ZItzeYPXxmKt3BOVUguiRqYT1sUf2PU1qeOMlEMuHbPRavvVKwfZaQmsDQce8fHVE3UhklHP3w4ekVYxfpLjDlJvXtmj8DJ+UROue//b/8l3efbXHVq9hyD1is89AlmwOPa9PEv7on/6Y7/30Tf7kv3wHk1aoy4r4VsKra5qhhL73xE3NsunRhDVqO2G9/xrV4QbV/jrrwzdwfouqGnF40OP1VzZYfHaX2Vf3uDoWJMkDtL6HDV+hmjssqz28WHHr0oTrl99GVeuY6YB3X/8Jsh0h6yHr2U166hJi1SesBrz1+g/A9Yn1GpP8CsNsGzPT7N9eIvYDzao+0dGe7U0inOiiT3YkPEe+JuA/Jn95FpnnsUU9HE394hThCie/fxMSePEtRSfz+Dvm5WRwHzx/9f6/51//7H/iX/x//0c+vfvx6fOkjxslwFvX3+E7r/yAb7/yfb732h9wSYzwq/ob079OtstpZwKnDcLnjLviwq9PLlz0ecrzF8rZuj6h0D7tv1MMChcpwL+H/B1R0Z5bd/jd5GwUF2mg4sz3F3n2giCPO+y5YeaE9nl6deA55Tu/0HAuE08rzjPlIs36XJafkreziTwl2L/4H37OR795wPywpL/e596DQ+4fVGhvUa1E2UDtFcNe4M1tyT/5737AK3/0rSepn7UuHKfXVebe7gF/9i//I59+fIco0hixiWPEb//mKwo7Z1DvoFyDd57gKkQsaFpDmiZoIajKBkTHHpWlCbP5ijxPaZsWIQRRrKmbADrBtJ48UnhnwYeOXjEVJDqwalvSIqNuNT5IgguIy0PaK2N2RGAUYDy7i/YV8bhAo9h++RIHsxnj0ZA33niN/92f/vGTpjl+Yc+U+2yVhydfvvr0Hn/x53/F7Y++JBKS5XTJfGeGaQ1aSJQS6CIhHxbMxYDs6jXmK4OvF1S5YxlLpLUUn+4w3FtRGU8YRNTf2aK+VODKhkhLciWYYZl4jXEwD+HI0mCIZUedulErer8+xO1WHQPLrTX8rTGHWrCeJjS9kpVuCVJQBIUOkj1l2GwUg7/aQ91b4ZyjSBOUEhzMlyjRAXRnLK21DAY9tFQcHM5Jkpggu/7am/Sx1/pMryXM8sBAJ6iNhHqxpAqGSdQnThL2aOhPV+hJnzjRLEzNhszQUrAXKoYh4rAJCBFxaErW2ggc7NuaVCi8cGgtOFSWLVlg5jVz5chQ+ERgWsMq8VyK+4TGMDUlSVAkRUqsFLtmyZbs07rAFEMsNIkPJEGyKxq2SGibilm9IB/22PjEMPy8ZeerHbI0xRpDXTcoJUnSCEG3HSpNUwjdZBXFEfblPoubGQ9lzSjExFd6sFEQtGAcZ/hVw4NyyiSk1MLQOoNINX2vEQh2WLEhckxuaH2LjQIboUAaz07UsN2f0CxAh4iVaxk/ridtGMmU1pZIEVgpx1qAkNVMs5K+ibFJjQqOedKwYXN0EtiXBwxtSmgqsjhjphZspFsYazjIVyQhIZ219BvFvNdwTVzjO9U7/PTdf3Ji4fQxqYY4M+ZybEia2in/+uBf8Gn9KVJInIwodxc8imaMmwEknsrOkHFEKnLy/oCHYp/JqkfrKpo+BGsZqD565XgUTdmoBzSuofIVNoJhtoFqJXvJnIkd4sMSa0psAsMmJ05SdsQ+63KdVjmMN5SmZBIGxGnKjnvEmlijNSt0GrGoZqwxRuuYfTVl6PuUTefErowbhtWYEHL23IyeS7E+Q4uCabtgMrtM++kGj3YDOQG/r4hJ2Tlo6UUVIjEsA+SZZjxfsC49XmriOGbqe+yXkkRBTzWIcoZREXZ2QCohSmKyPMHLOaow2F7C1RvbfP/7b/Lmq9fZ+/Aud3/+MUmRMbm5TVSkyFgzfu0yUkr++me/5Ze//IgHD/ZZX1+j2VUcfjmjLVvmjSFOetQ6JwoVo1FK2ksxjSFNc1wLhwvPZCNlee8+hzv7qDgiKyoa9mmkpacStCxI8h66l7G2NUapiIO9OcNxgTEdE15dNQzHPaSEg70Zg3Gftu3miOVsxdrGAO8Nuw/3yOKIYZLxz/6P/5TNVy6dHp2fM/kej+Hngj9r5eKxnHHi9zRA8gI472LfGhfI0w3sxxjhmbFciBNeMJNnwE3HlnZiJeECmHXysUcHD/m3v/hzPn/wKXGUcDVZ53//p/896bB/YfqPt7AFQse+JsUx/riILvh5Eo4iPEn082Rz/EXXzxTkonr4mvIsOPuiMZwxHT83nt+HivbvaFvU76dYnD7b8MTL5ol/LvhxBs+f7dyPVznOAr5wKtipaMOZH93vCx64KD/nlNhn97Ln9cGT3jbDRZn+BiWEJ5p6dbhkOS+x1gOBSEik9OACkez8Goyvrp/KzJO6D+dWRo6Vj2NDf1ca77tno0iT6gy8YrU/Q8vOw7I/orr0QuJDwHtPFEc0jXmSZzqq0bpuESpBK0XtLVJHCKUpqxYvBCLSeOUoVwZfS5rGYYNEIIi7cQkFKClwgFaC4DzxIO9uhkC97PYPv+im06cNyY9Xkh5boUzTkuUp5aoiH/SwxiC1xjUWMkm7rBFS01sfsFoddFSsSh772nDWIZ0kjhXL1mCdQ2mBD+CCp308NHqPlwItBbHWKOmw1mGNhaN6llpS1xafa4w1tM7hdLclzSKQPqBUR/sqwuO2DXgBOo3RLsFXFmMbnPdk/bzbFvNohnPueOnaOk+1qNChh3eeumpIdEAuuzaHgDvqMEIJZK/fpXOEOIPzGAdBdEoMIQZ5NJkIQQj+GBAY79FSdx57veuoYL1FRhIvIS0SKlcTjMXULUILdJag8hjhQHnVeUQPdLTEOuDhOD3nQegjylnZ0WvqpKP5FeGIgldJdKQwjT067wRpHHUe15uWQFeHdd0isq6vozvaUu8DbdUiqs55WWgNVnlCcBgnMEESWQeZANMRJATV0TDb4EnzBExDvaqQ6QBfBoSWYAXBde+mbQ1BPraMds8+pl0FEFohlERoi3cBoQXSA0ogE33UThLvfUd3GitE3Y3pzlh8WeNVi1ISgue4Eh6/SxcZAMWJ90U8thp244JvDaofE6Fpyzk+kwTnIBF4BcF271jwAbesCSLgXImoPGIUEHmMcIFQN4iooy0WSXxksezid8HhfZc3ZywhCtiqIvSjJ9ZmIfDGIBONa7oVKO9cl5dIHr/r3jtErAhBdvTZkSRY8MYjk4jQCOzRuCYSjR5kyMMWV9WEIAlaggCpFC60HYWz6bxYN1WNR5FuZcRpjnIOvOv82AR/PBiZ1mAbh6saZFZhqxXaFcdliXopl77/Mpe+9/ITPBiO+rGUxxwt/ih8CB5dFBRXY+T+gurRjKZt8SJBxpr57iFRso7UChVrZKQJ8yWHd3ZZ7k/RcUQA6rJGFoLB2pB+ryDSA6I0p21NRzt7pIB31Nkd3XgIT/pDgGNabeRRn5Ud7XecJ8Rpwub1S6zf2nquRe+c3fIkBjl14wJL4lPA87HifBF2OHv9LLo8Tv/3tzQfbzx/inGyK9YFczdPra6zQc88deLaBZjlAnXhqG3DUb9ztAczkqKHUBeDuPDYOi9PGPHEeaXiCb58eklOPvO0+n6uH5DzRXoxOYr28bv1u7f3eWXipNJ0nNdn5flryN/ZmYuz8sLa9rlQ4bj/HKscxxZiTr3k595zAPG4K50IGJ7cO53qk056OvLH6T3t+nMkcOx5+/eRcLIMF2nNJ8JdeP2peTjWnAB4/d3LfP7xHkUfxpmkOlywqB2xgKuDhoe7ngRIVMLmZsrHd++Qzw94482XSZL4GCQcHE65/dXnRFHEq7de5s7d+8zmM7Y3t7h+61IHXqRg89IVfvaLFb1CkouEd958ic9++wVmtmRrXLBfroiLAqk6AG6PrLPb2xMODuaE4FFacWVtyP50iXOBtVGGI6JtK9Jc0+/n3PniEVpCkqXdYcb5CukFN29ucP/BAQHB2DvqoKhmDSqWbIqcXZei4wEvv3EToVqaqgEbuHb5Mr/6za8w3nHz+k02JpPntN+J5ju6cOXGNv1xTm8jRktNYkZU3mO9pRdFxFGPisBqb85r373OopC0bcPWpQ3iL+d8NWuJY83LVyY80AarIkY2ItSOaqCQseatkPGVaGm9IGks10j4IDMIrXibEff8Eicla+OcW1uaT2f3kcBW5djdW5FYSz7Iub6hubM3RwrBy1sTltbSn63o9wtuTdb5/KBFCXj9B69TripmP/uINNZsDDeYm4YkT/CVI4kjTNb5DdgYD3g0neEay/Zc0txMWAbLIM94eZHxUX+FEpo3L13FBqinj0iU5K1Fxoe6JnUR61UEMmDwRKbhB1PJr7cS+laxFbqzGI2zCBd4p+3xASV9FBsyQlhJHbUo7/h+u86vxB4DJVmXKf2oxyfukKiGd9Uat5MFBQkbUU68krwvpiRS8H21zidqRc8GBj5i00R8SEMsEt7+7g3uq7vQt4iFZ7uUPHw4xXvP9SubHC6X+BAYbY25ev0Sn33wOdY6Jq6Hb0vyumUy7vHy8DrvpUusdbyyytnxjmXQJDrmbTHmb909lJPcMD1MKClbR+4k7ywn/NXaIc5bXq761EnEKlQkLfyod52/qj4ndY4roUdpKsqoIfaaV/YzPrm0Q554rpUbnVLjpuSJ5DvVy/y89wnCCy6rDZLa08qa2Gm+u3yVDy/fJ0exvhqQ9gbcdV+hjOdd+yYfbz2gMTOiKqF/mPCzh/+etOjxeu8NUp119sDzpuFjGasxm3qLHf8QgeDV3lv8df43NNUhPZFzuV3ng+wuQSu+K7/FF6t79K2iUAVvzLf5be9zXKR44+E69/WUOtakVvGafYnfJp/gVcTr5TX28oqyXpBUgTcObvLr7S8QOubm4TbzuKaMAonO+bZ+h7+yP0d4wdVmmzrxrIIkshHfM6/zK/kJmXFcT69TrirKWBAnOd8xt/hb/xt6YsDV6DLOJLRBkDSa74aX+AV7xFZzdbsP+xNW7T5mXvHdWwm/vV+SFw2X1zKW+3NsG6MDbA8Vh/sZy5Wlbw0vvT7GfHGILx1v3BzyxXtzTOOQwjJIPGUDOEdmDft+jljVyGabje0BP//1L5FC8urLr1Dk2ZGdqBuvH49jr712nQ8/+ojhWNIbKK69eomPPvyUfAg3N8f89tf71PWUXpoRJQ3T23fJioytq4advYpmd0GL48pEMi+hagw3r22T3SyYlY6iH/PyjW0++3KFUrB9qc/Dz/dxC82irrl0KeXj9/cRQlGEmrWbW1RVgtKKb799k/d/s0ORj9jeHgEWU+ckqebt77/N+79+SLk0XH9pjFKOL28/JM0SXnv7BnGsT4/Xj79fNH0+0SsvhqzHGP4Z1u2z1y7CFC+KL0+i/2dAjmM0dhKFH5flaYmdKMWFltiL8/o0+/mz0ODGaJNxb8xu1kOpiKuja/z5/+3/yuin3+W1n/59rm3eOG8oPi684LG6+U0oYs8uzRl5Flh/2oNPa6dT8VykCX+9Ej42zJwi0Dj77+8hv7dycRKCP0vCBd+ebr99VoInOv3Xe/JxBF0bXfjCiKPD5mf3Or6g6vksS8PZcL+DdPrMEx8dJ7XN48HhorjDma8iXGCFOJPSEw2OR/cXJFlMU3sWi5ZV03kb1gpMFejHntqCMCV3SsPerz8kTRMO9g7503/wE0BQliV/8R//kp39XeI45tfv/RYlIuaLBZPxmJ/84Ie8/fbLKCX5+LMFWVbRG6TosmW26vbkI2C+aomVxnqLd+CDo0hjGuco6xqtFd6AM4bKeASK/nBI0xisr4mjQDHQzPdnbG4MKZcVTVmTZQWRiugNCoxrSHOJaS2rtsU9MkROEFeBHTWg9gbqgp1DwVrPIgP0Bn3++f/4PxPlmniYc+f+Xf7h3/8HDHq908ovF4w1J2aqVVliVI3KAzhDKSqkjCkmBTGKJEk5+PQBwsPdDz8ln/RJJn2iUjHsjcl3dkmNYGcsaN8YYHA4FCHVZAq0ENyzNTQerwKx1jzMWkQmUALutytUC1IKlAncXyzIsgTr/n/M/deTrVl22In9tvvsMXlOuuuqbvmq7qrq7gIaDUMSJEgMySGlGUWMJhSKGc2DHqTQgyLmT9CL/hZRCik0xJAg4dhDgCAI00A32L7L13Vpj/3sdno41+TNm3nvraoGqZWRmZ/Z7lvbLbfX8rSzmiuV5mhVMx70xA8sV8RGYhg+6pkUCXQdwyJyp+1Jhhn5dEBrLYvbJ/jWEiKInZQBCce3jlBSoFONNpJBmbNuOgSSclzgJgleeNJhxs61HW7fOSb1EAcpC9fStw5rHUakfKBbDCmdgLUGw+ZAdFL3fNRXZIxorKeVnhADzm1Mnz4zFtWB1VDbjs44PA4t4WdqxkgmoCwhepYyYoJGO8GPT+9hCkMUnl4FGt2TuIhxnvf1Ah0lEoHSihPfobxCOcn7YY15Zxt/HGhmPYd/MkPqhEzAfL2Jdq6NJs0y7t09Igqo1jXhNLBjJLXouTmKnKiaTBmq1nK3niGNgACpNnwU5gxUSh0dy9SSdJsyjYWf6RlZ0DQycqJaZO+QWpB0kb+efUiaKVatZa6XxGGPSnqSLnLvpQWprAmpZZ05dC7JcigDfNB/yCDReNHi7ZoqaGIHxmneHx+TFANq29OVAcmcZN6QrgQfT+4hsgInalZVy78VfwLHisJNOLHH/MbOf/HIjvwSsFjqekViNUpqPrO3SQc5VDPMIOXuKKCqlCgVt7ITTK8QIaC9505ySKYyHHC3qJD1xoxLkHNrOKccTun7luN0iVtYYiIwVvJJcY+UjKA08x1P6BJEkmPcgJ/Yj9GdpFeSmWrQcgt8TsKAj8cVemnodcZJt8b3kmBylBvxU3GPvNjCugUrHKECIVJSn/KzsEL7jGRQ0PQ59tATTwJZZ/jpvQopGpCWVdNSrQXRgegcHy4kWZIRRhn91pDbn91DJpo0EZys1uTK03eO0NW4PMPj8c7R9UtE0YCwdMsD/uAPv03XdyilODw+4jf/7m9sAlHeX7cekDOns2Oy3KOrnjSzHM5/SDJsiSEgt8ZcO8j56ONj4rxFlBmJdjSrNR/+dIlJIsNUohPJqot4JLsv7DJ8aQeVJpj1mmGxxcGBoT5YMZ+tuf3d23SrFi8SjPScfLAmCEEg8pN7x+weQ3F1j/knx3z4Z3eROkElKW4Ow50B8zuBnb2MP/7920gJbRf42Y/vIsSKal2TFynL+Zpf+/tfv3jwPTj8feH4PEfkiUuunwXx/l79pNLgc5Tx9HrPatoenSU4l//cgydEw+fLFo9SPlMr8BwIafuWpm9QSpGahB/f+iELs+Tu6QfMfihRUnFt98aZQgWPxfASl9fz82c4Hiv88f9n4TLy9zHcPUog79Onlxf4+b7kb/S7+TkwF59Ts/PY1ZNahctn0BlB+tOtTsQ5Zl08mixnCfDLJv6DibAZmw9ynFWzbZ5deBbjPDyT0XjE5j+uSxGXjrtHUo/HVYuPeSQ4c/FI83imMeGyBp+r6n6SwztLju6taetNdOyVhTYolNGcdpYssIkCGx2dMKwOTjBGMxiWm6i4UnA6P2VdVxweHyKVIlEpShjqukYpyfHpKdffvgYxcufuXY5PGhoHXWW58/GSk6ONhNyFHvCbiL9GYb2l6Xus8wgh6XtLcB6EhHXDetnBsiHdBCRASji8c4JrA0I2tE1PXhiqJfS9pVo3LFcVQYBzjmLnCqve41RCCAEbNjbM1bwl/+Q2fi9SrdbMD2YsmwVmZEjqlKIsOZmdbJiLB+i+YC1+1F2bPj0+Oqaq1szmc+b3ZmQM8FWHc47WC7TsaDtL8IEuWGrXo5crnDR0xQ5me0q9qqlZE3NJoyQiSCSBtXeIeN98TUArAkfGITPJMgngHV5qlBKsvEPWkTIG+sUm8m6iFasaeucRSqC9w/UWYsQVKVjLum5YLxvScY6MgvZ4werOjOpgQd/2TK5MmJ0umB3PIcQN4xI9fd9jUkPTWNrOkoxy7jQLFj6nTzNuL05pVI2LgegTOD3GhshKelwICCMw0dPLgDQe5R3rDNrGUg8UxIbWBKR0WOdZSU8bPV6ADIFeCYIMtMJSp55GCjLZkyGpccQA0cM6OKIPCAGqa6mkQ5WKPnhWiSd6x0CC8IJabyJzKxlYSEvsljTLQGYSFtIy1BClx69b1sFjjADpCSJw++M7hOBBSzyRXvb4ALqQLAvBUb/mztISXKA0IIKj0o4T1WJdT4MlKAhElOiZOU/IUqLefL9NFBhDlIIVHb2RWOnQuqCiwdJhMqgzizURb+ZI1WK1RxgwqWCZ1PS+x2cRYQN1aIiuB5EyT1rq1CPNgiKmVKpBdT2tFqz8KSqRuCRCzFmpNSoPWBS9bUjqiqEeYmNPItKnyqAW3YzaVcz6UwBsmlIVjlVbIdwBXgqWYoEUkna5QhFZmZboTgkDqJLNuax2VIKGpenwcokeKVpd4V1P7WqCEawLDwRU6ulkTYzQq0jQsPItLnQ4Z7H5xstUCBr6jhUtPpPEsMKKBTY6kAk+Nazo6doeP+jBW5rY4SqJVEMWbU1LS2tADUe0eO7e63AnK05OLUiJkB0mi3QI5nXEi5Q2KLxKITo6C23taD84QiUdPktQUjDpGvI+UjU9MSpC67EeQhDIzCGlAwKzekl1IDi6d0wxLhkNRzRNw6AsH8aeekAEHR0fMV/MqaoVxI2nuLqqsE0Pq4ZktE8+KlkvK5ZNRRQKKQRKyfvCH4/uQZmS4f4OlDnLytPcPmS5bDm9fYp1hqqyWB8RzlMkQ2wf8TFgHRucBMAUnJy2rN2c5fESvEKEjoijmtdkByuWq5ajz2Yb00qjkMaws5fQtSe0TcPWzpjB8AI36g8X8SdE8pcT0l/YUOH8vv754aFm4JK4XU9oJp4mJN1IZnleTcBzmwqde3aeKZmtT6jbNfP1DCkVRmvU115luV6SzU85mh/cZy4eWF2cWTQefnZ8cPzisXdfBrdfCp5F2z+uePnP1swvCn9DZlHPw2aLCyisy9M/awifzfP4XLiQrXlUzTMH1+Pn/y/V0jzBrZw5yPyUsh/8e1xPcqaWyzI/mECXzN3L4Oy8ugzt51W+070BO3sDFic17fEJBkcuYWigiJAqhZ979q/tsnM9YbVaY4wiQd63++0ZD0cUec642CbNDEYrpDAILxmWAyaj8cP69nZzdqY5XTNEqZasaTflCYlWEpTCdj1lnrFsPJlWtDqghUBnKW3bsbe/zeK0IS9SpBQkWlKOEpZVQ3AOk2p8AFVkKCMoMkOVp2RpglCCtu8phjlaetII2gi2tKINAYTAAqnQTCY5MjqSLYOaQdVUCBHJ04zJeHIGsY965cJhd//BdDohzwuGwxHtYc1WPkAPEmYnc7RQxDZy4ysvcvrxAYiIkoJ6UdMfnpK/ts/uxJBdH9GPtqnljFu3DpnmKVFIdNMhA5hEk8TIiZBsywSnBIntSZwg84o0SoKMTMqUTLf46ZCu7hiWKSZLmC0rxmWBrSuclqDkhsD3HiME0ysTpi/s0rcd1bJiPZuRpobJ9SlFWbB4f8FoUCKJm3xCkJcFZZnj+sjoxphkXNDPV6RthrKQ1o7JaEztehofGekMoQXR1kxiggyghWGlPCMMaZQIISikZxQiwSfMrGes9eboQdSUDiwRqTSVC4xRZAgyArnMKIwhRXJKy47JsT6QGEcuNf7+maN+ecrISEKSYFAoHzC9IjEJMyzbGIQKGBlQEUwnyKXB6YSdScrwhqRiTl+3SBfRSWTeVuRFipCS1vUkRYKWkqJMCFPN1Z09Om3wMsWnkSwGdNsh+pqpNLRRUERJqwJjmaHRRNkzlSU9DuUcM++YJAXKCUQi2FYZfRdIt8asRgnD0x4dIocWdnyOyncINFSiZzsM0EIiZcqwTxEaYnDMxJqpzxFJgSwKyi6B1Yo8yVFKMJxLUu+I2ZDhcJuYlXiRIKNg1KaU60gtHaXMGE5GyCip3JpClRebZkQY6TG5ytlJdjcMhBQMEoUVK3ZWJZ30pG2OTgyJSEmTjOhP2W1KXKHIvUWmhixqVAfkhh05pV/VpCqCLsh7gaoB07Pd5EgcVmU47RgnI8La4lPHJAyI0uGSQBU7xmGAbAwxgWmboXJN4zVNaNhOxlgnCW7NdjoBFQhYZu0xE5ui4uYc0dgMCMUWIhkxqxu2JwmrrmeQBEwqKKcF61WNUJLtXFKvalQ6JE3YaM9CYO4dAx3QmWDZNWglSFOBXPYIHIUWZKnGRUm0Dp2WyMQSEsGV61dhlOFqR3SRRBuSJGFdr8mzAiklXddu9onJlK3xGGst29Mptu/BRWanDSY46Fom14YMXp4yv7tkvapwzqGEYjTKIC+Y7pSYwQSZZrS1ZfbRLarTFY0XJNKDSPE2YJKMwmiE7wiJYVSmWOeIQtDUDi08SaKJwZEIy7BIkFFRu7iZi74nM4JBvhFwSe9ZVzULK1GmIlhHdTBDNJsAgc88R/eEqP/xhf0xSf9FxPsXpRyfS/j8/DLqJ5yunIfzwsyzrx64e728GZfD+e8/J1AYlxPytGA62iE16eblwRzpNKPhFpPR9BGzI8AHR9M25FmJEhIQ988HXdCQx/D/DDXPf0L4G9Ms/CdiqL60K9oHHOGzUz34fQDx0a+4//vw2eeF58hztviHB5TjQ8I+XvBzcd5zzbzwXXxI9z8+PB53WysePBGCz+1G7invn4bJS989rkHkQWxwgBsvbVNXkXppaRcNwrVIqWh7z/YAVmtHWmRcfeUGpd/m4D9aDn/gGeY7/PY//3f89j//9/yHP/oRevUC9Wf7rD7a5eXJe1S3M9qDEnsyZHe6+1BV8tJLYzrrUUYyefkKWZLTD6/Qj/fZ2d1FRYH1oLRhMhzQ9R6FZFAU9w+HC2bHC8ZbBUp6tPTcvLkpv1k34CMvvXmDclyAhLLMNge7FdRdi5Sbg5VZmZIFi/AR14HziitG0LaBvg2kjUB68B4Qmq18i2jVJnhWrxiVg6d04JN4B8F4a0yeDyBqJteu8Nobr9DWHTHAztVtpjemkApEaRjlKV3T463Hn67w3/sBsz/9S5of/IhfyjN2D3punEbUn33K7nfukvzFLcxf3eH1uxYX70flCIJr1uCMpDWS12RBNxD4LOCH8MrVHYQQ6ETz4ot7CHqka4jtmlGiqKqK9WLJOE8R3oOMbF0Z88pr11gfzTj5+C5lbth/8xqdc9z68BaDIgMC0TumowGmyIlas2wsO7/4Iuu/vcv8l8Zkb2yjUsWqWdMnnrfKfdpC0JvIwCtyDBiwJvJWU1I5j+0jI5uiXUbdBla65LV4larrsN4z7AVbURN1pDPwlThE5AYfPVnQ7PqUSCRowdt+QqtAFCnleMiVnQldEVnqnq+O97ADCFnEecsNXdALS03Pq31OT48VFpkpXsy3sCbQmcgbckRVr7GupXMd2csDDr6mOf2lgu1/9DKLrw2Y/8KQ068WiLe2uf1WwsE7BflXr+G+cYOD3YI7W4a39m7SCUtrW653GS4KHOCalrfWA2z09M6xvVKkaUQkPTbvec9cZxUFUiVc8yOS4AnaU7s1761LVs0MJ3v2x1OSTtD1PTPX8MqdfZZrw3qVUtwakJ6WVGvJKmreXr9BpyMYxXR8hQlbWDYE9tfTd6hcjZdQphMm3ZhOONay4d30XXrTIVJJXuRMi23sOLBsj0g6we/c/Z/5nTv/M//m4HfofPvEvIlAIlN+befXeXfr67y79XX+6eS/BDqyaYFRkVfn29gk0EvHm/2LtBF6F+mj5PX2JTqg8Y4XT7ewrsK5ilAG3lGv0fmWdVNxU76Iykd4K7BC8Mb8Jms8LXB1MSUphzgJfQpfVV/FYhE4rnZDsmAIzlGHjjerN6m6AX2YMKyvUbCHDQNOZpZX7t5gfrjC9ZpxNyLtUzojWUXHVw6usf6LMf13txnd22GgPTa31LpjT60JSiGVwkTHdrnxj9wse66IBU3jAEkSI/uJQAVBDDCloXUeIRR5lrA/ySi2SoZ7W7z7tTeYvLXH6I1d0t2c3/x7f59Xr77Erhzz0u4N/uCP/hd+59t/wO//0bf58+/+Of/yD/4lv/0Hv82yXmLtRqvqrGN/e5/54SlRwN7VAp/cow4fk73Y8Wv/+9e58isZ136t5O/+D+/y0i9/ncGVq+S7V3jj3Zvce3/Gpz86ZHU0wwWBj4bOK7w7pTMKUWaYPNCnnnUGdpLx+lu7BApar0mThPH2kLr1eJXw0o6hk4raBTIT0XTkgxRhFNtZfz9grSD0PanUlMmQphYc/egWfdU9mzR5xvuzQr3HJNLn9/vn/I2PIuw+HZ4z2aWZPwd8bje1T6lXiMcJnEE+5Fff+XXeffU93n7l6/xvfv1/x9fe+CZfe/uX+cW3foUXdm8+7IP5+pTf/dN/we/++b/g29/51zRd87DMJwj2J2i5M/Wel7I+0cq/IQr9orH0ZVB7Ea14EUn+c4b/RK5ovyScZSbPq8jPMZrnk55Nd1m2xxFwCTrOipsfFiTO5T/HkDxK9hR4fjbyyWIu1xDFc+U+tZYLuZBHU+df/D9+wE/++pA7PzugqRd0RtJKQ6oiuQsk1pEMh0x3C7qq4/j2ApNIJq+mjK8nzE5WbE936NdDTg8dWaZAVth6xvHRkq++9xJ/5x+9yzvvvUhE8Pvf/ojv/NU97txdMc0Fn/71hzgkiZSk1SHTuGbW9RgpEQSqusYYg1ISkxiW913RKiUJzm2CxmUJfe9o6m6jOUk2hDmIjeYiN5wuV6TGELxHJZrR/hZVk+CLPQ6Wjt2Bohcbr0StD+xkDft7AZ/B1taIk4MjbNjYLb/xldf4R/+r3+T6jatc6vGGM+vXfWR/+tlt/t2//VM++uhTyrJg+ekcN+/oo2f3yjbWBZreEnvH6adH6AA2eFKliTbSthbuBy3Lhhl12zHd2SIGOD04JVpP88Yu/YsT1oVmJCRuEOnSwCagtiSXggPRcbVNGf7pHH+3wVqLxFIYwbprKdKUquk2ZmhAYhRCCGRmGE9HrE4WBOfoOsvVV64jpeLDH3xMZgxKbcz+pBSU4yEi0SzWNYNhwZ3XFfK1MSGRuOOKICP1SHB9NKHyPUiocAx7Q5KkzGjZ6hWtExhlqKJjR6YgIrPYMXKSvrMYH5nryJQEtOSwXzOKBkck14Yj3zKNGpFG5qpjmGyk3XmasirhWj6m6VruLWZQO4xS5Npwt5mz7TJ0mXLqG3TnSYTBeMGR7rkqC2wI1LZFRkEpNJnUnMqO/XRAva5ZVDVSSRIvUR6OQ82OLOglrG0LMbJVlpRFzoFb8/L+VRZ0NLGn6y1l0Mjec5r07NiENvZ4GWhkZKwkRRo51it21RaVl4SoaLxlWxm06DhMKnZ9Tu8hImmGiquDKXa54ogVI59hJRhtmPuanVZgEstRXjFWA9JdSeIsC5bsuAleGo5YUPYJ9CsSY1gma/bXBUkCczGjNCN8ZkizEcfhhL3lAOUCqzAn6SRpm7A1vsLMnXKjuMk3d36Fr4zfPbs8QQjEEJFaPZxA/7b5I/68/Q633R0m9xS1CKxld9+bXYkm51CccKUe4rYUdWyJwVO2msTCPTPjenmdmpY6NggNI7eFag33kiW7dYEfWFpaur5hf7APK8dhuWbHj/Gqw9uGVvRs9VOkLziUK7bDgN4M6OYWVwomYkjsPPfcnHGfEMsGIR2VaNjxG1e0h37Nlijof/QS6fIqp8uOcbRUR0tmQZLKgMShYs+yj0yEJrYZ89PA1ijFpIYsFZzWkeu7BtEtOThZgQwMXY+sVvROMM0V+VaBHA/RWpLsLdHba05mx1y/eoOvf+Ub7IYJpkz54PQzfvj+jzk4PmJnMqHtapqmQmpJoUsylXJ8dMx0MuX47hHVco3QkkQalFCsmhUvv/kKJ/dO6J3DZJpRfhPV7XJ8ULN7dcThpysOPjuldx5Fj1LgYsIgEyycoyeS5CXDXLKuK9ZCs5VoWCts7YlohiNBkkuOlw3jVDJMSxCCqo/sjhR1taJxEW9bQCJ8wKHQsmdQKHofN+f5ksj/5f/2v2Xv1as8Zm1xHi4V+N/feR+4QT2b5hk0QoQvHtD7QnrlPzNcaqlyAVzW7ksJmUcZ/uT7f8gPPvoeR/NDru+8wDfe+CZfe/UXNgKJS/vpsgrPPX9Cy/EFkPu82c6nu1/3eXO0eP/v42LrJy+fWs8l8P+frmifm7j+knCeaHtIrd0/N/FAxMXj8+08M/LMAS/O/X+YLZ5/8HjaC8t9NOs3V+eZlIsb9Vj7Hzx5KBI5zy7Fx7JfOh8venzmUNdmD484FzZuJoXcEIZKEVTE2wAh0i4b7q2WGwmQ0sQYWRzNKXenxBjxfuOyNISAtTC/d0i9Oqazgbvv36X79Tcf4sP7TX3EiLMBqTTBRXzcuJbte4+MkSg3h5wetEkIQd9ZtNYkRuNDwPqNe0LVOYxW5GVKmiWsFg3Bg5CC1GwI5RAiWkl67xFSIJWiHJVUURGjxQoJGly/YUps71geLok5DAcF+XgAq4rV6Yr53VO8948Qfc7e9bK+Dj5sXIrGiPeepEgxQiPanvWipl3VBKPY2p+ybzSu6ji8dUSIESE2+aUU2M4hdY/tepYHc7JBgbcB7zzpuKTXir63WK3xLuITQAq899ioiFJsArixaQcxkihBby0+BNquR2pF6C1pnoL3aKNYzlbEzm1cbkoY7Y4BuPfRPYiQD3KatiPGiEo0i+WacjoixkjTtOh8gh4VLOdLlBQU0wGxjFgf8GJjx+0IoASEgFCCoAXWhofnpJyzqETjhMCmChcDwgOxp/ce6QM+RBpvkUrROPcQ/70IRCFwIRCCR3tPW1kqp0EL/H33sZGI8w6pJEIpvPcEEXESZNMhdILwAW8t0Vms8igE1kGxlUPfE7QkHZcY4fHWkxYZRmqyLlLkQ1IF0qXEGCmSlOjjJlK2cwQVsDFggyeEjZvbB7hxUuDFxn2tIGJlxEuB9xZkjuscMTicVIREbr5XRIIUeOtwrcPlDjJN7AUBQSDQ44kKRGEIvgMRcdEjrUPKzdiyTUOwDbHo8SikApFKopKEQhMV+NbjhScIje1agvSE4IirhjiIeBnwwdFVFUF5fPT44J+YMcGH+4zF/dUqgo8ehwciPhGExuLyjctikxhiH8EFXLD42uLMJk4LRYJvLVFKetsRkoDKNb63BGtB6838SCWegJOBoDfunENTE3SPjR2+q5GlInqQZYpb3XcdvFXglw4n77sq1oJu1aNShTAJnVtipIUkElJNWG8O2ocYEYmmqTq6RUPjWnyMWOtJM0XsHSqRaA3BRVzviEjadbdxvxoEXRWoTI+KPVEItNbEvsNaj9YpUmtsY4myIbQduj8lx+H6Hmcd3nqK7ZLhlQkfzD97uB74EEBA13ZIKUmLFBfVZs8gQAwbt8RaIoREJ5oyG240g97T1w1RZLS2Ia6WuDZiW4vv/eYMHZLMJNjgSJMErTfurgURFzx10yO0pkxy2qZGOUGWpgidEkNN27RopcjKjLbZ4MW5SFt78tQwX69QIuLDxoWyVBIRoW47OhcwWhK1IFjP8xAxF6c4Q3zwlMPNTxHwPYwH8XnhmXm+AHF8CYPw3CZRz/sdF0naz15HiD7cl76Lh2TQhl7xZ8ao38w/NoH4HliKPNmmCzixDfI/RyOfEy6SCf8caOSH/gXOkoMXaUD+hhQu5+Fv2BXt/a89i7wHc+3hQWtx9vHj+S6CpwgPHkv08OrZ8v6HDy/gE85fPS4RuIR6f/CNDw6EP9GZj3r+wbiOZx8/pcFPjpUHx80fsCn3y3xw2u4pk/ppQpHjkxM+u/0ZeV7wxjvbfPKzY4osknmPwtFbhXOB/W1IfEHwEWJgdHWP41PP8uCEvdTQzQRFtsd0e0i6N6WZH2Kblqxfo/Ih3vesTioyZfneX38fpRRvvb7H9390xHArQ83n7JaOe43ARNifFLRNwAqNjJY9DXeDx4XI3s4Wp4sVWEc+yHnpzRv84C9+gnOera0RwW3IDtdZrl7Z5mSxwmjBIEk4tS1FljLcHrGzP2G97unqlulWoJ0vKbslRRyzPx1y93aNd47tYYZRBUdrWJ3C3/lHv8iPvvMDDIY333uLq9euPo7tSw7UbTph01/Xb+wzHJQMygFJkvDe33mHH3/nZ5iqoVCapszplGUwzXnrV9/l/R9+QLFfMhltsfzklM/evwUhMhmVNCLioyA1hlIZGmMISrI7dxyGBrGqmWyPGcaU2a0KpRUv7474KOvp0AyLlJuZ4zOzRhvJMEk5nJ9sCOHccOX6Hsu2ZTVbsT0ssN7h78eNeOWdV7l37xiTp2RKk6fJRrskBa++fIO7945wzlOYFC0UwgvyQc6v/51f40+bT+mO5rx17UXkfsH7J/dIXOTd5Drf4wjtHa+IAQ6BDZ4MxdfEFn/tF0gtueJTVNB0wpEFwdf6ET8TK6wXbJEgK89aCjJjeM0N+JmsyFGUvUQ5QSwFhUx4x23z4+6EFEcuevKomAswMuEbepcP4gKPYDskTHXBT+PGa9NX44gPWeN8YBI0U5vxvmkRzvNqP2LWR0aDIZNkwLV8ix+o22iteW/3Jp+sT1BVyl4x5uZoh+8efkLwgTeybe4sZzTWYtrIt67e5C8Xn9BJwRtiwjEVIURGMuW9bMr3mtsMlOS1bsA6abFCkLSSb+gr/Mdwhx7F9dMUu6eIQZJHzde7CX9pPqZQgv2jCNOCRs4phOCt9XV+PDglkZq9dYbsLC6BTOd84/QaPxx+Sm4jV1YDaD197DAKvubf5n3zCSObsssuWzqn6SuUN7zXvc0Pi88YZFtM8x2G92o+So5Ikpxv7L3LZ+IO3brDCM12ust3Z99BCc3rgzdJVYo0CoFgbZd8uPwZUkhezV/he+IH5GLIZLTFjU9rPni9QzjHV+zLfKJO6ULLOBtx5SDhx1dPUErxhn+Ju6tbNCNBwYh3m12+Hz8ElfF6tc9RWNOWkoHJeG19jf9YfAgm59XZhFOXY5uGYTnmrX7Kd6vb4Bw3kj3WXUPc1ZRZwdfme3zH30Y4xTU7YNUFQiLIo+ad5U3eH90lS1JeSq4wvxdpW0eaGr62NeavftrTtR0j48AI+l6SNpaXko6Pq4TUwiB3aCPwUqKcZa8/5nidkkdFmHmGW5GVVmgpuDE1fOwMq+BxVc2W3DDqishgJlg0C6yWdLLh5t99ga3rewgib7zyOsenJ4xHY8q8QCeSn8afsj5dsWW2cDjKMmdQluy+vsP3v/8+0Ue2BgOKawXrdoVONFe3rnOoViRZxgv7O5x8kCIkNIcL3NEdsBlaaoZpz5EN1KliMC55sW352ApIBNPgGU3GnKBJRoaXleSTE3DeM04Uq6YmOEm3cuznkdunCh8EQXhQknDfS8Ne6pn7jLpzDHVEm4DzAW89pgCVGs4QLve32vg44fm4LO+sccOZffbzUZCPEesXyQ8/j1T6vuDlS9vxn2/DRW19Wr4vU+8ZWuaxWBn3GQzuMzhvvPhVjhfHbA2nDPMhr157g0gk9h6RPo3kvcC84GH5PJTZPvH+y8IztGHnGStxztPnQ4b1eRi4/0SMBfxcmYvzo40zE/GC1OcIrYvQ9QCeax49DWnnqPt46c1zlneWpzi7xpzr3Es9JVwGD9Ve55I9hQt4MoDeuaggT/kOcclgXCyW/OGf/DEnpycUeU5YbpMVGWlhqNcBKkdiPImOpEJzddqRb4352//dP+EP/81dlj88hJMVs6XAnXSMrm3Rjgcc3LrL4fsHBGcROqccZBQFhNjwP/2/fof9r+6SpAkuTjDZFiwjfd9jByV0a1KtWZgCZzJaJONMcnzvU5RSKBk2B/NExBhBiJZPfvopSgm8j7Rti1Gatu6Y7IyJMpAVG+n9sq0wWjO8MmU0GXJ464R60WKtY328po+OAkHROdafnRIXDYTIus9h9yqVd5hZSowT/qv/5p9Q1w2vfOXlTeC0B/h9rjVd0Db9RlsjDGmS8ekHd7D9xuWqGBZMrpccHZ2gMrh3ckC2ldJ6QzbNMGaPVV2zOpjT+IATG02TShN6IlJtdrr1nVPKoxTR95QHPUmSsUVACsnp2qPfHKAQSBs4Ws1Ilcf5wLJuCeH+52hFT2Q9WxN6R6PdJhiZ84wnA47unLCe1yS5o9eKQZlR9T0mCA4PTmibjQcsk2TUx6uNRFVqPj45QCQOFxx2LMH2SAm5SbjNmtRLfBQshEMqRfQBE+FWWpN5qLG0RkPfg7KkSnFH1hghCYAVm0Bz0ihSqbkrOzLkRgsnBVGCCpJcJHxmV6Q6ZdVZgoa1t2RCkmvNkfGkfYoOHi0SFsKh0Oje81mo0CEQrMN5xUEqCD6gg+Ao6+nXgTZE1lrxmQ1oY1Ba8sHxPZTciAd8Z/l4dogSApVqFonD5CmmU5gouNXNyfMMnRpO1y1SamSQpE5wK25MkbyC0zwgdY6vK7JguDWsyFsJMlLnlrgUxERinObT7Rmliqx9hU0kvs/QJZQOjsYVJSl9bHGlJEQNtiNdWz6KnxF66FLJ3DqSpEPnitJk3DVLMlHStC3tesVh3uPTjDQb80m2JmXEOiyoW0tfelwbMD7yQfYx6SgnKsO6XvBvDn6HxrUYZThs7/Ibe/8QIQQ2Wv7w3h9wWN9FCoUrNKIwRBRRpxxvzRCNRWYpd+0RuvWoLELjOB7UJEajjOI4rCEbEWJE9hkf+XukZYZzluMwQ2iNip7EeQ4Gp4yLAU2zZpF4sFO06tBzzceFRnGF6CqOLGQjjUos5qTiVnVE2WpqIm0GIleI3pLKhMORw8QhofMsl9B+NiVYhy5zPlhEkghUloVvUV4jMaSJ5l6VkSuNbyN4SZQa6S2DMkVoxZSOykVyAisfWVUN0VvMtS3spKDrHMKCXDSU1uKJHLQdic3wBtqDyGrZsnNjs69sb0/5h3/vN1mtlpRFybf/5N9ikoSt3SlOeFTcrHmutdw6aBlM9qnma+RogCkV0UZUIulCSpkVSK1YHRvSfEDTdizvrVksFTJCkadYXeAGhuMq0C9bjBKkA002HmBkiVuv8bJA54p7645NeE3BoqopkgyExjZrDqvIKC2JMqFen7JoG0SSU+Sa06pChIAQEoymHGT0scHaHiEN+TC/eA1/yrr++JZ9Zk8Wlya6+NnZOs5L75+zLQ/eP0mPfA5G4zwd9xS6YiPcPBeB++cBZ8oSiI32+oz59gMB3e7WHv/ol/8pq2rFeDghUYboI/5ohbw+ecQsXPBtTzT30rbHh/TWs5q8Efp+ASR8Edz9PDUTX7Kcnw9z8UDsftnYvZBSvv/iIrXNsx89VtTZYHAhhI0P7gtn5+b+Aed3oWbigtunNUKcTf88nfGsAXNeuP3YYnOeG3hyhfnch4yeWDAih8eHLFdLDo+PSNOU/g6IdkzrwEZDYz3RBUyuqddw5d1d/s5//w+4d2RZLTpWdSCZ7HD62SGJUaw+mBEtHHx8wKpyZIlGS8O8ilgbyYvAvaMZ9c8qyskQi6ZzhtmsQQWJj5paaHoPhRR4JL1Q6G4TCK3vOqL3RAJt32+iODsPEbwQ2K4n+IjVhqbp4GRBhyXEgEk15VZJjILeOz7+/ke0tSNEgZISqQRSC7q25+ToFO82HSilRAy2WFYWpxP8qufPfud7fON//C+4cvPqRsX+mNZOnFkYLxoqmyeHByesVzWLxYqmaelOatYHC9bLmls6kowNqtS0fcdytsIIxeJoRrSRbt7Rx4AcpvStg7gx71mtKpQQ9G7jitZWLUJYpFY0vaeqLdZ6lFL0Lye0wrIiYuqeGC39fEnT9ZgkIQiJMJpqXVOtG3rnGIwKqqYlBI+1ltl8SYwSH6CzFhEjRZlR1+3G5CG4h6Z3SSoIPuJDZLlcc/jxxxwXLSLXfHJyRJRs3HWKhAaHjwEnIQpBcJ6F7+ilwwoQStBHR4wBaRSL0NMJiClIF1lHR4wNKhPU0uOlJRBJpKYmEJJAlFDLQNuvid6TyZSltCgapIJF6EnwzCuP8TD3HTb0xEwwjy3SB0yUyAhr7RHSogvF0jlChFpIZCpZxZ7QLoiVxw42B3IHUSOcZxV7Ot1vXHlGi5CCKtn4eK+15yQ22LqlSjfme7lg41I2WjyO3gZ6s4lm3kmL7mEp7f0I5IGQ9Xhv6dIc21nWImBV4FCeogZu4+7Zt/jYsYwdoYh0rUOGhC5YIg436KhUjy0kXvfQO2rj0ZOIki0VKxrfIbM5iTSskgqfOpCCpahYuZaj6hTlNVVmwTiEWjMPSxK3ZtWvGPRDalEjMsFytqQzDik1QzOiCx25ypm3p6ztkrvNbQBsklP7yLyfY/sGP7asZIXSCU2SEkWgMh1yADaz1DTE1jMwgTjMmLuOEBaopKaPDcRAuzUApVnEjuBnSBVx0hESSy8G9EvLurL0zmBTiyXgdYDEo2VNI3o6GWm7ihhzrJf4xhHoWaqWLjhs6MkyQ2t76tMcLwasnKKvHeG4xX6yoo2CTBa4zmOjRmpN1zh82yFUitYZvgt0JLg6IjJDeT/C+LK3rNeeOkgimpkVeKVpjWJgEtJeUa8dMtH03pF6T5QSOR5wUlW8cmalSpOEbHuHk9kp62rN6WwGAkqTI31kvV7TLDu6JqVzGy89s9kJ81VNLy2+j0Q7plkrYgjkUWGkZX5YUTfgKLFoFq2kV4JKKfokYx16iqyARLJad8jJALW9S7Xs6FpH3ktklDjAO4VAEqVC6oLVytLbQJIKNjMYtMlZdxbvE8osJXSWRdOwrltcBK0lKitIi5THFu8HF0+hVZ7QYlzEDFx0fT7t8xKXz5J+f1m4iOl5cH+u/ZvvvYC2e65qHthhPINruxQ2+bKkIEsKHjIBUpBcn9z3Q3vfiuBR8nO5n11vfFobnyjv56Qtuqjw8+9+ToxFJD7TQdqz4MszF/HRxbPDpcCFLT6LpIvo/M8RzVrIBw6wHjART9b3JAH+DH3SecnCRZM/cv7igrofqDnO62keTakn9KuPFXt+Fj+aiA+Z6C8xuB5YUo1HI8qiYFAOGAwGeD8g1gXYnsyltHWN1IIsjQyHhl//7/8B5WTANDQUg4TxJMUuepZ0yKiRQdGcnBB9wyhPSFNBkJEsl8wWLZkAYTS+9QyLAkyKFwXVyZrda1scfnKHQoEOgfwBrmLECEi1wJQFXdtBFOxMRtRVS5ZnaK3prccbQ5Kl2NbRK0WSJggEwfuNu9I0IUlSatezNSpZ0pFmGd45nN0wJpKIkYrhIMU6D1KSJxC0YO0tw1zDYsUnf/k+r//ddykGBY+dxjuvYDp3573HWsd4MiIvcoaDknKQE/IBV/d3mZ0sKMc5aqhYLpekSUpR5GipCNaSS8nqeEVc9xRlihkP8euWyioGWwN807E8WZBqDUqjo2RVN6RJQmc9WghSoxCVx1iB9IFpkpGhkEWOThOysqBZN/TeM96b0lYNu9Mh1WK9GYVREbxn98qUxUlFRNB1PUYrRNjYg2ujkDHBaIU2GikVOtU0BBIt6VeOna0hMVVM0xKhJKFdsi1zOhmJUlD5ljEZiEDUgp1gCFISI6yFZeIUIki8c4yjJiJRiUY6yUSk2LojSEHpFVJrcm2Y0TMMcTMH+pahNhA1qhM4JBOp6X3AG0MaNJk0JC4QhGHiIvXKIhKFwpAg0dajM8nICkTUGFWgXCRBkzhAw7ZKsH1L1wiKrRLVeVg7WhGZFgZvBIVMCTFSkpBGRSs6ro2mrGgp5ebcRUq47wXIsiNSlrZDCkEfHFtpThIjXbRc9Qbnc6xMcH3DVkhxduMCdaJyRFeiC2hFy4SS6DbnGrZDTggZvhVURjBRJdZHnO03+VIQBBayZ9vlsPSosmDYGlTM0EpD6JmK8WYuGU2+AD0aopzAxJZpHG3iHqQJucpJOsvAjRCpYqJ38NSoriEfj8hUjhaaKtQM9JBU5oyTKUoqeqkYKEM0kck6oTeRtDcoFKqGLBoigm07wGYw8Bmu78mcQasSi2OnThGFJIYcZ6AUBaKKeGHZ7krUKMO7jk5ahrIAU3AQVuwOtmmcRaSGJvTktSMfSbS0TLeGLG+vEbKgEp7isCW0M+wwMmSI3N4iQbLwDYVWYFKC7RkZjXMtvXCYomAoPWQZs4Ul8ZbEeELvaJGUgJeBYAQqWJR1ROtIhGGQCvrQk4dAJgRJ32FSSVACGRyjQYKtOnwCvo+kQqBMwvbVbSaT0cNt7+xWPCgHpEnKZGsLgSBVCQkK13mSaCjyMW0f6eYVuZRkpWbRrhlkOYghRaawnaXMSrTNaeYte3vXWC4ddd3TNo6qb6najqIcUypHgiPUFqM0o1yTJJp2tiZXkXKQInuP94LeQ1ctSYsRCsvWUNGsG1zvSROPE45oO3ToKTRkOWRZRi40Ve1orSNJJFkqeeiQ4yJp97kt/lIjg8+zL1+Y9oHwVnz+8p6LSHwoqSWK+LjpzedhjM7X+wXokc8j5d8YwFwmSH7waGOaHmW8nPF5jrbGGOlsS2LSn6NnLC4eNM8rqH5WOZeVe1nz44PXX14F8qVd0T6cdOLMkIiPfh9e3j+kGomPrs/ei4ucwT7I/aCqBz+c+fv4j3ws1eMQz5XyMN3DteNiZuTs9zxx/3gTH3v9JKMgHiCDh+5wYzxjunQJY/EAz2ev7y80Im7KFGfa8dzD/txc3HSjYHu6TZIkuODo+o53f/EmTb2mtzWTbc2g7OhZ0fuKt3/pGuV0E4V6a5IxGmuC8zgX2NuyrIPfEIVpYHvLkxWRpl/y5puGnZcExhyTJBUvXd0m1QmzO3PeeesqtoEkyUlVym5wKKvASl7NFFoppBd4D3uTK9T5NfrJy2TTK3SNx0dJcDAdj1lXHY0NDMuSfKskErG95aWrV6jXjmbt0U5SHS+oj5aUOyOuX9+mty1VvWY0LjYmBkSS1PDKG9fwItC7HpoVg3ZGMj8gnhwwNDV/+pd/wW//q9/jz/7sOw8Pkl205p2dIAcHR/zLf/UH/Mt/9fv8+Mc/IQmS/qShPlzzzjuv0646Yh8Qlcd9VhFm4OeBt7/6Bm1Y09olrl2S5DktkvmqZ2wy9FbO+PqUNNVILZCJwUUYFTk2OrwIqEQwGid40dGHhhcWAf7wEwb//g75dw+5Pphsgq2JjZlLMSyJEWzv+IW/+x7Vck1TNWRJQl7mRKCarbl+bQdrO7zrKYsU7+ImqnuUXNmZkgwG1K1nPBnR/tKI5d8ZsfjlIV994Sah0Fgj2JcDyiwjqEhNzzeL67TC4Yjsy5ItlRO0oJKBb4QpbbC46NkRKVMrCAa6aHnbD6iUpZOeoTZMZEKQHis9X4lDGmGx0VImCdvBELWkCZ5vJDvUqscaR4yeK0mJ0446tLxWJ3R5oBUt2I6XKzbasT7wlXZELDcubY0y3KxzXIx4EXk3TjaHsJ1FIHibMV1wzFYrXolbWCXpFNTA27sv0mSCJhW8Uu5ik0iXepo88K1rr2J1wGvPy3FIqiU+BVdIfkHsbaItq8ALfgjS4JRiReQb9ZTeBHwSuekLsvvf28nI13iVxnX0QnBF7jKkIKSChpavLyY08pQ+zpkEzW4cglJU0fHN0138sIX+lIk37OkrtL1nGRyvf3yFta9xKlC6jGvNGKc93RDeW96kG0W8caS9YF++wUqOOfUZN9Zf4ajrObXQyZyd6Q1ORhV3/SHG5Px/qt/iny3/3/xO92/It7aoxo710PHO+B2c6InCIxPFW4urRBOxXcU79Uv0MadtNd5mvPHZFJcEHB1fWe8Rm03gQZtrvnp6lVZ2uMTxZvk6WiV0RDoNX3VvsQwdte244bYRVcClhkXX8Evpq5sQhMJzpZ8g65y20ywrzzvLEc3Oii4/YWoEJR6X1dhRxy/vv0elx7RizG42ZXhLYA8kze3I68uarkvojh2pDQykJ/TgOnh9J1KhEEnG9k7JG1/bI9sbkO0O+YW3x6RaQN9g2oorAbIuR/cZL7WWdq7oVwplDeNMEqUEGxg5z1WT8fZXX+UXf+VrvPLKjfsyQYG/73ACNhqMK3t72GjpY89rr79BWyesZ4q2Mgz0mDv3Otay5OaNN2lvBapb4KqCl65ep11ZvJO88OoOi6MTZicnfPb+p4T+Mw7Thuaa5vWvjbh+xaCSNeOp5u2JJESJUobdRDCoevTK0h+u8Xc+okXQKkGZSwYm0LQVTV+TcwRJQCSea7sJkyyixebQ9jR39I3H1o6uqUloEdHifEeqHLazm+U6cAEtcPGe/Yju4RGdc2mq54UHFhfxMWuNZ8LnrEI8Ioi+XFlcUsbTkn9Ool08QPJllYlH/x+jT89fP+O7mq7hD/7id/jtf/9b/N6f/SvW9XN4Sb2oe59GOz5tODwgHZ/W0Mv67LK2XVbGxTefG/7mXNGeF+DHC655PM3ZMfJ5mO0ntAdnMp/9vM2kiU+l4R+9eEQRbq7OU4gPtBCXlXFxrjONuaDOyxpzST1PQ9JT8Hzh8zPPPv70U/74z/+Ejz/7lNFgiD0c0x9Lju/N2d0ecvTJPU7rljw1fOs33uZ/+B//MQC3P13y+//yZ7z/4xOMgs9+egtEpLaS0vQMTKTvPCF6rr02JB94fvrdDxgUCcMbBaJU5IMMxw2EusLduxV5aKmPZ6yqnkRJpAlkqeSo9QzweAc+SLRRqPUBRXNKby2jyZBm3RAjdNZRZAlCwLpqyPMMHyJ9YymGOc52aA113bC9PyUdl9jebg6CT0eYRHNw94TxdIj3EaSgrVoSbZjdXdA0PVlqELuQDAT57pC33n2Tv/cbf5urV688ZL6f6LP7OP/d3/s2P3v/IxbLFdNijJt7Tu/MGIxLog2YJGF2tGBrMuTuz27hw8bzVnFDk00VjevYmexjVyn3Pp1h6w7pehIj0MOMKzf2aZY1t392G+zGlEYrybppSI0mhkAQEaXUJvJ5jHTOMixLVJYxO14glcQYA0BVN7z8lZusZgvWx3OUlkipUVKyWK7Isgz1wBtVb8mTjCLNWC8r8jSh15rOB2xniW8O6d4bsRhFJs4QUonKDFWwbKmMRAmOVcteMqDyDu8CNZatmKJc4EB1TGOK8w4tJEss05iibeBQdIyioXYbk69KOqZk0DsWomeIIWpFqhOOu4pRr5BSstKeIii8dqRGckTNpFHILGGpLHlUiAC5TjjoV+w2hiA0lQwkQqO1xAg4MZatVhESRS09ygXSIMiU4a5dsWcTbCKp4sbrjbGQKMOJ6rgiCqyMtMKDgAKBkZED2bCvBtShxwlPiIGByjBBMCs8NwZTTk9nG29LbcMoGyKj4G5YccWl1KVFFhpvG7aqDOkTbpuOScjwOyvS3NEoy9QXqNZxr6iYihGOSKwtS92xGydIEu6JFeOYI4c1mW9ZyjW7eh+7bDmKC4Y+Q+SRMkmYmRV7apcoIidqSd5sxlouUo7Nkl1/lXqZcORbCpWRDgSp6zkVC3a7Ej2yzNpDUp2hVUYuM46zFTeSa+gAta+RNhKUQkjF3e4OV/wOXehpjUU6j6oLlBhzO55yQ0zo9YwubTdBNecJypfcLRt2uxKSFTazoGGgp2ibcEecsOe36ERNUJ4+9Gz1e4jTnKMxbNscm4APgco2jDqJxnE86thhSFcfIUYJja8ZNjmij5xkNbuDPby6gjuCeejYuTsgfL/k+BQK2+FmIDGsesGkFHjnWFSRTDqCVkTvsCrn6m6CHmlOa0+ZKcZtw7hrmC06XFtROUUvMoyI2EyDERy3kd3UMo4VorfgHLFb8euvTfnW/+mfsPP2zQ1Bc5/ojCE+FCSu6xX/+o9+l49ufYwQAuNGiDrjsw/vMhkPOZgFQp6jlESfHDPNJUfzJa9843V8I+kqB0qSyJy73z9g3kRkbKlHGTbTdCEy1AJjFMsg2M0NQRmkhyZEdrUk7zzLpcW2FZWQlMOSKBUD15K5wEnVEUNHYgaURYn1AkOHD5Y+SoS3VF0AD0EmlEmPYEVte/LUMCwM/9f/+/+B7Zt7T26gD9fyZxAsD5f+y1QAn4OIE/cJzHimvKdpFs6//7xVXkrAfH64sKjPK62/oNAovuRB9ecQ0n/v/b/kuz/9DneOb7E3ucK7r36Db331Vx/l54IyztPA5989pv06h50L+ikEj5Dy83/rZTh+ju/+z+uK9n7jojhz8wSIJ+jwswvWw1RPmSTxCWw/0kM8EUDzTD9deIjpIY9xgcrhgl69uCsvUE8+1lni4rwXFXbWd9h5Tcdl6c5Xdx4ue/EcnLoPbuNa874NvbOeEBUiCgIg1KMB7h64g4vgnMf7jdvZ2Ducjyi9Of/iXcSrjfBHG41KNW1VEUNAZZoowFmLbCVRx03gqfmavlphck0Qjj5EpI9460EIlNRYu7FlB0GaGHwdcc7RLGtcCPiwcTvqgkfeZ+1DCLjeo4y6v1EKjFJIJWmqluWiIi1S+qZDdQ5pNLN7J8zvniKUQmmFEDAYDZne2GF2tMDWLTIASKrTFc46rHMX4/9cxznn6G1PCB7nHM5uXOnVyxrXOiSCZt0Q2p6uaulaCwLsYWBVB9KtjHbdIn3CcDpEbI9QwpNnivnpkrZpOb11jG17BAIVNweb0zIjtD0Ev8F/3GgXhFZgNI4I3iO1RCmN8558mLM1ylgczVkcz9AKus6jdETEzZmnJDU472nbjiQxpFlCV3c0XU8U0PcOj0AKQbwfDT2iibnGi0AQAbQgCuicpXc9676i15JAxImAl+DFxk1uLzz2vkvJ3lt6ofEx4EWkF3FTlty0LRIQWuJdpBMeJTVkGhEVIkqsDxt3tSGCdOAFQUEUgRg22oAuRozU9OG+jXoXcH5jzmRDIFcGlNq4LpWRGDx9tJvD2VLSOLvBg7f4bhMEkOhJdAJqMzysCHgine+JgBQbW/IoAm3XQSqw3hOIWOc2keZLTW07Wu9weIISBBEhRkSM1CLQiUjsmo3Tg0xB0EjX4WTY4FU4nPAbzYcJBAK2b7ESohEP57BtekISsXjSXOK8wHeevq7wMeI19ApUdHQuYGOHTXqiBK89zgiQkV5uAhZ23uKFJohI73qMTpgv13SqwwlD8A5ngNgjhaGPFtd3VKtTEi+wg4joA6QpGEBLnI7EIOmrCmk0CR67XOALT1dGopH0vieKgCoH2GYTw8bpQJSRgCMIsTGNFAKhBV3bYkODL8DrgOsD3ve4taMzmq719M4SM0XXNvTS0zU9tiyxiYBg8ToiEgFFgi4lJIbmqCbGFKElwWi82Hi1690m/oJwkXRQkg4VxEBLj44b852IpG17Tk9a1DzSJglxBbqpKAYanScoI7BNpK4jvbMIJZBZikkEMW6YdhE2HpI0gmwyZHBje7NkhYiQ9/dN+WDfizjvCXGz3goBym9E+9koRxUpiY2sW8fy1pwRPWsHpsxoVzW+FvigICrSXJGNBoh2jVEpUSlQmixRBNfSx4hOEmJqsG3Ae3AhYmMkcfddIIeIyDRt70gHKTrJ6Y4XKKkQGIqyJApJU3U0vkHJTSBFgUcKTVZmBG1ItcD3DaHfuCYPIWxMbh+AOE8GPlsSKiKXCCI/H1PxiKcRTzy7MO0FxccHf+NzagnEuf+XwAPS6Tl4rIsa9KUYmGcS2xfi6T6CnqdeAc47rLP3x7vFefeo3OfSAlzyTpx/cHmbN4zFF4Bn0YJ/Q/Bz8xb1gJR+NFbuS+4fw8ajDn1gznMm8yZFPB/+7TzEc3ePcRKXcO1n0sSzrx5V/GD+X870i8d5jyeb8nyddWGaC5ici0bROSXT47i9jH1+fnhQ7Y2r19nb3kErjdaa7Zdv8JO/OCYxmr29Ac3dExKZY6Tmra/d4Gc/+ZT1uubKlV1G05TBTkZ975SRWrAKJeOyhD5CX5FmI4LzvPXOTX7wV98hHQp2rk3ZenGbw7UnyxNev7HL9/+6J/cdmYmME4c1EF3gpVxwb0MiooLjZuY4XqzBSa7sDJg3EiE1WkqGeclitaZINOPhgMWyRkqP1prRoKBre5xzZGmCUCAwiCDZHg9wImJrxzDPCQiMNGTGkBUpy3WHdY52USG9pF93TPcnqCJw6iPKCTQpSWr43g/+mrIc8MrNl5BKPb6o3O+q1157hU8/uotIFLtXdqGMNPOaww/uMJCGOsKqqpmUBcM83bhfzVJu7k/5rLmDQTMaFaRhSNccgo/sT7Y4+OQz6HqSrSHTnS36tiMf5bz19TdYtQ2rRUWWGJqTBSdHM6TRvPzmi3Rtz2fv30L0niQKJntbrOcr3njnVWKquffpXbp1y85oxOl6jck0L790naODGSiFs4Gt0YjgNh5DptMRC9Yk3pFmKXtbI05mKxAwXifIE0F9q2Y0kbz82g1ufXZMsJ69vQSvM4azSFakXL26w4/CKa23vJROaGOLdZ7cC35RXeFHHCNj5IZNAPASMm34qhvzQ79AA/shQ0XohccgeaMfcjiSWJ2x0ysyLfnAz9Eh8FYz5v1sRRkUO6qgcAYv1hgP72T7/CzMadueqcwoGsWHSU0qBa/ZAbdCTSkVY2HYdSmfZS0RuFEnHKmOvu/YUjmToPlkFBDO83qYcM9X9MozRnOlNfzUODCKm21BpXqMEAxlwg25xQ/jEUIIrjcFYZhughwuLDdXY35arhFpzht1xjKHxloyp/iWv8p37B0yk3EjmdDVPZ3oKCy83Nzkp+II5z0v1Cmu9LhUUgjFW6t9fpDfIw2CF+QWTghiPCbTKS9/us0n03sMvOBaNYJigIsHmLXlneYaH+4dAAN26xFJC37QkSY5ry1v8ElxmxgyroQBuhtDdkCSprw6u8qP6p5oUrbUFju54SMtSLKUt1Y3+El/i7wcM9Y7XJ1rPowHSCd4ZX2Nw50KLbcZtwXFPOHTrCfWnpdPptyZJFTNMbqO3Eyv8aFxRC15o7nKge4QaWS8TnnZXuEjcxuRJbx4us0xa1zSME4GXP1si49eWBCU4BV2OM4M/fIuRS74RvYi37Of4kLkRa7QxAUyLhkJzc36ZX4ijrDec6Mf01mFcxVGSt47HvHDRUACewb6laetLSZX7O94bi8UbV/BsmM0zLHDlHJY8NoVzY/eXzCb14zTgA8VdS9wWjPOe7zTpEVOgWI8UIR7NZVtGFOB2qUMka1RRrk4ZCYX9NHxymDKK7/+Dum4BMHG6935vVXAaDDihf3rGwcaQjApd/jsp3N8t9H4Xr025Eff/Slp6nn9xetMr444vnXE6U8/45WvvsVCGhCCl17d5W42xnafsjXOmNgZP2sbRltjXr62y0yvmI96ii7walVwr5LYzrMlLcbDIjokgVFYsmxSTIhM90tcoelmHZGAXN5lEQqikIxzSWEkx+tNHKSrA48bCO7duUsgkKcde6MMpRTXrk8ZbY/vf/M5geEziPPH6cafCxX95PXTirugyodf8EWa8ZRPEA/+fFHy44vme9iWp6hYLiz7AuHwZZkjvHrtdX788Q8Y5gOyNOO1668/N9n2TDiL1/PCx6cKyiNn3ds/8zD8czYmPijjSzIfX565uESaHs89fxqDfaEC4UGCh5fiyU54Is/jKgzxGDEeH9YlLhlXFxmIPRO/l02oGB8bJ8+UEpwt53ONDfFwrXjM9/PT4FIGZ4PjNEn5zV//DY5OT8iznJ/+1QFJuqAzlq62VJVBhgyJ5ic/OeCDW59SrRsGoyGN3yEYwaquaGSKiaCNZDAc088Fzius9dy9e4ylxgwF6bbBj17A24ZeKm6fGsLymFDV+CSwbCWSjRbEpgble4IPmATUfE7WV0gp8YsVQm9cqoKnbmtiDHjvcM4jlUFIT5JmmFSxWK4JIZDmA4qyoKocUiU0tdtIuS0cnlSbSN9BIoTCWwFoUmPQSrFetQQbWB0tSF98gXXnSY3m4ETw7T/+Y9b1kqIoWFVr3nv3a48tBg/wvjhaYYKh7XuOfnZI6D1dbzFG0TqHC5FIoOoaiiJFGIHOFMfNkuhBJwlCCpp2iU49xmiWJ4dkziJ3hpQ7A/qm5dpb18nKDHJFnpY0bc/WlW0mN7bJDmdoo0mM4fDTQ9qqZWtrBELQVDX7L18hnRYcfXiXxb1TpmWOLDOM6yhHJbOTJSiFVJo8z+icJ8lznLXMV81G6q4UpIaOQJIbBNCvGl4+3qEmwX+yxn98i51UUC8rsiGERNM0FblsOf2mJLkq6QPUtiMYifSCQqccy5YkSLpEY5XAdxZhJIkX3KUll5o2BnprMcVm7Orac1J4unmNGhqsDdR+485SKc2hchRJwdqu6aXExoA0hkQKDkSDcJsgblIbOgNpVBgfORYtmdJUoUdFmBsPUmACzEVPKhUmTRBeUQ0Uw+2M4APHJxXCbzQkgsA820ShjyLS5p5Caxa+IXGB5bBnlA3pqoa+qpFNpK0r0koyyyARBus9p8EinCa6CHXgY7EilRqRSupgiUm8r4qIHNctssuRJrCSGUquiCGSBM3B1JGFArs+pRFrYqoxo4TsuOVYA01KiI5GZUQPEYPsBPc4JYsbT1+MUjrTIaPEVIHTYkGCRvSOqBxNckiSNOSpZEFNVk9Z1AsambDIK1Rq0CTcdnNipbFYbJlyei3QHzboLGVd9owas4lc3gX6oSUJimADJ2KNYB89HhNOBEfKImSJ8JGZ7tCyQ8WWMkmY1ydkpPgqUrk1qhRIAon3LKcR1QtknrBMA2LukKlB94E7arZxx5pIVqenjG/m1HlGZiO3ZY3wOUJ5mqTA1hLvA4KMgyNNskzoekvXacKpJRUpKYJl74hYhDYEIzk8WRLzMSJIjpaeLINilKC8pRaO1KTYasVKSgrnWB+syKXHqBLfWrRwRC/Y0pa6D0yFZzk8pbcrRtOUq9+6wrVffetSoeqDh1IKfvnr3+LVm68hBKxOO+598FcIJEZp+tUpk4FkaHK6w3tsV2va2Yr3vvEWJ9Nt6nmND4HlvKU6rWjWLbFtWJcbbbhQgvW4R7zagOrQdcR/VjCVJYvYkBQ5SvQkeaT3PSJkZAFUEMg6MNjZpWhmrNcL1lIRCUQhWa4aOmPwfhMnZdHXyMWKGGqGw4yX9qc0naWcDvjN/+43KHdGj++b4twa/jB62bO33S9M9n0hQu8MofgAnmjA01r1VPXHo/dfhqm4sNZ4eZsvE+ieFyI/cfsYNfa527RuliglEQK00izXc3an+4+186mamYvgvKAxXvDsqU19csxdJMt/7OXnIWi/DI/Cz0Vz8SSV/5CLvd+6+Fi6zcB5eMDpvrrg4SfdZ0rOy+EfucZ6wMbFx0T3m/NN4tKx9yjhRfgVPN6ICxiRxwbxgzY+WdgTzJJ4Tk7y80zOM6v+gzn11Oxn2h7jZWNGnP00tNZc2dsH4O6nP+L0YElTWzqTUneCrhe0vePH3/uI6U1DXbeUlaAPCUcnPUcri3ApCQLXBEQQIDOqyuOc4N7RMXXXEHWkRnFyMOdkuenHk2ZFe2tO1QcG17ZZztes+34TnbtxdAraKDFdj296unYjFe49RBxt32OMQQtN13XIXtB3EaTG+4CPkeWqvh/VehPhe7mqCSEilKSuWqqqRUlJiKCNwrvAuuoQOqC0obWbQEzOenrrUEoxmzW0aU6nFHcODwiloG7mGKkpTM5773ztAuQL7nx2yMnRnLbpkD5w+P493P1o4SZLKPKENAyI1rJaVPjgWSwdInpGV0ooNMdHp4QWOrshZFOTkVzbpreWxWKNI1KdzImHkfnJirTIqNb1wym0XlX0dUd7vIQQKaZDhlemxOhxp4LZyYKDj+/hWkvf9zRlTns8o+t62q4jSzJMlhKkYF03iPtRrlWiSbYH5FojVzV5nlLN1qyqGqEkO1d3CVJRHy6x84ZmNicmGk+kXXeoxGBjZNVaZm864v6Q1vV4LYhIFrHHicidUCGloMETVEQlnnl0tEJxIDt0VFRYnJQYAmvhaHOYsSQ1mtZaGiBoz0J6OimYh4o0SirlmesODyxdi/JwKjqUhEXs0FoSlWAhLCLA0rdoD3W0KBnRWrMQHqkgSTZucVfKAYGubvFNRnCeXChi9CyFI3iHSRRNsokcLIVF+UCrI3Np8aJiHRx9aKmMRFvLQlp6rUA7WnnfVEtqkhbW2uEzxdyscDIgraVLIkJ4FrKjSyTH0eKFwYZArWuMaqj8Cis6nFsgInSFw6kaJWAeLcvE48UaGQVt6glhRbSBRdaTjCMLlhTWUmcg+ztQJsz7NdUw58TVJChWoSa6Y0IaWZqOpWgQHrwpqEXknpizECu6sEQ0YMyQkAuWokX29ygLyXJQIdwK0QsG6YBOeeZZy1q2LPMWr1tENDi1Zi4t7EIS2AABAABJREFUdeqYK0cja4iR2i0wOrJOOnRuEL7BGgmJplEdYpRRdR2hmiH2c6pmTYiCphe4aFikDqdaQurpE4/3DrvlcANoUotwsAiBKDV122CFxEfJMlqchLrWsIzUvcXNLKIRdM6wrC29EAQkTohNNPaYsDipmS1aklSQp5I2SFymWXQCnwicSVh0Ht85nGfj6MLV9F4jpCHaSG4FNggOFguKF4YMh8nGjft2jr8sQOy5jUVKyd50B4Cffv+7LOZrVquaGKE6PuHep3eRQvDq9StMv/kmb+7vkN3c5+6/+zHHR4sN7ueCT/7jPeouEnPNWiSQK9ZCEVQFpmfJEmsd7XKKuO3wShMbj123rCw0XmF7hQyQiYxbRxXhYI31ghANISrKYYHz0NcBbzf7RZKk1LZBuk2kdq8k05eu8Kv/5JsMr0wopsPH6Y4LcfI4gfkEuh7Q4E8Qi0+Rln5hyu5xCeVTY20987itOCdJfxaz8XOC89U8i8i+3z8xRjh7/kI8kegZBV1aOHdPbrOo5qyaJawbPpz/O1598c0n2/3soi6OZn6BUuLS95fU84TXrGeV+ZRyn2DwvgD8DUfo3oA48/fRsyc504t4wAsZbR6wHz+vUX1e4n/fuetD3kGcaeN9VimCtRvXmkIInPMbu1OpHhV0flG6qK++yCeckRzEy8q8hGN94mzKJRWcFU6MJiVbOwPUsmY4GLC6veLoqKEoDN1iQZHsIaViMsmoXcZ63pNiSTIFvUOpBOl7XNehokAnUGY5rlbkuyOuXBlz0uQEEUmMor01RylwqWJ/f0hWavjwkBg9wkcmmaQKUEiJ0pKYbqTgaSLxPhISw2BQ0q26jSnTMKeuLEZrateTGIXU6YYA6B1d29H3jr63ZM4wHBZkeYJ3gTxLCH7DQGSJxnqIwZEmGkJkOMgJq4gQAYNHqEheGowLDJIEpYYMyxLRBoLfSLrP4308GTKZjlkt14y3Rky3tji6e0pRpBTDAikF60XNZGfM/M4xJ0czsiylvJqzdXPMydEJwnrSnSHz2ZJ22VB3K8YvXkUaxXRnzL17C5rjFc56mllNOR4gUs14PMATkRKs0uzuTSiHBacHpySJZnZnQTtb4TqLVoo8TYgxEH1ES40pFc55TGpQSqKcZLy/xXB7hNCKKCJZkROtpzpZUlcdMQR2rm1TTAYMxyNiHzn9+IBymBODxjlLcJ4iy3A+kE8GrA9OuTKeoLfGnJwuGIgUgcKLnklMcGrjPneFY0qCEB4fO4ZOEVFouTmsPU40EkWIMDQp1bohTzXCO6YqxauA9DB0CowiQyFiy3bICASis5ReomVCpjQEwY5PsCIiCWgURiiMkiip2A4pPkq8A+0jCYrYWXymmJKxCh5mjiAlmU5I85RgV4zqiMlSdNuDkuSZZqg0wXq2Zc669QyKEWsXMAFGKiUg2PKSLmjyGHFBMVApmZR0sWIrSHq/WQCC9YylgSAJsWEnpPRB4IRhFRw7aYlRBhE90z4lqI3d+8xXjEKGChEfA2M5wPWWpCg4tksmogQCdFDGlCgVZeiRbcWk3MJ1Hmczhl0GIZBKAznsJjv0KiK6BVlIcb1BiRIMTFpNbFuMKilNhusEupbEkWCrL1GLDpluI32g8CkTsUXAs53tok2NrueIfEJ/bIlBY2XLjp7Q2hV51MTgGUtBhgK3YKtKIUnxawuTgsQYdMxo13N25YTeawYkNNaS9wqxloSBYVsNsEEitGTVV4xNyZbJESwYtJpUKnyQnLrAIGi0T6DyTIuUssjxJ6CFYlRKZCFZNJEy0TQ2bAQKbUN6X6IfSoVyHcJFZIhkecHYbMb62llyGSgyRWY3Yy3NMk5OGowQ5KneaHSrCmMy7LpFNB3jayPyYUGWZyTGYJ1Fa4OQAucdIgqUUsT75yy01o8CpQHjrSGjcUnb9Uy3R+Sp2jjhSAz7N6/y8q+/R7uo2bq+Q16mTHaGeBswMtkE6hRQqEgwglwJpIgMY06sK2KWs7M7JJ+N6D88pGu6jZMJlWG8IFUCHyyjPMeoyKJriMHhSTDCMS5TBsOEg6MFeSo3Vg0WdLT03hLpEVIx3tviW//N3+LKS3tEIS5mLC7YKx8Qi4/bSpzZguP5zfdsmvh4ugurfD6zhse3/kvSxme8f5jsAfUjHt5d/AVfUsR9Dp5q5XGe7DtP5zxs0/mXXw5G5RajYkzXd0yHU/Zvvvv5S49n6MmL+MoLv+WLwGXj7MIheGH+nwfmvrwr2nNwcWiJc1KQB9qBp7pTe5jwzNWjJ+I+Z/XwR5x3VCtA3H9+9vds+qdi+hxLFB89WS0r/vU//2P+v//sD/g3//rP+O6f/5j/6Z/9Af/8//ltPvjppzye8YJPOvv7tM//onARU/zsT70UXvnalH58l7B9wO5XPDff3CcEcDZwYzji1l+3dKdDSj3l2u6Y+qhCB81X9iSZ7BFuxUD1JLLHxYASEmY1JktJxyVpqnjp5j6dizR94Btfv0IbU9RwgsoHbG9Bn0V8Aa8OPdnsHvL2R5jFEVemKZ2tcL5lMMhoOo/rI0TJdDoiHxcIJbmyO6IsU5QCpQTlKKMJPdFEdq+MUblA5gIvPcUwoYs9Tjuuv7RDPkogichSc2V/iIs91rUMhppylCBNxGSKt/YzhnaGOrlDeTzn5cEOb7/5Fi9ff4m/9Wu/guvthf36yhsv0NPhtWP76pjrr1wjHaaYYcY3fuUrfPaDj5gfHLM+POHqzX2KcUk2KvjV3/jb9AtBbFOuvPASe7tjZBkZXS/Z2x5iZUMwPUI7plsjrN0cbt8uBzTLipPPDvnsrz/GNJ7FnRO8c7z93pu0ixXHH9/j8Ce3yZygW/dIobnxwjVMkuEtRAevf+VlVJaikoRBViAQ5KOMvZt7fPM33sP1Pc2ionSB45/cYn08R0vB3/rHv0w+yInes78zZnHvkCb29NGyPR3Rx8jk5h4vvfUCWEtX1ejU8E9feZf8e6fsf9LzlYOULasI1uGD55f7KY0M9MKzq0r2fIoLkTYGvtVvsbQdre8prWISDFZFOhy/nOzRCY/XkWFQXOszvFJ0SvK3uEZnNkzGUGW8IsY4JWmN4JvyCm0MG+1MVNzoSuquo/E9vyR28WpzKFsJySt9SdfX1Fjeakry6QiRGnoXebPaohGGKBN+0e8RW0vvPFInvF2N8ULTecHN5QBnBa3UrIPgK6spXSOIquC1sIfKM3oRiKnmW0cD6rXF1Z7XmSAFuCTiEvg1cZVWOmrp2e8yCmNxg5q2qPhmu4UNLUF5dtYF6rMU22zRdEPeO36RWm4OI19bF+wwoI8djWz5VfsaNTU+9UxdxlW1RW8craj5pfo11nmkTwRDSm6mL+BloC8E37h1g9a1WGdJDnte6vfwqaeTLd8KL9CLFopIPsjZPb7K/DRl0ZT8Svkr+NQiQkWZaN5SL9O2Fb1xvGZf4fT4LierQ+p+zbvJ25tDveuOb6lXGVyBvFiQNwd87c4uVWOo+ow3qtdxYcCiTlg1mq/Kr3OaaY67npfF68iVxPYKGw3fOHiN1hdYW/CaeJm8GOMI9MHz9WoCZYMqW14IQ3RjWM07qtrxC/Zl6mgJqeSaG1L+5ArtD29Q/XCfX7C7tIsEeygplz3Ke9Zd5GTVs5/MWbcthMBe5tkyS6xc4Yqer1y3VG7FbHFIc3yHYXWKaNbIvuFq0ePzDpvW9Cx4+eUdtq/tMd7b4b03d7ANrGc9Rpb404rlvWPqVcXOZMLv//Hv81u/91v82//wv/C973+X//lf/3P+xe/+Fj/4yff5/T/8fX7rd36Lb//xt2nb9uH+8dKrVwjZiljMEWXFu7/6MukrGn3Vc/XVbb73vc/4D9/5mD/8vb9m+8oejR3R+BEvvXmD7Veu4HPNOjjy9TGLznI8W7FzLMk+2oYfXUXdvsavvfUWyd5NYrpHKQzVyRoWUPqMV0rwImXVBBIVSBIQWUK+NeKVfcPxnQO69ZqxsZRpzWDs2Xkh47/6b3+Zb/76O/ztf/ge//X/8R9y/aW9CzQM534futN/tIHGcPmmHc/fPch7vtgzac667X9euNCd/hekJc7KwSMXkZwXEnt/83BJlQ9ouxgeBDF4AptfuMrXb7zJO698nbdf+RpffeXrvP36L2yI3eeh5c41XZzN8LxN+pz1nK9UiGcwFmfK/Xn16N+MK9pznNhjln8P331Bjvc8l3fZ/dlnTynnIfvyObDwx9/+K/76r37G0cEpu/tTbNdTrVuUlrz82nX+6//272PSi5RCDyQhj1ikS5sYz0gOnsXJf1G47Jvj45qL3/ujP+D9j95nuV4xTq7T3drhw784oKsq0kwRgmWwt8PV1/foheCnf/UpyvZk2iJcTeeh0JqqE5i0pG1bYn7IK+8OiQPDZLrHcTPheLnRXLCA9fvHrEPKZBio45JeRBIlyI4PKKo586phPMhofUdvO4QQaKFJk4S66Ui1RkhB3/cIpZAbK3vWTcd0Z8SiWRNFRApBkhiIkappmY5HVE27kQ76iFaKGCKdtQzyDCklIUS6tidLEoSE1aphWGZYEWmdp+k69sYD/sE//hX+4f/5f81qsaYcDTZRux/Y657B/e/+zrd5//2PWC7XTIZjfB04vnPCaDLC1S2zTw6YH84oyoKu6enuH0Lff+sFRvsTZscLdq5NaP2c08Mj0jxFm4SiKFm1NUVImH+4YHZvRXSeGPwmum/fMxyUhODxbMwOVYzIGFnXHZPJiKbq8BG0VkyubpMWGUe3jxlvj1jNltRVTYgwmgzZf2GX0+M5O1e3WZ+uWRzNqRY1RinwDhsDL739Er0NdE3H6nSFQiCNZm17MqXwIbL74h5BQne/DGEUL371JeREbSJQO0tXKE6vJxzKhp2kpFEBEWHuW3ZDhgpwTMvIKzxAFCxNYGI1IJhrSxkNvbcU0rBUlm2RbyKfa89ImM3hTpVwFGr2RU6QcKo6cic2rmij4oCGHZtgRWAeWgZJho6QBcWB7tjrDb0WLPoKJSQDlTHQJbPUsVUJGmFpdURqhe4juYd7vmLPGvpc41OJ84EiKgbGcJQ59kJGW/eEYYoXEbVukTpwHFbsqyHdytK6QCsjkyKH2HNsNniplEMqaIVnO9E4XTMvW672BbZLCSGl0p5tOSRWjlPdMw4JLj1C6Y66DOy0OXKUcM+dsNWleA1GGBZZx64fE3vLYVozCjkirMiBedawHycgA6dxTiEKZGbQK89pVrFXj/AqMlcrspDQ9yOSbszpyDPtClbLimVoyVBMr0oGynLgj9jvx1jRUqsG2QUyp8h1ybGZcUXtkxQ5jg1Tb+c1Zm/KgThm6yDlZKZppxNsbymFIE8V9/oj9vsB/Thgs4Dte6bpCHPccKDm7LYDepkSUkMvPEWXEhvJSdqy7TNi2pDvpKyaNXmdIDrBganZ9gVukBA7zyq2bM9eIP5wn8PjyDgRdMuesG5Y2shYa1SfcDqPJPSAR0jHuoOBbulVg8szEhFQUqPajpWHobTEdk0dA6NhQa482ja0SvLCiy+QiF2aSpIVmu5wTXs053DWsrMfqc3PMDuRvZevkZSGNDMcz47Zne5u9re6QkmF1glZmnEyO+Hq/lXee/cbfP3tbwCRv/yPf8V3f/g97h3eY2e6Q+d6+r7fnGvrpuR+l+N7S7b3xtSuoO0FzbIhUZHQdyzXnq2B4TB0VH3PrGoYK0FmNE2SMSkTtvQEZj3L4wqaNe26QYiCVDkaKZBG/f+I+7NuTa70vhP77SHGdz5TzplAAigUQLKKrKKKRZVIlkh1S9RFL2stu+3lXr73Wr70J/Dn8IV94eVhWS1RTZHdlkQ2SVGiSDbHGlEFIIFEZp75vFOMe/TFm8PJzJMDqkDpAQ7wRsSeYkfE3s/4f/BREXxFnoPXGbNJwfzePq7tSPKC6UhR2yW99yRacf3aFv/H/8v/nnJryON8XY/jKl7sIfGIc3q8pl9Aj2uLZ9xWXsJyPBUT+pTHwU+x2f+0HOMX5nURX1d9/vIxnPfe4GJd+8UBzq/Be72MvhBnmc9pWbmg2CM44qffqwu6eXTpJ3x+/2WhaF+DLg7OEZ97ji8se1HdZwX3Z6UycX5e45MLz032kwR35y8bYzG9xbtA1/ZEHzZMrJWEELDOvkC4iM/Ffj0VyxEfSrWCcx2+YnK+eAvgc2SspTNmA8fWe3yI5JMRbd1gTEBIwfJkzfTKhJCnBCS9DSQiIqMgxA3TLVRGvjWmO3IEAov5ikE2oe0d1nmM2cDYyh6a3mODpVMBn25gLZ2LJN7TW4eQAitAaUXoIxAoBwXRbxh/PdAkCEKIeGcpi+IxepE3DsEGBcVah+8CZZmhEk0yyvBVDR6EkmRFgtIJ9eEp66ohURrvN0kCg49YawkRluuamGqkVmR5BlKxWlQE7xlNhyDkE8Eybha3R4/NOkfXb5CrjLH0Vc/ZwZw0T/G9wftNHIUPkRAjwQX6YNj/8AEOcN5j+h41SFCDlCg3uSKiFpu6uUYPc4ppoJ6vkdYRY8SHQN8blJY46wjek6QJs0tTRNejk5TpZLh5x0PEu8DiYE69qHGtwUePDZ5yVDK9MtuMozOcfHLE6nRFXbVARGYp5bhESzi4c0DbGLwPRB8oBjlporDOo7VicnlGkIK+7TduatMSmSZEAfWqxgaDKhL0dEhQjqgERkMvIXiPE5EuOlSEHk8r5cbHNQp83MDcuhAx3qFCxEkQwtPFQK82cJbOGdq4CViNeByBVgRQAkMAJdERhNpY79roNrCviaLGk/mNlszFQOUtUilcrvGAR2F1JIaA1YoYwGkgegTQSvARumQTl2ZEwGvwQVAFS9Nb1gGssfSLHpVrCm/opcBK6HJJ10JrHSZAb3piFkE+3JBUxGg2kLAq4pNITMDGgLEBHz0mPoRTTQSttWRKYzNQwtMn0BNR0mGlpyviJvbIOZwK9DhEKXHRs+4bijyQZAofPX2wCAEGh9IWJQVhIPESusyDBKshdj3OG7ywGOPoYwKFwrYe7zxpZUn2UkKQtNHh1w1d0SO1IFGaNvb4XGJzRVxW9LZCT0cwTqmWp/iZx22n+AaavsE5j5YKUonX0HmDdYG26wnB0zYBrzU+errEEwtNR8ALKITajNFZ+jQH6UFY+mBIVbKBIk4lXkh62xP0RljsW0voLMYK6ijoqg4RwCWK1oEyHmNBKUU22GRUV1ogSwHO0vYOkWnsQ+hYFzbfc6Y1GRFvHHKgGF3bRVqHSFOCEVgbiJWhW7YEt4k3q+uK7GpOOpUbmOM0EqXHB0/XdwQfNrFrUqIbC6MNBHTfb77RRxuQsZt4LB8CbdfSrRus8Bu3STGj7w3eefrW0tmek/sVi9Mlg0TStDVepPSZohoqOi3wiA0QRJLggHrdEasTEp/gEJRFQSZSFpXDBonOUvoYkQGSJKG1LUpm9MbTWU8qFSmCLEuQKsVXzSY3z+mKar6m3HqWkXq4qT5y/XqKR4hPBJGLaz05Pndiw1sLEPFRyq3n6LzQEl/sJ/Wfh56775+SLlCufW56pu4m9vVp97Rni4tzpeE1Z/NZ/fcXMAdP5V17nUG8qMzrjOW/0CvziL5Y4eLzTP6FX9Uzx6+a2BdIdE+MIs+/xS8cYnxU++KCTdXxyY/3UUry5u3rfPS9B7gMtqYTxrOSux8cI6XgytVd5octHx0esXttwmS34M5H9wHBW29fI8vTx/6XL1RGPL6/c2a3V70oF5X5iYxDz8/QO2++TdM2WGsZlROqZIrvLbKX+LrC6AGddaShZ/fmDqt7pxxVc7Zy6Aj0XUdRFNx69xa1Tdi7MkJ0kjP3Ga5v2d1KmckdvKlRAgas6XRABE+pBJcul3x81hAlXN+d0bsa2kCeZ0iR0NcdQkmuXt3l5GBOqlPyNN3EGhydooDxZMhy3ZFnAp0ISpUSJBAj09GQrRu79NYx3Znw7s+/zZ0f3iOEyGiY0yxbRuWQ6fYYqSIP7hyjhODNt65zcO8YB0y2huzd3OW48lTzGtGsNvk07AY96jE9C2dI5K233uDeJwcor9i7vIfJOnwfGE2HvPHmNf7y9/6Cft2jhUQkKcGDkoJJlnP60T7JMOPGjctsXR3hKkt3WnF1e5vD4zndQc3lt7YZ75ScqTXbl7YYpJrjozOWy5okCkZlQdf3WOt58/1bLJsKpwNFWkDrWViDtZ40yA1KV5khQmQyGuIkzK7MuP3eGxx+fEC/bPEIdqcTJAJrLMPBYLOJnyzIs4y97Rlr6/AhULAJopxujbj+znXefPcGH33vU4Tz7LxxmUCk7x0yRsRpS7Wu2Lq+y+3BHvnIMFmtkFZw6fIlvlPvk0vNjVggRMS1llRIviymfODnSKW5EksioFJDEgRvxjF3RYUSkquiRPhIlJFCat4KYz6WFULC5TAgc4AKpFHypS7n09wQZMYVmTOWGR+JNRLJWy7jftJjY2QaNJe6nDt5iwiRd9SIhdpshtMgmZiUT7TDO8+tSnMkKmyuGXrNJZtz17fEGLkhSlayoxGWgZBcYsbH/RItJW92JYc6Yn1gVEXeS3b54eoebap4y42YpxZb9xRZws2znE/zNbJMucUWtlzzwC8YkPLVeI0PkwMqabjWzrAuYDPPIHpuV9f5qPyUtHJct2N8ENjEUVSRd+0lPpqekRnBNT9BRUnIBdFafiHe5o64T9RwyW+T1A5XOrKY8558m0+4Bzay108oshHR3ENbwZv1VT5JG2R0XI4piSnQBbja8tbxDjXHbO1tsaOHDNyMT+MRWiq+xE0OihorVgz6IVdPBA+2NToZcUPd5I79BBEs0ybh0mHCj8o1YVRw02yzkkusShi2mivdmI/yQyhybpst6gGYJjJqFLfkNX4o9omZ4KYdcxYMHZ6RT7nNTfbdKYUecCPssioF0Z0xIOPLiwE/yjuSkHJjoGidpPWWwkfe3dLcaTSxMoxUh5YJYZgh+56fuTbkQTXgbF4zkp7xWKPaiBZwaSjo6gzjPNuDhHIYOJkbxrtj3vv6NfYPKpJFx87OkFJOue8rYt0xyVo+Wy0oxxrtYbtIiXlCkqTc2rvB3CwIMTKbbjEuR3x85yOkkNy+dZveWibVmiItuDTceayMfuuNt3hwtM+gHFJkOXEW2d8/ReaKmzeus7qbYG1KOUiZ/+AeVR0QaSCPLWmW0KERvidfVoR8TCYk18b5JvbJSFLbsVvA8ZlBGI9xa0RQaJ0wKFJ2tmF/vgGYmGWa1va0pscFxVbWk+YZmJoxoOiRmcRmim/+o6+y++blJ1pg8WSdfk7z+1gr+GLN9wU6yodtP+0K8yp26bHLlXjaxefxVnLu19NM6ys8HT4Pn/ba/MPnEIIu8i75iRn3TQOPlLabYOnN+UdP6KeSCb4ooeoLps+VyfwiAek/g+Dxd2K5eIK2+frc7atKPjF+RZ4Ec4sLv5ULrRIPSz5CeIpxo108H5DGudfxfJumt/z+v/4Ljh7MUVqSJzmJKZGdR9Y5qzNDv+9RWnHnT8+4992aatUxnBbEUUvbtyDg7qcH/Ne/+U2UfMGdPhzn43Xi877YLxPOnpKaXmJGe7YZAV968212Ztu0bUOZjvi9/b9CFx3bNzPufbjeQIxKycGDM5bHS+rTHu0Da9tQjAOSjltfe4NhOaF90NCvG+anR+itjnpZ4YWnayB2AtP2rI9WIANRQDJKSG5skazv0lvHquvQIRClIAaP7T2jckQQIJICaxeIKPE20lQNMkbyUQGpYrRTUq0bOu/QWiFEJNcZV9+9TjEYcPzgBGxg+WCNazbwtXo249Kb26hiwGhckpc5kLM8W9E7wZtf/zIPPj4gL3P2jyMnq4APBeO8QKoElajHhtjNhvRwJ45PJrtZ9GifIozFVZ754YJm1TDdnbI8qyiGQ6I/ISlyskzSdXNElHStwRuDa3vu/MfvUx1fIaaKLB3Rnnrc/Q7lUtr9FhUE7dlGOze9dYl0b0J5tmI6HfHOjSsc/ege1bymmJQctWeYNLDyNcmwQKUl0TqsSoktBKOYbI25fGlC1/UQI2f7Zxz8+AGudxSDgr7fBNArJfHe0/UGpTST7QnF1gzbtnTdxgpx7eYOdddTDgsWR0twnmZRs7U95fTBCcZYjk/XFDoB6zmc7zMtRuzdnsDKMchyzuwx6ZbE4wnSYyJIJVA+cqp6lNAQHW6Q4HoDRLRUVMKSIhFhY6GTDzdyKSVHsUOy8eH13tLIzXNTMTJPPLiI0BvLyKpvEdqjYqQuFaoJoDeJIesigxCREVZ9Q7CRMIiEoFmhUCrDty21Cgi/cRFJZcJaepRK6ZuWXlukkMgAIkYqNgH2AcFaRKSLCCmRQjNPDEkGvQ50qSeGiNIave6oVYawAtM6VnToGImtQXaCarBPOeoReYDTY0RIUaIhC5FFcORZjnVrjHaocoS0knw42GQmby1taoixo517QtkxyEbMRYd2kmgdxrS4ssALjZQZJ6sjkkIiE0XsDa1sIdOkZUaTGLK2RWctiepwIiERiqyQVLYjqSXWSNJ8hLvqUF2FaB1nI0EoZ/RVR73fsPAePR0CkvniiKzYgvqINJ3SXzHolcMpT5e2+KqBoUXlOSvboKLAtZYaS+xLEDnCS870Cuk6YpLS2BqFREmBioK2bImrinQnw2UCv5CARi48Z1ZDpfC5pjEjXJToNENVDSdW4+Ye4TVCZQglwYFKBfcPl6SXthjKIZmpaNqW6CDPFEUtKHtF7xTTqDj79BClErbfmOBWBcpIklgS65z9+wecHrVMxjlVbKFYofKMLPacLM/QScaVt66zqusNYpaSCClZr1dE5zdJTgN88/1vcHp0xGS6RXfSEt/cJKbc3drhH//qf8XZ4ozpeMaf/NHfcuod0UWaY02Um7wZzsBnq4pGbtaR2XQH3cJiZSl9gkzHrPwGJGVkJCDpTGSkC4IN2GZFjIrJZIBAcnjW4p3l6LBBIdAhYmwkES0uQhois92SLnjqh+6DYyW4fvMSX//Nv8fP/erPbub72T3zlfvtRVzyC9p4JGA8ZFheb2v/O+BsvzALxAva+jznX8fs81p9R86xhA/1xE8QmT63fPTCy0+QTjftvk7LT5f+XELBI3pd68nnEdT+MwhNX5hwcU7Ifs4EdSGJCw6fK/40QsGjV+WlKF6vCtJ+aKF4FNx9PtDniaBxro8IZ0crFmcV9+4cIqQkVyU6JqxOG5b35qxPa7rWI4Tg7g/3yYc5MsvYvjkmDFvW3RohBGWZs1pWzLZGPHKREuJprcNFFOEc2sRPoiF4fhZfUeFpErA1ncF0xkc/uM961bBarEm0wqUjqioQpSSuPPO+22DmJCVW9tiuJh2mtF1kPZ+zOnG064ZYBiyGcnvA8bxhNZ9zdBTAe7xJScqSat6Su4g5WLMM0NuAXDcMjKU3lq4ziAiSTebm6jsfE0LEGEcUAhctbdtS1S1bV7fo7CZYVguBdYZyMiAd5FRNz/K04sGP7hFtoDcWawNCCOb3zxjtTGmqjq5qSJIUH0AoibORw/0zqkVNliVUxQ4xG2B9oMxTYlaeW4DOi9tPC6/3Pt3n7CEUbXCB5dmKet1wcnDGUXeErXqqpkMmmug9VdWQZRlRbxDLQghUumP1vU9AS4ZbI7qRQ2Yptu44vH9Kc7akMw712QFn+0eUl7cwITAYDyhv7PDP/tmv0K0a/uOf/gWTgSEulyRyk/tB2wQNpC5BeY3sDYPZkFXdUJ0u8dZzf9Vi241rV9sZrLX0vUFIwaAscG6T+bu3jrMHR1gBSMH0ypTWWNbLahPbUnWsT1Y47/nBn/+QJNFY4/C9pYn9hhH1gbsf32dolrS+J25P+Ti31DGh9wbnDSCZK8dARU5ZbXKS4Ij9Au88FZ5cao5p0UjWweAJyBBZSsva9AghSaOiCj1RBpCwiB0aybHoyJGsVYQUohLMg0UiWIUFKhMscVBKOt2wwBAjNMKhpaYlYlXAy8DaC1zoaR661DQZHPcttq8xQhM1BFEjkKywDxdZQ6ci3gdsnqIzybLtQW5crroy4EREiBrYQN+qJNLpnpBp2qbGxR6MxRYGLwOr8RKdBmwu8OOCrqpZZxZC5EiukCHSqR4la5RpOQkrOu05jA1J5ukzz4P6BJsJVhNN52vm6hgdHI1sCRGEbljohkZ7TkNPXgXqgSNuzfB9xUp2rNEc2yOUVKwxEBJs6pjbHpkKmlnPII1UzXKT0Vp7zuQCkQYW9j7Sjzlza6KO2CLi10vUsGCZDwm0rEWLO/mMpsg5tQ1ROFpXo0dQDR30LaQ9VWxAS7zRJMqzziKIyFm5oA4NMVb0whMTzTp0xBipdYdPa6QydDGhTzTzao1JU1qxJEaFSTXh1OHqlrpLaEykXQeEkaAT1lFi+54eTWwDyy6S2yVRJ4wHCXVIaInQR3QjGCHobWRReZpWkAxTFocN88UJsihoO0/14JCzg1OCynAGfOwJeFzXEEsQhWbVVeT1kl4ZtFdUTYWIG2SxdV8TXWBZrxBC8OYbb1DMRph+k+37EQ3KkkFZspxXLOdrTo+WRKCrSwiS9crSpRE/mFA5g7OeYR3IDbQu4oKgW3t6FzbIVAJE72iRRBNIrcTEZPMNWUXb9RgvsM4hhCRRAY8k15J1U+OjJ9UZ99Y1Tmzgw4vphF/8p7/EN3/9F0jy9JzG+xGc6audZ57ahV9na32y+L82Pd7tH3s6vLiBVzKtr+sV8kz5xwrYV7X3qMEv2nvldeoLgRDnkDOfVc5e5NHxk1DkFSBEF9V5pFD8idxIHvf7Qi8d4JVzf34eXmW5+ryWrZfQFyJcPG0p+BwT+KqHL55lzc7T82cu9Ay6gHHfMOvxqYk8H2x1vkoIgeGkIM00o+mAJNWokJB4zfGHByR4Mi0hixuLhAL6jvWqJZWG0TsF08kQIQVJoikHOd6FTdbTh+3HuNGUvpjODfS8wPBK/8Lz9V989dluHvUWQniMqhVjJIbIaDagKFKG44LBMEclkvs/OmVZGRItQEc8kSyRSCkoxkOGV2ZMtkq6RUZ0mkEhODwO3PjyVeQ4YTYZ4E3Ozi6Y5Zq+FwwKyWrhSZ2jlCnDTJFHRVFkFC7FEQk+IMLGL1mnmrbpSRNNlqdMhiWrptoEemuFqXvGO2NW65rtnQmjvekmjsF5QmOxi4Y0SRAasrKgbw1SShKlMKuWrm7J83TDbGu1SazXGYTawOFqLSlSicwENmqkigwnGUJeMPfPGNTGkyGT2QilFaPZkCRRCCkYjkrEAFbtGUpKBsOC5fGCIs9J04REKkg2/s+ZTje+632POa2wQbJ9eYeDD+8zTFOmUmB8S+JBH7Xo5SnLfETcmTGeDBCJotwecenmZY5Wc3wMbG3PaDtH3xsQgjQm5CLn5HjBzs6E5miO9IHDj/eJ1jPIM9beo5SEqFAipe8t+MhsNqLteoTdZEgXieTyW1eYbg1JBDjnmO6MqaVC+MDJ/WPyJEFJSW86BnmG9QGVJVjn8I3BVT0hWoqrGXuDkqWKVE4wihqNIOpI6SU+RFK/eU4zVeBxKDpGIdnkE5EKFx07SYmzhgCUKkUkiiIIVBDsioJebXz+B2xiQIYiAQw7qqCPDkEkFQphLGWQ+DJj0kRAIlQKAXKhGemcY2nYkhlV76H3iKBJImTGEwRMRY5Tnqr2kCiKRJFHjc0iE5dusrTHiJeazElGacZatExCSm8MGSkuOAZCUiYpvXWMSUisw0uN9AmFyxjKnJWPTEWJtj2JddRtx7gYUaaKENds5zP6YIjrlipRjH2BdNCrnGGt0fmQxDvWyrA93aOvQAjDICbE2pGqlCg847UmkuKVYShzVFqSYMA2TNUINwRhVuQiI9CTOg1py8zm1OtIkIo8L0iTjCERmSumpqRPHJEJUkSEKEiaDJuNmFlPOdK4pibximxnTDjz+OGI7e0RZ9bByuKjIneQJBnBVeyKEZ1OKYzGtoZSpAwoMbFi3GWE1lLKIVZaCp8gO41JI9uxJImKpBhgoiOPGQOX0PuEkU9JjEKEjN5LhgpEqjFLw1iDTgMQaGxgUAhINCfzjkx5lApI09DUEAzk0uEQDBJJmoEOgbYxdLalzBWDnQHDWY5DoUtFf7ZGtzX4njRN8L6jGGaYOlLmObd+7iZhUnM2P2ZYjigGBVmeEmJgMp5i2hZCJFpPORywc20XpTVKSlSWEEJAyk38xqM1Li9zkjRhMhsRQyRLE9KkpD6rOf3gHjGHgRakwaNlZCjBSjBti7EeBZRB4DbJv2kMpJkkS0uMjti+Y7A9wbRrEgFSbPbpqlqiUAjgyrVtDo/OyGclO1cm5JOcrrdcu7HLl7/+DmmRPVmXn9ZQ8nyy02e2ynPeEM/Xf/He+tPRT8icvmb1x0rW8/nDXipgPcPcPl/gGW36Cxi+152XF83hI4Xwy+p+EQzz+QTNr13nc5V+MT1rJIsvu+PXVEBfNJ9foEXjC4GiFREeO719AXTx+/M0mNjF0GLx6X9CeL5MfAnzHZ8IFqtqzb/5w3/Hv/gf/xV//cFfM748Yo1h5Xtuvj3jwQd3saYnyMB4oogqxaKYjQQIhRKa9rQlfFoz/yDS7Rdcml7lP/zOB/yL/+uf8j//y+/ywYc/4rf/4Lf57T/4bT68++GFc/HEEvRwjI8wxV6gqXj5E3j1ChgBHwL/y1//Nb/1u7/D//R7v8ePP/iU3/nnf8J////4Q+78+AHlJMGIli40/Oo/+RLXb15jKx2QdD2XZjk+KHoDX//qe0yu/ixNc4kk3ePNt67gjaJZeXaTCZER1SJBxZR33trDRk/TG3biGXXVE6MklZJ3djIim8zMe9MhMXi8s2SJYntrgnOetu7Y3ptQDjXIjWvMeFxuNN1CMCgKog8kySZo+Be+9VX6Zc/y/pL2aE3wYG3Ee8GtW1ceClQwmQzRiUAnEqUFb7y9Rz7SkHiu3Jiyc2nAYKIpx5r3byQUcs5AnHClNNy4uYN4KDQ+8uUVT44eP93bb92gO6vpT2smxYAcQTCO+nTF177xPtVphVIJwQSu7m0hRCTEwNWdLdI0xbpAphTbW2NGOxNknrC3O0WNc6ZvXqLcm5Lv7rBORyyyMYMrb7DWQ5pFw/r+Ce2647f+b7/Lv/q//08oq+hPe/qjjrjy3N67Sn/UYI8afubLb0BSE7MVsuz5yj/4Mg0dNo9cvrpLIGKDxzrH7tYUD6RFyqW9LayAJjpcItke5My2Suh73nzzMqlU9KuG5rRiVmScfnaMN57pZAQ+4J3De8/VnSlKK5RSTPMBN27cJCwjyztL/unuz7LzVy2X/rzlnQ8EO3qIFQGvBb9qd+hEwATH1CmuyZKWTSD2t/wuPZ4oIgMTuZXOsAn00fKtdkpne4zvGQfJu26Ij5Eez7fkFUy09L5HI3gvTumCo3WGb3AJPy4w0ZPrlPfMCCPASsHX1wNs19E9RNL5mb7EJo46tvzcaUb7WaTZL3GnA94+2aZutpifDbl2OsZ6R+cdQUTebwd4HbEi8I7ZBLe7gaeTPV9rSsJ2j582vBszUtFih2v8qOUX2wI3XhNmNV92OVsuYLMerzq+fvwGlYJaCC7fT9lqc4wzNPWaXz69RZcJjAhcrgp2wwaW1yr4+/X7NGlBZRXT1YBrcQvbNzSh45f5BUzwRKWZxik3212sUjTB8YtH79CsWxohybuSN/qb9FLSSvh6/T5BeLy3lFbyZXkDq6DtO7780RbzGqpQ4sOId5u36J3Cqoyvzd8k2JYQW7KrU26LtzjNPMftkneb66i8wPmILkr+XvY+NkmISvPe/BKyisSgEU3gF8+ub5hYDe/H6xRZQkgsNnN85ewKlTeYEHj7dEDhwZeRWML7R9dZNZLlWnCz2aMUJSbTWC355vpNzMc79N+bcUtcYtII/DpiOsW7gxpna6K2DHTNEIOPIJKEr95QuFzgC8EgC0yFwrSappZcGvR0lcNb2J2NeednbtH3GW2tuDn0VJ+c0h2taRZLtjJDkiuyQnElixuF17RkuDPj17/9a7wxucKtnWv8+i//Q1xvsK1Bo3jn5pcIfcT3kbEa8cd/+u/5V7/7L/mjP/lDfvjRD/nXf/C7/Pbv/y537t15uI9EslRz7eo1ukVOt8z50rs38VFw+GDOuuq47DYodiNV8FYORZS0i57QBb60l9K7wEkfGLoW3QbEIhCXnjdLhxQSGyNbM0UqKgJrEDVf+doOpB1erZF+xTe+9S6/8d/+Kr/+v/tV/g//p/+Gn/vaO/zsz7/FL37zffaubD9cfsUTBvAxXP1rbJWvvac+oQ1y6fOJfl9Y/qlensDSxhh5Cgo3Pn3t0fWnsW55CWP+zG/xIv7qaXqOuY3P/D3Xp7i47OvST2NxeKbyqyB+Y3x+cILz/Njn6v4nqPGSWp+3wfODPi/knX9Gz74Hn/fZXNTtTwtFu67XjyXdzf9ebXO5GDbs/K+LwMPOtfL4Zbmgpecqnvd5e1oAegzndb7Cw+M//vP/yPd+9ANO52dsTXapTzKW8x7X9JjPKqbZiOWqZzTMkbKk6wJpkaJExDYtJ4c1gww6L7FekuUpo2nK9rURVe3YuznE7N3DpGtiDNy8covf/JV/wqAYPHXPj3UjLzF7vhiM7fNTjJHP7t/nj//Tf+Kz+/cZD4f0JynSFawWNVu7Q6J2LJYrhsMSvxiThgn3fnBAuzpD5Dm1iexemZJMS4pxxulJy85WhrSR9bynW6xowgNisaK8OuXarRusuhnzZcQva5qTmthbVi3szhKKXcXSGPq6Zbw6ZtwsWLctQikIGwtJ2xqSVDIeFxyfnFEUBUpKrPU458iHBcSIKhNuf/UtuqWhOl5x/NkxiVBIpWiajjTdJIPbAANE8jwlyxMWy4oiTyGVoCVdZ0gShbGOpu1IlCTKDQKVsZbpYMjP/9L7/Lf/5/8tSuuHC/az5vbNU/7//b9+nx/97Ues5msEkc8+/AyZat7+6lt085bjj4+wLjDMNMEZlm27iWswltFowMnJnKvX90jGBYtVxWBYMN6bIRF01jIbj1gfnNFULTrRNPM1UknOjhcM8g2CV1SSYlxSTkuKYcHJ4SmTyYjTB6cUswFSSrKpQJWBdVezs71Du/K0dc/qaEE87WiPa3pjGeQ5Lm6ynTvjUKkmKXIaYyiKnPFsQD7IsNYxGJZIqbj343uExmB6SwgRmWhECKRZQrWuNwkMg2D35iWaqsXWHckgo25adq9sk41LCJHlyQp5a8j9G456W7ElNvkftJAsMQxrUOnGHWoUNCFRZFGxpGOLYpO9nY4yaKKEPArOpGEv5HgFc99RJDk4T5lkHNBwKWwyGi9dSyEUUmlKlfHALLkUCpyCBoewgUwqBlFwmBj2fE4XA+tgiS6QrwfIzxyHieZqOaRHsY4BCYynFj2qmeuerU7hVQQFLtMUEpIMjnXDtsnxwxpST6cj40qQCMVR3rLb5dSiQ2WSCsuwChQqcjbu2PEjfCkREWptmNkRtIHjsmeLEUZ5bOdpYs2OH5EUBcdyzchkhAQSL1hkhm03QGo4cwvykEPsGSQJc7Fiqx8SU8lCVBR6QIierIUzvWYvzAjSU5WWMhkgnGMQFCfmmG23QxUHrHAkBoKF0WDEWdlzLZnRNyc03ZJsNEBaQ4rggZxzrRvRp45GdMR1yyiM2L78Jsf+jEvlJc56y+nRGSgoRIKqHfNhx54fUps5JouEBAZxwCAdcqzXjFcpPve46HFYRk2GDhmnM5gsFa3rUamm14Gt8S6sLA/MnC1fUv/lLnoxpUExCQJ3t+KkgVw5Km9Q3mB0xixPEFay7gRptOTbmiQPHBytGUigldSd3CTKs57CWqzTzIaKEAPrxjGa5FjrcF2DI6UoIuksZ73u8c7g4hlZ2jHYnfHO19/hq1+5zY29GbMbu/zZ3/w53/vgexyfnrCztbOJO1nXhN6RjXLK6YDTsxN2t3fpo6e3PQjBras3+c1f+8fkaU7XWn77//0XfPrjY0KIZOMBXWP5wV/dJY09xc6EpMzBB8ZCkXu4d7AG11DuTmm6ns56pmoT5L5qBdNC0giHF4EYJVdvjJg/+JQ+gIiO3be3Wc3P6FvDVlnwj/7pN/mV/+43nvYmfmrlfVrD+2SLfcYScdHG+hxT8ro77E9ownim2vnDi1oUL/7xFEd0caUnvNFPFCPwRdDn9T567M72euOND5XhL76919T+vwaFEBBSvtQG9HRf545/mu4fMRwvY6ZfQf9FoWjFuQm4yET2JAjmiWhxcTvnfj0z1xfJLC/F9n1U6aEK4pGb3NMLystGEen6nrbfJHhqmo7eSNaLemMKLnJIMrKhIpsOOP10Sd9GpGoZTQvGe1v0XtMvV3gvCEFQV4a+ranmC9AJ2TCipo42tEQiIQR6YyjzwVNDeeIFFZ+eO/FkXr8oweJRS6Y3OGex1tB2LX0Xkb3A9JauN+AdfW+RsiU2Bc4bAmIDnZhEAoqjBwvCwRyRSHoLyzsOHQV9D1pL1AxMb9Cdpa4txjnaLtI3dgPxagIxKprW0K8Etd9AvnrvMc5jraOQCuM9ddWDlCRI1suKECJJpkjznOZo8RC1ySETRZqndI2hazoOPz3EdBaR54gQCYBKFPohNGtVdXS9ITcp1bqlbXp0obHB4X0gSRKEBJ1sMtUmuUZqSaZyrt2+zvu/8nPY3m6ECy7+PgD61tBULabbJIzzPmKajsXpkthDcI4QIi5IjPcbyNgsIcRI23QIIVgvKxI8UcDyZEGQgq3L29jW01lLs6xo1i1dvQlSdtbSdT0C6A7nWCL6JGHvjT1ijPRNjx3kFJOSZlnTrluSZWR2a4z1lmpV0cwNbWVQeYKeadrTBrXJUojve0zXE0IgVZLQ9YhUMdoZk2Sapu7wzqOkYn7/lJP7x2RaE4XER0iEINGK9brZuK+pjXvT4WdHeB/QUqIGKSpLcBHq+6cUowLrHLqQ2FRS2Z4klQQEMjha6UkThakrmofQp4mUYA298PQqEP0GMhXiZixa03tPFR1CKloiPvQkAFHg8LSP6qmIdYaBgBrwStA4S0TQYBBaPlRfRlxw1MFghdgIHjKShEAoc4IPGC1pXWRlPTJRCNuT9R1BBrpcI52nCQ6sJ8s1ndrAyXbS4H2PlwGnJSZV2L6jD4ZGSkwuicrhs02+lhZH0AErLUaIDTqX8rTOEDJBJyyN3KAhiQyslPROYIWhFw4tBb3zKCGpnGGARlhPlwZEsDjTEb3BaEs3EkTr6LQnig4RweWShkDjelSiaG2LbVvKPEcXJZaNYOYTSVtb2ugpdErjGrq2pyKFaGmVxWtLSsAFh/eGtV0TpaCfRGKSkC0i89Upbgx1aDFAK3qikKRS4YuIwbMUPS6FLttYiTICdeywKmDHEmd7emUxzqJ0QiICvXc0QuGTSC8tRkHneqzrMSJQYzA+0rtI03XIxmMbQ+0277wNkh6Fc5GmcyQqx0VB9GCrngwBicb2FhE21nEXIPqIFCneB5ZVRyDQWYmdtySJQOkUERNCtNSLBhsE1kWkFnTBE5cVy8M569M1s69/CaEkfd/TdR3OWdquIfaR1elysw2piEgE1jrqtiEqSdtv1qAQPMYasjSn7x3Bb9y1QohEnXL/w0NCFMQko+kdecrGChEiofM4D1Jout5joiQb5Ji6x5hAmg7oggGtkCqhGA8QicC4jSLCO09vHKNLW5u4vPEAPSrPb2xP0wVswGPWQZw/84Kd9SfecF/B3b2oy+c8Lh758vMYres5NfGjc88yUM/yshdIJ+f5up+aXsTcPstLv6jO+bovk80+h/PME6HpRULEQ4X5C1C4XhudCy5weX+x4PKF8nMXNfITyrY/CX3xaFHPCQZPs1TiBeVeq80LTj9JOPOMFeJ1XsCXLDC3b73JJ598Rkhhd3uGGmzR37cbLeK2pN43mGWHHme8/0u3+cFf3IcQGCYO6Sxb16YUb01ZHyzYv9eghGQ2yWhbw7oyrO6cceNWho7XEUIwG+7gnOcHH/2QrekWl3b2XnCvT4ujX7xeIXL16hXKdMIwBnKZ8qWv7HL3BzUKy6XdAaQe1+cUueaNb1zj/ocrolZsTUecHK/xISVLBZORYIlCeZhlilGA1ToSFeRpwpnT5DpldytD5Tv0yyOENYxzw3HnSFLFJFOMRoIHZxYZBTuTEd7ViE4zHg9xPtLmKdY6drfHzFcrMgFaKMZlgd8KNE3HMMuIWjDeGjHZGRFXPSIK8ixlNC6QUtK0PVoJskTjg6MYZozyHB88tkzRWrG9NeJ0ucJaz87uhPHeFp33jHfGXHv7Cvfv7tN3hitvXuXW29dJ8/Tc3D6RltfrNfcPHlDkBbffv8X9T/fRWrHuLOPRJtuzlorr7+zx3YM5rjfkWpGojCgirrNc3Z5xeLpkUBaMpyOuvHedj35wB6klb7x5FbJNcsCdyzPiWY23nm5ZMxyPyMfbNG2La3q828T9jMoM0RiW7Rnr0yWToqDQiuWiJlrPzt4OSdDY2hON483rN7j/4BC7arn+9g2GKuP+Zw9QCCbpiKppKccDpPMYAW1v2L484/obV/jkh59gOkNsPf2iIc9StnamZGnGydEZgchkPKDTkqbrSaJka2vIyfECZx07V3fIpwNW6xqzqNnZmhByhWt7JkcO/bXL0JwxNJLb2YxP/RyN5JoosSpF0jIWCbf7MXdFjRCSKz4j6wOf6EAmNG+ICfd8RXSabaOZpgOkhMwLbsQhh/REKbhESeEin2UtwgfetSMe6I7gDJesYpaPuMMaJRS3fMGhajfQrGpA1ms+FTVYw63Gsgw5Tkp2osR2PU4rRIxc7gsYWoI1jHTKXjJh357iA7zRj1moDiscI5twrd/iQbLCS8VNP6WxawiGcdRcCbvczU5xEa41OS6sOZCaoR5x83TEx8UZfWe5aSfYVCFUpDSK97vL3FHHDAY5V7sBQiVEFSit5lY/5YP0DCEie35IGgM6gbSOXG1v8llxQlqWXLIzEhvRmSDtJG+K63zm76Oj5ZreJWkEXmhyqXm72mK/O6PUU66OrpClV4EDbFfzZjPkLK0JJAwawU6+y4dNT5mU3GaLs8macNQw8yNmfsoDvyASebO4RtU2LNY1W9tDbgx2CUtHt2p5Q81YyBpDYGRybpSXub+zpj1dcK2a0ieBKANbRrPbXeYHnDDMR1ypUrxSeNExcglXuwGflCucD1xzJetW47OEYZDsSsl9H0h9ZBpq5niUSEi14tYwcuwyqtqwk3qiUJAnpEGyldQcrRtS65kWKbnWdLXHmZ6fe3+bxWGHWjREb1EygIokUjBMAn1QoBzTYcrOm7ucLCyL/ROarsNJj+07wnzFpatTfvzpR2ituXXjFnc++xgbHLPZFmmvqI8rJHB99zp1bDCpIRcZs61tjpbHCCHZnu0wGowQAsbTnN0rY472V8QQKZLAvaZmoBImg5TRWGEDeB8ZZx7TBwSG2SAhSXru1xaVgIhrJoMMck1ft9y+PsSMx+hhThl7Fnc9pIKoJFcmJVvvXcOFwM7ulK//k1982hpxfiUWkXgutuBpXvqJE83fueL+WYb4RbLMBbzwY8+dZw0QjxnIx34PD3/Fx3WfYl+fdWESnJdKfnom42W82OuWvfD6ExvMi3KO/LT0WoA78QVB7+euP2rrlZLUw9jWx+hlj04/X/JFvT1f6j+TMPEs/fTCxTOS6EXC40XC6kvpWfPcK7r/XK/VK4tu+rONR5kUOg21QqwFmUnAB0IAERS5SKj2a5r2FD0esj5d0VtBfbwinU6YbU8Zvj3h7OhjbG/xVhJsgoySdhH48F/XDK5MmVzb5jST/MHqD1g3FaPBkG985e9x69qtp0f2+CV9gYh+kZbiwqfxrCrhycoVAdeDPdzFnUroM6o4AaPo5ys+OVjQmJ4+SrYulaymNWq8IokNW2+OiH+TsP5ojvFwqhymTGmiIPaWzG+QShIN9apl640tyDP6lUE6i6ktwUPtA2maYlTG9PqE4Uiy7uY0izUmQJFkCDrqxrB9aUb14ASVKHrn0Immt4bOGJZ1iw8elSiCEsQQkFoRXWSxv0RrTYyRLM9QWtD1PcF7ZJoi/EZzHkuF8ILgBVEJ6r5HacVge8TNn7tN8JLVR/ssHiyJTc/RyRl9Z7AnFavvf8a3/jff5t1v/sxTmqCqrvj9//BHzBdz8iwnqVKkUljjaOqWwbCg9w6daZaLFVIGZPQ415OkCeKhBedsWTEc5sQy5fLtK8wPT5AJTK5sM740Zv5gQXW0QBvP6af7dD5s0FFi4OzwBOMcaZKQZineWvq6ZaAT+qbDtAbTGbbfvELVtBTDkks3L3FyeIqZN4y3BiwfnKFTSUwl7XLB6PaYvWmgLAo4i8RPj1nPK7QUJHnCeHtIogTVoqJbNhx+coR8mCU3xECSaNqqQUYYbY1wdU+iFMJHJnsjrr57k+Rewb0f3dtACjtD2/RkStFUNevjDtN0TC9NcGuD1godIo3rkVohgodEokRKIixpUPSpRNnNgwnGYbXaBPJHQe8tmZKoTCN1Sus31g4RNgn6JIKAwAZPkmpEBCUEa9shoifGAAiaviMmkSihTyNZKtGAjhGFopQ5CAXDFE1OSiR6T0g1mkiQkh67CVxNNdp47Mjj08071bQVofWExKFFik0dSku8NdjEI3RKsBK9NphQQ65BgU81uAEhRjApbaKQKif4SBcj0dUgGrIix3hDmhb0riMohZAbxhAbqOkppMACwnRQCIQ3pEh87hiORixjQzIukX2zcV3SOW03JxtmaFsTo8cyIwSHt4qzPtAliq7QrFuPyVtEEKQiY7Vc4IYOMoi9Ya0UQWWszzpWWYWeCPSoQDpFR49yHtc5rGiRBETXQdtRyw6ZpqjEUnc9QVm88jjr6GNNmgriIEF0BolE4hG2pwkl2meIVGN1jtIBnafIDvqRRESJwOO8xTeaYC2Q4ZISEQSu84SgSGYJpVFkOiJTTdmCjQ7TGGRsEcETcJiwppQ9Ec8Ax8hIll1kujNgMM6IOqFuG8osY3wpY7E2iBjYnhV4lWGCZOfSAFd7mvkpk50Rg2pEEwNohdLw13e/Q+dalFIUeb6BoRWbvcYFj04kMUQWZwvqrsJIh6wjbmVo6SgmA1xnzqEugTMBKQRBwvq4QkdBluXsTQb4ruHkcE4IkZBu5k8pQdU2BOvJ0oLW9ORSkEwLOr9JJFl3DX3TkE9H6CyQDgReRkqtyEXk2//o69gQuHptlzRLHnsvnNvaL9zvn1XVvYxNeJnC/XPTa7Iuzye2fjLu+JReVfAooRzEcwztQ3TM81mBv4iBvXLgn6Op+NyPF4zlYaNR8DDg99G/P4Eb14tMJE/mVT7T5ud+7p/TWiAuTFXwujnFv0AR66d8wX9q4eJpQfJJAhOeOb+hc5KweOgyFcVTlzYWiHMoUY8Drl5Oz5nxHrtCvWSGnnvoTxyPPrv7gMV8xXpVI0xCXHiqRU+3bBhPRoTe0zQOnSoa09IEhfcC4RyZhPnyFKkUUhfo4YRqPWexjCRZgVCCtmtROmH54zWLo4DJBalYse6WtOMpn+3fe064eGo6xQUv2yMT6bnbeu5bO4+CcU4iPz9PDz5Zsj7rWRxa+jXs3zlgfbxkddqQpBGfQGvg7KjjwacLppciskiJIUFMJgx3NX3dUGuHCY4mQLSwdJHoNH1rENuaPE9YHc5xvSIUc06XBt9DsAmZUpCmLLvAom45W/aYHmRdY1xDAJrOYh8cs1zX5FlKcIYowBMZjguCEjStxVtPiJE0S2iqllPOODlb4LtAmqcs5mt602N6Q5alGBzoDc66J+BDxAYHCvIiJ8/yTWzKjx8w319RrRogUs5yimnBuqpp1zV+a4II8ZzdevOM9g8PWSyX3N/fJ88yzKceUQlO90/p2p4ejxeR3jnqZUUUbLKjW0kbAsY7tNIsm4ZpOSEYS9U2yEmOlhaXCu78+DN8tYF4VYmkD4G2aSFGmrZFSblBb1ISqTbfXFN3ICXWe5z3nB0vqOuG5fGS8c4YGzwhgjGexlm8sjSLGlN1dE2DWkr6TCAThY8CnyjS6YAsU6RZQt8bDu8esjz4gOXZiuADWZIAEe88x4enuH7jcmaDBx8eooB1tG3Pj7/z0WZ+nEM5Sz/vqLqOPElpvMU5D0Kwnxnu7e+zGoMpBhyGMxIUK7FxrYsSVspjY+TAHKGUosYR9QaaZhl7cqk4VpZMSBahB8CFQCUdiZKcYdEWqmSDEhVjYBF7tBDUZYK0gaV0QEeMsMIjbaTVNXlUrLRFJxkisZw1LQ7HQiYIAusQQWl64NgYlBaYtKHE0niLSFLOYkebmk0ekWiIIVAphwdORi2tahHRY5xDAau0w4wy9vUpvZSIPMU4iwaWyuH7ioNshcdhE4+XDuVqVqkhInlQNMSY0EZDcAak5ES3tEXGITVJjDRZQDtDkgjWRY9JE47qu6SuoMIgO4CeuVpRhZqj5JRcDFjJChEyXKk47XryMmeRLRDesYot9BCrimqWI7LIfKdHREfrekTicaFmlRhEJpHpCYWN1AOL8J6+P6OTDhKH0CmpSlh7S1ge0Iies8Rgy55G9ghvmceWmHt6Ncd7TRhGLAF6wYoapxJsdNQCYpQ0oqEsclZ09IngNOvpo8dLj+1bXJ6wCB7Ttxwte1xX0phILxJ8gC4onAvMq4BygboNWK2RUlM7SZ6kdBams5QEgS7GkOQk0RHzks8OOpQUyMEAPZFUvqf1gWJUsFYFWaKpDlfU90+wUTNfG47PKibTSBs9zjiK9RnuQaD2a6RU5EmCFIKqXhNDJHaBXlpsb1kdr0nzBCsd+SyjpmM5XzBfL9jd3mFdrZmMJ6yXLfOTipPDNTFGquMK4zYup2fzjtWiQ4mMGAKr3uB7AzLFBYlLUoRISIqMhEAdJLWNRKH49GiNcJbkrEGoBpF5nNpkTc9ubHP15t5DnuG8r8R5hvqJoPHYleipTfIJM37B9vrMXsorCjxzSZxn/D8nPXs7j/mbZws9mwg4PjWu12K+X+V+9HnoZd3FZw/j4+dy/vIjp/qn5JRH8/h5hJfPSeI1rSHPy3xPS4JP86bipUriFz2fvxu7DC9/zj9ll19AzMX5l+DikV44MfECgeBFZV9EL7MViWcEi2dNfy9q6yENBuXG7cZ5JtMBxubkWY2VkSSRmKZHKkgT6EUkkxEfPSF6xsOM7qzDzBdMrw/ZvjKiSGF1cIaMhqIoEXlC13aMdMS0NdVnnuu3CxyG0WC4Cey+yDJ5kfB2fioeLZgPCz8OXHqB/fSRMHL+ymiSUQwSBqOU4TBh//AQu15vYF4zcAqElCSZQMVAf9agJ4HR9QyjCkwDLT3OGYTYaMfGiUbWEa03TPNoMmT78gizrClFJA5SphOHqwO2C+i4QfehdpiuQVtLqiJJkpCicI9gcomMBgVEyFJFkIJo4dL1PTrr2Lq2w/pkRZan7FzfZXG6ZDAqSbQmySJpkSJ8oCwyEinJ85Q2WMbTEXXdEq3n8s09nBJs7U6xbU89rzjbP6Mya6azGUpI+q5DCUGRJpg8ZzIq+c3/7h/zzjff32jyeGI6HQ4G5FlGWZaMBgO6mcVbi9IK+TDp3GBSsnt1B9caTFlycOcAjCVah5KKQZnjBWRZiixSROfpbUMiJds7M3zrgYTV2YpESIQUaCUpigJjLGmq8cEznY6QD+Ekd69sEyMkRc5ysWJnd8r6bM1sZ8ri4IzYOga7U2xj0EjSsiAfZbRiBcaRSk3wm0zevQ8kUqLShK3LM/Ii5c5379AcbZiN8WiIThXVskYKhdKaPM/oQ49OIsF7ijwjLzKccQyGBafHS4iRLE9JtUIkmqglZZkjhKBpO1SecP3aJeYcs65qhqlCpAk6bL6SESkhBIKEIQlGbGBIpYJZSAmJwLnAMCRIJciCwnvPlkzphUd7yGWCAIokIcaWSUxwbN7HRCq0lOQhYoEtcvroUHhUhKR3jJC4XDJLMpxKEKGn9xvI5MYHfIykwWMD7GlNGwLaSXITcUqSB40zgTEpUkhGMSIDRKEYhxyUZOglTjhGZKRR0znHLA42AphMME4xCJIsSTHAWGS4YJHW0mjLyCgSBniVMhUj2qBQPmFhPWOb4rWm9papLPBYEqmQrmNkBco7mIwYqpJutaIoJyAqyqWEMsPLgoEc4KMntxkuGkY+p48JM0rSVSTKBO0UpgiMybFOIdaRRKeYXlEWBcF6xg00BSAyEp0wHqYUiyVhO2MrGVE1Z2TGo/KUolcM4xCnAtM4JFjFTj7G5RadgDit8AnsugGdD4xdSSg0qQ8kRmFFz6xPqUlJRULfGaZJThFSrHNMY0ofI2nvMMDQgXcaK2CGoo0eLxxeRKTwzIYFhyuLcj2ZlBAdyTgjDw4hwCsYqg1E7nSi6YhMZyPKviQtHWWpWXx2Qr2sqBtPd9SjM08fIrppyPe2mNy+vFn5TwKH+0s0AiE8TdORFwKlFLu3rqGHIB0kOkGKSKpTTNczyEqCimidEIeBZlkx3plQuYat3V36vgcfsZ1BREGRFwAUZYpOFJOtciOgND2+NSgZkCIio2OyNaScjjD1mmq5pO49WSqJmaYNljJAEIKuaokyYzxIUGQECzaA0prRTo7eHrJzZYs3fvbNh2useLy/vZLEQ7b1oZDxFIP7EgeBC+lVLhrPChav7+tyrlA899/nB/AsB/b5DAePmN4vWPv9AuPAhVC2L+r6kTAlLuaHP/+QX8E8voTEw3Fsmniah31GV/7KEfwdiQxP09NM+ouF4i/EFPeEfnoo2odKgvNy2kVlnvpj82JFns4pcWH5+OK/+Kidh8rhzd8TODYRxVNS/qtWhe//zR1+6//5h/zOP/9jpoMt3FmOOyrJ45S33rtBQKATzZtXS6RM8E6Q5RlvXRuQGii85EvTjTYq6JxVa9katgRaim3N2+/lgGC96hnvTLl1e0TnEoRLEEeC438faf7mMvaTPbIw4bf+5R/yL/6//zM//uDuMxPzcNSP7Hbn/v+0f+CjxWJT9zG8XIyE4PmLv/krfut3f5t/+we/z51P7vI//s4f8S/++3/LwckDskGKsZGz+0sGYoFINH0I7O4VvPulBJUfodQxl8qIc+C6wGRWcOWtLQ7mZ9yfz7mVdUz7nNE6oegiA2nwQWGd5Pb2GIwgn864evsyX/vyFlupZaoNP78HSa5pTYftGq7vQZwp4kRy+dKYrrhOO/oSeudtJrdu0V55k+7yG4x2r+LzPZbJNe4fCsYknHx6SD7M+eV//A1SrZjfOyE4z40ru/goqNYdO5e2KYshnRN4NG9cuUw1XxN94Gu/9lWu3r5GaB318Zq0h4Mfn9AsLFvjMV3b0PY15TDhjTd36AYV2Y3I23//DeLVyG//+9/i3/3Zv2VVLR8/lb2dXYoixzmLsYa/961fwHhPVIJEa8o0wXqPNZa/92s/z+J4Ttu0lKMhW9MJUgm8gN3ZFKEE9WpNc7RA47F5jy8t7331NirVpHlGtIGr1y8Ro6BtWnZHI4J1m2/IenbGI/pVzeLglNRGTu/s0x0vWH56xHZasDg8AwnTvKQ5WbE+mnP3bz8h3O9Y3VmC0bx78y3yNMf1HhEF77//Nuv5irOjM2QbuP+9u5wenGKt5a23bzKYDWmrjuloxGQy3HzJIXL16h5KS4QQbM3Gm0D9QcbydMX2cIgzhug9RZpQZDmud3RNxyDNiBFkorlVbvPlZsTsT+Zk//GIX6t36TQ4Gbmcjrihx1g8vQh821/CKoGLnm0SbssJDk8dLL8sb9DJiEsE02LEl5JtjBb0BH4lXqYPG8vAsPa81w2wImCj5++vpwTriBJKnfHzcgcbHEZ4vrIY4ZDUxuFrw8+oGWYMDD2/kGWk4xqxvYDpmm+WPfnuCr274ks6IY+bjV8J+IVqipOB1lu+ovcYTlrYPqIcnfEPVnt4YQlJ5L1ml3FwiLImvSL5dv4zuNhiXM2X7DZjcvrQYTB8a3kbp1NcUvBGvce0G9MbRdNGvmW+jBUtYhC5mW1zvdwh6IAThn/YvUvMCrxP2A6X2F3eZH1/yPJBwS9VX6G2hg4YqS1u+UsYGWhDz7fM17BxiLVjJmaL9+JbqHIXNbnML63eBgPRaUo55m0zoXNrOrfia/YGZBIxyynHI7623oVhgi8V7364TeU0VUyI+YSf69/CpJHWdXylv00sJW3eE6cJv5S+BboH3fMzxxOUV/gYEXnOLy1uU7WGznneuT9Ft4aQO8RU8/WTHZz0+OB4+zAncxab1lhZ8832CnpUkaRnvJeWTMQABxjT8w0UZq0QNuNGllDaQLsMxF7zizcKLBpkxls3J8y2PG7c05ctb81SVjZlZXKyokDqlHuN5sBmqPaU9bKl7zcJIIWx9E3Kch5J5yfU8zUuOMqRpszOsMURoTjhVgk7OuHGcMgvfOOr/Pqv/Crv3v4SX7r9Dr/xy79BdBvgiDzL+Y1/+I949513+fKXv8x/87/6Zwi5yTyvlOK9t98HwPeWvckeaZoCgjTT3HxnigtrbFzzznsjIBARJFnCqKjprGGxXPKln93m+ntbbN3MufXzV7g6bInLBfL0kGxxj1id4RaniPWKJMxRE025lTApFVMluX37Cu++f4uv/9J7r9jon2HQH+6b592Kzu2ur+AZeJ7VeQmneJ4Near868k/G1boIfTs5+IBLxKOXhhDIJ5W7n4uPW98ij17ro0LGFrxzP0/Smz86I4F547FRtP/SEn62Dr1TJ2/awohPBrBs4zvo9t6tYL88S29phWJyOnymH/7Z7/D//DH/5zvfPRXL48DefbS8yzh08fP8shfkJDxBQR0P5QAXiFxPl/rZRWeiFevus9nDIHPtHSB5eL5yoDg9GTJ3/7Fj7n78QF5nvLR3x5QJAWiN6z3DWd3P2O4PSLNE/7mO8cIF3E2slo0LM4cOIlSgs9WGaIQBKnwMfA3f3mX7evbZMOCVTsiKgcicna0YrQ9pRxvXHUW8wy5iiA9E6n4N//DX2Jlg/eerjdcvrLNaDx4PNWPZP741Fvxghl99CKeW0Hv3rvHBz/+MfcePGAyHvP973yCiilV1XBwtyZUM0DQrWqWa02aKcokQ28P+eSz76BlRzEeIK/sUB5pvJKczg2r6oDO9MhUctIMoXHQRmSmaaJi8+QlHz2oGCMxy4562vPJ/DMG2jOcJBx0Eq0DiZZ44flBZfAKlJb8aJ2SixyjMmwm2VeGPrcQBXd6x6gAIaFzlk8PjsF6jj/e5/dOf5/r71ynWzf4znJWt6SJxljPg/0zBsNyg76C4LOjU7zbJEw73D9jOBqwPlhw2hqcE6Q6IQLzRYVMIyqBqq25Zx2hjIyvjOlmLX/z47/mbH3GZDBBa823v/4PQcD+4T5N22wYRan4kz/6c4pRQbpKWa0aCDCZTVBK8Sf/5s8QceOD3/cG4z0CaKqGfe/JygznHGylNJmBFJKh5gcffEiaZqRFiq17WhcIMTKaDjlcrVEP18W26bnz4V2sdUgpeNAdopSiNxv/6drYDaqP89w7PGKyNQbriSpw/87BJj/EZMCng1OEksQAUms+/PQzLr99jeM7B9z96DO03liFRqOSeVNv0F06i4wtabJJvpVmCYcnJxs/bCKnixXFsEQqiW0MZ95RppJV01N3HcZ4EGCN43C+QAiJ6yz3PnmAbntmp4Fs1fDHb95BjQcgBftujbcOoSJSwh9kh+QigSA50pFjsSZJEnRl+T1xh1GaIqTgzNQc4IkhoKTm9zigeBirUaeR78UFKgp0hP+gjyilRspA53r+SjboAMp7/na3JfUShKRqO/7EfwijBD1K+RuxJBGeNBqChz8tG4KW6Bi4VxgKNAiDD4Hv7qyRPuAlfGd7n5FoKLYDWe34j+ZDkjTFR8sH2/vk0ZIWgsR3/FH+XXQLSkR+XBygRYaKkUxr/mByFxU0kcAHZUWmI8gcFXP+QH2XPAQkgc/CPogRWaJIQsK/375Png6pguOB2sQsxW4AIuPf5XcomoC3hlO94MzXiLZH64Q/1B+Qhy0EjjmSedahKEij5E+nJ4jjgMTTpoYfXTVonyCWhr8ef8LA50jrMNeG/FU+J9Y9MU3588ln5CbQnnTUZctfTk42e7lU/Jn4DkN2CCrS9w1/Ofgxsu3IipTvTw9QJkXrDDnI+avtFcqnSJ3x/UvHpKsWnQpUkvNnl4+QHSgp+OHenLyQCLWxKP757HsMJzlN3fKxr+nXCik0ybDkP5kUZYAg2V9rEqkYaMUoifzVwQauvG0th07jBynRrhCp5C8WGxSsNgh++P0z2gWI0Q5u3rK/yNjOPSImJHmOUoqxjKhUcn+5Ynp4SrI9xQ40Yjdj7BqEA6kF/+DGO1z/9le48s33kFry1s3bgODP/vJPEQ+jTILbIED92re+TXNa8cMHH5AOCkSzpFtXfPe7f4N8tKb/6Md845d/iTwv6DvDp3fuIbRDxshJEynLglVjScqS3l2iXtX4JvAf/uiATPeQZcirJadrh3I9Vic4p0mix3uDqz299kyLjh7FYFQwzSW3JyO+8Rtfh4vt80+feSlT9sSd5fkYh9egz2WJOFfnFeXjowF9jiGcP/F6nNSmTIwX82YvhXp9Siv+8ODZybvwHi9Q84tHY74oxkC85Ojz0k9W+7Gr1Ivu87V6PqfoPSd9PWfFOUd/+cGfcefBh9RdRW9adiZ7XNm59qRAhE2OBvHk+MXNvWqAX4hZ5QsQLl7+0sZnfj0ryL74BXrZVD/d0MvlmkcvwQVDPXfcNT3ObJKxWeNIQo5H0K5alncPcT6QjIYMtoaMr27TnDQkeJJE4Qz0PhICRA2+9XQGhA7EEDi6e8Ls2g5ZPkKXBWbVIBqHMUuK0XgD32obhJC0jeHuD+4z/HLAlxsGzztP25mNcHHR4F+Xzk1U2/X0vaE3PXVTYxoF3tG2PUm0+NpQLzuqVU8QCcZCPhswP1rQ9AaRQDoqiEoyvb5DVbXUtaHr9QZCUWnq3pNa8BaM3DCd1kSkzllXC8RSsDpdcbe1XLpxg2rRUp2tKG+/gUwVsdu4KfhoaWNEiQ2ePlHRB0HVOaL0eCVBQJYmGA9RBjrbIztDEh1SSbRStJ1BJJKzwzOigPW6JQLae3SSkOcZTWtQidvAysaId471vKJaVOTZxg2leRi4qPOEEANdZ9APtd/5MEWXCZ3pwfvN/Kqarm8fP4Su7zHGblwKYqSdW7JYPlzAI1JrohJU6wZfdw8T03lkrujm3SZvR55uBA1r6dqOmAYml0c0oaFuG+gFZu0wxuLbHiEEPkTmJ0uKPMHYDWytSiQxCLquJ0RJIjc5PpTWxBDomg6hFbb3pElCvWzojSXJsk3QMJGT/TOcDux8aY/YaZaLNX4VMJ1Hlxlt0+FtgAjJIMdYx+G9Y8LDpIYiCox1rJYVSaaxzhFjoO8taelpqpZESrxz9HHjNtS1PSGCfig8BblJchid4+z+MeWkJEqBSBR1NNigaXGsnMB7R6MCRIEnYmKgiY5aGFTvaJQlzSXe9wQETbBUQuGco8Hgg0frFCMjnYysYkAgqHyHFIICgRGR1nScys3CU6WBBIEjUnctvfKsxWa+130NXjKRA1wOIUisAxckDRaRSHKV0McIShNQxMyzDoFoHbbIWJsWIwzrUU5/amlxWBnIdIrD0kvDsl3SJSWdsLhEo9uI1g6bBpaupYkbVzMbLTrV9NFSxx4VIWJwpaLFkiaSGBr6NFD3Db61NI1hHVtSNDH2NCLibEfIDS4x1MIwEC1SWRrt8aGGLsHKlDb21NojvaHNFD0O6zrUQNBoOO7WJHlKlThQPaVIiLaipWNeLYilYt0YQt8xUpowUHTOcLo8Ih156lAhkoQYJP7sgH7sWDmJIKEZRLypyIsCm0LbWRahQStH7WuoGsZC4MaCxjeo/pS2F3RC46UgyxKs6mmjodIRYRr6vsWmHrHqaUJPn0iqaOk8dG2gFRtI4qBgXRv62qEGGyG2tYHDgwV67DBRgAMvJEEpOhNY1BZEga0tjTOUSb6ZLwutDdAZjBEoC9k4ozMeX3XkVwqGty9jz05QQnLp1jW+/JvfZnhpBko8ZqaFgL5vadsGYw11XbM8XbDWC/JxQdd1NG2Ni566bfHG0TQtPjpM09HUDXme03cG7zzVugFgOBwTswxXdbStQyQJMslw0RKioOk9tqv57Ef3GG5PqZYdNgpyJSnTHOkiSka0grY1tFGw1oJrl/d46+vv8jS/8DyX8dQe+LKt85FQ8RKm8ZVeJK/DmL1Im/yfQ6B5qvJ5n5PnNfFPLr5Ezy7ODeC8APKw+YvRlJ4Z+Hl0qqcUpq++sadlm0feGp/H7HKOR3yqv4sn93EfF7Xzufo918dLqwla01J3FZ1pMaY/x0+cE3Li6/V9seD2uKsvRLCAvwso2mfoKSi4cx+ReO7HQ3r2eT67GIgnhT53+r8XLSwR9i7PGE0GTCcT0lRz5foex3crjj46YJgqQpQs5jXjQcE7X3+DxYnh8M4p1YNDsjTFWIGUkb2dDD8Ycni03qDcZIpV5aAzvPHVKQdpxuq0Ik88eRpIS4i9Ix1IBpMRRw8qhLPo2pAlY7JRyWw6QQnJD7//KbOtEZcvb/2Uty24cfUq3xsNGPcDhsWAnevX+OxHJ/Rnlqtvj7GLCYtP5igMu7OcNiYMtwuWdw/YG5csjWDv8jVuvLXNwf4SKTWX9gZ0dszZ9w/xIrC9HenPxMZnfZYz2Rvy6SdLEi3ZmQ1o/ZpUSbLouHx5ipI5dtVwdSxYDyaEGClty0w7jpuAN45R2hOdRnnB9evbkKx4sKiRwBUFlQu4AqYMGNRDFict0guuXdlBjgom2xP8uuPtn3uXVKes5xVlkZJlOVXdIvUm8VfXb5CmXGW49OZl8kGGFpKt2Yjj+Yo0SdjbmXK0OkEpybDMmckSkacM0xGXty7jpSE4wSAvuHXljccfw9UrV9iazTY++knC4NKQ6qChvTTj0+98TL2s8K1lcuMSl969xfd+/y+p85RLV3bY2t3i3qcHiBjZnk7orMGphNRorl65Qm16ymTAla9c4uB7h0QXsD5y+Y2rVKdrgvWMygF939N23WbebuyyWDdY49naGWP9JlO6tpG+d6zbljxNGA2KDdpW3FhPBkXBYrEmUYoRKdoLEpVQFgVjpTlZrdHTKWF7xOEH98mHJbOdKZjAerBESMF0UNL2lt54BsOCt95/gx/99Yc455htTxBJQt1GBlmCcIZ126JVpMwzEqEprs1w6w5coOp7vHWYeU2Unu1fu8lIF+R1w6nI0TiuqwE4y/3QU8qEK7HkRPQkQnFdjxDOEagoVMK2Uey3LTrTXCYntYHPFKQoboYph7FG2cClkFAEhYiG1MMNOeYIi88EO6Fky8GdCMFHbtqMMwmxbxl7ybYvOMh7ROu5Qcbc9JCnTK2iCIr9YYuWsFPntIPAPOsYLAN73YiDgcMqye79AnlzF1TFrM54S9zgXrGiDZZbzRR2AtErRmt4V7zBJ/oE6wJXVgpXpoRMMpUFe36bO+YEqyQ37ATjGsQgY9hJbppd7oc1Omiu+zHRa0S6ZhAUl802D5IWFeA6BVFPwK8ppORKf4VP7BEyy9iLA4px5EFU5FZyvb3CkVKoouBSXzDIdrhnAsI4LnW7HMUCnSaMXIt6UCGmmuhHXF2XrNQKl2omS8NQlqjJENlZrocJi22Hw7Ntcra7jHsOVFlwfZ3S5ZZoW2ZuwLTaZn9cE7HsLXLmzuKygqkvuRKG3Ad83XN5PaBLWoKzDNaeq+s9How3oAM3ui36sESkhq1Ycqnd4V53gp+VXDIFqz4nFopJmjKdKj5KHHmWsDcRmKqn0p69aclINBx6SKTg8ihFjCXmJFKkkskYFquNADtLLSooVitDmsJ0YIl9wIWIcA3DYY59a8agyNiNHYcnS+rjijGOvV+YImVKkiS89ZW36aTm8McHXLoyIx8o7u3fQ+uE69dv8eEnH9MbQ54WXN69zN0Hd5GHiivbl7k7uYsnMBtMKXTBwcEBtjHMhhPWJwuOz47Y2d5h5/KU7dUhRLiyO2M2m/Hd//B92mXHsNRI3zFMBFdGQ/oQuF+t8Lbm/a//Atdu7bI4mJMlknbVU697ZAzIROMUXLu6xd6VGf/4f/3LTC7Pno/JfrivP+EXPh+T+vhcjDy4f0y1brh2fQ+lFHfuHpJnKbdu7rK/P2e5rLl+dZssT7h755AkU9y8dZmjkzmLxZorV3Yo8oy7n+2jtebm9cucHC9ZnK3Yu7TFbGv8bKcPB/LFufmIp9qL5/p4vbl5VYnHfhRPO55cPPXx2cNnmXXB42DQZ3i9/2JJ/c7RhWzkY++Q1xQwnmngFap03rzyFr1paVZL5N1TLn/76uNmXshLv7rbi+kLmuIvJInes9aJp+in8d+Kz1QXP01jLxjLw3MhgnAK4RU4hbeS+YMlfQfbWwN873G24+DOGW7RkI5HJHnJ+PIMt+jRKj5sRwCeNJHYEHBOoGXO8qSlPuvJhzlZnqBCQEboqhakIDpP3xryMkcEiCcJ8wPH5JJiPZP829/9U9ZVw2BY8M1v/Sy33752wc283m1HIgEPRY/ILaKwRCfRYcSo1Ii+wFYd7bJCCjDGMtzbxvcW03l8trUZo51gm4cR3k4SrSTtIrpzxM6QZwkUGX0Pq7rCHBnSsiBRgiSNLBqLd4FidwvI8b0ly8bc+8E+g68MSScloyRn/ZlD9wHpFMpJEBoVBd2iZvvLY0ZFQruoaJWhSSy9lDgdKY8z+iqnaTqaZYsikk0GRK05+O5dbO8oBzk7ezOaxRoBFEWCTiTdUUUMntMHBwjtGewOWB7M0VYxmmR462jsBiVKKEGUkiTNGO/sYK0j1AGvFNHIjYtc/+SLLfOS3/jWt9k/PqTMc/Z2djm8d0y9bjl7/03+9f/n9/BqE4RtjaWrNxYWmWlGWyXF8QLT9hACwT20QGiNPRVIleIdGAx4j6lb2nXD8Sf7xBiQicTjQQqSNGHv+g69jbSNoa4abOewztFby97uDASosEHamuxMWBwvUCGSj3J8Z1AAQtL3Hr3qCSFiXI+cFUgnmM/PGJUl5c6Uet2wPqsxbY8SkigFLmz0KEmWIqTCtBZnPFEqxpf2WDWRWChikTHJArJacfTgmDzPyIuC1ckK0xouXd6msxYHuBSW73qmPz/EJQWnfzEnmBSyzfyLIoNokQhUkiK9Q0X3MEpUoAJIJSiKjKJvcdZjgkXnGdgNNKF3G/dGIQRSCrwPSK3xWtJrjXY90lqk9LgkJQiJt5bQ93jtkHqTTLJ3nhA2wbROWHS2OVCDhIHoKceOqCXJzOPokbohHRZkZUDZHkyPThQy1UTvEVmKHqckSuBMINYV/bFBXtbkVybEtQAncW2LvHYNETzRrXFBA4ZEg/OW6DuikiitUUrhugS6hBAcwWrEIBKdByTBW5QKKCKEQNTgOkfoPZ1NoBzig8e4Ep03kKcbPOqkRBdDkjKShBFaXCYRlgRLYoYUiccoxayU1OJ7KLUmAbSSqNEQFwPGSBoXUV4gVQIBhAsIKZBa0xyDHY0JlcTIkjA2BNETosC2NU5ViEzj0wiVhWgBi9WGoCG6iLAOkQhIElKl8Q/d4yKBmEXyUpFYh2oaTLJFH0cIUeL1mKAA54hB4mwkCEHfGk77FhDoLMXFQLlVIM8aQvCUkwkShahOoAc9SIl9t0mYlydMYiDJE2LXMp4o4t4Me1wx3R0j3h1w7/4pdnXK0dJgV4rOC3pTc3ayory5x3i7ZP/Dls9++F2aumc4zmDrjKpboZRiUBSIRCISgR4m/C/f+XOq1RoQjGcTopQEICqBVBqdJAThWFdr/ug//QFN3zLb20HnCWrabBxAhmeoVcrurZzq4ASlFYky9MYi0wFoi3c9yUTz/j+4zjCb4Jzn6hs7NFXHp9+/T55IymFK5yMqS7j2xgZu9rxjyXmQqMf86bPs4EPUk0fuKTypwjl1OyD43nc+4q//8gParmc4GmCFYrluSBPNaFjQNj110zEeFeRCUq0btFYMJjmN62ialtFoQKoUdd2glGSQDzCVpapaJpMh3/6vfpG9pxSGr8klitcrer74i68+3e/T8/K63OYz8/+Qgbs4E/gTZfNF7b/I0hEfMu8XyZIX17ugmRc5y7z4wnPtn5N7XtDJxfWfb/Bl7Tyhn7398+xM92i7mh01IU+Lx2A9zw/5kaAjnntHRHzigPV3TV+I5eKp+bnA8vC8oemiT/4C89BTc/Co5jnpWzx5QR8hD7zseb/MHHT8YM7qrGZ+XJEkitPDnpM7p0QUy3kLQSFEhnOe/aMecdCQlAOuvLnHoupp60CWp1RGIU2kc5HgFAuz+cCci3zvz+4zu7yNR9P3PXUnSXKBznLWtSNWDVIXSC1ZVw7nBfViQR9WjN6QrKqK6WzEnY8efC7h4iK6f3yPql2zbhb4aDn++FNYD+l7x/7dNScfr6gqT54nnK4Fe7ua1UlFayRi6elRnB52LOZnJLmnqXuiT4nGE1VG23V8tu9IUsu6siSJoHWBPvYoJTitz8hKS1AKORrx0ff3ObizZDAuObMSvvcAvTVluVrTd4HWRrwX2JhTZDl9jJwuOw5+uCKOU2IUrEJAaKhlQBpLOF1C3WJ94M6n+wi9cUW49uZ1lidzzk42AkVUimAsxnvs2RqpDUKBEpLOWA7uHpEMMnSRcDJfUhQ5dd2QNCmT2RARAoHAgo64WGJ6w/LkDFWmGBWwxvPp/bv87Jffe6zVKIqC2zffePRicuXGHhEwxnD1vevcv3fE4mzF0Z196qYjEFks1qw+2me1qkm0Yt61G7cYH1jWDcn+yYYRTTTze6eYdcPRp4dkacLieIExlhAjUglsb+l7wycfP0BEQdtucnzEh7kwuq7n7GyJ9xvXqunlGaumZrWuMJ3Z3IdSdG2PTjWLZs3qXgu5orKOzluCjNRdA0EyvDSlNpaQKkzjqbsOqTfY+cV4QHtQEXzgRz/4FBcCEHlw/5Q2pjipaX2EtkUQ0HnCfFGRd5aqacmylAeHpxurhfOYoUZdGnHAiokO3Nt25KKncg5UBC+YS7NxnXEtmUqogiESCAqW2qKj55SGRHhWKXjTQt+w1JZEJZziSDystEPalpAK5sJCiDQ4skywxEHseBAbKukh8YSRQMXISgVkNIg8sBAWkQQ6WaERVLFHJYKjsqVJOmQMtKolDYG2CMjWcdYeYZMesgCZJY2eRVyhhjnH3Y9p2wYvIi7LkHnCIrSQSO5POvre0dEh3AFIySJp8RFOk0OCcbTSEEREhMjSOozKOMwqNJq2AGhRomchK1yacSwMshM0yhKRmNqyFB4jA0fJGilS2hBIsxVp3rGQa/IkZTVeU2Qj1qYlyacsZaAOGXSe5VaODFBnGhEXLKNhqVuSPGGRGpSAWnm061lqT60sUgvWaYcMgXVq0IXG4VmlgQB0umYQI8usQyjFSdpSJR4QNOlmLpeJIYqahVzR0EDm8ZMeIQKr/z9x//V1WZKed2K/cNse+7n80lVluTbV3Wig0QbdINDEkBxpqBmORiPNkm51p79KF5q1tLSGIjUjECQMYcgBSdAAJNEO3eXTf/aYbcPq4mRWpausbnSTily5vn32iYi9I3acHa953ufVPWJRs6VhOzhSZpDyAbVJdHpExMDpbM0gMkbXMgaNlZKtMDjrudPUjKNk6xOjUFjrEIUmjJHLk91vqrGJj057cpXRjRrbW7ZDIs8yBu9pm0RhSnzv8UPiJNPUS02aTVkpz4Of3ONUeKraIPucmU5IIYnJs2oc7Ucb+ibQrDqKStNse6aHitCdsRnPkVJSZBkSSdM1SKU5bS1d1yCk5Ly/ROeGbbNFa816WNNtWsLo2W7XFKGi6bb0fiBlgm7sICXGldztL8GyfP0K/WVHc7ZFCcE7F2eIKiKnhumrB9x9eMrf+q03QOz4ZrLCsPjNz7/ISvbswVPfiecrflIe0UGJZ6Ekzxgw33/vLnfunNA0HZPFFJsUl6uWLNdIBFmm2G579ucTVIxsVy3GKGQl0IVk07Qs5xMksN22u/mVBTpptusGd7zPh+/f4+h4ybPojs8sPwN85blqL2n3SXzFf2JB9GVdP2vZ/yxY1c+ID3sWPpWegCj99N6R9LNe9uMiHtMS/5TPUAjB1f1PZL6XO0ie+eKFXpL/9OUXBot6rC584uL6xA6QPj56XJ4981i9ev6XJV5w9PhzenRaPNKO02Ot7flLvfzGU6KaFJhMU08KtJbYHjIt8EmgtSTaRGEgq3MkGeM4stn2pLHj6NV97r9zurN6RY1wgeAcpYHRBrJcY0QgDD11renmJWPsiB6iG5ge1YjpjM3pBYN17B9U+ADrywaA4bKjOlDkuWEyLanr4jMG9dmlKiryrKTIS6bVlGFaolRF24wUhST0A0JG8tIggmB5UNGertE6keWSofeMl2uk7iiuVpRVxmSa4YecvSszKhPZnPcoPHVlUAyYXO2CCcXOcl5qhR0sRoEoNEaDbbYcvnJIJwNCCdw4oJOgkBKfIkYI9uYZeamolOLEj9h+QCtJKiBHMJIopUSR0ErtLGsxUE0Lmn5gMq8YpwPVZiCrClSIZGWOdZ7ZYkJMPcOYCDFRTipigqEfufHGNe79+D6IHatTnhnyImNwDlMYDq4ektea1XCJtpFmc0F+bUFdVFRl9cl6fELxfoLTbgd7OJgz3Zsx2bTU0worBG2eoYRAI5nvz5CZprtsEDFhigzXDUzqgnpSkbSkKHPiaLHnW/CB5dE+l2criAkhJbP5BDc4VpcbjDbEmFgsJoyDxRi947rPM6qqwPcDSmv2jvboLppdMHu2E1hCgizbxZ1oISiyDEdkMpuCC0yWE7qLhmpSsjhYMHYDwkXcYB8lMIwIeHQ/FhkTISTKIqdte/xgKaYVnU/MFxPKLEOGEW89rrdE7ymrgqMbR6xOV6AUYwiEPlGaAhLMdMnVvX1EnxDSMfEKKQReaCZRElKiTAqbJJmQoCWeQBEkKUYynWNty54psSkStKYQGSIEaqFwPjATOS2BaQhkqN1zEhqnBYeipiHih5bMJUqpmCLpBOylnF4p5gGIkcwlaqUZM8Mi5fQiUCUBIZCVFaU2WLbskdGKSMSQZCIPihmKwXXMY02HIPcwCk+VTciCZgyBWSpQWpNtE9pnFDJDe0UrR+bOMPRhZ9yQiomu0ELh/Ia9bMrgLWmIOw/dKMjLHKc9s1ThpEIZQ5I9tS7IkyJqRaUkPklk0pA8edSYcaTOSqYhRzhJ6RNOSmqbECrh2gHTe6KUmAABwWwUOAdRGaRTGJNRI/EpsKcKRgESjfJgCFRRYK1n6g1dEMxcIkmFch21S/RSMekVXS6Zm5wkJVlUmDHSqMjM5YTokT4S7EDhBUVe4ZRgNhZYu0uw6oQky0tKFxiSYuYyOm8odUnjAlXS5CLDJVjkOVImilKCS0gbqGuNzzWLiWR12SFxZClhgkKGSCYjtZGUs4xykaNOG6YyYWwkEkjCoYViUig2D9fYTYvY88xqQ5lpTKHIp5Kxj1Q6EaOgXW+I6zWzL99kMpviXGBSFwz5llrWGK0fKRg5Pnom1QTLgAC00SAkuSnpTc90OsWmEVkLgnakKlJNS3x0FCrHi8C0npBSInMGI2rGzjHfn5CZDNtZuqZj78Ye0+sVl5sNsg8UOtspFk9ZJZ+1UqZnRIYXmA1fKJCKT9onnpNXnr5OoqoKptOKEAKzuqSLAusCVZUTQyQTgkEMaBJGCKoio5wURB3JJwbrHNNJRXCeFHeJQlXQFDrHjY6qLqiq4tE4njGwPpWTiqePecHxk20/cy5eXPkxZfrjYOOXeTs+q8ZLYzg+6eY/b3kW/fJE/MQLgS2flrvtuYpPXuNFdZ/UQp7Dhb2w++fW5lOX+Cm0kv9cWsSnlJ+bijY98++xnvBJNPwn6sXzbZ88+tlWWXrMPcvuN5he9MODp9xCzz6kZtvxh//4X/M//7/+mPffuc3+4ZzoJHbrefP1KcvrGUFcUlSWwz2NMpBE4OZVTVEXSKM5v3vKcuoplzVBJPayhva0gcajXeTGPGG8Q0tYVB227clnOcsrU5azkRgi7WXLr/zWq0z3Z/gkWK9abt0qyKczgjQcTmtW7ztW72W49ZS9o5rf+9Pf5Xf+2e/w7u13/zrTx42jV/jia2/z1itf4PUbb/Hd734LN4IfBUdXJtQzQ1aXJK353FsF3idCgEonJrlGOEN7NlI7y8OfjGwfZEzKGdduzIhaM3vlCn/rf/caerLB5w9ZHlmm04a8suS154s3K7zaoIotwZ3x1q9epX77kHiQ8Z3fvM7hW1cY/UBeSV6bSUYnCU5yY2oZxxGbAvWy5htvHpE6g28UN9pEXEO2zihdySvH19ke3qQ7eoXljZsopUgIHr57j6/9za+weG3JEHqWBxXW94xhwMeR1968SbMdSR5m9Yzy6uu45Rt8dCLZWy5B7OAAn/v8LbQUCJ0wk4yv/2/+Bvdvzrh9fUq9v08tNOd3HrB5eMbnbr3xgkX86HfyxMvryrUDFjcrxKElLUa+/Xe/QX0wxwGht9Qmp1+1pJi4Ml8wf/WA+nhGVhlevXWV4ByuH/mVb39lR6ebYO/KPl/+6ucQSpCXhq/+2lfIypwETKqS+WSCiztl7vjgYCdIaElRFSwODvAR2u3AjZvXCSntoExK8urNY2S2yzkyyypS2MVoCKV59fiQwTWUexlvfOkVqv0CsZDIpebNr9yiOM7JjnOu3zqga0ZGoQhZxq1bV0GDzhV7U8OiSLA5I1eWb37nS3gfGLqRxWyK1gY7jJzfOWFZVQwpkNU5r5f7ZBbyWYEoFX+zuEVQOxjWdVlxM1SElAha8G17yEhgSB7dJ466DBsio0h8J3sFZwQYyX40fCk7REhJTIHvcnX3nhOCSVT8spvvMqtmkr8hr+N9IAqoOsevxT2kFgQJ3x72CWkHpSp1zteYwYElHQe+1hUU1YDcG9ATz6+uZ4Qs4ivBV84XaBdJOqKk4G80rxJzRZTwq/1rTOopFJrx7hnffnALrxNRRT5/f8HEZng7Mpxd8t3m8zDxJN3zuX6PfTElsUsS+ZubN3DRkgzc6ucsXInXMLYNv/7hkiAsSQeuuRlXwnyXL4TId9svYCZX0fqYY455o3qFYnlMceUa3423UNMJ2XzOFXPMTXmNMUoGpfjWyRHBBUKCynpeaSVOJJwW/PJ7K5TQKJExDTVfvJxT1Fcpp1f5zfWbFMUXKPOvMU9v8dWHc6IPBCX4lc2rRC+INpIN8NXTJcEkkgr86vA5fCgZbE5MNV8/ewUXHS56vjJcozyeoJceWXl+6eyYgCWpyOfuL9G9INY5cn/Gr7fX0csRWa15yx9SjobBaFyV8x33Fo6BGAZunXrmLiNlGpcC39QOT8J6x5vXSqZTj812Ga6/PLeUekqppsy8Za8SRK1wMfHLi0BzMdBuPUUGmXFcTjTDouJoZrl72XM/AiHxuqlQbQ4X8EszRaZ2uXOkTFypDY3XeFPz1s19Hv7wIZuHI+EkctBWtO9F7HnON97+Nm+++iZv3focX3j9C3zhjc/jRosbLW+//jax9wgPOine/vwX8dLhdeCLb36BMFhiikgleWP5Kt15g+0sv/Qrn+ftX3qdL3zlFp//0i3+m//Lb/Br/9XX+O5/+23+j//X/5pv/I1f5stf/QJf+85X+drX334xQuVJiMdzgtMLNv4X7omftlHuNtGUIt/7jz/hf/6Hf8jv/ZN/wZWrh1yOikubUS33uXrzdS7tkvsPNdf1jPfeGfnwvsb6KeNF4J33R977yPGlL36RZjBs+oJAzc1bn+dhM+WkmfD2177Kua954KZsmeCE4X/8+3/G//Mf/Gt+/M59/uSP/5z/99//Q/7X//Xf46x/erxPKiE/Q/lYXPqYtv7Jk0/Omnjq78soTz8xHz83jS/+/6I6T51+kkr/p7AKpyef8acJgJ/S+gV6z8fL6/Ecp6fvZ3f8SClN6YXD+9TV9fxUP4fq+dnKy1xPf+1Of6FFpJcS5n522bY76/qz+tgLdbcnXJUvTzbyU2hln+YVe6btUz6SZ0b6z37/3/Gjv3yfy/MN+/sLwtbQnA9s7p7i5cDVLx3ywfc/RI2RaCfYASCihMZkGd5L8gz6IRLTDo9cSkEkYZ2iLCJCBoRSOOvwEa6/eZMhGeZTzUf/8S52jCAlx69fIa8z3vvBQ6YV2CAppzXWBoZ+S5FBMwqu3Zox+5UL1KLDeceNKzf4O9/5O8yn8+em7dMciU+X3ZP73f/p3/PeD+7TNJbJtKRdR9aXjtleSYiCosz58C/vYJs1ucxotp5JbYhKYoyg7SJlmYjSkZRhfjhheiwxuuPBByek1mJHgwuSTAp03SDzBisCx6+9Rpi8yvmlY7jc0m5HXv2l1/novTPkuiG4EjtKlJJIGcjx9CJnORH01jN6EDKBGNCFp0ezNBKLwMWE1orCrigvHyALjVGaftMyv77H9mzD2AxEFxicZVJX1GXB5nIDMZEvj7H1EW3SZNHBxUeY0NK2PftHC8gSVgQOXrlC86vH+BsTurZn/t4p2YcPCNGxODrgl7/9Tf6L73yXJ/zNT1gmPnk+J2cP+ZM/++fcfXiXuqwZ7nh0Z7jz7h1oHd1Fg087j4yYZ0yvzTHzEnvastxf4pzfWZXbgdv/8T288yyWM7RR+BTIihw/OPrGYscRKSUpRcpZydgOaKGQQtIPA2VZMDyisDW54eDqPsPllvOLNfPpBBs8PPIOFYsaUWisiEynJb1dY6aaCESbuPnW61xcrtjbX9J3HX3Xsz5fU6ma/qFlvdkFje8dTukvNjSXDVVVkOeG+7dPeOXzN0kCunXH2b0zlJQoKbHeYbRGVRlC7RSdyefmbH9JUXxpj/3JnPd/fIJ0mrV07KecFCIXjExlzigiZZRcCMssGKQWbMJAKTMSiakxXDJy4DN679kES6UMCEEVJGdq4MDlOOFpDORC7fJbuMR5Ztm3BkuiFx5CwiTBDMWpsRxTMBz02NKBVhQOJl7zoOjY6wsGnUi5QGiBcYIqKB6WHVf6km3oiLkgiEgVE7VOnC8GDuyMQYz4cWDsGuazA4yVnKQzDsSSoRIIKdh2GyZtiU41p1nHQb5H70aMNmxDzyIUCAcnWc9erAnRoZJimzkWqcJoWJmO6aCRxSsUcp+NDsxGBaJkpSLVCKNbU/iBVZGY+USnH7AxWyYxI5eH1HbORRE4HCtEcYPGQjYGTNQUo2AzL1kMPU15SiN7tJCoOKc2B5wFx3y9ZRW/T5cukWmXAyRHcCG2HMYpbexxtSJaj1I5mVNc1iPXwxRfdoQ8ApEyq8jbxGm+Yd/NaaXDjT2JQOYN5ZhY39RcyQ9ph0vG+6dY4ZjOrmCc5jzbcrA2dAKE0Iw55KuS1Cw514lFzBn/xZTwvuKidxxdq2nHLdskWZSS8Tygh0QXBBMTQEcu+si8UkQXEdHTecGyEBRFxmVj0cmziQlkogmKgyKhVcAmMDEwUzk6BDonmJeS7mJLM0au3jzENw3DxQVOGCYmEPWaKDyHb1zl81/7HP/1f/cbmMzQdi3/5A/+Mbfv3MZth11sVIDO9xxdvUrfN4zOQkzEMTCtSlZDw95yn2Ec6ZqWmBKvvf4G//u/93+gKsvn96KnooDFc0LXp+oIL6BYf26/+7iv579M6XHehE/2wgf3z/ijf/pn3L79gHpScTlooqm4uGzZX865vIB7d7fUGkYXEDGx9YKbxxWndx/SDo5FodEm8MrnDzlvBgrnGaxhkBoZI/VywnRRcef2JTMdCWOHqXe04dMisDeVnJ1dcvXqId/4xtt89Zc/9+mm9Y9H+lKB6oUOkGcrfAK1eUao+mks9y+7tcfNEyTxAijaE5Wfvr/PkgGfmJCnqj7x4bkBP/ZYPV8+bV5AvFTJeq79zwKreskdPMWy9cwP4pNkjy957j+FGP1ZZTqZ/rXb/kIydL/o+JMzn0zgk3P+8jGLpxblC/NYvLSDT1k9z5Su6dluWoZ+oFkPMCQ2Fy3t1hJ0z+psTbU3Jccg44SLey3BekSSDGNkGAPOC5QwWBeRUuMSGKPJtCYrBcPQ0LcWISR5kePROJfoukDwMFpAJNanDYviAFOU9HbA+0hne4qqADTOOpwX3PvonHb+gPpWQBiJ845+7HfKxaOhf+zh/anmelfaZmSzGRh7h+8j935yTjdKtmc51iaOXj3COrDuEUwsaVLKiCHSOU8MitF5hIK+swzdBZcXHcsbOXpRky8XrO/39FtPCIlcRAojCd5hfWB7sqLzOTYJBhu5++E5Mc/wSmObuAv6M4qiAEnArkbWXUAqSef8zvVeCVxS9CmR+QhS0SeBcJHcBVKmWZ9v2DuY472nudgiMsXBq0eIlNisGsqiwDYdSkvaZmC9aoh2gjcFutSEGBE+EEKgb1rkLCM/mIAQnJxdELIBVWZUagfzIFPEaUY39E8/jKe87x9rG7SPKCC7oSfEiNtGZKNRmaGcTlidrfA+7tJRBcl63VDnkjxXBBLttmMcLMIFSDAMlvWqQSlBEonJErpVTwwRay1KCuZHC1wMDMOIQpLnGTElRusIj+haXTuwenjBdG9K6SzDuIvRGKwFAXt1Rj7NCD4gSkO9t2AMPUKAFoL1+YrBjmw3W6JIBJUo9ydUZkZWSoaPzqgmBVGBSxEXPCpTbFYNPgQ++OGHIHcJk3wITCYVIUb8OOxesDHtAosLQ/nKgnAsGHRk7Tq2OGL0tARkSGijaVLAx4GUBE5K2mjJlUTGRCsDjhGtFJFEg0NLQdKwjXbnIfEwKk0bHQaIKXEZPJlSlELjZaDDowXIlNiYhBCBCoMPjlYGLrVF68imCCQ3orKSbe5xMtBFS5CSVliEUMxUhsXRC8dKCVwYabyFTKGMJkhLOzYYASEFOtERpwmjLERLX0XWjHgNzo+4OqJ8gGTptWcVGxwB0sjAiEoCqQWDsGy1xoddAHwnA3kQjCHR6h50hhSWEUsvISsyiDAKQO88Il7sEha2DFhhaehxwjGRC4KwjBKaQoG3tHmJEVD6Xe6cQQo2KjCmQJclZAzkRhOJDFKCGBmiY2MsSimKKPBa0IfAhesRhWSrB6K3TJUkiYiTjpXs0drTqAGRIslBLyOdsGSqIRjFJg2QAhNjcMnSDj2nW0+QA73piCKR+RZrcqwJbHRgkArre1JShGiIWAYh6fJE7yLWKqzIOD3bEpRnyDPWQyQ6QYZmDAmVPEYZvHesNw6VabQyUBjkPMOmSG9HkAKX58gYiRF6O1JkYBPIJOi9IxcaF8FGxZgUSRlWqwG3bVFRYoGQLClYovTI0xXWebwPmMzQdT0+eNq+xTuL2O7iMKzwXJ6dM2y2OBVIUlCXNa0b6NoWrTQ+RJq22SmzJ5ec3XvIzTduvRi+lHixUCaeRrI8ta0/xq2L53MEPGlr3KGLnpW0XmydbNuecbR03UAIkY0r8BLabsRdnnJ+nlg7hTUST6I0mt557t1fEVzCSUMrNXocufvje7QuIn0gyZLuUQ6Z7GzLZF5zuepJC0ORCc4/OEFpybIMhKOcMUbatqNt+08GAU8I1Dvo0nOQnU/b9D8ORH6xbPS8YvHE8c8jpD7b3af19UgT/ITQKr2w8iexEi9q//gwvcAr8KRQ9Ml++1IHwBN9vFS3e67hYyX5RQ/jmfl/VvF5UrUST0P/ny6PTz5q81nP6Gdz7PxCvB8/f8zFpyzmT8by0z+WT5vzFyZ1eaZuevbsSy77WFm59eY17r5/igyK/SszslBz/uOH5HKX6VcOgcmiZnh4wf4rx5SzOSZTLKY5Jx+uOT9pUHEk2F1QoBSRWSWwHnyCybTg9V++xem9DiHg+LUlQ9Q8fNCw2C/gwvDgYU+eZVTZwHSmCNen+EuPdwPbPqGSoCw9Wghcl6gzjW4i9n5g/9Y+s3rOwfzgpVP8stl/jK589a0Dzk7P6PvEsp6wuXtBCJG6gDx2TIqIuFqzvbemUBE3BvavVthmRVI5XmUUuccNDaJLEDxTIuvbK/Zev8HNtw659fmSe7cbjBJcfUVwvj3l7GRLrXYW7iAtx68uYK/gwf01SUmqqdoFiU8iZZ1x/dqC7apDSgnthkkliTZQ1AVTA1thSUMiJzBRgabewVympsDIknRzjm1btJLUs3qXy+F0RUQw9iNVkfP6l17n4uE5dnQIWfBgA01zQWZqDo73aLqCUTZoGZhPKvKDKdPplNnDFXEIFIspc1WRUdI3HVNdc+vGK8+8ET95GyQSJ+cndH3LcrZgOVsSYyLLDNm84PSvLlBasZhPOP/RHUZ2eTlmZb2LL1EZr3z5OiZpHiAwRiNsYK0eUmSG5XyKUYLVtmU+m1Hrku2qIXjPfDoldp6+7dBKc3y4ZLVq0Fpx5doB+zev8M5fvkdwnnlRkEvBKAS6Llkc7/HhT25jypzaZAQbGTYt2ZUDXv3Cq5ycPiSGwP7+IWNnUZcrFss5s705D+4/IKbE0f4RY5NQVWI2nbPICx7slTx4B2IbkEKQ1RmlNkzqmm6wSCkw7FjMcpNR1iVFlT/KmB04sDVZqegMTE1JJeAhPbkIXDETtFDElKjHwFU95QyLEYIroSBPAlVoCi+46ktOGUhKcJgKcg9CRjIU151hFS0qk1yTBTJJpG/JRjiOOU3uQAmu+owqSO4qRwyJ62LKKq6IMrI3Gpa24n63wo+CW2nKUHgoYT5mFNZwMR2IUXC1r9mmkSAVe6livsq4W7XYoLjuJ8i9QHSKZZiwGHPuyUtcclyPc6yMhG7FUs048kvupAfYPHKsDrCjJIYL9s2Mw7HkTmoZ/MDVtSQZjdyrmJBx4DNO5Jpaeq60NSGB0gumXnLYVqynJa2SHLWQNiOplORDYG+TWNUGVSgOfUFYb2GxR+3hpq/YZhVGJA5sRLvESenIesfxZqDPS4SHxdojajjzBcoFrkjHJt/lhphsFa4RZIsrGKNZDo6GS6hKjuWMerHHR5t74EautHO6zIMS7LWGxTrj4VKSJNwcJvRiJDnLMhbMQs09k/DBcrQtGF1CiJFlC4u45H4OXgaunhj8XoXcU8xcYjm5zp1wgrOWw1RiWw0LxcIrpqXkQ+EwmebooGLdrOiVRtmO6zVsXcEqOQ5KQWYSRhcUIpCnjjYZHJHjUtC3A1vtyGvDvrAMuqKLimWZMazO8DFDkdirIQSJCoFSOKZ7GednFtl3HC4MAsOmC5SyoAsrOuMp8sSV4yVdO3D37in7Bwv2Fvu8etMhEMTW0287XHIsjw4Y6i2dckQbuHJ8zOAHVJ2zt1hSFRParsUNloPpHvPJnOA8yrxA7Hji1RhT4N7mA3xyXJ+9xhAH7tk7LPU+R9nxM/v7Z3MZPadyJOj7gbt3T6jrkitHe9x7cMmmHTjan1JNJxTTPaoq48bBkg9PPbYJyO051yYHiEGhCCy1w6scbxPLLFJlhntWUWaKOQIfJATDLHdMyoILX+C946CMdI/iNXQ3clgWOFMQg2chBe60gaqgLCtu3rzCu+/u4vxevXnEdttyerbi8GDBcjnluViURwN+YW6Jxwqc4BMl5XGdR8HFn2Z0T4/qPNXnx1AU8VlCxieHH1/vU+p+fF588vHxfaUX1XtJP4JPEbhf3PhpmfKR4spjxfSz5fPH52OM3Du5hw+e61eukZn801s9pT28bPKfLs8q0y+9scff/ZxejJ+1/CfLc/GcsP/C73dFPPP3uQ9PKTDPLYGXXud5JeMxBR2olMG4ix+QPmPcDAzbHZuRRBItKGlwFi4+PIN6Rl2VWDFg6oLJsWF5VFLnhg9/eEK/avCuxz/KLXD5sGfcdqRsiikMF3dX3Lvccrly9OuCvUICESkjwQXGbYvMcrQR+BB3sI9xoFABLxQxRoQyTM0epxfnDBNBvFo+O3Of5W17vmoCVVlS1ZDEiDkoWB7MuFyvsIOnUJHN3VNm14+YvnrAg3dOSVERY+L4jSO+9xd3EDIjP8qZHR+iU0a0loNDxSg1Xe+x42wXNB1GVFlAPcPZgjRtyY/mzJQl3D0jDltuvXFAOdPcv3NO7kfsRLKxgWI6RasMhEAoSUwQrCOflEzmNVfmiu6jE3RIKA1h0tNnI8IoxkEzyiu0QlDNjyjufcC46Zlf28cgWd07I1jL9nTFvW6kGy0q01x9dcFkFnl4z5JLRza/Sk9JZIKXno17wNRnzPIJb7UTLn5wRghrlkhCDQOKsE1Ir58wDz22bOyewY/e/SHf+8n3GJ1lOVvya7/yLS7Wl5R5werultt//sfEEOm3PTozjD7sKOVsIkVYf3hJunENoSL4yNB3rD442Vm2pCD4gFYGpRQAmdb44DFGc/TKIX0zst62lHnG4mgPHxLnFxvc6JExMV3UXN6/AC3o2gGPYLqY4AdHMSlJMZFPCnylWc5y6sMZUghSDPjREpuO9t45DofLDa313PvhB0yvLBDH+6iFQ7oRNevJF1O0NRxNrrGczehXA+/+4D1i79FG49ZbfIgsphMmewvMzDNseojiEQMHDJueveNX6dzFTonQOSob0SJRSP3IyygRhcKIHCF21gCFQGuBlBEhJdKCjREhBG4IGCN3b8wQ0EWNi35Hu9o6slSiTUYaLHH0eGlxcmeRTiIjxoDWijJZ2tlImY3kukQ3liQ6lFTowROUJ+QRRaAup5zFDoRAS4MKCTl68AIz3UNUCmktKmTY1hKLEt9JpK+JU08SgbSdEItIyhIx1aiUkaQAIXZ0wI8sosE6xLBP8oGAAjUjn0wpzEgpCkrlQK2QMpLnGq1eo9UOHWFaH7OVgmQDWhq83aLqHK0CJZq1AJ0gq2u8tRSxRUdBZpfocoY2oNqAHh0hl0QiohsJKidFSElRdBN0pnbkC5uEOhYUuSZLgiL/Al22258nseVSrUlAFJK8rlCpwLuA2gaigeADXgqUKInRkXwgBQNyREhFGgNaBKQOqFyTDQpvSmIcCVphUo2sLWIc0BgiiWQtEYkOEfAkIsYInFEIo4idRwwjJIMICdsOZCGj6XfsT2qaiCLDO0vrO4p8jhYaFRNVaVj1gWbbc2bXeBxWGXKfWMwr2tmCeNGj25ErMaMJijg4VGdxKSCdwCSBFIlpVqAzSV051t2AzCQTKYhlAJPIDiKXwzm/+3vndN3AbFbzG7/5y7z+2o6m9trxdW7/6H3OLy44fuUaP/jJ93n3o3dIaUeKMQ67pI9oya996zs4a4kpcfPaDbTUuH4EBMqoT92T/uzOP+W9ix8QUqCq5vTTxDqsqGXNd2bf5XPV288YfNMTjo+nhVfxAomw7Xp+//f/JecXa/LcUFQzTi9HhtEyn9b0NmPtC7zLmeolzm/ot4mD2RHDoFGmwI8DKQK6IMWB5CGbLUiDxblErg9YD5ExCSKSajLjool422PFLqGikxJHYLWFrcsQMmcTPNoHNpsOoc74o+p7dMMAQrCYVUQ30jQ900nJd7/7Na5dP3yh1+GFW754RpTiE0PrZzEkiacm8/HJl0BRXibMvswQ+gyL07POlCfFuU910jx7lBI/K/rlyfpPDuWlOs2jiv/mL/8N7915nxgDR/tH/Na3fgujXiZqP5KWX5AA8BeqD/y01FSPL/xzei9+fuXirzn6n6rZs+7Qx2+QJ3yenzr+p1bgE8vwEQRFAO/98B6by57tqkckzfr2CusgjB4VPZWOhM1Aub+PVjNW9ztWd9a8ux12z0lltA8rynmNRWP2lmAnjBcNXWOhUIyrhHUNMUbkVOKLROcSDx82XI4gk6YbIVmJ3AaGMJC6RNtqQpKEKLAUGCV3LnYfeLDqGI1jvepYrbacnl5w9erhTzWPL5x8Ae+/f5v1ds0wjCRX4suSlBrWG4tVGme3jF5zcH2JTVuQkrOHLV1QVIs9thcDZ6cj4WJkTJpqltP6jMlS02wj6kEHcuT83FIOcN73DP2WBw/WnE5PWRxltH1H8pG+GynLAjJFdjBjbKG5u2L74ILtJqFkwWrrUQ42QRENuK1l8IpmFHQOsonhUnkaaTFSIJJCR0ETJCITbNc90zzR3z7BbTvqImNcbzBKsmk6mk1HCIGzu+cgIK8L5N6c+xctXlfYTELeYGTBaEcevneH1GmCF9jLDrMsiC4yVIquH3jnh+/w9tuf4+M30BPP4L2773P35C7d0JFi5HJ7yVu33gQEf/EH/5i+t7Trhg5BP1is9SAEZ9uGoi5xIXDy0SmSxPpshRsc56cXaClwzqP2Nc0w0PY98mzFsO3xzpNIXJyvCDFhrcO7wE++9y4mzxjGkdOH5ziRWJ+vsL0lnif84Bicp9v2hBDwPuyy+qpEeTQjZJLNZsv23TO2F2fYtmebXyClpA+WlCLNuiMWgj6M3H1wF5VLmnGDaAOnDy6IQeC9J8ndi3ZybYFCsHr3Al0XjOsGKoOsc9bvX+IGiyUQZcID73UP2T+vuCx7xui4JzagFS2OFLa4lFgLSxcTp3KkDIK1dCgEqMQaS6YkF8ZhgmIjPEkFzvBspEcjWKdzVIi0EUCTgqURiYSnmYDUiSaHcxk4iS1bHRFIumJNkVu204BKHedz2DhLkoo42aJcYqsDooiciBMas8upMPqAzAs2WQA3cpYPdHLES4/PIto7LtMIOZzOL+hcT0iR0ThIgtUjwfisPMfbLU5EvNF4K1gZRxpaHsqHpKxgSAlVQTmFpiqIfeSuuk0SDVZ7FHM0A5ssx6fI9yegraINifvBkxY57STHlonVJMe4QJNJlBgZcse2kNio+PFcUaBpc4GoFTFTNIXEFTkfFDMKq2kyDTFwqQWtYQfV0h6TAmMmcYsCS2JbGUSIrLi9y2arLMklTjtPW3ps0dMvHTpKNnoEF1hnGzoVdgqishglWOcjIiXO84ZhqQjdgJ97pFdspUPNBWfDfZy0xCLAQUSWjjYbEMuKy+KEft3iksO1GcxKzpNnCIk7fUkImiFJ/KhJPrAdBSEk7q978sIRs5zYBvpzSzt6cpO420YkgSEqLvxOddmGRIqJ750EZl3D5doyhhGbwPcWUmIICoHHo1mPbgcBDAkpEys9opXHS81pNuDLgF5qxH7GT37yEcIVbDYtx8f73Llzyje++SVICdtZXvvy57gVEx/9+H0uVuesNiuiD3xw+31UYdh2W7Is5/b9j/j2176z22I+tiDmRBcIKaIz89z2NPqeO5v3eH/1I0IMFGIPpySX8YJpmjEfprxaX8fMKlRuHqFMdnv6c5b3TxEy7t454ex8xYcf3acqC9b9GVEYmnZksZjhg+b8cqDMHLdPbiOjYuMkMUo2LQwJ8IqNzZmMga1VgKDvFKtRYSR4k+F8z0jGNgl8CxeDZBw1GwlSeFxWcel6WgvrKJFSETYt+3nicozE+5c4nXDsWPUW04JcC9brhsPDBe+8e4er1w5APM6w/tgzI55XBB5PzrPy0E8BD/pryXif1d+nCW6fqpCkp6q8yInxXNOfL5z46a5eejJ97BEa7cjdk7t8eO8DQogopTi7POPqwfELmz61XP8TexYeG/x/6rwlP+f9/AJgUS8EhP11O3vCAfXpfT6r1z2tYz5TKT3d4snvyiqnnhbYwVHWGRfdQFVousEjBexdWRDyjP3DJdv7lu78cpcLIAmEkIyjZXs6sDldIbRhfjhjfrzP4Sv7fPTDhyjf0zcRJUHLHQZfKhgUTEpNljxIjRs9eZWzOKw4fdARksWIQCUCtigpK4NSEbmNlEYyxECuNEWRo7WmKPOffoo/ZcGUZU5dVyQSZanRy4qyznCd3QXPZhK7bcj0kutvXuHOj8/ROjJuNuhcUtSaKld4mUiNJzYtfb/FryWthbARFLMJEoUWimHT056c7hJ9JVj1FxSzgunRAq0NdA63bqkO58iqQtU1w7alP3fExhFGQW0ijkRyIzF5epvIZGAQkixEnIRaSmRI5ClRaMngAnlU7L96xCRLrM/WDJ3Fxt2LgAieyGJvRrvtAEFWGJCCYd1iTUEoJVlZIOPOAldMS2ppCKUiRcVqdHijoQBTaeq6oprUvPOvfsDRa8fMjvfgiaC2Ii+oypoQAlmWUWTFx8+qrEsm0wpvHVVdcfHRKULsErklKdFK4YKnudhweG2fsi6RCLRSZJkmxoRMgnpaM3TDjq523MUGdMPA0A2YPEdJRaYlJoGUO/re+d6ccdtDSNSTake7m3YUtIu9Gc26RSSLkJJpVTFsR/pgGVHIqUd7cF6gFzllXhCGlslsSgyJpBW6zkk2IRRkxlBmBbJMCCTDYImDJzMFWZ6xWM6oREkaIs1qS1VVnH94RnSBqiwI7JKrOeeodU6dF/QqMDMlKzpU1AQilReMAUapWQiJE1AIwUCi9ILkI2OuKJIkJkUtDJ11TIRhtB4TIpXKUFGQo3HBM3WJJDXReZTI0IUmNxLrt0wxOBEIMZIJiSSnRjHahmlQjMFTeoXWmlxIalUxpIZZKhlkQApDTIE8GbJO0iaYhYxOWio0PgnUEKkwbLVn0iv60aOUwcpALjMKoem9p2oTURmEzemkI3dQipIuRSapwAoDcSewGQ+FFTR4sh4qpVEqo5OCQiiMEziXqKOGCPK8xRWKsg1IYwghUfUe5wPaBazKKHpPtJAPUCaB8Y7aJGwuMJ0leE0tJVkUKOsoOs84Lah6hysCTgoyt0vWZ9Y98WjGREm2/UihJTokxqBRo8AWitpl2LOecq6RgyJzgpksGUOg7hVBJyYDRC3Jk6JKkn7oqHqDjRFJIqAxVlKmnFZZ5qnivG0wxhCURDtBEQSuzJk0irEq0NHRDo5cSIrJnLbdMleKrtS76Y0JHT3zvQmyg6mJyPWAVpEhBuaLAu0FbhMwcSQ3kuliShMEcx1YXVxghUDJSKEFcegxWu08a9seYuJgb4IqMoyRrLeOWaXwMdGsLSIFeutwbiSIRDHJqa8foq9mu4Bta8jyknGwlGVOUWQfC/EJCKNDGcXh9SP0jwxVUZFiwkhNWdYMY09ZlBTZJ/vSYwSNVAohJB8z8TwjUWlpMDJjks1xYSQTObnKaWNDFUsqVYOAYP1OuXhmq3+cy+rpbh8bc3byQVHm5FlGkWfUk5IgBUnkeBcotOTko1NiH7He4WQF0qCVwRDQIpGJiMkSIYJODi2gVGBSIJORQiUyKZDJ49Kj3wsJQ9oRvIjENFesQ2JSyl3C0AyS37FwJe/JjKIUEhMi+axECMgyxaTK6PuRsiooH+/7j+FKHysJ6Tm4VALEc5br9IxH4lO0jBecfhIR9VS9J6b8Z0FQfFLlZ5Bon5HQX4SG+cWpFz/FvQjQSqO1oa4mOOdQSlPmxXNVn2n2zBz/nBimT2n6bNLI/9Tl56ai/XkfX3rm/1NF8Egj3EEehNgFdD4+97gH8bjqM/8+6eOZPh95MD7/yzcJDlIQ1KVhZnbJ14zJWRaKzYOR4TxRZCUHE/0okFZwfCDJFjV6b0J1MOFoqXF95PyjFVzcZVwP1MsFr339c3z3f/gqi+sHTK/u85Uv7TMrKgpylI28MWkQeJLwfOVXlphFxma7ZYyO1/dGCIE4DOThgma9JbmIHTzLmFHafbJxnyuzY5bz2c824S8oX/jiayQzIHLLtdcrrlydMd2vqCrN4WJE5QW9h+b+CVdv1CyvLZntz3j1asQ3I7EdqaRnUSSMMCSX2Mu2DDGi8py9XLM/tGw/XHHx43OOmzXKFxR+QukLDmPB9qTg8v3E55YHIPeJ4oiL9xoOB0f30JGbBf/9//lXeevLNzg+qpjowJtXBCnzjAxcL1qE2GXM9qPjVRtIW6CR3BSBlAfcPJKqyI3rR5zJKeLWG7z5ra9ijMZMC4pZycF8TteN5NOK42sHTGY1ESjrgi/vZUzcCrW5z4EWLI5qzDInvzrl1//udzj54AHbbQtrh1wnhruW5k6Hf9jy7/79X/LH//zP+OH3f8z3v/cj/vFv/wF//Id/yvW9G/htIDZQULLtGv7JP/9d/vjP/pgbb18nSAnasDxasn+4h55UeKO5vr9HFBJpcoQXvPrWDWKMeOt47cYxRZGjjGIcRq5dOXykbAReuXltl09iWjGdTJiWFTqTGBF5e7/EZGqX4C4lDvcXIEAaxdHBPkprELuM4J//0utotctbUvpdoH9KkWbVcBAqdFkhdMaBWpBJg2strrN89YtfIoVAdI560LjLEb+xDJcdX//yV3EnjnDqeev115nvTUElkoj82t/8VVanK4bW0p+siSGAEZQmcW0x5+rBHr/667/Ef/N3/havDnPq/9CT/6Dnb3RXCNKDSVw1E667Au8cNnl+s98nGoFQiUNRcstWhBjwJH4zHuOig1wwkxm30oxoFLo0/G13iMo1UUOG4uZG4TLPYBzfdgfIkAgI6mT4ur/K/OorTK/c4LfaN5jk16mK15jJq3xr/RZ5eROtjvnG2euU8ZBM3qCSV/n28DaZOiArrvLN7StMxJJycp2iusI3Ll5FZftk5oBvjm8yTfvk8gCT7fMbzZsEFFFnfKG7xjROEbpAZRV/8+xzCOfJ84yvmFtcVa9Tm1cwxTX+tv0i1d7nqOef53PxBst+gVbHmMl1fv3yi0hxC81bXN8ccOxKAgGvIt98kAhCk4Rhf+3YfziAKogYvv6jNZIS5Qv2Nzk3mwoRaxI137qbEWRFEhWzTvD6QwtoUpJ8+Z2Tj9/VtY3cOhlAVCRZ8ZX3G1SMhHFkOqt464MtKmaIlPGN+wuyZEgyQzrJL909JK0Nxk/4zvkt5vJtZuZbXJn8Kt88ewXnDb6XvH33EOk1MUiEFXzr4i0QEhEFX763h9wE3OixJ2t+7f5NfKYIUvDW+phiNIxDwCP4dvs5RJkQeeK1LdQ2EvwWkVt+8ziHSYLScVg2mGFLu2nZrBq+NhsIViK8onY9i9pj5UjKE//FlxdImSOCZl/A1VmBCjkm5Hx5NhCMI2YWUsN0klD7U7Yq8cqxoN07YLt3QP76Fd74lWuYgxn1zUP+1n/7FW798i2Obi156+uf52u//pvE1RX82T7f+OrXEW4K4xwdpxR5zu/+zr/k9377Tzk5u+Df/uDf8Tt/9Dv84N3vc+36TaKCIOGNxU1uzK/y5s03ee3aq3zhjbdfuPUIKXh4fsLv/tHv8rt/9E/46O5HH9dRUvP63tt4YfHS8Ub2ObqzdgdDSo433Zt0lw3EyBMb/8eb/AvlqqfoV+H61QOyomKwimEQ/Ma3v0LrMlZnES56Zjpn3SsGOeGbry1JZoq1OVmKHOSObhwYnONrs5a8GVgOgWMcr9UBgcIHwZemLWSSpBW5DBykLe04ErTkC6olNxVukGhhuGlGXEhEqfjilRmuXNIyJ58f8drikJNTxf07iclguH975KQp2bqSejrhH/72v+Qf/n//BR989PCl+/vjsjOwPyEUpcfz81mA/SeqP55o8UwdkZ4+/8Tz+esIteljKtj0gus9cw/PdP9TX+3JtfG44bN9JQjB86//4i/47d//Pf7Fv/03fPDBA/4/v/0v+Qf/y5/y43fu8Sf/8sf8j//Tv+L3/+RHHM1e5+LhjPOHC2pznb/8wRn/j7//Z/yjP/geH917wB/+8z/hd//oD3jvw/efvtdPFYR/xvJxP88/159Jefs5y89NRdu07Qv1oV8AZOuzy2fBo549mZ6u96e/8z1+9Oe3WZ21qOBZf3iJGyNZptn2O6aQrKy48aXrdJc9H/zwDklAuZgyPZqztpG5FshNZFyPhLizdkgpCGQs93NEWROi2CXkqjKETpyfDKRhQ8GOKSkmOPr8NcgN73z/PrnyVEGj2SUtSiKSBDQ9SO0wxpLXmvnVfW598Zj/7f/wVWbL+olBP221eO5hiOe/+oM/+SPe//BD2q5lqg/xp/tc3O8Z752xaQI+JoQpUb5HOYGPmukiJytLkrNcXowYEyDPGIZEpmDM0o6nX2QsVMJYyXprMUaQJGgl2FjBJA+0KRJUzqzURK0pJoZmFOxNdhlQhckgBQ5vLFjUkpP7G/rzM9JywgCkEFk/WFEKTRM1lfbYymNlhJgweaKaKi5I7Iud/dgNkfpgzlJbePARp3ceopE7i3mWEUNAP0rGZ41i+3BFNIqizOhHx2xhOPjSHvKgYDaZcfmjDeEycHb/BDHs8OcW0EIiZolXfvU1+mFgtpwipGS9XjOZTAgMmEyxbRoWyxlBeVrXUZc14wOBGkvWFxt8M3Bx94wE2NGC0kwnNdt+5PBwxt6VKd26YXX/HDF4QkqMfY/JCpSSxOjRxtBuerRSjM6RF2angPQDANoYsiyj6wfKosBZx3RZ065aimmFiImz0xWTaU1MAWUHXEyo5RQ9K2jHkVlREo1j75U9Qm9RWqMQNF3LcrmkbxsiCec9mdLUe1Ma2zGtp4RLAU4xdAPTowliKjg9O+P4+hX6hyPjamB7sWVYd+RZRtu0lEpRlBWfv3bMb/3f/i5jDv/8n/0L7t29z2RS897ByLinuUwDy9HQt54NlpkwRCWolOYi9uz7jJgip6lnJgxJQK4yLk1gOWoino2O5CikD2Bhm3uWDfREuiwik0QJRR0kTZ24Sk1xcESYTpB+F0uhgueiDBysI75OdCoQOkvuJMtixkPj2BskbiZwKhJCoEgZpk9clJHFoGjoQO+YcrIhUCA4UQMHPmebbwmhZ4ujGBSFk5zlPQexQsxaMmkZY8dU3iQ3b3JRCpYxJ7IPsaSLgVlIiG7gIoNlUdJtT2C7pas1y7IkuZ5LNVIHhciOMOeJts6Y9oHooZ3mTAIEm8iDYFMYZn1LJ89pM0c2JuRkj7pYcmFgdtoioqCtMjIXUF6S99DMa2aXDaHIGTKDth5BT+ZbupsLDquai59c4soC4QPj+C6hf4/TmWXpJtggSFpDiCzkNfann2ezqJm1LXfP/jlNvkV6TyGhqDQrs+WozXGzSFCRKAKiTcgOzquBg7bE5h4xK3F+oBoEcpBsrggOmRFmieQd3bBBfRCQ2auc+p49MaH/8yXcy9kMgSxEpM1ZDZLaeDySNFpkNaE0jqB6Vq1npiCjJHOJyy6QJwsSxmSYZDDIAVNGtjaRjQN7+YSuD4Shozi8hs4LTk57StcwSY6xd+RGUlSeG28fsF73LPcmRFPTdZ44WvJJgVGC+x+cURVgpiNRR4pphZlb8pnnfHXO3nzJ6B3WOYQQ7GdzvnnjqyxuHCGspTiYMzlaPOed8N7zj/7wH3H7zkf44Llx7SZ/97f+K+qqJqTA//LO/50P1z/GxhFT1pw3LXFm2Yt7vK2+wrfVbzC5sY8u8092sGfFmOcwJp9sgrdvn/C7f/AXfHT7lNm0Ym1zYsp4799/wCxTBDJWY2JRGcaQ7dZz0lShJ0hBkySTXDEbA3VrcWQUeWJb1ZyOCYKlKCQqjqyD5upMc9k6rNTIFKnLnEoJ7m0c88zTji0py5hMCpSMiHFg00VeOai4vGgIUiEFGBGQrqdRhoOZYTrxZJVEaMlrr17h//Tf/cYuId9Te7x44X7/7Mw8/+FT8Ukv//6ZC7wsEdynlceJ656KOU/Pgbmev62fRW5+SqJ/yVgele//1Y/4t//hP/Dw9JS9xZKLU8E4CLwPZEWJzioenm45OpjQdY6YIuPoyQWU05LzdcfB3oQiO6GqPKO1XDu+yt/57m+xmC+evdwng37+m59lcLu2P03CvU/pZjr9/zsV7fPq4y9asfiZNd/nFIvnqzTrgc1lR7cdcE2P7Rw+KYLYWVD6wTP6gYs7l2TLKcJkjL3dYVpbT+8TikRmBe2YGHpLniskEmsjZw9aPB0uqB3DTS4JIjF6ybTUdG5kHANZbvBCsT5pGH3CKEMUmm0bgIg04CKMfudilQI2q56mecDefkmzGZ9QLj7FrfkZ09S0LevNmtGOpFjjVgVtExhsoneJmCQCqLMSby1d57E2IOSAMQrrwPtIGC1B5oQIvQjsRhDJFaw3HTHmDCGCgqQSo4MQE14JutFjhWY2N2w2jou1pV+l3eaVlxijyE82pHnGMHj0YsH5Zksn5S5AMC/Ytp5oNE5LxhjoH9G5FSniQmDUkrWP5F1HTIb2wYpyX1BPcqrDGXY70K07VpdbtFIsl1MCicuHG6L3SCPpvcfHiEue3ttd9ucksM4TU0KXBcUs4/T9E1xMZFqRT3PO7p0QtUQqiVCCtumIIRKlRRnouwHfD7gwkBYa7x12pZG9o2163KYjpkQ3jOR5hjAZnXOQKcqDGUM3sF03jKPDtj3BB2IIRCHBgveOGFqUVAQfSERS0tjBMowWqXaQJx/ioxgMT2Y0TdPtrPnWoYsM6xxt05KI+BCQUlCliFICHwObrqGeZ1zcO0HmO5YnZwPjONJ0HT56urZDGok0ku1ms4vHcJHxQcS3Ee8DTbehiz1DtGijiWsIfcQ6jwuBYbVhCIGQ5whreevbX2Dv1SPeffd9hn6gbXfz298wbJSlcxbhPX1KbBiJRKTWDI9oTjUeUqRTEINDSkWPo8WjZQTvWHtHpjRaSYyBQXiaUuMTNNKjpaZE0QZPKxIrGagVuBxkIamsJ3nPqGE1gRgsQwlMClQnuXSeIRO0UhCSp1WBICI+SHSl6Q0wjkQV6bVDKMlESAbn6HVkUwtaZ2lpCSKhlWEbI73xXKYRI3tSaXcQzSHSi4HGCfCelM2RRuBQiPMt0Tv63KCCo88gThVWJeTYIUpoBLjoyLRATQx9phAuIY2kyzTOelSVMdpEbxRip4/RFpLRJHRp8BpaCSpXqABdrhiNJB8VTgg6LdHTEh8SQ6YRUpD5HpsZeufJtcRPctpsl5ckyERPYDCRXjhCB020RCXJjWGVS8Zc4862dDKyoiPpxEIInBzplOUiS2gjaYtd7EJhJaMeaRjREwWFwsktQXtQhlRJOpm46C8IK0tSHm8SxWxKEJHO7gROFxNxiAx+x+Lk+sCmC8hpRj84pNSM65FpbiGLDEEQQ0R0A1lSdGNiVpmdBzJpXKmIUhKqyDh2CBTrdiREjdQFl2tLby2NhYVMaCEIMoMkCF3PR9/7iPW253xScvDma/TDDgXgfM/ZBw/YtA6jLapoETpQTysOvzRhEJau73akJzHQuREBXHntiOWXrpNZQXllsdtb4s6T/GSxdsQ5y6rZeR+dtbR9R1XVuDAy+oHL4ZSQAmUukNNEE1sylTFmA0YqVJE9EUPweN9LnyJDPS2ObpuBrt8FRocQWLvEOFjaMaAitMHSJ41rPSYrcS7SJdAmR2rJMEREUlRJITNDGBM9MHhJ7yEETd97qjxjQLINmiF6RjTeOtCw2vQMIkP1EZ2XbGMiWsgIJJvoApw0Fh8FXiqkEOQxYLKcYQzcu3tBpVtUFpnsz7h2dZ+2HT6GSv1U2bFfWnYC6XO5Fl4gSzyGon3c7Oe85scX+1ng9s+O9WXy9GN42JOQ+RfVfaKPpm1p25Z+6FmtNU1r2KwDKSXqqAhdYtsMhKZne76lGyzaGNI4klcFPjcMFxsmkzOqekd6cLi/T9O2HysXz1/8r1ue0Sb/ugvh53Ry/NzKxWdPwc/pw0ifrIHHmDHBT5HU5Fl959EkPwlre/VzR9z74BwpBSIXXIwebKQsFdNMctoILtYD7fkF872Km28d8+AndwiMFCJAksy0JS8kG9cxm+ZcvTnn/LwlNY660uSlYXXpEQImU7AB2iFRFQJtBJOipD5acHitRsTA+j4sckElIysiWZZzfDRh8HBxPlKVgqFrCDJnGDxnP76Db77E++8OzBc1e/vzF4z7+Tl99vyNq9c5O13Rdz2He0tcto8Ma9YNJD8SRQmZQIwtB3slbRUgBMBiA6gYKTNBOZsSTUVZG4Lb8nDbc9n31HsF1/OSu+eOED2HewWxqrhYW+S4QeWSIiqCaznMNfJoAmqLbhsmeWRre0xSLKTAoNgMbocrrgJ37204uHLItV9a8NFfvM/6csNMlTDNuBg8wQfqGEgJZISJSExSYBCJmGXUxYR5IRnznOvTkjrAnXtrLh5cQtcyND1Fblgc7TF6T+MHhBJMdMm1V27Qhp7ZdML1subswxXVpGQ+KWHwPLhzQm4MVZC4hy2yyigmUC1nxDEynU5YXJmwPl8hxg15gupgBoucsirRdUF/Cf22Y+wsFx+dcPN4wWJ/RjGpWa23NF3H8dVDZD+QQiBsR45f2+PhnZMd48ukJqZEiAF8RApJTLsgbiUUs8UEVlAvag6PD9lcbFmvtlRlznxa0TnH5ckaAjB49g8WlGWBVoKzsxXOOowX6CDQDpZ7M65cm7O5XFEcLljOpmxPL4mjYyYNk2tXOL13gvWOw719EonLZkOdlywPDZui5/TeKeHcIavApMwpZcbVL16nOWu5+1e3EcJSzArGFHHWs3+05I3vfhmpJFevHTOZ1cz2J1RFxeZBSzadUgnDEsna9WSTxNJp9vuKCxMwKnDNVERAyo5KKY62cJkFVEwchxI/KsglVZAcjIZVFhAhcjBqdASTJfK84Gq5oOlajB/ZDzAbDO2gMSGxuAz0Epga9pHQRTZkKKc5lJquHYlJM/dQBbiYlgQh2O88VkpSgrkV5BbWkwofA4eDx6kMIWv2WsmVYcq5LrBacuQiPkSkjVRDYpkqxjxhveWKr0ijhiIyaRwL7WiXieZyy+G6J8SEEpLKe45D4tJBX2j21wNMJXFRUfWW496xkorMO5arcbd3h0Q5BpabLZu6QC5y9tYBnzxSFOTOszxv6PYyZKnZX1vU6FEWsgSL9UhvSgSw6Ea0DZy5gImRxaahLRMxJpaTSNpaTqVHKkm9LriUU7IsY24jeeO5rCVRK5anWxaHORfbnkkjKdeCfHFESInj4HBjA1XkwFfMRc5D5YjBc9AqNrbHFBl7Q8nMTzjPW8a+5bDJiVpypi17ekmxCqzNmjFPXMkWOLGHkJeUlzvWtdM60nWe41KwigmpNJW0vHI1Y9N6usEzySI6h9OU0NFxdFCyXkW0krx+Y4auDCcbT11pFpXmohtwYmBSKeqoGLICugHfXhIomFUl+1XOfhzpesgzBR66tqM0GWnomOhEcVCjlMQ/PMHbniLP2M9Lkh65GEA2icNiAVNIQ8n+rKaoNd3YI5Rib7mPzjQX45p9kVHXE+6d3CeRuHp4lX7oObs8Yz5bsL/c52C+j3OOPGkyY/jwzgfMp3OOqmucdvdwcWTPXGMdW5J1LMolN8Sr3O3vUqy2XJ2/ireBk9MHTCZT9hZ7nJydMtqR48NjvIvcfXDBbFpxdDDj3sM1XWc5PJgznVZM5jPmk4JXZ0s+vN3TGcV+ITkwOQ8GhYyOaVrTqhIJzJVjMasJzlMqmKqOrhuJRc0ig6zSWGkZR0sRerJqitEZpW2pS9hGRze2TMeGmBVsgucgF6TYkdUzCJ7SNoisILhA5i2Hi4wLC2GwzIQlGU3vBPuLKXXyjFqjnGJelbT3Ljk7bzi6smAxL7l3/5wQdxBgrdVTaKWnZaUnzzwtHDz31QuUlucUiydl28exH4+7fanY9shU/TFT1O7vTtRLH8t/T3XxaUrEZzle2ClFMQTu3jtDILh27ZCm7T+m+p1MSm7fOwXg2tFVflh9QLZNLGdT9mdT7twbGJuW68cLth1sHvaYvuMIeJAUycLV+YRVOzAOEjEVzKqMzUOPWdTU9YzDg4OX3u7TN/18rRcxTH1c9T9feMULyy+YivZnHNELoDqfulYeLdJn09N/WsefehfpkwubUhNSIpJoz1cUWnK5tfR2xOyVTCYT+lFgx57zD08orxwxXcywzRbVK4b1yMFMwdgipWIyr3FxZBNGfKbZP6yYFzmikAgpmBaey7N2Z23tA2Wu8LoiWIVximk9I2eNaz3DzGFLwxgde9KS5xWTvYy6EAi35WwbCV7Qd4nf/+0/Qy0qyjLjm7/+JW69fhXES2bouRcGZLIm9JowGkTI0QaEhnKe0w8bZG5IUmCdQ5WC6bxmuj9hORfc/egS6xKH+xVC73Ny5mnOVxjR4HuBCQppE4ZIhmRwEfzIthX4BGWmSdHjIxghCc2alR9RRca8KpFDpDvzuDGyumxhhMs2Em6veeObr9LLKdJoFpUhXAPfbTB+jdosUX7n1s7zyDZ3eCFIQiIngUFKhAqswsAqZVyqyGhqXj8+xMcLqoPr3DiacPuP/1cu7p0TJBy/tscqNJydXHD4lWMmexO6s4GYoJ7UPPQXtBcbxocr2ssVeS5RMtGfbklKMHhPd3tLPi+RVU7xSk4icvnjM2JuuHrrOr/5d77F2m+pq5obxze588F9tquGK9cOkFLy4P4ZZZkTZeBP/uTPcEZgpgkRFOv7F9huYDTZo5eyILiA0ZphHMnLjKMrBzy4c4J1nqoqqacVXkZmB3NS3CkyWWY4vH6IjvDwndsk69FZjh8d/TBysD+nNoYQEy4myryg7x1VVjLJa1g5xsZh5pHprT3u/Pg2201DFgWHr1xHmh0lp5YZ28tzQnBQluRTTVblFC4nNY7X9q7yq//9dzg4PuTG9Wu891cfcvuVY7b3L4idYxgG5sd7fOfv/TqTR4q10gpRJSgivd+i2wQU1JOapVR4/wF94cBElm7OhR0QGlKMO4pftfNA1bHgNFgCAecDRZIkIYhSMo+adQxIrchzQ+YEWR5RKVGejbQ6IQqDiIo8TOhTjhRQO8FYS5SQSCep0oKtDxCgMhPcEpTtkVGQXw5EpRGZpvZgqx6zzFB4JncTayWQSlJsA2k/33kQkuAgv047GZHRUw4Clycmk8i0h4NNx+1qSxSBrJ/itSGlkSAFM2VYrTvwEWUTSSgShugd9ZCzqjKkFGSiIDQevTcFadGXkbCfiCkhU0Chd+9guYPquKXESwnKkesjlFRI4Zk1A03td9Sl3qMHBcXunVx2kW4OCEFyu6BwMVN4D3lSbEhIDO5yoC4KkvVEFLNxxjj/MkOmqKRksndJU7UkIdizO0pav2kRKXGYf4EmiwRg0gw8DD8gCBidQvWKkFtCZshlRT1LtLnH6IxZW3JmNyiTU6SKPvNEafEyMYk153GNtwEaS5SXiCsCGQJ1tJxM6kdikqOelJxdeEKIXC0T2oMePZMwYPb2abae/mxA5Y6gst3z0ODHjnHwKDRGCpoHPb6XxDrD5oGttWS5YH9SMzQFfVTkeeSgKGjnOUYmzBA5FRLrEjhJluW4JAk2sTnfEPIMnVVQKupBcm5bxqjJxmO6s0i6rEhyxre//SW6eIkQkrKs+Kd/+oe0Q0uZl9RVxXq7IZGYT+aM40DbtZRlRaEzko/IBDEmfu+Pf4/e9pRlRf7KQEw7L2JOxnByj2BGIj0fbX5MM25gLVjkV4gParbNliIrmC+WrNsN3nvqYsblZclq3VHkhuVixul5x2g9i1lJ5zRjNLRBs19UdBcXhKhJUiIp0MrgwkBdCRq3I57wzpPGhPAKYQU+9/TTij6AqSSTeYQLj/GRmQq0xYCpDWnbU9qcdkjUpaEILa2uEEHQNQOzqWYzJITfUWVvk0FXNUJ4hNoxjRmVIURgJCOpRNQCz5wOiXCCv/q3D/jX//g/kB8suPHlVzhcKDbrDTElblw/4r/8299EKfmUCPCxyPox/uglwsJPY8V+mZD/7N+XionpUw4/JbDi0yBOL/JmAI8ZQ1NK/NEf/zm3bz9ECMFsNmHdj7RNT10XVHXJxaohJVjMp1xeTthsPEZOWB4e0/hTVh+e0j8I9Elz0YPVNbeuTBnurolJEExOMIGAwWeGdlxw0ndoXXDWXEc+EsGfk3ufVcbEo5M/hXi9E3Ffxgr114RJ/YzlF6JcvFyl+NnUp59eCf0p4ywe131iPh/39+73H9BsetYXHa6PRBdwSVDXFfdXgRS2IDQRzfnKkY2XlJOCdZtTpcg4CO7HSKUrfHD0o+ByDIxeMEa4fWfFnR5EysmrDHdQUe7tY8WI2244vfT4MJBOBs4fbJgezsmqKSIMnDQ9Tu8003fe31DFHkQGV6dsx4ph2NHhnjVreNfBPGOxN+UnP7rN9RsHZHn2M837e+/eZr3q6PsBhg1pa3n4/gVaJC5cQa4gSchkxv2LnswEnHdst5piWtCdNTy4s2XsPN5MCVZwOhhMnaGcoB8D94ZI3ycEhjvrRMwtNmrINZKM0UMXoWt3DCgjljDJyUZN1BnOOu5cWNS2pXGCpnWc/en7NGNAZRp/6TmYByb7JUVRce9EM0aNc4IHpSciaGMkicilhDE5ZAj0G4/qR4bMELcDDz58n+QEUmvk2DK5us+mablcb/HLQDtuCRW4OnF2eUnTtSQSJ++e49eBs7tnzKY1sjCEraXdtljrkVLgSaQAm00HStKdtdxbVmxWG2Sm2b9ySNNY3v7y2x8v1FffuM6T5p/9K3sgEr//+/+Mtm9pugbuRdxpT9O0EALnl2ucdQzjSNMqlJL0w0A3DPTdQIqJJKBtO7Z9iy4M/mHAthaEAu+5/d59mtUW7zwCEEoSnGewlvt3Tnf5H2IkKzKUVpjc0K9btmcb+j3NerNlkAk9yeiTpxmHXUb17/8VIjf40fLw4gyiox175Eawig1oRe97lnszvvibX+Yb3/k6MUbstufzv/Qmn//qm0QfdtaaR0QPT25adx7cpRka1v2GKi/pv3pImpdYAw9pOPeWjemJQfGv1RlK5VymkRQDUkvW2jES+XdFh3RwaQKRHmFgqz2DFvyFHtA+cik9KjlSllgrj/aJfgI6adYqkFcl4xRCblAh0l8pkSHRV4ZN47iYSjplICXewZGpjG5ao+PI5ZWKTgsSApu1iDCyHSOizDnbl1iZkYCw51FCsBG7DMBnmcPpDC9z4l5AOE9baJSCHxUbvBJ4qbkjAqqERimiiHyvktAIRpMBEpmgLQ0pwQ9rjRSJQSsElpAUfVkQg+THJu3GNDFIBDhoK4OzgtUbCzSRJk+IiUHqjLbIcNLzV6/kqOjZGoGsC0Se0RQF2kfevZahfKCVAnKNqAraIkOGyPtXZ8gw0uYGOThWizlNv0vy9u7VGVJGhiojl4H1uGKba5IUfCRnlCnQlznSBx7MpzSFIpF4R/8Eh2BlPOjI+bTFqkgyhjgdyKKlLUbUIDmtG0YiQQnilR4pEm0V0KHnB8tLfLRYHUh2SwqOtVd4IXnoLN7thNHUCUSQDMEQY+Q/vteQ4ekHz6V0+HBObwoQmvfaHKMzmsbz7kcrUvQMaKZV4N79XSb5tVfYZqQooE+RTApWrSYlgY2C9ei5mOeM7YgMHjsOCAHdEDk4OmBtJdtmwG06zjYJXeaMwrCxnsFpgs+wUvP9790H5xBlSaEDdz/Y8M3feAuhJP/qz/8VJxcnnF2eM5tMiTHu6LVTYlpNkEKx3q6YTeYE6xi6nhQjzjuCj3S+Z7aYMJg7DNUFIXkGHA+7h8RpxPSS728vYUgEndiLHeJiyvp8Q13WfHj/NiiJdZZMHtBsK07PWmbTih++cwZC0W575tMSqQ3n64HRRT58/0M2D1saL0ljRhSCzZhQSfFXG42RsLUCyFmdjFhR4GNik82YTgxtZ1EC2qToMg1G8lDuEiG2rmcmDb1VdE4QgqQXC9KQ6L0AmbPeRnoRKXRG5wSlzrlsPFEnzsZE6xOZkGxVTqEEl4PD+oTRCjd6Ukhs1xtmteLy9jmN97zjG1QtEUbv6FDPV1w52nuhmPSkbP50jrz0CWIkPWaWekKCejYI4me1Lacnu/vrwN6fgLU8Lp+G1HjB8epyy/37Z7zzzh0QkFclSSouVluWswk+JrbdCClR13MSGWcXIzEY3rtzh8uNY9tlVGMCldgmTQjwHx6MNMEQE6RGkMjZjjBay0kJIWS408Cde1s+etDwxs0ZPPLKvNQonJ4egng83Bdx2P7n0R9eWn4hMRfpM868tPGj8nS0xicT/Alj54v7fJwQ75MTL9JuX5xsLy80ZZ3TrDpQAh9geXXJ7HDK5UcX9M1IP3rqQhF6B94zWZS0q4EY7SO6TwghohUkZ5kdTfAXluAF87pAGEm7dbihZ/2gZ8gkajLnxtvXuLi9Yn3eEnxAJEFzeoGLGQdHBUJJVl1PSlBKg+o9XZ8YLwP1vMZai3URLSR226JzsaMNLHNMZp4Z6zOr7AULL8sMVZkTY6QoNSnkFFWGXW9RBNp2S8Iwm2qMNjTdSLcJlFYjRw1+R6MahoguNWZSE889w9hjTEWeSdbrlhgUk0lONssIOnDRBFL0lHmJDZGowOR6x0QTEqHvGUYDQVNkEmVy8kpCD7UQDD5QKEEKnvZsS2ktMlMs9iaM+YRwr6WzliQESYBMCRMhSoWPEZE8mc7Ik2AYHGFwpF4ggsB2I2OCvTpnfjhnPNsytgP5tGT/aE5ZV5hc0/WaoigIJRi/o7T1/YDWCts7JlVBUeSM1pOcQyu1ixERAteOhBiopyVJS4x5RC383IvhmYeWBHmWURYFfT9QVSV95qmmFat7F9TTiqLMGfoRJSU6N5gUMJkhWk9mDN4H8jJntJboAqrM2T9akuU57//VRyilqKqCEAIpRAiRPDdY50ghkRR4H6C3BBsQUtKOFsqcQhkybajqknE74LcDSmnq2QRTlbvEhkKQ5RkyKcbkKUzG0DtEkhRZzsGVPV79wi0gIYFiMfl4I5JaffJSfWx5e2RByPMcow2ZyaiqCj+ZkBZzVn6gDonmUpJJQRk0wgsyLxmkZIIhAYPQVDJn9J5JlLRCUDqBUjtkWJYEOkRyJ+hySeUFTkKB3NFOBkEZJK0IlCFiEqTALrljiJgx0ueKYgyMOeRht0nqBNnQIw8qSqHox5FSaBIJHaGI0I2BfNuCmKF8wpPQIWFcxGSSovcMeURsPGhBngQaSTc4ssuBkHlUtoOB6iAwG0e2p6l8JNgIfcArgXEeHUBlimz0j7xMgoggcwEEeBsobCBKiRwDXkvM6FFSM/pIPgasimQSjFFUCNLgcEZTuEAUEeMCXR7JYyKFRB4SxnoEicwFhkxTJXAhkI0O7TxKBPKw+y7vHDFz5DEhrYOYyEOgDZFaqF2gvNh5pbTzlOPAUGRUIeFt2BlNSCgnKKSiTYrcSmwuyFu7oxBWOWUb6LSgahOUOSpGxsFibEAbjZnl1GIX95YNEYGgLErEWNK0LWW722pjJhFBkQ8eYkAKKAuFbCOFEow8eiflNU1vWVQGgQbrkSKgRcTkCmUysuQYCRgtUTYykYLZsmYbInkMtBFSiCRpyJKguVghkiYFt4sfk5aqLDm4uY/PNLHdMJxfIolMjKIjUQVPijuKVog0Dy6QIqDMSOMHmsOM+K1XkNkO2lTkxY4e3eS44CmLkpQSWhtyk9N2DWVRYiOIEoL3KCRKKdquIdcFUedIM8WFkcKU3LzxOg/a25RyQhQeIyVORYwymKykNT0ySpzz1PsVAIUx2FZitKYqM6L3xM4yPrhk9eCCvCwRRU45K7i4WDExGU6AJuDjzhBUG7lbG0TamMhkROcalQQ6eRCJUia2JIz3xDZQmwwdA0JFSgMSwZydccENntI8YrL0kS54lrXhshtAQXQ9RZVhgkUnqA10UqByQ0qRusrIRcBKzVwHgh2RvSUrDNJKCiUhRsazLUF0TFKOmu3iNYo8+0yBUzwla+2MNs8lk3sS5vTkF/AZYt+LLv44A/YL5JNPu8envn786dkGj/eDZwXMT6TzxE7mkWInNwkB0mhMkbNte+pJQTd4qrjzcBgjMSbj4jTS3zlltQbyGhE8usgwStEHgdGRvh3JpMClHeplsVyw7Ue02NHuV5lmDAnb9riuA+ZP3Gd6Tln4dFDUkzWegLLBixWOp2s80To9ISE/gln9AjSTXwAV7RPlMynNPr2Ij/+L587z8fnHNXYWy8ennmKm/bT7ejRp7/7oLr/3D/4Vf/w7f8711/ZJMe1gABJe+8Ix+WLK5rShSA1diFglcSIxrSEJRUyK11/LGJTD5R45ERxf08TMsBkd1/dgbzZD9hETAjevQFUZykLzypVEjIHt+Ra7bvnO33uLvVePKOcVh0tPkQkIgfZiw6Fo0F0iGyTX9wT1ZMf40/eWq/uW4uqEUCTm1S6YqLvjsKeBL3zxlU+G/LLyxG8yxcjXv/42t167zptvvsLXvvkmx7dqiquJyTXF5/YCRfDIsSOOW5Z1QZRTLjvB4SxnPWRsbM38eMkXvn2LkDx92/PGlUgWIBsDFYHrBxIlBW60XC22iDFifGKWK64tQClJrjVvFgPaJFQmqAt4ZR5wwRO959WiZVg1uHZEeM/ri92KyJTmtf0Z43nH5v6G9UenfOuXXyGvZsSgud47cidQvcR4xes+YbWmM4ZrjzbjEDwhBt7U/z/m/rPZluy888R+y6Xd9rjry1ehgIIHCBK07TjdodbMxMy8kBSKUIRC30CfQN9GmpGmzUwPm2x6gr7ZJNgAUSjYMtceu03aZfUiT1XdKhQcyZ7uFXHv2Wfn3nn2Xpm58jF/Y+nkiDWWXCZ2509Q88Ttz9/lV//bf8jNV2+SzRXPPXuP1175GC899zzP3nmGX/7Vn4dMsbi1oqprYu8QKaJzw41bJ+8B+mZlwTzPCONIGEfurpf0lw3N6Zbd/Qs6t+c3/+B3+Mqf/TFPnpzyh3/4p/zGr/82r3/jDb771vf4jT/4TX7vT/+A23dPiMojssDy5oyXXn2erMjICsOt4zVjN5AZjVSSRVkSfCSFyL17d/AxQkpIIbl39xYxJvabjpdefQFSIsQ48UzmM1JKyExzcHKIyTNkZhBScLhcUc5qTJlzMKsptEakxGgdM1WQFTOEVyx3goN6zbJYMyuXfP7zn0VlGabIef72M8heE7oMXaz4mU9+lrt37/DJL77Gz/7qz/PsK89NF7eST62JT1/wP5hE3zm5TT0vUWUkMPAr9T1eLg94rT7hV25/klfUjCPlmGnHP2oOkblFZ5Yb0vCSOQAhGUbLl5pjrJKolDgRBS/vC4ScoBM/291gcfwcR7df5cbyOT4ln2F182PURy/wi/Y2xeERq5u3WS/XfHwrJ0f5mPjkWy0qJERI5C7y6js7lNbImHjt+1uUDzA6dIp86nQk2UCygVffsugxR9kaYXM++VaHyDVKCj52OlK5hEoCmeBz39ojk0IHxbPfaZj3AuU0ImV84Q2NGhaYdIO7pxXLToCLqFXN5964QlUGbQS3LzpmjSNJicgNX/zOFh8lMUhuXTiOryxiCAQEn/v3j0hIpBccXo4cPN6BEaDhC984J1mJspLF1nNrMxKdx8XA575zTiKiU6DsBp55skPEAErwie8/mZb3BFVvefbRFcSAUJNMrQgGGQxZH3n2mw8QSkFIfPr+Fm0DOkpME3jlexZhM0Qo+PjbDfp6jlRMfPatDZmQZAi+8KgmdwIRFJku+fL9E2TQmE7w8YcnZMEQtUYIwZcf3YJCIOYZH2tvsowl0npS8Pzi6QukmCFsxovdMQttKFcevfT8cg3yxS3mkzuee8lyXAeyRSAVjpdvRdq8YChrbp8suTkvmJVLtKn54j0JQSCjZCECK+XoW0fTBj618gQ/bVtKwQtGMttr1FXi84uReYwsR8s6SxzUlj44huB4+fk565M7FEe30TJj3rfsHnX0AyztBrfvYDegfOR2ESjyjKoqOTCWEBJN7zg93fDwL7/Oo69+DyEFr7z4KoIpoM7znM+++hlS7xAu8smXXiNXBhFARfjMJz5LsIHoI8/ffI5CFQgvGC8HfubeL79XFHyl+jRpUHTO4lTiZ/Jfpn/T0H5L89z6VZbFGhkkEsXLB6+wvcjZbWru3LjL4fFNAiVXj3vuXbVcPR7xqWIeBEcyZ3ce2J46fvWzt/FIQHAoLLfyhBCSiOC5eIoPoJTi7mHO4aIlHY6EleXV8oz+7tvkP3PKrZdaXpk5QtURZwM/V0OsJWEmqGeJF+cD3LTYw4FXZpfossfMGmK65KVlizQNOu/5WLXBiIEkOoQa+fytDI0mz0teO1RkOiMFDRZeqBIWQx8kr907BJGj9Rxpal5erbAiZ/ukp7Lw7e++xb/59d/nj//0q4zW/kA48MPCp/dg6E8FWD+K75pS/Mjc4KPe8q69wNOf4Jvfeod/8W/+iF/7zX/POw8v+I3f/Tr/47/6c/78r77HG99+zP/0r/+S/+Xf/jXv3L/k3/3+6/y//+V/4E/+4vu88d0n/E//5i/5F7/2Vd66f8Fvf+Vv+B//1Z/wx3/+Lb7z/cf8z//bn/Mvf/0veOv+Ob/zR9/k//Ov/5y//Po7nNy5wy4u2MUFn/v8J0l6hZOHJLngsx97kV2T04c5n7h7i/bByH6bsdsJXp0p9l0EVfD8ykAAN0hi1HxiDUKVCFXw3EKSy4QxOUVZ8lI10tkp4Tfe8ui73+HX/9ff44//4C/o+/GD3In35kxcJ0pTF/sDm8V7/Yv/4sbfixTte+MD2mHvNXqut737F9/976f7sz+uy/Mu6ecH3sT7F8PV+Y7f/Jd/xsO3zyjrnOQ0mc45f+cK4RzV4SFXD7dc3j9lBKKU+GSoMihQZGXF8saSzWbHxXaLx1CIgAwFSmaM3UCeSZbzgqvzkSoPhJgmmAlgjMZZSz8IqlKg84x8MSNblMR+YLjcsmsSuXJIaUhCEiOQPMZImg7KPNJkgfnJAhcSbnNFMXZ0Fk5uzPkH/5ef5Rf++Sd4b1l4OiD7wO/XcxPj+4HadZb+5PElv/c7f8GDB2dURc72jYHdk4HLqw4lE/XiiM4rRtuTlSWLZYWVGUfHJeGyZb8bIThCM5ILQTcKqjyCNlgHkkAwiiATnRXUJTit8EGSqUQsAjJzNEKxyhXjRcIFQwoBKSKlhq0VzLNIJ8ELickUZWwoxjM65zk6XqGf/wybK09/1dI1Z4h6oNGaBYndSjHmAgvMfOAgwE7CAZIhJUQCK+BIO26Znr5vOTo5xKqRYl0x2pHbN27zq7/0j1jUc1KCf/e//AHf/847dNuW7tEV2/sXjMNIPa8YBjcpNznParlASMH55RWlyagPFiTJ1EnJEuvXVpR35tRVjWsDJhm2uz2rwwUxCzR9Q1kUpCjIlOFqc8XB/IDxnZH9+Z6Lt07pL/cUeUa4PvdNnjGOlhgTxIjJMsZhpKrLKfAlYQfLybMn6CR46zv3p8oOE65/HCyRiWuz2zYUeYaUU+Ki6pz5wZzUDjx8+wlllrG6d0SxLNk9vmK+nJFrxePHFxgE+VGBN7Db7smSwaiCdrS89JkX+dQXXuVLv/RZhBRIeV37eA/29KH299Ot8aeu/0cXj/jKX/8+j84fUuqC5288zz/+8j8jSbiw5/y7t36dty6+R2ENTwYILmNTeFZdRjdOjtxLXQICEwWX9ByGgpFEJxwGzergHifLO+xywXJnsUYxZBIGhxIWEx2bMrHuBF7XuCTRRkE7UvSBy0XOQWuxShKqjDA6TJwkSq9WBaudJZYF1gW8FBQukPnA5cxwsPe4yhC0JGhJ3jmykLisFOudxRaKKBJWCorRk0XJZa1ZNharp2rsUChqP6B1w1VhOVqscW0JNsMqqPYOOcJunrOwkSFEZICmNCzbASEju1qxmtW4ixblYV9o5r0lykg3M5Q2kjDoLrIrFPPBEZggYXlISJVQ1rKfZ6zaQBoz+mzahhCY0bOZF6x7h0+RMdOYmCAmigCb0rBoBoKW+OMFYtshk0d5y+54wVGMbPePGfPpBlHEiirVbDPNct8zmojN5LRGjw9I8T5PFpaVLRGpByYCejnLqbXn1Ow43Bo65SDT+HVJ1ULm4IwN6zgnLpa485ZwUlG2ltRcMTyjWG4ztvdLojigU5H6UU74C8OV1Sxqzf4qIaKi6QJLA9EGepExrxXN+Z7lakbvJHnsGJ2lC4qT4xl+CAz7hjZqFsKy9OC8BDxZplEGmiZSZYGkBdaliac0nzMvMrZtpFCOKGC3G3F2JDGixEggY5kLhuCJQiIE+BjIRMILQ6YjJ7PIl167yS/9P/97Xn/rW3z1G3/F2fkZB+sDbNuzP71E5FNHo6wqTh8/YbVc47wjiSkYzbIcjWLTbMmDxH/iHHUjYsOIVAVXXcuZfcKLixfQfzPHvpN4cnXG8y++xHyx4PLykrqoePQQVLWid575fEEUFadnDfHxOZsrj8lygjLIvkcVOU2QLIxAVhW+t1wMgSoF6uUBT/aeuYZudByuZjzajNxYStJypBGJEhDPn7N4bqArPMt9SXt/xW6QZEIghKZIkvMYWXtPNIomBMRgKTpQe8+FjyxSxEeJMDneOmIS6DGxTYqDSpFixeAlWZkx7lsKI9gNkoMqMeJBicmDSQZqO3Jpp4KjTB0yOdp+ZFHBy5+7ReNGDg9WfObTH+Nnv/ipD8QBHxkr/MALng6xPrrrEGNEyPcD3qe3/qgYLqXE+fmWf/1v/4S3759SlTnWa4zJubxqOTpaYG2iaUaKfJIJL3LD2UXLjaMZg3O03UiWabSM1IXm7HLH8dGCYXCTepNSk6ldkfPkfM/J4ZzdPtH2HmU0GSBHz+OLjpWI7HrHvulZHK+IvUckw5BVFGGkcxEbEz4J8kxSJMXeaQpp6RNkWc7oIkVy5KVh2yZWJrEJkxhMNwSeuwUfO+4I0XN4vOJjr73IL/zyF39MpfyjDov44RP7d8w75rP/jFK0HxhPTcqPQTP9VCNd///+yfljnAY/1LJ797PsrhrGwbLbtPTdiIw5BsfoIvP1gtEGLs72dGOCzIAw2JAwYeqWJAePv39BlxyjUIxhCsx1TIyjIxMKbxO7q5EQBYNTFKVhtx3IMkNWZAzWk1D0o8N3Pf5sJK9yDm/NKI+PcWpARUuzH7BuUvZREkxeoAtJb1tGoD1r0VqjbUKHqSq63Qw8+d4ZP5hYXI+PXDPebXMKkBPIbLdvJ6m+fY/3gTSbUYYK0wasC7R2urn4FBiHRDIRLz3i8Z7UDOwbj4ieMl1/zyApZ9UkuStBShCVQWuB3TsCjr5ztCFRZhqUQxmJjdD2CSkM1iusTxwd1ph5QdY4YrIEO9K4gAqJaiaReU2REmK1ou0c+1EyOMGYoCwrfIjsCexDpEcRxFTJDCniIygBMQnGMFVl66Fl5zYEFdjvM8RKMuy2hOCxzrJvG1bzJcFHml3L5mKLtY5sUeJjQGhB105qKs4HILHvJ7ib94ERB+OIGx1RJJa3ZlxdbnDzhHWW2IKMmq7tJtJxHti1uwk3ntQ1FrtFOo3fe3abPVFAVJKmHxEiUc4q9vuWECMmN3jnJ9ncGNHOoFB0/cTDGAfLbtcxWks1K8nrgmbbEEQihsh+303fQzjqRQ6FQRaGsRu4fPsxw2CRUjA6x/3/+HCqvA8OXWbsLrYc3DzASRiDI0jIFzUiaoZdw5P7Zzz78j2UVu+fsB84Z59qGT9d1bmGSr3bBm/6Pf3Y0/QNPp9w2/KazLj3e1wW8QvoXWCbIqMStMIyifNqdirh6NFSoYSkTR7iiJCSvfTIFMkLxcbAYCSymAwH9xpEbRDBYWKi1yBzgUiJzkxy1EWV0StPl0lk0CQhGDIBWU5pHQOJPpOoeUYcHEOZkaQgpkivFUOmuCoTmElSNUqYR00fI52WiNqQSs2oIJJIQtDFRFcoiIaQKbyEoAWpbUDYiXw+NKjlmtBJogBsnDhBhSHhsdIgQmRUCl1qEIG+MJMHz6pC9J4xU9PKLAJdYXAqQNQoJabvLwSJSJNrxhARIqCMYSw0KmqEUHRZxpAmDocUgj7Ppscp0s4LpA3kEUYb6IocKRUpeboYkXVO7kEgaSWY2tCNivZapTuMGp/0JGkrCoLwNJkgpoRKnkEnWmkRImKEY8g8SQhG0dEqS59ZNnXEERkzhw8jngytEp32iDCAyunURIpPOuGLkX074ENOU2REPMPEXycWmn0z8RIIFckJmj6i/CSF3gyJSKR3CrexeJWRhYjQhhHFZRMYe0sKit4lSq0hz3AxMXTXXhptIArDEKDvelA5iYyr3ch+OzI6QW4i1awkiBxPYpZrvBf4KOhCJAqJD3KCOeWGclaybx0pekbr37s2d82WfbOn7VukFCQXacM4wSZDZBgHHJ52aHDjxAdLKTGrZ0il6PoO6pz9/oo060giUcwP8JUjqw2b4YK8FzAqjFCcPXzE/uyS3jvc3LLvC4JrcT4QUsbQjjx664JFpvF5SWsjY2cptUTZicsQkyCMIzFB6yEYQ7uz7L0CpfFKcz5AMCUXtqVE03qHFVAtJH0Z6IuE6GDUU4FKxEgePHufuAiRPkWM95ynCdK1jlAJBXqSqLUpMYwOBCgPuTSTOmQfSW7EqgoVI3NTsB1HugDSS3RhpnhCCELwtNbTJ4nwkUIkfAhgNKPveev1t8hOZmit2G2bD3IkPpw4iB/45SPiuCnGeNeT4r3ITIoPQpA+Kib8wHh/x5tdQ9+PbLctXTcSUo7Snt2+RyBJSbDZjWgtJ/UrHzh/smX/4AxTZQxKIlJCtC25hj5GQm+RhWF77VxvokApw35wdKd7tleWNiryYrq2UoLWwS55khQ4aRgvO3KV4UIgiIQLgsElWib1vuglg0uELJviJSRdzzWgLtJ3kb1lKjDmEpCMQuCGhsurhrHbo7Rkv2t/6Cz9sPFubPy/pzneTzr+HpKLp0/C9APPvjc+HCQ89Uh8xOOPGk9P4I+0Mn/6o7x74ic4uX3AbFGxOlhQlhnzxZzv/tmbDEOkwGOHwOyohDRSaEnKDa1NmGipBIy2Q8SIwRKERCbN8bqgEBnb7dRYVWLCp0dpMMJxeFCCVKQUqMvA2HtGF6hzyHNDO4KzA+PFQCoMyJyjZxfcFkveefOcthtZ5wLHQJlXzA5nXHRX9CmQfKQqQA8RHxJFJjhcGoiRJMWEj3xvPn7wYgdAfqijkQS3bh+xXM4IdyJlmaNvzmj3I2Y20L6146JpyPLEemlw0eN8j1AZjJZSBIJM6AwOa0nTGtoxIlJHGgRuBKXAAE4YhJMURUSWAeUUuYlkGYwyEVwkUw4ZPZiCQgVy25K2HcklqkxQlwIFpOAoUqIyhk5l3LyzwpsZcXsJtaS1k8umMDnKBZTz1IPAC6glKBJNTGRCsFSSvVK4GCisIQuCfW5IfeCZV5+hsZOXxLyesajm3H/wkFldcfveDa62G/px4HCxogiJb3/texRZRlUU7FNHCBM3Jc8yYgxkWjNThi7XCGWQ41QtuHHrNkVRoKOZ1FuGgVU9IwhPP+w5vHnIcr6gb0dUUhwdHBBlRCWFnQ1sbMAYzf5qR2YM63sr9tsGQSJbzGl3PYN3FFVBrhUiTtCnW7dPOAun9M6S5xkmSpSS6ConE5qIYJCK49uH3Hr1HpuzLWPT0zy5ohCS8mTNyb0bbK+2hM5OLuEJZusFPiXGpmdeKOrasHpmzeF6TbKC7rKl0pp5kX9onXiqbf5Dy14fvPZvHt5iVsxYqDWzsubO8R2uLja0fc/BwSErsySUd8nrnBvLiodXGy42p9SDwrsCKSPzqKmdwlc5bb5gMVoIUFcVmUscbAMFHuUCq+04QW1qjQyJmfU4AmqmWO1HsqTZLDWqd8xahxMCGSIHjcMwSZKKmFj0Hi8iAjhsHMrCZoQoBCsb8GLitaz6gGk9+9pMMrVREJwjFZpl7ylaz7aQOC052lqcFAihWI6JrB1pCsMoEwdbsCIiQ8YKwYGEqy7Qh8DhpicGDVEw60fyztMsCzoRONgPJJVQCIqhY71YsG0G9rlmvR+JcSKYlzYy3w+0dYEMgoNNN/keLEqqkKi7nn6m2QPrxqM6haoCmY/Mh8iYZUgGDvcdWgqMVsh2ZNaNeKUQUrLserQPXIWIARZtz6gnBcBDVbHYjFzG6TZ32LaTo/28ZNUM4AfyeUZEsOhrzjEIvWTtBXM/cFWMeCOpRkV9UHDuPes0p+wVl6ZlVJF1X6FlJFWBg1CjLyRbnxBHNYeupN90hKSZbRMnTc5+oemSZ70yxOWcZHeUI1QpcjVMgeVh5vHWE4OkTI71zNNaR2ctM22vscwZYr/nsBC0CJSXPHN3ycl6wf23t5SZRdkWqXOy9ZJaOc7Pe4aQUEqQJYeUBZ2TZKnlaK3ZKIda5My053KTKITBj3tO7hyw2Yy0neN4YVA6sd2NROkptGd3esW46bh38x4PHj3AGMO8niMCXKgMP/qJ0F1o5OaSmanJ5hlXm0tsP7JUFUGCV5b14pDlUtBmF0QdOCzusHV7LjCsxJKqPsDdGqmDJLdLkpeEpmU5W1EEw1aUOAQ3juY8+to5crQs65xjI3gSoQVWWUIEj5Q5BYFZHrB6xuOrjpV0hBAQsmSuoNCOAYgJKj8wi5AdSfQYuL3R+CPDVRw5CkAnkFFASGQhcDk4hJi4gQRPreSk4EZESEUUgson5ipxZQRJCoo48d9mRU4RHUYqmmQRITFPgarKKFTJUQ1pbOiMQijJUpbYAXZjYikjRQzYzKCKnHqA1UzRDolFPePenRs/sG5+IA57L2F4+kXiI+OzD0ugiutG8tMJxweW6qeAMu++9eJiz67pOFgvWC5mLNaH1IVhtai5ahKuS6SzLbnJME6i7CSbfXnV0W16bhxVpN5i5nOS86jB0Y0WmzL8sGF9e40o5uzeOUMMLXqxRntJISyrWcH9JqAj1DIi8hx6QRkieSlplAQXqJLDyoydc5zMFF0/oiIkIahFj8gMXkdUcGSZ5HxnwRieOappmgYhMsqUyNTA1it0grIoOVh63jm/IJOamyeH/Pgo+KPH3+5d/2nH37MU7U8/fpoG0PsT+OG0Qrx/Vj+94w/lHsYYNAasxAvQB4Z9n9gNkdF3IALbUZBVGaUKkGUIJsnYI604v3QE75lphXUFA5IqKCod2bpEEHDnhSWXjePqtEHlsNk/QZVzlJLUy0Q0JbudBz8gRMIOk6laVUZ20dIOnv7NHc9+7BB9u0ZtwMce2Qm22z1lOePWes63H+wRUpBriY0RiSLYiIrxB4sSP2X3aLGY8U9+9Uu8/fYTqrpgDHv++M//kroeufHyjPKPep5c7glRcOug4sFWENxANZNo52EURAejauhShteKVAog4L0kyESlAkMvCFaQRGKxlNggGEfLzeOMSw02WfxouTEreNJKpBSsKstWK+QQsdERNwNlfYSpMgrRcTVm7FyCN0e+8LmCbZnjB8diVXFmIpurgSIljmaCyzgZxh0p2GcglMSFgMoT1lyTvuY13fGSoYAdCi1KfLtjeLxhyFb87u/+AW3bkmWG5eGKtHRIG6hu5twQz/Pkas/Yjpi8QFqLURmL+Qzbj8QY8dai5odIClxILLOal1dHvPKp16jqCu8Dv/9HX0FUgiQCso2UswXJClbVAdtH7xC6hJxr8rmhbx9McrM3j2h2DSrPiDYgIgz9gASOTg7ZNwPSaKSQCCbCd72asby55p1Hj0ilJBYCkSkCihQTy9mMLCsY+nEikj/ecPrWI7pdQ6UNpq4wq5qh6WifbIkRoo9IqTl96wnbXUuuNfWqYne1Y5YJbt045jOf/wTj2QT7+uyXP/nBk/GjKmsfHu923q7FHIzMERcV8TzDNoqLouM7f/UHOOc4OFjxC7/8SzyJjylVQQiR3/J/iFEFB1GxD8f0+ZSwPeuOebysUQZuzUH4gVBadEg8Ny54KAUpCUSAGsmV0SQ8q23k7LAmRVBBU4SEi4GgBWVn6QtNiooYI6VNXCxzREpUvWdba/DgAqz6yOUsQ8TErLNclUCIJCVZNiO7WU5MkfysZVNmRAPBw9LDps4RMWH6gbicChwxN6y2DbtSg1LkwaGym7RSQZDMHjkuDktwCWMlPiZigjEJjnvHdmagUGQhQZwqcyEpsu+fEu6ukSlShAho9lERY2LejmxnE09FpICxILXGp8iyj3RzAQGk85joiJnEqcR809OVBUpIdBIUNuI9GG2Ydw2XhzlCghSS0g5sVEVSktmlp89yUhTEKCgHiCuDSJHSRtpKXkOYJeshsV1M0L7D/Aa9KxiMp0Kx8A84kw+JJPJek7o9LATRJ9Y24yrfQC5ZDoZeDIho8cZzYubsjhRyGZkVNc2jBePQ0MuMW/WcC70hEZiVgr4qSZUj1VB2jrOmJCbwzlHXJafNwHxecSA928tEUeXcPFmweXJFHAT1fMmdmef1Jz3Iqdi2cyOn44gjcm8mybM5NkJvR1QAP0JSgqOF4XRrSboEZUA5zEGBFOCbM7RSDKNndbjkxrM3OD19EyMNRYo8umiIURElZGoiT6cYeebOPUxmOLs442B1wJvf+z7nD56QXGRWztgNDd56bLQsy5pTN6LnOScv3uXi7Jzh4pRx17K+N2OXHjN2PaPv8EvJdr+nUAW3n5W8s33Edr/jbv0i4Xs3MEWi34wsZkecbkeiAOkSzdVANl+ybS23KwgoiAGNxGQLxqwi9B1ZGNlYSQo5JnqUjOx9omsHbt6wPDQCkwQL7Vh+cmQzE+QIDgfPQxOIOiFVQAbJ6GHnPLeAJgaCUgijyRFcikkgQbiBs1rQSYlIglkKdCojpcjMCMY2gQjIFMm6ERFzIokyhyHPsM2IDZFZ7LikQCYQ2QiSyWF9XlB6w9YlYozUqiAKQXOx5aLckRfVNZo0XicHH8bxf9Ty+y7a/8dEbD9K7ehDIyV4/Vvv8Id/+jrj6Fgsa9o4p0uW4BTH5oCLiyseP/IcLRb4KDnfjxTKsFplNDojlRWdzpmlyDCW+MFxszxhEOp6HY1kcsWlTQzJcbNccOlKdi5Rrwq0t8QU6MfIotTYbM3QjYgkmc96vApEF7mJ4GxX4HpJEiVHZWLTTvGDMZbRehyRGCJLYakWc9p+JHQ7SBrvIw5YS7DZbEpmZpr95hFKKk7fPmV7tv2QgtZPOsR/kdnFfwKfC340m/hHUN8/3KX7wTf+iNJleuplP+S9j96+YHfZsb3oKErDW2++SdQ5Xjr23uGv21U2JFzMWUgm6ccIzlnG1qOVwLmcaAMuKQYjuOwszZCYLWrOO82+aRmCoJKKi1YQmz1CCC7OBVprBgvzytCHEqkS3keeNB6rLEOAmZR87W/OyZYzhNL4xlAGyWg9bR9oZYHJoe8t28YjgiJ4QYiON/7yPl/6H0ayWQEivb8kvKdC8OF5/Ih5TbBaz1mt5yTg3/7+b9DFLZ3vUPKE+oVjSrdh2DW8cb8nNzU2CHYxoJwmK2vKWYYvJMuZZt94ylV2rTZkUWqSRywrgdtYgnI83liGkADJ2x1kK0UTBVlUPO4kg5+gaW/2El0E9mki2Le+pHAKrxW7URCEpAmS+HjgT3/7O+RlBQj0yTF5HsllQxYdp+Oe0SdEUpwKRwIGQGjJd3RiAmBKrtYF2dIwzDWisfzHb3+HmsmA7ntffR1zsKC1A4vVkrfPHoAWjOPIgwdPSHtFcbygPoT9gwustfgYUUpiB4t1jtnhikebkflygQuervMUy0M++fFPIITg13/vt+jcwCAcu75h2PSEUhEbwdf++htgE5urLTpp/M7TtB1RJNpmz3C5Q2rFaEdOT8/p+wGB4NvffossLxBG0/YDbQgEEuSav/nat+iDw2vogmX0cVL8qQypNoyN5eLBORshsNGTSETvQUhmpeHxW0/QQjAOFu88XQg8OL0gLzJCCESjOO93OBkQw4ATkcMXTvh//L/+7yilkFp+8Kx8qvP4dBPjB6/z9N6d8f5bD2k2HbvzjlAnvnr1Neww0nY9H3vtJbaP93zq5Qlz/G8f/gZjaPCyp3n2FpeNoBWGIki+UxQUsWLMFRtjsTHQG4Hyia/VijJpGgVqkbGRgl0uUMbwrbs1mVT0RrCNlkspaEuNUJLvp4SxkTZXKDI2maLLFaDwaurC7QuNDLCrNH0+KVg5ERFE9kZACmxvzxgkoDPuH09dyraYOiffXGb4TBMEpKMZUgq6zKAGzzdvLYgCnJY8OaxRItHXGaK1fH2pUXXBmGse20SKkn1hiMA3n8mBxJBrzg4rUohsC00NfOuZDCmgywwygDCaXZ1TtiPfeH6F9p620qhlgZQZTZGRm8S3nluhg6OrDBsfiXPJvjKYEPmOOSSLOV2m2YXIpRC08xLlAt+7d4QOgabMUAK2s4ymmDq2w40lOkWGMuPKWoabM7q5ghB5x2Rk3tDmGhEiF0XNUOUIKfhuGfBtxVhrdl3Hg6qnjyMoQbjpyI1jX3rEMPD1kz1OWnwheVi3YD2NDMhkeX3xGDu0pLFnHB1d2bPVAazlq/NHpNEz6gBjTYgt/dxAP/KdpsRbCCZn66HpBR2G1FouRUHCEaPm8Say6xRdMJSq4I2dw0bLEDXfebBHyJaNA41E2YrjItL0A7gBIXJUtaCoNFvviaLBekkymkdXnpGW4Dw5kiJO3iTF8RHf/vpjmn7yynnzyrJeLnCNJabE3mqCFNewQ8Gtk1vcOrlF0+x5cvqEpm2x7YBzDpVr2q5FloL7uydYHQndjrcfvD1BMv3Avttw2Z5is4bd5oon8oLQG+Iy0YuW18V/hHlgr3fsrENllu7KIkrFG2eXjN5gQ2B7v2U/Jq6cZa4F39iKifOmDbtksJ1kVAoTM77VTq7nzuRc+YEkIlYUSB15IyTyecRpw7YaaSpPOExUDv7meKQoBG2yXMiKbZV40iiCVHwnRlCKUWtOrUNJxT4ldErssgwRJgloGQNXQtJLgULBmFOowJAgecnG54wuIY3h7V6hO8veCYTyXGQFQ4DMaB70I2UO+5DQvQWpGElEnxBuYPOwZz8M2DHwZ7/7Vzz3f/tniHc5bU+treKp399DN4lrRc5rYZwfMGx7ag3+KB7G0+P99072AF/7xtt8/+1TtruO9cEhAwOPHnXEfcfrf3WKFpqt04hBkIykUTmd87Q7gZAGWxVcBs/eKfwI0QnOR0FlNFsLQQW6hz1tBO8zeiEIDvZRI/YRNyQ6JxFS02wdmbVsR4mTkm0bUMvJOPXNbUHwiiZoznaOU5nTuEBICSk1yMhmb5kZRTNkpBgZnOSddipqdx7qOufN0YAXhCg4P7sAE2nGAR8Cb771kJ9rB/JZwUfGuj80dp5m/Yca6v1tx9+R0vD3l1x82IjlJ8mkfshkfcBO/r3H0wn+/smbPriPn2CYTE96/Jkiyw1paNFCkylJrgxeRHIUhRYEC0Q3/dXgSBEyI5EkvIu46PBB0PUjISlm85LlyYy+bXDjgNEGo0CVk+RnTNMikBuD9R4h4nX1eqrIl/McVRWc7xwqWYyR+H5AKIkmogCtJPU8J5Q5wkwk5tiNaCmndrcEnSmeTn8FaVLEkpJ3zWM+WAn+wcTi6UxNICap1ixntCOZMai6YHlzxXyWEd5pGO2Azmq0jDhrESLD6IxExG52tFcWsZsSh7YPZGbCPVZVTpZrVqsc1Q3YTUemBLYfiApAsp6XuFaSbLjm9SY0CZUgzwSh0LhhIDoL0qOzCVaiNIxNi/SJYlbS3N+wiR2hnrG8MSM3Jfuuo921EBIKUGlyB56C3El208REhcQmyJMkNQPJKPJ5TVEJXDfSb3aUXqJu1GRVRgyBLDOQabIiY7VekCs5Yej7AWc9RXUtNyum4yqVJK9yQrAc3z16r2dszAShMpmhXNQUZc2uaSZYFQmTG4bRkuc5Pjhib8kPV6TC4AtD343URUG3b0khTt4dUlGWBaN31POK/cUWqcQUBLQtixsLgo3kwhAVHB4cTCRwZUhy4hcZKcnqafnoQ2BxsqS/6jCZIUNMiUSajpdATHLLiEmmN0TqRUVZThAoJRUm0wjxtMnTh85L8cGfH06P33sypalDaRRaa/Iix6dAsI7mYkdzscMY/d47jTTkMqcXPYXOmB2tqLZ7MhfRPlLERC88ajeRXLMCjJhs4hg9olSYkIgCTBRo61E+UhjFPkHuE1ZB5gMqRISUZM6hCkXuIlYKNB5xDZXKfEJlksJHrBHkfupEqpgwgIyJovdYJLmc4BoqRkwQaCCzAa8CMqZJ6SoEMi9QuSZ3AdLEnUmZRicw3iOjIfMR8MizHfqwxjDxkGRMZNZj1bT/oBVq9Ait0D6R+YhPYELEKYn2fvqOIZK7gPcBEwO9zKeOR4hoE8lcIMqIdgGZKTIX8DFhlCQfHCpEsuAnSJ7zYDTZ6NEhIEMg94Heh+mzCciMQks5yS73FlUYis7i1GRMJ8NUZjE+ohIU3oOC5AMoifSOfPTIQpIFidKKQhYE79DKkLuAUoZ8kIRcoJRmHAIER5YUcp6Rt4oULZnXxKCQly2ZE2gJmcggK1BG4lyLFgKFQMVpDhMRpQTNOGJ0AJcockMmHNE6tIJt319j/XPGbcTu91jnqCqNHaY1z+SaRZVD3yJcxA4dKWoyzWQAi0GJQN9O5HctNIWC3k3S5kWuyDNF2geUUrjLHX3bkYiEYClzxWxVsWlGNIkUA7UUKKOfukYF2mRIIciLAiUVWivyomDf7inqkqQS3jlESCilyMqMvCrRpkQWFSpL+HyCbvmyZJANeSxIKqGVohosOkYykxF9mPD0SmKqkqYdSXKE4NEYZkayt5FkJC4ltIQgE8FaMuHRCDIRGWNC4pFa0NqBqCKVUSgiHijQZFIzekchNERHHgSZVNRa48octR1J1k1dSSUZY0SFiFaaLCWkD5MsdZyCdOkdUUi0EUggxICMAQlokQhq4gRKEcB6ikzRKM18keNVwjcDwVtUodE4dKap6oxh6NHOE7WmqAtmShCMZKY0T776PeL/2aFyw/tiGT8Ysn0wzvrxgdZHv+KHV5OFgDzXlEVG143kuWbcOrrTDYvSoFcVyUYyJhgbYlLZK7QgkxNnMQTIRUQVhnFnUSkiU8T1HagCkwHRIyb6CTFEVIqIKMgEuBjRCdI1n0inyB6JTh4fAzKk665gIFOTHHmKjqwsMW4SaQljoComyeODWnDVdAil0XFCnecapEwoEdEkYvJYn0g+kdWasirIjSF4jw+B/KMOxt9y9v9zjr9fKdp3h7jes3jq3/uZAQApJqIPk1rRu9vgOvb94Cn+QdTfdXb2U8389Nob9w5YHc7QWhNd4JUDTYlgFgI3S8UrRzVLH8l7z6tHEuMcKzwHpeaoitihn5Q2Zj1ZbtCZZLEq+ewv3Gb20orOdyzMDkOkkgkRHCcHkuJwxeFLt/lH/6fPc+tT9zh8+YRbn77Hl//rl6kOc6QJLOUO+h7jLKVMfPYgMMdRjh23lhatRrJsxLVbDtIZ3dkpvrnioPaUhZwuIiIvffYuf/L77/Db//PrvPWtc17/6kN++1/9DX/2O9/m7NGOP/y1b/Nb/79v8P3XT3njrx/yW//i6/zJb36b88cb/vD3/prf+vU/53vfefCBGf/Mxz/JM7fu8vKzL/Kpz7zE5770Mq98+jaf+pWP8c//+1dZHIxE+ZAi33B42OOyU/bDfeY8ZuhHskxycFJxcksja0NQgsw/5PLJOeN+j726Yib2VFJSSMkXbuSsZcWsU8yj5NUDSWk0Wkk+9/yCypRkTpM7+MSRJMslUsNzC08WJ536zMPdE8neWa76nheODPQev7Vcff+cZ4KnHEsO8iNeWx+SjxLTaLJe8/lokH66KbxwmcifBOL3PfE08YI64bKZM4ibPPfpL7BeHmKsRDrFc03J8KBH7DV3b9zk8M6S7DAhZp5f/m9/nqNXT8iPS9bHc45O1uSLkpgSN9YZyYwk3WHKQHEDfu/Pfo8//qs/5e6tu/RNwdAtmNc3eebZe8hMkHTiF3/pS9y7d5tnn7/Lq594kY998XnqlwrEeuTuvSOKeU15sCAJweHxCjkzZPOMF1+4Q8wjohYcv3DE7XvHUAlSDq88cwfbD9Tziht3j/j5n/s8qvGwGfnEq8/RtR0xTgv9c89M5n5FVfLxT7xIUeYoo8jrgqMbB+THBXqdcfPOmuxIIu9E7GzkaDEj5CN92nP7hRs82Tzhd/709/n3X/8PWP+DMokfGNdmTonEG9//Nr/1R7/Ln/zln3Habvnti7f5X8++S39UUi9rTK3BwC/80pdQFo5mS24eH/PMM3feW0c+t/o0z9b3+NjiZT5bPc9Ls7sUlBiR87NnEukTmY0sm8DzjzzG56hR88nXN2gGtOipxp4XzkbUGJBB8NnvNTAmsiApLbzysEVHgRwin340oNSEGzb9yMtv71HWIq3jtbd35C5hbML4yGtvb5A+IGLklXf2ZK0lRyGF4rX7LQiFdImX3t5RDpNilJaSz765QYSICZHnH+yoBoe+DsA+/a2zqWARE89cjcz3HmWnhPwz372cZmXbc9dGjnYDRkbQgi988xTipKZyct6yuuymG2+Az33zDCEFJsHRduDmZkT1nhjgc6+fIZFkY+TIJW6c75ExkELgU2+cIpPEBEk9Jm7f36IHj4jw2rceklKE4Cl94LlHlygfkCHyqe89QoaAdIFydDz/+ArhEtFFPv3gavISCQnTe159a4uOU+Hg1e+ckrlpm3KJT9zfoIhIZ/nYO1tKLym9piDnS91tCg7I0gGffPuQyhuypFBC8cXv3UJgUF7zytUJ9U6SYTBVxecfPANOomLBc49yjlhQJkmmFV++f4jMJUYKnl+VnCwl+bMD4s7Izy578rkmryMH5cBhnQhjj4iBL92dDD2VgKW0LGNDVmiSgH/y2SXL4yVVqVgpx2vPLagyg0qC5xcNvUo0KpK0RaYtD7db7l9sOKq2dIXkKk+kSvHy7YKZmnxa7q0ixij8aOn2O47nEaESKKjElouHj7C+I2JZ547caGSmCSHw1W/8Nb/1ld/m9e9+kzt376GUJMXErflNYh8QFlIfefnGi8ggUFHyyrMvUVYVWZlTLmZ8+WP/FWY+pz4+4tOrL5KNhjQGFPBF9yuI75xQPHiJZ5cfR48LvD5kYMYvfvkzuFiSRM0nP/0sx6WhKAxRKb50QyOVIcTIgpbjMpEZRQI+v9hNd7sYODaBV26VVOVkDPqaadF3LPqZhru14iUSpmhQ9cCXz09wFyvc2wcs9xUfVxUzIBOCV4aRcYwkD2WSHO87ghd4l3i56RAhYRBUQvFakWH05BPyqWVOqAX9LJHqyLOVw6DIouITa4vUcbomh5HnRENRlBRlxStHGaWWFBGKkPh0NbnZ4+GOzEiDYBwUvZU8f+OQ3/3Dv+Q3futPeef+kx8dl76r/HktG/tDq+LXcduH47LE+3nJ02Heu62RT7/2PAmB0pqb64LiaocfHWNn+cKJhgTRByrvuWsiRBBIvnzDYERGFjSlUjw3V6SU4Z3mxbJHqUnNsChzXjrIyMoF3ipeXkwFiyrPwDlePUgINCTFp04Ei1WFkZApw8eFIlzWiP2K57VDeItRCaETr9QdRkp0StzTLWU2FU36oeXTBxbvHVrCbdMh3J68gH5oeKG4oioKZnWBGcGz5nR8hp27TSFz/uArX+G3f//3eOudtz/iWPDRCcd7HYsf1rX44Mz/xInI37EB8vcgRdv8ZC98OoG9PmHGtiefV09JTvIRGdv7th4fOSkf9el/yHNXZzt+8//7H3j45jmh7ekf7pllOfsxUheSEKHtPUlON2nnLNvGkWlISaJURlEZpM6pD5b0TnJ0d87WDZw9uKTZNBTA0mj6ETLhKJ47wSxrhBBkuaYoFGenDcfHFaGL+D6wP9+ze3SGJGK9ZDlTxOiIKRISE5lRCJrGYQz4MNWDw3VFQ8jI6KAqJMcvPk++qBkHTz3PyArYXLSs1hVDP+l3961jtsiQBrYXHYt1iVV7ZO5p24Fbtw/5J//sixydrN6b+RATIQaMNgjAu8nN+A9/76t87c9e55037uP2HTFJkIqyyol9Db6mGRJ1JZHLGb2H2SzHnu0Rg6O1gjKbVKhckAiRSBLWxzM2+8hBJRjEVHnSUnBwc0kuE2+/vWGRRYLWdGky+LKd4+RgQUPGQnueXG3wAkxmSN4ilKCJiqNCYcdE30/Vm/W9ObL0PHi8pQwj/g7IIiK1Ih8Epcu4kpJFgrgZCT6yfvYmhxXM4iWPv/kmi7KAIiMmwdAPHL5wjDlQXO02LOYLfBsRQbHb7ClVRtg67n/vEdhAUpooFDYEju4suPflI9pxT1VW7K8K/FhxtWk4OZlRzPd0/Y6yLHn+7rP8ypd+kbMHp8yP5/zmV/4dDx4/QAtN3Bm239qz3XfkWuKGjr7vWRwsqJY17dWeMViOjw7J1zXDaCHB5ZunLA+WOJ04mM2w5x19M6AQVMdLHr7+Dl0zTET/3CCVolhW7M53mDyj7QYyo3C1IKmEIKJzyBegVhk5GV4ETJVRrisWqxVGaq52G1aLFZ946VV+5lNffH+xENeFhPeqa1Mn5MGTR/zBn/8Rj8+eMJ/N2D1/i3i0Zu8tR12kev0xu9NL5vMZLz73HP6NK6qjOZ/7x1+gXNXTSnzdWYkx4pNnFz3/8vLbfPvJA3ILWZqR24xtqVjuRmyc4Ey5TyAGsuTYrTPWG08MJXulJkM7IckCbBcFq6sem0GXCVSYug+5Ulx6y3pvGTPFqECGRJ4UJgk2Vca6GRmNxmsFUqAHSx4im0XBcjcS5iUuRqIUFDZQGM1loZjtRpwUBMArQWkDBsF2VbLYDtjcgIBRyinpCIHdImc5BJwGQqTPFHMhEINjV2fUrSUmgbCJpjTMO4tMgqtZxqz3yCwhQ5i2NRahc7ZKUfWWlIH2jqbOWdnIGKDLNVlvr7s4gd0sY+0j3jn6OsOEBKOgkAXb3LDatAStGDKDdlOlOU+Ry7pgsesImZnI3wKyGDB24KrOWew7XB3ozQRtNU5Ru5ztrGC573FFYlSJKKGIEtMHLmc5i2bE3m7oL59gtaBMe3KecHkjstxmBDGQlKCXnpmqKKXhrGg5DAu2l1ekkBB3VphHFtHBZWZZu5JYaoLzdHlgkQ7gsuQiOWZeM/yZJp2WdFmGGgYyUXC2saxrxTBGpI8M0XD7uKTZ9uytwISRvMooS8nZ1lIli5KGZhRge3QuWa4qthaKfo9Lkj5l5EYgdELnkl4VHGeBVTPQX7YE7xAqkfxIlBm37i45v9xxuW1BJDIZkDg6n8hV4qW14Z//08/z/P/1H/D6d9/gr77xVc4uzzlYrAndiBstzVVD6B2ZVDRdy9Gtm2ASza5FGcXieIUpDY8fPOT45gnNs0+I65FgIjpomv2Ovbjipr6J/w9HcFbSDSP1bM3VpceanHmZ0/uS7fcvGH3i5Nlj7FXPO08aVplgdAKkorGJo1lB38BgZqihoagriszwZDtS0iMLw95LMhyrn/PYg0u6QnJPK5hf0C8dc10z3F9hH9RsVeJWkAxFzYNHl9gYGfpAtIGxLJl5R0AwSImJaUIgZBlXCdYi4VOihwmdkDzKjVylyGGUcL+GTqOlJKtA+oErKznMYfCTup1zjvVcUaqBbRe5MTdc7TuCYCpeHVSYNPL4as/KKE7uFeQLQ8o0d+6c8N/8H36J+aL+YNh1jXxI13DTnx5q81Gl9x+ETf36b/8Vf/03b3G5aZnpjDe+ekYfFItM4UyByXOu2sBaRfSs5vSyo3XkxYEAAQAASURBVKw00glyqTndB9ZZpFiu6PtE5kY656hKzdZrZtqCNqiiZGh7QhjJgidUS2ZxYNcFBjd1GOracLDMeft8oEoD0hT4KBn9dM5nOtKrirl0jDYh1dRxWa0zFJaLEY5nhqvtpG4VpaIyCYGnERkLHXGjgigYPKxnExJg0yVKHHfvPqbS58xOFjz77D3+8S//Q9ar1VPH44eMmN4X5uHdZPDDx/LHH633UULvPzmf/5ciRfujxoe+oNSKYjl7rwr53pf6gYl4vzn34Z8/7dhetgzdyO6qo7/YoUcI40DvwTtBjNCNkZgiMYXrP6/QeUZRVwSpUbkhn9V4NN2m5f4bT7ho9+x9vHbC1Ow6zzBEskKghWZ/3gHTybuXsNsMxNGTS0O3GWmvOmznyQpDPwRIkcwkrI+4EJHBo6TCOsgCIDXWJXSmmS9L8tIgB89sXTF42D9uCD5OLqw6st8M+NEzdongwA6ObqYQErrOYQePL3aI3DOOluVqxuaq4ehk9d7hUHIywHt36EwBgu1mT2Md2fGcxY01tnVsNg29D5AMEkNMkavNQNhvoKzwaAgKIwTOB5SUJBQJSd+PZJXmah9p+zgZGBWSPkwErf775yglGPzkgzA4T+MSSgqyJDjfebzRqEVOkhnb3iJdYJYbxtEzSMFlH6mynN4nbO/o4gXmUJHqkrYJuGDxBLSQzMTk3rxP1xAUG7GtxZ83mFXChwZvJHtrcf2ALAz9vkOcCjJRsB8aYoy4fUR4xTCMRB1RWlMezdFCsrnosIMjKEFxMsGemnFHbwe2FzPCGGjaAWMc2bDHppZu6DlcHWAyze1nb/Pw9CGDtezaPclHcrsmP15QZooi0/heMzy27PYtlJr8qGbzsOFqu6GWkcF7vHWMwTEGiw2R884jW8/+qiGblWy/94i2HfDBo4PCth5d5ezeOSUBNgR66/BJI0oJGuaHC0wRKW9keBMoihIkjN7SuR7RKkQS7K+LFNvd7oMLRoIknu5WTt207X5L2zXsmh3OezbDEm9zxugx2wne1TYt3nu2hzvu3jlidjgnn5fvA4uvFxIpJEZkXNqGPnnamaFvBjIbyCtNbwSUihAkTW3ofMTgUSLS6oScZeA0e2OQMZH7CfLSGUm6voE0tUYmyPc9rbe0hUKESTGmzRUiJeqkUcowaMmWRBKKvjDElKhSpCfRGomYZSQt6IuClBLeBDqt6TJJCJGEoJfTGhkkSKlojSTNMpyZiNZBiKlgog1toUla4YgkOUGf6C2sS1ol8CRckogsYadKCwJJnxu8VlOgmgKDmW6cIkm6usBpSdKTVPaQa1J0iGVFEwMmU4gE2gf6MkNaDxk0dYZMicJorMjplETWBUJAX5eIkMico0uJLtOIWTl937qABMXYoUxOX2ZAwGcj+1IhYqQec1zIGUqDkuDESJdPvh/eS5ScZGrTImCDo11O0EgfRvbK0xmPNxaRLGMeSVqQoqANHTvbgYoMpaP3Fi001czgg2WfB5LsiUYRc7AqgfUE0bM3Ap8Clhw3RnrryK/lUfuoYZS4IJEJRht5cjnihkhjBbk2bC4HlE4MUeC1RPhAFzRS5ORItMynv2dq+t7SR8koFTBBBa0U9P0e6z3aCUxWMFvlICJeatrBMQawUU0uxilQ5hmZSMgUIElmL95EKMm22bLdTXK0xISwkW7XMDQ9ucqwztL0HeHhQ7JZQTf0k7cDHr0o6OzAVXvFmBo6v0FKRSFLWt0wioGrtCX5irANkGvsrmMgp21HXG/ZdZbdztKPjtGdkoShiwJhwQeJDYkgJBdtJMWctovkomDXRJRy9E4iq5roPX3UeKkY4yXFXEOt2YcBmXsaMzKoxCDmIAKdEJxlknHfcZoSMSVQCmEUXUwkJAkYlEYZSSHAAb24VjoUgiZN5OpaSkiSIcLOTj47IWbIBLWPwCSQ0hBxIZB0jhWK3FuSzrDa82QIRKnofCTFhNr3yDQyaMUuBMKDC3jsqG+sODxcst21zBf1B2OrdyGtQry3/v4wTP9TzM6nnv0gPv4DkrUpXXc0EhdXDWcXe5p2oI+OIUJQhkZKui5SZZpBSS6TJ5w37L2gE4lZUWFRjMIS84yrjWUImhQUWsE4TvvZ2YBwkb4dSHEKeHuhCH0g5RmdHxmShgiu84xMqlDBeqILyLwgEBEp4jE0YyJqiRsDLk3Ho1I53gackFhTMAqP9QKiBJ2IMdHFhLcRggJhGF1Aj4IooPMSMkHvLbbbMQjHyY1jtvvd+8nFjxry6XlP790jP3xEfvz4IVDkv+X431ct6kMZgfjQEz+KryKm9PmpbT95erHbNrT7nvXxjNmyYnVYI3YNh1VOPybGbU+MAe8TJIFWk6t2XlfIesatFw5RSnH2YIfvB1JzRbsbaXcDuRQUlQTp0FKS64SIARcdszLHhIFilSEQVIUiWxSAY73IkSPY8wHtB4qZ4vYrN3n09ha72yCJk0zprGS+0GiVcX4xsFplLE8WDFERkuT4VkkUcPa45eCoRAnF1ZOO7XlL2m0Zo0cEw9hP3IKh8XQ2ErcBaQT9AJntWT1jwJRkKSfTisPDBU/ubyjrnMW6ZLdt6ZqB45MVyqj3jsOduydsLve0bc98XhEiXF5dUuQ5lbpBt9M8+f4ZNIKzqwaZJRZzRbCWvMio65JZ7tlv9jRjpJxJpIn4NEzypyogMgdBYL1nXUiETGxiohKQxgFjcqJK1BKi74DEUsL6RkV4MBCJVFKwmGWcbR03ble4/UCdeapcMM8FZWV40PScrGsG4ejChN8+vIbhIBNrJGUmGQ8KRtWxqA9ZVRDXiXyQPP7LN1GrDF94xtOW0XaolWF9a015UNFses4fnuHOtxy/9AKgyLXi1nN32V51eAS3bq5R64F0qZjVJcezNdtTuPRg375EVlv0YcV6fcTN4xt0XU/T7FnOl8zqGavlikznVGGB7ySqgOODI6RMHN44IFgPWqBKhQ2Wu3dvg41cXFygipyujcxNRocjRyKEokmR5fECdzklxaO3aCFZrZZ0M4ffO7JGEQqNOZHUNuPwzhqeq8hmBSdFTagdj8YLVtmKUhquaLHRc6xWJAFukbHI5tw8vsGp3WKT41Z2QEiBM3fJXM9Y6DmXbsMYR46ODpnNZ9RqwdLMOZofcJGVNN5xdFCTiy1iVrJYLbhz+xZf+Nxn3odrfuSylLilaxYy40jkiIuGZd/hZxkyl6yuhvf4DfkYqIPHZREVJQejR7gM2Q/oEKm8JAqBCBkHrQWZyEOAEJk3DhsDxIxllzAisrt27J6lhIieOM9Ybwak0jQuAlB3jsQEXzpoHUI4mtITBSxbh1CStMhZdR6ZEp0AqwSrZpzAxgmWg0WNgb6YjPJW+5E4y0khsuodanR0pcbmhtVuIGQj1Dnz/WT81yhFV+Wstx1RCFIsmI+Byjn6UmHKjOW2hahQRmN2HZV12EzSVonFtochIktD3lrK0eO0RIY0zaG1qDQZBtYDjNlUsFleNWgh2QbIUqJsB7wUxLpg1VtMSGxSRLlINQ68q4Kz3FlCZsn8ROieuQFhAwrBshlIcSC/JtrPbCT2gbgoOJ6V2EvLRgm8FizHObFo2Mw8i1aQuYJdPuKzxLpRpOhJNyoOLiRartjEljQWLE4jQythFVgOitkwZzhQdMKxTiXWa4TsWUSNmRs2JnEVAgsTSUpz2UUWpUKNA1bl7FNkLhyikmipOF4XGCk5v2rQXvDCvRUSyZvv7ChMwrg94aohBUWhA/M6ZzM46ixiZMCmROscq8OS5XaHqQqqecHqZoX3lovTllx4dJzgf1MJKKCCoJCaXMBnfu4Vjr/0CgK4dXKLtw/uo7VhMZ/DELgUBiMN82pOd9HgtGOWVYioSBKckJSyZLk+JIyepVmSjGGsF3gcK7Oij0ue2EccyEPKo9u0g2aMkYPlkm7MeeedDTMCN+6suG8TV1tYTEB6xhSoSGQm0hnNmARL44leob3ieJUz7LeMSWOkZmU8TdchZjXGO46cIfoR6wInQw5ZjR4jM1MTxymY3KTATWW4dAN7ozEJhB0Yk4CQWDHxwDYpMc80epj02JUQrFNEpEQuBZJIHRND71BKU0tPoTzWODIERRgnTx0LKx0IRFrbUWaChQiorqOPioOlwYhJLWoYHDMDuc5g9BxnikWt2DYNM1Myn9UsFzUPHpyyXM6Yz6oPLY7vro7pqad+MPZKT/3/VKN5on+Kp8FQ7+NQhBA8e/eYx48vuMoEh6s1dWx48nhHGAfW8xkBh57lrEuD3Q/IXUD6gbUUaJkTs0RJR5Y8oClKTY4n5YpN31H4FmPUxKtSiaVWJJm48u0kDU6iOM4IPjIbBYEWO9fk25E8GPwysjheEN6BzbghW0oqp8iFoi26SfVOrEnLSFQtRXTcnsF5bIhGUg8KmyysBdk+UMoKdSQZUkCcthR1iRSGQnqWOsfbgkpX1GXN8dHhe/P5oYn+wed/1HivifTDE4+Pirn/ruPvnlz87VKkD3Qr3k1of9gu0ocePU3j+HHj+9+5z5//8ddxo2OxnAGSEBLWBUQNV+c9g/McrSqO7h5zdtZTzHJe/uxdHjzo2J237J80uN2Gx0867GiZzwI9HlkJZqWmKBIPdz0IqLVk4xwYiFJDs+PJE49UkhtHNW1bsD9vGE8jS7Vm+2REKMnHv/w8sayYBU39whFHq4oH93tQkuc/ccxmbxkeNdQHJbeeW/DGXz3B9o792UhzNXJ+PtA+HjlZSu5/e8c4epZ1JCbBfvDM5zlS77iwAiEkRa4wQeBd5OqyJ3U9nTcgFfk254+Lb9G2Fm0kR3dmnD65wPvA+nDOP/ynnyMvJnjFZ7/wMeaLimbfcev2IX/x+l+wFS3ogdu37/Ctv2wwtaW5PKfSGTYKUufIXIcuZwiTU8wLhnZHuxlZzirWC8+IwUWojWBDyygMUSXyWaQrc8beUeaKwzHnvMvQIbCqI6f7SDN0nF8MvPjckvlsxr7pmenAZjfCKBmuPLeeyemvJN56Mu1p257kEpeXDc/fLnnTTUaIpTb0OFCJKDXr2xveel4RtebJ6bdpDku6pWAxn/PaL/88f/wXf4JUksIZFhvNvm+4enzK7Zc/zdWDPXlWEmeSmAxJZQw+crw4oO8LYm9RYU7sC7rLntAaPvHMDbrLJxQbQf/A4VY5QxtQItHe9vzar/0aPgbm8zkiE6QEgcjN5w558+37EAfUseMf/Nwvc/rmE0xVUC8rfvO3fpf0wBPcyM27x+zcBt/0fPwzz/Jocwmbgep4RXazoq0sYq249fwdNn9+hUBi8hz9+ZKmdnifsWaJXyr0THDz6Jjbd5/lGxfvsCeyPlxz1V9y2SrGaLmTLbnvNgijWK3XdA42TSSakjcWO37n9PeJJE7MAp16tn5PrjJuZkc8Hs7wKbA2S/pPCIYtyMzz4sGK+5uevh3pH7aIt+9jy8i4MizW1bt3s/fXmPT0g+mXXCgyr0gu4XrL6jzxoPBEpZDWk1nPVSkYU+DepeOdmxVRGEQ7ULR7wkGJEIGjzvNkWZCix6XIeme5NJPfx8HO8niZT943Gpa7kasqR4rEwaXlfJZBTCSjONiNbEtFAG4Njk1tiFJgleTmzrIpNUhJ3Y00VU70kdE77uxGmntrpI/MAzRGgBA4JLd3Hd+tMqKUVC4yDIGoFUOM3L0a2M9WICTFmPAexMzgZWR52bK5vYIkyF3Cy8mgb5SC2xc927trQhBkTqKiY6cSIZccnfZ878aCECfjsswNNKsKfODw8Y77d5aQaVRrycbJgMobyeLBhse3Z0DCkKhd4ArwCNbtwONljbyu2BVtj5uXJK1Znw6cH8+IQhIRHOwi+6okicRqN7CflddHXLAeE7uFAiFY9o5NZjCLiugiB5ee8xsJDyxGw24mkZUhZZ7ji5qLk3GCPbiaVu4hOkYtuH2huTrxJGEpZIE6kuzyHjLBrauC7849KgnWJqcJjnPf4KTg2dUxZ7nE+AS+gZCIGMg1q2B50GuMyUhhR5kZzkbPdhu5qbf4kCOSoL/cYjKFjwEfBa8+v+DBmGifbKkrBUNLvT4myxTPuS2XQ4nseg5ixBBoXWDcdMhwxeW2ofdQ6MB6AUnCMFoOTGKdGYpFyef+waf43H/3JcS1QMJzd5/BGM3Z5QVH60PefPtNzrdXBAllXtGrDqUV+aImT4b2/NFUZErmulIc2T0654XPvMg78i1IMEsHtHFHMgqnEjfNDR7urghKcXLjgLGNtLst3W7g0x9XfLcJODt1u60LaGUIMrGeCfZDjoqC2gRGwNnI5a7npuo5L06IrSMFy/pupCknwm3tz9nWHqUjoknkY4BD8L7nRX2Tv5GK5BMyCkJjGYXEkrg9eh7oDKE0mYCZUWx8IkjBXa14xwc8EZ1rZt6yQ4ASHOw9V3tBIFIkwUwmTiMIJTnA0fmCGCCgOV54hs6QQuAgF3Sxxu0tFsNMW/yQyLOMMln6AM7ClYBn1nNOY6BpJZdv7/mN3/wj9l1PkWf84s9/jnt3b34o7vopR/rAD+CpbseHEpMbhxU6jtQqcDiD7IUlD995gJaCmwnebgNeDiidUyiFd4FlteA49jwOBdoYROyYLQKN1chc8MxK892tRWvDXBjyoiPVS5IPHISWB0NE5SWlFqzu9jyqp8LRx5crHgwWb/fkreUmiYeVxNV77n1MErtmikGi4Mg5fBUotWLpNwyVYm4SJkrujCXejyQluSMNuxA49QOFSxy0e64OK+qq4EZvePwVjyoKdC6Z5zX7sSaOhvbUkansB+f2Jwx833WBS9dz/z687Sc8hn/HrgX8fXAumuZv92F+RFLywWTix8zmj+Fc/Nt/9RVe/9p32W1bDpZr6DO2px3D1Y44CmarGaODo9srQLA5a9FGEYLADZbL0xaFJSZPEhKtJSLrEcbSWY+RiSQn11YlBZnSGKPofaDKDSFCbx1KScq6IK9ydtuWUhr8fo42S7IqZ35UoYzk8rxjdVARWsHQBmJI1IcFUSbOH7UU0tNteobOE5JAy4DSisEqyjwRBo9IgiQUeZZIRFzMWC4NT5otophk1wpv0TbggqIsBG5I2M5hvWC2iBw9W5OqgiKTeDliaknbDDzzwg1+/lde46VX77x3pqZriboHj+/zh//hj3nz/ptkWU44W6P6FZuLhuHJnt2lQJkFRkb61rGY1VDWrA4Mu4sNZ+ctZZGRUsf6ZEZQBoXn8dhxlRJlZjAzSGqq9q6EQGwMwzgR80oFhEDrBJUKRCFxSSOUoBSgomDTJ4rM4wpPyATCaOZzjXeWi9YxUwl1S+OLxOg8tYQyk2wlrIFw+4JhNZIfzViOitiOnKc9J6tDioXBDwO9G7g7rigfRnaXW+qywp4lpDf0bc/q4BBExuXFnqoqCKNBpoxm37M4qXDGcr7ZTt/3kWO5PGZ7tqe9PGUoLI3w3HjhJovDQK4tTddyeHJIzCO7djupJQmF1obtbsvtG7f4mU//DJ9+dZJf/YOv/BFf+/rf8PjBI0qVoUvNYAf8YMmlQSbBkByLYoYfI7tdQ0yJo2ducP6t++zHnsXBnPQLJe3NSIyRw/UxRV1xGXaszYKrGNnanigFswGitZzFHSflAUN0OBkJInLgF+TZgrPYsbCKLuwYQ08qFffmKyoZuLRXLPUc7yefGaci63xFkopzv2Epa7abG4SmpomeWw8uqb73Do1tWN+9yasvvcI//5V/itDq/cU1PbVQXLfpv99v+I3z7/NGe4luLLGVFKJkl0mWrSOQ2FcTL8IIiRGKbaVYXvYgErtq4lzkXmKS4krD3E4t9S6XCKXIbUKFxK7QLMdAFNDqSTGuGPy0bZax7CaYXJ9pUkpUw2TSuZ/lLFpHyBSDFJO3wzipmmxnGfNmnGRoy4wgYN44QLAtDfN2xEkIajLYm3UWiWRbGWadJeYT1HHMNcvOgY/TPseITUASjEaxaKfuwGZRUPWepBQqRLrCsGgHhIw064qitYQkMTayLwyLfTcp8axKiiRIo0X4yK7MWLYWKWFXZWgfMU6TJ8VOK5ZND7OaRkpUiKgQ0NaznxUsmgGfoJuVSKAYegyJ/aJivu9wOtBVkzt46SXGC/ZlxrIdsFmkz6bEq3agXGJ/NGd+vmGvH9BkLVFAHS7Q+oztkWN+LhhTZBSeYATLQSFiYLsYWXY5Q+hglmFlpO4LqvWcC7GlvkhYJxFCM0rPIiywbeSysCx9jv2rj2G/XdN2njw6hBfsrEBFh0wG6RIhK8hcC0Ky6xIGT1FmVIXmfDsyLyLWRwavKAvF4ihDa8ujhxsOSsPYRKwqyXPJYdIU14WlVZmIBAY7Vfu17IEOlyRHN2ZUtys2Z1fYpufO0Zz/43/3c9z61LOUh4unzNLE+z8E7JuWX//d3+Bb3/0WIURmuiTsRna7Lcv5nP2uwYWp6LY6XFEsK84vL5A+Uv5qgbthCclTyAwXes7DE5bxkOY379C/WeNS4uDkBkMLb33nnPWyoGsCbowMSGY6kYRkbwUzDUOUKK0nP4NMQzR0qUBHC0YTncMlQ1k26ENPU0hqrVAfe8T8zsBQBlZWoNaJ3WIk20fGt+4hHh9wGSOrIDnbB07HgIwRfCATgkZpDrTA2sAOQa4U80wjQuAqJo6MBDxtghgCy30k2470KGYIhl3N6IqJc6EcksCoSjLXEJmgayFEamExMrELkkUpAH/Ni1ToMGJUZBSKPHqUcHg7EhEsM8+NezU2g/V6yac/+TL/9J98+aeIQj84PqrI/u458h6s6qnX/Jv/7Su8/jffY7drma1W7DrN977+gDhaVH1ANVvw+KpntSzxseSygYzIrCjxw0hLxkJbgvJ0UiNFIjcgkmcb4ChP+MIx5pqinIx+k7WMecHhXDDcuSLdFBAT+QDCJ7paMOsiyXj6bOK95sMkcrDRlnqQUFhiERESSqvItebKDMxaRSDHp0TQktqqyVk8d9SdwEtJUAIvEvXba8avz7i4FKznmuXwTWq9I0l49bUX+Wf/9T/gmWfv/FSx9Yelfl03YGbl9S6u4+mfglcwn/3n5Fz8PWQ4T48Pdn3enZIf1hf6MTtgkhU1xiClRBsNXqG05PDZE5IXaKHo3rli884pY+doGockEYUiIXBOUs40IiV6Gwg+IlSkmBmqMufk5oogPIN3ZIUhL3KKIuf8fMvJjRXj6GjbASklZZWTFxniyRVHB2uGyxLXSWIEu2sZ246mjWRhRMoaicJZy+atHeM4sOsENgukKK5xz4o8v5YAdBCuVXx8CEAi+MjyYE5nFWWlWciS3dgj1WT8FYioLCNyLRmZTxABKUaGXYcG2osBryyzkwqpJrdmZd7Vx/4gPUsrjZQSqRSZMTit0JlCacXJc8dE27LZjpQHNdoFrB0QaJQwzJY1TechBSSCOI6oVcl8nvPkUTf5dKRAhkZnmqa34CfDLqMEISVEiByuK1KbqLH049Q6Dj4hjOLo7gHh3DLXjl1q6YPD+ZE2jCwPa2Ym56AU7EVLGO2EE0Uw+XdHZJxw6rmD0FmkrpndOKDZB8RFi48Z1bJC5BIjcvJ88rQoigLygBCKQUzywN55+m1LkRu0LlBCIaXEaEXS0zxnhSFb5RijkFKQacWQIjEGxqsGeTwjL3LavkPJ6TVKKYw2E49AG4ScvFW01rx7sWqj0caQVQXro0Ps0NNsdlSrGUWWg0/Ybo/SCoSmlJMJpDaaO594jiePn3Dy7E26ZyVmYafELitRUZJ8xBiNSg45BKy1JDIKn8hLgwmCfpw6L1EG/GjJrEUoT2YlbW+RIuK8JwiLzCcJX6kjyXlEiJAHVDZBthQCnSSytchQogVwLbcrQpy2K43Q8qkF9qnl4qlfdRJIBEpIquWMYCRmG1FCkCFwAjQC7aebipEShSATAuc9Ok3yrjIlpPUIY8jt5FivokR6j4qC3CdEStM+Q0BPxA9UTOQhIuMk0YrO0QmIk1Sy9pEUAtoH0rVjdSRNErZhIgVlCUQCZQOjFogwkYFFodE+Eo1EhIkIrhPoOMEyTEw4F5FSTDwvNyUswl8H8yhUmsinKkGKCRkTWgjStdymSAnjA1FM16LWCtF7pJ9ea8IkqytdICtz3CAwYUKqKesRRk379AEdJj8RoSTaR1zTI+sSZd2khOUDIkEeIsJoZEwo56Y5TIk2JrSPBJ2uZT9BxkjWe2Sdo1xAKtABkgL8BKtKncW4iLreFpRAhslELdmAocAnT47BxoiWBjVGREhoJ8irGm8dUgRKFIUuEalBSzlh1y04nTBRYJYLtmGDGSXeOqpFST80FNpMOG+bUERC8GglGUZLrQUmM+zaAaOvISfRQ4qkGDBKYgOkYaA9b8mEnTp2AnRhGHpPCJEuCgxiMg51PUqAkQrSdJ1kRiOE5uDOAT6LVIcLZidLbr98mzs/9yp5YZ4KZJ7GwUz3a6mmjpDJMnRKZCYnL2v27Q7be0gCmSbenO0teV1OMsLqeu2SGUTQypCcQyLJhaFPUJQZcXSIEHBXPbMbKwoC3dZSGoV36T3p9lFOUqUuBowTOMSkECYSRimyAKNzaCIYxawsGNmTKYWKgUxqCiaxjTIrSWlEuUQmDUFKZExIPfGHvLUoFCpGpFKYdH1uRyiMZggRI54636VEWA8aRIzkSiGSR4nprponwZgSmRSQIlpKtAiMAopMYf10/KUSlLMKYXtEGzFjJJiEkIkYA3mdI9xAsIGs1CTrKPOMth+pq4LxqkUcl2RGTzLd7ypE/QQR14/KQT4gZfv0mvv+WYNWCmP09b1PY3JDfTgnbVuy4zmunWIZFSNCSYpCEe1A33XoGNBZTgoOU2gKqYneUmQakSLtAM73VGWJ8yO+6ShSotKKy5SgHamlxLuIFgLDJMbhUmIeJUOajDgRgtJoiiQYdWKlFUEnRj8S1SRNniuD1I4qL4iywAFOJUqtETbR6cSizBhTIgKDjGRKIrQiLzSKa9ltJekHy7DtmWi/72GafrLxnp/Z9DYzK3j/Kn2Kx/iT7/FvPf7TSNH+JONdbNP1mAg+0wORPurETvxEU/Kh4/CJT784Ea2L/z9z/9VtWZaeZ2LPdMtuv885ccJHpM+sLO8AFAGSYEtki2J360LqG11oDF3pp+iH6EJjiNKFyBZNswEaEGiiiEIVymRVVnoTEcdtt/x0ulgnMyNdARAgUWuMHHli+T3nXHN+5v3eN2F9OuXeszfQCWzff0LR73n0q7eotxf4vmKSebSBNBU8PIHpRJAXHql6ssSRZhkn90/5x//7v8e9l1/l+MbznN59hm//7reYpHfJ5Cnf/f43SMSaPN4kU0d87WtfIQs3SP0xX/vGV9BhQRJukuoV3/7B82iR0F20hPMn1OcV3Wbg8v0terjg/L0ztk82THRDQiQVkCjFC/cMWaIxRBaFxWDR3mKIvPxCeq3HEVhOArOZJk0E6STld37nlFwa0ii5f3fGrdOM4CoIHd/85owbzy6YLCKzSUTFQHPh6CqYDwOb91r6S4lyGu88f/Cvfsz//O9/webqwH/645/zP/3r/8zhyvLwzgOev/8c927d4/f+wdfRy4bybsOdr5d8+3cfMskD1faC5++AU54udiB6jpcRKz2qMBzPHUYrslSTS8majtUQWXvFV40gbSSzQ8LMG55RlqyPFH3k2dnAIVb4SUe6lrx8BEYptBTcW3q6zYZyaVjeXfL737nDzOSkTvFsJokXLdlVxJ5ZXshTKHKiNqx7T2ItOgqQiq+ez/GXC9xbJaeHY+RZho73iMkdvlHfw0uDMDmnRyesxYKky6EWfO973yfEE5S8Q31mqc4tanUPObvJd37vK+yEYq81wkbkIdD2Oa3N+cb3n2ObaDaJQmnDPIXCeKRt+d5XX0V4SFBkVnFneZPEJSir+M4r30F5RR5zTEyYJBP+3b//d/zRH/0Rt26eIiXkecKkKHjl5ZeZHS3J8owXHz5P8yCn+dYcvnHMwx+8Qv9bM6pv5Lz43Zfp7hiqb0xwDya8un6Z3pe0fcZL+jkObzfs37Ns3tzz0rszwh7EQfHs+YLEFogqwW8jv13dw0SNcZpX/BFpLaGJWAt/xz8kNxmpVRy/Z5DbEiluE9QRP5j+DoGHuOo+q7MT0rMlbncH25zw909ewMxzMqO5OV9z/MwDwjdfpj1d8+JLr1zPINcTdfyCiQK4nU15qVzx6uSI58sV//Xt+6iJxDR7JruK23uLCaCs51tv7BCDI6kHysbx4ElDMlh0jLz8uEdHQWEjxRB47sOaJEqSKPnqO3uUkKTWk1QdL35wQLuAtoFX3t2SBEgHP/771xckg8O4wAvvbsntqDJtXODrb16inUNbx7Mf7MhaR2pHqtZXXz9DeY/xgfsXFZNmIB0cIsLXfnmGvja8bz+pxnoKO2ZTvvqLRyNr1RC4+WjHYteSDo7oA9/4+SNkjKQucHLVsN405H1E28BXX3uMdJD3gaNNz+lljWkGdKL55q/PUR7SzjPddNx8ckD3jthZvvb+FukEZSdZVY67jytME9Fe89XXPkA6T2I9RdNx770zjPPoCF99/QNMjGQ+YNqeB++ekVqLcZ6XX/9gpPntBtK256X3dhg7Che+/P4GbT3JYDEx8sLbVyRBYgbBC29fkXaO3I6Ozdfe7DEukgyeZ96cUDjNRBdoD995chuNJukiz1wdUQ45WSxQJuP72xdRUZKTcP+dlMnre9IP9yRB8Fsf3kUqR1YaXjh6wM3JKYXOCS7wd2YGfeeSybdqTk92HGejM1nkBd+7PWogaAK3j1PurjVZqjFZwqurhqgd5UJylHmeO9IslxlaCZ5NGzzjXJ7FnuPCoqVFC89Xjh1DEbBzR7o2vPTijOK4YH53zu/9469w+o0XWb74gHy95v7RlO6Diua9PafL6QiJ/eg7+igD+JmluchzXn3pKzz38Fmee/gsv/X93yafFUyO5qjMcGdxmxhGRePb69ujs4EkNYavT75O6jS5T3k5/SrHHLPsj8hdzu/cepYkUZRlynJ3xdHJfNRz6Cx/58EEIQSpgJvKUoSeLFEYpfnafGQuSzPJvWPFUQm+a/DW8rVljdICguUkVUyyDcWDHnl74Lv1jBA65NCyjiUPuxVZp0hMzt+PMxSQhsCawG1rSXEYEXjVthACmRBk1nKr7UjEGIj4uncoKSgklMDzRHIZ0d5xnx5dQD4NJDPPw6JDB08aI3fjFZkE0XcoAa+uAkYLskTwbGlJbMe6lExzxXPZuIamieZBIUnVmLlBKL5+Y0ZSGNJcc3M6Q4fIsGkIwfPKy88+ZUuJjzNRH9Gcfva/Twy5zxh0T5m0n8y5n89sfPNbL3Hv/k1efuUhX//qA555eIPJKmdxZ8nLoWFoejIRmfieBwtFqgS5MXzreCAvMpSI3FiUnKoGrAMb+EbaMZGGmdKcqITn6z2TQTEj4XcmhuUzmvkLnqNbhu/KgjQBrQNfq3PyJJKqnryUfNstKItIlgdebUvKQpKnjmKq+dZwkyIx5MbwdXvMzAnmIZKLyPe3EzLdUKQd3711l+N5wiQfKNaS381vUpYbJuaMV0467j7bcvK991m+esUrz5zSFLepirtUjeH1n/+CP/zjf8cPf/yf6fr+0w33JYCjp6tbnqYGFteZI+/dtQzaX0/M4f+T7f93VLRftH0WGvU0Dvopl/jpVxTiqVO/7M2f2v9H/9OPeO0v3mC3rVisFohW8d7PPkDsG6QQSCKbxpIkCuE1nY2IGAgiIhV4oblxZ0WSzggyISsTpDToNOHyccPxzZKh97SVRRmJ1ookk1w+bjg6Lem7QN8Oo3iLEggjuLroWB/n4GH7/oZqUxO9JS0SdlXg9FZJVAltO2AHT6IisR/Y7R2TQhJixLuI0obl0QTvLednLYlyRB9BSgQaqRzL9QwrU04eLKn2FYdNxeaqZj4VhHaLj4r18YTydIHQisNljdu3XD3pGQbFtFTUQ8uIEDWslprZqUTNcyaLciy4MrDfN9y4ueLv/v63WB1PMVrxZz/7MT//+U/Z7Lesl7fo3lnw+OeXXH5wjtOG5Y1jzq86JpnARnBBkJcJ3eWGOzdnxHLKYpnyxg/fwLpAlhpkluKi4KoXLFLQvcBagRICv3C0a0eFZCEFYZPghtEZMtKT6MjeSu7enqLygu7QcfFkh4wWjaSLKYsCru5H2szSx0jhBgo8WwGnRuO0wYtIJ6BQgvJ0wvnQc3MxQ82vSBeOJg7M33ZMfzJgIyyPlnTDDWyXszvfo/HUwdJqwzTXXG13VHVNHcSojxIFjRfMMo13llQKznctS+OZqguE9KTacOvFE/J5wsUHj8msIIqAn+cUZY5KDCZJ2Gw3zMsZ1g50Q0+aphAhzVOuLi44Oj6mq1r2V1uMMexPJfXScZlaprGg8i3Z8RR8IB8U8arlTNScmgU2zYjLkma7Z71Y4z7c8sQdOO4NNom0GmKqmERDGCz7ieP2kNJnDmc7rIkUNkdRcq4HloNG5A47tFTCslQL8mRNVQiWqmBoUoLX9ArKPiJEYKM8UyeRuUQbqDQs0cjBctk3zLOcb999yD86fuZ6ofxkoYuf/PGpSaN1DiMlf7T9gB/tnvDhB49ZXVqCLqkLQ+LGirFESnYGFoeBoKHNFBqBIiH1kk0ime87vIJOS7QQY9QeyVWuWO06XKJGlqUIWQgkHi4Kw6rqcVLgjCJIgek9xsWR3ra2WC2wEoKSFMMoBHU1SZjvO0KZjCrcRpG3YwZpM01Z1AP2mtp2SDRl51EedmXKtO4JiSYET5tqZvWAjOPzyt4R3RiR7lJNUXUQIod5QVl1RK3RPnLINPO6JajAodCUPpKsV/hHe/ZaMakadCaoCkMmJTrJ4UnNocyYHVq8UTSZIRkcKoJynt2sYL5viErRpAlJGIXI0hDZzUomVzuc1vTZSFOrYiANnqvFlNn2QJwYOjUGrBIpyWvH1TxnWnX41OATRQgB01sSF9jMC5Z1x16+x5C0WCK525NkV2zXPcutoWOMhFsTSUJG4mG7GFi7Cb2r8b7H6cBk49GN42racry8SxsDvuvpyshcHePO4Eq1TLsExxLRGA4ZlG9Gmv95yrbWTDKJ7RwRaKxknkWGwbEfJIVwZBNBuTJc7XqSuiFJilFxuK3J5gnTVcbZRQ3VHtIURMJiXpBkEuF6ziqL6RqO0hJVFOSzHCmBYeDirKYQlu7ynEPdoITgpZdu8X/8P//3JHnyBWHrj6BRn2QyBjvq1rz93tv88M9/yJPzM3KRsnv/ghACfd+TTyfoVFPZhtV0QfZtgTgCGwYKPUEHyXn1mDlzLv7nElvPaHtHKlPqveSD93fMcsVwsAweGiTTTCF8ZG8FE8PY173FRk0RA9EnNNYwLxWdc5jUsHeS2bKl+K2aahoIm4blSU+iK7aF46ZZoUSgKhxZr+g+XOE+nHCVaiat49FFTYOE3iKlRivDTkiWMdBZj1WKRCuitaRCcgWsRcAk0MdAGBzGO/IQaLWitJH4eEm3ExR5jnMtSjoGU5KFFpEKvLyGBEsL7Z59G5inAp+nuBBxLrLINLZt2KOYaRA0xGgJQjCRntQ39DJw+5nb/O4//G1+53tf/RLD6jP9/JRd9ilTTgBRfDy/fjaD8VmzzTvPMDiqpuf//s9/yFvvnNN/cEl7gEBGHSXrMmVTKdqYIJ0dxXyBrZUcTwUyUWybgSJ6pBI439GJjFPtYSKxZYYUUDzwFLdrztLIsg64tKOOPUEK0iDIY+RyEll1Gq96XDpyfaUojPWc5wOrLmUgAAGXCophzEafTR3LMCGmDqkjdVeTXFbM7j/kkd9xWh7h6yd41zAknolbILspV3TkFWx/csqwnXPoPYvkwP3FE8xMMZ/PeOGZF/id7/zWFzT2F/WOuK61eOqcGDkcDmx3B4o8ZbVaIaX6zBr4+d78/xMqWvHJYPtkhH356V90SHwcW+TT/ARPXfaXuUKfOb653HF1saepOwiK2Eh2Fwe0EDgfEAKclGRFjpIpuotICSqRpJMU6yJ6NsU7zWHTU+17kiyHaNlftQz7Fu8C+22HVJLZMieGQL239LuGruqo95YQIQqHjyP29uLNSKI13o8qpibN2dct/SCoKojC0ltBCJJkYuhdwOQZKld0u4a+c6S5oncSoTNMLlEyUO8aYgAfAlkiePK4RijH0A401tF2HX3vkYywB5VKBqWx2x4hoO892XSGOrS0VcvgHEErvIi4ELGXe873DcUiZ3lzDYlHp4Km6SgnGdvNntt3jgDY7rfsmgOt67k6r3BVyqAMZjrjUFna8wZ0Qo8gaknXB/oGlJdsrnpEM6aDF/dOuXi0o+7s2H5RYIOgjpHCSTbbgURr8ls5Vvf01rFtA9JCW3mMkIhM0A+OLgjeeXeHUhWdG/VCMmGwHnoPl9Gxbz1VEkfGH6MIjJP/hYBIoAsRJxhpHJuOptA82h8w6Ra9axjwxIuIvexxlcVZT9Om7C73RBcRoeeya2hQaAJdElGZYkCgjUEpjbOBq94SokDFQK0MOvSjyqf0+AAXl5dMKKi7Dodi6Dvaw5ZEG5TRSCWxBBp9QEiBT0DUFakxtNZQty3xyTndrqZuWmQItLlhPzfsjKDpDwQcm6olhsCCEjmRNM7xxB5GrZrG0tuW/sMe3zuqdGQ08omgU6P6sXcWdGDrBoSOkEaGaUQmmuAz7HnDrmtxMgXb4pOAjX6k/EwcjVHYocaGEbZkB493Y4qzEpFAwLuA9J5WRkLUCOuodMC7nsebKzh+5ovn4s/OJxFyNU6LF7blMnR0i5QtCgZJlSpUOqppKwSNBlFqhBYcUolEkEdNHRXNNTVojIG6GPVhcqepXaBNFbtpOtZc5AZipBxGaFGTKmRMiAiafIQplMohI9SJIvqAV4I+00TAaY+M0KYapikxUQyZJghwUhBzqLUiCIhK4Y3Ca4UXdqSNzRO8EAQjcSISlAQhkUSaPCHkCUPnkEgGrQhxpKhsUoMTgiAlygX61DBiWQJNYbCDQwHmdEnbDkgFQTqaIqGOkWxSQBtpk+tIuIQqM6jUXNdWRNosQYZxTajzFCEF2eDoGJ/vpyUIaMpshJYMAw0jTW2c5ogEmkwhxJhJapHURuEnKRDpMgXSUEhBDXRFwgZLIyS7dEyh26FH5T0H0cCipHeBJg4ECbmVZKmmUhZhOgZh6avdOCYTjdSeZgabaUfddzjj8QZCvcNrw070uKmgbQdELhmiw6sZfRQ0VjJEGDqBVpLBS2Ln8UHRe02Uis2hQu52tDYyzwzKOuoejNDo2tPpgcMQIGqwghDB1p6JkigU7dATTcb5tsU+aTBGYxRE76n6gPEtSbCEqOhd4P23HnP5/iU3n7/5uU/oU77GdXwwHdVd2W637A976qaGPOITaA4tPnpi35CYlN52VKGiax2ht2OkNTiI0PgatOKqE7RXAu8DqVHsrxwHF/GVI4iEPozzs+88qTI0EZyLuMEhhKRzHhsFUmraoIktWJUS+0jUCV050IWAzaC8PWWf1SSloBWBXWKRzlEbS2M0rQz4RLK3FqskG+sYkhShFSFAtI5eaVDjN9KIEaaYSUmvJG2AHZARqXxAaEVJGOdMJQiDxKLZe0VVR1KjiAGGEBmUgcYyCI/znmXikS7SSTnWXLaOxoHUEtE5nBO0zpMWBuc8jjGCPV2ltIdA7xy7/YGry+0Xm2afnSR/kx0WP2u9fcHJTxnISinyXPHuB1cc6p6rbXVN36rR2uBMws4KDj00AURQTExKqjURwc5a+qrFJSk9mjR4epGBzrhSlug9QzeuS3NhaRKotCcWkYilSkbIVbSeTgkaZSELYDyDsRACEwwijdSJR0iLsI5WezwRnyZsTaShI0SPCpEuWFQpEcWSC3mgER0f7h8h2OLDgdiNNMJRQiUscZpRG003jIHFEsumbkjwuODY7Da/ocE/20/xE+s7io+/S2cd/eBwzjOZTEa4NnzGqL52TBBfYoH/1be/Befio1TClw3J3zCwnrr86fM/QrqLj8bwR1Rm8dPn/VW209vHPHl8id5K1kdz7FXgMtFMZjmL0zkqy6hry/GtBSIqNucNWWbIpwYbApcXNeuTCbFXuGE/Yrr7mv1FQ70d8NIRiPShRylF06cEAo0NqEHjbERESZYYpAz4GCFG8sSDHwhCkU8SVuucyQE+fL/Ct3siATwEHxm8RMSItxqvBbm2qAyca/CNIytTtAIjB2ZloB8iSE2iAiJaqt5ia4EWnhSBThXTXBOGsehtsSyZnkzoGke1G1idlBRJRn/oib5DGE8vAnhJqiAKj+sDiQucPHNE7xxSpkwmJUfHS86f7Egzw42jEy43V1RNxSSbY8WSIvEkLxyzv2p49O4Fm/0ObwNCG8q0IMkFSZZjdwfs4Jhpy/r+CeWsRGmBUIL337zgyUXH1HimRYmzQLRkXSRdSQiasgz0lUVpQZ4mnN6cUlcHnuwsy3z8cERrQSlKPDpIOgTTzKCFx7QeJwWFsKRGEHvJOpdEAS5CFSOJ9ajoyF3Gvfs3KJca2z/iEFqWk4RceKrlgFKWZHtF3EVcEEwmKYtSIa0nSzV6mtIrzzB4Sh2JwYEfSDRkxuB8QAfLsig5kj1dbJlOJ9x59iYyjSitWM0XDN3A+Ydn6CjIspTN2Rn5esKdB/dAwL45oKIkNSl1VSFXKSfrm9BantR7wr5lMniMHqkoT0xJtdnS24CREjkE2qYhnxuOOk2whnaAYZDMoiGGBJ0EjqxCWhhsTxs9swHSNEWEwFIkKCnp2w4mKceTGWGlaB+9zWw7kOUJfZEwGMFKpJSx5Kx1LJwisYphiDTAcoAggABzG8kVtFpQKTjpPViPMIHSeeYfnnM43tJFy2q5QiDYbDekWcokn3zplHUnnXI2NJTKMCsM3bsVsunJkCSNIxJRpWbZRrSWmAAmQmZ7XFSIQrPuA7HvMc4jQyQfRppUQcpy3yO0IrEeqRRF5xDWwyJnuRvrtCrriVIyGTzymrd+WQ0gBU3vCRKmrUWp0aBZ1ANKCdpUY41iWvWgNNE45vWAjtClY6R/Xg2IKCHAtOlJYqA1iiHVTHcNUo1G+SQ49Lan15o6MUz3DUprhAsUdoz6WyVpnGe2b5BmxEjnzUB62aMe3IKmZ76viWqs2UgHx1wW1PsGWeZMtwe0UUifkQ6WrLM4JZFCsNxVSCHRISBhLD5XklBkrA41IUaSGJHWMYnj9yOkYLqtkYkgKQ1KSvIAshoDPctDi1CCNo5BhPLQgVJspWBZeYrgSbJIMIJJN0XGFpEI1raEaDi0W2wqyOuU2fIEqvdZ2AIZE+p6oPMtqypDdB0iNZzmt+jPr2jEgL1dsHIF7ZnFm8B8kOQU1CTsfMuNpaLTElFIjHDoFJwPHCycLhLqXUOdjNTa7dVAtizZ144s9hitkEYxIWKw+LpHO0iUJUsknXNkzjMbDNE5BgKzaYIhUG0G/FAhZIA4Bl3m85xMAN5xqFqms4zljcUXL7YfRQZj/DjAOBo4kRsnN1gtVgghmE1nxGWgr1v2V3tcM5BlGdPFlNXRGnns8MWAC5ZcF0QXcRvPMl2S37vBVgiarsdcNqgg6XxLLsDIQJdo9jawzATO9vRCM9ewmuZcbloOWrMsFYlOeLy1JK6nUGCmU/oQkOctN+cTzn3D1EomTTZSUGeSEzlFDJaEnlLnxJiwRyG85fZ6jnt3w2U/oL3HeHBCMxjFZPAQRwFNFQIFAiki1noWWlIKgYoRDSQuMNGSvResdcALB0kkTRMSAQHPLgSOCoEbPH2QDMFTSk+aK0IXWQqYzHMO1lK1PROj0ZlmU1nmIhJSRUxy7OBYmASfGNzEsCxzjpfzz3XrXwU+83E8+aNx8Fe64NPbzZMFi2nO0WpCcXuFfaem7RWXXY8ZHCItScW1qHCscW1Ai4yZDoQ80KmIdgPTJBK0YusC2rUgA0YrNJH5lSNfCKzXrE0k5hlmNxa+Tyeg24hoHccqIgtFZQucc8ynEXTCcOk4NgLlBw6NYEg1i8mIgDlHsiYnGQIdFiciq3SJKnKEu2QZUpIhoY4J7VBzY7JAZivC7gOmLmF5Y8ZewuVmz9IXZFLjEsPi+Igbxzeomoqu71jNVp8IT38mi/HZBMTH5RdCUJYFPoy1cFrrpxL24pN177re52+jKONv7Fx8zr8RH73lX70+4otKVj7aN95NXBcwf/qaL3Wxn9p/dDpj8A1ROZICSrFgdeeUbJrx0rce8sufnGGbCmxCkkq6g8XWjtVJwVvvXLG5qNlc7plJxVvv1kgBx/lA24TRoMgF2c0NbmjQRrM0JZc7AZ3DG8mcJWeXjpgp7j6csT0Y4lWPsA3ppGW/D7hmz62HGdLMmFUQ+po7NyLvPulQRjDNI4cmxYZA10fu30r54EwQe4dRjv2up+40WRJZTT3onGw+5XgFFxdXVGctVgiOp4rH5yNHeugGNBN2FTz5VcXxcs75mcV5gxgU9A6jDd0wsD6BK1FSHzqE1kQxY2sV9sOeQrU82QeiVKwnOX/2x79muzkgleSr33zId776TQ5Vxa0bN0nklDd/cT5iZueC/+f/4z8y23rU9sD+rOFss4c24eGzJ7xjJ9jG8/iqBXfOoU8pliXf+Lv3ufywRroOmSWY2ah6KRBkOC7OPD5IRK5Ymp5HUtG5gTzUDLOEQhvC0LLWnsopZISJduh8QYwp+TzhFb3nzy5rCI6VhEBK30PQkuW6552lJnhP2jn2Hq66ikQm/JNXTvmFeExWBY4SSUuDNRXJccL0Pyie7FpMZlgezfCtw/UtvVcciYzzQZCnhgd3lsSq4d139uA8L5YZ7zUtiYmsVEKZC0QQzG6VPHj+Hq+//iva7YEwmaEbBZ0gas3p+pTtfkdbt+yeXPHgK8+yqXZEETm+u+KNtKPRGTqPzLol713VBF/wYJjQ654wOKwLHG1LXp/XCCIPr1IOqcUHTchKnilu8Qt3hvaaoybjYjqAgrjKeChm/Hh4F28j6zDjKgM5SxiqwLOHGT9ULbJpubN1bOMeqQVukXHa3ObdMkdrwY0woY+BGDoGB3cqzesTgRsCpY2464JmK+G5Bv5iGvAeki6AG4gm4LTCf3DJP/uD/xckisVsjpKCzX6LUpJvvPxNnrv37Kcnjus55juzG5TKsHU999IJf+ze5PyDLV3nuLcNvDXXeK8RvWfaJ1zlGVFp7py3vL9O8XYgeM96gN3c4KzjdNfy4VFJDAEn4GTXsb05RWjJ8eOa83k6wkCzhOOLmm1hkAKW25bNJAUETituXVS8cWtOiJFFZdmXkhjACcGNi5Y37y4ISGYHS5VF0AYr4M5ly6/vL4kCikOPT3NAEVTCjcdXvH1ngQhQ9h6nRgKD1gqeO2t4484aoiTvAiLxxFLSE7h9VfHWnRVBQBGAzrObKbxJOH73nEf3ThFZQrqJqD6wm2i8kJxcVPwKiGJ0yoq6Z1NkDEnCnUdXvH/raOyRECn6ju2sIErJ8uKMxzfXCAIxRta9ZS/Hdjm52PP+xBAZmbQWg+cw1wghWTc950qBVASlWW8PHJYFMUTW9cDVvCQisFJytAtcFp4YBcs+YzsROOupu55Xitv8eX5FxFPsFMOjMwZT0wd4drvil+VYgL0ySw5lIC4G9lXFc+E2P+I1aDX5YYIcQGcgTwoevCH4oTkQNBRJxAZPDIpBwcN15GePPRjDdKaInWdz6Khryal2bAYFLpIKxXSq2Vw6glF86+v3+NnrlzS7lrlMWRWSJ1YgQuBI9lwNisJCebDXmRtFmpXcW0nOd5Gm9Rhgvoo8uqxwmeOZ7zxPOss/tWZ/au3++ID41N/3bt9DCsHZxRmrxYobx6e88eavCd7z4N5D9tWOJ5dnLOdLbt2+yZvV67jouKFu8Qc//EPiJmPYae4ubnL25rvE4JlJT+tqJgsDXc+dec5PLzxGwkTAkGnqXuElLGXkERNMkTFJHCGM5CxmMuErJ46f7HsG5ZiLiNvu8GtwInJ8rnl7IRAyQ1WKojVcTSy2MDxnM35oBzyBNNOsi4wr6wlKcqPreKJHLaFURiYoKuFRmeLmMPBEGLSMRGvJRWBnBD4E7k9KLltJdB6tNKtMct5orHWcFgNPBoUxKYPruDNJeG0rQBpulJ7H2wapU6ISHMmGq7ZBS1hmCYceMJFWWe4Uhg8ODUoK5GBZf31CFVpkqDk5Lr7QmfgiG+1pE+yztRRfdM5H531ZaLjIE7JUEWPAWsvdleHPf3XBMDjKVJKplN4miBh5sIC39gmhtfi+o0gkV7UgNYobquVsKGg6S5FoSj/wuBVEH1hWnscfZrRJws46jnU2ZpiBu8pwHgSDHQVBT33gERGU5J7WPHaWPni2WvMw1TwRjiAFixsp1cvvQ3C4mHBHFbyVPcK7gRU5VZoipGEYAs/m9/ipaXGbhjKds29rrGlopecrt5/w2s0rlt5xMkxoupucNRv8QvKMcfzLf/8v8cFztDzid7/zuxhtvuAD/OKei0Ca5RylY0b8IzKGp32Lj+4jPt73NyvJ/hvXXNQf11xcv+zTt/trVox89kXEUyP34/v+plH8Bfv/xT/7Q177+a/Z7w6spkfEQ872SUuWG3yvaLctV08qslwQvKcfIkpBkwhsquijYqYioQvYoFFKkvqOBIsPinziyZ6pcEWLSRO0nyFdwWZ7YDlbQjWjugyYPCEvSkyWcXnWMp1IPnj7Q/Z1j5CSRZIwy0oOe4/RjuB3uODIi4wkK/HecGgEkwxs52lah7OBPIskZcJ270iUJzWGyXpKVJrpQuJdy27XURaKYa+QIqHedbi2QgvorEJiR5rdVOO9JDWBrunoBkliIu0s4rKIi5K5EUgt2VsQ3iFaTxIENirW88jqlh5ZEoqE5166zX/73/+dkZ2KT09E/+Zf/yl/8eevs90eSAbJ9u2ey50lhkCSTsnLGdUgKHXAV4G2jphUs76/IuB5+41LTpYJe2chzZBSohJH79ox6lMobBdo3MgWpKQF6bEq4XRV0B4sF9uWJDGkIZCahDYY5hlcuYpBjpzkkyCQVtAMmlx7NncHOFL4ECmIdHiuJCyF4OHv7Vg8cNTNnnUsiJstV/aMuZkjf/wA91PJ5nyLQNIGxVU7kCcaBygjcUpx82iKip5D1VAWGUZ47O5AZy2zImF2bHBJIC/zkbEo0WwuLpnlM4atpTo0I9zOOIp5xvawQzWO6e01Vni0Vuxfytkew0a1HNmStgpsho7oAoVXJE6wNT1lZwgamiyinGfag42ROgusfYZTmkEJQghkQQCeXeFY2xSSQCUHooiUfYJOC3ZlZFFLut6yHxqiFNxZHyG7gaukZ+UyhuTuCAsRkROtkf3ApR9Y9DAIAUrRisiii0gBm0wxcxGrAOdoZGTVDsg4sM8CZVSkr7/DgkDjetaLJYjIdr+lyAqeu/8s/+T3/8lvmEzG7f12z/9w8Qav7c9R9UA8eOQA+1yyaEEmGYdphvYR4yPSR/aZZNVFQlS0ZYawjnTwpAEuC81y3+O0oM0ThBDkvUPbwHaasmjGyFebjLCovPcYG9iUyUhFqwRDavBSUNYDMgQ2Zcqis7jU4IzGa8nk0IHz7ArDvBmNomA0VglmB4cOhl2RUjY9IR1hiH2qx4xHlOxnBakdEE4QfaRLNJOqQwvYlin54AhqjLxWqRrF6WSkLhPyzhKEJs1Tqjxl+uEVUSsORUpmPVEqTDNQlxnzpscD+yJFO4/wnhzBPk+Z7Wui0jSTHA3IwZI4z6FIme9bnBRURYYSgnToMc6xn5dM9jWxTGgVSK3IAsh9z2GaU1YNIdMM+ciiVrQW5SPbMmV2qNgmb9PoHUFJyrBH6S278sCsSmGh6IcKp2Gyk6BSLpOKdZgSzIAbWnwhmfYT3GFgewoLX9J2DWGwDKXgqFnANnKZ9qynRxw2Cf4gqROYvzXB/nDCxTYhTcDFSBg6BpWwUJ6hsWw6mOQjlCOJng7DjZVhsD0Xh4FcC8osQfuB88oxTTxGj3SkiRJMBsiRHGrPpJBU+5ZDO0KNyjxByUjTBCalR5lLLro9xmi++/e/yf/u//APyfPsy5mChHjaQvlk929eqr/wE/zpr3/Kf/rpf+KDsw+ZlwuuPkzpKj0yZ6mEw/tbdkKShciuTRicwkbJNJEEoai9pjAQ5ZSIoW48yyQgE8N5FUixmPko3Doow+KkxT+7wd/WlAOIdE+aO7Z64LjPRzpzGsq8ZP/OhLiZchUdN8sp7799xSYIjBQI6zAxUknBzEeCVNRCoq5ZiRJgEyOrEBBJYEglIkTyTpN0ki4qbnpBf1FwVUlEBKM9IVoqnzAzjoCk8SARLExLcDs6ZZgnMNgdPoxkDNMkIUTBZgjMc4P0HVqNc/mzr06YLGsuLx+zWq759re/z+9/7/e/dB78rDPxEUTy4759Ch3/hUPjS/s98ubbT/jn/+OPeO1XH5DnCdVFR79p2bUDi2JKO0w4hJxMC6SSCCKbNnJzliBMysXOEr1jNsvAWS6bwEQM6DynDQpvHfNFRuhqdl5xlINSmroPECPTGFEeNoNmnjii0DRO4kJgUkgigSd1ZJFHRDKySkmtOXllw/SbB7azniNdECYHBlnTtg1lXyB0xpVumDcan+4J2tIxsNJHxEFwofbMh5xQNwjn6ZPAUt/HtUvO+p6JTDjdNBS7jqZreHDrAT/41g+4f/v+l3h9445Pai4+f1K8ZtD7XG2z+HSh939ZKtqnXuVTKDvvEVI9JU3+V/RhPnYiPoJIPfWYpxMiXzBTReJIkSg+8bikHGk9hRjp8aIcOeVDb7l44zExqGtKS9DJGCEYaz8iwVl0apjmCicCtZUIJdBWkRlJXTuKac7iXk4dNtep+xw5pJh+oJgVDNaQTceXlYrx2YPHtxZjNNr4kfI0Rvp9RV8LdB6IMpJmhnxRMj1eI2TO4WdndFWDtRHC+IFN11OSXFG1FcLbsRjdOmxriWVKjGN0L5+XJGkKUTF0HjEInPN4L9BGIKQgekffg4yerMwQRjKZaDA9DR0OkNeYb6KgSDTCSdR1lLveNbihwUxS8vsn14wScQxNAiNdYhypQpXEJHpMk99coiX4d3fYfqBtPXXVMARDlgmydKQl7Loe1/YUR8XHtG04iP6jVJ8iCjVyghOJMaLlqG2glCQIjwuRw+UepCFPDS5EEiWQw4B1gdZ7VCFR5qmxFscPsUwNB+UZrmt1FKDiOMSdc+zPd6zvTVCJQQWDmBSoPkc0YLSiOJ4hUsNkOaf2YN98gmzHLIEYAiF6uqsKQ6BrWnzVcXRjgms6klnBzRduo3LHbrdBqWt6XDHO5jJE0iKl6+1IM5sbpJKkZQbCjdotIYyUtR5SaYi+gcYiu3Gx83Ecm85FnIE0SeijQ8dRU8UrgbD+OrLkUXKMnGghyMsM3w8IEXDOI2UgSQSe8T5hCGMGcUiRMVAIg1VgtzVFll5/O+CvoyxGj9oEJvAxjai4/pZVIkmMJHYOjEDEiAgepSRSRDQCGSIigvYRJQTaJMS+QwiJlFzT9spP0st/ySbl9RyiFeliQshBbQdwPTpA8GGkQ/UR5QJGjO+lQkRcq3MrMQrMSRuQwqBCIEQ1/jYEIgp0HMet8gEvBUpKYghIBNKPwnXKOaI0yBgJbtTRkAGEHJ+pEcQQCRFkBBFGClgFhAjCB5xS47xoA4SRzjZGeT2exnOEEEgJw6Ei1TkyXhMzxzheE0GHMXMkGNtbhDAev57TFBExONS0RMbr+TlGCGGkqL2OcMthjAISIzqOpAbymlJbhgj6Gipr3ch2df2e0nuiUONzlQR/3d7X1LfDYBGJghiJfpwHYKSZdWGkkOX63VUY4TxKipHCWEg8o+hoIiQg0F4QhoCKkqgkusgIB4ssDWbQxMIQ6gbvI1KMUWaaAyrkyMEjg8QLgfARlWeYRYq0iuAiwhgEw6gonI79mxgN3uH0+F0ECSbTpFJCHElAUucQKqVc5OhOIg8DMlG0bUt2jb82MRJ6yxAdEOi9GrO4PtDXHU3T4YOmj55URtIiGetltBrbSQjKeUm+KBBCjqvtU2HPz2Hyv8ix+EzI+nMmz9NojI/NAImSY2ZaKfXxei6lJJnlrF6a0J/vWWQG/yRQ7x0+gDYKowxtDyaRDDYgnRvHrYAESBONsANSMMKU+gE/eHBh3OfG+iERBCJEhPVonYzvEcUY/PQjfbMKkeViyuX5HsK4Jik14t1HSLNFGEN0ASFHOmEdIgRPCIEYrmHgIZCjkMZgRMQy0upCHLPlmaJqQcaANob++vrBWnIt6UIc1xPGcQyKclrgOse278iEwMVRXG9oWnbvX6C6nqTUFJMCrdSXT4LX/fe0Rfc5zqH4qVM/e+mXZkCAT+w0Ka8lBMb6rkQrfN+j9QxcIPiIlAaTKETnidFj244QIkZCVzdoEZAyJZEw9D0+aASRoa7JDeDBD5YeS+claWpG8hytCBb6YWCIniGOfdH2AzqTaGOQDPR2wAaBAup9Q3h0RRMivjAjw6AyhDIn1TnCG6To0CYlSgPeorQitgNSZtdjUiLkOCe3Q020AxKBSRPMIOkPHRMxto+Q4pN164u+sac7Iwo+3WPjSeKjAMDHUMa/PTjUR9vfYkE3TzkGID4epJ/LR3zBvqePPt1anz73c0mLz7SZuJ7Qnlb/fvmV5/n1zz6gkIKjkwXZ0YJm8x71B5c8XCk+2BmEj0ynKcG1tKMeFg+KwHuHiI6eSaHJ5pKzjSdYx0x1NE2KJieJBc/cPOEXPzsHIt/8wUN+9mcXZGJKlhS89I2b/ORPHgPwla+u+dWfPcZvzrk668jTgcFNMInhZOGoG43UkM8Lbi0THm0lZjblua+seOune6LtIXqeu6d5871AELCaO7bbFuEsWa5ZFy0fXlh8EGRuoA2OXSOhH/jBf/Uir/1FhW0rUt2ilMSUJUoGpsmBJ5eKskiZTQKzZU5lc4pZwne/NuHf/JvXkH0gtx1yprgMgcwYvnHD8MtGoUVg2ReoQ8+TbQRR83d/f8mP/uQ9DruOuw+X5BPNr3/+CJNq7t055Ze/fINibpgfp3z9a8/z/tsbRIwcH5f88M9f4/LqAlFBVqdYNIm0rJItQeesFoahq3juxPDafqB1Pc8oz1liML1Hp5K7U81PN46izHlpnfH64z3D4FCJ5HY28Kt25EKf2oZeFhg9Lkqv3kn58fsDIcKdhed8DlVwpCdLvuks/ykGTIBTHzkjsA8KgeTBG0uuphlycoObx0fo6WNcdGQm4YX5ip9Oa1SmuFce0VsPX92T2Bkv1Df5xV98yGHfkFnHIFrcrCERmt/9ne/zF7/+OUFHTh+sKFLN67+uMUZzf3WD199+g0Qbbjy8RXoy5z9fvU5z6Lnxy8Db+RXF1495Jr/BcbLkT7dvIQfPN7IH/MnwLrIa0DvP/cOan00HVBR8pcr4VVFjnWcaEl46pPxk1tCHwLe2Ba8VHRLJNDE87Oe8lu+RWvJtf4PX3Bm9kqzTjJeGkj815zgBr/Yr3my3XOqARvCt9gb/aepJpeT5g6JJFH2AhMi3+5IfzRRewHODogqKOksppzm/Z2b8Ub8lOsfp1tMMllpItI18r4IfzTpiDNxsBWpTj2rG8ynf/+Z3+XF7TuhaZuWKPNNcNRdYFA+eeYEfX/6Q2lXcKe9hDgVvvPE2aZrywvPP8Nab73I4VNy6c5MbMXL53gVSSr52+pCfn3wIV0+YbxSLzYpfCo9G8rXHll/fmZBFSeE8t7eRn2WjdsUrb21459ac3AaywfPwccVr95cQA6+8s+e9GyWljaSD55lHe1578RSi4PlHe86mKfngSVzkhQ8v+fmDY7SAB48ObJY53eBIXOC5X5/ziwc3MDZw/0nNNtUMqUL7wMtvXvHagxUGwZ1tQ20VfWJIfODZXzzil8+fUsTI6aamlxK3zhCJ4OVfPeIXD2+StAMnmxoP2MSgXOQrv37EL1+4RdEHVlcNGkeXSKTzvPzmGb9+9haFDxw1FtXVdGaJdp5X3jjn1w+OSa2lqFrKbsCmBukcX3nngjfvHZNbz6QbWF7seePuMdIHXn77CW/fPSYD0rrl1qHljXs3UFLwwltPeO/mjLTtSJ3nztuXvH7/CKEkzz3Zcz6b0ElB5gN33rrkF88eE6Xg2Q82nK0K0i4gB8dX3q750b0N0kier4+4mB6YR00hM17Z3eM/ytcwneSFcItH9ozOgrSCb26e40/iHuk1z7k77CY9revRreUH797jT+98iDxE7tgVQ2upzBV4y+/FV/nT6RbRNNxeOvpZzn5TI1zLK4uBn19mFEFyayIoCsMvHvWkKuWVteNXTxR5qpmHAS86nohRm+TbzxT85N0tSYyc3piwygp+vhuN6a+VknfOW2ISUIPjmJ7HtsFoxUILahnJbiWYoNFDT1K0rJ8/4ZnnT8nz5NMIhWsb5pP1eTRotvstr735GjFGXnj4AheXV5ydn7NaLnnl+RcRUn6xsfnUrZ+585A//fPXCO0JzuT89rdf5t/+xzfQacJzd25wdjHwxA3EYPhv/tsX+dd/8CaXjzfcLQVRafZtB17xjfzAW+IE3QXmbkOMBhlz8kTzfF7x2mCYJIaTzmBk4JIOIwNf/XXCmy9t0Spwk5xpk9CfjLTv/4tywZ+UW6RsOA2Cl+/eoHrvXXwfePio5C1hKDRMQ2QWI29rh9LwTO14XzmKVJPYgRN6npx6cJFv7Y+42KU02jAxnucWkR97Tecs903DlZ5Td5ZMwx2z4xcuJxJ5YSE5r0EkhlIojml5z4MgcNfAXinapmOqNfeLnNpo9HrGjVQSyg35i0dM5jNeefbVL7XNnnYsnu7qz6ISxMd/xU/Zbb85zCy4e2vNalFSFIYkUfzO91/g3/3b15ARiqrByAEfR02KI3/J435FJgXKWtaZoO40Cni+6LiUU1xVMUkiMxV4p8sJduCl3PFmq5mbgjRYHuiOX/YpEsvdpOHcJWgpCbbjbhF5xBKVBJ6dON7dBRa5hK7lW7dSfnKhsNazepIwzI/oXod9FvjuCxm/fmmgLCZ8JbnHk+pDfGgwnefr6kV+PP0FKlieG065ChXNVJJGz7fjV/mz5KfMRcZdO6UNAmcuybKC59JbvCWvULfmpPMjbh3f+tI++iRb8dkm/kxaKV6H7yOfsCj+NXMBv2n7W6CirT8ZRp/KOny0/fVu/+kKjs87F39ZGjXGpxoL+ON/8xf84s/fYrepWK3nhM7wzk/eY7g6gBdokzEMoLQjm5cErUkzTXtxYLerkDrlxipjwNE0lr7vyZIpMWiqGk5ulayfv03TDGitkEaAiVxeNqyXKeFg2Z1X9HVLtB0i9FgrKXPBYBPa9joamQb0TLGpA3kSMV7jnWBytCBPBM35gYvNwHqmcQHs4LEukugxit5bTZ5EfAgjplhoZhNBP3QcWsgzCL0nTRO6NqAZhYtkPqUwo9Dc/vJA03imeaR3gShSbj5ck96esXlywfvvXGKKgH9o2AQ30knqEZlXxcjaC2aPBbtDwHvLcppw78VbdE6wWGd4epq6GwWYsh49sWw2O05Pj/nBb32b4/UaKQWvv/M6P3ntZ1xuNszSKec/hUev766j0RqhcpzXJNpzqSwyy/AxkKqAjZatjaxTSYyCQ+/I84xMCqQQbNrARHriTNJGj48w8RLTaVw2oYiWvoloaRBpik1rDic9F95xIzF0LtCLUQin9IFOwAUw8Z5J6tETQ3p3xXN3Sk5W77IZHjMNBV1WcLioGZaGm5M1qXdsuw2zZMqL0+f5XvEd6k1NfXXJv/3Rf+Dx5pxJXpLOC6QU7A57VrMloYHddk9e5BwutuA8tW258+ozPHlF8+b5u2g7Ct5NJiVValm7gt5ptk2NaCyy6zDBcZEP3B5K6k1KE0fIURI8OYFHumNlE1ASqwM2wlynKGBnLDeSGVZbatGDkpQxQ+0C55nlRJX0xjHYFqdgSorfNFzOIkuX4c0NlMzxSjKLgtQYzrVj6RWutyMLlYSpjagAl6ViZcExRuNrBWs/rmpXCcycQIYWfE+lI8vNQPqLtxlywfreTboX7jIcL9gNPes0J/qO83rPMi8p3YfMxIHKHpi4Be4XKfVlR5al1yJeiv2+Yr6aEvKefV+RJSnqtkDeVlz2W6ZVzuWTBbugx6JuFCYrOJsYTjvASdrUjDS0vUVaz2aWsjz0uDKnDx5CIPWRJAg2i4LFpiKmGX1qCEJcU6U6rnLDqhpwSjFIgVejA2PECLWa7VuiyAjK4LWi6K6fN81ZtAMhiUQFfa6ZRkW8bNlOCmZtT1SBqCVtopg2PSE46ntriss91BC9pMoS5m2PR1BNcsq2Hw0MrWhSTb6rUMZTTVPSukdHTQwC+9xNsl+PQZZDmZC6gOwcEKkn179XK6oiJemG62h1ZF/mrA8tTisqLUd9CzfC9LbTnPnmQMhSGqPAedLg0cGzmxfMDy1ew5BqkJJMG5Jq4KpMWdY91kBvFChBNgyY4LnMFct2YOv/nEZtcKlk4SV517GbtBwvbrN3gbbv6IJlmU8QruNq2jF74hHLHGt7Ol+zLE4wSrM9csyeROyhw0tBI3tmNkcSOFd7Zq4gFDcxkxVXl+dM30uxP77D2XsD85mhaQJ95fE6Z6ocQVq2w1hjlmhJ8J5BGPK2og8DTiWslgVJEembPY/PK569f4ScF1ztOopck2eSLJGcX1Ucz1KGqwu2mx1GgBY9fbejk5BGSArL8uGK+ekR927f5R/93j9Eys9EuJ9CQiEEznv+5X/4l3x49iExRoxKMWRsdjtWiwXf+MpX+cpLL3+8rj+9pj+9rL/x1hP+1R/+mPc/vGC9mtIOimEIbD+4hF2LHxQf7ntKHVkeL5ndP+HD1z6kUIIoFVc9TI3AejMyJg2QSUteTthZTep7picZh2aPNSnT/EDx/Qu6I8+kgalqmSwMe1Ez6TNcVrLNHbOsxO1qJJHtNLC6AMop59Jy+GBD9V5B+3iCLVKWQTDgsYkm9KPQo4qRtkgo+x5z74q4GKGl88sTivdPuIiKpXMMHyoO1mBjQEYHwXHVC1bZSJVf9R6dGCba4dsdeydYJBDDFolFa8VUCbQMbNqOUkruZjlfuXuTl/83v83qdInIEwbhyPMcrcyXwt3itQDsRx30tEPxKez+0z36UXH/ZzJWn77x+L+r7YF/+s/+hLffPWNSZPguUr99xWXTk3mPkxO6qJBEvFdkpmQfFLLfI5Sm6iMSj5aORAQ2FpYJJMWCQ+ORBBItiG5g7zWrNCCTlM2+IzEaLRypCVRBk4eBYrGitdD2lsxArg3ne8+6EJCWXG46RGKYTTT4gcs+shSW4rffIB5vmN5dcvvGmswfeLJ/n3V2wk54Dt4RisjC5ci250m6Zz2U+N4SBfRmYMkC4Q2XYctcTOj6E5oLiZ0pXrp9n//u9jc5TqdfDjv8Kyqsx2uP8ctUL/4Lw6Ii8Ute7K9xi/F/17d5+ofGz5/2GzfxyQgH4PJsx+XZjqbuiU4SO03XekSSMRzcGEGOCodkMp+yu2rYPNlge0sIklxr9k3Aup5Da8eUtc5I0inDdsv5k47d4T3qxo+6GVnACU83wGM8JowCqlqI0cCPkr4P2CHi0USZobRClJLG9QwBTJAMfaRtPJ2vKRJJu7dEDFULQQisk8Q4pj4FI3OOUwKUxAXB0DuCtTgp8FJTd57QeqpDj5SKPEvotpbhcofAkZiUYjaDoaXqBiSStne8+6sLsm5AZBKHpokd3gUaI2iDJ/QBLQUxTZB1oLPgg8IIyeVVy/5Pfk02m9DdnqELOByasW5lNaAHR103HPYVm82W+/duEYlc7Tdsqx11VxGtJuZz0qMlzdUBW0eIgc5adBaxpWHwEh8iTYwEBFYoKh8RPjJIQ9c5CjUqOjcOohqZNgYFPkaCFagBhr6jUYCVdHVPXgiyFwv2tqUyYIcBYRQOQQA8iip4Oi1BjnU6MgbU2Y7VUYvyFa3u8c5zUI5+FmgOV6hoKbWkjgcGO3A0rMlWCdnNhJ3bwtRgK08tOg7bBgW0XUfsPVjFYVdRVxW2H5CAw/Nk2HLZarbZgFSR2XwGqeeyOeBCwAfDZb9FhEBRCASOXjkuw8CQGbYuEvGUMlJLT5sIDqVGDY5DEkcoQhghADsRkaojmsBODuADg4+EVLANwzW/ek9rHFIpOhdgBnvjCXHApAKrNUKBDxJNYO8DYfBECX06FuN6FYgRag2esVh5LOAWoyixGI85LcB5pHN0MmKGCj/V+CRyVe3YdUu8zWiiI7QOt9txSCO9jUzaMwZV0bqGYR8Jh4z9VYvWGhkFRmvqusUJixgcVb+nkgp9YpAt7LsdvrxLe3/O9qKDwTMRGlUabG64jA5tNE1qEIUhayWESF0kI1RHQ3NN15m3DiUltZEwLxDKUE8yiJGsisioqJUgzDJigC7RCCXx1iFEpMk0aA1OY81YGO7lSI/bZwk7rQjG4wxEo0AYXB9p0rE+I5pIlOM84gnEKOgTiZ1keCkQQTHoawVfIaizBK8lfkTJYFNDxBOlo841rZbIoJBeEI1imKYQBU2e0EfwqSMN0KYGMc0QSlHlKTI1GCFRMdJlhqsYEWlCrUZIa9cNCD8egykhRuosQUpJ3ndjW+QJcUQy0WaKKAVlVMgAdWoIREgkbTZqjJQ6IlG0iSCInipEdrqD3KCcpE8Huiywmw6cb1vqIhCVIMYadE9FS1gYnNzhVwpXD9jmEfnpiu12Q+UVsQAxOFyhxzXHWw6iwylN325RdaDTA24oRvimUAwdNJVAhRRlcurY0VQ9ISuQJmezO1BOc7bblkLrcUwJw2UH2B6lFTvref+iQl5WbPtRTHGWw2SWstu3+IMiSxyuGFWn5/OUvBfYpiEvU6YnhkH0XGzPOV6vabuWSTn5JAj6uawF1G1N0zWcXZ4BUCYz8DWHqgbgarv5UqvhaYWEJxc7Ntua7a7FeThc9dT7nvbQooVGaYPTKT2ex5cNu3iJNYa+GVBa0/SB6KHxgogmKkX0kqFX1E7SRUO1t8g0ZQiSOA34FGxisUQGVRO0otGWoBQDFTsT6TNJP9So3tJ6j89zQj/QlALz/IRwyOh2GpcoDoAPgl4LrBdoH0jMqNejpqAmCjtzKK1pHwv61LCrHcEqhi6y7SBGgYweIQWDSGgQNHWDUwl00DGAhyGC8BHDKJiWacXkeIrzlr5piM4jJite/l99l+PnbmKyFASkwNP6JF/UK5+oP3/aEnsKbPO5q+LTJzw1Qj4Lf4PIxcWequrYbCsOVUv9qKbZ9QxCsDAJLkYOflQkJxr2tad2nmmSkWUZNni6tmOaKkQC1lqqIKB21HZUf89jwAVNHySHoBGDoI4GS4IJnkPtGWJETzK2tWfTjkxSQ+9otKfqPUoZhtZS+wSaUcslRE9HgiwDnbKI6UDbbUgaRyYb9n6LTFIOueLgBpy3ROMIDByoiMri9YBUkiFavA1EC5XpcdFizYy+yOi9Y9PWXPTV6Fx8UXvDx1DuT1r8N/Xrbzj8N9j+FmFRT+fMvuRtf0O9xCe7xWf2/TX4dr/gtBu3Vpx9eIW+qlgfT3ny4yfQ98yWBSSG5tDTtAOrkzkmWvrtBrxnPkmZFCldDzL22OiYFAnrG3OOHt5h/7jj4gNHrgV+sGRCgYQs1XgBIsBinmJcpKstw+DwzqJ0oJzl3H7uCJXPqSpHX/dE1+Kkpu8thRmVpVMBLgxoBCdrw64WGGExqSZKzTAEUh0Jzn1spJlE4wMI70hVoJwo0qMj2osLZCnIypLteYViQMZACJ4yEwg6fOOYLics5xN2Ty6JMpDqgLu6QJaKRAwk/YBSBtkOEAM6NUgPtvGk0jM1Cb2MFFqQJprgHPvLA1fdgRsPF5R5TjnLKI8iMRmIIWE6nXB0tGJ71aC04Hh5xGKywHewXs/p/Rwje9T9GbFTPH7jknDZsprlVElk3zQoJUi0BAHVEFgkAi0NajLB9ZZUC2QQnO8tq0LRp46DHfABssSjg+JgRwEioaEJDu9qjuOS6e0VbzzakKpI9AEbBF5IZgLyCJsIkyiQLuJipHcD4UPF8d0FGz8w8YapmDPMJFsMxXsDZaKxhWQ+nXKSHFH7ntp1rBYryqJkcjJnoksSFIPziKFlnUyIXaQNA9pLZirHaU83cZwkC9CCXgdmy5LESXxrsS2sSPCdRMYEAczIkMJx5vfc6DS2NyRqxLLOVYIiIBi4KQqc9kwyjXCeIowwBidhPaT46ElERBCZkiGlQYiWtTP0A7ReIrxkOihEoolDy4k1SKPxUuClZNY4VO+JKSyGEY9vU0HnLfNBoqTkwgTmQaFsoI2BJlOswlj/cVU1zEVCYhTWK6oEFsslR+WUK9cxSzLmxZxKpVweembbAe89MQlMjOJILUilRKSa1WpJmOVEuSdPMnKfMnjHkEYWswVq5pBBkuqMLEvwqcf1jmOVU+ZLdF8R39+QBIf2FrTiaIhE60g6hwqjonUSxzZb7HuikmMmL0ZKFxEBArCqBjCedLAgJGljUc4SJgnLZsSOt5khGs2k7hFG4iMsDx0yJvTaYaVg3jlEHJfzaT0gtadLBVZLFgm4Q4eIgknTo1TEm5HGtth3iOioV45J62DTM8iENjXM6m6MYgrBxI6ZES+hoWBe9URhUaSknUX3kaAU3geyfUuIcRRk7Ed1cRsjYpKz6j1juEVcZ3ccUkskOYtDO+LdlcQoiak6RAjsY8FqX2MZ61ASJLpt0WKs6Vi1PV5A2ilEqkltRFY9YTFh1fREFcmGhBAjRdNiDIRCM9+NWaS0mBCynHnjKKNhV/ac6DVyf0blB/qZYTFo/BCJk57jOEFETbPtGIjMB416IrFJwmJvSKYzbOxpEslxeYKrG2SnWQwlNDmDdVTGsZgIrJKE00DeWOSmRaoMNwhSXzNbZ7RaMzGCqvckeUSSMpEWrOdq2zBNCwoNrbWsJyWLTGG7AZ9qpolEdh1FbzkcOpJgSAqPswNGSibTnNVLz3B2tePmyRKpG6pmhxKKwmTkWf7F6/hThdyTYsIkLzma3CACRZmhfIKwCcvpnJOjo99gBHxi8Nw+XbKclxyqjqNZgdj2qBgppiWq68lSSbCRiZRIJYh1jTGGMpfoRBPwrEpD34FTikPtKGRPlqUYL8hixGhLGy0uLTlhjq3PYQJTnzELmnRXIyeClZjhT9YkqmaaTYlNQdMc2PUtJ3JOQLKtOorGcDKbM9ydcqY96aWjGwYqNZBONBM5I9qejbbcL46Y3ZlRZQ1c1qS5RlQKCsVaDRxMJLhhrCHSkRg9+yCZCE+eeHo5spiVKmKMYNvDLESK3NB7D9aidw2r0xnli3dIPXzrd7/OzW8/++lA7F9if/5lp4zbUwZejJ8z9z76d/ySAzeOF0wnGavFlKJIsBjOugs6qZmbMQCM8xgp0DLiTITaclpkyGystciNZ64lMVo66VhoiXVgsgQZLNNEIYCL1lHEgIwSU2iIHYsyp20GqiGyTCNV1zBRESUUiY4UmcT5SB5bylJTuIBJEnIp2e87XO/Jh0DZG3RfYlBM64LZNCOIiiO1ZpaUHHzD9nDFUhYgcjCGpU2Q1uFCoFE9R+ka7zz4LSu1QPiSLsvY9g1pByuZc7XbkKcZeZ5/qn3DdY2U+CtkL/6GaYHfuP3NuKb48nTKX/MmH//Kj4p+PvrrryXk8QWvcnJrSdcNhBhQWqKcxwjF/rJGUo9eAA4TLYdHj0bqtkXJ1146RglB0za0XcfyaE5y44RwfMzpc2tMmTNfzcjzhMV0LPpTKOZmQHcBHRT2MCBtRdd5lNLcf7jk9MFtVvdvkq+WTBaR9999xLvvPaLdntM+qslayAbJOht1LhKluXOSorQerY4omCQ9h0NPN3gmZcRkIxxLGMWytHTNWEw/m2lia2kvanwTOVpJsvWS4+fu8LV/8CrPfec5pkdL0CmTqUdKRbWpaZoDp6/OmNxUWFOzyi/x7glGX3GjaFh/eMHqsuZk2/H8k47JO5bFe5b7F7DuIOkk/hBYCOj3ChNy3AGevL3lvde2/Ponl/SP4OKdnG67ptms+dWfbfgX/7ef8j/8X/+Cy7cjzSODuyrwm5zThxlMtsRywys/WHDnqyfMbxr64YpJfYWpKpJDzV3bMKkHyrojqwduS0U8G8hcyvM3VsyOjpmvjkh1wV2dQpcgDrCIAjQIDcXxjO//vfskJxliGlmZSHztQHkuKS4198498hL0RWC+dZRSQAhYBac9WA/BCfwjRxoNvvUMAl5O7iJcTZEpTm+eUreGJ5Xj3bMNZ6+d8X9599/yTx//Cf9j9XOGFzX187B5znLy21/l4oX77J65R//SQ+x315y94Hn/ecfkBzeo/oFn962a/fN7CqHxwrHbXnHvg0h1NWI9o6u4yYBc1YhbPbdVTh0HrBK4VHGjlIRFhThqeD5LCTpC9EQcL+RHOAFtCJwMGYOCZD2hI3CryrCDZah7bvUp1gTIBKGUPBOmDMHTWstNmyNsJNqAU/CCS3HJqJx+uhtQ3hMAm0ie3Vf08Qwfzzl2OxIORA5Ys+e+h77URBGYX9asfvIa01++Tvraa7z4XkVPAKM4fvV5xDde4fD8fS6fvcuDOw+p9pb6gz28v8ect/RNT7NvWD5Jee/yiksXGBYl8nsT9t+wXH214+h/eZfHL3vev1XzmvqQcBuah57qGcftBw/p5GgYy0Rz550N+S/fpthe8cw7l9R9TQgD3vacdJ6gBNYI7lYWm11j1hPN8aZlINITOdm0eCUhRmyIrB/vqa2jHgaOLvYMBIYYGUTk+KqhiYF26FlsKrzzWO9pgOPzDXs69rElPewIcszQWQ03nmyxanQQ596h48iKZrXk9MmWzkiCgFk7kDpHJDBkkluX1agWriRl75gwOvJOa+6c7bBSEnwk6RyTbsAJcIni3pMdLsuJQWI6z6QaCFJhjebO2Z6QJwQpEMNAuW/wUtAbxb3NHpsGghxQsmdxaMBorFacbioGY8YxIwTrXQ1K4QTcutgRUgXJ+K43Dj1ea6xS3HiyQ2iJ0AKnBDcuG1wc4R7HlzUOT1QRrwW3uxXi3l3skLLcr8G7UZxQWF5aPYOfOmRmWTcJmkiUgiG0PLyc4jJP0IIjeYzctAgRGbTlQXNCd5LiMskklKhLAarATUteqAvcqiJOG2bLHcWre/j6jvi9A88+67BC0TtHkgsmM0Hd15wfdrzwTMHQgq0d08SwMgadFgxec2wUVsxJJsfk0yNObh1hdUItU+7eWtMOCUJPySYrbp4uwaiRQei5Z9kdDF2b09QpJ8sjvLXYoWemi5EV4HPL7aetVCUVKx7iHq3xj9bc1K/A1RqxXeHP5x87HX/ZWn60muJHzgHa3nI7yWhEwa6G0+USfCAIhVWGh7dmNNLQWihmGQqwLrLZddyeRroB3ADraYZ0LX0/YH3kdu4YoqTrBuKu5yTtSMUVZlHzkjrCGYdSkfW9U9bLY2Km6Bh4Id5hGATOGkyTcCPcBFfS14rnO1CrC4rpE+7er/ntlyV3X3GcPtPwuzctp9+E42d6Zvcanjk+JWpNryV3TYrtHTEEBue4OQGUJmjNw5XB2kD0Edt7jk1P2/Ukqeb+TF+jLSIuwrPrGdm0RKQpC6G5uen41oM7/Nf/27/Lb/3+N5+qT+UTh+4pDMondtgXdMqnpJ9/cxeKp+y6T7bP3jleO6ApeZYSgqfvLV//7vOQpTRdR5ZIbh8lBNfhQsf9pSXKmsieob+Aw/t40RLVwFRc0bqaRHtS41mVA1F2uNhwq+jofEOkoyhgJfcM/Ya225DZM7wf6G3L7rDjKKkJvsG5irmq6KUjppHBeG6vLUNoqfsDsntCViSgwEfFy9NbeKXx2jDdlWg/oHKBEw3P2Gdpa0OoM078Q9L6FNEf07s1D9sHtHrAJZFCzRBeEKSjMz3P5St8ekDlDX77hP/4B/+Wf/Xv/w3//A//Fe988O6nWlPJa2KOp/vsU23//6VUxWe2vwUq2vpLXvU3ZC9+w7j85PAn13/O0/1Nj/jMvn/xT/+Y137y9lhzsVxw/uMzbBORYoTQaCmoa4cxEWU0HkkMHjuMLAzeK45uzjC3T9j3IGJAbAd052jaseai7xz7bQ/e03UdRabZNZAYR5lpXBCYPGFxOqFYZFydN+gw8Pb7l3QRtDYstCJxUNWBLAkMQuOiJITIJJUMnaUfFOsbOUMUVPuWEARKWyZ5wr6FSRoZurG6zntBkUWCd1R1pMggMMIZojKc3JqiE8XhEEil58n7l0gp8WjyrEPlHU4JZtOc/f4MZ2tsiGOdhUnobEADwpZon9BaKDPN0CmafizwjkRSGem8wZiBSnmaKEnUWEittACdcTLVlNOEbggkuSGdOZJJ4OriwNHplJA2VN0eKSV6WKDdjIuzA4t5wXAYqA9jZEcEh7eWzbajTBWDKBFZiVAS5y1BCdpgKIWllp5eRHyARDiMlOz7yCwT6CxBZoagFPPCsP9ww2XrSZXHp5KgBA5BvpR0ZeBKjrS0TgaQMAi4Nd3z8qsDNt2yWpxg44DUmto3lGbN1WXHB27PLKaEGlJTUM8Ut8spie7YhC0TVTCEOyhOuBpa1ibQxke89ejXTExOljfIfk87c6yHNV2XcRUHEisARyYFm7RlPRS4NFBNLCpq9DYhHQouC8tqAxC4kh0KSVqlmCHnQvWcqilRag4q4ntLpjRGKzayY9EpBhy9GLDes/SKoA2XpufYZ3g1Zlg8kcWg0MZwYSxrCuT0Hl4VuN6y6EfGq4tMsvICJ8/wqmNIJUufobziXFsWVtG5DGRG7SynH1wye/s9ds2WmcrYfeU+4vnbtIVinU1BaM5sz1wn2CHgHu/Y2p551RGEZV9CYQH5PrmuqFeC42RFVJKtbil0jh8SZKd5fLhidoisjjR24siTHCUkmTBc2S3Hwwpec+wfHdBK0d26Sa8zNsc5iwPockqtNNKPEXHj4CoRLA8dXinqj2oC+kASIpsiYXHoGYA20bgYmVqPcp7LScKqsQxK0WtJAGZ2ZGi6mCYs2zFjMRDxSrDuBWlSsEsT5lWLLSBogTWSuUgI5w2bScGkbgmFQohwLaJXEXHUd5aU9UDfaUQ7QpjmTY/Umm2qKbuRFlfGSJunzJsGpGU3MaSdBadJTEZ3vCB/40O8ElTTAt0NIxuSFBwSw+LQglbsJzm6GzDKYqJlXyTMakcMCc3RAlX3aOtRg2M/yZluK4KWtJlBC4nxFuV6touSRWtxCAYtkUaT1T3KBfarCfN9i000Vo+q1ZlrULbjap6ybDrqkw2H/pz20HDsOyZ+y/bYcby4xcbW7HdbvIkUnaHQmvN0z7ov6ZUjCM+QBOZ9AXXPZtIytwWDkUSlqUXPupkgnOZMNyx9jlc1OhFUqWV6ucZeLTkTkUkwNH8wJT6asWkDs2wAZdlGQZkqjE+QlaULmpsLje8HHl02ZJnGR4+Ko57P6Y0x03ZVd2SJRveO3HuqNrBKLUXe0BpPkiek0ynGGM4vD9xYJuj4IZYDSZnx7P3n+Ee/948oZzOkVp8syU+vzULQVD3/4p/+iDd/8ZgYI1lmsFVL3XmWq4KVcfx3/6ffpzhZfKE58NEy/qc/epM//A8/5813zljPSt792YZDC0IbJnqk4r5oA1PCCNmzgS4KFrME3wcOcRTRq21KmuQcGs9EDCDhEBMKHL4MpKWkR3F084LpV17HnWyZJrMxU2ahW0vm2Q0ak3IWKkwviL1AV3ARK270U6JN2bqOxINQkITARWK5oWc411ElPabzaC8o12uedBtOxBR/NOGy3Y3saT9fkLw759wK5tWA2xVcVQJnHYnwRDdQk3FSRDZdhVMjk1YeWzIV2FnBLAlEe4UQA8ponllM+F9/9Rle/W++T3a6vEY2iZG55qPsxWew+58zuT4bBY+fD/t+YaA8fv5en6+bHd/jrXef8M//1X/mtdffp8hTur2lerxj3ztuzEtclFxUPUaC0glGKq46x0RClAmVF2gixIGEyL4PLIxApBm1G6UGUiFQItIJw8ksZb/b0wew3pNpyJWhiopCeCwRzMgOZntPuZiz7aCQDlUUtH3EWc8kMRiVcLYPlLqh/HvvkTysGYLllrAs15aq2LJMbnDVzWlqRdMcWBcn6CTncX3JPGTY8kOEaei0ZWZniNaxU3sWcYoXa+KQ0WnL/B1B8q7DxcBsNuXFh8/zj//eP/ycfSzE063OF9je8XrXlxvk0+l/0ZqL6+1zOhRf4gl86gd/mW983QrXA+/zKL+/+vZRekgw0knKRDFsO5SMWBdG6jEf0elIuVe1A0pCYjSroyUWxfr+mm3j2T/eMtQdqYXEBtpBX6tpSwYr8MGBHAutiBotBW03MNgIVYtta2brgpjkuMFincUkGYkWKCnouo4YDeWsGOs/LmrqQzvqWRQppkjJMo1r7OgI+JFmtm17mg5SqRhcGAvVlRkpLbUC4XA+EBmLmu3Qc/FOM1LYecNqnSEYPd4kz5hMFFVdUR8GslRx8uxNIj37bc1iVpCVEzZXFdJ72gvQIcU2DuvsGLlHkeQpwXlC9HgPMYaxS31AaU2eJhA926rlqvccLgJESV6m+A5E0Pi2B19ez33ic6k+k2lEVPg4KglnhcYkGt7fkBu4uvA0VYcyivKowLvAoQr0OhAYqRSVlihlRvpKIQg+UFU14SCQRrMoj1jfPaZ6+5LERwYpR2pUIVEIjNIkBmQ/fHrUx0i/bxGra5pRpT4e+kII0nmJ2tfQC1RqiL3H7Xq6ykHucLLBikAsPOiIkGMrdNtqpDqsekQSMDbQ+pGqFAQigJBypCE1GmE0RqagLUoGdBBoIdARbNOjZYF1jihHvnQBROcIIuKCR08yRHQoITF5ihoc0Y8UvzbYj+lOQWDUSAkqegsyEBMgBBwKE68p9GyEwaEKQZykqFKN6qkmkpoMicX5Cjf0SGNQMhmjMIOCRo40kXGkDkUrhJTIeUFycwHzgs7bj2NwAgjtwPBkj44SmRiUGEbq2jgmLQXXdKQBfO+QmRmvHzy+G6CNGCGYlSk6OpqqxSQCPck/nlc+ft41jaKe5nTCEK1HIAkuoHKNaHqEDyNdqjBIKXEAciRFkFKgkHBNKfsRu4cSjJSX6toQ8H58dhQgJYGIlCNVqRWCmBpECEAk5glSGISShDhCTKW8/pa8H9GscaSVJcaRV/naIJAfzcY+IpUk4oFrikvvEdfLRwxxHHPhI0z2OAalGN9JGk30Hh8jkrHmRDMmYrF+rBO5FkkVYXQ2pZDj7xMj3bMT19/JvoUQr+mwP6LpvF4gQ4Dr3wTj7xIfUaGLT2J20V8/I4QxXckn7ILEiJ6VSHPAX3RIJZFBEHyE1kLuUNn/m7n/fLYsS8/7wN9y2x97Xd705X1VV3ej4UFyRFHBmKDMUBEz/DAxoS8T84eNqGHMiMTQiAJFQiJICiQBAWx0F7q6y2ZW2muP23a5+bCzqrKqs6sBNjChFXHjnJvb3J1rrb3Wa573eczYX1JhihzpRqphaTQiuvGPyfF912WBUAOqiwQ7IKqxTka4gOgdOhHoKMAYYnyiLO/9SIWqJELrL+i/o/O4wVEsE0TrkHGk5G12DSGpEFpha4d3HoMmUYp0kuOaSL+tEQF83eMGi3SBJDMIIUjKjPTAYLv6ydxgpDUWAnygOV/TuksW1w+JMRJ8oF3tKBYThPoZ4IfPbVYhiDHSnK6w1rFZdcS6phu2/OR3/wPf+j//FeLnc+bp6+OX2ZHP13zfDzgf0FmKc6ON8HmsXRj5Jf1reDJ/jCS0Y8ZOKoGtOyIaISN5krDtIMkNzniCs7gYabuBxHmSxCCcB+dROkPIz21wQRwsYWWJXhN8gk41WiR4G8faL9RIHS3kSEISAmmV0wgQeFSQhHpAEMF7htM1QfQjTXZv8YODOBIa2MGCUzwh/8VkBjoYrENL+eS9hnEBH2mssZ5ESmwEO1japuPuj+7y4m++QX68+HJwvm6j/ZzA71fOe9apP8dI+6nDX+Ckvnz3vrDXhMA3PcNgcSFS71qi0iAhTQxKG2xvAUiNZogSHQWZlgyDAzzGKKoqpelGCvw0MWg/Uv/HENmtd2RZytAPaCFJtCJNEurOIyREF8AHeutIsgwtJc4NROnx9YDrPTJNxvfwCflHORlVsNu6Q2jobIfcH7V0CHHcv5RBZ+m4PtoRWivTsUBMxHHt1FIgtX5i90iwYVx3o8AUKUoE2qZFTKY/Z/Ce/vefU5fwF9x+YVjUFxCmZ2TKvnQU4lMrO+PC8U0Jkyi+6If4DM/6z/FgvPbOLXQG5VyzvFbywtvXwDjQgaOlwAdPEIEoHdVEsbyy5PiFa/yN/+uvsHz5Gul8Qnd2iX1wD7vdUWaKb70zZzkvmC1zJpOU/T0wmSSrUt79zgGL5xaUNwumVyumE0tVJCRGYuSOZrUjdI7F0YIbewrlIwbBsrRIGcgLxexgwqsv5NjdjkLD1SNFUUii72m3Ow4mDVp4sgSOZ4JJLikUKBHYn9XkmUAoz94sslgY9o+nLA8r3n1nSp5rtAwcLCWTNKCxtOstt44GjLGEfk2VChZzSZL1NJtz3n7zBi++cYt3fvkV3v3NN7n50hWmBwXLm0v+5n/za1z51j5X357y0ncOee6VknK5wcsTrs53FCWUE8/N45LXn5tTaCgMvHIAKoGyFOg0YkRD4x2rbYPe7Tj7dEO/0tAmvPTc8+TugMzu8+67L5KlBWUxob9smZlIX0NXR25dm6IxTKolR7eu85/8V29zeFiRuIG5XTOhZxEbytDz8gSW0jCxcKuAdF8S9wKTGyXfu16xmGVoGUhWpxTGc/TikuuvH/PLNyZoAcI79tYNh0GyX0sWveL1xj/B8Srmmwm5S/FqTjcovjf/JRKZUKmCW+kRt8pDbk4qFlryS5cHKJGR25xlv+DA7WPEPrEr+NZpir24R9jcJf3skuNTQe41og/81eqXmSwWTF3Coc95JR4wMZFcB/4Pm9tkPqXsCpZuwlvyNjOfUA6K39hcJRtgRsJUZrzqjyiRVErx3XDIZKKYl465Cbw7TMmCII+Cl89TqqCZek05CH7VHTANkgmK19yCiUiY6pxSGH6pOWRmjpnlN3ndHrKv9pnJq+R6wbcvNHrTk20tNx+0JJ+tSE92iLtnvP7HDeKRIK0nvLAqmK0g2wlEHfnepWH5+JTDOw+4bjWzao7+zpvw+vP8xo1XMLKkVDNupnOumopsE/GfrPj2ucBkBbO04qqsON4KqiEjCynvPtonMTm5y1gOFdeHaxThOmbY45fa51AxJZNTsq7k6LJCugne5rx8epV+A66vULrg5vWXEa8+T3zxFr989TaLq0vKXcO0d7x0UpPFFt1tePXTC0zTkm63ZLuWVx5sSOstabPjlcdbVN2R7lqy3vLaSUM6BNIu8PJpS9FH8qBIouLt+xsyF0ls4MZpSzV4isZS+MC3t4FMKXLnubptydsG1W4QvuPNj88Imxp1uePg7imLzlIMA9o5XvvwMbQNarvh4NGaZWPJBocIgXdXDan1FG3P/vmW2eV2rKmwjrc+eYR2nmJw7F227F3uSOoONVhe+8l9TGbI2p79XceViw35MKCs4+1PTzAhkFvLoh24drYlHzxpCLz+4Smyt2Sto+p6bmxa8t5iuoHXP7hP5gN511O1PbcenGMGR+I8L398Qu6hbBxl53jh7iVF70mbgVfunlO6SNENmLrjxU9PMf3IRPPCSUtmPcUQKPcWvPGeYz5cZS/c4pXVTeY7w+RCYe7U/Kp5hyqvKAfFm/nLHKRLKp8hu8i3PzokIyXrNTcelMzXmpICrTPe/eCAxEuqmHKrnnPYZcyMpjqa8VvhHbIGqiHl5k5yxRdMhCdXgV+dK/IE9irFYRrYj5ZJ1BgvefsokGQKGXsSu+OwgjJPmc4r/pPvHVImCZUSTAhcM4G9yYz5bM6bVUTkCUrDfG/BizePsJtAe+l582iPSRnYP4jsX5vzq++8w3G2z43DG7zx+ltkeUHw4at78hd2y/iPRZly7daSrNBkhWHvKKO5WGPblqFrmRSCT//9j9k+vPzZIIcIr750lSzTTKoMoyTfuV5RpppMRq5Xkqn0zFKBxPPdqykqERQp3Eg816aSUvZkaeC7i4EqV6QMXJkEClVjVIeUlpfEJVWeMM0Ny92cm2pC0eWkrea7fAtz5Qom2+MwOeR2ekwRoMwSfvXsiMLAlMCeh+e6KZMkI2kHfm21R6Fy8lYy2UhunqfkjNobb53t4WtLGjX5IHn5ckbZT8i3Kd/JSzJyiiGhCPBq0pFIS6o918Qlk0xSJIFEB16uOiaqpYxbXqwcpeyZmJZcO16eJ8xLzaJKuLWc8uorN8n3p882u55CynwdTPOlyRafuvY/ItT7zEu+CtG5ee2Q/WXB/mJkuvxr33uRSabYzyUvXJny+kwzFQOl8XzrqKBKBPMkcv2o4oWZYKobcna8WHhKFdjPBVf3S26rgYkc2CvgpTKQYclCQ4bliJocxzQRvDgRSDeQ4smU4JW9hNQI8kTxXOqQfUuuAosy4Vv7iizVFLnhleMEbVrSoiP4nje6hLnsELsLpo8ririPMtdBLvi1xffITUZVTLjh5kyHhEopUq34K8n3yExF7nOeN7fY3y0p3CGaOb+avo1WUzK54PjqTebLA8SLV/DXF7xw64VvNKe/aD8FZxPfmLX4RdtfsM4FT4duvzKffn4C5hm3EE8jAb+h9551+MlNHj54RD6RDC4wDA0xy7j25nWKSYYMkoUTrM4b9q5MCDKh3lmywvDRJzXb8x0PPjlF2IaoNNOqIisT7twdGUn6bqDcS/BpSWkEJlHcXXd0omc9BKKQDDtIvKUqU7a1xZhIe7JlOkvJJldILs+JnWcdBEIJ0kmOKTXv/bt7GAJFklBvYXAttpfkRvLgUY8UmmxSgknxuy2ZMmgRcHGKSQErWNceJVq2TYtRjvfOx7oKKSSbXcCkOdp6ikqzcx4Za0SUnJ1ukPlmVAQNAds1/K2/89fo+oEQIv/8d/4dMoG00nz4ySfkCxiEJ9srSG8Y4vWIHBybOzX+bIuQhm4Y2Fwk5IlimhkebDxeBboIi0mFa3PyboSrndWjUNt2CJQTh/j9La7WpJOcj77fonUGOGzT8aNPNjgn8THy+//jZ+g4UjamLvLJemD/cMJ0ktKdnWHrC+gCSno2fkGZJaTTKUM60E63xLkmZpFHdcJUS/pTx6POoe89wqYp1cGE9XzO5KJlZz2NFJiVRQZBSeC01OggiEJynniSqJDKkLSaP7n8CWma4Lxl59fgYSIik+WMR36gWCc46aitY3s20BjP3nzBD9wD8gBbu+WyOSckAuUjU5PzXvcBZV7QhJqhb9nJB6RlJAuKn4hzsj5jJx1Bwv3hBOE8edC8n5+S1ArCKEh2OtlSxjFv8enRisSDSSJyO/BRc0bqJQHJo6In8REtIUPwcbojj4oBxV3ZkjmFJJCJlLtXD6iSHEJguzcWKqcJzDr4tIrkAqwLXCRg/FisbbrAp1lO2kq6LvLIOaSxmGVC6TynDz9hfnJBExxtNcX/ypvE/RyTZLwnFFmcMPiBxw8b3Pka1/dUXvHxJMNsLK5MsIcL3N6ETHkmKB4tHblsGWgIWcommSOdI4uKD9iiQwpS0DvHHdtQty3TScoP5Bn+0rIrHKeh4zxpcceH5GnCD02gwCAWGVw6Pks64nYgIfBJ3iF3Fi8MobPcLQTaBjyCTycpuh0IShHqjk+nE1SUBCH4bFlhfEBKjUlzPj5UGDFGN88mBj1YZCJR9cAHFaQ2MiSay0Qi1zscIKzj/alCND1WwJmSJCISvcc4x8cHCaLd4ZTgsoikyaiCm/aWu8sZ2cManyXUqSEqhQZS67h3vIcZRjhWrQXCGHQMpIPn/vV9ijyhPVnTpZpWakSM5N7x2dUFaW/pjMYKWE0ydIwk1nPneEriB7oY6Z0nHOwh2oHEOT47Xo4q3mEUcTzfm5L4gBLw6OoeJgpklCgXOT+YomxAWLi/KDHOEkjQSnFybU7iIyE6Hk4N0gfkJIfTDQ/MPhOTErVmm97DrA1KCPJG8JG9w/TokMsHj7h38hNMFKhCIlcNP5l3ZJRE7zg1lxirkDGQyYxPD85I24wgBefZBh0iSo1F+x+U9yiHHC96msOC7rJBuZ68D9yVcwoTGQaH1JrdDkLrmMwzPjkTHN/c4/FpyyAFQRmiqLFtzw8+hLhtaLcWrWFrC0xRoLY7Pug05YHECUkXPO/90WO6BvI85YfvfcDVlwtsMTCZeV5+67vs1Sn7r77Ii6+8RbeuMal5khX6WjT0yQbunOf8dINJFN57Hvzk/MnBgLeObR+o2p76csvk6vKLS7/cx0cB1pOzzRPhS0k1Tfnww4eEJpJpw+XgnwiYRioV+fSiJ42RNgrOu4EkOkwSMLblx7uADxGlNNsuIIxA6YBJPWflgmgHAho79XRKI7wm9YaPr/aofI73G1bK4zgnW+Qk68DHx6dMpYZFgmglp+s1MgSyvORHcYvpIAkj4cvDYoBdg9E5H0zOyS3UBKIUnFQpxglCiPyoNuhOISzQGU6kZjLXDF3PypaItsYFgzSe877HBDsiJJQh0+N7ncfAg12DSQTRRy63a5Krb5HuT5+yv54Rxf4agubZLT7b3vp57ZmGn/jKfeqmIfgdeRYpC8XDYcv1azPufnZK29XshoFMWOLg+fSRJ5OGDkdzeUlnm7GeVkl2VjI3GZ0SaGG58D2lMtBuOXGOTIxClpmMbHpYFgVd13PaBsqypGscJljWLqHKJM265pGXpEWKURLXd3woKtLMECJ8fF6jjSfNMyaJ5GxyylRZTObQzwfadIbFINSCH+4+QQ0BpyIP3QWp1GgNiQu8x8ekusL5HY/bDTKmI7OnL/lTGjQzdrblMjGEl5d07ZaVgx/157zkb6OE/uoYfplI/plD+ZeZxPiFnYufBjh9feY9cQ9+qsDk2bPzp7N18Zlfnxk1eUY7Pbnk/HRFW7dEpxGdpW4GeuuRwWC0wbrIdufw3nN52uDaUY+hGRw+Koq8JCtSdq1nN/SYATKhGazgYuXw0tNZgfceUXoooA2CJEiyfIJvYNNEgk8ISAYHj+5tKA9moHKadkAEiEEj+sijeztWlxYpE9a7SFootM6x0bGrA51TJGXBEAzDuoGQ0g8BZRK6No70ulJgLRghiEIT0IQYsC7SDR6ExEXBEBRJMDS1ZeggSTVoy84G+mCppgWDkqR5QpYnfPTBfeq6Y73e0bY9MYAxiqbpiYxQhV3TjIrZB3sUOnL5eMPFztH5jiCTUTW8kIg8wQfH+W4giQnt56k/FzBSg1CsLjuElJx9coJJDdX+jGw5ZbvpSXRO7z290yPMKVisg2bT024apHKYMidfVFT7C6pFiT3dImNgvXH06xZOe/wtWGWBOoVh11CeS2gEPkRSNRaANo2l++wCndU4JIMAGwJ0ni5AT6CuRnrBIQZkZTlPHdoP+ATq01MWexlWeiKR6CK7UGOl5WIyp24DTXBE4ZBzQ+0D/fYcMRPo4GmSgbhM6G3HVjh65+jCJWWI7EyLqDS9i6xDh5QKnc5QMrINFuFX+NDRFD0qgLEFJIrWeB6oDejIpvSE6JgMDu0sWx0RlSL0HbWDoCQtHl0m7AAfOnxw1LIDBJVJ2SrNloBQEaM9rfBILeiQKGAbPVEGohB0yWg0+yEiXGCrwZpITBN8qnFKEMOAjoGt7xm8o68vUe0GLyLxxg2GmWGFx/oe5yG0ke1qy3bdArBLFL2OBD+gEPRtj900yFKzyxStgCg3aLGhkRadeITq2QhJLRy96YCeOg5QCqQwbL1mV5+R6BSlNA0RIRz4nm6zRgCVkpgiYZikrIuM0A+s6xqhobwxJ2496+ChHBnmmnykNs4DCKHYSQiVwWlBm+mRXrofC703cdSpoEpojCTEyEAgOjHS1M4yKFPa8Y3AdQNIxy4xDEGANlgh8UQgwYiEJjV4LelExIaAVSOkJMk1faoYcgVZCtOI1YqoRjjaLtUMShKUREYYjALpEVpTF4ohcXiRU2rFVgp8lRGALjf0qUYEMKmnSQ3IEiklTZYgvEJFkAH63BBRmGnOtg+EWUVuPTJCk2iEFCMlcZaAFBT9gBQj49XFiCKgNXo81mlEDHRlylqCJ9DmY2F4kUIM0BBxdYucpAzzitBbglijppHGDpC0dFyyEQ678Pi+RgjYJZZhLqCSDFwiyhTXD0it2PgaX0i6Y080PVY4qDK0EGwTS1ArvAIra6yKMBkJFNZbSx8Crg0Eq9gOnkEm6CQhIDjd9PRDx/JKwuXOkaQFWqXYFNbAxeMGhoEOjUgUfTRsVgN258gmOe3Osek9H39yipE9vYBtawmiJrnosJlgtVlzWW959+/8ddQT8TyhFNG6Z2zcX7Z621Hves5ONuP+rBN61xJQ9DbQDhFTpOTT8qc37c+Nnih49PiSy9WO9abBh0BXVazqBoZA7gOCSCsU1gakifQ+4gREITDBs2sGYqrpfIITKTaOxCtZZnB94GTdkuoEk2T0QVDtRdbaEnOHy8Hbxxg/oQ4tPgTs0LDLe2QWkX1P5iSNDQhj6EvJar1DJQbjBaK11NoTS4jpKLAWY00a5UiDnDhE6CDUbJVEGEE2CKI2rNc91kLXWZoQEcqQKEEUnt5HVr2j0ppN26CMJux6lAisux5rJJmCpushBAopWUXHl2xe8Rmd/c2mlHj6up9hkn19Knyj//GMg2fnl9R1y3qzoWkaBpsQ81H1fhv8WJO1axDO0TqJVNB0A8JbwNKGQIdEOoWMHWpacufeGYMNDAx450mMJs9TbOfYhtHRHWwNUpCh2Gw7eqXRRY7LMy4vaqLQJNJQO2h9AKXxvaCRGikkuRyhiH1wyBRCanHZGj03NNrTJzUrX+NcoGksLsLQDpSkSA873eNFxOktUXQ44/C1QJYztgw4EeicJJLRxgFldwgiW+PY9paHzRr5TcrqP6v9JaOj/oIyF09Np5+qvfj6LPpygkaewIq/fuyn7vvN7WlF7i/vM/5+cLjgZG/BSmqW+xNoMiSGokpRUhOGgGsH/OWK7bqj3Vq8d0glOZoXdEGTJh5lxiJpETzGjEbnYD0Gh5GaqAUqgbQyUMG2iVTGk2Ua6wN9PzDdz0hzzcmDhuVBhkwiiXLINJInI3Y5KzXzpaY7HxmmrHUcHFQgIr115DpSqoR0ltJsOnrbkMqRjz9RDpMIqolBFzlht8N1PalOEL7DiYBzgdwItPAI36PkaECmOlDOFdZb+q5HpoHl3pLn3rzFlZuH9J2jbS3LvSlFmTGtZlSTDK3FWLsgWvb2i5EG7Un/JhRwNaFc5rDrePxwzarpEB5KspFSTkMuR6yh7S1Fomlsj4wSomJWTZgtMh5/OCB6i1tFiv0CZpr9wyl2N1BvHNPlBNH39JdrhFQUSWSwHl9v0dlo7FWHBSpN2Dss2NWCs7uXnD1eI3uF1hITNAfzBGMjVjiiSpgVmjRR3Hm0YVYpnA+4IZAlCbkZMZjKCgqgCIGNg1YJpn3O1PW4beTocImylvTMYvdTFnJGVCClYqInFGrOpWq48C3LoBBWku8doM462Azo/ZzVsGU/JqzcCP6tnKLaJGQiImXgaHJE0wyouCOxhlTMUGmJ8iv2dwmDkKS9JsOQWA2DRsSaA58jM0jqDjOryKQmqRvids1hSPC9IZUKJRWpNMyP9rnfXjDZWaxryZMRBzszBQpB6DyHTo41REZCpphHkJuWYAL7A5AZ2i4waEnVeIwP+EywHATCSKzQNL1jsrNkoYeZYZJllNkEvZfiljmL+ZymmBCiZyE17qxle+8CJ2DeutG0Lg2TJ/S2USp2maZqLaIbYJJQBYEeU3CoDObOEEkIITJJUpzv6C87EJqpNJhUI5UmpcfIBGMMF8ZxaDOcN2yGiBgcxjqEXWEOxmxccjil2CuITY/WKdGD3+6YrAeCERgX8VqhmoY8rRDCs9haei1Jh4CUkkmIY//GyF43ZqMyORZnT3uHEoKHPrLsPW7wVEoweE/RDaRCIHNJaUH5QO8crYaJgFwrooSyHZhGSx8sjYZ5F8jSnIttT9E4yjTS1x1NYqiafsR6+4S8GzBC4CPsMsOkHdCpQ0RN1g4kywK1brBtx6IZGGJAe0cxyRHbBjGMWibzbYNIElTwJG2PJCCCZR3gMM8IzYCoB3Q34qNVPyAmJfNdQ9AK7RwSQWIdJkaYFywGR0gMmQ2EfqB0Yz2DyFIW645eBhLrCEpQDBbpB6IQLDcDTFOs9YTWUboJulWokDEr5wx6nxJLn7SE3SmZNojcMm/GAFEXJaKYktZrkqwgWMeiMxBT+p1j2NdMa4Exmhi2LEIKNmLbyM71LFDkQ4bzHROXEE3ATyNCW5JuLI42icbankIPFLFjMTHkoSMBOukxYUAmDjNNqa3i+mFKLyLudIdIApMiIauSUWwzDmjr6GwgqwwTU5IPPSpNmE2m7O/tke59WdhpigTbPmN/fipMWk4ziirl6NoCYkBdm3Nm4OThmkRLqkLwwndfZXI0/1o48qlwq4ArRwuWi5Jd3bG/rJDrHarS2N6zLBLatkUbxbLIsZ3DemilZF4qYtujc8NelVFvPW2wdNIwkRbtAn0UiDiQR0U5qTjZtKjTSPWcIjSKXJfkbg5qgkJxKGbsNhYxBPJOYlqDjpJoNxzMCob5FOFA7wKq8YjOEs3AYgDrNWKekicZKoyaNSe2YdFrVJKThogaAuksIZxGWmdZplBLiWodWaoQwZPosTZyqjRaCBKd4Z1nnhpmU8PJumWZjdSqQ0iwMXD7lVu8+OtvcLHaMK0KjPkZZt/PiGR/tSLmPwIS9U1N8IXNuL83pyxzDveXZGnK4BTEhDxPWUxKBuuY3D8l1D3pZIZA8+CzU0olkEoyLxTDrqOcTEiUpk0Vdrshk5JBCJIiI1GabJJjH6+YGonMckKZIyL4zpKkKRe9pzJgdzWpt8QIVZpQ7k14fN5xdZqy6aHKBNZ6MhlJJwlbbSnayJ7NMMMRUWv2947woaJvNXORMtWCoY9su5qpEwQbCHbNNEhiyFGzjJqWuS/QTAm+ZuYTnEsIMmcXUvayjBA8bgvpoMnWgc3lBqRkOqtAwHazI0kT8izli8L9/z+3X9i5+EWm2k9n1552Uj6/u3jSOd/0h8XXHIwvO/Lq8VX+6Hc/IdYZxf4UM6t4/Ml96pM1U9Pz2cdr+sGTGshyBUgmueH2Ycq9c0G9a5CpQGceOaRINDdvGT678OjMMF8mzI4yPrrXEpxnqTvWFyCbQFJIqsLx2UaQzSve+q3r/PgPHxJj5PzhijIdsF2KVooq6bGxQKcppsi5epxx52EkCsliqbj3yRo/RGSi2F/AJ59dEJHcPs44rz2xV2R7FVfmkU8+6QmtZ1JC7QVt7+kHx9tvL/nJZz1DM7C31LTNhraHQQSms4ZL20GqOL69IJvcpg6Kps2QYsL/9//9A5zz7O9XI3XaKhJbw7d/5Sbf/8N7dLsUNV8yrQwnm8fQKV779au894MPEFXP0Qsz9o8M7713n67rSe2O5ryCIMlKRVpILn2EwXFtKjhrJAQIRnHl5h4f/uARzjqE23D2WUtx/RBpFG++c8Dv/ZOP2DrPO98+4IMftLjOovKUKxPH3UdwdtIgug2ndw1e58hB89avHfIfug06TdmfKP707sBAJKkiV0vPj9oeT+TmdMp2NyCCxNXw0o0pP7zb4reR+UTQDyndxiO04mo1cCEELkTyLqG7M2Uzk1RxwW/NDvi+/0OGTc/14japkqzaNb3reWN6k39efogPkpkeWSK2fSBOSl57OOEHPEYsU5Ih54owrGSLM4KX3U3+pP0hfRkRneBom3KxWBMzxVu7Q96bnpL4gSrJqewNfqjvMQjFO/Uh30/OCYlBuYQbcsp5/IR+t+W7e+/y/fo9IhLReW6Kkv9Q1EQVeVPt86joGbqaoYi8sJvxR+kaIQX7TcYD1xATQ+fh1TPLe7ckSsDhWctJGhFGEYBXN5E/mEd8rtlrYRcdokhxheItmfEH/Q7nPAebQLc3hzJhcILXvvMrvJ/2uOC5sjgkZAW+rbk82fLK++e8t5ciRWSyHTeErU6w0fPKgy0/ujYlCCj6gFGOzVTTBM87JwveO5oRtYaLDBMU/UIQ+sirnxZ8/0GDLzV5VrGcRzZTS5gp3homvFc2SAY47TiupmwKj5wqbt3Z8XEy0G08006QP7rk5EZJMin49aObvL9bky0rTLrl8N6WH80SYmK4te45LWAYHE7D7Ys1f3JUoITi+KTm0byEHKzvefGk5U8OM2KQzE5q1ssClWg8keufbfnxYYYXcKsN7JJI9IqoAy9sPH9UBbySVOuOrgq0eYpIPa9+csGfXk8YRCTrPUpEmt0OH+D13vInemShyroOrRI2RY4zmufvn/P+9ZFpq2wHEuu5qDK6BN6ZFvzxySXCRDLfUu48dbUkVCW3/+RTPr51BRCkQlJuV6wmU8gCr3x6yUdXl8g0J5nNyD4556LMCEZz+9PHfHZtjyABLTlcbfjgeI6QgucfrLh3NCcoOVIdX9Z8eGWGMIprJxvu71dEwCeaW5db3p9mxBA4PtvxcGkQREJheCkv+BMhiEJwZTPl6uNDzouSK8ev4LM9/rn9fUIM3HL7nMkNPjh6I3jlk5L3nqsxSjDfpLhZRYgbeu954/KYP977BOc8y2EPaQxruyGEltdWN/iD6UdYBoonDsRj39FX8O23DH9w/RLd9FwdJP0PFI93iiTVvHYEH67ApCllZsdMaVSIJOHFouczmyC0xPYDxjc0jacsU15fGP7Dw5qgDIkyPHc84SePLxnahttHB3z66DP605q9peRwuf9UFHCE0elEP0EjPAWv+dyGEaC14jf+xuv85Af3iRFefP0Kjz85409+5/vY7ZaXXr3C23/rl5FPDN0v7vSEJOHzGOWVgylaOIwYwHe8epTwv662hK5jmcBlVAyJxjrLL720z7+91xC2HQuj2Q0D50MgblpeyAQfBQ1xYDGTdJtAv5MkuuTlvciP2BLzSJUnTCSsp5KI5fXyRf5Q3MdK0C5hfplzvuwhwEune/zp3l1cGonecjxPOCstNJ5X/rTgB+WKIDuUD+xvp7x/IGixvL6a8+l0NxYto7jaZKzKHq/gTQF//LDD1ZGoDFcyy3srgZSCa6LmtBN4J/ExcCX33LEQjeagSth5SUwy5OGMt1874g9/cpdEwPyF6/xP//r7bHYtRZ7y1//quxzszZ/q988F176M9D6b+emLCtuf2cTXvn+lTOMZFeCjgPdov00mFX/1N7/HRx/fJU1TXnnxOX7y0X1W65rbNw8pi5w//fFdjBS89dpz/OmPPuPBxydcm+R88MEPeP/hZ0yODW9eX/Dj//ARXWuZJZ7Z5Igfr1p2dcd3njvm7qZDywAx8Py1Q37SQbeueT7XPOwcTd2hBsFhUXAu5+RJwo0pnIsEpyIXXeTWHry/7UBKjpYW/8YjpBrYMzkvFb/Bv3crYh25tbrJw/Mtq3pFUAnvVnv8fvsYHz3PpVPs4lNW9YZu3fDqg+f5STzHq4JZvaTTC6xJ2VrBO5e3+IN7LZthYGkSRJ9xcV6TKMmt5cA/ufO/II1mb3+O1nB2eoFSiu98721uP3f9K33+1fH4y3M6fmEq2l29+/xWTz7jU+vNz6pe/zO0OBYRjam8n5OHe+rQ1/2Qf/b3/oD3//gu6/Md03nFw5+csr7okTFC9EgR8F4wnySIRNO0DoIneDlGz3XG0Y05Iq+o67EmgCyCiTx+uCXRnkHCunVIIZg7gekc/aBGKtgkQc1nBO9pTy5IlaBuYDKRCC/ohxHGVE0MB9f3WK88iehZXTY4B0jFpFL0dYv1hjwJDIPHe4GPgqKURAPrFuaFoN0MiCCIKDLtUFrQDIroO0Ki0JkhSk2qGvp+TR/AqMj8OpRzQW8te/vXCW7J+dlAWRmQAqUl61XLclogQsb545ai0Owud7imY7N1TEtBkiqGoJkfTjDTHdm0Z3WxZf9gQewFJ5+c0a1ruhqik/ROkCUCTEHjFVJEpAQRHZsucuXqlMXxPvd//JDgAkasUaom25tx7flrtKuSz35wSt/2pLnGaMGmgStHOVIZTu5dPGGKEEQZaXpFkTqSyUB5WOB9oDg65Oxhw4PLnqNlip0IatsxDJ5JMjKq7HpB4gf6QY4p/j6wlwhyozm56Jml8OCao59GamCmPDoJbIzglZtXmN+6R2rO2LmGa+URudZc9hdM9ISzsKBrU05XFxy4jNh7VllgOZ9Tnz4iVZGVGTheHtC0W87FjsxpIpdM1MC66jiKC4L0XJqGzGt0TEnJOQsr9u2MTiVcqB4TFXonSIeEB3LHnstQeWAtG1QQ5ElOnmY89BdcdQuaS0UnR0hOEgVJrjmJW5Zbw2ChMwIfI5MhIY0JZ6Jjf0jwk6uEaoobHFVjSWLkvNQcDKMz24mIN5KZTNBS8yg6jvKMdvBE52h6yyIKdKo4l4HD+RSXjoZI7Rz7pkCgebipKR+usCKgiOwSxWI3ICNcpoqydwQpRhhNkTB3HsLARRZJW49QmlQZtlXCXhQ471glkbzzdB/uMC7lYnDsC4u6nbJbjJTRGo+Ogc1EsbeOuCSn1iOrh4mRZPCcK89yOzKabJQYIQppSrEsWeUJyx4Ga9k9YUpKLaiLhnMziug5LenGUCUzL9HGcKIFe/XAgMdKgVOSqR+ZOc5TydIJOgJd3xOUoBo8qYycTxNmXcDnhqgFXQxUAwihOcsUCw/B7Yh+oEskUz/SK54ZqPpIeXAdcdKNVLStRSDYFBl5N+ClQEdPnaXM6h0igVVlKKVCL0rCZ2dsy5TpqiNayW5vRqYV7mJD5gKbSc60rhHGsa00ifVIp0mcZHdjn3nnceuWndaIwY4Kxy6wnpcsmx4bLE1hkAi0C6Q2sJoVLC9rnJL0eUKMkFtH6iMXs5w96+mjpTXj3M6GDiU8F4ViiSRWM9ptjw+Rm6c7fvNHj1koxeRvf5ffnvxr3rcfM0RL+nggNjXnV2C5HrMJ0kj8LCE79aiq5LRomJ14eu0hS+hiy4GdUpici3THMj9gawZs07OuL9jTV0HPuH/+kEks8M0E2aSslWX6Y43/6JAHDwKZjpTVFLtpuGwCh5UkCsmqg9wIAh6tPOtBsswCPnjOt5b5LEcGi9GBiy5wPBOE3WO6vsEkmjwJ5Cqwblte+/bL/PpvvsP3vv3qF3uqbUdmPP2EberJZv/lx9e3/acNSx9wg0MIgUr1F9c7N+6fT8M7IpE//v5H/Jvf/wGf3n3E3mLK/Y821FtP3fTMsowsybiQmtxaBp0hlGa961lODFrBo1XLNJHYaBBI6iEwQ6DMlK1LSRmwew2h6KAqOVqu2X/1Pt2VHZVLcMcHCFNyEbYc+AnD+YpT3ZDFlOh3ZMPAZd5y5BYIpdgWljwtGB4H9FpxnrYszyJWSbZXRlFUVQcKU3GmWxa7jGgL6jwDH+HfJfB+ysk6MjGODjFCgIBUtgg6WpkwV46uXxENCKNZlCmx6bjoHIezDJELejvgYuD4YEJZSE7O1xwfLfnOt17ib/zV73x1eL4ybuIrw/lnML3+/C1+7fObmohfOT8+HXyOcHZ5zr/4V/8zP/7xj8nKArYwPNjSCM8kn3C+1qytIKlyiqog1gMnZ1smmcGlFavLjuADuZFE79k4OKxyWqbUVmG0IaskQgbOO5gaT8eAk4K8Kjh48Zz06mcMhwPHk6s8fniVzSqjd54ZGuUV97cNerWlFRaRQFSK28cDs/0L1pMds1jSDR4RBa2wLMQ+QS95ZDsWMaH/0Yzw2HCx6ZkFiW8MZ5tIVUnm8SMOJw1RCw4O5wgRuLxcUZQ5L770HP/5f/k3vook+nph8ze0/31Q0X7RnvZX/+yOxNP1YJ/XDAn5DHXub8rOxfiVE+ITB+VzpoPd2ZY4hBGIKyBLElIDfRdw3jPUDh8E1awgSXPKaUXbRZIyYXfZsD5psX2PMx6SSGMls2qsHciyBKkl7CzGaKyDYRjwUVIAu4sdwnl8EChtkFHQDg5roZwVVNOU9eMV65Wnykfa3CgiaZHQ1jWp1vQ2Yn1AKkVSZAQfsa7FJAoRI9Z60sQQbWRwo46HRGKdZ1Jk1MEydAMuOFThkFqBDUz3pgR/Qd966vWWWXWANGPfddsGOzhsNzo8Q5kz2TtgaDx+s+X00QVZZghBM/SBbtfQdNBcbljcDJjUjDUGARCCdF6SVhnp6YBrAqF2IAJ1P9AHTaIlmVZoYTAqUG8aFlchm1UMuxYdNN4FmnWDdwEhBdmspG8HcJ4o1UjV6iO6TJjuzeibHsKAc5YYRyrZdtfifcdgHaqaYoOHEHE+YC0IqUAEQu8QSILU6CIlasXQj0wpzgdMadDGoVNFkkh6ekIMCClx1uKFoKk7FkqOVKwhEIMnRvXEgR6x8VFAcAHfj4ab6wZsNxCIOD+qFw9Nh54V+LpBFgnBSVo3CtChNZEwbhJKjPNcPnmHYhhfFyWINgAKGzyCMFKfxrFWJmiFJ+I7iyoNPkiUEoTBoVKDcIHQWaLySJWO9K3BEz5/x568llErZGKw1hND+AKnjZS46AnEkfJUSWJr8Sqi5imuHbAuEK3/4pV2m4ZQarrLLa5IEAH6bU1jV3gnsakhMrL8RaPHHx2Iw2jUoxRRCmKIRCUJ/YCPgRhHrD5GoiY5YRgInSMET4wC31lEogm7kRoy7ueEQhP1uPDYwSEZKQ2DEiM1aqqRg0f0Ft9bWOYEnSASQxgs9I5+XcNqR7fI6YKCIgMtcb1FtZ4YPFIZlNFYJUBLhNH4AYQLoCQ2eLyAoEfF9BACuECQElf3OAEoCU+E7rwcKXKFFmPfK0WMEEREyVF8M1hLlGPhflRypKENcSSA0BE/uLEe6gm16JgtBqREKPGEPUgQpSLgR6jkJMdebPlcClUoSQjjehm2HVIpghurP6SQT6LW4319DHiTINIE++gU4Z/MK6VGukY9UjRG52B85RlDKuKL6Pfnzxo+/10+ec4QCUoS/BMjSisIivCEjlokhvCEcjU+uUdMDFQpelESXSR8vgEpAWWO1AMuBJCCKMf76lmFd2HcjSYFMEAMRKMhKvy2ISaBKJ/sclp+sR4Qw/hc9UC0YxE6QqDylCglSkvAjcJpPoz7pZD0TQcxJS0SdnWPyiVCS7JZRpSCrdvRNT1pKtBaEuIIo5POo5RCKQXOkU0zWi2oz9bj3H5qr1ZPshbi6b1YfG0T/8IM+BLmJBjnpcmTZ2zeT4KJT31+uY+PPyGCLnKG0wt0BNf2tFHSugFtFE5EnLVEOdYwBesJISKzBO1HCHSSJuRG0249KMHQOYqywCaB2jqEGucpAmSZEJ+IWvpuwOOw3hPFGJREMNYuaUmIEuk9vuuJKkWVGbF5MtaLfFygBIQYR0pTawnBjvBUrca/4T1SQugtURq8ABlHmuoQR7pn7wK9HbCVJClTmrZDqXHN/nwd7pue0DkGb+kHSysiNg60/YCbT/DWPUF68GRcnuENPvE4nspL/UfVcf/Z2lN3fWZA+qu1IuKLJxk/BeOYmTJDaImeJBQvTYiXa/LJHDn0Y63VuoYhkGXpOL5GEzpLUub4bkDwZA2LgbrvETqitMbHgBCKoXfEoAk2oNIRTjr2dU8+zRFzDUoRYsT7gG97nLOszhvO2p7MB0QJ+FFX43JTk5Ydg+ywcVy9otJENcJMgx3rZAIC5zxDM1JrBxexzuMDOAshBpp1DanCLSco/aXdO+qRxJHW+4v+/dw5+9KJ/MtovzAV7TNDFeLP9tCjMfJ5qu3zLejzn6fv/1MXPfPQ118SgeDVd2+SZIaySkliz62jnIOZ5Ogw51svL0gUeMaCoNsv7HPj1RscvXDMr/8Xb4yaC7uWy4/vMVw+xNsdaRJ47WbGYqLZy2FRKI6mkIiAtpZbVzSIQMRjEskLzxWovkfagReuJRSZxIhA8D2vv73k+PYeeSJQzQkyWFITUSpw7QrMrpdEY1nMPInyCCyTScqLL6ToQpBMFIdLAaFDa4dUnueuQZCerNLcfmFGeZhiK4GcG24dBMpCUxaCZSYpSxCZZbu74NXb1ymvvICsblLNK6rlhDArsVlKsnpMf95hrCazPfW9++zOzuk2O64tLWUukLFB0zDNLZMyjiJYqzWP3rtE1BWz6YKbzx+TZyXT/T1+67/+DsevH3J4s+D61ZLbB5ppUZPoDRNxiRguqdSKuWq5fqTZ29MUsuPWXkpmEkIf0NHz2rv7HL4oOXwODuY9qfQY2eP6hisTS14l7F1f8L2/9jy3Xr3KbFmgpOBoNgp/7R0tuHmouf3CMZMApnW8PpcoP/b11UqQe0vqPcZ6XqoclU7ZywqOFwa6HXkqcXbgl3JN6gMT4NBGFhEyF5C949fzVymykZ72KO5xJdmj0oZMSX5r8SpFnjIVioNGcrVNmQRN0ge+56+SqJQ8phz5CccrxVx6Sun5K+ZbTEzG1CYchikvuuvMfE4lcn5NvMUsKg5iytV8wavmOkslmTrHb+Qvk5aaSS45qEpejVeYaMMcwa+KF6nawCxopkLz9rBPFQJlZ/lut2SmC2ayZJZVfE9fZyYzJsHwlp1SekGJokDwrYtI0VqqzvPiWU/ZOKohkiH4ZZsxq2YU1vD8hWVBwoQU2US+9bin6j1V47h53rFsA2VQyHXP6+9dIB/WFFs4uLdm72zHxAVSF/j2Z2vyCMUQONz0HG56Sg+pi7x7b4OxnmzXs79xXOugHASFTvmezQgnK/L1jsmjHcePGqo2kAyB7617Cuk42M84Gjwv94JZKyla+NVNQuUSJm3KwhpuryJlL0hrz1uftZRWUVxa5uc9z3+2Y9bBHMO7MSOThmLnMQ833PjBQ8zDDcVm4PXzMSpV2EAWBa+eWyoH1RB56bwja3sm3lMFeHfrKayj7C23z1um1lP2jtQGXr+zIusDZR+4ddoxbyNlJ9Bt4N2zQDZIijpy66Jnb+eZ7RylF/zqLqUqF2SyYnbhmVtJFROKrOC1zy4R0aL6luVmx962Jht6kuB446OHJD5QWMfeumV5tiO3gmSAV3/4gCx48q5lvtlx1DkmUpJ2ljfvnGI8FINjVluunu0oe0vaWd54/yHVckK6bpjueq49vKRoB4rB8tqdx5huoGhaym3HrUeXFP1A1g28/OEDst6S7zqyXcPzn51+cd2L9y7IOkveDeQu8PKDC9KmpSDw3MMdZR8oo6YyKa9+ckFuLYWzzJqeSTOQXluS6pSX5W2mPmMWcl7cHDEfSoqNIO0E7zy4QUpJHipeXr7GUXnMNOTkXvPdx89T9IaZnnFtOGC+zkhqiYqa35TfJq0jE59zvSk5+MwxGwK58/zKWUmmPVPpuXpFckU65oeeycLzcnaJyTzTSWSW9Vw/0BRJJNqO16c1hRQkbY+5XHFF92TRs78oeGfmKHLB3jKhMIKXrkyYTQtmVcH3XroJQyRcdigrePmFL2EVkS8hS0/DaJ7VfkrE6xuaUhqp1FNohfHn5Revc+3qPm+89hy3bx3xn/6nb/HcC3OOF5K3jgvyGEisZ6IVb6YDRZGTFwU3jiZMyoQ0LYhovnU9x6DJnGQaOvYmgbLwpGXkFdWw/3xgfn3DzCbs6ZIkLVBZzm/kb6PqlrzuWTyyPD/MWShF5jy/snqeyWxB1Scsu5znmn0Ka8hUxq+IV8i0YqY1B1nJ7d2MScgofMJb53PSWlA0OXOR8/J2RnpHU5yVvOoaUqA0kUkqeXEykAtHrgKvLhW5gjJPmE1Lni80M1NQxoQrIjIxhjLPyacVrx4vKMqSMitYCo1oHAma+v4l2Z1zwuB+xkj87PH6j3UsnpXM+nOd9JWMytNG8vi5nC9ZTJdkyYREl7z99puIZILI5lTzGa+99hyZMUymFa/mBtY7Ci1Im4ZXSkHRr5ilA69OBNMqJTOwn2veumqYVYpUeq75HdcOC/bmEiUHXltGpgeB/ZuS79x+k4Pli3D+HHK3x2/u3SStHWkXkI8u6Tc1crAYEXktKnQbSTvITjO4X5J8+Dzp+W1+o/wO2foF0k9vc2O3z8H6kOL9ffSdKb9S5phGYLZwlMHxRFKkkUR6rpQpK7vgdLdkt9IsZlOyLCcxKS+/+sJPjd4XJvRfchnGX0LmYmxf9XKf9pb4Wsrtc0fkqTDIFwGQX8RPHu/7+P4lWW5otx3Oejq/Ja80CMf7dx7R9R6pNdXehOL4ENEGhHf8+3/4Q5qLll3jqSqFSTPyOEJ2zlcNWgRUiMR2YOdzhBthD2eno1c5REmRGM5PBtqtY5qlXFw6tNGYqDi8Ouf8cc/mrAZAFTlKRnzwTBYlTW4Ymp429mTa0PUtAcN6vcG6jKZ3hCiZv7iH4YK49ehEct5IpIF0kvFw23FmO/ysYKc9ipzlQcr6sqEJjk71iIlguix5lO0RZcmQJKzUAV0PqyDQQTB0EzIvSIShrjvqvsP5iMokVhX4oSPPJPv7E9pNTQgDRamJ6QF21XG67ZnlFntsETHBqIz79y6YXcvwacm0Stk+PmM4idiux3c9mkBdd1Sq5OEPPkBOp2QzwWePLwgBBhvYPNxwcnCHdNayn2su3t/SbwJaaPA9P3r/MVGkTBZTPv5xi0wUaZXh6WisgdAhYuSDP37I7FAzTQvCbstPPuuw0qEzQ5+k+OC/ENS5aAuS1tEGQaMMemZoT2oqDR/WA1kqcCGwFQFlJFJG6AZ+XD8kWxTUyY613xEtKOlIleTD9i6FKdloQascbRgzJ6aL3E1qsiSn95FOWlx4TErHNE25J++wNxSc+h4XWjZVxARD5gz37SdMfMQZS2ocG/WIxHYkRvJp80Pm1YRd36GaSy6KHUWh0Q4+tXfRvSOuanRScie9QEaFtJ6P1BqGbMw6dJ5PuxNS4dFC8EjWyCCR0aG95k4eSIPEhshpodBPoihZnvGx05iVx6G4yCuUTHBtZOIVj+QoQxOEYF1lY8jBQx4VD0tNMgj6LKHNIYpRMC1xnnvXlxid4hJFvycRTYcEshC5s8gxUeCVoteeVoIUCtU4PoxbEhw2kQwZeGEQPlJGxYNbU6Z2LJoWPnLRBoSQ5F5yF9A7ibACt3WslEBcdCTWcy9PkN0oNMi251RK5NYiETwMkMuEVkkyFblcSIwNiN7zmfOIzUCcZug+clYojA0EF3mURhQBgsd4x/1Kk0qJFZ6zUiHdSFOrQuT0ypwcRR9hMy/RUqFUQiYkj/Zyqiql9YF+EpHbHmM95RD4REnMOqISQ5tXJEiCkyRC8+lS4ZsOqyVr40kQxGCRneP+XkHmPL2SdIlCyBKT5MiHGx4elGR2YDCG3gi4dkBY1aSD5cHelCwEXBQEIdhUKSIEjPM8euGILEnZnG/wPrCZTxBRIJ3j8eGC1Dk6QMTI+bxEh4B0nkd7JXGwxFQhYuDsYIZREhEjJ7N8FEaLEdl0PFpkKDzKW872cmTnEUKRqIR7GWhnCYmmKzRWjnUaMUbOhzOKYOhDZLf0iFYihSJPc+7s71CqoB8GHm5PkUNPMkvINoF75Smp1bjasjY9cSawIeAvOn4g/oTEgjWG3WaNkwIlHZlOuHOtJg0JVjn6rsXfqEjPLGnwbH1BZnuGLrLtLNVkD6k9WkUetzkKR5VlaO25rAPCB2I78FHvSHKHUAmzmzMe310z7HpkEfng0QpdlXDRkOQFD++esVg+EesKT0QYpfzKXv1Tmz9fNWD+TMblF4CHL7MdZZHxX/wff42Lyx3VJOdf/t4fc3Czop5G/CaSNIbZrGC+LHnwqIUoCBZOH1uCTjGFokgFH55JiknGro30ZUQVCtlGprOCR1fv4ctL9F5Em5bzyYD3DjOteJ+PkA8fI6tAlxiGNEG4jtIbPq0eMlnss3U73K7lRI9ZZ9YDP/YfkOHZMaAWCeveIhqHHiL3dIfpU4QMxEZx5/0dyAJpPXfuKRItkF4So+PCpwTfkiSau2uL0QlKaFw7cKYKfOjRRnNBIKsUcdWTBsWdxzXWe6RKuAwSpCEqydB47nx8iqv7UfTxmQPzteBw/DnG6DPrKf7Mh/nSSX0qcvy0TfhMlMqXX3tn2Wx7iAYlDT/5+BwrC9b1DiMtQ3tJOs3J8oyNFpSJolvVzOYzLk7PyFOQyrMxCu0iqRnZMh57ge9btIIT79H1it5LisTzoHJky4z0qOReGZEPD6nrHVVR8v3NCrHuWG12bK1HaUUiBJmAh1aQRMWAoO0TxPkCMSlJ2eNPT4G+ot80PL5f0j8YaLcKieOP44DQI7X9+brH24EYxgDph5sFnjmNBXPm6XZ3aest00XFo4dnvPLaCzyVa/7GNjr3z8pm/fnbX4hz8Wyk0jMe7hue98us19MpsGck4v6cubmT+yvOH21odh1D57DAdrcb6VqDpJpUqCKnOl6wOm85u7eiWdVEB5lJkEphHdSDwwVBUWXoypDNEvzpjt5ZrEqwNtL3A1JJjKnQPjLYQLvzDFbS9gEjPEmq8VHw8NMNMYJzmhBG6AvAYOHR44ZuI+ikQKDZtZEQElwY1YzrQTE4gfWRhw+3CGUQiaHuB2wP7aDYnTbISsKkohsirYsQYH2ywrlIMod0OQM/4IqMB6ctIUb6aHjwqKYePCfnLdiBechQPuCCJHqJJyNIjUWxri34SFSCMJ2SFgX6/orNpmWz68nKkm4z8MEPH7A8SSFNMJuBdOIxmR+VN0XAlwlxlhGNQBtN1BY9WNatpb+s8VvHZDnFKUM/9Pgoefz4kuYHNaJSozLyYg/deJpLS2gDMWp6D5t6g1Yj/MIGRZp4Zoucbhjoz2qWx9e4OOu5OG0oJgm9gW1saZqBFoWIisYLpElpW01STAm9Y7drR3rTJGMbLJduoE8jTkq8Am0inYo8tgOzfkXlWmrdYbynbyydqulDx2lU9MKxyQM29YgQ2anIIMHLDpMYds4S3Rlm2rNly6ACMnQk0bJLek7DBSKmbGSN1NAVCVkXaWiIIqFOJKesEQSyxCAY6NOWR3GEDuwICBEoKZBVZK17glgRs4J13+OEZaoiSgYufYsPA0ELRgUFaGNCFLDDEpQk0Z42zQne02uBMYZtpYkuEKxjKFIIgZBKUNB4j4gBXxmcjDij8NYTItQi4mUgTEqiUAxPVKmFDGwzjTcSW2YopRjUqEIfvGWnYFAS/2TdGZQgYkDDVkMjFQhQITKkCmEUoKgLTWs9Ko6BgEYJhPVE79kZQZ0ITFTgwsiIhcADdSKR0ZAOowFba4GfgBSCJjWIGKl7UEKw0xIxyQiCL3H/vUMCTao4E54oBW2miEBvRl2BnZGEKkEYSSMjURi80QTr2RmJ9QEvFT4xBCFgGKFy2xjoFeAsbjOug50NSCmoE4Uljo6BUVg9wiy3IVIbQSSMtTW5xiUaGB2OtkiwyUgZrSL0T+AdUkl2zo9UsZMKTU9rJMJktIliHcGU2ajU7QNdaogiJRhoS4XKDUk+R7Y9bZHBLBARbPMEHSLNYDHALtX4ZQkG6nTU/OhqS5SKzmguhUAoRT/J8cNAqXJkiDSZQRYG6wN1NsIki1Qhjaab5Jxax5Ab2lSClMx2PetMMwc6BlZ+w2N3SoiBOs/p7Jad6ZDTgvp8gzeKoCB0A1IEtruaLk2xaSAAVgZkkeNly0Z2OH+BNRFUwGXgkTgn2CSOIY0MuzWoCR0O7zO87dgojXQRsQsQNNthoLWRVVNjVUnjHRJDqiWbxmG9INjIximaTpBlmsx5zk5XhLYmCYEhRJre0UXIM0lfpNz77IQf/svv8/o7z38RXY4xPsNQ+Wm0wlf8Bf4sDsazz1BScbA/x1nH+cWak9NzvA/oyT5DMKwvOuqPT2nVDK8NnfOIQdBvLY3zNCrgQ0KSSHyUWGsRu4GNF7SVwVQBtYyQCNamR016hkXEpRtc2+GLhi4JRBSSLbukocsNvl2T7Do2SUcsRmX2XdIjREdGjkpGquETvaObStZ1BxpyoRFGslWBIMAlil0d8PVA4hKkyNi5SD9IrB3ogkH2EiMdWZkxRMXZdkAb6L0kWM8kC4jzgdaO9Ly99fQ2oLXA+wGFp+16ZmXGyrkRtvkVG0v87EH6eQP357VDn6qXeNbFIcYRlvkMtNbXf4kRLi5WbHcN55frsYZHDFibsO0cUjva7cCusYjLmsk0x2QGV6RsM428eYBrWrx1WJXQ95EueFY7T7faUjtDkiUYoTBCj9okSYIyHj8zSNfT7QTCSy7qgW41sLvY8XjX4onkUoEQNEAIgBzf70BEOUkUCc2ZpdudIoXCDY7BRdrgCbVm20tsntHHkeijd5ZCBRCS3QCtjUQSCIEhCLbNBantcV1L1w/cu/PwGX34TYb4Xxz47S9E5+JzjKQQX11yvur8fpPb++UFX87vL32n+PRpT6fP/gx9sHc0ZXllgjoXdLZDeVhvW7SGK7eOOLh5hfVFR1lp7v7gHvVFQ1UkZDohuMCmCRgtWR7OkHmONooYeqb7JfkkY7pf8ui04ZM/fUClYTo1KBuJdlTQLpYVdogj5jIobNfSO8jTEfftEzlyJecG5yyXG0+hAxhJohQ6UaTWkyjNahupSokjkhjBYCM6Wmw3eu3TclxojBBYD8oEOmmRmSHVmnTXkVaCIYwF2sOmJsTI/MYBqwc1QkEcAqLekCrNQkrSUpGGiI4evCQtDG3XEKIk0RHCQJrAthtIomVxe59iltM8umB13hKGmqpKSLWkvbjEC8V0XpKUGUVmGFrPfFFivUMpjdGS2A5oocjur4h1TdtBXqVkiSQ7nFJMMx7evSDFo0Jg2PQcv3iVVM25em3Gg09OGc5WrDaWMhtFu5QSKCW53HoKE8kzie8lnXVoBp5/63lifITdrsiEYiElLgRSAllm0K2gTALdtmVqcmKZMSlT+m7N3bMdB4clUlpaBG2IpDGQeIHznqnRLMOEmRr/D1WtmKWw8TDPlig/pY0lunQU5x3CKpRyVCIhWkHcWNCCBSVplOgwMAtzhB9QOGJ/xl6+T4wSEySJSKmkIdMg/DmHep9VIpA6QW4cOgqkzxAyshxyfCLJ+x49QBoTdCcJpeDYLOhiRuo7gh3IrCFzKd4EDlSGDYF06NFSkqBJhCEIy5E3+KAouoiXknliyKuCR7Znet4QTD5S6cVIaS1KjpS1C6Xp44i3bxvHNEQ0AqVghh6d8bpnpyRzH0hiAOGYBgG5JIRAEwSVDcg+IA0UnR/x66lm6yKTziNEQOaKfAhEGdBKsbWwcBIfIkJ48iEg8CjnEYlg3o94eiXGTImMAWUDq0IztxEH6NCjHZgo0SEilWLhBTZGEkala9k5tPPEKmHROrwQpGP5DZlSqG4gCFg0DptoUhxRjjoiJgYYLMthxN1mBByRCaNqN1Ew9RIvJL4LWAlV7xABXAgsLAgkwxAZEsXEM2ZNQmTWOgYfCUOg1o5ZY8F5hBDMhKS0nuACtXEUrSVLCkQamA4eOYwF9OtUUTUWJQCfUAwO0TuEdMhMsjctGM632HqgcAEpBMJ7NgSmu46QOowIJL1DxZ5sXnJ2umGxbhiyBOMd2nqMlGNdS5Wy3Ha4TKDtKC6pOocSEpUnzDYdMU9pB4f0gSxEjPdEMhZ9oJMDSRgLiIs+IKOkVorp+Y5h8OTO44HMReYB0klBKhIqWXKo9unjQE5G0weihsWpIPcTAopOW+axQHtLiIHFhcIriTOCzjj28hleJBBgulOIaU5MFI1xVGiCBUnNxOW4QRNjyjoVTPVoIIssUqUpYTOgpgUxekxvid4ziIGq1IRuQOAImWZZSrzwo37Q0FMkAhkdfZEwzTWmafB5Sp4ZQtuQ9JbWBxZVzo0XrtKersn2pgTvx5qEn9PE1z7/rObK5+f3w4APnjwds5d13ZIlCfNZyeHBkrbtyauCYlKxPf0M4QeqMjBEz0Z6ykQyK1JOzltmicB7i1aCxgqqMJCXKaFxTASYRqLr0cncVxOSpKDJLBMm2G5Ht+3Z9g2LNiCMRO9VFD4ZEzf3HbEQHKo9XNeTCE1CihkUcheIhWcZFV2nUUOCFglGFYitwGPZDwKrNCaAyhKiceSZAiPIh45WBuZJhrUDhIByLYPXVGbE/acyIBzMMwPWchYi84mh7xN80FjrybWm0AIzCJZ5Sh5h+8kJ+eHsa6iRv8D2NQU36xz9MFDkOUSom5bEGBJjsNbS9ZaqzBBC0DQDxkjSxGC9p20tkzJFCEHddGg5MqV552jagdl0QlFkzGczEmMgZgyDIfrAsszYNYG01HSPLoldz+zmAVQFCylom5Z5mmP2M5I0B1WQPa7ZzyT37nSU0ZCVKd4GdBLwMnIkIb2ywE8TLJGJMoiThs3pFtEODE3HLElwwEQKBuuJQlA96ZcQYIgRNTjkIMlExlJIiJaeQCcERRowQhJEJJcDDBbpAyIqcgaci5Qmw8RR18cUmlXjyU2CCR5pNOW0ItP6i7H4KjDqp8c9xs/16MQXv/8i7Reuufj6AzwLOhe/PPkpwOaT7/Gnz/uy9uLP70PFJwVgn/+96y8uaeIOm3RUV1OiD/ggObh1jV/9z79L30q6tePhn9wjdA2JMSNLk9jSaUF1POPa29dZHuU8/vSEu+/dpX5wh+azO9y4VvBLv36LV2/NyIeAbCxLdmAjMoKMgb1ZoNm27DYNha7HAlAXKOcV7/zmTaZXllSHC177letMXj0kvTkhvTXnnbev4JxgaAOLIuJFJJ1lmDLjhdsF7XZABslBISjSBInCOcGi6NgNAyLVXFka8t2WbFdT1B2vXg/IYo0NDyjTLd7lOHPIalcw3e1oeovPNC986wbvvnKLK7pg3mqen0WCMshE8vwbx9x+bo8IqCTh+eslnR8jj+vTHb/2Wzf5zm/e5rf+9jv8l3/ndaYHESkuScyW2XxC70sePuw5fe8B7/+bSx6+7zj/KDJNj6gvZ2xXc24//xouHiPzm+TL57lyZYmUBmkSTBjwSJa3jrjx7ov8xt/6HtP9GW5wvPj6ktZ9hllsufqdkm//xg2KvSl9iBwsJXs3DylmFS4IMu+xckbUS/YPJ/joyfdL0mnObe8p14rJWvNSXlA5iR4EYie4eSi5f7rm4eNLVLtmdnVGtTejaT2vlJpBCYIUVEMkCR6hJTExvJ1eQcY1JtQsrWGaLQlGUtc73kiO2bhHWL1leZBRAm3as1UNb4sJvjhH5xcsZ3DdFGSFxbsL3tUv06gOMU3JMNzSxygDkZ7Xhtu0scWpsYD1BXUDGT2BgW9nrxPEANGT5Smv6usEbbFV4DVxE5sMoB2ihNtqQRvXeLXjncU1nLBE6ZGZ4HVzgE8lLhG82s2Q1U3k/Hn8lZd4rcuxuUHMcm51An824FtB0Dlv1AKLwGUJx7VDpSlWG7Za89ImMgRFlAn7O0itIiQZVia88sk5LZEgBfurhrLpicAgBa+vB4YQECGwsIHCerwUDBpeuRg1DbyMVIOjsgFfpAyZ4eXPGjoXCEKTBM3UG2xeMCxnvK5LhlzhZEQGx3S7pZcdLR3PP7yk1x1etCi74+jsE/rwCZ26w4vrE1zaEtUOKVuuNQ2D6elVz/XTS1wacNrilePwcsOQB3wZuXG+wemBqAdc6rm22mITi08d104vsUONUxarep5fOQatsVpztLEEBF5KohK8cdEzGHAarglFOp8ishyXpzx33mG1wgEHfUD5gFWCWktefLij9aPTN/VQFQVkKb1RvNyAzRNCapjoBIWn0Y6VGrj+6Iy1Hui1J683zOwOXziGynPjzhmdUDiZUFUVk4crglT0iea5R2fYMkIeSJVnf9NgpaBLFK+XGUPdj8XqMbC4OGeQlj6L3HpwgssEUY/QuOPTFVYGrIk8d3KJFyPMSirBtccXuMQwJJrrZxuC0XgfGULg5kWLlwqL5NpZiyoKYtS4zvPc4y2DBmsEi86hlcIcL1BCct1coaPBxZ4b8ggTJFFGOt/wxsMD6t7TdJH9bh/daYSEfiJ5+eSAvhRYHZjesRS1GgVYjePl8xvsbKSzitl2wqw3BOXpzMCb6wVD2CCUZa+C/ZuOcGPF8MKGN48su64nSMZaOuOxPtKFyPNLhzAZJs2YTXNuzhNsF4gq4YWZxpKgZYqKmmlWsJE5ZyHl5VdujbBXNRIzyDtnvP/b/5ZhO9Kt/8yN+em9/Kmt/ukSjW/E1j858YM7H/GPfvd/4B//z/+U//WP/oDf+ee/zz/6J/+Sf/xPf49JVbGrLV0fuHowJUlSZJJiipLX9gxeGLyHqXCkw4BQKU4lfPvVKVYoXIDZRJFNHWquCEXk6nlNml+SJiuuiMjBuUK1Ad92vNu/QJdavHAUneSgKbEy0EjLG3f38EVApZKJ1FztFvTWYjW82d+iLQ0uScBJ9k8Ng4RWRV56VNH+eIp/f466f8C1TcmwKdg9kLyIZ1cPdLuWGCNXkoGLTcuu89yqAjEIUpMyqSqOxZYoPU4MHKVjwbmPPXboeW2voB9GsdXreUohBUPb0axr9hMNWvIFRdTnDsY3yjl/w5h9fS58beDvP3zEb/+P/xP/8Hf+Ob/7r36f3/nd/42/99v/iv/u7/9L/u3/9iP+X//gX/P3fvtf849/5w/4p7/7ff7u3//X/D//P/+Gf/OHH/Df/v1/x3/72/+O//6f/hG/8798n7/79/8Vf/cf/B7/9g9+xN//x7/HP/gnv8fv/qs/Rqspm63kcgUv3X6O7bqj2Vjqh1vEpWW9FbRqwkxl3P2kZnMBjz+tMaeeB585Ht+x3Kr2GOqC1X3PxX3P6y/MsJVkEy1z07CbNoQrluTNiu++cotdA+02cnxh+fTOJY+2ngd95NBBExROZBRDQMZRhDYoyXM7j7qUpCvNsdMkvSbWhvVl5FjCZi3ZXAQmPqC1Y5CB7WB5/VjQupHyPleOWS6xNuCc4LW9wK7tcYNFack0UwgBXdtw/vEJXdM/e+jiswbvqfYL+py/OBXtbvfFd/GVyfmld/QV5+ILPFf80s8QX73qq3f5hsf7qUn95Pz4JIsSI//sH/0bfvTDT1hdbqlMwdkPL0nKKfPjBThNe7Lj8WcrpBjQiaKzUE0ysr0JOlOcPdwhXE/oPUSFVgIlWl57KeVv/j/+JuZwj3/23/2AP/23d2kuNgQv8EEyWM1ipug7Tz8EQggkOjI/nNJZQ1XC5qKhbUZYiqgClII6KGaZIARNW3u8D2TRMy0z6l6SKkeaV3R1z/aiQWtHNJFmUOxNNXXvSIsMmeekvqXbrIlCk+lIdtDT2w2rbcPeredo9B6nu8isMrRdj13XtC5yezllmU65/6MzlLAMEYSEtofFQpMYxclpQ1kqymnF6tE5HkOmO/7Wf/0G/9n/7Zfp645/8Y/+iI8/eszp/Uu6y47VZYL1OUVu8M7SDz2D08yLSDGviGmOMpKLTx8xX5TEfMrxzYIQG+q6RWmJrWtWj07I9xZcf2Efx4623SEQZHmCIHL3owccHu7j400u7lsuH11ihCcrUjpnkL5miAGVpVgbSHWkrFJ8UjKbaB5//BApFNu2ZzpNKZclp5cD+3s5l0HTDpGmdkyrUYm6zwoy33O63zFUgdZ5MulIUriUnoUxvPVLKxazNZthxczPSKcVl+GSiah4HA29T7hwW/bjErcRnAw1UxKUuRj56ReBK2qG9jU7s6YQJZ0GJVLO9Zqrfg/pPVtVkwaDCFCYgjN/xoE4wBUJl36NdAIGiVEpD7ngYFcRcsGGHcokpCEl2UUe6UuuqCusraBua5QQmL4gGQpOko4jX9G0no4Rgz3Vx5jsmNPScOQkw2AZ7BiFn/UKYyUnRcJh5+iVxBmFlYLSR1SEcxlZtpZBgBfQp4bF4NHWczpJmbmI6+1I6WwUi7oj1YqzKqUcAj6Toxqzluy3Fl+3rArDpPejc+Ad20SyaD3RB1aFobSBmCmS1LAxgn0xwgtXBMy2x3U9WT+wKQ3L1jGIga2JpC6gAyQILivN/GKLFeesTU0SJTrMyJlxWSr2GoFFstUCFQKJjaRecFFp5rVjkII+V0gE2eDRznNeKvZrj9WCLpVj1MuOVMCnM80VkWF1gU0SBu9Jz2pSH7ksDYvtgNUCK8WYnbAC5QWXiWLaWnoxOmc2UcxtHClsM8WsHuj1iKVvM8M8jpj6CyOZu8hAREhFrQULP67jFzpS1T0RgQnQGMlB7zGZYF0Z8s4TgsT0geZ4zlIk2LsrtkU5Zn+MxYSe9SRjtm6IRHbTFBMj5eEx4cMLLouUed0ShWVXGnQE1XvysuAsBPZWNU5H2sIgQiB1Et1FLicZy22LTQx9loIPZL0lcZ6LWc687hlMwBWaQKToIdubc5EZpnfP6FPHoCNeCW6f9/yVneDl/+w7OBX47zf/kA+GDxmipdRT+suak2rHsi3pyeh2A23suTJdIIaGVb5isUsZUkHMDE1oWDQZwgXOph2zLqMJCjEotqbnoElQWM6nLTNX0O0ksjdsysBe2Ke/bzkvNNNBYH9ygLybcLqzzLXEbmEbU1IVMVIje8u6k8xSi0oUq9qjncNUkXwClzvP4UzRY9kFSBLFXump9MC9uydcnZR868qSv/5f/RrTW4cjM5UEnaVfg1B8CWMR4kv78mmR3C+C5M/Y0j8/33rLP/rd/4EP73yMc5bKLBG24OTxJXvLOdvaYW2k7QbK6T4DM+7e3VDuGi46hcwK6iFSCEumDadNZFEpuj6SKk0XFKmuKY4NKx/JRSB77YfsPbfBFY59uUDOMzZTSyVKNttz7OMLdnuS/W5KtAOrAyhahewHcpPz2D3m6uIlbFSctOfkXiOcISHnNK052JVYn7IWFm2B9/cxn0y5lIbjImN3b2C1jeADaaLQLvB4G1lknj5C7QR5loCtST+nFk48XdwSjSQMjiodhXHPBscykSAknR1Z5abKUZnAyXrHrav7vHGw5G//N3+D7Gj2lNElnkCKnhqUn2dcPgMZ96z2j//Zv+DHH33MerNlPtunazUnJxsmkwLvI4lJOL/ccrQ/w0XJ6cWWqsjwUZJmKSfnG64eTBDBcnGxJs9T0gTKTHJ6seZgf0HXRc7ONqR5gtQp7rzl0eWOvSJnUwsaDEZLjBAIH9g4wZXKsGssFkGIkKuMqpryaOVYloImHynToxBQ1Eyva86k46Wbx+xaaDtPt20J9cBq3bI1KdPg8USGEIlaU+HJFZzHQOUC6hRUC0MQFEKjY8G205TGE1DgI3UfmCYBqQXnrWCiPAMCbSS7HmZJQAvFyiqqJNLbAaUibS84SlYclI9wbocOgsPZgv/L//3/xHNv3P7GoRQ/w7H83xEV7bNcgc8BUaNnHJ9QY/2sCMbnOhVP5jt/3iIL8fQihyCEkRYsxojJU45fvc720uJ6y/b+it15jbVQTRKs95g0QWcJ65PVKGYVFbNKk5gUa0faRykkR1f3WT5/xGZjQQrSST4WC3eRdtXSX9qRfU5L0iRDGUlZJoRhYHu+xe4iI1XkGGETclTfjT5ge/AuIhmpRjWBetfx/2Puv55tSfP0POz5XNpltznelvc97WaAHgAUJJHDIMWQRIqhC93pWv+VSFEkAIHUgBSEEYIACGAwMDPdY9qUP3XOqbP9suk+q4vcVV1VXTMDRkMRyogTZ++1c+VaKzNX5s+9zzt4DcrTba8opzNmxwuUtAiZcGuLv8Y6ItV40qceoyTtEFEi0V/tSJlldnNBfTxHqBk7YSmnOZQ5ItNcfXbJ+mRNUYHzkSASKjfEMGJFvQ3MDmdkW4ezI74yLwuadhTGn3x8SnCerMoxdY5QkmxaMJnO8d5ytUq0naXIFLk2DJ5RK3K1ozrOGboBpTX7bY9bB5YHGucaXIogNMWsQl8ZNmcbju9MkfmIjIQRIae0pl5M6DuHNhFVZJg8I7merh1oracuJVoKnItIrdDZOM+432wo8xnWB6QUICRt24NWmCxne7mnzypEVSEzQdNuKSrJft0QTbwu4qRrFOU19lMIgoCkEs6NzsYy0yPClUSQiQh4xukd3wxgKgQK70GkCDIRnScmBzLhnScUEbQGI8FGPAGjxLhuiugiwzsPAgKR4C0+uFHsriUuBDASschJBHzrSIDOcmw23uyds2iRQS4JWmO68f3iAz56ZJ4RgiP0jlQoUqaRWhMGTwph/EwwoiEzjTCK4EacalASLwU4h7AeMkWMiaggaD1Wn0PEC0b8r3eETCOiGvGQRcLHcZ8HIslfFy5iwDU9SQiCFITC4O1ApuWIIpUjnlnVGcpkJCIyRqRIpH2HSz2DBAaPFAlvNB6BHWURxDSif4MU+KogZRDrDO8kTHPQBsUcqebIMIAadRxSQrSeRCRISFoSMw2Mxz9JiFIQlEBJSdSAEWPwIEaBu5OSZCT9EAhdh2XAkyjTiNlNCJLRRCOIarz2JR9ISUIakxSUGNeVkhgdKUViHF83GY1PiRgjvrNoISAqrA04o0YsMWJE84pEQhKFRChJcnHUGolxLCkJMX6mBOQZosxw5+3142NnIaQRrcj150ti3C8iz8ZEUgpG0xsx7gMliSGijCJmmtTbEckrIaoRTRvD+NkBPIIk5IhqluP30Ipxv8Tr1/LX94lU6FGw7QJBjnPfQQmCGve/PJiM520KJOKIVE4Ru90Tc4UsDH7vCCaHypA6S1ICMTEkBEHDIBPSW6JK+DhiR1OKpGwUIYuJARHxTiCMgSqQTEW0jhQFMQQi19+JlHDpGmEtJEpIggsgDXiuoRee7FpXpPOcrusIQVDVJd7v6LcO1wX2PpGyRGM9aVLQeovUltBazNGc5YNjZBjv7TEEtPoibPjqSHP64u57Xdz76j35K8u3TCp8daV0ff6FEMZrZByvNyklvB+LbT6MxbroI15E+nVDHAaSnuKuceJSC6z1JKGxLhIDdM5hRaKqs3FbEXwKZFWGNhIvGL1BqoyIJRBICmImCZki6Yy4dcQUCGUGSWKHHkQiyUCUhhQ1fhj3hErx+jyMJCJJQsokMYEyhhTE6FnVOzwGkRucj0ipRk0bghBHiMTgApXWOO9JUuKiR2eGLjhIoJQipYiUEjMpGfprhDYClGIIDqEVfTuQtMRMixExnBLt1Y58PsEU5ptH68sDJYD0LX/65nq/sghGTen1MQw+EkMcv19fHAMZSCniYyTEcX3nAyEE7Laj27as9i3lxLA9ucIVOYsbNd7k4/dgcAw7S7PaofQciaHrLIN1xLoihYhPHoQBOWrefIzYOF47XBzPu6a3wIAwOT46ht5ipUDnBqUVzjuKGxPcF9+/wdFuGmzvQarxnE0RlxJRqRGdnGkGa0EJXBjR7xGBUBIhFOZ6FNe7hE/+S2SsUArvPUpnSCURMJ4L14mQtZ6YBN6NY1bi+hqIkbjeEaLDFDlJC4oq/1Y9zV8WWf+6yot/d8mFuA6svvl4+uXn+ou6bulbfkvpW0Q933jNrz35W35//e3HfPzBc1JMHN+ZUcQFH/3ZKetn5/j9JYGKrDQoFZjPDPtuZHvfOtbsfAFSUxeCPJOsWkHTtMwzSFnNj//5U24+XLA4Kpguzfi6Vxdcuh45NSSTeOPtm5yvBMOmoYhrNo0bcbQmUdeSq40ieM9EOVqZU0ZBpSV3bxo+fdpQmMStmwVDp9ntIrnWLA4Cz892ZEXOo9fmnJ5vMcJTl4ZJWLNpxjnqg6VEZ9BdrpBZxq1bc/ytQ5I2vPRwwdkw5ezshP6i5ZVbGZ+mguOjBeX2ijINZFkipMTrLxd88sLipKPKAwdTwaZU9I3l1Yc5zzOBfXLJ4bIkDWu2ZxuW9w556zsP2W1ajm7OqcqMOm3Brgg+UWY7vJiRREBLQZF5FAEbPY9fq1htNSfPtrTnK+4+zPjw4zXVnUPe++4tftwH2g8vGDaR9/7GA37+Z5eQEo8eTrm4slRVxeFxyY0b9/npT1bkJiJWLW2rSCTKTHAwS+wmB7jBMVcNppohThvyXPKDH9ziw5+vabvIvIg0w56i1uhScv848uHTKxYmY1oGskXJs5Vlmhvu+oYPQqDQ46w9csd01lKqmh+El+knU5IWVG2GLAoa1aKS5K3sHv9s+2eoqLhHRUwzBjoyIXjXvcL7+UeUBBbxmCMz0jEKNeW7+m1+EX+BkBNupAMma8knlUdLw7vhTT7InlCFyIE4oDaHePkhWmW8ld7gT4ePWSjNkT5mcir5BQqZ4F1e4iP/CS6ULL3huD/mz+Yrok+82y35bK7xNrHcJ27JBT9VO7yD13ewmhiG1lG1jkdXjp8tx4v/K1vHtsqwAQrg/nnDz+/OyUPi5cazC4FeCkoheGfn+OnSkHeW+5uOYVbTu0gV4OV1z5/GNUYkjmOJEJpBSarB8/LFng/vTFESbgWBL7Ox69dZ3jtr+OBGRYpwo40IH/DZiFV9fLLnya2KYlJwhEZuW9wEcJ7XTy1PbhV4ITnYB2preTqTiBB53RV8oiI1koNYUXRTPjUCbRTfP7rD07Ik9T3LITJvBR/EDpFpXhcZn0eLi4G5Dxx1gY/nGcInXlpbTpcVISkqHTnqIp9mhmyS85JTnCWHj1APAw+3gV/MIiLTvLpPXGCxOpL5wMuryIfHGXpw3N94tsLQTQJqCLy26vj4uMIYza1VRysSrQ8IF3lzveHD4xKjFHe3llbAsKzIesebZ3s+ujVFKMmdTc8gE+7mjFwI3r20vD/VpN6xbCPlEOh9RPnI6583PHt8C9kJ5ud79Kon3tJI53n8/JTPXppDKzjYO/LO8mI6xZDx0oenfGpKfNcx3bbUXcMzMUMBr3nJM2GZxkg9BA4uW57cXiBj5NHZlrPJFKcVExs49gOfxHE08KXTNafzihQM9eBZ7gaeHuTEGHgpaTaLOcO6oe4Dj65WfHSvJinBcu9wx2v+9eYPWZoFj/VDng/PCNFx6/OKzeMCLxsq4Xnw7JA/m11hfMbd9YLe7BnUhKwVvLU95GfH55gy5547wO6vCHkiD5q3PlrysxtXZAXca2eEFOgc5POSd08W/PzgEkngdusJ1RHJnKMTvFUJ/mwSWWaJIxSiUXy0ckwnBXdNx5Otoi4ENZ7jY8WTVYTY88Y0cKVrTJa4e5Qxywb+9OklRkZevzXn7OqcTAn68y08X/Ev/CdUF3t+4zsP+OTJCWcXG+7eOeTG4YwPPnyGEPDaaw+pJ+UXwQBt3/LRZx+QSLx8/xUm1eTPvZU/e/Gck/NTDuYLHtx6yKefrhAp8fD+Xa5OHOs9qLzkh2/e4yd/8jGZNrzy8iGn25ITc0KpNC8fa/7sKqFT4k4RGIbEkAQyBr57JPmT00Q1L7ldeTqxw+UZGYm3ecBz31DUE27KG1T5EpeekwnDu+Z7/Ev1L0mbgaNBU3CT1F+ig+Ttz+/zi+nnTMoFN8s78Mwz6AEdBG99PuP9aUMtDUe9YtLP+ai2xJB4Ky/40ArckChVz3HmsGREIo9mLScbw2KiqcTAoW550ecQEvcqxyZXxG7g5qJkqTwfbj0Yxe2JZBdzhs1APkReXpT8wo3F0nulpE0JpUFEz735FG9HPy6pJXldjGjawvBltPaNuOvb4roXJ5d8+uSE6aTilZfu8LMPntH1A688vkNIiQ8/OWFSF7z80iN+9sEJUhfcOD7CDxm7VmJyww/fuMsff3BOXmhmJqee1Vw9bzBZxnt3p/zBH3xCJhWLWUXabBFUBCt4rCvOukiezzk4WPDgQU3MPkcmwXuv3+XH3SfsNg2m73llPueDbaDMDPdryZNdJJej3uyo1HzeZ0gluLeMnPiESJbkLe/ezPk5PTY63tQad+cGF1IyTZo3SPyTs0uCjdwnshEKx0gnfFUJPiEhZOJOgj3gfcTEyH3pOSNDG8WDGnYtbPtAZeCOafm0K9FScKsOWB9wuz1KSl6vPR/vcqQS3Mw95IrYBwyBH943/NFJi84kZV5wg4y9q9C55j/+P/0Otx7d+taw+S9bfl0lzq+fXHz5Dv4ycOxo2/JFN+Lb1v5ldiy+Zsr4F+ZYf0l6dXW+oSgyhs7ihki3bTn95By7b8jMhDoz7Fo/Znw2MTQ9dZ2xaSM2DRRasHYDgxD4pJAycTlI/uQPT5hewOLWlBACKhOEfuDFqmEoBCJXqJnh4rKn3Ti6fYfXHpNFvE0sjiry2YzsQOIGD35Ah7EqFpuBYaKpdQAhSV2gWw/4ToK0rKxhUuTsh4FPPzglSciNRqmE0XPmMuKFRGaOlG0oZpb7rxxS3HuZdStoGsvP32/Z7Va4rWNxUHG+EjSrHclkmINjmp0jZYFcCrapIJsJfO/oEXz6wSkujdWe9Q6KUoOArMhput1YQQPuPjziP/xPf5Nm15HnBb978cfMt4HY92xXo9BTS0md5yQh2K8atILzC8HyzoyTz3c0256nHzu6K8cm7fjs4yOmh7fhw4HVC8+T9xXBLyBE/uAfnHHr8U3ckBP9hJPPe0wmUUcTrDyi2ZzioyZEOPcGlTz7fU/UidtzxWQ5o19tuGLC7GBCPFnTO40Cmk3LtFaoNOPxvYqTTy8xQqC0Zj4zyL6jrXOqrMeREKZjfvCcoR64oaYcz9/kO/f/czrbsFzOEFXOyl9RqpJ/3f2MRSyJosG7nmZIqFIyVQWf9xvyfE6rOzohOGtWiFJDUDy3T5hNKmyzJdme3fEMESuklzydrMlTzXp1ha0Sg1whk0T0nifyOXmrkJVCZgUrEVF+iew9T8OK3BhkTAibODE71LZHLyY8m1qUU8iUkEJxlgZ0D1IWXBqB7CxSBDKfuKgKimgIWrIvDXiPlIZCKS4PJpQROhdZKYlUApUZTGs5mVdk1uOFYFNmyBQRvaPY9zy/fApuS8gVW1WTlbeQSPIkOV+WaCEQmcYGQbIOqQW5T7yYl2gbUcrgM0PIDSIJTBKcHtUYk+GFptu2JHpSFNQSTm9o8uTppCKZwL6ukbkgD3CJok4RnxlUgk7eQSeLcZInlwGRD+h5QTHLcUeKSd9BM3CFYl4f0rueiRNYaZjJUSdmHxqWSuKDZxnG7sgiBXw/sPYBuoQqNVUx41y15CpgbcfzaEdjuJAhe8szkRCNR6TIJREREnjQLnA5zcgTDDGyN5IQIiQorOPzckTfJiHZiYTUGpmgiHCxqMhswJvEXoKXEhUSZUg8MSB9RNQZ1lm6wTG0Ad05TiY19cEhV7ueGNT1iFIg84HLG1Ny53G5wiaPMzmqmCD3Ay88ZGlAFyVBwW6SIwHlI5c3D1AvtlDnaCnZTiaIpNBRsFou0YOHJJDGsFJgQkAI2CxrchKNFCgS60WBdpaQYH1YYXxEuIC0jrOpQgdHEpLz4oI/yC/oN4GpmuLMQIZkcJFV1gAleMinC56vNig3jp5dtitkSoRKIhvDs6pFO42vFTvRo2uNDD2Vk1yU50y9okkRXyS6PsO1mrT1fJZvqEUgTCLR9Hi9xwwDtUicHlrq1tDvA4NPsFdoI8kyOOsS07nG7QO9c3iXITOJkYKTXmFMYGgCmzAwmIZCJnIRWG/3qBiRShBT4J+e7JDJoC/3/JufPyHXnqvVjuWswsiEsw4hBM+enfMf/Ue/jdKKGCP/07/5R7w4f0FKiWenz/id3/4Pv9L1+OVd/dmL5/yzf/37rDYrZvWU7abC9zOsdTz52BGipO0Uune83z5FJYHUiqtth4sZUgvS4HjeJeraMKw7Bm0IUlJqTSEdJ0GyPM7Z7C1tFhETSfAD5STnRdoiUsmAYOssPuxBCTKZ82l8QZlNGIg4Y4jOoqIg3weeFSsyNaGtI33ncAoUBXmQPKsTeaxRSZBCyc4UqKgxPvH5TqF7hV/12GQ5MyXJRSSJZ1uPUomYBBHHDphPxkLJaugpqoTRYO2OF8Gi1WiC2V6PbBsc81nNedNjlEIryW6wGOFJzjE/nnOx35FiQmqJEAJpFL4bO9dfeiF+tWD7tTn1sS11frHm9/7hv+L8YsNkUvJP/+BP8SHSdgM/+dOP8Emx2bVMqrFAG+Kcrm85XxmCBxdy1DbwB//kU/IbS1YvVqRtIJeW/SaQy8inOlDMl8SQGIJkMAtSHI1O//TznlwF3LSgHTT7tiNagZSCz062zA+mnDy/JPjAeR+RjMCHrc3QjOOgwQfWbYZICj94ThMwD0ih0ErxPhcME0FVGMK9I/J6DpuGuG74lyc72gQow1nryXOJTJBrxVpCLcAL6AUorcA6TIJLJ9FCEH3k7MKBE4hkiM7xuRdIPFFnbIeAlh4lA1UmWTlFqaGNMCSJC24kZMbAZ5tALixdkigNgx87x0e3b3B5vv4Vzf7XmhhfC62vo/IvZAW/Zu/i30Hn4i8RXotfriWuE4yvuPB8ZYTpGw+JrzYi/md8yK+5dMOL5+dcnq1pm57kNe1Fw24zYHSGdRIvE51LqB58ApNXbPcD1UHN0LQ0vcUUClnmbLYdVZ4hesdp33Kx+Zyj1ZxsmrPfD0Qf2AVFE0AGCFeWzd6SBglJkPIRZasKwWbjcBcrRF6RT0ucdawudtigMBrkWTu2tvuBXXCklCFNjlIZ+3Z0CpXGoOK4h7oBQohkmSKE0T0aPeD6DnRi3/WcPtuwayU+gmtbus7T64zYRmwf8V4xtA6jJd0uYIdRLLt5smV6PCEIw27wlOgRgecjn3/ekheK3gmaxqNySbdpAEH0garOybTk2ZMdvYM+SdAFUQW6xuIC2AAhBJLIgETvPKL2qHJC5zr6tWPwGnfpEL+4pDyYYqNhvbV8+McvaIbA7GhOu4s0f3JK72FzsaeeT9hctpjCoKWhc5qYDE5pXFKsnu3RSlFXE86e7tl1gWh7zl50JKnQUiFEQgqBc4JuEHz0wRXLu0eIvOSi60inLU1SaBFoB4fNx7EfXTSY3JJNHcI4VsWOqZ4zNfMvvy031E0AnvkTzsIljWzo4sAgSzYi0glPmvVkKdDQI4MlM3t61bKPHTttKKymUXtSoQgMrNIOGRKbbkeW5+wqizQroo+sh0tEhMx1pKDYOU+0glTNuWo6UpHYizWyDGy9JbLHm8Q69CQ/MC2WpMayVwOpAOdaWnE91lVIsiyxUyO1SATNoDRJiOvxDcVOS2wcncMHJUaqkbjGnmqJyxXRSFxmxrGHa+frJlPE0rDOPTZYhiRI9QHFJKfPNd4oohgdU72RiKRIQ2SfK5waHUxFEvR6HDNACdppTlcaiJHMR1oCIRckrdnnYGNCKI1B0mQSigwENJlARdjZgOgdXYSAIMrEDtBlRu8CYj/QMTBIRdKSRoHSgjIJZLenSZHoBclZ9teXxL1rICT2Cjo7jji2arxq1j6OiFcjCe0AWJrgSDJRFiBQtBn4iUYqzZCPiOtkEgRFPymQZWTDOL7kU8RFCSjaMgOjiHpsuUejSFqRIrRa4DKJKzVSCKwWpEyTyox9ldH3oyOyTjBISJWBTLEjMghoFweUvaNTilDlpDKnLTOaPKAyjWagzxVhWiLLKY2SYAP5skIzYnLjNAdhaOoMpSQu14TSjKjb2diRakpDSok2gug8bZWDHIklXWlIMY2I0hBoCkOiJDDQVjlCSsS0QgyBtsxIweFNoC/G8SnrdgxFx37Y0KgGmzoa0RCcRU1KyHI2esANlq7ssVIQjcBnPTEJ9nnAEUgzSDLidSKahJaRfTHgo8UfgZCGQXkGBzYr2UmPs5Fs3lDUgl4MBJvw3rLJHJ2Q2CcNYshoiESvsX1k0wn2w4iw1iHS9hBUhnKaq8ahlKDOCtK2p4uC6MFYTyCw3Q00O4+iZ4iRYVLilGL3Yg0JZmUgU57GO/p+wKRA3/cIYDat2O32LJYzds2WbbPj+ekzAOqyZrPbcLg4/JXw4PT8lNVmxfnlOU3Tsb6q2azHcddd7hAm4/TzFafbBiUcmQa9nND4nAGJrUpCgKtdJCjPEBV+n9BGsd575oXmfBvIK0HrFNFatIVGC2SEYdJR1hafC85CpHAdjehoU0erO2LpaXVAbi9RtWGb9pilIXmH0SX7zEN7TvSCjbBIIdHGoFPGSnmSG0B2rASoQqLbhN1a1vtAqAqC06yaAAJKUaAiNDbhxCjM3XcdUkpKJTDB00ZxTbUTtNah8PRaIBQ0Q4CLBp88rfekzrHUA8ulIljB1XpP//A25rrDlACpNaYUX51F/3Niq+sjdt21WG32vDi9pN4V9NdEpGGwTGcTQpSsty1lkTF4iUyS3aah2wzszlv6KNApYaWibhOr3iPLDLtpaVD0ly1X7tqFPSZ2EoSU9FIBgt1+h/Y9YbUndo6UEueXG4ILHN1aUsxKbIK1TRgp6ZHsu0ATI6SMxnqkHDHarZMocmSpccmy8wkvEixq2sIS64wzKWHTcH6+5Xzb0aDYC4l1noNJhZeK3gdW3qOvR3JjGse7pICtD7gkMF5AnxAi4YMZr80YopD4MOqQ3ZAYhEergFWKYCPWj2OfQ4CUJD4qLJIhKVabHqMFQ4DdvqHKIkkkmrbj8mL1rcf020YSv/zxK7KCX2f5tZOLr8nB/5L38i1jX19/JKWvZ1R8sRP+gs7FN0ehvvEKB4dzDo8XZFnDfD6hUhnbpxvmlSG5sTMQU2Q2z1gUNftmnLu79eiQri34/JNLqlwSdGKSK2YTjTQ5YrBs24bt84GDB0csDmqUUnhncduWqBOHsxyhEnbvCT5yfGfO0KzZXw1I4ZC6YjadUh1kRC/RYuDsquPooCTTkXa1I6sNEsnyzk0sOSb0nD1dUUnB4AMiBmIK4xy5SBAcs2lB30e0F5gyg0xxdGOBIaNf7RBBUBcak0nikMiERWuJUpI9cLDIkd6xDZGyEKRMUlWCnQzkKjLJDMoK6qJkeXuOTIH95YY8B6M9m5M19wGpFb639L1jOjNUdcbioCQvNTuduHjWI5WgLiQpSdb7AaPGgGCx0CRqlos5F5+e0Ox6Ih6DY7k0dLdnhO2KvtljtGYxU2ibM+z2hMHjLluGMNBdtcwe3aCeluxKweBgkiVa4ZlkiSwTmOQocxhsROjAwb1D3ODZXDVMS0nvPS5JcpXIZUK6hjuPj1ifX3DZtFRVTa0kuRR4IXASCltyS03RwnFUHrIsD79MmNP1l30IPVoajtWSY32ATppZaWi3oxld2RtM0gg8SsJBKFE+oQVMiinGS0qTwWBZxApnxmNdGI2wgUJURDwHfk4wEektRmSofIqSJVJuOOwrrCwRuUL0Ad0n6lohVeRYTWmFwWQ1cd9T9lBQ8zlwLGv6qCjdOAc9yyKVhKATN6PESz3OE8dENjjqaUmynkXnCFqTxMhin/g44l5TYj6MxnoxRgbvmPuEiOM1YeESmowYNNsiZ+4SJZLt4FgEQSQgRaQtYW4DIBEByn7UG6UY2UbBvHV4EsRxfEcZhdQKAczDqCcQUVApDQGySYGInsMEwccRRds61GAxnYMYmSeNsxEZPdnOAYLMR4LrmfSSOMnRWUJHEG0gD4I+81T7hNc5iTH5yQJkMRFqzaKL+NKM+FklKRLo5AnCcTRIQqYp2h7rLGMYPmpTbk5qKApcgoHINJPIoLkIgcm+JVwne1bLEdmLIKnAoU8ERhxn4yMTDyImkgjM+oCXI5Z2nymmLiJ0QkaYKA1KIbxnF2HWO7AeUWeUAfLOkXcRtGTa2VFjJhK6d+QmoIVnHQWLwSMOclg3mPUeLSU6BEKVMd93hFyhSWSzGr1pYD+MHhStxSVQISABg8A0llRq5rueqMS4D50j84lcCKJSzNYNPosUdtSbzA4kXG0YRGLaemzmyYbRXHEaKpZZIgXHoTmk1XuqVNJ0VxR6iipuENwZ8wtPaXNCljGIwCwUBB8gBg5cSdhYhEm0emA2ZJgw6jLqRoxeRSqjKxOL8oBuFUnDmlrUqEFQBssuTyzTlL4fk/A6FmNynivOVWLe9nhdkXJBISO6UOADQUQOCokXkUYHFtMc0fTMD3NOt57S9ywWJd4IYtsjQsf8YMku09y8MadrBKpxhNUe9h1JDGTTiqPDOcJZOiVRWpMXGWWR07UDZV5RZgUH80NSShR5waSa0A89mcmQcvSbSCSW8wWzekrbthwslgifkRFxPlFXBSkIutxQLyZ07Q6Cp8oyDhYFQyrpNwNqZcmzDCciNsGy1AydJU4MlQjU2aitC23PXAmS8BSTmtJ5si6j7go6AwtKzM6jFxXTbMq+U4Rdj1CeWZuj7djtzfoxDtCUSN+x3AiGThK1pjQlWhiM10QhWfaSlI1o+yrLoJT46Im5Io89LgXmRpLnmuQSGYkYJVMC5awg23VIDSLCzeMJl3uHGhpkoTHRURnNdFbi+x5pFFMNQWhKoQkhUiOYq4TXmts3Fjx+5xFSq19GZFKgjP7aFMqXsdQ3gjbvA94HDhZTpnXJdFqxXExwfiwybXcts6pA6Ix+2zGXilhldFctq3VDlgRTM3pG1Apan9DR00lBZQSLowlX+wHtPJURDE6QgmRZG0IM1FlOHAYykZEj2fSOmR11Uk2MlJOCPEaO5jXuYE7ZOyhyaqHpdh1CBmalpusth9OMhCG7xpVXKqAqSd80FDaAS9QGpgdL6qJA9ANXu46JGYtXKkSEUWSAtBYrJDM57qwUAkmN1yzfDtRJsJACpQVCjzocbQeMVjg/cKDFKMAnIOuKLEqIPU2K5NFTGU1ZKi72A5Ncgk9s7EB9rY9M0VFWBZXJMdeajOZiR5nnX3abvj18/mZZ/9dVWvxy+bVRtMAv38+/xfv6Qsz9FZzun/vkL9p04muJw1eemPhLVUbf/6tv8e53X+W977/Gb/+v3uPBy0vyWuBdz7vfuUG5mFDXBZmI2OGKfbMF6Un7z3HtFmg5mEleOi6YIPHbnns3C/RiSiwLdjEQt+tRHDdE3vvebcJcss0cOzVwdBjoZUAvcuaHiXZnETIjJcnxkSCqxOp0hWxe0Jun5LcuibNTMjboasL09g1eevcmsh7Ngc5OVkzrHTZEBud48LDmzr0ps4liVinu3wn0/oJmOGVae+riNqZ4iO2PqVcN4dwRXnQsty2TBNJLkpW8M43E0Q+N0G6QOmC1opWSWweBi5Md9XzCS68cc3CQY20gKcO73z+itxGhFNooJqVEmpEdf3m25b//f/wR/8Pf/TE/+cNPmcxLrFP0neDlxzVBRCKR6czw1ns3KbKMJCV3jhKXn15w8eQM3/S89MYRQWYEkfHgXk5z1aKMJi9zjg8FSUr2neftHxwSJiv85JI423BUW4TWbNYdr769JF+UMMtRy5rj0hGTxll4+d6E6mCGqGqoa27eMcjbN3FlzfQwoyrz0YRKKB7dybg83XP25IrHd2YomRhspA+C1+cO9WhN/WjD23dm/GD7gMf7O3zn1vf5wdEPvzyFYwr8i7N/wv/r6X/L33/63zEPUzZW0bmCaphz00xJ2jLIlt/YHeLMmiQ3LITiJkf0JrJXjvf8OzS2IyRBHSvuyrv0Q8fetry9fsh+t8YFj9hYHtnbUBuiCHxPvY6cB2TaUxaRx5cQuMDqK75bvoRtegICs5jynnmLoZNYWfL27iYhBERpiJngzXSEyzMGqXh45ogeklAM1vPWSYO9rnQ/bjyidaQkSWXBu22gcR4nBQ/3jhxwSjIUhjf7iNUSbzS3+0ARIWU5ti74vryBuPMa+dFL3C6OWWQlqSoZtOLdk4ZBCZySLBxM9hYHDEby+tlALwUeKPvAwZDwSHopePXpjsEGYhLMg+awUfhY0A+Kd18kuiFgXSK76rlx2eHbjr5vee2TNUMp8BnorufuxZZBD7Sq59FnnxPU+0j5PiZ9zKMXHzG0P6brfsJLzz9mcH+K839CTO/z4PyCXu9pzY7Hl1cE02LlBi+3PDw9w5oNVq15ab9GxJ9C+COG4ce8+uKKXlvi0vBwNqe+e5vsxjEin/DWiWd/NdCd9yx/dop4fsWwbfBK8upFS7hGyt7xkkmWIauMoTS81QeGicJncGgtc51IecLV8OblHpsHMIFlNzBdrXHNhsF3vL3qsVpCplnmGQdRMIhElyleudiwdXt2bo/od8z2DYMR+ELxymcrhswQlcJEuKUUQ9fTK3jt6TmDFiQFMkburLZYHfC15NGzKxyjwFv6xP2rPSE3uMzw8vOrUTDvAijJ/RcrnBSEouClFyu8lqAEItc8PNvhckk6nPCgt/h+gMIQMsmjsy3bomOf9RwM48gdKeKT5d3iHZrddtSHFY8xwuCsp5Oe99q7uNrhcscD5tRtJCZPW8Dbm3v00uOJ3IpHTMSUITgGFXj76SF96Eil5FZ9zCLWY/VzlvEd/yptATFTLMSEW8UxaarxE/jB8Qx7b498pWf+2HJPRJIw2Kh48wAGJ5DKEOzAjSKhdYH1kscTSxcUNkq0UtxcFKz6xAbNg8WCVt+kS8c0pwrzfMfnzwZeXCXu1gv6OONqY9g3BbeWd3j/p1s++rChnBzwD/7hv+Tv/nf/iH/we3/AvD7EDhY7WOb1gn/0+/+Y3/29v8ff/8f/b37y0z/md3/vd/ndf/C7XK6uRpFvCDhnee/tV2hay+ADL718G7/ZEfoeHz13yhnbOGPHghvLQ3YfnbG+6NmLjHduGgabsD5xUCQWB5JUCAYZeKVu6LpAFIpbZc4UgXUCHyXv2Jt0AmwQmCvD8YXBX+xwTcv3N4/w9SiUrRvNzabGR0usIj9Ub+InkWQ8tVDcH45xXtL2gffObmD1nBRniLTgweYe6fIGzQcFrw+Gpk34pBFCcaeyhEzSp8hts0XXGVmpSSJwpPcMITG4yONJZLvb0/Y90mgezxReaXYxcbMYUdQhCrxQvDo1hKGn71vuLEu8kLSNZbMbePW1BwgBfvCkEL+RU6Rfjauu46+PPzvl//Z3/if+y7/zT/jFRy9wasLGFVy0mnffe4urvWS1ERRU1PUhVxeJZy8stzrB2SoQ9JRCFxzN51ivsbLilXnOEAXBRSrGpNBFCFXBo0LRu5Khy4gNHBmF85Ihah4sa3pTEas55DW38xlWHtCqJQ+mh+zWilgfMzm+w0vHE1yRk3LD/crTtBHI8C7x+K6kqwJtHZhnF/SvfIr+rTPK39zwvTJDTRcMXvJOUbM7a2ikYe0iD4PDKUkPPFRQ52pkd0j4/qzCXXeV8vM1k8tEdSVRp4GXpMMDPsK9Gzn1JIFw2DDw0mRHlIFu2DPPeyaqJxMDiZ5373aEeMJsuuX2bMsyH0AMBGl5b2HRsYFhRSUHbjw2lPcD+rDl+Pb0m4H2t0TZX/zj624Rv+bya6Nod7vdV7bGN37+9kxIIP78HOlbxNlfJiTXbbwvp8G+Tcj9bRu9fuzFkwv+0f/zJ7z/46fYszUZGqcMq/XAfGkoSsN+P5C8xwdLWSiuNh1HiwllNuf0tEFrQS8T5aykcwIdeugc86MF85sLuuOcrXQ8PdtS7XsmfUZ7ZZECZrkmND0uGrSwTG8u2K0b+sZSHXdkRz2bfs+ymlGmB4g4ISXQucb2gc+fbFGxp8gzgk/oqmS51BgVuDjdE4YGVXuc71C54cb9e9g+p+s1dS35/KNTRBJ4IbFYwqygSZrj4xqR5exerGiD4KBU0Af2vaQ2EVPmRGcRZc2t45LNZxfs24gIDi1hOi+4uui4fadkIq74P/yf/xqPfvNV/uHf+2N++pNnXF3sObx5gO0rVheeolR0l2tWJ2fYoHn02hGyrDj58JKu7TBaIEnsOpiVCbKxE5NShOSZ1jmpnLGYSta7lv1uwGSa4qADs+Jy3zDVOaI/JviSECPT4wn79Y6enHkF66uBwYMxGbcPCqa35jx7vsP4jqbzHD2+Tbsd6E9OmFeGbZs4WBqGLtJ2djQwzAKtiWTHN7hxkHP+6Oeo+y1JJx4MU/6mfcj3Xn6D2VsPR6rTtebos/0n/P7pP+bJ/hNm2ZwXumTQNVd2y2KTEDpwIndUqUCJNdMcVnrHjXhA9IELtaVSNZUUlFawLRoO3JJewIVbUZkKKQSZU1xmG275AzCJvWzIsxKRJJlTnMYzju0hjcnYxA6NQg+CzGnOsw13iju0oebqaodwgUxklEPibOq4nebs12Mr1vvAVB1RmyPOZjk39g4vMpzSWAHTIVAYzXlhOLaRPnhsijgpmAyOTArOC81xgP1199KmxMKOHbnTac5yCKQ43vj2WjD3CZRkUxmWux4nHIpIWxmWNpF6y2UmmPYBnyIiwVbBQe9BSK6MYGLH9rFJowHcQeeJSrAxgtIGhAyYlFgXgmVjSTqxLQRZ7xEkcgSrecaNjcNGy8ZEMiRZeEHuL1nPHcumZEiOPg/ICIXOR1TqpOdgP6EXd2lNRQyR0kORJBdF5Hif6E2i1yCUpPaXZGnFZbnjYFfi6pcY6gVyWlL3OfmQcyJguekZkLgYcUIwtQGTBJcTw6IbjfkCAqslMz86dK9Lw6yxWB0QGnotmbtEso5LA4shMaiEFuOY0nIYuykrk5j0gZiVaJnRlIZlgCQFVxKqZiCSMC6wVnDDSbQwNLOKorNIkyhSYD3JOAySWORcrhpyF9BKkPvAalqw3HUEE2lqTX1zQXjeYZrIZjnlYN3glKArM2SI6MGRDY7VouZo1+O0YKgLRgd0iwZWs5LlvmOQjkGPJKhaZIhnGy5nJYf7jlV+wd70RC057i+4eWi5GF6wCDN29hJrPCEXFPkBoZ7w3J5xtC9ohUcZQRN6Fl2B7CXnVcdSLPA0SCJt4TkIE+g6LvMNi6EiSoH20N/MmLsDupOBM9lyMDtEFg10DX3WMh+WMF9y1q+YUuJWE0w74SL1LD7NsP+q5nJdoPVIlhHesrGKA+3GQNRKcg1h6Cl0Yu00B/mAjXs6IkVukF3iaDnnZB+Y+p4+JfZJYHJDrj156Nl5wYP7C9YnlzRxpDHeO9LcvG242uy4dXsBxRob99ediwojNCcvXnC4PCRJcM7hQ2BST9E65/zyjIPFEacnhq6VuJCYzyr2L1a8eHFFhWBrc8p6hjxeUPaOIQhOu8Q8Ezin0Cpjte25ebvC+4GrHg5ySQoF/c7is5JZ3SNnno0STESk+N4F5fGG9kBxc5uY+T27Wc9scshODlAVXA4XHF1IRPJs545ptYQio1Al5/6C+YuCvq25EoHCS3R5TL4znIueG26Kv1hyeWJh1xKeR7Im5yIa5sbhY2TVB7RR6GAxwbOLGTNpR6+eKMm0JqclpI5dUsxEIEno40gMqwtNLuCqCyxKQXQt1ls8iWWhmJSa89WWh49u8df+l9/h3/vua+Tz+rrQ+0VcJb5sVnwRp30RX6WU+C//9j/h5x88Y9/0LJcLgix4frJhUWj26xbfO7btwDwzTI8OOFl1LBclzaZDxcSgNHMtsRE2XaBWAuvHMbd1YzlaltSLKaveI4LH7yWih60X1PSYShDLguQsKTomlWY9RA4EyKS56AJagVaSRa7ZSMNSBboQ2PsxiYpNmZmRAAEAAElEQVSDIvMZV61gWQX6KuJyTQyR+tUrpm+0fC7X3GfJcHqMzw8IISKvevom8KmPHMZInxLRGAIwE6PZ7mVKLFLCC8ngPPt+4KATzPaKXZeYauj55XjTNFfgYO81tRhNTIsiY9s5atFhRM8uwtGyRkiHjI7NpmU2neGoON9FagOp32IYOydHM8fB8QandxQq54e/9Zv8737nP/u2SPv66IqvVO/F1wyx4f+vULT820nM07X24t9y/a+2bsSXj6S/HI321Scl8C4QQ0QqhSgzhg7afY+QEm8Dm6YjIqnnFcvDA4raED67oNsPNNstuiipZxXDesu+taisoKor9u2G/VVDPq2wVnGxuqJpLGWmkVqhjBorW50jV5pgI1k9Vrv61mHyDB/3GCWoFjXLuzeIZwX9akS3ZXXJfrXFDo75LMf2gZQEbt/j9z0iWaxNTKeG3vbITFEdzTB1iSlqNp9s0BG0zujbYTQhe+kmz67WdNbT7AdMpdB5Tn/V0AdPJjQmzwjR4XY9Wgv8tqNRkb73xCCQSTAMHtYd4Xr/ZnVGvZwghCCEhHNjG9X1nn7bY/uEFND3jhAS3kf224FpWSMyQ9h1ZGZ0Wy7rHJUlutYiRIYUEoVgsBHSwD5E2t7iGSsf3dWWfDoggHoxQbgZm/MRWdhuWkIUOB/Y+4DQBqUlREhGM9gwnihCjvO7pxuK2YSsLHDOESI0+wFrIXiQUqEKjZKB5CO7dUvK5IgulIkkYXbvkNnbj8ZK6VfOYR89IY1YSRctLhqG6HDW0keQJJIar/JBJKwIBDnyrFGCmAmss6gkMUh812GpcFIQNVgV0EKRhoGQAlb6Eb3rLcl6lMkJXpB0om+2hGqK154kE9IlXPCkFHGMbdqQS+IwoISiU+C9p5eBIBRDGrGaEyMYFOOMulbENHYRohIkn7BpxI1ao/DR45UkwIj3jCNacrheJ/qAu0bVJsZ/TowCZ0LEK0Wyjug9sTQMgmtc64jrc9ZDikSpcVoSEhASQo4jaYFElBKrx+MthByxpDoRRSJphY+JJCIpRKJUhCIjiYCTEZlpRBqJbDFF/CQj7AaiGnGxAkAroonIowrddojMkWIi5TnyIENJiSqmSFeSMIiYoBvRjEIrrAkkMepOkGns8lUKkWeIeoao5yRR0m4a8iCITo56FTF+Roe4xrRKHBDS6FVhQyBKOd4AU0K4iFOMyQgjCtsr8CkhtIJaEyqJKjQ6N+gYyKQmCTDRoVH4MB740Ftc6xBFRqwzwqQgWY+PCTKFtw5ZaBLgjULJgBOKJAW+zLGXDVFJ3BfTGmps5zs1XsBToemv3bbVvB5F8CSSGD+jFKCUJGYGYDz2ucZJAXGcvUZ8gfxVJDw+k+hM47cDSEgi0SvwIuG1ACVAg0sO31u6YQcHI545EQgy4pIDAU4nYgwEJUY8bhcI0RGIdK4jGY/MBJ6IxSNlIBmJFwLvA1EJbDuCP3wuCSHR9z2Ellw4vHO4oSNsNE4MDD7ie0N0GUmNEI+YmRFpHUZsbPKBJA1eSITSxBQZXEQrjY3u+nokwKix6q0VSkZ2u4F25ygKgSky3BBICVSMCB+JKNafXdAnTyxzYohsL9bkQTIQGJYVyoTra0nCmAgijOhcRjGtdXbElDrPCPRKdG2P7SIuFPgQCDEic42PkT4kimKGWk7pdj2u6dF5RUgCbzSuj+MYmlT0e0uUkZgkfUxEG1BlSXSQpKJ3IyzAR09U4HIBEqIMBAM+eFwYiBOFx+FTwCuBFBCMGItzV3uCKnH5gBOGWBl8a/GZRgrwRoDSRJ3jOku33pMGhybH5xlx40HLEVFLJAmFNjnOjy7oQhtwoyliSB6hIQaQeoQ+5HmGDonBO6z3KK0RWo1GfnY876QQGK3xgx1DLyXYPLvkTz78p7zzn/81iuXkVybKv63wm1LCh8BgPSFEnI94HP2u4/LCIssCYdSoo5qUbC/3DDaybyQ2gUpgXWBgRNz7NI4BxZSINpKUgiRH9DCQEKM2zDmSMOg8H4/HNXc1pURrHc5DJ8SIIE8QroPC/bXAfpMcaprTW4/tLZWaMsRESoKQRlGWjyCkwhFpo6WY5hAMosoYhsBwuSP1jFqXEAlCgJbjiGmIRMWInnV+jEViZPB+xG6HL7CxanyeUPiQCG5EtWuTIZIcu4tuoGkt1kdmpcZHQV7mhJDQUmBbi9YK1zqYKGQmSdevE4Uk+IjWkizXuAT1YY3Mvj6c9NVj+0Wh/psH/9dTWvxy+XefXHxtub5LfOmoc/3wV511vlyuP7b4+lO/nkl/yZz69s7FVzbzbcvth4dMD0qmxzmzA4NedXzydGQMa5HIVKAZIvuLNXVhqW7c59bj29SFoF1bdsUcrSTzU8dHTzcs5hOO5xnHxvPx0z0CeGlqePZpx2FWMC81B8FzTqIqDEdz2F56Bg03Hx4StxcsH83YbhvuvvSA4h242q6Zz0pu3XnAB3+0IkU4PtJcfNwzn2VILEeTgZ1PCCUpRCQ5SDHgXeTxK0uGyQyhDfceLrh44nG7Bh813//Rbf7w95/Rdx59ecHjR0c8+XyHDAMvSc/5fEbf7DmeXHcOQmA2nzAdrvgsOlyKhNAyqQVbJDIJXp4VPDv3FPMSoxxVLfnTDxoO2wteev0WH/z0inqaMZsY9p9cMDSK0AhuTB1hr0BJGFru3bmH7RxiaFnUjtUOdK25cbNie3bO3knq5YSpXXOyckiTyGRgUVp6V9AOjllmcKJE5TXHd495ePcBP//ZluZix0x2XHpJv/cQLI8ODJd9RthZXntYs+4SbaUoRM6havl0vcF6y3tvH7M+39G92BFT4Ed//QGfnSfOn11SiIbyMOeCPSk3/NbiDk/SL7DOM3GSYzkfI55vJNJ36weU+YQqzchFwY/qd/jX7hOEcxzaJcI70qwjT4lXutd4NvuULCpu65sYmaN5jg7w2v4eLxaXSFNweG7QqSIUiUznvCYe8EF6QvSJpV6y6EqC8sggeK25z7PyApEpDoqaKtzkA3GBkppX/YxncosdMmqneKW8zc/0Cb7SvHRWcFL3oxtwELyibvCz/gKhDW9c9KwOIj4L1D7y8GLgF0cVKtc87j2rKsfHxKSz3L3Y89FBhRXwaGvZ5QqroUrwzm7gZ4XCWcf9xtFqTdCKOiQe7C0fF5IsRG6vW4LWkHsMkteebvjguES7wOFVi3Aed2tOHuHBi4YniwytRuSpSqOvSBYSL28dTxaGlCRHvUdYR1xqigj3Pm/4/EiDTsy3nmkcCIfXr2dnPK07VA2Lc09+2fPkRsRkhkfdEZeHHlMGjme3OJxOuRoukWXBkV7yXDxDBs+N2Zwj8ToX3hN8YHbacm4u0KyoqblpZ3wWn6KV4gY3aYpEUSbmpuJAHvGz9jOmJvJgqFgncNFRuoFbV56PF4ZA4s6Vpa8ynJbUAV659Hx0qAHF3W2kl5GgJNonXr70fHogiV5wcxvwAoZBoX3i0S7w9KgiF4LJtiekQDMpSDHyptc8vbVA5hm3ukg43+JCTW4Mr1rF+1Lhe8903zMdBOdz0CHy0tWez48nRAnzrkd/viYup2jglU3Hs4UhDomDPpDt95wf1KSTDY8uBs7u1bimZdJ0zHvHs8MZkHh4tuViVtKTqBvL4mzNs1tLRIzcP1lzeXOKzSRl23N3vePp3SVZMtx+dsFlTON+6gO3zwY+upVIMnE/u4v2T2hWkYNbR9xZPuAX7n1CDNxXDziRls62VD7j7asj3l+eUqJ46I7Y2wYvBqZZxaP9PT6IT8kE3N6WpDwjZDCVFa/sjvmwfEaRBI+qm6zXPUOy5EHx+vo+nx6foETGXXNEaDOs7agXUx43Cz7KQKTEnWWC2tDP96Akb8xKfvrUUxjJcWXADgydYDareLzw/OzpgDaSw8KQa8HTjaIIinfeWPDzD3fUdc5xLah1xEWNqXIeHxc8exoZ9o4sEzy6OeWjNkIheVBqrN3iGo+0mndef5PV7gKAg/khTduyqOcUWc50NuP9939BInH34Cabdo8rS0oh+d53XudnH53hfeT+rOIqSFblHtkPvHdvwUfVBPfhCXcnij5FdgEqpXnjvuGTlUJ2nrtZIDuc8OlFT3I9b98v+MWLAASWzhNqxyoIloXmze2CT487bAeLruYgaJKITNSU79Rv8mfiE4zWHHcF+rLDsqWoJryxXvILdUY1nXNTztH7JS4GSlXwTr/g/YtIs4dJMXB46tmvFCkJ7k89p1uPyT2haziaaZxWiDhwL+/ZTDI2LlCJwL0bhl9c9SQJt4Vlp2BPZJYbZtLywnm0ggezgk3vGfxAYSQvzwtO+pYkErcnFQSLMpZpHXmwqHn+i5+jPvk5r2ZvMKknX4ZcfGM8/+z8kqefnzCb1rz56j2ePL9CZwUPbs65Oul41o3+Vz969y5/9skaXMNRJvHaEBpPISWv38j4ZDUgbeSoEghR8Pk2kmnJvWngs3OHSIKZSBzkihgzfLK8cgueJMmu9RzlAikEJ90ohn7tZsXTTcC7wGKhqLQibARSJh4tBC8uHbUpqWMiF56hzDk4mHJLR87SQJQdt80B2J6T4y1VVbI411g3Y7/XTJPk/uyIf/PBJWKI3CgNn3eJYfBUWnFbap4bwRAjrxQ5LZHeByopeFwaftz15ALuTCRu50gKSqN5KU88Ww9YGZmbEVgik0KFyDvHik8bSeYECz0mxlddQCF57/EBP/2gp84zlkZig0fqAZEC9xYVT7drtPCUsebeLGPVKW4d3eb1R2/8SkT+K2H3F3/7mvPln6/T+Lddfn1Bt0ij8cc3k4JfrvH1H8VXfvjqein9cpWvySrSV54ufuWxb12+kWB8sdPs4HEMkI1uzV1MiNOBPFfMao0JOYWDdt9ycdJhpg0yL6DMEG/eZn+yZ/30DHnRcFQVGDE6066tJkkDytB0ilkYZyqVjOw3ARUECsHlaYfJM5Z3l+yvGl6/X2MKaJaGH/4f3+RPPvs52gaKGlYvGrQZK0Yf/JunY0svBubTnL67wsWOup6gSBzcvYU8bZjMDNW9e4Q24Hzi7Knjs598Rt8lVPL8ye8/QQlDVuRYEdifnBGTIsskL7pIihsmk4yIx+tEO/TkXaB6fYLqrpApISqN3uaklUOkyPPWIzIFWtNYy0+fas7+4ILpsqHUIFVNDBLrcnZ9wHYe3wWebCyFMUipcDayumwxhSYrDbtuHCPTWqKMZBPkODZwULN7sUcx0LUDMh+rVHWZYXuLHUoSNSkrUemY83VAlhqZS7ZBYquIDYlJVZIdHiM+WWOUYGsFPnhIiazQ7Paa+VxjXWLbedS8Il52CAlPTluKw0MOM01wa7rJDiHB5JFNfMEsDTQM5EWHs/14Xsuvf0n71GFNGCsmynAmnzFRlo49WaXoXY8RHROt2HLBlJw9Hq0FQlqyACWatdhQyAku69C3l1gryMJAHjTnYU0lDa31xK5loxxRCGSUXOQNuSxobI8pa7ZdRLgMJTLOnEOJGjSkvuA8XKDN+NpX2R6TJLkZPSku/W4077Key7xAMpKYFImLmSbLNd5ItnVGVBJiJDQ9Z1qikTgSjVFjZyEJDIIXRmPkWIlpTAQ9uldnIbDORoyfFdDmo6CSBNkQOatzch/xCHyRkRZTqHPyKFjPLFmIWCXwShAARSIHNhODSdADTiRC5hAioUNgNQvoEElBEZSnXbQUxxoTEhftJXjHsG4JZU1z1CGLhEoD7U3NpK7p2SK9573pq6T4mMWtYxq1Ybd9zmADpXJ8fzGl1DfxvWVXPeVfte+T/IoDESj0wFE7ILWkNltKZUjWMc8StnhCnbb4EGhcgPSA4AYkjss6ImJEaklbR5IciEIhiKzmkInAgGCnLOJ6UDgHrsqACYpOwl5ElB5dmIuY2GiFaSM2U9ioEMIgoiF3gTME4WxLrwW71iKERPQO2TheSEkxKehzg2s8XRqN/ZQNrPIMY6ERCbvtcCZDMgoBzxY5xvdQZMQ40JaG1HtMErRv3EV+thlNIEViX2QIQCdY1yNtRzLizFdFNgIDYmQ7zTESJBHlLNu8xMgMNQi2UaAY95tyju1Mo5IjAG3uqbcDRmlynXFpL9HCEAXs9DDesEIk85Lzek+exNgZjw4Z0+hplOesw4ZcaBweVwTwbnxeVrA67CjyKd7taK+vDyImMuu5zDbolNM5j51VDPsOESQm5jxTAzoZkg646HDLFuUtuRJ8traYZNg0AzHPQBUsa020lpNdYnpQc7nx9NaRXMG0KiEFnq0k+XLO7ryjGwJDByYoRBu4eBbQMUdnJaaE5+uWmBuiT5y2iePlAt9csX7ecLt+xPfe+Q5JwOHiCOstV1eXzKdz/vm//v1x3DZEBunRRuK6jumiZNNsyczYbbo8XbN60bNvPAdZzrkqiXtLQrGPilQYZIowWC6SRAtFMS3Y2xZ1tcc7mFU5l4PCNzt0VhOEJxYKpQUxek7EHu0FIUGYGJptHNHNg+TCXlGZDKsy8uMZmxbwlrgWPCWg7JTQWtomYQ4NusuRbeDZi574tMIPBqsLuieJtIkYI1mX114KIhJUIKiaqpC4fqCJijB0CDKU9rzYdQgxmuwOSrCsK3YX+5H2VsJsZuh7y35oEdFT15pajF2FRSXpnUeVDZVp6XYNB8eWj8PHDPfg8oOf8Hz1gv/gr/8OKonRIFjrUdwNnF9e8g//8b/gcrVhOqloXYXQBW7f8MmPn9G0Au8Fk7zk/R+/YPAwBMF2l1DFdSA2OK42EUVCaYm1EWFyBBHjItu1IheGISasFVxcJtphTIhXEcoCOhuxIZLlUwiOTGkuNorYDMiQMTQJK9OIohWCy/VIp9quHSrXDOVoXNjsLFePBrh3hVSRNu5I+SWzA4NKifzeEWp3h23TI03J07MLrI1YITndDUgEWgkymdjLUdBdGMHWO0KKKCMRzvPRWYOKCZ0b+i5Q1xl2gFwkVrs9RaHwvUMpjY6WQV5jZoWBYUCjCUoiZE2GIMs1Z/uIyQuGwaOrnOkNSfe8JQ4dm02iFAKpEjJaXi5e46o/57e+9zd48PjxXxgqjznEtyQR/w7aF792ciG+mSTAl4H91xKFb8sxvnV7v7r9L5KJrw9H/QVjUX9O7nF2csV+27JZbWn2GtuVeKFJKNohkQXoOocLgsEKLl/sqI4kPs94/rMTPj3ZEnzgYT4hJcF63eE7x+W6J4qcfQf70wYrMtrOkUKgaCV2GxAiUk5K6uWC1UWDCo6LmebtBzN+5z/79/nFycesN2uadk/yiuFZyf4kw3WWzcWAKjKyxZTOdeyHiNKC9XaPSQahOvSsRs0Knj3Zst87hmZA+cB+59GmohkCtglIHfEhYaTAZoYBEGEM4AmJ4D0hk7g+0kaJ31men+zRB9B4T7zqyNtIayE3is4aVBtJ/ejo673EvuiQLxpE27FYlHRDpN9ZtnuwbkTJIQQxgkvQDx7701PUdEq7DyQvkSnh28DlxrPtJBbw5z21KOncwBBBKI33AdV72u569CgpXBf54MefM7k9p/OJ/XmLXiiaEGE2Ye8cn500bNaeXEpeXAwE69m2AW9h1ylcGJ0vTy56VCbpgyRKw4cfb5legcgMvnK0UtBngn2KnIgVWdEQM7C95dyd85K41hd95Vw9sSfswo5N2DCkgW04xQfY6T0ETyqh0Q0Oy1oniiCxeeI8XSKUYKcbOiNZ5z2lntCGbhwnKSUr1yGDQLsBvKfJe0TYkgQ0picp6ISj0DmNsqS4ZZ85roIl9lsmukDnJbsUiKHF24GegJKC7CCDXU/rEyEmXCa56Aey2mCTIS8UTSZIXoDR2EwQjBxHjFxgZxRxkrNCYNWIpQ11TiKxyxTBBUKpSLnBhVEzoJVkm2s84Igj9vZ6XApjaPIMD6yKCpE8VkuS8oQqY5+NxJg0HZGcvR7dnlNK7HPFkGAtxqrvYCToRIiGNkv0Wo6BS4j0lQbjiKlhu+3JshwZPAbBXlnOU0Icabbak9yoXShUZC8HNrrjqmr47dvfhxj5/1z9hLW/Yh83FCrjNLzgN9Mdoi75fLanFz12aNjHxN4LOtWAVETdk2RkMB0rsWZvO1apReSKdjInkdi3iegTMVNYrQhidDsXAtpCkZQgiojXoxuxRyKBnUl4Er4cbcidEkRhSAl2ZhytOss0UiisUcTr9v4+V9hMs1JiRL4qcU2hga2RZBrOBZjkGfIcdXtJO0Ss0nTGs0WgUmLIDdSRKAVNaZBS0PqOTJY0mURIQQSaTJHfmtP2AnJFk2mQY2GjLXJkjLRaQUy0ZU4yClJiKEaD0z4YpIK9gljngMItpxAi+WGFSJEm1yQd2RnNroggBGW6YBiusFXkyl7SCksjOpIWNBkM0rAvHdFtiYUnmkDMBC46kIm9tgR/gZ2MY0F9sKBGQs027wnxivMsYIqMTjbY/XN6L1lXgU55LkQ/4jS1I60/JwDbytP7FW46RbWeXkZ8nwhYtoVGW4+gxruEDZLzTQShaG1ECoWKkRAG+iDBZAgbadvRFbm0jnxSjMG7gzLP2TSWlCDMC5zvaYKEztMnsOL6Th0C7ZMVnXXkQvEnf/+PuPu//yss37iHkJIiL7hz6y5N17DZrbm8uiSlSN93KCVomj3SZOz2p2w3o4Mzg2S1H2hdoso1T5rA6qrHWrBKIFJka0ez17ONQ+YKlxyH8xJhEkMMNEqyWYM3E/o+EGqJERmtSDSDYz/tqSeeQQWkdwxVh6XDdWecuhYpNU1s8SGyzzq22qNT4lJsycjYRUcQAZoTNmlApsjZfkrqMvZ29OAYtrDvMxhAeo8qFHufCOT0G88QFALNuumppyXtENHK0OwGrJQIBF5HztsdbRQkJWlbSzLj6JhzHilhGHpErtn3DVFGEol817DXW0IR2bsdm/M9gxuIIWKk4ezshJuHtzBFjustKSZ0pnn+4ozVesvJ6TnbXcn5rqC3mvWLK7IgkUWNlRqXFzzpRh9yG0AFQdw5diGSkVgNkRg9g4uI6YzQOHZeMgA7neGsxUWN9mC3gTYItBQIkVAp0Mdx5IfW0YbxmtUEgUw5QWRsrQUSjYUYIr2TKCnok8INPaIXdEIipSZkW1Th8HVkEyLFHOJkhy4yLl5oho1l7RKhbbFJcSEETTdQIlBC0cLoUxEiVo73Eq8V/TASr3a9RUiBE2NBWXlB044xpapzQpJENxLNOjQuRFrv0WXFmdV0MmFtwl2jidso8EZw9WKNTg5rA+58xcwZQqkoJjO2FztcN6DKHAdsXeB7P/oBdx7c+3MC5G9fvp5k/PrZxa8/FvXVQP4bicTX3p74xo+/mkX8cntfZB9fbkf8yhO/fNlvG4365qavd9psMaEoc6bzmqoucLaAnadrAtN5gdnsECqSqTEgms0y8mnBbFHw9HyDdgPzKmdWZIj1nskkR4YBrRM3Hx+TFZrTZ6dIHSm1Yj7VSBspasX81hytJUPT4LuO5dLgbcfsxn2qwwmzdsZsNmNwjoPZhP2qIk8ZmxcDQy7QWUTrSLvZkWeCSV1ycbWlmBQc31vSO8H8oMTZhu1+h+88SsHRoqC1CZECdZWR0kjAEcERbEBESXIBowxFWdKkQKFgUeecrzsyBSZEpPNIo5kYQZ0pDImpkoQ8gk903jOtFNttj/I90lmCtcg+UtdTJpVgbSIK0DKhtKIygnUTyTLD7KiGMoN9IshxFlCpyPFxyWo1VoDnJjA7mrLbbblsArkSZHKcfda1QmSCVlicjxQotO2ZGE2QfkSaZpGr3Z7FokCsHYsKtJRMa43IIiFEDipBoQt265YgJCY65nVF00gK5cFkhGFHWc+ZHC64MpfsC8nEeqadYXI4p1cBEw0P334DixtxstfI40hgruZUqmaiJkzVDCMCrhsIoeewOCIkS3SRWtRkSpCj2GM5yI9wQ0MMjrxXSJ1T+gp0YBEqejNqBwyK4BpyNX6RjtQSKyOyTWQqRwdBrQrSRHLIHIZE8tcmbEExGzKC9By2ik4EjAejNGVeEhoLueRYVuytQjiFClAWgqL1oBQHXSBIgQ+OONPkPlB5CNGzsBGfEihFlxKTENBCkAQc2HitAxjogcp6jFREpVgMowgcEr2UzGxARgnJMu8sQXiUt+xzzaTpkS6SKJnsepKSZFnGRiYmMRB9IEnJJCZciqgEuxCZDJ6gEtIISj/iII3J2CnJbHD0xoyBaKdRwlAXOcrtmLcKJ8akWUVB4S11nwjSMSFnTk0UEWTiqDpm5mYMyjFTc2o/jrLpScmsXTBVM3rZc1Ae4gZHsTekkMhUTaY1kFiaQwSCrKrxKaDLgsws8MOKA60YnCfYxECk9hIdIlFYZk4RgGA9VsNEZjA4vEwstCGWObrIGLRghkENkMvI3EPXBsKqpzOB2kUEAe8VsySIatQEBgW1H3EjNoyjbDJTyLZjg6BIklk1ZeMDxbZDAhrBBlgMHl9n4/5d9ygTKZMnVYrZzjIogakLapPTPznDbC1xVjFvB3yeo0NCuYBynizEEVM7eEKKZM4jEBiZyAjEKmPRDnhTIITAdxbtIiZFHJ5pG6BMGJ+IWlCQcePwNht/xSI7wBQ9pZwx+IE81cSYM9g9c2/w0SF7T5dHqkaRJQN6pDz1XU8C9iExjTlysMSgWaScpAJZI9FlyWzIsdUcSke+6QkkSlmwDw2zRpO8Qk5KykbgXIZRJdvYc5BpBp0hJpJsFxiEg1yy8YLaBKpZzdlZgxYRmSI6T3QoJiric4lf9UxmBdF7KmEJE01tPbiBSSlH9KbtmKaAC5BFi1kYvBqLAJkT1EqQ1wXz3NCfr/jT//of88P/y39CeTzni2mFIs/Ji4LDg0O892ihKIucGCPL+QFSFhSZou8d9vkWbRT5RHH7xpS2MMR1i5tlFESkGN/70axmGCTJJtqQUG1LkQush2znCL3gYDJj5SNZb6kTxJA4mBQIn1M0Dl0IphTMgI7IRE5IcooUo8fLQsxQEVJUVE5DkmgnSVXJkS7ozzpSIaiLGWJWoJqazy8apsKRmwykHIXKyZIDg4hMpMcUGbvNgIiJvNYUZqTXlSYiSo1P433zYF5jux3CCyaM8ImYAlpJCp1jRORy31JGRT6vUQb2+47jWwtqXdLmnsX8AOsdEyYM/TCOqE2mDG7U35jCYPtRaD+fT5lMKqq6YjmfkkyG9RqxaaD1lNMCH3qmGrJcMcRIbySVAd97nIRpYfDWo6SmU4mjqaHvJMlJShExCmyEJiYOphn7NhCco1KSICKZgOgj8wpSksghEe1AnjKqwrAZHJVwDC5QakNmYDLJcG1LUJG5kQwiok0gNxnSZ4R9QBWKI5eTS4GsZyTrkVVO0Dm22XCkchqtQQi0GLuiBYkkBZMQIM/onSMCKkRmgLWOKoTrTpMipEiVScpCsW48dS4o5wt2zy8QuSEXkB1UnK07JiRyDfPDktW6I5cKLRKpjxQ4kvPo5FGZZirAtBYnIssHxxwezYmDp/WB+7cP+c7/+nscTyqC8+jc/PmB8f+Pl18fRSu+8f/18ivB/9f+KP58stP/7Bf+xqb/AvjV8nDK9KDAhYHetvzgRw8pCk3sOlRwzHXLYARNdEzrwH7T44ZA3LbofscgNSEvuLEcnSCD9zT7PS+/e0ycFFytW5ZmYEFJ2SqKHcxLO1J8Lvek5pRm3yLVWHmYFJ7DO4dIKbl/4z7hbIp7OsedTnj73fvYYaDdt9w6jJTLPdvmQ7LpjlcPK7qNYFof8zf+t3+F6s4N9sGwWnnybs3QQVlOeHhnghaBvh/HjA7rji4qnMyYasmEHOVrCjHjrnDgMsSgKYOnMoHicEJ1NOU3lhWDUnQhYFRg+cZA+P6K/t0r3v2eoXtJ0r0qEPcCR7cyLrZ7NjHwvR8ccrYb2PSO4qBieWDozWiu9ujm6E6MyUgpcv9hTd9HOhu5fTRecIYApip4cNNgA7St593vHuJzRSo1KZcsjxNtbuhyzUsPDGom6XKHKyLHsuXqxZ7eCWbNGpksWQamkLzx2GCnsM8sLz3U5GYUk4UIP3h1gplMcVEypScVHr9QDCU8eiXg3jCcTFbUk5ZsEukLR68t74lbpCIgpePe7Rv8tPiU/2r13/K31v89f9z+Gf/39d/l/7r6W/zMfkTUGVfKciE73ouv0/QrUhFZMOGWuYWTEV/A94sf0E4EjQzoRrE4KdgOAzsd+K55j647w/UXlDHwiGOS2EPe89uz70ORUDpSyIyXwj0wEHTkN9zbNMnQJEPSE97J7yKyFp03/MDfIEoxiru14s3NkqAiPZbXzyrKWxPUXFDczPntl19DHIAtB15ZD4DCSklUinfPOgYlGLqBV082qMGOIlcj+W7j6Y3CF4ZHjaMQiqA1vsh597Kll4JBSR40jkpIQmboSby36ujyAmsMN1pH3faITBMzzXtP1vR5iVU5x70cCUPe4bXg+yrHlppoJIvOcdBYnEwMWvD68x0uRpJWzPvErd4RKwEPZvzo1l1iDkw000nNI6b4TGF14jvNMbuuw2aS6dEBr8kb2O1Av+158/Qm2/PAfqVYf7Tj6uQz/tbZf83fOf/bhCGyszO2zYL9MKNTNf/V+T/jv/jsf6RtNf4XEv+nivgzyb+n/he8Xr/F6/Vb/Me3/1O+M/8Bb01/g7fq7/DX6u9ibEvW7/lumvBX9BF/9fguP7j1gL/ed5T8hCk/5vXdZ8zkzyiLf0Oe/4QfuAuyg19Q3/2Y77ymOHp0A/NwQf7SEb89u4UPBW4jODwNlKc9du1oVgMv/+IcryWxLjjYWybtMHZIROSNFzsGRoLUohk4aC1eC1qReP3pBm80QkkWLrLcDgQBQ13wxosNVgrIDCbT3FztGGxPJwNvfnyGlZagA9Jbbn/eEpcH7NeW19+/GMWeUiBD5MHZFkfCZopXTlakTBO1RHnPSy+ucEbhc83LLzYARC1AKV56saG/7pw+ONmNXXIlSUje+3RAS4VB8qZ6xPdu/IC3lu/x1uIdfnP+I3qRcFrxqnqMdgobPYOMfOfzW3R6FMnf282Zzw+gFHg/8P3TO0Q9QBm5t6tZOEPSDpcavnP+mLXX7LeS+WnJka9IxuGnkd/aPMDR4ZXlwBtuNOD1Fj8f+KE7wFcD3rRMCsedA4e/s8G/avmt+45Qg80tLm2Zug0+gC5r3jwKDMriq4CZJB4eaVA5IWreXkS6fc/QWkypuL8EJzVOG777oKRcViAFWaF5d+YRzZrUbXjzdk2Uim4IdEpSHE34w+j4b37vX/LHP/30y3hASc2PfvAj3nrtLd55423+k9/53/C9977PG4/e4NW7r/Cj776Ddz0Cy1/9nXd5+FuvUD9cQin5rccLehRDUjy4UVFNMqyH3W7granDikQQgYcLxc28QNiC6ApeKVp6FQkmMJeOmYqEBE4qfqM/pOsGrA/M3ZRlmNGqyD45fpC9RxwGZB84ZMIDP0GVA+qm4IdXN+iGMHpKWcODcAcn52xdzrvMaU4TbqXQm8TDA4WTiS5F7qk12hQonZNC5E5tsSTMtOCdY4W3Hd73CByPigEhEzY5jmiIBHywGCP5wZ0ZMTpsdDyeao6ngaODgEor3rpVkE13TA9a3vmNx8we3gStcN7xN3/4N3nzlTd59813+eH3/gq//4cf87f+3j/n7/wPv88f/uQj/pu/98/4L/72/8izz9f4oGka2DWR3/qNlxm6DpHBG48W5CERkmTTuP8vc//ZM1uW5Xdiv22PC/u46/PezMqszLJd1VXdZLNJDYck6GYkDaCB9E4C5lvo6+jNCJIgNUakNBxh6CSx2U0O2b6rqit9Xve4sMdtqxfnZlZmVlY3ia7BaAMXETfiPIETJ85ee6+1/oa3zwpc1AQnOSssZ4s55IaQSn7w9Tt42xBsg0qJmc74BEOEe+zoXSaikOPIeQW6qDH1jDfqEQqDaUq0zDSqx5WS3BR8+6FkLAWuhOq84NFjSPcS6ZHgdP2C/vsvEX/zhvnfGHj7B3vyb3zM+P13OR+fMz8LlPOO9R3DdxdvcnAto4n8+sU5+uxjqm++pPzaNd8z0PU9nsxjMZHuo8hEIXg8jnTeM4TAwxjxXU8GpFK8HsK0pkjJnVJSKEPAcDhGnswMzOd0Hl47mTErHVocsY3jV+8JxuMlIm84VTvK1BHpGX3H109LetHQp5r17BRrZ+wGw0fvH/n66QV9Lri99rh9xL9/zW//1/+CdnP8C3fNXwmJ+iWNv7wU7fHwBfI1fEqf+JR4PclHis/hzsXnMSKffbmvOI1P4VU/h7z6BayL/KXHL40XT6/4p//P3+GDd59SNyV0JfkouXr3ilWjaQ9bdj6TSMhsuXh0h6QLkh/54/1AW5Q0teVsGHhcG25fHhi7jpNvv0UfJNuPL1FdYC0lt71kvlR0rzoFSEFtJUolBqdYlJlFM/Jf/e//Hudfv8/v/877/Pv/7/s8++iW04s5/VHR3g5cfnBJvfZgD+yGgVIp1DCjma+oVjPqkyWpKPj4z26wYeCw87ghYgrLopTs9y0jJZVJODRZKvoxU9egrGLnJPNGEcaA1JKhT9SziKhhN8bJyOZOQK4yhxBYzhPz1zzHZqRyEv/xHHVbc5sSJ14jrjVjpyk1JB9RKeKTYb0yXH58SxIFKTgaJSbM+iBQYqBaLrDrFf1mjx9GtBZgGx59/ZRP3r9hsxtZzEtOXlvRffyC60PEKo8XGts0ZGB5p+DYb3i5GzktFGosCCMgJfWppDrXfHy1Y/2KNBZRDL3jVFrWsyVXm8DFWUEfFd4nDpuOKI7YNeyEZFEIXDlACaG0FDqh55IbP3DqM6vXn7FadfRy5PTiPr5SXMZr1mrNyISdPcQDZ/qUlOHSX7PSS7zrMH1kK4+c5TVJa67zhnkoCcljkuJG7LirL8gicSsPNKmglIFFVGz1jlW7YDSGg+6pVAUSClVyna65EOcMOXIULQZD7DTK1VybI/eLM6IcObS3qAhKLJFuxmU+cO5qumFLl45Q1cyEZlGXvLQH7lX32W5gSBI3jthwh8qfcd1YLvqIQ+KlJBtNM0SMz1zXhnOfGaUkMSUQiyFgpeSy0py5RBsm5Z1RS5ZjRCG4rizrdmBUGqUkbVNy0o4Y79nOKhbHnp5JvWlfWdaHFpUdm0YzGyJhXlKkzC54Vt2k0LI1gtonfAiYCMeZZbVvcaplV0YKlyjvntAUJZfdkZULDMNLdhxobAkxUWvLVTxwNpbkDK2OWGHIvUOPkX3lOfOK6vFIbHqU1BDOUOmc590td8SMdhwmOIZSnG0FpxvB9e0Vd0/v8t13vssPvv2DSV3vU4ypAB8d/+3T3+KD47vEHHhkn/DD9nuc5hny7pz/9vlv8ZH/iCE7KlUiVOJWbaiPJb3MxJQIOlCrt5D1t3gRI8s24ccKNUhaMgufwHluC8V8CESjECHRNQXLzk3QnMrQjJGoBSYmjoVmeRxACm4qwyxMqlxVYTkuStZ9QiVFWxVUo0cIge4d+1nJoh0IybEvFUVIaOloZGC/KlnfjPjZKe7hHeKHV+h2xMbIZlZychwJdcWo5cRvAKyP3M5KTm4POKvxhUEAViQKN7JZFKxuW4aigtMVYd9hnKOwko1VrI49zu5wciRpydfv3OV/fvcbLKUlpsD/dfv/4N3xA1z2E08iZj45PuOsr/E2kKPDLTTLVlPWDdfcstwbXDwi6pJOO1auhOPAZt6z7Eo6avJoOOiRk1CgSsnlbGDhCsJ4xArJoXKc7C3ZKDbVwFLOOWwV5VBzowZO+4Yc5mwV2D4w/p7BXM64dLAUIPuCQ69ZLixt2iJVxx7N3UVJ3Cv2u0ShBSkMzGeap1vHWgVsM2ezc1ir0dmhcdwEycOVRsgDh8OOQKZuDPPKcrNpOa0t0gTMaUNKmbe+dp//zf/qP2E+rz9d+F+hEzL9tsUdepKPUGj+7//0X/P+x8/xIVLPliQqPv7gknI/cLTnDMnQhsSy0YjesU2KMnlMXZEzdFmyshoxKPajYW4ig/IgPEPW3LlQmFN4cWg5KSz5yTPKxY7DPPPa7ARxuKErjtSxpLw7o7Il27hlbU84HLdszJF5veLwSUDsLNe65/RWkZq7HK1AjJn8x3PKj2e83HnOZMIJy8uNm3g9KlAa2IyShRzxZMYoMGrqjqvQs/OC0xJ8jsjSEv0kjV0Que09p7VBq0AiMYyOVeG5e2Y4qoDc9ZhZJAqHmZec3D3DWsPLFy9Ymobv/eoP+Ru/+Z+QM/zBn7zPv/jtP+aDj15ytp4zOk8G+sGxXjUoKbi62XG6XnAcMhnJYd9hezjsBdukWFrJEBQ5SwaXWVvBGBNHr1g0ipAiuhD0UrM2EpUNL28nM7gYBfjIKCwLEwE4eonJgagSWiZ6DDb12KZiF0DnSDOryMHTS0sjB8QSDjlglETf31HeHTnOM7N9JNiWOIsIlyhjZF1Y9meZVV/RyY64FJjCUlAgXnZcNz1nw5qr3z9hc1NwCIFSKozPXKbECUzKe3lS35trQ3aBrZTMQ5g4hFISMiw6QdNJrveBk0oiYkTEQNSa0zpT15EXL25YNxVjEKSQaZ2nlJqI4WaMNFog9ZyQBX2WnFWghGPbjcytJjrH6Z0lV9cHzkrND9845Ve+8ZB3/vZ3Keryy3oyX9oei69WiHq1p/+fVIr2y3hyeJUvfCGB+PxT8SWxqK/OBD7ja3zlUeLnXvnqt7/I7nDOE2PE+8DQj8jRoIRmDBPTv82SMTi0ksxPl1TrBTdPtxz2B2JpQWuGkEkIvIuMvScrRYyZ7fMNx6NjpTTRJ2IQ9K2H2qCKguAjISVA4sZItApdltSn82nDMEbG0RNjYuwD3mV2Vweci1Q50/YjdlZwenGC9guy18SQ8S7Q7Rz9YaDtWnJWuJgZWkeOAik0fgwQE33OoECbgqKxiEpjDgHIhATSZ0LMjENAKoGPmUFAIKOUwPmEF5FBJJxICJmJUmCNQriM0JoUMs4nwhiRKWEyiFLTd2EilRpNM6/Qw8g4elKGEDNyCOQhMIwJow1I6NqRlx9cM7qEjxC1IfjEGEEajfOBKDNKSHLKHHZHuuBBCKKQSCMJfsJFqtISyESfcGpyh+29RypJN3r8fkvnJBs8lDVeKJLWSG3pwkCfMk1pSdYy4IhtT1VB9IYUI64qCHja/oBYWxyeMTg8gSH29KEjOcegHJ2wpJQZckcrIPqBoDQhB0YdyUrgU2SwiSwFKWa8S/S+RUhBKAN9BiUynR/w0uNnrzov5SQFSeeIviPUntFO95UXgcgESXLSE0TisN9havB24lHoPoD0JAF99ORVzRATSimS1HQykCT0OIIyDESCiNhZiRsNQQo6LSEJei0REgoB+ZV030AiaoUDnBS4VwRrnzOHFAmvjotKMMpJPjQKwWA0XkiUVhPfI2dkYUhKMBqFQ5FjmAyKrJ4kQQU4I0jek/z02UNOkDIOhZSQqwJVGMLo6CY1RIIEbSRjisTbHS5N9wrVJFPchhEjJDJ7kha4DDlAHzyDG6hCBu8IIuJNCTcbgvTookCniIsjQ9ezubwm5MjxlSeBeRqQaUZQidGPjONAjpOHgFT6sz5zzJGYI0MaJu8XI2jePKfRpwSdkK4m7EFkiSoNwQ9kAfpOjc2JmDPkEW1mDFkQBxgLRQoCnxOjAB/CJLMrNcFOfiWq0AQyTkmElEQl8TqDloxKEpTEa0Uik4wmEIlMSnbj6HB9QOsSrySyssgQSVZPv7+EKBVeTTKTtRKMAqKEUUnk6ZzRBVLOE5FbTn4azioyGScn0itxOp+sJK4wYBTBakQG7UdcbQlC4IwmNyVDiGSj0NIQRCYpiTOCIDLOiomnoiQuTRjokCMhR/o0EomoHBhFIsnMoAJRBKIKBAlOCGK7J8wSYw2+C8gqv4IMJlhoYvkqXvtANhJvJaMS6HXBGDsGPfm7pBTwyTNKhSATdKL3HYmaIY0EmxgUk/N1ClBIvLWkOC2IPiTSEOhHYA+5zDTLhrgfSXmSqc1qgix6n/CHgSAUY5aEIRDktN40lWYYHDHBrh1QaqBLGWUUZDjeHIgZRFOgC8vu+S2uHTgJmaFzzOfNl/YEgnJeobSaIGpkpFG4EAg+MA4eF2B/tWfvPalckMsC5wKD8EghGH2kaApGJElAYDI8zVniXGRIkSE7TKOJCW5ujswKQzaaPiZycKAS2SqCjKATwU5SqXnokIYpNuNIjWI4dMgsSOtTwhAnjlgo8H3PIM0k15vAiwle3QoIaTL3UwIKrUFL0hjIxoIPKGuJORGYpKIRYKoSPw4cBg8pU5lM7wNaT3Om7wYSCW0naej9sUOsC+av30EVA2NoQUzxot2PjF2PX5S4YfhMmNO5gHOeECL96PFhkpodnWfsRqSShBAZRscwQsqCoRvpt4EkZqQsiIXF+4zwGR8z3RgnCJPSDGNE2olQPfavOBMRYpb0QyBnRV2WxCGBNIQQJhllBOhJKrbrHKqQDD4RmCSTU+/QElxOaCbBhOASOYOtDLJJSDPNt0IrOh3BKAoMo8z0fU8ZIZmEk5lcGAwCr6c9RRccXk58IpcSKoEwhtBHBpHJQjCmPHkGpYTUipSnGBbTtI9CKeIrCWWhFGNImEkvm74fqURmOLaEmD7rmE7Su5IkJOMr2dsgJTFEsjCElOkGj1GBHGEIEVsXHPY9wmiykhRnc6qLObYufi6x+Mqd9s9X7///g9CNEF/KiL6UBnwuQ/i0Y/FVROwvk7y/6nn+0vP/gJP7wv/uPbjg/O4JQgiUVpwsT/nwR1dUlxC6geJVO3t50vDDv/cNnj3tCR9dYZLjREm0SMSUePNrK/yHe5yPPHiy4rV3zhgu92QZuXtmONxIaqV57a0TTJP5yR9foVLk3qnl6mqEPGFUz04NP/qjK8pFy73Hp9T//jl1nZktSh48rLh99xmrxSQ3W5+ekKsFJ3dWvPbwDu/9eIcfAysR2F5uKdEIq7h7Yvngk56UBJV0DEIyW82pS8ETFXl3m9A2cedEoktDUViqUnB3AX/001sygdfWBcVFxbvPO0SOvFZaPmwDYVSsheFURV74gVlZ87WLMz5cjqh+4HyTsacF793ZooPkzq1mpy25TnBz5MG54bZNaEYe3Ze8uC1wKMabdqq6yIw3ma/ftzwfE36MWOW4ayBHWM8Nj1bw3o3Ex8jJvRnzVcHTS4etDEuZuA2Cua1QeeRklngxgkTyrTfO2KiR3cs9jZI8PJ/z3m7Ap8i92uJ3GjVIjAzMw4YXvabUksfnDR+HAVEojIjcTwPb0yMyDlyMZwyhpW4OlLLhu8XXuLp7gislr5Xn7JXjuM0or/jO8T5/pjdoIqdHS64LejS1LXg9LfhA3iDyjDtygdQCKT2VrngtPuS6fcGFXbI2S1SWbNsNoix5ZM954d6lCB3n4hzTrPkkPcNKy2vzR3yw/zFp2LEcSpaLC94d3kMGwdfUG3w0O6AQrF3Nyb7gvUZTFJavyQd83G1JFmbXnnO14IO1RmrNm/YO1/4lKWVWwfDW8nV+MrxPkPBwjGxVJBxesvIFd9qKj1YVgcQbXWCvFLEwLLXhkTT8mXOMKfKoHWmtIQDzDI8Ojvcqg4+Ch53DvXLWLkfP423P++sGYxR3Nx2y1IwxU4+ety63/PR0gcqSu5sOoRJR1VSD4/6x45OFQaXM3X7iDolSUWrJ/Wc7PpkbGi05HQQqRiKZWmkePXVcLiXCGO6EArEfKR68hhGKO7vIh+6KRmnWqURvA9EIclR8s5/zdHhKUgPzMXCSWi6RLF6/w2PzmKeHI6MYWPQdq7Tkhbokj46HH7fIY4341W9xujrj9fuvT3r3n8bQqWpDZWru1g+4dM+JRFbFCTEH/sT/Cat8wuPma4Q8JQeLYsmgek79FitK5mLN1XCN0LCwZ7wIa6I8YoncvYYPh4AWcLrp8VoStEL7xBvbgY9PG6QQnPWTilLUFZWUPGkTH9UKFRJnQ0QC2SaKJLh/0/HRaYUEVoeRUguwljImHl8feLauER7ODg7pWtR5hQ6ZR1c9N+caMSTWQnK2WPDTZzfkbuTh5Z7rVU1UkmXnmI89n6wbRM48vDqwP1uSdWDROdYZns4mf6NHt0c2K4uvLcssWB5HPtGe7BP3tkeOqxIXJc2QONkNPD2HXCrObM2pLIBMIS2PzUOepitCjjxW97jc39D3hkWueHhd8+H6hpAM9w81Lo8EK6lGzdevH/G0ainKgvu7ilBAEFBlzVv7u7x31lOvLHevSvxNx1Aq5mhe3z/mvfISlQ133AKTDWnsKKPkjf2Cd+WADnDmJHI/EJcjBs1rqyXvfgxJCdYiUVvNJ3tFZQVnReJ6hNpNEqCndwre9yPEyN2V4ukxYZVhKaAuM88PIHzkm/drfvrxnmA1y1KzEPDcBUzMPJIl+cEZBylYlwb54gWHPlBrw8pa1svZVy7RUivsvALAAG+++egzj4vlYsGzy4F+d2B4uWWlPdd4tIncW5WMbpIjrZLnwSzxvNUcWsecnhA0bZY0RcHXZ4L3dgGy4NG6IOVAbBVGJN4YVrx0kWIwnBdnlFLwcniBCYq3yte5VEeEENyV56RKM44D6pj4WjrnJ2aP0oEHyyVpU/DBDUjv+ZrJPJOT0MdJo7CFIHqoSstd1fN076hj5sQYmrnk+ZDQObMKPcdXRRntRx6UmcswiZXcqQS3nWdMkTvLObMouHJ7svc8OTnF2oE4M5w/vMfJecn2sCGFwGq5pm+PNLZmvlzw4OwBv/cHPyUrwb07a6qqZDZvmM8bXn94yh/+0SdwzDw8P2P0jq4NlEXJN995wJ++f4spah4+Nux3ko+uemyIvLZWvNgLtMucVJkc4YBExcj9WeJ5J6kinNUKmQUxgomS12aJj/qByirm1oOO5FqTg2ftO7bngpOZYnlUCNfDeqBWhjv7isNppK33LDeGUjjG0x2zquKNruTWtyg5chpr1qbhI7FDhcwbw4LregclnIWa+VDx4sShVMmjlyVP/UBSkZVQ3A81PyoScxTLKNj7wKhgLiTnQvPJPpAyXNSZo0sILyhInGt4OUyF3DuNIjqBzJJCRJ4UmZe9ZHZWswotmsyVqFBJ8xvfe8R7N0dGFzjXhpvNwCe3e1TMvPNgyY9vOtph5GJuUTlznRJ1Y3l8UvLR8x21UtSFohlGXvzoKa99+wnlrPpzd8f5L6jT/2XGL0Ut6meufp9rGExvfu7hz0mF8qdc7f/w1OFnKlKf+5u/4EIZq/k7//A3ePn8hqK0PH96xSdPn6FPEu2wR4aC+WLG+et3OI4T2fPQOQRwPiaUnir6xx9fsdkO6KahOj/j43/3PjoESgFjF3EhU8znmLrk5Y/eJ/eBeVXgDgFjDQwBKQU/+ulAVz5Fl4aqtsRQkWMk+oKXP31JipPBX9HMmD98yO4YEKnmcgNdyOyuj1zuWhgV0SXmpSWOkvNFw27TIZNEzyxtgqqUDFJRN4nj6Hnx4pZlURBFgRIF2zYhbYSY2UXHOi6p55M2+s3LI+XM0PeZlBKHYY9YJpSM3K4u0SKi04hYH/FPDJZIZQs4lIQ/C+z9yNmblv6DjA+BHDMdBebccn3bwVLijWY4jIhCsakU23xkEyOLiznhBiSR0HY8/cChFaDkVNUNEhEzyQVGKaldQaxq1AjRGAqVSCHTe4EqChAGlQUHERFVQmVJFz0mK1w/sjgpsBdLypue47anV4bl/Rm3mwOq1NhHG85mO2KOVOOBoh8oF4m7Dx8Rz+dEUTLGkU2aMYwH3EFRU3OdZ6hUkHXESYukQIsDJlYcRYEZBYN0RDGn1AeKICiD4KFZ85vyW9y2tzxaPKGwBR+OHyI3kq44ss8vcc5BykQ1ogCjJK09UiwWyHFEBM3RHQGJMpa9PKC7I0LsMUrRVzVK1YRjZLsIFDOLzh2ivWVfKRgkWSZ245YsIz47+s2e/dmfYe0RqTyD+wDcAcEBeQy0+i20mCEz9HbqLAkEWgi2UqCkoqwrnMvoLFDaYF3gVkhkmubzECJZKlJKmJTZFRqdIj4JRjIyCoRSCBS7WUMhFEEoXDEFVCFLpFAc84iKCVUWxDITEEgksvf0TYGVgl6JCZMsNeSA9Il+phEig0iExqLsBekwIhcz5EPDyTHwYneF0gpzbrG7FiskXZ2wuQICuQ8MZYQxkV2iFZc0JrBaB2axxOx6Zm2PiAeWReDb8U2a3/hb3H38iKaZfUnM4lOqWqYXR4TOiJS5iZf8y/0/45AOzNWC7y9/yN+c/z1iCpxX9/DRcelesNRLZmnGs8v3EesCZU/4rZd/NsGuBsdt1GijCSnijJo2fmR0TuwbSykFkcncS1uFFgITEoec0EmBFFP3Qb4K5SHQLUpKKTnKqZuQrcZoje57jlKgfZr+LgfkTKFUwhSaLhuUT+SQKR/foR0H8r5F5kS3rJCI6bxTYlACBSigrwzKO1AlqjS0ZEgJZRRtY9E+o5Bk7zmWGhkTiURfaXL2CGmQKtFWEpESQvJKvjhPSVPK7NRA1pqY4SAcbtchdEZ7OBYD6pVZnVMjMUwFKaEsu5knHQZShD4LYjBEpRHBsKt66I7kqsDJhEothUpoF9mlA8pPnauAJbtTBC16gF1Q1I3EaY/1gnzHY0RLJUq60lOU9VRJVobeTV2knDKds4TWIZLFpJph4FX3IZHrOYXfE5RCEBm7gHCTYtxHz24o5ppKGOpaogfNal5iKkt5OiMVBZcfvCQcjtRiumbd6KEoyK86b1+2ufpyYfGv/PBbPHl0jxAiQkj+0T/5XWbLgvvr++yvQBw9Sk/y4TKBFiBSZD9ohJhM/8zcoucSu4+kOHDbSVRQ1FUNIZH3juHo0SrTPinRdskwOkYvKGxC+YRygc62GDmpjkUZ8EZiL9aocOT65RVWaboSQheJz1aYPpP2HftUIIcASdAeR4IPhOgY+5HL6DAUNHWFlYk+vDIzjIFYluSuJTrIlaRL4bP9U9d5yiLTtSN+ENTzxCp6hIaGgd/8znfJj1a89vXHzBYN15trggvcu3uP0Q1c395Q6ZJ/9W9/ykfP3yeESFVV+CiITJ2eH/3bp2w2HVkqLl/0HC5v2fYDeeP48VYizleENjOoGr1QFIfITGZCFkThCCmCMpSrGTcvOrT3HF2FyAoRE8MukbxHqAqjJak2qNgRY6bPAbWI2KokdA75UHD3bc3Tw46qaajLQH/cU4VMUWqyCUQbWHqDDLDSkco6Yjqgs0dXAZl6js6TmKBNBzVQNSX77EhZEO42qMqQx8j19hpdK6QRmD5xLD1qgLKA0AdETmghUSkxXArKThNTpuwUhBGXBY2UhBQokkAogRgEMU0Gw7XO7ISFHHBdYqwbhJzhxh4vDD/+/WcMwiOaEvXagrJrKfAUGtrQonOPFJPBrfOT6WR2gf1th7USl9PUjZeSN3/jHaRSX9gxTyEzf26uTTH0ywihXxYL45duovd5J+KfU3J6VXn7xTlA/nPVn34Bhfs/6vy00Tx47Q4A/+Zf/RG3tzuCyvgMWkiq1Zxj69n/2TX7Tc9hiBRSEUXBsBsJ3hOToD5Z0rnEe3/4FFwkhGlTd32bMLYi24qnP73hsE/krGm7xHEEVWlciOyPiTFE/J9cUi4qZnWJkor9zcjxas/x5iU+ZDKReTlnd4hsrge6255D23LoHDFlaiSNsriQOXSRw85PLdmg6JRk9JpBCIQTHLMhmwkOInRi2zmOXU+7H+nLTCxgyBI3JDZPD/TJoEQkFGBlovMCdeHY54FsI0ELrnKHyRI/E6ANcXDss6PLIzedxiwW9L3jdu8pe0kfFCJlnjtJ0oFjBJzig+ORGAuaRcWzNuCNoReRj18cmbkGlw39PlIWkuWdBaE/cnP03B5bOg9KCwYhES4RuhErIfaRPgtyEnz4fI86K3DKcNV23OpIK9O0aIwFlRMcjhEtA8+2G5hVRF3w0TgQ955WZLSM6KKlqA4EIsoYqkVGrQSd3nI5KHpd43JgzBHX7tnpQGDkEzcigyGQ8SohU2AnA13oeSn36BTos8cYzzEdaUVLwPOUF/yq+CZ37zzA3lmRx8AbUiPGwL8I/x92bk8nR1A7fLfhYDqkk1z5SxCCo2wRWuKcZydbFIqd32OagsNwQBiDc5EjCVEKjvsP0dbQFYFwt2B48RH7akWxnjOOE5fhoHpEk7huXzIWPUJLDkIQhWFfeYQs2QjDWNoJ6uATOeVJ5nN4JVk4K8la4s8X0I7szeQqGqwkakmUgmg0+RWWP1cFl3lqewetiMZghKStSwKCy6ZAZhiM5lMToH1lGbXmtgwo30/OyzOLCIkDmaHUbAqJztBpAcITULQ64bPgYBxFXXCUkN0IOtOVhkPfsRcthXV0ZeLlfouShmOTSbsDu+4SjaBdVahZoCs046LD52u8H1FJMegOc2dOONGEcUV2Dente9x987/k4v7jL3SEP41+n0a6Lh7ZuBuu3UtyzpOfgjYcwp5edzwdPuat03c+U9dTuuKxfn2Kljnz4PQxsrL82/aSQ/ZsfE+pEnFZI5xmcB6Xp8SiLRRBK7YIhBCTq3mtyUrQGoUTcGMlEkEvINfTJvhQGpSEnTVTAlsabuoKGyYOxCgE+8qgYmQoNGJZIIzkOFNIIWi1xYTIcDbjdmbpn+/ZFQppFW3ImDQJOQilyBn6qpgkhSuLTJnOasSsnHDZlZ1gCYVCxcix1FNxojC0abqmY62Q2XOsNMhMKjW98eQS9tlxm0buqIqBkZfplhfpdnKqFyOj3nKoPFl1XFtHNJEoEn5WkKXhIFtiytycjiASo/D40pFtwS73+NJydZbor7a4XsDJBfl2x7FweKG5XmuQFYMKiOjJ/Y6DlgyF4Noe0TEwlBJ5ryCZwGEMDMOel+0JQi05xEwcM/4QGXNFiJIuakIUuKz54JMjVWE5JEEaAjvncCHQ5cSgMtIr2mGCDM7mlrLUHPpA2BwxY4dzPeyOXD+7RkrFPkTunC/YDgPH3hOF4OkHL3jx3ksevfPgFSfzi1CML4hOCsHdO6cA/M6//RG7fcuh7cmzmudecNtFstHELhETtEh8zOzGSbFt6CJu6BBKsR8z68pwjAUxwbiLDL1DN4IumimhKBzGBrzIXOdrfNlxVANGwAf2BTaWdKkjZIlLkg0HsD2u7tG+ptWSeLSE5LjdKlQwbDce0XmO0uJ8nu7pPHFFnJqjYmYMk09L/6oqbuWkmheZEnSnDfvR04aAEAKvApWdVJm2fUsOIwoHKeFXM9TZjLd/8C2EmmBVd87ufFawrcqa1x40tN3Azf7Iux++IKVEM5sRs2az62mvjmw3I2o+o922dP2ILQSd1qSYePFiR4Vm8/SWnTKQpuu7qA0hW4YBnDRcHjNpu8fpEqslz3uLQNBnSJ2jqSoOXaKXgs1NmFzFk6SoNH3opgIkgrbxLAuPM5ktHW4GrvSkJHB0aJ3pq8h2LKdOifUc88Axa4zUHNUwJcsejjYwFhYnIik4Wj0i14Z9fWAXe2LfU88DWmUOZiRpzb5wbIRG1paZtuyGI0cmhc3OSUIvMUqxHSMuSjqfEQWEpIgICJA8hAytByLsUyT6PLnU64zMkYMXoGGfA3noJkdwAcOx4+gcQUo2VztcBBczt4eJ+9L7zBgihy5iNIwhcdKUXG5aTu6fYCv7ufn1s731z6Zf5qtXmU8LWn+5lsYvJbkQX+44fFpl++zcvgyc+jJJg8/e/6rM6ctfUXx25KcHfEW68gsymJ91WQTzZcNyPSPnzNl8gRhLsjIUpWGMmsOzG7TMLGeWxiq8CPQhEZUgdEeCE5wsDEEkUiFJryQPH7x5yuAk/bMWKRNVZem6geVyhig0+31HZRVaQGwPmLnBmIwlcbXZgW+xVpBTolnPWJ3PiFlyuduTgiOIRCUl0ioqpdCDZ+c82k44fKlgVhUUS0tYFWyHxGqmCd1krNV7WJYGO7dcXrZEP6BSZl5U9ApUSiiZSD6wKBWpsvSho0hQ9a9A6WPmfL7C50S66ekNnNgGn0EmjT5Eok9YKRCFYTVL0ChEShAT42aHWUqWq4LlaUX30iGSYr42MNc095fwwSULIYg3oGJGKSiN5Oy8Yn9zYL2yuCiwXWB0DoOgmSs2+0htM8W8Yn8c8ClRSliuS4a2QW48RxFocgSjMSkxl4q+lCxKMEJxaA8IoymFxMwLhDCsEzSjwrqSQQXWyzXr1Zytu2Fhlng9o9Y1XRypo8QHS99L5lHQ2JrQJ4YYWCgLfsKrz5Mm+zi5dOqMbTNaR5rTGYtqyao6Z3738WdkXlEYZoupMr++us96t0W6DUu7opU9QliMk7hhRDuITcE8lYTZDNErLIbkE/NiRdCelWvocoEWk4yq0qC7jFBwcX7BTq4pFMSdp5SGBkWygXO1pDeCUM0gJWw9Q6cFcdiyGAV5VVINkxRonQQVgqwi684x6kR2kTgrqRAYJlzvuhtxhcLFiCssjRBYxCRFmGF8FRj6mKb34lRxn7lAKQUiRDRM8pk5EQTM+pGUPTomJJ4ZChJEEo1PJDI6Z3IULPyE/SdLSp8gQZEjLC2npaV9doOYGapZTWhbFtKSmgXLrDlc7snKUDan5GGHPhwItWCpl1RnirgMaGUoZEElKkiSlTwFk6mKBrJgUT1kfefuzzq4n3v8NC5moBAVVhas9CkhekpKSr0gpsjCLJnrBTnniash1M/inhQIKVHzifi6MgVzXTBXhtoIwjEj2hERIzM/YZmjEMxDIir1yn8iMQsZEQQpZWavjAtFSgglmbvJ2dvnkdJF8JmyLlFSUoWIFQIOHbMxkEWmCAkhBTOXyCTEACpMEBGbMmbeMO8C+eZITALzSj++9NM5zQePTxmdmUzngDILkhhYdA6vxGRoVRaI3lH6QJCCWTcyxoxEkHygrDSm9wQlaLpJRtPGiXNhpWIuJlJ4ISyVKDgVK4bcM6Okjg05Ck7yjBhGvBsJlaBJFtULYmFYOEOSGSUFnVU0FMhWkJrMkhnD5ciMFcc4Mo81uTuSk2chG3xQiFywl4l5myFaovM03USmt0JBjlT7EfXGEqzAbHeMKaBnmtANrHOkMxYZ3CRNHCOLUqJRFGFSuKtRCBvJOdBYwGfWjcKPcipIxchiUWJ14DgMzGeGoq6Ju4jI0HUtBZLTumQlFVejQ4lMaQ1D29P/5Cm8/eCLZMq/YCwXDfNZzWzWcXYyA1tj44btvmde1+SUURkaAV30qCypS4VKEbvQiA4aAylGylnJ7XagKQATKRLMKoXuM7NoGfBUo6YxA8lb6mjQckEhK0QWrMScLkN/tcEeFClXiFgiEiwE9GOkEVDoDDqTdaaPnlUFYwzUMmKVoCwkRczcHB21yCgDttBICcp5snckobEpYAqNEgkhwCKYC4FoCpaFoTEalQx+GJFC8uCbr5Nf7a7Eqzmfc0bJqZUYYqKwltJaTlYzQoiUVYlIimHbYlOCpqRY18xKQ5UjeRwZupFZZTBasZoVpMqwKktS1sSDx5IQ0UEKICSViNSzGbdtwOpISlO3UEpFqTOlyVQmMS8FffJYnck5Yp1ANYKjd5Qqo6Ni1nqEVSw6EH5goQWlsiAm6KoMPcvREK1GBonoI1oqVk2DEHBu5uzdMEEJ94mq0lhhQAruLi5oCcRtjyqXmCpR7DuSTJxkS0oaKSSqqWhmltk+8ME4sjST8ldVTH5BOUcWMuNTYmkU48RLJ0Wwr3h8MQlWlWIYI9ZKOh8phSANAyaCHD1GRqQSiCQpEpx/7R7V5siyslx+vAckN7uWRWUZfcSHyMwqZAarp85tYzVlyrhupPxMPOErRv7ZbvzT/bJ4lW58esBfMrf4JUjRfsWYWvdTpevTbsXPN0K/9Fqevu3n3bk/P8Tn/v3sFb76YL4yr/i58dbbr+HHgHeBi69d8PYP3sJ10B8S9yoYtj0yZuaN5cndBqMLlk3Dm3c0vnfUTcnqpKEpeiYqWuDxE4O5qBlUQDaSi1NB20VckDy6b1isDUYM+PHAk/sCH45cP/2YcPUuz376hwzjx8yqHXdOMylnqtWMd37lAukD425AxMSvPmqos8YMgtcWENXIqD1eeV57osgXNf1Sc/dhQZMS+dbRPTvysDqy32057jao4Zqh23IkEgvFN5YZ10EYBeeVZqYzUShcEnxjqZGU4A2zQ8m5LIgqEWzmP3VPmH3YsfjTI28Oc56UK4LqkXcUf/20JJ+/i/j6e6yfPOfhfUf7MJK/VfA3/sEj7Nca+pPA2beXfP/b57gMPgverDOH5y39HpQyPDkVhJxICe6blhc/fkFAUZ8seedbc8aFxNWZ77xZkASkQlPMCr7/m+f4FXSl5817CmVhcCNJwZunCt8IhjJx7yThSo+/0HRrxYM3At2DwHjX82AZePjGDatHP2F+531+hTUi9zRl4uv334HFOdezGZum4geLb9H1Pe3uyPlHkfnzROwyLkj+yvgQpAVRcjevOeszedwThj3fP17ggsX5gll3wvz4kNv9mpv9jDeb7362GOeYvnBff2/9Q95efpNvrL7Dr539Nf7Bvf8F31l9n+9c/ID/vPwHmGQo9rDal7x5eweyJw0tvy6+R9dCPyiKcs139BNcPOBo+Y3qLcpqIPmXqP6GX189ploeqOc7fnhcUs4TqmjRuePXxDuE0OOF5xvDGiF7Yt2iVp7vdgf2/JRt+gmPrz9CuUAsDKwafnU7TPKg1vB1n9AkQlXgjeLbH1zihSQbw9cOI41UxKpiEJJfeb4nSk3KgrvPN8x9xJUWVxi++/5LRq3wAi62B87akVhaXFnw3WctfnaCr9esj3DeTSZ7Y2353iESrCZqSTPAvY0myjlBLvjeVUFUK7yfsdBrvqaXBGvp9wPfed9wfH7DMDoWywXfuvM6rkyMM8H36zfJpSGOe7i65e7v3tBdv2QILT+c/TrfrL/DO8W3+JZ8m39w93/JO8tv8c7ym/zV87+GxryKauILEVJ8LtRppXlUv47D4bLndfE6STmO+ZqWDfLjI//4x/81/+ij/ws/2v4hAGn0X4i8CHhSzCnUFaj30PVzvp8jY9XhyyPn7Y5l5yfZ2Jz55tMdo8hEIznpPEsXiVbjleJXbnqCmjpO6z6ycnBoZnSLBb9y2eOkwPvAfPQ8CJC0xknJt96/wiuBt4bKZe5d7/EmEHTkzR9f409OGZLFf7ThwQcbvFY4BF9/7wovJrK3Gj2vv9wSJHgtePPDKzwZL6fr9/j5LcFInJG89WwzVYYlyLrk7Y9uCVKQSstbH92iRMTLSCby1//gyJtXmXeGit8o7tDIqSOmhOJN8RpD8HgBbxzOqbMiqJExdfzg+AaYRMqOJ7dz6kGQjYcy8YOfnhGkg0ry8LhkcdD4NDIKz689u0vKR4T1PGTFbL+kDwWdqfnBx68xXgnCdcHJYc7F0ZCSZxSRH27Wk0BFysz3ggeXARaedCH4q6eS8fEt6q+NrL7R8ca9RFpEXO349bcNQmv6YaS2kgezyOgSxz7w3ZNMUS+RokYmwVsPS7yQeASP/I7DsccZjZzVfPPOKYMvOPaSJ7bg7KJB6oDwA+9cKOrTHXp2yTcfNzz6wZtfXK6/tA34qpX8jSd3aKykIKJz5G/+xuuo5YycBHeFp7GSMWa8lvzmt9fEYoIBf+1ezaI0uKBo+8yTYstoIurUspxH1lKjQgWh5LubJf6DE/o/WVH+wZLZrqAFjmS+p77LKBxeBpZyxv1wwRA8zgh+/eUFXmVccCznmjelJNfA2vBrF4IuSES2yDHy+jyTpMJnyXfuZmLu0E3k9KLgB2/WKBuIsePrdyS6thSzAm0lj1d2EjJRhrdmFWUtII2sTmu+cb4k6gNi6Xnnr7/Nv//pH/Bb/91/wz/7V/+cH/3kPX7rv/ln/N9+67/nD/7wz/gn/+zf8X/4P/33/KP/1+9y//457QjHUfD6ek142bO7DQxB8Ve/+zq3L1tub3pWUnEyq4gpMyb41kxz2DqStFwUioUtccEQKfn23QJRzsmUnJSKVaUwZUOKircXA6rUDCJyfmYp7ZGx9nTW8ytvOtx3L8l/9YqTb+9463s7mr/1FPtXP+E364StrtHlU5bqwONg4SSS6p5fv1qCGEj0NBm+wQmi6RFLx68M57iyw886lHF8s74gLlo47fl+8TrqzoJ82hDGwFvvGoZ8wMmOb2zOUQawAWsjvzbTqLevUG+84NfuwTxZFmpOMQp+tbSMg2a/TTwpJCJKci4Yj/A4jUSvcU5zV2aUTyQv6PvEOyfT/Roy3KmhsQmpElkkvnt3yRA1I4Y6wvh8y+bFnuPR8Z/9/e8S0gjZMc8jp41FSE1C8c6qoNIZnR3usKcWk2fXf/z42WQU/IKN+H/E+EtL0bZt+9lpwZcaBp9+tPjCq18+hS8d+9VH5fzFBfYXiNF++uYXH3/B+Of/5Hf5kz98j831ntOzE+K+5HgzkvqBFx9eE3MmonnycI0YEt0QETlxu29JwOzuOXJoGYeWFDMxRub3L1i9cY9n72/wN7cYp+j7TAROlpLz1xpubnrS2NKOwyuTE4HRntJm+q5HpMTgSpanp8zOVxRNxcsfveDqauD8pMAHQU4QItQLhaw0z7cTtGEQAmkMPkGDoPCSbpA0JtKbQLaCwWdKq9C24BAUDB1lPaOsS/ogaCwce8fBSVQcQSeMhQHJ8tFA8WsbulXL6eqE+Xs9zSeeo+9YvXmf3WPD0/EW6wQIRy0EG3lktVlx+NMTbvqCujAIKZAxcDs4VkFSPCvYX0dWpw3MFON4YBckM5Mpe0XKhmpWImLCDz0Hp6lSx1GPxFJDhlk2VFlye8w8vDfDrQTPn12BUVQ5cXpvyYfPtpzODG4NHR5HZu4tZrTc9pm764J0KshlZrdrOV9uOTt9TjvvmOUGJXqqypIaSdFcMNZLXsYdJ3LOsY2kLrPbbZntM0prrtTAQtdEVaIxHEXgJAiMGrmJO+a5xKUC5QzHIrEWBdE7DnWmiYpvLO/zv/3e30G8UhD5c6bIF+73f3X1L/nR7o+4Ga9ZySWb/pq9bTFJE1KNsSe8TBvOhwY/y/TaoZCUKrMoCl6OzzkflgQd8TaTR48cEkUyXJc7Tv0JLSO99MjaYvwCNTQ8C1suwpztBpzQBBIr84iVesyV1lwMgV5popQ4KVjEqep8bRXLXTcp/LxybZ6PHlsWXBWGhYv4PDnBD0ax7EZUytzMKpbOE5RE+cih0Kx6B1KyKw2zbiQIMDlzqEvW2y1ZRXarkkZMvALjI9sUWG47QsocKk0VJ8OkQgj2VrLcHhnykW6pqZIk+EvKYcv+QvNgdYe279iOB6zQqD6iX+7YsOe0i2j7jHGVaB495En5Jv/la/87rDD4tqc+W/6skpsn7pB6FRO+CCf9mRCGi45//OL/zAftu4TgUSFj5wWX8QXn6g7+3T26akiN5rX56/yt+/+AVXHyhc8C+FH3Lv98+7t80H3CKs/ZdmeIQ8nBDSyPGj2W3FjNbAhQTo7dfamZ9QEpJfva0gyeKAXCR7pCMw9wMIZNXdCMgTIHGi3YFppzNFaUtCFR9iNZZqwP7GYlp11HqDqGRmLGSMoVi4f3uRxGlu9f4+XkZaNDQgsoQmI7LzgZI45J1ljljPCRKma2q4bT48howBWvsPjtQBEim3nBegh4pXFak8nY7DBx4HauOdk5vvm84zt7QfX2fU7++jc+u24hR/6P+/+OP3Of4LKnGRLsD9zMWtZjA2WCGBlMpB4MCsluMbDYG8bUo5WhNyMz1xDawOYksBobgnDo3nGYJZZuRdgrbmrPIlXEjcK0mr1NnOQSQmajHY2TRAtWKbbKcRYEedUzvGEpO0H/SYE+rrgymfVzQffHln1nkDkRjoIyKPaD5LSRoA23e4dIASkSjRVcHTPnazXBOvpIbTWBacN2kyR3aoVyI8O2JQwjdy8KTp/M+OTdp5wqCfMbvOrQ1vCNb3yT/+K/+F/TNF9B6uZnt/uXl+wf/ekH/M7v/CFPP7lkfbLg421DNype/uQFVakoljNuusiqUXQtEDJthLmRhENgsDPmOtKmgdm65DBE4s2OuVmwd5ZZkREXATNLjEpxMd+x+t5L9rPJBbm839BUFdu4ZWVPOUbPVXdFlUv8XqD3mttZ5Gx/gv/wHjc30GhF+64nbRWbNjHTI95An+XUUZGOSnl2SXJWS8bkGEJECYE1GhEjxyg4M4LjOIlaWKNpwpEiteyj58F6zupRJtEhCk3dNBhTcLO95XR1SrudZOUzGVPWoAqeX264OF2x7ycTxG7fI48OjWWLpM4RZwpEgkPvaFSgJHLb9qzqgj5YmpM1rYs0WZJTwdUh0ehITAqRBF0QrGYCUuY4Kgo8jogpFLthMsOTjaRVmlJk7HcPhOYKN5fcEQpRH2irjnJUGAXWwbEeOekbQlNwWAiKEZSAWhqu85Y7eQkrxSEdsFGRkBSq4LpquRgXDGmkZUAjkb6gcCXPwi0Xe4OvHGPpEVpR+0wdBdfVkbN+wWYQDIBaN1TP75N+2/AyKpaD4/iJYRwN3eCpTaSwmdseTiqIQtJ6R8yCmc5YCc+PjtO5ZghTV90lWNWCPBzZDJ5FIUlAToneB1alRotEmzNzrahOZ1TzkpdPb1BjIiRFlxTz0pD6DQsLfQisreVXXr/HP/yv/i7r+6ef7Re+aiv8xQbiV+8q/ieVooWf70n8xeMrgE9/QZIkPvt08TPu9l+SeTIMjr4dcM7THx1ikByuj/SbAy4khNIUZcnYB3QE7xOD8/gAqzsr/BDotx1VIXHeU1YFdjWjOzgOt0fSmJipicgmcubQ9ozvHkFbLl47Q3Ytt5dbcs5Y5RncZL5SWsP67BRdNIyDJwVoDw6jDSEIQgTvErwyLMoiY4yhLAQIiWfij5gEfkzTaynT+4mQncSEUR16jxeSZtbQDwkXHVEoyqJAmoKx89RVRWQk5+nv+uhJOeBV4hh7THCk/QFvMn1yOKFIjWIMjuh6shaEIhOXNfJ8QfzEcxw9goSGSRYySXLMJBS73YhVBlmXpDaQBQQh2V61yG3P+f01LkvGIbA4myN8pnMT6a2pDX6ELDPXV3vSCH2a5EyT0Tx/viEbgzMaJwJOy0nWNEhygpxg3zpcHvHFREYkjjid6PEYObI8rQkiErIjZ0+fBlzydGKgj5mxG+iSQ2uNlAEnIwMenycC7JA8Tgi8Hxh1oigErkuomYJZQc4Gf/AM2RNGx+aTKw7LFyy+dv+LXbvP7T3z5xPzV09dGhniQMiBQQfyScF4uMXjkbbGhZaoIn0RSSLR+g4pJUobdl2LY6S3I6kdaZNHW0MpDX0K+BToZI/PkV6NSAkoGIsJMnhwA94WHIMnxUiV4FCAt5pjyiShGI0mSUHfjqic8dIwFJpo1JR4WE0BhBCJWuJiYHyFk3dS4LUivJI/7bQiWoM0CS8miVukYDAKZfXE30iTrPJgNSl4nPdknRExUQiJ1xLXlKTR49V0ceWkWotLmUEJglAMKZJERsiEnBuGY8tW7tCrmojkeOwoAthFSRh7RjeSVcbXgl4OpJwYfU89rz/X2f3cyK9go5/+vl9Q25tADzF5Yor0sSMRKaylo8Pj6WKLbCReOnJwxBwZ8/jFysyr0aeRMblJalcMeA3eTA7HlVUkofHGTJt3CUpKRikptEQIyZgmSFMWAmmm36PPk3TsaBQKkCEhme6LcQxkPGNZQE6IFAlMv1mvXsk7KohWopuGTgj6fYeWILRk0ApVWErnSVLgpaQTCSmm31oAZYbBCIJWtEqQpWAQAlICq6YOh5S0Wk6SkGpy05VpSpK8lrhS4yuNOiZkU3zhmn0qRXuMHVFktMhE7Sbp6SIiVMQxEpPH6oZoNWmuGboJzurzgJMBpxOpAq8SfRFIekqCXO4Y4kgua3wl6f10v3kl8AoGF0giM4qI1JkoMl68kggvJIhAHzPJagZlkSLhRGYwBSFnRp+xViOUIEVFFoLj6AkHhxeWLDRVITj0A8IUHA8D2iq6PjK6jC4zttS4weFKRSElLmZUWZJKzebFdpKDnhmaVYMuFaI06JMZLjiaz4Wwr+JXfrE4CePoGAeH94GuGxnGguMIuSrwIeB2A61Lk2ZosiA1vYvURjIIyRDSFMerkkMXCEia1ZrkNcFByApSIuVM23vcSWTIgVAL2i4Quz2imEzsujQyBMcgAykOJF2gZhKnPN04krynHwWjC+SkEFkgioJ2GCibEpklpDRJMwePj4nNYQSZJnlmPdWLtTL4ENiHhPOBQUh8glJnggClNcdxoPISikz2Du0sznm8cxwPR9qbhBeTFGmSlpAy3keOh44hCPox0W6OlCiOYaRHIowkyczxOBAyVFbRe8cYI/ve4YWBwTP4hFYFCTFJzcZMEmIyiwuB9uAm3t4Y8ESSAq8gMsGIClvQtROCwEWHrgRBZYbs0YSJ+6kyOUR0KaBRpEVFNJZRD7hhpMyCHEdCkemiI193tHZgQKKFwVtPN+7YtT1RQFf5CebalwyuwxeOVoOUgV55ZHToLMEqok509ART0eWI1hHpIj5LQgCvDUkqHBqfIlkIfEykFOnGaS4mpUlAN/R4o0hZ4qLA+4wyhjF4+t4hwiszxyzwcYL1xiQIKSOtojt2CKMJuxYXPBQGQcYdAr0PSKBSChcc3keiydTLObb4PN/iZ9SFaQf9VUSDX/74pRO6vxAxvhJb+eW+6H/g+HRx/Dwp5S85vvb2Iz587xkIOL+3IL5UPN18DCGwKDO2XqCEYlaAsYZDN5LCyMVaMrso+eSnL5g3EisDUljuvf2A0/tz/ui3P0CPUydiPYO9FmipOZtLtu2e3bGjvUp87+9+i+PR0R86CpPpw45jOHJ6dsa909fY3YyklAmbA101aYn7cUCriDMDMUMZLTKXaGWZKcFJldgPkkiiLiCmyO54QAjBaZFpg6CwhtlcchimBKP2ktfuWl7soR881o2IKFhZTSETJ3XiRijGJDj1CwrVsRsHGin59qO3+ej2D9FN5MHshH45R/iEPVuwvLzg2txQ5pHTmFCLOertLeKYOH2heVmPSOM5HSruFCvefbEFH7mD49IlpIb1yYziyhNmicEN2HbEnp7izIjIPQ+WkpoK7wOneqQD1g+X6E5QF4lqXtPuWh7NLONcs9E91c7xcFnysbkEmTm7XRDkiLnbcyoWzKPlWf2SbDJ31TlSHXBm5OLiPq/XD/jAfYTLnkflHTa6xPnMXNS8JZb8iXsfHTX35YogEk7DnILXwppPtEf3kVNfYlNiVmiq0XC+uM/zlaTD86g6IZ9GPupvUX3iyfuKd3/87ymXlzxcPmFhV6+gg58uwxP8MKdPdYSm8frsTW7Ga5Z2RaPmDFVAC4uKgvPxgk/KgTxuONdr7KB4KgzGKF67rWkXW0QMLELDndO3+Wj/Z4hR8FA9YCuPmCBZ+JqytTydb5Daci+ecisV2XpWRcm8P+F9scfnwKN9i0+eJASzkLi7OfLxepISvbNtcYWF0rAoDOubI89XDT4k7g8BP/qJeNiNvLlt+fhsga8K7rUjISbivKLxgQcfX/P0zpLeGu4dB2LOJCUoXeTh7YFn6wYRExddQMbECyup+sCDY8/TqgCrWe8GtPeIZYnNcLEduZ5pBIrTYSI4CyUwIXLvSvBiEZk1NcsbOFmt0HUixZIn5Qkv/DXiMLDcK06zZLc2WFvzcPGEIhT40QOZGAJKqYlXkSH6gCw/XRi+FD9fkbxr3fCgeoTPjpQzda7YqmtiDMzFgvvlfV6KKyKRpV1xVl58KY6+in/la/ye/gNOjaLB8I36NX4a3mWeDpx1Z6QgieaaJklWVwWXJzVFeiUbC6SZofKJ8+3Ay1WBjJrzPhDKjCZTh8zrm5brmUI7z2rvWRYNTxtHOTjubwYuTy1aBU73I4XqeUGJkZK3Hqz46HpgthtZHxx1DrxY1ijgtZsjN4sScmbZB5reIU8bcsrcvzqyWU731qIdmY+Ol6cNpMiD/cjOSpCZFZLZ1YHniwIlJBe3R9omEkWm7AKvacuH+idYkflmfkDrW166S1Z6xWvqPi9f+V8snl8zSgslLAbBvcHw0ewanx33uhW+TOTKU3nFw90dnq42jNFzp1swpoyPe8ou8ySd8dF8g6bizo0mlktidlRD4rVhyUfRofcjZ0EjlUKWEpsl97qCZ/MOcuKcBVoKrkPEdpk3twUfGwgqcu+iQJyWJLdHi8DdmeTG1QQTWMuMjZkXx0DZWO7PA0+vEjiHjT1nhUVmg/eO+3PBIUVEVVK0HRcnGrFq8O3Avbqii4IuGZYXK9767us8ff6CROZkccJqvv7S/fzF/36Bb/kqkD1+co/33v0EWxjqsuCuOeH3/4enzM4sd2crbi6PjGFkbiX3Gng2ZGyleLSydHPL5T5TxsBpbPnIJZr1kjs2M249g0zUxnAhRl4cAgttWe4XnIWWZzcNRYQ393CcT3K5d9XZ5AXheoqkeXB7wseLDD5zoSRG1iQ7IoGLk8wnoyAPEaMSTe64jRYRI6dmZBsdhRDMSRTSMxQ15bzkycmM280RLQZmWlPNG14eDgideLCYk32kl4n7b9znwT3Ly81ThBTcWV/w/OMNoY2gLW99/SEfXbXElHjy8Jzrg6MfEzWSN9+4y08+vqL0gZVQ9NLyycsjM2u4N9O8Hy0+Ze4WGmdh9IJKCl6fWW6jwkrFWQUeSaw0lYZT63l+SBQisTaB9fmMD257aqlocke3mnNwgVMSgVtmj3tsMLzeWvYq4Rh4wB1MlFz7HSooHt027B9KbJ0535ekvSSvoJwveXJc8MF2Q9ePzFxkWa5432rKuuAbr9/lo7aj++glCxdY1oaP4wFC5nE757pIpGBY+4Jll/lk3CEzPO4XHBYOP8Kst9wbzvioTHAtudsO3PgaN0ITHQ8KyzMj6QrNkm4q3g6BuZUsi8izLqKM5WJpOYyBjKTMiYdz+OQ4MteSOzNDcAM6QiVgPS+4OvaoHFmXhhQipZI0heWbr11w5UbGlLiYNVx/tOfpbcvZouTUKEIYGIOnQBEuN4zHnub057sO4qsm3v9I43+E5OLV+AIk6gtv/PzT/5jv+mpP9SnL/QuklP/I4ceAVlPFK8fM/mpLjJGYIjoqGqkZNh3Xh8TgHT4oitJw/uYF188vyUyyg9Eb1vcuUMLy4b9+H3fbUoqCudUcjwNtL1Faom1CW6gqTd8eWZeZv/J3fmX6PkXPP//tf4G/dtiTgXd+eErBipwy1//uR3Tv/YTBD0jVE080Rkm8CywthBu43R6QQeH3ASU0VVlSi8gm3VI1ihwjxitm0SJzQgRHTY3vAxZF7kG4hJJTVVLLjBKCcOhwSqAbS+sC0WTsTCFkoqoV42pAD4pUQzx3KNFSZEepS+b3KmKYQ4BSaVz9kiIPqDFRv9VQPj9Q6kjhPbsXBbqyE6TAO1QQiJCJZ5khC44+sLgzY4g9qvEENZkDibpEuAQ50s0z/tTT6T0Pn8yxVuOvDwglOc5b4p0NTiZy45ifwNwOhBSpzm7JORCspwhmqgbUCdFoqhkgKsoqQa25UiOtNIw5cavB94lwCLjdjq1rUYVAWYNpKlAJ7UfUmOnGjHAZQkZEwa9e3iWdax794B0uq8jl5n1ycIQYQE0wBa0TT6tnXKsN6uV7nPY/4T+9+3dZ2BVj3+N8wGhNURZTgvG5afB49joLs2Tvt6zsCf/v639J4S1aGmgqZNuTMmSXcJ0iocjWMOZM7j2qEFircblHKIXKmTAOzGyNkz0LuyRbKGmR0pAOB9SiQJmIThFhCsRz0FJAU1BWAttolIq0FEg7kaqpFVhNLhRy8PjSkGNESoHvelLIUBlUzoyFRuc8dTNyJhgFSqA9jHWBjBMdLaqpE5Z9RKXEuGzQVYHMGZfBqookSsiRwRqkUWSryZVCyAPKauQY8IVE5Iwkk6SYJFgNlOsK0VhsmxhmmhwrjpeXyLOMrSTd9gZpOuzDgub+KfXsAX16gXAJz+RALl/5VwgEsXeoavoNldVfHQ4/Q05NW7C/cvI/43H9NaJ3SCn5p4d/jM4CPSa6YUuygWzzBPzL+VWX5IsfGekxYodRR4oIQvw+q8UGEW+I7sdQP0CoEVMo8uwhRjS4PMmz5phQZFTO9CojU4YUERLK4GkCzMZIUhklQRiFLBJd7IjRkmSiNz1WZgZlyLLHZQVJYZYLRmFJLy5R2iJVIOSpcyJ9mLoUmclcjsygE5mAlDAakDmTUiSFgFcg04Q/djIjREQYi3KRWGkUU0ruKgXFRHxVWvF75e/Tn32Mzi959/IlKSuO4UAjG6i/T1V9ExcDprxLrrboosXIgkN8QUiSiKITGTH6yfBrtiCdrFGXG4TORAFhlIiqpjSGoQuIpAlhIPQRgsQu19iQ6FQBQyAkifcZHRJYiREWVhaZOpLOjMEhpZ/WsxAZV4Hse6SNuOMt5BqqhBKCQ5smc7CqmOQtBzPdIz5w3DnqqiJoSekDPklsYREhIoRivqg53nQoY+nRpDKjbcHOSY5dZNdl5reK57+35+gDelbSbyfjUCU/wzV/abxayT8TMZgeVqs5f+/v/zVeXt6wXMz53d/7CPodYdPi5QljAGU0prI4DTJ74hC49Ue0WRC6SFFPanOLUtAHT7YKjMQUGiEiORmqqGlH6Ilcf3JO2zhyklzJG6qLHnGiyCkhFxo1ZmRKdNrDrSNaT6iWOBLRaAoE4zhQVTN6H1gsG1QBthfYSlLVmhQ64hAoC0FlYew8vu04Kg/DjpLEQhtC39OIhJSa4DqqMjGOI2I8EMQCqSXBBdo2Mvgl/ZBZX9xlmxq6NJmn3vYSHzXt7UBpLcfOsf/4miQl4u4pYRupypKcYHv0iCiYvLgKDl1GGEOhJKiG6MH5jOsFIUdinCSB+zxJGVe2QJeenTvgZUIuC7JRFEtB2ybELDD/9jWhdhRBUuTIzB4Yl2DbZ0gURnpKLfBVIuz8xM+TCjWzqNiRtweef6A47tYccexTQX54hzEMhE3gw6c1u1HQ9ud0okCdX+FqjVGKTtaI7EmjI/awS5k0r9Fac2w1YwdjHXGhou/mk2xxhr5bkF0NYVJPG3KkH9tpDS0E/ugQSuJDQDYlEocfHS0JoQWIjBCJIWfKQjOERE6JSke65JiXBVYFtAnoFMAPpDwVpIQUvLzccOg7eh+4ePsxp6+t2XmPNaCTpyoFoo3MFJw+uWBxZ/3lCfZz4xdu0X9J4y+dXHw11+IXHfWLxp/HyfgFh/Ppxcmfuzr554/7cz72w/efsbndc9x3iKjZ3gwMPkOWWFnRb3r2A0SRkKpAGkN5suDl8z27mwMgOHSB83v3cMmw/ck1x81AYUq8g20MRG3Rs0mRKsqR436PNoaQ4OVHG/7266eA4Hd/73c4dnuOww59FLz/x3/M3/77/xChFavZtxC1oSwtqrL8m/ff5/j+J+iUkKxIfSLvA5ujIyXIMpCOB0wxIspEEAlSmhZ1ByE6irLEx0SMhmOIbHImFWZyYQ4w9COdn5RsPhpGrAWnLNfqkr7fM64Gct4Thx31iacXIy/jDT5oNv6IjYZbcYtG0aoe0Vj2bc9t6BGHPVe9QBUL+plmey3xruMYLEIKDmZy6R0UXO1HZNLERcNNSFS2xkbYuYiZlxzHSOszUhkG5UHBEQfbA85H+lfumGnuULPMUARcdrwoWmTlyGR20aA0DHbkIBsOZcbZCCZwzQYlYMeR2EU+0Te4nPE50LeQtoLb454+Gz5WkHwmqIS/3JEqy65KdGhuSksKMCrPMgfcQvGDd77DyaMH/OtP/g1X7ji1d8UE5bgNHdy2tPo5p9WI6zbIwvCs/4S5WRJCwrnJTdUYM2laf5p4i2lurOwJK3vCy+E5B7dnO26QQnJZDYxWshuPSCmJWnFUkSwCIwca6znkPYTIxuw5sgMyITuqvKANE853sJ696En+wL6qcT3s4gj6hKf9JccmTVr1UlPONHuZSSpxu7SfwaJiYVFCcVSCnBNXy4ogJEEIwrxmkpQtiMDlrAIpcFqRRU1OiV1lCaXh8mwBLuCVJDYlMmfaeU2IiRsyKkb6WY3QihwTe6twPrIRApMSbWEQWiBi5qASWmS2VmBypis0WUXQhm6lCcuG3TCS2oat73B+B25LfzWwOFmysR0qOnbjALQcDj2t2KKE4np8Sd8M2FxNvCOlyPbVDyYEQqtfHLA+F/yUVNwvH5GE43/ofptj2NGyJxHZ2gM+BLyPLO0pV+NL7tcPfy4wfjx+wCFu2adbgu+43L0HlSbMI+Kdu/Sdo/M9ORquljMINc4FrgBS5mAVo5JcNXN0hlErNi6ClHSlJhSaWzQmJo5aEEuBQbMrJW0StIsFlRT0peKGGoSkW5SEixn77YEMdNYgljNSihxLgyoNw6xA+kBbTg7tGUFXa6QQdFKhlaFTErmsOGpBWypESLhCgMx0c0s+OLJWdNaAkvgqgwq0RiBo2bHBq2uk7Wl7gciavd8zEyuG8kAXK2JWtOtEbAc23UiaGUZzYPQ9UU4QBSVhz5EgMht5IJVHRh2JjccZ2IqefF7xor9BFpIhZURQ5L7jOCSKkHjOkeQ9rpSoQqCVYC8iLo/cmBZh4RA9Qjt03dOlgJaR67Uh7Av2qSeOAuqGfSdRQiADRJ8ZUsBFUE5xCJJ9HxhnFTJkNsdAYwzZZZwWRK9pNw6577ntAuHEsmszQ0gIIeh9QBnLUcCL2wPt7TUhHDGl5eLigs12z9np6heu5z83XrUy6qbk9ScPcC7wwdNbdgJGI2lftqRiMUEtW8/z24AWkiFBlAXaKw4xk/rEZRIkEYlSQxK4Y2KIlhBhc+MQBJIpiM3kb3HIgdpa3PmOO77FR0tKglEItlWPFpmX8wRZcWgE0hkOxw37rqRSCjaZtO04eMFQZmSXGYKE7NkcO3TpGaREBtj2A93oSTHh3YFCOFxKzM5rvIi0V1sYgTIxhIjXcLu7xT0/0I8Hogvc3giGoaENcLVpGa5aDu3kwbJ9saM4mdMbzb7Q3H58xW0/dX6HIAhe49XE03zZe5TQdDExukn2qIuCqGAXYBgSXgpCEqQh0gVNLC2bY8BYNUGhMlBKdiESDg55oqHtGTKYteNgB/yZIzj4RLXMZKIzIzfCI4SiXSSCluzPA6JT7EWPsIrQ3bJJR6RSdLIh+cQxK7KCl9c7NiEgY+YqD8gMmz4S6wOV6CfpWSnx5w1aKA77iJCBpAP9PKOsZE+PComdnKRoRdVzSAZKze6QUXEiwYch446JLkpQAh8EkpIxZ0iCd289g0vYsuB2dCgh2buAl5lNmNA3LoJUIyoM9MGRY+Ayg3eeAEipGUNkSJlxhM2xx6iMC4Gf/OgTinrGKASbbuB43LCwiWEYoapYfv3uKy7vV8ynP2++/ZLHL61z8bM9/KcVsi+xqr/qi326+c/8xV84f+4w8TOc+Wf5w19ACP+qMZvXLFczUkrM1w3yXsnh8ggpUUiYR8deKhbzgvpsSUgC3w+0hz2zStOPifmy5uThCcMh0D0fsAaWC83t1nPn/oJOGHbbCSfYOsdybglRIJPk7pPzz054Vs+YNTParmVWzygXy1cSboL53TXf+8/+yoSfTIk/vblkvV7gvaeRNWfNgqLeIdzA2HsQgt3NEaEi6/srUqlYLBvCftIGb3c91lh8nPS4x6GnkCVICVaznBlSrdkcPKWICClIYSQwSSgWUZEHycKUzJWmCD2iUMzVjDFLQs7UqiKRMFGSQmCpauRMk8cCNS8JrsPe9KRsOS3mDHWFTgIVEyKDLi1aCS6kou88xiiwkrK0lCRGI9BuIKMoUiTFTBkFpdHEGFkAXRaUSiIzFMdMMRdIrZnbObbSiCKQrGBhSqqi4CpvOBNLWuMnnHzylEFRJYnHMR9LhqyY2YLOdajNQO0X+GbBMlravsc0lnZsqYVFmIooR85Wa/xRkbzjGCTGZWYnK1Zv3kUoydJWnBYN2ktWtiIIGLoe6zVVrKicQGhPJUsaM0cIgbUGyGijX1XBv2J+vfpvoxuMNMzMAoNmFJamqnHesToWdCiEyKgkKEymSZ6gA7OuJglQegk5UVdzZn1F1IG1XrHVLUoakgzkAIlpgVp5g+gyHIG6YiYkCwc+Rma7gVAUVDISCk0xRGoFLsNyDLgwweMHq2hCRLmAN5rFq8RBpExfGGoXyDESjGbZDnijQSo6K6hiRCEILjCLGZcTpu9RQD0EktX4MEGtkpTYGMnArB2mimKpqJl4GjZDGjzzPsFFgS4MVdaMQaFECTPNxazAdZJte8sy1ch5gfEB528o+wKjB+zyBBUERpdUtiGFiDaanF6ZyI1TxVlY/efGsJ+rMinFTM5p1Jxaz1nLNe3+QKUbxjBgkpqq7T8Lo0ysDsFMLWjUjEY2LKs1Y7IIN+GNZ1VFs74At6cZNMdOUZiSw3ikiRlCIunMzEVGrdBpMvSbuQw5kqSg9hmvwaZEEoKFnxTfGq1ojEamwNxFsoD5EAkaTF1RZUl/eYMdI9lE5oNnJE149JRRSqB6hweWg2fQCdmDzKCFohojQScW7YgvFTJ4yGAUlDESlGDee5wUCD+CFJjkKWQgFJJZC7moiF2NMivKZDC+IEjHspyj0BiX8FqikyHejAwNzFygOJ3huxZnAnW22H4SG5hlRdyO6FGjZ5pZXZGXDcPmBfU2U59fkLcHlIHGS3IwhM3ILFt81MSQcUJzIgpEhkRing0+SkwAIRMLLyBGpJeU+4njoQZJRrDOmUEoGgKVUVBPBoJXISHGHpkky6LERYdwgboxtCKysDDGjJIBe1oQfERHh18ULCvF0A+UTTFxDo2mfMXxWFYFddEghkSKCS0FTVXyxcX+88/FF1/6Cli41oqmspzfWdLPK9zzAy4F5oWlkhErJ9NLowwzpSmMIWZBHR2iVFPCbQRVCmgtQSQKEQgxsFgUtAGs8ygmNZ8TFHPRUHYOkwoWNLQxsNBzypjoR4UYNVkn/n/E/eeTrFl+3wd+jnts2nK3ru/bvnvajenBYAagQCzAoEhquUsFY0O7eqGI/bf2rWIlBQVxKYBaQQRJaEVIIEAsQAIDjGt/Xd0ymfn4Y/dF3u5pN4OZ5Ug6FVWZ+eRTaY/7/X5fs4yJ/PgQdRaoSLi5RPSJoBS18mRFRhFAIQhCQ5oY2gmZSYSMzIunFXMlmGeSy10HVz2rmweU85LoA/O5YrFQXA0dh+slkYYsl0QXCKGkzOdEPbKscrgcyOYllxcNsR2p64JdbxGDJSsNR7MK5z2z1Qy7C2xsopICU+cEHyFKykwjY0JGRZ4Czk8UgBJ7fqdCkMZEHi1ZrigLQVUWyNCBjBzMcvZpoYjWkl5KylZQkjOMgTrl5ClSeYdYSg5X18AoMj1Q+ox+4zGqxDlL7RK9gzIvybwkE5KIRNcZ1w+WtFcdUzsh457DwORwci8tblyicBlVkSMvJ4o+UMaRdTZjyDSVyZBSQRGQVxabPMuQMUWNDAo3CvJSUc1y7DhRZ9AbMAZCSogYEN5hpGZRSqKUlE7irEOJQCYSlRYczwuudh3KCESKZB4KowheUCsFUiGrgsttS6UV6+WCJ7uRUoF1lkWdYWNE+kTqRpRUHB4vMJkj7K6o84zl0ZKTW8df4DF96d7gMwyFT60M4hcThfxCpGh/DFD69O/P0/6a8z+DpEqfgX/8+3AvXnrjNuFgQ7p2xeJe5MVv3CI/MAjjWR4EhiInCk+eRWaZ5eKjM9rLHbeul5AKplGzPj3mla/fIoZEtZhx917FLkXGQiPmGfQf4t0Vy9Lyjbua8tZAs/gQeb1l9VLBb//z3+G3f++39xF7V3N5WbNrSvzO8J//V/+c//y//hf82+++y7/6oz/iH/327/Av/uB/5q2vvszLL93jlZef5df/ztfIlwlXdMyeqfj1//Rt6pM1y+tHfPM3v87dl18Be4gIa771H76KPkpkNyQv/eo1br1+A6cEQSQW80u2ty2PjnfMb00cHHrc3BHX8OuvLcjXBTFPrKk4TIKoHUFOvOqf5Ul/xsV0Rp4Ep9ltdgGuuomXr25zftZxsXNwJXizOmGld6xXgb/h7/Jy/TxfGVa88TjxSy8Yjl59l6OvfMivP5tYX/+A9e2/4tqdM77+2kj2S++Sfes9vvragHjrI/Sv/ojZ1x7z7LNniF/+IfzS93nh8DH5yWPy5x5Qn5zx9fmIOX6IPH7AmyFSFgNqsWNxDG/lL9BFhTUlr9avodUBQ5wxiZpv5m8wuo4pdDw7XUdvctpzz9DC18+epXk40Z0F7tnrzPUMi8cr+Ga8ySR2eN3ybLbkWnUARuGC5av9GhstTgUqJO+1j/h//PBf8o8e/jE3qgWD8UxZYBU1q4uebvMYpwde889wqQOXtcRlBVfTFf/k/m/xe5e/y5ANFGWJlPILu86PJZ0TMDcLvn7wNi8vXuGF+kX+7sGvU04tc0YOlOCtdIIWW7RqeGt6AcScKcyQ5pAXzm7ixokgBC+nFxmUpREtTgfeqr+23xwLwdfnX2UtC2aTY2Y933FHyEWHmLfcvdyhkiDIRNKS1z7Y4ETERs9z5w2m7fdkVw1vfXT5tE8Kbp9tqawnaoE3iq+/d8akJB64vRtYuUjQe0nbb7zzCBcCIUZOL1uONw1eJHz0fPUH93F5jkdwuO04PdsS8wxfl3x902OLDK8ky9Fzs4m4YsFYLXjDZtiqwBY5ZZDceHdgeGjp7o9842yB9AcIf0K5W/LcdIpenzD4jG8vvk5ZJ4oycLCc8yvdL/Ps+AzPFa/wrepXyNDIxCefHQBKEibHfmWETzP204+pZnvF7qeJFuSeSP3i7HW+Un+NV+u3eGX1Nb5z8rew00TUkqPylL/c/Fv+8Yf/Bf/i0f+b3rdPIaWJ2/k9dNrjdQOWbx3+BkkZhMx5Jl5nLTKi2kLe80uTYdINE5cctFtWg8OJveTrV390SfNeQ/OjBvPOhtXQMoqGLm15+QcPGZPDRsusGbixGfFpbyD65pnFGcGkE9XkuHURCcWK9onlK997ggOshNw6bj3aYtVeYey1d56AFEQtyXzghQfbfZ8xgpffewLBE41EkXj+/iVTJrAZPPeogQhJG6SLvHj/au9HIAMvf7hBDnYPfysKXvqwImR74YaXxPO8dfw2L89f5aX6Jb4ZTohZRlSaly4zSsc+m+sD39zcJDIS08i93Zo5M0KmCCLxtQd3cNLjReDWtOIgFcjcEuTAty7u4phIeeK6z7lWzHDFiCtGvpPdIomEG0ZWznDD5fjgsMHyq80JloAXkao1nHRLehfolOBrPyyxcUesJ9bzyAunAfWNBl7b8DfeXiC1RmjFep3z7KFkjBFZl3z1WY0sDclIFouMF08C3nh62/LicqJeLwgONJK3761pOksyOa8eZojGI0ROGuDl29fZ9IpuUCx1Tf5l2dSPs4afb0/nr49PAZBK8PpLpyTfI9LIt75zl3UmcG1HHCZeLy0+gJ8Cd/OA3p4xtBcgJl7Od6i5RBaB45Xn9NmEu9HTrzteuN5yUe/YrDvWB4Ji57l47Lm68Lxy/iwP7t/kh392THpwj3vjKcYmVBL8yu4WzB3kO5ai4bmiRTx7H14859vfyAmVJy0Ci2PJcd0whg6bBp6vHTEoYspRUXI7k3grwZS8dnoNG2eE8oTi2k1ee+l52lAwmgVvfu0tnFyw6wqmqeDF26/RbAt2m4wXTu+iipLBwdV7F9xsHF0bcMnw1ot3GDeBXQtBVzxbl3R279n1+rPXOD5eMLkJIRJv3aj2Qg0JbuWwrEuGSRBkxvPLgJA5KUiOTKDOEg5ISvP8vGPrJ3rhWRWBo68MpLfP4a0Nf/PbM/K3L8m++iHX1y23SYhZj6p6vvboBv1C4Y9KlvMT7nIDP46M2y2/nF6FdUlalxzdvsPz5m22Pzpm984B35F3MIdHOFXC2cDyox2Pto7HbeR4a9k5mLzCbQXV92s+/O6S+99b803xTezmlM37J9j357w53sFGyWQjb29voqeSYBeI1vDme2uGHxQM39W87DNk6xgu9sqgL6wj/egZJs+9RaQqDChNSILn5pYo92I1L55kZCLgRWLXDTxbT0x+L8xxrcgxKiPpGaM3vDifgVHMjpd85dWb3DidkVcJoQJvnh7QDhP9YLl395hb64zcWFLo+OU3nuW569c4Kiq+9o1XuXX3+meG0V/bPpP//+z++t+n/UKkaP//4j18+vSftWohPnv7s//7UyKOn/DS/qc//X3+6v2/5Gp3yUF+iv1gxu7RBJPj8p0twgqsA60SIUliFHtlpzwjprgfcG/dpn/SERwUq4rN+Y6L7ZYxag6Xmu7yCVWRYSTIVcs032CV486925hljnUTKSZSWJDiikePrjg+XNA1PdMwkaRkvdasDjUXV5ccHRzwxiuv8O23v04Mke99933+9R98l/sfPuHwcM50lYE3TIOjnlconXHxuGN1VDKJc2RuGfqJ2fyIFNc8+rAlE57vVVeEI0XMM2Zbh3kSaK2gVqDmFWWVczl68uoC8+ZHTKuWa8tDRDWReUdjOlb+iL4taUSgCIroI7lLnKeeG2bBwQFY2ZLLgpvqJr9R/Ab+quXy/CF/MPtTHqSH6KRJQaJjzoW/pB4rdplnl3m01KgokF5wmfccjRWDsExqr+GfTSXVWHKR9ZzYGTYpvBKgBGUWUdpxnjVcz0/Y9nt8rFkUFKPARM05Lce+xC+viGbCJUu5K1BdzkUxcaxX9B7SGPdGedFQ1TPO3JYDPaO3Z0jpGaVlaY4RYsaFHFmJiv5iQg6STnoWTiMEjDdKDhcrnEooqbjodiyvHETLlRqYpYyYLsmlZTiE68UJpY8MbkepK56pn+Xv3PiPfoyD+rKx8vmhkBL/+uJf8RfbP+V8fMxKHNBEy5AFpNSESREaSTOzXM/X2PGMpCeEUugkMV7zxD/huDhF1AaPJ5EoU04+as77R8z7krMqoyPhoqcUz1KF57nSmoPOM0lBVApLohwCWZRczjJWzcSUFYDAKkltPTrBpZGsEvQxoUbHYDSLfkJIydWsYNVbvPnY2Vmy6EaEhCujWEwOawwmwi7TrLsRpGRT5dRPzcRMTDRVxnrT4aVgV2bkgGOiTJ6dSKzaieA9XSbJ/R4/m6fEZSY4HEZGfcYwDxQmI49nzFXPRm25YW7wNfEGX732Nma1Jx0TE76fiCGQLWvMUwK3O9+hZiWqyvhMcPHpue5pUCLkUyL/p/2BksBHz+989Fu837yDk4GZqTFSczGdc5gf8fLyNb59/GsAfL//C/7V+X/PR/Y9lmmFs4nM1PS2oWROLDLO4gUH2QFNf5vQL2l2DbMtCD9jVxjmUdC838H5xCYljmZgnlE0cyifSibmQdFVhoMxkqSmq3NKJHqmKKaJXaVYbT1Uh7jbJ8QfPQTnMZNjuyg53A14bejLDJ0SyjnyENjMCw6bkSFL9IVCJciDoBgCV7OcVTdhCxiLfZY+d4nCwfZ4xuqyx2cSmyJJQBY8OgauFhkHLuCufhfmW8Qy587sef728T+g3EAsNL9jRt4XARsj4qMPce1DLpZwMEnC8SOSu2AKPbNYgxfszI7FUOBrkJNnLCPzLkcEydXacyBXNP0WMQXGeWRxkZPMIU/GDYtRgz4kvT+w04EDUZJrwZUYmSWDX4KWkavcsUyGUW9p854yZUgvyazmsrYc2QXjKGkLSR4k/PAa2fdmPLwaWeeK7hKmmJGCgxSoC0kTFEvtaMYeUed7PtNoWc4rHm8dRyWEUrMbR6SU6N5yVOac9YGVCeh6xPct07bn2YM5/9l/9uvc+MYLe1ntLyzMX+QEfeYcsTc7/C9+6//DD957yDhYMlnRPHA8ahwHteFyjAijsUGwMqAyyXlrWZYaKk0IDqcNVQmsNOfWMpOCgUimFdvJsdaSoR/Zhsi6yNC1JJeRTglefK7m5KULevmEwht6nQhecBGuOOiWjEPBFZ4yacT7N+FPNI/6wCLf8+36MVBkEqU1MkXO+0AtHHYa8FKSVxlaRIyI9FJxbVXQXGzp+oGsyqlUJHcDdlVzerTA+44oEsF6pCkx1ZwHZztm/cS28SAUg/NkmUF42AXBwTwjphFBYHKeZVmRZQUfPdmxKjRj1FgXCEmQC43OSy52gYNSMTiJRjO4RCEc86rmYogs5oopBlQm2E2R+UmLfH1DMxuZW8jmjspAlzuWVpLNPE3ZM3cZrlBU9Ywr03I8zFDNRBt2VMUCWy+glVyqjgN/jc33Zlw2grouQZcUUfHhR+eUw8ilDXuYWdjzLysluYqJI63ovMdphRKCea25d++Ih9uGaymiX24Y9Q4i6EFTxponeuKgyxi/P6dv9lXDWcopdoIPHrYcrAybxpEV5d7FXCZyCVunqLFgFGNw+ACH64KxaWiSopIB7/fJ99EnZsZj1EQzeSoBwffMZ4ZN2zPPM4wUbH1kURdYF6mqgvOrHUezkkUh2Q4DdZ5xZzHn//p//7sILZmfLFGfCILsy4DiJ20GPj/Gni4w6ePhmMT//lK0P719vsb5uXTEzxBapZ807/y0gOKvOw4M00A3dFg30fmBOGaMg0MbxeLGIdPFxLgZUIWhrErGzjO2AykJpikyP51x/sEllx9dUhQ1CyQ+QUARImy3A0bsreCnySH8BNFTX58jas00TXRDBykhKRm7hqGf2IiGmCL95BBG4QJsNz3DMLDb7j7xFpFa7uV02wE7WdpmxPcQxoCzAaUNKUbG3tFuJM6MMO2ld7V2eGe5fLwFZ4lfMUxaYFNkdbQk2pHpciKvMtopsJ06Whup856VSljpaMSIkRavLWMc6eKEVxm9H/FiD9sJZYa1iV5O6KseqxuKsiIur5MdVsyurZhshj77AbZNBAIqGdxgcQTsLBGNxGd7GcgMjVKKoCRubkhT2PMjQiTPDFYnyAxOZYRB0HsLMaG1IOSBaBLbaYdNGS6XTH4gTYJ2jPR64jI4UDvEgce5CRklos6xMtHEkWmKOCHwOpCLgt3YMqSJbYCgHSiHVYFcOpJw9H5CpojTmuwgx7uEt5LgPENwNH5knByxs/RhwiSNMJEJv89iq4mYBUYSTbchuMQkB0IKjGEgpoj8mQuQ+4lmDAO975jCSCsafJnTji0qM2g9w1WJIYzsbEO5yujGHaGfqGLOlMBXiaa/QnuNrQApUQii3MsIutLgEOy6higFBmgNDEbRuECUiklKohboaQ9tslrRFYaQZXit8TGhBgty72HQjZZJaWJV4JTExD1JeVKS1uz7gwBGrci0AiUZ6wxZ5DgXMCFijWLMDSSYlIIQ933FOUagzzUhJQYlCAgEksEnJi0ZtUQIxWgkQYEm4EPAaUmXJax3TAScFKhKYQtJTBqfScS8IlvMCN4j055XkZTAx6eQIeuRmUYuSqILqM+hRcTHyZSnx4WSn5o+BTF40AohwD/9aUNLCAE1BQYSVg90vmUMwyfT4uBaRkamONA6QZgEk5uwySKLnGkaGFNHKw2DilgRGAtJPkqCUkxaokKiC5EY9x47wyxjzKEvBLKQRCcQMsdpQS8jQmiGXBO1JpOepPfVid4oslVFO1iSUmgl8VLglKQvMxKSIdMI7ylQeCOwWtLkiqATY24QKSKmRMo1VgmGXBNkYDByT6qMgaQ0NiValUAkBvOUq+QTochwKtH7AXLwhQUiPjlG11LVh6R5Tpgcjbd469DC43KBVYEuF6AdExNRB0wIJCMYg0UVipRJUppwci8HG73HFZLBRKwSROkYdUILSeq3THmkdRPEiVgKprCXxA4RemFJ0eOlRPqRsdDoFJnixGDcHlKrc6zwjDi2U0OMJaPWOARyCvTTnm8xjAkbBZMXjEMikwGUpLeBbCYJRtMPHiQsqpJB6r30baZJIjFJg1YScFwMjs4lTKHQ7bQXqMgNoTR87/f/nINnrlGeLD9bWv0ZWwAm59k1Pc4FbFRcbPd9lxRxWUFMkolEoRVxsLgAUwDbOSIeq/b4OD9GxqfCBFaCtZ5ucmg0yWhSBk1KmBjpRcBGyfnZGeWNFrsYiToy1IYkNbZJdJPDRbCLDD965G5EZWt844kohEq4FMGDJCL0fh5xIkGeMQyOfjcwn2m8UTSjQ11FQgj0MTG0IyJLqELTXjQ8vGooZpJYaaIP5FXG0I50FzvGYSLoginuhRT84KiqmuA97eiIbiRGR1KS3ATGZPeS3gn6Ye/P4BGgE3aMuCjYjYGIwsaERWJ0xpQkQUjazuMyyKVh9CO5SWgpiIXEG0XUI6IS+75OIBqPqxOjEIRSEeLIgKUddxjrGHNHjC3j1qPyBb42DI3ALwoG67HDiOhHRB/YdSNNjLiYcFKREBih6GLEpsTGOpIUDDEhUsJtG7q/aBCLktlJhbGWYZYgRIpJ4eOEJdD6fWW2C4CSiPOBbisYEWx6T5CKy92EVBIZPQH23iGAjw4XEyjJk/MdUsIQA6hE8JEIeEBbj1UeGxNaCZKSDHHPq1mtC7pugMww+kA/TEw+0FtHMjXbfmTT9UyTY1XklMuK4mD2uazij6+nj9eOn7Av+Mwe4eMF4t+z/UKCC/H07ydCmJ8EQl/2Vn5+bsQXTv3SAz//p3HvxrNcNVeM05o6nzONNfgdWaa5ef06T97bcvFoQ5Yivne05y1GQ55FljeO0HVFe/8RRR6YpgYta154+YC//Lc79BQ4XNes6oyr6ZLdtuNkecjizVs0k2NRLVgsK9798ApS4tpyxsNHEus0h8czjg9q3v/okhDhzu0VPja4s5J6XvHM7Tt8//sfEFPk+s0j8rrELBZUq4rTuyc8fKfDTh45NDx+2NAERXKGKmvZEDHzGddvLbHTgs15hz23zKPng2H/lYXmnLJT5B5qIXj52RUPNpZicFzLb0LYkjnFWpQ8q5+jGR7Tp5GlXGJjSWYfoQNc09c5C1uE1Cw7w6GcsZlH8lhwq75LXpQAHMsTlnLFujtCS8Xp6U2GpaOdGioqJpF4kB4SOsuyX+IWgXL0LGJBJdc8Gc9QSnE0rWn8QFlFVtFQs+R+uE/0lpOriuFUEZVmFQwrecq5aXDjwDV7xNXQEvTArPMcdSs2piVgeOboWUafkYZz5l5zLV/xsNjQ7hpOhowxeeJMs/CGw+aER8srYiG57lcMIcOnhjk5B/2czTKgNZzaEu8s21lG5RK3HmsemYG8ktxIc9LUo/SO0kuO/Q3acsOoIsuhpmo9l9neJ+FW+Qxn4yMat+O0vMHcLH7KBAIf707vzV/gR/33mcTEoTyhmB2ixX1wiZure1wMW4oBisZwatZsKknUkaNhSUuHSQ3LbMYqLnh89RhZ51yf3WZIHQ7PSi85Km7wrv8hfttwHCamYoR4xjKULC5yHlUjUcH1xuBMIkmYDxMHjzseLUtcWXAtRGy/l6KdT45ndjserWeMRnPaDgQfSKsZtfWcXDU8PliQhci1ZkSwl4UtEhyNnieFQZM4aQekj6QUKSbP9WbgyapEAyfNiGCv5JTbwLVtw/kyQ0jFUVZRiITGowfLtcuJi1oiEKxbRU7O5eGCTGie4YBduiTpa8x0ze3yLt8bPiD2lnv5dZ5sz7gQW66X1xFW8MB+hLKau8WzbPwlm3bHYX7MYX7048CCp5xvxCf7ss/MfwkQiVzl3KjvMPmJqBIzNaNrL0j9Q8qoua3vfPJ4d8sX+P7wF2gUakrM/ZxOTDgci+KU3gR0c59izHlhfp33fUuD5TSf4TvH/dRRWDh1nrO5JM8Uh40nd4arWFArxalSPHYWMXkOria0zGGZKJPjZkpcZntlp4Pes64q3n94gWxaTncTVzND8JZ576mi5ElKCOu40UxsFxpE4KCZyFPkLNUk77m+GeiKnEBi2VqKaeDssAIE1xrLkGdEBYtmYjk5Hq8rIHHUWIYy4ZcZdQur3Yz+tCBpySIukSrjh/49DvwR12XJYyamJFk9ETRqj62fO8l1ccRHGpwI3IwVDkcUicP5IdfSivfdO1hvOb7I8CYj5BNlTNzernm0LujHgRt6hXsSSYu9l8G1ruBJKWl2gRuyxnQDPnNkNnD6vcD9siOdrFh3JWY557EsKJLmZl/yOA+oUHDcJpSoeZx3ZLrg+qLg/mFCrj2rTWR75VG5Zl1nHFWCyzYipGKdRYpFwaNdgslxrfC4ek++XyhHgSWFQF4W3P3KNTYXLWkzUsfArXXF5RCZ+olKiP2G/wtcivQFpbsfz1VP+/bTvm6M5rl715msw7vArJ7xQd3wzjsPObm+ZqUz3rkY6MfAQYwEva8SLo3gdKZ4r08EYzgqDHYuUD5SCFiLxOMQMHnJOiW8dYQEOYJbSLZR0CSQm4L6wwZ3ckKxnPH8cslH6pKYWo6mjNiUmIVCGcFRKbmvLYtjwaodEZNn1zsciWfWOeedpMAwzxJlJhBRI1Li2CQmmfDAQktyoznzjuQD14ocjyMTcHS8YlUJuiIQfeDGjWPOm8T2vSco4GRecub289yqLPBCg1CYFDhezLjoJqaYuL2ukcsZ7nsfUWvDrYWhEYptP7LKAySJJFHkkiOdmCZHN04czCrGYUuuEsRIURguqobVEma7iO4HsqVj6TJOmwWX5cCUAsd2RmY8l9pRZzXXujkPp0foIDncFZRjyeOn6IYXzB0emBlpO3EQFdVG0D8ZMAJuRcX3upFoPSslMSlxHjwGwYmEBkn0gdPMkAnBWYrEkDiMknayDFcD05R4/saCq1DiJ8fpqNhsJVEqDoFZPuOjEHGXAwc60EZokdD13L214OFVAAHXCsVucKTgqSRUWeBiTATnOaj3PIYsCAoB87nkSeeJQnKoDQFPHwS5hNN6QSciuMBhnmMFdCJyeLRC7CY200Sh4ebRiu3DM4LOOThY8PZ3XuPCbeg/eMiNk5vMyvoLW3DxMU/5fy1pqC9pv2ATvc9v8n+eDf/nKhpf+iziE77XPpT51PN92gX8M4WSj1fnL36oz99+kcVsRdvvWNeH/MuzPyGcOYJITK7n/vffo92MFBmIKFAqEVLi+JnrmIMj3v/zjzApsV6XPHzc0rcN3hfgduRCEUdLv97QskHf0CxfuUFMB4zdlt4U9G3FbheIMVHmh8jS033UI7od9vHEbnLoWcHjd3vG0dKQk5k5f/gn7zL0Lc46yrJmK3MaMaK8xDzoOHvnnOpgidI55+KcUWUMwVKPOb1VxFFzyx2gY2B2sGBKgTa2EPaGQ1lShCZhZI7debYf7rBSo4sSF1tqOTKJES0n7sprXLPP0+uBsin5U/WnDHIglxkz2dDqgckPFKVGLitSaggpYpX/cbkuAR9o5JlGSM2ROuLlr7zCld1wmB3wB82/YjM8RhUVx0VOs9sQU+SARDkM+CJCgpmcEEfgfUdhIzpz6HiByCLKNYRgkDOJKgSZ2KDCE8gCMgTqOmPTDxgi2hQIaTCrOcEJ3PlElBD6iM0vSekSmQ1ks5IoJQqHShpV5eR1hjURJo/qd+TZjtJAltXEMCDTiJCKIB0hWaY2Ek2OrixWWFIKFKoj01symVHVCgpNch2zDOJa4SP0vuPd3fd5r/0+Y+hZmBW/dvqbrLL1XzvSnPA4HXExYlWkCGkPR/MO1Y/UcWKSkQqPf3iBOJrIypxqXpOswdpArebIQZKpHP94YDp/QluOTOXASM1x7DioNaGYMd/1WPHnSD2hvELNTvaYbpGI3hD8MUIGlAh4FUgigh322bVFgcwNIkYoDNJolJbEGFFKI9ln8kOZfzKNpBT32SYhUXYPr5FKErUiZpoYJqIAqQUx2yt+RJEIRpIJjeRpptsUaDKUMMhCg+9Aa5IQhMHtmecR9rILp4StxMfEdtS0hye0M9iZOf9d+8f0ZiDLM/6Ev2KQV7ShZdaU1FEyMCCARfZviNbvCdV6xncOf42b5e2n05tAfFmBSoDQ+0rGxxu0bx58i1vVbXzyVLrin6d/ilAZQhiGJ5cM7WPyoyXLcsXfWvx9Ho0fslitOJKnPBo+ZHQ9y9U1/sez32NHRjlJEB+h9EhWW7SyjBtPEHtZ2uLmklKWYCQrpTHXj5k0yPOWqelQC4kI+/4uyRFiv/CPvSMsM6yFUFaMXYPrGjQBh8OFvaxwTA4XJNFrtBR44RAigkwk6YjBICNIk4PcC1oIKUBJojEgFISA/5jjIiVCSrxSiKcVrPRUKlLIhCAgRYkmECPYTPF7m39JGztmwww1f5uUin2lKCVckoBESU1SpyQrSIXA24xRnOG1IZiacesJHiYt8UVBiAkfEs5FYl2gjzLixuMjiGJv8KWNIeLA5CSTiFNHMz5gKgRmuZcGlkVBGHuSqNDuADkMqKRhrNCxRxqFChIza5DFgPA98qBEmxkmE5QbT9oaBpsQWiC1QWIh7FX4Qh8IW0uuDEpoglCMm4ZFljC1JpeK/qxlnGkmJvKFITUjppAYJ9GriuW65uaNI7JZ8cla7N2+wmKeilJ8EmB8OqL+3LL9q7/8KnduHWOtZ16V/NftH7IdS8LlGUMxQwZJqQWKSJKR6BzCQdcI8rKk6S2qNsgxkJzDp4gtDFEIhsmxzDRJKZKPIKEdA94ofIwMSL733gnuMnLt7imrwqCOLzGzHLFJCD0RXUJgiLVFHhWoLENuHP7dvVhB8h5rBeMuMKFIhSRmCibIy5yZEaRgETEQEYS037xro1HzAtd5jNLks4oULiEETGGQJiDCXvp7fbSiXlTE+xeklJB5hnWSyXqUkUxpDwcMIjH0gcV8YnVSkvUO2fd4D9IHVFYQFaQUAMFCtHi/l8Y9FD0uc5ydt2gS2VfXXB44vIhkMbG6PrGreqqYU69rutriUofKIur4GFH3RCdwT7ZUtSQkSYbA1wZfF+T1guDv0r8L24eP0TvQ00h0e9GZXUi0MYJWRL+v4MWYSApUlhGGESUlMSQsgRASRitkUshkEFEytY7HDwVZUSEmiz3LSB9mOJEISpOGEvtgRxz3MF5pMrIoyI3A+T2kNgTPKBMueBIZEFjUBVdjt99di0QMFpk00U1ErdAIXAxkhcE7h7UTudL4FOn7ASHADh3KwHjVIBYFN547Jj26pLCGOAzEKVEUFWVV8XDzEed/8j42ONbLA3797V9nVs5+DKv9WPzoZw0sfkHxxy8QFvWpHf0vKjj6dKzwNHgQnzz4x/WSL/oNfrY9xRV87iV+3E7WJ5ysT/jo/cc0Tc9222CMpnm8V3MAgRSG0XrawVEva7qQsf3ufTZXA4eLnMFBTJJmN/GDP/+IYXSE5On9iNhdoY4iq2szLq3D7xo2m4Gh9UxyYjdEUkrsLh+ijObJk5ZewcPpij4msqpgWxps09NYz+7+losDgSj2Gu9ltcLGnCcXLZt3n/DBmcZtI8WFZf3SIVYWdAlkmXM5GoTSTGPiu3/0ActlxThG8rziA9fSRfbuxF3alzj7RCg0P+gEsgBrLfb6BZMc8WXPhkvemd7hrfFvoucFj25vCaNg6iyRxPenD0AYetPRVIqd39Kyo8gKPmjexS6/TaYM55sLds2OqydbpJSc1U/4Rnqbo9kRZ/aMjb9i488RCJxsMbXAOUtHz1ZZ2rDbOwZXE2jFYHpE9Fjdsc0Gkve0eY6ooFEWKSMNT+hTgyDhVSLFnFGOdDNFP2uxWcL7nr7Zl2Y32x2jVWzWDSHuiBU8VBnInMY3IAKX5gKRS6wMhLFHaEfLlugtj3KH0DWDH8FJXPTsJkepNVdlh0YwaIdSI3lo6fQO5xRduKQaCnp6QuzxOrHLejKZM+2+y1zP6VPH9TJwv//grw8uBLzT/4Ct37AJGwiCjevp/IBUkuA/QCPoww61nNGahn7qkFHhtEWlnM41SCNwjAx2QMwUtmyYpp5daGFMbN0VQTkiiW65pJsiO78DWXB+NKMnJ6RIEjUiaLa5xmvJk4MMrzTOWoJWJCFpS0MQcFYVCK2ZgHi8QsTEViu8dVwUC0iRqchIci9l3M0KnPNcLkqUD/S54UmMpMLQVBk+RC7nBcY6usKg2TvqNkqhneeqyDDW0UpF6jqECbQklEg0q3x/n97v+Le5ocsVTI6tatE+0I+S5DZc1Bf0coccFWXuEWpkG7esfIV2niG2CAHLaYWOmpaWo+yY94d3uVnd/vR09+Vfqfh4Dtz/VUJxq7qDEII/2/wxrW9o/BZh4Gy95ZVihjAahGBRHLAoDz7JHt+qnwfge7vv0vmGzu5IRcUH4V2mCYY04bOb2JWkCXshg4s8IaPA1RnGFMjoudxadEqcrxUKT58b5HyOrla0CWQzsKkVWYwMhSE/XHB+vmVrBFprtnmFtI4ul4hkMHlJXxaImBhnoHD0lXm6HuS0RYYSgvF4jgqRptAkEkEo+lyR0NjMkAtJlynELGcjMobCIABbRKTwNJlAFIFJjiS35xNOMpC0ZOO3zOMBNr9ikMeEENitIl5odmUCIbkoWhwJrwSh2BJ9yxUDsXnCA9EhZwFXSR6XjjB5trnFk3gituidoWcgKYeoBE3msC7yZNmhXaLJPMEPpHpiu6xxwPmtHOkkTSlRUbKRlm0u6GNiU49om2gVyNlAmvds6x4TJY3tSIOkm2WEC0EoCoYhY5oEY0jYPtF7idgGhJTsQo6SkrED0Q1sGo8sJecu0PiIUAWPGk8CdsGxrHO+//gM23foTFML+PDJlmuDxcz2BojWOmLaY9BzVfx4nf4J5VcBCCl55s41AP7o//sj2tHSe0sxy/irRz1JFcQoGGVEZZrWJ8LgOMtyhLPYJHgwONqho88VZa45cx4hoQkRrEdIwTYmJgFXIVIAfUokAzJExg7so47+5iVLGppqxFbglrA1oKTh3BfEUDBGUHmJrwzdpScIQ4g5QXhGLxmkYoyKUUQmJxh3E0k6uihI7YSII81gEVJgPxqYl5rRe87OLiirAdu06Lpg10lcrOm1JLYD9y9b+qeKdMIL+sHRRkFKgu1mxMXwNHBpuWgusUayWs94tOkZpoBPYMoF3iX6JAh94DwO1GIiOE+ztQgtyLO9AtaDomc4kqRSM8QRyoFpMaGk4vvqMdoI+tyzO5GQt1y4DXmb2M4stS7ZMeLriDOa/kTj88hHf/GI4R3NVe9xaAKJCyHIIrzTDSQpaUIgCkkUkpa9Ylw3TGRyr04lUiJEQS8FGoHVguRhEgJlIs52zLxAENmNBiZonCBNloeXnq6BpHMGEslFmklQGU1z5Ri8QGnNE+sxuqCfEsEntmcDXip8iLjRY5Rk242UStB0YGMkJYG7bDA60ttISI7NMKJlwoZAJXNi30OmaIaBd84vEUpwtW3ovEAmQdcODMPExXDJ9ZdnOOGBxIMnD3jxzoufGTji59mU/4II3f8bcC4+1z6fkfgMl+TLIVM/rkmIn3D84+tPj3yhCPLXYzurusAYzWxWkhcZ0hqKZzRn750jRMQ5y+H1JQe3Drn8cINvBmZlznyRk1wkyxVawdQNLMqMy3akVIb13VOKmwalFMlliKxmHB3HhysuB4k0ieHJlmnTUxi9l2kUCVdkmLgvQ5bLisMbh7gPnyBHi72wrE5qxLIkKzNyCjaPd5gUObi+ZEwdvXXk7Ksq/WWHIaKMQJt9OBb6gaQTxpSsjytO9IInYcegBNXMUDuD8IFZJsgyiVSCLkAZCjKvMCGntgVF3GOly3vXWIWM/LykLhYUssQUnjSA84EqlqA1BE8+GaRKyLT/oqqiRCtNXdYYrTHaYPReWaRSFVpoamoYPWpKlD5jcDAvZ4zFhJLZfvBEMKbABkftctCw0poo9oNfCo3zW5ZmhYtbMikJIlKoGsOcyUQO1CGTDmT9RN9NzJY1eqhoaFiKHNd16GJGkIlalWTlCts5lmpBKCIiRNppx0xVpKFnSppZMBidI32259yIHKoS6xvmKSMl0ElAgMpJsqAJZFQhR6ZARY2oM1bZAZNwhOGcMhaoKZBPkjgrKVVJperP9Okv4iz312pVM1Nz+tCTu4LkYFbUKKnJhKASGS5OLLIVo1aIVoCNiCkwX8yx0TLXC8Y6I4sliYQ0hrpaMF29Ty2rvblbXhCNQOqKoqwYdp7FkNG2AVNnuOTJfMDYiJWRpUtYPKhEHxOFC2TBf+K2PEiDiKDLnHIcUDYw1Tkz65meSg5rLLPBEpUihsh88litUFIgEszYE0PDJKh8JBiJ8pHoAuVoIYCrS8rJ42LAWEfQkvkU8F2LM4IiJpKAIoEViblPuOSIPqDC/kPPuj3ht3QBvGV2kKGSQnlBqQyTmFgWBwS/BecweUYmc2ayxnlLrWoqWX3Cs/jk8ie0fVLq89/0fvyUqqJQJTO9oNIzVF3s/0F8WTbrqQu4qshlSaFL5maJLRJuEoj2krL1ZPUx/W5DNUW8SFTaMCCpXCQ0PTmJ2kWccxgZcYVkuSoRUjKet+jBIjJJERI+SxSbgRDBJ0Hu95U/Yx3RaGaTI8mcJB3SR5QMFMHhjGQ+epzSJJNQ1qFConCeUUvqaS9ZLaf9prfQhqKdcEowGxyTkajkiFqSB8gmx6SgngQiSIyaE0QkkzlKF4xxpAwGmSS5MXSXHSoqyiCYClhqQz9aykkx+kipDKIX9IWm3kR8naOiZ0yBvAmIpJiUph40TkTMkBCznMoZVNAEB9Wo8CJHpYwQRqqkYHYNT6S2iiA1RlVE6VmmnITBesfMS1CGzEt8ipSuII4NXkARJNFHsqhJQbBeFLRS4lXEGIm3E0Ul8V1iZgRTDMwLhSQhrUPrwMHxjGUW6J1nniQpBIRzLFYZbvTMM0Gqcmb13lcmTI5MfravKSkhpr3a3c/Tno6HWV1Q1zlVuTes3Vy2hBDxZcbMGLSWjD6wLjQuSUxu6CIUzpEtc6TZe9yURcHicMajTUvpPXZy5ClRC8EUIyUSlWfMCMinxnuFDdSiYiESnsCiythddgSXyIPAGg1Gc2k9M6PYTZYq0wTvMCKwWma0ZNTGM1hHIQUiJYQElQJeKUolmHwkFyCFQItELmBKiQxJnhmyYoaZF0SvqbKKrpmQlw1FptCFIbpIGi0zXTClvWdpPwVyKbACMqOohGbqB+bXD9D3TpmakaGbWC4rwqBph5F5LpmLnHy0jEqxqCuGvkMImCZLnkpCkHStQ8fELM8xUrD0OUFCOVuQlxOLtGRqRgoHs9EgbKIYJU4L5pPBr5aoXFFR4HuL6iNDgrkAJxSTEqTRYkh70Q0hqZJnDHvZcJUS+1QCKL3fT9mngieFlggf0Ig9WsSBtBEzJsQUyDJJVWR0fU+VAmNUzAuD12B3PUWmMGgqk/BKQvSkBDJ5yjynmwKH85zdMFJkgqGPLPKM6EcyLTiaFQw27D2cEOQpkOuA9YG51kQMRibGIDFKIbRGCZgXBbrYy6C7fkJPkUxl5D6QJUiyJV1MRO3JbudURfWppWA/WNJnEvP/27RfoBTtp299+vcntJ8TMfX5R9tL0j4tn6an1z9d6vg50VkHR0u+9s2Xeekrz/DiK3f5zX/4dWZvRapvDJQvjLz6zbvMTpZ0Vw1L0bEoDDJ5hAzkxYAsEl5MPHOrJK4T09Jx/Popb/+NX6XdzNhdlLz2wivEKLFegFS8dHDI+cPIxYXmzedvI2czdt4wJsMLJyumWDPGimcXS4wq8WYBszV358dcXVRsL2peuHGbqsj2ostCcGduuVoIzupAFltu3bhGnR8QesVzC48LAi8NJycFdrJ89GDH++9c8PbxmnW8QfFwyeFgWEtNJGcaBb/2lYr5tyfKb+8oK8edJqP2hmoUvCpepnz+BsIoDrNj3lh8lRfrl3lh9hL/8MY/5LUbX+Or17/Ot05+mefUHdIs4CvP6XTAP9v89/yX5/9P/jz9W5YvLmhe2dG8uOP6S9f4X578Pr/9/j/izx/+G16Pr/CCeZ6Xqpf4O9f/Pq/e+jpfufM2r916m7997x/w8sHrvHTwGv/HZ/4vvH78dV47/Cpfff5X+Acn/ye+Ur/CV6pX+Y3d11g1kvmVp3gy8rXxq4w2x9qCV6cXmYkcbSRaCb49vox2ltrAG+o6x4VgfjRRrRy/It8gSIWdBHf7a8zGOT6VOKf5+kd3GXaeQMFd8zx3VncotSEvDP9BfIGMHVXcci+VPFcuOMxH1nXgN4uXWIaeg6nlrljzy/41XvJ3eSHd4R/e+7/x6p1v8Mr6DX7p8Ns8t3oJva5JGt60L7E1LdusJVSSTg/81va3+O3df8t703v8i+b3+G+ufos/7P6Qvxy/y3+z+0f8k90/ZpUfMZlEz97N/fniGdp4TqeveO3gDRpVcyHnTHrF8+u3aeYzmlnNXfkSIz19NeDLwFeO32QqPLYIvLF6i9eXb/L6tW/wbLrLm+4VmmlH0294rXyBZcipo6AQkrebBWx+QN78iFc3F1TpXaz4IyJ/ztuXO1yYSCZwzwdmk8MT8HXGL5/vSAaiDFxLgWXwBJUIEr71wRNSbghGc9SMHG/3Drg+RL75F+8Twx7HfLjtOb3scUngIvzS9x7uXd6PlhzUBafNOYM8Z8i3fPPDD4nmAuQD5tMZz56fQdUR5iNvX3YkM0A1UCnLM5cNQY94PfLGY4vIDOT7wP/FzTX63SHt5ZI3L7+Caw6Z2puk5oQX268wcEIXj3g5+yajLNmQsZsSear4nQe/ze88/G3e69/7mabKlBKPhof87oN/wj+9/1vEGDHJkHwk+MAL+gXsoyuC8z8ZfyvgVn2XV1Zf4cXFKzy7eIG/ffBrVMoxV4FnreE74hZfXdzhjYM7/P3ju6i7kbjacpBaTtqJkAJT8rz5wYB1Gi1rlo8GFn/yIc570JJvnzt8XRK0oWo9d7aWoAVBC966HBEmI0lN4RLPXHYEKYha8OoPL5BGgEpoa3nu4Y6QBC4JXvzRGVa3DOoSwpYXHm6wyhMKwVd2I1orogSRIi+/e06QiRgj9z5sUAKiTCA1L27WeCKBxEvlKxiriV6glOab5Sk+eZyfuPfhSN1rjFgg1ZyvPqpxUuGS5N5wwjov0IWDzPKND28yRck0Bm7t1hz5Cj1XBGH52vcP9+7hwXHDLzgRMzwdqQr86uwe3BoIR5esledGyvGLEb+2fLs9BTNDxop1V3L9sSYOgqkJfO1HBWMT8C3kFxl3Lu6S9PMkc49fujhEHFzA4kPq9TkvKgg+MbnIqwcOrTUxBapa8tXna+wYUMbwzXsVY9NjnSerMl471bjJoaTi60cF4WxD2HSkwfLqcU1KkSgTzz9zyuv/4JfJD+efyNlleUaRZ2ijP7Nu/7QdxKfzhS8+d523XnuGN75ylzfeuMd/8vdeZ571rPKOlw7hOLcUokX5hv/gRkFwA9EPHA49J0ah5N7p/Q0SbTtATBwkuFlkJLkn0L+WYHQOGzwrqbiXX3J8/T7V/D3+Vv4cunFkG891vea56ZCUWUIe+E7MiDOJLTwxtLx4PcOVFlEFnl/1jL2l343EbuCmGhi7yNgFbtiGsR3o2wnXTZxECyIiVeLN0zWZVkgjqQ9mPHd0i8u2YLMreePVF8kVCOGZzTNeP17ifULOSr7+6ikH19ZIIVFK8+a1BcgK53JulnOkKOnDjMtHjq8eHeKpSeWaYynI0KRUEFLBsq54z635MB5jRY1/yXH1zYb0K4LbFlJ+Qb3e8lw24+7yGG8C4Sjn147+JpNJjCmyPFfceJwjoydGxzffv0uHpBMZi+oGd8sX6drE9nHHLz+QeAdhSuQBDpzlahjpgdeVJElJIJGlxN2wV31LUvDcMBBjIghI1nHHe0KKDJPl2dFTtzXlRc1sW3PvBwW735XEP1ry+iPF8KMd/gIYFc8uAi7XDJPjtXsFeSYIIhK85V414ZMgIHlupRDOEtPe0+W5oieMG2RqODE9lerJs57RXvHCOpGpgcz0PHeQsawyQgjElHhpWRJSQBaa9azg4GBN03vOL3r+xusv8epLd/nGL73Cf/yf/h/46m/eZPXSgDq44NXlLQ5ZcbO6zivPvMKN45ufoQKIT8KKX1BJ4mdsvxApWvixRu7ns2efLtd//urno6svPecz533qlC972T+NtvGzvMtPPeb/8uf/M3/57l9wubtknR9jf7CkfRzYvH+GsGEvXdcHykoyJofUkiI3tH7HqEf08Zx7L96hHwJDt5ed1NpQr2acne84Olzyl3/a0VqNrnIq48nyyHnrKe1ElDnJJawLrJc5h4ucD5+01CbhvaDWOZP1zBaS5fWMi2Fi7jwPHg2Q5zSD5VCXXL92g4ttILM9V61DZk+l+iqF8J5mEuQqMAqDqXM6C4syIVJk20UqHal+faB+0fO421I9abhjtqS1p3KG5269yX/40n/8xc/5c4TTC/eE3776LT6Y3kVbhest89UxV2w4NifY5OhCixEZ1WiYtTkXwxNuzG/xjRvf4eWD1z6BwH2m23zqOT/5+tLH1asfn/AXV3/Gn5z/ax4ND1i4GWfK0SVPVIlFVlIbzYXacpIfMzVb0jQRK0WZCtQucKV3LMWSrQYbIlZYqrjAyDlnqWUZSoZxhxYwaM+JLlkWsHPnrGbH9FOHsJFOj8zbHJMMnRmo5ZzYDagu0uuR0+wG35r9ErePX8AczRGZ3r/vlDgLT/gf2v+BD92HFDGnu7xA2kRTDhznewOiXg4UskAiqUTFZbjkUB8wMtKmlkwYIhITMh4Pj7imjnCxp3ctKkn8tEbZQzaF5bRYM6kdTo0kFymDZV3lnKdzjvUJ3gdCCiQSt7M7/J3136NUFdaN/L+af8wPz7+LsyPL2SkzuebCXrI2a4awZRoGpqFHh5wocp6UI+uxwlVfQ0wrepGYWchVxrkSrIVinDwSQScSC5cQk+eiylmNjiAkKgq6TDPvRqTWbKuc2WixQB4ju8ywHKa9FG1hqCdHlIIsBJpFyeHCEFaWi3ZHdtkhXE/VD1xVgtXWk5SgLxVZkoQkKMbIdqlZ9/tApVOQ53sZ2XwIXGWRg6CwpcKKhBgcIo1kyrOZC65Xc5xomNJIcgGdHAWBczYcs0S6BlNKkkjcnd/j713/jyhV+VNzNj56/rv7v8UH/bu4aKlkTSZyLvoz1tkhL6rn+ebRr2IOZj87Bhf4Zw9+h3ebH9LZHadc482P7nEzv07+8k1+J73Dd5v7nF9eMDuXCHfE1mTUPhGEJEexMYJyO2CqnL42VIF9xWM1Y5MJFp3DD5aBPQwlCUW5G9lVhnXvCGWJKzO0j2g5UYaRzSJj0QbC8ph2N6IjJHaY2HAxlxy14LOayRiUVlRWUE2Cy1nGejcyZIqg95+BiQ4TLNtKsu4cIf45+XVJiA7lNcVsyUXYcJAd0K/exKs1zUfn5KOlcIGrdc7CJrpZi99tGGRkXTq0fMylvmDeZrRCI7ykTyPrkJPnieYazC8S064hL0oaepZpgTpe8eT8I2auwNaK8mDN+fkD5pcaLzN2lWMecvywImtrttqz7AQBaKKltOC0oIiCbZE4dBpxumCsJaXWiPwStXvIpW5YPz5g+/uv0D4oiNETRGC1zLl/1nPtKCPJkosnHUokwJKZQCsyrh3lXD66pB8d9aKiFJYsjFy5yLoQaNWTpCerCg6V4m8//wxf+U9+FV3kX9KHP7dwfOriJy7d6cdXUkj8l//VP+cv/uyHXD26IksSIQ1dSpRSEsolUxB0ISL8RHZtzi5T1EoyGoEuFE2MzIVg8oFLF8hjAAk6RdqUuF47Du8+QB9Y5iljffeAMi+48ltW+SGXYeJic0ZpKvr7R/gPFlxqOOgT/mHgyeWABoqxYuZKNk6zKhP9aOmnQIoBUg+powmCo1qilSWJQCYkVS5ZHtZcWMvRes4QBF5K/GCpFKxOah4/2XB8tGTXJiafcC6gnUQGw6PLgXku6JzATwGX4HBuIEw0PjEnYqPcm7KWBXqMGFNxOQpKGfdqTDFhvWB28Jji1fcI1xxVKOgri5ARc73i9Pg6bujYlgMHxQHT2CDHyFa2rC410geabKSOBWMy5PWaTeU4yY+wk+N8c46+skzvHiAerfjIebQPTEngMwOTQ0hBpiSXIXAoBENItCEgY0QJQQ60WrMIEbTEa4kCiitNvZW0XrFQER0MImmUFKjkqQ8rHm4shR8ZpoSZVQS3lwfWBHpyciZsTEQENkTmuSBXkSdDYK4jzl+hcUQERSXRwbEdLQdVTm/3qpa981RZzjR4Gg8zIxDKUxaazlrmmWF9vOZy12ESfOtbr/B3f+Or1IdzHjz5iP/pz/5H7p9/REHGreUtfvOX/jb5okQ+DdT325+PQ4r0JTXtn9A+m8H/31eK9ouwpE/f92UBwMcWTl9eWvgCCkD8hP3qp4/9JNTTTws2vrT9eCrrx452aBntSGsH4ljQXFn6zlIaQzMGnI8wJrKZZhgtXTfhK8/s+oJUZ2w2O+yQ2LUjQgrmS8121zOME1e7kfzams0TT9NOuDoivKePIJQGFxm92GvPTx7pDJ31hLB3yHTOE2Mi7nqsGhmkQJWGCYEdPBMSj2LXeUYvkCrfk9bG+FTSD6r5HCECUiX8lHADjFOiMIIoJWPY44i7dsfmamAykeUcxuCJvkctl3sy9aeJ2Z8m431qhehSi0uONjQoIRG5xrdPaGhRIhFipBEtSmpCXxEGg88Ck3YMcQD2FP4YIkLKPcH181/bJ5efMJn2lxL6NDCKEac8YxGxCXZDR0x7B+ZJGnoxsPE7RBpweiLYQPIWSIxiQqWWHkUXJoKISFUzMNK5gRQDNgyoWhMyQTt0SBcZxIhoznElRB0Ypg4VAiYo+jgQ/AgR8mWFS4I0z0g3FmSr9T7f8PQ9pRDpYo9Nli52WOHwa0HajQypZ9tfoKRmpzoyU1CamqA8YxxoQoOXnjY2e7LypEhTpBcdW5EhCfR6n7lTck5IPYNzPBkcPu6Y8hGZ7cu0l92OXnVso0GR0U8tpIRTp3S2paoqnAp4EehmHtdMyIsLQpUY1UgbGpz2TPOALwQxGobOMklLVxd4AzHLsCGiQmCSgrHMaONTrKrYe2DkyZOEwWaaNkSCNiSf8LnBxH0ls1eSVGQ4YEyRXkq01yAFvdGEp30nS4oekGeXxNEy3qiI8xzVGaSYEWRgWgZSiEy1JAiFHAP9dmTUic5AcInWSEYNeQJvEpORbK2DwdNnAnQiGyZ6O9KIRBYCYdow6BFpNDOV8Noz4Wl8S+EHunZAlTnOW/rQ74OLnwKR8snjkmXn9qIHUsm9PKntMMIwLYFM40eL+ZgE/zO03nc0bssUx71fw0sHGHGMWc/oLy07aZlKiVmUxEYwaEWSkZAkTkpGAbrOCBI6AZMGJSQueAY0SknINV10TCGRS0mqMsbC0AuFkJJO7SsHlY64FBkzRX5cE6KkyzRSCLIoGZFMmaSpBEJIusoghEAqRSAxafFUwlYy5QqkpBgc1kgmI2iLhA6ScdwQgmdeH+BjxxhGmjAwJU8fPVMmkZPA5RJbaFo7MhWCbgx4BYYRkzsGHKKEPiSCEEx4iiiZskQ7DXuIZPCMqWVMI/lqiTCO6SgjPmiwQ2JoPHYlmUyG6yOD8aQoiKNDq0AXLUprkg10wuOyvTP3JKCXkJUCIwJdJpiiR8cWNY8MRJTzTG6iCSU4gc4UTy4GnNBctYEUe8a4lzrOVWTXW0bh2J575KwiKM/WRczMkELAjSPNdqKuPTaOtNueg+tHhEI/DWi/TGTly3kWP7F9bvsQU2KKAWsk+nhOYXLa856uGfZjvxdk9RwbIsZogpCkIieoPUeus47h6cvyac+3kHmG9xYNWCHoxMhcBpK0+ELTixEXns6xqcNWmt4lJr+Xjfe+oAuQY/ZS8SGhpMA78ENkZx3BBiKRMUgEe5gYSKTZGxwKGejHiV6w5w89vmIkkVU5SWVsL1v6J1tqGXHDjNZajNaMKaMZwh5GM4KUJWOCTOz9hSapCSGy6yZitAwIomAvthATyY/MTcnkYPTgQ6AbJ0yekZShqgVyXeBnkaGzuDqiSoU8NPTG4oJjzDwbu2EYW4wU9GnAqD1crdd7xS8/O2BSjl5YLi7P8I1l63cYrbEhkuR+vk8x4Z8GF/1oydgH0k4IWiBIgVOG6AMmRtAaKwQjIKVgSAklBAZF5xMu7KsOeGhtQGrFbJbRXA00XYBM4UViaD3BR8osoaSks55oBFEKRg/O70EjLsLoEoSAIjHEQAJyWWBdQihJ7zzWJ1Ju9u9tsnsAl5Z01pKExSXP4DxaCPyTDe1oOT5d8+TBBR/+8Q956TfepJ8GJjcyTD3kkApB+WkZ2s/TCsRPpwV8vBf/eZJNP0v7hXEu0k+69YXI4EtDji+c/7lp5zN3i08f/UKG48s4Fz9P2z/SndNnON+eM68XzPM5xGPmpufh1FOVOVdti+sth7MaXRr6MFAWijuv3iPemPHocmA518yuV7z3qEckOC0S2ykxlCv0tqPeOA7LJepwycy2tAkYoBaOo1xxHgzNheNARRaZpNGGeSFYLzI2l5GEZKY883nOJikODypOVc67D0c6KZjniSpOxKzk4HDGszcDHzye2HaWgxlEuyMThuNrC14+qXlw5dlsRkrfEY0lHXvKoMh3EuECUQYO7ZzbmSQuFdV6xa3ZMzyeHtKFltPsOkpo7k8fkIuCG/ltzvwjtmHDkT5mpVcszTHaCU71NS7VDpJmNSwos5qH4REqKO7N7zHqFnRLnc04rW7y7vAOSkhuZDdp3JYrd8FxfszCrD7fAb6k4wjuVM/wg+Z7DHFkbQ44rFZ8lN9n3Oy4lp+C8lyMMN8IltMhfg5BRRaLA4RW7NyWWs0QpuJB94DRjxyMC1K+ooqaipyMNZZIUBLTTawJuLykVBV5tmTIR6aZZZFqtJe0dkcWNLNyyRQtUxhZ54fcqG9/MtBTSjwZH9P6lnV+wFwumMklpSg4UQc8XjxGdWec2BXGZ8gImcs4SUcMtSPqwIFbIkJCapBTYtXP2eUjWiiO0hFlEJxrg1KSQ3PKJYpMbZjtSspUcGYfoyzc1Mc4fUXMPLMp56A+5Ul5RRgts60iasdfiXc5VCuO1QnXxBl+tuIgzJieDKQDxbpcsShmPLaP8cJxWFxnW1keXrzPrNvLRl6WT5j8xKqp8UhC6lmEkvVY87jocCSON4rIHiK1wLC60lyUnkHCabdXH4k4Zr1lvh1p1nNMrjlp9yoiIkGZEkeblqvKIF3GtcYRmoazPjKbl9yoarYyEZuBaylRHs544C1FnnNjprlcOko8x06SrgbeH3fEbc/tKSPeMMyKiZkqUNFwph0pRI66OVeDBSFZNhG59ezWJSY3nEhFXzlCNmduEwdhziaL0EcWswUkyV91P+LIHLA2S+4PHxGJ3CxvMvqB8/Exy2zNaXmTMYyEFKjVDD85ampm5ZK78+cQWqLL/K+jcXym3Zk9y+AHbBxZ5YfcXNyjmK1ASJ6vrvFkfMy8lCydwbsaLQdM41i3mk2uQAlWrd3DOkRC2sj1KNn0DpkrDl0i8wGZCQqlOdr0DFqjRWDdjRgXuToskQhOLyxtFZFZzsmqxv3FORiDyjLWF5Zt7UlIDrpEGQwXZCSjONmOBJtIKWfZWkrruVgWRC05uBzwRYK5ZjlKVmKJqJegBbWe00pBiCMrkTPTSx44QdcH1lcTqdRIJ6iDYrExfNBGnBGcskRkEzH2zHrDvfwWD8UlvRs47ip0FTHeU8eMVXeTK3dGrw2n+RJZrUh4MmlY7nLOmy0qd5z4GWGSyLkg95qjrmbjJCrAUS/QTiOLSOYS606yLSPaR1aTY2k0j0Uks4lrvqa9s+d5HRpPTApmAZmgcgN9kSMnQa0ty6Lkg7OJ+byilpG2zGiTZmkiZRlJk0ORuCYl2cmSFCJFH3jm2optsKAlz75ylzf+z7+M+lKX7i/piB9Xo39SB/3cfK+k5Ll7NxhHi3WexbzCesH5gyvs+Y5uaxlkwKnE6c1D+hjQDmoBd2c5952kT4kDIfAkigS5EBzmmrNxpBSCuq8pdxtcLFjcOOK58hjLRB+HveRznhGKCfmkZyFKznJHqUaumSPUZg5ZjxsdayZSaQg+MBs9i8xwlix+tKwBh2aShrmIlJUCUyCBYyMJSjJmGYezGjN4ZF6gc8v1mWJsJ/zgUGrgxddv8P79He3kOT0taQdF7ANl8pysS+4/HkhScFhpfEpcdJGlFpysCu5vHSC4Phds2oA3GYrIYekYCkPnBma7gqpPeB1ZmzmzC4376gyfww1xRN9foGSi3CTujMdcssFIzbVpifIgqkShS66Ju5y5Ec7OOdU1aSwATTFElknzkTYEIZknmELirB9ZCzgWggaIQrCMEekjOtub0y5iwKIgJhYxUqNo3D4ZeZx7otFYKTisFdIH4jZQVDkzMTEZg5ORksitGxUfPhxIBg5LsD5ArqlkYFEJLsa9MtVKTHTOYU1kmWtO6jkPtokgJbeOlvRbyaA0B6uKgzLjwVXDbtOxKnJiUDzpR4zSHC8rrpotdZ1zuJxTlIrzTU/uOg7kwSdJxhvHN1kvDgHIs4J7d57/JLD4NPfuk/1w+jkJ3T9pTP6c7X8dtaifu/04GvgC5IUviU/Yf4jpc/f/IjFlz916nlk1Y9tuuba+RvHtmg9/eMb5W6eMU8tfvP8RfHhG33X4ZIiHhtmNNbNX7vLhlaAJLSUVroPzJyNhmOimkU4o3GKOnl1DmR1935MRuL6umLYepQRSBVSlCTuPyCtCDExWIyjwLlLOVzy57JBKQ4qQMkISTD0c3r6LeHgfhURnisFBP3oqG1ivM3QJlTKY3CHnhu3FxOWjJ9SVZ3IK8sThvQXu5Qds2w0CyWrcEGj2OtyLnLfsm5TPXqfMa5rU8C8ufpcpDMz1AkSiCTuMMNRmzjZtGFLPQi4ZhcAhiD5BnhN8BKmQIockCQKElMRCMqhA70bawvEH3R/Q+r0i1EoucNNE7zvmZs53jv4mx8W1nwAf/3E2TAhJTImPf+YiUulAvs5ZtQm3iww2MhcZ37n2N1BHM4KO3CmeYUgDj+1jlnrJB+2P2PX3yRSc5gVfm7/N4/yK2Q6qh44HciIZzaHVzI9XdDc8s3zBaXaD++5DhjhyO7sNJO4PH1GrmuvFTR729+l9x43qFrWZffIOfrD7S/7txZ8whpE6m9POHVYE0tgzNgpfO8gzUjSILuylObVC+4S92uKLCes0eaeIWYtIkoIlQwbaRWgGki5hIQFFRiBXl2S6Y34IdSzYhYDSmswnmqYnaQf5nqg/Sg+15gr4b5vfp3eRualZ+ICa9lm4+XIFCHb9I5zcoUWN9BGZEqXf16Smecksy5h1P2Q37hW2alOz1Rkw4aaE8HMikqgkSVlSzEnK4F3EZAWh1kQViWNC2kOUqRC5pYwTO7HHf4voEcIghUCEiFCaJNQelxolJq0QNsM/iowXW6Y7K/TJdfLlgiJPGN+jhCQ3BSr2qOgxMkedjhS+ILUT+bsPiZu/whaehVkhT9/gUu7VqNbXS/DXQDoWXpFf3KZ3u73L7kbDU8MtaRVRanrdIzLBw7Hktx//M9rUM1MVC1nQuS0xJZZ6RnITnWsodcXXT77FjfIOPjqudWva2LA96FlVR5xWN36mmTI9/fPxuHpj/TUOs2PGOHCjur0nmz8lyc9jwzw8Roaeg8KzNRnCDUgc2ZABNRHQKpHE/kGVBNWOCJ0hQ0L0FiE1ItsHjdpFhFEgFErnmKwnZXaf3fUjbixI+Yz+yUQ+eMjzvSynEAidECqSMoGWJS6CmALKgxf7jH4SAvmUpydi3CvJqP2UEYHXsjdYni6JBKrilN8d7xN8i1clWs2J3Y6kJVkSuKwg2YReLOD+O6TMQxQoqeFjN3UtyEeHyiNaJTIl0E6g5xXyKpBZmDKISuA3HXKwBL0lv3XK2h1z9fAHmDInGyq8LkjhHOEEmVXEp/KxqovIvkfgES5RxJpGyf00GALuUYNdJ4iCMDmmQ0cqM9AgK4+QCVPlqEc7gssILiG02pNhi4LgAvlBzvayg5gwhUHLiUQgGYnMBO1uwCuJPpgzdi1d2+Any5mF3VeeZ/3anb108l/XCb9kPv9C/uiTAwJE4tu/9CrXTw8Zx4ln7p7iXeSD++dUmeb973/EH/zZO4w+cP3Ogs1Wcvbd+zgJi7du8ChGQjsSAVnsxSCs8wQpCB4CCSlytpvbDC6gbc1bB6/x2p2KxjccmSP+mfxDssVexn15YunrHi8sVXK46S7xTDNphyscQ9oxeMi8Z4wRHzW+sKgAwxaG4KgXGaYukJcOrSXzekGHoTeaRz+6otIaZzKiKXEmo7MKWVX0VmDPJ5qHO7JVTbKJ5TOnnH/3Id4nQuOQSZPlOfiRJDKKTBGjp5QFeyqrQOuK6CdCgExnmMrDqmTY9oQ6MTusGdWECoH1M6dcrQOOCd/0KOtI3UBMGjMIIhExzzHVDHMwIzUToppRmgPi44cwKqQpiIMkKYFzCSEXBCHgKflcaYl0AaMV8zxjZx3ERGY0WiSkYA+Xkoox7lEXIkF5KZichBAoZcCjmdj7UBAtLu1hZ0RHSgqi2KuMO4+UAiEVxIm8LrnaTmS1QRPx3uFjRMwEyXuMVsTk6EZLSArvwDlJUhV9OyLtiCoGtpst+aJEy8RkB7wfmc1K6koxur1RYZlHsmrDOp/QyXFy+znufetFVKapheHXv/4bPDi/T1XU3Di6+Zl5++flV3waIfGFTP6/R/sFBRc/5VX8zNHPl5QsvuQhftL1zx753Ov5PALrZ3xN1w5OuXZw+snt51+/yfOv3+Sf/8s/ZPrQkRaK2fVj+iEhWsvGWjbfP8eqBRe7SHtxwe5JQx/2TzjPC1RMWG8QQ2KIho1z0Fh2jacqa652HrHUvLNJ9JMAXfCgH5gLT48hOM8PHnhGpxBBMkjB1dlepraT8NH7ARszus4TAaM1uyliz3rOrvaygqONuCkQpoEhKcxqxp++P+BSIiqDfmZElYGwjLTNhF41rNKALQJWDKTbC55fv4oQ8E/P/jEPxg9pfcPSLElEtuGKTOZ4F5BK0cQtC3XIFOHCXSGRNGnEIGloSSmSJFy6C7TMGIeRPBl2cYfsJZfZOV1oEQjmcUYeNDu35Ti/xnvdjzguTvjyUfHjGtcH/Tt0oaFxDUIIzrrH9HR7wuHYYHzGpCy2SDwqLvnVxdc+eYicgrVe45PjD/rfY2vP8dExZCtC6vjGjdfxeoO6prk9K1FlDi/tS6EfwwAB7mR397efHnhx/vInr/jm7PYXh1GCd5sf8qD/iM63lCxppsAFG5RPPAkfYTaKvrSkaUDKQFtNZMLzffUuJpi9/CsJdZjTCI+Mgt59iOgjfe1QhWSTNbRPP98ubtFFQStbxOR4IhN9PkECq3pUnmhiT7JPOK8HOuFJk6ftOoSu2bYdh9mK3Pc4vyOlSBgnpFRMlaexV1x89JAgPZSGGAJSCnq3RZoZFycNY5gYN1t85nBZSZdPUGb8VdqRgmASAa4tiS6wUyMRxdUykbTB6ohQS6QvaIoMb+C8mKFFRq8VUmlEEjR1yTRZrsoM7TxdkSFSJBlNWxisjzRVgXKeYWOJl48w10raWmMk7HxPJhJbAEYm0XOROdSBIiewuFJMuwuudE4XLrkUBQBt9Jgg2MW9q7xfCppQgY+8V3jS4Oi8IUp45BuGMSJyg433KfwFjWxZZ0t09NinDu0rUWNiYmc3rLI1HzTv8qs3foOUwNsd9fqA68VnM8afGS0fT73ic/d/6rYUktuzu18YXUnAe92PaO05g+8JOmOnWxrlUQTOQ0E+KcZMcS7l3i23UGRasMklmfX0QhBziSwMu0JjfMKezMmTojN7AqswkaZKiJjojiqMLOgyTdyOxMMZQ5lDTOwKhZSSpgI5q9h4xSANaMWDUmBaS1sYkg9sZoaxUCTA6hyJpSslKsHZac2bs2cAwR+7C1oEO2kAwUXo6KPDykhcF5hFQRs9KoMPVpZJRIIRCHWBkTs63ZO05lx9QJSaMQvIsEHHSCcj4aDk3NwnGcEkPMaMqFrQ+QDTBY/dOXKlGIrE+YHC+cTuwjMJyWW9o8iO2A4DzCVSC3YpkBlBox0qKfosoYTmUjt2IqIFbI+3ZG6iqyIhrZiEZTN5jDHgKkIXabxEK0M7SboJtFK0j0ZCgFEKwnZCjI4uCERMYEGmwFXvELViCJbJe3SV02aK7/7+v+PtO4fkB/OfwL18ujh/yUbnp3Ivnt4ppeS5e9eJYQ8HBHh9eQeAP/g336O1E8Mw8eGjhknUpOUClyL/+v1zwkzQAUkLvI9snCdLiUsfMcBAQqiEUpIRhR8S/+7BY3792W9xPb/OB+kBm7DjSu2Q1xLfk+corRlTx/nGcJVaNikxkvbQLefocoU2ksEJ2skhCsGDRpLLhI2S7eToHvUEtXeX/tFmIJ9rrroRPUQu9N5Az7qEU2EPzXQBl2dc/NVD+tGRu0gTFaJ9wG4MGBtodcUQILaBWktUJugdmCj4d2cTk0u4lNBXAZ9ydkMkFJJNKslcYNCa4WjicWhxtSXPct65cUUSe+jT1J4jxX5urqqSCx6irWDII+frgChadjl4Yfnji78ibjx9BcK2eG049w4j4X604BQXzmJ6i84zWiHQQvA950kxMci9HHJIiVHuswO9UmghGIRAW0mYwA6JTGnOtEF4GAIE7/n/MfefX7dk13kv9lux0k5vPLkDuoEORCLQIEBS1JVkWfa9w0Metj963A/+85yuRFISJQZREqlgUaQkBoAAGo2Op895004VV/SHfTqfRiB4hz3HOGfvqlpVtd+qteZac85nPtMWBV0e6fcT2yxRBKKsGJPjravIEAQxRVxtYD/RJ8HV3nMJ+KwhCh61ByOj9wfWw73KjD4jheTdxy2ZzKafcGXket+jdGZ9ucEtZ6SYmFLgZrtn9D2VEXTesfNbZmJCzAMiSKbjSHn0kdOxqWZ88cFLnzciPjasxM9uMIiPDbq/BT/9//pUtD9P7P1vcOmn7s1Pa/V0PNonW/5sT7QqC+qqpO9HFsuGLCMxK5SWeEA4T973FMlRW3VgaZCK6B06Rfw44bYDprDMjcBLQVNYpHOIlDARZBaUyZOUwhQKGT1WlcwLSbKg0oEDoLCW6EcIAVMohn5A64xJCdF7ZucLJg8lAe9GisIcsJwuwDThpowTjmreMKsKdn3A34zkmw4WgVk21F5TqxKJp5nNObp960PYTiVratXgk6eWDRHPGApqMcNLj1YGl0aKQZNyotE1hS2RQlAKy5gccz1nShOzYoHKiiJpmlwxMmIHTY6ZqqjQUlOIgkZUjHGk0hWlqg/v7qkG5OHLAftYUasKK+0B3iQ7RIIoIkVlqWNDSFCZhlLXH17q41VUJOpAF6rnjGFAJcny+BRlNerB2ZNx/DkdTPzNMI2lqqj1B8+3JshAFQfMlEApqqompRvm8xPi0JGVoVQVQmSKIHHaM1dLvJso0BhxKEink8SNW2pRMqWJyhRoZbDzGusV/djSTIZBOCpRIKTCJoEdM71RzMyS0UGtFdI2WFmjh4IujlTeoIKg0DNCjhSyplAVkwssq2OmZsQPEz45ROsp6xnDk/eS1YQ1FfbEYjuDHxWddDSpwORDEaROReyQ0dIyhEAdFTFrpBO0MVP5hALGDFU6cNPrcSRUlmqYkNoy+UATM8EqjAt4JSldIMYD9WPtI2iBmjzBKMq2JwwtallQNiVqZmkqzSgEc6EQSGYYDIJClcyKGW7pOC5PybMFQRVoKbFJUSWNH1pm+8gQEhhDDBPSRWwQ9DHTSMs+DpT7QB4zQgWaxjBaReUMyIyRNZGIxVBLwxh6Kn2gnf1gUMi6QJafA0XhY45fPjzlc+Dv4lMq9INwO1S6otEzUo40tiTImlpMzIyhdyVmkowuULtEFODlYdGDktgs8VmgB4/IgoKMjRmrFTXgY6YZAoFI5QU6ZIiZ2byiv9pjNwO5KBAhQTxECZRLDIWk8hHvA4XVyJSgc9QTjDZRjwFXKqoxkZSiyByMmghVlsxWHyQyZkoUlVBYJDOhGJHkPiDHiM2CMkGXoXaZPgqM0Ewyo6OiEoYhCWa5RpcFae/BCoqosDHhnWM5XyLXHaYsac1EMSrMomIQjiZUsNmgkHgfqWYakwylV5RBE4OkyRmnC2ofiA5KIaiiPBQ/8xmHoEHho8RHKALkYGimyDRMzAuLlBoXAyY6RKnwU8QjWS007T5SqIyxB7YhP41EJZhbwb4fWMxKpBTk/UBZCQqjKGJG+YS2BxbDalFTlBZlzUed7GP96BOWbf4kMuEpPfGzxz5uCGv1Ued+Mg/UdcF8dshXqkuDloZmlqhJTM4zucAEVNLiRMICtZBElTECYkyUUqBEJvlEYyWlTwdveYaa8kBTKioKrZlcRxEtk3TUU2LSlmUNdUiMzlFZg0uZBYeoSFISA5hCUaGZOk8jBLY8zJEpZdLkWN6r2O83WHGgQ5VaQACZElYd8gBmhWLImabQqJQptCT2IyormlITUqacWbb7ESkyOgQIAqszSWZU8khrSdGxqOe4DKVw9BwSm0t96L9N0nhbc3p+i0EGshD4tqeYFDqCm1XMXEksJdIFRKOYFTPiOFI6SR0kXI3oJ1Trs2zp2kCVJHU85EgVpSVqiQ6HivExZ3TODCFQCghSUYbIBJRGIQWUpUWPjqgUtco0tWUIEUmGFKi1xvlIZTIxBmojcc6hhKZWma1zWHsoHFgq0KWmUAmREk5rGiuYfMIoQQyZHANNIQk5UymBi4dPlKSuC1SKdJNDkzFVcWCd8hGVMrOmIkjByaJhbFuMhkJFVBKsTlaMdCyaBc1sxs8iPxX+9OnB8/Ht/KQ09ac9S39D+Vugon0aaOlThz4jT4s//M3/GJE/uNdnb/gxtlrgI1jMzyxPrv36j97jn/zWv+e3//l/ZHl8wtqveOxO8facV778Fbac8t6F5tauZ/f4gPEMQ+CXTg0RgfOB5xeReA671YQ7zzy3cvCcxZ0l7i8HZJ5QOqB04Etlj5EalQSvnGt0DoSUsHXBl+Yjsra4FHjxpODWndugVlCu+OYDTcwSKRVfebbBugGkJGvJl49HRufxIfCF25b7L8yR54bRBO7Ktwj3/pzVr/2YZ+62fGHpWIh3mcX3+NXwLGKRUCea+fkx27zhn17/L/yr9e9wu7zLIHtG3TMvFpxyl42fWI89X919lWFQDKNlnk95UXwV745ww4LXrr6G2xS4foXtT/jC9ll8Lomy4bXiV4m1wZUCayue88+yjT1bJl5Sr9DqwLoJdCXosuL/tfsX/L/3/5wfTT/mP+z+iH9687/wH3Z/zFvDm/yL63/Gv7j+LUpb4UxiKDzeJr66fI123NPFgS/d/jocL9nMYV9llrNT/tXuX/LPt/+MH44/5L+0f8pv3fwWf7T/I+7Pnme0gVEHFs0Z74j3+c3Nb/Fvun/De+49fnf7L/mt9W/yvf67/Pf+v/Fb69/kX+//gHend/n9ze/y2ze/yV91f8lfdH/Bb69/i9/f/j7vTu/xr9e/z29f/yZ/0f453+3/it9e/xa/t/s9zpf32R3D/pZksTrj+eIB+gAO4tvDV4lakKyhyXOeic/hhcLFxDfHr4GRZJGoUsGL6kXyXMNRwa8/+7+luHOEWNZUxYyX7StEEZnGga+sX0AKjdCGar7iK9NL5JjJMfGV7iW0tWSlMELz9fDqIYTtPF+TX8QUh9oV4+R4JX+JTgwM1vPi8mUwDa01DMbw9dWvkGcVuWl4+e43KCaN3w3EEPl29SuIKaGi4JdOvswzd57hyGia4PmNdxYI9xjjH/PCJDlz55jZF5DihG+/PierBwjzIvfkLW65EhE0YHnt7WtoFLKRnPmJO7st0jhQI9/84dvkeQWlYTFM3F+3CK2IUvDaGxdIe8AAz/vEc+/1+FYyPBx45Xe+z/4vrxne9ei3HC8/rpDtGXI451vVtxmqb7Cf/T1E9RVe9s+Q821SusW37TMIeQrlA5pbX+BbJ18g5RMiJ7xW3qO+9QBV3SbtDV98KxNSg3QVL75zgu9OaccHTPkuL7Rf5HqbWA+KO/kFnCjYKMVeCV5YvvKRE9iaD1TYU7We4Kdp3s9r8dG+Ly5eJSZPTonbuuHFsmSZ3qMOD/n7VUNejJijkRM1cX83Qj4wEn3tcUfUgaw8R8Fz/6on5QOF5DeuO2KacNJRhsDzDyeyr0ix5BubTI4gAlQu8uLjHUmClPDLPxoPrEYGTE68chnRUaIDfP3xgIwH7hQlJK+8eU1WGSECX3pjTXHzfdT1n6LdG5yJnn/96A/4/Ue/RzmtUUKBkOQkeE00xODJRF6YBKWLUChCP/LLP4YkIAvJ8/uzQ00dJLGy/Ib4OkkMCDFxv51x3NaoPiJD5n84/fuk0zneKs6uLMvHlqFPTFLxG3yTvFqQFwvO1An34jEpRkIM/N1wm9FO5NmBKvV+X5KQROBblwIRBxj2zC/XPL/Xh0giiV95eE4cIA2Kwgde0pZcR5Kc+PWXK6QSuBTIceKVB4ckXyEEv3xXYZQihUypDV+/Vx9Y40Liqw9mKC0QOWALxTeePz9w80+e8ONHGJ7ArD4z/398DXDoqTl90kn46VXGZ3pkFh/7Bzll/st/+wH/j3/y7/id3/9Tnnv2Hns/Zx9WLE2J3Y20G8f1e3u+2ZSkrULdGE728JxXzPaasld8U6tD3ofInBaWB7M91b2HcP4er4pIGj0IOBPHnOdjckqknHjt/dtkOUDjWJSOb71wxOKXJ4oXN7xaeWxTkpSgrixfyiCUICrBl+YCZzxxpRAV3CsLBhq8nPHNZ84OTkqlKSrLF2qBD5kkJC8f1VTzitwUxFLz5bOGICxRlPzS7QVVYQlZkDJ8cRZxQ0Yqyyv3F4c6CrpBm4rXnp1RNAuMqrh/rBB2YLQjzOCl5hL14g+RL3+PB8vEcW0RD2r8UvAbxTdI00jqB+5dV5ztTvHrgmmr+ZWHz5NKwAqO388s/xLG60z/eOLbb5/h6wYfDfVV4pk3bhH/5Bbq4Yv875rnkI8z6Q3PndbyjNFEdXDg/pIPICQ+JCopeU4JFIKc4NXRE2Mip4SViVtxIKcD8cyXjiPMPPkkIOeBO+yJOWKM5qt3NMYksnaYIvOFpqeoDD4Fnq0mmlohmCBNfOfZEuc7kpx4+a6lqg0xJoQQfP3+nKIsSRnuNBqZRkSe0CrzysmMvu2oreROVfD8C6fMq0waW75665QHyyW//LUv8n/8P/9PfOurv8yLD17khede5Jdf+cZP1NVCiE85Lz/yBH3ArJo/LNnw8XHz0edhyhA/IdHp55NfmIq27drPP/iJ+DmfRS19JsHic2MRn2z+6dYfNsifvcwHu3J+UoX2sOOpXuQPDZBP7ttuO/7pb/973nr7McZoBrmA6pjHVz3nxxXtzrO97phu9tTzmqbUPNxMnM4VvQ/stwM5JsJRorytuUqJeUr4lLBVQcwg1oGj1jKpkrmMjPtDQTihFHEa0CKzGTL3zirWu4lyVTPsJ06WDbjITZ+xbkAUBUhBu5s4mhuaRcGjG8dqoQhDwirJbgzMliBmkfUUMOOE+OIbrJ6fEHNBNUIROwbbcjQ/JTcKFSVuCStzRBCRTdwwUzNC7rFCsQk3rOQp3RDYxD21qMhZU6aam7jl1JwzTppWJ4wXZBepdMm17DhTC5zesMstTTNDhoGmtFzLDau1ZSoPFXSFy6gJCqe5KVtuFbeYdMSJgFCKWdKscsGVv+RUnzKmEZ89mYwRBVYVXPoLTvUZXW5x40BIntIsMXLOFRtOxRHSOCQJlx21qLHCch1uOFZH9HlPzol+almUx1hTc+0uWZljXBqRGfrUs1BLtNDchBuWaolPDo2iTR1LtUQIySZumKs5IXoMln3csdQrkshs05aZbBgqgSpKNnnLaV6Sh4Ht/gLTSxwZrUs2as+pOCHkiCsOTFQmJeb1nJu85kSf4oSnTz1GWCSCipLreM2xOqFPLUPsEQGMk1Si5jpes/JLRt8ypQlVFCgpKIXhRm841bfon0yIyXlkL7Gp4qoeOB4bXLxG2UhuDGVeIIeSa91xpo8RfkSRccnTyIpCKK67C+auIlQHSMPQ7w80qkXNJm1ZqCX7vCaJxH57Te0ewPxXWM9mzPeOiRoxZobaMh88KMFGCObdhBOJkkxXG5rdAEaxLzWz0ROiwQTJvrasupGAYF8YypwPnvQpsikNi3YgKEFXWMzkkAKKmFlXltW2I1rNOK+wRqGMplKCtTWcxkQ3TkxWw+TRMVFME/u759wuDb2AMSayD8jhsJC+jJHVusWljilMZCnQbqSQgfVScYLGi/dBDUQSZUjY7NmUPXeO7/HNo6/wG8ffOqivJ5OqUPITORRP061Pg0d9ePzjLD+faJD5Nw//JW9sf8De71jZFQnYhy21rLmejgnjkk2eqK8T3s9otcKGTFYJExNdoznuMx7NYDVlyKjCUPjIplCcDolU1gxlgXUBvaxRFxt2dcGy93gtiKVFhkiWa1Rasz63HI8GwilelGgJuhuxQ2C9KFnuR6INBCPIAuzmDZrtD9k2I6dn90hnFSknYo7o5nnU8mWucuQIxSgkw1vX+BBojheIy579WcPscs9OPQZ5YI2qpaNa9DweH3JqjhiHPdIHeuVYjTX1XrAzI6e3HrBfRpKA65tHLPuSPGQ2VWA2amJZUM4WbPXEiT5iuu5Yuy1FL9Fnp5gdXNMzv5GwzeyjO0Qxpp5SKDbCsRoF7viUrtKUUUDtsHJkUzuWuwXxR3fZXx2gT0wleg+P2sRcRnxQZFWQnEOKSNVItlGz0p7W7RCN4WDPeYo4cdM5bh3XiNgSpwFpNXOf+L/+41/jxX/0zafPvR+DRn2ilq58+kLnQ4frU+Z6gDfeesTv/eGf8fZ7F6yWM9bjgixrbi5bxNUaNS+43DvKFJCLGQpYd56ZTRSNYkhQKOibiJjBenScLALV8+/jmj11tnxV3uf/Uv4dzl77Ejdpw2/5P+Dt9JASy/R4i91HNkeB2WOJP32GTgr8VcvVdwX+3RpnDc/VNVfvXUM++Jw1GuFhlwVFP6JiScrqkFdAYtEYLqfAUsHNpoMIySqa2lLUkkvnOdaS2ApilOAzhZE459l5wUkp6UaLd5CUpjFQaMFAgUkj2RiICZ8Es5VGNInrKaKHnuW3H6LPN+Qq03jN8qVb7JaOpa9w4w7hI7u4Z35Tgj7lZtwy7yXpPNDcqlnvLllcGcJk2ZaZpgdn51Qnd7huN1R/OZL/9JSWU44fHLO/eIwaW646x/zIsD4K9IVExoDzAZUynVKsgCkdCg/KlNFKIUNgl2HuIvpakCeJtRpZJUwR2SFYSshbTfCH3DEtwCjBpk+sKsnoBUoZRh+x0lOryOXgOa4PtS+SEuQIs9qSyezHxEwkJhnJMRISLGcaMe6ZgFVdME09ikRIiVlpuPfiKZt9i+gD94+P+cqDB7z6P3yZ+Z3jzyx4Pxf4/TmIiPwktPxhNCMfxtbPhqA4LNj/f0pF+xPl5zKAPt/Gedpl8setlZ9ynyfmxEdnfOrhfmhw8JRZlcy+HXDOs912SCkJVYUbBm6uWvZvX+LGdCjJLgVOTOxDYucjYhT40TGkJ0mEEnof6Z4UbhJSsPaenGHmMirA2I+opmCYAmHwVI3CCs0QAk5IrvYeYSyPLnqUNZi9RybBFAQ5ahgzw+TJxrDuPEMWeBTrTQApSXt3SOqSkSwiLTCrS8pjRWjCAcaiBF47wkLQ2ZEYE6YscCkioyKJTBsP1LKJAY1gP21ICIIu2eeeIU5o2TCkyD730F6Tc8MuZ1QSaKDtR3o9IeKIPMlsc0c/jJQxMGRBZwekKqAo2YmOhKeOhlFpejly1V0QhaAz45M325C1pU89GzYkEl3sQEAtZ/S5p4s9Stzgw0SbW7LMxFyQfaAVPSpnbAhE5ckyg4Qhj/SxQyKYco/zAyE6VLT0eaJjQIQtIR/qmXg8CnWgwUyHOjAheWQWjHlEoUAI2tgScySlhMqKMfVIoUBAm1pC9oxZIfNEm3uMh7TZsPVrTFawaFAmMJLYTx34xG7s0FLTmIKYE33u0WlLBrZxe6gunDRdEOz9lhQHgors4hZpNbWYMbmRofQU80TKJb2bSK6lGgW+sXS5h+ECWS9ow4gsDQUVfdfShhEtE0o59qIlDzBTEnSmCz06gO4nMPngbVaZicwgHbKxuGFPSJ5sBVJaxmlD63dkE+hnDq8i00qAr0mlppeQa8PUBoQ2TDEicgKXGWtLrgzJgNeSMSdkqVFa4ZqCXWnIlMgx0ymJ9IEsJF1d4FJChswkFEOhUSGSJHSVQRqF8YEpJgZr0LMKpGQvJNIniq6jTYmussRuIktoC4PIkWoMtCnTX2xIkyc9OYaSLHLCKclYWTqzwG0mhpxIIVLGzCgifcjI7Ei5Z1I7IpnGRepa0KeR6/UFa3lNmkeklrhdj5qVGCV/okPqp7qYPvB+AeLDOjIH6XzL1q8PUMEnuOfO7/HK01fHhKag7xxqVeFdSZ8ghERMHmMVU23oK03yil7LA+QgZYZa02qJygKrJZ2RTGWFmTy6qRgLfaiIrqAvFNIqVD5w//fVgUFJpUwoFCIkKqVwc81oFXJuETkzNIeE5XkfiIVn0p6u8BBgjAMZKEnEONHnjBSJEAV7GUmVwpQaZ6AnkQwMhcSVB4rdHHumvGfQExvZEVRPVhFvMnYcSTnRp4nttKbNkmAl7kTRR08UglaNxEWFXGq69Q1dHEhTRwqZtoxMMwOxp6hLeh9RMhxollXGCRAx4UJg0AemOISjM5JRZLT1aJvobUSkSI6ebTJILbFtIOxgiIrZasa0HhmHSM6S2cIwPXlHuwlGlxj8gDaayg8EnYlI1uuOMu5JtSKNjoVQVA/OPrdu46en8w/gep/X5sPu+nFYx8e+7/YdXT8ciuMB68kwdp6rd6+Za4FQiskYMoppc6gzE4TEZMBKhgRuivQmUuqSYBKd2KNNItQJLyIxJ1I7klNiT4fLjt0TunIxTwdCkjSR6oYYBjYygXUoPSOWliwkrfOoquCmG1FCUokDJewYM8JalJMMQ0bnRFMcKkv3KUPOOCHZTw6DQNjI6BJTzKy9h1ESsyZOkdIDUjHFxCQMQVlGJQGJTgHvYDdOGBGpFiXTEAkpkwtPNwx0SBaFppMTtpiQhaI+m9HPInvX4vctYikQytMOI7KyZCY6CTF7RBWYwpZOTchKEoOjk5FQK9LCMviOm3bLIs9I2tJuAtNba3zXkbOj9Yfk685HNsk/0WUSpQ7PQklBlpLhybtvpCABowAVoUbhkmCcMlUj6EOik4IcBbXWjBNEH6gLdaDOzuDyIem76wJKSbRWXHY9DkkfM0FKpgikTB49SEnrIkFmMpGUD/S9egjInGjHiRACKnuq2tCPHiUSm03LmDyzZYU9qvnir77M7NbqM/lGh/XrB47xD/zoT8Wvfua8j3aIzxl/nzewfjH5xY2Lj0ckfpI8DQn1iYv8fHLQI08JhzzFk/EJCNlPsNo+WWwErm+2rNctJ8cLFosZi9MzrFYcnxzxwx/2iHXPSZFRS8NFfzj/qIbee+bGcGtmiHpi5xRSS+K0RZTVQdlm0N6zzoKYE/OckSGi65I87VhmCFWDMRN3lhU3W0dnCmoCx7XkUZbIxrDAU6mSvIvMF4azRcFNn9nuR44aiwsJ6WBZG/Kwh/uHaNNJXpEaRzcbEL3g1rDE9JBM4my+Qs0dl/KGhoqVOebGXdMbz5k4BXUIrza55Fg9w8X+XdLQc26WiNkJMKMpCo5CzfW4J4yZ2/UJplzxSG4wY+YoL9iGDetpw1lYYmYztPaoSXFmloxujcyZc06woeaxWiNC4JY+Ye87hN9y5BaU2fB4ukYgOB0aVANTWbBkTmPmPJZXJAG3OaENPZOMLKc5Jq64FgUxem4VpzhtSOMjZqPmdKrYmB3RwK3lKUkLgsis1Iom3+ZCXTNJxy13xNQHwhwWLDmi4f3+IYNynMlTkotMeGY0HIslN3qLxHJub5PJeAWNLzhuK250S7aCM3mG0IqQBI2seDafcDHekKeBZatR1xWpcZRUnEznbPMIBM7iCjVmlIJCFZzFY/qhJQjPsaxh6yAKFJKlmCOKA661TjVSS5a5QjpJkyqGOCGz5NhX6KwoCoWcGY5NQ+s2hBQ5Ghoat2I97xHRcCRP6KtI6B9xlGpWesEVN8QcOY1zgiyZ4kCVDLftCeu8JVnFLXNGzB6nYKlWLKv7XI2PcTjOy9soFMvQUqkaUUjatGcSI2Uq2A+QimvmuaR6P7KpLUOpuLU9sLxoFajHyGI3sV1V2FXD2ZDIbiJ7qHNmlSPbusHkxNHoUYNDpUSRBaftyFZrpCg4mzzZeXTOaBc52bZ0TXmg7931aDJ60aCd42TX01UFUkqOtnuKnLlYzNAxcrLZ05cF2lpO2wnjHJezEiEEZ/uBwSr8rGA1OAqVuCos0kjqq45JRFISHCdFJUseyQEEnIqKQkFKksaV3O2XvL17h2QFd+UxWqtD5PYpk9FH67EnQfGf4C3jyaT2aZX/YPYcrd8zxp6ZmhEHx9w2FLbmbnGXnVxwUs5YHBf4seThxVuItWPWafqFYpcCSy8oouZicBRITrY93apGHdesxpGFh+vskXHibAi0IiGagqNdjyFzIzIywrKL7EooVg2LYaQZMrvgkJNntR0PCdzyCRWtn1gLS06J43ZOGC2qUhzPzqiLGTf+mpQTR7KgVw3B9RzrAttNvLdx5EXJLS/Z9R4qwdxlzgbJeuHp/cg5K0SeyGXFijnNlWVdtkw2chaXFD6C2jPrFXflc1yHLX20LF3GjZCNYBZKTncVl5NDFiW384o4eHTpKEbJ7Nqw04GsBeeiRHpQcsI6xck0Y+s2SKk43g6IMKBsjfVw5Gr6VY8SmSMC2gvMSURXBccorvonRcBiT7MQ9CiUFFRpYoyZboqsZlCcVGynA/Pbka7wJMJ2ZFUUrJKhNQrXjjz/jRe4/eK9T3aqn5BU8bS++rR+OYwDj68umDUzjpfHXFxeMLqJu7eOmM8b5oslR4uKu7NT/vu/f4t5AWeVoGgM7+4iZSG4vZK0k2boE2cmUefE+0Mi+YmZ8MRjRZCZ87TiJI+00dMkw71dyWD2vN2/zbI4YiHmHIklJZYTs+CSd6G75nQsYW+Y3wKRBKYouC4slznh1i23VQlNSZw850qwGxM4yfFccnJ2xI9fXyNi4rTQZCmIwnJUgQ8OmQTV3DILHh8lwlqWIqNSokUz5cRCJlRjYR05UgI9S6yFJvjESoCQCs9ElTwrsWd/HtGzAnsTaBrPOBupQ8FxV5NEwJ4vuN/cwclEaDuOqiXzK3i0fQxFwx0WyOMHiPYx1X7itjrl0eN3kHrG6U6T9xUxKI6ePee0mPHOD65J7ZLTmUYoxftixPQDizlcD6Ckwo6OUgpSF6hLw6xSdGPAuEyjI0YJ9llgpORIQpcEZkosJCwbxXXvMUZxag+ONRFgVQiamBDnC/pdx8lMs133eAELITieK9ZW4p3nfK7ZJmhDYlkZiiTZuglhFHNrGHoHOrIoNVYZXE6MU2JpNVWludlnmqJgpkpmy5rNrmUxq1gsS0RjaeqSr339FY6fPfvsGvVj0KZPyseifE9d137GQvmccfepdr8Qlukj+VuKXHwuYOlnk6fhnj6ddPLUe34MMPYL3P7jcKkPzv/RGw/5t3/85/SDYzGr6fURvfRMQmIvE9dvtWRZs8+R0mcGLxEiY7JAZU12gjAIjlczrt7bkYfEshHsfAQOdIezomDjA8lFtM24W4JeBoyA80FxPXiiTkibUbOMEpFqZpGDp6gLun7i9IvHXL3dIpU+0L1lhwuSalaxnMNm2xJToNuNnL7yLvnFgDFQ7R9hxw6rPTNb8Zp+kaZ6HvviCffP7vNvt3/AzdgjVUktV7yfLpjciHMjvnWMRUtyIyemwYuIXMzRYgHtOXkCryx1POPxxqOMQokTinlE5AFRa+ZdZlOOMATIkdICOiGsYEnJkAVoSXaZtPW4csAUJeYiEotAIiKNZJZLbqwi+oCeNK2a6LPjpt8jMdzkDcIqZq7mym/ZFz0yaO6IM3yloDToqaTf3JCNJ0eN8Q2ehNv3uJsbuluKvW6RQlCkE4YVOCRpPifajq7viO1ELe+yrxKTgs4nUkrsCaQw0OwLbpotAyOr1RkxJHaxx0+OujVcqw2D9VSxQCvJzqzxxtPsFW1xjbOOsNWgFHFREVRJzZLruCc6DylidE3ICRkCZQftWUVyE74VHHclndJINM+Nt7krbrGbjdwzd5jlGW/a99BliXWWfzf8O6YYUEFQBkWcesSspimXjEWkjI6inNO0hr3KpDgy84leJXShcPsAXcVYKpIQiFjh9YhQkZQcYcy0TaC/uGZxNCMuNZ0SaJU4kRUpCZLP1KbhO/Nf5TpeM9cLbpd3eNO9yZhHTuQ5v/XwD/H7R+z6zFn5LGuzQNUWM4zYrGnLBpU9TfBcTQVhP0GWCFESsbjJYS82uNNEnpVoxCEBVSuSj5TTxM2sJFtFNJLCHdRO1pIyZXZPaD5RAjMGEIJsDJWPtBWHiJTSFNMBmodSVFnQakOWkiTEIbFZKFLOlD4xVAVKWZJ3VOsJThqYV8zVgpAkZIkbA3OlkDNFNIIiVIja4DcdY1Z8L77L/uH3yBLuL+/xf5j9b1BKfxae+nFNKn5KKuAHHprPrPkyXz7+BqvimN533KkeMG06rs01pSy5p+/xttuxJ3BHV/zR9j+zPXoMsaPZl2zFkpQkKiridUGoLDJ5ysGzLx1+25KGeNDRlSUDlfMHxqcEQknK5BFKAJEmWPp0BG4OqUIPh5oXCSi9w1eHiGI2AdNOZAxYjUGRpEDMK9CSUpUkn0kkrFB0LiGkAW2wbUvWErWsYduRywmnI5OaWNLyeHqfLBMqOkT0qMogBcxGzbo6UFsW9Yw47Akl9K7nQWvZh0DMiZU95nq9BqPJQmJdyahHSCPF0Yok9sTYk5RmZUs2pocc0VajVyV5jCQyZa+5UXuEUagQUf1ImnpyuaAeE1sVQUNOA8UXnvxW65mVR9w8KtAZmlqhisxueyho1lSCfhOJMZGSRPSO4BIAxUl5iMiLgDCG02efob9co5IgtCMXf/J97vzqKwj5FMPhYxDpz0UsfwqosGv3/OF/+kO2+y1lUTKvFmw22wNcrV4yhQqXLL0zHEmBKTRWQLGwxEGhnURmydIKnCnwRcKYQ+Q5krF1zem9wDt2JOeMlBndtSTdMputcHLPfz75IenyDRozx58eqJYjkUpVxFKCM8Q+cHr9CLE0mKZgday4uDk4I2WjGKJA1XPamx2yB7O36CBoqobj6piHKhJ9RG4OkWzvBG4hqSuFLgzZZuSUkfkwX0aRmTUlV9uIbioalZlCiciRyQnKmWMIHl0XKBnIUiOiQkqLv/UePG/IpWEZAoT32BeBxknuHB9zeb8mzwSJiH+8gYXE54B6RxKVIWWQsxOM1kBGnDRMPxzoGo2zELcVfPce3FowdYb00ONvjoghEWNCjQ4vBZP3zGLGJcE0RWxMrEaNlwXGC05dJnaJGBJ1DDQnBR6BSJHlKMgd+ClxVBrKKFmjyAGaoBjWB/atpBK60QzO4b1n2g5MvSdLy+Act+YlV62jmdckt6fQmT4+cfAUmcH3xCyYmQJdK6KKKAJVcmx7h5CSWVmxmtsD4U8KvHp+xu1nb/POOxd86cX7nL18h14mVssZz9y//RnD4jPD5AN46md86h851z9jaHzuWONvzZB4mvzCxsXH/5D8sf8/1uIp+/625KPAz2fwlz+PPCVx7Hvff5t337viZtOyPD6hE5FHlyOpG/nrHShRso0anzLRJby0ECM/XkNda8asuFgPbKNgEJqQIzdSEAZHZxUxZW4mT7CGkOGhCCgRCVXBzGje2HuICZng9fVAjJlUK5SLXPYS13piFrzxdo+VBdebgVkBF+uENAYfPImClAz7ccSe1HTPScTJlmQSWkX05FF2QJaC4TjxD175ewij+eHwffapZZd3xBR5f/qvpOjZj1uijrjgWMcdM1WzzWvqpqZVPXnY4AfJzeixInDVfh8lNG2YIL0HuWU7byltya7cHGj4mkinI+v4iK0dUFHQuy02ZLZ6QFcGX3fsGJF5ol/sUVmxKx06d1xPV/RyQJSCt0qBlIZ17klScZVb9mpECOgJCAlrO5KzZJv2TJMDofHZI6RnF3c4N7G2G5KKpCow6jVZWW5ocQIe6zWhj3iVGPcdAsE675gpy3+tfkRWklE64uDABdb1hJM1V4sbZM70YiTv3wRgXQ40QnO52KKypJUDoJBSsNE9NZnL6hqdFS0jVIdF1IYBOyluuKK0Ffti4PH+AqRha/pDgb5yRG0treyRAqYy0bsBkQXrWcevvfgNZqujQxYscJpfJmf4o+t/g99CP/RoobgqHNu8J2839L5FlwV70aGrgv1ioostCMEb6Qa3T7R06NWS7968x5g9QkAwj1EC9nZEGsX349s4En4Z+P7jv8LsCtoTQSoz3XiJ8BM+B7Z+ixOOV+avHhbuZF4sXwTgv4/fp5952ril9Jnvnit0KuiCR8wlRmj2ZSZm+O6zK0Q0tEoiQyYryX5W4aTir15o0D7SKYUoNRHBvioodOC7d08wGXaFOej8QrMrLTpEfvjgDB0jbWWRKXEzr9nXBSplfvDMOcoF+qZkDVzJQx6HSpnRGAiRzih0abhpCton1aV/ZA40qHuroS7YNIbeSpAKd1QgpogrFfu450ZscaInaY1PN8xTwy4PiK7nv5ktyUaSBtkbHo2X3KvvHCKznxO5/enB589vIYXkmdkXPlSg+XzJoj+maEqyC7xQnYOSvNm9Q5u27LlEVZH1y3PipGjdANEilg07qTAB/vKsxAC9FpRNQV/WDEh0hu8fUHZ0tUES2RhDV2tIksHW4BydsUgtaFcGrw7sQf5OgybQlxzoiO/OGCsFSpLmW6xIDNaxbq+4VpdM0pFzZnI9uQp0UqJi4B3pcHOLqjXT2BJUZmc8sU5cFjdM3QZfCIT0aBFobYApcXmvQ2jNmEfedxdQe3a6J4jEX3R/icEwxJH3Kk17GtlMHUFErhaPSH1mLCJF3RKNY9cNuGT48/mGUtXs957HoUcIz9ZGCi35HhN6KGm1I8012WR2DOgo2J0GbBXZV4FcC9bG0aIQfuT6rwfEWNM5xeU2IucFN7sBYxRRlAeIoh/YRck6KdoQEYC77Kkrw64LMEz03Q1eHihD33n7iu/94Z+z+uI96vPVT+1tH5fPy7l8++HbXK+veO/xQ2b1DDe+RY4wuQljbrNvl1yvB0KAtx8+JArBbgyEIJG65sZnZsD33welPF2UCKFQtWJQmSzh+35CqHyAKxY7bqoJu8qMqeWN5cTcHNG1LfV8yc7Djdlj0dy4DVJGdjOPcomx3MOgMbLmXbWkXzS0XWC2qHjnxjG0HYHMATg1SAABAABJREFU6ztYTZIxKh5fjFxeX9OOEikUD6dDAng7eqRMPE6BOJdIIXBZHajdXQQh2IZMHw5JvoKSQlc46bjetTzykVBKJIGoJUPbMuoSaTXDMxWcD3gmbBwpGVHNSFWuePu8g5Oa3m0IfkIdGzapxe873l8CwTDKiPQ3qP3AOrQMg+C9VUAJyViBwCLPl9ysNV038O5FRDvJfoSoMl7AzidEgs1NYnXcsG97ggDnJF0KkDJ7d0B6DFNClZLJCboUMUry1s6hJwgJWgGXnaebQArBm9cOmSWDiyhzqJrt4x6pDjCnsqgYfcZqyetXI4OHvesotceIRB8j2gl+2La45DHlAbWiMXTjiBaZbQoIJQgpcrnf03tFILKYN9xkx2/cO+OlV57h9IXb2Hl9YPz6mNfmY3b2h1ufVNsfbQiRfzqk9fMG1KcH1acH2i+4bP9fqUL3z3bkQ/kbwLs+eVXxEWj4b8mOKQtLXRW03UhTGcYuMV2sUTljVE1RaLo+UxeSkKGuLSpnwjhigidOgdlcM409OE+hBEoduL9FBJsTorRMKVMWhroukC5w5RzBe44WcyY3IiQHKrkcGFJEJpiVNZ1zpCTJ3lEfVUgSMkUkHJKlm5owjtSVpqktseuRDtIukotEky3LZcPQ1Bw1J8yXZ0hjgEwhSqy0FKKgUjUxBFJSTLlDe4Wt5gQydSoRJlElyyQcejwU6LFaUnlByBrbeXyZmSuFmyJWQ60KBIIiG/o8UHiD0IKKjOWg9KqY6QkUnUAuLVUKaKEwlaJMBb0IzNWMPkVsCGilMQGsMGitmMeSPk/MRUFKCRsERS7o0kglapL0h6iJNsgIZbB01nJ6dErIDgRMccKKAm0rujzRhJJQBKLzDG7EJokShnIxZyZKehEgQLZQUCCiwgoofUEkY5QmKkExKbLR2OCovcGrjE4Kh6fRNSlHClFQx4KQBYWw+OCodUMyUKRAI2ti31N6yVBpGjMjKYnzHhUURpfYTuJqS21mqL6lqmcYVVAfnVKulh8aFh9AEARQ6pLaNOxzzcweI/RAwh5wpUPCdhFhD6xmeaGo7KGYmsoaLSQ7v8cOibqqoR8ODBpG0RQl+7GnnjVIGzDOM0lNc7ZCXHXs9xN6CBgNVteMcURlSaHKTwz6LA7wnkoUFNJS1TPm4WBsGwu+sJQuoT0URlM6iEM4UO+ajPGBnDV69NQZ4ugxgDfqEHaPGecDjY9EDtGE0SjK0R940Y2myCBjpHCBoTAUPpGkoPARGyIiJqwP9CFSTgFvFJVKqJQwMRyob5OlcgGnFaUQSDImJCofGApLHQ+47jwdGGlUiuiQ0AHmSdIKCU4grGa+mjNTlm1ZU2dLUo6cPCFm8hjQk4AygxI/O4wVPjG5/eRG+RObAkHRlB+8MlJMaCUpVYGWmlKXVMuCdrLESTNow7KuCN7iXUaGw/VKYMqZImaEP7DwaB9QQlDFhI+ZOiSCltgpIAEVEtZFJp+oMvjRg86HY/lJFfBSUY4BX2isP9xLZ0URJB5FU85xwiGzIsaAyaCVoSNj2wmzH9GVJfuEDhk5BlSlqRxkF1Be42YWPQhKBP3OoUOBiBrhJdlqbDJoqRmlp4oGFRSVPSSRV8KSVw3ldUfZSaTL6GxIPlJ4hSgb9jeX1EnipoAxCZMVNZoUBKUyVEkQk6MUBVMKlC4QlKbwB5pVmTTFmBgs1KoiRUmsSnT0RANGZkYjsDqRYqBQGZE8oU8oIrZU1JWkD1BKiVQSqwQyOESIzOcWhUNLSXQelTwzpSBEPiQG+GxnO/SZpxAPPE0KW2BNgdGaqiwRyXMYSZnCaJySWKMwo8c97hDGoiQYkYjThFEWWwh8ShQ5E4TAxki/HphcRqqEXAQafXAuFMlQCI11kvlqhU2KWtUHKm9RMYlEiaOIGrfdUaWCHknpNVaXxJipVYMrNPJkRZs3nGVNmQou9yPT5BESSgWtj+gUGdo9tmgQAqwW6OxRSqBioDQH+mBSxiqJjYlCSQqR8AnqQuFDZHlrhgmKm+uRptIMBowVhBipqhIrJEpYah0IUlHYmt3YIaPgeLbALQuOZqdk60HUYGGmGvzFFlVGqlSj64J044gSTJ+Q44DMgZKaTMb4BIVkeWuFu5aodqDwHqkVBZJ+CBSVRiLRwVHXFj8FDJH5vKCIEeE8koTVEuRBnWkJs8oS7QFKrJ4UxiwURBRlziQloFDYQmOCAw06CGormVwiBRA5UljDclawWw/IFFAZyuLgmNBCoCWQE3VtSKZAjhklJPhI1ZRc7yJ1ZfAIjFH4lNA5UpWK9d5R1wVf/NZL3P21l1CF+aSj52Nff5KKzk/GzkfnfirS97QTf57Uhc8BA/1N5G+Bivbj8gv8op8XyvSxk34uatnPubkA3nzzbX73d/+QP/y3f8Qz945JSRyqQjeWcxcJTqOqBd/6Qo1pShBgnePlVUYkxdA6Xm4GTGEQWTBvSr5yVpCiBSpejZnKSKwU6Jx5wU0sjhrq2vLLi4q7t445OVlgC80zpcMdw7hKPLuILO4q5H2Qt+C15xzq61vUN2945WsRdfd9mn+4I37pgm99uWf16+/Bq3/BL/1a4OSVxzS//D1mr77Ny+uaL8o7fDHc4u/c/3V+5eW/xxdPX+GZ+Rf4wtGX+MPdH/EvNr9Hn0YqaYiix+eW35j/BikHVGU55ZS70zEqeQSBb1y/yrTZwbbjTrS8OL+HKiaoHN9Zz4j5MUE+plivub9egFTklPl2/yo5JESE2WB4ZXwGOXgYA9/evgLZIIKmVktevrgDUZB84uvvPEAOhzwStUl8fXiFJAw+S16LX8UUDUJZVNJ8x3+ZrBQJwTenL1FES/Ygxsh34lfIjcGLwFfsS1TLBb4ArzLfnr/G1ICfSX5p9iqr5ghdGkSMfOfd5yAFZAi8eHPMzDWM2xHnE79+/SrBR6bOc3Y14zgsyVISo+c7rz/AdxNpjNzZrTi9qmE45Ab8nYuXSEYgrOHcr3imu4VoFXlU/N3hNdxYkKY5x+0JD3a3yaEkOMmvX32FmCSZggVHPNfeIVcWOS/4TvglaBRJZ2zSvPTM1/HHlmkluTt/lv+y/xN+5/pf8F/3f8Y749v87s2/4vfXv8eJPUMGifGKKhZ8rfg61kkKWfJ37/5DXj79Ki/293nu4oRfevs+8aKHjeeb8hVm8xlmZlAy853ru8znMKszr+xvoaZDVeS06/nmo7uEsUXowC+5O9y+e4d6bskq8sp7D7jeZ/ZiRm1v8fp4xf99+8f8q/2f8dBf8Ae7P+Kfb36fFD3LZJm5RFMV/MawIuuS7BW3tpmTdSD0kVRYfr0NiDqhrON8v+fufgAN0U18680LEAKZBcet4zl3mDASgm+8/ohkFCImlpuW599fI0IkhcA3X394gDXkxNx7Xnx0g5CCLAWv/eghSkq0FBTO89L7N4dkBQHfePMxKj/BXvvAK29dIHNGJPjajx+h06FitPKBr75zA1IjleYrb20pvCLJmiRrvvbwGP/uKfHhbV7ev0BTN2ijUaXlm/4lYl8R25Izd8J3f/Df+M13/yV/fPMnjHH6ubXsT23ylLD7B9SI0mqUNWQEt8pzXl28xEvzF3hh8Tz/+PbXWTSXHNXv8eydwJdPV6j5BKbj1beukRqEiJi25bl31wc9LwVfe+saEMSYMUPgxUdbkJBT5Mt/fYHJChUkZjvy8ttbhDjkiL30w2tkCMgUUSHyxR/eIGtLjpEX3l/wbH/MF5df4guLF/nG+d/HL17GL1/li+V9KlUgM6Trli+/3iK0RqB44V3PbDegc0TEyLd+cIqsXsAWX+K59XMst7fI7gEi3+bbbz5HDJCT4VZ3wjLPCRKciPzy5rkP82Luq3Pu21OqZYE9LvkH+RVyZYhCUb+bufWuJI8RUubXXl8SWo8SBcep5tmwgCyJMfOr7TEJAQkWY+L564CQAlmWvHZxRtYZcmCe4IVNQRpbUhz5zu2C7BNiSpiUeL52aBdZGMu3v2CxVpCjw623vNokNIrYeV5ZSmxl0YuaZBXPL0uCd5iF5dlX7iEK/fkzdeYzCIJP7QLg6mbHP//dP+Gf/LP/iJ8MyS/ZrVfsNw3f/PKvsdsWtLsZz9y7y+nR8lBY8WLDbzw7R9cVyhheuDfjmbMKqSWmKviNrxTQZCg9t5aZ+ycRdeTJM8+r456peIvZvceslOd511CXBqkFry2+hS8ToYa5nfOifQ6tBTkGvrN56QClipky1zzT32cQisFq/t6zX+D0+DHPPfc+z97f8yvzitImirnmK88WuHuZ8IWIfSbz/HJCHgnEHG6bG1yckBZm85IvH5WookRoy6uNpbI1MWiik7x6LLHnNeVxwSsPDCcP5uRZQi8Vr30hoV/dYb+255kHHccvX3H0628zf/URX+smiv5NTuJ7vOxmLM/uMJ0esdeaX5evkURCZLj7I8lJX2CsRuTMd344J2ZASG7tLedjgZKRxMSv/OAcuf4SvPFFVm8XHL/nSZeJtIG/s4Rhd6gxodzIkXRIISALXpk7xmEgi0iRIqduIneB2Hq+VCVs7LBxz61a8M2ziqPYY3Y3vGQ99TSxdCNnIvDyKRTsKE3HC1VPIQf0eIX2W752t6QqwdjMi/OIH0cECS0zXz3RpODIwfN8JahMwopAHge+fPfoUA18VvB3/84voUTEGLBW8Y17Z+TowTueP1ry7NERD06OmAvDN7/+pSeGxc+gfj8cCYc1bv6grsLH9v+Mp3/+9ufJ0/T6zym/MBVt94SKNn9g9nwi5PJzQKJ+Ho/aB7cRn9JGH//8WS7zMXrazXbH7/7uv+bhw0cUhWWaCoSccXW9Y1E1fPcve7pUklSmKCvmdcGja8ctm2n7TFD24DPJgapStEFTuhYvD1jEZl7hiy2+2nBBZJYSU8qIwlDVJbPSEnYDe6s5UpJ2csSU0aVhoQWNzWwULDOouyPUgaBA7AMyJPyppu4EOl+jtSdXgiZo5kqzlXuaseC5/hbfSq9w69deoTpdPZl0IwLJ727/gNfHN+hix1yWpLxnHS6ZsWAYJoxt2FcTKz9DxcB1f0k5GnQlKLRlmzYc6zsMrNiEkSoa+ovHyKljb0eOOCacVLh5xkZN7B1F1mxMx3xq8MKRy4MHTgpFScGV3HKWlgzKMZURMSW0g0o3XMRLztIRY5UYpEcjMdlQq4r3wwXLXUFcasYwkJynyAWNXfBIbFjtNBxpIp6gMpUoqUXJY645lyc47UAKpjgyUzNsMjz2FxyNDanw5H5giAPFVCLUjMdly7k5xomIcJF9HpiPFhMyN83AKjYEmVBCsR/XHMUGOavYmo6lmBGCx5QFWzOwutQIr9mXgbmsmVxGJcuanuWoYCXpipE6F+QcsVqzZseZmxGZaEtP4RTSGoqouRZbzjhGF+CUw2IxSdLEkht/zbE9xWV3oJtFYYOiDiU30zXH5QkjI1OeDoue+gH/+zv/GOkzuzcf8jvt7/CefETOCWVLTNVwXXacimOm7RXRT+RKYcSM0Csu05rjvCAUjugmXAkLKhpbcyXXrNqSlhlelAyuZ65ryvmMazVwrOdo9lgSQxpYiobCK9ZuzULP2dkvMe5m9CLTXHVoodg1mmYIpEWJzpmdEazWHj9ZNoVhNgViktgk2MxKTmImhcxeCeoQCSlSGsW6tCy3HVFIhtJQTuFAXzo61vOC4/2IV5KhMKgQ0RnKGFk3FUfbDmcUg1EYKQ75Ui5yM685bgdGpQhaQs7YlDHTxHo1Y7nr8UbhlSQLgfUePTluFjWrXc/2x5e4boJZSXXec/ziwGVac8KMrs9kBy56Zq5nsdS09cit28/w1eUr/PrRax8pQfGBLnyy+Qkv2M85u/yEqeTj3uiYExLBf7z5t3x39xesxysW8Zy1f4ZtkugpMTyeMKlgWyvOJoG2C4K2SBcgRqosWDcFq21LnEnGSqN8wPhMLTU3q4bjq5ZRCrx54n1ME2Uc2R5VLG96QmUQ945wlzvuXE/8/XcC9/7nvw+l4Z9N7/FW7AgpUWZNbWZcuZHyrx8zSgFHM2JpkO8/IrsNm9slyytHmJVQGkYraCYPXcu28hybmmn4MTnuGBuYxQJjJOuyZ7YW6KuBxerscKxa4CrJOm2pR8O+TcRk2Awblq7ARM+2mJgHTcwNpjlmHTqWW00Ohr2Ih+KA40ThPGu/Yblp8ZWlX80pqiOYjRgzsJk5bqUVg5vT7XqssfD6Gfa/N7xz47l1XuL6kX3raBpL1qAbyeU+cD5XbMcWlxI5ZYzOzGvN5c3AeaUwaUMIAylEnjs/4n/+v/2PHD04PTjmPoO9+FQexsfzg5585pz5f/7TP+b1H7/PODqapkKpgsvrHcfLhqHvsaWm7yeapiaLkkePd3CxQVRHjP2BbW2lNeg51yMUJjPlkbIQOFvQmIBaRtbOo7yn+toOfbohNolbueJYjky6p4oWebagKBs2ccNRccKwSOxkh9pG4hBQa89N0XIyzvFjYCqhXi6Za8vCK9b+hqW8zY/ePuf9d0aGTUdQAuEjnZIHCubHFdMosMZgXMYKxc2QeXBec8OWoBNKKaqgEC5z02dyt8Oc1uiZBQSi9dx57h5vvrNmkQP2tT2tXVOsKio82q2JR5lqJyjiDqMyYqnRco6rltxUjqNiSTYT2krWmyuqm0x9MufKXbHYSiZfQCxodeSIguQnduXIYlS4976ESc9zebmnbifMaLh+3FHmxBgSpEzrBY2OJBHpEiyWBUPfMysVN2NkWUC/2+NTPkR55ciiyoxScDarcNNIsgrfDkivKYOldZFFpensgZGwmJWMXY/2jr0LLJcNzpUkaQk5HarTu8h6SqxK+WGl8sJaTB6waqAPiVoKRKlwk0MAx7ePsVpy3Q2cr2a013u89zjvefHZO/yf/tG3mM8qpNUcPTg95Bx9XPk+Rc1+MmgsPoxYfDggnkSIf6p82kh4WtYCn398Pvv/Gyrawx+eUkJK+Yl9P5N8joHx8VyODx7oR8RcT2mfPx9b/HnS7lumybHb7VFKEuKCmBK7bYfzmikKrnqPNorSe8YehiC59AEhLZ2XKClYNAUTmf0QGAKEHAn6kHcwf1YxGkOImVEIogKvFP3k8TEjlGLnArIw+JyZpECkRBLQkfHWYAQYGfFyIkrBYmXxo6dPDtNYIBHyCFKgw6GozFQ6ipVFLAvuvfR17Kx68pzzgfoU2MU967BmTBM5j6Tcsg9b+m5LbhqkzYx5QuWEiuFQWKcERGBiZMgDG9HjomGXR0Zl8CcgBs1QVdSzhhA9a79DJ4FRmiEKdnkALUg5MEmHlAcmnN6PdPSY0hBFZD1tERkaXbHLI52ZEGlP9onWTgglaWJF6zpaOZCqhJCavujJOjGbJEPe0OsRURtEHOj0CEKwzIlejrS5R2VFnByjmEgKQgjILNjTkbIjDwNJR4IMNMYSjGOQnhv2h6JTOjPJgLIGkSKt8uQ0EkREJHA6IfsRNQ3s1UTEHygtbaR1e4RXaDNjFwemOBFtBS6wjwd8fR49gw20acRoUFNkmIOhJ4vE3o6IEDBOY6NkZ0ZUANsHxjqglGYeK5wY6FKHCoqMYB9bBIK5r3B+oPctxEzWiTZ3CCk5T7cZ4sCyXKFeOEFvj+j7R4TOoVwkjT17JoTJqHlmCAcvuQ2KWBsm59hMO1IhCEeZMIwIl+mGjr52UAk6b3ACpuRJU8fad+yNw8UthekpTCZYgZQwRuhiRyaxnwmmhWXoJ3KhUFrTVoaoJMlKpPcMSiIKTUiCrrKEuiAOERMEg5SYeIBs7I1h1ApJYkwH2kJRWYTRtMbQm4CJEW0VvX1ChyokbWkOSf+TZwS6wiDnFQHom4Pnu5KKwUT60qAFRCHozcGjW08TaElnDaIpyWQ6q0lKMZ/kk0Wrpi0tg1Fscya3IydHLdfDnlb1SCPJpmBIgSwiar8lTdCLgHj8Ltvi7kFzpkMU4CMl+jNNVX9jER8gVwUoIcnANmzZhDU9PUlM9CbQJkMcJ6gUWhrCzLLfZ8q6ZsgSURgKF3ApMxiFnpVQZvpaQ9Y0QyIqzagku8aShKAvDDklmhjxsmAoJGJRoOqCSUEoFSdKMN6aowtLmwNTjtykQ85FQjElz34YmAxEq0mrErftsOZAdduZTJoJaCShlMRCkuIEjaAvFXkcyEeQRo+3oJWlH/e0eSDVBlt6/PYRSVdEKwlRsqfHW8u+FrjeszcBLQSkQGs9QXiSrSlq2O8cQkMOsCfSqYTSgSIFuhgQlSRZwb4EZQO6mDCloy8Dl+6QzL2tMiJPqLVDxzleWa5uJnIITF4SB4FuBGmCbkxcOIdcWNoDroR5IdnnzJBg5yLzQuL8YZ5WdUGal0TnnxgXH/W7j2Wlftbm+Ngk732k7Uaurrf4EIkJcnbstj3dxYYsEsWywvtAzIppdOx2A9InJjfgvWCKoJsC4WFKkugzk1TELJj6CAuQSFoOcD5ZJ/Is4cuEE4FuGhlyy1QcEt5N9Ae68WzwWbDNOzIOckbVgl4HdB4hZXrhaKdAGguy1PSxw7uWjmN2VhJm9gCBrAuGEFgrhRUCLyxt76mzpNCKMSXWY2QoBVsX0DpTDREd9aF6vLLELIg+I8gon3n4/pYJxV5FSpXZFZFSB/Ad2jjGoQdTos8s0kSmrsOUDe5U0YuMzCNJ9fjtniFOiHnFxJ7OTOSVZeoi2QdGPDImhA301YEwYDSK/PaezaYnuIwcMtsxsxUgsz7kVrkAGapZwdA64j4Qs8D3AS81224kK0WfIirBXEnG4OkmB4MDETFnc3zO6D6gdQFJMKaMz7CbPMIf4H0+ZbwUuCxwGQYXmXyg1JmUBFOWtEEQU8ahGKZwgLvpQ80iryQqSyYf0EYxvnOBdx4vBNO2R8oDfHeaHJcXG17/q7f59j/4KrNbK4T8FFjo08ioTyRc5M9t+zeWnwXlymdv/TeRvwXj4mNJ1U9+kFTyo32f+vbTfv3nBTDEZ97Cx677gW7Kn3/dp/9yweaqo932zI8WzGdzVs3ZAZunS/Z7ICTOT2rCxXhgMKgV95494vrhDg3MBUjn0eLAQHBeGFRVILWgmDQpTuQ7CXJEbgea2wce8BMhmEJgnxJIycp5AoIJqEbHMif2UhBd4u58Rsg7ruOWk+Ut7t95wF5e0e/3NK1GZkubPXVSNHKFsBVCK+ZnM4QK7HXLsjziS0df45LIuN3yYDEj5cw7245lYXlg7/Fw14KbOF8U+PGG9lKzNJZj5mz6jp2UHPslyjmizSzKJSfFgq3fQThEGaZ8Qi62NLJmaW+zn/ds6TiLDdO+R9gDTGcVa3ylsKLnFjOUlFykjkJZFtngrUCGHadjhTQCHSsEguNU4HPiKuw5ciVFVXAx7tAxc6ZWjG4iZc+5OEIPsNaKGCOLm4wvNHJZcTzVlIXhxrcEBUepgpBhrjjJc2phuArXjMlxRxyRZCZZODYzGi/Z6p5JOM7GJZMoyVmwdDVzaraipVWO+a5AZkGuEkexYZYbWtuzix23WZI3W3JKHFUrFuuCXTFhCjhNBjU2YDKzasHJ/B7vP36ESo5b6gx04NptUE5yPjthUAPr3ZbToUJbhXQW6wRH0TIagXAdp7GhnhKXbo9OkuPRIs8XeK051idoqZFxgxSSc7UgpIlg4aQ4RWvNeromx8RSL5nrgydjoecs1RHn4oxcH3IsdtsNsl1zrEoqadjXFUnBaXnGkECKxGI0mK1hjyPKkqOxJKfIBXtWcsYtec5N7OllxmwkRgtyGVhcdZzXNf08MSjP+fkp2hwW50s1446ecyEMN5sdx61HyozIiZlLzK9H9qXElIrjnSfLOcpPVFkwl5Y2RYwLnN60SDIi1lQpsRhGWi0RdcVZO0BIyGWNDZH5MJEqi8iC025ChoReNdiYWe5aJq3Ii5rTbYeMkZvQIEJgMXhGpQ5jftNiY2Qzq8g5c9wOOCWQAk73A8oHrhtLQnA6HFhURGM5Gh1HU6SsJVEJzjYlpdIIM+PMNBRRsS4GvHcsW4MOA/mWpbzOnCwKuA2xn5CFQTzx6j8VqvuxgqM/sfjohwr1YEH45LkcHlGqiiN7ws3mEb0aOZ/dpVDFh83vl8/wfv8eOmlOqiM6d4SOG6KILJbHpNmSG5GoH10wz46bnNA+shwCXgEULNsROyS2uUABR6PAyUMF78VuxMTMbm4hw6IdiEUkkznaTNSzGevNSNo75lNidlTy3vAeC7vkSFrOZElMiWNhyWjcdqLpAmU29EOiuxlY7ROjiVBqVh1UfaS73TDGzPFa4l2EVWbZS2ZuwU45hhS4t7iNS1uS37DsJOfFXbqwoR88txZHOGWQIdPIhvv1ERf9BXrYc56XaCm4cFuqUbAKC/zRDKqJ05tM6i2xMNQ+strvmMjkqDjZTEib0HWNTTAPNeFUYojc0gvyrkZljw6wPNcMjyRMgcYeYHqxXqCNYrVUdD6gElQpUC81F493aKWoh0QyGX2kOKpKmuiZrCL6TN72FO3EvhspljPEB2usDyf8j2b+nDMXl2u8D9y5fcLkAo8uNhwdNdy7c8yjy5Zx8tw5n9Ne9Gx9h2odKwtuyBTLBffOl3Rrz+7ta06PG6pixuPLnl4IjsqEd44pS2ZaUJWCzeiQSVP1jnKpUE2JLhR3g6J3E4NJnNoTVtGwaQyVrlipU4YiQtKcixOS0OQpoabIvDf0eEQSnHKEDIKtHNDBcroRFKuCWGnO5AzZrzCmJw+Kem9Yb68xekvhCmzK5NUOIyRVPGPq98iFY6WXzK2gKUZMoTHXJYKIO8+IR4ocE/pOIKtMeDNTEii0ogiJ+LinuB2pysjSrZAp0p4ozha3uT2vuNk/xM0rzub32ZmGjGIVK8r3MldppLCCu+YU7xIZwTIU1K5hPXT0tWQ1VBRzzWZlqDaBxZ0TLt5N5DFy+7zCvTuQZoqikOhppB8Sk4rMi4xJnpnO6JhYzhXdFEjOMVegSok1gkpJjmtLnFq0Etya19SVwc0N+s4xep8xseDmuuP0/pI40zx85wLfjhRKII1gM4zcOp5h7JK33r2BylAmgSlKHu56FkaxPJ5xue9IJFa2Ifo9OSuO65LKaIKV9MPEsrQEH7luB5aFoakLphyQRw0LWdAohamKD9fFn4jKfXJBymfXxx+sr58W1nuaDv589fxzyd/CdX5h4yL/hK2n7/sJDyU/QTp9KozziU3xCXPmk7mE4hMNfupP+fEPHvOf//D7TGNgviiJLEnbAa8kJ7fnXE+PkRKGRzeoeEgVm6aA2D8mV5qyrNHjyPnxMdONJPqASQPXW4fHUpWS5ctrticSYyTne8XFtaXJChkiM6nYSkGMCYvAaYkQghAi8xzZcChYF3fXlC/dYMVAFzes2tuExZ5iBS8uVtx+55xrHGfNjAdyxuXZhDypuFOd8seP/w3juEf4idcfT/zu5vv4lDgtK2KC636g1Jpb1Yz313cY/ESRatx+wUad4euGu7ZkKv4bISiUnpGCY5A92QVOxwU72zMEyxQsdg4xD4zJ82B6wJqeEDJ5gNoXXJmRrDTn5fO8mbakZIlhQSPnJLXGj4ITe593/TVhspDmVKMmqkuMVKz8KY/yNcKWKG+ZTXBZ7Ikx0+wUrQ3oRYlUBSfTipv4ECHhVnPGDTva0KF0xXxb87iaSFrQuBWtGgljZBoz56rivQb66LGU7Kc9wUSG4DjLd3hf9HgEclBIGcFm2jxwr1vwtt0ThaBkhiXT5kzMnqOu4LrYkURCToloa6gjXZi40624akZCyphqhjKGmAJxFjmpS96pe1JypKmjyAW5FPjJMdtXbGpPCJbsK4yb4biAJFmNZ7wzH8hao/QpplFM8V28zxTmNu9dXrGdgZWJhRDcaIfSmiOnaelwT7zkt8Wc9XSNEALdQtj22NUMMswGi2wP3t3z2QkcKbqrPWx6GnObS7c/UDrODM5ssTpSni+4K27x/favQSROz57nZuwPSfIBzols5y2Vypy6GZtNIBOJpUL/eMf6+ZK4LNm+N1LdLumsAJU5N4JHxqGWmXIzEadAxuAlzLvAelaTBOiUELSo2QwGzx1V8kY9R4WAaif06KAwhNGz6gP74xkkED5RA+t00D1nu4GHZYmIAIoyRRKQc2LZOR6dzD4MYzdT4DoDSnM0dFwuZodcBKNpRsf1k0mnmSLjogQh8VKwdIGrRQU5U/cj26YkK01uNEfnN6ybimwU87xgGBwueSZXcOx63g83uKHldOwYRc/kNK2UcOUg5YNh8bTqx5/j3fnpkeCDLnZx4t++93vcjFdoqTmuTrlx17jkWO2P+Hu3/xGlriHDXCxhTKggKaTE1Bdcrd+iOi34QnOXH4UKOYworcj7LWFVkoOj6VuujyukFagiMguJnT38hHo30ZuSkAQRxZEb2CiDkJJ6CmzrJ9N0ZVjNGx4/fh+hM1Pe8Z/m7+Mvv0+la/TRV8hZkUJmVhZsh4nQj0QJq6JkPQyknCjGgC+f6G0JR7GhUzNEN1LuNdEcYB9eSmZbzdUdTSSTrxxITc4HD2rdHLFZDLhtRwqOxWRop4CRjnvzgqtwQT0LVOsdpV5waRLMC+6d3OJ77bsI5RGFIsSXac0hj+NWvmJXXZLFCrEZKf2aXK1IcuQkVDw0kFNCSKhVB/MRQubkOPO20iSVwBjOnzvh7QvHFAJ3Sk03SrIHbQzxvbcojIGUOS1hsInkEyb13Dn3vL/eII3mZDGnPFsw9U/J+flUxOL/81/+iu/94E1SSqyWC9ohs931VJWlmR3R+hIfDVmtuLrYEaojzOwYNY7c7D0qSubesXv/gugzbet57o5l7yemqz1VlShWhm3niQqOasOYjyDAyQzKOtJNHiEEyzHhKo0tQXqJMAanMilM3G9OuG4u8FmTskF3Aj8MJC9YpDPW+TExC1IXKfMRrgDfB4qt5cYMDDPNvCq4+2xHu30fKRQvmSUX22uWw4YjX3LrWzPe2F6gjOYsbOiM4d3rSxpRclrXPBQHpMWdNOPxsGddC06+MmcZNO+kDaowvPTKKfd/dMb6cc/92ys2t3Z8r7kmGcczqztsj24R1IbsAkU0DEtBbmq0aVBRgU90l1ecXgguTgMiOIq6RtOQx8QUNHeuMteniZQDVjQot2JcOxgNz4lj3rm8REwG8dgjcsTljNGK05Xl3XVCm8BsKVFx5OqiRxtJLT0344hSBmNg1li67cTkA7O6YiMNOSeSEKysYr3vqU5mvPDVZ3n/hy3BwbJumJ0awr4lVYbbJzPeHzvoNYXMTJfvI3IgBTgqLOtxQueACJkqR6SYyClzUlZc+YSUAqEld8+WvL3bk0KiiAlbWFoXyFlw76jmnctLunbk2ft3+Mo//CrlUfNEkX6gKvPnxIqfooA/ZUt84EN/qkr+uE3yNF3+aR//T5Bf1L74W4hcfA5m8qee9XkP97PtPvnABFl8joHytPM/rL79gXz07Qd//h4P37xht+5ZnjTsr/f4KJjagTdefwc9lwwh0JmSi0ExZo2I8MNNwtaZth/I2vK990emVGG04b0kiWnkppsIq4muSchbDlEYLqoZ/S6xHj1tCExCMUlFyvBOBmJiNAat4d0smEQiZ8Hj+Y4ZO1w90k2GH5UeMTpC9Fy4wKsn93ntC1/HLmuk0Tx4YgH/9favGGJL6/eILPjzix+zHZYMIXBWVuQsuOgGjsqCv3qUECGx2Tl6GVC15spVLJLmP03fpzQdo5x4Nz4m2nSgShXwp/H7FLJkqyZyXhP3l2zkniIZ1tMeO5XsxICQkTRPbGmxWP7L+DpWrtjgkXnk8TixiSNSSK42r1OgaG1ChJ6sA7vkIAt6+QirFJtpQojMhd2z1xNCwfcWV+iUD7S1beLSbOhkJAn4vn2M9omuCKih4x1zzWgVkcSgLjFIHrs9SMFV/WN60ZNM4If5XbSW3LAnqcyfFT8kRs+AZ9ID2ms2ZmRhGv6seR2fIk5ErAooJJ3sUVryp/IHJA+DDeSFQAvJ2o7UbuK/HneoaOjMiNYZWWh2dMQM/2H4U4SKtLJFxwjWslMTdqH57/EdCmq25gBzwAe2JDSZPysuKXzBOjjI11AHdoVDadiHd9FSsM0BOa55Xzj2xYgYM1Pa0QhNpwIqaLrpktHtIWfW1Y5BTdjU0MU9F/1D9v0h0fYN+SNyYfBzwaQUPwjvMchIlvB6+32kiuznI/m647J5RJoJ/DTyo/guQSh2qUdoxV+kH4BPxEKTjiVTZRhTQirFn3+tJiMZ84jQN+jHA5tm4mh+yp+E91H6lLbJqOeWhMcDu0qQXOYvn2/QwtBquAgHlradjjRzzX8VBps0+xCRdUEuLTtjKFLmz+8cYXKmrUu01ayNZp8SJib+6v4tipxprUG7wE1t2VtDrxS7+8cUCLqqYJ0Sl8vmAJEi832t0SGylxI9K7lqClprkFLwulaolNlVFhkiN03BUFiygDesRcXIvipQo+PibsOgDtDIN0ePVpKxrNl1E9fqikl5XIqIWwlFZhs3kDI/EG/zjes9ojKoJ8X7nihKPq3DxSfj9DzVMfSpSe9h9y5XwwVv7d+g0hVv92+itWE/brg/e463uzf50vwV0uR4/ea7/H+J+9NmW7LzvhP7rTGnPZ/xjnVrQlWhUACIkSAIUhLZsqKjO/zGDr/wN/AH8xDhcIdlWZbUbYpUS2pJBAWQIIkZNdcdzjl7zHlNfrFvzVUA2KJDK2Kfs/damStz78x81jP9/083tjTuwBOh6PAcuKZrJP+hXpJNKjZtQ59JRGlpM4HKMsZCUkhJO7UYLdlrSVMcKTk7ZdGdpM40JlrenEq6QoEQ+DsVIo40hcJOMn6qOur8iBcUix2t7dg3O+b5GV1/TaPmRAlvxJ7YtDSZRAnBz84t3aYmVIZ3jCEpxyFPyGT46aQgJhiV5J3VMXVnn0WCgL+a3iCLQJcchDUowb441oj4K/8jdJK0ect769eZLk9o3A6054fhr/FnkrGu2RSeFPujx9wo/pP4BYnIzjf4yR1aJdiaOaYd+NHFDbNBcrAZ6vYJKUbqScQIz4+KNZmRHHKPGff4qWdrHTIkdm83qN5zcJKgIje/2tMGSXSO5jCSiUQzQOh6+sHhdXcEclcGGzzNdo8dNW/GHVHWmLzAPDujV57lndOPeGjfB/p8eA8Nw8AvfvU2P//l24QQqKo5IWmu1geWs4ptt8MFTbNuGJpIXXt2AqZWsI6GEKC5HugPHcJF2iQYDx3/+vu/ZDIr6VNk52HYdWzaSFVq/qbJKK1i30aEGTF14iASeUr8uNowyQKH1KMY6VaJ2gT0YeAH9qcYmbNLNXSBfrNlZzustvxo+hYcAvvMIXGksGYnPMomfnzWUITEvktImxPjjtrsUUrzS3lNcRJQY4PUGddhi7oYEGKkxiKlprotKfaejX8CqsenxCM6xHmOyFqGPvBIBqIYcSnQ9JrV+R2+eHLC2T9+jX/+9tukpicGz3uZZBQZe7fFdYYb/ZiUHJgMlx7jnWHd3JC7yA/vDggZGJTjbTaI5NmGAe88P7js0EpwECNibPE7z8ZrFssl/+7fvYdbR5oocd1A3zuaqDgceta5hhBoAiQfkMIxKEVIiZ/tPFpKvJCMSvHuTUcbE8l5/uaNmkJ7+pQwwaMZj5S6fc9PthIdcpptjzGS6+1AUzdIKXhzd0zLrbsekVkebXb06ZgC9yudobWlDQklJb/aHBhiAAS/uOqBSBM9ppP85PENh6YjxHSUk+1A7Tza5Pz47XcRIjC4kXrs2TYN07P5h9bAb4WX+HwDQ3wonD+/pffBBOLDwOAn5fZvmuI3nOFvan+PmItPn8rnYiI+QFF8wsAQn29sfQiBSfx6xMVv36zVZIVBHSSu6Xn8xmOmJ0uyQrO9aTBREI1G55JiXlI1gPeE0WOn9kiNagRyUSB7je8GwhjIntarYvBMCosUoIJEJpjOKx4OI1Yp4tPc44BAKwHOE0PA6COvtVJHKjmFxkaFnc+4W5yShxYZNMEkJvqEs7svkE8W7weVP/jBjDRoYdBCYWVGphSl1oQYsUohAqgQMb1jOAzEzuGHkSFB3DpGI6AsUQOUsxwXR3KV40XAyPHoRRcJ3YOMERMkymZoejKRIZSlUBmdClSmYhQ9agQrj0pCHjTbwSP6gYTGPi1mZTKDTZqOltzmeDWSEZEhkXxAoxFRYKPCyyOlLTGhjSFDozMo1YxBBJJNBB/IsgLTg4w7KlsS4Ph7C0mJxihDaQrsaImhxybD6AM2CUIIBONIEUypUENkECPKCYa2pUsjKztFFBXq0DOOHRpNOAzIhcB6RS4zEJIgenInSDGitCQTGVEIrLL0yaGjgiYcQ8BOEGRCB00TEmVQRJ3RyUTmBMlDngQ20xRRMUaJSZI8abTNKFRBHT1lzBhSwowCIzTaKGwQHEIgiwZfQJ5JjLWomw69cwQ/YBcaJQJW2aP3PglsUYGUKK+QQmJVRkrpyPYhc5TQzBYnpDggwsDYNAgvyKKgPjiyUCCSIrYBNZmgm4hKOaYqEXuJiBIjJUMTsEYdmasQTKuKLiV86/EioEZBlhcoPyKuOgQ92TwxCkle5YS5pB4GVO+QGIyMaCnJEtA7jDZkg2P0LWrwR+YY54kxYb0ni5GUEtYFOuPJ2oGgHNJojPPH7x4i2mhsCHjikfbSB1SM2NGjckMWjuwqNiaUP2I1jAtHWtRuJGiJFcfIgA7H/XSmyUIAqYhAjAmdEpkLqJiww4hXEZsgKrA+kCdJ42AymdD0BoJBTmfYvCLPAm26oXATbFGQtESX+dM0po8I318neD+rfQafhpEWJTVaajKZ4WXESItW9iiPpHnKWGSxJiNTGe3T58MLQZYV6CQwOsMkiYxgEYSn8kX7iAHymGhDJBs8IxITLEpL9NPfRxqFGT0hAzUe6zDIEMicpy0kxXxOuztgx0hUEiEMmQXla2xSjOFIAR6lQCdB3PfIBNZaQgDfuuM9EwUpgUZih0CaSsK+P0bJkkJGiUqRIs/pMBih8MOAjRKhDTIMZMlCctgx4bTBZiU6KrQwWJnj8NiqpA8dk+yE7q0tqnFMbk/pokRlOfWhocwzfC+xMZFFMBFsAIWkKJeEzNLrEeuPkTKDQkmwTiKSIosRnSTSSqQAowRlSnRSoGMELSAGitKybXqWp1P6YUbnWkgJMQRyk5jMSs5uL1FGgC2QuUFnFqPMh3hM8TFN6ekdlJBSHgHKuWUcPcZIjDBoJdECMinQUrGvO8YUyK1l65/SyYwBRcQYSQqe3BoaF8mVIiWJcP6De1oZRTWz5CkQpUK4Ed97vPUYD1oJCgE6CFQbsUtLqUu0GMlMhgkgk8Emy751yEcBnRlscpTFhDCA9CMNimwELySZP8pnkxsqnVGP15g2EgpD9vTZUNGRK43WhlwX+NSTPaVuf/9+MMayuHVCH1ps6EgxYnSJKmaM4YaVmzCmgd51hOiZVFPuXDzD+fISMostC6o4YYwOW07QRYZxPZXPGGWLzDPGGLFJwmZApkAuMkYRUWiiFMghIp1HR7Aj6FmJ9B5DRPeBNEbys4LcC8bdAaMn0HiEiWgt0FEghkDoAzIFtMyYGEXf9UjApERu9LGOzeixQiO0YnSevMqwITI1ijA6Mm3otzWkgBYSrSW5sRxkx1i31N3uSEU7K0laInONEFBOS04faB69/hhhNMWkxGhLe+goc0s3jEQi0mgyCUbB0Ebm84q+69EJtNWklDi9taR/9waTBEIpkvdk1lDMK4pZ+ZuNgY/J2/SUAEN8fOzv0H5dgOJTevdvYWj8r2l/z1S0T1vit/wx3veafbj9xyNAH4k6fBbO4rf4Ud6nRDxe3I9v/PLv3AWOVXlD11KoRHPTUdiKf/zffYvJyRQ3OHIRee3eCrynKCx/8NwMkRTG5JS55svPlZhcITW8uuhRSpBpyUxXvHKYE3++Ivxswe9Vl9z7wshzL15xdvqE10zC5AFbBL4gA1Y4MuOQjDznNxSn71FcvMuDYDitMs6qjDwFvlW+hl5O0NOK22fP8Eje8C92f8L/Uv8F7zUH/h+/+CX/l5/8jGFY0nW3eLR+nqvdJf/g9ivEQSJ6zb1oWLaRsBm5fnfLvasDN7uOrnXkvadwMNaR3brj4kcZ9V7i+ykX3OVeew+9W8K25Dvb12BfoOslZ/4Od9v7yOECEc/4bvdV4tU9xHtfoHx8l8uf3Sf+zRcY//YBX3/4EuGvTtB//oDJu3d4Zf0M8i9vI//mNt+6uQ8/mcBfrDA/rnjhVyvCf1oSf3jKd7Yvod46R/30PsXVfb7ZfR3xk5cQP36R1371Murn90j/4TnCX57yxR/dwf3FJfFv7vGl914kY4Xol4ih4uvNfUyRYzPLa5tTqhpyBzYJvrv9AmJMKKd54eqcSZdRpJwsSL780wtEgEqXfKG7w311zgkZWef5nTfvobHo0XBxNedOfAYlb5PMKf9QfA+pzrHhFnfDc5zWl6R6TnQzvnfzKkJKsqS5jKfcdueIpEi55Q/c7yC0IqsqTlnx7ProldTB872bZxGjxAyGeW14/maFDTOknPGd5h7DVSDtc7K24rntBaKZQzvnHy6+hRZLbLekGOa8ur2DOGRwsHzTfhVRnuDHiv17I8/xHN2spF9U3Jo/y0+GH/Ovtv+SH7ufcju/i5AKYQ2vTb/C89ULvFS9zLPFc/xvTv+YV5av8OrZa/zR9A84zc+ZtiV6J/jKm3ePv+8Ar5YvMbM5VjiKSvDd8UtYPFnX8eAdOCunFPOEzB3f2dyisIHKRO48kVRXoGUG1vC19zKG7S9J/RvcCR335hIj3oL4Dl//6RV+3CD9mtPdgVubFjXWBN/wzR+/BfExRj3hZNhwr92gzQZpD3zj7YfozJNlI5Ox4cGTDSYc2Vm+/sZD0ujRIVINjucfb1E+ohB87RcPP1A2y87x8ltXaBdQAb7y9hWGo7GQ+8CX336CTgkZIq8+vCETkYxAIROvvfkYmyK5gK+89YQ8RGyMmAjffDhiZIGRBV9qCqpekAVDcopv1LeQboV0Z7w4PMdMVFhboKqCe+6EP3v0p/zJ9Z/wdvv2UYym+Ns5a36NXH9fsl5Wd5i4GfLGENaCb65+DwFHY0PkPFM9+4Fcfu3069ybPssLi1d4Zf4lvrP6Li9Xr/CFxct893BGGhxWKqZIXnRH7FT0ntde3yG0QEdPrjWv1ApFgQyWV3++RgbI0tHwfuH1a7RwKOF4+edrdNQYUZCZgi/8eI2IAek9L4d7PD99wAvl89wzl3xr+gCtDUpqvuANetejY8JMC1792RoVPCp4nnm9ZdpL8nSsh/PV9waiPxDjnnsPB5aDJisXkCzfuX4GZS7R6RZ3NxecNzk2HR1I33z0DHGaoSYFF8UlK5b4WcZYSX4v/w56iEz0hLvmktvmFroqoNT8o/yrhOsa1SUufeTLpmehfsjM/C2/96RD5Vvy4pqpr3mwT2R2gy33fHt3gUxghGHiDC+tl+Q6xyTN790uyS4gv+vIpi2v3AZdBKqV4uWTkaA9soqEOPI7z5+iiylCl7w8W1BNS7JpQTab8PVvf5chntHWC84W9/nzH7zL//Wf/ZA//Y+/5J131vzTf/lX/A//nx/yq7ee8Fd/+7f8yz/9M37wN3/Ns8/cYwglY6p46YVnyScrHHNu3ul5iYjzCTOpuF0ochewQSKD4psPpjgfUVpz73zKfFaAsois4LsvXpBSRsQy14KVtsghR8sJ33ulRGiJtZILI7l3ryM9eIf04ppvpxW6TCjRs+wMt3YVYz3gM8N3zTfxD2vEw4GZX/BCfwetC1RR8vvuNWyIlD6xHCQvXa1QrUTU8K3xJUIy4DLkBr6YniNhCKPgy9vnSRFAorzgFfkSXia8EXyp/CKyUIiZRJaKr558Fbk0qJXld06+TC4TmXRkheQ7869SWU2lFc+sHnBzsuVPw5/wl833uT+9T8oiIkt8oXjArKjIJ4risuQfnf0DtDXIMXL3l4nF444ydRSx5fffuMQQyYTg3saw3CrUCEkpvhdeIY4RNQruHRQPeBn1y0ua/wDfXUxJfUQnwa1Kc//CkuWSvLJ8867G5AqRRqYmcpE7lOghdfzBi0smOWSiw6SOZ2cak0akdHz1wQnWCqa54mw147UHd5idzcnnJV/77ou0k4InCH75xhX5wXHz8w27N/d888svMlkEzu7A6kLy3/7x1/ji83d49fnb/B/+d9/h4iJnbgZK4/nuSyvOzjpOlzVfuTdjlsH5XLFaGL50UlGVNRfngVduT7lblbx895wvvHiHbz33gC++8hxf+/aX+M4ffo2T1eJTcvLz5OfRcf6JrX5bw0J8+PpA7/3kGE+jJh/a8/9/a//FVLR10/CpM/z1ZtNHjv7xviQ+PfTB2Pt/Pwvv8tE5f923SR9GTQSCf/8//ZS/+c9vs72pOTy8YtwE6sZx/6U7ZPcz5NTx+OGGqih48xc9h0FACqi8YHq+ZIcmCz1STDlsHcIHyspQlYInh8hUjfjckZUGkSInL2y5952ea38DDyO/fPec9UGTSCh3pDHdEJmGSH77EaLsSAYmKO7dOSHOAvMuQyws0ijGNFKqCiM0a79loWa8984ZfT2h856pydBJ8bhpOCsLmkPA1wO7usf4wNh0PBpGployDB4rBL2S5M6TgN5q8hQp7lxTnPbIueKOXWG9ZuNbJiLHe0+mNDs1sKCC0rKlp4ya8PYMbqZs2pFFkvSHRB+gKAw2ldhe8GTdszABPybaKJAi4V1PNZGsR1gmx2gUzeixUmAUVLniOiTOK4O3llErlFEYBIWCJ41jaQWj8LRDhxCSfNVg7+64Mi1nLmOotoTCIatjAbpcGJ6IPcs2p2cHhWCIA9WgSUKxy1tOhopdqNFaMSrPdMyxQ2Q7aananFiVCGF4Z/+Yc3XGJLvkxjUsRIF3HkJiL0dWsiQ4z0Y0zJyBqiGzI9t0YOUqQq7Z2gbbKUSCwmQ05ciyLYkysnM7KlkR/QSrlqxDzWpvCaGisWBRpDaQB8XWOE69ZVDQ6WPRLxEhS5K1cZwli8t7OtEfvT5JYKXmRrbMR0MsGtIkoYuciZAspGYd16zUitD2uKEnCbhb3uMPp/8IbTOqrEIIQeDIvvRm/Trfv/qPPO4fMk9TrofHuDgwqkCuK/Ss4ondcRIX4A7QD7TNjizNkOWUa3PgJDvF6xzRRmrfUrYG3yW2U89STkgcUzqaMnI+PcdgWY87yl2kGyaoOOWQRea9QgTNrpTMRkEQoMfIvpQs9gGvNG2uKMaEUCUGy77QzHYO3xtaY49F3YTAjJ51mbE6NHglaa3BpITygTwlbnLLqu4IVtM+rW0DYJ3ncZVz2XR4a+isBuexMVDFyPUkY7Vt6I0mGEMSAj04dEjcTApOe8egBgYZcbmhDBGz27G2idl+pM8DalnSuZGZrLG8y02+51TOyZLHSEGaKG6Vd/hvTv+YqZ6TAG3UBwvSB36bz/C4fSyT6hPtenfFv/7hv+LhzTuU+QROj9z6280jLvQFf/jKf8/t8t4H28cU8SlghIYEPjoEgn/z7rv8RbdlIyPzg6M+DOxHh/WRaWGYz3LWuWDlNeNgaLuAdAHtArkPbKcZ812LqzzeHMk2rBOYQbB75oQzJPXVO4w6kgTcrxb877/4NcKhIZtN+eduzVuhwyfQ25b4+hXbheXiYsXhl49IKeEVGOfQhWSzsiy9pI09vm4YMknZJ/LVlBvhWAqLn0AcepqhY9Z1iOFdtvORfCfRhUeqSKN6pnuDNQWHiWe1vDxGvLygDnsmesl6s2eTDiyW57hWEN5pWVeJ01BQ3CnYNmv01UBKHj1EdhPPss8gH2jzgTyr8M6i7YpruefsRuEKSycdckyIt84x755zPUSm3tMOhn5IxMEhgExKrnaOZy4r/Nix3R4IPlCKnoXp2Y8jp5MSfb4kWYUbPVk1Q2cVj65rLk6nDHVLcJ6QEst5ZLUc2ew2LOcLntwU9IM+4hs9hFGwGRKma5FViescTArEpsEozcZLJiaCUfi6o4+C2dwi/cjBQSUjAYUcPQcXWUxKfGPZdoKpSQQpMIWlC5LJSY3+zju0y568F8zOYHqase7XrMYSZGSvWubzU4QHcTNyoxtWbkLKPO0CJosVbBr0o5p11nDqlxz2mjbXqD6gMkNe5FwNa5ZjCVli0P7Iohg6JhPBvmw4Haf0zZ5eObRSGFuRl3PWZs+pPsNrh0uOSCSPBj1IrtINKzcjjZEYAz4FSpNjSWzcNUt7xigdMSXGOJAXM9Kk4po1KxZ0rsF3A229pWw1VhrW5sCiL+mtIBlNZwPF2qDEKVfDjtPlBW5o8duaRo+s+tvEd17m4c93lMGTekvYjRycQMWGoCOjlJgUEBqkSdR9ZGYCInUMKVBkhtgPVFKwC4FKScbwNMokEpmK5EQa57mYliwWBVHDWPdsxoLi7gP++i9eZxE9FyHB6BnGEXXRcft3pzjtOT8552tf/B2evfUsKUT+9hdv8ud/8be8/pM3WVQl1YVnt7kheM9sdkb7JDEayXJasb55h6QCRWUpKPj2M1/h7NYZq2dO6duBy1fvQQKt9UeU+k+rqB9L1xd8PnHGZ+38We2zdO7Pw13w9HjiM5K0nnZMq/+KVLSf1O0/6Py7TvKRucQnxj7MHvtwPH3ejy3ex2h8xkl84mS3Nw3bm5p63+ODYnCe0Qkev7VFjYE09QzeE4TBGc1mNxAT5EbQ7R11cKwWJaGN3Ow9SkrIBEOTOHQBSknXOpQ4FtSy45arw4FhMpJdLDB9zugghECmJFEJXPA0wYGJxHKgKDKmswnM4TAcwAZUcjh/FCr+WCaJXajxIXHTV+xqgY8RZyKxD1zXHc3Vnr6Fuhk4jJ48BIzV9FrhnSdpTS+gDxEvJUIKWgFjEoQi4PIREOTdnlwX7NJAGxxCHMPrjTtSFgYn2ZpAkeeMnUUcDF2ClARIyWGEw3ZE7RyyF+y6SJ9LgoAhSIIP5JViuxsZkDh9pIPtojjSfKrAevR0QRB8BBvp4vFaTxSIlDgEwVhKog40KSFlotQDOo8cCKAG1Awa00OIDN5jjGYnWkQe8crRxpokI8EUoCW1bIGR0YYjlSoBYkCIQCt6Uh4ZDQxJMMzARclNu2WLYxg6ovcgFb2OxHYkBE+dOYakEf4GQ8+YBVCRmBTb2JJbAxL6NNCOPYkRgWCXd3R4QoQCy4EeFIikqZUEP1LkhrYbObiRFCPJRw6jgwRFPKbo1SRII9DRlEcAY6UyVBiopYMsIsRAF1pEK0lZgYuBJtXHqsc+0Lma6D0rN2WoeubZ6oMgoUIhBOzGHQe/p/UNyQjGc0MtR3znGbsa3xw4iCOdoM48ngYnBoo4EsuBOnaE8Qo/ZEhl8WUCrfFFookDPkQCDqsFg3PIx45suWRPR18IxukS4RXdUyEgk6TOBM4eC/vZpGlVQkqFUIbaSrreo5LEiKNSkAZIIqO2GSpEdEoorWgzgwo5SR6paIUQ5P1IGxNt+RTTIKAxCp5GK7rM4HLLJkZQgqbKIGVUfU8XPI1RyNWEIBSdkqSUyDkyNjWZRsaIN4Y2AzID40AUOU1wxEnEqcQQelCC6HZks5FOjexNj+0HZHAwKFbZCdvmhul8zkfTKT8qPd9PQ/1McfpJ5xCwb7Z0Q8uh3TO4ASbHNIi63TI/P2M3brld3f/AMpFC8rRCEABamiO+J3r2GpoYCSnSupEmU0grUWcTvEw0MpLqjjhGuqJE6EAhR/pc01oNE4PKoCuP55e1IDPJOC+4fu8Gn0n64vgN/SxjN/ScVRWtgD4FbqI7Gl1dB5WmXxRcdx3eHmtnBAn5GGF+xIOITNG2HrdQBCVgoulzQW8NO5cYhcNrx5AixAHyyEF2hFIS8hGp0rGmTBaQChrh8N0TbIxk8Yg1clrTXWgOu5F+/TY+VqjScJAOnTztek93KlAKYu0wWaTPPHUmEGWknwuG0OFbSOlAYz0y9yQ8dXGkns6TIPUD2/6olPfNwL5LCCkolWKz7WkcPLxpCb6l8wmpNEYJGiFoQ+TResfEGgYpiD6Sj4qI58njPf3VDrev6cZjOqJ41hKD41DvCFGw3Ue2uyOxCe1RBu9bj/YeKRzjGGBoqGKCCM0QGBtHtBLSsbiiaD0iRuox0ntPKjIQij4m7CiQeUlIgjp63BBQo6cNAv1sQmTQZOORcrga8amjsz17H0hK0C5gjGvkkNC5ZlCOg2wQM0s9DbTDE1TfYzJPY0eSOxBMST3TBOkoMoWbRbpeIg49QiZq10JMLJRjcCNN14EYEUWiSTUpQZkih6GnCT2YiETRcExJq1xO7EYO8QBpRA2CIYwkEj4WCDx12BJJRCkY0kAiMSDwcWAfdwQ/MIwdQ98Qc1DzFX0z0DIgtKDLFFGH431cKKJrqW1A2YGu2ZIyjzcRE3O69Z5t7egyzXjTo4SlDwkjDMEP9CkhU0IioPd4JDIGpIy040jvwrFKvA+MPh7peZ2nDw6jFX0aSZWhC4Ft02Fnhv6moW96amXYPtzRuUQeE12IpCGA0CidePOnb5BflBR5wa7ek+UWgH3dsK8bYqHxlaDH08sRkQtGCWlmGdqew9BCJglqpAk9J+enrF4+ZzFdkc9Kls+co5T6uCD9hBr66zo/peqLT7z/TQZG4nOU6Q+Nl/eP83ct2fB3aX9PbFG/waz6rEjG53ynz/+q4oO/6aOr2ecd69ecx/u+uTsPljx8Z43UifKi4hfXv6IqM/zYkW4GxrpDLUpOpxmyl4TWk2WGvNC0wiONZSbHo1FRQfIjWdcQAR005RiZlBGZK6IPLPs588FzmFWcz5bY81vMZgMhRuZhQoqO9/orlvoOGIOf1tjccjpoTB0IesIJMyZ2xj52jDhO9ZKYIiHASs0pJiseD5q67TkZI+NhpBsiUx9h2z594CJLIY4FqZSiRGBDoHUBIQVLKdFCsAUqIVh0FfHQ00eYec0sz4kpkTeJpcnpmkCsPasqIuYlcS3QueLcaJyy7LrI0gR873F1wopElgtEXtCOA5dnUw7bhiHLCZ3nztmEq5ueVmvK4MhKTSOOgNbcCASJdQN5cmRGkWERJBYyEIXC7z1LHyE5MicQMjGvc8JmIPoZJxYKK9mniihhIT1JS2KuWA0FeVayDZpRHD1+yWpQglVz9EzXc8HAyEmTgfNcTySrMKWIcw7a08iMk43Ed4qwOBYVqnrFTjTUWeSstaSkuFKOiddM+yWu3HNQgVO/ILqE1orK5SzUlEYPHETNSVMgtUIUlkrkzPML+kEjPZz2BikrMmmw3lO2kX5woAQnTURoReFHlBBUtsCnAL7nZJTIaYb1Am00C2kYhSDhOHcZWWnY9BYEnDFB+55+7JnojGk1YytbEolFfsFkuuDh+IiFmlGa6oMn7VZ5h+l2Rjf2rPIVIZPs0h5fjpS2oNnvEG7PvM2ZZIZBlwxqYCEWBEqsMMxijokVdT/QpI5TOyXKIxC6GjTWKRo1MBSBkz5DvznC/YLFdEaZ32HvAuvDDatkkUEjhi1lJ5m4kk57RAEnrUSEhJxJsi4wdYpBRuSQWGwjshvRsxHjA2UX8UYhhWW+b9BColyOFYJJ2+OEQKTI6a4BIJsUqJSohpGgjwvPct9hJOyeYgKmzkGKSCFY7TsQknaSERNUuxbvIyRY1T26SGySAg1zr4hJgk9MG4/U0AyRlGkWwwwRtoQ853R1wkxH2nDAJU+lKlaTSx5fXzGbTJhMpx8sSO/ju1N8Gjv/tYvQh6vY6eKCWTnncnWb3BaYqSZOPI2ds6hOuCxuf0xIJzjm64sP30Pifl7yVtMTY2R601DWDltGbICTzJFSIOGY7h3G5uzHHu0Cs27Aa4mIGfPdQGZHDl6SYmTaArMpBxfIHjdoPdA0LUiYnd7F9AOPZc1czlkIzZm0OOexD4+sMPpyRfVwg6pH2iwxiMSijcQyBy2Y147FzlNPJKNOXK5mRBRP1nvOzk6QQ8d+hEPjOBmnIA4EPXKiZxRNpLENrbacuhLjNI+HDZMYWYgJcaHQecaJOqEzGWKSsNuawlzgLgqurt5lGebIfYvRnvnqgumioB0a1qLhUi2QqeNx+5A8GHI34SAtJvWceInsIjcc8WzVNKcvJdiWZWdxQlIsc0iJhRCMecXaCeY2YkSidUdc2qlVSAf9ELmzzJndOmEXBcOuY6YFLsBN36O9oBJQlAXOBYpGokJHaD2ruzMm5YqyTPS9w97U+OmE9KRmao4YyUOncAGqvseUCmJklmmsPjqWAop5FokOUtQsS4OViYPWdFpyMtPoJFFWM8ktjB37TUtuLMXjSO4Slc0pes2qnjI2O4QxnPsF5nzCtd+QHWDSZQwiscs0Z3GKsRU3qUZsB8qdBekg7jhlhspPWWcJEQryViJzix8blp0mKzN2RqCVYRY1Srds5I7L4hL2LXtdIMuMuV0ShORx85D51mCKDG0USQtWqSRZQ3IbTtSMPAq2roFCc5ZNCIzEoWShplgX2bgBr+FkmNL7wOD2LFKBTiUHVeF0YrHN8OtAXJWs5BLNjE27pwkNZ3HCeK0QJxMmTzyLbUYrJUOluJwbto0jTHPy5HF2oPURaRS678lXkt2YmOQWaxL9GGlHuDWdcNjWoBJTLTk/nRJ04Ppqx/1nzmg2Ndt2x6QssKHCFopuiEyM4PJyxUbkzOzIxXRGXy2o391yUmhWzjEaiUSQ6wmHUOO3MH1xxq2zyw+Uznu3z3nzrYcYq5nPJpiy5ex8QUoR4SyCGbt9zWxSIs0JPg3EELh1eYtnX30RrTTKqg+Ng0+KzI8YBp+b3CM+xBN/Luj716jbH903ifQRrfmju/96gyKRnkKi/ssMj78nQPffJQ/q87X/z58lfWz810/wOcf4SErU+21+muFiDaonn09QVhKCRchIqUfa0WFjQgbHrJrw866DFLk7NzwqZsguELqBqQBTlJA0zy4M71zDeN2iypyFjrx5MxwjF3XBZsg5HCKFmXD/fuRwOIbYX5wKHjcbDjePWE477utb/Gj/S0LXU4wn7FVD63vW3cjsqmJ75ogazoacut2wHTqCC9xe3+anj1uGwfHM7TOuUmC7rdn1I+cu4JXCZJbCB1yK+JhIUnGZEr80EkEii4nSavajP9IrjpbHhQGdyKLFuBynjuCs6kfwcFcyphymU9xWEvKcrMq5W5X8+I09XRuYVgoRIu4giEryzB3LG1sPKjIMLcp1DE6TfGK8eoKwOQKwWmNqR5A5wUVunRoeXo+MbWS1ypk72Gx7iiojN4nrHpI/ejnOcsG6FcSYOG/g8OYpXoA3mmIqeFJ4EDCdGOovvEUi0jnN+aHg4awmSYVtJowpQmbxZcX9bslP5LuEIKm6ki0HRqAWnsut4fH8WIhQt8DE4auW1mjudwtuljuEClji0YOUbwm64K67w89XHuRI7ipUn7gWLW0aeW5bcmOfQBmRak7mpnhGhsxwyQU/DTcwghWWwl5ybQJBDNw5dLzJnmgieMXFm3siB3SRcccofnlLIaVAGcmimbDODvhDYOEL3ps6UqkIzlKMOY8mEYHAbkqeFDV7o5GNR7Sam7MclOA8q/hXN/8jTajJZcEfLL/HeXYOCKo0Ib4jiHvBuA3cy25Rhw1EuKgueLNypLAnWrg4nPJG9S5qMmEl7hD2PX17g2l77spL/lJviTKQ1x6/TKgKVKZ49nDKj4ZfQACt53gXaTY7UuF55vSMtXgPMxmZ2gmh7vHc0InE/fZZ3jqZI1VEC7Aerp56kU/e2fOrlSZoiZQDeRAkOyPoyMW65e3VObLw5KOn2EnW6lh46aTpeHgyJwlBlJJZ27OZVcSUONl3PFpMkUiE1Czbjt2kIqXE8mbL9emUaI7P18XuwGFikcuK+aFlqy1aadCG5XrD5vYUFxPTKNjp43yitNzeB342SQQHRZNziBWdkuz2gktZ8jB7Dy8D+/2OP/3rf89+f8Bay3e+8XXu37v7OU6bj3R+ytD48POsmPIPvvJHvPXkDXJb8ODyed7u3qB2B+6U91nmJx9WA//I3OkDJhUBSXBaFAybgURAxMjcO/YCIpHlL5+webBCGI3KJIsk2MZEkDDddzxZVCQpQRumzYH19HiPzg4NzRfu4euOzEhOH71OP9+AUWR9wb+JP6dtOwpdUMy+SkiJ0I2U6452MUNETWgjq33N9R1FkAmz80SxRGqFG3rObwLbpULOCqpB0a4H7MWCSM7FeuBx6EhJkA+WwWr6JDk4z7P5fX6+eEjYrDEhQ1pIU8MgDJMnU97yD4lJIq1iJhVrkxA2cGcT+YV5jC1HZs2I9Dnr+oZ6uOZ+8QJXk4YxSfr1SNX1hAWM3vEgnbL216AiKmmqZHnCFqzkZDLw6NUW3daUxQLzH6ZstoEYAzMbedtpQlAYbTm3kr9+sgYpqM4LruuRLiSe7ASL05xWGbbXLRf3ptTOQVmRBCys4a1OkBQEFzj4jrYN7G4k91644FdvvEmICesTqfGIpEBpTqxlu4/EEDm/NePQJ1BHZp4XL0u+/8aeiELIhCCDqBnGyHO3DX996ElWoI1hfNTQj5aoEy+9rGhXGc2uZz7XWH1gKzuyRcmd/hl+LhpSMGhRUh3SkU5dSC7cLX6i1jiRERrFpJcEPZBcw6W4w1v5Y5Aa+sS0stxUO2QGtw8Zb+2vELEmtzPONPQzh8oVz8QLHvr3EEEzto4lK650Bz7woLjkcf8YdE7MC8r2lHfMQwKJM3/Cehho1ZS9qKj8gjpfQxRciPsc/J7GGXSc8KC6x1uHXzH0PSfqNvLiBoY9Qxc5ezLnannApUhZ3GI8z5CzPdFUnF0teRhvoMzJtjnBR6KPDG3Ps+6CH8sd4yEQR0WeCtKQaK5b7kwFr9eBECJVGZkZwb5zHHYNL15YHlp9pLfvRwod6bwnScmchifbNbmKZGPGva9M+cmP92hqXnvwJX7y5xti66jurpio2zxev4MQFS9/8QFvPeqYOQVdQzY3tP5I4DOuE3svmN6e4q4zptn8A9n1/LN3MEbz5HrD2emS87M5v3rndVJKPHf/OW5u9jx5suZkueDifMkv33qdlCLP3X+WPM/4lOb6ftD3g+7P0U0FH/R/KuDw6/T7zxv7qPHxySDIbwES/5ygx9+5/T1jLgQfXznEx8d+o2Hx8fH3LayPjf02IaHP6UsfuYAA/+qf/kf+5oevs9vULOZLfvX9G/pOE4MnW/bM7ij6EDHK0mUr3npjhzEKXVaYqmQfJBOT6DYjB6+OLAVJwhBoYsb5SkMeaGLEj47zr+6ZPL+hnjqWskDOBlw+kgRM07Hi55P+hhO9YEySuusYu57pqNFKc91fMd0nxjwnTCxRwjRmGCFZ65aZL3n8iwu6w4xQGFLdsr/eM+QZFQIXI0JJnBBU6Yjm3wOTlIhKIYEmRSYxomRiT6JEUL2yRc32uDxx28/RPmeXJfLDwPijOXpzwmEInBiNVjO2B1DB4Xp3pMHsYWoDSip2bcIoyGaSsWtooqRInthD6w1GC6qpolpqrrcDF/OCdutonEKQmJSKbr2ni4bLi4JD29K6SD7NyZIgz3Kudo5KOkjHapvBR6aFOFLIRsPMBHwJ3giiFJy8sCF/actN1XASctqsxhceLyKTVpMpzY1tmQ4ZQbfEQjDgmHfHiujXas/E5QQNKUR66Th1BVIKHmcHVmmKU4HkAo0eOXUTUkw8yWpmlAglMF6y0z2nYYbwgU3WUIYMET25MOxFzSKc4HzGhpYMi01z7JizjS0ncUXKbrGWGjsGxPUjbF+zNZ6zdWDy3o6hrVG5xT1/iZtXbOhZeEMSkloelbg8KaRQ7ExgGRUsIwfVHVPScEgxcJN3nPoJcUj0+pjrfMsYZgZ2YcupPeUr1Zf5/ZPfRwjBD3/+A/7iJ9/n4c1DlrMF/m6PqwZ89JjFlK5IPOofsRwrpPcQAj6DM3WOqWHTXDPxOftSMgjodGBRLHBuZK12TMcMbyUCST0emDUlwRZsdUfVSYTqyTJFmwdWZkVUkWt2lCED8YCCC/bas3KaFBO7PJJ7oIlYnbMeO1bbAMmyn+ZYH9Ehw4qc/SJnft3jWsO+KFAuHJmhQqQuMhaHhqgVhzJHCUHWO9To2JcFi6YlWUPzNJKRe4/0ns20YLY/gJUMmSJJwdQWiMPIxmhmXU8Xavpc4nPDQiWk61gzMt30BKnoASdh0l+T0hPWk5ETVUL+HuQtTjhOf7Fi9uiC3U3DYjHniy+/xD/5o3/4GwQsv11o/gP5/xExnI5pVp9cET7IZOUpi0lK/LObd/j+5oqbsaO6aXF1T50rdIT5co4xli4TrGTG8F5Pre0RVzEcQfb7ScGibRFZR5dHSIkiaMr7d3hytWG+3iAO32eMj5CFZX7/PtIYNsOGeXaGW36VTi8ZNjX5O3v0ZMphkpG/t6ar9vTZiFeCeW/Il6fsNJTXDZ0ZCJUkVJb5VcCknPpyytxYds1jhu2aXsEstsT4hMdqy8JZ1DSRLUu2uxtOao1Kjk3VMxEVMdPoQ0+re1ZdhT5dsDMtdu0YB4/CcjAdi7okpowb2ZFFTTKG/PSEtduxvHbISeJQNJguotQcGXI2smU15IzOsdUdWmnMOCFrNBs5cDKe0n1/xfWbCZSgNAaF5J3HDWXsj4UspSKRKHWksIJt66i8Q0+mjDanudoxKSRZZXgyelZG0e4DnZeQ4LzsydjT9D1nJwtqPaOXGc22xQ6BrJzw6LplZiRjykjS4HziZJ6jlOLJPlAkB+KYlz9GwaKQEBJtMGR4UhkJcaBXisuqwF17upgzzQTDsieVHmcN1fwh1ZfewN09MDNT/KARraKZJM5ihvQNe7unSBnOlYixYF8ETkROUgeaqkH3CSs0uovsip65m+MxHMqAUQb9pCf3msPUs+gsMne0WYfKLLko0G3ipn3CSXlOmmfsw57UOyZqgYmW6+GKJQsOwnDQ6WjYPVHoPmOjRpYhw0sYZMCHwDQapJBsYsNclKRpzkikrWsuLzOys5Er94h5n9PHgbFrcDqyEnOyqmAjd0z7jH3vcSEyZJH5ZkJsc/Y2MPWWZsxh1PQZnFyt8H9ZcvX2sSJ20AKpYVeP5L5FycB+DFiRiDIxmVgOLjKzHuUb6qahsIYyH5nnkVBqSpGY3Mlp+h0MkSI+QLcLttcNy9M5yVmu3z1QX++ws5zVvVPe/dUNuXLkItB3I0YrvNjhdEOQ8PyrD/juH3+db37n1afC6amfX4jP0V/f/5g+9LV8NEjxWdHdTxoX6eOa7meIyU93/JZa/sdkKE8jEB/Pt/p1O37mMf+rYi4+diaf1dJH3vyazY6X8f2/H17UT7GY/DYL2+ce4+M7K6UwViOlwOSG5fmCd3+5xRjJ6b1Ter9maDpOHpyQOKaI0I2oEJGjA50xnZUYk+MPDquf0pS2A1kxocoVLR7fD0gp0JmlyAv244ASEX8YkEREplFaYYNCCoEeYfQeFSV5WZJZ85SidUZpM1SKOAVOBFSUmAg0DUU1QSpFOclZ9wPD+sAkt3gEmqN3UABRCFRKzOYVQz+i+5ExRpSSJB8hRoQUKCWRISIC5MriQ4+NAolARtCmQC7nWFfQ24jVCnfd4Q8J5wd8TEwyjRKK3GrG0R/xJyIRhpHFosC3iXlmcU2CTpBZiRAOgicJGA41rksEr9FaIoWmzA0hWWQMGCWprDkCLAfH6I4VU7WIjD5SVBV958hzQ3CJ3klSGBhcJJuUx7QPn5C9R2ccqQKRpCCeUqwqZHiaN+wFY2YJo2NUIJVGhsgYAlkPvlRIoYkiYtAkH1EG9JjwwmGEptOCcfAkH3DyCJDUUWKlwYiRTBqSkgihyPSx6qrpIsIIdBsQVqGjIIsSpSTGJaQ61s0IISGDx7iEsJZMlcjYogVIpVBak88q7HJKvFzS9jvKwdI1PSpFZJLHa60VByImScZ+RBcCCUgpyIJARMiFYcxApUCKCd+MROdJ04DJjsYw6fj0KqHQyhzvbWWI0mGkOeazo8n0kXbZpCMuQeUZoTsgsoQ1Bdpa8smcoTzibly9IT6pEblCZFAUEw5jd7y3sow8FQx1INlAGgUy0+igiHVLijWisqhSYKVBoNBjQBLRLpIAOQaMk0QhyYsMnYPYtogIKiZMOEoTmRIyJKxSYBQagZECFSN5iLQCtA94KTExIZ1DuoBVGqmOfc55lBQQE8J7tHNIUWJdPD7fRh6V701NkRUIIcnCEX2jfIAuIUqDEcdrlyUYc4tphqMkDQmFQIwBkQLSSoQ7AtmV0ih31OyN0milPttl9TmLJk8l9Cc6PmifBCeKj/ieiIn0fhG/DyAd4gOAoRaCzGjEABZJTALh07GIlZIUSuGnGeL1NcLpIxVyTGgpsS4iUkK7IxW1TkejX2UWE47eViU0JIFGIW2GFBIjNcSElYqIQEcYmwEJ5LOSfdtjfWIMCeOO97a2hgwBo8P4hNNHmu120yB6SXa6orcGg0AOATlEVCHJigK3TVgpsFGTmh4x1ujiSEGrUkLGdLwXrUFFxSAUMinS4z3yUlGsVohDBzcdQgtMUvgkMAjypHBRwKM9yfaoYFBuRNuETYrUe9TgkHOJVZakFLJrsR6MMdgkj5SgLuKVxIqAUBIxBoyCFAJlYbC5pB0cSInJJNKPuG4kq57K5M0BoyUxRfDHtFtrFE3yWC1xLiCVQnuQQtBv9gxakt+Z0IaAzRQyRaSWlEZhhKEfIqMLjIeOLNOELqFsxIsI3iOVxSjAKNI+UBTyWFskBmJMSAXZNKNeB2JIGClJAppm4PYzc2xZMGSObAD8MSuhSy3aS3AJKRJGSLAZ0hvwjjh47EIj45HuW3kwUUGIlHlJ70H2IzGCCgIrDIJAUU5IE4cLARkkpsxQ/bGuj24joxrQmURVU2QnkPsRWWhMMNgsw/iR5CMygI2SlAJFWdKOPUYIQj8QR1A+QRHRMjGuOxIRrSRh25Nkj5weKXeVhszkRBNQTmKFBf+UxjwIlM6J0qGSxKKpiZgoj9SyEYI1CO8x6XiPmEITvSd0njQGylkOaSTTitJIBj+SgkdLhUoc6by1QilJnllmS0MtI/OTCSob8aogW2ZwozHRIK1Gktjf7Dhc7dFSMLY9N28/IYSEtoKhHY5rj0iYzKCEpvUOJQVaq6NW+AGo+VOu/k/LviQQ4hOaqfjI/0+JxN+UhvTJaX5D3OBzUqs+aah8Kv3p86b9Lw1RfE77e6CiTZ94fXLst2+Cp7liHE2Mz6VH/KzrndLHDvf+wjaMA9//yX/iz37wJ/zq3Z/z5luP+Rf/4/f50//5r7j3wiVeJVKpmKw0X/79uxTzPTrbsGJAdTlVPGF8fcurD5Ysdc8qd/zuSaScW5arjMVU8XzWo5wj1A3Pqw1nt6Yo1dPXW+5SU4gM0cMzVyXxV0v48zukv1nxlYfPM/z5LYY/v8UXr18h/GRF/MFz8NYdvhW+hn77eeQvnuOLh5dRvzzF/8U90nv3+MbhNcRfP4C/fJ4HVy9SPL7AvPsS4dFt/ig7pyLHbgP3k2KhJRnHlI+vaoFVglIJnrGCvGlQw4CU8JqKiBgoiNySgtvzwOq+Z3on8urNnPTzE/If3WH5s4yzn1eYvz4j/WLFN7whNQJz41k6z53yeH2SEHzlIoBOGOM5nQnOTUtZCopK8dqpJ449hp7lQvLysznaOJQY+fYzFhEGZkvF4sTw3ElkscyoKsWLpwPViaKaB5QaePkEcq1REV4+8WgxIGPDYml47Z4g0SPlyGm8YbrQKDkiZOQL2UBqE/4QuHxcYt9aIf7TLdyPZnzl9fukH5+jf3aPVx4+w4lYMfFzJBW/9949tIvkQXJ/PWexNsziFAb41ht3CM5hg+RefcqsK8miZXSOr7/3PClpVKe5tVvwbLzFUsxRUfPtm5cQSZHLiovDnPvNKZU3SJ/4/f1X6GOONedcnj7LM/EWxhYIbfhOdx/hNSUlpyrnuQPk3R5Nz3fHJdWTmtNfbFg1id9ZPOCll17hCy++xD9+/nfINMyM5Px0zu8+9yKTSlKowDfrCt078sFRdJEvb+aY1qK7jG+u72BFRuk1Nki+urtN1iTMPvLc5hKpZvRjRR9zLu0l/2b3P/OvN3/K/HLO3fO7vPTMK9yZXfLN299GJ4VNmpflC8zFjEksUU7y7d0rZFgKMu6n27xYfYGXVq9yf/Yc/+Tkj3ihesCXz77M9y5+l/vjlOUuYdYd3929hEiaPOXc55T7oWSuPWUe+L36ZXR5n2r1Gncmr3KrPaFoMvQ68J23psg2kQ2ak0Zzb1OSDQukn/LNdy3pAFO74u79+3xhsqDIBVI6fuenV4h+g26fUA47nn30mJwbdFzzjV++hUoRMwzkw8AXHq+xMWFD5MtvvIftB3IfyEfHF996jA7H2g1feueKUkjybsS6yJffuEF7MF7wypuPMdst04nEpsBX3t6SRUsZM77wXk+FZGIsmTZ8+d0ekxIZ8My6YNpVTLhDFld84+YLiKFEdRPuLC6YuxyLpt92vHDvAemzpO6vDW4LPlxRP2sN4LP7U3r6+lB2P2ze4d8++v/yHx//Gc8pkHKgMI55Jnl24zFJYYXhi+/0mGyCfOTItp5n39mjfUS6wCu/eoQNntKN5D7xws+vMS6hA3w5ZbBvKMKITZoXH1l0kuSTilfnXySrnsfOv4oq7/O1/Bayd6h64P5NRyEiuj0gReDVHx9QIWG94PleM60T2d4jg+CbjyPVo18wfffHvKjgJC/JEigPX/lBjZYZ1ckZL1bPsdpOmfhLtJ/znV/eQ8kH5OEL3Lq6xVl/HxNeRIyXfP1nz4DMMKHgrJlxOZ5DI4lo/sHyDymnFdOD56zPeFbfZnK5pLi34h/f+R62kkxk4sRnPL87w/oCJQq+9fA2Kg4UQ89igC82Z2RSYYTgO+sTtBop7UBZtLw8SZQv71F3nnDbXmMnmtt3Z5xMNV8Ma3KjsEbxvI7U6wEZMqTIeO2ZGdlqgpkVvLiyiBApbIZRmq+dGKwyZNry3HJGZQwxKIQ0/MFLF2QqkMeR5yaCSSbJtcSlyDduK4yWGBLPLwVTnagKzXRS8K27guXpjEzBMtacVJBZkCLx9UuBqSRWe24vBRe3YPacxN6RvJhvKF55j+XX32Qhe+6LGVlnUcHwvf2L5O2BZRi5W51xZ3OK6OeI6SX/aPld5JBRjjPOmjmvLr6ETStkV/D1N+6jUUxEyaxVvPDelCwKcp/4xqNb0FVk4zmT7A4vj6/i35kRr1Z8dfcl5LhEDrcx7oQX3rlDWs9IzZKvptfQfcRGRV4VfKf6EmVKqG3Nl8MJVmToNqBd5Hd2C2TbYlPk5WbCVJdkyaC94Bvj+ZF9CsEL9W3s2sAmR9gFv9t8BRUsdjA8U18y60p0qwgj/O57D1BI7Ch40JSctIo8jQgx8q13F4ifTMh+es69PufERUyWQCVuh2tkHKiMY8rA7TkY36DGhm+dago9kvkt0zBwZqDSkSqDL52do3JFlkmmKufB3RfxzZSxKfn6t18h5AE5C9hp5HwpSb6lyBPf/OopRiYUkRQ8qwrGfsSNnvvzCkHEWonNDSe3K/7tD/4d//6H/471bv1xufaZSveHKv37ku/D3o9k7YjP2uezxOdna/afq/umRHr6+szZ02fM93cxHn6dOv93bH8PaVH1f9kZfKR9GOT4aH7vb9r4I10xfUilmI7v/5cf/Vt+9tZPOLQHJnbJ4dGE/XakLDLi0xL0N+s9F6dzrPdcv/mEmzefEPsK6SoGp8jzyPKbK3bbPXHbMJZzsrt32DjBxTzj9R8+QuQVru2JznH5zBmPtyO2byiqFcMI9b7h7GKCUZ6rOnBuEswFsTha/BYoK8PVEDgtDQ5JkJKhGSilIPUjWwS3VxOam4gfImNMlDNBPvc8aTuWSjI4iFKw956h2xNzz0EJinCMXKSU6IAqgVbQSEXuA8jjWOsD0yJib7W0ZWQhLOGXc4r1hD4JTpsWWSxZe8FEQqoDRmtuDp4qS2AN2yaioqOaWpLvWLeRqXBgDF0PVgvsVJDGliYpzk5y2jrS1YEy02ibkGpkKxSlCNBZhkFSFBYXjoDF3uQUydHtFd49paK1EeE7dk5w76xkX3v68ej1Uhw9bZsezmaazXoAZUhRYIQjz6HTGfMwElYe5gofE8Wio3p2x7rqWQ2WsdjizUAvB6ZdgewF66Jl4UoaGqL0tKLnllgihOCq6ihbwxAgF5omDyyGHGM1G3VgFiuCPbJz1bpnsTcomdimHVMxoY8WGXPqaeBWfsLQDezcjnzUaDchb3K21nESCnwPezw5murtNeUba/Zp4CSf8Yf/6I944cuvILTiP29f5/s3P+dxt+EslYwy0oYB/84TJBmagms5sho1zmg6A8IoMjti9IEnZcelmxLbQO8DUQvypDFK88i2XKSKauFQeSJpuJ3d4b87+W8RQWCM4U/e+ee8Xb+JiyOmmuAnhofDI07SnLjeocuMpttxvpvy33/x/8hkcYKVFiklLjp8CqzHNX96/Wc87B4yY8I+efrRsaXjvFgghi03cc08VET7AGUvOdjIzCckj6nFnuxRh9D30PqcbSVZ7CJxKKlLSzFGiB4rYHtSsEoSH3Y0laDUBn/TINcN+1Jw2iSiymn00yiiL1FdyaZ8mhZlLK4sUKNDjh7bOzaziuW+xmWGQR8rSOc+YElcZZaTXY3LNKMSJCnJgsf4gf2dJYvO09QOlyTRaorQoSaBfSlZbjp24wiDw1lNFiNqdFyXgsUAoXwTIbe4LHHypGTy14ZDOEZJv/Tqy3zv219j8n4V5U9SFD51jX02XeKn/W+fHPuY4+wT3rfG7fmf3vlnPGrfw6qMRl0Ssrs86Q7MO0n9KNCGRKY0s/MLsp1nHSOLQ49Xis4oZAjkRIx37GYFy32Ly0ZcJklKMH/+DvH1J6xVZHEYEIcf4NSO4vlL7Px51OxlnriOE5UTlOXw7g3D9Y6yLMgyw5O2YVmP1KbFC4erDItyRV5rrtzAPAp091fQP6YLPfMHrxEmr3BYVEzbwObd95CXU8LljPy9LeO777GdRKajQtkKYTP2E8VyO0DsudGORZtAPUTIA3XlWQwVISZ2WcdUlExWE4okWG/eYzKU+LMFN8OGIuWYMkMG2E09s0POYdvS24F8EEg/on1kU3ScsaLtPHs1kkeFlgobFdd5y9k4o9tN6JQlblrS2yW8t2Q7ChYy4Hzk0I7EGLFRopKmFpbTucbbxBA8KSVMjPS7GpZzFiniO03n05GsIDSU6sBNP7DKNMXtE8gMV794xHQ2J+oJj3eeSXSMTpNQ9P5IMTutKp70sJABkWucSHQOMjegpaSRlkIEBnGgOs+p+8BiYlC5Yusjp/MC86U3OYif46rILeZkQVCXI5Uo0V1DdTJlG/dU44zDWnA4s8wXK2gk4snIk7HmTOTYF0u2YY9tI7LeUOrIbuU51+fsNwf2ww6bV8ibAnNTsDs1nIsp9aGlbhuy+QTZDeRWsp0mlrVkUJ7BRKQ1FPRUxchN2XCrvEW3b+m6FlHliIcR0VVsrOPE5/Syx4WRkcC0WFJkM25Sw4msGArB6B3NoWEKmMJzrWtOxBSxiMTDll6MVKFAhcTa7FmlGS5ThJDo1MC0yYltYmM7lr6k+be3ie8uGaYTiqbhsDuwCYJpoZDSE4aO0VhWlUTGnuv1gUoITHQIHelTYmoE2gjGFBA+YbPA6rJiMIl5OcOlku22pSiOhTozY3jyaEMxBGxb8vaPH1EVlvJ0Rd2MNG1imoNrGg6HlkmZIbOelNWMJJ770n2qlwxeDgjg9vkd/sl3/wnaaD4wLtLT9KIP+Lc/Kuo+YlJ8ABn7tMIqPpX7lD5honw6qPC+/voxcZo+aXR8/FjiIzN/qsbFb9s+oVdPJ/9V06I+brt9vI/PGPvsEfGpnt+wA59erD76g77/fnPYcLO7oRtaBhTtLrG5GdibY2VFLQXd4NBAkRJDDFS3lmzfgKYOJHHkLh/fWRMriRfQth7/aE8nNb73jDZjsxtJAWZlwTvv1dTuWBnWtDVeV+hixq7zjP2R79nniSITjO54rpVO1D6x84nQB0KCLggiiblV4AV1Erx33eJ2gm6UYDRppdi1HQ2KFGGMET8E+pQQhSVlCi8S7eB4mgFBkAKZjiXvm+DxSh6B3fFIQ2urRMxAzo6CPGpLlwxdTGyyKakOHHpBJxLJC6yFvQMvFaH37LtjqLn2PXkGQVt6oQgu0gaBQqDrEVKiCR7dJNyQaKNivxlZnhncGGglBCURQVI3gTZGhIrgI8M40ISIiIbOHcOyenTEEOlRvPmoRipDHySZMmgE9d7RJ0X/qMGWFU2XcN3IrBL0RlE3jn1ykDmkUkQSi7OjIVEzELPEaA7HnE0FKUlkldGKhHQDnRoJOJyKPKm3SCHYxAFvC6K1tCEwipFjSmfiYHtilRFkwm1aBukJOkPHwD4faL3Hmwk6RDo3krqREAKNHbGZQSdDkStaHfGHBpyg0QmZBlZ9g48dvfC4qabXHlGPyMJy0+247nccXIfQiTh41o8fkmJgcjIlJUnTB4TRBBmpVUQkR2EGUC21dlylBmUEnXIkH6kmM4Jw9CKwjQ39botrGvQkZ6VXHMKBi+yCfmxoXcNN/4REQheBPkga0SKkQJiG4HZE6VnYgtr2nKr8gwddC40Wmq3b0oSWQ6wJKrLRkb7v6FUg7FqKGWybLW1oMOV9tE10IpJcDX5PzQ5TRGQh0FrSikjSAqk0TWXps4hMCu09bfCIvieagToK9n1PPjeYkxV9cqyvBqSXNJlCxIRqLUllNNZALBEIuvyY7lZIgbSGNrckKqIU9EVGCpFqGJBa0yvJbl4RRaLNDFFA3neYIqfxAaY5o7TUT71UQXikdPQpsrfQJ8FBKYSRVEkyMnJQEGxCpgZvGpIWZKOiqWtilMxWc26ubvib/9u/5hv/p/8tqrC/VvZ+uv36MP6v3TXBdtzQ+ZbNcI0Uii6b4WTNIY0InTNODQeXaKQkpGOkp8ktCEEMkdpqlLSU44CSmi43kCxo6KYKYdSR6tVAk2nwDWr0hHJkjDsyAjH21CkiRSC6gU1wMLGIRUGzb+lKDTIxaENrQMxylIdGeLrKoLRE1DUxbmCRYyYZYwE1AZdGdnODOivwOLKhxlfQVJJoIGWAEfhKQz8gAuytwBkByqFDR68DKUFEclAdfXTU6xtmVUU3S0Qf6dortqqnFj1a5WipaKNjTD2hTLS5o0kDRkdSCHS6h7jHF4qdHpEJKq8RCWrrEKFnTII6OcS5Ib+q6HvPpols+47prKSOEuciOZLkoB4dPnhEkeh8AGCaK2Q1oR0TMUTiGGl6QXKBqByNdAwx0SlF/WhH545Mhv1NS7Saxkl8ghQUQRh8jCA13knqPjKSEC4e+42mHyE3ik3v8JWmU5K2dsc10wWMFmw6x6EdOP3yAXspSE/rInUOujzStgNWt/RhpAkNfe/pyil1ruj9FlqBRrKLHaoE1Q7cDGuUh+ks0KYBZ2GdtXSjYyMHpA7kxoDqj2vyMBCD4JAlRH+gSBEVoa5HnMhJIlELj3A9c91TuwONd7CPpCBpzEhqdhR2BTLQRAchENJIY0cwCqEch3ZNLR3RRCKWhh5vHTF5hBw5qAEAqSKubPEi4PsIJlFnnhRbBpGgMsRCEcKAj5HGelLo2btEcorxpqdIgbqP9ELRbgeU8thM0O173H5EipE+BoJRhK5jXmha79HKoHyi9444eualolOBuunwThBSYLvt2B8kmbUYran7AaUKoo8IY9kfRg5+jy5KBh+QfSSMCRcUg5dENaJMJIrEerMhHAratAdgNV/R9A1zM/+YWPt8dqUPkjk/8vmpsPvMiMT7lbc/b6aPfBZP5/qIUfN3iwL8htSqj2720RP4zLSu/3Xt78G4+Oyv/FEr6tcBJT43rPRrj/cZ2XGfc4jL1SXvPVnjXcfZakKfpng/UmQKcdgTx4iYzFguCwrnkSSKsuCZ+3Pe/OEjHj66Yiot4/WG1GuqPGMmYLSKx0Ngpj3LO1PEO3voI0sbkcbwuEmcLCvyrOQwQhhHbBw5XRmu2siJBZSjTwKjFDMJAo9zkoWMR3B1PLLNVMkjZSLUiVIFFIomCKI2LEbDmAaGITKrDCpGhijokmCCZjSKzEumk5woI23nGSIUYSSpI4VnkTx5Jml7GKLgtJecZUu2u8REJCaFodWCjRMsJu9b2pHSCFLbE6Uh5IIyDZjSorQgI5KphDBwCIGsa0khUc4LMiNJXWB2NuXRTc0kdBTnS7bbFhdH8v5YUTdJy8XEoGTO1dAwnQjcEEkqsWkdJxMJQtAZMApyFFk14d1Nz1luiFLSjBGbc8TIWMl7Nw1ny5xqlXF91SBzi00Ds9MJT3Ye2w3EFEheglSc7jPskOEbzTzTiDDDFSVjiMwHg0KTrOckTJC+ohn31Flk5i0xRDCGqtGUcso+tIyZ5WQsCcnDSrHaZVS24uAMOz1wOlTIFBDiwEJPqfJTmmZgE2tOxgnEwHXqKJxm5nNEzNkwciINYfRsUsKMkVNZYbKAmcDZM7e5uHuXTeHRMXBLz1mJimjgQk8I0aHyATE6JqFAVBOUklyUS5rGYdsRXGAqNEkPJBU5CRWZVzTWEfEUB4u5NedhuGJVF0wSHJIhbkeMlVSi4vH4mKmasshXnI4XjHFgIld0RpKILPoSOxga4ehNYJLNOSsuPi4vngrby/yCqa6Y6RlzPWNhc266HY0KzMaE6HqStkyNpUpzgpmx8z2nZUUaPDehYDqzlPk5Y6xY9y3zwaNGjwpr8gFKbwgyIEvJydYRUoecKUwSlCKQpCQtCy7PZ8gObpxDbRvsoSVEgSwEy/2ISoomehg9Ves+AAwuDy1SSmrnESGStwNaJNKsYrHdIwXUk4IAVF2HlAGvA/ObA2K+QO8PoCSLtkOZjusisagDC6XJ3chYZMxcwA/HGh6LzlOoitaP9BPBzOZUp3N2YctkmjM3Bbtdw8PHD7lz/z5SfcL7lY5P/tER98l83vR0Tf1I5Pjpfunp+OdzqidW9pSJmXFR3MYIy2gW1LpEJs+psIxZRmpqMh+Y1jtktAghmG8aSJBNMqSPVDGgRGAjEyeNJylHLUFPLfPW02960lQxazVmL0mTFdYsKNH4aInCc4rF73vSTUvSktOponu0Jy4y5vuRIAbaLEFmmLUBrgc4LVi0Ab1RDKJA3jllgcKpCiEFxc2BiVAkWXLY7smvA9Ef8YWzAYou4VYZbZuYr9NRka4EEyfIfEkwnn0FJ40CBCrPqJxi2g6IJsJpxkV5yZBLbFqTjQb1ZkvIBaoIrJoc0KylxPaK0muGNLK1irM0J0iLbrcoL5mrkhAcMrWcjRk+TNkGjzU5+crSV5FRHlhkBqUSRZEzjo7safmOGCMre6QAZ57T1D1TEclnOY8PnpOJJhlJoaE/BCZSUEwy6jExE5Kx77BSUF4uiY8bYq6RXWA5yYlOHRXFAXI8PjRUWrOcW4T3HPqeZA0nqxxCQjuJjZ7bpxWj7QgLhVp7lA7Es55447jcVqiTOb3pOEkzzKzivc3b5LvIsjhBVTnSwyxMcNNL1jqSO4XcB8Y+gSq4TDNSPZC8xYySJRZpOvZtywkzht4g6gYjM4qDIowZG+VZhZzoBFb0qN2equtIFsRpxaktSEAeGxCSRTZFO4mo98xHi0ySTEv0rGSxvEUaCt4bbjj1Fd3Da0oXCB7K1qFNAfnAsgmIpCmsYoyeZZgBLVInVr7C7hOHJBhSz0msEKNDGMsyTNAO2n6kF5q5k4x9RMqeeZ9xMs/ox5LdtmdWZlTW8eTgmRYZk8yyfnxDpg3nZcUwBHYucbqsmN1fsHt4RTbJuXVrhRaOq01NbjS3nlvi40gUDbdurXCdQdCS54ZZZfEeklCcziYUs4zUB/ZXO7JKc/tL9/j5f34DTUQkkFZhFeSmoEkOJQ0nkyWLVcW+P9YjqsoJRloePbphsZyRWcNu3JCARbb8eCTh85zcn0in+qSm+n4U4zfr7ekT/z9vm4/P9cGnj57Ub2lnfGSSv5f294C5eL99MuyTPvb5v6h9LAfst/vm7+fxZvp5fvXWc7z3+AWuN19kzJ/nxp/w7mFG7Kf86o3AWz9ueOtHNf26o06SrQtcfnnC5T9MnH5zxD7/hNwOtE3N7rDjIod63ZDGQLtpKWOPkJCsZD6DQWjQCm00c9Oy220ZY8eztzWd6xn8wIgjO7Q0m8T2iUNtR9obSegsw06RrXs2TyL1TiI3I+1VIg6WMORU0jMqyW7fkQ41/TrRrwWHG5g5Q7vN6B9Lpk8M+esW+UtN+rnlmccKtdZkO8PtuGS1W2EfluRPFrxwqFgMS+bNlHuHE8z3T/H/aUX775ecvZ2xXwtcq4mdIMmRITn2Y8+tc0UdBpqxxocDvl0jCmh8z91VYJQdgYbFqeRiuoP4GMQVt6c1Q7PGyhbttszVlhR36LzjzklCGEUMAVQiEz2D7xnCyEWWCIMmjhIlC05yT1CRQThun2m6/hi9aAfH3VuW3vfU7Z6zE4UfRqzRDD5wsYBhGIkyspxCe93SHxx2tuB2LOkfWbrHBv1WSf/9M8YfnND+5QV3rl5mbGf09RRxPTuC4tJIaxx3+zuMZkZkymI8Z6omSKkIRvLMbk7KJclKpiLHjkd/R51Gzp5k1KnBhQErFHma4oKiEYL7/ozeOqLwmNFRHixj4+l85M57kj76IygxCBbBEsKRPviMCc4HlLXEBP+5e5N/+vDP+R8e/kce9Vv6JAkYfFCclWe0h44+Cc42ERePRpHb7LmYvkA9e45D9YBle0kojkWmfBZYlDnttGY4c5xmgjY+IS5GmnJHFSesbWBTCOpDw//9V/9n/sXm/83/a/P/JOrESE8QnqWZolJCEHFiZMUtdiLRuIDIlmSy4Gli/see70pVKI6g8TGOPDv5ImN2iVfnzIqXmEy/jVl9HXnr2zw/eRWnMlQ5oZRLKvccsb/F6G9zP9zCz3L0qqIsFEX6Bd79NYP/Ky6u36SXPSl0aNcxrwVCFMRkufV6wLsJNDnDO4HqcCRZSPdOePbOlDDbIO01Wj1mdbgm0YEeuWz2pFyjiGgCJzcbAomoBLe6nmA0SQpiZjld7/FCELVmVXdsswO1qdnkDYv3foqbbfHZFYv2IX7YMPg9TdxzSwoGMTKODfnVDh0ECUnUltt1hQ+eFBKzxQTxxRvSV9b41x6xH9/l3/383/Av/uxf8md//qf44D8uVH8rgOKH+cDpY4vq5+Qwx0RygVJXfO/WH/O1s9/lq/Ov8/uz1xjTFYkt9E+4tViCNnQ+crIfGJQkhCP5xMkwkqwmZIrLQ0vKAqgRrwaW7UhIgTS1rLY9npEkA8jA8qBhYglElt4QggCl8VKyeH1LkBqmEyaPG0SKRCLOCG6tNSJbQZyw2gpi7KGCzjecdBlhVYBVTKVBFzlRQh8dd7YQvSDdjCwbTZE0Qh1TDy83Ci8lcUiUg2SaFUhjCUXO3e0tOnlJiJfYcJ+8v0eUt+nVLU7cfba5px1aXNOz1BXaCGLqub8pieMO0TcUwbFwAvoDyfTcPlSMOiOFDCkqVuqEkGV4o7j1JIfk0CKiReKsTyTrGIYtzz5Q6O+sqb52g371XZa5px0SUWWcFpLkPDJ5+n3HvcoyeoFHcXk6BZVD1LhecDnXuBgZnOPsfILMpozkHFTB7ZMJYehpn1zzwqsXyLEjdS1DXXNnJelJRK24c3dKda6IuaOLDRe3BpqyIcxHslmDWXlcOaLPFWf3dqSv3qBeW3P5Bx2Lb73J9Ntvc/7Hj3hGj8S+RfSeiSrQB0dUgXEueebsFVrh0cspk/mK5fyM4Dz9/sC9fXasJRAFHCLFLuFlYswi54cZYxwI3hOu9sx3imQSQXnu+Rw/VSQZESpwisbrhF9U3Fo8IJxdkLIckWmeO5tiZi3SbrkVLSmAFAY9qXhw+gLmpAItOEs5bVjjsxa3crz00hn2ssYudjz3bEX5goT5ATdZc8vVBP0uqrzm1A4o7Uh6wOcdZ9sZBy/wsiBvpmgKYpB0WnF5VdGOPePVnuogmcgcERPOCp75/zH3Z0+2Jdl5J/bzcY9njOHOOd7Myswq1FwoAEWQbJJq0dQPLZn+QL2qrdXWzWYTbAoUIJAUmhRAkCAIoOaqnO4UEWfcs096OPfmXAWAKLOWh8W9EbH32ftsP+7Lfa31fd+qZ0z7QBolMy/QBBIBFyN3ZgIXJ4apxcWeKlMUswJZF7z1lVcxdy5IZUlxtuDspXvo5Ry5nHNx+TJP9zUHf0Y7nWOqWxx9weagMFPGo8cNu2OgDxI5jchckaxgdSZw3Z6x3aJSh6saDmXHE7Vj8WCNsfc5tnPe+1Gkf1qxeZqxeZrR72v+6f/6/+F3fvcP+Sf/7A/4Vz//fX7vg9/h9z74Hf742R+SYuSL9rLiRdXYL0AifSpojviYavbXYCOkT/gX6cVlPvey9JmvL0Ru/dWAoE9ylp+/v78lY+JXxbn4ImjUX799jpqSPoE5+8VJD3h+5/gCA/zi34/kcAX/t//pJ/y7P7ths5+4dZYxtD0fPtqfSs/3DWoc6JPgovAUcUt2u6KoS+p1x/wC9scdlVyye6y4etqRFxbHis1jT2MzlqWmn+AwgYiRuiiRUnGYJPcvC7ZXW1oXMdZgZGC+LNgNYKcB4TXHPiKEYDWzhMnTi4yFjhzbiSA0zgfOKoMmse+hVA4KgxPQ945MTGS55qYLrCsFMcP1kWEIzHNQVnLwmkp6Qj4R04hLgkUQCJ9xdIZZJpjMiM2g9YmlkIjJsps0VQZegLKK7RBZVAGFYzcGhHcYrZEpsGkct2cZzXHEFxUmBly/Y7bS7DvPkhEVW0JxkryNXiA9jFJSC8BoWhcJw4SpZmSzGccAc6sYB9jdjFh5UqqyQnEYT1mU0Xt6BNooKimI00SbNHObELlg344IJSiQFCbnug1cnhf0naPrAxhFTmJWlDzde+YVpCDpR08UkrryyDLQRMFSRtK3rpD3J0YRWSmPLBtu6oZlqpl6hXeSlpFLLEpPXOst1WhxEkQSdNZxPtUgBNd5x8LneOlRQtDqgXO3JHrJlTwyVxVJCnJl2YQjq2PB0Eo2sqcmw7qKGTN2WeSs04QJtjJgo2Dxo2vqZx3TXLF++TbN/YwbM6CTxKgSTcbN1LLaO6ZpZOc7tJRkQ6Rcn3MdO1ZTznb+OjflGhETa75PaX/Gpm44dxWjmuhkT1KCOmQYobjSB878jOBGOunwBO4MBjVODHPHZXEL1TqS93gCRb0iVJqruGElFmw3LZOQDGnijfEW/5fX/1teWbz00Xx+0X5w/CF/uPm3vNu9x1zPOKxeYRgsTRxZ+QKd1+xzqL0gKYUKiS4XnKcMfOLZzZasOdXzsPOctlKs/Yjf/ZTN8Jg8WUS4jxrWNIVgdQikvOBQGUwE3QvsKNnVlmU/wlLQzDVicKhpIreSrQ4sPuiJXU5f1IiUyLzBenWSm921eCnp8wxSIu9HjBBsZiXrQ4s3ilZJhNbIuMWpA8/miuVhwqaBUGuigPqqQ/vIpoDVKIl3Ljk+2xOsom5Bobk2gnVIePF9otgwZXDLaErZseeKytW4/5zh3w+odc2XHn6Jv/vtv8v9O/c/bWw/E0T6nG3+rAPyCenFz2cuEime/hefkJIajz2/2/0p/7H/GVfjnrNwTlSvcLWPcByodIk1OR2CZTucqiaXFhETeezIpGOfS2btKavWzSz2zgr9eIvqB7alZLlrEe1/Rt8VoATZ4tdg8SVuSCzHSPPTG0atkGczssfXCDyHhWW2H/EmI8wKUpWRP75BmMimgnrTo45/Sn4ecCpSLd4hrt7iRkqy97b43GKWM5pnW4pjgxctuwXMgyblNbaoabxjvhtIyrGxnpnOGI87lAjsbWIdciSCrfVUJkeKnyGnKzrTctbXaGVo54FCFsTokM3EThxZDhVBwKEcsTLD7xViytnpnvVY4GeWne6Rx4nKRwok+9nIapjT7DVtoUlTpC5rcmN52t4wf1Zw/E+32T7JQEDlIqodeHp0zG0kFhmjUQghKQ2Uec71fmJZSGKAcYw0x57zM4NNnpvBcbbMGK8/JE0dKMntN14jyYpH7+9YGEUfa7oRnJBcri0+DmzGiBp60gJMqXEJVmVGZjM+uO5YaIH5+hXydoPLEivA5g376shc1tCNZFHSZhOrsSQQ2GUdxllU8KwWC44cmYdzhmzFs+GAvhmInSWbMg5qYjkJ4nJkO5+wQjO3jix4mtnIKq6Yji17O6CTxjwt0WHNjWtYhYJkcw7SI5MglwqL5CZ1nImMaK4ZshahFZU3mKQ4ZB3nxSU+OjrXEWNEuQyKkhvZcDblaL0j2I5IpMpuIUzF0/6KaiPx1pFKCDpSDRVCZWxMwyrUHDqPN4ZgAvUuYa3kph5ZqTlT35DcRC8d62mGnATbYmLmMrrfeRX5+M6p5pTq8UXg2b6nUKDMiEwTXYicVZZcw35wFEIgM0kxzzl0I+d1Rmw7WiJFbplEgalqrjctKyUJQ+TmMCBDwBaCwgr23ciF1qjrHiMtSQnKRYlMiQ9//JRiprgRHa3wCCm4u7hPHiu2m4F6pYhlQygFKUXO1gVVobje7rm8M8O8s8HN9yQSr8/f5B8++G9Y2CUfp2M/Y/O+KNH70bL1sT38qLTdX4HQeVHI9JPm9rP3+cXHPpEzES/gWJ9wgD6Zaf4El+OzOZX/XTkXn3wz6Zc+9S8+8rFr8vFH8kUp9PR8MfvksZgSKZ68LKU+k4hJ6bnc2KlTQz+we+8pUxdBRHQKGAnRRaw1yFHgdi3h0FMvck7bYEFW5pTLjJlTGKMZKZBPDsTJIw2ICeqiJHmPtYp6XjPuwymKI0+yZTF68spi7EnaNBzHU2YltwgEQzeyWJVMoyb4jrIuOBxHUkrkpWXaHfFOkpcaryVd25OVORaew2hg7AYKq7FW43yiqC1d16NMTlEqjm7Ae4+XGjUvUFNG3EdcCgQJQQkCnIp/+cSUAtbFU8VbBG6YyFYZx+2BcUosl8+1yJVAaUXwnnKW00ZBGj2ZNaRpQmiF0gZLRu8mjJIkwGQGH9JJpjYE4jjhJ4fJAmVmODYTRkt6P4EANzmqqsAkSVFajHKMLpFCRBtFcI7cKMaoyEtJP/SUmWEC0uSJziGNIfbjKZXvR4TVMJzui5DkVnE8ngheyQekkkiTEEHQjQPFFIjNhJwZZBQIeZKcTd1Echo5CVIOISZkDKcaFpzkjonQ+gk5RUgCKQP4CDqikEgjkD4hhCL4iIiAiAidTlKT6lQp3EZxkpatC8SoEdIhtT7JSwqQIZ0qTYdIGBMKhRKnCqVaqdO9OoffbXHXHUGCzMRpLo+R+OSaVAnEmBC5R+YJmQRCSFQ8zT8jNEF4NKc6IriA0grkSYY36IAWCZKAADYourEnugGrLUmc5q4ICRklpHSSA81y4ugRSRBcxD3dkRYvnd7bJ4ytFBIpTuNSCXXi8ViDGCZUElhjYOhJ+wmf0ql/Zppx01LdOye7mKPdAdcPhH4i3C5RuUTkGVrkGK8QZNispJcBNQRCTCghkM4j4olfgRDIweGvB/ygyDKLVhI5epJMFC9f4raa6XiCRYkYkfJkdnVKJ2nMeKpQLZVE+nCKkMUIUaKMhBCQMaCfW0gzOqQ52S2zKNB1Qu97kJCdzfBFhkIQmwErC0AiRUIiED6iFCc5aSQyCqSShN6TVyvcUjG4kRQTUsqP7LT4yGD/VQGkF7jjv0ag6aMLfxq1jJJIpVEohBBoJXERVDrJIRMiNnl6ozERnIiIEJEhIpV4Pi5Au8BkQBf2JKntPCbPEHFEu4DUGqkESZxkUEUSkAJpPyBDRGUG4QP4gBIJYkTF0+ZA5ZZxcOA8MtOIyaGTIFvOMLYnxvH0GUwekVt0niHrgrTvIYFMCa0kqjKoJn00tvCnYBODR9YK2fvTfJYCRUT4gEAg7YnTJ1JAxwQaVBSIfiCEEXKFXuYYUyC7AdVJUJykmqs5wxQRfQKrEElCO50KdZ4WAGQEfETbDEkkuYgKIKeIlgKpNcWyIpQFnRaEGAjBQ4rozJBVglHKU8CizLAikYaJFBNGCkYf8aM7PXNIpOhPCiM+IBPo3BLjqY98d3qddw5EJNOGmMAP08k2k8isohkHqkWGkPJUEFNryjpHTRMxROospwk9KkRMbU7jqfdIIdFCIYVEFRk6NygSWcgwziN7T8KhZzmSU/0MM6sIY8REQRpHuNmBzZErgxYaZcQJYmkMZTkHIZHDhBo9ssjQB4EuMqrqjFFIbJhg9ND7007HnOaALHO0nCAklFYYLEIOGKVJIqGFJaaErWZImaHSiJkUvhkR89OEkgiUzlBlTmVqptQSbGR0A6bIYODEfXkuz66FpG0O6KjRxqLzhG4jkz+tJUImpEvggZDIqpJOCnSmkTGSosf5AZ0EhRS03UhenuaxBRg9oR3JL+eQnXZZ3c2BrlEk7xmJ5OsZZlajEHTXR3Kr6JuJIQgKe1rPYjMgOHGuisww7AeM1ac6UU9ugIRIibLOabsGqzWkSLkoGaPGxI4pJHw7IoTAtRJZ1ZBAyZPtkUI+33if1plfzi07rQefO+OFnftICOOjP7yIunzixI+s4Gct6l8N2vkFxz/npHz2vfF5p+JzNTL+C9rfGhb1cRomfeq3TyZnvjCbw+l5P//2xccHvujZPh/8+ijN9GI9++CDp/zrP/hj/uj/+5/4+hs1RinqQqMOOx6eWapMY2XiH742JzMZ1mYYNA9XK6axxIsZL7UzxitJaheU+YK33rzP8jwwX3v+wW894GKVWPor8v1TvrYQlMKRSc/33q7RwlOZAM2R79zLqbUlQ/LNezmFFFQG7t1Z8t2HBWUhSW7k1bzn4lbJfCmYLQ1vrXts5sls5LZtqMxJnq3INF8+myhngrKKfOPhnFol1mXJvCj46nlA64hWgTuVp2Zk3G6RJL66FszyORU5FwUsdCBTIBK8oRqmYcQquFhJxLDHd0eUhq+sR8a2QU09axO4XYHwjsxovv3AUpSG1cJy+8zw9sMZ1vRkuePvvzGn1BNn2cDtdcYri4IcqDLDf/3dN5nNSqrMMLOa+3mO1QWZLfnevTlWa2xImBR4vRbUBVQzzVuXYFWgzBNGBN45g6qMZFXk21+aU2aJovBY5fnNV2aoFDAEXj8T1EtNXQbwPW/PPVY65NjwzgPNvBTkYiRNA3//60syBfPKcCuNlENCHwXWWd68rhA/OEP+8Zq7791j1a/Jd+eYbsFvPbuLUZGFSrw2nXEx1pQpwwrNbz1+magalG65NRTc6y6o+zOKccbf+dErmKakOK5Yb2fca2esixoTE791/QoqQDEILvqch90ZM1FSJMN3tmtUcBTBs54Sr44FhZFkVvLV8i7x3hnT/TX5esnDy9fI8gWajK9dG8LVFusSta34krwgny/JFmd8Xd3HmIIiGUrv+cahZzW+z3J4l197lCF1g1Q7RDrytetzyI4Ie+DXrtbo2BG4IboN397dx7Elij2vTrexogY5Z9IFX9Vfx9gSieXN+i2W2YqZrLDS8OvuLVQqyMWcdX7JdveU37/5Pf6k+Q8c3I4/uvm3/Jurf0UmDJXImGPJkuDvmlfQYU8+bbnzbM9lI8mODj1FvvODCdE6Mi84ezpw/migkJr69prv7grsCPmTgcUHglfSfar8TfLqId+Lt5nJDWf+Q27ZgTdWa6raUs5zvt0lFANFt6PuR155fyI/FKingl/7dzfoa8F8WmOvA2+bnOpOTj5LvPHj91FDQ+EaSuF458NrrHdY73n754/JnKcaJ8qYePvnTygSZJPn7R9umB8kF7uS+Vjx1T/bkQewAb718hucvXSH5XpBebHk18cK0XbkIfLWYsVCaTJ/2lx//cMaphzta+72D5hxizBeMk0zXk33sS9LVl+bsby74Pb57S80ub98QfhMNkOI04L7hcGiT1/72fCIf339e/zJ/g95s7iFkgtKeZu5qHhTzsncqRbJw59foXtH4TxFiLz2ZE/mI5kPvPVug5kcufPkPvLw3YaiyFHbnq/4AjN58iFgvOIt/wpy9Q5y8Q7vFHfIk6aYQF0fePtne4o6Q/Ujrz4ZKQZHPgV0hC8/HcmExNw0vHYdqK4ayiGio+RbF9+G2UPk/G3uhzln+ZzSaKyWfOMnLbLpySbPgxu4IKccNToZvvNewgD5MHH3mLhsoXSguolf/4HAiIzaW+7sJXd3mkrOUJ3g1398cYqGu4x5W3LnsEQ5RThOfPPmDYy0VHrGmTnjpeaSUpZk0fDdZ/ewQI2kDJbXN3NqcgpV8M2rl8iMpgiCRVXxzbOHzFXHrHB8r36VKod1LTk7l3zvnRW3vrfj8ltX/ObDxPLLgfmvt+SvdLxRjOAnjIKv3rLgBuaFpCw133lYIrUjL+HhWiP6SClnTAf45it30NU9EJe8cXlGNSnMmGPMjF9/NSdOE1YlbtmJ2a2O+qsd669Jvvcgo3r9SPXqDa8+SJyfP+Xim++xfOcZv62WZHHHQh15Jcy5aHOKaLCZ5XviG+jMkkfNXXnBq/IuZ6KibgJf/8ElcQyU63Nu1We8Zu5QhURV5/y94iEySxRyZLVtefVQMXOKVT3jN8Yvo4Qh95Z5mvHG9DJ2yNGh5FvTA7LVnNlqRa1z3mwyjN+SiYbv5vepl5plESh84J2bNdmoKJLlG/od6sU5ZXmGtTVfLb6O0rfR5jZfVV8iZ0GVzlCu5CvdO/jDAtwlrx1fooyWAoN0ie8M72BHSSEK3kwvc7m+y2q2ZL6a8Xe618g3DfPO89p2xrLXlJ1HHzp+6907qFGjx4x70zkXcU5pcsy84rdfXSEvPPa+Z5b3PFhkzAqNlpKvnVcYXZLbGevZjMuiRMkCN0r+ztdfY9h0ZGhyZXj5pTvEkKOKBX//Ow/xjacuau7cOeOtVy+Zr5eU8xlvL3Pq8zVG58jMMCskfRHxlWCpBtZvrileyrBLxdu/9jLIHFXM+ObX7yEyiVgqAonceXa7AKri4eUtjo+PhFESes07q28w/uiS8UeXnIeX+ckPb/jn/68/4Y//9CfcbA78/r/5T/zLP/gPPHm65S++/3N+9/f/mH//H39ACOFT29Uknu+PxSmQ8am4y2fM4udiMp9MknxyI/3ZTbX44i3z6b7PnYdPkTO+2Ca/uMgvhLH+DdqvqEI3/I0hUZ9w0j7/yvSFP37u9+fe4CelETebA7/7L/4NTx9fUZYF1/4Wh7jm8ZMj08/fRUjJYYRCRooqO2UznOCl8xzlezbdyKyyXKwFuWroFdx5cIEpD3TDHqMM7mhJYs3jd6+YR8HVjeJpFzFVRjGfUVU1T3eOrDkgTMnuOJ08wTRy//VzGpmxEBPNKGj2E1pr0tTx4I1LHm8nLueK/ban7R1uCMxzTS4V20PibCbZ9lu8hGxZUyvF+GxisjVm6okqoTPL06sDRToV7GqTZTVTTJMnLwu2h4FFISjKnF0vyNLE4BvGOKCXc5a5ZveoZQiW+3fmdG1PiokxKkrlGN1ALw11pagKi84Uj969YZULZC05hIRsB+Z6IM8Ch27gsi4xRclxcszO5sgsJzWex4+3rDLDtgl4aRjbjjzLQQiOQTDPBWEKTEoTgie3hpnJ2DlBNnYUlwWHcUQahU4JmoHWZpzJyDhCFxIYhYkBlQKttqxyiR8SfgiMITJb1cik2LUwNxGZV3SHiXEKrM8K0hS46RPnM03jBjAQgmC2OLL47YHrsuNsMPh8Q6xGOnoWrkArwbU5suozhkWLtyM3acft423K5jX2JjB3FhEDUSYOuWc5KaLcs58PzERNGALGWDYcOe9qVJqzMx4zSCSKLCl2oue8zwhec8ghSwozgmgjW+24NV9hbs04MiGu9sRNizU5GxM485agEx0eGRPWK2wQ3GSe80kzGU+nTsZSlle45WOeLvbc2s/wpWfQI5GAbBM1BY9mW+52ZzzutggrUVZxHm6zHG7xzBw5H2esgLzOcWGkKk9clKtwzUqu2G4j3RDpVeBM59RTy0G3XJ7dJY0OFQRD6E+ciyjZTTcs9JJdlXH0ge32hjVnlOdfYhMC5WZEhEgSgu4sY3HwpKOjf33NsqwQPuEebdhOA4udg1nOcLdmVpbkx/fJxmfs3J66LThkr7JzEYtAJ4HNMzbRsXwy4NM5XZafCkGNE9Z7NrVlDbB2DLVEaw3XI+rZxK7UrHYDXpT0WXGKvk4B5cMJFnXsCEoxVTkxRkw/omNgs6g423cM+hG9nQiV5fzOJZnRPPU958mw/f5jptERKstM5CQnuCpg3UUmdUVSPaOOrESGjSM3qmFllxSiw8SJMJfcq+/zf7jzf2JhF38zu/7J9hEc4POhs49s9vPfG3fgXzz5n3nSf4hJBpe9jFcPeNYduYgFY5+z3bSIwVFgKaLiMCtYHnuihNHqE2Qy9mSpZTe3LPcTU53Ba5e4D26Y3V8z/eBddrlkdXDoN+4SzkoSUMoci+HxzZbi+09I6xJ/a8H4ZEPeTyjv2C4ty6ND37uFO45M/UgxOZTr2SwNq6JE3V/jkqN3I6t6iSkKrpnIf3xDlBK36xk0zKQkFXCdBpZOInKLLCy7Y8Oyj2ATN4zM2ghSQmU5as/yCCrP2ZSKau8Q7icofcV+PnE2zQghcjAdxWSwUWDLkuYssh4qhpsd7TKSJUtsgUmxKQfOpxld52lqsJMglwGD54oNt4u7yFnO9tljjLIYVWLIuZb70/2soXGnzIANNemZ4pFrmQ0a8eHLPP1pf9r8ZYq0a9kFxe1a0XtPP3lkZsmTZHoy0RdzsqEhX5YEkZj6wMxKzBh50ibOLjIoNcfNkUkoLl8XuAeP8fcL8oPD1B5pI00YuFUViHDNDXtWqUTPDCkEBjOxVkuSVWxMw1ItiMcB+omj6blV3yV3ic3uEflREEuNeXDGsZyYNyXDNnLjj6xu3WZ6d0uImpvdIy6OCXFrTVtO1OUcpTwSz9Y2nIclk5PsQ4dJCt2XzM7v88wfWTxzpEVPpzpE57FeoQfY5gMXsQYdcZVAakWez5C24FnYckuf0w6GdgogoRQWFQJP3I5Vb+mGA1E5YqZYLUqyynHFDauhQojINHaMaWImZpikeKYPLJuM6CIhRAYbqZxF6MhN2bGcSlwvCdqyFxMXPkcnz2YZOKsuaP+wJG7XXB96zK6neezooqY2AltYTG44DpEqOLSKHEJksSyZ9hsKGdm0A4vMkC2WbPcDl69cIFBMx4mnm44KTxCCNgpyJZFuZFZoHrcj60Li9jegT0V/VZq4fHnNqCW1zRjMgqdPjzBMpwLF7cSYFdQWBj9x7AfOb6+oZCBsrzkEz9miprxc4jgVfiyynMxqbjZHzs/muMkRYsD7QFlYikyy2RxYr+d86xtf4te/+dbHtk58arv6iyFTfAxfeoHS+aWwqPSZn59fL33mpJQSQspfDMP6JZmN/z+o0P1f3tIv+e2v1T5TWXFzvaU9dmxudjTHjg9dRScKPnxvi+lBG8FhivQCxDSixImA/eFNjxUjU4Ju7xiHA5XqGGJAZ4lyOdCNOwBCtyIERU8kSsOTQ08rC+QIcRIcp5F2glE8J986hdYKIxPXbeQ4tXS5AjQ3bSTLEiZJ3n/Wcmgc/RGUtWw7GBpHQtOEyLGLdF2PqDVBwWE/MJUV4ygIk0dMAS8SWAdZhY8BqQ3BS26OIz5JwqFDVwWtizS7wCQt/SQQs4rBcapIGjSiXjAcPM+OgX5I6CTwwEBEasNxTJhlST9MqMHRR4lNgqmZTrr9CPpjxwrBsemRASqb0aREuzki1YRIkmOMEAVHFxlFxKMRWc40ODohEeMJHnJ0gYQgiJOC1nEI9BGmKbIdPXHw1EYRk2QYPCEl3BTxypwgWtGDFvTjhBAZ3bbDo9CZRTpBjILd4E48l6ctUWXoPOfogCTpnefxswG9zOh6D1LQ64G2OTKUgZDBWLUk2xF1IgwRoeCYTwQZOOTXBN3TygnTD3RZSydPih1OnuABAxFRKqKe2JmODk/KE2oS9NaTtEAFSW/kCcYRT1VS2zidSIUKjjohg8NmFpUSTYqIdo982tPYQAqOrFDI5Gh1IjGChKP2EKEiIgW0MhJ1IEpPa/0J/jM7MtR79tkRMfNEGznmDW5yWKcIKeGtJxBp5MA1B5SUeJ/hyppGTEi/Jzqwwx6UYIwnRZNjOhBSYqM1rQUvItJ1tKFlNCOxFaiYwCV8cjg1ISM07oiPnmd5waA1jR1ACXox0lYWX5SntPfgGfDIs4JoBM3hwGQlQknMvTljr9nLljBNdPsjRzcxc9eU4w196IjLOW0uaXVJN3rkfkR2LcO6gDsrwk7T2gwJZFZjUqQzEjm2pH6gMwIpLbM7S4IeaJ0nRkGKGV1RQEqU/YRMgrbMSVIgpaI1CoDKaFLwdNZCOTIqRVOAkB4xnIqzHeJIJNGVgn6eI8qc2CTIFQOBTZYYGPH5RIyB2Hco6WnURIxH5rMJ2TWELrLM12ynm7+2c/EJmhufMMefse2nZTUlPoIQvDiynW5ofcv1eIUSCicv8KFlHybQGR7PvtAkmaiTYcTQ5RqCISXoyxNvZYajlRl9rk6wu1VJPw2Iy4ooPVOl6TIBUpCVzys3A1PUiBA4NB3TKkfentOMPXFmcTohkPSFROQanUnaPiIqjdMBhKWtNWqZERkZwkRUgPRIJg4EuiziAdYZLgZSphmPe7o7JamLRA0iOcalIdGToqfJwClJsBKlTxLDYqYQWtJYGBaKFEfk1DDYREoCkUmazNONDu0i2Xhg6CRypnDR09aBZhhIXpEyyzG2BBHxueagI1ImZmFCKn+SnHbPkF3GsR4Q4pTB0YWnUw5leqau4cAIpWbma9wCxqiJTxLd1ZZBzolBwJhoGkdHRJcG76BzAiUTgxe0w2mUtJNE3owkaxDqdN7UB/qg8DcOLTRt0AQEInWYUtKnnrwAaTqUiQTl2YQBnbWM+cg+ADIgjcSbgNQWHwMHekY3AhN6kTEIR2Eb+nHk6PeMlSXemSHLni71TCLQTwPHIjFON7hsQDpFszSo2mBKR2tGpqrHFpCaI40aiGMgTJKmEuiqwHzQ0w1bDmFgyjwiNLTpCBbqoMhWBVMGjZWImGhCc5L7jpxkX2NL8or2IGniaS4VU0LESFsmQhwIeqC3J0GG2DcYG2irEUEiHFtG7Ugp4iePkJpGDsTMEzX4GPBa4LRHnRcMmWZ7nOhIeOGZZECXmtR3HP3IdHB0/mVCP9GSKJImFhrvJU2K0CfCsWMcI72J2ELRjJ5ju4c0kktHOzqCS8jhgMtzHt+0hD4yHCeGJGiTR1nDsfMoI9DBsR1GBimJhxErJF0/4ifPxVnGZnPEF5rBBBoXOU6C3eM9lc0ARXsc8DOL9yd5/A+eHFiZiUxE+hA5TJ5he2B7c0AazXJRobTm+tmOw+aA1orBOaSSLBcFWiYOx5YQI9fXu8+bvuc28XMIqE/ZRvFpB+BFKuKL0FJfxHX7ZNI4fZyx+OXcjl9w3b9l1gL+d3Yu0gs37r/4Ai9+EPT9QN8PnJ0tqeqSYnHOrM6wYsZ7j0ZKPKVJSBUIRlImR64FIrNshshcRgyRYxQUMnGWGbQ0KJVTpYyzs4JjJ9BSI1dLpkNGUWQsZzVMLY8f7VDBM0s5qjREN7EqgUwzoukPLcYmOOyIE9y7fYnMSuK2wQ8jy7lhUQpE0ty5KBg6R2oczBWLMlFmOX46sLKCxf0Fu92e4+iZ24Aznptu4qw0ZIXlOEzo5YzMjVgE2zGhXMBay347EFFUMjE0PfZ8TZVLTJE4OE03Bao4Ut5eY/MJt9vz0u0Zx+sjjROs88RsXfL0OHFWS9zekS8KQjOwUolJwNF75mcVup1OuMYEt1YzyosFth/JpITdxOADXktuzS2ZFxyjwOSKWaGYcsmz1nFLiBOhtZ+wlaVEUuWasem5qC1Zrkj+tFlY5Bo9y3myaZklj72Y0Y8edxwpS4MtFdvJscwFq1tzphAYjgNZ69DVjDjXVNFRrgr2vcPkButGgosMUnHrPINCcugSXgj0UTHzAnWUnOUFjEsmKTm4A+dhCcNINJ7zOGd+lDyJj5nyiL9umQeDXjpWxQrZQz8eONCz3M/BKPwCFikjFxUuTdz4PRdDhvYF+5AoJkEmDFEqILIeFEpkqODJXcKiEUmQCKwGfeJMmAnrJSU5QkSu5MiFrAgiYWSHUopaFDBOBLPjrK2JMqFEj7aWvDunsx1RR+4cl3R05IUiaRhuBq6ubyjfKuFpYC4Kjq4lisDtumYtZ5BJ1lPOyieEdzDPmMsVUQmij6zVijIr2bdHeuU484bS5GzChtVYUtZznB7pQsdarZFBEKVgqefkesZBJ26S48IpbCuRAuZBktk53fHA0TtmfUNxZ83Tw576ccv83gVJCUwpWb+0ZHi24+ZwILuemIdAdblCFjPWqqSq1mghMSpiTSLc7NgejqzTnIEC3TdYn8iCRAeHqDWL7QjFgJo0NjlyMWJXZ8has9gM+H4kd5GUoOw9KkRQgvmuAaPJjAYhyCaHHEfiPHLeOkbpKUdImWalBXlZgIxcqILGG5pDjyhmlDKi+kQgskiaFAri+YKmaZkNHXkGKnXMW8PaFsQgGONAJUvO7MUvjWq9sMEnKkYE8VegbD8DlxLAGAZa37IwaypVMbcrClUgzIzO53g/cY4g2oz0dItNiXLssDJDCVgeekRmacWEDIEyOKSYEBhWhwl9u2C3OVC8dIm5PuD3J5u6PARKldFLTSIxQ+EfHxjbicUEqo+o65agBHXvEcEBGcvBY+JIMYEbJqoxQByRczhPCqlLGgfOatbRIIUl+YF85xBBEOuMZgosjpFY59y0kfpJS7Fe0G72DKuCxTERYgQklRNor6Cw7Kaesz5BDkyeuo9oVzIx50DirD/V5pHznErmmGNDGkaEc6xEhQuatN1ThBzVa4LNkEqwnHJc1GRZJAsK1Q4YMSHywPlGkXKJLQu0thTqpCAk4pYLVzOGQGZLxBCpRkiqJonA+eUMf2/N/rphCpHcZWRlQuqe28sK5IynTzck4ZgVirPLil2CfAAlEj5PhOSYlQaXEp1QzEQgpgGVt+hVhT0m5HHCrjVLmWNHQZhaBg1naoZSCTk4VsywxhIINAys+5xoNGJMVI3CUhB0op1pln2F3gRiqlguLtGqxqG46a+ZPw6UcokxiXyTkE1JEBqiYB1yZusFm7ijFAW1LenDU2LYc95YvNfoMJKHDNMLZOdxWWA9VaRpIs8KbJazuH0Gx4k0bTlTc1QmyUfDuNkx6yAUhjhbchEqFlXJft/hdg11MsjguXaei2AJStIFTyCxHCLlMuOKhrMxI+4CQ14wCc8sFEg0KQmWQ46MmnEa6I3nLF9higUy3TBLGj84WhfoK806VYx9AjTzyXA+q+gHzXbyzIWlaxxj51jODJkSXD/uKGxBnUtsqZBaIYeessrROkPsRyrvsArcvKAUCaXhkCs2Q2BVaLRVmARSJ4zQaBHppKV2oOOIRFMsKuYZlJnkKBKXy5qFXbA5TFzMcoarI/Vsxk0fWNpE00yUJielwMxmFJnB7TtWeUbwkfsv3yaGgEmQXCTTGbfPV0xdj5wCY+exdWJ1NicEwdnZgtu31hyOHd4HVssaIT/rMbzgXfzi9lGWQ5xsZYqfjN58Gr4jPvGij498IkXyV3kX6TnHQrzgvv3t+RbwK5Oi/Wu6O5/Bib2Q8Hrx9YXkjF/mrT1v7733Ib/zO7/P7/4//zX/7o/+jE16mUfjA35+vMu9u3e4+nCHUgqjBffvLDDWMmD40t0KlzQpCpTW5DajjTlbZzkvlwyDoRs1Q685W6+JKeL8xDe/+pBf//obfOerD/mv/+E3+N4/fIU7r1jmRcfLcoNr9tAfUH7gtZmnOe4Y48TLdaKqCkRMCKO5l0ckmjglLrLI5vE12yfXdF3P3G/QWSDpkft3FTZrydcRr1ruyZZ+GEEmzuvI8r6lOBNE2/POqxlTjIzecfdBSTQto2hJdeT+3FEulwSXWBeC+Vri5UjjW5apY+oUsdeUQqEYcdGTnc94eD8j1oaoIrpIzGYKnzxNP/JKBZurA6oweOeww4BvR46bhrvrCrREiEQm4OK8wk8Dw9DzoDa07YAbHKEfWOYaJ6Bznjk9QwgoLQgaauPx3uF94EyNNO2RIB2mlNxb5oy9Y+gcK5UYuxbR9ygSD89Bhi0ibHlpNlDILbm/oog3vL52pHFHVTpevxDE2IOcSHlklXdgJcM0cGelyEuDtJJ9P3GmesYhMDWOW3pBiic51771PBRz9vV7jMsrCrUn2hva7BGPy59xZ1vhqoHDtCEPDlG8x372I57aP+FW94zN5V/QnP8MqveQdsOxeMRm8T73k2az/JDhbAOLI6tpDinDCcsrmyV9ExG9wY4F850gjBMTiVc7zVgOiGUiu1Sssg6/2DKuNzywnv5yg19tCMsrzhcDw+Ipbf4eZ/2HbF76M5qXfsj+Sz9kcXHN4eUfc3P3LzkXnmAdKQyMemL2XsY2HHA4Xm1ukyp4b/shqYy8sbtLNrdUq5LuZ1tcPxG9YxQTl+2cPjQM44G1WSJiJAbH6DpeV5dM5YiTA8uYkZxnYqKTLbc542AP9PmArQumuuBQCK7zwMvlS/TRE60mPzgKbRnbjuPVDXd+siOuS6JWFE6gHx+RtxZMtWH9589oh/FUqE4bbt27jb5/hqsMl5tznjXntOWXSKt3WKsFCYjW8Haeket3qcR7zNW7PJj3pGqPs9fcfvozpqIj6gZpOs42Fp9WjGHB+U8Hjo+f4doWcX/BHQa8HQnZyJ3dNc4qwnOM7t1nW5ySeK04v96TtCYKwaAM964LhLmLEJdcvq9JkyMJwSgSr+cr+gTt1ZGzUWOWJVhJMILX9gvGrkDYCy7jHQyRIANTEXlg7jBkI047YjdS6ILEx1y2lNLnTfALaK6UvGDefc54pxekwk97Ko+7D/lf3/+f+b0Pf4c/fPoHJJUxSDjgeDm7pBsCSIPOMhZ7T5AwTBN3bhqGXJ+cwiLj9jARDPhMcnc/4DIIKhIXlvPNCHVF0JrzRz1RCZIQiHnOy8UKLzQexa2Q4W4Op75fFZz9xROCOmVJL65HpBOIoAhe8ZLImOKEU4nV5kilPsDu/hKx/8+8OkGwJ4fwTOZYoQijYwiO+087hkLgLdTHATsEUjcwWXjlBqK2kCRzZ6m9QUqDt4Y34hIXBCIZ8mgo+kiInk5H7j85p1Mv43kF7R4yG95g8vfo/B1e6r/McHaLwa7onyXmfoE3kk447m/mDGEkKIExhgejxsQGs/C8NZ1hpad2gUIp7vYr8J7kJx48LRiubvDblulmz8UjjdMKX+c8cAVR3SCyA2Q3vP6VZxR//wOqv/Meb/7dZ1z8gz2r720Ir/+IO4s9aQnyTHHvNcP6rTWyBnme8fCeYpCOWEkWi0C2EvjSM80Tly99QPZ3r5Hf+pCLr2xRxSN0/QxVPuIN51BnG/KLI5dlohIKkyvE2vAGrzG5SBoEs33BbKhQqiIoy+vDPUIZ0XNL4RX5csW4tuxkx53mguOhZ9oO6DFj5QrQgoGRV7dLYrFGySWFvmRZnDEawS6NvCxfZswMCY0QGZehRJSJadrxUqsYzJFgB7xqueMqvEq46Lh3lRGaI1llYRq5HGYMbQMzzavLhyQu8c0MN855Zbqgf3bKNN65NuAtoZVMreDyw5qxtUyNZfVkSf/BnnE70k6e++19BpegqHlw/hZ5tYJJMYXEvcOa1kZ8ppnHBWqM+KGnH4+8Pl7gTUCoxLpRLMU5uBxPwVu3a8LbHdzfcv6VQJUkeVGTyHlQW4Sp8BhmdYVFMx4jnpxX1ku6qUCoGUV9RjVfMXrLfpu4U+f0aJQtKMqSSkAUCp2VvHVriSjnOCeIUVMXBSIvcEKxwHJsPH0bcAju3r2g6SKpnvHOV15i33qCNKSi4nZdEqNhcIoiatpgmVLO1fVElRRDhDFKcq9wZomc3+LJVaLIlvjZJfupYNgrnj4L3Bwkz7aSJ48P/Hf/47/mv/+nf8i//IM/JYT4kQTtX73J/QXtF2YXnkvQflY69rM8i7+mryBe8C1+Be1XxLn4lL/0i5/jMz7I50qZfyRb+EKa8JOvTZ/871Md8M9/5/f5wQ9/RnNssPMHPBvu8P41zCvNcXtkuN5xGBIz7cnynGf7gVyd7qFT4OAVt2qFNIqnh1NG4zJvyd2OvQ+c5Y47b0bEMqCV5rUHr/EP3vwudlbTK8U/+Wf/G3/5w/cQIdHvFV0jedI4bi0KRgz78QSVmFcW1/Rs0Ny/VdNuPNPwPOiXGsoarsfIyy+vOe4PJCVp+5FFZSiV4Nl+ZEagaSeiVPgEq9qiM8N141jIhHMZU1SIWclZJfB+4KqdOJtnjBtFrko2u56LlWCSPa0wiK5F6Qo5CXonuLidE4TnwycNlRVUq5LoHF0QzPNEHCd2Q+Tsosbte0RwHFGsskToWnqfyDJFbnvK1LHbt9y9XJHdWrLZN2TG0F0PKJ3z5ObIusgJImfnBUqCSokqN2x9Yi7BTZ4pCdASnSI6Rg4B7l/Madqe4+AQSpKJE/xp00zMdKJaKkLytNuG27dnzOaW6+2ebErEfM4kDX5w5LamDZqrIXG5LBgGhVI5za6jVpLkBa3KWc8VTTcihSRKxflXPOHVG67knvUkObz9Z4TFM8Z8or7JsFLxbL5l3tZEk1ABDqZhvp+TyZyrcs9iLAlyQiXJPm+5aJcIq7mqthR9xmHoyLwhrBP3mzeon7xGS4ZxAoTG9ImtmDgPlpgCRxMwQaAKyI3gxgycTZqp6jlkDUZojJAYB5uy47Y6YxiObNPxpCJlW4TueZxfc7tbE5Rnb1qElBTOkk2CD/MblruaZDxtPqKUoHI5h7bhSX3D/Kakqiq2qQUFi6tzXlNvsC0mLqaaom8wwuNkYLW8hTSaazas1Zobn3DG0PYNa2fJ8RzsnlWa4bIAMdCLkZlbkWLONQfWdsVQVIBh3x9Ydytyc5tNZSgPniQUxma0M838ekRKySZLLFYLGDzipqWdG27VC5IUbNJEHsDfdMj9wKFU3J7NELOcPY5MKIr9Dym7x+zclkXxEk3xEludITYNchfIvGK3yFgcEikuaPLqJKE4HTChZbPMWU0Rc+ucY9OR2hHTSawo2OSW+fZIMIYxz0hCkPUDxgc2i/rEM8igV4BWFM1TVD2wvTScZxXdIDh+cHOqIVDW2FnJU9cxbwJTcLjgT7K8oUHGJ2yrjrmoyPw1ZSVppyOvqlf5x2//X7lfvPKRA/HLQkgfrZufTP1/4uAXLTL/70f/gu9v/4z9tGVRnNEqz3XYksmMkN5EuHs8HjtWR5CiZh8S0gUqnTOLhkOdsWxHkoYmV8iQyGjJYsdmrjm3Ja6NhFcuIYH82YeooWNbK85Mjn75Hj2naF2+aYnv37BbFSynRD+OuMoSYmJ2dOgo2NWaM5sxCc/QdjglWOzfZ7E+cHXzM1aru3S3voorzphEYpmVqNzyZLujfH/LlEmEUYyZYL4bUfOMqzQwGxKinMF+YFgW1PsBoRObMlE7SaxzxLanyQXzxoMRbK2jcALnBpSPHGeCsyaBgl0eyb0g9k/IQs+16rgVC/RZ4riY0I1HkGNGyZXuuNUV6CxxTAeyrKDUFrXp2Ykdq75mFIKjaFHaoGKOcoqbYuDCXtB0gWMh0GVO3gbUpjsdU0tEmeh9Qwge01WowfJMdZz1NccfX9LvMpLVZAfQoeTZwbPQJ2e26SdEYSmSpyoynhwdt84s27t/jr7XY89L1iTceMO0mlgMGbEcsZVmygPzoUZGwdYeWYSaqQvEY6BXI2dqhVzOuZFHZqkgiCMyOA7ZyOqYo+qcjbtmVpzgz/II22nLaqghz9nXHnUzEZuKanGfTehY9h5X7NmWLWVWUq0rsinyrL/irM1IaeJQTigHci/RruC68pz1OToLNKpDRkE1Sgon2WY9S1fhNIwzUEZjwm2EW/G0bzgXBf1mT9O3RKD2Co3kRo2sgmXKNQORIGGRD9hZx/W846zLCN4RZIKzirWeI6bAVdqxFguaqWEIDm8Sy5Qjw8DGHpg3lglLwtDJiVVb42PBTg6sREkfNHY2Zz+0VD8ocP++4mpnKXNBdAEl4DAElnnCTROjMGgVMaUmNh19lMwzgclzbhpPlhIogcoV2/3zgrkp4YSB4BiajrLS7Ae4XQmCaDj2A0YKbHTY5OgFvPz2K3Sx4sMPG5SRVGXBeHWkSZo7lxW7RzeMLuG8Y5YlbAFXu47z2hLieOINZobxxpEVC7ZTYlkokoAhRNzkmWUSY6ENUMkE7oBSEVVYvvLOy/y3/81vcOfW+mPb+YUb5F9CiPioMOlHwNLPGN5PX+Zz5O1fdPlPGe0vPv63kaL9FRbRO7Uv7KLnztoni3yczv0kv/1jiNQXd7P4ZD9/5pD4OAsi+CgNJQDfT7jJIVJCC8E0jEgpkELwIlultMR7zzBMJOIpXT85UkrE0eGH07cQAiEFUkpUXTJu9i/EUE6yZVajckN0niy3mMo+l7UD86Lok1VkZUZKkTg6rFH4aSLLDJnVCKXom57oAlM/oYwixYguLFEkZKbRmSGEiHzefxIQKSG0YgoBoSXBB3wIhHFCa0VMEQRMzqGkxGQGqU4ya7awZGWGmxxJgMk007Enywx5eZK6Q4DrJ7Lc4kmUixJbWCZ36icpIImEnRUgwEqFFAJlNSY3CClPUptSorTEWHOSB1zV5Hn2vF8FSkoKo8nLHNLpsynLHJPbk9SpOElnJh8Zmw4/OqI/SfFqrZAhUhSW+bwiuhMZa7aeUV8sMIVlPPZkRpPNCkydY+YFZpaTAGM1xmpmq9lJJjEkCqtJKZ7kbrX66F5u8jTblu7QnsZfAqaTTGSaPLhAP460XUffdhy7li56Ou+wyiCf94d4UZfnOXZWhHiSLBUCqzSlyU5jMUZCO3C930GMJ4njBEnJ03h/LmsaEqDVR3KmUmuU1c8L1YGICak04+Twz+VG0/NnIiWQ6lR7QKuTGmpMBH/C5obBMYzuo0hJfD4XUkwQIjNb4L0jxsA4TVipUUJRmZxpmuinESUVSmkIiRgiwXmkUi+CMBAhdhNSSswn8rwpcpKTff675DRWhFL4biQODpEEIp4kG+NzUpwqLUJJ6CfS4DCz4nTNEPFPdhAT2a0lQgimp1uS8whASkV2McfMC/CB8efPGD+4OfXVc+PyIsBxmn8glcLeWpG/cok5W5zkZeEkK+v8SbpWSkR6/jk0I+HJBl1mqOrE10gugBBorT/O5r4YX+JUhCnGSPLh9PycCIN+c8Rd70/SvlqiygwhTjKNJ/skCd2I8wGsRksFISHj6RZKKrQ1+HY8BTuUhPjctn2hPf6cdf7INgcXTpG6mD5dMOpFav9TrxGnQnrhtMi9+Eo+EkMghYgp7Ulq9rk0rrUG5HPDG+Jp3qSTDUwJQkqgJeHYI8sMqRS4ACG9yJEjn/PCXowFd3U4rS9Kkpoe/bz/iKdVSz63r6rM8Mf+dI10krlFCNIUkPI0F4WUfLS6JcCHk3MTImmYeBFIE1J+9NmKEE9/lxIRT3K0yUdiP53GzQvZ4/g8BPr8uiKduoIESjzvPaUgCUQUxGFCKkV+Zw1akyaP1Pp0PxdPr1GSNDiElMTuJMuZXa6QixKMJoVwer/xOVwiPYdpJIGeV9BPhJsjqZ1I8jT3GDyx6RFaIaRCKUk2KzFFhpnl2HmBVIrQDoh+JPTTR2uyUBJtNfJ5gNF7DwKGZiCGk9StTKf+n+U5SiuyRUW2rE/2aHAwudPnHuJzGfJwGis+nNZMLSFGQj+hqwJR5qjMntaW9iQTL57btdRPp8/PKFKIxMGd7IAUH+0JcOE03sVpM518JOy759K6H6MypJRIY5BJoAQn+WwpTnLDidOcLDKSltj1jOxshnqeCSOejgsp8PuWcOxOkz+cxocMp2rUVipsbk/jkZNsOelkiyQSaTRCSsK+Zbw5ELvTmJRGYWYlCYFSCm01QsgThEkAz/uTmE62zgVEiITBESePP3QnifSYUNYgQqTbHBjaHpPpj9aK6D2T8x+t4yFGAgmVa5w78Rk96cRvsppsXlAtK2xuCMEzNQNGa5Q68dGihHxWktX5czl0KOriNBeezxcpOPFSOfV5jJHoPJHENE0IIVDyuW2QEptbhBAM7XAaOzGSaX2ah/G0R3T99Px8cRoXIRJTJC8zhmPP/umOm/eu8ONnipH+TdonDPCn+BrpU4Coj/agf23H4pcd/KLkyn9B+5U7F+kXvLEXurmfdCd4/vOn/vrJVepznfTCgfj0gS+99QaDOmcq7nPn9oqX766ZZ5rUjryhtygSVkZm0vP6uaEuDKTAd24JjBKURnBeae6qgcpArhOvlKe6GctFhQyGSzVD+xXKLXj1wevMb5+xePUu6+WM+/cXnF0mzi4i/+gfPeT2nYwzdaCeDtybdtRpTz5ueFj0nK0Ea9sykz1fng+o8TEzu+Nrq0QWGy6KnoWe+FLh0P2OpRh453bJnJ4z3TMzjnfqyGXpubuIvLGW3DovqU0iU4mvXQjKXDArBS+vNHdmOdYFbBJ84zWNLj1ZNXF3AbdW9sTLkInf/HLF6lbF7bsVKzXyYKWZZ2BE4L/62hqbHMs8sraOr7xzybwSTPsdf++rZ+SmpxiuOGPi9Ts589wxLwPfurUkE7CsLWdVxne+/gZf+dJLPHzpFv/ou1+iFJ6KkYX1fPPhGXPdUauOb94rUWPLTAwscnh9IalkTyU6fq1OFH4g8x167Hi9isz1xNx6vna7ZD3T3L6VM8sFX331nEUhuHW74kv3byEOA+v1gsvXb/Nb3/sKZZFTzSq+/e2Xefjll7h9Z0FdWx7WjkJLbIq8NEssCklZKJJzfO12Ik0duXK8Ieesh4Ligxr5NOe3f/CQasqo2pzw557rH27YPNlwbFvqf6bZvP8Ufz3y9E+uCO86musdw9Dx9n96Hdd7xC7x9E9v+Pm//ZDhWc/h+shvfv8dFnJG1easOnh9srjyZ/jZh3xnWmAc1NFwrmtejTMKJ8m94NuHC2zKqRvNYmd4p79L/bSi3NV858k9ct2Ryy1mt+XtZoHWO5Le8VvNl8mdwF13uMbzreHrLPI5czPj9XdfQfSSuI/oQXL/z86RbeC463jj/Vc5DyvucUk9Fbz6p7fJB4tuJev3LdVYYCdFJi3f3D2kmHLmac6b6k2WckGdSvKg+M3mDYoItVS8ku5x5mqKkKG94NfHr1OoilrNebh+g1vlm8zrt7HlS3xn8zJqnLGQ93k5u8X5wWHaG+L+Gb9+Y1CTJz8MLN47cKeTVF6iXOKd/7gjPDpQ6YLbizUXP96Se7BK8htqTXm5pK4yVhPc/dEW9e4Gsen4mngDUb+CXn2dUl3wMLvFTFpKYflufcFqPXFhr7h15nnYO7LQkvuGL//0hmxSFJ2mHCSv/OAZpunJlODL40QxDlRDR+FG3vngisJ7imHkzQ+uqPrx9O0D7/zkKaZzmN7zpRtBPiXSwTFcN3ztcaJEUCfB6xvP/DBSdAN2HPn2RlAKwVwq3nAXLAdFgUF5+PLNq0ijMXlBlUpuq1sf2fIxjPzpzb/n3z37NzzpHv3SNeC0cf/Yjn9kr587wS++3159lXvFA16fvcUbsy/xav0qlbJkUfBdLsgVzIae4v0rXmocWXIUfuStHz/FRCgHRz0FXtmNFEmQ+8Q7PzxgR0cxBopDz1cXa3IpyCbPGz/rKKZI4RKlzfiqmFF4i9l4XvvJkdIliqMjc/D10VI0E9UUeOVpT9U6yqSQh4m3/vwaMwXywfGyfZmX5SUv79c8KO/xG9UrFCgqoXk1laxTRt6AjZqv/ecj+SQodhMP1JzzXlL3EjPA1/5ij0VQHEfu7CLn1yNln8g8fOsHA3LyFJ3nchu4deUpJol1iu/+KJLpgmqyLMeClw8Zsz6jijm/8fQSIyyzYFlNM+5eL9B7iW4l3358HztBOUiqRvPabkVOjk6Wt69fpggZK7Hg/Pwe31n/Bm+o13l1vMtv62+xLpfcZsa5s3wrf8hFnbMcRr7R3qKMsAByBO8c75LvekqX+Jq6T12UrM4XLG7P+e37F5w9PHDx5pGvv664+3rP+deeMnt5w5fKDfOvvM/i6z/nrTc85fkjLn7zA+ZvXfNds+TyXLPMHW9wwX214HxQlAfHt3/2AD0ois5wvz3ntluwiDkZiu90b1IsF9TzJXfjmttyxaLMqBcZv96+TZmVzFXFZT/j8qqiUCvEYPj27iF6isxVyaVY8vriIWW2IqvXfLe9jQ5QjoKzY8brh4LaQeYFX//xGr3zVK1h3lge7i8oKci95lv7O1gM5aiZecub6SWyck1erfnu3d8ityXzcsmsmPNO9hZGzrFyzrfqlyiCItuN2O3A18Y1ZVDUwvL1sGQZNHOXyA8t3/5+Q9VM1BM8fLKkbDOypkYPBd/cPiCLgjIIXncXrFJFMWoslu+JL7OyOVVQPNifse4LZt5S2pK/p7+OFTllKnh1dp/bKWOZeYrC873NjCxuWOYNr1w47t2H9Xf2zN9q+MaDBGLClp5KDTy4LFnNKzKheE112MyQG0XpJmZhwIjI+vac33pniZGCea6YnlzzoJbIwaERfPVMkducOss4Wy95+6VzlNMYmfP1N+4TnSTPZ9RlwVurmlJoMqH46r0SowU6elI/8Gsvz0EkisLwemXISNRaYJXgS3dWzOo5VVnzxiJDxUAmBJnVvFYrMqUotOG1s4oqs6gg0MLwcDWjqmYsVitKbfijf/FH/Mvf+2P+w5/+CB/CF2ze/4rwzSfhQJ/dQH9kZn9pZP6Lm/j4+yNY1UcQ2L/BdX5B+5UTun/Rs32hR/VR+wVP8td8wL/80DPZWzTDwHuHGd1Nw9MfPiJLE2Ex43IteLofSUZx9JroR5Z1weOQkekjPoDJLM3kyZSkUPCoCawLxa4dWGWGRx84ZsUSVeR88LMjX3s7ngopjSNDfMZs6VFK8Xjzcx58aU5SDXKzpekFM22IMbFtJ2brGQ5HNsF7N9fkmUUmeNI2VEYThMBMA7vRU4eBtOs5Fh4tAlnqqONE5yO31jn9MHCzHcikxhDJQ+LGWzLhmZDcdIkqL8hMwgI/eNoACaHg8eFU1K9eFhQi8v61p5CBzbMbbK0oFhkCR50p/vxnN2SMyMwyBU97bDm894j5LOdH7zesZ4FtP1AZzfZJQ1lAnnqujx21Fewbhy0lv/bmPX7zW2+SWcsf/9Ffcnmv4vEHN9R5xnb/jFKN1GXG+1dPsA50PEWNnjYBqwRGSa77kXlhGZKgriSt9MxLQRAjm0FQFYmhglJGDmPDotL4sefdH/6E+e01vu/JZiU//OlTrLG4yfGTn1wzdDDuBmqj+CBkZLkhzQsedaDLAtpEbhUfNoIqlwyT55Ak4mZFv9+zVpa/uHeFOkjyVYV6PRF8YMha9CGx/bU953bNUTT4xcRTHuFCx5Prlu1sj7rWjHPH2Z0l0xQYhoF8VPz52U+oXMHPhw/JRsWTyxtiKbB6xZ+OOfP2FRwj0xSY8kSGIY+Sn+qGrFe0RuOD4tHRY2JNPhr+ov4J0h6Y9A2dcPxg8VOi7hFR8CfxXzE1gWB6hsOOP5r/MeF4iqQ+ufOENTVH2+C3nie3n6CcoMLwwfoRRW/Js4yFKXn//jMKn1MVOfq1CnMwZMpiR8HPzVPsZJnUCSZGCqgEucz4Uf4zyszQxo6b/AoTHCozZKLkx/yUys5pY8tN25HqVxCuY7me86jwLLynVZ7jlHCrA353Rd5Lvj/PqfIl49TTEmm9hEliG8/PzzRmiPSP92zRqHWOvzpSVgV/WUJuTxkMXc/Zv3eDcA75rOE/xQa7WOPOMqbZjCs3YlBYIXm/+TFV+4gh7ii042YpyYNF+ciHtyrUpNGiQMbAk1tzxPaIXFQ8fnmNedQgCSg/8uisInOOEBNPL5focCq0Zl3gw7sXZC4xIXhvbplSSSgE47tX/GDmUG2HSoFnScHjhlgkVDvy05UikwYnBdezHhEzdBzJteWH68cIaYjasU0dV4cr7uan6uh/fPWH/PTwI3rf8ah9n39w9//IMlt/of1Pn/j/RSVYxCm654fpVLhLCC6LO/zjl/7PdKEDIfhnT/8HtIioLvDj7DFZuofwIz56NvOE9iNaBH52ljFD0IhTJPS6ylBjQMXEo3slGR3d5NGZ4cnsJENNN/LkToaaRmQSZEXBz3uP9gr/dODxaoblFIm1SvNeJTA3gQDczAw6SHRZoN/f8uFLc3RIOAVTnfH31G/w+OnIl27/Y/5AH8i8I0XPVZhQsUYEje0E79+pyPpITIpmoREpILwg6+EnlzmZO3EpjpUmuohKEjt4frRKlGOirSTHXJCkRCZFHgI/fbikGgK+ECQj2AvIEhRR8dOLA9kuMQpHP16x1SNGZNgeflRfY6ZTYc0QHU+rEVzASsuPx5+y3NSoSpDrjNfnD/mtB38PmSQftO9ytdnAOLIwBdfpXcppIIrIE/MuhQ8cmxuyKHh0BpmpSDHwXvcBYlpCnTARfnb+fRZLTxSJXu2pp0QrB85izhQ3nPkOJwKODedjYFOOnOsFk4ZFrphsoj0+I99MqOOBKlS8e/EBta3ppOCYOkwPdm1YlCve1TtyWREzS5N7RPcItXBUWcH3D/8ZMUaSHWidI64XJ1Wn64kfhJ9TqZxYJJyHm9wjQ0kpNT+aD2RNxnHsmYDO7FEBSp/4fv8TcqXpoif6wOP8AB6k1/xk2WIOCmk00UnedVtiOqEp/ty/yywrkMohUfx4fEZKFp1bfjjtEUMi7DtMzPmZ7bFCI8eB98drxDjizUg8jPx5Suhri1qveVxI5FSA08gp48fzHTkSLxP7O4LhKuIHj51bfjD9hLxxqLmimzWIAXTvyFPBn7sfk8uSkHqe9ldk6wltHFUw/PzVD5mlwGAGxruRWCUKEbkY4PEft2RRM6ZElJrrqwknBItc8XQosAa8lCShmdIJ9ZEJ+ON/9wH1rSXtfmRhct573FEUJWnoeTRkLNYVwzhgbckP/uIx7hAxdcaPPphQuiQhGVvJD9/b4ceAlPCD91uMOZUQjZPnJtSc3VqRUuInhx21nEjeE7qBD3yGEhZjCvZGI70geI/rRh6rCmM1MQjevx4pKnMqUqkkP3jc4DzYzLDpPU/+448oHj/l8t45k/N899tvf5yp/8ye+JNlFX6pcX2+Qf6kY5HE34CI/Zm99Wdf96ugXfwKnItPInHTJ1aVT7Rf4lT8tfyHv+KkR1ctj657usHjpoEnP9ozxYzBwTgoQhgZgoQxIgbHkAxDG7juB6wydD7xwc7hXILM0g2OIglcMzCGU0XbqR0Yn+3RWcfF+YphmE51IvY7Drs928PN6VFdxA0TTgvM2Yz+/QNtP+JCZPKBNkIXI4PziDyjH0/VR6d0SjN2PpIKgx89vQ8k4ObZDqLDKcGmn9CZJYwj7eaIEgXj8ZpB6lPKXhmOY8DHwNQ7chXZNY5xTIh5yTAOdN2ELHKa3UA7JopCsR8HxquOkASNg+NuYt97ximc4AUp0g8NIl/w7L0bhiAIx4luGimzQJ8CR+eYQqSLgS5C7zxGBI59Rx8D17sDL71yF0hc7w7svcdnkuumJSDYdz3OSpQy+CnQjo5iVpOCoPOOcd+xXC4gCiYt2QwTxgiabiBJEESMTHhxSnVqH+iHDoDV5cmxODQdMQk6l7E7OJKPWNfSDtBEwahOGMu2G/HAosyYdp4+aJJzZPOcIU0c+w517EAmuqR44j1ufmCsbtCVpQgga4MMio3aMcZIZx2jdqgzCMIj1hJbGY6+p5Qlg3E0ZY8SmlAODGHiR/1jcp9jb5fstiMpeVhJGj8wl5eMdDQiEMWpOu6BCRUSRikya2nCSFLxJF8pBIfk8WdHhnrD1h7ow0g7HWlUi9KCkvo05arEU3dDbhp6PQIgvWSWzxiLkezejC45mqIFKflwd02tcp7pLU3d4YtIU43URcluO3DItrQmcC2O+MwjY09EcuOuCMlzDHuCDlwzMGnNGCfCMJLlgp4BZoqpa1HBMrmBIdSQjhwzzdTvkfMagmJM4OKBvt3RzCKjdBzMSG49bnUq3JWcpMklvbUkl7BRMJSaNAa0CjRW0LVHlOvJZyW9FYgyI71xQbc/0B0GtIvorqVLA8H06GVBmzwiSebjDdbd0E5HoqwYH8zZHwSxnyjyHEZJqzWsSiKRrgCSY5wm5L01zaEjUpOSpi9yREqM4yni1eQWpCSmSJefIDlNHJhMTVNEwtjTS8dYSYSQRCTEwNFCNAVTmEhJgLGMwxbkkSMtPkaivgbZE31gIedct4+5He8hpeJ6uOJZ/4QpThS6ZDNef6Fz8cJUxxgRCKLzSKNPMDIlsXXx/MTTmUZZFsry8/6nNKFh018BCakegA30KwtJgfA0KiIWltqV9EhGa9jNS9DQZgpiokojKEOnE+asPo3RFJl0pKgUlJau1twYSMlzHAKjgNnMoJWkzQRyXeDGgW5mTnBQqZDKMCjBaAVRW6bsBAt0q5Ldk47L+S1UnrObrnmWRiIRlwwSR1do/CIjakWKDqclwkRUldEeRoIUeCUQKeKUJiZJjJamkEyZJGiBDobeCvzKkoTgaGEoFJKEHuXpZwu4SFcq2gROdohppLUBVEPKA+5C0xxHzDggFXRZQMwTUkda26PyxKIbGA97glQUZcFO7Xmo3kIguB6v2Y9b2ul4gqjUhv1iJOgRcxiI84ze5lx3IyoOdOYkXqLHQBocx31iDAd0gm7qiJNjeXEbUWUcDgd86pF1zyCak/KVOMFHfSVowkQIHoc/Sa4PCX040MQWucoZzkdiFXHBEcOEioHeOaJOHIl4J/BWQZ6hdOTgNgzdnlAJlLEMYiSuJMGO7NoWrQQim8h6z4giKsV4cOzzxBFFCg47ZDRxIlpP0D1NnmjiSL7SZD7QaY/IB0QlOJiOJDx550llRmMCyI6QIkfjST4wtHvGeclxPJKEpBkibQbSK4rNyLgJNDqAdATnGPxAcgNVEqhbC7pqjnCC0Ha0/RGGG+qsgCrnqD1JRLRp8FmHIBHaZ6TCcBwnHm0+QJ9p3LnHx4EgI4iB1iRCe+AoA84pnAwgHCrzbNNJ2S/mICdHUCCWC8ZhYDeNjLmhVQumLjBKiXMCnRUc9p6UBE5rtIKmDzjhT3Uacs3u/T0EhcTSuIngEiFC07eUdUbAsn/SsT9MCJUITaCLkm7vyK1Ha/BJ8MEHO/pJ0UTFOHlSASlKOn+Cbbox0uuTHTVVwfVNQx8TqXPgBFMU5EKRBcnQB4YIYhI0+5HxOWw0SDgcJ4YoiEMgNAMRh4nghw4jI+3NnqQlT59tP72lfc57+IUk6ufOREqfcRx+ge/xS9uvIBvxN2l/a+fiY1/il7/zF0VBXmQwvtCt+IyfElNk7xpKmZMpyxgGhjgw1wsA9v5ALnPuXlQ83rZsh4FlEhzSgBMSm3mEG7GVZd8nzmw6Sc+2gYyEFAGlBBLBKoNJQB8HcgtZlJQ259g75jKxtBmyqihXNXVdorVks9lSlzWz+ZzFYY7JLDLO8UOJJHFxvmKxOmfz6AqlFSZq+l2L60ZyIvksZ1nk9ONIqU5qK0rAIkSGlDhbVUQEqR+w1rB1PeusoL53TrCavVaIPpGvL9jGRHkc6KaRfF7QDI65AjEOjCqxzhRJeTo8tlbcujWje3IDEu69vCS2icPOE4zlbGZppoFYCC5nBVOcQBs2u471zND1knKVUVpNcukkMegCFxcL0hR5+mxLnhmMlCzmmnKVcXH3nIvz1Ucf9cV6wcWixgpB6RPRWlQELU68iurOisdPt5yvZ0gDx32DC4mze2umqxYz11STwGjY4LB1gfaJizsLGhIzrTg+fkxWltS3l1R1BVEQouBiPacbDbn2NI93GJ7X0EiSpUqYDKQPyCzDDh2zzHDdORY6UhWK3Tiia0M+OoSLzK1gFRW6XdP1Pb6EujWMxyOPSeRPLJfZ4iT5Wk24RxO5NUwqcCud88GTK7LKkp0ZVscZSQSs1Jijpuig70cgcS/eJi8tOzEgDpFyF6n6QKxHztOCqAQyC9hRYSeN8YJgAxfjjBAEUk8oD+q4plctgci6mzMdRpqra9Z2Ti4ylFcchpY3pvsoo9m1DTiP20emJx75QHIvXDCakfcOHikl/bMelc/IzzL8u4Gz1YrcZAihyFuN2mh2tmGV32YxReSkSEXGylyQtAcSK32GTRO9D3SuYRlriii4CluWvkK6nIBgKCrmUwlihko9+TGSG8U0Ro4psnQlgyhRXrCoK1SfkTpHNwTO7HOCWttTTwktDb4bUSGy7iLp6BALTV3MYHMkXW1IC8tqqRBliV4uMWYivrchdSPEyGzfET/cIh6sKJczKrvGugE3Cs6FZShnqEzhfvwEe+iQXkMRWexbROnIvUD4gJl6yns5WE39ZEcSGXnvSEZRTAFGR1rPOds3BKXIh5GoDcZ7fOYgKPKbHtPesFivcPOSbNujjGJUgov6VDTweLNnbAOrmKGKEplnrEWBnyJmFjn6A2UqWdtznjz7gPXFJWfZBYdiR+c7KjNjlZ1/zAfkBHPyPqCN+XiVkwKZmee8gs+Gyp6f9PzvZ+aCStUszRm5zkCWJFUwhT3roPBKU1iFgo9sxmHynLcTQSeME2jACmAaoZKcX5QoZTHjwHR0ZK1HuAlZZVyYDO804nqH70bKEMjSSJgpLuoZ7WYgi46gJVUb0LniOATqw4jXnskkQqEptSV/fMV4qUgEltJyGTMGPDMkOiiGZqLe9kgV8SLQZ4q1FsghMTWOWXviA6RM09rEwkfiOCHmmqqPhBQRSiAKxWoUBOeJpWCGQo8n3sUxCdZDIgwe4SNFkojWEo4ZQsBZtOjLGZ0E6XtMN5BCQsiR8yEnKI9xiazPmNsZ2TBx0xypbMl5dskxdSgkZ9k5i2zFIAKX9pxWB7TMkUagpMftB5LznPsFEU+ZAmiJcRmpVSBaLkJGGhyVKvAiY9FabLkk5iP1kxO/a14smFRgPV9jAjzaP2N2iAibQVnRi5F6TFTaImzBeXWbIA1TEnSiZzZ6stywTQdmu4zaVvRNR9P2zKTCzjOSrJmlApkMcQjsQ2Al5vjBktyAmTLyVCLdSG8siyanPYIqK/IuwTigJwMxsDqOBKXJ5hrtFMWksFGyi4kLsyJVlqzfYKuS2AeY5Knvx4IpeWwm0LKg8JHyoHBZzqU6o6rFSWYZgdEGF09ZsbU3xGNL320hyymqNWbKCGpi3WfEVFPnGdNxQ91E7P0V0d1wEUoUkSg1Lo7UI+iqQpSa2SOHzXNiPaNXEytVkUJPHK5YhZLZlDEpQ+uOzHyO8hOprJl1Bi0kSSWa1LEMkWiWiLBlbmf4izn765GNmliEnNQlhNRUBmyVcf3oikJn3L1dUZ/NeHbTMw5w+9XbKK1oNkdu3a0QU2DTem7dWZOGieZpS8oVCx1JGYggKJ/zO/3U47DUMaDLjNgHrAqsZxqZEuNBspCJ1bpgfxiYrWvczUQ/WFIfuT0vGAIkZSiWFbJzjDISgfNCMfrIEE5QolycRGiEUCwziTE1IxNJKGwYuHW2ZNu05BHOl7+AIP3cifick/ER2kl84rRfjA/6BZf9Kx2LF2UhPr7PF6RV/obtV8C5+Gxe5/NnPE/0nIh6X3zK514whol/+vgP+B8++F3+7+//c/63m3/L//Tkv+d/efI/8rtX/5z/5dnv8v94/M/47x7/E/I3DrivtqhvjCy/NVFmjqgCZJqvPMgQJseHxGxeMFeBEEHajC+tJYMTCGlQIXBRBf5/zP3n0yRZlp+JPVe5Dvmq1JWiKitLdXXXoEfuYICBJLCGXXCNpBlpNOPfR9slSDOCXC64C2ABDIDBzLQW1aWrUrwq3pAur+KHyKrKqq7uGWD6A69Z2hvp4eHh4X7v8XvuOef5BSLCKF4+HnE1JLh0TnJ4E0LKp+9fcXbakhQp/+9/9T/zP/2bf8m/+vf/jiLNsf1Au97x8P51kmRNXmzIiy3v/NaYk4eBo5cdf++/ecA/+ttv8EcPb/Cto4p/cOuA/+qtl/jWjTm/e23C9VnBjeMRh/OC333zFrOTMZNC83vfvce9b025eT/n5ttT3vn9l3HCkx2UvPO3HjGeaYbzc7brBbcqS+86hPHcuZ6TV6CEwwXLXd2iUokqBCeHCceHkdksMKxOuSYucarGiw0pK6YTUNLijOfB2OFdjUksheq4NupJ3JJUbnk0ligGMuMpwsB/909+h995+RZvHs/4B+88ILtpGd+JFIc9x8d7pzCGyO/+zmv84d98mz/4w2/xT/6Pf4f/8//lH/J3//Hv8Nuv3eXvP7pDPpeMxhE9rHl0b47dLCkPDN95/Yg0XTAqV0yqFd95Z8RoviTLTnn7pZS//be/ze9991X+7t//LX7/j/8GZl4xuMCtG9doYkbtEjad4v69l1itIqtakEVFkY7IqhlmfMA1Ywla0rUd928WlEWCEJK681S7S2KSklQ5omkYqGEEfiy4fzGhryx1rEmfBJ58cEZrB/JZyfRHI1qzL6Z9vXrE9XgMAi7tipN3ZzTZjkH2uI1DLxSdH2j1gPjTQMwFWgnyRnG9n+ODo6YmfPwp787+JRfX/oLd8Y9R2XucH3+f87s/5Pbxjsu7P2F59EPW4++RTT5lcefHLO7/hPuqok8tQUXyPOd31VscX5/jR4HRBzlrsWPraxrRYn/csYlbNqrhpdMT0lyyblZ8sn5C/F5gF2qcdryxvUf0lma3w2uP/77jtF/Qx57sXHBVLxlCh80c99tDXO4JleCkvE4qS5RICQFeV6/QrJaEuuO4rkDlDIlmbRvuXB2za7cMXc/cKSZXn5Bs30f173P/ww315Q676Sk+GxhvZ+jiBk5OeS3eQN46RFYV5qKhWG4Rc0U/Fdx9tmUoPV61aN9RrR2287SD51U5Jc5n+DYy/OgZ+bvnDHbAjlLeunuXeLiPPIgQmJ31dIua1aeX3OQO9eQVwvW38PNH3DA5QffI+xUvtTu8jEQFwUiunVqsHDOIiptPG4bLBaJUyEnC7dMF1giclly7uELICNFjjeSl5Y6QZTijuLUKVENJaStKfcKN907p/A4xUhyaDG0SslmJPKh4PT8mTqfEvGLWTRH9DQg38foWr6s36LAMPpL0ij/v/5T/affP+Wen/1dO0mu8MXqbb83e4benv0ex00Tr9s5BiLjB7Qv1P38YPi++Fp+LnL6QKxy/5DJ+0QpVUiQzei3ZCsfLcUw/fIYIF+hwwbU+0gRLGywPHAwhYkPEEznerGAUsNnArXVLlAKyFFlk3BgkTkQccOvCIVSOLMYEmXLjfMngtsTMc3Nd7zG1RmON5taTLTbVeCU5XDSoLMFZhzOaW2c1g/K4ypALz3+6+tf8h/GP+ReP/5+Urqcj4hAcqxTjAtE5rIZbH67oU0nUMJMGvezwUtAbwUsfb+llJBAZN55iYwlKMySaBx+1OKWQKKoaxmsHQuKyhIefOkJaoFRBFTJmmwGvAq5SPHhW4mZ3kNVt8vIeN7Jv0dVz+v6Au09vsA2aziV4m3NUlwTjGUTDLa6zLixdGdj4DR/Gp/yz/v/Df9//j5ylDeel4aoquCozbmZ3sDgGYXl49BrZ7QnZNEO5hpfPRsgsYg5yXpvfpZh6sqRD6S33+gmdigyp4maYQHeFNDXJHc0b1SOG8ZhBZsyfVcSrdi/4VioeXs2x9RWi23HUZMSkxJ1M2c1SHhRv0ThF32vyiwIzaEKmsTPD/cdjHB49KqmGEXoBznpqLLefjKnbFc4O5JvI9LLDpA6TNjxqj+mzfbpa2sGBvobroG0cr4YTWhxBevTguU6OzDyqdDxqDwi+Q3hLmhjuyuvE1hGt563uGlH1aO0w2vGyLskmAzrbcm+T0YlA7wO7XcO99ICY7PB6wyvjGepaArkljjwvVYe4e0fYOzNumwJ3uCUcb+gPF9wXKW4E/tqMa4d3wV+hsppY7HiwHeNkixc9J11Bf9bTD9AmhlufTFjvBvqomfoTVCxxUdOnmjeHY9KyZnQQeSkojpwk9T2JaHn9dIwTDUI4Zn1gEheYaxtc+YS3HzqSP75i9DvnHH7nlOmRhwPPcBC4bmqK0YSA4uB4Sh4cu2VLNpvwxs2Ks0/WVJMphU64fnNKee2As/M1c7mlw+OUx0fL2EVEnyCHhFt5RjeUbJuEPpbcPKjwToPMeHBcIUWFdBlK5NwoEjYXA1dPG+5fO8CMjkFPsL5gLgydzWg3iqMsA20Q2lA7OEg8MstRec5RaUiLHB8lNhpuzce0PmXbQJVPEDHSND3PPrukcN88+42/Qvdij//+fPl+bzf/yoDXb9rtG2o24IVi8L/0AH/19htA0e6+uuFr0YcvXn9Te77q9bk8+ou/5Sfr9/lfzv+U93afMjdjhFyQKs/Ob5maEywJZ8MVEz2i7k5QyTGL3Zb0x4HFf9Qsl4ZcRdAaGQKrLnI8UvjBctXBKDd4ZykSRR00ma+J2rNpPYWRRBlIoqeNirnoMLGmbmvSRPPgt6bM5oGr1RWH8znetayXV0ghKIqSVBkWqysOD4/ou5663iGV5P6d+/yDv/UPGZUVrh2QWqHLFD84fvAX7/HD733As6cL5ocjms7SdQPeeSbHBjPxLJYLZtMZiytJ3QSGwVHpjMWHF1w1AwejgraY0QmDM4pJqqEeuFh2lBqSwzEi0eyc5/pUkdqaq+UGtWlxIgWh2Q6OQimKgwnL7cB8WrC+vEAIT+8jJ/OMxPfs6pr58YxuuSYtErZtx0ma80/+6R/xyu3rBB/495/9Be89e5/Vdsnta3f47W/9Lo/uPnreJz5PoxMv5FJEYoj8z//qP/GDn77P6eklhY0MzmOlIB0XjEbgrhasbcPxbIo5StksLnGD5eV7D/lv//H/lqqqaNqO//7/8S9594PPADDZBFTOk/MN144m7NaCxekOVWaw68lVxjJoxnKv6Bm0pq0Hrk0qfB9Z+4SSjk5YBu8wZcHomifOOq6wzHyg+Zv/EX/tCU05kH3mccFxcbglWWiyImdbN3SV5XZ3xOB6NocN+TbholuSiQRxKDlaTaiHgW4+wCoiMAwbT3Yz5xV/A5UbzvUC1Ugut5eYXtAfR24N10myhGW+JXMJWhoKci7yK663R/S+ZanXaKcQnaBSBaflFSf1lC6pOZcXrLZbRr5kFCsuRlfcaU74bHtOnESCjyRdykiMWM63+A96bDKQHaTY4BjbMabXnI2uuNWf4HRAjTQOR3E+Ia9nbIqe17LbjNuAbxqS4xGz7AAtNJfDBVM949Kv2e3W9LFnag4QScJpsubQj8F2qAidGjiWRyS9ZpU0jG3OtnyI81NqFZi1kRgD6wND2YOXiiQo6koz9wK32XKhB0ovQSt0bVlKx7zWSJmxThQZEukCaZKwHRvmXcDbgbVyGCTZKKdIEi7amtHjDd5FdoXZi1UqweTGnGUSOZQpjsAmWhQCXReEDxqu8oT5rsehaFKDCJHM1mjfsr4x5VgkNAtLKzQByK3HDJblpGC2aRlMwmA0USuyocd0O5ajlHKxZuseEw4V8tqM6nkR/TPXMCchFhVD79ku1owHjw+WdeKZRY0vf4opNjSx5chVZGnCMi6YmjmvZa/zj47/6fOhuye2fYHK46vD+MsMWfENecJ86Vh88aHI4/4p/3zx/+Ld3bsYKxFuQqbmXAxL5u2UkN1jicH0jiyMydqEZWY46QfIW9pqXz+gux7VtGxujrh2cICXCdu+x51vyLuAdpHdy0ccJxmbj57Rx0AE8mEvNHp1VHKSZtTPLvaOnRCUO092NOdysIyvaoa0ozcBDitOxJr4F/+W5sRxMLnB9ujb2OKYLnpmqiDWnrPlmtG6xyYeZKTLFMdHB9jzFQvtGW8tVgtkhCZXzDrwzcDmMKPqI4O1aCFoJhmTRYsVgvXEUAmNtJLES3Yjw6QbsM2G5RhyKwjeYqxnPdXMVg6vPKvMk1qIwyWiXrIuLSexQI9a6nyHGiBxkjQmXCUb5puScDhmKzuUUJg4Qdqcs7jmhp6h1Y6OLSAoZEoS4EIumdUFfd3SK4vIDJkqyIqC0/YZ44Vh1ya0MeISzdRotBi4yjYc60O2TtA1PR37fpkZx2JUcxAmhG6L8AO9doy7CSQVV2PHnDE9geigcTVHpsD4hoVcMC9O6HaeUAdq1TNVIwIdq7JhkkwZtmsSbdiwZdZVCOvZnggKUWJbD4uBldhxKK/TuYp1CmkX8VcDSa9Z9Fcceo+5B7uDDt1B2uzF767YcqwOoJBsZIvqAmYyQScFp80Zs7VGFo7hukbYCGcR2SesZoGDPseaDjfZp8Qk3RzVjfjs4ikHXUavoNWBECOVtCjTczntOLoyuH5MbyVeCcrQkBQ9yxPHYVcQRUMwDhsteTNhaFIWmWXuChwdUTjcLGGuCkTXscxq5maKVi1xtaVPHDM9w29arrIdk6GgM55oA7XumNkRHliOO0ZqQnMpiRvFxgzM1zdof37E2RLSGLFXAt1AjeaglAx1x1UbmMwz7NYhfaTFMEsD1kATJGHXok1EC8/OK27NM8Kip+shM5o2ODpv6UTKresl27qldRCCZzQuGec5Tx7XjI0lPa44fbpECMHRUUGWwGdPNoxxdB6C1KRJgpQWnQmuukCJx0uJUBrrApnc0/t2KErpAYd1liAkJTUj3VH3HdOq4L/6g7f43/2f/t5XpsHii/nQ5+bxy7qLzx0LIcSXToX4K1dWvPAF/BXn419tfx0U7W9eofvX/urPgy1fXrRf+mz8cs/PwbXOWmJbI7JITOIeIxYDrrc4b/GDxbcNITiCi6QmRycGgmXoLZnaIzO983vQ7PMcthDBhUhdt+g07PF2qSbIiFYaJSVD7XCJRHkQQiKEwDU9bWxB8WXBohR7SooQeP/83NoBISGGfTgthEC7bRhPp6R58sXPVlmCMHrvZH0OVAlh/ztDJMTA0PR7NGMIxPC5YmPEO7ffB9BGY4qUpvGEELGDRQIewOzRlq6z6DLDdnsqQ7ttGWtFkqR4B66zpKMUZTQx9PjBoZN92NM9R84J8/z7tcRkCUPT7wX0phNEmWIOSnSRoy7McwrBPloRQ9jnDkq5n1fEFyYmcf9CKIHQe0SuUJJ8WsG2JcSAHyzOCnSRwLpGjzIgoMcZhpxsWu7xrlLu+9kLA/ILGkKI9Jdb6mUkqj3St6oKhtox9JYw0ugo6TqH1oqm7SnKiuFyYFwZqlG2T30Se2RdVArs8AVSDwlKCpwWrNuOgMBFjxR7lfW0SMlIGYmUXg9YZymShELl9PR0foAYUXLv4BptKCYVIpWEQe3F0gwkWnM0mhIzeLf9lGyjmE2mhDQQifjBMnhBMM+jcZlBJgmy32NOXRcY3ID1e8wjz8mcRZ4Rtg4bPGfbJanRtLEnSRMqUSC9QivFbDSBPBJL2PUNi8WSIzNjWlQcmAmN7Plkd0qWZ1RG78eHFLjgiEru8YrPx054Ps6j9/uiNCWJw/6hqfQ+5zq48Dy8G56PAU8UGmLYp4OVKUkxoalrpIj4ttuPJbdPKQk24jcD/WYgmojMFMEGfDegjEZoEIMkesAopEmIux63qbHBYLuAqAxyXCB2A/2zFcJoxElB9uA63bM1MVjQCrqe7vEl8aUpUX4JB4lxj5lU11NYNfvfqyRBCKQSEBRSaOgGnAiIUblP05KCKPaLMCFGwud0D/bjSnoPShGlJGqF0gkxN8QQMVVG2DmGTQ3TdH8MIihJDHb/AIh7LHCMAecd3juilgTviASCd3jnkFrtEbWRL/GkSn0F7vd5ltSXNYefG/QXgB5fCf3HL//6sL8m7AsnnRv2oXqtwChEVLh6IH6egyzl/rBKEZ+jvjXsC56L9Mt85efpCxEQmUEkmv58RewsMdOE+Lzv8dz+W7cnQz8XBgwChFTg+y8dKgFCCnxvUWWK0HtbvH+ufF7EDmHYb9vbdvFFZBwlCP0ARuOBaBTBhT3KVEaE2tuuYB1CCdAG5P7+k2jiCxd9L4wescETY9jjpAUEKfbRmBiJPjx/XgGJRkSNTDRIR3ABZz0uDegsJW7dvoYtNUDALXc40+Ns2Nt/XzDoho5INvZ4MyDN/nkWtQQPssiQIjzvE5HQ9tggEJlCjXLEEEBpAvuxHPCEwTKsVniR4KVAqLjvf9YivCd6tx8HcX+dyBNCgOgDtmtwRkEQ+8iVVsg0JawddtgQRLq/UEIgE4XICmTiIApUkRA6h8g1wu0Lfd22wXtPlMkep6sMsixgAbZuSUxOjBEf9yxnoTWY5/040dALwmARI40ociJuj5HNDCF4MBJVZoi1JShJ8B7hPFIoRG6QacTkJcPlGm8Cutwj3vkcFzuE5917fz0CEWJAxEgwiogiSgUhoNIEEo8Qfo+klxCdg2xfp2RmFSodYCvxQ8TFiFs3WAUmOkQBdlMjqoDMNMEN+zqagwrR7IhyP7chMwjlCEPYU3/7gagH1HgKwiCaAaxDaomUe2CLF3sssLaB6NmjZAkQQCmFJBDtHplODLjekWcpPvYU45Kh9ljnUUBwERsdDk/0EZVr2qbDDQ5hEkIIKKXomz1CVkhBdB75HOrfbFvMJEVpSdtaUIbBeqzrKHLwO79PdSoNTki2tSXESGL294Hn8420TGmvenwMmHKP/ZVSUk5K0lH+y3PeX9O+cCM+X6CJ7BH0n9vNv8TRiMQvMOa/ZHJf/P7PD8eXKt1/3fabdy6eNwFfRiS+9s6vPO0XnjMvV3f40+WfM00Dalvzneq7/LD9czRwIzumI2FHQxYN75R3+V79lDhsOZ7k1KrCjyND57jVLbkUh5QiclIKjBSo1uCGnnfuGn78Wc80V1S+Y6Qcz5xGRnh9pvjocmAqYSQlB0bwZJCUScLkWc9abTDXZhTXptx76ZDzxQXROU7mx3z46ce0dUMiNLdeeol3P3gXqRQn02O2tubT7/8ph4dHHB8f8/7H7xNi5NqtGyQ/jRSHgbQKnMyO+OiTLRjBg9tHnC8uGYYZpjd8961r/ODPz/Ai8PLLcz6tJcXphnHU3D4s+HfvPcOkOXeOJ5yfrRlyS5nA60XkJ7t9TuzxfI+v7ZcCUff89t07/PlHp8QicP9GuX+41FsKM3B7OuJxe8W09BwVFbkU1Klh/tIJd49n/OwvfoGNgZe//TKvPHrpC/70a/dfZ7NbczQ9ZFJNuHfrwReOBXxtjvFFp4E3X3/AxeWKw/mU0ahgVBU8O79CALdvHrBcnVHXNaPpmPnhiNPLUwSC+7cf8OxswfniPY4O5ty8eY0PH18RA7z16DYfPB0Q3Za2a3j77nV++Gyg2XVcm0UuU0UvNYbIb9+v+NOPGmKa8ODEcHnaMyslB8cVr1yHf/ODGkLgWq8JiWbXRVJt+M6zl/nRo46m2TB+lnCUT/isP2OSV7zxi/v8xb332K5r5CfwrF3Q3GsZuYKbPzzk9K0FOihub07AKj7WTxmLgqM/O8S9XlFfWKpLw3GR4G44kqB558PX+P5LHzPaXKHPNKPTDB52VFLzzqcP+P6tjzE+kqw8d8UJP7leo4Tit569yU8P3qccEqo6RX+c8unJY4qYUvxJyvrlHUYI7GXP+HFJ/e0GR4/58Yj6Xs1yd4m7Knh5e5+Lb63oVpajH47Qryhmh2NMrXj9yR0+KB+TzhOmHyrKqiIxkkk24u6zER/NnmF0yu3yHju/ZqcajMz5PfMmf27+gmybct/eYOU8jW3IvOLt5i1+PNoiEsk1RkiVM+SeJEq+nb3ED+tPUN2OW1yjCwW2caQ7z6PHlvffGBO7jqNlQDjH4BLyMue1reLdqicIzcwFijZidYNuGt5ap7ybBYq6ZrqB4qLn05OEdFryhkh4d9hhH68pEsfdazf46focv9jy6kc9j08M8llDeWPESVryrtsiBLxpUj46jLTtgtK1HCxaPrw+Q4TAgydrzueGXEJa73gw1bwrLKG3PHi85Xw6YjCafHDcX2744MYBAcG9Z0sWY0WfSEqhePTY87PZng7zcDLlbNOwaBtSLXjTVPzH5pJpUXL9zLHW+0LILAheX73Ez046RIAb4ibaeKxzGG94pXyNH6//nC403FJ3OdLH6Cr7IgD5zU+4+NXXX3/IvTDmryfXOEwPmLsxcoi8lr/JT9ozKp8wM4ZZGPPjfoWMgTcvd3yUZ2hrKbrAtbrlA5lAiLz8cc2TkwSRFOQWrg2SH64tYuN45WnD+YPrDCuJ/GTHq4sN792qiETufbbj4rAgJAl6tePhJzs+vFMRiNy5bBiOoe56ssHx4MMLPrixQYqKm/o6+ewediYxMmFc3OF7wpHEyB1SrtqaXduTOM+j9zb84uWKdJpyfeFYLXra6El6z8OnAz87yZFRcnTZ4rqePlUkg+fl99a8/9oBMk84XAwI5fDXMvJU8ei9LR/cqiiA8ZMtpR/weYUeAq98ZnnvtqGqA7MNlGmC0wHZeN48HfPuEXgBZRO4Hg54T+zQUvGOO+Q9f05uEkZGMHnW8IvxJUjF66sT3tdrppWmcIY7z0b8YtSik8gr+gZn0zW5KCmTEfdX1/lZ+RSRaN4YPeDjy/cxqy3V9UMexev8KH6I8wMvPRuznW2IuWekS96OD/lR+gHWWW4vDunVJb7x5J3n4eIWP80+RmnBnXTGLgm46CiLnNffH/Pj2TmlUcxPNeoAViFHdYG3zSN+kD+llIFb6W1cEmnbJ4g+8F3zbX6w/VOyQXLUjVAywfVPMT283dzm3eNLYm857jTR58R8R1LAww+n/Gi0pcxT5k3FvI18VFi0SXjzcs578TGTySHz9IgpJe/2HyK85I36Bh9NWkaqZJpJiit4NuvQmebBKufDoiHrIRGG68MdfrF5grKab+U3+SRumeZQFZprmzE/MedEBa9uD3k6WeAaSRUzXukO+Nn4HO899zdHrMsFOMtIGh42t/lR+RHew/1uxlWeEzLIG8+3+zv8qPiUPsDJZYG6ofHdBVkPb9Z3+cWdBdHmXAvXiJViMJFkF/lWe5efhQ9JW8HNZk4nLV5YUiJvno15955FBM2dk5S+TnBHF+hO8rCo+DFXyNQy35bQBprbW/Ki5O6m4P3YUKQBs5TcPpzwc7sgUyl3d4bFsSWbKsqLQHUqeX8z4EPgZRH4uNXEiWJaSHIXeeoUPkR+637Gz99rSJQn2p4TBe1zLasDv2ZooEhTppOM49Txk8eOYbDckp4mzYk9pFHwytzw03Zv014+NJztOlwPRWJ4/VbBD+qewQduHY4JfSArU5SUHIr9otqXNWcv2McX67V/yZ4+t59/zTqIX2rx6//96zsVn7ffrHPxQtjl66cYX/AcPte1+FV5ZghY2yVRLlGqptCG9+ofQxexeeCy26BMSVLk5LHgo93PyK3H6RYqkDcSzOOetIg0ak5lNS7AMEQaIq63VLnh44WjTPdpUcIkbKyjzA1hGPjkoqWUkigF0Q5spUJnKUNneeYsiVT09HA75871h3z7jXeQUvDks0/57PQpKtFIIXn66WO0UEQHH376IY/PHrParplOpwQFjoCQYNRPkZWCvsWpwJ/923PaK0ExqXi/SahmJ4R1i0ornv0kMGLK4Bzthebk9k3sOjIKkcvzKyrXMixbdrEjC1CaQOZa3v1kTXE43qdqna1JZoo8hVxqLqk5mCncxRbCBk1HZdbMipJls6CS+8IyHT1vHD/g9rcecPDaLcajkj/4o29T71oODqeICH6wCB+4Nj/hf/NH/5i6aZiOpnunQ3ylm3zlnn/+xsnRnH/6X/8R213DdDJCaclqvUMpyXhUMjjLdrtlMh6jlGKz3SCE4NnpFX/yZ9/narlmMh6x3mkiKWjBh6cddidod5H54ZyPzy2u7qlGFRsEwVmic4Te8sMPIyZJGVzg8nLAdgNJXhH7hu/9oCE3KVEall2DrDtiCIySlA/HZxQyp20uaArLatjtxb8a+HfF98i7AhKPHffM51OcCZSuYP1KTWITdramSwZqZxFB0awHTseO6klKmORUZsZueomSmszlfHj9kjKMuF4ecefmMVvboaIncTm/ODnDNh4nPEYLTtNTtA2IPvAj9UPEGoasJUaPfQmuywP6ziLfEExCyYYNddNRPcw5zic456jvbEhjQpEZBtvzyfQJL2W3SKcJ63tLrhdzeuHoGsv781NeTu/goiO9nnMjTkgyRUHCk8M10qRYI3gcTkkQWNcRk4pP1WPG1QSdatoh4jc9UkI2SD45KEj0NQbXsaQircZY2VOJlE/qDxj1Fwjf0DU74sl3kIsVqdN8OrfobY+epdjME4LZF8wvHB9lnlQluEojnWcpdwhpMVHyYW4xSiEM2MaxSQpE1PBsx/tSUF4bM6hA/9EVnzU95vaEXCme1h5pI6L1dB8vOLt3gNYKjeBx3JFqQXrdoBctl3mO6vYiThfjEuUiwmtULzl1Ndksx141XM4M0npEjCjrOJsWGOvwWnE5yVEMCCJJiHw81sRPF3DniCdhS5rNyVJH2sBH5UChEra7ml2VEJBI9g7ax90vSIe9+vx6WJJ6gdCCXOX8WfPv9qJYruYD9xP++OAfc1y99NVno/gvf/R1ocWFmkxKtFQ8jqckmOeRAMHZ+hQzypEWPps4lGvxPjK0HaejbB/l6i3P5gnpeMIgDbHxfOwH3HmN6DyfVRVpm+CeDYit4rMqQVlHkIKLWYKSCpkYdD1wfpCRePBEtjcmmOG5wKobuMg+I1utEMUY/Ja//c7/HmsChS75N35D5na0eNbB4WyPIJD0A6e3KpIh4rOM1bJjUDxHCwc+nWRkVlEbRW0SkB4ZImaIPL5dkfSeYAxtqlBaon0ktZEnBwmms/SJxIlAM6lIRIIZBp6cZBRSMUhPNNCcjNDtFjNEPi01WTOiSyBLEy6UJNoRxgs+kClGPyDankDK5fgjtC5J0pxFCdM6w6otuRA8HQ0gC9zgeG/7EWmn8YeRMMDjSUvcAVHwiTgnmRyh1D7d81n2mCJYQqUZxpE8nZLKQLHLuMzOGA+SXnr65AIl9sKbicz4NNuQ2pKoAktbI6RHl4ZCpjyZLUktNDLQlJZsnpIwRp4Ffr77AG3GDGVkKS1uGxlaSdJofu7fI5UGP9cMEXy/AxdJyPh0ekU1Ge+zEboed9Ch+x1p7/j0jqEMKTWRIXOssm5/nk3gk/EVyVAyKEUwgmf1FcJkJInhs6zBBI0IkJ7M2OgFIhq0zPi02CI6hcs8Q99xca1Ch2PcYsu7i1+QCqBoMNmU02RFbjQoyXLiyf2UndqQ9AnPqk+ojMWmgZ0e0EFgpKcsEj6RlygyYrBc6BrTWsxcU1YJT9vPGKeKNjr8uEYNmuwkowiKD4Yz/FZhjeIi1hSdRBlFOR5zwYqZG1OnhiANQUEiCvKt5HHxjPRKYkcRXw74b52TtVtKqzi7v2JsA87XyH6FlDlTHJkf2KYd410A6RiZjEZckmx2+G7J9mhGmWY0CcSRZVNN6T92GAFnKofTAVKBGhsWlz2oSF4lnIUUb9d4HyiKlKtWYTR4B70YE/tI21iqqLnsNFWZ0qmBTiuEtcRub/GeXUYy9lHPZSNJUkPcdUgZebIM5EmKjJFVbTnIU+quY1h3/OQHH/I3/vbbX1Lzvj4R+tzH+NqCzZfrMl994y+zt1+JfPwV21+zUuKL9td3Lr741b/6hL7uDX0zKeqrnsnp8JSNX7NyCzqVMCSAUfShR9oFgo61r2lp6L3FmITWdVg/pU0EtTaooHAY/BCp++fJF1KwdTAMewVpvKO1gSFTe/Tjzu4VpL1kYy2th0kaSVrPEPdkjtQIAgKZJlwtN5yeL7l39yYAl6sFq/WSuq2x2xaZGpquRUhwwiFa2Gw27DY7SAROR6SSlGmFCILNbkvIpkxuHWPtwNVix/LsCUouGJzi7HMNCqP2KpveorTDVwW1GzhdrFm0HSHCYD06MXQhYp1nAPSmpestjCRyJ9judsQ0pd1uCRH6GHj85Blp6gnKsxOGUIIIHjcE5Djl8Lsv8cpvvb6/W1JgUkM1rvYq0r3FfB7CBTKhyNL863f7y3v99b7wfFOaJqRp8sVxZtPRF69TY0hm8y/2nYwmAHz//BdcXq1YXK2oW8uuNlxtLAhBsZP0W0Ht4MmiI0jDbhDIVUep9tx4KzU7ISAa+ga8Cww92CbQNx3r6PAoVKawzlFV+3SDIVFcCkt9tCGYUy6TS8xEgZZsyxqrHJuyZiV2BONJtASp2OotrWqxI8dRNqHH8tHVM7RJ6CuHThST+ZikH4EJLMSOodhylW3Y6hqZa2IbsYXnKt3hJOzSgS6ukVHQdw3bpOF9+YzNsEUkAisclcnwLrBNt/RuwEjJOt+SjA113TJ0PWIuKWRJLRvsyNL0HYVMWPtIXfVM7k/ofc9P3HsMWE5eOuLnm09ISdCFYVaOqbOewVsqOeWzfkEjB5KyxFHTiR6hEnxrSRDsRI23EecDXkcCnk4N2Jlg13cEGRCmAVVgU43SGulbVruW1tYk4ilJWDGEgSGvcLGhPcixssWhUDoyCEu8MyJ2gU10dEYSEo8cGrpW4xNJPNCsZWSzGzCJJgmRxkjEcQHOUJu9wq3xHrNc0R3kiIdH9OcrtldLzKSkeHSNeLphpyKx61Fn59jjEiElhdRIBLUJhFeO6T/21KaACEOiEBGazOwLxenpdEQeVfRxIPiEJk/3QtdK05Y5SIkzIKKizjSeQGcyNkOLqHeEpEK2DZtkj0Edzi9wpcZpsNoThWCnFWHwBLVGDAtCKhAKtI90al8gvWoXqBBZr5d4cYvVyZpj4j48/Xn60fO/vz4z9sWH45djf2Ev2IUtS7tA+IhrB1BTauW4CB1OtnRJSpSwHRxSRmqtWMwyTCJpUxBG05eS9MaIzdBjjWZoOlZGgEkYbIaJkZ1QhHmO0J6+3Ksq94lCljm9jHSFJJqEPtmnZ7oiR3SOpkyIcUCFgHU7VAjMR3N2suV6egNL4MoOnIceT8QLwZDDTmu8iPjE7FXtM4lNAm5iaEqN0wIrs70NyvQXRZe7HKwRBK32ab0pDPMEgaCuNINWRCNJoqJLFf3EoHPFLgExNQQlSb2jUYI4lcg8skIiE1CdRQ6ROlEQHWjJxkAtBYVzyETSaIXIHV46dqFFqJ6WHqEtbe5Z0tAHxy4dwES6YDFaUg8O27eI0Zhd1uJ3HetGY5KMdiIQtES/o7ZrcNAWE4QTbHWDly2xtrRDTYgee3yEzM3++Z30OLunGDOrNn0AAQAASURBVFImiDwixoat3OGspcksIZH0fkAVgVT3bERLOhXUvoa+xwJWWoJOOW/WbKImKzaUI4nNA4RAzCJNCv1mS9ANWejoE0dMDT5GNtuGRlh6pxEupy1gHQc2ScdObzFZxFiFUQlNs8M3+5SyrWhRacJoPEEKxdptEEowJFtaFRGxRuiBmGlqGfcprduarWgRWWSQAhMDtbb4YUmcjFm7FoAmpITo2cYOl1nSoieMBoSWeKeRStCZwFW9pE+h1vuE1L4XCN9QtwIrcvy0o/c9JBI5NrDd0DpPnxq6bD+PsC4QfUsuFbXbMciGWHdouY+MuREMuaD2nkEODJVABElv9kjkrm1Yyo5aK5wMSALtONLEnNA72tBjLaytQyaaPoNNsIQQGOYRJRKu4oB2lkbCsOqpQoUdZaAVbZ/hSkMvJIsu0kZFHySZSGExcLXxdF6xQ+P7SN1GnINpmTH0PV4aln1Aa0Pbg7MaiFgbCTphYz2u9dgoQSl2iwZVgBWKJgqaVc9uMyATTehr/NCzqXeMjOHxswXtsv6qc/GCKfxiFvy10MUXFKevq1S/aEq/HkX+3C4//89ftVJDCPF1H+a/qP2GIhdfJGx9YxNfZF5+udsvuxfiKy+PkmPGasxMzxjJCh8VQ+fZug2VzWFI8UlkqkeENEIQLOOKg1lGMyoJhw1mtZ9k19ajhCJzDVEJSBKUqzF6v2IdhGaq9nmuGxcpMokmQbSe1EquFZK23pEIQZYatLMczEoWm5ZcSI7mE9q2R0jBfHbAbDLDDY40anRmSEyCkJJyVCKDAB8ZlyMGEVCFASkwKkGjsf3A4eGEPkwoE0m7HdMuGpZP92J/dhcYdnuBqHRUIqqK8TQjBDg4PER3FePVlnrTU2r2uYO9JZcCoRVJltJKxTTXZLHDY7h++wRRFgQXKMuEIgSyPGB1YDQbE4koJdg1DSeHB1y/dwuh5C/XCUmJzpNv7Ai/up/ue8M39gnxlV2+uukbomMHB1NmkzGD6zmcTdEKjPY0iy2mbVFeM8kkVSHpB8gSQ3SeHDg4GXO2tujOogpFu7OIQpMKt18ZGgIzLWitw/qaJDHkPqIkkA3Mh5SxP8IuO87PnuKvBGWZsW52xDUcZzNqP+AqS3thGWzN+GYBS8W4LDG1Ip1luJ2n3vaMZcH1MOPAT8janKUeOBhG1E1NFD2VK9BOoHq4FFvG6xwxLshETt4qpI+oMOciXzO2FaeNoFv05H1CIVOGZiAclpy0hzjb0m57/ODpth15SFBS0nw04BKHqCKlLDG9QlpFlucUZylpUVB3HeuuJpeGebzJtq0ptxWijfRtz2w+wa8tM5eTHKQcxTl1ExiXI+p2YGwmpI2DsWYWxgxdRwiOXllKqwlZRswF414RekNE0GWKgyTDL2qcj0y6iG4hOxzT6p5KZbS9hHHG6LBguFgTVj3NccJo3aJHY6TQJOsGdh5tNEvvGe0GgnDI6xV5lsO6Q9UeUUgmu54gJUJass6jY0CFfY1AKS3ja3PS9Q4+WmKSlGw0gqZmtnG4bYeVivxwTCoNCQIReg5GY3bTSHK+IzhPaj2pj8SQMasHfOpInq5RRxPSdtgXfArJfF3j0pTcR4JWZIOFdkeQFdPasvORvFP4PGPiImLd0vcd0y7gXIPdCtpEUUmFDJGgPHMrCEMOtsBdyxmHEu08QgsmbkyqJEoL+jCQyYxilxKnAfE8Gvmf137Z+s/0AYUsmek5Bk3Ix4QwQbFhWhu6mGCaQHUwgbbHX/QIGZluHSrXmAxU5ynHBaVKsKuOkzLl6nSLsA4B5FGQR0kUgvnOEnJP7yxRCAoHptSs+0Cx6Igq0jWRoGAynsFqiTcwrQVYQxgKQiwZTedMkikAGslEao5kQkdghKarA855xhtL1JGYGoLQJIuWWA8AlI2DCEFounlBteqQwkLUFDuHkB6RatosUK4dIXgEGZUAWoeKCnJBuWjQIwE+kHiB1BG56xEjyWwXwQRi60mGgHICMYDIFNMmEmREGkEa9oKr2g9QCaZWEHROlh6iHOjeU1YHLGTLkaho1UAxbIk+kgw9mcmhXXLUlbRbS1JlRJlSmASerRl2jvnRIaLMGSWjPfDBa2QLMbRMdxovFVVaYONA6SvMUIKJzMyMfrHAEfFZwigWGGEgRmbJlC4ZiFnGanHBpC8oXEboWyaMKX2Pax2dlIxFijQjrFtR9AlVcUSeJ6zdhumQILIErVsy4dFFSdgNrMOaSYjYLMWLCenKE/uEYBMWsWMsckI7oLKUUuVoG1C1RDBwmE/huCBr1oirlkylZGVO6LYcZTMaozCbNUlZEUOHCinYmsM2o0kkWkp0CJReknUOUsOxzXB6SpbsdYnCkx3JIIjjhFm3x82ayZgoI5mVmF5AEanWCq8NZe+xJpAHjbCCUDfMRYo+PqRdrak3ayZVST474CIumaVjbKLYna3oZM/EZySrDpdJRiYjHx3iFlu6IjCRUwYlQQqqUUa3brF1R5NZZiajJUVIQdYrbGORUrH2luN0BChK3ZMFQ2wlcoCrpGPcpPjoyY1EbRza7VGnCk9e5sRaoscBOkuWZoQKNqJjqlKMDLRqYJxL8qCRE8k6BCbK00eQDAgpyIMjTyJ1jMwKST9YVAIkENuWWaFoESTBMYSAVwofPbMiRZSedR2ZFYK2twTt0YkmcQrpHEWiGBU5t24cUh6Of9kkiq/8+fVm8/OsKvHVOfMvHeArx/yGI39T6ds3vfdf2P76KNq/8kkIvnoFviH39oVNR8kJkzgiHxLEsuet/lV8ahBZzsnoFhM1xbtIR+B+e43F5pTWbslUy813NPqdjvidmrdf9vRDIMkMVSG5NjX4CL2Dt08UXnqC65nlipulwrnIYOHVgwQnDGhNQHBjPKENGRuf8uDBS5ytOuou4nTKs9Ml/8M/+9f8D/+3f8V2Feh3At8ZdCh46aV7+BR63/PS0W3efPlN3nz0Lb7z1m/x3/7d/4a3Hn2Lbz16i7/zO3+LfrPB9Q3bq0sePjoiUKNzx6PfOcRLu8fIZorjucIGw3LRcfqLx/zsP3zKpz+94qOfXHH/5BYxHJNVd3jt2+/w8u1XmakTJvIa3712g2QtyLeSo8ZQdQWT9ATdj/num/dQekdeDrzynZv81//dP+Cd33qbb7/5Ov+Hf/KP+dbDV/nOG6/ze9/5DoeTyb6o9hu7wF8eqNsvb37DEuev6R6/8sgvHOrWjSNIdui8Q2UNj+4dY9uW9mrFtcShRYMY1qS25u3K4fuaIXRcKy3bixXbdc0g4FY+0PXgnjuW5SzDR08bLN9+q0RfM4SR5+6tBPNbP6T7zp+w/u6f8M7kNku7oKhSHsQ7ZE2GkBE9Vlz/0QE+DfRY9KVh3I6QiWB8lPPdJ69z5WoWuxp5oXik7zOuRixlw/1nCavrn1GPP0bLK663JU47dnLHG5/cZp3UtHogzypeTm8zZJZN3vHy+T3azOMTSZWU/L54i9l8RDnLmfygZOlXrPoVwQ+k7+fELOITz9unr7N2Da3zSCm59enNPZZXeNy/hy4OKCHIqhTzA8MmtqhcMf2gQBpJmiW0oSb8K4EcZsTtiDf7t5hMjzAyYSDwKD6i1opgMo76E0QsGYKmk4rXkm/TjUpsNeIkewmuLMN2S6MGvpXcwpZ71vthNBSDICgYphkPFhO2z86xveUgGCYyxwVHpyO/de02tjQMm46D8ZTxosPjCPOM11aazgZEUJS15HhdMqwMbZ3yxm6CuHVCcjQn0wkHfqDPWpqi4/5pja1SolbIemD64wv8KINbB7z8WUt7sSQoEDFw4zLQrizbq56HIUGsfoRe/giz+QkPT3Lc1OPzjtunZ3ijQe8Lcm8+qbEyp60jt/r9on+UApsm3Hu2xCrFICU3Fg1aaqLWOK14Y5li5zdx1TXK9xrERY0PkiHLePm0p1cCJwXHTUQ7wBjaVPPq5hZWjfB6xkzfpSjH9GpgIzbc5yE2OKrxmIOjm3v72+/1Sb7hefaf3So5YqwnOBxWO16TL9H6Bh8dWsFL1RHWDvTB8ebkgFCa5zV9kZOlpd62rL3jdi24fP+S3ZVl9dGam59tGIxmUIo7yxaXKgIBR+D6Z0u8kYREcf28QWYG3/VELXjpyQ6fa3yWcCcohHVEAdZIHmxGWOUJKjBJp+RqvwopBNzSFb3RuEQz33j0VY0n0iWKex9vGWYpTsN0OVDYfdG1zwyvfLBhSBRRK0Yby6ge9pjaXPHgvQ29EQQpKDY9k04h8hI/qnj5gy114mjclsRbqm1PpwON9jx67LBGEaQizwqurSRRJ4Q849FjBdM5Jp+RlYfcvDRgCmwx4uGyJI5nSFUi+4zrT49o3DXs/CFvHf4xVt0hVg+Rs9d4yG1EEYmi4xV7Y19oHCTOeV5eTunchiG1vKSuEw8PCEVOS+TucJ/F2rJcDMw/qjCnO/R6QLrIt1f3Uact5mLgzvsp2VmLeromPjnnNX+TLtlhk46T4oBMpfiuoVld8uhphWvPUXbJSWcYbzTifId7dslbV3NC3oDecvNgyiGBxOwQ8Yw3u+s0omdwA0WTMM+PaHdbauN5I3+LYZYQxjlJLDhqSnzXMiSe7yT3UXckycyR24bb/QiTSzw9j84O8MkeCqCd4NqmxJlIOC54U71ELHqCaqHf8HB8lyBaQjrwJteJhUcZi6LntV0O2YBLBu4ux/RJQhckbZby0tWY3nb0vuNRdo38hiKdDJhpz7dGrzC4mnq94uRZCp3Fdz1eeh5ezrG5ZYgNN4cRqYqQWLq44+XTA9q2JSjJwWmC9gU2KGoBr7nX6dIJTk6ZNteQ4iZbO+J8JbjDA/obCbVsKELGQZ+jdh3R9nx39h3kTKGk5fp0ys0U1GiDPNzx3ew2roQoPfpsw82rDYlcIOUFv60y4uwpenLK4bWaR/dy0rs7ijct3z0ZUz6KFHctJ6/Cozd2ZK9/RPHWx7zz5oLxHz5m9PsfUb39Pm/+7oLyj54Q3nmfl79zSvF3aswfLNB/sOLlv9nDH25Qf1Rz8uqS5DjDph6bBW4fe1plGRLP8cyj04TeBmwUvHGnwCmJMIZ7JzmJKuh2ERtS7o4NJp3St4ZZljNJLZloMLLh9/7u2+jM/Aor+JdYT7GPKuyjGuIFUsjX/r3QPocifTGn+rpDEYH4OT7pV+z3X9h+8yjav6TF5+GZXyuiB3yweZf/eP6/8snuA8ZxxHnbMKBoM8c8TIg642JYMksn9G6DCp6V33Igb6PHD3nW9ZhFR/MnFfaDlMud52iq8UQ2g0T5ASEtifZcbixz7Yla0njBpExwgyXPFOfLjgMT0MGz8/tS/UJsOUgH1tbx4O17iBjYbet9TUApqHLJxcUls1HFkNW0rkFpxb2bd/njb/8hRTkiDpbRrUP2qI/I937yPf78+/+JJ2dPKTpDZu5idxrvA3k24dkvVpye1szGKeic3abDR0GiPJpI6xRGOnqpcXGvzDvJYD7OaXrB8Y0ROvEo6Wl2PVWlWJ8v6KPk4PoEN14gq4Hdrubendv84e/+Hndu3QL2/cwPFpUavkyu/mqQ7Vf2ol/yyMUvd/AXbvyXx/mr0BC+DGnECH/24z/j+z//Ac8unnEwPub8iWZ51rM5vSLPc2SQbH3keFywdSnr1mGBUmcYlbPympkONI3Ceol1kSr1JIVgsfOUWORJjqgMm01H+dpH9G/9J3a3LzjhmHAi2T47Z5f2zK9KtkPHk+Kc8a6iEz1uCISpZ7QsGJUjuoMWvTb0ISA6RV11HK8mTMsxZ8WK6VDipWdMzqracbydEmLgrFpT9Bk+eFQn2c06btprxEpzGs6pYk5mUvKQc5Zdcq0+oHU1C7PABEPiBbvVjiflOYeXEy7dCnWsSKJBdAozaHZHDfZ9SzEpqNOORGlkHXHNwOak5nAxw+QZjRoYVxXjoSK3CYv5hvRpgmxnjKpDlJbM+4KJyrnMdxyJGY2KDNEy4DgYcpIBlpOBA1fRMUBh6GLPVBS4puYyWTHpSkL+iHR8m/Vuy7XqAHfZslCOmUjQ7S9Ql0/YiZbp+BXC0SMulGCWlTjABLhcr5muHGqUsVSBogtQpKRRcDV0TFeBkOQsc0PRB4gdWXBsjwuOkpTd5TOWxpK2kVSVpLVkNVbMlhYfI3VlyCYleZ6hrhrOupr50uKVpi4SpI+M1VNm2ZIre8FBfpvd7G1WQ8LwZEG2UyQ2YTEumS832FTTGUUQUOkUtWq4HJfMNw1WG4Y0ISSGst1hfMdinDHbdNRG0OeaZrBMvCBtepYHI+ZImtUpnWvpjeIwybCbhqtpynwA695FxiXDccZxmRLsBRfhGdM4obSGKhvRxIaXypf5g+M/5rq4jnyuaP9F0P2/8KF02j/lX1z9c95r3yUVKUNfIYaKy7jlUJzg/AHrNpCUOWk2Il4NXKnA7LIlGE1tBMpH0myEaWAxyjhYtzgFXZkglKKSOXkLSyM5WO9wZc+Q7klOuQ2Ut48571omTzfYRGKNwOcJs6okfnLFZaWZdQ6u/gO+fQrznId33uaPr/8x8/QAHyP/93jB+6Glw5N8vCRebVjPM0Ybh8sk5mRMXxryn50ifGA5NUx2jj7JEUjaacHk2RIhHMuppqwdQUlMllJPUyafbpFpxmaWM5KaZr1EdA0LYzlsNVHtMbXJAImRZK1jOTMcWY0fPCvtSYeIjJDphKtccOAkw3bLthToKEilJh0ki1Iw3zgsPdssImOkKkckbWBRwTGCkHzAdngCPmJWAbWDxbjjoC1pTU+fefThmLwtiWeWU7PjoCvoRcSafc3hUeuYesuSBUfFNUIQDBcrrHCUpkIVKZdcMd4l1IeSoZK4mWFiK+KuZyGvmDUZMRHQ7fWBpl2F6KAeD1RNQn9scCHQpANH5hi3aLjSW/JLS28cZjxml7TMmwKZJVyFKwqfERJDEhM2Rc/kUhKtY53WVMmYHk/mJOtxz3FTEezAJu9JOoFsNInNWZiawzilcQP1BLIkJ/E9k+Mxz5qnHPZj4jRluTxFmxQ9pGifcsqK43XKkAt2xiOEJK339uF8ajnxE5qhY5ADGMk0SyhLxUW64jjOadYLWtcS8VSNIdEpl2bFvKlotcflEqs85VKiouSi3HHoJvRDJAhJpzzTJsUEyeXUcpgf0vQK7yR16JnHHFt3XMgds9aQz2qyIrCLNQfDiEQlrOOSSozoU1BJyqq9ZKYP6IPlvHtGJUe0bY60FUtRc3BpyZSjPY6MRzNsGhDtwEKsmLUjApFV0VOQIm2CcRmLpOa4rwg4NmKHdhKjM5KYcC5WTHclTmq22iJcRDUVui24MAOzWhGLnI0M4AP6vQrzScmiU5ShJwTYdhatFYmN0Hg2znA0UjgirQ8IBONUoYzgyVnH9aOUph4ICIYuMMvOOcgu6IeacVXyt/7RH/LHf+8Pv4g6fG4z4xfF2l/OhcQ3RSa+mCfF56jaX2NyI1/UNYtvSPV4kQr1S+rfz/f9/y8U7dfbV5a3v7wUvyYZBoAQPT7u8YDBCITJkFEQuo7BWtwQcDha3yLSiMw0otmrxEbvQAqchOD3aD6T7IuP+n5gsI5MK0K0DNYjtEIWmj0yL+xXbQEfIlIrPBGVaIZtj1QgM431HdZ7nPMoEfcYUsB7gXsulCJStcfM9h0BUKkhO5iQqARzOAbxHMmKwIdAVPt87iQvCNuI93sUbRSS2Y1DdrUgTSWrTUuMks97ZTtYeh8QOiJSiRSSGGBoBs7XNb1V2O2GaqapDnKCEKxPl2zPrvB5jjuscNahnqMUY4z4biCGsBfDEvtz/3wkfN6p93fz+Z0UX73dv9z+smTsF/sJvwo19rX21W/zPuCDB8B5R0QTjSKdlMggyccjmm2DlYIhBkIUyBBxzpFNFEYb0krvdTU6AE+WpQxDizEaJQVBSobOIqWk71uUjKAEskpp6iULu6V2NcZGtkNHLKGNHTrVlGnOVtVkWYqQkcZ1KG/ROieqSJmmZJmhsS1aSrIsYYgDznls8DShJ8SAMJIYBUMzkKD29TzSUy+3hKJnUJrYR8LgGMSAFY6oIxbPerdlmpToVDHOc0ICzjkGZ0kyg3KStuvobced6zdZ9luEEdjgCN5RFhlVDsFEhuBIRoagAi5aGgF9cFR5iSDBJJoOR5CBgT0S1ycC2w84HfBxj5X2RIL3eC2wg8dve1wCVvR4AsE5fLBEwFpLEAJr93HxKCBkmugl6mSEcQqRZgQl8CHSXm2Q4wKpNXpcIKXHrRp8KYmZIfQDXR+glDArCIMiSIGVoMLeBrhNSxs75OEYERr80OwR0Cbd9zvCHvsZA/1igxx5yqMJeifwzZYQBCHsV4WGyyX9aEvMIo7nCMk8QVQZoQt49jSRYPQeU6skUUps2xKTvfpseL7dS7HHa8dIUHuWsBcC6yzWC8iSPe65zNG5IXRujzpVipgovJZEs8ea+uiJIuCix3c9rYoo6YlyP5Yskr7riMlzPCgBlWhc0yMTAyK+YA/+KoP8a2M3+udH9Thv9yKDCkLvsAxEIl7A0HRokSFC2NesqX3esxcBMcpA6P241woORohMEcKeQx+kwuOIEaySECNe7uvGhErwWhKcJ2pFkBCEQBTp/hpLQUQQi4RwGQgqgghEyRc40gh7vDl7NHh0e+zyvtaPfZ80Cu88joAUPH9OPUfU6v2+Xu2vYRD711GxRwtbh5fPVyPVPjoQ1B69GgT779ISjCKGgHMOKyLRerwy+/EnwCmx79uJJviBoDRBCYIQ+74kJY4AURJzTbSWKD3BC/xgocgIXUO73hGTJW7skFIiJwUoTxQDNtmfl40ed7lE2gBOIXJF1OI5Pj0SgieEfb+LRIb1GrICcVgio0eXU0Si0K5Hz0aQdARpcXVLiAYhA0Lv04GCs4hcE8XehijLHvE6GhF0BKUIztGvNs/T0AKxTNGzESI8v/5a4K0lpnskbejCXoQxtviYIwsDURBSSVrmSAfRdQzeopTADz1BZ4TooWv3gphlSSIKts2CbrNF5gqHQ+UGmWU4EfY2xA8IJ4ldQGYBp0FNCmRo9ucSwZlIdI6+39sgKwaEFwQJvQgE5ejaHd4OiGQ/zKIENwwIDRwU0NTYviVMUmIicL0Ho/b3RES8jHhnCcLQO4tvBrp6yaBLRFLgvcO13R5HLcGLgLMDdtvh9cBQS0TqCFnEeUvwAtCIVO9tdzMQRMTZnigyXNcg5garLEmmcXHYP7+1RM5zWC4RCvY5yBEXLDJKpIp71HemCIPbI4AzTagdNgqkEUQTCb0lSIfSan/NTYqOETGA3bV7p1RJlFQEBMH7fa1HO+BCpKt7jquSrglfzIGGwaGKhKG2dNGSSINJNU09YK0HpZFKIoXY6+9o9SWi+gUb+cXaqoBfw1H96pRHfOl4/OV5It8wMft8wfdzh+YLc/wbKLR4of2GnItf7SR8fb+vrGC/+JmvffxOdZ+Ptu+TyhQtDa/lJ3xv9RcUquSGusX26RbrVxjteK2/x6ezJ6ArrlmDX0ncPOJU4LVJ5KeJQxaaqbaUoce7BPzAq7PIsz7Bu56pFlSp4FMXIThePzZ8ctlRxcDByDCSnr4TKAEPqpynq57x0QmpKpi7jk6kpGXGa4+u8fTsAtlIYie5dfOQ9x+fIbXk+OAm55dbzi+WHB9OefDg1hce7Ct3X+HZ2TOqoiRLc0b+Ou/+8AkxBu69MuOD751izJJ6aznWigun0NqQSotPBPm0ZHe5hrDFq4poFKWJxCFSDx68Q7YDpx8a0iLjxnFKem3KeudYfXTO5KjDjTWj0SFVMiEtE/7ih39GnhU8ePAynzQf0Lia29U9pJR8sv6ATOW8Mn8NI39FmO+FAs/I8878TalQ8Rv++5/ZxwXw8O4rnC5OGZcjiqzg9sEBP/jxJ8Rpwf2jOT/7/mfQOFSUvDkd8zPf43zg5UnGWedIoyQ2lvul50lWsVk03CxTepNxuvWIwXN/InkvOnQIXF/cYuAj/NBT+Jx7fzHh2fSUTGfEn0WKLCEkgSqWvPrDG/zwwSccjWYcLeYIGbHSIQbB8feOWD7a4HcOPvFcy+dsxg2pEzx69w7vv3JG2hrik0juCxptiYPl9z99nZ/e/hjf1mSXgkl3wOMbAypGXnv8Ep/deoraeLKt5Ka/QXfQ0G1a7j2+yQ9nP6NvHOpM83v+27w3+oxu0zP5Sc75rZ4kTzE7yYPTW/zo5AMORnPUjxz6Nc3FcsU1f8jh4zkfvPSEemg5+GxGcTeHUmFaxc1PZvzi5DGHsykvN3foK4lzjirPeT28xA/a9/BS8pI9ou5W2NKTC8Xb+bf5qX2XEB03+xOu4hJrekpdcPcs44PZKZVw3AglXpf09QITBt5YXuPDo5JsorkpxvTFATbU6GB58LMdnzwaERPN7dkUOZrxi4tT9GLLq03KJ/dLDJGTFqg9dmgxLvDgs4bPrhkyKZhtPPrpBvtgRHF0jYcf93wQ98SfSR+oNp5Pjw3KBl5+74zzbysmRyNmJ4b8R+d8fLQXSXtwMeWy6zGP7lCmBbeTOe+GHj9KufbDz1hUh1giedNzvOv46OYBwQ/cfnLFcl7hlKB0jmtnaz64PidIyd1nK3azBGskpRDce7zlZ3emOKF42aT0SuK8IB08D592/PhI4ga44yVbC3bwZD7y4FnFuwc7TKe5nd1kCOC0JRcp305e5z33HjIx5KYiCQnfX/05hSp4EB6hlf7KmP/17ZefFSfJDW6md8BFRICT9B4/WP6UEAeOVGAUZ/zCrZA+8uplw2dHKUEFpjEyreGDZJ+H/fK652wyZlCGShsm5y2fjXOU1LyyajjrLEMqyazn+vmGD24kEAIPRnOWvWdX92SD56VnPZ/cKZFScee847JxWCPJTcKdzwqW+ZhkesSN7DqdyvmPwwUzlXKfnKdxwIbA4YWlcQ5nJNngefXjms+uHaO3HYdnlqA8Lt2/98rPLvj4nZuoduD4skdovyfu2MDLn7R8+kcHhOWGg6seTSBmCYmPvPKzDT+/5qmE47CRJDYQtCQJ8PD9ho/v5EQZmYdAet5iDyQmwMMzz2d3E2wIzKwlvRz49FghI7y28XwyAicD1ZXlwCS8l3YoJA/PI5ev5zRNx6jPOXhS8MHtBD2teEPMeVJe0tdwmM24Hsb8lI+xm5a7VxmXSU8UPROR86a/yS+yxwSpuedu4cIZQ+zI8imvHrzNz+JHaBx39D3WaksdHKmo+J3iO/xk+CndcsW1swSbWkKmSNuOexczPri9RCC4MRwRMonPtxiV8V35Kj/JPkRtAjfiEa7rcPQkXvOW/hu8m32A8Q0nywLaSJsJEpPxxvqYn4+eUXSRYzdjev06v1j+lKSXfHvyHX6u3wcvmD/xlDHHVw5jMh7ujvnwqIXcMpMjpsWM9xKHv9zx6uVNnukLCiOp+shknTIUCSJLeeXygMfZhmAVs5hyy7zCz+372KHhweaA02JHYC94dzJc4735JYTAvWdjltM1bR9ImoEHmxM+PDjbo6qXR2yKFhdhnE95M32T71/+Ga4RPFR3uFh9gk0CSRt59HTOz29tSGTKPXWD7mbF0Jyj1wPvXM758UFNGSS3djkb29MWA7lO+Rt8i58lPyVTjuvTW4TLNUMhMTLljfAqH4RPkZ3juj4glidwNaA7eLm/zc/TMwoCxzfukz274vRwR55mvCFe5yfxfUZ9zqGbkF4GwqRHC83Ds2M+nC+ZJI5JGxj1FR9PWkwiedXd5cl0iVaSAz1mJCe8Gz5GesErq4JPTU3IOw5GEyaUfDC6IgwD96aRx8dbqHpmYcRkl/DTbkuUkvs+sJ1NeLJsibbn7iRwGXN2YuDmTOwdbhypG5gXA0+6vWM2H8+Y5FfsYqAYGV559d5X7OM3RXu/aZEmxvh8LvVCBOIbJ1RfHuVXLvb8yo/95hwL+I04F1/EdL6y6Stvvxjq+XJp+tceNVUZf3zjH7HsFxS65Purf89EC3bWIswGdV2QNQlFL3jWfAzrgBpLQiZodpf4TaRKDGfGUeSOLkbW9ZZUj/DWkgjPeSMIwmPylH7o0EiyROH7gWernkIEyDQyBjZ2zzAWRBYxwRjJdi14vF2ySC1N3VJMCv7k0xWTW3N2fYLdWC7OzqDUpOOcn/x4wbvyitVmx3w2xsfIqw/vQIxMqhF/7/f/Dpt6S1mM+Lf/3x+gjcA5ePrhZ3z00x/SDoFEClZdxqScEIBmt6QYp4yOZsRmYLcdSOnwQRBtACRpljJKJV0s8HiWq47d1Yo0DvQDGOFplwJ0z+xWzq4K/Ot//2/ZtivyNOeH6z+D+R5D+d7qZ0QCtduRqYKNW/G71/7mr76RLzgYX9n8nPX8YhzrP7d97mx/noI4m8z4h3/w91lv11T5iH/+L/6M1OxXDFY+Mn90h+7Jktm0oC8mHJQdy8cLLoe9uJHdOZwInCmFUJakkiy6AdEG+i4yTiNXZUT4FqkktV4g8GgpKWXOZ6NPscueMIrYiWaSVrTSoRrBs2srCrfPzY5lJIRIIgxZzKhv19B51nHLfFJSTDUbBcprzu6tqVRGn/YMuiUpBZqIbxw/nb3HtmnZmJrYWqbFjM415DblB+r7mFWKnXWcbp+y0Bf0XU+lC34y+pBZeoBVlxid8l54zLyYE6LD3bdMqVi4JevNhmWy4UZ5SCITNjc3DGvLLrTIoHhSXeLbiB88XBdstzWXLCkuUjj6iLySbMM5p2XOyJ+gEtBRcJovSdaCIXrWcYVMBiQWmobL6imToqQLHb4IhB2IANpJruZnmKGn9x2rdiC79i2EVxSp4dMkwa7GdGPN1fgAJSxCRspJzuXDhHB6RTjM9ykyRpOfTEnTjNPzGrnpiCMD16dE78mWA/qi5fIowThQKAYCLslIthFVD5zdKEmdQvQ7nLLUhzlGRkQMnB0kiMdLnIyY+QHtWxJ1foV0gfOjKZGKZijwx7e4iD06Wkyh2N2eIC8cggRFZDHKUS4go2A7LlHegwhoCYtJgXGekAi2oxwlAiIEkgCnBxXaR7wLLL0lrQoUEWMDz6Yp2g9EDSvhiLlEykha5VwcSdJgaH1kt9ugRhLhFQk5HyWn+ChoQs85S/6XZ/8jra8pTMnGrfntoz/4zx6/LxgDZBT8Qfx9lvkjTDQ81p9R6Y5WrKHXXOjNntLV9TwWNWmW0BmPMY6F1mit0VFwUQh030O67zdtmlFiELuey22DEh6X7slZTxOPqzukklyONarr9osww8BirDFpipCKpfBIAbpKUW1krl7itacTsjv3UaM3+F+HM67iwMhppClJhMYNHbUWRCGRIZDYwOmsIBMpXdfRJQZBQPqI6TxnJylpntJvtrQm7oUDAyQWzh9M0K0l9gODEQSlAYFpLGeHBlO3yEoTZaTNDUZqMht4dpCSWkGXClwMDCODDh7j4PJmRdI6VLqPsOxyiQKMjTzLLboXiCoF61lXKRqNRnBeCtj1iCJBXDkuJ9eR1kGX8akbMEYhZYoMKQvdU5oZXpb0Cko70GlHXu+4yj4mDxZnB7pqHzWWssQkEz4ZrYg+xSM5kzURifOGKHJO+2cU1iCTgpBHpI2kKmM6nrKaCYrqCGSHvzMnGoWKgkSMeSaWFCEjjCuGYHHrPe0r14an9QfkRcbg9qSk1qX4LoU64bOZI4klnYxYD1u2KC1IesFn9YckfkD4GqESujwgGksSM57ddGSjCa3cEqVg488wsaec5dR3ItkqpZEdQkpWZYfWe6DLZbklcQGjPIl3XFx9hJIDIkpW+YrCDTS5JXcty/wcXTcEKbjSFrYWQo12KZfpGuP30c31xBIdRBcIT9d8mnakaOh7Lu0FZAo5eEyQPL3eoRF4I7nyHbgpPuQIm/D4SJCoBBsja9UTXEDGgGksv+AjGBcE1dKMDTKr6HdrsmLEp8sPSEkZvMCHAYIjd4Zc5mznW2ZBsuyv0NrgyhbpethKHmdPyGNGPaoIpwO1GpAukCG4utEwCgKn97WUu7xDCofsAs/Cx8gFMBqQpqSe7vYCsC6yqXaMXKQNO3Rt2VRXZCZAKmhGF0yPI13YkbolTZwwcwJ0pL7q0Z+WFDqldILLc4vUkCYJ28YTuwZIiS5wFfcho6LK8MWOnV4xqIaj61NWwyV3uP3Nc5gX5saflw/w4ubPX8cXE4J+tYMhvv45Pv/sNwjrvZCG/uL3/HXabzQt6lf9zC9rLMSv3vHFH/P8rxaao+wEgNPuMxbDMzrbMsRAYwVbtviqpAs7jEnpupZBJgyZZkOgDpJ6SMAKdiEgY4JdW1oMjRNcrTvSFPoosAgWdUcvFVIKGufQ0dMMlr7cqzvu+r3i6LZrUFKwGzyttBQx0ke4eLIkIdAKwabuKXNNt7xCjVKyztJ1DiVhu23wPvDk6SWvvnIHgOACaZJxnOXU25bNuuH8bEn0kfbiinbYhwmnt45RvuTi4xUxgJCKXeswu4aYGfrVc3XZGHFC7EOpItAPkdYJpEkJCspEIbq98Gv6PGVlGDxP3r/Aqi0TKdgOK1KVwKgnyRS9b+l8QwTW3YrMZFSm+pX94as0tf1Nf1Hafr/51yZS/coWv77T8w1pknI8P+ZqtWW13HF6sYII6zpgMaytJ9YW3+xYX3Vs64FRliNipHGCYPfpCBaHtxDNXuF8b3Ijq35gKPapROHGhmHc0c4HHrsnfDT6ED8BazwXcY2eJ3TpQEwiC7HFCI3L9mQWJSTnZklKQiwDQ+/IZyld2/Ekv2KZ1dRJQ512lCKjTlqSmwm93LLJG/IqpxU9uMBW1rjg2MmBXdmgvSIZJSTBsko2+JMxXd/jq0BIPbVruQwLWj0QDyM+Rj6WT3GZ5fB6hfWW2rQooYlRsirOcd5TXM+xvcVXsFY9Skpa2TMrJiyv1nTNgB3vUxl9siKZ7dPSLrYNi9UzZJISxYphsLR5vw/X02Gip4kd3gTqvgW7VyluC0s/smy6bn8/YksUApt40Adot6KZJ0TrGOaC6DRWgb28QFYZzcjQSU/IQd6q2O1q3NNnmNmYOpWkM0OcTBDrjl3XEPoBfTiiPsxAeFZWoaygyfepQyIMtJVGK8XV5go90rQnJUJphFU0iSJ2iroJ6ChpupZwdoY5mrJNxvhVQ2siMkp2EZ6uV+hRxi7sFWPzu8f0oWGnFD6mBGno8hSEYNCCGDy7PNkPmUzRGgNKYk1ECE+daYJ0NKVkIyCmBhEEOjg2RHoCw0jRR4lXMERLlIFdKnFJgFFLcANORQjnGGlZs2MIjuAv0FrQ+Q6zVrTk1P2GzBaMzXSfn/aibtHnD8Bfkw0ZX6y3CgFhI4fJESLR/Kf637P0F9R6i2fMoDrWuiD6SKY8sl5hZyl2LLFDpEkMwXoqrVFe0yhYhX2tXBdBjAsSLMG17BJJDBKfJNTKIzODlA7tAk2m9tjhKLBHOchIbSJUijbX+LrmfJby4DRjnB/yc9eyFANnvmUnDTFonNQMdiApBGCoS4mVAp8WGB3pjMDOkj2SuNBYCUOWYkaaxiuCS5AEmspgswAHBbIfaCqNkAatEupS0QuNHeWETUtXJlxaA0JSV5omCcgMdIAmlzBEvNmLn6oQaXKNaj2NgQssPpPsCoGIkEeNdFAnkXCQEJWjKfQeq77tiXKgSQR+Am4Q1IlAKE/bLRDNBTvVQilQWtKEGgy4azlKJww+YdsKHD1t7oghQGwxSlNLh2CL8y21bYlEWl8TfWArG6weMIMj9B22b/GzGdJo2tAiREtb7THWFgtyRUSwYcOAw7YNwnlsClYb/KilyQaCNlypS0QjaUNLm5a01rLSjrbSLMIzMhFplCXkgUxaNuVATctVu0YLTSNaQpkhRMtm5mhNi0534Fvq2BL6HlFv2MntvnbGtYg0sHUb5CzF9pZtbIl2S5FpRBA0uiMkniB62tRDCmGcIbynFZarrKcPAzvRI5TEjzLidksdVmAEKk8YMksMkX7wyEyx0z3RbQlmR5d0RClwHXjfsBuDrxts0mPlPjWqvYr4q4al8mzaiEy3RA3OCPw0RTSWtR+w2qEPe6Jv8Toito+h7dmKLc5ohGoo+pyOHuf2ZIpatwwMXMoNxECTt0i1ISjLVnco33LVdCTFmF3SEw4UvmnZ6Y5GeXbaIeuBRvZQRLwU7AqHEJIhSkQf2NEQ7Dm+gV3iIEbykCK0otEdqjAMHlbtFhGh7/o9lU0PbEjwvWPzPMV9GAoIkZ2DfhD4mGI7Sd96GKX43tETaazEdxEXJZFAPl2THRqSREMRuNicfTFtiV+zhV/O6/fzpEhESPHFtr/KxOj5LOuXd/pLI8pfM9R/TccCflPOxfMr9U0hni93+XpByZdVF/Br55gAzJJDDtNr1HJL5kuKNENEQ9VnWJWihGEpBEf5FCcPYLuiDIZqlBHHhrgdmB7k+LFhsbJkOmFoBspccroZOJoY+iHQdZ5JYYhRkGjF+VXLVFgGHzGJIpWCLE0Y2p4QJXeOZthuRR0kxbQiDANVhE7ASEjKPGWz68irnFGW4tcbBiSzacXBbMxgHcRAYvaCUV3fkWSaPE+ZH00Ydi3NU8dkUjC+c8K120fYtUJFSXO1AyuohwZF4OTWIcPqKX3fo5QhMYooJLu2Z1QY8jyh63qkMRTRkoqOZZCoPCHVglJp2mGgPd0xvV8wnU/JdQrJQJoZartjlOzRtKFzjMyESTr/4h59cQs/v5m/LDP5lwbe4je8/vpnQgh0vSXLEqQQ9IMF9vcr+EA/WIo0Ic8Tjg7GhAAmzbF1YLNuUNuW/x9v//l0W5qf52HXk1bc+Y0nn+5zuk/nmR4MABIgiqRIWi7bZalKLlfZH/1/uYp2mRZlgCWRdEkUIJEgRCQSMIHhYFLnk9+440pP9IfdM9PT0zMYEZCeqhPevdZ+9175+YX7uqOumBUleZ2TF/t+9IDgeKxpu4glEoykFgGhYBkCE51oO8uojsQ8MXaHBHHBNiupn0eOdgs612JHAd0qqpjTTwum7ZjlsGWa1VxnW7IhozYFcgR6LZFGAZLkAukqMbtzxPqqZZRGVKkkFxkhT5TrnDzPUGiywex1CD6yKxrmmwlD8Ix8id9GiAmDwswN6lIwKUZ4GdBWcJjmuMaxzRsOVmNC/rnfik8ID81Fy/z2iBvtEZ0KxCay7TqEFUz6krpwuM86QqW4c3BMxV4Q793Ajp4DJsS03wfnbsfl5RXvqDfousRiyLFZydD3DNKxyEfkKXEZrjiUE5TUxNbvTcmCwZkMGx3zWOCGBDKjEZZFkmirIUVmToHKSUawk4GpFrjrnuA9s3qCKjKklmQTxSQFhmdbOK6ZVHsthpqXqNWa+skG0SXkvTnVUUnYOLhoUT4x7xMhgVoOFGWJrsf4p5eEw5zjyQz7bIcmYWQGQ0fm9jS18bIlri0H9w/3KNChx9hIkpH64hr54JCsNEghMEWOWGjCxYrZtidkkcp5olLkzpPZvd5ksR3wWU45eLwUlCJhfA/kTLc9ZpKjrcdGGGlDLSUhBOY20vmEHTw2V4yMoR/2ffzHmcG7gjQU7IxnJityEUkhMks1KUVi52iMZiQqxr5EGBibKfNsgU8BFx2lKn4isPjyNf1T13+CMLj9Q9QoZGEQWjEfDjjITxBCMMvnbMMIESW6qJC7Bt052mnGohjRCkVpNMn2yCQZJYkcPPPOkTJNLh1y26GtQwZPAmY7S68iOQFzOKe47hgphQ+WaQvidE5E411ENR7lEuws4/VA3TgGAnFRMEuacVLshGEhMoLQRDS7jcN0EektSRom230CJxea5WbYI2aTI8rEeBcgq5BdQOwc451HsBdsjvqIPsgIlztklpi2+4ymzDPKrcfZnu5yg7p5wLjzSKWQlaBYe0TwmCQQAqa7gA8eVQgyD3mImCaQCpguLc5EVACNINcC00VSCiwGgReBPM9RVw7RO4qi4uJ6x2IDPewreDKRD4ZCTggoJluDSIpCKZISjEROrjRRSA4nU3rRY5PDB0fZSbJtxGrDOBjCvKKMJbuLS4q+R1qw48TIO7QEKQrcuGaaT/d98gHmarZPJJBoUsck1KR2wLrEOApCr4ge+imMGoXODxB2xbjJYFYRNh1SOyaNJh9y0IZqZxBbh3YdnJbMUo5OEJSmsiVKClQQSJOYqwVhcEilyWyGzieINpCUY3QRMLMpmcn2/hfRoDaOWBUcVDO61GO8QApJVufo5cBFShzlR3TdgAFUkVGJjGpUIOWag6Fm23bk0ZJ8pCTDmBKRlcy7mtgNxGFv4FeEHOUEqfTM2hzuzXFti5WBuq6J7Y7YbljECc5LfAj00lLHEh9rXNxxZMYIqbGDpR0GRj1kpiDJQG0NarPX+nQ45uUMdiuoEuO2osjH6CDRsmWezcAoMr+lUhV9tyNaj9GKWRojxjmqX1IkReg0qhGIKuNoegOnt6irFxRWYYr882WJeWewlUHZDpOX6B7qeob63Dm9We8ox1NUEqTrngyDGMGBHNOGgP68wqW7SO4zRCaYD5pBFuQakvWYXCBSJOWB+SinCQmfoCv291+RQbvdcf/GlNV1SzUq2O46MipoAykKFtMDZqM5pL23zo/uiYJfUGP65fvof0Qbk/hSoPKLTLj+I8dfHUX7VwxxfigM/onxpYx3Solfnf9d3pl+k6/Nf5V/cOc/4yibIukJacsvH/0S3UEkHGgqpTjNC6RpsFzz3sRgtQIpmE00c+1xHprW8f6JxkZQhaEqFQcqEIShsfDaRNB2Hi01B/MJD6aGiKD1kXs1xLLam671npuzOQ0T1rHmzo1jNvkENztl2xvefON1dr5gtUzcnRywPItsXcXFS8/qfM0//q1/yX/5T36XP/7T7/Av//Bf8t/93n/Hv/rjf8X0RsEuNvSF52/8n/4m9/7W2wylYeM9b/3GTeq3ErNfzfnl//PrfO0b93jn/fv88t97m//8P3+PV++MOZ0rXjmVPHh/ztErmuIkclyvKPIViTNMuUMeK5hZerNBVVdsRk9INy45uCm4NYx568GbvH7nNf6Lb/5feGvxHm8ffp2/devv83du/2959/SbvLV4j18++fUfH8MvHciUvhw0/kiN9IVjLX72efAVY7Nt+Kf/7b/ht/7pv+L/+y/+gD/4d9/jH/3Wv+Yf/da/5o//5Pv889/+fX7zn/0r/tvf+QMW8znbVrDrBQ9ODlm+aBDVhPzGCd94cJtmlxOYcqPOyTMDQkFR8uhQ4WPGMCiOR5LRI0O8G+gOLHeOn9J84w9of+2Pefi+4fjREW245iP7CSd/OiE7NFAn7vYnLNKCfFLiy8jf2/46cbS/Kd4ZbnDbnpC0pj6Y8OoHd9CjRCphEeZMXmaoCvq8Y/FvRzzvz2lCx6itmL4subJXrOWGh9+5SyctSmuyLiN7YvCVZ6ha7n/nmK7s6ETLOCu5dXbETjfY2vPmJ/cpZzmDdFjvuffyJtY4XJU4/taC6cEUr8DGwN1PTnk5XNGojq+dv0U5HbH2O0yhmX17zDrteNlfcuvDGeu+5arbcN4tef/7bzB0U9prw+tnrzK4jF5k7IbEG5c3abFYGbm5nCFsQSdytkLzlnuNGAekgVfHDxmPv47Qj/DFQ75h/wacvotavMuxu0PV7gWCPZG3LjSDhJBgvg4sUkaUgu1ywxuXkiZZnIpMxzU3T45weJYvLnjw3NFYB+OS2eGc+fOW7mpDHyO/PD9B3J+DDORNz8ky0quMxiYefrdB3zxBUWB6zf3FAW1o6VLLu+M5YaxIJiE1nD7ZsTu7JkxLHg05IS9IMoOkOf6T5/TRM8jIm8agTnNE7RGF4+6zC1yW4Yzm3tMrkgIMOB155ck5Q6bwRnHzxRKZElFLbKZ4+7rFCXBCcNsKdIggBU4p3nzS4IxkUILDy4G5MchC03Q9j85LWhNwOnGojii6OX6o6VzJe+nrNNIyxEDpR0DJhWs5Ey0yq/nHL/8J/+WL3+J3rn4Xn8JPVNe/6lm1v19EfNvvgwslUYVBKIlUkm9Mfo2vjX6Zr1e/yq9Nfo03pmMQj+njJ7ybQxk+olx/m6PqjK/fOoZRIhjH66ueIa3p04rol9x78YJde8YmXPHq5TWeARu2OO157WrAjg2N7bnxwRWbqzPa9pp2WPLW/JDGJ3oEx892KC0JzuGMQG2f8fuvf8r/KP+Iq+1HCGVIQuOE4l05oY+J1joOLwfyIZC0wOWC15809J9PShbXjrpzpMLg6oyv+Yqh64gSDjaWSROISuFGOe9cSHqxF1qPVpb5esCLxJBJXvv2Ba40kGWM+8jBRYePjsEkHn3QMOQZISoKVXJ4GfB5wZAZXvu0o1EOqzyGxK2zgC9L0sGURx/2OAlkBi0kd156/LBn+78bZ/hdvwdLAK9fZIS6wtU1b/R3CfEGon6IGD/g7vV91umIVTvh5NObdP0xbbzFdjvn3vemrK/XbNY7jh9PGXantPEeO3+DVx+/zrY9wY3e4pb5VdTBu7j5m3TT13gQXmdT9uyyjoPqBFWXdFVkFdY8eHzA6uUl25dXjD5OFCuJT3voy6Ozm/QmYXvLpJ1idnN2jNhMD3jk36GbZbj5iMXpHe7cOEWMOkK55f36HdIrc3QtmATD0YUhRsugLG+f36I3ESehcIbTYYHVgcF4vpYewKFClpF6VnO3uo+rFH2yvPLJBJcDixqi5NbHGe1mTd83vPp4gc1zxNEhqax5WL1JT2Tbdtx5ccJm5WkHwUDOO+YRYIlYHp7PKY0hUyC95dHZMQMOGx23lgfoLCdWGlfAo5c36GxH3zYcf8cTtyX9zrBbRd45u0GsPCkP3NxIpuNIcWLxsw3vx2N8naAWnLqcunUk1SEmjq83dxiExaZAfakY2xIfLb1teJtHtMMGFy3T8oC/M/97vDd9n3fHX+P/evf/xq/c/7t88/jX+FvpV7h1vcAsPXIb+Afx1/jm6H3e6x/yy5/e4d73MupOY6Lhm+0byAAGQ+Vy7l+NEVmEOPDO1SlDvyFuVhjneL26i/VrwijwprsDk4o0ePxlw8PLMSG2ONXzTnaL4jSQ1xuqYsM7UUD9jDR5zlu3euq3n1G99zHm9Y9552tL+KWXlH9nyRt/31L+ypr6P9nRv/uCB7PPKOz3qPz3uD+KvJrfZ+4OefXodd578I0vzX++as7Lj5GzP1EM/qoJ1pfe96O51JeErL9IwPClzqG/apDxvzqK9sfjC5v/875BSl9IhO+39qP2A/71xW/zcfsDJoxZS4eoK5bDNUfhBDmUXNNhdtB95xV4cszlqmck4Op5h5U1GR6hPEpa1k6wyPZkqItlz2SUo2QgT5brjeNIJ4KWtAG0kWitKbOMl+uBw0riXMCaDELAyERB4FoapqHDBEvjHbmSzE4X0Ay83PRUYWBcWswiR41LDo4kswO4XJ5zODtkdSHpdgEfIlVVI3XGi7MlJ8czpN6AsFhneXDvHv/gN/4Oh4vFfp/GRLCeFBMffP8z/uRPvssP/sMndGdLYpI46/AxUmYalMClSC4VjLfIwmLxnNSHvH38Or/2v/+7mDJjdu94v++/cK6nEPHtgBmXP92elz7vFxQ/We770fjyC+nHZ4Pg5xY++L0/+HP+9M++z/OXlxwf7Q3Zds2wz/LVmrpUvDy/4vhwwXIj2HV7wkNRjkgdfPpsxdG4wMcJfS9xIZJngbKSXKwcR2PN4AztzhFRlIuW/J7nKktU/UDzK7+PvPWSdLPgJDsk7DZ8GD9k+4MtqlKMy5pVtuNws8APieaw46idsfYds2xMP/EsVmMyaXhRL5k2FbFw+57sasVpc0DvLNeTLeUux6YIg8AdBqrzjKACF/WSqi/o7cBpccjT/IzZ9Yhe9TTTljkTbGcpU8VytmJ+OWNUlbwwl2irSQMcyQNejC84up4jS8W2aFBJoa1CdJHlwYbJy5pslLM1LYNzlL5gHCquDlbMzkekXODLwM52HIUFhS1YHewoX+YcFnfRFDzrlsgVPFo84HpiOQ0TBjpCslgZmMWaTOaclQ0HTUGdevIY8JWkHr+On7zKc9sy2USCzlB1RacTMytIveVSW2aDwnYWlQTNSHEoC1JnOZMDEycJMmLyjN3UcCxL0hBZCk8dFfaqpaxKtqVk0e6vnSvbUyWFORhTVyUXfcPkWYP1sBnn5C6irCV3jvVpzcGQ4DhnOWzhbEMWFaPpARfSM33R4lH0pUZlhtF8hny+5lJFFqseqyz2qKA4mlHIkpyCZ9dLZp8tsYwZTEUUUHqLCY6rcc7seofXJc5kBAmV7clE4HqSM9sMbBV0WjIYzVwYSqm4lrBY7tjaJQ5HX2VMeocwcFUk5k3AyieksKbVjuN8RobgIm2YihqXXyGrfSvHgZsjybgSa6aMiCJhlGEtdjysHvAPDv82r49e+8lS9k+VHxOhs/huQBUZKjcE65BG7x+sak9u8quG87ThXwx/xA+aT9FBUjQN0+uW62zDzVvvcJ29ynUw+FWLaRzKRc61Z7y0JFPijCHTmjLsXccvi8RBVPs2BgMiU1SrLdpZrqvIrWpG9vrrNBsHuab47JJMSy5zmK974vZPEPIaeWtKUTxEH73NeUocyIze5LjWsT1fMdk2yORYzQyTJmLrCdnBjPXZkulmhxKW60XGtI3I+8fY5ys6A9PVADGxmhdMhCaWCi7XbCvFYgciz1lPCqpNTzdsEF1Df/OQg5UnGsF2pCjaQEyazAnWBwWHfcL2PbuRwtiAUIG8s1xPFEerSChz2sMatWzRLmBsZDk3LK4dXit2ucAU+wq3OF9xNdccbhM207S52JvFrnp077maKY46wTBKNKEjJsg7R54kl6XnYBNx2Wc4tSWIwGg4JS/vcbXIOHIZVhlsiFiVmCaFkpFz0XHgNb39DlKs8doy3hiyvOBCXDFeG1ymEEnRqoHD4gAGy1W5Y7zROBFRSdJklkk8IFVzzkXDXI1I2f45vWLLgRshpOCiP6fyJVEkij6yyhoO+glCJzajnrJXROfJdMF6Ypm/FASV9qaYVqGkpMrHXOcbjuIhXbtjl1tM0ugoqfIRV2rJ/DKj26xpC4suS3I9oTATzvWGg7amj5YmdpAg9wYTDGd6w4mboCqLryJ+GKgbMANcZSsWw4Q+j9g84ZNnFCuMzlgeWmaXhs51OAJOeKp1SfI1Z+XAURoT6w3mIKMddoy2GXRwtfDMw5hdJ8ErGu1ZtIpcRK7MjoUcM8gtQsOGhgM/JvOeZbljbEtkFOTJsJM7Hkwf8Rvzv8P9/JWfeP4j4GX7jN97/i/5dPkBWS+4I27ynx7978iO51xcP+V/2vxPPB6eUOQVMU9I61nlDQt5gK0Cm7zFRI3sA6aXXOYrTkd3cbVmubsiq2vESpDZggtWHLOgN57dsEUaTdkOzGY15+qKg37GajfQVYIYI8U6w3QFS7XjIE3ZpZpd3FM+R7JACcVzv2WyTdR/uiI+3iIyxdFiwdduPSQfFXzz//ArTA9+0kDvx3Ocn9ny8yP9xU/oML68837ilR/OpX6cuP3K+dRfOvNPjEdfYfj3C46/HkH3F77Ml8eXN/Sn1vwZG5gSIPal4S/vkxDd3gQrBZz0xAyiDJArQhvwfYeXA9l4RJByjxIE+t6ji4K+B5FnDN4iQ8RkezFXZjSqzAlKkaxDawmZxquE+jweHDoHpSLme2zg0DnyqmDdWJRRSJEIUuKcx+Z6L2DSiraziOfXJCmwPpHLPeayO1uSp8T8oMS5QEoJ6xzBSayNxLRH0rroiDFhB4cmELGEsMdQhvg5Ii0JhOTHJi16j5fL65zRw5u43tOuG4bBUhUZOtcMMTCZjhCzGll5+qHj5s173L3zOsk66juHP003AFDyR4HFT7z+pX6Ir7xkvhwZf6Fd+y+JM/f71TpijFjrCAGs8wghCA4Gud+Hw+DwTtKvOpIAJQtAo4ym7x0+OtpWEHykFJLkEt4GeiexLuLj/qbi4h5LHL2HTKBzQVxkpELSXl0TUk/rW1ShaBmwzhNMZOMbMl0QVcIpR5L7jLOLDiccje/Z+Y5xUeFMIkRLEwbWvkUrQRMHkhKEFCmKnC70TMoStKCocmJKaKPxMqC0pBcD5aSkMS3X7ZrSFOTGkGRiFxsUcp/Jko46H7EaNhijSVnkut8hRoKUoBAZxmREsWKbGnRviUWiKgrYQDIRYzSylKBhMJGDyYzRtuCi2zBEz8FkxtA7OimRhaEcZcRCEgX0Q0eUFqscPgZciiQV9wZlwhNiwBEIIeBFxBFIUjCIBGqvxXBtT99EIBFziddgFajPz4/Ot5hphQT8xuFixPU9AwOtCKiyIAhwRJiVDMuOkBXEcUmyGmETdj3gz1eIRSCNDfLeIelsS5DgtCClPR8+9A6fGQiBmGs4neCvLM3VkjAvEUcjWFm8ksQQ6K82lCcT0mqLU4JoJL4dsH2PKQusiKhpha9bQq9wah+kB5eAuL8/GEWUEmcUQQhC2KNDkxB4o3Ap4jO9R5Vqjf3c8NJ9jrG1QuxxkiRETASf9pUOAkEGUrY3mrMhEILDaQ/TjCB6gguE5IghEXWgjxZkwg49g+ho22t22xe40xPUpETme/HxDy/sFBOxt8S4x7fqMkNohVASXWQEF0jeI3ODEAI9qRCuJfYJTyCJRJVJfL5PNg3BE2LEk2CU41uLF/uf+0zsUa9GIuoMZRPBBWKW8F4RncOrfdtQTBFvBLLQhGmBcx4v9kkUowRWQFQSpyDJhMwFSURCjMQU9lx7Ij4luu1eZBvN53jzz7HoVBnD4IiC/fmgFElJXAZSSbwWBJHwWkLcYzbjqGDYbpFKkJTEy4gqDImENxLnEroqiEoyaBBG4QGnJSnsi7GpMPTbBvT++4tco8I+454EuEIhRzmu6fbGj4H9M46EU5+jlvOMOCvpz1fobP/scyLuv6/c7xMtwO+JyFjvGLaWIfNIrRB1gXeOJBI2Ay8FQ3JEJfC5QWWS0PR0PhDziM/NHlHbDgQNMQ+4CDKXeOeIuSLIiI2WIML+fE8eoQVRJGImSVrjBouVYo+dVXKPLfUC2zZ41dO0A6IacNHi9EDX7cEIcQpR7++J1keSFngTyQ9qom33iN8MhBv211JVEWMgZYlYGNKyY9A9gUTXbPEx7D8zQCFy2k2HzVvsUJJySSgkKTnY7vAy4itLPwhCpvC5QGqN8DnBgXCJaAJ+12CTR9U55BXJJ4TrcC4SRMR5u/936PdzpcbSh4DPBS4lglZEUeIbRdIS1w0QHWFweBHwGsggOouLHUGVkGeEfsApiUoRHz1tssQsIWQgGUmIAZs8gcQgHBqBDHt887DZ4ib2Jx/sn88DfAokmUiZhCJH13PKuzdRRiPLKVLXpF1GEAIKCSMDYSAVGnJBSInkB7RWiFqA1thkCT7hZST1Ldoa4pBgZrDWE6PH+gGlIVeJttnCNDGEnlQovN4nt6VRRLefzcZMAIrkASlJXcRav8flGo2pckS1f36bIuPZ+SWv3XjIaFr/dLb1K6sEX3gx/Tip/uNQ4Ysri5+cYwsQP9Vi9dfc7/QLjr+G4OIvC39+Kq/9C771J0s+Pno+3n6fPnSclDcZqb2ja6kq3q3f4c+7v8AkuFWdIhpJSs+ptOH9Rzf407QhdVsOrzX9Wc7VaK9HOE2Kp32OV5rCS2a1IjmB8pH3blV858WaUZUxE57TccZHjScMjlcmgmeDZVRKJiIxywNdEGQS7s00L3aBSkimRnBzMuKT1YDzcG+Sce5g0FAEyesnNX/+5By/9Nz71Xs0bAmhQKmKtx4d8a3vviQmwcMHR7y8aNkNirKuePO123znw8d4GZmOFwwW/uDf/YDFdMT9e0d89wdPsNZz+3TO0cmcLDdkueHwcM75y2tCiExnNTEltpsd2miO7tScr57hhoFpOeHg1ilPNxeszhwPygc/Rk1+4agChBj58OPP2DUtd2/dQEnDBx8/oygyHj28zcefnbPetNy/e0RZZPzgo2dkmebRa7d5+uyc6+WG2zePuXXj6EcnREqJjz59weXVmls3DplNR3zvg2dIKbh364RvffcJeQXj8ZhX7k/59vfOGK63LEJgGGmyYsZoXHPv9iF/9ifP2F1uOMkadmbKxJQUWI7Ggg8uEsknbo0Cu5gYGUEpE68cRz5Z7YO2W1nGZfkp6vSasp3w3tV9PhpBv9nyykcTHodnpImg7nOO/sOCDx88ZboYcfRsiilzrgtB4QpufWfK09cu6Ncd5mpOrgry+xnjOOLmd8Z8++YHTLKK4mnOKC9ZHuzIguLex3e5fH1Nu+2oryu6XYu4DWNRc/zdOdePNoxCQbWquB1v4sceuxt4+/nrPL99RlGV3HE3WH9rC7eh1hVvnz/k+u6Gl6szqnXBzeaEs9E10UVm3xmxurVitCiYxjH6A8PVox0iRBYfTlkdbJBJojaS/DND+7qFLGK/6xgf1OjCMvY577Vv8GfyKSYJvtbfptMKJx11MNxfH/Dh7AKXAq+mY3Yh4IOkGhRv+ps8SZ8ilOGOL1htA31copvAG+5Vvm97lI3c2sIQI0FAleW822Z8TzUoD0fbAE2HO82pD2oenEX+wl1hAhwOHtwGd7tgVFa8YWZ8MFnD9ZZJjIyOD2CaoYzlzl+s+KxZks8KFrMF5ckxH5yfITvHK09bni00lZaMXzaMxhr1YIoqFQ9vlDweXuIvnpFdSe4uXuVju0OExL0XLVevSKazitF5w+LC8vi0QF46Ht0tuRDglGAyryn/6CVPbh4glOL22ZpNLQm5YtQNHF1ueHzzkCgFd692bEcSpxW1jdxZNjx+9ZChd9waHINQJCLFELj/ouWDBbhcc8dqdmmNsy2VKHhrO+XDWY8PkltxStARqwKzgwVvjm7z5+tvQyy4GaekpHF+hRGG94r7/EX4NpLELJtwq13QvVxSVnsX7fTD8r3be0yE5vOKZ6n3fWz7i551v+Rx/zFG5bxSvM5z+xkrd82xvsmBLFnkEukFr7pXuRo/oYuaaVZwXJ8Q2hfIXHAzVnxmzwnFwFhkzAd4Ka6JPbyyHnE5dkTjmYSKxUrwiWiQheGeK1jW+wRSHRSv5zP+/Polrh04ed7SjgV9UhR95MbFhKevjFH5jNupppVjHJ5aKt7Ywp9fNWRCcOO8pzcOnzIKG3k9Fnx/1yJbz8mlxeeOYCRVkrzjK77VXWBE4uhyACUJpaFMcP/Pr3hyr0IJxcHKkhHxeUD3lht/9DEXv/SQrIfjXUK5nrRQ6JC491HH0/vjvf7kuqPsA/FGjk6CVz7b8exEE41gMUiqsx3hMEMhuP9s4MVCE5xgsrGMd4nn0xGZk5x+2HFxqElJMLGGA5vxyTAgPdy9gEsD0cC4F9xrDR8fG2gcr1x5lqclYVQwzyQnFz0fzmpSUrxypdjWAj8tGHnBzaXmo/keDHH3QrJKLf0Eiph4IG/xQaZJec0tH7HW0ucHFDbwrjrkB6JFkzhpKoIJDGpEXUpel6d8T62QQ8/xC0e6eYAsNxgjuPcxfHr4EoHkuBmjhYB0Sa7hwfKEx7c26KA4ampMb7CzGuUjDy8O+Hixxl+3HIgZtSz4bPkc5RwPhld4QiTbDUwoOLx5kw+aC7hueHApeHbYYL1h5EsWacST6YpwveOV3SnL10q03jK1mupqwkfZFtH3vOJGXB5mhPqAcmW50U55nC9JG3g4ecCmWBMKxbQacbwd8+Hue8QYuetOWacelitGveGkW/DRwZrQee6satZ44jgyznNeC3f4nv8M4wdutwva6HA4yi7y+nbBJ0drRpXhdnGLGDpitIxMyaPp+3wvfESVLCebHBUGWL2kUCUPhpt8as5IzpC3gryAf3f4bSqV81Df5RP3gm1suGWOqfM5Jh1hpOb+7BEfuDPWXcOd/IBxfoD2DQrNG6NbfByeksmCiVxQZ2Nse4YUidfChM/CJUVfUYWSsZWEaoXMDa/2t3iZ7ZCxZbZNHNg5H4x6ZFDcXR5zXV8g5xmzYsztFyWfTM9BG15JJ6zkFil2TGLk9eKED+KHeJm4N3nA0q1Q/Tl1Pubh0QmPyzXBwHEx4zfe/1Xuvn0fpeRXt2N8cdab0lc0dnx1gv4n52NfIXD7yhnbzxk/VSf4qwUj/8ub6PHzd8rPfM+XXNn+9OoP+XDzXfrQUZsRvewQQmJkxnn/gspleBy+bVCTHLWzaN+zPHnOwchgz1aM05Thf9SE3QABljJRlYaz7cB0WjJ4jW12nCxGXNqIzjO6KJB1xbl32Jgo6pxdYTDJQUioTLFRkkTAFIp1FEgdiT5SlCUXzuFToBoXXAv2y6xH1DkfLjtUPkFXOU+vFcGNWW0EeTala8GJCh8jzy5hd+XpOkEnI3/82x/TDh16UvFh1vPZ43/Pct0wnZTIf7OvfFjruHGy4P/4v/km7a6jrgvGo4rl5QrrI8c3F8SUuDxbUpY5o7Jg3WzompZyXPO7f/y7XF5eUI9GrJs1v/zer3zheP54/PtvfYdvfecHNG3Lt77zAXbQbLY9RW74/X/7fUIUbHYds/9QoURg13SYTPPHf/pdJJHNtmExn/Cf/ie/wo0bh5Dg29/9jD/4d3/BarVjNhnhk6BtB5RSaJMTqLEhMLiCTz9pCDHDW8Wz1sPlDjcf4WYVL14GZDZGl4JrbxhaR9tGlBasZKQaGWzv2Ia94VxmDGJwXLQecomWmuGVNc0bf4o77NBxxurBHC0jw/aai8Lx3cef0mQ9U1dj7yaKWKKSweZ+X4oX4HYD6l5EuD3BJdaeWha45NAWPqlekMcCKzyyVuhaUBcZps3Z3Wzodh3ZzGB1D1XEWYsWNcOdgTA4BjMwKio+3n5GyAMTOcLedAw7RzABGzxtPnBcHSKs4OXoErfxsBB0vmeVNnSrgQLDauEh7g2mrB2ob9ekPiClJL9puJsd81Rck8WM/JWK43IvLB/fHiOiovOXjOSITdGykGNCCgxGkJJH4DEi4yLboL3AZ4pl12L0HBkT9JILscUgiUAXG6J/johryiFyXR9jmr3B3WAkwUWUkOirjotRRaFy+jgQRIZUBlxAND2XByOqbY3tW5zdYzRj3xNbx9k0oxhV9LkgnHVcffQUd1JRHUzp3r9FfX5N1za0Lx7TH07JTiuU81yONUqVRCQuKprVgHu6Jb9xyLW8RqcXZNMt8nzLZTdBTcewatjUIF6uoD4kP52zcRGVDGnjuVhvUdMcgSOfl+xOKxSemCLbCkiBlDyGyHpaYFLCxUQzyhAqQUxIF9iUmjpTSLs3hNROoAtNJRKX4wyBBSX3lBux2uMrQ8ZlBXmUxEzTiUT0HjkqyfKCl90O1Y4RXrIdCrQwJOnI1YiX/oq6KvG2Y3dxxtW04/7idP99tCKFvcGoMAWu6ZBlhjCKFPbmpACda/i969/hcjjHqIw/2/4RQTh2actYTem1w6QdWmku7DO8yBiSojGS9fK7COXRSrMeWfJ+g5GW6WiMUJ5suwIB6/wC1QXIEqIzbKuMvJAIJWkOZqg4JySLQPOiXeOv1vimZ5U8sU8MWjFsLU/GB4SixuuaKznB9AFRKNSQeHq5Qg2eYCQ7EcB7ktcYD9eVRl16iAKbaaQRSCSZUFyogLYBlwmsESQJMteobc9ynqFsxGaROC6w3iMKhdi1bE5n5EnhA/g8w6cWAWgfWR3nFGKfSRYShlygUsL4xHKeYwJInRFFos0VMipkElyXCu0jAoUSknaiySc1admyW1QYGxG5pChKtm2H9gI5RHajDNV7QOxpU4c1Og4gJdsStJVkGHKfaO8/ImuusF1PU5SY0RiZJdQQuaokZZQMMdAWGoYcKUGtPc9ViZjew155ti4HKSAL5EXF8/MeaQ7QRzW7dcRdnBNvTmBQfNblBKmxQ0OTPGq7RJqBIhZcTXsMht62eNsgBKg8UgyRa3ONuhxgGokGbCVJg0ennKtjiekrUIn+uieYDkagyTkTGjEcEmVPkBOut2NiByoteDnp8b3HGkkoZ+yUQ4SEURnbSY9qEqK2aKHYmgojSkSVWA0FxeSApvRUecZL+z1sp4HIi90Lqlv7yrY2BX0VGDEneEeIijIWFOTUomKVB1SnCDGwpUeVAV04SjvwzD1FDHtoSut2e5RylZP1kl32gtJ5+t4zOIcqCkwVKULgsj8jY39uDr0nawZMnVGJEVdpR17P8KqnFYZ/dvbf40xNldf8Ed8mRtjFjomsiJlgEBVSFvyxe07oz9iGjpmqSECnJyRp+CQGvJjTI9i0hvWZw1dTMmU41zVG1kR/TbAZ9rgjixWi9az8BZmR5LWgHk3oQ2IUCwQCqwbkViJIaBRDtqSyA0iDrVZURaSNjmkGNnyfqd5hh54YdsxGBa7cMPGedrLFNA5vO/SrltNbp0ix15p+MdX+lbPiLxY10s9q/fjyW37+Sl9c/kNC3w/b3H+moPvn1AR+0fG/eHDxczf7F9mAz3/Bi/YJz9sn2DBQFTVWOlbumiF0dOIchKGjJ8kAQbIpOtq+5VmjyYtTurHlxVPL2klerATjUYHtHYXe93JfbCMqJbZWEVYBNh2qkPQeLkxCaM3aOTISW2tBSxq/f73dWloH652jzAQ6QRslT9fDHj07gOgcRS7QQrINoMX+xt0MkUIGuj/7lG43kMY1tgkMux1971CF4fr5mu3lji7CxkhiHPDBwcUOHwTKKJarhvnBGB/27pbOB4rMcLXa8uqdk73btpLMDmeE3hIHj1CSk+M5Qu7L3Iv8gDRb8OHjD1lvN7y8eEmxKxnVI375vS8dq8+Py9PnL3n+8py27ajLHus0y9Xe0Tqh0SZju+3YbVukDGy2DVopylySZZLtrgXgydNzTg/nIOCzxy958eKa5WrHrhnwUbDedgghKIoRyJzlsmV3vqVZdbQukucG3XfoXOGuWpw7Y7eCTQvGaHa5JEZJEyVCKjZNZBcsWknanSPPDb1U+1aQqOgluM6xzB8TFh390YprLbmeb9ldv2CX73iRn3N5uIaZ4NP1c4rDipRgW3Z46cmVoSt6xgclf2E+Y9d3qJHiubjCpA3BJAZtGcYdMURc6Ul5yye7zwhVJDcZaq5IvaApOsJBYNs2hHngpb8my9aYqGEkaEzHarfFHGmuh80+UAmKmCXOxSVqqtlOWkII5M7Qdx2MBZnJGJxlk+/olGY8D4gEq3zNcGC5cFvawjItR1z2a7SQbIoGFyNJrjETydZ2HMpA13jyo4KlbemGS1oh2PQtvYkoodmYjhADKQOvw96lNWqMzljHbt9uFK/RZoAk6foz4njCVrQMynGZtQRqHBBVQBSwK8ElyUtadJ3TDiCGAbxjlyS2yjh3K/KDnMYWRFpibGmEokNwdXVGPZ/TGYG4NSYcFayahu3LC4r5iPy0ZvCG62xHGFp2K0t+VJMyA12kKzViniOToEme7eUVq9EFhCt2tKSHC1yb2JmAPirpjEMlTdO2iNkYd2NEQwQhGNYrytGMnQygBd3tGZutQyqFz0CKRJtJBCU+ZvSmAMAHjRKBNtcgBF5leLVHV7owoDJNk2ckJdjmBW1KRKNIxhGcpZEeieRCtIhaYWNLipGIo1eQ7BLrHClFeiyOiBaadRwYJFzFc0xq2fktRbE/z1SV7+2qE4R2QNcFKQSk0ftSv5b8CO4g4Gq4YGPXvOifoOR+4i1kok071uEKnwtWYYkQEs2E5DO2oiO15/g+YxMcKjdUmSEWHTs6TJ0ThoZN3SIzQ9+yxxYfaDYoyCSt9ETnceYQERVNB1cqcNVuuUoWaoXLEkTPTkfiSOKVIhYCERxBBtR2gy0mBJnYYvFjs2/3SRkiSXalJIwzVjpiRxkuaoSOoD1NLUlZxto47ERj9ectVAi6aU6/6Ym3KmQEm0t0XhM3A02lYZbh58dUWUFXaSgScchoaol2ktVUkhcFnYQwVUSp2dUaHWEzVkgX6GuNcHsn8e04R0lJazwyOJpK7Y9PljMUEEygqQUyKNpKc5VJHNCUBqRgqAVxp2hyiGNBmiR2ARAKpwM6k+wIez+dtqMZKVKRE6ykmCi2tidkgqgirpCEAfrooVZsVCBONV5FfCYJyhBURAjYCnC2x89AFhofPLYIhKOMVbOl7RNpNkGVJbtlT5ruEFlL0y3ZOU2sHaYwDNJzLRPSO5raMYRIFA1aZfSZQ+aa6HZssp4Wz1U/YIqCbehII40qYVcMiK5FjY+RAnZJkmxLWve0pURMDTlrko3s6MA5jLR0NMgauuBQydAkTxoZbJVYOUEK0KuAatdsI4TMEW5plhsLPhBtS75OdNO0b1HznoGWpBNBgUDSB4csA5vk2A4dMUXiRKC0p2WLygW9t/v2VCIiVySf2ClLnGquFhZBxCZHzICwZht7nNvxrFsh8xFDsohZiYwNXRlwboWfKkxW0qcBXySGNLBdnlNNZqAyDDlN7NmqESTBOjaY1JOGHp0KdqGn0T0pJdahQSaB6a8wIrHxDV4mvIPN1YBEUuUZeZ2xkwE19+yKHTtaKBJd55BR0HpLkp6h6ehVj1CSYTRCmMDOt0Q8IdvR5g6UxPsBJQRNWu/b5oJj69agBY4K0UGjO6RxOB1oswHvHKvmgidnH3F38oBiVv+oBTx9YR6VEnudqhA/0lb8aI71FbKA/+jxVYHEz1vvr/jB/ytULv6KIdDnb51kM+bZATu/z2Q55bB9xzw7oDeS5CVru2Kaavx2IE1qsiESiorSjBEjT1UqitmIOFiKXBDLEt/1XDZb8kJTm5x1suQxUI4UGstaQBkjSShGWlCIhMw1UieGIVLqgEqSkZGEFBEkpgJCDEy03GNQK40wEg1UuSJuYSrAWU82Lkk+kIXIeFJx7QKcr5HBUgmBXzuUVpxOKs4aSykT+WSE67u9ydLgaJ5dEgAloO86tATrAn12yVgbrPcYpRBCkMS+l1SGRCJiXcQYhTYG21mSEEzGU+qyoqrGjKuK2XhKjIEQ4udBAzgbUVoynUxYzKYIKVlMJ3StJEZFVeXEKDHGQIKDWY0fekRMlHWBVokyV8QIk7piPh0RPg+AFosJi/kY5yOHiwldH/YZaq2QJietPVfnKzIjqI/nrK62+F3HKN8jKTcJ9PWGKpuhCwExMp+XgOD59UAtA72NzDMDCupZTews3bZjUis6GZnOcnbbQDbMUH3NMgRuT+/Rbq7JXpQEPGdPl+RdjtWO7MpQ24pJXnPRXjPtKyblhGW1ZbIruerXLMSEpGDcVmzXHQfFhHFfQ16QAlynLeJScMiMoQ+UTUHve2wTMFNN3VSUsqBtWsZuRFFlhN5zHZZkl5pRLAlXkcKWuBCYmxlD5Rgt8z2SkERBifeOeBkQmUBfClKWMclHiCAodUHpMlZmjTiDLDdUviJuIzFEFtkckSnKrqQVPd2mpVQZ0UWO3Axpc453I6LPWK+3ONczO67JZU70MHMlUQREhDYOjCiofUkgMTpfU4eO8nRKyDV5LJBqRgBGWuC3CZEbtt3A2IMZlcRmYKZz+nWLsA5TKiZCI1wk7gKjoSPlAt1L9FHF/MYYu94hXUe59Ugi2XoJN0ZMq5xU1sjCYF5uCY9XlLMR4qDk4OYJzcslYtuSb7bowwPY9CwJTNtIFBEGj3EDpg9UxzMIkkM9xlYHqIseFSLaJvLeEYVh9GJHPJpgzlcQI9kwUBhFOh0zR1NMStTZGUl4ch8wQ48fZUy2lt4ISq/2cAZvyRQkKZk0FmcEQQripCJ3ATNEfIRxOyC9o8okbYgUQSN3kVRKJsoQKFAUbLZLxlVOsgoDjLcKj0QIyToIDooJShpie03RGUysyBPIUjLRiz0WdLujmIxIMYHeQwmjC8hsHwAhJdF5pNovm+QLyqxi7GYUqiTpvTmliIK5WrCNe82A8YqYFeg0grRibgtcMUEPA3JI5EWBHteE6+eMO82AwGQZGE11YMij4jKuOWBCP3hyIYlRk3tPUeQMoWXhJb3f++H0ZUbpBUUSJA/TPmGNwJATVEZ+3VDpEU2EaeMR64GQEoOWVH1Ae4cYj6m6SCYUaTZi9eyaYufJ8kiSMA2ggqLbeJpCMmoikoQKkF/1hBRRIdIuSiY+4Hdun9U8WyNHJblyCCmZth47OEBT9QkvEhkQo2W8dvhMIhLkbs/PNzaxqmGy6vEyQymNcg7pIqZ3RC2YLB3ppKKw4K8GtPWUDlImGa9aBhExdq9zK8fF/nySktk24AowPZBLCqkprCB4z6IR7HaW0oxwLlHLjHLpGVJgsonEkSbsPKHOyFuLjolYw7Td6zxErbGVpvYR2TlClZi0gVBkyMbTioGqdSAsbmyYC41bevQQEFYwsiWSnKQqpqkgiYCOmq3smOsckYEULZXMicFjhGETWqZthvMesSioZYV3HuNzEjAXOZEAoqAqDaFTKAtiVHA8GWOVIJeRXEogkFcZ5+6a+UWEtNtjwwMoFzGDwvWWsutBdhzMD0AJilFOoQuEsBwMii4q8uqY6D1Fv6G+6gldx6TWSGUodUkkUMoCE/fa0bmagx+oqimdaxkJQ1kahq1l0hqKPCMkGNLAyGlUUKSYGDcaBKhc0VaJiRxBZ4kpMe0yhmDQsmKLoBYV0jmEDIzLMZ6I1iXbuGOez7HGo8MWc+7AJIpSI/KceSqxbY/zUCNJmabIRwgE81Qy2B67S+RJonNDYRQYOCnmtDHCxTXSQdYF8s2Am8DcjBFmnxROqw7l0t5batgwkyMGqfHFBCElmZfokKCQzLsxbjEhW16DFoyqGVknCMkxizOcseSmxtmB8WSMIedyOGMhDmh9RyVG2CoyKWeMXUm32ZFPq8+Dhx9PbX96/v7jyEP8JS1U/zHji+qNH/33r1ih+FnjrwFF+8Mays8af8k3/wX3393JA1ZmyzZrmVQHjLMFvlK0xvHL079JU0Y6E6ltxXF+hLNb0kzwq9sFkTN0seRo2nDyoGH0tzfob1zw9q0dm24NmWexUNycSUaHC8x8yhvjSJFPEL4gi4bTQuBkRoPm0c2cfgb+piIewM1RYkAyIHk4hiAlPoLJDA91YBgCTe95kEds4/FJEaPg1XFJq0psMeb+bETSBb4YIQ8PeOOVG7jRHF/OuDseEWTOkNXEasr92YyNr1l1OROfYUxFoGC1jXz9nYe0uqZLBe1lx7/+Z3/I/+s3f4/f/Od/yLe/9yH/7Ld/h3/6O/8Df/qD7/K7//Z7/KP/5g/4r/75H/Nnf/EZ/+9//if8w9/6A7717QuG4YCrqxkvX5Tk8oR/9E/+Df/wv/o9fvt3v8Xv/O53+L//49/n//Gbf0ReHPByPeZiO0dmpxzduMfaj1n2Je+/+warVnN5Edg87ci7khefwcvH8PrhHS6fD1xfeDZLz4uLHf/wN/8N/8/f/DdInbHuDTtbEFLFzXrCyw+vOf/wmjeqEc31QO8lWVnzS4/uIOsJXZLczPYmVJsWvC5487CiC5ImKu6YgFaamARIxfs3CkTMsQ3c0p5iqsmOK/LTMW/fv0J9/fvUf/Mj3slhNC7RRyW+ivytp1/n+XDJmo75xxPERqBKRT4xHP7hmG22YzIvmJ9PmHYjGt/R6IFvfP8RTCJW96TnkXE7pdeeje742vcfMqiebWq50x3zanObLg0MeuDRv38FMzJEDWalKZ5krGnYmB3qv9/TOUQmua1PuPnyhHyc44rAK392m072YBK1KLn14gaikDRpx68/eZ9Xbt0lyzLmasajp/fQI4MoBOPfr8mqClOULMaHvH/+FvmiQNSS9588ZDM0NL4l04pf/fQ1QhExI8Pht6cc2PeZDN8k9+9w4zu3qcrXeHDz13mjfYdaPqCo3yEvH/Ir69ewIhKV4NXrCh0EXnjcvOZ1/TdYT99mM3qLG5NfYRoUqm9RyvO1zYghE/haceQl1ZAIuaaPkfe7yV6onGUcUbIoanytsIXgvY88rQv0jWeeKu4d3sYcHZPGU77xNNKpQLdaI773nMWTDdZH/MmEX5reYLdqaa53FErz8N4duDmlU4nX/vycdFBDJlGd4+aZxZU1fVXz2gcVIdxAVI/I8vu8UZ6iTius9jw4H/YiTSUIveX+sw4/KbFS8MrjDvtyhXMepOCdeoyf5gw6cu/FGqkEQQuiFrz+9AqXgTdw7/kSNUSGKHFC8fDTC1zypEpzqx3IfSRpRVSKN59uGUh4Jbi9VIxjINBClfilcAvrWqKBm27EPBS064bd0PPe7iZtcEQSx3LCItOEbI0Lz3lvfUKTtoTQUOmM5/oZ/9T+N/zT3X/N8+7x50JDgdD7iYqQ+3SdzjQ/fJiOZM2ECS4ODLHnvfE3GWKLtQ3KJu5nj3Ax0jnL+/E9+iFgg0DIgvv9Ib3v6ELPu9xCjSRUEkXkUbhJFyNeCt4bP8IKxa4PWJd4qz2h7wO2j7xpDmB4TjIvidkFb14NuNyDttzfefJRidfgqoy3lpouOqy3HD/ZYG1ks+u5ulzz4Ptr1kGytYmDC89I5iSlicbw+qdbwkTBWHC8Hag7j1NgS8W7G4nNJVFLjjaeSRtxItGryJsf7HBVCbMJ45cNi+sBKxK+ynnzgwab53hpKK49J5d7XxSbKd76dCDmAi8ThUucXnlcJugNPPrBDldrQgzoCHdetvhSYKXnze9v9mJzJAbJa3pEt9thVeT1xy2DjrgCwtDzymcNvQE3Mrx2DkkqgtIIbXj0qSVogY+RV76712pFs3eNfuczCFKRtObBek/4SUqQMsk7P7C4UmNJ3H0ZMAlCLggZvPtZxNc5tnfc+NRS95KgNbEqeO/7jkEKojGcLBX1ShKcog+K96/HDDGRyorj6jY3pu/B4h3s+DXeuf46O3+Tzr/CpH+dQ95jKN+kzR7wbvc1Gt9iDZRiypF7k7Y9YX1V887Hr9L7Ezh4j+npN7nRvY0vHmHnb/P1+AZxNoGDOZkpecWOcULTWXjnOxXDRUVKdygP3uaV9dew5i26/C0erb4BN38Zf/AriNl7vGLv0Yocl1W8xwk+ZPiU4xrBGy9u4OItQvWAt8Z/mzj9GsP4GzT9XW59fJ/L7pirdIfj8DWG4i7r8i6b+ibvz3+FIU/EOuNh/Qjjx5DPcbLm6+uvYct72Ow+t+wbFMOYPmR05Ly7fECTHP3Qc3RZMZueEKYZfSV47/yYQS2RR5GT0ZyRyBimgeEo8bXybYaqx9WWmak5ZbFPxkwz3nx2wPK6ZbuxFDvDUXNMP9TshpL37atsr1ua8wb/6ZajlxI7BLre8c71Ac2wo3Utbr3lntKkGxviyYp35QE2QL/uGR7vuPXsLusXI5r+lLfdL5E6S2gtbB0Pr2/Sbdd0uw2v7+5inaNrWnwIPFJvYRcV9mDEw/xt0rYhxAGvAu9Mfgk3UfhZxivVWyhTECY5YZ7ztfmv05Y5Q5YxUaf8+z/7C377D/8Vv/2v/wfWm/VPT4F/FER8TkYVPyuwSPwUjvYXGeLn/PlZv+6vIej4a0DRNl965QtI0b/kvSn9GLH181eE//ri/8MPmu+yCRsOzAGusazMhlm+oFUCMCz7a06YIYNnHa8YqwneSowYsc17Zv2ci3PBEs/IK5pvV6SnBVuhmEQYdgVtp5EqkdqeRWV4vnYcTSV96NnaiBIJdVtjKrc37csy7IuA7UCkRG4kOZHLNnA4MQy7ARv3NJASKIBzqTkeGYa4v1BESMzKvdPwZYApHo+A3BCGQEkihcB1gIVKRKnwPtI0A8czg7Q9G+s5PKzZNvvMWTKaKvRMMugyyemdQ5TZopWn2TWMpscMQ8HL8y0H8xHdAFJq1puWo3mFJHG+3DKf1PjoyYxktWk5XExxTnC57piMCqyVZFnO5arlaJzjQ2Q1RGTXM3QDWUpcd54bByOcE1yvLSYElGypteO6t9yYVlRHY5q0b29KQVGORjw/2zAj0q53ewLO4BhPJsQ+cN557p9M6ZE0rSM4T/KOTMCVh9Mqow/77GJCkIaBIlNc9YLFSBJivhelukhWBqqF4qwLTKSl/BufIE+WJBExI4t/YDmbX3IjnnB+9Sk/+Pi7uCqx6CacXV9RPszJLzM6Y/eEnjrwarpDsvBidMVRv2DFhkplrPINp7tTNqsOcUORbzIO5hXKwVm1Yb6qWdoNm0VL3RZMRiNSJ1mPdxQvDbIQ9IuBkatZdxtkC+lGJD2Goixoxi1pm4gpYTqNu+GoX5bUVc2m7si8AZvQneZytuJoNaPRLWEakEHgdoFb2QnPJxfMzse0qseVgeQjmdWUQ8b1ccOd7RGNdshKoIRAn9/ntfQ32Y0M403kOnZMZlNipqhTSSkMF9oz7xKt/xArNjjpGfkxZsi5yDoWvkaObiNkja80R2ag6p9x1b9gni3Y1K/i44hWRcaDRHu4HknmQTM4hxSSnfBMlxY5yrieSMqrniAkWVRsasmsAS0V7VHFGM3Q7khXG1YFHPaa6GBTSOo8R89H5Elytt4wW/aYW3O2I43eDPizltwp1ocV05c7vIJtZTAxYfqGwlvah4ec5BW9cOxw0Dvis4bKZSxHmsV2f537kylx1WJ2Dbm1LG9U3Do+pZcF6xdr/Lqh6BxFTFyNMxZri1UFtiz22q7ekYXE1bhi3gzYMuxr0jfnmCdrskGxnNbMNg3LsGTQAZcpquvnSPeU9cxykM0ItcCvGvoS5nJEtIHztOGwnONiQgRopWWOIaUdS71mHCtcuKIqFBux5Tg/RSXFKq0Y6wmvj97kP5v/F6giI/mA7x3KKFSZAeAHD8C1O+d3L/4Fn3UfU6iSaBxGKy7tObN2QqdhV1h0VKRdgdYLLvw1x8xpO0+TLCkkJlVFZQrO45LZOqNTmsEIZGYwUSGbwKXccbDLQEIvAlJL6rrApMiL/pLbB3dow4LttSWkRIUhR3FVC2ZNxKtIysXe82MrySdHLGc5izbQbBxS7jUrByJRV5plLRhHRcgV5cmU1fMrxpsBZGI1VhxOxngl8E8uaSrNZDMgC8PqsKB8sSHlBSpI7J059cdXQOKyiJhVQzZfYDxsJhnz65YkHNuRpBgijHNMF1nmicXKEXLFJvu8ckGiRHKdw8HKE4yhnZeoTYdygdxGljPDkSqIxzXXLy/2vgI+kEe4nhsOzgdcbugygaoy9Lons4nrmeJgkAwqMBBJKZI7QV2XnDOw2CSsdLix2d8f+oQWmgtlOVgnBpXwmcLXhuqyQYbA1Uyy2ESskcj5iGbXMOlA+cRyoZl1gr2VqqTPBKOdI3nL9UQw2UVcqTFa01b7qkoYPOuFZpZV9G5ADY6t9BwOkugcyyJSewnFMzKWbLKWg/4Y2x+x1JLKS6SpyWTJepZxHA3W9qzoMTaRVRVFUFz4jvnFXrjfVBIdBdo6siFwOYbDQRNGJQ0OGRK5ycht5GomORElg4JN1yF7SxEUJmRcFpHDld8HebkkKEFhIUdyPdMcB72/xlXEtR35rsXIxNU4ctgKgj6HwjHgGIUSEzRn7orZWtFkc6IsGFRkRkLljjO5ZrqEqFaYSrLzO+Z9iSozVrOBmasZmh06QlMHTqa3CduWS7ViMT7B9h2yg3bkWAwzYiNYug0jWdE6jb0KtHPJjeKY/nnP+XZLGSRSQiEV13JgPmhiJthqi3Yg60iZC65Mw2IoyBaBrdpigkLuZmS7CRd+x/GQ0wdPl0WEUEynHdOJZZmtmG9r/EzQawcpYTqBSZpLveSgHdOPM9x0D6UYrR3m0yuWR46j8gatiVjlCTIySjUmGi7lNYfykE0zYEPCJsvi6YjRDwyrbcPh0SFvv/EWv/Grv/alCe4XNBFfJd7+CfnxV+Fo/5Lx49jlq6bW/EiD8RXLx6Px/7zP+sL4a2uL+mptyE+GDeKLCvSv2j8/KyIRYKOlix0uDAxiwLseG1vaZOiUJMmMUAj6XYe2ltbtUEYgyimx77FNg81nmElBbD29hpAShD2S0glNEgqnNGEYMFGw3FlCkgx9IJ9WrGxDAHIXUHlOaDsGGZFSYkOAwYNNxFyBlAw7S9IK5/fZOZESwWhChM4FXD8wRJBSsml6sionWL8PHoInqD06sa4yhpQILiLHFf2uw7mAyjMGHygKg3ee7bYjJoH1HoxGFTltu6VrPd1ihM4HhGvonSUrHX0vsc7T9Y6+i9jths2mI1s3uMGyC54sJiIRpwXWedptix3A9oGLyw12EJAUWxvwxd6ssE9y7/lhNFGA0JrtbsD1CaGzvbW9EAQhkFLSW4/a9Qxa4HqHXzu6vKdrLSk4NJ4m7LGZ1kVsTCQlWa5bklKsGktm9v3W1nsiiZ0L+8mDi2RljpHQWU+SEhsFIQrazhF9ZFJK+gRRCKJRDMFhZMCUGn1zhB1d46LlennGantJvijoU0NEUB+U7GjxKqBKjUoSM1K4LuBSIOWCy2aJGWsG6UkagvZU4wJbRFKA1lgKrRiEhaomywxWWqQGkkSbjDZ2+/fpjDa1DMHuy/dS78VwoxFb32ClI+WJSTZGZYKYRbJJRpcsTjm0Eogk6HHITBJH4HxAlgIpNbOs5mq7osgNjWywKeCURxrJRNWYXKKM4OlwTiZzlNZoIZgZQ+sDV4NFZQXTfEqvE4FA5h0qU0Qt8Dl4I+ndHgesvSVKtRd+J4f8XLSctMG2LYo9TnFIA04lXK4ICKJQ9JsBHxMDAmckaXDEcYZrA6kfsEaQzUvstifKhI8BnyB2nm4d0ZMRcZQj8xmp2WKTQJUZzjvaXYvsLb4sELOSmCS7syVdKCknNULm2Bc7nPX4kSG4gNWCGEFqiYvQL7e0c0nIYMAjc4m5Mac5HwhSYPfEUdpdi56WqKFnQOK7gd1qQ5rnhEmJa3pyHeg/10rYXONQuDIjtpZMKawSxFzjfCAagdMRvCcbldgY8UCvFVYonNkjRn2+f0wFkRjigBsg5eBkpPcWtCCmfa+3iwEArxI2BQQRJz/vvzaRXnic8Ay+I8sKfPD0qcfh9hDvuG+rIyVQn+stflS9gBAiUSRcsPtngAx46wna4/JIAIYw4IVCSIP3PT5FWr8PHodoEUbhoqcZdrg4YLUmSkGPR4ZIsAKREtb29FKiIlgVkEKTDxafJUSdsV6ukPM5cZIzbDsy66DUBJHoo0fUht72hBjJTckgErYd6KTB5QafBDZTOAVDKfEZDJ1HFjlt1+NSxClAQlACm0nc8DleVQmCkcTKEFLEZgqMgirDhYAz8nNEbEKNCpxRe32HFHsUrRBYLSBJVK6Jw0BQYDNJlPtrT4iEipE+QVDsr51CY2NAZoos7atLUQn8rMCudjgtkFog074tLKTEkH/+O0uFC4FKwJAJgoRW7hMcgwGERIdIS9jjqNW+amkVRA3luKDfDnucbhZxAga1T6h5LUhGEjNJLzxeK1Ly+HyP4fUCvIBeRrzYi3GdljiRiOpzXO/Y4MQeY21TZAgBRMIOlt3WEXRCKoGViV5ERKHxNdghgYn4rsPR0zu713YUNX1KaBHBCCgNzkuilISkiMESdy3eS5yJ2HzfjmwVeC0wfk/UihKG5CEGrNlj5BWR0HU4JdnsGmKmsJVEKFBBEEXYAxe0J6r9MU8CshT39Lwg2G2HfQUwAwqFNorQ77BtYNclIlui6wlEdNtjpcaGLV0oCbnElRlD29BbR+rWxIOEnxT4IAixI+TgfcDHAdu3dC4Sa0mwARctzfUVej4iouhjh4+W2PX00THoEt84et+gc4FV9d54cBjoQkvf9ji19xOj74l+r8/rh4HkI0MliFIhiUgJXiZ66SAGeuUJOmGIyEISOrAmkWJg8A7hAy4f6PIBn0XicYEbWrq4hwMJJOR7oMWgJNb1NBdL5KQicxDyiCcwCLufJ+AIwaG3gTgeYe1An3XYFOiCwydPTDV9dHTbhhed5+H9B185f/5hjv9ntkJ9gWD71X4XX/GGX2CdfVDxpfXEj7/PX2X8NWsu0pd++sloYb+5P97oH27Sz61yfL7gjepNXrZPyCycuAO8CiQhqKh5w9/nI/sRuVHcCAuMdTjfk/ucd2bv8Zn/lCLCiapIhzfJrj6AxjMZVzyb5CglWISAzg2fXTu2uw238kiTlcTBceuwphoJmn4fIL09rXgcewolWNSafBtwIVBowc2RoK0r0mXDsYLRRPPcSmKMvHJUctUFwrKjCoHbhyXfX7YIkbhbZ/R5jhd7O/nXTyZ8fDVgQ+RGIdgUGW5j0d7y2oHh7LIlaclhWTAMHb40TKqMkzLj4wtHVDk3ZpJUac53DntluTvTvHQ5RT3h3q0TVrucPm4oteCO7/nWpkMMksU0p/GRPhjymHGSLB9f9RTTEflVRxo89XhKz8C7pzWfoUjLHTfGJblUfHzVohS8MhJcUBBsZOI78kpzmfa8/jdvLDjb7rBi4GRUcOPugk/WPUoKjmi5CAqbGcZCMtMZT7tI8oE3Dwo+ubIkJRlnguNZxXe6FQq4YxJrk6EyRRYs8yLyvA2McsGNTPJsC37nqJLgaCx5nARKKg5ih1iArHaoleDwWrJ7zZHfrnhNvsrj5tuspOTygzPK7xv6NzMOMoX+vuB4NgcDE19z6z8c8cndFygMo2cVF8016h6Mbc3h/29B83aHSYrysUGHjLaIsINfP3+XT04fs0uOw6s5MzEmHiaGjeXVxyc8v3/NwXjE6HrEvJrwVJ6Tx4zsPyiu7l2TDYab3TGPP36Be+iYMuLo4xnL+w3zsuSomaGuBR8fP4cIix9M4A3JRRMYXeX4pwPpvYQIgslHFfpUcRVW3GuPqNY1n3KGFJI3ru7xtDzj3viUZujw3wuEt/Y3xOMXjuVwzfjOMadmyuyl58WxJhnNrZ2gLzQxM4xd5N7VgienE5x13FYZ26HDG0fpIg+XJS9vjYjKcLKbQdrhjhaU0vCAI34AWBG5o2u6IeCHlqqqeDWf81HR0nWO2/kEu94RNo4i9ryrR3xaRkzXc3wVkH7P2VfbDe8eHvJZZdCznJMW0tkSYfbY2ltnEx5XPfnOcBBz6sUhH293mMslj6aHPJ6PCNcrZitHFSVJSpSL3Dt3XI8grB0jLEenU552F4gEd8tX+CyPXPY76j5ysE48WySUKbjdKS5sJChD9mzF/dltPlKBrum5fdmxqjShMBSd5e7G8rzMCd5zc9mwy3OC0VTNwI3zLU9OK4LpuSVytu3AQKSIcOfa8eFCMLjAHbegcyuCnVJqw6Od5tNqg4lwmzFegygNapC8xS0+Dk8ISnLaTRBVie8So7zmoXyVj+JTZLQcmQW1qXFCU1Bwr7tN1B1iWqO0wu96EOJHlKgfOmYemROOzDGMEwrFNJ/zmf0BMhQs0hxjJnwWHiOD4F75Op/tVkQpOcomjIeaD8NzjMm57w44T9dY33GQj5iKQz5LL8AnbuubvHQrfPLU1nArjHk63hF6z+0mY51t6XPLfDZj9izx4lagawdu+xHx5ACxW1GIyOuzG/zFs+/Q7Hac6JuoGxmxP6fuDQ+vCr5vDNmi5BSJ9PskUdUFHh3W/ODlBfSW46UjFECdM5IZJx8t+ayMaBc5vnJQ1LihJe88Nz+45vydE9TGcnDVk5xnGEeqpLj/dM3jGzX4yGLpyPxASjkmJO5vPU+EI3nFok+Y7YA4ztE2cHctOJtLUpRM1o5xI3k2EsgINx83XB/lRK04MCXi03PSVCKBOy8GLo9zfEiMd4HZ1vLsdkUaHHfPLFczjc8KJsuBg13gyXGBIHFzlVhXPa5KjHs4uLS8eD0nuMi9IDm7bPEnBeM+cXRm+exOTnSRGxeRpoSQAlWfuHUReHI34lzkxkXYB9WZovaCW08sT04N1iduXO99PGIuyTeW11aCp/fLPSJ4J/AWolLkDu5daz4dW0yuON4JpEh4BMWQuPtywpNboFLkqFXItuaJySi04ZVzzfNTgVpbJp9s0L3FzgVKSu5vM14camKIzBpPbeGZlKiQuPsSzueK5AWHJqd6OvDkWCGk5N4SLoUmKsO0scxe7pdJLbhzGbgsNV7CbID52vP0RJNi4Na5Z1cJogyMWjheRh4fK3wXufMysB5nBCmYSMPJRvGSgZRr7pYZ7uySWVUwOTqkdIf8wEZam3Or8fRC4deJ0sFr2SM+VlcYHzjdQhA9XuQUneDVl1M+nV9jsoyT7Qh/YemPBJlzPFwe8XhygYmGg22O8DWpSlTliK+pR3w/e8r1xXPmPqJjgayXaB+50454Gj9FmJ7DcEpZHfFyskJ6wb3dIefFJSIEjuKUWSN5Ulm0MNxqJ1yUkXigmS0NkzDms/wlcttz/99vaN7RxGSYZGOO6wdcrJ+CVIwvExf9cxglRnXBQXmDT9wnxAvPXX/KripwckPpK+6FWzwpXuKF47Y6YDt0ONkzZsQr2U0+MZ/hU+D2zVP8WYvPd0zKGa+9+vBHs94fk5v2k+C/FH70P2v8FM/2K1b5QqL/y5WB9IXl/5HjrxxcfLGgs/87/cSy9KWazE8EGD8KxX6I6PrZUpfBtlQxJ+kCWkfUEaEERmT0bCiD3IucU0NYjJG7DDEotu0ZIykI1iL6FcU8Mit25EYTb4A633+SzxRu6NAG5kclxUjgB88ueJwYeHnZkZWGNHg+u1pjTzTFuERmmpQpdBGJMbIWgB0IJJoQkELBYJFaYpNAbHZgA3qkuR4GjJEwBKyTWPYtApPjKatdj5QKMyrYqj3K0ZQZ5cigi568dfgQkcmT6YwsMxzcPUAXR+TtFb1PvDxvKUclXVSk1nNWFDgyQsi42pR4VRF1JDQ9T1aafHpIvxtodcGQFbjosS7jLBgQhqgm9IOh1z19EmSjMVfTHJ8iURZ0SuC6iDAKIxTXbm+i5oceWVQEEwk+IpVgFyVqNCV0WwZdcv6sp+0tRZ3Tl1PyTBNebkjGEKoS6RoCnlWvkEIjjEZowWrtUNJASDQYRBLkOmNWFbSt3SPmOkdnMoiWPM+YTTK6GNA5KC0wp5HN8bfIjzPG3uCPXpLeVDT6iifLNV4Hdutr2t2apgqMKVh7y2gx5qpf0w+W8VCznjZUqiRq8NJRj3Ka1KKCQB5A1hquRKANjkU5wroNh2LKetIiBoEyElloLjdXrJsdZSgINwUlGVduRSlzWtdT6RrdKvQNyTw/IOVLmlXH+HiEkwE/BMrbJYMIDNEyBIevAkpKalFgTvf0kbLMCTpw87VTHvun5CJnaVacqhMa1dO7iKkDRmYE5znTa3JR0PQdvouc3D3mSmz3CN/FjIP2iHxxQtYp+pkgyzRoRSol0kdEC6pJ9NkpVZUxpA439Hh1Caony2v6iUakfRapi5Jgb9A0grwasyxLdBpwgDMCFgWyd4jdwLXdYGYZflLhri3BGHSuMauBq80OdVig6hK/bfdmZUru29Y+PUfcGCMWBbJSmOkF+fIZmRcMN18hT1M629FdbOiXPen2FKEVZ08u0PfnyFlO3Pa0QiJ8QCXYmYQSCgD/YoXnCQUrlJT0AYrFCeHcE2WgKQxSCNL1hv7GFPnUkdjrOK6vl+hZidKCxghk2tNEjJC0tULYAZFJOiMgBogJFRKbUqFSIA4D/mCEjRaC2FOCjED6hM41fSYZ7E2ETKiUsyp7hIogA0M0JNuix5IqZSyHa3Id2KWeoXPIOCfJChlLroTG5Ddg2OA5YDv0BF2QUsk2WPy6Qc9qkHsnZ/lDk88vPEEUkt9Y/H0u/DmZzrmy57zsn9GFATkoOlqk2msAdqJDWQVGokc1XbSYJMm1pPE7cgFZZVCZIuUd+qpFhMhg1pgsRwRNUZTskieliFSwsStSvyONIyIkhvE10gaM6umNRe8qlI4oHdmqM1RaocIWcVJjdCTPN2Q7zxX3oFhgvWaz7RhVDqIkQ3HxYonYdQgNTkOKIKsC3Qeu3bAXviuJVwKlJalP6ChoZ9kejek9XklAIWJAI9hUCh327UBJKnxmkEi0EDQioV1EFGqPTJYCERIqCppJhurs5wJ7RS8DhH2bUTc1SASizok+7I0cE4gIu3GGVhopIsIHmlwgfEQi9nQpn5Bp33rYjwoUkpgSnUkk2xELAR6aSiGlAqVonUeEBDYgomBTJFQIJCEZKoWIEZkEWdI0pUT3AZ8SVqR9QK8VxkZ2Y4UGHOy1STLbO7rrgubYoKzHOs8g2Js0kjAB1sFhUkbI9B5RrSQqaTIBOz1HbUekmcKjULmmPJ5QKkM7Ehgc29UaGwKpyFAK9BBYE5A2wVjvBeilQCqBTomuBu09sioJz1t6IgSJ1JpmXKB2ESEVSmT0ZUDFPQGzmxiUh+QTMqQ9fepzzPNQyT2qOkAmFc242AfxSjCUEhUTUimyXhJGR/9/4v6rSZo0Tc/Erle6CpGRmZ8urau7q1qiZwY7sJ3lkGukkTygkYf8HfwT/As0o5EnoNEgaFxb7hrXCKwBO7YAFjCIAaYxLaqrS3wyRQhXr+aBV3dXV9cMejFDox9kRmZ4uHt4CH/e97nv66aqM0kVbFnxv/rWI/a650yv+Zcy8STskc6hbj3tRlKJkabPXO976FYUGZlkBv+ENA3I0nGLR86Qc2IWoDpDmY4oJzhyQM2RUjze9eiLDbKWKCk4yues20TsatqcSbsZfbyliZq0jnSxIupMlTOJK3Q1UAlLaAKtDUxiwGRFUPVCjAyCsO3RKSCrQPXKBXE+UZWIPNPMqkH7iJgz8hD57mvfQ29/iCgwdyf+5Ok/IAxPaD6PjC/vqc5aoDAcArlekWUgesUp94hYkELhuwyOhYQ3R048o6oLgszsD1TfkNSTYr2tmNbH36iHf3n7d5c6fX1G91e38Rvdjd+FDPXVvfw1mMn/2joXX3eMvxwi/Gqo8BsH/KV7f+uJ/Lbe7PPxF9y4F7g8E9qMJ3GIB9w48dwurd5JDUsoUxg4yBOqQBwGOtMylRFZS3A9x3xAF8WeBwzbc45XJwoaF+DWF7SUDMeIJnPwiXw9oBrLaYooJRm6ilAizgdSH+EgmOPC3Z98omokXhl6ZTjdOFwoJFVwT3tMLAwhY7OgOJiyIMbCNCZsB4cxkh8fwCX6uMh/RpWpGs1xCOA9Rw7k6Ci54MeI0AWnNU8eH7i5ccyzIUtBpwrH6BhKoROC/sUJP/TopiLojqIjTz/bY0Pg0BeUsbgoUWPGp0KfJOEUF+KV1DBmdCxEqTiOkXVb8XwISAtDpRGhIENmKJIhJq58xjrPFCUiQG0NAwFRCh+dAloUBqH4/DhRYmLOoIbAbVtjasPRJ3zIvDgFTnNEa0UaEsZW9C4tCZsuMYWCEpLQJ6zWuBwoUXMKmiFKyhw5jYG6rehT4WrMzFkyI/FTZHr0gnoHcdWj0AzvBQ6rF4R5Yri74ebZZ3zkfsHm/or0UuRKO3rh6LYt/WFiWs+c2oFpHSAXJjkz3q0pQlDO4HA6wWuG6ThCA0dmVDMx1I6NTvxb9XMqobkNJ7JI9PVI86DF7x0/158xnEbiKiGlYp8nRulQViIeFlpZ41rP03FY0K67REqKX4gnmGQYmpG0DSijGduZYxiwjaYqhpMdKU1BmReIy6WgUeuKq3ggtRlnE6M44rvAOE/I9dL6nm2ge1TzVO/pzYxgwc2/ducCVytuckGsa+ZqIYwkDXjoq2VaIalCahQ+aga/J1WBWwZyIxirkdKuKDrjzxRgOKpEmmY+jwNqVRH0IidiLRlqQ1SRF8IjfSBWlnKvI4+RwzTiLiquQkQRmXMinFeEnDnViikUDlXB3uyZS42oPSbvGaoTvtJcVQ61bZiShromeskpR7QRHO8Y1PUt82WLeLQl9IG+1ggEk20wKTBUAuVPjI8/Jp9NSCm5bS+INjKvFPss6WvDaBaS2xwc6sGGwTtAcnU8kM4M4aLFf9G2HyoNnaUow1QbhDV4lxF5ORe5ZIotxAayUQgjmbcNvRCUlBmMwQmPt4IgCkkYeluIIfGk6pEqEEQm+z0iD8wBom4Z/A2CQKgKeSUQ+cSxOHJjuJF7yhQZ40xJLxB+4phPHHPPL/SGH87vUK6PrO6fL4jawvICprxIpAoIpTBYHlWvgBT8m/0/5xBu6eORmB2TD5yqASElt1GRZM3enVBWk4rnkA7oXHESIGNmVB4tNPt4YF9ukFbRi5qYawYdeBF7EJmBGaEF7oGCWDNax23tyHHkFGZC9PhNg2bgVMArx6m/Zh+vKHVC5xusc+xDz6w0/StbnNkxO08lA84mpmqRW1ylsMhHtCSbguwsUy1Js8fdrUAsg+ZEwawkgzYELbjdVdhOMRdBvqihFEZlKChudYXKgqkxCBIg6VuByXBQEjlb5lajagh1YVhpVCr0xiJPhanTUAqlJPpaIAv0G4lKMG0sz+NMODfLfUIs5D4lGYxAFEOqFKMGUMz18lqOtYCkKEIxNcsEgzOBHAWnVpBLRq4kwSZEVzG7CXaGvpGgBKmzuHZJCHdGInzhVC+S1SsyURWSkGSjUF3FsQRiK3hRLxKyIBfZFlIwrg0pwlUOi1Q5Z4ooCCs4GoHThZu1QZYF9Zu2EmEUpwqcEbx4IFFOMQrINZhtSy8ih9uepxSsMYxbA7mQlWBYSeQEhygxRjDWghsXyVkwNAYhFScdkUkymkJeK8pWMTSSohKuUShtGBq9uFGzZmwWX6rXGmbBWAmuSwGrGGymFAgWRBYMNcgkiEIxWIkQYkllj4WhUSgtORlJ0pZMYf+05/G/+JecdzXdH/+AJ/KWq0oSbY0bJtL1nmMn8GFJDU/ZEaQgNAPCBE42EcvMdXNEFI+vCkJPmLOG0UuyL+zFCaU0E4VyOEEaOcWZPh95Xh5TNR2T9agC6Szj2khOhX56jpgLcxM5iJEo4WQdKnmGBEZIJhk4RIcwmRM9hMip9SANPQP4iLCKwTpKnQilUM+ZUU6c8okn7nN+r/4DAP5J+ccMxuGawrAVjNUNvXSL1PvOmjgETmaiKME+H3DRgZG4OICAUx5IOlEMi3QqRVKcaIpmqiZUvuXx8CnvnX2T3yiH/0MKpl/d/8WNr0XF/uYGxO+y4b8cW/VXXv6aBhdf57CAL8ufytcc/S+t3L/sZAgERZQvb/JXy9psOTPnDLFnZbdMweP9yKbekRXozrAfrjmTW7I0ZJNRObEqlq3dIePSas9f7LMuFWJV091ZkUumOc5UUlJaSaUFSmpUnHGzZFuJ5YJrQYtCzgWbMjFmGiHJLLrGkjK7VYNWGZEFd9cVY++wISO0pG01JkpCr+hCIAuJFhK5qRY8q5DkIrk8M1x/esu2MZChkYKmVoTRc1YbUpQIvygK6sailOW6n5F5pBOa3eWK/cmx0pKmMqTJY2LCGMF22+GlZNNa3BCQ04zIiZU1CFVQapFF+SShD1jv0Z1Fh0wqGS0KxUpiKGy+0MEqKYkh05SCshKlNGKcKRmsEQgl2ZpC1Rim4LGVQsaEigkDnK0t0S2owPWqJsSImhO6ZDoj8DGxNpLNuiaFxOV5y/T0RFsLhKmwU8QIQS6JtRFMRXG5sYhTQqRIJNEZycYWMlCrREyZTV1RGk0jV6ypmVPh0fkDXhiBPkRi3dLcFh7/eECfSfJNYcKxalsu1zVqVtgbQyMqxK1guB5Z25bN2Ypt3mAwfHz9CeZg0U5wnncUnTgeJ5pQUUQhv4hUneG8WmMazSbW3OYTfT/T9pZIpHaWWc1cujN672mqGgZQurCWNb3S6GK5Hm+IKrOKNcZUC+I1B5ory2w89dpiS0XwgR0bTKWpY80kA3KA4hLaS2SvcKvAPVdzYORSnnEaNOd2i46Kz/tn3J3O+WR8TtVUXG7OuBQV56NiLwu7qRCFoM2CWDJNltipkIDdDHMtkFExz6CdJQdF6Bo2R4GRmarS+FKwx0ClDXmtWPuIPwXEkPGXLSsj0dZQbKETjukwo7RiTI7VukZWDVkLzCcHqCTKZ04h0s2RpDVCQjVEVMhYVxC3Dj0PNG0G29GYFt+tKFGSiuBis2I6JaRSqMOMKpkmFm5fDGxNzaT08nnJoEKkjZGMZjVKOMyopqLarkgopGoIq0T3/ABUqH5Bsirv6C62xASbISw0pMNMqSqk6zG+EI1imwSzD5iQYasxLlAFQdSajUskmSkT+DnSrguNUMQY2c4RRKIOAbdV1GNEhwUduh4isYDWmkEn1sUgQkC4zJnpqFSE5HEGVlVNcRUpC87NhlwSsoGD0mxkBbGQVWIlGralQXc1QkCOC2o654goEqkUJS15J0pohJTklImDZ603bO2OVBK75pKDOCGSxmRNETWqPmO+ndjGFmctqoAMAqMkJhRKHjhjRdIZWS1+EWlbONUkC9ug8NMRXQTFamwWtNUKYQ273DIR0FnRz8us6dlmSwkj2ywYDwd2viKSaCbJ9nxNzJHL3RnHdk0QNadSqPvC+gv/2+58xfTkGjEF5kqxCmC3FcVlVlNCDxGRC3MtWY8R6TKzy6z6RFYBkz3SCLqTR0iBF55VFKRaIWNBIujGTCmBUhRNLBSjECdPAVZJ4ueMIGITSBuxQ6IoybaPeJEQWWFiQZCookRKxepqYJ4TIglkzOgMVYrklWZ9CLiuoL+QdJiQqbIAVdieIsFKbBIUEtoXlCskDbtREA2UU6bIgsWgTo6gJetTwutEE5aBVj1GqiTIFDZjJlaQYyGuDOvKIp6N+Ba6oMglIxS4StJFgRRL92dzDHizzOQOsrCaCioXslC0fSBR0EhGldh4QXKRIg3NGMlaIYfFKr7yhfq8Ij2/pXGFVDI2RsSDlnNZMfUjAkVVNLiMdZkCrPeeaAxkj5UaQqZyiWQS2yETrESVgtJgZKLqF4/Uts94VdBfJNxrHamDJVI4m8DHhJoyVJpqylQ+k4TkbEz0rcKkQs6JxmXMFEmVYnUzIxoJIhIk2NNE+Gd/xqc47v7R92ml5BzFTKFShnQMJKFZHz2hBIiJeaVYeYUOiiItm1SRksEUGFKiGQNmEKQ7HetqTZYJTg4pCt2xUJQg1ZKOmqLA3EbKVlDNkSwlZb2htR2lzigvOMieXdwwEyAKbFTIlNBDxhtYBU1qFJgWLRR2e0YlO2R4wfbWEDUoL9Aoqipj50yxit3mkrVeL+8bBGuzYW02uDSzsxeodkbGHrTE0qBER4yJc3mGO15Tm4qyqaiSoiqWXCIX1TmzCHRk5unIxqxpZ0Mpma3ZsjKbX1fNX6px/8LaXnyNyfu3LRJf/8DfefnK6OIvMYD/j1n+yija8jW34JdDhS///dvQ2i8kZ1+EiPzm4766/pvd+ySfKR4eqld40NxHWkGOjt+zPySXGSEDd+QZ97tX8CtLPmv4fvt7THnAiZm1WfO3dv9T3qvf553mPf533/w2u1d/xsMPf8b7Pxx591wxR8+YIr//3tli/hSFNA289EAw7QrDJvGuiJgXAvlM0IWK17pFE1pE4d0NzAGmQyScPB883FJYk33LW1qi6xq6BlFVfPhwh6diCpp3dg3KacarTBgkH761Q9QtUxC8cm7ZbCpCDLgYeKtdUdZ3Efde5Qd//EPufvd95INH1K+8wrfuW/b9jMuJc5NQokHoS1b3X+UPPniHo99xGLasjlBPiqJ3YLZ8/5UNydagKx7d3bBtLEnVZNPwzUcdJ685jZJWVWy1JTjD5AzvFQm9Rk8V66y5FBo3W4ZR895KUKTGJ2hrwzsvXxCcwnvFKzLhoiElS6VqXj5fMUfD8QTfuGwZZpidwuqGV1cVMVZMvuKdy4bxNpF8hVEd79/fktSGbM54d2tJ0eLLGmTHBw9qMgKzanjrXOAqh98k8irxg++OiB/8CPfhv2KbXxDiRDyDtFP84NM38auMM4HX/tWWN+RdohK0Xcff+NP3oRa8CEf6fzbygDvIVjGKmXf+2SvITjHLwPaTLeNHE7qyzCJw8Q/XTGbiyMDLw13yp5GbcEQ0kh/++H2cmvHGo59Kyo8jQ+gZysgr//0Dmk1LUIXyLPPgyTlZR0IVuf/fnfPE3dJLR7pOPPjkElELZht5+Z/e4ZBO5Fqy02e8/slLiFZCJ7jz358z4TiVERsVH3z6OsUkeiZW/8hSVEHUEqMr/uDJNxnKhO0s7//kDYgS3TSEkPnDT/4nvKT/iHX4IT/47HVU0TgBRSu++UlkVov587XHHosiWU3Uim/fGDwQZOGNF2ecte9gNh+imzf55qeJw/Cv2bt/w0N3oNrP+BhJRvHtxxInFK4PPOg1Z8XiM8Sm4odhi5cQUmb3bOLCiaUweLDlw595QqVJdcXFbeTec0/MC/ryu5953NrgVopqtnQfn3Gb36DffIMfdt9AVBWyqjnfbHhb14iqIDrBhz874pTAVxp5PfDaIZFWFaFWvP+5x+ma2dbIasuj+XVu5escz77Bh+3byMNP0Kd/x7a95vXrmbCtcJXgnc96/G1P3rYUIXjroz3TaSDUmrefD8iSiRJiSbz/2RGvBU5kXn9+ROTF2JoovPuzPV5BMopXjjPtuqI0kmDgO88dQS8m7ldvPOu0SMRSZfju52sc5+Ryh0f+JbZqRz9lBpf5QX6fKWamKXBPnHPHbPFyMeH/4e5DgloyCB6093jl4n1C6JhGw339kL/v/z/8bf9f8g+Pf8I/v/1H/L2b/wv/xf7/xo+HP+W/2v8d/u71/5k/Of43hBwoKSMKvNG+g0+OmAO1qnmve3+ZmZeJH3YfkIynNAHlHN+zj2j0TCNHfq96F3G2wWlLnOHt+VXGqmHA8L3tNwBHoaeuCt/hLkUfkPbIdzavULUNQRaC83yQXmeaIamGt8IZ2t/g0mPYzXzHXRDURNAz7+5epZGWUCK+eP5QG2R+TN1e83Ya0ceePsycjj3v/NkNR+85es/u0wNt1PQj9EPiG/++J1aKZCQXt5HzpElC4LXk/R8dFpOyEmxPkd2NI7cV3ko+/LObxbQsYT1E7l07ohXMleTDTzy5VmQj6Dw8fDov6xrJt358ImhB0hI1el76dCDoxQD7/o8HcmOWQfhh5tWf9QvNykje+fMjObPIs4Tk3Y8dQSuC0bz1kwGKJGkDKN752YGoC8kU3v0koIsgK0mh8K2P82J+xvL2lcJkSdGaYjUffLp0x5PQvPakLINqq8i14oOfREJniKuKBz8+0fSGJNcU2fKtjyLRaqKS3L/KrJMiEplF5Jv/3hG1ImvNvV5xFqovjlvxrZ84ZgneKM5OhbsnCGqhVn3no7yY6K1h12x5uBd4KZiM5Ds/TUSr8D5SFc3Lo8VLhdeaD37sidaSqoY6Gd641mTbEU3Dhz8JRC1JAnSGtz4LBC0IsvCtn5/IFJJVSCF55/OAVwUvM+/9bEIoTZEaieK9n3tyZUla885ni3QsfZG39Z2fBzKQpOCNj2fqXCF0C7Li/R8dSZXCiQj/7iPGH/2YGAICydvUOAqBwlvVGV3SpKomVjXf+0khtB2pWfPyeMGO10jr90m79/jmp+8xmFeZ5Bvsjm/QPX2V4+2r3Dze8c4/esDx+BL9/A7b/n12h3dx5luM8TW+/eP3GdXrTLzNKr7D5dU5h2Phdu949xcv048jvXN09ZZ31m8itopSRb57fItyVlMu17QXd3hn9Q5xKwirzIfXLxFDTzIenRJvf9aS/BE33fLN6VVKl3G1Y8ojw+nI3x3+Ln/P/T/IjSI0mbmL5EbwYf1tJBIRMh/kd5FSEuaeeLPnG8MbOBmYxhOvz69gTYXH4/zEB/GbjGkiVHD/Zo1KicmOHPwNrzav/Wqo8JvV8S+L4qUYLuXL2Nkvh+t9fcVf+Cqm9rfX++11/gPLX7Gb8deEov3ihHx5w19zZL8xEPnKXsXXOVpK+aJlW/h/f/pf8vPDTxjCiXW9IRrPTXjBihU+zUiXOIRbzrpHhDs7rsWRNlbIx89ZFcPQzrzSvckf3v2f8Zp8HYTgT27+MT85/ohbf8PKvcQn/+Ihn32cqIwkTBO5H/G6QoWB+a6iNxLpI7vZIq48N8JwuVHEUohFIFJGlmXG4DgWtrZQVEdRNf4wsrs0FDNxUoa7jeZ4iPgMrp/plKFtG66uArutZDaFJMFNnrNGYMrM88PMnU4zHj3tpiN3NZ1WVF3Lk4NjJwtX14GMIAjFrjFstys+fzZRh5F5jmgpmBKsLRQhcE3Ltpb000S7rri6HrnT6QXfJi0XK4ubC2n2XN/MnJ8plIIhCbpaMjtPY+CYBI2fCVHhsZgUQWa0yAxKc6eWtJsVT16ckCWhhKDSgsMMaxEXHX2SNFYTc0TlxGGGrclkaXGBhXSkJWe15RAVTfb0QwK96C1VihA9rlpzby04uonDaWR9viYyUK/hKCWlv+XsD14gdkfmkmiFprWK8VXF7qS5efOKqTrS97eoX4w8Pe6Z7zlene7xaXrGlB3VmWVzalFJcn1xQDyVSzhQ0Yz1zKP0gDA6jhcTm2OHNwGLJmwT1VNDDBLzasOdcUVuMzZLjs2J3W3HmB3X3YF2rIkys9UbPpVP2e7XHKYefx5Qg0RoaJLlcNZzf7zDFCfcxjPvPaUIdmXNeDnTPa1Z7zqmzYwbI3EIXKodz9fXrF60S/t4C51sON3O2KmCVySbFy25gknNVNoiZs1lOePx6ppXj/co0zfo6odoo+lkR03L1QouB0mwBq8WmkwzFeoguVpJLk4J1ybE1jKfBtq5YLXmRZXYDImj+gg44HDcXb2DPd7lRgu2URJrS5kjk4FtAHNWc7tV7LDM/US5GRgayW4WiMrSn9dspcWHSH5+5GQK55gFY10JmimSjcAgOK0UZ1cOgaRvNJ216LOaTkhuCVzImiAKt+OAneLSgbiaFwTp3uMrzbSqUYPDFEHtM1ed4vxmIgmPrwVmt2LT7GnHz7nyL7isHrGfHzHSUmLBTJEqFA4PN5w9H3Ep4WTB3N9hTh7x9Mj+vOViTDghCUoRG0PXJ9SQuV3XbPuZtEqgM14UOjTN/Xs8frFnd5o5+CMpecZGcyYUop+4XWk2fWTSAqMNs4ZuOCDtLS90z2WzRbSBcuo5SccurZDZcMPIRjSUVYUVmptxz2W1RRrFdThST4LSLIX8rR54aHfYNHAqN3RmRREFmy235ZqXqzf4/eaPeHf9ISUm/snxH/Oj07/hxr/gvLqDkxOnuMcISygtpDUv0g13jhUmO8oKlNR40RLLimfhhrthzTBO+E4itEKdPLZ33G4T99UZUZ5waSCXjEodTbXjeTmyCx2DAzd61KZmpRUqBZ7nPa9cvsRwfMFwOkIFF3dfxoiGZ/6WS32Gsw8QasWUIxsq3OOeG52507T0L45oBKMVnCVD9fAuz0Nk5zOZiVoVxkqyniPm3parvqcbE1kbTNMyyML6ZkIayaGV1IeRWDXoCP2m4uwwUUTg2Ekan6Ex6MPMcaO5kw3zODOsNJVbJJZ2yuy3hrMXA9EKxlZiMsis6NZrDpc1q3//nGBgqgQyZXQW2Clze245P0WCErhKLSGQEWpfuNlVXBwCsyrESlEA4z3KO643gvN9oqyXLl7ZddQuUl7sud1ZdkMhtJrgAskIWr8ECl7Xmd0IsykIIfG1ZHVTMKnmZlNx5gvBBoiOyQrWc0JoyV55NlMhaI2pa3oiayfIonCoYTMkggSVCqet4WzvKSVz7AStgyILZo7sV5J7ZxeEm5G9iNRhqXlMKBzXknMnSaJwsgIbQWZJQ8X+zLJ7NhJszalS2JAQxVEFx36ruDgtBLKpliigsmuqm8L1ruJi75jEHlclBGC9pa033Bg433umGrxcVBF2clQxcb1VnO8jfl3jEWQh6JykcpKbXcXu6ElWIERhyI6zP/2YD//+v6Q5P+eH/8f/A3/f7PkZMzOZtc/4j55yvbOc3Thm6SFFXKtZ9xmlLLcbzfYYmfMBGT2HBs6dQsua/XnNVlmSEmgkxwp2YyI7z94sJveYAtUU2DdwERPJ3LLXB1oqUJ66FPa653JuKTrQ1xN1sZQksN6wX83cLTucO3GixwqDFpo6VVzXJ3b7ihgcvo4obbG6wkbFlbjhLhcLqUp6lDW0uaENFVfxijv6cgmwzY5CQdkKlOLJ9Dnn05ogHal4SqNpWQKHn8yP2Z1awlpCpQh42ltBdYIbccOFucPb+j3+83f+t0itvlQR/9aU+6+0PL9rgf+1CNu/YL2vrvMbfu6vdC3+/4qi/eWB/ergfnOE8ZUn/VV+1Fc29JWlwCJME+DTzBQHfHK4MhOzx2WHVoagPIhAVAsmzOV5+SAIsCYxjw4fE7MfmcOEWC0aZ49jShMhB8aUKeuK0iTmfpH0ZCQxZVzKzH7B60kKZZipUMQC4xRRgFvuQefEOATGJGm6FgIM/YzKEucjPi4Y3Kkx5GoZKMQElZbsj56IpB8jcqM4HmdizFQ+MJclPXt0GZcL0/WJvB9xdUUqJyZpwAimKCjaUoRCNBWHw0x/M5BFJpSlVR5SJhZJBobRQxBMk8eVgs9wsx+xqxoXC/vBE+eC0RphLUUKUk6EIpizwKeCqg0xZaLSlKxJRYGCHD1CK0KEKRbifmR0iUpCyAnvC+NcqOslWMlngRKSlCHGQkYitCWEjIuCySea2tCXRFSKOS6v0ThFfBZsG804elz0DKuGYgxRGQaXUBVMwJQyTVeRFFAXckwoYxD3GqKamdvMLBw3xycMY4+1BjYCWsHn0zW3nFifd1QrS9+PnOKAS4F12yEqQe8GVhcr/D4wxBmvA7fiQNPWTNkRVOQQexrdMQdPTo5WVXitODGyn09UVnNTjvSMdFXLqfTIWmC3mu16zU17pOlqYvKQBcVmbvs9VWXxVcBsJckVTmFgLDNUhePUozeKoBOmMRxyz8BE0WCs4lRPCC0xwVA1hlkH8rowR4/cSqbs2QiLI6BrxbPjwD0r2ReHIWNER6kkUcPcygUPWilSKZiQmeRiKJ0sRA0+OFKlMDkTQiDVBlcKYQ741BNLYOpHuKiJITHeLlho1gYvCs475psjY1LY7YbUGYpsiSTGEBCzoz9EhK1gVaMebYnHE8PBIc47gkjIUshqsWl5Bb5WyCxxWlCmGTX05LMO32kmIllIQmcJIaLahjwlgoapluRcmGNEdZZ0nEmiEKTG1RopC94Uwjhj0xHKRCyRSQTK5Yr5CBgQIVNyxk+OcNERr484q/DDyHa3IRwnkpLMjSAGmK0iC7BKEqwgSomrDNlC1AvxRvWB8sX5Pc0elwROLJ+/uK4psuCJTOaL/4vMDCgREdnjiRzdiMShhCeoxJwCCHAkRhEgCwKRoMHJBCkxh5kiNXE8krTCMTPkE1k6prhkI0ktSSUsePE4MboTrEFas3yHp5GQPaPvSTbi8kSUgYwllYlQAnNn4Rjw84ypa5JtcCXghpnR1LjsGOaE3XZYlcg1+ByY20TJmTFMSKtpG7PgTF1iloGkNKOMKD+hokZLT1aFPgy44nFmQYEO04Cx4EtkLJ5YIilHfEk0RhA3Ff40cJqXjlFQklkLYmUIp5HYWYYY0ec1yIwvkdR0hHHpMriqkJQk1xqfIq5WKCkJViK6iiAE5osZeGckhQVtK8QCq0itJijBqATJLPflL2bMcy0JWuIaTZJ5CahEUkXJ3GkCmbmWFFHwjUJkRZ4TudUkLXB2+d6eq8UPJKfEKCRRCyYriSLjNIshK5YlbE8LXKeBBZkrFChRiFYQtGA2hWwETi6IXRUikAlWMYVMMEuIZCBRWU0pimQlU0okkSmVxBuBL1CCx1mYrSAqQbAClwXWRUopeKEYrKAogSjgyPhNRfEeb6GUjAJiJUm1Zi6JWCK+lgi5ZIVkVQhWMoWyYHZrSfQZk9XyWuTEZBfJlreGQMbGQtYFL2G0kJPA2S+UGkqS6gWhO1WCWGCuBEIIpFDMGoKVDJWgGIGrJEJLRAgkIsEIxnqhU05WLZhaD2LXkIxgtgqsWHDTc1oQxlbThUjKmUhhJBEoWDLOSHzOTFYSlFy8qUZQVQohWJ5Dq3BefBHyCXNW2NrgRWYsieDSYkCPgmoukCOTWuSYKElpW5IpTLd70nBiqgZSnFAs36NzHRhCRnnPLGayqjC2Q3SakBLDdCKnmVkt6OsqGHKJRCK+tZQJZhORCoSUpOKIxTNXHqxizh7cjAyJIiOhBMY0kEpiyhNQMCzo/FwLphJJIRBXQPboYyK6idRGXB0XnL6SxOip2zM8iegKozvh8oA/DtTnm69Wur9RUf+uTYO/fFDxhe3gSxkWf/mk/1f/+Kst/z/Juci5IOUvn8gvOVC/DMz74j8CfhlHKH7ZyRBfHrd9eZuCN87eYY4zIXtWdkMv96TBYUvFq3c/5DPzc+rxwGW+IMYtKnoq0/JyusvT8guEgba0vGxfRWiFAN5Yvc3B3bJLF3TbM3bDfc5NJL44IK+u+cgemPSMutWkZJA0SCO5vyn0lSLkRD1HXll1fNIHRK2510qelUItLRetZGs0nx4SYvK8c2fFjx8f0bZjaxTndxp+9vmJWUTud4XjIVNCZN1qzrRDmkyqBa81DWO03DjBKgfevF/x8+cRe7bm1YcVT5+eiKeEzoL3Hnbcpo5YJJdNIqRCOqvRyXG3FXzaB1QteXmjSGieBoWNnm++3PLRPmG15O5WME+OFCtWjeW8Hng2CXa14FzBetvxybWnKlDFnsPQsu46djEwTSPoDmvgfp3pqxYxJ84bkNOM1zVKZHZy4EQFEs5swVSC20mzaWt2MvPsBHLOXK40cZh4UQwlCR41gYMHo2qqUmjP4DZWuNnx+pnisYaDCGwaw0omcpakHDhPnrSO0E10g+FeXzFsKuhWvL56RL+e6P3P2K4ecv+j+/zT+HNuZsfZs5Zm1eHbFjtJ3nhyn7iCufeUJwnhBaP2rFxH/W8sxzcnunpF/fFCcdFak46R+k8rjq/0dGc1jw4rYpH01UweCt978SYfXT4h6IbdbYdSgmnrqX3F6z9/yGd3npNtQd5IuqAZ7gvWsuLuk0dcPbjCzY7ueY2aJONLApMt7794ieODidv5iP/Mc1m2pEYQpsBrN4940j5FyQvupQvaF4afhs+X2fMfa+QjjUiJ64/3fFC9yUktA9s7n615KkYu7z1iGzTtLwrDyw0ma16eMv0ZFKVYecGDUvFzDSEEXrpOzI3Cy0Lr4O5N4skuk2rN3acRV0vExtDdBl6+WfPp3YqYPPdvA8J7yoOGppVc/mLk853DbCoeZos79qSSMbd73tIdH60Eqq54ebslHifS6URTMi8/Szx/bYM+O+POPDL94kh50NLIirsf7Xn6oIFcOO8z1RjJdyx2Trz0eObFZaB55YI7mwYjNSKPFDQvj4rHbQ2nExeHROUKj7dLR+6l5zPXGwsqsTtF1tPM43OLyJn7N4L47h3S6i5n0tC1d/hpf03ej9x/6ulrTRSB9aZiPQo+zwUGxysEbosmjYFVKJwfAp9va7JR3D145qIotWITIxdPBz5bL8bWB/sZzw3plQ32ReClm8hnHYQED6486e6KcNzTJnjzOvDZWcEayb2xJcU93LtHlRWvHBKfVTcYKXiQOrANOe5Z1x1vrx7x0fQcouCBvUTJQoqRqsDL+l0eh4/Bw0V9zlaCqKA2La+ZN3gcfwFCsjZb7op7/Gj4V1hpebV9k+vpGVu9o5MrcpX5zAm0NDzUb/LxdEMicOZa7ppzns6f0qzOuNe9wcfTLaOHc9vSqQ2/4JrGrnn1wX2eXj0mjNe0o+Xh9nU+GiGfIi/XO+atQeaZtWzZ5gt+rJ6iXOBle8Hx8Cni5R3NSfLu6i1+xqeEHHl53DCjiWZmg+Kl+h4f50DIiZd1y83oGF2kmwv394nHFwqVE3dOPfKlNekwsCqK18eKz2JPToG7ZzXzkx7XSCqfeHSauX63RgwTd64dQktytuhh5v5zz9O7W3CZ84NHhZnoamxMvHKaeXHXQspceJCHwNOUsQgeXiVebC1FFnanTDVMPL1XI3Lk0VXm1G2RraY7ZZrJ86xUqAL3bhL7GopeJFrt0fPsQYsQ8OCZY99qslwwtavrYflsCbh35TlWkaIM6wnuXE88uVejzjSXnx04lUwyifWYubzOfL5dZEN3n0fmTpBkopsKl59Fnl1qghY87JdiP0pBNwTuXQ88flBjNdzvM9F5ODdULvPw2vH0ocVWmss+UXwEJE0WPNhnHp8pdCzcR5N9oiRPFeCVx4HP70ikgruhkK8TnCuqCA+feZ5eGoQQXN4GzJR4+rBFJ8HDm8D1uUbkxPntjKXimdJIH3n43HN9ISgSdsdEF+DzbYaSeXUYuTEVyMC2z3S3js/vKqSSPHo+0Z9r4rlle/LssuKzMw1acO9pZKwyuVKcRcHZU88n9zoKhYfPR8LOEDeK9Ri4+yLz+aag+pHNzcjF1UC536BT4bVS8VQEPJn7Q+Bw64hFsZ4Kd688n99VeAP3biK5EuQSWCXB/ceSTy8MVRY8PGaETeRNoZk89x8HPr9v0LXk8joiUyTdMTSp8NITx+MLSV5p7oYNqsyY9QOsULx0PfG0cUhVuDND7Uc+VxkTCq9ew9Otpq0u2B4SdbKky0u0z7xyKLzoJmK27MqG9pR5bE4IFC/3l9zIPUEl1kPNdt7xdKUpwfPw+YbpjlpIj2XNRXXBp3wOFB6KB1zJA0UVNrNlVx7xmBuoJQ+GjqnKlHTF1tfsbmqeygNJWx6V+8QmE2Vm02159fgKH9/+GEHDK+vXaHT76/7FLyfjv8w4+u1xx69v/w5V+S994L/hqvjKDP9v0Ka+tP3/qDTwLy1/jbSoXx+xlOJXZ+fL47C/WC322+dK/PrBALx//iF36vtMaWRl1vy3T/5rjGqws6K/3mM6i7Y12nbI6LDTRBMVcbtC6JakHXnTLS3BL/Rrr2/eYlvt6MORO/U99KOKnz/rEU9XPLu6IvsDL9yJZlR89umj5bhEwW8lKRUKElEMLz7vScKifMALQ9PUxDFjIvRxRGiD6TRDKshYEwZBahSuSeQckLWk1JJ4dExkzluL7iwGRymZm3EmTRVBWGJWhPUKXQdiUFw/z/gZSlbkUhCmozjBeDsytIWSQdUtTJG0kmiZSQVyK3A3mZw1lTRMfaY1LSVnrABhK/ZTRIwFuaqweGYfEUbhbgKph9JISuqQaOa+4JWhXhl6J6i+6GZoFCnnhW4zJJS0yJKQdoNKZTH9JChZL7hM3VAAqUakKeS0XEiVMEhVGEePMpbgBXXd4JlRlaRC8/h4g+siulsxqyPTEJFti9Sa6mLCvfxz2i5zWWqarPCbFtlZfDNzE3/CfKdn78AdbtCtQqJ4Nt8SQ+T80RnDnBjDkempZ3W5YnYzWlpWxtKOFavzFcfoKLGAElyszjjmxzSqghpWckVlKrp2Te/GRRomNU/8DSopksj0bsbaRVN7Vm+o73XoZNDKcDMeaSpL1dSEPnCVnjMcZtTlcvFZn3c4OxOHxKfTE+pTS3O/5o17D6mK4efpOW5OXPk96+0ZRQy0piOaQnaS1raotaDvR0Kb6FTDQQQeP79i26x4aF7mzfQmz089Vd9w75VvcThryXIx6CkjSFJAyByCx2sJ1jC1i544V5rkErMCiSaLJV0WbShFIdAUe586L7ODqlimsWe6melsR/nGJfL6inQ84EtN3LZgImpI3O5HRG7wk+d4mqkvG8x2C0979rdHvPTEB2vEgzOsVKTpBFmSXrpAxBmRgSCIdpFMoCXTxkKG8OLIHBTizgbIVNuO6XqmahTKgYgzuW6RWiJCwtca+UVLO2vB3LREKdFKMtgd6aoQ39iS6w1eCOy2IhxOpFZCkUghyNcD6d4Z+XaPUJrTsz3ifAPzTMmJsa1AKkouJCshLGZtKTMjklIW/OgYEiocSUmhmkRoFUovoWuhd+RBImuFDonRgvrC7J60oahHCBQ2Kea4J5clYCrKCm0tZIW2Nb3MZCRucIR1IWtJlIK6qgjGU5FwJRPnPaHbUsoyyXSY90uYZim45PlH4b+hH45Y2/BG9S5//OB/zcHdsilr/jv3DxBiuViOZUCKiNARtGc+eUpM5JBwecBWmXqrkH4gdWsqDDJlvIhUZxtEOCF0RZ8kenuJnx1T7xHssfVIg2YcrmkqtcwwTz3htifvFHGuOYgRe7amREcKguKP5HQklkxv90jbQEkM+z3u+pZkE1lo3EoDi+Qzr2qkCpR5QAjN7ewJYSZVkiEMxGMgoslzYvqiKBUxksjIIhFCIotgQJCGSEzg+gRJEbRABcnJF6SUiJyIk8OsLUIWmAOhsdgkmZAgDalOKBbccTQFjgPyokIaSQoKkZZrsVcgU0EqSQmJ2BhEKcvnpNaoUhAFhA+4WoBcdA3eLBWTVBKRErMRCLmEKfovQlUlEhkTDhBFLiGDWkFZfDgmQW4rdIFcBDEVci0RJSNzxlUVIqilw14cRRqQCoPAnbdoaXG/1FAIkNKgfSYoiZbL+94PCeFnRKuRc2RuFIqFfBWyBAxSWFTJxI1BxQhiQStnW5AYrNHkLiNDAiOX78e8hMBqpYl1hc5lOd9CEpRHAMpaZi9RZamZlBSEdYOSCxHK12IJGE2AysxJI7MmT5lsGoROiKQQYaHKFV2RU2aWGTFN5K4hl8ysv9g3kLXEl4KKSyfPC5BCIhDE4slfhAQrkfGtQgmJNAqx1uTJI8Ty3pwag9IVwghYS9IwIopECXCdQkuFkEuXqNhlwClSYWirpbOVBe6UqOR98r4glWEKEuEjdJC1YU4jyR9RSXBSDQhN1os/ZVSGgENqGNRATo9x88QwFIqKxDGgK4W/rBGuRZiIYE2IkHqHsgbfFsI44ESPx3BQimgSaMmpPyBVgOzQdgVthckG309EuyHPDtFKhK1ITUQ5TxpmvNmTVg2506ArfqaeMtz8OcySjw4/5o9f+V9gZfXlcnj5VQBRvlYa9eXBwNd2LL5GHiS+euNL64gv3/GXEKj+xy5/5cHFr9syv5QxLT/+ArvKF4/59c+vW8SXbgnxy8GH4E53D4Cf7n9EH0/0ZcBrzQ23iL7gTaREiDlwynucn7he9YiNoZ+PrIcrPl1/wm61+9UezqsLLqqLX/397ktbyoMNP/v8z8kvQIwRf92S9go3L0mkU1kGGaMAEQRVXeH6pXU2zQljDb0riBzwEiYiVioOnw4YXdMPheh6Ht8GZiuXAiFDlIZYCw5BcPV8ZCJhuhppW0pS9H0GZbj5bCZbS0EwTpFq0zLGgGksP3uRKFFx6jN+ilhrGOOMypnjSRAo+ALxOlCpNftDIqrC01hYbTT9EJhPM7ax9AHyJDip5ct/loo8K+JtYIgGnwWBBpHSwlcXy4WsT5Ci4tppWgunAPY2kWLFLAxEmKJC6QXLa7QkZ0k/g7+JVLoskqkkeDJ7pKoIosY7z4RAZUlgQaf2XhN1QasKrF1SoDUgJNQdoxfEORHqW5QZSbXjRGS+s8atFbk4rssnuMue6+aG4eoZ6f7MSc8oqdCtxmZDv5rRl5LjbmQsM7dqxJ1PXG52pEt4wYnjQwcUXogburs1qY1MeqZuDfOdjBKWF2pP+7Cin2b69YRZa34unxF8ojqvuA09UkPfTYTwgmerW1RQDHZi81pDLwZOtqfe1YRVoKNh7GbSvcRkZk5dT2kLdpOZXcKpwNg4urqhX02wFux3PTJP7OWJ2UTCOjK1HlVrdudb9Gx4UR3pujV9HilWUGrBzfVMPUzsCdTbHZ9dCObOIoBQg4yL5phW8ExLxkpTKPgzuaTQd4psJYdNIZNIuuB2S3L3ZCGuFFcrQxSS1GhEpygh06tEmU48kTPlXJFky5PriCiOU21IQvD8oqUkwaygJIc47emVpbvb8KxK2JSYjyfCzYBaNUzbFeFm5HlxmNow6UV6UEriuFKYkDlWAjtFpkpSbq7RNjB2CoXk9lJDPzOd19y6JfjuUElk0YxtRkXB0ChKWXCxJyMgL2myJjjm3iOrRC4jfVVI91tm4RFB01cSQWRvMv1FR3YBV0CVxKk1FCG4tRVTgSIFuRNL5sAXwXSzrRlloVhNfrhClYneT8Rzw2hh7mcii+ywhIm+s8Ra8nynERqchFQKpUgGKYml8HzdI8h4E8ilh7nnpCNuvOXz/gqJYLSBXxyeIK3kxh3pi+Y6PKEWpwU12QmG2HMqe0y03IjnVLpmpEcFCRROZY/2hkZ3/IH5Y3b2gs/7X3BMB67jCySSqzwSs+ZEj5SRSTp8F5nLnsMcCdow2pk0BXIe6VVETieGEhBSM7WFJ7dXPB4zsc6oxlJaj5j2zDhKBX3ruZ2WdPEpZ3IbGcY9Xm84MpICZFlI1pOTZ89IzIVr9wLEBaFkpiSY27JgW1NhvxHkmEhGLVfI/sSplqSYeKGXAW20iuQccqU4aMFUCfrLmsbCpMyC7tWKcWMxteSZdsigmSpFWltAcLASozP9HcmqkYx20XeLznBUGdVKZtWgpsLUGUTO5JgYNxoKTF1B6UxQGX9RkVrBUC/SIX/eUo4DY6cR91pCzkyNglwWDGnMjK2CuAxypm7Z96wzQmgGK5Cd4nBW47sKQaDfSoQw9K2Eork2Cm8WyV8gIVSmrwpIuDGGpBRJFLIBpKS3iiTh+lyRC4TGkIsHYelXgqgTN3LJkXBGQAgUYTm1y/m+2UlELMxrC+lE0XCsChOC25VEo5jWmqtUyJeWvtOMIbPfLBSisdVLTgfQbyx9LstrIDQnEeG8phRN32m00Qx1QcXI0CoEnlgEfScROePaGjku3x3ITMIy2IVWFdYaETInW5D3Wm5GwdhUlJIXqVYKDGuDqMBFGGtFFpoilxDA3gIbzUkpopH4JtNd9bhH5+yCIuTM5yLwgkikMMWBdKbpG0EWkqudAqPxslCyh9ZwaiRRwrPdMqHiDIgpUozkWIM3cHVWoSKMVpCLRmrNqQZfwc12IXeNlUBKjZCKvl0w4TdVwWTNoBRJOHKV6W2FTIXjymB1zbA2qHNDUZJBZ6YM01mPnCS9EJBHbuXA1DoEM/McliyiMi/dK+8ZK49UEnc3IX1iSB7mPS+Ga6YuIZVlsjXaWkYCYr7lOt4wSUdWgZACKTlGIlllrjf9MpmdE7Fco+o1B3egZDiNNxTvSTFjtOHF9IxHq1d+VfX+KvrtL7JCf50N40sqoK8bPCz/Fr/qinylyOartCjxWxv4j1v++hK6fzmy+DpfNvyqPfOllX91+L/qUvzG+r+UU311H9CZNbVq6MyKVbNmLiMyF4bS05aWGB2BllaulyAd05EnRz0rmlHD+ivDny+9kAVACdarMy7SPYqVbFaX5HiH+IueojVTiJgvZt86WSAXtJHIlDFVhUmJUDIrLRmFQOQMKbFaN6ytJd8GLiXMUmDMMvqslVxCx4bExsLV6NhtW9CCRoAo0B8Dd7Y1xzmDFeQkMFJR6cxkBDsLI4VSImZtUKnQdpr5xnHWSrIuiNow+MRGWRppmE8RMfesmhYdRlbWUGuD0YLZFxq1GNxdiMjKYqfANM9sdnexJSAbCzkyIljXkuIzuRTWNZxcxKTEpjasZOFw8pyfr4m9BzLWCkKEs7VmmAJYyUolSsmsNpZyijQ5IE2NExkTFlxjVxVOPnHeVcsMlsw0jcYLzfrccJthmzwuZoKHtjJ0wbJRLb6reXD2gLkSi27/dCIh2bxyyXA6sP/ZFaITXKy3DDJwPJ6IY2TKjtfjA3IurFVHMjAGzebU4FeJyncMaSZ5QdNY7rBj5Wpu4pFqbIh+phKas8tLNnOLHwKDcDBkoozoqLBG8pJ+xIvxBl1pNr7lduipo6W6Y7GTYog9LTWtq9G6hakQS8TuDbIR2GhoU0OYE3mfUVIibwRzE1DZYL1kHh0vNXdZrRrklcDpyL1uRxtqCFCFCqciF9OKYgWNq2iiofGC9iSpaskG4ExSzQWhJLUv1B6iKmydYMiFGogsJs9GCYIvrPuI0MtFMkiNTRk5BUpt2AwJLxOUQjCCdorQB8JOsQkwH/xSPKwM66bBYMg5sj455hiQWaErSTdlVMoU6VnnRJUyldb0KNrDDEeP31astSVIhbydyI2kmxLZCLKHekyIkGjGSBGKdkykj6+xu5rVnR2y1tjVmnQ8cr5ZcbqdKFqjRo9EUrtMMpK1X+hOIoDwEZNhHQTX+5k6DZT76yUEspHE5KinSJSazZgYxcjucoM/TKgYaW4iYVuzmTPOO7SUFCGoEVRCEIms3YJftgKCz1gJbS6EIbCWYLsWd/DMWtCmjAyRpANnXYcrYeHhp0gzZ8iJLGGrLV7UyBwYUmaVDMklgi5shMYXsMoAmXXQhN6xaStWpaLkjjoXZOVYyy3kSEoNjWgRRtKpFaTC2pyRcqDEQiVqahpUUeSU6WSHzoq12mKlxUeJrjYkn1iXDiUkTaUwVUNUGnSHz5GtrpiSQCsgFPRU2JxtCCVxvqno+wO5CJgKXbtB9xEQrHOHOjtDq8DUD1RkrMyUktmVhmKXwbLLARMKm7v38fvPWZ80pbGIIJlTwpwCdZIUDfWUSMGjlcRJgTpMWGUJrWbjMl6DNZY+RDZ6CWsNYZHM2KyoTgF0oRnjMlHeQR0K0hWUiyAFW7f46pLQ1C5hTaEJDnY1qzETs2e9Mug+okygCoqiEqsxMUVPKxcvhkyFKmXGB4UzWzMcZmReMjB0nbAO8hjZ1S3H57eokBGARWCHSLGKbTH00aOPAZTEeLApk6Vk1Udim6lrCUkgXcYAwWRWfcQ30PiFJmfnhJGFIGA7C1zOCCGWxPkZZBakDjZjwpvlOumEpBkTqgSSUqzHQiBgth1DyDTD0uVL2rCaM4FlYkQAqzGTYiIa6BwkElVlEa7Qnhw5SgqRymVQgioWhC6sh0jQkjJnaqHIpxEbCnGt2fQZbyVljFgSMmSqmIlasBoWX4ogIwsYOVOPhiQFZ0NilAkVQVCwMVJluaCUx8AYNIrlPWtcovGRWGlWQ0IKgXaZWGnqUGgTZJVYHyO5BubEaRhRLqJPjmQqZM40RbITC9BF3jr0FIjSLOdFV3AITKrQTBllNUEtiGCnxeKraCXNsARRRgkbD15FjLCIklmPhSIXIEbnIJSEjQWBZjXnRbIuC5UvZJGxfvFmbPqCL5FSFaoEqlXUrhDDTDs5nCi0rcKUpftWJUuoM7vNiun0BOVAo9BjpnGCdCZYx5qEQJ0y0hisVXS6I+rEbrVjDD2NliSXMCNUReBXmvPmDuPcY2ZBaddUyWCsBnnL+lQTZEaVBo9fPIyhxeWRVW+RAYxt8cVjZEVn1nzNcOHXIXa/S/Ng4R4hRPnCb/DV+3/3DsSv/BniP2wO/w8tf2UU7W+NeL54or80eZev/PyN4YIQX0Sf/+Y2xG8OO5blSw+73zzig933eHf7Td7evs//5tX/Pe9ffof3z7/LH1z+Z9yXDykhkVPkB/IHpDwjbMF4uHryEX/n+d/mv7j+e/x8+Cn/8LP/mv/nx3+Hf/78n5By+tU+vrf5kPfW7/DB5bf4g9e+w/fefgt1p6VUmbdCoJRCKoWq0rx0DsN5ob+AN+8XhMwklZAm8837NSXWWHvG995YU0zAqxm707x9F0pXCE3irjri+gkfC8En3l1JQtAEp3lZB+pWIteG0kq+/RBUVeOT4IF2ECemacJ7z++9WTO7SBKSVy8FZ3c0uSmITvJe48jCkovl3dc2XN5RqHPJ9s0d7z2cOKmJaRW4vIhcPkrwMDOvJt5se/JKkTvFS6+0fPPbZ5T7iXQn873XC2EbyJeB3T24d+7xO8/cOV6t9owlkFvN6lxz3vYMZiZsCm+c9YS2kM4EmJlHdwPcKfTNzDdfzvhVYugcrp55eDniz2fC3cB33suU71wR/9bn8K1rvvG9PeX3f0b+/Y/45jtH1Nufwjf/HfbNT/jOm3u6v/FzNn/zE/7T77/K+dsPCCvD7DzvHFqeNj/l+sFjvnv+AeV6or+9wWXP6h9oPnc39Ix88Plr2EFTr2tkrfjPf/5dzEpxzEfufbTGX0VuQ8/enXj9nz7kWCZMU3Hx8Y7VixZjW3o/88Y/uU9fekbhCT/1vB4e0a1qSi34T3/yAbKROBwPbrd8ML5GkJEX8cD3//Rd9uXAs/kZzY3i4rPNknRuIj/402+QFQxh5nzc8tIv7i6BdZXgzX/6iCASSRVe1ff51vM3KDoRpOc7P3kHT+Tz/hkqaV760V2cSEzZ886PXmGc5kV24SV/46e/x6X8TzhTf8jfuvk91pu3OLvzAV33Mn/jSU02hqg073+eKULhbEVWmg8/jgQFXgve+mTCRMFcCi5nPvxZYCoSh+Lt1NF5gU+JJOHbPwkEpQlZ8nJfsZo1MWhS0nz/J1BkRcyGsz8/kn/xHK8C+UHHD64iLu2Jec/l1YmLUyZqxZwS3/53PWPIzBEucs39XuBiYuhnvvuTgXJnQzSa1VC4/8zji8Bpzfd+NuNbje8MHZqHV5kRxf524Nu3mkSh1AqbC++qhqwC4rLme08cSULUgqoU3vj4sOBfa8U3P5lxKJxtCC8m3n4SCTkTpeDbo6ZgcKWiFM17P73FiUTaNbz7bEQLTZKaLATf+PREMpJoBG89P6LUgam+IrRHvnMz48XSgXj9OlJREZIhnBLf32vUg3tgWl6bLesk8CUTYuJv+o5oDDEJ7l1HdrMiqRo3Fz74accc7uHnh9yLr3HPvEe5+AF+8w2+7z/Ad+8Tum9zad7ngf0AZz9glm/zg+E/Y2r+iL7+X9KJP+Ke/0MO6Yfczt/iO/l/zmnecPJ3sfEVHsh32Ue4dYF7+lX+X5/93/nbz/9P/Ovj/8BWXjCWmT6N/KD+PiVN5DxQV5rX2ne5UZFbHfnu9nvYfsLcnmjGyHd5GZMGbDjyneMFXRxYpz0Xa/i9i2/iUmAKnnf9K+g7l8yrFXm35vd3b1G1R7rtwPfuvspmm9HVZxj1mG8fz/Fmwouet+IdOiSJkWAcf0CLSv8Clf4H3hifcVZZkklknXj3sxEv9szpipdioOkHknXMxvGd28SUBrycOL/t2R1HvPQ4HXn/3+85jDOnfqK7dmyfjhxOA6f9wIc/2TOTcCmyGh0PDw6nFF5J3v/piEs1w2iobgX3fjoyDYrJW976F1eUShG1oPbw6OMRJytmVfP2TyZSKXgXqJuG1z8eSXpJDn/3T2/BGGLMGGt593kmK0lSknd+3C+ZRwAh8cELQdaGpDRv/2RGpwVhW5Tk/Z+NpBSJWvD6xxNmDGQpKEryrT8/ESkkIXjj80A9QZKGVATf/tOBiKBIycufjmzmQBaJpDLf/rNrgskEFXnwfGY7CrKyRCTf/nd7nB9JxXN5NbHbJ6JQRKX5zr89EIwgUrjoC/cPiqxq0nrD934hSUVSpOXskHn5aklJT5XmO392xAtBsobVWHjlsSOkjKfw4UeOREXUKyqneP2TgSjBlcw3fnwkYUmixnjNO594ohIkJfj28wwIolKoJHj355GkVmSz4b0fO/CesOiIee8ny8RYkpL3fnpCFUFWAlEK3/l0plQCROTtnx0wcyGZmqIt3/x4JlYa0VSsnu55/mjkX33vxJ/c/gmvuEieJ/Iw8NrnI2snyboiCskPPgcvFizwwxeRs0MhK0uqKn7wUSTYhqRa7p8q7swtpT4jtFu+++PMJDOukpx7wcODXgiaQvPdfztSqhphazZO8fLcEHVD0DXf+XkiG0sRmu2see3WkG1DMjXf/3O3vH9FphoCbz6OZCGIOfPdH7Vkd0mu3qAKD/lW/D5ev0PYfpPvV39Mar7BzLco48u8ffUtpvZ9BvEGb918yBwaDrFi9jXfSB9wco7Jed4dXse0DT4H/P7EB+PbhAacCrxv36ftNpRaIozgg6t3mI0iNDVv8jadWhFVwSXH35R/wKviFV5OL/Odix9wVp1/qcD9pabnS4ikv7B58JuF/y8HI4Wl6/HleAe+Wnf/ZrH9RR0ufiOVu+RM/lI9/B+z/LWgaH/5tH71xPhivPDVFsxX2jR/+fLFif6Lju7rDC/Ak+kz/tvn/xWfTh/TxApvMsY2HPKe7dwSJ8ewjqzaM/Qk6ULL3t3ysHuJH977T3hj8/av9/nF7xfjxP/1T/+MHz2/Jtz2nJ6NyCDYA5uUF9IRUAlBNSjqA8xFsxEFNzdEllRVW3vqNnJ18NxZScY2UZqF6DA/czTOMIqatnhml7DrhoygyZl2U/HsGLlsJMNtQQhNlhqRTtRt4ton7m4qolzjDp6UJUZ52p3i+cFz0SjmLDBG4SJcnFmc99y6wloVxslR15ajT2xMotlZriZPPJ6IEV5+5R4vjiMXRmG6iuvRI2NEKwUpMmrFnUZzfbMnVZZVbbj+bGBnO2Zt6Uok+MyQBY2VjP1EbSTO1OjhSLYgu4bsPHWtEQQGqTGnEzSWbA2UwuoVhzo/cmwTD+2ak38Bq0ycE5bIWhQOq5mLqVkkBgaKklhhsFlx3EXud3d4tv2IsTrhpoH8dEQOgdOdifRJ4FacuLM751gG6tEQx8B433N2WHGQJ+bk0VuLupGsRc3N5sD6tOIkJ1a6RZ5JDj870omG67Oe+kYTbKRVNewE1bVGScW0c2yGBtNZ0hCZtoHtoWHdtVyvDsijYh/3WC8ZLwLn+y19GritD2x9R5GSs7jicXdDc7X4Ok7NCUaxzOKfNPVrNWf7NYOYSKuEiJKSwE6a+ChTP6kQVhNtxM0eEw335Dm35yNvjC/R8H2yOkfkjMwSGQSnXcXdQeBWa3xTUcqCZKwCvFgr7gyZWUNU4EqiDtAVzfNWcL4PZOLSnagVZ22DPow814ndMeLU8h0y1ZIOReULt3Vhe4w4tcxKTa1mNQekybyQjru6ZbQgQ6R3M+cngRQ1h03Feog4rVEoTo1kO0RETpw2lnZKxAy2SI7nDed7RyiZfqVpQqGkgPGR40qwO2WiUvSNpgoFlQJrqzjd7ziPmmn2HPsBPQX0eos6BG5axfkhECrFXCmET1ghqObETafYHT1ZBXi0xawaxElQfjFwXRt2R0dsE8GCOl8hPz9RzZLbbc3uMC0kLqOWIC9GdN7zosucn8CZO6RjwSnJqmQqAbcbw24/49Yd5t4Z/fWJZhgovudGBna2QXQrSihc3xxYuYLWmmOj2LjCrAWyFKZKcSZrsq7ZN5azInBKoIDeai5jJobErYRNWdKBdcycKsXdkiD3HIqjKRIpntGKI7di5CJZUntg715Q65YKTzNGDquBu/UjfPGc4hGDWbprueZW7tnlC6YsGYLDGssqStZHuJVHzsIa30piK/HXJ0wQtKamXzsum/s8TZI+Z3JK2BBptOKFPXG/vgPTNclPZJFpGot0jqfjZ6yHhqHaoLZbfHKsisUqzdP4gvO0xqwcKgemMKCHlxCb7/LUO7oXE8HOKAOjiKxiQ54N486yOnqSkihp6WVi65ak62Orls7QGFC6YlRw7gpi3XCdAhuXCUVhiuLQKM6HSJKG23XFyhiE0ayK4DYHdvuRIAp9u6BobSNYWclhbdhcTcwUxlpjhUKVSD17TvdaHty95PTJC8YS0Qmkj9RIbiu4YxtCZxluDpSUsdZgp8jtWrO79fjNEviWYsL4QJUyN2ea3bUn1BVlVcNZi35yQE2B/c5wdusJtSGxvHdal5AI9ivJ9hjxZpGFeQndEDFSsl9rNgfPaBYfwbwyrA8eXQT7tWY9JLwoKK2YW83q2oEy3Haa1ZSIevEZHmvJzhWyixxXik5oYsqYVDitNGdXM0kpTo2iK5KcEsYnjndWbJ+diFLQ15I6g6rXqBcz+4uW8/1EMImplmgE+EIbBDdry+4w4c3EVCVUgbo9o7rOXG8tF4ewUNyMRAmBDiN26rneKS6DxQVLNJaiFGaeqL3jZmc5P0Zms+TchJyonaAphtttxdnNTG4BJXHJoX/8r7Gf/RtOm8jLH36P4d6HpPoOjoTZO9J1z81Zxdkp4NYKfGBuFJshQ4DjxrDuI6GpkX5JAd8NcUn/7hRrn3F5QkfPoZNcjAIpa06NoR7DgqNOheOZZXdY3r+nSlGnQsmB2kcOG8PZweNUoK+X6wyy0KC4aQq720TUiqn5onMRl87S1Qruypo5TQzZIZWiVg21qLgykTtjwdnAWPyCWfbXmHTiZjVzL3RwmQhlJDlPdYo0QbLfjJxPa2YbyZ0ilkinV9Sl4nl6znncMvmBNM3ki4pOb7DC8iI+Zxc2vHP9iN8/fIC43NC9fAfbNb9dHH9dnfuXlMF/YQH/pfn5X5sLvrzd367Cc0rMs2OcJmIIvPXWW3/5Afwly1+LLOrLIqfFdLc8kV95K75y3v6ygcWvzSq/g+Kr/PYYY0rjgijMM2jwpAWp5wequiblxDAdyGSa2ELM+OxwaWaO05eeya+XwXtCyvQpka1aAo2mSDaGoCU5J2YhCEKg4+KtHGNCKUmOMPpEjhnrJyKCkOF2jOi1ZkgZqQRNXSOFpXjB5AtCG04uL+i0HCHXOJ953k+IXCONxg2B7VrjWQK0ZqFxY8AHwZKzWpBBMPqEpGBXLSFmDocJP000Zy1zyIiUKaZiRhBFISjIPjGlTJEK01l6l3AJnvc9dUhM1lAphadQdzVxcDy/7Vmfbzj5xJgKtutwUTH6jCiZqqlxQyC4TLdZ46eZKCWqrrGt4hgTBcl4GmhaQzYSZwxaKmZAK8VMROtMUoXnxxuU9Uuqe1WQPhI7CZ0ibyqUtsx5IuWMFou+NlaJkxiYpOd5/4TcT2ywDK1nUDPnd1cYY7ktJ67mAw/MGb4LzCbgV4EiF+wkrWTFBh8ik/WYVUBpCRXkJvPgwQWn2ZHrQn1hCSqzujzj1t/gDw5rKtRG0eMJjLSd5SBHtucbBjGzVyNVrYg5MuCJKlGMYC4Tvku8EAcUhqJBrzVhDPjiEVvJrBzrskZXml5NCCsQUpDWC6dejHBipPcTIsLGbDkxsd10rGINZEQtGHNBZXAqgxA0UaNrTTSCvhYkBaNaWpXWR3xtcBpOdsFFjjKThELnQs+CLRxqiciS5fKTGY8DZm3JjV3O8ewXPTCF2hVGK/CNXnw8QlCEwBuJmTMET1oJDm7ChUi1XeHrajExC7WYRmtB1It90VWK2UUkilkWaBQZRfCZOUXGSpJTYTLL8SmrSJXAVzD6SC6FqZJEC9UQKMNI/9xjN1vktl5ClHJEe4+5WOFSYGwyojKMS64YZEEEvJbMjYIYmA8ntCp0zTnztjDnzNAoslrkMsJ72nVDSh7PQqorWjJZufgmYsHJspz7ClIuuMYQKdi8+EiCUQxKEMnMITIbtVBbZMYbwUiCnEg5EyqNEwWPYBIgVSHVhpIS3iqmOZCKYlSLjyQIgcqFKWqqkAk+0HcVBUGOGS0Ek9T0PlLcTC8DUWl0GslqZhaegQTZMSlPLJlcIsVkvIz0+UQumYmR2WVsqQk5MJeJQUxEWTFJx+Qm1KSxbUcKC1KWtmVkgp3COMU0joyHE7elwlVrTtlTSmHdGGKcmbPndrylKZ7ZHSiiIO0KuS6IpoKLNSLX9GEiyUhVVfhxIBTHmAUmBaQO+OJozxqihaQtcxfwpSBMxpPQUlCEZJYFta6IuaC1xIeEaxVpTngrGAV4B7IkZikZW4NeW9wxMLaaECUajTOSwUIWkrleZvlrLUFKXMoMzfL6OasW6EL9Beq01rjWEHNmrCRRGyqfyULiUqQPjnTWMA8DsrAg2EPEW8PRzZh7KyZvKT4sUhgriKuKcUqkFHHbijIXKJKol/foUEvQgtBohAJLQdYSbyR9LSlG4rUki4JOmSIhVIqxySQpyZUiUDBhAQf4zjDMEWcWWl0wEmskkQV3O9glvE8ICK1hPnqSBG8kE5CUIJRFujSl5RrkGg2xUEQhSHAiM28s2SXmSlGWhDqMKHiRmdcVJSTmWpFixtYaVhavBGMlKWqZMJFCYgWMRi6fpXYJS5xrCaUswJh6ef5Dq0jA3BoQgm5WBKnxRjBQyMYwmYVWJbJi1BqnBX0lyFYzG8hCoaVgFoZgJNNKI6wgGAhBU5tMrgVRZ4YwMpeEK5FAZrVrmWPC68JQLbQ/aonTYCsFGpyR6ErijEBKgbOKMRYomdlKJOCRyLQ8bpSgjGTe1hSjKN4RYsaLRdqNlMs59Au4IPPF69RpYgqMZoEK6FQIbmZWFndeUUJhbhU+ZowQBKMIteAwOSiZUWWkAkoitQIvBH1VyCkx6gwy05TCPB4ZysytiFRjwdczpV7Svcfe4QhMm4IbJ5yUFCXg5gZvK5ya6aUht4VRBNLs0JUiKMc099TGEjeSvC+I6xPq9fu/LmW/4h34XSVJf2mNLL5882ukV1+6p1AI3tP3Az4kvPfEFH+nY/iLlr+GwcXXjbi+bE4RlPIFL6p8nRvly1v6ijn8q5v98u6+1DX68ioP65dZ6S1bs6OWDXfUPR6XK4S23ElnyFrCIVIPFS+ZVzlWE8lCa1bcae7xs+OPMdLwqH0FKRYz2sOm4UHTEO+cL7rC/hkfpZ5eZNZzoi6CawNaFB6tFdiJ2k5sxhY7GsaLATc6LvIZe64plxOr2NLpisPuhFSSB2rH4GekGcgvCu2k8a8adK2RP/ecP1wztnvETeStbsOz6kAi88CtuBU95Rwan3m52/A4H5GNoX6RqS9AvwarWfCgKD4RPam7pXkuuLvViLsHqmC4GFpeNEfaFi4PLUGMyFcn6llz57Ziv7uhehBZPakhDRzveRpR8dBdcmuPNOue7b7GCseLuwM1hgux4rk80VQz69sO5WbkawPKw/pJw/5sIl3C6kWDFQJzf8CiWX2mGM8n5rOebl/TZrhZ76mV5jI0DGKg15Gdamid4XkaqDcNr9UPGLueK33krtyxEzt+Ua4oZF6R9zhwIrrnrKea3XCX4fgcSc3Lh45wHz6LV2xii/pF4dCduJAd5887XJVZtQV1UFw+3/LTzSdUZ5brf/2C+/fuIM8U1im+U97no90Tssu8fLzLyU8oLalOgm9Mb3AyM89vnpJ/Enl4/y5hC9PVCH8O+j1NXVvUbeHu6gzOBc8eX/Hw9g7PLw8c3cDquuastBzEBBO8dHXBs80BXQyvuguii1zVB5QX3H92wdPVnhMzr7h7jLcTj4dbWl3RfqwY70Q0Gn0r6H/kWb/+CnfaDd8KGz6Vjku14e5JcHdu+fzMUknFo0Fy6gwk2KFZHyWPY6JQeHgoHFeFImE7F87HyCergpCCe8eCa5ZAvbMxcXEMPD8zRAH3n48EMzPtDJum4Z5t+aTf43Lh4QST9+StZp0ld4PmiY44U7g3LIVYFpZmDLx5zDz3E9W25p7QzBHSNNKNhbt7x/OLGu0z924LEoGIgioL7u8zzy8alMjcufXIL2g3VYGH+8CLrYQIl/uIRfGkhP8vcf/5LFt2pndiv2W3S3fcdWVuVaFQKIdCAdVAwzXR3cOJoTQjhSakD/qkP02fFVQoZkYxGo6CIhkcchQUKZJtiCYarlD+3uPS7NxuWX3YpwqFgulmd09oR9xzbp7Mk2adzLXftd7n+T2YkHl07dgVmQQsn96y+tJDqCrS7cjFJ0e29xXZwunBUU0D8qJChsTDW8++VmQ0my6x2E1cnllE1/LC86ds1xX+yRWbIbJyno/rWeP9nLIcx0i0gdWU2NyOfNRocml4sE/0FoKwrKJieeu4LOcOwqOgiQRibVlNkZPtkU9UhVGKe5NiGhNyVbFIcN45ntQC4wLn+0hSCnlSUgEXn/Rcri3eCO5NiSmMZD/RZMXFwfPJwqKc4Z6LxNEhsqBKmUf7kae1RrYDJ4cB7VrCwlKkieePgquTgmJzyokP2DbDyQkWwYvasKtaSB1nYoMVmuyfoKXkWX2f27wnTprTvGZRPeAjc43MkhcW5wzugMuJs+o+i+UpH40fIYXg4eYRrduTu6ds0pJ7zQu8O1ySU+K54pxd3OHaxEIveKF8wCe6JITAs/Y+bbjFK8Wp2fCYh/zi8AtyBffDPbztiX3HUix4sXjEk/gLJjXx7PKElgbch9SnBcuP13wc3ycuBc+Uj+i3cKV6Vrbmwq/5qP0QGQdO3QYRMtvqSJkKTvYFN4uECZGLpCmTZhod1RR5MJh5fKPiok+ARtaeSmvOdxP7RpGnkfO9Q6fEkxwxPvH8daJ9WCKUYLkbkV0gLBRlKXnUOvZVQhBZ5ZHlcsFPbg6YDA9ue/YLBVKy2jpO6rmr4vYD928nuk0BZeAUTfHBnltTkLzg7JOJroZ0p8NfX07cmBJhBOunE66UJCFYHiObzvP0rCBIuH81zdQpIVi0kU07cXU6p2vfu5yIKpFKzcLD+v2eywclzkTObkYkkphK6mG+fHmqCdpwMUHoRoQQFEPg/nbi6qJARcH5zYgUkoykHCMP9p7LpUQGw+neo4OALKlC4uJq5Pq0hOw57SK6nxAXJWYKPNp33GiDHCObLlJPI09SgU6RB/vItrZkMid7TzlNPDmVyJS5P3b0RQN4NvuJagw8vdcgheTe5ci+ykRpWO4nzqTnkyqTlODBjaOziYBk3WXWTzuenFpSoXjwZJzzsFaW5RA5+Xjg5qJgcgPNjSEdDH55QVM95LE55X0hccAjVdJdWPyTK5Zd5Pw68PREMarMg2MiJokQimbIXNw6PiklYwUXtyNCQqKgcYnzy5EnpwlrJfduZ9/ZZRJUxnDxbsfNaYnKgovbCTSkBMWUeHDdc73RIDJnOw/Ow1mFlYL7NwPbWqEOsGoHls2Cj2LCRMGD28TtiYaYOL2aqJXio0pitObhKNi3I/m0YH3jafrIJ2uBVJaL44a+BqEDK684/ejIzb0NsrY84yQjt+Qp0xwFj9IzfCJuoCl4oE4Z9juCnTjZnHAmTnlfvYfzE/du16RSkl1POcILzTPIKaDvrZFaf2bc/rwn+1eK3d9VM//a7X9ZR39e4vRprfzZzz6VTH1uMRO853A44nxAKUldWsTnKVZ/g+PvztAN/Dat0udDPPjcLb44Lp/2PPjCdb/q0/jC3YtflU593t2BAOcyMUhSWeFHTWUzxhpEF5j8jmM9MlWeYz3xL6/+GZ07ooXmxeXLfOviewDYwvB/fOtVfrrdoYWke/4Z/s//4v/LMAzYpUHHjIhhps2srqnOLlElrJ2mHBM5ORZKsTElaMgMnFdLipDxeUBKgcm3VF4y2Ii/7FhUp0wnNbqwnL4lcXxCsb1lLS3SvA/jSLWo8OMNVWFxMqJ8Rtse3R7JSlJ+GVCgCpBR8vHlFrcylDmySQKz3FFrTxMVm6QY88RkMg0FqfJMqqfOliYXDGkkmcjpqzV5nPCFp8wG3X2MTJGigmZUmLLAioFSGOrHsLKOLB2nscBKCGKgiIJ70VJkT6scJ6PGCIO3AS00917XHIvMDQPrULAUFs+IyFBRkkwgNIHFmWVp50RMAaSp59jtGIuOHoUM0NESU2Qb4ej3tOIWO3YsBsWmOWNInuQsN+2HHMSBX/z0fc7GhmajuI49u9TzbPWIneg5q9Zcc01lS2KIvPbsi1yOLYUu0IMiyYgKGZDspo73bz5GrRRru+Dy6poPP7ghl5l7i1O88xz2I0tR8ejRQ/xaMNWe07Bi6h05KWQuqM2SFzcbbvSe8NRT2nqGFGjF/eUjJqsZ8oAIGj9FgpvRhOv6FLWu+Vn+mGlMTFNGRcMwOk70KcfpyEIt2FQLHj38Ph/LQOkNi+mCx+cl13lCR4lsHlJWau6g+USOM7lEBEE2mjtuIkmLuWiXguADY4gIYUBKkJHsA6wsWUucUgxALgyuqfAkvLUMNyO9G9EvbHBtT+wdTgh8TKQ+4gdPPp3pS3JTIVuFlKCyIuYBXCLue9wuMOUR8cwKaTXhtoMQEJLZi0UBokAKiDkhfEDWBaLUpHHerck+ERJkL0hSELJCpQxKkb0noMiqAK2JYaT72Ufw+jnmXoM4tGjvMJsK2QpikrOnTguCnuelDGQJsW6IaTaiHv7ifdKLG1TpSPsO5wvCpECLuXOy1GQNohC4UZBiIoweFyW5L5CFnYPO8kTGIQyEfiCYEj84Qkz0FLhh3sF1ssFag1EaEyJZTGQVyAUIHSHLeU5DMKUZtJBTmsPKTKZcFJhdT0KBtnPIoPNIbWfPDoloNAhBVoqkLL44IRiFFoppqnEJhkmx7zIb+wB/6MhZcpCSsXnK6KBTK7zNuFyBMnizJsdIjkei13iVQCvIAoeg94nJGsbaUghPFpEkBF4GvFVESpJZEvPduUnMIYhaFhhVEG8mjlbQFx6XE63MDNnilMExu42NGXHJI0yNCCO6DJjoGdwRrxOBhBctRv45RlxidIFaCYp0izipqGyJUEu2bosWFXH3IUIcUXlExVukVUBAdpkYTtH1fUyjmD64xd4vkVUmDCM9EaVqBAmshOgQLiImiQyS4AORTAwekTXRSWSESUoQgphBIYhOkv2cpu3HjKxnP2RoR3p7guslwUe6UaDWGvKs0Z4uD6hXztHXR1J2ZBehd6j1GvaOdJwQlSVLybwUB3KeKWeTx5YFojAQIyJLRBKkJBBCzh11pUhhLrK0UHPhFCRZzmGrUUEeHHLdkC4HRMwIDVIZohPkoCBCRCKlgnZErReEeAQSSkKWczdVRIGQlpwERD3jdb1DKgUIYsiYpkHmdHefGpKGpMhJIGxCpLv5MATQGmJAxkjKEoFGpIQnfabuEEIQAZnnAFkQCDvDEQCy0pAymUQyBVIUCDRSGkI/wqJChEhMgRwMgnnzJ+aAEJLsIrE0xJjIQkCIRDGTv6L3RF2Qn3sH7tekB6/hqoboW2JOeDyyWaIWC3J7IHqHzAYlQMRMFhqyRhhN6jwSjcgKIQxCMuOE45xwpvJcqElmjLBeVIjtQEyKLEsyMwFMRBDSAI4oDFlYYlaEqLFyhZIFOiRwEdNIdGGwPs+POfYg54WhcAmhBAiNtBYtBCIK8pRQaBgSxXJFHOfJV0hNEgU5L9EmUOkCKsXob+AocdLAqidNEtIcUiiVJjpPigG9bhDjgdxNDOMWsRSYyhKftOigsQtF5TQ5z7dtvvzMjOD9Yp38hYr4dzYwfst1v9al+Oxuvlh1zxV3SpGhH0gpobWiLAzLxeIOFf03P/4OFxdfMKD8hnH6/Irpd43ZryZf/IZVyefu8zPE1t3x8fgBh7Bn73eMceST1JIHwUBC6IDoDxzzDrsoORRPYUh04ywPOSRLNx7QUmNVgU8eIw0IKLXmjYtzyJl/eH0FF0vStaefIrcxcNQZUmSzOSLqHtaRQ6cRj1cwenJ2HHLCJ6Bw+CA4Rs8oRoSWHJCkIeELT9NUHLOnF7vZjyELjt1EOBc4ofkotfgTQetumXSBlJHBRISTfGgnpsKRZCYdM4QwJ/pOkvBcAj0SVaIf5nZoX02kYNmqiJGKUUxcCYesEp1pIVp+IVtUlvR64mqadxCOZiBQcKwVajIMakIvlmSb6O2EcxNtDVVtGaeew5RARkZ1xAfB6CUqSlwxcTwaoinorJuRhsmgtWaQPXoI9GLgVg5opUkqURQlo4rsp54tLW3XEceJGyxCZLZyJEwTUe7YCY8UMIQDQgSOlUMoyc0qc1TgfcYtbrjklnwGxWhxdeBJumbMHvFI8XPxhEl5UpW5fWXLoCYGJv5jcphVgbzQ6HXBn/AzYo7oRuHveezGsF/2iEIizjV+H5ALzU4P1DYRNpG96fDPCJbLEy4Pl4zLibSAthqwDywfck0tSkLtqV8qGaLjpjzSlAV/unoXxkxfjMQ6wgKOa4dsJH+Sf04eM9uixdeBe/fWrFaCFGHymRN9xtYccLLmSR8p189jhORHnUcmx6Qq7EnFe1YyNZacYZAOmSTHejYNXhWJtpinkDkVWHIoJFMNN0sz+wzkTHYRCA4a8kJz3SgmBVFLorSIkNg3miwEu3EktwdYV8hVhbvc09cSWWR2Z4KUMxORIBLyfsWwssgg+OnuEpH8nAKsMikaBjkwecHNqw1aWvroEVIihKUtJS4JbusSlSSDAZaauFDsraCoBbtNxrjIsZxDN4WRtJVClpJDYSiDoKs1ImdidAzHHXazoH2uRmwdrRvhXkVIsBMZmRK9LlFZ0hbzGG4bQ2fmuW44dMjbW45rS6oV13XBIUuyUYw5U60L2js051OgvytMgopIClojiRGuNoIRSAIiBoGccdKN4ePNAm8tQUpEYykmOFYFSQY+pifg6E0kntfobDkoaJAcHtSknAhWgFSQEofgaNaWJ+uGLAp6o1B6zunYWsWQ4eqkogiJo5klDinBri4wKXNbGYqYOFo1o5GniX0XsTnRFtdYt+doHMhrso4ccotwmWPuZrS3GOaCaejpyoBI0E17rDIc4hHlb9h5TxcPCLhD0Rr28UjKij507N1EzjCFYX6PpoG0MPxcXNOHAyhInUMVhh0doQ1chQGve2KOpOwhBY7qgNCw5YYQHR5P7kFXBYd0TTJLrk9HUoh4f4ufMsgz2tiSUsflYkCkxJgncpGwUnLUI8HC9b0V5ameTbFNYj/saSsQ1ax5LxEcZUKKhLSaToJznr3KyCwYDdzUkigkh0pjQsJvKhZ3spybVclkYKckVhumRaSQgWOtYBQEEbgtLVlH4skspekX887wrpA4mUhnFYPKM7WxlNC2qFdOaY/d7KG6bxBEukYhlOKw1AxaoOLI+PyStO3oVpaU4fZkltcgIUmBJNMXs8TremEJShG0JIsIOdKWghQnbt46JxxHvJFzMS8srVVEFbndCFSOTFaSwoh8vOboJoJJ3K4MKgnGQoFUCKlo7Sxb2q8VOsb5NV3UiATHpsS4yH5ZoiMca4MUI1lZjiXoIDnKEqsK2ny34JDQNgYJdMsC5SJdrZHZEJcFXTPnYAzLCmstxxgQuSQqSV+qeSFXalSI9LVGZ8l2JRlrRUYxKYXC0DUGENysYaokSEGu5s3Frpm7AO1FgSMyGot/fIbM0J827LTiSWoZ00ggEcQdKnhV4FrDdiNAzobuhJo/S43Bj5Hrh/W8aC3m3fh893q9jtwuCmSa6AuBEAaZLUNjUKPj5sU1Wmh6IxEZUJK20djasF9aTMgcK42SkiQkx0phMnQ1aO/ojERUkVwJdtGgEAxLjYyBrhQQEzcy0lUzKnesFEYYOiu4dBPxuYpDnBDMfjIZBcdKQxeIamSoC0JM4D6g9Ld05YTIcLvomawnhkBMATll+oVH5YGr+BSXExlBXln0pWeYIgTPu8Nf8tpb7yAL86nt4bcUzL+lfuaXtoNfrZd/rYj+lbvNn7titi7MdXPOmWma8DGCEEghZjqaVL/7+fw1jr/jzsXf8Ph0XfIrA/0F38VvEpflzw3s3Y0btaCQJZWqWagF2gNSEfsDi9MlFJmcIpWs8QKEkoQYqIJCJUktawpTUaoSJRRxcKjK/vIxBawKy8miYmDDg7Jkd3Ngd+golOLBA806B7b5yEm5RJqSsiqRShK7QA4KXfbct+fshwONyaAETbXBTpZ8vOTc1/TSUGfw40QRFCuzYCs9m1HilCUniVeKKlt0kAiRWXvJlCKNMIwyUmWoyoobJk7LCmciIgQGFVg2Bi0CCVhQEZKnUJpWCJo0Zxd0rmfpLblQaA8iJVa+IKuCpBWLVJG1pDIVOzNyok8YvScgqIsCWUFjLYHAiWiIJqKLioqCHBPFJLkKN5ytN4xWQZwlU4WWVMmSZOI0V3gtCQlM1thBYNuINI6qUzgTaLRC6iW2LCmKEscNJ3lB5xMqzicpk6EImslGVsOs78eU5KQxUlKrxOVwxXDQKJERraAsDIwZFQST8JSiYGOXHK6OLNcldV6gJs0wetJtRFlFjSHkjOoVsU2U1rIZF3STxxwMSkk2qeEkLTiknjqV0Etq03DTSap+7hIIkzkJNTFPFMmyMwMXbkmLh5CxvZqjPLxlWNacqAWjcGyix3rFFAKFt5SN4VSuEGNElgbjJTYI1GDpasXFVFDrFUMfmIaJ3jleXj7kJgk2XuCUQI/zhFQkSTEGvIaVF/PEPs2fwMJnxDQiUJw7xWQl1TRjWM2UqJPAm8SyDQxWYcgEDXYMFEkwuMhiiGQhkX1gnI7YsmZxuiHGiaYdGVTCuIQ2gnKIqJuB6byktiXF2Sl5u+PgJhbHSJYQZKIeIaZEXUpEXVGPESY5+37CrLdWIZFEoNw7sjUENNUUSGqWTgWVacZEineEOJ8R+Q71aDONz/gsyNuJMmqK5RrdS7ybaPY90/0TVs5B7zEJqigIRrIcIk4miLMkQkaBHT1joVhrTTdlFgDG0mhBNUWmQtIcR0igksBLMFlQDQGnDcsh0qsZQRsUFAhsFIxJsAiZLDNNzPQxULjIMmZCTCzijBPNU8ZoQZVBGU2VIosxEHVGxEwvA4usSGnO76lyRhQZqQUiwSpLwuholGTFHNRngGRKVlVJzBAFVIMDkSljImrJKghygigkxkUKbbBB4a2lEQtC7EiUxM6hpkhdFEy2YhkWjM7RSItMgtIWLMsFYUosckMSHVItEUKgZEGhF4zJsTILUkhkMedMWKGptGXUE2dqReciOlVEkalEgfGGIY4sRUNWkNAE6aloMFYyBcdKbJhEh5RLJkaqUGCnklE1NK5GJYk2lj4dWdoFaSzpxcTaLJmERowepebwzOQjLicqaWhOT6iaJbf9kSIp0nbCVoLCiXn+rgwhOKyHHCNFISnCfEItMiQFRRR4JSjdLIsqxkidBFELmjGQJmiUoowSawS1i3graQKMGRo3o5mtyCxSJtpM0zkiCnlwKG0h9Ngx4K2k3k2kqmClLWHfMecdRlwhqVtPqBTaJ9hNNOsl8eMW32SWHoYQKXzGWYX1CRsTziqaafYjWRK+UBTTnBfhC0O1H4hSo0xFN/QUQ0AmcKuSZgjEkJAxIJKi7CLKloxS0PSBoBUqAkJQd44kDVXWVEMgq4SJkaQEiz6SlSVOkWKYEdXGZ4KaMdbexPn9OwWE9DRVMZ+Ph7sxGSMmJGSecaqh0DR9wKmMGDMyZnR2NBKGlGnGwGRmrwgxUWQoBo8rFE0f8CWoLpCVoMgC23tGI1l2nqnImBTIVlNOGTtFJiNpukDyGR09cezQvcO4iKsstU8orSikYcyRmtlrMBSWKoCPCZUzY4LKZciRUs+PF6xEThGRofYZQSIYSdN7vEzoOBey9TBfR++pgsD5iE2ZWGuqzs9ZL0JQZwgxYV3ES0HVz0SwLAXWRUSK1H7GfS/agMuShZboMSBFotIKN4Y7FG5GaokMc/5QbRUuJhZtYNSaZkxIMaOSiwCTUpyUDfvdDWJMUChqWVNNBSMdy7zAy4QNATcOFFjKrPE+sbQrdCmww0CwmdI2GBUJ8ciiWnPvwZcxJ4vfXgT/tkXG5wrhT33Js93gV3fqf5Oy6vP79L/sjsxeSe8d3s9UKCklUn5Kjfotmqv/hOPvAEX7hUPw25/T77ruc1fP/35rz+d3HvfsQ1aHE/iZJr0v+V71bfK4hWnHshW80LxEErMZ9XubH2A06BBZqQWPxH1acaAreu6vnuMfH/8Z/7D77/ifu3/FD6ef8H89/A/8N4f/J89eRJb33+f08Y959PiW/+L7Fzzz/T33vrPn773+GsWr90iPFzSvPOTtR28S6z2h2PHtx++wfFhhlo6iinz30TdQZwKxiHyVR5gmIB9F7Islf/Di64jzA/rZgW8+epaz5wz6Yk/xwPFdc4Gvr8jrW96oGlabRD69JZ0PfLd6iDzbYs5u+ep6zYP7BnNyg1xs+R730RcD5rzjxXrDo/snFA+gfEbxR9WbBDPvADwunuE1+YCHwbIMkv9s+BoLn1nfOF7aLfhKuk8joRSJ798+D+MNerrmfpf4Ul6jyh5ZDfxg+gpue0MaW5a7zItP17hty/D0lnd++pBxF3GjoTqUvHxzTtQZ1oY/sF9H1xqpM40u+erxPnYpkGXinePzWJvQa2gerPm99VeRLy7huYbvPvh9dFMgGkOxrPime0yoI0FNvPHBikI3JDRKW9548oh+DMSkeOODL9Hf9PTOs9INX/13L1JXC85X57z8/vOcpBVZJWQO/OGP3uLZ04dsmjPSvwnwJKOlZgiOh//8hFs/IqTm0funvM5LDJPj8rjj+X+6mU37UrH8sCL8InLMgR7Pw39c4XZbtFHYq5Ly5wInPIMJ/OBH75C3L5I++Qr9n59i/vUJ5e4VFsNXeOP//Trm+ALm6sucP3mJt372Nvb2ZeTxZZ75F8/QJo/LIFrFWz9/G3v7Enb3An/4o++yGd/gIn6P8/5LvPXRGao5Y33xHP9b9wJFtUYvTrDFgjc/SQQl8AK+9glgCrwpEMLwzieZJAVJwpufBOo7GdQQHN94f8KTSVLyxgcTRYBwl8T7ez/pSEYSZObFjwaWXoA1RAFf+dGOrrSMVcmjn3fYn29xQsHZmt9vC2KhSFry6Mqx8YKYEuOu46v/r49wI4jNCff3lvNLDXlFlive+UnGhUhWitNJcK+7Ytz/O7rbP+Eb//GSbDJZJU4OI89ejbNsSUu+/RcHUo4kMisHL34yke4wn2//uCWrjCskZRB86VYRiyVjB2/+bIJSE3XGDI6XfniFXGhkIXnjxy2hDbhjQkySl37uOLgl+7zm1UvDyBl7f4+4eMSbV4JpccFQnPBSb3GxptWn9GrJV97raYsNvV7z+KCJ9T32+j5HdcrXPpIM5oLO3udxW6Dlir44YzJrvnE50mGYdMkzx4QJmVYbWm35vVvDUJwy2XOeGyqWk8FtLpjqNV+/0QzNCWNxyulYcJYb4uKCoVjzracjU8yELLjXB54fIz7BOHq++6Rn0pZxTGyeHnnuSTvLWQrDt3cTky0IpmBZNnxp+RD/8EXC45f5Zv0WYf01uuIbyPwKj/3vsdffxl/8Me+ov0+vvsbefB9VfoOvbv6Ivn6Lvvkqb8hv08eHdPbLjOkZnj+8SDspumB4Xb5OHgei6xBDz+v9Bf5wCRx4p35MpSJa9Ig88J3qDWQhUVbx9fvfoLJrYlQgC95u38QdR3CJN8uv8c7i27xZv81Xitf4gfzPEDGjouDL5jVWYQnTLMn7Xy/+a74sXuEr6RW+xze4pxXaXiKrW75vv4RY7JD1Lc83Kx6fb1DLHea85/v6hDD8W/D/mufOOh5Xgazeg+oTfn/M5JNA4IbT0PNo8Ph8xKuBN59OjHlgCi3NOPDs1oMCYQSv/8WW/tDT3rbo7ZFnf/aEEDqcP/LaTw6MQ6A7jEiXeP2YSH4kJ8drP2vn3XAtUDHz/J9eMewC06R49ScdMguyFGgkL/+rj8mFIVvDS//xQN5Jhr3Fd5bXfzKQSk0YHV/uFPWiJsWIqAxv/McD6e48//iDnqqPJClAK95+4kElMoFnPzyyHMWMV1eWN//lJyQDuVQ8vOxZt3MYXFCSr/7FHq8Koiw5u46s371FLCxBw9d+eEsQMxzhdBd5eDWRhCRJydv/YU+Uloxldet5cNkTiAQNX/8PV0Q9J3DXfeLFj0eSUERtefsvdyQxd17qkHjxwyNJCryWvPGXW0LKhAx6yrz8856oDEEZ3vjRgewTWWmUS7z8kz0RQZKSV394g4gQs0Akwat/eSCagpAUr308ofL8nLMxvPaTjqAsISle/MkeFTOeRLaS1/7smmQUUUnu//Bj7HEkK0HImf9SP+JVveENfcIfq3PWQs+m5XXJ23/eMsmCiYJH14nNIZC1wgvB2z+6xRcGLyX3doHTrZtRv9by9T/viKoi6yUXR8nD3Yj3LbEKvPMX13ilCEqxHjLPPB2JWuOS4Gs/2hKlIilF03mev5oIUhKM5qs/7nGqYJIFhdM8/klLQBCE4vU/a/HOkOtTdK748lUm6tnc/9WfjwhtiUpjkua1n7lZN24qXv+ZR/oMhUUmyVffh6gUCcmXP7hPdC/ShTeZ8pd45YOv0unXcct3+NL0zpzWHRxhGnnj5w9nqW3veCm+wGvmDV4QL/BC9SW+du9bcxkrPvvyWVGbP79Zfrd4+K1Hnn/9i12L32on+LSm/nQjPzOH/IVIyvPmoZTiLp2dO+rr77SL/5XH3wGK9vi3egJfPD5v6p4v86uLui8u8PLn/e7w9PYT/vm/+6d8dPUBTdngHnTIhef2+JRFPiGXBlc7almTU6TIhn24Za1OmWxk299QiJJUlpTVhpu85cJc4ISgyyNGGIqcWKC5Dtec6wuOKtAzolDIrCmouIo33JcnZHeJD0cEAq0bSrPhKlxxmk9o/UAfJkiJ0taURc2l3nM+LWl9R0ieJDOl05S25jLfcDYt6UwkG4m3mSY3FNHyJFyzmWqC6jEKQpVZ+BK2A7d6z4k5wxUCLTVHf+RErhEJturAOjQMUVAUSw65Z3kTWd10DKmlyTVJg4zQ0bFggasze9uzNCt8GlEu01UD63xCXxkOxUjZS0IKFFGzLwcu0gkuJ45iwHpFzgXWV2yriYtQM9UTRzthosSEzDIZrouWC7dm1I5eDKQsaBZLmnLJFbdcyHM66RnyiHAJlRR2l3haHLhwa7o8EQtB6kbkqKnVgqui48Iv6ZkIKhGCx+iBpLY8qa9Q7wfyOnM17Dg9WxN2ieNhoD3p+bp+GWc8h6HnRnXsPzzwsL5gf9JTbjXVukZlwV4dOT02bMoFt6sWtpoudOQAbAQPpg0yJq4WR1ZDzaXb8bi64LJqWRwahFb4E896KOk/uEA/OeFQwkO9wBtHbz1iCNRFxTJqbqvI+aCJWtKaSJUk4eQput5xtep42N4nXT3gMGa0z9TViqpYcdNkHg0GVhe45QIlFSaBnRLXjeS8z4wKplJBzpgAZRJcN5KLLjFVCpfn0EQboAqCy0ZydvD0MpGMJsgZNFBFeFoLTtrAVMwSGa8F6jixwXK1kJweAm5hiM4zWMmmzxRj5GapWR8cqZZIMkeRWB08WkpuG8mmi3iV0SHRn5ScLNa492/YLwyLPhCVwxpJW8K6bcl8yO3wlNpr9HNfp0gP2LqBzSGQTMGxUlR+DoEyPrFfas67PKM8qzmUKoZAETLblebkmIgCxnJO9pZuZHOx5FpHNh8ecWpG0RYnC8InI2qbuKkUJ1OmLdb00iBzxua503C5XnCPSN97nJCIRYnyntIHroTgkVEc25GQM0kqitFRKMlNaTlte5xOoMBZTZ0EJsHT0nDejozaIIWgV5KNnzB+4mZRcBISQc7dyU4KNkKhlOSJyCy6iWw1OmY6rVgPDqxiV2oWg8criU2wN5KzwZGU5FbCYnB4KdEhcagMZ1PAS0FbaJopkIzGToHbQnM+eIIRtFpSxgQZ6hC5riwXo8fVlq6xlEphrKCW8DQFHkgJTabPDp1B41mkwGUaOHeQup/g4h6pFDZ5ljJz7a44U2f0VuLCTICrVEmtC67CLRf6jBFHSIFApKBGUfLk8IQzscL5j9E2kmrJ4/ol/n7xDzivL0Ar/ofbf8i7/U+Y0kiVKkTI7OSWjT7jtdXX+cPVf0EcPe/2f8m/GP8JH8b3OdFnjKFHK0Mb9qz1CTlntumWRV4QRcbKkkPcsc73SPKUHSOmzUR5Rr16xNPLp6xHS1aWvYiUSYKQKJ9pbeLMGZysGApNERLERJkEu5IZwWwVY6GxCUTOVFFwUwkuTEWoK9rLPSplyvOG5UlNKyPLD3bs+0g6OcGsa9TNlgbHdm05OXiclcRFgagL/Ls7OCRuVxVnnUNdKHIjSTlTIlkqQPEQAAEAAElEQVTeO+XJzS3rY8CVmjh5glUUU5w/Z0vNau9JD1ekfg7NrAdQSbJdWZatw9uIUBCfWVO8uwenOKxKFkeP1wKdBX2pWHYjQnjaM8vKlIz7Ce0FXWNZt44sBG1tqKZIUAKb4FAp1oeJaAVdM4eGpiSxDg5Ly2Y/Eg0cK4V1swy0LipuCWx2Dl9ohsaiXUTGSOky23UxI4KtZypAxYyMmqpeca0FJ09apkLhi1l6qTJUneP2ouH0tme6yylJZIogKLLkupRsdiO+UnN2hoAqRMzk2W0sJztHriU5JW7ba6rjhHWR9v6SB/cf8K1HL/KdtALgx0z8T+LABziWO8fx6RGZBb0WrMaAyon9WclqN824b204pMhmiAhg12iWU8ILjw2BY63ZdBOJkUOdWHjwcoUeNIelndHcepbuVS6SpcSMnv2y4Kx1eKM4FpIqZnJKlD6yWxpO9iMTnrFWqDAv7AsH7eNzljcdPtwwqYAyGkNBmSzXVnB2CDgDUyFRRiG6ATtO3JwZHqqS/faGUElkYdAO9ABXZeTCS0Y5gwSykaziJevykiv3MZuxgezIo8NFxzP6Of6g/y4ni/s0z12g6oLP8t0+NQyLGXr0aU37ean/r/sw/tOq6U89CL/0bovP3OPBeyYfSCmR0vx4Ss6yKK01QggWi+Xf+NH/l5VF/RWdnl+76Wcv/q+/Zvpih6MbO5yf6MeemCIh9CidcSbglcdHx7E9MKojKiYKVTCKHhklPiTGwuNDIHUDfT/QiiNKJSgKWutRSrMUiphhTCP7dMBLSZtbSFCJBUOc6FPPNkS0OzDELeRMZRJjzgxioFUF3krGnMgpo7TAMzIxsRcQSujyNGNWM3jdMyTHwQ6ExtwVq7N5rk1yRo56j9SRQXhSBDF5ch4Z5cQxt/ikwBom6bGhRzUFk5wTeV1U9DeXDHmiOEqG7HDKk8WIMBJT10RR4k3JlEaczrShI8URbSWj9ijl8I1iKBLBAmMkJnA1HPqBnCR9GRljRk0aVySmUtAKCNPIUY5Iq1mbmsNhYBSOPQeEkvTGwQwRxfWO43SLjANBS9pFAh+pBkMPjDqwD0ci0AlPMp4qFPjQMmTPLZCUYCzmcCsjR7w8MhpHXkVEkSlOSg5ixk3ubU+xLvhFd4mRimHhaNPA8sGarTsSysjitMRXgf3YE2wikfgk3rLLPWVp2bmOxaKmWBmmo8dmEEtwZWKhltxkz2AFZU6QIwczMomILe6jliVZBSaRUIUilomiMPgoGABvmQ3SwFDCCFBMyHqiN4596lGp5yAFpjJQCGIJoRB0SnMIHWW9RoRMFWAqZ532sdGEnDgWd2n0E7gMgxFsTSYSOFowSlP3kUlmBpXZF4IkFL2dd+5EFjgFk1V0zYypnfQsj1mKil1MjKXiKBWONAe5aUmfI15JplLRJYh5QuREWJTERcXUT4wq02aIcpYVTRqsiITGMJYKqRUxRabkGaVCqwl3PNCpuVAwKsPDFW4PQ5FIQ6IvNV7PiczKKAYt2Ju5YOgKxWQyyoOPeUYvliBSpisk0ggqobjd7pnuN/SPVsTtwFFl+mNHebaiT44hRXRWjFrS2pkcswwZ5yNjSuxiImlFiyD3jhUJr2Z05k07wrKiQ5BSog4RLyWDVhwqS1bz3yLK2f8wAaOQHOqCaC3OR4IQmCjRpWXQs1k9KshaMwnQUwChmaxCWk1UCqHAFRor562cTktyoUlG0bvIIAVFoUEKeiXIWhGlRMdEpwT2bpLvtMSjQAisUQxG0eZMFnDUglErTMp4oxisZh8iafIcZKaNiZpEVyi62rATARsFR5ORQrIQklZKnLD0o0OMicPYkh0scySZxKQDfeHxUnEU42w0FRI/DHShRckMRjEwz78RQUqOUQdaekytaac9KYAPE5MdSC6QZWISjmM+EERAFYasI4MbkG5HF9p5h1AIutDijGfKE/u4Y0oDMgmGPKCDJuVEn1sgElPGlp5RjljhCaHj6Hu0kKTY4MYjg8nYNKNTe5kJOSNn1TeTgaOYC5lBz0F2Ks1BdE5EuoUlpMRYaYYQKQN4BYOVtAYInmMhZ7O0AqVhFCAai0+BwUqUhEUh6ZTBlYpjyCQBo0yocvYNuXL2UrRJUWpBsPN7JB8cyU/4RcFxDOTGMJk7v0WG2CgmnTmWgjQMiPMFznnE1QBCMRUKFTXeAjLjhxH5YI27GhmsRCzMjDwHRiPRSYFIDAqkjPhNhegCo5Xo2iASDMWM7E1K4GJiKhRDo0kkhkoT5Ays8MU8P/XRkokMlcbZhPGQDExS0dWaLAWdlUgtKCaB15nRSI61BpnoSiBnylERC8UkM22jyVLe+bqgngLxDm97rA1JMXtRgDxmPAJXao6NASPorQQBss9Mch6ntpaoyhBEZBIVKkRSZfCV5SgznUi/rKWI9CQGErLW9LUmpzl3wwgQKTBIkI1hzAJZGIYosCEh5N3jA1mqGdxQKGyYzyVDpUl6rquElLNUtprhD0OpCVpBTlhlGK2krTUZ6GqDCxEdBd4KRjtnD+UU5/m3khQD82JZC7QIRC05VhLB3flNJkZraGtJioHezL9np4yrJZPMbNOE1zDYRI4jhZ/9K6NVtGomHw5FJsuE9h1p3DLqic4o2B8JcQQ752CkGuzZCtWU5JyRX1gw/Brd6TfUtb/qEfjrHZ/Kpz4DJX3B65wRKCkRiDndG5Bivm3Ov/6c/lOPv/3iIt89Efm3eyK/bETcYWs/87fnz133xdsyY1Y+91wenj3Dyep03k01lmKjuTYfoxrDhbhHHjzXoqQqF5ybMw5hRxv2nHFGzAntb7HCcFLdYxuPyFGwORisrpF6h86JR+aMoRyIZsFZWqNVgw4KlQTn6YTDeEBMB06cZRU23BCQheFkt+RYCMSq4cQsqeuzmdM+jVRHS69GhPKsfU3DgqfqGu8c98Mp3TiRjOMkLlg8qfik2DGGiUfTiomMKDybznJxbLg66wkSLoaGGEdSn1jIipObBZfrgYLAA7Ehbh1Oe2qneSGe8FS3lHXBo0f3WfvElX9KY5ecmQtu8i0qHXlgHuCLzCc8pQyWzV5zU3RIPXA/nhF1jdS3FBgehCXXukWLI/fNGh0sn6RrjBPc60+4zSNmHNlgKJoH3PRPkFPmoVjTCYnGc+oWLO8/w5PwhPj0wPnQcDADzhhOQ02ZK66aSBpH7o8bDrkn+x0XoqEJDR/rG2JQPGiXdM6RVWYxFpyFmqfLI0lmzrolhzLBVFD3gvbnNxxOE9pKHnQlT8dbdqanver4ln6ZD6sjF4t7lHvJh7cfEaXmYVixuVrzXn1JfVLx8Lii9R0+eNy149nbNeqxIfnM+U3JwpYICWoouXfYcHN2pC4FzdMKqww+eswoefa6ZCoc1BPnx4bSW6xN1FPmYafYnhUok1kdI8uiwOqMGiNnl89wlSuMy5wNsAj3aco5ZOisLxlNSZkED3vBS+UJT7cDMiQuejUvJrLg5JCpkuLJRpNj4uER+qWZM2JuepoxIk8NvXdUe0exWJFXhpO9Z+Hg8sQQyTw8RAYz566cDpl1H3m6MTgtOL8eyFojpWLdBda3E1dnFmck5zuHuCMtLcfE+bXjcqMY3ch6O6EfbMBm6r5n87Rje14yeDi7OoDUIBKNz2xuPNs6Ybzg4rYghAa9XlChuXcsGNcJURSc7kbS1iFyxo6B833gdqmRS8vJ1lEKiUKiM9y7GbkpNGkSnPYBGxJ5VBgED/eeQ6lxH0bO79XoDB8cAiImHrodh9MLximwFonzIaCiJ6XIw26kk4ooFKd9T+UDTzcLwuB40PaMTUksLCf9wHLX8nFTk5XiUT8w5FkidtINrKeep+uGKCWPBPgpEROcpMTquuWTqiBIyaNhIutERLAZA+fjyJNVRScyzxw9ea3IQrIKmbPrA5eLki5kHvpATJmYYREy93YDT6VEl5r7vYeUiLVhKQUXzvNUCqSR3D+OGCkRSKqYuN9N3FYGJQMPhoDJiY9rQxEy948ju1IhUuR8CBQkPgZszDxse/a1JrWKdTuyLCJhUWCU4HmR6NYavyy5MEtWi0d8UJyRB8ezIjDKiSkF6i5SIpBCkXLmIWtCDdkaTuWaRSx4mp+ScuQ0zpjwmBOrSXLWnbItPUFmNsUpddHwC/Eui2PDw/yQK/URXgXu2WdwaSJ4x0IseGxeJqcEpeHx8CI/9H/OiT1lkZespxVX6pp22nE/P4CUkBka0XAq77GnpdAl9+U50a1ZygFrNWU85TZPaNVzQokMBquuMV5zIR5yK3b0euQ0nKKD5WalkO3EhTdslSPZxKZP6AjX6ojJkvNWMSwThJ4zFGU25MlBiDx4z+GHgLewuDlyNhgu1YCxivNPeqaVwgdYDIG691yvLYqS5XXH1s9/+5MpceYj16MiKHhwDIT+QHi0oWlbVoeeq6Ul+MjFccIrSbxYsGhH1k+OXB8c9bOnrLoWN0VilCynxLrt2Z5oxi5yr1A4LxDdRNMHNofAzbpEaclZ6xDKgbTUw8S5XXE1ebTPnN+OCCGBkmIInB49u3WBinC2dQgxbzIUPnG2n9gta0SInO4mTPCIWGJj5t7Oc1hnkhGcbAc0EpkSJiQudoHj0kLOnB0ixg3cnBfgI2fXPeMDQ1oa1tuBOgouNyVIwcV2nDM2BKyPgXqYuNoUCCk4vx3ptSJSszpMrHrP1XlFkoKL3YjXGWk1qzZyuvXcrDTh9sjm/StEUZCFoFE1L9wrPtvwfozlT5JkSWatNc/tEx+n2ff1YDsSRSQjWLrEMzcTu2c1xjnOtyMSyLmkHiMn257dicFEwfltRDUaqSRF5znt9mzvnyOPjvObHikVIoOdAufXHdt1OSNldxMmzoVy4QLntwPt0iKz4Hzn0cGhksEqxdnHPYdVg74QrLcOMwzcXFTImLk4DhwXS3KMrHeO2nuuT+eF89lNYijm174ZAmUvuEWTrOZ0P9EvKrTLrPvEchI8XUmwivvHe2i9I+nM0hecDEuu8lPkomajL7BtwfvDu5yNz3BWXtzVqr/0Cn/Rmv0bLQFfXFj8NRYbX7yfz8uiAKQUgELIjMy/9HDMiw1xJ9v6mx9/J52L37rC+Q1Gk7/KJiK+MGqCzxu9f/nL+Ys/uPtJXVT80Tv/OR9dfUhlKw52y9XVE0RWaFugVINqDwgPha4gHhBYVNlQ6YrDOGGyZpkXjNKxtA0bsURFTVtYcjshdiOj6XHlyJQ6pPAks0dEge7AmhZjJgo8JjVI3aObBavmEen6Ke4Y0DLzztPn6GNPHEYWneR/PvkhxrTYkClyQq96VGWohMbhUUqiyoKKEiEzOoOVgmQzUmV0ozCTJTMQ2gGmklxaRNGgRE1Vb5DakZMkTxEXw4xNrBXaVMhVRIgJlRV5F0mk+b4biwuCkCShUAQr8UGjS4ta3MflS5zQBHmCDokc511fmTXRRQIB7zM2RxARWResigaCR46B1WGP3Uu6akBFgTzs8asRWSUsAn3dI3OPjFCiOCiJMIqcJDoJ8B4pBbpzkAdYzu8ZmeaPq7Jz8uywKkhqwhAoYiSJTHKeIi2ow2MacctyEGz6C45nmWEaedBXjNbxbnfNs9U91O0ZF9UZBEXZRkTt2eqORlfUrWVZ1KQEH+/3FAaWVcPJWcmDuOKy6TlWgaavmdJENFBmKLcJyUQMA5Wp8WGksrDb3vKx/3OKhw15rYj1AdN+g6q2aAuFKLEWSps5OS1nEkc1oSysdvdx4xGhEvUoWeiCroFCSk6F4UYnDnnucOWxJRqBCBndZVAGhkweM0KuiOnuk5kyYzeRdYFShpUtaYVAGs25KfBliTICKSM2BogRrEKmhBBzmzXmOXE3pkiOgpzmXeMYEwnQQpDEvKtqspxlV0qSRUKUJV5lYm1Ju8j0yS36K/eQpQEkWSoyEjoHZUaUMyqwMgW3Ks2vIZeY+NwcqKQKCrWh3e9xuz3JGygsMUeCyPOuntDkGJFCoBLklBBZIERJ6BU+KcJRIHWB85oUMz4VHJ2gNwXX70dWp2cMdSTvOrp9z7EqCJsTnAtoGUkxk5FoAlkZklQgDVpl0uTnOVMIckjkUhKTQLkMixmhKpOYcZBCEaVCJU2UFp8htiO+nik8cQpIH8m1mHdlcyYkhU8SnxUiSnwArwRTBqaIl5EpZlICLyQxC3zvEVoRgyD4OHdxKkmQs89EhkQWihDnhW4sFElkQEKe8acxQWE00mqEEiiTkWMgC0GWGZPiZ/hSITMaPf+NRUInSY5zVkgWhtjNcIuYMsetZ7/K7BdghwEnz9itEmZd45szOjHSh55+YVjGD6D7GeE44EfBcX9gqicGejYbiZQjwkoWRiC8Y8iRRUqY24jQCeLEkHb8k+6/5yiOVKKmDBYfHIHZZ6GYkZRWVhg9n24ls1leRZB32mlTN/jhKUJrtC6QIaGDApcwQ0SsI0plqtLyg5M/4OPxlipbRr3lf+r+JaXqWdojqo8c0w1lUXJxknHdE0I6UqglZvVtVClw+57sIBUB7zxBQIEn5gh5ltmEGAneE9wOuXxMkiNZRLyTdHtFX0qKEXTy+CzJfcaPE32xZJSC4ZgpRwgLRWgdiyGjVAbnCQl8VAz7OTBx3AfcQjI2ATUIqtYzCTOjjY8SJzNTmVBOsZ5mSGu8PlA8PGf8RUuYYJpABjXjk5GEy5bi2XPE8QAykXvPqDSjkfguotezxyJJAdcdbCpIYsanivlzngXoMHeukAoh5IwxzYbMnDuCnDdiyJDTPP9kMb9fQsgko0hSoXNAqAQponIgYUk5EWPExpniJ7OcsfZ4pFIIHefXJOeAPekTVHreic4J5eY5LSGQ6VOJzWzUlTGTkyBnUD7jlJi9TkIgpoA0BVLOKeNayhlskDLqs2p3Tjv3eSRkhyfOqGM/P+as5lFkBDFmVBaEEKEwiDz71pCSrDMmS7KyZNScnTAGcqlJUiNdIKWMagq46ZEpk9Ic2moQM65VqruSFyQChMRmQVJ6/hsKiUKQBGQlUEqBVghryEKhxIosSrLMSDfN/GJbzZezvPNhlqixA32Hms2ZyhTIlInHgHYFZbXCqIjGUwqBlnLG6k6J8UYzlppJ1eilJU5P8GPLtBn51+ZP6fue+qOGb9z7Do+XL306xJ+rjX/rsuI3H/8pXYzfqCASSCn51Nid8/xdCIFS8m/dtYC/i8XFX/M5iC98/+Ixn0D5nUP8xTXG58c3f+57XTZ8+bmvAPD/+PDfcHA7unBEZoVEcJQ9Lkf+cvgRRlqOoUWOikTm4PeorGj1ESUMXe5Q9byT3KYWtZS8t9iTxszRBFQeIOw4phYpJa7sMEbTiQE5JK7TFa4E6T1TmCB6uqlHxsyH6mO+e/o9RGH4t/2/xU8Jnz2dGrlmR8cEQ2IyI9lYDnogDzc80U+Zaogi8UG/R8TE0YwIL7i2B4IGrz25UAgf2YuOGAJPxRXEzCQ81JK0EOxlIIWBPzU/RU2KLvaI3S2NEwyyJ8jI1bBDGEPPQEpzAbLNe4Y88YncIaWlTUfSFGGa2ImWIhuecoP1goPsEBK2CtpioCjgp927lH2mzwfs/QsGEfAhErPg+qxH2gKfJ44FtHo3YyQX8As7U0E6JFYqdnmkjS1ZJrqTHpkVh2pGDl8WO1rjZjnA2iGUpdMOLRW3zS2tCggLQW9RytApgWwk8RXDoAJjMrxX3BCWmo1dsbvq+OHDS1ZyjTEW/zgQpMSvMtf9kU9e2CONYlSO8pkZYTyuA1vRs3ulJ/iIqzJ+PeLzxN70VKng/cefUGRDX00oJQk5sa2PqAeSm/M9yndMTSLlBTdpSyrO0Aq6laTKir0KZBHQtaFraooE758mdLI4k9j6nqPRDIVkzMzY4pA4yIiqJKqMdCYjrGCwAk2gLQAUTwtB20jI0MlAIQvaUhKDZqcVowKk4kMdUSlwUAq1sdycWI565tlHVdwhHBUpJa4Xc8p21pKs5l2jYz2j7y6frUhaEiTkU4tK0FYzZ/5qKUnMJ0pxPodzjdGxPm+4KSQiJMZi5vdLJTmUgkpqfrgWaCHodJ7zEUJBW0nKLPnRwiEHz3iv4rqX+An2tcb6xH4177Z1pfrspNYuDDZkrr1EToa9kohSEqXmUNdIHz9DgB60hRh42noOqxoWitbW6BDZjRmB5Lqx7KcIKeGNRYZEay0iRJ5Umq7QJB8Jaj7B7gsLMXG9qBnLedEQlEJnOJQW8t11VhOApDVSZHalJaXMk6ogaoW/W1wIJdlaTRCCJ7Um58hkNDkLlBDcSoEziqcXSwR3qElZk0PixiomKbgsLSolOq2QNkE5vzcGH7jaVJiUaY2cT2Y5sy80Y9TsRcbmTGvUnGmgS24LjYmJw70FRU50VnKb4CmKfWnQUnI0ChUi+8IgQiIvSg6lQeRMbw06JXZaI2zgUibaaBA3ju3Tj9Cl4bAqoEy0cceoRvIyk2xLGmdppgiZ3e0vmOQBtaoIuQfnacUeYSO784m+3RFt5qP4PtknWtWy1Bt8cnNBFiM4iUzQhh3IzHvxp3xFv4Uwig8O79GpntbtSSLyJF6SFQypR/EEpaCVPVEnfix/hs2WPg7sxxXb6pavPXgLGRP/99v/C4O9pQ8HtmKCJYxpS8Tyw7DDlJZ+2oIpoDhwmwqC8XQqokgcVURluM0jrfFopZjKmTbWMXKdDNdpR7uQ4DJTZdFB0MpMqiTXWtCbhEiO7rxCCkmrFanU7JaGqdYgoNsUiCRotSBrzTYHpjwXtOGkwlpDKwSxNGzrAldoIhm/mTMZ9kIQ64L+XJErSRCZcOzJz5+yb3t8EnTPNQid8GZOP9cm0Z9WZDnwyTMLohNMRqEK0CtBt1SkIrNf6BlHrWZTayLTNobCJ3brEp0EXalJm7n4OjRmRtE2FhPzPD/cEXb2jcbETFuu0CFxbAySxFYpukahsqIvC2QQdI1B5cytlHS1RKTEYCVaJ7oik9YFN2tLV854WWclKiWOCwM5c7u0jNUsF/JaIuPsCcvrgt26YihnOVYwApkjx2rO2ThuNKnWDKwIyWOlpl9XWAM/VxMvxhLI/Cx1tNmzzRMRzdXDkngz4Yy6G6dEW2uSlNysawTg6gJxHgAxY2q1ZPvSBpVm1CspzcjyWmNVYLtZoj0MC0s6qxFS0DaWKWT2jcGmTFdbPgWj7huDSZpjbebxrTRyqUEWtLWgl4LuhTUqKAYjCJuSm3VBV8/zw1AW8ziVBrks2a4zfSWRpaZ/UKKjp6sU5MjxxNKlQEaRVhplJQcSqVLcNLPHLklBsDeoMnIIE2LKtOqKVHeE6DCH9ymmmta3rMtTfnH4CS8sX/otde1fx0fwN6c4/aqvY/4qBMhPHR5iXnB8qkL62xq6/5dH0f7Osfjllb+y+PiVMb6zt+Rf/Y1f6Wbcmbqz+NyN7o5KVTR6ScieSteQMib0NPWCRKJUJT45KtMQSXgCBZYkBaVp8CGyMEvGwhGTwAgLSWHqkpS2rM0ZrttClmil0RFqLJ7MRi4ZhMeahLIFVihMWeElrKoLzk4fszh/BoDT9iHL3UccJ8+JPUepDuk6wjBgg0JEjdWahWhm8/iYCAVURYM+RkYCS1EzuJ7Cw6QzZZrZ12MpWIwVnok8eVSlKU0DveeYoZ7mcC99N7lXqqYeJlJlaGSDUqBkMcthZIkWgiGPVJ0iJ0/RWIYhYXcTEClMpkGRlKTA4giUg0QRCVFRq4KSzEIqfJpoRE2QnlrVGGnBzDI0FyNLtWCUnpqEUoqIImMZy8SiL+mnlkaV4CMaifWa3ngWo2HUATFqUgiUUlE4w1ArFkfJVGtkUMQcsRMUWXCsBAtnGHXEOCikoFArUoxMcqSUikqdImKFQNJ4T6kbej+wcjVDlRFOIpuCtbLkcaJ3kfO44Mm0QyfDlHv8bWBTlizXS6pJMynHeBgJm4iaFJOPGG1YjCVjDjSp4XraIbqJFSWDgzRMJDGx2dxDrDTnoiIWGq0SRYQ8OaqciTZyrz7D5chRRoxLCDd/D4ycjJFhSpQJdMoYaSgDjFawnDK9EaRp1onqJKnHQKcU6ykxRVB6NqNZl6h8YtCZsk2IdYHwgpDmx1IuYQpJM2YGHVFeQjk/lgkwxMzKQxcj0iVGI7FTpIjQK6ijQISEStAVUEQwDtLRob2nWdfIHCBESpeQYvZ/1OOMK1Q+4WtFFQQ5SYI21EdP2g4UUkOWlAh0U+FkomhHIFNMCa8E1RiJMlNqSRkyIUq0i4yloPKBsTIUPlAgEM5jUfRFphGZISWqfkKODq0kdUr0LlC3HW5R0xiNcB7tI03O9FaziJEhZ0RORCEoUqL0iV5rFiEyGYEaJpLWWBcoY6QzmoWPDBlsTkxKYbynCIFOK5qU5l0p5xmNpogJ6TyFFFRuRgxLkVExUd9hJ49GsY6ZkYSSktZHyikgUqaXgoWPhEJjmGVZ5RQQUjDmzMJFopIzSlRLFj6QhMDFTBXmUL4KcFKwTBkvofGRKmVEztQhMErNMiaGOyqNjQmFoGLO8lgxe0qSC2hm83oVEkOGRRZMUiKURmlJoSQNMIVMeeORaaQuLEJLSiMxtibEW07W5wztgA2RcMyomClVzagGFmqJi5JiXeBloEglWmom4VjIJUPosEEw2UBBiRGKUXaznNGZz5QGzWJD0ZYUsqRRK4gDIMk5U3iDymC0Zdmc4dWIjpoQElZV2GgQLpCBKhXUucYpR5Uacgx4WVPJhqQEpa7xMnC2PqOPFU1QKFMQuh4VBWMpKIUmm0wQYJLCiEThEm5RsnAaLzQxgZIKjabIkillVmj6NJuTpUjYrCh9ZFCC2kOoDcpnck4YBEYphhRpjp5RzZ2dpObPXaUMfe+oAzgrMFPEK0GRZprjYASLBMlnFHNehekmhB8o64Jm75A+I8McxldMEXXTUT23oXrSEYIgurkwKGJCT+DLGQ87xYxBE42kGAIYifOJZpxBESbO8Il6SiQJhVHUIZPyPE5eCeoxELSkmiLWzTvvpUtMNtFMmVgKoksz8CFKSidwlaGZEq7IJJdQcX6vVS4Slpl6CEzWkMdAZh6LYoqMZaQZA6OWSAJZCoyf54fBRVYuMSqQYyRKsCGjnMeUinpKYCEPiTgE8uBQ0WEXFXaaKNNnO7zUQlFmRYlkITShLAhuQISEHjwyJ0YrqcaI1ncKdaUoXEaSGL36bFx0yATm5y9ExNoZ3xtTwDpIzQz9iFOgNIpyDHMQ8BRxRlNPkagVlYuUPpEyFKPDGUntEl4mSgVWKhRzPlFK0AyeUUuqMSDTLP+rQmaawjy+xexXUdmjQ6IYPFMpaYYEC0XuJzAKQ6Ik06pMPUZcpVFTIiqJcpIqaDovWIiSOMm5kx0ySkJjV0xhohQFpap+WaL+htr98x2N3378zRcYn93Dp+sMKZiTZD634PhrPYe/+vi7R9F+8fis9fOrI/kroKvMb23zfHq7X0qqfhkh8qmGLH96q99wH6+svs4xrznmezT6Be5Vr9Jyyp4lb5//EQc2tOKCwj7HM81btJzSqhO+cfpHDHlNG88w8iFfKr7O4M4Z3AnfXP0BUZ7i4xmWe7yx+n28esiU7/HO5o9IxSMGHiEXL/G1e3/MqJ+hixe8efYD8tmL9OUzuOIeTfmI//bJv+G/+eTfoDlnTCe04R5jPOXr1Q+I4llS8RKvp3dYdZbicsLeTHz75itoZ5BXkVc/vsfi9pT0yYr4tOK7N28SXUXsKl68fcQ6LWedr4Tv7t+ATU0uDC8MF5xPS7KQpBT5zvEtggCU4lH5HKenz9I/rGlX8M319zhWmWOj2JgLzsc1XdfTjT3ffvcFxltPHC0nwykvDPcQypJ84jvvPkcWGpEM5+mEF/YXODJ92/P6e8/QKcuhaNDNBc+tXuem0lwXkjfCm7Rk9pUhipJX9Ku0Eg458vbxy6Qu0F8eSE96vvrxMwxTYkLzjf1Ls1ExJYzUvHP5LLlS5Erzjf3zlFkiiKgw8e0nDxDao6vM12/OWCLRxmNq+M7H98laIK3mrd3LXIjH1PJZ7q2/xLfef0xhM7qArx4e86h/RDmeYdIJr//L5yimDXa/4pVPXuDF4Sus3CPoV3zr//MW99R3eKz+Pv8g/Fe8uv0u6fIt9PA2P/jTP+SR/WOel/8lL2+/xwsffQPbfYsV3+b7P/ljTjb/gOfu/5/41pf+a7714ndYvvwKD996m//dM98grE8YRUm1Tzz82cjx2tFejnz1Xx/prhzdHuLPDzz3w5ExFLhyzXfs8+gHj1DPPGb98it8/ezLyAePyeeP+L2bGi01ICgjvPKTLXLaI4Yd7/x0h3UdetpTDEe+8fMO1IyiffXdIzJEophbvO/8cEdMCS8Frz3xLMK8c6K15Ns/HWfjnnc8//Fwl2IPMWe+97MR1DwtvXzpWBwd+c5A/L0fHUl6ltY8e+U5cQqvLR7Jm//qCUOIhLrg/iC4ON5Jc6TiG//+hiABITjZR87eH5ieDgRd8t1wTi4a4qh4WG549IuWcN0Suol3/v2OfigZDyXlreCZ9yLHYc1xXPGNn7VM2eJEQ5UML0+CoBucqvjm0z0pC1KeyTFvPLklh0yQim++/wkiJNLdYu7NXzwlRggovv7RNeQ5aM4keOejG7IwCDRffXKLTXfIwJj55ntPSdoQU+atyy1FvAttQvDNj67xSJJQvHbdztSbOMsav/PBFd4UhCR5+TCw6t0sq7CW7390SxCagOLxwbHpAiErnLL8wccHfFa4JHnYOi6GQBKKICTff/caFzIpCR4MgUf7EZ8lk5R8+70bXIYYM2dT5MV2IpGJwPeetjghcMDSZ17cjkQELmW++9FhRlnqgrooeEsokpq7Ld++nLGTMWXKBF8/OKJSeCX4/U+O5DupgxkTb//iwNQl+n3gq//+CcOHB7qtY7r2fOWj+1x2L3MTXuPF45uk5m32m79HV7/N1xb/G3b1H3Kwf8iL7gcY7jOFM9yw4J36DxlCZpgSj/fPUaQKR8J5x+83PyBXmhgiL6mXWcvNjJi0kmf1Y/7ZzT/iHz35vzF5TylrooRA5Lv2Bwg5L4ofpAecuVOkkQQR+Pvr/4ovn7zJa8uv8frq6/hN5h/F/45/6v5HXj3/Pb60epNXm6/xdv1tnpcvAIIYIt9f/jFCSbRSrMfEqzJTqD+jXP2UPygbtPoQJX7Kxhx4NQpM/gXV8pK/1zyi3Owpmo84rVveCAplLkE/4Zu2QBpFVqBS5tVtJiGYcuata0d2jhgm8BNvXDv85PHDxFeezPNGZE/OLa8/nXAigcq8eNWjO0dOkFLmzQ+P+BgJIfHi1UAzZXKSJBRv/KSj7zL9LvLwo576oy3JTaQUeOuHO9wo8Ee4+GBgedkTuwmWNe/8fE8SmawE99rERS9JUeOi4rV//5RD7zkeHfVlz72bae4ICvj6X9yS7tQj6/3Is9cjiEwU8PUf7YhqlnA2R8ezH7Uz5l5LvvYXN3xap9c+8eK7B1JIJCF4+y/3s2cpgZkyX/qPe9whMewjb/zZFuHvCHwp88p7LVEKkPD6j28hZlKeZVBv/Gw7h+WKxBs/36N9Jok5qf6tH2/vMOGSl99tqf1dNZkSb/5wO2/Eas3pn75H2Y5kMjEGXp5+ud/8JWoaWaBUhZCWP5hKghJkJXj4tGdzDHNSuhS88+dXROZN3/uXR85vhlm+JgS/92eXRAVCCc52jvtXPUJC1ILff/dIlIIYE6et55nLjsQs2/z6nzwh3u0214eJ5z88kIEoBd/4y2sQc5epmRJf+qgnpUwMkW98MCDsPDcWPvPq+8fPxvutH9/e2XQz2kde+/mBdCcJe+O9AZElQSg0ktfeHcjLBh/gtScBWwqy9giT+PovRtIdMuFNnkHIE/qz5xnqe7xy+wZenDOlcy76lyg+NsQPIF1JXl689vmy+Jdl8qcWh98kRxJfvPBX2xB+5/GFPXghxGfBeuKz+//bry7+1ijaruv+Wu2TX2/4fG719Rud2p//2eczu3+1ZSPubPCfN35//hH+xyf/lv+wf4+bfkezy2Sd6W2kUgVYS6UKblzLhVkSdOYYR0plAUkpDNfTgXO9YAqR49BhsiT5SDEmdmXkLFeM0TEmjxYSKRWVtmz1xIVeMqmESwEhBLYoqE3JZThyr1gxuhEXHCkkSl1Q6oKnbs89vWDInpQjUWRWOrDKR67aj1n7mn057/hM3ZGiq1Fuw3aj2STLuHak5BjiyNpoCj1w2/RsQsNgIzoLOgYWU4HoI7emZSNWxFLDFBkLzybUSJHZygPLUOEqhU6averZdCUhRg7qyCIURL2gas7Z5iObbUKqgaPsqHtBRFA2J+zKkbO+YOhvOdqJwgmUXlLJFTdpx/nmAcM6cZQDJmvEFCmT5sZ2nLYFrm8Z1Gy4k1lReMl12XGvb+hVZCoFKoONc0DZdTOwHmpGRjKRbBQmWepguNJ7Ti8hPqgJIhKSpwyGMhquqyNnfsnOJVISeD9QSkvpPVdrx2lcMs37pMRKsBg02gmeFAfULjOJSGVKnE3IQ6bEcKw9577GFc9xu4uszjaYg8PairbRnAl7l24N/UJz3zQICQebWQrDZBqMKtlmx+bgcf3IsRCUU8ZPYX4f1oqzvccrRVtqipARIlOEzG5tODt4nIC+VJgIWilqn7ldGc6dwDclrtJorSnSSDN2XMuJ022g7Y4ck4M8Y2irpLldCk56QV+tcMqQJRQ+UYTEzdpyunc4q+b0aD1jSsssuKklpztHbyWRjNOCZojYJNhtCtbtjIxUCEYtqIeAdpHbteE0KFwOyCzoRGI5RlRW3C4Uy9bjzSx9alVmcwxoKdiZzEnWuOQRPjA0htV2YrrtOJpMmSTqbEFVlRxUYrkdmG5ajoWgForBnGBZsNWKsykwqYqjtRQpgZTYlLjSmvNuICjDUBUYMoRAFSM3dcl5NzBJySgVIkakc9Q5s10vOe9HxrpiDLPe1XhPnRNXdcVFPzFpiVOSCJQpUU2OJ1XJvWFk0JogIEhJGQI2RG6aiovRMWk9F+laUbm5c3FZFpyOI6OZd89HKWn8hI6Jm8py7iODlqic6ZRiEwIKuLKG9eAISmKkYCcFJ8OEkIJtadhMgYlZ3rQvDadTIJPZGk3jPD5H6pzZFZqT0YORtFZTh0QEihC5Lgz3Jo8HjlZThIjSktoFrkvN2XFkVJLBKGyeteBliFxaxcUYmO6IU9IHTMo0IfN0WXL/ONIrxahmaY0OgcJ5rpqCRwl6wAnIUlJKwcJqnlaa+0CwEEm4nDnNT1l3P+aaLae5YTJXkOY085qS5nzD1fAJJ2FFNgmZYPAdS72mKBtu/VM29hzfTWhb0qeOWi/JJrIVt6zlCc71iDHRcWQZFkQh6JqBld7wJb7MPzj/3yO05qn/kH+y/+/50P2CRix4yb7C/+rk/4BQisv+Y/7x7X/Lh9N7VLIGCaUo2U5XrNIGpx2D6DBOErJFxgXX6ZZzcUI/7omlp2yWKJGpVcF1uGTjzhjyKSMC4RK6fEy63XCrEps24shMdkZ5yilSR8GNSpx0EW/UTNoSYEJPlUeubWA9CAZVgdSoVYXtM6YXbGvDaZYMRHJhCAIal7BJsF8WrHtPT4CcGMgs4lwgbheW9R02ViEZtGCVAlbDfmk4Wy3ZfXSYSXC1YVMU2NOa3TSwGAPtcSRNka6xXGRBZSRdc4eiNRLtEseFZX10RK3oKkXl5o6idZH9wrI5OIIRHEtF6WffYRlhty442Y9EGRmsQKWMNCVm79itSza3A13v5i6Ej1SVoLGZ3UXN+nZi0iWutAgXMBHKkLhZFWx2Pd7OHZUswEZBOWZuzmpObnsmLYlaEQSUk6PKkdul5mTvyLVCGkkXR9x7H2J9YnywoRkSf/it3+f75gwQ/ESM/HNaPsRxgmYYEtN7t/RGsOg8Jmd2m5JF6/BSoFJiWFXUNx1CCNpVwWIIBAXKBfplwaqdEASOK0MTwEeJdoL2tGJ93RFhxgDfLbAKFzmsCzatJxpFV6gZpUzGDoHDynJymHDKMRSzRyZnzWpzwrY2rN/f0ufEpCUqZbSAKsN2NQM8BjvnZmAkepgox5HtpmCzd0yFRD7cMF0e0NFRVrA/t6wvJyYsgXl8qzoTtldclZ7TTqKOP8cUgVQK7LsTZ09g1+05v7jPm1/7Ft9+4zu/o3YXv/Pir/kBfq3i/SsWBZ/9/i/NB5+qgMQX6vBMZtn8/xFF+9dZmeTPvv4GZ/YX/pu/0C8SWXz24jO/et0v7/8LXZFPne9ScPA9O3+kCyM5JpIL7McRgwKhsVnTS0+KR4SRHNSEFgojNAbN3vfE0JJi5iBmlrqNkhFFmz0pTIic6XRESEHpFIMYabUnhVla0emIEFAly14KDkUGNZB85Oh7YkwsskUpxUF5UjiSiAwikCVQRFI94atMvxCMKXD0HbGKLNCkSnIIA2EY8HomQAWdEcJhreOoZhecj3NuhssOUkA0iqHIqOQIsUcawZjdrG/MkU5PJJGZUkYKQ58GJJ4cA52dCATC4OkzHLQjxYQVgcGMuKWGIAm1Y1SethGkRUGXBsYxoY8H+ujpm8zttCMOcKuOiJgxx1n+0uqR5EpkjByLgNSCKhYMMtPZMGtBtWavR0TOrINmMolOT4Q7t+RURDLQuMykI51JqA0INdJrB0qQu8yU58sqzCjMLidSyV3mQmAwjjYeiCoSKklUGTEZgg6MZaQ6tUipGUQmyMRSWHJWxDLSu0jWsHx0jjcCayyxKMknBYM0JAkaSZKRzkdSCGz9xBAgWI8PEqcFoU8IKTkAvUzIRjNZ6K3AJEmKmbaSjAl0zkx5XlDYmMlCcixnXW/tMl4IepHYukAKnqM3CCFY+45RObpaYC4qwkowjD3ZeRgSQQp6k/E6MClPXFaknFgOmVEJOgNioUkInJ0ThJcOnBL0hUQuNZ6MM4qsFTp7PIJBc+ddEAQ1L55JEllI+lIhpkwU8g6fOQf9iDtuPcy6YiFgVIJSaZQQTCqx+/8x92dPlqRneif2+3Z3P2tsmVlVqEIBBaCwNbqxr+xmN0njjEayMelKN/oH50ImjchpzlAkRVEa0kzLsEn2DjRQWCorM5az+vatuviiCoXq6o3d0sjTwjLinDgeJzzOcX+/932e3zPV1FzlDKOTYCC3irMqeJ8ohxPNPDFtWzCCvDScS2ROiWQ1k23opUAqTcZwaCwmJlQuGASjNRxCAqU4GY3IhaYUZq3odV2wFSE4LVuEkjT3BzyCs9Yoa6FrOISa67CUtQM8WMOeetI/6ao2TqNncJbRGnalYmYHq2tXfBZMWtf7ECQpmaQkycqzH7TkbDVKtQQpCUJU1ONERThagxICryRFCryseSIIwdnoD7q49fhKdKnEnJPR1ZxNlVT2RqFSQQg4Oc2sBIWML5mTFKiUkFpxNIrpUderBQxGcsiKLAQHp9FaYHNhNJKzlqjG1PtsRea6kBmsprcK8ziwPmpJUYaFT3gjGJXkobVE4Og0QsBylkxOMzjN3RyJpdDbChrY5swUIkcSYgogE3OjKFri4gGUZyyRgz+T25k5HcnRgxXM8x19PiMFiJRBJILwyCCZ9cwoRmTaE0tEhIFAAC3wfqLXZyjgw0DJCa8C0hnK5Nn3B1KX6M0r+PsToms4smOKAye/JzByKk/IISEL9PmIl4FzOTOnGY1iVhOjmtBmIInEyR9QUlLKCqEEcwocw7H6MMoJNY4stWXWkqGcUaol5QV7H5ESOq0InWTwCeWqmbg3AkFmqSUHBYOSqFQDNEctIWW6kgmqMBmQpU6d4sai1o44TiRd5Y8iZ5Ks6OqUM0JAcIqeAloSkARZA99UBlxFRUvq+aQIgVcC7TO+lUxOciDSXy3w+7pg11ZgjKzn3lIYoqnTl9YyaE0WmXNTJ2FZCpSpOTUqGYQS9K2uWTJQ99PUDJhCYVw5fEjomAmpVEyvkwhR6FtZSXSpIK46eikQnSHExEmB0BraigkfJMilIWfJ2SkwgmUozLm+X9TCUlRm7BSlFJZjYdKCqdGclo5YCkNT/S5FVPT02Gp0LkgNqZFE0ZCWDoTCLxuUCByjB1PrqBOZ/vFDkJhKZu40QQlkyggh6I2EThNVzUKarYLOUET1qSQhyLKgXT2GOqpaE3WaWAQpyMoPcRq1qL6wvjP4VJCAj4mxNWjquezcaqZcsBm8lpytQnR1mn10AumgiZrSafqcqnIhS05OIQt0ueBFYWoUh7Ujl0LfaoRWdNETjGWwErWsoa5BQ1xq2vOE19CngLp0pGDohaTETPQnypOGfvToRaJThtPpHiEV2ywYO0PIkl4E+vHMB7kW79e4H8q5+Gspov6m24eb9h+U4b+smut640O2gv/cn/OR7f/7ngt+OV34649tysePhz6yz8fZxa9MQ97/UTxKpt5avMJ7u/doY2C16JDnmSMz2kNTDIMYORG5ygvKJBEyYJLgKhvOOpGU4MorTNEYlTBFsvWWUWcQmavgcElwVyaUVFwGV+8jcxUdDYa7MlJK4Tq1TKqQ88QqZJqgUI8Xvhu/wItMJrGZC12x3KlCVnB5smjjCTcbLjZXPFuseFGOzMlzM2/odwZ/+x4XXrPA8XI9ElLm5uyQw4F81bANLavg2LcDsw5cjB0sWxjv2cyGbVlypyZ6l3malgiRkPHE0mu2oePWnHEKbsK2pk+yp8sNF8OWh8mj1prL0bGQgZc50yTN1bFhbBdIq7nuW8zKknce6+H6wXJaGBhHrncCd/EMOT1HjJn1QTExkJvE03lBpxveG/cYobkZF5zLgMyJ7cnQ2jW6PSEKvHJq8c5TkFz7ji4obkUkxcDVyRFlITeFm9CwnBe8lw7kGHh6bAlEslZclRWub7k1Z0LOXE0LkvTIolhOhstk2A0TsynYu8iYMhevdmwnh+kVP1U7Li9XPI0rgi9oCauxsIgN4/WKednw6qYlZXgeZhZj4GqAOzzZSbqHGZES08bghsjVGHm5XRCXjut7X/nia0MzBm584rQ0yAhPjhGRJbKAi4Wbc6RfWaRMXB8jTijeCwmdBVeHGkqWc+J6yJiQuCsCfOLpYWaWE36tWaVAd72h2a7IIXKVJ479CZRkmxT6qLjz54pJ7AWzEmSZuO4zevAcLhpSKVwfPFEBNx1XXqAeRo5rSzCJm3MmPr5vtyfPeoaHjWWWkZtjqBcnYHkKbE+B3YVjtJJnu0AsApJiOUYuc+HeKXotuTlOVXq0cqynyKafuWsMOMn1qZAPmbJqcbPnavbsvSD7hN2f2X7qCTlm3O2Ri+cHdhcNtI7r84AoAV0EZvJcjxN7Yym58HSYMSXzXgYbI1fjSG8NIiZu+hGTMi9SRhvJ9WlgECCk5HqacOOMXS9hCrwyTzWPwCiuzgNdSrxoHQXBk3FkVhqk5GqcWcbIi0VLRvDk3OONAam4GCfWKXHbOLxSPO1HfIGyFFx6z9pHbpcNU5I8PY/EHKG0XMbEavbst0vOKfNaP+IzsOpYh8CFj9xbw1lKXvOBnDJFtiznwPU4s+scNhdeGWagIGRLOwcuh4lTo5BK8WyI6DIhVi2LVHjqE7daYqTk6RRQpUptTEw8G2ZOjaEgeMVnZEyYYrAx82ROnI1CUHg2BJyUvCfq4uXZGDkqSRaC6zHQSMl7gCyFm94zSUEWkusx0qXMiwK5wCtTrAVtq7mZM5sUuS2VFPRkaNHWEW/eZEliM1oO0uLjzLPmCchEkYVt3nBtLrj3LwnW8yQ/rcACIVnLC1ZmyY49kxi5yU8ILqJ4yXJuWdtPct//jLPxPJU3hP0enhrW6oJXj094Pv+I+Vpy2VyzCB0X4oI2Nbw6PIWbWh48mS5ZpgUbtaWZFNfmVXp9RgrFE/PskQBTk4kv5Ss8xB6RM1dii2s078XnWCxX5ZI+HBFGcBXXkC8xZo9Wliftkl1pKMOeq+RqsJhLCCm5CZoxRLKFrYeFtdxSF84Xs8WngdxmLl3HZvuEw8ow7U50Dz3JdAgV2PrCqkhuXSRJwc0MqMyUYOFhEzJ3tkIdns41r6jYzDoJNmPkzoA3kqujR3hBioZmnni23vJ8DAxKcPUwohOk7FnOmdePnjtZ6IVnS2HR1oqimyIX58B+ZZEJro+1kVhySxOqjOfYakQRXO1GRAElJNpHtvuJaekosWJUbcm8cGCBbT/Sb1cUJ7k6zajjzG2nIWWe7QL+2lFQXBxmnCi8HBMiZa7GXJsyG8vlMdCEmfuNAym42E0EbSAJtn2gDZnbxpME3JxmkiskHJtjYD0HjpeOaMH/9A7jKjnK7Eeur0f4RC2fPonl91BsUGyLQv10x8vZExrD5W6iCBBkFn1g3Sf2a8foEzf7mVhqZsJySmyPEw+dxnSay92MkpVK1oXMxSmz7xzGaK52M8SILB8+vhKJ4OYYED4ghgmb4HIunDWkRrD2giYGmKo38MlpJrRr0jxxcZhosuK2yYiUufGZ0SlELFyd66Tzdlll49cPE94WcrFcnCNmjJzWS3I2rF4G8o0ljZGNk6ztkufTSAqZi16QREYcT2zFile2r3PUknkeWCwdl9Gw0gtWl5e8/vT1X9aw1AZSofz52vijE4q/dGLxcSCkv2SK8ZH9/kVN+7/t9ne0uPg4PdNfvX34168Di8rZRbzvXxd/3kshPnKcxS/39r5JpSCQjwdtfYq0P9+R/cArmyU/+I3/gufpgJoynHb82/H/gRomtoNk0s8QOSCkYEnHuR2RpaLSrFCgJLlAc/D0q0CJnhIzImrSKpNDwkyZQ1NAR3LyuKzJJYEQmLkw6xmSpyQwWZNNqPpK0TJNtcMtpWWRG25NRlgFU8N5LhzuJ4xseGNzSUxnstDo1FCCh1w7hFeioZSxJp8KS5GVZBFzYhUaju2AApZZMx4VUiiSl5hbSb+KDDbjx0TTCUpbCHOhnRTiJiNywY6JVCQsLWkqLJPkrgukNGOkIHmIOoBWrFdbTl0gmwIGhgfPiKS0DiEMZ0bG7On1kmYfmEJF0V6mS263GSc8yoNLmrI2jzhbi3AjykrMwmEngXrE77VYphgpUyGfA6u04aEdIAjW85p9GzBCQDQ0BwlX1M5kNgQLomnJo2brHA+LEzlFFrvAqBu0yYg+sZjXPF/lmlehnpBXnhe6R0rNTVwwXglCiTSzRdnX0U1Cbxa80r3On6pQQ+JGgWgMSdUuvh0ToQkkkQgpsXQrxGPg0sonbpUho1BCI3OhaE1xku6cuM+Zgqqyu1xD3yiwTHDUgjkEfKwmOBYNMSfUOBM6XbsVIWFjJhaFlLnSvTZLglFMc6b58Uj/NKPXHcubS/z6lsP5gLCSyyTYxYFCoesF02pZpVAULotip2q3qSmKs4QSMnlMXIyJ3aZUM+dUzZoi125866suOaeMmUt97VB1voskeJETaIsInjIoglT4KGhOAX9lSRHKUaFSpojC7AXyVjLeLJmzwo8aaZZMzuFe37IsitsQ8eOEGk4kvyF0iuwcN0Iw65YkDUJl1BCJSSBcQzt67lVFHVZsYkVQZqVoc6nEnCqixQJFKXKopsVeSXKGLDV28qRQUbdNhpOtmmmkohlmcteShcCGzCCpyEilaH0kI4myys58qV3kLBQL73neVj2wSZmgFELV/IxmPBOcImWJTYn8+DyjlKxS4dZHilGoDEbX3y0WWM6Rl42lyGqsl0KQcyEKSeMToRMUUQlTIiVSjCQJq5DYNaaSSEpBo8hCEmWuv4NryI/IVkchU0AJugz3j+jbmGCbC1JVRGQ3BQ4ahFTIxylHVJUS1ojEqTFkquHWTqFiJ4FFLkxGIUUBJVnETJHV39Plgtd1H0kJ3JzJKDAKJVac4uc4nQVuvWEhnnM3/Cdy8fBcExd7vOpJxtF0S0J+TpQF2bUIEiVAImKzJjSeLDPKWcgS4Qs+zCzthlvxC2QWaNOgn16h3C2IxIv+x/xo+yd4KdiEDVmmOp13kjYuKOe5hnOpKu/IUpCcoVFLHuZbkvDknJEsSGikNDjRUdQDJQVUJ3FRoTUoBVuzpp+PlJyRSrDuZg7+DolkIW446QVSvURYRxfWCCuYY0R7TbQGVCZTsH6mVMIr2s9MKlFEQRi4fLZmP5+JaaazMBIAQSRTzoHQtGStSYcB3zmyUHiRsRmSqpk5JUSi0AQhCUri5oJ3MJdEzJkySCaVEVPiOg0kEqSCGD3p5560ttV0ew7ki6bCXoKnKENqNV5K1JyJ2zp9TLGgcvWYRFHNxrtVzYhASOQcSalO9Uwf2HeWUiQURd4NzJsavnu9j+TVAmRFuVoBpdGUXGg3a6arDp8DQUrc7Yl5bZAFTJ+YrjtKKYSSWQ2ZuBAUJTHnRF8SIWb8lFiNgXBpSRTkcSRcWBCSbBXNyXOQFSGuwqPBW9T3b344weu1njLva/BFnTQt9xNiYSgFTMoUXSu0LKEbPLuLtmJ4U0Y/Yk6TKDRjJC9NJdBlSPeeUCRTyDRTIS0sQglEDNUzKarnovOJw8bVZ5Ez8jiQomCOGbubGZeSGBRlyDBF/EZjW4vtI8PxSIqBtDshiyOubT3/7GbC2hKywp88C1npWuIxKX4S1YyfRYWIHDPIVYf1iokFQkTSIWP0jH5lSd4PLL1H/Oj3SbqnGxVP7Vv46FEx8iR1vF0+jf71Sy4vr3n15rXHCvWXpm4hflnPVnn/r9zwVy4sfqUM/ktu+Wttf4drjL8jz8X723/+rn65uOBXjzbvH/DH7fFAf9iM8sEeykf+FgX+2b/9J/zxO3/AeTzziSev8+0vfZ/Pv/lFAP7Fz/47/ujhP3L0RzrzhGNec+dnjFBopzFSsZuPXKolsR/Z+zMiZlzIGKU42sQ6OrKU9DogpcJlTfGJs4msJ41Qhl5GpJS0c4EQOZjIJhl8l+ldoKTEuu8ws2WvI5dJk7Rk1JlcMlvbEXNkXwa2qkG8DmmZSCRW/Zr0Eu5OezoccRtJcsbrwqWRaNGzb8+sSodoBLo1DP2RxaGjTJqdGlnRcpgCKQkGGbiJFqcyx4WnCZqyzGhXU7I3oyNJyc6OtJOqxtQoOTrPdW+RqXBsZxps1TEKxdHNbPYGLxU7M6KTxAiH8pK9mdiElkRikD1OW4zSGOBoRi6mFpSo0qdUaGdBZy2HdmQ9L4hG0y+BnGnuMyIKDq3nKi0RAfpQmduL6CDBbhG4UitmfWaQZyiZ5eiQAR7amQu9IavAPJ+IJNanFbIs2amJ1WgICqIRpFZx1S6QKvJQDmxyyywCQsAsPRe8iWzfZGcViykzBItoOwYNm1OiDBO7VrAYM1FkdC4MjeJiKpQi2HWiypcQWGU4N4qLUwQp2LcSF6r8xMTC0cFFX83Up05jM+gMOgsOTrA+zihtOC41MhXcnLBFsu9k1bLKinuVQDtlTBHsG8HFOVK0rOm8pbDyI92lYa8Ci3d75PWao5/JU6D1liJb9ivDxVTTpHsDuRTWfcJIya6VLPtI1oJgJElJ1hFEyOxbxWqoGuckIBjJZqr+hV2nWA6R2BpyiISFY/UykHrJzlpWBWJOCGBsDFenET3PHBpF5xOD6iArzs6wnjzZWY6LhoWpccNd49iHxObUk44Dx3WLE5A8WFUlSpvjQEFzaFsMBRUitsDBWS6nCYxmZwwqJlwM6Jw4NI7NMIGUHBqLpNKQlI/sW8fF7IlScnb14rYoGeUju8ZxMU1EAb2zACzmgEqZXePYjBNJSQZjQEnWs0dCvW+aCEIxK0mUgovZIwTcNw3bcWKSmSAgKMmFDwDsWsfGB/xj82RWkqs5UHL1Y6xCetRUV5LVdvaIAg/OsPSRJAumwMloLmcPJB6spo0JBNiYODaWi2EGUdh3DhcTIiUaKdkbydUcycDOSGyu1BxXBDuruZo9lFwnIFJgUl0Q761ic/Zko9l3DpULXcz1OFnFxRRICE62ctuXISPf93/MlVx1tooCbGJG5sSD01yM1bQ56erHWE0RCTw4xcU04uR/QHb7en6YJ5Q4cFA7VnFBcZlkIcnIhbhERzjrE4uywssZjGQuM1t1CT5zyA8sWDKXiEAyxDMX5hJhBYfyQJsasgKFZhADm7JBCMkh3tOIjs+1X+Z/s/nfUc4zP9U/41/N/5wfzn+ExSFTRkfJYAbW8oaIZhf26KwRpaCy4JD3XJYtlMggzmhlsKpBITnJE1t1SY6RniNKa1T4NKI85X48s5wdIa44W0cJiS5ZQlScnGAzF5CKQT+eA8YBGXt6m7jsVsinN/S55jy0R+CYeSiBdRRELZkfSVKLkFEFDk6y6D2pMUQpCEqw9SC1Ymclq1AIWoCUDCWzngqmCI5WsvCZKAvKGfoQWU8JUeDUapqYKUKiimDQkgsEYt1yXNvakKGeY/uFYTvEiqvvLC4XxGORfWo1m+NMzoVjqzCZmlMSMueFZXWcCOPAXlUi1KLtcM5xahSr40QKFRNLKiyWHbZx3JPY3A2kaeZUEkIIVtZgG1sfd5pJwOAURQrahxHGxLHRrOeINzCaCkC41AqtC+eLhvXZo50kNxKcwf/JnyFjZrpe0e0GvrS84X/7pW+CEPx7Bv6NOPMzAospcXp+ohSJt4r1aUaKzHFlWIyJWSikrBK1TV+vg4elpZ0iiYKKmaFRrHcT8ezZG0mbCmrb4FpL32lWuxGk4rhymDkihMSlzNEp1oeRdOo5ENGP71WdMicn2cwVeb6zBecs+jjTXq7Y58h6H8E4jlajcsGWmqV0bDWXCURrGFYWCizmGREDx06x7iPZGOZ1g1w49Dt3aGc5WFj3gaQE8emSlAqXP/w9Fsc/4Zx3dLlFX3cEAilHXvVP+eLDZ/mN3/lNzKL5oKYVf+6TP3/DnxP8/DUWGR+7fcw64y/c1a9qpVgt/2f0XPxNtr/MbvLBouIveqz40Pd97E4/fnrijKN1LXOYsdrirHvf2IGVjkZ3jHGkNQ1ztLSq4JQlTxPOKKy2LFyHFwo/1vAqpRIuCkYmumSZRcEhkKFgkBihmUqmzYqQMo2qAyuVJWZKDKoiLmkkJSiKUPWkXjQ6RvRxRiwMi4Ulloz2iUXjGHKgnQRhP6GlIlmFRSKEQhXBMkmmKCjWUcKMKQIrJMYp2mDIfsaKliwcresgKAZbWC2uSMNM3E11nKkbRJhQSdNGQ8kFKy1Rgp01SRas0nRYYk7opBhjoAkavKeR1VidW0HjGsYUaESDABpZsFGCh3YUnJaS5SDICmTr0NkiC6y0ZdaJpV0x+ZFmLsgscT7TzdCXTFcs4XIJMlBiRKaZTnUMstAcCrlAF6tnR2foNhf4bWAjtxyOMyJYosiYKHHZckgBtwuEZUKZDi8iRljsJOlXlvV6zeRqcNkoAnoGqyRuUXGSWlZph2DEBQ0PI8oJGhx0lnLweBJ2SBAiRmlaX/DUsMCoC27KFCFwVtH6gtUKGwteF9oISRScKbSPiMc2FCataKZUF6RzNUFrpVlEwagVzZwpKWIV6FAXD40PGGNYhMJoBG0CQsRlSRMyva2m75lCKwsSgRwj+kcH5LOGzcWW4TiwfrIiignpa2DaudN0c2Yw0KRCFuCEpJsyZyNYjdXYaDJ4mbBRYlNdWC0TjBJImel97KjP9I2kEwo/BJQQ9FOkiZkc4KxL1dnLir7LKeMyqFTQqerzswQlJZ6qGS8xM/tY8atpgmlH0RrdDygpaYRgIQS+RDorGXpP5wNBSZqScSEicqaJNduhC4kAdFKiQ0BRcD7QG80iRrzWNCmhUsGkTBMiZ2dpY2ISmU49Tp58xMnCWUCXMqOA1geKFLhSaHKmL4VVToxSIEIkoTCl0KbMOWUWITEo0BTmLDClYGPmZDOLUiBnHIXxcZ+qFE4p08aad/A+tUSnhMoZmzJtiGilUCWTk6TN1P3kTJcSMQsshaALXUokMi5lFimTSjV7T0AbU0V8h0gbEoVCOwcG6Whj9fO0j54KkQttEZxNwYWE0IKQQYeEktQpnVAsAJ+h8xFVwOVCmwo9sADGlGhjvSzYR4Po2Ui6WL0oTahBaCpnugynXFjkQszULqsApyQuFc6l0CVZkaejR180dAuDOM8MUtPJBSGMKOeY8ohF07oamNmKBUJKJKouuIJCSseAo1MrZJpgKoSs0aUGtuksaUVbmw9REdtEk1pKzFgcLjeYVAuj4gNWWGRW2OLo5AJ0orUtISU61TFngROORjXkFNBZcvaCznUIkym5YIRBCoVJhpGBJltCLjgcCoPMAqdbztazmA3zellJTtljpGERqm9oUQRBCEqqrUEjJG2SzCnhfEEISckF7wvWGkhTNdsmmCkYAb7UBaZNhSFluiKZi8DEGvamp4ARCYWiRSNDQcj6fm9y9WToVIliYwE7BKIWtNS8HBETdq7SY50hyJq8XeaI9pIu1CmJSwWfoQmFQH09tj6RKTRJMDtNEx/vS2BDRuSMmxOzy3Qhcw6JRmt0TuiQsDmgjaSZM6GUis8uYA8DzdljF5qFj4yp4KhZBDYVWiEZdDWNz1LQhkwSoKnTzd4VOqkRBsowVtJUiCw7y5wKrS+gCjJCkpmSBaqf8ZsW2c8Uf6LkgpDgkDghMQiaUPA+Qy7VQB4zioQOEjcGhAElIJZ6HhNCYGKm8Yn4iMqNRuFiXWhYJWgKiAwWgUfgYgFdZb1NgiILTSjMFrosmHMlaLlY/TwuZgZdjfNR1vOSOwdKFjRjQsmKR/dUTK18PAcoo1FK0lnDVDLNXBtTKmbaOTE2qj5OZBgjyhpkAnOe0VtH6wuTpU68WoMsChMVCkmjWpR2GAwhexarDZ/8/K9hOverte7HFrMfUxP/ZUXzX3f7aG4DH6qSP06O9Rfd9zfc/tYo2vKBS+QvXlL98t73kwD/GjsWH/n4az2TOuH40f5P+Ofv/FP+b+/+S1594w1Orxj6NzvEK2uGTvG/f/5v+d0X/y9ulp/mLDvO+oLOXfHW9g2KLkQ/8vVbh1j20O4wx3s+8ZOaVhrKia/erylKUFrNYrvmqzefRa0csjN8Iz+lWWaa5cTyQvMbeYMxB5S452vHhkXn6cwtKzfx7V1Hpw8sujPfsBd0UqBMRlnJt/YtiEgWkU/tW2wQyFKTMX/9RxdMP/b4X2S+ID7Bul2ijCalzA8erlEtSDKffLhkcVqSjg5/gG//4i3iIZAHwRvjDdfb12C9IkjBP77+LqwbhIJPjGue+ktyUWTr+Afr36QsL8Be8FS8yhu3G5qHiDlGfvCnr9eEzSzY+jWvT5cIXWAp+C35DeTNFrVaciFWvHV3gfIBkQLf/fmrINeYqeNi2vClw1MoilLgBy8/RQ6ZePK0+8Sv3T4jZyAXvvPyTUrRJNMgouaLf7TGP3jCMfLN8W3UTiJ2Gj01fPX2GTOJSRa+mN/ErRyFiTz0fPNnT2paak782otrFnGFjR3GLPn+6fMUqxHO8nZ+lVW3gYUhlMS3332NVK7I6Qmfun+N9fwaeX4Dv9/ynT/7NNP0GjF+lld3F1zLDVlZpinwtf/pSAoRUTJPX8zc3IeKFZSSv/ejSHnUzD85F14/CZCCrBXf/aOelBOkxNUp8PovzhTvKTnyvT88k3LtAG/PkU//YkKXeqH57n86kmOkpMR2yrz90zOyZBCFb/7BofqgUqadEl/+yYDIGS0UX//TEzJkSiqYOfGVdwYAckr8+k8SUnQk7yi94Neea6Zzoawv+PbqCUuVcOGEGk98648OGGqK6ds/OaOnUKeMAr79pz1ZgDCaz/7oQHf0iFLxmX/vj3vKqSDuI5/+Yc/FbUAdQOwT3/2f9oTRkAfLq7ee67GgtCY5ww+e9+SiKEnydMhcTJbBXjNcvsJ3pMW7jozl2QyvDYVCS5w1f++de5JoAcd11HzyPJHHQBaC33z5QA4REQLbfuAz9zugThO/+867NYWewjIEPv9yR06QheJ7775ECIUoki4WvvzuHWQJUvGtd18+mtHBKcGvv3dbQRMp882Xd+g5IVOmaSzffHn/OMUVfPW9O0yoHXQpFd9/cY9QNdzvK/d7XIpQEojC91/eARkhCp9/2LPMAXIkk/jB83uKlCghefswcBUzmtpv+c3n92RASsmnjgPXc6inXqP5++/eImSVDb127Hm1H6vpW0l++/kDkfp6etZ7Xj9NkAWpSH77xZFUFCXA9Zj41HEiZchC8lvvHsmiSuIuQ+LzpxlRqrzs+z99QFAXP9tY+OJDlXomIfnuO3tULigB69bw67uxXiRK4bvPD8hU5S/OJ759PyIyiFL49ntnrBBVYpIL37091ytTznzjtkeFhHhMKf7O855YJDFJvnzKtEohtQZr+YF9A31ZkHbgSxdfZtNcUoqhoPid+bd58/QqnxNv873VP+BSPkGOCikM37F/nzwEyiHwWvok1/oJTJkUIt8K30FqiW0bPtF+itfaNygZIplvpO/Vl0+RXJ83vBpfQ2WFLJI31Wf4v57+B363/C4Pesc2LGuwYIp8c/oW/uFE6gML3/DG+Rny1CNz4O9t/j7GSKxSbOyGLy2+ghQCaSS/dfGPeXv1JT5nvsjb6kt8pf06QitKTHzTvIXVDzTmF2y3A9++2IL/D+jmR3zl1GPES1z+CZ2851vHGRV/ii4/5+2jp5M7rHwXOT3n10+CLB4Q9sAXCiy1RFqQKvOVF4EsNUjFpx8SKy8xokELy3d2gqINWMOnvWQ7e7SfSP2Zb//JA2U6odLAm/dntn0gq0JU8IPbWIM5jeTplHkWqaZ6mfiNnxzqRE9m1seJmxdnwnFgOvV8/fdeMJ4H/P2B9YsDr/xsjz+cmIeRr/3+LdO5J9wfWDz0vP6TPf7UM/U9X/3jB6L3+MOJ5jjw1vOR7BMhJH7tTw8k7xkPJ8Sx57M/ORDniTCN/Nof3xH3R+L+iDj2vP2Te0qstKkvvZwowePPZ8rxzOf/+I55GAjTxBeen7AxApnkFN+cDRiDdJbPvdNjYk21z1nxpT88VIn36Hntjx+wZ48qgJJsfrHj/+zf5Z9OP0OmCVc0AgNZ8s0/3AEFWeDZ8zOr+7ECd6Tkm79/R9ESkTLP7kae7iZErhLXb/yHW3zvSYeR64eJVw8eBMRS+Mbzkflwwt/vuZgTrzw/EA4H/OnEV3//Jf58JD7sWB17Pv0wQ4nkkvjGzwZK6SGd6Iaez94OMB0J04Gv/eyM8BEZIsp7PvNyhDgjS+TL+4BtJErV/JQvvRiq6arAV94ZHoOWNbpovvxOT0kFhOJzPzljY4WIgOTX3+nJPiBz4a3pGa8P17w2P+VT27f4R5/8r/jU+i0+vfksX3ryGzy5euUR9/rYP3+sZ8sHBuGPKXTFR/7/z9nKhz/5C2r08ld8/C22v7Us6tyff+Xrv3Kh9eGxy19w90fv+igNSvDB8OGDYcf7Mqi74QX/l5//c573v6DTC07GklTLPp64VBtiMpzSTKccRRScUDyEE9d2w5wi+90OM0XMM0F3IXn34edsXyiiXTFvDFYYRLYsmy33YuCpWTOXxJRnNBIjAwuTufX3XLNhOu4ZxzOCx87Z4NmpAxu/IrSZvFQILRHTBWW84uV44GpQxEaR48w8j9jiMLplt4T1rJhyQORMVLB0HU3bcFt61odMWI3QFYbgWWSLaTru8pHNpMDMaCKTjixSR1EN+0vBNrX0xxP4xCmPrCaDVJrejKySJT9ZY4zlqGeuR4O5f+AUDixTw3khkI1l38xc+RbXJM7qTCs6fBJo1bIzAxcnx+wnztrjvCT2lq5c8lIOPM0NfjVzNjONcUgibYSXecfV0eF1ZnQJLTRWWZxy3JkTT8YloxCMRETIOG9pTpoX7cy1bxiXE7MOzPPMdr3i8mLDL07vcrG3lC6QRCDKTDMtaIaO+03iIrRM9kjCE0xmobfYo+ZlOXAROsr2MwixYMyJNkikz+zLmU1p8F1Xk6itYDMllJ+5bzKLU0RdXiCy4mgFq3NEJDgsFSsPUQuUVJwayWVfyWJ7W1gMlVhkQuahEdyMhVgyBwerrEgpoUPmuLJcnSJBwrlRuDlBKTQRHlaK62NiVjB2BpeAVCcf92vDkz4zycLcVJ298LWzeLvUXJ8jk64yMCklLkEb4X4huToEhlYSjERqyaKVrC28d9qxvfX0bkXS9rEbmMAnjheO62NkspVrHrRkEQomVizu5TEQBkkcI6FzdD5jUubBCLZzYjSWrA1TY1iNAaEld0pwVQRzBmssBwHbMRFFx8N2xUoUwjCjTz2H1nE5zoBh3ziWJZNTQZfMXhuuhjO5zJysYrNdkI1C3J04OMNVPzMlybmpAZACgZsDD23D9eyZlWEwFpsfyXA+8NJZbvqBSSkmo1GATpk2BG4XLU9mz2Q1PlfNs82FNiVu24Yn88RkDXOuE7gmJ7qcedE03IwTk6242SgELkWMn7ltLDezZ9BV6hOUYhEithTec5qbOTA/+igmpVjMgVYJXljDhQ/MgkfynWI5eyyCh8Zy4SP+kRJ1sIbtVD1e+9ayDpFUQJXCXiuufCSXwsEZViHVYLaYeLCGm9kTSRwazSoVEIUmJx4ay5MpMGU4GUWbMpRMlwu3jeZqrJKtXktMTFjqMby/6tgeJlLbckoFI2qAYZcK7znFs8cArklXWZ9JmTZl3ms0z3xkFJUuJqSkS4UmFV40mqdTpFdQpCAoyaIkuhB42SiehIxM/5oSfk5ZKi4ur+Aw8ZBuuSoXfEX/Gr/17B9BTvw8/ox/1/8bnod3uVg9q0nZOTObmYXeooRin+5Zqy1J1fPbOZ9Zmy1ZZO7GF6zygjR7nG05m4GVX6GU5jje0+kV0YHRjn164FJfE8PMMR9ooyMbgZrhIT9wJW7IMTCamcYuEEpisuV2eM6VfkKygVlMmGL4hHiD/2VX8ban6cjvhv8D76afIVEYbWlFx+30nGv9lH2YmYkIQKct5rzi5fTAZVrgG8mUAiJlOilYhMBt2XEZlxztCvHKVZWXPC8syhUvZOY6KyYahHXMKdEOkS4IHlrD6uzxXTXPBqdZzh4zntk1kuWcSSKhpGRQmYWXIFoe1i2bCNlUFOlZC9Y+I4rgYKtpOz4GiZ2crNKnWGVKS1+nyO9Lny7Hes09WcEiUSc9Gfat5CJAiKmiUlMtRlyCnRNcnQKz1Zy1RMeM0gInFfcycTPUnz8pgQJUSDSpVGz3I2J71vX8q32iRXG31Fz1Ee8086NPqQmCJkv2S8v1YsGYM0XAnDImF5at4+gEFyePWglEiYSS4G5H2u8Zn25obk+kC8f2C28yk2nNCt1ccCdg8e6BfneGUphbw6L3qBTZLTTrMRGEQHUt5xRZDbWRdFpauiHg+xk5Ro4a1nNGLBwnK1kUQWklRhR2KbA6ziAFR1kDAZWoU6uDLmyHTNJw1lWmJvKIDQO7pnAxCqLW9DLhUIhs6JLlrtNspkLUismoGnBqDa5x7AxcDZnYWLIzH0w1rM88LDXbPuCNIjUGFpby7o4Oyf0Hxz4TRaF0llf3kd/54cxqu+CV738e5SqFrFBQUn64av2VGrh8UL/+JRXzRycJ5WPu+7vwSXz4OX3oZ61W/38ki/ooKxf41QXFX2cUxEcWGR/ZZ/no5x/ajv7IGEdO/sgcZ060+GngcN7jpxPQcFIRnSWm1TTLBec8IVGknNkzYVaGpvGcTgfO4YS+vEB0hpNKSAWN1wz9Pac8URgB6G1CG83aFXwJDNpzoKcsCr2OZB/ZOEfZakKQjEKCVQxqouSMzVtC9ozAjkxKgUnNZO1ZJAVq5oQgS4XQhfGRsZPjyPE0ctI1CTNrTzSZIAKlKKSdGUQGoxAiIGXEE4hek0g87EambPGyoJxkJmG0BgIHnQgyE6cdepaMKqInSaMDg0lEPNOFhaYwpEBjFF4GTvnEVCaiaSHOHP1IkR3FFg5yQCmJCpJZRo4pIvPIHHvmNqLETFvgJCLnRULajEhwtBFREoucGUSg1zN3IpOD5CgDRRSWuePoLCcVwBYQE4MLJJPRsccfRs5mhjaiVGRynpgj5hxZbRt66YHCrCbCwoOWpNsdkoZzm8Am8uO+A4I4gdSC3nSIYvDOkITEKwFiRreWwRaElERTEFoyNgohJUIrzgbinEm5IFNipCBFlWkcrWSWCiRoLRisYJcyAug7hU8FUSQqCsZWomM1cp46xdDUi9iUoG8VMlH32UpkKTgPo62I1/tcQEpOrUIUaESh19A7ic6KKAt9q1AI1rEwxyphkjGTFJw7CQLy0DPNgXGl0V3LcJT0RpGlYDUWipX0TiGXlfAyqWr0LGOCR+0sS0NOhYAlaUlOGSEFvRaAZmwtuWnwsna7MzA0BpkLc6mTvVkASpOkoleamCqGUXUNo7PoBAXFyTmmGMFKTM70SqNSQJTC0SomH2k2C/SrhtOuRyhFcZajsfS5GkvN2nJ+nB4UqTk6hyzQxsAgBGdrMVTd88nZ6v3xnqExnGX1v/CYTSIQLHxgNJqzqb9TEXBqKm527QODoGJjcyYrxVlV9OZyLojWcX4c90chmLT8IGMAYHCGByFIWjMXSKpmq4ylcFKSohVeS4qACRDFMgo4aEWkBlcJoZmUrCFqRXDUikANylK5MBqNyhmhFHujmWTdn9aKo5JINBQ4OcOUMpqMTdArgXo0lu+M4pwLjswQE2dbE3eLkOyMQqFZeM9kYBCgr1eEMbEz9e+wkIIx17TyeyEoSnEyFZPZ+UivBb1V3Il67TibGsqaYi0868+DJGEwdZFWfGaymsFKdirSpExsZmgk4nQHwdPrEZkkx3ZCttVfczqcGIxnxCP9A7PqyTYzjz1oBRlO8UhREGePEAIvHvHYqjDqkRIT0Z/RxTLLgjIKkaDXA0HWrBBZNH05I5Mip8hhfqCPApENWhoGBlTeYVrLqZzpw4DOFi0Noxo5yQMlJXrOSATX6glBJha2xYtAEoX9dKi69NAx6ZFBDDyke8YEZz3V+2SHaD2jEexPY/U56UCW9fXqtWfMkX0KjGVmDEcoksatmVNmEvDgE2Vl8UhSyBQpiEYySpCdYXLVzxUkpDkhneDcyhpGKAsogUeSuw7cgp5C8dXXJiTMCh61q5ycqmGTWiGyYGoUvRAQJWfzeB7PmQZN36gPOvEnK5mFhJwxmboQTRk6zcnKR78QjCFxMgK5MoRcX2vSKNqcmVvJKAV7gJTpXX2NLnRNtz87iZQSSmaw9TXaackgJL0CnARViUniESYxacvgFA/zRAD8qiElWElFajQ9GdVprMkkq0lC48KCoBJh3UIuzNKT0kQShcSCUhLHnBnGibAwCCkq+CBX4tPQaYoSBKGQTjGl97vzgtMjzjfk2uwaFNBYhDOcrWAuAAldEicSNIoUAicjHpHXBR1KxZt3kpQSJ6cwOqNTwSgYdUY6RVaFs8goUTDRMCjoZUYaQZIwOcEZcDEyDJmzUyipMI1m6ur5t/GpXs8fsbVZwNhIiIGmM3gpmRrFHsgyMjoBCq4kHEvkE2/cIF3l+Erx1yh2HwvYDzLbPqKX+sDc/aF696/0XfwtfRniY277z93+f+K5+JvLxj7imH88Yr9y3D4yuXj/pqeLV1jaFRu7oTMLnnVPuKPHCs82LmHS6LTH+kJ3cMQnEblVPGvWCKExVmGzZBUE+5cTpX3C026LiivMPCOL4FIuGKaZEiLbGVzXcT8MKCm4LpJoAqMybJZLOmu4axfQFC5niWgLqXU85RLnLC/DkZwS180rHA8NqdyzHsFNmWMnia1jfe5IIaJUzyYtWJSWvQ54kbiMTeWBk9nMhk4aTrpnSpnr5hKBwqRIO2g29il+4+nnExdig3ctyd+ylUu60nJyM72YeKLWFCGQas8iNrTectYDWgxc2isW48C+tSy7LevtEx7cyO3+Pa5fFBbG8l5XaItjqTYcpjNKJm7SCjEVVFNopGXh1wzCElXmNbUhuyV305G2KK6yYVIzd/HETVwhIwQVWZmWq94RdIQ28LTvEMFim4HsI9u+Y87AOvDKpBG95igqTeMqrUl+Aue5Olha3XFqJ7wqPDVXhN5SWsF6dnSLFWer6R/2PJkgT4riLReDYGEKx+uak/B6MiQpkaawPiW6Q+JhAZNVXB+AnMkrxWZUbIvhoUR6X7jeRXIqcGFZhsLqHDhaSd8Wbg6hSoayYTUn1n3i1GrUQnPzUDNIRIQuFjbnRN8q9tFzvQ9IBDpYbCps9xNDoxHZ8uQQkblgNxpTBNtDxLcGSeRqP6MzmI1FZbg8R4aSycXQ3Q9sbcN9KKSUeDbWopRSuB4Kygfuo6GUwpNTIqWRcOlYC3jl6hnvnUf8aeT6EOqCoNTfdSU0OycYSTw75dr3LHCVJM1h4qA0g5Zc5hrEmIxlmyKv9JF77+mN4olP+JgQyrKeA8s5sTeGXiqezZ6IAtGznGYugmdvFEcpeTaOwKPmNkS2PtArxc5ankweFSd0cbQULu8OxOsNwikuXo5IPGrZ4WJi6wN+u0LExCv9CKhqRC6Zq3FiFFXCeN0PGAoPuZpIL6aJ2WkwmZtpwoyZh7ZBAldzIIja6boeR2xK3LUNSMH1WAuGUgpX/UgjBQ9GE6XgZvZ4aujUjQ/YmNg5Q5CCq36iyCoZupwDyzJzrxWzUjwZp8fUa8dm8ixLZq8VZ6N41lfDaGwtlymznAOn1nJUilf6iaIFWkmWc2Rb4CjhIUWeDRNSKkRnWYbEZgqcncZaw3U/Y0i8FIJFLqzHmV6CTIXLwWMLqIWjiZmLcWZqNEIqnvYeI2WFbOTMVT8TDUgpuHGKOEdsY5BT4MongqhNrqdTxMjMbcqIApdzIIl64b+aIm0pvLQSpOCJL3gJQgmu50gL3KdMFPB0ygh6tOi5ih3roaXXHWLZcSW3xP5MV1o2csWn9BvcxfcIJvPK5ae42P0ZQkna3CCt5MieoZx44l4lDDOpBC7FFatmzVGcOM97nuhXiTmQx4kuOJbDhvxsjXeBZVpUUpSRLNSSTXPJ3u9QQnEjbpCNRKZC165YmwvO4YjOhifmVYx0mPgCUwxbdcGYR6SW3IgbtNXc+RcY5XginxIJ/NT/mCVr1mrLpbjGWMOWS2L2CC244BqE5Z4DlMJFvmZWFlTkUqwQx8yD6Ukp8jRvKGamZMGVWkLe0rcNfp6w751JyxVYz7XqcBMcpp6pZK7O1R+Qt5rLrGmC4jbOzCVzeU4oI9FTYTEXFoeRwxrmVvJkkgwK8sKzHiXtbBjbyKATN4MFYxFSsPCwPQbOC8tRZG7GTIn1fdaFzOWUOauMKoUnXiCV4j1VWACbCc4yI43kasyonDFbi0VyNSSGUptBl2NG+MKtA4fgZkoc7wfYtlz3Ea0Et0KifOR6ysxaUJzhYkw0MfPQ1WnjVaxmahkj11mjpsCtLiiluJoKUXhKUmynggFOQFKKbUzI0wTasxjgQgn6lSYYxcUxc74f6JXC3fcs+x73qU8StORpkUQ04TzQ7kfakDl2hslpbvYTRWRKcWzGRNdPHNeJwSou9xPkDMvq6VvuPbsckY3kSdNUn4UQtEWwjoJjigifeDbUhG3VCtpcrweDLKgSuU6WMmVsGTBzYRMEk8sUei6nBRbNcxfotGEVJUNMyOzZDAIjHPsikEJwGQWzrNXi1idWsuEQCuTC5ZwJWpBTYTtUTO0+lYoT7gNeAsVyMWXMONGrI9kIVn7LdZLYy+Wf66l/bN0rHivZDzsESgHxqy6Fv9Cb8Tf9+v1a+n0Tx0cHAB+3GPnb+jz4O/BcfLCy+rBG6889sb/+Uqr8uR087vhxFfHL9eBHxyH1mVhp0FJQZCKWmSunQD7HNnuW1z2bG49bn3AXZ67VyByeM4/Pme7fQU892XrGcsa8UwjDNZTXUOotlvNT4oMmvgfLHyviXab0CtEbmjtD2EPYg32vo39YMB2WnH9uiL/Q7E+Fc24wzSd4eZ7ZjYn7WCA+5RRaDr1GDB2iMUinMc/WPH37knI1wcXE9TPYvDKz3J5p3B2LyRNloKjMAonUhaIyyRUuS8aUA06cuHGJrZxZiAkz3nP5Z7cIP+Bk4XLRsVg0dNcLzLXjjZun2K3ELSTLxlRyTZiRZeImSVQzoOSEmHtiq/EbyXQBa7MgFo8QBakMOq3BrMjtmu15SVYFpEAMgQUKqQtZJDaTJJPQSmCd4SZdgrfEWbN9WKBmiZ0VbS/ZzIaYAzEGLmZLVglUoccj5hllPabxPDOw3J5pVyPqWeL1ZzeYjcC0kWtfyHFC6Yy5cFzZp5SLC9TlFQuxRrcttA51veHZ6qv4+2uE+Axd/iK6+RRy+SZi/SabuMZLjdAW9on5bsT3kSkWNsdIUoqcM04ZlFlSVMOsW5bPJ7zUxKzQUWAfu01BCLajIDpD1gZVFE2SlFJlLZuxBp5lBDJLTFJkpYhScXnORCUpRUACO2QSNWhqfa4mN0o1zXVTJOZEKpltH2rmBxmFYBUgUzs1qzEjbQ1/W1jLaqiGYuUs7jQRRe1CBgnrIZNzIQtJOwqiXZP1kvMgKH/ygryxlMsOl+riJKUMCLbHQDEaqQx2hNw74tky7CTLXjBJQ1SWZnuBubohtivGzSVdt2VebInJkQeN0SsSLVGvuKAhtmuKWyCSRocIKROFYHOeSNoCEi0kOuXarZaSy3HCy4pqNUJgM0Sp8Eg2dyeSkejNAnvRYnN6DPmTXAwTs4+gFakUGu9JJZMKXHhPVrpeLKSkDREvqoRpM86/1NoKWE2eTO3+r+eJpB4vPFpykSNFvh9EWPHOUCk6m3kmSepkKAS0EshHQtR2mkmyaqGXJdfRvJJkJbnsJ5Ks3bwmJWTOZDJewPVUk7iFlHQUnBQIKQhacp0S/vE8a6mehYqihYt+ZCq1/2ZyxqRITJG5ZC78zCQqFlaXjIyFUCReKK7mgteGLDUuCzoAo4lKsp4SYxFVDl0kdk4gJLEILkImKUEpGVEya6spUpKV4CIkgqxhi0EI1iFRRDVmXyVIjxOSBGzmGn6YpWQdEiJnSq4m9ItxhhIgB9b+nkb8O5z4f6Lyv+VKjJgbiTQzF2fJP/bf5wf+63yj/yq93/Pfn/+P/IvDf8v/e/63fH/zO3y9+w7ff/aP+PzlV4nUyaTBYhcNSkl8mFhOC4Kfq/Eci5kEZU6kYeZrb/0XfK/5Lb4lvsvfF/8QYytsog9nurzC55lMQgqFky0YRVSZq+YpkVivnVlgkiIRSQS26pIoatK8lBo7WXKGEiLeZv6H+E/4V8Pv8i/H/46UZlCZGGbWaUny1S8mMmzdFai6QLvsFiT9QNF7SrPnYgvoHcLtWS0EqQhCKpTNgtff/ARKR7TwbOWMUi9R8hbiz9nevyDHA1L0bPQEuifnI2Pcsdg9kMIZUUYWKaBzPcHFkliFM17fEdUdptuzbn5BPv0hfvxDrh7+CBl/hB5/SDP8EBkjSRSihPUQ8boGmelYKkjCKLKSrKfMrAQ+V/yy9IFSCnOMbI4zUSsKBV2gKzVQMqXE6jAxy5q3okSV3UlTyU7bKVNcRVyDxvXVAC2MZjNDUTUYVBjNWhqyFEQBy/DY5daK5BTLKIlGkaymK6UGhJZAIrA5DqTTiTic6fZ75p/9MdP9O0wPP0a/d+KUFWPWqOhwqxUZKEajH2rWzqQ1UjuEEKQ5EK1mfQokXRUeJhRkEhQksxCPKd1VSmhToezOzMcT4/FEe7sjloAqCdOfcYczcXckPOwxP71lOtccsBwTLiZySWQS62FiLEdyOSPjgSb8ghx/Tsw/Z9X/hKB+hBDvoMw7LJsjtuspasdNPlLamaIGdDOzKTVQFw2bLEiykFNEktAvToynCT967G3PfBpJ55Hp2LPoA7nUqW07VxojuioEnrz7hzR3v0fz3r9n/fPfo3m6xay7DyrTfBghpI8UxO/Xqr+sct8fcAj5oVL841YVf5UP4i/1TVQJKu/7nT86VBEf+fg72v4OPBc9POrL3h/jiMcL5wfbX+Gz+Au3xwPzYRkU8KEAvQ9r1uqNPz7+kP/x+b/kJ8cf0uqOsRnAFo5xzzZcUoLmkI5Y4YhNQxoKR9mz9Ruy6Di4iJwLZt5i5IZzK7iMhtxP3PfV7GqRFdVnE5fJEkvhJGPVYUuDNYaDDlwmQehmTm6uXHUZaTp4kEcu04owgu/q8GhxNJjkODSZK7cgtwdGeaKIwnVqaEJi5+9Z+o5933GaKhN8GaqW+956NkGjuluEPpMdXIoLtG44qIFFcJxvX6LWLV5FVqtXiMsVL+YH1qUlNwKlJD0z12WFTIX7+YHOa6Krid4nf+TCVy36vT6z1AtoLaYYdv0d275DBsV0o2lkQ2JGTZ6dOLEdO0qjODYz8jjT7x0brji4yLVYUoTgLp5RRbAqkYVVHOOedbCMF4rDwiNjpvMCfOC0SVz0jlgCU1vfxKvcYJVmZ86sTpqUI6mpo/Juciip2bUjV+6mJnGWQIqBTd4iS8t9OrLxLVO+YZYdWSvWY0ST2NnEehSM3RKPIjnN5hAgZh7WmtUpEJ0GIZitZDsJQHLfCNZTJeGUnBkbzcVQdfm7hWLlCz4XVIG+UWyPASgcVprOZ7KQmFQRh9ujryjElcH5ggJsSBw6xfbgyVJzWBpsLJhS0L6iAi+OniIzD03BIbEBTBbsl5qLcyQAQ1d1p+1cyVW7pWFznCmqJnsDLKaMSYXdSrPpU5WOuGryXY4JFRO7tWXbR6KVDKaQnGYrLPIcuCOwPUeyM3irSErQ7QTlpHhoHJspEJQgikLQigtjyamwU4p1ysy2I84ZD1xMHiEV+1XHanxUfadMbzUXU4AI913DKiZCKehcODeWi6kW97u2ZZESpVRN9bGxXI0DJXkenMbFiCyJ9dMVR2u4DJn+7sxOGmyMNUwvFw5tw8UwkZAcmgZFpRWZmHhoGrbjQKJwdhZRqqfClsyDc1yNE0nC2dYciGWsZu6ds1yGQBSC3tTJ0HquFKp7V3+HqASDVrVITgFVMnfOcjnOzEriH+VR68kjKdw3ju3kCUqStGIqcBUCOScenGEbE17VtN9RSa5ChFx4aAzrmAlSIjP0WnE516C8O6tY50wEdC4cteRq8gDcWc0iVd23SYW9UVzOASElD0Y/+ioSLYIHU4MBhRTsGoOJCZ2rR2LXGG6mQAb2jUEDXZppc+ShUVw5R7IN9/2E8JE2VfrMg1Nc+0yScHxcoC1jwgjBvRZsxwhGMjhFSpl1qJ3ne6e4DpmsErOui76b+Q9oxB9x7PZsywqle4I/EHPkM/5T/P3993jj6ecoVvLfrv4JfzL9PlFGPtt+kd9u/0te1Z8kx8j/afhv+NPxD5nLxEZtEVry4F+yiF2lAkrFKGa2+oLkA3t2LPWKz9kv8V+Z/xq1XfCj8Kf8y8Pv8qfH/8RCr0ALTFSc1ZlLfQ25cIgPNLoWOhrDIe251NeUkjmWA1ZYmAXOLjjGHdu8oeTEWffILLDaYbVln3dcyEuSTBzTjuITTVnRFMeBPdvmKXMRHFIPQCs7hJDczbdcxhVzjgxpAC1ZpitEaDikE9erG3KRTERySrjJkoPgoCa2qWXOV0yiIZXMZgRhDDuV6cZCVoLII6p6zEDh2EoWc2bWz4nyxKgy195QcmRwnlUPWSuUMQxlYhmfkfXr3C8XLB+noyrD2UoupkxBsGsl7ZwpVMzyUQuuIggluVeF9rEbbHyq5+YhgRIcXaXf6QIqwd5JLudCKoWDriGRTZKoLNh1hssxQg4cDCgh6FJNuz84ydYXCpkTiVwKS5/QSPYry4UvRCkZF5oUE+u5oKVgpzPbMRNTxKsqi2wPD5Rw5NgV1l4hnr1FXG4pSnIzzzgR2NuAvTvxkGfM514jt45rs0ZGy8t9z+I4Ex9lgrMWrPuAKJnDyrF89ESJAlNrWL48kfuee1Nop4rRFakwGsk21jyyfVMJhV4LTCqcG8W2DyiZ2et6fEs8YwicReQyFXK6ZydOWKnR+YAVMyc7suUaaTac0ozMAsU1Ii856swmNRSW7K3BSEk3Z2QRHAxsvaBIx2AN5EwXM0bAvlNczAVWLePSgqxhgILCYanZHnrsz/81efo5mcJr/in/5W/8r3njzc9+kKKQ9wOitchG8/HFMB82XfDLqv8j299hsf8X7vPjVgCPT+d/ZhTtL5/Zr2Zl/y2Oy4fWOx/nX/l4YVhdYFhp0UJjpMGphiQjQgpUFFhpyUKhk8Rpi1QO83TDNL1kVS4I2eLFTNMamJc0aUU/7tHHSJg9NmZkqaSVpkjGkrG+UCQ4UXMCjFI0RXLM0GAocaYxsnaOtMScAnJJzcPImRIVqjUYLSm7QB5G1NIhdMFpRZIFhcIKjZKaxWqDX6yRo2AcetqgEVNAE2izphSJxhFTQBeJHCL6StEt1mTv8ccBYRNCJ0ynEKEgTgF0RLYNQszI4tBao4uka5bM5YTuWkILzakhhkCjLEu3IOSCnkD5QodlKpD3M26zIHUdzi053p9wQZKsxhmBNYZGG2wv6GXB+MhsJTZlrDKoItBjQipBozpmImoGJQySwgLFlEcWXjHKhJ8jRtZAoEYI5ErQTpJgauBPSaCLrMb4tcKeJOHuhJYFiBDOKDLCetxZMJtA00AQBasUOhaUrEVjCgWlJdMc0alyy1XMNEngY5XuJVHQUwKpUEZV7LAWqAI+FabjiaVrkKbggkQAOhRmXbCxUERBx4zzmSwKJoE2AuZqlDNBoeeIlrLShZzA+swsAtYpmlCQpWBDQiaFmSLJQpsVJmZUhmYuCCcQ5wndOWwElfMj0rBAiLRzZnaiUjJyRbvaOSFbSdN7JqdorKakirfVdaCE85VU1JYa3qjihI4FryJtEfhUkCHjs0AXSVESRaGJCSkVJheEyJhpRCAxy4Z2DOBHbChkYzA+oaxAhdrtEoDMBR8lNsZqPi2FJsaamlsycy40JVOQ2Mf7klTYVJnpLlSMqi2FNhfIGXV3RD7ZsugsqbE4nysGtQiaUjjnjIuRIDUup7qoi5kmZXQpdCnjJYSUkFSEahsC2hhcinihsLmiV1UpuBjRztKGxKglLteOvS4FmxMKcCkhpKLJmSQEFoEJCWUKba46dZkqqtKkOjFQOdOWjMgCYiJLiUkZKaoZ26WKIhVAFAIZErpkdK4LLaE0WggC0BQoJeOKok0FD+icMFKgUybnjDGqdiEfDbFaCRqqCdaWQpPrNLopGZ2rDCJTtepNlcRX/CsVLxtlRRO7UhfOLhWUEJh+rhO90aMR6FzohOSAoImJSUnqzIq675g4aMNKVG27i5kM9W+F4EB9Ll6AKDVA0AiLixKtDM1sSOeZRhu8ltiuZa0ukbEQn3RY0dCqlll5ZJaUcyK2AUlBF43DkonoIFHKYJTFlRamiWaxIJaMEfaRWqUw0dQJx3ZB7Cds4x7BFo5GtaQQcLJhzAMmKErJaGGwxVJEwUSNFooGR1IZWxyuOIrINMlyzhKnO1Ke0XnCqgatNa1ZcI5nGtkyhR4rHdJIXHE0LDinHiccPgRs0ZQpUspM2yzQ0tDojpJnYvAgNArJolsxBI8eC8lKdBSEKUKUuGjRC4XziqINAo2XBWMsIhSUCCyUYBKPRYuoIY8iV0xrQw2m1Ohqjp8ScZgwTzSL1Yo5eKy2FduaajijihmXBD4XTBYoAaaAMBora6hjSrmibBX1Wq/rNaEN1X9hkfRInKROpHKhKRKpakbDOReakPBC4MRj/tDj4xTQImpYHrnKU4EGyUkImpAJZBpbmztaCTql6YWgCYlBZcxY0CkjfcIJhVpItM+gJSCIKaONQ+E4MWGLREiFzTCVipZ1UuJsg5l2yBzQY4CuQceM2I/IkLCpTohEqRNfG+tjVc7YUFPYZYbU1WNQikA/ooQpFevsEahSEEKgM9gEUkkMhSlXzC6P72+dCrJITBb12EuNLxqNqu8j19IIxaATLlYlgckZIxREgUuSUUOTBaMU2FTxuTqDyaAMNKm+zx2CXARFCrQ1CFFwJZEKuCLIsTbyTCzIDLZINAqyJpIxy4bN06sP1gkCkNvuI/Xpr1bwH5S4peZVlcIHhuVfSdr+KLno/V19ZL1SPvaxH62VP+brv2Ar4m+/rvlby6LeN6SID/2Dv+0Te/+v9Li3DymvPvz/+19VvG2dcDxbfIJPbz/PZ7Zf4JOrt/iH1/8rVBDIQ2FzaHmj+Qw0a7Ju+cr4BUrRWLdlpTZ8zr6NKTeIuOX7+i3y3Ql1N9A+eD6zsygkWgi+m29YrE503S2r8sCX353RfsSkwHcPC4xOWBdxTvGFXUfOE5SZbxxew8wN6tggDoqvp0/BHMnHkc+fr1jQoXaB/MNbvvCna+Z9IpzgEw9PiefAZBS+kXx38Rna9Yn1U883PvtZXn/rhidPYPuG5Qfb79A2He4seP35gkt9gZaWUuC7T34HefUJWL7GJ/SbrF6ukbcr6Jd8b/p1OK3Q5xteG1/jen9D2m0Zbg3f3X+ZcGzIuyVPyxt86vJLSFbM+8R3n3+GOIMIlotzy2fnG5TriELz9+TX0LLQZcGVWPHW+QYxzBSn+G7/KlId6S4825Xhs+cW2xzRw0/51r97oNiIvDZYJfmm+xzr6wUuR777zivYuZqS85j50js36CTBZ379nSfIMWGDpJENv3H3SVh2yKst33r6PVZPXkcfHeX5zNd//AYyvYHk03zynQva+AQpXyfLa775EwPSQVR85ieJdifAN8Rs+d6feIgFnSRvPY+sjxmVquHu+z+cq1wgwSdfzFy9HDA+UnLiu7+3g5SxsfCp+8QrDwmbBCUXvvfv72sarg+8ug+8djsjQybFxLf+w56cCzIVXj0VPvMyIENCIfj2fzxSckH6zMVY+NwLj06ZlCJf+4/3lFjQIbOe4fPvDMgIIku+88cDFIlLgk0xfOWdCZkzxMzX/+CAjgXjK0/8S392QqSCTJmv/fCMLmBTwRbBV/7kgJojMma+8sMj3S5jbxPmWPjqH5xRDxlzl/n87x9YPkgW04Y0OX7990+Uk4OD5e2fntn2oJJD4PjOO3uSaJA0fHpIXHiBjI4iHN//0QsQFpMVnzr0XB8GlC+UJPitn7xHwaDRvHYaeTbUCylF8ls/fRchFAbJK+PMG4czJgNa81s/fxdEvRBez55PnXp0LVP5wfMH8uBRU+BKCr72dEnjJDpHfnB3B6VgS2btPV+436Eej9P33n1e0+xzokuRr9zd105mLnzn+UtUKegUaWPi6y/u0CliSuZb777ApYSKHl0i33p5h4gJFQO/8d4tTYyYlDEFvvHuS0RKiBj58u0Di5SwqS6yfvPugCSjcuKLp56tD7hcJUS/+fyOkgI6R94eR67HGfN4/vztlzsEBZMSn96feDpVIoyg8Dvv3kJKmBR4Y5x4dupROZFz4refP1ByRqfEa+PMpwePigkhBf/g+QNSCmyBJ6eJT5+Gungsme/9/B4epzxbn3jr/ojLM6YEfvNnDzWkLMM6Fr54f0aGSPGRb72zh5RQIbPYD3zx996hCR4TZn7w4lgXwSnTFvjWbkSVgoyJb74801BoS8KJzDdenNDJ40rg2/uRrTpy2TywMEe+9/IlXfkDFuL3+bVjR9cv0McNalryrdNvoGVD06557fIzPLl6E9kanLZ8Lr1dFzs4LvIFL29/zD9797/hf7z/F7zpPodQEoXi9fIGW3EDyRBC5jvND4ghAppXzCd4ZfUGylqyEby5fJt/M/0r/tn0TzmFAxu5xdkWIQTfW/4OUkqsaLgxr/CG/TRKCZCZb+nvo4TECcNGbnnLvI0uCikk37/6h1jp6GLLlgu+uPwqrVhgsuU769+uWRc4utzxdvgSOTpKdnyt+R4og9AOqzu+tvw6SgikgK+Pb6MGhRwUZtJ8Z/EdnNtgcsMXwydRwwkrzhg98+XxCfn4U+xq4hs3b9FYT7M6YTYj3y4LtPwRhj/hyf4BNd6jxLuo9sC3JoGW7+Lku7w1TtxwpNW/QJt7fnC8xIhER+bNsOZVfYHEEHPhB+LtOmVftLx1c8kbW03nfoY27/Kbxxmt32ORfswnznd88uEBN/wcE17w27cjVrxLl37MK/6BNw8PtPOPUPyCr/30Dpd/xmL6I27653zusKf1P8LGn/C953tU+DkL/yMu/S1fur+j8T/CpZ/w/Rc7mvknrMY/5KK84Et9RhuFNJJvHkFriRM1h+ZLzyeIGZULX7/L6DEg+xkVM18/KTS1kfDld0fMHDGhYIXgK/ePYH4p+ELesrIXaHuD0iu+9jwShwExDLz2zhl5NzLtAiEZPvevf0w5CWzs+OygWfz8APuRMgW++ccPHywMXrkbuT6HCsgo8Bu/9wJRQPrEqyPcnDwmZ5SCb72MNWtIwfUET/tcG3si850XHknGxMC2j7x694Cdf4qO7/LNlwkdf47hp6z9iTcOHiWeY+wtX313jQg9TsxcNoa34wZj7tHunu+KLbo9YsxL1vLAV84aWzJinvnqi1jPv6Vm+by9C+QUoAR+fYSm0Rgtka3ly7cjqniMTHzxvQE3nWnGAzZHvrX/BM/mG17zT/iNT3ydTXv5K+VrRc9+TBVcPrRe+HA9+0HJ+zGrgY/e9nHfwkcWFh/3fX+D7e9iYPK3lkWdzuePmSh8ZMn0N5JFvf/Y8pfc8svtl8bvXwXWxuyRaP7vd/+cPzr8Hvf3P2etnzC2C/ZpoI0GXINbX/CQj6z2jjBtOJVCE6pmzhwGdiay9RovMl4lWqVwqwFjjrwnj1ylS6Z4w1RUDdGz0Bl4rw1ce0vfjfSxRyFws2FFx30XufINwc7kVjDNHjM0rKcVt3ngau8ZnhVmWzndm6XDTCfu3IEn+gZtAkoJkkos5YqGlvtwz4W6IKRAngLTdMZNBvfKDfdxxzq0nPSKbFrOeWLDCjm2vHd/y0Y4csmUMXDyI6uokEZzsJGNXZCWEbVQHPLA5hDJ4swuH1ipFV5mGqG45ciTskFYw8kF2qDRxtPlxDHvWA0dQycZzIgzC6RSiPueczNxo59wngYG43FjQmZBt9iyW01cxQ3lactYRvLtmXSYaaNh145cn1t8A5NJiJjRQdAE2G1mrvqO2ZZKzdKSNnQ0fsGtOnHZt/j2TcrFNVGCiZCPEy9s4vKQKI0DaxipjHUdCndLxWWfiZ0mx8xkBMsxoxPcrzXbcyI4BTFzNrCdMhrJQydYnyvJS0nFycDmXHXQh5VhOaR64k2FQyu5OEWygMNCsRwSRcs6Xm8ll6dIVpX61D5iOVyC3UJzeZgJUjAsLXoK5JTpkmC/cVwfA5MqzAuLSyBTwkZ4WBuuDlWKNFhRMxSyoBsj92vL9SkwqEJuDAKBDYk2Fe42hsu9x2tBtKoG5R0S3VFwu7JcnTxe1G5z1BKbFQLL84XjyeAJ1lKASQoWvqCj5LZruRwnYmtBCAYpWIV6fF82DVfTzCwlEsFZKTazR5bC3aLlwnsi1ch67pqail0K+2XHevaVqAOcrGE7PcpvjGUZq9zGpMy+cVwNI0HA0RoWPkKZsWnmeLXi1VXLnBJnKZHvPkCRGCT3TZU3eQy9NtiUkLJ2zW8bx00/4pVkshb16DtwKXJrDTfDSNCK6ZHcZEPE5MRt13I1jGRjH4lLdX82ZV62DU+mmVEUklYEQQ2lK4WXi4abcWaQdZo6FVjFjM75EVMbGbWgpMwoJZtSUClz6wyXsyeY91+/is0UMEpwaxVXuTCnKt07O8s2BGTOvDSKy1KzWmTK7JRkM81IIblTkm2uCccauFOSq9GTdE1K73wECTYl9s5yM89klRgaRVsgBdAz3HWO69ETFPRGY3NG50gbZnYLy80YmHJm0hIdE0o7LIr3WsOTkAlKMIqCKAVHDfl74RRP50Q0BS+qZGWlJjbqzH2XuZ4EU/gxMR+JBrrY4eaW23zgejCYV3pQIz7NvNG9yf9i81/T9RqM4r9P/4Sfip8ylYl2dogZTrZnIzZkk5BKMYQTi7ImJHhgz5Y1Oc3opuHMmY3YIGRhF+9YlhXR1gDWYzqwYQsCzhxY6jU5JlRS7POOK31FtpFDfKDNLUobnGjZxTuu9FPmMNHPe7pmhY4WN7fchzuu3BOyzfTzAWtbihFoqbhPd1xyxTHODHlCZYHOAhsVd/mWp+s3iDIxxpozokeFKy0vwz1X4gJvBFHmOuUS4ErkXj5wY54yq8A8TcQUWLQrjGq4TbdcpQuGYSDFzCQCi7gGecEunXjaXTGHCu+YZaQ9F3SRHLaJ5UEwDRMoRVhIXC+RumNvZjqvka3BOs2oI1vdQQo80LOIGmkcMkoOaWAzGLBLjhZclJRwxuTAvgxc5ZYInFSgwyJI2CI4momrtGCcA70K2KyQ2uDQ3HHmarJkJzkJj84SB7TGcbgoLPqWefUFRrtA+ojqPXaM3HWSq6kwl8JMrlNPwGXBXSu4nCE0Bk/Bh8AqFuwUuV1bLs6R5BRRSwKFNoMtgjuTuRwSvtF4aqp1Gwo2Ch6c4KKPTDkin2xwbz7DvTiTX+x56DSXRRE7i1SS0SqWQ83G2K8ty5MnUoNW+86w2vWE/szBFla+0gEFgp0ubGMFMZxMofO10pYxc9QV4iD4GSfVY5NC6gErI4dmYnnWJLHHLzxtt8YqhZwle7XnSt3g00wvR5ywiLzEyCtuy5ELv2aa3sDrBTpkdBQoadiZwnUQeGWYtKx+DySN0uw2hsuxkBcSYauPrRln7DSxa+FygC/ewts7weJTN7zyrf8Pc//ZLUt6pueB12vDpM/c5tgyKNsooOAd24BNtigtzZoP+pta+jBaM1oakRRJkZwmmw1fAApAAQVUodw526UL99r5ELssqrrJ7qakKHPOztwZOzN2ZMbzvM99X/e4aPCRovQzit1PLot/eNMfNBXvF7x/W838WYXxP9D2f6ks6mOSsQ9epPjYH//Zo5iPffvHx0mfffzyBwf4o8dZCwMItu6KG39JVzh8d03vW/bGc0QT+4JKejobyUaRYmR77Ml9wHqH0ZGDDGQD1iia5OlFpIxbKI60lUeJSGw8jZbkEClJtJXgqD3kSCo8u8pBysxjJsRMKwWoRMqOITiizCyM5arvOMoAJwXBHmmLHoxE6QRFS2Mdl/6KMnhCaMAqovG00tIwel9ijAQZCVUgVpY2bjnGI1knrkPCDS0+B5KUxKsD27ZlSB0+xFFWIhIhK4iBowt0nSNmj3KJ3mSCyFB49kR6GvromChDW2W2XYfIjn0YaFBUDPQGBptRa03Xdez0AGlAOUE9MzRlQg1bYpk4FgNtKaiipbctNzRgBXG7pREtyMhkUeO9py0i2zISYuQy7dGVYr2Y4zI0IqLUQNSSo3GknJkdFSJlGhPG8e7C0haQfKTsPYOMHDXkKqMKGErIUpPbBFbSlBIhIc4s3oXRTHvrxjqUciTrGAXK0OcIIiCE5FAJotAEq0dNqhqlIQjBvlYMt0hWmaCzgpxAyMyuUvRGgJCokEdvw+06wKFWNEagGMe9Ta2ReUSzHiYaVY0NkYuZQyVRSZMk7KYai6AcRlxiUyqi8yPutTYIMlUXaYViZzNioshK0NYjXq8eBG0eH8fcEJRkKEfT+HQQdB4aCbka6SatlmSgyoasS/rCcAMkoWnNaHZOCmKUHCo7mmmVxktBVJKQAlJrjnb0HXityQi81ggpyTnTWEuWcqRDIRi0Ipej/2pvLE7IW1RqojPmlg0h2BnDoBUpj1KEVmtEGlPP92VBZyPSZ6xPHF2Eyz1qUXMzeIq7a8TRI1ziICWiKEBZtlIjbwvYRpsRKVtlshAcCosAJmGUyxyNRuWxCdhrhQCmWiFy5mg0sipBaQ635s6Z9IjMuE8gkmjtiKmdAg23SFmriXLEYyYEvncooTiYUb4WrWIQgijFGBAYBXujSMKOicp2hAwIxvNyb0dNdzASUh4xlFmTxeixCBmCBC00Y4k5HvuD1YSUyEJic6KRo/xPCMHeag5aYhjlVEejkSJhGLXtB0DVNbmN4/EtDSmPGEoRJdMQabWhMRJtSoRRHMz4+WuPkSw0Bz2+34WCg9ZAZhYCrVE0WnIJZBnH8xCQIhN1prEZkQNRejo9IEpNvhpoho6jjZi1RvstQ94ijaKjZx93TMs7uOw5ugNX4mIEUOQJmcQxNiSdSN5DyAQ8PkW63rPPB6gT0QRkOjKkAfQoyduHLb0/4pNAZskghxEokwXHtMWJgRgjJhua1IAbG9s9OzrZoqPGioo2HRB+fL8c1YHGt5RuQpFqeu3YqwPkxD7ukO6IUQVIwTEeyEIwANu0R2SYFROGWjE4z3W8JCfJMR4RSlKbGS2JJvWIsCVFTZsdUivmRtOJnoM7IrIi+UyjOlDjNVFwZOe3ZCJRw6AcSWQwNVI5hhi5Yc+QeqKJBJkJtYbg6FQiFuBtJhtBEAEXFLqKNMnjgofUY4KijwHfNMQUGKYJbwpS9hih6LQnWwnKsyNQSkU0HSoMDDqicyArxVEn+jiMadspj58V0eFl4KAcRo0y5zZnmhhBenRhOKpAjol5NcUruG53eFuCzVweGnJMo+eiVjRW3MIWBAc1roJPIijgaMb3WRaRxgiyVog0omkbI1CVJCpo7WgOTx66lMZzPQNylHklAUlKDlrQ2NE7J4oJcVZyaDrKriNXmkOpidZAaZFG496/ZknBsdJEMRrOAZxVZD8COQ454PSYwyGAXoC5Jdcd9Lj4IZSAPtFpkHFABMdB9xRWI1SH9C1dHL1iSncMVU8vPSYZrDU06YhIEqFgz2GUfKGRYs/OHxCqJpWZVmREoTBtQosRbztuiaMWCC2ZCc1gFEcfEAJ0ofFTQ5aQhKdXklaP0qptCXpSsn7xAULJz+4DPnbHx2vasQf5G6YNf5Ok6b+kofi7Pu7vuf1XQdHmW13df+n2h4Kqj08jPr1J+4zW7dZZc796ksf922ihWZg1x05hywNqUBi/oD9I1FxynmrCUZFaMEdB1SmiNiQxcOo1de95TKRQimljGZhBkTkJJeQ5N2S0Vsz6THIRpGTlDHLfYfQYjjNvFMZMyYeedSwwUtIYS4yJZSzJgwAOrIeM2HuaiSds5pzm6ajfbxPTNGWtLW064G4a1tIgTUGwnnmylJMZjfIMODZmQ5TjeHQl58zzjOtmRzsENm7AHTV9DixyRRVKOunpZGKlCkAgfMscQ9UVtNFxFI7TQRIrEGrKrJhQJMHgWowfOM1TNBolNOUgWW0tsXb09ybcre/StDsK3VBgKXvB0B6RQlHtNWVUmLnCJMN0sAw5wKTg1BUI4KZI+MPAvJcUVYlUktNdjVCKelqhjWF2A6nvYV2yOZZIbdjrGdF5lkdFklOYCk7ajNaGfRD4Y2DZZrw16FqxzgF7k9gXEW8E6+P4u0QIVluP7RVtDvRWsbkZiELAqmBx8JQ50hSStpCcbMPYb3vJ8uiphkwz0RxLzeY2kVqkzLQLTPpEVyp2hWCzH8khcp6YdoGpE7RWsitgvQtIORo4qz5SDxmvBTIYTm6GUfoTwfaeuQMnQSbDyfUActSMZudZ9KMmNyfL6T7gQkDMDBWKRRPGYlxa1luH0JKjH1NZp+0ILQhecnoICJFvcxgyqyYR9xGmBeshIDLsCjuatl1HtgoXYdn01EhurCYZw2oIhDQW9ifdgGo79trQ367sZ6nJCdZDj02JRlnawnLWNqTbQfDCOUofaI3lYC1nbfeBV27uPFX0dEqzj5GztkXkjJhOmPnAZHC0RnFjLHe6Hhixk5X3zPsjAx6RImdKMJ0UqMsD+p0965MFx+sOURScHo8IW6LLEhsi08ERpYSq5LzrEClRpgqVYeYHUk6IsuC07ZA5URUWIWAZIiFnmJRs2g6NpLYGhGTp/PuzbzZNhyaz9eOF/WQYiIxEptPBY8jszEhx2XQO1FjYn4SA6gYOhaZTitPBk2OAnDmJmcIF9kbSKMVZ78lylC+tfaQKmYMUNNZwZ/DEGJGTgkVITEJkryV7LTnvPKSEzAVTF5inTFuOfo3zYbxoG6CKiUWI9GI0YJ83A0ZGVNJUKbGYZw6AHBxnLiBCoEwZEzOzfiDrhMiasywxhWUrjxQTizlmhqHFZMeZKxFCsVU3CCTzUJBkQFWOs6FECcnetaSUWSMpTUL6wGkxxdRn7EOBbzxraWFaIvody0tBGQ39ySnUFYv6hFV9wqN8hT4Y1vKME7nD6YG1WhNVRIRHrNSGSlccwp4+tZxWd3Em8jg9Zp6mpHd60qmkFy0nbBAmk2WgVjUTs6KJe3buihOzQSvDRY5M3JSaKS0dCsFJPkEZg0JTpYq5XOH6Bgmc6nNyBKMKCgpmakUWAuEuWOsT1O1k1UrLxMzpRU9MA6fmlCA1hSlIQ2IyTNFWEEXmzJyByxQBpDAs7SkxabJKrFkghWGfjogoWOQK5EAWcMJmPPayI0TPmgUhJWIKbNISEyxHM9ANDTNXocopohQsjgVFueYojng8azknesclexaTOaaBferxNjKRBQwGKsFiUlIlSzsc2SvPSa5J0bMLB2a5osoTQhXZdtecTVdEZ5D5gklQlGHJkHbsaTnVM5LUqLjFeM1SVATp2OaGkzxBTioudUPhJRNKPBHInFYLpACrNFZpFrHGdT2HaDhVGq4D2R/QQjIZJkjtULll3dUoU7Hze7KQLPOM6Dtk5djECUJojqEhDY6FXpCHiDADG2dQSXFImagSm6TwUZBSZN2PfoajSTglmQ8glAIiqwHqlOgKaK+3nPSZmCJowSJKqmPHYAWdVWy6BBKyc8yGcUo+ZsgI1k3E7R15KpklSeVhh6eUiROvRplvjpR9ZpLN2LzKzDrPkKFA5S21KZm6DUNp2codK7OhqD17u6eIljpVJD02LSfyHHxCKY2lYMopQVSgPSfJotScrdakzlM3iagSWQs2PePEogKlFRMyYt+RasEyKibHSN/vyRImrkS7RGlhFiUPVYH66pq9bbC5Rr6Pkf2Yemf0LowLWh/tM/6G2vjTVD6f+e23e7z1bIiP3/rp22c1Gv8VJiB/f8/F+5v48D8hPvRefGz72HTjP3+3H324+Oh+8tjIvE/Y+rRdL+wal8e4+Wo24ez+DGWOJK45H2aEbo7fVeT9lPLSE5oeLyLnek6YWrI1JKUxbSQNPUOzZ/2ewLOBfIoQ50yFJZtAkj1noiLmiPCjTvL0coHsakRXc/+wIYcKWk08KjYHTVYRYRMPnzij/FxEnbTIxY57MaNKQa0CZ9tE2SuM01RRs7lZ4jrATJmdPksMhqFLNC6zGNa0MdD3HhMKGCAMntb13JssUfcU9omCxZnBLDx56QmnnnuzydjZK8EGw0JpjIIgIvcPNbER5B2YXUl9tUZ0S1I34+HunCgnSF9S7gxTP65qehG5I0/oi0x7s8O9fsnmRjAxhqoyPLt6BqcSMUUKW2KpcSkRZOa8XRKd53hoGdqAftfTDwM737Jua7yOxJSIVrA8WOLhSL/dsrg25BCJLuIHx+LRk/j+ITl/jlX7IkE+Q6qeZzj9EvVNQSMNw2RCXUzB1pAMWVfcE1NiWRCFYtIkZFYgNLG0nL/bMVhDQFA7iRIapCIYxdmlw8kR61r1GTlEspA4qzndB3olCTlhG0/pI5DoReL83T0+ebIfsMeeSdND8Dgi5+/t8aFHRk/lHLPeQ/Qkmbl/42hEwqeIQDAZAi4HOgWbyw6nBTElSIlpE8fYRa1YXfd0AkIaUbJnvUBJTRCC9f4WyyjEiEPdOY7B44DTm4Tva3JX4Yaak3cT+SigkawvPFIKsgSnBFMquuWGYX3KtF4T7JQsK6KdcdImnK7w2TDtEypDlgpnDHf7hC8mJFkwdaMRP0nNYArutQ5flkQUehiDlJJQOKU52zcM0pCRFDFi00jaGpTmzr4ZSUhiTMEuYwKhGKTivGnx2oxIzhipYiJJiVeak6a7lSwJRO8pmo6oJb0PnB1aXFWTpEEIy2LwxDTif+91HUFmBAkpMqvgiVLgJZx3o/Qq5ZGktHGjhMwLWMVRwpVvj8f62OKVwElYDh2eRBaZqGDTtwQFQWWWwZNvFyUHCedNh0eQECxCRDOekwOCe7dY3JQTM+ewt7KrQcBZ09ELQZIwywmbx+lHn+Hs2DFoQVJj0GIpxn32SnC3GxhuF4JsThR5ROQ6o3iQE30a0b86JeoYx+RrCXd7P8q+GM3TdhD0SdMkw+adHUmPAWcKwSJmPGMWxVnnb0MABakfOL38Ebb9CfLwA75w/pjl6e+Yxleoh+/xYP99qvAKZfgJDw8/xqafYdIvkemn3Hn8c9Tul9juNzxwF+jQI6639L96g/L/2NK92jH8NjJ9vcC9fsC909E/bpn+tmT7pufmN4HjbwP/Yvv/5l/u/xf+Rfc/44mE7EkpUckp0hYEkWnTwFrdoY2OQWSUnqCNJfQDzkTuTu/hQkOIDis0Wiqi8LjCcVackYoBYRNWSAqpiDgG2XEuN3jRkLTH1IZSlgQ/0PV7Zoeaw3CDcw3EQK0mRBFw0nG6uEtnGrx15DJQlRVODXSyY11s8KIDCyl2zLMks0eqA/erE5ooGKSlTZLTeoGoB7I6cqKnxBhBSXIhOa9OiXKcdi/SGh8KUqoJVJyIhyQM6IqlPR+nTCnjo+fcnBJkTy4Sy0mNNR6RWqJtuZMtKe6I/Q1T79AkwJON406uyOqILB2rUlJJQRg6XOg48RX9bQhuZUtK0RHbS1z3HndFxIVfo/Q7lOn3TNSbaPsGTH7LE9NMrvfoqsPaljp2CNUg7ZE7SeOKniwHbCVZzucIBUMcOBsquq4lpRGUMBeWEAZ86DjxJZ0IGKvJbmCtfoU0P0So73On/T64/4iOP0Tzfc76n2OK1yntb7h7fBXTvUIx/ALtfsadm1eR/auo9GtOdr9E5texvInIv+HM9QQBMSVmR4fwkYwgSMl5P+a3ZKNYZYkIHpEjXXJs9j3N5RXD0KJ2B3A9cWgZ+iPr9244Hvb0xx3i8oZwvaU/7Nnvbpi9fUnb7XHNAbE/UsZx+uZE5jxGfDoQ0xHtjhTtNXm4IakjZ9sbhrSFfKAQLWV+j6TfJdl3OEsBZg2iaJktM3M7h5zINvOgfEA0EaFGOe9Cz0kaoorcyVMSV6i8J/YXlO2Acx0pO05CJpSZFBwIzypEQg644Fg/2qHrhJpmijpy/81XKN77HuV7P+Dp37/Kty80Xz0UfHuYUj4x8Ff9X/Fv3vmX/OW7/46U04dF6qdsY/H/fpH80Yr2M7ZPFrSfWuCKP/yb+Hv4JT7xwL9vr/EPgKI9/ud/8ye6sg+6rT94UfkjHV7+wxf5kRv+xoYrw//67v/Iq/sfsfc3rKpTenquwiUlBc69QD6cscUxu3SklNmriEoCqxQKxc4ENp0gty2N36GdxxQCvZ6z2xhWwUKhaKoELmKdQLvMjR1YtpaUJY3O4BOTQSK9YKs8S5+J6xZ/NhYMJ/M1JmXeu3mLVVeSUsSpSCazrJfYuuSqv2J21Ax9hy+BecmyWJGOjuu0Yz09IWRPJDKEnvlQoAvDjTgwN3OONhONYsAxd3P6beRxbph7S9xZZK8ZZOTUaYSAK+WYeEHSI+1qj2MRx5XUGx2ooiDNBvRcsVeOk1yA6Lk2LTUWa3pqmdiZls3WoFKmP5GURY0rC4JLXIUbZl3JYbcnzKCUFhs0Jiiu1IH1MCGqyLHo0WVBHQvcvqObBTbdhEigKRw5Zqa5wji4rFs2xwXJPE9rFyQhmMQC7IQLnVk1EZdhsGOxPz9GdBbczBSLfcAbgS9GPfuiTUituKoly73HF4ogwCvBoh2N1Re1ZNFEgpXElOitZHOMiJy5nGlmXcQpgYyZphy9E5IR6TprA0mBionGCBa7EeW5nRvqIQEJHTL7WrHae7KQ7GaaMoyYTBkEN7XkpEkgBDcThfEJkyWFT9xMFJtDICrJfqIxKaOGSCkk17VifRj3eaxGepkdAhOpuZlqVntPUoqdgURicSxQneF6UnLaOggtnR7faJMhorTiZlYwi9DVK1pd4H1g2ga0F1yUBeu+JwiJ0+oDVKoCrqc1y8HRYwnKMEjJuu+QwGVVsRwcXimylPTasGxbZI5c1RUL53FiTFVtrWXVtUjgqqqYhUBgDLc7GMO660FKtlVF7T2JEXm6s5Z115KF4KYoxgwIf8D6jl1pWXc9+mzJZUyYY4+2U2xR8XiInDQdSUturMWkTBEdNgauy5KTfiAKya6wyAylHzDBc12XrLt+TFU3oxxqdutduFKa9TDgMrSlHVG03qFS5rIqWA8OJ6AziohgOTikgAur2fQOpxSDFEQpWTkPMXFdFSwHPyajG32L8x3IKXNVFSydx+tbFK1RbHqPFILHWrFwYZyCAQcpOQsj+vmyMMxCHAM3Y+JgNSe9JwOXhWbiI0mNnpa90Zz5QE5wVVmMCygxkqGurea0d2TGvxsfUSFQG8VVXbA5diQyN0ZiMlTJUxO5KRUnxxtq/wp+eSRlKJOlsBXX+cjiIAkkjmKAnClEBShuKsfaV9AJ+hxJMTJ1FjtIrulZBsOQPIMaV25nXUIOAzdFYnHs8bXDlZk8m3I2kSweCm64YJ5mBEZpzRA65npNyoKreMnCjItcKUb63LM2G+g9V+mamZwTUodWmiY1LOQCaTPX+ZIJE7JKaGXYuS3LuEQZwzZfUaVqJELpkn3esUor4jCwL48YpxE+YZLhUDSs4wahNDuxp5AlWhbYXLCN12z0yYi4TtuRtKgM0mW2XHNS36EPHft4jcwCKe6Q45TLcMO5XWH1jjZeQMpU8Q5KrLl018zdhEiioSfFxFxOEVlyqAYWcUJUni61ZC2YZYPMgat4xYI5sci41OODYynPkKHkij1zprhhlPgGEVnKNdkLLvKOtV4QlCOnQBd75nlD7A2X6cgiVzgyKUInHCdFifDX7LhkmmuYBaxKHOOepV+QCsNVvqZOFVKMC2dH2bDKKxKKrW5HQlGWGGE56I5VWhKzZZu6kUypC3SUbHPLab3Cu45dOGCVprA1Ikq2omEVLarYcsjXCCEpQoH2ip06sIwrhKk5hAGFoM4VaoAb3bJ0FU5kmtwjyEyYokTBjWpZ5DltekgzOwElmAeJ8JmrQrAcEoE4SpsKzXzIiJi4MplJF4lG4hmljvODQwvBdSVZeIi3OR29FiyGRAqRQ6WYDomgx0TxVgvWYfT1XRVQe0iiQbiOViY2qgA3sBUDlTQjaVBI9iawikeE/zl7+y61mYIUVPWEfd6yzhuyEOzylkKVqCyxWK7D6AsKJLbs0FlhRYWOhhtuWPEEQb7MUc3AJ4wT6Ky4yZ51UERd0hQSfGIhMoWVHKaKVe+wj39MGN4FKXhCPuRPim+zKJbUnz/jXzz+3/j17lekHHlm8Tz/5OE/Y1OefFiVfrLCzx/WsR+qej45Y8h/ON14vx/5rCnDx5VWn7397RaQT7k7M5/O/5Ydf/b2f0pC9wfb+wflw2nO+EX+uEdDfPLrUWH44S4+cbDFpzUht24ZJRRGGKRQqKww2lJgKHNJzAJdFKTLHVZX9L1DWkUh5GjAVpqDiKgsQSq0UOjoRjTbsYXZBCMrkk9oKyCMyDUdx8mNQRGVoiAhpEQLIGQYjhQXW3xVEIcClCA1Dtk4pJLYakJKHuF6fPJoqTBRIYSkms/HULNKETTILJFZkUJEZ0WKHoEkKkMxnyKODkQcEaOlIQqBCw5jC1LuR7RaFHgx4tXcLW+dEJAiU3iBv0W89UpQCEUQEqUyNiuSSGif0TmjOo8oQYmRbiRiQhuJsgpb1sgQ6PcH1KRElwo9maJCT3GdcFkRb1dZVYRCFUjZUmZDNJrepNHk1QamwTDkiO0Tgx5RhKjR+Gy8GP8MoweiUJqsxiJcHB15qtCNH8PRckaI0ahqQ4KsxoA1rSFCEJkcAiqBKAUmQYog0qhBlz4iY0ZWBUUYpUYqZLwesaLvU5bsMBZZAoHwGe1Gqo+KGR0FiUxpLW5mmExnZAGdjJTHQC4UldY4naiNxzcDSklsYsxv8AkZR8lTEBkZRh+GShHjx6mLCRnBiEg1MaMYMYxSaIoIQY+cd5mgkCOnXeRxn15kbBqD+lKMVGHUsis/stdVyIxVohlN+kqO/PLeoxhXrIss0IBWkiJmhBpXtRACTca+f5x8wEuFzIJkDEqA9gGZMyZ4khDIDIOImJwQKY333a6WipyROWFSGo2COaO8JyuByfnWFDl+SshbulGWAh0jIqcxkIuEygkbx5U+m8b9mAQyROrFBAXEvaOoKhQCw2gKNilTpHE/JiUkI03KS4VO43tEp0RxO00qYsIhbqlW4zljySNdKSaSGvHMWQoUEpvGpHXjAsEqTIgIIZF5RLgqIcapQRpVzk4IFOOHvAAKATFnUhjDHpUQqBhRt2hYmUbynosZGSMyg9SK4tYjREwYK5G3x0SlTJEzgRFjLHO+PRaMZLScCWFs3pQZszBSBhkTVc4f+DF0zlggxDSeBxmkADl4pNXYkAhqlE+ZlDCMQX5SCEoUWkjCfqCwFlsZTJIIJSjnU/rgsAgICY2mSIZddughE4aI9B5BJnYZ6Q1JeuSxRxBQaszioB/JVOP7OxHjiIcOLoznvRNIKyl0BRFyFoSskGnE14oosdISQ0RGAT7hjx1FUYy0LKGB8XlrFAWaHCJKgFUFUQR0NoiQMHHME0BADgKhBEYZcAki6KxgSOggIY/pxCI2yKAQSAQCJUeAgEaSY0KhEDojo0RrgxYGU2jEsCU3GVNorCmhG4MGpReInJBDhCpgCjtec9uAJiOtpsgF3dBTmBF7q7KiFJZdd8DqGV5LrC1xbgAfsYVFIihlyYAjJU3WoKJCMnqLVJQUZQXR0wmHkgoznaDbZny9QoIwdKG7PXctqh/RoVmJMf1ZCaw0iHqCCEc0E5QdsEYwhAGTCrLSmKgoTUn047VXaY0VBVFIZB7QWZOFwEQJJIzWEBTCRdSjHXlzSlHNEKkf6Y2VZjg6lAcRM6WySHqKbElxNNDrrCiEprAlB9FSqhKqmr7PyCzQymKMQRAwsiQGh02GLEB5gYoZUWSMVGhrKKQkSPl+xiHkhHn/8zokvEwInzFKoJSglODSGKzaCbDWkLuBLDWa0SsohcSFhApjU3CIESMUOSZkAmHHhUmZIHcOkSRSJEoUnvFzNCGRQozvKaMwQiFyxApLvj3/dNboylKI4raJM2AU2mssZqRWeYlEYjDk7DHKoDFILzBZI4WgQI94cyHHxTOpEENCaUGRJX0GzahZkglsGjM5pL/9M8mR8FZa1s8/ZHN2B58dUki01KQ8+mG00H8gifqYGfhjVewfFKqA+KAM/ltnD5+caPxdt09bmf9Is/Kp6qP/gu0fThb1d94+/gI+zVORP6J7er+z+2DAJOB9PvDHjTLj/z4//xqKgomYc6bu8SA+pKBEDIk/iQ+RoqGuPAsNTzQFNgo0ki8/LiCM5Khp0jzbjfxulTNf/43H+CN16phkeD4vkHaH0Du+cpyjbEeh9xSm58tig5067MzxlbCgrgRl2mFyzxfeKin7yMTDV3iGgpKqmDM9P+Mb5guUsxnTsxNerF6kjIba1Oiq4o+f/C7aFqgBnjVPspqumNqatGv54sXDkfEvLU/pJ1hNTjFOIaLgT4uvUfSJqZN87jjlvDMs255iaPn2zQw1cdhy4F494TzUFK0nHff86eMSMXhsH3hwNfDkLlAmh5Cerz/eIJyg9JazuORz+2rk+MvIN994QA4FsimpjxOe2m6wUUHj+MabD9FCULeZ1dHwpZu7VEHAEPnWxTOozlFGwVSUfLF9kolT2C7z1d/fY2YKlqpksVzzVf6ISTWjpuTlt+8j+xlmP0cPJV/vTsdiZAh88fWOatcz2bfYfuDrP9ti+46q73npN3smvWfatNgQ+MYvDphmoG4Gnnv9wPy6pT6OgYDf+v4jVNtTNz2fe2PPajtQHTpEP/CdH19jBsekdTzx+yOb6466HTAx8sc/vsZ4z7R33H/UcPq4QfeO7Bzf/v4lft/DVcfsp49YvfKYvHdkpfjGL470lwdEE9nIihfvPqCYT8l1yV9MzilO5kxRbJrI848G7C228Du/6ccGYQhMu8BLbw7UWygPgj/99UDdShbXsDjAF95xlCFTRPj2bwesy5RdZOIzX/zNATtEzBD5yls3lEDpAiYlXn7ck9UcZmd83lu0K0lNRT4Ivv76FdJLbDK8dLGj9onKjzKnb759gRGaAs3zF1vmLlFEhciaP3vzHXSCIiSevd6x7gaqME6I/vTN3yNipAyRp3Z7zruBKoyLE9998/fIGCm85+F+z53DkTJ4VM782VtvIxOUPnLn2HJ/u8V6j8yJP/79W4g8Zmyc9T1P3OwoQkKmzJ+8fYEkU8XExkeej4FKSwqr+LPrS8QQKL1n0Q/80eU1ZUqYnPjTx5eYLKmjYBYyL13dYEPExMQ337nEpEwdIpUPfO1qi0mJEvjmbk/Re+pbjOo3Hl2hQ8DGyFcutlQhUKdEgeDb715hQqLMiZev9sxcYBISRgr+9Go3NjEx8vltw9KPP0uGxD99tMUOA1UYeOHYsomJKo2N2nffvh4bjRh5etdyeuwowxge9d3HW4wU1Bk+1zruu0DNuIDwZ29dIhAUIXF/CDzVOeZCoKTgT9+8GIPDfOS0cTx37JnIjFaCP7/YorNnEnvOu44X9wcmDFTK809v9izCG5y1r3DHvc2Xr95m0b7C3P2C7z56zLx7ldPDf2DRv80f7SpkkNAlvimfxUZH5QfkruGP2hPK5KkL+M7seSpdMDvCNGu+2pxQWkMREi+9Gyl2V5T9DjkcePnNIyr2qOx47r2OMgwUMqB05qvvwNQemPp3eOpRwUxNKFSJtJrvbP4pEtBC8ezkBVZ2Q4klH3u+NXwNTaZMiqfVE6zCgokuMVbz9fRNQg5Yo7kvH3C3foJCVoiQ+erxW6TDQDEYTsM5d/w9KllSlgV/rP78tgEs2MQN9/Z3MS0Ybfnj8i+w0wm1mbJiyYPDA7TXZC/4WvwGmURVVcyKOc/bF9FCoMh8o/4TtDJUqmIaK57ZPYc4Vqg051v+y5Qo5sIyK2d8yX0ZsauQ/ZSX4xdg22OHQGULvlF/ESUjSkS+6B5SZkuZx+LvG+klVAvWa75UfomZvUelnkCLNd9K38KwpMhrXpDPsSnnzK2mKhV/XH8TK8csnyd3C2Z7mAElge/sX6B0kRmaZ8Up57FgbSKTKXzLPYGVLXM7cM/PuBfmzKWl1Jo/tX+GQTFREx7UT3KfB5RUyCHznfaLFCYy03BHTHgm3WFVFlRK8o/ly+jYs9BwiuXZMGcqeyrj+er+DJsPLFXDzDme7jbYNDbRX3dPMptI5gwsheaL+WmqJCgTfCN8gflguCtWnIgJfya/wrPmST4nH/CP66+ztIozKznZTPlvH/wZn18/x4vzZ/iz2cssV5b1JDAtHN+pZ8zEL1jGV/ji7obl8C7L/leU4U2+fdVQu98w7V/jxZtr1t0F0+Y1yvgu/+iio/K/Y9b/mqcvHnPW7Vn496iqhn8saqw5UKdrPucDpz5QhSNS9XznBlQ8UnVbzpqBRbOjGn6P7d7iG+8MyPQGtfwt5/7Aw9RRyd9g5O/4Zm+R8nfU+VesO8/9fo01Nbaq+OPiH6OkpmTCSp7wufg0Nhtklnxb/COEi5SULOSCl6ovYakwFHxHfQerLZWsqXPmC5xS5IZC93yxVSOmmoRMkc/vx0U0GxLPvxeQbYfaHdA+8ZJ9yPRsxfR8zbPPfJ4Le8W/ffdf8cvtqzwxexKrLEYWnNf3mNvFp9e1H0Rwj3//uBdZfOz+j0Y5/C1F8adsH0quxB/8M5bIn/zvU/f7d7AufOYz+j9VFvWfvX288/vYM/zEsX9/ajH+mz/45bz/kP/w+F/zy90r7P2WhVmyH65ozJ6JnOLUKdEteXT1HuuuZugmNDJReNAhIbXhWkfWnSTGgT62mJtrTDFQ1omrB1NWYolb9vTLjDg6CjQ1lsdcc5bXxGpK6zypcxSNJjWKa/eIzbVDbCpSLVCVppousfWMR/GaU7Ui3Fwjl5YgEoXXVLrgKt+wMRuGOOC9Z0gDCzvDKsOlu2TuJ3g7ypj6NDBTE4w0XBzeYzM9IyVHdJ5OOWapZnh0YKca5mpOLw3Bw156pjuD2FkODMzefpckxuO6LyWrxsFEsFtVVLmA5XJEy1nPSdJIc8NhNjCZrhiagHKawyJwrz5FDzcc948ooiHMKtJyxqPL33FnPyEbaCcRHRVSF9gu8W594F4zp0sDw0xgtaXUlkpY3ksXzG8sfYo4CzlHJs0Efax4NBk4SzPi9A6d0GNQ0CDR0XBRZda7RCzkbQIv1H3CBLhaKJa7QDDjhMdbxcRlpAtcTTSrQyBqiGoM9pkPGZUF1zPFYu+Jt8FFbSWZtePq9G4yprdmOWZhbHVm2QQcsFsWLPpEVgYlBLupYXndkzNcTyR1G1GFRrjATSlY7zxmVnHY1My0IaZEXRZcWVi8vWfoBraFoHIRKRSFz7xTJe4ewA4FnZRjeFEGFRLXE8NJ6znO4FgAOWNdYIrmam5Y3fT0StJrMaI8g6UYDFezmrOjoytnNEIhpKRyCRPh8aTitB2IRuEAJwQTH9BCcFGUnLWjjwGtGayhantsgstJzaptCVITc6a3lrkfUDFyVdesum6UReVMawsWQ49CcFVXLPueyDhuPhjDqusRInNVlizfx9Rm2BcF674jS7i2hnpwSDlKba6t5cQPhJjYFwV1COjYYULHTWnY+IA6X9AuJ9jOM1z16Gy5yILTpiUoxdHeolJvw9kuqpLTpmVQgs4YdB557sY7LuqSO8NAL/jA11EhMC7waFJxHgJDzvRABKqcsT7wuCw46wd6LXCAB6ZxbE4eTUcUbU/G5zHlfOYjOmYuqoKN80RGCk+nJYsIIgkurGHdO4JSJOCoFct+zGy5rgs2PhBv6VxHa1g6P8rOrGbhPEmMJKl9oTkZxtDSK6OZ+jGBWcbEjdWcDB4UHCYllfMonami59oqztuRwLYrNdYFav8WE/c2N9axaiRORVodsEJjU0fle270gbWf0qmaxkIxqymsHFG/8ZqTvMARccIjlUJ2BhUn3MiWZWMYuoEhO3IIYwPtMlfGsWwyQTFKaRRUPmFi5GYuWR0zpnwHYQfCrGJ2cp/ybM21vGJTnON9SwqOXgxM0wwpLZfDeyzDEs9AEtClhjkLtLXsyiOLOCMWgSwSR3FkKVbEY8+Vf8yCJSkGpDbs3DWLtMSsJ+zElkmoxhVgabhq32N+qMlKcJx2zOySFMbgvl2+ZqPOcQn2bot1CjsvKYuCrbzmRJzjcTTxMK7SR4Wh5EpccMo57ZBppEclgXISIy3XZs+5POXYtQyxAx+p5wuUh0uu2IQlcSLoY0/KGesKKqZcqB2rfkoqM0FEYo5M7ArZlVyy50yv6MMWLz1BJebSUujI43TBKi6IbkBWhj60TBqNCHBdtpzIFf2hQVWWJrcsxRwpNVu5Z8aMEAaGnOhkx9Ks8N6zZ8dKL0myQ4vEIe9Yyg0BuHGXTJkhfKAoyvG+tMEFQ1d46lQiZURKSaMOzPOKpunoaLHJIqVEJslB7NioM1pKGoYxYLDSzEvDu4d3WTQVqhgYSodKUPsJlZtwo/as04qvzL/OWfUUpMzN8pof7f+ax+4Rp/aMr66+xdP2Gdq3r3jT/5bv+e9zkS+Y5yW+TPTJE4ND7DSyn3Aljqy7glBCjAGvExNRY2TBRdGzCSXOD0QSXXJMmCLEjO0ks6IkBkBpjjhmviAmzdYkNrIgxkTykYMKLKVEhmt2HJk1kM0WoQeOtWfhSpCeQ9kyUzN8DBhrOaY9q7QgiUxTtEzUFCElRhRcxytO0oqUAwexpxAVSipUlFzmK87FGUNKHFODxaCVwQjDRb5g407w+mk6YTBaE/cS3VmuisSkBcr56EHzkSo5StdzXSfO6imb+QUp7Mg5UcmSQhbcDNcs7RKX/C0RLnJ/8oB/cvIX2GwoPgjPuy1WPyLC+aCM/Rsr7k+xY3+a8fhjNfH7o8zP2OUfSLQ+evsnpFif+PH/Fyd0/wNvGT7TlfKpU5o/UKl9bNu6K27cFW1sSCbhpo5jbuiFp3UWqQxNGcjHI8ka9jEhjaDQAhX6EQNnABnpTIa5ZrqQHBaSY5WI+UAqIl0ZScIx6xSd6OhM4Dq05AzNDLINlH0gzAqOZolcCUw6EEw7agudQBWBIx0KReaI9+NZUA+atio4pCPJjxryPg2j6CSD9JlDOJBkxEtF5xy+63B6jlSSYzqSnSLGgSwyIYx43XhH0bSRJDqGuSUMcNx1ZCug1hyzxG3mxH4/+iUKgTAl3NuwrxJNkgg5oDJ0MiDUgKkGunlgMAcGFzGTKV2VuRR7VH+Nsy0aRVoaojnQzDKXdaYoNAfRI0SiQKFPNFFbdkERveEoWwg9M6dpfKZTDcoUxCw4FB6kJOSSVI26cJEgSU9fa2TK1FaTo+SoE1IokhQc7Ug1i1aQIjSVhKSI1tCPNhOcyAijOFajsTgp8BKSkiO3HsGxlCRhCGYsfp3iNuFyfJyXkPUoZxgUCCXHPIVajaZrIzEoukKQZ5oUR49FpyBJsFZztHIc08rIMXu2xw4tJKZtaaaWuC6gnLJtjhxaj4kZXUj6QnMTM5U2HJEM3jHLkqK0tIXmcmpxE9ipQHCOVVkxALtCwqIkAY2VDCmg9olJbWgKRRYVAc3BFGgpCXqUg7RFwZWQZAGN1iAFsXOQBceyGI+3EPRak6RgVo3O4L0tiBmikAQ9mstH1O/ohwhilO6NZuDRnA3j4zzjPgWZQWtSGlNP90WBU4ogFCaPuNmcxwT0nTV0SoMYA96OWiPkmAGxLyyNMagQKHygsSPWmmagn5TkfgCp0argmEepVhYjtlVmqGNCmMTB2lFrKzJ7a5E5M3ECtGCvFZKClALH0gKCaUwIpUfcrBjlcgetyBlmfkR6HswoO4g5cTTjKD46z17AXgqiGRuEVssR0SsCAtgXhqTGi0fQo5QpeUhJsNOKVJcM+dbMLgQpaZIQI1JWCoIUSCFu8b2jSfVgNU4KfB5TvrtblK4Qgq2RdEKRGCVhByVRt4b/o5YchcHKgEWMKMhSQU4ctEBKxTx1dLqjk4FsBKjM0XoEjklo6FVHYwbktCYawUFnDunIxEWia2lzQ8qObA29dAgkpVkiRMduaAhJkWSgEQFhBZUAoTONEiAlMUV6A6REJIBJNDIgJoJyIskrC/MCVQXadMl2uCYDwbd4HElmfPAIpTnkI57A4BqUUTj8KMczhkM6EnD41CO0oA8toW/H061oiSEQRURlxaBbpFQo4dinLYNqyWSMsDSmIVcRWRgO8kDnGvKQUL2gKweCiAhTslUHlIaJKNFO0KoGoSDHyCHvEQjKWMCQaIseoTUujRkN2QVKXyALSxNbpNS43NOoHiEz/RCQhaaRDqH2xH7E+WYpmKg5LYlODaTsIUo65RBSELwBPWJjHw2XxNzgyjCe2xFE6Nj6G5zo0FpByvg4kO0UWSkcA9fhGmd6hNCj7yVEslJ0csC5gWgiWcDRNUglSBaa0BBjANmhcqTzR2IOZK3Z5z09PdoIdFQMuUVoi/OSIQZ60aL1mLjdDAeSSnTZc0xHNBqTNUpr2nQkR01kwsFEcoJJL9gfHcd0wEVLScbTIcyI6B2EZ1Ce3gz0y4R1hsXDDb/bv84u3NCEA4W03AxXPF+8SFFWHIuB46GhSx3JRUKAVvbIUlHXZ/S9pG8zN9qRRaRPPVkKQgK7tjgN+5TpG4fz/biIlkazfGMzOWaClCADPkeS0CA1jUyk6IhqfP84CaI/IuhojSNMBEk3aDvQiwFZBMDRFj1BRrLIaKFpc4NMAiEFe3GgTS0SjcmGIw1CZESOHMURmQ+YbFFC0YiGy3xFTII9R7g9f7WUHPIBVE2Mezo1ShaLcknOiaNM5LklhEgjBdpIkssMBjoDbenR7oj3lwB4NUVmwdEfSHmUBLehBTKbYsPjt37P+eYBRa4/LGM/IrV5X1Pz/tJ3/pQe4hNF8PiID2U4H6+BP/bYj3YwtxLW9+0Gf2sd/aGlQPD+Y2+fxd9v7vB/w+bi/e2jB/8zOq/xuH+acOzDm87L+zzu3kV7zUqeMPgduWuYlAsEJzg5w0wHJjtJ7CsKfRwzGOKElFuMGA1oMip20mFdZsIpGY9WHWs3I6dEmwLCSKouQzsgZ4qztMC1ijoElK2oi4JwPfB4ntjIOdYL4maOKAxTvSAiEeKa2bVC31i6kMgiclJvUMqSY88qz9BlzTE29MlxatYwBNr9kdVyiSmmHGg45B2zpsDWJdIIpl1JIafEMtHljqVYkowmpp6ZLynX5xyyo5oKloMhZguiYW5qynev6W3mYGCTV+RYw7BnkgoKYXEMtCaw9hVWZq6blsoJSrWB6YwLd8PkGqZDwbGeUPYCa2bEewvswrB6KyOvHfZkhsFgvUH4QMazbD0ksKWEAeaDQpMR65KTfkoQitIkhNRU3uKvJWliOG8TeV6wvzWNzduItBY5qzivC5SU7DUkI1gnRQ7wXu7ZyITSBUcD3bFj3vVkn8hSstoFNNBXmq4QnHg9rohqxSoLigStlRxk5jQxFloa5lpTZUlLYh8jmz4xhAgyMTtGCu8YjOa4KDjdjwZZkmfaBEqf6I1EV5LTvUckRs/PEFnVU7z3yD6yOgyozZwYBmwbqDtPtgYxVZy1mbJTKJOxyjArCoIUUCvuZMmgbn0YMTO5bhFSkGaGk0Pk4HpSoUiu5ySULHXNIwUnh4YkEtNibMLmvUcKjYiZ064DkTkYQxCS1TCQ0/iWPG27McvBGrxSLLvuVgsO665FAZ2xdFKx7lqkGCcSy6ZFpcRgDY0xbJp2/PBLmeXQU6RIJxXHsuC0bci3Hou5c1Q50yvNjdacty2JjMyj2buOASc1yljOumb0k6TIJEUmrifhuRaSTdsjB0F7MkMLKGWiOx4RpuC860gpoauSIiamwZNvfQPnbYtQkiKOidnTfkBmj6oLzo49SYz4R4RglhIyjReE896TcqTU42Ro4UZsbKxKzgc/XiBjIgqYDw4RI3lSsTl2aC1o7Jg7sRkiyiiUyKw6jxWBTo1ZO5shEbMk5cy6cxQZjkrSWM3Jrf/rsZAsXUANHm8Vey056wMpZ4zMzEPCuoRTgp1VnPYRqQQ67pl4SZkMQXpujGfVjSFc+3DFBEudLFl0bGVg05fknCn9DUWQzEKF8IadcZywACWwusUIzaxYQD4gueZudYrPUyw9MmbmSpPLjmt5zXl1j5wFV7v3IEPVSbSaorNgXU4IKuGiI/mAJUHs0WxZtuPnQSgLkoTaWFK7wxQDS7lkulijFxkWllpPSHJMI1/rM7SRBNczpJ7azkgxk0RkZdZICd4E2tyyFicIIchJsNQrTBK0ruHgBZt0clsXSOZijokGJx1Hued88pBMRmrFxFXUxYy23SNyZmPPRt17kFSppAwWJz03/oa7q4f4JiGVxmKZM0PIyJYtp+Kc1HdMdI3GYpQlSc91e8WmXOFlSZlbkBkpDIW0aK7ZyDU5OxrZoiclZSxI3YDIjjN7QhaJrdsTZWalT9HR8DhdsalWSCHZxz0xRuaxRJoZ0TsWXYm2BUFFnB8oD4liWo/EuzillhUqCZwcbpugTKEtUzVDziTNcU8TW9bFCUobDqKhLmpyijgxUOuKWZwjjEIYmIkZ07okio6d3zIfJkQH8jBhogyVlQQiR7Fn7RfoaoGbgjgkaByoRKlK5nlBKCW79hqdDNJntNFcesksTYjFAu07rDDUokCmgakqmRcLbJ1ofIvOmul8itpK+iqwKjbcnT1kMztHCMF5eZe5XOKVZ6lXnJk79LuG+u6GB8Mz/JY3iAOsqjXD0HHMB1JMzOIUMVliJpKN2JC6yKG/wmXP0p6gbYkIj1mKCbKYcBBbQhGZthNEteJC3rBSE1Rv6ELLkciJLIiyROk902gpguGYG1rXsg4ThPDc5IE6GGy/Iq0cnTyySUuSDmzlgbmaU4gSLzw34Yo79T1EBOHeYarn1NR4AiIJNvkUGUf/aSFKJmZOEgkZLzjljJgEJluEg6makYIHmTg3CxAbrnOHjYqKAp8VObScZYVLimMOKAlTb7BpQA4NxT5RlgItCrTVbFYn4DOhd6wnJ0il8MmNtEtnOL/3gMl6+UE9//Gq9KNip7Gw/bCG/zRZzkdGC/9F9X3+yB/iD3b1adtnL8vzd4qT+Oj2X6+5+BukTH/j9ge9wnjD+3aY9w9Gfr/b+gjg91Mexro4Zbhd5beiwKg5l/Y9XHfkhWLCb8q3KUXD3efvYnrHa7vfQx95dn+H31aPqAvPer6mbNcczZFU9twRmkeLI4IGs5xyb/2AX/A6Ugie6Fb8zr+O8QHRNzxxXfLa3S3JS+74c94+7THyiBgCZ8OUX/lHKG25d5xwcxIgNqSQeHj2kB/n32ALxeTC0U17KAeiaHhi+Qw/bl4lCZjaBfuwR0xKOpV5ytzjp/4X6KnlTrrD5WE7pot7x9OHmtfm75AKwawqGJRCVJbBOT4vVvwo/JKyStx9asPlWzsCHc1U8Kx8wM9XOygEZWso1YGhuKYSludvTnlteoERnjMjcKbiOu9JU8vz5iE/Db9D0FHEguk+crMYqRPrNzSX6yNCRXQUrNKc7fCIwXc8e3HO68s9Yirp3cB9t+BQHZGV5OHVgrc3u/H3XyhOtisuiwtE1/P0e3PeWa2wVUQKw2JY8N4koecFD1ZL3p0osgoMUfFUq3jXOjKJJ0LBtlJEbfELwzNU/Nh0qNMZ9+5aboJDS4/Iiue85ccTh5KCc1FzcI4QO1okz6cJP56ORvhVqnA5IuRAzIpn84QfyCMyRza5wvUdu9SSDo6HP73m52ejKU7vWoQcQ4s6LTj/zQ37Z0/IQlOESOEyl3NNVIrzG89vNpYoMzpo5r9ruN4YZDY8eTnwy/sgtEEmR9kf6TZT0rzgmUHzmk0MOuGy4NQJHleKwSgebAfe2liOrsc6z/1j5o3VFCHh4aXkejHFY/Fa8uAw8POphQTnxz3vzuckCU4rnrrZ89OzE6IQrJot1/UE5IiGffb6mlfOT4lSsnaOvS3IApzRPHdxxc/u3CXJMduhN4qMYNCaFx8/5mf37pIQTEPAiTF/xGnNC5dbfnJ2ShKC6nZlPQK9Urxwc8UPlxsSYINHC8FjqRg0fH6348fLNQkoUsbGwGOlGIAXjj2/XE2IUqHxTLuO60OLFoIvbWb8ddd/IMRce8/VdIIXkvs3W367XJARJCE5axoeLaZEMg/7I29MNAhPEo6zY+C6XqMqy/m7V7w7n44r4AqeOPRcLWYIKdk0Pe/V9nZyI3j6MPCToiBKwWnruK4tWQi81Tx9aPiRnpCE4MQ59hJytkQZuH9z5GdnE2LOrJzjMJkBAm80L+5afrCqyWRm3hOyJGFpReZLbcPP5xOydyxzwANXjIb/zx+OvHI6Q4nANHTU7e9opgkdEp/fCn4+O1D7xF1vmcvA79KRMgmeOy54ddlRhMQyFExaRyiPGKl4Np3wm2KLkj1VUTK1Nbu0JSfBg/SAt8wOLXu07Tmpn+Xq8FsSiZNLeE+/hdpkpNhznk5p6gEhBF9efZ5T+TzXYcddvWQ1THite4vgPOfe8O/5S2LKzDYFf26+y4WFQOJOLvl3/CuC3jG1mn9W/gXNbEBMDPeqJ/jnN/8viIIhDXzX/Pe0kyN9e+SBfYp/1f1/EUrghOP52cv8vPshWUkmeU4vPEFKGjwvT77AK91fAYmSmhwDWWU61/CwfZHXildJRUb3EpEEaZLohOOpmxN+Id5FzgxFbxFdQR8e4fuWp+wL/Cr9jIxEdJqVmLJLOxCRp4YneTO9gQ6aUlm+9vjLPD7dURY1m3yHfx3+NUWMFN2cE7Pg2P0CIRRfmL/IW/JN+ggTlVkXp/za/QrRep6aP8nv/W8Rlwe8rXhi+gxbtUMpyWmccxkviOmIN4Yn8wMu9SVZZk78hJvYkvVAKgTPFU/wi/43qOB5UD6g3V/RyZKZKvnH6rscTEOaKJ6dvsjAwNvhLRZ2SQiRf/f4XyJSycPpM3z59Fu8PbzFVE0hwP9x8c9JQXDH3qe3e3Yu4fs9Z7v7/M6+jgiwNHdQr57SXr6LRvH0c+e8tv4JKk2o05zvnv13XCwPFBvLc+XzvOFfZx+23BMPKFXNr4+/REbFU+EJ3h5+x9vNuzwonuR3/JbXul+hFLwcnqcUNTfiwAN9l3ffueCXu9dIQvC5O19gs5zQLxNn03s8mD71wWryypyMC9NREkNipdcYaUkxsZBrcpSQDVkpHq6f5ifND8g5sfSWq+5tct0QdOSZk6d5pfkdWiTuasM2bjFxi8iO56Yv8JPd74lx4NRM2fl30PKGlAqe0fd4ld9RqsQqOQat2acLYpY89Hd4tXqEyD2L6pwkOvbqmpjgKf0Er+vfokxiUc1IUrATBwYGnlcv8NPwCjknZAdFUZMkdKnnGZ7lV+JXZAkmSCZ2w2XaktLAczzktfhLQoikDCu94DI+RhWKe/EOr+ff3NbmkY1ouMhv0PvEk/lFXrc1Mg/EPnA3rHjNjqTQB16wC28wrRw2FCx3Je/oFmYlS7HkKl6CFAQR+Sdnf867b75OCIEnyyepZtMPi9APBgkfmSh8ZjH8fgORP3LXZ40bPuwUPqmU+gM906dORj6yj0/pQ/6ht39Az8Unuq6/Y3OR0thACPmHh49P3vKhEX+87VNeyT9/+3/ml/tXOPgdczvH256t2VJSkTMUqmQbb9joU5JIbOM1xks4eOhgXxxZc4feFWxNhGbAGMNkUrCbDCwPBWlecBNusMpSHwNFEuwm3W2IUqJRLQwe42tENFxXLWs3xadAk1ooNHNXUK0WXLFlzRKHp6cnkVkcM4US3OgblmpDh6ZXEERiGRfoXnIxXLNSc3wew6+GOLBQC/pdxxV7Tu0SSQt9j9OB5fQOSZdchhsmrcb1LXY9o2VgZtYcrjveUw1TZ5DCUUrBQQ9sWkudHAdzxHiDcgETFX3pmNandCaxnTkqXSOExCjLdd6zvpbge47zgBGWjGS6XI34wfckkshu4tBZoYPCeMFN0bLpJ4QcaGcBhaJoMkXS3Cwci2ZKOyQONiGFpOrvoDnnZiZZ9ZphtqGdllAZ6iYhXORCJZY3jiElOjV6LhZNoMiC61XB8uCJE02sDHFqWSWD0obHNrOJkjZ4Qgz0KTK/GYkllzPFoom4GEkx0RnBph1JPhcTyaJPOEa5SGMFJwFUobisJUtlSQmUi2z9wOp6wB8HrqaaST+iO02A3URz1o5UoutaUYVMFxxTNLuZ4d5hJIpsNejWIaoxUfyqlmxuBrJUbKej7rQ2BTrDrhCcY/AhsRUR2Xts67E+cTPVTHc9GE1XmrHgHBboMONxXbFuOqLU9LYcm9zBI1Piejph3XZ4PcqOkhDMug6d4KKu2fQdTim8UngpWfY9IiUuJxNWfY/Xliglg5Ss+nHKcVnXLNsWp8ZMhl4bNn0PKXM1mbDoe4JRSMYE603XkVPisqpYhLEQlilxsAWbrkUIwVVZMQmBJMCmzFYbToYxfO+6LKlCgNhT58B1YThtWpIIHJYVBWDXp8S3j1wpw2nffYCbVTlThECREldVyWnb4kVkqyUqZ2rfUWXPZaVZHQe8KGjmI3axPvaYlLmsRoStk6OUKwFT51B5xMauuwGvFL1WJATzYUCmyOPCsBk8TuYR9WsUm67DyMRlIVm0HmcEScCgBGtTEveOx0XBavAMYlwRb4Rg3XuQgsvCsOgd2IjRmUPObNrxvuuJZeYiSQp0yuw0nB8vsf73bNWOOipILSY6Ghs49RojerqipcyW3liELjhUjpOhRGbPIW4RXkASlLpiLw4szYpsEjv2KA+FiMyXNdfxkrW4x9HPuAke+kh18QbTdGD7RMl5eYccwpjiKxXP6Rf4b/I/Y24XiLpAK4U/dOjS8v3Lv+QV8VMex0es5YYvTr7Md07+HFkafnj4j/yn/b/l3fg2G3HCH5mX+fP5f4dZTvhx+z3+w+5f82b/Oou45GX7Jb6r/hsQ8Jr6JX/Z/1ve9L9lzhKvR2lOT8ecFQjFpb9gnmdEcUCpTJOOrNhATFylx0yYkZVA9YmjbVm6FZnEvjpSMSF7j1EF3XRgdpzjB8ll+5iSEgXYKNmpPWf6DsJodmKHToqpmDHJNdvhirvmPl+pv8mL8vMUqwn//p3/nZ8Nr3LtLpmrBdSZQ9whk8Aag1aKa25YxAVZQStaiInSzsaAv/4RVVsTS01nA0JL6lyjs+IiXLCKS3yl6FJPJDH3MxQ1F8MVp2aNLQRuf8D5gVWskYeBthrYVCc8V7/IP3n2/4GalrelxXjxjznyv7z5P/Gb/a8YYsdTs+f4kzv/lPuTh5Ay/5/f/0/8un2NNjTMygnedlyG95jKOekQUIPkGPdMfn+O/smG42WmNBrx9S3miZ6DaLgTzvjmne/ytZf+7MOS5tOKtPdvyxkhBRf9I/7Vu/8rrx9/hRKaZ6cv8N/f+R8odMn19op/+df/gtff+S1SSJ48fYKv68/xuT//OrK0H6udvvf4L/nJ1fd53L/HaXnOl1Zf48uzr5PJ/KT7Md/ffp/3+ndZ2SVHs6VhT8yRqrdID9fympPynKA9Pg347FnkJTIrrvIlS7nCSUfKo2xqkdfEQXCdrpmlGegR7tCnjrk6IQvFtdozF3MG7xARDv7AKtQIIlu5ZarnoMaJf2t7NvqUIBKX7jE1NYmETopd2rFmTZJwna+p5CgvKkXJNm85lScE59nLHTYZtC3QUbPN12zECdkItvEGGQQmFZio2Zodq7whA3uakSyVn0bGu1wrzyZUDL3B6dGTt3aXLMuGo9hTtYYYBmIRUVZTUlKWNdtww4olT7cP+Orka6xevI+eFH9D//C3F78flOAfKWb/xj7jH2L7G2VZH27/9/VcfJqc6dN6ho/cJsVHphL8Ibrrow//pB5NkD/2IzIghUQJBYCSBtc3IDLKanLMSAdCCVSSoAVSKHRRIk2NuBqQNGg3Fm4qgypqTKEoZlNUJSjNgiH2mDQy6qU2GKGRZcSICmEDKgxAQmuNFAahJDoKolIYXSC0RCSNDIAGlUd9s0YRZUJVBnYNSQ5IG8lxZKJmC6lrCJ0imwDJI2RA1iN6V2ZBUZWY1NPtBirtsVLhicgsEGJEE9pJjet7pM8IkcjDgJ1PUENPgUXIMVVX68BkNcO4fhwdGoMqS0pZEHRLWU5JJWh1QAszJsAePUiHiCP5RPqIzBGzmiDaQB56rFoQlUSKgArj61fvI+CSJttxjCgRSJGRWZJ9RPqElAoZIkJmRGUxqkbVmaqoSJMSmTL+nS3hGNB9Im0sau8RpUIKSSaj84gQJmWUT+TOEwZH6gdcm7FS4xeG4bInyEQUmWAkHANEiN6StwPZjPIeUSloAlJrhNGIxiGURKQEUZJ2AzlnwkLjhxHdaaUiTzSyGrNJhBsQabx4GiEQUuJ9R8wghB7PNcB5h0oGJeWIydUKWQmyBenDiGRkDBoyIaHdgGDMcklzAz6Mr/sW9WnlKDtLZLIPeBJJCwplSDEivEcwFth9FsjbtfsR8zq+6UxKhJSQIoKQ4/smJQS3yFIpUYyTBZkzMqURBRsjScYPPgdkysgUR+xpHlGpo/Y2I1JC5BFDrG6DNEWKCK2ROY0X9vf3Lcb3rrjFp44T0DH7QiAYZfYClTNJgMxjSje3z3tEryaEyBACxWIyTkxTQmhQKYPMt5Kq8XVqRpyvJhNun7/OGSVuj0UGKwTZanRhSIf2g/sgowWjl+G2KZUCdByDmozgdp+3BzzlEaMrBDolohQYxsUWyYjQxQhUymjEiM2tS8TBIVxElAJ9i5QVMSOtHI9JGqVlKmVyygg/SqyMHN+bMo8/199OlJXSSEZzt5AClcYwRqM00mRsMUEjcSaiVUW1mKKKCZ27RsqCvB9IPlAVU0xZooJEuCMqgCchC4UtDYWMaGXIfUDo8TlroVC1pbx/D+X3KHNAo4kSNBqBRBpFsVhSzk8QYvQ+6eVk9BLIJeZYIp2hqKYUywVmPR2RxkeJkgZCRimNsSV6OU7iBALSeM2xxiK1xS4mt6jMEh0MeIHWhijHq5TMEhnGdOCcR4Qv5hbxKyTKQ05iRGOWBUlmEGEsjrQhpluUdRYkoZBCAQKFwg8BIUf0t1JgvELGDmULsgTFiJVVQaHSKOnUxmLrivJkM8qb0ppyN8N2LbWd40SHicV4bdRm/H26PUYVuOhQWSKkQg4RPZsgraGWU1oRUXJcMMwhQpYIpTBoIqCUQagE2WDceP1UElLrEUIhjYYhYScTwkRh6ynVeoWeVh+7yN8KTW7fy+qD65p8v+KXAqkNSqjxc0Vo5O33yTB6xbQ0GF0g237Euk8nVKsZcREoz2pckJimREn9YfHxQbHxcQFMFh+VvoweIiElQowp6FJJlDUjtcdHBBKlFFIp7KTk7te+gCzNH0jtlZAoOQI+lVAIqdDliAGWg0SJETGsxIhhVYweQBHzeP6mTO4johg/m6QU5N6PxxlQAYR+/3wWSKkRMD4vXRLFMH6mSo0tCzIaui1SZkiMuH9jMLYmB4fWFh0ViYgtSwadkKixvpEjOEDcAglEGglnUSRUGrH/QkhUUuPvFQ0yocSId5aJEeGcQEtNzAmRQEuDCONtGYESmnCryZVi9D0WUiNlQGWBLTTe335mF5ayitzcXLIs50SpyCaRyRS6JveJftfgVcnk4ZrT5z7392oqPvjOD+rYzEeL5Hx7DfnQOvHp+/xYWZ3fd1B8YnLyyVpbfOKBn1Rk/QNsf//m4pOv7P3tsyY0H/niMyc3t/fmjx2VP3zMByaUjzUYH99enH+R1/e/oJYTTvVd1PI+v2x/iJGGL4Uv8/Py51S9ZZHmTJuKftpiguIr8pu8evpTohds2jWf00/zM36Gkoavl9/ip/lVqh4mXvOsf4KfqAZTWL6avshr6jeUfqBC86B7wI/tz1FlxZfDF/m1+T2+FszklJd+Zfnh+e8RWvFS85D3uKESCeUHvuye4Af1L5CF5Nn9PR6px1ibkLLim4en+J79GbaNPHM5YzePhNNMGUpeuLzHT/zPmUwMz8j7bMOWUAVKZXjxjQe8+uA9ilLwwDykk45GHZBD4I/rr/Kz+nWkFDwV7tC6iPOPKPqWl7YPeW3xBroU3JudUliPqz11PeMr9ut8r/klKQ5s7F3OZ4Yu/RrtBC+/tuKV9ZvMFxPO6wfUbzf8Ov4ebUq+nb/Gj/UvmbgJszBhdWP55fItdJK8/NtTXntix2wwTJ3m/PKMH51egE+89N4Zv7lzxLiKUk15ZnjI99cDAsFXj0t+V005RE9uMi/8es+PTiM6ZV5+feC3JwV1n7AJXvrFgR++MCcBz/3mwMVpSWkF2kW+8nrPXz1Xo1Li2d82XM0tRTLoPvCl1xu+/+IUEjzx+5Z2btkVI3Ho6z++4nsvn5L7yMNHPUOh2csC6TN/+uqO//hsTZkSDx47vEgc9ZiV8a1Xd/zg+QWmdyzebdGzCf3DOXrv+dZvDvz1k1MqFzlvQbc9v6ssRYJvvrrnx09OcQfPZB/Qrad/YoXViq/cCH46zcQmcNILTm6O/HQ1Ekm++Gbk108JZj5QNgXPNHN+fseQY+TJ17e8fn/GRNcsk+aZR4Lv3Z8hXebLb13xq3XJ1HmKEHjh8SU/enCXLAQvv/uIN1crJtZhQuQL713w1/fukWTm85eXvD2ZMvEOHSNfevc9vnf/PlJmnr244npS05QlJme++uab/Kf79yFIPnd9xaEsOdoCFSP/6I03+OsnnqTOnid3OwZraYsCnRP/6He/4z/cv0/lPA/2Rzxw1AYVE9999x3++u5dJt5xr2/RKTOUJTZlvv722/zw3h3qLDhvOyY58FNtsCnx7UeP+eF6Ru09y96zGFp+LqYoY/gTv+f/FyJTKVl5x0nT8qOTE0zOfOfyMT9Zb6iDp/KB5443/HBRo4XgG4+3/HIzoQojqvaLSvCXTYf0ka9dbfn1YkY9OKoYeWl34K9PlqSUePlyy+9rQ6sTVUh89fqKH500hBj4wrbmUZUIomMeLC9eGn5w2hGHyOePU250R8hHps7yxcsZP3qiJbSBz71t2OsI6kjtLH+8XfL902smMfDs1YLGJpI9UGbNV9+e88Pzx9jgeHp/iicR1tcU3vDyow0/fbDFDD33hjWlc7xmrlDG8uXhWX61foNaZeq+5Nwu+K0KlJMpX1t+i786/hLbFFQ3lpm/gz+ZYpXm6/WLfP/qVXSCmV5xOj3hZ+ENZILnDue84V7F5pplOeVz6hl+PPwEieRr5Zc56rcZGJilKaY3/Kp8DWUtn1v+EdNqOTZGt/Q2oUbPybPVi1zkCxblmlLW3DcP+I/v/u8kDQ/rp7FdQR3HpuHpxQv85e7fEJLnqepZCkqKPEEKw1Pqc/xV929xeB6mJymoqfMMQ8HXyn/Ef2r/EhMsD+VDWt0y6AYbFV+x/5Qfqf9AbiN39xuCFHRlg46GL7uv8QPx11RZcmoeonqJ73+HlQUviy/xM/8T6ApOwx20KcjqdQpb8WX1NV6J32culqzNKQ/t0zzmXRSS51ef51H/DiftOZvVPV64+3WMrgD4/MmX2cYdm/KUmRlTp3968wOkkHx5/U22XHMW7jFhyrKf81Z+E1kYnqye5Z3Dm2yKc6ZiSuFrfnD8K2JKfD6/wFvxLTqvqYqSr82/wo8OPyC4wFPuIa3uyRyYBMlXp9/k9/4tssg83Dwk2cA+7ChUyUubL31EqfAhHVIIwcubr5NIxBQ5M3c4K+/AbWH24vwl3mheo9QlD8sn6UxP1w7ITvDt+bd5Zf9D3HXP6cma+ukHvNU8Zugv0d+PnL94n7uT+8wmc57ZvARCfPaip/iwqHtfxL22J5wWZ7zTvInwmYf2SX61/znb4ZrT6g7PPf0Cyo4Qh5eeeYnpcv7B/q+HS355+CkSwb36SdIxoaQg6cjp5Jx/v//XZODJ4nPkPEXmMwRzvjZ5ib+8/DGpH3jGn7FfXeBiR5ULPi9f5vvhe+gQeE5/nqt0w0H0SFXzbftFvtf8NTpbnime5podbeyxheUr1bf4vvtPkDVPlk9xzI69OJJ7yZ+W3+JH8SeIELnrT4ku0KMwuuQb1Rf4fvwRqhFs7F3sxNCEFisMXzNf53vD96nlknN7jyJYnEzorPkGX+XH/Ii5nLFizTTX/FL8AqMs3xTf4Cf5J0zylAlzzvIZr/ATVBJ8Q3+Dn/JzplRMc8198YCfyFcgZL4mH/KLcKBKW2rWPCdPeSX9muwTLy1e4PF7P2Pup0zMlGdmT7OttkDmwfRJHu/e42Ryxmy64OU7XyOnBPIW9vqxYv1vNDh8euGbP1L9v9+33nYVf1ub8sme5pM4WwEfydD48FbxkTr8U2U/f8/t7y+LOh75TFP1hz+GD5YY3v8S/vDrz9z+cOTx8Yd+tiTrPz76t/xy+xN27oZFtcYvPDfuEeVBYGaTMeE4X7PR53jn2McbKkq0smht2aobVv2CICJ7v6OsppAKUgPXdcOZOgUCjd8jhcIMYKoJF+4Rp3GNs+CriJCSIhh0VFyKK9aHGhccvY1kqymDQTu4rg6c9HNcCd5kfHRUnUElw/WiY91NyL4hi4DDMTNLJIbHXHNSnTE0DbHryWvDQm1gC9emYW1WNF1HSJE4FSxEhYgD19wwGUqKWY0sDQe/Z5nn5D5yGa5RjyNlZKTDmIG1LxH3puzMkamcEOo7hFBxHQ+c2Tlm0nA9PMZeB4qqpFhOuU7XrNoJw8U1h8pRtBkhDcViwU3Vsr40xLahLQaMF+gg0brk2u7YtAtaUXOQAe0yVliMsFxOHKdhgV99jkYbYu/RfaI8Oi6ngrNdYJiWeKtIg8O2Gekll0vNybXDa8lgFFFJJn1Eh8ijuWGz9wQliVrgrGTaBIxQPJ4pljcD8RZR6WrL8uCQCS5WltXOjSZpo+lKxXzvECFzMTcsm0BmXBXfl5KT/RgIt51q5o0nxYQ0miubOdkHtDFcTw1zfzvJ85H3ysz9ThBi5KqElSjwbYtuA+205NQLgoSdhVmSCBcocuY9kzjvEsldcpAOkyUyNsTcc1gK1gdDsg/oywodM1oYmhhpVxOWe4exdzlKhc4SG8eAyKvphPO2x2tNpzRZQOUDJsHjSc3pscUpQy8lUSmmw4CKicfTCSfHhmQMTkoGpZg7hxXwqKrZtC1BCrwQ433DMKZST6esuo4EJCForGU1jDkel3U9GsbFGEJ0tAXr2++9qkoWg4OcPqBHrYeenAXbumLqPdnHkW5UFJy0LUkKtmXFLAaUa9DZc1VaTtqOkAO70jKflZSrFf6dI4+F4k7bEaRibwyWMUDPhMBFVXHat6TUcNTjVEJHQSENF2XBfQWtEDQukkOiJmNT5lFpOWv7EWGr5K0sasAmx+Wk4KTp0bxKSDcEElMv0MJwUXjWnSSocXrhNEy6gAEuK8dqMFAIxLzguNszO0aMTjw2Lcvekk0mKkErBhZ+pHld1APLVgMeaRVNGVh0BcoqrsueRafHiVFhOdqBNTNCDNyIPTMzR6PIHi7cNXfECi0sXTEwnyxJoiYNmvf2FyzjBFFYujJio6KsK9LRcZWPnOoFQ9vS6IF6MqVOR2paLsUlZ+YOQXuaeASXOevP+Av13yLmisl0xr/p/iVvh7cAeFg9xV8s/58Uyo4TRcE4BZZyhBiQaEOD7DL/5vC/8fbwJjEFjDIInXncv82JPmdIgRAiXkRKVSOj4DJfsFYnZOEQSuClp4o1Mhqu0iUruaILPS4NOONZmSVSBK64YJWXJJFJMXJIO1ZpjUByFS6ZxQnZjWnIR3ngdPIERbXkurmgjiXJBeT/n7n/erYky9I7sd9WLo++KlRGRmqtqrqqu9FNQgwwM5ihkTQaX/gwRv5tfKLRZmDQBBpgT4OQ3dWVlZmRWqvIiLjq3CNcbsUHvyEzMrMK3SC40/LGude3u++zfW3fS3zrW1qySRtmTUmUjo3ekpIPXtwoWcYlB/Iifzz5u+yPLjCazTC9HPaKsaRIJkgh7+2kAnzwNL5GCcW/uvGP+Lb6CiU1jxXX+G8u/u9ofcsoGSOjpPU1AJkucNayqZbkowl/cvsf8FXzOaGzmFbhN47jZMUeC1SWETRY21PYjFxmHDWHTMOEF2ev8sL+a+h5yaicDPTTbkuqcvS5N/0B7eBOBA+wocf6nsKMH1DM/s3hv+TT7YdUbsM02cFLw9Hh1xRtQlaWuFVNm3Qs9AHtuxU3j05ZnVS88uKr/E//0/+VPvTkukQ+wKZzbww/lvtau5p/+d0/4kb1FaIOCCspywlbVbGb7fPLvT/igrmMEIIsze6qO33o+Rff/UNuNt8OEfEESCKH9jZ7+gDbe2zwCCNQfoHs9rjdLdkzMzariq5r8CoyTR15ecpRuMmu3CdIiRMBi6VghBAJh/6IhVygEk1wlravGYkRSMmRPWKu5jgxJNm3smVq5iAlJ8mGhZ4Ra4v0UMWKqdyhrwynccMkFkTliDjWdsWOnCAKy4rlcH0/GGFruWZX7BG6Idm7CBlaD8VXz+KSBTv0wrNiRS5zDAoZFUu5ZJc9et+zEVtSDEakKCc5jkfsyX1s6KlViwyCXE1Rfc7tuGTRjSnJ6KLDVT1lmyK+sWxlw+5olz/65d/i6aeeBQaIZgie2tVkOh/QE+cCoM4p6L/X7rB6/Fdu9wdGfkhLv59k6t5J/38Bi4r3/fuoyXx0RONRvR599g8YL3cn4vzM+OCxCJx2h5x0RzS+JoRA3zSsOCUpE0R3hnKKNu0hSKIMbOSabdiSmAyNpnIbonQErdgkNWtfoXxJzFPqUeB4e4xSUJvtgDs1GTLxVLTglshRTiVrYu8YiRKVG7b1mqA7YqbZ5hZCpHQKmUm2qoEkELOEOumJQBctEsXWWISE4Bqc7Ije0YehEuvGNER3iEgDPvN41eLaCF5QGY+ve7oEmqYlbAJNL5Ha02QNzifQnCF6RddV2HYJCDayRqeSph+Uop6edRERiWCjK1rXUVtDCGMq3yK8RW1WrMMp2aJA+oZc9KzbE5zdEnLLVlTIJKKTApMItqHGA5ieJveokSInR2hHJQRkYaBtTQZRHcUcoqTCIbpALCLL3hK0J5cBUUi2mSS6gFCWuhgMhUJIYlSsMkmYaqLU1MVwzVYNUbJtqUGCE5I2lcML/pwwYJMrfDQ4ATZRRC3xAoiRTTEoYlZLAhGnJS5oQjg/Tw2Kv5AD1t37gcJ2Uyg6LfCSgc7XnIeLTcI6FXQeXAik0WATyRGWznn6IqFyjiRPcN6is4ENKIZArRWND6SZRMZArRTHwoMSbPEIEUiSAULVJJY4SkB4bKkJ3lGqFKc0dSJR0YBQrE2OQDDxEolma4ZqukEptskQlh/1DhFhk6YA+CjZJimIgTpWENlmGYghybk1hsAADZRCsElTImClwCmJQwzUhxE2SYKHoc6FEFilBppaIVinKV5KnBqgj71Ud4PL6zSjk4ogQMVAq4aqukRYmYRaa3wKJkYqpQeokxRs0ozKe5TyJFFSaQVZAlGzyTWNUqQeQpmzdhEpIEQx0M0ChXcIb9imKUSHiJaNHqpfZ04gvaIqM6QS9Kt6mMMUxm6oir02ipAlBAkbrYY5NEM1941WyJFCN5ZO1SAiVhikitTGAoooAo3yQMSlIGWkSnowIHJJ127wqT+vDWJp0h5ZSJxy+OBwOoLQRB1plIORJGIRscMKC3rwntamIaQpiIBRjja04AI+OFZiS+NaVJqSSEOveta+RtqGumtodI9zBYScrbGYMhCxrF09VCM+WaGVYuVq7NEZ0TuqqSLVPdO4plY1ja454YQYPBvWYODC6DLZaMI4X7COK9q247Q/IsbIjt6nky2pzBBqWN9CSqJzBD/QYJaiZKtX1KHmdvsdMQTytCC4nnV/BkrSNT0NPVHCSExBwMqt8ESkdng/5GWNwhSsZNWf4YxjG7eQSly0BG9R2rP2SxwdXd+ilKJX5wZvEKzjik40BDnAi1rdY+IStanZ+Io2yXGhQwlN1VRY0aFFZOtWaJWAV6io6WRLLStqs2ExexWEJEpLvpife16/v7sqqRnJMYfNLWpXsewGSs6FXNBs1qQxh+gJ0ZE4iTCa0HcIpSj1hG23oerWHLe3ic6TxoxgPK2sOe4DemuwwhFjwMkZjaxpTY/RPf2uYHbl4t2xSCEYmfGPuC+Hd58QQw0OI9PveXxP+2NOukP60BGEJEjF1rR0oUduz0izDGc8q2ZDLXtcAZPRlOljU4waGLS+1+6fuIeUsvt1mTN7SuMqzuwpwgjytKSub9GIFiMNp90xT4yf/t51N3ZF4yuO2lsAGGnwYshLij4SmjBQtmYJWUgInWbd1/SrBmc9tfCAINgztv0JlVhDjIReYhOIBHod8AE2YUOwFtlLXHD4YLGZxzvPhi3eB7rYIlNF5zt8FDhg1a7oRI10ER0lbVtR2x5rU6okUMUWpEWKiE0twZ0i25atWlPLevCoB0lHdxfeto0VVdhgPGghqamGdWd7trpi7dekwiCDpI4VQgq8CKz9CoEgFzkSyVZsEVESvKOSDUIJSiGJoqWKW7QRuL7HRkuvLL5O0VrQdi1VbFh1a7LzaB4MkMWRGQ2qZnhYGuODD+/haMZd7f2n2g9pwb9t+/7599neP9juDu1OQeoforH9Hdpf3bh4INTzMEjptzz3vl/vL4R334Xv6y4emr+7T+/ub/dfey+/wGFzm3V/ykLu0iUtwkYKOSYtMvrDM1Zyy3iTYCYFCkniE4p8hpAC2cG8GeOVQAvQTmLUBGZTDvvjgSaxbkkkmHTwwNBC1J7FmUakE1KhkUnCWJRgA8HV7M8fw0XI7YoYI0VUaCeJnLLbTxGTMVW9wuEo+wzpBJENO91AF9iKFptExq6AoAgO5m1OYjQ2CXTCM892oI4cV0uKPkUkmt5pGjomoYCuYts7pr5AVAqfQK1hke4MyfLdMSU5WZpAptmqmp1iH19KJCcUfYZ3M9qYcFRvyL8NJEWAcUrpC/I+Il2CbTWzKkOZ0VAoyBSksiRYRex69pmipoY1WxIvydMxAU1ULXs6pbUpqvIo68kdsLX4DHaaHn+2QaQpQirKbSD2HrxkvvRIDYVXhESTbS30gYhm93RQkOo24CSMKzeEOI1mb+0gQq2g14LJ1iHikCcwWzvwHptIGqOYrO1dMZxvHUpIehGpMsXO1g85PRHmjUdaT6thWxoWVUTYHgmM1z0aQS8FSS7Y3XhUCqLUTPuIdB4fIirXLCqPRLK0Pbrz5H2kt4HGeMZ1wGhFqkFbQeY8xEBMYbINSAfGpCQuoptAzArWwjKrgcSwbiMmSUmrjhvrI/TBBcxyg5KSbCSRAiZeIaIlFrBbN0SpyLuOAEzsUOU5hMhuVROlouyGwmyTpkGGIRl9r6pBSFqt6bQaErpjJE7GA70skU4rWm2Y1fUgh0IwrypEhF5JmjRl3jTDYg+Bxfk1nBkMn526IYrBJTFuGoz3WAmrLGevaxDnOVhTZ9E+EIzmNEb22oYYIjoEcufI+5ogPCox7DU9EY/WkKxq8sKSXrmIaQOL7zYEF0lDxERPdl44TkTYrRqEaMi1R8ZAYhOk9yzHPXtrSV87ysQjlKS0Bi090nfs1gqfpIy7M6KSjEKKcQ0y1OwzQjaKXil89ExkiUIj3ZK5TQhC0muHw1KqAiUcgjMWqkQ6TScVreiY5SNk6DiWZyzUDGs9UnlqOkqXI4xCisCEEdqP6XxLn/RM4wgRBdJLpi4fcsNw1KlmnuwQlEc6RWFTTJWee1YjC6akWcqJ21D0GYma4LMCYzfMugykQsRA0gR0HZEi4FPYS+cDXaxvSJaRUa9Iy4wwg/30Il45EjtGBsEolGhdsAwVWa/JfMpC7yKiYJxOSEXK4fJrpsWCfDxj1S2BwJgJQhsgUOZTRnLEpfQxfHSkOiGYAEayI3dpjRuSkbVnauZIoQldZD+/gDKBrt3S0DLTu4ggidIx9lMW5Q6dtmzqJQu1i/KOCMzFbKgR0A9KzYwZUSqoJNN0hjISK3o2ccOO2EWrjFyPyciGuTaKiooxJc12S1GWpGRIMThBlv0JUzNnv7zCsj8h0RnjbHK+l8b7N9+7//a+ZWM3ZC6jVGP2s4uIIBlnM8aTBSKKcwPt3l4tMURAZYZpNEyKBZfF48QYMSTEJrDsThjrCTQWT8RFx7jcoShGrN2aSTpjf3TPsHhIOXi0GiHEIDv3wzweavvZRZb9MVu7YW52cHaoEl8uJkOuQQys7ZpFssfsAM5mS0bJmAu73x/LXRjJjyiL96tF82SHUo+YmR0SlZDJAqEih+ubjOWYvewCd0kvzyMWa7emVCWFGjFLLgxKs9E47fGdYmFHyDRh07b42jMpRkTGONuzCClBCda2oWstpZ6i+opOJ+yO9whBYF0gFopSTQluyKlamDkaRdNUdKJnGuZDTRsl2Ul3kRJa37PxK6ZhigUCsKfn0HqUEWzLnJmd03QJIp4yYUwmJTY2bEXNVIzxbo2WMGaCChrnPVtTswg7gMdIRUY2GBApnPSH7KcXcHlk6U8wVlOaEt87TvwROyyIAlSUpCrF+GSgZFaCfXGApSOLDSZqcjkDDCIGdsWUlJQQHVHD5OqUfJNwVp2xmOywPz94WNDOc/lASHEXtnTniUcGB9IQrLhTy+K+cEGMD6m835ef+zMuvtfvd7ZNHqGN/yRa6He410+0v56ci/s//9igHm0zPNTl4T/eIaG9Zz7cMQQf7C9AxLuG1522n13iN+E/EUUkVTlZUnBsv6NanfDM+A/5cHRG7B15UjDqJyynG6wPPN4/xsf2Or6tMPkeO3bMOt3gdOQZ9zjv97dwIeB6x95RysnBGhs6nnbX+GZ8hNIpcpZyUV7mXT6AquUZf4lv4rfEMqXfVlzcLlju9MQQuLS9yK3JeghJJ5EnDke8Oz7Cq8iB2ONkXBFERe09r3ZXuR7fJSjNvrrMzfqUsJjROLh2OuOD8iNCqZlkjxOzSOVrilHO86MXub65jnaSx8RFWlsR1BFGj3gufY53/fuYoFgkB8RUsO0tWmY8W77MdfsuPiZkyYRgJNaf0iSRV+Ml/vL416i4YZTvUJCxjGc0257nN0/yQfcVMfGkylBsNIeTSO0bnj4+4KMLJ8hJhulLpk3JYbrBZZJrX8z5aG9EmwdslzI70dwYtwgfeeI7yRc7kT4XtDZy8Vhx68pQ4fiZI8eXC4UN0AFP3nT8JjfIEHhyAzd3EwJDRe+r39R88OwUJFzYBm6PItL1OBV45puW3zxR4gQcrHqW02TwsKnAM19V/ObpMU5G5htLO8uJUlIreONGy9vPDuwu4+OOGog6odKCl79qeOepEoRg3HhCgBAjfaJ46cuK3zw5JmpF2vYU1nOcSnopeemrLR/tFKQR5ptIGnrWM40Lnv2bFTeujFFaksvIjhiK9sU08tS3ji/3DXkqmQXFaCO4sWMQUfDUNzWfLxwmCaRSkZ5lnB1MOXM9r7mUarbPoZA0SvJsJ7iR5fgIl2+d8NV8AQi80Tx+uub6/sDJf+n4mO+mU6IQOK14/HjJOxcvAoKLVc3RaMQdStlnDo+4fvkKTkr2qpplMVy/05rnjo9468LFgcK2btimKQHojOHlW7d469IlvJTMuo5Oa6KUtEnCq7du8dbFi3gpGduOIBW3Y6QzmhdPT/j1OU1tYS2SQMgKGmV47egG7164OHitJSR9y7HMabXkpZMN781LooSEyMh5TqLEjgp+Ps5410tc1aGiYNE2nI5HgObl9REfTqagJNIYHjv7ik+mFiEEz687vp6sydeBvIJrdcn1mUcGyfNL+LbcUhhHEQ1Xzwxvlxvwgme2OTfNMZnxiEbxeJfzyYUTlBBcsgWnyRmKJVElPLnd48PkFoLAJXmJVbJG6yWCjmc3j/FOeoiSgYt9Tm0c1SiidM8L9RN8JD4ni3Blm9PUS7psTdLVPH/0OB8uKoQQXBBzQi5oRINKNS93T/G++ZyEwNwX1GcrvGlxmeLZ48t8XH6L7RqSRJGZi7QSHIrfmzzHu5uvaJcdZjxnpBOOmlMCgdenV/i0+BrZ1WhnmArDKh5iO8sl+wTfXthgk0gTYL59km+aLzBaoWeP808P/4JGOkY6Z26mOPcNEDEh5V8e/wO2fsMoTlnYfb6tvkRKyZP5s7zBH6KNQSL431z47/l4+y4heA7EBf6k+Sd4Ai0918rneKd7Ey8DB+oCz+kXuVF8zVzO8bHn39g/IYjATrnPilOcs1jT8sLkF/ym+nOE9Oxle9R2i++OqUTPy/FV3vdvErvApCl5hZ9zOj0hTyaUesKfrv8ZSVIylTN+If+Qb/mO0XjO84tX+bz7lK1b83j+BDoqPu8+IZM5Iz/in9/6n/HO4WLP++u/5DjcQirFG7M/4oXR6/d22TsOywgn1S3+w+Gf0YWW0kz4vb0/4rvmG6SQPDt5CaU0cI9u5WEdW0TQQvO39v4+H26uE4k8W77EkT3kdvsdC7nLBXmRT7cfEhU8M3uRdX/G7eYms3TB09PnHqky/K7tfj1qLzngHffnxOiY6jGvjX/Jd/4WRToiDwl/dvNfEEUkL3N4OnCyrGiMY/fq4pHXvHPde4GL87l4hPqYypRSj/HR0/ueZ8Yv8vn6E0L09F3HPFnc7XzSn/Cnp39G7WtGqsSIPVbuDIDHxPN8cfoV7cpR+5Kr4oCb8SuiFDxhL/Cd3eL7gPWei03Jkb0N0bOj9jhSKZ3VbDrPE91Vvph8RagsjyWPcerPBjILaXncPMHb/teQK8o2Za1a+tDTpB0Xbx1wQ36CLBQ72QUa2XLWbeh94DlxjQ/cOzjjmU5LSgLrZovtKp4OL/CBuIENHeNsThrmfNGf0lLxevIzPpQfoF2gtAIjc5biEKc9z6c/4wP/Pj6RSJ2wCAXH7iaIwLXwMh/H9weSgWiYZTscxxN64XhWvcCn8YOhQKL2XFJP8EH/ATFVPGMv82X4GiEDRM/fdK9zKFeMr+3x4oVXODq6xfHqmJ3pLk9eeuahp3xPBu5CjR6SjKH3fUb7Q3ruw67yh4XlAX32p8INj5K7Bxbjo+/xwOefvsV/dvvrybm4ezUeaXA90o6IPx15+X5M4nwK4w884Ed8lT+58Y/5+Ow6K3vGbLSDzVqO/S2SVqGUIktLzsQZ83pMzBQrzkhEhrSRlISzdMtOP8XZnnXWoJwkqgmSEUdiyZ6fEWLHNqzR2lBYTTGdcSJPma0LrIls0w5soOgNaVJwalbM2jF9aGlSR7SWYqtQted03DDvxoRC0itL0FCKKQTFIUtm/QjZtwQcLvRMplfpzhync8/0GEhW4Gt65djtFhRyykpsmJgZNvSIKGh9wzSZIaTktD9hoqd0cqCXrH3FzMwRWnLqTxmpEX0aEFqxCRsWeoFVcMwpZcxxmwotNMv+lEVd4BLFOq3IXYJwgUSlrNKaxTLBi8hq4khlhvKCVKSchhPmywynJOu8wwiDEs+g2z2OC1hsBLVKWZUJwkeKLpJ5OBlLdqtI6x3bbBCCso0kUXI7i+yuHL2SVLkmEpk0nlRKjseKnW2gl0NdB0tk2toBlz6SLM56+jQZKg8rwaSymCg4nhtmy55KeCyCLlPsVgEZJSczw2zVYYshKa9J7kQ5AocjzayNdAyMQdtUslj1CASn04Rx7QhSQO+p5zm7yx4pJCepYNQHdCdImsAmkcxaS6N6miIhtQFHxCCoCsNuE4gisDKQBMgTTSElZyPNfGPxQFUoTABva0TfcpbBrJZUekY7n0JjSW2BqhWno4JF3RBNOlSCBnIPBslJkrK7qeiVojGGKCWj3qL8QBu7U9d0ytAoQxCCSduc506ULKqaXmqs1vRKMWsbTIwclSWLpqZTaqCi1ZpZXSNjHGhqm4buHEJVac28aVEMx2Zdi1MaEQLbJGGnHiIgx1nOpO/xUqBCYJ2m7DYtQUhOsoyxc0QBqYSzJGW3HSquHicphfcIW5G5ltM0Ybdp8VqymY0YTXKwmnCrYpnn7FYVXknWWYYBjHOk3nGUZlzoTkncu9TidKgUryoK03NzdYvdfkSnUjYmIrVm1LekruM0qdjxI3phqUQ70NQGMMJxnK1Z9GN8GrGJRygouxTp4dSsmfUjXOhxOuB0YEKJThQn+oxFnGODx3Y9znh2k12k0hzZI6Z+jG8c2mQ0vmFKQrQbluqYsZrjbYLuNdvEMtVTRCpZsqS0OYSAEpq1XzNVMyrZcRxPKWWJjhrVSZZ+xV72GL0tWdKTOIXSCaqOLPsNl3YPCLHltF9SjCaosEFVK078kj0xx9ZbNqYhMTlJOSJLCk7kGRfMZXwzZt31KCFJvSE3GcehYj8fkepj2rhEIMiMRmvBcX+bHbNPHxyNH2TlmeJ5/rv5/5Gpng/sOeIOrCHy5vo/8Oebf8M37Zcs1C516OhDj8XxjH6W/zb/H9l3C1zX8Q/t/8zn8TN6OmZmQYyRY3/IlDlW9gMdtd8yEzsIJEfhiKmcEfoebaFyG55UT/E3y7/LY6Nncb3jX/v/F5+077Nlw9V4ld9P/pjnD36GmZV3C13d8aYH60AIVKL5Fzf/IdeXf8lxdZtRVyKzyFaeUeYTnp29xv/p4P+GFvrBfTZG/v2Nf8X7m+sct4dcKh/jjd0/4LWd37u3KcNdL+7dLfjOXv9D0YUf2eN/qs+9o7+bqnK/cfFPb/w/+HTzPrXb8nj6JH+0/99ytXgSoRX/8tt/zKerD9jaDbN0jhc9J81tRsmEp6cv8r9/7P/y4J3vfO/78y9+wLgAOGoP+dOb/5zPNx+jpcbIjERlHJ59xwV1wO9f+1u8sfMLEPD/Of23vLn5Dbe72+yYA5qmYN0N0OmsU+igOAlb9syExna00RKJjEhJpOZ2t2LSamy/xSVDZH6SBbzasDRL9pgjTQQdByrafEGiEw7bm8zCDCs6gog47SnFBOsjp3LF2Ba0LoDUdLQs9Axc4IQlE8Z404DvqEXDvCtRk5TD/hZjOcH5gIqKddyw42doKVm6I0o5QqcpJppBf5ALvHIchyPGyYSgNUblnPRHLNwcRGAVz0hFgo6aNGYsOWUhdnHCcexOSHVGEjVJMBzHY3bjHkFkrNo1SmkymZKIlJNwzEV1iZ/3L/DL7BcUj+1SzEd3Beau8/pRiQh3xWCIXokfk+KHdNwfMFO+1+4wRT1gLPxnGQP3SeQd0M99ds8ADXjEdc//9l835+KHZ+6BLt+bxt8C0nVnEgQMtKZ3biKGp3+fufHIe9+551AB+LwO8Dmtp1J6EBwXwEDwEDsH59TSUkqkMgwu5kHYovUgFLhI9JZoArgIvQMznC90QuwsIXSIPkVkGqk1se+RiSGebogLh04MXkSkgmAdMk8GGkrZIl0g9gFhPNF5xEQjZYoKhkSkBNcTOo/IDXZTo4oxgoYoBTEO308YjSRBosHdIeoTw3cW4nzmzm1owb2/CzEk94k79rXgXm9BvPvznNotNdAE0AqRJmgBQiloPdE6BAkiRPR0TGwaovDEtieiiDYS0jjALxKNzEE4Sax7sB6CGha5VkP81Z9T6PlAcBFhI5IAYaCYCz6AVINs+QgK5LkRK6VE+POwpQ8IqYhuqCYsI4jcEKJFKXWXSlNIgZISFc7pQKVEEFFSDFS+PqClGChJY0T4METYtADvIZzPXQhICSLE8wDbUBH7jlwjJZKBEhYYnnmi8D4QUQM7CBGhFLlK6M6fo1aDsSDPaVfD+WIJfqBijWL4DoPwxqGUttak5YjYSiQd3aZHT1JoeoT19H1LJgoQAiMk/Z3vdr4epfOIhIES9k6yWjzHPJ+/DOWdvnfWrZAoMdCoyvuKXg4yJAb4Fuc4VjXEKO/J2L31Lc77DH+/o/sNIX1kvPf7nfGKe4wY4nycd64r7rxPBAg/JHyLO3Mmzp+pvHeylIKoFLrMBgrgswojxT0F4/ydRIgQ7sw/4P15ePx8NQmJTDRmkiMrg2CgaRVCglIIcZ4XIsTdsUQBMtHo3KBiRVqUWOUJvsEHN6z3cP7dEQStQAzzErwf5CuV4AUxRJIiA+0QUhM7P6y1GBBxIA8QWiJMgi5KZLtECYmcjVAxQ7stxhREA7Edcpui7VFEVD7MTyIVql0jLATvMcqgtUEqhbCCYAPKJPjWkqgEPcqgbmlvf4srAkFlCBVRwiDzHBEykiIhkRWJNOgkAw/4APi7sikY1nvoPN73xGAJhTuX1Tt7hBjysTT3eRfP56q1iKkchCtGoh04Zn0/1Jshxru0r8RhnYbzfUCev3O1SpC9RMSBpJkQiD4gtSD6iFDD+1VKwR0KFxEFSim0VEhlkGlKkJLoA+msJNz2A41oDEQlMNMSPR3qAAQ/XF/Ic5jSfXuhlAKlNSZPGU9nuNCyqc/wdUcft4RpTzDDdw3n1MtSSYTW3F2kcRj3TUQBWQABAABJREFU/bCdB3yvdxSxO//frws94EWNj/z4gzrA9zyHPOhU/C3ag07ac8LsyEC1KoeE3OE98NBeyLAOMA9CtO8pad8fwaOMivMh33d/HryXHOTofrTFnfHAIBcw6B3ReYRQ530F2DDoM2F430V5vv/FiLQOnSW487oUQdiB4ljJYU8SIBKNsH6I1AmJ0nqgbfUOpcAFN+x/RoOPA+W7GGhthYTQ+/OyAeeP3od740400Q1jiW6QTSkUAokxCdJHZFQobXDOkagEpTU6zYihQVmJlJIQwdU9zg9jufs+93GgdvfDHCoh8QiMOacbjgqJHOj4gx50In2+bqUk+EAIII2EAEpKfGcHGT+ni37wET/62d7rc8e8uA/2dN8pP2wPPHzdeN+1fgsF+bdq98zeOwP5XoGHRw3wryGi8ddb5+JHDI0H5unRhuDdQ4Mxcmdh35uKe6f99rPx3ORlPl9/TKnG7IoDZCJomw2q97z81RU+uvQd+SRjVheM1oovDhp0pnl1+wofjz8ht4ZRmzJyV3kvuQlG84v0Fa6LrymCoYwTHpOPcZ3PkUbzUnWNz12HYgfTCZ5qL/CbuCYGz5Mf1RzunJGua5Ik4Zlwjd+Iz6BPefpoyi11Sj5bkI3nPHky4q3yY4xOePrGjOMdR2tSkj7yYvMib7m3UEXJlcMR22slXluSTHHt5lN8celLggxcjgd0vWW1VxIxvGHe4E37NgjJBXmVTnSchY5Aws/Nz/lL/w4KxZ64RNCBVewgJvyCF3hTvk8SExanKb5q2MwjYHn960u8u/iSQhsWq5zMa9ppRRIUL39xwEePLcl1xvRUUGwWNPtbJJKfHR7w4TVNnkomrWd+GnmPgFKC125kvH+QkXoobeSxY887+4NR8drHFV9eySjNULDw6Vs1bz+VE4FXP2n49nLOVCoKF3jlhuXNJ3NQkhc/33JjrillgqksL96o+M3zU3CBZ79uOBy3VPMUVTte/2TNWy/O0Frw+Odb1ouMtQLdWP7w8w2/em6CCoKnjh2bLFIlA5PS771zyl88XpJ3gSu3GvpUU2kwNvKLLyrefKKEJnD5qIM8oTIWZQO/vB14e08izxoOjlpSbbAxEK3n9e8in+4LCu+YdylZ6OjkBuklr90c8/5OTRF7JnVJ0Sv66QrlBa9+M+Kzyxbd9IyYMTkWfH6tQBea39cL/vzmbRIDuzJlZ+X4aOKha3j+u8Dn8xKhjpk6w8GZ4vr+UIjo9W+P+XJnTqmhcI6XDk/4zcEBUcArh8d8O5lRtz2J9bx8fMibly8TEDx/dMThaESdGNLgef2bW/zq8mUSL3n69IRVUdCYjix4Xv/qBm9dvozxgSdPT9mkKbXSJN7zs6++5M2rVxFErpye4tKUWg8MTT//+iv+4uJFRkSubNY4oNGaNAT+4OZNfnVwwMg7LjY1Rmt6Y0i84/dvfcf1hUPFyMFKYEJBt5igreP3lydcLyvmwbFvM8p1w5fJdVKd8cxXJR/tZMTo2Gkki07w8dQhpeKVE8ln40AkMO0VV1ZrPpkeIRw8X+1z+Ngh8zQyVwlX5y/y5vLXxM7xAte4qb7GERlJwXPiCd6VHyGN5tX8BW6mN2nbljQkvJo8y5vxHbzreap/nFNzRisdhSl41l3jveQDMJLn9POsu2Pi2jEdT3hGPMEH4RNs3fO4uMhZvaSlITMFr05f4R3zEUp6nsifoY1Lml6QipxXeIPr9n1KU/JYcZVee7ZhQ6pTXrcv8Hb6ManquZRfxUZPI1p0CPzc/Iy33LukIWVHFuTlDjF+inKOF+un+FB8SknNrN1hr0n5en5GEjb8PHuD983bIDPmtmQedvlY3sKkCb+cvML79afYPqF0BRf6C7xnbyADvBYP+Lg7JrER0dZclJovdip0nvLC/s/4Wn5OJgoSkfNc+QrvVG8SfOBAXOBm+y3vxnfYSw/Y5xKf9O8SVORq8RRZlzGKY5Jo+P3y5/x6+e8wTrAwO9Rqy58177KT7vF08TJfn30FXvCEeYq1WlHHBi0S/qj8Q37T/AUqKK6Gq6R6xE5ckKYFF/vL3HJf4pVnn4tcUJcRicaUGT8/+GP8Fpzt2FF7XBZX6ZuOJM/ODWBBqDtkajiyh3y+/pAsLXmqfJ6PNtcpdckiOaBwGps2CAePuycJy5Y4lfi2h9QMNRO04vnZqyzbYxbJLiM94onymbvOvLs/HpXgcNeAftRefM89+pPRirt/fLDnj+36Amh9wwerd+h8y5PjZ+l9zzfVl4zMmKfGL/D19nOiGFGqCQLFn6/+A6Ue8eTkGb7YfkpOyX52CVSg8Q20cNFepWs6kmxIEj9sbvH55lNSlfLM5Hm+rD5jbddcKa5ytbz2yK+ym+6xyHf5pv8KJSSvTX7GZ5tPBtajqJmqC/yb2++gpOKx8gnecp+SOUGhpjwhL/Lr/jMImhfEAV+HM3I3OJWudVPeCd8ireXJvuRwryKNSzKV8ri7xPvFlwQJ19yTrMW39PTkWcHr+Su83b+Fkoqn0qc5rY6o+w0JmlfyX/B2+zZaaK7JxzltTrFJSRY1b6Rv8Fb7FjomXPT7+DLilCUNKc/7l3iz+w/kJuNCvEQInsZvSETC6+IXfBQ+IPGay+kVdooFt+rvSNKUx+RV3ux/RZmM2M8uoK2ijR7jFD+Pr/Kefw/BlAO5zwV5wO1wC2kUTybPcDPe4EoSmOk5fdNwvXoHZQw/L37J++17jGNgoubsh0u8G66Dhxfdc3wjbjOWYGTJs/Jpqrpl4or/DGX+IYX3fsv3kc7uh6Nb951wn8w/4DD/EZ36d2t/DdbC79j+yrCoqqoeEer5ifawcfFDxsYdS0sMr5Z7V773ohJ3Ojx00p2fvzr8d3ywvM7KLplnC/pxy5k4JTmLiHWPylNWo4a9uIddrtnkNZkqMCQIF1kmK+bbGSu34Ew60qIk6SLaCG6z4tLoEqFbse3PMFmGdgfQ7nEyFey7lLCYsbU1obPk331BoY44EqfsdGPi7i6N8sSuZxRTVIDb9U0Odq8S/SmtqAiJpFyD8nCYrZhXxQBd2KxRFyaYwwY9n7DecSzEHN83dNWGbqIY25zYRY7NmpktYZQRSjMkDfoRKkRO4ikzOSNqjbWOjd8w2yYIHGd5zahOBk9PpjkLa8anGh8im7JjdF4YTxBZm4r5MkEYyXovUuqBhhIpORErdrcTnJ6zUj2ZUyh1QKhTjmPL7hqCFKzzSBoVWmUQ4LiA/bNA5+FUBqT1lL1H2cjJTsbByg8V0E1EIigdyN5xNE/Y3wSckNRmqMJdVg4V4HBm2D3t8ZmhMxInoKgcqYfDRcp8ZQkq0ieCRkTGqw4VJMeLlJ21HVihlKBOFfPKo0LgcGLYqTwiSqx3NEXCvItEKTidaGa1J0TwRDapZHdriVJxVAhmLSSdxYfINoH9ykHsuW0sSZBMFIRo2SSBWQeEJdvMklsJzqOThKVoWGwkUcM68SROkCUpsvMsJ5E9NSOofbaTnNGoxH1+jKjcML+tQOzlrDOQm46sOoc3ZbBbC5ryGbZmjARy59EucFhk7G1qnE6pTQJSUbQ9CsmtsmRvWxGUojUaJwTjvkc5z9F4zG5V4RhyL3qlmHQtWsBRUbKoKpwUOHWe0N00yHPI1KyqhqCA0VRJwqxp0DBAproOEQJWCbZpyk5VE4TgNMuZ9B0yDkXntkXOvGoQRrHMcka2Y2Q/w4RbrJLItDY04iqnaUnpPHn8jsQfcaY9OwFi8zn1TqQgIa4LUAec5rDbCZzzbDKJiZIsRFSUHGeR/cbjwhds5RoVBKNUM56lLNWKnTiHRLCp1/RVS9qqAdIjl+zLHXqlaLUnRk+hhs3vdjxmhwXCCDo6+r5lxIgkTTlWS3bkLgpL7xsclomfkMuCk+6QGTMIQxLttlkzUXPIS5ZyzW65h80dneoGaKSaIYXgsLlNcQKy8QQRsXPJYrSPV3DsjpmqKRFJiIEzt2JXLwjRc7y5SdYlmFGJ7ywrtWU3TjFpZK3WlDGnP7WEJnCmKxZhihQdzagnNyMSDATBUThmN+xj7ZRtFtFBkesUassRK/bDDL/21DgkiixocJLTzSG7W4+aHdKOO8JozOLiBbROOHIDlWd0lqpegxGMiimx9WzMhrle0PsWGy0+WIxLSEg5sreYxQUhOJxydNJShhKtNaf+hGmyg4sOFy1Vv2GR7iKD4NDdYi4XQ/Jq9HSy5VK8yH+T/PegBKlLyE1OJ3t6YZlPL6CLZIgAn3trW9eyXZ8yL/aQeiAkQMm70TqAVXXMv/7uH3FkD8mzMV46vPAs+2N20wOi7FnaE3Iyrvon+Dv671Nc2UWYez7G2PYIo3AiULktYzO5VzjujoER7qEHHqbavFcQ7KfaPTfiD0EyHvj9AVfwvYP3qw5/dutf8OX2M9rQUKoREsXarhiZMQFPiJat3TBVC4TSbMKWkRoRz4kotnbFPF3gpWdpT2Ej0F9l/L0r/yPP/vJZtm7Dv77xzzhsbpOpoZCfkoqNW7Ob7vHHB3+Hi/nlB8YF0Piaf3r4v/BNPdQmyUWBiSmHqxvMw4I2v0TtA0oojFQoJIf1CfMuxYbAuqmIPpD0Ah3ghIpFJYjdhs4PTEpFaBHjnpOpZSF3kQuFN44gA3koidZwmxMujy5jFHR9Q2sb5nqGcZqVXLGT7eKjp/UdTjlGYkQkcHN7g6kfg1F0rqcWDaYeiBo2RcNOukOMPS62bPyahdyFEDmxh8yTBXmfIXvBNmy4kFzil+pvkKuEZDThA32d99w7nIWBbjZEzXFzRGYTyiQdYLjuhEv6Mn8o/piRHJPPpuQxo91u6SaRvBjxT4//F75yX2GCJjUlIDnsbp1T0XZswnYoztuXaKacxCWX0gv8Dfkqz4orjK/to4vsrlgPsvzTcnwXGvhwyOJ+Gf7ByzyEvvn+4Uec+7vE7v6KLcJ4/F8RFvX9Gtp/pYvda4KHjLrvc0h9z6y774EOHwXH7dE5FW1FSDzO96z1Cj1RkHq09NSyhrOOOJJsTY2SHUnQSCWpwhqbJmydYqkEwvfkWmEirFRH2H6HshVbVSOdIjO7yFyxSSVEibcVWxWJmWA292zqLZVxeFETtrdpSgUKWh0heNaJgvYQXbZsOUNoRT/NETZQaUvs1ki/wRYOrQRmFJB6RR08UXqs6enHHV4EOtETSsk6Vljh6epDiAlWOJqzoQLvNm3pzJZOQvTQKYuTOSJ6tqGhLXNs06KspFU9rhjoRDempXUdMYkYYegmEjkaKEdXdsW224Id6OnqUSTmBt/AqusQHpRMkSzY5uac4z1Q5UPF2KwdQpRbo2AqsRbOlCAEwaiWmChY54roh/ohzTgheM+4HXIgtqWG0A9UnkUCIdDoAf60LjVRSKIQ1LkmSkFvFPjIOpWEqcFpqE3EM/D+BxdY55IgE5wEqwROCqKWOOuoCkXUiqg1wQa66PESvJFsCo01iv68snRvFCiBiFDlCmcCuhAYG2hE4Dg6BIqu0MQoOYo1JkAlAyF2CGGpk5Y6kUPlVOmoCUOVVCXYJh4pJFkK1JGN7sF3BNHSJxmnh7cxBNRYURk4kRG6ik1hMDuGVDiEj1QqgCroU8MqGZ752HmED2zTBCEEHsMmSREISmUQSDZZNgSHhaBKDDFGOqUQAdbGEIoCh6TRmqgkVg0ys0nTgW5WCFyicfF8jn1gm6V4IeilBCkHlqRzyNA2y7BS4qUkxkBvDAEQSFZJQqf1ec5FpDUD5Cgi2GQpjdZsVaDwlloGXFrQCsmqSKlCJO89me1pTUAJB8LSJg2N1CBHxKajlucwgAS2ZqDjzYJARUFt4JiWaFsquR0oE1NDa1c0oQEd8JWlkS0+84x0jhX9QFtZZFgUG1tBjDSqIwqodYtkRZRQxxpRKoLUSGlZ1Suc76CtcaIDLbG+waicKlQ4MUAVg4zEHITpiImg8R0n7pTKVrjoBqV6IIjmrDmmRRGNw5QFVnqCk/gQWfkVXWix0SOipgkN3jt827KySzKTE+wKhaIOLfgOHR212rIVBp8alEmpYotGoZSnlhs2foMhQauEmi3LmGKV4KxzROsp1cCEVCmLlDViZNi4gfI37w0CxaaQCNNjRo6mqCD14DUiSDZxM0BfOksVN8ioaZuWKGHr1nSxw9uOKm6JITCKE4QXVGzxwRGCoxOW4Dy9bAk+svJndLbH+Z4u9Hjh8f0AZ9qEFX3ohkrNSJy3jOWEk3jKc5OX6NcNUUp0SBjt7KDHOQ8rEKnKUOmC0PSEGJGZQebpfful4Iw1je45qY/R/gxvhhoulVsTbA86sHKnYCPTfIqYJ/f23BgJnSX6gMoSjFDM1IPJzNyBEqpzRMEdWBfftw9+uj0i8vHw4R/So8Q9o+ROtxA9J/0xt9vvsMHS6RYQbOyaxle4aBECetfilQdl2PoNldwQw5AT0PqGIAJBBjZuhSkSHrs2ZdckeBc4qY+oXMVJd4QWGiElWmlqV5GIhOP2iAvZ5e+hpk7tCZXbcupOEAjGYoq0inW3IqYpTb/krBvW20hng1Nzu6K1Em8DW1cjnGPUCwieRjnO+khMInWuz98PIHJPVTrQDUkSaGWFMIreR8hSeu84DsfoGOlCQ1QRGQXKQys6hBU46XE4vPM4Y7G2owpr0IHe9UQp8DoiFxInIjU1IkIX1iACHQ2hdwghWLPCOkvmMzKr6ZVj4zZsioonLj5PCJHT/pTj/pDKbfEhELzkzJ6hoqZwijRqGmo2bDjVZ1zRV8lmC6QUmFHOWEluc4taNpzaY/CRxBcIoVl1SwKWPlgqWSGVomCXEDzb2FCy5TTd4mo/jLn8nYX4Ee0c2nQOMxRC3IfC+b6Qi/tkPIaAOK/Afn74+1e/L2h4524Pdn140Qzwqh8MJt656EPf4Ifu/7u0v15Y1G/bHh70fW+nH0qMivc63Hfa/TN9B1P2oLmzm+2zSHZZ94qZ3KVXLSJA6lMUEqUMy3jKbjbByoARW9KYYbxEag2dY+EK0jDGKGDtCJUnzRLaRLBnDUJkJGVOEiSpE8jU4L1lxwZimZE5B05QdmOSdoQsJ8xrOGsdRTIixshYZJgQCc6y2+QorSkAu20Z9wpdjInBszvZx99a4UeGKBMyBdza4pHMyylkio6Oql0zthlSp0QlmDUJodbYVlGZnoUaY0Y5sbrNItkBZejbmlW7YbwSqCIjtp5RHVEuwYshsrBoE6JSBBMZh4wkCkKEleuY2WTYeERBGTJkVJBnLOOanY2iqxVSpySVR2WCmBiwkb2NwwHGQxoDaVRQNcj9jAMyqtMNQkeMjyRdJAvgY2DnpINE0NiICJHSRaQNBB/Z2wSsayimgiAEZe1RnScAu8ctzmjKxuONZFR5cEMAbGdlCcLTJ5K1CMybiOwDUQh2V5YoBK2CLlXM2gguIIVktxkgXc5ZtjIybtzgWYySeevRRuOBdRKYbYeNRMbI2CuyNmDblmQEC29ogsU1NXM5QnUSgkMUllkywQZPqiDvDUanBBkJtmc3mYGRJHJLRoryKTE06BjY6RXrEAjqjEWnEJ3ARI/IWnZtgWsi2q7J92boVqGiQKSW/RipjMHYmthbRsFg/IBT3mtaejyFC4QIpR1ociOwX1U4OVCr+juRC+uIjNirKxySTkpskgyRixgRAhb1UPzOxpQ6wtxa5PlGNW8aEAInBFWWMa3rIbeDyLztIAacEGyzlN2uJYqhjsGk75AhEPFsvGRaB9ASHdeMrKB0klymbISl6HoaEUhFR2odSVSkvaKSmkU5RSQNtrCkOsV1UzAjTrozpl4TkBhqjBMkYjDOpWzZ7QtcKMhFT1qOSVwgcT3GGKbdhKAjuepRQpDnOZnMUP1t9pJ9GiEokhZvLaUphjwhe4s9sUMg0qkRfXCMmgQjNNZmzNoSQYqXPSFTTGyGCQVBB2ZhihlneBNpQ8tEz0DlBAsLs2CSTOhEx8ZtWMgFND1dfcpMTMn3pkTJcEwvsNHhvGViRyAktu2QIjClxHcSVKC0JVpqQvAoIZm5MWkpMNFQiBKlUyIJyp2x6HKkdCSiIM8KEiEJXiNsyq6Y0rgREodJDJlO0Mpw5Fcs/JiuDSBhNCoHxqgWvG/ZqQ2yXWGMJp1MGcsJOskILeyaA4JryGJGCJFxMkEqBTaycAu8spS+xGIZmSmJNBz2NxmHGdIIrLL00TISI0RiiFawEDuE6HHGs7EbJmGCipIoIvNsFx0U3jpa01FSsp/vs4ordJ4wygs6YdmILbOYD04ad0Ymc1KZUrUbNs2Kg/kVELB2Z2Q+kKqcPnY0rmaWLChkyUhOSEOCEooQh3oni7iDjxZtNIk0TOKUGCJLe8zM7A05ZEois4R7JsOPb+L3szg+mPj6CKvgkV7cR2g893uAxXmfh85tfYMNPSM1JhJZuRWlKtlJ91hmJ9SuYqbnCCQ+eOZmgVQS2/dsxZZFMgdtiI1iRE6SJfgA637DwkzxyhPRjHXJlfnTSApO+1OKPqNQBaUZU+oRRpnBkRITRnrCwuywdhVGaHKd0oee2m+Z6RmlGjHT+yQioZAp9AIrPPujPSo3Q9MjkagmEM5q2hDZcyl2vSajR0hF5g1aJESxYeETgtFkweKkojBTTNYQ1Rn7ag8ROpzIiUqRywlhGwmJZ4c5wjtCMsHimcYS7eBMrJipOSLV9LGn8TUjSjyWUEQmboKPDlJJTcNETgkCnPPMwgSpSoLybPwZO8UeMUDqckZyRBIMKpFs2TDO5lw5eIIqa8l0wcHmEje775D+iF29i0WANuRigD5nKNbujLQyTNIxYaEG+J4QyHSoPbLwe4ySKRf9ZZSXCKlot5bgOy6Ul+lix8avUUGSMEaGETIG8tqQNRq1SNFFdk+ufyul+k7E4lGomfs83D+ROhEJbKoNWZqT6EfUUnmo98PRlO+Bfe5XiSPcocJ9pA3/Xxgp9f8T4+KRGMsfiFLceWkNMzL8MYoHz7lX9uf+ENSDoKk73S8UV3jr6C8IEXKRU6qC4+4mAnh1/SzvpR8Qkh4ZFPtyj5Xe0m63PFO/yCeLryFPUEeWJ8qCD8LHiCTyzNmTvJs1CB/I9nfZ9Vd5u1jhjOa5zQ4fpmATQ7uJXP1oya2doWjaU18XfDF/nrYY03l4LsA7ZQcCnl0Zvmt+g5M1beN4bjnm+hMdUXkuxguc7UTiZkmzWvKMv8pb8kuUEVy7/AqHk9vUy0853hzz88lr/Fpex0nHdFmylIK2NGzNiNeSF/kL8znWBEb2Es1pTe1zwknN64dT3r5S0aVQdFNC7WgnWwiC108v85uDQ3ofSZYZUiTYhaUSgmduXuD6hWOsE+jtiNL1HO942iTys+5Z3lKf4eoWVaXsf5dyeqknKMFrtxXvPanwwYMTXKhgeUnSusDzX9R8cklADIjgeex2y9m1HKvh5a+2fHwhH3KUleTxmx1vP5siEsULH6744mKBQ9F4z9WbnutjIAaevVHz7YUcJwRdpnnhm4o3n5sQhOfSYcWtRYqXik4Fnv1sw9svLZBScelmw1EWCUSaVPLKR0v+8qUF3kgWN7ZsMg1a0SaSN25bfn0pwUXH/pnDZhm11wihePnzil9fStBOcHDmcbRUUoAXvHS74a3ZEb715NuEkV6xTZd0MuW17iLXp7cgjxR+TreqacotrVC8bJ/mnfQLlGpIMezoKaf+iFZoXl8/zvvJIV53mKnksZOeD/tD/KjghVsjPi+PUb5H9wUHG8HHB0t8m/P00S6fzwNITwwFj38H70+HAnNPnyR8uv8UXgislDxxtuU3+3tEAc+fLrkxng6RIK147vCIX115jABcOltxOCpARqyWPHPrmLeuXMZJwcW64rQo8ELQacUrt27zq6uP4aVgf71kk6UD3awxvHrr1pDHIQW7XUurNcdSURvDz2/f5C8PDvAIpv0AX7udZzRS8nu3PuSD3ZrUCvY7R9Ic0fsOHQV/fLyPK8dslOPKGZis5YONJVWCl2rFjf0L2AsTnrv0GGMdeef4PWQd2Ik5/1b8itmoZzdOSTeBT/QNpBY8t77M5/kRSWzI0jkXdcmH+haCjhf0q3yjbtLYDiNTLoQDPvQf4wU8NX6BL+rPsB4663mifIq3+ncI0XMtu8bX4gZSKlzwPF88x6+rN3F1w6X+aVa6Ie01Jmquysd5b/wZjAwX9l/itD+hsxV1qnm5eJFfb/4CFz0H2Ywzt2UdtwQJryev8J82/4m22rLflHTthta0bLKEp5vn+cv+bVo6psyItmfph+Jwv2fe4De8j0cw0VOU2WHZfoZVgufbJ3lHvgciULiUvB1zM67oTeD31au81X6DiwrFDvM44vbqM/o04/fGr/Be9zFdEwlxwUV2WKpbxCh5envAh/4rOt1DKnhqOuXtzQfU21N+MXmJD/VXYM7wSnNQHbA0N5EKrppn+KL9DFsPFYivhsu8K68jtOJK9iTf2a8IjcXpnufKl3iz/g9EIhfjJY78LXwEkSueLl/izfo/4bzlifQyp+GYrmtpTM1L5jX+ov9PeBwX8itUfsVJf0RPxwvjP+AvN/+RPvTIIuff+//IWbPGCM1T/dN8XX2Kl5796hIxeo6722hpuJo9zdfNp7jo2LUHCKE46m6ihOLJ8lm+qj+hDz2LZA+vDFsd6KTnl4uf8+7mz5FOkidj8mTOcfMunYdMzviHX/3fkYuUWbbDH+m/zWS+9z0E0o82cZ5EDEOy8Pd3+R/Y+H/o+A/c+M7+HuHT7Ue8tfwVIQb2s4usfMXSLklkwpXsIuu4wQrLpXxKFTu2wdHbJa8nf4N34pe0ImWHSxAVGx/onORn+Uu81X1MGwU76hKJkGz7r7A+IY4n/BP7p7THHbtmh057zsSaOrb8YvS3eWf5NdsQqOKEd1Y3+K5+C6U1T433+NZ+TBsaZnqG8peom5ouCp5Kn+WD1Se0epfWz7mUHXBr+TH9uuGlfpcb1Ai7xTUNl4zg/b0tIcITJ3vcmizxYoublDzZzbm+OEQmmifDU9xOKzJlIWx5kqd4x78NjeBxrnJLnRKipfFbnu6e4V37KV54rhRPUo/P2DQWpVuez1/kze7X9K5hP71Ek9fY/phGOJ51z/OOf5s+9FzOd2jjhhB6Nm7Fz7qX+Vi/jw6C3TDjZfNzvoyfU4YR03TGvxX/bzCCbJzzG/9rbp/cRKG4mj3Num/pHWhVMha7HMmvaL3iD+MfkGWOQ3vIpdEVntx5gXxvehcqeEcfLHXJ39v9H/hgex0qxwV1kX/V/TMCBWkb2Ssuc90f0RN5yT/DLXGElRa1XXJlvosy6geM3t/Vdf+goirud3w/3CJ0tuPfvv2/crY9xeiEP3jxjzlYXDg/fL8+K358fdxJ9xAPGTs/OPyHFOr/Qu2vh4r2x02zu8bBAybBIy2O758L3C2INfwu7ot0xO/P00Mwzn/9zT/l47P3WPdnzMYL+knHcX+DQpb4TUMSE9bJhkXYoT88ZjuPZMUEKRQJKct4zE43w6eSjd4gtx7nL4CbcZZ17Mo9mvQSq+kICSS9xHjFzb5m/9SCimzlwOiS2YykmHJoYL/xsNA0sac7q5icfklpb3A8rtmrM3y2Il7K6OuaiRiTT2bcWn7JrCqws5QudISRZprsIaLhlj1kdqrxpidES288435B6FKOspa5nNBHT2gtjbJM+xzhBLflllmjYerRqWBNzW49QF2O84aJy3DeoXXCJnfstiUozamqKLbg2h7jBOsp7DcaMXKspy1pNTwn0yvOzJbFeoJtM5aFIAuaMLqG6macZJGDbcSJyLoQaBcxvSd1geVOwn5I2a461skAa0p7SCzcHiv2TntsItgUGhUhqxyJheNZwt5pR2sEbaoJREadJxGCw7HkYOOxBjojcATKrUcHydEiYbbs6KXEZ4ZewnTdEfqek0XG/trTJgKvJH2mma0s2sHRbsGiCXijECGykYGDTcAEw2lumHcBFyzCOapEMm96IjW3U8e4EyBuk1CxzTzTPgAnnGVLCkp6EUlIqbOWXT/HR8+Z2lKEBCECWdScmg27YU5QgpWuSJyCPpKKhFN5xoHYxVrHmT8jkQlFUmCayLE9Zqct6WWDWwSUMshmipIzzlTNdDPCiYvUJoUQMepxhLzE7SJnr7P0JNRCE5Vg1Hu0i9weDTkXrVS0SuOVYtq3pN5yuyzZ2VZ0JsFKTS8l874f8lZGJTtVRa80XksqKdltWlSEw7JkXte0aqhn0iQJ86ZBAMdFybxrcUohnGObZey2DTEGjouCad+Tuutk9js2Zii4J90tVtmGwic81e7z97tfIosEM84oH9tFSkk0GlMkSGMQ6v7oaGTz5W3+3fpP+dh+xFk8ZWF2aXTLmVhhhMHEBOMNZ2rFnt6j77ds/BlKajI7pkjmHLdH7Jpd+mipfAURclOQ6JTD7ja7yT596KjjUNivKEeko4Lb9jZ7co+6r2i6LSE45ixIK81SrJnEMXXe4GcaKxxTNUNJxaE9ZEfv0IV2wFXHdsi18oKbm29ZhDFt7AidpaJhJ04xSnJkzpiJGa23CCfY6IZduUAEwXE4YRJLYoik5Zg1W3aZg4+csGJETggdRmiWfsmO2sOFwCmDp1n6ObouOVMtu3JMEIKl3ZJ4gUk0mTQchzW7YkoATl2F8pCISCIlS1Wx60tiWLP1K5RSjMoSYxK+624zqwpiqImTgEwMZTJC94Jb1Q0OzD4+dTS6xcfALJmRBsVhdYNds4+Tjs41+Ogo5RStU479IYtkn4aa1jUDb7+aEiPcqL/hUnqRjh4bPVb17MgdNIoje4u52qGNjhgFTWzYKw6GnBZ3m4XZAWcxQVL5DYtkDxEFJ/1txnqGjx4tNWt7xm4yECic9keUakTEY2TCmT1hnlykj5rj/pRCFRjpKKRmaY+Z6wM6LTnpT0iDIYuQdbBO1jyeP8XP1O/zxrW//ZAO89PK1QN0tPe338r9+6hki0ccPjcufPT84xv/Tz7ffkTrWwozwwnB7e6QhVngRYuMkdpVQ/6L8xy5Y+bpDs4tEH7MxtXsJVOIgsN2yUQWuOiRHs5sxR4FrrOsRE0hUkJ6hjaWlazYT+Yge07sIYUsEO4CqdvluDljX49x3nEmW/I0I8k35Knl2B2zJy7T11OWTY8JAiMNqVcsTc9+NqPZ1CyrNYnS5E2LcpbjzLITE+x4yTbd4F0kCwm5SjhVpyzcHJF09KZDJYrcZ2gvOTYn7MoDnLDUth4geGKGMgXH4ZhFmFM7QS8ENloWskRLOIon7OW72NzhpaMNLXNmSBs47G6yUDv0OEDQ0DJlTLA9Jxyzm+0Rqo7UCSq/4YnsWf4g+99ywV1Ga8Wfun/JF+IzNn7NLN2lk44jd5uRGGE9qJhwFlfsmyv4PuOkXZHrgsf8Af/n+X+HCJHpzpRknA8sUd+TrfOIQQTf9vzZt/+c91a/4TSeMNMLTsSGs3CKFIpZWzKXM5bhlF32eTF9jd8b/5LpU5cQ8n7P/18RE/Q9kb4T1bh33Y+/fp+/eP8/8s3hV8xHc56/9hJ/6/W/R4wDPOqeUfG73/Jh8+hhk/63Vfr/q1LRDl/kx1GX4lGffxvj6eHOP2Zd3gcquzORd4NUMXL3v4FTcCh1P0oRnYREE9uIeeyAuL1JaDoQCjkrEU4RthaydCiKNTJolxDWg9EUBVAk+LYn9A5JSjyrCCNBkCC8J+qBElROc3wzUMiSCdympesqCBGpFRE1UOQpgZyWOBUQqcFvLa6qiUoQUwlaIKPCbWrCqCcGT4iOkCT4GMFIguvxTUdwkiAsrlvTB48wmigCsekIwhAzgc8SXKzx1hMMeCERvSWmQy0FpCA4j69auk0caOJGDjGZofIE1UVErAgSVAzE3oKTxCwFJQjeEfqOqIthbO1AU+etg9KA8IjUEKMdkvdjJMphpft1M+RIKElw4ZyBMgyUnVKAEITzqpmReI6pBycH+tkoIQhJwIGPECUhBGIUgyycu0CCt4Sg4ZzSMcoBzhCJGD3QCfs4UOhKeY/j3YsB0hOJuBCR52NwDFSxQQo6NUDAhBV4EbAiDlW3tUYEQGiCY6DVSzUkKQiNdwElJFqqQY7FkLgenSfEgEwE1vphzEEQvccHC0YjtUC4eD7PFpkblDfEIInRo/MMk2WY0RjnIkFUQECXCcIqhNFkF2b0jOmiIfaOOBTMJsaIdx4vAjEZchhiHJLyBWJ4LnJ4Zndw2uF8nUYph77n6/PuGjqngR0YPwfKVoQknDsQohyuNTyXc0LZc3fNnRwaodW5/0EAkiAFUUlikATBMC4lh2dPHOR1UWCYUl6Yk+9Okal5IJJ6HwH2+R8E42v7pN+MME2GtikqTRDBIlCAPKdKHCJvwfvBH3JObSyUGGgPw7Cu8OC9H56T8NhoCT5iu46AI+CH+QkRZy1EcM4RrMU7h9ACJRSkBikNaT6iTwVO9YOzVwzvv+A8tm3oXY0NFqs9TrT4xmJtS0+Kj5boPdEwjCE4kAJ/vk5iqoj+3ltWhEhwQ5Xp6B0YQTj/7tFFQhwgc1HGYf7P3z94gfeOaN2QDxwhhogPnkAkak0UYL0bKJhTNVRgP12BDTAuiUlCdB4fHFIJdJqgtYZMo/IULQxpTIZ8NtMO6ycEnI/oIiUKSR88zvvhmThHCHGgrDSSYMP5+wGEkaAE0Q/rPARPCH54DyUSiSBNE6IUBB+Qang/eO9R55+ds+fvE3n+PNxAtdn1uGhRDHDOyDm1Mudr1zuijHffN4EA5/IbYZiveN//5ysrMtAQWxfwYaBbj3GgSO67nkRIUAZv3UAHnqkf2Yh/uj3gK7zrVv4pzehRxx/ldYx33xVwTpv7AARlkDXf94QQ8LiBHjgZosZRDO8r4SzhvKCg6zy2a+liIBBQURKwWOlQ6vylJAUhnPuQJfRVgxA9PnRYBNK1RFsRCPjgQEWi97i6I/oG7S0+9DjREX0gOg9piggCWab4uqY5XmOdHfaNusE6i56WCGp80DjAhoA2ikQM+4XSEmMUGIOjv/eOyTTCRtADdbAyEpEkaJkilUG0YqBUVuKuA9b7Id/AS0sfOzwOJyxW9HTdFhEFzvY43RMMRB9xocdHC3ictzhtUfL8WchzsFyMmNRgpgWmLWB7/rTiwKIXQ6Dvh2Kn8pwwIIQwVASXw/shzRKwjqLMSUbZPSKDR8rLwFKmsgSdJ4haIYIc3h3+nFo/Alriz6NtUoJWiuLC/B5l+e+kzMe7P8UD8vqorgJEfKDHnTVLHArqxju0wj4i1e80kEeM6sHPv42e/tfd/uoJ3eInBvwTUY27//5Iv+/bqfE+IYgPH7zbXwAvzl9jazcchItM0jmVWeG2Lar1vLLz+7zb/CWjMGZHHpDXCXbk0EHyAq/wJV8yEhPm5Q6T5AmuiyVRwmtHOdcTKIqcidVc3ZS8V1hilLz0ccuXc4FziknrubKMvH9JYHYKXtskfL35BtOsKZcJV6qUDy4cghA8ezxhWQa8Esz25lzzu7wbv8FWG658mbDZiSQ6QbTwezs/5033ATImPH4y57BZkY8MSSd4efsU784qpHNcWydU2iNCR24lb5zMuZ5/SabhUrVPZwStsxRe8PL2gOu7R0gpuLDJiWpOmyoSF3ntLOc3O44kRPa2Pak2NIlAecUbpykfXpWURrDfSLLjY7beI0Lg58sZ7y46UnOViV0zDQs+KgzSNbz+teSdPUPZQLHsmVct3aUEGeG1Dyu+eLqkW3vKtefyqeOTx0tEiLz8jeWLhaZrLNPOc/BVzXuPFwgpefnzmm92UjojGLWex7+ueefaULPhpS8rvtvNGCeKsodrX265/tQYHxxPvX+bswszukwx6uDpLzf85sUdMi157jRyOtY0HWTC8Np7p7z78h7GR65+V1HlBj+DPAj+4LbjzTmI6Hl8O0hml6VkieLFTeS6bCi8Y28diLLDq4ZMJLy0mvH+/IgoPRfEZbROiLLGmJRX+xd4R3yIFBk7fUniEvq8J/GK19vnuR7eRUjNjhwzn13k/fojpIOfq5f5KP2M0PQsXMlsOeXz8QDPe5kX+Cb5CisKFmKHHf84n4uPQUpeTF7h8823COeYyp5L5T4fxs+JOnCtm/GpWkOyZtZEDpaGdxcLYoSXDk+5MZ3SaU1pLS+vTnhnZ0EQkmeOjjgph6rXubO8fHiTdy5fIkrJk7ePWI1KOqPJneWNo5u8eeEC2kuurc/YmoReK/Lg+dl3N3nrwt75sS1O1QhpKTG8cCK4PlqS0PNYtyBKwJ+ShpSfbT0fjg4RtmHfXkDLkphtyZOE53icz/Ov6MVnPBleILUjPm4+JxUpL5bP8FnzJSu/4Wp2hULmfNR8RiIMT+29zGc3PiPzI6Z6l8vFk3x4+h4qCl4av8rnzaf4LjBPdrisLnCiT7C95TF9jU82n+BizygZsa/2+bD6ACI8m7/At+0NetWRiYI9u8vn6lO0MTyXPM9X/Q0yWVCYkmflE7xj3kfmhqez5zmzK1of0Crj5/kLvNn9BuMtT3KFo80t0h6Etby8vcaH6SeYRHM5LNiqhg0blBX8zL3MO+mHmKC44g9w0mF9IDc5v1Av8pa7jhIll/sd/HpLVyTkKuPV7jne679ihOCin5KM96i3XxM6zxv5E3yqbjGJMy7oGYaE3qXgAr+Qz/OePKFtLbOkYGcx51P7JcrBq+oa77tviSphrxgxCzmt+BR8z8tnF/nmwhbvLYskY7cp+Kg9JSrNK9mr3DCHzMdjdqb7XHYz3mveRmrFS8krfOE+pY8NshU8mTzL7fxbYvA8657ltrpNJRpSVfJC9grv1r8miMjT+fMc9rfZmAIjDL+X/wFvtr9Cu46n5NOchlMaVZGR8Ub6BtebN8mD4qniKRq7wXYbcpny3OgN3q/fJLWei+ICNjbYdknaeV6b/IL3ql+ROtib7NB3HbU9IdiWF+e/4DP3PonTLOQCJTR1t0QSeG32B1zf/hoTUmZqijYLGgnSSV7qnuPj+teU04KZH5PEKT4MRQOfrp7iRnoDzZRYC2bTff789N+jpebF0csU5rfLbr1jSDyIf4g/uaf/WGtcwyerD3HB8eTkadb+jBv110zNnGujZ/is+RoVE66VT3LiV1S+RvXwhv451837CJFyWT/GtnasNiDRvO6v8F44JQ+afZHjwhCZKlTCi/GA95JDCIL9MCZ0NVtTQbD8Mn2RD8V1fFAs9B6p9VhpyZKM55dX+YgGpGAeS/JW0QSLFpI38tf43H7JRM2YqwnTeJlPs0OElLyaXeHDzQ2SbWAuE3ZayQfxJjIxPOcucjhpqLuaop1yzV7mc9OitOE5+wy3stt4LKUY8TgX+ID3CN7zfPoSh/o2ne4ozYQn9TO8tfoLUPBs+QKH9oRab8h1zlPHV/gg/ZRUCJ4Il1n524Q0Y5SkPMcrvOXeRHeOJ5PHaUuLq1uMVfxMvMHbvIMArojLhG5g7EvrnFfNK9wU3xJUZCfs8tjkKXSSkU1HPF+/yqfthxhRcpBdxgnPtlmhMbxhfsF1+QFjEdhzJambI/oKGSPPFI+TZimmzO7VcPlJeYQXd37G7fome+YSpRxxRXveO3sb3zqej8+zlMeE4MnTEa888fuYUf6QrN6PjuF+G/c/vz0iGnLt4pN8fftL8jTH6IQXrr08OKHVX0+2wv1LMN738+Fh/ZcyN/7qsKjqvgrdvy1U7VF3/IlzfoiVSjzw6R4e6m7vCK1raHyFEpp/feuf8O3yE9JWoZH46DhLtyxYwMKwjCdkIkNWAhEjZ2XFvrrCqXyZY+dITMIoZAPtpmiZf9fDpSlnKYiTinEbCVXLyVSyt3R4Gaj3c9LdCbOvv6b47mMO5YZFk9KPItUoEoxklpUYIifZmgO5R0fCuq9xMjDaDsVzjs2WaZ1gLi5oZEfb1czdCNlHDpMN865E50/SjyZ0OHZdpKi+5rD+jsmpwG5W1O0JrbFMV4JOpZzsKCa2AMbY8YiqjOy6GZSP8V3m2ekEQef0SlBNNBd7g15vOc4DYytQfcSmcCIt+50ZErh1T94GEpkgUsVJbNlZC6SSrLQlbR2mF3iTcpIL9o47vIBVqUg6R1b1CGB1sWDvuCUowzKXGB/Ja0uMgpNZwsFZT+9hlQz+5SJITOe5PUvZPe0QKrItNEhJ0QaUjdyeGy5uhsql9TjFBsd0WSP7nuP9gp2zHmsdXZ7SJYpZ5THGcLsQLKqhoFyrIl2mmZ31SCk4mqfsdALdQ8+QmzGvPTrCcQbTqJCiw9qWVgamnYOw5DRpGPuEJN3i9JYq7TkwM7S2nHFC2WcYkeAUrMSGuZ3jPJzEFWM9wtQOEXtWyZaF2AOdcpa1ZDEh60BnmmNO2GvmoAxn7gwdNaXU6EJyqs84SC8hRWTjzlBekIcSesGhO2Q37hCNZCN7lFEU+ZM07UVutQ27lWDbP8ZKTYhEJnZg6ro9GrFf1yAilVI4IRnXLSJ4jiZjdtuWiKBWEnteaVsiuD0aDZW1faDRhjYxA4QpwtFoxKyqkKGlM5JKKQ66Jan9hNMsMPGSxC+x1GyVZ95rhIRD0TGNCVm2xauKddqyJ2ckaoAQjURJqgwmT6moGOsFNmRsY0cu06HYGYq12zDVEzyB2tckMiFxFtX3nHbH7KUHBB9YuRWJSsjVkJB73B1xsbjMH+/+beblDrH3fFt/xa83/5GjdoA+2d6xtVsEgkKURCs4DSccjC7S2JqaCpkoRsWcPkhu9bfZl7u4rqbqN/hEMLI52hhO0y27eofgLNt+S983TLocLRVHcsmsK4hRYI2nFx0zOSXGyEm6Yh4miNrRKUsjGnZYEBPFkThlwoREpfRdzcZtmK4T/He3WD0xYlbuo1sJZcYqbthzO0hzmWO7JfUa4wXIyCrUzG2GV56lPyOPCcV4ineB427F1d0DYMXNbz9Bby15PkIfXOCMDftmjg8Vm7hGtQFzWmOKlNOsYYc5tbe0uQUbmY3mJEZxFI/ZF7sgeirO55cSGRQ3qm+5kF0kz1NqXxGCp5AlEcFt+x0LeYCSgdqusd4y0jNUlvBt8w0X88tEAo3d0vqWhdkFD0f+FnO5Q9pB22zoRMeUOSYKjvpbzPUu2EAvejbdipncQSrBWTxhagb4VOs7Kr9moXYJApb+mLGeIqXB4tm4M/aLiwQfOAsnlGoMOsEbOO6PKeyMfHyZM7GlEAVj5dGu5iycspdewMfAaX9C4g2SgpgWnMRT9tspSSpxRcTIhKvFNf7+wf/ht6Li/MGS3MADVbx/8lp3oC2R//W7P+Hb6htcsKQmISjLmT1lrGfUQlCFjsY3zM0cESw31zcY2xLXO4J2dKanbBaYcIlTauZqhHQCa3sqYZm6DJznzHSUYaiga0PPVnRMKwccsp45SlFiEo0cKeqkZuZnWB/ZijUlOXEzxjYptbLsMqZZ91R2Q9ZHknyEXpRscsd+MiMIWPka7UGsHaruOPUb9kJKWFSswhkmzchDJJkn3OwO2dd7SOHZxC3KGLKYo6XmmGPmboaInoqKoGCazjHGcORusRt2cYRBtg2MmeBd5IRjFm6GNIbGtXShYxZKVKo5FEfspQfEfqha3/Zb5mJBkJJDe5O5WGB0RissdWzYE7sUlWYVzxjrGU+Ip3lx/CLOBC5euIbJsrsO4D9b/glvb37Nql+ymx5g25aj9halHJElBZ13rLoT9sIuk75kHQdD/fH8af7mxb9LuTcDeS+K/OMyNPTpXMvWr8lVyT+/8Q/4Yvsp9JHS5miv2Jg1B+Mr/NGlv8MT42cfIbs/Kqbfu98jz70L3f/hcfvgWW3PKLOSNMl+9LI/2X7kvN9+HT7Y/utW6L6//fbP/m7/eJ9F8ujTH7YWHn5W3zcr40MfMp2T6Zyvtp9RuQ1rUSG9xbsekyU0vkVOE4IRrMOaTX+GjhEznVH5DTf9lpXYcFKMULlmjILThrW32KmALHJaV0TjmIghIX1rAm4UkaOUeiKgXdPVtxipFW3SsJpI3H7GtrTE6BF0SGvZyobYHdKpnI3uINH0SUFsLUtpcRJiOB5oH1UkpApUYKN6QhRYNvheERMF/Sm53lIXnpinND7D+T36tsYtDE4qNkXA9hqn5ZDwhcWbEZieOksJRtDlmuihcY7YtEjpaAJsfCCUimycUSvD8cZhqw3bUYIUDq0hH42pswm+XiKcZ5trTJKAlwgbqRIBM0MUsMmHKsLlSBHbnkp6/ESC1ufHApmJKCGpSkUMGhdheQ5NGNcBMsk2V8S5IRhFnQ8YzXEdwAW2o5TvhEVI2OYQ0bh0jCKwUp6YaGzvqIwCrfDaIYVkUxqi9oQipfMOGz1OpggpWJcGbyIxCESI2HMoibSOrZK0tieIhiQL9IqBJjT0VKan9x6KM6Ss6UWPxpNg2YoVXVITpESJlDps8QRcFGx0Sy16tKoxLlK1W5zyCDNm1dfoKMmkRFlJI2tEJgk9bNgSfSBDUsqEmhrpJSpG6rgFKch9jUBSiS0qM/gY2dg1uEieXCTOBU0lOFKGbZ+yEgWESGsDQig2aXoHqECdJHepaAHW2VB5OEj5/6Xuv54tufL8XuyzXLrtzz6uPFBVQKHgutFmukkOzSVn7tCMGCKlUCj0qBf9W3pRSHoRr4KXjJnh5QxnONPTDkDDNIAqoFAFlDt2n23TLaeHLHigzUzfuKH1UHV25k6zM1eu/P3W72uote6UoWTnVb5ME0KMWKlolcKJzu9CIlimKU4IbDRE4XBao4UnkVCaGm8M3q0QoaRRnkDS3ZdY4qJBpjOUqal1ixGgo2TFmipskAJSm7Fxaza6xYWcJTUajfCQmpRNqKhCTQSWboUSil5rMa1jY1cE6wHB2ncSp7nOkQg2bkVGykH5iKdG10FF3ti8ypmbsQpLQhPwbecnECP0ZGfutXIrRCPx2rFyC6RVlK3HJ4YyaTgKM2zcdLOrESrdQ0bBsl5T1Qu8a2mzCCJiVQNCUMmSaDpfGIvrJDeNxAXHMizxwuOylugdFocjIkzKwq9x4gnsI3oaUeOHA2IxZJ1bbDwlGoFyaSdjHRJ0dcoCTyYNPnpE5SmjpQk1QsA69ZSx5dTNUC20WeTYzmhOPmKdNahcs0kgVUs2sUI4hzCWDStET1D0E5QSVMGzkA1V21JlLdEHvAhIF1nFNUIHhPSs/YIIZG2GEZo2KVmEY5arSCVqEILc9PHRs3ALgghE37Jq50ghqKnxteSsOUWIiMdTh4oQPNY1Xf8VK4KIiLbCfyJFG1ti5dj4BV5Z2tB024SWaCLNpmLtlsziKSYz3bFcRatqlNGs7JxNtcBrurE91kDoZD7tnNKscUikzinlBpkX1JyxjC2bWLN2a4po2dglQnUQw2WYI6UENYRYs/JrpAzI0mKjRWrFyIypQ0mufk314suJheAzJ++vvMU7Oc5fF+Q0vmbZLni8eUAkkoYEryxLN2fjS1YIqug6v5C2JDYti7jAKkeb1kQCDo8zPaTdsLQWFzd457rAOVgqX0PwbFzLxkEQLUoJ6tgiVAsTwbJwVLFE0GCs6MZ32cF116ypRUNMNSIaSt8S3BoXWxpj2YiAbo6RJyvKvsIXHrRg6Sp8ZSlsRCtB1VOc0MLAsvI10W0YDnN8O6NOK86UIgZPKUqkUuSxABfZ6LKDTLqGut/JDbvoUF6y9AtCcATopJRbqFXXx1csCVhCCzUNIQScqhExsmINLuJDS4sl5IEgNa5qWKo1PgZ87GCPXnqME9QipfYbbOuY5tuMBtMOWmr0ZzAhAY+bhxw2j6lCiW88tm2YhzNKUeGbiBYJldqgnaSNDY0tqVTCtt4l3+4/MYrka6bZv5mzk+qUVO9yUD3qnrH2BGKkDQWJStjYDVl7xlH1+OuTi99oyv2bIvnf4DtPmhKSyWDrM/jtJ8/Pb0Oa+Px1+RUT9393oNXfrf0OkouvT5da2+BDIE/zzxaKL/0f+ZS08gmK8qsQqE8g0F/UC+6W/+pqRvxSZxwnWxS6z8hMSHNF8C04IGmZqm2scBACSQsaha5yYpKw5XMEKXLQJ5MGPl5glo6QBy7u7LCYlYjGYoTCVJakDCAk+zElYCiPN9A6+m3BdrHDetqyk++z6nty0RBaR15H9LrBScd2vk3VCnp6TGsD+cpi6OF1YEeOsJWjigk2WPoWYiOwqWarUYRRSjQ5dRSM9YRBaIlCsCUKXGzwqWZRrRgkgnbeEqNn5CSuVliTs2yXjKs1MYDHM24l7bwkusgqEwxmNXnwzAeaocmgkWS9lPUoYZIblu8+QPuGZG2Jds34mSGLUc7QrWhOVijZxzgwziObiBwqpkuHMxLVQmoDpnFo65glhunMEZJAYtOO7G0jibUctA27M0eVpkjl0AiyNmLaCCEyndWESWeGFpwjLx2JF3hgbx2wRlBUDisiQyRFv0eoVuzFlHLdMFCBNhP0W4GpLSIxbJWR0Da0MbJ0NaMmoqIgCsFk1UmxgmCTScYbh2gdoZAM0Ein0aJlrR1DmyC8RoqEsSrABYITrBLJUIzIgkVpQd+MQCoEirk3TBjjEoVxc3JZIE2Ddp3e/jSOCL6HiJDLnCxL0DYyQzGNE1wq0TYhUYos0WRSceKPmaptIg7jNcakJCZFBU2IgW29izWRnh91z1RQGFkg+5FhNBw3kqxaEgmk1pAgkbTslI5GSfquwcdA4QTKOogNW6XFKY1PNI1QDFqL9B4RG8aVw0qNF4FaSwauG6BEbBg3niA8IVbUOjJpFUkb0RqGaILvowc5G1HRdz0IAeECQ5cRfCQxjko3jOMIGosQkb4ZQ/AoqwHBVG9hyZB2ReYTQhuQaw+DhGGZgRb4ssZ4ReYlhSwg0Uz1Fj54lE5JVUqCRD/BOI+zKdu9XVbrOSZNGKstxmqLVll2k10qX2IqgcpSEpmj6cjz22zRiIY8zQnek/ge0WYE4dnRu1TpknwmcdJTkKGcIhjLdhzhdMB5Txsa+hToqJkrxUgM8G2LI3SCD02BUAIh6aRnpcdjWTULRnqMbyWOhqmcEL3vfFRYMQ4DXCoQYcFIDEEodFQsXMkk5gh6+GZDXyb4xhGsIEpP3xp8ZTH7PdJgiC6ikDSJZbSWtG1C2k9JZEGa91BRYpcl+VqQnh+QGt1dX51gkNDAtp/Q9iIrSrSQJChSJ9FBsOWnRN2SxS6BTXVOKlJOkGzLXYII9OgmdzJVIKIktJZtMcWplpQEVKRQI7TOIIdtuUvVbhjKIS0NfTlAowketuQUaVpcaKnshpEaoRKBdJKBnPD48AEnsxnD7QEi1SxPatKtHNFqbOk5mR1jdUPsJ9RNQ8wd1dmC7e0dkqJAGk1qe8zXc47Xc6iX9CcjelsZ/dGAaRxifZ9mdcwgGlLTQy8WiN0pW2oHKzwEg4kGk/ZB9girQ6Z6gl3OqCwUWY98kKHQrNyyM6MTksqXSCSpyvDRU/k1hewjpaT2JSDJVI6PjspvKHQfhaIJNQCZygmxS6QLXaDQNL4mxED+ZF3p16QyozA9trIdbGwpTNZN6uDZMttkQO0t682CQSjQyRBfOiZxQKAgZJJW1vRDDxl7EFcMrcZZRVNHpA5skSKbEi0sA5dAUoD3LBJBP5tgshatVhQxQ6qAwrNyK6b5DlEKEpGSU6D0lKgLjtenDFxKg8IIQS9Nu8k1FzhtPb3K4RQMUkESUoz3aAQ6N4yXEDxo0fEmTAWDwZgTjtkWu3jVksUc2UYy00MGgRSKaRzRZhaLQxhJFjOSpouSxkyxsRMbcNJjgkF6g9KaiRrRyo5r1MqWvumjhUCiGdlRxzuxLTZa+mJAkEOEkIzskBAEKEVpl4zTLYqQsomafjpmb3SB3v7WE1+Hjj9RhQ1GpGzrXXaTPeb2jKHtFBqjgD59QoRMZyzcnK10i17MqHxKbgq2+rtfhAj92oD/s4jch0DtS4ZmRK56TNNtJJpUKnKRE1vohT6TZPtzUeZvCr35zVt8wgX+xqnzLy3+7OOXouEvb/7rPn959a+qWHzNoX4XUKnfgYle9+/nL94HD27z1p3XCTHw1LlrfOfZ7//acoz4cib26Z9PkoknmLXIZ6SYX5VgfLqbz82mDMyIXhwR2g6S8cKFP+CvzRlLVzGQEy6oA2bhFJsJrh6+yOvneyx1Q9JmXB5e5LWkpHl4zPdvO355tUeTRloXufjBnDevSJxvufH+hg+vZIQiQSR9bv7lL3hvcgAIvrv3Ig/31gS/wqoNz+hv8ZPqLezGc/H4Ig9DoJ4K6v4+z57k/NicIAYp12LBo/IdRGywDVydP8NPd1qigt1ZyqIfCEOPSwd8S17kr/KKVgSulDvUYsxZUuJlyvflHj+yH2MH8PTeDqvZnMeLR2wywytHGT/ZdoS2YutEEbzi1EhaKXn2jQVvPp0Q0YxWDcmm4jgvqPsZf3iQYK5eYq0DT6sePxmXvLo5wCrPzVeP+ejqOZz3qE3L9MQy2xMEBS/d2vDW9T5RSZQN7J9afvFUhtOC37tV8s7VHvYJgff8/ZI3b2qUhlfenfPBsxOEUVAIrj3Y8LPrfXyMvPDhio/O9/AKSBXP3F3w0+t9nIjcuL/mo72MKFNaFXnm/TmvvrCFJ3L+1oyzpwKhD42zvPy44UdXC4IRXHxUc5IJXAzUwvPK3Zof3xgSTcr2wwV1kRBdpFWC79+vee1CglCSvVZQ+Q0zHQhB8e1Tz+vjxwTv2XZjnFKcUdNKwffcBV7ND1HCMmoTcjNgJpZsQs0P1Pd51b5KCI6+6WNKxcw/pGmqbp34GaVvOF3M2SszzuQjYjbkJfdD3pXvEkKDzgTb6hwH7gSbJjwfX+D95i2c8NhVw4X0Em/WryJlxfeyH3Anvt8ZKeH4o/yP+aC6Q5omXBAX+cuz18j9kn7scTWc8ap/SAyB506G3B1OSZRAuMDLZ/DatoIYeObI8rgvSaxGhcCN2ZifXnwKLwOXFics9SPWRqFi4OWDltfOJaQBrswcm0KzlgIZ4DsnM96YPESGyMVlH6fn1GaF1AXfGTzLLwe3SG3J/kpgo2OdHhGzlH9a/SOWvkL2DE/Hy7wmX+fMrWgTxwv1y7wt7+EQpGLKIAiO4yFCW15JXuLnsx/TuBYdE4bVBQ79mhAEL8nneD9/TBUUTRixV0x5XH1AJTTfz29wZ/MLfIjYGDhYPOBn5V+jlOJK/xqVtbgm4qTg6uh5fmF/ShSRF4bPcWf1AaiOuPts+hyvb14jOM9z6jL3Ng8RvqFxM14c3eTV7HViWXG9PcdBOMQ0FkLNc/YpflHcJgTHBXeRpdlwVlucq7gZbvKz/B7eRXbVU1SccebXeBl5Rd3kJ83fIIzjnN5m0WyYS4dlxcv227yWfYAlYSz3aNgwVzOcsbxc3eTnzW2c0gzzKarJOOCUddtyfTbmg1GJx5K4hK3xgLvuiMbCSycTPhjfI64c/eI8w3Sf9/KHqNzxrewar7dvI7DkwzHn+/u8Wb1J6TZ8b/0S74bb1KbBJZLz5YQ35Xs4qfiB+AHSS1b5hp1mwll5xGvyJwgEL8SbfJTeB+8I2vO0uc5ryx8DcCN7no+P30E1NciSq73neC3+mNB4nu99m4/DIwKBNtZ8y3yLn2/+huAtl5JnWbgZum4Qec3z4kVeb34EoWUnPc+6PcUFx6w+ZX1PUg1qlocrmqA4//Rl6t6cB3ceslNewYxXbE+mXEyf4f2HH1Kmc7L9IdcH3+Ve8j4nqzlJG+nl+4zHAek1/2z/D/mLx39GVQYu9C8yNUPm/UPqcsWN8ArvDw5ZNw1JM2K/v8+D8gO00HxH3uQ9+RAht1FiynSww5vrt1ierbm43PAfmv87beIYmQnbyR4fV3cQCK72bvCoeUDp1gz1iJ1kn3vrD0AIniquc9Q+Zu2W9M2QfXOBe+sPgcjl3lVm9piVXVLoHjv5Be5UHxBj5EpxhbPmmIWbk6uCSXKRQxp89LycX+I0PKASgYWveF49x9+s/waH42L/aeblojNFa0teqK/ybnEPGxxTcpqw4KQ/p2w1z6x2eXtwgBkZtmce61tO8wWbmPC8u8Y7vQcE7ZiaHYwZcxYaamX4vn6Wt91PEET6LkGTcioOiDR8J97kDXmMzzy9NGVvOOaWfUBpLS+sd7ndP8QJhwme/VjwXj7DC811d4672W1a3RDHY/bChFNziC40r/ACH/LBk4nXyBV7ibfFmwQluRau8r6/hbUtPoVn62u8Ld/Bb1pe6H+fge5zok7Yzc6xtZ5wy72DkIpnxLMcxSNOxSnTYgdVRf5681fg4an0Emf5CUsHwra81P8Or9m/RUTBBXPpScXojCg8301/yJub18lCxoV4jhvjFzjyB0y2dnlh8u1PYzwXHH99+qcc1I/QUXEuv0wdSmK0DGMPouJIHFFT8a+Lf0spa9bpmqf0UwxGA+6u36c/2eLF7e98YSr5GyK8r7R5M+NHB39O5SqGZsTYjPgotsTQcmP6D3h39jZNrKko2cvOf273vyHxN/7mScivg3J9Zf0nkf2viPC/2ZTv64/w5a2/slx8cVn8dSfwmx75d8G5+Pytt87yn370H7jz8AOsa7l6/jr//Ht/xPZo56sbf5HK3n383G/69OeLLxJSvj7H/GwnX4ZFfdIONg/5y4d/zr3lHXJdMDv3LG5ymQO74cJiQeHfYRPvYyrByj1LNNc5GiouyJwwSDlaL1BnFbqKZLJgdrHH9qMS60qWRUT5iCk9fZVwcnnA3ocnDB6/ia8OkFLQf+48uq85co/ZTi4w94a18wQRybmEifscFLDnE6rgqUXAxcCoPCVtDzlJV0zaPuXwKm02xmrB0EIW4YCaaSlY9wtqBOu2Ybq0ZM5zPBBMqoia9pBaUhWKbZEifeRxs2LLa0oRkFqzVJ49EkyEI2rGJGyso70/Y2EC28cVylqWWymTnW2unsD/7aXfR0jBvbDhP/oHvH3yEPV4gY+Cohiw2O8xubvAC5j3FZkXHeTECU5Hmp3TBq8Ep4UgeSJFmwvFwUCyv/DY6Fn1FMoHzKalj+ZkK2HvtGWjOrduASSrltxJTnYL9k4b6kRRyoiLgWHdmfMdTTP2zlqqRFKLgJeCiQ2dTO3EsH3WUItAmyT4RDEqPTSBo0nC1mlNmyqi0VRGMlk5ZOM5nWZsbzyubdE+UOearbpBuBWHacPEaWz7kMS0rGTDKPSwLrAZBEYuJcpDjKhZ6Q1TtpBGMU9XDNSAGFwnKetO2RE72Kpm5k5JYwYxIq1izgyzTqmaEp9ZBsmQzGRkScGMU3bTC7RpwkKsUU5gNpYemlN5yp45h40NK7dAK0M/HZCSchKOuZhc5ru9H/KD6T8BIXj17Cf8cvMWB/UjpmablW2pYotvWyi3CXGXw8SzU2usETR0AgW9VqADnGSeSZOwSJ6jMdtYo9hef0Te3OU0a5g0CqsjQUZqGRm1EikVp8YysRrCu6g4o1It4zZHZYLFcM3ADQiJxSSGRTNjiylCKo79MUOGXNlc5t9f/b+SDnLuru/wF+v/yvvlbQZyQGMTjOhz5pfsqCEkjhN7TBZThAkYL5nJM3bcPsGOmLsGExRKKHKVcqo2bIshQUaWVCTKUPiSQfSctsfs5nu0bckmrFFSkcgcozJO2g7j7IKltGtAkMmsm1m3x0zNDi0NZbMBJeglA7RMeLx6yJQxjW+w0hEUFCHFeMEJp0zlFqXytNFiQ8sg9FFOMFMLJoyoTIbTCa3yTDAk2nFkDxmHAV6vCK6homQit5HKcGAPGfshjcwIwbBwKyYipzfUnHLCWI1pmwzZZizihm22sJVgLltSq3A2oINkZVrO9UYgKmZhTl+ksDlh0MuYsWSabCNGCZu8ItM53nqoI8f+hF22CSYyDwsSYUhCSuISDtsD9pN9rG9Y+iVaaG4Uz/HH5T9jtLNNMwj8x9n/kw/cLXCBnBwdE87kCbvJedbVitptCAIGLkctA2f2kG2zx1o3VLKl9Q39bAud5pxwxLbYITQVzjbYaBn5AZlIOG4eMc32aZoNMQaW9QLlMgyaU3dIKBU+tCRpSmXXsDGgBC6rEJVmuDVka7jFyi4YpNu4BE7DCaLWNMGzNdqhVTW7aocgYaNW9OUA5xtiE1mwYDs5h5eGhVzTEwVtNSSPU07ZsGPGKG04a1akwiCJJEpx1C7YN32sWLCwMzQa067oS89ZOme/uIxQgo1fooQmVTmJyDhuD9hNz+G8pXQbBIJM5SQq5ah5zE5yDu/8k+pEpGd6GJVyXB+wk+6xkjV1bPHRMVA9tJAcNo/ZTvZYOUMdoA2WSZKhfcPB5gETN6TNLFEFqlAxlTsIbzhyJ2zFIY1qQAs2oWSrGqCSgmPm5JuExlUIIWjSlkk7IAbBWbJhqAZEITDCsJQlUzklYjhp5+QhJStKcjxLuWTChDZazuSCHjneTjFhi1lcsyuGuGBZipI0akIL0ipmYs0OA7z0rGSFEZosqTG+YqZm7MldnHCUqkJEQR41qVfMkjN22aW2K2pZI40mCymJyTmwj9kVu4S2wSWBKOCqeYY/lP+SPBmRFimicYjMEEJEJRqEQCYaGx1/cr/jILSuJiFBZ6KTm/Vj6sTi8bTaMpJjRBDMxAljsUWowYiEypc81b/OP7nwL7k4fKpTwftcGPbh5hZ/dfyn3N3cYmgmVKJCSMWsPGISpwQtOXZH9OWQG+Y5/o/Z/6kL36QgKoUXMN6bfDEA/C3ajw7+gl+evs5xdcB2sUvNhqWdgYfE9MApjpsDLiSX+Lb+Nv/0hX+DUIov2GX/qvbJbPXnPRb+Du3Xpijxyfn8ZnSlv9e5fH5Xn9/F/6aciy8LPnVSfZ2EXif5GT812vlK+7qS0NekOvHzQM5PhCi+0vG+ZsMvJV8ueOIT6TkfHT52M4t2WVKfLdBhhe87sIHYSwhpCiYSjKE5W+Ns03luCAGTDq7Q1hVBOHyURCJaS8Igw68rmrqmLyMxeoI2RBlxsZNubDYb2sbgCtM5ORcprpWE4Gm8wytBMAqhDTrJoc6RokHmBShFTDVIkEJ2coLW44SiWZc0NhJkIDYOGyPBK1xtaY9aAPxOj1Y6aCxBecKoAEknFykEwUt8CMQITkREkaD2R9jTGVErQvC4ELB1A14TQwChsK0laoHcHqCCwM0rrLXYqsHn3UAXpHgi2RrwTzC4UQm8gCA6qVYpoG4bgk9pbUPQCifAE0kEBBFRRuPTThbSAzF4UiBqAULgtMB5j9eKiCQqcE/6Tqs6OVunBUFrfHBY54hB4bXChUiLJ8auvCq1JCIIRUZQdOeqZCdtmnSyrSET3Ywo4EKg9Q5JQIju+15Gam/x0UMMBBHZlCW9LEHIiBeBTslUEHVXTvWyk5OU0XaOzE0N0eOCw6iAbS2J6NxKdaookoJaV0gl8TJ01w6HU51xoY0t0QlUDDTe45WndhvqtuK0OWVYDEhlhtKdJK8XnqifPHPOAd1zDd3vkYkitAGRalTap7YJYPFOdPdZPZGWVZ1LehQBLzqxTK8kHkFQEq8kUYCTsev3xE5CWCtkaojR4aMA90SqT4McFuhMgt8gjCLQUtclqG4MkonEyAQlDb2dbbJhQTNbEQsQWiK06O5FKolBEFyg9RZaC1oghMBai5CK4B0eD6KTvLQuIFJFGz22anHG4r3DygakJxEWr7v5Hxc7udjQeESk668q4H3AeYt3tpOiVBLvPU5ZIrGThHSOID9hsIRu7JBgvcerTgbZe0fAELRECk2QnTt2RAIGgoYoiV5BkhCiIqhOvjkQaduGSCCaTjrb+0DrHK1vkCGChNq1+KARUaITTaJTXFtB2kEnffAdTyEE2qZB6IIYI6owCB8x0qBjxFqLykCmhoAiyYedpHEbcTKidPf8euFxzhJcANHd7yAhxCd+MXWA1hJFoG1qguxEeyHgygoffTeOxQ5+EZ7cu06CM0IAHyzBd89SjBHbKESA6AMu8VSuoRY1la3JkiEium6MxONjJ4Eb6OA6zttO4tU2BHwn9Rssvd4ELRVyIciKjPmqpN/fom9ycgY8evQQoTXFqI8xmkW1ZOPXxJCS6x4RyLOUXpKQpxnW1ngCUqruPasCEYEuDNpqVKqJQuFah1MOQecNoVKNkJJ6vqZ2JR6NCIFGCKyqqWuBHESC7p5TISU+OKL1NItF9ywkDcEkaAxOdr/Xhe4d74N/Aofp3qsAPnYywj56Ygjd90Q3htjYbe+j6yRkY4AnMrk+OJwXtNZjbUu9scQnjtwu6a53EJ2kqfcOScclsdHhCaAkrmo72eYncConAyIRnQO7AFEkiCgQqul4BCGgNATbcZGQnXSwlxrnXTe2C4lME2QQ4ARBQLBdD+hkpAPhk/MXspMzjxGJ/FQyPcoOZ+EJmEIhgiKE0I0PRKSgk1uXnTRp05aIVIGWYCQC3V0rL2ijQyeqc9D2gagCcpSQqBRTZMihQiZPwjvxKQOC4EU3XqoIQpJkGUE6ZFCETBOixXcjAugns7oeogHJJy+/JzGYll8rmfqJVHN3/5/IaXvfyT2bQFCCGAVBhifvuABSILXCJBqqBtdYVGp+awLyJ8f3T+Is5x1RdX1FIAmETpFJSkgkMtWsDs4YnJ9+BXr/zU18Mdz8Jv7DJ5+/eS9faZ9H5vydixN/j/a75GX8Tnwu4DPORKITnrl4A/8kkN/t7bCVj341A/5XpXCf5hVfBEN9mtV9adXX83267+73zpEP9gmFwSP5h+kl3rCHxPIhW8eGLTvizrkRKsB3jgb88qJmHKH34Rm7jxb4qz1oIy+faD7e05THM8Yry/bScuuyQQEvL1Ie5ILVbElWCZ66r3g0NuTn9nmm/wr30hU6XqSoBRfcgF8mDqkV1w8UhwNDs91nojKesgmvhRU+eK65c8zxbBigq8h3GfJq9KjGcvFBw5l2JP1IplKeexR4dVeQ4bn0qKZOoFYpqYPn3i9551oOrWL/tKYqGxYjcIszvmtzXs1qdHAMTizKKFaXeySZ4od6m9f6Z9A6hh8eMKhaGpNhjOOVy89w+/htSt2w37vEjrWs1geoRHNtdIFXZ4eEwyVbZ4HMSfy5BOMiN2+t+fDpPk54tuaeovL4CxmxaXnxgzUfPjXAVZ7hyrO7qLl9JUf4wPPvznj41IB4ecroUcXFxxW3zieEELjxwYLH2zmFiPTWniuPNrz/zKhzl7635ngrpzGKXum48dGc965PcDpy7XHNrBcpJSRl4MbDineuDgjac/VhyaqfUsaAqh3ffdTy7tMDMhu5eNxgjSSomtzCi0eedycOFSIXSkMdS5yZk9uEl1Z73B7cJxGCp4p9yrah3JzSHwieWdzgo+F7ZMpwMb2INgnCfoRuNc+Lb/F+fA8pBbtmj1Qa2taiQ8LlapePuYttHFmjuHnxeT6OH+Jrz/bJHmfDk86wqUoYVAOarCRVCS8kN7nX3KYNnrHaYpqO+Xn7GutZTfFxIFzYYI0l2c64KC/xxvKnRCE4l5znMD9ikI7omT5GF9xevUuMkaeHl1iyzd5qSW+o2TF9HvoNrrHshoQHp3fRzSl5m3F9dsK9rY8IKnKhmmLdCt2eUMgBz/Se40BVYCTb6QBnJLNmQ4rkYhxyGO7gCUzNlEjNNNkhUSnnzT4PNh/ipWfMhCqUYCWJyriun+ONhz+iDGsum2foxx4jeqigeWH0Hd44/SV9JHt6igmB+6FFR82LzTXuZvcIrs+2HtJnBy8/QkrBDS7xsDhE1JHdpMdADrm9+QBaxwvpMzyOj0kTQ99M2ElGvMc9pJA837/Ox/aQQhj6esxeMeS9s3eRSnNzcIPH9SNaHINkyNV0hzv2DraxPKWeZmHW1NGS24xnzAXenr2BMTlP959hI9fUVcTEjBvFdW77O1hnuej3UT4yzaYMJ1sM5S5vzN+m3ljOt0MqAXXqSGWPb5kbvK1eQ4uEi+Ei67aiZENGwkvJK7zt72FCyjm3hw8rgpYUIud76fP80t1FtZqLw22wKdgVufJcV9e4F+6SSs/5/jlUveb++ohia5vr8WXuxncQxYgdtcOkt8eH/i6yidzMvsU7vIevLFtiQr9MuNOsEAFeEM9zl3t4Usaxx066x+3wAUpprhXPsc499/yb7DW77PodHtk+QkmeS17gQf0RDS1FHPC0usp71ZsAPDN4gZm/T+sqMtHjorvAXfsOu/kON/OXmYUZsrIMdJ+LPMeH8W08nivZs5TtgtZXZKrHtcH3ePPkx2z1cy5kVzmeHTJOd7Ery7n2BpOtPmVbEk8E+5OrxG1Pu2rpzyZsdhbkyZins2uoYU5Wf0xcB562z/CxuMdIDNhhl1xmPFKSTGc813+RX5a3cSFlW53DxIK19eSi4OXRS9wKR8S2ZnjWkLghVnsyk/BicZH33THaloyajOHKEXoJRileHn2be+UdfLPNSPUZtxl36pNOvpc9HjFDy210OmRL9HiYPYQAz6Y3sdoy0VNyCop0wDvrdxFGcL1/k+P2cdefTM613nXeWr2Nd47LzUVO3QkJQ6Q1PFdf4pZ6gEdx3u2wkqf4XNBPRjyrrvCWe4tMpzydXKMSDus8eWl42t3klv4I6eBC2KOtNaW39FTOC/oKb4p7JHrIRbOHDxEXNXkwPMsV3rF3yGzGuWSCzgtaNyOJkevtTT6W98izlK24hzEKLwRGaJ5LX+Dd1UOiVoyabpy16YYs1VxtzvGBf8gwF2zFnEl/xIPkPsLBzfR7PIjvIOuWQZ0xjbvcM/cQPvJMvM6hfkSIju3ROXbNHrfdexAjN/MXebi6i5cjJnLCxXCFM3+EI3BJX2Znch6ZmC8kE1/+I9Up18c38bHzSppmU9ZiyTTfIZU52+keD8qP8M6yne/R2JKp2yVRKXvFhc4FWwUG+Qhk5Mez/0Zfj7hWPMetzTuUYcOl5DI906fn+iQq4/nku7y1+CljNeK8ukAUBi88SUh4LjzDrfZNNrrmav8m57JLXYLo3JPkRf3KBOPrBAJuTF7kpD5ikk7p6QFIx+22gQA3Bq9wt7xD49ckFi4X1yg3FZ/Mz//mcKPPtU/jzy9BbuLnP/yG7ZPwlm4+5NdxNn6rc/xdECl+i/a7VYt60l669m0u7z2FC45xb4wU36BR/LU/9svskk8QYF8sEXX3MX7yla9PFsVn9xsipQgc7lxi7ftEYbjnHjOef0B18iEZY04u/0NsTyEtfLg9IBORs8WSarZko1rcRpLLhMNnB8hHJ6jUI1XkaCiRLqKl4ujpPjw8RptALuE4XWD6hqSX8Fi0tOlNWja4os/BUKGoCT5wuN/Nprh1RXu65q1NQ6UjjsCdTWfyU+4MGcqC29Zh52usETwioG3ERw1e8fGljLSpsD4wz7uLYCOYoLh/oUeCpFzVnMwrgtI4rxCrllu2RqqAyyRrF1DW0zx2KLvkl9OS/NyIdneEedpxdPegSyYry+vtO4yaY9bNkv7yXaIQjPySXOacjRK2rp2jPjggrDaso0NbSerh/n6CrFpianDRcZZBaC3GBh7tpujaErJu0DgZKmgcOsDjHUOcLxHsk1/cYt6eop2HKDne7iHbhhgCysPsXEFCRy47287QLqJixFjP4/0eynkQktNCEr1Horrj7xQkXtAIwdm4ByGitWYoJI+2JUkTEMpQS1DOkVhBXkUeFw2pd2xCw5mqybNDRJhR5ENmSUM/GqpM0pgKa+foUJKFmqN8TSFTNrLGxxpft8gAhUg5VocUFDgRkEZSPTHya6vAqZ6xM9gjJWU3PYcNDcYmJKlgWZxRLktCP3D/6GOEUDAUFP0tDtIHKJkR0NQu8OrR2xRbfWwVedQ+ZGs24vbpLXaf3+V/cf8zXneOoReKK/wPO39EJWv6ZsBfHfwJSehMkZSd878/949ZTixjnZE6wcHjAxq/gaHFhQ2iXjIwFpH8mG3fYuuWpNUkUtCqDZPM83Th+P3BSzTRsZcNqcuK1b6hHxUDk7OW36es1+zke6AEM3tM2hj6esC6v6KONXHl+G+Hf4rykp7Jec3+DU5YNmHD+7P3sAKUEKRR89HyXXq9BOtKoqqooiBUESM0p/kZmUtYe0EQnpU8ROuGLE05i3fJW0cl1kgxY2mXGNmiU81xbwV+QlPP2IiMKlq8GQGKe6EBOcLisKLPsV+RZAUAh+0JShhAIFGc+hOM0KhUspQrgpdIpUlEwcIs6Pd6NHVDmTUIkaJCTmHGHMcZKSlSSdJexh9N/gVNL9KTff77o78iaS1BBTZqjVMJuuiTJxMeukNSlWODoxINIoFQe6KN3JePyExB6zYsqw15odE+IZM9HsSHJM5Ri5baz0iVJKOibxSlucu0rVmKErm4g9eS3ER6bcM8/ZjRsE90lixVzKtTkJDonAfuEWlMECja+YqFtSgZSEXK4/gRuZbURpAaxVzOUAG0Ddxu3+UjPmJWnbKVTHD1AoVGBMlhc4AOhmg9MpXMmgMy11UBFptDlNQIBMcHR1h/wHBSkMucspqRe0iqSKEkc/GQNGra6FkzQxsNFbTLmtePf4IoJG1VUyUlEcHJ8YykTTl3eQgywysHQ4XJFQw925Mx+pKmH4eUYU3MEhAKLVLSNKVM1ozUmJWdI1XEakuiUwrT54GdYdhCJoaWnCoIMrNFpgo+ah6QGEeMS5xoqX3EZBrTtBzka3KRsnEVxqQsKvCNQkbF+6cLZLZHkCW163EoBZgMJRUPWo2IKVVzStkW+P4C7yLRBdZ2zT/t/QvqpEYu4K/5CdZH2lXJvfARSSJoXUvE8+HsQ+pVTSDwMJ4QPPg8Qco+x/mSJBiWmxXzOCfNU6RISHSfj6v7JDqh1Z4VS9Aa4QKpSXhgj9BVgiSj1ArXSkQ6IDUjPtIthdph7VZUXhCdQyYpeTLg4/URqdeEIsUmniiPSExF5iPH4hATh7ShpgrQtBVYQSISHolDMg0VDfgVTaJQMtAb5pTTmt12wFyuKaJkfvQuFCWyFRzoklRFkmjJtWSpT9BGYrKERTyjUAWlWyOs5bC9D8ERleQwPqRIe6zrBXlMeCq9yvfyf4iPgYvTp5Bp8sX45wvts6UvTV/hcv9JfJZOCdExa0/oqyGF6TO3M6xvmCYdbPN4/Yi+HPDq5m+RicQ7z6k84r+c/AfmzYyBGfGjs7/E4Sl9yUAPUDgQgXZRck/9kkKmBNkQtcNLSRJysjbhTfdzlJJUsebh+gH/IvljdvL9b0a7/AZtJ9/nX17+d6zsgkL1+S93/99IG5BWcFjeIxtkaGUwImEtF2Q+J/rwxIT1MwzObxTQiy99iF+NRH9DsNWTLbrM4hNj3u7v30E94Tc9id9hAvI7Ti4+uTWCUX/85Ap9mUDxyTc/t/jLN4gvfv7sFn0iXPsZTEp8/uPXIKQ+6SYAj2PFQliOpWMuIht7n6J6QKnnhMmEahw4MQlGaXRTIVctKxNwIwHZgGUa2fRT1naDSC1LEwhjiEKzKiRqWNBUJTELrEcZJ/YENw0k256qPcS15ymbJctU4WlxWrGMnTPtul4T1g3LFOrgaHuSRSIAhdWik22VEJOIHSgWqSYKQSscGlgVklDVtDpQK3AoPJoQYifbaiDqrizcSmgnhoBk2dO0MuANEAK1kSAtElj3NXUbOKnOKE4a7N4Ae6FPWRXMk8imaUlXj6njnMqV1HROpGu7ZCMMi9E2bbJFeXHYneuyZp0LpPOotMMpVQNNNBrnHMtCI6Jm3QQIkXXfdG6sUbIpOjnTMvFgOzdVYSTrkWKRJhAjZa4RPmddKA5UB/WoerpTjkg9KghWPd3hOmNkU5gOEpFIZAgsi8712wpJmymQEp8+kRktNC62xEGGkxKrIIwTtPOsdKTJIohO0ahG4NoluVqxFkva2CJNgRIJVnqib3GsEePA8eIusojkOsXSooQGo1m1S+pYMQunJMJQ+grvLc5HFnFJWZcUqWHQ9Kh0jS8dUgqWbtGV7jOwWGpRoXoJq7pCCol1NQtRok1GKSokAjtxNLpGbgvSVPPe/ffobWV8dPYhNqnxxiGUZGCGOO3YTfdYtGes7ILT5oAYYSvZpvVrziXb3TOfCs5fuQjAa6c/Zr3ZULIkGouXLW3mCSGwcd3A7rSnShrOihWvTKeIxODrhp6UDIuCYB3SaEZqwtCMaU6XJIOcqdsC2TmzjvUuCMEt+xZN0rKpNt29dxUutLShptQjghKs4hITE9qo0aHHOqwIIuBqy5oNZdhwGiImSNZiw6lK8TawYoP2mrU2JFJQiYqZTnBBskxqRIgsFw5CRmk8Qqywq5qNqJFakVUbRIysXYmjRIc1lZt3fTsfoZViXp/hW4s0go3tJILL2BKlZulWRBMJTUul18QicNweEYJk6ZYE5/DR0cSGGAPjwYiVabiUXGKzXnMaZiySJYFAzDWta1n5inZtiWZG8GssFh8cQkgqVSETxUf2MSFklL4hZo5SwzKuaWXElmuUENSi6VxvXaTUFUE71u0JxgnKUBKyPiJRtNQshWcez0hcyiasCU7gEsPcrbpnoPUQBQs3J6gWLQObuERpTa4yJIJ1WBFdN66txBpkpGktOuYs7Jw6bgh2zYYlAtiIFVIplm5BcB5ZWqp2SYyRWpXgIrPmhKPTU4rhgCAGNLYz6xNesmrnBO3xomVtl9RNRV1URCFYtWcMsgmiLyjrNetmTZxHqmVJ6VfExHMYH2OaHGUk+bhA9WDhVx18RDqI0MQa6Q0iKlZ+QWtylnLe+WCYGqEW3W9oO5naZWNIswkbV9L4FpXnzOOatW9wixm6aSgHQG8PR8misRT9gqWddXr/oYYAIpNsrEcQqEIgbgKltNShJUhHlQaUVgzSjOgcZQpG1SyZs25PUFIyZQpJZKsecaJmLNsFx+KUmEd8azE2sgxLbFlTB0VpOoiKl5J62VLWFT4JeCIVLT7xneuylCzjBt9EglxjXYV3nk1co5VmGVfUscQnKc4KWtHgUYgiZyUafFzi2hapFU201G3XTxebFXXW0LoVWZrQYFExoF1FqZb41LKIASUGbFwJPkKoWdgZCy8RcolRBaXf4JQlICkpKec1WZogXaDRLV5tsHLGxq+QWuBNSZKm1NKyMp34yoo1Qghqu0Y1gTXrDsqLZ96cIVFEusm5lVughWI+PONZ8TzZ7hCp9a+JHb8IDxklk0/XSJGwm50nPgnoJ8mUGLuoScmU88On8NFzuHjMkX2MDS2h9QQCS3fGOiyp8SAUdaiZ+CEyOObNKTpqZjGSibSrJntDiIaFX1AJw8I2pDGhpkHbhCN/wHgzxvRz/JPJR2UU4hsmqL8p8P7EfuBw84BVM+d0cwARZvMZYSNYxxUx1nzo32CvN8FVDcmg+PRa/Z0C+q8Gs3x+yRfh/J9r3wSj+g2TgW/ko385ofj/18rF54P4b7pAn+/eX1ul+RXwqG++Lp8nvHw97+KTBGQqMnpoJiT0Y0JfTlGn92nDgN3BmHmriVmOOauJx0t622PiesWkkgTfkTsH/Rz76JikdMTthO0luFRQTPoYq4iP5hRohBWMyoyd3fMkfdcNHCgGyRBByY431EpjFivasqHvBGod8SEyXXg2wpIpQSsiIwdp4/DBMWo9TaFJW0ujJf21JY+SEAOTucU2gtY7ahUYrSzSRaQUbC09PhEIBFWmGG4cvg0EciabgBcdJnxdSIZLi5ayI6GvLNG1mFrgd7eYGs3Ka/yqJFtU9GYlo6cmCJkx0gMiAakVuSxIybAiwyjJ9OKQetNwenyKWle0dU1qYS4F4zOLNRrlwLQO7SNpGxDeM521WC0wrUc5T2Y9ZlVTnXPs72xx4jfoeYvwgaQN5B6kEuysA00maayljZ5eFUkqT9SKyZmlUZC3Aa8kReVIPQTl2JpbWiOItcEmin4TSYQEGdiqIk4GQvTMcRgbGbmuzw0bqGJASEeWSUZ+hKyOoVcwMmNU1kfFLjiciD7RJFC15GqMqysmwyG1rhmZKTF2/ISe7CMEpCZjGRYM9JA2emIQOGfJU0NmUhZhjtxohIpon7A6XSMCXNq5wEouadaOPBtiMkWhOrnTLBScGsHEjdnqD1nZJUZoSB1XnrnIx5uP0WtDWick+ZDoIikphe5T+U4DP9cF2+kekUgmM3riiS6+lN0g+uS5nGTbjLItWixjM6Gya2zbYKWllxUkac7MnjIxUyb5tHvJxYDqpVCk1LFG+gA+4K3H+0A2HSK1AiE+HbA/mcfY6u3Q702YyIqeGdComhAca7ug5wqCkIAkFwUxTVE6R7SwJUY47VFOkJKhlUQLiQyKcRzR4IgBspDSSzMSJwD5RBZSo9sNIghU1iNRYw42B/Q2Gj2a0qNGODDKkMqUYzdnz4wJ9Ql1pQnWk4eMQX9EELCtpzjRkukeMUZSnaNkhvOBYduHzNOLOU1VUTQpWmY417Dd26ENFUFE6rYmExljM6KiIe0XDJdDtuOUhpaeHhISjZs/ZGhTfFugnxgKpjYlNxleOnpNgY09ZqWl0Jq+KuglGoInr3KCSEi8Z21qtsKwu25Bktse+ECRZiRJxVa6TZSOhZ1TiIKoBFJohNVsJTvUChCKLKZEExAOgvJMGRHqEhUCiUswWUpiMkKM7CT7NMKio8FoQyILEp/isUzVNo2UZKHDbicyRTlNUI7tZJ8QSwpV4J0jI0OheLx+TE9MuHbhOjJGovAUaogMikW7YFLsUsc1Rua0qiElQ6mEdJIzNtss12dEJ/FRIErJlZ3rbIddhsmEZDoEpaip6ScDggool3SSodHiK0utSoZxSLVuGPe2GWUTfLSIKFjZM8ZyQqDDuxemIHMRwwgjFeYsYEyGMprUa+IwJREwa2eM6BGLMWq9xpSavFeQJSl4z+i0hVEPJTJUaVF0cqvH1rJDwiY+kQ4XkrQQ9LI+Uip2VB9rGnIkMkAv7TMoxtR+w05/l1G1xU69xkdPHhWJF2AkW3rCuvX0lcBGz0D0EAZO1YqtMKSRjr6IlKJlqHJSneBtYCuOCMrgQo9WWQaxh9YJwUW2zZS6AZmlbMKGkRgjKRD+jL7NaFoDrns3DOihFThvmfoBZAXCeZZ+xcD30BqC7DNSW1iXInyGty392MM7aNuUnu6j9YBgNTqTjEUP7yMGTUGCdhJRWc5Uy0AV+GSMUZpUZeRFTqELZpwwVTuUtkSbFOVA2UjaSkRfM5XbVLSYmCCEJIspfZeijGAipkzzPXQ/x0lPEhUBaEJFKjOklJ2fCpFEpF0CHSpSmSOFwEZLiIFUfrYuEQnSx87XBk8qM2KMVKHGRM1QDNnWu5ShZKhHxNBxPUZyQkMgRFjHFf2mB97R+ooefXSaYoRiGRdM5ARHxzXpxQKdg7awURXDZMxETaEJ2FUJUnYcTq1+lQ/dr2zDdEKmC7bzfUSUzGenTKZbSCsYqxGjQ00ljpk8c+mTcPGLGcAXAvTPJs+/uX1ugy+DcD5Z9ivbZxv9VlCor/vqb3vNPh9//w4Skd8Jofubz+WLS79Sk/hKNeOr+LKvc+YWT474aRXjmw/5BVjUVkwZk2BFpMTxA/kd/ntWs84CW3KH83bCo/kZqrR8/z68s+2xeBIb2H5Q8ua3BpQy8J27nrefNnitUCLwbLHDz3JHczDnB/cjt28mWFuhLkz5N+d/n8fr9wDBxewa/2Xxc+pmRlEmXCiv8d8HnQ/FzQ9a7u0ZWqOpjefm7RU/eb6Hl3Dx9oKD/YJWaxqteO6NE37yrQlOwZXDhsORolU5VSp55a0Zf/OtEY2U7D/aMB8ltAI2ieD77y758YsjrBJcO27ZGDiaBkrp+eHbc/7m2xNqAU+f1nitOBwZhIbv/WLGm98ZI2zLNO0zMD1OEghBcv61DbfPbREujemJCeeWjzlrzmho+cPkMsdyypyWq3JAf6h5I59idhzjn9zjfxovAE9aN+w/LnnzW9s4Efnuz49597kRTiuE9zx9v+LVlydoBS+/dcKH1/u0VQNa80Jl+MvcgoOX31/z4dMTvFQE4blxZ83PX9wCEXn+1ikf7Bc4wGnBy/fW/O2LE4KEFw9aDnczIgKXaV75YMNPryo8cPXAcZwLpEoILvDdg4afXpBI4bk0c7h8w5lpsSi+ddLy5vQO0gt21lNqGZnJBnqe39PX+Xn9UxJj2ZfbRJOwzg5JpeAV90Pe9r/AicA4mWBUwlKe4oXlD8b/mlLXbOKay8VVtDW8dfQa+XaP502Hcz1tTtDrhDUzflb+lFQlXFhfYbM6hTSyl+yyOSnZpAtEKvkWL/Ge/ADR1ORGcl5f56f8ghDhh6Mf8F79Btp2CiObOy3L5zulI7WQ/Oej/8jKLxmaMd+d/rCb5SLyTPoc5gm5XHxpbL3Sv0brGw7qx4yTCRD568P/SgyCK6MbnNoDQnC0suLy+FnUE5iQCy3//exPOG4OSGXGD4t/ytAOyLaHSKO/MqZ8ctyd/Bzf2/1HfLy6Q6H7XBs9x63NW2z8isvJVd4+epX1ZolQ8AfFP2cmS46bQ67Ii9yq3uKE+yBqvmt+n1fta3jRUkjDyA9YZqc4BVfti9yKt+gkEhLOL3q8HR5gdMq3+jd4T39AbhaMgmG6SHi3eICMkpvh27ynFrRVy2ax5orb5y1dEaLiOfMiD9UZlW6p0xHXzEV+tnqbQOAH429xtzpgtVqjguGHF7/L35z8GJfmPN9/gUfVfRyCja94Ll7n5+4tWt9iqoS/PfsRp25GLjJ2sz1uL97C4rg0uc4xp+h+g9s4XjEv8jPxY0LiuRjO4UPDUp+icsXLq2u8ObzFpm0YV4o0Szi2a5yOvKJe4Zf2NUTdMM1HJHnOWbvAm8jvbf1D3ix/hnUNWVaQuJRH9hCrIr83+mf8bfkGa5WzZSbsmZyH859RNvCPRv+I1+NbkCpyMWQ/v8Qv6ldpbcuLzQu827xHK1uEhqf1U7wWXiVEy7ezl7lt30G4FTEWPK9u8PP5XyKV4vnRt/jQ3ULWNZiKZ/Ob/Gz5l0Dkhe3f40H1IcoohuOCC/pZ7rS/QAp4pneVQ/uQzOTY1PGdS3/IXz3+M5yHlyY/YO1W3Du7zcPjE25ULxN6JWIU+c6lf0yQjgP/gH4yZjTZ5c8P/jMuOM7ll7k2fI6Pqw/I2pQr9ine1b8kpJ7z1XnETspj9YDCDNgKI/5i/qdIDJNmQtLrUbZ3EEryby78ATNfsYolu8WI/mDM7eYjcpmw0+T8RfNn5IlnG4loNautNbGOXNtMuVWsYaAosimjxxVvD2qksPwgu8q7ZoY72RArz7V1wlvDDVFInr6f8eF2RZV3kzfP7HyLV/0tRIhs6av86fwvWNRnTPyESdzlvXhIVPBS8jwP+ZimbGhkxrd3v8OPVm/ivOMpdZ1H2SHOtdgk43l/iZ/Ub9BUNdviAotsjTOSKjhejM/xVvYOPsKV9DpLe8qJPcYJx/f6r/Dj8AuicOy7IZt6yeN4iCuGfCv7Fj9r3sG6mr3sApjImZ7T0vAdnuPn7nVKWzFtRvQGBSf9YzZuxQ96r/Cz8mdIvWAkxmg55iw5gJ7n2/Ear+s3iKqmnw4ZrjPe8w8I0vDd3g95a/BLciKTrMdUnucX65/ibMlz+ru8K9+lcg1eRy7Lp3i9eQ3p4XubF7k7foRrLEE6nlHX+HnzE6SQvGC+x1AWnIlTdnsXEFHwPx39PwC42nuOI/uYhT2jrwdcyp7m/dU7RCJP957h2M6Y2VN6qsfl4jrvbN7FR8+17CorP+PUHpGR8bS5yrvNO7Rtw9P5dTZec+xmZCLhgjrHon2fJkguq4uULKn8CTK0vJK8ws/Kv8b5krG8QOsaTsUhIQm8wLd5x76BFIap2kW2hnU1RxrBt4vf483Nq0iXkMac1Bn8IJCNusmjvy/XINc9/vHlP+bdk1eRUrF/6Wn+6+v/CbloCcFwaXyV4eU9VJ5+8hb5ajAbv/Dfr2lfA9H5raoH4ksxr/jmaoeAT2RkI+IzsasvH+O3gUP9DhBYnx72dyFFC7/m3H4Ne76jT3wO6/YpnEo8Ufv60sXm86z6L2KhvvJrPvf5o7ji/+s/4t14Rh+DLy3u3Ydsrm2x73NcqjlanlGgCeuKtHQcD2F/Hjr1kP0+WijU2pK2cDJWXBAFYafHydEJsrLkUpP6yFE/cGP3Av9EX+D35T6hsbxRvs6b81/wuHrEWO7yoT/PPB3iQyCrA7rxHE1Tdk8q6gRspmlFpL92pA4Ot1N2ThvqVOK0pNWS4cqirOdoN2f7uKLNOmhPlUpGZzXSBY53crbmFp/oDk6QK8ZLi7KOo7Fha+VoU9XN3vQN2wuHkpKTccJw1SJ8jW5q2ufOc2GyTTlbcbxY0K86NRBjA+urW1xLJOOT22zKR+S64On+Vf7Vuf9d93B8jocvpOA/+0f8ZPGA+7NjJo8rKq2ZD1Jk05JGSVo5jncLpkc1IelgSVhPr7b0Gsvs3ICnL17i7GjJoiwhRIoWMi85GGl2jjb4IqNMFT548o0ljZKTrZTtk5o2N7SpwkoYVrG7Z2PDztzhnce6gM00EytQjeO4r5m0ERdq6tBgtWDXtmjWHGcVo1rj4gcosaJWDZNkC1NknHLCRIyR0pFIxUZumCS7BCKn4YiRmtC2Dk3Kws8ZxxGJlCziGX095JneTf7N+P+AeKL4Io0i+oCtW5RW3Wx+a3n38D1+Uf2Ij+s7NKWjLSuqZUVvP6ewPY7KI7ItRc/00ColETmH9oAddigTxUo3KKEofGdGeGAf06sHHCwPGWz3Kfp9sljQ621xLE65mF/m++Mf8I+2/smnpLroOtUYoeQXH79PMaTgguU/3///cG/1ATa09JMBSkmOmwOm6S43h9/iH+/+IQDvrd7gb8/+Kx+V77Olt3lGPc+/GP5rku3RbzwGfnlcelDe468O/xfurW7To+Dp4ln+9bl/TwTuLt7nL+o/49bmXVKfEoMgIWNlFuyafaq6ZiWX5KogbAR9NeQ0nrFvdgHHqp6ho8ZkgizPObSPOZdcoGksq3qBjBKl9pBscxyXnEunlLamlhaBII2GXGcctGfsiiFNaDvHcQE9kZHIhIflMdv08WndmZcZyUh2z81B+ZhJGFEGC4kkpjBuNcYGztScc6OL1HYDRGpf0U8HkAgO28dsqSm12kDwlHFDryrIvWapF+RxgFhZDBnLsKRvtsjHPWZxxlCP8W2L8YrZ5oRpvocTgblYMExGiCSSKM0izJmaPWzrmdUn5CKnNQWmmHDsZuzpMS4uOa0PycjQSUomMg6bQ/blDr5asLBnmKDRUZOJgiN/yF52AataVnFFKpMnUp6aE3vArtzrpHXrFTFCEgyZLpj5I7bMHo2rqO2GICLLWcnezgUer+5xaXodEqhd1UmlpmNSnXFYPWAnO8dCNoSkc9Me+Ql5yFmJBVtqys38ef7B+H9AFyk6Tz99FmKM/M8P/198uLpN6dY81X+Wf7rzR2xXI5qyQvdzTJF1z5CUSKNxm5pQt/z57E/4SN1nXp4y9kNUkbNwc3q6z9Xhs/zLS//u0/4enMPVliRP+S8f/wfeOn2deZwxkbuUUXDGhtzk0PZRm4KzpOHCcA/rHItQYaLESEWG4eHsEdsbTRwOmJ+eoNYVSQ3GK44Hmh1ZYEeCZhAxRUahW3JlOWgO2O+dp9YpZXDE0FWUcyk5Zsa53jnWjaDxAessPQyy9RwxZz+ZUoWK1ja0oSVrDHmacKyW7OktrF8hjaBqNmwlQxIjOWoP2RJj1rImSsHCLulXOamAUzOn7we4kBK9oTYt+71dpHpSpQo5iIDftCzFmi3RpxgHFvGYvhhAIklEwpw5O3IPW1tmfkYhCoSM6GiYqTPOpxc7p2s3JxUpSmlSmXHSHrKbnKONNfP2FFlFVJaR6B6H/pBz6QWcb1m2c6SLZCGjp3qc+CO2xS5WWipRI4XkaXONf7vzfyYpBaVb82fxT/iwvgUSct0nUSmH7UN2k/Pd9fMNLjp6ZoRUKQfNI3aTfdbRYqOnCQ0jckyMHIfDziCSkqig8hvGnId2wKGdsxX7OFUjiaz9hmk6QgrLcThmrCY4uyQzilVYMhFTlBTM4glDMUJ4hYk5Kz9nS2wTG1ipDcN8jCtbjE9Y+gX7Yp/v7fwDXrj6vd9JYvF17afv/C1v3nmdg9NHjEKP83qHP/73/xeSfv73Ot6vpDR8OtnWxaxfdLH/bXkdv8UJ/V23/Vz731SK9os/4sslna+rO3y1fTFJEF9ZGr/ync8v/2p15AupiPhsexc66ThHpIkeu6mQo6LD/CedvGu0hnbdOfha08mjNtEjEo3Xkth0koTWCMg1cTKkOV3QOotKJEmIWOdRkz5101DWG2LhUVmCL0Mnw0fAahCjHq6BEARRRFoZcd5Ty8443KpO0jNqSUsgADZROC1oVCQoiErg6F5gNlV4Cd5IvFYEo/HCdfsyHU8AIlbETtox0QSjqHWg1RIlOllYpwReCrwEZxRKKXyQNMs1bW+Eng4RymOP1zjbGX41sxUbLH3p8LEzKXLBdWoHUeCtQxmNkN09tCLghxlJbxuzBdXBolPNjBpbNZDqDotsIkiJ1aKTYAyBNnhINLW3tFWNTzTBeYKHKnb3zCYaJyI2UcQgwIEL4sk6iVeCVovPZGIjeKA1nYSgE2BDwHo66U4lsXisCFgtEanBYYkhEkSklR50dx8ZZIgkwztP8AEnHEoHvJadDKtwuKYlqIANLa231E1DEytC2icYibcBJz11U4EEv6zQo4LoPEhJ0sufjFIClSXsyG2SkxwpDcNeDxnH6Ce47Z4cYDeOSq5Yu5JcK+pYIjKN1xqZJ0QcbeVIbKAVEpSgtBsa2xCrAIkg7fUpqzVWNtRsKMMcpzdEKVBPyISfqnd8/in+HFoyxEAInXu0jx7nWlzrCZ/0mWg/fbI9Dh8tIXrqpsSZBqHVVyaCfpvx0wVHiJ2cpVOxk1hMNMSIHqZECxgQBgiC6Dw+BmpbdVK60WFji04yrLcgI9Y3HSJaBKL0qMRgtQMPta0IPuJlAC0RCGIMEAStt91z720nGhAFla1wrqUOG2wMVLIFJUikxOGIIeKkx9snMtLeE5UhJqBFisKQRInTEYdH6AS7XBO8Y12uQHewPhcdNjiC72SR29BQuwqhO1lNlUiEUMQIUkq8U7RNJ1NJInB4IhEXWiIOJ0Flmph0crYueCwWEQP47j43boNH4kXA4bA4vKvxwdP4hkgnvdsGS2gC0Vt8tDSU+LLC+pKgE6JPQHaQmkU5Jx/lXZ+KTSfaICLeOVpVwxNZXd9YTDKijS3WWcqw7vxUYgOAyQx1qOmPh8hU0biK+WpGVmQEApUtCcFztj5jESr0IO1kV1VAaMBDkIGQCLLpAKHUF+F6opNCb0ODcxZnu8BPj3ok28OvlPGjD8hEIyS4RaCxHfk5ZoogQjfGRvup9Ct0yb1UmnTQvdZjrpB9haglQUWCFzjnqW2Dpofsa/xmzdnhSSdVGyta6ykGA1TRkVt9bkCCSxShSJHeg7NgPb6uCS7QhARrLWYokaIFI2mjw0eNwxOCI0XhZDde1U3dOWZ7j3WWRApkfCJTq0InTQ6ENuKbmjDoXOvr0OKdhejxqpPqtqLD/lsVCLrrl1IqVJQdF0spRBD4NhCDo21bVm6F1oKgu3dXxENCR/LNU5rmjNATtHgEHqW790sbGrwIeBVx4olgqxB456j8ChE7vgcSEhERdHDlNjZY39K2NUprRCJwJiKtpPU13jsa36CNJvFgQ4v3Dp8HohTdmBkDItGgIvm5KbYCf2BpXcfl8tHRhE4qu3E1PnT9PoiADe5JUBtofI2NnjpYrG2oQ/f+88LThIpWdtfYxhYrLNG3hOhpgu14jqKT8rfRok0k+kjja4TuUB4ejxcWEJ30vnAIHwD15JxqtE47Se1giRqapsHZltgXJFu9TiHqKwTaz14iXwzOf4P2uS+74HC+g6ln2wMuXL35WWLx9wjEv7Lpl+BUXUT8JIr93edMv8EJ/Zrl/ytULn4HsKivYsTEl5Z/Vrrh0/VfaZ8fiD/hgH+FrxF/NS8jfsbn+Lp1l8WAi6KPRKAQTCl4tbyLXln2RxPyjWBzWCLrlhfWGbfDkqLVDE9advsj7pxZZIBnPnY8uJKjxxNGC8/eG2f48xpB4MaDwPGNAThFHgTf2bqIkgaAa8MbPK4eMdBDMl2wu3WVX5wd0x4vuPbI8jCLOC3obRyXDktuXx0QleDaxxvO+oZWdRyI5x5W3L7eJ0jP1fsVZz1Nkyh6VeDqxxtuPzvCWnjqoKYyEZcaepXlmbtrbl0fUdjApccV3iickRQ2cv3WGe9d66Ndy4VHJTIxeBnJm8DN95fcuZISj0q2/IrBtUs0usQuTvn23ZJfnjcUUpKctAxzwebaTRCCp/LrfLS5y8qu2M/Ok7ucj8p7GJFws7fDOyyxMuP8IONqvssvPvoQNg2X3jriwVMThlIyWTim8w13nhrgfODGh0uOdwyxjRSLlvF7Z9y/MiJax/UHJcfbPbwSjBrY/XjJ+08PEUJw7eM1J8OEhs5Q7/zHSz640AcleXrWMk8kQkiGLVx5WPLhVOISyeWlYK0bnGgoGsXlOXw4fYwQcL7aowo1TTylL/rcNC9wN79FTCMX5QUaXxG1JYs5L+Qv8n7zS0QU7Kl9XBqxLWQy54XkGT6QtyhUxnl5nklvm6Wfo6TmhnqJe/4ua7HkQn2RJOtxb3WbRGZc7d3gfn2PVTtnV+4xlAMKeiQq4Zn+89wvPwQPO8k+V6bXuVu+j0JyLXuONw/foCy7mb6nsqd4e/EWvWzAs8llDuNDgobJzoTz/jJH5hhRCszMkO7ntL4liymXuMBrBz9FKsnV9CpztWamztjOdtnLz3FrfQsfA88ObrCwMx5V95mmO1zsP8395gEuOi4W11iFJetaoXWfp4pneWP5Lm1ouZDts6PPobVCecXNyXdAyc+Icb/tSwY4X1xmN99HCYWSmuuD53n37A0W6xMuT59hyJBRHGBIeCbe4I6/TYw5W4zJVYEkYkTCc/2XuVvfI9iGiR4x9D28aZHKcNPc5CN7h8L1mGRTRnLKPXsHGSWX5WU+ajcMBPS9ZD+5wK3mYyKRa3GXx+0ZrUkZ5SP2zZRb6/sE77kmdpmLEotlQM5ls8979gFRwrXsMgt3Rh0lulY827/MHXtAkIKnk102agF+yUBlXO+d5+3yNgrHZbnPWi3wsaVHj5fEC7zj3qUNDRfM5S6IEx7TGl4Yfodb1bvk+YALyRWCkU+SUc0LW9/nvdVbBB3ZzfaROoHNh6Qy5UbvJu/bW1jv2c720SLDukhCwiv9b/OO/RDfKMZ1wSgb4eolGsP1cJUH6hGRhmkYMUy2udsGNIqr6lk+4j4FDTv5HhfyC3x49jbaGK7mNzhY3aH1PfpqxFRPuW9vQxa50n+eR/UD+n2QZYI/DpgtRVEUXJg8xdzPOK4OsWu4nDzDneOHmDRyaW+bk+aIRkBPZ/z+9g+56z/ER88lfZnUFFSipEj7PDN9ifc272Oj5eniCpvQ8FH5iHEy4Onec3xczYixIfcDtDC8vnqVgR5wbXgDJeSnQc6pO+Hj6kN6ps8zuy/x8OHHxLTHdraPkoY61qQq5anBM9yevcGymfPU1nNs671PA5sb/Re4t36fmEX20nPkyT6n7Qxftmw1W5wpxfZoRM8aZBk4bhaoENhZ9Hi4ecTYNEzkkF6Z49I1RLi2GPC4qPFhw6D2TOcN92wFg8jl5hLr3Rk2zcmc5nryFO8s7wMJT4ct5uGMMh1SJD2u63O85x/j8Fxc9VmINa2GtE652bvM7fiQxjWc84bNJrLRA7KYcb3d4Zb6AK8E280ItSOp7IJMJdxMXuTt8hcYp7miLtC2G0IWyUXBK+Z53g6/RHvBVtMjFZKNn5OphOfFDd7xb4OCqRuT5wMe+I9JZc4NdZMP/R0GBHbUHqnJsatbGJFwzV3jfn6fEBxTtcM4n3C3fJ9EJjyXvcTd6jZZzOlVBYWb4FWLlJor9XUO7COcyBmHAWM15W5yB4XkunmOQ/uQOtYMkzG76TneL9+FKNhPLnCmF9xavseO3GVXXuChnhFD4LK9wEwvWftA4vtcMue5Fe4SCDylr3Dslmy8I/U9rqcXec/dwqG5Iq/Q6DkxOPqqx0vpt3inehOH45Leo4mGENYkUnBFPc99cYskBHbcNjoP1JszEg/P977LXd5FK80FcxmVGsLqHpnMuNF7iVlzQt1u2NraJzU9lm6BFpqddJ/j9SHWt0yKba6Mr349mfrz3IWvNbv7hsDwS7Pb1y8+y+HsgGFvRC/rcePKzc8SmS8jbH4N4uYb26fZz2/3dnLecufhBzS25sre050o0idT6PHzJPPfdkrt8+f2m6z/3ZAu/leRoo3f8NcXEE7feG2+LAH22T5+HXTt6/rD52FSRkj+nXiKR6IkR/H+3oLbYslJaGjrhvm9I2Ia6J2bcnDvDL1sUX2FzDTLXCK9Qzs420sZXNmnjo723hFtIdBSo0Jktq3IpyNOTg9Iz42Yi5ZdckAwTbb5H8//MfN2xsCM+ZNwTH+rjxWR1XJGGiWJlBQBTscJynqshyMTEN4Rg0bawPHEIKyHRLHoSSIBEQOJCxxtJ2gXOl5JoYlEtIDURk6mCaaqwWQ02SfmPpCjmO0VpD7SakmdCISOnTxr6zmYJmgvwAg2VYtxDSYx6F7Go6lF2YgP0AC3lym122Lr3A4/X8/on7zNxq7pqT4oRelKjDRYf5FkuI98UllaJ5Fse4w/q1ieG2PazpxIIJj1OzOuIgqWOz10sPhNTba9z9l2Dx07JamzftIZfwlQERbbBQaBd4F5BlgLXqDawFmqSVYNMTWsXCTREl0H0sozKzxpsCATqqxGulOUt+RWskofUtg5LYG6eR+VZqRpySgXlANJ4UxXgYgbog6k2tDzGQftQ0zUWNFik4gNkWAVWuaciVPSBpzwyFTwe/k/pPEN/WzA3fUH/OT0r6j8mveSEYFOjStVOa+d/ZgQPWu77Er4MUIMCBc5aQ8wOkGEbvZs7TdIadAYTlmws3+RZuYZqS0auWZc9Miygk1bkVRJ97vUEPN0pH5wyHK9ogXOrXeodYXQnv9W/zmNrRFa8gv9GhLBxlSMzBhnBFXoHHhfn/8MsCztnIEegTA4CW0IHIY5PqbUaBqf8qcP/5ImWmx07Jop/2ryB9T5mr4aMsi2ECF89nR/5f3yNfws8cVRI5EJ/3zv33DSdLKrH6x/yesnf0vlV7zXvo0zARkESdScxsekKKoYUMrjwgYZAibAUfgIIzyIFus3nKkGJyOpljwKj9ExIUaJayMrtUKhUMqw0kvS1mHXZ3gJB60lCouQklW/oZ+MWTcBIwwL2ZAWnSFdZQRiDb6skSrh44d3YTvDNS0H1RkhB4cmTcaclBbpe9jgmJmIUCOsCyBGfBwryPt4WpYaZAzQeEwQPLaHJDLrKiZNRaAlKIsOGQfqMdneiI1fUeuW1jpcaEEaHrh7SCPxzlGKDdq3SBFRbeSj0w+xOtBqKIUjssZ6R5JkPHQfEdcbvJ3jhGS1lugIqYe5PCJXitJ6ZGxZUSMjZGnGMs7IZU5PNxQmoZwfkrWgXGTjj0iDQbqIcI6lOkUKhVCStSkRsWC5OePC+Bz53pCFnWPblnmogYy0N2aktikl3HzhO9hgQWVMxC5CGyZ6h0pasnUP62tM0PyzC/+KNmvpqwE/efxTHsQDLJY3Fr+kjjB3awayQIocL6Y0smSW5PzZo//Myi/p6z4Lu+D7Wz8kSlg0Z/zXx/+J0+aIXBVoqdGZIbqSKizxbaS1FYlMeG35t8ToKOOGuyd3+IOdf8tWsg3Ayi1IRUrFBiU0v7/9Q2yMmKCYhAGz+SkLXzJYa8wwYT30SBt5fPY+s9X7NPEM7SLrzCJwICInu6DLBBEatFMs84gSFrnasHQfEfsJ9ARpWnC8WRGqDltw4htk0sNVnuBSjvMGRUI9X7CQltCKrhogPQ82J9AzSATttIf0AS1BrRWPwwFGBdpmw9I9RqeG2AtIAo82t0m8wwtHKZaQRrxvkLLgSN7FqJoQ1rTqGKNTsliTyYQj9z6JdlhZ48Ucb3pIp8lUxuH6QVcJ05HGt1hlkVKQqpTVYEMeCko2oGCxOcE5hzEJ9xcfghZdBcIEqsQinUZHw0qfkUVNKbtJzpWfoaVECc2pP+ygpYkkishpc4gMHZT4Xn2bj07uMHdnDBljXY71ORA5CoHY5jTW4Mi579ZYlxI1HLUW5w0+pgjd57g9xUhNsI5NOEMHj1CRIimYhUMSr4hYWrdAeUkqK4qoqbOH5CESvQUWNKvOzHWkMxbJCZksOqNL4YiVRLuEXjZiq9jlZfkdqqLmyoUbCCU7+KPKGadbLNsFpV0zzfcwTyZivxDFfbmI8SsD689hcJ9sIj73Wtgd7/FHv/evWKznTIZTsiT/Ffv6FYf7FeTnL8e/vxZu9WSDn77zt9x99AGNbbj36A5/8L1/SZH1PtvHp0H0k2TjCxnXVw7+xeVfe54REb/yEv1s3d+zjPE7MNH78gn8+sTgG1v83P4+TSa/dNU+lxF+ZZ8CxCf4b74+AdFScjn2gch/iQ+Zb6eUSA5bj7s2ZGMC5bpFDBwqK6gmOad5QGSCeQQpFeXWiCTzHJ+cUReB2Des+4IYIvW5AtUsWKrAcb3mXrHmWTH+9Pi5ycnNBWa+YRYaDqlgrElf3KV+vGCVCiCjFpFV2pF7Wg3EyGrwpEStBHWqiFLSKoEElj1FFBGnEpyRuCcOyYTAolBYEvzUEFyLzcCZAhe6fXrtcFsFhEBlOkiUAJZ9jc0CZ1uaxHnKVCKqDat6xSqH5MqYRwnEsmWTKSKgomRVrlmeaax9wFZ1SOk3DHRFRLCyK5RQrAcjmjhiieugSnhOh4p6OyXLJbG1rPtPSLtCsO4bBII6b8EpNrni3ukp6sXzHJ4uMUFTJV2PWBYapMQJqHIFMVJrUFGwziWNr+gVKbWSRCFoiCglWKUSL8GaQEgjMfG0oUJ6x0bWhCiI8hQXT5CphN4YEs9he9wleu0RSnYSsBDBKDasCNpx0h4Qrccaj68EQWrOwhxH4NQ/QtGVxkdxi5k85dn0eaTR/M3Rn3PYPqT0G/phTSSydHOMNMQgMHSytQMGKN3BoCSSTb3GyJS1XdG6lhBg6ZeICHO/RGhDm7Ys5RLvPGuxYlkvWNYaqTQlFYRjfAyY/RS9qDv5RjHndHPC6mzJ7vY+VlpoI0PfQ0TJplqzSpa0wrOiJEYY6hwp4xPFqwX2/8fcf35bcqXpfeBvu3DHX5fewBa8K6CAqmq2oRtS9BwuiZq/bjSLXNSSRhK1aKQ1JLspciSSYpPNbjabXWi49Hn9ceG2nQ+RABKJBAroKoqzc92b556I2BGxI2LHa573eTy0viemQGM9MWhWboPVPZ6AfaR6bCrNUXfGDxbPEWNC5+YLWN13ak+bIEhopblYXSEluL3+mAf2Dl1s2IqaCJz7UzZRcRxBR02TtgNDD7AJa1RUnIZTjCnYps2g9K0UW2pEkKzjEtVDrRpSEIgu0aYaKRVrEQjG0GY9Z2JLUo5N6pFK0jcB0ShWrsaLlhAVy65GCsFSnpOPS7qx4gyP3xdswwrXt7R0RAdbY+mVR4uSznpiGpSvhResfYNzHhtWeNUQFHTphNx0rOwpPrV0AlKSuGQRwoJwdLoh6MRZPMf0OVY6nPP4EDlnSeNrDs/uYHRGJ3qiDyg0W7/GkGFzgdSGOtbgBD5Elv05q+4cWRyihWYrN2gpiLZnE9aAoFIFWczYskFKIAXO4jEbt+JEFGS6ZJu2xK3DNI7OrYe52a4G1jt7PkC8YqQXHd55uhxMUaGVYp2W3H54G5HLQTm9Skgp2foG/MmASc89SUR8sngsVnSIKFltzwlKEHCswpaGLdfKZ3HRca7W3K3vEWIg12O6JFj6LWNV4bwiJYWNjhRqdFiyCedUsmLClHd3P0AAD9q7rPoz7jd3KFVJFB4lFV1oBhVoYM2Kpq05jYfkWU4Ttiihud/dGZyLBPeb25zbE2q3YasmHLZ3eX3+7hfvx4PRVQ5SJPmI7y0zKRBC8h/8v6aXHV3XsNIlPQ0bItEHeqNBKxorECmSpGKbD++nRm0RxtA5C2isbVmmQQm9Vx6RJFtpSe05xA1NsjjR4XOFrBTbLiKzgLfntJueSKLLekCysltslERzBGWHb1tcaNGtoCsCHkvnt4/gNpaoEyJTrP0anwJH0UIOtdiSjTRN2LBhgw09x9ojpaJTFuEjqtGsxZaOlmgSRgwMVERwtmcrtmxlzcn2EI1hm7aEziGVYCPWbPyalcrR0VDLLTIpko+s7TlSDvODFpI6bkkyEmJiGzeAYKuG9+PKLYcZK0Edt4gkaWRD8rD2SzZig3UVa2+H7WhQUrCKDTFGkoA29SQEdbLgBxrt3jkSG6yoUZki0KIFbMIK0QkcHSGL+ORQUiO1pnlUp7UWZ0QZcMKhjSRFT586Nqw5T6eICF1oSRF0zKnThmA9t88+4qX8B+xfuoYxGQLBxerqozk5Mc1mTLPZ0ybsb21fjeY/vuAbXgGPDOyqGFMV46f1+Gi9pxjt39D/45+TSI/AT1/CcL5muz+tiUFV/OHZfe6d3MV5S6YzjpZH3Lz07NM3+T6wp29Y96lQsPRVFNIv0n7xzMU3ZLA+FwD52jpfOA1fLnyq7/TIM/s8BZYeWyYe62HIhjz6JqUvBv0Ll+SpGZ7hi11RsC8KBHCQl1iTEKenqPsNdIFMZiytYLdX2BAhJKq9imo6Q3x2Qtv27GwStpDoGMmqjCqr4KNDfBlZTDJ2U/7kzgEYS00pNBdESRQJPdKIqxXh3gMWS8s2kxRtokuBqnXkNhKVZOfc0WeCkQBbaCZtIAsQSOyuPZ0JRAQ2l0yaIfMQgcVqEM4KfU9dWBb5nFA7UJLJsidoECGhK8W8DgiG+oHpdqibUM4jRorZ2lHNG+TVGZNck+sOt+lQPjJZOUieGALVwwdUO4H5aA5CMc9muBRBKHKZk2Fw5IDggIxtHITs/NKT2h7dDYWs8zNLLA0qJHQUFCFiGkuSMD0/h1iwX+RwVpO1gcJFkpLsbAJ9Lin6QU+hDIKitWBGLBpwyTFSQx1N5QUmQlCJRRPok0RFj0uJkc9RrcRlMI0FKlsgygJfRGb5LtELZJmxo3cQqUdJSZsapmY2YIZFYKfcw8keVKKWNVM5JwpNj2UWZ4iQoUViK2tGYsRMzPEioD0sqn3mnCCcZCZmeBlJJCo1JqaISYYUYSF3iDIikRinUCKjUBUxRhZml0Z0CCHJRA5KkYmCkByTtsIqh5ISJRRZZShMxXF/xK7coc8CuS/Y39sjVzlZ0MhcMw1TpBzw32goRU4WDWiYpSmr2LJbjAgiUgmDah3WN5QxBxHIZI4TDtMJposDUjdQVNposU1HW69QIbC3MyMVEqMyxGBlPvV5eurX6dGvp74sholhrhfsmj1WccVueYHWNfSxYyInBBEos4ozd8xC7ODwKKHJRQFaErqEF44dvYNNEcWwTClJhoIk2Mv2cKlHO02mcpSo0MWMJBJ7eo82Qe77gepX5ZhgIBfsyhnNtsNICQLyqJDHHj83HIwWdLll1Pf4wpO1HkkiusjIGfJxxbzStHXNqJWoNtAlz0QX2JQRNbTSsjOfUciO6HrmzLBagFBs05a5maK9Z5kU82yXKBLCJbZhzYScmOeELDHVY5zfkJmKZXvClAppcjrbsje7QK8CUmWIFuZiRtAJEROlz0EolJMQAws5x9GgtCDzGVoaclGQJMzigqgsshzokKOU5GIEAvaLA1LYkmNQKLQ0ZCLHGsdYLahtTVlNEAhyMyH0Gu0MczNnur+D845IoipGGJkTmsCUOakSOBzWWQphGE8qTu0R8zgnGlDK4JRjXu2yGO3hkkMJzdiM2TE79LGnUCNGwhASLMwEhyR0ka2FPA2Uxi5qpuWUqZriuw7vPZUrKSkZywkTNSNiUVKzSZqZXhBSIhnBiAp0JE9moDLOK2Zqjo0eiWAip8zkwIg3MlNmZoGLA+mClopEHNgQM4PJND55og3Ms11mdhcXPbvFPmtfILwjGxkQGToKDlNiqsH5LdpFpBDo0YRCCjZZz06a0mYjdG8JRLIgKPMKoRTz3mD7SJHlNAEmsmIyGaNKzX4+Z9ts6M/WdCJQtpIiL1FTzUJNqJsevzknScXYjMjLjPP+jEmsqPISEjSiZqYXEAW97VmYBT5aZJJk0jAPUxCKhGSiBnixRrGOaxZmZ8D8B8VITIkEDDkCwVzO8dqhkqLwBYjhflRSsat38dEhk6AQJVIqdDQgYCF3cbFHKlBRY7Qhf/TuW6g9enpUMhhlUFGRUxBUYB4XBBkGilghUcGQqZwgArt6l42VGFHiY0D3EiM0G7clX1nM1R0qChrbUamcTGYkmdjTu7ggkfmUPnRMixGlMiQHM+YE40AK2tgwSmNMyIgyMtc7eOVIQBu3TNUcpQV0iYmY4bFIFI2umckFYi0IvWNiJlRiRHlph6wqvqPR+mWA+Fuj8+LLtb4+v39D+9ry9MS749thVT8vafJ4xD8hHkGk0qPySPGFXfykUySEZFrN2J3u0vYtRV4yG82/z4n8ctpj9vMvCoz6Buns798ezyV8gy3/lS8EPO7jDZkGkQbvTzx+U4nHtnpah8PyGCMxRsLnyo6POxlfS64IEIKX04yWgCUxEpobZ5F6taFWkXc/S4RS44kU2nD14xo3ywkXZ7y3rtieb3AKREy8cNtiS0G8OOHd3+95+5PEO2clP51c5y2x9+ShApAJxZ8xl3lH7/JDtcvfkNcoC0O5P0IZePMPzonCIqXnpQ9P0c6TJFiVeOP3TuhLRa8Fz326Jus83ig6LXj7353SZ4LeCC7fq6n6gM8kXS5589+v8FVGNIqbqWC27vBa0GaCt37vjL7U+Eyyd1SzWPbYTNMXinf+/TltldGWOZNNZPzvH7LZ1DQK/tTeTdLcoFVksW45OOxo85xNrln80zWfxj0eXHqN9uB1Jpc+4MHFl7h/4TnemL5KLxOWiEHwXKNp645OJV7/3cOheF4plPM8+0crXJZhc8Nrf1TjVUZQBQnN9X95myjBjQ1vHEW0MBAlwkbe+NkGHMioeP2jLbpLyDAU7v3o0BELQdCRG8cdsjmFdEaUG948PsfG36fvfodrJ0fk8Qih79Gl27xVvkqsFJbIVXmduRoBFu8b3il/RJsa+tSxKy9i/IQuRLbO8pp5j05YXHTsZxeYyykhdnRuzZvZe7Q6YiXoWPKz9Yf8rTv/T/67w79DkU04Z8VK1JhizMXqKjZaGr/lremPhqI7NTgbv7Hz53l1+jav7v2QP3XxL7NWHWtloSy4OX+JXkW2qeXN0Q9xtiH6nmpc8creW3Q60AnLa+O3iAwF1iImXlMvEbsOv615M7zGi/ZFflj9kF/Z+SkfzD8gCU+SgVcv/pBsWhJFIGXw+s771FFRB8kL07dR2RQnDD7PeXv6HjEPdL7hstuj8B0ynhG6Q55/MCM2pyjVsW8q/mP/e/xPn/wt/sFn/x2n7fEj5NM3h5O+lrH8Chbz8y++3P7F2eugFArDgl2ucpVMa6KMvK3fo/EtfQiM8wV/bvev8droh7y58yP+5Ogv4FI/YJXNiJeyH6BsRFjHu+lthE/QJXKf8WzxMpvoWLuOF3iBvu9wRKQUvJpdo+tPadOSH+jLCGPwEZwLvBgu4LNEbyJvHDzH6NKEoC1O9LyurtAZh80CL41vkOsJZjxBZSXvls9R1xt623PpEMThPdzqHu3hZ7z0O0vazS1COOZK2iVvJdZ2OOV5O3+b2q8IouOiucKEXUIXsNbxkn2DZbuiti3TbsZkOaLfOOq25638A5pQY4VnPr5AESc0smedNrydvcN2c07XbRmlikvyOp2HWsBb+j1cFnEioF3GDX0TpxK9dLyTv4cXHhsduSi4Lp6ll4lGed40P0Q0DXLVULSRF6pXsamnSz0vTd+hExBMhhWaA/0DjjYrmhR4uXiHH1/6Nd7ZeZ8fLt7nzfmPsFnEmcCL89dJOsMaTTCaN3ffxXpL37U8l17g3fGPeVm8xsviVf7i/K/xYvkyr+29w7sX/wT/5+af8z88+G/4h8f/PVOzy4lPnHrBhfwmVVrgG01z4nj5+IC2sfg2sLuZozvJNlnWoWE+3uN/Pv4f+e/v/W0+XP8M6TVd21E3W16Rb7H1DV1yjJgyjlfZxIplynhBfcCSBVtxEdvt8NHRMX/7zm/yd279JrgFZ2nEUizo0oJb9Za/ffcf8d/e+Sf8u+M/4H88/F/4Ow/+Lv/L8W/x26v/g//3w/8X/9P5f0teldiswWUtOk+8vnMDIY7x/gHvHdyAXUmceexUcT27QTPO2U5yXtQ/QGQFbRuJJuP10Qt0ODocz/o9/KYnkHBEXu4PqPsaryIvTa6RlwYXetqu5kc7LxFmmiA9N8OMyXSLLO5g6w95c3sZr7a4rOPZ3ecZmRFeerxyvKvfxaWWEHou+YuM64t4O6NtC37Ir9G6Ah+m7MXn2Ek3sH5CEwre9B/QeYEXObv6KhfSBRIR61s+mP6UqFuE6tnJZlwzV0D2kFk+GP8YtEVJy1RVXJc3CDhsbHireI+oLEF6NIoXRi8jjUCYxDvF+yQ9EIXkecVL5euE6PDR8bp5CxE8KgZyqXilep0gLC51vDl5h0waMiBLgh+WLyLSMWF7h2vnBTIsqWY10xsZ789fQGSnFOM17154lt09RTHaAqdcP7/I2eldGrvk2eo5cmMQmScVnncmP6G3NcF3XBFXKVWJTy192PKWeY9UR8RKcM0/w4/zX+cV/SYvhpf4y+pv8nx4iVfFG/xq9qd5T/2Y58SLPJe9zE+u/ZnHHIv0xM9X5+MvZ3Px+B9P2G88Qks9vq3gK+JKnzsNP9dCFl/Yg1/hUP8m3P3jr5AnfoQQg9PwxaE/eic95v8MAfOvn68Qgvdf/Skv3XiNV555nXdf+oD5ZP7zDv67tS+G+kur+8l/T45D+sp5/PHaL0xFWz+iov0yu/B4nuixD9+xRP5ppSqP085+Qef1+V7T487F4Jioz+n/njicJ3fwd8Mt/k064YiOiyFn9R9vc2YCZVToBJVNnCwUe+cRp6B7YZeyLPG3T9APN5zsZhwsIzYXuCsTFJJr/2HFX/4Xgcs/eZXZT1564mb7ct9PCpf/K3fE/+GPuB227G0SJw+PaYMnKMjXFlzi4SMq2r7KCFrQG8l049Ehcrxbsn9u6QpFFINQ3mI9MDWc7uYsVo4gIjoGNrngysXLtJ8+4OEsZ7+O2EyiomBZwO5Zh5CKk7lhvvVYxaCuOsvYPetQKXK+Y7hw+SJynKO3PQ8fPGRx1NEqzekso2oDKlgqn2hevsjV8ZwoI2e+pYhyiF4myRE9i5Oe9bpnKQPKBvKswJxuOdmv2D/c4suSZpyjpSJrHUUfOZ5n7J92NJnETkrQgmzjmfeSo5Fk/7zHa4VVwz1T2MAoz3kgHXvnHb7S+FwPBe11jUkdp4Vjv1O08Wd4d4IrYCErcqM4lWcsmJOmAkSkDS1zMSXTimN3yCIt8MahhGCbGmb6gOQEp+6UnWKPQIvykZotE+aEmDgNJ8yzHVz0lKZim9ZMxAIyw2l/wjSfE2JPnjRn/owDcwHtE8v6mEqP0UVOLgvOumOuVc/wwe6v8eLkVQB+8+wf8Xv173JsD7lgLuKSZe1XKC/JkqQImjO1ZD+7yDZ1rO16iMoHzUSPOewfckFfwPYtvW9JIXI9e4a//sz/g1E2Zn1yzP+6+Qd8Zj8jxkCVT8hUzlH3kF1zwBJFJ8FFT94FRkpyEk6YpTm9XVHbGplLdrMZmVKcpiN21QHBekIf8CawyHfQQnFqj9kp9/nB5DX+zHN/9RvUU9NXglBfDyo8fZt/cu/v8+H691n2p8zNLja2nMczKjkiiIQi48ydcFle41cWv8HrO28jc8NvHf9Dfn/12xx3D9jXF4kItmGDjhqFJgsFx/aYC6NL1FjO+tUQsTQTMiqO/CkXzR6NaGn8lpigjAvKtOAorrmQ79CEns52eOsYmZzxfMy91QN2XIXD0T9iL5uqKbksOZINF8ycbr2hb3psvWa03iKj42wa2Wk1/XwNU0EcwULNMB6OxQl7+QG9HsTaar9lT+9hyDjtD5mlGdtQI+KQeVv4XVQx4didDhH3tMVIyZk9ZVfvgdKchVOqWCFzTZYyTrsj9vQlwmjMiT1nlApkFilQHLtjDsQuKXnWekNBgYxQyZJDd8gFdYANHWu/RKIpusQ8VZzZQ/ayS/SxoxENrvcEr8izMX3WUtkxPRZdDtHiZ0Yv8Bcv/Q1c7Wnqmn+m/zc+2X5ESpHcTDCq4tAec2D2cL6m67YkEXlu/CJ/fve/YCymyJTIphUgkIXhD7a/w784+y1ut5+yaw44dzNczGmDZcEEznqOuhUzNSblktQF6q5m1rekece5OWfHLFCVIFOajVuzl+0jo+SkPmSWz3HKoZViZc+Z6UvEYofT0DCRJT5pslhw5tYcPKqtWaaWUmYIOYzvWdxwkO3giZy7LaXMkdSMcjnQAJs5iRXbMCgqawmlLji2D9kJ+3gETWgRUSL0HirMeWjP2Y9T6sbSi4DMDSOTMKHnWK24YA7oU069bvEhkDtJgWY5Dewxpqlr+mAJGnb39tAu8bA5ZjeMsMoPrHwyMA4d80uCh80tFnZGExuSTDjtmMsFmdAc2gfsmn360JF8pE41Uy4j2eHIrdnVU2zqkSFRi5YdswMxcpLWzMQIGzeUmWbJlgt6TqYC5/GEiZkRlCOTmnN3wn52Ede2LMWSMpVIJcljxjKesF9do69b1mlFJiuEFOSq4sQdsi8OEArqtEUljVKGTBachGP25QHWt9SxRkuNCZqRLDmNR+ybS2z7NV1qSSlRxJJClJy4Qy4Ul+mzjtY3RO8ZVVOMKjjy99lTF+lCzXZ1TlQwK3aH/aUjFuxThwaPJ+rITE8pdc6xvc+uuTiwVzlPF1umckEmM07DMXOxIFmN8oY2NFw113iv+jEXpteRCTyJYjaIZsbe4RQYoymqEpXpb8KnfMvc/N0Wf4lW+U8Uyf957efBpnjCpv2OKYEYwgAzV+oXObpfuP3npaL9pmzFl4v4fhf+SfficR/2y5TTl1Ijw/pSiq86ro/v+hvu415E2hTwRFoCnR4oZkWS5DHRpiHK0hmQF+e4QuO3W9J6S5YNVK2NTqhFhS0U4bwmKklaZJSvXP1Wf+orhf+AJdKniBfQTzP0+CL24QkpRpSXBOcJaii29pmke0Sn6hREPdDTtrnEmkffa4HTwCNq2S6TCCkISeA19DHgD+bYbsNWCZKRkMAbQZcNNIpeDxmPICCqhFMDpW0EooDlvUOKGxcoR4awM6LdBJyQ+FzTJSiioW572qNzTm+fkURkmSfyKFAJOg/NWJH7DH19j9jUhGU9UN+WmqgkfVWQlMDlCo9ABkWLxGtFkwlSpumz4a7IpGCrEkFJGiMQUtAZAUhyBK0WeKloxwUhebrkQWhUcAQdCSQaLEEGXDnQy1oV0YUiCYVXkpB6YvIDvaBwBNvhcfSiJ0QHAnzqca4FlRNCpLU1yTgkASc8QQ04Wx89bRiUSK3o8cER80hIFieGZSk4YpJY19H6DVkYlFc735A9StJFORTROeGRj9iUHI4+dvjoaXxD8I7W1SihIBmIjiA9dbPCaYEVHpkCGkHra2LydG47FBOHFqUUelzASCOEQSwKUivo2haEIEuDPkgg0kuLTxndI+pHFQal+Zg8cqKwZwHPYMg2rhkUW1UiaE+IAzWqT4+oFJUaPsceLxzRB6T5Bg50wZfFe0+bez6fCx5b5pKlD91A7ckw7n3okUIRQkQ+ovv0OOp2Q3ABIcVAISwsgYCTjhQFTniiSpikgIFmsQvdQMcpA70PSDKi1kSZaLEklXAqQYQUJH0cKJUb39M3LXXsQECVl6zOz3E4nA7YEOn1gK0ORtKRCD5Sr1dY6+hCT5CJrCyQQhDzQF+MsKMOaVq8GggEUpYIPtCnDpsCSIFXAzUsClIm8GLoO/lAUOCCw4eOPlk23YYUtggiJ80xUUNZlFjVkUKALqGCxKqWbb8a6IbLgFUeESwpDfShfegBT+86kkqYKMEHXOhZ9UuUFFjhiNFRiIzeN4QU6FNLEMMz1lnL7uLywN603ZBXGUUxYmtXQx2JlgSVmO3soPcK0r1B7wMh0ERCGmhim1QT+oZttyEbF3gisZBkMkNXBcjPo49pgPE9Ii7oYoeNJa1LdF1L7hJx0xNLQcwEfd8Ttw3e93gViMITZMQqT2o6rJQ40dOlGtEnXBzuTS89IUlccjgZCdHhkqNxEJ3GxUDvezZxQ3CJbWroosSIRIegHyVqGhID/bEsFEYm2tgTCHSuQXxOQyoCCE2fuoF2WTt8P1AkSyExKeB0GK6bSOispPEtIUX65LHJ4mOgsQ1BSqyOhOgxMqMjYJ3DVomgwco0UK2KSNPUBCIdlmjE4Fx4TzCJ9WZF0AGXDxBXLwIWR+9bfBzUpltbY7H44DlvzxlNLg600yrRC0/nH9U1xYBVAaEE1gaa1INJ9MrjvcPGnhgtTrphPJLFu54gAl1siSoQ8PS+QyeNzBTBJfrYElTEWotQCpIkBvDJ04t+eAZSh5IGk8C7YQ7sREuSERstPnmULGlCg7Udm+6MaCBoP1g8dqgBVLnEqR7nLV1sQYFxPc4Oc2Qb66FOqEggIIhAm1p8cLisJ+LxwuEJ+OjoQsDjabr1I/rvMMy1OmKFI6SIlUMdYSANz7AJqN0Rs4OvIjO+Gs8RX1CTP2HS8Y02ofgSUv+1Of5p/sl/Jp/iK8fwc9pXDvFRAOwrhFdP6UNK9Z37/7LrxyFZX/5+chyflgiKKSKE/KUO5y9Fofur7ee4Zt+WbmIY9C8G6TEKW/H5RXmC1vbLC/RYSuoxrv30lQ+wtRtubz4jUzmvThb8IUsScImC3bXiVhnIU+K5I8GdBQQluDSZsbe4xM/6c/qPz3j+lufBxZzYRPZSzpXigA+Xp/gTx6UTwd6rz5LNx3zxtD15Iz2ZyUjwAzXj07BhlDQjocm15g8vKUJM3NwtuPUHnxDaQHG64drPzvn0xV2ckly/vaYd5zglmdSOqx8u+fiZGU4Lrt1t6EtFUJJxG3nhszUfXavIdOS6d9j5iHZzRlE7XjqGP7pZkVnN5YctUQyHOrKRG5+s+OTmFOUiB0cdeUoECvLW89rRMYc/voaYL5gfQ//JESkGCg/PfLrh7tUKVSdmRx3zScXRlQV5WfCymvGZ7ChxXFEVhaiQ3SH9yTnPry23TUR4z955x7QL3L+WI2LimcOG43mGiIKdWrDzcMvta3NESly/veJuJnCuYKcT7G89txYKIQTPNIKTsqfNI3kfONhYHswaRDJc7Uq22YYkNswYcbm9yO2DRO87rrgDUoo44ZjKimv+WT5W98iF45q+gg1bQoKxmXLT3OSj9g/RwXCtukYvBN51VHLE89lzfLj6PZTRXC6u4sTg4BUx5zlu8LG7Q6E1B2kfpMFrMEHzYvYMH9uP8Sky246YqhEhi+Sq4Afj17nVf4pNgUKN2Msv8Durf0umcp4rX+TD7YdYHHM/Y+Qzbvc9Smmer37Aob1LSoK9/ICp2mUp1qQQ2VV7HLV3SckxVzvMxJTb4RZCSi6Nr7HxWz5uP2Y/P+DS9DqH/ghi4sboWZZxRegiMz3hurrGz5qPCEJwWV+gjuc4E1GN5Lq7zmp0TpSBA/bJZ4rD5h5TPefm5AVOmxP6vmV/dpFNvyQkT5EKXpgOWZkUE0I9mTYXXz5P3zC3PO3vF6avsnErbOgZmyl1qAkhUaiC6+Nn+XT7McJJurOenYu7/O7Jv6ScTHhu/DIf9x/iRGAh9xiFGbfDHVRSPD96kfvtfbxM7OQHjIsdPmpuIQI8U97gfnuG8565nLAjZnwaDiEJns2ucH+9xZucUS24qS/zqTwjes/Vk4pVJrAZVLHieij5TJ2hcsP1tMd2c0xMZ1Rhxs1wwK30EaKEg3SJzmxJ+SmzbMTN0XU+kT8jqMh1fR2bGhyBUoy53lzg4egBOYYr6iqJhNORUo54efQmf1j/B7LYcnVyDd9Far+lVCXPqOe5rT7DjEbcKG5CgNvdZxS64Hn5PB+2H6KjRi8F0+mMfNRRmIob/SXupM8QAvbZo0RzJ93DeM2z/jr3w21gxJ7YY6Sm3LOfkJLkhfJFzrlLTJGF3GWS7/Ch/0Oms5xnihdYsYZRYj+/wLw64HbzCUIKLo6v0aqO29tP2S0ucLG4zP3+EIBnipuc2DV1vyIXmkvmOQ5nD0DCfr6L71p+Z/svuXDhBhfLa3zY3MInz0F2lVLvUEhHKUfczF/gDza3KKm4IOakueRIbhlFzbPNiNuxxeqMi2JOUBsSMJZjXixf41P7MW1oOJAX8NLR+R5jNa+MX+NTPiNGOBBTktjDx1NymXGTfT7u7hFjYN8bVFCgtpgoeSZc4JY8I20cVYiUqsBlkhLFc+Iq98wRXR8om4xFlnEnF2iteXn6Avfbj3DSsmDBmBmfyc+QSK6LKzyQliAT4w72zB5/1N8m9o4Xqqusq2NS2zJXhkvldT6Vn2B94gK7bI1DZB274xlzcYFP7QNErnm+usbD5W162zOVBZe7BR+bUxAZ19UOztxFCM80TbiiXuZj8TGd77iuruFEj/eBSk54Kd7gjv6EyWTKlfwCmyZDyJ48Sl4Iz/Mph4io2fVzsiqjbTukFTyjnuG+uc9YTpn3cyaVQBgoRMXzxTv80eb30FKy2yzQMsdaQS5znnWXecB9vKvY0fuYpAnJUqoxN0evcqv+CGJiz1xgIqfc7j/B6Jyb8lmO4hGmN+zofSZywp32E2QS7Hb7nPpjRnrORO9RHCvO9RppDBcnl+nChoVwZDanHM25e3SL5DwXFhfx2rJj9imoKFzJndVtRCa5srjK2m6QvWIm5uybA267OwRvuVxdxaUeETQjOeLK6BluPfgIHzwH5R5mlDPP98iiZscccOJOoRJcnF3l+t430MY+Pi9/bu88bvd8m4n4bcb0U5Z9xXD+pm2/xYj/xduTketv8HieiHE9Dc3ylS6/r5X/uDMmHrOXnxJce1pCX4qnVUj8YgP2S6Oi/fnZnu+YD0LwZfn2l3dF+uLTk+P+NZf46389+tD6ln967x9z0h4PBaXhBtl8AYDrHU6CRCJT4rxMqCSQsxKzs6BODn//DNl5totsWCYl+aUFTXTE0xodE30pmdzYf+SBPw2e8fR2IEv+WnaD49ixQ8ZvxSMybYZIQW4YvXgFfe8e0gdWU4OJgijBVhlRCIgR5SKraY5J4ICuVCAkEkEWEufzQQQpikhjG4rFAdl5QXbecD7JMVHQqyHzEGMc0nI+sZoVmCBok6AR4IUiiQyRBEf1Fv/ZIeLZPYqbB4TzDYVIZM6znRXIlOGFJlaKsDchW0zIhGIFGAyCCElim4RpJGkD2zqSGUGWKWQNVhaYXiJjopYZeScwmaBQBa7SZE0YaPV8YCY1XhlymVhVw+ymgDqPqGZ4mes+4sw5pbR4m+hiQLYrZBkRVDQHhrxQiGCQY0EKoKVAR8UpHb6VBG1oDQN7URCopDntT3CNZ92sOWqPKMqcEHqEyDlRR2ATIToa3eB1jouSfmv5mb+H2ivwxrEVAi0jMUnwgsPuCELCu0jnI6YahJuE1txf3SVkA0XianPO3w//M5t+TTGaUMgS4TTBMWTDYoeKkEvNpj1DIvFuyLS8O/4hQutBEMtuWPn7yJDQWuKKgJEF0QVuLT/lzvYea79hXiwgeCSGKCIbvyGJOMAShaKTpxShI2qBs0uUBqUl42LMaFLiO49LjqIYE2xLbEFGyZXxVd46eJdUSaSX/NOH/5DEQPXcpJrvCKT9antKqObz6Niz0x+wk+9T+zVjPeUf3f17aAw6GNbtmkIUbMOWcVbwW+t/iM0dFROybTZEUaPHqkhQFh8VBMlxe4aQhhghAsfbmkCOEpLDzYaEpG8cVljOC08KBgGsTY8xgtB3aKFYh3rIcCqF3c2RaaBkFs5g54Y8FnjvabpDYn0Lna3J3YZWnWDUGq0SOmvIRxmZrqlMwQaPTuCspRU1IfgBTmoTK3uCIBCkZ8sGMyrxKRKT4CScYnRO73pclsAISpMz1SNcIRiJPUJYE8xwjIocWsH99j5GSFoh2DnYgVKxDT3CC2pxRiUy+tQgZRoK5lEYDK2qyXtogkWkjthFtHcYmdNzjpYZKUSigXvLQ1RZgYuc1+eYLAMkKUlqux6KlxPcW33K/c0t1n7F1MzplQGVk1JknTqUD8gQGRU5MbPoIGnXNcf+Hr/pTtjGDZMHf4jL5jQp4lJgJEucG9F2FaWccBrXaKXorMOXAhUF+IAKimXWoKtiqBGIA1RYCUVlxqzllrws8SFAJpBaoU1GWU5Ymg2SjCQMfYj02wYnIqWSnNXHKN8iTE8se3SpyREUSVKnSOGmNG4DwdD7QHABd95yP0Q64ekUWFFwEltcMgiVc7JdEzoPWQKRaLIa2oDSiqV/iLSg9BrRtpy3FiFazMjQ50uU26BEC7Gg13fI3Ao9g7g5pRhfQOPRUhJ3NFU/HQQqpcVMR3C6RAjFKrVoG/AatmGN7zb4ypGM5FytwA5zeid6pFFIkWHEwNyWi3KouwyOkY40oWOsMzrZUcgxwYPQmr6zaKWHLBsOTUFnLW3y5MESXUeSBct0SiYyerclBE/nJrg4RYec8zxAG4garO1J0aKlRPhIKzYUsqKTLVrndKlHCAlB0Mqesq/ofU8hK3zTk/cZoRtE8SbllNR5Zns7iHWOWUq6uiNOC/76n/2vWLlTpnKHf/MHv835qiWmyG7+DG/dfIPD5gF75QH/9qN/S366JKZIWCvMpCTzFXmT05ueIhq8EAgrMPkI42oqNaU9tGSrCaHZEosRr19+BzvumBS7XLl5k41c4aLlwugSWmY/d+r9ivPxHaftPzZT0bfY9l8s//xA0lMCv09r6eet8B3s2u97Ol9zNr7M/gxQ/6/uUzy+0WOLPh/7r6z9f2Gm55dARft1R+Dp7YnvxdeXfmmIP+k+PFI+/trmXx+px4/myct+1Dxk1S+5v72HkZrTnREdJavQY5cttnJsRwqN4GyUKIqM7uKIh8LiNy3H9MiDjLoX6JhoLpacjRT3bx+xGiUkgoOoaOcZ5SP38WtswU+7uGK4f8bCMFGGVXScpI6HqSORaEi4MrEeKbLLO5wpQT8qhkJmIxBJsJ4aopSETOGMwkmIahBlWk0MVgqOFgqZBghY7FsmxrG9MKb3Pcd5hlCazgjifkEKkdU0w+aBw70S5RNNLolJIIVkO8moc816V5L3DW61hPkC/9ZlVscn6K3gZC9DBEVdaXQWWMuevt+S5zlnwmGSZIVDBEUMgeOuIyxG1BNQIbGtMtgFYQz1OEMqRV0ZtHOsjCDGgCw0GxURucGaKTIzbIxAFJIUFXVwpJTookcJ6MsBItZER5/VA7WjdAjRs5ENQVjW2g9qpWmAaeRas45rkobGLemTJ4QE1qHpWdpTztozonTU2w26MlTFmGVjWcUlLus5rB8iJTT1hrZz9Epxrz1kms3oD4ZC9Lqv6V2DlpJlXJMHzVEI6CA4C2tCEanTliZtaGLHsT9GWMmyW9JnPSrkLN2SQowx5KhesrYrwKOipUkbVNyySRtkEDSiZmXPuW/v8n71U2QG/6z7J2xY09Cw5Bxvz9jGLYiEjUCvWbv1QKMYPY3b4K1nw5JiUrD2K2IMOJmodUNKka1sEFKzsRuEgOPO07T1oHTft8Teso1rSHC3vc3rl94j+sjv1/+GjVuzDWsQiTubT3l1/jZSyq89P99p2vnagzjgdRfFLou0y6frD9nYFeftKUZlnMgTlNLUbFGlwKaOjVuhNxkpJspixNot8V1EyIJVbJBCstwuKYuKTdwS6yOsyln6hpQEYeOospwtLUJocI516DFKse16BIllqgkyQeap1SMoSBpeFo3xKG056ZY0oSEJ6O0GwyldWIPs8CR6bUkE7HQXtGHlzwlugHg56YgEbN0jA6zlBi96gnYQoU8D3Eu6nFVcsbIrpLyNFHKAgsUASbAOS9rY8FAcIqWhcVvctiX5wIoNhc5YqhXaQi0aBMdEp1irmiwZ1mpJrgpq0UI8Q8jEyi8xUrPpjsh8YO1XSAXCR7Z+NVCGUqPR1GFDdIdscaSYyIxBmqHmZRu3yKARMbING0jQqhqhNRu7ZOM29FnOKjQgwLqWsG3pRMtSrTg6vYuVLSEEUhZRtWTLlpGfU9sV25QIKTAVYwiJ836LjR6fTnFpYGESURGbSK0GqGVjBviYlxGfGoy21Loj+VOOfYuUg1I6AoSAVVrineeeuw9S0aaWaAqsDGyio60bDkWPMZFGO2SuUZlkHTeYpHlYd6g0os08xgRCTKw7j+g6VrJBJaijRWcbEls2fqBZbreHaBp61ZKkIHSedVghoqQUDSkZNt2aWM7pY2IbHFpIfH+KzgJbapSU1P2WVtYAtJWm3z5kIyx23aCKjC4bHsPOdbiupTEO7JpjMcBwUoI+NiBOqB/RzJ7oY7pU49MAmcLBOq4JKnAujsEPkKnoBBLNJm1IMrLF4lNB7RqctSAS67CmUC1H0iFipKElpZqN6+iyhm1Xs3T30UnTyBYnDDY5zmKHpmUZ7pGLnjZsB+VtmdikFRrNdtujQsYmrEmbQXl+K7coZfCtJ+sy6rAlNA78oFUklKQ3gaIoaDrL/aP7iGVGvW4GR3ruEUFxY/oi63rFarvk7PQMgG1Vo8qKG/kr6FLgTGBjG3xniWVCouiUY6VaotzQug0xhGFeCYpWNAO74fk5djkwfCmxprg84+UrP0Q8ggKWVN8w0f5f3L7N7PwmdMzjFvbjWZRv3cmTWK+ntW9LQzze29NhSt+468+7e6zQXDwWXPsqIOZR34+fY/ryvz9e+8U8kV8OLOrzX7/AsXxl0y/6E48t/2rn6bFBftwf+eLzY1C/zx29STYlVwVjM6ZQJZGcPmhc3TDbBLYbj8oNRZdAKeY7e5zKxKJVnH12zkQkTBLImKhMTlaNmdxvEGuHzAQawXh3waQcPdJx+X4DIh4dbCUUudDskRFI5EJDH1j3sK9HnG9WjPqh/qFqHNomghLsrh22SAOONpeUtSf3CScFi7VDqIgIEa0D1bpj1iZcUZI10DQdmcnZFJLJ2iIALwXTxhOVRPmEqhSL2oEY6jeqdhAXy51jw4axzZEHMziAdP6QECLCgZCKRZMQLiDvbZldyFBjQynUEHWRmk3tqI43GBvRUpF7IIvsBIUbF+RZhkSgZSJTEo9nxyZq5xlnAp0ZTGbIG4fPE5Mm4jJBlmlC3zPqB8peryILXdKSUaYKJyKToiI3Y3w4ZnoKIS/IpMFLx0hWlN6QssRCLigKQdBQdzVVLNFO4tSY6WROH1oKX3KyPKIclbioic0SYSXjIsc5T73qcP0Si+LmC9eZiCnD1K+RITK1FUpAEI4qlaATRVWiU8WumKOSJ9jIXM+J2UBtKJVi2o2IUkK2oIglvnGM5JioA/M4I6QtSksKVSCQ5CaDIJjoKVMmA3Y/wrTaZeZ3scKxyHapQ4eWQ1QtSznlIyG/Rb6LdTWiiZAi4+mEQudY17NjdtnSkqectmvJRYVWJVGmR3SOPZOyorUdRcgZjWbooNitDlhMDpBagRAsRruMNhMqNWZq5syyOaSEby2mejrF82MTyJOzymOTbSLGAWM6TCPD+hM1JRc5IzWh0iM8gUzlJBWZqQVWNGg0GTkueEZqQgiefbVH6yMpSjKdIzUUvsQLxzyb00iN1Dm+HrIVNJCXOTvFgtZGMjTRg06SUVkREsxsibUSrQYBuBxN5gTWd4yjofESRU5SMJaJsXAs8exVl2loh8BDshgK8JpKOWZql8Pz+4zHY2K0TOQIFRUBz9SVRDWMaVN4RjZH6BKvA5UaIQmQJG2qGasJUimCd2Q2IwSIfaTShpkeQ2XAKUqfk0REI8AnpnJKzIcMTEWBKjKKkEGAuZg+wnt7Cp8hY08pJVFHFqOLhK5BZ9lAF+sDwkpyXTEv9qDeIJXCyAwjcibVnNQJZtkOPrbIKFG5GZbLAtv3TOWMRmuUyPHek1k50IoWmt3ygF6X2LbBe8som5CFoS5ooeakqDAorIiMVYUOgiZ0zPQELxO+8zTJourETjVHhUFEL/cQ/EALXElFZTwxRaZxDFKj4qBpMKZCKoOVlrma0yqP0oa1WzOVI4KZEjYrMivRRmOUgFQzbgyh8RRaUUaNdwYdFFE4CiJiUhBTRzmekFzA9ImUaiauxCuLFCNyU6JjQ4WhTpJ5mtObHhEEUmjy0YwsVKQ+sa92qKMhsw5CJFeRUgiCjOyVF+i7Nbk2CKMwckRiTrLn7ISKuvboXuBTQCfLWOb42LIrJ9S+ZZQMNnjKkMiyGUIJdtQu1neUMcMZT+ly8pTj8UziBKVASUmTmoEqlYxoE1VfEFKOzMcIlZinEt9sSSansAVeSkazESf1KRUF09LTihWlKECAThoczOWUbSpwmSG3CuMFKihEFqniFJIHEiYYlKoYVQvCNjBlgS8iwilyUZBFwzibk7o4zNFFIK9KpFDgQQZDLyzz0Q6+g5EegxDMFnOqokIAZV6S6YzFZEFMicxkzMYz8qwgRE9uMhbTPcI4UI5zskmO6AXzYpcubJkUE2zoKfQYIzPWfsksW9B3Doygdx2Xdi6xt3OAVN+fVPT7IHu+l9H9efvcxvvG4NE3bPOdjufRqp+LVPxxYEp86QJ8WSf8DZ08BVn1VKmGz43bJ32e72t6f9v5/DHP9Wntl0ZF+53bE55mSl9mfT5/z39+z3z58/V/X3Ynvuw0PeamPWWAFvkO02yGe1R49ivZDSwR5yzZ4Zbn2xxnJJ1O/Gp+BT/KsDHCrTNe+NTic0XIJe/f12QXZzjv4XDNn/tdePUuvFFX/JWLr5I9KsYRTz+MbxmW4bcRkufFmE4kWpF4TUwRKNrC0OWK1377AX2ucEby3Cdryt5jjaTTgvd+9wyfS7yRPH+nZtLGIZuRSd7+d+d0ucRnmgu3z5nWjlgZwsjwwe+e0huFVZILhy17546QaVxuePffnmCVxGnNztJz6czjlaLXkjd/+5TalDQiR/9sybVVwuea9Mwe733UghPINjE9j9y85XFrwfqjFe98InDbhF9Dvk5c+9e3cZnCzUreOHGksYaJYnxhwktSE4wlyo43zx2i2yLsFuNbXr71EBEe4JvPePU/3ka2t8F/hrb3ePXeZ7jufyfF3+b5o9tI9Ud4+W8I4T/wxkbRcReXP+CF+WXKiSLoLXGWeDd/iyAsUSV+kL1InnLq2NNIx0/2foQ3LVHVXIsXUb2kqdd46fjx/FfJxwVRJqbdgpIpa9ty++geV49uUMdEHE149fI7/PiFDxAGrGv4SXgD3ddkXcP1OOdG3CPHkyvPT/MfEVOLsFsmp4Fr3QGq73GbDe+0r2JFYhsdD+6csdvt0kpPHTrez97GpwbXbzABXihfJJqEFT1vTt4jkgghIOJQPPz3zv4uf//875Kbkt57+pRAGl5fvI0LPS70vNjfJCWH9TUkx59e/Flu2Bu8fe19/osbfx2FBAJIeCO9SqgbYtvysnyOhS7Jo0fajj83/tO8fuEdfnjjA/7KK/81H9z8Dd648B6v7b/N23vvIcRA0HCpuI4RiiQ8AcfzO68ilfyOQnriqX+mmPjth/87/8NH/w1/7+O/w+H2HrEfCsVnaoeJmhFw9KHh/b2fkvCQAotihz93+f/OG7N3eW36Dn9l52+QuohsBEWf84J6DkJPaLe8V7yJyFqc2lCOJK+MnqXpN2zthtfzF5jNSrI8MSo0b42v4M0h5Me8l11AcUaUh2RiyQ+Zk/RdvP+El9cSsb1DaP8Q0X3Gu36GFHcgfsrL3Q65UAO1chF5vXyPVvQcb04xDzOm3iCbGpotv1b8lJgcDsdNcZNRLPHJEVTi/X641iE5rslr7LKLsz1CRn48/hVs6uh8x3hVMloa+r4muo53tq8gHl2jfb3PJXURaxtsaPkg/XAgK9ABHXMu+gMCPY6O99PbuNUpcXnCeBm4cT5HnJ/hzo55V70LGoSGkR7xzM5b1LngodvQ3Cl5uDnH5wbn4S/f/K95qXyD57KX+EuX/yavLt7htb0f8vbB+7y5/z5OenrX8sr0LaJSOCPAaN6Zv07sz5FseXPxMip5Eg2Cjjfnb5ImgTSJvLT3BnI6ZyslNYn3xm/h9ECicM3tETeWZAJROD6oXiEYgSoMzxdXKRL0YotTLW/nV4jFQ8jucXM0ZScf43WHMz0/vfQbBK2I0rAXL7IICwgR2/e8X3xArDtE3XPQj7hiNco+xHDK+9wkdWcIe86kT9xQY6Q5gfyMX919GbUQiMoyTolrfUHIOvr+lLeaKX50TtpbU4wDL4pdklkR1JIXVjeRnSeuO+S553n/Isn14Drelq9DEqQEMgjeyZ/FmDUm2/DB7luMRhqlLTL0vJa/TuPWNG7NK+V1RuMNuryHLo95J41JfEwSH/FiDaU4QcjPiPIOPxS7hMkD0vgBr+zfZHdnB6kTEct7vIdsO1huea67xqzNkKstsmn5UfkB3taEruaKusREj/FZT6wcv3rxLaK5jxkfcnNnwo1LO6jxObI64636Ct7eJ8/PeGaxx4W0S+8aOul4d/JrBD3AH6uY84yao9MRSp7wtn8VjyOJQN4ZrnJjEJnUntfjGzQ02DJQzCY8L19BOQW94L3pT3mu+AHP6hd45+pP+Asv/01e2n2Tq+Z5fjz587xx5T3euvoj3nvmJ/yVD/4rXrrxGi9ff40fv/qrZHqAImU65/3XfsJLN1/l5Zuv8P6rP6HIy0HDRBk+eOlP8PK113j52mv83179y7x54V1e3nuDl3df46889zd5afd1Xtl7kz/7zF/ivSs/5ZW9N3l57w3+6rv/JS9df5WXr7/Oey/9hNl4/h0tmM/bAKX72gz9tUzBE56BeOLnG6bxr/X5+Pp/DMTs09sjG/Npx/P4fn7Oj0g8RQH7W5p4/OO3IIGe7FLwhYzDcLzpK6bwz93+uy77nu0XpqLdfkFF+4274Gun+bkzIb5M43xxMZN40kF7fJPHenvS201fcyy+OLNH/x82D/ln936T25vPKHXF2YWb2Nllbt+7x96pJ80qljjKoqC8vEslNHfPT5h/vMRninUlyJMkn1TMZ1PunB5z+b7l/U8EL9+Dg7/6HpMXrjzhaT5x3uKrf36RoElfftvHwN/yt/hZXA86GyJDScMn9x8wu7NkGzpSlmG1YFo7Cp842i/ZO3c05ZCM6nPFdONRIXG6W7BYWqIBGSO1SZRHS6bP36S+uaD6o2POVw0ZmnWlmC97AM4WOfM24lIi87CaZMzPWrTSnE8MozbgSeQBVtOcg9ph9nKaq2PGKqO/26Bv15xlsFhbkhZsS0UehnOezEYsZxmz45p609MuKgwC6T1jKTg1kV0nsNFRu47Mg3Ee3QVOx5KDJuL0mq3qSG6IchUIViPPXqvp1ANs1hAk5DZRSM1ZtWaXXWweiOUQZSt6Qykyjvwhe2mXTnqsdQQVmIgxWV5wLM85KC7Q2S3JBjabJSNr0MAqX7MjdzlzaxSSB8v7VH40MEXlLbKW7Fy/RqYqatFwZXoJ5SNn7oSpHyGjpQiCrW7ZLQ6IIbBizdhMaGOPFoaz5oj9foqej6llTZ4KeoBOcFbUzNUOvu9YpQ1VNiJLUHrDmT/hQnYB6zp63WFEhhGaLOactIdcHF+hsx296JFItC7IVcVR+5C5n0GV6FILMaGTocxGHHUPuTy6xvP9C/xo/ydML+7wOw//Bf/64T/nfnOHg/FlWlsTVSQSKVKJjopje8h+foE3L7zPr1z7MxDTwP6U6ceCDemLSNmHZ/+Bf3X4W9ytP2On2OOF2Wv8yRt/6Ytn/nNF1K9MED+n3d3e4rfu/kNurT8aCu3nL/MXn/kvEULwsLnHP7n79/h09UdUegQikcuS8/6ES/l1fuXKn+S58csgBP/84T/m989+h7P+mB21Q5ccm7jBRI3KEnmWc+QPOdCXaaJhKyIiCDIURTSc+jP29Q5tvqX2azKlyKKhNBUP+4fsuDlW9vS2JilB1gqyHlb6jF11gM0d1nX45BiJMcZr7va30OuMUEraaHHJ8sz0GuNNYKlX7Jh9tqUnZIpO9kyZIJPiJB6zl3awrkFJRS07ZmJO5yN1VrNb7NP7FtkHNrJhoXdJIbDknKmY0rueTGZsxJY9uUsicepPBiFCInlWceJOkGtDNS7pdcMom6C6nrJXLMMZO2mHJCKNbsj1IypPUXLaPWTXXKTOBQ/qQ1IUnNw9ZEzJ7o05zy5e5L3dP8EN9zxaSUZ7M1RuSAnONyf846O/y6erDyFBlo/RuuKoP+RCcQEnGvrQklLEOI1xmrVesVddoqUemINEJBMzoOIonLET57RaEyK0tqW0Bh0VZ+mcBVO8ykBqnImUVqK8Y5k37OULvD4EX9OEmlm2h5YFx/0JC70YsnFxUDKfMWZ5eooYBeblDi5ZZBvYpi072R5RS443D5mqCVFBJjNWcclOsUsaOZbplCIUhDQnL69yGlZMVxonAmvdU3pFEC2GwKlaceBmCN0PdTYYyjYwJefUHrFXXKINDZYWpQwqn5IXe5y4I3bFDj7WtHGYH6qyIjc5x/6QHbHHNjRYLEgoZUllCo7tfRZhh14MLFs+OkpfkImMU33Kjjygz/zAwoZl3BWYqDnVZ8zjDrHZkqzHYpmpOcrBWTxhURzQP2L+6kTHYnqRpDVn8uxR1nF4b63sOVM/QxnNmT9mzJQQeozKqMWaedwBYCmXjMSE6B2ZKjlzx+ymXZKEjdmSW02IcYD3iXOmfgEGmqwlJ8d2AaNG1LOOg3gB1hFLjxGGK+IqvyJ+jZ2bV8im1YBySBBDRErJF7W1X8WKf9WYearxKb5l+S/BavwWe/fzBV/d2zfsU/CYcfYdjuvnQpceP6YvIfS/DJXpp+7v2xyGJ83dP84hfNMl/T79/ZIu+39mKlp4qgPxRRuM/vSI6upzL+vzm+/J1NHj6a4vnYyvesJfUUB8/BjEl6rdCb54aD//og89PvpHtIfQ4umSxYmEvzrHbVu6XGAujOhFwK0b2m1DNjIIkbCZIJUZZlay2jZ0wQ/4fZOYvfMMk+cuff9r+RQHxBHxRGo8gQEX7r2lsxYlA9YYXKGJSuBdpM4EziiaKuEyNVDPaknRR0DQa0lTKJIexrlXCV1otrajJ6IPJljnccrQ60SXDdfJZpImCTyCEBiyI7lGCElrhnqOAIQAvRnoX03dsDnzpJ05clHRrwJ9cPSFRqRALxNBCDJgs6mpXYtsI0lLeu+wMZGHwIYB41+3gSQjvQarE+MsJ2iPN5G6GO4epxMoSbARJxK9iGyMJxLYpGZQklYSbwK9Hmhmg+QLHK+mpE0eLwOd7LEkatGQYiRTBi8GateNXePbBmd7mthQlAuEBu8Djd9yvj5BG0NQgaqqqKqKs3iGqBSiEKQMkk80fY1Jid62NEIgfA95QdQJSw9G4KKjoyWYSBKJKByuGjR1LRa0xEpJRNK1W8J4jJOB3nWDUrPKEMkRVKQTPS52NP0Wk2WUosJ7j8fThpaAp/UNQkgKKQkpYb1ltT4lVwWtbABBpeRAaZg8nWvQE81oPiI4R+dbnPJEGelCQ1CRxtUkIsro4ai9pct7+tST4nDtpNGQ0vC3+OrrwAmLw+JxtKGh6+uvPDNPVW/9Oa2PLTZYOtcijMCmHts7stzQhxYfBzpKwlCY7v1QdxMqz2p5zjbUjOdj+tTTpw4vPL1xRAG2H4rUcxQheqIKA60kI7pkkUIgnKZvanrVsvZLkJ5edgShkSnR+DhQDcsOHyyt6klKoLOMoAYqyD629NbSaTvAjlzH2XbDw/UhsRZkoSJkcHCwh/CBTjuC8HSxoTcSqx1OOGzypGjxKlD7hqAsIiUsjg5Lj8fh2No1m2ZNYXLa1JP7Bkh0qUeJ5hE952A8takFKeilQ8gW7z2rumblVxxU+3h6utSRPOQpkaTExeHelgms6wg+oFWGD46mr3HdIetNwI8iUij29nfYK+d0YrgnLD3TnQmyyAbqSyEgRZKOQxFuaB+9AzJsiLjQs3UbUH6oY/CecRoRZcAlR23XOBytaEkSUCO6ekUvOhrd4mJGFwJ1U5NCwWhcEW3CykgqBM576k2NJEOqgMPTSkuSFnI/0FCLiAsdNnSs/DmiHzIBVjhGRcH0YMLKndPREWRAjSTeJqwJkDyikHgdiQLQkeAFNvegPS44AEIMhNQO9MpG4u1QMByjRMgeLzxeBLaqJRdhqD2Tieigtg1OeGq7RmRymB+cpMxKfLfCCUcrG1JyNKFGCIFKCuctNvTUbPAy0dIBoJOi8Q4XLW1qiJmkxxFSoIgCJwedqj62uBjoGGhyc20IwQ/PhGiIsUOI8OjOtAQ13DNbu8KmnoTAxY48HyPzEhctjdtiaZECbGrxuiKKQNABLyxeWOIjets2tUPtQ+y+MGlcjANtLB0pRBq7xGUVikRMjj71+Hyg4u7slpRFYqbBhEHw1A76N62r6ZKgLy4w/sFFsqr6AvktxEB48TVM97e2b7M6/zj4lp9jkX6PMPRgfz1miH8t2v5toXW+3aT82opfXf9r2YJvG4Y/Fgzo84jwtx/St/eQICbEk/WDj2//izgI33n8/tO1X0JB9+P+6tfbl9fuywjj41XsPPHp69s9fZ0n9/i5A/KFY/GV4xs+XBxdYrfcI5HQUvOsucLv9uCykmf2LqLGkU/TmkpX3NwaPrx1yKSAA6so1h55WTHem/HstuD+f/wPGN2w6Ce8Mb3B7p94BfHzsIlPuUke/+pBarifag4ouSYq7siOQOIZKu6fnHF23jJbdlw86bl1fULQgkv3avwoB62Y1YELnzbculrRa8G1hx0u10SlmDWRa3e33L1e0YjAwcOOWJ9jn7nIuBpz894xd/cKattw8bgjKoHwkpGHq4ctdy9UGJu4eOYRwYMtGDnP1cOWw0tTTB+4uA3kyXK/j1QnS16YX+DuYkT38R0uyhGZE9wTDiMV12vBLeMYecGsgVmS3As9KsKVWnIyGhTX94IhaxIPy4COcD0qjtMJIa2YNRPKNnI86pDjiutql03WENWWOSW76hq/t1myM5pxc/dZtmrFoT+itAVXyqt8lm4TU+Squkzj1kSRmKQZB+ICt/QdvPBc6HbZdDV9nlNhuCZ/wCfqDjqruFpcZ7s9warASJQ804+57w/ZrQ74QfkcQQuUkIyKEVez5/nM3aIIkUtxgUoJgaMSFVeLK9zvb5GbkoP8MlU+YmWXGJExyebcbj8G6dgvLg+R7fSAwlRcLp/jU3sPgN1ugjI5Igc2lhdnL3GmjxFoduQ+JsCd/jZjNWK0mtBmDZNywaLYZa4WbMIGISQzPefIHpHwZDbj+vwmZ80xOjPM812O2yOS9IzFiBvVDf7w7PdQRc71+XP8bPv7TIsFs2yH/fIia78ieM9YTehtx6LYY5RNeHHnVWKMaKMfiSBJvLODAR0dny1/hvU9u+UBC7OHnmbksuDFvde/nfrwO7Qr4xvs5XuIuSBTGS/MXiHLDSS4VF1jYubMi10ykXOtvEETa7rQsih3eenqW0zUFITghfnL3HokwLafHzAqFiy7M5RUjGPJ0h8zY8FYz0hxxP10DyUVN6pneKjucxY8O8w5mO1yJ91CILjWXeQknOF9zSJULNQV7qTbiCC4lF1l2RwSRaRMYy7LPe76zzg7O+X8KLDtV2SjDLsN7IYDLv5ggYqCS+YKXq04QTId73Elu8Sn3AID1+W1QSCxC0zEhKvyCnfEfbZuy548wMxK7qf7uHPLD+IPOCuWmNhwmYuI4MlCoNIjrqgb3PW3KZNirvaRUiGIyE5yUV7jTByyYyr21QW0yHho71HkFRfUJY7tLXRhuDC6SiELbp9/RFGOuCiu8gcPf5/NyrGf51yd7FOrmlxm3Ciuc94f0uQl03KHq+Nn+KPuQ5TXPDN5AemH1Ogi3+PC6Oqg3ZBgpGYc+hMSkUW2w46ecXvzCUi4kl1hK2tSFEzVgh21y61wjygi18obnEpL6o6YiBEX5WU+i/cwyXF9dAVVGYKP7Ix32PU73LZHmJS4qndgDMdqw9SMuZZd4DP7Mb10XBYHdJ3FOUulRjwzusad8JBeOi4Wl1HCQZcoKLhePsut5mOkgP38EjrTxFZQiIJr2TPcbj9G5YlL5RWSGoqTddRcks/zsDtHycD+aEFynge+RgvJpfgsx+ouhYCL06tMRcb91ackF7lZ3CSMetarE+zKU6WKEANaGC6Jm5ymDd637Ix3WBRzbm0+Rgi4WT7LeTiDJFnoHaZyzl1/l5QSF8UFtqnBqoJ5NmUv2+F2+ymJyGV1mdqvCcKxKPfY5YBb6w+JInK5uknvB92PWTHn4vgVHqwe4r3l4uISTbNhubT0SZD6kiY/p5qWXIwXIBsRQ2Akp1yWr/NZ+yE6GC6qSwQXiNJTqjHXi2e55z8lSyWX8ssgFHqtybKKC+kCD7mLTJG9tE8xm6LcbWSduLzd57A8ximY+x0Kch7ygFxUXM2e4YE6QQrFTrbHtBnxIN1Bobi+9zybdsPdk9tcWFxgZ/qYVsRTMw9PWjT/Kdp3tES/LXvxeXDoyWU/N+PB00/razChb7M0v6GPn9e+5zYJ8fP1oB8LaKenDIj4ApbzJIzlyW7SV+zlp+7ny06/st/v3J40tH+JDsl/Ap2Lry74XNhOPO6pfsuz8vmYf+Xr9Egy77HI5hcX6IvOvlTv/tJ1eezo0pA+/vUrf4qH9QNylXOnUPz+9mOyvRlRJkSp0SJHhMTpx3cRIaL2KuJpTSg0+e4UJQT9H/xHdh/8ESrvmdsR4195H5mb7zlyXz3HW2z5B+EO5/RMMQiZE5AEEudHK/rDc2SKSAR2lKETCKEgz0hCkhgoU/tSP8r6DNmMiEAJgfSRtpDggUzjs5LYNoRNQ75YIOcTsuUQL9LREKSm8JqscXhl0F6ggkSGgb6uiIrMRlyErLaDoFDjh3EuJGLZslkeUjy3Q5ULhO1IWiJKCSFQy0RmFK4QqH6IUIoI2kdsAB2HSG5ynkgaioNSZNM9wKcPEapBpzFJ7SByhcx6zvtDsskYrQSFyLBuw141Q2tJ254TjIVkyc2cNloEmmB7rHE4n8AoBJpeB2TSNNsaV0iUzSBKEJq6AGEzpEy00UFegeqQTGj0ip3xHmIkCFrjo0UgyHRGtz3GxB5HDzQIU6AjZFpDnqADQiLPCn794l9g5ZYYqziTJxzHBzhp0WiiGuokhIAm1cg0KAULPQjjZblBBkm9PYU80MUON/Jkk5xc5YgEeqzIs5Iu9ZAp3t35KSlFgg0kHfj/nv4W0geKPOPdnR8RRx6hFZHEP1v/f9BBkMuMf735FzR2A+tElspHURiBlIpXZm9RFhXBew7yy3jpOekPmWcLFsU+tuvxeLQZpiCdGSDxfx79Mz5e/yE2WPbzA3798p/ntD5iPtlnf3Th6Q/SN73Mnvw7QUbGn732V3nQ3KHQFfv5RZKPpBAIZhDwSwmkUszNPu8vfp2Wmgvjq1R6MFaiC/jYo4UCEjIKfrzzK2zbLaNqzJ7cZxOWHDUPmNYj/nn7j5FxgxSa3t6nLHuyZKm0x8U1yllSiHRpgxQBaQQacGFLLhIpRoTsKLWhjgON7CaesdqcsVyf0xz3TMYlIsHzV2/y3OgGjdviQ0CmDpFrlM4QUvFw/YDGDGxLLrcE5wfIG4I2OdAl3nVQlXg5nKtMoPNEbgzBSaRIqLUlC44Mh1fnmOQIOEaqB6XRtqOQFWXmGVlBEpE8F2SFZizLQThTRybVlLU/h5iwIpGkwdnEw7CkrBYsouOgvES1u0ArgxaadtXiu4QsNEjNP3/4j9l2K6TU3Jl+wq9f/PMoo0kh8dP9P81xeAgRfHT81uH/inQBnaALPSkIYkzYKhJzgbcJJyK1ghAMIUXWtScog7WSrrYs1UNE1pDrgKCnXSVkWaFUgQ+gUOR5gZAaXMLVHp96lnnARkFrLVtbw7ggqhIz2aFVmmRLAgJnBDF0ROmQumTZHdI3W7zqCbIj5hU+JpLRNKwxfaTzHTE0SCeItUVLTe8ekJpTVD4wSslxSd615HgKs2YXjUyBqqtJZy05CRk1O0x5/cZPObIfUyfB/fHHLJfnpM7z737nX+HHicWlMcLUNCiGt42kSx6ZCmTK0aIiRonuDZGEFwZvdrA24rMdOu9IbSSkQJykQUU9GTKtSZuWspe4FJGupwiKrJWUqYC2JK93oGsJdYFrPfvmGWajHeSo59h+wtauafqaWFu86tEjgTMW7TJk7PBthzBD7VaW59jUoUUGmxU2tmRphmwMRVXh84hiECaNIpIygUwK6T1N2CLzAq0ctgmIHHRZonWBjRYdB1r9FANWNsRkUabgwdkdHnx0SN1tmY5m/Oobv8HB4uK3TGCfT3LfMrE9dXn6+qrf2L6nlf1NBuk3GbjfBvV5cvlT9vWFW/GLRuSf5uh8y7B90+bfuM439fVkMuVJh+FpgeevILCerMJIT78dfs7YfI2/9JtuqV9C+8VhUV/BBX7Pq/4taZ9E+iK99Tjz0uclIk9mPb5+TR93LIaDFECmcq5NbgDwm/FjlhWskkOkliTgLHakky1iZKnmE1a+JS0UcpLRTAQ0NS4+YKFrLC3p8g5H2SnXePb7nfsT7aO45mFqeUDDjJxOWDaPDIvT1SmRjs0sH5wNrejyAepjjSI9oqJNWnNyQeCVxGkBSoKQrEYaGwLH8zFJikFlO5bgJc61SEY0F0v8/UCTAALKGNalplOS01050GBmEpkAH9kUml5LlhODsY6mMpwKSYqB2oASgk3hKDYr6onifhcxWrCKnkRkO9OokFirRBoJYiGptUfExMoktBjqR05lInhPW0qEkmw5pAgrtv0JSu2RZhXbykDs6XcrjNpSi44Ue0iH1OEU33tqs0ZGxVY3SL3kJKypYzeokNYNWVWwjhuChCN3RhM6XOG5w0NModlKC6nmxK8JyuOEAylARtaixdtIuNhBijgVcP4euRSs/TneW45UQAro6SEJdDJs2eCcY5vOySYZraupw4aT/pDnq5cJ0vPvzv8VS3dK4zegIfk40HWKNff6E4Qs2MZ6UF31HZuwwWjNJq1RbWQrahQCoxUNW5RS1LpDJsk6rMj7klvrj/hg8SeIyfMvl/8bG3tOL1tG4wl3V5/ytnkHNR7xb9b/klYOdJ3n7hTXd2zdmhQjYzNHCMnGrZBJcnvzCb8x+3NQyoH9KSUmxfSL+cLk5ouAQ4wRqSTWd9xrbnN78xE+eTSKdb/k2flLqOJbpqovojbfkOP+HJb7aO4wZFyvniUBSilca1FacdjcZm1XLO0ZW7fhvrnNr8z+9KBqHhOkhFSKFCKfLf+I8/aYdX9OJSsebO/w9v4HCAZti5nfYXf3gMPqLts7G87TETIqWrlBJ83anyMFBBvY+jUCQSsbhFBsxRqhAtFZ2rgZlOZdh0yCpT9nfb7BOkvUDpd7LrywQ5WVUAXGuuA4PMSGntB7GrklL0qW3Smd7Lgblmy6lrmZo6VCpMAyrfDJ81BvIWk603Okjgm2ZeVOGRUVH6lPkU5gsejOo4Jjm1a4LHAuVxiV0aWWZbYhxjhAX3Tis/gxWVHQ2polp4hOse7PMSrnTB6itWbbL3E+krSikQ3RBkJ/jA4aMdU0paPhhI1bI6WirXKSDJydnRBcRCrBNqxRSjHKR2z9lomcQkrkRcnVdJPgA//HyW+y9ues7ZIUEy54lv0anWlc8GAjS3dG27cItaR2PTFGGhMRZsRWdjAu2cZjulhDJkBvENmYZb8ldJ6HQmGDo7c9dWwQIrEWHV2y3LVnRNETpCcVCmTLhgZXH3PH3oGQcCpQ+1NM2LIJ54zyKaYQhDjAu3yd0KJkLbZ0oeO8vo3uI41dg3Mk71m5cxqVcy6PkELQhhYhAq4WrNUGIzJav0Rb2Pg1ydbQK1q7RQnJsVjQn3fslje5+HzBrTt/QCO2NKFmO9lgqoIzf4pxOcEec27XFOMK1wVU0mz8BoEipcAmbEgx0uSavjec9TW+cxymM4LaojPNPX8bpQQbf4YgcdJ09F1NJEBICCep+zW29zw8XyFcjg8emweyIqduOkgrGv0Aqzd0puOuu0uo4cQd02N5qO6DjbSxQ5RioD3uT+hjyzH3MSJjw5JgQfgtVlma5pSo7yLzRCO36Cxn7WqW8Qw1lqwnNTLpYQxNRKk1636N7hWn6hRjCtZ2iUgRhWArlihhsCeKbDVi22zwwXHn6PYj5+Lziey7YnWemj54+ve/aET6u0S308/5/5fRfsG+vrQfn8gafF/z9UmIzOMH9wXW7clA9/e33L/I2KREjGmoyflc+fy7ZPG/727//ylzAXy7U/35Kp87Wt/xRJ+8+I9R/X7jPh4XF3ncyxPiSTWOYb0ZGQsGg30hDH2KNA8bzEmHmo8YWUlXe+adRFyeYnwi3m/IQkZlM8SuYb5/MFDFPba/bzq8b2tTMqbCsE6aXTLWKPKUqB+coE625DbhlGBnE7GFoLDgTaLqE1lIxBKmW0+fK6SI1GpYlvuEV4LZ1uOMQMfINleMuojqI/WqZ7FvKAtJ360RBMZdQAWJFYlpF7HJoEhoKRn1CZUkyUZGfSDGgFZDBHGsFEQLPpGLgWKyeFgT9gqmmiH67UB3doh+ukRSimmbiEYhWotJg1heISTBwdgKnMkQIZKpDCHGjPuKYCbkcUTdR0qlqWYTCmnIrMAnxzhWuJih0hSbLONsSq5ykoBxk2MLQ65KPB4lIyNXEPLAIs2oUwcdiFIyyqbIOuK1Y8qExm2RwtBLwygbkeuc4GCRRtjUoaSiSQ0jb8g8BGGZ6wUOS5YbzvslJuaM1IhIZKSmaAVVViGTpFAVYz1FaoXQitF6zFTPAZikMS5aghxTmTEtgDPEFJjGEU5rpFRUxZjUOzKtif0xMz1HqIBGYlSOQJCnAp8GeNM0XyBSQhnNyEwpU0WbaspUMJvsUu7uIZRk6uZM8hltaJjlC7bdElJEaEGuKgpT4ZNnli+YZNMvHtoU4/A8SEn0g2ibzg0pRISUCCTRB/BQyJJ5sTfUdGCYVosvC76/eLyfjMg9Pjl8w2z6xXwvCCFgiuyL7nRhICbGZkKuC8bZlFJVjLMJks/rxCCFOFwXJZmUc2b5Dp7AOJ8xMhO8D5jcgPNIIQkhUOoJxXjMbLuDkhoVJaUe4YRnpuZ0j+4ZIQRGGHJZ4ZNjJ9tj3Z8SfcAYTZ5KHtw7pFE1qwdbZosJ09Euo1nORE+odMWpOGPOgoCljCW+CBT5GK0N55tzhDBc2b9KMJIkA2M5RnVDrcRcLfBZhvCKRjVMGCPIsHbL1MxAJlSQbMOGKlXklSIFwWy6TyBgZMaqPaUyMxIRLyIVFZFAaUYAlGKMdZZxMafUo0EXo3VUxYTdyQVq2+I6R2oURTVmNtplI9bM9IKOHrQgUzkygAmSTjZMxBSXekZiQm4KjMwGelAphhq/OLyYlVKM9YSJnlGrDfNih8Z3ZFlFSkNhrpEGKzr2xgdsuohJGUEnjFcIr8i9YRRzogxUymCDJXOgpaaKhlnM2XZu2H80VMpQZjnBBiaioAsFymSEPFKlikwVxBgZ+xJlGfR0QkMZNKWUqEywM9nDuQ5VCE43R4xUgd8Iijxjmk+JSVIohcgFEz0nSkeIgUqPCcGTm4KUlozVHFsyEDaQEbc943KMXVsmekaKoJBolVHM5uxcu8xkMqULDUYaZsWCiZ6zsxPpe0esLPNsB5tJjC0RPlJmBaUaEwjMswVdaFBRkRQoPRrG3vbsFLv4rgOpiSEyzqfk2uBjz0zt8P+j7r/eNLuuw27wt8OJb65cnRuNSIIAARAkEilSpGTJlsM3Y3ue+S7mYv60uZjxMzOyZcsWRSWKUaSYCYIBudG50ltvOHmH7+Ktqq7c1UDT41n1VNUJ++y49kp777XKYEKapNSmRDYKl3uiMKETDKhCTZr0aVxDK24RqADnLN2kj44KfJIwzrdRRIhIUbqK1KSzVfcGpJLEVYRvGpIgpeN6eCVQRtFQkQYdQlJyVdEfzFFEE1AW7UN6ep6qKkmqkNjFuEjhMwcpzIl5bODxhZsFMNUB2kYY2dAxHWpvaOseIQFKhnTTPtY6WnGHdtzeOxt65BCyvy/D7H/oD8mxDyVtnKJ/PNJNV8dZ8ffvWDnFuPxQZTwKgfjj5nGqQLr7eNfUfSTq2QMWnMTerXMOa91s94oQMzf/QhAE+ghLvH/r9+3w4Xj8YtcQf3Rl5JMeiP/kysWesn3MMs2hZMBBhHpQP+/k7fdmGPu2RvmD6ffy3fvoYLm7SfYN3Atli7d//V1MMebi/CXyOuJGUhBeHPAvWlf5x60PMFrQ7rS5Fszx95vvo7E8f3eZSGnk1WVWBxd5vPvkLP8Hzs6Dw3c9+4hfDn+Fx/NY92kEMx/uyJA3ZJev3/6AZiPnxd+W3JiPUKFEV4qXfjPl+88OEFbyzDsZm/MJ27EgqDUv/mrEPz/TQSvPkx8UjDsBm1pDLXj550N++pl5hPNcvl5Th5J3B5Jq2/HFPOIbNIhAslw5rIDNUNAYxwtvrvOLp1IIAlYzS1BZtlc0Rlhevwv/fEVgTYEeW+YDzVbXoozl87cFP182VMWY7rakV5ZsdIcIr/js7TZvzmfY2pI2KSujjJ/2b+CU5o3weX7WvIurJ4hmwPPxJb5vfo4QMS9sLPFWX1C3Avou4fPxZ/lpcJ2iynlmY5Xr8QZ1XGBtwFOT87zZ/iWNqzk3XGErXsMEJdK3+Zz9FN+z/4TD8rnOK3wwfp/S5eQu5DPy0/y49Qus9jxhLrCVThhWI7xpeFW9xD+5n2Crhgv5PE2/YdNVCBHzRvAF/rH6Lo1ouJo+TVFP2LQjjHe8uvAVvp9/l62tMa1mDhMKJvGUMIz5SudfMo5H5C7ncusJ1orb/PPw28Qq5an4WYTSZHbMhegqH47f5pflTxC24JXOl/nB+Hs4M6Fr5hj0rvCT6Y+pfMUfhK/wZvUzQi9YiOdZDpf5yeb3scLz5YV/Qa5qtpp1VpOLPJE+g9eKIIl5Ln2FJnRsVesspas8M/9ZpFQg4On55yhsznyyyEK8jKlL/u7X/wXwfPby57nefIjbcUfw5MJn8HikkBjb8MN73+L29CPmk0Uutx/nNzd/SW1qnuh9inE95E5xk144YDk4x9vNWxR1wcJgmV44zx59PGZOn4m4708mBUEYYIoanYQ4YxFCIKRkPlzixblX6KgucZDwZPdT/PUHf864GnK5/zgvzb264yZX8sLCKxjXsF1usdq6yJPzn0buGDdyl/O9O99k7EasJudY1ud5l9/Q1DVf7H6Nt6pf0pgGKRTPhZ/ln7JvIqTglbk3+HX+JlVd4qTlpf5r/LD4DnVT073VpiPGeJmxdP4qL/qv8c57H+GB5659indGJcP1bcJeyotXzvPd371FYx3PP34Z00zo3+2jpMCPSibPbdCYhmvhk2zZm9zhLjaAV+RLfMd9h1pUXJLPsLV9fXZQNXB8Ub3GD/NvIqqM83OfRtawnY2wtePVpT/l/bW3mNzLGbQvcPHiZW5kb7N2fYM/fu7PuFO9S6EqznWucbe4zpsb/4SUkjce+1f8ePM7jJsh3WSeT+tr3Jbvk/RTHl9+nm/e+zqmamglLV6b+yrX6/fQMuRq+jh/e+vr0G+Rdhd4Y/GL/G7rTQKleW7+ZdK0hTeOum74sPqAX27/AiklT3aepLY1tZgpuM/1P8+3xz/Ae8Fn2y/zQf4bbCVpKsdn6sf5qfkpQgle7H+W65PrTKoN0ljwlHucn2Q/QmrHk+oaW+RkchNpSl4wV/gZv0K5isv2CSZuDOoOwnV4LXian0Y/wlPxRHyZLB+xWdzE0+UN+SK/aH5Oy2Z8qv8Cnop3Rr/E24KX0y/w481voWvLCvOEOua3o7dwyvP5wZd4c/IzZBUy110mLhO2N96kkorXr36VqjNlu9zkXOsqG80Gb258Hx8LXlv6I35y/VuIStJK+jzdeo7rzQfMr6zwwvnXGXRnXpPaussrF7/GW2t9pFA8NniWb/z0v7JxZ42o2+Hpc1f5p+k/IDw8rV/kd5Nfkdk7zC+1+Uzveb579++QKuDVwcu8U31AkmxCbXk2fpZfyB+A9DypnuFufh2fNThV8scL/yeuF+9QVTnnoicpXcZEDOkl81x7/jP87vpvqU3NtXNPUFQZN9dv0E27XL30p7w1/CFVr+BK6yl+9OG3KIohIZKXktf4wdY38bZkde5T1E1DXl/He8lnu6/wpvsZyiYM3CJpO+Gd4B2yUPHK/Jf5weTvKSYZi9UiXbnAMLiHVJbP8xr/HP2MwtW0WysMaPOz4J+ppeO14Av8vPoRXhlaqsXqaMD7+l2ayvKZ+FOkiwuMsiFLg1Uev/DUnoX6CB3bJwOdXdg72bhy5NnHsYZ+XEv4SasfD9jW6vH3lavDXbR/deQM9XpkHqTOoIwcDJnATpiFnXHcp2SdugjhZ4qlEGLmEESInfQS59y+Eg5W6KGcnVi/E5Ti/k6hR6Fm/k9wRXsQTlrBOIgz9zHlvs4yG4HdcxX304tjEPi+cnHEmLmX1vPdX/4jv/vo1wwnQ9K5JW6sLDC9OqCdpLP95+9usN6FywvLlOMpW6MxkYNLa57/+8ILDJ66MLOqOgdSgnWnHOo+OJMrW/Hfb32d69lHeDwueQybPslt17DkNKM7mxRbYxocrdoSNZ71bsjCpKEMJV4KKiVol5bQCzY6mrmpoVQevCNTgl7lCbxko6Ppj0rqSIP1FKFgYCWytgy7IcvnlphujfDbE4peQic3yFAxCh3tCpq6IEEwChzdwkEUMAkgnTklIbSwncBcBbWtmLagE0Y045xQCMYtyfyowsc542ZE1AhQishJhnHDXAZW36UMJoQEeKFJZIt1t8ESc6BrTNggvMRXHmckd/Umi+E5vB5gENR5SYKmRchmlDFnWzTmFiJp8MKjXUAiUjbkJvN+QGEKrHI0GJSJSHWHdbdJ13awsQclqKhp2xatqM9avU6rTPDxrM2lq0ibgFRLRmnGQPaZ1BOwgrGdMK8GhLsuKqM57gxvY6wh6kestlYJtOZedpvEpHym8xz/auX/jIhDbk2v873R33GzeJ+W7nAlepyvDv41USvhTn6Dv938Sz4q3yNRLYwz6Eay1WwwxwJGBExEQRq10HlNT6Rs2U0Wo2WqpmRcjQhEwLX5Z/iThX9HGMY7xM0TtOKzLbPu4W/BX771/+D9tbcoi5LO3DxJ2mWzWWMpXuXZuc/x0txr6CDgrY2f8KP173In+4j5ZJnSFTjvqW1FK2gTELBRrjEIF6gp8QhKk3O5c40/vvy/sZAuH+WDB4wIp1Dm+0sW7Lf4mbxC7pzzwPnZ1i0pZu5xncMbx7fvfYM37/2YbbPFlf7jvLr8Fa61n8FZh9Cz7V7eOfAzi6jfsZL/09q3+eXWT1gv77GQLFIEY6ZujLQCaRURCWvNXZaDFZoqo7LFzD+9iNAq5m51h9XwHLWcebWyVUVSa1omYsgmC8E57M/O4ddiXGOxSZ9p3OP6VsbKQgdTjgiUwDpoqZoLcwnDjRGmKRh+7j3SpxWVKej6NnJq2fCb9ONFKluig1nk4I7r4CY5k7mGgehDlhEVnowpc63ziEIy9ROCJmBJX2RueJnFxWWuPf0E8ytLmLJmNBrRX5hDBwHOOe5Nb/D3H/05NybvkOg2XmtC3WKrWGOBZV5MX+Olq6+gk5hv3/xrfr39CzbLNVaTi7x2/g95svssUkm+u/Zdfr7xE9brdc7F5/nC3Bf47OKLM+cAO/TXO09upvzFzf/Ch5P3mZ19UiRBwFpxl8VohbGHAovHkzTQ9pJ1s86CmqduChyOpqlo6QSNZstssBAtUgmLNTN/RaloETCb53PRInkxAWMpfEVLtRFSs+U2GQRz1HoWyDI3E3q+ixg3bNZrDOIFfOOQtWCYbzKXLCGRjN02/WSexhoCGbA+uktbdIhbKZNmm0S2oNFEPmU736KrBzS1pPKGTrtLV3T42qf/BUm3QxUWfPP6f+G9u78iEjFKBaS6w1axxjyLXOt8lq++9u+QUh5h0DOnC7NnP3nnn/jlBz/l9voNOnGbrLWGCQtsY4l0TBq1uJffYj5cwXYD8nyKbRrCypK0W9yr7rDYvkQTGbz2OOFIm5RWk7A2usGcmOMz85/n1Qv/guloQjho0ZnrH+Kfx5irD91+OPwt3/7wr3j/7lu0mgQvHN5AIUu68QLELeqgotVEmNCiw4ipHdMJu8ieY9tt0dYdDIZQhKyNb9NruhjXMA1yWrqNkSGh6rLlhizQB1kyMUNCFyEEtHXKZrPGolihvJEjBilsFVzoP86/+ez/DSU1Qs6sz/so21Eqttf/p9G6B8AR+efBsGvB3rV4+30WnpOF9Ee+/jELWcAJ2Z65PWfpgI/RSafArCf8fpHzyOrBgxSL/dWa4cFM3rXO7hm6DhwVOBMPF+yLAXEq/C/givYgeO7X/bC2ehKSiMN3R5b9Zhncj3Z4DBLvKhanZb5vkhZ1QVZmVE0J2iPP9yhiifU1LivR51r4VDJuKsrhmDKB2oFLNNnmiGSrR7oy2HMntt8DmmfG4OQJAb8qV2G8ZWqyvWoVrqY0lvV7Q+pxTpFoPJ7AQ6NnrmAnicIHilKBE4LQQ+M8lRJMY0UTKYxpKJUkCgS10pTCMEkD/M6h3CbU1IXFB5o6UoymGVlRoHsJVayI/ax/KyWQEVghsVJQaUHpJOCpglmgM9MYQiEogYkCEQjKENAeotnyXWUteeBAGIoYbCTQ1uO0oJZQeovwnoyC3Jekqo1zE2pqMjcl0opClggkOgnxWhDKGBlqTANZU0HoiBBkwtBoR+4KZOQp/RShJKmHIqmp8oKRDHHCUImKtbV7DJIV6ChqZWhCSyMspS3xCpKkQ2ZzGmloYoOxBuMajIa4FVD4htJXTF1G7gqcs9S+nLk19YJKNYzqMaqtSYOYmpkL06bxNLYkjAJKCjAWpSU1JbWrKGyBB8po5prTe09uMhpqcpNhbDNz2WkllS/IRA5BSm4LmsbStpBhyeuc9XKNINBUqqYxNaPhELu8s10kCpFa7q0InkRrxC5+7ySoTIH1zY5byZlryGkzomoKiiCbbRFTCo+n9CWlLahcxaQeY72hsiXGGiSKRtXUviK3UxoaGlNjMDS2JisnDOQA7z06DmcKwP5aHdE6TltrF3vt0HGIsw7vPLaoUUmAkDOFQQiJl7P+ruRsj3xhcnJTILScOZzYIfK7Wy53l6m98xRNxrSeULxG3D0AAJxoSURBVNmSSTOibKbkwRQ8RCTUdUXtq9l5laZiUm+jtKbMLJOiRLY8LTWzvudmMlOOdUpGSY0htwXS1tSFwEkYlTk3N3JqGdOuDSGKrKgwxtJua0abU+qqJkxD8iZjOByTphGBVzjfUIqKqRnTuAZkSSMbAh8g5jSVmzAVE5QtqHf2uefFGC1iimpKaRSxHfFvvvYV+nNze3gUpjGLabxHC6UQlDbfcQ2aYZ0FF3Jvcx0ROnLRQq9qZBDgzMwRQdZMqF1F5QpKW5BtZyBgWkyYNlNKU5I1U3JXYOsGFYf3R1oKSldRlSXTZgpC0CLE+ILKloyaMZUMmbpyxuBLqJqGnIyslYKylDbHSUugArzyOGEpVImxlpIahyPQERZLVc36sKaauTj1hih0eNnQGEuhK2oKsIbaV0TNTnDI2FOoElc20Di8shQmQ0hJLerZO+Go6orClUgdosOY2jUYN8XWksA1VKImVJYwjXFFTVEXDHpzDM4tk7Ra3Bq/j8VgAoMzGSKXlL4gq8dIHdB7Zn7Gxx5gtSyqgrzK8MJjQ0tlKyblEAFUTYmPPC7y5C6j2nZkzQRb17RKT1VPqAeeMq5xWCpf4p0lMIJxVlDXObmKyCnZno7pLg2I0uSY+vh924WOJ1qFyaltiQ89deCoihxvZ66GtS9m26lCj0kkRs08R1nrMbHF+YrS5WBmyk+FppENhctxzlCSz/bA24TKC3KTMRUSHToKchpXoWqP1QV11FDICjGIyaspInD4SIKCQOszCYPipEYegeNp34EI2B9HfvYHL8RxdPcw7BitDpa7T2Y7i4x/+PaIbnkmH1L7Pn5QXz8apWIX9qq5t+vmaA3OpAvsKiX7znIopY5m4jm+CUfK8LPD4seV8wjh96JcHNIH9h7uaV4fM9fZqsVJSsWhqbXzR3h/5IvddFdXr7E9GTLozNGK+2zGfaLJXQIRstxZ5U5gUMWE/gcjoqFhK9xGeslKsYxsDPFi76DeIuVeSYKZ8NY4w83pdRCCi61LDE3NvSZjSafMR4t0UoPHsxq0uFXBdH1I627G5cJzry8xCpYKQdaUeGEZlDA3NNzqCIyauW2tMLhE0fGCubWK9chQKlguFLYzEyDatWdp07A+0NS+YWlsaJSEOKa7MeHCds1Gr6GsJItjjw4VtDxx7ZkfO0ZzmsB7lhqFlII164gbmN+0bHUd0jWs0CGIE+4EW6gi53zWZTPaRjYZCT2SWqN0QyJClv0yd+o1jJ+yGKzAdoZLKoTxXOICo7TAes9SeJ7F+UVuuztIobiQXODO+C7SD1nWCyR+kdvmI0Qcs8wKUzdE+YKF1hydIuWulIgw4IK6yKgZUficrmmzqOZ5Z/IuSZXwWOcSxkmkglaV0A8X2GQN6x3n5CqNNSgaOrJDX81zu7kJiWQ5WMU0Gd54eqrLNXmZ2+oOWTVhQS6jtcJUt+jIDhd7z3LP3KJwOctiBaHAiIqW6nFFP8bt5ib5Ws5i7wKdaZeu7hPJhMvxY6w3t5muT5lnQE/16Mk+ETHz9YC6ZaiDhtSmjLZrWmGbiIh53carmkG6RCvooqUmJ0NYwYXgMu1Wb0+p2D8rBPdjz+ze7yn6u/MY6EZzLKbn2dCbM1eTvfOsZRuUtiJyCRfTa3wwfQfnHavpRRaTFUIZoZuAdtRmY+seItH02/MgPN1gQKpbhCLiTnkT42t68RztqMM709/QDfqsBBdQQp/MI44ubxyd9OzoH1IipcAZyz1/myLLWU0uon3I9en7RDLmSvo4t8rrSCNpB10uRJcpxwVhEiKU2IkUPmNwlS35aPI+WmiuDp7kTnGLrukhMqhNTDgfoZTmHOfZ8msIJ5jXS3RUyi35IZPJhEHW4vJKl6kaMZ+s0HVt7mQf4YTnXHKBcpQR1m06cZf5c5e5MdrC4JlTlvbSNW7fyVHDkn5UUVYK4RSdwOHKiokNGIQxL557iffEm4Qy5HyzNBOihKMreyyxzG13h9JXrLKClxJdG9qyy6p8jA2/Rt1YltrLuEwgCalNwysvfpXB/Pyx7NvjuTO5zqQesZCu0I3n6KcrxCqmzyL3kjs0omKxtcy53hXeGb2FFiGX29f4cPIOCOjEfVaS81wfvUMcpzzWv8YH+bt4V9PTHc6rFd7P30FXmovtx/YO4PdUj6V0iaHdACE4l55jYjfxwtD1HbrpRW5mN3DGsCD61MGESAX0fIe5cI5bxU1EJFiNVqlFQeMMPT2gJ/vccDfxynM+OE8taqqmoBf2mGuvcLv4iMbXnE8uzc6KTC2pb7MYXeHu5APKJmMpPkdjK1SVkoYpS60FJmpEbgv67QXSVput8RqBjmjpLlk9YXVwiU48QEiYlLND9F29QJbnlE1BN+4hm5hpPkHrgCcvfIqkNTvvsty+yHy6gnUOLTVt3Wc8GZLXU+a7yzy+9KkTefP+51eWr3FneIt23KEdd2BwjondoqlqbObwztEJ+7REGx22ubV2C9UKWDq/SKEnbJtNemqOuWSRO+u3scawOn8O3xT0VA9da1pmnrlzy+ggOFSnfbTqOOF2X9KL3Wu00wFttURHdVjWq9wsPqLwORfiy6i4xW1zm1S2ORee45a5ibea5WgVF1W42hOLlBWxyo3td4EOi8kqlJY1d5dYt5kvlxn2akIpWGQJZS3SWlQtmG+WmDZDIt1hTi/SlV1GZkjYa3Fx8RpxkDykLHSC2X5PwzrtyxOsuQ8Q8GcC6H2JWByOWbGbx4G8xPHvj2vDQwjWR57tXBzXhPtx0cShNvqjdT7CM+7Lqd4/wLPSKfh38J2472vkhD7f5bknrgidpBv5B3TjMS+dtVjrUErtBaw98s0jUDR+L8oFcKyG/FCT6dj5cOwSxPFP9i0jnKSsP37hSXqtPpNizFxvnu+ufYciv0UoA1rzAbLXxW5N8JOCwb13ceEEFUX0HSy9+kWU2i+ccaAUAQgJ37n5D9zNbwGCn0QrjMIVJramLQNUME8RK7yHTHQo37+BoEG5GoTDGY8OQgIN0huUd7P4CKFGKQ9SYBOBaSy2ztCFJagdIphFOQ6lpsobdCoJcAStAKXsbAK1JWEYoBOPtJDMBQQ2ozEeWzU0MsJKjUo0KrNY47BSICKNDgTeFAgHTbfC6ilCe7R0uHsfQrtAxy2MjtBBQRA1DFSFXRti/QivYqSt0XJCrHMCHRAs90ilQXlFuz+PMRvkpUYJS57l1LFAWEfRWNy0wUUeYw1KbxMlFa7JobQIn+PdJq62iO48wigQHqscwimapiFMIxCKoq64eOESc2GHxjcYAy0kPQe5F9jGElcZQjsCU5C2O0ShxU2mWOOh08dKCUrjvEQlirACG2i6YUhT1sRKksYh1BXKeZQUKGOpTIPX0BQl77l3eK/5HUWV0c3mqESD8Y7AO97dfptf6bfIywmdqIe1JUoohBesJBd5evkFtsd3Ode5RNDV3BL3iMOYFXmOod2kCAqW03NEKuV2/iFKBJxvXUKKXdw9bMLYNQCcTFSFny3nMk2RWWdGhLMEJOTTDNHy/HTze0ybCR7PUnKOPzz/Z6znd+mF8yy0lrg1+ZCqqTifXqaRNevVHXrhHO9sv8W98hY4mBZj/uH2f2dqRsQy5YWl13hm8PzR+XbA2np4tp9Mc4QQ/C57k1+OfkTRZCQuxknF1GcEPqATdnYOBoMIJDrRJDrF1Q3l2ohkdYCzjsbU/PX1/8xms4ZWAVfaj/MnF/4Nw3qLqIj5XvYPbNuZN6FRNcJh8cJhzSyImVcSHYRcOneOvJwgaZC2JgwFKrMo6wgCCcUyegKQcvvWOsmgjykNVQa3fjfk3nrGIFHM91KYWpwVSNVi2lsgy2uaqSX79YfwKUeVFTjf7B18Fgi8sCjE7NdDkFuiGqKmQVcRUTPANhmpmOfxzjNM9IRQJ7x05Usn8qJf3/sxv7j7fQqT0wl7mEgiVYR1EhlGtLt9RtUQH2i+ffuvyd0UJQI6YXdmnTPgnOFbt75B1oxRMqAVdAhwaBzC1Pzj+/+DqZvQ6nW42H6Mr1z4V+xscEYIi8CCE1hTYZqSMsvoRG1kNiEsK7yANNJQB/i8AVfhOg1KK5yYrbAaDwaPCxVWB0gZUZsKEwusrRHa4HyFEyVCOpqqoq5zgsYQlDWhbDDrY2xZIYQjbIcEwy5FJdFELK08ydMX5kkHKZcGj+OF5/b4Q9KgTV8usG03KZopq93LSCG5NfqAJGix0rnE+uQO03LCSv88SgTc2bxJGEScm7+wx3MDFfK1a/+em+P3CVXEue5VNrO7jIotljsX6MT9E+fJfriweJmvxn/KcLrJQneJNE65OX4fhOB8+yof3X6PD9feRm0r7m3dJWra6DhETQNke8a/lPYoE6O3UjAGvdnmhSe/yGZzj4XuOR67+Kkdrzi78/iIvXfn7yHate/aKk8zpzGFxuiAMtK4MsFZRx0HONFQlAapDOOgpig9WVOzlU1IA4nBYZqa6XhzVlyokIEm7vaJ8xwxcfisRMkCRY63U6gcVlZEaYd+Zx43FPiqICxjXtAvkPcrkuUBV1eeepgdqCfDkUl3eqYHKOIDhN3dhOLQ/QMz3mc935PX9g/h4ev9n591VeUB78W+v6d+e5hl7NVjp+YPGiRxynrInh52RoXKn/Zyf5qHhEMV9N7TmJly4ZwjUtHBvB+RYgG/B+XiSGefog8cSLuLaOLos+O+PXlYj6qPJ/eVYHGwzOJgmdvTm0zKbabTO2gZcLPXY5o5tkyBDjNkK6MxQ5QPaK5cxQ/CGeE+IJ/5AxNmu9pms9zg+viD2cN2QO0ihrahFyQYVzLxs0M5k2pEI2qywKNaiknbkSuHVxX+0gDpFePJCBcpNrWgtA6vBI13aCupQ8+2F2z1A4zwNHhULPBCkkVAqNmSnkZALTzGNyjtmaCwqWRDF1BbCgWuAyrx5KrBNw2bcyC9oAjgjquQeMaRo0axVo2IqakCz5rNEf2SMUNCUTDuKyIHU1kgTIlPyx33lRW5mnkhMYFhIjOMz9l2GUoqyuJ3SGvJ5ZShDqhFxrCYopVmMpkghGNUjEBbto2l8BO880ysBCRTOcE0FZvNkIIcDJSmAicYmiGxT9i065RxybYcob1CO0HmJ6hE85G4SWVKvHLcU5uAoNQVY7/NWnkP07dUpuL69EMaFJnOsaFjWN5G4ah8iassSupZLAqhGPoNcLPtcE5bjHBsm21SFfNu8RYRMYXLadshPpi5HM1FzLrYIKhCxmbCwPcR0jKx22irWAtv8yX/VbpTgWq1aS/26MqZv3QhBCndA9PiSufJQ9Pk+Pkh9h/DOuEg3SQfszXeZDgc4vFUSYbrllhVsT69x9AOKXyB924WU0EYnph7FlPWCC+4PPcE3jmcdbR0h35rHmMbbt3+iM1qHWNrrLdoqxg1Q1LRYhDNH6NcHJrzR6xlR9u7/5vr03e5U1wna6a0VJfGWLab2dmUQClCGZCZMW3T5frkPT7TH+AqQ7TYm+WiJFvlBmO3zYfTd5FCoX3Ay0tvsNhe5V51h6zJ2ZpuIBAUjNBeMmqGVKYiCGaH9UUguFG8h1IBo3obLRRbk3tk1QgVBoh8AzltkeUVpYWNu9vMp4qmqNjaiNiYSrxKaKTk9pohMjM31O/cyxiPHBMvSUNLKO/R9iO8t9wSApxni22shC2xifczHLVFQSICpuUWlpTRpCKgTWUrNqdDLs85Xv3M14ii6Ih8t58nf7D9W26OPyCrx3RbC9AEbNfbUHtGZkyko5n74nIWM2TcjNBSo9EEMthz02utZWonSASRTmf0sN7GuBprG6ZuTJzNPJZlZkJbtRk1W2yVG2zk9xBSUTLGNBWFysjUhKnJydxsi4sVzczdtipRUcjI3yA3Oc47GlHjhWfiJ8has1at723rs9MSbM3YbuFwrE/WaYzBKcda6VG5YVxuUtYj7lUNtTWUroI6Iar7jLYnNIlnGpT84VOvHDhM+fj8s3s4m/jWAePctYVP710v986z1N0xagnBlZVrx8pFoY55bO5Te/eL7XMsts8dM59Oh7nOAnOd+4Hfrg6e2bt+/NKnuHbxGbanQ/7Hd/4L2zfGkAm249uEypO5WcTvzfWSJpvFueiG84TtLp9ffRap1H2hdv92nBMEvZNMCDeqDxm7MduMMN5yr1hDIsldTp0bvJCM3JiCgjvVOj6zZGZKI6ZEUxgzRJeCde9IREzhKwIVI8pttustNIJRMkRaxbgZYZQh7IazyOLS8/bw18S+yzQbE6G52x/y4sVXCdspWqljavwx4GNkcWAR4TQh8kzbaw7l86D89tusTqLTO+9O3eVygt3LH/v048FZ5esT9V92V1COEXpPyufjwP7+P6NyJqXccWt7+lboTwqPQLk4vXr7O/jwGOxXIu6/O4ZcnKYaHi3wwMVpCvoeHfeCVM/c2rV0i0jFOBEQhi3qeehm0O73sSjiOCVptwlkOMvTHcx5f+1jncyWoMMOIGaB6XRC4aGnQqYOXGPxzsO9MXHhKKWg6ySlVKjG4yzojZz2ygKZDOh6j6k8kZAYIYgbR1B7SjxdrygtCCGppSPKDUppqlDTsVCJ2SpHraAVhAgnqBtPC0EjQqR3KBxtAUIF1NbQEZrGe7TxwMz9rEg0dQPtxuIICSvDBEsnbmNlQUNDK+nihCH2EmMsiYlwgA88IRGBDmjHHcZiRFf0yIqSjm6jvUa4mnYQY62hJzqMvaVFSiwiZOVICCkp6NABWaJ3XJqqRBKpFO8hpU1e5vR6czg8sYvQpaKr2/RlD6MN03HBXDxPIlskNsA4S1f3qG1FHCYYYUhUi1DHmNrSC+bQ5FhrCWVJErTxKqEe3YTSEccRUaDRStNWHQIZYoyhIzoUTY4Ws/38qWxjhKVSJWmToCpDK26D9LR0B6eh9jWpbGNxBCLC4kh8ihAWQ0WiU9qdAUGnRdBKkXF4PDE+hWodceVwyJI0mxv3V+L2fxOFMVpqOmkHhydUkiBJqVxOXy1gtEW7EOsNWga0gjZSSXQUIINZ3Au/c+YBmLml9YJIxXR0j0qWRDIhDiIqV9INB7TCzjHtOanN+81ox9MfgFS3aOse1lvaukdJTYMlJgYsqUppmopYJERNCN6j4gCUnBnHnSNVKVoGtMMugQxJ4pRAhdjGEBMT6pBu2EcagcQQuYA6qJnTcxR1Tmhi4iAkiWJSkWCoaaseTVgRqADrZqsc3bSHk4K59hJzLsBMBFUYkBeeORVj0h5yOiYsHbEWM8HYOagLpI7ptiKCuI2YTogHCZGPZi5dg4ouHQwNQkiUz+jqFlElaGxIW7WxSYqyLXCKbn/A5WuPE8URR21zB4g5adCmE/Vx3tIJuhgtycqMJGyhQ00oIkpf0tZdalOSypRYJ3g8sUqpbT1T+kQ126cuQqRUBEQ0NAzC+ZmbZ5MgESj0jstpMTu4LDTdqI9AoIWk3+1D7Wc45szO+RqIZEzoQ8qgoh/NUfhiNoZYEpWghaJyJYlLqVxFKEOMNCQiRIuE0uakrkVlKyIfUdmaOEiIAkFZTmkHXWhLyrwmdiXduIeatnF9Qb8zR7/bP0GY2rHDPoz0cWAl78Ew86Hv9nzof1IQQpDGLVrtDgvzy3jvCTuOoOcgg366QF0H2GiGo735AQsLCyitDjDqk22L/v7DAzRrhngCSFWbRKUkKqUju2TD4SygoYLAeHwgkNYR7QhYqgxoZEQkW4i8IAwCWqSoUBBUAosj9hqZxpioIdIRpioJvEZoGPg+1juIJYHR4CByMbWqaXfmWVg9R9LvHNua42DvvMKp47FL187gSeo4/eywYLRf4D/VsHtsNQ6Nnd9REsXpyoc/mL0/DgFOUWr8oftHCQfOqpwGh1/v78NjjVxnKvz0/Hcv959rOan9++ohhEArhVZydhj8mPz8TjyNTwqPQLk42KKjfXn/lMSJK0L7VitO2+N22B/vybXx+/Lb/1/w2w/f4r1b7xAGIS889TLzvQXA048HPL/4ImmQEoiQJ7rP84uo4XxUcuVTT3Jh8mne2/4tWmqeX3gRJSW7o/bh3ff5zYdvIaXg6auf5oa/yVa1xVKyxFz3aX5lZgP1+tzT/KLKqb2j2ZzyxM2G77VzkJIXbzluLkqcaLBe8vyG48erE0Qgefqm50Z+F5fUKBvyzHsFP35MYJXk2jhmK1hjy48Qus3n77T40fmbeFtzrT7PlhJsViOMiXiteYLvR2s0tubCpMsUy1a3xKiEz66H/GTuI6ysWdarlOu3GS2McCS8Nn2MH6pfo3zFSrlCWAWMgvdxLuaN+Hl+3L+BVBldcwk3VkwWazwZr6sv8HP1S0INy60lur7LL/gVKkj4YvuL/HDzB0xtySKax+vz/Iw3Ac0Xmhf56fSn1EmN9pLP+Mv8RP8C0Tg+Vz/HO7xN4BtSAZfKq7yZvIXQks/3/oC3x78gMJKF3oBL9Qv8yPwIJeDF5AXeM2+TthKUh2fNs3xLr1PnOS/1XqbX73O3us0gnOeyvMTb9W8x3vBY52l+Mf4Ra9UdDIY/Wfq3vDP6DXmT8zjXyLVh0c/RcQlPJk/yrv01la94vP0079S/Y1hs4oTl1f6X+P7021gc5+LLNMqxMRljlebz6kV+3vyEJmpYbK0gVMK9agstPa/3/4AfbH0H0zTMRfN04hZvTrZovOFx8SSuNnsHWX83/BW/3f4loQx5afF1ltLVk60qJygWp8+r+xAGIZ975hWiKAbvefLSM9zjI+bTJXr0WAku8Xb+FkLB04Pn+NX6j7hX3qanB1zuPcFvNn+OFZYn+p9mvDnk5vhD5tIFPrv4CqEKqW3N451nGGVbrIW36SVzvLD02umVPA0E9/cM74MX51/DYpk2Y84Hl9Ei5O3Jb0iDFk/Gz/DO1psMonkuhld5rPMkQisIFFk55of3vs3IbHMuuchivMyH43cQDlaDC3zr7t+xWaxzoXuZ1fAC705/i/WeV+NXeTP7GZM8YzFZ5qp9kp82PyCQgs/2v8w7d94maLrEaZ8vn3+D3wx/TlbkPPXES0iZsL69xlx3jgvPPsZvfvE+1lq+8rV5/ubrb3Jv412iWPL40hy/eXeE856lUGDjlLyG6bjk2XuLlCsjqB1PBU+xXdxlkm2gg5rPiZf56eSXRCbisfbjLHXmuRnfQLmIxy68yLDZpLY1V1eeYGVwnmOku72+3oUnF1/grbUf47AMogWCuMPNjeskvRafX/wDfnjnW3gcnaBLv32Vnw1/RO0tr698hV9s/TNWOFphixcWvsbbm79CCc2zSy9xffoeW9Umq8l5ClPyzxvfxnvBleQxAjFzMRzagIudK3xQvI1A8PLcH/D29FfYRoITPJc+zw/q74GAZwev8N7oLUwzpTEtPtN+jh9vfxvnLc90PstHW+8isilWhDxmn+R9+RauKbnaeoGt5i7rWQ1BxVfn/5jfZr+mMAXPtj5D3ozptQcMBss8vfoSb6//nNIUXJt/lmYiuLn+Ea2kzQtPvMx+x43HCZWnCTv7038cd5ufVKk4bGmOgoiXn3mFeJc+XH6Ge+UHrE1vMpcuc+mxZ/jt9d/gnOOZK5+mnXR3K78/1yN1O+w56fAJsd3rS+EVUgKEKagmDc/d/TT/FL1DLkMuNovo+YCtTkVVST5fPMvP+SdCVbLszxPoZd4K3kYnCX/gv8APx39NJaaoYp7F3jyT1gShA16f/0N+tP1NcJp+sEx/Y4G3bv0abwSfm/s8xcDQxDXn2hd5Yv6ZR6K4HdPzj2INZDer+3BGK/hp1tvj6O3hfA+cj9hLcoYWnYF/nVk5OENR941r+5SmE8o/cMr3wOVDuBN+sE55bNkH3p/A+w8qDv5A/YDjz2F8DPi9u6I9aeXrYeDIqs9+IjyTGo6W4g/dCFgfrvPNH/8tt9ZvEEcJl1eu8iev/tm+Se/vkyvvd9yE7UcSf8iVriArpnzjh/+dm2s3kFKilkLClYTNapO5eJlNtUpOhGDmHSJ0kuv37tIfGmoBdawwtSFVihaCjcQxX0BtNjA2x7cCWvEc/lbDRuyYKwXNIMQ7Q42jZTIiNWaoR3TziFqPQBrqwNDW88ihZphU9FxKLVv4SlKGjraNEDUMdUW3CWjSbaTJKaKGXtjFDbcpwgxbClTg6aUdRm5MYlKiQDORU1LZRgazbS/TqCAt2oSdhCkZqUjxCoJKMElLeqZPaWuyoCJyAU1WEbuQUVqwEi9TjjbJ7BilQsIwIrIhG3aDReapfcOoGqOcpB1EtIM2W2LInBtQNBkumo1bQEAiYzb9Jgt6icznNMLOLOtWkxCxZtfpVC2MaJgUU5JWzGPzz/Bny/+RdtCdxT1wHpVGgOe3ozf50fA73C6uMxcu8lT8LK+03sAC0oPJSmQcIgOJq5rZtZTcrD/ke9vf5La5SVf3yU0OSDIzod9axjjBRrFBV3WhyghzQ5ZUDFqrGK8Z1kPaqo0xJYkMGdZDBmoA0pLLCbGLuaSv8C+X/wNxO2HoRnzjxn/mxvQDYpVwpfs4//rK/3XnbMVDTLL98DEsVrNbTzktqPOSOI54e/prfrzxHe7kN1hIV8jrKShB42taqk2oYzbzewzCBZ4ePM8XFr5MU9SESYi1lrid7vOYIg6WfVLd99fxOOJ7TJ1duRN1XciZe2kh8MaSbU3QWhH328hII4Dv3vo73tz4CcNmk75ewPqG3EzRQuO8II5aDO0W89ECmZ6QuQwqizaCkJgtt8GSXqIoJ9S2RFhPx86TTnpMzISF9hKP95/kuWuv0JsbHLMP2O9Z7n79y9/xrb/5Hndu3kPmFl93KTNPnMTYVouy22NtavHFhKWX3uLSZzy1n63GqAa2xnfoih5mHCLriMpXrHbP8cq1L7K4fB4fB8wtLhyyfIpjNNSdmu3r32++/xe8vfkLRuUWg9YSJY7hdJ1ua4AXnlBEbNdbzKfLNFgm1ZhIRgjvSYOEYbPJanKRV5e/zOOd2ZYe52YxLFqdlK3ROl+//RfcLK6jVcDlzmP82YV/DzW40PEXN/9ffJR/OKO/IiLyMfcmt1hurZCbKZaZ17VAaFpJi/XqNvN6ibqaRYg2tkGVAbENGfshHdmjyMuZy2LpaIcdoihhs1hjEC/y5OA5Xr78VZJWis1rZKQJknjPV/1p4L3fh94nKBf7edLHgd+HhfdMVvZHJAsc3i6zF03ufiEeuF6+zbe3vs5H+Xvou47cdfFNwpiCQdRCL4eMwgntJkYVQ1rWM1VTWnKBSgQMw5xu0EVWE4K7Y0Z+SF8sI3xEFRl6c4sYVRNIxXazwbxdwb2jmA4zhBFcvfgE//Zr/3EnQOZuZX8/ysWZ8j7RsnvGYh4k0J4VzqBcPLDsh4SHixFy9Nuzqif+AC7u0EexqwI/YO4eVtIeaoXjBDq8l9XZMts7r783UT2ddveUL06H3/u2qBOb9TDLbgesExyDjKcj5m7/52VGbWryMqMxDWVdgHcgd9x6+d31lWOI5Q7CHH6UVznGGqbFBCEkkUspq4bSlmw3GYUtGe3Idy0JufUU1hAmAqc0ORYXz7yy2FBResNEgheGItyJ0RAquNLCuZrKKawwFN5ijEAVDbUoKSKLkhanLEbW2NATVA30NZX05BKqssG3QmrlUZVDJSGVm53zaESJUDl1KAgpcFFDGTRIqaldhXEWoxuKrCJymqZlqTBoqei0OlRNSZzGVL4gJ8P4GqkDgiSk8AVKKIzwjMsRygrCMMYpSSUaRm6MFSVTmaFUTWwNlS0obM4kiJFa40OBcY4Gz9RnlCZn4iVoyOsJIGjJFBM2VK5kZLdxCiZmdh4j9gmNKGlkTRNHOO+x0lLIAusNuc1ImhAZaGQc7AywoPA5uZlSmpypGM9ciiqFcn52yDdsowKNCvUMX5zHNobCVhQuJ6snCC8oXInzULoCWWxjkOS+QCARLiMMPJVsmFRjnNfkZoppapxtKFGMqhFhK6DOc5qopFEVOQXWNkBCbiY0riFrZi5QSzNrlxT33XM+LJxopdmbD8eDQBC3E6IkmvUFGVk9oXIl42qIcQ21rXHeoSJNVVczV6N2QiVKtFbIJEQnEYHYX9THZKAP+maXJyiJaywykLNo8sbiBXRWBrN4EtYirAQpycyUzEwomoxQhHjvmVQjBIIobs3cj5qcbTGksiVTMQbviIloMFTMcFQIS8YE8ESmg3A5lSmZFGPUxYj+/CyY2X1vlEdFtKIskaGeuWkWlsmkwoqIYpLjCKhkQ2FmynDlazZGW6hYIkNJWeWMfYaIQnwoEV5Qu4YqEailNv0LKzvutI/DgaMa3o4NZnYnIG8mTKptCpMRNBNqbylFia+30VpT7szzUbGF34luX9mKwEvKYsrUTegHc0ybCdloSqvXJogCpFZUeUlJiROWqZlAA6vJBSpT0go7DJtNGtswbrYBZtuWxMzV7thNcKJhPNlAhpp20GLUVBQmZ6JGOFuT5yNM09ClizGC3E8RgcALaHw920JgBCZ0VMxc0b5343dcbX+Wq4M+QRSdPH+OQ8WzeP15VJa6/9mwa5w7a2+coIkc6aNjDBwCZnPTZpQ+R3cDJuMSGwhKYUk6ELQ9WV3gMQRMsaamFDWq1acONYVr8EzR+SaBy6lTR17nBEKQmRwKBbFHKchNhh5vIYuYSZYRxBHEEu8cYs9l6KNXLB7WMn8g/f9P8eD+7enxMuBR9NvHXrnw++bcGfprP4nek1GPGLGA3dW3g1t2Dv4/ydj3EOP2sK0W+8v1e08+Nvz+vEXBycs1x6TzzHjVfQXu/kLncSfuz06m7ldieW6FQWcO52aWqotLlxBSHUL43SB9JwtUu2PsgbnuPL1Wn35nDiUVi61ltpOCppbMqRatIiboFYBkhQHDcoOi3GCubJO4NhvxFhjLfN6jSixEBb1M0zcpa4stXCBYrjQM5qAc0c2gtW24K7dwqeLywmPU5iNuNLeZV23mzIC78To21azEKxgRIYrb9HSPxdZF7voNtkebnIuWZuc9kpwWCYvNVTaTNcqgYYVFVNtyu75LWyQMTJutYEilSpbnVpFKcbe+RSwSVqNV1up7OCVZ9ssEYYJw94h8yKpYZihHaBWwKJbwlcCVnsBJLseX2bRb6MYwZ2JEJQmkQVSaVbXKqNnGUhFXEQudRbbcGkpqFliglDkiFCyEK3TjHpmZgIeWbO34XJfMBQu04j45OdYYWqJNZiYos0ZPDOjIPqXIqeuagZrHTRvebd5ivneOOb3E7fwGVljOJZeYj5bQMiBVLa72n+a2vYlRloutazSu4kZxna7vsRAscyu/jhGGpeQcc+EiUipinRIQc6++TdZMWVRL1EYitKalWiyIc0ziIUXY7Li3leA9iW4z5/pk+YjFwQqDdI7x+gbEnjRp81j4FJtiwkfTNRbDeVq06YcLBDLkXHwRLYLTp8ZhS8mRJcITvjk2n8Oqv0AohVCSK4OnuJ69S1ymtKMuoYqYlDtek3KIoohW0qEddrgQXqYaT5FBQLATJ+HUsk97fvj9MQYN7z1rxW0m9YiV5AI6CLgx+R3Kaq7MP85Wsc54vMVicI5u3MMbC9JzKX2M9fQu3bBPJ+jivUeqAOUVy+kq23YbLw2L4TIqUtwuroP3LKtlCjHzob+olmjJhLX6Jt5ZVroXiWTCdjGi1+pzZfmJg/K72N8YAWLmr/zSlQt8+N4NgjCg1UrQrkc+tRTTkiyruFECpaM76HF58XGMv0Gv26WbDKjbJaNii1bUpbuwTJHVNLZhobfEhdUr95fQH2j53GfyEbC7XeVy/2nuTK6jpGY5XsGHEW77A9pxh+XkHMNqEwrJYrJKoCLW6juEOmY5WGHUbKLygJbusByf52bxEWmRsmLOsza5Ry7HLERL9KMB/bCHUprFZInGV7w3/pD5aIX5YJ4FNYe3jnmxREmBNSUD3aWVdlmvA5Cw1DqPV4Ze1ScqAoIKcjXAK09sYkzgScmIZUq7N8CpmcevVtjF4+lX26RBm+dXX+ex1ccfenXhJMvmAT53VJc7c+6cUUi6zwrPvs5w5rbuZHmmnD+hTHkxfoy2mqclS1qtlKVRwl1XUKeCVbVAFGjq8YSOiVio+mT1LbSs6W4nhJcvIexd1EZNf22JPBmjbMFALxL5Dti7tEzM+dZjbJg7YDxd1SbKY+bOLxO1UlYG5wj0A+jvJ4WPY+U+w1g9ihWmk/P294X233c99vXPJ94iddxnR+bS/W16B5PtX8Hg/hicVpWH4nW7zOzo+6PJ90vXD1Hux4BHr1zsq7X3nqquwXuiKESwb4vGfqVuR93z+5D/IBJ4Dosuu+zrSF8cUB13VZPZfRzF/OHn/oibazcIkFxYvXLwu13C5++P/1Fj4c5C3r4VsF3i6gGvQwptKI0mNxDHN3B+hHAes/0B1doaMizAx8RhG6XGuKYm1AOMS5G2RMuIoH8V7yq8CIhbi5TOg5AgPTp/HxHfBqsIEoVvamQ5wUtJ2D+PDBKstOhQ402G0BkyDBDVHYTaImjlRHGK15rATYmEI7Y9pIAmmyJUD29DvIzxOqWVzLGdb+Jsg8fga4u1DY0VlFVNk0g8GhfEOCTWeZwAUYOhwOoaAkOQdGEqqYoGmUhEkSOagjAeEBOReTXzFNNA3ZSEgaRFQFh7tPBI70mSGKsNupQEWvHq3FfY3FpDGEevPeCbxV8hrUCFmlc7X2LaZEgpSGTCt7b/GtVItJS8kLyMTDReQS+Z47trf8PEjEi326TjFhM7wnnLUnKeryz/GRv1XXp6wLtbv+b95h2ssHSm/4w3lqkdE4mEbjhg2kxpfM1CtMiXV/4VG8092qrLvfI2m1t3UHhCNC4McY0EqZGNpvYOEwic1AjpQEs8jqeXnuVcco6JGbOiVhhONynncmIVk2vBNza/TSkquqpDRIOzDmstw3tjNsQ6CxcWD86lw5PmOKVi9/YkK+ExsJfFIUFeIFhKVvnapX/L3fFN2nRYbJ/nVx/+hFY/pdObw9uGbbVFP13gXOcSUuujdXwUcEw+v93+JT9d/z6lLeioHgi9E8lc8+bkx+RmTF5P6ao+f3zlf6MtuzjreGrwaXpxn2GxyUK8wj9tfgtb3kZqgYoCTFViXY1TJYFJMGVNoDSBDhlXY5xzlE3FnG0R1AJEyEq4wHNPvs5UFcx3FlnoLh2quD/UhtnN0vICX/2TL7J2b4N+v8vCwjwffbCGaRwXH1tkUlg+ujNhrhcxn3pujN4naEku9p+gtiW3J9fpRQOW2xe5tXWDqik5P3+ZOErO1qfHcqpZ3bRUOO/ZDUUrpMRZC0oQBjG+ASkFSim01lCDtxYdSayfRUK3zvKde//AuBkTjgK6YZ/cTMmqKe2gg/cltckIRMBWfYdvfPSfyOox7bCP8hpRlmAckbbUriEwDbKsiK1HVx7rLIOgw/OLX+B2+QHdsEcsUm6Y6/hI8Oylz7OVb1JHOfOtZRZaq9wYvodxDZcGj1M0OfcmN+jFc6x0L50JFQ/C7nbcM0j+nwTOaH09fPVJYf+h00dlMD949oKjBgQfUDYDymaKli2UUUjd4OoGZwxNXIF3eO9QXmMkOD/jMUqCtw5XVbTafSozQliP1BKfgm88PrQIa3HW4OoaTMPzF16l/fQFwiDi4tKl35+EvttkMcOZsxpa97aWPsAq/UDl8hGuepy8LWpfi86iZZyQZndOfawYa2c1WnHfCLAnfor9yU6YVYfrfFK/nmbsO5CRZ38IBs9xRew+PZj9CYvinwgekXJxPIfxficCrnMoawn0TiTr+yn2dfyD1bgDfbwb4OQkTW5P2jnYY0mc8MSlp9hTZk5oybEdfsyk3BpvMZxuM5wMkUIwnFpMK2Y926YRBS4YM2WCrw2ZjHGtmkxOCNM+WZCT+RwfO8pKoZ1jqmuCTsyWnzCtJb5xmM27qDhkFHmaLGNjsEETjfCdgJvmQ6RQ1K2aXJS8xe9ompmfdUcOjWEsRzjfcMveQAlJEzTc8h5vFEO3TUOLNW6C9eQi57YLEDJh22VURc2G/QCaiiZxSKtw1jI0m4QuYl2OSEWXqZsijUI4GDEmIGCjuUcaRIyrCVhBna8zFGNUBL81vyHBkQc5IzlknDimFAhXUKoKHShqU1AwpnQTMpmjZMBH1kAjGJttIpnw0fhdXpp7A2rDjybfJXcZmZsS1wkfTd/l1cWvopKIHw2/Te4zMj8lkjFr4V3+YPnPAPjJxnfYbNa4W9yko/tYZlF0rbcooal9xVO952lMxT+ar/NB/g7GN/TUACVmbkXbqsvN8iPwULsKgSCzE55qfwZvLT/c+ke2iw0qSm4VtzBxi5GbYBrLXbtFHETkeY5rPEJLtpshiU54b/o2VydXaYklOgstkpWIIImQgeYvNv+Gm/VttpsJi7pDUOZM6y0CGfJB9i4vL72Gd34n2NsnhAdk8SC3gYN4kblocbaVBPjc068foMAXjyvjETCx47LcT+zfG/+GW9mHTJsxXT2HbTxjPyEkRE09URAyrUesRhe5nr3Ps90XQIK3nqVwlZXWRW5PPmJYbbFVbaJ1wGQyBGkZu21EA1VZMSy3CIKA7XybQGmmfoKtDXm1iammCK1ZL+6Q9Nuc6zx2vGJ33AHJHRjM9RnM9ffurz65uncdJ7A4t7sKJPj03It77xJa9JL5vd65tHjlfq8d2/8HdyEfz4/ua6vvbf2acbnFtB6B0phGMLYjmnHFcLpGHKRM7ZiN8i5OwLjZRsuAyXhMKDQTM8bWDhGus10NCYKASERoGTButunZLsblTPwWopaUwwmBV4yqTbp6Dl80ZHYWobuUOaEMyeptfG3ZaO5Q1BnOe6IiZjBcQpHAoEW0Mscry8+glUYoybxYvr+9Xwiuzj+919pIJ/T3+vDjgNjL9+ib4/Dg4+X/KOATnfs4iV1/IjjUITu3H+Q3GdUZW1VOLTw3GCO9IhcGETqoSiZhhlOOKbcJi4q8niAHbVx1g5GYIsOKwq0Tu4ZM5ghzF0xEnZRYX/OryRYhAZmckEYJm3LICxe/9vtVKo4IKLsPHwD7rT9nwiFx7OUDi9tft2PSHcbnT3rY+tQ6ifv5P9Tq2pkTnTI3D1rOjzGOH1zF2S8T7/07ZOHe7xzpYI67Aab3ct2rzP1tXSdrLgePXd8Xdj/p2Dxyb1H7BXEpJUpLpBM7vp05pNWJg9+cqbSTDwAdtvzM9haeooDA/eESOzrdPuPgAQXjBIijGCUlaZSilMKIkFinjFRIUkcUhSHtRQgREemQeNCnyBvaQY/KF3ghkKFCqZRYzWPllLZPySqNt2AdhM4TFBVZW9CqFU0UkrbmMKFA+5DIBcQqpqf7SFvgrKNQmtDFSNsQhyndsEfkI7CQk5OIGO8UmdG0REztQHkF0pPaCOFCyqYk9RHWJ2gVUqqaVthhOhpT5wZnBKqlaMUJjWhIbIj3EFpNqhKc0CQ2pPIlKTFNWRP6gMhpdOloqRaFLYmbEB8JWoAygiCOiUWMaTwdsYARDTiNEhotAsIwpnT5zAWo0fi6QYcB7aRLWraZ2DFJ0KbVGqBbMQJIVDqLAK0iEtUiken9MVQtEpUSioi26lCJktCF1K5CejlzS2odPmtQVtHWXYomIzCaKIgomNJSLSpTo0SAlHLmklSlMyRynpiIlmiBhzRsY4OUnIa2bCNkSVsleO/RjSKMEgoyUpuga0m2ts7Fl5+euXJNYrwUSCVJVUJbtyldTeJjhK1xuSPttlhZWWFheeGTKRYP/HTXT/YOIdpHUPcO9e7Nd7FLB48hWo/QFLZXs9NqfB8SldIKOjS2JlUtjHc01pCoFG9rEhJKCuIgJWhmKyour/GCmRtdKUjDFlpqUpUSECClJ9QBlSto+RYI6Lfm8LVDK02qWzS2pp/OIWyFtWC9RwhNEreP37lwhGk9mh7xu4zrrMx3l5weYJ7H0OKdcU+ClFbYoXE1qW5RSU9ASEyCDkMSmVCZglS3yIqCgJBEtpBSEIuEylX0kgFFVRC5kNDFhEFIolMqX9LyLXJhSGQLrQJCI0lVi8yNaNGiDipEoHD1LHKylJq6aMjH2zhn6fY6RFFAf3GBTz39Mp20Pwved1zTfy/efh4CDtvhDuDCCQLP4e/9MdcPVYWH1xB+H/12YuTundtEx8Q6IlYRbVJEaPFe4VRNmDl0ElP7ikS2UE1BWIOLPalMsSIlcjVB7dFNQ+JCalcT1RKnFLrbIbYRpq5IWz2aqiE0AarSWGNnLnVnlXxErd2ZTIeHeD8tPSzUP2hs91ftlLQHLPFnxZcH0Kr7MtyZqsAnVUH84U7ZJ4MeNJTcX2E7msfRaTdja7utEQe+vd+egyrBfjh+ReN+XQ58sTP+x33xoLz2G8WPF4UPy+GPBm8/uc+pQ6sse7c7AkUYhERRhJCzLVG7AvzD5Ln32AN+NlReeLw4qkzs/7n/3e7i4c5qhT+4POQFB4bygB53H2+OhXbSYfXyCu58iV0tePnCMwg5QiVDOouaz8onaDY3sWXGc/YplPQEMYQ4nudTCO3wyvDS4FlaqUFGm0TdglfSHuHgOjp9m8+E0IruQf0ThPyQl/2TiEgjpOfTrU/TIcW5GisNb3TfwMsGScOT+jEWu6t4a7FNzWu8hvESaxQXqnP0mjZIMKbmdfkKFovznnNyiUXZw4YlDRkvqc9h2wGNEsypZZaDC7RXFpg7t8Kfzv0LcA5RGgZ5m8flZVouIG4Er2TPI0yNNIbOVPOsuExLWbSveFm+iBKSSCr68YBnus/hrUFqweuLX+Na+jRPtj/NpzrP8+n2C7OxE54X59+YRaiWIISkl87x95O/4m+2/5JWPKDShkwWVIEljbv817v/ib+4+58IVUyFIPOOAk8/WuKvb/1n/urG/wflFN4xi8rqLM+Hn8M0NdYa5qNl3pm+x59/8P/m25vf4mrnUzSNwLqQx9JP8aR8lsejp7kcP8GXF/8UJw0OQ1d3uZV9xH/76P/JPw6/wXlxkRqL1YILncusRktIX2KbjC/13kCIGknDhdYqF+QKyhlcU7DSLPOLwa/4y/U/52fDH/Hm9F3+/N7f8t/u/SPnk/NYD9ZAy7W5xDmCSOG14VMLzyGFnAnA+4WSw0zlIQSM45SCvWXnAz8cQxPupz1Y8OE5fOjm49A5P6MVB34P1WP35+ne8xhn8N4x0AMuJJdxduYl6Mvn/iXXek/zZO9Znp57jsutJ3DO4yMNUqJ2Yot0VZ/F1jImaaijmpd7b2AbS1M3hD7i+c7ncMaAcLyoXiIqPEFhCUr4TPB5xLSNH8U8NniOJEyPNua0pnq/Y3l60O8JfSr8IabygA7fdXqxx4+ONxnuCn9PL7yIocKJhsQlpOMET42VNS/Pv471Bc4V9II2zyw+g6TGu4KX+6/gbI6pJrR1xKfnP42WNb6Z8EL7RURVQDalRcgLnc+jM4EYNrxkXuZqdYmnkmd5qv9ZXtNfYZAtsMh5nmv/AZf7z/DU4gu8+tRX+ZNn/ndefPwNnrv0BV557GsMuvMzwVDs47d716f1iz8DU9vXvft/HwAH580jgFPKvY9L//8Fx9X7WnqROaHoupKEktflNYJ4k7S1weW4z9ImhNmQoB7x2Q+v0rR6mGBAZ9JnddIlqHK0aPiC+TykM/fTPeZZVZdoXE2jDJ/v/yFGe6wSiNJzWV8lH+fALs4cM/8O1vzI+6Pd7w++ODCt/cHPTxPqTzJYnEEnPTHPjw3ifvV3p86pZGt3DuzymoctTeyg/X0heje3A0L5sYYv7tODXdK36/lNsJfDfhK6Plrjmz/9Bn/7o//B9bvvgRA7dEQcTwOO+RXyUFoOpxGH/p/0/iF+9+DRDPYnd0U7nc4Gfu+sxOlwoi/vPYH/MBIcklIOFXJUUzwkPx1Wvf1JDPFwITvfiqNt2l9WZqZ8/eafcyu7jhQKqz0i0Kw191hUS0w21qlEgwo02ioSnbLJBot6mcwVGNfgJcQqIlEJ626NRblEZiY4Z2l8Q6pahETcy2+zqBZpOoCEsi5ImoA4arFh1+m5Ho1s8I2hlDUd2iij2ajXGOh5SiVwVlHpmo6N0WnIhtmg26Q0vkFZSR6U9PzskOKW26ZlYogk2kmmumAunKcYTZmGBR1aSOdpEzPVOQP6UM484QSNwsWGqJ2wVa4zHy1RNzWTapvIhwgvafmEcZQx8H0qVZM1U6Ig5krvSf5k8T8gjSczU/529N+4XX2EEgolNJGM2azXmAsWyZuc2s+2IQmt0UHMen2XxWCJwhU0buaVKPQJEW3uFXeZl3NIGqTwWG+IwpQQzabdZE7MU4sCIQW1rwlpI32LjXqT+WiBwuRgHZVsuNy+zB/3vkaniAnnOnxj4y/4MHuHwhe0aCG8YMts0gsGVLZAqZBcFXRkDy8kW/UmHdkGaQnQbBcbLERLuMYxtWNaQYcaS6gTRm5EP1gmdwkjW5KqBGtrYiTr2Sb9JqLK7+LI6Q/meWLh0/zR/L8D50l77eNR/VhTzDHXZ4XdCfOgcj52/mf89qzMFfjmrf/B77Z/yXa1RU8OsAimdkoiUy5Fl/nXj/1HVBTgKkNdNgRxiI40TVmjA42zjmGxyV+O/r9cz99He42ZlCQ+Zui3WAgWKW0x81KU13RJ6DSzCPFdFgjGbfKsYXu0zUvPv8q/ee0/EAaHPXyd3OD7bkAPP+fQ80djjXpY+IcP/zO/2/gpo2oT3SRcv/kR3eUOvdYcSkOqEjbze/SDRZzyZHZCEqTgPaKW3Bve4MLKNSwNWT1Bo5FGEPuUYbnGXLhEVRRUTYmSmvPpZZ5rfZn33n2P3uI8K+fPUZmGS5cv02m3kUrN9qof6LfDhqWH3RJwVsTcl+yMXHf/JoeZUHaydfVM5R7M/GhZ/hBf/l8OjtKY41zh3px+yPfu/gO3sxt0gz6b0xs40ZD5CUkWoaOQTE/oxHNsb9UkgxXGdsKcSxDFFlWvIbUxpiqIZMw2I3q+j29rCqYksoWTkMRdhvUai5M5Pidf51z7UyxfXUWq45Xuo23ZbcO+VCd4YTucw9Fnp4zbnrJzUObaw0WxL0//qKjFCfzg2AocqezJcFwnnJTmlCoczuaoBOv3vRMHnhxe7dgF5yxf/8F/48badZqm5tzCBf7o8/+Kbto7udB9A3lgDj6EZH54KPdjzbGx486Yd6fTeXCiE+CRnLn4WEF7TmOYHMWHWYftH/7DqQ7roQfL2uvmPR1jdxBnzw8i1w7K7J9wHD8NcjOlcbvuDgXCawyOzExx4wbvDbkukU6QipSKhoyCQI2xwjFlOlvx8m1KU1DIgm0/xNiKzE7xUuBrS64D6sQy0QWmaWbxHYTHVhElJZkfI4THOEPjaowzSMA2jsxOkQhyp7FI6qYBaRF1xsSM8a6m9gaBoPEWbzwWz0RmOGVxzqF1SO4KZCUhcOQ+o3E1kZNYUZE3JdKCbjyZz4l0DMpQ2YpS5EzcGAJJZnJKVyEqgU8FpS8ZiynOWSZuTN5kLJVTjK1IoxZGGaywjJttBIJEpxQ2J7dTlNBYbxmX2yAEEW2cz5g2E5RTGFszNRO897Rth4yMqR0DjlagMbICIfBCUnrIXYZ0gHIzV6nOkEiJ9YasyWYRXn2D157GNORlzjidML+whNCCgoKxH1G7GqFn0S+zOgMrZ64rS0spagjBK0lOjsMh6hpRW0pRMSqHSC/JmGKtpRGgbb3jESuhwTE2BUVTgDPoxjOup7g6px1BZQsmjMmqCd43RPFhS/g+ZD44uQ5OqYdRBHa/e0iCeGY4Lc/T5LozMKFpM2ZUD8maKVIpPIphtkkmJvRdHxR44/DeE7fj2Rmy2uAaC1ohA8W0mFCbku1qE4EgkiF1PXPJPGoCDIZRvYVWmtAKvGgobEbgY4zXrI+3UFrivJ1F7N6nXBzPG/cbaE7pm/2C8yEmdjS7QyUdujzzsO7lNYNpvc2o2pwdsI41siModYGWY2RpKL2mcFNCHeMaz8Rsk9UTQhWgnKLyOaNiA6EE42oL6QRxHVGSkZkxGAEGJvWYsqrYuDNh7urTvPil1zh/4cKJgvKJzw80/kHC0cGvzgwnyVTH5rx7aPe+fezjw+le+x+Jq9vdkvwDcPNj5Xm8In3cWE6bCYXJyU0GQJVWNDanqKaoWOK0o1QFuCFlGlPVQ6rIMc5KhMjIqymlTEBZtCnI3YQgUARJl6zOybMJWE/pSzI3oR20yLItrMuZbk/ozp8lPsD+SeZPQLeTjbYfR+o6cru32nGfOPzP0y3Fof+fIIvj4AF84/DrI+si+/pn/wr9fecLB1ULATRNTd1UbE+GOG9pbEOWT+kk3QMKw96X/tDB9d0mHadvHWeA3/f6+HYcsynrJFR7xPDJlYsDlrEHU74DQel2/p/F28FM2N+vXhzstGO/97upjpmiR3jpUUQ5HvkOwiBcoBf0mQsXUCiiImDkc2xZ0nc94rDFJhtIpViQi5RyZmVfFItEQcK6vIfHsxSsUIsSUcOcmCOREev+Hj6SLKoVKlPiKkff94iIGaoh1tTMiz7Gg3GODl3mkwXWyjs0smHBLGCEQYaClmtzXi7yfn6builZHSzjTI3H0nUJPdlnS08oyFnRi/hAsubXaLuEnuuz3YxIRUC/7KENtKMUYTULpDg98/XdkR06/S6FqoiChFBrtsy9mQvZYAWJwmY1cZCy1D7H1M5cyC6GqwQqQBYaYQQr6Tkyn3PP3GM+WKIbDOgFcygki9E5JtUQLwzzeoFIt8ijDBAEImLix9iqZk7MEYuINXMLL2AgFjFKYquaxWiBOd1lqLdpTMMyy9S6wXhLnz493WHDrlP7ikW9QmUVdWNp+zZBIRnLEWk7ISgU3bDLR/X7dOU8F9MrlK6gNgWpaGG9ox23aCU9AgJyX5LXU1ouxSigNrR0l8XOMpuTO0zsmAW9gvQKodqkKmE+GLBRbeNFxGq0SEMPZ9eJnGJgEsZuRBDBQjxP1ExY95ae7rOiV4mCBBU9pDvEk0xkJykd/pDl8EHC7sNStbMatfbX+yzGsh243L7G7ewGCs1CuIyrJaqtCHzI1cHjrG/dYVgPuTi4gnYBd6rraBlxLr7IZrPBdr5J1/XoiC6L0RLSCubVIrmeQHYbs2FpRR3SJCQIQ5aCFchq2r5NJ+yTjQULbc35CxeZ7y3SSbsHqvpx4H4spwPc8X4H7V3vY0OHlIIjl2ew/h0Hl3tPcXd8HU3IQnyOdGmB62u/YxDPsbRwjkm2yagaMh8s46xEVy0iFdBvD6jqkpQOvXBAoAM6pkMQBmgZMC0LxpMCEcaYyiFswiAc8NmXXuWPPvun+4JHnqYlH0b2nf44VTB+RGz5mME9KRjd/n31B7b77vw9qhDt3B9hYo/s+OwD4WEF1DO7lj8h48PegM61LtKPZjFiEp0i4gtM6k0ysU1HdjHKoco1WiRcjlbZEhmZyun7FiLssy3XSVxCz3WZVutoJZkXK6TBPFQgpKA9Dmi0JIgiUtdhVV0mgH27M87eCQ9U7M6S1YOMMGewWh8r2B6uw5kJ0ylE4+MSt6Pm+QfDw6bf991xWxJ3z0McfSMIg4jF/jJFVWCdodce0Au7VMMp8Vyb42mQ2JfDCX3mT0lxrE1InEyqHp0N4VR4hN6idq0s8MBRPMC47p9o3w0Xf/Drg9g0u9o/5CcQmwMp9tS++8/2eKw4kPqk+XOY3O8imBQSLYKd7Y+ebjLP1t11lHYkrZRuq8uwXEdqQSds09gK6QUoRypCnDVIKQidosbincNrT0KCE+CMRVtJpSUoAQEM9DzDcoj1njiZeWoSQiKlInExs0jijihKkNTImln5ukUsAwLRxWU11lX4tseFkrZvs2G3AIuWEryDpsAhGZiIRiiEUSzYlFfj17nOXQadAZfrFdY6Iwpd8tjKM4Q64kZ2nUjFNJR8c+N/4LxHK4UrQYYKoQVBEJGbO5Sipg5mwd4q0SC1ZNMP+cboL8jslK7uI42nNgVSSKT1NEWGsQW1mfL6wh+RRQVhoAmJ+av1/7Kzj9PTySXD2uDxDNKEYbZJUBbYbJO6FTPtlHjhEXGMMRWVayh0TT+IKYTF4CGOMY3EEyPCNisrC4w33mKST+gHPf5h9HVyPyESMZ9f/BKvxasU5YQrvadoXMPN8jqdoMuF5CrXi/cozJTFcIV/vPtXjGqNNIbUJqwLiVQBWsX4cEDVOISIUXqVsrYYKSnrlDAQuKbGeE0/mceIMeW0RlGClATdmEY4wrSFDPR9UnRWA+w+pf/Y5wcn2b68xdHnJ5V7VoXhONgjmAdn6l4VT1KOjvsvIFQRFoP3FiUVYRhC7hDSs2U3+bvh1ylNQSfv4lzNVIzQIqCn55j4MRUVbdHGOQdm5l2sq9vkZhvnHe1Wh1U5x5q5jWgazs9f4Ory0wyrdfpykeTigCkTgiDg8vJjM6F4r3oHucZ9AeqQgeZAk/Z3rj9ma+dBk8zes+PG+Dh8ODM6zVLEooUzEmE1roBWo9EGqq0JYekxGFzjaGrLxm+nTNyUdtLiwtwS/RCiLGHOLmBGNU1i6ad9Nu7WvPa1r1JdzXj83LO0gi6/u/1zOp0eVwZPzc4a7dT9wecljoeZgnH0u/sC/cdkzyfpNw8NJ03Ih6jXJxHyHhnM6nx2V6onvTuYXzfs84fn/yW3sxu0gjbn0kt8WL5NXk/oF32+de9v0M02OmrRtQGjKEPm26Q6wNWSoB3OVsmykBHM+KuI8PcMzjoCo1iML7Oe3aPJzczphxdY3RBE4b6heBAxPCM8inE6FT3OULdHhSufNJ/95OthFIyz5Hnk8Sk4d9wzIXnl2TdYXbiAtYaLy1dIwmQm1+3KyeLjq/kP9dXHRbdHNM6PSLk4KvLfh+MxYFepmPlq3icv+IN9cv/rXSJ0sMyT4Kgl4H79di1T+93g7qoYB1iv4MBeSPb26u7kI2Cr3GBYbTKqt5BIJmpCkzQUvmKsxqxX60zUBIGkqgqCKGJqxyinWK9vk6kC4SXGN0gvmLoR2io23D1yX+C9x3iLMooJE5RVrDcb1L7GiIYPzYcoqRjZESDYcOs4YaltBc0syNbIbmOl5UaxCVrT0GB0RRAEjJmAhDfFb/BFQ0GJ1BKahrEbYUTDbykIqoBK1RRhzYgxr6y8StBJUVoxCK6gwmBnLzM83XsWBPz1vT9naidkTFlr1rE0TMSYwhSMxAipNSOzjaw1zlu27RZKan6V/ZxAhmzbLebUHL5qGJVbCATZdJvACkZ2myiOuF2+z+f6f0AYBHxr/Pdsl0PGdhtde8ZNTVZtI7Xkw9ygpaYJcuow4EP1PtOqxtQ1RZkRhCHbZgvvPHfLu1jVYIWjahRSddn2Oa4RrOfXcaqmCHNulR+ytakpwoyu7jGXL/Evl/89Yt+K+CCZxzYWX1uuxtfw1vHO9NdMqm3G1RaxSPnF5KcoqcldDmobU9ds1BNS2bBRvYUmYNxMcUrgK8tWvU0apfzGvo0qSrarbQgbgsQzdtsELuDD4j0+L75EiHowkdm10OzNvWNNIafPtVPyfhgid8R6eyID8fff7959DAby7vjXTM2IsRkhSg1WsF1tEeuEX279hCAIGdcj+mEPK0qGzQahDAnCmCBIGDdD+noej2Vst1BCk5UjlFfUusDJiNvldcbZFoEOuJVd57P911hIztNdHKCj4MwddLx72sNNEwcELSFO+ODA01M0hsPPTlQW/aFHM/r+7uZbTKsR02qEiAXFZIyILLnI+HX2S4RXTPMhNQ7jNLZ2VDRsmG3+3Rv/F3q9HsZYRtvbBFpT1TVRFNEf9GdxMXbgxcfeOIC7Yg+ZT+vbExonTkakT2TxO6l/d8dQnDDvTphDM9n1MLc8lPaE+bO3veLQucdjlfJTYT93Plz40VRHacVxBe4aGXcNB2e0jPiDk6Eb9umG/T2aci19BlJ4W7xFE1nypsTXgg11B18aCjHlnhDIUDAxU9KwxXut9wicIlcNm/VsFX7ixkQy4rfVr4kKRaYrWkmXW+Ymn7n4OnErPkax+F8EPsmKwf48TsSr0+fIQ7KD48s/9PzEzX4fu7BPBloFXDv/xMGHan+HPaBSx+ijfseN6cMoJQfO3Z1o0NtvWH8Qz304eIRB9E6qzfHP97uuPNar3KFH3u9r8UlLo3t/j3d2uZvD/Z1ZxxOv/WkOzqlDbfEQyQglJLFKkCiEFAReUKiIhAQfCFpqljYkpBW0yJoxqQuohUMohVcC3WhiFzBxs0PfXkILhcEQypl722mTkdqY3DqkiKi9JApiAqcIVUhLtii9wFuLUIJQJbOD2H52AK1yFYGIyFxGK0gJgojClrSCDmU9iyNhjSGqJFLHlComsQlREKOMxAqHRtNenCea7xGk0X1Nzd+3rO72daRiEjU7I5GohEZowiYj1ilOQSBCMjMhIaGyJSERoQ/RXpO4mLGRBC7EGkvkI7RQBGgSEZGJjNCHhEajHMg4IBpF9Fp9JvmYxLcxxYiIBC0VgVckYZdc5LTDPlY1CBFhZEPoQ5ImJFMhqWqBdzivqWyFc5YkClDGIwuLqSrSdojQKb1OmzjQFHlGHKWELsBkBTIK9vZXCiEQu1493Ax/IpkQ6pgoTGmrHpVvUDKkaQyJjmmIiERIGqRYDwEhRZ0TE2JsTbvVoR20cNk2oQ2Jg4RBZ4CRJVVdEssYMkMznBIuDo6fVEfm2COiKB/TQnS0Lg8oQ+y7Pi6JP9ll9X4IVUyiWpS6JFYp1rs9vDVYtA0JRECiW1TOEboQ7UNsbklCCc4Teo2VgtCFxFELgSe0IbnLSFUb35S4uIOSGuEFSbdH2uqgA3VfODzRcvaANohDdOnIofqzaAcPASeO7x51PVBKpGMS3aYyJUnQRrShzArqaUO33yINuhgaIpsQ99p0pCaOEpaXV5mbm0MpTRhCmp5wdmjfytWZ4Rh5dv+2nFPx7/C23hNqdGwOh4WG0+bK4XdHMhUnf79fhjkhzYynMlu53a+gfCwSMBPs9/PN4yv1cLj30Jh62srGvutYJ0RhQhSltFR3FoXeGpyxRFWIRFATEtsYYxxR2sECQaWRMiT0AbFKQUvidhurprR7A1aXnmRufvn3f2bhk5Dqk+r2EAssu146j4/LwqnKx+xsiTiFfh8jgJ+pPw9IeA/x3YNzPNNLD867GS4dI8gfoCnHZbyv2cfPo1Pm+5GsDsm1/iB9O1Deo+L7x8AjUC4OVe6MytlxPXzcpwe7aXc70mmWpaNv97O845SFPeZ8Ut8fLODA2atu2OMzc59DywApJI+1nuJ7698knxq68ws8s3qR74+/hasbXkw+x2/tb7ECVBjzgnyB7+ffwjnLc+pFPtA3kEGMcJJX4zf4dv5tvBU823uB2+4moplpr6+1v8j3y++gneAz6We4U99mq95ESHhNv8736++gveQKj5GJMUM5RIcBX9Qv8c/mnwixPB5cZmoyRmoNV+d8JXmD75lvo71nxa/QytoMemP6nT6Xm4v8oP4mAkN3MIC5gL8b/SXJNOXpznP8butnTJptrnSeIggSfjd9k0gmXE4f5xfmn2lcTUt1GMQL/PP0DlLWvJ78IT9Z+za6MbSSiKv+Ij8b/QDhHV+Y/yq/mf6CtBZ005RL7Wf5yb1vgRM83/0C14fvE+c1qtNCRwn/cPu/otY0l9RlgtyQlJDGEU+lf8BP7/0Qanhu5WXe3vwZTVmjFgK+0HqJH4y/hawNz3We5U79EVvjChmWvNF7je+P/h4vLM+n11gzI7aaIRLDZ/On+W30JkoLHu89zViU3JMVtUxYdpf4q7Xv0oSep5PLNA7ez+/Q1S0+1bvMrzY/IDMF16JVtFoi92MUCa8PPse3xz+iUYrF8BJCxazXE6zzvN56nu9u/QxbNwxUm8XlHj8f/xxbVLwSvcAv5Y/RwtGLeixwhbeaX6IbyRNcJUzOEGH5AI6fKuGeToMeEUM9duvDSeWfxsT2p9mfxyF4evACP5/+lBpHW3bpJXP8kp9jlODVua/wo+F3afKKmISLnSt8d/I3eNPwWvpl3pHv4UVMO5hjVS/xs+r7+LLm5ehLvDX5KWEpaScpn+l9id8Mf0ZZVwQb88Rpe2Z197AX5PMETub3/T3dsnx0a+dpVuHDpRz1LnUYzmg9PgQvnv8ilSnJ6lUu9q6hpeZ3a79gvDnmtaf/iFuT95h0z3Ou/xg9v8IHt94lCEJeePJzOwfsTzJOPahes+fHnmN4GF66F/jowUrF/3RT6cMqKLvPdtrzyQ+I71bihHl7INXHwZ+H68sTD7seqtuF9ApP9D5NpGNilfBk7xl+k/+caT5iJVsiilu8P/kNQSl4ovscN7t3mDQjBtES/dYcN6r3SZM2T7Wf4/roXab1mNX2Ra7NP81sV+PvGQc+zpidhYY/KP+zKCa76Y6R9Xek3DMoFg8HR/ez7KOpu/U5rqgTFaCdfycpXP7Q/33PvT9mdW7n+W7gh4MxoY7msaeg7ZbrT9WbORD7bd/8Pis5Eof76hHpGp/cFW02PfrwQY06DhlP+XS2ZeP+kHlxOFrhCcWfglx7TOc4DdmfwNJO6XjnHQLBm+/9lF+89zPWt9eYG8yzfX6TPJrgKov0ijhKWHfrLKgl6mJCXRV4AUnQJlIpG2KLBb1IaWosjsbUJGoWEOju+CYL0TKly5ChpDYliWoRELDFjtvLegpSUFPS8m0CF7LFFgM1R2GngCc3Ezq+i5ABm3aTvu9gTIP0isxnnJfn+JL8Csud87RXF/mH2/+VD917TP2EfriAk7MI2S3VpqkLtJOM6i360QK1doztiFS1cDi01WyV91iIV7AYJnZM6CNEYUgqzdgPmY+WsXVDXk8JZYRCk6gWW80mc3qehprSl0gvUU0LOYm4tXEDaoHpjlk4PyAIQrQMiIOULbPOQC1hhhJbzya1jGE8ucfd7Dbn564gWhYZCKxriGVCoGI26nsspisUosBZS1ZOaIVddNpiw63T9wMKX6KkpHQF7XgZL/ts+jFzqkfN7PxNTk1PdtE+Yasc0w/aVK5GS8XUlfSCFh7H0E7oyBQrLVoItpsJfdECV7NVbdMmxitwk4YsqlntLqJExna+gcpBp5IkDBmaLRaDZUIbURRTZOa4PP84f/LMfyDY53noAE3fFTD2zYUDs0Hs3yK4S3z8wZiUu2ekTtlGcoapcxQexBT2Z/gJlYtvrP93fjX9OcNqgzk/j3CSqc9pqRZIQyQ1a9M7zEfLVK5iu9giFQkiCAhk6/9o781+ZUnuO79P5FL72c/duvv23mQ3u0VqJC5DCpqhZsaQMRhhYL8asP1/+dUwDD8YGGBswxs0lkYSRQ/JIYcUxUXNbpJ9+/a9Zz+15xJ+qMrMyMiIXKrq3KaB/D6ck5UZ8YtfRPzit0RGRHIRnXPfO0UEE6bL1ZfpvcBlEA05nzzlwfAVfv/wm9x8HHL48JT3v/JlOg2WQmV1UCdAisargJKZMRPtpAgTeXPG+pBSEssIx/FASuI4gmi9f8R1kDLGdV0kEMcxjsiWyxb4V9gpfEDMxLI0zM5vgzKZVBhJZx/rTrbZHBn1WZMqmJyFpk7WTlDt4Wx1vO4WiGVEsjQ7jiUxMa5wQUrmn10Q3swYvP4Q4bvMFzOiMGY0Gq3zOTiOSL+h5YjihxdtG/TvCvl21Nq9cR9vJnT5XFrexE40HYu2CRXVoOlpBNnb64btr58k2hgaPxIJMcRRjOM5G8m5fmBBgV8s46dOUSVB1Od+FG0BVRUqiYD1/lQ/vKXqcIm9sQVqNGcuMLcnI50Y3FzDOmL1OuxmcsPN5JrpfAIzyWRxy7V7SRyF9OgyXt5yE1+vZjiCgCljhOsSSZjEc8bxDY50CBYhM+Yrvpx9psGYqb/gyrkkdiNmwRRJRBhEOJ7LlDEXSwjlkiiOiAhBCBxnzjSaQAgLOUESsWQBCIJFxNSbAhGhDBDSYS4XHMs559EFj7zXEa7DYhhyfXvNLJrgRD4yhtvgimU0J1zMcGPBOLhFOg6RhMvgnLG8RkhwI5cJY9ylRyRjxvENvtehKwXLWHAbXOHi4USC2+UVURzTd0bM/AW3y2tktDo7+mp2TrfXpT89Ip53iD0YHvQRB4Lns8/wlh59Z0C322MS3eA4DnLeYTJZslzM6QwdIm/G/ukecTdgPL9mPL6m1+tx2D8B5kzkGD++JCRgFk2JvQjh+cTxgqkzxXV9wmjJcjkjjEPiZZ/Ig5t4ggxjQuGBdFgSEkuJG8+5iWZEQcA8Wq72zzgxsR8gheRaTgmcgEAuIYwYB1MiOQUZcBnfMKGDlJJ+t8eyI7mcX+Asb7gJLuh1+jhxxDx0GYe3dMMOnbnPdDHG7/cJ+oBm71LpVmaSchIvigclmIxFkY4FSubKkWWbZdUhDNc2w1k6c7vCdXjJ+eI5N4srHBw86TOOx8zdGa4b0XFclv6CsbhhsZwzjq+ZO1PcsE/HD5jICdeRizOfMF5c4Douw2jEMpwxiyfczC/5+1//HQ94h/fe/xJ+xycfodWF4kgbbonEGjaZdZSqYbKkSYuscgDtO+6AtfO1SuE47srRWJ8uJnDTvI7jFPJK5YdRp4uMx8L+EVHG8/aQ6ZsNcgGMKFyYMitpytJtwr5pnJTx0WQyMKFpkbVsCcadRSw7gRoQOI7AWU8tS6D38AQeZoHBoJ8syxM4imIVQiAM3yIum7NVm7v2KVkNEMdxbhylhSao3TVNgxOBUN/EFrxsZWymydaOfElEndtvYJtEsP7esG23CCxSztW3CEIiXFEv0NFmVVbfLbXnU3cMl74VyVNNc5ZPmGyOrYOL3CuZ8oQkH9vLy6nBaCmzpAnl3JaL9e8yndjkaDfVeOYTNGjhddKX773Kk/Pf0vW6jEb7zPbG9EWPaLFgKPaYhzNiYk6dU7qOx5V3SYzkRJwSequKnTqn+J0ul+EZYRRwEp4ie0AYcsgpA6fHtX9BEC04FqfIjoMTCI7cY4b0uRLXLOSc++I+eA4EggMOGDqPuQzPmAQTHvRfJkby2fwJe/GIvhhyPn9OML1g/94x77z0Fa67UyLP55XhGzybP+FGepw6pwjPQ4QxA2+Pve4+1+MzmEWcxidEIUSzOX7kMxT7TOMJwpWcuPfw+x3Ol8+QS8GD/j2CaAwhdIIBTujRC2KGg30ORyfEkWTYO2DPP+Dm8hZEh4E34Oj+PXocMF7cMurvE48mzOJXVqsXAsFsMsGJXOKJgxsMePXB6qz7waiP7C+4nV8y6h4SexGfnv2G2WzG/dNXETh4wYBD/5hOz+Nqfk4QLjgaPmDpSdzpJxwEB/T8EVfOGfN4xrFzysIZQhhw7O/R55DreMZMLrjHHiLyQcbsR31G3jHX0ZhxNOM0GiA9kDKiH/n0Zh7j6Aan43PSOcQVIU4cMJR9hnLEVC6YTG84cob0/Q6+B8PuHofdQyK54GZ6yXDaoR/0WI6O6I32eDB8hC/0j7HlZdV6XxQTyUql+IKciU2HqZImCAKeXT6l1+vzWv9Nntx8TEcKTjv36cZdPps8oS+HHA9OWTDGW7qcuPcIRICPQ9ftM3CPWMYBThBz0j2l7x0yjkY40mWvv084Del0+hz1T/nqF/8p7zz+AOG4m5m6mvYo9wKpwmEshgLC+Kxo8us5QznfVrV3Irup+BiVtLIpJkW3y2KaNNCyzI7KYE48H+P0RohOLyO6AcIgBMBxHRyht59QnAvLLLDKtPpbmz3Mpd816tDU+akI6kUhoR2fzzuLcpgnLQ19Z+yofDojrXR/SvGULNv7gjpvd9JnjmGcGhzwHE29YNP4sU4+JDP9wpDPsGE4P5irdbjYXD42mcfZVhrNyw3F6qvbYD7qOjfBnf9kX723riau7WOwso47GJDbv7lYR2pC6BXJYvPkf/bxETUcUQeAzEV+OrJOq+7+1MjkuklTB/mjoCB9jUb6Sk0LIgu10vH6wzfp+B0ubs65d3Cfv1v8gNurCySCk+CIT7wZfteHSLLvHfA8fr4qK/SInDmSmEhEPOodcHX1G+R8zv7gJW6mN8TzKaI35bh7wvn01+BI9kZDxs4MSUQglxx0X+H57BkRIX6nS0BATETohRz17nM2PUMIl67XJwgXIGMiEfKge4/bxTP8OCZezPnzi3/LTXRNx+tyzAk3V+csxIxweQizCcvoGtcPeWl4n7PrG+R8CVFAr9PFDSIcHI7iA6bhJY4f0+v7jMIhl7dLut0BD91HfMKH9L0Bx94JXz3859zMPmN0fMSXXv0Gz6afcDl/zsPRq4y6+/zq4qc4wuPNo/c4u3nGxfiMe/sPORge8uHlT0AI3j7+gLPpU84mTzjuP+De4GU+evZLpJS88eAdrubPeTb+hOPhA06Hj/iHix+zDJcci4f8n9/5t8TTLkHXZf90yGLxW3AkI2/IRNzizSRChJzKQ24Wn+ELwbE/ZOIsuVpcEk5nHIt9zt0ZkQzw4ohgKQmcJRNijpY+c39GJEJcIYkW8erDeoslj+QhkwMXX8TsuQ6dKODWmeN3XV6SPX4VPsUXc4aDQ/rdLueTBZF0eX/4LYbjHs+uP+JeeI97rzzms+EVveGIN/fezguqycZlAyEzDtaF2CavR3f7NLwAj8G4xrUEy2DBv/v+/835zRme63H48j5+LOguHYaiixtHEEyIgoARDxiLW+JojutHDJY9bqYhjrPgRPQ4i67ohUv2hoJvP/4veXr7MZ7b4Xj5iF/LX+Ef+7z96D3u772S8bjrNpEGPWpLmutCkUyoVUDp4+SfMJ/6Y3OT8lf5dlDLl4ULZeKvUJniD/X0vyIk8fSW5W9+AsEc4ffpvPolnMFB5mjVDVJFZjtW82AS0o2csphez6xWrk5kZSC7Keq5/HXomGacVW+xCUcq6gQku5/tb4xCQ+b15mZLoUoCiAYdt1XbbChnuckNVcekDqKSVlkuZtSLK4cy5cVWm8omEbVSNYfVQTU8l0kryCyJLhs5fWeZFEmeK2UYT8nKieEG9d7h/OD2ey7G48Tf35HSWkHUuilKntvpCzDvuUggsg2OtZAalTytq8UF/8cn/4ZfXv8dADEx82jGtXfLkTgiciKmTIjjmH33EAePy/iCY+8EFlPmyzFhFLLfOcYVLpfLM/bc1Wz1Ml4QEbHfPwXX42z5jH3nkMiNCOOQpVxy5B7hCpeL8Ix954BlvPquw5IFBxxBJLmKzhi5B4SzGR4us3jKUf8eeA7ny2cM3T1kGOBJj3E85lAe4ixjLhdnDP0RSImHx83yEi/qI3yHZW+JG3sQSfrdEVNnwrF/SrQIuV1c0PF7dOjRiTpczs55ef91/uDgm7ztvEswdHnwxms4jslRUIbTqhPVD4turFR/8PP/wPd++l0+PfuEXqfLpPuEpXfLdD6l5/bojvosvAmHvVOW8YxIrgK5vcEpsZCch2f0ln0W3gkxfZaEHIgjoqXHuBOw7/YJogBmSybRnP2gg5CSS2fGUPSInCnCgWkv5pguPX/JTXBGzx2wlAv6vR4zZ8qRd4xwYq6Cczqyw1vB6/zL6/8Mb6+P+2Cf7tEevZP9emtFlRkqKeP0piNEjT0Uphk7889q7W8oq8HYS5dHak5qWj1tnH/06Yf81Y/+go8+/RX9bp/wlTHukeTy9jlDhki55Do4p+v0EFLgxR4Tbjl2T5FBzO3yCk96uLFH1x8yDq+55z3i3YOv8o3Xvs00WNIfDRmMhni+n7ez5RUpqbzd4AjtSqeSt3d5p6z4hsIynZZL1UDZ2lAiPsUHJv2s580pASuCT35G+PRDosk1cWcAJ68weO19/E4XkomvWqK//j5vLEHKdL9IPrgoYcQc+zRrUtscgA1JUKQ7sHU+pZ0bUHUT1mdM3UGpBg624zdNwcXd72/YgdzXLsci8/p8ThOUsS11XWBJnJOBDdtDCeRL+yopo44t27ZrGtqbVVH1ClvZp7yqKqyqUcu3msRiICHX7SMqThzcGPJz3nORvbGRiuxvHjurpi8znQbBlyINcGtwidpr+cCyyUgV629fSP02ytLbFL7j4+DQcbsIHOIOMHe5ZcKgu8dkcoknXHB9nCV08XA9l67TIyZA0sXvduh6PbzYxZGCgegzkzFCCEICnMjBxcfFpU+POQG+14FA4uPjOz6uXB+V6wqIV/x3xepDP27k0aWL60rcAALp4sUe4TzExcWPPSQCL3bxpEvX7SGcEF94dJwecRziBAJigSM8YsCNHAbdEVJKhoMD5tMZbujiuC5+p0/PH+BGHn7cQcYgZxFjd0L/g/uc7I9KOlWP0oX19WLSL0UkDkT2sON16HY6+H6Hw/0j/MGC0OvTX04RsQsOTMNbFuMloufS9TvICDx8hO/R8fqM3D1cf4h0RsjlhG7oIqXDNJC4S0nsOrhul6WI6dIlXgaro3XD1Tpzv+cROCHDzgAvlnR6fUa9A2InpOP4BIuAjttDiBA3ELizGNcRdO7t4790hDfs4fe75sDCpLDS4aU453XGkmpY6jiJpYq/xtirMKammS9FJWX/1zc918d1XHzPo9vp4jgBnifodHoMnT0Wi1s8fDp0kUh6bo9pMMb3O0gnxold4mi1CXQ+XrJ0QtxeB+F16J8csud5BgZW+iHhw+zImyueuFz1nOwqampbSYi1BLVgG3DVBNQ1wVvNPhfqK0qeKXBccD1iKZkuAp7++gnxLbz5+mscHZ2sNpEnRwGWli1AyPUEiJP3tYyCWAPNfXLj2LA6P2nX6/drFKw6tqXjcYP+TJe8iMzxSh+Z6W28cfV3AZXBgaUiUvu/LYx0KpjbRdnrPpaYfSZzmYr+K2PRpIqUrLqvV/k2ucyXqBEQQCbDQkmbjlF1uZNKX9XruXLz1sDKv4nv2hMEBnobYgcbuvMtUOaj1EmZ3dVbex0YFF4piGKjGYVJV7qykDfLrgUhApCZI1uQJTUaVR4M/T1+7/gPcR0XgeD1/bf5ztVfEk9ChrMO70X/iL/tfI9YSr7i/z6/iT/mNnLoBIIvdr7Gdxd/AYHkC967PF3+mm7g4gn45tGf8J3n/xcidnhbvM1lfMF47tDtC77W/2P+9urPAYd3T96j74x46pwy6h1wP37Iv1/8FV3R5fXueyzm19xOzyGM+Mbon/K9i39HR3o8jB4SiYjp7AohIv7x6T/jB1f/nj59Xhq8Cp7kenFBsFzynv+H/NT5AVK4nHQfMeoe8Zv539Olxx+9/Kc8Xf6We+59TrjPyD/g4+kvVoHQ+JAzPuODV17h0eFrfOu1/3wVhJUZuzpCXzXJEYNQ97pJePvxFzm7fsawv8dosMfLr3yTn5//RyIZ8cbxu1wFZzyfPsGXXV7qvckvb37EzfUlX+i9z8fjT5lcBPQH+3z91a/znfO/QSynvD18leBAEN5+yiCc83viA77LD+h6C17130YeOCyjX9J3HL7R/wbfD76LK+a8OnqTrnufn938R0S04J+c/DO+d/aXDALBA/cI/8xhcnFBp9Pjg3e+Tu/RfbqHI4TjNDvdQij/VQVsemtR5T9WGT59wNTxq02/N5ih0meJHp2+xFuvfIGO36Xjd3j77bf4ZfATHvRe4mHvFZww5sOLn8Ai5g3nCzyRH3PPf8goPKDf2ecX05/gdjp86f5XuYw+JXCWPDx4zLde/1N818uxmTGx+tZJaicdUyKtsrl/Nicro6/TE4Yf+ZWrKwc516ZGp33bacEVquxZcWZu996id/oYOZ8QOR3C2ZKLG4fF80s6fpd+f0Cvb/uWRhGF9eMmlBnDSifTTjQXlm1MpyFszo8pTQ1+0m8l0GBiI5dv/Tcx47s6DSwpp8CS7rGa7tckfBeoavuKcsuXFBpuy7X+aFiOTq787Wl52xZm7nUekmDYnNnMUNW95LbNRgHFbw3pZYoCC8aicrFHA81okoX6zbozbL0s6jZ3FK1l1qSACm0is4t050PiI8jM9U+FMdHzSk1UATAHtEVec8GF1FiBzHlLluPkOlHmLlUnOYxDBPD31z/i++d/w2eTT9if9Lnqj5nJGbLjMKBHd+nxbPmUE/ce82BCLFZLnPqyR3fhchmfceSeEjoBwXLBeHZLzxkw6u9zKy85HjwgiOZIR7CI57yy/xbfPv7XHPYO8dwO/9vV/85H4UdM5ZxR4MP1DTfxOfvOIWEwR4YxS2/OiAPGtxMuFs84GdxjuL+PLzpcTc/pRD0mi1um3NJzhuA5HB/f48nFx7x08DrRJCDyQwadEa+N3uH9+KucnX9GZ7THsD+g77rMiDg4OeXo3gmxiOm4XbMcmCLypgPDJN2mcS8lQbjEd32EcIhltDpKV/gALKMFvrM6QjSMQ2bTCR/99kP+6if/D59dPuFk7xQObwm9+eoY4N4BOJKr5RlD54Bo6ILnM5Zj9jnAE4JrccuedwDhAg+Hm+UVx51T4ijiennJ0N+DRYQXOlzePuMgOkaM+8wJ8FyfB6OX+S/++L+iuz/MN47NJ1THhxbEmQJ/qQ+Cuopav1eqiJWLHSxpMAX+6g25ThRFAY7j4giHOI6JZIjvdJBILs/P+J//h/+Rp58947/+b/5bLp8/RzousYTX3nqN/cMDPM9HitXpbB23V8pPcmVautH0hDqzbm36/lWd+K4xqEyzdE2dWi2ILRQh9eCihI6Nt1qQEEfMZjOePX/O7WTG/t4e9+6dMhgMkEjNjmgFmpvfXlbeQ9gahSY09MMmarJeYSXpSh+p4ZA2zhv2X9UpkLtCedWViQLQJnXkeqXZHfFmHXdbBDwNUL5BWpkisPTrqt2ykz4rl2Y2qYruk5muN4WJhmliRu8fPe5JxL9JYF6Wvgyb1lsp6/M9ijbxsm0OjRH5tZU5cmTk9FZdPcscHp2CsHSQMShdBynqsi4zDwkXibMlS6tnOqXKczxAch1cchNcMZVTom7IWI65cm4QsWA57+HFgnF8i+M4RPGSSXhLJGP2oyFOILmaPWfuzbi8vSR2QpbLJX0xZD88IHTnSAHLcI4UMbEjOQkeMpE39G769A48bp0JF/ElQbz6OrXTnTEZ3yKJid0QIWPmyymxL2EgiGXIWF5zdXFB3x8yDSZML+eIjmBw0iESSyJH8unZr7haXLLX28cXLpP5mMnsmu6sy/uvfpP3v/CP6Xa76zPsHRzPzQZYWWNuoy/LaBueCSHo+FmQ4wg3d+TgKgBaGQ7P8dgbHSB6Ar/v4808AmfJNL4miG4Jo4DQjcCT3MY3xK5kFkhwOswWY6S3OirwNrpmNp8glnO8WDCPZ8TuEiLJbXDFhAucQOLHPjNmuE4P4cHV9TVCOJwcPsQfdFP5VJsq33RNG0+jUJW9rvLbQsGbbWqxpkY32+DXeK6fPnYcB0d21kkFo/0D/vTP/gzXdbn/6BEPXn0Fz/NWxzuKrD2FgA5VgUXGo1BefaoxlREWB750P0yVo6ZOwqQ8aI5enXkhlYiljFVSuZ4XUipcymOVBS/+bAwhEK7PYOTz2mDIcrlAIvB9Px+HNpnYaBRwbIdCUSXivhWk4XqDehYdxu24e1EbuctLyY6mAV00DEt16xSWmwCRhQlK5WENYtW3jPTKJg5E7l81nTLunEwfVPanTSWU2Rdzx2xWTll6/Vpo/w0QpjTaBFhpWeufNT4ttTl2NMR29IVu9bqi1mm0bwgs0s/EZn1durlIN1g1OlcnkWdLGK6y2Zf61IqQCB72H3Pg/oIgDDkenXIrb/Hnz0BKDsQIr+sRLSTH8oROt8O1d0lESHfaZzjycbs+3rhLHLjEwxhv4ODPewSTBWe3n+KOBsgw5vDBId1hl5G7z1H3lGlvjNfr8kr8mKvFc6Zywkl0SDRzWUxvGDgD+t0RUSdkHF4irx0ct8Ox/wgncBkN9xFdh97imjf3TxjPbnl2+Vv2Tk7wQw9/v8dxeMu9g5eI55Lu7JJhf5+3H3yZ19/6Qtoy6cZHyNZbpiOlSiNVNnE+S6K/NjX8VU6MgIfHL3E4OkJKyag/It47IvAmzIMpPW9IKEKiC+gtBpyOToiRTLllyD7MI/qxS98Z0hGCWKy+eTLiAKfjMvL26Dl9Ok6XOIq5XlzhzDv47j6jB8fsjfZ57f47rNZ4rc4Xz9mFXIwr9Rur3+qJN0IaJL8B6rSzqU1F4aKQ3v75BlsBGv06DqnyrNPp8PiN19Pfnu+ZjadB6adhnsgvrhRaQrG+KW3EcjKfnWReirrjwxQACJGvl9ZHthfc5c6unSH9zXE16yYZpp64mpw3QDgu3d4gd7dyM2sVi6ZMGw6plGaTft2V01ESD+T6rmmZZQGazbHdJXZGP9O5jctXkTiWav3r0LDJmgll9Kt+l5G2xP2ljdLAluf0qZqhKq+ix1IaZa9cbMFITXthRU6e1+/ctA96FtjKOaUSU6RqM7Vlujh/XDBFGdKd4cw92BjbBxeqfhE1IlEN6lkRKxKapIosZbUDD8jsyNvEyKcdq5oPkZReoKBdGR/bhdDSIQI4iI+Rv3Fh0kEOO7z81mtcB8+JlxH3/ft8Jp4TenAbzXin9ypn8zOkgAfHLzN2J4hgQO9wj7cef5lfTH+M4zu82n+L6fU58jygz4CT6BFP5r9iIWfcTM/5n87+O7wDl9HwgJPeA8LZBURzurMe82uQk5CQBQdHr/Fp/DGu63F6/Bgx6fN0/Fuc2OXAf8gns5/j9ByODu/T80c8vfgEGUq+dv/bHD94yNXkjBP3EcNHBzyLP2HQGfDOyZdzrwBNTWOdhCg4lIaUJe3efFwkIwrSD3ypil/Aat9Ndkb5vYMH/JMv/3OenP2GvcEBr9x/lX+4/DGLcMbrx+8RxAt+dfUzmAoe99/ik8WvmAUTXhaPiYn4zP2UvhjwVv8LfBx8yO3ymsf9t3j22Wc8DT6mJ3t413v0H3ss3QVvnL7HXveQj8/+ga7X440HX1g7fflZNL0NxFq55RVVljJV3lIqQUYe2cnb+iCQhrFKeQfYxpEteRMHywSh8VlZoIlG9T2RRrOyUEfjdyVqaO9Ee+VS5tpDcfW0+4pStgZYYm3wjPUyeAui8NAeuRm7zOYjWNfMFyKDagdVJV4SWFpdw9rWu0a+Os+a0Cz0jYIdOecVYVael6p20bsucZhMjg9ia96LBSuOHHLHezOyU662JJMbTmVLqlQfJ3/X4jybDEMZbHKlInXR6n+0rZR+jSzlIiZTvsz7Lyr6Z5ciYaEvE79Cq0zmiyqQtgdKgpUTkv60rdpJbuZW1JgCvNRHW1sTqXrlm2H7o2jXey5UMsa3Emg2zDoQpLFh1fBAhb5novC6KG/ByptLpj5kmrWQXmb3rfOJql5ThOlvf/LX/PAX3+P55TMOjg+YPL7kynlOMJ0z8kdI1+VCnnPAEXG4YM6cOA457JxADJfykkPniDBasAzmSDfm2DnGX8Ll7DOG3iHLcMYyDrkdX3HUv8fF7RUMY+7vP0I6MXEYMlncchycEN9EzDszRoMjZszoDXrMgjHHzsuEFw6XN5c40qN7H/ACIi/gqH+PYLnk109+Qc/p88FLX+dPTv6Mabjk8Rfeoj/MNkUWjnPOdECuqQryYnMEKhTvdijxQhQIsjW15pGTPx5XFY44jojmAbPpFL/j0xsNVkfku6uvF0dRjOu6RFGElJI4ipBAt2vY6C5Axqu1q8ZvFxmqVjgUShoChhpOmY1+jkZRj9aDLUDRB2OdQCbVIyonBq70jqwILvKfOKqR10RLZ8PoGOo7Iuq3ZtWpQTk+6hG0s2CM/rQMVaxb+bBIka245Jm0/KekbUrraLn/eWAHAUQZKoOLqrHXMMhperxnXaqsqdqfb1de7phrod2z2ak6equkPCkTnW9SHjWwgexYW1KhdRd9mAsa1kGM8RjiGmWrvnhpmcp+kIbMapd52VC/m1a/jfL9urnElgSfShJT237Oey7IGXEb//UbJTPcuuteHBOi+EtxbEy5snjMdN/0bVrtznoWNJ0NtlVBknXY2onzXA/P7SCEwPc6OI5Lt9vHCQWu28HFw3FcOlGHQET4okMgBUIKem6Pm+h6ff6+RBKxWM4Z394wcvpIZ3X0bOxECOES9AYgBQOnx83iivnNDEREEIVMwwl77gH90ZDb+ZjlMmLveB/HdZkuxszGYwYcIxD0u318P6YzHHCzuIRIIJcRnnTwRYc4jOgd7/Pw/unqXH+hDiDNNVoPMjWgEHq7Kf2mD8RszFdFqRqVWkGJqHQqAaRydGL6WlzqGWSWVZklcB0Pd+TRGfWRMl4rnsQqCTxvdYyV562Hpe9jxJpw8i2Quuvw1bX2CW+FTdtGPzFxEKVV5I1s7soJ2tRe5TpHKnS0YKOhnU4mOsT6rzE4q4KeTmj/lYAnY0lhrqiejAFQKZr0jYWc3VgajFlZDJJzEWpEtnq8WFVOHZTlUftnY5mu/U6gisydYivZkRXPVwWQHzJVOnw1ynIKVVNbakqDZbEwsRtsJG6FOYkaznniZBu9/M3KNZLJOcqGZUk1aO002KiQlXSyJ20axdDVpJu/r8laFQmpN50mEeryY5S2UQ/2kHl/N/Wm02BHcfxzpBVa2pgQ6f5kQZ2l54WjcbfUM1sHF3Ec4ThuybpoBSUMS8icl3WYaQ4myoU2M/TrISHXnaR8VVYfLEmRRec2X0YiIgJVkIUqGQaOMxrvvvY+59dnHO4dMurv4Z++xXef/Tk96fCB94/4cP4zpjOPYcfji/1v8f3JXxOEgg/6X+HT5W8ZLbr4Lny5+3W+G/wlN9dz3t3/CqI3Y3Ez5umTT3l79Af8/ey7RNGSB51XOdgT9LwenbjHW7zHz50fsTcY8cX+BwSXksVNQPfogD95/V/x8e1Pca98DtwjjvYeczR4wMHxMW89fod/uPoRQbTkdPCI2c2EfjDi4PiEb7//rzk9fJQbi+rMrv7auHBcqrCLhchdF4dvRs9CwESoDDUHVCYHyRI7qby5E5lfJTLOVamM45jxeIrjCPqDHo7j1ivbEHwVHOOqeuT0btFC61mFNAQgVfwl6WLtvlK+8X4ZZJIlkyh1Zqt23VNeC9a9+NvmUK8DZCfZpyDXhW7q1JqwVqipFlxF5pnxKSqsfBtsXC6VsqOWY3xTbHIwCzwlgaqu51c1DMOAH3/4Q24m1zw8eYkvPH53bWRFjoS1DjrfCv87m11tbIDvaDvyDhyBRti0LKFd16Kz1lTpUDcPMpGkEYnVsX9HRX9m+1hf+gyMk1PGCSubU1pV31SPlCUxBRY7RN2A0FCXzSS7PNjO+WlVToJUdZFZPqxQaNvmIAtSp5ieYjnFu3lvUyMqle6X2qHAxo8JK5RVP1mPPRIbYZJJqXKSb1j14JFtsPWyqE8/fcpoNEA4TnViDUY1oRmk/DZVUexgXeiTB/pANRRkWrmYv6rWgDl/SvdXDAIYE7NYLnBdh//15/89v7n6JbGMYRriCocLzjnuPiByI4JwwSJaMOoe4C4crpwLTroPWIRTwjhiHk4Z+ft0XZ+z6ROG4oBZMCNYLIndED/u0euNWHZnHPfvEy6WIGASjNkPT3DPBnx69oT+aJ8//tq/4Gvvfovx5JZhd4Tf6TBfzvC9Dq7jEsuQIFrS84dIKZmHM3zXw3M6igLWa1vD2ykJLirRxDmtiyoHUVVmKfOJqy7TqFOVi1z9BERBxO149WX20bBPp9tB8fjtZZbdb1r/qm6qcrZrBHVSo9tIV9UxxtaCa9I3pa/RB3I92B1h0nl6QylhnE22GvVdqceee54F4DvySArCnD0ocxLqkM1dSfj+z7/LT3/1Y67Gl5wc3ONbv/fHvPbwDepIUems6S6aYhd6Z5e6Sx+LdxFsNAmcy5zApvmFfjRwU2J1iisJRGp9+dsUYTdEDX2aS6v6qCXB0bZoPF/SoB5Vbzfy+2Y3xMYTPooPufNmXTNVNjFTmnutbdfpa88pCdbLs2x2o3j/c10WFYZBpfHKTE++AvkIa3Uj+UJq+pZB5g99KwT3qQOveT4in8QUyxbHgcmjyuex9b79icwNDkc49Lt9rmZnzIMpZ5OnAPj4hMGCqTtFhA5xEDOLp0gkMlgpj3FwDUiCMGCyuEE6EMkAj/WzDoQiIPAWSE/ge11u4yvGk2uiKCSWEQjBcjEjmkiicYfbeIZLn6vJBb7b4WjvOG2vfqefVs4VHq6zEhchBH1/YJhUMMfxRvFP80pL3obYlUGty4YAPYjVZ5aSiYNc+C7BcQXdjg9Srk4iKjZkHlUKsmEe61KxsnI2cIp3b+pq4o4LXr2wSAIL0z4uS8NUta2U+S4w6tWqyomUhZ03g9D+q8G0aXYlSaxH2nqKJDhPngu4Gl9ycXvO7eQGGQuubi/XwUUdNiuOJG6C/NxWds9ccE0dtPYIDK/7c01UFUfa6nMXgUWtZGZnUULxDRfVam2VaDdSXObIljnlm62/l5axS26s525Y2lgile9rUWgwKSVhEBLHMZ1up5pfXUZLZDYtrmkT1JSXOnsnClM10t6PpfwI44/sVsbU+l4FfcMcUvqBR20vY7acKQkqtOdqn9WuVt73qJNP6mXloDsu22Pr4GJvb4gQq0/O2nVuwSqVILFUdY55Ky6WMSsPM8pKMO/NMG8qT8+70oxP2ReT97tH7HePeOXgTUDiuh3Gl1f48ooT5x54EBISE+KLHjKQ9PweB/1TYhGzWM4I44CBNySYzlku4ahzyiKacT4+Z+9wxOnoJXAcLibPCa8CDoYn9Ps9JtMLYulzdhNwfHSP1155gwdHjyyNVtVnK0Xa+NzlNHi3CLVu0G00rCzWnLIw0dBnAC0B7cqvksr1+pEsps1BCPr9XlFzp3Rl+rtUiRYcE219bIkTVHnKR5UjVQd1Yk0b/apyq/rNUHShb0zl1xAZ07SEjZz1SepYyty9qibLyq/Qj2rGXDmivI41hk1WG5HJcK6BtcKlkrOq/dfZHxw94tnhZ/Q6fY72j7l/9LA+g1jGjZK1VHWY8kFus6dcL1HLvb0q65ASPWKFpn8qN6LvAmowZXpW+GnYAGvIb94oazpDrb793iU23sgLFJRQrfElrO1sOsPS5EpIKZFxjNfxkHEMTpFefhepYfwZ6Kb+S4EBc7q7QuHk0M0JGVGolrBc22iqSkSAflKVVZtvKdDZHpPi6Wdl2rF2sTsacFsvi5pMxiQtXTDeUI/RxP5ox0mlJspwKsMqj6TYhfqsgX1kGF0Dm+NTWo+Gntg62XR5y8/PfohE8vbx7/F89ikfPfsZnSuXvcUBz73fErvw9tFXmPtTLuQz7u2/zOP9t/jZxQ8JoiXH4QP+l7/+N5xPnnI8OObxyUN+MvkP4MJ79/+AztU+58ETHp2+ynH8EtfBrwlYEo/77O2f0D/tc7h3xNsvv5u+maiEgPynJiscVVtzqY3Bep3sJq8iC81fw3Ww9W1hONj5WS+Dz55vqwTTmEKmzWpdZ2tw5tRj5Gw8V2KbelQ1uym40PPW4mlHlm6jumbhW35CI+0w9NOTzBpIalTs5WXNlrr0FX6sohe1MZHTmHXlwxgg18yblKvGUBZvRh1LUsZ8+MkvuR5f8fD0ZV46eVmbDDY4tCZe1fs2nlUHXnesLHbgbk44KkdxJjR9sMtCGifNtVXyoMHYMsn17tq1URj5O4F6y4XEyi+SEhxhSWvWLY3Gf71YfjdQdZWAXb21UvmXdyBhzVGxjLSkzdUJxNLN9hV0KtOum2mbZVE7CS6MPp1xTK9qoO6jKB7rmDfepv+ZE6a3XWLg84wUbUNyP7/ZdkVCqln1jAWsfIk1neS1mMaRemEjq9ZRxpLFfJ5Wo9NffQVYfROS1OonH/6Q//fvv8NvPvsIAsls8IxJeIHbcXj/pT/kDe8r/MGX/oiDw0MEsFwu8TvZ69N6a0ktisu0rKYKBVKa0DR51Wf2UbaHrOh4RTdLNckuyk9jNS3AkGRLBoXOwAaw5d1FkLQtD587Mj1lMgBxvFLqjrPZSeB1Yyo1Qxqz1EBqulQFqZ2AUrbO3ECwQSLLYCjTM8ppKvlU+bCqeDSCIanKjt7QNVRdLllVkKzka4wy+1JK02r1dgeTHUe5dyfQI7zdBxefR0D4+SI/Vu62/juWwpKhnhanp9PTprZU1ySZTS3kKxt7G9p52zvmIut2X0OlUxqU6MSrusRWl3X+z/coWhXCfJ1vXDWg0A8dLLZEYlYSGomRWTl1qkJS85vnQCSZjZUioa4ImZA5AVLXypn9sMRB13nWLwzPDGlTNoSgtw4obBKdtJfjuLiOi+t6HB2dMB8IDt09pssxYRjy8OVHHB4drf0KQbfXw4xyh1o/KNL4ar7KWTQKuiY0DfST+qKrfLxXjDIr3+UzAqVB9aZI4waRr6DiGNZylLbR803qUTttGVM1GLYkqW0wa7ZJujlSyupl0zp99WEFK7USKQU1ESvjzKRWmVx7mXhvJMdSYzfpE4WoLZAtpDR1VO5AahsL+QthKNcqA9lEibDxaiveFNSUYYtxaWP/zv19q9GqQJkzZh1Egl3WKDe322CM7qr05JtIDXLs0PkvGfM1edk079YoG7f6M5R2U32CtQnNb2nI/SiiTjWbNIVB5vQ9GY1oqf5BejvReUq6BmPUqha37PKtgwuTgVVn8FNH1FDZOnuPkEkgkdwTig9aJihm4nkjpR82mxkkiTR2vqprk9dShVRlHWtTcAVlW+aIZc/ffOkdnpx/wqA3pNfp8dLLX+fDq/9EJGMeH7zFF1/9/bxjaoUqrMX2LZh3odmdHHnNwFcVuaFDXj9bDcczd/2CFGll/Q3SaZKbTdqvytlu4mjW6kdh/ZlMG9i/npsqlkLe2kavbrLKY/hWp3RkRwDKivQWGuu8Nbt+e5Q5eMKglCzWxmDSUI9PXOkFzbHXZdTiWO7C91PniTbGNgxsqdOqSb9A3aT3n7A8N+XFkEd/brkpIZ0FLBvfTWfi7+4DrA1Qoa9/Z9+qlKlmQXoMsPVbCaoM6fVP1IWU6zjfbitsvFjFLFVFFUuI7gprJnJDyBAgGKEGCSJrlyTf6jMQzvqDvpYZKF3vGtPkvz1myroJdvaF7gTWNW2FWeZVSFnWvFL9o6RN88ss2ChD04nc/AdNlB7RiWwx41cyxpR6lxHNnCAZSybzMb1OH8/1WIbz1WbvjuGVVqFg07SAfXDX82WlRqZB6zftLBsNtdi6Br9O31U55E1n9eqWW4cXm5jYBK0uqpwILO5ynRngO3DCNkbd/lM/rrIB/3WKsQ2DXRtJI71djMFiQWYojbF13XRnJinX5BxvijUticH5bSILm04K7Cq/DVvQ1I/ILEVJmpx932FAkD+1csWE6S3bXR7tWuRpN2K5OlVKbNXulfmM5aq+Eqvgok6Fck6vzKnSZOLGOkGgDjmZd9jtxW2gW+p2jsmF0spOIzDNZla6ScZ5H8F8PuN2PKXje+ztjXAcN7O9pokcE83C7WTMrTJKJPt7++bENbDbZVGYB6RcPSBbS5lsSEozpSkL9RZakvTavt45UU7CKk7mObIsspTK1gvl/YRtak27n45fy0DO28BsaNYZ84l6VG8IRzDqZ4FEx+vRoYdxZifn+8nczVU6c2CRDHYjj+rMQ0JHaIXVwYaGreBHNBhQjQpQaVWVYUqjdvym3qWNJ/WeiQ+b7NaBLsei+DAvz8aRXF125UzDjmArp3YZSkJbkJQ2SHFphLUYYbzMZaq13tZEwNL/jb4F0cgTMm1aVJjQFbrU3yJX0895Fbp8qryqY24T+VfbTh9bnyeaOIp3ETAWIIovq6vGh5HK+u/O+U2CBxN5hdHKcpsp03rfylCpNw+sKk//y4jfCTYOspX06hvP0pprzZ8GImIdRBgcAeux66auNI3xqq6oTGeuVGUXG55LKYnimCiWzBdLBoMIx3Xr82p5ni3FFtnvLbDz4KIAmf4BEnsgCm1dtI3miuUiZQGmhU3mkEJ9jb/qIEcLebMVEZlzvGLfMlpMilMb47kzqpOwRzkHu+CElXnva6UjhWa2TYY0rYl9pOfOoVFHqIEfY28YDUkxDCzCYukaynKiG9LVMlJ/UpOm6ozUcfpN97ZxnDdIn59/ywLqXN66gcxW/OQL0cTPnLSOiJjKNznQ1qCnRtm7gK1tRXZRfMuvaz5t87jUwzVD2+qbXisDyHU5az2UFxHDW2ETGasllKDNWMpkwfP6uUyz22iY7q/zS6GsiNPqbQsi1P/Cck/9XcaKUVXZBalUHVTJfp2xaqJRlc9UJ1vdpeF/XbasQXZNPhvB1tLmgZCykBs2xYa58xgsV9pdKaYXgxzXjfs20TYN21ztP0VOC3sPCgySJRbqc4Mu3ZAfW/4Vm8nfxIMt+4p8zoTk2lYIQa/bJY5iPM/F87wdjqvdyeHOl0UVYHIIco+zfQv5oCC7Y99tXwxPJEI/LKqEAvmEQuchz6ddD9iXgJnKzs7UtjvzNuQ2WZmMfVPjpOQpfXVokbmc3Nd09LZZ/pDzoUShqUuYMxSny0lZ2xX9weZoYKireLer48RZTa4pkdu6TKnn9DRQFzbHYlP9ZWqPmjJXq+kbVc1iGLYJgCoLzRrQuAzCQjsJKMzQRqKqPBXxMai87GFF+Y0DwMKNLQy/hcyLxiaz0Y3RxIHPnblbqqy1iw35L5rqO8TvQIcraPrm4vNG6XhHad2GwafBtWO13j+/lM565HIl3xa/ooTHFykpKzWcjbsmIZXeJ8UPMGi2nlxiAyP18PmfFlXoIaUphElYi8soTM9Xy3CkZltELlWWW79vD0zUpUi5ChQm4LTcVUGFrUTVuAuhKJn6TnxZiWm+uk6vYUZP1s5sIGXKWjJqt5kbUmedzGNEGqIOJcMutEgZjSoDb8pr49VGotRZS0ZEbqojJaqqbSVMzcm8epVXaPk8tbVUQmjbtjflL3NaKmXFkL4wE2Aut7Qq+sMm9S6VUaFcGWTcxqvuQJbJpmFNYWVdq8ZV3fpXeTTbBBbb0FgHBtVrGCpw1x5M3eEoJXEcA6w3hCoNU+KE5di3Df8K/WZsxp0HG787Trxxb04Th7xmKbXrbNKXGj96EtWW5P0hzfm30DNmXvt2IvkAb0NTYkLtJaO5PHXLNUwmNe1DQbr5Orc3RbfnUvtv4MA4Xa7nW/9X9xBp2z7uFHe0LEqU/FrdMeuXvOjoX6hQY5d80JG15srxSjpO5gR9tcBAP5VEK08q5Zb48RkjSqBirJTitm9qnOroDt2IbkK37Hxx0yyF+ls3ILYyVKydGT3Uyz038WF7pjpRevy2iTJP8zZQ3k2Citp8mBbSFIstH3WrFCtDkVzrT/N/s+5NQhKddkXjft42viDfyrXVwdEErIajX347bxBys3Eya990FJS0WZ39mmtyzZ39BgbeSK9K7ksCv1KoekXd07UD1B/ViuNtG3gVxAo8b+lgbrvpeOXksNJt6lfGLbJRa9a9TM+bkmxQ///ff6viDthuFDOb7Hglsgy1jqC3BZ1Sv2VWaFYnXhjqWaXTa4zNOmgkbyWmQUqJjGKE69rTG/LXKl83y7n/a2+3LLhUdfWW+gl2FVzsYMCojkxKLrGm60pKIdMAYZ1Uay1TL8mscWXWSRlZs+QJJX+uraXe5tJ4mRHJi0Xaf1bnxoANDHElCrZO1HMSTOXVdeAF2r6IPHmp37hLlAUppjS2oEq9V6vMtTQJRcaE/t5ILcAgm0blUwVd4+hPMw6Kf8vLkdYftuI2WWZlq6E0J6kTbBubuKwczUuq6elL0y+NXOnq1HVaUwp9r0YuT+FHPrApXBsLRkloo28ow5quRjHWWNXgpdoc/soi6ygAja+y+y/Y191miU32AVWzLjHC1M7laurOsElRmyxN2kUgs/Vs9yZlmBOV/67MVuIxA6ogpKKiykctfVMP0ra0SHeQ1XslAYY+sbnr481V9hBitfm6Tt4Nxe7T8yf8+umH9Lp93n3tA3p+19zkNtd5RzrthWzoVt8EFNeKmXRU3ktIzKdYO2dCrCdcTLW3ORiiWohkLu2arzSwsdbQTtPohMrc48zg5zecb4RceYbRtImw2NoT+32hXkjlXu7jMatXg40/JNMETQMAq+ITWd4kKq1yNgq3swcSCt90yPtKhiV7uYR3MW9XoYFNSALtxszU6HWb85parQRZp62u1r+reKoTfFTlNxlPHbWDThPxahpWhzuXr0JPmpzzpJ1NBtuoE4SZTlm5+j19bKnBeFXeqnuFJHese6rwIos29Jsok40qOk2f2YrawNG0rTVv4mCbzjHbJertr7k7LoyUddWu668y7NIRNjj72R5UJU0ZbZGM35Jyy4Iprd4v6i1Yusw/0au5h8q17VmN+1fjS/7mP/0FZ1ef0e8OuJ3c8Edf+RNjDXP7iA1e+LZK6s6Ci7wMifSeKQ1p2qxSUkuZ2nApcVCX0hSbbeXIFmnojaYqJmnYnVTH+AjlSj3aNRf8CJlFJ1INKZRFWhso2nKGNhwwm/BRVlSq0Fd/9bCxNpLuaVitshMZcrR11A0m1OQiC0ZNfJT9VnnJPTGWW6tW9ZGbarI8MkHsTmxrYxWZ2R+Z+LHoykLdTM5zgYgFesGVnWPgVB272zTqLgTDFnyVGW0b6tqqTWjXhXGuZdMCSkZF3X5rEvzWyVO3XH2s15lPyDmD64IqZtusS5pttJtgk6DEuNGjvA6by4fhSN4dUq+HigmKCn3VfAmiMFwZyjXcr/xoXiGrKE9WNXZi5XfdoEuYEqvp1h6OIH9kv2A1iSog+56HLD85r6zNcpsmRCH9xe0Zk/kt5zfP8b0ue4N9M98pcyq/em9vJ6HbBxdqBKrcFjnnXqSOiAqzvGcWPv97fVcIhZ5NwxTvJ1GjKUCUypGJBX5sTOeCB4VjCXEsidfntjvuKhR6obNkpU5SDdTIl55W0xBJsPmi2qPy/O26IpST8+LMlKyipTtYNZRuOfLSbMqWLyoL7yzxit1fSipnss964bt2bHeUuTCWTZM0Fv1rJZ1OnUlz2qYOZH11ViyvDsp4auyc1suXNnOdujYI6lZs1GjkiiApN8FU5VDpRr0uu2VtZNMHtfpWqX9zH3DDfFp5VXJTZ1LIpleq+JGmvipXsKVvOjYJdCz0jeVvUk89v9HpzRPNud5lQ8Qmq5mLVa9/G0M3iObAL/sL6oazXAs30EVGFmzjISlOCx6E+rPgWmQnlaZ8J5PJa1sh41VkI51VLrOukcrfTFb1E6FMxxgf758y7O9xsn+PfrfPYffA6gPt2mzr2Poo2tvxOKdvUhcmrXctTzW71CVaCQEzYyKVU53sHlGhYjblUWpLyh1h/YT4XHAhktM4MM5omzZ41obyrQwDYb0SdjQpt1KxKemsbSqyBErZ6QZ9m26ucsptdS6rm16eOcYsFpVsptxm3XNJx+RVi5VAOiIUxtJnhcTWXxjaNt+Y0kS3TgBrcuCNdDRZrpJHof8wDq5S3PnGUJvNxHBffdYETYOZRorBkLtsE3FVAG3gT3fmM92vHTYgFYepDtu2AMjIthJc1JAJYzNv6zRWl2DGpo7VHaBxHzUijtk2mHR3LcWU5FG/v1KSp4FtMZ/Hp9i6ukHZHaH6nfdul2ut1Pu6TQz2Uh9z1vbT8mzEn24qTL8Tpstin+R+kbVKyDgrUBR2V6seNBb51mDwg59ePOGjTz+k1+nx3mvv0+30mzGpYJujaLcPLtbfuVi7/FmnGxtfEVyp31/nFHpqhVnlr7HPpXJfJMZL6ZnS4KL4sNTvLgbUq9/KvgLbcbhCvxLFNGoZd4Oig18riw01Ag21PXRFUzineZvgQuUpZ3Qs9bUZjJIB3QiJApCaA2Pr96rya5aZXWY/bPYZZKUoNLbh9sJqBBymtGsObN93UabHc86OkTXNkdzEWFT5gar6sTlHuyzvrrHp2LSRS4OVLKQwi8MdBoIWQ1LbwdrEwS/JYzzjv8whKsULEpi7LqaJfEnTD0tblhoCnWx9Gcxsf1GONhwqO0G9sm2y/4I5/7z03A4mgMzf6VgvlU9sV4ndM/pCFb5InYnO8qAsP4iT4vZHn+N3LkTuWjEOaRsWNWNxPaYyFJUOsBt+iwQIKO7AVspK/UuhP7HUq1qTS7166dez12UYYjdJEpQULAt6J9eCyXkrlKkLlta2u4RaBVF8kAWiBtiqXtkkJs+1JgGbQjFmyYKUVT1ETggEFJffrLNIZTGmue8N5djSJArLpi5yYq8E17biLPey4rQP89WxPXXEuHZXiYr+kI1kubbjuElArT83jgVz/rxuMjhHKepVtnCQQEnach9WrjMbGmVDRyDR86ujGR0rqdJlShvqL4mEmPyHCBOVuEnQ16xwKypPF6pRltVcqjdNdNRA2JSmwhEqC+ZLH5XWSanNxkFWRirftTUMZ5JS+wJ9aVplwJuC5M/Fcy5Tn+vnq2vDaEvH/YbQZaqOHFjMeWHzdxUdhUb1sM4fqpMe1ywMTdBQR0g9v83uyWw85TOvCrTVv9ZpaCaepRoMaaxs6RzudkN3MluYGA2DZkwVkJDpWu68a0Z+GUaOhFBoGIpfa7jkK91m/ZOUAQJZcARL9xKUxTS57jB0ijK4VBnKnFQ9YU0UJcKSbDcKLalfenRtFU+FZ8X3OIVIvYpGg4jemtf2rMxpVjWEpLiEz0g+a7HScvUbtQypwMCCOd+mjlha3Q0yV7W1pSxzWoPlMXpPyaMtxtHnCPMbzM2VfI6eMIuaOZ+dYp3yqvctkOlbx8SYlqdsbJbd20APGPW/zZnYzv6aUYem7her9iW9Xuvo2gG8dr9Uj2f/5FqwpJC2sxbKUTr28l5hrrolOi2ZyDFuUTV5z0kZdezJJrpUGC/N5dZxYsvSm1DF767luCwotjq5WUKb/qj9vRVD+yQeWi4IlsbLPA2NXwmlq/2TJZbq1F9CzrSvS3XuM1UvixPXSnoZS4TjFD6om+z3Nr1/Kq4YUu4r2JUo7Pi0qEzDFaumQj3nSW3k5K8e8a//SoPrnmuvRNXJEuUrczKjt2S+3DILpKRLCK0rlauXKNIxjbtNfb8yvnauMNZMbhqomA8YyS/HKdXvsqxKGvFN624JICudH+uztYDajEQdgqrCUVNVnY9s8Mf1ZVmF9HXumfCinPMyfsr6TBcy9UJ33lNLoKVV+sHERP0mWOU3BaImo3OnbasZ1oLmXj+QBUtXEUQYkDl8SsEppXxrqGlkbjavofYpU66i4bB8USgwZFNKhltNgoNNdJ2BUOawW3RKFS82qJ2T2lZtnrXM3ml5SyG0/zofZb/rQLWbujxq9AoOqE2PbcPPXaFuYGzsk1zP7q58TQYLQUR6WZTfRCemp38KrAG02etNShPpahXT20n1BWqygkca0qSrehxDK0kQ2sqZTcb2RsdUG7Db4EJhqsiW0sPpvoRiDJAjg83BF9ZnppkK48y4CUKlUHKmkcK4yNVlJYSZz6dEpLYyE+NdmbAGNs27LrcQ1VuSblFEDgX9IsqrUFW9RmuzqwxOphPMo7wWg1ohTfrHKAuKU1dJSz93zZikOABtAQaG+wWkglQPmwiTVVkmjriwp9VhPze4hL4a1MlcMmP3F26t20eYz3aXxLmswsRmajeqPCHNmSlpD7HOat6sbdILZmJlYy9tN6X56ozVQpqaclMeh5bIic1JtaGO3t4qitlh+JPwanNuE52n389hwz0pOg9N8lp9C105JfpRlJdju18mC9va56qyC8nMjmj+YkeyUdVWOVUl09OPgPT41VqsaPFSvot3UBeD7KrSWts3MN0WdaTe4tynFS7mTgMGmU26SwEO6lLkBq1TlrDMtpf5ABvg7j+ix5pnZVBkPlumAHIHj6UCqPWyMIcV5s1H9gCkAKOdUTtU6fRcMdnT3LOkwtpASujrvNcOfmxo6sxZ0ousM4wGVv1cRyUvhnSJA6OOs7TlcosbLTRL7jduujqDx0hUYBaGDcZkLaZtsmwrqRjQJEctZ7ubKnjYWLkonbtL22dTfMbgi/wbnVxaqemiDSAtOsUgC2UCmr2+Xj1MnHebyNVHSWKTIanKmihk/VmVo1Wn/3foM9cmXyPQqk+soOob56+CdVeVbQxUBUp1ZL+uTjD79WaS6sdjC0YkCbhF47GZrqC2BUVinSihn7tvIli8FIZnd4Gkr0XjdtjOG1wFC2X2BI2+QN2CIoqPi6xpLAqh0a0hQ40g8j+2VaGlkxG2UgzmWsYxOE52O22fbJtAnPpC2dKobAm/UMkVIOvoojr5dtAPLyS4UDlNXz0llVGjtTTAUGqWNOhaQax0RHkDF+NhaZ6kNMqLiWrGXbFeIh8g5HIUkfd71sd8yo30asZCDQilcGma9haFi0I5tYqyNR9ky8dyCXflhZbN8uyAfA2ogakamppQcBp0hZzc21goipmz4HcdbAhhdl6q7ExtLhLZVgKyMnp1DIy1SbMBJG3CKtV+qSt3ecazXPZpi8zoKlZVm9pL/Bx1BjDLo9NrOEbsKkzzCDaklehjK9YKTXca65RpS7c7NVENkxxa+HoBasVctK0eTYK6JuPZ5KyZAk6dD+W3+r0c64fTyvrexJZmOKVyr/J43LI22tBJK0WV/lPvV/ZRBXe6+i9NrjwsmI5i29UllftdeLWxjTJoBtvYqYrLC09MLovu0+jtrgdVjkhXHaSer2KupMzyrK5XT6RY59N8t2zvruoT29utbHXKrmPnFxJc5IwsyaVMo6W8c16sfMEBksqbAqHtz1CNnlJcxkdGNZco98TQzFZ/XO2uvNOSfe5dzyXXwqO4Kk03bW4w7uI4QgiBwClxjQx6TS+rrGyLE6mGl+ltjQVhuGfizRwnbmP5VY2q8pcsXTG44KV86mf+JGct5Y+izeko84dQ8hdKhnqnTWmX2qaVpEwrLYOhKOx7qXIGVF6V5jX6IVVDwGQs9TyxlqZgLLX6Jn6/QlMLA3IMZLrJIHEq2fRhhTdf4eBoxLT7aPVXrZJeSPbWpswHzLOVFaCZtGysCktX5F7NrIWmLHDQieh9Xc5onpZ+35TXrETql/NCscFxCmUZGjwra5JGdFWKif2vIlBl43QnLiUvtduyKE82eqYK6/frBgl6nhrtY9KVlbRNTJjqUFqu5ce2HmeuHrUaQNPbu3Z5DeUVLwt9JwsJDL91ObPIkzr5JYXS30lxuTds6nXR6gilbRPrZNLYZrZL2nYHzb71dy5atGjRokWLFi1atGjRAsCpTtKiRYsWLVq0aNGiRYsW1WiDixYtWrRo0aJFixYtWuwEbXDRokWLFi1atGjRokWLnaANLlq0aNGiRYsWLVq0aLETtMFFixYtWrRo0aJFixYtdoI2uGjRokWLFi1atGjRosVO0AYXLVq0aNGiRYsWLVq02Ana4KJFixYtWrRo0aJFixY7QRtctGjRokWLFi1atGjRYidog4sWLVq0aNGiRYsWLVrsBG1w0aJFixYtWrRo0aJFi52gDS5atGjRokWLFi1atGixE7TBRYsWLVq0aNGiRYsWLXaCNrho0aJFixYtWrRo0aLFTtAGFy1atGjRokWLFi1atNgJ/j/sAPATshQewQAAAABJRU5ErkJggg==","text/plain":[""]},"metadata":{},"output_type":"display_data"}],"source":["# First we define a function to calculate the umap reduction\n","def umap_reducer(x, dims=3, nns=10):\n"," \"\"\"UMAP reduction of the input data.\"\"\"\n"," reducer = umap.UMAP(n_neighbors=nns, n_components=dims, metric=\"manhattan\", spread=0.5, random_state=2)\n"," reduced = reducer.fit_transform(x)\n"," reduced -= reduced.min(axis=0)\n"," reduced /= reduced.max(axis=0)\n"," return reduced\n","\n","# load the features output by our feature extractor\n","pos = np.load(global_save_dir / \"wsi_features\" / \"0.position.npy\")\n","feats = np.load(global_save_dir / \"wsi_features\" / \"0.features.0.npy\")\n","pos = pos / 8 # as we extracted at 0.5mpp, and we are overlaying on a thumbnail at 4mpp\n","\n","# reduce the features into 3 dimensional (rgb) space\n","reduced = umap_reducer(feats)\n","\n","# plot the prediction map the classifier again\n","overlay = overlay_prediction_mask(\n"," wsi_overview,\n"," pred_map,\n"," alpha=0.5,\n"," label_info=label_color_dict,\n"," return_ax=True,\n",")\n","\n","# plot the feature map reduction\n","plt.figure()\n","plt.imshow(wsi_overview)\n","plt.scatter(pos[:,0], pos[:,1], c=reduced, s=1, alpha=0.5)\n","plt.axis(\"off\")\n","plt.title(\"UMAP reduction of HistoEnc features\")\n","plt.show()"]},{"cell_type":"markdown","metadata":{"id":"ixWAJc_ZSANt"},"source":["We see that the prediction map from our patch-level predictor, and the feature map from our self-supervised feature encoder, capture similar information about the tissue types in the WSI. This is a good sanity check that our models are working as expected. It also shows that the features extracted by the HistoEncoder model are capturing the differences between the tissue types, and so that they are encoding histologically relevant information."]},{"cell_type":"markdown","metadata":{"id":"J_1pb6BGGbVu"},"source":["## Where to Go From Here\n","\n","In this notebook, we show how we can use the `PatchPredictor` and `DeepFeatureExtractor` classes and their `predict` method to predict the label, or extract features, for patches of big tiles and WSIs. We introduce `merge_predictions` and `overlay_prediction_mask` helper functions that merge the patch prediction outputs and visualize the resulting prediction map as an overlay on the input image/WSI.\n","\n","All the processes take place within TIAToolbox and we can easily put the pieces together, following our example code. Please make sure to set inputs and options correctly. We encourage you to further investigate the effect on the prediction output of changing `predict` function parameters. We have demonstrated how to use your own pretrained model or one provided by the research community for a specific task in the TIAToolbox framework to do inference on large WSIs even if the model structure is not defined in the TIAToolbox model class.\n","\n","You can learn more through the following resources:\n","\n","- [Advanced model handling with PyTorch and TIAToolbox](https://tia-toolbox.readthedocs.io/en/latest/_notebooks/jnb/07-advanced-modeling.html)\n","- [Creating slide graphs for WSI with a custom PyTorch graph neural network](https://tia-toolbox.readthedocs.io/en/latest/_notebooks/jnb/full-pipelines/slide-graph.html)"]}],"metadata":{"accelerator":"GPU","celltoolbar":"Edit Metadata","colab":{"provenance":[{"file_id":"1Ke0YSaLwsoiIc6ZlNj3MNm7fMdGdL2M2","timestamp":1699972954536}]},"gpuClass":"standard","kernelspec":{"display_name":"Python 3 (ipykernel)","language":"python","name":"python3"},"language_info":{"codemirror_mode":{"name":"ipython","version":3},"file_extension":".py","mimetype":"text/x-python","name":"python","nbconvert_exporter":"python","pygments_lexer":"ipython3","version":"3.10.12"}},"nbformat":4,"nbformat_minor":0}
\ No newline at end of file
diff --git a/_static/torchvision_finetuning_instance_segmentation.ipynb b/_static/torchvision_finetuning_instance_segmentation.ipynb
deleted file mode 100644
index f4b58f7ec..000000000
--- a/_static/torchvision_finetuning_instance_segmentation.ipynb
+++ /dev/null
@@ -1,2605 +0,0 @@
-{
- "nbformat": 4,
- "nbformat_minor": 0,
- "metadata": {
- "colab": {
- "name": "torchvision_finetuning_instance_segmentation.ipynb",
- "version": "0.3.2",
- "provenance": [],
- "collapsed_sections": []
- },
- "kernelspec": {
- "name": "python3",
- "display_name": "Python 3"
- },
- "accelerator": "GPU"
- },
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "DfPPQ6ztJhv4",
- "colab_type": "text"
- },
- "source": [
- "# TorchVision 0.3 Object Detection finetuning tutorial\n",
- "\n",
- "For this tutorial, we will be finetuning a pre-trained [Mask R-CNN](https://arxiv.org/abs/1703.06870) model in the [*Penn-Fudan Database for Pedestrian Detection and Segmentation*](https://www.cis.upenn.edu/~jshi/ped_html/). It contains 170 images with 345 instances of pedestrians, and we will use it to illustrate how to use the new features in torchvision in order to train an instance segmentation model on a custom dataset.\n",
- "\n",
- "First, we need to install `pycocotools`. This library will be used for computing the evaluation metrics following the COCO metric for intersection over union."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "DBIoe_tHTQgV",
- "colab_type": "code",
- "outputId": "de73add6-c54a-4d53-960e-ac0032ab4009",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 10356
- }
- },
- "source": [
- "%%shell\n",
- "\n",
- "CURRENT_DIR=`pwd`\n",
- "echo $CURRENT_DIR\n",
- "\n",
- "# Install pycocotools\n",
- "git clone https://github.com/cocodataset/cocoapi.git\n",
- "cd cocoapi/PythonAPI\n",
- "python setup.py build_ext install\n",
- "\n",
- "cd $CURRENT_DIR\n",
- "\n",
- "######################################################\n",
- "# TODO remove this once torchvision 0.3 is present by\n",
- "# default in Colab\n",
- "######################################################\n",
- "pip uninstall -y torchvision\n",
- "git clone https://github.com/pytorch/vision.git\n",
- "cd vision\n",
- "git checkout v0.3.0\n",
- "python setup.py install\n",
- "# why do we need this?\n",
- "cp -r build/lib.linux-x86_64-3.6/torchvision /usr/local/lib/python3.6/dist-packages/"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "/content\n",
- "Cloning into 'cocoapi'...\n",
- "remote: Enumerating objects: 953, done.\u001b[K\n",
- "remote: Total 953 (delta 0), reused 0 (delta 0), pack-reused 953\u001b[K\n",
- "Receiving objects: 100% (953/953), 11.70 MiB | 29.29 MiB/s, done.\n",
- "Resolving deltas: 100% (566/566), done.\n",
- "running build_ext\n",
- "cythoning pycocotools/_mask.pyx to pycocotools/_mask.c\n",
- "/usr/local/lib/python3.6/dist-packages/Cython/Compiler/Main.py:367: FutureWarning: Cython directive 'language_level' not set, using 2 for now (Py2). This will change in a later release! File: /content/cocoapi/PythonAPI/pycocotools/_mask.pyx\n",
- " tree = Parsing.p_module(s, pxd, full_module_name)\n",
- "building 'pycocotools._mask' extension\n",
- "creating build\n",
- "creating build/common\n",
- "creating build/temp.linux-x86_64-3.6\n",
- "creating build/temp.linux-x86_64-3.6/pycocotools\n",
- "x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -I/usr/local/lib/python3.6/dist-packages/numpy/core/include -I../common -I/usr/include/python3.6m -c ../common/maskApi.c -o build/temp.linux-x86_64-3.6/../common/maskApi.o -Wno-cpp -Wno-unused-function -std=c99\n",
- "\u001b[01m\u001b[K../common/maskApi.c:\u001b[m\u001b[K In function ‘\u001b[01m\u001b[KrleDecode\u001b[m\u001b[K’:\n",
- "\u001b[01m\u001b[K../common/maskApi.c:46:7:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[Kthis ‘\u001b[01m\u001b[Kfor\u001b[m\u001b[K’ clause does not guard... [\u001b[01;35m\u001b[K-Wmisleading-indentation\u001b[m\u001b[K]\n",
- " \u001b[01;35m\u001b[Kfor\u001b[m\u001b[K( k=0; k2) x+=(long) cnts[m-2]; cnts[m++]=(uint) x;\n",
- " \u001b[01;35m\u001b[K^~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K../common/maskApi.c:228:34:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[K...this statement, but the latter is misleadingly indented as if it were guarded by the ‘\u001b[01m\u001b[Kif\u001b[m\u001b[K’\n",
- " if(m>2) x+=(long) cnts[m-2]; \u001b[01;36m\u001b[Kcnts\u001b[m\u001b[K[m++]=(uint) x;\n",
- " \u001b[01;36m\u001b[K^~~~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K../common/maskApi.c:\u001b[m\u001b[K In function ‘\u001b[01m\u001b[KrleToBbox\u001b[m\u001b[K’:\n",
- "\u001b[01m\u001b[K../common/maskApi.c:141:31:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kxp\u001b[m\u001b[K’ may be used uninitialized in this function [\u001b[01;35m\u001b[K-Wmaybe-uninitialized\u001b[m\u001b[K]\n",
- " if(j%2==0) xp=x; else if\u001b[01;35m\u001b[K(\u001b[m\u001b[Kxp build/lib.linux-x86_64-3.6/pycocotools\n",
- "copying pycocotools/__init__.py -> build/lib.linux-x86_64-3.6/pycocotools\n",
- "copying pycocotools/cocoeval.py -> build/lib.linux-x86_64-3.6/pycocotools\n",
- "copying pycocotools/mask.py -> build/lib.linux-x86_64-3.6/pycocotools\n",
- "creating build/bdist.linux-x86_64\n",
- "creating build/bdist.linux-x86_64/egg\n",
- "creating build/bdist.linux-x86_64/egg/pycocotools\n",
- "copying build/lib.linux-x86_64-3.6/pycocotools/coco.py -> build/bdist.linux-x86_64/egg/pycocotools\n",
- "copying build/lib.linux-x86_64-3.6/pycocotools/__init__.py -> build/bdist.linux-x86_64/egg/pycocotools\n",
- "copying build/lib.linux-x86_64-3.6/pycocotools/_mask.cpython-36m-x86_64-linux-gnu.so -> build/bdist.linux-x86_64/egg/pycocotools\n",
- "copying build/lib.linux-x86_64-3.6/pycocotools/cocoeval.py -> build/bdist.linux-x86_64/egg/pycocotools\n",
- "copying build/lib.linux-x86_64-3.6/pycocotools/mask.py -> build/bdist.linux-x86_64/egg/pycocotools\n",
- "byte-compiling build/bdist.linux-x86_64/egg/pycocotools/coco.py to coco.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/pycocotools/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/pycocotools/cocoeval.py to cocoeval.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/pycocotools/mask.py to mask.cpython-36.pyc\n",
- "creating stub loader for pycocotools/_mask.cpython-36m-x86_64-linux-gnu.so\n",
- "byte-compiling build/bdist.linux-x86_64/egg/pycocotools/_mask.py to _mask.cpython-36.pyc\n",
- "creating build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying pycocotools.egg-info/PKG-INFO -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying pycocotools.egg-info/SOURCES.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying pycocotools.egg-info/dependency_links.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying pycocotools.egg-info/requires.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying pycocotools.egg-info/top_level.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "writing build/bdist.linux-x86_64/egg/EGG-INFO/native_libs.txt\n",
- "zip_safe flag not set; analyzing archive contents...\n",
- "pycocotools.__pycache__._mask.cpython-36: module references __file__\n",
- "creating dist\n",
- "creating 'dist/pycocotools-2.0-py3.6-linux-x86_64.egg' and adding 'build/bdist.linux-x86_64/egg' to it\n",
- "removing 'build/bdist.linux-x86_64/egg' (and everything under it)\n",
- "Processing pycocotools-2.0-py3.6-linux-x86_64.egg\n",
- "creating /usr/local/lib/python3.6/dist-packages/pycocotools-2.0-py3.6-linux-x86_64.egg\n",
- "Extracting pycocotools-2.0-py3.6-linux-x86_64.egg to /usr/local/lib/python3.6/dist-packages\n",
- "Adding pycocotools 2.0 to easy-install.pth file\n",
- "\n",
- "Installed /usr/local/lib/python3.6/dist-packages/pycocotools-2.0-py3.6-linux-x86_64.egg\n",
- "Processing dependencies for pycocotools==2.0\n",
- "Searching for matplotlib==3.0.3\n",
- "Best match: matplotlib 3.0.3\n",
- "Adding matplotlib 3.0.3 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for Cython==0.29.7\n",
- "Best match: Cython 0.29.7\n",
- "Adding Cython 0.29.7 to easy-install.pth file\n",
- "Installing cygdb script to /usr/local/bin\n",
- "Installing cython script to /usr/local/bin\n",
- "Installing cythonize script to /usr/local/bin\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for setuptools==41.0.1\n",
- "Best match: setuptools 41.0.1\n",
- "Adding setuptools 41.0.1 to easy-install.pth file\n",
- "Installing easy_install script to /usr/local/bin\n",
- "Installing easy_install-3.6 script to /usr/local/bin\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for python-dateutil==2.5.3\n",
- "Best match: python-dateutil 2.5.3\n",
- "Adding python-dateutil 2.5.3 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for cycler==0.10.0\n",
- "Best match: cycler 0.10.0\n",
- "Adding cycler 0.10.0 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for kiwisolver==1.1.0\n",
- "Best match: kiwisolver 1.1.0\n",
- "Adding kiwisolver 1.1.0 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for numpy==1.16.3\n",
- "Best match: numpy 1.16.3\n",
- "Adding numpy 1.16.3 to easy-install.pth file\n",
- "Installing f2py script to /usr/local/bin\n",
- "Installing f2py3 script to /usr/local/bin\n",
- "Installing f2py3.6 script to /usr/local/bin\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for pyparsing==2.4.0\n",
- "Best match: pyparsing 2.4.0\n",
- "Adding pyparsing 2.4.0 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for six==1.12.0\n",
- "Best match: six 1.12.0\n",
- "Adding six 1.12.0 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Finished processing dependencies for pycocotools==2.0\n",
- "Uninstalling torchvision-0.2.2.post3:\n",
- " Successfully uninstalled torchvision-0.2.2.post3\n",
- "Cloning into 'vision'...\n",
- "remote: Enumerating objects: 91, done.\u001b[K\n",
- "remote: Counting objects: 100% (91/91), done.\u001b[K\n",
- "remote: Compressing objects: 100% (58/58), done.\u001b[K\n",
- "remote: Total 3006 (delta 42), reused 68 (delta 33), pack-reused 2915\u001b[K\n",
- "Receiving objects: 100% (3006/3006), 2.50 MiB | 16.98 MiB/s, done.\n",
- "Resolving deltas: 100% (1927/1927), done.\n",
- "Branch 'v0.3.0' set up to track remote branch 'v0.3.0' from 'origin'.\n",
- "Switched to a new branch 'v0.3.0'\n",
- "Building wheel torchvision-0.3.0a0+684c064\n",
- "running install\n",
- "running bdist_egg\n",
- "running egg_info\n",
- "creating torchvision.egg-info\n",
- "writing torchvision.egg-info/PKG-INFO\n",
- "writing dependency_links to torchvision.egg-info/dependency_links.txt\n",
- "writing requirements to torchvision.egg-info/requires.txt\n",
- "writing top-level names to torchvision.egg-info/top_level.txt\n",
- "writing manifest file 'torchvision.egg-info/SOURCES.txt'\n",
- "reading manifest template 'MANIFEST.in'\n",
- "warning: no previously-included files matching '__pycache__' found under directory '*'\n",
- "warning: no previously-included files matching '*.py[co]' found under directory '*'\n",
- "writing manifest file 'torchvision.egg-info/SOURCES.txt'\n",
- "installing library code to build/bdist.linux-x86_64/egg\n",
- "running install_lib\n",
- "running build_py\n",
- "creating build\n",
- "creating build/lib.linux-x86_64-3.6\n",
- "creating build/lib.linux-x86_64-3.6/torchvision\n",
- "copying torchvision/__init__.py -> build/lib.linux-x86_64-3.6/torchvision\n",
- "copying torchvision/utils.py -> build/lib.linux-x86_64-3.6/torchvision\n",
- "copying torchvision/version.py -> build/lib.linux-x86_64-3.6/torchvision\n",
- "creating build/lib.linux-x86_64-3.6/torchvision/transforms\n",
- "copying torchvision/transforms/__init__.py -> build/lib.linux-x86_64-3.6/torchvision/transforms\n",
- "copying torchvision/transforms/functional.py -> build/lib.linux-x86_64-3.6/torchvision/transforms\n",
- "copying torchvision/transforms/transforms.py -> build/lib.linux-x86_64-3.6/torchvision/transforms\n",
- "creating build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/coco.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/__init__.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/mnist.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/phototour.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/sbu.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/stl10.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/omniglot.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/voc.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/semeion.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/vision.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/celeba.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/fakedata.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/imagenet.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/utils.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/cityscapes.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/caltech.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/svhn.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/sbd.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/cifar.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/flickr.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/lsun.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "copying torchvision/datasets/folder.py -> build/lib.linux-x86_64-3.6/torchvision/datasets\n",
- "creating build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/roi_align.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/__init__.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/boxes.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/poolers.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/misc.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/roi_pool.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/_utils.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "copying torchvision/ops/feature_pyramid_network.py -> build/lib.linux-x86_64-3.6/torchvision/ops\n",
- "creating build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/inception.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/alexnet.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/squeezenet.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/__init__.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/vgg.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/googlenet.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/densenet.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/shufflenetv2.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/utils.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/mobilenet.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/resnet.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "copying torchvision/models/_utils.py -> build/lib.linux-x86_64-3.6/torchvision/models\n",
- "creating build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/mask_rcnn.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/image_list.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/faster_rcnn.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/__init__.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/transform.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/generalized_rcnn.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/rpn.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/keypoint_rcnn.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/_utils.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/roi_heads.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "copying torchvision/models/detection/backbone_utils.py -> build/lib.linux-x86_64-3.6/torchvision/models/detection\n",
- "creating build/lib.linux-x86_64-3.6/torchvision/models/segmentation\n",
- "copying torchvision/models/segmentation/deeplabv3.py -> build/lib.linux-x86_64-3.6/torchvision/models/segmentation\n",
- "copying torchvision/models/segmentation/segmentation.py -> build/lib.linux-x86_64-3.6/torchvision/models/segmentation\n",
- "copying torchvision/models/segmentation/__init__.py -> build/lib.linux-x86_64-3.6/torchvision/models/segmentation\n",
- "copying torchvision/models/segmentation/fcn.py -> build/lib.linux-x86_64-3.6/torchvision/models/segmentation\n",
- "copying torchvision/models/segmentation/_utils.py -> build/lib.linux-x86_64-3.6/torchvision/models/segmentation\n",
- "running build_ext\n",
- "building 'torchvision._C' extension\n",
- "creating build/temp.linux-x86_64-3.6\n",
- "creating build/temp.linux-x86_64-3.6/content\n",
- "creating build/temp.linux-x86_64-3.6/content/vision\n",
- "creating build/temp.linux-x86_64-3.6/content/vision/torchvision\n",
- "creating build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc\n",
- "creating build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu\n",
- "creating build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda\n",
- "x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/vision.cpp -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/vision.o -O0 -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/cpu/ROIAlign_cpu.cpp -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.o -O0 -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "In file included from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/ATen.h:9:0\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/types.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader_options.h:4\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader/base.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader/stateful.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/all.h:4\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/extension.h:4\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/vision.h:2\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.cpp:2\u001b[m\u001b[K:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.cpp:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:84:52:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " at::ScalarType _st = ::detail::scalar_type(TYPE\u001b[01;35m\u001b[K)\u001b[m\u001b[K; \\\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.cpp:406:3:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kin expansion of macro ‘\u001b[01m\u001b[KAT_DISPATCH_FLOATING_TYPES_AND_HALF\u001b[m\u001b[K’\n",
- " \u001b[01;36m\u001b[KA\u001b[m\u001b[KT_DISPATCH_FLOATING_TYPES_AND_HALF(input.type(), \"ROIAlign_forward\", [&] {\n",
- " \u001b[01;36m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:23:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " inline at::ScalarType \u001b[01;36m\u001b[Kscalar_type\u001b[m\u001b[K(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.cpp:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:84:52:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " at::ScalarType _st = ::detail::scalar_type(TYPE\u001b[01;35m\u001b[K)\u001b[m\u001b[K; \\\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.cpp:456:3:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kin expansion of macro ‘\u001b[01m\u001b[KAT_DISPATCH_FLOATING_TYPES_AND_HALF\u001b[m\u001b[K’\n",
- " \u001b[01;36m\u001b[KA\u001b[m\u001b[KT_DISPATCH_FLOATING_TYPES_AND_HALF(grad.type(), \"ROIAlign_forward\", [&] {\n",
- " \u001b[01;36m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:23:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " inline at::ScalarType \u001b[01;36m\u001b[Kscalar_type\u001b[m\u001b[K(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/cpu/nms_cpu.cpp -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu/nms_cpu.o -O0 -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "In file included from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/ATen.h:9:0\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/types.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader_options.h:4\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader/base.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader/stateful.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data/dataloader.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/data.h:3\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include/torch/all.h:4\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/torch/extension.h:4\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/vision.h:2\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/nms_cpu.cpp:1\u001b[m\u001b[K:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/nms_cpu.cpp:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:71:52:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " at::ScalarType _st = ::detail::scalar_type(TYPE\u001b[01;35m\u001b[K)\u001b[m\u001b[K; \\\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/nms_cpu.cpp:77:3:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kin expansion of macro ‘\u001b[01m\u001b[KAT_DISPATCH_FLOATING_TYPES\u001b[m\u001b[K’\n",
- " \u001b[01;36m\u001b[KAT_DISPATCH_FLOATING_TYPES\u001b[m\u001b[K(dets.type(), \"nms\", [&] {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~~~~~~~~~~~~~~~~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:23:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " inline at::ScalarType \u001b[01;36m\u001b[Kscalar_type\u001b[m\u001b[K(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "x86_64-linux-gnu-gcc -pthread -DNDEBUG -g -fwrapv -O2 -Wall -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 -fPIC -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/cpu/ROIPool_cpu.cpp -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu/ROIPool_cpu.o -O0 -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "In file included from \u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/ATen.h:9:0\u001b[m\u001b[K,\n",
- " from \u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIPool_cpu.cpp:1\u001b[m\u001b[K:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIPool_cpu.cpp:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:84:52:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " at::ScalarType _st = ::detail::scalar_type(TYPE\u001b[01;35m\u001b[K)\u001b[m\u001b[K; \\\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIPool_cpu.cpp:152:3:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kin expansion of macro ‘\u001b[01m\u001b[KAT_DISPATCH_FLOATING_TYPES_AND_HALF\u001b[m\u001b[K’\n",
- " \u001b[01;36m\u001b[KA\u001b[m\u001b[KT_DISPATCH_FLOATING_TYPES_AND_HALF(input.type(), \"ROIPool_forward\", [&] {\n",
- " \u001b[01;36m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:23:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " inline at::ScalarType \u001b[01;36m\u001b[Kscalar_type\u001b[m\u001b[K(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIPool_cpu.cpp:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:84:52:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " at::ScalarType _st = ::detail::scalar_type(TYPE\u001b[01;35m\u001b[K)\u001b[m\u001b[K; \\\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cpu/ROIPool_cpu.cpp:206:3:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kin expansion of macro ‘\u001b[01m\u001b[KAT_DISPATCH_FLOATING_TYPES_AND_HALF\u001b[m\u001b[K’\n",
- " \u001b[01;36m\u001b[KA\u001b[m\u001b[KT_DISPATCH_FLOATING_TYPES_AND_HALF(grad.type(), \"ROIPool_backward\", [&] {\n",
- " \u001b[01;36m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:23:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " inline at::ScalarType \u001b[01;36m\u001b[Kscalar_type\u001b[m\u001b[K(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "/usr/local/cuda/bin/nvcc -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/cuda/ROIAlign_cuda.cu -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda/ROIAlign_cuda.o -D__CUDA_NO_HALF_OPERATORS__ -D__CUDA_NO_HALF_CONVERSIONS__ -D__CUDA_NO_HALF2_OPERATORS__ --compiler-options '-fPIC' -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(83): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"lowest\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(84): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"max\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(85): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"lower_bound\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(86): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"upper_bound\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIAlign_cuda.cu:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIAlign_cuda.cu:337:120:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " AT_DISPATCH_FLOATING_TYPES_AND_HALF(input.type(), \"ROIAlign_forward\", [&] {\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:1:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " \u001b[01;36m\u001b[Kinline at::\u001b[m\u001b[KScalarType scalar_type(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIAlign_cuda.cu:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIAlign_cuda.cu:396:118:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " AT_DISPATCH_FLOATING_TYPES_AND_HALF(grad.type(), \"ROIAlign_backward\", [&] {\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:1:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " \u001b[01;36m\u001b[Kinline at::\u001b[m\u001b[KScalarType scalar_type(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "/usr/local/cuda/bin/nvcc -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/cuda/ROIPool_cuda.cu -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda/ROIPool_cuda.o -D__CUDA_NO_HALF_OPERATORS__ -D__CUDA_NO_HALF_CONVERSIONS__ -D__CUDA_NO_HALF2_OPERATORS__ --compiler-options '-fPIC' -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(83): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"lowest\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(84): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"max\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(85): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"lower_bound\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(86): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"upper_bound\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIPool_cuda.cu:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIPool_cuda.cu:157:120:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " AT_DISPATCH_FLOATING_TYPES_AND_HALF(input.type(), \"ROIPool_forward\", [&] {\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:1:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " \u001b[01;36m\u001b[Kinline at::\u001b[m\u001b[KScalarType scalar_type(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIPool_cuda.cu:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/ROIPool_cuda.cu:221:118:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " AT_DISPATCH_FLOATING_TYPES_AND_HALF(grad.type(), \"ROIPool_backward\", [&] {\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:1:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " \u001b[01;36m\u001b[Kinline at::\u001b[m\u001b[KScalarType scalar_type(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "/usr/local/cuda/bin/nvcc -DWITH_CUDA -I/content/vision/torchvision/csrc -I/usr/local/lib/python3.6/dist-packages/torch/include -I/usr/local/lib/python3.6/dist-packages/torch/include/torch/csrc/api/include -I/usr/local/lib/python3.6/dist-packages/torch/include/TH -I/usr/local/lib/python3.6/dist-packages/torch/include/THC -I/usr/local/cuda/include -I/usr/include/python3.6m -c /content/vision/torchvision/csrc/cuda/nms_cuda.cu -o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda/nms_cuda.o -D__CUDA_NO_HALF_OPERATORS__ -D__CUDA_NO_HALF_CONVERSIONS__ -D__CUDA_NO_HALF2_OPERATORS__ --compiler-options '-fPIC' -DTORCH_API_INCLUDE_EXTENSION_H -DTORCH_EXTENSION_NAME=_C -D_GLIBCXX_USE_CXX11_ABI=0 -std=c++11\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(83): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"lowest\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(84): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"max\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(85): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"lower_bound\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "/usr/local/lib/python3.6/dist-packages/torch/include/ATen/cuda/NumericLimits.cuh(86): warning: calling a constexpr __host__ function(\"from_bits\") from a __host__ __device__ function(\"upper_bound\") is not allowed. The experimental flag '--expt-relaxed-constexpr' can be used to allow this.\n",
- "\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/nms_cuda.cu:\u001b[m\u001b[K In lambda function:\n",
- "\u001b[01m\u001b[K/content/vision/torchvision/csrc/cuda/nms_cuda.cu:95:134:\u001b[m\u001b[K \u001b[01;35m\u001b[Kwarning: \u001b[m\u001b[K‘\u001b[01m\u001b[Kc10::ScalarType detail::scalar_type(const at::DeprecatedTypeProperties&)\u001b[m\u001b[K’ is deprecated [\u001b[01;35m\u001b[K-Wdeprecated-declarations\u001b[m\u001b[K]\n",
- " AT_DISPATCH_FLOATING_TYPES_AND_HALF(\n",
- " \u001b[01;35m\u001b[K^\u001b[m\u001b[K\n",
- "\u001b[01m\u001b[K/usr/local/lib/python3.6/dist-packages/torch/include/ATen/Dispatch.h:47:1:\u001b[m\u001b[K \u001b[01;36m\u001b[Knote: \u001b[m\u001b[Kdeclared here\n",
- " \u001b[01;36m\u001b[Kinline at::\u001b[m\u001b[KScalarType scalar_type(const at::DeprecatedTypeProperties &t) {\n",
- " \u001b[01;36m\u001b[K^~~~~~~~~~~\u001b[m\u001b[K\n",
- "x86_64-linux-gnu-g++ -pthread -shared -Wl,-O1 -Wl,-Bsymbolic-functions -Wl,-Bsymbolic-functions -Wl,-z,relro -Wl,-Bsymbolic-functions -Wl,-z,relro -g -fstack-protector-strong -Wformat -Werror=format-security -Wdate-time -D_FORTIFY_SOURCE=2 build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/vision.o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu/ROIAlign_cpu.o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu/nms_cpu.o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cpu/ROIPool_cpu.o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda/ROIAlign_cuda.o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda/ROIPool_cuda.o build/temp.linux-x86_64-3.6/content/vision/torchvision/csrc/cuda/nms_cuda.o -L/usr/local/cuda/lib64 -lcudart -o build/lib.linux-x86_64-3.6/torchvision/_C.cpython-36m-x86_64-linux-gnu.so\n",
- "creating build/bdist.linux-x86_64\n",
- "creating build/bdist.linux-x86_64/egg\n",
- "creating build/bdist.linux-x86_64/egg/torchvision\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/__init__.py -> build/bdist.linux-x86_64/egg/torchvision\n",
- "creating build/bdist.linux-x86_64/egg/torchvision/transforms\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/transforms/__init__.py -> build/bdist.linux-x86_64/egg/torchvision/transforms\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/transforms/functional.py -> build/bdist.linux-x86_64/egg/torchvision/transforms\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/transforms/transforms.py -> build/bdist.linux-x86_64/egg/torchvision/transforms\n",
- "creating build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/coco.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/__init__.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/mnist.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/phototour.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/sbu.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/stl10.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/omniglot.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/voc.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/semeion.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/vision.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/celeba.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/fakedata.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/imagenet.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/utils.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/cityscapes.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/caltech.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/svhn.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/sbd.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/cifar.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/flickr.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/lsun.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/datasets/folder.py -> build/bdist.linux-x86_64/egg/torchvision/datasets\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/_C.cpython-36m-x86_64-linux-gnu.so -> build/bdist.linux-x86_64/egg/torchvision\n",
- "creating build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/roi_align.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/__init__.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/boxes.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/poolers.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/misc.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/roi_pool.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/_utils.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/ops/feature_pyramid_network.py -> build/bdist.linux-x86_64/egg/torchvision/ops\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/utils.py -> build/bdist.linux-x86_64/egg/torchvision\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/version.py -> build/bdist.linux-x86_64/egg/torchvision\n",
- "creating build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/inception.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/alexnet.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "creating build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/mask_rcnn.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/image_list.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/faster_rcnn.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/__init__.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/transform.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/generalized_rcnn.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/rpn.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/keypoint_rcnn.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/_utils.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/roi_heads.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/detection/backbone_utils.py -> build/bdist.linux-x86_64/egg/torchvision/models/detection\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/squeezenet.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/__init__.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/vgg.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/googlenet.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/densenet.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/shufflenetv2.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "creating build/bdist.linux-x86_64/egg/torchvision/models/segmentation\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/segmentation/deeplabv3.py -> build/bdist.linux-x86_64/egg/torchvision/models/segmentation\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/segmentation/segmentation.py -> build/bdist.linux-x86_64/egg/torchvision/models/segmentation\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/segmentation/__init__.py -> build/bdist.linux-x86_64/egg/torchvision/models/segmentation\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/segmentation/fcn.py -> build/bdist.linux-x86_64/egg/torchvision/models/segmentation\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/segmentation/_utils.py -> build/bdist.linux-x86_64/egg/torchvision/models/segmentation\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/utils.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/mobilenet.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/resnet.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "copying build/lib.linux-x86_64-3.6/torchvision/models/_utils.py -> build/bdist.linux-x86_64/egg/torchvision/models\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/transforms/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/transforms/functional.py to functional.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/transforms/transforms.py to transforms.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/coco.py to coco.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/mnist.py to mnist.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/phototour.py to phototour.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/sbu.py to sbu.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/stl10.py to stl10.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/omniglot.py to omniglot.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/voc.py to voc.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/semeion.py to semeion.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/vision.py to vision.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/celeba.py to celeba.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/fakedata.py to fakedata.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/imagenet.py to imagenet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/utils.py to utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/cityscapes.py to cityscapes.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/caltech.py to caltech.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/svhn.py to svhn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/sbd.py to sbd.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/cifar.py to cifar.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/flickr.py to flickr.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/lsun.py to lsun.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/datasets/folder.py to folder.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/roi_align.py to roi_align.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/boxes.py to boxes.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/poolers.py to poolers.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/misc.py to misc.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/roi_pool.py to roi_pool.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/_utils.py to _utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/ops/feature_pyramid_network.py to feature_pyramid_network.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/utils.py to utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/version.py to version.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/inception.py to inception.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/alexnet.py to alexnet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/mask_rcnn.py to mask_rcnn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/image_list.py to image_list.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/faster_rcnn.py to faster_rcnn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/transform.py to transform.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/generalized_rcnn.py to generalized_rcnn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/rpn.py to rpn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/keypoint_rcnn.py to keypoint_rcnn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/_utils.py to _utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/roi_heads.py to roi_heads.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/detection/backbone_utils.py to backbone_utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/squeezenet.py to squeezenet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/vgg.py to vgg.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/googlenet.py to googlenet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/densenet.py to densenet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/shufflenetv2.py to shufflenetv2.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/segmentation/deeplabv3.py to deeplabv3.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/segmentation/segmentation.py to segmentation.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/segmentation/__init__.py to __init__.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/segmentation/fcn.py to fcn.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/segmentation/_utils.py to _utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/utils.py to utils.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/mobilenet.py to mobilenet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/resnet.py to resnet.cpython-36.pyc\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/models/_utils.py to _utils.cpython-36.pyc\n",
- "creating stub loader for torchvision/_C.cpython-36m-x86_64-linux-gnu.so\n",
- "byte-compiling build/bdist.linux-x86_64/egg/torchvision/_C.py to _C.cpython-36.pyc\n",
- "creating build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying torchvision.egg-info/PKG-INFO -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying torchvision.egg-info/SOURCES.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying torchvision.egg-info/dependency_links.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying torchvision.egg-info/requires.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying torchvision.egg-info/top_level.txt -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "copying torchvision.egg-info/zip-safe -> build/bdist.linux-x86_64/egg/EGG-INFO\n",
- "writing build/bdist.linux-x86_64/egg/EGG-INFO/native_libs.txt\n",
- "creating dist\n",
- "creating 'dist/torchvision-0.3.0a0+684c064-py3.6-linux-x86_64.egg' and adding 'build/bdist.linux-x86_64/egg' to it\n",
- "removing 'build/bdist.linux-x86_64/egg' (and everything under it)\n",
- "Processing torchvision-0.3.0a0+684c064-py3.6-linux-x86_64.egg\n",
- "Copying torchvision-0.3.0a0+684c064-py3.6-linux-x86_64.egg to /usr/local/lib/python3.6/dist-packages\n",
- "Adding torchvision 0.3.0a0+684c064 to easy-install.pth file\n",
- "\n",
- "Installed /usr/local/lib/python3.6/dist-packages/torchvision-0.3.0a0+684c064-py3.6-linux-x86_64.egg\n",
- "Processing dependencies for torchvision==0.3.0a0+684c064\n",
- "Searching for Pillow==4.3.0\n",
- "Best match: Pillow 4.3.0\n",
- "Adding Pillow 4.3.0 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for torch==1.1.0\n",
- "Best match: torch 1.1.0\n",
- "Adding torch 1.1.0 to easy-install.pth file\n",
- "Installing convert-caffe2-to-onnx script to /usr/local/bin\n",
- "Installing convert-onnx-to-caffe2 script to /usr/local/bin\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for six==1.12.0\n",
- "Best match: six 1.12.0\n",
- "Adding six 1.12.0 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for numpy==1.16.3\n",
- "Best match: numpy 1.16.3\n",
- "Adding numpy 1.16.3 to easy-install.pth file\n",
- "Installing f2py script to /usr/local/bin\n",
- "Installing f2py3 script to /usr/local/bin\n",
- "Installing f2py3.6 script to /usr/local/bin\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Searching for olefile==0.46\n",
- "Best match: olefile 0.46\n",
- "Adding olefile 0.46 to easy-install.pth file\n",
- "\n",
- "Using /usr/local/lib/python3.6/dist-packages\n",
- "Finished processing dependencies for torchvision==0.3.0a0+684c064\n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 1
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "5Sd4jlGp2eLm",
- "colab_type": "text"
- },
- "source": [
- "## Defining the Dataset\n",
- "\n",
- "The [torchvision reference scripts for training object detection, instance segmentation and person keypoint detection](https://github.com/pytorch/vision/tree/v0.3.0/references/detection) allows for easily supporting adding new custom datasets.\n",
- "The dataset should inherit from the standard `torch.utils.data.Dataset` class, and implement `__len__` and `__getitem__`.\n",
- "\n",
- "The only specificity that we require is that the dataset `__getitem__` should return:\n",
- "\n",
- "* image: a PIL Image of size (H, W)\n",
- "* target: a dict containing the following fields\n",
- " * `boxes` (`FloatTensor[N, 4]`): the coordinates of the `N` bounding boxes in `[x0, y0, x1, y1]` format, ranging from `0` to `W` and `0` to `H`\n",
- " * `labels` (`Int64Tensor[N]`): the label for each bounding box\n",
- " * `image_id` (`Int64Tensor[1]`): an image identifier. It should be unique between all the images in the dataset, and is used during evaluation\n",
- " * `area` (`Tensor[N]`): The area of the bounding box. This is used during evaluation with the COCO metric, to separate the metric scores between small, medium and large boxes.\n",
- " * `iscrowd` (`UInt8Tensor[N]`): instances with `iscrowd=True` will be ignored during evaluation.\n",
- " * (optionally) `masks` (`UInt8Tensor[N, H, W]`): The segmentation masks for each one of the objects\n",
- " * (optionally) `keypoints` (`FloatTensor[N, K, 3]`): For each one of the `N` objects, it contains the `K` keypoints in `[x, y, visibility]` format, defining the object. `visibility=0` means that the keypoint is not visible. Note that for data augmentation, the notion of flipping a keypoint is dependent on the data representation, and you should probably adapt `references/detection/transforms.py` for your new keypoint representation\n",
- "\n",
- "If your model returns the above methods, they will make it work for both training and evaluation, and will use the evaluation scripts from pycocotools.\n",
- "\n",
- "Additionally, if you want to use aspect ratio grouping during training (so that each batch only contains images with similar aspect ratio), then it is recommended to also implement a `get_height_and_width` method, which returns the height and the width of the image. If this method is not provided, we query all elements of the dataset via `__getitem__` , which loads the image in memory and is slower than if a custom method is provided.\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "bX0rqK-A3Nbl",
- "colab_type": "text"
- },
- "source": [
- "### Writing a custom dataset for Penn-Fudan\n",
- "\n",
- "Let's write a dataset for the Penn-Fudan dataset.\n",
- "\n",
- "First, let's download and extract the data, present in a zip file at https://www.cis.upenn.edu/~jshi/ped_html/PennFudanPed.zip"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "_t4TBwhHTdkd",
- "colab_type": "code",
- "outputId": "6aee5a89-b16b-4651-88c0-f050fe3f14c4",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 9095
- }
- },
- "source": [
- "%%shell\n",
- "\n",
- "# download the Penn-Fudan dataset\n",
- "wget https://www.cis.upenn.edu/~jshi/ped_html/PennFudanPed.zip .\n",
- "# extract it in the current folder\n",
- "unzip PennFudanPed.zip"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "--2019-05-22 13:33:18-- https://www.cis.upenn.edu/~jshi/ped_html/PennFudanPed.zip\n",
- "Resolving www.cis.upenn.edu (www.cis.upenn.edu)... 158.130.69.163, 2607:f470:8:64:5ea5::d\n",
- "Connecting to www.cis.upenn.edu (www.cis.upenn.edu)|158.130.69.163|:443... connected.\n",
- "HTTP request sent, awaiting response... 200 OK\n",
- "Length: 53723336 (51M) [application/zip]\n",
- "Saving to: ‘PennFudanPed.zip’\n",
- "\n",
- "PennFudanPed.zip 100%[===================>] 51.23M 65.0MB/s in 0.8s \n",
- "\n",
- "2019-05-22 13:33:19 (65.0 MB/s) - ‘PennFudanPed.zip’ saved [53723336/53723336]\n",
- "\n",
- "--2019-05-22 13:33:19-- http://./\n",
- "Resolving . (.)... failed: No address associated with hostname.\n",
- "wget: unable to resolve host address ‘.’\n",
- "FINISHED --2019-05-22 13:33:19--\n",
- "Total wall clock time: 1.0s\n",
- "Downloaded: 1 files, 51M in 0.8s (65.0 MB/s)\n",
- "Archive: PennFudanPed.zip\n",
- " creating: PennFudanPed/\n",
- " inflating: PennFudanPed/added-object-list.txt \n",
- " creating: PennFudanPed/Annotation/\n",
- " inflating: PennFudanPed/Annotation/FudanPed00001.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00002.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00003.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00004.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00005.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00006.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00007.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00008.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00009.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00010.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00011.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00012.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00013.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00014.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00015.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00016.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00017.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00018.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00019.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00020.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00021.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00022.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00023.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00024.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00025.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00026.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00027.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00028.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00029.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00030.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00031.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00032.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00033.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00034.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00035.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00036.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00037.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00038.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00039.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00040.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00041.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00042.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00043.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00044.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00045.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00046.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00047.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00048.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00049.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00050.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00051.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00052.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00053.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00054.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00055.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00056.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00057.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00058.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00059.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00060.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00061.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00062.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00063.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00064.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00065.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00066.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00067.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00068.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00069.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00070.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00071.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00072.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00073.txt \n",
- " inflating: PennFudanPed/Annotation/FudanPed00074.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00001.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00002.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00003.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00004.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00005.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00006.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00007.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00008.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00009.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00010.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00011.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00012.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00013.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00014.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00015.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00016.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00017.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00018.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00019.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00020.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00021.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00022.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00023.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00024.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00025.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00026.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00027.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00028.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00029.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00030.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00031.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00032.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00033.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00034.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00035.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00036.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00037.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00038.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00039.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00040.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00041.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00042.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00043.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00044.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00045.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00046.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00047.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00048.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00049.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00050.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00051.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00052.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00053.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00054.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00055.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00056.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00057.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00058.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00059.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00060.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00061.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00062.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00063.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00064.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00065.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00066.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00067.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00068.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00069.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00070.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00071.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00072.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00073.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00074.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00075.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00076.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00077.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00078.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00079.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00080.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00081.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00082.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00083.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00084.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00085.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00086.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00087.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00088.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00089.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00090.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00091.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00092.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00093.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00094.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00095.txt \n",
- " inflating: PennFudanPed/Annotation/PennPed00096.txt \n",
- " creating: PennFudanPed/PedMasks/\n",
- " inflating: PennFudanPed/PedMasks/FudanPed00001_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00002_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00003_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00004_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00005_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00006_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00007_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00008_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00009_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00010_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00011_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00012_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00013_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00014_mask.png \n",
- " extracting: PennFudanPed/PedMasks/FudanPed00015_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00016_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00017_mask.png \n",
- " extracting: PennFudanPed/PedMasks/FudanPed00018_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00019_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00020_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00021_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00022_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00023_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00024_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00025_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00026_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00027_mask.png \n",
- " extracting: PennFudanPed/PedMasks/FudanPed00028_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00029_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00030_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00031_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00032_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00033_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00034_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00035_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00036_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00037_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00038_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00039_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00040_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00041_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00042_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00043_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00044_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00045_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00046_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00047_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00048_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00049_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00050_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00051_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00052_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00053_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00054_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00055_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00056_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00057_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00058_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00059_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00060_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00061_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00062_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00063_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00064_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00065_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00066_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00067_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00068_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00069_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00070_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00071_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00072_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00073_mask.png \n",
- " inflating: PennFudanPed/PedMasks/FudanPed00074_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00001_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00002_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00003_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00004_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00005_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00006_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00007_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00008_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00009_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00010_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00011_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00012_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00013_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00014_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00015_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00016_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00017_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00018_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00019_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00020_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00021_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00022_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00023_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00024_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00025_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00026_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00027_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00028_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00029_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00030_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00031_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00032_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00033_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00034_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00035_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00036_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00037_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00038_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00039_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00040_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00041_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00042_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00043_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00044_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00045_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00046_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00047_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00048_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00049_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00050_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00051_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00052_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00053_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00054_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00055_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00056_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00057_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00058_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00059_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00060_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00061_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00062_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00063_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00064_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00065_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00066_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00067_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00068_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00069_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00070_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00071_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00072_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00073_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00074_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00075_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00076_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00077_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00078_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00079_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00080_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00081_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00082_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00083_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00084_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00085_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00086_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00087_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00088_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00089_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00090_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00091_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00092_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00093_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00094_mask.png \n",
- " inflating: PennFudanPed/PedMasks/PennPed00095_mask.png \n",
- " extracting: PennFudanPed/PedMasks/PennPed00096_mask.png \n",
- " creating: PennFudanPed/PNGImages/\n",
- " inflating: PennFudanPed/PNGImages/FudanPed00001.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00002.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00003.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00004.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00005.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00006.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00007.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00008.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00009.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00010.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00011.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00012.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00013.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00014.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00015.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00016.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00017.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00018.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00019.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00020.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00021.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00022.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00023.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00024.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00025.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00026.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00027.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00028.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00029.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00030.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00031.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00032.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00033.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00034.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00035.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00036.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00037.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00038.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00039.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00040.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00041.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00042.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00043.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00044.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00045.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00046.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00047.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00048.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00049.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00050.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00051.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00052.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00053.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00054.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00055.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00056.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00057.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00058.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00059.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00060.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00061.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00062.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00063.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00064.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00065.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00066.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00067.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00068.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00069.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00070.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00071.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00072.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00073.png \n",
- " inflating: PennFudanPed/PNGImages/FudanPed00074.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00001.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00002.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00003.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00004.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00005.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00006.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00007.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00008.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00009.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00010.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00011.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00012.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00013.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00014.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00015.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00016.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00017.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00018.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00019.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00020.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00021.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00022.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00023.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00024.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00025.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00026.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00027.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00028.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00029.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00030.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00031.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00032.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00033.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00034.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00035.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00036.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00037.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00038.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00039.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00040.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00041.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00042.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00043.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00044.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00045.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00046.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00047.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00048.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00049.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00050.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00051.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00052.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00053.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00054.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00055.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00056.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00057.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00058.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00059.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00060.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00061.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00062.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00063.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00064.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00065.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00066.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00067.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00068.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00069.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00070.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00071.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00072.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00073.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00074.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00075.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00076.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00077.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00078.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00079.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00080.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00081.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00082.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00083.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00084.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00085.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00086.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00087.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00088.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00089.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00090.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00091.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00092.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00093.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00094.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00095.png \n",
- " inflating: PennFudanPed/PNGImages/PennPed00096.png \n",
- " inflating: PennFudanPed/readme.txt \n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 2
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "WfwuU-jI3j93",
- "colab_type": "text"
- },
- "source": [
- "Let's have a look at the dataset and how it is layed down.\n",
- "\n",
- "The data is structured as follows\n",
- "```\n",
- "PennFudanPed/\n",
- " PedMasks/\n",
- " FudanPed00001_mask.png\n",
- " FudanPed00002_mask.png\n",
- " FudanPed00003_mask.png\n",
- " FudanPed00004_mask.png\n",
- " ...\n",
- " PNGImages/\n",
- " FudanPed00001.png\n",
- " FudanPed00002.png\n",
- " FudanPed00003.png\n",
- " FudanPed00004.png\n",
- "```\n",
- "\n",
- "Here is one example of an image in the dataset, with its corresponding instance segmentation mask"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "LDjuVFgexFfh",
- "colab_type": "code",
- "outputId": "ad7713d2-9c54-4e2e-fe68-034d283ab478",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 553
- }
- },
- "source": [
- "from PIL import Image\n",
- "Image.open('PennFudanPed/PNGImages/FudanPed00001.png')"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAIYCAIAAAAqyZsGAAEAAElEQVR4nHz9V7MsSXImCCoxMycR\nccjlmVlZBAWgCqRnFj0iMyL7D/ZP7orsj9jHkX2Z2WkRTDcEjQIaBVRlVSW5mZcdEhFOjKjug7rb\n8XNv9kSmHIkb4eFubm6m9NNP8b/+H/8fVSUiIiqlxBgBIITAzMMwpJRCCE3TqOo0TSklVQ0h2MEA\n4L1HRBERkb7vz+fzixcv/v7v//6v//qv7WBEVFV7g4gAICKqCgDMrKo55/1+fz6f3759+/z585Jy\n0zTeexGxS6iqiDjn7DzMzMwiEmOMMf7hj9/8zd/8zTyPSAAA0zR0XRNjRMQQggj8l//yX/5f/8//\ndynleDy/fPXs1eeXu13THy5CCEzeOde41jn3j//nf/3Pf/9/Erjr/UWZcvDegwPS43RCRmauNwIA\niOi9t4HZrdkEMlJOMynUI+vLjrf3Ng+IqISqWkTsPHWWEDHnTER2ZjseABQKFSVezrAdT/2knmGZ\nOgBmJqLtaO209ef24To2X8/JzABQSiml2MzXJwgARERk75fB1x/WY+rjq4N0RNt5qDc4TdN2Zuqb\nmHOdw+232xVl/1wOyuWjwdTj7RnZkNbxExGllFJKIkJEHz1o+8QWqohkKY7brCIiNnK701JKCKFt\nW+9927aXl5fOOREJTHE4/+ov//zNmzfM3Ibmhx9+OHQ9M3ti7z0phBDmYXTOdV03z3MTfCnlF7/4\nxVdffeWcCyGklHa7HRF574nozZs3FxcX8zwT0TgPEFyS5Jxrmubbb78NIYQQROT+/v5wOMQYQwgx\nRiK6vb0N7ILgZy9ejuOoqqfT6enTp8MweO9LKSLStm2M8W/+5m9+//vfH4/HIskRM1NdOSGEnHMp\nxWa167oYIzO3bXs6nbIIUyNIpZS2bYnofD6HED5adff39//hP/yH3/zmN6TCSKCFiJxzyKSbh6eq\nU4oppbZtD4eDIkzDiEWuLi7fvn3bdR0Qishut3v37p3zXkSavhuGwTk3TdPf/U//8e///u/3TVc3\nVOh6770oXl5eDvMsqt53PoQCaAvAE8bp5ImUyJbBMAzswrNnz6Y5lVLmeZ6mKYkCQIxxnAdV3V3s\n5nmOMXrvp2nquu4v/uIvfvOb3wBA0zTOuVKWG8w5p2GyB2SC1FZj0zTjOOac7aKlFGa2h2KScCtk\nbM3/3d/93W9+85sPHz7YYQDQtq2CbVXZbhN7sv/z//w//8M//MP5fD4cDvb027YtMUGRPEebxlJK\nSsl7P8/zz372s9vb23EcbQssEiB4cjinaGOwcSLiOI5933ddx8zzPIuI6YWUUnC+HpZzds4550yt\nmEiPMYqIySj3hz/8IcZYSnHOVQlFRDlnOy6EYJLUVqFpEXsY9Sz2E5vTd+/eff/9923b2re2heyW\n6mxWOeKcA4Ccs51WREwV2ejrPVet9pEItvOfz2cA8WG5z8NhZ/c/DAMA9X2/2+3evn374cOH/aED\nuNwKKZM2RHQaBhFhRhMuCQAR2JP3HnmRmFsxmjdS0kSViAigY/5RbVQHv5X+IsrMsFHSHx1mn1fV\nAigEWH9eFZjN0lbE1+umUmwz2MFVjG7ncztOE8UmiO0ebULqU66aRkSI7Eey1Rb15x+9/0iD2nsi\nsiHZStiqHPunWULb16djfjx+/OifW6W1UbpYtZFduhpJddo/el4PQgFpe0Jb24fDoUqZGKNtFnF8\n2O1sW8YYTWvbr8yWckgpJUkZAGKM8zwP5xMRnU6nYRhMQaaUxnE0A4uZ7+/vp2kyNVM0w0ipRGb+\n8q/+6rs/ft20bjyeu65ryHkgJNf5xgOFEDxQ8N4DqerFxQUA/OIXv5im6cmTJ4jYNI1t9pTS9fX1\nF198MY5jSinOo0iZpmmapv1+X01SALB7TCnZQyyl+BBiFlCwb1NKphiqlLB7N1OSiLrQTMNICPZh\nKdkmkIhwNcXMFIgxFpVpmvrQ3N3dLUawKgDc398DgKnJ+kRMKx8Oh/k0YDWPOJZSclERGea5lALI\n7AIAxZJNG7WBEmJahzFNk+iQUppjNgMxhKAKInJ5efmLJz97/cP3oQtd15kINaNqGIYXL17UBWZL\nyHu/73otEkIwDWGaxqb9/fv3IpJztnmb59lMnJSSrVj7iRklzrmvvvrqeDyaujKFNM+zqjpPny7+\najDZIBHRHI95GJ9cXiVAm0BTBLYZPxIytotN7qmqqQBbAHaD9phs5HYLy8FBUkp2vL1h5hijc67q\nkXoS99lnnw3DYF+bOWMTZG/s5m30JjVM0FdRYrqKiMxEmqap7/unT59eXFyYaqlrER7Z1GQbrO/7\nKhcuLy/btjVPQVdD3rTgPM/2cxuSzUu12b/99lsiANSc83/7b//82Wcvx3G0bbPbHe7v729vbwFg\nt9tdXFyAIpEjdITOOe+9J+8IcJomu1lmFir1BhnZtFEVoPaAbVqqqbLIR9GSo2mj+uGjAzYve8gm\nILfyusrKrWhe9DEo6CPnAD5RP59olwdZDOuFYKO9PvoJomyVbhXT1VfbHo9os/HgpmxthU9VMgDg\nY9+oTlT1pT56sfc/+nnVxFsrQVUD81Zv1Q1Z/ex6ZF1mAGDWz6e+I2xcKCIi0Bij4MOkVTPLVo59\nYgsLEbvg0zjYFnDOdW1nImMcx2fXT1JKnjjnXHdyjDF4ZxuqbdvqL9p6M/u9bdt6+54dFNFYAMpP\nn738b4J78sP5Jvh2HGMRLDlLgTRN3LYYIxYQ5u/evbu6ukopPXv27Ouvv/bem/iA1YP/9ttvzdbM\nOTftEgNIpTx78eLNmzeplGVhALD3yIyI5Jwn6rt9h4TIJjFjjD/96U9/+OEHk4MxRttTXdd1Xffs\n2bOLXX+8u2cCVZ3neZjGlJLJO7DwA2EV6DbJKaXz8WQalFfXtm3blHMppcyzjVxVh2EAgOvrawCI\nRUxWmMw4Ho++bRcBgpHQOYTCDCopJSBKpQCACbc55nmeQ9OZcUZE8zCeTifn3OFweP3D9/MwLmsp\nZRAppbx5/b05GaYgTdC3bXv4cvdv//7vNhsmSEspOWdzR+x4Zm6axpTHq1evvv7666ZpTDLbr6qS\n/vzzzy1o1DSNCUlEbIMz3VOtK3tz+/4GinahbVyQptOgzjkGQqQ5ZyKClGJKuZSsioixlKwq6/ZR\nIgUgE01gEpEKZlVFBUfcNa3ZrwS4/I8ExLAR+3XfmSqxl2lH28XObE9TWdWvNPPH9lWdBTtjCKEK\nKbNxbIJsZgFgHMeu68zxzDnXa4tIjYfYdq36xgwlC27QqsyrcWoPrO/7Or+2QO23v/71y+Px2Pet\n8xa+m/7qr35VLxpj/od/+Id12MPxeHz56tJu1nzGEIJzHjJM02QnVlXnHCFqWfa8yoMIg1VVVJul\naoLlwfDHtjlsVMInghJyzroeWdXbj2oX26KYpUr/6jZtf7g15+1EW5W2FaMfCfc6ZADejsFOvo1N\nwYPTUFRLlfkfqYrtnX46J9uD7V7g8ct+mzef1ykCAJv/j66LqgKPtKB+Err8SEeaB2+KpJ6wRoNr\njNH+MmB76JUe5rkaZBY6g9Vlt1h314QvXr549fL5Z5991jRNG5rj8YhF5nkejqdpmi73h+PxqLno\nattJySJyOp2qS2qDjDGO4+i9N3vZJLv3vNvtChQAiFKilCmnpDLEub84AIAyUfBpHCCnoqIlX7St\nLRU7v7lxZowCgEnD+/t7U65EdDoO4KDzHXn34vmru9NxHOaChYQEwXHQoFiwgKY5I8+qWMpiO5/P\n52fPnv3xj3+0OVmMd+eGYRiG4e7u7vricHdz690SDnXBHw4HIhLVYRhCCOQdAFgIBJm0F8jlYn/Y\n7/cAQI4B4MmTJ6fzue/7GCMw2YNQ1VevXonIzfsPDolzEZFxHLMUi4iaXV8EEBE9EhEpyuq8VqFn\ns6SqgGymvSmA3W53eXl5cXERp3mKoxYRUC3im8BIc4olZSLKMSFTGxoR0SJ929md1mWmawD5+vra\ne386nUyBVR/UJs3EZjWeiOju7m6/35sZ0XWdiMzzHEIIjkzwfmRump9nUtd8VkR0xJ9//vmbN29s\nkm292Q3u93sLNdnwqs/ade0wnQkQmXZdrwiMlEomQCRyxE3TBOfJMSMVFdrkdGp4zLwXuym7HZt2\nZzdvplwV/TU4ZhbxVifb+Eyd2K1WD65OmSn/avF9OpX1nPZtztlCqIiI8Cg3UCe0Ovv1iiYj1qB/\nEMHq/9qORUTmVMWKRbeBHbJ3zjM75xsfWkYnksdxLCIpJRbw5IkozhFAhB9kZb26jXkbW1sEJSAC\n26i3n+snbi+svpGI6EbeVauhmhKPtBEo6BIHhI1/ABuFtB0SEUnOdn6tCmlN2n2qpVQVFBHB/l/W\nMYICkHcfiXURUUXRRf7WO60Lt0rz6lRV52Orluy6NVL30WurdepSRkTJuY7/4ejNk9oqQlWteb6H\nyTdLY2Om2Se0RgV0teO25xmnXI0hu3FJuXgfQnBIRYoF4sdcVDUG9+a7b7/79utlQymUUjofEHHf\n9THG64vLnDMp1PXp3aIa+743s7eU0jTNbrez6PzTp0+nabIQPHpyfTuk0Tnnnl785G/+8nA4fCa/\nFJGvv/465yyCYdeMIyYH4FkQb89HS+Q4506nk4Xs6nq2rV2fERHtLg4CGlwT8yxIKcsYU9G87w8M\nAuyKJBVVlTGmAuhcMKFhIqLrOlPVVeWbme+93+/3Xdc5YpU8p1hK0ZREZI5xGIa+7wso5SQiArps\neQWJ6fJw8fqH7220Oeenz55988038zzHkhcbF6GU8vqH79+/f9+3O5tDZj6dR0R8cn0g75fnq0uE\nhByXrDnNu77tQshrPiPG2Gdpmubu/mSR2JQSO9+2LTNb2ka1cEABKCmRc13T9NDffvjASMCMzJ4Z\nFbSUGKPJpa1vZDrg9va26zpTeJaqt/k/HA4552maTKabDW3qylwu+0rX+DC0QfISNKqOu8lnc19U\nlABBVMuSSbGooD30pmlMq53P52222FaIqr569fL+9pimGR2TAjAx4JzTod8BEymgEiOpohYtIt3F\nbp5TKQWAFhkJiMjX10+r3Kgb0/32t7+t9le1Us15rOmcrdFnfoxJ/Co96yI2X+p8PttEiEjXdbQJ\n08HjrK+5803TNE1jSn4axo8E6+rBONhkXKpYRPIhBAARLTatt7e3tg2GYShFLSxwe3sbY7TBOOed\nc+zdshCB56IxF7tTAfMUHWIyg+lTEYlrnH0rrYiIkaQk1a2rARtd8nHeCPVRHK/KUNPonxryCAJF\n6LE8rYKjHraNONVPtrrHzI7tAfVsusZCP72EveqjWTYSbwN3uP1J9VBho/N+RIWsv/10ngHAzJR6\nTH2ZaNvegg3YuR+P1OFj17CqoqqV6+fVpvloYPYTW/ZVNbr1VcEOsIYNcs4lU98EAGjbtpSS5lij\n3BYeR8SUEgNajIGZT8fJhKz33lasDebt27fzPO92u2maPnz4YAMrms9pLijOuf/y9//n8Xjc7XYm\nUJxzFvyhHjQXQGJmUnDOXRwuq2H39OnTKnHMKAwh9H0/jiMAKCEQZxFSmvN8/eTZn/35X37+2aSk\n3339HefgyM9TJqTQtipMRMf7+7IJc93d3ZlMN1tb1uC/GcHjOOc4F0kmo/u+7/reh6CWSrKlwsTr\ngyDEKUYgtFR5CCHlfHl5maQAEwM754CWp2m3Y9ZzSsk3waJn7a6PJd/c3CCiwmKbm32cUrpz1Hov\nq/E0TRO7YPLEOWcpAKVkuvyPf/xq13aOiJGQqQDGnErKu8MeL69c8FoEmRofbLPHaXr16lVFgtiE\niIjF4syIt7t+9+7d6XQ6n8+21Lf2XEppmiaTP0RkUnTZdKq4msJ1EdoPt7FoWIWwYWds6dqRJrRt\nNuwnVfjblF5fXM3DeM4LzqA6BiklzMu+UABJxYKuL168OJ/PNUhmN5hzPp/PVUaZC6Sq7m//9m+r\nsQ8bnJuuIDpTBnVMNlBZs7XDMJgpNAxDvYHz+Xx1dWWB7+PxWHf4VkqO42g7cxgGUxLH4/FwOJSU\n7XK6ieznnC8vL6vo2cq103m6vr6epsEidaWUDx8+2DSN44jId3d3tiJDCME3TJ5dYBcIHbNnH1AJ\n5pRzJu+8D5DLKmvANUFLBFoecJX7Ji+2Um+RblocI2xUZhWIdcy6YgFWMfcoDFjP+KlsNhmoova7\nrRSu01LfVOuekdYTIhnuENCm1TygqkJWVw9xHVNdu7BmjG2gizlTSskZgQCglAedvSx3QFlzjQRo\niV8RMQtpe3DdHtt7qccwPqAhzK2rihwA8KOJ0mUBf6qNtpH0qmtxTdhuTQr7bd2K+tivlSJia9g5\nREIFLZIl+c5ZPB0RPTsiCs77wCjFEETMLObf5xJj7JvWwmIi4p233YSITGhSyeyzOuYKzQKA8/m8\nAIvmiVPZt6EMc875hWuazBJjKNK2NEXsXXjGfdHgxDlyonp7Pt6nYqGSCscKIczzPM9z13UhhJ//\n/OffffddjJF8KEhACAKKmrMqKioi409/8QsBCS6chlNw4XB5GM/jPE+N81LKOI525qZpPv/88/v7\ne9uDlmzH1Yodp/Hq4mBRppiTKOYsKZV5TkQEtIRMiUgApAiqhKabxtg2fcwpNC2SK0UBiJmLQhaF\ndRXneUbk0ARiLnNq0DnnOQRzlWjFR5RSVASQmUAZS4yneVYik0Ii0jh3OBx+/9UfTWgCANFiUmgu\nKUZEnWJCpuD8NIzqy/Pnz3/49rWAEqDFrLIUED2fz+SYnLNgWtUiTdPgiuqqMK79fq+qT58+tQ+3\nyUUbxrAAr7iKjhxjG5qScqZsC77u4nmMtm0tSZFz1gLBNcfTcB6mrutEUYoglWlOTQuAbLIpFzs5\nKKwxsCySRUBkhS+Z8SQq1SbWolpURJ3zCFSygJa6JaWoa/wSAgUERYMBOlydIVsu1XWyzWDuKqxB\nJDMfygpYtPipCXoAqJsnxng4HPq+JyIz7nQNa1RPq5TSdV3O2Qy6Usrbt28vLy8llx9FeFc9XGXT\nKonvXr58eX9/27SBmfu+9Z5tzBcXF9MUDTTYtm0pehzOT/EJWoSTHDIROgBVhDHODTlEFNVYMipk\nlRY/xsVVKbnVKA/iTyzo/EhPfGS/bz8HACkPESfcBCerWHwsVbUo/CjCuzqp29AT4qISqgqEDRjk\n0WErbsUuVeV1Ha2JP9y4rTYG7x9J/3p8Hb+dv55Q9OMprYfBj6lYKznQjf2xnc/tr+wYS6h8qo10\nE0Ks46lGMayu/9YMqjdSz6Cq7W5f1djWZd+uDVxdN++dAzcMp+PxmFLSIofDwTPb5jJrr5TCTVvx\neDmnGqUpK1DKhm3OqKV5lioLREv3DsNg+HIiurm5Mceu3oUJppxzyrnvewUw76RpmtvbW7PQLy4u\nhmEwsXh5efnNN9+M44gpDzGx87ah7u+ONQNvnkff9wZcevLkyd3d3d3trUN0zOZa2TBCCOM47nY7\nU6iIaGGutm3HcYSS2xCarkXEvu8PhwMwTdMU2kbXWJMiGlhLcm7Zn+6Pu8PekNzDMChh13XIBONo\nd5pKMXvR5jmlZFkoYDIEmnkYNrEVvmFPf39xMU1TXA1rXWO5NpP2c2BnY2vczjFLTkM8m/1BgN77\nZ0+efvOnry3s5p0HAJvYcZ5q4GG7qu3DYRjO57N9ZeOxoBmsrp55ybvdrm3bvu/fv39v2DH7672P\n05TmqOVx2Qkv2TW7FwOYTNOkqvuLQwhht9s9ffq04im898+fPx+GwY6vQby6omjF9VU8AW5gbnZA\n3RGmMmpiEtdsmelUXQPjS3TX1nHFJtAK18s5X11dffXVV//L//K/vHnzpm1bc4NqhsA8NVkhSeZF\nzfP84sWLf/7nf/6zP/sz21R1/29xtHY/NriLiwtzpQ2nYB6xGQ423P1+PwyD3QNuimB0NdKHYdjv\n9+M02Jmvrq7Gcby/v2/btutY1jS1QVS99943zjfee+8aZq+q3jUlC7WsCOSdlpKLGFKllKLyICtr\naA7WGGZ9YKaepVgYXatErre8Fe71hIRowuyhZkdV11oEAKA1gQOgCuKcA3yQlfVUNi12LTN/7Kvq\nW2xnntcCgroraJOT2+yTh/c5x3UGqjJQ56hskOXbNzXMXbXdMkgVfOwbfaScPnqPj6N/9X5pk4lc\nJmoT3dVP8mp16SOiSSJTJ7qJrVWDzNZ/Db7DxpGy0gWz3kwrdF1ntQ0VjKOqpRTLxcZ5vry8tBMG\n5y8uLjofUkqksN/vGfCv/uqvoCzIKBHxjkXEFvAXX3yhqldXV3d3d7RC0aZp+uKLLwDg7du3WdLd\neI4M9zK+evXc8AIzRpKcPtyr6suLput5umgWxzehzzEghxAuLi5MSdjTmabJJuH29tYEnBWL8Pqq\nIqY6PXd3d3abv/vd7/72b//222+/9d5rzrIC/4ZhuLy8PB6PIYQPHz5cXFwgoomRJ0+epJROpxMD\njjBbaOTi+upP33735MmT0+nkvL+7u2t3vYX7mqbZHfbHu/syR0nZYuxKyMz/6//6/2XmXAoRxZKf\nP39uGJC//tv/8Pbt267peIUjm8I+n88//elPLd1iQqZxDhHP57MVPoqIEomIvW+7PudsEa0PHz6k\nlO7PQ4zx5cuXwzSC6mHXm5dpmm8cRwPxeu/HccQVD2mCnpjnGIlov9+bmrThmWliER1bZracELEO\nFQAs+mpyrIb7qqICgBgXHEApZRwnu+g0Td1ufzyezEqom/3D7V0pBYnG6TVuQuvDOD9//vz771/X\n7bYUPzl6+zZO0+ScI8dZCjk2a2a321WIgJ0qtI1d6NmzZ5eXlyaXzEpIKV1dXdl9mSw6n88pJWf/\nqMLCTDD7pWkCC9FudyM+tvSr9MS1ksD0ip12G9+v8sV0g2xADfZz770WMYPRQtg2XIv/1lHpmvYg\nIsMEblW01UYYBnSaojm5FYZE7Ik9P/zPdQY30DAFRMMMkHuEPcPH6Yft5w8y9BHuAKoy2M5YnRB6\nnKGpZ6sR5McvUVXYgLDrpeWT7P1yM6LVp4SNmfyp3F8u8BjDVt9/VA/00b1sv6ra4tMjAYCJt0ql\njvnT6y5PAh/UtP2qLndYA8vbnzxEFx/7UrZn6qXrQ6zm13YkVT3jpsQVVmybblCqts63ECZcgw3z\nPDuCy4u9uSzzPJ+mOaUUiFNKKHo8Hh1SKWU8nQ2m7L1vgp/n+fPPP//d7353cXFxPp/btjXdaVrh\n7u4OAAx/hQyub/uLXSml1rHqWp9umuzFixcvXrxYQAS5BCBIS9GJJaurDC2lmHtkNZI556bryjQX\nLXGKwzS0oR3nkYC6XSelACoCEGPfdcfTvWMWKaUUWVeFSRKbosvLS5NoVSTZFO3azhDwSng+n+d5\nfv36NTHv9/usS9qjlBJz8jHmnNumKUjOOWCyx+CcU4DdbgdM6f7+/v7+fD6Htpnn+Xh/utejY7bL\ndV2nqvM8Hw4Hw39771OKgZ3JAQAYhuF4PI4xmnGZc767uzudTobwNgF4/ew5InZdx6DjMBwOO8+u\n6dp9v0slM9KzF88///xzAZVcUskgen86jueh3++KStogwgzEH0L47rvvTFpaUNcOqAk280VsXcUY\n7+7uzOK0ebYFhojIXCO6aGESIkT0JkybxsB2qppLUZG0zkndVrCmTs0Dq0Y/L3MocZqR1AHMOZWc\nOXgROQ7ntm3nnPIcswoUSVIM43B3PlUbcSsNDCNajbYlb6SqphiqOrGtZQk059wPP/xgGVdzPK1E\nHNaSVb/W3No6s8DCmzdv7OC8lojSiuuwwywWZ7Np/7Tl0jSNZ2fb43A4qKqF8ir4h9bC4LJWaSHi\nPM85RwUhommanKMYo2XJUirbiuKu23kfvG+8D+w9OY/sGIV5A+hCBEJQUCimoODxCzdEAFU+VqlH\nRObsbAVZdc8/Ep3wkP9A+wIAFBQA1hzPJ9eucLfHsrtKz48ukUsmBXYO0XIcRUqRTeAO1tTLqtXS\nw/B0M9Sq7T6KWCpBRUxYLRQsvtF29S02BKjio/DXVk1+dEf2csQMaFBCmyiCFfRHH09RVVmw0cf1\nZSZkjcBsVyauAYTtAOzDbQyAiPxj1AMRMSKI9G2rq+tZlSURVFPP7KR5nh1gKeXQ706nU2CL4Jey\n0qBM4zDP869//WtYU9YmGmw/2k4xIyyE0Dg+39w9PwQdykts3x3jNN3nnItztvtG+v57/NdqScSU\nuA3DONonv/jFL3744YdxHKtqv7u767ru/fv39j5Mo29a59zF9XWBi7/85V/+8O4HUtpd7Pqmz5q7\n0PnWD8fh+avnh7ZPKbVNUx30lNKTJ09ubm6I6P379zYDZtc3TWPxpdPxPExz27Zd26eULq+ub25u\nnlxezfNcipQixErsgm+8C23Xp3FSBUYCAVAEov3hwmQ0EwHgHBMgdW3P5BShCDBQTAUAFWiapxSj\nSRgi8kQlphmz9+ycaxv/9dfvRQTX6AIzhyY0TWM1s4ZAE6Sc883NzatXL25ub+9Pd46YHBNgKjnN\nMUtpQ4NMfdtNce7bLuY0nM5/9Td//S+/+c1Hot8WkjmpFk/CNch2OBxs+VWwDK3JFOecUXKYMNQV\nDs3sT6cTiqJjZo4lE7FzfHt3N8Y5pyQIDomDZ0AzktLKsOM3tX1bywzXiGUqpWuD996zK3EWKI5c\nzuU8TC9fBCqiWGyjIiEhsXfmSDEzItQN6L0/HC4ReZqmVWyCiLgqCHADlDINoaovX740tKWVIjnn\nfv7zn5vLYuLeHFhzKk2XTtP0F3/xF1W32UM1WWkoC0PT2VrMa3WY7bqmaQiQiGqc0SYlxmiRzWrM\nlrUyGackIojg3FJ+aBEYS5aO42wqzeK2FmlkdrjWGznntBRyLLCIS1YA1QIACviJC7I1rrefwH9f\nG8GKMIaNF1J/UlL+VATDxhd5ZFOgINGP+kb6iUMGtv/4IXBXU4D6SZ7m4eobQPP2jT5+Pdy4PlLP\nsLGLt7dTfyWfKCQ74KPjH8ZPKo/nbRvH3+7qxX2BH/HVcK2Hqz7Wp/eyPRsiWnaB1pI7+9A51/pu\nO+x6IQMO6Vq6Z4uwaXxeq3ksU+Kc80ilFM/ueDyCD6WUJ5dXsDIwcQhm3h4OB9uGtGbUAWC/3/NK\nvpJzLtMEog4JRRvnHRIUIQUGlJQJIM/R8GywhoXHcTQXyuSCUUKYGbca0I2lgi4vL0XkfD6xdw5Q\nUbo2jOfj/e3Rv3dpzuyJ0bnAkvWf/+UfHfmUUimLCLNM2JMnT969eycipn62SRq7hSfXTwHAEiHj\nPP3yl7/893//96unTwxS6EMw/yCE0HRtSXnXtDkmm/BhGqdpury8vLm/sy222+8BwEqOpjgDkJRS\nCGLMRLCAqiQDQN/3ALqaJkWVajIMEdE5WNkxAGOM0SqT7C7KWkDzy1/+8ng8xjgVlZSEANj7pmvn\n00lAU4zOuZu7u5yzIqaSn714kf7hH2qAx9aJrPD6mgeRTemIBf0sDAgb8hqLVVrIx6SrrYpf/eqv\n5hTncWq6VkqJOQkJMqECMoWuJceNDy6Y/nXPnj0bT2eDtNhis41gwpxX28tWhbkuuURVbR254E2s\nXaNScFQYPVMBIUQRRVQEv3Lx4BrAt3/a+O3GYXXInLkvuAL47J4r1sCABjbKKsJMi1Q4g63pKnwN\nniArBsG0wlYbVWklK5APNiQTOSYDk1gazYyR77777uc//7lsgH8197XmsZZsrak3q2lomsa50Q4I\n6yYHZCDH7IkcOU/OCxBhEpGsJuVRECqGTFa02IOyQcTHCSTdgIMRfjxS95Gc3crErVDbvq+C8tOf\n/1+8cBtLVPDek2WnABCAEOmxc/CR7ObV33g4CQAA0LqFProdkceunp0KgDfKpl5CVvdoe8WPJPuj\nKVJQ0Qqcw4cUGuSUEFEf49pFVelBA8kKzajLuy6/7czjJy8A6Pu+rMWP1XVY0q2A1URdTiW66/pt\n+tD2dtN4YgjBLZEx59u2dYA5ZyjS9/3Tq+vb29vri0sDLKSUVErTNK9fvw4hWAjLnAzLb1tuqRZ4\nzjkWkndpuIP0erj7UKbIoqTBg9nTJSUobmRbriWEsG8vQ9NYqJxWfCwRGZJot9vZyU+nk4XsXjx7\nFiU6wCgFpSCI5hQhTaep2TUxKXpsuDkO9xf9hYIZi2TqHFbFY9NSP7SXRb0sN3MehzktoZvjcD4O\nZxHJaxFClmLzoEUCMQH2+515KkR0/expVnHOIdHl1VXTNDEnq/Tc7y980zHz6e7eOaeSh2Houyal\n9P7Nm1IKITpGosDMJc7DMMzzPAzDnLMpyLZtpzkdj0diX8VO1RYm4opKyqWoEGDDxEjk2IUAUpAZ\nCIsqICiizbM9u2p+mSFlDHjVI8EVvWzYd1mx0csVS7GcpaxA7Rp6ccGnosM4FyRPDOSQGIjG86CE\nDChF4pzRsSdGRO+b9+/fW/iXVz5GIrL0m9kx5YGjSH75y1++f/9+nud+7+0nIYSXny3VzdVXM+2A\niFAkr5rCe6hpoOPxHGMUAWbvnGua1TfiDc4N1jy2jclSahbnrZF3O8YCjgY6MM1s/oc5YlUbVX2D\n+LCHYa361jWxXN0aq2G2nW/aqDpYH71snE3oAABRi2Q73oIYtrJ1wyixze3jCvBjZlRAx9t8wyKh\nAOETNVAvXYVU/VxVRZVwqU7FTaSuLr6PhGCVrXVd1q/qvD1SAP9934hXNgF4rJBMN1a3oE74R5oS\nN94GbJTlR8dsvb3t8Z++ttHLB4UHQISKPzYPn0wCAIAo08PXH2nr7Rtb4hZFNOaeH10wthLwIZJG\nnw5jOyF13mqEIWupp1pDEAhgXB5gK8qES4xxGLBIIlqmrg1N0zSskHP2xAZJff369TyMxn3lnGub\nkHN+9+7dxcVFKcXcKRExE834BU6n0/X1ddd1RTM5B6Tn8/nlF58XBACoeCJETCnt9/v379/bCLu2\njefR9jszG/DabjDnbFwP9/f3FgKyAbx99wMiWhjnPBwdEjsUkYvLvQHqSinssPWhSEJg8mwZ2JqR\ntbkahoUvrmxAnkTk2LdtO8W5SuemaY7How/Br7iJWhrvvCcFSy1Xbfri+Oq7776b5jmvPHICagGi\n/f7i/jQgcp6n3W43jaP3/NMvv3j37h0ua7hU11NSTGl+cn19cXFhCG/DuyM5Vb28elLWF4dmmibz\nhr/82U9LSeZiVkW1vzi8e/eOmRVhv99b5s97fx6HasVu162J0JopB1hcCgvM4iZBXhOWh8PBnp1f\ny7oRsagAOfYOmLKUUkqWksgIgNAFT4AqJecCZZFIbddZpko3qT5EvLm5sfCV5Uqdc6YX3314/8dv\nvh5OJ/benMquadh7RzSnBCKKSACpFAssffnq8/PpVMMGNv6aajGQRdWm7g9/+EPV1bhBrFny/+bm\n5unTp4g4z3Pf96ZC6u6tWsrOVeHgtR4CHyODbfWYOLBAhF3UFK+5yVoWwFLF4CGibQw7EjexFGY+\nnQ00Cbk8kFhYdZj5W7akzORRVQBCZCLH7Jk8k0c2UU6IjIiEBIgkQIBotcaP9URVZh9rLzTkQ7Hd\nWBcc/l96AFuB+OnrQaksx+gCrvvv/KQucVjxFEXKwiW3nqS6xv+dC8FabvToq5Ri9bgR0TCAIuoc\nbw+r77f6bKMaQRXl8fi36uqj6+JiFvzI7NkGridflCIiIpbH46+PrGJMH0Shucs/dvBHCrhKDRbe\nXrce0Pe9HeM3vI66lJI8KPWcM8DiqPV9f319jYh5Ddw3TXM63pshcn9/jyscy9wUQzrM8/zmzZu3\nb982TTPPoyc+He+apvnjv/y2lGKwI2Y2Ss1Syq9+9at3f/r2cDiMw+AOB9toNmaDd5u/st/vjcix\n7/vnz59byaCIlBydYwstXF5eBueuLy9NuJg2Mq1AT5/e3t6Sc/enyYJ1tvvCyiBu6sFmhlbUkgEZ\n6j06547Ho+1rU5kG01r0Rime3ThOWqSVYmUbqmoox7ZtTW6cTqeiS7b/fB6BnCoSkSAM4/h89+Tl\ny5cfPny4ff8+5+wd5Zw1JyIahgGYAJzRgd/d3f3www8i4kPbNM2//fvvAWCpoPdLIuAPf/g9MrnG\n2TitrNV7//LlS0EgwjknJZzSwpjwm9/85vr62pS02e72K+PdsOdrMBm7qb7vP//881o5M02TwQVt\n8b99+9Y2QjVlSin3p2OW4oJHpjTHouLIAeE4jA1BcF5ApRKurC/eFLrCpuGARZssYJZzFlVyruna\nGKOAiigQplKmnFDBaqrYO0YSMP46mqbJiKBsx1Voq+0+8/vr1nO/+tWvcEWFu5WJxFwiE7hffvkl\nAIzjeHl5aYlW2ZAu18SUfWjKyegVaCFRj2tex6hOzZDHu7ubutpssZpzfdhd2HtDMZjJOY7jf/pP\n/4lWuuWKaOy67sPNrdkRoqVtw93dzc3Nld3L+XwGoNvb+5TSNMWc86E/sKJTdEhVQQIuTisDMjAB\nEQIxMqBqCd6bRfIgfZAQkJ1f5bsgskkcBICySPMqZBVJRILzn6iWj6Nw2/dVCG5/ogDMqMggqgio\noAgEqAglZSC0T1ChqFjZAQMCAZEDEAAEEFUSyfaJKta/AKRaUtG6SpdbQAAAAQVQogU7gEhSiiII\nFNBHJEb2tzoN9at1fYuigKBAIWAgRWUl8RzscyUBQUVBZVUtudCPqSvZVPZVraAA5B9pqe18Vqto\nG2VFLWBYEkJGQkZHHhBZAZCCNxXECuCYHQdErvZpxTiggombNMdIMzwgwok4mG8kIiXllFJgx0RM\nLCIp59PpZMOLJcch94f9zc3NF198sZCNIpzGgYKPFu5gdt4jkQKknOc5XT493N/dNKG7u78JvkXE\nFEuE+OT62Xk4TmN8cnX9J/jas5OsKRZAEqQiysyncbK9Y6hlVZXjSVXvTufb29s37z8gKokias5S\nShIB703h8jyn/b5PqcQ4ed9cXh7u7k4hhL7tU0o5i6KiKKJ6773ntm2bxtuqa9v+cNgB0DRN+3a3\n3+9Pp1O33+WcD4fDqxcvj+cTESnhMAwGshinaZomJhpVc87MBKAiBqqOp9NxnCezA4yx4urqcp4m\nJAagOGdm9sTTeE7pYHHIRRp6ElBgp6jAjpyfU7FOOmYf7NqWbKcTtm0LTL5tpmma0/TsyfPzeCql\nOA5xzjmJd1iydm14/uzlv/32dyGoyNy2LSKoYBO6YZiG09kAFKZvTA1fXFzc3t6aTrX7NUINU8lT\nnFHBBQ+iWcqu6y+vn/RdL/COyLX9DpHJ8a7rpzhrkcNu/+TiygVfUibHF/uDvW/7rvEhSykpI5PV\nfrSOVXLjWAlRdJgnzYW8c0iI2jgGEFLX9G2eKUk5nU4qGRG1JETu+5bQnc73h8NVTFNOAigqoJJF\nEMTYPVzOAVFNwgBwCG6ek/HulpJyFgAhck5LthRJ452qzuMAAG1Yor1aMoGKiCMsKUpOWikS8kMn\nmJQX0wBV7m9vSs5p5qZpShKR1DT+fD4jBBMBTdOkNHatQ8S+8wa4nOf522+/ffXyuQq2bSC6qsg/\nRPzpT39SVlhkdVfN0dm/efvZZ5+p2v1QTBMRpTSnVEop+93Fv/3rv3dNj+pgjwR4CO3O++CZHaFD\n8MjZM3uNsr/sdcpZS+O9IHDjS4Q4zVTFGiogChREXIAOqjaPRGDmXClrpwnDliASIjNqWU0AAKxq\nRrRduYQBAFegWZWh+DGyziGqoJBpj+1fxwJLtwlGNH9ZVSUXK/e05yZSTEpXbg1jjgJQABTgmLOu\nvp3a/zZUZkHMAMYHAqqAqKUIocgStMQNnSjQRk8wIZIaPqcoGOMMES8pOsmlFNECQopKQMbFCAAI\nQrSc63FIjdgDAOCjYCmhxpS2HS6qP6cqqqaP7d5BJOcogVlz0SKKgMSkDKCiqs5JKaoknAQJCJW8\n+HJ5/fTu7m4cR6OzirmIiCdGVYdEbrExlyAeg2/5cLHf7XYmxfu+Z8CUEgH2TRtz/Lv/6e/MhXLO\nFZEC+v7mwzAMu6dXcZoLITZ+1pJRXRtmLV+//vZ8OsHpvu97APj+7hb67t14Vsftrj+mpN4r0Nu7\nuyJptz+8ub0N+/05JWrbqRSznkQVkHzXW0B7v98j4u3trbLLOT9pu9P0g/c+kFcQyZKTXlw8TSmn\nFJma4Tw6F+ZJEV3fXYXQnI6j404FTvdHQPGuiXG+vnxyvL0hclA0K6Q0qmIp6TxO//E//t/+7d9+\ny0g6FRQQEQ7eksQhhKLivS8ihu5LKf3lX/363XffN10zTmff+v6iBSeXl5fzPP/23/756nr/Ijwx\n3+LJkydd193d33/+2Wevv/shhPbqcGkVS69ePEkplRhfPH16Gi1SAo3lbOZRnBtTPo5jkaVzzzzP\nu+vr9+/fP336NN7fcSEgPY+nEMKhO0xxDCGA0jzNec5MDAUCB0/+dHfqm15E2qZFwBSTJ4+Cwzh6\nRzVWzGtdFwCY92D1SSEEo7ZpmmacBw4+uKaAztOUVZwLwxR3/aHt93cf7sZ03/qmpDIO94gwj1FE\nUFQJDWn9DhAdtz7MOUERY5ZLUqCIUaaoqmkpR6wIaY7XT5+8fP7s5rfvZynkOOWIGvquiTl5hH3X\n7toOUZ0Lh8PO++Z8Pj558mwcz/OcEJXZGzJDJaNg03jvPTOKQM4xZ5nn8fr68nS6J4LLy6uUyjie\nVdHVOFKFc1hM2bKLhtmoCdsHf2I1fqtyqgAMs7aW3UhaoiBaSNSJQIxTKSWluW17RLVEkp3Se08E\n3a4vWXWt0YWV0nFb71If52qlgnMeURUKZmRGAN91u5yzd+1+f7DjY8yayyJ9TbIZSw0jM4MoiLIC\niKpYH7xFthNIVR7GKqpQVltbARBBEOiB+mILglv/3yaZYOP0mJ9XYY3bxMyPxa8EEQGXc336d/kt\nIiIaFK2sFZ31ogaONgfOuBHWCykguOAFgQGXnCcCKRRQKGLYUHTskASBc0lSUBSYnIISemIltOM1\nlwJKCnYeJeSCqopMpt23MTG/7eH0KNuEc0n1w602+sj1WVeFkm46tqnqGlL3j0l+7RWIHCCyFrDG\nRUywVJ5pESyCiKyAYEUiIGu7LzNv7YQOiYhktZYWt1sBimgR3/k8zu+PZ0szLOSqpZANWKsX5RCx\nqPiuRabr6+vj8Zhj6roORaHIUqiren11dbHbGxspIg7zZDN/dXVlFjchWk4rTjMANM4739SKKHQu\n5TxPk3l7gFRybtqOEA8XGrw5YYLEKeWUMgM74rnImw+3TdOklCm0Qo5CM6c0Tee+75vdoWE3Zcnz\nZJaKQlGR5S8WVS4l1+dooTjvGZWUgQlLKVpkTmNKyVZamiMygWrwnok0l3kYp3nsdkG1DMNwf38r\nIjFOxkp6PB4B5HRyNzfvm6abpmG/2/3p6z9gBueCIctjSufz+fb9+3Ech3lCRHILMEGRnHPchGf7\nC4v0mjn+9Plz14Tr6+snz58ZasDWgN1L3/S7/oCIJUkqMc357nibY2ma5tWLz6Y4mvcfpxTzDIJt\n0wAIgBjE3K3cns65/X5v0cIKesa16FBEkhQAIO865t3hcHl5WQCJHLJTkZiXTIwjKAAgBhnwK3oJ\nGIgAIRUDSpgM9977EHKOzlMIvgxJFbzzGXU4HS9++WeMEOPUYAMgaZ4yoiK8+f67ae22BwAfmgYR\nj8fjT34ymCNbRbeloC77fV4JeVfTUJum2e26cTzHOA3DAyLM7Xa7WgspK/cPraXCFxcXluOq269m\n12VTditrDWAVDaafoAAAqSKzRyTnOKXkfQMAOcvaOZREQBVDaBF5GpfkE2/KZnEphXngGasi6Xg8\nWpqKGUXzNE0hOAA4n+9KKYQTrOwyZmtskx+rCCNlNn3MiiDqGBWBGZXZE6KUyn61Sn4iZvM6VRVJ\nDYwMn2T1N+N/jK8zH+JxeRBtcGgfaa8HTaP6UV7nR4/5SJN99Mk2Wli/QkQglFwUQZFAUWFhVCeE\nUgQJFQQRFUFBJRdQMd68pQxIwWqaAJRgwWigAgKAKCioqOPlm2pV6KYE+KOpAzD1/OMNxLbe0jp1\nFhDn7Q3a8Q/iuN4vkSLWVlqgSiS48m50Xc8ioFQzqQBEjoGQHJNjRSgqYDp8jc0CIjDBYgoISpmP\nZyEyNDYBBPJdcBSCqsYYtYhzzpPTrCKFEabp/vLq6hcvPr9//bYQNMAJhYqm8zBNE57n1Urj8e6s\njND4WLIwI8A3X3/tnEtzNDGHosxMq4HovUciBiTELjRN313uD2ZntLveLAZPLAiX+8PPf/7zPEdB\nmFIk7+7v79+8eXN9ff369eviaBY5jXfMrAGOMs3375by0sbjpCCCujyyuqQtMGUvKovY1QKukCID\nADAh4WHXMzN79+HDB88cmqbtOkTk4NtdXyQzeyVDqlBOkrM45hijFPCBS9bz+dy1KpovL66lAMNC\noZnWroDv37+/vLz0UgBWXul1/RORJWMscZVzznOc5zlNs7Ffygr6L6V476+vr7/63R8uLy8P/cE1\nrvVtkgQFFNJh1/mAgUN/6D35AqVv+v7Q39y8r1qNV8oPSzgZPs0IPGnt7BDznFJKKRtQQlXnYT4f\nj5cX1/NwRhXPxExCAM47T5qSFXkrgqikvGDbrporF3zHi8TOOc8pzklACzOqqhVlElEp5XQ6mS60\nXLuuNanGNF1FaF47slr/oC2wq+oeKyeodQ62351zV1dX5/P57u7Okl42/+79+/e2kmAFDtqmtTj4\nzc3Nhw8fENFwAWXDxFcfTFVIH2WSqPYKYpACCiX4dhhPT588R1JC5zyBEpJOY84lTmO8uz1W/MwC\neFtF8xbUABsD+dmzZ5ZhApAiD5nz6+vrlFJOYB1TbPMXQJNBuDbaYGYQrCgjjwyizjlj8laXiZDF\nKchGcFdvxK2qRTZrmgCAFMyrqJ6BwwU4bp/bX9igKnHjd8LGeXqsaEShbKXzj+qbrYehq9KtXuz2\nnPUqy+AV1MwxEEQ0JuNStVcBQQQR07tSihF+owIiYBFF1aWUs4QQLIyLC63w2rVPH9Zrva48JpLY\n6J4fV+31VX9ST0UMVvtU5QutqJmKLq26PzjHCqrFcmcEXPNwjW9yKSBo2TgBJWD2rpQCKzxpuQUF\nsODj8oSUasqNCR2Rd00buA1aBBDnkiVJ0zQFARgxOHNQlAAdO0+FwHVNIeAmZNCkgqL7ywtl8m1r\nuAAMrqQIiDnGmBM3bdd1OSYCFBEGNKYcQjQWorFkFE1SEAiZCLDp2nge5xSH0xkIh9O57TvjnLbK\nzXmcFOE0Di44FYhp/vz5SxKBVByA903Xt4SsIKCYEH23u7q8uPABtPgmiMjTp0/P57PRAVjpgK2N\n03B+/vx5KUULjPeDFo0xppLnYXTBf3h/Y9jugjBNkzXcC6djCIF9f3u8854dU9v0IbSllBDa4XbY\n7Q7OUSEVEefCNGVmj8hhrfMrpRg6wnq0G1a+rKtx2R25eHYCGpwHwpLyNE3WirMNTVExZhNGUtKu\naa8uLp89uer7Xoucj3eDHlOJcUqKcnm4mtOkBXzjtMB5PO26/ec/+eyrr77qdjtYQcVGDmRgK1rb\nK5u8ZebdbmeNfZm9kaB779u2b9uW0F1dXSEad8MCz3HO3d2+l5S3QPBa1VDtb1kxn6qFyZ3Px7q5\nAMDCWqZFqgteUZohBEmwlVS4hhatJXGVNgDAgF3TWr2N6QKb54onwhXvs4zfzmuYGV5rSojI8nhf\nfPGF+UZWEMcr24J5moho8e6tyyIbou6NcKEYp6bpbm7ev3z5GRGkVJyjUtQ5ci7kHPUJEi2+19Zy\nt2v5tWtvnVM7wHTk+XzOORZJ5/PZZNT5/EcAcNy+e/duHMe27ff7/dIykj2hM34gIocIuraTAkAz\n3VXVUAAmwJd5JwUERLvNJdJl3ygAopACEKqq1YkrIhAogKKyJwBFRQAFUSK0dhKoiyuCCGT+xYLg\nMnfhkdr4UT1UD6iuRn26Zq1vtZE8BrJvPTNckOLuo9OqqoISP7J2AYAABaViLOvVC1JBIjBqJah8\nFoggKiD16rr4FQDLh6r4kQJGa3W4uomI9X9aVJGAqpgVInaVh+dFRCIKpEQ0noey1tasM8zMBKoA\nssYkqUYpP3+xLwiSREAJwKwn9j7mWUldY2leVFUbfM6lKIgKKTkkJiYiYI6BtHHeOdAgpZi5nXNu\ngAoLM5eAoJK0IGJoeIrzu+OH3fdfv43nq8NFSkkDOue+H+/HOF51jkUz5HNWZfFMmooWsaggFFmq\nX4luj0cGtGqHHBPR0pmhZEECLSXNcVIc43y+PxbQXdsF53OJ8xwhFSWM4wSqV22bx1kVL0LzIvTv\nM6QUuWQRiMfzPCfnaL+/6AhyjqdhvM2xgBrn6fl8Pp1Oxt5/fz6ZiwYAwzR+99135/OZ0WlcKvva\nrtsd9j/7+c+///77OadSSr/fDX3P3iGib5sX3ct2138BX4bgm6YFUOf8NI3X10++++5bVRApORdb\na+/evU0p930/3B8NITYMQ6kw/ZyTFBFRXOpbrEYshJCSxJw9c1ElgHmcDrvdNE6H3S7mjEVEFFC0\nCIgQwHA65zinOacSu6ZnT54JmY53t4pCwMzqyHumfd999vLV7373u8XNidFEaxuCyfqFQ2C3Q8Qh\nxna/f/78+e3v7qwyM62t4KzCz3EwJcHMIlA9iifXlzFOeW3KXuW5hZfzpln77mLXheZnP/3J73//\n76ZRdAVhG6D6yy+/NEVgct7AHcZXKytmzc5myJFKLm5C24y/aRjNf6rqwCbcqgtq+ZAN0tkQ4VG4\nAxcdKGKo7kow5TZNhmRtVWLfViFVD9Al+ge6dutxzs1zsthlCAGARBKASynFmEII0xQtjVR/bkaN\nFUVXLboVu5eXl13XighAQwy73c7AeyG0OWdQ99VXf9jtdjnL4o1eXy0Ab5NGzFAEAFKyQCeJghbI\nUsAa6xJidTWgEuo8kun1ri1yBwC64tBQQRAQFhPb/rMWLECIgFJKrU+CNcj5o+6LXfejSOCD3N5o\nnXoGIiq5VFcAH+elYGMQPTw4ePDtUDSroGhBDexqHsghFVAEyljlOACSxXmQXHaCosVI5tb8k51N\n4CHcuo3Ube0P2ChIK4So91jHXCvSHofsHk5S501WaoBqe9YlykxS0uIpm/5aJyoW40V9sCtVMBCm\nmM1aFwTeXAsNfLhpbUVEQDBNUy5JfbCgWWDX9t5+RrV/eVnquMm7Fy9eHM8nBvzi1WfXl1dGkcDM\nJed5nn/y2een08lKI7qmJYXWB0kZEZ8+fZqmGQFSSq0PL589P5/PqHA4HL766isiytnyC8LOlVI4\nJYcU2LnLS+fc+/fvbUdrLn7XLtY6AhFoklwkEJ+Go0BxgVmB2QNIjFkkA+mc5pRKg95Wc1lr22OM\n1iO8tiGvtj8RMXF7sUtxqXwXVfLuNA7ncQAAZBrnicQBwP35FEII55Nl++sTTCl9+eWXf/rTn8wq\nVVUrvb+5uf3Hf/zHm3fvg3dWQGKCr+u6i4sLEekPexFBplrv4rwxC/A0TZ6d5fOnOL949vzm7tY6\nmc7jlKUQYJbS+NC33eXFnohmnn1m57iUknJk5dA4QxfnlDKk+7u7eZr2h76knDYV2TYtiHh5eWnh\nKFyL4bz3h91uGsaiS+JzTdUjIkp5SIiUhSlRRfI0DVZGvd3splTKhstmlZ+ZvTsej/M8G7hc1rKE\n77//3sqTDfNpRWAppZ/94ucWXrNL2wM1+VyLirYej1XLquput5NNCWnXdbgS4dcfOquiKqVU38gG\nbbTEprisOKCslOM1ko5r9tU25NYrquY5AKqaxY3OeUTyfjmbqvXFsaGrc36e5/N58I971m79rSq2\nVmnCp9MJQFNKzIbdwpW2NpZSgg9Gj6iqi8NIbJ2NyAey+GwRwcU14RXXBoCOQBjdYvvb7RAiIumK\nAhALJa0OjZW8fKQllv8tuS4i+pBjADB/y1IvCIiKCItnhXXLPeSKVkn343kjO4kuBUmyouoUZfHT\nQBeeCPPtiIiQ6t627MniiOgycMbljhCUTMmaLkFQFVRBJFQFBRAVVcs8E6xNmAiBkMCoSQSBygry\nqLtF1/Lvx/dS1eTHVBSrD0eqtjAelcSiwprkewSIiHFegtorWgcRETiLNQ0yY2OZXEREJrNall8h\nCmhRKaCEi+FlUUerhwKj5aMlFCwAWcSJXghzVpyiqmoRsfJAIs/Oe+9oQb54RNSUpZzhjpnev75x\nzt2/ORqBaUqJEWOMqYTXf/jDfr8/Ho9Pr67PcYoggovBN00TAwJA4wMi3t/f92332ctXaY6Xl5fo\nVQD6/c5KW+q+NgHx6uULZr64uDB2aiPeVke4dwny6TjkElWwd69U8Dwc3767abugDceU4jyc01EF\nr3GPQ9RceHaW7T+fz+YbWfWuya/W195OEEsuUASFUACg7RrnuZGQcwZGQSUC59x4HE21hxAYliIV\nUQGB1rcMfLw9mq3s0InIxe7i/ua+67o4Tzlno8o2afv8+fO7u7t3796VUuSBHEjVzHZwp9PJsyPH\nIDrOU5nT929+cMTsXUnZeFGtguLtD29yiQ4RRAIzE2nOrfcXFxcpJTPlQwiXl5eW3v/iiy8uLq9d\n8HXxG7bFmiiKiCVKSim1I8/z588Nd1dWjnBVtBBf9R+YOXhHjUPUfr8jxxwXxv2l7g2AvTMvk1aK\nh5iTSDbKUNMHZWUKz2uPvtov3HwvvzZZLStNRpXSlW3AVHsV113X3dzc2DCsn6yh2O1x1IJfS5Q4\nC/aZ62P2pv3y/fv3x+Ox67pxHJ8+fWo5wJzz6XSyJJ5ln6xC2NhEylrHW81tRFSlnHPXdcfj8fLy\n8ttvvwUAM1QtAl7Wl0HslxLU1ZCveq7rOjunbrIsiHg+T+bGIapojjGabrCHHdaW5Lr2ukbEBV9M\nROQQF2qAEKgNoUFn2ohz5OCoaOMDbJNGaIkrUS02VMTHsvITkbp1emDNkaxfoPMe1g4UuDoxsnKf\nb2389c2Poxu2fm29OiHyein9JFK39UJqhtmQ1bDeliVRTMYtBK8WfTP8uoLzS//Kxe8riyaomGy0\nOkDF5SD6mOLho+BhHdK6nR5qdasHWSdk4xVhVUUAlrEjBgQmh6SEjfNZxSFZLUVWIQV0rCgPGUpd\nwKJE5H1gZuc2HBbonHNMnphpnU9EtMkZz0t9H/OC0xCRLCUQKaEjrg/UEk6y1jAWEUdkAYY0Txn0\n2eUzYy81w9nCOHYwe2cVETlnYMo5+64BppTSOI7t2mOUV0bqEMLLly+NrH4cx1TKOI5NtwAK7Pwm\ng8w3urq6Oh6PNzc3XxsgAvIxDZfPrmyGLZfQtu3t7W3f91IkxdiE8PTqWvXZNE1O8eJJJykjk6q+\nePFinmdABIBnL1+klIyxpelaQ8mmlDyHGLPFqe7v7y8vL5u2BcT78ynGeB6HUILV/KpqnOYSG6Kl\n44yuBOGGQ6vFEqWU6+vru7u73e7aWo5ZWc80z9M0PXv2bJ5n1xgubonilFKKSM65YSwpo4K3ejLi\ntm2D86fTySD1BOicY9UocY5jYFeFsogYyny/33/zzTciYlowpXR/f393d/fdD9+za4qKCSVEtAl5\n+fLlN998Y53Ijf/Tbu1f//Vf9/v9nJKsMcbdbtf3+77vTfyarxNC6Pu2aTpmbppminNlcKjggg8f\nPphWs0hY0zRd1/Vtczrdmwqwl/X3qco7re0UbJ6txNvcEtq0OUfEvu8r8ZusIGEiurq6sr1Q00CV\nI8qOqclsVXVd11mykTb02LbDD4cDAHzxxReVY9suXOPvWwlomlNEzAqwWG2MkcgbpO3Fixc552Up\nOJdzvr29NfVWShnH8Ztvvmma0HXdMJxs9ZsBZQff399XWvW0UoY751IS5xgRU5pFjRR1AWKVUpqw\nIAbbtr25uUspwdKYnQBREAqYoc2mIHOOkAozCwKrSi7CQmh6HpY8iAIAeHarZjK9uMYP8zK59WnZ\nP0spSIS8QOoXSSrqABHXR7LmqKyLqP1DFl/ELHKMaTZoQpXF9iBUVSVbo0ar3lUtOZcmLB3T7TZr\nkm8r1mEDGwExcraHBon2kC2ozRsSKVmOxKrktufEhxdY4a0Vgc557YCuWmqIeONM21dVz8gjKnCo\neDyx82wizIsOLaJatIgKFAXNkEUVoW+7kmIRdcUn0VRycL7b9WmlAvPeMy2JDVrrrJ0LbuXwVkFk\nmtIU49IFoPWulFJyUlViEMmaQYoB9dR7z23zIY1KaJzTNlRPTETTNO24F5EsuQ0Nc06adMeha79J\nx3DVDiVqo83+8uvzve998PxuHH9yEfDV1bfTKfdUypkacjk1FLb6G1fbwqawtofIOROzDyxarPoq\nxiXAXkpyzo3jeHenqno63Zu9RUVe+F0Ylt50XkGGuXwYXvY9DJJSenVx+cMPP/z6y7/4zW9+s/Oe\nmcd8FARDTv/2t7+13Zhz/vb714aqUtW2737xi1/85//8n4moDZ1RKoQQDofdb3/7366uL7z3zjhy\nCJn5fD7/7d/+P/7lX/6F0TUupDnf399XA5yRPnv56ng8WqG0YweiP7z+ngDPx5P3/ubmpjIJvXr1\napFmKswsKkYSAQDjOD558iRPD113oXY1Fbm6urKTGGeSNRS9vfuAzvu11VDdHSayTJDGGK0xoPXZ\nmc5n51zbNLYGPLvry6un10/urdWQQhsaC+ESkSKklByRb5oYY3AuTlOcpr/+9f/9H//xHz98+GDx\nHhFhxnGcs4jx4NnkmOjrum6327XBj+dTcI5AAXi/31so9ebm5i/+4i9w5QSys8UYr6+vc87jOFqE\nzEAW0zQNp3PjA/Q7XbucqKpnF+eFfhdU04pliNP8j//4j23bWh9wuy9Zmd66rrP8S0rp8vLyw4cP\nLq9dX2HDOlqftEV+dQ0EVwcIHsf9YaU9FZFKk2rSzeoz6pF223YbVX/GGA1D0nVt2wazdCzWSavZ\nuBVwW1M6JQnBmlMUBfPwzMfMKSVQd3FxwcyqEEIwUD+SVZUQGsBzpTWKMbpcDBfLCIzoGOM8IiKD\nWiWNEqIWAWB8+ARKsWyK2fIiAqJW2w9kuXu1an+CB4yWuUTsPOjGut8ACnAJST0g3QG1c03VZ1WC\n01pR9OmrxEL/nVTTj770ITf2qLLHiEyq3KeVS9AGxhsK0ar8PropAECFxnmDn33q7nx0+8sye/y4\n6zFlU6FVr8IIOYvF2h6gdbSWB5jfVsTsAFm68ZSysBwJQq6qaBwtiM81Fg1KRNT2TQQoMc255DWg\n7JxDBSVFRIcLYISRELU/7LBSrG6Qr1dXV4fDwREDgHHkW6h0TlFEDoeD8QUQoCnLw35v7AzWeMaQ\nq/M0xFxSjADgvT8O58DOLl1J629ubvKG+zVPDx0Ft7Nnkqvy9CzUy541Zc1FkqgWZq9SUBCKABAU\nyXNunC+xkIIkYfZENrVLUwnTRrB2kytrM/UK+rq/vzd8MG1o2Vzw8zzHnAHABW9q7F/+5V+0yL7Z\nq6JViZpo6vvenKoqlKwtIRE5R/2uswXZdR0g9n1vVSuXT65VtaicTqcFZt000zQRuJTSeB4EdB6n\nVPK7d++sZ6uR6dlPUsm73U4KCELekLDZSjufz6s1s4StFjkGcNj1Rsxjdr+J1pSSNTm0PApsmom4\n4E09GFytlFIF+prFL4hgS8w5l+MkQIxop7aO4aUUR3Q8HhvvY85oKIOUEPH9D9E97pkia8LPtPhC\nar62ZDRmd9okn2wV/fmf/7lR29UQlLmGu92u0njXCFyM8fnz5+au2Qy0bXtxceFU1S65VTN+JZwv\nGxJ+u/8KD99qIxHxa0fRyvfnFrJ0q05dfLoYYwieN7TfVbRatSmsEENc89tu7UlRcSMmeS2KOs+5\naUIIwapfycBqYFlWsMNOp1MpOs9pdTA9oQNahLiU5Zw26Y7JOwZC7z2S5jkCyEJeR8bHw4oAsjLz\nLtA487UQVEAFVVURVA2AI6Ce2Nh8RGqwy9ipFbepD5POK21gFc0IS+8G5iW/Yfwb9hWKjpb4fVxm\nBECew+L0rISVuMaOf1QbIRHxA4KzRm5XPbTksaxuhXRhCcI1WKH6gPD+dDwqmDaRt0df0ceoiqqu\n4HFQ0f7mOJt2Un1oeFQWnaRrvu5BHTITgfXTIgAoBM6xdwTZWI/sOS5E4IKYijm4IGvYDYHVMQIw\natFSclYhAWRmZaY1beQYVaEAMCgXlbvRIfGmQs7wl3MRtzvb+jz7QCtLlm+Cc2738uXNt9+GENIc\nLdTzQSTGePy3r60ktgvBOZcw0CFkUGZ++fLld9991zZNztkT931/uLzYdX2/3/3lr39lig2ZVAv7\nxfSWtUQRAIwK7/7+XlWPxyN7GoahII4shaB4UIC+a2JSFYwNn45DlhhmcL37Jg23LaWYr3wTCsmc\nVUFXRK89TSv145WdcxzHlFJJ+enVNTMbHY7mhAjTNHJxzjlHgIjec/Bd8Lzr2xTLNE2tD613zEwq\nqrrvWgYtORGRqqSSjeGMCbXIV199ZXnytm0BUUT6vo8x/stv/1VEmq4129c595e/+tWf/vSnaUoA\nILnsDntU6Hb9OE8XV5eMFCW3bduqaJGe6Sc//XJ32DfB5Zwt8GWTaV0Tn718WSEJJnYQcZqm+7tT\nVVoQ1IykaRiD84gIotlcbaImBLfz05zUJCE+dP/58OEDEThHvLCzyzSl8/lsLUGg5CIKhCCCKmme\nVEshlhzFBJdomsc4zYadw03iv8JPXr58aYZCBalZ9Oh0PNadLhuggIrc3d7e3Nz4BQwCls0xfkUT\nQdV9NG307t07WIN41g7DvX79OsZ4eXmZ1v549gPzrSw+a+MwxWA9hqv9SxVavrGObf3ZMc7Relgh\n8uN43u0OpSTvvTG8GU7MOQLAUpKxqtsZ6mBMX1aRRCsZhIiopnUSc9VGqlrKhIhN2BkpoQg4l9qu\nR/bkGJgQjCOVAR0A9G0bnEcFXkcLklG0CY60CrVVhqKImAOxDUkpIrJIhWFvBeuPOBwMAOCds8DO\nNn76oBseuwsAUsoDbcHWN6p8sh9dOselv9xWxP+oPrDzq6p1+rOC0FyW7nxodDKqJunrX0K0Cptq\nTSAiWoXAqhDAbA0AUXWurf7Q1rf+KH5YBykPcJhHc3J9ff3pzRLoNJwAeDtv9DijVm1V55wnBs8g\nZDkkBn7gm1jeO3RslToMTJ5QoWHvOwYA0qWApuQIzCLCsLTGQZsypL5pmcgh1R2hRQCg3+0ty61F\nLHGhpSCA5ELOt6GRXNjDlFJwLok0Pjy5uh6Op+JLKWUeRnFOmSTnUXLrQ+ha82lSzuDg5v4uz/F4\nPL778L7xoaigQtE8DAN56kJD3knKY5w1F0M8FtB5GA9XlyWm/rAHgKZrQZukYgi6q6sn5/PR6s1e\nvvpJzhGALi8Pu92h6dphmK4PexrnPEcgLKUYTkxUc84G2jZJ1PYdIu73exC9vbkx7JmoOubdfh/H\nCROLGLYeQ0pE9OHDhxKTFiVG69ngPIsE0eKcYe89MaaY5zjlnK0Kao7TbrczdLL3npitcSgzm06y\nqhXzbL788svf//73zEEASkouhJISMr9//353OLQhnMexb1v71lPD3inC3f3pdLoPrnGBx/NUNAfX\nzGna94cpjsE1ijINs29c41trmQhrda2ZbqfTaZ7nZ8+eyUpubdGji4uL/X7PPuRSbOp8YBPuTeOf\nPHmy2/XmRYhITNM4jk+uru/vTzkVta6vYLwWgETTOAbnvXOsbHsWg15fX//www8fyW0TQZWqNeds\ngSvzzKwfYN2w1ZoxqnK/9lA1HbPb7eLaWgI3BOGGX7Acm64FRW3bus8///zt27eWzjFwJK7BNMPk\nmUtUt7SNsqIY7Kt6mTq+uDZsnqZJoUiBIslxeP39ty+ev0LScZiLJCmApCqYSzRCILtV0z2mIC1e\n2fc9bgKAVZA518yz9TaOljcyhLdBupuQDL+IyBYPXHwjcgBgdfWQyZbjIi8AoEiWDIRSUmAHgEBG\nAreIbABgolUmL1i4Rd7RxzG3B/Xz6LUI0MC0wu0elX8iPnClbwQu5xzrOW3MZigYveynL+bgrNMJ\nAJKaZrXGjJ8eLIhZiiCIalGBIlmFwOrkSUBRQEAN/83G1lqkIrkrM5AgQK3zBTWuoK3ShceIc1v0\n+Dgot75/hNpAXFThMJyqGnsI+im0wRFg7ZyLgIxLCy5YQBPL/pFcEiZygQERgJGMMNcRM7uu6YoI\nCCITWA2xEiGCArMjbyx6C22VpCwiatE/BQsaWEH1SRMAWf91QREUM0ve3L3d5R0UMUuraRrqnHPu\nPE0J8+B09EANzeJc7zPL8TxkCDkgohfhUgpYrYZKUYklzymOcVbCeZ49cdM0glCkpFisvIYUsuac\ns3nzgQ3lQgDgHTc+KIJzrunac86p5GmeYhEU1FxCv1OVrtXj+7M98Q9vjjknEZ0Pe1UYhvP5PLzv\n2q4NpSQXvMmg29vblLOIHIclMz1NU9svSQjPrmmaNjS7rnfBB+c/++Lz7777Do05wrF1s1bVqyfX\nF90OAFrfMrNVK8aYS0ldt7u/vy1FEXWe0zieAch4yOY5/PDuLTNbu6Zg2RfrH4EQY2TvLCVm5nlK\nCcgjExABoSKSY2RGpqbr/HBGZgTVjEVlmKa749ERpSKquaCmIuQYiAXw7niKeW6DksNUxCG50ISS\nja5pG8q2QNz79+9pzcta7M501dv3H4yerW3bENw4jinNf/g9hRCQrNrSUFomsX/y1e/+kFKGIuiY\nAa0qA5haH9CMJBXnfAZpfXj29OmnctU2ZgjhF7/4hWkX81yJaJ7neZpMX8pjPNTbt2/NkfLeG/wB\nrVXxGp2rIS5aU+mWx7G9bzg4x2vfLd1A0S0mVnWjbErlLQJT1gICWJvvVZetis5FZx56K9vPObZt\n/+HGXz+5VC3Pnz8vJZWiREvtggiUUggdIpqCrcgZw+Ntw0e6xivP54nZUnZeNHvvm8Z4hptpmqSQ\nbXXnAiLb1MNyHqrEICJCaJzWaqEqVGQCBNYiao2OHsxzAQuUVREpy72Tgh1JSEDGsa2EhEwquuSK\nNtzbQGgQj40SWibQbrw6B7pJm61Bs+V4W0lPnjz5VJQjQBxyjdRtdQD9WDJJUBx6YMCVqppXOEbO\n2fx5+5mdjgDQI28UDG1CUtszu6oz8gP+AjewyU9/si7ZRx036hrb7Xb1mPpChTJPsGba6p6vE/jx\nVUQlZ7OfRASRVTUTueza0OaUStbNqYgyIK3bRJaZCewAOedMCoILQQkDOufQOXFsPaHrzDASIl4/\ne7rf7zUXS9WYiLSoiPf+2WcvC4HlvRsfSiklJhEJ3pvZYZ3NhmEIzKEUKzPyTbDSKSW8Ox01lxDC\nYb8/n8/MbCHaxrdJUpaCUkxaGZz/7niPjkFkSpEcC4ILnoA8OSnY+6aU0rLHrLRgbZQFPTFmVZGG\nvOv3SDDPM4CQY9u8ZSUMM7yyzaShZ7uu8+ziaRDMAJBUS8ogero/KkIphQ1zWErO+fXr18uaL4KI\nMeam8cYY3HW729sP5nuXoqUkRLYKIhF5+nTpLdt1nQ+Bma3pxu7iEGPs9zsTi6r68uXL//E//h2S\nBwAr8DydTro2/FQEowgAAJOBioBMx9M4p5JUMSMKMpMoIvuubRvoHboChVDYe0AOTadlIVGrsaWP\nxFo17uvGh5XgxhT8fr+PMYoWFBzH8zRNFn/a7Xa7vu1C45BB1Bg3TM6Q4zjNqFokKyiQ01KQ+GK3\n/+qrr8qmiLNG8sdxNF+nhu+YuWkaJqoZrzpyVf3w4YPlO/u+N+yDuTGHiwsr9rLEjVu7SHjvX7x4\nYT0t0woadLLiDmTlmrMImDXTWzb56spVNVA9zZqmY35kyy97HiXnSIsdSd5zKYkZbdGoWlzVsAxA\nxIjkvVfBGl+2nKpt0ep71ekAgKZpmS0FJ6JQ1but4zincRzP57NzyQpvgdjcjgLqN6Ndkrq6kGAS\nL7KSJJMqqsG3llIZANBHzKUAiIAqAKZ9EFSKGhzb5C2tqYwiWktxRFQ/yqMsdTroAi8WSH7I5yEu\n5ASwdSOYQXXadPPbCveGO13a6jw8HVkJlj56IaIQkBUgK8G65ti5LKV2RNkKdDZ1sRoHuMag4zxv\nL7H8RLTxneQiIoTkiAlJVFTBr2jDerCdx5Rm1V71b47po5PbbRMRr5gOrDB3IrfinbamDCAaCTqs\nXLpitVmiDAhF7CrOOUJUUQCVUsitSThEBM/MoMqEgCiIjplwWQKQ83Qa0K3Fcwq0jsR3HbokKafz\nkEWHtRbHWgWe33yo+9nolxjwfD7/+te/nsbY+NC6lpvd0O2aw06ZoAgze7P610LAHFPTNK+ev/jt\nb39rJiagjPM8TOeSs6gi4QLBRBQEEAnBx5SC9yln750UOM8xleJQo+Qe9Si5bnkA4BCO86yqQOBC\nMw3nq/0OQULbnE6nLSGbrHZtjLHb9TFG732aY7CAUimWb5SUh+OpgHZdpzVniZim2XQbERlMBMkh\nADtuGt/1TYpFbBcTmzfOxN63x/PR6tIQ8XQ+W/fCDx8+fLi7jTEiLyQs4zj+13/6p6zSdnvfNjZm\nE3TmrrW7vuk7i1NZlOnp06feN941ADCPcYojKqUScyxAOg1zGzjNeZ4HRI6ppDg0nlMqWlLJ2YZk\nfep4La0xPqfFDF1dAsuVOOdSitM0OdfHGK+uLxGxFGue4GKMMU3TNOWUSs5QrCgZCqgnZvUECoa6\nUqUlzSbecdd1aVWN5ujr2qbLe28Ak7ZtrcDrxYsXv/3Xf3X4YHHWrWTjN7LgGKOWUkTneQ45G9aO\nVhSDBWaNYtXqhUzd3N/fOxPfBrazRJOttopnlw396mquPqBx3NpBy9bKNvmBuESDENloiph57cQl\nISxAg5wtuEfMC75QykMJPa2Iu49yJFUGMQciA53nXGQjblTXVrBN0zB7AGr6riAUBFlJrAmwAKpq\nIcmoAoVUSSCl2VwljxZ6M0m8lcJGXveQI7J6HLS0CyJV4JAqqQIzGdXsSr5mdoVfWzduFYlJQFxx\nHNt7t8mpS8EOFhGrNVEryrWvzKqCWNQo5oSBlZSU7L2g2Pvt3zlN5J0xLxgPt0MqLleGPTUFYs3a\nVUsqYH3HiVhVVAx/uQuNZZVqhsnG45AzqBRCUuuhgoAKEnxrCEXj8lOwGMPCvAtLr4yH4Gcpj3hg\n7T0p5AiOmckrFAQGFCbvHMc5AwACI6qK+aekABwa5YIK5JjAohrEzvm2mXKBVICQvSfHFn8spbhm\nE51mLqoiBREzqhIQAtVmuwC7tluo4gGs9oUACTANk7iAAA4JGURERRAgEKeUhvNZRErO6MMwDJ4d\nER3v7xsfvru9eX0cxuncN72QRibXupJ1jmMbGju/GZcppcvDoWv8t9/8ac1FQ9d1eZiWTs0hOABE\n8sj94dIy/OM4Hg4Hy6mUon2/TzE/e/Ysxvj555/v+67vewNBFBXn3Nu3by0y472/+fA+ICIsxSUW\nqJ9j9N7Hkk0zpZJNmDBzyiXlZOk3c+mavmv6DhEFdKH+WLl8yLsyj8EHYiAswFRiyaAup1hy03VW\nn8sOUywxzlgUmEx/mJS7O96X4i1Vw8xZxYRJExoCPI/DZ59/8e33r/0cSpKiGZWypKvd4ds//bEk\n6XZt49uiufHt8Xx/ebgahoHI7bveYoa73QFAUiptG87HY9+30xSn8dw0nSFxG9/t9z0x2E4MvPyn\npLt2V6B0oWt3LQoO84CCLoSLq8taRXt7e3t7+2G32x2Px5hm55xhx/q+P5+P4zjO82zMF5JFQLSo\ngIgLnpCAkFABVUUAU86CmovEGGNKsBJm0gahbga9FTlZj3Y7IPhQC3gqBttqwqzkSFYMd8nF+6Yo\nGIq4FC1aStGY4zAM5HiaptA2kgs5/vDhg/tvv/1XZv7f/4//n2kty7OZg2als33fm42z6CFdeCaM\nhLVpmmma2rbdSgpeX0QkutRJAcDp9O7585f396emaVQRwLqDB1hLYZgZlCpUH9dOkVdXV4b+rNEM\ni1eEEOaYxmnY7XYu+OPNfdu2+353Op1KTs65+/uT894oRrp2x84V5rGkFtQ7tsfcdd0PKbWHnRC1\n1/ug6gh3u4YRRcRxMHP1I59DVREePAy1NuSgCpJXh6mmzwFxqVolVdVi6qeoqnZhydW5FdyyzAYR\nrjqsXkIX1OwaXdSlyLeUAmqpQlBQBNWFTYFnSWqwNzauGgVBtHJrAmQmRBBQlaKqWhp2qEhZABQE\nGJEUsJiWUFQQEVzBhAAQiFUVkioWAiEEEC2qTovpmRoxkFyKSsIEAKikUuY5mdZB0jkVe08MhM40\nk0DJGq1QSVXLJriR1/rBGr5ERAWrE6KigEjsHaICUMoS2k4kA1DgJcLjfeNDOOcEgEzkQ3DMRcRi\nrXfjiN73V431WiLHFmGrXiY3mHM8pygiHFwcJ0R1gEWKk8IG3gBIKbNz1iFXQAAQidk5FSlG2SJi\nohyNSawUFQUk4+zIYnTV2PZN0Z49Fc1A2u+7m/c3X/78y9M8j9Po0O1DECmW400pBVTv8Obt68Pf\n/nrXsGoBTQ2HdDyGAk8un0zTlIfZfIU8JdEoIvOcd11HU+KUj8d3KHpKb87n8/uum6bpt97t9/u7\ntT2rgHrvj8fjX/7Vr19/+42F5sacTD40fff7f/8dM1sruYvrq2manjx7Ok3TxcXF51/+5Jtvvnn6\n9On1/kJFmNnK26+eXP+P//F/cs4lKefzeB4Gy0CY2d7lvZQEIFMcTvcnRidQYtJhOCNH0QxKPjAg\nKxIizZI1l77tAOR8PjMCgtzevGcCBLm62M9TAlHNQooth/l43ofWBXeaTpeXh+E0tL6hknvvOXDR\n0hAihxzjoW3j+XToWkmFJTrNnsFpjHEO7F5cPz1+eJuGuGs7Fj4c2vP5RJ41DoOIC244DUDQt/3d\n8c6z/9Vf/eq//vN/Zc8lFUXt215R53GWNTNiLoGqDuPZe//y5cuY5pubG4tgnU5D24a27b97/Ra9\nv372dB5jlnR1cZ0lgeCrz1/e3x6bLngOqcRdtx/n4XwcXNu8+uwzCxRbZNJqby04aQ/FAmZPnz71\n3psWT1K0oFUjmZyfprGAWiH8Up+DTqSUrEUAuZmHc1ZpnI8lT/PEgUPbFVVHLhUlhNvjfbfr3Z//\n+Z+b67RYK2kJTcAaPG3btiI3iEhysdV2cXExDIM1+TYDpEYYtwppm+pYSvCsd/3qDViocDhPuJL6\nfJToNjV7PB7NBDNn/3Q6nU6nGOP1k+cxzSGEUtLxeMfMTeuHYZAC3vuc4e3bt4hod5FKdsFTYyWN\niEoqqaRskB4BKYpJBAVYSREll0kmY7yvcs/eMy8Rv+2HAOJIzWswP6ma7SbLGB4OXmAJwFXTw4bx\nqF7OrY2d1Gph17yF+cXMbIGO5SeGeisrMzEhJtJqmwMAIBAwuAyGOlUEFBRUUBQEXNrgEimAuWw2\nXPuEVhIkWX0vTcX4F2DFFwIAKzAvkHTUlbMVSS26b82gAB1pAUJRAfCMBdigaIyqiAvfLKCgMoDZ\nBAUUVQtoCKEiJoznlBQAKGUFVSPqIUzVM+OFAapY90EFUI0K4NiXVLIWzbE8jjYTlYKiRj/IXIiQ\nqWk6q3VXRCBEH+w3YYcE6BECcoPMxvOBqERu5VMx58C2g7nsiLjb7y08bhvEDAWzC0tMSFRKOedc\noMxxfv3622mei6Tggm9czplAHRIjaJEYx3lSBowxPr2+FlXvaDgfEQQRgkdE7bpuHGbbk13X5VIc\nQBHZ9X0uxZ5yznma5zjPUMQjB8LGO9SAiKjCKqgFFURKMZpcKc4Zwx9wCLTpfyagViNlE2tVGcao\npKrDMPzw+ntaShc4xnh1dXV7PIUQikCMMXSdWej/w//wP/zTP/0TA2jKBJpL9uAcO6LAwTvitu+q\npcLeW5kjO4RU7BHFGKWYZCOr+vDezyGVUkqWNMcnV9en06mkiCKkqjEzACnOw9CyX8zHnNOUzSfY\n7Xanu/t+1xaBlGcRKZKWBj+szmPOqQgXScN4nOYxhDCnRM5jQUVlYvZsxDzOOd94c7hLLnOaiQgZ\nW78AiQnNbsRW27Ztd7tdpecwJ0YVY8wpD0A8zmmcJwA4jsM4jiEERf769XcWf7Msjs3A7ek4n0+8\nEpBW5lar/8U1qq9rhY/B5Hjl1jocDohoiXljHzVsfWWcUqCm3RfFaR5MRllVTgjBUEiLytDFb16C\n9cavblK7KgleKFJ8DcchIvuH3EANreImHV3WBIYJU8vS01pqYCfRleTVzq9rsz5r7/FR+KVKfFth\nprRU9XQ6HY/HZ89fWZ5DJJeSiEih5JwJnYgcj+PXf/qGmWPMphIcsaelJA8XqaQl55WebnV0LIUo\nEmgp5qINUHhrIz/sAWYgzmWufsyWMyimGQAIHs7DiADgHFUVXiOcbm2fUaexfus9G2VDyVnW9JWq\nGjcBA9aIHyECYhOWRJiugXs7W7/rt6etFzJwy9ISz9yR1RmsM2TFT8YQGpq2aqNtVnNJ7JlfaBVT\ngiykhOY/IQKI2ntFcOxoRXnUqmFVIF3qhQkU0FjREQhLWQjBFUEUVGy2FWmhWa2ke2zJIQRBYUQl\nVTAqQAGAIChmjiCSc49mG9FgsqZoyXv2wQccYh6GsyK4xtHKd6KSSaGAZMUISApkM+Ycm9O/Irzr\n+vl0UQFAEwKuFP1QpO97Wusuuq4zxiBpGgPUdn3fEyrCrutN0DBzG5yIXF1cxBhTnl+8eJHjkiWO\nqYwl357OVqAHqsfTSZgl0k2aiworsQoCJJbsARlvbu9YQZLLUlSV5pJJg6eCkAEEtTCOJYmzNkWY\nUnaqSYrGaFIvNI33Xla4U84ZiphZZiisSl5V60nato2plFKszuR0Or169ep/+9/+t4b5SbcnKQ15\n732xCv05d8zp7uycywhGOSFdV7wXKKWUDLlktYhLKcuK7rqd6mAPJcV8Pp//7M/+7N27d6FtgKnz\nHhBd0wDA3enk27amN0zu5Zz/+q//+vUPr9EvjAm0Vu+q6m63u7+/v7+/N2a1Ugr0zX6/Px9PmtWR\nQyBmDr5JPhNRivl0PJtXkHPOaakF7LpFkIqIc+qcA0UVKFnGYSpZmAAUgw9t01lnihBaU/mGEqw8\nQ7rhbysrL9z5fKa1px2s6eQlW7kpTq/vSynH47Hm8i1/xszPnz8fx9GaIVm5qxHcsQvTnIBd5btL\nKYnkruuaxgOAwgPzFgAsasa0kZVxVcjHRyKyCmuT1LWMFgDM49nC/nRl8cJNYzTa1NyYD2T/zDlX\naiLzTKtAh030b8kqrcCMemZv9FyobRsQMeU5hOA4OOfaNppjNwzDxeFqv99rEVQgAAMsKDu3VMgQ\nIzEgkZAqOWIB0YQL6EAX8bYiGbYcAdZlDgFRiYCtVbkdU3Vq47wdWW/K5mK/39mjrZNm81ApLbYi\nXlWJGNF0UDZeNQRWyAslODBAsSog6ztZciEH1lnJqocMY3O8vbMEl/FEKIIjRiZAVKs3QgDRrGI1\nCwxYVGpnptqfaU6xamslEFwTfm5hNqorRxB11YtbHLyuwcm6Tux4yxosmbhNiqhKcPixV0U3uI1J\ntETD1wvBilsJwZESZaRMyOCcg7UXOgiZs4gMBIwMwQffhLYNMTU5ZwE1c7WgAoBzjACogmsHYStS\n9mukRTbkXWal2j/d0hRgyZJa6Hghqctlt9uF4Esp59N9CME6xS1bL+dpnsc4I9Ou65nZDPPGs4h4\nA7UD/Nu//dt4HkQkhDDGdHj2NBe9v7//7LPP3r9/bxQJljnmlYcCEUPTqCqovnz+whObkZpSEgTn\nXL/fee8LLBx6L168OLx4CgBM5JKAqJX1INObN2/YYhvDGQAkF6vzNxkdYwRRlGXNpJS6rrMUBSBP\n00Te1zL56+vrvmllmFJJAEAIQ5ydc6fz2ZQEERaVOScpSR1RSfM85xxziQi8uCDeW/uIYZgMW2/7\nyzn3k5/85I9f/8kCCaYYTMIcj0dLpxltjZUrDcPwi1/84rtvXyNjTFO1uS1+Q0SfffbZu3fvDP9m\nsr51fjpPwYUsC4zTeK8B4ObmxgjYbLlaDl5VK/wa1lyGSf+rq6tXr16ZrLAm3ar6/v17AVV8yP3z\nWjmqql3XTdNkdanmHlmAqg2hGqm8VozAmiWR1ditqRPv3JLGW4lG7WxXV1em3qZpsjS/qiJlXXBF\nNcqliH63203ToKqieSvknaHxjJXIJKAxmeIKkLV/Vmv3Yn+wb/PaHbziF6qkqEpLV4L3epNVgleE\njOWczHazRvc2uOqg2HKpnqmxly+Y441pX0qxXZ9LBIAfbt52XcfcmEVgF7VlwYCMhKAEiNa3p8hD\nYSsirtTWCN6h1OpXgEdv6giXXwACYpyjrudRBERkw6oZu7YRpMoqc1HSHPMKMq4q3OrQDThhSW9E\nVFBRWR8NlKJWAEWglcgaDSsgAACWqi/FSrtVQDWXhdtbdNd2i47ZdBlXR+M0Lf4VghbJUrSIIqDz\nYiTUK8uRI0bEmCLbOmOj81YBySU7XOvw1+SWjX9rmjDZcwBVLVrsAICl46yqZlHARgDtJIszYdC4\nT1B2iEigBbPhIasqNHEfY1SrtVpAekAMBSE7iMgaEBwpezX9TLBr+zlHFEBHBKQE4AKHZppmUG2X\n2SiqYhy85/ORAJnRExOxd26BJq6qVDfkMbrh8K1b5mE5rawl5/M5llxiBIC28SGEkcnIUk3xiIgA\nEqEiFV3YuXSJ/fospQ3NPM++CcwcnG8avX93czhcTvfn539+8e5P3+6cO6d5v+/n80REgJh0ESX2\nqI6OOHibw2maTuezc87oaoDJaA5+/82fhnF0zjXsQtLGeWb2Tfjss89yzv1uZ3ERDh4R53nu97u+\n7588eWJ0DCUmK8UvpTx//vzN+w8pJSQ3jqOs3DP/9E//NM/zMI7EGEsCpo79RHp9uU9YuovDaTiX\nziNi8giIqW0BIGra7y8kJlnIRLiUkqWUJEabCEiAhKzIBMQANM9TtXRNoFdfoZpBVdB7JF8AJ3CF\nmZmAlL2gpJTwPtIxOSys1EHjvX/eXIYd3o5DBhVQS9caPnOK89u3b40Zwa5osvEQD2/evKli1nSk\niOx2O6ugMoR013VN0/T73fPnz++OZ6JFIJthYb999erzYRgMa2AuaddlIkjjUG8WNmhbWsnhcEP/\n45ybp8mOMYBYpQw9Ho8mxCqDLSKmLApARVAUVFEKKSAAgTTWZSppybmUlZHL1L51m7Du8bX8qHpF\nVT1apsv0uf1KVc0vqwhvXRFiZg9+++23NUVkxoXpeTuPc84YpcxOsbboW/lSdVvlztIV+V2xf0Uy\nM5eSLFLnPKmqrfVpmq2rrh0/z7NnDsyenUIhVFIuOaZUpIAACEFRcIiFEABQlZ3jjSisKzKvfaV0\nG0wjfPrkmbIRBZlKW8RNmuZVOi/HOyREIIaco+RisamiYr7LPE7Wa1JAQWT9FhbeHgXnVAUtVgqC\njGZ3MANbp12z6BvHRiPrVIW4LqwYoxVEwZrtKwCa0AcPvNymoJCQ8mq8KAogbYJyRCRSzLak1cY3\noKEYwG8pOF2dbACsfHFEqAuso8roqt2XfyoAuaU/n8VCFQzibjCWj9cJqgNVVSSyZ4NESEoEJaZl\nMa9BM6WiqiUnLQoALAQoUGyQeNjteMB5nkmACCRLljgXvegud6G3Zy2SrQ+Wc+6HN8qAzpF3zjkX\n2MiwaBwms0NNIhuPdc75u+++M/liiADedKSNMTYrr1Jd7dM0WlgbEW3LeO+V8Pb+WH9oO8I7r1Di\nNIuIOEkpYUbnZTwPzjfsXX9xGMaRm5BLKQgKkEFF1dAjWQoACCECFS0C6hyj4/3FRdN3BVQQknUc\nsEAu4jTPSkv0Ipa55KyqcIK2bX//+9/jams3TZNVLMIDhCklRmp9MG/JHqL3/v379+fzWRSJyDWN\n9/76+vp4PH7++ecxxm7XlVLIyKqn6Wc/+9nrNz/s93tybJOT88KIWkrJcyznoaQF65Wz2PynlOJs\nFTxLPgIA3rx5Y3A7owE0X8GunlIy36iuT+N3cM7lKcacEJEQshTvPaPLUrIUIEwlZ+sPF+f70/E0\nDkUklaV4yIShqo7jaBSaaxLIvG1X0WFVqJoctk7cRDRN0/l8Ph6PAOC9f/Lk2W9/++9Vm1bFNgyD\ncU9YLLGsFanPnz89zg99p2DtJYFr93pcCx/Nt+66Ls6zmSA2CeYn2WxbxsjGbJiUcYqlqFXjqRbb\nAgrGtlxUl4BkFSbudDq9efPGeBsNRGeJr6203aqZrlm4HKr/VB1JWF9VFanql19+WRWbRUUt07Xf\n76uHKCvO/SMtSGu63nzPOpIa+vTej1MSNc5zOh4n59x+vy+lSFmSctYkCgC6rtvvdo7QMAwiwkvk\nbCECAEJFEICiQIYpE815JngI+NAm0L/6Nwv4GwFB4O7mVmoLBkSu9tRq79OqqBwxkpaSS0moiweR\nSrFc3PXlZRYxh9SEO6oWVWZPjlGxlAyADhEARQojEyMowmoMMBAiFJkr9k83paa7tRpx+7AUIGrB\naq0T6tLAaa0k5UfJPABIKyH/6p4uPnEFqsA2QmuoPFwQMQtDgYp5LbqU/UC1yESUCEUXIiYyrLyq\nqnbew6cvFM2ZiEhBxPgtAEiQ1KwzIlwcU1EEdUlcKo0YckQBFiPae3+VAM5Rz4PtW5siYPfm/Vmw\nsrOXWDIRsXclJgXMSWLNCwIgYppTta9tt9suePLkyUKWaqRkTUNrSwIiarvu6bNn15aokNK27fl4\nx8yXh72uvStNjSG7LOA9l1LOx2NKs13lw/u3iLhrO98swf276bbtmnenu5xONzr967tvfyjDNM77\nfneXToAaHAZHAmQMFKigRTQtbKplJU4khZTSbrdLKaUYTRQ473NKMY0tsJRFZHd9H1ayXdvgeY7o\nGADiNCOia9zxeKz2e50o731Mi8S0fPuiJMb50rcsgEyJ6HQ6vaT+3e+/ug8hrXlcEcnLipaihRpm\n72wFLvUeoVPBTBpCk7OY0G9bubm52e12z1686Pc7Q1SXUna7nREA/urXvYVn7Mw556btXvzk86Ek\nPd3bh+MwTIgAcJ/K1SEUf5icq31RE+fkUSfI2YwzRFwIvaZpappORCzZKgI5i2qapti2PS7xKgUo\nOUuMWRVFlnq+UgqRizECkNG22TgfsnQA5rLYwlBVA521bfuzn/3s719/L5KrXDVJaE/BlFZZX/bD\n8/lsscHqcpRSbm5uLLlQBbgt4yUlojmlxRYvsvSf9Z4t1tc0YRGtDIv6NfPNInW6KWVdBOhKQqyq\ntLZgMP1smcatf1ClVZVZVerhCsAwh0w3sTjblqaB7ebtVLJyN/HaYCqsoB2TGuyaOU5t2+a8RGxN\nu0iBpmlC6K+urtq2HYZbS+6hKoiibpoMIYIisgMiQAApgmjUpgLYNB4QQUEQVCHj0vInx7gUFq0I\n5iX7EhrrIgogqGQ1LQgC5FQLCBYoBsbLwAgFmBULAQMDAZMkVAKGpJC0SJEkySqBULCAlikanE8k\nr/A6kpIMFc3AIlkEQKz9knqHqKUqcnhoZbSgM2nTwFAJRcSIcKotQmR4CKoBClzhYaL56nBZQFBA\nUB0yMJKifVJAoKh9vkTAQDoKuSTJoqiOnKJKloTJkRMQa5fLyIoKAqKKzjrQmw0F5vPUHEy1XaBW\n+zpvLmlBo9oDFiCFhpyAMpLJ2YJCgI5YPNDq+5ZSAJAcu+AVoaikkhWBHKvB4FXYhwWVgQiAbADK\nIsF5U4d1UZkTaV3mbLbM3LY2OSYOnHPW4NkgSWa9zvN8Op3S2ucixdl73wYXYwQpd3d3ltsvpSBT\nKqiqIThmjtMESww8xWn2gQ3BoiuBadO0z9g1Te+vsSP/y5/+/Hg8/uxnP5vn2baJZXNlxRNLKQ5J\ni9zd3R0OBxHZdT0RWeniuZxTSigCuTA5SWk4n4dUNC9F06fTyVo/GBbLhFSzmpi8Up/5tbumKWPj\nq/ah5bXSKMZojRIacnmMRl8cS55zEoRpmsZpcs7FskhSsyyd841vpxSrHVAWSlAzuJumaYbhwcP+\n4YcfXAh3b344jAcr3bXwT0rpn//5ny1HYlWodnfzPFPwGctxPJv4Tin1fW+8D8Y/a/LdVA4zO+J+\n30rO3vuu69q2vby8tL6mhswyCWYzbLrw+++/V9Xz+byhmUbnnKkZk5ze+/P5PM+zrQ3r1mry3KqM\nrR8SrTWqiGihUWbDdlNVsaU8UP7jiqmrsAjz5yoSzcS1995WY+Wf1ZWW+3A43B/PRWDJv9BCqZzS\nXIpJlYe0jmh2AHBxcYErTMCSqFKri1Ytgms9nRXiWbDSVlKFw8mKAUspWUbOpsOtbBA1uuKcq21F\nSimHw8GChPf395YTWkXDA9mMPTxjTLJLm4GWCxwOh2EYRDIiXl1dyZIRzbvd7vb2ZHZBzvnq6oqI\n2tDY5nQA5l0ChrvT8TwOjXf349QwNew9477fiZS7OfrGBefP49A17ThPl4eLcZ5821gGBZk8u1Qy\nAc5z2gcLudAwnBrfEqCqHvY7Fcx5Pt+fnz69TqkcT0dmCQ2VkkVL34QkmUGEyJNzjeeuPZ2iqOwu\nL/Ocjsc7hzzF2LY9MgOQoCI68qyKEjUXuL66imOK0xmIEMH4/8m7IsnsmuPxuNvtTnd3h8Nhnudh\nnp9fX59OJ1Ft2zbFaEVFmsUO3u/3c5x9G4w2McbRLIl55aESUNA8TGcCdoHHWAQKo8uSPAdDOyiK\ncCCHknWOo+suTufj9eH6zYc3Ty6eRIl5ys2uiUNs9+14Hptd48BNabroL87zmUEyFERbjVBKQgDP\n1IawtYGWLKui46CKVqvLDVqnDyVsd40xd5F3nvg0DijaXB1OIJkxrQT+RFScy8yZc7rq8s5lgHl1\n3yFJR4yCAJBFVEUJEZb6dgDTWCvkh5B0Yf61lEA1P2tYo26rahGydywlS2m6FhX+/2z9V7NlWXIe\nCLr7ElsdcVVEZFZmVpYAigAIoogZdhumadZPnH6YX0wbmyc+0Dg9TYJogiRUqVShrjpiq7WWu8+D\nn73jVrGPhYXde+4RW6zl4vPPP5+mCRDQ0fF83u/3PgZ0dDgdu66TSUopztdFmFkRwceaOYMJZlvN\nrIoW5/X90G23+TzGmel5vgrh9O63Nzc30KdT/1tEPDeHt6dT0zSvXr367rvvzBuNeYYmUgyHw8HK\nFRaw2jjwrutiqJj5f/5X/7f/+l//q6Lu717bEIFV3uXHP/6xkawsl7Io9i//8i+//fZbM6+r/zMT\nNs+zi1VKKWUupcyLObowCHL2MYw5iUhVVf6q+SafpuumCE/TFOogIrG+VPtjjGWeEURTQnSINEzp\n6uZumJ5CXc9zEchAJACpCLOwIhRBdCyQiyBJLhJYc5GUGUlEMWUGdAAwThMA1EW0799UNQnJJETV\neH/+/Mc3RyijqHHPANzxn767vb0dx1No6ufSU6xOp491Xfd93zRNjPHHP/7xt99++zJeXFFBu30r\nFMSKTbe9vb19+/atjVliZiS6e/1Z0zSHU9803Zs3nxsatNlszGB++eWXz8/Pxt42GVlehrG+evWq\naaqcswFjBmle6HZElsdYmIILrdpE82QZmVaWgeCrqzOuhD0ZQsBSqI6qyoVVJDgKzntv6gEgUlSV\nUBHII6IlbjYBENchzYhr863h0XalrD12hWVWLnJZlJRstsfKdIBFVmAtGll6tEJ8pjzx/Pxs184g\nC11EZAHAwiWbX2IAhWVjIjJNE7kIaMRxtRfHytsxG6gqy2iM1aUvUOAl8xMRVvnjf/Yn265Vlq6K\nEZ1KqUIcxjMFp4QmkmHhUtu25lbtrHHpowohzMP4/t27OlYxVhrjLFLmXArPyvM47692VFXHaQJF\nbGpE93Q+KeS2rUfV58MpxmgzCe8Px3cPT3bZnz/c2+a36DWlggxWxUNIkC4lvUCuygJEEGpmFsFA\nhA7PzJyLqmZ0Cah2QXzM6NgFDZDRzYo+VCNrYo3OVTEyM5JHHwE9eiUXXQRPjoF8qNBHJyjoCLBI\nKaKIARCZUQCJovOeNIgIAhrhwdSY0Imjakp5mnluWNRNubACK+jMgMRCDFgYTf+OAUVRuNh6NQrF\nCuibCbNgyJimIQQAEqZLMWrJmdYU39bhEsaWEIIPVZrPBUEFwFOM0dBOAWEA8OSpsmcUxBUB0SZ0\nxKiqqOAXegkAjP0JAAQ/FYEvYR+rI2fo0wVbQwSA5+dn28xd1/nLoJoLxHHBNNjIepf1X8dPimE5\n52EY8pyAXFd7KSostrmYuSiX4qoQVVnl95hRpXDnoubSkB9Fa3R94eDCXFIqIimTj5oLpiJkJHXg\nVIDIKUQfAhKF6L2PpsoqUlKuQmxciECFSyQ3ipqJFJHD4fD09GRqe1aBNz+x3W6///57qxy/vFMX\n3ywqIrFqSillaWG5XL2Umt1mh+hiaJrGov7Nbquqddu4RU5sztko8ppLA0QqObPZH7MewzCYlTeD\nYDWhUkrmIqrTPK+noKrWVWm/ypKnm2EsonXdenexY2v0bMGcWbC2ba1iPc+zkIOlbWZFjCx3TMvs\ncDuLZQldwiwzXyKycrgMwFzHLDDz4XBwzqni6XSy+U9WWtvv919//fXvfve7vAx+hU+aeIBcYrzA\nj34RNrU1uR7hmpYw8263M9KEETvNXN/c3Hz//fdmSy3j16XUYlU3WejTljP44BZZ7fJyXKePMV5f\nX1tCutlswjJr63w+m181ZEyXPpjNzaX7aa30rOdmzxtb0QQarM62Rq8GPhpANAzDmnLZce92O1W1\nnG51bwa7pRczdC1pNVd0PB5vbl+P0+C9FyneExHVTUwpgRIzpyTH43HN/EIIiqK6tMIACEIRyMyn\ncShS5nGKhA7JA+4328Spa/b9eK5Rk7KiFk+JIBGsiyzGaHnebrcb++Gnf/LP8jTPc47RO/SAMk8Z\nUI5Px/1+O4/pfD5WVSNS2rprxnNwYAT8m88+sysv0/TF7W1eBnwcj0fXNN77YRyf7x83uyvmCwir\nhZkZAYiolKkXbmzSa7mkld7TdtOqJ1WdALJ3s6PZEXNBR0XdIaenaTRdKFXdei+goppLGUWwFNsK\nSbVxjtVnyxKYswgpzKXUddSIYp1k3lMI4D0hSimLHAGo9+A9iBASKrqaXdN0hv0hRoBiglHOi/fJ\nehCQZtVZlTmpstVYFVUcOucwhDxNguqDG9OEGEbOrqmUMaViMkJ/gOMZ4q+qUIqt58Y5VNTzXErO\nmYkghMp7UkXmLG4yPV8BASBVRiAgPM3nLCq5KItDJTFdKdm0tW03BTDAEx2iQqBPkRy84Bp8+eWX\nC+H4glzZoca6Qr+g4gqqOk/jOI7H47P3vmqbjbBZjRxCrNtxTixqpRqjbBKgimiamTOrxBzTnJkV\nSVSYCQuWEqq+wkfKz1QmyqNMV9t9qaqpCUNNfUOAqCKqFGOMPkQfYoxcmEvxik4g9WPOmRCvt7vO\nx6g4noc0TliFVLL3HgSVsKgYWGLmHgEc0aW9D6DkHBeI3q6P996RA4CyNKLg0kovIk6h3J+D90X6\nno4i8t0whBhVlVWcc6GuzM387Gc/O707oIN+0UaOMV5d3+Sc91e3wzDYmo+xJqLzaTBT1ve9j5cR\nNuM4mocwK29gz0o9uOA3oIcygqD3Pmly4AoWX8ZZ5ryt53kGIH/VccSzaonIzkFWh4COWEVA55zI\nu3GegFBVAUFARcW4JIakIyLBpbPTqVgK3m03Bk54CRaTzfMMhIGCCoISIpUsObF3sWu359PgnDMl\nWUSsq9p7Dyh5PKsKLx1IsuhinE6nVSCblzaeYRhMf3KtEpnPe/36tV+GOaxUZ8uigiCXIlqWooiN\nC9Ouac0OqyrgpW7iTd3BMrW19mVUN/voi4rBIrNqYo70YooELtUdc4n39/dXV1ePj48W0awlKFk4\nIfarPf+yRGwrZrvdvjQiukxvs6H3Vr81659S+v777//0z/7F4fjcNE3Oc1WF0+lU1WEcR0Kfc356\nOn37zXffffdDCD0AWPIHhECo9g9BQLPo8XxKqZqGgQCcTREFZC1cx2+/e2ve2uJBuxoAD7vd7ng8\nWsZdVdXV1TQMQ9tU1nR2c3OTxk/q65uum46HPKdpmm679u3b+6tt8t4r+cPpVLO2bZsUs8DDqedQ\nTdPlrkPdXt9tbH10t3OI1YphqkgpxQEa5jMMw2Vml+raJhyds0EbNt+sbVuoL4wsu4Mb5+u6xmEI\nIVzt9mWcQRVFcbeLzoMjB4glT+OUnDKSFC6FTUVunOdjGldzYyAyvKC62X00E6yqnEvlAzPrOKpq\nnmdbACmlzWYDzkldJ7NZzmXmWTRWNYBYyUisTdg5jdE5D8yubTnl4kOilJ1nUHbo4HIMn1Y/QGYG\nvxRFkAAh+phduLp704/DNIwCGpxHY527Lk2zi8EhFWHOBch5cuKw2mw0pzzNWhhBTTYJnfJF3VzX\nraiqoDDPc16O5SUFZg2HL5pvzETkYxiGoe5a+6sWJqKS0zAMu90m53yqYylFcrkAJgLofIzR1w4u\nkkzqyXnvr/fbUkqMPsYohZ1zzmPOWQWtbm+g2ZsvfgQLrcvAAwq+6lq7p6o69sNM8zgMRHQ4HEop\ndbgMAyVEQdTCfd97ctGHDCKqOV96P2wRmlW56JEv3VeIeHlLSvIiNyKiC6VFLxZ/xfMvJiJ4j5RZ\ngMUhOsBN19nFLaUAIbBM4+gAHz58LCoQUFEtGN1t+6enp/3+2tKL0+nUtpsQwuH5ZIWc4/GYymzV\ndVvPlsztdjuzOW7p9L9Q2jjvt3cMvNvtzADO82xTnYy5oKrWcuScq+t6PPdpSHWMBgvb/97729vb\nx8dHXnp61sj74iC9X03lGtmcz+e1xrOW3NpmM0+XytNqeE+n069+9SvLY4z/bJGBCa2+vtnnPK8u\n3zLIssxkoBekdrtHqxgCAFiGZD/YlVkrTLjw4I/prKpIlx0hIt67GKPxGi6ByFJtvaxLW/1rgXrl\nUSw7+lP7nrVQ4YumRby0Cns7yvjiYQEp/L7qsx2EudAXGEKxjqo1HbavXpPWFcGwBdo0jffe6PZw\nkfzz691S1VjFEMLh0B+Px8PhgIjb7Xa3262CykpI3iERIxSVORUfg6tiHSuHyDkn5n6a/uxf/vTD\nw7OPUcABeSJAFxw4Irp7/fkwZfIRXVb0w5THlIc8+xCgqrZ3d+/evh3SHJxH7x+HARGj8zPA5uaG\nP3yYEEillAJVncl9PJ6cc3/y8z86zunt45NxDqPzU8qnxyfVR+fcL37xi7/97/9NFoU6u5eE6NP8\n069/8u7pCQxcVWiaxsDD8/loPv5wODBzNU4WVTh3YUNV3eac0mig+DimcSIiZSHviIt3Ic/znFPw\nnh0WJFZhDT4GBWQHbV15gnEcvYjV51e3va4/ALhoFjALUhOiGNEuJfQenaMce1VSgRhGLqpSuSAi\nxfmxWNAjpliaL8pVyZblkcdDP8esKeUexlJkGmZQWt3huoCrqqrgstgcOkRMnDVPM+lILDUpoicy\njSLyLm52EAKrDtOUZ1XEaPOESIqD4nCRkHUekASgZAUgWAkOcGH5O/dSgEMXyrt/MZRMVS3d9yXA\ni86SohLIxarShTdkBs4F75zLwgAw9GPTbSg6ESkTl1KKJy/8u2+fc87hEu0V771DKnPyArvtFhFf\nvXr1D//wD1ayNQK6sZ/7tl31J0V1d3sNiDHGzz77LFQREdu6sX1d+dD3PQCchn5/ffX6szdC6Lft\nWFIdYkrp888/3+y2++1uGAbrlQ7ep5SUhQDrEJ1zApoXnqHZsmFOOWcyFem6tptue5ZiwFgXoHlC\nVS0q4tsnLSUXdJRSEoAQgpAOle9rL5w77zkXQjeNk8rhcDhYFtq2m5QKYcqJzRMb3lVVDYOC88KS\nWBKncRwZMKUUghCRAJLzFCIA+FLO7+5TSng1m8uZ53moHkspH0wnohTLKrbb7eeff/7d99/Phck5\nw36MaKCq33/3tmkaWZA6YXDEiFjFetPtLMKjF4JqVVXdXN9ZxV1VjQExTdPr16/fv/0QX4gzrVum\n67rNZmNcjAuFGKBwEskr7hWXiaa0zEvjZSDIyoVZHZUsk/D6vjf1NUNBeeFeXqw6ZyJy5BEx58TM\ntPQXi4hoUVC5tD+z/y//5b+UUqzRZ4V37XPNPdhwFF7aqYLzK53JLTOUDFAybBcADJ2DlSbwAjN5\nmR5dvIKqwXTGPrIsZLVlzPwHL7ZVa37RWjdWH2aFOMhSSjmdTpZcLzGF5JxPp9Pt559bVnQRrSEU\nUFbprnZViNM0MF7crHoi77abPbMCEwA5CBfN3ain51PXbTmpeNh1V6EOHn3VtJnKaTh9fHy4/eKz\nBOKaKsZqnuem3XrvUfTD8yNEj1XwbT3Ps6i6GOvNTsf+eDwfpul5nCmETP6chi5U1DR13TJn7+NP\n/vRP/uYf/p6CM0kNIgrOgUgu5dUXn//m+29FBFS5sHiaUikM4j22TbO/PqSZinIgB45RRNBHDxy+\n+KOfffe777SuylwmQmka74lZ6zqKgGuqqR81+3Oygk0QKRpCtWm9j+Hoh3kghBlQPXkfhnkAhXq3\nOd4/gQMUNE4gKDtwzEWK3nbt8/PRFCVcSQsDnAJB03RTScyKVciZwXurEa4rbc3IjUEjIjf7OxG5\nqWvb9j/Z7de8+sLAxwsnsKois5SSEUmEESlu2mkYXPTR+bqunPPMRRW8d+M4UQyFJaV5JkIEsytp\nPBMriCILleJYnYITOD8/oRo5GnURi0DELjb0oonSLQqERqKzSHOFvgGR4RNd3la1szG1l7LTp65M\nRCzyieljBi6lBFmJaNu13ntPpKopFVUVlZwzkDM9OkCcpqluGvveoGoKdYW5qqq264iIEY5Dzyol\n5au720N/JqJcSgjheDh0Xdefzjnnx6cnANhuNlllKCmDeCTD+X/1q19VIaaUmlgRUTRRmVxSSsYu\nSSWLqve+67rXr1/Xdc2AzKxAVVXVXWexr9li5/2YReASvJ76/urq6ptvvhnHMVRxmqY5JxHhnN8/\nfDyOfZnGQalMo7XVq+p+v1dFM7trmcQKIXVdo6Ms7E0Uf6EKG0q0Rur2v5WaOOVXN9fHp+fahVwm\nZXUCxFqRH8fRh4BA0zRxKVDzrumsu2AtYBsh2+L+0+lk9AGrUa3tlZYbvaySGnZlBLGbm5uVw20s\n/F//029WxsHKlH5+frY6+lqUssaguq7nPvlFuMFKdLbw3rx5s8rluGV40G63yxY2eW8R3jzPNnzO\nIv5VWK4sDzO/C73gIhNORBc2I32SRwEg//Of//x0Ot3d3Vmbrp05EZmVJ/oUZl6qavnCVrC9FJch\nrZvNBpe2yhDCZrOxmtvqmdZSlb3sdDrZQRgYaADgOI7v379fvfcaM+IyvNa+2i63VRqfnk/kkJlL\nSc/Pj1VVkYOcMxeNMaYkVi6mRY7lAhvacBdCARWRLDym+TT0Dx8+ci5EEJzbtF2eyzjODx8emqq1\nGcOxDqa449DvN/uSGDG1uy76UBJXbbPZVxxcOJ273f75dBYRCLHk3NZNKYW80xg3NzeFKAFkREGc\nS6kAQte5VKiuxbnd9b6p24zqYl04F8RZJJ1Ox2EsoCFEBBRmH2PTtlr4dDq5pmHnfFU55/KcsK45\nJQpBESFGrGt2jpxjFFGa0hxczMzzmOrd7uPx2HR1UtXCSTSgS6l0gZhVIfYqWQVjIAJwgRnNS/tQ\nOWWJ6L2DKlFwVdUMR21i/eM/+WfHv/kv6IkUQQopUnAOSFXmOV1/9cWBiwg75xGhFG63m+PxhFV0\n+41KynPKVZhBnXP3w2TeyKrWiq5wsc9p0PV933XdMM+v99d934vA+eHBZg3bRAly4F0kB22z8Zpz\n4pQnQi9auGgYjrWv56E37+tcKCWVIkTQththAEVMQhksNJrLLKQx+jrEiA5LxrlQERLdbTsnQPCp\ncwAcAoBXWh2GXx4WVxk6ZOd1idgQ6q41cTyzMs45Ui2l3H9833VdjH6eZ1hGpSD5oZ/rpgkhEBXa\noIiIsogcj2ddVIJSmrz3ntzEuXgcxuN+t4PplNvwrCluqn6evYrzfgzAxAiQIfc8AeJut5vnmRHi\npi2oCCJpopJmLiFndLRptqiQUurnKXPJqC4GAVDCV69eff/995wLEQ3nHhFLjASYpzl4X1WVEu7q\nvbEGSil93w/D0E+zdb96792iv7lu4ZIvrR2GVv1P/9P/dPxwj4jP7z8SkSCEEGpy0/Pps+21bnZd\n05xOh5ubm3Ecq6r56quvvvnmmxjjfncNADZudIlZAwCgR5GL0TgcDsb1ffv27dXVlfkzu7kGZ4nK\n/fH5/ul+BDaDpqo++RCCqHgBROToMvAhjSPwJIUFBIGQxjTXJQ/ztHoOG6RDKkU4cRGESiVxUUJL\nFUzPJXNhUAq+zBOD2qgOABjTvLilZPFdzhOzEFFdN9vtdq3cM/M0zcxSlZjn2XsqpZh7M8RvWgQX\n5KJhgTlno/9987vfrZw6+1Pf9+/fv7eEbIXWVjdGCspSOBHRRYyNc5q0rWsics6u/AXA8JbKmPM3\n9g4sNR4z+ivnz0IJh2QhmCWMdpmsQ8KStRij6eNaBAEvyCFlGeWEiEbbMC9qKaRJDRo13o7HLo2d\ntu1bk9WyvM0anubEdVNN08Sc379/++rVK9NiIPTPz88//PDB9CVz7gGgbhpRFVVFE9FBULWZs9dX\ntzYZHaQQEYh671nOvooMavpXOXOfgBMz8M3+Zi75h3dv5zJfba8Y+PB4qLbNx/7h6u4munA+n//m\nP/+f3373XVvXBlUOw/z5m1cxhsPp/H/+7d8aRSCQxR1RpFxf3/6LX/7FlPL/8R//E6JT5Zubu/P5\n6H1smur168+++PKr4zC1gB4dS3G+ciGyclFIDEm0rdqqirNPVRVj5hiDTrPzMdR1Vbd13RAhAPr+\nvNlsmctDedzurrLIddNVNSjBME4UnNAcmhZLqbpNVvBcrUFNzp6IQlt7F2kK86SETkNA7zNiYm2r\n6ubVG3b/zZETRBQCRPIXgVEuHLpNRiwKlXOImApDrHzLsWnq3c7P8yykIZYk6MLudl8KI2JVVQbi\ni045Z/WRqqYMk6tbnlLstqcpCbIQqKKiqE3zi8H7QN59//6Dj4FzYS11bMgjqApX+11zHvrjuYf+\n5DEUTlwUSb071U1EcNM8lCxIWrKMacjI2+3m1f46NF3lIkVyTj1oSVlRGGzEHzgAlKVjg7kstKKV\nxcBLn41ZNwshATFzLqXIwpRFxJJySlPXNM45beu+70vKFvOSD+dhspgXABxhCAEVpOSr7c55NI0V\nKdmqv3NOVdeeh/6LL74AgM9+9LnF109PTzaMte/7VVrl6enpwrBQKcKxrmwYq6iKigt+yPPYD1va\nAss8zzUCepemsXGuCOTEwTci0PcjCjvnVEopCckPWgL5GYFLqUoYU04pVxWhDyEEQucUVIUBWC+4\nCgAoF8gFGQDAZ055erh/AsJpTN2msUjR9HJLkY/v3rftBlHPOj0cjuTrYRqrqXz5E//x4Ym8+3D/\n7ENQBlbx5FLJeU7oyFJVi/ftwt69eiOK45TGcSqlVFUVvfeOvIsuePTYlnL95k29260am6tqzNqO\nM8/zqy++eOr7qr5Izz09PW232/PpZGbQyFmG007TNM8Z0SnSlPIlWVSlgOScQ1o4FJhFEy99NaIZ\nQEzXxrvo/TRN4zwZ7XAYx1KKJ1c1VYUxc/HkYuXTbBKRkPMsYuszWumTuYhACMis0zSFUFmag6U4\n73VJo5u2xcVlMLMlCVabrPylXYwvBGxHRIWTQbILfG0QPjOzr0Kcx0kKVyHatAiDjGNVlVKcd76q\nE6a17m0FIQMWjIduEyXMebRt+/j4aNOZDKZzqxDLkhVZp0Xf93VdW8ZjJauVLb3uWFkY3qpqnwkA\nNohQVdu2VdXNphnGPsaIGD58+PDmzRtTnASl/X4/DAkXBojV3NAHdJ5ZY4yEHlTq0KQxadGqbj5+\nfLi9vZ7nHGMUUQhhKGkoEwU/a6581WwayaKkp6nHymnA69vb6CJ6jE2tpK6LRFDXrQe363a//Od/\n7n2c59G5MAznXbdT5de3r3/05vOULirOOee6bhH1cDg5Fx4enuY5Pz3d73Yb788PDw9V1TiHzDhN\n5Xe//vb5+TknrurARecxuUC3d9f/6//6v/23//5Pp+ezAgdf+UBN3VV1AC5ffPn5jz7/6te//k0V\nm7qJhJ4cpJmdxzSXtu0cBREVhqoO0zDfvrqJruKSHZAWARFlLqU0TcMlRe/GcSTdKufH+4er7W6a\npqur677vH+6fvvzyq5TS0E8qWC6Yks3dUrY76+I4zHXVdjfd09PTdrerKyGM3unzU7/d3CBE70CY\nHNVt256Pp9ub62EY0jxd7V9/8803TdPkJDF4BP3szevz+Tz057qK49BXdQ1gOpwAgJlLSfLmzZt3\nH95XTfQxzCBVbDlzrJucUrff+O3m+O5tc3vz+HRfBUdVw6mE4KYp/+KP//iv//pvYvRjzuRgHOcp\nTYd+8LElClokzTmKRu+cowLCZOkNkKAAeDX4HACUbCChAQwAaIAzc/kfZLxjcI1zaNj4NANAE8Ju\nuz0eDu1+HwUF/ShZplQpljm1zhXOTRVEBBHOz09XV1csPE8DokrJiDiee8N5VNVVDgC++9WvLLwN\nIfxjKTc3NyLyJIKIf/mXf/mf//N/9t5/8eqV8x59qJvGmjrbutlut1ZUkKXX8He/+93V1dW33367\n2WyOT891XZ/Pw/X1bV1t//4ff/v81HMux+eH611HnopwcUSb7eSrGck17Xwed9uraZoG1YmxDn6G\nPAButvvz+RxiaJtmGvt5nq+uryRLHieHlNEVDNA1p5zb25th7Iuz9MsBCGcJMRSBOeeILkM4TaXp\n9v2575MUDAg0zrnxYZ4nF3wRKKAYA4WYSqlc1V1VM/PDc391dZWY5oKUAV3tULb76+eHxwsNlTMG\nxFC9f3hCxFpxnuc3b9785je/2e/3Bhpd1Kyd++H//f8pzN1uu3Ky3z09AouIfP7555urK+995S/I\nrScbiKWM4GKwuGSNzg12+imitSEb3HctMqrcffnFPE6Hw+Ewjt4TKp6m3qcLZQZ8kCSc8lzytu3a\nbaWXnmya53makok9eU9tu7E5AUTgHJVSSpGnw7EIF9Sn89F7H8iN8yQiIEpEbdPM88wpmyzQPIy+\nwZQmRIxhmResSuBEPwkyAQg5ih5LKd7suyFsth/Mj1lyg0tv7cogWDl4qxs032CA4yrJt6a0pua0\ngubmluwO2fwkg0qNEb52Ua11sBXfM1W+sEw/slhy/XZmttkt9gIiQnBrWrYe/PrDBUsBE73OwLjf\n7y2isSmxMVYCmrnUbROq6GofC5BzApo0k1LS7IKvt83VzfXlSPhYcjGONbCUuTjAQKEK0Wb3kkLb\nthYXd922bdV7fzyebewvEe12uNtdXV9fd13385//sZ3jZrOxd+33+91u9+UXP/7iRz9eT6csXXJX\nV9efvfni5jpZjcEuERHev3urgvM8j8M8jel0unBjzD2XUt6/+/jDDz989913T09PIuKr+Fd/9VdN\n0zS7/TAMnMtwGn79m1/9wz/89vq6Y2aRUlXV//Kv/6qpu/fv3//Df/+HaZpub28tnjAX++d//hfr\nbFZEcI7cEnUOw+N2u7+/f2yaDsBE+FlV97s2+OpHn//4ePi7uvZt2x4Oh/NpsNAypXR1dbXqs9V1\nbf0ctjI3m42l1wCgQFUVDJRnZgV+9eb1x4d7321s8XvvZphVFRCb3abZbqiuXR3rzdbaGzhlZWFQ\nXzftbquqXhQRUz+4qt76sNnu62rjuIBkEClJMmRVFRAbZYGKHhCECLWoItrsUUQTk0BUgM1+t/Id\n4NNssDKlYkIhAOAAiYgZVNmwKYO+jVwbyCnofr8dpyk6SlwQkFQ4zXmaiQiJSIEWhS0zZ8eHp6Zp\ndk0HAK2hN+SHw2mFZfrn43g8q2oZZwHtx5n8BRcxdgMs2jOWK6eUKh+OT8/D6Zzn5ADHcRJ96sfM\njAjh7u7qze0tl6GqY0aeAUu7SVXd1ttut8/9CKL1PBLRPM9jytS2RPS7jx8JAabRnU7Wvn0umXO5\n3l3P4xRjzMLnkv7+22/efniLiNEHBo0EiC4xiyprSSosOim0MRymCYN/OJ+TIwAQ76SUsWQoeWX/\nYyrOBXaMiM57v91QXScArKpzSpdiT8qzKjAXAIc+5ZwvIsjgFChWoWl3N7en8/libX3wS4MRixz7\nXhAqQ+eQRGQeJ//0bOJ+l54NBYOvLoOqHZLCqqYfyIGj/njyVbTpzHWIDIqiIQRlCd77GMg7lYKI\nUVVVP7u5UVXvyXuf82y5xH67vdnuqxgv/PulMGYdx7ajeemTZeauaxWxyIVQZqPiHaD3/unhcVok\nya2bG0TneZ7TDMtjXe2wCOLB0ggYQkB0/t27d+M4Pjw8PD4+WnuafWJK6Xg8GjXTHM+6beLCUDSs\n0L7bfgghPDw83NzcWGZjnsytc11fqK9eX1+vKdFms3n//r3piFvGsxa+VkYDM1vhRxamuLHS62az\nLqbr6+uqqlKevPfTmGRp4ZalpWndQvSiBcSO6ubmZq1qmjO2kcnWzLVcrwtl2XtvAKAdf1mUXq2y\nBUu/lLEKzVetwEuM0WSd7GE+eCWJmINZNVrWa2vO+7vvvtNFZ36aJkTqunaapufn52kaRdh7Z3Xx\nUoqqMENVVU3TuIViu96Frusswoox2i22y/7+/uEnP/mZnfjbt28RtW03v/3tb//V//2XxjKf04SI\nn3/2Rc5c123zWWNGyqzJ09OTcfnevn1r2KwtFVnIk9ad8B/+w39gvnCZAFBECP3Nzc3nn3/x7//9\nv7+/v7e70HWNcI4xbLfbX/7yl4fj8R/+8R9N1feih1/X3vurq6tcyjTPIjLOkxFh9nuYpkmVu3Zr\nFBtYhqGUYogavHr1KoYWABSh6dq2bkSkbLcxxrfffb+/vjJALFYVAOx2u6ZtP9zf+2VIvCOqgvcA\nuYj3/g+8kRNC1GyKtv73CJ+qepwvKqhWP3eXVvasLKLFFowFMZd9N83JIyGUyoGr0DlAIpan5+dx\nHE3pwJaNX0RaDd6kFyNtAODu7s5CzI8fP9piM/Ex6/bzizpZKcUaburYUFbImZk78piEiDz4MhVm\nzsxt217HtgNfphJCJO/a7c75qu4Tq3pPnLIAB3/BSICMVURzKcMwBaJhOHtyTbcxUtlnn302DOeb\nu9ur3T6XlOdkr09pijHGWD89H66vr5k5zXPXdZu7G8vbcs423+t8Phs0Os1ztdl047zb7R4eHpxz\nx5K1qe1qjCmVGHLODlRAFZR5Hs/HFUcVkWMan/N4PB0JLgMXZHSz5CmrqkaPmQvaUGBmnRMAPB6O\nw5yUnK4ym6I26CQzU4hESLEqKQE5T5RZCyCbsqICOo+AWWTMuQi72usyyZsALaxzwYe68jEwFQQl\n70WYpaCKA2CRUFXEMg4TLuIGx+ORmR2o9z5Lzjl778/HY+pHeoFImRXa7/dPT0/GjOVFfyGlRB6L\nCDrwL1pOm1i1bXt7eztNU2PgRL54Gut01uUBLwRS12zPvtFweP/mzZvXr1+byoBtciMU1HX9+Pjo\nnLOU0yhAiDjPs+X4ZZkoYVUlKy9VVXVzc/Pq1St30fBX0/leU6XV+ltHtH3dZrM5nU63t7f2OWYW\n18PVRU3VvMJKoLA4EdA7fxniZE8ejoemaeYpq6q1QC+04AsHfbULuAihAkDXdSbZt16j9ZjtANYq\nml07XaRjDZO0n9eebfMrZuUtZbTI3UyGZSG6zBgMiziKRZ3n83m/3+/3e/Od+/3eCCaGQYfoyEHJ\nPKfRUYiVR0QFi+ZsvE7JWUWLd9F5nPJkdp+Wifcrot33vXX12wW/vr5uNtu37x9+/NVPrAo4DnO3\naT7//POm6ZqmM2XGm+vbUgqCPx6ewURoFqqL3U0LL4ztvZ4XLTuzqqo//dM//bu/+zsrTqhqjBUA\nqKCIfPXVV3d3d5999pmlRKpMqKXkEMJutzMug5lvq1aubB+jmaaUgGia5r7vp2k+nU4AiugeH55N\n78s5F6tPk45/9NWPC+tf//Vf26d5uiy/uq43TXs8Hv/Tf/pPdo7M/Ob1ax2GVY1bRILNogRQyGwT\nPhZvJIAoACAOEcAquZcOT7v10XsV1VQyq8zZ1kbhVMdKF13B/EKevIlV5UP0YVM1lydZcs67z3+U\nUrq9vbXaMi2DO20FGmtrXaKlFC7JAAx73gKmzWZjcnlVVd3f31sHugEP03TR77FPE+HoI/mw22+Z\n+Xg8isOJszhkgRjDx/v7/f6amlA3cUql7jrNqeSiJY2TDGWSuo5V2yd5f3wcUqpCPDw9mlc+Pj8y\n8y/GX/zwww/zNNzd3aVxXPtXTsfnr3/ys6z6dD5+1r+Z5zmEgB8utuVqv5/nOTrfNA069FUdyUFp\nn8996OpeC3Y1ELm23Ua3ulsbWbBiCaraNF1ehhghooPLuT/c31tAY+1WZtPauslpMkRnzdSdc7vg\nTLOGmdM05Zwvw1REjoezHfBlrENdz/O8mQbnnOSLco1pHiqqEqac8EV2C1nmnGGEuq6RiEsphcEE\n6EAJNKeUprnruk3X+RCQhYg8ueC85GKN5Aj4aQ2HwAtfxsyXKVx8+PDBTtxec6FGo4ADeKEfbdBa\nXdf96Xw8Hr1z3nvrEvHeD8PQNhfdHF0qNWZ+zcKYHzG/4wzTX2tutPRMGb3NingGAppBN1O+5iLr\nu2hpB/PL9MyVZbgGg3+QrJlukklaEZFZRjO4vHSBrYmUAQKwcA3XVGwcx88+/xIJUkqlpK5r2rad\n09i2rfDFyMKLqWvrMay/rtc0hGBu3E6KmUUvRMaXTst+cM5Z6oqLSuN6gmt6ZJli+f0BGbL0l9hp\nIqLIZbaheyFgbCMjjcRiaZD9CgCbzUakrBwwIiAHbVvHyjdNZWqqzCpiQx6IiFwMc8kUfJ5nEHYI\nIiI5zSWDo6ICjuaUEpfEUgq/evOmahpEBCIk33bblLUfkgKj86GqWaeqacmHumlPx4P3Xlgsr3Ux\nyAj2yc4592K2OjNrSu8+fjiPgyDEpra+Ai4iIiHGx8fH09DPJbfbDQC4GBz4KhrrWonI4iT7NJPb\n8ktzoqWPRA7JA3lFx4oCxMyx7ljp5u4NS/HeI6qtJWa+u33ddJs3n3+uC+RbSiFA771H+vLLL6c0\nX11dbbvNMAx/8qd/ejqdxnluF/lzWLQ45zQ55/5Hb+RUGvTEy8ipT94F6xBFRUVBAIuoamBlBkiz\nTQBRVTUyETnv/enxoYSQfSAihxfXnqT0x9NcsqpaiCOLsrIFtmvHxZr3eHdhPX3xxRePj48hhMfH\nxxjj7e2tgbeGfNoyLqjUNOqo6zojOlvIZUvU9G+Y+e7VK7rZImIk9/XhEDBMWc791J9HVMigKlmL\nkiPvo417L8KZy2z5XNN4T1lYyPkQ9zfXv/32m2a7cVUMAFXXqXApBXz48o9++r//zX8eSg7j8Pz8\n3HWdMiPiw8PDv/yLXz725zzNbummF+ZhHDHE29evPnz4YHP8rq6ujP3061//epqmn/70p+uiMhx4\ns9mt0poiYhX3EELXtOIAALJcrBYzK5TMqSLQcqEB13Xdz7M43NxcmQEM87wSnYHwCyJWtUp2jLGp\nqnmet91mHMc0TuZ6YwgW8oYYjWu3AkLrLX54eAAj5U7TrDrN8zAMTqH2Lg0jAOy22/1+X6YZVLz3\n8zByLiwZbPyxKqvknKlkzsVsr6qBGb6uYwiOCErhnGeT5kopAWHVVmXReDOtkHPheZ7reLH/a0xv\n/WREn2zjam8Rka2oDHAZOIaoAJe5TOst5EWhxPyV3RULpWkZAraGBi8fttaZ2Uznan+NO7Fyh1Y/\nWdd1VVXmwwDASj5WQPoDb2TuxLh2637WF3IvRoEvpTiHVpESEdMMXmkU8GJGyBprwEIbtc80tHT9\n1Sa8Wciwhgl2srYnbRHLwj+0/jKTPDA5KViATTt4twxbs3VvB+ncRYHUXNfqyGnRL7Cw3SLfGCNz\nLiWpQlWFhZGcRErOMxFUVRShlErORZVzvvQcLIGtrPmloUPGfjEoz3vPrJvd9vbmVQytSFFBIlfF\ntqrqGGPbNsw8z9Pjw5HI58x9P266rQ9uzf8sILK82VaOpfMG9ppERV3X1qm+poN2ZexmdV2HiEZy\n6brm+PxosPvLAS2W75r/K4tGcowxVNWUxPuw6a6apiaM/XAi8s4F5wJzjjEWzk0dyeE4TO1m+/j4\neDwe27r2i3yAQ2JmI1VaYmQX7fr6uh+HXbUjAGYORM4Bl6z5ktko6kVIV1EUvDpRiYHkRbXSWTmH\n6NT3uFAYLiFOCD5GQLEFWErJ05xLYRKvUnctAKhCEc5aLrNzvTPZm1W3BpeOctuMawy0rvOSL1oD\nP/rRjx4eHqxBxHIjYzBblc66pzH6qR9mKfvN9s2PPv/h2+/AZtQ7moex22055Sz8m3/8pymnyodp\nGH0poIS+yoXbZueQYggI1VSGECP5akJKKqquabp6tz+djuCdOizCvqmcc5v9zlcRfZg5s3IT4zwm\nJcggzWbDSL6tJRB7LA7Qe1V9mvrsYEZJKNF756K3Uc7bdnt986MvvzimsdtsEikHSklZ8s2P3pxO\np89+8tXT05Ot0tg0AHCYB2b+7O46hHA+nrKUMfNU5On+ZFWZUsqrV6/O53Oa5zpEKEygxvUNIRhB\nce1Xtc1rRiDG6IK3i2xcxxDC41GHc391dXFdDqmOPiH086gXwTNh5lJElZ0LITjvIxHUm61zWHUb\nkeJcmOfxfB6Qy1XbQuGpH+aUPAKXwiVX5OtYsfMsDhHRgZrksei+qUG0LNq+toQ2m82rV6+89xeA\nbpnrXdf1eTiN6dLlGcitMdbYD36ZhmqUuZFGBxjC7w01Xx/m8lc7bIbO2IQX8M1WsPlnK7fY6nzJ\na7Bqvx3litTR0vpr9YnFbrIsMndr4r+WcNZo1/A0RDTIaM2oVq9gG8ktyn1rQLo6m3EqIQTE4Bx6\n703X7/B8Wr/UXkwveqdeBqr0Qr7Q1oqZ5pIuaVl8oZpuhsPOy67+Ku9hJHWzrbRQBHWZlrY+b+81\nX7XZbKqKHx8fZVFdstWQl7H2vIjP2nUbhjOAhOiXuRZILjBzYQcgPri6jqIOEZEEwTofk4UILwMr\nO2x7PD09nc9nS4JFsqPAgEqOhU/DWLVNYnGhAnKCKIjoAjhXt5tQNW27mcfzOIr3ntCBoiPftZvt\nZnd4PpqTgItObh18JHQsxQZgj+Noo18QcbvdisA8z2/fvjVVFcs/Pn78eHdzNU3TlNKc86nvM3NV\n15vdzk4txjgMQ6iqzJxKIRe9i1yEyOXEznlQmqccQjVNkyqqYskcY13FMA4JFKtYV1UdqpqZ03iB\no/u+v9rtD6fzdrsjcnPOm90uxmq73YnINAw5cxu8R0IugBhDfHp6eumNnIJXByADsLhPcDkRIyIC\nQm36mda1OvNFcgK3u46IEEEcMnkRsiC0qiIAmCQ8M9t4HE+u9R4XMqrtiLUca4vHvsLueCkFlO2O\nnM9n67jEpd9FVbuuM3XgC4FWqQY39HMj6csfbz4+Dtv9Ls9pzokK03RElir4sT96hLpph+dDdbMb\n8tzVrbDGGJ8eHoPDeeq72ho2pJCDSApQhNPMFDwFb6cGjg6Hw2mcZinBVUUACRVhLqXrOvRuzEkc\nulixQFW3gA4QRViB2s2umzP5EQCmec75omvsN2Wc83mYBCjWbRFtN7tSyrbphinFuhU4FC4pM1Au\npaBzrNputog4PjwWVSQnIk23sTAOUrq6ubF839ssetEEEGJs23Z3d/d4PttoJnSOVAlRmcU58R7J\n9XOaS54BYoxOdRzHeRhD11mu01S15aAGvYQQtl3HJjBOEDwH8b4IEgz96DxxEeepazfkfd11HrGk\n9OMff3V4ePzuN7+TNAekMs/JBWWxydiCgA7Ie3SEAI+Pj8HRak5tdZ1OB1s8vIiQ5WUCOqtwysLs\nQkDrExJFQMueL5WkZWDQbrvFJclZEXsz5pa4r4vT9oa33h0z6xY7G0poT67FkhVVPJ1O/sKIny0E\nWJnZ3vu2bfMyXdFeY+59nmcjI1qaZTmQmXjzbTacY202lhdaDIbM2BQQyxgM/jIo8/Hp+PT82HUd\ngBBBCIEcNE1D6BHRtF8veeWSbfyPDgmXWtHqciyutxG5bhkCJC8EkKw/wC6LeVlT2rZqmX3mmtzo\n0q6oi9aT+fKmaYjyH8CeVpm3e0ZEBtBdlNyMguIul9T8nA8OZyycSykpz5Y6GJWAiIxvZpmf2Sla\nqPN2I+q6NtMfYxwnA+ukrmvnuq7bdt3WORdCRQQmLrnbb6qqSikfj8ci0nSb4Xxa74sV6kopVuax\nlOhloFPVkZlNn9fSxPOpZ+bzebi+vr67u1uG9k7X19f7/fU0zimnuq7fvHkjIvf39yuN0Hr01iJQ\nCCE2NagfxwkApmmuqgoAmblrt8IgWpzzIqOIqOI0TX0/WvOgRceWMq5aWafTyXoGU0pWCr25uenH\nMc8zojjnnEIR4VKcd/v9/v+SxaDBqUfvHBI5IlEFVfu/quu2aZz39owNm0O6yPpVIVpU55wjhfP5\nbNKldlXF0F0kzPnw+PT69WubxhJjLC+EsXWZBSVyGXvqCGwAj0m/WK+6BYLrdbBNPU2TeN42G7ut\nn4aZscw5bTabYRpBtaqqeZx8DPv9nrUAoRS+ADvKcxrrTdc0TVXTnOdhHqBpq7qqhManh/fHQynJ\nBWcwSR0rAaUq3Ny93u12ngAAQnAUw5s3b8j7bre9vXnlY7D5YTlzznPO3Lbt8dyP8wRALlAQAMI6\nNi74q6sr2wLMbMV5I2Suc91s5Vgxcs4JAK31ygoBtsFVlXOBF/PoYBW6ZXGO1FHV1Nurq+31FX7v\niwggGJGWNEhBdE4dqaPt9RWNQwwxVJEAKSVfV5urfQGd5zmXkqeBmQV1c7W7ub6+f//Rbg0wjDlL\nLxZV/PEf//E0TY9PH4w3ZEX0gKjj9P/63/6flfNF2Lmqqeo+5zwnvEhS2Tg/ACJPhKQiYtHA6nhs\nn644lpkLs1eqapO37PmLL+FLn6ytPWNm2ZbcX129/eF7yRftO0OzwjLseE0D7EoCgLcoFQAMPLE3\nGJvOZARxUXh0iyTdy1TDgEK4yEiXtm2NoGz51s3NDVymE5KR9ACgbVvLA6xzaAUZLKx7acHbtn1+\nfn54ePj6669hIaq9pH+klObEr17fhRBKSX1/+slPfjKM5/1+P42p7/v9fvz48aP3fhimFZgyXMU4\nZpayrB24bdv+0R/90ffff388HttNNwwXzrp93W63q+vaopjVOb1+/drQcyIy4dv1pEwBzLzXNE3T\nNBmyZNXjzWbz+PgIQFYlslswDMPt7e3d3d33339va2JtkL65uTGL03bNWrJeuY52R8zirHCfc67p\nWlZx5M5DH6po2XfV1Da8Y5qmIoyOfAhzTgYh7rZX4ziSgxgjAJmXXUOnNBfzi3XdHA4H54ILEZ0r\nouR8u4mKNM5pzqUi52PlQhQRVlCkqqkB1Q5JEaqqOvXn3dVeAeq2EdCnwzN5B8KhikVYEdC7QE2o\n6mFKRYB8jD6aJd3ur8dxrJous576EV0QAWEmFwDAefQx1G0DRKaRTOiKcNNtAGBKuela55wWdD6K\nIpJvtxUzT7lUbRedj3Wj6FLJPtYuVLFqfKhCVX344Yeti+M4eudNFmGex+12mznbUOoYYiTnhEgY\nM2MSh6qIDtHGtLOqJ3Kl0Pk05wwi5D0gTnIZ1J1S2m02YwjH49F7X8dqmqZN0xqckFIiRFWdylyc\nxKr65ptvLD6zWq/33kxq27bn85mIbLWHELgkk0DMOf/5n/+5LupERnwYx/Gf//N//sMPP1jcidEX\npPjFXSD3VsftH33JXYvbODyUTDASlTl9GJ8oguD8ePxQRSfDiZzrz0dlfP/+vX2yIx2GqUgJPhZ0\nfT9qt+l2WzgewLtuuxuGQXBm5u3uqrB+uP/4/uOHNI2lFLNLv/nmd//iz/75OMz/7W/+65zTOE6I\nQOTmeXIh3t7dpDH99X/8z88PT6GOlY8M4oCubm7+zb/5N6fn49P9IzM/fLhvmkaLMPPUj19/+WNS\nrEO1ht1VSkT+w3QfXdSi+82+rut5nLquQ9Gc8+l0ur67VgZlqGMjUihGANhfXx8OB/L+7fv3oapy\nzujcbEF8XXchfPz48Yu7u2mapr4PVV1V1anvr/d7GMdQVUUkM1dNExYNwxjjt99+e/vqFcUKFQyA\nsXBlSuVw6l2oZErDlBTdOI913UypTHkOhOTd/cNj13UIcDqdsHC9aQmMMgCZSy45CVdVVdWhruvj\n4dnQub7vbW3YarEEwzIEw6tFJPqQ50SAytL3g9W2zbDP87zZbUMIrMIqOS3TwwmV0ARCbSwJqyqC\n1TstdrfJ2J8mvqx5g9l6S19W9+UXHdlLTWUZvbpifxaxWtDql/F/a6Vk/di1ILTdbi038stwF1go\nWLjUh9cikIVmL4tPuij91c2GHCLiNIlBbUZLAyWzodaOZ0GQhZbmlp1ztBz8GhXe3d19/PiRF3k9\nItrv96WU8/ncdV3XdRY4GJXWQEjLvVasb81GLTxchZHMedh1jjEa8bpt25SKDWO22fVE9PDwYBVp\nWEZDrXhjCG6/38cYcyq5JBVAguCjiPBFOoREhNABKSgKq+W1a8FsDQ7Wm7jeIACQZRqjiIjKWiOU\nRcR29XwvQ29YRBXt17XIac/8fibqvL9cohU1Xe/pCziL1mQRwL383pfX2dwtLDpXlxqMd3CRNvxU\nMl0eXjHTC+qNko0/v0DH+PutOZZkrLwSK+wxsN3HABp9IFAP4At471kvo2jGPCYFyAolv9peuRfd\nBHQZzQcAgKo2ep1VpRSxclRVGQFhDftA9EXjOhKRX1BrD5E10zLT0w7Y4lN+MRXe0jsDZqextyIH\nLiNE7WNtzVsR7ttvvzWyJUbvm/Y8j0RkRHA7NpsLDgBV2+zr2lxOSglz/vzzzwOQQFDwgD6EEINz\nDjZdxSij8Md+eHeepsQsEKsmTz2rqCooCgIRAgCSR2XywRPGuloXJzPf3d4KX3goIQRz/9vt9nZ/\n9aM3n2/rzseLyLSFmMG5IuIBFRBEOZc0jOM8Hx+fmq5Dlm+++06ZM7NDTKXEWKuq+xe/9Ipvv/nu\ncDgcDocqxrZtQZSZ37x581zXb7/7fhiGLLy/3c85X2qxbYuIj8/Px+PRzLetzO12WzWNC6F/eop1\njYiGPllSVtf17urKdIRZxaB1dLS72n/5k6/nKY/DAEWqJhD6XGYfqv31Fbkw5zTNWREAnYCKoiIe\nz6dxnoGwaptNjJGhJnd3dT32g6oCihKCAxd8qKpY+da5eZysans6nUII4zh+9tln3333XVn0Ui1N\npBfS5rY+q2XMvEmYW/nGxvTZi8k7AUVEs962y9ba0Jp1wCrrvgIpa33FlqYlAdfX11ZDWhMX2xgv\ndyws/SsWla8bz/5kFakVbYPLpGReE50VKHsZ0a9Gs2mazWZjUVtYJhbDUqNS1WkusBhQy89s+8lC\nk6+q6nTq7cX0YsjuavhkGWvNzLe3t1ba9d6P02TqD7awzH+o6t3dXYzR7paInE4nXdje+GLskzme\nq6srGzb8ww8/mJm2FMqiCVUNoWLmtm0tCra2D8PZzG9ZWFAuior1PFszNgQfVbFt6xCqh4cHVUQg\n54KjbDPIbd5l4lJ3bd/34MjFgIiC4KsI81RUKPgsbPNQRAEBqqoKlXeJShEWiXW4TOZWRjTXJQgE\niEYhKyJAnnw08ymqmTUVYUVWJDDCDCAiqCpk9C6VoohAxKro3EXBFmzABwIROoeLi7PoBYAQXSmW\nWuhFUgydc0FVvY+lFCJP6E3u22b4KaEgCCqDKiGgApAiAikSAlv3DwLZ3BcAJCRCBQSDtgHIeecd\nua7bog8qzOlS1KwcdXUTm7pyTjSdTqdLiANoSB0SSHAfcq/LZHd8wb1sYuM9EpE4FKElxnKH0/M2\nyFhGx2OMkYlrT6pMjnrKzrkUREBN0kEYddZmWckvKaAW8VhXmW1704JzywybFSGxjWYgAbzQ9Awh\nRBfcLGFGVdF+aH2AQZxzV35j/UZEWiUKQZk5Z2GW5/4dgxb1ok7BIbrgyXskVPAgIZxFT0K5aSn4\nUFc698wKphipAEjFJuoKOu89eHMPqgromLXM2VFw4ADAo3felVLmMUnRpmppS+gul2KaJmVwSKys\nLJeFKJKmeRqH6ENwrgoxODfNiUsm54Nzp+cDonPgoq9KYk/h7uZVbcmTaAjhj37+R6rKUzmdTkCq\nEcMSPdze3pZSvvvuOwAwMGntoDAu34cPH3Rp6rDocxiGq5sbIvr//v/+d1s/zDym2Yzk559/8fd/\n/4+Pj4/TlOo6EvlhOJciMfpf/st/NYzzMM1tW/tYAQI671HbTdd0rZSShul5GGBMFZLmkoZRRBIn\nFhFgJmBVBXalEF7IVpZ+lFKcpx/efr/WLCwxMKcSfSTjvzlXV5Wqxqq6vr4eptGyummalJAWpdM3\nb96YzbfYnZmNrX1/f69LJXt1Gf7rr7/WpW6/bhVLRywJsPR/u92eTieDU19Gx/Zxqno8Hs1/Pjw8\nmHyvOacLsLDw8czI2MYwRCIso6JMdMROyTln8xm99+fz+enpqeu61RWtyUcpxfmKnOVSibmcz2dA\nEZH+PIYQPn78aCGhdaitsLj5P10Ewld3yMvEX0SEGUop7969M1c0TZN1At3e3vKikGTDgO31Rkww\nqIQu2skXZp25JasPbzYbWkp5dnbrIZnUbillv99bDdOSOXgx/LEUiwAoRo9Ibbtp201VNWapiTyi\nA7DBoxdd57quzfm9zELMKlmws6YviFo1l8ZJJGUx3qc6hwAewNJWp6rkPvUcrGXJP3Dz/2P2I4qq\napx+u0p+mZWyvoyWNgMiyszOESmsnh4WTBIWFXnz3Jf0FEEQkBR0TaesZJXtsxFxGaaiiChL2vd7\nB7x06erK2yxsZQZVjfHCvkspnXLRcfAAhSdEZOUiTIAOHVza2sDHWkjXzGa91G55rEkeEQHi9ZvX\nNzc3xkusQnTO1bEqy5ixQI6ZYaXkMHcxbOs653w8HlNK4zhaAfx4PFpUa5A9LQPJuLBFP+afzPzZ\n6dsas41sTLA8p3298eREpHCJPuScQbQKsa0bC2Q9OYeEBEpCqG27zSqivqgTQVF1hCG4kueUU2Zm\nH3xVU9U89+Pz09HHKMsYaLsU5TKflIgUl83+MgOOISAAMxtBUVVZxDpGWEVSISIkKsxlnkXRKoKw\n5smAuHSqWOKrlbjgow9IftNd2dh1i/RtDyJASonTZTuYuqsh3lWsYluh6jBNVQh93+d5DiEEs6gW\n5uaMiNMwTMPQVHVwPjhfx8r20G6zCSE0VU3eXeLgcczCzHxzc2NcIefmi1ECsKQkxjjPOedcVdeI\ntpcLiHt4vD+PwzCOOs2+cFD1wbd1c/j4gIgCLAguOBdcESl8KWMbKGcFZhF58+bN3/3d3634hL6g\ngKVx8t5bF5SZdJNg/+1vf2uF8JQSBU9Efd8fj0dShaXH4yWkgS8abFa/4z9+/EjLRIaX1souiq3X\nFQcwD7lGeS+90Xa7te8Yx3G32/llGLkRc23jmckww42IRqBAxL7vzdBbJcmSJKvWWE3Fe//8/CzL\nQFhbsrbx6maDZNy5GUAeHx9DdMzsXbReCqsxrGDjSotY0y972MV6fHx88+aN3ZKu65izHcPL8zXb\n55yzT7Z9i4h25FYiNsqm+VSjzL5588aMgr0yhGAsA1p4ClZGstbFl7CVbZhL62sIm81mnuc0l5xZ\nmKcpxSBEnosCmB4SgdIF+lgm6BhX0GoDsDQsv/RG9IJqnDmlMgNK5gSkw9SzFveCKK9o8/hElU14\nV5ZSue1wt6hv0At8iRf+sTUAWPQTQmCWdTnC7+NmttiAkIsAYeZi0xHtYASUHCmDC94KUYCCeDlO\n2z6ICiAKjEhICCqW5BEhgKkeZACwYhWojaAARXAh5AUqSCWHKtIyMXqN5tbDttMhIFJnnDoCREGn\nKEMi/L12N3s404awHQcARGCdg7kkcfPxNI5jj4iI0YdpmkhhRcXp037WKY3X13u3DMlcndwXX3wR\nY9xut9aPbGbCe69SUkp3d3cppefnZwsN7bwMkLEFb2eXSv7d44c1nfJ9sg1ogIfdviY2wVHiNOaR\n89wmQGXBCkMF6lkUHDn6PdjWe88hVBU0TaMkqux9FBFUIEBOhRQUwEbuMjMIOuc8OURs6i6ECnDW\nlMgF9M4jkWrKDOicp3JR+Y6ORS86/SSKiI4IFAmRXKh8qAQoF0lFWIAVc5Gik803YjDBQRTQKc1p\nmvf7vYigd3XXnobeBR8kxqaeptE01zlxngsnBsHoAwJIFgRsq9ahCxRySpt2O/YDgQNBECyJ05RB\ncDyPXd0xqKfgnHeulCKceJ7naZoInXdB2KYKOyTiIo58mrOwNnXryJdSSmbhVDV13TaaCgO5OWmZ\n0zQdDodlJ4IuulMCysxtDETAnOf5sg2nafrw4V2MftmDsHYowFKsIQVd1L4Ls8lkE5FdOm9SKaqb\nrjsfDvZ+i3XMI5j0wcvtc1kYRGQ+YGVsm8Fdp8EbimUpES8dDKtDo6WPgZdGpfxCCJyI1sntKyZA\ny5git7D4VgDRnlm7r+3b7Y2vX7/mpUXR3Kex+z7/0VfksJRSSvKe+r7vNs08z/OUnXPb7bauaxF4\nfj7iIoBhVnJNs2DRCDCQrW3b0+mUUuq2F2Vxu0NWObCQM6V0c3NjeGZaBtpbZGGEk5XuZWQQ+3x+\nMXHEqn8rP2ee581mY3RnXMQAeZlwo0vJp5Qyjck5X9feYEME1/d9motzLobaxNlkYcIwY121FtDZ\n1622xkBXO6pP2YwjH0PhxJIXUBiGYTDSxsUVAduscFVVBMVPcoK4kJTMTrnf17xYK2Er2GsXRCQv\naxJX1/UHCRAsvWV2WVag6eWfLu+1sX6qAOIckgNyl7IWgAAIgMGBZH15ArouCZuPB0vqnxdZEMvj\nDWAxXqidaSRHoJVzomEYBkPkEICQLENyhMFHwk+uawUVogsv4z8pAgKAFJyP6DI6oUs3m1MISCXn\nwpeSqkcSu6So3l92iqVEuohA2tq2lk8AWBmVdRVsxU7T9PbtW+M7WGHMCE0GVNiTc5rvXr9C71T1\n9vbW6gq2em35GWwQlkEtHmRDCFLANS7Uom5OmVRDdMfjc4Eyinzoh3fDPAxDykpE6Mm64koplrYw\nMyKpXhoN1/V/uTWEWThxKSrABYUFNMYoDsGRghI4AWAE8A4xXgY9e3Le0ndlAvIOowfCggqEVIVg\nVcNSztMI3rngpzRj9M776MP2aj/1Q1EJhKGuWASDl5xSzutkOEIMIXRta89YYkrO1d4zMyHmnKMP\nECsb9YTGVQtx03apZJtrnFgwu5KzITSegr6gur0Mg9bI2EAj++s8iaoiUbvptte311Udirpcrrvt\nPE4eKUse8ly0qKckPKfRpQR6Sf1XqprRYtfLvmI5Dmnq5zWml4WDbdmFLjmQiPR9fzydSs51CLCY\nL7Nglq+nRRZ1faiqN4LAJV5bNrm9zfAiW8SWB1gIvKZX67akF5Vht5RY10osL4CYuRkDZyyTMIO+\nmgMzmnagYZFttT+tdIAVVDFeJjMrXHjxpnZjrLarqysiur29raqqFLE9uWICduTBe0txjsfjMAyH\nw+Grr77abrd2qLurvXNo85YsOzE3Y/W3vu9/+OGHlZJnZouZ7aIx8zAMNikrLBJHsDBEzaIZue7q\n6maNam9vb8/n89XVlX8x631dE1bYA4C6bqzCRAuHYrPZeh+qqq6qOueyrhVzruScqPoQpnkm52zA\nmnNOAXwIYpOfl65M7y/rvqqC94RLIouGcYFeLDnZcPAFP/HOqXfOxbqicRBQHz8Nob/YEQRRrdsG\nCMnbdIkcHaEjQuSiSISOyDubAGMFAMPZcdG8MLPlFl0T+9PabIh4YVgDAiiaYihYoQgAHSGoigLh\nBdEERUS09rIFsUT9xKkxPg8AhBDM9RpIQkR5yuc8lvPJqbLMqgoE5J1DcuiUHIAqwcz5gg2tuRGC\ngh7OB/vYqqqQUEARxaOwMPE8SGKnRJgzRyQJ5KrGAhP7CFUFUASFhTu7LkLr1F6dt18mMhtgNY7F\nUnNeupEsQjIxFF4YzLh01E7PJyIqpbzZXD1++/bq6qrv+1JVz0ukSAtaW1VVW4c0nEQLUuOqpjD2\nwyg5+0DMGTxwCL3iCbx0ex+qum1LSolnhySXSbnBDBGIWAGOwAlYKQtLEeejCKAPwQcyQ++o2W4Z\nqQACkToQkcuoBZCZSwFVRxSDGGSHoI7GnMC7mUsSXgImBO/aqkZERjiNw5xzEZlz7rpOPYE6S7Zm\nKVQFl72ohhCmYSQiR5TnVFJGhTTNu90OlwHNhaUK8ViYUwZVLVy0UPAiooUdYJ6TzY93zgFiIOdi\nMG5bCGEq84IisJlBQ2ss0jVQ6lId5BSbWkROh0NfngcfdJjz6dy4UMa5qiolTSWLh2rTYvCiJR+P\nKhd0ZBgGK/+/e/fOonBY2GcWczgk/zpwLiakCwC+iiFGVX392ZtSSjQdINVhGI7H48319fHpyZpe\nzDxe/JZNmLPxK8s/APB//dd/bXryK+nZeMkiYgoC5qUNnV9TqtU/r+EwLvOe1yGwaywsWhBRtOTE\nziNAfQm9SXM2FAUBxdKvuq6naSLyRKBqboaISMSwF6fKqlhKtvgvxogEACBy8aZmR4xsbQmKoUPO\nuRijRzJujKo654lozvlwOr1//2GYp6+//olzbr/fA8B2uz0cds/Pz2/evHn9+jORMk3p6urq1as3\nKU1PT4dXr17Z5CEbct+2m3HsnQveU123qjxNiQiI/DQNXbfNeSbyNzdXwzCVkqqqORyenAvj2G82\nu6enh6pqQnB/8id/0jSVvasU8Z5Kkb4/3d3dMfOXX34ZY+xP51JycJ65VCF8/vlnyizCICLCyix4\nGXIFKLnMKSXRMk1T4eQozGncdDtAcc7Z9bfB9USgLGka8zwhbEFUuMzTyCXFpgEwmSpBR8GTwd8x\nOCbw3iFICKGK3jsE5eCtdmWO34ywgGpb156cJ1dKMcdBgIQEpIRIgARo01oNVRcpJnttMJVb+JAv\n6z0X9AA9EWYVALD1TsLIQsIgevFtqqpCRA49gbOv8wTOOU+oirbqQJmIPEEVQh2tN1OlMOcyTUNK\nSchF7xvvkbDyiMJjnnBBO52gB/TgkVRREdW54BzaqibyAMKs3lPXbbfbrqqapdM+sIhl57aSh2Fw\nRKo6nHuLEta4GFgAZR6HZtto1n7uy1QKp5JFtAyDiJa6anOZY6gBRVVFC4tmLmBdpTkZiQsIXfDo\nKEIVqphzllmt0GLk5oTparvTwtH5yQpzCiFEy4CtIWnqhzwjl1FAffC1rwsggyoiIMa6miWxigtx\n03TQbdKYx3EM/lPZAJdWdOecFJt1aDCGByARKJlLKcW0A2z4k7BDoOC99+QdEbmlRqCqRH7OpXBB\ndOjIaRBQIq9Ygouxrqqq8TFwFgFGRUUq5TLUHAD211fOufP5zCouBFYV0FTyOE+KgNEDSy6FVeq6\nIaJU8pwTOnLBW3+CIhRmAGjbNsZ4tgFU3oml9ZZhN7WfJ2aOoQqLVrJM0k/j4+Nj1bTDlBmkqiKU\nUsbBkWva2sKOtm1NdEYVmXWexk23RR+mKcE0+9iEwhZvqQf1IIhzziWJjOhKUGABILyQjccphVhX\nrKLI+QJK6UWXJ3nvCVHmYrYUHJU5xaZ23j8/P++vr87nMwAUvXBknHO77XalIKxER12Uq14mRpfc\n+k/+7E+tBdKCqbJIiKuqwVAW9dgP3nvOxXv/7bff/vSnPzU04+bmBpd6QErpF7/4xfPzszmwqqqm\nebAcru9PuaSqbmPl+340ICfuOlUm8rfVtVXdxzmRD8+HI0vp2s33bx8+vP/446+/auq2H85pzs6T\nIy/KXAQAfvOb31jLp3WAlVLIQVVVddWWUn744Ye+74n83d2diFQxEirnQoAqQOTJOVZ3++ZH5ylX\nVftPv/onVGDJXV2LSC7zZrM5ns9Phz5GX4q0bT3OfD4fT6fehfD4+Mycr65uDoenGGtVHscZQNp2\nAyCIrm3rec4xesQnkRJC9f7jx5y5lLTfX9/ffwjRVVV49/HDZtNm4b/9739bisxlVEVVTqlcXe2e\nT8+I+sP7Hz68fffm9SsReXW9y8JpnHb7NpAb0/zx/fc/+fqLOkSGV/MwUvCbphWEzfX24eH+X/8v\nfzWOAyLd33/c76+6rj2dzt677XaX0vyjzz4nwr4fiOj19em//PVf13X9j3/3X//4pz/d1FX9xY+c\nFgDYbNphmKZpCCE41R+9fnWz25ZSDofDikTlnD9//ao/Hm6v9mtibnGJg+BJCeB0eEJlVK6jl5KC\n80SEwm0Vx/7UVJ/Etj1Vyo6l7Dbd4/3Hpor96Ry9i971fWrrpiRpqy5PBRhBgIs2m6aUBIWDYFDc\nxUZnvtleH8e+io0iTNMQyJ0Pp03dbEL9ND7e3lx9/PBQRb/Z7JjzOM6SU9ztlcumbQ5Pj00V99uu\nzFNd+YeHiYhES9+f67oOoJxKSlOIvkgRVUFE8ALIwiAaajfPI7OG4BBdKQnRxeiJPHsaT+fvfzcy\nKxGYxqAnl6YLSL42P9hONgjISjve+5JyEUbvfvO7h91mp6hVV/X9eXu9Yy6bpjufTz/58U8eHu73\n+6umqY/Hkwu+qDRN42JoHP3P/4+/ur+/N8kM8+7H49GQ5Ou72+Px2DU7zXo+nepNexz7ets9nY/k\naSzJ6ky6aBlbTACIGTEzO2ZLTwsgOoQQXAU4lVCH4zhSVU9zT75ykUopTXcRgokxXl1d5cQILsY6\npQmIkFwV/TiObdOpIhGhChEF54Lhe4AoKrls2m4YBhUJzqGj2vp+lEritu6meYy+KloIHBIqw7bb\n5bk49IWT857AESGA5lII3DTMqJSm7CkEF1XVxs2hC6Fq+nGeM9fRF9TQNSPnylexbQ79OauAd+Za\nfQgsEmuvCJmLAQbMTCEyYmKmKpB3ioCOWAT50j9ARMFAqTmDD5WP0zw7j912Mwx94nQee18FF0NR\n2e2u5jnPc766vhvHPmVB8ORgGIZK1Ise5zOgVN3m6fDcbltIuR/Hr67vHh4/SlFfVVMqpcx1uy2C\n5CtWtHI4EXkfUinjPLRtu9/vH57fgWrOjEzeOxbRUjabTUl5t9mez2dSCOTO5/Nms7m9un76+DF4\nz6WkeTb0UlXtmTW3WR/eIM41PV+zHFzqzGu0sqJ7+YUOm9VCc842fqosQvTm4VnyCqw55wAMAtYQ\ngiqLkGq+gEBoBQangHXVVLGWZXRFyXx7c2eYxkrPk4WWvd1uWUpKKaWJORNRrHyM8Xg4A8CHD4/X\n19ePj8/WJ2Hv9YGij4goDOqwqprd9upnf/TzUsrf//3f13WcjyO1lOd0Op9+8vXPilg3FeSc+16Z\ndZ6zZWPm9p079bY8mf0ytGKec0qj0RlX4oPtt4eHh1LK8XgehrMCh+CY9XDwfT/+8pf/4m/+5r90\nXWNxOrPO83g69VUVcs4pTX//93+vytFFQSlzUVIHrp/6/WafOAUK6FGLuuiii4lTKrlq6++//94M\nx/l8XkU0AMAOjz/1mlTbTfvDd98XTvf3923bPj583O+3VYjn83lEyCk5JAQtKec0VzEQwvXV3r8Y\nYD9N0zyNr1/draAoLeTjUkrTVPriYWAAAGw3u5zzfn99d3Nr8KmIIKoPDlHHcb69vcWLooSJTYj3\n3jvjLmZmqarKBZe0CKgHdM45AUR6+HjPKVtTnjWhx1i5DbU+zmOqQtx2m7xPROQRRDQ6otByTsxc\nRz8S7a4219fXeU5Ph+dpHn10+92+IHpWybNDqqsooE6REUiBDHxQQFBlcUjk1CEBaHAeAEDUOt8E\nRZxHtZ2ppOhB0XvrnMdFkcQBOCLbP8AMtmEQgsXXiloKl+IrJAWZU5rn45SYORI9fvg4HE/WIBHq\napwu84oMCDJRtSWTIBHZbrfDMIQQ5mlin1VwmufCrAC8NGYi4us3b2TpyvDLCDRysN1uGNTFrmm3\nRL6UQoB1dG3rzsN5EP7th48ngfvEGTA4108DUaRLHiylFHKXHjubzaKKcGmysuKOI/hUhyAAtVQY\ngBQcoFFRUMH+ESCBQ0SHnogIrJZJDKwMgoJKiIhKgID66dNwqZeY7VqYfgAv2CuKTsBESJFtLAXC\npVJF1k52GbioyxsNGH/5zy4s/mFvnAELJEgKpARGx1BiRCTvkFSBQ6i9946Cc+JdLK7MuahgXddX\nu3rrfBdc5Rw5mXPudu3tNNZ17dXlOd3ub76avnQOgXDsh2EapfA4T2mayTs69zYV1wUvhVPJIURE\ndMHb9VFVFkmLcrlfpuEgokmGg+g0jJZllkUmHBfeslvqu7pwJIjIm1jAWsderzgvsnIW8PKiXmpk\nuZU3tUoHGavbkEF6cWX7vveezL6Y4oDla+vdXdNzAFBFHyrnQgg+pZTynPIsyiyl9lWsgvOXT5al\nbeoCBKvmnEWKcQ0AwIp7hniO44jozOzqwm9Wo5Z5skogLJXe29trnpKhOiZ7bmU34wJYsK9Lld5O\n5EKHXa6S8d9WWf71UphE7N3dnc03yjnXdVtKQtQqBkAZh/mf/bM//Y//x98Q+dOxD9Gp4OnUz1OO\nMcZQU4hFerGmHwdKDh0wQ2ZptzsZTlyUABVRWFKazsPp2B9/+ctffvvtt7SQzkXUggYLt61wvei+\ntE7oyy9+jIh11R6Px6ZpHh4eSknb7dYS0BDCNLF34f2H913XCSsRQYVrMp5TeX464NJJutY2VbVw\n7nv/Irhxqiqshi8+Pz8fj+dpmrpuayTAEFzf96Y90fc9ALx69YrIH4/Hn/7056rqXWTmq6vr7XYr\nIi64w3Ri5igY0UFhRLy+vv35z/+4L2lIk3WYVs57ASoyTdPHjx9Xkv3InFLySE3TeO+NzGK3+/7+\n3hSDjIVxPp91HJtYe+8llXkaYl2JiICCAisDIAiiypQn214rmVMXJdmVoqJLEzGKUgix7aZpWuwq\nqQogOR/Iec2FRcucyKYPkKtCqMG7rHnKAaMURC0yzBkghFCDh6kQSToOzWbLaYyOpml0VSU5K/oo\nGMR4wwrAbV3vYjM+HYGhUpLMgmQbyoqguGhoffjwAZa6l8X7pRQF/uab3xERhgYoGKHfKRBKrKBI\ncXX94dxPseoxlKpjZiNoovcoF7iJHYLzKIAkyqKCQqhAiE7EcCci/cQIh6VwAABKpqMOa9B9cVrL\nY4224UV39mr6aOmFX+3SSxRxDcfXUu7lw9ELACiZbPza7WdIo7X9AZDaP0UjORMRkdgrxXAasvcS\nXTRx3YuvvhwP6KWR0cz6dlOHEAIFZg4hFPZNVTuiNM2HfuhTplKQWSEXYd8EK3RVoYbC3+s3McYQ\nnJKCCDpXhYAqXVNt93u8vcnMwTkfIwHMORNAjPH1zbVdIrOKskgE2QQN2yPWF6RLOw284GCbwaQX\nzfK6cByIyNvotvU2rHeoaRrTUaZF6NNOWFkWKpS8lDOKy/yeVZJZRErRqqrs4pq9My4ZERnTTF90\npFpuNKeiemmPMC9qRtw82Xpi6zGXzMZrXY/cNsaF5Qxgds0U51ZegL1WRHCxCB8+fLi5uTHmiLHS\nu66zypO9y6BVo5GY+zTPZwDuSkcEAHOB1i+li7SrOfJSinm+xRtd1NftA2Osm3obY40Qdrur1f8h\n5Cp2Xbetq02s51KKJweOvFP0Dlhmlu3uqgCWOSmhIjMoCAP5um5/8Ytf2Pw609J3zhkLP4RwdXVl\nAuFWw/Q+zn3+N//m35gv/7f/9t/+4p/90b/7d/8u5zyOs7twF4uRRIZ+LPlSyrbkz2IUo+odDgd8\nocKOi6JErALR2kRCqzd6+/Zt3/e73dU4jrvd1UJgQVVux2Ycx2mcz+dz27bex/P53PfjPM9VbJj5\ncDhaq5aiVtuOJYMiofKcYoz39/fM/Nlnnx2HMxAxsweM5HTK3sWf//EvfpRG21R2tSsfuq4rKW82\nmz/7kz+xQMp6A4Ho1atXeRpbpFJKUzd1UxFrmqsiLFKKigP06hwgMRDortk1TbVScoxisPJXddHH\nWw1cfzx12808Z/IIguQJCqGj06lPJee5DNNI4ICUwGlUy7yJMAmLQ6qCD6F2OI8TBn8eh9jUzaZz\nMYDq8XTaX91MR/Z1lVWSsBBmvXC1RYRioBjGnLyK9z5zQbzIjhl/xxbAyktaH7ZNREsVYghBKOai\nzAIAoMCcp5KVIDRN2zTNdtdQNYdmzLKiHUTk6BMJ0y6UIL/8ilwKOrKRKBd/QEQvqPPrVlq31epO\nVpBmtX1rVP4SELL8fo2ilihZ15e9jOXXb6FFx3L9E/1+l8L6/0vbtb5GXowOePl4cVKL3DteJBlh\nGZZmFTNLDHJynhyKKjOIOMTgXQjO+/rYH7mwj0FFUAEBx37wDh+Pj4qiDKHywcU5T8FFInj3w/si\n2aH30Tn0rAXEKEEXg7+KFRnB0iJy67Y0tkXO+d27d2ZU1zVj5AAzsH+QGDkr4+sLacXVX/V9f39/\nb51DxnA1cyOFrVRg340LbdqIcMMwGDFjSbpt2OsyTGyZamqEaV7Ii7rwo0KoQqyZL3PNzTdYUGkS\nai9vrS3Q16/ehGjogYqUuq6RdJqmnNjMYs55s9kcj2fTx1v9LjnvvUeiUuZxHO9evzLk+nQ67dvN\n03N/d3NbVdV2u+26Tc65qmpDIG06XCmlqmrLXokoLENpzYGFEHMuC36FKWXvAyKllAFQxMTNkt0I\nu8Ih+O129+HDx6qqVaHrOr90ARM5RHLOI1IIURQUEQAF1Fvx3nkGELX+FVJSQvSx8lX8/vtvm6YT\nsbiPYgx1XTMrs4RgxDUPUJg1ZxZJKeXtfm/L63A6scDz4ZTLLKAVBVaRokju9Wefv/94X0px5Kwb\nhnxQxHFO3vurm9vH58Nl+yx9siQChKEKn0JaRQBFh0RaSum2u+3+as4lF/MNME9zjH6c5pQLOp8K\nj0/Ppr/AQuM4xpgtUh2mEQCyFBrOLNkLVOTLnOoQXQxjmr/7+H5Ik7XNe8DKeVd0v98PPM1czBzT\nMh/anGtVVQ6pruvx3NttRY8+uL7vt9tdKeXjx484j9u6beqQUlLlosIKCl4AnSCqnIZT29ZWRrVQ\nxpg1q0FfrZhdpLZt283u6fEEpKqKzqMIkN9s66qtUHB7fVX5Cj06cK72heTm1V3btg8PD7vdDgCM\nFfb89FTXdR2rX7y5tijwdDpthv54Oo3p3F61E6RTnieeJIuIwATMvJHpyvHb6dg0TRMbBB0en/ab\nrV+GBcALITV5yVAXyww1lwSqilAYRIGIQEBZ6iqmkkrKKWUI80w6zHx8eq7rmlUtPotV5WMwnXIj\nFasq0IKYrcRddNYzo0jOeTBm5IWS5xHFsiUkQFIRFbnIP9k/YyQ652H5oguVctGdYpZSWEy70BMA\nOudXT2OKTmY8nXOKgo4uI4OWTEtEgBAUjINHL4ojDEqEJsGlZLsVGRQcWT/RJb1DFARrPyDShfFK\nCpfcSFVNX8d779CtHs4hIiuI2sR7KZyFuUBwTkshVhFJpSeAnObxqO2mKlI4M6iUPI9DP8MYInln\nWkrMRQBFUUGAFdemSXzRQUxLw4ZdhBU8A4Affvhh7Ry315gCwNPTE7zQ7rK94Ncc6mW8ICKbzeZw\nOFxU0XK2dgTvvfFfbVLq+Xy2v5polXVjHA6H169f26c7j1VV5TyvzsMyDBPiXOLfS5ofY+y67ZzK\nNKXVG63NOqZasW5dWITscs6ivNSEjDdc7HKsOZx9qWVvF/7Vovqs7tMMksPhYFtu99ku5dGIeYLo\nP00ZKdaZgYgfP35cYy57/oKZ+k+luLDMlBQRA3+s1cZUW+yKOQpVVY3jHEMIvjkezpvuSqSAemGo\nYh08B9+UkhACoGvanYszglPgkiVEh+AaharZVimTYyRNcwGUEJsKGcjlnE3RnNATkaMQYyT0ITrv\nYsZM6MlD126rqtIWHh4ettvt4XDY7XZ9PwDgbnulqjEGgCRSAGAVzqiqqqjUVUuBtGjRMxrljjw4\nIHCCQuDAASoSee8CoIKiqhqvE5fZcVXVtG0bQ70GDaW4ZYmjyfqN42xs+3nKa8HDmunWxgAP5AW8\nIikA0d2rV+8ePuaCtScXPOfiAZUFALb73fkx8fKwkcxaGABubm5U9Ye3P6SUgOVf/+t/fXNzM+X0\n7fff2E03PpY4JKB5nuc0qzKDOkAAFUARJNCVI2C7tCwC26v5c8tASFuQpUjVtAyXvg0gJwgCeDj3\nIc/KIMBVyAIsRV2g03i2Ff6b3/wmhJBSiiE450zrs8wJAJ6enrbbbc6Zgt9fXwHLfrMFltPpRHrJ\nMzabjbnk/X4PLMYBC963P6u7urEtfzgcbJzxOv3Z3iuL7BCCPD89EhFAFKUsWkrBIoA16Jxz4pTL\nnKhhX5GJlKunzExLodo5B3JpzFo99ErxJ/KOLiaLl0Yx6zlQVXDk1Jlj0sXDrebiZTZjW88AmBWm\n40Xc2fK/1TrZV79URFsNMZJTvZhU88drYrR+qSU0n7799wUIXmZRa3Sy+ni9lBXAOWS2WPzT5DMz\nvM45h2sDpVTBb7smvH712XZ/XdU1qFNxXr979zaVbLPe8zxHH9rP6mE8Pzx9BAeqQAohVNuuJfJt\nXeU5OQQG5ZwZaFEaWyA1/ymNWZMkWsiuVgWgRRzILd076xmtScX6sI/y+KLZEFfFTBGz0S+3zQV8\nSxkWXZO4zJEzqWC7QwCw9nKTgzUkXFNgWTpvdJF3Mx09Zg6hMi6Zrbd5Tjap83w+rsdmqRIAzPM8\nDNMXP/qSl4GBFuyYZwo+rBnbPF846y8Tw8uaWILTw+FgyaP3zvyflQ1Op1Nh9iHYyNuqruumEZFh\nHAuzqAbnyjyLsTKIxmkCAOc9IJJzUEqsKnJuTsmemVMS1VwKINpQGwFUoMzCRRVJFO1/EXE+Vo0G\nXx1Pz+RCjPWQekVHLoCSlJxZASSzChIrFgVSZEBh1VwAym67L6yb3R5AAOeLGgg6+wpDlFNhDwTk\nyAcW/fjwNKUCAFXTFZV+Gjf7i9AGOvXep5SKwDAlRJdZbdxqYQZF56MwDOMc6xYdoJIAo5KisIgi\ngzOFIYfL3lNBAECnmbUI+KoyLw4AbQzOoYUIik6AWLHMeZxzVVXWWiGlxKZy0Uue66YZkoklknXY\nl3Ha7a5++9331aZxoKxSihD5eeiZ1cYMkg/MWooZVlA1qg5vNg35EMk9Pz4puafj6f7+AxCcz+f7\nXGiamm4bQpjPw+n4tN3vABDBJgmQQ3KIBMrC81xWe2fNUmsLmlm61RvFWD89H8lHFkUgUREglqKs\nIVaKUDgXFUeSuKRxdoTXVfVZ3Hmk+wlhKjrOCAmd65BiTlSK9z5Sh4OG0JD66f2zP/WvfhprrEMZ\nMnsACD6Mjz0i5nycDhP0PVfTMWdXxQ8ACjDP89dff/3rX//6+vraWvqsZX5FOM2dI0hXVcwMVKGL\n1ucnhb2Dm+vWe++qKioAucwCJMpCIVozOgAgOC4KAEheAYHAoToXyHsQIbp0UIEjAlVmMu0gU/ZC\nICWy9rKLYsil9KYAJpdgQSgiqojzHolgoQ+oqnU4kSVhLwAy8xu0mtQX0BIRqQigI9JSRAAVSdEp\nKiiBqgKBMR3QKTogjyIIDpSEWQXROYTLP0sKkEhFkEgFRSw3AsuNzMGttsvCAu89rcotiPM4Hp8P\nz+/ez/f3H1jL2Ms8A0qz3WROmUtVVafDedN2P/vi68eP98228QFKEeYcPHnyIlDS9OWPPjMKiUix\nghqRByJ03joOX7pPXQpC9oMRsK1B6vnw9LI1CBf2tVs0seBFhcividFLBEwXmUX76xrZAcC6edYm\nJMOvrMfI8MGyTOdU4BgjgKzFW16Eva0oYt7IXo+IOc+5iNkF816yqGtbMqEvJHNKKUQQok/J5gMh\nAJZSWC7HufaZz/Nz1211aQl8eY68RGFGZA8hAMi7d++q2o/juN9dW9JmbWircqvVWnRhi9Ey3ceq\nJmuZcQ0czJETkUHwYZnuiohEzrtY1yQicxmur26d+7VzkZlVkIiq2MQY+z4QEbmgqkjeea/qMLOo\nAigLiGphFdXgq9oFOzZQnqo4z9kohcw6TRbBmeSXUVGic9b9XrhIzhJCNc95v9+ez+fb29uhn7w3\nnDpZkrfqHG63236cvHdAOI/ZOVdVjX1R5uLARihYcOjVM2ngonSJXxERVVBQVLGu23EcU8oWeI7j\nCEpVHZgFUQ1IBCCLyu36t22rF/bKRfa36VpbG4E8ACPgPM/b/U5Ax2kSh1NKnHOo2ywsLHXdwouH\nuQTnwxreEtF2uz08PatqVVVffPHF/ePHrus2dbNqPdZ17d312/fvVFkQHGDE4JG8EoGiR+Zsm1MW\nHrP3fhgGi6usBmB2NtbWfEpZ2GlgUK9QVLwsUDChxxDqymt0zgfEcRgKM3pk0BhjTeiRnHPKS0nG\n0e2rV09PT0B0Pp9jE3wIXdcVZnc4pJxte9d1Tc5p3yORdUzbCg8xppyJ6O7u7t27d/v93qB/Cx/h\nRd3FOecIckqlFPKurVorNIKTqvL39x8xuKu2qWMFdc3g1YcQQvn9BJGX5npnq0TELTMqRaQIKy0E\nABEgRLkINKxi7LgmQ/BJkX0NQFcz+n8ZoQPAKg+9PiPL+DF8USZYP7MIrmbzZT70Pz7zB18Ei+VZ\nP1D1U1K4/v8/vOv3VOcvBDT9lHvFGMmhcmEAAax8cCGE6OY8OaKcNTiPClUId3d37979MPSnUPmF\nqJUQsZQyDPD4+OheaKmYTQPyKZVceOnXvBDZiCgu85d1UXe07lX7fjN6VjcxMQErn8sLpgIA+F/9\n6lcGItneMDjLcO39fm/FYSIahsHe2daNOSTDc77//nubuZBztmTi6uoqLYPlQ3QAYFQ3G0+33W5x\ngbNW34aINu4Tlu7XnGdVrevoHE1T9t6GtJdSsqoa+aCUvMZl3vtpGkRKCEEU67oe+kFEbm5uzCft\ndlcr/TrGOI7jzeYOyAnIyq0w5xqCg8wh+K7rTv0ZiQTw1A+bzeb69s4ud9129fc/jHMKVZ1ZqqYd\npvnu7tXz87MLcZwm8qHb7rz3iiSAQM5HSoWrqrIAyodQStlsN+MwoyMpGuvq1J9P/TnWl+SglMIq\n4zjC0J+HfpxtCGryIVxC0QUs3m635ncv5boldAJlIp8Lzyl7750PznOI0SKAaU5fXV0/Pj1XdTMM\ng4mK7vd7VUwpj+MsAnXdApC11RpWbuWuvh+9jykV74ILXlXrplXVZEq7ddO0F30UWAQuyWEZx+1+\nt+bsKmpYhYURRI7QN3U3TVMVm1KEizpPzCXGykB/741TUK26SpvNpmmaVSoeyXnvCYiVvfOI1J+H\npmn7PKuAc75tuzLNVVWrJOORqyo6cu5SUGQVVYh1nZlF5OnpqW6bzOU89NM03N/fR5uLGkJJBYwT\nEePPfvYzk7EmhYjBAUIWKRmciVZ8Qm/WBW+ALS2a9E3TVE0LStM8/8Vf/AUuKiTGHrJ485tvvnnz\n5s2rV6+GYdhsNofTYeQ5eSdIn//yz56enhwzFz6cz+ixONf3/RdvvvjH+3tBKfPoakrz0bfxbz98\nex6Hj8/vv/jxV2+/+95RaqsavUrr7vO5qxsl0V0Fqq7kKoTdbvfNN9+EEKyV0ChF5lbXGpj3XvUi\nVJgKtG17Og91XffHk6rruq6A5Jwza+N9wDDyJdCsN5sLq7OUqm3HcfRVVeZUSuma1tId8pgLO/LO\nhZSzKgbT9gZG7xxZ/0NhZhe8lc1VFNGh83MebLavIsW6ERFSBXI+VlaMNKPv8aI84kIc55RZyAcR\ncSGanQHEoe/PwyiA5AMqhCoAIbOIAjlfWHJh45aj96BK5DabbUppSsmFAMY3JhKRdrM5Ho9zzt12\nO6UkAC4EZrY8rJRy++rVw/2T9z7lWfVSYihL/eJ0OhkohYj9cayq6ng4z/O87TbjuW+qipRJkRMH\n78qcAFRRmrZmKeSgPx2VC5dUVVUqs6UTbpFMs9thTSn2XeYO3n98IPJmKOxhsFbXdY+Pj/Si92Zl\nNwxjnxe5EEPUzGLLQsZbvVfTNH6329nobrMPFqRYoehlNLFmSNMwIuLhcDBR4aZpjDlmCCa9GKzA\nzApOREpJOef7+3uTRqWlsUAXJo+Rdy1vIBcsySil2Fq3AgYArMngGhqYAJ3Fm8NwFikxxjmNRFRX\nLSLa0Gs7VePyLae0BE2Asqi6fSLFKzrnZp5WJoXNTDIvaw+3KAqv/9sFXNNS+yj7tViDWCl26buu\ns64OUPI+WoCPC3Rjb1/lNAxNMsuehcMy2R0XsRw7cvuuJd+60MMKKy8zh8wryAvaz8u47HJVnIel\nMTvG2jCrUooRUgGEkPBCc0Ij+CgoOCJRBnUKRWWJ1dCE5W0iOjhCFiQngAgWEjq4/LCYaV1F7TyR\nJypERAiCguDWU6MXpKk1xrz8utBjrdUDF/B9WTOIsgSbREIogKyfmL6XmFQvClK8dDWYwS2lWJNA\nEU2iUAqkwnkuAghcY2MzBYmcdz6QIwfKPkt27vc4q+sXmSbmeniIiOhS5izs0dm8OEHlVNDT1XZ/\n8+p2Hsbf/ObXv/7Hf3o6Pu83u9PUh65ST8FdyBHe+0Auc6ljFb1/9ebNOI7tppumqdtuSkmb/S5G\nv9nvtlf77Xb75Zdfvnnzxi3N87Zo1xqtR5IhO0ADuq0eAADTNA3D4BYBddu/KaXg6Xw8iohAEHAi\npoPD8zwLT+oQOZqSgnofY7Xd7+bT+Q/Cf/z9PGZ9Xq1W5JxbNC11qR6ZjpTVkNYCxnqd12u+hgKw\niHjy74u/LT71EwDzMtfBT3jGypdzzsm6DpeV9alS8gcfQotovVxIW8EOb/06fVFMQkRwtPDVF11j\nJYRPJEC3KGO5hdk7LUO5ahdqJeaMoCKMDmyknX149NFGqh77o4Dp3QgAOWf6F1qK9fYw0Wx2gFmd\nc6GqSr4U29bA17pZ1uuDi64/Li0Nq/tYexvWm2IfZVfMmzqqxWj6giNgwnR/sOcBwJOzxOirr76C\nReb9JUX1D27eS7jPe7/f783z2W633GgNtURkTmW9YaYzRERff/21uTdzs6tDIvKqaM6m70+Iut1u\np3lgZmHrzD1b4Gw3fpqm3adW3E/eyLgJqtq2bdNUxPr/Z+vPmm3JkvNAzIe1Vgx7OPMdMm9WVhYG\nFgACYJMCxCallrolE98kM5nM9KQ/qAeZyYwv4gOsSRkJNgWSQBND15BVldO9eYdzzh5jWIO7Hjwi\n7qkCd147tnOfffYQsWK5++eff58PFIfRez/EVBSBXFHox0SpVBXU5Fyo7XFEnMdXoCh6ckBugYnJ\nGV8Hx1TadlXXddWsBAjI1e2azUQHYEhRELJKkjKkSCUDgKhkFUXw3rkqAE86fjCPMS2JzEKgXE6t\nzLIa3nsgVxQliyrYSIQAkGMtBcgJkH0eIEJg50KoGiKq69oE3XJRICQktfCiIiKADMjMXlQAWVER\nARSIAdlbJwkVgJgIiyASq4p9BQXTILLwgWASNCRABYhBFUmJPQOZXhGqIDIgIzkkIvY4z18Aznpt\n88tM+Z1iIaM/6XLBI5PMKnvECMtAN7La6ykAioICIhCXXARIkcdUgFwZ4+Qoica2chVyFZxTJLSK\nCsGs7UrMCphVSwYG1cXYfkoJLcmYODhP7CVtBK2pgmRFAM8uS0ImJHi4/7Ba10yYYpSsdXBtUzNp\nGRMOQlgAoAHkAp4AIKTDSET/4IuXf/VXf3VR137QbQjdGDUlgHH32DHz4XBIr+9tU3azDODNzc03\nX39tGICvwrEfZBaDWEj8i/vlOI5XV1cyi8GHEC5efVpKQaxEqWpXqhqQRdPlRZMli+PvD8fU1Oex\njDlNuBwTzTpmMO9lyiwi5BjRRM4h6zRbYqOmZE9QIGIih6jsApoQJRMhKxZVLYpTw8bEbAFUZOpZ\n2nlnP21ZxoQSsT+Z/moZhZ12WT/9CmFSBneMgkaTo9nvEZnMaxWYJh1xnH1wyCZe0Ty3VGFIsYCi\nY2SezAYRERT4Izb4MbYpEU4ywUsCMdu+MCL6yinhmBKMmckHonbVMOOYxgIFCE1ubt203XDebLfX\nL+4ExeTSVRFAmG0Gw3nPfT8SgYjhW6tmtRnGaIrdS4ls6YsJgT4NFrYvLXwQnLU6lyc8beRbRj6h\nfvrr6O3TiLJEdbtjtdHpdJKZqLqILS5RR54wxTebjcjkHb5QL6wGhNnyzz6fvVSMefkVAFj+yLP9\n0pLRzDmIP597+kiJmcoRAPDO2TOXKa0Fu9eZlEEzI66qqu12awT0qgpU1HlExBBC13Uu1FYR2zct\ns/3rb9AilhqLnkjHwixznmdbX5ibBDThvA4Rm6ZRLUS2JhRAQqiHoRvH0fjx5tBDBKoApA44oxAg\nMSCwBC45AykCKRQEJrahc6zr9mm5tqRgSyL2a18BoWrqqqqJyLabtl2bRQWzEzWGjAeYGwbeZfO7\nmgi2RCoWFSZM31YNEyIqoQKJAsHUUZ6XmWngVqqRiFSQaGo0AphR3zQqi8jLGKBdt4C6ZEJzmDHV\nQiAiVFSArCIIaN1vmU4HIwBnRSB2rLP+t8LTV5N5CkRE2rYdFFL2zMyojOQAAmMFYtGoHwdEVNFS\nRItAEUiiJZMnkY+r184CM1upveDVNGucf/jw7urqKg1JUFb1KkkiJRG93GxQBaUwQm3CrSqaS1s3\nhCgpW6IqRWLMiEgAJaXKe1RFheA8iAZXkUORPI4js2urGkU37crIPiklUtiu1qQQeJJRCCGknJcW\ngm1Dhn4joqHcNphoWLGpryKn/bHbXFyWUlahHofzw6MULVhXu5jc1fUIDuqKfUUpExHQr5URzAxP\nhGBMW11VcxZmLwIwu4pYYQQA+sQVRSfy2sc51gWD0ifa8Mu5oBli4tlD4GnButQ9y0F4UvRYblue\nbrX2GUA+mlo9vcR07lrZwXwKrfOTsacFyFq236cVnh35PNtW8Wx0YuOeufbE6tg7dCWmYRhE0/F8\nEMKiUtf12EdJ+c3u2G7WsldhAIGYY45ZUetQhzqkMTWr5nw8K6ojN6bRs085X11dHY/Huq7ruu77\nvpqtim27sKxlqTIR0VozTw+4fa/JgmBOPuyAOAPKFtPxJSpcX18v33z5A5ypjZvNxt5+UdrXmdcg\ns+y/HcS+762dozM9z8LDUugtsdA+sdUPABBjRFLRnEvMJdqsLz3BxBARIXpf4SwGgahN0+QSc85V\n4OVll2/h5hCFAXPOLkzndRkeBpvPSkX0o2q4TVfYJ7c/tzSwzG4XdmEsLAaae3rpo5u9M+md3W5n\nNn2bzcZcBKuqqutgRa1zxIwhuKoyERQVyTnHUkIpSSSbjKEnZiIAhCIg4MlR8J5QCUhRUD0hOueB\nAIwYiWIKycTMaAorMF9JNgxvcLAItM3KeQ8A7Dw7v728QCZFq6XAKEYgFlMY2UMRRbZ6QpEUxcpE\nqyoUGRAVQXG6Ds19FYlwptobQOeDL2JkKkB2QKwoAIBEIKyLvAoysslyIxHrtP2rAiADMDHal509\nnhQtmhIyMIui1ViOSGgW7Sa2iZBpqRRBRMfeNBCYuBRpmjalzKlyzpEWFc2ljFmkJCqqkoBQtQAC\nEXly5IA9okqSZJ3mZSuxS8loaUsWuOzFV9uLT1+9POyOWdK63cQ8MjpF8RyQ4XzdkcPK10PstUAG\nHVWr1dq2ocBOVeM4WtVyPB4PDHRzuTt3o6Tz+x0xrFZNKUlEaJiozBsq1tAdSoFSNmXYaRyFxzRS\nGa4urmHEZb+2BNSwccuxbA9N5lxOumoaS9qBsKimUpKULCU4F1PWkosKguZS+mE49+Ydw0CA7BCL\nKlq1IwxQlGlOpLLxu8TSGotPyATlYzJu6ZQu+DMTgD7NzZe93q5WmYcsaeYfwxzSlpT6NxL039hP\nAMzY0pEKaMkCWcBgbVUBUEAWBRVUQbsivPWizAmlDiICSnXVjuNIyEgzoQwEgZcYRjOPQ0QMSbYP\nbDutTXCqasp5e7Vt2ybucopx0IR5rHztObgUyHGfInvfAPuqAj6HujoPPSIDGhXU+cCr1bZdN1/9\n8mt0nLIgA5OxRB3RZNhtnYUYo7U/mHm/3/PMqf6IRiAC/lfgSiJ6/fr10wNuocHZBr1Yxtmem3N+\n8+bN01C8RAKL+bvd7uHhwcgIBh/p7ASjqjbuVEpxnkIIpaS2bU06yAybbR+3csGWMs+wyZKT0qx3\nsF6vedbVhrnEsyNScqkqtwz6OEdVVXllVT2f+qW5alI9S/oJy4QagIUfS/fskZxzHkZRXqg1S9Up\nsy8tP7HeWOBN+619F54VmZbsTGYnOgvDZq8JAMPQObOaJp5rvyQyhVLvmajy3tZ3yTk7G4UlcEBF\nCyGxQ4deVU3sGUUViqdQnHrGc855HsBa8onfQFaXhEBEV6tVCLXRwJh5s94Ssg3JyjROYbvGE4B7\nHh1blt2SBy0ndN4IWI2NMN8QESaVF8OOnepHLaX5Q7JqAaAJjAO2xrbpbVsmi7+J6QMRkYKYAfpU\nrtHyHCI2Eu3TT/v0tvQP7IpYrjpmJlGQpx9SVI2RMXWrJkkfIgLkwADT8rBXtoN/Pp+XjU9nVqcn\nfv/mdcnxzZs3fd/bVbOcL1uNtlaNL7e6uIyOb7yLMT4+PtY+IKIZHNze3rYI5N3v/cM/ANXValVK\nWa2a/f5RNNvwUNd1psFqmfU0ZdHW18/vpg2uyNu3byVN9k52CVt9b4V+KcVa3JaYElFRMaG2etXa\nnVQyMB2785hGqqqM5BCBib3zGdITE53lXNCTGz4pJoqI4Md9bSZmTkuFiJin65qITGxl4eUu8UNn\n5wF7ZMFdYLbU0VkNYHmjZXtdsgpamkMwTWovT7PXEYVl/SzZ89OvI/ModH4yT/p0y53+CpjIUJNf\ni4V2x05B5avT6WTvdTwenSYZhlqkYhfIpmW5HwcW1w9DUfHgUkpA2HUdh0qZkBTEKcZUNJU8ptKs\nWnIh1IDm7qHOVyGVabenmR8As1zcYgyET7xcETEXk/T8NQxs6dEsp8/uu88++2zZapcD9/R5y0G0\nv2GcoK3T6WTucFavWUiwi2Sz2diBZoeI2HWnqqrMwsueKSKr1WrB66wys5BmqI4VgMxsagjb7fZ4\nPMqTW4xxGIY45g8fdkYZTGkMweWcYxqIaBxS3/fv37+3q8XP9qluVtgrs/biEhRlGuUzsNHwmUYF\nRcB42ohsSAUiDsNQijJ7mwaz4BSCJ0pEbDXHHPhZVcdxrKqmruuqavp+fHjYGdo+jr3VfwpcJNn9\nmICZAWWaEycFFEBB0hAcIwKoghLb6QdVkVIAJukLQVCmktIsu8ImOumc2XyYPYf1GL1RBkykR0WM\nnJIzORfMsGPJX0ze1O4sFZVjBSaAxbJPEWk+JsjsEa0KsufTry0tYASEmcWwrD1QJGSEMkcQsr+1\nGzPTJJEMyy6wRD6Y2QdPL24ikifvu6TPyx4hNncyzT+Z6REVnXaxpXouJRMRATEDI3rkwAhYVDDm\nhEgFVERy0SJaBAm0XtWlyG90yxdNv2XfWb5+VVUX283jw32KY/AujugdE0IppQreMPoUR9vFspRM\n/mpzmbt+991bixBj1yPi+HgYx/Hh2zeqWuI0GFRKco6cp9/6rd96/fq1+WzJEwZzKeX0/qHrOpwd\nwZ/d3ALAer02vcelKrL3YmbbBAyuQdJSshIW8FW96rohpZRjqgPHeOyGLjHd90Opm915GFMccyHv\nZdl/EZZjPp13y1zsLFusQsBJeoBVhFAUAcnZkgMigFl6QYQQZqdcv8SVZTdnZitN7bqw5bpcIJNC\nK7mlLlmuFHtBAEJUmVfXBBguHCtWmIVol4XHzMikUoBQRIEQAM3XYzKunFesgCKowBOITyeYkWHS\ns9alV+Q9zfwIcnx9fX3zyfr5ZnPhw3jcpaHvuvMfPf8jrsLxfHLONVUdh+Hm4uZ0OidRNYXTOI79\nkKUE530V+n4sKkCOzcDJ+bpdx5z7cVigIPt2llXnWX3uaXSBmQ2wxHKcSXe2NS3H1k6HG8cRwA4p\nqJJqca5yjs7nHlERHTMyO4OSEJEAje1nRpALgrx0zmEmiE8li6euG+wEI7JluM65UlQEVKWU0nUD\nAISQVbWq6yJJBYskUDJlgd1uJwXscSRl8nVNhM5xfPXq2TAMITjrTjHz6XwAgPbF+uFh9+bNe4MC\nBKiUMozjij1xIMdSLGWe4nZJecaLMUkhpaIKM5K7bJQisrjZWnazbGdLzmVS5VbumNl0Kamqqpxj\n32vOkYgAjGWQRPI4pKGPIQQE9q4KvrZyHpRUMCchFCmAwI6DxexSyqSYYtK5KZkovZnzGLZmTsMG\nDC5wv7XQrO/1dH/HCfgW8o4DIyo6VC1KqPMSEwACsBZwgY8oMBChKBA5pGxlP6JDUlKHpIQoqh/5\nbKwIiqiI1tFduAYFtEARGxwkAEZVBQYVJYVJfJmN+0Og9po2cAI6j56YOCXY7jBfzdMljTadCobL\nmSKL7Xm0kAxFC82z3rlYxQkAVVXVdY0ij+TIpu+ylFyGlCDGXEbv2dpkCgAoE/IBoGqTtXa9mSUP\nCJSkqDKnkDQza0HGPo459zEOKYVSsooZL6ESMStATKmuqu3mouu6lLMLYV1XmIVRSaF2THWNqM6c\nGJyPQ+98GIbuYnO53z9KKejoYrP94N4nmow0CankUte1ZzcMQ1s3AIA1snd93wOTS0EQzkNvzaGl\nq2cX+7Lb5hKrKiBTFry8urm/fxyH2J1P23WLkFPOtGqPRWBb+lxgFdp1Mw6ZAEQJFXD+SYAFCABI\niW2eeM6BcKmIyPo2pE8fWIR6iRBA5qi2YC1LNFrG1JZiSD5aidpXs3LfyjIx5NwemTMhstezN7HN\nDZEBkNApohEsVQvO6AKReu8UwQVvjpSlFJkv2P9KNFI0Tp1+bJcSI1m5vLQhn1YLiLg/nB6++/6r\nnFtAiMOqCsQ4psHV1eF8QsRNuzruD7/zxW+//u4NEJILloiYCYMFNu/9OCYiqrAionW7evbsWROq\nw/6+XTWgmHJ07H1whOyDe/bsGTESMjsiZCSwnzZXJ7PxI82sq77v7WPn2XSGmR2TEbSAGVUxpTIO\nXUR17FVL8OwcxZhU1LmQy3T97vd70xoxhyUDtWyPdrO0OM+Wmt5VUoDZK6EKelfFGAkhJ3MB8D2O\niFiFJqXE6AA1x6KgoNq0VbVpz93RcRAtCOQdE7qUR8+hWtVx6INzkouCIFEceyuzDucTeRea+tid\nh5hd8AVgtbnsYt4InYfsghcBX1cxRpt7lVxC1ez3e1/Vucgo+Hx9eR5GmTNZERktpDMbpcc09hUg\nl0LMwzjGNIjkUPsh9kSubessCRkAFRke9w9XN1v2pCjI4H1wtDqfz6vVRd/36/Xlw8Ph9vbF4XBo\nmhCC9ScFwFm3+3zuyTE6Nqq4Z47m01rXKjIYCM4MzAKg3q8utvvHw9j1TahMgs+q0sr5wE5ESkyB\nnUNKUtZN+xB3VRXW2/WHd+9ReUgjMoamYk9KSg5FlYizSqiqqm1SzghSUrI9OBYBUHI+jb1K9kxS\nUslidqjJyCx1BQAKUBAFTNBYkDDGBA6jJHZeQKMmrjilERlICwIgZ6EMoILCTFKk5BKcr5paCbMU\nACKAoe+Dr0GFvRv74fLu5sP+sWpqABhjcoAOSJljjM2qPXXnlAoiMSIYtAIMFpgFCZjRlTEHCoEC\nK9ehbqp2GHdpyDU7zwxFXAje12Ps0U08oIBcO+/BqRbw5i4eCANM68AEjdB73zRVXQcfGBGhFFUd\n+v7Fs+d9oZubq1/88ufXL59vNuvj8eiItMj53H3+xRenwzGl0jSropIJBGV33KFDH3w/diKgWvbd\n2Lb18eH+9urydD5WlX/cPwCIkAySB8m77uS8Ow9D1lKFioPLCOM4Cio6QsQioqDgkZlSiWXMRXPR\nXGI2mMUSUIFShaqUkkvGeX/px/HVq5fffbuvfWivVpoLs69C05WSUznuDrJeIRXnQxqx5bqAenBO\n2YNTzSUWAvLkPYcYh6oKIHjYHZmZgo+lR2ZymGNBBsdcSlqv21IKgFoFGUtOQ56zEJdFiqhxv1VV\nigRfl1KM8oLAVQh1hYBSSlqtmnHsq8oDJOeMyOrM95IIuu5UVR5AmAkAVSj4kFJCYO8rRC4iIdTW\nM0YgJmrbddcNzD6mguTIoQD5qolZQqiygAs1ZRFVdjy1gip0zmUV8q5izjm2bRNjBJbudGbmMaYY\nIylcX1yeDn1T1UMYT8fjumUiSiJVVcEY67o+HQ/r7VoRY8kCulqtdsdzHOPN8+dfff01ZKU4WDCr\nJiupoa5CSVGGcbW5kCGuQ/vdL7/5p//4T/+/P/uSWB4+vE+pMGMINREMQ9xu1+dzb76gzGhOkjc3\ndyml+/v7tm3No8QGPRe00+KomRO1bbvdbt3/+D/+mY0pWRRZUFcbDDTm91L95JwRvCUU5thNRNbS\nt1WIM65NsxBcCLXFPcvoDYJLKZ3PvarGaAOSxOyIXF37EBxRs9QiKipa6qptmsZOME0Tr84YnG1d\nI2If+5ILMzIzOa7renc4GbB2cXGV8iMR9UN82O3uXn3uQsU+EHEsuQza9/04DMx8Pp9P3VlVfVWn\nlHzdNOtNN35M/XgeyLAusVXKS4UBAMSwCk0pxTkySHdpoqqqc+umqZqmqWtz8SjBhWSqPkoI1jAl\nKKCCkkQUvMnKcQi+ZmDvqzEVBjUlSFUtIkZQOx+PxOyYRTWlpAAIgIimImEnxc8e1Qb928kqs7Zu\nCCGPEUl3u4dQ+3HsqyZ4z+TQKBsLWmITJGrFNbul8yEoYC4DPoBMpBWe2UHgNUgppSBbFkWMpAio\nszqkYyJCNga6EgEx5BxjGkWkjnXM0aPPkrWoc06yFJUpu0QERkRsq9ZyIEQEQhUVUOt2GBmLicqU\n6EJRWUAPVTWFNDvRbNpiCjKPdlUhiND5cESRiijHOBRpUAEgjiMgoGjWrDkVxILeCYgIeABCAZRC\nRQGUkQKyXzWNTJTAlEtM45ByLKUEF9ar7dt3b7bbzf39+3ZVN0019t3dze16ve6Op2+6eNwfGDjn\n3Mdx1LTb7Yzj6oEcs6+8qr68fea93/7uxug/KrPfegABAABJREFUMcbgvCIIKzi+vr7+rd/9nSZU\nSYpD4uBjPyQpUCSWnMcYS9ZckpTh3AkCIykhC5tmfFZB0SQFRV0Vzuez1b7ee7PvU5R+ODeVQxXI\neexjzqVabV1dNy4Ux2Nw53E8n7oa1iVlEcDgg/NNVXsWIhjHhCrWjmqaBkDqulWULo22NSzXI8wG\nB0t9s1ynNSIDCrMpudA89YVP9CNw7kSIiAI452JEkayqxtHN2exbrTw36BgQrSGEjqeiB5FVEJSY\nPSJXlSulWF+jJFFBBbQ/wKIIqAillJgTI0Ub5EcgJCOj2rVAs/OciGQpeRaaUZwmwIw2tZTylfPe\nESOJSN/3NIxDjrXzh8NBGDmwmNoIMwd/f3+fUlpv2pKivUKyDhbjuT9XoUYGRRGFXEqoqsPxSI5z\nGu3IAICZDqUU+55TGkW4lALgSynMQbWYpuWCUS8Aks7qnXbiYoxTDHr16tXNzY1xBEzzA2bhH8N5\nLHzZ2c05e9d0XXc6nV69emWUaNP5t7mi5ZQvsJUBrwDQdd04juv1erVaxRhtDDbGaACifTLv/du3\nb0wy1RbNou/w/fff285OT/RiAaCtaxHZn/Zd1yFqSmlMkYiO5z6E+s2bt0bQuLy8fP78+SeffDKk\nLDmpZ0RyCAQKIIgaKoekQ38WESJIKTmEEJxqUQEpH/tyCEKoCAKgpmOFIPYgAT3e3wPA7uGxpKyq\nBOjc1HZ2xIJl7IfudCYi770jTwqemcC8wNgzl5QdURxGIMwKknNJGUTOx1MeYx0aJkIwYS4Aewvm\nynlXhcAuSRm7vo8jihLR5fYKQAzbM4JAzjHnKcQ6RyKZGQHEeyaCu7sb0HJ1efnVV1+pZNCS4pDT\nSERMoAqlFASJY88E3n1Ub1qWnXviu7XAIBM2kotnRkBHhMTOAHcxQM280YDM7UwBVVE0hICgIlL5\nUJsEA+cJFhYVKZKLKRZP7zUPX9NMVJlBnWll4q/LX7lZEndJgBbQY3kOzAHJLqWmrevk9XwiU+zX\nHMeik1anlKK5FEXIAlokFCRGRiIBVixSAEbF7NkXUJBMWpxqzR6shV4Q+njpG5/h+eayqjyirprt\nuDt9cnUXqRvPfQXuYnOZc44pPRwfYUh1Qe9rLwgiAXUcx9N5RMRPfv/mV1//dLvePD4+tm1bCLLT\nDLr7cD+MIwLElAgRENumiSk1dQ2I+90ul8JE567bbjYpZwRg5whRS5FSFODy4kJU66r69NWr9+/e\nNW3rnVutVkRYVdUQ+81m86PPPkfEmispZb87AIfHof/m4SFLcavGOcdDgujYYRlzkZRSHCMOfVQo\nhn8gYpHkvY9pQMSi2QXvGB2jd2TxMeccS2LyjhEn5Hw6g6JuGcwEAC1l6ZPFNE4Yl4FsautQfXAM\nbP5JxFT7OmoUEQV16JZ/iKigGQQRVbL9K2kEyQQIUpKN0jtHqATCNpgUgidWVYeUVUxEj2zlW96j\nKlqgmG+fLuQjRXDOFc7sAojWdZ36weQ5+r4H5ZSSjflLio6aVdNumJsNlP706pNP33z/7fb6ylcu\no97d3cUx185ftJubm+uoaYg9s180e6rQPD4+ppRTSlbkqeDVyu/zsLq6ONwPDLwwa6xQ6fvehvSt\nIQpzN9SKh+X4L6OiefbsWIqkKV6YfJAFAH2ixbAkGjrrkAJMgpIxxsPhsHx6m8peyPIwsybmnKW3\n7Wm329kouyF7h8PBlLlzzkb4iTHaEA/NUzsWrszBxezUlibh8l4EwMy36VZEzFe0HwcROXVDjLkU\nXa1WD4/7rut2u121Wq8ub3POrpSqqqxFb5wI0zy2L0UzOfC0P7RVvSDOpRRQYEAGJOdtNds4MICI\nKopeX16qanBus1qN42gcAy2lDqEOwTNX3m/Xa1tnDJhKoWlRomdHgCkXAmyqWhGcrV3iOlRapA6V\nZ+eQChQUVRCNWZk9UHc6h5gkBEREhYocOTKa1hIwLJmyrt6yR9uJXoaLJeXYD5rL+XDsjqe2qtdN\n24TKrmqwCMGuxOSQTO56WW12yqz2Wriey4KzPNc7b4iyfc5p2o+wICkpIxEiIAEiARJgTglFHZJD\nMsNpyZkUHHO2wEG8AI8AKPQxiiw9VXwyDvI05OhT+oMxQ/7ebVlpIqJaRPMwxDRGN4wg4DIVzSmO\n24sLJXUihRKIBvROSaWcur0nDlUVQo3IJYspHpEnEMmgKaWUo+YkkkVku7lJKdXrJsbBVUFQYxqr\nqmo26/Xl1eHU9SkragIYS1HHN8+fIUNOyZqCKSUG7eLYVjUAhLZJKlELeB4lg2KWErUcHh7rVeuQ\nQNWzyyrd8TTm1PjgqoCihNiEKsboiQsWzQVYHTG6aXLTaikSRYAPb99x8JJy0zRdd26aZn865hyr\nqgKRVbUSkTiWdrMtwQ+lcFM7X0UtwzDcXbz0XDk3jdOuVivmXlVtc/Dep8ShcjE5hZJzdlUAAC2S\nc9YiAiq5jOMYnPfBe3ZAaIaxht5XIRgZ3Ho/1sUBkK4brBdnMpOWrqgWax4vSxpn/n2eFZ/tNoEl\ngME7QWAIyTEiBs/eVc6TCBGq9x5KLs4xG9cAigiKAikpIAADkjVZGXRegqJKMwph7Q8b9cg5I/2a\nPaNhTo7ZNjHbunNMaRxHRI+chvFye/Hh/fePH+4FpUvj/fsPwxBXddPvTqt165vQDecQatsBqqq6\nubl7/+b7H3z2eQnFuRA5moK+jOnq4vLV8xvJU+/ZILS2bc/ns2WfFpxsr7A4al1G444t3MuF1GPi\nUgbejOPoiFwpOgyxTAaxpi4MNlw9d/94rovTbLQxeUvXdW1iB0YxXC7dJTh5P+mfW7Hctq0pdJnI\ngpuF4yyALe04fEICtmEdeeKSaZupLQstJYSQxPxYPwbFqqos3805m3yRkcWbtvXe205nCMZpf3j/\n/v3f/d3fEVHdNtvttq7rUsr+cDDtrKXas1BqofepaioA0EzJyzmKan/uGMneRVW1yMPjLo0xhJDG\nWIfK4v35dJxcMBKkOIa6yWmMQycIJRclFMCYkwN1jCWNTV0b80tUwTZ6EUM5t+s1TJQwQVW2YaVS\nqotAiJURlIlMehkAbMUwUV1Vdo5LzjaeU1eVjaSa4bxjPh2PNq1WSvFW6zHXVZVzzjHmeXp0OUp2\nW6qK5TLW2bEYRYtkVQAmBgRChyQgNvgAgArIgIIoWYg4hFD5ioAki2RRVAVFRSYmJs/ekUslqWod\nasTJMKIQG/4muZCp6iLCHPidc975fhw+Vr3z7MESxngesdRJSSHfPLsdj3tQWNf1BTlfxGsmhO3F\nhTE+cs4sGIhZqEC5az+Diqqq8r5y5Eu2bcVYdlm05BxTGksac04i+rDvXeOJ8ZiSQ805xrHbBBwO\nJ33/+s3Du1IUFB/7krM0qzoOB+eolOLU5ZwBQesmineVR8SHMsimPmDx15vT+eyYVlXrU9aYAzsC\nBAFUQFHvPCLWofIhVD4UleB87UNwHgAEi1kMgUpRIADPjpmbqm6rOjgvonEYtYglT+umBWidcwb4\np2Fs63VJeXc6P4yRrq8ub6+fX91e3D7H5EOocs5maXF1dWX7viWvRpKq69qGzzhS8FzEMSA5QkJ0\nrN4pFChZhRQ0Z0FRYCIFLQpOYEoyirHgzNOvrryxtwBESpIiNj/ARN65uqosPzbhBrZpaWZCtIBh\nWxMilpyLZgIGLSVHkIIgOY6OHamSSi4pjUNCyTGllKp1C6o44+xqZE+A4IMiaJFUMimooaMInpiY\nVcX4pexIy4Q02IjkklNa0nl3fbOp/f1uf+7OoiBDV1IihZKzomgusR+0KIgOfb+qqtjtdYwasuYc\nXMB+WG2w6sr3/8uXIsI09WUuLi6GIdZt9b2mMU+iB6Yn8uLFi7dv39pUjxl/z3GxGGy2lESWDTdN\nk3O2nFhErMtjgc1dXV0twqtzAjjt4EthJE/ES6xJaL8VEfP46/t+8XGxsmYZPkekMotY55yNPGoF\n3VKK2aBDKcXkiJaN3javZXbHVoDOS8Fe0BsBYZCu61QLM8ecRATZ25saE928Ifb7fbO9XoKZHdNx\nHNMwQYhF5XQ6HY/HYRhO57OK3FxdM7NDKqBQbKrfqZN11RRQT0zeMaBh7sAEJScpjQvPbu8k5dDU\npFBA9XlRQkm58sGvSBCaUHVd530FQIw0prhZreu2OR2OLvg0RmNoFZW2bkJdVT4IlMfD44KDEZF1\nBa+vrxs/6ePmWQnKMmVzyrCxFTv31iKyqbLHx0eadTlVta2b4/6watqj7kB0U7fvvn97vbmQXMoQ\nC6jmot5VzsdhpKIl5aqqHHx0ZMFZNWupvj9WsUQMSArTgVRVAPMyI4VUCuQiSAxgGUAhLSnbqD1b\nIqmQVbGIskgRKcUjiVkv2J+DxmFEpiWRsuzMz9ar8ARDtsdP3fkjkjMzrWWmAKF8HNCz9bzf77vD\nIw0j+pqRKY1B0Xt+PB4MUZEsVNAjUcGoCRpOYO6uyICTsZOKTTUQAbtJsAZQRKltLq9v706nEymo\nFqhCdL5t2uCSI79ZbTebLZNnHxjdet06r5dXaxM1t0tvu1rHGPtzx8zXV1f8e79n8MPhcGDA0+4x\njXG73pxOJ1UtY5mGjcqgqofDwTk3+SyLapHdbmdXnBdf5hKTmQ0Ric4f94cJm/WemUvKOeYUY902\nXdeVlNl5RBqHQdlVzl+v1mWzHrrx/uGr94fjZn1VudpInjaEm2Z70HEcQwg2FmJWwiklAzCcc1wK\nAHj1AEAKF1dXPCsp4GyJLSICZI1DnBXkbGEsqijT5OKM/JeiRNS2rRVJS3vJNiIj+sMTBYeURhas\nqgpRm6ryTCZL4ZBUyTsiDO2qIGJgN2bnQ5V10gfQIvZ5vM0kKCgYQR08O0TUecLhozQkTSOhNo62\n3+9LKUPXTQqKMe0eHt22hSKrumkBwVF3OoMqiJKnpqqJqKlCE6q82RCQkvMVEDMjrNbr0+kEiG7m\n36qigKpIPw4pp9RlcljmYTtLxG9vb8/ns83PGYdg4Z1bMrEADJZYWD23xA47nnZ23M3NzRJyluKD\niN6/f79QwueyiWOMTZ1t7tfM+/b7vWkp4mygkGcFT5mo6LSwiq30tq3QdqjF3tvPLnaqU8eI5/LT\nmtKWKD3lEVjy0tZ10zRjHodhqCofQigqiDiO3TgmVR2G4fMf/qhtWyuPhrGrU4OkRZIUp5Kryl9c\nbNrN2pbRzdWlC5NGelVVx4cdMztmBTD0h4mQ6Hg42H3D01POKgKIJed+GErODFhE0jCmGMcYpZRh\nHE/HIyBKKYB4dXnZ972YNJdqP45XFxehrk+HQ6jrOgQgApGYcx2CC6GkRM7VTSgiy4zU8XhMKR13\n+wXJZebgPXkqzpdQ0HFdV4wT32S1ahmhbds6+GEY6uA/+/QTnadq4Pbmr/7Tf/zVxUXbNClnx/jT\nv/vbz3/wyodQV5V9cmKuQjDGxBjjvutkjjoLlTOEgGK5yLRkyzyJ3B1PAIj0cc58KmdFUcGzIyLg\nBY+1wjENqVRVVVImpiIqKTdN65x7msULMjKd+xEVGMmzM9fZyofs0jAMZu4npVi7yHi8tuanUDRP\n3OET22l5YosMAEWlbduqqkPWkjKApiLmJQEICIjAyKDKisilbKlOKWab+DFrTiQCDOsrm4oFkGxv\nIlmV0mF89mx1un9Tm7RP5dNIOI4VkcMuHAaXXdcnZI+ie81t45rPPzkcDu/fv5eU1ZC3nO0rvPMh\npcSI7w2RllKcplJevXr1oevrug7OC/HTPRcR/dU1zlMsRje1n2X2ZzKU246P976pamNGLZnHue/u\n7u6+/vor59y6bh3x/mH/cOrP534YMzoWz1VV3d5WJSMHlyQnyaf+nLXY6xy7k7WlLSbZqL9tYYZ8\nWD5qQcUySJ6HTOwTqg35NSuZVRVsf1xO65Jk5Cdm8JeX1zmWOKScs2QFRi1QjNsFDIKMjiCjkmQF\nmIwHN6t15YPhSU2oznSWUuzgAEDlpmHHPo7nbvCKjp0gqZuEWkgnorygSTuSbYwFtB8imjIrAjM7\nRzA3+G9ubk6nk3POYpKdo+2muru9pNXmbrNuAalED9R8+oqCF9aY06nrHLqc0qZq96fjPhcOrYiU\nQvXV6r7bbV3uN15EBs2qqmxqA8e6rWN3XkFwSFVVmanuOMbZRRfsEfuHCDmXlPJms16u/XEcedZr\nWNI+O/hT9DKriAWOyLNw1jJbu6j+TLL25E3em2c/paXDNDUeRAy+s9XgfWVRbYk6CwZowckyMu/9\ner0WEeap3LPgjIhLxFpo1rYvWEspOLfZbLLmruts0KcfhzzfxnHc7XYA0HXd+Xweuq5eb4nI00et\nBO/cer0mnJgUVVU55w6n4+l08uzaUPFckxUAFckiVo4sUVNn0SAAMJNc25Ht1SbVlhBm6NKrqtFI\n9vv9ql5ZvDcBSsMwV6sVz4IrSxt2v99771VLksmFVlUfqup0OjVNY6yqBSUzfb8YY8rZ19WCzjVN\nczgcbJjxeDwahml57vl8rpz/5OXL+w8f7K3ruv7yyy8/+eSTqqpef/fdIldhb71arYoIVZXMuc8E\nbSPaE2QmE8Ii8zqj7fSRijihu5Wb7LIWmhAzRx/Wq6bvzymlzWrNSJYsq2rTNLacSinb7dYOvve+\n7Qalj4iBzNZcOvMslsYAM2MhS0inJ8jHhoGFpTIL9S6vkFJatfUKKe2Pfd+7lCnnXGKoKu89swcA\nVAacXqHre5Vpbik4N5kMCpogYYGiqgJaQBRQkFzdbK6uyy9dVQfFvm5XzsWx7xARgLwP7IJirpsa\ngY+HhzFFNyuJKCEUzVIEVGbIUYt4syFfrzFOgM/V1dV3330HswyYFTemg/l0jNFWr81aqWrXdeba\nbLCMAd02IKFPpMkQsahcXV09PDwAwAMQCN5c3hg+o+zQjJulFGIRUyn0dr2s55aqXYyGBbnZQkwV\nPDEz11VLDCkWYihZETH4OlSOySsUJk8M3XnYy95Aflsbdmnbaf3uu++WR5Z1iMiPj/vz+WxzwUvx\npDMfuOs6s7yBWRE/PybVMmwvrIlu0Wi/3/tZlhMANBdb2N04VLOl1lKCW+JlfDGdlcaM5JxVVtsL\nYEpDTwySiw902O1fvnz5fRGz2HbOGbYRLqrDdsuUY4zn+/v+8YG6oSLtjqftxapPsZCkkg+n08Vq\nS4Av7p6fz+ekCZhyTEWFAIdhGLq+lLJuV4jo2fkqBOdjTi+ePT/s9hVQW9Wr1cqE23e73WeffTYM\ngzmsGrHCrru6rne7HdGklmLfzkKDNewN+rIoNSFqhG6MfQjBuxBjrKvWiAk5CZP3zhugLCIpFu8q\nw3mM9WD4j0Upc6laYBC7EHi+WTw0e7TFz9gQwjz7R1j6c3GxsXBlezoRGQrRNM04js45++35fLZz\n4Jw7mZtLzs5N4w5t297cbd68edt13WeffXY8Hscx/TT99PX3b7e3dxzCj370o9vb2xcvXjz/5KX3\nnPJ4cXEhIlwHQVUo65W5xhUAsR2DiJgJ3Tz3VzJaTZnAGjDeOyIqKdc+EBGIoujY9URU+yBFrHWe\nx6iqBBD7oa3qOIy2HCsf+nM3dL2qng7Hjwn7vDMG580VLYgsCcTqk08XdHRZ5TDfBKFozvpR3XVJ\nDPmJ9+JyI4XgfBNmnUBEC6Lm67Hs+Lb79H3fjfF+f1D8SIWw2xIDDAZ5+qBnp7NbFzzpM93e3tLM\ngLCbnf3TcW+j+O+Gd4jYoe3LIEkAoNNOVY+74xS9XBbVYYx2ldpmqqp3d3en0wlnofslBCrCzc0N\nLqFxNtZkZgL88Y9/fHjcVVX1+vVrsza+uFj/8PMvqCQ5ndHHcEEtsxPJMbXrRkTQ+doHD44Qa658\n7WMFFNgzgSiCMGDOOcWh73trNZHjIY4c+M3331/dPD+d5DWX4WZLTTWeuTC5pnFX7f39/dePb5hc\nHo8+1NqPXTcw45p83T8+Hu4f87mqKsECYKM6gQH7vm/auuOsl3VmFcR07lZNawpjdqVbKxFnptNT\nyRbLIexKtxVip95yDpNbfPv27Xq9tv0opeR9lVJSlMvrqzGltm4gQy75eD4T8Wq1OjP3Y4wEuGqr\nptbsvA+q4JwPofI+iIwmPVhV9TCMzrkYExFXVS0i63o9DAORk5JNbXrMw3ZzeTye27YFICbOWfp+\nYPbOudVqtfjDgk2VEjK5UFdVVRlkQrN9gdkmnbths7388OHD3d3darUyl4MpVa1bVa2b1RzA1Hk6\nHHarzfrDV189e/asqKDjqm00l+CcioQQ3r17t+B71kizndNMqt6/f79arazUsxRwGIb9fr9er7tx\nGHMJTV3iCCgEuN40x+Px/fv3h8MhhPDtt9+O4+ioIqKSZLvdvn/9q2cXL7uu215eCEBVVYfHXYxR\nVBTVm9FizpvVuus6l/WSghyS5BLq6uHvfvm7d8+H1w9bx3o6hJIrH7phB96nkj95+cX33/30iFhg\numZt8/+X//Jfrtdr25BNStUoCf/4H//jn//851U1KXcs+fovf/lLmoWzrWKxTKiua2eVB8w0fHrC\ni4XZ+dvuLKWxHbUlvMvM37UbPrlZBmGfxoLK8qtZtAaX97U96Hg82hNoUliabvZ2dhksFQAiqrkW\nsT2Z7HJi5nfv3p3P56qqXr169YPPv9hsLtari2a13vfDr77++uHhIYTw+vXr8NfhF7/4RdM0kosR\njRknETQickiSp6+vT27wxAMXZhm6ufCcx2ue8OuXR/5+wLBafnl86aJPOklzM2Z6oycGIcvryCy8\n8RuvbB/06SNP3/3vPw4AIno+n0tMdkIn+A7ALpKFxPFxnqxOLz/7geLHemKBfM/n89NabVonCqaT\nLU+05e1Xu91uef4wDLa4VTWOvWkrLCsKn/R4FnxpWiRM7FySYsW9fQtLaBbv4PxEbF5V2TsTo5rQ\nwnntmXfq+XCs69rypziOx2PouuG8f9TzsEH0wH0/cinO0cPDQxI7Ph6zQNaATJWPXjMUkKJFEAQA\nPKF1JnanY2ja/ekY2ma12WKzOSXpVK83V1fP+3VVnavDdlVpipLT82cvrm+uUsxKyD6wC/v9vutO\nAPHu5nqz2Vzf3TJ8PGv73Q4Arq+vh2FAJjVEgQkIU0qHw8FyR5kbLZYUPsUnZebrw8zdXxY5zP4X\nOWdLQ2mWQEwpKYIo7o4H7/00Q4asSOTAYQieinfFhUysBXLJXJwKiogUKObPTaqCdp+ZETjnbBxu\nJVbySjwJWSABO+DAIZOvRQSZmcQMcF0cBVBBGB2Qmq6wCipK267ZE7MXsCGOAoKiwswueEQkxxa9\npuK1lKKiIgJKgGINQJOQN7EinqUiiJ1z6CuHIALec/B1qIIj74JfDqwh50viZWlTmV0YljuqRpOL\nxACip1OxeIaI79+//+TZpznnouCcA8HD6Xh5eWmLv5SScupHaZrGe19yAlITTtbJXpI5eCwSnD8N\nI47IzP25s0Bo1TCbtAIiKsQYJRfwDp+wexb2wBIsrLCrqmq1Wm2325QmM0adAa1lLS07xgKfuD//\n8//J2CzDMCy6wsvmy0883Pwk9caWJy42RVVVIaJVajiLXi8VKMBE8rP9xSpQZjaPBp07FssFcH19\nvWw31pZfYMenCTXNEuuGMpPSMAzMCDBpUdzd3Rmp4+c///nj7vD8+ct/8Lu/f/f8xd2nr7785S/j\nOP7Ob//28xcv6rrm/w//4qtfqbHUaFKXQYDy6xN2OtEvJx5w1o8xe86z7ZNNdiZoTGVVQBQANd2B\n6aUUbDoVgPEj81hVRefuHbA92whBy33Qj1ilPOnM/0YcehpjaObf2VPtf3G6mj+qp9t3zDlHm6iX\nQkQkBdHsZMhUlLKK5GTBzzn34cOHZQd/+u7OOSAWYnUfTbPmD6NLLFn2uLu7uyXYPM1mKh9+40vp\nPNami9joE96EwGRuAgB93x8OB9Niv7+/X4LQxzAJOqZotRHA1EC21f54/7DZbIzecjqduq6L4+g9\nr7fr+w87HvPm+tozj+c+l1LXQcSZ6DIRISEweCBPVOWSkrEcWUU1F+eoacJnd599+atflrPEw7G+\nDrvH+4LaDZl5Nbrb/s1+zPm0e8TL7Xn/oDltV+3N77if/+3fnLu+lLK9us6l5BJB864OYzfVLjnn\nuqrGcVxVNSK+evXiV+9/Fdzk6oZMfHGVSs5S2vWKiJpVi4hWHxgit6BkdgrcrOxpB2y5Yw1L59zF\n1eWHDx94Zg+NY/IhxJJfv3lLLhRFZgKB/fGoRMn5vvhBNDoScagCykgOWZCcYgZkICBGJAQEIGQX\nADUXjbkws0ePZPZaJlvHSI7YK1ARyFmmjIIcEiv5IqCEhAQICCQgCFhUfaiBAZCLKgoIIgEBI6Fz\nIQAhe29DhUAoAIogCgomTIdgpo5IogLkkBz7yvzAkJyvaimABFBUcJKYJOddFUopuOTfJYem9nHk\n4E1qSxDIO1MdIu8wE2Sxw+6QckwxFeO/iMjj4+Pv/M7vxBhLgtPptHvYf/XlT3/rBy/6Ybi4ulwT\ngfOYx+byqh9O3lGGrIhONWkRE+JiPOaM3h25BMdc+Y5g3AZa+cexK1pqlOiy91i4fA/noxMcB0Zn\nKQKTE5EqNKoavC9ZS9acJSdR1ePhPI5j00zA5pLW2PAlP5lchsWpZLvdvnr1yiBj42pbfFu2jAXZ\nMIgmxsFMZ6+urha4eRl4XNJnnPl1KZUwW18vG8cy279kW9ZwUtW//uu/tjsppfP5vGieLgO2FsyW\nCyZYjUJ6PB5NSOpwOoYQTt0QQn08Hs3j3LL1w+Gw74fb21vv/Z//+Z93fX91dfX111/f3t72cUSc\nJxhFAKCA2gApAKCCeb8JqPEvtQgQIkzaZIpTwDFFT9O6sp9okUxEARjRyNlGJwOApLLk/jBPaC57\n9N+PLk/3/eWRpxHl6Z/oTNTRJ3MzS/T6jb+aokjw5hXG3pF9O0BkKqUYu6aoaJwyRGQKwc/+Qx/j\noiU3f//zf6xvRGXZG0TFTA8/3leb7VXVk5wsTggoiBYV027w7LIUECXHwXlkklxSyTZzZkfJskv7\nAL/927+9pDJLviUIVhvZCqeJ5k1E5Nk1TVNiWq/XKaWbm5uSMxK9vX97//0neu6vvZfj8d3+2Pdn\nRk2SpqkxABRlAVAUZk0ipQTnmiZIxvMQY0lErqqqrhvUa72+GJX7IrcvPvnxp597v7m5uslF9+/f\nV00O9arbH4OjkuRivamdX103fd97xhyjplFVuxRLzrbI0bkmVFDEJrpurq6/+eprzzNy7l2f0nns\nx3G04+mCj8PYrNrudK6auq0bZCopZymMRI5BNEuxR5b5nqKybldDHEPxd8+fxdevQ12lIQpoU2+a\n9Ypj38dxc32puTQupDHfPXuRgc453+ckKsUFZTOlJASPkBG8yiiFVESRAUAKSBEED5qlUMkKCApY\nkBW4IKBqBlJgISdKUSAnISBPJMioVHSyeCiKxo1RIAUVhVQSISOAuW8BMhIhYSnigk+lsHdFVSz8\noMlOqYrFSCJngr9QBNjV4LzzTVIg9EWRuALNSqQl5wJRlAsmBx6olGguZCYgwt4558gxF7Ya3QVv\neYP3niOLotXcc18/qWpd19vt9nA4GMvDoIeqqlLJ3dD3++6yaQDA5yzDsF6vT/dn8JxKBMfmspKk\nBBEid/f8uqButpfOkXEaLy43x+Nxs9mUMvnmMGMp5dNPP3Xk166GDCLSdZ21V7z3h8Ph7u7Omm3W\nT7EMpq7alOL5fF52/r7v1+u1oXkLYL5QFpz1DK1SWXZ5K8Ge9n4XwI0Z9/s9zLoyhoQYzrZARks7\nrpRic1XDMJiXjzWfrZ+5wFk404Kdc59//rkFKkQchsEU7zebjfWWrOGxJMIwK25mzbvdDlG99+e+\nq6oKyO12h9OpM37zarWp63qz2Vzc3P7oRz9CJhF58eIFIn73+tvDcR/qGmY1nQmyAwBCVREEAiii\n5lBgU9OmyYlIipOWKAEUAJPQZsDlpzG83aSCo2JaODjVSSJ5kpd+qm0NUKRM9dBcGM3B5+NQ15MK\nA4vIx+cD/Np9EbSaDhERbSDJfv0b0csUegqIKmS1Jocsn18QmCdxxymmKkBKAOXpR5J5rgj+3m2K\nBwiAighSZuliBLBZDhAFFVAbNFVVa1SgqKnRqP0EFTuSCEqITOiYEU0knxZ6GEBT11NkmmmcsCio\nEilAP45LNDKkzhZwL3o6ndIwPjw85JwfHh6MCTnmIgna0DIRumG9vdw0zaoJUQa0VSlZc8EiJAAA\nCVGLoHfUtCiZGy6lSF19Hzu9uRRfYbt6+7B/9sPPf/CP/vi//Wf/+69/+ZqU4P2b+8f3frs6ebd3\nWjOX/vz6/Ph9v7u6uoiV9Nr1NIZtZRdRjjGFUHJOScRJx6V2DAAHzAfMPaCoQBGHbr1pHZRJCyAX\nQchShhRd8MCUpaQc0zDGkh0SeaemTamghIbPeu8FYYyxgALhartp16tmvRrOHTo+HHtI/jyM5dxt\nNqucUnGSx/i4P6CvIrmjyuAwB2eSVoosMFnC289URGByiLBfATE5zz449qlgMfcsUFFBxaKoQIoM\n5tZKDohh8iH2ooSAimhtW1GwkbOYMwFQYEKylSCqqiAiyC6VguyKalFAZgE02xTzLAIiRQJEUS0K\nipRFFWlMOTiXSmEA7wMAYFEA88ScdfgVAXUG+gAQFSHlnKUwoYAWS/gA7L7MTa+ne7ftlovDXs46\nDAMoxhhvn93t3r7OUg5dVxelEn1VkXfnoR/zyHUwcgSWnKkQMJ3H/nw2SOzh+++qly9vru+++eX/\nMtSV1b65RAsVD7/46uFhpzBJ+6uqcUw+/fR6HNP79/e2pS9NHCI3DMOz57fOsfX7nXPn8/nly5fv\n3r3TeViT50kMZp5IATL7Hj6FgHh2mNeZH+WcG4YOnqjGutk1xwaJlr9a6h6dDZjnYMb2Ofwslba8\n1LyxirWX7JlGYDfV+gVyfZqDw4xCIqJz3DQNMtV1DeQeHnZWWt3c3Pzwhz98+fLlZrPq+357eUmO\nVfXq6mq328UYX716dTweYXFafAIZCZrXgpIdHNUCCgqmXJXBAGcEBXOTWySuTbzH7quqEOD82+Un\nIrB3BhAtxaj+PdPJpxt6mWeE4UmJs8BWTzd9C3ZPH//1X/1XQoWCCk7Fs6pmUCiQDdWFQkSTQBUT\nT1cTzjHu4wdecpG/X41NociEQ2T6DwAQ8Hg+LZGAmR3NostFpmMFKKgIqASowN7hXB9nFcwTBNc0\nDc4HakLjfh1xXT4kIipAVVXIc8sNP56CMGv6wSwPSkRIzqkP61UtJR0Oh4fj7sND6c/EZbWu2CMx\naMko6i1rUVRfDTmOcejHAXVq0oyE9Thsbm+7otlVz7+4/uf/w/9xfXV9342/+4/+GwbyTTvE8bZt\nfRmvrzYVyaZyz2+vz91xtapKKVkLEF1dXz/sD3Vdn89nVYUiKSXv/TAMOSYAAM/bmyvL5KAIIr5/\nfEgpbTebfhi8c1AKOlaAPo5UcmQuIlKKqJIjBODg7Qq34yKqgMgGlhAx0TCOY07lfD4eDs5X7Csg\nVAT2ThFENUtJIOyDaxvHYZQ8SC42wtLnm+1zJldACNmx9y6YCpf3zkZBVKBkQSAEGnPxpEUR0CkC\nIAmAKAmQ/QR0iixKWQsoZAEmVtCijAoArCiqCCQCjoiBAjIp8JTtQEEAF/zYD74KxWpBAEJQBQEz\nZtZiDVnRoqKAipQyKFLO6hzFDA6UiQEkAzMBUEDnBVzMhR0rqWV4BpelnA0PQARALJYkMiGRTcEv\nm8CCZ4iIEbusJKo8Hw4Ho6Gfz+chjojkrfRnylKKSrtZU2SqvHNOu7HENOjowLEjGQt6AVXMIGOq\nyJUhZoCcErjJBpcB4rlnpKpuUlEiMvzteDze3Nw8PDyYCx3Ps6EAYEyZx8fH8/lkjEFjzbx48WLx\nd7V270wJQTeO8ZtvvrUM1IKhsWZxZhZYW0imqTfabtf8RD1oaZ5blxjmALPEm74f7b6xipm5TOb2\nv9adgpkf3DTVEhRTSqZut0xC4EzLXv62qSr6aKFGzjmv4r1PRWOMxkk1uMZ2qLbdiIgVmza01Z3O\n79+/DyHwTBaQIgBglg3o2LTdgdD8R3EaEJr21znFmfnLMFtoP1FjFDEXFjNQmHpBaBo4hGqboD4p\ng/A30bnlviGbS1kJJgMxP/s3Y9IkSP+bSN3Tl/378WnyYZj9WizaiJhE6cdumWmYEPB/9cWXt3ga\nOO0L4jzngfMsMyLyE/VSUS1z7ye4yuBGs5cFC/qqzlcyTwKlPHVEEaTve545IzgPzTz9GE+jESAO\nJYFOf27l2PRkUTWBltkbjQ0ijrmIKCL5UNdt26yEwHns+p1X5gAgxQESOwckosH7AJTGCDExUuUC\nAheB/fcP1cVlUc4O/+R/9c//6Z/+88f96W/+9qcY3fO7Z5t69d0vvourWocTdAdK8ZvT4zdtrWXs\na68q5+F8OJzQcWiam9tnh8Oh6zrPrpTi8KPf9pcP+67rzAUGAFLJ9aZxVbi9u3v74f12tY4l1z4U\n0MAOHZsDCAOiY3ukcp6888RJiqmpkgI6ZkBfVyWmdrP+5NNPBaFpmqpdvfn+3RhzSqlu226IknNJ\nknPeP7yvNhuqVyeEWAW3brfblXCNic2bGMDqrqoUy33Z+0oVzZDDTBlyTORBEYEdEQgooCixIhZA\ncg7RIYMUKJLRXEuAAFTUFH8BCO37ITlAMpEvVbsDAIBEnmEYBsMwBRQIBZSZQFARzEJQEVRVjJuh\nWhSIvaj4UOcsxJyKipacpfLMPlhnKxdBD0goMoUiRSigRcQ8GIDJCv2p3GcehongvuwqOk3O+IuL\ni3fv3p1OJ8/1w8PDut1cXl66Ktw9f35RVRvmkAvleHd1jax9jt1YuSqEELqqH/reAzt0acy0qgcA\n9nT58llf0n13hCaMqBGFQYkJQJm5L4XqMMRoSj3MbGzMm5ub/X5vFLaFDY+Ih8OBCELlFk6dbSNt\n29ITX74lX0RE90d/9IePj492VXddZyWV2WrN/Y6iqjbkj4gpjbv9Q4oFSUtWQCF0uUQVFM0lq0Kx\n7om5CC86eIa5me3e0qCyom/RZh3H8fJya/THhRpuAXKpw5Y9aAowFmnm7VvnGREXaiN12Je3kqKu\n29V6O5YMKWcp4xivrq6fP39+Ok0q8QoqombVDADIxMUXVVQ1FRFFdEQK6ImKAk6mpAqIzlZqKQXA\nHH1YQQDMLtshKwjrVGwJApugjpLttKA6uf0gIULKdvwREXTqPSEAIAgSEaqA2k8EQCIwbg/Aooo9\n9atQBYoiAgkAW09GoBA664ItLCMVNJNji0ZLBbZs6zLrFi7RziIEAsIC3T1JMvDJbS6MNKVJU2OJ\nDQpAzLKYtcyY5RxUly6bKYyZvosMQ1yUx1SRCJwLTJDHAQlpbnwqQJ5feXnHJVEwjpnlEECi6BCE\nyCFalC1EDkomcjlHABJNIQSJKabiRZLKKcbU91XGdrV1FRFZbVSM9JU11xwcqApIYZqnwmNMZibE\noXp/OLWBx8ODjAl1BI3rTVj7T8auPxTJh0NLIH0MUJ1OfVO53cOeHHrv1k0LxAC8bVapG/p8cowI\nCKomfYaI3elc1/USn4YURcQxOeb+eMIi5/PZ8JbfqB2Xm/fOhsph9i2zHgAAbLfbnHN3PuQ0hBDa\nJmwv1i9ePAOgru9vbm6Ox7OIONBSyt3Nswjw7nD82es3v9rtDg+P/emYhD+5/VxQx35ARMlFJJcc\ncyndOSJqydkCSVVV63ZFNBYFI+KjcuEpWSLAEELlA3gigpwFojA7E35UVYACQoAFJyMsRBBUAi2o\nJnxM6ECBQAs7x+gc+aQJFVQQERxzIVYsCkCAbJpfWByxKhKS54Caq6phTM65HCMpEQiz995XVSO5\nKErJEafKClQnoBkEJsNyRZDJzsr8nEzdHtgjKAARetUxpXI6dm2zBoDNaltV1cOH+5xjKem037We\nd91pFJTT2WtO3XlMY2grZm7qerPZrOpVGsaaQwgBkYOvD4cDM2+2q6+++gqZXnzykgiHYVCYTLoR\nte9H733ErAW8N+c2FcmqJcahrmtzhHKzQ7Ft+F1/srQ+S4EMRcV7L6BVVRUVLTLly4TM7HIZFFJV\ne+/rqmaj1fV9bSWFc261+ijRb7Xz1fXGOfMdaZjxfO6bphKBcexjzMxY121dBwASyVVVpTQ6F5aq\niNmbDywREboYY0qpaSqLQ8656+vrZQjJKBLDMNjMszHFLbZ9/fXX2+127Pu2bR8PjxcXF6r65s2b\nqqljjIfTu64bdrtd27Z3d3efffbZdrtFYF+tGOmTly/7sUPE8/l4PJ3rJnTdyYfJ0J4IguMiaeyT\na1asigqOCRVEFQuYH495IjgmRgJFzBarPKuanBVJsU2XAEhFsvU4yKoZKaVkDU2TUmL2RFiKIigo\njGPP7J0jVSwlIbLdzzkG75LknIoSBnbMRKpZkiMooKiaRaznP8UXJiRFIkAVETU7Oyi5iA+MAGMc\ncxJ2yOQt3pGR74rIrEpAgCXlBfgyMHYqE1lVU5nL2am8myo8BMQJkZ+ELNCRB5idvKdgK1qUQJf4\nJyI6yeY6FWNPgSiImFQKEzkCsSadWBNLAAkJGR0DkSDqUsY+IR8uFZzlMioqc/QDRUAiNQFlMd1W\nKUpICkg+CBCKpHHf1EEkZS5niIcyCsDu0F2zX1FgxjyqFGAAa5feVVeCUDD0sdPUe5+9ZwA8n0/5\neGgvNt3Qvbht79/87N//xX88x/z82arv7im7P/3n/+1/+Q9/ef3sB+PukWrnWBjGYTxVmwvVUlTD\nqn14ePCeEfF8Pl9cXJg6i5EADYtGplBX5/PZOXc87Ji5Dv5yu02nflu1/anf1q0jRygghhy0NHO1\nd7sdoA7DQaN/+cUX7969647H7XZ7POzam5uu684y7vf7qbGHuNvtNptNLoroif32j//4L//Df7ja\nXhz2j01Tv1v/atd1Gvy5KBW82F797/67/57Dal1t4yhDd2bvHu7fv79//y/+T/+HlPPLFy++/uYb\nR96FcD50X/7yF6+/ffMHf/gPnz1/KSIhVKXk87lDhOPx9OWXP//D3/3dUvIwjA8P95t2dRwHVt1W\n9eH4cHV7c//u/bE7P7u5HXIy58artv32zetnN7fjOFhFGNhlKU1oWLhGTwkum80Yx4t2sz/tSd2m\nWr2935F3zbbJWbTkwC6QM8BmW9e73Q5Tuli1pmPEROS4qcIRIcdxs1odz+e2bven43a1PvXdp89/\nMKSIxZmWf3DtaX+o2qqM2bWBNTDVqoOatiohUtaSU9TunJjDMKS6bo/7Q06JQDw7QvBE4/mERXen\n40VVp3E86EMp6f59FJKdd13fb1bbl3fP7vcPu93O/NuXEY62bf/nv/rm8vLSxpyLifWphuCIXBpz\n5YPx1OsmOMfbi/XPv/zp9mLNzE1bWWYjIl988UXTND/96U+fvby1/DqXUoWARI/73e/9/u/3XVdE\npkwTpxkRV9ch53ouO7IhQABi5ntWTtkj1jRxjkoxK0qzRCTT8jGUbL7sTdhUVEtK4xiHRTsgpRHR\nuBIGguSUx74fDc6yOfBFOWqRSTewTmdauu2J1hZb39y0betrv1qtvOe6rn0VEPH22YvvvnsTY3z/\n/v3r169Xq83x0FWr7WeFm/VmuE5SoGkD4jrn/N137z799KX3jggVEgA4B4FCVXlURJ1J3mrbn0CB\nKkxDggAKWiRZQYBKH/sli/s1EcUxwqxyDZOTLrDHoT8jsj6ZH7L6gCZ0SlREwfY3EM2k6BDA2+yq\nasnJ3Dds2ArBIwKhGS8LQtQiExntY9UyVdMlMAM7R2wHNpecvasACMVmMEQQNJdJgxLUIRlrsKhq\nLkmSU5obR1MAokm/K811CE6ENSBUymPBiXsgCAww/Sy5KBdEp9aIM1dXzaAqQMavg1JMKy+byqpV\nmWaijmheF977j+jkDKVOQX6+/Rry+dEoWpeHCY0TvAhuCoCQaoZMKI40syoAeKQ6sHMc/MXN3bpq\nHFMy0XHnAGWIMbS1hXMCrIOrQ0UgKcXt1eVq03733Tffvv3u//3/+n+OJf+Xv/nr/81//z988+2X\noal/8OJH//Sf/9PXv3hz0axwfeE09af7ypXzkVFHRMw5IXGz2dbV1N+a1EaG4f7+vuu6RXdgGEcR\nCSGYRWQ/Du50crNzMc+ibavVahgGU+gwrKJpmiK5rl2oyNAzEfOFSbvdzvuq6zoip6qILJLbdo2I\njeck4ghzP9TOg5ZARFK60yHHkf2agYJz9Wb78vnLZnWVBsU1pe1GoZyO+5JjSglA7u/fP392C+pU\n9Wp7/W//7b8tpXzy4uWLTz41hT1mfnZ3V1XV119//fOf/fSP/vAfWlA06MUUy375yy9V4h/+3o/b\nf/KP67q+u7vLs9Pov/7X//qHrz79F//iX1iLYdqgBPf741/+5f+ch/Qnf/Ind3c39/f3y8ZVSvlb\n0NPp9KMvvgCAnFMp8u79PRHXIXz77bc5pTgM/fl8PB5tDKuUErfbt2/erNfr4NzQdZJzGlJPYxpS\n1w37/X4c06tXr+wz5DqDwHZ7SUTncy9JNpsLJBqHAUCDr0K7BsHN5uLx3YeryxsQbJqGEJumAqNE\npQxSPHkkJtFx6IeSco5hVSUFNhUU0TiM4zCY/baZo5ecAOB8OoLocX/Q2UYdRB2zI2//awQ5q4FK\ncdPQp8rp1JVSum4S8358fDifw4cP78mxXXhlVqawGbUF38InVINJvmKZzF+APNNeNTb2krTaM02p\n0xB5ml1+l8GgBTdkYzmZyrWiPBmOsagLC1NgpifYi1ttaDIbFucW2QyYOdDMvFqtqqryT1TAzajR\nXrkfk8mkjuO4Wq2eP3/+/NknFzfP1hc37eZyu932/dkGaL799tuf/PRv//zPRx+YCEUjAHjPzjER\nB9cg8NPeg32FRXr2N3oSVVUv3Tya9ZPcZP1CTwkkM0nEh2qa8HAzvmR9aQISkVyyqrLO8zSqxMDT\nwPLEEFHV/nReYLHlXRSxlDzRKOaZO0JEwjjGqJN1of1VzjmlUvsaQJHAmkdqJnaMJeVpSxeZkEMV\nAkgpMX80p9CZVTF/F7Em3BxoyVFAnTtBxvAABdAquLl6YUGdYdFpbsnUY4XJWN2KkIwLB+isijGX\nCtYxJSP648xGsU7VgtH9Gg5FCFIMaiTG2T2cUCemoi6+5hNOSkTIzIWipGlKMSB458+HY6lGRpKU\nEcRWbJYS0yAiRrlu69oRj33X9ec/+V//6X/4t/9T3YT9h8Pr79798ttfKcJ//v/9p9/6gz8yFujd\ns2cPu8f7t+84Z85jHfRi7U/nc87nEMI4DkTMAN9+++3jh/d2Ed3c3BCRCVOayJuJ2dhiaNu2gG4v\nN+QnxHtp+NnyM3eAr7/+erVa2WoxgMR734PT+oK1FtTgtxnk4XCKcWjbdU1+GCKihtCMMWLuYox1\nVYw3ZawKRGWmuq6pqk5D7vq+f3x8+/atr7qL9U3la+ecTuNwGkKo6/DNN998++23f/WXf7Ner/8v\n/+f/a1VVTeNMPKxtWxNH0JlmYl/WBCMsbTX1Mhtyv7u722w2pZRxvlnr5ZtvvhmGwXAXe+vuPHhf\nich6vd5sNojYNM1msxnH0bmN9e0Ph8OzZ89CCDZ89Xu//w9TKnVd/9mf/dmzZ88+/fRTS5SNHWYb\n3b/6V//q5ubmT/7kT2zTMN2Bt2/fHg6Hf//v/33TNH/6p39q/Yiqqs7nc4zx4eHhJz/5yQ9/+MN+\nHNmhKeCgFCnlV7/4hQXU58+fH49H7z2IFkAUzVm890TVyjcFdM3OSXaEKWHX90NOVVNb0m8SUN77\nc9c1zJoLsDRN03Xd3fWNqf5MALuHpVeytPzhyci/HUxj91mpwMxd19mxDXW1PHNRqzrPvDvbrEAV\nnQNE99d//ddudgVd6Nqqukz8uln1Ume6wX6/tyFW23cMOls2ZXuDaZrJkar64MYhGlzQNA0il1JW\nqw3OfrJ22kzJm2bnvY+Fwrx9L9ePbcGW1BiibdxBIiilmFANuWDajhY1TWyDq/b5J5+HqlIt3nsk\ntXG/J1IRACBIKpJTIgA4y0Dolk/Cs2OFpQBLQFpwqq7rJyBrFrCwQ2ETgvxElmYOV76qqmlfC8HC\nhn0qeEKYnt9IaUpneWm7MDtm2my2iCYigfYIs0OEdrstICggqA6ZPAf26KitakGFotksWxlqH2oP\ncegRkYEFxTraBITTuFSRrAUKKQGDQ4eEOSZB9sRKwMD2Lugo9mMBgaIFhBQFlc3V0uqEOah/rFfm\nTpI+GQGefiXMNjclRaUYK8qRKE68cxQVAFRUQdRUVBkQHKOAsZPFsFFCm3D6yL8XC64AWEQRMU8x\nU2dmo4IsBEsFADidjiWGHJOkHGNULaFqKmbM4ogZUDyBTNcCga7bdYwxjSMqSMyCoqWQYkXeozvu\nzqfH0+/90R88Pu6/+e7br37xzevX37/64ndP3flm037+oy++/cWvGDHLWDX1xdWm5NPQS13XiCCi\nbVWtV00a+qqqHh4ebBdYslcj79zf31upaoNTv/oqLYxZW8Zl1ldExBcvXrz55tvNZmMtZKuTFm1A\nW/Cmt3S93YiszMTyyy+/NJsYSamtaRzHpt6s1heXlzeIGBxriat183A67Mfxffe+lLJpmru7u9Xm\nBopDpZTGUsRoR6fTKSV/e3tbVRWCZ+b1eh1C2O0Ofd8D8aKyYaMt9pX1CY3T9jET0QCYVLqt820T\nviGE58+ff/fdd5vNZr/f6yyY5ly2Y2ITL4fDYUr1+n69bm0jPp/Pq9WqaRpbv0WgFK3r+vvvv3/2\n7NlqtQKAq6src9ixGPnmzRtjwZlonm1xdV13XWfa03b8bRM2gaXLy8vz+fzjH/94vV67EIqktqpR\noR/O5+Mpj+Pz5y9fvHjWn84AUIo6Dj7wer1JUjDGoSCkBOycc8GxarneXPcp1m0DTBWFyodS57aq\nBaFpW1M/ury8PB6PX3zxxdu3bxcpryV1tjB26juTjVDVxWzBaqYlQafZmaWqqiKyhDFbadZnWfJ4\nenJzFxcXm83GaotlwRl94Gk6uZQyIvLu3bvNZmMKDjxrodrE+7LF0MQlx/P5fH1ztd8dzHXi5ubG\neOiXl9cWRRExpwk0GMfReH0yq4/Yyy6b+zIzC5NncLy/vy+lCMq7d++uri5yzoaYP+wOfT+eTifj\niNu82KeffoqIOcfJNAUm6uDFxcVqtSoyihQzwJ7HpRTBI5ItpjxzJwzlsI6InbZlPOtie2UHIaVU\nRFLOY8yIw/biys7rUj7OQbeMYz+zAyaZ0WGQhaYBC3duklEfAQWUjJPKDqvQhMp9+bOf2x6LpISO\nGAgdkMYiRbMWECgEjAyOvP1UFFQyirqiOPLOOU+OiBid/RZIGR0yELA9oigEDKT2ar4O7Cm4ij05\n8uwt3pHnoCjT33IIwXkORJRSIl3AsY83UxG1Zs80GGzCwCUhFURiBJ3mTxQIs2QkIhBEEC2gWkSB\ncL3aWP2ETFpEc9IiCGRH5ONMMiEZ45BZnigbTXEIJlzPeIUWOW1Y/upy6z335y6pIIgWyTERldQP\nybFnRisZ5xfsjwdVRYXgnDqnxITcVO3j/e7dm3eC8OnLV//5L/5qXa1//Ft/8NAd/82/+Tc//sN/\ndNHenM/nP/4n//i7r79RKZrmmargOTurulLMAEpS8jjYxSLzkL9dGsv1i7N/SonJpWSGHVa9lQKl\nABHFh2PTNOtCW3VNAo3asKt8VUrPacA0OuccOyKqPSfIcexCCCs5P2/xJ4+vPd/mc1Ggh4P0UZw7\nib5lF0rOninHPmum4OrLaw6+FhrH8csvv9ydfvLy9iUBO0eb7appmpubm5ubmxDc8Xis6/qP/uiP\ncs7Wker78fLycnOxtW0qBFfXoW3b3e6hbWsiWK9b06RZHCKcc+t1e3t7a8IxtueeTqeU0rfffmu1\n4ETLTCmEsN1uva/Mu72u66ryVg+ZdpxxNyx77rpOpIRQMfk6+MvtxhG2deWZ9vs9SGmaZkxZctqs\n2tvrq1efvLzYrGMcm6YpKfbnExHdXF3eXl8h4sVmrSrvvn/zk5/85PLyEgB+//d/3zPd3FxZx30Y\nQFUduyo03lWxHy62l7e3z749f10ExphjLkZ58D7k8TyOo/R9dn5ZAzHGYRyAsIAO0hNgHtKqbrpx\n8N5bx3G1Wo3jSIhff/211QZLMTBtvyLkp76J4WG2tS7SUEvNbUy0qqp8Faz5YrZGttk+PDxY6IUZ\nb1vQP2epxzK1ZMWynYYl5f+YqCIaKLegbfZxjUSwDHks9Y3Mk0zWAVogo67r7Ds450yF15ZL27Z2\nyml2MCqzdKMdEWMlWTaRc764uEgphSb0fX97e4uI7J2INKvN8Xg2FrzVkufzeRi69eU1mSlh4PO5\nG4bueDqcz+f1eo2lmF8EgOSi5nDVNq33waKLzmZxJmyMv95+sKNkhZQ+oZYtx2GJK0tAyjm7Ohia\nYcHYTmGaDX1p5ojbAfHepTyoguikKq2ZAPpc+OJyA09uS6m68X7qtahxHsX08dPQW+fWeceEsaik\nmHLqo40eE4BOegVIiGDTYs55ZgJAESMuyBB7qzOMGQxM1hNefqJjc4Ey3fTNZmO/Md6ERU0kfXb3\n4ikbkxhACUClRFCGxd4ewJQf+tyzMjrHxKFxCwra9UPKiYEdOyYqJIREntIQBYWBlZSBRQSs/iOC\nJfhMIXGKSaBqc1fTYCQAAHR9rkMlOQfky8vLlt3FelMRxa6vmCofeJH2QkSVYewZybvgnDOZQVRC\nou3FxT/73/53u/3+zdt3n3zygw/396XI1dXNw/64Xq/JucP59Pzlizfv3m59CAy70zFU2o0DIhQV\nMkUuUDuklnLZkrALc4IKc7aBDaPYZimbtjHHXponruyLNW1bVRUgsnNjjLmUXEqoG8SgUEK1XkJd\nTALgFVTB50IxQUzQ9TmlJADNqq1rKgqa1FJGlUJE62Y9lrQ77L97//ghwcUP1u1qwxXFGLUAohZJ\n33///c9+9rOrqysAscuhqTfeeylo4kwfPnzYHw8WSi0qOOfevn17Op0s3bYL09jGdV3nHGN0xhC2\n6s1k3Ihos9nc3t4CgG04hrVIARG5urp69uxZVVVddzLNaedcSq6qqvV6/ezZs7ZtnXMxjqvVqut6\nO+DsEBF94LZt6yYwsyHwRdI4joauN21lmAUAxDS8f3f/5vvvbq7vxtivV9t2VVdV1a7q7jwAinPO\ns5MiNOFMjhFKyjnGw+H0yYuXKhBCpSqIOSfRXGLMzjkhsp04paQpMUJKSd2UzScppaAjtidYQTOn\nJmWz2bhZmXrpiejsKe6cA8RxzoxtEdoBtO29LFjc+WzFpgn3xBitNDda9eFwwHlIZimPENGdTqeL\niwtEXOSPlmW37LMLsmTFl4UyC2BLbruUCE9b5ZbsL+tm9jsX23x5mYedpS8Ms7I3si/sZlHnpapY\nxqGqqrJ+poVPADBw03QWqqo6Hs+2iHGWmcg5H4/H9QUXSaVMCvbr9drmyOZvrTkXk5gNvh5TZl/7\n4MkF+0ilFMVhTHmpYdkocYgAsN8fdRYyD35q/dnuYIgBziTIUkrOEbVA393c3IQQ3r59672/vr5e\nZqR4cUGOAADIZKnT05rVbpa4LWFvOdN9101KRarGXpdScil1VY0xphIrIl9VRJQ0llKcJwI0t2YR\nsNEaACEE0FIylCwiMDk6k27W6zHGFKOkogCaIIoUkVXbAqIV1KNxsQEA4Ouvfglg4yNqXOrlvYwt\nTwSmzWzsBJjrqKdltx2TZXkszTl2Yb3epJIZXdUERpdKRKVQ+7ubZ0Q2rGv8PSAbHaFJWWOpxgAQ\nRHMuc9sJmT+S3bMSM6U+9Xno9sfjw/3+/XssgkU9o2cXHNnortUSbduWklRRVcchDsNQijrnLrZX\n33z3+vknLw+nc6irrPr5D3/0t1/9rL1bIWLXddvV1d3Fi2bV3t3ebmp3fPgeHTertuLaI7VtU/kq\nxdERfPLi+cPDwzKoaxpaMjkR52cvX5gDWYxREe4PDzJ71JZSVFmVDD5ilpSO+wbHMUqDJ05NtRn6\nEqNcXFz0fV9yMV3jtm05cCnlgi7KDvLlDx+Zfe0lniX2TYCcpKhKjHVV5VIAqesGcORDVdf1qnLX\n19fPnz9P4jx4AiaCqvYi0g+nH//4x6tVAwCbzWazvlLVw/78L//lv1ytVqvVCpmqqrq4uCilWFeY\niNbrtZ2g4/Fo3SNLphHRctbdbue9Nz1QS8zv7+/3+/1f/MVfGJ5vF0scM7N/fHzcbDbffPPN4+N9\nXddzxxdF5JtvvjEJ7fV63XXnlFIdKhDpu5MjKjky4nazco69D96vU8qq4hgZkQnW603fD01VNVUd\nY9g/7jar1Scvn19ut4j0yYsXm9W6rqv7+wcQubm+dJ76bnTUcph05cVNEp1V1aRUNuuLmIaSgX3n\nyDer9nw+Y86N8+g9EZVZu2GUjyrVBOycwwKIWGIqk9sL9KfzzeXVcO7yGI1aCgAik14oInLwTdva\n3mJ0O8uBzG8BZpeNZc+v69quhSiKampqGpzXIkiTkq/ahY4CAO54PJrFkb2iRSOrm/CJaBs9GRBZ\nSh8rF3Cek5XZ1Wrh6qiWruvsMl6tVtYYLEWapjGta9vKM07iQMZcsHjz1Gf3aXRcChFrS1bewxNj\nFaurYoxEbHcQ8erq6vnz58E3Bvhut1vnnA0mNc3G9F4t+LMja7aVrMH71Wo17s6IyOztzKpKSqXv\n+6ZZEQGRY8Ynuyos8Cg+mX616seQbnvQkhEiGPuzfdlFIdBCsh0rO4wpJSN3OOdymqaJLcWzjvcw\nDNvt9mmJtuTy+/1+xsSnGTo7d6vVynhHdVVtNht7l5SS+RwvzTCdwVua6Z4xRpHMzHVdhRAmAWwA\nnQ1ElrVhf2Y0bpoWj2y3W6tAlpJR1ewDggjPy2kCl1RNcQmXYSaLDqqacywFY3z6OBK5UDXjaDwU\nr3P70w7+skKWRWW87iU64qTOTIAy9hFRHTpmZPbMyOgQkRxXVYVF1m0TgMoYfb1iUO8IQVDnJp3N\nMjIqypDTOCYRybkUKewDBr8fzs3l9vsPH9Tz7nR2vvr6u9cxl92bN3/3d3/nsP1Hf/hPLtt8PJ8/\nEL4fu1WNUgqkc8WSU9Kcm6o5HQ+So2f61a9+FUIw/fu2bc25SkS6rttsNn3fG9bkgi8kFDwDjjmh\nKHln00j96WxsyRCCQ/J1BUXa9SVf1Odh/MGnPzh2R81ar+rd/e7y5pKBD+fDy2cvs+ZPX3x6Hs53\n13fd+VH6h/WqOp4GKZhSaZqmOx+ZVCQXxhHwscDhNGaZsOiqqlBJJI/juN/vTZHZRFKY+d27dyKy\nWV++e/fu9vbZ9fU1ezcMg9WCRkQupTw+PtqFYwvbOWePAEDdBCtlLi8vLy4u1uu1uUj85V/+5Rdf\nfPHDH/7w6urK9lPvveNA5H7yk5+p6qtXrz777FPbvu7u7kpJh8PBCBSbzeb6+to5btt26HrvvUhp\n2zbnZHOg9gmtSttut113Pp1OP/3pT1JK19fX4zh2Xee9N5PAb7/95l//639tKM4CtKaUHh7uf/7T\nnypw2z6MYxLJwVXMeDwejYbQ933l/Pl87rrusD81dZ1i8ZvQVtvnqwuK42WoSn9etw2iCmuUwt4d\nzicq2FT1eB5IwZqClst++PDh5cuXKaXVamUOO7al2Hshoq+rZZYDZ17bk91eDWCzPXAh0S2pz6JT\nbpXrkuEtscb9k3/yT6xnbmCr/aKUskzC8hNXadv+/vRP//Tx8dEGg0z/bvqs3lsr1byIcs7D0MUY\nkSCOqeu6+/t7mzf65ptvVLFt2/P5vNlsvv3m9WeffWZq3DhPuS6B8Hg8Ll/JUjwrHn/6059ut9uH\nDx+I6MPjBxGxyGqyY6duGMfRFt9PfvKT9+/vb66f/eyXv7p5/nJ9cWmUG5F8PB7/5m/+RrVst1si\nEM3jGL/88subm5vr69tSdLc7POz2UialT4VSshZJL198+stffZliUSg5iT3eruof/ehHthebaH9V\nVZvN5nw+X11djeN4e3sbYwTC4/nEzG1be6lOHz48e/Hy8fHx6uZWVV/94PO/+Iu/WG8v2rYVkRDC\n+Xx2obq/vw+Nu7nYWFmgqqvV6le/+lVVVav12o6ezhpOVj3EGL/44os3b97Y/mslFCKax0mMsW3b\ntm39YtemWreVJRa73Y6M5luKIber1er6+vrx8VFVjclye3u7Px5SShcXF5YHAEDf9ymlH/zgB2bB\nYg/auT6fj0VlvV7ZyxoVx07uOI7jOFxdXVkP0ns/jmNbNzkWnRFgq4Rg7r3b7mP7r72v4QQheAAw\nolRKMQSvqm3bWHQ3k0bvfSm5rmvnqetO7Ei1nM6nqvJN1R6PpxJLqJwLHkByGlMs1s7q+/7q6uq4\n2/+D3/6t4F3OJDlmlRAqh8iEhOCYmJBUclYHVah9WDVVVdXNSkR2+8N+f6zq2jGHdVvXtffh+++/\n3++O/+CLF2/7x2+//fb//n/7f1TUEFHbtkOM27YBGXxVkSv96ZEVHNH5dELRYRh8FRThYfd4c3Nz\nOBz6cWDv+nGo67pumyGOoa4E1AXvgeooN+06xbg/9cF7yCol+hBScZL1suZ379+v29asPdPpbZHo\nUG4+3X7z8/8cXLXPIwHvdx4ED6d9fn0BpEM3CpRfJvFNLYSK5EPz6Wef/5e//Zvtap3iACDeuwTC\n7eTJdnf3/HA4uWZDpQuuApCuP59Op7Ztt9vthw8fvPcxxu12+/DwYJHVaqAxDYjqHDHj6dRdXGyY\nUbWsVo3Nzuecq8q3bW1KAcxs8fh0Oq3X667rbm5uDKE6HA4XFxe2y4Eh/0lUJ72Atm2Px31d1977\nx8dHIrCCTFU3mw3Mfev1pi2lXF5t33z/3R/98T9sV7VIuLq+qOvaeN7b7bZd1S9ePvut3/5CZ1E0\nu4T/03/6T01b/ei3fvjP/tk/Y+bj8WgFrsGP//kv/+Nv//Zvq4JzLo55vWklyW73wIx1Ha6urs7n\n8/biIquQd904PDw8NutVSt05928OXUvYFYE4vAf1nkeJSYUcn/puFdqri8vucDZpQWNdWoH4l//l\nfzZm2eK1bVcNe2cVJz+hB9t0mohcX1/b9fjw8LBarQyXswrJvAK++MHnxu+wP7zaXljOahejbewA\n4GzvWAClJbM2vop1MpZoZICe5VyG1Bk/0jYLmiXzLPdvmqZpqvV6DahSJl8ZREOBIGcxx9K2bavQ\nfPrppwvvApcRyCecK5OdsBNp3zPGeHt7i4bpBY4xXl1dWDQCgP3x/Pr195bOe+/v7u5++PmPrp89\nb7eXF9c3bdt6zwBw7k5t25qGCBEjsPfBOT/higq3z+4EaOmLZBVJOZb86tNXNhiphFDE9CU5+Laq\nq7YyZ/Eco6+qq4uLc9+XlI7n83q9PnVd0zTITADOBc/Oe9+265TSMMScowgMw/D+/b1zjykV5yil\nUlW+6wZbpofD4XA47Pf7uq5Pp9Nnn3326tWrv/qrv7I1lLMygwGqmsvl5fXx1E3uTaKhrhgpF123\nq9V6C6IK1J0HZFq3K6wxhIAgqrjZFBFYr1sR6PtzCHVKSQSY+erqJoSQs7x+8/bq6ipUZeIIAJNj\n76qYUxWadqXB+X4cSsqi6F21vXDn7phVxjEVKM4F8kRKSdKzZy8+PH5w6AoUIqeETbOq6hpxlGwS\nXNO0HJEjkvV66z2nVMaxH8cUgmvbNTL13eir4IgVoT935Hiz3mwutsf9QRGC86ZCjUxxGFNKbdsS\ngU3nbLeRiEA0pfHibmMdowkun+2Db26uXr38ZNc2F+uNR6rbdl01pPrJs+ceiZGY0c/WtkqaGeIk\nqARAnKTUmxV4RuRQ16UoETWh+cR9cnU9hE3zonmliJvViqFKY/zkk08qpvt331nimfvzcb8nUY8I\nSRAh53w4HJY5cWN1y+xVPwxDmaUocs4qUCPGGGHugC6JS13XxHw4HDabjZQyDINjLqVIyUA6juaF\naslyTgmaqmZmkSyiRBBCnSkJSM6qzCAlpQJAgjQJHDAn1SSacxYES6GazeXt5ro/D5vN6nDcEdHh\ncHj37t3t7XXbtk3TvP3+HhEtkPR9/9VXX7GnBZ61QtxCi9XBC33O2vKbzUaeOLQt2TYAmP+WdUeW\n3nsp5fr61tjPdjXZnrZarc7n41dffWXm3+aVXFWmveYQ1QKhHaLNZuM9x5hXq8a5kHMEAPMvvrjY\nMPsYh5RSKeY+Z7ucjGNerZqmWXXdCYBWq+b29pYdpliI0HlEhLr2V1eXFxfbruvqOlxcbPp+vLm5\n2e12Zn98//23z19s8inncYigHokRpZRxzBlLksLwEe2w5LUKQVSZSAHiOKacmSgb8m/mc0QO0dRS\nciljmbhcC161HFJDILquSynd3t6+ffs2pZTHaOmsc27pPljhCPNogcWXYRicsU1g5jYsMWN55ClG\nZ3moc85+LpGD5wEXK2tg5nkj+tPppCaJ+MRH3LAfu2MNp4WVsSTCT4s4AFi6bZa5W65UVdVht0NE\nyjQMg/ds0UhEUpa+740rwcxG67Q1VFU+BGcvWNXheDy2be195ZwTIapMy883TTvEPMTTZJwNrAhF\ntKgW0TFnYuedM8WeumlySop66ruwanLO5LymkkW7IY4pO3LIrihm0ZilKBRRjTE4N47J+2q12pxO\ng2oVQi0CzH5WZgLnwnZ7IUJN0xaF9Wb7xY8qETFEom3b58+f0+waYGmOFbvDMGwvrw6nM4gUVRBx\nITiium1zSr6q+/M5j3H38FBUf+8f/APnXB2qcRyYuWnXwzCGqkGkt+/ePT7uxnEwDC8XOBz2+/3h\ncDh0Qz/EGJzzVRWcq9t21TQx5zdvvo85r9t2TAlVm9UqOLe5uLi4usmScixFgZgQKAukLO/vH8eU\n1m19sb1gdN1wBsF+GNqqyZxzGUGKmvUNOSbMSRwSIKQiYxwEqrryJOirQM4jYi4li7hQmeLyarMZ\nYkREUPWVyyIuhFN3vqmvBYo1oGhWtvdV6I3TPHeqVPV8PB2Px9oHYnCEQ38eUpEQAiAW+eoXvyRU\nRnIEBDNoDJoZCoICqaqAZpVcNKtcX9+0UEBJRCRHVQXN3fk4DOXd/b47nT0WKCE4p1JSSp998jK4\nMhzJayJRT+SBfXBD7ENT3zy7M4H81TCs12vjKBsRwMCrpUjtY29Mk24czoej2aac+i4B+rp6/PZ4\nfbs+7Q+nvqsxJNLKXwnQu7J65KuK/ICxlFSKrqA6pKbBaswJhVu/LprKODRenKAKDnGERaQRpB+H\nqAWQYpkcZi182pW+3+9D5W9vb7v++OrVK3MvtMKiruuSIef8ySevPv/889fffxcql0ukDFXti6T9\n4XGMfcpjqNxqtSqltG3bruq+7x9398+e38rsdLzk4BbaF4s1G99JKY1jfHx8NA43M19cXLRt+2d/\n9md/8Rd/8YMfvHr9+nWo3OFw+Hf/7t8h4vX1FRFISbV3TbPyhB/efp/Hbr3e5hy320vv2TD8q+2m\nrQKU7BAYgYMP7HKOgalyzKAOwXnX9+fAbrtqUyrfPj5AyYGpXjkiN0g+H/eGiCiUrjuHOqw364fd\nIxHtDo+pJPbUj93xBBxjZa1i0ZxzSVEkq4MkRXFqZEyDVznF4zGr1D6gYyQKwTehMq6T/QSmECoO\nvsREUnjekO2mM82t73uDxA0Vs2gkIs2kNcNPkT3DGJYwYW0LAHBL7mDRAubp1CUILe8H8wCNMSAt\nkOgTstlS08wNUrWxniKZcPK3EBFVZObzubdCSmbrWGsXLb7IS/fCPsyizmAfxkq8vu+N26Y0i28y\nA00hzYKQDcm6WSl2kcVTVQVZrVYiebPZ5LyQFCedzbquh2gsCVFVmi3+DDlN5sE6D9sGkSJSSjl3\n/UUp++PBez+MA0Y0kNe2g9JKznmkaVJYgBm475J3VfFK6HxovKtSVBU0dUqDLpt68yHtTl0P5FIu\npKSgpQA4P2RNChmYGIic9+xDTQRjgayDAJPzjjyQagFkKElSkRgl1D4LAeju0BXN5GpFJfZA0blA\njvs+AlHw9e5weP78pUDxHIrmm6vbUFfX13dFxFUhS8mxkEPJSg7benXuT2MfU4meAw1nySoAMQOy\n+/IXX/VxiMOQSnFEQCQ5jyn94R/8wf3j8Wc/++UQY+U9e//f/PEfX17fQBKkVDKI6YO54IiL8qYO\nVgOtNps0xlBXwfkxRV9VY4o5Jhf85uKiWbWP9w8Pu8ebq2uJY0455mSV3MV228fhPPRpHA2XAABU\nCCFcXV29ffO9IdhlsXwkbJpme7FeNW2uhtWqlSGyJVUg7IgVGGd5cski5gIVgJGdI+8UIJU85uRB\nf/tHnyOiFLBhgv50zpDGMV09u3vcnaDI1c1lf/r/E/ZnvbZl2XkgNpo55+r23qe7bXQZGZlJZjIp\nJilKRdM2qkqw4ScBBvRgF/wiVD34V+jZLrgA+1cYMFAPsgQYsvRiWLQJqCElFZVUMpPZRcS9N25z\nmt2tZjZj+GHste6OSBa8EQice5q915prztF+4/vKd7/73b/+yX8C0fv7+9qV6bAdjkenKIgCrMlv\n++2+39uIt3V/Dae7Wq2IaBxHazVb2w8QE2QBXa1Wp1po27ZtG7QgYtO23/ud79d1jZ+gxZ1MlRSW\nQo8ePbp6/GQRKrNWjdl9yxXqus45Sxp2ty+ACQCmaSJia2MaRMU0gh2H4Nn5SpCmlPr7t9/7zndT\nmoqkh4eHL774QkTGMT5//vxwOKSoKaVnTz+cpgkAfvWrXzx68hhJDZVweXlpVsjqaar68PBwf39/\nfX19c3NjN27XTDOv/DLGZwbHcPDnfdYQwvX19be+9S1DgVvx01pxq9WqWzXOucPhcHd39xd/8T/s\ndw/XF5v1urNe709+8peWnh4OB5jnYZqmefHixTj2v/zlL5cqtCHR3717l3O+vX37H//jf3z8+PHh\ncGjbB0NIvn37VrXc3b0zks/NZkO0QsT9fr9atd2qetjeHft921Ul62rVmXG/vLzcbOrr5vpRvVo5\npnHK/aGkCCBDHqMUF/xh6D24Vdu1ock5RympZFRIJScAZIolH4fepiBAVDOUUlzxWsQa2H4WtFvS\nLDhjWDjXql88iLkD+6Y5CHteMs/GWGrh/tN/+k/nLmsBiS7J0JLT6WljycPDQ9M0q9UKZoDTqeVQ\n14fDwVbcGh6Wt6YcVU4QQEQkcvbZi1e8vLy04a/zNvv5xVjdbPFSPItcwKzsl/WUoaeUBDTGOKWi\nqvaelr875yzk8cFZa8FyuxDCarXabrfOBZHsvQclFQy+LmXvQ1VmKR8BBERyHoh9VbtQEVFRAABk\nhyalwuR8OPbDeu2InXOOmIldTDmE0K3WMWVEG/ZHR8zsFHG12ShiUe3qmpw7DsOViK1hyhmIkHmM\nEQrdPL6ZDmmKuUhCYPahZHWhAuRUUh5H0ezd6ANLgawwxjzG7AmVVLMqaZ4yZw4cgJwPtaAAsvOu\n7da5xNC0SujQKakPk6+apu7GmE2OzIc6xyFlmVKpXOUbH3NyoS55QibNeUo5eD0O0/Mnz2OJpNSk\nlUOXJJVYrm4es69SyZILzFNRxvHaH44ffvTtjz78dqgrLfL5l1+03dUwjpu2AXIqWEwlxjsCFJVx\nSscpNqEShJRFYs5JdscDuf4w9GmcyDtSuCF6+dXrfhp//vNf9tNo3fvKeSX87rc/++qrl1+9fqVz\ntI6IDLherx8/frxZr+u6JqJRBxJgjwAgVVyv1yJlGPvL1cohSYqF2bOvQ2WTRqgCKCJk6HACSpNI\nnCiIspYYc4oC+uKXv9ztdgCyajtU7Q/HElNm/3Z7H9ZX0zC+e/v2f/df/dfXl5cXXfu9zz45PrzR\noGo4FyUsJacEIqu269Ng2bD1Du34mHVYQLcW/dTONwXjOLGMRYfxcEj8MFZV3/dXV1c73X7ve9/7\nD//2P1hibZGf906hdF1nA0BWBZF5c7ZXV/nh4eHNG2s2I2LdNgYzMVSUQSSJoG5CBpWq8ZCckCHZ\nBPH6+vpnP/vZatUCyvX19Y9+9KOcMxHc3t62bbu6Wg/D8O7du9VqdXFxYRQMbVMvQOSHhwezj2YN\nTELbOXc8Hl++fKmqzGz9SytaWjfRakc2f2rND4P5VNUJOPeLX/zit3/7tz/++GODOD169Oh43D95\n8uSLL39tduz58+eqcn11kcajd5TTtF6v7+/vUxxBS8kRZ/hSTtN61UpJD/e3hmI4Hobd9t6eiHf0\n5Re//vlf/7Su68vLSwP+WcMmxvj//Gf/j6ap7+/vAdBygKqq2IWmaf75P/9nKaW///f/fow5VO72\n7vD2ze3hsHs53O1YbtFXKlURyhFVRHLGkkF9FbaHvUZp60aTeO+nkguod855362665sb79xuvz/s\n9857JhJVQjRAt6oG55umsQchMyGcVVMvLi72+/3l5aVVVj/77LNpmg7bXZmdUIzRfrmf3YolGClG\nMQS5Pb9ThnGmB8ozS81SH9R5eIiINpuNDRi5s0nVtm3N81ug5L0HkJSS8xynZI6xrmvngs5zvAvW\nawF2j+Nog1fmS62CZ17XsBI6K7DtdrthGMa+B4BY4t3d3WazijEWlWmarh89GYbJuoV2LymllCfj\nXHAzHbh1Dq1JFkLIGZalWJAhRd8P/y7rY4u71B7tms1TmiCjNept6y+KTUuUeipyig4FStb16qJk\ndRyuLm+uLm+YfPB1jJHJjyk6hio0VWjQ8bEfhpTbOtRtDQIuuLt3d0PK6Jwj5wIICCMjI2QhlbZb\n1XVrE0KZChG6iqsqlCI5S9W2KUVgXq/XVdty9nXT+SpMwwgIVdu0q3UVqqIATEXKlFOxlM2HMcY8\nTrHk1WqVRDpXE3mvsrm6SlLutttSsoHpVquKQDNp1bTpbltMv4VIgUSEgMhRt7rYXG6mYQKCVNLh\nODTtmn2ofEWcpJATBFEkNr7Ebr0+9EdydV1XA/RAGHxoAICIg89dturB5eXl7tHNzTyhYpN6iDhN\n0w9+8IO6q589f2oC9oxkDdGubj766KOHhwcEGMdxSpGJjHasH8cPP/zQE+3vH7quCwiY5bJddVXY\nPWzZxALn+gMzolJw1SQpl0KKqEjsa+fR4W9/+9uff/6r/X5POe63u/u7uzLGRIzXN7uxfPHLX/3R\nf/Y//8lf/uV/9b/537LK57/81apGJ8hSHBIDlZLyFCVj3axgVmCy87Wgy2BGD5aZE8whQYxYRCET\n0apujI1mVTcGBmtDNR6OV1dXVd1EYmYqMgFAmXoHBfIEyuQciICIA+4qh+s2jycmodDU211vBY9x\niERExBgqlNQ0TV9Sse5XBsv4laonz57+t/+H/+Pl5Samsa7r1br5J//kn1SVt9L6m9d319fXTb26\nvr7+F//iX2y397FMVqC24ZhHjx4Nw/DZZ5/9o3/0j0wXZrPZWKv8+vqamf/0T//0Zz/7mT19a2Yv\nedLhcPjpT39q/skMfU7SdesnT5781m/91nq9Ph73JiP09OnT29u3Nzc32919VVXPnj27vr7+y7/8\n8cVmtdtuc6qdc5vNZrEzSxBv24aZj8ejFYd+/etfG87LmlKms7OAxSyXtQVcr9dv37459rv9fv/o\n0aO2q0opKUVyBCjOw3Z7uLy8tDC6rutQuW7VfHC9Stu7/m43xukyVBdNRaAxjj6EDBrqKquIK01V\nY4C6rvscp5KhSCzZxTjEaRzH1+/exmF0VfDEVq+zqUFETDFay7DMZKFmSB8eHiwbsWGAH//4x+Zs\nLrrVUimVmUDHZmOt7WJvZV7GLQ/JEnDDLBmu4dwb4cyAYAGjraCpTZuHXJzWgpQwb6SqSCelIkvx\nEG3M06f3KoEnb2f2gmdy+0XZyOIX85HTNNnDs5qyIwKAJOn+/v7q6qKUogjjON497EpRu7XNZrNe\nrxfgODPPzKVuGIbHjx+bx6rrOiVcLmAOuEgADBlBZzJ3yL4oIiCxB9VUNKXiPQuCrytBQMelZJWC\niEqYS0lSppz6abSwAhGhCGQoRTebyxiz99X19aOrq5sQ6hhzSsU5HceIyCb04hwAuSw6xTzmlMa0\nvlznoqFuHrZ7X/va10qoRXNOecrTNCgSIM3CeKapCkVUgcYpXl5ej9OUstRNG6qmaZqua0spQz8J\nQLfarDaXDFgUkZyIFgHLqNjHFMuYhrpuqrqJSUQhphLj2LRxfzg+efLMGgw5R+erlHPKgkBV0w5x\nUFNDA0xiQuwSOAji/tgnSZr1MAzri0sA0VxgHGNMMo2qUkRIIaseh+Fuu73aANfVGOMQp65uYinM\nJsHEIiWmwi4guaquwcpwyKIICv0wxVQetvvNujMsgAIAYSpyHKcx5dC0DIjkFMgRV1WF5NI47Xbb\nddukNB37fVT0QAeRYQ95jKgFFRiVAE89VySKGjIFQiZfUEgVHIY6vPnyy+27d5pTqOq1582TxxW7\nfRF+8sGv39w74t3D9n/2x/9T59x3vvVJ7b4bKK0qDDJ5SBWyjFOZEnvuNU4SYR4Yt6AVAO7v7+2E\nMrONFkzTdBRhUGScptNAm1UUiOjm5iYKfHn3toeCcdB54NEHdzqqrppUSZCLceE021RcP5UCI/mi\npZRSJ2AX2PkUyzSNzpyiKgIcx2EqOZEb45TzzIoJQDO1GDu0nKCu688++9SIElbd5Xq9fvvm7sMP\nPxR50bb1mIb1evW973134Vx4+fLlNI1Pnz5p26brurZtt9tt3/fH48GqXl999ZVVlhbsqHNuGIb9\nfv/ixQuLdE/RsOA4xtVqYzgIC0x//OMf//jHP7by0O/96HcfP378ne985+rq6sWLF9uHZjzumjqs\n12ud8c2GpzfEXdM0x+PR+IEMiWdB/MXFhVU4jc9tvV4b6NTA1sxsDHsi0rb1OPYAst9vRSSEum4C\ngD59+pSZx7EfhmMs+ylP5OnY93uvnBIz+xAsYybQUniM01RylhJjxAI55zymmJI4UkZkQgVg8lUg\nwKqpc87IVFSLCoASaJKiqsG5nLMxRS1J0jiOhqO+uLiwAqmeSDsr8xFzVew00hNC2G635o2WXoyI\nOCnkXKhCp9pLISKHwAmKFFIoUvCEGyNVYVUd+tQP01WhIpCTsYM5571KRnKEARAQPFJmqoghpcmx\n8x4QJ1PQ8r6KMSOwlFRM6fuUljFAtr4rzYxwOA8zmde0Z2znxLxCP46IqGDZBnvviAiUPnq+efHi\n1TTG7XZ7PA45neArzpPkYuk2kRtjXm0urcThQq2ErqrRectAFWEYjjpzKQHw0pglEC0JEIl8kRLH\nGGPUEu7u7/q+N6SilQcXXDKeIbDtO6K5aCHv2vUqHA/o2FXBPK6e6E+C0f15z4hqvHIMWNc1EeyT\niYVnKOK9d2g1yUkEmNG54F2Xc7TjRxQQk4jEOEzTiRW3ruv9nkspdd2GENq2bZsq53yL7xBh1XWb\nzYWkbHWDosKMRoZkp9f7MI2paU8DVXAaYfZ1XT883M1JJDD7lAoA1HUrcltiMuURZQ8qJhwlKAyI\niJ4YKw7sTqwtXEpGxV4FYxbSE82XEW6HprYDMKUiQM65oiXn91RsJrE8jqNFx1bLtczYmg12WoZh\ncI7rmfOwrmurDlmCm6aYUkak0NQp5bquLzcXbd1gEa8qIv1+V5EDUUYsiOgY2bGrHPOwj04xhMqx\nK3Hq+6NqyWOdPOfDiKDHfjv2PUgpsXxx++6jP3S37+6vri/qJvyf/y//3X/33/6f/od//+/XbYjH\n+1UAp1OFuXNeYoZcQgiRkrCWJIfjruKqqv00JnAwDjHUXgRKSVXVOEYmDw4o+FBXVUqq2rZtjidY\nrM7SsR9//LFJLTd1fdK/qyqr++FMQWmVrvv7e3MJF5tLM+6IGGkM7EpWKQMWKpKh5IISp5QQpG6A\n0Ht2nhi0lDT00wcffZxKqZsaQPth+Na3P6maer25fP36bagqcm61WY9xGqa+aavL9WWMsd/v6lRb\n8tGuuqqp7+/vFWFKsX/XW0GMiIrKxeXl4XAQVQAwggkD2V5cXBh3pQlgppxPjWcPm8sOGXIpmCjG\n1Hab7//ghw/buz/90//P7//tPzgcB3bhydPnT55+9J3PPon9Tkpi5pyjc8E58t7f3NzYgljXyvyQ\njWq0bfvixQsre9r3d7vdw8ODTb/YyTJwGjNvt9tXXx222/ubm5vb29u2XT16FEBpf9h/8MGHTx8/\nSzF2zQqG/mpzwcBfjj/FTfPh02fPr242IYQiLAlLyTm6yo1xQu9ijATsve93xyIy5AiIlimWUqio\nSElTnA2UgCgiEqAYNixomqIRtlXVKbMZxxGZ7rcP64vN67dvLi4uqroZhsH5wMxQTmfWYGmmMrOe\n5yNzKaRKqiLiQP2XX7wGfesDI3DKU4oFUMYh2iRNkWQ8LjnJFIdQNUnSw/3Puk3nyQPDxeqiQKl9\n/ebuwZMXlFWzAsbddtu2dZzGqqpSKghVFToVn6I29RoRh2EKoV5aQSllG1m3xKjMY72Wli1xjWE9\nbRah73tyqKo5FZPWWDUrUGIpIBiHfLm+fhd2q9UKmYCwbVsUlZLa9sIFfxzGzcX19jg8fvxUEbJk\n33QXNzeiOMREPsQYHRO7E/6ilGzbmhBBCpsMUIoAUHmvJWvJN5eXj6+vmxCglMAMqsY0wABpHC/X\n6zevXoFqGkerznvvjsNhtem64ypLuXn0hENVtd2Ysve82+26rhnGow9UyuCxAaTGudz3omVTtxLj\n9WrVel8hgggaIQWQguSUREvThgKpqZqUkoAc+gMzZ0kxT+2qEShZEhA+fvrk6fNnw7EPVNc1MbrK\n+6Zqu6oTVzw5VPTkGLk/Hh597+bVq1eVDzY9t98eHLMWKTnGaWTSnEY7fqVAVYexH0IIqIQKJcUU\nJ1QkZMkJCQgxTlPlg0qRnBSkCm4ah7aumFkylnTfNN3Lly/brlaVnCciyiX5ADEO3hOAIimgTXAT\nAcaYiMizyzGhQvBei5hKE4iCKCMRYI7FVw4RvK+co2GaXAjD1ANp01QAMmVRwlDX3lUxRlC+urqy\nCjAiasmICFnqUDk9xW2qmAUlkyAWpNC1w7EHhGmKIlr7rh8OWPjYD0FDznnoB83YNl0smTmEin73\nR9+PuU9pfPr46qMPPvjil7+ovXN1IJ1My/w4jQzIAod+ogoliRO8rtpAjgCbQFlL1TAFTiLO1WVM\nMKZN3R2mIYl853vf/fN/+2d1Xe8etpfrDYlOxz4OY3D+fkwxRj2Oh8Nh3a2mFJNkdu6HP/zhv/n/\n/qkVAC1OMotZVZWxnOmMTBvj1DQNI5HkODzUdV1XVUHMUbpV9/Y4CoJK6Sqv037VPVKlrM4HlyFP\nsb+6uri7e/f8448IwwdV9+rl64f9oFD24yF0YT/sa2wEIaybmLMnHtKopEmSaQDFEr3j2le39+/q\nun76/MOv3rwRR3MECc454mrK+ZhjBuG2nlSICCqfStGSBCKFMuXBhTpmdWG13U8546Gf2DfkQtV0\n14+ejRNeXj0vpXKh0zKmlEQRiRWgaVfDGBVhfbERERf8cTi64LLkqqmnFB89fmpR6TBGEdlcXFkY\nZ7UvC+yGYRjG2HRd3TZX149SSh9+tEbFpu6Cq7XGtu4wD4FDnLIHN07D7u3Dumoacl99+eXDy68o\nRycSENIwNMHnNLFziJyk9P34t//wD//qpz8rpYgUs6hG9z5s96WUVPI89CkVO2b++OOP7+7upmmo\nK197F2Nm5mbVpVg2l+urm0tR/PCjjx49fXpxc+NDePr0+f39vSNGLTFOln1aHpxz7tyFm1niROR4\nPG42m91u537v934/pUnV9HEo52jyRX0/es/OBdPWVC0ikHNMRZRUCrBDUDJfJZqnMRG4/jgSwxhz\nLlEK6HEwjS/rBtkVGLLFmFytA2QT4zln59jGgM6bpZZWW7NnyQER8Xg8hroqKSmhTSeRmpAOe/bH\nYez7/rjvh2EoWVQ1SZmmgeiGyDhiFJGzClFQIHYOhZiZmBEJ6QQRRDGRIePNFDgpZwOCIrxHG4IK\ngiqazuEpIV06cDBPhp6/VBURXPDsSUAVhcnPgOFZhUFVNKsKYFYtqgWKgighqoBKMWEkAiQ8EXmA\nIKCAKiEoKCqI5FxiLglQiU94ZSvcW23B8k6r83hfMRIogSCTd+QFTSIPjMQaZ7XN5S5OX0ABUEQl\nBiQTdS0nROLpC0WTIAO0C1MVEAQSVCAEVFtGABUCdEzMpobjiBaITRYR0XyS8YNCbNdgQBP9xlUt\n//zGd/C9OMi5UPr7SQYrESOqiLBadkspjOMQCYrNi2AuY8kwjjIlVCIABCYfvKu4cqSoCofDYYpD\nZ2tXJJc09KN1hksRVGQXimZBj57a1apZr47x+PbdaxDXVZvDfjv2w4Mkp1NF2bGG4BuqHAIKFijr\nRxfjOIy7w3QcUh6ICD0rUwF1vipxAilIkKQMYx+nyV+eJjcRUXOJ01RiEhEHVFIGIMjFBWzYe6QC\nME2JQSEnj+BshzMzsxG4+LrSFCVOiBgIXdOs1+u6bRzCOPaSs3OkhEk0gKPg6wJZMRdgAshTmUba\n0DAmQHQkIThfkQGRri4uctmKgM6ydaFyglUWKSKYMOesTlU1pjROExLxjPLFWYE+l5i1KICKZsms\nrKggkErKOWfJpZSiBTOCceiSgiTFHIInhyVSLqICSI7QmUywrwIRIztCj+ARGJARs21RI3VENEHm\nU3lfVd6jlIXgb3otPemznakqeKK9EXXOeQ4h1FKgZG1Ck1wiYIRMwARMiCSUxkFS1oACqqoFDLRG\nWqRIUiiK4ObpGhGRUg4PWyLKCl1VT9Pkg3fMzntETDJPf+aSY5KY7nf3tfcxJgBwoc45A7FzDtlP\nKd69u9sfD86FHMubN+8QNVROpCxnShcCTzrBFMi7qm26zbqAumE4mucwnsoiSQWRdLfbrdat954Y\nUyyiWRWJIbCrKg9ApSRmX4pLqRCFddsx41flTV0Hm+Fqmi7n+PzZEyK0Ci/NMkgWUi3txFevXj1/\n/txwEDGOMI/swtxVWrASbduaPqyqPjw8PP/wg2ka0DEUyTl7dCEEFCsrnUSArFzTtq31RfE0CHVi\niMmlWBRQVZUIE84V/zOMu5zRaS9bZzFw9oUtMSBa+03OtFDPx6fgTBfE/mk9Z/t6wWssm9IaTAvI\n0DyHKC5dwTLLU+EZ7nHZ1oRkvUSrUPFJUYnLzPdu7cRSigGC67r2ofLEyCSgddu44BEdEgGZJgMA\nITIpgm3393Kq77v3pxm1ZfXer88MwlzmrJe/XR6NvY87iY+Q4/b+/v7sr4qIKBSDHuhMaK8zbOzc\nJ52jTt57zfnreYXh9J5qC3ga67PQx1ad1UhJSsnten0BMqW+b9sWKUHJ5BzW0lQtqiIwh6quWlfX\nzF4Zr39wGUuy1joUKZLiOHVdx0h9fwARAMkx2bUd8vSnP/2Lu3783/833/vwW9//qz//MSL+/h/8\n3njYtl4x9yyDpAmmaeqP43Ec8riDacpJxigpYSwiUlQyaia4co/2Y8+Aq6opKilHdKQpDceeZhJI\nIiLD2kYj65EYY3Q+5QzDMExD23XsSWbuY0sKyUgixtE5Z9w5NI9qFclA6AlzzpJzKZpVplyEmI2k\nkV1bheDrqmrIe0dcciL1OSbCKacqjn3X1I+uL/f7g5YkAMyYpmk8HsY0hropUlDJEdTBERFJaZtq\nHMfALoKWnL2j4CsikpQ9oSBYKMUAJhMqCiAFQRitGAUK6sizo5xISm7rQI4gaZbCCEToGVHBEbRN\n5YkcIZ84pVDPsMdEZPJaZ9/7mgoazOozc3vi/T+Xr3/TRVn4vlldtG2bkyCiqSMuJ335IudshAAE\nTAo4Sypb3F8EkInZ2xHLOa9XF/3+YD81ihaLVKLFqXoiB7IWVx6Hhn0NzpGFpEzBxyKVq3JREIzb\nQyCUMdWCNE6K8HDYAZ9uwf5vd73f72VmkrOs+u7uzikUInyvuSN8ojqDAqCAgojEYKMqqhhjTKye\nfS6JiXxwOSUfwtgPdVvHaagb7xgBtanDMGSRGS/hyPsqBKeKbVvvdgfnKMaiWsZxRDRO67hcrs4T\nToYCtIt2zpnAlE0DtKtOJHPwUMS6c845zRhjRD5J2Nk7mDkuJ+EGAAApyswxnYYVQggAAUGcMwY5\nOr+GZfcsPa1z63aKXlRJcfl6+ZH5g3MLeL7blrwE53lmyx2/4Y0WT1NKUXwvS3HujRZTizOihOAk\nT2VMFucoDCv973Y7+yyjSGGkpbUoCOv12tcVgxYw8R9hVWAiIiU7i0BgdWA8dzbLpyxXXkqxBfvG\nT+lMRHEBd1geGUIAwLbpFg8nki3MLHICidnty4zqnBfpPZXW4qSXEtP5j+bHahoXvHzHe19SDiEA\nECgycFU1zomkiIi5lGlKcZoolYowhFA3fjwMpRQp4KYpTpmHQQCylM9//QubhQSQknIpqcSyuVit\nu9WbN19Nw0AEKZWSIiIOJPXT68u6AaL7r756/Phx3/d/9fbNpg4jFy09y+AJgqoi+LpC9cOUmLFt\nWt+SAyKAolpQw7p7+sHzh+Nei1xvLiBmKuq9P8bx6fPnzrnahzhNVVWRAgGigoisu+7u3W1gl1IC\n1ZhSkgykRgpnG8lWMudsODEjlDPExBATOx8NQ6+JwEhpTwteSpHCMUeoqmma6pwR0zQNDNrUIauA\nJgIpOdXBbdZd5R1IYSbHRCAlZ8k5xymXTKJFszFfxBjr4Dxx8KzipCTPLtQelQAkeAZCLcBi03RE\nwEFJixIhkncCJYlACY6dAyiQpsE7AlBBBARHqKSOCbUgSFdXCOLo5M8s74e/6XX+/XNv9Js/ha9T\nz+Dc8CciBbJNHkK4uLhomub23T0ArFar/X6/nKblD6+urijWm7bRFF0ugaG0UxP8cbdFxCKgCKWo\neTJENAKL5YxYeIGIPOMO7GBav9AzlmFIKgUUAaSktmqHYQAmV9V1cP0wrrpuGCYKHhwDigPmcGJC\nMlSaYQ6XePrcYrhh6K3jbaWjWXknE2EpaRh6c+Ezo3N++vT5NA1NaPoJHTp0mIk8UyEKjtuq6pq6\nq+sYh8AcGVOaikDJCig5Z8u9AHNKE2BOqbBD77mqvU3RLryi3whmzZ4aHdECugOAvu85e1JIKbGS\nqqJwKSX4sBCl2Ekos5QfzGUd553GZCyKxlVlFCZLOGP2S2a7uXwonQEOzy8SbMjcOe8cG8IQkYiU\nqJSCJ4lrNE+FAAiwDCcuTx3mRGEpIJ37wiUdWfzT8tPzy9ATUhG994ykopKLmqrq6Y2KZ4cKRFT5\nsFmtPTsrMlZ1rYSAsL68CHUFUrIUQRDVAopE6NiEUs4v5pR/Ey2VwPOLEc2lfM0N/Oa5XVym3ab3\nXvWkAmehnI1qOec0F5Fsu3lJ9XIuzPSNZTlz6rJ8vThsnVOr86siIu994lhVFSJLUQauqso5zVOV\nc85TNOZjECkKetoYgio43ywULAqQy3Woi0BTsBTJMYsUybopuAF+GOO4PSghFqGciIgDvvjyxa/e\n3qlqVde742EYhi5Uu4e7D3/rW/EIqU9YUtICSbQAEdSKkAvaeLAie19XAYM7bo+p2Q93t8Oxl25b\nxshFOfjb6fjm7Vsj/E826qCACrYTnjx69PLlSxAVOc3hs+ck5e3dvbGuwRzKXF9fb5A+/eyz8PKl\n5ZHWEnA+sGdPDJDdCfpDBTApDIjHTDCOWG+MJhicPx72hFpSBCpd16y7tq0rKbkO3hGCFilFCRxj\nUwXnAJmogCeasmpJRTTHMU3kfYVAqIIgDsE7ggypZD5VlhEAGYgde/IFaDyOROTJZQVByYoO0TEU\n1uF4ACmimSkQkXdUVBhBJWopdRW0mA5y0ZIRvqYM+d4anJXxz39hCcXOk6HFGZynU+aQconmjVS1\nrk/ke/b1eRS77Oq7uzuKw3QMEidfpAmsUxq905yccwokoCmVu7s7i/m895tuZVZoHMfvf//7L756\nJSJVXSOimtJxKY8fP27bFhl8G2jOZmKMl5eX+Oqruq77YQohyDB2lxd5u9VN8I9WBJjv7msfxiKB\nXZSxcr7EpCLTTDPvkBxS5XwTKseMVe2Dr5B0YQXNJRrmEoEX1RkpkEu8ffv6yy8/v9xcCZSSxAU+\n7I6+cruHfd1W97cP9duq8vV2/1D5ekojB8+M05RiHKuqcY6sRxVCbQoCVeW3u/3r16+GYSKipu6W\nIh7M7ETL47GU05CgNom9Xq+BSXNBRFay3MgA7Db5ZLS7eBr3qVUVgU3WjcmLHBfSIEQEYURGYEQy\n1hZmLiUvFv88kIevU5ufNtlZfU/PZI0W+3i+OxGxFDHQOc5DTnpqTSHAe/7s8018vvG/4Q6/kRPA\nnKcvh+X97gdduJoWQUxbcBe8IhSRpmuRCJRSyYAooKKKTMgEiKKqy7Wc8rdi2i0655SqiqiIcwap\neTk2iwOwXzaSaXvc1sjtuk5EFzgiM0P6WiiweKOlUsdsz0UXf3PujZY/XC7gzGMRAiOyakFiq2KF\nUBNyTkpqWidiG4mQQwhd3SEnTElyzpoOh4Ph39mnIMJBkBwiPDzcpXFqplGhGOsdKRiKpGjJUBhZ\nUcEhe1dVvky73/ndH64vLu/v7nf3h+Gwv9/vvvvpJ9MwDn2fh8GBOEZEIMfOOeeEQCALpSIpT5LH\nMUtE3zUJJINOWvZDD7lUyDJmUdntdss2QFEw/aYibmFJRq2qCor4uprSBHoispuDJCilGAbMkM3G\nawwAPoRhv1cEUlUtBAIgSihISalXSBzuU2mvQt/3q5xBk5TcVOH+/j7m/fMPHj2tbp48fVQHr6pM\nAKBxnHIam55jGnNOLngUQdZT2Q0hOK4rG8YsqIUBkBRKKbkAqGQLXokschBAYo8wgThAQvUAmQAF\nEBVUGXEcDoClJEUltH6gKjNqKaK5Ck40o4pqAbQ8/GueZjlfyz+/noj/zUW5b/za8uKZt9QK6TYv\nZQhymoHHOpNkgwWymplZEZ1zVRVEkQn7/qiqgCygImpsETYmzIDG62NEyfv9PqWUjSwGwdoru91u\nv9+74JFB6cSqkFL68MMPP//lr6qqmnJpmiZOyQi0+sPxsNsDQMXMgEbMel71sZ1DM1ur0S67fjiI\nmk5XMV1MVSwlETk4zW4ms7qqqDldrDe/SlNd+fXF1TTEuq3WbUcOP3z2nD2lj7Lpio5xkKwu8LHv\nOfDxOByP+9Vqs9msEFkkE7lx7KuqIYJHjx5tNqucxTmnisHXS4eJ5lnfMGuQ2HS0RQfINAzHkjSN\n0ziO5o1K1GEYqqbd7XYG4X/PyzRNbbde8h4iMhFfIodoyczXIxpBZiZ9n0Qv3mj5YkmhTltKAUS1\niORTAxJExega5yB0+c9ik2X/Lc/mfKd+w6oyu6Jf03pY3ORv7m8AswYIcKrG2H+MxMyO2TH3fR+c\n9+zqUGUp7B0HX0RiyT6ErMKIAqAIYsgNRCQSBDQrRoCnQykAp5KdiKU4RWeHKvK+nrm4zPP2kiGw\nDRAvNufftqW8dzZ4mnhbWkSncHKJDEopAB7+R0LRJbv9TW+0rJ6YvAUSIjsXQghMLqWCgt5XhOJc\nyDnnmfUDYpRxhBgzcwj+hGJhUyX0zntgqm7aYerrurZ2AjNLLuFi3V5e3ly6dYzMXGIClKZptGo+\n6ZpfvXhjMyv/9id/9vf+3t+72aw19qsKj7u34+EeJeWY+n0/9mNCvddemVzFlFkmzCklKRlEy7Ad\n93uIoxNXRke0qcLUD5Xj0TqvIgxYoNh4hGd3tozgmVLOpg4CeBpANPmGpR1rZnF5piJiMWP52nlB\nKSAkxI4UmqYZXVmv1yFUhC4XuL19+/Txo/0B+wHaOgSmp49u2jqM/SGwu1xvpjAppK6ptBheISOi\nY1bJOQEjqBRHAMiEKgDeGVVoklyAyJ1qYyqgAAIqCIIAjhFBVbKqfVMRBEQIpKQpOEpDLmUCJVRx\nBMERgaCUyjGUQiAEuhSxz3MaayaJvpeFO/vR+77RN17LWTgPWC08XTp8Jm1nseNiFmhWJZ2r3AlS\nYhXJWeiEn8rlJJ1XSjFcSM45hJMAB6JNjNAiPHgW5J0aJabKHYh5KlTUlWKtjY/C5RbrCqshT36E\naRJfRpeA7vtrwSgleyi+LGwAbpZ2W5SGDOAmIrvdzs09N9tAhYhNhU9E6IQrs7o8IioxF0m7h218\n9NjzZcSJAJlRioyphxGcc5JFnTBS0VhVraK4EHLOw0DMp9u2eReR3HWN5TFLd5TIGYWRwdhVdfH/\n5l3tp/Zsdrvdet1lFVJAxEC+qirNWNf1oT/Je1vhxXATlnUxO0QGLYh8XoJDZAVDvpEKAnzdzcz2\n69wtnW9E++aiPLS8LZ/xGP3mn1c+LO9vxVnbQGH2UnTWAtVTZem9o/rG3v3GdZ6lAu/fBOeqtH1n\nqXw650BOE4hZJeeshFDgpLtKqGqlKFiaRubu4FRTLICLULu8XzdSqzJahV2k/OZ1wlz/sSbfcrTg\nzPHPbkPs7C0oBjwrd/ymKzr/iL/pReZgzx2SwHt6RybnnIMCzAxq6TXrdCp5aykI4pyrQpAZiaAi\nRZImVBQChwmnYZScLHotpfTDsW1b1RO3CBGNY6+qXddR222RQncRp1TVzZ/92Z892lx++fOf9Q/v\nPv3keRweHKRNV1c+NKsu+CaxPLr5MEqSmHRKVDR4X7WNb+rd1FddO6aYUir9WLG/bLrd/cNF15o0\nXynF2P5zTCklyWUhE7LNMA1jzCnJSYWEmW0axg5UjLHv+4eHB+PdsTnHcZyIvaoyKDtmZEApqsQs\n6FBUBPrjmOj+r//6r/3L14dBvL949OjRd777cS5HxcisticPh4Nz7vGTGztJ1zeb27s3d9s77yog\n9N73fW+YOEeTyQggonpR9Z6xFFEtzOTVkUFjRFTVITEAIQXjmhFRERSx7BhRLcxxjgAk5yiFRLJj\nYrYSuxABoMys/yRqGLrTXkW0Ajwg4FIEpvkFAOU0dfPNbbl0H85PtIgAniRMl2IMzqE5fD3YkoUp\nzTnvnahUzldVJWPMJdssf85ZQJ2jXAqzyzkTwv7Yt22rqlVV2aQjEfGJU+q9DbRvMoBNxJp6pglt\nJyl1XQuAlfXss0JVSYro+TyNO4fVwQzpsnMhIg5Rc44AJz4FsWLCiXg0MbNqyTmdCHdTmqbh6dPH\n3nPOkRkBpK5DjJHZ55yrKsQYicyIcIwjIhrj4aw3cxqTNMD3wlkCAEbj6D2keFwsr3XYbPVDCAYK\ntzFGS5KmabLi5na7vd5cxRhr39pUcNM0xiALM2UsAKjiNE3eV4i4CEQ655u67YdjjpPz5L1PKXZd\nt93umKlZdQsIzW7BFtTGAmytDRRgnnK1Whnvkc2+2a9dXl7udjtr5VmA8+7dO9NqfPz0yXq93u/3\nFibYma/reru9f3R1vd3dlpJtu5RSiEoupyjbemw2x7e488Xz2Q7Ybrc3Nzf9cYQZyQ1Ax+OxlP7y\n8vLnP/950zTOHT744APnXEkiIvakLBAbhsGeZs758vLyeDzarZk20njsQYAQAdQ5jikBiPfeNAnb\nth3H6Xg8du0658kiL9uFdpu2EwDAEiNbqM1ms9lscs6Hw6HrVlZuHYbh/v6+aauUJKXUNE0pSVWH\nYbR3s0djRCzjOF1eXr59+/aTTz6x6GdpR03TtF6vHx4ebm5urLNqOl5mcC30IaQUcx0qBAIgCxHq\nup7GiMAlSU7p6vIypSQxcsmO3DRNjXclZREBOnUMiaBhaim42GMSZj9NQhT8urXh6K44q0+m7BDx\n+HY3tal69uyTb3/29vadu65evXrVsB/2267y27vbw/ZN5eHNqxEEV6tVTppz7u7qNA46JQfIiigq\njMqUUccUwfM0TStft6E6ZhHJvxx2f/B3//Df/bt/13VdHCdmNruvRdq2/Ysf//j6+vpwOAzTJKCa\nc9O0QPjxJ9968+YNID17/sF+vze1aFX96vWbb3/2HTvUpvc4TqlpGk+oIMfd9tGjR/e7LQV3GOJR\n4X6I74aYUnrx4tUxfkm+Xa/jmzfvLi4bhXF3uF2vGwD46U//er26RvA5S13Xw3B82L7b7u7QYVMD\nEBq9k2XSTVVZ6gZfj8+89+1q5b0v+l4rB2fs/qc3n/R9b7vRWvp1XRMJcYkxfvXVV5vVY+/COKaP\nPvpou7s/HOnjjz+2/Xl1dUWEXdcdDodQITHFmC1fGcexqnzOuarDdru1elTfH63ImXP2vl4y9cWL\nyDysvfCKmtqOuaTLy0sTFTPWjHEcTSwthHA4HOzPTUft9f1bvwq1X5VpNOvf9/3lxQWUzsbGQ9Vk\nKTHmpx9+8PCwDSFIyQb4Xsacf+/3fk9EfAh932cVRHz79u1nn332V3/1V6uLjWuqN3e3DmCMsW3b\nnx/v9enVUErJEQih9jlnEUugMzpM/bg77EMI0zimGKsQhr7fbDamJWRioUQ09P3V5aX78z//88Vv\nnwetd3d3ZtAtUDJxeAK4WG/GOA3DYHyXRUVyKSqucFHp7/t21YmIwKnu4YJnZucCc7JcxFRqYsyI\nmlKxrlLTUEozvaO+v5glRrAdY7sQZ7o9e34F1Mb4lw1nREc27WxOwuRS4KyFQ+SYmcmrnmToOlxF\nduMwGgZvu91fXV2Vki0VV1UzataIsvj9GxkJztIpC5WRbTsjuvezsq1hK41cXBSMRcmiy7quX79+\nfXNzYyURk2mZpmwmONTVNCWePc05p8ByCGHOfojIxmXGcTRSrCXs3Ww2bduZj18G03LObd0UYFXN\nU+TgV02bUlp3Tdd1gR0AOCQNwVlrBdA559jN1Ttr8iGALji3Jemxz7XEy89yvcsEnB0G89nTNBnu\nfLPZrNebcRB70E3TMOM4FgCQlIlOIaEZGpmBXnY4LRHJOY+jacm8F7ZZ+nlWwg1VjchFBIDIONPV\nomMXQnAulKIoCIqWtcdpLyKBfeO5iOpUQErJCWZeR4dAZPx8pZSiKMF5EbFVKqXIKADw5Mmzt29f\n930/5eScA9QY4y7FZ9/9zkcffnJxcWU5x+V6c9XU7159ngFKjuCDc06ypphTVGJg5gKYiyggIQOi\n5FJKDm1TQAto5YOqDsdexkgOu2697ByrFthOM8VoWxO7fdtIU4oWY5mVHIbB6DvNOFrtZSGTTKko\nUAjhcr3a7R605BcvXsSSlXgqOrGb0AHAZ59994d/9++urx+360c/+9mLf/yP//HtbV+kV4wXF52I\n/PCHP+zayy8+f/WrX34Z49uY+ptHF30/AsN2d0A8qS0DENk8EkjJ6jxJUkBh8kVS4JBVtvvdN7Jk\nOx1ffPGFkTIsnH7e+1KmuuG+719/9d9L9lJc06xU0OqoP/jBD66urv7pP/2nIbSXF9dmVcZpj6QL\n7DOE4P0JjdY0zeXlJRHlnFarlaqmlMYhnV/GclV3d3eLkTHnZD5mf9hamWuR9CUiyx1jjF0DM90a\nmv5WHzIyYCma0iENpFltYqxkVUVyRaUUBcd3d/dElOLEgLYH7EPJO1W1iqIS2jvf3Nz0fT+mGEnH\nFO2MxJRontao6spOesVs1OmqWmIKG19ytlNvBEjPnj1brVYff/yxWVGrAV5eXpZS3H/+n/+XOFvb\n8w7z559//sknnxjBwUIGzMyay9NnH3RtW0QI0YcwDgMSHQ8HBbi/3948eZpTUgAil0sZYwaAGPMw\nTDkPu93OZmwfHnamltY01Zs37y4vN6bkFqeM89iKzjythh65uLgw63ySVXYu1BWAJCkMeDweJRZV\nbaujiMRcbGbWEg57q77vLy+fIHJOEiWHuVLH5Ikcs1r5sm1bAPniiy8sbD+Ow9KfsBhkgUVY2md7\nyHbV9cVlGqenjx6fKjOSULQJ1TRNbVWPxz6wY8AppraqlTCnbOqrfd+bgN5ut7PPZcY0TqtupSoW\nwJoTglPVDS2z7Pt+t9uZPuZvuEZpqgpFQcR5n0qJ41ioOOfyFNM41T7knLu6+ej5B3d3dxw8cRXY\nqUieoor0+0MgPOx2T2+uJWUQ9cRSCilIKUzkZgY/AOMfglIKO5R0IkBiNtg3OMd2IwtK2DyHeQsR\n2W63FxcXlsvaChwOh1V3vTzBlDIAdF0nmm0uLYQTIHvJb9wsxWZVWZlJFGFGn9NM2PwNFyWCS2ih\nit5XVdU4F1IqkoSZVdF7Px4yFGFPTdOQ91zqmtgjrOoWJBNR3a7qtmEX0DGxm3JRoJiTgQCnacoq\nVeVTSteP11VVjdN0PB5zievvfnL5wQc/fX27utiUUg6HQ92EImldB1Q1+WpCqTynnGPKJaNv6x3m\nA8WMsUJuPCFizDJpIR2xdikXZiYFjQJIbfCV42kYtUiOJ/4kWweuKhs77cdBRJyUMU6qWtetAk0x\nx1SmmAGncUrsYlVVRcCHWlV9qBGR2EMWULCQK8bomfb7IzAJJmUPDKWUlE9pSt/3+/715eXlMEV2\nIiCbi/XVo8dv3rwJdfvRJ5++vd0CE3nXNRfXj57I7ZtxHJwNRbNDBFUg69Qx9f1AzjGBSEEkJnS+\nClXTf/XmvC697LoQwjCMRHEKaRkHTHnIMHVd98O/9XccdXFCpuqnP/3pMByH8fDu9qvdcff48WNg\nent3Nw65ruv+cA8ofX+weD3GaA83l2gCY6UUq22YQahCu0TYSyy7BGf2OPJMIa2qjx8/NhY4C90M\n6SMit7e3x+NxOI7OuWk8hWsffvihHt8SsecAhCUX77yIMJ1KZLkI8fsGlYXIpKeulVULzM5PMS5d\nA7PGdV3nKcqhvwiVtXjLEFW1DR4AYBxTSpImh1S3bV1LzvkwTgeirCIiFoIPx15EhmOfZ51DVR2G\ngZFev37tlraEziV4+85+v7cUwSAWcxJahRDYcRHZ90eHRCn2+wMH75kFYbvbCUIuRRAYsAAisvc+\n+LZtW2NwQOAi6ZOPfVX742HoVs2vf/XFk6ePchLDL8LXFS7MfBwOh8vLS8N+rFYrKxldXF2qmqYh\nllJIMOfsqfLef/Xmrc6KGlbXNg75JVtnQBHo++Hd2zsg/PzLLxARtDDT7//+327betU1H33y4fF4\nvNvem8mz8qBl3w8PD7b5bGNZRdHW9+HhwYZYeWaUMPtYVdXhcLDlLaU0TdNP45MnT5qu/eKLLww1\n++rVK1Xtuu6w3yOeembr9frt27eIOAxD03RFv/a8rHho6ZcFVjC/VPV4PNqDX9rOBhI5Hnt757u7\nO7tCI9C8frw2UwWEF+uNiNTBgygTxZQQgInTFAlRizg6JQREkEu0waNx6vU0CJmYnfeMiJTJSiLW\nwLO1snNl2/TDDz+8v783kLfF3Y8ePdpud1dXV0tbywxZKWWKI9Gp07YUTgHA+JJtee2AWbiwRHBL\noRXOqIGJkMmTTfYCEcHSYgQABGYjLdRizy6m0kvvpXApAaVpu+D9V69fSsoA4KrA5ItKLppU0ddV\nU0+p5BK999M0pCwXl+u2bT9/8XlKyQXXtatQ+Skm3W7b1fr6+hERbTabEMIXX3xRI8g4fvdbz7Ac\n68B1XedKShEprt2sq6uqXTUw5dr52nkCTCoFtV51N8+ebI8HAOCiNXvKUjs/HvbPnz+FWYLT6g3G\n15dnVWXLeE5VIMVSym63OxwORudoi3Z3d2d0cJZ2wyxsNk2JmW22URC991mFmYsdOkRNJ8YvVZ1y\nfPXq1+R8VcGUc9d1F5eX+93x3d39tz6RYz8CoAvBM4e6AaWYct02HHzgoKQoCCDM3hHWSt5RikUl\nefTK6igI4uXlFTAyYAElBUGQlKecPvrgw7vtQxxGG1RQwsAOvXogQPxf/i/+V4djjANcXj3+6U9/\nWjX1MB7evru7ubn5h//1f7NqLsYY/2//1/8eEVetF82HQ7CYspQSgkspVbW35dput4hgFgARzRvZ\nUT2fgLTa9VJIwFkH6NjvSym2nk8fP0spvXz58vHjx3m12u12/WFAxDjl9Xq93W5bRpgDLxeCFrlc\nt9P+yKB5GpkZQL33VkE4ubehpxlUYXXsaRppEVWgU1/HnF+JqXJ+1XVGBdsfjgpg8wCrtk7EyZpJ\n7wsXqW5WGfBEBOqcKRlaDGrBvR1/+5GLMf+NuRGRU0URMHwRMyNy27a3t7fsXAzh2I+O2YtOuQR2\nACqqUy4pSxJFMr4IkQJMzrkAUM1z7+aZWQVL0ZwkZ1FBi1kNpbPE/ufVGLMjVqNLKe12O/Zumgbz\nfN57iaWUQhotgymlDMOgs+yFnbFpmkLT1nXtAZPoNE1v3rzpx+HQH4lIJQPo1XrVNFWK4zD1T548\nMXiilTgPh8Nut4sxmmoGzqSuVjVm5iZUjrhr2nyRrbmqqkZwawPPqmpuqeu6Q3+8evz4ixdf/st/\n+S+vr68//fTTf/Wv/lUp5eOPPzZcwLrtchmvr6+GcV/5cBz6+/ut4olSwbadTSH8+te/XpqB+r7D\nKcy8Wa1tcDDn7NiB6PF4aNtuOPZpiiVlQnzz+vU4DNc3N4ft7uL66umjx7vj4f7d7fawHx17dqum\nPUDvkEw3aN2t7GzHGEWkqjxEce7UcbQC9HmFxEIBnmeDltblEgM+PDwgYkrp/MGp6na73e/3FqCF\nqnMOnXPj1DdNq6rOqdVYzNnbbKz90wTNrAZoTst8iUXuVvFommacMjNaxdF+wTleGP7NNHtyJild\nilxf3+w12xisiCRJ4zjSCZphyAvDa4iocCGZRl+cpEJSQmCYxAm0E96su4fsDscRJ3El0STTMByi\n/r9+/Kcfffu3n14+XVfd2A8wTsHRxx8+X7UnoCmIiqIIxqR+GO/fvYScWTEjj0giAoTK9MDYqX/7\n4kXf9zLGi26FqYjk/XT8/Ppiv9+bNxKRVPISepvQl6221Uu71caOmx0fi98R0YrJn3zyybt37+xI\nWijdtitm7urqo48+0FIuLy/2/dFVlRAfRF/cPuxevDoej3e3D9zEpNWbd7fdajNN2ywaUz70w2pz\nQex8VRcFdmFKse/3F/1FFvVVXRRBoBASEhABiAAV1VA1hBrTBMi+btgTCIpi1TaAqCJaCiEykTqv\nkcl7YgfMqIpOvfdVCB5Cyv0Yp5jL/tDnidYXkEXZuxevXt3e311cXeZSdof98w8+jrmISFOzpmT7\n2bJznLFCzjmL8OCMECHF96rWdKYmahnbEnxbOU5ECF3XdcYE+P3vf5+Ihn767ne/e3VxMQxDU7UA\ncH+3BYCvXr1Koh5gmiZBqB2zatd1/cOulCw5hxByUedcznGJ0jabDc2g82EYnj59evtwX9f1Bx9+\niGjaiMFYclarlQu+T6lqu+pwNHX2tm3jNOacj/stQuVLLSLAKMworm59TgICcga8tDVZSl+W8xyP\nx91udxLkPl8OCzOfPXtmnWEz5WbLAGC1XscYfQgr4wB3TpvGOWf4t7brSilINFczuaRlpMsRgYhN\niztmJrJj79frddN0ZlB2uwf5ujSLPTzLSGw0x2p3C9LUe4eiTdNkTM45SVBVVT9OFn3YfcUYY4w5\n57Y1ZSNIJRWlEMLNzc0N4e39XV3XKY77/e54GFKa2rrx3r97927K0bZIORMus/2xGNxlY02Hvus6\nQ+5bp6rv+6Zp+r63pba4+1RCTNHVtYi8ePHi9va2RFBV45YP3qc0eeLt7hZAUx7auhmmsa5rRV5q\ncUsS+dFHHy2WXWc6JWasnY9xzPnUPXLOSYH9fv/s2XPrrj179uxw6N+9e2dtm/X6Io2TiHjiGOOq\naR8e7i5W65xziYm815j2+72bKUKJ6DRmFI3G4mTuLTtUyQBZ1erppwk+nHnQccbYlFLu7++NoN5W\ncrVamXJjTtliiL7vq/okqmbwEABQhWEYlnAy5yIiRLB0gw0voLP6pJlgnXvX82ohqCwFTp2pFBHR\nEIDnBb23d2/3t28dQtisayJGBgBTG7LkiTJlglyKIjHjyq89eQ6iGgCAAjBzHZo85bbuPId+PB73\n+yySc66df/78+e/8zu883jz+xU/+GhGd99PY7/f7J9eNQywKIqJANuEVY1zXK9JSATkkzCI5KyJ4\n7nNchwZipiwlZYhZxlQ0E6H1jWmWn2B1S9jUtu39/b2d66qquvVq6Cc7gG3bLoAda0aa6bSkyhIs\nZv/w8BWiomjbhmkYbm6u393fhaahUE3sdpNO06TGt8TMrs45C1LKEuqGnL/f7mtfPbp+nLLEXJpu\nhTGmlMgF572rfSqCzC74ZSpRi5RSgAkBkRKjD3X1fodAIgSbQQMiG6pDIpu+NC7CZAkfgCiOcaqa\n5osvvwz1BRB/9fZNt1rfbe/rpktFnz3/8DhOtaPD0LPznrCuKaHYMbSkPwSnM+LAXt6792P7npc9\nRrNKzoJXXGrUc9ZO4zQ652wbr1Yr+ysL7MySLEf+/v4e2vB0VeuQc04FgVQN/ZRTcif6g2xmc5om\nw9mOKdqwJs0Ifou237x9a2mO0bSf0GRNg3Wt9E5KaY/tNA0ftR+9vnuHiF1dee+tCuhwVhIX9BxK\n0UVj1xBJ8+E96dtdX18/ffq0lOIO+96WY8m1Tw3hJK+/ervEsGbNVTWV/Pbudr1eE5FFT2ZWLLZK\nKe37weJTEWHAVbtWPTGwGVmccy6EahgG1QgA0xSd8zEm7yGlw2q1sqdilaWlpJNzNkkMi1jttNiJ\n4uCnfkgpDX3ftm2OUkrZH3tEXHgWTHHZnp/F4MM0Ioeqqj744IPN5UW3Xjnn3r19/Ytf/Pwnf/Hj\nY99XT8LD9kFVybPOSHFbRJPCtK1jhnWpjF20q8vLy6+++soiWUvVu64zhUpjgrI+8PF4dMH/4he/\n+OiTj3/4w9/9N//m3+wf+v/iv/gvfvzjH7948aIKQSRvQ3Xst69ff3V5teoPRwH1vhKg5UNtlczy\nLitmzZKqqqrKa8rj2FveaRs9+JqZb29v7S5SSjHmf/2v/3XO+a/+6q8O+/Hjjz+O4zT0/T/9v/+T\nGOOjx9f/kz/6IwBZ9NQvLy8uNxeqmqUISiml7erDYbdarYgwVM4irxijkaCWAt77rl1bhrTEGUuG\nZ5gOy3d/9atf3dzcfOc737m7u7u6uh7H2HXdUmmMsYzjKHqqMyxFOWYOoTKwrRHvzn31ZBYBT8OA\nlc5SHYv9ReSSoveubVtm1JLMHHvvETlOeSkbgHWt+rZiurl5fNFUAaUmDqT45KmUJFJiTv049eMg\nikzVvh/jdLRriCUTYdM0ceyv2/qQ874/xjy1bbuq64eHhzf7HbbNOI661j/7sz/LOQdiH1yK47s3\nb4/Ho2MlCnqCFOuUkxKR5iIYiBkhoxQRLYXbSgIfSmxXLTlOgAWlrqsA3I8nZjkLNFPJSzx6grmC\nFpUsp4NPPgAAsSuAMWVmVjIfkQvgEBMiltPwqDRNk9JUVT7nCQBsgynRcbfPoSquNb0xQ/SUMoli\nP4y+rjkUXzXE7n67v3n6we399t3tvecaiJUQmZOoqigyAmYBh4zsQDWnKaaCWbxzBVCLpCxIknNR\nLchEzIpEgOycC5WqYpGiYJNhiCjGa0WMIk23Yu/2fd9oKDGKErnQrda+avpxfHP7bnNx0VRdLpqK\nOlURWMpuZh9KwZwzEiyQUT7jgM75hFCwFEFm+VSaKUjsOJiNsqjI3tmsq7GjmTW3mMCCkq7rmqZ5\n9uyxjw9pImvNlXkexmJiZt7vj+zdNE0ZlNmVUmxwGOZRCgtQzMAyc1ZZAnrnXBwnytKPsa3DMKY4\nDtWzj45v7uq6fvHFC++9IwQAR3bLmFVFOaeTsSqlfPrpp59//vlCDrRswsN2l1I69XIXTAjOnJ5t\n29oNWK/FAqKcc7duv3j54ubyqll147Hn4AO7Ajr1Q1ZZt11W8cTAlMYJEVfthXWhraLiHDtnvZDV\nsvvrurLLMsWRmMaSVaGoYJEESsSw6javvnrR1J1933pOMY3jNDHz/f29itzd3W26jUVzTdPu9/ss\nKcY4ToPIBYraAKwl8kGDIKlqLNMw9b4KOUfrS0WJzrnrR1f7/qHACYafUrLnJ6KrFZlmAc4ihHP4\nrKmUpuumlLz3krNzLosoogvBed+t16o6DAMxp2lq6lqntF5f/PEf//Gb1+9+EX/5ox/96E/+5E9U\ndbfbVZUHkKptDtvt5eUnDw8P3lfHYVLAJQHygAyICMdj72chRTPBdco5V4Hd7nCUAgsy3vtgtdpv\nfetbKcv+0D9+/Pjbn3327NmzYRiGYXr58uVf/+JndV1361XTtS9fvR7HcRx76/qMU7++XxvrQc45\nq5RSuq7Z7/ebi5Uh6/KJANfCQzeNSVWJHtIs+ETzKMbJIKZ0f3+PiIaaubi4qKrqT/7kT6YpOq5f\nvvzq6dPHFxcXT589jnFKaVLV9aazY/bptz5D4BBOYkXMGEJAVWS+3GwOfX9zdUXOpWlyIaza9tD3\njuj60aNpGJqm2x+GnGWapqYKCoWZxrEPISCT9xWhOpdKOXkjIhLVYRoPcWLVo2dMkxejkC02gKII\nOUlRCaGuq4CIU07eu8AMRV0ITdcKypvbd0B4eX11OBxiHEUEmC66zaff/a1Vd3l1dTMe++9++9sY\n44ogsD59tL6+2azXbdM0DIwcpqkQkcIkKbFC7V1FQbWkkgvo63dvr64vNqv28ePH8TgMh2OfU3e5\nCprHu6mUkkpm7xShlDJMY46pqDwaHvXjoKrjOB6Px+1h713lpYjINJHF713Xee+bplItzpFqYTay\n8yySBfI4ju11dTyObddMMbZt66oKqqrPkEAVnTCq0YoGz8GLSN00u92boebr6+e3b+9KKe1mw8Fn\nBRHJgMxMzICI3iGTdy4E11SVFplKkZJCCKGuQnQ5Z1c5JgRFAJdyLmQU/LqUf6zguQB0c85AFJxz\n7ERhd9hfXV/nRCVDW7X324fVqk0lr1arl69eOefe3r57dPMMmbJk76uSmMgROWYPIERu6ThKMYSO\nIhKzC6FSWbqVtEQAlv0s34GZG5OIRE9adiGEmBKo2ukwP2cDelZPHqeplJKHIY99mSImxjyllKZp\n0JzIsSKIZmb2tTeqBo2RiLINTDnm4OuutentfX+02omBKn0Vqqo67I+eHclQsS+SyhRZod8fPFLX\ntETEgCKZEAlIS5EsHLzQCUCUUnry5IlF6iJins+MwEmi0KCHS/nSkHky03/hjIK3pfGBpaSmYikT\nQeVYcxoEgoIi5M2qTdMAhDFJltI1bUppiscpjsM4AIBoBVjlgsulxHSC9Jg3JiJiCOiodjnHcYxd\n03TdGkBylk8++ShnQVTvq5yjPSFVReCnT55Y4GCxBjvX9+NuOEx5cB66rnPEIOpdRYyimtJE3hPx\n7e27qgqiZZqGqq3XF+vXf/5qtenu3r2dcppyCr7ORQG5qj0xK5Dznl0g9qUURGD2egJ/o/ehKBbF\nul1N09S2qxgjuVAU2VdZ5NGTZ7/61a+cC1OMQO7d7f3V1U0c0/Z+t98e2ra9u7vLJSJpu2pSmlJR\nElQiZD8lRUfknYjklKqqVlVFWm0uYow0RQFMMSGir+pSSlEITddUNe/7YTwUTcxct2t7oOyrbn3x\n9nbr6+bN7d3f+v0/OB6PzaoTzb/7+z/49//xz1eXq7//v/77u93h4uLqH/7Df/h3/s7fKcCClAp+\n/K1v/8V//A9d1w3jWE441KEIHg4RCaqqGobp7v5oe4aQl/pDVVXv7m7P9xvMZuLy8rLv+3d3t916\n9frtm1//+tf/4B/8g9t3d46qcewfHh5E4PbdvQ/WeZLdtmfm4/GI8OtxHK2pTkRtXSOq5IJMb19x\nqKs4TsM0MhJNPB72WcpxfzgcdsOxr+qVc66qw+biInhG1N1+W1Pz7u7h1eu3wbmm7na7ffB1SdJ1\na819Rbm+WMuRvWfNhRWcczGN7MOUU0zZe0+hSkOsufngg49+8dNftJ6JsA1+09QP2+39MFw/uqKU\nAgCLrpzfDkOaBgR4ONx+5w8fpwjHh/3nf/2LJ6v1eH930das+Sd/efjwo6c//9UvU0qeHSGuwvqw\ne/jh737/y89/vd/vg2cokPNJx5o8/fVf/WXTNP/hr3/WdS0BBuc+//y2MP3e7//oJz/5CTMBYc4l\n1BUH75CA6Tj0T54/s9Dz8bOnzrmua+u2sRG0pQK8lC6J6A//sz9YWrkqMPZTE6pc4pMnN9M4MiN7\n9+5hK1Ko8iVKs+6aVcdN46qmUJ1UyHNOMbCjLCzl6c31NPRTmg5xXK2vmDSkcBiOwXMqJWqCDJ6p\nduyLjMdepqlh9sGJlCxJUW0OUnICAHSmBEEMxIAqyOiaqkWFygMa9bgAEBaFFCNizjE1db2bxsrX\ncRqZAEGlpBxj17YP9/dMIcURQYLzMRUXavaVAAE5QFFiV7WqGksmH+p2pQBAjj0MU3LepVSYGRji\nOIkIOpQi6LzlQClPiBhCNaZM3kkRDn5McZqm0NSay7u7208+/VY/jmbloEiWkkreXF6Qd3XdAJV1\nU8f+WCG+ff3m5uYqOAJR59zjxzfE3jVNqGtyXkQcseZ56JMJiH7nR3/LKo2iut/vY4xKJ/SdAnj2\ndXVdSiF168vN3fZ+fXkx9MMyEmBTB8bonHMOeoJxeecQwPhfQE9MFYRYcjZ3k2J09tUJ/5fzgvEw\n22EhoZt5oEVLVfGqa4kIVJxnyFokq2rT1t6xlFn9IaoRx+QcRTKzdfvZzUyKKcWTtSJABO+ZCJnJ\nSGVmZtFSCqU02UUa4ygi2jwmszhHUKiUMiXj4FPnSBGKpHbdVm0VKoP5ZjH0hAg5xw4VQTWXJGMc\npmmiwuQcTBin4TgcVETRJq4RyD7XlppnbllEZCL7LgMYGxshMjIr0vIfEJPzyA4QVUGRBFAAFa3P\n5MYhpljGIRqoJqVkUdICSUVEYhYFYgeEqKyIAkWRRQWAFFmAkD0iIhAAADkVAHKKLAKKhOzIeWIG\nYgEsCipSbFysSCr50B93+x2AFImhdqEOgHjoj8M0VlMi9qJo/ylCFhVFw0sYqRIiMhMiO3YIjimo\nVR7kRNlgSZJzDoGQ3nsjSy4R8dGjR19++aU15GwTfvrppx9/9IlkNRIRy2tjxCIJAESOzDwMfV3X\n+/12gYT1uy3NwmU2amZ/uDB+IqINLWy3W9wPQgFwBBDniQD7YW8x2fXlFSI6tEIHKUrf97uHN4+v\n2vGwc0mK9yoKoCBQslIAVwXQAAAqpMQiEKcc6gpEh2l82N0755CxClUI4WG/s8M1pRMDluWajx89\n7bq151CHqqmC69q29iA0FbfdH6eUry6uGPXu7TsdMqEOx34axxRHhFMD2HmyCnIWcQBX63XXNTYo\nvVq3wn51sWnXq8PhMOUEhIKQp2mYU3x6z+ePRDgcDqE6NdWXqBRmfPAS41v5pGTlEEopTx89fvPm\nde3dceg3m83d4eCaLkOZUqIYC2AqBYuknBUBmQCKY6qcr5wvYdbUAS1QCEjpxIeIiOQAwBxLQVBW\ncaCKClKAEUCUAEhBFLUIAoATAAQQUDZ2FWsQWaMXsdCp8QtEgMbtTcwUQkBwS6IzTYMlVTln4FNV\n7bQIqKWINUMBQBCkAJJZBjEBLYBltIgQv6lQA38TO8Op+A+ks5SBQVQMM5WmaEGA/X8YhoeHB6/j\nOvUuHTTFNBymAtGzxCk4UhNgBS2gxBUFUwUqfKJ1VDBeL+P+myOPmJOqItHFxcVwOE7TlHTSGRe2\nHKWli09n0m52zV1V06mHzdY5e/To0dJWsPKdddMR0f34xz+2boqIWD3K3vTt27dXV1dWxFy68UgK\nIN6zNVGsoG+NOKuBjuPYdZ3V3Ow9r65ullh4MT3W0VnKNQvW1vLW5VqXNNZKBGZlcCbktrybgGyE\nCgC8Z+ecwKlgakHckqEvoIMTlkM0F7RxP4+hlDJNU5ymw+HQNs1S01wO2/l2Ob8jPJtlgRn0oaf2\n/kn4y52NeerZgKoVhZ0Ly1G3Ot5mszmz12x/fmrbCpqgH86vpU64/HO5SJhhIHzSjvsajdDyC6p6\nOBy22y0zqpZjO6y6NSLudrtxjN41Fqwsj28pJqieGFGXhbWHvizasuy2TU9Tung+n4v2h0Zj1bat\nzPqKVVVlKq721v6Rs0FXImJ32oRVVQ1DcO5Ef+6RaO60d91a9aRHaOjbUgoR17VbrTbDME0xp5RE\ncykJSRkpptFI33/0ox+pqmZ48+ZN116IyNhPL7+Q63W1i/36on6yWq3JNQyVD8PYc+XqtgFnJDrB\nKXahvbm5+eXV2lVhmqb9fh9zMizJ7bhrrlbMnKS4GFtVZBrHsT9M5F2M8VB0mqYeYdzupm0Zp+Pl\nzeVutxvjwAROsd8fhH1T10TkvGfvgDCXokUKEACUFFVVQJEImGLJUMB5H0LwxLUPvZ6ONiLGEru2\n0xko/36flFKx84JaRJJoNp4bozOmXKAUq1UQEReABOKcfxiG6+vrL7/8YtO1NnxaVRV5L+wrIXXO\npiCxagvWy2zNIi1mW2jZqOebGRG9f684Iyc4xGzordxk9Dl64mc8kZp+bZT+PZcxzhzE5x9kO7Ou\nay3Bu1NrsxTDRlsT0TiyTjhsK5yf+5XlIOqZfuNShVt+vJgR/TqP8Plb0cyEaWV2+wXr1suMwfMz\nG5n9qKLKe09S4WjJVmJmQBszmhfN3hzQibIiIqmqdZus+XocBkG0gDvG4eLR08/fvCsidV1POdtw\nCyJut9tSijG4L2bwvOZxeNi6WZyilLLdbhdEw2JD3DIs+Ed/9EfmuOyGlwX6yU9+8tlnnxnQc7Va\nIeLxePSBnaO6Dvv9cb/fInLfH+7vtznnqmqG4ViK0bLWIhJCDQBffPHF+SUur+PxaC1lc3Wmr2PM\nLnpSE1AD6hhDpfHK4Bkl83InpRQvXlW9d957IBSRYZp+U9MIEXPOnDO7IgilnHbke3yOat/3q65b\nRilxBsvBGbMhfD2KXDbc4o3gLIS05TU/en60zEAjkN07EVmUkVKyHo/Vye0dTpkynj7G1lPO4tnz\nd16cjXUjcG4Ynl/5UrHN+YREjzF6zyE4ROy6bhimaUol69KetYEJu8HzBVkuw5quRr/2DWc5bwG3\neKPzk2a7bpqmzWZj5mAcx77v97tDU60Oh4P9vvcVwOkEFjH9RuaZVvUEqGEyirBSSl3XNujAM1GC\n+ebzDemcKwILyR6euN4X4ZJ5esO5HEspZeqH23fvaHXxMMXCbkCtq6rvj0Ma6rbNxvtHgQGdkPc+\n5uni+mK9urhar0LV5ByzQl2HUrRt6yw6DEcFUij9cXw0pvV63TXt9Wr9gx/84Pl6xSnVpCkOLvC+\n3w7jkZlZ4IMnT1lgGgcBJcehqiywKCpaBERTTuv1Ok8RAEzMAwFEZLfbvXz50oyC2RFbfMvIlwBi\nOWi+dUkFADJoQUCEoiIiKAUAFEFVSk5ml2Mqj6pLPODSGjQ8JBheq2pK0TRNYECkoOxO8+OllLkc\nckpelyCSz7S7bNMUUAAw/2pCJqZ2fH7oTn8CRETGBQ0ApEhEMPOZfsPu47w1eZ5vy4IhVEvMZASj\nzIwz88tpL+HJgS0HBBFFM87z6ctuP/+s5c+Xi/mGffjGtYmILYsVUWCWPjH/7ZwLITRNs335pnBO\nMUKe5DgydOPxmByZWLOAJinEGZMjcpJLjcx4uoZyJgzWbFaWFZVSxpya9SrbTmtqGcEOCH0defGb\ntkhEcB7HtC2x2+3M2thpNeNsqyoiLuUppnFxzrasRaAfDkWS81Qk2TzjFEeF8O7dbr3uUioAtFpt\n1uv15eUj04k4HHYPD7vNZlXXbYyjaUY8f/78PHdbvOJqtWLm7Xarqvf3913XGQh9vV4DwIJ8s9zI\n+uELxvrcAJkjIW/FGdMGZO/9dn9cRkF/0/bNz/4UJS0Og4gWLsvzbfSbwcuyVue+B85yI55lTJcc\n9tw6n3/Ezc1NCLUIVJULIaRY5ovxdkfOhZzFex9zQisIzpCTb9zd4iTODe5y5TLD8GzWdbmF9Xq9\nbOu2bZq6RWRVDSE4hhBC07RGp2s0dDCTPDKzFSLsrXLONkplyRycpYxLuISIAIiAaHP0gAAKoN4F\nFUgxlywcHJMjPFGtOBcsQIE5kyMiERbNzjnvTwySlmKWUpRIVKYU2bvUH1PJqsrEyIRiDNOgCOSY\ng9eCzKTKCnCu1WFP0Dl/PktQVdXFpnlLvGo7FgHRolnZaS6oACKlCIgE7xyxTkXGsSXUu/32/rAF\njTHt97tQ1R98+PzV6zfrzSpOaX/YiUIpWURzu/rbf8+N4/hunN69fvPw5a9Lf+Qccxr/4A9//82b\nN1McPDGIYpFhd3jY3n/7u985HveI6q0OzswOQfTx5vHHH398d3s7jmNdhytVBkxSqrq7urm2cohF\nD5YhGV7Jwn+bN3LOKdPd/kEIVXUJ7AwM9u7du4Wi5YSwVw2lRCmqasSsNiM5DAPVtSowc0CaZuwS\nq/r5aGuxLGLuWE9xMRfnBhoRFQhURSCLUAFzRpJVUBCpiFXPVLKUrECipSiYKMSJYP59YWq2Bcs3\n54fuRBTVAhoGJSMPMzyX4wCGqkDHzKCmVnp6LebiPHmaT6iJZH5TIIbmks9v+kiYEzgz5ToLbMrM\nMGL+z8LuaZpU688+++wiKBN5lLzvnz663t/feUbzRllKLFnBKZMq5lKO44CIyISIziI2UFU9TlMp\nQgSCevB6DBBrbkL1sN/lKVqtwvaMFcn5TBbu/EYkJvNGMMu2mVu9uLiQmQpkyQQcnGmR8Tz8oTOP\nDsy0N4vnv7m5ISLHYrpHpSQbYiVkZs/kEZnJ1zXVVVskWVv1G9YcEe/u7owZ0AZTbP7OtLF1rhic\nouBSLF2Aszrb8lqgFiKSUk4psXcWLNjG4q/Lii9RjBJiPj3acwO0XIDNqeDXfc95LENnhSZ8r/jA\nS3Hs/RH6urN//8CUYowmUz1N0zKKBErz4zhl3/a8NWVCtN2PZ6/l6SyBBsxcI0YQQF9rBpxYQJbT\nvl6vjSKhqhrvq65bT9NUil5srmLMXbeyWVHnWETYmel3NloLQOcfavnu4onPnfGy/stlnG9ci56s\nbmO7vJQiAobgijHarJeqGpMpEZXCdWMz8EHnSSbNhfikKWmTW0uhYDn5Fu5UVaXIuT+BTRVAy/uC\nfowRAArKOI45QYwxTXkYhlTx4XBwj5+jFlRAVc8ueJ+mVEqRLABAgIyYARAxpjRJKXoqQStCaKuL\n66uv3r0tIsM09MMgCIZCfPbB867rtKRhnFJKZRgdQFVVdeU+/PDDL1/8KudcN4EIiMGt15uL9eGw\nizlZRquEAEieUfTu4f7Zs2e3d3d93ztPjhgRY05S8MWrl+M4GrcvAAzD0HXdNE1WYx+GwTghnXPA\nlEGU3+evAGCGj4hgtdIQzHud9n8uPjjn3MPDQ13X4/FgFCEUAgJR0+QMhyk1cyWciCwHlfw+pg4h\n0Dgtx/x8kyhhtiIbQCklFiVRVS0IkgURshSx60ylpIRMwzQBEVuxy1KlYhzwHHMiooIwTRMyOZEi\n08XqNMGDAKXMjIsFxnF0zudkVYETApnZl5znEtfXnJxdtlVf5r1nY0a6nIVzq7i8lnU+Nx3nlXac\nKUiWKFnnjNY598UXX+yCqkgbOO2OUNLt668IxLS1BDSrIAVwrIrpRKMMwLPUrKoh+5k5GwWpKips\n7x+s6Hl1eckzy2op5cmTJ3d3dzorXyxR8mLr1k1rDEl2C8a2t3B9LVNWp9zIrPmio7Wsgk2/LrrU\ns7lP69XF4XCwfnVKJcaEyDkV1QRKRE4K5CwAmqgMw9C0lXn0b9gg68UZT6gZU+tanSclZk8tZl/m\nGRePag/ADobg+86QvZbeGv5GMe10Jcxw0jh4X6R2zNY507mqs/z+b26ab7yhvcN5trTctQWhi0HE\ns5Q8xth1K2Znzq+qmtN2VJoT4ROFtuUrSO8d4/mnLztgcU72GodRZygUvM9OvlZkM/5We6nien0x\nDBMCbzaX2+3OOYdwCnzM3eqph2TERbxwUsgsi7JsmOX8LP9fHNVyC0voY8AtiySWQT8FKgLZXJNp\nKiEguzgNKSUXfBGZYowxhUpiTiBKQKowxgzkUtGYhZn1BN2UUoSIskDMMo4TwOIUT6wqOLf0lpgD\nTgrcp66YYa4oYlDErIGdOH/3MMiE45SSlO3dLk2xjJk85RrIn0qC5F2hcsgkD6/ufRoc71wcW2Dm\n43EcXLzYhPZqNU1YdKybgFK1hB6yaBTNOWcGjHGSlFd145gQselaztkHdkgxp1KKxGIMbuQ45kSO\ngWBKUWdxFhCtfCBAEK2qKk0RRNu6qUNFRImiuS5U0CnXIjg3P+w8lgJRlIDa7FgxRi0FTHV3zJrS\nICeyx6aUYrxBpZQkRcfxOJX9MJ0OV0plGJZeyHJIq6oKYVqO5PmPEFEEkEkFRIDU5LpUVVUsYwQR\nzUmwqAAyUM4TEKnteVCAmZRwaYKeLICaUjpizYygxI4BCqETkSIlJ6lqZ2to5wnga62H5SJPbmYO\nF3UWdSWyT/waYAH/R3Kj5cZPx3zu2i6lrXMPZHAzN+vAeS8pRu+9zmzXkhfIGDIhuxq9U8WSsh8z\nnoDKxMG2ukxJvGcRijkT0UoreXV/kZGk7PcPzaqzif7b29u2bd+8eXMe5Z/fFxGR6JJIqeqnn376\n61//OqVkZn9Jm05FTgNF+Jli0taFiJ48eWKm344iAMQYt9vtiy9f3d09mL0w/7agPxHRGD/RIPwA\n261Bck+jvEsIb0bn8vLycDhsNpvb21sRsTDWkN9LZmrXZioM5/5sSVQlqaoCgnPO4BXsnXMuH3qc\nZ56XR0hzf3tZssWUzzHIaRRgMZ3yN/Qn8fwP/8btuHgjnZt1v/kOtmtFxCaClxlhZm/oBgQL6RSR\nl0orMPz//ehlK9uDkDPY5OJ6F5wuIprntsWPMTZ1l5M45+q6eXjYlqw5G7X8Ka1R1VP3F88qHmcZ\nrZxJ28GZC8Q5VZrPxntgiz3rhcmpbdv1en1zU0s5+QbrcOSMWWIpxftKVUMIIdQ8T8Kn5BVPiT/N\nVfVT0emMhtEOsOVDpRRULCUrFC3vY5rTEYKUUmILLBSJSEXyzOfWjzEd96kf++EIDpxzK19x8I1r\nJJfAYX25fph2WLHJ85lOWtM03Wb9wQcfhLqapkkAgnNv3r0DgO/89vdFBADbtvns029fBv9ks65I\npEwXV5sf/ehHXdcOfb/f7jZtt3139+rVq67rXErs3i+jlZ3iNO6OB+PhxaL7/d40I8YhGXJhmqZx\nHK+vr2UmVrCimUmfWcgsIk3XaSk2jYSIVisQ0K5p2DsQzVJAjc5Ccy7chOCC5mKFTaN2HEphpjwf\nhLZt3WoFoVEOMUZLr5fX8rzOvdH5gT1tQlRFQLD+0IltGq0AfGYQq6pCZkcEAMH4KYucZqIzExGb\niyJk763QN9sWh3gKjkULIlZVY9T5dprNPBIR4d+Q4sCZ9uv52Qd4Xy/5G2/t/PwCGKmBGgw6zTKP\nS69XtdgOF5Fpmg6Hw4VzzklOic5wQ6onyU2Ya10iJWdJU7ypVwCFFNCxNd0VIUuxnVlKCXVVNfUw\nDE3TAOFxGpdavemXL9juxawt3TIiYgWLxa3Ac3l5+eLFC+ecDbMi4hL028pmEe77EyWiJUnGw1ZK\nSek0SJxzzjmGENom3N09fPzxx0R0OBwuLi7smqwVcX19fV41suawSLaR7PV6bZgFM0m26Mz83e9+\nd/EZtrJ2wzaLambFruF9AQ0REff7PYMHgON4bJrGey6lNF07juM0pVevXtl7WsF3sUT2VqBiK9J1\nHTM773POzGSsdMsCETgL0q2ksFqtjNmCFwUB5xafZ3+VUjJiusX14qwybo7WIgBVpco1jTD5aZrq\nuk4pG1mD91U+iSMAsZnjEGMkdN77Aidc2dKeWSqEC1urmzmqrZcDM1vonFaRmR67KWOp2Gw2zrm6\nalWxqhrLIVbdphS1Se+UJ5ijGHtzEXGMRtkHAJvNZr/fL9mtNcmXgObp06f7/T7nRUnLDpuBJ3NV\nNSkVk4pXRSLXNJ0ItKt2fzys12sBVJAsxfmKGHPOPtS+CjEn9kGR9scDAXofcs5E3LYdEdt/BkZQ\nPf0nojmXUkQVnWNZWl/M7sRZRaeKK4KIIEgIgdEdthrjiaDFnmnbtiB6dXXVpyGD5iKac9JUUiZP\nXqC824fgK9E89O2Fa7JsX7yMTY2IX719c3FxkUs57Peien9//zuf/q2rutPL7v/9z/75z3/+M+p7\nGY4fPLq5u3+TJakWF1xOU1fVFbnjbl/V9frRxZcvXwKKVduccyH4/X7fdd1Pf/rTy8tL51xM4/X1\nNSNVVUXqjH1YVa1itnSkz40mGvqm8m8P23azJoUk5bjbJymXbbfvj56YvAvsnJQ4jP00ksLGuXic\nWkfD4ThHJBpj7KfJt6vVavXueGsDzm0I+2laXV6qailZS2mCW2y0Hczl3BlxBhGJKrPLUqYsLknT\ndMeH3fryQnJCwoLA3qEIAoa6Ih9yzp49mXaeCIKl7Ce4FntHRFqyAXENXZkz1VVrFcvVah1CHWNe\nrztENj9KRHHKiCdeJUI1WePlaNh5JAYzpItzpZNa29ciYJn71rajrFMOMygg51y3zW73YJJZFxcX\nr1+/Tikdj8e2bkQkBNjv9xaomVuqfb3p3PXV1boJueuJ6OOPP648l5QBYEoRHa/WV8o0TUkBlFBA\nCfDQH+uuOwy9Z66I3r17F7xX1WEaU0rcrXJdVz6sAouIMZ9+/PHH9/f31hq0Zopd/+FwuLm5UVX7\n5sPDw2q12u/3ZnsXJoQlK1oC5VMpDM9a3HLW+ZcZ546IdV3XNeQEdW3lO4uvVVVN+kwkA6BqyVlF\nMiIjqg+8YJTprHuxOBU4y1HsPCzp29ITgjk/W1KcpcgDBXPOppsn4kWE3Gm68xsHDM7QX8v3F1y1\nbXfbMctnTdPUrRqLu8272BLVdX08HuHrufkSeuhcVTC7Zq50OWk0IzJLKaInBbwlvlCFnMs0Taqo\nKgCAwOfvnHMW/NqNLKu6JCh2v/bgzAWeP9PzDIlmKclTcY884smCS0FCR2T9ofdy6fYeiEiMp0GO\n98UuOH80Z3Hi1xpXyzfPg8Gl2bYskf2WcwHflzuWRt38Dvo1mAacAXbljHTxN/fY8icyU0baz863\niqoCvgdiqGjOuVrVRDQMA4yDm5KSYpYpjq7xy20JqI0ZWILliH0Vcs6S5XA4jONU17X3AUX74zDF\ncRqj8+zINVWdUhrTvqQ8TRNNUxfC8Xh0SOyDUqnrUIqv2DnFqqqaur6+vPry5cthPJLCQgNThUBE\nnlhmhkktElVjjFBIVXe7nfVOzBSmmdd82UKns+mIV8366tLmbOwZ9W2fUtput1Zst9d6va7ruvbB\nKxOahMpYOVYEIooA77b7UjW98q9vT/YLOcw4I1xOx4LvPd/VC+7gdIX2xVmwr2psC9ba0AIiIvaP\n05Y52wPfsAnnWwKUECyfYBuRXK6BT+iGrwn34Un29Wvld/iNz/qGiTg/CMtP3x+tOYlfPprmieMF\n5N11XX+whugpNFzM6du3b8uBQNX6Rl0dNEXPmGNi5izFVWG9GcBxjLkgpJSA0BKd24d7NTwzQNt1\nRASEddsYd6r33ilefvgJAy4mGgCsLWSRkF3G1dWVVVlUtXbeOKytnGhcHsx8d3f3mzBjF+M4KxdY\nJc2svxuG47JeZz7AxTQRg0h2nkJwPrCqd57ilAHFsWeHoFREEdgHzjmaXV7CSTvqaZaxKbPywvKM\n51zyJLNmlppmNCHR+4abiLRdN01TmEIIoapOErEAEFNayP6WHbDciO0ji7yWzeGcc+690bTrNOQr\nzkNOOA/9LXHQN9526Q8tNwIzHEPOtHzswRh+um1bRFRBwpOIRozROYd4QgoQOgRGYJMrfD9gcWZ5\n8awnB2du0qABSysLz7wRzMHHarUyj8uGM3MVoUMsRnZCpIuZ+8YyAgDo+4NH85jbbzqexaYj2jSx\n7QRSRVU4Z4u3t2qazj46hIDsikKxagM5OWF3GVCVUJHFbBO5xa4oQC4ll7JAVk8/ITJUE8wb4OTx\nzyyUvWzXVa6qqsq7ppRi/L9931urnE/9OQhVDaj74QCOiqIjVERyjMSJaKq8VOgcHmsiBzmnvcbi\nSmDZ1+QrV0Ilqzpr2ebx4HEqeUxxnHrJESRXVReHYx04a05FENERAwgAemJmvrq6WrVtmgYC9Oxi\njCVnBpSUGSkbfxWAiiJASXnVXVhhdsn/lvN1cs9fV8mihJfJPWwPEGNXVSLic2qIHm2eikjJpWxj\nvh+T6kFVVNXzmMePP/jw5csXXV3FnEQEqyoBRRd2SW9vb733CfHq6srVm1KKc0FngtoT9OZMlWox\n5SfTAQpgOB5F4AKoiipo8+cKIKKImAW8bSp32oLfMHznm/P0z/l3Zj7+JYg0nim2FK2UJYZmlYIO\nCb927mY79h5Eimd0xrbZzn3hcn6X7y9+i84mMazSZSWN1Wr1cHfPzIjgnIsYrXrsnBPnmFHOet7W\nJTu5+QJW04tDGYYJRGslj6c5iXHc+6ryPqeUjrBVkxwHCCGkEERkTPHHhwN5Z95xOexLLc6MpInV\nGixrO0VV7fveCsLTNO12O++9TRYuofmpB/bTn/7Un+mSuVnxyRpN1TzHILM8GiKbSE8ILmc59iFG\no1pwIpnZN03F7FULAOkpD2PzEG6eQgCA1Wq17AyeESMyDyhYsIyzXoOIWA16+abOU5D2zWXdSymU\nuZSy3e7OyWKXvAQWXBmdJiKtu0DWUjoJmPLie5ZdskT9p2L01zffYqmXU7TYXzjr39gymr8ppYBS\nKcU4VU9PlExWZzks72O0ucaGeCYdtryb2RTzLjQjFJaLPE8RlgvWmdN6vV7P3sg7F5xzzL4UNfYE\nVXUuLKpJp0wL9fytzi/3G7nRsiZL3nO+LN+wDjSPZxuUDpCXUTARNU0jBBI1wo7lfRiNOAMRZsKM\n5a7P07IFW7Gsp86gW0BAfX8jZq+9ESU775xLkImIHV5dXT16+iTkrMfeQ7naXDBT1MTeGaNa8I0W\n8crtqnv26cdJRVVTSnXb5Jy3h/3jx4/v7+9dVVd1LSJZJcaIXH340Ucxxjq0t2/eIiIqLEPfTddM\nD32M7IhPHpWIFG7fvJ2GMcdkKZSqZsmSi7EJTOOIAHVdqVeHlKT8ZqK8FJlpxq/KPL9MAI2rGTBP\ncRoGhzRN03FWMbaTshxS57wSJlSJ0nWdPQLLzAyeZ1dsWW8p5Xg8wnQKiZRZNetcbjrfUWrV1ZMn\nIRUEnAkNZtYAgfdWXufm1vmpXF7Lzl/+f/osQlUFZBFpms6iXtATqNruJfjakAsWM9kOW/bSuUFY\nDtr5Jtd5vGG5mPPjeR7dnrsxORtl4XmyZXEGIictriU+jjFGQlBV50+hfGYAMd8goEhMRMExIjti\nHrODEwRp7AdW0FJyjJWpd9pwWS5JYyklxmm1WtmjXOytzGiyZTvd3NwsetMw1yGtB2TQTWa2bba8\nyamQ88d//Mc4R/F6lh5+9dVXXdctlKnL8TY2zLZdEUEpCiAxZuMKHMcegFartmk60zFCxGEYrGmM\nM/2D7XtT3i2zDLYdfjsGy40tGk0GKh3HcUHgLA+pCR0R9VNfVRWAjOMY6irnXDWdzFQOy0M9t5JI\nZIcqhMDOKeI0TainQ2P1uqUBs+ARlnVY7Ps3XudFMDdzKCCijXAurk5PNA2hZK3rdr8/5iwG2bCO\nPQDM1aP3Pd7TO58FUOem9m+8nuVJn7vVxamYN7KxvpM34sq5QOSIhMkxOYUZoopeIZ+/j6rmr/vs\nb6S557/8DRe12AKY/eLyZEXEaJ6JvWNPtLRJT9RQIAuc6dwhoU06ApGqArExMyEDWoxJBqpCBZh/\nRKh6iozxfaVudvzvYYeLm6y6hoPvx2GaJj32lK39Fo/TEZknMxZcScqYtKlqUpJcgE5dtJRSktJO\neHx4ON7f94jH4zGVHGM8HA7xbi/YXF0/efHiReUcMg+H4/W66YfjZ9/79jT1AOA8sUBgJwKIetwf\nri8uN11LROGks6Vpis+eP91sNrv7B0TsukZVg/cpZ+eqrutMSQ8RbYpjgWifLmOhEwU9jJNuGh0a\nqplXK+i5xIjO9X2uKkdE4zgOh2ExEW3d9MPh/snT3W7HsE75VEE6Ho+geOgjIuac69UGmH1dz86A\nzIecH5z3Jvs8SUIwGm/bTaKoQJaWWwsE0ZIVUlSluaB9Oj9fO7w2ZLP4DJsPF0l1XZei3qHBxeUk\ncl+qqkIEInLspIAKlCxV9f706Rwiv7/a30Dezi3Mb/7o3D+dp6cWPuAMNcK5SGOGYhwjzaqVtrC/\n9Vu/dVUjAlyuGhzTuq2n4wEkB+cBYH887PtjyrAf+mEYAdE7hwpIpKhlU+9FREti2ZeBiJRVUJCy\nd0iBNdSHfmCk82Nuz7dpGp3L44udhxMMUky9hYgMDWGucfl9nUnpnM0cfO3ZA8DM8UWzCKD1NuzP\nqqpSLSJIhKWoPVAjwC6lmD0ps56uRcN6Bi2zqMosoJH6EJEB/uxOljLCMucUY2zbdpqmMkPLlquS\nBN77IZrYQTwej74KpZSH3WGZOqKvV3WXooSbh+/sPMx4cnbza/m4xYYuy7e8CZ6l4apfGyawrGWJ\nNM+92nIlSzpont7SR6u6ApxijeUTELGUjPI+AVq60Is5WF5LOjubcjy//eVHhnqCmRtiua/FIst8\nMJxjBcCZs2B+rGU5isuCyBna/txrnt/74qiWj1vWTVUtXUNa4ODvf3H+2+X9z6dhUFWW4PrcTJxf\n8/luR6STJ8L34HmcK3UMvCxL5gIA7Xr18NbtjgefUq3KTAqwO+wpMDEhgJQChM45BGD2ZcweXFU1\nVjicprGpmw8eP3/z8i0JMjmPDomzZE1Qc3VU7VbNw8PDJ9fX6lOJo/eeBnx8ffPixRe5RIdk/REz\nTF988UVd14CnsnZT1aolxnjYbZ88efLixYscU9vVBpyJMcYkNoZlRt9mvUXkyZMniJhSMm9ktxyl\njCL7adjtdohYEKxBG6WsLi9Wq5VtVPNeRASqV5uLnKZvf/Kt9Xp1seqsb0R1fZjSxP5Xr2/h9r5p\n/n90/Vmsrdt1HoiNMbu/Xe3uTn/ObcnLXqRESqREy3JDl5xKoSpxoRwggF/84MegHgKkkgBJkMBA\n3gIXUEmlDKQAI3aCqrgaNbZs0bJcokhKJCU29/I2557+7Hb1fzO7MfIw11pnk3ItXBzsve7aq/nX\n/88xxze+pmCt/bW9ndglGqQTuyiK6z0cXDt7Ybd3YNjKfLaPkUII5LTdSIOctANjsStDTLwldtOO\n4f1q57QvFQzp1dMfvqoKMW4DNmGLo+zXNCFh//P1s4uvDXH3lx7s4mD218j1S+PnLt7rFS5VI2be\nu4il7ytBR2mdiTF+/PHHV5qAeVTl2Pu6yPrNmoKjEJN83sUgVR6AmdFkWcp5UpmJMZ6cnMxmM6KY\nZclSYBtnxTv4SiAOjo4FoNZ6n0Z2fYedFszxeHx0dJQWbd/1iQeY8K31eq21TrGlqSNX13RUyu/m\nOnsuQzocIXofHOB28iGVCJFjjG3bJuKW2CFd6agZY7RRGEBpCcjEEZClVF1n9S4WKH0HcafCgWu9\n3v7MuL5mXV8T9+leYsdST0uG1lm6U0qJqLMsSxPjxBfaUxL+7QgAoLVWCBVjBOaiKDK9/ZNUjFer\nlTYlXtNCM3MCPc/Pz/fvbb/k8U4WcP2MTLcsy9q2TWVjv53ZV+jEMynLUkpJEYD3vETaXSxi91fh\n2vuH62cDXLv9xfKzv1PsxmDpGZL90r5kpr/YGiWkF4o/o4q/3p7/XIO4//r2DeL16/lV2SZETBIK\nASyAAUEmEIYSYoRYlQOBinhPrtFS6rTH3T4VAfwMHA/7gy+vicyuX+T7I/Nzv75a8n5mcoRCCCVU\nalUR0QkfYnz6/NlyucByMFQKpQjBA4APIZITUdkQQwiZJgGIAWLkTBdtCM57FMxStEA+ho13C9u7\n4E2mKDeZypzg2Pe0ZbGHNA0mDnmRJRg2xuitDRwypb33KEgSMLNWaktAJ2Yg23aRPCKClJk2HMlb\n6wR0XScYgvda5+mL3iMW6dM1TbMnQKqdbxgHFAJMFAO1XXqMFimdOfqIfYzO+r5PfOIIEGN8MlsA\n0vzyyjl7ncUQUHYo5314eHbRtq2zvpoc8s42RlI0ZntaSilT/u+rM+dnzQsgcU+udzk7kHaP6SXk\nbvtF8/5cfLUK7ffvP7P6I4mdghv3rTyIxOLZHx9mDnErKify9LM6h+tVZP8Rrm2GXgEAfG2TtF94\n97Vqf7nBzj8FERPyuV8A0zMkGhfvVA1CeJ+2CM57Jbz3FHySZeE1aIQZmciAiEQ5i965e0c32quF\nDzErs67rZASUAtL+G9EBENHGh4SipfNhz21JvU6MMdVysXNm0ShStNtmsxkMBqlqdl03Go22zMZd\n3SEilfwx95v3vu+ddSEEgVJJbXSm5Fb9GkKwvSvysiiKtEWSQsVAwMDMtnfeBSIKPgL71HNota9z\naWagiAKASE5CiMkBGoVIvglJ4pDGVCkEmpWKUmrnXApuSJ5MROnLhhiZvGXmTduGMuhdvBUTphW2\n76y1lgiU1EqppIMjIQmBGVOQtjIIBC6ENL1sm26z2UiJxLhcbVbLFqUYVEOCSIED+Uzn/VHfbjqU\noIQWCgVIgsgRIpHrPQNwBKV1keVS6CLPpVIUo7NBgBSoMmOU1sF7BhHJM8cQHAAZYwApxpg8bwDS\neJ92tZaTTNxIFZggbbyIBQskVonyAJIxClQABKi0kAIVCAIWKRcKABCkEIAgmTkNrqTQ6WfErfoC\nkAEZxfaH3a4HiQmAQ6AYIIjEWNvjEhFAAGxLrBAKGIEVMAOIdAKkK5WRAGWCyxgFCE7p0pEDAwqh\nBKIxBkAQRRaMyBLSiBoBGFEAEkcgiMRMEBmBmAGBkSKRYFapg3tV4WBf+ZjjtTcMO0VXWssAdo7L\n3kdmlkDA6UPJEJx37uhoeFy/8fb9BwdlxU3bLZfHh4cnVzdWzQaF2HRtZ3uJKsYYXVRCljq/upq3\nfZtlWVnXMtd9313Orzab5aZtiNh6Xw1qF3wTOgfUBrdYbXrv1n2LfZeX5WK9LHO1bpum66RWEYVn\nQAYUWgghoPcUnQ+IYIwmImRTlrm3Do1CKUggCUkCpdEkZET0gH2IEMkRW+dyYiGllAq0kQCCGJIn\nDHMglkJHH4AYGWzXhxAybYL3WZYJQAox+oAMWm51DsbkSomub7SUW2sLxL7vIS99jEU9gLOryWRy\nvm7zrOwjpYUVkAAlIURgFKooKmYAYsFC7nYJjMAQBRjYnmdMkIA7SN69QK+GMswcBXAUhCBBEDAT\nBkQAjIARUAkJKCMCMRExbL//qDQqo7dbMhCQvPYVArDUAl2MHASpSAggUCKRJ8lMSMDMiWSBjMCE\nidPHCAAi/ZvK3/Vatd/3XENNdsRA2Nq+CkQptMA0fYyeIgsMxCDSWGGbECZAZDLLy8wQUoyIkkVI\nq3ja70oUQkmDIEymgSNjmRvbdBCImZ1zdVaGzvWd1aCjjWgAlWAElMCCYoyefG6KVN+VNsaYZNzA\nW6ELeeuV0bPZrCrKGKPr+ihlb21RFMQspSzrInpCCTH6QIGZGUkIQUwMrJrG7olnyZk8VV1E7LoF\n7yZJab8WY1ytVilsAncIZirvScEA1zruVM/TnuLyYlbVRQxcD0optPP9dHIYomNCpYVWmbWWCYmD\nFDrLdde2xyeHL1+c3bh5bHtvsjwGZibvIhHFkHg1ElgYoxGx7fukxt1nu8XIWVYYkw/qEYIwJt8O\na7QJQqCUTBhCUGZLVVdKRG8Hk+Pjk5PLq/lnP/vpH/zgB5nOpRDMbNcur3P2fDG/OJ4eF1n50U8/\nUrkqdAEKyJFnL0iAFH/9L//17/zpnzz9+JmnqFBsulYwVMNBdP7k1s3j6cl3vv2nHKLOMw4xK4v1\net3btuub3rZllTtn88I8e/Y0YSmTyaTv+8997nOnp6cpijA4P54MgcVWdwjx3q0Hzx4/qcrB0ydP\n796533Zt37nDo2noA0SQqDbNCkHmhYmBvPNKAgquywEQrhZrLY1EFT3lWQoKkVoKjkFLEZw1Sgpg\niTAZDTebjRRKm6zKR2XWpXmeC1YIpTU7H4g9YGSOxuQUhTJZCFSVAwYvkLuus75ngSyUURlFsM5n\nWaZ05imyjMKwp873EVEJJQGFVlJpCRS9s33b1HWtjCKEpumUzlJDtVgvPAfrbJ7nKISPLvS+zKvh\neOIiocwoQIxU5UVvu0wrH5y13WQ0fPb0kVRqtdkMRqM03UdmRpEXZYikTQYAfWtBCk9RKXTB1nXF\nXUMQ//x7fzqpBn7VFMr85IfvGaWFEMQhJv0vRIKkzM1E7GXYDPKchF8tT1mg0eLy7Ont4wnRyJg8\nMC37dt6uzThTA11k9fjG0fGdWzcODkoKh4O6NpgbXQ2qr//V3xBKSqk5spFGour7Nsu08zbLsqZZ\n266v69p773y/Wa423o1uHIv12lprzNAhklGOeN6sA0UQ6NddZ3sBmBV5cP723Tt923W2L/Pi9Ozl\n3dt3FusVhFYIMRgMNr4HBDRy0W3yPIdMgVZ923rBxpjWOWttURQhsA9BikwrCQApiDUvh8veRmGa\nTV+UAwYlZLZpu3IwDc6jhnJSN+1cZnkUsg3ho4ePXn/znUzkBkTKpqEIgbzJsqTuUcZ4F4TRqFXr\nbHKu8hQVIEhFRF3YBmyTZQFBCAGATNw6SyFGlAgiuhB2SfMy8S5RoEKda5MVPoKUJjK6EF0IIKIj\nawqhC+E7p/SIwSglkaOQkVHkReV8zMsMQBJFRizrwXrdEKNUJhIASh+CEEJInSmzWjeAUunMx6C1\n9tEJgQRAITKy1AJAcCSFglkWpsjzMkZWOuutdz6OJge9C8TYNt10erBafG9Yj/quqzKppR4NhwrB\n91YilNo06w0wVpOD+fxqNp/Xw7HJs0237oIySnTQE0tTFoum0aqKWiNktu9G41FU8fDmoSzlex+9\nd745mw4O5vP10fDYR+eZy7IM3jWbdVmW66bVWvYhgPcMKKRiH5RWRFQOyt51eZWDYBe9d56QdkEE\nzEy967MsU1KoPCu98FsITxqj8127J/YA6x7cIKLVapVlWcLB6JqkIz0stV2pfUtWYAmbPpucHR8f\n8844BxGTgRXtbAJwp21K/V3TNEVeJo5Znm9dy2DHyGLmiqq0p+ib3ofQtm3VVQyklAJEIgq9d9aH\nEHZtVhSohFTORxlZyS0QFWOkEIMKSRv4/ns/vXv37mQ0vn//NY7w4sULLU0ytkJAmcs7N+7Udb2e\nr+/du7d/wwGC5iQ3wefPn/veG5Oj91prpUwa8wohbGu7znLgtu0L3roHdk0zHA6EwMPDgzzPiqLw\n3l1dXQ2Hw8ViMZ/Pu677whe+MJ/Pz87O+rYbD4Znz8/SoSjLsuu6XJsP3/swBb2/ePpsuVzWdf3y\n2XNE/JUvf+W//m/+aQL9EyEFEfcJ7l/4whe6rrs4v5JSFkXRNA0zF0UZo99sVmVZlmUeY7y4WJ2e\nvnj58nnaghwcHHStPT+/FEIsV/PRZNR1ndKwXM1OTg7KMl+uFlqV3gFCFnyUcsPgUIQv3/vik2eP\nAkDfO62qPC+YZOw8c+/cRut7QkDX997HUT3VOus6PxqNYuiDsyQEUOyaTbp0tdbOewp0dHSkM+UD\nSd1S4JQ02vd976wxeV5UTx4/V8qMRuPF1YwoZNvc2605r3duMhmBUCEEsyNzGpPnpoAUd7PjrKvE\n4gWi6IFjYq85HzWQUibL8na1BiBUUhmZawNK5nleZWb58qXAqBU6ikKyyTOIgOmUcp6jtzH0wbtg\nrWBPQQhBIbab5oJIbNZrYwwGo9BTdORQahQyetJCSzTWdvfu33j2/Gk6w5FpH75uu0ZrrdWraVwf\ngg3h+OZdFCaYsGf3pBlA0zSDalAVdQihLMu6Hp6cnExG08loMBoMkw497oQKCazb48N7IY5SyrrA\nAgVxjJ6DD0wAIkqp5ssWEGzQfRAomZEiExEgSYVCAiPaGCwFoZQpSudC9AEIxNaTnZAYkIAEAHHc\n4lpJCZ72wRKQABC21ghBgEgEjZ2nCV9ToQkGAiRGZhAoiHdIHwMiRmAEiIzMSAAMUWglJUulEBkS\nio4CUYZIgoCAESXKLdiDJCMREzCCEAqlQJQp3x1oi5jtJxRAIMQrXCG1R/tfmTHxfFFJIRTv6DmB\nkr+iAgrAIlFahJTdak5kRaDgvFGi9yFX2rlQFhWCGA7HRVEdHh2tmo1RMi8LIeDO7XtVWS4WC8p4\n+tpUKMmCj+XRye2TJ8+fPjl/8vbNT3z9r339/Or8vT97/xOfer3Wg872LtgirwKHw8lhUWR93wOx\nt1YJLO898L3drNYMhEKwYNf3NnE1WSQcuOsaYGa5JdB670OIWzEKXzMaEjsGwR7cxB1XajdX2ALu\nUr4SZibGQVqR90w5IlJK9X3fdV2agyXcMDk9X3/yfTVK75WI1uv1er1OUhjcWb3usWO5i8BQqGKK\nJnJOaSGEkNd0nenZYE9TYc6MkgLSicEUBLLS0uSZ7fr1ajEeDf6n/+7frIryt37nt3/1q1/7+q/9\nWr/pB4PBcDhMx6TruidPnvz0pz/9O3/n71wfhyQJmPf+Rz/68VtvvfHlL/8i4jY8aRt/rvWPf/xj\na7svfOFzSqn5fL5YLJRSIDE43zVt17QU4ma1/vQ7n4oxXl1d3b977+DgwBgjAA8m09xkRDQoq7Oz\ns9TCKqXG4/HZ2dmbb7753nvvjUaj9XoddwqS9CqJ/ZFWq7jjv6VjeOvWrd/93d+11o5Go6urq0R3\n8d5XdTGeDLMss667vLy8uLggDulXAJgevBFCsK5LU8qri6um2ZSVAQz3794ZDcbr5Xoxf3n71oPg\n++BjiJ7ZM7pMG2/9smk3m1arrq7GMUKMQSmhBGnMXj47DcEjCteiVnmeDZiU0XldDqy1q9VmvV4H\nilJKFpyZIitM8XrR9u0HP/1w3ayU0MNh/bJt67KqqkFhzKAa2Na2sV3NV1oqpURwoWmbq6uLvuts\n1yevrWSOWZeV620CKV1vE1VLoTBSKanETnkbA0cBRuuErmxCaxiRIcs0M4MUQiIAJ9AbgkeUdTXM\n6nLZNQpQSh2C8zEoFiEEH8lRDByYGUEKRklCecbeAwhoLQUiCFGhlEKGgApRMPlITAJZeH9rfHD5\n5Nl602daa61FBAyc51qylBHlDq5QSoE0QdPYFNJx433s+5CC2phbpbIsu5yt0iTY6lWM8cpG2/V+\ntqge3Pv4/fcRMY0Y4y6HIlUysSM6IWIfokeUmVGAXddEZ4VWUsoghGPsUK09pVNXCMiyrKoqwZAp\nrVBIRCAiHzKtq7zwveUYkTjN+BUKgp0dFSL+LKkB9ib6WzbCbkoKKKXcjnWA00GDFDFBgYk4wbhb\nEnkiQaCRSjAIQEAUDFpKJDZSKSHKPFdCsEh5QT8jckigmZQSgMQ273Cvj9w+MFUXIABEIATafQxi\nZAAQyOk/RhYAwPCKQW52cFRKto07iQ8QM8QYPSW3gQiaQNjAvZV5Bj5KEhkhN/18sc7zDKUwjOvz\nqxCdDni1WDeDJhuaTdxc8hlWwgxUkHEymcwn0DSzp48fhY9C/CFVppYdfvyT93OZqL+ilToZqy4o\n5HnurJVSNsHf/dSnH59ddquVCz4vC1DSuxBDjCwgeTBJMz6ZpPPHOXf31u2Li4sY49aRYvvBABLJ\nLXU2e3xz/63vR8T7QrUfvqmd71nad+87nqZp9quhuKabgWsGmunBCXfeW+zFGMuyTMwN2I3iaeek\nl34OIUj1ysl8PwPknadsURQxbPlRkMwdiCWB1hIRLUTf9mlKnG6+txpEXZTHk4MHd++dnp7GyPvC\nycxlWY7H4xTfnubAe/1E0qsvFvMbN05u3DhJ/jHpYwohLi8vX7x4Ph6PPvvZzxwcHKxWq6ZpyrJ8\nfvoy8UQS1Hl1dfV3/+7fres6dZ/e+/V6/Q/+wT/42te+9pWvfGUymbTrzWaz2cccWGv/8T/+x3/v\n7/29tm2ZuWma/aoRQvj2t7/9jW98Yz6fpyFn2jXvOevPnj378pe/nGXZbDabz+chhIODA2vty5cv\nnj9/9uDBg7qurO1fvnxRFHmyLKqqCoCbZnN4eJD8pg4PjrXKRsN8NB1AhKur+e0bNzOz6jaNj4iE\nIEVuDGr1/OljgYiEWhVaaGu97x0imqoUArTOrPVFkQk0y8Umz+rhYLqcz3ru0sq+Wa036/VgNATA\npmkwivV6fXl+FZkgQqkr733fOClU13qIzWQwLbOy6yxHyvN8vV5T8FeXFKJ1XUuOXGddZ0EqCgGI\n27ZdLZYptD5YJ2GL9Kf/0tY7U3p6cJBjPJ4cTEfj8LrPhRqYXAA3mw0HH4EJ2EfXeRdjRKDZugEA\ngrQqbRHvQV2nasSMEkEBaCSQUmh1dnlp8mq+XBiqtbOFFFKQBGH7rgu9UEabjAGVRKkkqtzGQBJl\nbqTWmBbeKFhgPqgAIHrnvecYJEVApsibpmn7PinwtdbKaGRAKZSQTddmWYZSBB+Ekn3fCwmocDid\nBGCjNTLJzJD3LIX33nnHUgjgzvaJCuu8j1IaKRWCEIJ25tMEUGYFgPQyZr1TWorwSgu/oy9tK4rW\nWggg2gpOUkeTdA0AoIQgEAoFid0GeWdFhvsYZkYJSIAA24EW75hp+9HDX6QaAQBylLAVogjc6o0S\nlxgFA0DiMe8XHAGohADYe/anRXL3oYDoGssOESUqiZJgqxmQUkqhASBltex6I7HniwKARAEiqUG2\niSp7+oDWWioFxJCs4QSBBFZCo2ltr4Sw3ikhG9cLCSbLbQxolLXWed/0nVLCWnfn6M58OZtdzGgQ\nVrPFarFoRWuh/6t//a/9+OXT+ekCC7h168aHP3zkZgtp4Wg8tn3vQ9/1IVqvlCrzXAD4TWP7vqwr\n22wGVeWDJSIAWrfN1g1557KRBncXL8+JKM9L2/VHo6Ors5lzTn300Uf7jcZ+j58M+PZ6K9yLS0JI\nx2K/+l/fGiT2WlrWYUervXXrFhG1bXt2dsa7rIE0TNqzOxI2mI611rrv+1QC93hgymGDa46c+7ck\nURZFMR6PR6NRiE4IkSzlr56ftm2bECp5LdTAdr0yucwLrbXr7Xq5uri48N4nguzjx4/feOON+Xw+\nGAy++S9//8mTJ/fuPUiyp3RiHRwcFEWBQH/y3W/ve7X0qZNY+C//+tdDCOdnL58/83uXwxjjJz7x\niXc++faDBw+890+fPEr1YL64isDf/s63stx842/8tddevz+bX9Z1PZtfhouQTDbH4/HNWyc3b504\n37//wXvjwdB5lxcmyzUzCwkoeDIdDUf1ZrMpqzypSU5OTkII//L3f+/f+c1vrNfrfauaYK4Y449/\n/ON/+k//6d//+38fAB4+fDgajbz3RZktV/P1RtaDUkj46OEHIYTX33jwv/3f/W9Go1Fy2/zt3/7t\nxWLxt//2316tVlJoCLLvndFsCvH/+Sf/aHE1+82/8e+YrLJtDBGjJxCsJEewP/7RD37pi1+yEbxH\njqK3niOXZQnI88XZYjb/xS9+qaqqtu1nl01VVIvZIkaK0TWrTde2o3pYmHwwHtnel2WZZyVKOJoe\neoqL6SLxFTOltc4uLi5IwGgwLbJSCd00mzKvOFLfts710+nk+NbBoK7LvLi4uBAmAwBP1Kw3fdMe\nHxweTQ+8c5gWrBAhUgriE4BaZ0Tucrlwvb84u+yWa/ahkLJdrvMsIwoAIBQScB98qkZjaWwMijkK\nACmCc4ji6PB4s2qymIAjjxEpBiJyFE/eeO3w7v2DN187GpSm70Z5JskqwZ+4f2/TbVDpvCglKq2z\nypTIxCK8PcyKPGfmEJzWOjovhLi8OBNJP0MEkYjIur7trcpL3enYKh9D50PvrOutC14AuuDX4ISS\nwXllNBCXZek364P17MVmXpZljDET0VqLDgeDgRMSDAJwpzjPBOYqkKLwikVGRD7YEEIXoyKwQod4\nzdRqR0VLa6vY+aannajUe8gkMsTdXhe2lBbBuKO3XG8odu0RAZKA5OH7Krvoem0AAGDClNGHKHaM\nPN5aZQapmClG8rjjFROFLNNEAVEDvsJ1gD1QRCaBAnnbaWklmZlCpOCBciAWKRUJxC76aFuPmFmg\nBA5p/7MrQ7u8NM3EgSgks71IPq2czBGAhJAogANTOlmFyKejqlSzq4vReNK37WA4ml9dlFW9Wa0D\n6DjIG7Jz6PsCtVa27eLF1Wa5cqbPjJK5NNIE4QD1f/ff/PbJweEkPxARQ++lh0E+zEqzspsIXmdS\n57nOtQahlOIQOZJQiAoDxjb0a99a8GgwuEi7qIRUQdhTCEEJHTlKVBKVEpnGDIRQX/jCF1JLtKcI\n79ujoij2qUIJGt7nDO2/3f1ynPCoGGMKJoCd7jJ5j5dlWZZl27ap6njv5/P5vtLALogpFZs9k9ta\ne35+nhiBe8aE3HlRpLNBoTLGrNv10dFRSgWEFJYKcrlceu+lzLa7DCkViiLPtZQQYgSAEJUQdV5g\nVQFx7+w7b719cvOGZDB5hgyf+uQn102XOL4JZtxsNskBNuzSDPftmrXWGNV1Tdc33kVtpFaZkJBn\nZVnV7733k7bbONczxK61yT+JmfOy+N73voeIk8nk/fffTzHkaR+QLtGqqk5OTp49e/b06dMQQmGy\nzWaTjljqzH7hF37h0aNH5+fnabqWfIZSkvenPvWpx48fJ35jOtoJuky7iq997WtJr5DmT4PB4Ozs\n5XQ6mc0uyzIvSxOCq6qCKIzHdd93IfRZViwWl95HZq+1zFXuGVVpUISD6VAI4Xp79+5drYqqGlHc\nytFQUIz2p+/98I3XXvv057/kPLsuWB8ynVeDej6/+ODDn3z/B9/9W//hfwAAzaZn0keHdzab9f17\nd+ZXFhFHo9G9e/eEUFmWNV03HA7n87kL3tsQQjgcHdhyYJSWUva9G9YjKeX56Znr/YN797uu6zbr\n6e07SqL3th5Ufd8+f/J8VI8mw8nLi/Mkfdueq3m+Wa/X6zX5LY+WQqSdYlGiYBbrTYMETkpkyo2Z\njkZaYAyBI0spdWakVoGIgBVwaFre4lggpCRgIcVoNOqaXkqZOA/phQIyh+itC531Xd9LGdpOWYu+\nQw5CiIvZRe+DSnbvIA1qIprPL4TE6XTqvbe2S1wmInpw7w4zx+hppyhABiNknRV1VuEEjTH7DjvB\nEnVdp946XYCpFZ7Pr+7dveet29PBE5/27OyM8oKZ+76XKDhS33be9hS4E0hSEQWRuAEMUsrFYuGU\n7lj0vU1TAEQUAmL0iEyUcP7kdUkxRjQoBAiJFLbc6+2emSIjcySOAWkrOiIKWqSeQyAQMiATEAMA\nbMlpWzRvX5D2cN9+UgAAKJKJF8QYpSDeubGF4FIm93b4+kqvEiRC3CVuAABDosax2MYFhFfFLzVM\ne1kgpc9zTQnO4ud6I8GQfHu3nZCUAJAGGdv3z7BfjdMt06bMtM3yOi8qZeqqcJtiXNf3bt1i5uFw\nuGpWg8Hg3t27QohmsRmEMjNGFLCOy151cz9vqWl9e/y5IwHy6uVytVoLK6qszoVBJYXJQCqO5HxE\nQdZZbjwSK6EZAaKNRj5dnveCXY5FboyPUovoI0QWCnOTAUBuivVqA0whhMi0XC598oXay9/2TOJ9\nk5T49ftvLp2yadK7w0BfSSxpJwulnaIoXRWpDu1XSbkzakzuwnum/D5HMsuyvu8Tzpbsc9Iyuk+V\nTidE0pAXRUGeUjU6ODhouw0RpWr0o3ff3zZqckuET2+4zHJAAI4cWQqoy6LMTFGWwXtAHI9GHz96\n9MlPvFVWVZHnHz969ODBA9r5tyZOPSKWZZl6x3Q9b5et5PpDPst0VQ20lkkQVpZ18gC+vDxnxizT\nAMLarm17YwwKtV6v03MOqzJhlenIOOAQwuXZ6eHh4dmL52GX8JSObdLiWWtv3Ljx4YcfTqfT4XCY\nWjHYqYiMMX/4h3+QriIhxF6lmKZ39+7d+4f/8P+ptb5z587Tp08PDw+vrq5i9MNRrbWM5P/oj/6N\ndd2zpy+KMivyCgXfvXM/L8xwmH/zX/3L2dUCSbLPMmVQhLfeflDlxdtvvqmlWC/nP/3JT6U0eVZq\nI5NH6MFkMhwOXb9xAYBBCqTQto0LYZNlXFWyrtR8uTg6nsagfGh662az89PT51LgycnJ7du3pZQH\nBwfOufF4DCDOLi7+5E/+5MbxyWc/+/miKrVUV1dXeV4KIdbr9b/5g3/ddd1/9Lf+w+GwXi4W3vvp\naGhdhwgffvj+2emLz3zq0/ce3PW0PZJpVnf6/IW1dlBWrrfMHEMA5m2fRMTMZVlJlQtlovfknA99\nodRsNhsOKoYYiUREEEjMkSl5AGRZQQI72yFADMTIgWLa0BBjoO3ZZfJ8WA76tTNLp2adtqC6Vhsp\nYi8g3r8/1qKZuxUmg1MmyT56d4I5hTjswVrKHA8ExAgxsrpqvPeub7x1YptUIiTD6cOzxLaHawMY\nZh4MBvndux+/9x7tQqqSFT0AbR4+TUSYBHukLL6UiWWthXVniACCtRaJIDNd10UhhQAhBGz1cGp8\nfNwQLm3oZkutNTgfgvPexxCkEAxITBTAWYsMAjkGhwwSBaNAEHJLNCBAJCaxa48ASDBJZAQSQLsI\nWWaOyXRYiOSmveNh4Ta+fMvnB0AEuXN7YECBoJUSiHI3qVJCEjstlZJYFjkyCEQgpuBJKymBI8Xg\nmAKmUHJAFBKImQJw4mcDAgFHYECSSMAckVlwgvMYIQGBIEgIBmYQLACAtk4CfodqSCFASvTeboEZ\n2Bc8BmAZY/fivDFCOLeabY4PDpuLBSzXdmUft49i9HmeEzAqGchLKZu2X6waY0w1qEPwN27fWp03\ngaIA/eLdy9FoRD1XUG+o7Zv+3pt3P/vLX7ygpon25cdPLp6/jL2LHaPGUVkH66XRUUBt6iXY6u6h\n8K4wJrabTAgODABlXiEiRDDKnNw5ZkItDBEVWTk4GElEtUfk9uOcVCFSgUlX6R48TSTOfSe+n9/s\ni9b1eravPaksJeqO2KUW7V1T+ZpVndhZi+K1iNKU9556hVQS9p3cvkyGEBJfIMbIAEKI0WhU13VZ\nrhH0/k3GGJpmnZVVZkxRFGkk0PZ9jHE4HPZ9v1gs7t29671vm6Ztmps3b1ofErSVCmpq5vaCxAQG\nvjp6SBIUAGw2K9oJCbuuu7q6aJpmNBoh4tXVBRHVdc1MIThmn6rF06dPT05O0iYgHd69vby19u23\n31ZKXVxcpOqeMnNT0vNms/nqV7+673vS0U5tEwC4GJRSdV1rrdNOIlWjqqpms9k3vvGNi4uLpmne\neust732W6bLK0zLUtm3fr2/cuJEOzmKxCCE8fvJxevOPnyym02m0zJ7RwGp91fbz5epyNKq+9a3/\nYbFYGV0BqyzL+74HiJFs065+/JMffutb30Ip8qyKMS6Xa2JnCi1k9GH1L/7Vf//s2bNPvfPZly9m\nQpRVPj07O3/tzl1G0lqdnr5cLBa3bt1KZgHGZPfu3RtURW7M6emLi4uLw8NjpZQQq7Ztx4PhrVs3\nnj9/zuBnVxdCiKrQUiH1sa7Lo8PDJ48fSym9j1rL1PIaYxSKJDtNrQYzwzVzDYgUI3XWe2JjcmUy\nVpptpzLFglerRbKq1MZIqQMwMwuAsGlG4yFLsVqtZJaxQC1kQoZdCIzbKCYjjanr0WSSuayq67Is\n87xQDEUmJSmJsWnW6/U6vU+tM61VJgwpWQ/K5XKx3+PvL73UwewxcOectb1t+7oeJpfPPeaRJr5a\nqvFgGF06GwtmzpRWmQrRpVK09xdOl2FKI0uXYVoTAEAKwKq0kSSTVCgBY4rgNGa7dHLSTW+181mu\nieJWhcNbVGaP3REHIUAqRBJSIkeGZLLAKCQoFBJBCSEFSBSQ4k0TSR9oxxaAxNgRoEAwEu50QXF/\nD0oQaeJECAhCJDtNkBKTBlwpFWhLrdRao0hZTpGIgAKLV3pVxKSHS+yHuBthXHc/YYkKdtFHeO0G\n/yO3tPLQzuQsPdXeyelngEeA9O003pe5Wczmd27eevniBcZI65Dnxrl+vV7rzLjOSa2MMaYwr92c\nnl2ck/BVXbx25/76Yrlar4uiygiKUC1mSzQIOSklfvjTP/vB0x+FUTE6mogAMpfTyWE7W85fXi6a\nNQAYQa21xaBevpgVg3rZbJSEHH2hBRAKIWII0ce+tcxInpBEWi2D4zzPlZAqWTWkTyh21m1d19V1\nfZ0XkFbbRKERO0O55EkTQhgMBvP5fF9v0mKdmpv9MU0q4v28cZ8qm0wWUs1LuUpFUaSKmGLo0uOT\nY3m6AFI7lXZwaZtfFMVisagHZdM0o/E4kZVXq9VqtRqPDp1z0+nhnp+qlJASre2I4mazSteSc71S\nQgjRdQ0zp7dprSVAslYJAUK4vgcAJUTYemzjVuWdSqMQAjGEuOPHIABwDKmrLjLj+g4RjZIAMjjL\nzN4jgAAWfdsdTKbBeUxzSwAASNZSqfvumjb94L1Pq0NKuEg9ULLI3Z+auJseCyF6/8r56ef+ZeZn\nz57hz5h/02q1AmAhsK4r5rLr2sGgJorT6WT/t4g4Gg0RUZDO1AhB3rp/uGlmRzfHh4fjGOPNOzeZ\nFJMkSkY+jCIyB+JwfHwYQuhs71wYjA6MUQE66zZjMZ5M84Oj15WmG3cGbccHo1znh7P5+dGNgz5s\nAKAo9eXVaaIvGaOfPn3CTMvlvOsarfXs8tx76ylOp9OfvPvo6OjorbcffOc737p18+Zsdplrk1pD\npYVEcfv2zdPT8z/74Z8LAb1P8X16uMtct9Z6634WkyEkHg6HuRJZXoTITbOR5EXwTbs+PJq6posU\nKMS8LAb10AMx4bCuqe+7piWJR7dvJWVVmeX1cPTpzx653kaCwXR81ayenJ+ePLg/22xmvo92dOOz\nn7w1GY4QDgqzXlwAexB0/+702Nu+cwDCKAOeu65b206UE0aURL5vLzZNEAER5dAsl8vIXhnpvffk\nSUZvqEGbZdth+NXV1XQ6TTYGilUVV81QAsCaGh98lmUUeinRmqiUsoKUCsaIqJVSqgnh5P7xhz/6\nkcqVEA4AcKD63uYUEGUMkQG0yUL01jopwDoXTB4jjcfj1WrlhYhNUwxGiBidL0q9WK7e/sSDFy+e\nT0aDwmR9F4dVLQCIuMiy5eJiPKl8jEwxEis0qGWmJQXvgSnqIq96G/u+r4cDFvri4mx6dNi2PYdg\njOHgbbBaaOIAkZVCCeApGmlYcHROgDDS+BBd70Z1hWy8td7GPCuUQIpQ5nmzWh8fHEbniZ0UJtfG\nGLNeXxlDid2glEyuoG230aiLojg/P51Op8YYgLT1RAEyM3qz6aMPQgAyZNo07Ya3PkYRiDlSjFur\nBa31auXzwmizhek626NgH2w9KH0btdY+Wh9sNhjOVhfFSHdA62B5lD21i7kKWWls26Hr0WAITmuU\nubLeBdsMBvVs/hwwoIaGYzD2vHmZlflFc1rVQyavhlgNqovVmQu27bvx6JDIX7x8IQLkQjm5VBHK\nImMfMpU3m+b4xsmma2XgQmosh5F6xt4M9cHkcLlclmX+6OPH4+F4NlsAYFlVUskQAinqsBMg1O3b\nt39OXZRwrQSX7YkGqRRLKc/OzvZhr6lfSROUlLyw2WxCCAlGA4D0g1JquVxOp9Owi1Rh5mQEvi8t\naTSXipbapdIlLFtcS2rYM/rSqxtjyBMi9r4HgPlCNk1zcXnZ973QuXOuruu0j1itVsdHt5LUBq45\nSvE1hsz1Hcp22YUoUPIrb7RXPn7XZ2Z/8df9FnX/6/7Y7jc1AACULIl//n7+WYek67f/sT3RHjK9\n/hixcwjcv/T1v8KfvcF25Y3XLOBe3a6/+qsXRVqs5ogoG+9iq1QIvBEgCbBvArGAKGHrOU1MntgZ\no0AmSIW0lhGVkF6ir2ozWz07OTnp7LwLoRpNP3r6E6PK0WRCBGknGkIQEQBAEKLw2qBK8jiVSSkR\nIJBUmdJa3bx7XGYGEfPiOC+kyaZEFF22692FUbqqBjpTL05PldrydDxF6Vw6wcQe0L8GRyPFl+cX\nMYSjSYlApUTwNriuWy+NTK4T20AQAhbKKKXaEGKMnfNr2/XWb7pWC1kVZZ1Xfd/b3ueDau37pe2y\n8ahpGl0d9n3/8OHDcyF01wwUQ3DMvTLCQ/AxRGYjTaZzxSLGmBdZ52ywLpFYhZIaEQASrF0URVEU\ncquaEs65qqiYMYRQFMV0Oq3reo/9lmV59+7dtDlLfbYQEChUVZWUA/vGWkrZdd3R0dGnPvWphKAk\nQVLf2761Ugpi9N51Mbqkx4uBVbZqeyfMyYNbQsB0Ou0CLhaLWyc3EDHLsqOjA0Qcj8ePHz92vr+a\nLRO9FhGZt5xyH2w9mHjvgRlipBCTgVUIvts00iglZfCOGIxWtu26zaY0GSQT6hgpkcg5KlaRffTe\n7WIhFSpKkcFpeYlhuWyOD+9T5Pl8fnBYI/LeKluActYzxK5pB3XV9cuu6/I8K8tCax3JJ3/nLNPj\n8Xg4HCbnQKVUrnPX96wSapJybVKbFaTUCXNjjogsZMrl8Yhi36mntevg4CDNL5xzmTF920kp5/P5\nqBwKgWVZFtKEEApj6rzw1uVZpg+nmdKJZcMCq6paNytGyAtdlca5zvqeZVyaq+mnB4A4NIWUcjye\nHowPHj18dKP8xNXZVZEVTdd7LaTRmVTCU2is63qjjSk0BWbr46otBJqsEhYMSMjKhV8umkVrW+dc\n020WmzlqAZqzLJ8t5sFdVlU9GIyQuWutStbfe9XqHg1DxNTZ7BGzRHpJoeAJEUoU59RzpOTQNOpP\nvt2ImJJApZRVVR0eHia8LlW767y76wtikuakqd3p6emNGzfSO9mv5tcxQCLSQhPRul1PJhOpEACk\nUgDwb771neVymeclsBiNRt7HtOeti2K37L7yidoz/a6v17v/C7jNwEHcGWEhIsfwqnwxACJRBACp\ncOcus3PLSv8RcBIoXF/rARg4GWO/YvpsC9L1EpTe26sHXC9a6X8JAYlgypywgm3aC3NyNd2+120s\n2c+U4fRGXz3n9bcBsK/Br4iX+3eLAHmVoWDXt0qDwLjuFkYa64MWBZESQrBggCQhBALsrJMShURC\n4hijs0LaiN34eHzVWF3B5WZejMYUe1URk23DCklyJGYABKEkAABx6xohki+TIk44PALQcjWzvi/L\ncr70AJBlur1oc22UMtGTFBpRxMhGGgRprT04OiTaD9V3h4NZ7qsR8auzhfmN+w9isGztuz/8M0su\nl2gwZEWugAVgStj03kcmBSKE0DQNR0rRhELzQA1ynZd5YVtLEZxz3cKvg/cSiqrMlfYbJ2wbXi6k\n0SXHXNHBsA4OBIre9z4CCqHZoBcKUAgzLScLt9hYD0B5bqSUwBRjtOcrQ5TlWraRI5GUjNC37fjW\nreVy2batzfO2bf0uNtQ51z8/Sxa6fd8nO1QpZfT+9ddff/rokd6lSKR2fLVaLX76OOlFmDltXi2T\nHNSmMIxAFAVgprQxhpTM6lFo++BotVr91m/9VsyKxkXPcjQav3z5krg3GT58eCml+IM/+AOts/Ho\neDisyzInCigoy0dSkRDQNZsYI+ZgtMiL7NatG2VWaiMh4mBcu0CRAwp198Ed76P3vl03AjBpARPv\nN7FnQwhy50sYgKVAJRCVqAbV5dXFeHhLSmSOm6aRcotSKiWt65hJGdlsbFEUrrdKKQ4BiQSD4LRD\nE4XJpETf227T5FoVRtdFiYIFojFKCMF99MHFGFWDWZYhshDpiiNAEjJdzowp8LMqYwxVVWa5btvN\nQXUcYyzLous6ZTBGPx6Mk1Zd9oFm6yxDaLtyOPSzFlZL0roYDLtmbn2fZVnnuuL4uJ/PpJQrzVfC\nW+WhCOZQPzr/gCbxojnPBrlSKmyo3tQPbr2+WFy8mL1wM/fgzuthvmhsB56NUpnMJAMReu5znQ/R\n+I2fTqd5USwWqxBCLGJdZcvYr9frLMtcCKgkCy6GVZGXx7duGmOcC84GJcREKJXneTqfEipKO//8\nNKJMPQrswOJ0Roqd5bvYKdWZOVWgFEgFuyijBMfBLtIxdTPMe8Yk7SvfdWlOInkbYxLghoi7gSqk\nerlniIUQirJwzjVNMxgMrPOJ4a2UGgwG6VLJjFZKZVmxr6+RiZlRCojJ8Y45eQKn9RqBk4yagffB\nq9cWYvjZ26uSdG35vt6R/Owi/rPtDrMAoH8baPxzj/y51/2L/YrcJaP/xQK/f9j1N8PXLLfhVQl8\nNSb5i5/0+sN2vxJBDxS6uClzKRVGH2VGRokYIoAkZEQkRCaICMxCpOxARIBI4Ck6iR50ZAyDSRnB\nrppZXlRPXj69c/vN89Ol770ACYycXAqFBkiudEgRI6FhI4RgQmZmwXklNKjcSGsdM0sVlY8RnfeO\nAyupAZTrQi+UksaHIJVAKaSSqfAkax8EIJH4tshbihMiAQOcXVwVWiI5H0OmZaBA3hZSxOAliugp\nURiYIZBoNh1RsjpDooiIIDAmHpqQWZYRsKOogD2HsiyjJwkSI+VSD+p6CATtRoNoe1vqHCIhg1ZK\noojOxYhCa/ARGVIcp7fWJ2sZ5kFVAYDSaRBrmaMPvts0B5Np17QtMYUoUUQftNZaKs9uvVxprQUg\nEBulKUSjzWK1Lkxm205VIlgHSnGIKNWgrNq2raaFDZ1SKtemLMuocNa3ALkQSESIrKRBlFGK1Wrl\niJyjdjkvpOkjR1RVVWdGKy2ctwzY9a3SYmjGaQUIIaxWK2s7IVkbBvTe2ywrmIGCsx4u2x6ZG7mK\nMW42m7IsrXeBSGqVFXnii3IEKbZm/GlAnoQTeZ4nOkZaFtICSOzLSr548YJCXhWHz549a9v+zTff\nnC9PyzJPpsZpCx5CY4xxfcfBI2IS6fe2TS+a52aH+myJXUKIEJ0LQYAEAKkgPSbBT0oLaxtmjhQS\nZ0FszxnqulYILKqt8jKhRyk8N43YrbVX7oqI2rYtKADE0lTUWRG5bRsFGHvXijUSQ4jSULROo4AQ\npRDeuo3f+MyPJ0MyvvFrPRCdXIe63azDeFj5tR35UT+PVVX253ZxenXv9o3VYta4TkRWEhElQ4wE\nbW/rvGqXTeg8iswvWiAOve98G1SwrTOYBY4aVLCBQxc8P3z4SAh1586dsiwvF/MY47a52WtgASCE\nwNd8y2nHE8drY9I9wWFPc9jjbLAjjO6XvPTg9JXzzhVjr0i9vsDt8S7eiXiSj7rcBaeLXVZg6rH2\n48HtrI9JSplwiclkMplMTk/Py0KuVqvDw+idG60AAQAASURBVGMAKMsycFRAIEAowQiMHDkiC4mJ\n+ELpTmISW6OQLV2Cf+5fgbtp5L7MJLplimZJSzxs2whEYHGtz9hzOhmQJCRD65+pCvSzEdrpuSl5\nRALDbmK1U5+/Ml/fHVVIVtkpgjLJ2Pd/iIKZaJsCg0mkRwAACALT+/+ZqgYATK86tm1lBQARQUAk\nKxQRRubgY9evN95BWUwZkLeTXcHMkZgIJAtikdhWKWNIFVIX+mJ2iQpIRlb8+OVjG/FqNQsQTZZp\ngUwYIwEEFsyMEUJmiugjM7MQIFXypZSS1+08q+SqWafdZdcGJXXb2aoaRGBUWiBq0ghKKY1StN4K\nsRViw77zBkxl6VUjCZzkKN47JUyZ5YeHh+NCx76lfl1m+nAwUBIpglKmqoeIIpAoTBb7jpk9k0eO\n6cuIBESnT18KQJ3lDhltJ31/cnyjHo/mnVj3tstVq1CBCDIaGVcyPr986aOTWuRQGmlCJEFCxXB1\n9ZKIULBQgiHGGKUWSul57IlIMgohSESlFBodMd9oXsrYlyooAXnir5IUYXjrMDZNIGozsQnAmlsf\njQg4rXmU+UraAjtgIWLASBkXRRmEaw1tVNAaPQTLXeiZUyjJ9nxOPWWMLGOMSmeV1mZy8O//L/6X\nMcs9iqKc/P3/8/+VIxFbKdThwUHft1/+pV9qNu2zp+cxBA/OOzcY5s62PrSBvHMBEVkbIlqvVpnS\nyNCuN+PxeL321jtptCC5XC+klFJqIFRCJqKg7bfxm2VZLpj3BjFJni+EiOyEjN7H733nx7k5WC+D\nc6EoMhfW49Ho7PTFP/uds9/5rd8t84Pote3E4eHhennZdUsAajYr3lrSQMpDyXJ9dHg4GAys7Zzt\n0mySA+d5abQ+mGztqokoBEZSUglmY02ia22lmfWgZOaiKGaz2Wg0Ojo+zPJcCLDWHhwcKEYp4Pzl\n+XQ6zgszLqvmct3nsnPIKvSZKIZFsP0y+OGgDhn7Iutj22bQZuAUWxtGo8mynwHhi8fPl3oRffAF\now6Hk2Fo4nQwWc029w9ePz07P6iOhI0ff/gxCpY601ptvHexy0wxngy7tqXS+IVctC0RxEiFMgwI\nvSirAYLSzrDAWisldWe98/5rX/5VqdWPfvSj0+enb3/ynVu3bqnf+73fS21swtkSLyCRW9I+Yj9r\nSa1Pkh2koc6+MUquB+kPk3VCaoevzy1gxw9JV31VVdd32ftVb59xh4gJ/ZNSJjrD9RSftPhmWQYR\n0vuMMaIA772QMoTw6NGj5XJJO0+tVLGk0du8yKQVT4WTkwkvI0Mi5XCa5fxsP3G9P/i5luJnysb2\nJnae1rz/l5kQJXMyoeI0I/+5tuMv3q7fz5BKCl8/qn+xT7r+888Vuf3/2t/D+yk94h4LZU5hFqmx\nSTZfyBwTGpY+S/qMxghiOjqeSh20YSEml5ez4JECUhS0Z86CFMRAACRjTFIQRIgYGAIhcbNcqoym\nJ9Pbd+/86Xd/9Plf+PKPf/Th26+/Mzu7AiWRMJIjYgQlhBGabewpBomSUMCOaKOUjK4FYQJaKSQi\naglloUEGor73XnqvVRVJCAFMMlKUSqFgIaW4FhEtAGOMYld6ASDRuwVDaUrbbJbL9cuz84UgDa6Q\nCFE9vDjTSlEEKWVRDpmhs16C1MBEFAQIo0FpEKhRGqWSJDkQBORV3141q67r1pvGVMeXV2egZOtt\nJkVe5OVwUA7N1E+jIGWkyowRBpiRUKKaHhxIKc1WqB5ijEpIrfVoUK3Xa6IgpYQtKosu+PH0YHx8\nuCdoLRaLtI9cLBb1ZHR+fh6APdDGdp3rm771tnvvww9OLy+yLNtrDCrveLkQQrQzG0LIkxN2DL2z\nRV6HEERieMpt8qFUKmBErXvH8/m865um7cBkWTH43ve+d/PkWGkErI+Op4vF7Pj4+FHz+MWLF++9\n925VDgHp9fzu02dPmmYZySmda62roizyvF1v6qNjLWSHTdu2MUYWWBujlLq8vLx15/ZiNqfAKTKG\nrw29xuNxGm+npSMpSZRSgCFQ/7f/9q8Gpw4P7lbF4Q++/6Pf+Z3fsn4FomPoP/3pd7KsKPODs5fr\n98+eBu8Fbtp2obVMeFKWZd7brut8sKljK4qi65qkaSvLEgmbpkm8bdhHISNbaxNzamdbs71IdV54\n788vrj54+NHx8fHzly+EVM+fP+cIdV3H3hV5Hl1Mn2IVui996p07x2PXtXmWGZQSBQXXNA0CpZH8\ndLkcH0xMWTBC8DZ0ljFoUKJVx8c3ZsvLsTaik2FN6xdr587vTh7YxtuFp5U/Pjj04KMIojRYFoG5\n2bRrto1rUHDnO19qAKkFcJFvetd0DecIiNLrrrE6M4FJ10VselTyD3//Dw+Ojn7lV37lrU+87WNo\nmkZ95Stf2bcyqdVwzvV9f3V1NRgMEt6FOyaolHK9XicWA+wkqwCQZdlqtUrfaIoYT63xHtADgMlk\nkk6FdIUnDDoVv/QMcpf/TTs30sQzTq+VTCLSotn3fSJBVFWVqSzZ58xmM0BaLpcoxGq1chFms5kx\nORGlypeMdsqqYMTILJgjUaCti2/YGYekRT8t28nyDvnVyAf3dFR4taDjKx6EBEIETEYnAAI4GTkC\n06vWCiDNXZC2hYGuV5GfqzTXq0gKvmP8t1SUnwPW9r+KXfQ7XZOOXX9yupYfKFDtgrwhVSPmvZ0k\nACAzXi+ajDRbLkC6B28eKx1H4/LgcPThBw8pyo8+fBFJxMgUZUqUYGYklesyeGYiRs8cI5Fn66IP\nEFfd+ri3OstNkQNK570pssnhxEjlnQtz6zqHSFoLKbBZrKWUWhdCgbd93/fG5CrPhIbOrrXWTbNU\nSk3G48iuGhWSdaRNsEwQQSAKwQiRiYgTQUJey5NGBqIUW7P9RrbxALtkmiLPi6LQ5IZFngvo13OB\nIBLph5O3PXnvCaiuK+ccowCU1jkfQ5VVg3KQFRX2PRIpJSwwt5uqqqqyJJR+1Y10js2amVDG7mqR\n5diuF6jQCY7AIplKgoRIy9OLV9nhwDHGVHtee+3+ixcv2s1KSkkhRV8CAWdVuW42g8EgfePz+Twx\nY2/dujUajZrLmZQyE0IRGJNTiHlVK093D0+uQxTJ5vL27dsXFxcJft9i+xRYapVngggRi0wTUvCE\nWXY+X26IVesN4+npKWVVMRrHGLuuc86hSCiIwt30Ohm5CtQp+v3Dj6xzDjBa1wDAZrWuyrLbNIOq\nRuKzs7PtxSvFYrUs6urZs2evv/nGxcXFxdml2eV2p0VmPB5XRfbBB09SHHP6+EkUgQpff/PewcGB\n7XC9XnPM67r8+NFHo3F5cFQWZfmVr3ylrodFNn33J4+ePr5kZmLKczMcDvepoQCklBqNB+v1GoDy\nPDdGTafTtHs2UnVd17Zt2Db223rkXJ+WIgDIMi0VhhCcjX3fDwYDH1eHx4eHh4cvz04nk0nSMntv\nUx7GYDBo1hsIsYDw4Y/enRVKSyzLclBU86srjiE6H7wVSjJz03dZkfV9H4gAqcoLkGStLe3gJBzz\nuSi7AoSYz5efP35zs2mrMJgvF2/ceGspFxF5Cb7HWGVw887h3ZMTU9XlYDAYjp8/enb18mJMolbF\ngJVwvL6aV10rFTFHoaS1thzUl1dX4+morftqPFysFta5j99/8uLpOUpZ1YVi5n03w7u8phBCXdfJ\nkC3uHNhSnRgOh4DkbCAOzoHzfQycF4YJretijOnntttIoY0xqVtKJJPrFjsJYE07FESsqkprnURI\ne4JfWZa7nYJIUlzcUcOJyBgznU6t9YWoBuORc/1gMFhvlkVezRbzq6v5D/7k+z7ibDYTQsXIqYgm\nvkayTIG04YWdOg4iMhKSAIjIMi3pFBkAWADy/l8UTASQiAtIyBIwStQAcUc2SHUiMQiIAXg77LjO\nVgipGqQ7dxViu/yJVwa113AzYAJIiSCpuQBiZgLCECkVqi14KBiACESuBgiS2DITc0QBuyBV2mec\nUwRmSGoLCZKBIS16zAgaEwchuQRv1+RUwZmRyioj5PF40HSzrl+v1/zBh+/2HQ2qY0zhM4ACkpFl\nynHxMRkJCmChkTJ2FECQqNp18/zRShupsfzut//UO3706OFf/tqXAXi1aghCiI6JCBwKgKzL8rwa\nkFIhrBofNlI5LKqDk2KxWhwcVv3zM6nkwa3D9aI5mI76BtoWggsxRgEy9TrBclGbuE9au5bqJpMC\nhQUgAUvciVmTazJK0XRN7FYaBqjE2dmFiDxMDr8gVUYAGInQlIvGeRdQCQkQgo/si+Hw4HDy+NGj\nrndCaaVzUsojstao9MXp1cXZuRBCaZ0JKpQKMRiWShlpJIMgawHRqCwTKsZY1tVqtUpXVqaVlDJp\nKfZ+KHunLqWk1MqFiIwCRG97iYI95WWmURmhp8OJRoWMRhqKJFAEZ1Hq5XJmTE7OC4XeW+cChFiW\n9bgePP34CVFwLgBQnpcRoUu2zRSllLlRnet664XJiuH45XI9t2Fy9/58uZ7emfQuPHn6Is9KZgQM\nJpMoYpZpZ73SVVUNnY2dagCiENC2rXNBKSVRem97cpkxAFBUOUcAKZTJmdm6sFptXKD1ej2sB865\nPC+FkN673jmXIjqN6Z3zkXsXiNj66L1njoGDMSpE9/z587u33/LOL5fz8XTS2TYuuqObldTq+MaJ\nzioFVQT54nxO3mVZMxzoAcJitVwsFlrrvm+rqnKuN8aMxgOU4uXLl89fvuj7vsjyVM61kKbIjNQ2\nONt1vXPDunQxcIioZF3k0mjX9cvNunf+jTfeEEp9+cu/PJqMP3r48YN7r02nU2RgxnE1mF1eLueL\nP336bFjXB8dTZbMQOqNyLVVuzGI2F0xKSuaolIpEuTbAWBWlDzEzJjpf5oOL2aUxZREHmatlk2kj\nj3ThLsLITEITDwdHTz56bKQxgyJJQ4HV/GJ5erUEpY9u3rh7935VDX744s/cuitYZYSVyP26KZQp\ntLCur+vaU8AKF5dXwNF6d/byhcnzyDQ/u9DaVMPBJZHaJ9Tted5pbpQE6qmZFTu3Qa21VOicFxKB\nwLleCDBlRhRQSKJQjUZEoWm6osgQZdc3RV4lb7Tr1GoA6Pu+LEveRZuniyfdEpo3Go2Wy2V6e4kD\nk4h8acLpva/r2pjceSLmsqyYWUpdZmWRlebA2I0VIL3t8lGV5+V60xKAkEqAkCgFIMU4qOrlfP7g\nzm1l9MXZeT2sXO9Nrvuuy/IcAYgCICMTMUcfARCAhUhqalBK5lmGmGpnZAoshEAV4raoM7NzNmHW\nm2YznU7X63XqKZum0VqbTFGg5BkaQmBGipD0W+v1ejvDULgzACaUorO9KowktrajGDOllcyBRZEV\nzaYHKSJ4kwlh2NqGSXddLlBLJdtuPhxlvW36pi3LWpmsbVqjayYRAkhhvKNofTHKN5sNMyZdbZGb\nvu9NngEjsCBBABSCJw5SSilYSVa5OT6a/Ojdj6Wl737/jwSqoq4X61kmhky5QMik4cjeOUZPRAgM\nLClIBUph6Zx0m/bea2/S5mF76o9vjD//5lv/+T/8z9751KfuHE+ePf/xk6cfU8iAM5MNnQsntybr\nzex0/vSNz326t1eLxUKN8/ny+es33oY8lDezwb3Kh7mbPRlNJyt6nwv16OXLSXWbwNeDcbNkJJmb\nqtm4UTXq+1YaKZVMnr2cuIicJm0kRAp/8EWWSaO6rosIwmhUUed6Mjisc6UjvPPJz5W6KEwhpZwe\nHeZl1oXW5CqQhDhEklLEEFvym7zQlcl777/2a1+9Wm6iMB1zzDQ/+qC6cQOrcng0kMXzfFjXoyKj\nLtq2LIoQfVkezBcrabKOo9t0Q9Bru1itl6ODae9swprSzFxLpbUmI6+alSnM2lml1NGt4/l8JiU6\nC1KV1oGQRd/1eTEi1sSiyEdG11IUSikO0dmQZVlVjqSg8fRwuVxJEByp7Z2UyvqYAwaCtrfMVJbV\n1dXlaHK42qx1YYqyvLq8MMZ0XUcAUmqU6mqxZKGFkpHEYDjteleOhijzbuPVgdHKKh2t22y6lXUU\nycxmvdIlQcgMC5mYGoUEwwxFnvW2SVEFWZnP5wvHkSN7F9vW5rmZL9ZKmbDNL1IAWVaa9XphlADk\nZbOuR+PW+qYLZVlv2qasjPNd0zcBFAPUw8HVfBaD9kHMzl+ygAgxImVV2YRQaHBRtF62TlAUnuxw\nnHmK51eXiAgkQIqrxTzLdLPqjm8do5St7ZlZa71sN7nKrbVSiHdeu39+enFxdVUV5aZt+95mRU4h\nLlaXX/7FX7qaz1brvncxIDugdrV2wccAWVZRwFJXrvcAELooWGe61EIPB+PNZpOz0xluYp/LamE3\nWKi+7WQkKSXFqLVWQkTgSAGUDh7G+kgFcWOcz7pL1rI6GbSx3VA3mFSho9nmqiqqRTfXBktlNvPN\njfEhKcEBZaNyoPVmdXXa4NPl0cHhoZP14PDF42d1WcvYZygzpZx1znkxBCXE9GBwMB966pj7qhC+\nXxk07MJBOW7OV7kpVZJS8jWpSuJpTKfTvYKSdzSBEJ3xar/IJjufRJo0Bo0xCfo0Zlvkqqpg2hpv\n79l6vDNfSBvzVKVSs5yssRJXJHVFWZYlNG9vHZQMbxI3r+laRFRZjoiAwnU9M/Zdl+wSvPeb1bqs\nR4nC7mLIUnechochNE3z9PGT6F3f9/fu30mUGGMMIofgIDlBCJHk2VpvaYF7cZL3vu+bPdtQay20\nDD4wkA/kQ5eOpzZaa5nloxgdgxdCKA3DUbnF2WIUILpm1TRtVQ4ODo6cC+v12ii1644oJbYAyICx\nqvN1vxFAZVVIpq61MfRlMdqsWyFEXZXni/Ojmzcu5y9UHpTIDRYU1Xz5LC8w0PrkZr1Y9AB9WRTO\nh75fnhzfaZq+aTaTyWQ2m51fLIuiQIEMqDX60GqjjBbz5Yo5Jv20lEIKQBGYw+XF2ee/+M63/vjf\nlJV6/8Of5mWplNk0NnjF7CRIBSKEHgAkRmauyyKE4B1RZCQUQhnIWML5y8Xt49dfnj3aLO39++NH\nDx9/7nOfPTqc/PTDbx8fjd5//8XrDz692YQQehJhfFS9+2h2tXokTIC8b/3i+G7RwUUA0Vw0X/jS\n2xfn63pKkK+fn348Hd5Zd3Z2Pgc/mRQ5wNZ6EYm7TZNVhjhyiIiJjRKYAQRopUJgLQRKKTFIKTOt\nBBeMOrjeu67rOuyDtCojGaR7dvWyzIrAUNbPSJKLTVZrJhVsDVFnKkqwSO2gMlVeWB+zcuhAQ1Za\ngN7bJE/puo6oJIDp4eHNSXGQIYa+VMJ7PxiM2s5qnfd9DyEMB4UCFoKjgNbZtD+L3iYakZYKlLh1\n947WcrPZtG277lrrnQEs6mqzaYOPUgkUMm21iGg+X6TW3Huf/AoocgCarWaj8YCAKUYfYyDKS1MU\nhc5M03UgEEFGJqFU72xnbQiWdgQBjp4RIwMKMRiMQ+9931nnI1MksD6Ac0VRD8qBMAQYpIQYfduH\nENh5dIGEIgJKrgrs0QUWEhhom40kAAQHipFIgQABQmYotJQx5QwRcAgQOUYAT4QxCglaShZIICKg\nj2A9o/XOWxQRQpqFI0dk5gjsg40cgCgCuxhC5EAMBD5AAJkot5EoJuNugEgUKDJu3SB27CFIe/Dr\nkLtAxQAIkhgRJINgQgYhUAmpgQWDYCEAiZBCTCwiEEIYYYAFgkBCTyH6dPYiMEfg4Wg0LgXHWFRl\nLvXB8RG7AMxhd+u9o63NODLIpxcvpJQ+iyta9RaWvLSqc8Jf+kWWa4EyIkiUWkoEt1gub/JgfTkP\nTCc3T6aDoezDplkHtTqdLfuuM2U1HVSDvCLn+7ZbN7Y+mp6fL30zy3PdidAJ58myIoEscp0wqM72\nRVHlOleTyUTs/Ll5p5dMUx+8jqSnihXhBz/4wWQySnq3siyFEGkoR0TJqTNVkTSkybIseEjw9GQy\n2atfaWcUlGzZEnGO9wbyzEl11DTNdDoloiRySu2a2rmXhhDWTauV0XkBMUgpfYyJTJFqGxGt1+tj\nAGu7ejCJMc2JiHZR80TUNM3FxcVyuVytF4lYmFhAiWMjhMAY90R2sYu1TZU4vdVUolJBdTGURQXi\nVcCE2EVGJbX2aDRi5vV6nZ5hOBz4rvXeF0U1nR6s1+vz83Ots9FotFisdix2p7SoqjLLNCJKpYRQ\n23htgBijD5FpU9fjq/lCWVlVxdn5UxY21/ry8rkRVsns5PbgcvZUaT69PB+PR+v1crFpPXM9np5e\nfVCVg8lRfnb2wcnx8WK+mRwNFvOVja0p89VyXZa1jX01EETALBLbB5EjBUfuV772hSfPP7x97/bZ\n2cu6GkYWjx6ePbj/CUITvJCQSUTfdxJYquhddL0IIUmzgAQzuQCEIioj33v/T9uwqUL2O//ip8Pp\n4DOfe+d7P/j+rVsHz1+8zEw1Gk2ePn1fCKGNWC7PQ7DOtXWl58v5+x88vHvntSIfHt283cdusbzK\nctl2ayJ9dDyFwK+/fv/5441wpYhkXQuelDBZrqTUkb3zjojSIDoBp1Ip8iH4HpTSUnEMnoKgyCwQ\nCCOyZ43KSIEMyIIDG5MVReVpi80qY/KqECwa20PokCKTZ9daL0F33vPmcgWqWDnfAy99f76a18yu\na2OQz58+fvTw4YXwA+mobwoJQgiUmQ8khGrbViPkWmiEg6OD2Xpp9yd89FtyrJBtt9FC5rnZY+MC\ngWI8vn1MdGpbm2W6LEtElqiIAjOtN8vDwwPn+0xlRCHPywjx1v2bk4NxCiXasrzqOikIAeDTRZau\njrSN67ouMNWDwezqsizL6C0jBmKS8nLd9dhqF/I8L8sy6FzlOZNWShVFQbpN2Hu6cAClj2GPo+yn\ndyEGiCRha4aJiAk1SctXkmtch1i89zFCcnNL1LV9YMT1AWp6Hm1UVZnrtN7Eetjzj5wNRBR9AI7O\nOQlIyIiSAjNRQniD90loxZGAWIAUIBJHlnfj2z0Uvx/o4rWQi+s9wLZ0Ee2jANKoYst25uCtc8Hb\n4EGKVO3Oz85wmLneLvCy0IZClEIE66qqgkjkQ4LBpFJCSZKc3R46GVC6jCEcaedFS+Q4zpaLuihl\npkrw9bA8qcaT+ig7Hd4vb1eiWjebdbOqRuWN1066vl+slicnxwiwnC+qvGg3beitaLGLcWUC3qzN\nsGZBXS3huGang7cKlRIy9pGMvth006p2CGo2m6ldCuSeyEDXRvo7+XpixLGU8tatW1mWJRgtTYCq\nqkrMHCllMshKFWU4HAdPAHB1dTWZTPbE7nSi7OVNeZ7jzgYjceqSQcN6vT4+PkbE5F61N04loqOj\no7quA/Fm3bgYvIuHRwcaRFmWm/UaES8ur6SUyU+IiIoyg2vRsXvgMc/z5IGU5TqEUJZl0zTWdukI\n1HUNtB0s8c4QNpXbg4PD9Od7Q9K2bdu+X23WZVlWVZX0DamlY+bnz5+/fPlytVql8VUynXv8+NGn\nP/VJk6mnT57+6Ec/unHj5ptvvK2UePfdd7uu01rGGNtu471DZB/spu8CSJkrCRy85URL9ewsCaGb\ntkeFRzcm7z/88e0HhzdvT5tN53qT6Xy+ePG5L7yFsv/6X/oVa7u4Wn/nO9//7Gd+4Qc//ImzYTAY\ntG07mY7W3eO6GrURnpw9ZMYbJ7c7sqVW3gUIkJgIzGkrhjH6QM352bNPfuL15y+foYAXz1689fZn\n7t6smjUVOuMAKAQgcIgko0IQktartRSZ1lobCSKSiJkAoWC+ejG9WQxYELjTq4uT25P/4dv/ejSu\n6uHdb37zX735xqfffffdEOOgrE5Pn23a89ffuKN0PDt/Npuf5xlMpmWRlxdXT66WLx8+am/dOBoM\ns8KYQVmu5/7xkw8wTpl6JeJ4OpCx4sDO9j7Ysi4IkVkoJVMCAKLIpAApmJQRSivtGTimUAkIfdAg\niGWdlaWI1LXO264PuS62O5XIjATIjOSCG4wL3zkgwMiECAIZBUNUmXFEbd+yliFaJj8ZDxoHBQxt\n1wJFa9sqY41Q5NlgMLiaLREgBkfRS6MjeQheigMgFohGa4kCMU+XsFGKoy+yPESXZ5nWmkNEhL63\nVVUgsnO9lNvRZmAfyQcXneuPjk5Wq0Wuc+aY/IR0zLpoLy8vrbUpnEUIsV6vk1ni3ltyv7ZKKQeD\nQULqgutRyshAUrIpZ51rXMi9t9ZaT0YYo1XwRATMEEIwecYoQWCWFQCAUjESM/E1zm2MESKnHbM2\nMhXC3RW9pQTsN4ghBETDO9VKCJHhVVDQHg2SUkqVlZUZTyprbYxb8EZIkzaUqUh47xNrADlY2wFu\neS57YGlXFIMQIiUi7HmqtL/h1tcj7TVh58icljXceXrtOUppwUlcj2QCII323gsQIcbO9sE7763W\nUkgQkbQUmTZsfbDOE2iljFSMYbVYbhe9zGQmE1pFIsfucvbcZ5Fz4JKc7x33HnxArwskGUMICOQ7\n2/ftfLN05x3pzs5t03VZafBSztdzAnF0cvjR84+Gw/ry/Pz1B681q6au6+qwHNTl4ZtvFNNRJP9n\nf/b9F5sLa3B0cIRMm+VGCgU61APd0nnIlY+gUgOkd9l6+96IrnnnwC61iJn7vncuSKkTUUoIBBDG\n5MkqDUAAiB2cJYui6GGrLLveYyFisvzZelMCbC2Nd3ES6Uxq23a1WiWuXSoq13cuzrnOurIsVxfn\nzWp9fHIkpGi7zXI5T2ez3BmwM3Oqgolag7tCu3/C1Pp0Xdd1XdJdj8fjxADcGzYAgpQodZYjAkDT\nWWH9uulgR6tTSkmpptPDdDKFEPq+mc+X6TQ6Pj5+661PHB4eOueePXuWrPNu3rz57rs/Ho1GLrrb\n924Lob75r7/pfUxFsaqqqiqUlnmVS4khGNRq3bkiKzOtfOiCtQAgckUVMMjX33wNJD58+sGXvvzZ\ns8unk6P69bfv/vEffl/q4uRONVs9O74xfPzsp7/4S1+cHFanF89+/1//93U1ds5freSbb76xah9v\nNhsCNZ0f/ujP340BRvVkveomowNg1W56rQotZIyMjElIyNjePBsuNvdByNPzyz/+4+/883/+b/oO\njRr5TgJrLbQUJMFrHXPDAk2mD6QwKpdaI0vL0uW1LgYGpPcXrqjyz37xc/nk9e9+b/7k5eM3iweP\nnz4djifPnj9frdqvfe1rUvLjFx8+eO1kvn5WDrLciNGovnXrRKk4mRSnP/34/t2Txebq3fd++lf/\n2tf6ZjObXfz6r33jX/2z74hYLk77zeblpFZSmb7rlDRlWbvQo4gCEdBH74O3UsroIOHVpBRFE2NE\nBqbAAVXI8qySWXnn6NZkYLjvKp1F62wf8rxsXQcGAloP1lTYue58ftY7KxgUCiWxMIqN4Rznm67p\n7dy39WiCUTXr/rKfty1IVi+fPgm2Ydd0Pq6axYW342FdD6cQCUHlWg3qXAvBrsu14ug5MhEhECCl\nFY19mI4nHKLliMS27aIPUoqubesyL8rMtloqZI4+WAocgqvLAZFjjiE4x0AcAMCxz8cVGsVKBMeW\nAlBg5lXXkMTW2zrTgaJ1VgiRBsADle2BBCmlzjJGQVKuXdRaj8v6+Ph4MpmsPBWDQV1N09WhDTBt\n64TWWoDZL+VEnGKoEVVSAKYrMoSQF0VCSnbX6LYcSZBqFx8qpYy71KIQAsRtIsN+fdtOysHHuBXU\npwUBRAYi9y4ygfMh13nnmi0dm8jZTgAHjpDiWUFShJ0n7Lb87CF9JqT4yrtrDz79xd4Id+zl7SLM\n2+UuNUZptcyyLFhHTETknAWAyKSMTnxZI6RG4QmIQRCzCxSBfCizPD2/UGo7ZbC29W1VyhhYgMyz\nzIY+x6zg6EhEoQRgVuRHw8O49ouzpV/P+6vusWveuPvW8HhwMb9ASbdev2W9ny9nyhhZS9lrOdJX\ns6vL+SVdkanr2Ufff/PTn75586YohJRGIwVgYJgtlxIwehrVU5Zi3W9CILU/RnslacqIS/aRdE2G\nkr7sBw8elGUJO2kqInZdl2j1e2u7BMTtD3HqN3EnU933pOmZw86Pdg/T7eGvZESdGBAJD0x3ws7f\nWgbPQM65SMFaawpM5URK6b2L5KVMaZDJ64HTywmQiFtbvMT08953fXN2dpaig7SW9+/ff/LkCdHO\nKYGFkKCkUVooaaTC4WDMEJkwREcRtJFFXuWFiUTO93EXqZ5wDGNM4i88ffqUtyTOzBjTts3t27fv\n3rv9J9/93o9//MN33vnsF37h8zHQbLaYTCYxeuetc1tXWSGhruuDk2EkNlqYTPXNZj6fC5D1YEQE\nl/NZZPeNv/Ebf/y9b/7Vv/H1Nz5x59133/3q138REf/4W998+1OvrTdXprz9J3/y7YvZ1YcfffTl\nr37p4QcPp8fTt9547YOHP52M6t/8937zd//F79cjeXSnlMKs5o0uqafVuD70HjONABD7ECMrlgoV\nK/Xrv/7r/4//4h8oox99vPj0Z1/PjItRv/HaZ3785x/m2RADUvS5QYBegC+L2nfaB7Jtb00A3aks\nGmVUUXz85IPx0ejhh6dBr77+63/lT/+cRtPqanH55Mn7k+HoB99/eOvW+M9/+F0Gx9ISXl0tnn+2\nfltKKRH7vn/x4rQs6izTp2cvzmcvsxwmk8HLZiUVzuYXy/Xs5sHRur34+MNZZS45mKvz1aAcHkyP\nYuRdMohGBsEgpeqlKooCYgAhOQYBoI1m5nbTudapjF03X1ycNZfQLmbDsgzWAwhpdOedKtBL18d1\nPjAsQ26UcxYDKsy1UlplRVYiqLIYLVYbabTJ80IV1nYjU4zLgaBpXZWHx2/UMtyZlCr2RuCt2zee\nPT/rXVA6Z+ZBkeWZ9t2mrusHb7wZIvPOzw1p65vV9+3lxYWUiAyLxQIRy6ogoqbZEEWTKa0VMwhp\n0GCMyjurtFwsZtb1wgAioGAJct02w0xnWZbwa+tcnmXD0WgxnwspvfcuucYlsEtrVHKfxLNdfBEC\ncwjkCaNQ6c6+71m3WtUA0HuXSSm1QiUjk9Y6OPY+AgtEEYFd8D5EYokoQGxVeqlsSClTNXLOSalD\n4BAE7RwQvPe5wWR9q5T0nmOktK9NxXK/cQzRSsV5Jw/GE621AA2kURprfXJV0Fp3HWkpU9/jbQ9M\nQIEjpcUq0fqFxN1qk1ZOmTi2+/q3r0A/1xulH/aNXVoqI0dUmPJh0wOYuSizpXMUgpIpQRsJolKC\nkSLEz3zmM0eZ6rtOC6ml6psWd88cY/QhpHlYZLLBh+A2q2XsrUAss/KyaRWSioEhIkWOpDJZgZY+\nE0TG6HgYbB+enT8KkQfTYTEorpYX674tqupyfeEWrg/9RX85DyupMEKcFMXnPvsZF+j5s4e265HY\n99YMJ/du3p49PUVCjiwZbt644bq+63o1GAx+rnFJBSPlHomdgfkexPTen52dpf4x/VXa3Sil5vN5\nEht1XZcI2USU9ICLxWI0GiVKfipCKcovFYNkr8A79n16Gykhu2ma/YKeNgg7y22X53mgiCi1UbkZ\nx13S+XA4FELsJb2p7CX/ZqlEjBHlNjp22zojKqXGk+G+g/beHh8fn56eeh+LapCKqRAopVJKKqWl\nFB99/DFsfegSRIBSKiHwzp1bV1dXqaVLG0ZmTtXok5/85PnZZd/3yWH2S1/6ksnk+eXZeDrqbD+a\njMeTyYuXL9u2Ozw87F3XdV0IXipEKRAgy3RR1T6IhJQlnUdRFLhNv53euX+nHOd/9O1v/u//D//J\n//v/+w+fPO3e/+CHX//VvyGlfnvxltQ8HI+fPns+GY/zonz7k5/657/3nbt3Bq/dehDBf+M3/0pd\nmadnT0ZHmQsrkduTk2Np8Gh6O/R44+jOk4cvBBtvY984ICzyKtdZRPdf/ZP/9lOf/NLl/Oz1196+\nWsyPT4ZFObZ2dufedDq52S7brukHZdG1TbuZDeppPhlv2saHjaqCqQtd2mwA+VC8PbrRBfurn/4i\nCvNH3/79dTv/lV/+1d/9nd+5f/tmOchee3v81ltvnJ+fEvvXX799NXs5GdfNenV68bLruul0alTx\n4snZpl8+ePv4Yv7y7t2bT589uXh59sm33rm4OHvr7TftSt64eaRgOKlvNyvfNc2quZivzxF0npe5\nNlKq3BRllnME27kQQqpMAFtxt7X28uVlXMab0xMtIlBvJgOl1HQ6FYyr1QaUxFxkg8zLXhIc354c\nTuvm6enGee8ZoxAWMwvGp9yjUPXMHc6vLmSR1Rb1RV8fTDYUrs5ORa0vm9k6RxG7QqvguoePnnbW\nZUXlvQcKgzyPvo8xEmgXCZKgFwhoO3j4hS9+/uOPHua54RhfvnyZ57mUwlMcjEfrdi1B+iCYUEgw\nMgOkg8PpaDR48uRZPSjKrNwzth1wXVWZ0gTMkdq+K/PC5Bnfuz+ajG3X984WWQ4CBaAxRgJOJpOb\nN06klMH1OssigyV6djE/WzWryFmWVVXVo5J5rrUGgc45pUyWZQIlABhjrGPrPSEoo4G3enkASLl5\nzAzAe4Au5chQ9MwYAnuPDNvxcNwmrm1326kMpDUhsRBhp8zbPx6kQCkRJUchhfY+CpBAqKVJi4NE\nZKDgeqAQnJUmGqmN1GkqY2QOuFe2gkyGkcQQCQJgRJa8X2d4Z1Ujr9l67acJIYQIUUmldlhOQo+U\nUgyRmYTUqFBqSUgoIZDnEN5///0zpBjC4WSqpbo4PYshKKU4EgGnfjACEzAhqIAjKMCyaNWBHse1\nOywnUUTUTEgxRogwXA7Zce7NsBj0Rf+CTk01Wm2a+WbuNZXTgQim7fv6cGjZ+Sxc9rO1aOqyjMzV\nUXl+9qxbddGHw/GkMEUTbJytfb6+MzqQqJqmy0z2qXc+E0JYrxu1nwntwStrbdd1BwcHqS9Jx2sP\ns44nQ9jpXtOIKE19iOj8/Hw8Hif6ckqt7vve6Dx5LI5Go77vd2ovcXl5mdqpzWYjdxZ5qTNLIEnq\ntROCJ7ZBipSg6hBCEoUpo4mg967Mcmu7yWDYdV1ustTexRikRACSEmP0yQBmr0KHXeJtasVWq9X+\nVEjs6kQ08N7v7DSTZd1WFVQURXoVZpYShdj7nUOqN8k/Il0qqVUaDAbPnj1LNTJ9nOVynef50dFR\nOkRpK/Dw4cMf/ehHCTAcDgdHxwdCiPn8qmnWIGRvuajqzEhENkoURaFV9oJPpcmyQv3qr//K53/h\nszY0o2n19qdef/Tsw6Mbh21rP3z8cV3nkdy9e3eaPpTl8I++9YefeOd+npvO+oPjSYQYhB+Oq7fK\n1z76+KGlBnUA6cfT+vzlwkcLEjhSoBiIMpWVZZVlWYxZFPTwwxejg+LRk6f3Hpyc3DxZLpe2p7bb\nmGLSNX2ETukaAKxHRAWCiXsS1pRidKBFQaQ3FvpyosCCLoLzYXI4mBx85sXLp0VhpIoo+jffvmnd\n/Pa90XJ55cIyL1HrzJg8M5XtaLXwR4fTF8/nk6N6MV9Pp+Ou62ZXEGNct023jP0aRRwRlnmli4EB\nEKNpoXNo216gMgYFEEfHIAFM17SXl7OD8QQQOcYQXRBCKm67Zja/OC6Py8oYjBAJgFbr+YVC55w2\nBRBa9jEPjd90tJnIQT2ueF3EvuNI4AwFEVl7kog4n8+yIiuG9azboFBFUTkbnY2E0XctVjVQ4IgU\nIiFIARx9jF4J8EC2a0sjEdl7W1W1CDFgYGYgoBSfjXg4PWiaRgBpreuyOj4+DsFv2sb5XkqZaZ3G\nsUCCZYrPEXVdt+2mKIomrJ1zQiwjcOe8Oj9vmybL8zzL2q7TSqEQUgjX9acvX67W67qqnPcJhPLe\nHx8fb9aroigkclFVBOiYD2/fP1s1TbM1TUhrThoDOx+l1Lu0GqmzHDeOtjZgAjjutsty7xx8fZqQ\n1ujUUpBkKSUgC+a0x40xUtIy4ysSLzOv1+u+d5kpQwhCwn6AlFjyvEXfJUWWUkupESTHRG5FZAjB\nU7AcA9B20Ug1DxERFVEC8NWu2gm+dttj+/uf9x/q50dN8POIYuoBeKf9ECp5XSWbxsgU+mBFsAIQ\nlVRauxi8taUQve2llHKbkJS8OkmiqrKR9z0FYivdnFQvSLIwcrZc6swgIjc9+ciR2Op5e7ngZSt6\nZi4GtS7MulvbGLI6b72dr5eosG/cOmxipKZrilVRUpVro0yeacXWUmdXm9XzPkYb8jxvNptOiNGg\nKIpi1WxUosrwzoluz7feA2L7HnPXG7HWOvh+z2lZLtYpD+nZ0xdKmqLgrrXAImWQr/t1etrlcplO\noFQSkjlHWZYfffTRL/7iL15cXKR79g8QQty6dSv1FumFkllRCgX/3ve+97nPfQ4EWut1nnHwMUYj\nZIw+hV2++9P3E9Ja13Wy700bIpMXqTb0fT8cDvfWD0KKoijShx2NRqncMjOAKPIqhGB7mw2LtukS\n9z0G7tqUwIgI0vaeyN65e2symfz5n/+gqqo0ckzHM0GCiYYXdzFLVVXVg3yxvACA6XQ6Go3Ksjw4\nOCiKoqoGbdsqJQB4sVh84QtfePHi2Wg08pGK0iiTAUUU5GyX5/nh4eEHH3wEUshc/N//8/9sclis\n3em/+x/8xsdPfzI5GJ9fXnzn29//P/6f/i//6X/6fyMOH3707M7te0+evF/Xx9PpnV/91a/+qz/4\nPR/gX/z+N3/t61++nL9kidWw/uWv/XKzsqPR8a0bt0MU4/Hkv/x//fbRtB4U40E1/ulPPypM/tVf\n+dXFpv9v/7s/+MznX3v89KcHN/Knzz++99bBOBPv/uTDv/nv/3v/yf/6v/jcJ+66Vv74h39+cnDn\nwb03PvjoUdet8xLHx8Wjdx/+2p0v1hOp6nJwcPDhx++99c7bi3nz8UcPJ+Nbrz945+WLi7v3bmZZ\nzHMYT/O282UJEeV4kgFkVTk6PDg5fTk/GN9dLpqLl61S1cfvv/jlv/zJdr7svdea2tY+e3o6Lg+f\nPX2xvHqymsWvfPE3hKT7b9x5990fF7UsB2PrIwDmypw9v8gy3fWbP/nT777z9if7rlFKrVabPDdt\n3/Fl7Jw9OT7MSHpuh3WhRakFndw65EgCcXo8ffz0EWksi8IovVzZZxdPn55+6FYNWRwUx4hitXHT\ncXnn+DDG6HU4X80o0KYWqGjTW39woI+OM1HkJvPWGSGNUQQWxdZoI8FBSU6ulOzazloL0DBjoqdG\nJh+CDeH27dur+WJQVgJYokieJq7vhNHMwQdbFRkzCwFKiRQkKiXO51day75vjVLW2aIoog1GKkEw\nKQcETJ3LhdKopFLRh9jZcVGzCzJCVQ2C853tq1GZdngnJycff/RB7xwIGYVYf/zx1abLB6PxeOy9\nL4pS5JVWuTF53/ebjTiIpZQ67QuFqtq+U0o51yN4KTQIVEaHABAhy7Kuc2mJSOAKgEhb1SIf9H1v\nXXPr9slyudwu7gBCiJQU6oOtqipdjwmtUUoRuaIommb92ut3mBkFUwAESGL8tu2bpg3ODaoq12a+\nXB6Mbo2Gteu74aByfdOsW44kAKuisn1vjBEgjVHGGC1N1zUcyahMgCjzrHddIjclc7z9spambqkZ\nqOs6TT2UUgQkdvGY0UdEtM6ZLAPDy826Hg1Pnz9TRhNwWWZ5NoizxjNNxmNT5H1vCdjFkDMrrRM/\nYLFYVMOBs84UOUp9FRrIkosgyukocFg0i1xlYjBadOvhcNhKwVrGGFdx43M0ed22lonP51djgGo8\nvLhYgN3IMq9Hw4vF5WBQc5DecF5WC7vOy+Ls/Dx07qu/+NV23tjgszzr+z7YsGkaFkgQ/6vf+v/d\nuHPr5p2bag9w7WG6VHuSYU+6DPYPSPupVF32FTv9sF/xUy+Z8LS9onY/YNwPopKBLjMn6nPiniUs\ndV8U9wMn3NH8dvhsTK9IwEoZRE62BCHEuIsMT08iVSLMCClRSikl7hHYVIRS5QPYjm2v3/Yt/L5x\n5B3JcP9r3N14582zZ2fSLpH9+sbn+k4nIQ9aZ8lfXAhVFEXTtADCey9FyqkhRLHTOSlM75tIACBK\ngSozhdaZygwx/Mf/8f+q6ed/8Mf/7Jv/+g+uNk/+0l/5pcvl7Be+cDRbz0/PzkaHh6fPX9x/4+0P\n3v3ww4ezr3/ttQ8ePn3vp//l+ezsM5//j77xN/8nAjuS/mp9pZV6/PGTGOQ7b33u6OTQWb59cr/p\n4aaRl4urT332cy9env3P/ud/6yc/eff9Dx7+2td/9fHzh3lVV4P867/x+W9991/++l/+lb/0V774\n3kff/eJXBqFprpYrnRtTSsbQuwaUe3p2Nrxx99e/8dXHpz/50hvvONm/uHgcRXx6+pSDPDo+qIoB\nx1iW9cX56dHRpO9m683s6Hj85OlHd+/d/INvvvu5z55oVXz3u98HytpN/I1f/81/9I/+yc0btxHK\nvgWjq/VmcTApL9Yzjn0movW8XDXvfOpLj589/eSb4/nyshrlm82m7zerph8OxzcOj46OD9770fvt\nrP3CFz7XN73a6rUpqT6kydbtBg0CBQ/NvFnVhcEYq8wAgyn1qpvffeueg7gOSzMwIuDGrw+m44PR\ngaF8XN/K1cR3ojDDYVX7YO+Im5Z6kDRbrlatf/7iklWx6V2tzf379z//9n2wy5y6DL1WeHx8rE3R\n+UAg1uu1ACoLE/pOSjm/atu237fyCZlIKcZCCGe7hGWFEKJ33AtdZ2kQku6sqorCdo+ota6qKoSQ\nfAnFVsGNyCCYAViiAEQFKBi00pKBGIyQSkgFiCjYZBEx1cvLy8ssy3SWBWKhlN9dTQlxCVKGGK1r\nWCADolAgBEoRGRkFRYiRIzGBkAIJgTkhNNuMTSKSApIti5QyeEq543jttiUD/9vdH7eDW+BIFFO2\neFoK/v9k/Xew3Nl+H4id/Mu/zjcHZAwwGEx+M/Mi+R75AvXIp1XREldLKlmiJJfL3JK8Knstr732\nrkOtalNZctkreVc2lSiuKFJ85MtpcsYMBhkXN6fO3b98ov849/aA3C4UCmhcdP/61+ecb/oENVPJ\nAhQYojWghDnMgwDt7+8DACjGjUZje3NDSc5YHIdt33cB0EEQWCMoY4zrusPh0IIFLKrLXrNt/MxO\nFXslf4o6Ak/hzVpraGDFK4xoEIRKqbIU9oTRWlNCOC/TdJyW6ec//7lXPv/ywd7OD//w966fXVOT\nMQAgFRVCwK/HBkGulO95nHMFjON7RVXmeV4KjhGFmBgAEYZYUEmkgdpBHnTw8cG+AAoDR0lNXGoY\ngARmOSdAMMchjksF9+OYMrficjAcGYzCVrh+/pxhZqryw8Fw7cxCUfL9cffyhUvLc0s8F71sunRu\nPR9lhzt7UVTTUhpkBAA54jLvDo8y8u6777qua4Fn9lu0OnWj0ejxL3U20UGIhGFo03xwSmJVyiBE\nfD9EiEiplTJKGSl1VeWNRs22s2bBxpwiF20fzCK/bfICT3XEZ9Fitnr0qf+sLddOcdUVAEBwZaQC\nQEOljVGMUvuFncQMoB6PmnbJ6tOHXdDGGKXN42/36fsCLbUAAGiglJEAGYiBlJIwjClSSp3ShgEm\ntseLECIAIGOg1p+Gc4wpY64dgUEIpdSMuQYITJjnhwBSiIAfxCwpAcRSSRtltdYQAkwcTFyICAAK\nQgi0QQggA7QVEwMQQQwg/L/8X//vo+lxezlcO7P6V//nf+1f/O4/vvTElf3jnX/vV3/57/8f/89/\n82//lRs3bkzzvOT65VeeGQyzb/zSn/1H//C//dJXPrO9t7d+8cWjo26tGdMAp3m2urqKkZfn6fbO\n5mRYTAbpV752JU/Ec8tn8zz3684nDz7Z3NkK6kFSpoBg4tKoGRmsnnrmiuPDZjPa2dvOqmR/H7Qa\nTFVkWhyfiVcKOQprJO+Bv/f3/1e/++/+2ZVnLvlNV5Wpg72wHRd5Nc2zem2uuz/MRwppFvrR9vbe\n9acvCpVKwMPIHY17n/3CSpGrra2tZCI0d65fe/HVH7/t0bhIpJQoDuenuU7HA7wUS4HjqLO8dK4V\nn1FX2b/87X/77NOfu//w4d7e/kJnrqjS1956gCj4G3/j13guVhdWvved7zb8FvOwqE7cHRGBEEKD\ngBe4VbdgIYZlFXVCU+YKVmWV1OeWqqwqyjJw4+7keJhPfv2v//qr7//0leuvfPDJO2Hohwk1iR4c\n7avyWHGKkeN7juNjiKq0GE+z6XCSIRIQpx4b1wNBNs3u3LmTDw6wTBsOaIVeWaRpNnXDWBsoDMjz\n3HUowwhqsbCw0B8OOJc2pw48185isyzb2NqURkutfCeIokhK6boOQLA+3xxNJoycNEUajQYC0BhT\nj2u+76+srAEACETWIAYhRDFTShuphFbQmkNqKxsFIMFFmk3SxEhVSSHKSmOYiQpSIgUfDoe1KIAI\nAa1sl6WqKgXxLGmDmFbc+stZzC0imM16MDOgE0IEQitwrJU2hMBZwup5no1GgiuMkPX8NuaEIvlY\nFvipfPAs0bQtFimMFVWfJZoQI4QxNhgBDAGRUlKEGSGe69bjBiM0T7PtrUeB51994nKSJM1m6DBY\nVVWnM7+4uDidjouiCEL/3LlzNthnWRaGse36cF4CDmZDIHDasptBG+w5OZvT25wbIxSHkVH6xOKH\nIgC1tcsL46gS5Y2PPzw83Pc9Z3F1ZTDpYlECbVJRIWU0F5Y+LIqsyPNaGC0sLkzSJIgjz/O80OOY\nayRd5gEAXJfZWkIDvX5pYVqmGc/3uweZrBDDYRxhaohml85ejsLa1s4uc72LV64++cxzW/vb4ywZ\nJMMsr5JJcuHSpcO33uqPhmEY09i5ebARLc4//8oL86uDg62Dna3tpcvnDw8PJRaQYk2NQKD0+AhL\n8txzz7mua6XqZt+Z7XHZZ2aTHnuDxuNpHMcWrXC6jKA91l3XtbmV1joMQ8uG63a7ljpnqTnmVKF1\nOp3ayXCe56PRyNbOJyjMU5S9fX0bBWd1DOccITSdTgEAaZ65rjtOpsjoIAgYghBCz3Vdd4IQQAhg\nfEKWsmEJAGDMyczQll8ztVb75On6+HQpQwi1UQhiiIBSygANIRSSQwghAsggaNV2gQYAIAwfb2za\ncD57KXTKyQCnqrJKaYRwGMYQIqOB6/qEMAgxRgxBbF8TQoggwZhAiI2xuBK7Y6GUkhAqhBIKIILD\nMAZYfuELLx+PH924+fETV5+kFN67e6tea3/x56/fu//xzl7+zW8+def2w/mFThyrosz+8l/9jX/5\nO/+///Dv/LXvfu/bTz974dU332m1GsvLq/V6rSxUI6oNB9kHH7x/7uxlxMxXvvrFj27cqXean1/+\n7Ecf3ax1AkrcjUd7rk8gEZ2Fxt7h3jMvXP53f/hv4pp/80ZeD8H8Erhzk881+UsvPPfZz1559a3v\nAddZWAeD9CCok2k5XPTiO5/cbi+0eCrKQizOrXf3hr5T/9H3P7x66fx4PMaOufXJo1c+d/3+wxuU\n8PMX1judzqCfLM25mxtHH77zMEvejsL2o42DKHL+/d/41Tff/dH+0aGUYG1VQxNq6dy9vVmV4IN3\nbl976rnJJHlwf3N9df31t95OUvDU03PNxbmP79xYX1pfWl/8j/43f/f1H76hK9DvDhr1FoTQqzxE\nMZQFpghg4EZuBXPNCkz18uJC71ApWuUq8WtR1AyH+wfrl9f7SS8VyYO9yfK5pZXG3Nv/5o2armEY\nu45Dg7gsy7QaldBomGIHUKQcCEquiIMk0JVSnudzzpUyLnXKKh2qymek057vDseIORoiTJjnBxBI\npMlcZ2Fz48Cm+WmaIgwxxo7rBkGQJBPf96sik1JWEKZpqpTPjWotdabTqeTcrtJer6eEJIQUWe77\nvm2JE3iSGjqOxwizMKXZzN82A+zCtkLGszko8z3qOcvLS5uPNuxU1e4KoRR2AkKI0PrEqBNCxhgu\nbQvBAIwAgphRAwGCBGJsNLSANA2EVSGAECOkjZHGaEIIxtpOrGe5su1/WHFIONMFthKQj6ndz3ot\np4eMVloBeJL72ggHJEIAEUw5lxBircB0knLO9/f3p9Pk//n/+CfQuGurlyUv93Z2HRcVRUEpDcOw\nqsRwOEzT9NLli1mWZVlhIV12hMw5dxzPYodnBx04xbzZy7MUYDij5UJsmcXgMQ8ECOHi4mKvd0wI\n0qY+Gg0Gw179/LkXnn5msHX/4NGDg719bEA9iBzfwRhpLkPPV0ZjhwW1uDccFEWRJAlLsWJCwcpl\nXjpNQi/kVeW6bllVGmrkkUyUjWYwSEvqIyFTDTWg3jvvfwQ18MIIE3dn/2eYUSf0NEKEOLVOfbg9\nLQv+y9/65vMvPvOjn/yYEn93c//O1kYlgBzztJ+MisLLU+y7UiPDtEA6UYUyGgF0Amy3Qw77UdGJ\nIuefkIg+bRHpLMtmAER7Q+1topRWVZVlJ0o5RVFYNEQQeBaG4HmehYbbaBRFkW12zyKNRWbba7CZ\nFACAnhY6syLDCtYZY+I4Hk8neZ5qqAlECwsLoesAABilAIDReGrjn9UGxqcPG+HAKRvJ1lhCCMrI\nLE+B8HENbKChRpgAA6RRBmqDQCnKUlRCCwCQQUYZfYL2lpJzrpQ+JT/MfNNBVXGldFVx+5GrihsD\ntAbAID+sAUS01tTxAMIQM+pSIYQxSBsNAdIQKQOVQcoA8liKp7VxXdcqi0ipCWBSwx//9NW/+7/9\nzW9//1/92T//jcm0K2HaXFi6s/EQI/ar//7zt2/d2dievvgyPnvh3M2bN7/1rT/zg58Fo6T78uef\n3dm/u7TScJ3w/p3bZ85c8Bx63D3otJfOXVwFRhY8+cPv/N7TTz/Pq/zb3/8epc43v/nNP/7j7z79\nwqX+qNsfHnNTEAI//uRObwD80OEqX1lfbjfnBsMPv/xz15YWWpIeXHsx3t2fKgr+1n/4X/3v/0+/\n/GD7k6RMFlaXIYb9w0kjbu/tHskcHfZ2oQa9g26t0UYO3Xy0MU3evPb0+sOHd555vtXrDkajZOvh\n8WjAAQC7u0PfGa+ttsqy+Gf//J+98Lln7947bDSAlm4UzBEUbWw9LHLpufGtOw8OdpKLF9aKqnz5\ns5/5+OYHr/6w+6u/uXRv80EURW+++8Yf/d4ff+75L/hhFNcj12MAANd1IIFpCfIqRw42RNIanMpe\n4DoL51uQlcPeUDK+cnFpd78bL8TIQz987YcL5+dTMXrrxtvHOwdPNp8CSokqUWWB4BQh4ASo1qLE\no62FWEGge9P+xmgokh05bjjuglvHlEGMKKUEUGBEXpaVEIQ5BhOltdC64tJoToCRxiBKECWQYICR\nhkYoWQmOS+wFvh8EVVVgSq1ovVCSS4ERLYpKVtx1XWN0Ms0kF/V6XWtQlhxjbIzAANqj0/d5EMU2\nGp20NxAyANlOgNYaG4YBmKkDeIFfSL68vLzx8EGz2TRKIAhdP6i0rgB2HEdBXKvVZqltWZZGQ3VK\nMZxZfWuIldHKaKU1Ou2UwNPtaYBmjEAkbRS0zRujTzpddmvbTgyE0Fr2/qmGB4RQSnlq4Wa00eC0\nQWfTU8GtVSAVQiBkE0Hje+F//p/9Z7W4sdBekQL/8HvffeKJJ1zXjUPPIY7jOB5zXMqyZFKW5c0b\nH/u+5/s+Y8xjTlVVBhPHcRDBVhFmFnJmVEh7MM6iEUIIImgnTPazwBMwuoIIjSZDZXSeZqNxn1L8\nxJUrlJEbn9wkIq2vLj75wrM+dfY3tx/cuQuUXJqfGxx3s6okDtPAYEIc1zXGOBRpo7SGjgSyAgxo\nUyjCJa5EGHgUMJlnV58698lGqY3pDweIOTRsLK+cFZXM8sJz4+XV9UrwDz7+CDmwsdDMpoXPgjzn\n3/2j7732xuv1ZmOhs9BqtXbu72S9lHESO7V6VB/0hq1OU2klsOa6GhejJE0Vk8Qi7mcpxqwYOmWz\nfmrUbSOzVTi1BTI61Q1SSlnBD3MKXrRLhDGmtZy9vsVW2te03oX2+dkymkUd8BjCZFaEzTCdtjFt\neUI2wiGE/MD1HU8phU7NHP9EdQI/Ba7YzfB4bQRPHZsef2tg1bIhVsYgDKCC2kiEEMJASmmAghAi\nDKG2rUWDMQT4U2LB7K3hKY/KflJ0CmFnjBloILe1EQYGuK5n0TsIwUoJCBGEGEJrbGqdtj8VarKv\n43thXkpKGcUIIVirNQbp7n/6n/7f/st/+J/sdx/mPHE8OUl3z5xrjUbJYLTVbDuNJth4dBtCsLV9\nb2vnwlPXL2VFvxJiPDlcXpmvh6HHzkAAut3jopRllRFqlpcWOS/ds6utTvTBjY+DJlVK+HXyZ3/1\nF37wg+8/8+y1+w+m2NEAomlWzHVah0eJ54LuIF1cWGvOgfnlcGXdy7KDYTa99nxHAfz2+0dHg50z\nF9eHSV9BYJReWFozldnd2XJROO4VnWasSuOz+HiY1aO1g73N608HvAJHhwOCzP7e4fLyar/7sNGI\ndraTn//W8/fu3as33SvL55YX1mvRg9B3d7Z6DsPpdMArOByk9Wju+PDwF3/hixjTjYf3CUFPPfXU\nMPlwcXn+zfduIAfevvfJhcsXpBFZkVaCK6Ck0Bpq13GYx7IirTVqXJXNjlNvxg6Ek6pfgKQ+H/mR\nX5iiszznhxF0yViPdw62SQQ0Uuvnz4QgajuL9doCIp7guhJFKYeFHoYdpvwiLQtUQ9FiQOiCN1/H\nwCUBC4NYcNVPJg0XugHN0zKbJE4Qc5FVSudlMaVTioFD4NHxcSV4lhV2ROH7J6lVASFEznA45ILb\nnei6LnUZ0tTuOOp5URSdJOaYRFHke56th5RSDJ/IfruBTz1HEYihkUYbAAUywBiJTBQFGgKUF6Xg\n0ujSSMVFBZTjunZlUkqzMocYF0XBjUmFqaQRmHqehzEGCIFTGonWACECTsS6AMQIQ2KFtbQ2doJ8\nOm01RkMNNEJEGzNLXu3RIYQQ5AQ6a7NYhJCy6vQnm/HTXv1sdosQsr6UCKHZYWiMsczTIq8scfDw\n8PjoeNtxgOPSbrc7HCTtTgsCANSJJw5jLM9zO/+GEOZ5XqvVbCad53mapkEQNBqNsiy5PPGztnt5\nBie21zazz55tcyFE4If2M9qoDyHUStfrsdaBVNVkMqp4nufpoH8Y+gBpMcnS564/fenpa5iSezdv\nPdjebMd1J/QpY+NkKrU66RwK6ToYGgIkCXDd0YwABytEkKsKbSDJ+xUoqSmI0ZrhMIoaw3EqZe44\nXru1pJTpHg8cz2/U21mRJePUqwdRUN/c2/DcyHf8Ozcf8bWyGdRBVs0vLDFByknhYC8KG4ODXgVK\nExjpSmQEJQoRczK1m1UMsx6dNambTWvAKcKkqrKiKI35tMsJIdTaJMkJ9tp+qafcNDSb0c16evbP\nURRZltLsmLayQJYYNBO7m+U4duVZtrb9Iu1fjVFVVSFH22cqXkADhPjUBcM+ZkHCxiEpBThtH8/k\niB7vLM/CEoRAawkARQhobTXrkDHKdgIJQVZHBEKEMbIeMPAxBgOcwTExnpFhbfBzXRdiyHkZBAEE\nGCEQBJHr+BBCKbXWgBCIIEUIAgCNhrNEQRs183ullJpCAIOMhkVecZD3+umZy7Xf/u1/Htbx1adX\nk7w3mO4/ff2qRsV8Z+39924RF7gBALg8c37h41vvPP3sJT+SJe+3F/wk60INq9xEYW1tdfGddz6C\nEC6vLW0+eri1t/mVL//iv/7Xv/eNX/qGAoUQIm6yjY2tcT6uz6GLdAkiPJkWcW3+5o3NjQf6N/7S\nV370ox+2m/0/++e+cf5CsygOfZL/3Fdb777XWz2z/NyL4VF/v7EUX7h0/t6jh3OdhaOD7o2Pbi7M\nr0yOkxefe+nj924zzG7ffBg1lksln7r6mQ/euxPFTp7JfncvimIlDefG8cCvfOv6G2+++4tffSVL\nx3lZHR32W82ldiueJsPA844Oj1YWV+/fPR4P9uq1DmPu4uIihObNt974+/+7/2j9wuq9vUd/7le/\nfrh9fNw7nnTTr3/xa6ZA9XpslxNhtNVpx536/tH+0sqSMJP6PFlYikSWbe1vQqHOrZ4Xrtre2nbc\n+uaH76yeXx+Vo6jtT+UQu0gUpRD5cHScDnIhDZe6NVertQlW+ujgvhsTDkAQLfg+NVKNeoe9tEeb\na1pr3w8rmZdlijVqt9ovf/aVh1u7eVFCyoQQCAHXYRTqsFZ/5rk5XnB7hgahRykVFa/X6wud9t7e\nHkSGoJOugz2L23Nz1HUpOhH4SZKkzIsgCHzXG41Gtrj3XRdjPJlMwnqtUAJADTTVUlidAYCABnBj\nb4c6TAkplHQoA8hq3SvI+dbWFiFkOp0aJV3GJtMpZIy5ITZyhnUiGCNCbJcPWMKNhvCENwrAqZYP\nxphSSKmDMYYKWu6X4EoppY2aNeGVUhg7AAilFAAQohOYlZTSGAof286zU94+EEKEYKCwbePbgw5j\njAg2CkipraQkpXR/f98Y4THaPTyqhXNRGLYaK/1+PwyCiucIoSAI8jxFCAV+5Dq+7/uNRiNNk6Io\nsqwoisqqhTmOY+AJVttWSLMcfVbY/am5EUIoiiJtKcPG2J8nhIzH41JU0si0SPf2dtNs6lAwySZG\nVmmRJ1la8wKe5m4YNGp1FxFmoEuYkWp9fR1j7FAmpawqBQ3AGteDGuAaKCBKQSkdTEc0dIg/V4/W\nOu1qp78vFTw4nEZxfW6h41K3quRwMHRdn1HUPx4urizu9/cebm22luuL8yuHw4Nsml1cXYoAnSdh\nEEAzSLIx95FPkejMNeL63LgYccQFEa4bV9RRnj6R27HBQwhh1XFm5/isPLKpB+dcCOV5HqVMSqG1\nwRgZA6QUSmnXdaRUvu95ns955Tiu57kA6Gky1gok6cR1fCErJQ2hyHX8NJu6ji8VZ9QVsvK9cEYz\nskFxJqUKTwd95FTWwpwqGtgxEsGMMYaMBcLSGcDfeuogRBA8YRrZZflp649ATAlhGEB4IrhrlLXv\nPimoIDDGWBtQDCBCiCIMIQYKaA2MNEobZIAGgCKEzAlCxtq1zfCKp4Ht1EnWIG0gRhQCgYhDmQch\ngQh6bkAdBgDgsgJAA4RPAOQAaHCihYExtiZKxhilpAKKcy5kxVx/YW7xaLi3vrImitHdW4+eeubi\nnU82mOfXW+HO3n6j3v7u9z94+vqZM2f97vEw40dxi+RFPs0PU15xMSHU1Bud7fuHrdZcb9C/enVu\n7cz8YDTuDXb+6Dt34wjc/OSDP/er37x370Fv0F9cWHr/gw+UFL/1W3/to48+UBrcv3t3fmFRSu56\n9G/+L784nU6/+vVXHMcomN7fOpBymGXHSqPnX76YJKq5eEYDCYm+t3HX9bw33vzZk1ef9nycFqMv\nfeXnbn9w/5kXnrz98b32fJyXHGN844NPIM4vfP7qnY92geFnziw9/9Lnf/aTh0YkfuTSABhaeA3o\nGOfg4KjZiBEGu7vbaVbf3Bg88/RLEN+ocvPOu700ee3PfOPreZEgLD748G1AYRyEo9Hk/Q8+DF3X\nj0hlkjPnz/3sh69dvnAF4sohpL0e+5EDo+LJp84edLfdmuhNe9loUvK8GdanRVFkKudq52jr4qUn\nNvceaaoORlvPffb6zof3vvK5n6cDqsbQACdLucnLoOPX5r1qPFCFYpHPIARQ9vrHRqaMVecurgfc\nqwSfpknsOHXfqdJxVVW+H44Gw7wSQVQzEPCSGyGmVTbuDyDESimHMnXqKMEwWV9fP9jbunnzpu+6\nCCHr3iIVhwBLrYqiqEU1AExZVghBKRWj5NLFy5PpOM+KNEt8x8MYDYejcBwbhtWpyww8kb/CBKHF\n+TmrYmz3rG2hQwgxItPpdHl5+Wj/oFGP2+323tGhV6sJ6hyMpkV/jCjWM/VLbQhFWgCEAIAaIqOU\nMEbBkx1qKKWOo20vxgA73wW6lEojpSRC2PbQpJReSKoKQqROCIFGnVwbYtgQYzSyFlYGIHDyOwbQ\nIEgQMhpqA4w2UENiKMWeoVhopGWVp1MlOAIQGtSstQEUQBuKcK0WLczVAw8DaI6PC4Sw5znj8dCG\nriAImEMcx5lOJ67r1mo128URoioFt8An+8veNCsGPRtraa0VMMYYaHBZVRjjIPSVlmWZAiApQcAo\nglngxb5rytI/4sfpKK8qEXciKJIwimpRaAQfF4XiPMAMMtbstLAGPC92Hm47jFVFiQFMpnk9bkOF\njYALLVElBVIwm2ae56VVBhkaZqNJUWQ6m6TJ0tnlQpZRs767u1uV8tLFJ+Y7S0fH3f5wd3frcOfg\niPrUi+sHh5ON/UPI9JXrV6jRdehko6ruNubmW6alRcqnw8nlC+dXz61tHu/sjfeG1WhQDRKTlaIk\nFh1nb8GMBmRVFWbaNvox9qstJO3RihABQEOIrUPPW2+98eKLLwpReV5QVQWlDucloQiABYwpIQgA\nJERlDEQIIESKImDM7fe76+tnhsO+74eccyWNxd0bY+y1WQUHG4qyLLPf6wcffHDx4sWSV9PptFZr\nGKm2NncIgEJUCGAhxGg0cV3f6KnDPKMBQkQroDVwHCq5gBC6LsuKHDMqoSGeo7VGDi5FCY1p1WpZ\nlmIEhdRAa4dQXgrCqNJSCx2HNVltKaEd4iAAhVCUOthYm23Ey8plDBqNIWSElmVpLReVNIEflZUg\n1DEAllzWmy0zIZUCGjCpIKIupmySJtRhPJs4lGoktVKu6yMK3MBNsqnv+0oZXvAw8iEEBhlCMfOw\nhoa5tNfrRVFdgUoAvLJ2eT5uxx0M/MkoO1aSpylDGCQZx5i3FnzXU4tLzSwDm1ufLMwvTac5pU4c\n1xttZ35+oawS4sL97sNz589vb+/++f/gzDtvbT3a3vvmL/+5P/j97z5z/aV2e2Hz0fZkkh/vi82H\nk49vbl66UsPInDvXfuONSsPN1bNxWaVlmb33yf6Ln7m8ub372c995u23PmBlqgFtBm6ST/v94yQf\n+sH8tevnNzY+CuqwWYvDFvjyL790/85m2If943Ectba3dinCgRvf++jIdSOHNYZ77r999Fp3D1x4\nwnvn/XeWzvm1JXZwuF9vNJ+cn3/91fdcN3zlc88eHvR7w4GG5Be+9o3tzZ31s9M8nd558PHifOPp\nZy9s795WGo0Tfe3p54wAWwflX/0rXxqNBrf33zjzfJMFRTac5IJvJ+k3vvS1ni5vH/yk2Wrc39nJ\n86Lhh8wP97vjiQMcGOQcX77yzOHxcaVAXPcB5MPREWFqyrvt+QVYp4f7h/X1BVqie4PNmHhJ1gOU\nBJS1ms333/14ceVCOjZZtm1abYMdzDAkwK95usoA0MaoOAwwgD5z0/GEOY7nMihkSLyqzCE0CABR\npEop228oi9RoAaBmFDmMpGmKEZCi8H0/SRJCmO+wssghNA5zbXEvq7IeR71jKKoy9FwIkday1Wpi\njB3qQW0UsbmpBAZooZQSAaF6mkHJqVLaSGkMhFBAlELEXG/U6wWuI7Ls7tGhMPp42E8hoI12KvOU\nl14Q51UZ+zHGWCnBGIJIFUWKMdRGEApFxYUsmIO14a7nSlVxURCDMTbSFI6Puaw4LwHEXMgkzYMo\n1EAaJDBljkuTJMEUaQOVUgQqwQvKrKuDqsqsFoeCl9AADJEyWglutCYEQ4CBhAzGMevc39xYmF/5\n4z/67oN7H2NEfUbjuDE/10JAKslbzQZjJE8GWnEA0cUL50ajyd7udhRFAIAkmQheOo7TPTo2Vuu5\nqPI8l1w22y3PA2FQK8p8PB5LrhDAWmvKcCU5YsgYYxAsBS8qThw3LwsAAETIGMFFKmWKENcidwk2\nEno0HA6nxHggZSu1s0Hollk3bmJZjdV4Ei16lZFRMzJAYWZuPfr4zNq6X/ecOff44BhDRDGRrgYu\nmo6SbFq89LmXXvvRzxbb80RjCQVDREMZBrRMRm5Il2o1ORxDDHvpPpIaK3O8f1TkHFJ30E8Q9kqp\nD/dGS2eXRqm++OT1c1fOlars1GvT/cOsGlR5ee3Jcx+99W7AXO3BW7v3N9KD5vJc6bi9iXq4O3Jr\nwTQpyUy1yVZIFptg5y4zqYLZ9AifqllYzTdjbFmttIZJMhFCVFWhlMK4tM00qbiQBgCNMZ9Bt09n\nNpVSivMySZLJZCSlVEqUZU7JqRbyacU2q2Nm/TobqKIoinFtcXFZQwCUpJQiraSUCEApZbc3ghBJ\nKS1HgRCCLFLAfgoIIEYIIUwJpVQBhAGoZIVO5YLAqQc5RBBBqICBBhhjjNJaW0VnCA0EECKAgEFg\nZnDCJdDaygSdJIAQ2kVJqS3aILCdBIiVAQgyo6EGCFn5eQAMghhjgw0AxiBoYRQAaoARhNZNFWit\nDdIQ2iJNAaDTNI9q8WA0qNVCLfHx3hgo3Si8BOwvnOksLzYPDg/HQ7BH+isr7azIDUDK1D3fcb2A\nUtfzKMOhqLxLly5vPLwLYLXGaJqnO7sbSquyMleuzh3sTb797X+3vLx88+bNc2dFmmYYs7fe/LDI\nzZn19sFu/4tfeuW9d990XFAUo8GjzetPX90/Gly6unjrzr0wDF99/cO5zsrrP92q10l/MHry6Uu7\nBxvLa3PpdASJIVgurs+LQmVVP0mHCiYkEGsXO0kPLMzVFUdFwidTBWOHa5P0xvV2FHlQlqg+34CQ\n379/l/nQILW5dTtJKkx0mg3DmreyCqbZeHlpHQB9/8G94Tjb2BqH8fl6HHidoHs80kP98M4GL8DZ\nc6DgE4PL1YtL6+vrg8E46Lh3796tELj16H2nrnvpMKlkvV3f++gIKIBU0anPbT/YfeLsk1GjcdTt\nh3FUgkLoUhqOsHf23Ko0FamxnY19t93YOT7ozK/tPuo6JZE6rdfYrY1HtaNuY24uSZPPfv4rBpRb\n2w+eXJmr1+OaTyCoXJetLpyTZbH9aLPTbpeVRIgURVFwWRYJz9Mw8ITiiGBCcFEUk2QCIfQD1yB9\nfHycZFMDdSlL12UAgkpVBkMhtecFM9vlLBeEEMbc4XQqDGS+b9NNxWGllCx47BGECDLYQIAQMsgw\nwIxjlDLKAAgxJIgaqqHGACKMuVIAIKW04sIAwBB0XE8yyqtKQKOBsRoaEjAjDS9KjKFBmhDiuMDz\n3Jmp+cw32bbKtdZSC6WUAQIia1BJKaUYn9gIQAgRApRBjKGtEZVSBDOEkDEaGGOM1FoqIZWQWkIl\npHE00AZAA7QxCkAAIMQMuYPDAQb4D3//D/7Vv/rXGMIoCF3XXVxYqNUiLUVZJEKIPE+n476UWgMC\nIayqwtrcCCHSNLXTI4vDyvPcinBjjIuicL0IISC0Op2TYQ3UbFACAKAMY8owxgZCQgRzPQCA41LH\nYQZIhCBjjCCZlgJp7ZKAl5UstVFACe0w5oehcDjAQCI9LidH4+NSVAjopaWVD+9+YpRqRrWwHSfD\nSZamDvUH2bioqtZcQzPTWukcHXWJwaHneoErZGUki1yv4JmBsJIAAZ3kBcKkSnOey0roWrPDGInq\nNVhVX3nphRe/+NmjYdcws3O4y4Joe6c/2O298uxzR4+2+9Pi+c99IZmMBoPevUf3v/7yr6xdOhdP\nx3uvJ8Rt7O32tFRk1v+ZASVtB2zmAjJrs9qfsXMd9BgfFpyiEqwWjh2QQAhd16XMBo8T1YbZ/BBC\naB3wtNacc6vbBk51iYwxdupjl6adRdm5qP0xi7vnnDueK4TIq5IiqJQygmutgTYWbTELLQihWZFn\nO14AAosZxYhS4iCgLG0QIWKMsj5ZRv/pGdLjj9mQ6fFGHDpVJX/8jgFkMQsUnXLc7PO2c2gnYfAU\nXaNPdfMgMlqrk1c4jcQQQgM0REYaBbWFvxOLbuBcRmHjuDfodgdhjUqhm+1FzzMbW7d/8NOtr33l\n0s7+wZnlFYPMwzv7kIJmnQLjIaN3d8ZHWyWmQeCYcaBf/9H7T1w967jg5sd3tYIIUYyRw/xBbzCZ\nVPMdl1HSas57bviTn75dq5G51sLy4sK9h71r1y4vdFbuk/pTT8a8FMCEh3vp8VFSFDyMA5c1Dvd3\nOw3HoSidQCGqQT/NUl6WHGNojOi04/XVhc3NnSwfllOuJESIuwylxtTijuIwGR3wXOGICSlGwxHn\nsua3RF4EtIFAOTzuLSw3u3tjyeFnPnMpjBq7uweeFzzz7AUusqPu1mgyOTjcIgQ2mtHK6lI6mQzH\no939A0rmNzYeOQ549pnn5+Y6WvPWXEdK0++NGWOUuoIbXshGs9GsZ1KrySQdDqfTcXb1/EWDzHA6\nODje971abziAzpwy3PccSkOpdRTV9vb3eeFOR1x4PJmWo/FmnomNR49WVzvQcNd1ykqtrc4lmh8d\nj+7d/umv/tJf2d8/7Ha7JnRgOXFNiUQ7G4+3H21W0kgFMHWklO1GsxZ0gK4//ez1G7c/LiRnjPla\nIwQJIUKIXjJpryw5tSiMfGv4YnNHjByoHWROBrGPt5FrtVpzftUuXQuItZhYpYwyECgNjYTGWPwq\nwEhxro3WQlayUkJUXBslpeaIYCV5nqYCIs4o5yWsmGCExVFa8iwtOOeUy1IBo4vJJDHmRAYTQUop\ns314xyUaAgyRZX9b6yI7PUBQYQitWo8l8GkNOJd2L9gJkzEQY6qUIYRAADUE1pfCAGDTUGigUFIq\npYGBACnLS4TAHhSO5/7Bb/+zH3z/R1lWLC4uNZvNqqqkUkmScF4pURigijzJkikAwADier7t5VhJ\nMIvPMqdUFnCKsNBaT6dTz49PzEjhKRLdAABOsLL6MTSZPU8oRrwqHOo61CkLrpTGiCoNqONKBTDD\nPCsrnSFH5WKEnKo7OXJjcuHCuVar1dF6NOhJLmRZ8qxsLi1gZYgGAXGWmguqEnnOg6gZRQ3NlYCm\nNT937tw5JEE6mbYazYpnEJqF5bmj3gFziVASOdQQ6gTB/tFhbziaVlXcbo+ydFrmG/v7dzc+eeK5\ny0FIl8+sNVs14jqu627e3xBVtXTh4t5g2O2P7tz6OIqDv/CX/nJrefHdjz+EzLl2/YWLl55+9dVX\n97d3yc7Oju114sf8F9I09X1/dmLaPp7FRM7i1gwXYP/AGKvX67ORj81WDFB2KKdOJR7stwIek2kI\ngoCeuqE7joMgs0GoqqqZx6vFqFiQnoWgNBoN261mjGVl4Tiu4zgSAq215MI8RlR6/GHf0RijNVRS\na2XxBQQAFEW1brdrUy2trJcPtF3pxwAQJyFnhov7k3gHiBAC6uQPs5+3/0HP2LinYB5Kqe/7wJyU\nUPaAsPcHQogQVOoEEmJOTT2gxZ5bjUVoMCXIwkMxggZt7e7EceyHThDhm3c+uFiur55b/uz8F5j7\n5ms/u//0M2c8FhRVGXlz02wgCkeXvpC8FZ092O1GcZgVJGDRxQvXimyyu7t/5tz8ubOX+4NDKdWZ\ntaXd7YHWwHXZwvrq66+9+yu/8q133nt1b5c/d72zv7d37ty5ei3e2tx3nQaAYtA/ElJORt0giLtH\n/U6nfXgwrMVNoL128+zO9r4fevvbXS9yuke9tTOtvMqazVpZTot0TA2UHFWZoRB0D7oirxMTMuQ4\nJCAMhl6DY1lgPu5O55ebgutqAqJW1HAolc7m9oP19fU851JM6vV6ENan0+k07QXhUsWnz790PQ7C\njQcPe/3+xQsXyrLY2R01W529/W4QOOPxlDkwCD0l4TiZJtO8Xnd5pc+fXz88GNTr9eOjQVSrd4/H\n2iAISBDFLmV+6BAPUtcsrLXTLBGaR/WmG4cpH0oFpEJZqhiJ8kRWpeFSBH4NoWMAqeuzRt2fjIa7\ne4et2ur2/mFAOswNQQV5WUKf1aKICAghjMKwVqsVpcwKTqgzGo0oJlrLIst81+NVlaepdl2EECaI\nAFgk6bDbO94/kFK6LpupfJVVHvn1RtRO0zzPc1uCAACsLoNd0p7nWWqLNbfUSszNz2VFUZYl0Rgi\nA6Gt+VG7vfQn81HbSgAIOw6hxXjIIPAorqpCEVJA8KjfrdLM87IwjFwvABIFfuSHMYBYaaA0EFpB\njCDCXKmYeRBgiLEGUgNTcgkMNAYiRIBBANhQZTCiFhGngYYAYwKNhgYZYJDjOIIrC/8xGhp7fQhi\nTChxCManINXZBoYQYoiI43sffPDB9773nfF4eu7sJd8PmEMqXmgjx9OEVwVCAGOoNMDMwRin08ze\nTHOqzKJPBeXAY7xJAIA9P8tKUEpdjxGCFVBK2zuPjFU0PdGg0Vpr+4Q9EywltKqkVgggqgxm1M14\nQSktVaFQ5Yc4yaYYyysXL7o+vXDhnKXcJIOR4FU6Sl3CBv0BEqAT19OyPBgcYgNq9fZ02N/t93Y2\ntj/7/EvHu4c+dstJcnZt/eBgr8hThE2anbl7/xZ1WVnlmJBS6ubc/CQZT0UJPebVPYC5oWLt3Nz0\n/vB3/sfffvLp60JX29vbl688+cmHH9+9e19y9cWXXz4ejqs09VutnPN3P7nzYrPRS/Nbd97vLMy/\n8uIrywsrBxv75MqVKyfuDBgbYywqzII30KkKAzwliymlrOKFhTxYlpK9y7Ys6PV6lqnAOWeMaWN9\nokr1mGq6PYtnhkZWMMoKqhJClDyB2BdF4XmeJbhBCKMoIqceFgghK0JFGJ2bWxgOhwQ2EUJVWWqt\ni+xEltFWafiUHQUAwIhoDexCtGo+CGGCGYTK9wOl7FBTG+sNbOCpGgL8NLScQtUBqGbPgFO4DsYY\nmhOAu/104BQIJ9WJspFdl7bgcxwHnIgunsAOrcoqONUfmnVHwSlBCiHCGARAK6BOcwiNMQ7CcDRJ\nlBLD0bQ7SJaW56QqNh49eP29N7sj8Pwz7TzhjXBuOqmyiYYw2nwwxnCghFpYXB73jkUhs+mY4ea9\nt9/9y3/1V0fvjF796a2vfeP5Jy4/dXR01G4vlMX7L730VDqt3nv/7dW1+aPj7Wefu+p5DzHRAMq/\n97/+O7/7u787neT1eP7GRx9gSuJ43vWYEOW59TgdV8mI90Ry99YQiUae40ky+szLlwajrfPzc/3e\n0PUNJej48EBLrUqOtDMejFq1+f5Oj2jXcIqoE7tNbgDSHhQVwzUOAE+I1LS/XxiJ40ZYSeCadp7o\nhdX5qiq6x308HHu+M7+0uLm1FdWD0bA7GveD2N89PDrqDrNp1mkvFXlFHNZsRf3RUBouZDmapIy6\nhLi97jgMGkZTBOn21r7ghpFgNMgpDoPAHU2mMI6iRhg2HGj0s9ef/eDGjayXHPcPWIGcCMdu7dqT\nz27ePd7f71YlOD4eXbx87ebNj6Th+/sHeenMzT+5uLo26k8Pe/1Off1b3/qfOW4YqMhnLkaIIIAA\nzJJUFUXoB0mSFJVkzkk7HSGDEPIoI6mMOA4dygtelhnwZJMwr1GTilsQjTTSSIUxLhSrIQzTvlMU\nSApjDKiA1tqDMCLEiu4jrfiUF0WhCCkIyUXhgjOD6dBK+loWp90EW3fTWYF1kp8BrCFmwRylbjro\nU2M8hqXkipAc6JLSfpomSVaVQpGiUgSBcjJJKHWM4BhjpTQEmFIKDHL9wECAMdYKAIOEkAATexgp\nQRBQQANjANAAGmTNVRFA0EDJpVYQGui7geTSKGCgtT7UxsATVVmL87bOhxoCYADEEGsAT2yp/9E/\n+oeU0rNnz47GvSDwlJK+7yklJ5NJnqeUYYyhFSJC2lSCj8cjeIoGVEpprcryZMYxAwlbAgnnQhso\nhOCipJQAoBUUjuNQ6soT1BWAtgEihTEQGs0YwQgEQeB5ATAIIxcCB2FWFFICgLGRkHOYMoyAWwYU\npHc3Si42HhwJJQ2Cw9GIMabLokQkZl4hi0cPNxmh7WZTKXVv69HTn3np+c+8ND4aIGkGg4Hv+FWR\n7R3sEgCrIncoMVIBqaDSWANqsEs9JqCplMiz0aSX6uQoGfSScW7kQb+cWwg/+vi9RxsPLl++8u7r\nrx8cdgeTnBLnBz/86bm1VRJGiIDlVgvF8U/eeafWanzpa9/Ik/R3f/ffTvtDDChJksTyDOAptMPq\nHfi+r08l2mZdKWPMdDr1fd8CDWz8sI8oiuI4tjfd/i9KqTYSY2yj0azpZE4lsGwdYEXtsixTSnme\nl2fcdd2yLPM8t+IO6JQZZ0OavR7LcKIOGw7HVkp8RhualW6zv5pTZSBwKu8GoIEQQ4gpcRhjChiH\neVIqCBGC1tuCGA0RQacq7CdlEDqdBj3espu1KwkhUlSzhues3EanRPEZ+kifOu3acItOnXMfJ73r\nx/hYxhhCiFYAAUQY0VpKpQFGBmplFCJq92CrMz/HHOMxurXdu/6ZFyiTQUQaTdhewFLx0PWl1Lvb\ne81mfTqeagWScZWmmZZeVSIjtZLMIbV6bR4jr6rUoA9uffJg/cxiWfJ7dx/Gcb0sy6Pj41Zz/sMb\nn6yfWXI8vbbWno5615++0usfff/732u05iaTZG5uTiu98eDYDxyhyuWVBalUGLRcI0WZljkZHo+W\nz9Q3H+298NITg8H20mpNqKlHvNiLXRMaQSQn055aqsUB0QjUiwwDQwn0heLTUV5klaxMQBvJYCRU\nlY1lOiqoC8OIrZ5fWltaGIyPy5JT5Cslt7a2gjjwA1fKqtluGIUwYsm0clmwvzes1aHjeVEUhUGc\nFwZjWlXVg/ubcdSs11tloTqd5sry2e0d5XmYVwe81MA4c512no1rcWM4PL54+cLmxiNj4A9f/U5V\nCeqyuBVDBqhrdvcPq1w6uiYrRbD/xBNP+l6ggXFd94knz7733kc//+Wa57jzcyvJSPp03vEDiHGW\n5A6hQJssyWoMeoyNkyTPc8uXswAco1RRlUqKg4MDiBEiWAMDEHQ8FxEslPQQJMiRKldaAwizPPd9\nXwOjlGnENTtCoYTYMsiubbvwCISEsYAQ26tn0ndClwqKSmQMBARJoI2CEBo3CO3611orDbSUxgil\n6ULLw4AqZURZag61UYAZDo0ASGvgOE4QRMSPqKGuE9jUFEIEECl5opQCiNhtrjUAEGmlAcJSSgSJ\nAghBoiE2WmlzYpMGTvYfAgAYDSzCVinlMHdSTLQGCEFgoNFQG62NFEJxLrVSGFMIkDklS0B4wnrc\nfPig3zsmhKEohEZn6TgKQ2PMaNgfDHplWVrNbEQJpcRIBZW21mWzc0CfQhCtqsBs+H1yggIlpZIK\nCAENUBAaCI3jEDucJhA9TjWBEGp9YkkDAQYAG6MqrgAgBkrX9xBWgClu8pSXkBbQoJAbkikgxkAr\nBY2nNNHGcMJ89+iw63r+c88877rueDyO4/gXvvnEOM+HkzF0UBD4V5+6euv9G9qIIIxUURHHYRQD\nJWM/pJQKRChhGHm8EAygei1KJ5nSJfOAA9BgVK6e9ceTdK4WptPR9sbD+dZiiJlywBc+/6VsMs7y\nRCnRare3D/e65aQ3GdU6jYcPHykh56Lm2XPnxt3BpyIFsxxnxoyZxSF7o82pSat5zIjIYhMsNNw2\n5R5nCAlprMiuesx9zm4AOyuy57INe5ZEZszJOa5PH7NYMit+7XrNsoy5TlWJ8XjcqtcopUVR2DA5\nqydm8WDWIrMrDwIDDIIn5ZODgCKECK4AQBBa53EEAAQGIUgQAgaZxzt+j0+SZrW+/cillPoxlVh4\nOmOzN3hW5ZzcJSXxqaSevdszKO0s7s66fBBCY7QyiCIXgBIoDiHURkpdAaLOnl/YP9zdvzv4pX/v\n5f/gr/4vmK/eff9nSXq4uBxyLou8uHzx6ffe/fjX/+Kv/oN/8NvnzwcORchAAsn2o+1mY3E6zhmN\nRqPJmfVz//F//N8tLYP/4r/4e1s7dz748G1M4MbDnXZ7fjgcUkq/890H167Rh4/uFEV27sz5//GN\nd//st375v/lv/8Hf+tu/+d/81//o2Wde/OjmbaUMZSwO55qtqNc/yMpUm1JIWY9bTq3lsPrW/oPP\nvHy+3x2duXCm23+4tNisErU6f35vu5skAsrAlN74GIEqkiUup1IiXuayzBQBkpcAAiakBsoVaWUo\nzis5ycZhRDHwN3cO6wtBu9P44MMPgjryI5Ym5VH3eH5psT8cQ00accfzm0d7veFIfOmLT4zH0yiO\nsyIfTya9/vG1a9ek6EFI0nEx11lKRuW5tcuv/uTVr3/jyz/6/o+G3WJt+UJecM9TyuDOwvzSyuKD\njbtFnlPqUObefvBgPm9Fdb8x1yCMlYXZ2NjMx3Jp+Wyr1Tw6Op6bb40nh/WGf+VaB1Fz3D+Yay2t\nr18wwt8/OqT1kFS0Ua+3Akalt9IO23FQpktXrlzZ2N4rpTYaOp4bOK4UBcFgYWneadUqKewKt7on\nk8mk1WoqpSaTCUSGENLtdmu1mpTcYYFHa6Y3VuMxPtXZStOUc96ca+aTScK50UYIAQSAEBZSp6Ea\nZSgTLoQYars+IcEsTTO7lWx3wa5nTFApgAOlFEpLrREGAAKAjNYQIiUNr2SWFRTmgAYVqAaDgRDC\nShtXXGr9qU65EMLz6KxJYLcG0OZEXMHK/RhkfwH7DILaGA2UEhpDIvmJMZICBkKgDNAGSqOFUlpD\nSLCGQBoN7RVCI40WQmzcvdush/v7h9CIRr2lRJmn4zRNeSWrMkcQAqALzh0MGXakVPgUQ4FPFZ/B\nqd6PPD0KzKc4C2SU1lKBk3mVtS0HFaOe5wGgATAYAAwN1MYKukjOMYAUYaghMEgrVBRCG0Soo5Hs\njXtSl0HDcQNDXWC6o3ZjvhY4mDnMD4qypJ6vMRJaAYKfuPSERniSjHd390bjMYDm7taGX6/F9aYD\nsQdZxNyLF8+HmGWDsQux7SNRBDtxvaoqaATgGhOTjRPqk6ARHWZHBU+MZyiCZ+c6G1u9RtsvqyQI\no5WleV2Iz7/4mTioHewejnZ2DNTEY9lkdPvWR/Wl9qjKxxu3XNdfXVrGiHSnA4egE8y0ndA8fnzb\nSGN7QfCUbySE8DzPGuXNAHhKKavWzhg7ce/W2v58UWa+7yt1QrTGp/oW9hvyfZ9zPrPXnZ3ys7Pe\nBh4bmSxt2wIlbDg8cYk/tVC0C5cxBrSxfhCzvA+eDnKUUkZbuxF5esRjhJBd26eFID5FDJrTYgho\nqGcvOBv/PB6KZu/y2ODnpIQ6GTL9SeNze8OFksBA/Rgtd/ams4t//FNYSB5CRBtijYaVERJUBhdJ\nkfzCL72yvfdgc+9GodZHg94T11rdgWDuHMFe4De+/92f9YeTwfBgYRFgogPXiyJ/bq5z+/a9K1cu\nfvzRPaP07u723uHkt37rW9Ok973vfe/u/Y+Yg+r1WqPR3tk+9r2Ac4EQmJvrPHy4e+XqysbGvWef\na3/3e3/oueS9995yXfbDH77TagZSAl6VRS76emwMajfbl6+e/fFPflyr1XjuHR1ur68s3Lu38Zf/\n2jdv3X2z2a6P+9nYpMvNS+Ojw2lfx17s6aXRnsmnRJZVNq4oNWUhRAmoT1zmEIgGg0Gz0dYldBgg\nBOYTVY3V7Q92adPkhew0VqZDEPhuMipvffIQYvDwwb3F5Xihs7y1fYi0ywUGhvX6yZtvvDY/3wpC\nlxDy8L767Cv10TAtC1Uk08P98TPPPPfv/uA7jfrczvbR2fWLn9y6d+nSwhuv/fH1Zy5++9s/+bt/\n5y89fHS/0W5Os4nj+F7o9Ebg6jPN5TMr1MV5lQ57exjD4bB46unm/sHm/OJy1HL39vnR8e6586vj\nSS+uRds7j+7f2j+z8tTLL351KVw6ODiEEGqlsiw74snRdiGrcm1tbXd3txCqKHkYhgjAPB0zAj+5\nDXNeYZdBCC3vh/MSY/zss88eHBz0+z2EkOPSnZ2dVqslpYQAa46NQQQzyrAUuuIFRjQIPd/3k3Qi\nhABQGwMwgZQwxECRp1Cp0HUdx0UIaQUIIZ4XeF5w0vMyNiad5F6xFwSu04nrDJp6GBCCgEMTJTd6\nxynpDyub4CLGGKMeMCdtD89xuMSEEM9xTkYDUtlEmCBsjEFAS6kM1ARqCP5ECjjbjzOUkE3pLJXn\nBMcEP534IoQsDRGcajFb9p79j9PhcNQbXLp0OU/SwdH+0tJSd3+7qIQxhleCuQ5XJsmykldSSl5W\nNdebsYWsPgA6pV7ZqYTNJm00opRasuPJRFsDraVUSPJSu/QE4GfzZiMNQNZPyYIeEUKUOohoe+gV\nUqTpdHt724tle77ZnifUKfbKdJzr0uiqnGJZdrvdMIy0gZBghJCBQGsttNBaB75XFNl4NBgkk2A8\nRlI/eeHSgwebVGhcypi65TjxmUMh0lpbnqxSEkEqlMyyKq7F9XodHZGCTxSDEgqgVHOONeP64V4v\nDFxeZroE2w/uLUQdR+jR9g71GWBocf7J3/i1P/+v/uj3ls+u6t7BeJoeDQ+++Yu/tD63FBKHLCws\n2G/IBhuruNPtdpeXl+19sSQy+7AmHNPpdDwe01PDLhsVut3uwcHB2tpat9tVSoVhaFmZjuPYrtUM\nyGC/eNd1LTQuz/N6vW4hea7rQkDjOM7z3MYqq7dhO4E217CaH9Yx1vO8ySRpt9snYkW+HwRBLYpt\neAMA5Hlud6ldHLaS45xDDCgh9l3AqUiUDRJVVVFG7TJK0zSuR7ZYzvO80WgcHx/7vl9VVRAEvV7P\n9jMpQTYSe55nw7PdJGVZhmE4mozjOE6Tk0/UaDS4lFmWNRqNoiql0JZWZYFPUsowDKfTsVI6jmMb\nqm3rWWstpcLYwcSdJEMNZRi5QeyNJkd/82//9X/8P/y/fu4XXnz4iL3zQe/iE4297nG3v2lo7vid\n5569/tMfv/XEk4vf+DNf/ujG7fWztSCIarUaAGA4mF5/+mJcp9eun79ze+PLv/jlDz96TWt1eLgf\nRo6U5pVXXnz//ffHYwEBEFhPxrzVBJ7nf/nLr2zvbACoO+3Ga68++JVf/vl//Ts/Xlxor69dfLSx\n6wWeMYZX1Wg07izUnnrq6W//0R+ePdfxXEIA8gKY5cPlxcb3vvPH62fnxv0MI4A1eveNe1XiJF1z\nNOzXg+W97WEtbGEtJ2VlKq4lCNzQIV6/P0QAR0GdQLcWtdLpUBgZ+x0pucayKrL+fnVDPApo3Duc\nfu2bX/n9P/rhtWcW0+TQo/HOVnd97cLu1nGvO1Xa2do+uvbUUzu7G5XMfvM3//r/4T/5r7RBWVo9\n8/SL+9tdBFngxoNhT8pyI9vWAoRevLmxAzS6ffNuq1l78413k6x76/bg619/ssj55u7OK587iymp\nqmr/qDu/NB/HsYilNtNa3d3d3/Jj5/oz1+KG1ih1HHV0tL+7Vcx3ziCssyz55KOP4RrtHfWllKng\nPkJS8loQCIwG4xGXoigq7LjTLPUd149CWeZImRpwxLCMoigrSsag1k6ZlR1Fj3tJlCshSoTxeb9j\nCoUQpRRzmBmgtTRQAYQwpADCyhTTmmT90XYdwFot5lxACChV42RIAKx4BiHUOfA8D0GSjXInjJvt\ndq874FwyxpQ2lbXERM4xcIQCHiIMGiAFIUgRNBE8gWZYCa217/vIdTUARVEQhALPL8pRVVWEYs5L\nx3EIREWWYwB5UToe8n0/CPzBYNCIlossi+rRcHhYq9WKopCKF2WGyYkoyWQyabfbVVVBZPzAtZMz\nYxAygCIMoJZKIAMCz0umeTqZLi3WirRwHZeLrMyLc+fW79z+JE/Grcjn6dgjxCNUFXnkEMDLSZIa\nAzKeA0w85kBMqqoyWnPOEQbaSHkiZaRnMVIbbYDmgmutDTDGgKrSFFOtFMBQSgWARhBaqH0URRBD\nTGDoB3ZsD42hBEMCrSSrHaVHURQEwWA4aTabd+7fzLLk8lOX/uCPf3SNrnDVR80wW+54reWjrR0g\nTO3Ck6P+2MNOI4ohV9l4xNMcGwIlV1XpExiErcNkIiQ3lajKghEMKuk4zGhNGQHA2ohALSQCAAAk\npJ4mEz+ORkm63rxcazfLUpkaAjpzY3+6s+UGbr0RV1XB3fL4oNdYuzjd25mP6ufr9fby/PG0t/Hx\nB/QwWltsHfUPMBDMAQYJiaoS5AxD0uv1ZmWm/VLzPO92uzOEt61pZiMcm0HAUw+hGXrEliPr6+tL\nS0t2GgQAQNiOcz7Fks3GLXme2xHfdDqN49gGHoRQnp1UV3meWzSEDVQPHjywp7wdTdkY4/pelhV5\nVSbjURRF0pLFDBBCTKa5BezZOFEUheMJrTVEBqEThQaMsVW1AkDZGDMajYxRodu2hGpKidJSG00I\ntbWR1UuGEFroBzpV9ptxs2ZDI4wxQCcVmx2YWVf1siyVMb7vW2WjRj3O8zwMQ0vYzvM8z3Pb2bMA\nuhO5LWXbDqCqqqxIgygohEqKqUFybqHRXqhdfercq29+97nnr1yR6xJOFZxWqr96ZrnMhReY/aMH\nayuXL15a+e53v11vNC9ePHv37l3PC5ptjxLnvQ9e+8qXv/7aa6/7AaSuef2NHz91/YmKp1evXr51\n69bCwlKWbksBDw+Ka9fO/uzVTdcJm425PE/ZAu0fDtZW/FdffRUA0Gw2jw4Pw9DXGjiO2x10l1fm\ntCoA0JefWD97bvmTm/fzZBzHmCty3BvNL+AiK4QoHcbOr14sp3p/bzDtAV24XLq4qgtNEdQechlz\nM11prhQQDmWe52VJjiGCGnpuhIARshKlEcLwisRewBMc1uciWuMpXGjVqhQ0onnFceDW0klJsFcW\nulFvW6u3p64/mabjBw8eQAjG4/H8/AIlruDm/ffeXl5cYQ65eOlMWU2Tadmqd3rdEVTYC5jHcJIU\nca25uDA8PuqHtTpEzA8Dg6DjOEtLS1mZVFVRFAnzQW9wlKTDMPPG40PK9CSZUka0LoziZZp097nJ\nAnVJLcwtjumEECKLPJe5MgWFSkmeFbnWGmKEKTEQKGCEUnmRI6ObXmwQ1BBogCohLE9lmubUdbAU\n0mgDoQKGc6m0wMCEkauUhNZFQUmAIDTKQBCGQRCFVVFWgmdpaiDwXQ9oA6R2sWOPBcM1ogZKXaU5\naWGGsDZKV0IIqbU2CHGjlYO1QRAbhJAySillMMMYUwxD6gyrCca4KHNA4eLCgtYSaiWqEkPABScY\np9MJgib2PaMlwQwDWBZZkTkIGgS05FUyrSAEjuNACIIggBAwxhCCeV4YY7VzbPWAEEIEQQOQMtpo\nIU2lhNBaaikgBFHoKy0lF5yUvucpAHlVEGM8DH0KI0YJIUYqBgWCWGOQqgpARAmBlGgEldYKQgKR\nMQrAT4fEs9GGUp8a2TzWP9EGaGBDlYIGam0UhlBrxHmJEFLK5EVqS8bHqzdKKQRYSo45h9AwRniZ\nd1ptQsXR/oHn+EaB0I+iThPEi7c2D4ZFsjq/FHWWFs9foAaXo6nOi8tXL2Mh7t+6ub/9yPGwQ92c\n82azriBRuMIUQWhKVQAJuDI1xyPWNV0BbQCE0CCkIWSxO8gyHDHsuYXUfhy3zy08Ot6qzzWzinte\noBsQC+Iy1/VpWaVtGpoiL8ajvspLU0UB01qZIot8x6GMcqIB6A0OXYalW55gaeBjFCI7xbG+qPaQ\nFULYGTtCyFK6LDMGnLp0WDDYcDhstVrWWvFER52ioigA+DRfmPW4bFVRVVVZlpYZahl5i4stQkgY\nhraDjE59D9fW1mZIOXtJGGPHc5Mkc3yPYeS6ruZVURQYIs75+x987Pu+NbawonBWT9cYy8o2Sgup\nuNZSa6mBUUoBqKMo0FoZo4+ODrvdY8elEAOllOsQO+uy66wsS6X0THH1T3XYZmtIazOTOfc8DyEU\nhqFdsEEQ2LrHtvUnk4l1nrVgkDSdAqi1VhBC29OzXw1hCAM8Snqtdqh0cfHSel5MVs4s/uz1H/3K\nt75x58GHP3vjx24o3vvwLezlGqmt3Yet5tIf/NG/6Sw0ENMH3Z2v/ZlfeO3Vt3cONp2AeAFptVq+\nF7Xm2pjIL3/txR/86A/Wzy0oYCoxpQyWVZ7lCWN+s9k62Btcv37544/uXTgffOePb/yFWu3e3c12\ns8UgGw3zPAPPPX3xo5v3rz/1bL3W+re//4MrV9eKLN/Z3frrf+M3Xnv9h889/9TG1t3JZNBuLZ4/\nf77XP/ro4wdGKyXk4Kj0mLjVfyALp7uVRc5yTDqg8gLiGaW1LBlAxECGMDCIIEAJMFq6vmP58wwy\nAlGWZbzSFLk81yanh71Bp6oFDTo6qp688LzCYpIMbXcFG5VOUgxg4HmB50CmDFKTdLp7sPf8Cxcc\nxyPQLUseRfGf//N/8cYHNzY2HhZpUlTjV15+/u69h0hHFDOooUv9Ya9PSZ3R4PhoJDVdWlwdDadh\nPaiqClGwuryIjaYSjoeP8mKyujZfa0Zb2w9czxAmhoP+XLtRurqY8Gbc/JVvfOvJ888Pj0eeF5w5\ne3ah5i81/MgxPgHDQa/Vbq+fv1RJg5nDldRCOgyV2ZQQNJokaV5EUZAkiRV+5LwUTX9/L811LqEk\nhCAEBdBKAYTI1nGitYHaAIwcQjEjFGGAkTlM9ifKSEQUrjjDjDZoDTnNYTJhmHjMy0AGFQzcoHQq\nrXWv8lOgOZZaa4UNcQjGuOJcYwCVBtAoJYSoDNBGS44Aoj5GsOJFnqelcTQHGOPBYCBFpXhFIRDA\nEGNkWUKlEDSMYgQMxTBwmEdJ5HkOwVHoG5VDDIs0LaucFwWAuspzQhFFKPAcoBQhEBlDMUTGQGRO\n4LBa2l8OowiawHcdSrQUlEBelYwYocvucdLwHeLQmkvrLiGEKAFcijGmDlCjruBaG+MQTAzGRmsD\nESZEKamVAKfzbPWY4Kk5Zb88NsPGWmuojUFGawPgSc0EjLKS0ydZrEHEohQhRAhrgJQxlGKlBYBS\nqlLJqhT54nyn03b3uw+vXb4WxEqYMayImlS9e9u1qNZEvhpmtObWfa90VaMzf+fmjf3tbYcat+ZN\np8O0UrV6i7CACwMIRhQhBwMCpVEIgG4yZIgig5Q0ECJCCIJEGDQuiwoCDGA3zRSmGqHJpJhOqsY8\nYzSYTrIqr7AhVcFzVRz09kO34wa1TqtWqkpnPG4FHMOmF/Aqcf3ICTxh9NHhviwLDPAJBA6d8ofs\n8RdFUZqmszoGPeYxYZuk4NS+8HEpttm0yf6T67pKiyAItD6JWPAxqLStLWyQs9a8hJCyLNM0tVWX\nxXPbFrDl9J1O8s3svWxU86OwzNKqqigECCFGmYVLKKWyLBuNRu3OXBMhAEBZloy5EBkDoFJCKQGg\nxTVoqbgQnBCMCYn9mDEShF4Y+pXgFu9vA7MNKhjjsqyssKyaeZmf3iV7/ZRSqE+ccGdIhNljNt4M\nw7DWbNiP77quLUPTdMo5t9Ku9mHrQkwQxCoIycHh5tXrF6hruC4w1n/0nR93Fmp+HBclv/1wb/0c\nhMR8/ouXDw/38rycm5+fjjgm5Dvf+d7S8pmrV58YT5Myz86cO8MI3Ts4NhJWmA9HxwvLLaGS689c\n7HaPHTcwRp47d/bunc0oaAZBLU2qxYXFvb3DxYXwpz95a219cTzKx73jyQh87nMv/st/8e5v/q1v\nEuz+03/6u0uL8d7e7rnzS0e9w1u3bj7zzDN5niTT7KWXX3Qc1u0dtufC+QV09crl73/nDoagtuw8\nuDMOKFWVG8V1qpxhd0RAYKSSogRAamUowo7PiOMiZNKijGs1Y2wyBLXRGmrHc4MgqLfawlR5Wox7\nWZYBpdQT1y9oDAEnoiz7/eGZc7XDo91a3Kh4ClEkZZVlMox8qThEYHN7y2PR2bX4maefu3f30d07\n97/xS1+ba9f++//hH9+5c68WNzGsi1IV1ZhArCrQO55KA8Ja03Nrvle7cPHK7t5mv99vzdXefvst\nChFStORgmowDPxqN+sNRN67TM+tzS40Vh9IU8UnJu0fF8HA0ibLl5sLtrTubm5ubPHV0QXUeOrjK\ns6heQ8yrpObaaK1FxVuNyGgRx+HuYbeoyjgMiqosspwwqiS/s/EAIyQUhwZogJAGCgHGXNf11tYu\nKfUp7W+WztfqdRoENmmzqV4cxw5lDmVZkli8AwDA9/2qFACARqNhiep2GGqXblZmUosiT7EUUIgq\nT7SWmtIc6OM8r6R0HCfPUxZ7XOvRaEAJxghEvme0chjRUjTqMTCK55nPmJHCCEkRMkoCrao8JxB6\ntVAqLIQgBHk+lVISCpSypqhIiMqlAXMQABpAyTAuCw4BMEZhoBEGhDCjJCWkzFOHBY1aVJa5QzCD\nDCHywrPXd27cCCAIXepQrCm2I4CywpPQnaRFUmTSGGwMIcxopYWGQOtTo2ebvutTBbXZTp/FJwA0\nUMacTIYMBAadlgFKSi4EQohAoJFFQAjCqB+dCGe4rus4zPWIVmXF01a9U4oiSfLu/nElRs0ORUyC\nnB9s304+fuQ25+7ePtzd3qMYY4i1Vu12s92pBbGbVWlaTQyQpci3to5azTUhjE8dZ4KB4AIrF2MA\nUBh5vuMTRIVQUhmMCUCMAjgZTdfX1/tJf1SVC2fO5iob5MNOa+Xt1z7IeZEkEiHgUegQ6jGvhOTi\nc081aVhkydbu1uF0oKfTQTctqHbm6x6mGIJc8eOjLtIGaEjeeecdY8wMBm1Zb9Y+ciYZMIs34DHd\na3NKNrY/Zm2HLNxgBk0uykxrLSW3s8oZWNm2tvBjBnczUICl0NrQaLXAZ/PAx4EDj6Oo8zyvigIA\n4DNqyzV06hmB/iRN9URLDgFtDIAGQkMIpgxDAxqNulJiNB5oLcNVDxMXQpNlGcTILjIbjQghFj1I\nKbW2Lvb+2IBqG3GzaxDyhFxllZa01rYQhAgBAFzX9aUYj8edhXkppe/7vu/3+/00TU9SJHAywzyR\nqiSEMFSqbOXM3Cjd/Oznnv0n/5//76/9+jfffPtNQuC//p1/8/xLz62vPXHm/JneYCtqon5PDIdC\n62pxKRxPilotnptfuXt3s1mf1puNT25vtOeXfviDHwgJfvErnz86Ho0mw3PnV0uRVHwyTY/v3jdL\ni9hzY4zhdJryEg96+63mwlxnaWfnYGm59ubrW6vL4eSozBPwkx++95kX1rMJf/fd15eXWkfHg5KD\neiOpR/H+zq7jkq2thyuri7c/uXX2/EK97tTr/ksvPds77L388tKwl2DtUJSLUugK8TJFgChZtBo1\nhpxBdxCEEURIAK0RwEiGEQPU5NUEISKFNgYapUteEkSpS6u8EpVo1zpJ3ue8zCflwW43qLsKmDIt\nqrI0WiIIXBfkeT9JCfPhw809YxTFzKXu8tKZZCyklNvbu3t7B+323N1bdx9ifXb9zKB30Gkuagka\n9TqaclFpxnytJQSoWV+Mgnh5afnu3TuD0UFZTQ6O1NlzS9k0MdKsrLfmOkv37t1LUx7FME+qychJ\nRt251lzkNGpzyy3sPHf1pcXG2ZrX2drcSfIspMD1PRei0CWEIAOBMlpqXQkJMeJaEdcBBkdRFPcm\nMaQhCxQNBA0QwVoqZaSSUiGCEQAQSi6kBgEmNcdNertaCruhZqEIAHDY21JK2UbCTAmFMffKpav3\n7961k0ubEnFeWR76bD5qdwGEZpqXF596ut8f8mQCpZBlboySGGdGT4zKmVOv1yjDnU5rksvJdHzm\nzNrksE9QVQ8DQIAoi7WlRQJMNp1CrShFSpa9o8NiyqCSRpdC6zRPHQdTSjEERZZmWSZ5ZXeoPbW1\nwxAw4+EgTxOtKocxCKHSxACtjaEUTccjRj3PcRCCLqNloYq8kqoAUBhZnV+ex1VFEMUIGGlcRiml\nJTCX1pb3e4P97jDnJSCMYqqNKStJ2J8gkMzwR+rUG+HxJp7tPNmTyyhtMLBoZghhVRVCCOZ4jDGE\nCEFIGE0I0do4no8Qogw7LqYUSVW6DnYoSiaFKnnNr7/3wU0tWp4PKDHnCq/jrXkgKCp+eemJsF5P\nioxDDX3UXGkVOjsc75Ywn1vtUOAOtw63B/uAk0atnlc5EoIYExCHQoQNqFFAiV8ZUUhhJDSQSgMy\nbABPj6fj3XSIXVyacpyN3ci7cP4pSOBw1MvLLJ1O8jxHgFey/NHND0gJVVUiaJDrRp05XQQ+0cfj\nYaXBqCwmRdYf5sywelwnL7/8sgVpWHk6z/OCILBlxOw016cUV1uH2kTe3mt7SkIIy7L0PK9Wq1lY\nnV3ZqED2ZU9TgxMsg+3s4ccE4e1fpZTJ9Ni2wobD4SxNg6e63eYx1yIIIcTI84JJmoSeizF2MMIY\nF1nOGLO1V61WazQatoixCUtZlsRhECNjjNJSCFGWRSWr8XjIHDI3155MJgaoosjKMuecG4iMMTYf\ntBfc7XYtFNBCZYwxWgH7eXu9HkLI3kCMsQYQQogI1lrPzbUghFZ4ws7iRqMRl6LTjkejkZ2N2V7i\niZIFOoHXCyHKsrRwHanV8rlmrUm/+HMvLq/PMR802/W9/cH8fO3M+fOjUWEQXV5tHx/dvf+w/8u/\n8qVOy8/L0XBU7ex0V9caK8sXbny89ZkXr3X7/X4fKIMWlzpXrj3ZPej9zu/eunQO3Pj4zosvLU7T\nY9eDfmDKSgkxopTt7/Iza8sEyWZjPo5jjJzRuMco6PdSosJknAJkXnrx3D/977/3cz//1M3bNx2G\nrl49s3pm6Q//8LXPf+HizY9vdeYaVSmfeOKJw+6D+cVzC4utIi837j944uLVgI0f3t1bXW4fbw8k\n0qJKoyBqNlkjRkCq2tryysqKAuaof7x5sDdOhlGjzhzYG44JYwBArQEwRCEFIRSKjwZDpUTcCAmi\nCEOXujwTnbnWKMnKvKiFESXg4oVlA3UlxlnR746z8RTMz5OV5eV+d9Tv9/NEf/2rT33vD3/mutFn\nnv9MEHjHx7vD0WGR+1VVlQmv1xvhwvLm7kPCTBiHOc/7x6OPbtzFFFy4eBYYsry8PLcQdfvbaZZQ\n2Gi35lZX14SQBwf7QJdFxvMkf+Li2cgLu7uj3Yc7Km38hW8EOsfbe/ucCwNBURQqL6jMysAhCGgI\nENESIC6lyzwFjYSmyvNpygAAjNAZg63MC5vA+YFrjDmxCdYGKug4ju9608nAAImANshYEWvrLO45\njgIIKKW0QkAhrDFUhCAvCIQyRVW5rqvtayEIMDIIKqUIJgQjgBFCACLgABpGfpIkqoAYEgo9CI3E\nEADdmZ972B/18vz1118T6P1poeOolSVFq9mgqOLFuDLjzY0Hg16XZ3cA2P35L36h2aqVvKdVEgb+\ni88+5+BamqbMA27oOI6TpunZs2ezLLv8xCXb2J/lxFVVXbp0aX9/fzgYFemJD44BXKoSIbi6egYj\nh2E3zyqESJJMhOQVT4TMm3HQdClIUyOVVoqXFYKSIYIobq0tB0FACdsfTAQ0CAGjcWUqXkoN/sS5\nNIP2/U9DEYTQnJyEtm6yP4GM0jbAM8ezUR8hgAHSWhsNfS+w4ZYQhLAu80ng1ybTgeBlLarXw+D9\nt9/QJeIaSAJYDtaiTsmFrkovDJECGVeIgvFofJwc+XP+yvnlo6T7wf2PSwPm51q1qI2l24rj3uFB\nnk2xVgxiI1XkBxVDPoGSIECZ4waQUCWVh1gvSWizzjA4ODgoVaUM2j/agxhE9cAgIQ0XBhCPEd8B\nLtxKxsw4ocuevHgRC5kkk9E0E0glaUEUyHlZFoUHoa60LBSZFSizs8/K/J1iH+EMlm1RapPJZFas\n2AGSOpVjsoiysiyDILBgtrIsyanN+2war091cewCiqLI931bihFCmo14NqFpNpuWG2vDJHgMJH0y\n4gMmTfOsLFZXVwkhRnDf98fDUb1ev/9gM8uyNE2t8Eme5zRJqGOlhjQE0BhVVcU0GU8TMEkn02SM\nMbx27Wq/3488nxBMCTYauH5ACIEAI4TsaGdubsF13aWlZYsJZIwpaYwx9Xo9jPzpYGTACWu45IJS\nSh2W57nvhWfPnv3qV7+qlMLUekoiq/2apOnZs2cJIfv7+51OB2M8Gg2k4hgj24r0PC+OY8aYAtnV\na+cBLpZWl5TJv/DFZ5JkMj9fI8TZ3+tJZS5dfrrKyyuXXvmXv/PveBln0+l7H+0fHIGvfuXiZCJ2\ntz5CKPzRj9+cX1yYX4x/8tO3wsBdWTn3w++//rWvXzg+7K6uN4eTnXPn5lutVpoWo2EyHYuH90fd\nLnDIses0Nh/tPvXU01rhPOML8wtH+32iPaDLK09c/uDd24yCyThd6CzsHx09ePDo7XcexXXw/PMv\npj9NVQVMQDcebs8tuW+9feNXfqV55+6d9fXV3/u9t566uhAG3ovXXvnIvaszIFMYOEZhIGW/yuTT\nV56/ePGykBIRsN/dy7IEUCMRAFhCQoRQVSUwYhBBqXWaTRwX+9SXUDqMSWBkKZJxVWZxkecY4yBk\nS8sdCFsGVHnRdV1w5tLlh5uPjg/E+fP02rWrmw/2dne3Dw4OptNphvjR7mEUBZ6He8e9xcXl44ND\nhzQm0py9eCadpJCBqFZHwHm0sUuYK5Xa2d6P60xKsrm50Wz7ezvyaL934RxyvbgztwQB3tvdYBRj\nwA73joqghkCwtnB22vWAIJA4Z1fWGfXPnDu72qotNP0Qy8glUvFpkiDmSYDyioe1eDqdrizNDXvH\ncRD2D3ue4xVlbvdUlmXGqCiKtrc3Z9R1rIXW2vE8FEU4axgpFRdcClnxUnBZca4kgbmGQHGhgHEp\nMwgSyB0Phb3xzjDXGnjGSKkpw8ZQVYgaC3IpMDAOZgoCrTSBGFBc8IqLUimFjAZGGaANQACY3d2d\nMZcLa+e+9KUvKep3h5nnxj/44x9u3X/kUBk1pUbJpFU7PjwoQwJhvPlwJ44DoYcIVaHnOtRFJhBC\nKFgCohzHGY/Hjx49tK0I3/dns1vbMXvw4F6WZbxSvhNCA4oygUgqzTHG6TSFkEphpOCEmFocGaO0\n8SgzUeiHOURaQ6Blxae8AloyoylFNd/zfd9xPIN2uuMUYIQIlYZNi0x9yqw/qX7+J1URsixXhDBA\nBiFkwImrhEFGQgiAjqKo3W4jTDHGSsl2u02pk+ZFc2GhMz+XlwVxYL1e8wNXaa5kaWeoouJlkakK\nIOVgDQGiTieOHCfQYJ4yjbEwejX2gUvu7d57ePRwq7cfGC9c8C8/czkTieS46cwxEzZr8UHvMJEV\nNpohWJVFYWQKjSsq5nhRo+23a5iwquQE4aLMaoFrNOQGFYXWCAiOoppvNEYYC1lCTILQh0hJQ0jY\npiSshbVnvvxlMRq99dprlYHGYN+Lg6hWIyQp83qtCQCAEJGiKCy4C58aJtobatEN6tRu/BSBhiil\nhCIIkDbSaGiAUgooLapSOC5V0kjFa6QGoAYAB0FgCyNg4WWP/S6EUkox5kIIAUCWVccYG40HGGPB\nVVFmStUowwAALkqMsQFKKyAVBwZBZIyGymgIcZqmNrCVhbQhrVar1et1AECappZmaxWPtNaIEOow\nQohQUhlYFjwri+FwWK81XSd0/QihMcI0CHwhpKj4eJo4jmNpFrYrWJZlvz+0tEEAQBAEZVnZHqNS\nKg5Dh2IpdWUR867jut5kMpngSV4W1uDERyEA4K233kCEfkg+dHyvUYv2D3aT7w8QQk9dvSKNLvOU\nug7Uut6q1+M4juqe43Aw7TTp3Go8mYwwhs1m8/Dw8NLFi1xobRim5NGjrfmFxtbug9/6rd/4wz/+\nN+cvr126ePaZZ4IbH95uNeaTaVmkVVWqz7xweXCc1Pw2QuDWR1tn1q48fPgIAOAQb/9Id16cj6La\nm6//tN3uHOyPkgT4IWi03CxNqOsamO7uP3zi0uVerzffnucJyUa9ubn2o0f3l5Y6nMuyFBCAwI8o\nzWv18OaNWztbh2HIlJRxw93Z2p9baPaOyvGQP7p7d2XBqznNpSC8snYx3ZqYEPSqHgPKCz2PBbhF\nIlTWKa+Qbvio4Tt9CqFS6TQLa3WNcZonSZ5TohhjSpmy5GJaLC0splkRxBFiUWUKDaTiiGdV2PCw\n4efWlvJq3Gov3rn/bq3uqapcW1x5cHNz6/723GeWfTeoxxE0aDwe8lK+8OwLBwd7EJJJMmGOEUK4\nQB5098+eW1NCaS0xxmHkV9uqsxAfHBzOz9fTdIqPZCVSqikzBGq5tnwRalTlJk1Emem5Vn18NCWN\niFA/H4v9R7tIzi12lhiM9vZ2+keH08HhYKtyQElU0Yj9KPBKwaWCSptJVoZxPJ70V5eXet2DyPeM\nQlEUJUnCGLPWooyRIPCWVxYtJeO0tyEQwpTSs2fPg8ck+f/URLMsS9uOtrwOTNjS6vm8UgRjQmlZ\nZI7HtFRpnlGC0JgCo6lDeFlVggOMMMZ5nnNeGqUMBEpKrqTBSBDUaLeP94/zogrDUJEA0XBubuWf\n/9N/sbu/X4/Jwvpy1Gxcf+ZpoenK4jXPm797558dHvcVmCzMR6WQ+/tb2cQEQZDLqYa8WW8ABBlz\ni6qqinJ3/4ARKrVymSOU9By3PxwxQgl2CsWNMWVVEQoRRhQTLhWCOC+40gADBCDK8qQop37AjmRR\nCzwXKwcRrlAJtdACA8UYU6KoN9oQoeF4lCdTbQQh2HUJEKgyUCqtgAHA+qAhra1HmoYAYKOxMdQA\nbDRSxgCNDZTGKK2k0UJBDLSGYm3tzIUL5zDGjLlKmrWVM1Fc7w0HTuBDCjnnSnpzCwvNeoNAUhbS\nGMSoy4ghEF27cq3dqvf6+5PB2HVAryzKgjebzTTPR8m0NddJeKqocjFdas8BTyuugOREG6RA0R9S\nx2Df42kmipJ4DmGuUIYjZKQqioIBTAHUjEqEci2o77B60E8mo8FYI6WxwZhcvXq1KJNKFAYJWADX\nZ3OtjjJCITZI8NFwcHxw9Pzzz/vQjMs8tQTTwCGEAUKJ5nEY53mJMSZhGBZFAU7ZqTNqDmPMnvK2\n72QjU1mWmEBjlAEGAK2N4Vxb76K4FlZVQRmhwBmNB4QgSokdDmkNKGGUOrySBhiMaFHkgR8BqJU0\n9u6HYQwMMsA6ndOKCM5LP3Cl5AYoxogByhgFEXIItUrbShmoAMZEn6pi246W1no0GqVpmiSJhULY\nK4c4C+NICDmdJp7vG4Tzgp+7cMX3/aIq19bW/vH/+7/b3no3nUwvXTy/t3d0dHAoJfd8xxjDGHMc\np9c3SqkvfOELN27cGI9D27HM89QY43ne9vajz372sx9/9BEhiDHXcV1KqdYyy1JEEKGkPd8+Pj5u\nha3RaJIVaavVGg6HQRAoDqoSNuIgz7Kj/b1k1G912lqqNE2t2PjOxrYGBghDAqKE+eDdG+1O6/7d\nB5//4ud+8urP4jh68HAjjJuNZu3zP/e50fjYkMHewd2V9VjqSeQ3ily1Gq3xYLi2cvHu7YeNsLH7\n4HC5eXljY6vZbN778LjeCJ88/8y777/13pt31s/AcVfev7kBRLz5YCIEBND8/FdXkslQ4dJlZWU2\npAYQpIwgilChR9deaH5y+y3maj+gg9EIQgwgq9XmHz54uLRY39s+qPl+LQ7Or67duXfbieaKSfzO\n63sea/JMp5N09OD21bVzu+r+GdaEUq50HKxJ4Ndc10UAdmohyHYxZkshXG8H3QN8NBh7fjQd54h6\nGPmUAiGE0hJArYSEDhxWGcSkkMijXqs+t3/wSCSgHXUctxxmvZ1HtzpL8dr62uKC/8Lzz8kq3Hx0\ncPX8Mc/Umz9+Fxqy3Fn+0fe+Pxn3CSRRzIIpwQT0R0Vcp5Npsnxmfdwbj4b9Wi12QgKRPOjudxa9\nSgwvXFoYDAYMM56iKnP7BWZs/pkn5gdHRZ6Xo9FIiqoWtEMQx43lmsPKg1IWqO3P55mzt7/rRWpn\nd3vaOwqQcQmhgDIHEIQQgK0g7nb7SMFIGzOdLvgBKtL5wKuqQnGQ5imCEGs52kvyPG82m+7c3Hvv\nvW/HjXYXuC4rS+66LoCwKAq7pC2oFWPs+369Xt/f37fdjiRJHMcJgmCaJg9v387LwmWOF/ii4lxW\nruMwx3niySc/6h/yqtKSQCEDSjTnAMHj3V0EIcEYQxTELqJEIJQDrf243gDHo2w6KZBPgHG6Rz1C\naFCrc52yKOqNu8jxBaDc0LMr5z+6/bDdrhuUX3/u+uHBdm+SExOIrFRG5FUODM3L8sUXPnvU7f7s\nJz8BCImqoo6DIeRSiqr6i7/+63/87W8T7GSpKPKq3vDH057j4LIsf+3Xfu3Bg8379zYwcvRJl60S\nMp9Mh9/6uVdwbNphiAGc8CKkBDnMDXzEHBZE0nCPmacuLK80gsFRf9AbkLxkQdjNy2lZGggBZspg\nbYABSElFECRGIilcDHyCoZKtWr0ztygU+Oju/XqzXkCQygpgBLHz4OFDrWWR5XOtOSWRMhiTbiEr\n4pusSGq1Gsb0+Ki7uLhMiScqaaSCACBlAp8pyZv1WFV5VpUyG7latjyXSlXDzPEDkxUdz52WE0aR\nREwJbaDkGJTKGA5wwmO3omjy7Mr5hxJ2h0MuSeDVn3nhxXc//Egh2ppbJa6flapWi7Gjbj96YDDw\nmRMtxEc7e8gzl86fpwhmiZomQghxNJrMNdZhYcq8MliXE+kA6njexx/f8CjpJuNEcUppWZRH4zFj\nTpKm+0fHQuo4rhPbf7MdMM657WuNRqNarTadTi3mbVbyS2Vll/QMzjib3c0Uvu3Q3oLKpJTAEBvb\nLMjEhgeEUKcDH588YYwh1AZYiKS2/FkANCEEY2gMsV0yfSKdZ5t1gCJaVcK28myr0HVdozRjLEkS\n13XjOLZCfEmSPNra8wIfF2V/NAyCqNZqCmHSNJcKIoQ8N5IKao00RIIboQBjDqVUK6nNiTv7pxgK\nDKbJGCTAXvnMwLHixe7uNkLIktOBQcYYqZXWutmeczzve9/7vud5XIr5+fkvfOELk8nk4oVzu7u7\nr7766mc/+9kv//yXjv/J4f379z/66COrX0cpXVtbG4/H1joFUZnwI4OLX/jFnx+Psts372NDP3z/\nQyFlnpfd3kFWDHcOHly7fu7wePuZ5y6/+957cdSMgujO8Z2qBHu7m51OczwoB73e6nIDKrxxd6cz\n10wnR3GdnVk7e3y80YxXb320R0jQPSovXryyd7B9/anm9tajpZV6JPIL5878/r/d+twry1DX1pdX\n7ty8f3b9zOHhYb0WlZVCiJSlaLUbUmnONXVwq9XZePjJcFA+99zVGx+89/yLL23ujsYDE4atw/1j\nF0d7W6M2BdvZ1tef+jwtDTWSujXfCVzXUxoIXmA+QQgR6PtE1T3WCP1JUXGpGaJSgaqqiryUUlKG\nCUEQGuJghSSFZJok0ySfJpkQRnEwTSc1A4wB29vbF69+odvtPvfcczdvfuLReaDdV154ZWFp7Xi/\ne+vuvcFxVyhz/uzKw82NH/zo97/2Z766vNA5Hm0oUVy9vr7WWphOx4+2HuYyaa+sT9JRUHMrUZ49\ne34ymRpjqoI7MCgTEJMAGIKFO52M+4NBURSe6yJKZQorKEHNp9zBGmvoBvU4bsSIkaRKAo/GhDCi\njAbIaIOB1CItVBzHWhrOhVISAa2F4CKtijIKYmP1t3IJACAQUAShVh6jSikjNTIaGa24qPIMKMkY\nQ1oZY4AU0BgKAYYAG+1g5BJsjCEYSUooRthooCQl2KeQEgNlCbXwCMJAizzVvHQQQAQZpYDRDoSG\nYIBgXgptTZMBhEoaKSTCOQIKllJqZeAkyahEzEUE08kkqaoKEGMAAgQrgwBCBjOAqIZUQQIMVhBx\noSsppVIQQmWklLrkUinDpeZcVkIhZIQyUGqNkDHQQIwxNRArAzXAGkJpkDJIaqQhUgYrA6VGXAqt\nIMZIaVVxgQhtz3UcqqXiUOMwDCMvtJhrjTANXAURkxJqDX3Hb9eXQ7+EdCNJSJYzgpOiKq0cEsKE\nUqEVNjoOApmOV5pNrPl8o9aJm6vL63llRqNJonVaVcZAiCl10GQy2d/fF0UROH5V6sEgVYYAAqI5\nd2ll/sUXXzIavfHmu1HcXl1ejcJamWYIGFEUybi/cf/2w/sPqiKPMQhcl8kKAwSVBFyBUmgjuYCh\nRyWAQiOtlVaYGkgANEa7vqdKWWW563pn18925pcqpUuhu0f9K5evddrzQqkirxp+vUyK+zdvrV+/\nNEzHZZp2Gk26trTzaONgf/vc2ioleK7d0kb2ukdFWmitlTIGAwaIAiCdJpubG7UgBBBSz8mS1Bhj\ns3khBIEUQwQMJN1u1wK3bNPTdmCTJGk0GjPYjIWEEUKUFgghq01gTjVvZrAc29+znCR7kmqtlYRW\n72Cm5sQY833fdghtWTOj1BigEELWLCuKIhspbTi0KsLq1K7iBMtHWJYVjLGDgwOttarK/f39PM0s\nBG5lZWVhXrthGIah6wejSXbp0iXXD7iSEGJA8HichmHoeoENJ1mWWQiGEMKiV8EJFA8paYA5YTsh\nSBAkwOhTp1rEK3nCCCaOjcTWT89GI8t2o5QuLS0lSVKWZV5UnhvMz89bGYvFxUU7GIui6N69e1mW\nzQpWC5S30IY8zxEFBrmLS8s//sHbYT2YjEuIje/Vh+PBdJKm5fTa05dYn1Y8u3DxzP7BltJ8a2tr\nfy/ttLwgAMsLS7dvPzizdjFL5O7+veXV+W5v3/PnBsNeA8/tbm/4gdM7zqfTYmV1EeiqyODd2+NW\ne2l18eLKUsu7QD/5+NbZdXx8mF67eu21H9+g0F9fWjpWaZbnB4cDIcdcmosX58Iwlso2SMlLLz2/\nuX2XefD6c5dvfPy+H5zhOejlE4cG/UE3CCHPzLTS84sLKC1xzqmByCDOs6LiklfUGAQxBBQhEoZh\no1Eb5NWkVJBiCJALMICOUuRURoprw4syp1EHGIExkqJyXJdz3u4sptVBc34pz4fvvHvrlS++9N6H\nD3d3DgDvh0FzfXX9gxvvEuQwF8VNbzQZezGImpBgjVg2Lavrz6+++cbNi9fmDx7uXfvMpbhR+5e/\n+3sbexte7MlKvPTZV8qyhEk5P7ccBzUf+5tyM03TUX/QrjcCRGljztSNEkLxQqgSem4rbrSXm5Ff\n7/XzYaIVVwCZNE1rc+1W6AYuNLogWPgOoRBoobtHPWAgdig0Cv//2frTINuy7DwM2/OZz51vzi/z\nze/VPHajG90YGgQItACQBExQJMJBiZLpYARNU/QfOaywIkxZirBDFi0roDBEy0EFZZAgAIEwCKDR\nQDe6q7ureqr5Vb0538s573zmc/boHzvv7UeFMyoqsrLucO65e++11re+9X3YYAKIJrhpsqQwCtT8\nAmFDCOGmPBifzevCNl+NMR5FCIAaaschSZbhpQ7WirFp+8F1XdsmvP2jheU9z6Na2f2rl0JcRVHY\nUW6EUFVVNldTSgEECXWNMUhfuFNKKQXUEkMphH27uq6FwRC7COrFYlGWJXEvRIHtJaFnLNaMIUuz\n6Qu2tAYa/EjRBy6nws2zDZsVYYpLZQyxHFd7Mc9SDDgXSgLHYUore/dand5m1zeLqSwqCpBLGAQY\nYmQoFQZAygwElLpAGck1lwZqOOwPjJsjSCBMZV5JLTEClFDTmNj3rlzaUUVrb2MwPT7qtWKX0ft3\n77EgLoqshsiAi9l2C64IIQCArVYrQw0/nXEpmM/sfKfv+8BgrbXjOJ7nKaU45wgYo7Xtspel4zls\na723HRLCK6CAMUYJzTkXShpkxvNRA7kxvG5kw3ltmlo2wqiKEa6Nr4kLdWlkIRqljFGI5+XifCEn\n+ZXdyw43ow8+TdO0h+H+ex/Om3JjbRgOnIarzf5we22jqou6KIu6qOqiqErsOVDhsqm5KMPWugFI\ncpHneTKd8aqMozAKwjRN4zAihGZJGkaxMYZQdjHjgp9x1gFLtwi7Juz/tbFHSDtmfBGKbGUAltre\nto8KlzrzNhoJzjHGnHMr8GN7ORbRftZYwUYjbSSllPPavpRtzNjF53neKmrad2SMUebGcXtz5xKv\nSgCAg5ExxijdNM3R8XnTNPuPn2pET8/OlQHHp+Oqqbcv7cadNiGsaOrJZLFYLHbitj3JqqrCCHie\nZzeGRdsZYxCqVcRdBWBbu9i/rEQZVizBJYMGQQghJhBCS3y3t7Sq+YpSn2WZvXuTyWSxWEgpW62W\nUioIAktH9H3fQqaUUtd3IWtli8ah3TqrC6ovX9394MMfxp2WMmrv8qW6bG5cuwZQVpdlp9VezNPT\nk/LlF24WZbJYzOfJ6PqNHcWbRXrWjTcMzG89t5tlSacb7+5tldXCYTQKukWKP/zhfhi3sgXotjsf\nffDoJ3/qM1HQLavs8cNZmYH5KOnG06YG12/c+Ff/nz955aUXXn3hlWtXigcPH5+enyxmKaKaUPAL\nv/DzB0f3rt64vbH7WS2LVofeffBIK6AkzKsqGHSFUJ1OV8KE1nK6mLGKe8oARLRUnHOAYdQOktEc\nAGk0UogRCOLQj0O/VlWtpZbcKE2AwVALpYCWCBikVZbnDSRCQBrgphGYuafnc+h1/E4LYA1R0Onv\n/PFX3nIcp65BnfOoZebJtBEqT85u3L61//BR3HWv3lzfuhp//OF7mizag0F/Z9gdPpcupp/70hv/\n0+/9SZrnThuEsb99eXeeLM5Hkzdee9OIe/sP9qenSTZd+NRrB631/vDwwWOoIXN91/eBVKZWJGQt\nL6oW1dHk2JjTojBrO7faUTsX+O6dT2aPHheh5zEjRAZA7RKoBa+KOnQDYBAAEADDHMQ8ionBBjBE\nCcEOJvaosuEnXySbwzXLDLqw0QJASrm+vr6YzRm+4BPZlNHuyk6nU5YlpdSO1tknNlIQQpIstYQd\nm3IZY+xe7na7EMIsy6SUlsEEIK44V0pBIZEBSCugLayCGGNYas9zCCFgGUWs3hgg0EYjm5zZpHM5\npQet2P9FWmiMAReBBy99W+w2tP+5yiAt0sMbRUkIn7F7YA5ZMaGglSFWCmHEGNOGl2WZedjRQGNq\nhOKF1ZkwCoLHB4fUdR0/cF3XgThst7AfcwB03QiM8bKtvsgLZSCBADt0vddZ77ZZO2j5bgq1rKtK\nqKLIvbjjukwa5EJkoOayUULaU5dCRChFSChgDIRa61arZe8ARtBOx1NKp5M5AbAoClFVil8cJmVZ\nLhZ48vCI8ApqCABA4MJqQAMVdWOkMAQIGqCM1soAY4CBddMIqSh2Ag8FLGRtz6UuJU7T8PhyCwMM\njCYI7u5sn52dHU9HqqxuXb1cpOmjjz5pR6EHaJ0XnXZ8fnR8en62yBaYIoSIEEoKrbUp8wJC3ArC\ntWG3SvOnTx7LugEIh9QJCEMId/yw3+6lRc4bdaHhbb+wC/twKQEAtp9pV8bqK7dTCHCpRWjDyTMA\nmlmNB5mlkfkqnrmua9E2q/pu9wBcqoui5QDRCr5bWfDZg97ukNWMkVpaVMzn87jTtbGTOkwpRTGx\nE1Fpmp6cnLz8+mdu3X6u3e1RJ8CUvPjyK3GnrTU4HY+U2j86PVn1zDDGBEM7crHiE4LlbNMq7Vp9\nTLs9rEK5nT3KsgxjCiEEEBptpBIAAIAUQqjrenleAICUMpZqmCSJ67qUuQcHB34QeX4opMaEaQPP\nzsdRFBljsiwXUpdVU5S1EIJQp8gbTGB/uI6J6q+1wqDbiofXr1/7/g+/N1s87k6C3rq/e6WTzKZK\nkpOjPEsA7+s8KRxGNrf60+k0iuL/8O/+rd/77T/84XtPv/iFVybTs057jdfNF3/8C7/zL3/vzddu\niLqYT8ee64zPi71Lt3/4/tuLefODH/wZF5USIJkDSsD4LGlK/s1vvP38rRdcEr31F9/tdLvDwUa7\n0zs+f6ohl6B676P6lVdv3r1/5/NfePX+/UcGcKGl7zhNXcZxezyehGGcLGbDKKyrxWhyTsvG1yBy\nXAcTpRTECEGDCJQC8qZptJBCU4wCx/EYZ4iAslFSAK20FMRoQhFjjCDlAImQ1kAbyeumdHxYa57X\n1bVLtyszc6lLnXiW1Ag1zG8BkMXtYHR++oUv/uT33vnu1Rs78+Tkzc9+4ez08PGDBz/373w+K6cC\nzjzfi3pma3frzgfv/fjPvfrf/j//oj8ElSk/ufup6/tpUj5+8LvYIFXLbtCqDN5d39FcaC42e1uT\n0TRPai2Q53mu7/bCsOe3RZ4robVGRS7smGHohaISpBIUQiYQA4Bg7CIEIPCQ8Q0FAGlllFIYABdp\nZhBEZF4WLsFKQWOQA5FtBQnQQNaIstQYSwgblNjp7Db2R+eneCnxac90uBSZ1lrbsXGbLBJCAEZX\nr14/PDoqisL2mewRYZ9i80grZFV7vGkawmjc6dR1rW3csNSypVgO55z4ruM4gDjPvrV9pC2zbIpm\nh0mklFpLCKE9i6CdMDUSIsM5t/3g1QTuqugByzPEvgJGGiyHx5XSdjTFnloYYwmNlNIh0PO8JC2P\njk+Tx/d3WvGw1SUalGmRzOZpkRdN3RuuVYIvpjOKcOT5geN5gCpoXArb2GEIEkIwAsiYoqy0qgOH\nDSIf1IXrOdl0zMuCA+BGeGdrrTPs33vydJalAmJDCaHEc1ytAcDIQGhpyfZQaiSv69qmCBix1cHo\nui42oC4LG2VXBKs5lB1CHOgggwAAGBKKMABAGs3LRiMNESKIBhA5zFXIQAiLWb5YlPV8VHS4F8We\n7xulkmb+8d1Pr968FUShVc/q9AanKr9/djDc3Jw8Pe73e8/fvlaWeZHlUKiP3/8AYxR6vjYSEpin\nGXYwc12XuL7bms+Tmhew0+pFLbqzK5tmPpkSjFVRGwM9SHxEp2mxmKXk3r179hPaoGKROlsrrDAx\ny+LHGNdNZT/56pheRRTXdS03z5b5K949BLAoiiWdQdt838qzrg56+CPfCrS6udYeQi4dFlY1x7Ox\nQSkVRZHruhgYpRQERkqppbJ70lYYu7u7QRBgjDc3N/OygBCWZUmp0+l0omhSlmWSJFY1DmOslKjr\nWoUXyACljPOGEPQjoEBru1tWE1erPMuGzIsYtvSDMMZATBBCvV4PYxyGob2TruumaWpD+2g06nQ6\ng8HAqit1Op12u20FIKqqsk+xbwcwi8LYcen52Vl/0Ir8Dq90v7OBNF3rb42mR932cHPYgYpvb1x7\n8OgDj6LTRJ+dzl997eXR5JAx1uu1X33llfsPP+Qie/6FznR6zija39+fjqaRHxEUPHxwPD5Nr115\nAWJwenYcRsH25s54NB/0N58+eVRkwPfA7AwIoRBCYcDOT05FVyguur322vraJ/c/Pjk5HWxHAIh7\n905eeGlPI5UWGaaYC1XXgIHCdRwjBcCwETVziALG9UkQRRBhIpTjuJHnAwCKqqqq2iEeMIbzC5Eq\nRrDnksAhjQIeAdDFxqCqkllW1EpBB5e89hhTWkSuZwikwigoiYN6671LV3cORvU0y977+P3uoL//\ndP/a1d0iIXWT1bz49O77G9sDAJvbL1wdDNsPH39UVvmjJ58Spnav3E6zcbfX+v73v/P+e/Jv/frl\nl9+Ex0emqsHe7gAYqgVJedbyW9iHDBDjNV0/TMqZEVAuSsZNBB2mHdhAXUuNhHI0ljR0XccNmnJc\nl/zx4ydRbyfPCwShEKKG0GEAY4wIwNAhmEGDMCBKGaM4gFojZDDBGBJKAUIWfFLAaGAgwVZny0Nw\nNYABNaaUeoFf1zV8BmBfMYBWocgstVeMMWypaaKWwmD2F8dxbOFlU0n79KZpIEbWKlNKiQHECCKE\nIIB2KryqKidoIYQgxkZDewIQQuxuRhBalBsuR0TtlrcEP4QQAkhrjSBCGD6L1Nlf7EFhltP0YEkD\ntniP1gohpBSw++giUGFqA5VtXhtjirqGXCRl7TDuQlJzXUsjDXbckDCfYgqkxBgzN3Bc10HMgYbn\nuQHSMKSUwwO/KQvVlE3TBC6LPcKgiV22SIXitURAUBJHHYRhw+uqKJXnGoIJxEEQ+L5PMCQIE0IU\nMJgihKmoL1oGnHPXuZDKzLKsLEvV8LqqpJRAXSBMvu9HraAeHyKooEFQaqE4BxegJSLYYAOwQQgj\nCDE2EBtiYCca9lFLAK0Q1I0xUHBk0jylvvv4+Mlwa/sLP/2Ts0U6W8xFTF/9qc89+vhey48+/ejj\nTz786MXnb7uuW1fVWnd4fHbMMIEKAmPqvAjbkefSsqjCcI2ELSmESAtjyo7nsyDm8yzy/LquMYA+\ndjyDcCVg0ZAbN25YWMwqBVwM/XS7KyE1e+DapZMXKaUUoR9JIcClskVVVbZdtPqjXetFntoRpSAI\n7FvoZ+j5qzV3USQRW3AoKeV0Ot3Y2Fjhe+QZGz278hBCmDBjoDTApVapACKElJD2YYSQ9fV12wCz\nF7mxseG6roaAUsooCYKALH2+LWKmlJLyArxeRVCt7bq3s2rI2vRhTKVsAICMuZbPAQAKgsheMCZs\nmfcZBAwEYDSabG5uF0XRarVs4xJC3DQiiFtCm9F0VjZ8uBERx3X8QFdVLSRxXIMwwIQrLbQx6MIq\n/vj4uNX2J5PJ+qJ7+8Vbf/zHf3xpbycI/Ns3Xv707ofdbvfTTx4i1mxstmUhXKze+ebk0YNv/dVf\n+Qww1dWrV2teHZ0crG8Prl9+4Y//zTeLXCwmAvDy8YOjN179/Pfe+bTIayEkMuDq1d2SZ9vbmwdH\nDxqeHx3pfhdUJWi1wcnpU1EBB/mIgLyY+iE2oOr2Hf/E9Nfdqs7yBNx+Jfytf/GdK9fBIht1O8EP\nfjgadkCazXud7UWWhZE7Gc0GrbhOFoNWCAjywzjQiAGMiUOpQ1nMPZ6O5xBTwhAxwjEw9Nx2GChp\nTicTJAXTCmIEsJFYE4fGUYhVQAh7cniGHIN9xChqeKEhd3zY32wfLOQ4OQ1j972P7v7a3/i5LJ13\n27DIkiFpjWenr77x8sn5EULgq1/7k8ViogzYvbx3ePTw6cGR46KDDz4kFP31X3vp6OTu3/lf/drp\n8eKf/w9fKfKFbmiVK11BvVBdLy6r6ura3qXehgm7DqAffOeHcRB31tejuKWAAUrHkb/W68qyTNO0\nzhqCnJvXb92+8Rzw2pBg2A5SkUEoqJFEcNNwCABF2EhEiIMgUUZDqIkBjiFEg4UqsCYXObIStgiI\nPVaWqVKKYSa1RAhZz25fFApDIKSdeQBLJ55VBvmsH4pZ+pmtjvVV5dE0jcU8VpvXMsIdz7Ubp6oq\nAhFiVENgINJac8XtxJ4xBgLAGLMq/owxiC5Ev+yOu+h+XQAhF4C/jUb2Lxhf1DqraGqWbg5wqQ5n\nlppvSmqEkDYGEywlXEUjs1Tnsp/USu8M19a2wiA7PzubJi0vQBpxhQh143YLEhJ4roFACFEUdZnl\nDDGH4rjTwnWllVIEtn1Ht2IKQFnXgee1fBY5Thwwp98dH++34sBxyLDfcVph4DO/YcL1C6CFUEoa\nY2DTNIZQAJAdeKcMCylbrZbneVVVIUgZY7a9ZK+cUgqkFLK+8NGWsmka33F8AjBERkjNNTAGaKgx\n1sYQiDSE0hpHGwUUQMDMx1OPOb7v1kbXXCEHAWMapdOqlhRVkzPwwQ8Pzk56g34uysPDkRINyI0X\n+MaYo5MTx3EwNKenp0HgaaOQUDs7OxM04YLjSoWa5OdTz/EHUbsV+7ysGIRUI4fr7bVegQuXuRBC\n1wl53OuigJRlaYyxXRBbDFnuwGw2swf66rzmnM8Xc8/z7LrQS4k2m87Y0aIVuoWXlts2zXccp9Pp\nWM7eqrf0bHSxr4PJxRyyLaF2dnaKolhd26oqAkujVUxYnpeLLG+FAWPMwYhSWpeVXc1pmuZZOZlM\nrl7r9IdDpZTv+5RS6joIkbyuVsZOTdPkeQ4vRPaA7/t1U6bLVAssBcifhRZtZF2RNWwgd10XI4rx\njxzHzdIE3XEcOwJld47dPHmeWzT/9PTUkjssRmHRD7JUKy+KwjpoQAjzItna2hxPjj2flmWZLZJu\nq4shqQpx8Pj85pVXzo/H3Wgvzc9VFdRZzgv9/K1+Xp7/i9/63utvBh98+NFwGEVR6+x4dveTPyEm\nqDLx2isvzidZkahkelDXTb/Xaaq8M4iee+Hq19/6s20Sb2z2T0+rL3zxkkPdh/cejs/0zkaUJYXv\nOGeHE4Kb7tra0ekdGtVno4e9of/4sA574OQ0/9LPXXr69GA4WHvv/cetGGQZ8EijTNHtBcdnx3HL\nm84nEcY1b9K8ZE7YSDibzJNpApRhjDFCI99xKMYYMwY1NBoSLpRSgpLhLEnTIgcAhNTfGXZ2dnau\nXb4ybHfPzia/9Tu/N684QSb2ncxo7aDNSwPq61vPX9ZO8vGnHzgemEyPotBFhAhuDg6TSzvDNJsd\nHDzhnLfb7SyrGENP9o8dN2hqNJstjo7EjZvtk9On29u7WpVS5n/rb/zsw7sn9+4cOr7X6/XHR1NY\nyvNHZ5e89tndJwxBD9OrG9sEMAwIVcgh2GCjCzGuxkirPM8BYaIWmps8K7HxiqLoEWQUopjGcRB6\niBLgO07oh5PxgjGPYKaBAVBhBgmFEJphZ42gizYtxrhpGoRQp9NRS//lZ8PJWq9/ZXtblLXd2kKI\nPM+11qstZp33EEIWwMCMAgBc1zVLKTawVE5ZxSHb2lRLt0w7aZ7nOUUYKsdgJCBqNAbMtzwdm4Cu\n9p2DPYDUCkhY6WA9i//b0xYaJaU0UAEI7F/sKaGe0Sd7dtMtoydYAf6r00kvVSLt/jWGS6k8z9u+\ntNtC+PTJ8eJ8YnooIk6S5lVVVULvHx74kef5vtbaSNUJ4yvbvZ2tDa04QUBLgQGgCDoEhx5tOIcA\nRA4NXaaaOg5dj7G93R3PCww0UvKyzJuyRMwjGFPH6bTbGGNea4I0ZpQwaiDQABCKmqayxwsw2Ar8\nE0SiKMoXyeqjWeyuLlVd1x4wCGGCiTFAa40MQMaOlEFAMKZEYqghUAgYBBFCuD00RgmgMTLtwCNx\ncLyYJOeHkBHEcMWbs9F5mqbPv/KSEOLBJ3ed0PddnwRur93RUnz8/gdVWexsbiohMUB7Gzs/+fkv\n3vnwo3fffZdoduXaNQTdg6Oj8STBaz2PsDDwh62ufwUwTCJIwzCSUmLkoN6a6SBiayC1lOu2dnb2\nnF3NHq0Wh+u6YOmqCyFcaUvbRWmjiy1lVqpudkvYxMcCeks+9wXmZleGvQYtNADAtvHTNLVqeHYD\nWCdyu/St4nVVVQDyphF5nseBr5SqBZ/P5912Zz6fc87taHqr1bLXHwWBrfoZdBljRAoL5dk9Zl0n\nfM/RGlgOG6WUc04pWxZ8Fr4ASmkplVKKMQcAoJRGCDuOrZCsgIe77KwSYGVZlLa7NAziqmxc1zcG\nag1c17cCtWEYWv91e3xYhyfrNIEQsiaHAAApuQG6KKeuhyFSDsMI2bwB+F4ACX10/wRTeJBP/BBB\nqV284REuKoV0+NLt8Pz0+MZzm5gYIeFsVq6vbb/73SMGQJkrjHyfxZVqoiDIygXScvTg6c/8/OuX\n9roQl+02KUvn5o1dI40S5dnp0Wc//8IPv/fu7s7w8GDixNyQ2c7V+PZL66U+zur8537+xre+df9n\n//Irlt6RZdVPffGNBw8ePBwlyK0Jrg0UV69vPrj/KOr41zcvPbnz4I/+9M9+4XM/w2pw/OioG3Xn\n08Xe7obnOcZUDZfKCAmg1ogi0w69IPSqmvMyE1BZr5NOp00w+PT9d8/8zvb23ovXb731w3dlXU2S\ntL/X89eieXb6r/+/H/7YT7zieBJTc+O2u73bmk/GlGKl67U197XXX57P0pOTkeuyra1LrWj46d3R\n+lqYzktGgsn5xEgw7F+Zzw9cBz26/wnFcZaWu5trPoju/PD+40/u9YNuM0+/9ObrHsRrrU4xTwLm\nUg/XlaSOr4UuC7G+vt6KwtHZETY4CuK0rBHAGxsbUkqGsWlEaGgEXAoVKSXhjcuwUwOUazjKNK6S\nqgnj+OTsOO5G7XaYp4lPWNlcOLnZKYtWq2Ua9PD+fVua2z5oWZZKqadxWMnaLDlpFkCDELbbbUrp\naDSyK9Ae9BhjgNF0Os/ywoYEx3Gsbxljzubm5snJCaV0bW2dc+667tWr17IiD8PQ933nytXIDzpR\nSD1XQJQa9cHDJ8nJmUW5W3FXam1FW1RtirLUSzlHu81tI9bzvMVivGpFUwQopVz+6OIppYvFwh4F\nts1s+bdxHC+7vAgiRAhRWivV2He0ZZzv+2maI0ghhA3na91uf9C+cvnapz9814u7/4u/9tcf3bn7\n4KOPv/ATXzp8+vTB4we3rt/yYv9v/s2/+S//5b+8fnlvd2s7n80owel84lOqPBfCBiNAMAq8C90A\nAk0UOBS5Z0dHn/uxz7iMBkE0nszPzk4G/V4BYWYNQh0HIaSkJoTYbndVlZTiRnKuhbWuBwDYeRvG\nGNCgrmvHcaDRRZJQQiil165dm4zOi8mpkpo3ZnN368mDR4HjZkkauJ4UQklDPb8oCuQ6kJLxfCG1\ncjvh3NTTYlE2NfPc4c7WxiCC7SheX9NFUvHGxxiWvO8ED777njFme309Iw1Xqttbe++993hdRZF/\nflhcv+4bLkPmBth9cuc+yJqd1qAVRm3jJFkVGky9CJdcIyWVoVEbpJXGWHGeF1xr7bphTJyyaMj+\n/r6VpLOld13XK2I3WA69wqUftlTc9/0Lqti//ROGoVpqm9pD2aYe1lt2RW1YFQerEmeVuSCEALxw\nqbDnr32ifYrtZF58H0tFcG0u8ikLlEMln7VfNEsnb/tBVq0m+2PMj+weAABFcdEStI9XS7Mis/QF\nX7XKVtf87M8yuF5g6EtpPrTKxVZ9Jvt4Cx4CAAhhq1JvJYSh/23B72eeqBHSEAGjBIQQE0OJFXvH\nwDBRmbpSmGECIt3AiK09PT4yxjFIAs3yheQN+PjDk1YbBFHYirsP7h9du7qNpP90/yR0WplpDg4O\nJJLMA2+8+eL+wae/+7v/7Md+/DWu6ytXLvUH0bvvfn9vZ7fbia5ehscnj9tdxwv08y9jDUEQwGly\nvnPlJ2n44t1HDwws/8bf+kKelVLqKIiNMrNRFnn9a5eZ5+CmqX/wvcUXf/LSSy8/l8yS8XTy6uuv\nsxwenp7/2HNvigxUabO7c4tiP01SimuEBSIUU8YohtKa0vB24G32IhcbynCn3R2u9TnnzXzmGZCN\nxnubm3cfPTCBFxLvKDnfuHnVD/B8lu8/vetEkBCgdb2YnfK6yvJ6MBiEe63ZbOa58WwGtrecP/mj\nDz/zmesuG50cLc7PZ9s70vO6BBaTs6rVibMkJYi0Ar/l+ItxUyVzoiU1YGsw8PvOIGyptFwcjwat\nTjdqpWnqEooBKhupucAaOZg5mBVZKpRs6oYrSDCGEPKmKorCCQdUKC05l40WAmnrIkIJxkoDh3lF\nUdg+6Gg08l2nrGotLgSIbaFgV75Np2xabYVIAABCSCEUpmhVS8mlg7Pts1pK96rvIrSBAFnDlxU4\nYTev9UaxkF1VVWVZVlUltZrMZxBCagDDhCGoEeQAFgiAoGWZEfZ9ASKu64ZhiH1KSu15nusB3/cJ\nRZ7n2fzVbsDVXrC/MMYgWuJUywPELHWfV1v1AncxUOulrQPQq9PAEmiNMdpoKQUXPE1TQsEsWRjM\nCHMePzkqypo3CkIUhfH1K9cb2RRp+edf/TOGoJZqNhkX88ShxGhlgMIAMoIAxAgBLpWAxnUYMppg\n6FLaioIg8LQSTVMpJT2P+T6DEwAhIAjbCXcAAEAYQGwAMBDo5d9s7m4T8R+10zAwQtovC2pujCmK\nwiYcQgihIa/q1RkoOIcQEooohsZ1JQDz+XwyGgtlcFNMUNUwHfc63X5PEfTBvU/neSq1oo7T8Iwx\n13UdBOBisdjd3Z1MZpXWFW9yXmuCDMUc6PUtx3F96pjj/acb7d7BvYevvfBSAclma6C4Yho8d+X6\n2cmJUdwB2Ifk9Omh4TJotamGQRAqo3mjm7op84JsbW2laWoLFwtYXVQJS+kne2TbxWHtFAHQz8ah\nFXCsl8p1NlTYlWc0Nkv6pi2zVgiejQpgCVsDAADUq+1hJettGJNSxnFs94xdzWhpgWEL1YvFKqWN\nFjZiwWcIe6t/66X2u83F7MO01kmSLKOUNkuKkS3aViDAKjyvwtgKwXvm7YgxRittjCEYQ4ytnRJG\nVEmjNUCIGGMcx0GQICQxxkoDiIjj+szxCHUQppxzALH9xwBkAAIQAwAAsgQlDYCBCFj6CcWEYgYN\nxoAwQiBAGLmiqTeHNx4+PBdSsdDx3E634/dY9Pjooee219e2ppPM9RqtcJk1eVoJDAMW9jv9UqYc\nlCenT1557fbJ+NEiPW9kxZy9yXQ0GPRms9nobDzo9wg2TZPtXn55//AuAODqrZ0XW8EffvV3n3vh\neT/AG1tbdz7+eGd7b9Dqf/DeHYa8TquvmvoH7zza2wM7O8Nr1/Dm5uaDR48c4jteIDUIPK8VxHc+\nvU9q5DmRAbQ/2JxOjeQ150KWFYSQOi5z/XbkYxyVdTXsRD7BmMBOuxX7zihP8ukkarHYCdb6A2bM\nPJ2pCCMItrYHkMhWO5zNRgMaYgMMB/PxiEBS5vXo7OHnP/e5xXTRiTbW+g5F3pVdb3peiAqmM2kE\n0Y3nxV1ekjwx7Y5bZgsp4GxUbAwud9rth/Xje3fTYQiaIoOyOVs0XTcEXItSni5OEAKQMgiw4I2S\nRjS8qirBFYQYQ+04Tl40AAClBVASuzQFokYNQBIYQbF2qeZYOlgWPhZCe643nVfdYQ84KJtUrBvx\ntAKa2vVZQSmlhgwypHKfrizEMEYQQiEM0rwVBVDJpmnswrYAhuXUrDirK8KbUpJRQghzHNf2/CGE\nCBGEkOv6hDAhKquE1zQ1QoJQuqJFGGOahnOtFCaSkaYoAACu69rhd2OQbR0x6DYqU0oZg+xBYa/Z\ndo8sZ/2C92t+dObYaKqWU/lwyWKw72uWg4lGI0tFU0pBdDFobzc+QigIAqNR09SYePZN87xstzul\nRk+fHA3j1s72buRHKZpTiDF1aIiPnjx9+cXnW1HoUepBBLSaTHOlFIAaIUAgghgYqKHSjGEpjVLS\nEMRclzosmedC5ADiTivsd9utpMDIqSHRhDDqKi3Q8jgFF66rxpiLL8JOyFjKhjEGQqC0phg7jtOU\njcX2LQcNilJrXZalQ6iSnFKspXQch0uRlZnj+pgQTEjcibWBgoEuIzDAi7z45MNjJ/DcVgS1KYpi\nZzgQ0PhhhDEu6mp2Xt3qd2enx8PtzXpyLoCEDk4XRcJVx/OPz88C6khlqOu1Wh2lzNpgXQlNKfUo\nGnS6+WwxGS22Lu2en54Ueba9sWmjjBcEAIAkz2reVBUndsh0hdLa4n06nXY6nRXH5kdfsGwYY9Y9\n79kfW7vYCOR5ns3FbIzJs9p2L+09tUWMPettOvZs7q+10loLwbXW1p581aB69OiRzWgQQlZQxxhj\nAEKI1ELOJ2MIoeYNQij0A71kfFrMYVXTGGPg8hcLjtuVvUTYrIXgBadoxbAAS84ofIbat0rWbO24\n+jEXQ8EXpFXwDFljxbhb+cYiwsBSntxxHLtXn81DV3jms5cEIQQAQoAxphhTQhghjDfSc33PjZVS\nStZ5nm+ubbs0CAN3+/Lm+eyRVuD65ZtvfO41oau7d++OR4tBf3NykraD4e6uc/DwKHKCRjbD4fo0\nOdvfTw3+5Mq1QTKfIQoYYw8fPP7Lf+nnv/n1t0fngIKsd/XyQX66ub3V6cWPDtJxNhu40PWdk7Pj\nW7du8UYfHi5eebELFAUSIUbv3XmoBfyVv/IT+/t3jo9GDw4AZp+cj9JeO/SMgxuyc32L1GSaJ2th\n7/xk1Lrcvnnz+p9/7dF4dBoGuN1u20kLmyiopmHAtDzHJ4gQ4rpEFFk6Gck8hUFnvddqTEOR1nVV\nlXqw5gNt0kVy48UbDw/vnB1PL613gVGq1OuXdh4vDhDUf/yHb1+5ulOm+48fNbdvYId56SJnNHBI\nEK/1CCLTSVZkRavFJuN8PDlptzvt1vDR/uPzw+mjO82Vq/Da5nXaUEdQX7nXNy9fXts9PzxNp1Nt\nOGTE8+M2oI0CYRA7Dm2325QgZaTBTB+ftttt3/e9bufy1b0XN4Yh1o4DKVMMaYQNQRghXORCSeB4\n/mQ26w46hCGAdVVkkBuk7d7RdhDVtmdGk7Gtchzh2syaQBq4YTFbAClWg95g6dpsn7tivdqZ61pI\nz1WNkKsEzp4JnudZ4AgsZy3susWEXOx9AKE2dlQFEWoYraS2Yc9mk0ZfbE+HQXt6Yo/Wde24jsW0\nwTP4/EU2qZH99iHSeukDsIJYVjLEdotZnAbBi/AjFfxRfmxM0zScC8fBgsu6rh0X1nWNiTk7O/t7\nf+fvnj8++v43vkUhavfXeC2GnQEdDI9Pj+JOnKaLThyl83kNoKiaLE8Iw0JxrqTS2kAAIcAEAStS\nB42UnBOECAQYCSWFkoHH/CgYDHp7AJfAOS+apKoopbLmBiGEiIHAaLAq++xRZmnfNtxKJVcZsD1F\n7W0hhHT9cGNtiHkVeS4eGi04hqCp6iAIuBSLNAviFvG8RmnkONLoXFSH46Mnx09Alj13abc97B+O\nx3WxGPYHdc29IAzb7Zo3TVmRIGwQ9nudNE2T+WJ7e7vMckJIp91d6/WJBt0wfpgkhyfHdZpHUXTr\nyrXp2WiRlK24PRqNAABn49GtGzcfP9lfXxt6cUgpbYBCjJZ1NVrMqqaWGpL5fL6q2RFCljBdlqXr\numhpJ2HPQa01UYhSapP91Rltf7d1jI3k9t7ZxQoMsXHI3jhrC2RhBEv6NMbYEGUzRAih1tL25exE\nrV1GOzs7q/gxnU7b7bbjOJgwIZSGCAMDIZR1hTEmCAMAvv+D920tZd8aLE1HXOfic9ku7ooZgTH2\nPE+KBoALqqstpBh1bZhRSkEAESQEM0ocIQQARmulAYAQQAgQghBgC68TzFaVk4EIAAQAEkJdRCOu\nKHHghcs4EUprAAlzAMIaQICwMgBjAhAGCBuI7D8IIQSJMRQDbSDEECDDMGAEMYpZJSqFJYHKKImM\nAUYFnqNkwxh78vjhojr7hdd/ynHVnY/v7h88aHU7t2+9kMxKweepXExOplVR+utDzuHjB0/aw/hL\nP/3cpw++n2XV1u7OD969/z/9zh+s9bafPD6vK3j18tbDu8cEn7mO/3T/LCv18y9d/uF7+y+/gje3\ndiveMDdUut7Zaf/zf/61bgu8ePPVx/cPeSkpdL//7fcIVZu71xt9UGRmc2MbQ4S52bt8DWCSlcV4\nOmqxYHdv4/j84P/6f/svfvzzb4Rh2Gp7nW7bdz2lFK8rpDUwhmCIGTEU2gNoUVahQ29d3xvEQ5dq\n5rjXLm/7ZXzaJJzooqjCfvwHv//nu1d6cTx4cOdwrR9//jOfv3v3bifcKrKTQYccPZkik7z43G6Z\n1m7b5eUCQ9JUlTZS1kho4TmUUnp8ery2td1pd+uiPjobddrdjUvjttctRW4KsxasKa0m89ntqy+c\nTz92CdGaK8lVWVLXlwpN5zOEAAQaGlXxClHvbHReVAXJ0kyC2Xj00ZOnLSRdBxGmKJTaCKCh0QAC\nByGqNOBSPDDSC9ybz9347tvfDpkL9AWQtUILbIlQL3Mjm8ZFUTToDk7nKQsC3/ft8rPpGqXUju/A\npX2M53m+70sDup1ezcXKk8UyayxMZ9szq80CofXnVlprKKSRCkghjLZIXXZ4SiBeNYwxxMaYqqoi\nt2UDBlpKMACzVNviyvOwhesRQuDfpiQwxqxGzOovVgnMHt924pBRDwIbjTBE2sLhFtK0+pY2G2bM\nAUIwxpIkWR+s41pvbGyoRbrd7Z88eDTsdgLfKcOYYtrbuUQBgkojBLHRFMGqaRothWik0QhBRLCd\nzzUIMkwghAAZQDEgGFLmOcx3PIeSbq9jok5hHHU+qs7GNqLYzBMu6RUAGoCMrRftVKeNpkqoFaJj\nzzQ7CSOaRlB8cHaksoQShIHBwLiM1lXhui5lbJ6nYdWplEzLivlBLaQQDYPqaqvXJ87xwdni+Nzr\ndXf76zU2JI5YKzKMlZORYay7vfV0PJEGpaNxs8guvbreLDIZxZd2LhFIkAF5w/12582XXvn43fc7\nW5tneer3O0xqIHXWVH4cuoFfKI4C99KNa0GngzGukSGdUC5kAdWcl1xoEkWRXbv27LYWDEmS9Pt9\nm1LZKGWRXBt1VtEIPCPdZqsWu/pXrAcIIVoW0fb2rXpItrmyouTZrwEio7W2e8OGB7wcg322h7Tq\nsiCMlTLMcbXgGGMgBca4KsoVdxMt5yHwUg3PwhEQQozRs9HIpopNrS58ypccUEros+XRCsW2oPwq\nKq9qI/tHuKR3AwC0uTgg7Ke2T7QSGACY1dwVfcbAUC8dY5+txiCEACICHIIRggwjBYEDAUOQUMpc\n1wBgRFMZY1wPx6FrAJeiynM93BrUavaVP/3js9niuVeGnhf4Xnh8fCob0O12m1xsb28OO8356SGj\n4dWrN6UWVa5uXX/hZPyAns/jiCxmst/xP3jvIdSUaNxU4MGnyY1r3a9+5Vsopp+8tf+P/7P/7X/2\nX/zfb92QQjZFzq9fv84b9fnP3Tg7nDx8+LhOBQFeVfDLe9cfPX6YzVXkbhgGKfbiKCwXiw8++vRL\nr//YcH3QzNNrt/aS0dxxwc5uv5HF9VvXKTbGqKqq6rJQkjNCfUY55wQobTQ2ysFMUsoG3V67hxUc\nTWa3b10bFTfMwdN6YU7q6bA3PE/P6gw8vj/FeLq9Pigm8jtf/6Tb7X764K5GJku4NmB3Z28+Ti5t\nXz48OonDFqYoTeZFmsaRB6FEEO7vP750a/34bHw+yS7vXdm5fCWdJtBF7UELlNBg4/sebaiU0FDc\nCOP7jCJTi1pKwetKASalBkC7jEBjiqJgPtBaDwaDcNCdlqKqCkYpkUpzwUUjTQOAQgAjhCFAiOKm\n5lGrPU9mBOH14dBzXAIxhsAYA/AF4q2fmeozWhOGCSbIcQed7pVLu/uPHmp9wZK1HWJbEtkfm5gq\npewApgLwMD8s62ZFq7OFhe/7FkyDK/s4ZA3DNHGJEELXDVAaGy2BaQzIgDZ+DAheAfsEXxgiw6Ue\nhN0RjuMYzWylBaGy/QLHcYQQEDFjDFQU4Qv/mlUrGiwbBKsNbjc+pVRJCC9GABW44IgDKWXgh0Io\nSikAxnEciGS321VKHR4ejp+cJLO5r8G13SsgLxkA8/H49Oj4bHS8tb0RhoHR0sHIcIkobpqmMlJK\nqYHCGGEEIDQKGCM5cV1tjJXXMxAAin3XdykyUAeBT1pRDmmBcN7Is8n44oBFEACgwI966rZVBsCF\nKQ9jTDTCEKiURuBCm811XSFEkiS0qdYwI9TxXacqU0IJQsB1GaaIK+4FbqcXi8XCVFpBJbRwA5cZ\nMZ9OWOi/9MJz87o6nU2bIsdhVKcFhETCppqVDkJR3D14epgnM1cjRN1OEOmaI22S+Xx0PiGEQG14\nVdN7nygC5qJilO4/fTQ+Pbu2tee7DnGd1vrg6dlJ0O/QyD/L5tPpVBk9RKZSnLtYCFIbTvb3923B\nYZacfaVUnueTycSuab3keUsp66bs9/urvhF6ZozOwlCWCbPSX6CUuo5r/5dV3DFL0gFcMphXocUY\nY4A1ezXGGKs9bM/0lSSJXfr2xYUQvKytJ4VVN9BL/9lV9LLY16rrs4KVtdaYXkzVrZBZemGoYWz8\nW326ZyE7tBwMtLnkqupaPZIQBiFe0Q4tqmbJilprpYyF3S3upAS3MLotGe07roIxWVm+EmLxCoJd\nrHxGHG0qiCRGLgCYIuYQinxiXVAB0IxBhIgQmecAQOBsOhr0Wl6re+tldeP5Kw8fP5wlizoXnhPU\nvJrNZp2g4zq41wkHa5cOTyou1Hj+4Nf/9i+3usG9Rx93emsYVk8en2eJpgidH511273ZdEpJnE1T\n0ZjNzbV33r7z5puvffTBu1yAz33u0p//2TcZYqNmIrlqha2dbmd0Nkun46OnJ1d2X5imaXfYGWwO\n//Rrf6Jks7M+eP7y5a/9xTf+u//yn7xD/pwgsL7Z+bHPvswI/eSjjzmvNUEUQ7sVGy2rqqgK6VDq\nUGqMVqKBhDqMQm6QUUYIbITvoiuXL6VQmpj5oqskBIZ6rkcw4pyLwgUSHR2nW5+9dfOK/96d97aG\nO6ejsc+iHInx6SQKor2dnUoUQNUAVZ22e3x2pkX+9BxU9Emr3w7C1sP9A63E7DwddKJZMd8bXsYh\nhg3CmLkwGCcLGke1ksViSghquCm5Ik7ImAu0yXmNISirCnseVxwSaIziopZazaqqVhUEAiJJkaQU\necyjFBVVTYwpG8GQaZARGByOz5Hv8EZhuBxQ1YoBDBAUENAwYBf9EgQAME1TGH2+WLR7XYpgXde2\naYqWqnSW76CWupQX1hKO6zAfVEJwtcq9lDRaAa3soWkAAEabRjYIIT/0uOJKKaM1tFkjxgYiF4Fc\nKcTQKhdcAdCrPWivAUJowEVD1ABgERqLndgOtAbYRiOrDbEKPLYEtEH0WRfwC1GJZUq3Kj6klGVZ\nEexcIJyyppSWZdluteZkVOaF4jKZLzzCDG9Uw4FUquFlkvVaLaG4FlJyzispjVZAaa0BAsscVGtg\npBSE0WWMd7SBSgNIMEIQAOM5LnIcSIIbcc8QZ5oszDOUKwB+xGKwsA2E6tkmGcYYUWrUhV3IqsYF\ngKVJwqRoReG0qIFHq6JhDgGizquSug4rvEW2UAASDIoqVcQviR7DyhTN03zRGLO2tQUJ/fjug6yq\n+sO1drff5oYyz0lU4A3fv39IPYAgHD85WowmYRwtZvO6rruDvlJq0O0cTSdxFH3t++/s7VzK0rTV\na3/w8G7L869fvUoDL0mSUTL75OmjJEnGs6kfBBVFAEHhYCkp14rs7u4ukhmCJIx8wVXdlMAgTKCS\nxjoYIQwocQxQWVok6bzX68AlO2CVhsB/29fV/tGesEmSGaAAoI5LIcBKCwQJwsD+LoU2QEGAtZFK\nGqUFQsDyoSeTSavVsiHEsv4AAFYRxEJ8nPMsL+uaY0anozFCACrd6/WqoqSUWtFr++VJqZtGcM6V\n1JBqaDQyGgMkjVwtUISQ7/sIGoRQEIWu4wOoMYBKGYQQhkgZDbQhjDqOR5hDqQOQJMooo4HSEFv4\ngTDHAwjaAuoiimugjGCuow2UShkACCGO7xFCDG9Ws34WW1iRmiwcbwOkRc8xxhRhAyEh2AAHQAQB\nhYACRCCmEArHYYQwKWshaw1g3SgvjAzAAjTPPX9jnB2XapbmYycEO+3+vbuPi5ojQPcu7zy88wAI\n89rLr3z6yWOlWusbmwCF3/rGOwAVVaVElQZRu87TplSI6TCM+v0+F9n6znq8Htx9ep/r7PD0YHdn\nq99fGw77xwdjw0kpZFLNPBaezc5zVhVZ027HZdFMzidrm1uT6Ww+X6SjYvfy5vH+ST1K5oflP/7H\n/+cBc371F76cjkanB4/HpydR2IKI1gVPeKUER8BgpAkhCCCtFKXUSnMSRBRSi3yRLhKHQub5Z+eH\nveHmm51Xh4vZjIvf+cofVEBASdw4zJLJ49nJxnB7Nis0Yt3OxtZwniRJU8iz03GSZP1+H2qTZdlo\nfDIZnzk+aced8ehsfTiMu83a9UvTbG40kVJf3r08HX/Q63XqpBzPT/tuT9ZVU5faiO+fjj3oK95o\nU/fiDjJIFXUQ+Z1eV3KRpgvJa4ZoaxjTxdggKLUh2O111y67KAKSOdBh0PVI6Du+7zPq+H6sDKrK\nptsfJNnCj3yMwfb2NpSCImxFdVcltaUUOY5jlsM6VskeUggJxoy4hGLZQICrusiLRpV5FLYKXoMG\nEYqqsjFAQcoiD6VFPlvMLaqxwkgIo1VTm+VcPELImhe3vY7mEEJoAARSAW0MggZBjImSymBEGEMI\naWOdjRGEUAGOEICIYORpQ7VhAABIjIZCqUZDRwrNpZZSa8211kor+5IQI20AQBBhggimhDW8ruoG\nIoAwAQgaAJXRUgmItDHKikoCQyDEwGDG3LqSrusojQCQCKEwDClheVEFcau3sSUW+Z1H+5Ojo3I2\nLbPF2clTiBShcAesF1XmUKaRWaQpcD0DDYQQ2WMPAqUMNBIZQAyUyiAMyBKCAwgaCCBGlAGDJXbU\n5nofUn3/wSeLJMOAakO18SSgBhCNgAZAamE/hxRciwuhGQAQIkQDLYCuZaO1wtAEHuu0YyCbFvW3\ntraaOvccVpR5FAXKyKjXEQg4fsDqJo5jNwzG2aKSvBUEmLCNja3dy5eVAcR1Z/Pk6eOnlzd2Nja3\nd3d387yczRaHB8e76xvfmy3Wr18SSI7PJ6IW8WarnIzXh+tXr18bz6Z1UTaCj8Zj4jmj+RQBeHxy\nEgGazBb+815v0N3Z2/03/+ZpUuSNUSz0WRxClzZKG4oVRJUSBGHgOBQAJCWXSkFoDNBVVXtegAFm\nzFVKKKXC0KeULpJJGIardtEKZV511VZgnTHGyi4wxs7PT3d2dtN0kedlqxVVVUMIwphiDK1TkS05\nbIJkiwNK6dnZ2fr6etM0VnPILAePjDF2SlRrPVxfm8+Soq72dl6VUhohPc8pstIYY6UfjIF2qAhC\nSAjVEBlMGqU7cZTnOXOdrMiBgBhDjHFRFHVdX758+fD43IvaZ2dnoecrKS2d5+R8vL2xSR3/9Gyy\nsbWruGCeiwEUWhmpNAS8qgFiw61LeVXSJbmIEJLnuYuQ1KBsmrDVCuK4NxwiQvKqoo6DMWaESi4c\nyiaTSa/T3drasvIqSZJorZWQ7bjlra1XVUUIZdSFEM/n006364eBkLrXX3dcr9VykiSpuex0e01T\nKaUwbrXizcvXdmf5mQLSgLrmEyeIy+QYKQBoGrc7k6NZjMPuoLcY54eHY6kgY3o6PWx4PliL19c3\nr+7dFEJ8/Mk9JCk2QqqGOfDh4b31Te+j++/83C/+xMwo5qIoqE5O7gcOLRZlOinLTDHMCCRlWnda\nnSqtNTCYYZUV7babzs9CxysbcWV9s1k0HaeHuG651d0P77/xy79MNHKkSUZnsdZdiitNJFDQAIIQ\nuOiLQIyhAbDmgiIKASpKCQzx/X5Z5xzlfstpAG8T6Aq821pr1Wqg26Ns4Tge5jQ3JYmc0/ExjPC9\ng3v+yOF1s1hkQqgyr+IwSuaLsiwdyk6PRzeuXS+q/OmjES8YUu2Dh/d3r/n1/BjWKnQDj7KXn79W\nJOmVyzvJ2RQZoWCjDKKuEzkurGoc4tq4tO+rmvcG7fF04hGQVYkJdZZlwGF3z+7VGMSDXsmp5mZ+\ntuiFAEBeVQVzCKGQEPDaa6997RtftzPpACApNYAwDMO6rqXiwAiHkLquLevHdd2bN28eHR3JpX2z\n1YeklLoEKSU768PeoF/XTdPUnU4XISilarXiPC8gBMZYJpGBEECIgDZAAaXMao+voOM0Ta2SgtZ6\nsVj0CPF9v65LSDAGBACogVRKcSVKoXPAledXQlDPz5u6E/YAJEIZTKkClSGKa0TdbtUYgAJCWZJN\nhM4MUFmODKa1NEIjDQSCoGjqLE/6vaEEwGCCHScrm6JpYuZRz1PSGKiZH9RSOkGoRGMgb3jlOC6E\npCqbOOot5lUc9auystHaGIWwCb2wKKq1/poyEDled2f3QBy89+BJL2h/8uk9XSwIRqGHg5DOswl2\n0IJnXCvc9qQ0UENjDFIGQUMAJAhqDQ1CuqowIgQCoHS+yH03ENw0BA66cVItCPOBLn0cXNuO8vHh\n2trVWcLb65cw7Tf8zBB/noxabUfpmmBDkKnzLHQdagxQEGIstJTGKGw0NpAB1dShh3m1cLGSRjo+\nbTRHCgKMp1mmgUmK3G/HqqiMQ5MskfkCBm6ZZs6sMnN+7cWd++/f1cb4USyV6iOX1k1+fv60LE/G\n57wRTw8PimLiuDivG78dz9MUQMd147UeLZsyXWSy4Mls7iJS15XnkLVuvyzLIq27NASSffaF15My\nARg4lBZFgRyKGC15XTQ1ZX6el2VWtfw2SZK55WNojVegHMaQEIQQwRiulKm1lr7v2/W36pesoCq0\nVEkwS5rZqq6k1MLR2HWl5e9ZCA5CaJs0xkitAQDPUMmltAi1lb62TabVa9oiTCmFeWO5qnZ41kgu\nJbaoRZZl4ELxyEgpXXqBE0KEIIbKaGX0qvglhMRx/Ku/+quO4yRJ8uTJ0y/8xE9EUYQAdF03nS/C\nMMQYl2X51a9+tTMY/MSXvrS6D7ayqev67bffTsvy7/69v1fzxoqo2htSFAUh5I/+6I/2rlzZ2tnu\ndDr7+/vr6+uYEjuuwTlvtVp1Xfu+/4/+0T/a3d21WgydTufo6Og3f/M3/+E//IcQQsvIsLPJYRhG\nUfQbv/Ebxpi/83f+Q9t2vnv3bqvV4pwfHx9LKdOs2draHY1GpVyUsn56+uDWazt5MWcO7Pf7Uurx\naSakPDk57fobqOMtpsXrb3z2L976uuuyIHSapnl0/8Ha5oaUuhsPkiSrDAfKMMo++9K1g+MHjx+B\nh4/ubqzHAMPA8+48feySrpHAd9rppMa+M5/NPYf5bpRM8rXhppTAoCxZTKqq2d27cnQ08f0g9sNk\nmhCj/ahr6urWzReAgaEfPv+Zz77ztT9rsoLEzgUOYyCAQGmtjQYAYwSV0UAZYzSBGCOKCWGeqnTl\nBC6AOk3mxIm3h7tuUpFKOw1spEqykmvx0z/7sweTww/ufnh0dtpyI6OUVqjd6ndabQA1AMjzvGSe\nGmU4V1lSdTqdqlQnB+OdjZ0HHz/MRLJ249pg2G0HEUPQJ2w8HpfJAlSmQ1vtuNVUOdQi8AIhhUCq\ns9V9553v7u3t4kAnzSTsepPZuIR5EHR0ozSHo9moqpw0gf1OH9QjhAHF2CGUYMQYZphFfoAwqOsa\nI+p6DGOKEcSOCwBTsiIUGS0xAhBoJXlV5nVVWHFI2+C0UJUxRgPDFTg7O+dVLbTymFPUlUPo5WtX\nnzx6bBDEAEqjgdIKGFvgu8xbRaMVLA8AiKJoMpkAAOzUtiUgGKMIw8YYpI0teBjDGmKDwEJBDRHC\nmDJXGTtfSObzeevKmgESAqolRQhDQIwxxEG1LHzfb3c7nhdAQIyB7XY7CLy/9OLPSsmNgYvFDCB8\n4+ZtzuXdu5/MZguEAGMuMJAwBxMGECYOi6OQ11VdcwBgFLWaWlHK0jTrdDpCCM4bpRQmSGsQ+BFC\nxPF9hHVvayeIB08OzjMDtRsELg1gHTHt+xhAKTUUgNdaGaF94i8VNg0ECABotAGGQAsMWvAeEowx\nwgRD6DgMYux6lItSK2BE5nnOay+9+PSoYiTq9XZqCbr9vQdPP93cvnx4eG99EEF8AT4hA4DSQGsN\npYZaQ62BMRAgBIxRUqhGCRcCKUXVlMYYaTRXUikNEYrjloFIaaW5bHidVIXQCinjtuJO1HOJ7yBX\naw1qZYB2mdNudWdpwpU8OTstqioX1cHZcVpWxXh6e30rittVI9JFJpRsmuZo/xAiIysRuB7zkUOZ\n77oedTrEaysXNXL/4aOT6bkbOq1Op7exhl3KtcyqkhK3FtzxfFfowA2IFfnQS0Fue4wWRWFFdGzf\nyIoaWMH5Z1MkGx7s6rRN+GfLJrQcNKNLNW78zADps4yAZ9kQ9vVtWlfXtS2w7E5YPX3FkH42EFow\n2j7gQtcEY5tRXjRdCDHGXJAllIYGKCERgAhCRMj6cM0OFfqu9+jBIwyR5EIZXdZV1dQKQ9d1ASM5\nr8/n06uSC2jquraDuhDCMAyhQ7Miny3mouFWlt8eBzZjXR+uOZRVVZWnWRSE0ICmqs/OzhCAs8m0\n2+6UeTGZTLrd7mwyFUIEQaClCv2gLiugTRiFBOE4jAAAuNNVSvU63aooRcOvXr6SJAljbPdnf44Q\ncnh4+O/8wpdHo9Fv//Zv/4N/8PfPxk/Gi8Npfgidz773ybeIo70wcF2/G9NHd+4kU1Atqhd/8srj\n9OnasHNwcOAGtKqzzW57vpitb65pKMu6aWp5fjbf2b0ynU8fPRiXJf9P//F/cnT86Lvv/tml21eK\nOqlLSKArauNRDyDQba0pIaAmkhvZaCVRU+nJeA4kLOtqb+8K5/z0dNTvd19/7c0H1UNe5FIqnzpB\nFPMsmY6msqzu7x9evkxiv2W5swABAAFCBAGNMFJKKSOBUcZAAjUjABFCNHMUJRAYJUVTYOL4DhoM\nWs8/d3VW1vcOD8KwK6anv/vbv89ajtdpzefTJp1iDSAyMMIZKqzTPGPk/Cy/erU3ncyLMocQNg2/\ndu3qdD5K69wJvdlocfj0IIrdza01StDXv3706vNhnVVBK4IhE7UkFCgC5kXutr1Rctbd6OQiH6x3\nMUbHJ09LXgwGPQDpweG54/Q9nwVhZ3//bpbPY3wxgo0x1lpJaYqi0FpHcaSUQpAwxoyBZVkiRLSW\nBF9YZVp3BiHEbDbLsswygGxeaGf4jDEIQKqQ5jmWilJCpABZGXd7u+3BUXEXYEQRZghCDaUxyECD\nEBIaa42V/p9Fo7UobuaLuq59FwaeL4TAAALqVKox1m3PYuAEOYgoDKkERl4IvlRV5QeunZcvisJx\niW1RM9eDECtliAKRH0nJsyQdjUaMsU5r8+qVvSAIsizzfdf3wyxJoUFrg/WmEQ/gfUYcKTmGhPMa\nGqSl4bWgFM5nCwBNXTWEsFYca2Bc32OOZwDSVmQWEUxIw2vH82suhTaEOq1OZ23gz9OMxS3H86hC\nocMcWCnVVHmNGPVc5rhEGIQUMhBrqA0AGkINgAHQEpcggBhgAxAwy/ULEQCoyquwE8U+y5oqz3js\nsF/767/+/Cs/89Wvf/+f/Ys/kJAYqh3anS8KCAOEAoR8ACEERBksDZBGAoOkkk1TV1XRNLVRiiLK\nEHYgwpprreuqIhBRgKQyQANGiFK6rmuXEAm10VByQJgbtVqT8azXG1DXo56fF0VSFEEcb+5dnuVp\nKvn5+LwUUjrUj4dr25v+enL45HA2OncDHyqdJ2mSZ4wRxliW5pTSKGoZJQXnRVUbaYgyTuQFfXdc\nLioguDAcmUI2WGgn9A2v06qYz5IgiLhsQA1It9u14cFWGJZ+nWWZjSIrwqhFxqwL3LO9/VUYOzs7\ne3axwuWPlHKxWNgj27KfbV9xtUnsxjPPqM/ZEGIFrS0pfMV9sO2TsiyjKLJMFYQIw+ziei48YZGU\nMgiC3MaR5ezqs3HL9gb1crYZYxxH7TRNOefb29t2ZEpKyVzHi8KBe+Fl3mq1Ni5tM8ZqJYJ2DCi2\nFZLVKwracZ5mg8GgLitbAq5ip+/7b7311ubm5vb2ttbaohwQQgAuFAKNMYPBwPLrrFysHadotVqX\nLl2y0Hxd1ytDWHs0WH/0MAxtxM2ybGdnZ29vz94Bmx23W+GDp5MP73zw4uvXCHL3drYb1Xxy7z4x\n3mwCXMzctved73zvL//Mlz/54NPJdLy20a0l1kgMN7r9YadpRJpXSZ4N1zc/+vDupb09hxTZXP2X\n//lvvPHZV3qtS8P28GSkDk+OO/Hao7snwnOPnpy2212CcDvuJrP5Ypp7LDo7Om9qY4w6TbJ/79//\n6bfe+na717p5+/Y73/8e1JBhYoxJq+b//T/+1lbcKsenmNeXBv0rN58/SxYKKIABwgRe+M9DAw0X\nwvaLIUQGA2ggBgZh5WFHVg2h0Hcco8Rsetrf2vulX/zL//F/+n/CUZjnEmiIDAnc7mKaOjT0KMII\nKqUENxWQvFFCSK31+nqYJNmtW7cODp482Z/sXe7P54vRaFJz1QbAH0a3b9zmunz06P7Va5d/7dd+\n/N5Hd7woUoRxA/rb6xvddQ+yYDGvdA0Y2mhvfvTBh9SnCGji0hduPD8eTZ9/8dWdvZujUTWZnlEq\nCDVf/vJfZrOjLjWcc9cldVMhBLa2NqSqtdZBEGBEAQBagzzPgyBK0wUwHCIDltZidgcFQWBH2ldw\nut1oLnO0VEAZY4yLsUGGYUII0ULafS2Xo+sAADue03ApjVZaAQAguJANMMZoBInrQCW5VhhjCYyQ\nAhrlBq7SGioNtFFKKaM41A0CEkAhLnJKG3s4r+umJKQXR+123PYdHxHGCG0aYdX2oiBeX9/cXN9q\n+aGSPI6jssrX1taWntQXtyIIgtu3n79//36SJAghY+wEoUEIQQ0cz/ddR8dASo0gCYKwqQVjzH5e\nShmEgBBY1zUlDBNaCekSpgw0CB8cHvmXiesHOqnqplGy0jwxqnZCtz3oMOZAjZQtgjDSCkgDjDFK\nY2kgUBohQIwhwDCjDOAAGIiNUaRpVJu4GNMojoDjQ+hd2r35h//mT3/ul36FhFt//Gdf/+juJ0HQ\nFwUaDH1tkDYOgMoApo029mjFsBWFRWGaEnsu8+JWiFDMWAhM1wG6KjaGa5HrO5TVZQkA8By3amql\nVBBFWZFLaBrOHd/z2+0a4VKIQknkuZe2N7MinyySo8nk6ekxdOiirjcvXyolnyaLecPvHzwdRq1k\nOkuTpG4a5rlIG0aI1rrf73POOefz+Xw+XYS+147jXtz++OG9QbcTtMKwFfqdOD/bp4qHzFtkaVGV\nZVllRRpEoQa6akpiB83gcq4IY8w5t3YmaimKaisYS7Vcqb6vyiMbftrt9o9kP5Y/dvENh0P7ajaW\n2NCCnrFRWXHnLApnX8QetXZW3GZ/VtDBNnhswDAQlEWNCV7FmBXEF0XR2XhsK7/V69vLoIyCpW+F\nvVobGgeDgW3V5nkeBEEQBF7gN0YiShBCMWgRQhZZEobh+taGTdPsyOrFhyWo5vX29lYyX+Cl36CN\nakEQKCWjKLx8ec/OOVkrWwjB06dPXY+NxmcHh0/sFAgm0PXYdDrFGGsTnY9OO92WUsrzHYRgWZZZ\nnuzt7SEMzkena2trdVMiDI5PTpqmIRR1Op2qLrI8WVsfMEbufPip49DN9fWH9x8R4L791rt+HC3m\noin5oDNEku3fOxr0hl/90z//q7/4S996JyWuvLV75d69e1eu3zo5OeaNKevSD/3xdNIfDs9Pxu12\nT8raJd23v/FBdw1zOZ/Mj04O54HXSye1CetsISngjJHQdx0SAIn7/XWs3Bc//9q/+p3f+9//J//g\nN3/zN6/duHV2ktTNu0EQUczS6fzSYL0Bi3sPnm597s3rL7yaj07bvd7RdKaRMVBDDCEERiOljJIS\nQyO1UkrYowcgoKTGBlMIWwxBpT2fBg7JOS+LudFrt29e+YWf/5l3797XRVkqfyNoNcq0vKHnuWU5\n81zWCM55jSDtdELO66apMEGuF3z08Se3bt8g7Hw6W9y6te4myeZ6+9Le1ng6+vY3v98btqbzfD7/\noEj12tDf29oRRf3o7EgjSlzPSI0w/Oo3/uzV1185OznXUqYPFlVR9gddzHBVVU+fPj05nWkVEALW\n1vvf+c77H3/3e2E261LTNI3rkrIqMIYPH8bjybnneVorx3EFVwgRKSVj7ng8RlAiDCwzze5We9Zb\n4VS7AW00ulDiIWwVnCwPzXGcCqnXvvhjK9gZLj1imO8XDbeY9irFtImjlDLY6NuZWfgM37UuSiCU\nllxLBbSRQCOIFAKjRaI0CAPPc5lQVPJmPh27lBmpeF03ZdXUNVEGGmQlH19/9XWMEQJwOhrzpqqL\nnGLEKNNCV3nFMKOIMsKAAkaatf7a5HyihSaEBG4Q+RHUcNAdVFXBea0NxgQboKXUQRgeHh5jyqQ2\nhCAAtFSCC40JA5B2ukNCHWEMB4ABk9Xl6Wi85rt+FMbYoxKbWmtNXd8JmKsNFFIBCQyABkAFgFSG\na6g0UAABBTCEyhgtlTYSGIShxkZjPwAANLWoy6a/vTO8dG2eoySt/9LP/1KrC770szf+7Js/ZCyu\nRcNI5/zssBP1jQmMUQpQACQAECGIMMyypMjmabJI5zNTlBJiiXBl1KxJdZOPTs9EwykmomkoQI7j\nAGMIIViDo/19rqTUihDCHVqHPu3ERVGMRiNzcvz05EgZSFwWD3qTdAE89+n5+TRLDMU5hCz0ed34\nDqOMlVmqMey0Ysfznzx9OpnMGGPR9s6gv+ZQt2ma6TzLktxnOFW1aMB8nG75JG2qFoJC84pXGgJI\nsBv4rsva7VgJfaFwuooutl5ZwWIrmR+LPtsZoFWkWUFqNobZkdUVSG1fU2ttjeNWTAS4NIddWTrC\npTgbhNBOOOFnRLLN0h3LwhEIodlsFscxAEBqxZhDHAaURghZDuiz+om2pFshgRhjZfT/39qoLMuL\n15QSAGAH64SS0CHIaGvhbi/VcZw4jm2l4vv+Cgy0OSl+RiT42Uqx3W4zxoqisNXMSq77d373t8uy\nRAh95StfsTMc9iZ3Op35fD4cDimlf/7nf24LRNd1Lef14ODAcZzbt29vbW2dn58TQnzfHw6HZVnO\n5/MgCGwwK4ucMVLlEgEUem0JvH5HQsqmvF5MU8UhUEjUoCyLXiv+xrf/dHtvmNZnCsm446d12tvo\nfefbd1qRX2W5ULKu1OXLV4+OThhG77/zweXrO7OzdDrfFwa4hO4fTH03MpwMe+tNWQtl0qaK/Nh1\n/dCPN4a7/+6/++u/9Vu/90/+q//65ddffPxkf+/GZpKkizQPvRBi8tLrr0+Ojovx5N7+kWrUdn9N\nUydveJpNCTaOw1yXQQQQQhgSg4yqy5UYDABaI6Q0AQgC6vjMC1zPKEEwcHymZZNn87/2K7/07n/+\nf2nHHUM5DVvvfvRpa7B++OQkiojLENTUaIWR5zqBVrCQVVmWvX6LMXc8moZRvL29fXJy0u8OgNbZ\nrJqPs2RaMMyOD6UbgBdf2kNGX75+u0yyp/tPBEMznhsFNteHmZRH45Pjs5PXXnx1Pl189tXXfvDd\ndyDAvGmAcQFwL6Z6OZ/Pp2WZe0ooBKXkxth9h6XirutqvRydhgIhQCntdruj0RklBkC9mnKzi80K\nidoQZccD7B4PguBg/8mK/QyX+pMr8zr4jJeE7/tBHE0WC2HAiqa0yk3tuwghngVLPNet8kJLZZQA\n1owcwxrBGmHX8wshGWNVVTpeG2JMKfnyl3+h3fYODp5iSJABs8n8IbjPpap502m1CSHpYp5n+dXL\nl+ezkZY6LZK6rgGCTdOcnJxYQeQ0TS1uAZc6zkqp8/PzOI6VUvbfAIB2O0AQGwMdx1tfX7c3p6qK\nqioM0L7v1jX3vAA7bp4XBmKD8cbOpTJZIBZGbovpylWG+pghzTwMECoarhouNQRQG0iNMVwBYYzU\nUFsdFgORARIoJIQCSEGtgNFaZ1WFfS8c9J2g1UjsBu29a7edFn1yBNa3wS//yq+M/vv09PyEurEf\nuFpX0rjaNAZQDYAGCCCIMXQcapRX+S73PF5zzVUjtZZV20WIEM45sE19hABE8gI0gn4UAoodRoi1\nZcBwVMwbvjg4OHIcp9frubGvIahqPk9mo/Ho8z/1Uwcnx8R3g3b86YP7LeZRZLA02AACkZGqKUrH\n8XrdLnOcRZYuFqmV0nCZE7favW5r2I+14gbq/YP9oEi8wNPAHB4eOp5nDBR17WBUlaXHmCbgQipj\nharZTCeKIrtGV0iUjR9lWa4k2mxuZU9evXQptqe/WaouWuqnnVODzwwYrWKMXDrVrwKG5cLBpSYx\nWRr32WrJ6o4wxsIw9DyPS2Ftu0TdIIQAxsYYiplFA+zgjg11q42HCCIQAaURRFrYWQTIMDFCNGUl\nhAjD8NLWdjuKm6ZhhFLGMKUIoqasAQAeYRSg0fEppbTdbkOps2JhyTnZbDGfTLRUyAArrEsxQQAa\nACnCs/HEY86g27MeekJwCOGw15cNl0196dIljHGZNUYK6vtFmiCjz05O6iLvtVvf/PrXVpIqVuJv\nsVi0Wq3ZeIyMPjk8MMaEYTiZTAaDQbfbTdN0PB73+/2vfe1rQYTm6RhSJ/Kc77///el84vhBWcoi\nqTEkeZ5GHbi53RJVznVdVDps+0VVEock2ey5neeoCxCTwnA3dNJZdXT62PNDLfgXf/qzuzubjw4+\nybgQqomD4fjkCDKnzpXROE+abq+NDZDSiEaJGnCi03nViqMkyRzHGY3GG1uX5pP8uRduZ1nBCPv2\n2+90/MDF+MnxaZ6kxe6uTwmDCtSJ78A4jjAMKcVQG2AMggBaJQwlgMEQEKMhJBoCbBS1Y5BaK+qw\nMPQgUlyUcXf9M2+++dYPPhqfTV757O3rV/Aiq5+79kqSnToUC8iNxhg6vNK8VkZCQthrr37mu9/7\ntuv6AEKpTBCFDx48GkR9wDGSrEjBxob/you9vEzPTqcYwwePDzCEHMFcNrzWjNAC8O1r2+P5PK/B\ngyeH2TR9/eXPFJXeXIsGvY3ZNJWCUwpPT8dat5pGtFqdqEY+0sYoz/MgAr7PDFC+7y2JPIAQgiAq\nyxIhgBBomgYiY7O91RSEHbixWZ0xxrZRKaVQqEBCrCEhBGIopUQAGWNqpZnESgGEEIEXUIQnUCRx\nVSpp9CoagaUAMQDAFQALQaQkhEgpKKX9VnBScYkw0hgagBACBDkYuxTPlcYKYozyPPWDNkWYMvxX\nfvkXMdJ//Md/1G71fupLP600ClsxRNgKGaRp+s7b3zl8uv/Lv/hLCFonAYUpBQCMRqPf//3fHw6H\nr7766ur0kBdXIu/cudM0za1bt7I8JxRzKauqCsOIc/7DH753/eZNi80QQsoqV0oYYzzP/eSTT4Qy\nVVNLrSAgeVN95vOfS0ejNc9Nj/abRqqmcqHALlYSNpIXddU0AiEEsQYYGgOANkZDbaBZ3ipgNNBS\nG6mAMpBopPOmKBseKN3zW5gGGrDOYM1vOydTwAKQVGBt0xms9eN2a5EtZhOhjQbABbDRgGmjDLzQ\nBuOibppGct40jWwklAYCwohjVEkwrpsGatNYzSSElKgNgqrOIz6Yy9pxnJo3WusG44Jw3Apo14lb\nrUY2hci63a4fukHccj3aD/0nZa7zrFJ8LfAD4kQObrJCGuU7DFJWVGVTVlEUVTVXXHGoDESIUEQI\ngNhAUNSlkFW7HXf7PYTQ5uamMYZhRxQNAIAXZbfbLdO01R80UpC3337bMrVsowIAYIeibRzyPM9G\nFDsNk2XZykViyb67sBO209pmKbsLnlGfxUsRVQtbrYA+q11o8/1VpW8jos151VJlFT7D0Fs1mS7q\nLf0jgA5aTxd8QfbzfV/wC2UU2xtTXFDqWVjZPt1GO0IIhzIIgiRJTk5Ozs/P5/O5/Ti4Ifasp4QI\nIZqsAK7vE+YwJxlPP/7445OTk9u3b7/44oux69fMrfLClji2YLI/xph+v08IsQp7EELf9znnSotf\n+ZW/+k//6T8Nw3Bvb8/eecvQ01q/8cYbnPO33nrry1/+MgAgDMP5fO77vtXoC4Lg93//9z3Pe+ml\nl/I8Z4y9/PLLEMI8z69du/bw4cO6rnvtbt0kVa6IC/cf73/2jS9+462/UEr3W8Px8dwAFUfOi8+/\n8vWvvfc3f/3z3/nWdy7fWEtzQVzv7snx9s763QefbmyHhwf5zuXe0cG0t+4Tzeqy2NnduHf33Xuf\nfo9Ls7nX5hWY5UXgtEUJKKa8Ee12jyESt4LJaJyp0nfi/cdHGP3rbrd//fbOfJZsbW0DhK7cvHR8\neoIhGfYGxSKNOp18OsulqsazshZ721uOFj2mFAJaaiU00EaIRimFgEIIQW2gBBBoAKTtPVKMjYFc\nKK0MYIQQBjFClISdNmDs7/wH/8Hf/l9H+8fT3/nXXwEgvPfwsJgXhPqyaepKNFJKUSnNG15ApIfr\nvbOzke+Fm9tb4/F5uxM7Lp3G0zCIRmcTP/QwAE8fHyOGgnawe2VHGj5fFIRB5rillkmea62n+XRe\nFJ3OAAEPYY/z9OvfeKcXrzusfe3K7bdPvmsU3r505fVXPhOGG1/Bb5+fj6MANaYpigwiXZa5EE7D\nKwCMLQJsZYwxmU7mSZKUZcnoj1qh/zPCQXTvAAEAAElEQVRez7MTgTafI5QajKRRmCCIUMNrySXG\nGBBUSa61JpBARAyECgCFgIYAUUKf8a9bZZ8rSHDFKbU1vZnPLgqvC9F5oCHUCpRFKQHwfEdy4Pt+\nUfLJZNLpdKDi88kUKBMFoYGIc1GLAmMCPc/3XN9xgTYuo7y+sF5DEGFKoAFKqXbc2tzc1FJhSoA2\niGAEYFlXn975RCn1wnPPAwQbzqnrWOiyKKpvfvNbr7/x6tbWlhTaD1x94ZKjlVKj0RghXBQFYY4B\nJs2yl19/lSpNyuJPn9zb6fd0DrAoKYMIY6gNox5lXp6lEEIAFTAIAg00QBBqAJAx0GhgjNFcqUZp\no5CWCKmm9nv9BuEnp+c7Ye+ll6+5rY1PHh7H3U2/BYUCwzXw9/83v/rP//lXpKzdzc3J5BACZoAD\nDDVAGI20QcZAjKj9uhHAlNJW4G2E7ZZLmU4dorI811pLozElAMKyqaNuO0nTYHc9KOeQ4GQyqZra\n+Lg2Mq/G++P9a+GVftTpr7d6cSuZJQE2vUtbzWziadnBaHJ+/rnP/dh0PGuSor+1pYF5enzEPD+I\nwlI0T548iVutvCpdowEAUkllKMKAUDqdj+sq8zxn0OunaUodlmV52w+LNDdAQ8wGre6oEm0/TERC\nbt++jdCPZqRX6PBK39ou6yAIyrI8Ojq6efPmsyS3VZfIMgssmOY4ju0wWe7ye++99+abb1rsy+rb\nr+zmEEJFUSRJYoOQEMI+DGP8+PHjra2tqqriOC6KwvZpOedxHPu+PxqNpJSdXncxT8umxgAihKCS\nCCGCqI2vi8UCGGJRPnv6I9zE/a7SGmhAMfnw/Q/Oz89ns4Xneevrm9Pp1PqGvfD8i3/6J1+xY7ZR\n4CMEWq2WRefanqer6t2337ZV4PXr1z/32muTyWRxfp5PpyGlZZG5DpOiSRYzKaUVg6jKfGd7k1HM\nKJ7PJr7vK3mhnlfmxbA/ANrsbG1b9rYNNvayi6LQUt24dt0Y43nevNW2+rO2QiIIA216nW4rih3H\nyfO81+v1+/3pdHrsHB08efrTP/2TdVNev3Vb6vpN+NlGVugL+P2PPjg8PiqLAmP40su33/zsC4jM\nhJreuB19+PF7SnmUxZNx3es3WZYdHnPXBcKUw63IZ3E+K5OseLj/sBsDYEA9B7PJwmiKofC9DnIc\nUSsFoBZ6kc+BkYvF4j/6j/6j3/+9P0jT9I3XP6OBfu/DbyvIvcD3fV8oFQTSKKC1aqT49OH92PFL\nKUOHsag1yYprW+shU7pYYOyURdPvtnnFlTAaaC0FwsRz6WIxowT31tchNBgAqTTzfTcIgUsBJgoi\njXDJBaF6sLnDc/Pa69dfe+MnFACffHr+87/4C15kfu7LP/Od73zLN/Lk9FDpZrjZM0Y6jpfnOabk\n9PQ0SabMI67Hbty6/uiDfYpZmTUbw60kW2BGgYLJokQUnKbn/bUegHJ9Y5A3BcTmvTv3W9TNppWq\ntc+M57abHMQt7/TpdHbyg07UT7K6yZRs0KRYPLz/tNMeFIsDz4GWksAYW19fv3b9yttvf4cyvL4x\n5I30PA8AuLW11TRVt9cOPG+41rfLxu6pra2t09NTy6nDS1nuCxwPwe7eFlnaXWqtkySxBE4LbFhK\n4Ur6JDUGOW3bSF5Zrlj1ZYvU5VVu4QQpJQEVzGcCaFk3sqmB1oRgxJikpFHIGMUcL5kvDPPKMq9r\n6ZCAIGg0QBBGYdBUhQaIud56azCdzZAx0IDFfFqXBYbGaEUJoQQBACaj0c1r14DWLqVlnrejOCsL\nlzI/DGTDoyBwKa0RSmazwfp63QjZyFbUaspm2Ov6DtOCOwRjAI0URmtkWF1zSikyyBpNZWXRH6wj\nioVSinMXmLWtbZFPHC/AFDKHKKWqslaQGqMwcYRoZCOdMKxKLoVgjqeAoQYiYGRTNXXZiX0KjVKi\nqU13fTvV2tT8yu71K8+/pF1/lGftjWFRN3Xuxm1AIAhD8KUv/dj4bAwAEFo8vP/p3s52mpS+iyjx\nQF0KrqUCAGCtoNGQENY04nB2fA64Cwtk6o3trVm6yOsKu+xkMmKhLyfHxHfff+upMDpqxQ2VmpL1\ny+vZkzO35b7+hVd7YZyczQIfJbPTkHmOrFmtxucTkqYBV2tr6z1l1je3yJXgBx98UNSVhnpze2OW\nJhFtS2CCKEzyDCGggXFdxhwqtIziIE1OA89L5nPNRV2WZ08Pb1+//eOf++z+oyedTmt9sF5W+cP7\nD8bjMZKarNo8KwbOCgVGS+s8G6VsqFhhcavW5Sods/C3Xc1lWdpHlmWZpulisbD0cas4stLVtsSH\nFei3KnoQQoyxnZ0dIUQURZZcbkOX9VMBAFjmdKeDI6MdQhFCRnAIoeTKsm6KomDUt0pFQggvDNfW\n1qbzOXEYwQxjvLGxsbW1BSHudDpWrEFrXVXVYDBACHmepwQPPRdqY/tGZVliZbTWDsTDQXc2m4mi\neu+737fEB11zQ/Bf/PnXvDCwMKNtMq1kg8/Ozs7OzmwctXklhOby5cuTySRN029+85vWJMaqTg2H\nQ2OMEKJpmvfff99OwhJCiqKwgtbXrl2zNeWTJ09ms9ne3h7GuKqqLMvs7YrjeDFLTs/PCEGAKMfH\nxNFGIqCglvrF51+YzUdaNYcHj3v9mMv54yfZ1rY/OWdVqVyGHz867a05X/jilW9/+/Fwo10WQvGG\nm+TKjRYUymFker5Y90Cvu1tW0Ch2ejIddKO8Tn3f10bGkfcbv/H/+MN/8we/8d/+Nzvblwdr/f/X\nf//fRa0IANA0AmNRlROAietQjOjp2bmROvaCrC6pQxXCZ8m8G8dni7kXub2g1Ujguy5XuOYGGaQ1\nQpA2RZk0heCl77IizaIocH0vavULrk1e9qJ17HrcYJf5GztXQasPEINIG6UVAJiAbrv1q3/lr94/\n+PTrX3trNp9EUdCKu1vbw2ky2doePHpyL4q8imeYIWl03ZRxKxClYC41HAvFiQSUesxxKlkvpvnm\n7tps+uTS5b0P73y0sb2GHPzRR4+ubvdhAZsFj1uhyKTPWtd3rrqIYQ3yJE8mVZKWr7240+RiY2uP\nYRebJvB9ijgXAABNCCIUGaMxgcaYNE2l0GVZGgMwxpQ42sgiy4oyK8vSasfZNXB0dFQUBVqKjKy2\ns0awMYobZWU67f/q9XqXL19+99137f61yMQqN13rDlf8I4sVWzqrRRTs69j9hRCK47jf6gEFkNEu\nI57nUs/VDq0J+Vdf+ZPamDxP3RZBCFCKjVFVXQQEtyKPIogg8D13nqTpImGuQxGczWZVkfsuy7OU\nIgi1Gp/NWt2O77IkSUZnJ/jV1y7v7ty/97Dba3tugICOomiRzB49etQfdAeDwXwyiTo9LlWR5X7o\nlUWBCeJNTShezGftbsdoU5al4DyK1u59ev/mzetNU0nFk/lMCGOgNgQS6tRadlstphy+UALjWpY0\njLJFXlUca40gZR7L0sJAAJVyCaqbMllk3W5MAPBCv6oqFHgQs7g/OM9r5Tpf/NJPf+4nvlQolNYa\n+WGtNI1djICBAADg+WBnswVlPTqfJPNFFEWRH0ihNMGMBg6p8yrRkBpNgSEQUUIgBQq70DFQVSlx\nSCP42WTcGLXV322zNcAIcAhgxDR+KXlu1Nl8Pp/PP509OUkPr17b4ZAyLSbjk0u9dYKhoxQ2lQNg\njCCiTALtQuQ3kov83v7h2XhEGC3r6nw8mqVJ1Gkzl+ZV3h20iqIwSjGH+gHx3ODk5MBxqIORUmo2\nnvmuF/vtdJb8xVe/EYcR4Hp+Ms2yhHPOy6rIsh/x2Z4NRRBCy7WzMQA+Y2llYTdbHtl4Yxer7Z1Y\nDsKqTWo5bLZBap6RBLUzTKtNsopD9q3tC67Y2Db45Xm+EjiwanhBELi+d3x0Shi1uKK2/FGgrB2I\nPb4tPb2qKsyYbWJ5YQABtuWdNTWZzWZJkoVhaCdV86ywBDxo9PSkwsDYlhVCCFg4SPD7n9zhnC8m\n4/l8PhgMsiyL4xgiUJS5AsoC9wghy4E3xmxvb8Zx3DTNcNi3vEEb8DDGn/v8Z21/y1pYWlsaG9Tr\nul7fGHa73c2tdbvbXddtmubo6ChJ51Ec9Pv9Gzev2efaokpp0fAqCL31jWGaplsblxzX5TKdpePj\npyeP9/fnoxnWyMXsV//qX/v+D74znczLenJyfrq1g0+OSw9HPvV6/c5kcUAInc+nN28Ho8np1Ss3\nCXKgUb4bpJOZ1HVRg3YMOOdGuPPZvClrEQnXdcsq57zcu7zzf/g//scAmL/97/8v/4d/9j++8caP\nfesb7wjDq7LCDDVlPVukm9tbWmslOSHIAOgGXjZf+H4AlRlPZxqDpkjX/N29/ppoOAmCSsqSQ95w\nqARBWnCuGtFpdzutgDkk8H3suI2B3e1t1w8rpX0WXLl2kw02ACS6NmWW5ZUKlOOFLjRgc9393/2j\nf/C7f/j733nnrYPjA8qQ1I3vR5/98c98+ztfj6IoDF0iQNGkEJokS4LYSabpdDHvxv1WqwUJzotC\nAqOBwtSpcpnMAQQ4WYCqbCjCrgfCMHz66Amq0ZUbV4yPh+Hazb0bx/uHxSIP3XgxOgmduBv367yp\nizpLsrLOt9YCR0OpBKUYgAv1Nrsq0nThB64QQitgtwmAxmrh286uld638sfWQNmSklZ0HqO07zKq\ntasAxgRooJRqKzjETh9SjbBxqGE/ohphSJpFhaVaIuTKGOm6bhD4RVEIUXtWw5tfQBplOZoDoDRA\nWkGgEYISmsKoAporVy4fTOdPHj+cV6LVfQwgcUjoO26TJ8lsCg347ttvOV5gAIIQ+WHcVFVdl+Pz\nE9ehdz/50Hcd3/OSNJ1MRwbCPC/3Lu1k6eIbX/8aY+58NqLUQQgoZcLQv37tiu+7RZ5ijM9OTtc3\nt7QEZVHUZbm5vtZuRVWRuw4lCEIMDYAG4aaq9y7ttlutVuga5KQFR4jGrUjVnAGTVBUQOsTAYMyF\nTLIKY7rgWhocuX5ZVVkmjIGUIMZYniyqOmu322WWQQxIGPqt7iLPoijqdtd9Fu3cfLl3+bm5djhg\nc1mYgre6kUMAAkAAUFQioHRrCLb7a9P52sMnZ2fnY0Zwv9tthWFTySKXzIm4boziDUdNo7RogDHM\nKIAMIog62HHdzrCvMIz6nSbHDVDzqtAKKQgEAkXdVFrksilGKfFBN45E0VRZujg7v95bg8Dgpnao\nH1KIiRdFxABECPE0KKqqEbzkwoimkrzkFTciL7NpMvN8nzhMQ9Vf6xGIknTOHKw0NxJBguMgXjQJ\nMThZJNlo0VT1+mCIr17FCEquAi/M06zMC3JwcLCKEKtftNa9Xs+CdWBpOm7rhv39/RWhwCb+tpPU\nNM1qCMb2Ei2OrJTq9/u+79vYZg9iWzfoZ/xYbUYGl3p3dhfZC7AzfUEQoKXGot17UkouhVXfQUtt\nLnththvU7/c77YHv+67rdrtd6rpVVfFKGwSBQXqpPA9AaWOJhQTX1tbqqrFTQUYIj2CplaVvrLpi\nlrTdarWKogjDMI5j6+WMGc2ayuALI5bV/UQIjcfj+XxuBfc450EQ2INmMh3FcWz7PasoZfPNqqoW\niwVcEhqtyJCNYUVRDIdDzvlkMvnud7/LOV8sFsvZQL8oCvs6x0enedbEccwcKEwhZK6VWh9uOB77\n8MP3/+gPv7K21hsO+0+Oq36nl8ynQIH5LN+7vGNguXfpMvaUhmVvvX98fPTJ/XvP3bjdGw6mo2lW\nloHrdvsgCnrnh0ngOWma9nprRZF1u/0sn/fXBnHLv37r2o9/7s1/8l//Ny+9/Px7H/4wjL2iSIo8\nGwx7VVXJxsRhdHJ22tRib29vMpkoLQAyEihMkWEwqQoJwbgoE6EwcY0GRV4pgCdJETisyjOGNQKg\nSx3qhZRCRF2uQRhGpYau4+/s7Hb6azBsA7cFmI9qrWXj+BhiiiDQBkgJLm23//7f+/cGw+Fb3/r6\nyfkxROrT+x+NZ6ezxfnla1sAyfZw/fF+wlXTFPzgoMwS3m53lFZpXkRhqzvot7ud8WQyTcZCCIJA\nvsg2+mwxm4ct54uf/8zBg/03X32Fz/iw0wM1Xov6m/31NX8AhFFCRixijq8bCZTO0nTQ6fSjDbN4\nYiwZFyNjAOdNlifGmKoq0jTtdHpSSq2AUo0QsmmaKAiEvNh6RVEYY4qisLN6dkOt1A5t8sfrBmqD\nEHIo0VpXRb4YT0fhqax+5BVkjNEX9ZcJXUdJY2EMi3xgAD3mVHkhG44QQoRqIYHSEIC6qqDnXdCO\nLvB/I4HWEIzPz2slIQTDYb83XNeGKAFUzXvdOO13XN+TvFFKBVGLMSp5BYAKfA9BQxCYTcaN7xaY\nGAS5FBVv6rqmDKfZbL4YW4KcTRazLIuiaJFMRmM+X0wZ9QEk9+/eLYpMSjEY9pLp5M6HH5ydnayt\nrXFu0QuvqcX5+Ygg8I2vf/073/lq3I2rWm/vXL1x/XbghVEUSQxrrfMscYFp6hJTp1KGM1chk2rK\nwhiKmkF1dvwYmaYp8+2ddSV4GIbEZefT6TBsR8O2F0VPZ/Vf+lu/fun2K40iTydVexj2NljagEyA\nO48erg9bg3bsOIZBggEkCHRC8OZr6w8eBovxvN/tdaOOaoCoIXP8Iqt4bQQHAJIgbA9Cp+s6HRcH\nVMom8+NocGkra6p5maVpyqFGBGGAPNexODftr621e0WdPDq6I7NSF7yqeIjZMOy22luIm3qeB8x3\nDYcQE0o1RFIpWZTEdYnvSq0oRcihBLBG8rzkXuxubg03t4ZVVZRZHkaO68FSKoCQ43jXr99sKl4s\n0rOTEYXk1s0Xnjx6LKUerA2F5PP5fDydTWcleeONN+yJqZaGxFaQlDFm3Qbt4bsiN9sayKbtFruz\nYcA+ZYXy2T6853n2WE/T1LIYbLhSSq20c+y5qZfTTjb+2WhkkQcbrtI0XVH4mqYJw9BxHKlVWdT2\nKfbot59CCDGfz2ezmZJwOp0iTD0/1hACiKNO22OOnVN56YUXBoOB0VAIEcdtjPGdO3c+85nPNA2X\nUo7HYy0lkEIrUZaltVS39V9d11auoqirk9PTII4sUmEgaJQ0EKzi6wrttNz0pmnsZKKFOzzPwxga\naQFqTikVdWV1VmwPyXVdRmmrFc/n8167pXgTRREhRPGmKQuGkUMwAibyPd9hCCGgZBxHgessCfru\noOsIpao6JQj7UQygPD4+Ongy77bWHj/ZB9pTmi4maH3z+njEk1mGBHSx8+DgvhfDjb3ecHvtne+9\ne+v2taPjqcHOYK17fDgTkp6e1R6D6WKOUaQhIA4DGE7mk1rUEIL1rf8fW/8dLlt63gWi7xdXrFVp\n187p5NO5W52klmSpZUlOMjKyDQ6PTYbhDh4ww+XeAWxPMOC512MQA9yBGY8xNjDAjHGQo4QkK7XU\nOZ2c9tl578q18hfnj+/s7YbnVvezn3r22VW1qmqt7/3e95e6aTY+ON7+1f/j+vFwn1BkkeYBVwAE\n46qowaI49MssF1VNMLZGUYJmswlCaJZN4yiKWvF0PPOC4MuvvtWfTC+cu9CIozovCaCbO4cegY21\nZcwJx6YGUmrjNxrE9w2gGjD2A689F3UWUWcReATggaYQ+Am3QJg1gDBYA0U+bnrt3b3xD37/d//m\nb/16EIR5MevNzVuizp07lxWjsk6b3TVrtTGSMtQfCWQgM9OFubWk2+bMn8zSsqg85q0urR4cH3Sa\n0XQ86zTboqiMT5tR7BES+TSKkamKxGuLLLv62uvMMFHU8/PzTT8EypMw7HU6LAwx0qHP185uJlgR\nijEGpUQYeWHk+z5PkmQ0GvV6vbqWCIgQgnOv3+/naaqNdDM0J4Brt9sOXDy9Fk5n7EopR/+VUkqD\nCSEmYMojJTaZfbAdxAhro621HCPL0OFw6OYE3HKpZK3rUluwfuVDpQHAaKattZYhQggGUlYCWWys\nMc5WkAAmGBMcxyFChDHGOAdjKEWBFyDfn2tGr778UiLl+fPnCGOUeV4QAWBjDCEIjGCUr60u9bpt\nF8GOuZflRRRF//hrX/3IRz7y+OOPX7t2bfPMZlEUhJBzmxuz2ezN117d3Nx89tlnp9OUe83pNN1Y\nW7VggoC98frLUcgfefiyQxY49z0eCGGQRZz7aTZaXG4krcZgWnR7vbleRwo9K9NJOpvfXNke9hUn\n4yxfW12vitIAr7BVgjHD4jA+2r/X7C4TUyAEg+G4EQcBY0fjdOPio9tHw7n2ykjjs08+N3f2yZFp\nhBFwHBxMoMtAInjn2v1WwpU1FqSPOTaVFBhZz8OgLGysNxLfn+90MPII9n2vmc3qwOtYixAOysrK\nbDzr1/d1GYBsciuKKY8CFvjYYwqDj2kc+toaLw49z5umqSlNYDEhQcV0yZswrj1LRKZXmwtMoCRs\nYLALqwuc8Nkss4hQz5MW0qoglRgf7rLQj31fGWkwUmARw3GLR43w8Hi/024yDkGEi6zsH2+3ml1k\nsQKEuedhlmcVob5V0Gx35ldq7sdeo1nPJjtHh4PZzPqIpmn6n+yJTipTt9t157RrdMxJtMkDyzlC\n/jOE6eDgoNFouHqD3+Mi7NZlF5HgWh+3yXIWpQAQBIF7oVO+nJMiOd82OPEKctC9K5YOeqGU5mUR\nhQ2lFEUPxolVVRVZmabp6urqNMscey2OY0ppEATzC4v98YhyhvEDe1aMMSDs3rhzVXHUcEcmJAT7\nHkPWnFL+yEkIehRFDkv78pe//Mf/+B93uHElau57pywmdCLOcB+d+yRbrdbx8XG32zXGUIqzbOae\n0PM8J8xyNg3WWtfuuMr99a9//aGHHnK8RzeT0SfJm2VZkpOEKtcbuXp5fHzcaLQRcCnlJFNKW8ps\n6AfNRhNjUglz4eyjaVYMj7QVzXzq99qP9fffWWrPHx8eepiPBoOoRW/eu8sjOD4epDm8+to7863l\nvYNJgH0h9drSJsUs8pP+4ajX6wphNjc3KlEnzTAvZnuH28STrVbyyKOXXn3lTQPk/Pnzb77+diOO\nq7wKgsBv+Pt7e2EUJUkyGg3CMCxKQIBmeUkoiuO4VnWuCG741/b27xz3TS1FJRbbHU5wtxHNpEGU\ntOfnMNKKMuKHuVDY9zyPL6xvzq+ekYQziXAUA/Aiq7hPEEYEwDpPAWKSZoDArC23DcCv/It//hN/\n7W/M0jFjLIqjSTEoy7KShdJirteplYcZ0uiIWAi9ZimL0XTSStqM+WEYjkajyXTWTpqVykEaiaRH\nsKzqd956e6XT5WCkkfmkJMxASSFH860eBXLz3Xeb7e5wMn38yfcpWTII9va3dTbs58cNpoIgwNhI\nVVNKKMN1XbrWJ45jIQRnoVJqfX3j9u1bWirKsCOgOmW6m0C41ZmepP643trzvCybuZGdUoogjDFW\nQo7H4/m5nraGIIwIttpYBHEYNZrJbL7AJ5kOpzN5Z+rjpn+n1zXnPI6TKqutBreH01pL0AJBQdAr\n1674nXYcx62FBc9vGGAImKrKo4M9StDiQjeJw2maM8aiwBNavfP29eXFed9jnVZrrtMiBGkltOZg\niLGaMrK4tBDFoQWzsDgfN6JWu+muozSbNVsJ4zTL0zD0waJWEq+sLPf7R3kxxdbMddpzc53ZLOt0\nOh73AbCozerS8m/91ucuXNw8uzHPQhZEtR8lYRhkJq/S2oviD330xeHFi3PtZG9np9nuSmWpH0XJ\nwrPvf/Jg1+zcufLf/r/+GvMbWJjO/PKovxs328PpbHnz3LX7++sXH7t7NPzUZ/7kEx/69jHEaQn7\nM5jNYDDKxI3aDwj3vM3zi0iWStWKGo4Ix8jDAADCQOBBuMyee/bp6VjkmQDLwUKWFkojQsJG0vbB\n57oAQTxTE1s1/bYb59gSiMcRgnI4IYzGQUyFzaelN6uRsRghsOqRpfO1rXxEi5rPRe3p4RQmus7r\ndtIlmI5maWWMJbS2JpfyzvE+bTcCQwknFPFaSR95Ugtco7xMB4MckOi0m/PzXbzQuX/vDsKaeb5C\n+P7eXpWW6TTjYXSwvf/6W+922+3jycQyMk0nw1lKwzCOfHrKnXNnrQM8HBbqlrnTenBah057lAfm\nVxg7Dp4rXW7VdppQJzBybkCnRAkhhHP/PQWZTgd07nbaNhVF4f7eLe7vNRJOkqTZbOZlARYrazih\nACDBOl2F4wg9YHVr7V6RVtVp/InnBU7b5JoqSqnT7Z7y2eyDkCurQCNiKaVOhyGNJgSoRw/Hx5TS\nRqMxqzMSMi8JLEK+F6haWIsACMYUIewS7hGCRiNijNV1zTmt61IpoZSqa+scyt10zhkyub7QGdSe\nVkG3543j2BE0nHjWHbPDFdz36A7b8SZu3769traBwGOMSZUKlWKiNWiEUBAmlbB/8AdfefFj3znJ\nsrt377782iu37tyca1W9TvjGW1978RMfyHRP0QKNhh/4wAvXb9z2PXZ0IEU2qiqaF3VdmEnDcqKn\n+nBra4cSVhSyN9fzA84YvrN167u/5xP/8Yu/l9ed8+fPj0b2zMWmRjLPZctDnVa7LMuAezllBOOy\nypeXl2d52um0sqxgnFgMQsuwEVqDZkoii2xRLc4vMKEOJuONpeUr9+5XSvrENOdaIcPCIkFwlZUL\nvbnNyw/TqIG9IFxcBwiMBItJ2Gg4vrEFQASs1WAUxkbIEkikDAgBv/ALP/83/9b/8423XjZZ6fx3\n4jhM0+nGxro0VVGnlJnJOBsejwMeAabKyNFgOhpPtFRhGPo8mKXjZqMpZGqlKlOhbV37/htXb/gS\nVufWfb8VRIEfhVAZLVUnaYi6GA4OPQqTUX8wnVKsGMc6Va6NxthY0NYaITVCFmMIQ9+eiLittUtL\nS9vb96UFz2PutHHK9Kqq3NlyevG6jQulNKAcMOPcR55FlHiUVVLIqsZZaZXWRlsLQDBoYzECaQkP\n9m/fwye7T7evchejm4U44o+bdvi+v7C8cufODgIgYDGyBJAhIBmpGFFKZZPJ4K23zJUbea0R8Vpx\nGwGI2dAaNZmMvvrVPzwaDBtJi3GvKApjYDYZZFk6ZPjVV1+eTkaqFogSzAMLoLWWdfX6q6+8/M2X\n1tbWXHQ6pdRdHXVZDPvHk9Fwc/McssF0Ort+9eosHcUNv9VMxsPB1StvPf7Yk1YrraRSWgobBkld\nVozQyXhgxjKrrRwM00IURV1keVaXh/0BYdRQ6ieJwuThpx/3w1ZzrvWtN1Pfi+bWL5999GlPTqcH\n6TSvwrg5mmQPP/nUvcNBe2HtKBN/+b/+O3FvWYfxbAolwN1t0e9P/aBRa5lQfPnRxZ29tMFL1iA+\nCz1AnCHIpTbIb9BCQUDgfe/bzCdw88aYDtL+eCK1NUYZTaS0YKUxFZIVmBpUhTkxYDljgBCyCBNC\nkdWlSoDh2ha58q3HMDZKC8JGRYoQYYDarOkrjhTUmTYS5ZnwIq6xXxlZSlMha72AtbrQ9D1RaNDG\nKim0RqCsUlZPh/WZzc58r0MxWlrura0ud1rR1776amehhcEej4ZFWtS5XF9aGwxnlTF3d/fWEM7r\najDq56oO40AzQuM4dv3QfybrcaEG+j3xr27o5Lg6GFMA45IgXDYEIYxzTgiTstDaEoKsRUopY4Bz\nKqWmFANgQgBjF6vldnOKMSmltlYr5QB/54CHGXMdjKWUc061tnVdSun2ZNo9s5YmCH1ZlUIIBOBm\nEYSQMH5g2xM3EkwIYBQ2Yj8ISlETDGC1rKuyrCejMeN+FEVJ0prN0m63G4ahu4YDzw/DUBkptHBv\n3PUlVVWBxYx6rWaHedQYQBgf9/uIkuFo1Ot0qffAA0kaTQBZjCjCQHCVZV4YqFoQzoQQiJLgJNMW\nADNG3QQSIcSYByC1tg4kqKqKc39ubt4Y2N8/bLVa1krGPEqVK1d1Xda1dEoUACjLylrEORdOSgLG\nQm3BhbuHxqqqFHUhfd5gQJGG1d6qqe3hXv/Hf+TP/PRP/81uk1qBF3vrPN546/pr3/epz3z5a39Y\nCblzTUIJehn1WovH2aDhxSBZnlXW1M0w4czntJ5OJutrD124fG5hte35bGGxRzmpRNnoQW+58/Ir\nby9uNtJ+vnn2/M1b14Gh5dWlo/5Rf6/41Ke/53d+77c7nU6aZ37ocRZgjBeX5/KsPHt+sUir61ev\nES9kHk6z4n3v/8D1KLayHueTGlFKiPIDr9XljeiRZ56farKwvBYuroJBICXmDQBsDFgAjEEpYBQA\niAUNiHGKFQCyEAWgAH7m7/zMj/zYjwxG/cG4HzVJOwwGRwcPP3rGYib7Vbu1MB0Iho0otBA1RZ41\nGAgoY6WUVYXyabaxuuQTW8xGBsmLl84e3bv/wuPPzg7G7bjb3xkOs8Hi3Eo+zBjhRttpmnWS5pn1\n9bA1/+pb7xCwk0G/i5GQGkmBMRCCKEFSGsZInpdhGEohtdaEqbIqLUZpmoV+QDGTQitpGkmAsC1E\nzQJfSgkIrLVCSS0lIYR5HAiu65paX2utiqp+wKcFrCyl3EpprEEGaQNgLAAmCGtlEXZm0S7ajlhr\n61oqpYOAYWyUEggRtzX1GbdGAUKWEIOwRqAwSKDCYgm81Z5vLa4srG5gwhkLfC+oqxIbmeUzhBBg\n+v521w+CaZohhAimRZlHoddutXyfb2yu9Xq9oigKIbtz89tb92/fvbO6vLKytnq4f9Bst+Iw0tYw\nQvcO9l/+5re6vbluuzOZTKIQKSUt6F6vN52Oq6oaj6ec+bu7u7u7+4QQhLAU1hiI4+hw/2AwkLUs\npSWlsJNxrZWpRaWV+PwXP4+t0Ur6frC4cuaZj35XUarBDCxvbB0O925fqZEPUC1tXt67+27UW2jF\n4Zs3dyBubZx97M/+6J9tLM+lAu4cw06/2D9OhUKeF2BGz260l+ZBVmCV5qHnc88CsgAWLPIZQaAA\nwBpAmHGYm4cwbG/vtY+/doBBW62V0FIApYEXhXFzPmEQqLzOxlWdx7GvVT2djT3k95LmeDhtWq8s\ncjUuiAVMsKorYECs8gOiK+VRXqRZHMRSCozpcDxuYSKN1lYJITQBP/Bbzcb24IjHfhBEpSj2RuNa\n1n5A20mrGal0nBOFvvu7PjHXab/88stbW3cN4Lt3doOgzTGhmBVF7QVB0m4tzS9sb2+vbq6mRZYe\nlIRzFkXUJaOcViNXchwRYDqduvbItUpOKlSWJec+AGBEEbYICCADFgMyWtnRaKSkcbl5gAyjHuPE\n40FRZkmjhQlYgzyfaWUpw1Jol7bXaDSKvOIeFbXyA46AYEy1stposKCN0soihLSyGFOP86PjSRwl\nGNM8K92AArQ57YQAQFtjrZVGF2VpqQcYKWsKUQNnAY+N0NgYixQCgyy0W60waFhrGfVErZ5+6umy\nLCjDkyLd3ckQQoTxvKjKMm82m0ZrhFBV1w4PAwIW4UajefveVppn3PN29w9cDOdoOKyFEHW9sLg4\nm07jRqMsCsqYqOvFpaVBvz+cTqQQvu97JCCEuMRlx3Fw9wFEkYsH+FmlJ+NsbZUGfgMsNVpjRAgm\nCKgxWivUbHaEEL4XZlnW7SwURWENocQ3BmqVNVuNOjdGGs2gyCTGJAwijPB3f+Jjk/Gs0Ul+/9f/\nrQH4u3/rtx86t/n8s+9b7vX6o6N/+29+49H3PbT17hiypNMIV+d24ziRArLBLOHR8HDQ27yEAW3f\nvTcdFCsr7UmWRr6/0Ov9q3/+Hz74HY+82d9bXlnrD4+Rx9IKWgvNpTPBdJRefvKJV998a35hzvo4\nldnahdX2Svr6lVexhySoC5cvTCf58vLarZv3jGWc4dHR0GqIvWhve5cB/W9/+mcO9nev3fqtbrvJ\nCbtyb/fDH35+8+KZlbUF7hEZNjeWL4SdeVkJ5gd5lUaeD1pgwtx+HYMBwGBB19QYwwNCERgAAsZa\n247jv/r/+G9+9u/9w4bfwpDns4kh5u13XsmLSV6oOFiZHFqRgc98mWcF0q12GxHY37u7vLI4Gk0i\nP2r5zWxcy5zOd7od2RR1e3grn4sWy6N6o3cWt+DimfPbWztgUFnWG2ubuweDbJgqwZkij51/SBSz\nlSZr+IhSihAQisIwbDYbTveaZTNnQZKmqRsAfOqPfV9I/TLLpZFBHI3Tca1lEPlpNlUO8XU+xUJr\nIeM4kUUVRg2t1CnW67wiBUJ1VZ1KXN3uU9e1yvJcaYzQKUUITkywCKGjotRaK6WtscLYLC8WlTS2\nNtpgHpUWsBfSKMnLugDwmq1S4hb4d29sEcJEVQceU8ZoDGmRGmOCICLkXlVVBoHneVJoY1USxVvb\n95VSzWbjxDzTYkY9ytIiF1v33rl+tX94tLK+poVU1hipECVx0jjsH+/u7nLuI7OHLHaBzr7vz3Xm\nZa2FkEYVxhgH33LmB3EQhxHnHCErlEaY+n5AMCtFWZR5NwqDkCWtRGgtJV4/8/DusBiNKubR6zf2\nD/YOZFG0OquHW7MwDJcuPTMaHqbKCzYe/64f/OHO+oV3j1NU1Zp6sxL2RnlRqySOOq0oDvFCG5iB\nw53DC2fmmyEKMLLWCGMsAo84j1rtMwAAREAZYBGcPQ9nzj//1ltHL33jW3VexP5cIwrKvJhO8ylR\ndtw/u9SzWudpURWDgCEiZD2qEhTeePMKp37IGxYUJoYwTbBdDDos8AnCdVHr6IEXrRDCCznlNg6j\nbHc7xGSaZUoUcRRe7PaWz5/zovDNa+9ua9Tw4jgMZ7OpTz1TG0zo7o3+r7/xu5iSsqqp1/UwBKQ1\nHU+ajUAJW1cyioL7u1vc57fu3cyLwm8EtTbE8w3F9FT680CRYIzzT3MD6FNVkAN4oiiKo9YpXHQK\nHcF7DOveCyk55nFRFK1Wy6ntHKHudIYghGg0Gi5HHKOCMSalFLVysiTff6Bq0uoBwzsMw2bSBgBG\nPcfiq2VVVZV2aG1VEkIwpkVdKaWk0SFCQDBlzGWEWGs1aGUVslQbo4wVUmNSg8UWE2k0VEIZTSyi\nnMWNkHEOlgd+/MYb248/+oTzzQMAwqjWUlljwHZ6c81ms6hyqZS1NvR8WZWbm2ePjw87nbkoCqxF\nGEMYxgBGCNVoRKPRpNVKjAHGmMhrAOxmHWmaOgAJndiFOQjaWhQEUZ6XdV0rNXbzRufhJITIsixJ\nEucj7jTIjnPY7/elqkfTQdwIsiwz0hCEsyw7PjxutVqO1IeMfe3VlzdWV4y1FOyt2zfSixcaYfvq\n9Rt/+sf+ojDV1771Na3wvd3dtY31w/2DyTg7s7555c3r66vrk8FkNp61ko6pwKMhw0xV4u033zp7\nuffhD3/45/7+//LYs9KLOPX4Rz7+SCmy/aOy1+Hv3nhLAhAP+uOjJ558pCyLlt/K8/zxJx//+ldf\n2t8/XF3ZvHr1apELgmk+y6mBwPe1kd/+7R/7gc/8wMOXLv/vv/iLf+kn/srBzo5S1Z/4wc+Ietbr\ndaYyCyjttRfD1qLVmFBitY2aLQADCFSdW0usAYy5tR4CoAy7slSUmnLI6jQKk1LAd3ziA9Ox/7d/\n6m/7iRd4AfdDZMsLF8994Q9uHNV7q72zUld5WvSaSyvrK08++/QXvviFxcVlUZUYkKjquzfvLLaa\nCY10psZbw9XWKq0YFSzkvs4kxqTVSHa0sRbNtTt3t3cPjiZ+FDc73fvfeHl7Z2dlvjMYDAYyq8sK\nMMx1u5cuX97b2b9x6yYYW9aFxzimpCwyQIgzJgoRkRC0sdhij9S6ph5bXFva2r6ntTTGCKE49URZ\nyVpFflCWVafVPt16OvqPo8XWQlJGT/Ub1lpjISuKhdVlwjw3M/EY09b6nMdJUhWFMoZiLLWOgkBb\nC8asrS1RpK212A9LIElvsb2ynitcWtja2V/d3AzDsKqqPMs4IdiaUta5EtTjCBEhKnelVJXIstmd\nO/d6vS7GTu9I6loqBVrXk8mMUkwpn07HhDD397PxpKqESw3VZVlmpctACgKLrSSEUUwsAplKNdXI\nAmAUa6hEXRZ1JWqX6SxrwTyfYE4IswYZAwQD86gFIVRZigIYSYtqbmH9e77/x69d29ndG/t+tbO9\nn8SNW/fvcaDdxfXR9DBg9KPf+yfyqvy+H/qh+4PZcWnXLq/sjOBwrPqDKfei+agVBmyuBc0YjIBp\nPmv4pMExBwAJDxzlMDIACDSAQWARIIsQIuiBj7qBZ55eaDW/vdvpXL92u65U3Fz0I1OND7udjSDA\neTEjyHiMc2aQ1EYKwkKfeBhRZKlGxoAGCojiPM1CaxnhWimtNZwISbM89U2AOYpDj4cB46AMKKuR\nta99/Zsk8GpkVCmztODEC1kYeRGUJh2WN6/c9nGiwQAiBEWtJEaIdZq0yFKwZHt7F4GazsYA0GjG\n2GONZsKUBsrKqnxgHGdPXBTdAFop5fSe6MT38xTPcORsfJIkBCc3h+44/MnVoVPWuBugnVYst88i\nJzd7kroNJ0FETuztSpeTJQFAGIZuZu1UR26EzRjLirTVavXm5jjnWtRCiH5/uLWzffoq+D0aXmMt\nDULiBwhhjJBlRCALVhutkTGWQC0FY1hhIAQjzAj3saXMQ3sHB41mU1urteacGWMw9rQUyNow8EWt\njAaKWRRFUgilTBwneV6ursZSiihqFEVWFJUxCiEym2V1LcfjKULEWkvtAycxa61T9bpPzylbT42L\nXMaEM8dz8U7uQxNCTKfTOI7d1s8N0B1OcP78eYSsECKMfFfvCcJa6zfffH19fX1+fh4AqrL0/FAp\ntbu/98xzzyOKGo3wn//iP9s73Lu7c/fWndsXHzl79e27Dz115uX/+M4jz14Qhd7fPei0OqKSZT1p\nNpqj/sBtsT0v8P3Gve29tY3ul770h8vr0bVr+2EDBpPxxYfOZUU6P4/TiYhi/vij59955+rFi2dv\nXL/m+/5sNnv6fc/cuXUPA5mbm5uMxt3WHENlvz9cW12+ffM6ZmCpXlzv/X8/+/f/i7/wX/SWu3/+\nz/+5uzdv/et//atf+cY3fuhP/OD9rdsPX77YbDYXFtcAh2AA4z9K3gIM1OMACACDxWChKg1jmBAo\nckCEMAaWhABYCGUN3Vhb1VqPRqPFGFdZdeHy+uXLFz73mzc2V5euvX73wtoqA3rr+g7G+NOfXgWp\n08m0EXmD/uShC+sBwa1mo0E7893W+LCvK9FmETPQ4P5kMqG+H3keAqONvbd9v1KGBf7xZESbXRRw\n49G7u9tLTAUgkdJSqxxNG543Lipd1EkjCliCLBjQ3I8MWLDG9zxSG49wi21V1SEl1JL17sLB3XsA\nDBNsPAj9wHoJsiiO47ooRV07HzV0YiYUeEEYhmqWM8Lc9WixE15YkRa5UsAIsoAIRhZqKaIgRMgO\njvtFVRKEy7rSUlkEdVlde8ePA2+azgqpo27vwxvnHn/yqVzB/mg6zMqnnn3OrR5ZOm03Ewa4qKtK\nST8MMCZC1ACIUiKEzLI0iV9+7rlnKWWTydjzfMYoQthaM5vMMEaM8SxLjbFhGFgLQeC/9trr7XbL\nWhiNhtPprCwLrQ1jbDJNARNXjcq8SPMMjGUeL4pCKOlzTygJxhJG67IilEupAz8GwEVREIQbSYSJ\nLussbARH/aMzZy889sijSug7t243m0vT8eQTH//A//l//vZoNHj00plvfPXtjdWF9z392L3d/Xdv\n3tCNuWc/9JGFLlMEwhDUQQlGI2KCgDEGhAIlcDSeVunw/MaSxwEbMFoBGEIpBUQAtDaYAAAgAAsA\nFiw8+B8DbKxFs/GZo/29rfGulhXGWKkql8WEkllacCas0GAs0QYMklmuLbFSWiWVlQbVhFtsQBhL\nlQFrpNB1XWNHTtYuJU7Vo2mhBQoCyzggay3K8zIO4t3jw4PJUGMLBtJJurQ4X2WV74ceDfKsTDrd\ncTbBmPp+oCUpyzr2/dHwyGOsP+rPdVoIY9/3mechgi1CbiBnEaaOHqNOgkpP8x3cIuiqlDpJfjyl\niuH33NzqefrH+sQJ2P3eqTgdBOXqk5sDODaBq2EOtjXvcWZ8L2HPwbaOKnZK7EEn78GVMedBYKRw\nYiNXw+x7jLrdQwzC0yw1lDDmAcYk8Pw4DPyYIDyZzBDBpSzDRoswbIwSWllRYzDYIifjKIpCGaO1\n0vBAJuUHQZFmFqOiKltJUyuFLSDkOj9nx+KqrFWqRAiFIUcIO7SZUlqXlRvuu7fsOH4uxMh1fu6N\naK1dBxkEwWg0ckTB012CIyg6qoijxbtq7eRQSZxYRbRAoG0pK0zg4OAoaiRx0nTq4KIq+8NxGCfX\nb9546603Fld7m+fWf3zjx6/fvPbwEw/duHX9Z3/u7/zs3/97l546e7C7f2bjbF3I2Sh99KFH79y8\nZ4w5e/b88fA4TdPj4VF7Lllc6Dz99DO1qeNm3B0cRq14/3B3687OcNInBEchRtLc27p+/sJqls9+\n4id+4pf/xb+8fOmRN19/J4oaGytntrbuU0zuDu5Yay+cPffO1WvKgqHVwkYnaNK0Gl58dKPR9b73\n+7+DADHKdprdRx57dHP9jFC+RU3ACVjquCMIg6hLbQxYzb0AgZ3OpmDIdJYeHQyarc7ZzTU/BERg\nOi38iAGGZkyNheef760ur1SaHfevPf7suSIvq1Kvr3mD/uDTn/nO43uHt45vLs03n3j88d/+rd8q\n8vTM6upkOjizvnRmY72cjseDfs1oEjBC7fHeweJqiwOoqmTWULCT4cht0qKkkQ2nApnaakntqMxq\nbHkjNCqzgL3QZ8Yoq4nPa6v9RlRbTSkVqnYxklprIWpiUDdoWm0sBqM1JrQSJWCrjPZ9HyECUkll\nRCWsstpAnmVRFLjLSxujtLZaASVIUo0ArBHygU+K28ApowOfK2SRRoQTpJFUNTKWYMAWwGqPeYCM\nJYwFTAeRBZ3nWavVavNQMi6VqaXyG62Ndvfave1Wp5vmuTEmBFsIEXi+tLbRSKqqUtad6kRr6fOg\nuZRw6i0vLhsDBGHOfSlrQpgWddhblLL2mN9ptoyylBOCqEXm4pkLq+srURCn+UxLgylihFPOEONC\nSXd91XWdZZkbP7g5R7vddpCwE/MBpgCYMw8h5tRUnFNtqqKc9UfHX3/pG08+89zjjz9nAJ59+rml\npeSNNwe//Eu/cvbs+eWF1lNPPrJ7cP/hhy+9df3K/tFBe2Hl9774tWT1wqXHN65enQ2yopbQjKOq\nFFWZW4UzzGRh66pIYr/dDIwGai0BixFQiwgyAABWI8AWnBkjBkCAACEwGBCA58OZzeXpU49oVe/s\n7dvaRpHXZkHo2emsjzDWKFdWY4x8xnJRx3FUS2OtBQNCC8wIIhCEgeeHFBMADBrAWIQQYoiFAfHY\ntC6toQqj0qpCyrysPRIfHRxKIz3Pm8zG80uLi4uL49EIrEWaYgTWkNksq4VGnJZlDQbyvMBIG2sx\nJdZawJgHvhd4iOBaClxVrjXxCaU3b948ZcedlgFrrUPF3e29qlhK6tNq9N6hnJu/uZboFMIxxjhx\nuKsH7kQ/Fcae9mSntLf3ViY3xzult53SSU8bMifoccdZFEWapqBVs9l0DLRTm17XKDywHkco6c7x\nwJdSp7N8e3d/7+DIWmyVdn3Y0dHByvISxmBBC1ERRLEmRtusKL769a8LIShnjFDmcddBNpvNra2t\n8+fPT9JZ1SnG41Gj0VBSEkIGx8O79J4DgZyXF0LI6gdmr059VdciiVwVd5mYuWMlGGPa7bbWQAg6\nEYvUzgAwCDwAIAQJIYxRSkmlhHOYV0qg9zhZSFmDgSKV1sqqLiknSokoCrkXEMakkVLK6XC2urq6\ntXf/3LkLH/jQBzfObx72tx597KE//MMvjWfj27dvD4fjn//5/+m/+i9/4pOf/M5slv/0f/NT68sb\nV47fvXvjztHBUZK03th9CxFotVqLiwulKAlh9+7en5Wzu9v7UQOkAaHhufcvIoTu3jtemPOyol5d\nmpOiHBwPf/Vf/opRKIm6i3O1NWh4nFLrnds8k84mZZm/8dK1oAvteS/NaygPf+8P/68f+fOf+Zf/\n/p898diTQRP9k3/0//uFn//srWtbB/1RVeFnn1m9en0vL3ir1WIeTxrUGOA8sOjBvnI4GN26fTfw\ngkbSOu73v/SVryZxsrSy9MgjD83PzzHK6tpgjLMcigKef/bpb7zy+ZDHjXiu1sc3b9x//rkPFTku\nJ/VHPvKRZpgMBsdKidls/MIL78+KcVENO93G0fFuO/IfeeziSq9HrFmen6+GszndSEgwm6SOJMn9\n4PHHHxMGaNDY2jvcPh52lxaavW5vbekssq2AN9RMTAeEEN/3AZn22dU4H+qEO7cnIaq6rjFB1lpS\n1yBNVdkqrzGlChM/8vNcTFSFkvBoMsOUaGEoIkIoMChkNJXV4TDFBE5FftZaH6uQ6IkqsMGnBFpq\nqMOuqFFGSjDgE59RzgkBq2VVgdXIGAQGW6utxpZaZAFQFDUI5WlZWw1B1Gg02xWihZBxs1Vrgz3P\nKNVqLhzt7/E4xoxrIbHFWlttNUInSTQGWWVlJY0B0ECAaIuxxUBYFMR5DqAhjCNkkNDCo54GHfDA\nY77PfMklEMAMuwRbSohR0unKvSAgjD2Y0Djxu++f8uCZlAgR7gVKaaPBj0KMwWpptXWG0YSQzfUz\nZV4dDYZpagf97Ohg0Ot1L1w4s7A4/3f/7v/wnd/5yZu3b2SGGT8ZZEqx+Jd+9d+/8JEX185dsMqs\nLi0zHw6OMyHqwPcAdF0W3XZjYzFuBCAz6XHsc8aRpidNEEH4gSLhJOcQANy4qqqAMpjroY9//NGn\nnni4PxyAgWYYp/vHk+Ojl01d533FkIcVyNpYWFjqLS4sFHmljASks2rGfWyQkYZw5lFCrFBWKgrY\nYwxTKrRpL82Ni6LEaiJrPT7KR+PZdDY76gc80kotzi984nu+h/peURS9uTmQ+v7drf7RcV3XB4NB\ns9FWGPqDURQSY1SappSRqiooJ1mRSVULVVPOtLVBI3ZmnnlZ0bNnz763C3G9y3sncu4Gp07ylv7/\nxY3G4/GpNtYVNoc/uUrg6sqp5oZSur+/7wx73K7fccodbnT6JO9NyXNdkXMosNY6+xzOuQEdRVEj\njlutllWSEDKZzAaDATkJDTvV5bgDNsZoizDlSULm5+ejKPIop4TEcWyUJmDOntmgFDPGkNGMeQRx\nKdSTTz5JCDFgHY3NZf2Nx+O6ru/fv3/x4sW6rnu9Xv/oOAxDY7UxZmFhwUmdHFHeOS25LvM0S8lF\nvLtq7dRCp/dv3LihTkI6pJTT6dT3fZdZ6SrrCbkRO1Wg7/unXFullMOQ4jDpdVYIEItNEDLAptVt\nWCIn6aDRja5effcrX/vqz/zMf3c0PHjuhedG09Hlhy/kbw3+p3/08wu9+Q9/5NuuXr+WJElZ1L/8\nS7965+b2c888c/f2lix05EeB5z/6yCOTycRim5cFQtBotqpBbQENBiMe8JWFrjCVAdnsNNJpXpcV\nUsAI7XVplqZZWlcV9I9H852Vq2/fGvbH/+Zf//vP/sI/SBrRa69/a3tr/5lnH/6O7z3ztW9+I63r\nP/GnP/61P/zKpz/ziVqOv/rq53f7t/7q//u//MVf/SePv+/y57/wJUvw7mH/9r/7D73OSlmzp5/q\nKq0Ypf3+uDvXTtMJY2w46m9vbz/33HON2J/N5Nnz6v0vfFAr8/Y7b/3BH3xhY2PthQ+/0GoFd+6M\n6goARX/uz/7p3/zcv3r4yct3bl7dPN9VZTbV+dLSmc+//B9/51e/9B2feuGhJy4d9Q+b3Wgw2b9z\n58bS8hxgIWQGnIZNHwd2686drBpn+8O2DLu8eXzUb7ValPLZLAvCRFk8nBXTst4bTq7euD6qxP7+\n/s07t6mqWypF+dTzvCAIsmw2PDw+ODgAOEF6kLEPci+5tVYWNTckn868gGuttJJZNr157XqRpRH3\nOfcNtx7zrUEBD5rNVpalWTXDGNwI4RQ38jzvwrnzTuBxOqUIgiAOQlVVRkslDfcoZ35VF0qauBGK\nWtWiJJiVVS6FRtg6RtJkPO70esO8vHF/950rV3ZGs5GQJIq39g5v7+56QWgAFnrd46ODXnfOKinz\nupU0GWNlWWKMHa0gz/MwjiezjDGGCKOcU84xxoHn5WkWx4koK0IYpdhI4Jwb5EBoVeMaIRJGvhcG\nBJBCtjIqZvSUM2xOsqrJSYKaG708yKTmRFkjtAINbrlQzorMC+fn5994680kiu9tHx4dpYS2PvTB\nix/64PI/+V+GK6uLQODSI49+6823hda1klF3pT8azs0tZqPR1775yjMGLa2s7G5vTdP8/OWLBdJR\n6MU+QdwsLQa9BhQlgFEUc4+CBwS0AeMyzRGAq/KuEBlkMQBgBL6LmbNgDDRb2A960+ksm0wvPrl5\n6w0oBUoLRa2PsZJVJcpiOi2p549GIylrQmGWj3hAtTUGcYwptQQbjYSlYCkhmJBSCc3w7qifI92v\n0rGqRkV6MBk2aRBFweqFTYHx1SvvKEDGmMFg0PCj470DDCROmtPhFDEeN1uNSBVlpbXMyzwMg1rU\nSTNUSlpkmBcQxpA11OOMc+57wljqvo/TouII1EqpTqdzyrFBJ4GPxhgp6veSFNwJ7TAPZ0DiGh2n\n2qnrOkmS96qUXMtCCFlYWHA5CL1ez40BnfMjALg0VVeNThVIzmTIGDMcDgHABTR4npfmM4wxd2CS\nchkW1mlL3SbIXb3qRCdR1hKQAACjrBLCEIY8jC1QY0VdFeMx1MsMB4Hr/SjjlNcII4Sk0VZrrZU0\nBkmiwUqjB4PRcDiejKZCCKsBADn+BSEEI2K0nYynjmvurv+6EoxxJWeMcmvAjSsJfUAYoeyBX5GU\ncmGx50qXa/Xu3LmztLSEEIrj2O0fXcyH80qP49gVLQcaVVXV6XRu3LhxbvMiUowQghlQjiuZEg+a\ni0FRZS+9+sXv+q7v+ht/56/+qb/wo/uD7Z//7M/9tf/qJ197+5V/8Su/qKx85503q6peWVn5wPs/\n+A9/4bM+83/z1369v3f8wvPvv3Ht5vd9z6c31zc++9nPNtutWhTSiP4oQxyiKArjgFAstFhf33jt\nrddFAQApjCdnzm3GQTSdjIlPCKIPXz6/u3MkCzweFdNR+Z0f/2P/n7/3Dzqt9nyv97P/3f94uL/1\nUz/9U5/45Ic/9X0vvr390uqF1vevf+LOrTfPbG7WCHqr/j/+5z836Ze6/uJP/fd/+9bVvTpna0vn\ni1LdvLl9+9a9peUFpaTLqXvssYdbrdbc/PK5C5t1DdJA3GSbfGM0mnqe/+2feOH9L7zw67/xa2+8\n/s6LLz63u70XRq3Vlc54qj71Pd9zOLhTpXr3/mBhtfXO2+9+7nPf/Mt/6cfTD0zPbZ41VmZXxleu\nvM0D1FtNjke7gc8W5zvHk/38+rDXaiGtPEW0ryojUighpjNRMKsEskbWgBkP/Gw0ruv64UsPL61v\n3r67TW7eXIhbsDNs4yCiITGECSp3B/PYQwhJVTtND6UYABI/8X0/hYnKhfRRGPp5nmFDEy+pDqZz\nYUCBU8BCSGwrJQFTDRUx2dQDYUEjUrswMGOMQcgwNipLV5mcds0Y0+128fLiuzevGmTqWlqrKeVO\nZcE5tRYBGEq5UsLzAoQsIezcuXPvXrniRY1UKBSGL7zvfU998NtShWwQpEIh7iFCtFYUE6UFMlpW\n9WD3qDc3FwSBG9o7wclsNlvMc8IY5VwpJZR2K0yj0XjjtTcuXrxojZkVJaNUSMkZE1LuHx1P88Ia\nk+W564aVlBpBf9yPmokLBnQer64gOWsxl6bm5IYPDGhq4fmhz0KCEBgLYBgBQu3uwe6NGzdfe+21\nZmfp4sXLftA1Bt54o8zzNIjhi196GXO+cvZCIeT+0YAnHa7JoBALq5v37t154613egsLzShuNZPQ\nYx6POEYeRc1W0Aih0lBXosEpZ4Se9kD2pAl6UIpOEHrkSKGuUIExFhCiHlCOPL+Z+d7+fnkwmM5K\npY0PYIUWUnOLlMWWMk8ZXcuaISSUYpYobQmnxiJtAFmEACklda20tcApRjQr8pGuRrLASRhHnSjL\nh7f2H7p4yXK6vb2tCRIIpWnuUVblBWNeK2oKrUI/2t/Z58OJVIp6XBsNGFnQhJMoiTEGKcNmswnE\n5mWNCHZr1wON9ilD4dQ44LSzMSfJEQ+6Cq09LzgtQqe3P0KM3yOVdfs7N2E77bHc6e4GEc62xHU5\n7hRxOxR8kr/n7rjDKIrCYVpu7+ZqXpZlhGGllDUGAIwUDkM6hancIRFCtMtitZgjzDFBFgOxEeEN\nziPPC7hn6wpLicoitChCJCRUK2ukMhpbrfKiSFpN1ydzhDDG4/E4juNms3n27Nk4jo+PjwdHg16v\nm2YzoVSr1XLDASfH01o7YwUhhAONnNmlsVppZUG7N3tKtXcfu9scMMYctucKz3g8dvXJeRFhjB33\nwcmh3KSuKIooinZ3d+fnFuqs9jwviH1moZAzKWrC7fF0+/7+9b/81/5tezH44td+78f+zJ/8nd/5\n/f/45d9lAfuJv/ZXvv3jL/7Ij/zIV7/y9Tt37nz1D78GCrVWOnSV7e/sW23e98STn/3sP/U4rC0v\n7x9sa2IXV3rj8VjIilJalmWn2z7aP8rz9JFLDyMEg8lxVWeqMkbAQm+JUuwzf6G3+tpL1wmOIr+t\nqnpz49IP/eCPY4y/9KXf/4M/+Pzdezf+9J/7sZe+/pVvf+oDabh0MLr91BOPkWCl1Qgac3D50VWp\n8hc/9pGvf/lNDeWnv/9Ttm689q2r07xuYGK0XZhfefPN1xeXer/9ud9dXFycTKZPP/3YdCqaTQ4A\nQgAhsLDQNAakhDCCz3zmM//+3/3aP/6fb7744sdFbfZ2Dp5+dum//smf/HN/6Ue1IK1kcff+/Y31\n8xcv09/7/OeQhRpleZ42O9G5x9a4h4CaqTiojeitb47zPeMh4wuCcF/0m1GSiVoZ4A0+6E98iMIg\nmuY5JUFRqk57bjyr79/bqoRuh3FM+O7du5uMGFlPRxPGWMB9zhnn/Lh/GEVRKUpsMba4qirlCY1Z\nnpXYWOZ7fhgXVYUwbsbNPM8jPyiL2gJCBrmeink8CENlZF4pDcYYYxEgC9oaAvhBLrWSUkpldF1W\nBuwcQkmrWVUVZthafSpUpxS7L5pSqpQ4NY2kVJ5e3QhphCkhxAAyxmBECAWptRQCYzzNp0uL89PR\nuKqruaUFSihiNAp8Y0whaq018XjT94bDIWLUYuQeb0XNAr8/GT3VSgLPL+uKUya1AmNVlj75zNNB\nFBqlaykoJi7riPvel7765Y0zmwsLCy5YAD+wpgQnG3d7OzfSdyvMW+9eWVxa6rTmrLKyFoQggozS\n1aWHL33fZ/74cJxKSRYXFzCGd98dG6D90bAzD0DZmUuXrty8eziaYj+iUZIeDrwg2D3q95ZWW0l4\nfHj49FNPhTFWCAinZSqMMq2EEQzZWHkYfJ955HQRRYBOyHPwR0yxPypICMAi7cZXhACAlAIAWnP+\nW69fyWrRmlvkqCuLia1mHLGA28nggHCmXCwqI9ZaQAQAiqKyFjHAAWEEYQREKS2NJBRjSgAjo600\nmiCb13V/1P/Ih99fzrKDw5EyioUNqxVjBAPm3BOFqMp8OBxvnDtf1jVjng0CYTSyiHNmrfY9z/P9\nuOGXogYMlDJuAWFcltV0OhXKUIffuCwiQsju7m6r1XKxBaf1yp2ID+A+wuDEN8GRF04XTbf9dx3V\naVApOokHTtP0lNfg+36WZc4ntCiKZrN5yrI7rWdO4eTuSymdxMfpT90Izr0EYGutravKPfY0zyJJ\nEnJ4eDrCYsx3Nawqq06jXeRpwPg3v/TlXrslymK+0z2zvpalaQPwZGcv46zTaUul/SislF5Z31BV\niY32KRVSagyckGYzYYyNtGw2G0VRdFvtsijcqIEQfHBwgBCqitwY0+l08jxvNmIAiAK/KvLQ9wbH\nR6fxg5g8oGufvq8oitxH53qm0Wi0srLiSBzLy8tHR0cA0G633afh7Jcc4+60YXJfHOeUt4jHkEbF\nYDycX+188WtfWz27ePXO61EHPvX9H/vlX/6VL3z5N/7Un/3huIlff+2l1dXVt9/51trGsrX2xRdf\n/MV//kvzc/NIobdee6fdTpqNRFb122+90YjJX/yLf/5//6VfNKCDRjTLh8rWnMVVXRDNGJvvdnqY\nwFtvXO12m2k+9Xw21+69/PLLxkBVwdJ8a+vW8Nn3fejG9a2PfPATH/3IJ/7BL3x2NJz93P/4937p\nX/xv01k/zWf/7H/9ldWVxsHx9tMfunzn6J2dw2tREqXl0ae+79H9/t2Nc4uAyvMX1x59/EKVpRGL\nXvjg88XMXL1yq9fr7e8fWmv39vZbrc7du3fPnz/LOWjD6xoYA85BSqhqQwn2PFAGuAcf+9jH/9Fn\n/+m92/cee+wxz/MQgqWFEAOJ/Ob23YNkLp5M0rI/MrgijKR6OMz7BQmX13vjSb/daWQ39NqqX+I0\ntaYu87ULi9ksbSbJ8WDg03AhaRCv0UwCVSopMUJ+mUnEmDWoGTdA6flme3Q0tlkVeN6ong3rzOUV\nQQmTySiOY8/jdloBgI8N4wQwpFWKRVmYKs/zJG6I/ng8GV48f2FQ5lXs1bLgEVdKFKrudnrTaYqF\n8pvL2+NUmIIwbLTmzNNKRXE8Gg4DFvKAaUMpIRZAMg4IFQ02xRr5TFYVQsjNz92Eo65rN+t3Nr5u\nnuyyIquqUphw7gtrG41GWZZJuzdTBqxljHPuaa39dscqHfoBWA1ANEaVUbaWhBDmc3zidxV3WuQk\nLRAh1I4CC6AwkMCT1mqCDMXKQpIkhhOC8LTIXQUyxhoMnFJhdFEUC715ionUotlIzIldmZthGKWN\nMcpaEmAMKE3T2Wzy+OOPl2llrY2isChz36MiN7WszXQKQD0vaLdglkK/389rRVmwtQNPPPvUN15+\nezTL42Z7nBazog4biTJGm6KRJK1W7LrbuuJ+gwz7M1WVjzy3UOWACVR10eompxQuYwEjACBgAbR2\nam2wAABlUQRhCMhopQilhKKTbgkoe7CDX1xbemd4Y/PC5YZPZDYlskI6Q6pgD13Gtmq1Y8+jgJS1\nhnI2HI2FIZ1Wp84KpI2PqZXSJRZO6ox5fGVt7fjujc1zm0ORHx2OMEW9hc5BtaNMZRBC2HDOImOK\nrIyj1mw4TJLu4c6BFQorHRA2Smck5GHou513VlZLwRLxOUO61WlnWdaO4t2DfUr5NM0RwnRra8uN\nUAHAoTJuD37nzp1T0rZL8XKFBCOOTzIg3JLnKAwOq3iQ7GCMKxXmxLTGlQR0EkDuKp9rdNzDT9sy\n583z3i7N3XFwkauIDllxM0ZMH2SWCyFUXQFAGIatVqssS+e0/4DqDYAQohhH3KfWUANQVoO9HT0e\nyqouDo/2rl2ty8qFGxljuO9lWYYY95MG9b3e/OK93e1SCh4FP/an/8zS4rzUinnB6tKyUhppo5WV\nQmgtiyI3Vq+urhqjGPPC0AfACNm6ls6xAiFrDBijHmxa+QPPlfdyDo0xLtAMnVjQuu8iDMN79+4Z\nY1yYjZMnP9CL/KfsjwffZpWKuljfWNre3dvr33/3/pBG8PqVr02z8TSdfOHrn0vm/A994Nkf+1M/\nEAZJr7P0zruvE0L++k/+1V/83355dDx57JFHdrb2iMUXL55jhHqU6Uh0Oq2/+Jf+zEsvff1n//5P\nf+TFb/vbP/tTd7fu3bmzG8c6aYbdTi/P04O9vYceeogzThFdW1zbP9jdXD735cnL6+u9OG5u39+v\nynJ4+BbB4R9++SuNuPMP/+E/3Dyz/uM//iM/+df/yt/4mz+hTf3Ucxdbif/yG98Mzl/ozId3t68/\n9cSTB7sHl85fvpnfO3du47f/wxcXu+efeOyxGJZGM3W0l7WT5JHLD/ucKwVC1D/1039rdXW5KLKn\nnnoyy3UYkpPxBiDk6P6gNBAKQkDgR9/73Z967bU3XnjhA3EEdQkGwQ/9yR/+H37uv+8stLfu3Vw+\n02y1kv50aj0ddFhEAmsFTxA3yLLqzKWo1+uWeXZ7B86dgdv7dzut9s5oP2Dx5pm13TsHk+3b5zcu\nNjvJwdYRqnHkJ9moiIIW9ThBOJ+mvXbL1rLdaBqsLaONJvF9X8r66Wef393dDoKAUqq0OLn0TBzH\nLhkyCCNAliAcBZ6UtZI1QihJGkpIIYQQMoqT2awAixYXF8Mk8HxCKXZmjPokCOY0tAxOKoGbYjHG\nVlZWjHCXkdDaSlkbA77vHxwchaFyEzzOfUopxrSWAjDK8zwXs8pBnnU1m82OZ6nXaFKLMCZgNGAM\ngIk1HBFLKKaEOC39e1zyfN+3CKw2BqzV2nVyCCE/CqXRxhjACBjBQIER6vG6rnngW2sNAsIpQkiB\npQg/yJu2FiHEKZVaE4SAkFaSCKWs1g4wV0pFQcAYowgbKQhGlHDOeVXkQgghqkbSMGDrXF66uFYr\n8EN499r1q7fuPf7s0zsH4z/82kuV0kl7bpSmcas9mU29IEiHx08//XQYcIaN79Hr169+8INPp2nd\njMJ4Phn3waNQKBV4flGUXhRIAxgDRYD/iLJArAFEQEtDnEIOAVhMKAWLLTh5kAXABrRWxhh87kLn\n+HDxS5//Qj4Z+doWs74PMvZ1Ntn3qDSm4B7WWlprfD+YpTnjUavVKdKZqSUFpKV01E0IuNi9W2KT\n15kak4NJH0CfO3vmG9/8WrfVnFtsj/N8NDu2iPjMj0OWzUZGVfe37rQb4aR/2I6isihbcZzZ2lhl\nQQMBWYvRZDic6DTP1e1bQRS2m500TRkNMMatVpt2u113Crp5mjsFrbXtdtv1K3DifmaMmU6nK8sb\n6D36JPwekeYpO+WUcedIBKPRqNlsuimcex73cBfB4i4wdZIxMR6P3QTvlMXnpohu6Oes3tzTuiZp\n72C33W5jhLTWsio9zwuCqN/v6/fcjDH4pLZxQk0tPQAEthyPvboiFsoiR5xhrX2jocqN0lWZy7IG\nRqosnebZ5U+fu51n1tphNm0njTwdcz/MZpMgCBCQssh9P+h0WlVVdbpNpUSv1yvLEgAHgTceT32f\nPwChEXFnj7XaWmSt9nzfYdTGGoQQAlTV1Wm6oFLK2csSMu92oy4eyemxFhfnHdnXdbfOqst9m4SQ\ns2c3/YAxqkez/beuv9Jbae3t3xWQVTqNkiCk0O55t25u/9pv/tv3P/NhI/E7b77teeFcd/7v/t2f\nbcat3lzn2ts3GmGLE+/o4NBn/Du/4xPdbntnd+sPPv/bn/pj3/XutdcOxltvvfPNqJV88rtfAKD3\nt3Z393dkqRqNxv7eQa8zZ40pc5GPLEFsrtMYD9PpQE4Oi0arzYi/uXGuqurPfe7Xg5D+yr/+lY9+\n7INvXvtmeyG6cuNWYMgzH/zk+bC72385AbSyPP/Vr37tEx/99tdeeaPXXr57+16z0Qq8MMvSJF6a\nT1qLyUpZgs8hnQHFEIfeB55/dn191Q9YIwJjiWNiWutkR25/qerahrGPCUoS8v73P/qtl172PQgC\nyAsTxfgz3/fp//mf/FNk7drquUoebZxdG757P26H1LeBxnlex01O/aZW1flLm4yRuvR/6Eebd27f\nW1/ftBa6/tLe/YNru3cazcTDjYnOgXidtQVPB6P9ybTKhUTprDw4OOQsOHfh4ng8DnEnBEYt+NS3\n0qapfurMI6N7+wxgMjkGAGcWIKVULM8ZE0JYi/I8pYQszncP9/d63TYlaFcIq7WUEhHCqFdVlQF0\n4IVKKUCKM3KqssAYLy4uHhwcnO783M7StUF3CMlUhSmSQhOKwiDWRvpeOL+4VFYqCD1e1LUoCeXa\nmrIS+3uH7XYbc64wHRX10uKi5wck8A3G/WlKlXLu41YKBEZLVYkyEwJx6qoRGGvAylpUonZ1yP0G\nA0IEU0wwxnme3rp1YzabOeznNJ1yZ2en1+u5eYyzPNZaB9zrHx1du3LFPUMUhFIrp3612iStplE6\naTUJwkVVNqK4qEoj6vFwhAyJ49hyZq3GmIRh6Hne0WhQVdYAHBxVc/N+2EjCRntl40LQaB8Oppvn\nz49nabPVOTg+ysuCcxpw1p1rE2wbAWcUXTvcHYxSjKAZNjwMVoEzswEASnjIHjRGgEAjIOAEclhJ\nSzAyFmEAyjwHJ1nAxlhEMHIeQoAxZpgjIQEoPPOBMwf7D7/2jW8CgnZ7gdlSpMcYE8/DSkkCChDU\nyihlMJDQ8z1KFCIKaUDWEoQYwozWVtZGeXHUjdrDMu/v782qghD07EOXGo0ok3IsJ2HC4kbTKDQ7\nHiVJvNA6MzwcBTwYj6Zzc+3BZFoaaYys8rIUtedxi0CDRQT7odduLyoLVVHXUmDiVVVtx0DdYm1P\nkvRarZbneQ6NcNXFnaauGKAT50RzYsXoGiCttUsjdnv804hYh3A4iYxL8nZqGAcXwYkIwNmTuCd0\nr+6Gfi4/6ZQ17lhkrq9yNnqMMcB2cXHR9zytdV3kGGMAXNSVA5nIScL6g1ZLK0BUisqnhBNqtKDg\nNwIOUlIrMQJLQFe5URYRHFBCKGW+L4o0QLaYjJDn5bMJKFHWZZ7naVlUlTDKckLjOPG5J0XFfUYp\nxhhO+OiGUnA2x1rrui4dMf3UhvKof+gmmafTNillnuevv/76o48+eubMGReYCwBCiKOjo7m5Ofex\nCCE6nY7v+64qu8vSSYNduxmFkVC5sNOo5X/oxfe/c+PVN959ZVb1z13eqDFL0+lwcry23hsep7s7\n94pUtZvNqpRGCZ/x48OjKZk1Gwlo0FJdvnCxyPLt7a3+YP99zzz+8qsHb199DWF97dbOD/7w977+\n1htpPrh7Z7uZzHk+Ak2qquDUL4t6Okk3N9fWNhZ/77e/wFGgDRK17fVWgiCYZunrr768vLZskf6t\n3/13q5utt659/Ztv/d7B/uTTf/KDPECf//rnPvSxx6sqX0uWD/b7nLCXv/FaNhWjvbvl1HYbK2dW\nL1DwpsU0ZCRkASdAEA59QAi0hB/7sR/SSlSirCvlBRQBGAvWOK05WNB1VZR1lVd4eXERIahrePjy\nQ1parZHv4zyTcchWFtf3R7sXzl68s59KVQmj253GeDLQWgpZSFFFIa9qiTEp8+LatZvYQrfb29s7\nNBrPZvlcd04SPSonoR+WstLZ2DeByaYUeQtrK+moJgHsD47Xzp6bW17y40hTTHBEmQRKRV1rQitj\nhUVZViDuY4xZ4CGErBCAkEJIgOKYtdo9AqjIa2txEEQUo+l40ghDQ4znedpaxgkgUouSc1pkFWjq\nNn/u4g39QAnpipPWWitFMGacIYSEVq1mm3g0T3NtNSG0EjXBintBWVaAkdbGWGQtMO5bbbMiH4/H\nXhjQoGG1QtZKUWlCVa18ygMv4JxbbZDVHsYIQCplfYY4pYhq0FZZoUWVV1mZNcKGQQZbbJCh6MF/\nQODhC5earcZkPEPY+l6otAiDmFD0u7/z+w89fCkM4rLKfS8EZKTQcRw/cuFSI4rdrjcIglNC3Ztv\nvrnUW7DWJklirZ3NZq1WazweP/XEk81mM5uV2EI2nY1GQ4wBsL76rZcQJc9/4EULML/szzJodjuL\nhQ6STqHgY5/83m+9/FIQhePxxGfUGD7qHz751BPIiCAMotgvy/zMuc2yLJYX5hmB2aQ8eybIJkAp\nmU3H3bU5C6AtaA3Yxe4ZwACEgLQWABmMNADmyAAoDQgBwggDWAQnDT8GBBbBLIckhBc/9kExK+9c\nuS6qrMjzajYLGGCMkdUWDCGEaUsR9RnG2kIlVS2UloQQDbpGILTAoedRJowaz4bTMlvqdJbZfFpO\n8mpqaDUpisP+XiFgAan5zkKythBAEABbbnfLNO/E8eHxICRECt1uJjNRGGSb7aRNm+vnNhqthhf4\n9+7cLcbj0WRqAVqtFkKo3WzTJElOrYBcC+JIJo1Gw22d3Pd3Ok1yNcOt7e+lhOZ57tZBN6Nz7ZHD\nBtV7vLdPadauxXFYPT6JJEcnIbP6PSmxDkmiJ7dTcMURmqMoCoKAM6aUckFBRVGOx+PTY8DvMYyw\n1hKGjNHuWOq6FD4z1Ki6cuoKhFCZZkobZQ1jHsYYz2iI0eTwQGYptRrJChs512l/7Zvf8uN4Ok3z\nPE+ipCrvjUcjQhDnNGnGjgfoRm2uy3Rvx8mq7Emqk9a62Wq5N35avx0Xsa7L27dv7u3t1HXtEKMo\nijjnN25cO3/+fLvdphQXRTabTdzI3vM8a7WUxjk1FEURhcHWzhbQfO/47vbBna+/8tVWL/a03tq9\nbbHmnC+vLfzu57afe3L+xo17zz7x7NuvXg2DOB1NiDXdZjIZ5lgbjv0yL24MrjOKR+Ojxx6/dPX6\nm7Nykm+NHn7kIgjxxjsvTbNpq9nbPLcU8Faz2b5/e58SpCUihDSTRAsdRY27d++ur64USoEAAJiU\n03Y38QM8Gu9dfOjsuzevf+q5j/zm77yzskG6G7A7vH754Qs//pd+4N0brzz66GOUab/XfmfvCg7w\n6Li6sPHovaO9w0m68NENhsKARkhhwkBphQn3PQAAhWAwGieNsBLC95tCVA4RQRYjjAEjgpA1uq4r\nq43SYCXUNZw5u6FEQVAE2HicUArPPvvcr/323sFBf3NzU+md9z15URh9cHDQShrUwPHuftIMPY9W\nUiZRoxu1ZrPs/q2+VvD0009WpSzKPAjJ4f4+jUk5nTZpZ35+oUJydW5d5EiboRe3jtJJRey4zqPF\nrrJ2qEqOuVJKe5hGyWvHO3mnMZlMLGilBJQPtOSMMe4xrVSDIVvLKitmk+HG6uIIjK7K+7PRcsQ0\nVhzhStZCKUxpZWpco0YjxIwp9aAx0lpXASl97C5PrZEiCCEgxGithRa0UL7xhVBAAWFKPS8I4ihJ\nGPeBEGIJwYAQRQwZa6qqnut1KiFqUVHGfE7DRiwxm2WFhz0OwAGstdgCt5YAwgBFliNOAXNAGmuE\ndI3LGle1xyODDbFII4ON0lIbjQw2EfdVUTCwHmOcEo0oA0ssBJR04rjZbGcZwZgqJaRFIaNe3FBK\nWa2VUtUJPwsYA2NaSSKlrMtSSqmlxAAUY2JJnRdGasoxJbSbtIhPuU++8cq32r25OEl2jiZe1No7\nFNLauZW1rEYYwd3t/bzS/cHuyupCXZehFyKZP3xpkxDkh54xZjyrLlw4l4RAJHgIwPNDBhOlVC2E\nUAjBtAakNSOEUAALQmhjDCPUYxgh0BaKrPJ9X0ptjAkChpHDkkAbAAC3yBkMhMJkCr15eP8HX1BF\n1d/dCRr+5vsuHe9fbzdxVRxTAnEca20IDpCGZtzwORtPp4ARC3lthEGQ6+orX/8qCqgwQqqyGfmL\nq4vG2t1j01mMK1sTY1vzYWzJ/FxrqTfXCZtMEFPIGAcgkZJWlq935uYhDn//9W9lRkqjXbCBtVYZ\nTa05e/7c4eFh0uxWRUkx7ff7spb06OiodN+H1nmeE0Km06nbfbvF0bU+jno3mUwm48yVB/evp72L\nC9X+zyZ1brPvjNdcOp85yS93nDp3SbgRtuu03O9P3R9OmX4u19LzvFOanzu2qqqm0yl20iJR25M8\nCHWSwXxaCBFCiGBjLUJGGYVAGyuVqZUCo2rMseexIAgIRYBIWUvGmBZK1VWStEYHe70kSRbmvKkf\n+561+uyZjZX1jbKu0zSLg3g2yyajcbfbVlo0m8loNHLsDwdEOeKGG6M5EO6B1l2pqhbu83QqV8fC\ncJKmN998czgcrq6urq+v13V9eHhojFleXnZTfGcL5N5gXdfj8fiUhe/wv6qqbt68TiO9vNH9Z//y\nn5R6un5h4cab79LAzi90tNYHB/tPP93Y2TpeWpj75jdeObd2YXdnP4x8zkiRivGwWOy0wViKydkz\nGxhDoxUdDQ4uzp+Z6zXv7Fy/cj1vzjXOnF+RZnHr9g6l0db921HQ6Q+GnHnYes1Gp9fp3bhxY9Sf\nrK9saKXrQnSai1rb/vFRmg0fefzC0f4B9+vuPHQX6YvfuXE8Pmh0ojPnV6bF/j/9F9/8oR9+Pk37\nBMH+/jFDyRuvjObb/rU374/6+Wp3s5MsD/ZnjbX5yIvAArJaSwVAtLXD0aCuS0a10TUgZY202GJM\nEDaAEGDkcep5zBMU+3iWTig0O220vwdFmQMJ6mK2t99vNJf+yl/+y6+/9SZtil4P7U/uGlWBwbZS\nfptjStPRrJymKysLBOEkaA6Pps2oRRq221m8c32XUd8LiTW5x2mn1ZzUuEqLwaiPam4JvvzIQytr\ndRg0s7RsrSxkVj7+wefAGGIVp6SqBICJ41jI+omL54ejAWNMytpaq7Qo8spYpbWuphnkshXG83Od\nYjaNfJ7NRquLl178xMcm4yEiCGPQ1kijgyhkXpBNZyIrOWUu/8VdGgsLC0DJqSUBnARXumuzLmqM\ncV1WtRTIQlbkjFBtYGF5SVtjlJZaOaRHEyUkZFmmlKot0pS/8/ab7YUVGrcqBcyPwFpDGWhDwSJC\ntLFCSkIxAUSoYhghhDzCaw+4NSF5kMmCMXfJLNaCRbaoaiNNTJlPudWmrmWdV9Yaz1iTl8gLubZG\nCg6WY+IBAGOZ0ox7SilkgXOOAXHO8zSry4oxJo1lhFKfWG0YwUmUCCFCBhhTqa3WUtSilkop1Wq1\n2kkSJFApaHV4LqpSodUOvXO/vn5rq8in73/mfXfvXFtZ7r362jdf/Ni3xT7xAg8zasAu0AUvgO4c\nbF+rOrG/soSyDKqyNKpeXFiQBqbTLPA5Y0QDGAuVsUYaoYTvexpAGZhkeWxwVuQe417E6hoAAyOA\nMSAABUAACAESgJJgESRJyLmfpllaTurZocgPZEVn410Lohk3Ra2NJthiqCvP88bZDHPCYq9QlSRQ\nyRoFFHMMEhZ6XUwpVnp/d/dosNNavJBWk0oVYcyJFyJmZulQpRnk+vzSZno8rLJ6PJi2k7jhs4PJ\nEIEJkzCKoqXVJYtts9MEjKSUltqiKsM4opSGfoMQIipFXaC143dVVdVoNPr9vpuTnkJBbojkOMSi\nNqfEa8f4dDDPcDh03UBRFA/4KsY4oMjxkk/NFNwM0LHp3LLrFlZHUjj1lHOVzOleTxhi3JUlAGg0\nGu8l7D2g2IFVSlFqnYzAnNjZ/VE1QkiCYphIq8BqwgnhBAhQH0+yUaxDwnAtK865BQmYaqPajQbS\neuvmTUlAIT2eTjmjeV0dHu7XSiLClNJllgPgJImD0Nu5f1gWqbW2PiEHTsZDrTVY7TKfXFV2TZ5U\npt3puqWh1WoBgPv0rLVzc3NKqe3t7bW1tUceeaTZbLrak+e5m8udjjQJIVLKubk5V6cdc8TNP4Mg\naC2EF9bOxs3k8P7O8QCHcdRZTK5fv7+52a2lEnnqe3T7/mAu6RwfjJAlW3eHi4vh7v1iaaHRbnSu\nvH3n8sULg6Pj5194/pXXX1o/s/h7f/CVsxdb585v3rh7a2412T/enl/oEQ+KdFpWqahtr9dMGr3J\nMD8+PrYKgiAUSM7G06qqkqR9cHC0uLi4sDhf62w8OeRNyOrBxUcWC3Hc7KK1S+ePRgc1DP0Eb16E\nKzffXplbQMQzNWMobPhpEi5tbR94pDM4rDZWHwpIjAwf9cdamnbSJh4GhgigdDpcX19N0ykjUKQT\nSikGjBxZ1mhAQCiO/EBbhQNcV9L3HuRAHhzsrW828zxdWlrY3Z+cuRDfv79X4f7hzLbWpI/RZJxz\ny1WuuId9HJTp1BS20YgPt47OLJ0ZD9JW0Lh7dStO5ra3Di2odg8wQC9MP/yB94vM7tw5fPixJ77r\nk5/GEPle4vmNNCvnF5cVoO9c/D5diZixiFIhFIDhQZBNx3HSymYThJCxmjHmGDFCVFmWTY4Hb37x\nm9s3bu/e2oo8yrAFXfW3tkaj4yjwOGdS1ZhhIWWr21lcWrl75w7TmGLqIFgpJef8qjHuzumE3J1I\nrVarM9c9Pu4DphRjRAgG8ILI51wos7i8UglBMaacE4QIYx5j1sq6mBpjxnm1ezT8ype+mEpbI64M\nKmvth2Hg+T5lsRfEUcgxklIaawlnzv8UY4oxKGWEqMIwRshiTB33hxCEMQVsg2ZTWZU0Wn7ArUGY\nAFiMCcwlTVNX1Sy1oI0GyjCjHgipABupQs8HbbTW1O1HjKUIp5Nps9kkgJyWscoLzmiWpnVdB37E\nPE45jeJAGSls7eiCwpqitnvHxeJS49z587kMNIAXeZNp/uz7npZSLC70hv0jUOLi2XWPIgxKS0n9\nYH4xRgQO+4AQwgCcQpVDWdSdVqOZoOlEGYQxJQpAlqauJYDh1KMMFwIiDoQBIhRTVgtlLZIKpAKL\nACNAGIyFNDcU4yiE6UyHPjk4MIzgs2fP9ne3UUWnx/c4xi6fTgotqjrPKyWIT5lPEEUQMKopAQBp\nNDBCAwaEYIang4lKBQbkc0qlOru6sr1zF7d4s5tohLJCFNXMC2kYJ3k6abcao52jOs/LdHL2/EUp\n9d72fa0lpZFbrISV2hqjrdAyorG2ttVqjYejKIqacWN7a5fOZrNT+wOXFzkej50lmgs4cGetPXFG\nqGtJnJzyJEtCCl2LEiEURr7vhXEjNBo8n1HClRbOZ4Ex5p78lLZnjJnNZo4u4bLjXOvj7hgN2kij\nAZAhmGECCIgfcN8LR+OBNWiu16GEU4ans5nv+xghSmmZpZPJxBgB2mCMXSCs+4lOBFGEMMKIlUYr\nQJQARsJqBpZQjiixGLmxhgFrMTLIuM2IHwZxHKZSDMeTdrvrG93pDLUxQcAbDd8q7Xmex3me517g\nS1m3W63pbCalRBgfHh4ijNutFqFUCjEaj8uiwIQwSrWB3sJ8VdZOBXyqbMUYHx0dXb58+amnnnLA\n7HA4zLKsrArOKee80Y6bSVwXpWdNm8ZAPPAC0BKsAiVAVnVZHO3tBqO+9eNf+42XPvXxj/3G52d3\n92/yBssm+eOPXS7SYnQ4XJ+f39o5DhCjmhljQj988iPndne2Hv7o5ssvX50M00ef7FFWzoXM79Rr\nl5rj/GDjUiMVs1zGa2fW7u3scV/7YTDXW7iX7p+9cOnWte35+ZU8M5NxCpgMx1MtdBwF4/F4eXlx\nMpktrC4MR/1KTVY228eT8cc+dW5aHV5+speJyfJ8M243cFQNx+NOq9duNy6cvXiw3c+mY1nhN9/Z\n21yeP9obSQGtZmNn56Db6opMSfkgZZj5/vHBQaPVUEYOBoej0bHn80ajMbdwCQC00hiItWAMEIIR\nAPE8ZsFgYBzCCJSCVqfxzpWdS+MlITRCpixFXcKzTz/zjTf+gADs3DnSOPW9BgZ8dDhpJOHyUq9M\nRV1AHPiXzz/00jde3b9/kGX9RtzZOT72eIN5Bsvi7NnVeqbu3zqoU90/nG4s6C988esf+eh3xWEk\nNOKNRiZEWYlWs5VLVSuJMUaMEKAWUNBIgBIeRpRSIQShCFPKY4oQngNTLcwev/A4Fho4m+3s/OI/\n/cf5tO4miU8IRtrz6SwdUUqtENyiJPBVWTPiAVgKiBFKLIRROB6MwiiwSislhVKCYKs09XjkeYvz\n81fevSYBGKGOX2CRIQhLreIwSvMMA2Iet9oAtr7nIQT5dIQxWMINZUVtgqjhE1tbE/qIYomlsZWp\ni4mdUa1EWZaBH2FKXF6ayzNzzL2BAcf0ATBO8UgIAwIGk0qUoR8pI8uyphQz5jFGMKbWakKYMUpK\nzRghhJVS+EFcSjXX7RZlWVdVGEWirhHGB/v7N994hTNWC5E0GlKpLE3nFxaKMiuynHMOgLWy1Oe1\nlLkqt4+Pj46OPvFdf8zn3KOEUZifb93ZngwG4SwTG2c2ESV7ewfznUgp8fAjl6uqWlruSa2KupJl\nYXizNQf376QPrTWwgtkM4gaUlUo6XlbD4TCfm2saDLmAySStqzIM/V4nYB6kU8k5IxiCsBmEANir\npCkq8H1QBgwFDZAWsHc0lsI2G9HCfMA43N/bv3xmdWljoz+Zxkgg5tcVIMwpC4xViHmWaSCUh1E9\nnfqYWYItMpXUlagp9Qlj+4e7K6ursdewWoHVMYuwr6NO1O20h3I6zUulTeSFzOeiUPcG9y+unDsY\nDnaHx/NJb27Nn5b5dJqOi1ky3ybtiHEitMhFkegm9z1GvXyW+yxcWVrNJkWVFs24gS1QVwPcdrvZ\nbKZpKqV0UIdr3l3b7lD3uq7DMDiZtim3l7GgjVGYYEqx5zOirDHAGHFDTc8jQgjfDzyvIYRgDCPE\nrTWOSQdgKQXGkJRKKelm+xgjpRRC1vO5lLWQlYeZkAITk+d5mk4JYWlKGPOcnE0rpWqhlAp8zhkb\nVxPOOTIWrG0lzcDzjdYUY2SBIGwAKOV5miNZj0ezdtToDwftKFRFzZhXVoowXtaCME9KqRFIgoq6\nxNzjgBTlfpyUQqdSHB0PWeCHcVNqBdZ6BOdFUVSFUNIPwsOj/o1bN+/f2wqisMjyuflerztHGJW1\n2Nnb7bTalah97vlh0NHd1994LU1TzvlTTz21trbmeV5VlZ7nzdJp3IgoJWVVhFFAKNYjMUuHa5tr\nhoppPtpcWLn6pW/8+v/1extxuxwNpCgb3YbFkmDVjUJPySQi3/zW/q7NeIdDNitH46pmncV5XXj5\nceXV/p03jrlhEWu042YQh1U+Kfb3V2N2tHv1xQ+tNBfi16/dOP/oWn8ySy5MN5YCcaevFR4fmFFR\n3bs7WFtvayv3jmb9w50iN+2YK8snmdjbGXAWEEJ85hulszxtdjsWgSG2nx0ni4EuQYbjtTW48Fy4\nsP74nZ1rncjP851yHAZhY9VfPT6a4sq//e5+WWpOg2w629xYmvZTo3HUiGtZ5mXRaEUlqrUWURTI\n2lR5Hoa+rMpZMZNC+EFwdDhYXt1QihiLGGNSg9KAKPRHdafrKQQk8EQBvg+VAoYhaJLDwd7RYBaF\nyWK3tbObSwnf/rGP/v4X/n3STDrNs5kYCGGkrjrddlkX/WGJUHzYl9/81jcD7zq2HMy8lfnwSBOS\njKdlsxViS7/15Xs//sM/cmHjMgNvdensQw89iXk4nKYs6spKVFXlGU0AjQ6OOKUzIaKl5mQyqYos\njmPO+cHOzsLCQpXnVVUFQUS5BayNMaJWse//q9/41ScffnhzeX1SCx0mSMjD4XhprpFPjpEBXZcM\n+UhJW9dEoYD6zSSZpamxmoIxyGZF6oV+WRedVnuWpRYMZbhWEoytdZ7lkyrPuB9gC0pJaoEwbLXR\nSumq8BBgZLCV1hqjNdEoDMPCglEWaUG0aROGVGlVHSJQ0hBFCCEUY6utqTVSIjKAixIh5OqQq0kU\nEQ+M1tZaDYCdAhQpixCxyFDKfavsJLVaBMpiAi4WGxNmjNIWjHEur1YDxgjJIaGYpoMDZYzVemYt\nQQgwnkdIHe5oAIqxHBGLUGTMZHIoQSmljAVGOCXcIsd5w7QomszTWZnputtsYAMJt50GK3KRzgaN\nxA9jrzXXBqJHWfbJT33S4xgQYEDEQKvRDDyoB7AQhUaDHwHnsHVfIR5iH3Z2AHtNHMD9Y+AUJlO9\nubEICPp5CTxoNtlgaueayGIoFdSKzWaj1lwLKNQ1IIBcA4lgUuF7d3et0u9/5rGza2Tz8mpaQO8s\nOffEY/ORx3SqZ4fETNnmJmVKgs6qqpLKGlX0j3rtVl5UpRQGk4aspdHTLH3ozKOe57W8lhIVRmCU\nDiNfCFENUsxwi7bH2TRkMUb+3a0bdSF37k845rKQ+7Pq4YsP725vjydj2gohYdozfiuqhahEfffu\nFsN+r7fQaXYirHWqHj37yN7Obn/32EecusmPY3XDe1JzTtl0ThXkJkJuRnfCB3PTO8K55py6cZPW\n0nHutAaEHlDG8yLDBNW1UFpSRhinlNLpdIowIEAWjLEaYSAUI4SqqvY8j/MHbngnVFU40dU+sDel\nlGIMjBHPC6y1tdZCCKOlowkQ9IA1roSQUiJjXWkUQih4kC3Lmd/qdBcXl2Ucd5NYl3UcBoHHjDHK\nAKUUEWyM4YgbgN7K2v5gMC2KcS2DpIWliOJkfmkRYYwQqmWRpmkraeRF5nq+b73y8ttvv310dOTC\nzucGfd/3e73e0dERQqjf7wNAp9Pxc395edmJscbj8VtvvbW3t3fmzJn5+XmHvZ0SCKuqKooiSWI/\nIMNRn0XBwlJvenS0ff3GAvN233jjmQuX2r3e1e3r02KwuNQ5un/78vLy1beuNh5evrTe++IrX6mZ\nOr+5MRbFzp09JQ8C1GQm8S0HAUbT/v44SdT5jVUPVYyKy5cvbh3dCRN27lKTxmU5KwflnbXz50vc\n2t8d93B8fDT42Ceef+2114qRShI8nZjRIUQXwBJaCxVFEUM+I/5kOBJ13em0xqPB4CA/89C5rf3d\nVMiwjY6m9tlPzhkv62fDxhzHGFbPnH/95ata0iLN8okoU3Hc76+tnzs8HmBFSpGvbmy++/q760tn\ndIkogzSdJlE78hJiuecZMIhIwjiWVopa5cWYMM8CBYQZgaN+xriPKR0cTaazLJdzy4t+noOxIBRE\nAViAoiqKuprl5eLi2SIHygKt4flnnn76qWfS6jif9WvF46Uw6YaE2un4WEgD1jLKNjYuRX736tu3\nxoMxsogAQkjN95YRkTv3tn7wBz6t66B/mNXp5GA727o3anZ746ycXz7w/bDZSNpxhGpFtAWjmkH0\n1muvnj1zBrQZHx0JIVZWVm5dudLpzGGM+9MDBERbK6XkzD/S4qnnn23EYSalZqzTm188dy4fHBBd\n0l6TE2W14B7Ns4qwIImSpYUlTAllzHlFGmMAmW63e3h4KLXinDLGrNWKYc6pVGowGBCEkDIWA9bW\nWGUsBrAMIVEWUkqpamMMgGGM4UbkMWIdywkAjLFaWfGA8XTqbmkxdqxc0Bo0AGYAxCIECBmE4MSH\n7NSj0pzqQhHCCAGuKDJgMbFKGgvGICWQBCCUIIsBG6tcTiemnBCCNEZGACBqtFKaGO1kZ5QyYo3b\n+xJCEXLsf00p1FYgqZmqCaKWEMpCz2Pc6OeeeF+dFV7cAgScAMPa8xBk8s7dm089/tjR0U6ez6pi\nevGhy0EYepxqDRjjJA49CiDAByAhYQyqGhCBo+GokfSGUzgYVBhTS6lGsHOUznU6h6O62fAY9ymC\ng4lWeQ0QGg3dAACzWtmD4+ncQpMwsAClhtkYvLi1fi557eVX7u0eNVrLlMLOsFLg39i+f3U65DI3\nswNmM44qhIUhWhEQyFprQg9lqB5PprNZpgwA4CCMrDZG5xSXRkoCNmAUtDRCMYRDFgUcam0k1irT\nk3wsK2uBR63m0VEfAy7z9LyHbx/t+Yxbn7GAZGUqRFUWUgmFLRWlHh+Py6zEQNrNTuj5ZV4YqwCA\nLiwsOA7CKSuh1Wo5hMaJKN0dF1Uwm82c3adb6x09zBkLOV4yOvGQdpgNQsiRvtrttvsnpzpCCDn9\nJgBIoRzy4X6vtXX4vzlxmeOcN5tNa+1pVoIx5tSEFAAHQdBsNpVS1qg0TZ3+6b2SUniPyRAPQkcl\nSot8Mpns7+/Xs8ks8ELKJxgxggBAGbDWWqeRrE0QRfOr61tbW6VSh4eH+XRaWzMajZbXVoWUQRBQ\n8sDyxyFk1tp333333r177nKKokhKGUURxvjw8LDZbDrkzBX7+fl5a+3i4qIrOcfHx64IfehDHzo+\nPnY6ROetYIxBiFtDQ7/d7Swe7h0ve/HR/gEZDX78r//knS/+xzeuvvXcx19Q3N68feX4SKD+cffs\nWjbn3Ty68+yzj2yPj373G6921zq7O7rd1GWZxbQlBba15R6bTqfakihZgLIMInrUP17bfHLv+E5r\nYf1+/3YQsp39SVZda7fnogZ98vFH3nrz6s7+uytrzWa79/u/c/0T3/HYq998Z+v+0aWLZ8qpGpbT\nyLOz6QgMqorZjNhep5syXhXlY488/Parbzz3wccXNrwPf/yh/eH11995+dzllVar3T9IsQnAMo/7\n26OjD33gxd/4zS9s72wtLq1s39kO/cbR0cGFSxeJ4dfv3dk4c7aWKmwnBJgSBhmihALAqla1MPOL\nS3lZ+34YR82qErs7+4srq2+/c2V7d08Z22nP9ft9Apf3947G05pzfmZzfnkpSpJWI26VRS2kiiK6\nuNiZTnWj1VhZXbtxZxgEsahLikk6HffmW+trK7s7W5EfAKCdrft3b767vtJ75OGLR3t9pYWoSs5Q\nmuXf8R0f/5Ef/dHESzjiItdGAqFhu7dQCE08T9TKIxRrVJdVzDxT1Ie7++d685PtnVarNcvLuSg6\nvnn74sLiwcFBkiS2qjzPB4wkoIDiSS2DuQRTKmd1XebvvvtuvtirxwNdTj0skKkZsYzRSmhAbGvn\nuChrxom1+pQTixCcPXP+3r17TkbteVZrWZalUkbrgRCHlFIEyAG0FghCiHMWBIF1tozY1Z0HXi2c\n8yCITvFad8Wduie7enTKyDXGWIMY8xB6wOg7Jb6e8qRc2frP6LgYO+YZZcYaq60BQHaWppQSRFwm\nurHWEGsYMFk4PjByARrGKMfxJ4S5rsvhVU4FKEFZRoxRRFuFrAENmgAQw0i7mbzwwffvjtN2Z85Q\nIACU0oAjglT/8KD9bR/c2ir7/T6n9qGHLjUSzgjISvmcxBFWAmqhwoBGERAGkwkYA8fHx6tr8/v7\ndjSaKGnqqh03/HRW9rqNqpTYmt5cMMrh5rUbl85eBAyMgQKY5YUBDJQVpeKIehQswGQyIzReWSEv\nabV9eNBbWTq7jjQhyINkrrs/OCTWEEZ97DPQStWAgBNirc6VuHnUX6RLllqV+FaDKIWUlSrrJsQM\nYdDaNadaCCuEBUuwop6nKhMRb1rUs+nU933EfD8IvDBwYtzaSuQRGnBEwRiLpLYKiNYUEYSoMkJV\ntVWacm6kGBd5WRRub0TdaM6VE+en4M6e0/Aht46fxhc5dqmDglxv5E4jSql7oD3xJUQIUUqbzYYx\nZn5+3r2ecw2w1ro0udPqcsqjw5g6BMutwo7Z7IqZq0+nbDRHybt16876+nocN1xv5DZ9DvE65fid\n8shdDXAPdMfg+z7VUeAxD1OjHnCsH3D5EDiRk0XI87yiKIjvR1EUJQmRYn5+vtFolFVFKWXUwxgP\nh8OdnR0pZaPRKIrCFcLt7W33KT355JNHR0f37t1zxxAEwWAwMMY89NBDDlJeXFx09l+O1jEej4fD\noZN/uZLcaDTquva9Rq3q48NRL2lGQdQ/Ot70+B/8m3/JRH3h4QsoZG9ee+P5D3/A7zZvvv72Aovf\nvvLaufdfur57j4T8ySc2t45Giz1IkuWj7bTITVloJAkngFgAiPZHMx/TUT65vnXLXq8bC7zYHj3/\n4jPIk8PZYO9wb38vf+GF940Hw+l4xikepfkkKzfPe/3BYJpBt0sPDrc9EhooATPfs62kfWx1XZQ6\njEDq2XhyOD78mV/42wqGqdy/v3VgKL54/pFsNs0nkzhqvvv26OFLjXyWpjP99a9/XWvIp5p5/YXl\nBYo4w8Er37j50Lkzc3NzWOOte9vzrdWI+xaAeZhgghAA9dKyWlhaOzrua61936tq9eabb+cvvaKU\nMo5CZnU2next33/t9bdrxcI4Go0PCX2s04yNJV6QRA2/P4Sjw9H27s4T73vszLnzX/r654FUlU1J\nFPSWm+PBcEZ1FHitpJFN8scefvjMirh/b2/YPzJafuyjHy2yWZ6nrbnLZ86tf+tbr3z3t3+3R/yQ\nUSWttqwoikJoVNWyVobyKGm1OvONZlMdHC9vtmAy6i6sAsZdTVSezm+cg2yWnLsA1oJSoDQoBViC\n1q0wHArhRWF7Lo4xUbJGFsIgAGpMPa3yDBASldIGAyaqLv0wqoqcUDd1qCnlCNkkaRoNUdjABDjz\nAXmONYAQsVYyzwMNhBDKsDHEQXSNRuP27ZuEEMYJIcTloZgHhl7opJNBp1tVp0g9rTR/9NNiIdRp\nHXpvNTrFCNwvT9X0QgiMwXmaKOsKofNvJZgAIMAEkOtOCUYIkmYMAA7htgZZ0GAxwtYahLB1DAgE\nxN03oEurMIYQe4xSMFZpKwjR3GutzwfNhM1yRqhGAAAeI4yBtXUYhlmWYQxFkV147HKn2w48QAAK\nacYpIVAqaUEzRl10HmFwPCwrIeMEXntzz+PxdDLU2pZlMD8/V1SmEcdKCiHh3u2t/lH/0UcfVggw\ngUpBVtWYMEtoIaUWyFKCKRDPn4ynjaTd7HYPx4fXt+4nc5soYuMSVs+fHx3tcZ3VYogYASBgrAEN\nYISoRsW0ZHZCtdTSWOVR30v8hh8TDf3dg16rFRAGQoA2PqaaWmMEGIxqpLOK+yExStc6TJqWskrL\n3vJilmVJ3ChVdfbSGVFVZV3vHO/XSkZRjABrC1YJUBqDYYADxikhUghjjFKCMUZd+XEr4Ok2/JQv\nh07cFtB/GrX3XmHQ6Vrv/syt/m6y5yhAjm3szHtcEXLNkHv+9+6kjDFS1qfeNq4fckl67tVdfXJO\ndE7RNhgMFhYWpOePx2OthHt1R4XAp152J/Q2QkgQRcYqW8taa2NMWZaqLE1d4jA2SmIwhBADWGsN\nGGGMO50OOmndQGvGmKrryWya5/nNmzeV1kKIRhyWZXn13Xfu3Lmztra2ubkZRdHly5cdEa7b7fq+\nf+bMmX6//23f9m2Hh4fuSADA9/35+fnj4+MrV670+/2qqtxPa+0P/MAP3L179/nnn3/22WfTNHUk\n+7KoQq9tAF966qEbb7/hhdnmynJ0PGxxH9X25q0r3/MX/sT49T9sP/l/s/Wfwdal2XkYtt6488k3\npy9/3f1193SY6ckYzGCQGGwmFSGKSaaKpCnTsqwfLle5XK5yKPOPS1USyZGoIi2KESAAASAxCJwZ\nYEJPQOfw5XzzyWGnN/vHe+/pj5D3j1s3nHvOPme/+11rPetZz/OifHyfrfTe+JkvffeffAfZwpg8\noO3N1ZV7j47SKCtmFUVhWRkHHBCa51XAmaPs/tMn7SzprbQuXLtyMHzUWe0RQSiLH+3fO+4fd1fa\ndTk5eDrgNNrZ2fzxm0edLoRxEsfh3t7egwfHnW4jYOHj+0dr642DR/M0xP3TfDF3nTQWVZHE8Z/6\n2Z95Mnn69//hf/P5n3r5F/7Ul4+Gd6NG63jw9MXnXrh/7+FbP/pgd3NzPKyMNIMTuPRGb//p/t6l\n5mg8G/Wr1W7j0t7ahQtdh9BoMt7o7J30B+PpnLZSZCkAKA1CAgvAWlqWZV6IZrM5nuQfffTRo0dP\nkiTZ29s7Pj3N5/OVlfArX/sqIfDuu+8PT/trdOvkpF+VSiWgDCZBbB2EEewfH9++e6+z1r1y+ZoU\nttFubK6t8JYwcrHRWw1C8sF7b6tuvdJdE2WRL8rdre0Xrr/8q7/8q7/z2/92d2er12snYbC1s3f/\n/sPBcLSxsqWkJkAppePJHDDlYRRwirVBykhZ1qX61q/8ajyduXxe1zXnvNtqV1XRajZnswmnbDwZ\nJmHkjA6CoNFoEATR7mb8mU8Vi7lxzCrJGImiSOt6MSs7zYwgi4mVRoPFAFwDWCBxmlGMzu5oRB0Y\njCnGhFJWVaVWjnPmLFLWEIwZPbNwRAYhhbTWxmpplEWgndXa1qr2T7XUSy3z/Nng4bcLci7hv+S4\nLosh5zx09klAOn8AAnB+bP2cdO68fIkDsBYBssbCWVcJuSgOfN8IIexjlXHIOVeWuQ9nng1xrkNq\nrQWEvBnmJ793yBaixgQZzANCrbW11BIjzcIvvPG6q/M0ixF2AEgb4BwwoHy+WF3pDvonshZbG2vX\nn7vKOUYYnIUw4pyDNqBNHYZhGIG2AA5oACfH/UajRQhMp7MbL2yf9kcOkDK20cRlAQig1eSDUf3k\n6XHMmAMYz1SzwaIEaBzXdXk6msRx0InDReUYQ1HKDw5HwzH01lbH5fzpcLI+vLCxAiePTGdjS4At\n8nkjZIY6pEESB8hhhjEQcGQkhDKVtZpiBBwjhyqrXSUe7z/m6CKJYrlYhECyOCIWpJLNTqtUwlaW\nEmeUtdoppSohJIKYEYcdDbBxKozDgGHGcHMRsQpTA1prbLDRYGupkI3izEixKAulFFirldVan2Fi\nfoRlqbizVN7068AXPf6RnnK9HCxdLiPPAkfnJns+M1pyxM+Vfc805c6Xl3XPKNGdS0KwpdDDMwvR\nelaF/5N5xl62KIozGp61nm3hznW3luvb/5d//qIorNPEOUrpysrK1voaszqiOCIMg7fQNFJbXxsh\nhJx02tp+vx+GoSOk1WrRc3sIDzxyzinF/X7/nXfeOT4+Xl1dnU6nHkj07ytNU4zx0dHRZDJ56aWX\n/An7k8mybGNjYzgceusND+gNh0NPO7x7964xZm1trdPp+CIvCCKMSVVUjx8+ubx3gc9nB4/ufbq7\n+ui99zdX2j/7tS+Aqf7jv/Ify5PD115//fWXX/uVX/3/vvjiC8eHB+0s6+eLu0dDWUmpyHwqQGdG\nAw8jUHY2mVisAqBCLIKGvb1/EDeDypaTcnrl+asW6Cuvfv6Df/Zr7703+epXt548GJULcWHnUoAB\nmaiuzN7mxmQ8u3p1u1jkk8nguRe2b3900OoAc4iGwUo7pjYoc1kV5a/9+r8prPjan/3CZz/72X/z\nb35tmp9u763WqvjJjz6Kgzjia+PTYjKeWuO6Hbj58X6awuHhbGe3w2keBOwnP35rvbchi7rb6a2v\nb0ihHj54cszGSdhuZd04SKu6TLIwirPT/kgK0+2sFkV1+/bd7e3tk5OTa9euffaznw1DPp/OmglY\nC5//zKeFfA8h9Ojhk/dXb770wvNR3EQoEAZ++KOPP75186OPPrr36O72hXVjQCs0m1bDp/c6q8HR\n40LpUmsxHx9/+O5xGkKRw+gUGmHn5ZdfmU3GSRqFYWyt/fDDj9fW1t9//0O4gUGhNMqyJsUYlDHO\n2ABTSlDMA24gcPjo3qNesdjJsqo/6m1tnXz8cZZl5XRmZR2kWUsobqyWtTF6erxfF2XxMPnFP/V1\nrCVWuKpVwLkQlVXKzwaA04Q4RKixiIaAcHgyHBEtsYegrfbp4MMHj2ezRRAEi8UMIeT5rhgjn6Fi\n+MTGjDLCMfPqqH4TAPjEqNP7UMRR9CxMt0TqfAN1GYqWgYcQHxXwMjYAEABvpWbAIXDGOWSdsQaf\nl1zIOAUA9ixjtghhpYTW2jjfbnAYY2WN1jpmHjn0XScEgJ0Da925OxsAIOesc95PCKIwAGPBWWuk\nNYDBEEQdBefM4PQ4Wd814NX8gFKw1p6eHjfSbD6flfn8s597bW2lF4dgLSCAKEIUQVkKjFEcM0JB\n1uAApIXBaHzpyvOTKSBM4wSENjEinEV5AQTDcKzTlB4fjYQ0a90uDYEpFiQgLQDhFkuH3bQsW7hl\nARal4YxQzoqqThpNoHQ8y58eT67stmlKGs22ZERixxBYXepqKuqJA4UUEkZPdEXTIGol2CAOJLRU\nzqvRaLToj/Z2di/tXWiFUT2dEmezOMbW1LIxV3leFk47UUshFEJE1KpQNY7Co6NDThlYFa2uj4aD\ntZVeEtLdtbXj/qCupNU2DmIcUSN0LXUSBrVUdVVZ55IksU6XdU1v377tywittVd8mk6nXnXUxx6/\nv/vgVNf1cDj0AcnHGD/UiRDyqsOeDr7UblgCgEkCCHkeJzbGWWuyLJNSWmuWyJtzDuMzLaKlZ6uH\n5vxAADqfbVpqMfjErSiKiAf+8UIID3z9sb7R8scgjITUSqn5fD4ej6nRWAnqTMKCKOAEuaqqKqEQ\nQhactTYNUgvQn84lQCFl2O4YKTHGYRgmjcxYyxgbDk7ffvvtO3fu+EGr09PT8XjsoztCaDKZIIRe\neeUVKeV0OvXqfFmWecTD10lpmnplTJ9FTqdTf7ffvHmz0+m88cYb7Xa7LEsENA5Qq9VqZ+l8PFol\nBquqnPT/4v/ub8JkCKaAwcm/+EffeP0rX3nn3fefv/z8z331Z39w65sXdi79zve/W1Iapy2Kpa5t\nHKaTU+EcU1pgQEk7MFALNO/24nTFPr49uLa3CpNidXv3vZvvVkogQtI4fvH58P23DidjWGmGf3jr\nXpbFJmiWsgSHoygZj0Zr66srz3Ue33/wyss7zbh5//bjw0c5ttV0BDub3ddfefW7P/5evEq//etv\nIia+8+077RWY54Uxantnr5V0TwfDC9s3RHErToL+6dHaWuvoZLqzk/VPxyEl0+l0fb1npVXKYkvi\nOK4q8f6HH5kKdVsb3ebK+urmfD6fLSbS1vfu3RsOh1s/eev69avg0JUrV77+tZ9pNFJjDONkd3cF\nAIyGV166zNPek8OTxXzy8ce3iqIqSjkYTq9dX/vBmz+UWgVRuCjzOE5fvPHKw8f3hqfD7UuXnh7d\nQqAdGELRWrf3qRubi2n50Yf33nj9qqjN8UFfikpUctgfvf3Ou0m39frrrzeDtBE3sripMq2MQ4QS\nFipRIcScQ6oqnTBhENfzeRKyT//UF568//7Nmzd/8U/+yZ/86EfD06Pt7c1HD27tbG7OJ4M45MzZ\nqip7rfRgeGhG/TmChCZlvnDajEcj7gwPA6ujKCTWacZD5VCrs7aysn3r1q1mHDglCSGcM49SpGnj\n+rXnsyxTWiwFq5Ik8vrFZZEvubWezcQYwRiPRht+c1gmiHVdV1WVz6dLdG6pd2et7ff7z3aGlkVS\nEDAfh5b9m2Wl4r9f6jqCl+t3Dp9HEh8Yzn7EGMBiDBj78OYIQQDUOm2d9bgcQQxhBxYh7KxxgM5c\nNYxx1mkEBDmHKTFWgwVHEMXEARgwzuhHD++/8LnPR1b7aVNnzt5I//R0befqaX8ahXxvdzsOgXOw\nBhACjEEKI1UVBSH1iJcBIDAe6SIX3U64vy9arU5ewWyep0kDEbaYu3YLIaBHJ1BVptFa7a2vIgaY\ng7QwnoDQzmCWpmFR2tG8SpPIIowZBFGolQ1DWgtTlPLxk4PRy+20AyKHUVXGUWCorgRxmNkwtlgJ\nW5fK1gp6a6uttFHPS5XXtQJUm5gHUavTYKEWMpdKVRUFp4QwWhpk5qocF3mQZcK4qpaYMGUkQlhL\nYaUyxliCqtkEZB0YgxBelKWpKpCOIsQxIoQEBFtMJqNhGCeMEWNMEDJKQxow+uKLL/o2iVftXSwW\n/X5/fX19KREEAH5a00+/+l3S7+xwbqfo12IQBEmS+ADg44GnhJVl6c2slqUVIWQwGCxdXH3B5Jxj\njE0mEx/efCVUlqV/UR97vGyEj4JePJRSOp1Oq7wQQmDkAEAIlaapP3NfgviQtkQFl1+XmhHYujzP\nCUpDfvbSnHPCqK8uCSGj8bS9tjaczXAiPfmiqqqs1RxPJq1WqyzL0Wh04cKFXq/n9VJ7vR6cz/D6\neOkh77feemt1dbUsy2636z+fX/zFX5zNZnmeA8Da2lq3282yzFNCXnnllfl87jl1nseRhBnDiTPa\nWp2lYf/BHUZsKw5+9xv/7eXtjacnB/nv0s7GauTQn/m5X/zxd3/sdJEG3ePR6f/6z/zlO4dP/8mv\n/p4L6e1b+vKVRGmBESzySRQFG1udQgiL8vZW7+j04cZFdjzuX7qyrZHZ3ds76Y+f7vcpQciJNO5S\nqzlJL19snB4Pnz483X1+4/DpUavVTJPG3Vu30bVLQcBu3tz/wmca29vrqtxvZ6uLkTw5Hh2fHCVJ\nBDFka8FwOMgy+PSnX9rf3+cYq5LcOtgHAFUcBbS51usWi1zUamUlFkLtbq3ls0oiN+oPf/Zrf/LH\n33u3fzpZ+/x6q9U5mAzG/UU+k3eLB5xG9x88AKRqVadpaqzaf/zkpZdufOELX2i2Gp1OIwgBHK5K\n5T1jrJYB59tbze5K86Ub19955/3BYNQfTmc//PHm5k7ayA4PD4WWK6vdXq/XaLSqQu5dvFbmR81w\nhTAznQ04IoOTuSiR0SgNmz//c3/64w9vOUvXVrcfPXpAGfrs5754PDzpnw4//wtvdLrdzZUNRjgA\noSzYPzw2UjeiZi9tMoSc1hBhRrEhenT48OMHNzsbHUjoG7/w1f7jh9PZhCRs4/JW/+1DZwwFY7DY\nu/bC3ZsLkgREnEmgpmlqikoooWyVxHES80WxMOCkNJiwVqeLMZVSyrLwKLEQtXNuMpkYY5R6wjmn\nDHuQvNfrJUlUVdV4NPSEWz+fzhgDsF6MyocZD7n7+90YY7VcEhCWiBwhxLd+/ziLwRnGyLNo3hJu\n8cMbftvxII0/pNTLBxv45CWcD0vncmAIIYcRQohY7FtZy3oOPaNMttSaWeasQkmwjmOU8JASUmtV\nGL1w6OHD+4wRqeoQIa8I5xBYQMV83sjik2O9stINKDAGCIBgQA6chVpUSqlGmlkLSmgHlFIYjufK\nQBjB8Um/01ufTOV8Pl9b23AIA0YIw9o6fPjBMEqbnGara61FCfsHcx5mZaUAoFLWllXSaAzGA8xW\nmyljDABj51wUQqfVRYRrbec5bK3AcAiDfLbVDY6nE2LmHKswY5hTqVxRCIXg4a1be1t7IWIRkAAI\nwhAjZhgkLJBFIZQkGBBnQgttNIt5XusaXNbIiqKslbbOmlohinVVrzVbdVF2o7geT3Y3N1NMailk\nkQcEt9oZIIIxkxoYoRBRzt3upYsO4HTQV0pJo40x1PdyvKKBv/ZeAcEX4H6p+WvmkTpf9/hFsITF\nqqqaTCZeOtfXLr4kstYCYEJIWda+YFfqDMJK08ZoNLHWtlqd5aStB74QQmVZelMsdK7zdp6yJe+8\n887LL7+c53mWZRhjQpgQwmkTx/FkPOScn54Mnj596pe7t5F9VleirmvKaJmX8/ncYxF1XkcUL98R\n51wZUZYlIpgQwoB5vkMQBF7IVUoJnHlzF//1/v37u7u7Wgqt9fr6+qNHjzY3N/09c3Jy4pWWrLUP\nHz5MkgQh5B2kvAiTMWYymXgJ1AcPHly9etWH5+FwmOf52tpaXde3b99eWVkJgsBYxanlnGpTWWQc\nqCwJR8OTaxd2dJH3mo0kYpOy2mx2KdCgNq++8dM3n76D6pXf/I3fOy3n169eHRTVyspBEPFrL1x6\neO9h1IA4sSSuX3vt6p1HH3z3jx5trMLPf+X1yXwmagWIWSABb1zczUbDxWg0Hd4tsvUg4uT5qy9O\nRvOLFy82W8nHtz+oS3jhxoao4eYHD3c226+8fIFzLoldWVkJSHL3431w5LnnrjWnzUPxNOrx8Wy8\nsd09enrcba0eH58uTC1LNx5P81RpXVd50VvtDSZHvUZ7e3er3+/PJv2AJHGYfef3/9AqijF94YUX\nrly5Ui9cvTD5vLASlXnV7jQnkyFjbDoeOudms9lnPvOZJA4pBc7BKLDWBaFXSwbOqTaQxBAnUFXw\nta986l//ynfef++D1dXVH/74x2ub661uM4oDhFxAyV//K3/1D7/9neOnp3GT5AtTlOOXXr5x7/7H\nnAaqhCRp7Fy99o++8U/eeOPzV6+8cHS4X1d2JWsbjV751Gtvv/f2t/7gO6/c+NTdm7c21rf29i4e\nnZwC4E6nNxkPVhrpYHB8efvS/OkRprByYeOP7n1gm8GLX/4MbLbh0qUW07Ro777yXMDxz33m+Qfv\nvsOx23n15X/69/7fsLqqlQjDRFe6kqKSwkoRYxQGMRAzmU3TNKmVEsqEcbTwmws569r61e75Sv52\n89u0VzTu9/uf/exn7t69W9U1YbgWtb+V6rqmlFLOtDUYnLMIEEEYe289QsyiKpZUoyXkjs+Vi5cs\noSW8zzm1zmilnDwrdPwDeMCttUpLIT9xoEaACTmzpgUARMnyaT1jD/D5jwCIEkJISAKvfuL3N/QM\nifzZLsDyJYIorsvKCcEIIggrZwWhKuCWhfPFbGfnknRWGowphBwODg7WN1ZPjw/3drZWVltJDOAg\nDmG+sHGIF4sSrFmO9gOAVFpV9OhwsLN7ab4AbTEPGQgwDpW17PXoZGKCmIynEEZJlkbzaT9tQn8A\nhIXKWMAMMIo5F7oqKwmYV7VilAUcGGPYIWRhrdubTOaY0iKHfQ1RClm3MyxPnFNRSGgUFSivTOm4\nVSSoByUU4pWN3XyyaASpExoTCDFHoeWYYEBC1UJWjmKeZVbKQTE9KWf92UQEQbPXuXzlysf37kQ8\nAIwyxkVedlnU4XHUS2PE2kG8UHZjbX2c51nadAiDI5iGh0fHJAi3tra63TYPg83tjXv37hV1Za0+\nc1P1S2ep7eYjinOfrI9lQ9L/6dk0x5fkvvPka/9ncxCljH/wktP8bB/onLlw1uZZ6rf6BywX9JIr\n4TMaX1QJISildS2VUk4bT15ACAkhllKt9hlxoDPYGiF77oURRVGWpSkjCacrzXbAKCNISllUQkop\ntTLGgAJECA7ds+mb1Ho6nRLOZvO5X+UbGxsYnHNubW3NPaOn50Vd67ru9XoIoZOTk8ePH/u2UxiG\nRVF8/etfv3v3rp+090Go0Wikafr88893Oh3/wXoKfrPZDHk4OB1iggFZoepClApBZdS4KHAtslZz\nUM3a6xvvvvUOo8mFrb2P/uCHcrOhbba+eTVU5f3BUZI2Wt2oPzjBuP/lr35+Muo/fHTv+otbb3zp\npZl5cvvjGWLw29/8EWVw8eLl2dEgz8sozIqiurhzieOkmj2yTgZhnKZ4URx1ent3b91UEtZ6iaq1\nrEEZyNJOHKVS2MePn6a80WzFa+u9J4+GP37rxwKLxsWEcpo10zRJBienFy92nz453lpbX0z2242V\nPM9X19fBqShs/Imfe+27b/7BbDgTueo1115+6dXf/+a306grnJvkY6tsr9N9+Qa7sHkJNJG1uXf3\n4Z07d2pRKiWm07EQotNuxVEYx74jDgCA8JniMWCHEBAE1oEDoAS0gY21Na3tYDCazia/+Is/X5Qz\nQoETzBjrtrsXtveA6JPB41c//cajx3d/+OY7z1+/1B8cLWbzOOp89OHtSxev90+nW1sJZVGn1xsO\nB7dv37HEfP3rX3/5hRuz4bjZaLRb3ffff3cym1+5fE2IggTwe7//zZ/5zJdAVYQgBHbcP33x+efe\ne++De3fvvPrqK+7DD/nKWifL8vFQV3WKXLPdcqqGssiaDb66QnmgtI2CyFnodLtxF3OrqRNVNaNY\nM8YMAGNQFaV1U3+LIaOFEADOa+0rpYpiEUWR923zeIa1ejAYVFXpwMxms6qqPGnIs3LsmT49dvaM\n6eqFE51zxiF3rq38SeHinB8aeTYyGWMYI5Rib0L6xw6/gz978y4PfK6DbJ/tNz+jsHe2z/gtxZ6l\nxc8WWD4QLmuyZ/6Ez0Op4xgRgpADh5FhVMjaYQQIUUwxAqHgqO/2D4+zLCmkAaeTOGQM8lzLhDYz\n7KwP9hoBZews0jOG9x9Pp7O83V3PS6ilxBScAguu0UgXBaysEyHBAmzvRo8fzRACpcEaAEwAiMNg\nEXhfLgtAGCeUKwVaQ8CYp3RENOCISOVGpxULg9U1DBhrQFvbO3V1WMmRcdpRhAJWVyKvylXE8aQ0\n/ZkKJVbISi2AgoEawICRTilkIaCmtgtZzIpcUqQI5LKOrEGAmlEihMSApBIh4put3oWtrSwKCQJZ\nlSMxmuRzBY4FlNLQONzu9BBBVV1MZmMeR2mzkTSyrNVEJS6qnHoozCvF+cDgzply7pz4D+eQl+/o\nLKMROp9TY4xlWearmWVEOV9PZ6HoWbjML1+fjvnqyp07fcH5bMFSC3xZqPlI4OXHlwNSAMAYc9pE\nUeSs5pxzPvEWW+eU00/WtHMOE2ytVkp5RbiSYKwENupef8gI5hRTSgkLlsldlmSEsZQFhVJxHKdp\nmmXZQtRhGG5sbz16/PjevXvvvP1Ho9GIEdxsNqfT6enp6XA49KcaRVGj0QjD8MKFCzdu3GCMxXHs\nvW6VUsPhcGdnZ2trCwB8n+nk5GQ6nQLAO++8s1gs9vf3KaWeWHj58uVm1mg1mmHEMEVag6U8W1sP\nHbcGKFePRiO22i2AHj89ubhz6cPb9w8nE9XvuZVkMBI1t2nWmqq8klWrGzz33HMPn3z4pS9/TuLB\n2k4DaHUymTW2Ics6d5+OV1eb3eaViJVPFk+oC6lD77z1btZIeitZsVggPK31YSld2pSrqnF0MtaV\nGpYjYkAKUBUMy8Xp4amsZGVn62sX9y5euHt3yEM2zaenDxYv9nbqul7pdQDs/v5+I82s0gdPBmka\nNBqNkEeVED98872PP/4ga0S2BmTRbDL/Nx9+s93MHt45amWN9e7a0dOjiPGNtXVdHY0Hs5DHz12/\nsrnZIwTNFrOnTx8/efJkd2cnjsAaKKsqjiPr9HnXATswgABhDAYoBsogV8AIUaKyWoaMbq4n05mr\nRR4GnBOepcAJnRU5BuYU2V7fq4uckqDZ6DLG80XV7qzMFnmaND++eavdaYRRsr0Tv/DS1e//+Lsf\n33w/+U//N7/xq7/WzBp/5+/8ndv3bzbanR+/++bVS1fng/n46IQGP/Xeh+90eXb09MlGr7n98suw\ndSFgMUyrO99/O0jSR48evfLKy5PR4PFiplUVUJcIl0g8OhgBjYQQCQ+E0jyM1lqdajYytd3a2rK6\nJARrZ5VGQdykLAmuXe9kIbZaShkEZ/B4kiRllRtj/AiRMSYMQ0JwGIarqyulKIpiscyW8jzf2Nia\nTCZ1daa7qrV2Dvyt7YyZTcdWnxnKLAsXez4guNw34GyiSIchf/aXyxvW39rozJAbEELgwIFHa4gf\nUbLGBx4EgDCm5yksJuQMqQMAzkMAvER0tD5jMwkh/L70x/h+mDAHZ60ni8ACGGuVUZVQ1oGwlgIA\nAmHh1r2HRyenjmdAeBiQditLYtCCggF95g1IACgApgxpDUZjHsBwnEvl2u1mXUNVCuegrNR0Pgui\nsJYaoTMWuLUwno563YbXstIKNDjtEKaAMDjEpDYxYwiRM1EBBoDAaIjDMGIcpF3M5rRim+udkIU1\ngKhr5HASJtrqyhgwLmZR1OheIaSLAmNJrBB11FhLHXLOWYykQ44xFlLJUKnKSlkTYh7yUEcGTEAZ\ncnir3SvzEjtA4GbjERFaTBfVZGKMRsgBQtqayupZvnCoUBpWtzcNtiTgw+lIIZdVza7pIQJhEqfN\nBvXTrH61eSQKY5xl2WKxgGdYbb5g8hd1efHw+WiOL4wWi8VkMsnz3C9Ef7FHo8kSf1v+r1/xPgr6\ngoycW55Tin0F5vMpn3N5Gp5fwXEc+1Mty1JKqbXNsgyfTyD5Zsyy2Fqe6vLfKcZaWd/LEULMjcZK\nVGAjwrSzzjilFFaGEGKclVIW04IFAU8bo8ViMp8HrXZRFPOyUEoJIfb39weDgZ8XXsymeZ63Wq3h\ncLis0sIwTJLEO3Uu8XcPdyRJ4tPJ3d1djPFoNKrrutFo+Guxubk5m81ms5m36hgMBs8//zwhJC/m\nrU5Tg0uSxvqVaw0Sted1UClblLgRf/TgLmtm9uTkyVG/3ep86sVXRK8xwZL0GncO7wRB/er11//c\nX/mzs9nk/fffv/9oPpmfXLyytbrZPug/XV3HzSb/8bfHm90NTvjv/vb3PO0Qa9h/dMS4Y5i022kj\nI1U11XaysQ1xCheSndm4WkyrZjNOIjyp8+ODiZHqyqXr8/n8yqXrxwdHslbtFX46ODWBDWI4HZ5e\nvXRxtphOpmWn1T46Oe5c7b726gubG9tCqNPBEQW+vbEZJNBuNpF2J0enYmGuXbw0Gc6eu3olwOHx\nwSBLkiSKaRSQve29rZ1W1qprPRqNHj68iyAgu5shQy+++CICMM6FITdGW6sBwIFz4EcugAA4qxEK\nHYAz8Ojh/TgMV1ZWLlzcjhKoBcwXc7DMkcjKtNNoLOYTSumdO3cos9evX//hj767vrGCEOqPhlmk\n17e279668/obn1GiuHL94pVLF+49uo0J9Hrd/SePn3vu6mw2++73/yBuRLfufnj9+RvvfPh2N2mV\nqjw6PUgsPZjMX3nxBf7k8Vu/+btCWoPQ3bc/funVTzdefOnip7/05A/+YG97m25enJzs37354dNc\nrURdiANw2CGqnJMGjSaLjXbvtD90YnF6lGOQzllCiCNMWwIQhEGwX8wQGK11EDKvOpplWVEs5vO5\nVyUwRmOMCUVlUcdJyAI6mUz8yHYURYvFwjm0v79PMFsC+ABn6aYzJktjsJ9AKXBOUFp2Up/dQJxz\nQcAA7LPRaHmrLh+//KVzSClDCKGEI+y0Ba9uhzFgyoxRxgHGQCnHGBwizrlmki43Lp8C+vOZz+fP\nns9Z4HTIABDrABwg5/xXBA4gbmSIcaEMCkABaAP7x6faumaapK1Wo5kRgqyGNAXGIc8BPHMdCMEM\nARgNRoMLYDrLtSXNNuwfABBqLJR1VVVVJcpmO1kUsL4GdQmPnk4wRu12U2uoKzmfl9oxEkQBxRiD\nQxgAaWWF0sQ5Tz/EFrCDNIEoCAHrkAcODMOQhpEkoS4mKSeNKEYYVQJrpC1BNCMtJW1VcWOJMxQh\nUysfSDHF1hiLwYErVT3Op6WpMWec0jiKQBnmnKnqFgkj6ijCAWeJRu1ui4X8dNxf1DnllDUiqGiZ\nF3Y2AkxrYSola62yLFbWzIt5XlfTYhEEAQsoC879h3wC7i95WZbLYaDlypBSVlUlpfRS08uyduk4\n7usVL8C6TDo4561WJ+CRp+Qt8TrfRfRByH/vo5GQlY9GUkrPOlvKNyzRQh8+fQMGIfTgwSPOOcPE\nLzUAWM4q4WcGHdAzPoHL2BaGYUAwpZhYTQFTjAg6cwsEAOOs1jrAwbM3RrPZ5JxzrZrNZqfTiaJo\nZWVla3O9LMvT46PBYIAQWiwW8/mcUloUhS9uEEIbGxsPHjzwMH2n0+l0Ont7e+12mxCyublJKd3c\n3PRmegDQbrefPn1qrd3a2nrw4IHW+qOPPnrhhRdsy7SbLUxZpREKaJy02lcaQaFhXuG1NVhMnUFV\nSHeuPr9Zy6A2l19+CTg5yk/j/Zvty73rn7783/1P/+D3vv9bn//SZ+89ev+/+K/+9v/9//aNX/zT\nr05m47wutvcu/OavP8wSyOLkuedeSD6bjYaT6XQ6HJxyGiLQs0mOQF2+ul0KtrLe/WwDz0Zi2h83\n4oRotLGyNRyOsRX5RFFKf/Tm+71e7/DpmwCwsbqGKXn91ZcPJ0dlUDz38tWbH7332c985ujpUbfX\nstLU1eLhg/2nj58MnhZXX9nOmnHcaLz+xkvf+da3d3pbYuEmpxpkX9YSqQA4XkzmqqyL2TQJG2nI\nrAWjhVYVx/q1l18UstJan5wcbe/tVsVCKNlsZgY5BA5hjIjn9PrWt6PEaplrHTJEnz6+/+KN5/cu\n7u7tblEEPEBS5KIwNfCEBZcv7PUHRw5ClkS3bn+QNJkBAwT2jx6HSfRX/tpf+vv/4L+P0uh0ePCf\n/Y2/PhyfJo3w0tWdF1+60ltpD05OB6CPjp9+/4d/ePWF6yvrHWXL0XzQPzr6+he/9vLrL+3ffLC1\nvnX32996ZefC/M79XrtnMb376GkjaUOhQRKsKI070G61MWs/PS4Xs4gmFDHQiIWJtpiH4XgyLSvV\nH465EyFVFBujhUaIslBKq3QBSULAYuwAWa9NQAApJYSorTWUUc6ZseCcQ8hhApRixhjGoLWsKm9l\nCVEUZVmmlS99gBCKgJwB/s7UdQX2DLH3K98f3hPy2TLIf5WyfhaOW97mfguC/7DH45zTCgghlPIz\nMXawXv8bEDFWaeMQdl5n2QK21h5Vh/Z81tCnzn6z8nuLj0xLmMeCi5KGQwQha5whBAghFAFG+JVX\nX293O5RxDaANlBJmRd1qd1/+1EsO4bLMnVZlHoQhYICAwWwmCSEhCwgGo8EasA7qCganU2mJNVDX\nspG1nANrLY/46fB0Z3clTqCuYTpV0tRJI9reYXkORVFUVQ0ECE8oAetASMMZFboOhWacEQAlHNLA\nGEpjiONQLMokisoy1wVkQWRZtN6MTHHCqjnDqI0zhExeVvlEII0KW2JKnHEOnLUWUUQwtoD8Hiil\nmIvFvFgoDhkNibMZZQiRyDhVmzSEjIScUocwS5uEBI+f7h9O+52tVZwGE6sKkJUV4Gin1UGVklZV\n2jKjokZa1JXQsp6dmaYGQUA9cEzONeh8/r6cClqCcn5tWWu9qg06bxotWyker1tylP1fGWOLebWs\nrnxV5L/3WO0nEPC5HINzBEBVVeWrHA/oLfFDv4acc2VZzudzHzmW2Zbnwi1ZGMsV7w90jlZ7oSOv\nNOH/C2k77A9938g5ZwETQjAlCKGyLKnWlXG1MT6fms1mhRQnJydps+H5foyRMAw3Nzebzebm5ubT\np0+FEF7MwhjjqyKEkPfLwBjneb5YLGazGWNsd3d3Pp8jhDqdjhDi+PhYa91utz275MUXX+Scn56e\nFkWRpun27o6VJkrShTOlIbVyhsQRNhqBPRx/9ODu1qc+NVVFxej26urBzXsfPHmyvbcZxNH25d2b\nP/hg/t5wc6e3ffWnhsOTP/8X/1fvfvDjP/MX3nj77bff+OJnt3f2Prz9UZrCpQuX333zPiHmUy+/\n+vGHbw8GI0aDZqvJORkMD/tCx8lwNB3FSfjKqzfqVfvdp+93Gy1bu2JeTPvzKEkDHmNM19e6D+/f\nb7azRb6ghCet9NbdWzSjKMZ/+N23Pv+5Fx48vPfVr32+ESXU4YOnpwHDGKG9q90rly5rKx4dPPqd\nf/f7g9PB4rjCGq+vrMynixdffOX+nfu1E1VepXESMEoxaCkXixw0xHG6u7PxdP+xrAWlOAppSFFd\nzmnAEcXU9xEwOgN5ECDkMDiCHWCnnUxiyhl57fU3VtZXms1ManBWVsW0zAtiGWh3+eLed3/wHRTa\nKA6brWQ6G65vdMOEtHsNAPwrv/YvL17acg59+ctfdEh96w9/b3tz9etf/5nZdPze229trK8XxWI6\nnbS6zaOjA2H00+PDz376s1/42uf/9T/+F0f3H/3VP/MXV6/sAUVzVSerPQlIWLd6ae/h4X5W1Rog\nx+jOvQeUOE6h4kEhmAuoiyPpEOUBKId5YBzKq5IQyimMT/sBNdZIhFwYZZhwsLgqcgyGUX8bemlK\nYoxWWmgjqcWArHMGY2yMbTYzY1Sez/1tspxn93kkpcwDX1pro9VZtLA6TUJ03nL2W7/fYZboyLO5\nLEIIY+Kc9hxuhAiAHwWBpXLP8itCxDlHqQdX7Hn14azRmCDnW8zOWWsANELgOdhZGC+j0XL/8T1j\nD2/4toLfHBBAUdUAQIxCYIhBjhPhXOXsl7785XZ3RdFsAWAB8hK0cWvr63Ecz/OZlHXWWIlC0Aaq\nCoIAALDWgDg4B2Vx5kI0mYIQBlGeF1BL3V3p5QXM85xSOhic1ur5rTZ5eL+YToab66tlsYgTmA+t\ncyjgEQ3TMIEoAqEAHMYYG42WyhfGGKcsAE8a0Gw3R7M5Qq7I5+MBbwaxwSx11iiMpUOylqLEoGOM\nqKIMgwSbpYmtJXGMhybmobYQpjGIwjohQDiMeBTyhDWydKe7wrULgLSDxDV0wqIIBz4ALLQY1ou3\nbn5YWv3ytas6QMOn9wurHMGaOBwwhvGszEkIjoCwShtDObfWEoYXZSGNpt5a1Ncoy16fp3SfV8du\nWQb5nOIMIz5nTvsw5nFYv/h8Ce953s9q8yzDAzpHnH0JxRg7Wy7I+g6qjzHPQskev/IgHjkX1/HF\nkO9CGWM8w1tKWRSFj2TLdpcPqnDuvrzsG1lnEcVO1uvr6wQBBquUUsYhhBwCa23ciAFjCbiZpqP5\n3A+iRgQ3Go3ZbPbgwQOEULfT8m/TD121221/YovFAiGUZZkxJooinyEuI7H/jZRyPB77TwyfG8D7\nAosQsr6+fvHiRUrpaDQqy1LU0khjHQMWkCS1BtMoDDIIe12p4YUrl+5Ph+8f7b/97ttIqf/T3/7P\nxXg4kYvVZgwlpJ24sGOeYqEXLHJHx4/2Dx7+5Iezn/35qz9480eXrl81lhMC2kxuvLTS7cS1OJVi\n/ManX+qfTu7ff9xuNwPeuHJ1b3tv/d6Dm4Nj9YezD510FLisRZHnUizAYiMJ4ZGo1PruhhRmNpts\nbG4HIZnOR1kaL/RidFiv7ca3bt/8/Gdee/jw/o1rz80Xk9lslOfm2tXtS5eu3nvwCLDZ3t4djY8/\n8+k3ntzeHw0nCKG13uoffvsnvU6ytb5VL0SWpqKqJsMJp0ESJiTAeT4d9A+RsWf6h1opJaMkCqIQ\nkAPnznsQToM1ziBAGAEBQxhKMAOATrPZbbeCgBEMGLkgJJwhRRzBYJT81EsvIufmi/HpbE6Z064W\notTzfG195fD4dHNjdXVlc2tr5w+/9+248bNf+doXnZX98VFEwziOP/rog9XVlfWtNWnk5Yu7v/XN\nf3fthRuT+eQ3v/lbL7x84+d/7ucQRcV4EHazt27d3kqbGhFgQdZb++jwoRseOMYYDcI4SJPIKZUj\nKTms9xqtK5dqgpQDjkhZCRaE/cEwThNmq62trYg7BMo5l6StZqvrHFksFgTbIKCf5J2cxHE8nU6N\nMb4S0lqGYVhV1c7Ozv7BE0RwnKaEMOccpVxKGYVJu9uVUjvnlNJ1XSt5JnxntayLBXoGhPAUJA9Q\no3NhF/cMPYoxBoCcRQgTBATAOYssOCm0A+Ms8s41CDsExO8JxhhrwDrtEMH4bDPBlCGEvW62swjA\nYkQwASHkUllmCZ9gjDkP/EC8bzsB+BYXMB4AwdxxZxXCTiOjjC6lunL9OY2RAywdOARVrSgLuytr\nk+nIWs0obmZAKdQC6hqcg5AFeV4IzI2GorCNDAPA8dGUs5iGcVGAtW6lB7fvTieTCYDFBFGK53NQ\nWvKAWqcAzCIHv91FEQdKnQNjACEIAuKc5TxgjFrrjAGGiQYrSmG7QXc12j+mGEOVF/mEtaJkVuu6\nXISiiox1tTbTObE2ThMI44ma1U6zICpFmSCHnJXO1KJOOpmTUFd1aSuNDQs4DjhGaHJyEgjb4Imo\nBkzi3OAsTKWU3c2N/mIyJ8YgZ0M2NfX+yejjx/ejgAZJpI3LZQlA52XR7rWdI6JWDgHhBAwEcVRK\nQTmlm5ubVVX5ZozP9L2Kjz0/ln1I/0vvV+QDgP+rL3j9wKbPg5YVUhiGxjjOOSUckEVAvCqUdZqz\nUMiKszCMuDXgleGt09aeaUMscxmMsTEmTVNfcHgw0I/EKqVarTrLMlFWUkpOGWcBAJbaSKmMdtqC\ntdaCF6xHGDvG/TydUVY5ZxwgjLFDRBvjC1VjNEIEEQznJA5jXC3rLIo9Zi2ENATdu3O32esMBgNr\n7aB/EkXR9atXdnZ2OOcbGxsrKyuEEC9o5GPJ7u7uxsbGfD73I1NFUYzHYwB49OjRgwcPfCTzSrKe\ndz4ejz2s5ylMKysrfsKj1gocxhaBgWJeYIkLjTGQ0XiSGykTSoL4+o2Xitl0XNWD05Mvv3Z9Pt1X\n1qyv7/7+999vrMWt7oqo1MHp0cbG1le+mh4fH166dOn09HR9Y2s8hitbJu3Fi+lJRNGF67317cbt\n+x+nGVlb6/VHw8WkuLW41x8MwjisqmJ7fWN0PKhy6RzhNIybjaPDoQPiLOoPBuPpJI5DKeV4PE3i\noCxFmMavXt+tTHHxwku3PvhI5MXhw0HEgyo3ayvZ44ePD56crG9uaGdPD07DOHzv7Y+4C+MkTZJk\nvshfvHHt8OBgPstlrbI46bTajBTFfDEaFn5Baq1no/4ZKQZTbVaTRgMoVZWkPLSAwCKLwBhjNABG\nhNgqL9MkBUzyRY2RmYxPKhl1erF1jGFCSRgElqMII7KztwfIMobySqq6DhDMFzPCodXtrKytFmV5\nOjihnFy6tns6PgpiWpQzfVhfu3QtarLhvD9aDHq93nQ0ee+D98OQP3/9WrfVrRbip9740oWtS1vN\nNVvov/h3/3PQBsoKghAs1aW4PJ0vatldWxdSt9qNJA1lueAMA0GgayB8RIlSigKbTqeEkNPT0wsr\nbSO0koWRBoGWqq6EJIRax46OjsCJIODOWoSx0RIwCnkwHI9ajaZDFgOqpWik2Wwxp4S8/96HhNFO\np5PnpTHebQg4C7XWhJylpFYbADgfQ7SqqgFZDMghAOsIIZwyRLCshY8dFhxYZ8FRTBDBy9LEyzEA\ngHUaDIQRX8YtdC5LhhENw0RqbbW24CG7M0ow5QxjjMgZKoPO51XAOmstcoAIRg6MsxgQYbQqSmWU\nNcYBUEIAIWuM0oaGEaWUIGuN0lpWRomipE6iqDHLFW2AUuA4aONowButbLGYNXstLaRDUAtgDJwG\nIRznyDvSOEQWeRUmiQXoj6dAKaE8L8EBbjZBSmWk4TzstLvdFnrydLK60qakfbj/uNFIZzPQFjlL\ntANdC1mQWNMgBkpASRtGnHOkS2U0YIawxJUslA2yDoRpxDkHi5yEjGemUGnMXW1tXUUAcZASbAGR\nRVFEaVSpGlNiHXIYMKeIEVUZwghg0FobpcKIJDxAmBEDMeVYqRDTSpSBC0RVM6CTxXztysXDh6dj\nJ0qjalCHx8eFlXvbO48ePmqspYigAJGAhoFBq0l7Op03m+0pzAHh2mhigVoIEKGTyQhjLGVNKcUY\nzedTa22WZX7g9H9Z4RrjPNPBNwa9ibhvKcVxjDH2agj+vzzcFwSB1laICmN6hlYTpLW9/+DJ3t7F\nqlKDwShJIiGUX45+Fx6NRr4p5TG3o6Mjz/qbzWa9Xs/LFznneBhUt0uKGUIoCRMERCorhQHMa2EA\nYYewBWcBpJZxmEhThgkVpZ0vxkHAdVXWtQ4o0c4SggmhiGAACxic9cQrYpVtZm1R6yRKKaIhD0pr\nMKaUcG8xPpmNT/qn+/tP/afx8OHDW7duxXHs2XQrKyt5niul1tfX19fXfX3pw0xVVVeuXAnDcDwe\n53ne7/c554vFIooiP/337rvvcs6ttZPJZDAYMMoRYmHEZVmxql6LuVYlAA7DqNMNTu89kVOzYq3N\nxcW1HZSLiPJKV47TmHbSsN5ovyjK4ng4cDQmunF49CSKSdKIhcw317sPH91ptIA3LeJyNBhFhL3+\n089znMCbcmerO5ucrG92VV2PjyfXrlx/+ujp8xdeLPJcl4iiAFFCGFsUi95G++R00Oy0+4sTHEBR\n55zSNM6SOA4ZH037db/6ytd/ajqd3th9dTAY5PNFnpettHH/zqDZoGEYHx/2syzLsmywP9YVogmt\nlFB5QTHZPzrO0galPE1TYywAllXtDChpnNMWnDUyCLHUlXZIS4UYNxYTRzGlgAADGOcHX8l0IufT\nGWMupGCqigU4bcZSzqWaBQ6m45NO66IB0mysRkxOJwuLUNRI9w+fvv5TN249mhdlVVVlp9NYlIta\nqJXVdW3RYrEYzCbaCEXrwMDR8ZP1td6w2r/18W1FbMSS24/vdFpdK+y1K1frfHH35Pj6ped6K53K\n2ZLRiShacUPms9WVjUpo4dBxLnWzOyfV1BINTp+OrqQXsu76aD5JKGU8rJSolW1mDTkrZ+NJFISa\n0aoq54NBt8mttYyeqeAnSTybV4yRgCZ5scAOWBhQRB1CVtkkSpFF2lpjLGO8XJScBsQxsIQ4ZjUC\nQwiQMAi1trKQhFDQFhOijdJCUEqDgGFslVKIEWuR08aCI57t5sAai6wD5DBCZzy5M2VTrK30EIjn\nhC8p10oJeOZY5sTTxdw6ZI3R5xRtX2/h8zEVez7w7qXznHFSaqs0EEwxGOcwOIdRQJmyigDCjFIM\nFoAghwhLsTs5HiURk0YaZw0LgAbrW5tAUg1aGeAcTucwnZetThNRhMNwvCibWSQNBBSsAkoAMYQR\ncMq0s4iw2uKDEVy4BINcTBb55dUNL+05n0NVql5v7e7de1/50lemY8ji1v7jo5XVVrPRogxhCvOF\nKMtaa0soBUYWC2xd2mzhiRBOsaDBNWCMgXGoK+IYyjXEEYRxUJZ1I+mEOOqPD4hkQi3UrEhcZQMt\ndKm0ICygAXe1IAZNTiaMUIcRwqRQwnEkrETYUXAxxgEKTG21EGHIpRTtrCGEQphixjEPcm3jrVXT\njOhK8+D+TcfRzvoGx8TWZjgdNRlt8NAsRFJBKw5cpZpx97RCzlGMAosQbWWjyXij2cnzxVknY0mG\nXl74s+kBY/wFXuqQSnkGoy0bSx718v/l0SffufHjRHmeY4yDgMRx6CsbTxUlhCwWO3t7O5xzb/9a\n1/VyPXllIHQOrCGEvAmQMWY+n/vZnSiKnHNCSZ8FWGsDEiml5vMCUx4EEQsDzkPMKELEgjPGGDAY\nEHLWOQ3gEPbakRhjrLXBDgj2InsOABkwDqGqrKzFRJrayLqWzjkh1KIukiQJw9Dz2pUWCCGwFgC8\nxoQHM+fzufdslVIOBoPT09MoisIw9JCdl5bwM0Z1Xdd17dkcSZJ0Op0kSfxv/N3l263GmP3Do1dn\nc4QRUhgjF1FiwFkQRTmLOGqHGaW0QRljAUghquLeg/snp09WVzbq2vzpn/ul4eTk0f7t9z/+4e7m\n1SBki3KUUGutNcb2Wu0vfv769374/cuX2xu7rUH/dG19g2Z0c6/x8P6o2wjjjB1PRhubK2D1ymp3\nNByOhpPN9Y2Tfn9tY72sK0srILaz3siydDqdIod5wJ20eV7WeZVGGRh87+b+4OTX5/Oac0AIBUEU\nBMGkmD3/3MWqqrK0eaHZjON0PB6rcsBZXAslpDDEMcDWOWtBa6202VjfCpNGEktGZRAmxpi6kmVt\nirqqpIjirNPrdbs9Z5GUgDGUJSgJotLD4fDpk8fzybTZSFdXO6Ker672ej02qmrr1Hw2JhTyKJBS\nJUnGaGw56/USSlizxS9evfLeB+931uNazbVEYRLSkB0eH5RS1EJvb+/2R/1WO0ME7j24t72z2uik\no2l/59ImJfEH73wMBP/4j261Ghhj/PTho1/4hV+YDAff+MY/vLT3/J//s/9Jo9WbFkJhqoQ0Do/n\neYnItKikti4v19bWVJEXhAOiNaaYsNrpSjvKsdNKCDEej6fjIScErI2iCIwyyFB6JklXS6GswYxW\nsjTWGgBVVR409horLoqMsQihkDCLCELIYhImaVVVZX8YhpG1lpLIWABMEaGALKaYY4wQEAwIGQDk\nQIFByDlAiKEzPgJ4FOy8nYydM9Y65xQYsMpYg5Bb9o890dxavOwd2GflVGggaoUxQhhjuoTxrXPW\n2PMJJ+QQ8lmoA4AoCAgQ43XLsTPGOGcRQl6d2WGHndZgrbWejFdjrGVZY6qdBkRQGFEWvPq5L2ph\nnQtqBdKCMiCUbDQamCLfu3GIOL8BWEAOCIJaQKsVnQ7rStRpI5oW8HAfLGbNdsc5N1+INA3e/MGh\nMSaKMsYCq+Dmxw+drb/y0y+cnsx/9KM3/9bf/hP5HAjjhBilah7Q1fVm0oC6htlMhIwxTjCAs0hb\nAAyIIByQ/rB/pbd66VLnyb2iXNRZErTTNmgcZzHEjQjbkNaKWOUoZaEjeKW9qpQyWmGMA8oYYw6M\nMSZL0igJkyTSzkZRgAh2zmHONLHIgasNszihkXOo1toQZBhOu+1L7rLCJkhDA4YpjXky0iZUuNdd\nX2/0GjzDBittGyR67+at7e2NeV0OJ5NelG1tbB0eHZyZLyxHpuu6XvZ7niWc+KBFKdW6QOdTY/DM\nAMFS8scDd1VV+bXVbDZ9L2fJRMAYB0HgzZB8FFz2qHzvxC9EH5DcuXy4Fy+QUuZ57pno/q+EUaWU\nUVZKKbH2Onuj0WhZ4PunBS/+YazUWnnBv/ORCIwxAdTIGpRggsAhQMghgi2yTqOwHSHEgjgblQuJ\n6fb2drPdKoZybW0ta7euXbuWZVktSqWUH/p77tq1jz/+eDKZLOO3b5ZOp9P9/X0fpxljUkpvFeGZ\n9O12O01Tr1BujNna2jo+PjbGrKysdLtdY8zx8bGXYyjLEiHEOPd1KkKgjCqKYm1tRYjq8PB4PJ7U\nQqyurmfZzuXLl1dWg92djSePD7Os/ejhfqMdjQezZtrrjx93m+tSSuPEpQt7QRz9+3//rW/+1vdn\nOSCzv9LbaDd4s7Fy8PRkbW3dSHK0P3Hm8OC4LsvCGFhfXZmWUxSgUuVpI32y/2h7b3dcTrUqW63W\naHqMHBaVwJaCxVIKB1xRTTjjjM9ndbvd8mBmnpcY48k41wpPJ+ViLupaZ6maTmdlIdImt8ZpZZG1\nAI5T7pyT2mkF1mJRCkQ4DxlzSEhtkbIErXI8m46UdhhzjChChGNQBmaDyd279xezeTNLemnQiVf6\np8ff+/ZblKHt7e2tne1FnoeMI4SU0kKIxaLotLM4aSJcYyB1XVcCXrjxUnl7xlKz3QySRjAYHnaa\nbRrgwWi4vrHTbKWLfLpYLGbz4ee+8Hlj63ff+tGlyzsnh08m47yurBZ2c6OZxPHOzk548UKr1crW\n08++8eXLF15QgtSFjuO40V0jhGHKNJyEjgwmj2ezxWy+eOmF58s4aDQaEcMhcUlAndGUUqktAHg5\nlXa7ff3CHi4WHMtG4KwpwxAJISgL0qxd1sY4uygX2ip07kPmJVD9olrOeHi0I17prF3YpZQMx6N2\ns12WJSVhnudZEBdFUZe5QQAUDMYWAaLgnNXIlkWJ3Cd2REsuw7NzigAAyLMY3LN7CDwzjOEbPMuS\n6PxWJVprwGS5/7hzfYelzgKc82kxxgSToiiMPncNPS/MMMaEcOfO8lHPoDp7ToxpwLU1xoFxGqSc\n1/NPf+YNaSwNuAWoJSAEQqvNzU0eAOS+nsMIgVdexQgcBiklJpxzzhgOE1jUICoAq4WopKwzlC3m\nxfb21vvvfzCaDMfjcV4W/X7/5Zeu5zk8fvzYaIUBpmMVh0GWBAgB5dBsQ5LALIeiwGAtxmAtODBK\nY06AEGCMyUpqDd0u9PcT/+HHnPsdmIHxTRCtlCPOWiuFKBgWQqha+OmXM04AmHF/aMFpLZ1zC0Iw\nJdZqYfX67uawP5B5HeEgRAxjahyUVs3v351rUYHmMQcH4HQobAvxnYvXqqpajRqhJeVoShArK1EW\nRbfdubi9e+/JI1VU3Tijys4P+/TRo0fLaOQ9igAgjmMPEC3hV7+8KKWMBWc5zvna8itYCOFJnN6R\nyBMTfFjyMzRLDwj/coQQj+yh/1CmwZ9GWZZxHC/DoX+5IAh8858Q4ltHPvItORGUWkpplmWdTmc4\nfOhDoL/rwJ7FTo6pwRg7wAAYiAPtpYDH47GPRgAA2FFKHbLW4rkuGI1CZUbz6Xg88UI+R0dHiGAp\nJeccn+ugACFSymaz6fvDviTyod33vbywQp7nS4qdV5/zNZavmbx2EWNsdXXVy1B6ZZF2u72xsbG+\nvv704CSKIi+s7FebD6tHR0eeobe7u0sYdc5pZeq6vnf3KGtEV6+8MJ3OtzYvzIvpZ177AgvNL//6\n/3j45PHByXGtKlG6Skhi4xvPbf3ghx+OTlw5GzjjrlyALO1QJ37/1t3rV1oU0a/97OXFYiFr0el0\n5reHAY2KqthY3T4cnczryc6FtaPj4/WtztHpyY3nLx8fD1TtQKEAc+SoFAa0zZot7WSns0pp4CyM\nR7MwDNut3nQyA4eMhpPjQdWUSZK0213CiVXOWMUxs9pFUeSksRashclsPhzPs6wZ8BAjAlXNIpu6\nxv6TO0Hc5g5lWTuIsmJenB6d3Lv3wCg7GQ0ZIZOj4uH9O2WxCEMuhFAO+idHh4f7LIzSOOm025WU\nGFME3ojEjYaTyWR2//7DVrOdC7Gxs7N/eidOSJSEZEaA6N5aS+iqFou6zm/ffvQ3/sZf+r3f+53p\nYL67t9VKV+pcUhJGAVy5uPvWj95rtpPnrj8/GQ8vXdj9/nd/0G11d7avhKzJaSONOhjh0WjEeegQ\nrutaWIwxUErTNB2Px1rJnHPJkJOllcQoaYxhQSiNBWvH4/FwPN3otB/f/JCaMg2dlXkUUqFqAIp5\nIIXjYSBl7WsRv4k3Gg2EkBeH9FKTfshvPp9PB6PBeMQ5K8tyPphorYMgyfP8pRsvH+8fGCkoxQgh\n6xTBYAQghKxR3W4X7DPycedK3n7wAz8zOO8Ph+yztRE+P3xPyN9Z5lzcwWHCeOjnR/xNBOc6eM9i\nessDAWnEqRRaKaW0qOu6KAqvzldVBQD4aKT1OauCUUwJDyKpSuTAWlMLOcjzzvbOTGgUgpWgNBgH\nUspWC+UFIGcxBorBj6kiAEwBLEQRv33nsTSYxpk0mMXNGzcgSa5FDPp9GA7H+/v7Fy5ensymzWbz\nueeeOz4+brSyvb32xx/dtVpdv3K1zEGJGmkZx3EUIsxACqgFlCVoWTvnOCXGggGjFGMMHAKMod1u\nLxZgKPR6MM6yiIZiNuKc1/UIlCKgtBFa1phhbaCq61arBdg4rI0DcM47wDvnvCUjQs5ZK41hjjln\n6rrqNDrT4VQ7SYBoaRhBQRiCRUAws1xiBwSBtUoZDkEW0L213Xv37tFCV/WkKmSr3aGYNbPW0XD8\n8P6Dw+NDDrgZJSlmG80OvXTp0nK81O+bnq7m8xH8jEOdh85arc6yeejXlt9kfahYcth8elVV1Ztv\nvvn888+vrKx4kz1PjfN/ms1m4/HY8yaWyZqHuYfDYa/X8ynbcgV7OVHPYsiy7AxdRJBlGUG0rmuF\nDMbYq0s8CzrjZ0R9lBKyFnVZl3lRF6UTwjgnAUeMOgCvYu/FggEja60VxliMw8g4izBudTp+doox\n5vkIUkrvq5TGEaf05OTEGLO7u9tqtfr9vieFNxqNZrPpP9WyLP2MlwfrMMZ5nvs52bqum82mP1vv\naeTBSW9W1u12G42GV5+shfDx2M+KJUlinfMsEmttEIUeXGWMgGuBc5zGnJl2YyVNmtM8RlT+nb/5\nX/7ut37zgw8bD5/cszU7eXpKCHv66N56u3s6HGFLd7e29x/13377vSRO2i1ABE/n44tXdws107rq\nbWfmoWs20OGsSNrRymbj5GT64qvX+tOD7Ysrx8OYcIOwDMLAOKcpIoiJusIIn5z2MSfKAMZ4Y2ND\nO5jMF6urq6PpLAxDSnhRzd08Nw4tFrkD0+k1wGqCqNQyCMKyLpx2Dshpf3zr9v2Nje1mq9NqdZQl\nxmBr3dbutbJYLKYzBEE+nh8eHBilO2mSTyf7o+Pp8FTUVTEbUYyMQZPhCIeN+XTqnLlw5WojSbut\nzmg2X11dD8NEW3jwaP/e3Qfz+eLWrVutVidrtCeTfqPTrcT4yeHBxlZP6bIWeasbL6bVwwd3d7d7\n8+lC1pZA9K3f/cHFS5tpg7z9zo9/6S/8J7/8r39tNqtfeG7z4w9vybrKZ3NrTBY3h4Px1pravbKx\nmIr5Im8kzZDz2SLnnBfzotNsxVEjyVJwlnMaBIxhZ53XvUYsCGopnAFusVIqTdNmoxUEAdEaY+W3\ndkopAMWUOYtiFuFKYGvPagAaNGhkjJEagTa20jEOqLMYU4x4ohFmiZSi1+wV85xSHiBOgL20e/n0\n7iNHz0kHANhaYhwhxBDkpNbuP5BM9eWLF11158o9y28wRRbBs3HFB6HZbOa/WYa0cyCOWAtLNq/f\ntcIwnM1mS9bDJ89vka6lc87PPnqehb+/fNaP8FlgNsZg7CxgA8IYpY0DQihnzoBFBnhQF9JqqCQI\nDZWEWgoAKEvls0JrnZZIW2Dg814gFKwD40CWZSksquTB/sp4rG5/dFsJEcbpxYsXHz561G63jTGH\nx6drur223hkMhFJqe3sbIxUGkCZBvaiMzA1LkhQjCnkJoi6tURhjxgkhwBhxDjAGY5WxKogDrWFW\nwFoLMMZZlu4/LDmnEQ45DphlCDMMHDOMCNXG5IuFUVpr6WsPALDOWGvDkHsqGcYYrCYIMx5o60aj\nyWJRuFowhq0wCpHYEcAQcK6NMVI75JCzxDlsKUJkjcRjFISWKASEQIipklpIiRA6ODjSUq2urhJl\nSa1XeEK9JYQnyHnmgq9grP1kQHpJnPMp/xkD5nyA2XOZfNDykF0Yhr5C8mGj1Wp5QwRrrR9l9RwE\nT897djbIL1DO+f7+/s7Ojpe+9icjpUySZMm1C4LAk6Ens2mWZXGYCCGQIZ5A4RnVS3da5vWwMAYA\nKYQS0kiFHApYwGgQYswQ6FpghBA4ZxUYsMg6B9ZgSgP/9p1zBhznXEgphBBKDUej4XA4Go2KfE4I\n6bZbGOOf/umf9qVhp9Pp9Xo+YqVp6j+3tbU1b4rhHQgZY15wgXPuaY1exyFJkps3b3qXKV9Tpmnq\nP3xfQvkgdNbwQ0ApLavKXw6EnTFKGymVNBoTRCnl49G83e6dnowRsv/+O985Ge7n5emsOCWURaxN\nHGtl62nSmoyklcFaa8c59+jeaRzH16++FMXBu+++zTkHDAfHTwjHhZpvXVzd2o96rbWjg4fD6XBj\na/VoOH/7vZ98+jOvHBw++NznX7398R3GoZFk83ElRI3AOAQ8DDhKMHVSSspYo9HY3dt78vixVGp7\ne1uo2hmrXUAQlqZyoLJmZq311CyjDEFUKQPGAeBFXn98885guOj0Vi5eumIAaeWkqrrNxBoGODAa\n3nnrnV/+F/8in42wta0sVlUec8oouHKhkCUIqJVa0nmhrj1/bW21R4MwSRIaJDvbe9rAfA537t5/\n7733nUXTRYlJ0FpbWZAxN9i4tN9/iBkw7LRBT077yMLzz71czOT777y3ubJ196MHs0lxysaHbnpx\n6/K/+63faTW63dbGvdsPW410Ucssab3xxqeP9o8Wi4W1IISYTGZXLlybjieACQDmnCo1FdIMJ9NK\n1Gsrq4xS5AXctHbgVFUHcdTIWkZZkLYWyiE8nk6klNQaUEKr2lgkpXQIE6aqyi7IohWH2ihrgRGs\nna2kUEpVUoRhCAQDwbWSjDGLoJJCOuMIDqJwMpliRishhFJlVeVF0Wyk5y5EFhxYZAAc8oRrQMss\ncLmBePh9GaV85mrB1apePv7Z+iZN0yVY4ncVz6kT6syoYnlXLsdaz+qh8wNj7JDrdjtLO09jtJQ+\n6TWEIGutOx9sX+5mSikNDhC2gAihCEGznYIBR7gwIBVgAlICY8w5cGADRqy1Vpu6pmC1IRghbC3U\ntdvc2a6Fm5f1apLdf3z0ve99UJV1M0kv7F5NsuZJ/1QpnTayMImAAHLqcP/olZefB4B8Pr10cbtY\nQJXPWmkWx2GnAwGFmYRBIbQU3rM0DBGnoDWz2mGCjFHKqHIuGp2OsqAUlGUZrnWkrAEgCBjWCPmP\ny1HAGCHKWODjDQsoQsgzEq011tq1tbXB8NTvxrKu/F6kCRBCVldXQ8QSGmHtnEWMMUcxi+JcllIr\nSnFIKUVAjXPOhHGCdq5Qyi2gvJKls4vBaDSdOoQ555vbW1cvXIoJub6zh2pFfSPdnJvRnV2P8+u9\nrIKXLZwl124ZpZbdF19OeXxpeY339vb8PuvTdl9vLdV97JnDHrHno07L+MTOD4TQUoHbF0a+5++5\nZ75oW7aX/IM9IW0Z3pahTksVBSEoI8KkkaTtZivCJKAkxMgI5SdfpZHWWkSwBWcNIMukNoRRHgas\nFnGaYIyB4L3NPcr5dD6RUk7Gw+l0Ohr0vWne22+/PZ1OPVbuAZAwDLe2tpxzGxsbnsjgpwhbrRal\n9OTkBCEURZHXAfIOUv1+X2vtrfkQQs8999z29jYlrBYlxuBnCY124LBzTtTKW0ABslpLqSuMEeeE\nEoIdnw7n3ZX1QX+8vr5aifrP/9m/OJmfCjn9ve/81m9/8zcIw2FI52N5enhATKIKK5XZ3FpHJsIY\n8pkMWPTi85/qjw47nZY0YrXVVo4PJ4dhgvdPnlgC11+4/hu/8a1Pvbb14OHhk4OHX/z85yaTSW+l\nSRDO4kxWKl84SrApjLCit9r2hjGVFA8f30+bDR7iIKHKVNN8rGohtA4otgissg0clpU0SiNGfEdT\nCk0xx5Q3Wu2iEOPpbJaLUjipNSYBBvfY1EnA57OJzBf9w6eHTx53srARMZNPAqRRbYWulaowaMpp\nGiQzpSbjQTNNwGij9GI2D9Jmvz9wQMM4KwtxfDIEAESYdShKssnTfLzos1BRzvrDfhxjhLQDSJLw\n+ODwM6998Qfff8sxcvj0BIy98rnn33zrd3e2dlsZvXrl+fv3H2lxeHTY39vdLhfFZz/9ud/Y/5/r\nUgz7o05zPQzisqy0Nn7wGWhwYTea5mUUp4SzXqflAWojLKaEIkvBhXE8mU4pZgE660RWleh2V7LA\nhVganTPqhBCYsiBKFwtZG2WQVbLCGANj0rkKO6DUdBtHs5m0MtLYK9NrrWkulRaE4MNhIXTdJASc\nw63w7rwv2tGxKjEGTDDCFjkHyGIMHCMsFD7nWBtzNh9ijPGcJoBPyhqMCXKOuQA/o5kCZ1rdSCvt\nb204l1HwTxXG3j3vbH7InptwLlkPn4Qi55xzRVG4c1kWX0hRij0aKaW0FmFECCEOO+ecBTAOWeww\nIKkVJswStrV9yViLWSCUERoRhoVSSZIgBGHIASEpDXKgtXZGIccUwkoZAAyArVV1XcdZ1u12KQso\n5d1GtrEB2sLd+/MsywbDIZoQBzZgqKqqOCbOmsW82Fi9rpXjBLKYtduQUcgdjE7r6WjgzuFMbzyA\nEGirEOIADiEkaiGEkTUe1H7uC6QSQlY4wUopI0VAtDVGa4UJOEClVADWIW/erT3a5MDSLK4GTisR\nElRLiZQKlFhU5el0yjlnjlCHQsycAXAYB6zV7c3KeVEsnNXMAVbKCWWMwgEDSqTUjjJLWeHsTMlF\nXZIoCnHKo7AUdV1UR0DMvKTP7uO+2bOEbp+96uQ/dB9ZbvHLC7/0noBzMkIYhlEUiXO+gF+CXt3d\nLx18zuVD57rafvH54mlJ5/O/Iee+XkvZCADgnHvFbmdAax3SeNln8qvNz/ZqrbFlxhilDAJbV9Vi\nsZhN5sPhkDvEAVFwWRwRQNZpoaVxFrCz1loDlESlkIG2whltDaLE4TPvJcbY2tqaUsqrtVqtvKoC\n5zzLMv/S/tV9HNXn3oNewN/DiXEcz2az5UcXhmGv19vb2/PpD5xrKrdarSRJrLWj0Uhr7VtTCBBj\nzICz1lZV5cBwTqMoUFYAWIS0UpphyqNQKdPtrvT742a7MZ8ttLTf/d6bDEV1ZeSsyMt+FCa6wmtr\nm5VUw+GQumQyPFlZ6VmlDh4fPT06eOHGXpzxyaJfFHkQsKeHj59/8dqTB6cxI7/2q9/67BevfPTR\nfWOh12nfuXu7mWb37j0Y9qGR9scDAAebK51Q1M6Z09HR5tbq9esvWGtv3brFuG1206wRjkaDMEJR\nHGiD4jgmhMxmMw2VFMIpMECNUsjPjhBEKUuSrCqNUubw6ODBo6fD0SROs0ajkcXB1Yt7ZV6Mjo6L\n2azdSLoJn/T3s4ByhsAI4lSaEACkjbROcBbN5hNnTf/0lMXZeJ7Hzd5Ht+9HceP6jRtJkjWbTR7G\nOzs7e3t7V29c/If/7L/mTTUa7q9vxFs7zTjG+Xz8M1/93PBkJiswyspCHQ6OOllnb/viH3z7+z/1\ntS893b+/sb73K//iV4rcXL580UVGVfpTL74ah8nhwemrr3xuMpl98MFHVy7dGJtxlqRFUVmH5sWo\n0WxrUbeaGee8WOQOTLXAUtQBpwEldVWkxlJKOQ+oI0KocpEfD/qRU43AgV4gW4UBVUZGSbPZcotC\nVaJ2BGpZ+dzuGcsi8H3NOI4B4NyrhWitGSfT6STtJmmaitowQo+OjgghSdTw23rACUIOYYMx5hhh\nhfF538h3c4UQy+buMsE9g1Ws7fR69Nwbetlkcs55lYRlpmuM8TnokmTrbwHfkfIot3lG6WeZLns1\n/WehlyWO50GdZZg0xigHmnhkH4TUhBoSptt7eyRIjHJFJcvKhkEihKAUGwucIR5AiYhRZ4UaAGgH\nyrhGA40OF3HWaEFLCJvFQa8XTMaWYHj8ULOAvv761Q8/OrzUvpKXhRD1/Xu3tjd69+497baa7eaa\nlnB5HYm1lQiAAhQWJiNtpOi2mhZhpf3JA0JgjDVGA+ZAgVpKOZ/PcrFwxHi3ORBCCFGTJpXOWHdm\nhmCtRdgBxcpoC8Y6Zx2AAYesAeecUxTnRhqtCQFLsXOOYgIE0zCIksyUdVnUiHBCiXYQcl4jK6wT\nxjprMSBCWBhyjNyiLuM46g+OSq0gjF0UpqvdjSx8eHJcGzVazBhGXNrRaGQWOe12u570BQBCiPl8\nrrX2/qTLqOPOVVONMfN57sOSL3d8r8Lrs52Nm52NOnPfgfQCCowx327xAWY8HjebzbIs/WOWkjnG\nGB9dvGaoXyiEEN9xAQAf3vwp+daRb5/4hEsI4Ydknw2lfukveaKgTRzEfv7UGGMBV0I24sg4CwgL\nKZVVhFJtHUIozpK6MpQxZbS02hewhJDReCwdLIo8CIIgCHZ2dsIwDBgVVb26unrt2jUfOIuiKIrC\nB5ssy8qy/Na3vtXtdn1JVFXV5uamMcZ/Dvfv32+1WteuXcvzvCiKq1evetljL5p348aNCxcu1JVY\nX1/HGCNClveSzwMcckW5ODwcv/zSjUVVGauVkuDI8HRy5fILR4eDIIg6vc5oNOx0G0WtX3v1dcDi\nn/+rf/5TX/7aaDR58ODRYjpAlm+urufTajpcxEEzS5qPnz7c3OqNJ8PDg9N5WW9fiLXTu3sbL750\n/fD4KcZ0e3Pj6drJdDSLQwgjnEaNhw/v3p08vXhhI43norZ1XS1m8NzLV77zne/2er2VsIGwefPH\nf5hl8cVLF+eLWaXmFjkWqVrnKyu9unYHB7NPvbJl0HxwUjSiKBfCN9jqus7SGDSKouD561dXfmrr\nJz9+ezyZzfPCr6Kjg32C4fDRg3I6ng6Omxx99lM38uHBSrTpZIlsTSEEoEJWlag4pSQNHY6vXbvS\n758gNmFxs1KmkHeL2iBCP7x16y/8+V8KorBWMoqi3d2dCxc2qqq6cG1XVtNWq9lIs6ocNtLmD7//\no3IGf/0v/6f/9B//60a8srLW/rmf/RNPHu2nr77x5P5DHscfvnfrT//in+311n7jN35jc3OjyOf9\nk+E//G//+9XeWqvR3tm6dPHC9XwqCGZeBsYhiKLEAl5dWQEAB5CEkbPaWovimCCHMSRR7BDUSlZV\n1e6tU0qF1q1Wyyxmcczy6SKOI4IdIiCE4DyEQhOLQotJbqMoQApxnjnnqqJijIEEAGrruqUJs6rT\n6Wipj45P4maW1bbTSftP+532KpJ2Ohls9HrVLOecKlVKZK3TnONGozFbTAuh7TnF5tn+0LJq+WNc\nhvl8jsj/nxx3GU7s+dQj5zxOEyGU30zrul5iOYvFwg/qkfPDz+BfvXr1zkc3PR+qqmo/ouvBG2/G\nxnm4NHaK4zRMk3ldKbBZllpwuTYobr726c8JKXmYxA4OppN6ytrtNE1TZEHVigesKMpGGpelCXik\nlLLOIEJmc0cIW8xLQEzIuha66RoX97CsQSs6GE7zWoRhyIIIkTP+yKMnj7/8hVe1mC9mk5XuWqkh\nooABprkbT6alVCGPCQuFNkbLMAy1tML3iRkjxLfoLKNBEMaP795thG0QGmFAyDWbTWtnhGIjnFKK\nYowd9ToUQhsXYBbwIp8hhCjnQskwCfdH/Zkoq6KswHBMrNW1M4SzKGscHB9Th7uNzmRRWgtJliJO\nKCMzXdM4AiUxpRGm1WQahxGypnau0ety5xTGuTWH48HBeDQVtcNoMBmLsmgAa7Ag4Zx6ryB77s6w\nLJb9NM+yVFouF63PYDrPYI7j2FrLOW80Gp6Qs8TolsUyOufjPTvDVBSFr3j8LK1/LT9ts1y+yxXp\nT8PT9nyl5UsfpVQYR7PZTMuxEMII1263vYXd8r+WJ+PfQlEUVhtrARHMw4g65wAhyqwX70UYYYIZ\nQ0YJpUxdgSVCG4usQo5yTig1zgoh3HweJXGWdVdWVn7w/e92u12OcR2eeQb6APmseLnHGIUQ3ltv\nc3PTO/VhjGezmWc0LKM7xjiKIj/S9PDhw9XV1YsXLxZFkaWNs48UgBCCEeKcO4wIIZUoO53O+sbK\nLB/1hycXLmy/8+4H49HsT379L9x5eOfurQfPPf/i/ft3dy/sLIr5Bx++N5kdhxGO4/ijjz4ajSbz\nWdHIus7BeDgBi5qt1r13/qiZZpcuXBmOjiOeFPUs4iikKcaqXMiDJyeLorQKzfIcO4wsYEeKqXn6\n6CifCiPhcP/05NQSApzB9l6GuexuZI1mKOtiMBx1unFelg8e3dTWba73DCowEUEMLJBBwn7257/+\nR2//pNVhnKEGX+vjmShEo5nm85lSJo0az1+/9uqnPgUIz69d7XZX7j948pO33h6eHhVFwQjUYJyo\nObFr3U63GTZxC0kmc6Sl06JW2ilkA06TNI06HWKz4vHRu++/V0pNeKocImHGooTxuLe6tre3kmSx\ntVY7m0ZxHEK33R6cDhnhRjpdGVHa/ftPZmNY7TT+0Tf+SURbg5PxvdHBozv7lFJMXKPHf/qrXwzR\n0d3bD3/nwR80m83pcGasXOttXn/u6tra2pe/9BVRg1I6DKNG1qqKGmHkkF+u/qvXNXiGqbZUEwUX\nhqGUWisrlZrN87Td4ElMOKSNBphSK4EZDYOQBtxaK4RglGdZ5omaXtvXl0S+KFnmlO5czM2dW4l7\nPACsDcOwLEtrjNagtUZgtJHOYZ+tamvO1ADPwTF/eJ7Us/0e/yMiGJ+7ASxvdnhGQszvSz7GYIz9\n8/wvo5ofgiTnosx+w6GU5nnuzkVVlnsCnM81wrnR0fm5QRynw+nk9LSPGCVh9tb7P/6v/h//nzff\n+eDiK593CAIeGcLqUi/ymY0iACCYEYQR8lQpBMAQQtZAVdUOE8KwscApBUBFXty/i5IwlkpFUWAQ\nXuRVIWZlXc+LPMka49HxBx98cOXCGgOLHWgJQsFkNrXWcozCRhZGEVCY5VQKK7Vx3HkFP/+ZYUQJ\nMZwSqW2aprrWfhpMa4mws9ZgjAmnIXWc0AAcwgyH4Upza1LMaiXlfDqcDCwCiyCpk9rqUZGDNc2A\nr62vtxpNq+V4Oj8e9JVzypj901OM6d7eha29XYdRmKRBt8kps0KExkUIidaUMdqjpFJSWjdZ5MN8\nMRkPplKMFjNLqTSmlnV/JDWLhlHMsuaZ+NsyGVmuA3+1lkFi+ZgwDP2yc88cAOB1Tv0jl1faV9zL\nGmUpaucXt19G/hu/yHzFsEyOlpW1T158qe453B7IUkr5xMrb1BvhgiBoNo+bzeZ0mrtnWqb+MMYE\nUWKliKLIR1AOgLQNCOm0mxhsXddCCxJwh5wymmLqNK6EVBbVRhnKgyh0zgklkeKDp0/b7Wav1/PE\njVaa1nWdNjJCiB8eyvN8NBqdnJx4cDLPc1/ujMdjPwm7tbU1Ho89FaLRaDQajclk0ul0fPp2+fJl\nznmSJM8999z6+npVVRf2Lrz/0cdaa+xltQxgTIRWhOAsy9559yd7FzbDiExnw1u3p/PF8M7dOzdu\nvFTK8u6Dj09Gx1/50lfn5WRyNPiD73/rZ77+U//jP/0fMAap6m63Swh7cP/RpYtXe+3ez/yF/+ib\n3/zmSzderKuKEJRPi7JWa2ubRTUbHE4QVvk8yCeFMlJW9uiRrHIIQMQkmYv58eOR1mAtDI7t/+vv\n/R/+/be+9dY7H9Z6oXF5fDJ76dVLTx4VGqDVTYHrjbWVUpSz8fDgCXzuSyuPDwad1bjda2MuBtP5\nn/szX71/+/C9Nx9PJ1IUsLbWchbSOJaVrquCUbAWLl/YevnFK89dvbK9teacK8syS8J6PlXlPB8c\nbbSSBrO5m4v5PGkGujY1d2VlteMUQdJsNbo9p+OsmeW1DEjEwtjUUkppMSU0jKKQB5AmoVKqEqWo\nF/kiS4NIOr22vn1wdA+rYndvY3TQV0U1UYuEZZ9+9fMP7jx97lLr9PgUAMKI7e6t3/zwblno09P+\nbLI4fjTsrMZ/+S//0qdeeZEHeP/x/tGlo0bWJQEHgJOTfpo2wDmEPLjkZdSIQ4AdOM9tR9Z5WxYA\nA1DlpTVG87TRaOhW8ZnPfKbBIKZ6PjpkVFMCCLlFXsVpK4k6mNNFOUcEpJQRxrbIVldXPbBhlNLn\nTFTtnGEWISSaoUDWuUARXSUkd5XROm00Dg8PsyRijiinwGmpaoZQoak0lZUWwyeh4o/tKs9GEf+j\ncYApwc9ILS9v1eU+4P/HIWwBLZPmZV7rtwjfZvcA+LIJLaVknFCGAQBhhwkYq7y+F0IEwNhzfyZr\nrTFWA5Raa2sWi8ISFKT4l37pL5WLPEubhwenLuliTIwBinG70QwpKcsSO8BgMQAGQPQsR1DKGnBB\nwAGgFg5jSjlMp4vTk0ExLxAiYZyQIKaU8jhIG62skRwfPvX6yDsbLYRqikAaUFpyihgJGI9oiDGB\nyoAzoKQ0Djt75upknLMIMCXYYgLESt3trvQPhpxzjCHPc6KEBEmtJgDGmFpp7SxClji8vbtx0D/p\nTwb94XA0m7AopAE1dTl8Mg44b2WNUorbd+8ShBjgUtRAaV5URmtkUbPRnlTF/PGj/niEKLPINuII\nKR05yAjVs8KB6WxsHI0GnPPRdDap6uF8Rhpx2myNFjNpNCJktlCILO6VD6dJeia8/clmHQTOOb/X\nLwvnZ3uMy9J7OSTk4Vpvr+BRWh+u/MP8Ey7LneWa84WOB5o87ufTmWcf4w+/dv380xJHXkayoiox\nxozwIAi0tUqp2Ww2Go2W5+CTPrzspmJSa5OXxWA0WeRlgBBxtnYwnU55QJUS0mjCsHVOGIkRIZYa\nCyyIBZioHTuMaMAbjcbO3sWbt28xxsqy3NjYeHjvfj6dFkXRbLdOTk58ZeNDrx+32t7e3tvbAwDP\nUDDG9Hq9l19++dvf/rYH67zYhNdluHPnzvHxcRiGBwcHr732WhRFt2/f7na7B4f74IW8rBeiPWvk\nEoJHo9EX3vjcb37zVyfTfinmPICHj+5NJ7N/+Sv/9OOb94zGmxu7zU72jW984+/+3f/ta59++X/6\nZ//YYRnG5ODwRAmzsrr5la98+Uc/+glo/b3vfqfbaT58/Kjdbg9GA1mrC9sXT/tHgEAKlzWyAKJZ\nfz6f17MZbLQTAbqc1chBMQdCYG9vs9lOh9PR3/t//tfPv3z18196VZryydHtr/7Jyx/cfLecAWOw\nKGenfRlGY0KRQfDTv7Cb59MvfunGbDYejo6tq1bXkMNq9+Lm7feO2+04J4tiMUOWZnES85ARqMt5\nwMIsCQHDSrfxpc++GoTx8cnh0eHTCAKatUzidjppPenHOqmpEIuJBIqBOwAJoBxgHuIgIpSvrK2S\neU6DpN3ZiButtLmSNJtHx4Nr16+EAUyNqKuFEJUxhob6+sWLb771vUZEelmvEZJqIpvhyvUvbp4c\njnvtzUbcXuvp8XjSTLO9C7vDYT8Ok42NLWvQt/t/sLW2S7fISy8/v7d3ud3u9HptRoMLFy6BY1Wp\nQx5bg59t5p99dYgihAm21jowcC4e6pwDcGmaylpJrSfz+c3bd1YaKS7n9WLkxCwMXBQSjPFgOKI8\nrmrT6XU10g672WyWJIlSKs7Sk0G/KArPekXn/s5w5lOugogTip2zUZogYJTS61euW3BGScYJ0xpj\npwRH2IRxhJBrtFJs4dn71x8+6Vz2pD1+DhjFafYsdAHPDDL+B9Fo+b37BAD0O89yutbnu95fzTcF\nsizb3t72W4c5twC1BsIwnM0Wn4g1w1lrnCBqtWI8WFtJaqtnVf0f/c2/8/jeftZcfbR/mq4GQFOj\ndaPB1npYlPBoKsAmfqe01joHCIHRILWhLKAUHABWyBhAzmEMIaeXXnxhMs3zsqqUEtrqqq6lns0m\nWgnOeavVqsocEeksILAUTK/X9AvCJx9WgdXWaIsxJQRjBwYRD5YghJFXAbS21QpO9x3nnBAoqzw2\nSjmBrcXOGWus0lJbTDBGaGVlBe7dMkqHYdhjvUanTQMqtUrTNF/MwFhCSJimDGEjZFXVcZgQwjrN\nDqNBKcTd+w8kQjQOK6NYwOdVwZ1r0QCHESVEKNXeXj8o5rW146oshDLOxjzqhqEEG1lDMRJ8ttFs\np4isN5r01q1bS24bAHgpbj8T5xeNlw9YTj4HQeSvvQdh/RX1DhQeefO/9DPe4J2PEfINofNMxPmG\nx/JJ4Bmw2AfCZTCDc36OXzee0beUOQAA3z1y5pPJ2SiK0jQdj+fL8LkMqxacQyC1FsosirwUtXKO\ngrNCOWsylCAMzrs9glXOEeeKfIEpRywQWkYAdV3zWAHBFtz1F57P4qiqqtWV7mQ4evTwwWw2K6ry\n448/9mghY8yPGbVarTzPDw4OvLaetXZzc3NlZYVS+jM/8zMAMBwO4zhGCHnFv+vXrwshiqKYTCZV\nVfmvQojHjx8vb2ZCiCOYc44oCQJeq+Ib/8M3/tpf/0ucul/7t7/873771//L/+P//r/5B3//6eF9\nFtmYRvsn97dO1i9c2Xrngz/Ki8nXf/4r//xf/VMMenN39emjg0f79z766KONtc1azOuTWRQlG+u9\np0+fAkKiFPWicgLRMEZKizmKCO0kWy9d3djc3P6f/9VvBDhyGNKomVK5WCyqmSsX085q797p6N13\n773xpavXXrw4ro5oIsMmlDlgDLUUnR4YZ9MkKapye3frzp1pGIeTmZnOp8aJzZ31JwePTp/OpawP\nnypMIQuh1U5PTw6bcYbRhYA6DMbIXCsrahnFSUAhwPq1F69qUVAj1GyUIP14fqBBUFsDJ84iRQgQ\njChDgFEQAQ9bSe9G2j3pj0qhHQoA41pWcmJfeunGtcuXMEDAsKJI1ErWi7q0sizW2t1u0jo8msyF\n293ZuvTidWPQF1/7xUbSQsDr5+tOpzUc9MtqfunShZPhIEmyo8P+/+X//H89Phqc9o9XVjqf+8zn\npvNBGmdp2sCYTCfz2bRsNyljkajVMhohsMs9esmQRgh5625rrQGHKVJKC+NdcCqjHbLIGBNyXtez\nupJ+1CHNMgc1BqRnZZrEhMQxjgptY4WbEIQUAolAYUopI0wh4pzjhCPqtKqRtlobxpxWCnOeWRLU\nxijDLHDjGMfSEmsMq7SulFS1Q5/0m5e1kR/Q+WOlEgCo4xNwn/QIlmvbt0ufPfyNTDD8sUDl/+oB\nfw+u+Gcoy3IymRBnz5joAIQwjHHAg1arBeABQBoEAcFng7RA8DYPFnWZNZvawePT08Gde9u71x6N\nSoKIqCRNXEAZJ2A0iAL8ED1BgJBP0wEALIAxhmAsFBAMlIJSNs9zLWWWJcYYJeq6rpVF2hHKeJrG\njJHjo3yxWATBjlKq2Wk6A06pOA2ssoCQAeQ9yJEDRnDII+0wJWAtgKMOtH9dCwhjxGjA2JnJIedA\nKW1GzfL4EBtB0ZmgASKIsgiHoZWKA26EacjCXFUxDwBjh0xAqKEh5cAxFfM8F7LbbG5d2bCYPN0/\nLKY5C1UUJ/56hWlWLGa1VtPFlForo5Q0W20eg2M1QOW0VkYYAwiFQSzyWhEAqbUQ2pl8VrRZ2Eiz\nMAzp9evXlwt9WZqkaWrOZeKWM2jn+NuZDqOnGHjENgiCJEl87MnzPM9zr7HmzR08f8EXKz5c+aTG\nd+/DMFxi1stiy5wrFS2VIFZWVpbr2Lc0vcROVVUYY+T8uAAsQyD+D632znBnQgghPAzSRkZZQCg1\nUoQ8tA4YDQmjdV3nZQ4MsTDgQRCwMAlTAEzDWJa5n4GohSjL8ujo6Opz1+uyQAhFPPjc5z5npNxH\nqN1uN5tNH0u8byHGeDqdcs5PTk48ebfVanmZVE/38ORD/3bSNJ1MJoyxXq9njHn99dd9jXXp0iXP\niZ/nFTqnIGpljDGVFErxOI7/6l/7K+9/8Nb+wcPv/uAPfvqrX/ntb/6mVMW8mtVKj/ozKW0ty69+\n9Wu//du/9bf/1t/46Obb6xvdH7z5vatXr/KIBpruvXSxf9w3lRBVHYSb04m4eHHvo49ufvmLX3r3\n3fcXszKzWcKaCCGkwsHB/O6HT6IgzKKmrvV8uihAIuDOMk0IMHLrg/svv3L1af9eWZZ/+P1//6Wv\nfabRizu9RjHgH759p98vO118dCTCkDebSVEUL730KUDmpZdeOj7ZL4q82+0ghE4O5mEY/md/689d\nu3r1m7/5b+/duZ8k4cbGmlG1s2qRz4xGlFJGKNa1w2at21wshgFxThdJiKiQDOmIA0vCslBSOGO1\nMtYAQUFIg5SFCYqiaxd3NnYqhLlBjEcNyiLANG00Vla7zoFUpRRFVc5EmTeb4dW9i3dufjyyZnN1\nG6x8cu+wwbubGzt1bn/r3/zy3/27/0WB8nxeNBppEtN+/9RZtLN9kbMMHE6SbG83fPW1l6yFy5eu\n1iKfzxfT6ZSxZGOjHbAGAGaN4JMqAX1CD1tuxwihM+lXa7WzZV1ZC9ZAvig9mh06yxgj2AYQgMOA\nkda2lmcMz5AHSFtsnJM6ZgF1iDpUS015GGBKECEOWQvOATbOWt1IE2uNBOWs08pYp0RRIeMYwtg4\nZx1HBFOmtSEWwFhppffcwecyK/6bPxZdlu+Ls3D57p6NRsteADxjuAcAzzrEomdawvP53Dnnh1V8\nRiuEQMgZUfveASEEY6q1jsIkiqKTkxMA8K+GEfUZsHY2TBra2eFwqBFeKPsv/+W/fPWnfv7ipz7P\nmZwVRRI00wyshv6hE+W822wSBJRS3yBzDsCfJiLaWqtsELAoAudwngMAxGHECI6iyGKa1yqfl/Oy\nojwA0I1Wp6qqfr+//dLFq5cvUQyAURbg8WhMADkSIhphBsgBOft0qVcB/v+R9Z/BlmZZdhi293Gf\nu/4+ky9dZZks11Vd1Wa6G41xAGYIQwgjCAQIIUASEiGECJAMIhQB/VAEQ4wgAAZIhkZEUJShPCVS\nIZAECIAcDGYETc8MgJnp6enyJqsqK93LZ6/93HF768d573UOdH9kvJf3XfPde87Ze6+99lpEnI4+\nZgzBm8wUBYQe6GL+Haqq3J0MZ9feGvKmwFqBRWJGKVWFWmVGvP7Sy8JoS2HbbhMhW2pVFNn77763\nPD2ZziZ7t+4UyrD3fW+r8QQ8b5q2btrZZP7iC8JJ0QnqOHTe9dtNjshSgtKD8YgRPv3yi0VdK5CD\n0XBYTgaj4cPDp6zlyelRppRQ0gyqXGojle16dXGuhZDyr9SMSTObV6sfnkFpx+NpvHTouXJZbds2\n6cillTGZTBL/MoRweHiY6oP08AthXeb0QqmTdGU1mywtUlRPgeqK8XJl2Hq1RtNrnZ6fDQaDMq+U\nUuwvQLwkgncFaPAzLPa27xIPYrVanR0fR9sf7O1Xmdlut1munXM2eJNlxLxt6pXfDHTpXBCm7SlU\nVTUcDknqJI5Q1/V2tUREjTAYDPb3913wSqn9/f3ZbEaXZipEVJblzZs3Hzx4cH5+nnDRR48exRgP\nDg5Wq1WCRtMF5nl+cnIyn8/btk30vLquN5uNc269XifRP0rNA2bviZk72zOTa7rpbDCZTMrq7q//\n01/+8MP3nW+eu3Pj0fHTx188me3s9l1478Mf/Ok/8yenO4P/w//pP8lyMZ5U3/ixtz///PP7X5wP\nh2b58VqCeP7GzZMju7s3PT1Zfnbv09lk+hv/5DfruimKynUkhLC2r/Lp/s7U93JYFquT08yY2XAH\nWGZmSCA39dZ5d+vghfX5ZjaZ60xf37v++ZcfDzb6h799lrvcWZjN8t2duXNP1uutycTjR4fb7fbu\n3eefPj3+/Iv7Bwf7x8fHy+VyNrtRxepv/53/ar30ZQ7TctAFf3568vzN20CRo7Od65kRZfqoZ7OJ\nEjEzYr3aaEltswC2MViKNnqb6PaAUhoJWSlMwdJM57PRbLLaNjH41toswGhsxqPJdDqpqpwJMq2C\nkVoyZGJvNnnh9q39+U5V5bZtQnRGluzF4aOT8YhG1dx19I9++XvzneF4Uq43J0VROCeKfNT34dNP\nPhuPp9eu7T1387lPPn3fuhbQVUU5rEbMGkCsVqvMVBvqAECkKU4gRBRAV8ueQKRoxMyBOXLUmcFL\nuvN0OtVaF1JmBTbro6IotCoChbaxzAggiFHkZts1nnzd+6qqFrap2W+i3W5cmgpKcJZSSkZpbQd1\nILrw1hOsc5EvXculqbdrjjH6UMrAHCO5GETt+yo3V1YseOmChpeKlM9G1vRDJAJ5EVGYGSJBvDAH\noKvpVCFEikKRlMQr+P0qVqXd/c943Djn8txkWQZwgcMx4xULPHUQYqQQAlNMh5WLobcxG5SRqO77\nbDx3vf+17/36az/2097aEI0WEhEEgtHoGJABL3hewMzeBwRFF6cluUBCqLLEsoTxeGQ7q6S2nfPB\neh+fZWkxU57ns9ns6eHjnZ/8xt5OCQjDkSGATGkmCsRAjJS66UCeQAERBJ8MkAQwEIF3EQAGI1jX\nkOf5s8H73XffHfDSxK2gDiJFRoaMAYQkF10+LG3wjiNq1YVeZ+bzz+/1bTfIC2j86smxQlFoI4RY\nfPBxNRiNRpPz47PjJ4f3Dw+5KoIWq3YbEWKM5WiU6Fpt33mmz46edOTdtpMMXdlrIZ88eFiOhkNV\n7hzsjsaDyhhDPBsMpPcXlcdV9kFEybH0io0NzzDTECWgZGBiZOZIoJTKtE5F1VUAUEohcozBewtA\nUqLWEoBiTFrUFwwFAExG9yGQMlJcRp1n52TTskt11UXC+Iz2IjN7b4ly761zLrqopGma7Wq1UsoA\nQHJLusL98FLrlohW283T0zP2YbqzO66qt998c293Pp1OBqOqGg2bZvvpZ/ceP3xy8vioX9UhBgKs\nBoOiKrddt9lsZvP5w/tf7F/b5UgU4oMv78/n88GwPHx6PBoNQiDvbd87IUDrbDodE9FLL70wnU4f\nPvyyrusYvVImy/SDB/fbth2Px4kUNJ1Ot9t1npvXXntlMpksl+cAMBoNrO2zTGut0xVJxcZkSoIQ\nQuemrPJtg7Ph7P79e8TxZ3//H/nFX/776033/R+8g0bU23pczJ8+Peqa/ud//uet6/q+efONV7vW\n19uNt7Q3HazXDUcYDSePHz+synK1WUoN49n40aPD6we3R3ayXtVamjwvN4+eLE6XZMfd2u6NdnvT\naSGFUOtV3RkuqjKQUznXbn14eAJjuPPGVEi/2tatj8MKnn/xhWjNBx98cHjy5Pqt/b5v+6btOjca\n4MnR8vDR04HZWR53169fL6bz1XmrWH797a9tVuvNcnN0eDIdzjJTgMgiKJMNvdsuzxcABBSRAUe5\n356HXK6fPhGlas9O+mbbN7Xvu01dd9YGYqVMoTIyRjAE6548fupB1/VmMtmJMfbN0vZt8G3w9aCQ\najyqBqWQWHctgMiL0de+8e3/8u/8N0KpTJYq6rrpz1fr6WR+/+H9+d58uT6XGgjC8fHTpt2Mx+Q9\nHj55sliuszzr+/bO87ed60MI89nBZrtEcE3rECjPdOJhI8e0uBEQgOBSp+Byk17eCSAZIqB3QYBE\nLW3oGXmxPt2GLgNfKvKuBQrGqMFgMN/dP8GF996HKLUYDid123hvzxanADTbmQIxSlFkudRKAJaD\nKtOm65o8U4nq2fc2xgggxpPKh/n4lReis865alAiMlHIC9NsawmS40UvmYiI0n6nZ+NEulGIkWky\nGEgpk/rlVcoLANbaGJNF72WBla6YRSSPICN6ioCCBSoUaQy8Q5BEoe+cdV3X2txkAZIkvwAQzORd\nlMJfHTIxUiBSQoAQQisjBSrT1O1kMrF9H3H99HxhJvt/6//+nz7/1W/NBvNJTj5wXuJ4Do99eXR2\ndjDYZ4gAOsYILIARUFLEGDBYanyndTkYwGgEvcmiB6DMu9V223gWCkWZ6YDc94G8O9jf+/T9+0Vu\nvAUHsDuGVd2PRkPnINjAiCxAMCgFUmc2UIjgIngvEFAwiADo2YZ+Z5avEQaDSjiKDHXfLTcRpYBL\nJymWQoAMLIgo01JITc7avhNGRaTFyamNgQLPZjvXdveqvOibmpzvI/WdXTn/4MsvCbhu+28cXK9G\nw6P16sHJU51n2aDUQlbDMSp1sly2XV/bjqoCRbY8WUXrGsfT6we1daO82JweVXYcV5uNgNXx0aAo\nQ9Ood955L42/0KV2gNa6KIoQLgKA1jp5AKcunYuAaAhQSDEYD6SU5F2IUUhJHIhJIEQGYiCOQmKZ\n60wLQFZaZlkWAjgbhBDamL7vOZCUMlJwvdNCAsrUUlqv1/v7++v1ejabbbfbPM+dc4PBAC+pnHxh\nZ45FmXd9a7teax1sMCZHBKkwmdcRURosAIAQohFSESpp2EWB+pvf/b23bt3SWqOS0Zijzi15NXK+\n2DYx+nwwfunV8dtvffvk+Gy6tzOeTGrbnS+XEZnIP37yYDqdtnWNHNu68c5tnJUSb968/vKrLz56\n9GS9XtZ1W5Z537vJZEQEea6uXbsmZdJ6WnsfpcSjo8Ozs7M0JmWtvX79+p/4E3/Ce7teL/u+TSBn\nKluzLLO2CyEwgDGq6xpjjPNRKAyhLzJzfHbc1t3nX9z71V/9ld71H3xw//kXXnjvg3fn81mJs+XT\nT4tieP3a7Uj05YP7zRa2m02uM7sR/Zak18NyePjl+Rtv3eld1/a1zIqW+nxaPVk/7Tu/M78WfXx8\ndFhWBQCQD4XMTg5PvfejUWGjv/78jS8efLHanLz6xt0P7r3/1ddehumCVfj4k89me3DnhYPz85MM\n4sni0Vfe+BqWL3z4/icBm7qrh4NBVzsxzz5//4nviUJfFoPHi3Z5vgguPn308FvfeK3btvc/f7q3\ncyBUdXRaf/e7z6tylzXJXgDWfb0yijMJpw8/v7UzXD89hO3y8HAVuq1ttt22sX3bdj4QhuC7biOy\napiVpeIYbaT87ORUMpwfPXSp8an06ZMTCDdOc9LqhdF4TtmwGl4rKnAwGO/dkEW1rLeDoWn6Nko+\nPH/ShLrrukX99M1v3L334D3f+yLPi6JYLDcxRob4ycf3Dg4O3vjqW9dv7J6tTvMq324bBCNkbnQV\nQvAUVS6kZIEgOF5iWeLqB5SSCJBRSimFImDvPfsYWFjnDNJivby5P/FgtSajtUQnOY+2dy7kuerb\nujSqCZ0R2nuvWMvojdaZxN752DlgzvLct35rrbP2O7/n93z80Ue2bSVwYTKQFwCG1vqL1bn3fnUk\n275LDjKEhIg7Ozv379/PZPEshZohSlBCgrhgplPKDgFACVBS9tuVtb0QMiE0UkoljXMukcspMhHZ\nC8a2UUo54hCCd4Ev3F2RIDCQklpLA4xC58CYZ9lsrKQSCgEvCeIhRiVzZl4u18PJGABCCJFoOplY\n5zab7e3nnl+sOiWNVDjf3fEUo0Q2eTz7/IPvPcHB/E/9uX/tZLsxxU5wAEab0dAzVMO8bR0zR095\nJoFBgibmPDOIuF71qxVNJmVZQo9w8rTWsqhyWDZdEu0VWmVGjap8Fbdlnoe+253C+ryV4zIz+aID\nk4NWSktoHTQ9RISm74txsdjCfBeKSj38bBv3hkMFde1s6N3w2nQI97u6UDlr8CJ2oQeFm01dxoZD\nJ6XELG9cb4ySzL1dm6xAwdvtug8x+jAaDnpjinIQleok9tostnVd15aoJu9zuTw7f/7OnY3klbfr\nplYoSmVcZw+uXx8MRmdnJ4um1loLZbTQxIjT+dmTw2XT7ASvr80/PnlSe9scPeZI4/EwUDhenuzv\n7qlvfetbV82VNIIAAOPxeDgcXiFm4tu7TgABAABJREFUV5NDgDKyYhQUovfWWR9i2zTbtq2NVICU\nhql9cM656B0RSeTNZuMpeh+1ygGEd1EItW3qxKkzxnjyiJxqcyNQSpnmt9OseJrKTpV4GtS9amVJ\nKV10SoncFMaYHqxSWmlhjOnaLf//3YBYoajbBlhMp1Ops+PlcjbdefXlV1erRdNu6019vl5JJqaA\nFCUqg9l4POn6/vFHH47m02vXrtV9e3R09Mqrd2Nwm+1KAgrkPDccove+WZ37OByPh889d+vp06df\nfvnlYrEYDqssyyaTSYqpfd9rLVNYvX37dtc3UmGli5/66Z946623ZrOZc+7k5CTP88FgkFpKQgJD\n9ORTtxYAhAApUQgJUgBSmvz9yle++uKLd1984VUAPl8u5vPpf/gf/I3pfCKkfOWlN37mn/vZf/BL\n//Dd99+Zz+ez6QE7/OSjD23THuzudU0T+3Dr2nRxcipzkRUzITmQD2zzqihHw/uffVbkAyXkcDxQ\nHpnIdS1HyMtCCLFertGgKgQDHa8eTfayxi2u3949Pn167froza+++s67v/3tb32DhOwi/Zd/53uF\nASWhqooP36+v79SzyTxTA4xbwRoJVid9s11oNM/fufPw3rtay8ViMZ6MeudtcKizvJqgAEJRDUcG\nqdto266NoFFmmtPj5uyoPjtp6o23ve2avm299z4SCMGoQ+x90zBqlEqJrIu9ZK2UZI4YA7HnaCNg\nUy9cvxuDi5EQhdJV18d1HU/OV188fPgTP/Hj//CX/rsf+9bbg75i8ufnp9cOdmzXg4qz3QmyaDfd\nerXVWueFGQzKt7/2xiuvvFKUg9PTpxH44OCg62ygaPvYd44QjKAQgnWdIBLJLx2TQSCk8Z1gL36G\ndB8ACGQQIcRMZwnMWK+XxbhcbdecC0muVEpJ1FobpZHJ2a7ZbtibPM+azUYAROeaZPfctsaYaC0z\nQ4xI5LvO9723zhgd+k4IJSVAAOuskFoZmZksBMeROtfFyEIAjWdKmgjMAOqS98osJApEpOivgPMf\nkRY4IhFyFMQgUCTwij1QIGcZAQkR2AgllcqMVjrrN9skOJTodTEwcyQiMBdFJP1o7J1klCwFRwLw\nSQT5QoQTIVjCSwHMzXZrvbPeBqbFci2EkgjELlCIEKPEqHXPKp8fQL8Y5QNW0FroQxBG9y5kmcpz\n4x12PcUICKAEgMauZU82BE/s1+vYOUMesiyrt5v1amuDz4pyVBaM4H1fr1eDMp9OJtZaRJhPSk+w\nWm06yMIWovPj8aAsYVgBCyCO1kJWQF2DbQFAdC1ID9PBqKQcGCQCAAmtQIPOM452OBwKmE3VULGP\nyA5E5qEalrORXp0fKZMJJYGFKrIAqIwWJhNSRsTG9cfHp4u6bhlq71au23TN7du3v/7jv2dnMn/t\n7Tek1J998vE777yncx1j/OiTD2WWf+3bP3bzzvPLzfb7v/U7dd1b52+88AJRWHT1su9kmSsIeZ45\n5zryLjqdZ7HIVDr6Uw1BRKkZOBgMknznFf52CdkpBiWU1he9RmmkgrwQTFopY1SeG6UUYFoNmMgL\nUsq+d8HHPC+FUNYFAGF713WdkIm6HRAZlYzk2V04kSdthfS6ibctpUzUsivhBilx02yUElUxyPOc\nHI9Gk6TFcFXy8yW/HAAIGCRGjo5coBjb1tVBoEo2dxIwOm+7GoJHJilAC5kPzXa9xnrrKZZ5sVos\nPIc3Xn91ujNPFA8jVaaNVsp7a63trQ8UnXObTf3w4ePvf/8HR0dHDx8+bppms9kkgZ/BYLTdbrOs\nuHHjxqeffvr1r33zzTffbNv2ueee29nZOTo6mkwmt79x59k+2QXQwUgEXWeZMYQghEJkAI4xIsh6\n27Z9Z4x67s4Lfd+ikJ9/8ZlUZrOu777y8udfPvh7f/e/e+OtN77yla/84i/+wru//Tvj0WCQF5O8\nXC+X7ENussXpcme/it6FttVcagAJ3NfbtrM3ru9DlN2m65u6Xm4z0AJhNBvVbeN9T+TbdlONipPF\n5tHH6/I63H31+dZtbt64/uFHhz/9U/vfePs7/59f/PU/9Wf+Bw7E3ec+KYrqnR88iTN8/ZWpFubo\n4fHd517vOrs4XUnQmc7LsgSWHog0sFFg1Gg08lZs1nZ35/pkXMUACgG0UAYDcogBoiPGerVs1uvt\netM22+isD9aFEGLctD1KZQNvbYwgFaOuhuOdPdcLWQy1liEahN4GG0MkgG3TR8K8GOpMCABY48nZ\nonN1067SiPf+/v7Z2dl4XO3s7/zkT/74g/ufe+uSOcjezr6SWd/0eZ6fnh5fu34wGAy+/vWvV+VQ\na73absqy9JHIMTMHTnDUhQCx63sBgCAIAVFe1kZwQf4WyMzJsEdrI5QRoLTW3WYbna19U+xPifJR\nlYduK5ghRu8j0AUCJpPYjx62bVeWZVpXZVk554uiTHsky0SMkRm0NgIwN5mzXYiglGQE750CNlIv\nl+vIoSqzPC+l0BGiMnmel3XdCMGAKeLwVQsglVYABAB40RRgEpAZLUhJVCAFQgApJEoESvgKMhGA\nQAAphJRCK0JAKcRlO4SZmZgRIl/yDy/8ZVEomfyNLtrGSTf5woYPt9taKJlm6m3ifQOEcDV3z0Ki\nNlIiRiG9lM2q2cST1WpV7o5Agm3YWiuMds5rLcUFM97aSEYXUoASIARKlEKoSD/i67d909k2xB4R\njZbGqEAxeCIirVVRZE+ePCJ6eZBDcDAsq9Xpsu36Zr1pFsV4PKnGU21gWGZBwGQKR6cQIpRl7jxU\nEvJKQMibJgz1BZ8+xfe+76Heiu02y8gI77zviQLq4agQgOvVxsUQmbyLqsicj713QhtUUmkTgJum\nazdbQbHQqvHw3M0bg7J8evRku16fn592nbW2Iw21b1GoclhKZY5Pni6Xy3W9XR4dtW3Xdd1sdDcw\nnRw+7rquKLNcyRDdtl7HGIeT4atfef2b3/ymSoQFAFCXdqt4KQx11WzkS2EPAKDghRBpMA8jE8Tg\nbQwueOu98t4qpfBCzi9NrYLODHnixNUhDoEoxguynIBLsyQACUCYVVXiCKQAeSV/t7Ozk5YOEaUB\ngr7vmWM1qgBICc3M9aqRUieyX4xXcMePYHdEZABT5JHo6PRIKpNlxRP3qPu1RgkJHJEixsgUgL1G\nlEKdH54XVRkjsxRvv/32bDJ98OjLL7+4v1wuh5PxfD7X1QClUFoXVY4gA8UYY9v21navv/7GCy+8\nEAJlmX7vvQ9++7d/6+nT4xCcMbmUePPm7aoa/sRP/FRZ5nt7105Pj4VQMUYpNRE1TaeUKIqqLPMs\nK5ij99G5sDQ1XlIE003nmfdW60xrOQyxabbOBWPyH//OT7722mv/xX/+/2Lk73z7x//qv/Pv/wf/\n0d/4Y//9/95P/tSPI/OWws/+9J/+4Hfe+eTDDzKlBoMq9u65a7u6QhZcDgemKPMsK0y2bXoReXO+\nMCovdDEdjKSLGIg9AYWDazvL7aqs9NOT9a2BGI+rneviq19788NP3n3u+ZvL1enX3n7xF//+P9ps\n6zfevPvLv/irNsJ0vJtlxUvPuVIPHW2djd/97k8++PyhFHpnb3+92GzrNjd5WWppdGBYdrWuihCj\nB4rsKbSb9akSidEKGJ2GoDIRutiu1+122Tbb0HfRWe+999EFihEDi74P29Y11gtT5KAsSItaF7nM\ny0zrDEuT2Tw4AIFS6GKgs8p5Ug4Wy/DRx58+PDwFCL07d8796q/+6q3bBw8efvbwoT07OxwU+fnZ\n9o03XpyOZx9//PGX+qHWmW1tlmXDYZXn+d7eXtu252fLwWDAAp1zymRKKaHVs0uUBSalOMQEV8iL\ne/ni12ejkVJaKNPZIAXm2gjE0WA4HY3ZyFJCOSwFRfaOQky6XIgyhPmgyKtB0fd9QrBHoxERNU1z\npVGZaER7e3tFUUgUEoW3fe88AwEjIAuUQoksywnImMxFT8SrzSrPiizfXL9+I4Tgur5pmqapm6bx\n1oUQJuMhM1/Y612VRszL9cp7K+WFUaeUUqB0zjHjFaSBKNMlaJV11kVmoKQcziAQGRjBOQcCJYr0\nbxoFJSHSFLGQWmopQEYOBAhMWV6y5FzlQiuBKkOSqPKycM4BCAEsFaNiFhyQbPC3bt16tKittRWi\n0nDZvJaIFCNHRudc3zvvyGssirxuvBDCGBUCOW8B0MVgW+sclGWRF0UUIqIgRogRc+M6SCn4/fv3\nvYe1A3L9oMhfe34HALZbSBpjZ4etKiautT0ZwsF62QmhJMS65XKqtusetVmu1vlwziiJIXVG0PpK\nao7kbQfgXAwMKHNd5gYRn3UAUShIgEJRlRUxR2bvfLSOrQcbQPDBfHeyP3M2rM5O+6I9Pz89X63L\nQeE5nC7PAMRkMrLWHj19lKlsNpsVAopBcdzUdr3qnSNrq0xBjEWR2+DT0Ju19uOPP370+LHiS2HB\nK33PtDrzPL/iC/Cll6JSqosWKKJACslkIQbrovM7OzuAdEnQvACOPUXnnQSJUnCESADAwCilShmJ\nVILoAifUUkbA5P1zxYJ7lr+XsERxaVCIiELAYrlQSgzKYeJJC6FSb+nZOVm41DcCxBAjaGQBne2F\nCzHGruuOnx5SjONyMBqURiJHzzGY5EJriRKLApi9i7bXUh3s7nXeReebzdZ1/dU0HzNPJjNmjoHq\npqbIWmcIcbFYvv3W177+9a8LlNb1UigGOj9b1HUrhGqa7rPPvgCgxWJT17VS5v79B6+++rpzIYSm\n73ulWkQOgbwLwMLbQIaFECEQgDAombFte+8tMaLgajA6Ojp858P3f+VXfuV/+e/81evXr39x/7Pv\n/fqvHj56+t4P3v/f/s3/pO+aX/qFX3j42Rfnh8evvXi3224p+qIY5oX47OH9wUgXWvc+rNYbG6ko\nh8O9veVyS4EhkO+aersaZGWZF1mmIvU+1q+9/or94N1Mi+V5U6D64Q9/+JU3X/eh//Y3f/zk7PjD\nH34+nmQPvzhbLJbFcOBr8emn9/7gH/xumZU7I/vxhx93G+csMQsptFKGhfcx9M7WfWemYMYD0bud\n8e6733//lRdeeXDvwenJk6cP7unoc4BCBMN9067qxXlo19vzRbteNvXGOee8733orQ9EdecbH3uC\nYrIzP7hx/dad3YPrxWjHYc4y8TZDcH3vLREDojIlCsOoI8PZYvHD997/6KPPZSZ+7Nuv+8h5oT//\n/PMsl0x4+8btplm/+urszu3nyizPsgwIpJTlcDAcDr/77W+98sorSZaeEKTRxpjNZmN9uJrhS/Qw\nTPMM+COdArwYdJWXrB9I8xVCX4yHU3ASBQRflbkEns+mHAMFf7pciOBzIbREJaRSpm37EDl4e8bk\ng03ZnpTy5ZdffvDgwbM7S0qZVOeTtm9S/eg62/etMflgVDFh3dfeReKAIBlpOBz3vp9O59v1+vjo\niJkFXziiFkUxKCshRPA2ZahwOb7LHAFoMBpdKfQTsVJKKZM2OwAwJVTmwnxPalWhjAAcYmASDJia\nPEoWJmOBEjCxGlDJTGmlVJlXiV/ASByBkbTOTGGs9YF8bopAHlGyYIgwn+3u7dxiZqYAGAlihGg5\nWhCnm/6s83lu8twEAADOskwXMpIE4Bg5vcO+62q7aduOWM5mo+EYus744ADIJ1Vl0lpnSiVrAudC\n9DEyhLatMYMs00++eLpcBxV7LWJXN3XdzufzQZ5NBhUEv20dCswU9jY8fXrmIlfl0AVLhRrPYLXF\nTAtP0QUAgTFGRCCi0Whk6q0XAhkQKZMiShklcAxtG4RQUmpiRvBJMbSqqsVqjYggZCalqqpxUUgp\nhdFQZU/PT8ZFEQU/PjrsvBUKHx0+Ho8m1aBs6vb46WEm9HhQVUVVSTEcDSOF+oSwq8FZIzDXmoCD\n65qmMXk+2Z2zwEhUt4369NNP08RPEqxLpJfLxXFBqONnpJ+0kMYYLQ1KkFJLeSGY/fToyVWzPc9z\nYzSiCERlOZA6cy64aMkHyYIIlAIppVJGKSGl8N4yMAZNRPv7+865tm0TygeXPPKUsl3NvaajP8v0\nbDYjCgKEc67ve6UMM6c867LmgqvcE5ADBOscCKyqMkZq29b2/Xgw9JEzKYyUkikEL4gEsECoBhVG\nhhiUkoM8Ax9zpa/t7fsY+uBt12+3W0Jg5r7vm7pDgtTCSR9a13XGGOfcB+9/mD6ZRBJJIo9nZ2cm\n04PBwBgzm80Wi8VmUw8Ggxj5137t1yaTyY0bN65du5bUmNp2td3UVTXmEKPzpC4kuVSvmrYDAGNM\nURTbuu7bTkp98+bBz/3cjnPu3Xffn8/n7/zwB/+rf//nf/A7v/Uf/82frwpzMNudFmX99Pjs8Omd\nmzd2d2bnRyeR7Jsv3SFJSpk++KE24yqrhhNAsTleDIpqMBmVeaUJqrwAwq5rrOu97/NC5oVSWuzt\nTV5541UCQkCjq8cPjz774t6br3/1888/e3yyLAqzPe2nd/Zv7cc711/6x7/2T6qqqvRos9wOiuH9\npw+cC5kpBtXQe+9CcBxv331u47qvfevr/+R7//Qrb712/OBwf298evjl73z/10XfXZ+MXrx53UBY\nHD5anh5lArbLRbPd9E3jgreROut7H3vmNnDPQpXD0f7N3edemOzf0MORlyaQJpJa66wYlBWX0SUt\n3aIcTKY7eVEwQ910y9VmuVmbTI5Go9Vq9cat157aJjdG5brr61fuvsoUqrxSylzbO1gtt3levv3W\n13/69/2kQgjRJSGoohqmmn673SqTXXJwEZ8Z7PPeC74s5S/uhWdRCkgZ3WUn1KjCdS0Ar5erfpiv\nMGbkow/DokCKwInrHJI9CkMcDSrruuQulrQTu67L8zwNV1zpZydTmOCJEJRSnsFGEoBSZwCC+7ao\nChZMnmywjNJav900rXXDwQABkPhH7zzSs2zmKzZsIqmz99ZbGYQkxZEVa0PgY+BIqRJjBCAECioG\nETQLES9psgggpIxZJkmdnJykGVRKnF1EJaUU2kgTQoiRiQKAyMpsZ2dvOp98+slnvW0zUwQORCAE\nOBfyvGB/8aYZAiMRUpTohTKjad+7JEG5aUPXOSEKY8AHiBGVgqo0xNo72vSt91ZIY21RRo0IKXsG\nKYqiCJas7Xq38QygNAqBzEQ+BicKk3jLi8Xqxt5kd6rqtd3bnQ8KkAAIUBWTdQN9hGUXxuPh6fap\nNqWn6Jztg4mgWMjhGPLz3HoAEC4GkwMA7u3tXb9eyWvFVLYGHAqISjSB83IQo59MR4CY1gMAxMiz\nnbmzIU19XgUFwYBGUqau78xJwGePHrSr5el6aarizp3bWZYh8ersvFFyNhhNBkOy3nV2MCgXi7pE\nmg+KQHkAzop8srNbjUfvf/zxYrM6OTmJwCbLhJLqueeeS24fVz4FSS85HfeX4OOFroaRajQcCgHI\nwkfH/CMLCaV1WnCX0h/AKEHg+XIrHHRdb63VOgi+mLKezWaopBBIRNbaSD7xwt979DiEsF6vJ5NJ\nsgtqmibN6KTR2qRxkHDwPDcuOgDS0iiloqXxeJq04GKMzOJH/AX40Za2vu9dh1JIAATSAgdV4RFz\npQRFDl4GFoiSAULc1MvRaCQobtdb8i6T4uTwyd/72//1H/sTf7woMphOldFZWRhjIpPrfK6zxdky\nyVCmC0l240VRrFartm1TWHXOTcezWzdvTqcT59xyucyz/PbNW2n6dXe+k72apdr8/XffQ8SyLEej\n0XAw2N3ZKYtMClBKJJ06jtRu66ocrpabpu4i087OTlFUq/Wm7+1/+/f/ftM03/nOd/7Ff+HP/ONf\n/fXNenl9fu3VV178wz/7M3/xf/o/ia395lffdu320af3dubzr3/9G48OPz9fn243TQyxkNLoLDTt\n+XKdS8iQBYe+2fTt5mB3Z3/nmqf+l7/3vXIsGPz1azuBqa/bJw+fdK7TmTk+O50MR4T45WdPvvys\nfe31g+C8Df7ee18Ci49/+LlveNt3IcB4MHzw4JG3VBaVFKrp2q6zZVmOp5NHi8fjavrOB+/sH+x8\n9uEn83K4PH66X+Qnj744GI9KNaBuvWnW/fqcutohd/W2a+u27VyIjrgLZCNYFNlgFCJEYVZ9bB8e\nfXq4iIzESmUjo/PpdHrtYG82GSulIiEBo9AuwOHR+XJVPzk63t3dn8735rvTt7761mg0uf/ZF4Nh\nNp9Mv/t7vlVvl2+9+fpqtXj08CEyfPfb33n1la/s7V3zkb333jbAPJvNRqNR19rzk9PRdLK3t7dc\nbyCd2sSXnaHY9z2CTHILeBGJUDL/CJ94RkAywbQQIlIM1mVS9E1NORL5YVnE6CAG8oFCDMTMLFBJ\nhZvNRghRtz0zt223WG066wOBc4HgQmESEQWKVM9FBgEolcnLSus8MiCgzorNpi6qXAglFUttUCiT\nF1mW1ZuVFGCkklIKgWk8w3ufZ/qCCHUZppiBmYtBCVZKRBCCAytjjDYQZbABpJAgIzMyR2YAGSH1\nDAAQWSAQE0IkAmCTZREYiQMTEl/8DcJqWwNcOAICozRaoMxMgSgiI0gJxMF7JSQDhhCQpEj6pyhA\nICqFWQZZ8eR8ZSPihayMB0ClMM1AxkjAQisoChwMKyKIAU/Pzh8/rs8WhTHGup6IQAJEGgyHTdNY\n3wORFNJckGazhZYprf/ud79bDcfjqco06FkWeqgbIAd5DkrBcAA5wLgbnWw8gNBZsam3yNBa9+Co\nCBxBKpS43dqEceY5NE2j1PwH3/9+bk/muge/ZY6o1cpaUJoimDwTQnRdl5uLyetBWX344cdXfJCU\n9UpAoZWP/XA2sRzP7j+gukHrBtPxz/zETxwfH2/Wa9W7a4PR3mSmCFTk6Xh0vjyHth7dvHHt+vVA\nBEpGKZ+/+9LRYjGuqggRt7Vnysu8651KDuKJO3eBJxClHtJV4naVyxBS02wlinTcg0CttZSaL2x4\ndOqbxRiBhNaoRNa0Z0KS6wMRGq0jU9v21tqEaAkhhUQhBINITq03btwIIRhj9vb26rre2dlJ2gQJ\nvptOp6nFlQS8s0wTUlFko8FYa71d1syY3FGJiAGvml4XMYkBJETgvm83m1WR5WWeOcDY20JrjSCZ\nJKLOMq0EAMUQylHJTMNqgIjvv/PuarVSWf7Kiy99+sFHk935zu6+Usr39mKAF+RwMHDdhU2tMWYy\nHo/H4zTieuvmzXhp05LneZ7ny+U5M1XjyXg4SpIWiPj+u++9/vrr0Yciy8v94gq3uQDAGVzbdcxK\nKUZIH/7h4ydf+cqbCXvZNPVmtWGEk+Pj8Xj8L/zxP0kcXNefH5+cHp4wuZ/7w//8199+4+z4aHc4\nGQlRLxYK+PrePsdw74MPGJzwYaCzQnMAoaRyyL3RzXozqYa7k0mMfHp4tN2u+7Y5PT8djsTuwX7b\n1Fqrvm2VMq63o+HkW9/5zqef3Xvy6DAEUkq99Hxx8vhcSikACxyYIvveL//6iy++wBJDoEExzFWR\nGRsD977T2gx2R865x48f64lcLpeF1MdHh8/d2Pvgtx68fXcvg75dn+zc3tsZlYvjJ6dPHpKz5Lvz\nzSb58vZ93wd2jJbRsfRSB5AWwEVcrzu37h0xysyYAriR2qw3Tdvb4+rM9Xa1WjVdm5eDl15+ee/a\nTRB6NBq9PpsbXeSluXZt9Gf/h3+m67dS8KjMXnrxdmlk17c3Xzl46/WvvvTC3c1mW9dtCCRAAFGe\nZc71QohMm2ycM7MScr1eS5QcKTifkjPnXFc3LgYmZAQB8gpnloAAYK3VUiVmaXAOEfOsLPJcoSmN\nUVK+8Pxz0rfDslodPdGl7utNafSgrMqyRKmIyEcGgOjtbDJOrdn1ej0YDG7dupV2R9plAFCWZZZl\nZVm2vSUQQkklJFw4j18M/Cmjkyjc2dlZyhR3dnaGVTkalAJZcDJ96DabzfJ8Udd1ZhQzM0dEVBej\nRQh0ATkm4dIYOQ2whxAIATkJfnGIMcZoyTOCUBcqPhfUJE/MrJjW282PjqlLlF5KDQGlUFLKGMF5\nV2+b83whlKy7tm07FDKJlploEiSIgYQQESNDiBxAgiQSAGWZWwcpGgkhB4PSK6h7YAZnAxFAZgAg\ny/RkMlESAsXjo5N20VVV5bxt21ZqXRVZTRvnHFMMwTvvneuzrDBGCWDXtxLwj/3cT9+YggQ4XkAm\noSpAI5CEPAcEsBGsg3bbO8dVVU3mmWeajgslAQVcu5Z1HXjvm84ys0TUApbLZV3PAEALiYi2t4Gs\nxhxiJIHWU14WFx+C0heBR0ojVYQIADIZLERCRClwdzh//PhRPh7uD0fr1aKczWbznfXJyfbsrDRZ\nPp+rwEOduboNbU8oZ3lG47E0OtN627VFVtnocyk++J3feXh0BFq6EItBdW1nt+26CwOhVHzISyO7\n9H2nwi2EkI7O1WplpHLOaSWrcqCUsj4AQIjctu1gMFht6ul0Ssx978tBVVbjp8cny1W9s3ft5u3r\nN27ckELNdnaePHj4/e9//8GDBzdvXldKNe0GAPI8RyYK0eTZdrtVSvV9f2XgneqM0Wh0BcFVVaWU\nWi7Pi0GRZVnSj7C9U8qksbsYoymKNMmbeA1CCGIKMQgBDLHIjVHaNV2h9CAvJEMyrhLAUTBHBiAk\nbtq01sA7+9F77/36P/41qU0fnI3U2H6+fw2l2L9x/U/96X/xt3/nnZ3ZrND5D37r+8PhcDQanZ6e\nDgaDg4ODhIckdYmqqtJuTxp91aBUUqosK7LMWhtD+PaP/ZhSKjXz0jhwvHTAVEJKptj3IAUzKaN9\n3x2fni5OT853dm/dvk0ovPfzyfTR4ZO33vzqvXv3dsZTCsowPj18ZBBWm/US4MMfvvvic7fY2tj3\nvm5lpvN8sNpswEtkVxZKFbku89W2WazXMstzkNH6YVbU27VARdFLgadnJ9b3w9mw6xoiUplZr9dZ\nNRgOx7/1G/eeHp62theMZTEwBp0LRlYSRfJTYyH2ptd8D0fnJ4PB4MnDE4lqs9zkeW6KvO97KbVR\nmfN2cXQW2e+Op81yOWa8eytrzk6++tZXf/zH3p7lGdlaQSi0qtt1smy33oEULE3fN6DLyKK1cTCe\nbT2t237ZtE2IfWAbmFEoaYLH0Wj0RD2N7707GY5u3b45Ho/LYpiX5Wf3vvj40y/uvHD35dden+3t\nZ1ne2S4SvPzyy7Pp+MsvPjk+fNRvu+deut13eXTWk/vw3fcQBUotZCaEBACVyzRwvV1vQiCpldF6\nJAbW+uVymWdFcH4+n1vvRoPheDLLyur4+Hg0mgyKcrk8V0pNhuPNdlOWZd+2iGitpRAnk9F6vd2s\n1oPhyHdtDN617e292fLsaHc2982qKspBmbvedl23u3+taZrV+XlRFEDh5OycmXmxBIAf/PCdhGXQ\npY2Q1vrk7PzrX//6u+++65wLgCbLBaBQUqJIfndpNiOlfYlYpLU+fPI0eKclK4mCgZmFQKUUMmRZ\nplWaoAdxiZ4zxwjMGic7c60zuHTpFJj0IKL8keo/XiEcjCI+Y7mZHMq7rkvSJ+n/U4CXUjoXDGYx\nUELOY4xFUejMaK07Z7XWeOnTdonqCwyw2a4kQog2Mpoi8wg2BJNXm7Oz3b2d07Y7X9h8qiPoECAh\nMWnWHhCEAET2AYbD4ZMnTwaD4WKxkFIiiBiprltkSphYH6JQalbuVFURo0cGo7PGLvamsO1gXEBW\ngEJIFg/GQNOBYMhKQIT1etMGoUzhPRRZBgTTKWgFSgEoqEqzXCzKfLg8W63Xs/F4PChKXwzYnYUQ\nBoNB7xCVGhTFqm7LspRSBxdzUwgW6STXQjMFmTpPxM5aIB4MBuwDbbv9aryp27hpZqrAQb47nlck\nWhJuVY/ykqOHut8rRxEy2/VMMMpzH4NvmjLTikkq8/De5xh8pbUHQiE0Y7feRIoXIoN0afWRuAzp\nrPxRdiblVYgajUYUAxF1trfWi1QPgdBZMVTZ0fHZarWqqqHcNidny2owevvrP9Zbr7We715bLtau\nD9P5zs/9qT/9t/6z/5tzTmJMtQ6RZ4paa2s7uPQeRsSk3oaICbHlZzSBkkBq13XMUUuTCGZX/V5x\nebuq7YiIgIQAIVFKqaXIlRRKK0bJtDubB9uHvmOKCAGAKPgQQpEP2DvvbQiOotEgAFgQ7Iyng+hX\nq7XMTK70H/lDf/jNN9+aT2eHXz585zd/65/86q8Zo5lBCARAKUVRlCF457xzloiN0YPBMM8zSFr3\nz7xVvJSITWXrer0+Pj7ebrda6zIvjMq01lqZrMiHw2FZDUEKH+nLL+43XX/jxg2ls7ysXvvK648f\nPDx58jQjiCHkWu1NJspZ5XpNJH3Ynp7NquFpUzfBV6NqNhpKiO128+LzL1Bw26aBgDmq+XA8mEw7\nHzar7cHu3vly/dLLd5fL9Qsv3NlutybX0+nok3tf3nlh5H3Is3Iymp4cne7tl33bI4hI0Gx7q6IS\nGkCEEIusjOC1yJi51GWXtYJlW7fL5bIqBmVZNU0dXPDCgobBuIy2IcHnh8tvv3H37OHjbmW//ZUX\n/hd/+d/MiWWM3Xa7Pj/brpdt0/R9b507Pl8Q6pOzs6waZSZzjsrpbOvpbN3UARxLQkVIJAiFFsbk\nRqbsWwjVdd1n9z5Pq8UTmyx74e7L1w+u3blzWyjcNta7VmHx+OGjLz795Pr+7puvvf7+D3/w2//4\nV77yyitFUTBHRCm1KfJhVpQ6y5VS68Xm+OiwbduyLGfz3el02jif9ohgEIAQorc2ek8g2qZ58uRp\nMRgeHR1xiFVVZTo+3jzumqYsy3qz3dvZjdG1bRuDc10/Gw0Xx8fz8YTA7c2mRZ6ZnZkKlqTk8Lt0\nh0EIbTJltO2iALrCPK4WHj9jGZ7O9DzPQQgIEQACRXBRCIFSCCGMMW3bXvFsk0oyE8XgQ/BMcBWN\niAgZYowUEwwYiEjApRuQFIvTlcmz1O5NKaMUGgDatr9iG14qnEohBBN4igoFC+QQpdEKRdN3hcl6\n77SQLJB8SCyGEAhIEpGSOlIIPgIyMGZF1jQtSBRCMjITCIlGZ0Zr17m2bSUCYCTwOrgoRceUCZ3s\nDvp+s7Ozu/EUIxQFIJbeU1L2ywvQCtaEm3UzHle3bt0KFJVSIYSu6wKTEpgbnReGGEMIkcWwqnKj\nnCOjFMV44/ptR2ByeHwMH7/3xWf37p0enWZCjYd5aSQFO5lMXvnKV15/+eCdj889EVnKhZAEGQJG\nyDOAAq7tDD784F5VgZJiUMJ4MLTWTiYTpXaNFwY77ZXDCCbX1SAG1DrTUsUYJWD63p1zWmtrLURi\niYOySuW7Bu7rRqLQgAOdY4WYmRKkstF4liR0YPJkWAgb2MdRUa3sWkhWIKQUzIg+uuB6bwc665Wy\nzB05EQI1rfdBXb9+/XKaUjBz0mOfTCapmZQSjUQo8N7n2sQYrXVEEEJwNiijhVBNZx8/+cAT37xx\n+61vfIsZn7vz/GA2A+LT0/Peu1s3br/zwx9KKR/09pW7L4J3J6enTdfkGeZGmkxE7yKFsixjSF/t\nhTHS1extQuqklMmgoW3bpEw6mU8ACFlIKSNeuAtfdbyujvgLsA4SUdpG54BIIbAUghiBkCIEH4MH\nikoLLVRMyL1CiGx9b62VEolZeKDgt6ulyk1p9Nly9dmn9/7uf/3frLfb/d3dv/wX/42m3uzvH8hh\nRQQA5H0UAoJ1UiKAEEzBh9Z2ruu1llmmL0bTlUpa6akeSvg+XorVFloLITAGa71P1u8hAAhptNIG\nhfr044+W643R+WQ+29s/+AO/76fn8/kn771/sLvzt//W//sf/MJ/G70blWW0fb1aSo7IPjp788Z1\nDJasPz0+LstiOhrXyw0F31urs0wSy4h20602q1sH17um1UJ+8sknxpjP738hFPbW7e/dYBDLzVZp\nrdAcH50LpREpzwqtsxipby0F1rkWQrhgY2AgIE8xRg4sQHob+r4HAiEFBTbKDKshAC9WKx+anYOx\nt5vJCOJ6PRL4yt2D//Rv/vzTz7+oyqFtm3q92KyXm2Zjre1t3/UuCh0R777+5pdPjp8ut7NrN1eN\n99KcLJsoNJhSm1xkokChTZllWZ7p9XoZnBMSnHXJnC35HBot93fmt24f7M1x3YCzW6Bw/OT00w8/\nKfPs7ddevXvnxvP7+7bZ5JmaDEfe+9575z2zZBDJhWi6M9kZjQLF1KBWSrFAyaB0Vpgsz8tcafYR\nAkWK/bYp80qhZskEHhlsawHpYP/a8nwxGY2D62OMGkS0fZWZo8dPru/emMymj+993G+b4/VZJoht\nlykujZQCSOFlD5WvPBcAfiTidXXLjUl73IXAzMv1uuk6770yGTN579KTFEXhKTLzcFDhpXpvlhmt\npOt89FYiEHDiWSSknyOFEIDFpVAQiwtfcOSIRhoBEohjCCEQIiJEAKguxqGS3p1IuyMZuIgQpBDE\nHJAkoEBUKJgIiZNAAyAqIY3WSkB0USgdAklgZXRrWyIwoJSSkTwS6kwhSkTO86wsy7Xf5LkRCEpB\nZC20JCVCCNvtlhm9t13Xznbz46Ol87EcllpDCMK5Pgatc2kMAMB2uy0H1cHBZLHqi7ys6zpGJu+k\nwKIoCsyE1ETkAmdZJqX27LwL68UijMr/6//lt8i7k6PHZ6cnR4+eaKkzZKNooAVyQOQvvvjijbe/\n/tIbbzUBeu/zKrOdNSHrmgCoRhMYlaCA+mZj5EAARB+ePjkyq+PCLpQ9M9iiEj07VYTJzu7j4yMB\nImUPCYYxuum7TqkL3SDvPWZaCOE7d/3gxvrpkZYq17IYDizHKFFlmSKcFgORg0IRUZc6kwwg9cHN\n6+LkCUkm5giIQkQBeaTc2aOnxzJyJUVmCmWMLrK+c+rs7Cwtx+Q6ulwu4dLQPvEFiCiV5CEEMkZJ\nqUkLoQAlEYFQMbKL8NIrrw6G49defcOMhp9++CnKjAJ+/vkXz7/40scff4xw+MJLdxWqPDfLxXkF\noqqG8/lkPMrzQpdGMgTmmGVF8FEpc4nPigRnMXOiMJyfn6fyPIRQVVVRZNLIrmu8DQlUdC4kdO4q\nMbzKsJgZ8EIIL1jH3osMjECJMhPCCBRGawFCQq6VNgqRA1MkqOIg8Q4ShoAoi1Ccr9d93d587k7b\ntq6xf/2v/rW27/Z2dm9fP8iz20qp09NT7/1gMBAStNab1XnivOVKZVJ4j94754m9jBQostLSK4MC\ngo8+OCmUd54JpBJaGSExhhi8EwQopUBME0h91xKIiLhcLu+8+NL5ah1C+PDDD//m//o/+umf/unv\n/9ZvmGgfffFps1wIoOV6iUCh7fKqIIqDqmrWq25bT2djKTE3eb1deeu0ElrIypQ58NZa60O7aaUJ\nTdc/fHK4d/3GycnJcy88zwD7N66/994H48lss6jRKEDR9Xa+M+z74G0gQiDkEJnR9VYIAREieUQM\ngfreFkVPngiYIr/55hv37t3bLNdE5LStqmJ3sjOdlU8OP7x1fX522pwtT/6tv/Av/St/8k8+/fyL\n3UG1Pjnut812uWqabde7ruub3rbWdUB14z4/fP/Oy68ZyLZ9+Pp3f0IVo1fWjWfpSdjIzsfeh8Qx\nY/aT6VALORmNy6xAAUVeTqbjw8PDsizfePutG9f305xd166993efe1USrM8XZEO/7UTk3elsXJXB\nOa0wkzpmyNKgkIASkD549wfjYbWzv5fneb1tQ+9Mnk2qofUhz7RRhqx3MVHO0Mb+0ecPeh9eeuml\n3dl8u11LISDyowcPx8Nhoc2jL+9PJpPhoHz06FGmzf/3l/7hj3/7J3yzFzp796UXbh/M2bXo+1xL\njE4bGUIAlGU5cMR9Z5XRHMLFCOqlrWoqSlIKn3RPnHNJQj4yEQExp5EJ7/1kMunaFgC0VOmUgEhK\nKSWlII4hd66/aNEyX7j+JA4U0NV2lhfKXp6ulLmJmVmhACkUKgLomiYyc+DAJEFIoznEmEWIxERM\nTMDkQ0SUUgEzEiOAQoFCSAYppUIRMTKyVsJbJxRqKa1lrZQSSBJDjAAoUSJy73tk1hKd64koUkQU\nPnpvO8z0tu8H831inef5tWvXSGGWZULlWkPXASIwofVWdWWRFMmRnzx58tprNzqbIWLfuzzPQYoY\nPRFJlVRuESFcwJYRiqxs1LYqx4eHx33bdG2zXDVNa2O/2puM0flVaMeFRggf/85v3PvwvdZzlCYr\nB1/92tvT8aD6+luZxJ29veOjbrRX3Lm1//mXx+VgKgGCsz31mllKjVIJaXSmnGNQejydnR4v0zeY\nCo/UHHLOMUsAMEXe2r73LmVRN59/7ujxEw+ErKIgTxys7zrLggGElIiEwVvIOTgrWFzX2vkYPfsY\nXAgohdSKEQXjMCskQ1YWMjN5WSij622rrmr5dILTpfLuxbq59BJOyJgxxnV9JBBSopIYJQgZiTyL\no9PFH/n27zWDqbe9I6jGU2a8++pXHj169Om9z7/zne/8Z/+P/9z1fnl++s/97B/49je/+eWXX0p1\nx+hxb5tOgjYCgJqm8Y60zi6C34UO/IVnXd/3yb88RUohBCLbYK3to6dEAUhhzHsfQtCX5IUr0BkZ\ntFKSib2L3kGMEkEzaBQnR8cCQQiQyFskRBASUIjIpJRJz+l6J4VOCsujsjo6Oz0/OVWM0/Hk8dHT\nYG2zXo20Wa2XUspMyqTzsV4sqqraGY1iouNYK4RQiFIIQkZmhYhaIXJSjRUEmjlTypS5UsZ727a9\nbXshlNZSIgggJU2RGSyEi8FH8gzT4W3v7Ha5KK/l+/PZL/y9v/uD3/yNRw+//MH3fmmQqcrgznTX\n1nVuNDg7rEoE9t6en59n2uzu7npvGSEEmpQDcwGwCKCYCVPklZ3GVb1FwiwriqIoB1UIYdv1ETer\nZdP3cOvmC6erBTHu7c6fHh9NZrO6brx1ClWe58gQnQcmrbMYI0hMOptJ7CPPMpnL93743mKx2N/f\nV0otFgskNpaaxfHB7rg7Prs5yv7tv/I/f+vuy+dffjlV+vCzz1zb9W23qZvNtt20XdPb3nnL7ED0\nIG+99MrT5er5l9/8V//sn5PZ6Oh8rYtRa6ntXOe88zEE6vveuX48KZUSRmtjDBJ621vrQ3C50bv7\ne1/96uvDCgnAGObY1ZvN++9+/JXXvvKP/uE/+Bt/7a/f2t95/uZBu1l17aYqciGE1MbkhcoqnWUo\nNQD5fqu1nM/n4/EY5YUzS9d1QhmttVQmRQWttdSaQAyne33THT56/PDz+xT9zZs3C5MJ4rOnx4e2\nE4DLECVFBSiIXn7+xel4dHZ6fPTg4Zf3P0dXP7j3caagzKQC1hIDEzEqZSIKigwCkX4UihIennZ9\nKtDTIeC9f/ToibVWKJllmhGQIbWIMqNOjo6ZOVzq9wOxEEKLC5BcZQqAL23TL2CJGCMCXvZm4Aok\nJKZBOZRaJZaEElpnRksFAgXLxIOLTEnRVUsjlWIKgaISMjIF53VmMm1c8LnJAsVMG2V09EEoqaXy\n3lOIWZZtNrXUAlm0fVMUFUFEkJ3vJEtTGiZs+wZZZEW5t8uI6F1XlNp627nOVINF255tOxGQiHZm\n0w8fnwMYpUTXATNoBVmW9X3vHEkhtIbpdPr+Bx+++uqNwQBDgOQUo31s2q33gQgFxjTIrDDJOAhE\ndDYsFkv2IQSYTfcPnxyfn69Ds57lqsjQ97X3IEWg3gZcjSfzbb3dnB1+Eeq2Xn3+T365WS92buz/\nvj/+czvupddfvvnk8ekgzzlCvdmOCkAUIAWgZBCOuHMuglht6sS9EiDFhe09hBh9CAQxhJAF42PA\nAATRBdsHLwcFMTNhIE8MBAIIE9WRCASLSGCZPTAKCEq2LgCAJwqBIEZFDIjEtDud9X2flbmUUijp\nQ9g2rQoh4KV49hWfL9nwXJUUV+30NIoUgQmBI3sfQXAkAUIK1MVwCiA2dff93/6dxbp++uTofLG4\ne/fuYrV2jt5+++uPHz76uZ/7ucmgAnnRaRRCEdsQopAymWJJadLrJl4fX446nZ+fpyptNBpprZum\n8d73fVsMCqWUUTLPc1IspRNC9H0ff7df32WgZQnIkbx1rreUe2AIhI5AICgljFKIMXBkJKlQSMkk\n8jIPgbTXFCjLDHlExK5pqyw/eXqUD6vV2fl8PNm0zTAvNMdyPFJCrjbr7XIptRqV5WQ66dvOe+et\nI2AtlVASiAN5JaQ0QgkBgjkEZi9IoOB+u7UKJChUoFiq3AiWKFgChOC9d0JpZrY+dt5HBqlMZHzx\n+Tttb5WUJ+fn9Xb90p1bs0JBcCeHT2NTS6adWzfXW/t0cb7ZrEbjwXA4FKKwXX96flYNy8l4SnWL\nWgJx9BRiBIFKqNxkzz+/t2rr0Wx+vl0Ph8P7Dx90Ptijk5vXbgshnYtlMXTObdbbTBVVXhqT9X2P\nhJk25MPWW2cDE0mliIAFXvUp0wDWbDItsnwwGKxWKw5xNJsXRdE3cfnk7M//y3/0T/7RP1oZPdbq\n8PFhJ8DXNTnvu75vu67rmrZvvCMhRVZooTJNQao/+z/68zeff+VkuZ7tDuf718/XDbFgIbUSeaal\nlCHEvm9W25OyygEkB290PpxPJCrn+rOzs73d6WSUdS66YJXRZamcNTevXfO97etmf7YTevvRe++z\nt9PJYHl0AsAgNEpFQgYAHyCSHZW5862WSmcmaSh47zdNXRQVIDKjp4jEIIVASSgC6G3XEUWK8bmb\nt27dvP7WW2/9a//6X/ry40+Wi3Btd++v/7V/9969ezcPrm+2a6N0prPo/N50bNt2Op6cVVWhOLqu\n7TslAKSIBJGtUBqFZGYpEPlHzmFXu+MKsktbjzmBSNK6HgTqC8a2SFIRElEYk7i1CeSRKLTWUmHv\nOkKZ6HdKSSEEMoQQtFZwRU+/7OlmKLebrbwUpBDiQn+SmZP8BDNcmUcgSiHERefpEi9JBKsrmf/U\nXb4ScPHWCQBjTBq0TBO++/v7i9UyhOBjSJ1pZu6cJSIpNKDRWnftdjDMXXCd64az+XmzjbqIomjb\ntiqnJycncjCXsqxbXxQ5AkgJiQponREIw2HuvVsuaTQWMULSjmEMzmtyF+NSqVmslBJCaamKrKyq\nIfsAQtfN2uhCinwynltyrtlGkkMjC/Chq5V3WhvenIg+VMxyc5LZTqw5a9awlv/P//P//sbrb/3k\n7/9jfb3Nr4mDfbj70kuvHUzy5mnhFyYstbQsuQ4d6Wwyng50JS9gVYgcnHMArLW2rmv73mSqGFRV\nVYDA9Xq9dY0aDYmIQpRRSyJz2XoMIQQioWRk0loLykGg1yoKbaRSiMyRgC+WQPAHO3td12W5SYVQ\nEzsVSN27dy8VIlfVeozx+Pg4NY2S1VtVVVrrvu+T+gUzK2kIuLOBUQCrpu1AmNX5cjzdGQyneTHc\nP7jBJLveXb9+81d+5VfKanj37iu7872maQqtJmqcZUVaQ1IJIZiIktidzrIQ6IrIkLpHyZIu0RCT\nRx8zl2VpjGptKwQwg3MuCX+lSd6rku6qPRtjRCQAT8FR9MgsUShEpDTDwDEZFEJgASgBEIk5APgY\nbN9DhL7vtdbeEyLGEObzuY+ssux8sbHeR2avZF9vMyNzY7brlZZyWs37tn1w/4vJaBSZtUSUSktJ\nAMwUGYLrIyHICBIgQuAAEQipyqu6q7u+FloMioEQwvW265oyyzlERJSGUAgBnEmJQoos661v1uvz\n5XIwmozKAgDq1WqqhoUWZaZyhd229X1vuzZ4e/vWre127Xprfe9pIIQAFsyMxBIkSKGUEUKSEtrk\nQjREMJnMvnz8ZD7ffffjj/f2D56encx39k+Pzspi9OnT++P5VGvduO7OnRd611EgwSIG13pHCejs\nbV038525D5aVYsEAZG2HDBLF4vxcKdW31jk3GU5879eL9f6kOLix81f+0r/h23Z5+OT+w0fXplO/\nXVvv+67tu7brOutcZIooWGih9OHRyY3nX/yp3/cz8/3rjQ194Pc/vndw83lUBSqQATy5EBwSO+e6\nvq6qEjB2XdOEoIQelEVhCpBQFFmyjdmuz22w852dqjRaToxSwJxpU2R68fR0VOXDqlotTy8N14AZ\nkEEhEiIK2WxrBi8MxBi7ziJinueDopRSuRgoEFOMIfoYiDgyimKIDPPpHJm89+++8/7J06O3v/KV\ng2vXRtVgNh2TD6G3SorxcCQAjdRtCH3bZcacnZ3FEFDJxINVAoRWIbL1UWojlQ4haCWBOEEdVxpa\nRJQO5URLS1TvBN0oIzmZpkT2rpcCKDgQgkK8aAslZIU4Bie1YmTiHw1R4aXBWIof8LuHLhI7KRVM\nMUYgDs6nnvTFxGhi0yVxOyBm0EoRXkQjINZSZdqQJNdbCjGg50g/ikbei/QUMQpgb/vxeLy/u7PZ\nrp0NAgABEl1eC8GIMRnqgkrnYTpDslxnIdu4MNoZ5bnpvauqKiiV5ZKFDB5CBO/TpbH3XkktBIxG\no6dPn2b5DWYoS9X3pAjKYtCFECnEQCBRKSlRIUhmPDk5a9u+UEYbHQMeHZ/3zgsh5uMB1aeEcrwz\nKJECyCiQyAoJRnqhNDYL8J2nTWzrmvvq5m327umjRwLj4vy83kzPz88fh61YPZbNUQ7bTNuARAo4\ny588PRnJTAljvQUApUT0ASVOJpPOZYX3KFgqZTJFzCY3juL85gGDAGYMhMRSCCVk0j/sbG+yzAMF\nYJJIzGY8uvHcc4XUQgi+wIeZiCh65/pMaWM0EQFSlWfgnXr99dfFpf5bqodSAZTWSlIQSWXKer0u\nimI6GqOSRVEBytY6JggR67Y7PV9N5tMnjx9vts1oPLhx7cC29vnnnz8+ftq27XJ5vre3Z233/AvP\n+a5dLRfL5blU1DbLYZUXuYrkJHBVVdYvus5eNYeapkkpT0rW0hDPpfij7rpGGyUExMgSBILMssLZ\n4JxjFIkPmg5ZjmmAl6QUCFIKnWVZUZUKBfioAKuipOBCcESCBYBgFEzMg6zIdBY6jwISq82xi4wh\nUG87FOy6djDM15v1aDrLlLRKJDOLg4ODpmlSV/zatWt938u0D2NMUx1CCKmQpUZkIYARUbBgkSiL\nzvVKqWygI3AIjiIoFFVVBe8AWRmtjCTGEC0RIEK7XRVltdmu79y8frZcPHhwePfuXUG+Wa+iln3b\njPPCaJ1rZbSUnHV1027r/f39LNODyTgyWefati+N7pm6vgfbsUBdGiVzoWC5OQ21UIU8Oj/OyuJs\ntRLGWBeA1XZd7+9fW202UIoXX7y7XK/Oz8+rqpASCThGryVOZuPg/bauoxYuAgBKbaTJmDHJ4Kbc\notlsBftJNVqcne8Phv/6n/uX/8K/9a++/wt/+4WbtzKSXeDF8fn506d9WweCddOte9cSWJFZiB4E\nBXj17W/85O//2YPrt5ebZrU66xwpo8/Oj6UuUekY2HnPgQEgRCJyy/M1QJRCaK1B+q7x3rZCq77v\ns1pb65hZoFJCKzBSq7wcDAfT05MFj6vZZN4sT89Wpzeu73vbEVyMYyIrRK0BGJAFh8hAUYAwiKik\nRGCmGHoKxERGSjBCRMGBvRCWOiH1bD4+Pz1eny/293ZcvfmPf/4/3N/dAeLn79yejwZ/4Ce+u1wu\nx+Nx13WlycTuONc61zeNxL1pYSSsFudGCYGsdGaD71orlJZKO+cEAkfiS62vBNCl2OC9T/srzR0i\nYoxeRvTBJZ7qZrNpNtvNZqOEtNZKQCmlunRYFkIIJ1AC4YUWQ4wqEaASL1yqS6cihhhj8D7GyHgB\nGAIAAib4jph9iFec3iRvmh7bdU1kkiQiU/AetVTBRyadGb6UtEcSKIWSCgQyRZYCSBJC3Xf5oGIp\n2q4DRCEv6FEpNhMCBpBSKZUhSmCRxNSVNEL51XJZHBQe1NH52pTDpmcdIXEWQgAiAik0SmZgBmKY\nTmcnp+fX3Y0sg+EQIghClRemrVfEaRxXCkhW1957u7s7b9u67tayF1mmraVr1/a6Ul0f3qL6dKhi\nib1bPNYYB6X0zqPoM0Nlqa31aIQREYTGHLyKGXcPPn9/vveis7XOIS8zR0F4H9uGYu2k7XwrCo2F\nbep2yWqgs851iFhWRV3XSuvJdPTJRx+hlICktba+J6KyqnrvWBqUQqJAYkGMDCkaWWu3TZ2XRQDu\nggMlPVOh87xnIyQAxBhYoDHGKIEMSLFpt0opZhJCRIi+t5fy1ZeM6vV6PZ1Or4ieaVF677fbrfc+\nN8pTRA+2qQEloWjqruu9NFmRqXp1lhv5wcP7t2/cePz486Zen50fKmWGk6GQdL44rgZZ224VxrrZ\n3Li5t7c/m8+mWjBwNEoIgECxqIwxbYpAUsrkU3eFEiRhwbRzAGCzkdd2dohISkXAUugYOQJLpYJ3\nAWjT1C74yAw+SKGJvfWhD7Cqa+vjut4OssJ3fZlns0IhiPOTrdJSCui9H40Gtu1i52PA2Fip1Gw4\n7ptWCAGIWaEiuywXgThQnE4rAGutQ4WFLl3wACCUNEoiYqCojIZnxFsvjgCIQgghQACCQCCWwJgD\nCPTWCYEShRIoABN2zwgi00m03wtUSpWFoggxRlOoEPx4mPftUoO7uTcCtynyiet67qFQWb2pM22O\nj08vnGaIx+OplNra9vTwRGems1YZ7YnrerOzO9tuV9WgWPbLfK+IupeK1+vVxoXTVZ0PZxizpuld\n3wx0QcHW2ybPC63NZ/e+2Lu2b703ZFiIrFDdpiaGLDPW906FKMEpqYyuVxuKwIxFWRERcYh971yd\nS4D+bC/3P//v/pUf//aP9R98eGd20J6ujh4/NgLb2jLo85VVRflk0TilndLO5FsfzHD8M3/wD/34\nd36i6+z5ctn42Hl7ulg4H6vROC8GSmdCqBhC53zwMUbm6IG64DrUerXpYvSJsDMYTax1yqD3PgaU\nqgxeDYt967jrILCRqvIO6q6RAPPZxPV13W2VkTrLAUQMjjwgC0T0sRUCiAMBEDD1FCwyAhFZHxFR\nZ4aI2q6jGEGbGjivyi8ffsTeGZS+XQ2zItbL8fXdh/cf/MbnHx0cHECWb05ODu/fK0vDwUqJWomu\naWfjUW+7XEkAaOtGKZFUcp577rnT0+O6bpMd0VXVctU9SlhZYbRQEgAI+ODG9cPDQyEExzgbT7bb\nrTHGSHV6fDIejpKKedqhSGyMSYrgfd9nVXZFf+26rizLxWIxn+8gojE6QTqp6Zs655PJ9Gow4wqZ\nJ6LMFFf8WHkZ8AghK/K6a8ssBykgUmI3BCaIiZVCm6YWDNu2GZbV06dPtFHbpqmqKkqhqtwh3Xt4\nf+fGteVy2TsHCGZQHh8fJ9kXZ1nLyZPDw+mw2K62bbcZzCebum49ndX2Z775e50ZWelQF+z71oHQ\nsG0csAApmLh3IXjS2pgMhqPZO+9/+vyLoRwoF2FnDx4/sZNZ8egJuUhGqizPELGzvffWBbvcnJoM\nYyDnehSkcuYYs6q0UpvxNaaGaTWaTZUF4VZgSBskYkZbFWB717atAhCRBjSaaNdD39enKh9YgJ1b\n15onD3OlhDIKTSFZieg5xhAKI2UkR12ISRfKM0dgEZzlGKRErTQTK5YhcrduWKBU4GMwZcmRttvt\naDQqsvz09HQ4HGoltBQQg4FErsMSoBDabup8WHWRBYpcyWDdeDDcLhd5RIhRGg1C9oGyolI7OzsX\nVoxEaQY2JUrp16uFmwpqpRSFQDEQI7MPEYTEQZVHlA+/uP/RRx+u15uHDx7duXNnf38/z/Pjk5NP\nP/0sL8xsNmnaut3UgD6TAgWZTCECBx8kicgRJSTfCu//GUZcul29SURMYZKIgGi9Xisps7xAxMDQ\nWV/X9bbtQuSsKCeTSZ7nIcQQorXW+X44KBAkCCmkAhQoL4hyymimoPTFxkDi6DwFNhIVC4VC4YWI\nLAAQRBSIlDSJCZAS8soM0YN/JuTAM/NDz/7nJbGCOEZEFpcCS1eXDABISEIk++H09ykOpcgkhPAh\nXHSSmRExeg8AWusqU7lCpYSAUOaZFEKDAAAjpDFaokC+lEQTYjAYVMPBeDxuui4iy8w0rh0Nq2k/\nlwasa6/fPChG+apuopRuvXn14OV3Pvj8jbe/+ff/wS9d379ZPz3XUldlyRKFlMPh8Pbt23sHez/4\n4W8zhEEsQaBQMgIJLcbFBIrB8vFRt97cvHbdbdvcZAi03a4l0nw2qiZFJfn6aPiX/vyf+/YbL/Zn\nT3NpotQgM8G4WTfp4Fh1vqtXopo0Xc+qyiazf/Mv/88G09njw+M6oI+SUKPOGLvO9tvt1gY/3xHV\nsNLK9L4nCibPiLhtXKmN52iMYY7WcgjOE2NXM2Pbd4NhJXS5XGy7jpj1b/zTf9p7fPzkOAY2VVFE\nJmcFu0heG0TNLGKkSJEpgIgCEaUgZuYQCS6pNEKAQAEsMQohpCCBrCRHYFBcadV0NSg9G401Yd+s\nsGvm49F2cQqu0RzB9S568i0ECxEKg0KyFhAVC8kA5JNJskCUSlyGnET5IQrG5M9uq6uxvCv+wrML\nNSWC6+UqxigAp+NJEpBMIxZ8NSZPkRASOwPaTUphpZRt23Zdt1qt2iyDS8s7uOw0JKD+8Oj0nyH4\nXeF7Vx2ji4rq0jCi67rEsbpCca7EzCCJVmjtvffT6XbbGKNC9H3fpzNks9k0TZNlWbw0MvfWKiGK\n0ejOnTtPHp1pM1IqqzKJ0GsDWZULrY3AvYPnbr/4ShTSkmpc9IwKARjSGyBmvBB0EoCACFKb4XD0\n+PFjpe7s7MG2hizTxNBZ6xxFQCm9QEZk8sF5670NsWeOQpAUKKWCKNloITLJmWRWZDOZG6ml1hi8\nkkgsUApgVMoIGY1AXZYyE5WkwajcIOxd2+kjTPd3Fw+/QO+kjy4EKV2ILshAgoko+iAAQ3BEAYBC\ncMxxvV53XSedu7i6y8lopZTv+sDBC6kQMqUVAiKWZd5s675vOMQIEVCG4K0LeTnwXZ90pT1HiIDI\n3roMpQRkloAEkSITA5g8U5999lnXdVfTy4eHh+PxOHkLpaZR4tclYNcoMZtMgrdC6hhj3fQqyxHk\n+Xo7Go329vaIuK7rzz777KOPPjo5Ozs+OVmvt6bIu65LzAIARURZnhlj0voQTCbN1CFKBL5Q/5Va\n6ysZx7TyUkmUguKzqxYvHRYYFKMcjUa7u7uffX4/yZJmeTklLMsyLda6ruu6tvbCjTgag5fWMkwh\nHfqpU2pDJCZrrQCRAqFgstYiouOYnvACTEgMIub0GaZ4I55RQOcLp1p5tc3oQrzkIorFZ/w7riLT\n1dVdtb6ICJUERIEYL6FtvBSPCc4jYqZNbi5mCSnGzndaSULBzIHROaGkZObhcNi5rgt95zqzzYbb\nYW9thGiqIsS4WCIAOdtEjn3nVpv1elv3Id7/8vHejXBtOv2NX/2V56/tf/HF42vjcYzsvbPWSWUa\n137woT9bnj3/4p22b/PcABBFn4CZ3Ajr7I1ru0/uPzo/PsyFwkB5ng2MGI9Go2HZ1/7bb7/5l/7H\n/8osz7RWmoE7v91u67purLMhNt47QC5KjrS2cbx38C/9hb84f+4FKMrVejsZ7+XKKOmlzocxFPmw\n64OQq3JQMQuKKItiMs2KIjBKZhyUY/ZdDK6qqhh977oQXde7YlCtV9vFpnEEDBiZCcVgAO9//BFC\nRkRJKcN7zyGUmVKYQWRIyMvVTQAiCCkJKTXkgAEQBKIQ0nuPDMiAxMAsEBmRiMl5yVRoVWVZBsJG\nnwmVGbVcnIUQjNI+OOs5kBcCmeO2boSAXJtkUBljRHFhDJE6Q1fnSJItEJc6wr+rRmfu+z4xLNLW\nS4r4UUkgssEXRZESnbT+0/NcnVNXAyHee8DfNcyUXjfLLgqmxCFOqW2qgbTSV8A1Xg4wPatMdoFp\nS4mIggGJtczSCHsUQgqplPLCX/alwJEwxgQR5sVQDkLXN0qXKaUbDabp/WvUJC7eue3tSOZFVrx0\ncHtxuO56KyU61wN3jKFtW/KhASX1ZGdn5/hocbrqly2RzCjOIrDJBFFiql8k7kQQIygFs9ns0aOH\nWZZdv3lwcurLUl+2oiApJwn5o7T14ljTWimhlUxFJxBghAwwJ1OwKWSWqVz6UkREIAYQSjMKYa2U\nmCudDYY8GJRlmU0mMWTXrl3rWjg4OHi37wqhpJSSJaJElFKi1BqZtDZKyPTtpG8qHVC3b9++OnlS\nQpBlmTHm6fERACRDwjKXUiIQDsrhwc51F52UGgTnedm5rmvtczdu+lUbrNNlHoBZgVIqWFdmeWga\niUIqBMQmuCZYB1E9//zzfd8nCgMiVlU1nU7LsvTej0aj1Ak0xqT1IYAEgLOdyYoQwmpdS5N1rT06\nWzx58gQA5vP5/v7+9evXu67b3d9/4cUXP/zwY1PkKVqooiAKZ8uFVPDll18WhRnkmTZY6izLtRKC\niFBKH6MQItFjrrqdqbO6Wq2klKnjmjwrq6JgIrneICIKExmXy+V2u62qKm2Soihmsxki1nV9cnp0\ncG03nSaDwSjLTJ4XEopMCCEEkSyqAXIa/qAEBbDjqqpAICFIKVEIFijjM5EABQgIF48CZfKru8Qz\n46up1hSXEiyXewxBiDSNeFktXWSOads8W05drWNIyvkAkYiZBQohhTGGUAohyixPQAoRCUDXd8jA\ngMzRE0NEIgVIm3odo9d55tm7nkSudKYHw9GqXiFy27qqKpyPMcbtpj87Xc9mO8L2r774Ut37Bw8f\nQ+93blRv//O///Gjp84FYl7XW5NnuleATBCtc977FG4FMqJAEDHGvm+nk/l0kEtPN3Z21yfn40HO\npI6eLp6/Nv3f/B//C3bN3mCgo/frjUaJWd513fHZ6ely4UJ8ut50PvSRH5+c/9t/7d+7/c3vQB8h\nH63PNqYYZ1WGxEI4gS6Q110AoYlVJKlNvt52qKr57j6zPDtfuN5X5SRYwxyH4zFzzIMN0aumybKs\nGu1u1jUIcARCF6v1drnGT+59due5l6Y782o0pHbtYhAxMouk2w8IxMCMAKi0kKylEIGsvJj7u/jq\nBYr0pSoUePkYcUF/IMVw/cb1nfGcnGUfZ/t7mVTk3HxnVwthtFZKEHCMc2YUgmKwUkCZ5THG2WzW\ndZ2WSilVbzaIycqSduc7aUfDlYbNM+VR2mIpw0sxKQWwtBq11mU+TU3cRLW11prLHO5Ks+pqlT5L\neEusnyTbk5xsEqefmRMiqrVGwBTJ0odzJdjPl7f0Jq8qNgUIAlz0EiiEIEgUSnThAsBHRA8EHG1w\nXXB99KiVvBQsL4YDiEEbk4THYoyA4JmE1K2zJNAFC9KUReF7iyyUyXqOBIyI4/H45s2bn500mSm0\n87oaDQay9+B9ILooEoUQEShGslaggOFwGGM8Ojrq+wMpNCIwgVKGKFylqkpJBlRCDsrKaemlIgoC\nIYVeJkJHBmPGmLHMhMrQKMyQiKIHRKE0CJlyHZNcrIqiLAdg9LCaGJN7D7u7+xe0DqWRFQACo5AS\nlUJgu21IqiueV6pZU/vmKglOyyMJ9EhUcCHuzkpJ5yxEm+fmyfIpAAGICLEsB13XhEDX5/tffHk/\nxohasRKMxMwUYiaUiEExSoUsheXYUwiSVdM0RJTUd0IIiThnjLlSlU+tGkT03iPH3Ji+a7Tpiahp\neh1pvd6enJzs7l/TWq9W62TSysyRKFV8vXcPHz7Mi6w0uZAshKiq4oUXXshzPSzyvFCVyU2mkj6x\nMiYVQ1rrZ+vElHkNyjJ1WVOGZa3NjenaNiTVetTWx1TFK6W01mkXnZ6ehhCeu/PC3bt318tlUlbN\ny4IouhAMogthuyWOpCQyp+ROBOckIF663CZmjxACpIhMIQS+3NUCheaUfl1q/sPFz8/GmGejy1Vd\nFWP83eHm4oEXyeBlMpvSw6unkiiYOaJgZoVCCBGsS1AFhejZXfyZkplWWgklFFESY0ZgQcyEhEZk\nVUYGQMp8WDICGw7oWUDrmwxzVooihCi2m346Vn0TCHBnPL994/bR6dFytfnNX/+Vm7dfzHNDwIen\n9abdOA7D8fjmzRsoQCmBiNZaiSLPcwDXt3a+M7btFqOdVoPm/OSlW9cV4G/+9hc/9Xtf+hv/3l99\n7uUXYL1052exa916rYejuN1uNpu66WprLXGHKCbT6WD0tT/4R/defA28WLd2XGWmmAHKvoe22QIk\n5xuT5aPJZD+yUcYMh2MfqCin48m+koahqDeNUqqqxsyxLMvOdSb6Qko0dUJBpzsDBthsexvi/YcP\nm6bJq9IYszffKYqiaVZKKfLQe2ddjZIhcloDgiQDCGDmGJwXEi4as4Ax1cExCkBOX3wkJhKRkZEY\nyPYDqQopF23TbWouSwu4Xa9OD4+UTt97RCmUEiwkxKAVCsTCZES0WKy2261EoZTKlE77OoRQb5q2\nbVPgSdXSRbvoslhP+VnK//I8l1JOp1MpZZlnfdsOh1Wqmdq2vXPnzuPHj5P5GV1OKaU6LIUrKS5U\nXWKMm82mqqrlcqmUSjEpCY+lRPuC0Rc4mWqm5e2c42ccYa42S9oIJHFdb0HJzluJsnc9M480bLpN\nOhO01qDAaLAEuYYuE867TMqabR96hX7p6lKVvvFCCOttnudUKsx10zRHdhtL022bLJfW9VoGjOSC\nE4UOIYyLwpjc2pWQOSJRRNtD00UhiTkKJaQUUgKwtI5iZIGYZWY+ny8Wi+NjN50aa0FKUCgi4EVh\nTajURalaFIVUKAGDt3gpuYQohPIZYAYyR50HrVFLkEg6JE93IYSSzAaJlRRCCCGlksbGONmdWGvz\nSs3mxmQFOXcJ5Ei4UKpRkSkwcfBCCEbwMShUBNzb/kpNmxFQiAt33UBN00nA4CMK0CpECpww6Jja\nDciePNjQe61NVZQRgZTwFAQrBvLeK0DrXamUd976gEpyprKyKKtMpTiUsmm+VOJJePHVsZiQOmaW\nKNOvaSFe6FON8MaNG9VwNJ1OV6s1MxdF4ZzTWdZbOxqNhL54lbOzMx8637U+jLbbrXMKgo9kyHrZ\nIaRh1Wfks65QBWauqip9+sklKAFfSim4TKC01gyqs77v+7qu/+Af+iMPD4+apjk9Pb2m8yzLttvt\n0fHhZDSKwHlRFUXRbuqu6yIIjiEYTcEXeR6CAwClZFLwM0JprVvbe+8BMVwyaEEkRWNgvCjRJUCE\nCwj7akNeJXdX6NxVusHMAEQxJinJqyulS529Zwujq+cEYgnJDQNYyHT5AnAynSVsM80hCiFMEtYS\nkFgSKDixX5jZR2eMseQTI1MoiVqcn5+frM6EIULwSD0FYTJnKR+MVTZsbHzp7uvr9doGR8EfPnzw\n8qt39/d2HOuAghCyXGljWAmhRVYYYpYyl1I65zghVRFCoKePDn/sa69/tlkVilnQ6ujxoCh/6b/6\n333tJ7/78L134PxsfXTYb9eVlEePH50Jvdw2p4tNR37RNFsf1pGeO7hx6+5rWxd/84NPysE0y8b2\n0Xo23a+KwWq1yozQWjIzeGDW1WBqIzKItgs6K0KUZ2ebshyVxUSKqm1bF32M3G/tarXSWu5f2xtm\nFQBtt9usyG2Edz74sG27R4dPJMhvf+c7O7P9ndHoe/+gPH/cC/TRR+A03cmRiRGYGYkkRYIoAEPw\nki+HPYlSjz4CX0FVycOUERBREkyroQgRnBuaTOYBgmcUZVkis5SIDMSUSmEWyJExSYk+M82aFsyV\nfZFzDphTinlpB36hjpqwu7QgV6tVqkgAwFqb5/n5+flgMJBMeW6Wy+VgMIgxDgaDDz/80DlXlmV6\n+1eFS1rwSv7I4rLv+9lstlqthBBJaDVthKvlzcxaZSkrv4o9KWil5tOzuKIQAqXI8zwrCyWlMcaX\nJTPv7++vqipVflcxqW3bqiyZSMphURR+OosxXrt27aQ6SREiSVwOh8PEbt9sNlqqF+7cEWwGZdXV\n52UhAV0TXDndPW5ieeNlreR4PI1ZGSTbiFqDDjISAQhglBKEAGAgFiGAECClnM/n2+328ePDvb07\nbQuIafboYohKoHg231VBRBTxMk8VQigEwaEQshKyQl1GrZwGVOw9ChliRCmNMVobLwUyoJQEwhMx\niKKsmq7f0dWghKqq7OZMRYoEHIMLXkQpY/AxKmkouISOJnph6o+kn8VFgLvo2zFCrjIiEkZenGNC\nSCN9JCUEpyo5iBCCAKGEdM6jUSgw2F4pwQgUUWe5CEREoKQERK284Lbv+n6rrgYLnk1zUmWdMpSE\nPierVqHlBURmvXMuEoa69i6WZXl2dpb++GozFFU1HA5DCKPhoKqqLDehd+NJlUlRDXL1zE1K+f/j\n6s9iLU+3/EBorfUN/2lPZz4nphzvnHeo8ZZrcJly4QY1XciAZB4a4ZZ4QzKiEc2T30C0hAA3ILW7\n292AG4Qtv1gIRGPA0Ha7BleVb9353syMzJgjzrin//RNa/Hw7XMyqrZCqciIc3bss/f3rfE35A8P\nEX38oo29G3YBQG7UMsfNe59fcIwRdx16Ptxwt3D7B//gH3z9W9/55V/+VWPLi4uLGOM3PvrW/fv3\nz8/f5Fs6nU7j6JWwURoiWWs8sLGWIYmIMpqCKmyB6RbSc/t6tDGI6ILP2eiuJcp1REpf3LScgfJR\nuysk7+YPO6TGF3XQF2iFt9PS2xViXjMIIufylghYEieOcbNcZSEvut02GVJEqLTk10gEuddOKY1+\nTCAh+bKuRaEuC12Z5WbZh97jyJDW6/Ziu27MfLXs944fsCpeX609Y12Xo+v7fvOX/tJ3//RP/+Qb\n3/72zx6/iKRQKRfGyV5TVGXb996Pl9dXPnJdT5iZhJL0DDCbTjnx+Ysnj44PVq+u3js++Tv/7r/7\npW99BzZrWK8fnR2DG7Y3V2f7+3/6B3+gk7x+dR5IbUY/iDy7uLgaxk3k6pHfI/V62/6z/9t/pqg8\nOniwPz9+58EHla36tjNWANNms9l2G6VUtv1mkSigTQGiBKmuZvO9fWvLGGPbtt6Pm3b76vXL+Xz+\n7W9/cz6fArLWpfNwcem+/6MfLW/WprBNVf/Sr3z3/vG9WUl1XacUQAMAaK1R10l8disCAGRFkiF0\nrM2urkJERYQZXpArD8IkEIUJkYzOheA4DuuLC7duS6shsY9RIeb8KoJIlPEtiYMIArNCEgZhQCQQ\n5CQCQiRa6RiTUpoocRJOArIraeFOtlEEAPIClW5BBPllZIZf0zQSPLOUZW1taa01pkBUAJRpGLcn\n8859RsZhpLeklnPJeHek3x4A7JJxcvni5+iRF3J5d3BXj96NBDSQX3Z1VGk7VlX2NsWjZHTUbTcy\ns9Y7sjxst+CJ+t55n24Ztc4pd3FpsYkvbpy10Xvf7PiLKaVPPn1VNJMeQBfW9cv5tBxd26dweP+d\nJ1ft73z9V/phbNs2BdNufeukqSeBRRu1KzFYKQVKgdaACLoAakEpNZ/PLy8vx/FdREgJyrJkhuB8\nSmnnkIs7JrJoHfJRyaLJ1loSSK4hrpVqSFfJkGiOKhEhaQFApbJ6RTSaY0hKRaV8CHVdA2nnvY9g\nKmCB9957f+b3FrLFuHF+S5WiqvApgvdj3+fIkOvv7O2Z+5O3q5z8WVOkEBIZnWmdZV2VZdm2rULK\ncTVbauUT30wmh/dOxah1uy2rCkii8/vTOUVWMWokq0kU9dGvXN8np+fzOd2uzcuytNYuFoscRvPg\nLqXU931exhRGcYzWqGH0m81mdLF3fhx8EDRF2bZt5i3lnJTZQvlMF0WBmJlMBYBcX1+vVqui0BJ8\nTIVXRmk0ueuCrP5L+b9wiwvIvdHdX+36JGOzMhRLFqnzWWhLa312dlbX9evXrz9/8uz5yzdFUSxX\nG2PV/v4+c4rj0HVD1w0GgQqRxAToBqeQhmEAZIA6ywRwiD4EH0Je5EThgvAOkCMAwDsXlt0jISt1\nV3L+hUqQ39JlyREppR2L8O7nenuO/xewhQSILISokFDrvDiFxDHGpq5zYodb1a8YI3MqKy2SQFIu\nh0UkSQqcIgdBBMLBu+h7G8sIUs0mbdtGSSNyHDrGcu2dbqb1wf7Vk2dFjMT8g5/+9Dd+/btPX754\n90vvkSFT2MKWZCg8c1dXl6IhCS/29prZhPqxrksAcr3ruo4DTCfVwWxx/uz8wbvT0/cf/t3/xf/6\n+OhkfPZ5OZ1BGC9fPVcIU1t+/NOfWVIgfHJ2+tmr8y7GPqWBGat6UjWLe/dmp/f++OfPki72Ds4+\n/uzZNz5Y/NEf/mm/7YDl4uolQFyuV8PQn9w7e++9dw6Pj4qqccNwebnuRweiSZuiqGbzg8ViEaJr\n+/7N+atPPvlkf3//6OSUgQD5yZMnzPH999+9vLgWhC+/96WyLD/88EG3CcoQaSqqclJpD15pBmZC\nJEqMO1CJYkRGZMn6bHi7F7zrlfG2e87RM6+Ilaamuo8oiKhv5RKyhBIAW2uNzdSNlJ9IIQKLJM5z\nubqu27bllO4qub8wjgshVHV5d8xybeecy8rIudrL0+O+76+vr7uuC24E5vl8nlKq6/rZs2c3Nzd5\nGH5XMt7dR611U08B+S/QmLItwN3vcwG+CztJcrjIqSuPPfJA7+3KbJe9ELTWyhohTCA+mwl4142D\nECYWEGZhEmAEUERG18XOs807t+27dugZwafIAQAhCvduLKBomuZ6tdRNY4xF2mk1jW7Hz0Xssvmn\nMHDaFYhFAbXFtgNOIMxKAeU5rQIAsBZylT+dTi+urroOqgq8AyJ9V6omFBEBBBQorR05aq0Tq1zi\naK0LhYysKRVaDKEGwFs2L6m7zZMubKEJkhePWqzxiat6EjlFhn6E2IBz4fGbZ4uwmcOWwtr5DVUa\nKutDqI3pN+uyLIuiyOPcyWTCzJvN5u3juvsUhAgohFTXtSBsu27/8GA+n18vb1Cg7/tJ3YiIhKiU\nis7zExkNiqXVel02tSZIITrnTJRuuVQ5eiI4Eqjs9GChLy4uZrNZXhRtNhtjzGq1SilZay8vL2ez\n2R0OeLVa7Z8coQgCT5IcHBwAaiGVogwh3azWzJy9TfNnkE24u6578M4jZibEqqpSSmVhwcG9e/fK\n0tTWZBRDWVnaXQaVy4y7/dBdcrbWjpNpTpl5R3pxceHGwXsfExMRi8p+5ABwcXFxdHb/xz/+8b37\nD4FMURSLxcIWuplMunZ7c7N6c3FhkLZdd3L0zna5fvTo0Xa9HPtusViQghjjZDrTSgnpKNzMpkVd\nZfAPACRhw6y1ZhHnHADkyzZ4h2SFdqetrut8yXOCpFvOefZTz4ECjHlbU/nuDucje3cVd3UlS2EN\n3W6gsyiLVkorpZSKMXKIWmuFhAAgO1tCZZU1BhF9DJETc4ox2tKqwpJWhSqBfQYNDt04hDjdn21H\nHsY+Dn0xm/zk80/LolncO3v82adnJye/+Bu/9gf/6o/vnR29efbs6Gh88vzZvfuPnn/2vCgsWVKF\nbvtudL0LKUr0cYxRJpPptuvqphFJ568u3n+0/9nPzv/Rf/J3ZBx4eV0iyOomBCfO3WzWMUYO7H1s\nV5veha1zEWk9dI+fv+xQXQ3uv/Pf/7ebg9O//jfee/bk/OOff75/cPz6/I0Bm4NpVVXDsJ1Op3t7\nC1uV2213eX3z5uJCBJS2PiZONJnNJ5OZfnNVFEWU+PL1K2Yehq7run/8j/8xAJydnQ5jRwRFYX7n\nd35nMq2Pj4+IaDaBscfNxk+nUwC4vLieN3qzvjFWhBIYEYKUUvKBWBQqo3QY3V2D+3bsLqy96+MT\n89Y5ACDCjdIIjIgZA0VEWeRUSFJKk7rc399PKd3c3GTh4OjDbnir1HK5RMTgvXNuPpkS0Xa7BYCz\nh6cXFxd93y8Wi5iFO5VSSuWJXF625xdTlmXXdd/4xjeePHlycHCgteaYqqoSkdls5pxbb7tvfPPb\nXddllF0W5um67utf//rjx4/n00YTIn2x/UbE+/fv51uZ/92c/zLWLsbICTLpPq+OXr58ub+/nzuq\nvLrI35iLsyH6gLIWCXt15z1ZU1XV69THiQkheJ/lUyRGp+fly9B2Y5e9Kqqq2rgwQgiL5mc354MB\nkeC9N+KHND46PP75q1fT473XXVvGQgGQxKurKxY3PTzI2frRo0d5EihKhRCIihCgG8F5hyhJ2I2p\nKIqqUoCQEgwDWGuPjo4uLi729vbevL44OzuOEUpboEAYRo5RmdKPbogxhwUCNEpFQCAyWmtSKEFJ\nqrVURlUKQtvp5Oez6cX5RimqqgrVzpKmaZpkdHKxD6Gua61150LikhDWG+gGd2Dserk93C+79qpq\nmi6Oy8vrw5PD7XqjSHeDcyF571er1UcfHb148UJu7aoXi0X2qldECpBZOMSiqW9WSzTqer06fe9R\n3Cydc6oulkPrva+M1aAFWQiwKpbd2pEM3XbsW2IIo5sXdUHoR08Kyqbedlsm+YWvfmXXGmeN3vym\n3HHQ1K1iaS7f8oGoylI4YuQ8AGHmGFMIEW+Bm7k9yvSgu2rrraSSctt0N4LbLfQgoUiMEQDzN+Zs\ndPe9ImKtHccxN5XZI2u1Wt07O0VEnbnfvCsnlVLT6VQpZW157969D788XywWh0cnzjlUwJJurq5v\nblYfvvsOVs1nj58cHx244H3kkFhElKiUUoZt3gGp79hODF+0OIk5/3n+Gh88oNxlo1zj3CUY9ZZI\n5e0UDiWlO03lt4d1dzqB+SG3qq/Iea1ImOF8AISY02Hu/Y0xmm61bhWWkz2tSSORgsxSrKoKNYUY\nQUEEHoMfgh/j2I9jG3pvkw/JFtXeftl3SYi64B4/f/7w3kM9rbDSn798SVX14uLi6nJsXUgszXTa\nTCaRo6lUNatNoa/Wq+PT49VyY4uMJ0+TyWQ+mbHrPnzvne7i1b/zb/9b6+ubxqW5AHpPgI+ffoaK\nBuc2bSuJDakEdN22r1eb6uDg1c3qYrPV0z1V1Mtt/4vf/UiArJ3FgA9P48HksNLl8vz61asXnz/5\nJIRh7IZhiMb1zBEACHgMCUkTYJLUt+0wuKKoZov5GMbprCqMffp08+b8vKqq2aQZ+9nJ8ZFSeHx4\n+ODe6cnJ8cEedj0ED1Wlx+iNtYJQVGWKmV2Wsd2UDbWFCDgxc5SI+gvdYQVffMQxJRChP49tMaQQ\nJM+DkQARkwgACiSNmkgUmbezWgpRIaHGjGTJJ98aU9d1ngLlf/ruruXbnc9ePmbxNhTmJ8xyDF3X\nDcOwM68DzPEh45vyvRuGId2aRBtj2raNMX722WdVVXD0im6VUhHvzn/eIN79+FlRZRiGFCVnnfxs\nV1dX4zhmPbA7YknOTCmlzo9U2gg77wNEdHG3CSuKQjIWDUmrHSJXWdP3Yxb+IqNBkSQERbqwAKAL\nq5QyZdHMpofp+NGjR5vlZtgMhrDQSVNCSuV8iuXkhG0O8Sxj221Wq5XoGkGD0lqZ0Q0xpfxTDEPi\n3DlZytuHoiiNLrJFU1FAXeq2pa3WueAuCpuUkhg75zPvEBFT4ozmt0pdLc8Pj6cKQUkSBTwGj5wn\nZ4xAtOOGgiREUYpsWSlTCFJIkoCTgCnh+PQkPN8obZMIauVj6schcHpzcVkBmrzRFMmCUsMw3C01\nlVJ5IZdZXD4LPmnVjv31eoVWH5+dRo2v1zfGGEjAEnVlojGj8yJc2LLz/ZvVjQu+tEXiSCF1fiy0\n0UqjVsoQGq2rAip7eHqsMxUg3vIo7zAteU8jtzRYa+1kMskuqyAppVssstIgZIGk68uyzNDJu2uQ\n1e3enq2xRGbO3AitkRVBYh85RKE8tiadQkwpSWJJTLeiv0VRcExZMSsKZNJWYexms2FmUjrD0PO8\nu67rthucc1WljTF7e3t7e3tN0yAikCyXy7qui6q8WS0/eOe9GFxeaebdGCskzik5pZRu5Wn5buaW\nP7Z8VfJ2LzHH7ETOEiFlq8q7RuptRMMdLu52eCLCfIfwvgtbADtPyb/wIECTW/QIiJgDocYvYg0i\nJpAMZEBEYuyveyDhlLwfc+eUgQ7aWlQomrQ1uizIkERmlwzaEP1iNi2Lyes318JKGVpu1i66oiga\nX7548fzD9965uo66Gm09nS+mi8X+k2efd27QgkNyptAhgNakDSClmOLYj0Q6AXfdZizjtKo/+vJX\nP/3eD3/79/768vWbg/ffu/jhj4ZNp6uCRRAUk4qAg6hR1OT4+Eeffb4cRtGFqZo3T55/9atfJyAG\neO/Rw0U1f/H5y5dPX162fWOKDz548P7790SS0hhi3GxXl1dXn3z2eLW+WswPtSEGUIYUmapqHjx4\n+P6HH95/dPb0xdPri8vFrMFvfUNrvby+GV2/WV//yq/80u/+lV8qLLgAKQJyKiuFCL6D+WKai0ff\neW0taQ4xqTv0jQATURIUkLcQkyyACHkxANnd+XZHnD99TUoSZ18FQBBEgQx4QW0KEa1sociAkNWF\nJFComRkAE0tKybmAiBmrUhgjgrdYpAw/1ndl012Uvxup5QCU52PDMORwLyJaGefDMIzOh1xLjc6z\nACktkFiABZQ2+b8iyNmd7LYao9t5493UOvc9u6FxSrtvua3Ysr5DXlTnmR7eSuoBQCFUJYUsAGqH\nWXS7nCdd8n5345i5LNEYUWOYUhFTNJ6mUhSenMMChMgqpZDQOReC+GcXYbUyzcH2xRssygDg0XMa\nWEZeXjvQy6C89xZxOp1CbVeDJCyJKHISQTd6BrG2YOZhGAShLKsMv80R6RYfD7MZGAVu+ILqrpVS\nAglgNpvF6EcRTQowSeKh7WLsVhfn+rAwgpBcoWiU5MbBWMUC8rYIJyHeeqSZogTSCFqhzVToxcHh\n/cNZ1V3sU4/hIYtbj+tyMTu/vKgJsth5LhfyOOro+CS/4X3f54ywXq9zoprMpterpcd074OHQRgL\n07Gbnu7348DMiIUuSkDsYp9SEFN6QCkNQxolsqTS6iSy7dpqOiOQEGNyY+9GgIRa7divGaKWF0WI\nmEFxSqm6rsdxzMY8bdsO3dYoRSgCBAB5Uhd86n3MDbWI3KWffBazRFVKiSXxLajI38INtdbGYra8\n0ERKKU06w4HynuMuseVQm+GhcLtuLcuyKG1KiQXyLVqtVpeXl69fvxbIenGTtm3p6mqz2czmG0FY\nLq8nk8l/7fd+7/T4+O//x//7Fy9eNEV5c7MqTo4FQXYLZkJkAAUgeQSXU8vu3MtOdDL3Ovle7UZn\nSgEjKLobtd0N6OAWVgu3+9t8cZRS8FbJDLdNUs52+BbAAREzyQhup3a7rJalgwDuqoeIuCPkKhQU\nq7Uu66qqIOXMp3I3xswcGbRY1Iq0gCim0hSScFgO67Bd3qyr6exksfjwSw9fvHiBqHvXb7vQDoOP\nEhNcXq05bHyQrvdnD+41s+JyeWVKNZ11LOHevTNEur5ejhAQVIhDUVg/ht/85V+waGpT+H40SD/8\nJ/80Rm/r0vkkmqb7+zHh9XLVh4RVvR76T1++Kqrp/OBoM0Tv4vsP3n/6+nk9WTCjEjk53DucNk1R\nHuztz2f65mq4Xt0sr68vby6rYN55dP/+g9Nvf+ejrh2UMUlUTBKDJIGTo9P33r3XzMuTk4/m871h\nGH7ygx//5Cc/eXj/6MMPPzw5Pjo+PjQE23Vqu+3+/qwpFAogQlHa4+PjkBJajaiMKROPRIpBQBBR\nUCuNqAgQMcQktJupwu2GMDe1rDhP2BARckRGMDavZJRQ/gaVS6i2Hylj7wAoiR9dCuzFZ+7drve6\nrXUAIAMB8t92XXc7sWAAkJ08WsrxJX/L2wvOtxUZCOku5OVQlevU3ArcJbOcwGLwChMqfHs1tQu7\nWt8NSO4WablgvQsXKaU8qrm7BXcowS9wdyyyY45TVsPO2d0Yg29BgXJW45RASJAlsSbFcSfMaozp\n+qEoiugDIfrRKaRJ3Vhtt0NkZENJUrSFBlRGFe89eJgD/V6pVYS9YZ6I3Ag+wnY7EOlcYOR1F2mV\nF8qIgAjGFFpb50LXjnVVGtjB7QiQY4oxkoDWejKZ9O1mSLudccbHDzevYdhqZEgpxrHU5Am898Yq\nEEz5vgvHGCOCUaS1RmWUsYBkjAUzCQnaDrSyP/rB9yb+RrcXVtrIw5CGh1/+0qefflwpVepd2xpC\nmM/ny+UyV+f5w2LmPKyr61oZvW63y3bNiPNKv7y8uFheFZ9NvMSyaYrSamVaHyTJdtxEF0oKq3aT\n8tovRkN4tJgvyiZt+mrSqCQpBVBUUuUVLPb2duzX3JRlhWxjTDYTKssys68zGNR7X1odnFMEnL14\nEriYunbwPIYQcjmTc2nu6AUg59vcXMjtGj/G+OMf//iOb2RRkQKjlNaaI+/we0R3CD1EzPlyGIaq\nqjLEPDdqWf3EFmVZlkg7DKsxBlABQCZG3JVm2ppf+IVfWq+XZVl+97vf/fGf/eBnP/7R6eFRHIfZ\ndJKqMoWY++VckwJAdDt4T7oV17r7XxEhyFJyO1A1KuIEqHeas7nkVG95ROFblXLe0d6NIu/Kw1xe\n5zt/9y230xm4i2uESEgAgggMQITAKCIsApyVJwUZx+hLsSUToqAgATKLpFTXdZKoEBQjJsQoEBid\ncBfun57wFHRV2I/Kzo/L7aZQfO94T5AQcH+/6rphOtnTqt6uNgcHB1VVHx4eN5OZMhBjpATM3Pft\nex++F3za9p0wjqPvtu3JbH79+uqv/e5/5dnnT3/z137zR3/2w8tnz5Mbp9Opcj4ppZpaG/CJWxdX\nPq1d+Cf//PfVbOKJXr54eXT68F//1/8NBVSgwpBCNwxdzzEqpKEfHl+/csM4aWao6GBvdnq2j4im\ntCHGm9XKGFPWk6KcaFt4z5dXN9HH2WJWNeRCX9r08N7huw9++2tf++Dm6pqZf+2XPxIATMBhLFEq\nhQqh7R0UxWQCJycnuagCACH0IaJCEY4xiSQQzpkDEUUREiHsPGBEIGs75coMkEAYYZeNEBFIC6KQ\nSpAywV9rrY2q6ymAlNqU1hikSd2QkNKISsUYNVFd19niK0t010UZY8z6p/PZ7Ohom/eUmROS7/Xh\n4eFyuZS3kEE5e83n87x8zSOujJ5KKWVG+Xq9BoD8+zzhjzHmRZp3ox9brTBf2LtnzjC5uw4sYxkA\nIISAoPJX5nIzs2vvvveOW5JXrWDUte/TLdb0DrNqKbnOpZQyxwERS0ElamCXpVnzXwEAEgonndgl\nVzKKEmO0c1FKfSOhJwgCCjQhZCytC8GF8dHBwfHxMRudPNzcxOvr63pxCEhlhcOgq6pClVNR0Fpr\na3AHo8+/VFEUIfTDMDpXWgJjYNpMog/5bdFIRWHdbRDWWsfgd6NRN9QEViOklNxIDWpFPp8TRNhZ\nGnKMHCBp0GSqDIoWEa2NqWtO4D1MZtPn3jciIQRNAIIAVBQVKp1STLgbpd51CFrr/IHmFJtXfW3b\n9uMwQtS19SzLft36gaaFntW9ay/GzaKea4VuHIBRTEoAjt2IHFPUWuvSInMfXEnaKGy7zggmDqIo\naXQp6arQdxujXLDjW6gBIsrnJtc+KSWvSVJSBAKUUooJBh+2m27Tj3Vd5xOWh9d52pjZ1xkseNtN\nQs5GX/rSl4yhaVVWtSlIA/IORIQq11N3BdTdeyQifd9nhF4uf0IItjApJQFk5n4Ig9tphBij+77P\nT5WN1ZvJTFvT9/3XvvaNdrtezBZ/+2//7b/zv/xf/X/+n//Zl95799mzF5CicNpFfcjGoDKfNIgo\nt8I8d9l0h4YCfKvRgVzjknyhCXQ3o7/Dqv6FBzMr9edEuvJvFovFX8hhuyOeOQq4k0++A00RYIwR\nWe7wsiACiM1sCgTAwjFyTAAMcScirsmgImVUYYwpCquLUpchiIn22evnjv3BvUNR5LoNuy55F2Ly\nETTZ66tlc382KaeD8tdX674bheLF8nK238wW89MHR/fiycePP0UUlojILB6AQwicwv3Tgx987wd/\n7dd/89Xzlx//9OPU9ZXRRwfH18t1c3ggqG7W2/Xot31/sVx/fv4m2WLdD0O/+spXv/H5k+f/23/v\nf0cA/Wbr3VIrBYmHrms3Kz8OebtwddNpZf2kss4qhUUsBVHYbdbbELz3Y93MjSmqkrYhde3NcrVp\nJlVwrcHUNLP7JweN0U+ePPmTP/rjhw8ffvj+aXXQdK1q16tJXTZV5QgQwVaWiHyKBWIIISXRChiE\nU4rskQUl7Zgo2qAWIsrGJZIYb5WcQIRvaxEGUYACNDhPRIIx8w1BgRHQwl0aNeCAZIkMkgEgUKTA\nR+dC0ETT6bQsS2ZOIYoIsmTRhBBCVZZ93xdFwRy1JkCx1vZ9/+jRo9evX/Nb5MIcyu+IRymlW0OG\nBABHR0dE9PLly7uuJaPy8mV0zrlxmNTW6B0yO9dVdyIOeGsmlFNdXpwo2vVz+TXM5/P1ep3vVMYZ\nvp3YSKu95ggU5Tsobwmq5go1x2IAyDGn7/vCNjmO5UXsZDLJr3nX+RFl6C8zN9PpvQcwqfaN0pXB\nob8xBV+sl22I3/rWt5AopjgMst6s+qGb7B8KoLUwnRprIAmIWGZWipTRORQYAzGAUqqqquCFGdwg\nltBYqKqq7/ux79q2V4AxFIawruuqKFcrvLm+6vs+N6OFJ4MAHIQDsCICpRFAELMA4u5T8syWEEWs\ntdqawCAi2oAbgAw8fPjo95fLwsZaEBRVZcMRAbGua+67u0gbY8ylRjY1zccgZ/Hdvtkqq/hye7Pp\n+2gAS+XcYC2oojTR2L0mMrRhIyzaoCBIikf3z66urjSpw8UexsiDE8LF/r6NqVaGUwgoQWPv+tl8\nfquQcdt/3B2g3J3k0a2I7PSdlBmGIWcjZhbYUQqMMWVdj+N49/UxRluWMaW8/8itCaHKlVTObSJx\nAEFKoAwg+wzxtOUOLwvAt4xRZUz0PsY4dF3Gq6aUOEbvfdeDiCApABhdukuuANC27Wq1Oj8/X+wf\nNU1TlHVZV/fu3Xvx4sV3f/WXn37+5D/4u//+v/zDP3zvvffOz98UxhLq7PGFOwVElVdcecjAIjvs\n7G0TE2PE204l5xUUYiF6y/4836v8ocpbiO27R0qJbtc8eEtCuuuN4K2nyr/Jlt75YUjd9VUIEGME\n/gIrgSxCqNfLXC+TgDXGWqMEYvSlLZBIAHznXO9AETMHn/Yme5R4v5iCEcWUSGbGXoXxy++/i8ps\nW9f3ScNak9Gqmtbs9DCOw2J/6loXY3TOPX/+3IX+3r2zYeiHYSxK067bxd60tEUa/HzvYDaZX7y5\nvPjks77rli9e/dqv/Oqnn35WTBvoR0S1GobL7fbyZvPs5avP3rye3TuOfbfYP/2Xf/qnf/JH35tN\n5+vVan+2AObNan21vFpvljEGAo5BYuj6NhRFJanRhUWSwpVEtO27xBA5rNdL0ldV1cQkw+AF/GKv\nqEscx8G5TVXa6aSe1RXH8eri+vzV8zhs7t07s1ZXhbKVAYQI0HsYhkEbRUk0Uu9iURRJPOSASZoE\nUIhSEsFIOxFFEOEYITevGd6SOCuoAmFGqAhhJglprQUgcWJJITKDqN20T0KIIghEKMycisoqxVqp\nPMf23qcQ89nIJR3d7qhxx7wWwN3kLc9h7tYz+Q/zzkbdPiELICIpIqLpfKa1vrq51lpnVW/SCmi3\n1ynryo0FJp+LObqVU8lVab7Id23Q3Shbbr3+chGZB4D5XuQm6e2ts0pqs1rnr8nDpYz3y5flDhuV\nf7QcVa2ti6IYhiE3jkdHR23bdl2Xvz7X0DnuD8OgTdkPT4qimJTajavpzC6HjdiiqqoYQqSotC6K\nYjrlvT01joAEkwmMA2TgZFmWiHkoA8xgLeS7W5Z1DDCOwbmgSSsirclaG9yYxhRCFE7HB/ukICQv\nzBITJGZmDUzAwl4TCAHHkC0emNPbYYSZo8QYScNOxYdzU6YgBECEk9OTj7717Xs2zNK2wKGZ2q1r\n986OD44PCkkGIY+UhmEYhuHs7Oz6+jpH9bZts61tPiRj8tRo9ypCaUb2TtH5J5+PBdlZxVZt49AP\nbtWvOYoCQaFC6VW/6cdRE2162xgzn80OmvnM1jXgrG5IeIh+RI5bdfjggf7+979/1xXtKm6tlVJ5\nUpcnuRmMYK2d1GVpCwRhgZSSACVA56P3oajqzXbV9u0YRh96F0ZbGpbUjV1KISWdUtIaUkoBJAtY\nATARKTJaa0DOkfRupUQAKaW8KMLMlUmJAe5+ReaQkia1M7oCQmREhaQUGWvL0fVuDOfnl1X5pGxq\nESyK4rNPH5+dnT178vR//j/9nz35/HMlcn5xRYIhRXU7RVOAgogMzKCtUVlu8g7IIJBTUdolS7rt\nZySHDSBERSQKduq0wCIMwsJ8K2d3m0J0lFGhApXVEjDvgPPMDXJLDQkRGSGrmeVL9QUiUTCxiEih\nDeRJHOW5PIMCRNTKIAkKGEWlLQut4y2D2BijQIlg4qgASFFVaPYhCc/qRpX05uZC1frk6KDrus3V\nzWx+EPtxdbH2rXuzbq2pRfBb3/nOD370faURWCSmvvVCabpoFtP5i9ev+n4si3q56ZvZrJiUr97c\n2G13/9+8/2d/+q8WqvzZJ5/98je/eX6zIlNer7rLIeC0SYW53rafvX7x9PWr5dCfHX3tB3/06WJx\n+D/4H/6P7j98tF5v5/P9Vrab1ZZ5x9xKKQyhD3FMUTQaoGA8Y1IxeWoVAKzbLZEuq0YpbYuqrlRR\nWGYOIY1D69x6s2kP9o+QxZp6f3FwenJIKMuba+d6W1DZFJIAohtioKrqN7JedaS0UVpBEpG6rtvW\nGyJSWimj8qIoRWZgTcra3dLehxC8CCCCvrVryWNeSQICglzWhTHGFCWihCQx+Ry4k3eQvX9iEoEE\nKDHFGBOVSRgAQkqR2e8m1bobBueDKjgJgEAEjICeRQsigUrgoiRQPkFMIFrwFq2Tn8qqbBILzJmy\nTTGK9y7GsNlsdutPBEZIICAcgy+oSMyFUiB/DrZ3t3PKENxcjiERZBNabVJKSAREnBIam5AYAbQJ\nzDEmoh3HVmJSib2P1mZdItBaaZ0BArEoCoAvcEM5EeZSUKmsGC2QmG7ZVJPJJHdXOYdprbuu2z9o\nyqpQSolE5wbrhJmLqjx58EBPp4yl0aCMsTZUJXDKSpaw7qXbbsu6qOoi+2drDc6DGGCBJFFrqwvN\nzvk4FrFksEpBWdoYyxBCkIGIXExu0203N1279SnqQquAYzdaTjFGKomVSuyYmVALCkj2yr4FRAgE\nZmAIIVSodGF1UQBBCD4mW1fw6efP1ziU41XsLuuaVt1NuZgKBHCDQcxDWh/CZrP55je/+fLly8G7\nuq43m818Pu+6ThkSwYDpJnaqMuW0ub64ptIWZXl0dJCUWvft0A5D32OEjKKy2ixme+31WmszDMPl\nJ5+WWn9w72Hs/cdX1zNdHO8dGE1D8B74arvaXl7p3/7N37pT7LgDveTa3DmXwQt1XW+32x//+MfT\nunEuRB9G78bBu+AjA5ASRXtHB84NpjRR/BD6pELrN5NmCiBKUVkVbj2OY2BmIVRKbTYbkTQq5Zyb\n1VVRGBBJydmiEGGAHVvTGgsAUYQAo4CyhU+sWYqyAgBDUFqrlLq8vCqrKQAVRelcqutpTKKU2a62\nRVG7cZxO52PXXr15fXOz+jf+tf/q3/ybf/PlyxeFNlrr5IIAK6URdsgCYUkgiAgKggC7kIfddwO3\nu0Ur3W5Z801OIDlPCpAAsWBMQkTGliklAMI7BaD8LyGDUZGk1IpA9cMgETRpSaK1Nka7GIpaD34Q\nSc20dsNY6tIPHoiMsWVdnb+5LJsaAUZmMkZBBtuQ1kSAgKkoNXNCAUXAnHyIHBMK7/hJIN77oiq1\nNm3fV3XRDVtb6Oh8HFkRnR6cnl9dlVJWVeO6qD0czWYne1abwnu/6frLi+dnp4fL1dWkLCQln4Ky\n6sXTG0RT1rPRiU8cGLajOzg4evDOyT0qPv705/vHR9/7/T+qJlNHxc16s910qigfPnhw0a2fPn/F\nk+LJ1ZstOpkZB5EKUzXNh1/+iqaisAYEGMxi7ziJbLZbsoVBn4Lvt6Hz3f5kkbDv3M6VMYnEwKSS\n1irENrEC5fsBqqrSilN0HLEoikKr1c1VZcv6qA48zvaawGNV66urC7QAmJikH7pJc3y1gqN9FNY+\nksLUdeuiKFNKBoGESAC9MIfIDIxAYrQJzsVxREStdVVaRCWS8iI2qybnDqCuS2NMQTbGGEKK0Veo\ntC611oqoqqqyLEtjF7O5G4bZZDoMQ9+3pDGBZINw731Kgoiud9vtNoa7GTKayZSImsU+AQLz4Nzp\nw5PzVVvOD5Q1226TQTEe+XK5mtbV5dWV0doAJD9wTEdHR33fvXr9Isa47ds8EcGxK4pis9n4mKbT\nKWyh1HrddbU1SRgRJxMkSsMwxsh+0yprTEhZu4QTc4ghcus6QVWWpUbVDSMVTR+kqmo/DAKkSKHW\nm+12Mpk45w4O9h2vAhkiUrVeb1ZmMu2cq/f2xnE00wkz930vkhiURoHSYIKRo502kdNmvXlQl9fP\n1qYu2SiqCqfAzCfjOA5jV+7P2+i9C6U1oOJ80Yxuy5JMWZXNfHBpKKFLsB6GZlqvrsd5U6LA4GVR\n+loTadQaEqCPEhm0QmDQGqrKuiSMAXQKkhLpwWNljbYGFVVNrbXerG58CCn6lCIqAkqBx8AONCmr\nhhRqUTFEgmTIhJi0ssCShFOUKAyc4ZcUmBNSBLTGOODkoKzsagWTGQwJOqAU1cH8OKbVZDJFwm7b\nWRSfUfKcSKuY/OnZ4WfPPtUFRnKR3HpcmtJ0rkWkHhNPbYupDb2ZNW03nJ3cK9EQWWH//OWrZjpd\nnV/XdV1WFUVs5vXF+qIqCo2aE+wdHl6vtg8/egRaY5Ku1IR4dbM9OD6ATvsx6WEY7oAob8+F8tQF\nEXcaBDEWRTGZTOqiZuaYUowxsiQRQWLCJBKSD8Exx+yWwQyJY4guL59SCiSQUgjC3vvjo1NSXCpj\nC1UZqxRmobpxHHO6yljtnaMXoogUdZUhEogYOANqgh/Huq5JK2buBrdabobeCeqxH72PQGl5dR18\nur5a7h0s9vb2fvO7v/HXf++//sknnzx48CCyzypefd/v7y0Sg+xc2EREkIRAWIAJARCUJkR9qzJy\nW3nxbTsFyAzMyuis8oKIpizyTCYvjektitUumRGgYkApTEFCVlcS2JKJMXJMptChT009TZCKxuZu\nVeVRnFIM0vY9Wt0NvdKaEDUqVAicJ8nJkFKEm80GkQ1SVKrUBpQigS+2TUrl4oMBkjAzV01pbHYI\nZBkhuUSBSlUZZZJrZ+VkvrdYrrdt32GMR/Ppth3ne4u95v5ys7xeXpdan52cLg73Xl9duG6c11PP\naX9/2nUdAEnX++3ws88f79Wz0/fenVAVTEHTBUR4+P4HHvhnTz6/HNsf/NHPlj78l3/vd7//0x+/\nvHq+dzC9vnn927/9GwxcVPpH3//47PRh69qinN97UJib8uIyiXfTvcPD45Pl+aUlMqYoqsKaUmg3\nnsoU6XyqrXF1U84mMyK6Xq0vr9fDMMxm836MT569Ksvy+Pj48OAwzJNL7CJoi0CmqGeb3s2mxdgD\noW3qWRrWtm7iuNlsNoUCRAYGASBBZiQhBhn6PsluMJW77wQ7Ml+M3pZFJp4DQFEUmlS2pN2tUpCU\nUlbpOxBNYe3BwcH6Znl3Metp7aMjUJFTcJ6UqYo6CafASVihIqUU6iSMAkopTAwsLvjej1HYR2/L\nsh+7siiGoZvNZsrQ3vHhtu9MoTXi0f683axzPzF6V9f1fD6dTCYhJAax1tqq1GqHewJOTqvamix4\nP51Otd65eqfbH4qIyrrKhiwxMuqCkQwpRhjabnaw9+DRQ2WNVTpwQhZlTRjdfH+v37ZVVVVf+ert\nuxdDCJNJ3XWdMcoYo41i5nHsY4yIEmN04+j7L+aQ09msmUxO7t9TSnVDD0ZprUGRobLM5j2eT8rF\n1eW5d84qqqpiPp999Zd+abnZVgvfxbCN2jNMTFEXtJgACTQF9l0xjIYRBMAFBk4psbYFZYlIBQpB\nGdQGUMCHUREYY8hQWZbJGKO0D2O73oQ4JtcLZK0KbQrDAUmKhMRKkTaKWDMIR5GUotxi6WUHJkQF\npEVpRsjjUyEQYUTSFkbPNCnHLQ+KlZAgDttWEg9hnE8nzLztWlTUzJrt0K/7jTFGJSOEYMhBjChF\nZZXEYtp0rnM+BO/dMPYhLC9uxmGYNDPofBJXRKrF1FRMZotKFTrhq6cvq6owoG+ultH586vrQptE\nPPTt6dHx4vRkGIfXF5ez6UJnq2y8BfXfgUTzlcgNU24LJpNJ0zQc+IteGDAyJ4EIQkTAmHwi0imJ\nAkVCedK0e8sQ8S0frXEcjUXFwBLi6ACYUHLrkECcc123W6/lb5lMJn9h+Z+z0d50miM+4Q6BQ0SS\nf49KEFNKq9WqbdtuaNu2/UfP/tGnn3769a997enTp6vVzYMHDwiwtMWkqlNK3qP3Xna6pUAEYRgB\nKAMbdlAWRBEhpVgyaJ3vcoyIuL6/e81yC8HIk42cA/gW9qqUQo1JfErJGqOY3BAxgUGdc/+mdaa0\n1zeXzazJxmXWWiAZwtgY3fctKGqaSTf0RVUapYwurDE77+vEWmuradIcEkGhtFLKkjLGWNp9ysys\nrWHmqqmVMevtpiyMxGCNMqYgpbpxWOzvtf1Y1tXjTz+/r1XgRFoll957+IiI+m4wRRkZUgoWpSBQ\nhSpNWZOZ2+pqfbO/t+9inJWT1+dvLOpiOq/q2ZOLcznVgfFm7B+d3D+/Op9O572Sl5cXem+6fHKx\nCuErv/iVpW/7NOzPZ6RSCupgfzL4laUporTd5v69kxCgbamp9u+flagkYYh++ODhR5JCjOyii+F2\nS0fkvY9pR6fTamLsom72i6KY7z9sjzKpArKdNJG+vh68356dTd999x0AWG36qiqtMWUNmzU8f7IZ\nXT+6HqKra+MChiBABEiAIpJYWFAYQARI0d1ScIdGYU4QAEApU5hSKx0gMrMkiMyUMkwS8/guxhgh\nImJhbIzJkpBQjJz3Q8207jbbKFxoowubhBAgOBdSUqAAQWWdYyCODMwsqTQmuy5ZQ6U23RirUitd\naiI3xKYyCsrTw/3rNy+q0lCS6+trFGia+f37D7u+z5yNzXJTFMUYfAoppVRNSgUYRjf03WxSo9bR\nub4fBh/y5jUPM0MIPkal1GQyqao+Q/VCSKgIWEir4Pyz558H51GRJhU5cUykFQEe9yfL65sYkzX1\ndtuVZencUJYlAHvvlc4Ytoxu8PnGZb6KAmXUjiwRUlwuVz7dKnPeml/k5tIY03XDjbSbm+t5QTGy\nwrAoi1//9d+sTk6drQbQzEikq4rqEgoNiaExkAASUmJIAApIJSDZwbuVBs2AgsHq4AmE4ugCUUoF\nEWVMR0LlQx1GJxCTI06QWby5zJ1MFkRWGIk0QkAkZIkxMGNKzCIZEIMopADV7Qoge6tThmpCWcKD\nBw8eTnUsYWpGSzOA3seexQvHLM4yPzoSBFDQef/eB1+5ubkBg7VSyqqb1TICVNaEwTfW6n4IY5TI\nVlQSGbxzm6FfdoiY+iApgq6iuGZhhpt1Sdq3fa1tYWx2OXnx9Flh7Hw+X69WyNI0TRQ+Pjv1GZEI\nt2SFvG+8Ldt3+0C8BXRZazmlWxlijiklAR9jSBwS7x0ccojOORQIbgclkFscWn4Q/jlpHGZhZMry\nxburCt57xi+k6nLlnu/A3evMfxhjZEZtjY9hHEfSYK3NgJZhGPrRsSAAMkKKIgj92G2325vz6/39\n/devX4vI6empiKzW6/39/Qxk3GEId9wLUCi2LNQt4+HtJH3XTd5tZe8OAbxlq0y3akA5U959fUYq\naiEgFGaJAjtspTLK6hBijGQ0AGex5EndtG1bFEaShOQn8/pqfTWdL0yhCrRFZYZucNEZn61dAZgx\nqJHg+qZXCFopBYgCmshqY5TOl1MpJQiT2cwU9ubmBlE0iEBSqJFo23eTyWTb9k3TDD7YovDek1bd\nenvv+MQ7f/ny9cnJ2Wq5TCmkMB42k2YxGVwf284kUYH9pnUxgNa1sikkXVaXN5fWlv+P//y/uHdw\nuLpYlaQfnt5fL1cffeebVBU/f/r4R08ef+UXv7r34Pj//v/6Z7/1l78d+k1I7enZAcNgbUOS9g/m\nf/wvv//jH1Unx2cHBwdaNd6JC2MCjVJu+t34q6g0iIQYY0xJOIZBG9DEUQBQjYPeYuw17B8d26qo\np5oZxsFbW4rA5eVld9GSmRiDxgCZWhkIAs+errZrvjy/LMvyenm9qC0joKJqUilJhAmFQSgLl2Va\nD/POIOeLIw6glPHJ351tIg0QERUJE2lCQVACCRKIJABClBiZCEAobw6qSkGBdVVuNitLaLSe1bOW\nW6VUjKyQyrIWEcIsWoqYnw5YkkMClORdqnTpx5ZUXi0pozH4geO4WV9zcv3axxgXzV4MwXt/N1HM\nIILsVaEAiZRBUgIQE4d0s9qYQuetaoml1lqXhVIqMoNWJrdqikKKfd+3bWu10RkARra0NAxdXVUA\nkFK0BEkJIRNRZahVEl1S5U45jEhXVTWOY1FUxqiMIE8pAaDWtq5LIi0x3VzdaK2ZgQhIG+dcXU8Y\nGYQAGUnH6BVSVVVKmaEPRObg8HhaSLe5bNu+f/lGKeMjbLv+2ofLHlertqlnKUDQ4Ic0W6h+gN4B\nAJAGJCBDBkkyPEVAERBAZSgYTQCd211/fWuEqCxWVSWzaEbSIM4hJydgqqpCnO/PbFEQKa9UgSmC\nBABKUYAEkHcTf2RBZGS1K/d3mvEiEGNkZY2Bq6ur9tlqBt3leG2N57Q9PN27vHwNuNMimM1mLoxA\n+LPHnx8c7r9+cw6KmmndTCejS6BMUTU6xs3NZtxuvQvAQomtMnVtK1AEVNd1CAkQi7pBog9OHzx/\n/rw+ubdXTSaTifc+BNc0zfX1NUt89fIlIi43a11YbQ0G/R/8J39PTycTuAXUDcOQIXCZP8wpcUpZ\nBg0BrDFd1429y9oNIcaQ2MfoQvQxHRwde+/HYSAhP/oUUoI0ks88pCwrIqRSChBTBm+Q56RMUWo0\nVmvacWTykvP2cRfls8ZdPoh3RO4MnsmxXpDykkkppbXUtUpZ2FgRCDFIXtm8//77280mJH7/3feq\nqui67t0HD0MIuZdhqZgZ0q3hHnIIIXupCWbghghIEubgtdbKaFQUQuBbNlK72apbd2QAIJNdtiQ4\nDyyidplcEgOSiPhxjDGKRtbCMeOqMEokQ3t7i5ubq9PT008///TR0YPL6ytjjDLivD66d/jq6tXs\nYNoPg6C0Q3vv7HQcxxCSJmVIpxA5JWSuqMq4Ckg7eLGIMIg1JqQYOQNDJHDq3Rijn1ZlCIHEK5vJ\n/IZAMYPEtB5Wiszp6UFTTFLvx66rlFm/fiMpGaNm2iggGkOJShuzN50d7S1WbVdJcjHuncxWy40g\nFdP5i+Vmdu/MCcaioGbyyfnryWTyyfmrjz//NBr4+ne//Xpzdfli+MXf+nY0MFmUVsWb8/N/8Yf/\nv1/7lb/SqNIYNZtN/ugP/+xj+1lha2V0URTNtG5mk6YqTo5P8pvfdi6GAIhFUenCzhd7ymgUyOJP\nqBQAhYhX1/3FxdV0On306Mho03WACIeHp1eX7atXK+ccgGgDdV3O5/O2ixcXV5NJs7f4cDJrppMy\nhs6xn5Q6xSCQNIIIg3xxgI228hZA4A4POTVTpVS2Vy71KMBG28QRJXtzaiIkQVJolCHCsqyM0VaZ\n2Wy6P+8m04aTsKTCUI5u8/nearVqmgaA7oDROQ8y71BtChnEIXFeGS4OFi9fvyrKUkhQxBgVnOeU\nSmO/8dWv9m0fI8eR+37wIQBSXTcAYFRGJGk2nHmaChBZrNJQ1YEYtQo8hBDZeRldZmVNJpPcsjBS\nYEnAQspaK2E3QeUUiGgceuGd1NZOTZUoMA99Ow5d8Czcut5VtgijG7UZho6IoChIiHNVB5wwOnCI\nIcZYlnXO0JktIoIpCksKISGKMgBAu0FOgpQElWilhmELSPcfvjM5PFC6SEDCJEKKbFXTdAaVgRIB\nRF0uYRjF+dyQGUbglPnFKAKQF8gEolRjlAjEwqQkMQYAIcBMJhNoJEZSoEG0xuCVgJlMmkpmc5NQ\nBgFUugDxRKYoqpQCcDKEglk/V3ZE2FuQFAAklpAghpQEksB0Nr988/z03qwbLlVK3rn7Dx9cra6G\nYdg/PAnBOee2gz86Pm596F0MghyjjF6MH2MySM5zux29JGSZmlojRecVoLV2ris3+MY2TpwyWqON\nzDOyNIY4+sN6ashcD22lTeyG5eXVYrGYVDVqtdlsBjfOZrMY46/91m/pO2vhPEEKIeR53V0hnxV3\niHLqC4vFLCUJIdz1Ri5EF2JhrIhwYKsNMBNgSinFmD13d+RTpDxlSylNJpO8NypK3RSl1kQonLWr\n6YtJl9zKHGTtwpx47hYwAPDixQsiIm2cS4Dm8ePHr87fkLIhsTBm6KhSBgCiRIkJ9uTm+vqD997/\n6U9/Wtel1vr0+Hi73abcFJLALWpOJAFAWVnEL/q5v7D4uZtD3h2Cvb293AbdyZnjLQ02z0LlloR0\ni4stmLmwVpEJ3itArUzieHNzkyQenR4uN8vj0+Pr5c17773z5s2rsjBlbYvKLA7nk1nVui0qxS5M\n9pq0jrGLiCzIQikGzzEVSpNgEkEEJGSBJCwpspeQIhChIsnm2NagVkkRZ+MTTkKoCotWB06BU1VV\nhPry8lIp3bYtEdW2EFB2YgbX60JHDu16Xc8n0fn1erk4OujWG9Bq9F4S9G17vWrZFvVk+vT1+Te+\n+rXJ7OCHf/bDR2f3t3745Mcf7x9PDk72P33xtBf/6PRdsQQG7p/cW52fv3528R/+h3/3L//aXwsc\n6qb8jd/49R//6NNPP3n69MlLVHR6cu/k7LiZTY1RJmsXECFSWZaLg/3Tk9m02gshEGkRAY4ASKgA\nCREENdmm7eNnT9d+TOtN60eXhDerjTLq6OCwnlbrm9XHnz3dX+xtNpuC9MMH906OZr/wC9++ePN8\naIfYcSIO7Ak5gigUICQiJCLSmSXKIfoUJaa7gW3btojoRg8AWa9Eax28V0plaR9ERBZEVESZwKeU\nQpayLPu2WywW3vth7BdNA8gpyunp6eXlZdM04+gz2ybGKLdqdSklBKVICEckDimFFO89fPD554+1\nLYDEOTebNNvNRgGmEA8We23biqA1NWptSBVF8fDhw9evX4/9sFqtmluVlpRSHF0o3TgMoJULToFV\nWs/Kcn9vr6yqLJ1wfX1990pIQCMVVQ1FUSgS3mGs8/Is+/LlbJTfK+/9/mIPBRDMYu+0H0Jdl5l6\nISIphbxd3g3GVW4LUggpxgiMRCSMpEAY60nlfWRkZkAUY0tSgKDKyhLqTdfWzQwhpX4Vhs10Vr/3\n5a+6kPzg3ww3N1xuuO4DtC0MCDpJ3/cRitFzjAmIUWLuVpRSRV0ggDAjgyIyJIVGIMWp7J2/xdyT\n1lhoICohpSIap0gpGAdkNkpjDSyuG1ynETRoTGwANBERKYQEkYRYYrYNvgtBSBqAQggh2SQcBZyH\nqp6Q1qYokLSAB9JV3ShToI8usPfMooRV1znv2Rawt3eQmAOn5IETuhRvrtfXl9cMYq2ZzOtCG+8Y\nWApGADOpC0WqtNmEmgBgqotGWWPIoGafcAwjj6/P3wx+ODk8ev7qYr43I2uQ6Or6+vNnL379L/9l\n3Q0t30oGJImoQBkyhU4pAeXAmXxMzKwMxSgujMzAwkhAsksbuWXJ3IWc2FCEAwf0b0PO7qK2iLRt\npw2wMiGS63oiIBRAHMeRjL5LgXQrJXLHs8uPzHBWCjMY22g7DAHJNk0zn8+VLpbrDQglALk1bDWC\nQGo+n19fXV1dXYUQmuZgGIbPP/98MpnQTp8n0yC+IKIOzsEt1ly+UPpBAHAhig933RsKp+THNGYB\niGEYvPf5R7hLovTn3cOI0L1xcKsZMQ4Dc9TaphQePLjX9tv5dPbqzasvffmD5eObr37j6y/fPPeC\ndVNeb27KabUdt6DFlrZZNOW0cuyBkAAJMXlQFjXStJhSFhUEpFvZ7wygAsKirgSgmU6UNVRZa22U\nmLd6zjnXO7Zm5Oica5rpbDaPIb389NPT09OYYmUaFH5zeTGfTa9uLk/unRSVhREmk8m63/gUy6Yu\nqpKsqWez5Xozmy5WW6eLZjv4Zr7/5vLm3vFZOZ0uh64orGr0JvjDunrx9Bk28JVJEyQOw7haduvV\neHhw9rOfPu6GUYuaVnPvoO97Zq6qgkGuby5fnT8nrafT6dnZ2Ww+WSwWpS1Dklevz1+9vtyt7kjn\nvlCRyYg7Bll1WyAVXRRUh3uHe4eHi/19ZY0w/fSTn37/+z9w0delne3NHj54dHBw4LthOm0mE/jt\n3/nt//Pf/49VoXVlRDOb3SQuCSOhoAgJoAyuFxGOKaSYwo5MppQyRXm3cTSmKIrCKO1QI4nW2mqT\nO7wYI8cYU7K3HmgWSwYZvcs7sO12W1iLiNYYRSTMfbd1o6qribwlsZMPt9IYfULOfrNQVY0xBZEB\n5LrUWpdNjcjJVKRQ12Wjte1c0KRdiP318r0PvtQNjpBsWd1pWAGACKcUAYQUFqpEpbz3KSTfu+Dj\n2PV3UkOZWgC3vkck0sYQ/Qi3UkPvvPPO+fL8bmWQ9XjGcfSDX6/Xpmhuln2IO00HZp5Op3nBDACI\nu6dFxMQhxbuSElBppTAlef/9d1+9egMKYuDIwdrSGBUFtCatbQgh8jNJcVFrjv35lfzm7/5rKYkw\nCpOiwpomKkAFwUHycXDRM926SSIkTrBLohoBAXL1rZBIkxgC0qlEF3d27IAgstP5stYCslgbY4kA\nIQwsMTGEhHGU0gIaC6JzDGVmJCQUEtFIETjDJVARotLaIKgY2XMCIBFwDvq+b6bTbdePwQd0iuDF\n61feewS9XW2dc5PZrCwrN/rK1JrserUqqtKPjrSyutBaa6P3Jvub7UolwDERa5NII5VoAYAE+02v\ntZYUY4pE1N+sUzvMmulqtfUpdsuti861/b0H97brjQKMMYpwSGrVbucHe46DNkaPwacUGQWEEzBz\n8ilA4igpeh8lReej8KSqffR5nXN7EBGSiKSYgo8OOfWujzGO4+B9GAevUsyN0a7rQtrxtGJERK2V\n0QYxy2BHRZDJZah32/6s+8S3Wvc5D2WKn9pBq7msir7vhfvRpdlsP4H4GOLgQwiCKuvX+cRaa6VQ\nEZ2fn0+nUwZ59913X79+2TRNPZk45yaTBgUAOYdpJZB3TggsCCQCeXKilSYlCJrU4EbvvCAYpUkr\nYAkp+XFUt2659Of91N/eMN09cg2ttSYF6CGTbknBxc25tfaHP/vhvfunn3z+6XQ+Ccn3YTxcLOp5\ndb25Kuvq8uJCV0VpZH64eHnxcrvtQj8Skc66DIKVtkM75H2Bxp08WooxT1qMtVX0LgZeXQtC27b1\npOlcr6zhDAaPbKbNSBJIDMrLm0sUxMKcvfPw5z//+c1m25RFOw4Hp0eFq/ePj1DByrXNYhYUb4O3\nRWXLMiE209lnT18cHJ8Aqe22Ozq5t1muNuvunfsFkJrO916+fF42pefw9PmL3/md3/jolz76ySc/\nHeIw9NC3MvYqOBEu/9E//L/+m//tfwsQt9vut37rt/6Lf/77FxfnGehVm4IMFSW9fvPi4lIDgPd+\nGD0AVFVTVZVk+QCliciasigKIPQpVk396s2bFy9eimBVNn0/aq0fPXpkbbHZrMuyDMFt2xjYmdLe\nu39oAeoKtIFv/8K3/+6/v1ksrCo1k9e6IIjACZOkJCjCWdUOhAjRkooGKKEIgspHQkSicBbbzrNx\nIGy3a0RkrfN8XLJnvIAAjM7dgl+UiwFEyqpSIAowa2uPzmljANEWxeiHXUcO+q6bJwaFCmiHwqqr\npqwmlF2oQ3BjNNpG58uyWd7cIJC1KUUxpVEALvjJbMogiIQajbFJkjJKMDOYIEFC0dYaQBJS+fAT\nogNIMbLfaflrQEVKkQKGGFNV1jusj9Yxpun8ID17DSCkdYwhiQayQJJERVYWiQFQYwoJtUKRZjYN\nISQQkh1YcQweWRKIRlLKyK0bmY8y9r2gulmtgDCjMFxMWusQgiAUxgqCtury/I2flRJHNwxHDx60\nwSwTbNquM4UvOQmlCD4A+Bh8GpJjUkSkgBiASIwxVaXpLQkwAgASowkJA2cMEQMyS4qRkcn74Ich\nhBDdzr5Aa4rRoxvJlmAKU2aX5i34gSBmsvQXzVCm6xMRkQApMpl7zQyASgB8hE3XH87n2/PPUkwK\nUlnS8xevnA9azN7scBgGSakppvv7+/V08vr1y/KwnO3czji70ymlKl1+6b33nXNakBAhpMLY2haQ\n2Gh9eXmZycjjOCLRvKz3J4uDw+PgYi0SRkfF/vsffPCt73z7//3P/3NUVE4aL0k08GZ9dHr8t/7W\n39K//0e/Lwh1WbV9d7h/wCBWm9VmPXR9M50opHrSTJvJ1c312clpjFEpDCEMgwNCIu1jipFDZKVo\n026MUYmz1m8aw3i4N99ut+M4ltbGGAMSQMJbGrb3HkLSBktttLYInA0aiPVdJcV/XuqNbiWBb998\nlRHqqKlWxXa7vVs1TSYTFxILKKUSYIwxcsIMfxRBgE27baYTAIicUKnejSQgsssWmS+tlDKFZQCl\nRJTmGEMSESatB+cjgy0rZQwBjN5LYqX0bLrIiAFbVKRijDGmnb3Y7a5rp0YFADH5qqpW65v9wz1A\nfnOx2j86uL6+Pjjaf/DgXjv0L66fD7FXRv3wJz9594N3T86O62nx/OWLswf3J9PpzI2i6Utf//Lz\nF6/GOFbTahg64Vg2k2E7Rh+11lXVEFPfthFlOp+GEGLb1fWEjI4xbtzQDT0qKutaVUUvESelF765\n3p6cnCzPz1dhWEevteLoU4yFNsHQH/7Zn5VlKYWW2t647khifbB4vbxSVnkSKorr161jfvr6VTGd\nCVDv471H763bbTOdpc24vlppoqKcfPzTj93g34wXk8nMhXG7dfcX04uX5//08s3NZvnq9c18Vsjp\nB42dK2CU/n/z7/1H/73/7t8CgeDTr/2lb4gkpWUym4jI508/68ZutboZhzSbLbz323ajtK2qKsS+\nu17Vk0nf9y67JKAWESBErZKwMma+qAFIGG1RE9Fme7VY7Bcl+tACyOHR3je+8dXprDg8AIygCIDg\nvfceuRS2Q9h0awQ3nVTTprRGBTcGF4hIk4IEBAiJtVLWlIgYvE9xFzq6TScotio5iU9egSqbMtvS\n59lAjNETAYDVRil1cHw0jmOhzbZtv/LVr66WS+fGyui6LMZxZOTjs+PLy8t6Wm+326IoYoqzZpZl\nb7JXjdb6gw8+ePHixXq7mS3mnz19Icpu+z7fsrqo+m2nSa23I1FJoNabbURZ9tumqh8+fPj81XNd\n6Ms350gwKKU1VUXVuV5ELOmAcW//IAbQWoMwItZViSw9gEYMKRS2Km3RdV2hVCYyFtY6zyw6uJSY\n57P9EJGoGsauLCqltXdRIGpVrTd9VS0iR1AQogfASV1LYiAZw8ggkjhyqoqSlCKllKIUeLXdWFNm\nx3FT2MvLy6Iq276zVVnq2vVeGT16V1VV23VE1A1tNamiuMOjez/50ff/W/+Nv54Gt2x735SAxnne\nuHY9hqa+X2oom0qQrC1GD8ysaDf1UQpFABAQwRrlOAY3GmMKbTyLtTSZ1H0/hpBAIKAnZa01GnEY\nhuRGZuCYsiwZKoVsm8WBgT7xptQWkwljp5QKMe4mHLfQKp9YxUQiiHhwcPDm6U2gUqmSsudsVflx\nRcrUs4Uiy2k7xpgALaj1cq219t5Lgr3pXllXL90z59z5dkcs0wlj9JvNZu/w4PLVlUjimBRibUs2\nqfObvu3m8/lmvR26UTLgi3C5/AkZ/eLZc2F2Icxns2o60WXx4x/+CEU0melk0gVnqvL45OTJy+ev\nX5/rs0en2dixKIq2bff392OMD9T9tm339vZCCMvlcrVefv2bX338+PHDhw/bzbouy69+82vL5XKz\nHUJIL1++Ojm9pwwxCgArQ8wRFAHKanUj8oUZCWbNMuc2m83V63NjsdJWG1QCzBEk5anapmvv/Ljo\nVt836yHmQdntU7FI2ttfhBRjSIImJdx2rYhoa0cfXIichIxWyuQ1X4xRQAhubeezb50iQCmy2Ymm\nPFJTgHmHpIy52wzhW4+8GbpTQiqqatfisOSFUD4l8db9KIuGqbek9UUE2DKn03snm+2qntbvfPje\nxfWbcm6/8q0vPX78+Gp5/et/+bv/9J/+87Ozw9/5a3/5T7//J9/85jfOr98EiL13p3sPDk6Pr5c3\nry7OA8Qxhn69evToQd/3StRUK0Nqb7porzpBFEUJYIwhxDBKAkkUZbaYD8EfHywCp7bvtCnW2/UY\nImk1SNz4gZoyKEiagMjHGKJzkiJJOamKphmGoU3x4MHZZbfZbDaL/fnh5FCbyYury+cXl++8/14E\n3vRD2w2DDwLIDEYXk9pwFIkSY+QgwkiI3semnlRV1W/Gtn0hiqtZ+Ru/+osP77376Y9frm5CUzT3\nTs8u31z/p3//H/6N/+bfODycPXt6vb+/96vf/SWgtNmsbcUR/PJmXRbzqmr6blwulyEEF8Jms+l7\nubx4NQaPiJPpvJnWSqmUJHLoRkeYK02sqvrw4Pjk5GQ6nR4cHM1mk729vboprdVFYava+AAQoKkA\nAMbgdKmn+3XR4NHxbBy2BDEGD6CMVgSIIhwTAAgJg4ARowyQpHH0IWECMKiVTsxt1zKL9z4jMsYw\nLttNjMEoY6yWwM6PddWEa69Q/fIv/5Iu7Ms3r87PL5qqvApDUxbwhUcJW2VnB5NxHMexlz4dHB5k\n16JiYs7Ozm42Kyj03B7Wk0YVBcWAISbvm3pitBFBo/RsMl9d32DiRlMxrbLUTYS47rai4Pjh2WIx\nE5GY/GwyvYf3skbctt0cHhxFLxzi3C+MUZN6KpL29vZIgVGWOUqCvm/nk/lkWt9cr3xKZb3QtsxS\nCMy8WCw++s50NptltbodXILZGNN1XZJoCxr84L3XWoeQDg4OqkmVB93BJ7hVDJrP51dXN4cpKaW6\nrlPKpBTq+TRwOLp3OpnUL16+ZkgswiTtOESJCgwqFZL3ybX9tiztV7/+tQSyf3T4dBVfvLpw1VGH\naQhydbPdnzd1QQeHxavr5P3O6smaLIMiKYHEnSU5EXGKOxkXUpn1ld8xuN083I3ujTEskRF2JOHI\naBQJoHgEnTt7ITKkEiZEJJYEko21EAhQkTbOhewaRarsR3QBWMCUFbhtEvQpEUQGRpCYRG5Z24Y0\nMvjBISIwFqYUyDIvAixDNxplt6stGQJURCQpBc8kERhIq67rtDHOe21NMalDCKqwdT3ZblsCUEox\ngvd+CL53TkSm0+lquVG10UTr9fbBvfv/4//Jv6NtowKM7dBWUEWMrMIwdnGMb87f1PNi021uttfv\nffDezz/7yf0H92+2l8I8DP1PPv5xSmk229Na1fNatDge+9AlkHpaqQJnk0ZbtV61k8kEEbNHOLJk\ntz1mPjs7q2ozKSptEGKK0SMwIJZludpuMtMzi3/fbWvu9FL5VrrU+xE1KqWMttrW3rMPDABd16Ey\nzJwSMwIACQDf0YgAAARAEgDuUOOUhGNIo9uJi6idzAK6EO+w2nfq9xmFkYGCcAtnICKF5JyzSt8N\n6HLuyayLrLKcCZj5+CqNCEFH2g7tIE4wbtrlg3ce/sGf/IEpzYcfvX+xufyNv/qrl5eXq3H1a7/1\n3Zub66KpT+7fc8F//yc/ONg/msymF8urpmkOjg+asdn03YMHD7r1ZrvdLvYOXj59OTFT1LqYNlrr\n6WSau8y6rvu+74Z+7/To8uqq82M5qW9Wy2p/3q2WQoo1LdvNYr7vEamwRpuXL19C4rqeMHOKkb3v\nnUNJhbVtuxlRKkUXm3WCNFxeJKKrzSYxuJh8iCIkQIklxlgZCyAuhRAiJLHKgEgKqV33+0cL7/2k\nnNjKaks4yA//+IfI8+BtRNNt+fpq+x//vb//V3/7ryHiOA6HR/unZ/uB3fX1+eKgIovexYP5KQCt\n15v1ep1SciENw5CEN+t2s9kMw1DUzf7+/mw208owcohxMpkYY7wPWtuD/aP9/cOyLCdNpTQgQmKI\n0SNKqaE0oAwsl1LWOJ0Wox+W61Eo9K9WSglIVCiEQpwnpaCRMEUQQVDBRxTiGPNQXKPWVlljRNAm\nm8E63dib0pIhYkWYTFlMJjUJDWPnBr84WHSb7vL64nJ5rRQuDveGriWrRghElCm0i8V8EKdBm0lx\n/3hvvV6P4i9X57lCulhfjWMoyloptR62qV2BIkQUkvPrK6O1AjWpm0cH+9fLG0hiqnK1WVaTikGW\n7VJEAFkptfHbGP18PrsZ1i9evJjOmnfffdfx8PrxTyzasRs1GWt19ClGb8gohQSKo0ehENxitlfV\nxfmby9GHIYIomw9kvh13mmR866wWQnjw4MHTp08BOIOlsrrrMIz1yzob0TIzAPGt/fSHH374wx/8\nOOuuppS0tohyvb753g+/t9522pA1pSp0xGSMGnxoFpOUJIZApIpSLVdXR6cHH3zz69v1MD2arJ48\nb5rG1JNupMLYyKwthZApiWS0MIO1uiqACARQBCQCESACJZNi1nYBIkAGbcCyZubIkZkTJCIipDwy\nYTEJJHPRhZSxBhOAGIgaM5E3O1KwQokAIoIgJECIBtEQ6WFwzGCMTYhJgJMw4r37D5wFXYrlBqUF\nHCK4MDoaIlveMZ9SiMI6cV3XXddl1d+UUooqRXn0zoPzywvKCuUsjJ4ZQ2JNpIqSiKbT6cXFRVQK\ngLd+0NZu1jd7k3mMTBKFMDGH5MnoxXyfleiyqOfTZt5s2jYJv3PvkUYLYxiqWbnZrOfz+fnNG611\n27Wdb//4z/7lZDKp6/rF+fPF0fzJy89PT08vz6/v37//848/rapq2a6efP7i9P797dAnkOubNaH2\nnFabVd1MIvNqs8pUVqs17DyKEjB772fzRmvKLU4GOQhHAWjb1qeYkQt3HNimaTKkLfOBMng6xujc\nMJlPmDkJELYhQtd1gqALS8qQNpEFCBEUADAQAKTAQMggKBwTA2Q5N5zWk4wQzRCMCBwTi0hpq1y/\n3GEQci7MSoLwFlWLmX0KSdhxjFGU7P4wcRIRVVoqjGhiQdGkSNuiKIzu2pvD44Ovf+fr22H98s1z\nbOD++/d7aIXk8xeP5/N5CcXh6f73vve9B4/uv7k+DymWZXlydHZxedn50XK9Wq99igmg3WyPj08Z\n4Wq1vH/v3ounLw5PjzcX28Qgwj4kv465BNNDq7Uup83PPvsUlRqCW52/Oj07u1ze+BgghrZtl8vV\nOw+RmVGwqSoGqSb1bL7ous73XtwoCLasN22bEMvFnLV6vVxqQ+v1+uGjRxeXSyFUpLWptDIp8eid\n651SgkIcQwoRs7WzyOiciAx9SIGTl2paLxbzia2dlcX8oXPoOhc8N83s88+ffvzxp2Vpnz59cni0\nOD07uvfg7N13372XTlFjY5t224uovcVsdEeaTEgxxohKO+cYxOpiMpvWde0jr2+Wy80yxjiZTJRS\nfT8yQ1NXGtn12zcvXzRNtb+/mC8mk8pmFqEkcBH29lAAGODDL3+wHa6ev/hs77C5vD4vSr03nRRF\nEcbgvFeApqh8HxQhgjg/RheZuTRlWdQxJABBQY26asqiqEII3XW/3C6t1caaoigA2SVnlLZ1YSsL\nhKL5+P4JFerZs2d1XU8PJt4PwQ2oyZA2xhydHZ2fv3YpvLy4eOedd8bUF9ZU0zJbZbb9EHxsGmOM\n6Tb9GFxRlFabqKAuakLUoG1lF0fz+DiMYax0oUpt6iKlFCCUZWlL470f/ABKXly/ribV13/5o/39\nxc1qebNZ26ZY3bQxxcZqodT5TjhqlVzboZDRVJUNGgiKJY5dHHxKppn5xKJZlTQ/mC2XS43Ks9NW\nQxKySBYBZHE0f3mhlNJtt1ZKrDUpRVY8xMGLJ9be+8KWpAkN6bJYHB4kYirUEDyiACpr9WQx7Xxf\nTErvRzAoKNuxbVSVgKtptVm3nesCQ1Xqi4s3v/gLfxWqwl2trXfbvts/fYB799WgAqmx70KE9dA3\nseCQAECTAknjqAR2DMvFtBCBGCGEEFJERhAGIAFUCoyhGCk6SCkkyVgtTaSINKFmTAgJgZAIlSGI\nyHqn5XxLwNcIClQeDgIIoUEwhCb4xCFqbVMMfQgpkSRigWcvXm6efVLHdY09SquM7/zGdR0MAcJO\nqNv78fmrl0VR9EOXxc6VwsG7yhbt0H+0mL++vAghiQgwh+AksUJUShGBiLCmbXRWF9F7O61Pz84+\n+eQxjF10USSR0QwyBI8KTVloo/dmzarbLq9Xk1nz4sWLzz59rD9/9tlsNjs6OooSXr55cXV1NZ/P\ni6LYO1x8+umnulAF2GHoT+4d3yvP9vb2yApodjLsz/cP9g+pMEYXL1+dH5wcoBKWoAu97VZDHEHo\nZn0zDF3f93VZaq0xo71D6LruZP8wpTjGEYmJJaWQok/MRVGAojtsTB7WZVpDxjXcCcLvGLVEnD24\nRJh36shG2ZvlmkgzIIMIY5ZTQERblF8AxCXd7p9o23VEZBRqazIKLvgxxMC844hI+sJxHBGbpkG1\nczl6i70rZV3drRYBICvM7/pxQiAkrQxaRARCl1wza1btOpx7IfmVX/+VVXvz+fPPmkWNWnzUYxxE\nJzT6m7/40fd/8mfvvvvuOMZPPv1UFAnher3p3Wjq6vjsrG3bo3unTx4/vXd2dnR6dnl1U8+mq/Ua\ntWZAbewd0ByUCsKC8vrVi/nRwXKzVqa8f7j3/MWLsixTFEWoUScPKaTgnFJqFNBkFGphDD5lrCAA\nCVAEjIgxxM6NKcF0Pr1ZbobBWVt4F72LruuINDPEwBI5KI8C6RbrTEoxg1BUSnVdXxTlatUOgyNB\nLeq9B++/PO+2Wz+2w9HBwf37Z9GN/+Jf/PPvfOc7s9msbftPPv70Zrn86te+vHewGMPofDTKaq0L\noyMnFOrHoes6QBWc2MLWRakJgxvbrl+vbrbr9Ww2weCTFx4colJF0ikR86/9wpeYQQAQIQVI0SEi\nGlsVcHXj9/ZtN/bPXz1ftxe6VKvtSpVGtHgJBpRoAI0xpTG5srEsMYXEwJq0UkoDJQmgEZiTRB8D\nxyQIWutyWgFlv8SktRbm3vV56cghFkUxJvfm+ny1Xm2GrSnNOIQQR5FUENmyEGSqFVa60KqMdRt6\nB6HZn0IJl5eXYeliZFtUUCRTFxNTFcFoa5LnsQv90BGiRQM69bEdYhfEG0RBDhJGP26HbaKom7md\nlRrMZNZc3lxu2vXVsOQBehmb4/n+4vDj4bEuK1WVLExSlOXMKJOW2dM5OMUKEWqNRuPEgnMOnRjq\nU9eNHW/Sul3nEQgzS+BAPnHsQ9+GbZ86i6qeV8k7IBn6PrEAiSl0WRejHxhYREIKKnkfXUg+STRV\nEZMfwugYGDBw2KtngnEIg9YUMQWInqNPPhGjpt5t5tM5afjK177E62tE2W43RWFCSlVhGwVtBLf2\nbccFhNmkjIPXtrRK5Vo5hyaFGAXGMYtNBNxRaASSZBP03FThrTANImb2C94SV3ZxBhQiCiGKYKa7\nAiOKfOEuT4hCQEQ624z0/WCmqSjQOXez6U2xp1Axw2QyWTIIYCZ46IKICK0uTAGMSqGIQNCAGDUa\n0wRCz7lnUoN4J8EBb92gbZGiZLM6QsqjOgKIkobt2hOLgmXbvXNytPfo3vJHP2Si6ENKSYsljYkA\nERXCdr1GrSQma83+bJ9P5d0HD/WzV8/2x8XFzYW1+uXL10Rwvb6eTOpvfOObh6f7APj46SfWlp8+\n+fjhw3c++Sc/Pz4+Zubj4+Ob7fWLly+jiAZ79vC+rWzFaexDUZagwEdHqLVVx8fHxhjvvUhCFmOw\nsDaLLSIli8pYqoy11oJRLNlQ2WVVt6IoiCjGuN1um6a5g1l/QdmxJoSASllrAQ1LZJHITJAODw9R\nmWzWK0Baa0RJO/cJpXeGLomIDKnMQYs+eD8ys9o5PAkJRJ+MUnfdD9zyRe5MBfPYLc/xUvZtFM4u\nnQoJCFFAENwwglY7VyKWJBx88GFo2+7k9PArX//Kk5dP/uwH3xOTLlcX9x6crrerclo8fnx+cu/w\n2Zvzs7Ozel5frq5mzWIMXllTFYaRAqdJVV/f3GQd+Pe/9OHjjz/5xtf2GWG5vDmcH2yXPYGa1I2x\nlpmttVmRvR36Zn/+5upydrCHRJerm/2To+vLK0pQkt6bzGQ/TqvakVKAzGyVTj50m+3Y9Uqpqqr8\nGIZhGNxIWnPifujruo4MgsqNERGDizFkJ25JkTklFEDKUJFEBIIQhVl2is6jC/WkKbnWhtwYnnz2\nbLMNs4P7p2cL1w2ud9fXV+vN6u/9vf/ogw8+KIrir/yVv/Ktb3/05s3l48efkVbVpP7wvfc/+tpX\ntTGUIcKIdVnVZaVNkasBEcghwyz29uYLiSkGZ7QiVCGkEBInYJYE8uLpFTMrRUVpRJJzQ0qJtDm6\nd7a3b5+/vPhP/+H/MaTwpa9+ZdNdPX3x6enJ/jBuN30bUpiW9XQ+jT5yDGDQjyFEp1CXk6Iwpetc\nu9k+OHuAQgDUbbvt0DHI4f7B4fSADHVDN/YjUkZga0gSohc2pyfH827eutZH9+DRvf39g/PzN0fz\n/aoqELGuq6urK7K4OJzv7+8380prYmaysN/szw+mZVn6FLUx1lpGmIVwey9USikOQRFJkEKbg9PF\nV7/5YVYo6AdX1FVKaXA9KFSGbFnU8+blm5df/fbXr1Y3234TNM9OFyGET158fvjojBiFMfjRVMZa\no8lMCzg+PLm6OF+tNi76WUF1UxZDA04nEKVU3/fNXjFb1MV0Z0NuiDDucNuFUh76yX5ZGtu3XcBQ\n6gKtmtgiiUQfej+QoYgJWAIwpbAZ2sl8Vk0mXdclYUFOgCxJNHW+33Tb+Xxuy2JiLWmtxpEJJ/NJ\nVet2TdNF897DX/rwKx+27RZ1047DdD7Do6NOZL1xG5fKsqwnpYp9P47b9WYyxaLWSGiMLgpTFKA1\n9A6ykt6OdEhaUCFhlvJByjUu4J13mtq5fiilOGmilJcagiAIQjvUHGSPuGzzgUi7zZQizPhv1Q2u\nHEetAIDGsSOdJJELqpnOY4wuOO+74Nd7qvQpJZY2OkSVRXPyugETIKLEFDkaU2lVOj9gaa7adRed\nYuA72hxAJtQDACrVDq2yJkpY+2Eg3oZx7YfFYg8FIUYmBEJNJvunmLLYbDZlXSDLT3/0496Nzz97\noo9OjwCk6zsyk9nerCyL5XLlU3j64ulmsz48PCrqMoT4X/rd3/njP/6TX/+t3wjR/fjHP95025BS\n9On45AyYtFU+ep/8arOaEWptBxeUUkhy79697MTl/agAp9OKDO0kFaxubFlWpjJWa1IEWQJuEUPW\n+cjCqTno56F/9oDKWAAAUIZevXoVmV0IwUuKuNn2AHBwcNAPLrKELMBjCgDwKY7jOJnOUatsAyHC\nu0+asBsGNwx934YQNCljjLFKIR3OD+4aH9y1pUREtizzfjU71d41cwyS8aagyJACRRlvKjEpawyp\nBIIsjNm+xj0420eKj9596NEtf3bx6J2Hk4O68917X37/5z//6a//5i9//vnn0/msG9p3P3j3k48f\nH5+e3rvZIOmXr16WTcMiDx8+XG03n37+5Oz4RNviwTvvXt1cP3327KOvf/P06KQ/cpCgqWoiyrYu\nKaXt0ImmN+fnoOj5ixcBWBStX72sbSEbR0VVlmVJety0IgKo89ILkYzWZVFYUzbVBFIbXXKjL6eG\ntE4MSqmbmxUkIFDb5RqArC5LWxHoyDEyIyVjyftREEirIBA4ghAVhda6BOhHb5WZNJN6MtvbM9oW\nn3z6073940lZD2PHUR4+PNuutm/evPHeP3v23Dl3s1p+6UsffvsXvnNwdNxv3OOf/nx/bw4A/TAo\nZcqmLoqisCURlXVVlvWOts7gvfduQOHS2sJWzLxeb1erjXdBKbO3txeCI4XTadM0lS30bDKpJ7M/\n/d6P/g//l//TcnlJJR8dHXz++WNVwtHJiTJSqybFoBUqq+qqQqYYXD9sbGlIQYoSOShWVKh6Pikm\nZXBRgZrMJgACgMqQsqobOm1VIYVzA2naP9yTBDfLq5vr1fVPL/b3D+/fP6vr+tWrFxfXV0QQcGxS\nvd1uz85OrtbXrd+KSAA/mU6UwqZpfvbzn2a7ZC9x3a4/+NL7N6vr9XrtnEuCRFTXk6ZpgAWirK5u\nxnZ8/NlPt6t1VdRW2aJukBQiKqtB0XbYJonNfPIr3/3l11fnL69el3WhMJ6/eV6W5fxkP3gOLjoX\nEFgIl+sVR5nU5cnESqu5x9aNV+1ykLHl0VaqXd1MJpPWrWezGatQTs04juv+hm8tQDPF9dnrzwEA\nOUZxLowTrE2h53uzYfSb4Dft6mBvPzEoJNCkSXVDu3ewp62Z7c1I68KYyDwMQ9XUzrlm2kwmkzH4\nsiwBsZ7UiFiWpXeo9SKE9q/+7u/VTRnHFIIjO51MJrOz/TcD1K7s4rh/VFYG0Fd9ty0KY40yChIA\noCjK9ErQGoqiYNlBfDkD4UkL7QT8b0c+IkFEeNchGZOJKACcUkiEDAlIACSzenctESIIgRCAKNSM\nGpGASBh88GG7FYGyLAsbAWgcR+caIhqDN0lwlyNtTMmlOPgxY9xTSlVVWrPz1Qkh+uhL8YDQBae1\nvlhdJYUxBCU7eScfo3NDAtGaROF26CxWRoOdNl7B+Wa5f/+0HwMRJoVj8JgwL8s5+JTyPj6VZVkY\ne3h4aJTVaNU4juW0XnXbpmmu1zdkyI9h3a9Zxc9efHpzc/OVr3zln/3h/3ccfaR3z28uNn3X+3B4\neJiQxzC+++77nMBYVYAK4FBHtMLeMyMoCbEf3UZS0oaMUoCy3q5fvHgx/XKlpWSEGGTj+pQSAQNR\n23fVpLJKDz50/WjMgIgxxrKsBjcKgimsMSavkazV9x8+REUgysc0DvHyenX87PVib3+P7ODcMAwx\npaIodGGHYRCEm5sbUDtGqsQkkPKCd+h6RLDWlk1dGpvBOYPvJGYgQsJbYVm8tROs63rHRb/1K9sB\nLnF31KLJ1iESORmjOUUfd441xtqyLCttBhhTGv/gX/3hGMZy3vR+ePz0ycnZyXq9/c4v/fIf/dEf\nPTi79+LZy4ODg5/9/OcA6uNPHz95+vTw+EgX9vj4+F9973uz2ayoq4++9vXLy8vnz5/fOz27uLj4\nxjc/arfd4yefG1NAAsfeatOPfd633WyX0/ne7GBvs90WdcVuvNmsAaDv+xqzbJiQVsMwGGu1IVR0\ncXFRT5qFsSGEcfAxxr7vQ4qmLEDI+ZFZ6mrStQMAeR+LomZmAi2CLMwIyhhjSyT/BU9CABKjMkVR\nbLfb/f39dtMBymbbjS588P67StvF7P9P138HSbbl933gMdeb9LZMljdd3V3tn59n+pnxmCEIgABI\nEALXUaQocaWN3VBwnRiM0HI3uKJEYkkuJFIigiTcYDAzGPdmnu3u16+97zJdvtL7vN4cs39kzwNi\nV3viRvWNzOysiqp785zz+32/n2+y1ai7mpk0TIiB7/sxjeLIxxi7vgsAEATc7nZ+/NOf2razurz0\nlXcvz89Op1LpOGZhHHpBGIZxRGIRC+Oc+DiOGRjrYgRGYl1TRAwVWYMQu64f+GEikcqk04wCw0hk\nMilFV5ut+o2Pr3/++Wf7xwdaxgxJKGnC1oMn+XJGM6WYeY1mO5FUkqahaUocRSPbchxn3CtVVdkw\nDAzRcDi0Rw6jcS6TT6VSvXbPti0McUI3jKxGKfdpMLIsL/anpib1rN7vUypFyIQYcO7HWk4QIkVN\nCl2vQynVCpryHIcCIkys2FkqLM2kZU1TAQCSLGxtbYVxcObMmcJcOZ/Pt9ttykBCSwMNRlYUgICJ\nLIqp7/lO7CZ4IpPKYADpiBKJhiTUCkYxXxAE2XXC0WgURGFaSSZSKaIoIYmkhLh5sO0F7tAdpJW0\noSQUJkMMncAWoRIBQjExzYQgCF5khSTIpTP9oE8lJiZFRnA/HNnMA4xn0+nIJkY+EaIYi7jrdhVF\n0QytYBbiOBx73qGAIeN+5CcMQ8CSkJDjHiUqCIMIGIKkABlpskACTBinoigzyDwS1Ts1hFBkRZOT\nk4zHMQlsxxkOh5PKZAhiaEI1pw4bwzDyAQC5XC6OA5+Tkd2UaNBtHM/NVYa2JSsp12Nq0lSUZBiC\nhAlOpIDWUAQRuE6cVLGRSeSXoCgADoDrAd9HEQERAWHEZRnKIgBAZIzFMSFhQDnnXFawAiHgHAgI\nEIwFxAgmgEHCmQgxlkQMxgT9GEWIjm8TwAXARMhFxCFEBGEGhXGolcgBghRATAGkQKJIIkAMvYgw\nYGiKoYUxJW5gx5EuahJWZVXCIkdRCJJ5FfqEB0QXs+OEAUppIpEwDINzyBgDnNq2rWkaIVEscF3X\nsKLkNAUyKGJpnE7nuq5t25QzWZaRiMRQYwAQyA1F8Xy/OxwosgQ4kcayZN+nlApj1zmjApcmJkph\nGELIFUU5Ojr6p7/73woH9SrnfH5+ttes+jQMIu+FFy5+5zvfYYyev3D2eP/g7bff7nbb00ul+/ce\n/vH3/2CqNDe3uLSwsPD973//7bff3tjY4JidPr2+s7MHAc6XE+1WzUzpMXNlWbH6g96gjdFpy7EY\n46VC0Q9GKTMVBF5/NMyhjCjIvuczxlRZFgWVMCIbqYBGju9LimKmNcdxwsBPp9O240BZBhBiVXVd\nJ4qiQqEQRr6gSI1WyzRTYcQI404Qnjp7DkCcSmUd12eMyZrseV5MY9d1b9++zTmnIWGM/aIpiDiD\nnHNFUxVFjuPY9QIpqeiGSh1enipHniNLzxs/GItjYQUAQNPUwaCvKlocx6qqMsps287lcpzSwPOx\nJAQh9wJXkgRNU/zQv/DiBYxhvVnjURSTyI6HUDB6rksdUp4u1+u1hYUFQ0x4gUsoHA29QqH82ae3\nvva1b/zRH/xhsVjkTBgNrfn5xVq1df7ixQ8+vnr27MknjzcW55c8x7csx7cCAACGQrPZLhRKjXYn\nqSds256Zyem6/uDBAwiALKkQwlwuJxlKs9sURZEjzimVBDGXStu27fqhoOshYSnTCGwLyiKQhONm\no1gqAV9SEgk3joEkeaEtQIWJiI7BM5zSmCQM07LsRCLZaLQ0FUZxrKp6GEUActdxTNN0XA+GNGFq\nlEJKOIRIgAgLAkACZkgEguf4gR9xQCGEmXwhnS8dHh5DIKUT+cBz2u2OLKuKJCNJjCM/Is8beFgB\nQewABFUDH9UOfu9f/xsaE0LY2CoxtqZxCOZn51bXTpw4cSKXy5mahhAa9IfNVgPjcTgQCoJIgJIk\nKQdHzWbz49t374xGIy9woQCRAEQRp3PpwlSy59WxRFUzcfLSzGjYG1pDhFg+Z2QyqYlS+bh6mM2m\nbds2VM0wjHa7qyQy+7Xq3MxsjP38dEpRlMcPH702+ZJRTNYHzWQyaU4mOaEIIXtkBV6syapclKMo\nmJud/vzzz1AYjwZ9DnjXab/22mvHRzVV1eMgyqSzo9EocMJStuz7gQYNDwaHzV3N0CQZPdnc6Pej\nr37t9b3+IQCo23QURcVYTCXM7dr+1FT5qNfQdX3YHji+U05NutwXqAcZF/OaBYLh0CkvzHQtK/YG\nYUj0rD6ZKVarR6KkRiyKcTy5NPHJJ5+cu3BWSc3tHe6nmE65l0vl9vdaumJgQVA1yQ+GEpBKU5lW\nq9132k6kiAj3vX6imNJ1PQgCEtFHe1uvv/bqwd4el0C2lG1sdY1kstZv67qWyJgja5ApZwaj/vHh\n0frZ9X63Bzk+fe7C8ecdOS1ELmRZwbG8o0ZVT+gR9admJyBH3W43dkNBUnRTzylpEfNerwcwKC5M\neEeWp9jtXpcD0Gk3CuUCFlBlanr/2Q4SeKk00Wy3EAlXl0t+bEvJZEhVc2oyAEnRyMQQRBYgEEwm\nAeDAIlGv3bBHVkdOLq8uKApAMUjoIIhBFINUBgIOYgZcF/a6zB4MQ8/HGCNJGYxGyVRG1kQAgYAh\nVEQYwiAIRFGKCAm8EGMoCYIoyyjwiEcIhAAEEgx0HsqIMgQjIIaMiJIQ2raGKQBgaI2EdFEyMnWf\nu1zkSAwCkE3CRiuKAAUaVDUABUhVqeYO82lIMY2NqNrcNTTJiZACVTfwZVkeBLGaVvv9YafTkbBo\nmoY9cGRFjBFxiVuv1QUBhWGsjEUAEKqqKmdl33Jq7QYWZVEUBVHq9/upTHrcLWt5niiKnDPbthOJ\nBOc8IyVH/VEUBbIkjYgz/hwGlCmKgjETuv3eG2+8sbe3M7ItgPjBwcGp9ZOvv/n6vXt3ypOlVMY8\nqh4mk+bd+3fTmTTlQJAUNwhu3rlTmZv1o9Byna2dZ/tHh6+88spHH31cLEyaZrLZqc/PL7qOv5Cc\n1SRVUkAlUwqDOAo8RVO6g8762dO5TFbTDEVUGOGMMAghJRyS0CNep9fnnKsx6Q36lFIB4YF1pKqq\nrqutTm8wsnVVFkVxMLIAYAGJGeOMQwFLge8LgoREEQvKOHt4nCPCOdMEhbI4DENJUhgDgHEGOGeE\njnHqlKUSSca4gHAin8+mM7Pzc1Hoy7KY0BSIqO+HhJCxpGK8qecMfgH+GZfsCCEYIUEQQs/niIeh\nj0VBknEmlwaY1ZsNRRW5WOCQMUY8zw3jqO92BE3uO4NsOR9DCiEa2g6W5GyheO/uI8NIfvLh1Rcu\nvQIh3N/fT6Vy9XrTj6J6q7G0NBvH8dz8jG3bC/NLR0dHURRIkuK6NsbYNKcty2p0misrK/vHB5qm\n+XGQTCYJpclkst5pMcYIJwkj4blBEAQAoGw6o8pKoOrW0KEx4RgBhAoT5V6vlynkkShoSdMN/Cgk\nCCHCGIcwiCIIoSSKhBBFURhjnENKecJMGYlUvV4PYyuOaTIpUAR8ElHENHX8Ms4YYCzmHPDn3AuE\nMQ7dkBCi6zrlJJPND4aWqhmxFyMmUDEmhI1XcAAwLAqExACM8ZQAwOfFaw64gGUAEIDjXCqMMIQA\nAch39/ZbnfbVK9f8wIsjIoiYM+BHAcJMUkTIBRIzCcuyrIZ+NBqNsrl8EIeERFwACHMRiCoJnBCr\nCTTy2sDzKpVpRUurBvR9V5Sw73qUhSSKxz8Jg4BSmsnnCIOFiYmI0nQ+iwCMaVxZmt3Y204kEol8\nYnZu1rZGEQk4oVCCo8EQUGzEuqarHvPUtEzFuDCbz+bSjx+HkeCXFvK97oBDPn9qbmdnR0vrAhYZ\nceWE3LHbF1453+13Dqr7ek698OoFQRe3nz1mHHCG19ZOybpik4AJwAmcuaX5KIoCEhYnS4Zurq2t\n3bv3oN6sY4znF+fXs+csy1IlQB0nnUsOh8OTCxNNp+kQJz+ZazWbP/rgR2++/sbtu7c1RU1nU91e\ne+XE8qDXT6UNRTZUScnlcp9++mmlMkt4WCjlDg4OllaWtre355bnZ2dnW82OZVkYi0pCG7i2T+PF\nxXmAkZlNpicKuemyrEq9fof4YBBYetZ8e/297Z0tKaVIsrp5vMU1fDxonDp1yvODUKA28xNGupDN\ntzsdRrjjWRPlsu/7HnVPrq1dvXIljsNcqdhxOuWlSTf0comibmqOYw3sQUpL1AbV1IRJgvCgvq0a\nGI3Ct978Ur6Qi5Dpx4ZZqsQgMQwwiTljAEEoASAKQDJkDWfCtBm4REKAhiAMIglIjIE4Ip4rxAQg\nBAQI8lkxqReDgEZhGBOGoMIxjn1ieT5jQJIV3VQ0Q6EUwAgRGI+jrcfEDkkSWBwhgcmIS4wKlIaM\nUg45EjmgAkKYhwhyEXEBC0yQmCggoFIsD20rlU6oIorjSBQgB0A2VCAJlcmFRv1xPmtW+wdYB048\nyCSLCEOARQ6BKMAY+LIqJLMmI9wlPiFhFAqEhYQhrCAGuaapHHGAuSBKUEIxpNgQU0LO9/2YUEIj\nIKLecEAIUVVVkCUrcGVVgqrgMd91fS4yQRbSmXyrUWcC4JxDzgEAqWLm0sUXhWIx73lOs9lcX19v\nNGqrq6srKyv/4l/8i1QqWau2isW8piay2cLt2/cr0wt//v2d3/4bZ58+2VYUxbKGr736xtOnG4Ig\nplLp4XAkS+r09EwYRJQyx3Eo4Z1mNw7jg+MDWRDT6aw1HKmKHnjhzEwln80jJMiCrCiKIqkIIRrT\nmMYQg3avnU6nE4lEv9+XZTmVSo1Gg8DzFEW+Fl/zPC+VTCeTSdu2NU0BGKSSgDHkB2G30x/ZHoSi\nIAbl8gQWhDFBHEKYSaUYiRHkcRRxBhFgHEEBIkmRJIwARrqihiQSMZZFSZEEQ1eJgMdZKQLGQMZc\n4qqqjkXeoihGYawp2riuHUURFjFSkW3boiiKSVGSBM9zkumUHzjjOq+qqmZCE2QhphGlsZEwoiii\ngAIRB5EvK2KpXNh8upFOp3d2tlV1IZ/P1mo1WZJUTXYcx/XswHMuXLh05949XVdHIxtj1Gw2pqen\nu732k6eba2tLiYQhSUKv13Ndu1KZqtfrhmGMWR0T5UlFUcZ9r06nJ4qiImumkcRIVFW11xv0+33X\ndYu5fBzSgdeP49iyrHy+aFnPTdCyLPd6PRI/58BijD3PH9s+XNdNJJLjqYKQSJZVxkkymRzjLzGG\nGKMwDCilQJYJowBxhADnkDIGAEeIIzSmMDHGCWUxByCdTjcaDVlWxwqRschqbDce2y0oJV9Ij/7i\nZJyRiAAQxg1w9FzFAphuaJzTMCJRFFDKIWKSpCQ103VHlFIEAMIIQs4YEUWcTiejKBREpKgaARQi\nphqqruuiKA4sK1/Oq5LMCGm1GqapQ8BGg9H+buPM+lpPV2u144RhJE293+97QaSnsq1Om8akMjPl\nWrbjWDMzM6oqiwICkMqaMhz1ypMTAoKCIEQsEFXFTCZkWfAD10yaYRxpSFV1DQnY8VxF0Qijg9Gw\n2+9qhp5JZUEMG41qMplMJLVPr34iKDiOw3w+a9nDdq/90ksviJLy+PGTew9vXzh/ydQNJCAkCoyx\n/qhPONFMLQjDzWdb7V5bMzXDSHAE27329vb20tJSOp1GCA1G/f3DPVVXoiA8PD4ydaPe6Nca9aPq\n8UsvvNhoNZNm4rhan63MdDq9hJFQFO3O/QflqWnK4cHB4fLyaiKdAQinszk/jPtD6+yFi7Va7eOP\nP65MTm1vbp04caLZaRNKs4V8tV5bWlqCAuqPhmEcVWYr9XpVVpR0JhMGwekz6yTm1Wp9bCR6dLA/\nW5mbfvdyr92RZcVIGOfPXbh29Wq2lKOU5tIZhuHquXXP90e2RSBV0ykeK9s7W9DuiyKWVVlUFd/1\nTF1tNWqObc0W8rEfnFg9FfghVJOcwziiWBGjKEJYxAAABBACggCwIMhShjEWGkxRgOeBsamdcUYI\n8Tyk6SiKQBwBhICigEQCI6hRBjwXhBQ4jiBEQhQRQkgYsSiKxk4+xggAgAE4vuYxYEE/eN6uBs+d\njgAyhAFnHCEEOeSAC5KIRYliAYuSImkhkvrDQSKdUHWtN+pirI5X0gwCLImWZSkicxw7n02Iog4p\nDkkEMA/CAGM4sPqKqIoqTuiJTq+n6TrAiITI8R0kAMsZiVQam5E1jcfjGZYQBDFhJCKEUsoAsBw7\nlUqJsuiFgRfYBMiAcUGSVV3hiNuePbAGmqyFMQnDUJFkSZJiyh3XF3q93pjF6zhOrzdYXl78s+9+\nH0Fhe+v4b/z13/5n/+yffe3rXyGEZNJFxw7feH3pB9//aSFf1DRDlvU/+qM/WV5eZBREIXn0cOPs\n2bNPHj8dDq21tVN7uwdxTAvZ/PT8pCTI7UY7kdDTyYTvh5XpaUZBykxFQYQ4UlVVlRXOYQwiDnkQ\n+el0ulwoiorMYsIRVEQJJdK+qEAIJycqiqJks9mJiQnLsjRdcXxXURTP9QEQ8pkJQVRMM6loRhCE\nY602FjGlMWPkzt1bgJJ0IsUYIFEckRhyICIoiSLE0BoNRVmSFZVEwdzMbDGXFxBGGJi6hgVEYgog\nVxVt3HcZu6nHV0wURYPBYJyQFMcxB0wUsSRJjmcXCrlGq+HHPudxSZGNpE4YHVk9z/cZJ2EYZOJc\nd9QZDoeapo0rS3Nzc0dHR5IkGYZxcOCdWU88fPhwbm4um83Wj6udTksQkWUPKSMIyy+8cDGfz4dh\nqKpSvz8cjnqlUtkP3IPDnUuXLpmmPhz2FUUZI6Jd100mk7VabdzoCvzINE3P88blrLGQCWOcyWR6\nnS4hxHGc0Wg0dvtKkhSGEQBg7D4eu6/Gxi9FkTnnuq6NhY6UUkkS4jiOSfhFC1qSBMYEhJCiSs5g\nAMbhVZAhABkAEHIAGWNE07SQxIQQTdfHWyjLsiI3wkiE6DkQc/xN+S+Spf7yVMQ5BxwQNvYvIzhO\neWKUc8g5dZwYISAIkqJIjIEoCjzP4YgjzAmJEaAICRHjYRgigDHGQRjIWEUMU0Ax5AgBQmPb9iiO\nj4+PFEk6d+6MaeqERpTGs3Mz+Vz24GAfIja/MAsZHw6HoihGlqVDhgVYKk9ks2lNU5SRMBj2MIaU\nxAAwwmIGWb1VDz03k8mkMqlqs+HHQRx5goQlESEBOq41srVUKjUYDWuPn66dPLmcWwxin0T0waP7\nLKRLq4sIgcPDAz2pZfOZ0WigGiqlvFwo7R3scoiWVpYESXy2s7V+6uTBwYEsLRJCSqUSY2w0GkmS\n0u/3K5XKaDQihPi+7ziOZVmDwaBUKh0cHiCEsIgYATNzsxElVz7+6OXXLuqG8c1vffvpo8eirFi2\n07escmnKD0Jr1BCQmDBTvW7P9/2lpRXHcQCH/X4/jmkiobuue+PGjXHpYmCNFpYWj6rHCAHCWd8a\nJZOpoW0NRv3haGQkTEGUMrm8H0ZQEG1/2O51H9x5uLKyMhqNDg8PlxeXHj1+OD1ZKZfLw17f8lw/\nCmRdm5qp3L59GwoY+t7B4bGWSGJZkhSxMRxohpouFovF/MNH90sTZWc4NBW52azv7+9WJqckQXj1\nzbezmWJEFUkxGdV8P5AlzijwSUyBIEgQQoAxABBADABAqowwBpEAnudfcA4AiOO4Xg8ghLKkmyZW\nFAAA8D3guMA0AIAgloEWKRDG5BcBcF/oGuBY+8kIxhiKYiwgBCBgHHA+rgEgDug4OgA+p2oKogxE\nkQPEsYAFURQV23E5BrKqhRFRNUQozRULc3Ozk2V9pvLVXvupbfFee4sBVixM2LYLAOAu0009imLF\nkFSIZVmEI6olEhBypovQZaZpqiM5ZhRhLMuKLMsQ4iAIPDeIYypgSBEjAZUUUWHyxEw5DOPGTn1s\nvXBdzx5YIsIcJkVBwIIgKkoQBAwAJIkM8Fqj6bihwBgzDOPevYdvvfUWAMBxvGw2f3xcQwj87u/+\nq8nJmY8/+iyVSs3OLO/u7q6dOH28361WWwcHrUqlKElCrda6cOHFn//8/aWllb3dw+Pj2sWLLwwH\nTjKZGkP3joKj0PetoX1UP0iZKWvkGJrhWC4nPAgiFgNJUhRR4hySKCaERHEgKwrkKCIxiWIv8OMw\nEgQhkUj4vg8QnpycVFU1m816nkdpjDE0DMN1fd1MttsdVTPy+aIsqxBCgJAsy0ZCj+IgDH0Sxbls\nttcdISgAzgmLMUScIRoTFjMEoICgKCDfjs6fO2ckdAyRKIq+73Ma27EbRQFFVBRFRVTG0vM4jmVB\njoOYE64reuiFxXweCojSOKZEYfH48uLRuOeECSFYFEzTTKZSWIDtXteLw+PmESHRiRMr+/v7uq4e\nHOxls2nfd/cPdldPpExTr9VqvV7Htq3Tp0/6vl8uFznn1WpV14vV2tH+we7W1vaZM+uKInW73Ww2\nq+vaaDR0Xcd2RrlswfMcUZS7vY6u657nDYdD00xSSpdXFlVVPT4Kut1uGMamaUZRtLu7u7SwMja4\npNNpSmmlUrEsS1GU0cjWNA0C7HneGL6i6/o41pMDyjihlHDOGaOExFEUQwgVVYIQxnEIIeQMMgaH\nQ5/EkYghwgLgCHAGKCckJowiKEDIBQEVCrlCsTwajQRBchw/DEPOojGliTEWxzGlMWNMFIW/mIqe\nb4AA4JwB8gsFJOeMc0A5hwAyQRAYJ5TGAELOIAfjWDZMGeGcM0Ahh4ySOKaQj4ODGeeEUEI4QVhg\nnPq+T0LHpR0zLQyH/adPHwNOT58+2e21arXjYr4wMTHRbbcfP37wpdfe0HXdsWyE0Gg0yOQz/VF/\nZ2czlUoVCzlFVKIoVDQ5DP2RPSxPljKZDAKgWq022425hVmAQa/TMpImIxHAoNdu8SZIGAZWRACA\nmUo6I6tbr2aSqWTGRAx9fvMzw9CgAL/+ja/+4AffW1hYyOQy7XZHM9TJSklW9Tt37kxOTCfSSTNp\nXrhwrtWsV6vV2dnZqampIPAwRrl8ZjiwstmMYZjdbjcM/RdfvBTHsW2PXNfO5LJPt55iUfj5z2+8\n+qXTX/7aVze3tzjChPJ6q33y1ClNVbe2tx0/ePRk69zp9TCMfT84ODouFovH1drLL7/caLR839cM\ns9PrB0EwVsFks1mI8Mb21ttvv/3ZZ1d10/AC79r1e6+8evbchbP9fheJwsOH91dWlgFCj588WV5e\n3tjczJcKyytLH3/0iW2P9g52/dCznNH+53unTp6cXZh9tPk4iKNh4Jj5tEtDazggknTU7Q6H/anK\nVKPbPHnqxHG7dVA9np2ZtG27Vq2eXlk5PjwCjCcNM5fJv/PWVwFQpGwZcE0REoTIMeEDy3ZDgCRF\nNxKKBiQ0ZrgABEAMAABAkoDKRMoBY1iWEQNc17HjOK1Wq1qNFUkxTdM0NEUBvj+me4CxnluWZU2H\nGKueBwRBgJLAKec0jqPnVhZJkhCPKKWUUQFAEUMEICeUc4YxBjECkEFR4hAHhEWce1EMReBFMYdA\nUgCHgAGAEG512k82nu7uBpMlud3aSidjLOPydIkxxgTCGeQC4wIhcRSDGPCYUxpQDwY8CAI/cD3P\nydKs53kcAklSIhoObTrmwTqOO+iPstn8yB5FEUkmUjGNBqO+67qWP0IeVFQpnU37vh9HkRd6KTOh\nqrrvh4RRgDBhPPD8IAg4FIVHjzrf+MY3er0eIcS23WazuX76TByxFy69/L3vXS8WpgSsVo86vY7z\na7/26//23/7+f/r3/nd/8id/GgTe3v7O0tLS3OziH/7BH2maVj1uTE5Onjq13qi33nvvq73u4ODg\nYHFu3tDkbqt54cL5Z1vPUqnM6upqt9OfnpajIGYxC3ziu77nOK7je14Qh1GpXIiiqNvpc85zuZyq\nqpblYIyHQ6vb7Wq6MegPKaW6rmMshqEfhL6iKLZt65rR7HQdx0mls4SQfD4/DlgUFdF1bUkWNU2L\nAh8wJquCLIgMAgwgEjGn1I8iWRQC38ccBKGnjGPZwjAOQkmSGICSFGOMx3HFAICxlA5C2O/3xxuF\nmIRRFOm6DjAPIk78OJlOAAgkTYqGges7S6tLvUHPGoxc3xElzBHc3d2t1qvzS/M7e/Thw4eDwWC2\nMjNmBt67dy+VSJim6bnezMzMYDCglHqel8tnNra2Tp5a8wNHUcXPP38wN1fodIAsi71ePZnSASSd\nbkPTJQCY59kwnxMEIZvN+r6fz+fDIDJNU9MUQlin0+n1emEQj1WjnudNTk7mM9njw+p4rs3n877v\na5rW7XYdxxkvCMbL5/FIpZKWZXFAJUkghFD23FrBOJEkkXOO0NiYFWAsEUYgREEcKAIWxglVlCME\nCKOEMBLHmiYFvifL4vLyciqd3djYQEiQRUnQ8ZgI/4uG03PL1/jk+SQEvwgZG8OexjlVHCIAOIAY\nQIiiKGSMQogYRwjhMfUfidj3Y4QBAhBCgATIAYAcIMwkUYQCGNsORXGcN8kYY8mk2R/WKKWzc1OQ\ns2rt2LYHqiZigbfaNWswTKUSC4tzD+4/GgwG05XJDz69/tKXXkQIzMzPJE1zOBwUi0USh65rK7ri\n+E5/twN2QT6fhRBOVibuPXig6UoUhaIiRHGg67ogS4IgKJo2ajdFWa5Wj2RZnZgodbtdDQLfcvSU\nVijl9/f3v/u9P220Butn1x89eZzL5ba2NheWlk1T/+Vf/na1Wg+CwHGH2WSy2eCVSqXX66mqmkgk\njo6qiqL4vj+O/hsLRzOZTKvVikg8OT15WD32fPfVS196+eWXD4+P/6ff/5Nf+bVv3L9zX5CVM2fP\nM4D8gIQxN8w0h8gwkzvP7q+trVWmfUmSCoXSwcFRoVDodvsYi8fHx4qiTE1WGo1Gv9/PZDKZXPYn\nP3tfEvHqzBqEXE8lqtXjve9+7/XXXyNxnExlGp2OoCiSquWKpXG0OaV0+9nWb/3Wb/13/+3vZbP6\nN37pm9euXev0exMT8tCxCoXCH33nT06dOqVp2ud3b5emF7rD0fnzZw+rh5lCcf+4urK06tpDWZYe\nPX6sIKRiMXK8xUpltlR+70vvKIoZ9gO5YNBRRAWgG0mHIMd1CZQRJTGjnGMAAASAARBTwABgAEAI\nFAVQDgQAZA4ph7W6yznXNA1CKCABIeS6PrOAIKoAAcSBJCLOYRiTMOSMwzAMRSzIooQhZ4BBCDBG\nEpSoKOEYQU7HaZlgHGjNAWccYwwoBAAjUYqRGBAacubEMRZjPaZhBDgGgiRDiEVFmJiclFU1ldSg\n4Jkp03IPPXfo7HQzmYzneYTQOKI+8SnlbuSNk8ACFkAGYhj6xPGIE3Z9y7Jn5+aQCKMotF0bcCRJ\nSgxoDOOhO2j3+xhjNaERSA7rh6IoFifyQ3sIZWYYpqhJCMDRyB55dr3TymbzXhB4jq/FGuIICiJH\nUPjN37x8//79y5ff2dzcvHnj4d/+279TrzcZQ3OzS9NTD+/fe/SlL73x4z/64OV3pt//6UeU4P/i\nv/gHv/kbfy0IvePj2tTk7NMn26+88vr9+3d3dvbCgOZyuVqtsbmxDSGemJgSRXFn75lrW8lM2gsc\n7OJKZWo4HCqqXCpNpBLphJ6AAEMOJUkSRRkDGIVhp9UOwzCdTqfSWVEUGQOUUk03giAQBOnJkyeJ\ndCqVSplGcqzBFwTkeZ6q6pZlVavVycnJcV8dIK4oiqLIg8GA0phz/vTp5nDgyrIKOQiikEQx5ST0\nA9f37t252x/2UsmkqitxFMiKiEU8lgJzDlUVAAAMQxsLFsZWKozNW7duTU1NpTNJ13UQBgDwVqvh\n+Jbv+1OVSc/zIORhGNq2fe3atcFoIMsiEmAqndATpmkai4vzO3vbpVKh1Wql08mnG4+z2Ww+nz93\n/oxnO/fvPwEMvPBCkTFSKpV+/v61lZUpVZOOjg7W1tY+++yz8oTpB97JU6l6vRrHsSAYGEPHsXRd\nj+JAN1THsSRJjKJgamrC87xkMl1vcEHEcRzHcTQaDXK5wlia0e8NBQHZtk1ZnMllXN/VdT2Mw6E1\nMBL6/n57dnbeMPR6syZIIsRSREJFUcI4kLGYTCcURUYCjONY07QwDJOJ9NHRESFMVVUOuaorcRzr\nup5mydGgjwQEIUQQIEGQoBjH1MchR4yAOJfMmKZpjUYiljzPH1dEScwYfw7jYIxBiDDGYRj8hVIc\n/QVenwMKIQIAgbEDGTCEBISAKAoICQAgNoaDURIEQUQjXdcR5IAxQigGcFwq4ZzGhAKOIIRcADHh\nwGeSJHGRDAaDVDaVNBOMUMbjhKyrSta2Lde2+v3+0tISJeyjDz4slSYuXrx46/7d1dXFcdKxpinN\ndrtaO2YQFHNZLAqDQU9VVVVTJyYmXNc+OjpyHGt2foZxKgiCJAkoglEcIwH3h4ORbQmCUCgUxoDj\nIAj6wx7n1LKHq6srGOOZuel+v59IS9euX01lMwNrcOWzaqFckmU5nWUje1gulw/3j+7cuJXLZN54\n4412u80Y832fca4bxom1U1evXt3e2VlbW1tcXqo16v1+3zTNgTWanZ853D84ONpPmqmYkhMn5z65\ncnVqYnpyakoS5JFt3757b3qm0h+OJqcrP/zJT9ZPriNBvHDphU6nk0pmLMv6yU9/NjMzs7G5WZmZ\nmZqa2t/fp5wUi2XG2OqJE9li7u7t2zt7e8sriyPLKk9OiKL4+OmTRDoxNTV1eHwEED69fqY/GJZK\npXKu8Lu/+7sIoePj4wsX15aXl/+r/+ofv/bGxUQ65YVBaao8Nze38Wz7sH6UKxYWV1f2j1qianz0\nybWllcX9/YPXv/Ta3s62iJEuSjBiyYSpI3F5aubiydNnTp1cmV8BAyZrWeBzHiOGEIaiG4SapvtM\npBATQnwfYwg4A3FIoygSZTUiFCGEZQgxQCLAGMQUTE2ZrgusURRFEUZYkiQBIwiAZccAYQQRxkAQ\noB8y1/WCIMBIBLIsYIgQ5pwjDrAgCABGEEmCIDAMGGUkYnHEOcMCojEUBAlQkQCORSVE2CcwYJxL\nOGaccOAEQFGApMgkZhCCiYmUkdABcmuNmoAtScTlyiQhVhgHgopJQBFETmDLshqDWMRgOBwahgEl\nbhiGYkoTUsl1XcPVKaKUBhGJKWSU0TgilHGsICzjVD6hKKog4YyW9jxP103T1KWRFEaB6ztBECTN\nlCBhjNUgjgFChLMwjmAgiFgEAPSHI2F/f1/TxkLqaH5+slqt3717X9fMl156+Z/8k3+rqWDtxPri\nmRvzcyvtdvvxo2MMwfvv/7xSqbz5xtt/+Eff/fa3v/zwwWNRUBF0oij69NOrf+Nv/NbTJ5uTk9OO\n4230O9PT+Vw+0+u3EumEoeqaoWUL2cANNEPN5jOpRJqExPciDBGEkDM+/rjP5/PlyYnAjwAApqk7\nnu/5bjqVwRgP7WGuWOAAuJ7NAZBEcXxTeV4QBF6v1ymVChijIHDDMOxzpqoyY0xWxDAM2u1mPluW\nJR0hRGksCIKmaRhjQqOzZ063Wo10Om2aZhiGqqqM6z2CqPhR6Lp2EEcYQ9VQVUVWNM0aDhRd3d/f\nS+dSpqYf149VSa63xHqr2u93B6M+QNT27HK5rGiiCc3uYVeWxcnpCSShOI5d17EcW9bkc+fOERbv\n7OzYtq2qaqfTGS9LZUEslbICwr7vV6vVYrE4PZ05cWJVkNGPf/x+NpvO5TKZTMZxPEJIrzdYP7N+\ndHRkJrQTJ1Ycx+E8rlSm4ph6btzvd1966aUPP/xwZWXlyZNHyaQJAOv2Opqu5vPZTqczMzNz4sQK\nY+Df/bs/v3huydD0vb0DQUQcUM+3T66dtqxRImGIohiGfiajIqRQFscEWrbFRmByMjdOaWKMcE49\nz9F1vVDMDQeWIGDOKedkNOrHcSSKYkQI5RxDSAGVsABFAUMkcsw5VRQpmTJd1372bL9UnBgORxiJ\nNKJjHuDYozfu9H6xSfoF4ekvz0ZjVMdzjQOEEAAGIWaMQIjHCXbjhp+iwJCIADAIIWU0jiMGsCRB\nCCGlkSDKAAGMEZSEMWgXYyxpmqkXvGjg+z5EEhZAvV4NA3dk2QIEs7OV7e3tfm8kYsH3w51nu/PL\nK0xA9588MgyNc24mjNcXXh+NBv1RP5VI9Ho90zQI0QUJ221nqjI5O/tyr9/t9XqapgRBYBjGmCV6\nPBp95Stf6XRaDx48GK9XBoNBOp1GCC6uLNy5f6dUKhFCdFNfWF6AEB4cHN2/f/DyyxMIIcuy7M3N\nmZnpRqOVTSUvXbq0vbn5/vvvT09PT0xM7O7sq6qayeSazeby8nIUxWEYWpYVBMH83GK9Vdd0vd/v\nT0xNdrtdx/ay2Vx5cmr/8IhxXqs1+v0Bxvjd975yeHh4XK0fHR6mU9lqva4oysi2NVl7urU5USwl\n0qlisUgBF0WxNxyUSqWJ6alhr68apuVarVZr5cSJiMSD4dC27VQ2nc5kkuk0EuDnN24pqtTt9yRJ\nGg5H6+vr927cfOGFi5XK7LgUcf/hw7/2m98ijD56+OS1116zXOf7P/zzs+fOb25udnu9F158bWe/\n6Q+s82fPfv75Z7/2a7+yt/tsZqLijIaxYy9Nzwf9nhiBiyfOnF9aO7t2dnjYSGmTIJWL28MIG7Zn\nByNw1LOlZGEcAUUYhZAzImFAosCP45g5nu0HgiAohi7KiqQJSAARAaIERBGYpgShJCBAKfBc5rkB\nB0Lo+TGhUMCSqJm6rKoy5cD3YlkSZAEyBkhAIgA4pxAADCGGSEAYQcgooSSC46AJyjHCDGMIOBBE\ngnAYg5ADQVEiiDlCfhhgUREEwfdCQkAEgCzLGEaiJPlBZCbliDi9QcfUVUVVMQUcg8DyJE3mgCBJ\nLE8WFE3ttju2P4qjIJ1N+6FLIQEcEQ6wCFVJJ2HkBgEHVNYVTlm6kBERbrQ62XRaTWgI8uNm1fc9\nRZVyqZSoSIqmjgt9sqo4tqvqGgCIxKxvjSilmWQGdTq9paWVZ9s7kiQVi+UnTzYUWSuVymFAdQ28\n+OKl6nFD1xK+HyIkuQOwuDBXPe61291UKiMK4PHjJ0EQxTHtdodTU5VKZebhw4e2bc/MzDSbzYgS\nSZGDyC+U8ulsqjI3u7m5GcWxrKqj0Whra+vBw4eCJPlR2B8OShNlUZElSQKA5QpZjKFuqGEcjOyh\nLIuc0yAOn2w+zeazmqFgGSmaDDBQNBkJMJNLc8gESTCT5tDqRyQgLAaYJpJaTELXsdrNlmPZjNJy\noajKoixiRRIQYL5rh74bB75rjeIwyGczsiiYuoYh5zSO49gJbNd3/MifmCrFPOoP+xENHd9SDfnw\neG92cWpo9SxvODFdUAyx028MBp3D6t75C+tLy3Nh5A+G3Rs3P3u2s6lqYjaX3Nx6OhwOMEZGQuec\nFot53VAB5LZjVWamoygsFPKOY2cy6UTCTKWShMaSLKqa8uTp4zAMbt++OTtXESVg2UMOqCQLqirL\nsjgzM91qNQxDUxTp6PjQMHXKSLNZt6zhzMzUW5ffMExtYXEOACYIqNVqVKtHYejb9qjVbmZzGcse\n7e3vHh7u6zqQZVFSxGw+AzFYWlmEGAgSRgKMSOR4jiiLru9aziibz7Q6zURKE2UQ00hWJcrJ0BoG\nUYAEhAQoq1I2nwkiX5AwYbEoC5qhjreGlJPjWkdWJTNlYhERFjNAwtBTNXlycsL3/WQy6Xm+Y3tR\nRBBC+C9BwMaaxjiOv8B88V8kGT4HwoooJmEUBwgDWRERBowTxgkWIIAMIi6ICCI+fg1jhDFA6fMK\nviQLADLOKcYwJiEAbFygG4M/JEnRNCNhJEUsBr6PAISc2dawMjUhIlDIp63RIGkaaydWyoWyqeki\nEjmlrm2/9/Y7+Ww29P04CD3bCT0/l8kUSqV3vvze+UsXjWRi69mzbD6/d3jgBv7Kyooo4s8+u4Ex\ndhyv1xt0u31r5HQ7fdf1RyO71epsbGwghCRJ7HQ6HLLl1SVJEVudlqIo779/rVqtV6ZnTp+a3d+r\nb25s1WoNVdYAg4okj1c8fhhrRuLwuNbpDXLF0sCya41mIpVmAFZm52fnFyPC/DAmHARBZJqmHwaC\nKBPKI0IAgoIkcgj8MDASpiTLx9Wq5diqrlmOq2qGpKgMQIhF2/Uqc7PJdGrkjCamyljC1fpxMpOk\nnCytLs3MVUIS6qZmOTYDHGJk27brupl8zrJsxlir037w4JEoyhygKCRPn2z2BqNms+04jmEkbt6+\nTTmXVc0wzFar06i3DMPY3t1BSEgkUmFE2p1esVgu5guB6wkAOoPR0swc8YJBq+N0RzJBwI2mk4W4\n53QPal979fLZ+RPD7WpKywAmAStkBAGOrZEnSDISRIDg4eFhp9fudFoja2iYqFCQctlkuZRLJBLJ\nZHIMOvE8z3Uj1wVRBCAEhIz7Q4AxQAgQRZROa5m0lMnoyVRinHVLKSCEkShGkPu+H8dcEACEcOy4\nH8fQjI31jJHI9yiJIeQkilVVjWkEEKIQSZrphTTgMAI4ppByThkQRVmRgSJrAhIopaIIXMfBApJk\nIZVK6qYmqUJ/1B85w4hGgiRceunSO19++5UvvXL+0tlsIeuH3mH1MIwDKAJJkWIW66bGICOceIHr\nRz7lJCCBH/p+FNiexRGPaTRyRkZS7w66oiyqhjZVmdJMlUNwXKt6gT8YDS3XCaJIkuWYkrGxI4wD\nRVOy+SzhBHXaFiVsZmbGNJOtVqeQL5XLE81m+/Hjx6dOnbjy6a3FxcUH9+qKonluMDGjel5QLucp\nYXNzC6IotVvdM2fOzs7OrqwsdTqder2eTCZnZ2c//fTTX/7lX+ac2/ZIUqQPPvqw2Wzu7D0bWKOI\nRvuHBxQwRVNFWdl6tpPP589duLS9sweRYJp6EAUYY0VTbdcSZCGVTTU79YiHvWEzYG67X79645Pe\noDnyBlCgR42jiJHuoJfOpTL5lBdZkiaM3MFw1PU85/Bwz/cd27V0XR2j5gUBaZqiaYppmtlsNpfL\npFKJTDadzWWSyWQikdA0ZbwWhhBSFgsSVnU55lGn32SISCpsduu1xuGP3v/hcX0fisD2BjsHW9lC\nYvHEbEi8RvsYYdrrt5/tbSPEP/jo/fJUUZIQpdGjJ48Wlufz+ez+4c69e3cmJkrtdrPRajx58uiN\nN95YXl5cXFysVo9835ckwbIsAFkymez1OrOzs9lsenJyMpfL/ehHP7p8+a1er3fu3LnRaAQgSyQS\nY9Hz2traxsZGLpcRBEFRlIPD/SgKHj1+8ODB3R/84M80TeaA5PJpxmNNl+fmp5MpfWKigBAbDDpT\nUyWE+eRUZmv7qWUPfN9utWqplCGK8NnORqGYGQw7mi45rpdIagBQxxlxTlKpREwAFuD+wS5EXJKE\nwaCXTicdx/Y8VzeUTDaFMAhCL4x8QiIsomK5UJooprIyY8T1HUIihJkkC/lCNpVKKIqkavIY4zs1\nNVWpVHRd13XdMIzxiaqqmqapqir8YvwFLgWALxiUX0B1x1PU+Kkv5q2/dP6cmYuQgP5ijJGUnD2P\nAieMsTimtm33egPOYTaTHxfxhkOrUCh0u91iMQcAe+ONN9bW1p49ezYcDi3L/vrXv5lN5xzb+x9+\n79/aQ2d+ds7UzTGo33ODzadPCSHXr3/e7XafPt1uNBqZdI4Q8vDhw1qt9t57bycSqcePn3IOHcdL\nJrPJZHrQtwFHGOMoIoeHh/fuPUMYJJPJ5eVlWZZfeunl+/efvvfelww9aduu50WzsxUWg3wmv7O1\nkzSS2VTW1BPDoSWK8mhky7LabvUUWe33Rnt7B8+e7cqyev36jatXPxOwYugpjMSZmblut5fLFjzP\nEwTx6Ki+u7tPKa1Mzx4dVR3H2dnZ8bwoiqJSqYQQWF9fJ4xpmub6nqqqtUZdFLGsKsvLi5vbW5cv\nv+mHHkLAC9yHD+9PTk/U69VarTaWw4z/cOOcwLt372GMZVmen59vtTrFYjmO45dffjWVzKi6fv3G\nzVKp7PvB3t7e5OR0r98/efJ0vlSWZbXX683PLaaTqRcuXrr66b0oDFlMpsolkcNKaeLx3fsvrp8r\nJbLlVDbsO7Xt/Ysnzr114bUU0vgolCMEfA7sEAha4LPhwNl+tleeLM3Oz0mKfHL95NLy4nRlKpEw\nfJ96HhAEoKpgoiBOThoTE/lisZhMJsbRJLbtbG+32+0BIVySgKYBRQGcA9clhAAIwBg5HJMwjkPI\n2Zh2BiHknCIIxkFrkAMaxZwyTiinFHGAIRIRFrEgyUIUBQghWVUkReMYhxyEhIWEhYRaI6fV7R0c\nVYdDEAUxQogTKktAFEVrOIrj0HJGvVHPcqzV1aXpmRlFUbww+Pzzz2/cuvXo0aO9w4Pj6pGZShaL\nxUQ6BSGMKBljBCYmJjjk2Ww6nc0QGhFKc7lMvlhACA7tQbNZtxxblsV8seB6drVe63a7qVQqkUio\nqgohjKLI8/0gCLwwMAxDkgVVk5PJpKYpAABBEpBpqtPTM0EQHR4em6a5sbEhiuLCwsKNGzdqtdqL\nL569e/duKgMwxplsqtv1ZVk+ffp0IpHQNG16ehpCOBgMVFUtFArlcvncuXPPnj27fft2Op2sVo96\n/c7QtkaOPTk9PbKto+pxGEXD4TCRSOiGObLtVqtVLJVkRbt7/wEWpHavu3ewPzk94QXes70dJGKI\nYbvXNDNmz+pZ/nBgdwUFSobQGbXssPfJ9Q+q9UMKojPnTlrecGtnQ9GkTq8Vxm6+nBFVND07HcTB\n+rkzWBRSmbRuGEYykSvmEulEMpNMpBOJdFJSZUXTXN93fIdwgkSEJWymzOJEsVjOpbMJJxgphkhA\neNw4ICCMmL+1+2RhZYbjeHPnUaNzxFB48871q9c/SeeNbq8exe71m1f39rd29zZjElAWQcQmJgsX\nLp6p1Q8Hw85w1McC//HPfnj7zg1BQFNTE4yRDz74ma6ryyuL+XwWCzCdSRYKuV6vk0olAGDlcnFr\n69nm1t4LL7yws7P7ta997fDwcG5uDmP85MmTpaUl13UppaIoRxHpdrtjGbph6rqu9vqtkdV7+Ohu\ns3UkSlw35ERSOzzcO3/+TBT77U4DC+D651c73ToH8fq5UwCzgLiCAp/tb0uaGLFQUDAUmZnWVAM6\nvpXOJ/eOjgcW6Q7ba6dnkYiKE8VEOmGmzInpiZCEgixgCQMMgji0PQcKSDP1mMUjZ2S5jiBLuUI2\nmU6qumomTVmVIeYxjUb26OBwb3d3d29vb29vr35crx3Vol+McWbjcxr6mP/9i9zFL8TllNI4ooAj\nCDCJGYkZggJGImcQAjw+xs8+PyDkHHIGOR8fvxiAjjUL42bV2NUbBJE1shXZIBGtVGZyucK59TOA\nAlEU33rrrcuXL9+9excDfPb02WKxbI2cJ4+ePnm8dfHc+a995bIsioNuz7XsKAhVWdl59gww/vOf\nvq8r6vTE5K/+6l89d+4cIWQwGDXqzYW5xVdeerVRa0xNTCmS4jshJ7BZb+cyhRcvvZJO5GjMEMBv\nvXFJFpXdZ3vXr33GKahMzbz7zuWnT7YUUfv3v39XhHJlYm6qPHu4V7t47sWrn1w/2D12LN+x/ctv\nvd1udY6Pqo8fP332bHdiYuprX/vG1FSlXm+qij5Tmbtw4WK325Nlpd3q9vvDXqcnCVLghcV8rtvq\nu5aHAJ6bmZ2ZriAIJ8r5Wzc/7/c6yYRxcLB3Ym2lUC4gEdmeTQGFAoxZ3B30kplku9dxfDeVTT/d\n2nADr9ltdHsd33c77eZo2M9kUul0etQf9Hq9XC4XeAHGgut6SwtLhwdHjUZrb3vX90MEhYnJ6YnJ\nac8Pc/liNlf45JPNdDpbO6oVc0VDNTBA7//4p5lk+jd+7Zeq+8ff+MqXme9/8rMHIkCvvfBSUtUf\n370vUIQiXkhkS6ncmy++Xtupbt/fVOUk8BjxWdTqP3zw5O7dB1tbWxCCbEZKJk3Hsykn2bxRnjR0\nDWMERAwAA/vHzvGx1W4PRqOR7wdjBsHY/iGKIsYwjkEYPtfdybLACcAYqCoYL6ie+yUAF8aBEIIg\nCEDThOcrY12BkHPwC/EC4ggBEcMx6FlVdUUzBFlhSGRQZIIMBBkJckRA5EfNWtNzoiiKFFHilLk2\nCD2X0zify+RzGUWR/cBNZdKu67quOzk5yRgzTXNcAI8jsr2947quJEmpVKpUKhmG4fv+aDRKJpP9\n0WBgDZKZZDqXtlyrN+xJqjI5PZ3MJKEALdcSFZECKipiKpsy9EQykU4mU5qmS6Iy1h9FUUBIHIY+\nIREWIER8HCEmnD9/cTi0Hj58PBqNTp86MzXF4pieOnXqv/x7/+LNry/PzFYePXz89tuvIwQg5Jcu\nre3vHm5tHSwuTvf7fc/zKpXKcDi0rNHYG9ho1IvF4uHh4dOnT8MwzGQyQRBQFqmKFseUhCy/XD44\nOhaQWJleSGdzzsjv9wfHh423L79769btcqm4+eRuLpcplEtYQd1ey0gm0rnkyB6aKaU76LX7tf3D\nA0lVgm0vk8k0m+3f+o2/dev+jXqnOhz1Q98LQm9na3thYeGotp9KJGuNaqlQHo0GuWJ+a3NncnIy\npvF4j8w5C8MYYxyGoayIURwgBBIJQxCE0WgUhn67Pax3mlziMSCHx4fb25uMsfZgutlsGqb29P3H\nk5PlydnSyBpSHG/sPqKU7uwruVK6Wq2ePHny7oNb09PTMQuHo67n+1OoVG9VJRk323VBgFBAr7/+\nahiG3W57aWnp1q1bc3NzsiIeHR2trq4qinJQ2+t2u5wyQsj8/IQsy6+/8RLnfGdnZ3V11XXdcrk8\n9qgKgvDhhx+ur5/d2NgIgmA0Gs3OzoZhePbsWcaY4/QBpDOzU0+ebGMBLCwsxHEoCOK3vv314XCY\nySb6gzYHPJdPTU9P+77vewGhoSTjk6dW9/cP5ubmHNsLQxdjfu3aFd1QFxYWjo6qp07Pr6+v379/\nP5VM2/YomTRVVZYVUdOVWq2nyNr8/DwASFEkSrVUKgUAcF0fABAGkSyL2UIOQh64HhYgsYMoCudn\npzw3eh4Ixdi4RRSGoeNYbBw89QvePud0rPAe734opeNnn/eNGJAkaSwHp5SONRpflPi+2CT94vWQ\nEsbH2a9wDC9lkLMvRHoQQogEBAUAMUYYCVwR5cXlc5ouPXp8FwGCEGIc/+QnP9FUVVXVw8PDfs9W\nVSOXK21t7nzzW7/0o5/96OT6SXfkhnEgCfJUZRIA8Gxzq9vtXzx/6eDgwLadn/7oJ4srSxMTU4am\nKAI2DOPKx59yBk+unrx5+26v7cQxBwRxxBmNp6Yqek/98JP73/7m0pUrt86eW7p791iWu+VSZXt7\nb2XhZByTV18qf/rR/v/7X/32P/9n/6/Lb7954+qtv/t3/+Mf/vCHFPBCYWIwsE+ePDM5Obm1+SyV\nSlHKfvTDn77yyitvvvH2d77z3Wy28G/+9e+/8sorve4ok8knUsl+v3t81Eil0u12++TJU7btViqV\nsdJS17WZmcrdu/fiOBrXEsZxz0EQiSKWZbFUmqrVamHkb249OXv2bH/QbTSPRVH8+te//sEHP2OQ\nGLq2tLRsWVatVsuk04uLi1eu3Dq5vtTv9wVBsIajt96+fO3atbUTJx3bRghbrpdIpFqtTiKRQUgS\nRXl5OYsgrkxVbt+4e+nCBajAN19743t/8v1vfetbu8d7lanK8uLCzNTkwf7u9uPHAgJvvvJa6Hrz\n03OI8r/6S79ysLVnt4ejZmdl4STAKPLp48eP7j54ZDF04sVXbDuIFUXWYJIkI04BAH7A7V5fQjyb\nTCAkFIuGFwHbDge21e0PnMAPY8YAn5mdFwQhCKLBwKcxFUURI0QIEYAky7KoIFkCnAsIIUIheJ79\nBhECiAOIgKQATZJilAwIFUKMOMDgF1YGyiCAiigBDCGmNGKCKBtpKSeWRWioZko1fVPTAQOiIHHi\nIAlSQgwNeK6rKWGj0SGsJSgjxohtjxhjum7atj0xMfHo4caJEycPD4503ZyayiSTySAIHNuSJAki\nQCkXBGEwGIy1Rb7vA47y+bznBa1WB0EsSRJCgud543stCIJGoyELMsZCEASiII8XlJ7nBUGQTWUR\ngmOzoyQJqkoFQRDm5xatkXNi9UQkwDEAAQAASURBVKTneQ8fPtJ1/fPPnzabzf/t//FX/+W//OM3\n33zzypUraydPrK6c+Nf/+l8PBjYjqFRKi6L46NGj6elpSRJ+9OPP5uYSCwtzR0cHk5NlUZRVVaGU\ndbotALiZUtbmV46OjhcWlg73qp7nq4ruecFxrbH5ZHN1ec2yXB7Du/fvq5oxGA4JpTGN9g/3Ihox\nRpAM+1Zn92CXcuL4zlHjsNo+BIirqnrc3Hv11S/9b/6T/0UxXxYEQZJEWcS5XGZyYsIJRqXkBMSw\n1Woxxo6r9ampSr3ZOLGyJgiCIAkiF8eGX93UJEWUZTmKYwZ4TAkSoKoruqnpoQFkePPB59VWFULo\nhdbt27eXe4u5XJY67vlLpx49eqDooNrYE0Uxk0+trZ34/p99T8TY8+2p6eJh1SyWMtOzE/l8XlaV\n/rBXKudd1+WQzc2vjhy72203ms2V1aVrn1154YUX2u329evXZmdn6/Xq8vKybY8wholUyjC1jz/5\n8NSpUyLCyWQSiQgA4LmBJElXPr02MzMTRWR5eb7XG4Rh/Pjx4dJSicT00cONN9/8EmFElvHi0nIY\nxPPzlc3NTVnGYeQlEokHD+++/PLLTzcerZ1cisJ4NBrt7W2XSqV33n1TluW9vb1sNjsxURpnfxwc\nHKTSZi6fHo2sbq85HA2zOfPBgztBEHbiOJVODob9XD6bSBij0SibTfd6gyD0PDcYL3ksa+g4ThjG\nqVSKcuD6HiEx44REYS6fKZUKmmYEbswB9TwvjgnniFIKIWZfRLkDOp6NIBzbiPjYAzuekPhzL+Bz\nfDJjACHIGIBwfI7gOEz7C6HD82N8jn7xMPtLL0EIQSQIAhYYQpwBwCHGIpaF+/ceM7Q0GnQTKdn3\nw/X1dRIHd+/dTCeSr7zy2mfXbiQSiVHfjULAGHxw/9HZ9XPXrl/99re/ffPOzV6vVy6X7927NzUx\nVZ4sd3vtUr4EMPjG17557frVTDI96I8gi8rzxe3NZxjgm9fvTFWmU3rq6rVNe82dnpl+cO/u2Qtn\niks5x3E0VU0lJFNLvPmlU91O/8HdB2fPXCQRW5g98a/+myuVBfCnf/S9E8un7t58MDszc/vm/Xcu\nf/mP/uSPw4AORsNCodDtDZZWVjjnhwfHxdLEzu7+vfsPv/zlr25vbxfLE59cuTozM3P9+nXAQRSB\nfF7JZQpvfOmtu3fvJhKJVqM1GPTbzVY+m7NGg8lyWVWkn/307le+8mZ/OJieng6CUFFkL/DG9/LI\nGpy/eC4M/SByX3zpxXa7dfvuzfnF+d1nuxfWX/jsyrWpqam//uu/cf/+/anJyRcvxZZj04g6jpdO\np/d29tvNzrnz02EQPHjwIJPOnzp18smTJ6lMdqI8qet6PpvvdfpJI/nOW+9sbmzU6/XV5ZXf+a3f\n2d3dPbW6ZiaTvu/fvX2Hc/ql11/99KOPO51OStFd1/vVX/v1erWhqvrDveP5iSmgpYHlD3ujp0+3\nWs1Ow3b+9//ovw4ACKOYSGIqgwOKNREIACooKwsgJQMKAAdAlkDCkJPZvB/mIwawCAQJNJqhKIqi\nADnnBJFx4zMIAhkDxljMFEHECAFFQTEBjAHXiTHGjPEggJREsiTIAgKAP8++AXQstOOcUcAhAghh\nBjijAAAoG0ZezEC5jIismiktwbKptO96ugoGEGIOAIdJDeiSsrg0tbvfJ4SRKFBUsdWsT08tjEaW\nphoISouLy6qipdN5jLHvhxA6juMMh0NZFhVF0nU9k02bifR4bYcxFkVZVdUoJPlMfjAYKorCKLAF\nOaEn4iDGACMoIIBEUQYMypKKMTY0EwFg23bguaIoIixRzgRBVBWVcy4cHx+nUqlxE6VUKv/0pz89\ne3YxlUp9+umnigJu3ry5tLSwvb25trY2soZLS8u3b2wmk0lFkTDG6XRaVvBrr50gJBqX7Le3t19/\n/fVk8vytW7f29/dXVhbr9Xoch4uLyzvP9gQkb2xvTZUqyWTq+Pg4JPQnP/3Zi5de+j/9H/7Pn169\nuruzhRGj1L24eHZ/f//JxmPXc4LIp4AuLM1/8MH7J0+vXbv+8cuvvRjEEWGxExE3GL382guPHm4M\nGt3Tp08WCnlK4s3dzUwydfWzK7pqzM0uhWE8N7vUaXd93x+MhqvLJyQsQAgNw/B/EXEYkxAibpqm\nrqsIIUmShsPh3t5utXW8vbdl5kzIWHGq+IJ4PoiDgdVdWF748JOfdvrdqZlCImv0Op3Pfn6z1T0G\nOIYQpDPm1rOnmUyi2jgql8u1pu8F/nA4nJmfmVuocM4/v3Vz/PE2MztNKV1YWLh37161WjV1Q5Kk\n9fX1ZrOpKEq/33/nnXeuX79++vRpz/NOnDm7tbUlqUoQBO1Wd3V19aWXXvrss8/m5xd93w/DWNf1\nEyemoig6PDz8lV/5Kz/+8Y9fePHSYNjq93vjPtPEZPHgcK9SqUxOThp64gc/+MF7713+0Y9+omla\nHMeaLidTie9+94+z2Wy5XO50WoeHh67rvvHGG9lcmnPuucHa2srnn3+ezxsIwfn52cFgeHhQ03U9\nk8lQSkVJSGdSg/5QENDk5OTx8THGKc75mPIwlofFrj8aDTmgGEMBQ1kWJU2dmqoc7lcpZZzEqipy\nJlCCBADHcwylMePkC4PRF4K653sXCH/x7xhVx/6y3O4XS040FuZ9sSt6/j4AQigAAMb/FQI8fisA\nGMIYQgEAxCighEHAGQOYwXy+GAQRYzyTzjLg7+7up1OGrpm5XOHq1auSqM5U5vbYUeDTOOJ3bt29\n/M5b1tA+2Ds0NfPiuYv7R/uaokOOnjx6ohlaMpFutupPvCdnTp999uwZgPTi2dP7uwf5XBECkUTs\n9o27iqK8/OKJz67d/JsLy/v7h+l0uljKXjx3aXNje231JIno7s5+uTw5OZFvNTq97qh21Pm//qPf\nvnPz7qBrP9vcX5yfe/pwk0a02+qW8hPtQY8xjpE0P1dpNpsPHjw6derUkydPMpkc53gwGPW6w8r0\nzK2bt48O66urS91Oc2lp6dmzZydPnq5Wq57nGYYhCMLy8vIrr7zy8Scfjn+3nU7rq197gzEahn6j\n0ZiamqpWj86ePdvrd3RDbTSPm836+vppXdcePrpXKpVu3/n80qUX251Wt9v+1re+9eGHH/77f//v\nXdd96aWXXnnpJd00Hz9+3Bv0E4kEEgXP85qNRjabjUOSzuS+94MfyKKCsXT7xs1vfvOb777zZVmQ\n3//RT1cWVzcebzZq9b//d/7+1StXRIghAwBwSRKNhHHixGq33Z6ZqWiaVq3WMqoREyrq8s1PPqcU\nLC+dAG4AJL1W263VaoNu/+HmtpxO+24giGLIQL3a4xglTCOhibICJADCiHkBAYJEMWAMhAREEQ9I\nTH0EMTJNWRAAgsAwZMBkzgGJQRwDFgMSg5hxSgFCAECAAKAcjDccIoIxiaMgxAiISBxfvZwyRijg\nHEFOn+frIUmSGOQIEAEgRVVjNSFCnUTEsT0IEY2JKqmQAxGLAhI1VaQxUGRxbnbWtncpjJwgQgID\nfhiGYa3aUFVdkpSpyWnPCzASe93e3l49m9WTyZSmGpTFrusDgFRVzeSy9Xo9juNEIuF5XrfTR0hQ\nVVWSZN8LfRIahjFGGSmKYhrJ2nFDwMxxPITccXtMkSTG2DgfjqHnO0LOESEEcQ58P7h9+84nn3w6\nMTFRLBYXFxePjo66vfagDiRJsO2RqsqDQQ8A1mo1wghcunQpk8ns7++PsTSDwQAh1Gw2LXuYL2Q/\nvfKx5zkvvfRCImEWi8W5ublasyGKYqfTyefzhXwpjingaG/v4MTq2t/5O//JX/3VX9vc3Tl99lwy\nmZ5fWPr6N78xtEb3Hz7oDweu76SyKc1Qrl6/ks4m/Mgeev32oGW5XcvrWV5vY/fJwO4ms+bC0lyr\n27h55/P+sNPpNbuD7sUXLxXLhXa3VWvWrt+80Wy3eoO+IAiyLHth4IUeg8wLAwZBRKNGq7X17Flv\n2LNcJyQxEvHAGt57+OD6zc8gBnsHO41OrVjOmSkdYpZIG45n7ewfTkwVA+I5vpUrZiuzuWanwSAp\nFLOe53i+gzCYmZlmjBSLeYzh3NxMLpcNQv9HP/5hNpsJQk/XtXK51O/3BAG7rgMAv3DhPMbo/v17\nqVRSlARNV9vt1sREWZalbDZz//69zc1N3/fLpclarfH48dONjS1NMzAWAUDtVmdudn5zo+o6XhSR\narWuacaf/MmVl19+qVjMnz59kpCoXC7qusYYPTw8GAx75y+cfbrx+NKlCwCwUqlg26PDw/1Tp0/E\nJApCX9fVxcX5ixfPM0aOjg4ODvaiODg82m+1g8rMlChiQiJJEjmnEPJsNj0c9oMgSKVS3V4nJlEc\nh7Y9oiwmNHJcC0CGELJtu1gsioqMJVHWVCwi13eb3dZw2CckGouICIloFIeeH0VREAR/SVzwvEs0\nHv+/j4znJ4TQuNczTiMbo7MwFjgH4wMA+MU55xBw9IvtERo7Z78YlNI4jsfTGACAEh6FpNfrS1gq\nl8u7u/uAQchRFEWu6w4Gg+mpmeXFlaODQ4xF00xWj2q5XGGiNMliag+t2zfv3L/7YHFuMfT8QqEA\nGIzD+Onjp5TwlZUV23ZVVbctZzS0reFIU9V+txeHxBoya+gJSFyYW8ymc65NGOGBFzJKraGdSecy\n6dz5sxc4QSQikU9Xlk7k08XDvSNNMVOpXLlQfvJwI/RjTtCwZ08UJ3rdwfTUzO3bd3d392VZTaez\nAKClpZVupxcGUa1aTybTjx8/vXjxhTfffMs0k4OBfXxwnE1ljw+OIYPZVDaXzogIIwCODg6Kufzx\nwX7t6DCXSVmDPqXxzMwMYTFhcbvXIjzeO9h3fQdiWJmt3Lp7UzPVQimfyaXLk6XSRHF9/dT25ubh\n/gGJ4oRhLi8ubW9vf/75591uFwBgaHroRykzRULeqDZMzWQU+H5oJlJnz11YmF9aXz+rKNqzZ7u9\n3mB1Za1UKotIKBWK9aPa7vbu6dVTkigCyCRFhBhY7ggglM5lD2vVTDYbxtRMpR8/2RAVNZXNSZoO\nCO1Vqzt7B416q9frjUYj4HkQQkkCAIC5SnZiIg0htG03ignjAEJomhLnIAiA49AgIAhBRZEkSQAA\nxDFwXe664PmsAwCEQBQBxkAQgCBAjJ8/TikghHPAAHyOpZdlWdclTYOSJIlo3N38xRLqL3qZHABA\nAaeAQ0FQNcNIJs1kyjAMURR9P0QIcQ7Geh9VBbIEOKHPNrcO9w9oTDglw+FgcnJyYWHx4sUXCGGZ\ndPb4uKZphiCI6XRmaXFW03TOIADQ90LH8Xw/tG3Xtu1SqTQ1VfH9sNvpC4JgGEYQBN1udzAYWJZF\nKe31emEYdjv97e1nEGBZVjVZFaAAKIAMSoKoykoqkVRlRVbEZMpMJ01DUwxNQVEUOo598uSaJInf\n+96f/c2/+VuLi/Ozs5VGg1/4Uv7R4wfJZPLUyZO9brvfA2snVjEANIpz6Yzv+4IgpVNZVddEWTh9\nds0PnZHdYyAulXP/4Q++9+abrxNGHc9bXl7e398/efLks2dbnVb98HC312/n8qnQd3r91s2bn6ez\nqScbT1946aV2r/1k4yEUaAQ8CqNUPmG7g6dbj91gqBryzz786eV33qg3Dr3QWVqaCwJndm4SCSxf\nSOwcPA1ixwut3YPtdC4BMWOAHlaPFF05PD7UTeX+k/u7Bzvvf/QzzdQgQoIom4mUmUjlcqVMviQq\n6l//m7/9xuW3JVXb2nn24PGjZ/vPBvZAVKVcIQMRffTk/tbuhhu5buBRRNP55MWXT8/MVyDmyaQe\nRnbCVACMo8gL4sDxnE6vlyvm9w73AAa1ejWdTtWa9StXrrRajZMnTzRqx6Zpaqp89dMruqSn9FQp\nWxK4YA3s+ZkF1/IOdvdN3ZQEqd8fJJNJXdchhJ1OZ3p6ihN+uHc4PTEpIiwibBjGrVuPTp1aO3X6\nZKNZ/3v/6e+srq1SHt97cKda71ZmpT/4gz/8+c8/dByv0+n1eoOvf/3rzWbz9u3bGxtPFUX+xje+\ncfbcejJlfnb96blz50qlgus75188V56ekFShN+zYrn377u33vvKuZQ3b7ebVq4evvrraaDROra1m\nUglr2I9JODtb8X1XkoRk0qQ0npwsQ8jrjZofeKapQ8g7nc5wOEQYyLLIQew6PcfqkyiAHEGOBaQm\nE0VCBM5EyjBEIhIULMqSqsiaSlnIOOGUcE4R4AgBBAFCEEEIEUcQAsggB5xzwDhg/AtNw3iqopQy\nCr6QLYwnsPH8gxEXAGM84oyw5wdljFHOKGeMAUJIRGLGGMJAxAgiTimNfNppDp483BaQXCpOvfTi\ny0EYT1VmKrOzlblKs92ozM4sLi+pmpbN56IoerLx+PTp03fu3P7qV79arVY3njz9zd/8TWs49Dxv\nplJ55eWXTcP48Ocf8IjUj6sXz10URdnzw8dPNk6trx8c7a+dqkzPTFrOiIGYsLjeBJ9evbOxuY0F\n+eVXvnTl088lWe8P7PWzZwvFSd00G81ms9M2U8mpyuT+4V55ajJmkaRIG1ubtjPyfR9C7PvxmTPn\nIMRPnmyUiuVbN2/PVGYRQq1Wp9vta5ohy2oUMl0zDw6OvvH1b2ZyxVQ2+3Tz2fUbtyen5/YOqrbt\n3rv7MJVMf/DBR/l88Z133tne2glCj3Naqx/GxN/celwo5B48uCfLAgD83ffe5oDqun50dNTtdqMo\nWlhYiuO40+tKqnRcPdIMDWJ44dKFU6dOxXE4TtrMZvOqqnqOvzA/n0nnzqyfe/ZsV1XVVCLtuu7e\n3l6z2dzc3Oz1eqVSKZ1O9wa9iekp23GebD4J4qDb7+wd7DVbrY+uflycKBdLpTPnziqa6gV+q9tR\nVfVg/2hmZoFz/PqrlwHBziB4+mTn6OioP+hSRmZmpwGnSVMWEaAk2N45qh832s3qcNiP4ziMooFt\n2W7MMPAC2h2OeoOh7QZxzAlhcURd2/Ucl8RMFIAgAkqAZYW9nntcb3b6Iy8IAABIAOj5Woj5vhv6\nXhRHgHFJkpIGMAxgKIKKoQo5hghwFHMUUkZIxEg4svq2bdte6AUMADlhZqfLhZW58pm14vzUZEJT\nTEMVBCDLeIxzFQQAGD862GcxKZUmDT2zt9fzfb63e1SrNc6dPd/vDy9efOHosDo3NxdHFGPcbnWP\nj2ujoQ04ViRTFJQwYEf7ja2ne41qG1AhDunxcb3Z6GAkra6cWlk5kUqlgiAaDAaZXG52djaTyTiO\nQ6N4fDMSQsLID8MwiqKxfZAQIguiICBKYwi5UG0enD59utVqOsFwYXbh3/yPvzcxMeX7XsIEE6Wi\ngHCpmA89n8bx3/zrX3ZGfi6FIePTk7NHR9XDgyrhwfLq6g9++KPwzsaLL1Uce1TKZf6H//GPTpyc\n+PTTTwul4srJhXq9lstltreeFHI53/WSpuTZbUXRsUju3b/5v/5f/d2fffT+TGXxP/zpH549d6I8\no9268+lBfTuOQ1GfafabmYIREdFx+ydPrUoyLhRyhEaNWvXU2glOQy/olRcWXnz1rCiKnutvbWyP\nnGHohYqmzsxVREFZPrG4vbtl204c00wx+3/5R/+wXJoaDq1kMjk1VfnZlc+iKBJF8ZVXX8pk8uV8\ncft4z/Xd73/wY0kSYu61No8kFb/93mXbdYbW6OzFdVEUh8N+u9uenC6T2E+nTECDhjtamJ2aKE9t\nbR4Up6cmJ6cb7XYYxbt7+3t7u+WpyfX1dUVROGW2bb/80guWbR8dHa0sLAUWefZgP6bg1OKZncd7\nKtLsrjM3MWcY+rA3zGfypmYcdg583z+9fvLpk81MSoAcuY4zMzMzNVke2ZahKT/68+9PTE+k0+mY\nemvrS+985Y3/7D/7J1//xsmtzWeQKRgK9+4+vnz5TYzx4eHR5OSUqqrVanVc/02lUmfOnFlbW7t7\n966iqpNz00+ebRQKpZnK9NCz0snM0B3dvncnkUq0GqO/8lfOHh8emppaKuQ//fRqs1579eWX9w93\nU6mM4zhR7A07w5nKnKrKQeBlMilJFgfD/srq4nAwKhaLrXbTdzoZUwwDRH1fS2SK2anR0N/baZNI\ni8IIABjHjAFIIWQsQowixAUMkCAwCCDjhDNAEQWchBHlBFDAOIGcj3ndEEIswDjyFdWMogAJMsbi\n0PJkNSHKehz6EEAEWUxDBIggIAYB45D/onXEnosXEAAAcMghggBwQCklAAERMQECDBWrG8SM+S5p\n1LsPH99bPjnT6dabg/anN66+ePGVs5fOtWr9dn/wlW9+9Xd/93crixO2Z7359puURydOLh8e7U82\nS0Hg/c5v/9YPfvD9Tqv+4ssvP33ysNdtm5qqq9rQGlEGAURH1SNRFjmK9YT86msv//7v/weGgsvv\nzBJCisVyr29xLq6cPOsEBCnG7mFVEpWJmamPP/rktZdfOTqq5jLZueWZ67evJQqJZC7R6/XOXTq/\n9Wwnny/sPNufn5+tHtcuXbr0wx/+8Nd//dc//fTTpaWV4XDY7fYZPSiXJp8+3XQc/5WXXw8i/97D\nx2dOnwlCGhPAOHq2c0hJND091R86I9urzC7cv//YcbwTJ060e+1LL1347ve/e/ny5WfPnkVxlCul\n/djd3N72PG9qaqrT6VRmF0e2K0nSwVF9bn6xlMk9vP9wZWV5OLSebD1SFT1XzD98/EAQpGKxTBkw\nzMTs7EKj0fjen/3o1ZdeazWaCINcNh24Xs/QcrlMEHgPHj/odruqqsaIfPXbX4vj2GPBxtEzLWVw\nAa2cOPn5Z5/lcjlFktdPnH4tmydW8PDzO925/osrF6vg6Hi34Xct6ka1nYbnBYRE5elpMhyOeq1k\nQlWgkNYEZaYMBFGAgAPQ740S2STlLILQC7lPaUBoGIZeSGRZBQDEjFqWVSgUGA1bzUiWZRIFnudg\nUVU1DSLJCfzucKAZpmkaljc8ODgKXM/UTQGicnGCQuHIAccHx8AdycPWtCliTOyQIChEDHijLgfU\nCXwgah7DZnFua7fhHXp6cdhzw5hGxamJVrs3cemCpIHRiKkJgTAQhCBfyJCI9bo7kEqqnPd9FMc6\nBrEua4aqRX7QbbUL2dyg2ysVCr1eT1f0dtt2RT+XK3DOA4epKhahjgHuNu0xeEVCwqjvxQHY3TmG\nEOaKhfnFchAEQ2vEKUtmUqqgIIAJwRGGnIsIAUoiEodJXTM0RVXVo4NDURQNw1AUBSEEbdvqdNqG\noc/OVvL5bD6f7fbaU1MJQcT1ajNlJgqFnCiKURB2u925+Zl+v48QYgw4juMFge/7mZxsJMH+0VFp\nIvf5rePL7575W3/rdzDG/X6/elyfnp7u9XocsMGgn81masf7lIVx5A8HHdNUb9z4jDHy4cc/X1tb\nbXWad+7dun7zytDqzy5UCI+wwFuderfbanZavu/Wa8dT0xOZTCaO40ajeXBwkMun2p26ogj9fjeR\nNBeXF8IwHDn297//8zAODg8Pmu3GCy9fWD97SpDQjVuf9UfdnYNn5alSrpj78MoHtUZ1eW2ZQnpY\nPfz89o3v/ORPf/LB+ztHW9lSemK2lC2k3cBRNfmoehiGfiaT8kLv4PjgzoO7XuDu7e+YpgkRTySM\nmZnp2PeGg4FuGpKihXHs+iEUMEfw23/1rxaLRd8PCCEYi4Swq1c+e/TgcTadgwzGLtvfPhaBPOw4\n2UTh/s1Hk6XZUd+VRTUOmGsFnhNKkiqK0mjovPzyK6lE2lDNXCYbh1Gr1bp3564gCKVSodFocM52\ndp9BxD+/8dm7X1kcWoNf+tY3JienO21ncnL66dPtwWBULk1uPN2amZktFkuFQmE4HIZhmM/nG41G\nPp//xrd+qd3vqAk9V8g+3HjUHfRv3r7x7rvv1utVx3HOnFuJgkBRlEIu/+TJE1FAhUIBYxiEnqzg\nMPTL5YJh6K12PSahbsjFYn5nZzObTVvWkNBYNzRZgKJI5+anOh1rcrJkaKappQw9zZnAqAC4iLAq\nyqaq6ppmaJqm6hoWIIacA8pIFJOQxiGhESMRgAwBACDD48Ld8+oaYzRWVAljSDjzfJcBnsokkYDC\nyPejMI5jCIEgIIwx4JzEIXhOGhsfXwxEOeOc03F1hBPOyJjWqilmFNKUmTONjCjKFMDNje2V1VVZ\nVb769a9wyP74O3/0bO+ZG7hB5H/zW9/oDboh8eYWZvf2dzLZ1NraaqfT0jTt6tUr6XT6l37plz79\n+MPlhaXzZ85yQn3Pq1brqpFcWTt5687dZCY9Mz8j66KoiEZS8SO/OFH88MfVo2qt2x+5QVyvdyem\nZn7+wZXl1ZNuEFy5eq08WS5NTjx88jCbz8Q0mJ6dMBI6BbTWbO7u79y4fQNAmEwm8/ni/Pz8tWvX\nf/VXf/XTTz/N5XI7OzsbGxuTk5PdbndycjIIAlmWFVW7efPmhRdeOHn6lKxo7773Fc+PZVmdX1iZ\nnVm4e/dBsVBWFK3d6kxPz3z00Secw16vd/nymzs7277v5vP5u3fvMgoYY2trp2q1BqUcY4FSVq3W\nctliHJP9o8Pj2mG729YM1XacoTXwAl9RlDAMt7e3b9y40Wq1KpXKpUuX0un0wcGBgFAunXlw997Y\nnHTt2rWZmZmj6mEqk/RDDyC+e7S3sbO5eGKJC6Ddbd26c2dja3OqUplbWDh9+nR/2Ns72Nvc2ZyZ\nmalUZgmjhUKp1xsgJPW6Fueo0WxmCtl2r1sqFX7y4x+OWi1GYmc4hJSFricDEIVM1xOWEwuSgiQh\nZhCKopHKZAuTyXQeIMl2w37PnihXSMxsywcARlHU7LQdP8jns4uLibk5ZW0lvbRUxhDVanVFkt65\nvP7uOy998+snv/HVEy9eSJ5c1lfm9VdfXL105kwpqSVlxGjsur7rhzEYS3hiURIGg4GoaE+3diem\nKwndONjaTIrIHXbrB7uaKgEIul0O8RicyikF2VR6b29vdXW13xld+fTmyZMXDw5bL1x65cc/vn94\neHz58juU8F6vPxgMqtXqoD9aXV1TVSGdysURE7BMCQj8eHtr3xkFmpzQ5ARGiqkldD3BGFQVwzQT\nlmXfu/dgZ29f1/VMLu/7PuGEcoIQEAQUhn6/3x9DRrqDfqvV8n3fMIyxfHwwGKDzF84Ohr23Lr/B\nAf3s+rVHjx59+OGHlcrUl7/8rqZpv/Ebv3x4tN9qtcLQlyThq1/78smTJx4/fnDv/q3j433O6anT\na3/ll7/1D/7Bf7m+Pjs3V04mk//wH/4v33vvvY8//lgURVlWbdvd3z9QFM33AgBgFMUnTpyAEFNK\nHz9++OknH1+5+snDR/fq9erVa5/83/7rf/Tf/97vnTl1NpvOsphvb+08fbppWU6v12/Vm/Pzi4Ef\nPdvaQVBotzs7z/Yc22vUO4ALGMtn1s+/ePFla+i+9vJrc5XZ//w//9u1Wi0IAt/3H95/4HvOybXV\n+blKt18LwlGtsbO5fT8IRxx629v3b978+P2ff7/Z2nf9bm9Q3dp8wLmvakgQ2fT0pG3bQRCEYZhK\nJfZ3dgPXe+O1Ly0tLOq6fvbs2dFotLy8vLCwkM1mFxYWRqNRqVyQZOHO3TuDwWB9fX17ezubzSmy\ndnR0XCgUS6VyFFFVNYZD2xp5lAJDT0mi8eMfPEFQTCYzM5V5w0hZo+D8uRdVxYhCWixMNeo9RoWd\nZ0dn1s999NGnzXYrlUk/ebJx+fLlZrM5ZrkmEgnXdZ8+fdpoNK58svPaa6/92Xe//zu/8zvf/OaX\nGWOZTOZHP/qp7/tvv/32d77zU03Tzp07L4rSo0ePIYRjIOz169eLxaKp6dtbmxhBVRKz2fTt2zfL\nE8XVE8uGqQ0G/XPnzp45ezqZMhMJY2FhznGsl19+8fj4MAi9jc0nGMP9/cNkMuG6zqPHD1ptKwi8\nMPSnpycdxwppqBkqA1TRgBe4+WKOsFgQ0FiKLUmSLIoSFjCAnNA4DAPPpzGJ43hsORrv8cdQBv6X\naEB/qXX03Gnk+6GqyooicRABGB839iamCumMIcmQcRLHMaUcAhELCoQY/s+NLwR7X9Bax5Jx13VN\nM9lud1dX1wCHBwcHgiAcHh52Oq179+7dvPV5v98rFnNTUyUOiKwIuVxmb+/gxz/54aVLF3zfFQSc\nTCa63c7a2lqn0/m//+P/bm5u4cvvffX3f/8PJUkZ9G3I0VRpaqpUSRpJEsQpM6NJxtNHT99+8+0b\n126lE9lzLyZeuvRK4ERHe0fFfOlorzozPX24dzhZmpydnU8mU/Pzi1FEUqnM1auPVFV97733MMb5\nfGZ2Yb5cLldrx4yR+/fv3rj5ebGYv//g3osvvZBMJWZnK47jEBK12o1sLi3LoiwLmWzy1KlTmqZ8\n/vlnooh3d5/duHF9TAMqFAr37t07f/6irplbW7VspoCR9PDBUxHJkIq91mi+suwMvcuvv6MrxvRE\npVVvnjm1Pjs9AyjAAMuCXMwVOQUbGxtzcwtRFD9+/HiM7k2n02P6EUJoujJ5eHggCLBWO67MTJVK\nBde1Pc/J5TK2PVpaWlhcnH/69HEiYbRajUIhd3i4/9Of3kEIdDqt27dvFov5VDohiRgLcGd3+/79\nu9VqFUK+vLxUmCi2+52+NQghOf3CudLcBE7IW0d7iWw6jOPF5SXKwb/9/X/X6fTv3H4gC6osyDQE\nDAAMkC5DGYuQgigAjht7fsw41nSYSuNMVi0WCzMzM/V6P50xllcy+XyiVE688sLyqxcXi2kAORh0\nQKcBIAG5pKYLaq/eeXynCiNw92bnj//DjT//s8fbG/b20/792zu//2/+++P9LXvUQDwQBS4JSEQY\ncB6HkWe7yWTSsezpybI96CoCWF2YMFSkqeJgMEgmk4UCkGUoCKjftzudDoRgY3vr3XffdWwvDKOT\nJ09e/dObCKBarb66mn3yZKPfGwZB0G63FUULg1iW5TiOx7uWXq9nWdbCwpJpJjOZXKvTRUjIZDLt\ndrvXGyAoHB0dhWHY7w2jkKTTGUmUj49r+3sHvh9omiFraiqTLk2UM7ksxMjzfc/3FVXVTEMzDd00\nNEM3EmYml0XDYX8cQW8YhizLhqkvLMyJoihJQrGY930/CPyd3W1VVY+Pjz/44GcTE6WYkHa7EYT+\nweHunTu3mu1aHMfvvvvu3l5jZmbm2rVrlmXpiQQWJUmUFVGhIXcst1wod1s9z/Ft23VtR8BSHMeM\nEd91Hty9AwGpHu+fO3+mMj3jeaHjeGEYZVKZbCbPKWAMGEbCdzzf8ff3Dpv1ljXyPI+3291MOv/g\n/tOjw5pleX/6p98/efK0qmrTUzO3bt2Zn1+cm5ubmppkjGxsbIxdpZQFZlJodQ4eP7kVxsNO7+jR\nk5uCFEMcXLv+82vXfz47Vz53YS2RlBy3l8mamiKJonhidfXg4ODo8HAwGASh32jUbty8f+PGo9rx\nsSQq7XZXFOWY8majHUXRvXv3ms1mOp1cX19/+PDh0uKKImvb2zszlYVGvePYweTETDZTFAX1yqf3\nZEmnBGxt7kxM4ampWdcJo4h12v1ctri8tNbvOZ326N7dRySGnhsO+ta169chBJVK5cGDB1/+8peP\njmuj0ej119+cn5+/c+fuyvKqhKUvvfaGLIODvcP5+flcLnfx4kVCSBRF58+f+/DDjz0v+PrX3jo8\nOB4MBrpmZjKZMAzHcpdMMhW4nqZpExMTw+Ewm81++1vfMg0tkUjougo5WF8/Va/Xf/zjH4VhIMtS\nGPlYgLXacS6XSybNYjE/snq5fMIPbEkS+n13eXmCA8I4MRNqFHumqWEJHxwfzCxONJvNVCphOyPb\ntjmnjBFCojiMAt/3HdezHXdke9bzdcC4xPwFSeGLLu4X+oUvvnKOCeMxpbqpIZG64UjSuW6iWmOn\nO6j5sY1FIMsyggIlMI44+P8z/r/eH4zdsIxhJNbrTdNMlsvlzc3thfml0Wh069YtjHEiYZ48eQIh\n8PEnP+90m7l8Qlbg/ELll3/5m8Nh76OPPjw42M/lcu12++LFi3fu3DFNMwxBu9VrtztvvfmmLGm9\nXn/j6XYymTo4OFRkY2npBIKiJKqeG01NztaqTUpApTLfbLQlSQ5DousGxmK5MOk6oeuEK8sn2q3+\n9es3ksm0bduSBAQsGYZRr9eLxeKYHWxZw3rjOJU2CYmyuRSldExDaDabqiqPRgOEgO+7lZkJQUSN\nRi0MfcPQEkljZXWJA9ru9DwPZDIp13VVRdc0vVZrKjLq96yV5dNhSD2XDAfu5MTss+2DKOTDgXv/\n3uPNjR3HDh4+eGqNPNtyO+2eoSfu3XuQTKTXT58LgjCOaLFQTqVSjuPpuh5GgWnqiYSRSBiuN2q2\n6u1OAwAqSigMQ9/3h8Ph9vb2WIcWhuHExMTq6iqltFgs/v2//5tjOvhbb7317NmzVqs1/khNJ8wg\nCicmS0hEUITdUa85aBKJI0MAutALrFAkQMdDz7ID76B6LIji9EzFsl1N0YZ9W4AgoWsYgIQMWAQU\nAYx6gASgWBCzOSmVBoYJZAUgDEQJqBo4ey6XSIAoGl9LoDMAj7bJp9fbd2+0OtXRqD3ae9J4en+n\nW29GjueP7Ps3HzYPDngY9WqNn//oz//p/+Mf/+CP/2D76b12az8OBorCDB2PJQ2yIGqyaqgmiehM\nZRoDVs6lHty5qorRsF994eL50kTZcd1OH7g+GTku5SRXLAgSoJR2Op1CrijLsmN7M+enHtzf3Xi6\ntbiw7LnB8XE1k8l2u6Nmo33mzLmDg6N+fyhLShAEZ8+ejaLo+Pg4CAIAgCzL+/v7e3sHY47i/v5+\nPlcc0z1UVR8N3XazEwYEISEKiet5jus6vhczqplGqVTK5nOKpo5GI8Y547w76Ld73ZDElFJhOOxH\nUZBLp8qF/PFxTVVVUcCckU8//jgMw1/9lb9279692cqMLAmFYs5zA02XsQAePjooFOVsLmnZgytX\nPvnk6s0vvXHiP/qPfs33/ampqRs3bm082Rt0nGw2PxwNkkkTMA4MY3Z2sd/tRJ5fyBbs0YhGcTGf\n54AUipl2pyHL6qnTy8NB7bt/8t1f+ZVf2d3ff/pk+9T6Sdt2FFFXVfXjj65SFq+fOXfjxq0XXrgA\nGKzVeprceuHCK91u9+G9xy9demlvb+9g++jixYuMwIO9fciR4zgzU5XZytStG9e73e7KymK/dyzK\ncq6g9/td3+9Hcdzptt68/EYB637gPrj/2cgZRHFgmgbGmDN0/+Fxa6WxvLQ0LgNyyAeDQTarBUGw\nt7d3am3tzq1bZ06fkiRl7+DAGjmFcjkMw6WlJc8NMuncaGRjjCcnp2u12vRUJQqpLBmpZPqzzz4r\nlwrTU7MsFjq9brFYvHnjzt1bx8urJz/76OCNNy8fHdUQEvP50v0Hj1577bXvfOeH5Ymk59qOB1RF\nP9ivrZ85k81mg4D3BgPfC0+dOsUYW5hfjIPopRdP/E///MZv/ccv/eTH75cKJcd2f/6zp//8n/+D\n/+af/j+//e1fvnLlk4mJqWajHYYxxujz6zfX19cbjQcAwmqnISpis1afm5urHh9xRqMgfPTo0Vuv\nv/H9P/vkK++9ZNujty6/sbe3Z+qGKmrlyYnf/Zf//jd+/euDwWA4HBaL+V+sm7orq5PlcrnX6x0c\ndKvVQ0EQdEO1nL5u6gjDE6dP2J4tqXKz3tS1zGhoe14YuDHnHHHEKRWgADBnJAYQ/M9S6b6YML74\nCvj/h6//DpLsvvMDwd/zLt976b0p731X+250Aw1LkSBBN0tyOJwZ3YzmdmfmNJJOMXurvdgISafY\nu9uVQqcx0lgNhwYgSAIEQIKw3ehutK3q6vIus9J7/7y/P5KEIGrvXmRkVFRlVWVUvfc+X/MxsGnZ\nDM0CBOiGKkodykWOTcRgNJ4+ytjAAZZlmrqp2ZYJEyiFEYRpq58KpPjUqA6GAQA29F8BkuNAhmF6\n3L52q0lRTLFQfmbx8v5hHUXR4+Njj5cbGx6fm5+SRW3j0cPNjfX5+Xlf0Adhzvj06NDQ0P7+/q07\nt06dOr22tnbm/Pl+vz81O9vviX//3e9fvXpVVs3R0VFR0vK5cjAYHB2dOD4+1DXT6/O+//7HszNL\nNM11O6JtQbKsmabZanYInEomhg73jkmM1hXT1O18tjg3OTs3NfeT1964eP4UTdOvv/YGDMNzc3O5\nXBbHcYwAQl+amBhbX38oyyJBYM1mfXZ2+u16dWp6EoIgw9D293c9Ht7j8am6YtlaqVyYn52tVquN\nRi2ZDC0vrpTLZdu0VldXy6Vqu90+e/bCgEw1N7vUavYZlqZI7oXnz//d3/0dhtJf++9+48GDB2Oj\nk5lM5vjoJBKJlEu1brc/PDTy4Yc3XAzlomhF7liWdebMmePjjCRJGIZVq1U372k2m6Ojw8fH+9Fo\n1DAlv9+tW2o6mxkaGmq0m7Vm3eVycR5eUmXTNCVJarSbf/afvhuPc5Iq+3w+BEdHUkmeY2HHFsS+\nKPbrrbouKSgMEBu2MZCvF6LeyMbxli7rj0/2qlITYjGKZGwU6SuSLMnf//73SXfg7BNPMaxfkA2C\nooJBADkAg4GlA0UBbhZAAEAAmCYwdKCpwDQAgoCjQwAAkCSl2Wwahu5iaQBAv9NO+gIhnkcQcNTp\npbd30+l0qVRqNGqhoF+VZF1TKBQP+P2m2BVUoVU8WfjsYjRIUZgtKSpkGxiKYjTrUC6AInqtQSKI\nC7cDPOXn8e//3Z/5EhMahLg8YYIheR7QLrRQQpqKLogiN+aygSUIUjq9E4hQbtY9OzUviW1BkAxN\nuXz5iXa7KwhSNBKp1+vDw0o8nsznCsFgEEGwbDavaQYEkOxJPpVKNRoNkqJIiup2ev2+iBK4IEgw\njIqibFkOjpMeD47jOAQg21ZsCAaQLUpSp9sFAKAIguAYAADBUBTHMALHB359ti3IEmpZFkVRDMN0\nOh232/07v/OVYr70wQcfTE9PTk/Prq9tnDt3pt8VCoV8IpG8sXsDQ9HJ6VS72wtFYq1Os1yrDY/F\nAgE8nT5SVWl0dNTvD+Eou7G+R1GUJEmmqXfbncW5BRxFU4mhVrU+khpTVRXHEJpiRFEeHR0dGhlP\nZ7KGYVWrZYpAKJKVRO3Rw0eCIEiCbJtOrVGnabpR67/4+WfXN9YS0Vi/J104e/HWx3c3HuY5NnB2\n9fwHH3ywsbHd7/fDwdCPf/z6008/PZwaKperi3Pzfr9/e3sbgqBYLNzpNvKFTDAc9vl8bg9NEIRl\nWShuYqhTF1oull45NQeh4Dh92G43+72+aUBzMzFVVd0sV6tUU6mkrqsfXL9+7uwqRVGKLG1tbU+M\nTzYabVnSDN2anZ11+3yxWOzevXtTU1PFYlmW5Wg0nsvmJ8any+Wq1+ulKVcmnbctNBSMPn78WBa1\n02dX33nnnVKptrwajcfjn/vSWZKkB7Lnzc1N07R6vd7y8oxl646tzs4mZVleWV0yDOP4+Pib3/r6\nf/7P311YmLz+4f1/+Du/3mo1OM79eH3v3//F//BHf/Qnn//c0kn6ZHl5ORQKNRqNYkGJRePdbj+d\nTn/88fa//Jf/17/6q7/yer3vvvvu+QtnSZq8efdjiiEYhikXS44DnTp16tHa+ujw0PraWjCEv/HG\n3ZWVhGnqFy6cu/vxnZ5Q6fTaL754WRD7ktyXZLFWqz3xxBMURR0e7p87d+6NN9584YXnRbHf63Uu\nXbq0ublBMARFUUFfxLGx8eHJn771QSo5XsjXHAcA24EcC7IhGIIQGHEgGABgQjYEW4NmZSCGBZ+S\nDX0yqfvkYxRFUYI0baUn9ggGHZtM+kO0KPX9QcoBqibZg6AJx4EsB0UBDEHwgFkLfqE6+uXP/AUm\n/SqD3LZtDCM4jvvhqz++cuXJ69ffu/bMBUFuIrh9nD6AEYBhqKq2zp0/DTtwPlfgvS5RFINBX61W\nCQR8DMO+9947ly9fefXVV3/jm78pSRLHej/zmc92u31J1BCYSB/nQuGoKMoMQ+VyhcuXrxwc7CUT\ncU01Y9Fktdrwer3zc4vf+c73TNOcnp7ttQWfL9TtdqemZrInuanxKcOwV1ZOZdLp2dl5AMDt27en\nJidN0xQEURQFkqbOnD316g9fhmDn9sc3z545D0FOsVg8ffo0SZKVSgXD0XanheO4P+CjEBIA59z5\n0ziCSnL/c5/7rOM4m48f93odisSDwbiiaAxjxGNJgRPu338IY3Cj2X7uhWd//vOfz80uK7JB4Ixj\nI35feHf30OPxMIzaaLQGDtzj45OFfB5DScsEPl+w021Xq3VFUcbHxzc2Nt5443BhgUgmk4GgF8Ug\nDENq9fLmVm1qZo5lWa/Xm81mMQxDURRBkAEWlsvliYmJVqu1tLQUDAZLpRIMwz6fzzTNaCzi9Xl8\nPl82k7ZZlsSJ2eXpZqm5c7L/YH0NUh2OcEmYhgeZerMNYXggErEAJre6mqWUM0effenLP3j5FYLh\n52dXj/YMSVTb7a6LZkjede9xw0LhQVgJDGEEQTE0S1FMKIhCEMAgShEYyu2PJ6hqVdt98Oin3/me\n3O22e13DMHAcJUkShgFLwNVsmqFJW9dKrbbYLKIwbCiyJVbGhwMMJKliH3JUhiZQgGsSZBiGblgj\nqaF8vb5y8ZLca3z1C8+1W+WHe2uAcZ96Is4wlCAAzQYkDQWCHgwCxSIYGxtDgdRoNAjGbTgCTFpT\nk9OG2SVJmiRpUSjDEIphmGU5m5vbsWjc6/GVy9VcLmfbIBwO67oejUZbrdbi4qIoitVq1e/3G4ZR\nKHXDEdbFcqIoMrQrEU1JqlIqlQzDYBhK0zSaJmEMMx1bURTMQgiCQGCYdfOyqrZaLVlVIAiSJMmx\nbNhFU6auffD+u1evXB4dGfrbv/mr9Yf3dUU92Ns/2NsdSiVgyDEN7SRz3KzXWYaBUbC4NMtxtKZL\nzWYdRoCmKQ6wea9H1uRur10uF19++UcERcqaqqo6z7qTsQSK4BMTk9uPt7xun2ODSqlSKhYlUZQE\nsd1u37v3sabLMGzbplGrVpcWlpr1ZjgYHR+dePft9/ttcXFuxVDtC+fPnmTyGEy26l0CJcrFysVz\nF7/w4tO2Dv3g+z+enVp0UWyr3hb70tzM/MP7a2JPtHTjp2++tbezm0zE8tksReI0Q1y79uTZ06cQ\nyLEMVRC73V5rbHzYdvSJ8eHZ2alOt3m4v6/JSiqeiIbDFEF0W20YhmVZHiwwJEl65to1URRpmiYJ\nut8XT58+a1uAohiv12/bdjadeeO116cnJvd3dzcfbbhZtyLKAW9gZ3Pn1NIpD+v7+//8XTfrWVk4\n9faPNxgX3WhWLFsPhnynzyyMjg299dOfxBPhj+98JEpdhqEQBH722Wcs27h69YrbzZ27cP78xQv1\nZiOZTAqCdOnKVVlWOY5aWlpZXp7lXDxF0Azlmp0eL+ZL4SDweDzddnt+Zj4eiWfT2T/8H359+/E2\nR/NnT51jaZA5yjz95FOOaQX9/q2Nx71O99yZM6eWV4ANhYORL3/xS9//7vdokrQsK5GIBwL+hYUg\nisI8z7711hs2sHierdbKxXz22tUrH9/aZkgiGgo+Xl/DYGhyfGztwf3nnrnGUOTE2PBvfevXD/d3\n5uanfT5fPJkoVSqz8/PbuzvRaLTT6ZAEgWMYieEEhpMYjqMoAsGQAwaZ5Z9A0acHdL+yMfoEMBAM\nl2TZMDUEtf0BnnNjotyAMLUnVgWprRsCQSCcm6cZ1rERUVD/ixfD/9/jv6huHVjXDVXVZVnJZLLT\n07MnmdzY2DjDMFNTU51Op1jKT01PWpZ28+aHE5Oju3ubo2MpRZVUTfL5vKOjw4Oku8uXL7/33ns7\nO3u6bhI40+sKiqIeHBwGgyHbdBAIDQXC9YpSyJZV2ahXW9VyIxkfrlda5UKtkCv2Ov3zZy/IsmpZ\nDkMyLM3ahr23vTcxNvmT116HAQQAyGaz5XJ5EAulKEowGBwZGQkEfIoqjIwMKYo5Pz9nWvpgg2ua\nervdxHE0Ho+qqtzpNB4+vLvx+GEyFVVV+eBgj6bJzMnx4dG+IPRSQ3GXiznJpnVdhSAEABiBcUO3\nH9wrnDl9ydSg2emF3e2Dmam59NFJt93PZvKRYEyV9IvnL7GMO+ALYwj+N3/1twiMLS2tTE3N2DZg\nXVw4FAEONPAb+/3fvzY8nEJR+MMP38cwBEXhc+dXk8m4piuzs7Obm5snJyfNZvPRo0eTk5OWZV28\neHFkZMS27S9+8YtHR0csyw5mdMfpo5NMOn103O/2ALA1Q3XxLs7LPXy8nq/lfYkA5WdxP1UU6yJq\nCJCCePDUdLLUzIeS/rnFKUHqSFL7X/0v//PjtfuvfPfb/+7//f98/Yev2IZ6anFhamIMccxowDM9\nEj81N7E6N3Vqdnx1Lr44yU8kUVMESgd4aRDzee9/dOMPf+eP/8d//E9uvPN2u1KQO3XcVjjcQSyl\n3yx3agWlU4cMATFFEtZpVEWsPkvoNKo8c/WUoTQMpQk5EksjrIvEUHigLcUQnESJVCwKNIXCbBdm\n/ePf+9Z4MnS8t7Wx/tA0VIoAJA78AYCgQDcUSZUUXaJd1Oj4SC6X63a7kANpmsaxbuDAdz6+h+Mk\nz3u63b6umwMHln6/73a7Z2dnPR4PRVGjY8OarpiOmcllTGdww1d5r2d2bhhBUFO3ouGY2+3N5Qrp\nwzSO4H6P3zCsTqfX6nRlVSMo2uPzMxyPUzRJMdFYwuP1ExSDk7SLc/uD4UgsjgaDwcF6dmNjw7Kc\ny5cvYzC2t3uwvbndaDQ0zSBJ0jCM5eVlhmYlSbr/4N7pM6clVcKBiRBQKBiAUciBnXa75Q+4BUE4\nyeQhGIhinyDIqfHprcebo6khGIK2Hm/rqqE6CjCAruu6YvQ7wtzcXDGf64vC0MhYv9/P5XIsy0IQ\nZBumYVgeDz89OUXTdDFXfOLiE3fu32m26jAKra6uvvvu7ZWVyUgYkAS99uCDf/Wv/tUf/dH/bXl5\nKhqOqopG4STvYvP5/MzUdCIe3drasmwjEgr0er07d++dv7g8PDwMQdDw8DBNk3uHB5VSkef5k5N0\nOBKyLTAyMtLtdjEMs61e0B+S+urzzzy7/nh9cnqC4Vw3bx0GQ36/39/rdGVBjEajP/rRa71ej2U4\nQZBQRB8eGY5Gow8erCEwNjEx5Tig0+5OTEydPes6PDg2TevJq09ZpnPz/m2SB6oq6ob0/Zdfnp0d\nc4CFoEwo7C2V89FoiGZIl4uanZskKLLVRrZ3Nvx+L4Zh+XxuZWWlVqt9fO/uD1/7+J/9s28+++zz\nm5vbpmlGIrGjo3QmszE0NGbb8MREKhlLXH//w9u3b8/MzO3u7r7++ls0TZ8+farZbPKcJxQK7+3t\nEgQxqDdbrTbBUL1u76tf/kq32z0+Pv7SSy/pup5Kpf79v/v74WGOpZn5+bm7d++OjIwcHR3lco1r\nz1za3t7+4Y9+kEqxgthzHGd6ZhJANkmh0ViQ51nGRUUioUcbD2gGJ0l8LDC2sbk1PDy6vv4Ix9ly\nvsxSXt2yLMtyLBsBCIRAMEBMBwDbsR3IMHUbWAPawsCTeyB9HcjUfwUzbAg4ttmX+14fRTGUA6uV\nei4Ic1euXJqZHdtY2znYyfc6LVOVUYelcC9JU6rR/v8FP58MAz/9aQCAbQEUxSVRSyQTlVr23IX5\n7Ek+Eg882kgnEzGKoorFvMfjW1peqDfKq6sr7733TigUMQztxkcfuhj+c5/7/Me37586tXr/3nqh\nUEER0uViQ6Eoy7o3NjZoF+U4DsuyhULp6tVz169/dO7cOdOwDw8yKEI2m+2FhaV+XyRJcnV19cc/\nfi0ZT7pcrsxxuhcOuWhmcHeWZZXn3KOj44eH+5IEer2e40CdTo9laYYkfT4PwzA4jo+NjWma7ua9\noVDor//6b6empkKhULvd3NjYu3BxURAEAiMBsNPpo2qpjGHIysryzs6O1zNK4JQkyPfv3wcOAsPo\n9MT0o/WNfl8kcfBo7dHFyxf7PVEQhKeuXX3ttddIkr5w4dLW1uOxsbGjw0w4FFFVFcfJz372xfWH\na/c/fkgzZLPZJEkcw4h4PJ5KpW5/fCsWi/l8PsdxstlMNpeBICgQ9CIohCDI+vp6MBg8OTkpFovJ\nZJLjOF3Xu91uNptFEEQQBAzDarXawsLCm2++efbUKs/zsiyTJF4qlURRNE2zCUHRSETsCNvHewSM\nd5vd4dFhWVQRNxHwe2mSSUwPi4Km9DWKgWHMZZq4LLU9LlKT27kT4d//241EIqVphgM7jJ+anJ6Y\nmprxeoIoQihtqNsRWq2O0Jf29g4ajaZlmYIg4JbqJmBVaKOmiEMmAMB2AAw5OAPbpmU7KkU6mlQn\nUdhFWJCtKv22Jkunl5839S7ALQrDYYDYuirLEgAOz/MAxhRN9XndvXYLVUUCh1RD/8aXX/w3f/n6\ng48/8gV9DOsyYDzBcwQJ/B6qkqslU7GP3n9T0zqJZMyBVUURHNgWun3TUjjODQCoVqvLy8uZTBaC\noEG1jaIAADA8nDo4OBgdHeU4l9vr7XQ6zWadICgEQQAAlmUDABRFKRbLtIthXXw0EkcQTJIkoSsM\njaY6/ZYoioNgaFmWdVWDIOgXKygMtywLwzC3263rOhwKhEzd9Hr9k5PTwAK2Ye/vHc7MzMTj8Waz\nHY8mlhdXQsFIp91DAMzz/NBQQlGlkdEUhqE8z6EofPbcqu1Yum5bjpkYSiA4KspA1axQOHB0dERi\nuCRJRweHQ4mk1+v1ev2qqi/NL48Njy0vLyMI4na7Ty2vWIZ2kj5KxqOjw8PdVheFsfmZWZ/bt7e3\nXyyWnrzy1M72tt/r7bZ0DMFlUWk1wPPPPr+/e9BpdYL+0IN7D4ENvG5PIprInZx8fOu2bVokTpi6\nunb/wdL8godjec7lmNYzTz+5MLd0dHBcq9QrlVo6faIrum0DQZBIkq5Vm44FbT/eNzVw5+OHmeOs\n0BVt07p18yaBYYauS4IQDodLhWKz3iBJnOO4iYkpN++lKZcoSBPjkwiCHB8etRpthqInxsf73V4q\nkWQoOps5EfuCZZjlYokiSdt0hJ7o5kEg6I7GfF/68nO7e8e6IUxODfkDHO8m/EGXi8ULxTSAjF6/\nWa7kxieGPF5ua3cbQpH/+JffJ2jK6/H5feBHP/xxIp58vLG1unpmf++g3ep0W53pial+pxfw+nEU\n41lOV7V3f/5OOBhJxlLRUOzGB7cIlF5aOPX6j950LCeVGMIQNB6Nib1+uVA6d/rs3/3Nfxa6/XAg\n9PD+w1e+/8r1D67Pz0RGUsOTk5Pb29vRWOTe/bu6oS0sjH3w3q1TyyuqrPi9vvHRkZWlxaFk4uhg\nfyiZmJ6c2Hi0xrOuaqUEOTYMnK3Hj4+O0sFA5OjwhOd87VYXw4jB0HmQIECSJIbgwLFsy9AUqdfr\nDUh0g67oE/OFT5qVT8zrfolSQDdUhiFkpf+Zf/DMyHg8FPMkRyKVRr4nNbOFQwi1OC9rmrrL5bIc\nW9ONT0/hPmm2PrFYHcwGHccZGP7btm1ZjmFYCIxZlrO9vTs5OfX2z96LRpMIghUKFdsC2WxWkiSO\n4xRFTqePr9/4sN1tMyw9Oj7mDwSmZ2dkRZmamT48Onr62Wde/Pzn3V5PT+irmubx+n1+vyLJNEkJ\nvX672TJ148K585njdCKWRGG01WiGAkGapN78yQc4ismi1Go0spmM2BcatXq71dre2sJRrNvurD14\nGI/FGrV6pVIZGQkTJO3z+wmSRHFMFPu3b99yuznGRW1tPd7d3b1+/fra2qOvfe0bMAwfHx8fHx/P\nzKYqlTLLukRJKJWLGI6SFKFqUjpziGJQNBoqlnLH6f2hoSQEOwMH1W6322wKLhe4dWtv49EajmHZ\nkxMEQr/8xa9c/+DDk3Tm9Kkz6w/XapVqqVAeGxnHUVzoCclkSpLkSrne64oQwJqNbqlU29s78Hp8\nFEUFAgFJkp577rnNzdIXv/jFt9766cMH6yRBozjO8ryqG7VGqy+KjVaLpOlCqTQxNYXiOE6SgVCo\n0+tJinLx4iWed+cy2U8SDUiGRnCEclGVWvneowf3Nu63lG5Dbhu4nW0Uw2PRuly//vCDvZPNw9wO\n6QL58pGudXS9C8MqZIswkCBToAhT6JUcu28oTVOo3/vwZz/8u//0w2//p1f/7s/f+8n3cntraquE\nGX3M6DpSw5GauClgRtcWa0DtYJAEO33I7kFWD3FEFEg4rBKI7lh9HNFgR0QRAUdFYHccu+2iTQpz\nMNiCYROGLBiBaIakKGpAKwUAyKLoIknEtsonaaBJI7Gw2m2++NzTdz764N2fvvbzn/74xvsPtjcf\nSrJaKGYsR65U8/FECIJtj5dttuoEQTiOs7S0MihG6/V6s9nkOM7j8WA42um2e70OgkAc56rVug8e\n3INh4ADLH/RFYuFOr91sN1Acg2F4oD7WNA1y4GK+VK82Oq0OAiFDqbHd3d1+T8RQgiRoAqeAA2ua\nYVnOgPllWU4wGJZlNZ0+MQwL/vGPX3e7vQiChEPRlZWVcqnq9XqPj9MTE1Ozs/P37t27/uFHEASh\nKOZyuQAAOI7TNMlxHO9mCYKgGNKG7PHJkWCYp2kSgqx4IuzzA0UDqq6IUq/TFTEEjYbCx0dHjumg\nMLY4v6BKKk3TjunQBE2TVKvRbLcaDE2yLFuv1iAH9vv9lmHTJDU5NtlttQmCyJ7kLcN+4tIpXdFl\nQeQ4YBiGZTr1ev3s2dPp9NH8zHC31W626sl4wrJMhmFKhVwmk/nMZz7j2CaOYc1mc2Z6evPRZvr4\nhKbYZDLlol0Mw/K8R1dUSVQsHbC0G4GJUytnJVHzuAMuxhOPxJKxBI4QjVr95vUbnVaz32nDMAyA\nTZLkzMwMSZIQBPO8lyAYw3B03ex2+6ZpVio1hmYhCBrEa8bj8e3tba/XK0lSr9eTZMHlopeW5rq9\n5shoIp3Zv3BxZnFpxnY03k07wEymYpGo/zh9QDN4p9OybA3DIVUTC4WCz+cjCCBJUqnUwHFUVdX1\n9fVQKJhKDhUKpXq9OTe7YBp2KBjb2z0AALz44ovVah0AWNfM7e0dj8crCOL29g4EEK/Xf/vWHUmS\nhoZGGo0GDCBDM+/ff/jU1WskTlmGnc8Vg4Fwr9drtToul0tVtcnJSU3THMep1fooina7QBRFXddZ\nlh0fn3z99fd6vZ7jONvb2263u1IpFQoFx7E4niUpwrIshnS1G8L8zEK5UKFJlsRoSVAdCxiKoSia\nJEmCIMiyrGma6diD3KbB8SsxRZ+e4A1QBIZhGAHxVJThCNWwaBfG+1wn+QJJo1u7GxxPfeZzz0fj\n4Wy+GQgFJFVSdNUw9E83Pp8QIiDok9wj+BNk+mXPBEEQ1Gp1DMOcmJiCAIbjlNCXIYAuLiwdHqZr\n1WYmk63X68PDIwzLWbY9Oztbr9dhGJ6amtrc3KzVajiO5/N5r9dbqVQIgoAg6Pbt26Io+ny+SDQo\nSt18ISvJAu9mu90uRVGyLJumOXglyzEsBzjede/+bQR1FFWKRcPFfDWTOQ4EPLqubm4OsqZwgiBa\nrU6328VxXNMMw7D29w8mJibOnjtdKhX9fr/b7S0Wi35/kCTp9fX1Tqen6/ro6Kiu6wiCoCgcDPpb\nrVahkPN4eBgBu3ubJIUep/dlpQ/BNoqBixfP4QQcCgUgCBJrwOvlSQo0GjWSxDVNAcA+ONiLRELd\nbrtaLe/v7y8vL4fDYZZlA/7QIPKj3e6Kouz1+nu9PkGQ7VaXpl17eweZ9AlJ0snkUCaTJXCgKrqL\n4TCSUjSNY904RgYDIRzDO+2ephoETkEA6XUFj9tXrzUhgBTyJVlSB+41Lp7z+fy5QlFUZIIg/P6g\nIAj+YPDas9cm5qdPqgWUJRXYJLy0Q8OeqN8m7KbUYny0qHdJCur164X8vio3NaVlaF3L7AG7DwEJ\nhRUMUW21zWGm34V5SMfvQkMczuEmUFvdalpuFy2p5igNSGthVp/FdA9lYZAMQRKwRNvsm1rP1Hqm\n3rX0HoZoOKrDkAI7MmTLkCMQmG6bIgAa5NgIBFAUHoR52RAwHduyTMexgeMA00AtCwMOMHS123ZT\nKEc4PAblDnea1ZPH63f6vcrR0WavW+72anPz4wQJJZLhZqvW67VYjl5eXdnd3a3VaoNAZEEQFEVy\nuznTNBmGqdYqsiIJYj8c4Sgar7cauqmyHO0Ay8WSBIH1+12SJFiWxXGcJElJklAU7fcFXdebzXa7\n3eZ5D4IgqqoOois0VQUAMCQ1MK0eyI9omuY4zjEt+Ozq2Wqp6pjOqy+/WsgVR4dHM8cZQzMRCO13\nhN/57d853DsAlpOMJYWeaGoGhmEMw7jdbl8gQDEkhmGVSsXn842OpUYnxrr9LoJATzxxbnrGj6D2\n0FDc73fpuipKfYqiZFGyDNPn9p09fW52ek7o910Ms7K05DhOLpfr9XonmeNivpCMJ7xuTz6ft23b\nNq2nnnxyd3t7fHTUtm0EQeLR2OlTq8kYh8EIRWB+rwfYJoEhPOcqlwowAEKvG4+GWYZyLHtyfGJr\ncwNDUEPTL56/0Ol0IpGYKukIwLyeYKPe2nq8pan65OT01Pgky3LlcqXV6BwfnfR7ipcPBgPRXk9I\nJBK1SuXZp58ZHx9rt9vj4+PhoD8QCPA8n8/nM5msrpuaang9/rt37s9OzzGUawC6pm64aCYUDBI4\nfv/uPZZx3b93Z35udn9vu1wszM1OZ3MnALIUVQiH/adPLw8EtiSJ7+xsNZv1vb2d559/VhB6ALIX\nFuY+/vjWnXv3QuFwry889/y1o+N0owWee+H5UCgyOzvv8fj6fbFVb8mCLIvK6PBYvdo4f/bCztZu\nu9mKRaJXn7jyb/+37wX9oeHU2JnV86eWz2xv7oaDETfnsU375o2P/F5fu92dGJ1AIBxYIJvOdpqd\n2anZaqka8of+L3/4R4FAiCTpt9565+M7GxcvXZ5fmKjVat/85rMe3nvl8tVUIlmrVK8+ceYknQn6\nA4okH+4fPPvM026ekyXRsWwEgk+fWuUYj4vicYRuVbqKoPfagiSqgiBZlm1ZjmnahmUapulANoLB\nOEnACDLoSz7NI/iUY/cvNkm/bJuck+yhZgpTs5FQzK9qwte/8fliKffVr30lfXJcrhQj0VAkQneE\nlmkbFEWQDPnpluhXQGhgVPyJ/OgTQNI0jWEYAECz0TF0Z2J8ZuPR9p//2feFvhwKxqKR5OnVc0eH\nGVXRn3/+MxRFR+Px/cNsLBFHcezU6mqn1z3JZj//0hf2Dw44N3/9oxu3P/747Plz9WaNd7MsyzSa\nlXI5jyDOzs5Wu9PcP9i1bAOGIZZjwpHgoES1bb3VrhEkIgmtzPHu6dUJGJgYAp2kj1w0gB2nWCwM\ndCc07WIY1jAsr9e/uVktl8sDLYcoigsLCzhGhsPRXrdvmTaBkyiKQxAyPT09WJR2ui0YBmNjY/6A\nV9fVcDiE4XClWmRZmqZxQWyvrd/1+z3bOxvJVGx8mc3mepoGcvlyt9eIxgL37t8KBN2JZMzj5aem\nJwKBQLPZ3NnZefXVVzOZDMdx09OzX3zpyzTlAg7s9wcBgIPB0P7e0fjYtOMguWzx8CAdDETOnz/V\n60nFYi3gDwMHnp6dO8nlV8+c7fb1ZrvTE0RRVvqi1Op0c4UiTlK6aQ2NjPZFSdNNzu0hcGbj0SaO\nEblsod3u3r1/r93tHRwdbu3t5MtFSVViw4lGv52t5V9/56cvv/4q7XaRPC3oYk9oh2N+t4eZnR3l\nGJR3ITwN0YRJoBqGqhgqI7BoKx0aMVjcJCGVhBTUksRWsXyykz141KmmTamOmD3U6hNApGCZwjTe\nBbsYiKYBRQCSsHHcInFA4hCwNcfWIEeHIRPHLYpEImE3TcEYgiKfIpQCCIJRCEFRADsIAkG2ZWi6\nqRuQbmk9uVUs/d63fv3mO2/U8oeW3G5XTg53H2w/vvf2Wz/c2rq3t7uOENZJ/gjAhmrIlItwseRP\nf/YmhiGxWKTbbUuSEI9Hm8362tqDWCxCEBjDUIVCbm9vZ2pqAgA7FA7UG+VGp1ZrVjkPG4uHNV0S\nZUHRFI/HEwwGI8FQwOcjMVwRFU3WdFUnUMKxHE3RVFk1NMPWLVu3DM1AYVSRFKHblwUJWA6OYLZp\nw7VqY3xs8mD/aHFxqdloFYvlQCDE8x7Hhp555tnNx1utVu/b3/5Jryesrp7pdHosyzMs7+LYYDDo\n9/spF5XLnei62uy0MieHuiErmrSxvV4sNR3H8IU8I8MJyDGnJiZ67VYsEvZwvItmarVapVQKeAPt\nRvv9dz+oFCtjw+NzM7Ner/fMmTOKIuVyubmZ6Z2t7WgsbJom52IpAh9JJQ/39nu9zsnJCYbCQr+/\nvb0NAXN97b7HzfJu18zs5MzsVCIRu3btSYaik6l4uVL0e33dbrfdbne7XQSCZ6dnhoeHZVne3drW\nNG1hYSGVTFYqlaPjQ9gBQ0ND6XQ6mRwiCMrFuFOJoesfbB4dHsYiUVmWRUFIxqONenV/fx+BoEKh\n4PMFSqVSPp/XdbNWbcIQpsgaRVHbW7vBQDiTyQiCCMOgWq0SJDbwTt3ZeRyLRSYmRx1grqwszE7P\nnDp1anh4uNFoBINBGIZFUVxZWSmVSqOj461W6+7d+7VaLRAIQRDy4Ebv6OhofGoyHA7ncsUvfvGc\nz+eTZTkajWazedO00+l0q9VJp0+KxTIEkJGRMVmWSZIOBAL/+l//2Ve+cpmimEw6a1vg6DD97LPP\nF/LFCxcuHRwcURRFkuSp5ZVysaqKGoaRFy5cpihXrdb4+td/fXZm8bvf/f77731YrdRhGKAouHv3\nbiAQwknKMmxVVY+OjkqlimnaFy9eNE07FosFg8G9vT2hL25sbMzMzFAUlcudOA40PjR5YfWJYqbm\nc0cU0eh3ZYbibN3BEBJDCYIgSBInKBwnMYLAcBL/FdftTz7+b3sa27ZN0+A8JO+jRyZSKAHmF2de\nfvV11VBzuRwAYHRsbGZ+hqBwB7J9Ia8Dm32h/Sv07v967gd/mlk+OHRdBwCmaca2QL3eVBQVAEjT\nzGvXLhAEg8B4JpN7cP/RqZWzoVCsUCi98MI/YFn+M595ppAv3blzr9vt8jxvGEalUqEZMp0+kmVx\nfmHO4+ErlVKlUvYH3J1Ok+OZaq0Mw6BQOMEwxLZNw1RgGOTzWUHodbrA4+Vs25ieHDt3djXg5xeX\n5jrtRqvZ/P0/+D/zbqpYygcCAcuySJIsFpumaT548CCbzfIc+Oijj91ut2lapmHDMPLFL365VCzj\nOMmyPAQhuzt7g7M3EokEg8FkMgnDcKvVuH37pqapl584zzDE2PhQT2hYtuoPeMYnhiHYnJ4Z6/bq\n09PjFy+Njo3jly7PjY0nIdiIxoLDIwlFEVdWFg8O9oeGk9lcZmZmxuPx8Dzv9foFQfj+97//1FNP\n2badPcn3ukI4HLUsp1AoypKaSo7Ozs67XG4I4BuPtiiSwVBqfHxaVYy52UWvJzA5MUpTrMftZ2hO\n16xatYnAeK3apCnW0G2G5nCMard63W5f1Y3j4wzH8QRODaVGGIbh3B6GYSamppbPrDgoXG7VYiND\noWRk9eK5lizJpjk8Po7TlCAIhqmpkojAFobYGGKikI6jBkM7PIf63GQyFhhKBKNBb8Dr8nAECqmq\n1FKkhql1KdwKB1zxKBePcrEIFwm5/H4SwywCh3ACwgmAExCBwSgGISiEITCBoSgKkzhKEDhFY7Fo\nBEcRAiUQmHBs2LIcw7Ys4CAIghIogkIoigIATE23NQsyYVMy+83uwthIZmfDRyMjMZ+t9XBU39t+\n4GKgYvFQlBqy2ml3KsfpPQg2h0diBIlGo2FNV2zbjieizWaPpPDp6WmWYx5vriVT0anpsbn5KQcY\nR8d7jItgWYogkU6n0eu3YAR4fW6aprrddrfblmQBghyPxzOITq+XG71er9fuyLJsWZZjWqamQ7ZD\n4LhtWa1WSxZEqS9omib2BaHX11UNRRDY5/O/++57Z1bPbG5sybJ6796DbLqgiJoiypqsZTL5f/bP\n/tk/eOHJ73z7nXfffR9BMMbFYRhhmiaK4jzPu91uWZZNU6dp0ut11xuVYil76dK53/itl6bnJq9e\nvfw7v/tbi0uzfaEdCgdPsmmKon76058e7h143d6R4VGSoCbGp77+9a+PjIyoir68sOJmOY5xZY6O\nu+12t91WJJkiyFar9eGHD03T9Hg8v/e7vxsKBGanpgvZnN/nyZ2kga1njveBrdME/nh9rddtv//e\nO71ue25mulIqzk5NAst2TKuQzcEw3Gg0JEkiSXx6ZnJhbtq2jWaz5vd6bNtUVJFlXYuL8/fu3J2e\nnDINY2975+zqmNAVAADAsj28u9vtFovFWCxq2xZDUScnJwROBvyhbreXSg0zDCuKUjyW5DgehpHh\n4ZEBz8fj4WVZBJCtG2qxlF9emY/Ggvcf3BqfGOY4rlSsWJbDMCxFMR9+eAPHSQwjxsYmut0+DOHh\nUPzqlae/+51XyqX6r/3W6dTISKVaZd18LBnVdbPZbDsOlM3mbcNuN9orS6eKOfXw4PjmR7cLuQKw\nnZWVlVAo9Morr372s5ckSUmlUuFwpFyuEAT51ps/OznJPX78+KWXXhrIlWAYvXTxCQIjs+lCu9F7\n8/W3YuHEh+/dcCznmWvPjI9ONJttx4bmZuf+1//1/zU6Mv6b3/ptoS9hKDE1OSNL6uqpM9Vqvdvt\nc5xbUbRKpd1ut4OBEARBXq/3G9/4BolRAW+Eo3ylfIPEXaYONMkCJqQqpmU6EAQhGDZw+HYgyHIs\nw9As2xiEun4iff2EZTBoiX4hDLJty7JMS5cVkWFRxoVev/HOw4f3eR751re+9bOff7R65sz3v/+j\njY0NyzJCIX96b4dmMN7t+mXQ0a8ev0LV++RXDwwfO52OphnRSNxxoAf3HyUTI7aFmgY0PDxO4IzH\n4//JT9763ndfabd6hm59fPsujpF+f3BoaIgkSZqmx8bGqtXqQFzx+7//+/Pzs9ncydLyYjji13Vl\nZmqsVmmfPrU0MpT47Gee/83f+PVrT15ZWpgzdXlhbmppYfb3fvdFQ5MYCrMdbXw0+fbP3nj9xz+a\nmh596tqFWzc//Kf/5A+npiZSqYQo9h3LhgFYWT6FwGivL6ysLg0NxV955ZXBn259bePkJDc8PFoo\nlI6PM6VS5cqVJwOBkCyrm5tbPM8TBBFPRPv9vt/ve+Ezz3W77Vz+JBj0OY4Zinhb7cri0kwkGvD6\nWJYjYcRaXJrxeelup3L34xsLc5M//9lP8tm0KvdrlUK3XedcVObouNNqmLrebjaLufze9s6FC5d+\n/vN3V1fPfPazLzIM26i3MJSIRGKBQLjflyrlZi5b5DmvY6NnTl8MBiOZdO7+/YeW5dC0q1KppVLD\nm5vbluXYNohEYi4X53Z7j47S3W6/2+273V4UJ3GCtC0olRxFEEwUpWaziWHY/fv32+3ugBouKQrF\n0DCKdAQRd/GjU3NtQfruyz+sNTo2gBwL4BgmtLtSv6dIfVXt25ZC4cDNkwE/y7A4ggLdkFVNkqR+\nrV4qV076QkvTRQdSIUR3gGrZkgPJAFZsoLg9Lo+X9/jcPr/X6/WyPE8xLEVRLhfncnEkSeM4CUGw\nbQHWxQmCYpkQMBHHQQCAHRuygW3YhmGruqUbv7w0HAdGIAyHcMxGutXipVNz7fLJycFjxJKTEd/j\n+9fv3/3QsESMsFvtcjDEH53si0oHoFalXkJRmCTxza3Ne/fuBIJcv9+1HdPrdSeT8UIhh2FItVp2\nu7mRkaFWq1FvVKKJCOtm3F6u02u2ug23z43hiGUZvV4Xgh1FkTiOw1DUxdEIBOu6DmyHxHAUQVRF\n0TWNxHCGpBAAKZKsqxqwHV3TFFl2bBtYNuz3B5PJoUajdenSEx6P79LFJxAErdebh4fHd+/epynX\nT996e35u8X/84380yJRVVa0vCqVipVAqSpJkGIYNHEVRBEFotZowDDieqVTLuiEHQ15J7jWa1e2t\nx7LYN3UtGo22mk2KIE6dOlWt1Au5oqJo3Vbn0doG7MDnTp9jWZamaQDZn//C5+7cue33e69cuqSq\nCuuih0e8j9Yfjo0Of/TRdQSBPvjgjqoqVy9f7vU6Y2PDCAJ43kXRWDIVXVqaSyQSJIkPDQ1FgqGd\nnZ1YLDZQa3c6HVWTvT6OpPBGo6obaiQUQFBnc2vdH3DzPHv5iYsYhnZ77ZOTtGUZhmFQFBUJhaW+\n8PDhw2aziUDw1PhEwOcPh8O7u7vHx8cbGxvlWh1F8P39Q8eBIAg5OcnOzs72ej2CIAiCaDabtVrN\nNM3x8ZF2u/nUU1cQBFQqxUuXzu/u7sRi8aOjzNkzF+Kx1Ekmb1tQIj4kS5quWSNDk9VKw9DtZGJ4\neWl1fm6lWmkkEgnTNAfDonq9TlGUIAiSJJ0+ffrg4GBxYfl3f/dLX/va18+cObu5ubm1tTMzM/Mf\n/sOfPvXU1cENHQJIJpNdXT2zvr6xsrLyB3/wBzCMHh4e+ny+3d3dATHG6/XHY0Oqqn/hC1/meQ9B\nUB6379Uf/KjRaH71q7/23//3vx+PJ7//vVcMw/j2t7/z8cd3CoXi0NAwTdN37tx5cH9tcnLStoHX\n633mmauO45RKpX6/P8jIWVtbRxziYOvIRXBSTyUgmqE5TbUsyxFFSZaVgfOCpmmKpkiqJGvqp+15\nPg0Vg2HdJ73LL7ZHCBgdi7Y7Nc0Un33hGZTAfv03vvn/+ZP/AAGQyxX+5//lf2p3et6AX5D6gWRI\n1qRuv2X/17y8T5MjPp1k8clqCsfRQSz6AJkcG5IkJZctEjg5PDTOsZ5IOH58lEVg4uyZiwhM2Db0\n/POfQRBsb3e/UW9ynBtBsEqloqqqbZuWbayvPywUCjAM9vZ2SBJ3sWSjWf3KV59rNCoOsFwuJpfL\nGIZ6/vzZiYnxVqsJwValUkimYjRDzM1O5vJH83MT584vhINuodeCIPvtt38WDPh4lul0OrFYbGFh\nEgBw+vTpCxcuNRqNWCwxPDS6u7sbDIbdbq+uGblcYXnpFHDgqcmZZrOta8bY2NjTTz+9sbFxeHjo\ndrspmggEAhDk/N23v7e29ujNt163bE3TpGarf+v29WLpZH39fjIVm1+YbjQqyVQEwwFFow7Qz19Y\nXVu/MzY+bFqG281pmhKJhAVBGDCGu92uqqrFYvHUqVO5XC6bzXq93oF8slFvNeqd9bXNxxs7kxPz\nwEG7HTGfK1976rnt7V0UwR0bEfrSmdMXTjI5jvVWK3UEJhAYW146ranGzPRCqVjhOV+t3rQsJ5vN\nDw+P0jR9+dKVer0+MzO3uLD8xBNPzC8uaoYua+rw6MjC0mIwFDp77nxydLLa6gciiSevPb+4tApD\nGEUypm54PR6vh3e7GBrDENiBIRMCuu1oHg/Pez0ETcAYgDEYIA6Co7yXm56fmJqdHJ0YSgxHkyPR\n0cmh8emh8YkRkiYIkqQoiiJpjKAwjEBRDMCYaUGWDVkmZNqQbcGWBdEuVhI1UdAUWbdMYDuwAwHL\nshRNkSRRViVVVwzbgiAEBgjsoAhEUhhZL+R/++tfWZgemRlPAV3MHe9GYn6vh3LRiKb2quVcOOIL\nBPlQ2Gvbeq/fFqW+ruuzs5MIgkCQY5rG/Pxso1HXdS2RjFqWSTMEBIH1RzuBoJeiCVHs27bJcowo\nCo1GjeNpj8etG6rjWCRJ9vt9jnMxDD07Nx0OBzmWJVCMIkkCxYBl64pq2zbPctFwxO12u3nezfMY\njADLhmyn3W7DlXJtcmK62WyXS9Vqpd5oNJeXlxcWFiiKWVle1TTN5eLee+99giC3t3cGe05dM3u9\nfrVabbVazWZT19Vas4bhSGookckpxWJf06T9/d27d2+/+dbrH13/cHZ2ZmRkZHpmEkHgUCgAANjf\n24vFYoIgBP2BS5cucRynKAoEQcVcsVYts4zr7sd3pienDMOoVquNRsOyrNnpmWeffZam6YDPf3Jy\nsrQ0IYpitVaenBpbXlm8dPlCMOSHIcCxLlWR/T5PIhmTZGFw16AIkmVchqbzLiYWCVumxjBkLB5q\nNCr37n/cbNXCkQAMO5NTY2//9Ce9TuOf/tN//Ef/5A8kSfB4+atXrjiOE43G/N7A+MjoIAX8ypUr\nNE2Pj4/DMByPx30+n6io/kBoeGg04A/JshoKhQYsZEVRNE3tdNrhcOjh2v2JifFSuXD/wd3NrY3F\npfl+v18slCfGZywLevfdDw/2TyiS39o8CIeSqmLnc1VNdcbHZn/20/fHx2Zv37ofjw31ugKO47l8\nfmx8XNX1crl89uzZH/7wh4ZhmIadyZyEw5GbN2792//t3xEEtbCw0O/3x8ZG3nnn+ujo6KNHj7PZ\n7J07dzY3N7/85S+LoqRpxhe+8IVerzc9PT0Y5oyPjjkW6La7qqzt7x6MjYx3Or2Tk9zk5PT42OR3\nvvOdbrcXCAQnJ6f/5m++vbS05PV6P/OZz/b74ujo2NbWdiaTmZubOzo6ajQaDMPMzs4uLi7atk2S\nZDQa/9IXvmTqdqXY8LsDkI2SGBUJxd2cx0VzsqJJsiopiihJkiIrumY5tgPZzn/do3xaaTSACsdx\nBvxvDMNoml5cmpudG83nTzYer1M00Wg0dM26+tTFbk/4l//yX3/uc59TFAXHcZeL7vaagYB/YJb6\nCQh9An6f7I0GBIpPyBQkSWqaQtM0giCNRqvfF8fHJjOZ7M7OQSQSu3vn4fT0vGUC03B+8pMPSZIu\nliqFUplhuUA4cvXa03cfPMzksr5gIDGUYjhWVlVZk0vVkot3DY0O3Xtw98ZHH87OTdbr5XPnT4dC\nPgCZly5fSA0lXn/9tdsf32x36rncic/vHRsbkuReq1X3eDlVlWgKHxkdnp+f7bbrw8MpVVUAACND\nQ4FAIBQKvfvuu5pm+LyBYqE80FFAEHJwcEDT9N7egWU6/b6YTp+QJD0+Pr69vTsYF/v9wc+88FmO\n4wYGMJlMxnHAxYtnLAtgGJLOpFMpb7fX+vjOOgTb1WqZZZlkKrawOBONBZaWZ8bGh0xL9fncFI2l\n0weyIh0e7qua3Gq1SqUSBEEsyw50Ant7e7YN6vWmYVjDw6M+X6DXE0iStm1gWU6lUkMQYmZmYWNj\n+/699cOjk+m5+Y9ufdyXZIphIRQrV+uVeqPTEwLhSF+UJ6ZnJEWLxBOyqguCJEnK9Ox8TxBkTXvl\nlVc5zl2pVG/fvo1hGM/z09PTkUjEMIz9/f319fX0SW7j8basOBuPD1/94U/yhWowHA+FoqFgzOPx\n+Nw+D89xLprCMQQGjmMZhtYXBcM0VV2rNxu1Rr3T6/aEbrff2TvY3TvY3Tvc3jvYOcocpE8OD452\nt3Y2Gq1mq9VpNtv1Vrvd7nY7QrcnCX1FkXVNtTXVNnTINIFpQCTBSrKm67amWYpsyJIqy4qsKqqu\naIZuOdZA8IBAiG3YQlfqtQWlLylC35CFYibdrhYxxOq1a6unFjiWdDEkx9ORaABBnaHhhDfgBojt\nD/pIkmBZ14APBICTOTm+detmIhlDMViWRd7N+nye4ZHU1FRcUaRqtegAq9fr1OtVnEBxAjNNneUY\nyzJlRZQk0bKNWq022K26eR6CIE1VHdNy0Yzf66NJytB0CICA3+/1eCLBUCwcoQgS2A4MINu04HK5\nmkoMJRNDKIwyFGPIqtSXSvnC4vwCx7tkTcYoaP9kp96r0D4SYSGcwRmeIhkCgizLMhRJtE2n39J6\nDYGEXSQMUhGfJlqVfDUWivs4n4/zkgjebXbFjjCcHIIgaGJiwuf3dzqdhaVlzs1XKrVIJLq0dCoU\nigaDYQJnYtFUMBgeH58mSRqGsdVTZx0bTsSHaZKlSTYUin3xC1/hXN6VpVWfOyR0FdjBPVyAd/l4\nzpvLFtutntCX6rVmqVgbHhvHKVpS5HK1Um82DNtCcURRFILE3G4vQVA+rz8cCGuqIQny4f4hjhLx\naIImyWIuPzUx5vd6lk8tfPVrX4ylwtNzE4mhBIpjvmCgJ/RzudzW1lY2W+t2uzRN+v3ufOH48Ghb\n0cWRsaFarSqpAs0Qii51e03Ow6ia2Bd7LEdF4xGXyxWNx7rd7tmzZzc2t/yBUCadTSWHY7GEYTsA\nwIZpwxDW6XQjkejYxMSli1fe++BGMjEEABwNh8dGRyOB4N7WLgJBBEaKgtxtqWOjE41ag6Kovb09\nl4uempo4tbokyyIEEIZh5ucn2+0mgjjFUr7ZFI+Pj4EDp9Mn//HP//LWzTtzsytjY5MbG3v1WvP1\n199amF82DMsybQzFNzY2BUGgadq2zXKlGA2HRVEI+D1HRwdPXD6rqXIoEkIQqNNp5XK5hYWFixcv\nZo4yE6NjbtY9NT6VzeYpijl/7tL+3oHQl1neV600e3211ZFU1azWm6ZhwyiqaLLjOJZt6Lqm67pm\nGABAMIqTJP1fGhSAQAABDgwcFDgoBBAHQhwIsoBlAcOGTBhzKBoem4hBQDVNiaHw1dWVXC7n9/sN\nTTdNc3x89KOPrr/wmWdRBFQrhXg82u21AQCD9siGwKcXVAO0G0DRL5AJQlEYdRyIIChNNSAbCgSC\nnWab571DyeFKqVotVy9fvqxI8tWrVzVdcblAvV43TXN4eJhjuFar9Xj98crKCoEQ+/v7Ho53MRyG\nIIqiSX1JFGVd0cPhKE0x5Wp9ZGSs2xcJgnD7vOnjk0ar43K5AIxWqz0HRkRB8vhCO9t1xsU7NuwP\nhHf3DlVFa7U6oijzPN9ut2/f+mh8dASBnLHhkUggaOpGpVg6u3qGwBme905NzimyLknK8PBwMOTH\nMESW5Y2Nddu24/F4p9NLJoYmJia77X6pUNcka2R4MhiIkQROE+5YNF6tdCbGZ5qNHgTQC2eWstkc\nQWDbO1s0TTcbbY7lFxYWtrc33W5ubn6mWq3YjjmIZeM5z/zSom2bAAEAtVVTTiQSrVYHx/F6raGp\n+rf/7u9ZF0eRLsdxBEFYXl6+fft2LBYZFA2GqQSCPII4LpY8ONiLJ8IXLlxotRuRSESSBa/Xqxsq\nSeLH6X1B6Kla3+WiF5bmx8fH+/1+JBIRRXF0ZJwkaJeLpylO0wya4oqF6vb2LgyQVGqo3+3m8zkI\ntmZnp8+cOa3rav4km81mq9Vqo97qdbqyrJqmCUMOjuMUidMkZdsmRRM4jum6LiuiaZqGYUiSBAD4\nRf4py/I8z3EugiAAALqq6aqma4alG45pwQ7AEJTE8MH5NjgJDdNSNUO3nZ6gwBDiWEBTFFEQxL6g\nyoptOggEYwiKIAiKohACK5rR7HWqjWat1TYMw+fx8iyz9vA+ZBmddlWWWwyL9KRaIMyvnJkr13PV\nWv5gf7NwkmUpfGJyxONlXSy5sDgDIDMWizSaFcexYBgEg0FZFmmaxjAEgiCPx2Pb9sLCAoqihYJE\n0zTP86IokiTKuCjD0lVNDEYChcoJTkG5QprlKQy3m52+JHcpFxZN+D1+xrAlRe8iuGlaIkY5rIdA\nKNsCCkI5Hj8DPfPfDc/MzBRPcsl4CnKcWCSaTMavX7+OEfi155/5m7//667Ua/Sa6bz+R//8q4FA\n4F/+3//kCy9eVFXVsqw7tzaGhyO6rhu6rsnS5cuXH62vT05Mpw8zkVBUkdTJkcl6oR7xR1EIpmkG\nQwlRUSEb0k3LNmx/KIihhCCJtm1DKOI4DnBgx7Icx7EswzRNGIZRFLZt2zA1giAgCIiiWG81Lcti\nWQbHcdM0ed6D43i/3zcMrVar8TzPMFQg6ENxzOv15HI5gsAGybO+gBeGYcc2IciJRCI4jm9tbeEE\n5jgORdOWZblcrv39g6mpqXQ67XJxuq7TLIVTYGgsyfPs+sajw6MjkmXmFucVRUFgFEXRve09ny/w\n0zd/xjGumakZ27ZDoVC72yZw3LJthiYdCLSbLa/ft725FY7EdFUXJNmxwNz8YjZzEolEy4XapUuX\nwuHw22+/vbd3cPHyJUVRODdfLlXz+fxTT13zBvx/+qd/OjI6GvSHItGgofcoioxH47/3j/4ff/zH\nv9ludWEYefDgwbPPPvvh+x+EQqFgKPDw4f1AwJdMxYeGhgbUgNsf3/zxj+/+kz/6xl/8xXdmZ6au\nf7j/+Revdrv9cDhsWuo773wwNRP91m9+7e7du6VCO+CPNFt1iqIsSyMpAkEg01L7/S6ArC9/+YuW\nY9Zr1cPjg2efuSbJ6tFhxrIckqRDgWAul6NwiiapXq/v8/n29/cj0SjNurLZbGo4FY8nTJ14/dX7\nYh90O31BEAzDchwHcmAAgKqqjuMAYEMQhMEIBA+AwbJMBQbAsSHHgWwAAfCLeDKCwASpz7hwRRVQ\nzAkEvY127UtfeW57971nP3M1XywCCHH7vOFIpFgp/+xn1//1v/4Xf/If/qOpQssL51tl8cYHD0wF\nhSEcgWAbOJADHOiTdRECAEBgbNAMAQAGQ04AIBvAtoVQjAtAlg00msEYHvcH2WCIr7dKtXr+t//h\nt95867ULF86+9/47JEOGQiGaYerNRjQcGR0fKxdLh8dHM1Ozvb5o6mZqeGRv+3BkbHzr8Va90eBc\nvG4onBuZmh6lCEpRddt0eI/34b31p56+9md/8udf+bWvvvrKy4ZlRsLBz7/0+Z+99ebKyoqH57OZ\nk2azOTk5blp6vV4LB/1LS0sETv3N3/zNs8++cHyUQVHCNGxZVmvNWrVVvXzlEo7jmUy2XmsgCCLL\n6pNPPimKYq/XY1l2c3PjhRdeePe9dzqdjqZpY6OTJElHo2FB6L36w58/9eQiiqLBoL9RqyaTSV1X\nG7V6Pp8fGxtrt7uTk5OS3BsdHf7gw3dXV1ccyO52u7FoyjSdZkt0HPg//cc3vvb1Z+/e+RjBwDd/\n4+vra4+3Hx/HQklBEEZGxgZhev1+f3Fx3jC0XD5L0ySGQzRNBIK+hw/vX3v22p//xSuf+8IVGEZ7\nPUFVdFXVIICcOXNmbW3N5XKJUp/jWE1XGo0agkBXL19972c3psanUAKtVquWbbjdboZlKIpgWNfe\n3k5XEFEU1gydYZhKpQIQEI9HAoFQPV+lYIpFeRZjlbZCwKSl2o5uKorS63dwCndxzPTctOM4OE62\n221ZUhmGdzGsKKjZbLZcrvp8PhxHERSyLEPVJNNSEQTBUAJFKNMAMIySJOXYkKrqhmEhCCRJEgwD\nGFiKKsCQ7TgWSaHnZ+dm3J4QRbjdbgA73W6nJwo4jnO8G0VRWdM7XRGGsFa7T1Nst9vvCn3ezy+e\nXdnKHL7+wTt02AO5GcBgvni40q4AxNIUBYFtHIY6rboqiV6v1zBtgiIFQRgdHZUkCQC4XC4ztMvt\ndqMo3ul08vni4CpoNps065qbn79x6yYMw8PDo5FIpFAoaKouCJJlObIgsyyLoUSr1YYgiCRJQejT\nFBII+jRNxXAEx1EcRz1ed6/XUxTJ7/cDAKuqCllAUhVZkOFYNCX2JZ8vZOp6s964/sGH24+2MBTt\ntBv7+9tf/NLnP/vSZz73pX8wtURpkLif3QrEwNbuRijqtyw9EKSefOrKb3z9G7/5zd988tK1uzcf\naoKzubZLOPTe4wOpo7Tr3aA3zNIuCKC6Zsqaruu65TgwCiM4IitKs90SRdGwnEEWSKvVEfpyp91v\nNXv9niyJmqqatg1jKIMipKbapgG5XR4P60UcHINIHx+ELFSWDBfJDw9NzM+tuBheVc12R4Ah9O69\n+yRNqZbR7na8IV9fEnPFHO1idNPKZvPFcoVleRQjERjHMBJDCElSw8FIqVRBIFTTNEWSy+XiYWa/\nUDrZ2H6UGktduHxxbHI8n897vN6dvd3d/T0EQTY3NxKxUDQWFKVeJBrMFU9kReQ9HII6qq4YhpIr\nZLa3N2gX1e21GZZZXFw8c/Zsr9cDMByJxqenpzOZzP379zc3N89dOG/b9uj4mGVZ7Xb7zJkzpmP7\nfL6te42xsbFmu6VpWrlY8vEeAiN1CdAkNZRKCT0xd5Lvdfr1ev306dMjI0MA2IlkbH9/Z3p6cn19\nPVfIq6qqm2D/YNvjI0dGhpJDTCgUSqaGV5ZPN1u98fFhQVRazU6n24cgiOW5hfml1NCQJEntTmd2\ndjYQDGYy+YmpSUWRJFnEcVSShHq9+s47b3t8HhfHJBKxbP4EhuEvfOELmqafXT3t9/jnZhdo2hWL\nJWZmFz+8fhPFKFWzqs12py/rpgVgBMCQ5di6qam6MpBToCg6cB5DYAyGUBhAsPOJ3OeXUOTAwIEF\nUUZRFMExCAUIDlfqxQuXVy1HHhtPNeqF08uLm48fpw/Tum6eXjlNkuDu3bvJZBIC9v27t+KJqG2b\nPMtiCOpANgQ5Ayj69LDO+uUxwKFfyJkQDEEw07B1zbAM2zRtRVQ6zU6z1iQwMhFL7uzsTE6Oa7oS\nDPoH2Qe2bU9PTjEMu725xXFuDMG3t7dlSWo0GqFA2LKsQi7vdrs1RW+1OgiC3ru3eXiQ7vXldDqH\nE7QoKFefugbD6HG6r6nG4tKqm/dXqk2hL5MUJ8kGywVffuWDeqMbjw8FA9F6vQEh2EcffVSpVDrt\ntiKJp1dXFUmanZpMRGIoBE+MT4uC8tabbw8PjXAcp2laMhlfW3sgiv1sNrO9vfncc8/95V/+5fjY\nxOnVM+fPXQIO7uYDHOsncB4BoFLq7m6n3XwIcigUZqS+0ah3Q6Fovd4cSiSPDw4nxmdazd7kxEy/\n31dVFUXRg4MD27YRBE0fn/z6N1/odDq0i4rFI99/5XuLS3NnzqxqukrT9KNHawPKot/vz2Sypmn2\n+32v180wFARblq1+/guf0XRxeNSVL6RZjo7HwwSJeH28qsn5QjaXP2m165Ik0gxeLucDQbdpabl8\nJhT2Q7BTb1RFqT81NcXzfLvVqVYajVoTx+hkNMlS/FByeGZqdnZ6jkLxdrO6+ejeqZX5z332+bn5\nKUkSNE2FYVjXdQeGGYZheZ5lWZIkB6cqsMyQPzCUSOIIXMjmKqVCJBT67AufuXb1yQvnzi3NL0yO\njY+khuLheMDr410sBiMIBOmK2m406tVyp9WQxa4qiyQOo7BjmJqqypZjG5Zp2QAjcEmSNE2zLAsG\nEAqjGAQDy7F1Q5FUQzX6/X5fFGwIKKYGE4igigAA23TOrqyODw+5KFJXxF631WyVNV30+bnkcIT3\nshzPRCMhlmYatYoDjF6/g2Lw9s4mSeFHRwccx3W6bRRFVVWWZXnACTB0i+c8sVgslz9JJuMrK0sY\nBmWzmW63DSMOBNsIagPUgDGb4TFPgHa5MZR0IMx0+1zRRHByZsQf4gCi25CqmQKEaqMTCc6DO7Ci\n6D1B69iQijEQvLu7/3hjS5E1r8e/uLg8NjY2UEEbhqHpiiQJuq5mMseLi/MTE+M0TT311BPlilSv\nlk1L/8M//APT1N9//92f/OS1fD4/NTVF07TH4zk6yj/99NNf+8bXE0Mp3sdTLINSGEwgyCA9G4NR\nAufcPEZiMAbjFO6iSRyFMQQicRSCAAxDNE37fD6vz41hmGmauq52u11RFDVNGZjFabqiarKmKziF\nO5ANEGA5Ju9lOY/LH/S5OIag8HgqwXt5iiEhFOr02m4vT1K4rMkQCglSv1QtDb6RdlGGbdAuinWz\n45NjDuxIiigqoigLlmXNzs62Wh1dN9fXNjRNBw40NTnd6/VDoUg6fSIIUjgc9fuDAyIcRTHBQDiZ\nGBIFWddNhmHcbm8yOSQIUqvVIUmyWCx6PJ50Ou12u4eHh9966625uTkURT/88MbKyqrf73/rrbcg\nG75/50EqNdTt9vb39z/44IPf+6MvvvXGT0+dOnXv3j2KZPb3D2Kx2NIp/m//9m8nJyfT6TSCIJIk\nraysnJyckCQ5NjaWSqVSqaEPP7wBo1ilVh8ZHU8kwfbO3v/0P/+LntB/8tpTf/6nLzdaTRs4giiu\nnDplO84rr/6wVCk7EChXSx/dunH3/p1sPvfs889xbn53f++Z5546tbrq8fllRa3WG1efunbz1t1A\nKFyvN3b3D9MnmTNnznU7/Y8++uiJJ57o9sVgOJrLFdbXN4ADP368tbS0cufOvfsP12RBNDQFABvH\nUYrAKQLHcRRF4UHdROIogSEICkGwAwH7/5DPDSAbgh0YsXECaTQrNIMLovjMs0+Oj4+WSoWVlRVV\n0U8yudXVlVAoVC5XHzxY+63f+u1crhAIBM6fPx+PJ2dmZliWFcSerIi/wl/4hLlnmqZpmr9EI/DJ\nvI4gCADZA+kbgiCGYUqiLEkygVORSGx//xCCkMOD44WFhcuXL2ez2fn5xcFwr9FolUoVvz/Y7fYj\n4SjPe9bW1q5du5bL5bxeb7PZbLUaJEmEwx5RFB8/fjxwWhuEzhm6lUpxjgMRBBEIBAKBwLvvvru0\ntBQIBP7iL/5icjrqQNBHN2+6vR4IRu/cvcfyHklVMyddACPlSiUaj91/+OD+wweVSiWVShUKhatX\nrz548GDA6/N6vYlEIh6Pj46Onjp16n//3/9samrK5XIVCgVd1wEAhmGsrq6m0+lAwD3wygQApFKp\nt956KxqNfulLXyIIwufzi6J048bhw4drtVptd3cXhlGv21cqFN1u92CXMDe3MDDsuXbtmfHxcVVW\nfvCDHwhiT1GEYinHcrQgdE6dWvR63Zom7R/s8TzrAItlXQNa/L1791RVf/qpaytLS41qTeoLsXCE\nwonBTWVpfqHTbBmqdv/OXch2DFVLxuK6qrjdXL/f4RhmbHj48PBgd3en3WpWquWTk5P9vb3Dw0NN\n08r58u7mLgSQz33u85cvX4mEYyiKr69v9Hui1+sdBPy4XDTHsTzPu1wuBEEGdyHDMFOpYYIgut1u\nt9sdnC3lcvn+g7vvf/DujRs37t+/n06nRVGkKCoUCiUSiWg0OjY2Njs7OzU1NTY2lkolgsGgy+Ua\nxKYoiqLruuM4hmGIoqgoimboumnopqEZuqKpoiT3er1Go9Fut9vtttgXWo2mbei2ZTEUjUOIqWrZ\n47TY63MU4xgmR9Cw7SiC2Gt1apV65vhk6/Hm1tZWpVIxDAMCSDAYnpqcAQ4cCcdq1YbX63ccB4aQ\ner2uaVoikThzZnV+fjaeiLpYWlEkj4fDCci0FJJC3B4mEHSzHElSMIY7DrB1Q0JQOxT2Tk6NnDm7\nfO3py6Njw9VqNZ/PAwcOBEI4jg/CWlmW7ffFWq0hyzKO46FQKBQKweFQdHn5FIrizU633xNFUS5W\nyu12OzU8ZBjGcSZ94dzZJy5dYF10t900NEUSus8/u7yysrS6uqKoUqVcwnBkeCi5uLiAYciTT14J\n+EMzM6PT09O6rrtcLhsCNgLBBEq4aIqjcZqCcBjAjmJqpmlCkDP414qiaBgaSZIsx7hYmuM4j5fn\neZ4gMBgGA1MWnmf9fj9FE4yLikajkUiEZCiA2AgG6ZZ6nDkuVYqqrmAEquiKIIvxZAxCgKzJLg+r\nW7pqqIzLBSBI1TScIhmXywJOvdGwgIPhOMOxhmnu7O/ZjuMN+BcWF+OpJO1iFFmDYdg0LJ/PryjK\n1PiUYVhbWzuBQCDgCzabTY/HR5EMBBCapkvF8u72bjabgyC41xXS6ZNCodBotHjeQ5IkRTIHB7lC\noRCNxlEUy+eKLppZW1srl8vPPPNMo9F49OjRH//xH//Jn/wJSZIIggQCgaGhoVqtdnBw0G63a7Wa\nZdmKok1MTG082lxcXHa7vbKkUBQ1NTX16NGjl176km3b0Wicopifv/3uuXMXLBv0BalYruqmceHy\npf0t/eD4KByNdIXu8KSX87g/unUzmog/eryxevYMxdC/9vWvqbqSLWR1SznOFj/3+c8VK8U3f/pG\nMBLm3Hy71y9Xat97+Qc7u3uT03PNVieWGCpX61/60ldQnNw/OPIF/A/XH7Xa3UtPXGFZttXunjp9\nVjeczEkuGh/q9ARF0XAcH/A7Br5VFEW5XC6WZTEM+8SSeUCTsyxrQEIBzmA65wwSWiHIAcAkCFxV\nRQQBALIABL7+ja8apioIvQcPHpw5c47huLNnzkMA0RTt6pUn08cnTz35dDZ9EgpFGo1Go9HI52sw\nioRCoU8j0K+QvAcd0idfdRzHcSwAfqG9RVEUhlHHgRwHQmBid3f/zJlzxUJp49HmzMxsvd58/Hhr\nYWHp4cN11uVmaJeL4Q/2Dx0bnD1zYWJiyjTNg4MDiqJmZ6ffeuvN1dMr4xOjOztbqVTq4cMMiuIX\nL1x66613ej1BkTW/P3jx4kXDMBiG9fv9EEDK5SpBUB6PR1aV2fmFZDK5sbVlWNbY5MT09KztgHQm\n+zv/6Gub29ubO9vBYKgvSJZjP/HkU++++64syxRFhcNhkiRJkjw6OqrX69lslud5HMfjcR9BEJub\nmziOHx8fy7Lc6/Xy+TyO4+12l+PcFMUQOLWxsWEYRrPZ9vuD62sbw8PDh4fHv/ZrTx7sH+VyhWy2\ngqFEOp1OJFL5fLHfEznObVnWtSefrlQqkiSRBP3cc8+9+OKLi/Mzc/NTV65efPa5p+bmJ9//4J3j\n9IHHyw0NJSOR0MjIUDwen5+ff/hgbXX1jKqq2ZP8wf5RLBbjOC4Wi01PT+fzOcuyAoEAwzAjo0Oh\nUOj06dM07RqcS7apilIXw6GZ2QkAmYyLsCyjUipubx8LgsBxXD6fX15evnTpkt/v/zf/5i/u3Xsw\nMjISjyfa7XY+n6/X67btjI6ODqZVpmkqitLrCu12u98XNU27devWzvZeq9VxHIemaZ5n3W6O5/lQ\nKOTzeViWgWAgSUqt1sie5I+PM7VabVBY9/v9TqfTarWq1erATUrX9cFFQZIkBEGSpLQ6XdU0RVXr\nCGK93Wm2u+1et9PptNvtVqtVr9YQAPU6XUWWUQhQBJ6IRSHTblertXx+JBEP8B6eoXmKgW2Ho5he\np99utizLNgxLklXKxY5PTdsWbNvA4/brmtXvSbpmGLqp6/rApfvo6GhtbW1jY6PTablctNfrBpAJ\nwSaGQ26Pi+UIt4cOhX1T06MvvPDsE0+cGZ8YYly4ooqlcv7oeDebywzUkBMTU5qmdzqdUCgyMjwa\nDkcPDo5UVU8kEtFITJKkcrnqOBAcjcbC4Wg6nTk6TMfjyUAw7AsETcsKBoOyLMuyuLb2AIZBv9OR\nRSHg806Mj7oY8vhofygVu/7hu+Gw3+fzYhgCwc7FixcZhrl27VosFjs+zhSLZcuxLQhojqE5hoUA\nCEMABsEoAiGwA9kWsBzHgSAHQaBBdUySOEqgNmTLmtwTe4IsmI6JUzjn4UiGpFyUi3fxXrc34PP4\nvbzXzfOs18+HYoFEKhofikbiIV/Yx3pZhqUUXUznjixg6aZG0sT45Hi335V0xRvw9SUBwRBf0G85\nVrPTUjSFctGFUsECNoqjwUgIQqCTfBZG4XAsms/ndd1AEMzt9g6K3+997+W9nf2bN25pqtHrCT/+\n0c8syxZFqVqp3blzD0XxzPGJrhoYgkXDsfHRCVXWCIz0un37e3tPXjl/787derXm9/ri0Vgiker3\nxUa1kc8Xl5dPed0+HCWCwRBBkKIgowg+NjTWqDSy2Xw9D6Lh2OzUNIYRpWLl5s2bAIBz5851Op3p\n6WlZlhEEKRaLGxsb2Ww2Go0qioJjZKvVgTHM5w9ksvluT3jhSzMP19bCsYiiqZ9/6aWfvf02QVG8\nx42RRKVWPXv+fL5QyJdyALFTI0P/8He+BmOw1+8Zm5yIxmOBUKjeaG7u7AII+/JXv37n7sN4cpQg\nXYnkyO2P7w4NjYyNjSMI6nZ7X3/zDUlRjo4z3kCwUW/X641gIOLYcDQ25GI9JO2CIEhTVEkQFUWx\nbRtDUALDCQzDUfQXlgoDy9RfELuhT7dHEOQAyIJg27IVRRPCEZ8D9KFhL4xYmi6MjA6FghEcI09O\ncpFIoliszM0uvP32O6vLp3VFAwAWBOG3f+v/FI/Hz51bNgxDkPq/AkWf6F4/sWCwP3VYlqXrumUZ\nDrBt2x4UyLYNYBhNJFKKrC8trXo8gYcPNkLB6Fe+/Gv37z20DAuFsYO9w0Qsefni1WymYBn25sbW\n/u7B7PTcy9//PgTA/NxM0O/PZjIUiQf9wQvnZsdHxx4+eDCcSsEAKRXKJ+mT6cnpmzduzs/Ov/mT\nd0ZHRqYnpzRFvX79I6/Xmy8UKIbWdD1XKJbKVd7je7S59eqPPtjdP1hYWk4kh+7cu3f63Nmh0ZE3\n3njjueee0xT9zu27lVJVU/Repy+LSiwSV2Xt5o1bYl+6eP4SiVMojOVO8sCGcBzHMGx7e9vn8yUS\nMQiCJEmKRqMEQdTraqVS+eM//uNLl57QVOPJq9dEQZ6dmlVE9fyZ1Qd377Msf3ycMU0rnT5p1uqL\ni4svv/xywBf0uL2maeI4/sMf/uDgYIdx4e1O7eOPb/r8/MVLpz/34nOMi4ARmyARHMfWHz3MZrMj\nIyOCIBAEYds2CiOtRtO2rMePNrKZky998Yvnz52tVStzs7OGpidi8d2dHQSCK6Xy8PAwRZNDqThO\nIAeHu8Ayu61mr9/heFcqFfD5PIauv/D884VC8ec/f+e9n7+7vDTscfsEQfrg/esIgg0kwJqmDfzC\nm81mu93u9XqSJCmKMuhmSJJ0u91ut9u27VqtlsvlGo2Goki6rkIQRNO01+sNBALhcHhgCBsKhVwu\n2rKNgUm2rusYhg2sogEAOI4TBIUi2KBoEyVF1o2uLNda7Uqj2ez2ZEVTdVNRNF3RRVHkOQ7YtiSI\nkANs04pFopamSr2uJisBt3c0OZTLnJiK1irXapVqtVASRZkkaBhC+n2x3mg1mu29/aNmoxcMhnGc\nrNebvZ6g62YgEDIMi6Zdfr938PB4eADseqOCYhDPUgQGIEeHgRUNB8JBD00iW5sPS8VMr9NQpB6w\nVRQ2KQLx8C6e5TqtbrVcMXVDV41CrlivNmiSjoQiFEHZpo1AKOfiXTRraDrM8zwMISRJhkLhialJ\nDMNgGJYUOVcoMAy9tLSkaVqjWTu1umzoOs+5vG6XKPb9Ph5FAEFguirLksDzfC6Xq1aroVCoVChS\nLiaVSpEk6fZ6aZ6BSER3LMVUNVu3EYCQKM3Sbp/bxTE4hVMU5fHy4UjQ7/e7XDSKwgSBkRSOYQiG\nIQSB4TiOIJDbzTnANkydJHEMw/r9brNZF2WhXCsXSrlqq0pQGEFhAAGGrZEsZTimqiuNVt0f9Nca\ntVK97Pby7W5L1iQcx2EULZfLpUrF6/XaAPT7fQDD3W633e3Ksuz2emVZNm273W6Oj09SuGt8dMIx\nHVFQ9/YOOIYbG51UFQNFMVnSTp9arFRqi/MrnVafc/FiT4nFEvl8EUGwSrn62o/f8Li90WjUNKzF\nhaW9vQNF0cLhyPFRxrZBIpaUBfHy5Sssyx4fH0ej0f29g1gk2mw2NVW1bfvx48d+fxCGYdINAoFA\nrdqIRROlUqVSqZEk3Wq2+/0+SZKqqmYyhWKxGIlEYAhxu70AwKIol0tVSdRomuv2RBhGl1dWdV1H\ncSyVSo1OjPj8np7Q4zhu/3BP0wwEw2OxWLFsP//805ajX7/+wdjEaCgUCoT8hmF0ev18Pp/O5MbH\nJyLRxP7eke3A1UpjeHQiEIquP9qUFM3t8UVjCdbF67q5sLxy9tz5YrlSb3TOXrgcCMZKlXq10iBJ\ncnCl/Te7mV+Yzn3SjnzC5/4vXQvkAMgBwAaQCSDL5SLanbrHwyaTsVIpRzPEyNjQpStPfO+VV5Op\n0V5X5Fg3gVKWAQRBKuSKC3OLtXKVoqhyuZwrZPtSX9d16L85Br/qV5IsfqGuNU3LNgdcu8E0z7aA\nbQFDN2dnFhr1FoaSPOcVBEmWVcsCs7MLC/MrN2/ecbncGEZ5PUGa4rodce3hY9uCK5UKjuMcx+E4\nrumKA4yBCgdBUFXVhL40NTWDY2Qymer1hOPjTKfTkySl3wdej18UZQTBFEXRdN3j8ViOPT07p6ha\nKBTpixKMYAQBkkMjDMvLsmJYdiQWpRmGcbkCgRCKoqFQJBwOYxjRaDRQFFdVlWHYVCq1tbUTi8U0\nzYBhOBKJDSLs4vF4vV4XBCEciqqq6jhQvd50HMi2AcfyEIT4/UFF0URRdrk4HCcj4ZihW8nkULlU\n83kDvU5f103LcmAHgmF0e3vX43YPXnzliScmpyaCIZ/f7x4ajgLIuHnr+o0bH+i6Eo2GWNZ15+7t\nSCT02c9+VlGUbqc3khqBAdLvixiGNxoNTdNcLvrwcL9YzO/s7FAUoSgSRVG6rnMcr+tmpVzGcVTT\nJYJAisU8jDiqpiSTsWg0XK81YBge+KSVy2WKohAE03VjfHRSEtXDw2NN1Q8PjyVJoWlKUSRVVQfU\nLQzDKJrAUMK2bU0zXAwHABAEQRRlGIFYlmUYZuDMZhia4zgwDKMoimEYiuIDYiEMw4ZhmJZuWeaA\npT0QJgIAYAi1bVuWZQBgHCdlWTYBJJuWoGmiqpm2YwPYNG1JkiAIonCCIAg3xwHbVBVJFPvAsWiK\naNcahUz2aG8/Egj02x0SRSRBpjCSIWmaoGEHhmGUc3t8/gCOUankqGPDJ5mCqpihYGxqaobj3Pl8\nfkAO7Ha79Xq91+vJsqwbGorCkVBwkLdLkuQgHE4QBMMwBrHlKIoOrujB8ICmadO0Q8EIhhHNZluR\n1XA4GgpFKuVavdZUFX1Arul2+41GSxRluNVodzo9Aqd8Af9bP/tZ+iQjyfJASSOpiiAIFEXt7eym\njw4/vvlRrVR65+dvFwu5Xrtz7+M7CIAoglxeXiZxjGVood/7sz/5U5qmCYIgaAoA0Gg0EBK3YFs2\nFEEVZV02HAPGUYIhBxpgiiIQHHFgAGMIhiMoBrtctNfv8Qd9Hp+bc7OchyNpwoZs3suzvIt2URRD\nDp4xAoVRCCMQnEINW4MxoNsqQaEAsQBiqYYcioSK5SJBE32pf5Q+dGBHVMSDgwPNVPtS7zB90Oo2\nWberUi8Lcr9YKVQbFUWXJVUsVYuGrRu2nkgk2q1Os9k+PDxWFf369RsM7eI5N+/i45F4KV+ampgG\nAJ6fW3zn5+9FI3GKZGZmZmcm53KZgqUDAqPbTSEeTTimA2wod5I/f/YCjhBv/uSNhfn5drPV7XZH\nR8cPDg5tw4pHYkK3v7b2iCRpWVZ5zqPKWiyWcByo0+wlop5KsfLuu3csy7569SlBkIKBkM/nOzpK\nV6vVyclJmsYgCJqdnacoCgKwzxcwDAsAqFiqdPviuYuXXvzCF/OlYk+UPD7f6Pj49u5uMBKGUOTx\n9lYoGpFVtVqvm4595nzMG/DWmrWJ6Yn7a/cb7caHN25wbvfao0c2gIdGxnhP4O799eVTZ4dGJmTV\nvHPnAYqSnXbv5CTncnEkzYyMjX/nu9/f3tm9efO2ZUKHB2kYwnpdCYEpnzeEAIQicbeH83h5miIg\nYBumphuqqsqqKmuKrCmyrqumqUOOhfzCIA4ezOgAsAEwIdgCwEIxmyBh23Eg2PJ4WVkRotGgbqgb\nm1tT07O7O3sYRrz00pe7HeF4P10t1X3ugJt1z80u7O3txePxYrozMTWOEhiK/YLG/WnPhcE9Avwy\nffzTzkC2bcO/GCU6EIAxjAAAUhTjww9uwjA+Pja9vbVfqzbzueLjja3VU2cODo6qlfrC/JKq6Ddv\n3pqYmBwfn/B6ffl8BUOJZGKoWCwWCoXl5UUcR2mahAAS8Ic8bh/L8jhGHhwc3r59xzKde3cfXL50\n5fatO7/1Wy8Vi5VKuV6vNZcWV1ACL5RLO3sHumnWGi2cIFEM1w3L7WEJkvrz//iflk+d9geDh8eZ\neCoZjkWvX7/+uc99XtOMycnpg4O0JNkAwN1u/+DgiCTpZ599/kc/em1+ftG2QbvdXV4+1ev1aJpe\nW1v3+/3Hx8fhcNjr9d64ccPvC05Px3d29jJpa3pqhiTpTOZkYWGRd3l01RwZGWddHjfrdrt9GErE\no3FRkGEYxREcgpAb129KgriztQ3DsKIIhcJJKOzv9duBoPfsuZVTq/McT+YLmU63EYmEEonYD37w\n8pUrVzAMu3H9o7Gx8aefehpHsVQiefbMGZqiOJbpddunT62QBIbAcPbkxOv2aIq6srQCAUQQeqVS\nodmojQynLlw499xzzwynUqqqRiIBFEZSqdSN6x/FownbdFZPnVFkrVyudjoCiuKqqquq6vV6B8Nk\nmqYJAsMJdJBNOnC/VlVV13UMI3je4/F4WJZlOZfbzQUCvnA46Pf73W43x3EDUf/AyKfX63W7bVkW\nByAEw5BlGYahIQgyWEY6jjMgiGMY1hOlliB0ZEXSTQfBSBfLsByCoZphAQDcbrcmK6FQiKbpfr8v\nK2KpVPB7vCgC1avlUqGAOGAoliBRzMvxFIpDDrBN2zYdBCZ43seyHhtAzWaL49yTkzMIguu68aMf\nfjgYjLfb3W632+v1LMuiaBJGIAzDBj4JiqIRBMUwbLPZ3t3dz+eLKIpHI7FUcmjQYzkOZFmOomj9\nnlQqVuqVmiIosXAMg7HN9ceVYoVjuEgw4uE8CEB8bt/q8uqZldPRYAQeGxuDIKhUKpEk+eDBg3gq\n2ey0D9PH9WbDcZzB0slxnHq1GgmHjw8OFUnutcWD/f3nnnkWxzBFUVwUnclkAADlcnlhYUEQBJfL\ntba2RhAExdCyKomKKEhdaeA1ZGqWbTjAhhDIxbv8QZ/LRUKQY9smjiMM52JcNM1QKApbtmnZJoYh\nLEfzPKsoEoYhJIk7wMIJOBoLJ5IxjmcCQd/QcNwX8ALE6vTasiYWSoX19QckQw4eMAqNT44tLy+3\nOk2WZYulUi6Xy+VyhmG4XK5Op7OxsTEQ4hEEUS6XW61WNpv1+XzFYrFUqS4vLI8kRxmSLRUqU2Mz\nMMBU1URRnCLZX/vqNyjSNTk2FQpEKIIK+kKLc0sYSvV78qVLT8TjCTfvHRkZOjnJ2TbY2dlrtTrZ\nk3w4HGEY9q//6m8FQYIghKYZDMMgCIIhNJctxCPRZrOZOS6Pj40JgvST194YTEiajQ7r4jQNMBT3\n3rsfTk3OMgwLQUi/3y+XyxiGzczM7O7umqZ5cpLb3z8EDrK3ezg2OpVOl25+9PHY6MRf//XfAAAv\nLCz883/+LyRZGPh/YDgySNscHh5GUWx3dzeRSNTqlbm5udnZWVEUY7GY4zhTU1OhUMQ07WAwODY2\ngaL40VFaFFRFNp55+vkf/+gnKytnGJr3uAO6ZhYL5VAo7PcHU8lRBEEvX37y4YMNFKEMHZRK1YGz\nDsdxPM+TJOk4jqZpiqKoqjp4HngxmKb5K/4Lg1UOgGwALACZlm2KknL6zGyh2Pb6+E6nlUzF6/U6\nDCGsyx2PD/39t7/XbvVRlEyny6n4MAxhhXz55CRHklSn05ldSeE4ZtoGhCK/gkb/LQJ9+m3oumoY\n2qByBADAMGpbsCJrHo93b/cQhnAMw1dWzjAM3+kImmb4fL6JiYm33vqp3x8aGRnTNbtaaVqW4/d7\n79y5u79/UCpWnnzyyZOTk7GxMd7Nzs7OfvjhDVXVW62OKEo+X4DnPDs7e7Oz8wRBFQolSVQuXrg8\nPj5pGObDh+soiluOHQqFDg6OUqnh9z64rijaU0898+KLX7hz5x5Nuz66ddvt9tbr9WKxODs7SxAU\nQVAjIyOPH2+xLLO4OFOpVPz+II7jW1s7tVrts5998ejoKByOkiR5/97DmZnZXC6n63oymUokEgRO\nXXvqmVKpAsPohfOXtrcb09Pszs5eIV+mKdf+3uHIyNhnXvisplrJ5HAqObqxtnH+zHkcIx8/elyt\n1DGM8Lk9siz3esLo6FipVBrk0yuKFA4Hb926vrKyJCsCgCxB7B6nDxxgZrPZVCr105/+dGBoAjsg\nl8thMIJhWPrwqFar0QRJ0zQKg2azSaCY1+sNeH21Ws0xrVKhQODomTOnLctCEKjb6XQ6nQ8++AAB\n0JVLl0+dOgU50NTUVK1Wk2X56PAQBsCxYY51h0MRCEKCwTAEQblczu12wzAYkAsGUmsIgoADOzak\nKFqj0SoWi61WayDpZVw0gBwMwyAYWPYvuh8EwWAYtW0gK1K/3xcEQddVANm/NPjAYRiGIJggCIKg\nIAjBUJzASUXVc+VyudnuKoqDYTTH8T4/zfEERRq2xXBsp99zeziGoSVFNE29XC31FcHFuQACkSSZ\nK+Yoijo8PNRkRZZVRVJpgh4eHpmYmHTzPklUCvkygTPxWHJrcycYCNeqLZIEiqK2W91UcjgSifl8\nAZ/PR5F0q9XK5XLdVrdaaYmCVqu2jw6zzUaPdXltC9ndOTrJlFpNQVNt4GAkwZIEa1uIJKgkRlAU\nAwBEU65gMOz3B2mK6fWEra2darUuy6okys1Ga2/v4N69Dfjo6ABF4ZVTS+12m+W5nd1dX8DfbLV8\nPl/6JIMgiGVZly9eioZjJ4cZyIGuXX1qcnyUwom33njD0g2v2310cLi0sKQoGkO7CIIYHh4e7AM+\nvHFDUaRCIScpEkpguq6urT2wLIOmcQRxOM6FYajtGKomK4oEQQ5OoKapq6qMojCAHILACAKDIGfA\nuSJJHEC2Ayye5/x+n+PYiiLTNGkBC8EQF0sjCNwX+7dufZRKJU6dOc2yrMfDExReKpVu37792huv\n1VvNUCTc7/fdvHd6anZmeu706tlQMHLliSc/eP/6jes3bQtQJOPYUCQcMw3b6/FLovLKK6/ev/+w\n0WiRJF2t1huNFkOz/Z6Yy+VzuXyr1Tm1cnpne29AvDJ0p9XqaZr1+mtvWyZ0//7a7k722WeebzRa\nJEFHwjFBEG7e3D19+nQwGHzhhRd0Xa9UKl63r15toDA2sDA53DtMJaPNRtvj8ToO4Fk+EUuQOPGT\nn7z527/15UQ8xTBsrycUCiVRlNPpk5GRkfX19Zdeeunw8JCmXSzLb2xsZjLZer0JwxiOYRCEtVrd\nUqkS8IcgCJJl8PDhw0Qi8fDhw0ajUSoVIuFYs9nUdb3RaI2MjNTr9Wgs/O57Px9kiIyNTRwfZxAE\nu3r1qVqtsfbwkSJr2ZN8s9ny+fxra49cjBuGsPRx1rLs8dFxFEZxlHhwd93j8c7OLFYrzfv3Huma\nrSl2vdbudjrNer1aLlfL5Wat1mu3ZUHQZNm2TAg4KAxhCIwhMAwcaMAQgKABPECwAyDbNHXbMREU\nYBhkmuD06VOmCXien5waX19ff+qppx5vbfsCwe2d/URy5HAvQxPc7NSUm/Xdu/OQJpmTdDbg87/8\nyisIhq6snvr0dG5QEwwqsE+GhwOgGlAqLMuyHRNBoF+ag0GaZpiGBcOo48CKbBwfZQVB/uav/1Y8\nlqpVmzPTc4qikRiZSiQs3WjVG5ViJRwI723vNSotxMEgG+l3+mJPAJZdK1cunDu3tbG1u7X71JWn\nsum8JumGaqQP06l4Ckewk+MMx7Anx5mANyB0BWCBWrmROc6MjIxMT0/jOB6NRk3TrFSaBM4cHmR0\nzd58fOjYyGCNPDw83Ol08vk8TZAszbooV8gfCvlDN6/vvvgPXlQllUCJ0yunT45PUAgdGx6rFCtn\nV8/Ozs6iKLqzs3Px4kVFUarV2vz8fC6Xs0wHANjl4lQFYBhx796DkZGxk5NcMjlyfJR9+HCjmCsH\n/aFCrvDUk8/s7x+FQrFeT9AUPZlMqqpOoITUF4q5fDQULpfL3W7XxdJj4yO9fufevTseD8+yDEUR\nY2MjANiGqY+MDk9NT/r9/jNnzgiCpMkay3CbjzYlsW8bOgKD9OEBgaOry0ulYr7dqLs5DwIQnnUr\nklwoFB6trS0vLH744Ye9Xi8Ri48Oj8Tj8UePHsmyjGEYz3GjwyMwjOqamUoOuxju8CBNkq5atcFz\nbgBgFEUdx0EQhCAxDENgBKiKjqLoQFwIw+gn4VuGYQyQxrIMw9Q1TRtMpLvdrizLjuOIoijLMoAc\nBIEGOrZB/62q6iCPbvCWfD4fQRAYhjEuzoYxybDaguQguGE7um37An4UJy3HzhcLDEv3ZYlkqWKt\n3JMF2VAbnZZkKqIuq47eE/oUQ3/tG9+EMdQ0zUQiJfYloStQOHWwe6DKOsu4p6ZmPv74LorimUxG\n1/WZmQmCoBKJZKlU4jjOcSCGYUmSDgZCraZaLlU6bREBVLshYjAznJxsVHtiT/fyYdghCZS1dMTS\nERSiha4W8iVQmIIhHAJIvdauVOqSqLTbXYZhK+WqY4N4LCEK0qA84jh3Ih6HO912q900DF2SxIFE\nwLKMYCR849bN6amZarWqyLIiKsOpkeeeeV7sSw/vPcIgIhyKC30ZghBdsTTNaNRbsVgskUh4vd6/\n/uu/HjSzp0+f3tjY0DT1+PDgJH2EYWgsHm3WqwCyc/kTANntbsuyDF/ANzSaJEgMxmCWZVjepaqy\n3+92HMtxLEHseby8ooqGqRIEThC4JAntdtOyNQxDbNs2Tb3b7RaLBdM0VVXGcfzevXs/+9nPWq3G\nnTt3YBien5/P57PDw8MMwxweHn7zm9/K5XJbW9ter/eHP/zR2tpaPJ6Ynp6+cuVqLBYbHR1DUVTX\njUKhcHR03Kw3J8anT6+e297YEXtyp9Xpt4VzZy74/SECZ95/9/qFs5euf3BTkfS52aWx0Yk7d+59\n4XOfn5yYOn16NZ8vfv7FlxYXZ3jerSpGKjXEcXwmczI+7u92+s8998Ldu/cf3L2fzeTare7K8urG\nxsb46Nja2iOCoJYXF998862gP1DMFyLh2P7e4fz8/KNHj/LZQqPRzKSz42OTJEkGg8FAIBCNRiuV\nlmmafr+/Wq1KklQsFjXV8HkDzUa7VzEs0xEFeWlxRRBEv9+fTHJraw8wDKVpstmsT05OVqvVgZFX\nPB43DGNycvL4KBOPJTudzssvv3z69Om7d+8GAoHXXnuNIpnz58//xV98B0HQubm5SqVWLtUjwUg2\nU9AVff3B46HkMMPwmmZANni8vi30ZBwl52cW33rj5+sPNlv1XqPearVa3W5XEARFUT5J0vsVPhv0\nqfwIGAYoikIQhCAQTiCOY0mS5ABrfiHV7XZfeukyz/P7e4fZk/z77324v3cUDsVlSZ+bXeI5X7XS\nRBGyWm3YBkgf53LZgsvFnZyc/H/p+s8gybIsPQw8Vzzpz3V4aJlaZ2VnadHV3dO6Z4aDERjQgAUJ\nI7HLNS7IH7tmS/zYX7tmXNquwcDFEEvskiCxGA5mMNDdM9PT093VXV1dXboqtYzM0BGu1dNXnP1x\nPbyyhwa3tLBMz3D35/fde8R3vvOdq1evPn26qVAaryOlNDOEDI3bdd3/9fU88/h87h8hDJFoRdvt\nXrlcGw3jaqWxvbWfJvLWrbt5Ju/fv18sFrXWnU5ntjG/t7d/+/adTqdrWfbJE6e3tnbm5hZ2dvZ8\nP9jd3f36178eRQnn9tLisuN443H00ouv2LZjegnyXHYP1HPPXet0uic2Ts025i9duhKNxgXPT9P0\n7NnzAHTQhYsXLz9+/ORP//TPT57c2N7enWvM37//8O233z579uyDuw/iOI3juHnU8n2/3xt84xvP\nbz5+cuPGjSiMNzc3KWEffvjh40ebruvevnVnd2un1+leu3btRz96a3FxsVKpPHz4aDQar6+v3751\n5+TJ09euzR/sd567+rxW0G71Hz3cHAyGUuCZM+f+7//1/2N2drFarrmOf/vGrZPrJ5882Uqi5ODg\n4MGDBwsLi8PheHPzaRQlvhdoBZTSs2fPhtFIyKxaK7/y6gunTp0olQLPc27duuE4Tr1eHwwGgV+o\nV2vj8VhL9cYbbzSPjprN5qDfW1hY8Fy30Wg8f/36nTt3PMeN4/jixUvloNpqtrWGX/v2r6VJrhS+\n+uprB3uH5XI1jdLhcChy9cEHH42HoziOz5+/uLd3MDe38NOf/Mx1/Xa7vbe3t7y8nIuUUDSjFw3P\n07Ic13U9r8CZRQlTUpu+nMGg1+t1er1eliVxHA4Gg263OxqNkiSJwng0HB8dHbVarX6/PxoN4jgU\nMjO50dLS0tzcXKVSdR2fMQuAIhJNSCJkLwwP252ne3v7nc44ToRC5liEsTTPMyUfPnmYajm/snDn\n0YMc5N3tR/WVRe1wadFBHB502z95+6dr6yeiKJqZmWk0Gq7jf/ThZ+NB3O+Nq5X6p5/eqFbriCiE\nWl9fX5hfun//frFY9jx/0B8RYKbRuFptKAWEWJ5bShNV8Gq72y1OPZmTpYUTNi8uLa5vPT3kzF9c\nWL9983E4krs7zSgUnc4Akayvn6hW6oiQpSLPpdGHTZJsfn4xzyUiaR61ldI0SSIp86AcUIu6BbfW\nqI3jqNPrzC3Mc9v6+S/ezzM57I/2tvZlqtaXT2axzFONip3cOHPh7GWbu9E4KRZKjfrsnVu3f/Sj\nHzHGPv744/X11R+/9cOTpzbSJFpamIvGo/3trZPraxtra61W07Z5HIeOa/V6nX6/+/jxQ6/gcZtb\nLg+Kvus7lJPV9ZXBqM9tLrUUKs9llonUcnixHCDRg1E/SkKkCFqJPB2O+mkWj0ej1dXVoOifPrmh\ntZ6dnX33nZ9/97vfXV1dv3rpajgM69WZD9774Lf+ym+dOXVWCeW7hTiMP/no01/8/Bd/8ec/vHPr\nzmef3HAspxSUz589P+gNa7UZRHLz5u1z5y5wbg8H49dee+Pdd9/rdfq1Sl1JbDU741H0/PMv5kne\nbfdOnTr9j/77/3H7ye6oN16cW2ofdTdWTj5+8OTN199sHbYCL6BIr125Blr/yb/7bhJGS0tLR4et\nmerM7tZuq9VZWlr58Q/fdh1vcWHp8oXL9+49+OpXv771ZPv8+YuU8qWF5Q8//PjoqFWvzyDC9//s\nB6dPnxZCFIvFpaVGFEVxHD/33HPf//73v/Llr25snBBC9vvD8qxXLdXaR+1qqfrZx59wwt984w3X\nspsHh6+/+mrzoFUrV37w/R/90R/863Onz51YO/HTH/9UCz1bn5WZbB+1ZSa7re4br77x8Qcfriwu\n2Zzvbm9/51tviiwd9vrjwVDlMvBL3/s3fzLXWEiitHXY+tEPfnT31l1GuBZ62B3duXm/fdT/5IMb\n0SgjxIrjNEkSmeUolSELWJzblkUR6F8iKwAAgONYnHOlRZ6nSknGiOvanm8VCr6p5RaL5Xarc/v2\n3RdffFlpUqnNcNs7PGiH4ySK0n5vpCVksXQtN4mSOE5+9KMffe1rX/M877DVNGibZVlmkN1xC5Eg\n/6tpsJ+LqDKgDBgjjBFKOQCgplpDqVibqc+PhhEidexCvT7banaEkEJkg15XCjHsDw7299vN1vzs\nQuCV/+Zf/1s3Pr11auPM0UHTtd04TH7+9nurSxury2uD3kAJnadif/cgT/PmYUsLLBXKg+6wMsMe\n3HuYJfmffu9PF+cXW4et9dWNaDT+7OPPSoWgddiaqbEL5y5YzFqYW/Qcb2VppXnQTMJocW7x3u07\nq8srjLBHDx51270T6ydQQZZkd27dPXfm3OWLVwa9wcmNU3s7ey+/+IpjObVKfX5+MU3zbqd/7blr\n9+4+uHr12vb2bhCUAAjn9qOHjzm3hIBOp/vxx58iwt7e/isvv3Hj09uO5f/qt3/t9q27SZJtrJ1Y\nWlz58MNHhULwi3ffr1frX37zK+Fo3Gg0pFB3795/+nT3/v2HT59sr6+dOH36dK1Wu3fv7v7+3v7B\nLrdoqRScPn36T/7ku0GxMDs7m2VCpGJpYcFi7OnjzXJQ/MLVq1/9ype2nzzJk0QLCUqD1uFo1Kg1\n3vqLn7YOO5x6M/X5cqmexXkaZSvLG//Rf/Sf2Ja7vb2ztrxCEK9du7a2tnbq5Ml+tzceR4N+ePbs\n+fPnL7zzzruNRqNUKpktYaIi27Zt29Zaj0ahUX4yD0OwNKOKhch6vc54PByPh0mSAABqGI+jVquF\niJzToFhoNBrLy8snTpw4ffr0uXPnfD+wbRsA8jw3qLXh7GnCEoX9KDrqdPujcZyLRAhNiQQdZUk/\nHI3zNNV5Y2mO+NZY59XVuWY67KlIuRQKVrlRPep17ty/N7+4/OjRZqvZGfSGezv7J9ZPLi+uHB00\nXduxbT4YDB49enT58mVEfO3VNw4ODhqNuXa7c3TUnJtdeP76i+/94oPVlTnUtBLUomHW74yX5tco\n2ionh7utNBSDzvibX/3O9ube4/tPX3/lzaJfaR12S4Uqp7zb7m092U7jzObOpQuXhv3Rowe7c415\nLbEUlC1mi1RpCaAJjeIhEFmpBhpzQlWpUkzzZByFcZKkaTo/v5jnCpBfOHexVmmsLm/8ype++cbr\nX/nW138tHKbDfnTzxt3RMHzrrZ9+9OHHjx8/qVbrnud1ux0zO1JrFY+Gy/NznaP+uz/fZIB7u9vj\n0SBL4jAc2ZwtLC9Uq+WFpcVqvVKplKSWQgmlZZanGhVlZDQatFpHiKpQ8PI8HQ77SotqrTw3N4eg\nHm8+FEJwzmdqddu2i8XiyvKyzS1CSBJFlNJSqXJy4wRB2u/381z2er23fvzT9977YGtza3Pzqe/4\nlPJBd3D27PkvvfGljY2T9Uo9TfP9nf2jo9aVi1cunL3Q6/RBkyxVnLnjYZwlea/d23q6NzMzu7K4\nOugNqtXa7c/uuE5BazLoDb/+1W+cPn0WgKZJXqlUkySzuANAS6XK06dPFxaWwjDsdQelUuXx401O\nrUsXLgRBsLW15Vp2rVZPU/Bct1qtuq7bbbVXltcODg6Gw+HCwkKWic6+TJOcEPbkydbc3HzzqG1K\nHWEYHh4eLiwsuK67tLgyHI5efvnV3d19g3J3O/1+d5Cm2dFBc3d3txQUa7VanmVRND57+mSz2cxT\nsCwAjc1m88K5ix9+8PGJ9ZOFQmHrycGbb355f3dvNBoZ2fIsSZMkEVleLpf7vW40Dm3uFP3iaCCS\nKF1bXr1z627g+FuPnohULC0si0yGw2hv58BmBYo8GacWM/yiyc+J8gJjz9r9Z1ISTSnVKAE05xQA\nsiyTSjiOUyqVVldXZ2dnt57unDx5emP9VPOo9/jx1sLC0oOHj+eXlobDyHMLIpO7W/vxODk8bJ/a\nONVpxZRwAMhkFsbjS1cvheHYSAZY1oRWa9o+/v2J0S9nSUi0BiVBKzoexcPh+N7dR0FQ1AqiKO12\n+71O99HjB4xRy7J6vV65XF5aXBFCVSq13p7q9QaALM/0zs7u3NxCt9vPsrzd6jYaczs7e6+/9sat\nW3eODltpmnNud7v9LFPzc4tRmBweDuI49TyvVqtRSmdnGtVyrdfpXbxweevJ9sP7j1CTclCmSAt+\ncOPTm+ViqXl0VKvV0jQNx7FSamd7r1qtAtKFhYVwHNu2XavOPHnyRCs4OjpybM+M9A2C4OjoCACa\nzeb777/POW+324SwjY2NwWCUJrnv8zhKB4NhqViZn13od4cXL1wmQAt+cTQaHx40Acjq8tqJjdlT\n66cWFpak0O+++97q6vqNG7eWl5fjKFtcWAFkT5/uEsJGw/BnP/tZFEVpmgqRx3H8Fz/8c0Rl6FtZ\nmtqMX7hwaXtr9+zZs51OBwDLleKHH364urb8yacfcc4ePXr05ptvbm/tNhpzc3MLpVItiXNG3Vaz\nv7iwqiTZ2zvotLtJlMzMzFLKCSE3b95UStm2HUURo9be3v7LL7+SJvni4qIhCFBKbJubBN1wKdM0\nHQ6H7XZ3PI6SJFNKmRTHdV3fd4vFoiFeaq0RlWO7poPQiCxvbGycPXv2/IVzJ0+erFQqWZYeHR0N\nBoPhcDwcDsfjMAqTLBNSaqlQEYqMAbdSIZMsj7O0O+gPx1Gci0ESNfvdYqXcHPZGebJ+5lQz7KkC\nHzNx6tpl6fJeGo3yJKhX0WKHzSONxHG8Bw8ezdRmGNBuq7M4t2BZ7O7d2/1+f2lp4eHDh71e7+bN\nmyvLa4P+yPcDy3IYsxFpFGUnTpw+2G+5biAFaoUFP5ACUdN+f9jt9geDMEkyRp3hIAKkWsHpU+e2\nt3YP9o/iOEGEICh1Oj3bdtutDgDU6w1EEoYxZ1a/PywWi1Jq2pitMK6FSLMsFirPRUopXV9fX1tb\nW1pZe+mll8Nx/PDeo/t3Hh7uNUWqhv1x86D3/s8/jkf5Oz/5xXxj4YtvfPmv/e5fPzxsFotlz/MO\nDw8RcWvr6d/4m3+DgH7zjddnSuX/7D/9G//w//V/Hg/7/+X/4T9vHhyOBsNwPHq8+VBKOQyH5Vr5\n0ZNHcRoBA8u1hBaO7zx++vjU2VMHzQNN9OzC/O7Bvltw10+uc4c/evJoc2tToqxWK+12s3V4FI/D\no4PDcrE0Pzu3MLfoOX7BC3745z985cVX7t2+d2LtxK0bty9fvDJbn33tldcLbgE0Odw7jMaxZ3uP\nH26uLa89vP/o048+vXj+UjSKlhdXfvrjn549fe6jDz5ut7ulUiUM43q9sbS0IoW2LXdr8+mpjZMX\nL1ze2DhpJBjOnbvQanbiKP9v//7v3b/zEBUpBdWH9x/94R/8IBxFO1u787NzcZj8ype/+uMf/mJx\nfokglILiW2+93ZiZu3XrdqVSDcNo+8n2/FxJ5Mp3Cz/+8U+WllY6nV6n05O5Ak267R4wWF5eXVpc\n++zTm7btvvXWW/Pz8x999NGZM2eEEPPz8/v7+y+//PI77/xi0B/VqrNSINFkPIwsamVJPlOtHe4f\nhKPB1SuXe+1WnmaNen13e6daYqsrixTh6OCoHJTLxcp4MLaYvb6ylCW5ytW9O/dPnThx787dc2dO\nReNRu3lY8NyDvZ3xYPjitRdufXonjaBaqjrM/m//3v+7Xp0pFkrLiysF2xt2BnmUhYNY5kom6DCP\nUsopUAZGbQFQaS2VEqbJiJg/FAlFSpAQYkJOSmmxFLieLUQmhLBte35+4eKFyxcvXj59+szbP333\n8eOtXndUrcycv3Dl8LC5sX7yyebTbnf44MFmlqqFucWFuYX79x/OzBQ+++yzQqGwt7f34osvzszM\nTCmqUxzfZEvw73kQ8ksoImqiFWgN3W5vNIoJ8FazC0CVQiVxNAw1yjSNhcgODvc6nZbneZRSy3Ie\nPHhUW/I67cHi4vJHH34621jUimSp7PeGr732xnA4TNOUEDY/t5imuev6WSY+/vjTQqEwN7cQhrHr\nsO9+97tawcHevmPb1557rt/taYme43db3TRSnu198N6HSwvLzcNWnqRzjcYXrj53++bNQX/kun61\nWg/DuNGY6/eH5XL19u27SuH8/KLnFZrN9oMHj2zbTdP8yZOtubm5crn86NEjRHz48KnjOIeHh8vL\ny2trG7du3VlcXD5/7mKSZJ5buHr12uFB88MPP6ZI9vcP/+2//e71a8//2Z/8mRR6f//wm9/81h//\n8b+UWe5wq1QqPXnypN/tnTpx+vnrL9+7+2g0isul2s7OHgBtNBpXrlxpNpvtdlNK8dxzz4Vh+O1v\nf/PRowdpmgZBMD87l2fZwd4+p2x5aemjDz68fu25zUcPO6323/jrfz1L0tXllVdfeSVPs7nGnOcG\na6unolH24794+43Xv+K5wXvvvJ+m+Te+8a0rl66OhmG/N6yVK/ON2Uaj/vTpU9t2VlfXb9+6+5Of\nvP21r33jyZMng8HA+BKD6Jp5IlprQhjnPI5jo9xDnpHZJRSXlhcWFhZqtVq5XK7VapVKpV6vr66u\nl0rBaDT45JOP/uzP/uz73//+p59+amYUxHGcpqkBrj9PxCnPpUaghPEoz8dJOo6To063Px5GWSq0\nSkTaT0b77cOjflvYgJ7dlUlpZba8OncU9VrRMAJpB/7KifVyfSZJkmq1FvhBNIoGvaHOFCD2er3n\nrl1xXfvs2bO1Wg0RZ2dnhRC1Wu3osNXvDZeXVvd2jwp+6ZOPb66tbQCAX/BOnDhx//59RMU5XV1d\njeOYc37z5s0rVy8tLs0/fPjQdV3OWZIkvh/UKvWrl68szi/Mzy7Y3JmfXThzaoMRJnMpcxmOovFw\nFI1jgpRev37Nde1W+4AyaMzWNOjeoD8ej89dvPTxx5/+k//5n966dZcQtrtzEEdJp9k72Gne+Pjm\nndsPl5c2SsVavzf+kz/589/7vX/ImNXv91vNTqPRWFpaOnXq1Ozs7Ozs7NbjzZ/88EdZFP+d//1/\n84u33/now/fXlhbPnz+bpmkQFPqDLqV0c3OzVCohJcViwYwUarfb/X43SSKj2FaplM6fP9vuND+7\n8Umv17NtGwCFyBHRtJ4FQRCNxv1O99NPP3348OHu9s6Duw9t7rSOmrXajO/73/r6tz758KPlxWXX\ntu/cuvvXfuevnTl1dmtz6/VX31hfWR/2R6VC6Tvf+tV3f/buTK2x83Tn9Vff2NrcCrzgwtkLUZg4\nlv3xxx93O71yuZKm2YkTJ+7eud9ut5tH7W6nv7S09L3vfe/OzTsizVdW1v70T7//pTe/8tZbbw0H\n47W1MqVscWG51eqYyXtnzqzeuXPHaKWsri7duHFjMBi02+3l5eWf/OQnBc8zDRNm8uZ7771Xr9dL\npdLm5iYhpFQhm5tPB4PR/PxiHMeXL19ZXV394IOPCCGu6x4cHHBm371778qVy6NR6DheuVjhlBdc\njxHmcGtjfR2U7rTap0+cHA2Gq0vL4Wjo2nymVm/U6r1uN43iG5/eqJXrW0+2Bt3B81+4/uTRY9Bo\nM/7w/oPF+XmR5Q/v33/phRfD0ehgb//ExtrHH37Sa3cdCyql6n//3/0jkLA4vzDsj1xuHe4fDfvD\n3e29PBUUWalQ9myPAf0l4Ou4APPvs/6cEUO5NAfV87yFhYXTp08bJPajDz/Jc/nii69Y3N3a2u33\nxoPBaGtnz3X9SqU225jPM5HG6fvvf8iZPTe3kEbp3Nzcz3/+85OnTzx9ujk7P3fu3DnHccyVPGsL\nnr2Gv8Sv01pplMbfKKW0Rq2AEGaaJ5RC1OT0qbPlcnXY7y8vL4bREIgWIjclhFOnzhSDksVtkcti\nsdxq9s6du2BxN4oSx/GuXr3W7/ebzfa1577wb//Nd/NcXrhwaXd379TJ06Vi+X/7t/93N27csm17\nff3EcDC2OM/TtN/txVG6v7N34ey5/d1dkatGvSpzubyw3O90GZBTp04/3XyyurxGEDzbKRQK5XJZ\nKTUcDpMkMTmQ4zimafprX/vao0ePXnjhhf39/fn5+c3NzeFweOnSpX6/f/78qZWVlb29vTAMoygy\nZbbDw+a1a9c4t+/cuYNIWq1Wmub/5J/8i7/zd/7Le3cfnD17PkmyjY2N/b3Dl19+mXN7MBgZotPF\ni5f/4T/8n86fv+T7xcbMvG35ve6Qcxs1OTg4mJ2dLRaLBwcHFy6c3955enR0tLCwUK/Xut2uZVkb\n6ydfe+21paWlbre9sLDw/vvvnz59ul6v3rt3b2lpaXt7O03Tu3fvvfzSqwQsJdknn9ysVGbCMN3a\n2nvttTfbR21Keb1ev3z5crVaPXPmTLPZ5JwXi8VisXzp4pWtrR0p5XvvvWeY3IyxLMsAtOc5RhzI\nsiwhRDiOpJRaAyLRCg0JK07CKIo2NzcPDvf6/a6pJ21t7dy+fffhw4efffbZ4eGhYXtduHBudXXV\n933T9/ZMZxI3GbxCBEo0UAmQZJkGBEYzKRRiInNmW07g77ebihFwrUhkp66cs2tBL4+PwoFdKUYo\nnVKAFts92C+WS0vLKwf7R61WZ3amMVuf3dnaJYp4rv3uu++urC71B939/X3HcYQQjx8/7vUG6+sn\n5uYWnjzZ2draqZTr83NLeS7TNGWMUEa4xTQqy+ZxHALoNI09z9nb23Fdu1aveL6zt7/TmKnZ3DrY\nP+r3h48ePS4G5U6npzUc7B+lSY6IBb/YbrcRyeFhu1wu00sXzl27evnMmVPXr197/fXXr169fPLk\niUq9du/ePd/3X3vllauXLofjeGdnb9Ab9vtD1ExkuLS4+qMf/uTMmXOW5Xzlza/UyrVOuzceJfPz\n85TSxvyMW3De/tlP3n33naWFec+xd7aevvHaYjiO/+Cf/v5f+Q9+44P33t168ljlYjgcCpnt7Gxp\nLZ9uP/ns5qfN5iGA3tp6orW+deuWUuLhw/vb29sT8T4hbNtC1EmSSCltm9+7c/dgbz8cjSuViu8H\ng+4gCRPPLVy8ePH69eue55eC0q0bt/b3D4rFku8F2093rly88tO3fgoKXnvltX/1x//q29/8duuw\nZTErGkVpnD559OT0ydNL80uloFQMSpuPnyilsyxXUtfrja2tnSwVnXZvMBj1eoNKpTY7O//eex/s\n7Oy98sqr4/H48PCwXq///b//e+vrG4jE1HUePHhQKBR2d/cBKaOWEJIQGobx2TPnu91u4BcOD5vP\nP/+i8cSVSi1JssuXru7vHc7NND587/0vfekr7713Y3l5mVJqcbvdbtfr9cODphBif3//4sWLRimk\n1+sZiZeTJ04TQu7fv99oNPqHY8dyd7Z2be5QIDa3njzePDo49D0vTZJKuXzqxMlXXn7561/92l/8\n+Q+jcVwt1zqtbrvZqZarWZIxwqQQnVa7XCytLq/85Mc/Wl9deXDvrpbi9MkTJ9Y37ty8dXTQFBnU\nSjWt9XPPXey22hfPnX/04PGDe/eEUIzxSrEyOzNnMXs4HBl0zubWFLKzGbcZJwD0c/zr87oRABhv\nEcdhnqdBsVCrVXzfX1hYMGVwreAX777/0YefpYkEoEGhmOd5vz+M43Rzc7NSqXFuD/qjmzdvbmxs\nrKysXLt2fXNz9/Dw8MGDB2maXL582RDNTauH8Y5Gn+0vuaJnmd+TTtjjzl1EIMBGo3G32z84OOp2\n+7VavV5vmGb78aBfcJ2VpYW15aWtzSdzM404DJsHzWgkRv3hoDt47vJzj+4/unzhcvuoufnwEdHo\nO+7tGze/+pWvPH7w8JMPPyoHxdZha311VWTZuz9758Ynn7qWTQEASaFQQKkIIqN0plYPR9Hmo83O\nUf/e7Xu1Sg00WVpcfPTgoZbqn//hH73wwguc89bhkcrFxx98+ODuvSsXLxGNgee3j5r379w19bzl\nhcX33/2FFnI8HH388SftdpsQ4vt+FEWFQiEcx8PBWEq5t7enNTiOF0VJuVyVUkdR/LO3b926dStP\n4E/+3fcODo4OD5qdTmdne6/dauVp1ul0OOfD4fD69eu2bb/wwnP/3//P/7ixfrpem3v8eHNxcTlJ\nEpN7CSHK5fLs7Mzh4aHneUJmAPoP//APB/3+/u7e9tOt7/2779Yq1SuXLkfj8NTJk2mSXLp4sXXU\nvHTh4ng4Wl9dC/xCv9erlOq99qBaqTu21z7qvPT8yz/64VvD4fjpk+3xKLp39+7+3t7du3c9z3t0\n/0GaJLZt7+7ul0qVkydPf/jhrVqtNuVYmo5Ow70UQsRxPB6Ptf6lpjRTfTQSwEaIwbjVNE37/X6S\nJIhoWVYQBIVCgRCSJMlwOBwMBmQyvos9iwMDALcdyhm3HMtxS+VqvTZjux6zLKWB2BwYZY5tF7xR\nEgXVInGsQRY/bR3EkPv1Eguczd3tDJRd8MZJvHuwb+jvvXavediaa8zHUWRZ1nA46Hbbr732SrvT\n3HzyCBHn5uYMQ4cQ1u30atX6cDimlHuuPxr0kzjsdZtBwdFSgFbtVrPge5zB/t72g/t3pciUyAe9\nLqckjkMAcF3XzB6TUvZ6PaWU67phGFLCzRoaElOtOsM3Vs6/9tKvMMuOokhqoJRqnHBYwzBcmJ+N\n43A0HlQqFa2lw51okFrc1lp7QSFL4p29vcD3X7r+ptZ6OOrfuX2vVA7CKOLKtzH4yutfT6NRrTJb\nLlVff+UrjbnZX/zi/Xfeee8bX/3OwcFBlstqpb6/fTg3s3D/zsPZhXkg4HDHs735xmKSRDnJKXJO\n4HCvKWVeKpUbs/U8zfNErCyuAsDdu7fPnzkfZ/Gg12vMzRU822Lcc9y1tbU4Tebn53/01k82NjbO\nnDrt2u7Fs+f3t3devP78P/4f/tnf/Jt/9ac//en58+fXVtZee+21t99+mxBy/+791dXVs2fP3r9/\nf21tzfO8x48fDwaDRqOhte53u5zZvV4vjmPbstZXVsPhyLZYNBrfu3fvuStX9/Z25+bmvvOd73x2\n6+aDezAej0qBPxrFO0+3oigaD/unT59+urm5vr5+/+5dKWXR93a2nszPzd2/98B1bSGyEyfWoyjq\nd9u9XuezTz/+3d/93dGw/+7Pf2Fz+NIXrz99sn3m5In93a03Xn3lD//oD0SWuLYVjcZJOG4eHNYr\nVS1k6+iAU9LrtN5++53VlXUl0pl5f3114eH9O76H+wdPNk6sMmAFx9t5uvXlL5/cvP/w1KlTNmef\nfPBht9W+cPbMzVuf/fqv//onn3wyU6lsb2+LJNp8sPPctSsXzp/95JOPSoG/vrxw69atYrG4uDC3\nu/3EdcnSwszaCv/hX/zZxQvnXMt+/OhRY2bu7KmLg/6o3Rlb3BmMk3KNJmnaaDSyfEQpUjIZH46I\nmgA9JtWhGQxOAEADUEJwHIWlUuC6dpKiJpIQ7A/a3f5BY26mXHF3th6fPfeN93/x81q9cuPTByfP\nzOVxQhTO1mulQunD+5+c2jj12UcfOK6FiLdu3PK8QjgKr1w6/+je/eeuXP3jf/bP/vbf/NtxNCKE\n+n5AgTiWrYSWQhPybHqEiAhEEwSiuUYEIIASAJADaIWUEg1CiNlafdAf5rmTxGpxYa3faedZurS0\nOh5Ho2F7bfXUX/zgneeuvBD4/v7ejlawurziee4//8M/XliYe/p4e2d3a21tzebueBBVSvXPPrnh\n2p6WcPLsaSnEyvLGw/uPskQ4lnfrxh3HsbMwl7GcKTcIoZ9+ciPsJdWgbBNrrjF7sNdKonQ0GjQP\nOs9dvJqE6bUr195+5+euV377p7/47d/6LUqsONT7e0dPNjd/46/8ldu3bhXLRYI0ipJysfrJJ5/N\n1Bq3795ZW19jnN+/9eDNN9+8Nbz13s/e/8oXv7ywsPDOz34OOchUhIPx4/uPLl68+OD2vb3+/qkT\nM51O79zZxc8+vb20PDeOw4JX2tneXVpY/Pijj772K1+5dftGY25m5+nOxom1KIo2g62nm09OnzlZ\nLpayJO32WsuLKwd7R8P+8NGDR9/85jfv3LnDuW0z7y/+/Ifnz5y7fv36pzc+Ixy++vWv3blzS6O6\ncOHC7ds35xeWdveONGChGORS1GrlKEzOnD17cPD+f/Kf/mfv/vznv/rtX9/b29va2vrON75NCHnn\n3XfOXzj74rUX/vhf/vNisZjEschzQohIk7d+9N7lC8u2F3z7G1/c3d6qF6siEY5ry0waivY4yqSU\nrl8ICkUpc6WMH6KWZdk29wuu5zl5ntu2DUDyPJUy7fe7aRoWi8VC4Lqu7XkFy7KU1ISg53m2bSdJ\nijiV6GUGMmAEkCBQQhnnFivUat5MTfW7YRoTi0pNR2laXlroRYMHm4/Xr5772YfvWbVSKsXuwX6z\n0379tS/ef/jvqvWZF1544cd/8ZPxYHhq7eSjew9nZ+a6/V6tUm13OiMx4txaWznxve9+v1KsV+s1\ngvDw4ZNapcaoPTszv3ew32m1n/vC9U8++nh2dmY8DJXOapX6ndt3X3+9LoRYWlpijEkp2+32uXPn\nDg8PS6USs+j+/uHJjVM7W3sFv/j40fbq6srebjPN1KDfStNktpG7nr29vZfnmoCoVqqO4/D1+etK\nKJUqF4rcsjnnBqYQQlStXCe6YtVLlRWjLGuDpUhsAwcK6TCXqTtXOuk7ruN7ZiDbc2e+aPzh3t7e\n1b/yai7iLB/1z3aiKLZtGwW/fP7F4XA4HiTLC6eWllfn5+c9zzMwfbPZ3NnZGY1Gh3vta1dfqNUq\nRtG20WgcHBw0Gg0jmaW1DsPQSNgWvlCZmy+HcTgcDAztApR2LZsBOdrdL9jucmNWRnGhUChw6+TJ\nk51y9+7tB3/rb/3u8vLyb//2b77zzjtPnmz93b/7X62trSHqRmNmPA4PDg4c28szmaZhuVRl1CKE\nUM5efeEVo/nBOW922pbWZ9fXuwcHURR96fXXgiAAjaWi92Tzvmvjb/zGF3MhPnj/5xtr82kSN+rV\nsydPKNQW0KNW02I0DsfgyiAopmm8urZCCPng/fcANWfUdfjO1ub8bPXP/+zfpWl65dLJ7/7rP0bE\nmWohy0b3bn0kkkE87Io4+skPfiBlniSJhWTQ6vjcfnTnTpJkO48f2wS6zZ2Px521pVLn6NG4LzqH\nuzbQd35848qV1UGzN2y3nz54cO7kxt07t4bDIQA8d+FCa38vGQ6SUY+jGLQP9rceXbhw7mtfeo1Q\nuHfvzsp8jWNGZMohe+HaS91uV+YDkffrtXmb84sXN1zL3d89SOLYdf3d3f3Dw5ZfrA/C4cLqcioy\nt+xrAlTbBKXSSAihzIwhFkoqwgkiAgKaKBM0IACA4xUygcAgSpNavci4vnL1/Gjc7fVbrdbO9esX\nT6wv9Lpt27UbdfvSuXPZKEl6Q3sVth7dS8LuRx8dvvbq9U7rYKZWufXZjYuXr7YPWjuPt1yv4NVp\nreB+9N47841SFGcAilNQuWLACCVKIcCE3odEGiUICgwkIQiAFBgwphghDARBlmcZ416z2Ww06stL\nG3dubX7hhet3b94fdUfLy7ObD26cP3dx0BuWS2655D998vDll18t+IAiY64d9sev/8Zv/l/+q7/3\nG7/9xdF4LCJNFbt45tKdO3e3Dnf6/X7RLfX7/Y3lE8291tFBUylV9muMMRnD0XY7zaKV5dXTq+dK\nQfkH936Yj2WtUHsatmZKcyKWTx5svfzyi5989O5LL71IlX2w27l0/jpF78tf/ObH7/8ep96X3vja\nH/7Bv3zphRcH3eHO1u7GyfXf+PWvfPLxzYWZkssK+UgEgRN342yQ+bRAJY268dKl5Ue3N5cXFj1a\nsNEtOZXWbmd5du2jjz761e986/d//09mapnMNSh7ffl056hfrzSaB03Pdr73b/7t8vIilXplZW3z\nzqbjOxfOnhmPh2//8M9PnTqVh1jxSukwC4IgaBSfO3d97/FBozifJMk7P/r5/Px8sVC6eevWMB6v\nrKzcvHtPKo0Ie4etucW1x0/3lpeX79x/dPLMeWo7zW6Hc37z3p35hZVOe5jE8qc/eufihQuW4v/L\n//BPX3rpJRIrHYpbDz794ouvbW5vHTaPGnMzO/t7lmXNVmF+prI0N9877HjMLhYLB719AUwLjQod\n22bM0VpTwi1CNME0j7XWjh0UPJ9bFBUkUUoIsX2rXC4LIZ482RoMjhyHFItWfaZhWZbr+gDQ7w3M\nECnObYs7piRpapeEmHHDJM7jmbmZ0Wjk++76lUs/feutcqV4f6crVXbh8gUhIlEp3Lj7yXOvXPv/\n/es/+o3f/q2HW09kEh4e7K+trv/srZ88f+W5zz69vf1ws1KpS9+/c/s2s6yjZjMIgkjk43G4sLx0\n9+1b/QsRSmt3e8t1irs7O6tLJ0pBsdPrvv7yF3/yk7fnZ+ca9VnX9na39y5fPJ/E4Uxl7uSaaO53\nxsPk2tX1zc3NTrdbKlb7gxG3nDjJqMVnZuePmm3O/HgklFJb2WGrfbSwMDfqZcvLy4FbLfgF1aDx\naLNSrNZqta3NbS5TC5EDIgBoTUU+QfA595jmnBCb2cCAY6615oxarmfklQLb5z4nhEgpZS4lAGOO\nhVALAkKItVSoVquaCEJlb9gZj8cAYOSZLcsy2EgQBGZinklyGzXOwCsUCoPBYHZ21vf9OI4JIeVy\n2eHFacO81lo7XAWMaMd3i+3WoevRYlCzeLwwF8zNNQBor9e5eP7qwcGellRrORyOB9lo324SQr7+\ntW/3+30hRL1e+OY3v5NlmcUd13XNKEPbdj3Pc12/Wq3meR5FkdFfYowZhWOTrQ8GA8/zpqJqJn83\nMppKZVmeUMJzkd747JZfcMulqtKiMTNHGaAmWZ6kSa604My2LAuRaTWBpZIkiaKIMVYoFJIkUUqZ\n3u/PRdKUSqJ4bn621WpFUWSStjAMEbHX65lsw+jvZllmRk8aQmqz2fQ8Twhx/my4tLQEAN/42rfL\n5bLW+twZBIA0TcvlcrfbLl0OfNerV2fyVNQqdVRAgVECM7XGwcHe/OzC1vaTb3ztm0KI5cWV+/ce\nu461vrFSCUqOa+3v7O/s7MlMeZUACIuSjFqZ6/rctsIsQTST9ChBhjjJghBRK+N5CIJGQCTGDREg\nCEAp4VLmhUJJ6bRcLlIu7t2/tbQ0v7AwB6CazcOtp5uMg+e4juPWKrXW0e7CzGzRcx8Nu6iywHcZ\n14Ro13XK5TKndDwcDntJ5iZz9ZlqsdA62jt39sLHn9zMMjnXWI3jXCn0vSBKM0IIgAaigBAgCESD\nBlSMAgVKCGqCoCUiKtSEUqKUIqY5vzWkFI4O+0ks41B4bnHQHwVBsDC3+OnHt3Z3t4OiO1MrzTWK\nWoksjWfq1aPDw5kZerh7WKwWx6PRk82th/cfHR4eaa2LQeA6lmPZzcODcDS2uUUtN8/z8Xg8Goxt\nJhuzVc9yd5/uHMqjUiHotTtzMw2b3fcdt+gXGKDM5Kg/unPzdrfTP3HizP1Hj9dX1/M8pxSePH7a\nOmq/cP1FxlitUpeL6vTJM++8885cY77VaoksG3S6vu2cOXGaauTAKEAlKD+4c7fo+cXAl0IkcTjo\n9zc21giA7zm9XqdQgGKxSCjGcQxtbDTqjFApMsuySkXPdawsSTqtdrfd83zrG9/+le9//09ffP4L\njx49Wl9fT5LE9/08kbVaLYtFp9lbWFiwqDM3M1cpVmZqjR++9eNX33wjDMMz5872u73heLS8vLq7\nv/fzn//iq1//2vnzF9NcAEChGFTLlcODDuWyUqkVg3IajlHi/Oz83c9ufvjue9/+zjcVqmQcJcWo\n4LhPN7eKxcLq0mJvOFpZnhdJ/HTzsY3M8kuDwSAIAhRaEUUYaAUElNCCAGitOSGcM0RqROgZY4YI\nmiRRnssoiuIkMuoStmOZyZ+27RrqphCCEOScWxajFIAQADrFhAlhQLRt8/F4aLv28vpaomU/S+Kh\n2u71tM733333S1998/7O0/mN9ZWTJ/faR4VKKUlSIaQFrOD7DCFPxdWLl0ZhnIQxBZYncSaUY1nc\ncRARKc0TYduQRVJLahFX5mAR12JOGmVZInrtPiNW4BXv370feAVOKNM8cCs6w1qlsbm5WXCKR3ut\nNJGeEyABkQmNxHVd23UZzVUOuUDLsfq9Xm1lrt3sMuo6PKjXFgbdkHPHol69NlvwPNt287TDDw4O\nDBVkCknAMaV1Km9u1k4pxTktOO4zsijU8B1NwcNxnDzPC4VClmWmykcYMGKVio1yaZZSaoj5tm37\nvm9yUqWUVsTg9cXA8dxKEATVSqS1ti1HWsy2bdQsKNQNJmucQbXCcd5MoMna/X3GUCnsdFpS6tXl\njVptpt1uHh42y2dnu+13z507de7chb29HcfxBoPBhQuXDg+ODg4OCCEba/ONRmOmPjtTmTlsHxJC\nlMLxeGzbrsW8ct2vlISh8ZgWfWPrKTCbYzROAYBSi1KaJSocpYjIGLEsz7VdSni14rxwvVoIPCVR\nyMyxPcqAM5tblFGLUASkiCgEAhLTx2D8GSHEcZxpJ6bpuTNLRBnJktQIXqVpagoqo9HIJJfTJTK7\nmTFm23aSJPV6vd/vT9+kUCgcHR3V6/Xp7ahWq0YGcTTuJckYiOLcdl27ElSf7j7e3d395NOPSsF8\n4/JqvV6vVhYdy1MinGss/vZv/m98v0iZ0zo4KhbLV86/UCiUQVEp4Qd/8WPGXUJ5UCxa3KE0M905\nTFOC1DBfTQFGa601EEKAmLERihACMNmQaRqXy8V+v+t67MKFC3PztTDquZ7lF+woGqdpMxyn585e\n8NyAUl6rziTRqDFTqddqpWLR5g5jzHNsUi3Hcax9T+RJGkdBAXzf8z02Pz8b+OXnrr5w4+Zd3y9a\nlkWIQA1pmhNgZvo1IAFCAak5HAgKACgYGSGttUYNmoBl2ToTjuNQwpMknZ+f0xoWF5ddp/yTn/5g\nfWM1iscP7t9fWKwNet21leXt7aeUglHkK/rF2zc+u3T5nBBiPB5qLaN4OBqNCMVi4BeDUpKEaRZu\nPnlgJmEncWaY8UvLc7YlatWS79kiTw72m5VKZXfnyeXLl8+dXQ4Kzv5+3GruOzZlFB2bvfLS8z/+\nyc+WVpZ3th8JkZ09Pb+/fxSOumsrczO1uVarJfOw3dz9+OOPv/Wtb7VaLU71rZtPPb9VLHkPHt4e\nDNuVStlxyY2bHwHJ33v/7te+dj1Ohn6BZ3n48Scf+L4NRLkeNFt7QkjXtWynUCr7UqaFgksIoQyH\no15/0EnSiDJdr1f/+I//6Otf/+r3v//9Wq3Wbje/8IUvmEBKa53n2dmzp8MwrNdnfvGLd2u1SpJE\nSotyMdg8OvScs0dJlCXxeNhnBPI063XaF8+f7/e6FiMWZxT07vbTF76w8d7778RhhEI0mwezjfpL\nL1//F//iz95664df+fpXDKrWHbT9Al9YmPODQm84mp9bRCHD/jgT0q0WXMsVUiilAChM4kYFQLVC\nIEipUXxHziesHCDAGJudneWcS5nHUWJEyMrlcr1W9wsBY5YUKolTo1ljzrjjWIQQ1MTM1ZqcZU4r\njVp/NFBajcejzz77dDQezvlzvu9LySknUZjEcbq0NN9q9UrF2rs/f19KpYV2LNe3A88O4nG6tFDf\n32u5tlcuVHWGqGOLOShRgfYdXwk9Uw3iMImjOI2zve29cDRO07xcLBFNHj14XCqUsiTf3d2fa8xW\nSrX1tZMff/RBEARRHK8sLEdpAhq0UFqpTIosywilnuN53LEJR4+oKCZIQWmR5wzI4f6BY/E8zUSW\nGnrUTK0u88xitsoVv3PnzmS+OiFmCaZTxUzBzVTbjDeiFESWWYwhYhzHRu4iCAIzgcq27TiODUPf\neCNuWwbEKxXLjsvyVEVxplVq2TEBqlERoNxijHJCFSWMcSccCcbdLEttywLtAFqjQex6DgEqlVBS\nARGUMAQtcilkSllh2O9prcORevz48YN7W+vr667rVirVzc3N69deDYIgS+Ds6ec2Nzcf3Nv5+c8+\nW1xcXF5e3lg/sb6+johxnPaGkeuUEUmpXqpWctty+/0+I57tsWjcsnkREQkSVFIJTZBzWpifnTOJ\niylpZjSjlHqexy3qeZ6U0nf9UpCbmq0p5ZkyyS911SC1GJnwuAgDogkwJVWqkRAOjBFgBIDRifQI\no8wqFKIoqlQqtpUJISxuuQ7xPG+6sycBGoApqErBRE45KwQFl3MupXQcZ7Zhaa0dm3KmfN9HzfMs\nJwAUCosLs71eNwiC4bDfV8mwL0vFua986dcODvYWFhaUEi+/+KV2p+X7frPZdB2vUqu7rpunolqp\nV4oVABZHebcz+PO/+Hm5VLOdArGcPM8JYZ7nSymolIahoJSJAtEUgI3dRwQgFMzkCKCEYKHgZXmS\nZemLL73yd//u393Z3Tx9ZuPW7U+FyKWUnU6nWq09d/UlSvlwENYqxX6nGY5jx45WV9YtyzGTbyzL\nqlQqSZIwZmmtv/6Nr3me4/tBFMajfqYkdV3PtvxOp+M4hSAoxHEKBAApEDBe09SyAI9ZFoBIiAYk\nMMESbNvWgIiYpiLeP3JsLxwnUofNePu3f/s3/9W/+leXLl0oBcUf/ehH58+ffeeddwqFYmN2hhGW\n57nt0CSJr1y5cnR09PDxY6WE5zm2XXMcx5S1u92+X3CSOOWcABAEVSqXXNednan2+4dPnjweDvuM\nEcpQa0koqc9UV9eWKdPlcjHL60rnjUYVUUXx8PyFU8Viud/voxZSpGur88vLy1rL7a1N27avXL50\ncLAn8vzWzU89rwAoX3zplNFB7vaOyhXfL9it9v7DR08IgStX52r14nd+9Ru/8zu/84/+0T9680sv\nvfPO+5VqsLY+n2WZZbH5+QZjdDDoP3h4b25uznVtk6tnWZbnqVIiSaN2s7e3d/Crv/rrP/jBD55/\n/vk0zSllhDCjG93pdIym+PPPv8AYk5k8uXGqc9REBYNON09FJSi2jtqXL1/89je/aVlsptYAjXku\nkyQaS7QYT5NoZ2v7+rXnnjzePDjce/Tw/ne+9c1vfGO4v7+3u7u7srqaZHGxWPyv/2//1+/92Z8G\nfuHE2omd7b35mblfeeNrR3uH7cOm1qA1CqFQAdOUEEYpZ5QgQcZ5rsQ0fDfgBKFoLKfRwO71elLK\nIAiMrKrnB1LqKIxHo5GxnybctCyHc865kcHWxrAg1YNB3/E4EivLk1EY16s13/erxerT3adBqfDg\n7kPCYX/30LYdLcjTR7u/9mu/9uTJk263++ju49FgXAyorkPZr4yGY9/zdKEiUyVylYYh57zRaHQ7\nXZd6436klPbtACSUC9XAC3zbd7nfbw/XFze63e5sZa7olU6snbCYncVyplqIMVcCjnabFPnqwtoo\nDPM8j5JYCIE5RIM4FXkWCd/ytMRGfTYL44W5xe2dp8vzCzpTBCnmOk1TAN3r9giSOIz57u6uAcFM\ncG3yJM65oToYLgSl1AhZUgqolOsajlMchiGltF6v1+t1AzGZXpAwDA2NxLYdhcx1Xd8LLJuhJhol\no5bt8DyTCIpRy3Et1ETITEmkDCjhxVIhz2Qh8NIkpwzCcVwsFQp+UapcCm1MtkYpcpWLGKhO0qRS\nqdRry51yNBqNxiNJgP7Zn/7kxRdfPNg/KBbl+vp682g0N7v+0ovB3OwCY9xoto+GQikVhSnn0vO8\nNM1RuY7j5Jq2W+NiERqNxuNHu3k28dCWZQkhbZsC8E57nKaplNI4cq015wRQZ1laKnEppQoUAEPb\nIlgoFApCCBNOK6mmFB1KiZKICJSa3n6LgkUZfC7iqQCMVQZEhbmUru3IPNXSAg0iUwQZQZcRP/B9\n0wbBKCNAzGdIAMcqKYEEXQqelpAlUgnFaYEwUiyVtFKUsSSOGfEp2JzxYT+PQx347kxtlVJK1nxE\nrFZqVy7qOIm63TZBur4y6zjO4twZy7KAIqVU5gqAjiOZpens7HyxPL+zfei4geMFqVRpkhgcPI4j\nn3OqifE2WiNoQpACIgECBAkhiJQQAqhNEVdksWWxaBz//b/3/6zVyqdOrO7tb7/60qtJkgRBEIUJ\nAK1WZhizOu2ekNnFC2f29rfL5XK9Xje518LCQpYlJq9VSpntTSmkaT4aRgz8ne3D3/md3/lffv+P\njFBYtVaYggSIGoCgJkAIICMI3KKgUaMBFye8XEqJEAKBalQ0FVmWRVGiVBwEwAjtd3trK6v9bk9K\nfebMmW63W61Wy8USI6ByxYrFQqFQLldOnNhwXfuFF66b4QJG9VkIxRgb9EcA0O8PTYShJNbr9Var\n5Xr8pZcuP3x013XdjY2N2dnZVqtTLlWGw/7MTE0pNTvXKFeCJIlK5SCO48FgcObU6TRNbU57vV5l\nfXVubu7WrVvPP/+8QaR93793p3vm1Eav11lbWbHt2cOjvWrZ55xfPH+qXC4Ph8P9/X2CsLFev3Ll\nQrfbfXh/f3am3Dzc+ZVf+ZXD/Z0njx8k4TiOY24xz7EXF+evXr36heeu7O/vA+hqqSxVbqDyPE07\n7d7zz1+PxomW8B/+7l+/ceOG4zhCC8ehSiAj1rWr1x8+fDg7Mx+H6UsvveS4LiLpdrqU8O2nOyJX\nuWvtbO/5ridS2W13Cm6JMhj0Rxplpexdu/qFcCTPnj5VKBTSNF2Ya7SbrYODg7MXzmuCpu1paWXR\ncbzt7V2ZyUFv2O+NZhtLcZh+99/+aTKKzp48Nbe0+OThE0psJMAYIUAJUEAGlDBGUpEBaMYmGB2a\nZBrANPCawWMz9UatVqtUy7blCAlpkg2Hw9FolOeSc661yrJsOBxaluXYnuHsTRJxRNvh5Uoxy2WS\nJGkaA9DxfqiUXl1ZH0fhbGMuzkMp81MnL2xubp4+cb591NeC1itz4/F4vrFCKd1+uqsVKAHE5Y7l\nFwtKCp3xzLLsUlAJR7ETOIQQixFObSGEGW+RxtlkgJOdyFw3Gg0A4GAV7GBteSNJklqx3mw25xqL\n434UuCkDXrBt1/INAqmV9qnnFtxxL2GM2dySKi+WSjO1eq1Sz/O0Uqna3JFUISqRapkrTi3yD/7B\nf/Msc2iaGxk/Px1EOEXq0jimlBiagyHCTqUyDE3W4D9BEKRpaln2OBS27RgCgokgTO+9qRWZD5JS\nGm83rSoppTjnpv9DKVUsFg05cvpy4wCUkhoUoVgqlRhjhj5o27YQYmZmpt1ur66u5nkex/HS0pKx\n71GYUMqN4fY839R7KOHVanUwGDiO53lelmV7e3ulUmVtbeWHP/zhyZMbxiP4fiBlTggjBKXUUuaI\nhHPKuX0cyxPX9Rm1RqMRAIxGI1PX8TwvTVODLBNCnvFGVKrc+Dnn+GFGcx9jx4Rz7jiOwS6UUjZn\naRZ7bkFpkSY544QSbtmMUUvITCswz2iUWgGhaHGHcYKaKC2ML6eEA9HjUVStlbNUOK5lflrcyUXq\nec7BwYEhphcKvvkWlmUhKM55sViglBqRR8aYZVlpngCA73q+H1jcC8PIc4u9wfDXfvU3uOV4pSCM\n03EUM86ZbY/6g8B2AJXBJIUQUkpEZaJL85cpudtkIUokM43qX/2rv/l3/ov/3HH4YNhJ02RhcW48\nHler1TQRSZIVg7LjeHGUKZ1Xy95hc5dSWiwWwzAkFGu12t7eTqPRoGwSwCKiUkJKqSRYtChyEifp\niy+8Wi7N7O0d1eqzIlcKCCAFoo3eAgASigS1Y1nm1mgTJzDKqAWMpZmwLIcwWgzKmsDS0jIgrc5Y\nG+tep7tVKpUMQHpi49TSwkKWZcuLy0opotF0eCwtLRUKxTRNERVjDIDOzMxkWaa1dmzPFLrNSTG9\nL77vt5odIZOjo62Dwx3fC4rFcp7L4WC0trZxeHiY53m/3zeqo3EclkoBoRiG4aWLV9rtdr1aK1dr\njx48XFxeypJUKClz4RV80BjG0fVrX7h5+xYFMo5GQBS32cHBgYF8jVzF4uKiEKJQKNTr9cPDw2Kx\naHCR8XhcKddNdi6lHA6Hg2GfUhqG4crKilKTjjHLssychSAIUpETQvJMnj5zstcddLqtjfWTw1G/\nUq7lIh30R0oLizvVWlkKHUYjKfMsS0ynlKFcGUwbAMIwNM1AUspSqRQEgecV41DluQrHcRyOZmca\nGpWWSogsSSLGWLESRFEklBBK9QfdtfWTmaSUsl6z61i2z90/+oN/1tw7KvoFEIhSg0aT1gshkADn\nNBUZorJtOwgCy2bTMwugsyyTMjczjQoFI9XPRuNs0B+2Wq3RaEQIsyxLKZVlmRCKc25xx+ilTsAq\npiRJqAXFcslzC0JjEoskzRYWFg6brTiLbdsehSNKYWl1iRByeLQ/NzeHUhDCdnZ2OOeO442G4dLS\n0nA4ppQiAmPMsT0AMIPt+/2+gUwQ0YjoW5aFiEYVsFwuDwaDSqViigKe5104f3Z/Z7fdbo/jKAiC\nmZmZVqu1u7tbLJVs22a2pbU27cCcc8ty4nFccAthGAbFQpqmnucgokbZaNQti2utlRZHR0fFYqHf\n73Pf96eHf5ohGT9hbvMUxLMsi3PqOQ7A5wKCxqwrpaZFo+FwaEQnEfG4nuROm5mnNToDfFNKjUK7\nuQcGa0rTlDGWJInJySzLStPUtu3paw1ENun1oEApxFFrGvkqNU6SRCvg3Prs05uFQmF2dvbJ5pbW\nGpFkWWbbjsHNsrRlImUh1HA4JIQEQWlxcTHLssFgcLDfOjw8bLe7pVIpz6VSIghKWZZkmVBKaA2U\nAiJBVJRyxggiUUpl6WSObxAEeZ4b38Y57/V6RnvGVH2mC25ZfCoUbeJxkxgZcUYDmTqOY16lUWqp\nXNeWUhOCSqFSwnE8rSWlXCkBQC2LGe9orgqAIirLchCVmSGnNXBOEUkUReNx5HnOcDi2LMaYBaCl\nlJbNPM8bj6PBYDQajUy0YVlsPB7HcRwEgVG4YYwBoNEvIIQOh2OpUErdmJk/arbDKFtYmmWUEyIs\nblPONKK5iQQpGFraZB0YmXgg4yqOgyMCiMg5/Z3f+s2/9R//x6PBMIpHc3MNgtDvDvq9QTxOtaZK\nYr8zBqBKEte1D/f2OadpGoeF3Cj2Ex1pYXVbI8qMyII22j+MEcacVn/ftoKgWFpeXh4Mxp7nEAK2\nbadCAjHpDxBKJxIMRAMDQo1SBAISNPNhlTKzALJcSqkA6P7eIaV8PMJXX/7qG2+8KNLM9OS7rj/o\n9SuVSsEtmNZ327a77Y7v+0opVmOmkieEmKvPtXodY7vzPM+yrFwuj0YjzrnBIdZW1gqB+/y1K1Jl\nABSOh8qUipVms1mtVrXWGmWep1mWPN16kiRRtVpFxC++/ub+zu44Tl68/mJQLi3MzoVJXPQD1/cp\nQH84rFUqWSpdy63MlBXmlk2Nlr/p00zT1ExaM7v61Zdf63Q6Wmvf99M0U5IohdOSvmUxc8BHoxGA\nNh7IbG+lVCakBsoY8zz/wYP7q6trc7Oru7t78/Mr3W4PANZWz3Y6bcdxx8NxEBRtTnxbkwJxWMlE\ntKanx9jQJEniONZam+AYJHSOhjYvOlbBq5YLKyfazValXDMWUAhhLGC9Wi5VSmEYXr30hZ29A5vx\nICgVrapF2Wyl5rvFwI+CQjEajvC4UiikFtJMwNKEIKHAOGGckMk4Lg1AkyQ57om0pdSjUcg5t203\nFzgeR1kmKOWmYmQG6xEitNa5SBEUoR63KOMcKUFObJd/+9vf+sIXrnuFshSQ5cL3gzQTxUr58PCw\nUPQtyxqHw5PrJ7d2n2ZJWiwVXMc3kxKV0qPRCIASYEIIzysUi8WJMVEohEjTVGtthqwKIY4RIBHH\nsSl3tdvtcrlsqtR5mhJE+6Uv2ra9vbtTKBTG43Gj0Wi328aHGeOc5Jk5YoQQUGgmJgdBYTgcFovF\nXq/n+26WJ1pL13WllCsLq45jp2nKp1Zv6pDNRjlOGMGkSsY/2TYfD4ecs+mTpuRuWZbJbDzPC8PQ\n932ciPBrygkhoJRUSiLitNnYhHuccykJAHLOjOqG49hRFFmWA4Cu62qtPM9N01QpOcWvKCWMWYTY\nlNJcZmZfmhzOuHcz2dfI1uZ53uv1SqVSnufmPEyFyAhF2+EEmBkpZmrmvV4njlPGmJDZaIRCZEJk\nWZZLmbuum+dpHCd5nmoNlsUQSZYlhDDPcyzLMW1wURSNx2OTzRg+giEHKqWSJJlmn4wxSkkuErMg\nZsWmGPTUMwmZJSmDyeQ3mcbJTKM2HkXcopTwNIt9L0jSiFFLaUGAmecJRUYtkyeNxgPX8UvlgFEr\nSaM8k6VyIIWOkyCO0lI5aLe7QLTnFsqVYhiGJmiQUhaLxeFwWK1W4zjmnPb7/Xq93ul0hBC7u7u1\nWm0wGACAlBqQRklaKdcsx+n2Ru998Am3PdcL4izNcqFQK6EVoGVxyCU88yCTpr9JXo6/LOZNQcdR\neObsKUphb2/f6Cjnefrw4cPFxcXxOLG4UygEg34YhnGei1KpFIXDRqPR7w+KReV5znA4dNxhtVqW\nQkkpGc8Zm2guAGgpI98rtlpHo3H45a+8+fv/9A8rlZKQGCcRYdZxgY8CJYQgIYRQAqAIQdONpJGg\nBqEVagpKWhYoobQNtmXnWe66thCyVpllxFeEorY3H+/Nzs66tv/wwfZMtZalOs/zhYWFamXWBHNx\nHBOgBOxwHFp8vLtzMD8/7zhenqdSakri3Z2Der3OOZdCA0cpkAB4dimTQikkQDij3e6gUm5EYVyu\nFNM0Ra0KvtvrjrWWz1095dnOcDi8cvn6o0ePZmdnq9V6FEXlgluvN8bjcVCqKslcJyj6VZGrPFYL\ny4v9UTcolKMosq2C75Xtht3tdh27EIbh4sJalmqt2Pz8klJKybAUBEk8oSGgAmZ7SuelUsFzKkka\n2ZaLmmpNEKlruxZTYZQFxcpgMDh14gpjLImy+dkN13LnGqUoisKRKhbm4jiuVZazLPO4XfDd0Wiw\nMFMtBMHR4SHVrH0wcj1PJtp2Sk5QSrOs4PvNVmumXq8WLUDLst1Ws9ltjeu1xSgaj8fR4uI8eDAc\nDRbnT+Yi63f6s/PzzYOjpbn1XON4HM5UGxRIFCWDzrDgFZMwoYQTpkxngkFoCCGcgxQ4FYt6tk8a\nAIwVNoYRAIrFYqFQDMNoCgKZeB2AGmM7kUnV2qAOjDEgyBjNsswYtDAMS8VasVQdjULP8fNEVIpV\ny3HiJCqXGtvbexb3vKBACQy6w3q9Ps5j1/FnVucPDg6yLGfAi16p5JeiKDJqWzLX1VI9jmPP8xAx\nkpHFLUDQQlDk841GlmXrKyfyPHe45zhOyqJiITBZ/rWr1zutdimo+K4311iQuTBJAufccuxp7mFZ\nVrvdrpTKCiWnTCgRh3G1XhV5mmRpuVjKRJolKbM4AU3+8T/+vakrMubeWAQT0ZjUYcr1siyWpqmR\nrcyyLM9zs+0KhYKUctqlbBZ0AqZJbRyeYVGbdCdNU5N1mQjLqBAa5UGjgjotxkwr/wYVnPZCG5dp\nwJJnAcZjL6imqYbJSADAXHChUJwaO63AEAKVUq7r27YthDRNRQ8fPuz3ho5r5Xm2trZiWU4ch4xZ\nWsssE5xTAMo5HY+j8Xi4sLCklPD9YDAYFvzy3t5Br9dzXbdcLhu2m1kWs/kMFGk+17Y5pROa1rQQ\naq7cwJUmgz4udVAAoABTzI0AM6xxBGWqbr4XZHkCSF3PzlJh6nBANCBFUBPoCSZ0iWefIRTNz2m2\nSgjRCsziTJ+cpnQGL6WUAcBoFNpOQeRqOAyjOK035n/2zrvAeH8wkFJSi2RZkuc5pYQAQCaVyMy7\nmS8IoE12GMVjALBta5qmS5V+65tfvnL1QrVa5ZxF8XhxcXE4HLbbbcZYUCilaeZ5BSVRCEUpG/RH\nnDGbcbOBCUHbti2bUwqcU9d1h6O+UnJ2dhZRJUlSqVSoRYvFspB6bm7+C9deWl1dTzNBwIrSrBiU\nbNvudHpewTfxo1K5xhxRIU6H0gISRoATwgjjlDBKOSWcMWZZDrPk669f+cqXXzEpRRony8vLnu2Y\nRLlUKpVLJcuyUEnDdSwUCkmWGtUyM97FmD5EVS5XCwXP8zwDKgDAeDweDgeFAnct2/AdlERCGOeW\nCXVN8pplSZrFRnjUdR0lZaVSUUo1m02l1Ey9YWoqeS7NNO44jm/fumvur8SsUPKZBeafBk82R97z\nPHMAzfUcRxXMtjxCmEGfTPRpMoBn8ANhcG+lMMsyjdTiE1zEmGnHcVzHzfJsqrButp/5LE4gTiJQ\nWqKulKtRHHJCqcW1kEgJA6IAiUYFSBGQUAAeJxmnrFD0TYSqlLJshohCZIQwy2LmeMpcIMFEpgDg\nMO7aTjwa/8N/8HvJOIrDUEulcqGVAgAziIQQUzdKKNOlUslwlwy6YwxaFEWUcjM9cnl5eX5+fjQM\nt3cOKeVCiCzLzJc1pskkxEkSmbZZAzlSm4zz3htvvv6bv/NX4yhj1Fld3eh2hqVyNctyI/mqtCaE\nICVayFykjuOg0tO4FhGl1Eops3MIsKlhN3Gk+e6EkKmCuEGYTIg/qVMqZXAyx3GicUhQaa0laptx\nwpkWMskz33GN4ZoG01PTrUCZ+0U0aqIpUqRoc65AE43AqEUZUiQa+VSk65ktRcw2mrCKj7t8Pg/q\nYQJ3Tj5MKZNLGRcCk5k001cJyhgAcItQhpQit4iNTEqJABqpRgSiKUNCCWMUjCEiCgE0KgQEAkCI\n7TAAYIxyTtAoJ2sFAJQdN68QBIKEAEFNAZ9ZTco4IKJlU0I5PZ5bgIiUASdAKNUaKNMIgjHCOdFa\nFgpur9e1bZdxi1vAuCJUaVQaNRABhI/H41KpBCRHEM3WrlKqUqloDVnOPc+amakYYFPrCe/Osjgi\nIAIhilLNOVDKHJdLKY6zBGCMTm8k52a12fFdAACNoCyLEwmmbRtRKgXTu45IEDKtc611nsssTw3U\nO3XqU7c93TFTn/3s45k3RCn19G5OkdJnEDbie8UwDFmaa0W5ZXkFaxSOR1FYqTaQUGXozwAAqJRW\nMmcKtRJSavMVlJIAgKCyOLMsrpTKsoQxSynhed7KylKlUrEsS2slhDYAgmGOeG5hNBpLqZMkyzPJ\nmEUpE3nuB2VDk81FrrVO05wxhqg4566XjcdjITKtiNY6TdM4zmqN8v7+fr0xe3h4+H/8P/0X//P/\n9PvjKF6YX3Z8RwgVxWGtVrEc+/CwmSSJ77s4mQI4KRMSYEgpAYpGzYgY2YZJhEwlHuy0Dva6hCIA\nEGQiBw5gW4UwDJUa56mmlMhcCJmhJqbONxj1pdRB4FuWI2XOGAuC4PCgCQBS5SasMYVYRmAnHBoo\nFYAKIY1DMgZRKaWUYJwYf2EQqmq5sru7myRJpVJTSrVaLdtyV1ZWZmYarusyZiVJcvvWAwBwHIdZ\n1ClwbhPObc6pZTmOY2aYSq1Ba2mwX85tM1+DEEKJTemkxkkIcRzPWBLP80wjuTGFxqUJoTi3CAVC\ncvOSqfyogU9MEGAMolIKNFqcopKoIYrDrj8ehyOL245rO7aLoJXUSkutUKNCbWhZPJeaEOK6LhJt\nGuoJIZTBtJvCsexj66lH8YBxAlIXPDePE9DEZjY6biIiPVFT1Mc/GQAyTihl00L7NCsyEblSmhBS\nLpcrlQoAhGEshABQxluYY2ViTbOxAcD4CVNSdV2nUqkGQZAmWZ7nBEi/308SgXqIhBKQAKA1UEop\nZ6BRS7LfPDKn26wbHnfgDPrh9OM8z/M8jxCS52KSkCkAotMkD6ORyBXjxHV8pQUgpQwIMMaJ7wV+\nwbW5GeBJplYCbM65rbU2XXnT4o6xsYRRw0o95qZOHkqpaW2bEAIatdbc87xnMZPpY1o9Ms9PScO2\n6whBCKUmSOacIwC3rGnIxgCIQQwBKEVCqOkmoXRCliUELYsBaEKMVQUDm0x5ZXBcXqLUmO9Jajy1\ny1obcHaiomHqDcepBQBM6jHT+w0AiGBZjHNqShSIBIAgIkXCuY2IlmWb9y8EThjGlWppa/uJ45YJ\nYY7LOedK20opRGrZlHNuO8yyrDgZlyuBCRU9z5NCj0Zjz3dKZc8kcHmeg9Baa893AYBxjYjcMoxh\n5npcCGW+4zQgOF55c5F8emsMrYFbhFBKKFPqeJWQaI2e5wKA7zvcIgBg27a57ONk0Szy5zLDSimz\nAjghj003ilZqQihHREIBkVBK8lwCAUKRUQAk0zDFYsA5YZymSvl+YCHb2TtkFgdKkBKkBCjlnAOg\nFJlUEqXWSmilAbRWCrUCAARiMUYJatAmRddKrywvfv0bX6FEAmqR54goMhmOIkS0uUOQNA+PKpWa\nSdydwEZUjmMBGC9tGhLoFDFIkgQICqGEUGEYm+Bdo+z0m0BUf9gbDEaLS8sXLp55vPlUo1BaWLbd\nbndS1y8EpSDwGWNRFDGbAyWAiPqYbqHARHGICEqDaYtFZbbdcDjqd0euazPGPMcZD6KIRrZtU2Ai\nE6NszBghhCglZSYymZdK5SRKsyyXueDcSpLYoAUIJv4wJdvcOCTXtVFJ2+aW5QCQPJN5buYHUkKI\n6YCRMs/yREoTafEH9x91u10hRKVScxxHKe25tNcfDUcGQ+ZCiPsPHkspC4ViseRLzB2XO7bLLWZb\njmVzAlRpKYUyFp9Q4MyyHYszixCS55rAZM0ZY47jGttk6PXP2l9ElAqV+hzYmNp0RDToiwlzTeZk\nUC/Hsilo1MQwHZQWju2ZzF6qXORKaTFFC0wNabKtCSjUQogsz4UQk7nmhLiu69oON0JQRNoF23Zo\nHEbFggdCjcdjqlBJSQghoE1IBqARtYmyDGYxCRZRIWqtTV7OOLe1zh3HmZtdKJeqw+FwOBxqDUoq\nRKSUoSZSaNOlnmWJ1mC+LKJSSmgtOS8QTiTC06fbUmpAq93qEbARCWMWAWZOLefc8VxOmQZtghXz\nMDUCU+71vAnn1kzeMR2faZpSwoUQSqHWMkmyMByZGoRtu1pLRAKgEQljxHV9z3MaMzUjZSSlVLkA\nAItzg2kBAIPJzT02ZZpwhuTz+SzPQlaIGpGA0lODPzFY01+a4kUTwvtxwjWNmhlnUhLDgjNHwpTZ\nnwmZn3ELhmp2TI6YQqiIaGBT855Tjtk0hYTPQdjJR5t8n/zyw9wJs14ARltMU8qPwR8wKIfWAKAp\nZWa4vfFGiKj1BPOllHmul+c559y2LUTlunaep4iaUFBKmLHoZk+aY2NSQ0ohCApxHPu+yzkDAErB\nspllMUQklDHuWJIJIVzPppRaNjMHzFyGbXPbZpOGymP7fmxx5PSQPuONjAnUlHKcKBrAdKlNZZ5z\nU89DU2JljDJGzC8/e+xNhPiX7hcAEIrTrNfcMtSEMZYk2TOfxaYXRrSulF3Prw7DmDArydUoGhWK\nQZiESgnjDzRKQpEQBKI1Sq3VhD4HCEQBAKFMKzUajV3XLZVKSZIwRubmGisry82jHRMjm080DBcT\nOPf7/ZWVFSllllHPs+I45RalDBEUpdqygXPKOdNaZ5nWqLSWnFNEbtbNhOdSZ65rKy0pw729nVdf\ne+n02dObj7feevtnly5eXd9YpYSPozhNM8/zGGO27UxyRKL1JCAAAMUYxc8FJiQAV0pQAFQ6SRLP\nc8wtjqJIiKxUKqGWWZbJXDBGzfEG0ARxOBxQShmjhrXoejYCDcMBpdSsp23blEKapUKmQtoERS4s\nizuIREolchOB0jRNzW5PsziOIyEyblHbtm3LrdVqeZ4PhwNK+cxMgzF2cHBQLJazTGitCdBut5vn\nMoqSPC8lIvY8x5ApDP4x3YpT42DAZ845ISzP5PHhBUqpoT4TQlzHBxAmn57SdrTWSZbS466SabGA\nPAPFTy2GSY/CLAalhRDD4ch1jJa2MpophlRFpjCvAcMtZlKrNMskaqAkFyJN0zRNAYASksaJTDI6\nORrQ6Xc83x71B55rc0SLWZRoDqjzzJwpIAbi0IgagTBGKSPTr4OIZMK+4cbmlkqlmZkZQshoNErT\nzOIeamEggckxp2jbdqFQMMQBQohSx7K8KDmwJE43N58SYMYPBYVqmuaUcEKoAcYcxykUCqZ/dhSO\np2bBFKrNkGWDBJp6SqFQMPOi8jz33KLJF80Km3qSEZ2ZrqQ+5kszxvq9nuc55uUqF4QQfpzpIiJF\nmN5fgoAEgJFp2fV4YxBERYhJSD5XiUVEPsVwJmnXLw89M0v8THiuQJNpNE0I4ZxPuG2m8+uZ0S+E\nEEoYojz2LjB9K0IIpcR8MiEmCaBgFMHkFBJk5Jfwx+kkAgagGZtAJYYJZr6heRNK+bETJGZQNE4Y\nAZwxcuxlyefuExglDIAggmnGnEjEa9AapVRJktm2y5hl4jjGOCJKKRzHMeMqhsPxYDAy0kFGuCHP\nU7MjHcdizMQX6hi709MIwIzGmC7m1OsQ0JkUE9yS8El2SAGIlrmg1IZnHtMXSik5t01ophRKqQnR\nJvQ2YML0qAOANS3SP3OvATRlhnKiCCFKacYYEmKqGmaPfL5hNGhQIou4xV2PIvOSHEWcDkb9JM/T\nNFMoOedAdC7SLEuUzPM84wqVFho1ACAgolFeQMuits2r1bLjWlE8Xl5ZWltf6fU6AKDyzOEWJ9S2\neZ7niIBAlMgJ6mq5FEURaIEql3nEOXd8S0qJWkqVI2ZCQBJnZv4Kox4hhIDSymxOJaXyA7fXby0s\nLifJ2POdOIpOnV63LOvl116+f//xWz/+aZbl9Zn5UjlwHd9xXKEQyZQaCqZWP719z/h1bfQahEwH\nw06t4lPKKdV5nkqRaeWKPM3SVIiMc25z0ExqraUSeZ5bloVaKpkAMi0VBeRU2TaL4ixN8jwzamaK\nMUbQYJ1Kqxw1KIVKISAlhPgej6IoSSPGyEy9yK1KkiRhFCGwOJdSSmQqE6LZOTJgGjAYjyMhlMWd\ncRxmWZ7kSSYzglILD6WybVsc4x+TwOi4sss510Ie03amyLDpFzalLxLiyLjJaQ6EmmiipVaUwtSa\nm/jSmPJpL8fUQGkNoAljTAjR7XYlTjxfGIamvG1yevPyPM9VLhhqxkgmRZTEEjW3LA0YZylntmNZ\nnLJcKiWE0QXgnGY619JKojiPI8filFJiYviJ9QHUGohGVHhsuCilhIJG9ewpNhfmOn6tOuO6bq/X\nC8OYc04pN/IjAMRgk8aJFosFg6waAS0AUFoKIYrVEiIb9Ee27XIGQihG/STOOGEAhpIH0slBaelY\nSIlSqFCr495yITUQRpmVZqZkAAgglSKGPmfbuRSjcGyU26YRP8smdX2zkhMHQwAJDEejJLUn8bQp\nhQDRWhuozTRcsektJlrRz8/GsUNBAJRSEWL0YT83SvzZgj8ci/1Mj9Z025nn4XgiGWPMdB6YzmpT\n45q+cLp7KKUE+LPvDwAa0WRK+pibTwglQAkQwMkcaFO/Od61xkBTQAJAABkljBKYcCqBIlJynO6A\nYeCafmhNCaWAhBhBaKCAFFFPP45MrDklhAJQxixjcF3Hj+O4GJRt283zVCughHPO80wCEEq4VJIz\nO88kJZxRq+AXtdZBoQQAdsUzlVLz1QzAaNovyDGRxtxjE1ROZfqmLp9MroyYP8cJnNn1nNK/vMjm\nn8fUDcM2ZIQQpdB13TzPCaGMTXjk0z1h+leejR4QEVFRiiYFnfCtJ1Ufo4/ACAECk0wXGADBeNzh\n3M9F5HpBKrM0T/I8DePYsV0knDEmlRBC5HmqlZQqB4lKHrM/AQA0ACGUWjYr20XKoNNpI+LZs6dO\nnToZhQPQSh6z8AzXnxBiepUsizFGpEq5RQlRrsdt20JIgQigApUw30thpjC2mQ8kZ5xTRiaps6JJ\nFrebfcu1hEykyl3XzfK42217viWVWF9f/rVf/86HH3wcJ3kUjbXWSDgiw0kYBJMapEY8zvun60kI\nUkoIlVKlvX5zfXVBI+YikSrVKKO4TxAo055lO47luxbjRCkglHDLSpJESGE7VGs5HLWllAaa1Zhp\nzLXSjDHKEEHkIncdawI+G+8OkwxtPIillAiaEaY0yEwlaZxmcSIixm0zRd2mjFvM92zHc2WeS51r\nrRQQIBqoFiIfhwPX4pZNLMkIRY2SKjqNNRljQABBaQQhM6mIEIJxopTCyRYy1o0xxrQylFFTVOAA\nAIRyClLlCKCRaS2VQgBNqEO0BKCMcyAglRDCJNMUEQky2y46jh9FYylzU/+3bU4pNf7PeDutNeeU\nArEIJaARiHQpR0ZtDgCEQ5qmwBilBLVCFMYZSkXTNJbKAq3DKOSlMmWglBIyM0xuUAamU8fVI0Lo\n59iPPmZvEULMfigWi0Zzst/vmzYYIWAKrsAxB8QAaJ7nISqDpyGiUZlizEqTPE1zAEZsVwqVpqmU\nGojRydPTXpc4JppAqVw3KZd50pgXcsyONjmK+V/DCFNKGUoFADiOQ44TAGNSpumm4zhmUKQ6brAB\nADrpmNRCCArEeCNCCJsWHYgWqKeQ9rOlgYlzp2hu6yS3UcfzLvGYkmB+dZqSG/ydHtPV4jQRSph+\nINu2bddRqBFRiMnXnpbOzMchEn2cTpmvapbJXAFj5ropgPGZBIAjglKmWDU1iwYZ0VMrqfXE+YE2\nJtsEqlM/SpVSWuMxZ8EcIZOi/tuyAAEAAElEQVT6TAw7pcS4SAMmUMI5o1kmtKKu6w8Go2KxTAm3\nLMdcu8GACCGcW4jAGIzHPfNZnFt5nnNupWlaLJa1Bs7tKYUfgHJup2lqxD+UUoaKhojHaRwaI3bs\n0ZEQ7XmFZ6IJfcwiZQSQEgOBokZtxAIASJpkQghGJ7EMpQSQEKAWtyfRBxy7fOPwjnPgyZUQolGD\n+SVqAgYKlAJXxk+naUrA1O2eCWeIsm1eCCyhJKXY7bWPmkfAwHVti9sStchFmkVpGkspAbVSiqIG\nVAQmQyWAgPGxcRi6rjuMIo3y7Nmza6vLBDTnPBwllILr+gZDMDmB1jpNY8dxhMziOCyVikopz7cZ\nIyKPNORIJFAJAJxxjxDGLc4JY8ri3OTonFMEJWQcJ+HizNJwNGCMRPFwplHp9ccWdxhHy3KXlxe/\n973vKU0KftmyrHGUAtpAKHl2Ih9+DgwwOD5sDDQQIErIeNhvSZUgMI0ZoiIExuGYArFs5lqWljKK\nMyATPNy0gEgpzehrbimNQqMcR2POmetRcxwAQKo8zXMpze1gWoFS2oA8qInW2nEty7KVEmHUz/KE\nELRdlkphew4FCOMEFGEOyWQ07AxKQYk7xLJtQhmzgCIqIXKJlu0hSkSpNQFQRinDAKdT3hOlCKCk\nVGmaWBY1FpBzDkCV0gQY51wplFICUBttpY4jbk6zPCJUE6CEAiWMUECNUgIlTEqmJBUy1woJBdSg\nlMpyneYxpXQY9oMgyPJME4dSmsUZPFOWMH9nqCUoQC2Vlig1EJGD1lpqzTgBIjRKjZIyxSigViLT\nxlgXHCeJwkKhAFowSnOG0Xg0taGGT4QICKYKCxPofkJtmNRoXdetVquU0k6nNxqFx6E8ZcwyLoQx\nbtsWtygAGJqxmbQplaCUGr6x1hBFCSKIXDGitIYkTAhQiZIQggqUUpIKJSShqLRutnpST1hzx8yy\nie1VSk2HVuhjFTFK7WmTzzTGndZETFH2GXPNTC3AbH5iCgRSqVzYJltSmhDC6XFSSyAnhk0yuS+I\naBoNTQJDjmGqSVpsLPXx7ftcEIVSIGSS+2ttyneoFPZ6gzRPUOkwjgK/QCmzGGcWl7lUqCkQbSFo\nlFpRIBK0kciccCeAIWglUSrBqIWgJy2QSLUWSiIQOdVz08dULrOUcjL9d7JexqVRSjmxjKdRalIH\nogQoISI35JzPc+fJihA07ogQMKISlHBGudYagJp6mBE3AoAsE5SCEErkSIgSOXILATkhuhiUEUlQ\nKAmZpYkcjXqLC5bnWgSYY3u+FxgK7Hg8JsBs29YKLO4wxlALk+0hmjI/R/icOT25TooWd8z2NbiT\naRclwDQIAOCEI1EEGWHACAeK9XojzRPfLSiUWqJCKaWe2ovpipFjTp3RjnumWGWSSwCgYKR6JsEL\nNxGGoaoDEgDU2uRzBIjiTuAXG+MwzRTZ3j3YenrAXb9SqYzHUZ4mSRTHcZjGISVICAghbM6RMAA0\nGSwAo5RQzgijtmvZrnXm9OlvfONrhUKh3W77vh/HCaXEdROttUklHccxh8pxLSnzPM8IDUSWIKJU\nqe87oAmAVihBIzKglDKLoVZSa6KIRlRCK+R5moXhyC8Wnm4/AYBCoUApTbOEMkvIxGOF4bBTry1w\nTjny0biXpbHnVeI0J4QRoIocQ6xaTQ+wJsSMQdJIgaJGjGJBGCRZbmrxts0dm4s8dlzH5pRSyEWc\nZZnQijFiIhi3YGcZRnHEOXUcJ1OpGeHocQcB8zxXShgIFClmIqWUm3AKKKBWBrFzXCcT6SgcGLUL\nyoCSiS+PohAMDmZRIWMhY0pZIpASTpkDoKXOpRRCSi2l79mGQKG00EgYTKAzJQ2djGpUWgGCyvM8\nTsaMo5QC0RR0wQzmMBxupRUASCUQ+AQXAUaZ0lprlIwwU0QQMjV3WemJKDOl1KIWglZalEulME7i\nKM1F7DplbjkEIRMpAYVkMhweNBJGLc4txlSWKy2QgUWJBhBKKpCUoJIotMi11lIxIIoQmeVxnCJj\nQilWqYbJSGJN5alj2YjKBLTHoS0F5EAANVDCKGUGuUFtlJANRMEKfrFUKiVJ1u/3jUxaEmeuZzNG\nOGdSCkqJZVmMEyGywWBgey7nVAEKrRgBTQARGbc0gs0dyk0FjuW5sLgjRE4IoUCAIuEUmEYABdrz\nLSGZcTCISkrjfLXjOKZ5hzKDkBEClDGGqBkjtm0TMmnmM531juMZ/qRtc6M4Qwg5zl8n+ZwpmaKa\nUPOVUuYZQwcmhndOiURtyi3GuxCkQAkqTRhlhGtAVKZlj/AslceFbfY50kBA5JM00HgtkRvfwIp+\nxfcCQJypU4tz0EQqTJMUEKVSlBBugamTcEaRwnA0MLoAlE4qN5Qxh1tKISUEiBYiAxATJgLqLIsm\nboZzI3lkED/LsgzamOf6uNkFhcikzKdufOLSQaOWWZqQX5YRMkU8x3EUk3LyDlRK2Rm2jfiN1jA7\nO2uXi8NBLwpHcqJAxbxCUSFkubRdj1IQShPCBqMxIWw4DoXIqvWZvYP9XCqlVJabBJxozAghjDvc\ncjnno/2jWn1WKRVGqRERSdOUUkuInJEJz20Kh5qvLISwHYcXuOGrAECaJ7bNgRoNaYoTrrtCRIXS\ndm0NSoNWqKSWlsMVKtueoKwmFWOMIRIppe1YRlCLEDDApoGaKeVCJLZtj0ajIAgOD/cWFhaGw74f\nFBhjRoKDUGJbFiJJM+0Wl2JVGMTde/cfdLqZ51fTNN1v7oxHkVS5zIXWklMGGpUSlFip0IQwwhAp\nWJxyTglqIfNiOTg42Lt06dLrX3zN84Nury+k7vYGUZI5jtPpDVdWlkZhVCwF3LHDMOUOL/mlTr/r\n+M44ighFQglnbi5BCNSKItiIKss0AyScKyUIoRZhUsssz7TIVC5SkcoktT0KALmKiSaUMAYWY04c\n9SxGB72j2ZlytzuoVoooMY77gDYAhal+BKKBiFHryVJSalFGGOOEaoqSUGqX91ujUyfXbUZlHqPM\nXMtVueiPI5OlKcAszwkhjmvZti2i0aRuhxCniVS6XKlyy86lMvg2AMulqaQyTRnlXCLmWabkJFyT\nWsksNbdTESI1ggTGgDGKChjjAChVHsWR0nLS3pdSy/Jcp2DxwomT66NhHIWpktKmoKWWuWKUatQE\nKSGQJAmlQIF4nsMIxHE86RdkpNdvai0Zs0wl3CArGq0oMXRwmsvJ0QMAyCYgOSEEGUM1cXUEMU9j\nMiWagpZ5avKJaDzIRC6yjDMY9luEM6JRojYdLSiVAuSEEs5QEEExjkaEINBJTCaOcS3ThSOE0GKi\nbc8ZI5Qy2/Ztuz08SFUodGR5NI4GSkrH5QhWLpSQCODYlqeBIqo0w7LnaCAKwXYKSqk4EQjUcf2g\nVA7j5PDgaDQO8zxXmtiuY9kEETUiZToXmcbcch3OKQFycLRv23alUiGUaQQgVBFSrtaREUY4ZUyh\nQkBuA6GSoJy6R4Eo5CRvE7lAwpCilBIVTmkIHCzuWIQQpYXWSChojXGWcG4RToBBLnKtAYlGikrL\nejk45u77lPIJF0xpAFBCCikppVpPUhzXKyAiIZMoFijVn/OiGYDBoRCU1oCgUaFGrcD0pDDKOEGg\nRCPPsoxSwrllXiGlMdrC9wuIxp9pU18w/lSjNDgsoJLSkLaJ2X9aCYVEyhyAmh43xsgxamnYdM/y\nssg075n+HUArLfGY8jTJNCnRqBh3CCFUkSzLsjydxvuO7ZpRBeq4V9T0oxiGaBiGphBlQFLGmNFW\nMa7b7HUj8FwqlYQQhiJs29y2eRRpAtq0uUgpGSNaT7SlGSNK6WO1OmkYKSZ7C0pFQ0U1ZZwpNajX\n65mpxiZLNYQfi3MKRGmhlDIKcghKK9AoLe4oLRAdpYXpY7Ut1+JcaqUBpVYTmOs4oqTHaRAoogFN\npZQgUsIYJ4AGpzbZEkNESphGQwWmANRIN+Z5qrWjFMZxOhiMDAeEc14ul4+7jJlhgpjOiVxxavvj\ndrfZbLY6405vPB6PszjOskyKDNGEi59n6ASAMM4YY5wQqkErIRUBDYSFSby0unbx4uX5hSWbW4PB\nKEkyIQQltshRyjzPtZRaCgUO4ZwLwbRSWkvDuCWEUAaEECl+CVswZp1JkFJjpqQNiJjm8vi/mBCp\nyDIlNWXE4jbnpsUq48whYGk1GYOCOgNkRCOgIgTIsXo3ATAtcRPE1SiQAyMagQEAFUqFqeiP4+Eo\n8m2OIiMoKUgtRZanCiVjRBPIhSCMKtRxmpjU8zjkohqQMCqUxGNGz7Pgu1FzQcRpnzL8MiF2uhUZ\nY0bCnBCCKJXOpMwJ1QCSEMu2XUSBqG2bB4VipTwjBaLWO0820zgW+VgIlzFmO9okPeNxNOkBAm0o\nakopYNqyGKIGEFk2USMkhBiKtoGD2HErNyGEEGZx/7jH4/N+DDiuaE4XAY85dZRmRiETEcXnmf3k\nXk9v/bGZ0ULk5BggMQGrmgwxmbA0mc3MazMhhFKQU6WEzAWjAFxTBrbPibYw11MnqhUoiQqVRlWu\nVbTSUk4AeaUyRGJZ9szMLAD0e4PhcJjn0rT6IqLnOYxxAJ0khqmvgAEir9ZrSCDJ0nEUEkKCIPCD\nguMVuO3AMfEMANAI5aHi9i/V48lEtYAQyhilpk/I/DQalVprQlErorQCNKjQZKmP+4vtae4BMGkm\nkzLXmhIipwieTaxnlveXGI+TZ2Ci7qW1VqiJEOpzfvTnDG1EJAqRIgXUx3eQ9/pNxohRNlMK0zRO\n0zzP01ptxggu/aWf9qRqStEA1MecdEKYEJlSaHIg46UAQElNn3lMd5uJ959dzckGNbdbKQAwE/AY\n41KqTqdlGhemp84QVOI4np5GcySm4kPmPR3HMuczDBMpZblcNsfJSDOQY67BcNgHgCSJjHqSbXMA\nTSkFI0mmpFBKSSQUtVSmIwxBiVzlIkWllcyTKEREmzNDvbMdh3MuhDAEyjSJszSxLc4ZBdRSSiWF\nUgy1NmtIKTBmaNCEAAqZaS1N2TAXOdOmnY0k2aS0ODVYZkk1m7QqAxJGODCiiZ5wKIHAcS+aGWan\nNaZ5KqU0rWCMWhMfqbRSSAnr9rqHB0daYZqm4zAzn6KO5RiE1FmmtAagbDQMD1q9o6Mjox0wHA6z\nOKaUaiXpscnBz5mZxvtbDmcISuhM6YwCYZyAwPNnzp86dQaRjEZhHCdSKou7nIs8zwkCozajWkpI\nU5llEjXVaGZc5Wa+mXlorZUCrScJnzkaiBSA5XmmtWCMSYmTdBO51kxkmOeKMcJ8BtSSQmWZsDin\nhAIQi3kWzaVUjHJGmNQTGvczD/LL/wQEBQTM2AmbcaVUHMdRFBFlg8wAJdE5aHXsjZgmWmlN0WJM\n4nE0hgqIRQkz1RRq7O+zRxqPz7wmRh9MIqJBvrVGdey9piYGFSADRi2llFS50sI0b4JmWhKBSisU\n6RiUXfAtzjxGOFK0LTeGWEnJlEQCOkOSSyGyKI4VSqmVQX2zLDXVTSklMOCcMyBKacPoQsrSLDfI\nOUOQeFy5BSDUlAMMb/ZzcH7iVlFTDSa3Py7XC6WUEHKKPJvNaXAOcTyd8nihJJBpzRWmCzKNWc0D\nEYTUeS6Ekg5xR8OYEvRtiwBDDZblqFwwzjk3ehxaUgCgDKhpgJzK/h4zpFmpVCqXy51Op91uD4dD\n84nGUz6rNTOhAzCqtfZ9PwiCwWg4HA4550EQuK7r+T6nlmm5nMTo5FjtU+pnKWZAQGutNGRCcs4Z\n4ybON/gHakItNtm2aOb6UWJUBpRizHIc26wJHtf+TRgBMAXwJzA+PsNxO65zfy7oRZ7RxCGEENOE\n98z5mNr/ae15UoIyDO9We3/qeE2Ybzhyh0d7JsNwXddM0uOcM0aieNLTq58hV5j3ms77mQZoSmKh\nUCbqcyRqeulGrW+6dSYXSpBzaox4lmVG3thIvRntUfM9n+1OoNQmYGzQ513cRpw0y7I4jo2k0LQn\nq9PpmP9Vx2NbjXMyX3Yq9oeIaZoiYppnSRJN13f6+41GQ5kgSuRaS0ohyyNCiOvNmNwoFyoXYNZT\nKVWuFLgFlGmLEEI0Rc0BKINxGJoqqNYmrZw8OOdaK6UyQgiiAOBa54iMAAPUJs9g1OJsQjYRuaIU\nTZ0MEVAT1ASR5kqYCrBZN0DQWgqhAEBKnaVCSglAjjNRo8pDwjCOogSROE5B5CpHHUUR5xalVGkA\nAMZci1NNrd6gNRqNkiQBANd1gyDghCBiniFjjAKaXX68/xhnLiWUEEqAESIBjUwR9f1gbXW9XC73\ner00Ts1dsywLkAJSxrjr+ohESRGFSZImlILR4daoAPTxd9eMMSn1tGtPSuPpFWNWnkmRI+cqSYRR\nFwSiFVKRg8hAc8gpotJC6CzTggrLopRwzy36nh4OIyAcUP//2frTWNu27DwMG2M2q9vtaW5/73uv\nXrGKrIaNaKtoFisSRKqJRMmC7ERAbCZBggSKhAAJEOVHgPwREFhCAgTQTyF/JMdRY6lsU1RD07Qo\nySQtymSxKRZZzat63X33vnvv6XazutmMkR9jzXnWffQu1MO55+y99mrmHM03vvENgPAHY8P8Q/5n\nTmCM1hQpjG4YBkUhhkFzVBiRY/A+cogxsig1oA6BjNKRXM5ysvvJaC2//sIkhhKT2FI2u/mVTUYM\nXNRW2P8hECqapKaIjS5zi4X3QhnXADAGHyb1ZJsNqHOOGYOnARwqQQUAQLGC0QcNRqFiQI6KADUb\nBkNRoVYQkQEpMmrWyKhYqxgocgRGUqAJIrJipAJLgsgRIwcVtVRDA3kgJIjMGEi0i6PVhTIIHgN5\nChw5AiGjaNoqjjRNZEEAAgJkUpGJIo4UvSNGhwyRCYgZFBESsdLKO5FZ0nVZtX6HwmHj4L0bQ2BC\n0TcaBt00lTFmGAaxHqvV6uTkZBiGw+Eg9FppeJKn0LatGKJ5BSHG2Pf96enpnTt3ViuZ+oha66Ko\ngmecSE+QHUCM0ZgSOEraZ5KOmorsxl4IIrkywoyCqgGwMLkARL3gtrtRFMKAFeLUvCyKYjLfGFhJ\n1d8ojj7MF3lebPNNcftXYkwJSE5hIXVGwwwYk9+bv/xX/nf0+it/jZh4cQzyijGG4LJarWBTOZAR\nZxYT1X0cRzfS8TACIAOFKPniFJtIyCBh/jxD9H4sCiP1f2aWGIGZz8/PITU6iOlExBh5szmRMxG4\nAKW5uqpEcF7QOSLq+/54PPZ9//jx435QGdbLbcPr9VokirXWy355bA+RgtJVWRYxxnF0RFQUhbWG\nmWKMz559JJcve7Vtj5eX2hgjhE5pZIuTOEpZVZW1+njcj2OfbxcixugYgtLWWiPuPBvuSEFMrTFG\nRI9C9MEPoyPhlWitp4IqAAAUxa2GRYyUbqxnCpKnaq3LsrRWhxCTriUzg/chCVVVZWmBHCCJ6uti\nsarrWmnbdf1u365WG6O1c4GZdaGD98du//LFRe8cJJbOYrHQAF3XTQNEeEpz9fQqS93EyBQjYJjU\nGpiRWYS8CmOvuysKsTDGj+M4dELmZubk1z0iejcpKTBHRNZaKy3UW2lC8MIbipGdG2JkqcoejwdR\nF5TsX2uLyJGdDxw8xAgcPWKIMYZACFwUymhdFk3T8PVVR4ghEGqVNptssNQo8Po+zN7Iex9BVIgG\nN3IYOgPBGlBAMQYSZtQEWgXjjLU6K0BKCCh7MAeSmJrS8t6WZz1LCG6lNPK2ki2PSACylX2Io1Jg\nrDSJY/BKoS4Lw6U0VAh/1xABaquNYdQ+BO8DEXmKDEwhOtHUIJJHrABClDG5FF2IPoidQ62QARQp\nQEYQD2GURmVGwwQMBIyspBQaOXIsbcnIyIga8+8DBY0aFMisr+ACAQXF2urgQuTIIkXFKGgOAVGI\nM28k38UEHP3tz0As7wGFw+7oRgKL49giamvLoigGZbfrlRCgiSi05ClE8sxM1OhpUq3T2q7X66ZZ\nIuKrV6/atlVK1XXtfZQ1rLUeBldVvq5NUVRlWYtCIAA8f/4CUZ+cnt45vycjm4lotdwEUEKIl9YU\npXSKPCgzpUNgREmII6JWrFDyZSQkBFAcGUHK9ICEABPfBhgqW8UY463upWZCooisGAD5tnsAAVlB\nsjy3KxCTSlCOxrLLYekNTNmRvCW5JsGAAJgRp7+Zt956S5gSM7zIKgXHY5fZBxmpY45df8wuOu+H\nfELZyouHcGNYLU+Z9XyLyvaQ2y3vz0guAEkfCTO3bSv5kJRD8/tjUnyRGO3i4kZcQpbLzSOCuq7b\n7XY3NzcSnkjMImHI8Xg8Ho8hTUYhIlGUCCForReLBSVq++D6cey7bpBoWmsMgcax325PZdaRTJSI\n0Xf9sSiKrj9GodhyCJ58GKUqt2hWN7tLYCWTyLVBmUfeHduiMEVRIUrkEiSiIYIQXFnWwmkRHbBx\n9IBGeoC01s69pg2YA2F5yV198fEzqUAqpaqqKopCIGyBNLWy2X4httqA1cxM19eXWuuuOzIzMe73\nBwBFESKwj+RcGPf97ubm5dV175yyJoQg48UgcZTLwkCCuSUzNsYYUxaqGAYXQgQU3I+MUVVlvvjF\nz2+2y647Xt+80miKwgASonZ+8D46P1xdXR0OO2NMVZUxxn5o5eNTbZIgBzqioiZVPeEIAdDx2A1D\nJzGjcwGRrQWiEGiqNBABRUGPkYiYPLMKCsuyXDRK61da2YiMCJmNnX1PRhc+6ZAiA5GPwbngnIuK\nhrZFdoVFBJL2b0CS/mI1KtRKa+3cICtTfFL2RnO4Oz9reZvEPZhaSeT32UZkVARADX0MIfjgmFnp\nqXwCAF17sKakRVFYb3RkExBYKb5//37f9xKGOuekMVwE0RluPaLEBKiV89EYyt+eIt+Yg7B85ilA\ncZ+4mTGJvEHqu9SzHlhKnWpiOiiVf3AaeBbzoaa9QJgD81sTCSCipQlWAhZmvCjIEUeAoQ8G9WHf\ntofj0B7LohCDYCtbEymjYyAGyrKnzLxer8/OzryP19fXYnaKoogxOjfF3HI3pMFZ9Be89+M4MPOr\nV6+YOcTIzKItWdd1VVW9U1pXOGPVA3tgSh1dAAyigUREzFDaSgKmGMXn6CQFMF2r3Bytp7k2Ck1k\nZg5MoDVIR6aMy0HQDBMhmwkBmUnmCk73f/Z8b1n1NJM4QET6AzlTDo/mn5IfjCxXrSXskjkuCgEW\niyVM4y0BAKchmEx1vZAgFBGncgRMaKxYxqlurDQDh0Bd61Pv5K32MyIWtkz+8jagk3K0sJXEx+TV\nJksBZ/qtNM1Yul3BPFMF1Wk8XTbTcjTRQRDXpZQqikKn0Q88y/ZSzgc3N1cy167rj24MITo3htH1\nV5c34mkYIhPKRLuiKJ49e4ZKxt6o4HzfHg+H1rlBKdO2B0RdFEZUMUR9crFYSBasNMy9lDUlcShs\nZaxyYxCOg/d+udxS5PnFyuv6+nr+S61zS5OSqe1ZBF0l5p5SSvqi9CToG2L0QB4weNfaevny1XOF\nWptqGNxytb28uSYCpYvg6Wq331/fdMMIZoIOhDPCzIpZYggiIuAM6yulANi5IQZH0aEiZG81LFfF\n9mS1XBY316+ury5fvfzY2rKuS6usrmqloy3Ae2rb/eXVS2NMXYuCmSciBlIqk4mnSCireRKB96Mw\nVgU9lYqm97EoRJl+JCLiSa1yKpiTyHBEjgQcEVVZGK2wsAhoiJlZyZqHmQDXvJjEzIiKmRhBKwWO\nog8xsLIcY4zeeUcApNLHVRJjjBD1pAIMiORvVXZYzHd+sqmIQjL9iNKImhBipqHm9ZDL78wEOWFi\nZFYhEkBkjkVRcYToI5CokWtm5EjNYmXSwBtbBFNY55w7+lkdi5KrC8wcUgcop/ExzDS3xdlnCMLB\n5HKInRYJMLMbJ8ZTdjbZJmTfP08QsxYDp2bPZFJyLsswM3zeSxulSMxJKEPMoNEyhxgIQBW2+uC9\n9w/767oor6+u8rnFwCGGEEi8gNxwKfwAwOFwkOnjzBwjZVRJTl46iowxuTF2mjc49Dc3N8S83++l\nUUlrfXV17b01RdDTAAtjLXgXxt5VVYXJHrpx4h5L+y8GysF0WcoENeOcm7ppokgPRFlFfRzyPRE5\nPk4kMp690r2Vgr0SE0ozPWWdxIHyc8TUXfqJQA1TXfATTwQRDZNGNEopnB4bR4rEjKjzLruN/CQD\nnohSKJQDZmKKWlmNFgBQE7OkyoxAq1UzXyVaa600AIbos/9UqFQGQCDG6JUy1hhrKoBIDArB+VBY\nA6BB5i8CIWgqhIfGc+8YKcYYhcYTZ1q5eY0abSYyFAAAEMtceiuFTczLF6jv+ydPHinpKgcv3ih4\niuSrsvFhBFaSA2mD4+Al5Mk6wTlxkUUjymOSgUkZQM5zGLuhdzKXfT6nlSEWtiIOx0MXyUv9WQYN\nOueE/g6JpyQOW/ZA3tUAsNvtiEj4BVLdkcQxHwGRRKgxxOhDF/2gDRaFbhZFPxyZ9Wqti8q66F5e\nXPT9uFyfKCzato3Am5OtCz5OXbFTfFAXxXq9VsgxRlK3FWkiijGMwxBkioQCAG8tLlfl2fn6w6ff\ns1a7sQ/BA4bYdopxGOuirLQyzjEqP45tP8Su14fDrqoqqRshCq4+AVYhBGZSShujhSMaI+WISint\nvXPOV1VpbdH3nSQfkAqHWsunAkVg1hS7sqyJdIwjoEWICjWlfIgFbX/9lf4UARBQA3H0NI4ueG+M\nIuDBOY4OFStghchMagL9JuFIXQj5zY+jl/xbeEZScI4xMmOMXnBi54Jzg6geaG1DcKJcUJbTfE/Z\n+2LYAaaBOjAFkXFy6szeMTO6ka2py6IROmXwtN/vZdg8EVVVZQvddd319S2lRSxDjvxQ6xjkyFHr\n6E2MMQqEnislcsOttcHfkiyUUrJ9JCwQ85ozIU6VMJXYsPn3cibiHbMDm+VSMGkUzQwfgDCtWPLm\nZA2VRmQKzgWDYJSuy2Z/s3v58Ys7d86CLWyhy7I01mqD5DGwhxBEo7IoChmXc3Nzc319PY6j3LFx\nHNu2HQbHWYYYUbZeRnFkPwaKRHQ4HITFgIhFURxfXIVQFNVaVqYMOfTeH4/Hi4urTIXouk60HBHR\nFNNNZmaRpBMJwcxjnKfOAhSJAmG+Y3/gBt7KPRAFRBQ9+IyvyDtFqjQ/yhwAZWLB3BVBkuHO3zh5\nI6ObyfaKtwHQqXqaoQCVPBMz5VRYmMEgkjtGTvr1Lk4ihOBTDDVdJLC09Gs1XQaTEGRFYTJoZbSW\nBYQAKlIAUIDKWp2QAUrJ1rTNRJYvX4VWRisrjZpa3ebpIUwIQOA4X83MoJWhyNYUKQuUBFGVZakQ\ngUMMAZCtslZrNigMbGwaAA0QOQIg4daITMRmtcp3b9o5SlGM9+/eFSXzfGMR0U/kC5NZi5I5MaNC\nJOZh6LyPWQEWKMAs0OMU6o7jKP22MnVQ9sMwDNWi2e/34zg+ePDg+fPnEr7JmoYp2PQhRMl9leLo\nezeOowsACrVVaEFpQLNYnQxjiAH/wT/66u9941v92DsXrnY3zWrFPA0Y9N5XVdXUtdaaoq/r2uoF\nM4/jKFMQI3mKrqysAghhWG2aN9969INf/Nw4tp96683lqlqtVlqj613bHsbRE8HoyY1BPvvZH3gz\nx/hd152fn65Wq67rRJS6bkqRnmSObdvvdtcxctNUZVkzx93uMI59348xGsGfEfVqXWlA54IkScG3\n3XEUEoQ1pdamLBYXLz+6c/7w9GSxXCzf++BZUS6ZFRFMemIskig0cWanvvcMoMe+GxXg2A/e+2EY\nm6qkurl4tbcKl6uqMNY7R94bY0pbMoL3XoO2yqA2GoxXWnS9FGMYvSMviIV4Vmtt1/XMBMCewdS2\nspXrD1dXV3fu3BWcgyKFcQCYlB6JQIrSAIQAGkRliA0aBqAQdlfXrveFrRAxMAjcJB3HMrNHRl/2\nbaeNMsYAYiRKqapyw4BwS1kKaQhnZmFkhGOKyXCaf1aWpSLoBw+Jc1SVpUrj0EIWXIZpI/OsNiZQ\nvEryEMQhhhhCiIFjZAEAJF65xbsAJBpTkySBijEG5xUgUKiaqu+Hw6G1tjzZnlKIYGHRrKqmFm6U\nj4GYCbioKxG9ZebLy8uXL18eDq2opkGCs+YpgvBax9G3bb/ZbO7evW+Kar/fn56cX19fd91Q1/Xx\n2O33x3v3Hrz//jv7fajKddM0fd8zs0xfu7y8XCwWAvDILp4E1Qqr7fS9crHikKbhRrNXtsne+6mR\n4HVsaZ4Y5QI/UZBFPjOeuU1e3eYbs2HW4hSVUvl8xLPCDMyQhRFjNMFDinFeOw9tjBY5ZwLiHJ6g\nLarbIJBymRS1tpnJJ7+PkYlQm5ISGzFGCZpYKemrn7y0SPtMp6WQSTRjNAADC4NZIwCARmSeAr3s\nIKck4PYIAABgjBXK/a2X1fK213w1wKS5m2/sLJAEEbgD1NqQlK1zzTo4pyS0nQRYUSlWSoEy0n2i\nszoT4vR/OZ5MspaGFQbRXAAAnlSngHlib6PRCrEomqKAiTvHQWGE1AdGxERRfj49PQXE9nhkJq3t\ner3SpsTdtQ9BJl5/97vf/aEv/vDVzaW1Vil0blRKWWusvcVRUXFlToiEgmsYrQ9xHOMQYtePm9Oz\nr/3Gb3/zW9/aHXaRWJni0B1uDgdZ0xIo5QRcAEDE2+eCiBqgWRUfffTByWa1WNQ+dP/Ov/tDf/an\n/6cffvj+Zt1YmwYNOOf9BgAUGtSlmqSgkZmlFti2rdKwWq1EiK/rHjGztTJ2y4szFjpTVVWS/eC8\nPzqRcZ1zfvCyq6VmMP1MSARa23EIV1c3J9s7d++e//zP/8J6e0a3udCtSE9+pcSIJWdiVqfb7eBc\nWdkQQozh8ub4qTcfLVf1i+fPQiA/tjEEyRf86JnZlkWMJB0emZA5LbmU+ELCYLXWy+VSfhAh56Io\nttuTk5OT58+f5/g0LUMU9Q2cHrcV/sLMsmAyAgAYGRAJKmsChcNNd+yPYzeOYdSIaNR2vSIkiODJ\na2DQWJqSFa7sWrrrfQwUog9CHafCWKmjC9uLUUm/e1WU3dAFF5RCozQoQEZGXi2WtrQatTFaZoYK\nKwEIyGiZdyj/E+aCcB+iD8JiQI2FsViqsQuggGNgBAXMyBR8jN6PTltTGAMKKfgArACLwoztAEBt\n23LwQsaxxgi2EqfhkIqV5kioodQ1JfXYYRgOh1amjwtsJXfVGGPMtAW01n3fZz8t61M8zdX19WKx\nKKpyt9sdj8e8VjnS8bh3bpBVfTzujTHS2CDpY4Z8JCMnMpSIrDmtkZHT+ZXXqqwxY5RoT0vdmhmZ\no7Vl5grMf+/9OBWg5unKpE4AMOH/Jof7IuiVz9Ak4V1B8uOMU83Mxuh64gVhXrUAANETETFPoL/W\nChRoLSqXefOBSv1+MYDWmTEBCgE1sAohDkllfApedHqfUgI4mnxzJrSdKbmQfOuUvCHR3m9f0voK\nAFq/9oc409/LPl/u2+zXDEm3TWuVf55tYBtnuR3MfLZCiykIFo1WaU+h4OdvTt9F2ljgW/+EClPJ\nLC8OhaCMnuYdDMMQgwSSArtpZo4BlNYg7EwgNT0P4ZhoYK+1reoKAGNwAKqqmmVRKVQ+jJ/9zA+8\nfPVK9G+Iw9nZuVJKQXbY03+Hbl9XK1CGmbrBKWXOT88I1Eg0uPg7v/uN9z/8oGmWgVhxDCH0vcuu\nyKZXURTAEQCIYgbQxHn2fXfnbHN6tt3trv6Dv/Dn/8//p/+jG/o337ivNQKywKwcJZM2SmtTVgDC\nwJos8hwIncd0AEAUiIKUEPLsUQDw0+jx28RdqBbjOGrQU6MCityiizECoDVl0yzdSMMwrlenu93h\nH3315x49We73EUCm2KbehtfWI0g9CQkBgBGvr6+DJ1ovjodusSwR1Wd/4PM/+IXvX62X43D0Q68B\nrdLIALItlVFG62kYnZ+TVClR18T8yc9C9FJpkrJgXNI+kVMQIenJI3j58qVYVRlHK8PWYoyHwyEf\n0xo9TRFDAlQcvBt7Pw4UQ2lNU9VlXQTvRf/AR6QQI6MCDQq7oWVQWimjlKmtqMcDYgwhs+Ah99Uz\nW6O1gsDEFBAKYzSyIohNXdnSaDRKs2IwEUXvyg1e2pIIiImZo0KtFEobmBwVQYkQIgKUhZLBnaDQ\nWiuKC4xQGNv2Xd92TFCVJWrlRzcM3XK51KjGvtWNHoaurmvXteJFpWxvjbUmjs6HQNpgJnxeX1/v\ndoe+7wUikrqLQm2MKYrbSMK5UBY1sOq7sSrdark5PS2tLatmcXl5OYzuzp17m83J1dXNu+++v16v\nX774MER0fsDEDpeITaw5ACS9R2aASHzcH7Pdk/8OM4v2evDBskFQsUKDioV7NaXO3ArDe2J+K5b/\n+knHRlOqxMs/hQI9t7TyLZigKXnnFG5mIeRbM6601uaf//NfgBl3JWdYTdPkFGxed6mrZp5ri1Eo\nikLQSYF9by9egfNuapVXSmsQCy7f4sYIALpSgEgxAiBqRZEAzISBgCh6AMBkuyG5Qkxpipu66pQ2\nZn55mTQC6d7LVcs/iSgfTC6NkopG5oqI666KEkSzLx1KfsYYc6o0c+WgTPGJeHn2KYZJP2Yq0UGm\nrKS4NH9isag+cQxE0BqJHJDcYenQFjlkDajGwRldAZQAMA5jszRFuQbAd9999+TkZLtdV3e2bbuv\nyuZmd10WhRBzmCV9mWxr1ZwAMMWgVLGoFwDKEx/afr3a/srXfvU3f+t3XeClKdkFH2m12Vo7yAAV\nSCCMmEg39jHGmNoDhLyOTN6P202lFD569Og/+U/+H5Ut236vDVqrAUAoPwgaOK1gWwQKed2bhTnb\nWgBOxQ+CqZoJkUMIjuGWTcMJH5eKYDbocsMnxkrMZBkAgKlrHTSiXi7XMTARLprV4dA+eXzXOZmi\njWktEUjAjbeHZYjAIJMykJXRWpe2mOJZLXPe/vJf+d+7oe+6I7mxLmyhDYQoyl2orXgjSFSFHAxR\nVs5Oq1S93n4o78yUgRT5vca3NLMBRbN6AEmddX5/iIgCI2hm5hg9eZkbXdlCF1oDggajlHQ5jcFx\niIFYGSs9IW3btm0rokHhdYFzmBEQcvcIIkrTuvyeiIRMK0idrB+ps+LrnDq50uvr608cnIgowsnJ\nWUzEXZ6xH588eXJ9fX11dSUJShoEPijQRVEcbq6t0VVpNVeHaYwXhRApsrYGlB4dtf1oFBVaS4Om\nDLVjZiIWrUsiMvp2UvvEOjGlJEbMfDweF4vFyfnZdruFj3C5XF7vbsZxXK1WElXcXO/u3DlnQNHY\n1prX6zUiphhlQjXk2couLq0mBGFFZR/DEHPPkHgX0XyRDD5Gz+wFrBH1aGutXAsqYGbpalKaERFw\nGqwq4X72RjhD/2DGjcSZxEbOhEIIUlDIn5JwykxWINWdsh8bxz4/OUpUbGaUuZ8SDshNkQMJ/mhu\np/6JXeGiUDJNbjLWybHJ7QYAwVJkG0i6h8ifqFUCwGazmdnl29disVKTwA9nblUm8GQXnVe/SU5r\n8rLJAUSfWRWAKDcElIrjEAqjUfLQGGMIABKJK5jFGskWRKXUdOmIkxsT5XCtgSffM/k2ZgJWtgQA\npsgsB05W2Bh+jSObmgt0Gm4k7plSaK61VSqGCKYc2haoZKefPX/+O7/7TQB4553/9o/80a/cOb/3\n8PGD777zzt275wqaCTxUpCYgmOUaQWuF5McQGWxpjbKb1eoXfvGX/sFX/8uPnr5s6m3Xem0KimGz\nPi3MMQdEmZ4nyy6jYbkbBpit1sH53/rad37zt/4VRxhhrOuFAs0CSYOQnDSgwsjIEQC0MqZINxk4\nRCaKhS3lwSIiADIwMGplEFmJQrkWR4WgwGjSaPJdm34/HZGiD8ysky5kuucaQTkXxiEaVSwb/ef/\n3H/wT/7pz4NMNmFMy2BKj/K+Shq4slJJKWUL2XgqhEDMv/GbXzvZnl7fXGqNBpZ1WVlUcXDAbK2d\neHizumZertnyZld6u9GSFc6ZYh5LiLNyNACN4yj7K+93mT/i/Zi3CQAQxxgjRTZoECWfIBLuRIwE\nkSMpo4zSjEAhVmSFlBYCUWnWq+bO+UneGoi43+/zjp5vGaNt3rPzLPB4PIrjyf344lHats2hcLY/\nSqk3nzzOx5x7XyKQuleu28v92e/3d86352cb8XNKqaqqyrKOLtZ1fdwftMaqtLury3QaPoTQdQOO\nse2H46EfQzRmmu8s+aWsf++j5OX5TOSpSZ2sKsuQegqHYXj16hUa/eDBg7ffflsp1fZd0sykV69e\nlUVlymq/OwY/bDYb73omP4yj1rqpy2ycc2wRiJP4pJZenaybk6fbwTQNTmqfUWkMYSJAYmIsG6Ox\nrnL+dLsCAZBIzyav4yxdmdvDGKPck6os66KUy88pETPn6RW33CsGczxOSulzNDA/Y3XLhhK3hkVR\nyfeFGIhjmlEX60a0tynSFKbJ8vJ+QpOkewkxCAVeOsdlWKR0OCHqHsYYo7CchdOsDSLoSP7Fx5fi\n1aVLS/6bLXXmHUnPYwiu70e5+9KTLN08zLGqGkTW2hqjrC2t1cYUSkHTLI1RwiYQ5BNRE5EFg6UR\nD+A9iYqBUqpaVMCvpUUIgGQBASa6ESJqQAClEThneQAABJN2DaLAC0TifUEmPWhUFEFqBGnwgthP\nxeOt9UEhQsqBAyhjhAxRmLUqlOvcL/93v3F1uX91ddk0zd/9z/7Lr3zlK7/3je/+6I/+aGHqOM2x\nnZyomE6Dyo9k6xJA2QLYRT8yoPIM/9nf/ervfP13z+7crRer997/cLkpY1QugNLTKMmcv3PC5bIF\noaxCxqqyzatXH/31v/5//+xnPldX9W5/VdqlD86aGpiAEIICNIAaAJVhII+K811GQISIYGJEIhY5\nYU5W22hkjsCQPyBrVSPklp15RMbMWhutAzALe0f0HoVBAwRFrQtLoCtt+C/+z/8X//gf/4J0quOU\nu/NcFQVuoy6RdmREPB6PTQMMsFgvELGqqo9ffPTi4sX56alGtqis5Ou1nIOGQDxfKrfPeho8BUoB\ns0kFeUyoHaSEDwC01pvNJlsr6SAWQ7zdrvO1JzsGNJvYDRP0SMyMxMgaEUUfgSP56ClQ5LhoGkap\n1wQgBMUalTI6xpj7TKWPX+pDTx7cZQT5jVSSKERi7LvOWGuUFbUFRgLCyCG4KKGFC2Nw4v8gkLe6\nkHfK7wN56Zode5fV68XqajSo1clmW9ZVVZQ+hsNuf3VzfdjtR+9OVgtQooE99cZKW05ZLKy1wXmj\nMYzDe97JnEkiDpHbtu/9oeuHwQdtCkkRcn2+qqzWehhcMkqTQo1S0yShYXAOXUiiRN77i4uLMXjv\n/ac/830hBGn2994Ls+7xk0fb07MPP/xwsS8/+9nPvnr1qu/7/X5/fn7etu088U0empxnRJyuZ3oC\niAooMkhXsEx0Aqk4U1la4TCXpQVQfd+OowegxaLOGqRZ2YQQSjCcJpzlLAIRJbvNfiSzfJd1I03c\n4ow5FT4lFcFZ+wEiGklcREuGeAo6Mkcl5xYAIHNthuGYx8eKzHj+OQQKITKDMQZRAZCgQOkkMenk\nGkQex84YDaDG0SnFIlfq3DCOo7VaqmpKSeqmpFMEphxcCGAkm7+u6xAkGWJjSGsEUFKC9n4MwSNy\nUaj0+9h1AyJrHbVGrUM+n6dPP/4f9UZx8GUxcWYkzJcCSTYTn/DZVV2EMKkwmDRtj4ikyQARJWqQ\ncExbGzx5ivn9GUgRIkpm+0gxsCzrUhWQqs0mvWRd1nVdVQAAblCVhstX7Xvfe37n/EFpowJ7un30\nr//l//DWp944P3t09+756enGGFBawFDFBERAEay1sQdmMDUUVo8O/sW/+NVf+u9++b3vPW/qEwW1\n0Qtrmhg0s+pab800KCxbeT8MUtrJJHKalf7H0X/2M5//v/7V/1sIAUBv1ndc31tbAhhABUoByUgL\nnCw8K4pTPzUiKqW1LrSWJRsBlEINiJxmXyHEKclLCaj8oJVRM8R1AlmZgYDjhBUAorRjgFIQ4zj6\nstnISCkA/MxnPnc4dPWySv5m5ipez2Ng4h0ppdSyLk1RjM4VRUHk3eBQq5/7uZ/7mf/oP1JWE5KL\nQREbuV7vwZbI/yPeSE5ZSKPTuGIFoG5nvcmlGdnkWo99ryfwXeuqqGoEpQCIQw+SCt8SdgAAvFgT\nBUnSgliQIBFlIyQlIk7T/8gHQlIMARRGBAOinB2lbWdWGZL/LppGolTJmn0IZGIkasqtKazVBUHU\naJRBIBRPI9G8j44Cg2JkFTkYZQN5PwYfHUcQ30MQFejIQX4jvlOjAYXt4VhWxWqxqJq6eOMJaiUe\nqD0cj13bHVtQWJcVKOzb7nDsiFUIwWhttfLDeHH5arlcxhhDiIag70ffDs4FRKtVgQjBx6wMKxMs\njTF1Xfd9r7WOgZxzZanrumbmYXDDMHCaMT2ZguubcXSvLi6fPHmyWC2/8Y1veO+/7/u+Tyvz7rvv\nvq21tWa9Xq3Xq2Hot9vNer3abrdiiCBxW1LGHAGt1lprK+MkYvTiFrPic/YxEp0zR+cHJixKA6y6\nvpTuRtHhFJRPdJyZMAIaXcY0EAdmmehqtcr2cF7xiaMTIzZ3PMxc13X2RjqJbcr4itcKsYgMQEVR\nZgsbU0MGYqGNbAkZSMoAgidx1x2T1rWuqkqGnMYYmmaZtysAxTjxC0JwxlTM0TmH6DNjCgC0RknS\nJIRNBIepdT1Fc8Lx4KZpmDmEqdtAqcIYEYH1MaoYR55K3FbwAGnxlo9PLWPMcncQJQRgohCjlvcr\nqa1ziDGG6BhYaWMLLc2kAJOEMzMTR+I4DFF6klCx0XK7VO4lkpzPexChAY2oSsOegUJkokBj9Byj\nj7GpKtQaOTLi2PeHtkXmwlYyZpCDzHFGNKhBg4bSlL3rS1NWi+rm8oYVu97t93tQhQvx1atXm5Pt\n2dmdl68u/+F//tW33v7Uw/sPisoumqasKqO1XDZzBIpVVWllBu8Ox+75i5ff+P1vPf3weVUtyqr5\n6PkzUzTr9bZ3IyIChOBGU1vFHMOUNTIDSf+58977EF1qAJ+6m994403nQl3VAHB5cXF2fg7MYfBa\n62keCQNEGWInQ50m+RoAYCIKCCBjWgwRMWpEoAiiWAGvF+E4OUKFBhjSpJVbWioAMVihHMCk6EcA\nCrRSagDW0YfgfFHWi2YtBMiJuJDoCzj9W0pZU/lNSpkImgFEVlyhYebgx4cP3vz1X//dn/mPC1AG\nGEMcNaMpCkAE74E0MUrVXezmBCsSE8t0cw3SJi+/D86HgACmKEAp1BO3pmzMbbGTCJiBZLLhrB4p\naSQxAVu7BCUUwSi5C3IkZj1B2UppBp4oCMQECq01ymirlGT3ooAmj2DynrMXxSjpv5Dr62lFsB9G\nies5RkAFrHzw40DWFkopRlaEaDjj/1pr5R2ww2DAysVRTr6zsRNbFEK4e+9BCMGHGA6d0IvLsjRo\njC2rkmPgYRiObS+n0zSLolwcDoeyMIWxXPu6rBZV7SbmmdGoBheCXL9G751HCsEKoQZSPW/6J2OE\nqe+lKIoQCPHoRNrKxzh0SmlrDRHtj/v1ZvPs+UfFVXU47rUyPkyB7wcfvvfgwYO6WRI7Bv/kjcc5\nw9BaZyOmtWYSnh5ZW0q4nFW1EoBGyRvdqseiVm17HMdRIlpjVzAbspz9TaovMupSusQ4lS0lO8RZ\nJ5lSKLkMAHChJVHURilVSFYQgiuKSowwIiNqEc80RVFJO0iMUcbNFkXlvbfWis8vywITOxamsF3r\n1DEOACFE511RFrbQcwdIRNrYuRLovA7UNFO5SFTpvB8BQHRQ66YcB+/DuLDWhzF4Wq4aoy2DcmMY\nxmBMUTerGLjrj8N4DMExMCp03g3jxCMkopubGwBYrVZKh0gBAEIMRdkICzO3ICBiWZY3u4Msmq7r\nZMqI9JTdO73bD33Xc1mWtjDM7PzB+YP49hijd/F2JyATA7Hrh75ZVM67ZdWMw6A0RAphiBTBh9G7\nKP4pRKkHBmDSMjEZwGhVVmZ3/coUNowWtQLiqmSNClT0zjECM/noSlsWdaGYurHzw1EX2pE7XF9o\npW1li9L+0T/+41/9L362Waxevny16y6268325PTd977z4fMPf/zHvgwKg4vnd+7EEIwtri4uI8ft\nSfPh0w+GfhxDvLy4Rm20Mr3zo3NdPzZNM/YHY3RleBzHSK4wPHTHkcHasrAlR/BjiC76wUcfgCg6\nx8gx+idvPPrut7/14P69P/KVr/zrf/mvU40Qr6939+/fXy03wkciT+PolFKFrWKMrHh0g9zeXDIV\nTl3f94KiLJrl9c3Varmu6lI2YbYIaXsoCTgErA8hiFWS35dlWdlCWeWH8dmLj7vDsWzq85PTtz79\ndrsfFpvGjQMaGNzoYghDt1gt9/u2qqoQgtZqv28329U4DrLGJyYDUwgemE1hkWi93h6Pg1IKoHaD\nffrB9dhb9qa0WmOJIv1BpLAGsKg06gn5c95rQF0YilEVGhjc6DWgLg0Q9MNQNyvFQSN6H41SaAww\nA2AYR1OWkjO5oS/qOjoHGjRgO/SLxfJ4PCybBWpF0Yu6my4sAIYwkg+EYFAhABgMwRVlBQbjMEam\noq6UQhqdKiwQE0WlDRgEhqE91ss1+0hEWmlQCpIhs1UVxpECFWUJSpHY0NKiHY3sRD91GumSTTXh\njRmHTGwUpxRo8gutxWJKR/lyuRRCvwgfr9drEVUaur6u6zC6rPsnJZkQQlluvfdV1bZtKxsfEV0M\n2hTr7RnH0B8OpydnFx+/ON+sj8c9ujIyMOn1wgLQEIJnD0yRgnOC3CgpZBjN4zjWVePcpLXmfby6\nuimL+tGTJ+++/4ForWFg58LY9YhaGfzw2YfD0N25c++HfuiL6/X22bOnF5cXROH09PTl82ef+tSn\nXn78rO97jfzpz366qqoQotZaoWEW2VyWWe+FlY77CZ6lJAwtrV0xyHCASS8jEklnw7zvh5ICdYZz\nM9uFmYfRZ1+Qq0RTGpRqctkxxxizTqb8V/KzqZ8y9VAKrg+gjPQwC5tF6nXyZXlwg5TmBHLx3jdN\nI4U7nLEMRFYnh4pyNlOylrqgJFqVBpQY4zD6iXRAERXKHElNk7CQ0mDAaIOKDUBQSvkwUVFvFbiZ\nisIMQy+l7ERyl3sERLGuK2OM1irGIGQ/ZjJGG6MRwVqjlNJaRMHVyclWZqsbo5l5GPpxHIqiGF0n\nRw5xHMaWk4L44XgDM+pIzrGmtFRRWRbDMHRdu9/vAUC81zwqCeBHB4KoUpILS1VEs1hWIYTRdTm0\nccyRqSoXRWGj4TjwEI6+05Ba2IAsM4foAgA5S0RD7z7zmbd//Wtfe+ONN16+uPjo+e7YHRh50VQ/\n90//8d2797/w+R8sy2pxumjb/smbby2X9ZNPPfjJxU+enKzff//5P/ov/vFvfu23x9FJIyqL0jKB\nipFjYAgKCIGtVlpbRO1HN46+bdth6IauA2CmcH52tttdKo0fvv+9tz/95o//4R+/e/duQvDAGCNy\n41dXN4KwI2Ig0oiEQEjeeSIy2goqEqeJVurq8lppjIF2+5s753eruiSi999/f73aMJBWxljNBKMb\ngo+owGg7DIM1RaTgXTgejxSZOAYfl6tF8PHYHrQyZVUo1MPgvv3Ouy8uLq8urxfL5nho79w99y40\ny9qY4vrmpmmqGD0Ax8hFaWJSzp4cEhCwrEXpvmIiZgKlrVJodK1V9Q/+3n/18NG9MPQcA4WxLJQB\n1FoX1fp46EXzt2kacZkSMAnwUJalmI+6rjeblfNjDqpUouSEEM7Ozpj55uZGHPDJyYkEl/LOoihy\n8Ns0TVEUT58+zUagrmsREdYa+7aN5ENoM9Egnxi4sSzLYQhKkTDB6sWZGzyARUQm6a4DVGgMBM+B\nCiKiEQFYBL/YKVMso+gXF0sAkGb5omoot4hxRERAbaxSpnSuH73jMS5XZb04rRdbJiAOJ2cbgAis\nLq9eOa8YrTY1Wmay9aJerC1FP46+H4O1ZbVY7G72iNqWqxoMgCpLWxQVatUNg7GqQjyUV6VWjx4+\n7vc33W7XlBUhaGuJOcRIY+TIrMCP3jlljJgXjjEiqKqq+n4EkIoLI2jJ6p0Ln/rUm5fXV5eXl5Na\nXdXkeQUxxg8/fP/p0w+01kVRnJ2d3blzx1r74MGnDofDze7qs5/97GLR9H3/+PHDsqwRFbCSllME\nNc1656AUaFQELKq1yIAGRLuWI7ngKXjhnvgY6mbpKcruzhwHojAMTijcIThJQ7LkneiaijZxCC7j\ngfJ7FvxcgRwNQMY/ReIIjMZqawpj9aJZyvxZ2YPTX3PKkigokzWE1GGXC7/yEpXA7AM59d/O4T7x\nnLJ2RYE7e6n8ttyuLMc3aRxRLsrlVsrMr49JElswvRCCMSpnXTp1FMs/Y4yr1aooCmGIygGdc5Lx\n5FRXrlQ+KDRlkbgQSuVqtRrbTiWRj1zs/UT/ikpdL8ws1UX5jfSLyHw/qTzNAxCpzy0Wi3mUgYlT\nlz+ulBLkM8bIwbdtW3Kdafs5Xchpsryym/zxL//YD//wD//tv/23vQ+73e75s2ePH70Rg/9DP/JD\nlxfXv/Pbv/HP/9k/WS7XhS2/8IUv3Ll/9t/80j9ru4PSdhzd82evhsExqmHonPOIaHAqFSqlrNKg\nOYZRyocxxq7tjsfj0HXe+6Io+v6oFTk3yCVVVfVn/syf+ZEv/sjJyakwviRDlTsjjNKy1JJiAoqM\nLyuNo3Pee2OU1C59cH3frtbLtj0Qx/V6WTeVVBwRWQZMgCgBal0UxlorTJZx7A+Hg+wiRLa2LEt7\nPB6VZudC1x3LskY17ca27feH674fd3s9jt6Hwfv4xS9+4Z133h3H8fz89HA4KKWcc7aw3otEQm4k\nz31pGtRUA8u7IMY4juN777335I2HnpmBpFCBgET09Nn3lovVcrlk5uvry3Ecm6bZbreXl69EOCCX\nMIuiWK1WL1+92G634zguFgsJ/JfL5X6///DDDyWIlPt8cXEhKaNsCtlK19fXx+OxruvVaiWt/oJu\nCdiutZZSrrFTQinpoBTbpVdps9mI67q4uHDOeSeW6DXZQClwZupslojUWiNy3/eInNtoMu50PB4/\nEZ8hIkNkmXaIChG0Ntaaum7KsmAGpVApfXHxqihKRFgslsPQY+S6roqiDMF3XR+CL4qyqsqbm521\nBlE5N3oflMKyrGxRrE63TdOsyqLdXUEI9WLZ7nZobF0WWusixMg0ihpW9DFCP4KM3BQb6L032pZl\nSdSnGgFgovORc/WiOj09XSwWbdsej0fRTFksFhcXF4vFYrPZKKXquj49Pd1ut1KRvb7effzxx5/9\n7Pc9ePDg29/+9tnZ2Ze+9KWiKJVSwLIpChGOEv1GpVGqAjIpQ3DXRd0ogwowUBSV7OC8C76TGcER\nhDUmjHBAsqYUTU4fRvmr6GeKYlmUObuBfRhFL010NWPgEB0TKg1GF8YqpcD70bmQuRJ1vShL630U\njG4+J28iZM+5T0VRpKrPxNPN/MWqqgBA1GWyLoUs4nk9KqdvsiJzJ1OG7HPh/RPpFKdynJpNQpKV\nnddr9nZ4q480scwzDKiUkn4pgezEecSkmCRfMe/G4MRQEKxWYhP5uE9TvEIITdOs1+sQwm63yw44\n7xk57SxDl0clyYCoqqrirPE4h7G5i00n6VK5RTc3N3LakpvKTR7c6MbICuVTmLgMkFSE5cxVmmkr\nD0Qb/GM/+Ud/9md/9vHjR1/72m8KDHs8HmOMwzDuD1fODWVZ/w+//m92h5sf/pEvXt5ctl13PHa7\nm6NSpqwXMRJwBKVQiXY9heCcH5gjQmSOolHdHfu+74PzRFGpkoiWi/r6+rKpCqXUV77ylZ/4iZ8w\nMLEzZMeWZWk0i1hWhtcmlACIQVJ40lpYkUL30MyRKGiN1tqytCG4/f4mRrZWG6NCCMPQAUx6w0oZ\nIr66ugKgplmenZ1bW3bdsW37vm/v3DmL0Wutl8tKKXM87p0Li0Vt7XoYutVqxRzH0VurY4x//I//\n8X/zb/76ZrMRAGTirejCOSet3HlJq+mlQWlglcsewXsfwzj2X/vN3/jc5z+rKBoNIQSvyIfMeUMf\nXFEUJ6dbAST2h51sASI6tgdpdA3Bf/j0A1nzXdfJvhMU+sWLFzJXJZv4rJn77NkzZt5sNgJyaq33\n+72IK+YygLyUUsKjXq0XEveIG5O4YbFYhBBevXpV1/X19bXAFcbYtu2lB2nqMEsIStd1siWzNr/W\nOkbftoeHDx82TXM4HEIIEpxJK2Ve23m/xIj9OK5Wi6Ko+r49HFpEdi42TdW2PSLX9WIcHbMax957\nAqDri2vgKP03wsUVS7poVsYqBO3DOA6eOGhltTVPP35hCrtq6jB0rt333TBGXm9OGKISEpe1RWEa\nLtGjc47Kkil6740xiDrGCIzGmNxBhYgx3N7VFy9enJ6f3b17V0KE6+trMa2SmIrbPj09PTs7A4Dj\n8SgY4FtvvX1+fve3f+vrzz/+6POf//w//If/aLvdVmVTFBWAUmi1tgJZgZ7MaV5yKSsoBLaZG1Xv\n/WazyVEyzkp9Yq9C4sdmIpJJ6rTzqhIRGA3AWilWZKO0N6FSaIgCgNFTDUcIzAbAbDbr+dfJOZgc\nXGcWBKSOqpwz5bVYVZV0bMnt9t4LkiAXJvtP7qlSSjJQ4ZbkTiBKHblZ5VDWZbbOkOYoi3WWY0pz\nmTxaKbitViullBTKc1iaDb3Y4q7rBNmTmE4syGq1yvFXzmBijCJ6WCTd+KqqpHdPUgG5IsGdxXMs\nl0ufhg3O86Tlctn3fdtOmJ5YBAkMMXW9ydWZP6A6LD+LmxG359OE3IzmWavyk8rbNc44kJ9IE1+9\nemFMcffu+V/8i/+zf/pP/3mzKLWGpim/+a3fbZqGCTebJRFstg2iWm7u//7vf91WZdMsN6s1APbd\n6Mc+EBhjcGKURCYKXtTDxs16GZzI0Lk02gC0xuNhZ41CJquRKDx4cP/Hf/zHtdbH3VEUfYqiaNse\nERlC13Wb9UkIMllcBttrRFYKDoejNlhVBSAdDx0gVWWzWNYvPn519955Yat+aN0YNtuVG8Nuf71Y\nPBpGpm4MMUAEBojj6PywWm3a7nA87kMcqrJRGqqqsEXtXYjknXPSPzC6XqGp6qLvxhBdWZajc947\nYbV+4Yufu7y6/MEffPLixfOmafIW1VqL4lRaBrdYAgNpo7VWqIAoRIreBWYeh/7q6uru6QkiF0Uh\n5R6tNQEPw3A8ehHitNbWdQkAwzCked6ktRLdJaIqxig/C31AKbBWi46nc0PbehnzwcxVVREZALq5\nuV6vl33fao1laa+uLvq+fvr0AxE0SyZsWkU5xBRipyi1i7iDMLsQ8YMPPnjw4IG1drPZSGcFUWSO\n1mrBEkIIbdtKniroDYrM/WzlO+eyqm9GFHMAd0scrRZFUZVFbYwpi4XUlW9u9otmNYxd8KS1BVZt\n21NUVV0sl2vBmrRGUbsRndlD2810TBRRBGB23pRVd+yC8xricddCiMaWi7ryYwdIzjmtoLQaoEBk\npqDLahxH76MxsSgmOza1FlVVVcm1kPegIkTm0dPNzdTieu/evfPz8/1+fzweHz9+LA5ss9ncuXOn\naRrvfVnW7bEri+rxoyfnd86ePn16fnb33t0HL1686Lvx9PR8vdYoJ8+OiAbv6kXDzAARcRKcnaJt\nPxozVYOydY2RPn5xCXBbaMhPBF4vC+XS0VwdVc94110/Zn8RJ412Z4wZ3a0okVJxGINqB0REvMo2\nM3+RES8yL/nmREGnEas5+5EfxApLqi5vkFA9G0H5rCzfdB6vDZUQvyKpVV5nctcEW5NTEiMrCT4l\n3Sf5IlmyWQEvW2eYQSIZ2ZB0Qf6aveAn0hRErOtafJg4HtkehdKS3EixRxSfpB4un5r7g6Ioci6Y\nT4mZh2GY50bzmyAICafuhAxUnpyciHaLnLCckjL6sO/mXy3AaZaknEUr02u5ahDR7Tpj1Je//KW/\n83d+/6233g6Blsu669qu65erJ+Tj/nB1PHTrzVJpcG4YhkEpg8oYqw77tuuGZrUEAEMWVWmMKUvL\nSBQ1MnjvRRQ1pWuylHm5bK4uXlR14X3/xR/8wuPHD4eulwvJ5RBO+l0Sv0vpaLaWgjbY9+0wDGVp\nRXqImQ6Hg9LQ923f92Vpi9IsFjXisKQmklcKysoWLJARDYNjF3f7awAqyipb6sNxNwwdgFqvl0pD\n27aIWrDf3e76eOxCcHVdI3ICHDxzXC4aAGjbVpaESsOIYwx5qQvvejLrFEUuOsYITIFipMhMCPzs\n2bN7Z6fOjZU1MQbkWJbVvu3KSi+XjbGKIhA7q+tmUa3XS2Hirta1zDQpi/r8/NFutxNlTFkJsqG2\n221Zljc3NxKeS6CtlMra0nVdt20rIZcs2rt3765WK5msk7tKERnVNBgib8/tdqu1zrC2wEqnp6ei\n+idtK5LWY2qEFG0CsSfSmpbHYJallTmZsgC6rqvrerlcLpdL2cJyKNlcktMHT1oF70PbtlI/k3mp\n4rSmnWirpmmaprm+vNTaWquISPBGZgbA5XIp6IXs1ikPIIiAkdToQ11YVVQxUlEtRj8qra2yZRms\ntYWxAhsGrzyrkF5ThwZjjrnFsqVAQUGMi8WiG3pR1i/Lcr1ey1yJvu/Lsmya5uTkxBiz3++HYWDG\noiiY8eZmb619++3vG8ceQN279+D58+erlagiGWCJgMgwm6KW2JxSl5DWODVGJslmBADQChGU4jgg\nGjEbMUbOw01iFGqcpCpa32qoM0dmMbw8nzetFCiFABpR+lbRORqHqLWWabfAKgb2FCmVybNHkH+a\n/O95epRNP0+qf0Y8hyxuWYgmtXmHNCjIJE0weZscJMMFYj05zaCVoCnbHXmcnPSXVOJHZBMvTG5O\nhAvxlyImCDOsL/sY8ZHZKIj5E/uuU2dW/qBJWhI5w5WNnb09pf4yScmFeifoR354ctrZQ8ubBeWX\nJBLT1KUceuR3Zr+l0zSg/X6fHT8mNX6g2DSNsiZvdfn2TwChcqNijMzRdyHGqBHrqnj08P5f+ct/\n6W/9rf/P+fn5wwd3Li8vmcLlxQtOGhA3NyNqVRSFj9T3o/cxeNLWbrfrY99JRBJ8WS8apVEhgIL9\n/mYcRz+OJI3WyMzAQHVpgXwkr1Tx+c997kv/7h9eNgvvvS1LSXAlPZJltlqtYozgiZiQheJNMXrv\nfVUV3g+iY43IiOC9G4be2mIcB+9DWZ46N97ceO/DYtFcXLy01iilmQnRC58FEbbbjfeu74eLi1fW\nFnVd1XVZVbZtO60VIheF1dporZzzIfi6LgGKui6JDBErhfv9Yb+/+amf+qmv/ebXJRiS1ShbgF/T\nQoTkaFlgwBCci44ICBgkHjTmo48+/MN/6Idi4Lop3UAcwVpbVYUk5U1TrddbAGrbw8tXz956622J\n8cvSVnWhNCmlQnQnJyfjOBaFIQrCMTscdmL6ZYAvAIxjLxmS7FytVd+3Mfq63jx7dvj0p992zr14\n8cL7cVLVn8YrG6314bijNBxP0MLVakVEZ2dnUrvd7XYnJycSojnn0rzaQrBNrTWRYo5lWRaFQWSZ\njS25kTHq9PT+MAzyzhBCHt+83+9VKreIa5TCLTNKaVhrKzS2qmru3Xvw7rvvIqLWMAwOUdf1oq4X\nMZI1pXiFEEIMMkAAtdZNvVQ4SOwIABSBKTKy8wG0HpxTEIwtwYdlvXjvnW+fn6xtU9lCj2PvnANH\nFFW0BTBBWTt0RBR81MoIlC0NlMMw5IUBQCE6QJ1Hqb169ep4PC6Xy7qu33jjDUk9x3Hc7XYSxxdF\nNfT+9PT0+vr661//7Xv37969e/fb335nt9udn59XVWNNZUyBoK0tmHB0nrAHo2SuOIVIwBqNOBNU\nCggDRWRQRjpXfGGVFv1PgjQpCFBhDBSBPMxjLCU/IbA0+SEiygeBFUIkikkEDkAachhYMymK0zsB\nkAiZlfMx21itJ6tlZPXATPkK06SsXKvPwREilmUpK0bEg4/Ho5BD5rmeMaaua6110zTzYkl2eBKn\niDUXD5QNK8+qUJR7+JMXJKKmaYwxEk/JKs9F47x2Y4x1XQv4JiUx2Z/DMGw2G5PmguQILt9rcR4C\nPIpbFUxS6HZz93Z6eirbQ8IxQQUlR8lFHdnVcoez85bTmzv7mJiROUmSna/TS26a994Ff3b3Lhod\nQsiAidwx6T6jpFFN0/RMRIS6KZVSCDrG+Oabb/yVv/KXfv3Xf+NXfuVXHj168oUvfv93v/vdvhvH\n0dV1fXP9CrUqyhpRg9J1XY7KH/bH/X5/eno6jn4cx9F1/dCBkoq3G/uBpNdkUroDYAYg52LbjScn\nG2v1n/yTf+ILX/iC0AeYWYgkEgNOpZdEdYmJSQVI3vth7IpCn5+fbzabcRyfPXu2290sFovz8/Ou\n6x4+fBhC6Pv+8vLyzp07Ips/jqPg4+M4ukQNL8tSGNh5Q0lME0K4f//e8Xg8HPayxmKMRWHPz89E\nWdl7fzz2RLRYLOq6urre/+RP/uS//Fe/st2uJfrRWkfy3nul5hHMrVqXhDIhBBeD95ERjHy1H58+\nfUppDs04HJ0fnR8F75JH2bYHiedOT58cj3ueBiCpO3dO1+snx+Px448/7vv+eOjkcoqikM+enp4C\nwGKxwERVuL6+Fv7CixcvHj58KCQdInr//felyf/09FQnVpiEgJLEhOjknxJoylLsuu54PA7D8ODB\nA+fcvXv3vve972mtu67TysoOlfsjW0bQ8hy5QhI11lrf3NzkWEq+tG3by8tLQSmVUkLizZAOp67E\nk5OT9XrddZ33/tWrVzc3N1nDTW5FCOH6+tqgyjo9OUoTk5X1KeC2XquXy0bb8rC7jsRFYQ3jarM8\ntMPp9qSwlbF13XX2sHdu0Bqt1YGUNlYpJRU7uXD5wXs/DC6mkRwhhHEclbbKiBSTF0F6qfB99NFH\nKYK8rf4eDu1mffqNb/z+OPZEYb87HA6Hp0+fbjabGKMb/TiOAMpOOZlxkXwMWhmlC2QGBCBiVABq\ndM4YA4CTdBUxE1LkIXiNt7Kc2f6UZZ2i4ZBcgNJate0tlqOUQoR0A11OnnLJKsfHiIToRGdAuHap\n9xaVIqVgQhD/9b/6JSl/EZGsaUHhxMHk+xInNXUoiqJtW2ut0HhEwUIaOHJ9SPaklOYELsDZ7HQJ\nVU5OToR+hojH41GW5vF4zMPnxc5mOy5aVbKUF4vF5eXl2dkZgAzKM8wsa074ArIJJeKW6fQPHjx4\n7733mqYR0MAkcUaYqfDVdS0QnLgiuYpCaQnNnHMyyESEpIZhEOhgnpSIB837Te5Yrk967wWRwFQ3\n0lpLUVfIM5lIIicjN1m4TLLcfQzr1Uk79PO5eRkRzZtBeApVVQFQd9wJs0S68FJZO37wwQd//+/9\ng4uLi3v37pVlfX19/eLFi+Vm7UMIxAAQAzOrqlkCqKvrnZRJiCjwNF9VBEYVq7Is2/ZgjPFuBKCz\nk8319WVZlgC0u7n5q3/1//Jjf/hLZWX7vl8u1ohqnHZRblecUkPzmlKWkTmtXdfuDzdEJIV3uUXG\nmJubGynjCRAkVrtpmv1+L4GwFCwlZhrHUVhqEprId0nyKoVASsXRKeBL1Vp5miaJhfvATXX2P/kj\nf+zTn35bkCWt9dX1xWazEaQuX1FK09FH0tqiMhGYCJTRRVkWRVEWhtj9+T/z03/yT/yx/c1VVVqM\n8fLylSmqxWIhJyyQ2vX1tayWm5sbyUIkztvtdjHSyclZVTZ93+d6+GKxWK/XJycn4quklVB8yXK5\nlP0o8aKQkuQ92+2WmZ8/f77ZbA6Hw6NHjyS1unf/zvPnz6VYG0IoimK9XkMqBUluIcDGycnJgwcP\nPn7+sixLIbJmECJvf1nzMiJI0ilZkH3fy8nIEAcx3Nkpwowz1TTLy8vLqqpWq9XNzc0wDGdnZ6en\np5eXl0KvWC6XmTQoWqgAMAyD9CRVVSV5uUjs3Llz5+XLl9J9EUIoyvrysFemUEAP7969ePGxRXh0\n7/xn/6uvPrp3DuTfePJguWi+9e1vPH36ASJHhmMfRxdlXyfLext5O+cOh4P0QimlQBtADepWn01O\n0qZhdxmp4okGQghmtztst+u33npjHMcPPnx/u93+8A//8Ha7rcp6HH2MfP/eo/v37zPpQ9f20aNW\nU75OE7GTiJzzzGxNKabm+fPnZVm7sbUGlZpsFCSytDyjmESP8lYVWy28Adkj4sAk2+NZeUl2jSTo\niJjVbaS7KAQnKm5ZnUf8k8kZAM1YE5LZ5INi6kHjNIA2hCDIr8C7nESvsxGn2WDBeSE0JmHEly9f\nhpk4uaxak4YeSqCakyR5rk3TQOqJS06LV6uV1koOKzSe4/Hovb93796rV6/W6/W9e/eeP39+fX0t\n2ILcSrHdlAQNtdbSMSd9HmVZCvFBtG3EteQCT15DOrHgxMbJhef6UPZGMYn+4azSI+5W6kmQBoRn\na6iU6rpOZuLJ103Bb1W2bdu7Mbu0fFgJLSUsFUeOiN4H59x2uxY33La9YJ7bbc3M/4e//Jd+/dd/\n/atf/ar3/gd/8AeLwnz08fOiKPw42rJoFvU4xPawI1DWKO+GKNETREm4ZchbCE6urqpKrbjvW+9H\na3UI7uz89I0nj99++y2lIcYoFy4VKfFtLlG3JcSRfZhul3TwObkulWjusgEQ8fz83MzIhJJhC1VP\nih/MLHWC09PTO3fuCCE7R8Rze4EJjM33P+Fst1CtPNMQwVq7XK6urq5OTk7E4M6XZUp5KQWGKDPu\nlFITsqnEXEXnAiC9//77z58/r0s7DH2hcLVaobYZwJRYJ3OyhWsjI+/CJGhdXF5eNvWYF5s4CWZ+\n9913RXhUohYJaCTJy9cl2IAsMOHUCaIAM0LN5eWlnEnev7JHpA5vrZWHqLWWKpTsFwGddGLuSHqU\nc3drrQQHEjlhwuTlW8SF5EI1zebjyRHEVhCRnIDkQLKiQpo+J/dHTkPCFOmVlGuRntntdktEMvNb\nKH8+htViCQoLY+u6Xq427N2x7bUpX13cMDki2m4WSpf37z90btjtj0qNxkwc19SjCUqpw+EgC3K9\nXtd1PYGox70yFpKymrzEyGRnAIktHGMkAop4crJZLBYvXrwQOuVisTgejy9fvtRaN/Xq/v2HWqvd\nbseERV1ZpZURzjDK0EilFIDa7XYibxEDEVFVNU3TMMemMRonQq9sAXn0Yg9zM0x+FpKz0sSomgAG\neYLiLF5PidDaMgX9oBQDKLHfACAz6kRSR0TAjJgJeaghyf8JFEZJJBgTrsXMTdOIwZVHK+POEFFm\nEcpatGnYn6wquUhIAo6ZmyHJOyLKD1Jcubm5kd46WUwSCIvhkK8QqFD2jEBkxkxPV0oR4jJvbm6Y\nOYdRQuffbrfZu8iZzHEwk7qCMnHAGFMUpWwS2SfL5VJwSxF6mIEzU1wsR8gBRS7QyXPNgKQ4VHHV\n2d/nTDlH5VVVUSIThxCQpwpzXrL5PCWLEkuULQsA1fWibfvd7iC/kRt7fX395Mmjp0+f/qk/9Sfe\neuuNv//3//5v/uZvnJycPXz4oG1bZXQIoT3su96XZb1ZLRj1brdjisSRKCACIMl43hijHx1RAGar\ncQTyYbCF8mP4oS9+4fOf+9yTx4/3+31VVZUtjvt9WTf5zgvVUJy+dCVrrZlJKaUNUgRZb0u1NEkb\nnogCkQ9hsVgoVDFGiiILBDFwDNy1QwxsrV00q9Vyo5Rqj/3V5Y1NU64pgncRcVpXovCfgTUxi1rr\nvu910tKOMcqkF61UXddf+MIXfuu3vnZ+fp5xthBC09QZl8tpdwLrggzcUQoBgTg4B0ahNvj+++93\nXddUa+89MTVNo22plLa2kCzh6upaFsDJyQkAeh9EBw4AZWaKMaYojVJF3ZQZ+TTG3Ll7tljWUQYX\ncdAGAbXSMIr3ZcQpcMaiNGVlJXe3hY7kjVXOD2Vlq6q6vLyUiFPweYnGxGFkk5QhZSLabFfy18Wy\nzgtbJ/kM2RQygVvCkb4bJT/LpTgJCiUczN5I3XJuqa5LIrJWn52dxRh3u533HoDmFSmZz0QUyrpA\nBYz08uLFer0W7x7IhxBWq+XV1dV6vR7HMXIoTRFdXDTLYRg0wnF/oBjLoogcP/OZ7/+VX/5XVjMg\na4OI3PW+61pGtV6vnee2bZ0LIfTimGWxAYAPDgCM1Uu7MFbbqtwdjmGWPajUYZmBxPxPpZRSZr2e\nIIH9fl+U9sGDe3Vdv3r1QhIOBEU0IUao2FilIyqNaVyOMhastQjaubKuF8zctp3SsFjU6/WK2JXF\npP1ElPSCGQi4rCtQk2KiTWqZ3vtmOU1zRsSiKgGAh4EBMLVv4oyGTUSbk60Q3CF118gy8GnS/NyU\nGdmTspJycCeWPQcyOVPJyZNAecMwSFaeLayeOCRZrB7zVs+fzfB0XtMS+glgJYlkXdcSUslfBR/L\nWEGYNeLVda21mp+8uDGBFK6urrz3d+7cuby8FMrKMAwqke5zXiwn1jSNiBv2fS/gjzGGnM83MTt8\nmNEfVCJcyA/iLShVjLINlWv8ROYrZ5Izp3xwscKZCaJSl7FsfjS3rU75U03TiKPNCWVRFFpj3x4F\nD5FQQADG9Xr93nvvrddrZn78+PHP/MzP/Oqv/uqv/dqvvf/udz/zA99/fbMHYLM0ytjg6XDYex9s\nWSIqICbSgMQMxISEpS2YORL1fVtaXRRGmrpX68WXfuxHP/f9n2eOIbiy3ChA770pYg7k0+riEEJZ\nVrI6RV9KbpQ2E1NAbKWYJ4Fx5g8lP9AY4/n5eW6vydsDAAQtybBSfmpyqPwscnghKZqesT0RUaHa\n7/df+tKXvvnN3xNFGUQEzsqlWdFriioAWGkjY31BBO4YZEZcWZTG6GO7v3v3LpArCuP7wXsfGY2x\nUvJcr9dSVtFaSzgYUmuqRIH7/X65XHPqClCpYUjWsNwugRMxNZDiLO0zaUCiStiy5FJJ9GjaxfLP\njETJDZdKnvCYxVdJ2B7Ca3VvSjIzklHlvWMSUzerCYsRV4luyq8ze/Pu2+/3SoMf/eG4a5oGkPq+\n92FUamULXZalKEOikuJIaBYL6QNBnOacxhiLQrbtpOPa973W6L23VmsFTKGwdfSTEo13/PanP/Nv\n/+2/GYf+Znesm6auiqv9fnd11TQNaoHAQUCOYeiks6VpqhDCOA4xdWouFouqWaA2owuZ3cep8ZH/\nQOXYWmttWRSFSIAaq5fLBoB2u+vD4XB+fr7ZrNbrrdYYyReqcM5dXLxanqxQIRIHCEAYIiEDalVY\nrTRxBGO01TrooBVURSH6TfKah2UZP8DZ6DuxaTm1yE8zW6dsyvKWEd+a/Wu2WuJiQ5o1I65rKjbS\njD8uO1B2b17EIY2ryhw5SkwbWcEC2mb3nq3kHFPSs+E3+Q0qgYGSpSVqI8tDzXZfDMSkjDvRTzHt\nvalFV6UCmtb67OxMpscbYy4vLxHx9PT0448/zis+O868FATsli0q+HLbthZVNp2YphEzs5j4HN3E\nmbA8zISbINWlsifLN0E223K51KmGNM+IxR/LU5DvKsuyrKsj93o6/K30Z77PQh0UAyFpR13XRmm5\naUAYY+RIHGlRN9GHxWKBa+BI/8v/+Ge+8hM//nf+0//0gw/eWy7X5+fnMZLeHWNkHyiEIPoIWqFC\nZNRErCNHjmVRI6IewYcei6qsiqE/gIHP/8D3f/rtTy0W9X6/XzWL0ui+H09PT693x0WzKtaii3Ec\nx16a+Z0bu/4IAFLp6ftWbvKrl9eLxVLgx4zlAuCrVxcSgeboMoQ4DBOTuChKZh5H13W9PM0QYvI3\naIzND04pmRChEJVMqiWSGcQwlXyZQ4jeB2ZGhR9//PGP/MiP/MqvfPo73/mO4KLR+aqqYgwZ0MuL\nFhG15MoMhJwmTSDA7TI4Pdu+fP7s7HTToVJK9aOPEbT2MhbK+2nUrFKmqprEAVMhEICShvYYfUKq\nJ91+Y4xzg6TyVVUYY6Tg75w7OzvxSUI+97kT0TAMMXpjdNPUAj90Xdd1x7knsEk5TLomiUgckk49\n70QiEhPl97KnxN8wM2IpUe8wSMsReh/kbXk7iO/s+369XtOMQpW/Yr1ZWquPx865ARXHGGyhq3qB\niGVZF0Ul3crEoA1CBKKgNFjUn/nsp7t2CNHt9zfGqkWzCtFtt2tUbK1erRdXlzeLxQLY12Vx5+w0\nuig0pePhsFgsvv8Hvvjs+Qcvnj/3T5/fPT8pyrpsmt6565srhcYYU1ZWIsi2PUhRytx2UpL3Ywgu\nAq5WqyqQmBef9E/nIXu+aoGmAVRRSsQAIbj94QYRF8t6t7/ebrdNUymN+/2NJIgEsNhWkoYbzZEi\nMFFEYFSIbuiB0BpljdrvR1+OqNgYncbKAMBtv4r30r0rYFoMISKiUhiCNO1MrFexc1rLCGlK/YLC\naZqo0Uozzvjck7+DyBABCRUDs0JAhWbu5XTqA2Dm8/PzkKZCSWI1N6k5BpdCkZSRslcMSeRca304\nHEyaCatSa5jUPHMQJL8XS3p+fp4HKguSk8djxEn8O0jtWg47DIMxOodgGc2UkpXQ4QTlOx6P4uQg\nCR/kKIATOpdD4wy72WlOK2SoR9ZKSDoU+VMww/rlYueZuLxyWiAH1GmEopphfTnYR0SxtkJNHMeR\nZL59CmSyyZMj5NqvJAEAwIzLxaJtj0I8SVXr9ubmRppLhmHYbrfb7fajjz56/Pjx3/ybf/PrX//6\n//fv/v9+7/d/73Of+8Lnv/ADHz9/eXWzW6/Xl5fXUWOMHgAZYuphRLF9xpgQJxiHmc/OTv/kn/oT\n2+02RG+sXq+WfTccj+2jR08GFyWA9aldmoicG0OUABaF+GuMYY42dY/nUlyObPIdy5m9hEfCDJ5C\n0arq00usZ16ZmaQg2bAccI6CyqpTs2KePGtr7Wc+8/infuqnPvzwQwGXcNYqnh4c58AoAoo3CkxM\nzCSDr1JFBOHly5eSCrMPZVmelQ0RxMBF4RSaqqoQdF2X+92xrusYmCEOvSNym/WJUqosp5F0+Txl\ny+RFnqvlQsherVbzXApntRkpqsktksWplLK2lERfyKjigWKMFxcXArgJiXGz2ch2U6mQmR+NSf2I\ndjbaVb69LO2d83tVVUkAmnerUioba57j3gaJ2DkR4qTjcR+CZwatZUhPoTUSoTFK64qIQzDKCOWa\nz85Otd45Z/q+LwoLSMH7k5OVc+Ny1VRVqTSgYguKmBXFAFNB3ppSK/vpz37/+b2772++896773z4\n/MX52Xa5PWn3h/Vade2w3+/jdbTFxPmq67ptQ1EUNklCyw1nnOjBElzmfJcS9QlS54z4YHmbGMlh\n6CJ5YUQhImIZyfd9G0K4urz2Pm42m8dvvtEebsqmrKpGK1CFwkkyTik03gfQYK0tS2s0KwWF0QwE\nMKFwOT0Sdo+e9Y/GNL9UHnfej5xad2jWD8oJ8UbEqqrnoXPeRxnCma9Dk3+VjVr+G6cJFtnaIqKU\niIVvLfCdnLH4EslgctphjNlut9lJiJ+TspNAyXJYaTiVS5VMMFtt8ROZ4yfRqAiZLJdLKRgKi0G6\nFuQGia8SdpBYImPMxcXFgwcPXrx4gbMW5fk1CmVObLpcUdM0/eEoiLmcszQEZDKJYPoqKVBwYnnk\nI+fUU4ZoUZpkmCM+4RNmg6sS+CY/S1Yk1xtjjEyFrXPbf/ZezLzZbIS+IXc+1/zbti2Kcr3eIGLX\ntX3fG1Pcvbt1bnj58qW4OuFZPXzwaHD9kydP/tpf+2tPnz77r3/+v/nab/1WUy8f3Lvf9t3JycZ7\nP3jnnAuBMflL8hy9LwprrSUKPgx3zk9/8id/8od+6IdCcAZBF6XsNwF1p4JB72TFi8KNCC5IqimX\nVlWF4Ip13Wgtw6eVtJEyo1L6/PxuXsfz0FJqhIfDgblrmqYs67KsZVnK3ANmmesjH6Rx9Nk/xcgh\nkNZIBMYU2cFYC/LVgHq5qAHgy1/+8s/93M9NIjfWdF1X19UsqrgNaBSg/CcwBZlUhxO4YYyprPnt\n3/7tr/z4vycepWmaq6sbJhxHv1jUTN6akgjKoo7xYLRYF6CoEFlmtfRDqzVmu5B/WC6XsjdlfS4W\nC+mQ3e/3YgFzJJ4DL6311dWV8IAePHgg3aPOBVnwEsqI5xaQUPaL7IKM7Ik7yTinxNqSCsjbZMWm\n0dr6/ffflzRIJeKunKfsLJ7NkgcAbXC9XoyuL4pisay8i5G8TGnZ746RvHMYyYuaBrAaHdii8tER\nwc3+OhAx0snZibW670erTOQYORRVMbh+tVkhgwXl/NAedoFgHL215XK9Qq0229Plcnl6ut1uN9/4\nva/vD8fVeqltef/e6fX1tRSq284VRVGWE9veWqsUZsjLGIXG+sDEr7XNZE2yuZ9GxFzIPxx2zjli\nkX4WQDvcv/+wLKvD4eD9TVFUTS36OP3zlx9uNqvt9rSqKmtKY60xqBQqxNKWzEiRjYKmKpqq6F10\nnhghMvkYENEAA0BkKo0GREYAhagVAjOzTNKYfoMgdAkiQq20nrKfuelTSsWZ/GkO1wDApBFxc0zI\nyIqRpZALHphy8+zistOSlSHmWGBiwYUyXjw38RJ7+vTKDj97V4GthZsgoTom/C1HvrJGbVKEZGbp\nJLfWWqv3+30pgoZFIetesDIJ35bLZdM0z58/F2rs8Xhcr9cmdenOq00CDEpwJzdIugHu370bSOYu\na2MMI2iti6rUXos+rhgXYSpiavvNDin/fDweMcHB86A1y1hw6joUzy2WRbgksufLstxsNsd2YMKs\n+U8ASBwoun7w3htUpixk7lkY3fFwKAqzPxwOh0NZVYW1RVX60V/vbjSqB48e923Xj26xWC3XG0T9\n8uXFozcevXr16s6dOz/zMz/z6c983y/+4n97dXXx5MmTtu77cTgejx3yCCEEAI3MaLT1YygLY3QR\nomPST568+af/1J82xux2u+1qHUI87NuTk7OmaS4vr/fHdrFYWauJZDTLRGschq5pmqIwqWfLEMHN\nzY3RdQhBFOe01lKUMkYNwyCawaIuLJN/BXNA5M1mY60OgQ6HHTNWVZFgeZnyIjPiTVJYAGNUWVpp\nkpH6x24nzFSV9wwiImgf4vOPPnzjjcdlWUpV8nx1utvtknj8rRaDvFbbE22MMTYQjN55HyMTIgNx\nXdeNLb77zrv//k//2eCHm/1RmE4KjdbDycmWCJSC/f4YY5SF7X0sCtFD88JGMXbyrDlHlMxGeHdS\n/SUiYbvl/JiTqEpOgyRLlpxSiJdyKO+j8Ckk+c5Zo0gBidnd7XZCF5IMKVsPSsq/gnz4pMgFCa4H\nUGVlJcAFAHFRGV3I4XYOECGC9+F46Oqaq2oTFYeAPnqZLSJFQeeCtQhcEpEbA6oQiUtb7HaH1WIZ\nQa2XCxd8XaK2pm+7EKmp9K4bHj142Pc9DQ60YoV1WSljEbRSE7d+v79Zr9Y/9CP/DgB881u/13Ye\nKAIMSim58H5oh2Fo2z5GXxSFJ66qApU2ZQUABMCBtC6Cc9GTMliXjS5tVZQujIfdMUIAAkBCVjF6\nmXXr3MDMVV0sFmsi8t41TXP//n0itta2x/5waB8+XN9/cO94aH/zN349sOvOT2Lk7Xbb1KhnXERb\nWQ7cDQNoBRqUVbGPWmthhIsXyLI1zDIaTIpYVqkJnRK8Sh5lZhJyatvHGfNAKYWorbWZxZBTHUgN\nZzmAmzzWb37t1+W7xUV/4og4q3nmJSJuPPMRMk0uV0Q/USmhRKTOsZUk9TFNrMi+Qd7jvZdOGkSU\nSvtHH32U56hTkgkBAO/HqqqkhTnfUPl2yd7E3Ge6DibytNa66zoRP879vBlLzDkWIh4Oh9VqtWya\nwbngXLNcWq2vd7vVYuFCUAASfAYikKcXSfylpAIZBjTGiLiyEFJFNhFnzXpqVoKG17Xv1EwSgiK6\n4DmSzD0KFBWgtqYuq7bvFKApbHBeJlqiVrvdDrSCSC4GxYAGIcLgh/ViiUYbVJ5idD4wWaWVNfv9\n7vzO6YuPX8klfOc73/l7f+/vP3369PHjx4EiM3ddt9/vQ5BGSKAQvY+5Znv//v3/zf/2f/3g7j3R\n62Nm0ZaOkSXVkwqBJLLW2rou5ZHtdrschdR1LSq/bduCkoKzYiatTVkWxlgAds6P4wCAVVUiqnEc\niNgYHUKU2ioAK6WVQpm6LH8FQO8dEReFFaXn9rAT+rsxZr3edl3Xdd2dO3fGweXATcZkEJG25ei4\nbpbf+ta3/sbf+Bt37p69fPmyKIpnz54tFo3WWoZGTlwVJIXGlNVqvVmtNsoYUBpRhxhDCEbrvm+b\nwhZW/b//X//P4PvTk5OuO0quBqxkNiNxcGNwfgietifrrh3Kyio0Ibq6WlxdXwi8JlyMk5OTzWbT\ndd3FxQURbTYbweVyp7mAKtLVZ62VRyzAw5hen1h+0kibaeUZbZMkRhYwJL3jpmkuLi4kvrTWbrfb\nvu93u51QkwQIlRYi2RSCP8tpYGrzyr5KJZhULkS6feu6vrh4mRlJTdOsVit5OjmQlS0j3LyyLH0M\nVVEWVRmc9zEgg4/BKE3AQ9ebwt45Oy+qsj0c277brNbH41H24/X1jgk3m41SZmg7H0YEvdtfI8Mw\nDP/kn/wTo6jQXBWaiA6Hw36/H8cxMBEFAEA9aXVmkCOSFwiBIxBEo6wtTVXUptDie4KLecI6EBJw\nTP3+Ysqk51eAoqurKyI4PT0ty3q32+12uxjjYr0oimJ7cvLgwYOzsztlWSljjCkWi0WgqEArPZlo\nmUdoza3uXDL+eZI1m9TribfyOjT3KDmBExFe/gPFDphNp4VU3zGJF55djBhtM/dOORKU88vvyz4g\nO6GMU+U0KF3hJJjGibQm3AlOtZCQxMLjTKMhryGJbsQZiP0VyrL3Pus55t0inzoej9LegTO6ToYQ\nMwWDZ1qBc5+crbz09FFqvxDkTSc+YmTOXXhRa2tt5q3rdCsmLD6lRGEmiy5HFg2uw+Fw584dcUIC\na+TLocSMBABRfBGHqrWu63qxWBRF8fzZSxnKhyzTRlFrXRjbdZ0bR3lGk0CD8wRcliUrDBgUEzMr\n1KRIKbNvu9Rvb6BQIFkGgVJ6GH3TNC740Ibt6cnnP/+5Zx8/67p2tVmP/QDAD+7d8zFcvHzV9V1d\n101VShH1wYMHP/iFL9y/c//+/QfDMACMzo1aO60nhqg0YcgEAdEYDCEgau9Ha0spgYbgxlEIKXax\nWLV9z9M0XhHIcLLShHackE9h00x9SxnvjjF6P91/yS/DazM4YnrWikiGeA0S5Sil6qY6Htqbmxtm\nFPWwoigYrTblr/73v/bP/tk/u3///s3Nzf3796+vr5OuhKALWfNXix03tlCmsNZqWxiDSmlrkWIs\nyxKBq7IOgbS2Q++MKbSeZE0SXAMhBAxSvbfNYgJDFCviICZ+tVptNpu2bff7fdu2UmyQBS8rQbZt\nzjPkTmbwRMKCkGSFTVITkFhKcvqYNALkDZA65PKnZPVmGnfGG2TrCUFJz+T55VM2KbzkLQ+pW1w6\nFrI1EJBAvsjaElETAaJ2LhwOrZSdUkFRW1sURSGkhnEcNYJSRqOJSAoYEBSw1tYgRksU6XjsdD92\nXedDCOGq6/u6qsqyBERbTlPfysrqgBRhsz4BwrryRlcUBk+DxqnqJjXIsWu7rq+amlwYvR+dV0qZ\noqyaclEuj7ubKTsHZI4U0OPIbJbLJbONRYxx6jIMIUQma8sQo7g0mSEgF3V9fS2WYbfbOXfZtq0Y\nW4UGWBGB99H7YExk1ADTaA9gJAo+JiqZQoaIqHItFqZBwdMcI2DFDEwIiEziI4SwAJAY22pW6s72\neb4MssnNP8uCzGlPfoPJTgxTiyvNJuVkl5O/GGcYffZsSqlc78lniQno49dxQ58mEn7ijNXrlXxZ\nxJlH+wmvm79Xay1uJScWnFpwdBr6IAs6437yQ5YjoiR/kJ3KPC5rmkbqMVkPX1KZzDUyiRA43Q0K\nPGNG5FtRFEXXdcvlUhKjjz76SII7O+sOxllBK4d7AuhjoifBjK81v28SQMkrV+O9SEFiBkamG5gr\npTlhzcHB4zeePP3oo+VisSq3bhyrxeKn/9yfe+NTn/rHP/uzX//db6yWy8dPnhz2+4vLy7Iotqen\ngvWNPvzYj/17P/3TP/3Zz36WiK53e++9scWyrGKMN/sDM4tY6jg4WxiFmhm9CwDA5Ec3VGWNqLVC\nUhQDOResUdqoRV3nxZkXoVyLFi7WMEASPOQYx76fIPukz6NS7cR7H71HAKt1IZW/GAWFUAqMsYfD\nYb3aAOM4uMPhUNeL7fa078dhcM4FpVRk/c533/vP/+FXP/jgg+12/aUvfen58+dNveyHdr/fOzeK\n0mVG+IgoC4V470GNWmtUhpkRoCytjyHG2Pd9Veqh69ebpcje5P0cQpDMRtpi7Kx7t+/7uq63260U\n2LTWIpYaQpD5xdmLiK3k1Cok5yf2ThCRXPXk1EQswVyOAsVjcQJkOE0dkx9ka8hHzs/PVeppzUs3\n48855Jr35cgizItfQgTJ6iT6jskcS24tRh8RxebILst167z3JZzPWybv7uTmg7Q8EpGgoHVda2O6\n/igMV5V6OYXXWhWFUir4sNlsOE4SAW6IGqMxSi5E5C1YieToNKpYIMrdbnc8HovCnG7WWufRoJOF\nVEllak7bkTpxjJPhs9auVitjzH6/v7q6ykZD1KsReblcbDZrHxkRg/ND13d1p7UuEQmTJtOMZYba\naK2ZGJEUTn0+PIkrxrxOACCE6fFFkm6TmC2PntEp4Q+86HUW+NxLQYLf8mpXSt3eFHgdF4qJRQ2z\nREdec2IMpsuTtspcssurNntLWfHCBZDFnTPE+cskiVWdhvpAaoCQc5ODp7Uiz2/yRrLKKUHnkDhv\n+a7JEhGSuuwNSEQ4We75+JySx8VioVI3Sb4P8p58x+Z3L8bbZIgSjwgAiqI4HA6iIJIiemlQvc1q\n9WzMRJ7RJ6BBCKHve+dcWVbAKj9XOU+pyeUEKz9mWQ2U6Lnz55IX/Ws5HOLheDwcDlVV8TgOw9D3\n/aNHj7785S+//fbbu93uF3/xF3/t135tsVjcv39/SltjAIA333zzy1/5iTt37hy71g3j3fv3Pvrw\n6WK1tFoPbmzblmBavvv9flHVShk3eiK5dqNQj6MXjRBrCmakSENwzPF4PGpzG3xkMFbGYs7X/fxu\n4AwZlldeG3mF59UePFNkU1k3+sG6EAIzbrfnAnm5MazX66qsX7x48c677/2Lf/HLSqnPf/7zFxcX\nL19enJ6elmX5zW9+syobpVRCArPjBzRaAU60KkAAANSouDAWyBZGtd3R+1GGm8UYRW8QZohFBkO6\nrpOCfybUyJQ8KdgIMCXY1Onp6X6/z/HNfI8Lc0Q+nrew7FkJdwQnhwS+ScFmjl3Ln2TImRxQPJZz\nTiUdINnpmectdjlHPPl7c0ikZsWDDNOJqxP6j4AEcuYirCDeLheVswBSPrKcs5n1Y4akCyVfp1Pj\no4hexhiV1lOjEpFKM9KAbovisqNd9GKstdYcp6JIDlKLujo9Pf3uu98bxzHQ1F+fdpnaHfalndjb\nKReZZpOKUZJoQIrxjOB8zBxj0X86HFqROIIEaVprc6xc1gsiGoZht9up1Etaai29K0rb7EWUsQAQ\nfcxrgGcvPetAFdNhrVUk4TvMsw4xKeL1M9yVX3MLCbO5bp94WJNJx4QA5uhePi9c4Wy8sueYpwWY\nuH04a3fK3mK+7PTUzDWFV3ld4qyHVOyF2E1IrZFyj8qylFEO6pMv6fG+nWkk2yAnSflbMpiglJIy\nLCdmgVxUSB2ROavLOye/HwAELsOkqjJf05AUYMVuismwU7PLpEIkBWFpQSUiQe2zJYVZMio4LKQp\n44hYVVVZliGk/C8Rlpxz4+ggUoieIWqa92PFYRgD09x7yc3JN+R2dSoFCj/++OXm9Kxeri4uLrTW\naOzu2A7D4CLVy9Wf+XP//r2Hj37hF37h41cXp6en3eG4Wm+HYXjzrbcfPnpyOHbxcEQGU+6MLbt+\n3N0cfAxWm7IsQuTrm/04DERgdBEpImgXqVBKF6UbAxEpZm00sArRBR85+u12q5PjzIaViC5fXfIs\nCdaoiYgCrZfr6Z2gGDjE4Jzz6IuiQEaN2miDjNFHZhbJfBcJUKGx1WIZGUEZZYpXl9dN09y59wBA\nEdGLFy9+9df+7a/+yn8PWAaKfT/GyL/4iz/3N/7G3/z5n//509PTm5sba21Z1M4PWVQNEQbvIkdA\nRQgiCaOV1nryqXW9GIeeiIqisEZZhdfX1/BaHXjyIlI9lh0hS19ygpia8GSHCsjjnBNlqSJNWJZN\n4b2XRF/UT1Sq2sqmmO9HnMWwGVqYw9eXl5c5KJRV6tKc2byJMutBNlFWGZY9ArOBLNlmUaoIZMha\n7EZIDR7zGJdmLY8iUo6z6m8ORyjxp+fpteCQMfG2mNl7T87ZQgNORDhblYgosFm9WCDiOHgiyn0U\niDiM4xCnirts9rKpV6uVMvrq6urq5lr8HCcgse/7GAsCrGAKEMV4D86rEE2ILkRrp/qcUqqqZIJJ\nf319fXNzIy5fay32MIfaiQU+yIn1BHK3dXoWmgUdJa11Udap7h5nzyILAkgTgvCDjFKKLRujrZm8\nUR4xfWs3EhI+Tz+yTdNpvA7PkiGVOpAwJU8AME1eodTMkUOA/DPMkBxKuiOcCONlmraX7Vr29vL+\nfJaUiiL5vzBLOGSDybKW9Dmmea+yXOSX8jZOYsDGqOyNMu4k4VK+2nzXOHXDqMRApcSbyInaPLeT\nG53bYgT+kvJvpieoP4CW5pwp73bxXhLDIqK02UtoqV4X4ILZYD18HYjLVmAcj/P3y0LMseT8U/LB\nzWYzBi8nL+FV1lvK5kCKikTkYzi2/b49fvDBByGEO3fuDMMggsonJyeHw+F4PP7oj/7oF7/4xV/4\nhV/4pV/6pRDC/Tt3AaBZLgR1FF3Or33ta2+99VbOlaOOOUismyWQDFnRMcbDfkTsBO0JgQI59NMK\nBABliuiJNeX1lu9DRkHzkpOvOzk5ySYmL6r8Q058s5QfaMMEiHjYt0ZX3ntEFSMCKCZ1fbV/5513\n3n333evr664bTs/v+ABKmEIU/sP/8H91OBzG0V9e7jebDaLUTope9T5MmUeEyWhabVghS9uMUUqh\ntbosC3LD9dXFg3tnECHv6nlomdewrBybWlAnAZ7FQsRDZY41AHRdJ6YqIz95o+kZbqYSDCB8Vxm9\nyklUPod0eapkzkrlNuYRX3I+uQ1D/Iok/RKPS0dHviLxRgAQJqm9Wy1tndrA9TQIYyodycnLKZVl\n6aahjlOzo5gjEZmFxH7MsYsUaO1soJpggz7NdRPMTS4hEvkwGmtDijU50btyaigLj5nrulZgkbvu\n6LuuE3dorW1Wy6ZpHjx6uFgs1tuN7BrBRdq2rcsKUs9lptdmgylZGs6Gt9piasMXm4MzsEqg75xZ\nIqIAMMwcCORbtNbKmBjjcrHm8tZJJMMVrS1lDAwiIkysacm3mFlrKxbYGGN04YOK0QPcsqzz7jMz\nnb1sDznVaCDNiMjXm/Pv/E4AMDmoz7aMEnSb3wQz8E1uitg1Oe48qsJZppU3ACfN9k8wFEziz8iy\nky8Sjg0n4bhcBRFS+Nyxaa0RpV9qsumyrPNl2ySvNPd5Ej+Kb4gxiuSBrOx8bvkG5SSJEmlCFnHO\nV7J35BSnh9QyLFFq3tiUSsTZR8o9yR/PPkz+KkpINglexVR5nt832f9KKSlKhZlkpGzRw/EYYzz2\nnfTh932fxzJlBSNMAKb33gXfrDcXl9cib7xcLkXC5NGjR1pr2W8iS7zenPzJP/WnP/jgg4uXr1ab\nBrX92m/9jlhMMSjvvv9hfgRyb1er1dnJCWidJbcD8bGbEBjGWyn0nIWX1pJ3KFFwjKiU0qABAfH8\n5PQTUVhUMarohzEKlUZpBoBIRqmqrGKMTIyIGmRhQ4xEqMMYbFmFEL73ve+end4RbelhGG9ubrpu\nuLi4EEFCQTmYsCzKm5ubx48fO+faY/fq1auHDx9ut+txmr4TcrwfY2SIdWGdyKFrw0qFEJgjERil\nRShktVp973vvfPEL3z+OopHDkjnh60A3EWW8Wla7SH0LKVRSdgnbhXklZD+VgJEMJkjHhU6EApXo\nHkKQm7uKkBToc06jE4LNSbY5h7Aq4cySqGX7Lu+ULZZTEzNrllQzoDvvC0wDw4RMwUnuS+xArrYK\nCagoipwm5vWTZQ6ErZfj2gwbyB0TJyrpyzAMxByiWyyXFKOE2lproywAOIHylBKjIQs4+r6u67E/\nZmc5jmM79MaYq5vr5XK5WC3Pz8+Xy6UQ//q+dcPo/SgeLgflIXV6ZFuRnXeInNX3hUgl79EaQ3BK\nAbOIoLdq0qv0uZLddrzbyywPAoCGGxkWjIiFFUczJcEp/DYAEINw1hSRMkZba4ikuIWRFPNtVGdm\nrUE4S6bnPimnnvmLPuGN5uCekVs8Xw2U+NnZu+Q1lMOW/H0qUdTzEeKsrfcTwWl2CTqVjiRpEAbh\nnA7wCV8aUxGVEsaas+/sBnjWQKq1FpKJBHrzPSz2VMgRzGzTUEtI7bryyrtUipCIKEFcXkDZ589f\niDgk1T5ZcJkglLMu4ZUJvh+ncWS3ZO58G/OFuzShMl+s/CwQfwhBymAmzfLI/lgQG5XkDuX9MTVy\n1XUtSkh5f8ptvLi4YFBiQd555x0BWD7++OPVaoWIXdcJvULevNlsHt5/sNvthOTz8OHDy8vLtm1P\nTk6UUnOGNwDIZ1f1UiQyz8/PdRo2LzqEeS2F1PvNZWGtRY7zlFo+lefl5JPJC1h+kDdnqSeeATs6\nz9kCdC6UlRmH/jvf/m77sG/bFgBfvnzZNEvn3NA7ihBjdKPU7YIFfXZ2JqOP6ro+Ozs7Ho9VVciS\nziyyvIaJIkfPqBUyIrK4AQ3a4Ga5RKDFcvXi42eF0a0bjTHkA9hb5SpKLwCQtCDHhTJS4eTk5Orq\n6ng8SgldFtuY2JUTXJMMRzYWcszsoohIUGvxPTBTOxQpZE54dfZSAm7nxgw1SQwXmZ4w/66cWulZ\nv11+TDBjmohBlzUPM1kglZB8Ti3notQnP3RdNwc28sFNYhLnNIgTrUkWEs8gjbqujbXD2C0WCzeO\nsllCCG3bAcB6uRyGQSsrnkNmdHXHPce2bVsJ1CSv9RSdc8euRcSyvu3FFL9Y2mIYde5rFB8pORzN\nXpOBZoU6L20MgQCmKpFSIH50kneCOLpxGBlY5WyJQ3RpLoFRRilVwwQwSueyKlXwXtgDxhhjLDMD\nT6yuGCOiYEhTaD6OozG5JdzmVBhmdSB4nXSW0YhsYzGRnOdRyPTBr//Ob9Gs5JPPA2ZYUC4USfAl\nSbEM0xWahxi1HINAKgPaNKFHzB+mYpcU57Pmt/xTLK9PE70oCe1RGmDBM3ZDskGqKIoQpjhIlnJM\nYhDZP8vxOUmPLBYLIR0JNUCwnXnWSbNZLOKKcgZDtwVqFV9nrsv1sr+dDJbdsE6Tm9VMk0J2nfgk\nTkLpEuWJjxS4XM5fgkRJPjjV6jPwOH/eOXcEAGX05eVl2/fH41HmkuWYVAyBOKTsX32MDEpyKbkn\nsnR8EhOTMWuSe2GSFlwul5vNRnBITPNaYBbhqjQamAmX1UIOnim/VVVJC4XsEEpMQkSM3lmNVSHw\nvVdJgm9OUM7xk3imIk1EzFtalm7uaBFvLadkyyoQtN3wzW9+62d/9mdPT0/Pzs66bjg5OenaIYRw\neXk5jqMok0oC4fzEkI40Me9Xq1VdlzHGw2G32+3atu37fnQ9MyuFfbcHxaitMYUprLbTCPYwOlSs\ngD/15pOH9+7++T/3Z43C87t3vKNudDG1u8qDzims5MoxRina5yTMJK0EiT+ECCqBjviS3Ce03+9F\nYJeIpJlP0kHJdbIpyFZGJRLsrQtPYsoSb8lDyc744cOHQqbIxTOZLH51dZV5feKTQppBlf2QnGre\nrTjDgmQRCsNCqEDZzFGaMS07F2d9+p+Iqk3qTpHj4GxEpyweBrh779x574WVygoRFWgAcMNQVZXR\nRdd1yKqu67/1t/6Wxvjy43d31xfyOGTzKmtijMpoIgKFVVUtl0tZt0TU9630tMUYi9cnG8WZ/KbM\nGNzv93W9cKNnZmMnNqlSUBTFMHSIqPRt8UaeWlXUYrSV1tJ8ulwuF+vV+dldUFgUZVVVdV0vVquz\nszvb7dYHeeK3ygbCw2LC/GiS9Nxtjq61locru1j8hZh6PZusrRN7Yu74KWFvf9AhmcwUwFnTq07V\nyBxuwwx6lqBbwi4xIjlC6bpOpomII93v9zK3mBLTKVtenkGKNBuMBLMUj2cv2YTzgAsAiEAmShCR\nhCdm1mw0zyfkFjjnZIqduRU0nOaq2TS+Nsee8l0ysi9n1iYpR41peuY8HIgx6pmJzF4zJqGjtJ5U\njuspkYjyhhGnLvYiztoAc1iX4z5M6IdKffI4Sw4QERQ+efKkH0cJo+Qb5ZiSi3BqCpHfu+CJIQJD\nBEKCCC4617sxjOTJkx+7sR1aDqysMmg8eURdFKauF0VhtLYy21EpiJGt1UoZogCgrNXWlgaVUpMB\nzWxDsXf5fDjV27TWzHHdLKqqsNoQsNUGFGpUPgYgRq2M0spoq7UpbEks05e1NUbpyBR9YAR5D4Wo\njJaex+hDoBhCiDx4hhjjO++8o5S6d++eUsra8oMPPqA4OTnpzRR0t+97xmmPWKuLojBGeT/GOF5d\nXQ1jN/TOhzHEIP22PHHPCBQyakQAChRVxLhZr9bLBVC4vrp4dP/udrvWCt5/973Ts7uROOVVlCNC\nSn05QkMQ/yp8s7z8sjnO4UjeLBL5EZG0Rkl8gwk8CUkWPYe32cZJ3JDRGPmgCOGLT5ojKMYYmQhu\nEj1MVr70m8fZixOMJvFo9nycMH9mFkw4EwSkPc4n7at5bK5mapCy8rOPyX2KlHAwsQPSl2Ze1+AH\nxJubG+d9kIqULrTWCjQRmbRnQwga8yTG29Qqr15RD/VjkA0oaXR2M1VVbLdbgb5zFih/3e/3Z2dn\n4zhK5c8Y8/jxG8HHDBUAQKQgMhxSeGaYMhKlMCEcIO2rwBwpStRrOnMoDlprXwbJlpxzAtVp80mv\nzCxXNFlI8UaQXipBc/IEc/0FZuo2c0M0hyLyF2HqB5i/GYTFIF+ZDSgk8AQTcp3NJSYep7X25OQk\nh9iU2C9SIcy1xyKJpcYk3RhT0WhuPfMR5s81J3p4O1f7tkUcE1QtjoRS24H4bWnRyH4lO1qp++W0\nPR9EjjMH+nIQnR62krAdEoSYtzomHIAmZnkxv6h5iqpmNFZ+Xbszr8i8AnIKlfM2nBiMQQa4GaO0\nxnxDcmlg7q0ZgShog3VT1o1MuJqe8t1754K95MAwxhg8gRKVIw0KKJALLrgQKBz3Rx/90A1t30Yf\nGRkIIsemXsCkj8RMQByDj8Sxa/uyKoy2IfoYSBtljSgxW53mK8rykPu8WDWZgY2IAAyKrbKHth29\nt1oHIqOUbjsFMHq/WixAqcIYbW1hDCilEQmg7wcTi9LayOJ1qLTWoBqHUYVYGEMAonoNRIx+cJ5B\nEdDghg8/+rDv+6qqr66uvv+znzPGSKfhy5cvRRdxuVzudjs9USULYwrvx8Ph0HYHa22MwYdRGN6I\nXJaFsRDcqDRoo3VRGF0oo0V2j0L8zne+88bjh1/+8pd/4ss/5v3Y+/He/TvjSGIIMCmVydf1fb9a\nrfI4sbzkRI8uRyoxjZ3Mk7zzL3NSKEfI1WlRzch+KHu1bAFz7iL+Qykl1cc5AJg3Rbo5lUCpAhuK\naEJO5nIGlsd36USvyIGv9F3JoTLBTI4fZzIznID6HM5m05b3mnq9NGUS6yHbh1tcAUAmr6Nwek2p\ntQZCIrISoTJqre3kCq3G6UxyDZ+IItxOqwGFOeeTd3bDsDu0iChRYNM0d+/e3Zycbrfbp0+f3r3/\n4OnTp3fvPxQ+QpikZCZtOgDQRsmTFBEsmb8McDuVxhqLPKkwymOfNM9cXxSF8opCEJhRzPViuS6K\nQkoEIpEltzaEyADMKkfVk8MwRc6VMc12yHc73/xsarKd5BkomuP4T1hFE9IA1k94I04FRpohHvn3\nOZuW9Fkldo1kWhLvSBqREbx8uhlWptnwnpwz5WUn788os8SD+TT0pA1sdCKVZdJq9qY5xcn7JF+m\nRFWQ2IcmzUudm3JxTpl7k+9G3tVzT5P9Sl7fOMs183VhmkkBKY0Twb38zPKzl7OVjZpvtTHG+1vq\nI8zEyPOOza6dmSMTERm8ba/JXyQgYa4EZP86nUYEQAKjFqpUaFAx3QUfxnHwo+slg6IIkQOReCUI\n5ClwIC+qJ3wKyiCyGv1AgUGxRsMITEqpmhmJgtbWGOkbHxG15FLWaiIYx14pU5blgL02BlEhQojk\n3Ughjt5J4GmU1tZoVKBQATJCVZSRyccICkEpRGBEUOhCQCbvPSNMeZXWSqvtYtm27Y/8yI88ffp0\nGIa6rrU2f+gP/aGPPvro1ctLIlou10VRbLdbrfXl5eV6vSSiGP3+0AnWdDgc+r4bhkFrFFSqKAof\nRudcjJ4hMqPATIGBCRkVAJ1stnfvnZ9s1xzji2fP9YM7y6Y2RjEo1EUObrKb0dPAqkmPWLxCrg9l\n+y4LJn98Hs+pVF4VnEpQ6NzaIlFmziogNQhmLW1ZrvIeKUHPc4sczNWpW1ngBAn/837JaZlAVdZa\n6a/KKaAs1JAaeGXUmZy2nIkcnxNqFBPtKP8G8yyPVGJISYPKW0BuZraDIbXckZT0tDYCqxB77wWp\nm8xIStzlwqUWOE8FlFKAYIyZxo3z7UOUtwkaL8GonMPNzc1ut1NKPXr06C/8hb/we7/3e9/5zne+\n+93vxhjfeutT7b41qZGDKGitlUaiIPp1mjFG2bwEQMwgcqaYspocnZAPnGTbBOqsqsqWJRE1i1W2\nNsyMKNeLSimFr7Vazr2OTmUdsdI8k6rj9Jo/oxxoyhv0TL37NlCYf9M8n8rNcfm75SXR2W2dmTmn\nRJKRGGOkACAp4RREJI8SUhMrzypDekbKzCsm2+X8sPNfMfVkSaO73BEBvnNZ++TkRFLyXF+R2x3S\nHPEMPnAa36lnpSNOcLNQ7+RQcpA5UjfPY+JsWgTm3H92RXnf5ruKsxEYMREWOCWj83VAMxB8Hqrk\nm5MPmB8lAABj0zQRUmt3CpM5oZeCuOail9aafAh+FNF+YwprNSsGYq0MKNRV0VQGUQsiB0AukjJo\nlAXFQAiKrS60VdFT5ODH4MIIhMogEPoQrq73aDQRDEPnXAAgg9qUyrmAxmhtlYLgAiFpI2qnbIzR\nqAqccjCOVMVAIYJCAqYYIiAjIAMB7/f7QBEZTGE1KlG2FaQueywFKCgfaoWILy8uXr68eP7yufTz\nDoN778P3i6LY7w6LxaKoi7quUeHusHv28bPnH1PKeie9xKqqVqumLEvnB1lsN7vj8bjvui4EJ6rb\niJoBIyAAoDJKKT+6L3zxc9baw3H37W9/8+GDO1rr425fLrZ5edjZDGVmFpbw9fW1Ukq6bgVem0cS\nYu4FwZtbSUyIVnZXeSnKB+OsxGKTtLFEacI5FhKavG1qCwWAlPTnwDQmoawcJKmETsMMPpGlKDi/\n2BN+XWfy/v37nLI0nwb95Zgv76Z8jbKDMiABKQyXwka2mzk2ldxubg31JENNEgMSkRunblljjJf9\njrecWCISSapP2F89KYfFEIILfn5jiSimsqgQ7bLVevDggdyQH/3RH/3Sl770ta997Zd/+Zc//PDD\nO6d3iqIyxpSlD8EREQMpBcY0zMwQYwwxxhCmUsIwDAhpLwPLX2P0h4NhZq0kLw/BucNhb8syBCJg\nmYWBIMF6jIljiaiIKAaVIwBO6jMSzWSobG5/8oLk11/ydLI3gtdzJkQ0c7uW13S8HWv2Go4sKJye\nsVZ4Vn/LGXdIM8hVwsT+YKyHqYY0T4Zy0sOp8TOv7IxBfSIyygGRmRHebZLxDql3BxOWLR/JJCud\npgHlC8wnKbs3f7tNk1gpUahN0qSYuzGj9CeeihxnTFw7nYSW5zd2jjl8YkflhyLflZTwbv86f9iy\n625tBAGRMGJuu9zlaBJj5kRbrJhVCNaEoGLFACR1ICKI0WuNCMhKkmsDQAAKkbvrHUZkQ7IWlAKN\nSkU1jmMIzvsYo9faKlIxsg/u8ZNHBBBC7Lr2eGxF+VTr0vsgN0zG1ilVVVVdNZULdNuSJ+GfQgQt\nuJxCnGasAiAAAixWy34ckVk64yc1W6Uud69AKau1rCT5fSAS2+Hc8Pbbb7Vt/957752cbF69unz4\n8OHZ+emiWRKFi4uXiHqz2Xzxi5+/d+dcrnQc++PxuD/cdO3g/DCMcRi6YRhCcCEQc6yqQumy3e+0\nMtpYbY01hSmrql4UhVmvVucnW6b4uc99rjS6aWpkWK1WQyCaNWLnzEYUdwappRuz2WyUUkLrz8Yx\nZwbjOGYR7mxEVGK72KQQr1PXJyIKezgHoyrhb5IeYdLyyLVrmr1wlhnEpLylZpUnSes59XsopZqm\ngVQPy4UAcVSUuKxx1sWYT0kCSn6dyS2fFbAupupyNlBz+5Yhwbz15r6EAXwYM9wilfzClNZaFngQ\np9JGsglSOzT+9fFvSink18Lo7KRVUqk4HA6icHj37t3T09O2bR8/fmyMkbblN9988/Ly8hvf+L39\n/qh1LyqxZVmjDL3UGGMEFDGz6P3onPFhjJ66Y880tcwTSJeepLBGa22KqkgCzSGEoWuVMmVdSSub\nVsIRuy1Op9v4moOYBw2Uypmc0p1P4Kg4I5XkO59z5bnrQkSTwascJsihpeknr+989MzgzN5ecGHn\nZLaHzNychgDJmsuBidh0gYaKNKkME3iVLf78oX7CzWbTTFPlaWLiz62wXJFgozHpbcj5y5nL9vv/\ns/VnwZZm2XkYttYe/uGcc6ccKiuzqqu7urt6IogW0IQBEgiGRIgERcqmRIsRinAEn+gHUU90+N0O\nvzrsBz7ZlCIceqBE0xESadIiJVCiOIAgQWJqAD2gu6uqu6ursirzTmf6hz0sP3z/XnffLJ6HjJv3\nnvOf/9977TV+61tqKpABMPdzXFTRzKiNhENXA15N6fytD2RtjeqzrW9wpd8ilfmBmopFdUpTnRrq\nyR00mdiIpbs4F7dtjPHeERG4GtgIG2GBUQH61unaGmPQIJlzFknGkDGUc5yjeGcccnPEknPOiTIZ\nkr7xMZFkss6QcESVydD5xWnJYWRaakcxztI40/qOehbJ4NJOKY+z32xWY5iNMc5vvPfHYU9imtYd\n9oOxJJlDnLquI84kJue8Xq+TEGVhEkk5pyjCZKy13jCZEhVx+VeEyFgSYuuScEiZhaw1ZxcPyXCp\ncBGmhKQUbm5uzi9O3/zMs0ePH5CYL37x8+fn59fXt+M4vnjx4r33fvj8+fNxHGNYcLGGUtv5Vb9p\nO59zPh73u93heNyLyMnJ+tmzZ1985wuPH73WdminSG+8/tQYQ2yTZBJmZ7tuhdTf648fXb580XcN\npbjZbM43J/vD0bMlc4ez8oXPCUzYprBBiwh4m05OTvRg1pZpriYH5qoIFKvWFl8aaQEa1iDMlJRy\nrjCKtiApNDms6j6VKYi4MVf60PUg4ODYgvFTPw99DlIS8prqMcYgBLRVAy/uB0xd+jhmaeFaaGHV\n3kghYsYv1ZdV3xe5DfVrF8tNy4i9gNFrclcSW6/XOWcSU6M/2tajZhGrwaRq+9u2bbo2Fahwycq0\nxi2x2jzPn7x8ebPddl339OnTs4sL6323WhHR21/4wpOnT3/6p7/+T//xP3/54upw3DEzc2ctW7cw\naNAySd1Yy76xKTWUmcWkOczxbsg3uztcYgqT2EVTpRCHYSDju1UPXGXfWWyHiC11fSMYa8SC3tgY\n74oRkEbVeFpxyBUCU531XCrcn87r6KK58vV3XI+xNB5r6kl9fymzTWHeuRryaIwBbgeZaHhPuKym\n9bSwlKpZEsYsvOswG3ANNPGlWl6vJtULDm7bNjnL8XgQodWqx3wB7wESxVy7JucU44LsVLia3t48\nz2gtTAWYaEpCDNVXHFR9Cmut3ucrwSUOm66vWiNNUeojpFL4hbAys84Zk1J91aBHLbS1hpgNO0wc\nIM4x5JRD1658Y2PIMcYI4moxkkMSYUxCYqKUk2QjlAxzFrLs2HDTWGJMnYgSU0qWmEhivKtvNX7h\nFSYiZm8ME3q3mfu2A/Un/CEutfcY78aCVK6niXOYxxHmvDlxjVvG/npj1TXGR/b7/c3NtjtZwUsl\nzpI55SCZ2cg0BlgsoaT/1g6BL/waxpi272a7sFHEsMyVN9Y0vn3zzTdvbq8ePXzt448/7vv+wYMH\n+/3+/Pw8Jfn6178eQkJKB4nri4sL58w8jymEmLO3VoxIlJBD55spBomBrPHGkjXeGuecpFzcESbm\ntm3X65Ou61ar7tnTp2+98Ya3LCnPYWzazs/JmZadl2pIMU4NYnEVKvweGDNTKiJYQFdwzPhepAFS\nQcTtdjtM0IClgXnQj6hasWV2DBLvVKXZYahc6YJRbwxERH3f22pYF3YBODE9LzggwHnaMhzWVNl7\nIrq4uFDvUN1WYwymBeLmFVOnrqq9AyUv6kszdYodlar8rMZJz2/MSw6fgKkzBl4R3GiM9g45qKfe\nutb7xrkgsoDKKOWco4j4tmmaJuY7qBeTiTGyLFCp1WqF9NUwHN9//71pGp2zf/Lf/ffOT0+HacpE\n73zpK+vNg9/73W9+61vfOhx2x3GOaWaWVds5j2y5GBZjrHOePTOzITscRzMMU5gpRGFC5paLy2KM\nybT40CnlJK5pusa1ROSto1Xrrc85sxAxG7Ji4GovPgoUNRYcyAAoN4hozpkox7gMnKytkQYAr3jq\n+t+UEv/g+3+o4XAJOBZZB4UaGjW0awH4camgLCklzHbEhqEhC/SO+/1ec3S1LsZ+q/HTmEaq4r+q\nYPwpV3UUFU1aYIURqGLUw41xbeuXCQmZUgqQOswo896hlxuNCwpsdQUUL6XWKiKIUTS/p/BWrtqe\npAKF55wl3E3VlCpT1/c98irYPxQSmfn09BQJd70HPCYQqOrrHY9HETk7O0spAUsd45ySGEMiGBAO\nsI2kFGC1vW+dM1liyhkm3RqTckYW9WSzESKMaiARYhb0MIVFg9cekCtQbKomW8MrhFZCdwuV2VTg\nScMwkc1mA9233W67VY++bkDtD4cDnKH1en11dTWO44MHD2D4YaQfvfba/njApAmiDOwD0qU3N9uc\no3ONSDoex5wjBoJJNswWkNSk43StxSmC6CKbzwVvCu9Z87pUUDC51NWoomfc7/ebzaZxfpjGFGK3\nalfd2jgeDsckGbOmgKqwbJw3RsgastYiZa/+4NPXX08pOabVatW1LRGFMMeYnG/F3EPTQZurUVd7\no/+N9+eN1d4MlbTH0u9V8nL1naiOEBH0zSgnt70PboK7Zu2d36AHNpcJEdrXqSpYz1SdeaOSaW+b\nHpVLLlgnHK5hGHLhwNYAyFrL5q73A8oHVpkqCAPCESoZe01O6P0QEerfSOqozSMiY0h7D4gMpYzp\nt4iCvG/Hw9G71nv/1//6Xz8/W9++/Phw3O7322maQpjmOKccxCytmSLStL33bYxxnkLM6XZ/EBFj\nqO/79cm6bRdf4eLRQ2vt2dnZX/s//B+Hw9CvV0TGuzZG8a598eLFv/j1f/47v/XbMYbW28Nu3ziz\n2aycsdM4ODbrTZ9Sut3tMhfXOWdnrfPeuQYnDnFC3/feLw18c5T16rzr129+5mm3bvrWn5ydta49\nOb+w4oY5NLZhxynNbJJ1lJO03dk4LOuPazaNg1LCOqccwpyyRGuACmbV7fUR+7e+nIYIuTC9032k\nli2EjFLIkWCckAqIZRCD9j3gizFxRP1c7btUi4JMnR4DtZM4LbUJTQXbpr9RP8guwARYLyQEBLU+\nnChN16bExmQiCiGqYeMqVa1nGJZS14RLGSyXV60mpEpmLo9fkQLo2WNmnVSEJWVmdD6BV0qvrGpC\nXTwNhNMy4Ad2i3JG3tIYw0SACDprc0o23WEumcRYcxcxwCOwWi0rgHKcYWv8PhzxX9CEyMKx1FQr\nKURGhGLMKU3jeNv3PWbZIfpxroE/Y60dx93hsHD/rFYbzExbrVbBN9ba4OaT9SbnbI093Zw4Yxvn\nnbHeOiKybCxza41brahQGVnbYVlOT9bQOCmlYbVorhhzimae4hyXZGyMMUlmZmpbLGMtbMYY9D9R\nxZ+Gt8GsNk2DbLP6ao8ePcIHu1WPD0IIpylw4Zzuug5Z67b10+E4TQMLtYvJCdaY1Wq16VcFlOyY\nrIgwLeDHXHkAd+Fd29YuvP6QCxpNA4Jaretv6k/Jp1Aw6vPhMRFOIa4yVa+bwi9V2muLnquBMiq0\nlb2/xzai/4Vt04eNpREbmUP9Xi0hG/squRkupRpGzbbmJPR5a/MJrhZYsjtRScmYCoUoZL1vmm61\nWs3jREQSl5ykMUZyPu4HIjJilhYfIqaMdY85iiQRJlnqsoYtGe77k2EepmmKMRyPR6Jute76VZtS\n8N66xlvHxtmUUkw5ZdP2m+3uuDk9+VO//KefPXv2O7/zO1effHJ20VAMImYeQ4pknYlTJuLOd+Io\n5uAKoiTGiEGXKSW0GTVN07YGAAQSezwe5ynenq5CaAbPRDI17TjOJ5sHDy5eCyHENMeYjE2rdTMM\nYbfbGe4AHC0zMy0zhzCR9j+ZpWkxi8RAkPNc6FQgGL4i4Nd9dHUGiSpHSYMkU5Gi5qq5qbYWsbCU\nahyjzr6m5jSix9dpK36+TyugVVAu2Tl8NepsVCGwNSIxpfVX0whcUXGraVGpNaWjSK2RjpOAHOOW\nNItdW0G4mQqiyxXkD3dyPOxUEeQqw6YpTa5A3vWfckkeQrshGJIq/1Cvsz6s3nYonBH8qXqbNXdj\nA4XEOOcdHQ4Hcdhfa9gyQV0lTB3UuDOU8Ym4Af1efcDj8egKLwPspYgg4+oLnSvcdpiT3W4Hdz7n\njAk90HFnZ2e5cNVoKgDS5Qili8RMSFyprc05G+NEyojFkGOU25sdSFqLNhdjTFM4y7nijWZmY5yu\nVX0QAAdVt4wKVeB6vUbv52az8d7joZxzb775ZiiTh6SMWx0G0/smxmhooSkxxvRd9+DBg8YuqDY1\nJNZatialhNn2dYYNRUrchnpFur+675qE0FhWJV+dGwT9egX1RYD2xuHVeMtau9vtciFfMAUH8YrM\nq6LPhYXIV+MSNI6p70df9dhl9cZc4TnV9ays5l0FAhdEnkPNWK3EuMoFqVTjeY/Ho6lYyfUgiySN\npTgvN8PMlo2IcOau67q2hxEdh6Mt5lAPY87CbLxBEwtRqZozGSKepkgMFBVzOfXYHTyIFLwr0VL+\nMMY4Z/u+//rXv/7kyZPf+63f+Te/+a+t5BCCFfbeisj+OFgm3/pskrPGusa6QllSgsNpGlAxt5bH\nMYQwMTkWG0KYhiPTzFa6rgkhXk+H3/3mH/78z//ixcVF125WdpVlcp7m7fDwwevb2xFpnlwgDDFG\n9D8ZskyL34+Xsh8g60sFPFJ31KgD4UJFAIpfcfEfpdD4a4UDGqdOT2s8AfRnLpyesXS/qgek2lwP\nhu6i3G9So/tejwpTLGy++CVupi0+L5UOifq45vtYnRiB/bOaN7CF21txGWrPcNt1Xl5xhk0hJq80\n4+KLoe1JqrKQXipXbUxwxIBthVmlKiUihWpISinbFT5WPedqmPEptJ7U+pRKvc1U8BVVXvq2un4W\nY+z7tlYx6lkjYVWbZyiR1WoFOJO+tNCiR1TDboT2+KySaULrweypPpKC1RThYRis8cayNT6lhCnd\nqCfnRGwEDC4kRiTV60NVBBxLkGGMoYINFhHmu4yTqiERWa1Wml6QQsKLbk1byqhctcfp4dSlY2Zj\nlp5zb52KB/of9rdbVaA5LmXaTGKMEcOqIlMhMar3Wnc2VwSGtVmiqn5Zn3Yp5OXq6OiGukIylKqa\nMRemRyoVLF3YWpuosNUrr3f1ynfpXyE/qQDkirFZ3ETtL6QKmsTMxt4LraSUJWoHUVejjgv1W0yp\n2WABEWHr6YtVpweVzjwRaX0D+2St9c5jK4fD3hWXVe26ISHKJIixKOecUK/KJEzjGI2HPqR5nud5\nDHFq23Zzeto0DfhrrGmICKSZ++PUd+sYpsvLy/Wqe+edd2ymjz/++OWLT+b5Zo7Re0/C8zwws/U2\nxmjcPagUCRtjQBdZVDGASybnbA3FGGMaU+powcLIfjd/8MGHX/vq/qtf+anDYffJi5/M6di05vHj\nJ5vVeQzbOYx6BOC0pwJlRDZVt6DW56Zq8PfVeDl9OVWa8I8gBMgd5wKAecU4qWzVl7OFYLEpHMB6\nRKVEM1wFGagzmdKLYCu6qk+LuCk4UT0htrQs1KfUVugDqjCv6puj5VNvozZaqbQF2FIvUROo6447\nr9yoO8JWVUau8LfqKundqsS7woCnyqX26fBcekLqCEyK7dfTq7uuZ163tn5/fd7Usqr/kSr0ERrx\nfKE10625vb3Vuosir6y1IL8IpUcYXwdUCOwNKm1wddG8BU2HqhJeqDvCIupFYAxOT093h4MI9d3a\nGHs47EOIzL5pfOM7ccRMhqMxTMQp5aZxbdvGvKhUZnaY/lJYMplZq0oiQnQXN9eG1lWtxFKlrTBO\n3pTUh+KetfypZXNjjLXsiL23zizZYGy9BpRLnsosCAJ0KxMtKTiF1cB91jvRjAWEU1FCtkIb6YnL\nhZtKJYQq9Je+YGlwxGD88NXaD6RXkCo2UpHDIXXOqXLnqm70yjfWvzk5OVF8kHq36pTUVgG3ZOlu\noK1UqXU1ZrVeylXqoj4UVACrar34/mtRVsWpy2WgJcmC4uNCpXjPDlWOYCFPssYYeEtJcsrp5OQk\nUULJ6jgOIqkLTQhhQJcxm8vLy4cPXiOiLMGYqbEmhYWgchqnF59cnp2d/cqv/Mp3vv2t733nuz98\n7/3b3bZvOzKOmOeUGPCD8hQ5Z5GUJZ749Wm7McYIpWkenLc9tdMU2CShME2jsWK9GcdxjjyNWYT/\n5//5n04zfelLX/z5X/jjZPLvfPM3v/f99x9djDFQ0zSmsPtY2xgDDVayNdSICDEqIwErb0pgqkbr\n32KNmmqeCpeslyrHXHmU+ADOpPZX15BQPb3qtuBuagupd+BKF7fKXCxo5k+7M6rl5T6XIpXWJVW1\n6s/qRfRBoDK0m1XNpCm4c00S1qJc2ycuYSkurp4pVRFGGEddXCoYBJXU2vbD+VUfTX26ZWPcHfhe\nS3+1T6C1gfomX9ld/Y3aeCn1MKqyK7VmUXVWi07OGeMP4ClDfeBLceqkQD/gxiIGsqU5VOUKDwIM\nIcCKgAnAMYcu09303ocUG986N6ckzIbZMpucEzK7MQbnGmMYfVHGOO8lJ2qaBp0WqP3EnEIIrrBv\niEiSXGlnqVfPlLYzmENXukR1B1FJYmbt9VHzoAuuHoAxdHFyutmsvHXgCfTeW2NCCF3X3xm5uwEz\nbIyxZWIQ4kVsH8Iy3cH6mKhKpcrhq7FtVDH52wpFXdsGPHJtbPAVgNvUMas6KGqEail6RQ7pfkgk\n99FJqr51GdVvS4W0V58OG7paL7mHWoZVfanSKLmQ+On7oYKAl8q063vAsYDr24VA24pImGZN6MWU\nYB6apjEy1aZInxTPgqpkFptzjgG0ql6MMCbDOQu2jnmep8PBGNN0/fF4fPa0FZGYeJ7nVb+epgAI\nviGOMfrGP3ny5OGDC+fc9fX18w8/iiH3q9aQnY9T0xtHS0YdffpYGTCIusLJ2fd915mmiVFIJM/h\nyGNa+804zuMsq+7iyWvNt779vX/xL3793ffe//D5T/74n/hjX/7S1/6dn/6Z7/3h+zfX29vbW5zx\nBw/PjTHH4+g9BIyI7jQVgHhYEF0iqXAGtUVYrFEswbK2ScOKqOOvm63XUqtDJeIO91l1uUoa6MdV\nUGxpglNLRgWADypi/aB+kUq2iEBnvXI89MHUtqkBUB2HeulUWqy59AD6Moyr1jt6JnURNV2AgoHe\nmMZY6kHr/eup0zVR1w+HX+FSqUBC9LTbAnNPpTSttQTVmyr6UnVOpAqnbi3YYHHglxWTJR7iuoyd\ncxLhzWZTWzvNK2r7Pd6d7qOBqeKkwnrqnSN+IqL9fg8QHawOxADQXle4YjGxhovVPxyOOXEiyYmu\nr28VO51SSDFkSUxCRGFOxpI1IpkTJedcZxgaPKW0Px4Oh4Otcqp1kJHzkuCl0v5lSt3FVsVLXSaE\n/kSEB+ECQMWgDSoYtrKJJoQwjqP4ZXA17qHrOmDG8F2GlvFawqSDhrHyXdfB5zscDpobx5tt4RZR\nX1CKd6UaVuVQnYxXMq760jDCVPk9U0YYu4oByBbePC5BthSYktYGaofGVHWCXHVW4E+oj9ry0vup\nLag+oMp87bbqseLSWaVnliqnTbWW3lttv3WhFE/By5Rem/OCFLXWximWs7Mwl/PdXI67Uy8izTJn\nB9kwqypumrbGGzDerr1LKUzzMM+zE8k5YyLfcs+RUlqSLnEOKURr7WazkRxvb28fP3j4ta/9kRDi\n7//uN58/fz5OwVCKMicSO3PTZOi6xjeYrX51dTXPc9uCbKlbr1fOubTKYU7e8BjGeZZTe5ZSioEe\nvvH4K1/5zG4X3n33/eub/e32JuTwi7/0C9bTO1/64nE/v/fee++99+5ut9PMMzyEUg6XapHv8jcq\nQmo79G2LK6CAMW1rgDhiHp2eUhVWeLJcmodMwR2oolEX2JQanZoNlU7nHKbJ4b9N4Vq11bAfVQQQ\nX1wcChqWADew2+1eOYp4wXRzwQriCAHGNs+TurGp1Lr6vof3Wh9mV0YTYUHrG473iUbuzIO5OwxY\nd4Upqp7N1dAEZHtMxagPSd1ut6+cauccJrKrb8hVRlG/Tk0aV6mPXLKIqo7VTEoVQlHl16t2wAWB\n0q5VM27j5OREStEeVwbKAwZpt9upQVLt5ssIvhACWu7V2mm0gdXY7Xb7/XG1OWVmnNKLi4u2bcZR\n1qd90obK6TBPyZgM8J733ptGSlXP3FjsrK1gx1RoFadp6YtCwkefUTN1OCCuvEIImIMANs9QiAzQ\n+qN5ibI7i6NmaDFjIQQDbl9aLDpio8XIGUYLTi6BPnpdh2EAWyt2EAcWwaiSqNaihfOoz6tbj0/V\nMlNceIPu2loGYHhyleyKZbZIDaCFu43Eg+aEpbzUk9PfY4XVkVLzpkdbPcX6JqHcU0rjdJQq5DIl\ni67LG6umIrUrXGWtcWPr9TqWKRVcZReMucMWOYNBduPhcHjt0WP4wcaYeV6YOVNK/s4mcq1h54C6\nnWFm5xvvfdvmOQYiF3KY5znn0Padc8swX+MctAGmhTVNY61nphhiCNH4BnnvYRjaxp2dnV1fX7/x\n5psXFxdd1/3ar/3aRx99ZDI570MYUoIZy957gAuEkoaDp6enm80G2WZr7fE4pBwO0z7PC5NLzubk\n5Ozx4yef/+I77//ww/1x/Obvfzsb+YU/8QtJaJ5lvW7eeeedly9ffv/737+5ufnSl7704OE5DE8h\nzSORJQnU90tCXqpX7bzWL6fgLvXB1aeoXSR1T2oFp5VMNCHRfUQ/ZAiZHDCaUKGHggsMiYSNQeuP\noh5MhTHzZdyWRg9qQU1poc2FZlQKbR1VDW6+8GGHMNVaSY8ilVjKFrQ31kFT0q50VkF73tzcqFbF\ne7Ca8zy7soBqlXEbsXRvvBJ5QAXUeflhGNCzRSWYUwuNa+qCVA7IssfII4EhMC3QEpz2hqpA0zk/\njqNIco41AnPOXVxsiO4Ix6gKiLFlpkpq4Xt1WBFXZDN4hNdff/3m5gbNpAqlgyHHly58JNbq4Fo8\nL2zkfr8XkbOz0yksEMRxHD/66CNYaywpLB84teBCLX5AWRDvPezlME1SWkpXq5WShujXMbPSHMD8\nqHMApY/ijStEnLr+kEZTzXOrtGF++fLlZrNqS2xkrfUlELQ6fygtkuycOzs72x72bdu+/vrr2ERs\nx4MHD9SHgKRhYBVuQJHooNojInRu1faVSzFMQysYVFyh73s8oBRaVSQAAHpMpXMLIB1ccBzH3W5n\nKpRpzhmrrd+LxUG/Bx6QS2CdyktKuF9rD2OMMosjtILI+UbJPVkPKfYLF0F/Ehe6MijxmpnClC7O\nuQxXIyL8t2kaY0i9scyZeRlQdNjtQwh900/TtF6fwPnu+z7N+6ZpmthM06Dp65xjERJnjKEK7piS\n5pawDpJBbewcduT58+fwzK6ud48fPznsDn3XOOeA8IsxjmN2znXrzX4YnfU/87N/zPn27//9v0+Z\n53BME7HneY7H4+icOzlZE9E4Dk3TbDadiIzjBDGDX8VMDx5cuNZfXV5ba1f9pg32yWuvj0P40jtf\n/dGPX/zGv/lXxOGbf/CtX/+Nf/Xv/6l/11rOmdrW/NzP/dyv//qv//CHP3z99dfPzs7G6dh1HSbI\nMHMIKaUMfJMaoVc8m1y1BCyuEuoWsWpK4oo8W71pKr5/KGRQtTfEzOv1WlUtV/h9XFO1WCoMRVoK\nVinMpXZNn2odNTo7pBwqLkgzjDVSR0nDlxohLfdfRK8iofWdqmL0yCFfn6pmydoBzBVconzkDlxk\nCljAlEGouSpuxRg10KT7eaFXXAZTZSpcQSdrZIONUJifsiZTAT7VbogUoASVcE2fjpaS4+IE6PvV\nJNd+CRXvRv+qXqq6zLp6UrC/phppg2o/XAdFN6i82jKF/fLyUgw72/jGOtfFNMcYj8NeREKcmrlr\nWkdinDfONlwoGCB78DDQ66pND7lkSssjLIhhuQ8BQuuiCl6dbtWVlyrClvvRqlmqIByGMZfhW2pr\nc85UFYG4jPOZYyCikBaCR1tKmJq+qx0CHATE0Llgw7hME0csq3ciJUmuW4mPYP01e6b9GGpl9Tao\n6nDCI+if1JwbY+BDqNyqxMJrUZfX3DH33zWTqEcLR0qjWK4wgU7u0J66HQjEpYAUYgErSpWV1XOt\nPi5VmQC5q4Etwp9zzowrkIggg93YBpGxttzqyujrlcMrIsx3GUtjLHpjjbl3V1LuFoU6pIv0Zird\ntbxwdg5hCiG99trrX/0jf/TlJ5985zvfcpZsNpKpbboQwoRJfa7xvnUFbnM8DsfjERKaCm/ner02\n7MZhjqmNWbxvJKa2WxnXhBhDit9/991f/MVfdI1DwdEuuES5vr559OgRkYK8CGOf8FIGJrmP4awV\nsv7GIX+dPlWKQHeYqbpb8EoFHa/yDaHUDJItsCJszPX1tcKBuIqXc2lrwFrUfp/Khwp6rlAVpuSg\nuKI80n3iqjpaL4FeJBUOm/p00f3AXyqcHrRnLIgsjYR01ClVYFMi8hWZP1cgAlf162DFIBlqabgg\nNV45P68oSr2gqXLo0Bp6wo0xAB0ws8ikV9BdTwWVRGVGli3jaI256w+trbWa+fqpqdjvOimEF7QJ\nJtVq8xmWWnuSiAjip9MkUynjLVvpXc55imEO4xwyWCcgR8aYeR7neXaTEeG29U3T4dmnaZrC3Vxn\ntO8gflqenUndLBxXFT8Fy6BfSvW4r2Z0atZLCj1aLo0NuYKiQB5XqxXoL2yhMMCC+MKua62lvLgU\nIcQQgmsbpI80bgajT6UxpfYnIE5gNNCFVXiRIlchPIqWrFVbLZy5pMex7+g3qt+MVVWCMj3RantU\nhtVu6Tt1i+9kle/1gXFJALiKrlu/V0R4vlMjNfQuV6WI+obrpCJVLpRKslTeg3Numu66aFOGwZOc\n88tPXlhrO99N07Tq7+YA6O3x/Zepko2qQq21QDHknJmxLMt9IteSc95utwjxqUxT1YOWUymHGyMh\nxSRZOBM/efrGL/yJX/z4o+dJ5P0ffDcGmcP84MGDEA4xyDzPJydryYbIiaRxmK+vbo0xXbtqWpdS\nNkZa19izpm37MafGdpKtZBNCRB93yEOW/Lu/97vH8S92tqFsnSNmu16fhBA++uijZ8+edl2XotCS\nlUCKkpityFzr53qh6H6+jpkdtIZU8BIVJpwQruoNIQTwTWk4zMU3wVJquqnmgqPKT1HdHQsE/BWF\nm+4De/S/6vurBOTSo/qKms73MRRqUOm+k/Vp01ifLj2uUMRqsDWBqQmuXIWfRORaF+/DYXE11bBq\nurjqVpHKcTCli4Lu+3f6OHpjdeiZCgaJCrGNKbksPdWmJLtF7gHJWCd/l1TbK9aofkDdLFM4ldWY\n1UEVMnIaCjTV3EVVE1yh+6BSbQVw8t6zNScnJ4dhGMcJ01RjDDkLkXRdIxJFqPDFW92LcZhjTvje\nEAJbU/O5CchXK+0ZC+VlHXOATIELJxaOAE6ELRxIuQzKqrO1tYARUd80KbGhajx2jPM8s2803Zor\nBhAqTFRoC9UApRZjqhwdvQeE2vpLWzByplS/8BSoS9VOHpa973tE1YpyBND0ld3XI6xCpcL5SpyE\nJ4rVCFq9lB4uY4xho2YeNwwwoVoU9YHwKexjrazwRcpBTvczHPoItTtlqgkvpqpB1IfCGGMJZWxj\nrX377bedc5x5v99jrgRGXqV0p16NMbl4fWVz7/rQ9VVcYWziXRICO3J7e4vZTiIyjmOMCzrDWpvT\ncnittSlh/m+f82C9e/LkyaNHj9br9X9/ON5cvtxud2HOkpnEhTDMczTGeU/orhuG6eZ63/dpve6N\nMW3jvPeO2Ns2tWR5/fLyyrq4288hi3GWDIvhH/3kRymjLJdCWILjaQovXryI8W5OsdCdW8CldF0/\ne+1AqPeznLvj8YgLqfaHUH7mM5+haliDKl9bXlSS5pq3VVHTrAsRwe2VKsmgOUBsWCiM2npmqLKf\nuWRd9Btru5IrxKqew1S4h6mKWmpDqEpQ35/KoCNVDXrDqHihXp0quI6WQON9mK9W+2u5V4uCnzWX\n6stko1Ty7Kp08v0coO5F/bCqRlHN0nXLOaNuP03TgwcPJZfWCWEikkKVz2RJMLLONL4jouQTCH7q\nb9RjnKuMrj5vrqrEuiNQqVB8anRVYSmonZkRPKWUFGVHxa9nZjacUnLenDYnvrGG3RzGaQwph75b\nt52LIcc0D8eJjQAiGMvgag24EQnN1UTBejt0kbkgsvAgqCHl+0G5ioeqzlyyc0DlaEmvvFAoZY1I\nQggxhBjjmDLqTBmIKWyfXVC5sKO6p1TKG6r9bSlwAtsGw6mrfS/4KBEwF/43ZeKpvRnUGhUFYAum\nAKZOt5irNIBaUFOF6Zgor//VBFquKru55OSttUx3MUquMDj5fsZCZd7YZb+w2lLmKtX7qIdIPQO6\nP6aAlB+hXFyfyBdSSmutEVhWa61FaTzN6Xg8Sl7S2tvtdt3d4+pV/VBwdCbfVzXMJlOd0blLouiG\n5oKyUZ9G/2Vma70xjtmO49h2Pst4HCbggN767Nu/9Et/8rvf+vbxOA7HkFI2TJLNOERmcG14MpwT\nHw7DPMcQwqrrV91ahFOSKQXXrinb733vPd+cHo7hZrvNmUDfYNgI55TScFj8SExvABkpMnVEJIIx\nSfd863+rNVJlpTrfbTabeheRsYV7Ukc2VOBnCPxV9aiixz35QsKmxV6NNKWChkuZPVqb0FyiNlMF\n0SoxcLTV0taqQTWjbhsV902fsygOcs6JZH0ovb7eDFS8njGgaHBy6lS1PqCrOGSttZLuuOlyFWPZ\nCi6o2g2X1WWpT1H6VF1XbXMtu6p94CioS6uaIsx3ac/alutj5mpCSc7ZmCbnO09H1ap6vvVD1ada\n70cfH29TT2KaJpS49VMIQerAojqlaLy3OUfJkiRQyMxRRJrWGdN0Xef8Aj9p24GQbooyjsFaQ+au\niTWT5JxR14RcYRIa/jrPCwVOLUKLoiz6lyrwN/p4dB/VymrXwV0EllLOMh2Oq1XXt52Gj8vWG6uS\noF9q3F3+mcusB7Ucai/VLNW5AX0blh1TXXS7QzXC2FQdEbqP+/0e71H4DBXgTG0MpOpGylWRT4Na\ndLXXJ1GqvkN7HwJTK9lXzr7eucoe1qrrm3qerC15XZUZqlL9UthaVZW98u21rqely9hoLc0IQigh\nomGcrLU53PUgnp+fn5yc5HBQa13HRrSEPszMUmk/5pzBZceLNdJVxRtiIYNofJdSYomoc1tr4UQ6\n1zRNI8Lb7bZp7wC0IURm8ws//4vrdh3m9P0f/GHONE3BGh9jPB5Gs7RSSM6Uhygix2PrjM2Z+vWK\nbWMNn3QXZP1HH34Y0uUYckgxU7KN921+63NfgIEAdCWEcH19PQzDet0DE8RsoFqliihgU+V+jKH6\nRwVp2Sz1hsq9LhoWpQ5lLiAiIKRRj1XvXqOcOlKWUgJNKaG+osKRSu+kdk3WuruW+FzFKNCwemOv\nKK/6+VWnaHCmTmLO2RhqmgbzENXe2DKMXJWRFG4F/BfYYgBdEPpg9V1pAKrDhelwrE+vageq6iX1\n6aL7xQaVWk3u6/OqXlATgpdajlx18iLPozNA9Za4OAo6YdpU4OBXhKZWWHcWoqRicknwyn0aTX2P\nLQBx7NowDA8fPsTWhzIlS5dIod5UoT/I8Pn56TAPCPWAD0SLwzAMiDmIGueW2hVydSQG9oZKui/n\nLBV2Q6rYSEMZVzg1uNDhqMm0ZQ6CItdFpLajEI8lGrrnQ2R1X9QdwYKvV2tNNnhbkPckKaXxeNRT\nimuicq6bwlWXur1PbaVY01xlI+sDCKZLSIWeglDYEDTBSyXfWwuP+qyIpVxhoZTK+UXgZavMrSp9\nlVtfjSxiviMe09OqxlW/jqokoS14B/Xe8IMvo3K1VUMvUt8k1qF2qelTPN+L8yEQ4ywiwBzGKXrv\nwxyHYRiGYb/fr9p7RB76sKkqTVUV/myMgBu3Ss4tmfxYCF5VQWMdWMigKpyBL2uaphEytiA8XdP6\ntktJ8hwa37311mdF6HA4Xl9fXV69WK/7cTyGEMZhNiYaS97HlBZojyFufHuW5fS8Z17yb+M43myn\nRFZYuq5rLfk+feMb33Cty0NGSfV4PMIaERnv2xAmfVImK5IXmr9qOmjteeQqVFVV4zb9apiHOMVE\nibOIyZY4Uj7u9u2qbew6U05zihL7pnddC8QnfBMp+XRTcagg/4DiP1o7jTHeWO89ZwkmcJac86rt\nuq7jLHOK3lhQvkZBeJRFbEoBExOc67y3OWfnFvSkiGCGQs7R+5YoW2KibMmJEfyb5pBzNOKyiUZM\nzpESCbMznDMbokSEMZDOGAzlyMZY5LtDmOZZUhLms5OT7XbbOHd+ft56PwyDpOTW65urK9c0rffC\nLCnFnC1zMuZwOPgybpmr+P14PCpFGIYYQXFAyutDm8vsSzUGmktk5tPT01hIaLRAHcugCix+KgWt\npmlimq1zli1bYjFkxFsPJqspjDmKb13ru0zJJOPYQDzUXqoY1bpAqrC47/tMYtkACYa8izDlnK13\n1topzFZkjmEcR+udc+4wHGOMbd+1bTvOU0oJMUFIcR4nYerbzjWembPI7X6XcwY1eF4K7BJCihH3\ng36XJZaVnFYrI5nHeRmvvlqtvPdJ8jiOAebHGBYWk3POhlhyIibLzhhKQXKOhiy5TFlSCoZs0zrK\nHNJs2TZNIynHGCVltiaFOEwjCzVdy0IiQmAjEzLGWDbMkkha36gLwlVhD4aBmT2GJswhzHOUrBNP\nYiFmxPk3BUJpSitCKDzNmieHsMGKSOlY4hKrqelV4aRSN1JwPGrD+CAMYR3pcoVNB8e5lEF/UvgG\nVTzU/NuCV1JXwxWiSNjCWM1RUztK98Mm/BcEx+olp2VOT0Kc7b2fpgkpRwWhSClr1VbZlAR+7SIw\nc9s26uRBnWLFpjDHOYzz6NqGPVtj+3W32vQUBqJoJDMLG+LMmPpKMeeFYN+yQdoZjyOIl5iZRLKI\nZM45r1ybkrBQTiQChKTJiVrf4WOGnRhRX6Rpus1mc7JZ7Xa7FOa2bYVyzPHDj3/SNe3n3/nid773\nh2T5anvVtu08j9Y1iwdJ4hxIxxMLtX3Dhpyxm1UXEs/zmLKd5kNMMxtHLKu+Ze+b1n31nS921gfK\nIKmbwrg/HEKaiZktUWKCVuVMRMSZhVhyrCrotUGSKsWlvoLb727JkLPWGScpxxAs282qj84nSfM0\nGGe8c449SZqHI7uF8YVLtAVtiGo5RFmqsMMSS0yWzTyMlk3nmxyTxNSuuhwiZSHJ0xQwi5OZ2lWb\ncxIh71vvG2ZKKccY2tZba4gykVjL3rfGWJHcWE8sKaSQQiZx1hmSlFPjrclCmUgyE7XesWMylGPy\n1hKbkCILGdg+yZKycCI23tpuc7IhkZRjTo3zT588yTENh0Ny/vz0lIXmGB6cX4QUc0xsyDvfGKYs\nOWdwYL8SKMCK1EcLARYVBpRa3eOkxTIMF6tNhcmbyhzousYmBZSx2+1QgIGrHkJYn6wzkRFOlFkk\ns8xxykla11h2zlFmOY6HKc6cyTrTtx3usI4yU+FDMuWlCUbrnWGmnCVz23dsrbfW913ftplIUjKN\nj/Pcr9enp6fjPOcYXdO0bUvGHMchpNT2Xdv30zB0dtW2bczZGSPMbI1hzll0IoZqkHlKTE5EpjEG\nk4k4ZxFDbdvlPBGRb1Ynm9U0TeM4pDi3XceS0QjIwo6ImBjkuYJUYIhE3nhuXJrTcNz3Te+d8cY1\nXUOJaI5GyDJNYXLGWOtizmyoa7whypK9tUnEGbK+MURzjBgwYZz1zqFowES+hLxzipnJYFyvZCNE\nhn3XeqKTkxMqDRkIIuGCaDAnJdaH0aojV9iw3W6nDgo48TDKeZqm8/NzxKbTNK3Xa1CSN02z3+9R\nNZnneb1eK0nz48ePb25uQgg6REALvUB81RqfK+aRVCYh4VnQDiVVdqRt29PT03EciS24UEuOhG3m\nOYzee2NsTHOId/lSrvggcml5hKa5vb1FEHN2dgZ6vVRaF/RlC6+EtvQpFhGitd3uVXdlRpw0z2m2\n1q5XPVuKOTRt07APFG1DTDlTMiZ6l3PkSBppuZxyiEkkCpOIZMpN60MIEoktG2uJOSWmzNb4YZi8\n847d7c3ND77//W984xtt08xzzFmsdZQphAUHn2M6hsM+72KKLz4+WMOGJYZJRJylzeOHcZqnafoT\nv/QL7777btPbH73/wyg5x3gYj411602PPXLwSdJ83F633l29dO369Pxisz/uXDOHmxcnZxci6cFZ\n//rrb7z12Wc/87Wvvvu9dx9ePHONtd78+MMff/TJR8M82s5tj3tnbcihb1trXErCkQxTCsE6F1O0\nxvhmmdRFTF3fHY9HNgQfTlKmLIbZrdcrLZZmk41ZMnWN85qKufMpmCSzFAdZfStTGOnX67UWopY0\n6DA559iVhFLKRAQSSYivN46sQ9FGeKmTiwiRGINOVcwLH3O+I5lPpew/HY6KuM2UmMl474ydKXnr\nyJYajIixC62nNRbjSOAdG2MMmXbV5oKAgGDiThKXWgIxM1OWmFIKkR1GX7NkiTmqjlZTVKcFcmGu\npPv1fw3n1UfQT6krretvCnqithau6gSkKr+xrA+JR0aCiYWFiYTEEAkN87g4DcbaxrWW4fbmEOuq\niXqOaF6uH42Z2ZpxHLnqlDI5ByIR+Xi7RV6LsX9ESSQDkksE1jkyBuPzeJ6t95xzMoZ1BsEypl1e\nWQfsu/celzEGbj5Kd55ooirxYgq5HFegDJyKGCOJtL6xOUWKMcZJllx267xzhpM1hjhLTDGHGHMm\nyiJEKcViACx6xcrsn7mkfLGDhrhfdZp4UZi4ShpVyShhthVOUr2ZWipMafeuMTVyvwRiypwFKo+s\nLgXSpEQEmhWYru12CxKzWJq0XOFrEBGw5aLdGC1NQP3q+zWSkJLnVLHX1GssJA7qn1FJnCLRoiUr\nU/iR1d2RkvLF1WBCNLWgaiTGqEUBGEIAKWvhwXJxKUaYwq+oyM9Qxs28cipx/UTCzsYY98PeOUeW\nMovlJBKIIuUklBBCwjHVeECVQEopYRon26UQS4CgGTLLTULP4CrLKolTj1P3d7GXbskbp5QAxwph\nYsvtqn3cPzk7P3n0+MFv9P/ym9/8ZphT27aYY0Jk+r5pfeMsz+POe+stpxzDNEzzaCw9uFgP4y7F\n/R/5I1+9vr6kNP2n/8lf/P73vvfk8WtXV1trbdM34zhu99vD8Xj+8KJd9ZJCJglxytaaTNZaK1m4\nzHSpglGukNIq2EumTXddt42K567K6O4zVZHK1K1bJQ+gzlG4Twhf1xL5U8VMFf1MqW1bkxdb5Up7\nHZRsXXFRxRTSgh5GvK9HtIYXqxnQz5oqtYg/odsxl8w4NKkULhBb0J+masjgKn2fS8EZJb5apnVh\n68NjSn48VyggqfqcXOnboCpfkatxBlLhaEMIyPghtKISaTnnQgjaalSfsbpyVk6O5JxNOasqNK8Y\nS91x/FdvSdEcXMrv/m6GJuktmar6jYWCFtCy+StSsV5v8JtXrFFdBeWSlbIV15EtI671rnSvpUzS\nIiJbiG0UWMylBwhBc+YE342FJGVr3D3JKSWBk/VG+RqUG8k5R5L0EHFx47iCKqiKxHVqC1Q/nf6L\ntIQeELnfAKCHi8tQBk3nptIQrerblCYbJermivhRRT2XMaZt24LrFgNwc8X7RRU/vWbPsMhchTWm\ngH1s6buqJYorNJPuF+wKUi+a+a9PLiKwYRgwBESHrKsq00WuRUgXXA8UTKb62VxcQLxg3eFPIK4q\nlUInxhnj2DrmSHcvQyTYSfOpzsh6r5fzZe5+5or9kvleB4v+AL1U+6PFFTam0G6dnp5+9atfRYno\nD37/m+hugsVt25bZEoEN2UABHod5jEJmWcO3Pve5OcX/6H/7F3/uZ7/xg/fetc69++673p+07Sql\ndHNzg5D3nXfeaZomTCnnHLPknFvrmdmwySQAf9cWSCrY/Sua8A5erM4CJOkV0CQOQMzJu06lhCvY\nGMQF2ASqQAQK4yG6VyrUkp3eSs45STTGRLnXVl0/Q76PdBARwK9VtvRStdLU86lgca4cf76jIfi3\nQCpSAX/XF6zVHxfesPoGqHiyqspNhWjUtU0VhFcqU4STXwNMaq2k51+XCJoFPV5wexdj42zOWe4D\nh/Q86H9zNZaxtU5/rg1huo+twnsy3bVt6VbiGRW6HQslhyKPa83rSrNwvYBcIeZThYaqbfanHwf3\noBdUrSr3XTAqUA5guKd5xl6AD0J9mhoOwGX8j7XWmLshLLWaUFuLoulCqcnMdOfjx6o7rXYp9N4A\nRlBTpC8YlVekRUrTm7lPDKFKqi43pgIHpWpSEcKCvu83m82LFy+4MFmoi4B0nwpqSgkNSYCV67bq\n93IFzrzTysaYMqJJf7mc9yJUtY8F1Q/DQyWEwgLCa9E1qaVC70clsP5BbZIuqWpzUyqvcEde0Qzq\nmeEj+rBYunme19aKs2zLCcW9lYB2OT6GjTHowhZPGaDpCrhhrc2l8Yir4nHO0jbe8B1USkqSti4W\nqjUyxsS4bN8wDJLCer1+6623rLU315e3t7f7223OyXA6HA7zOBmSi/NVSimkgW3IYrbH6ThO28PR\nNj7l8Mu//GdjjN/69h/c3l4bltceP9tuZ2Z3s93+5Cc/cc49fPjw7bffnqbJ4GGrNU+SkaLEK1XQ\ns9qhVO+QmZeOClugcbaQtaBaqO4PDnlM0XAKeYk/VK3j48gpa+RblPvSNsv3e91V9aiqzTknsSkl\nMsrHfmfY6g+qM4iQSOWVi+9Z54tNaUcH2IYKnEMV2aKFCyYQ18epCyHg93qHtmrxq1dAUaEXFxe5\n9DClwrBSi2Yq1JBUqtn6valq3a1dJNWtRHQ8Hlnn4jhXO5u5zKPSp0P6IlXYetWMAN1pMo0V9xWT\nmjd8BVe8A/XOikhGwbYUlqQkVaiQLKg3AyWiq6cK/RWDoUcOD+i9v73dq6rVXZASO6qeysXbxVfE\nisnwFWOpWkyPsZp8zGTC1psqs0oVS7oK1St2hYq5RRZLe4YML3KiaasamFdbytq23dNlRDkvlMy1\npOmzU+Vq6AexWfivWlljzHa7VXo6MJVdX1/f3NxcXFyICCiFAASA/cDRWK/XIrLf70GuenZ2BqSD\nEs4qFjFXUUttcW0ZSKYiIXfu/7IXygBrCkO2Hv+5TJ1XK6WfDWUmEwIChQXmaohtHeWrB6nCXJsi\n7euSyjeFkGBcLNxu8AQeDoeT800yTthmMpnQ7soiKBwQV16FE2uIXe9DCJi/tQj2gt6+Jw/FGi0N\nwvWf8PgAp9B955uIUDHpuqZtL1gEkvPs2bOf/Zk/9t0//PZ7x2Eccb6jZdM25upyZiPGudXJWdOv\njofxk5cvt7vdl7/21WE4/Bf/xf/zV37lV54bPj8/ffLao+9+97vn568zu6urq+fPn4vIw4cP+76/\nurrarDrnnLeGmSWkEEKWzBZwCVIxeOWe0/3ZvnfIFqpcPC6pgPr0GmMo0TAMc4pcKCb1/dhOtUxV\npo41TvJlxkwu9MC5CmBzzoWKYzF1dVrDVUwhahiccxTvykgq1vqNapDV3VM0Tq0coZ3VxKrTYcuL\nqzwP/lRf31SEKFTJn+osKnQDXEWTtiLqp2pCEm5DKhIa9R248l71YVVjmtLnqF4qhD5Xp4urmh/f\nz2AsSlNmVZRc4miVdf0I1sSQOOfYWin9mJor04kDyK9q5kdXpk61UTUHq9YdVHoApQoK745xpdHU\n/3jFStky56YuD0AklsSa92p+wI0PXquaOi+XVEP+1CA455wvzPe6oa6Qk+acYwq+sIXqwcPj61Po\n3tUnrjZOUkqPao30wKb7jNe1cVKZTAVjmXN+/Pgx6kChjAYXEag2aHPlTsQ6qCzB9uSSg60FFZ+i\nAu9WwAuXPg2u5pPVckhEAFnYChFuqpnL+hXqmw7DoItZr1iuEA1SJlxwlfrL99Mq9aHGyqjOqde8\n/qFWowCRn56eihEyzGwRD2US0KKmOiNHd9JrrRORHO+WQhWUVFa8/JVTSmTuOiNVL+mDy/36fc4o\nm3Hf95YZzmvTNF/5yldSSsft8fnHH47jmFL01hvrJSWybJM0fbQpHYf9dns7h3g8Ht97772f+7mf\na9tmPO6vr68P++3J5iKVwY/Y8fPzc9h1qjzLtMQ9YvjO7dN9l0IgIp/KqdwlwZVhk0tegu87XOWv\nS5kB+50qCkIF2GCyIfQvVdpWd13uF7VwrzHGkOaUEsUlqa3LLSJYAr4f/Xjve7+0RGi6DPcPIgA1\nGHrmNeZQ0wIhQyzoCr+yL5zEGhG/oiNgcdUldGUmzXa71YOqQlZrWKmmudjStao3po8MH1BNsm7Y\ner0OhfaNS7ORKf0ffd/rb/Bc4zhK0Z76LcwMkJWKvi6dKlPVF3ogVeNXp/euSGOqiFtE0J5VL7hK\nmi8joGp3BCn72tiHhaD67tzWS+TuEznrvqi2MlWtK9/vKam1vGG2xljcZM4ZljjnpmmSMakaRowV\nGIfZsAFJREpJUjaevXUiYtmwUJxDnAPMXgrR2Huujx5IW4CUatvwQ6yodF5RtZq65AK81ANYp81f\nkWdlNsKz42DudrthGMBCjXOqxCI5ZwSy6ABDzAE67aZpTk9Pc86Hw4FKpIKDrwnDWr1yiTu5ZAhN\nxQSD7VD2Cn1ePAtI39WsavVLvcP6W1Lh8uACdlANY6vpglJFHjUKQ79U3eta8+ilUEq3hS6k7/uv\n/ZGf+uH3v8M2GhvZejaBjCPjyEhxnrOIEL6XMxp6VG5VLaSUQMmo504dRLn/0tNRH4paexhDKeUQ\nsohY5hACs22a5uTk7Itf/GIOkYh+/OMfxxhTkuNhXHcOyKFhmKYg19fXMcaz89OLi/PVZvW1n/ra\nt7/7ndefPH7ztceWeBzni97bUqRv2/bJkychhPV6zbJgUvQ+qXKhdBlVgfgyiZwr//KOJ00zS69m\nY0oQgPecnZ7xaFVHqw9S8xMj0rcFCK6qJxZWR2utzg2ypW/GWmuzMQYd0PfqKHqMbYUZJSLv/X6/\nR2yON2v2IBdyIMT4qmRjxYxXW9nz83NVyvCaIaz6CLkqb6SUUMXFmTelz04qNIcpaUZtCqnVvSp6\n9K7rx1VYkXxQnk1NbakUUpVEstYOwwDXPpR5AdZalEbzpzBOVEIHVdCqMiimV7YMgqFPJ1UPo3P2\n9vbWNY12Qapt0/fXBkMKgax6pnXCypRacZ2xlMozra2RXvMVba5Ouq0YE7iKmKE3FWhABSSmy6JO\nhj6RLdj6lFKYb1X151INQq1IPRIpxQ/vfcpB5UEfB7osFj5Dql56t7V8Qk5AAwEh1/ksuSqh6ZuZ\nGYMrdXHwjFJFnBirgfq/Yj2wMn3fw27t9/uTkxM0Hu12u3EcN5uNLc1DmhhgZlQrvfcIGuqtwY2p\nJNxTwSUWyZ9C6yBzCGOGK0MOdV/0IKsGA1Mw0JKqBNL9Geeq+IAnjFXfgh5zvh944a6AklAhiTGe\nnJx86Utf+vCH70mOxiXnvPHeBh0R2wI+IIIGIyZmYkG1n4qfChnKOWu/WO0y8qecVF1M5e3U3+Bx\npHTl55zHacLqQTLfeOMz3vjb29vr61vZSZzTYTik6Pu+ZWtCHoTH4/HYNO7JsyfjPP3013/qgw8+\nePvzn00hfvjhh48fPNysz7z3IQSQ6bV9i35255yhu4k/RsgYY4TqupFUNhg6VhdZH9DFGCF86BPC\nQ+52u/V6nUp7NnKmImKcVYqRXFLtXFAAOAOoxCIhEEIYdwdVForOlIp1NBVKc9zZMAyu9VIKVzr7\nUg2pnjrUBqiAZXEy1d2WkjNFz3wIQc1S0aQLmAobtlytKDJY7/V6refEVnA+Zr69vdXbM6VtHnYR\nDixgSCCwwBdpiiNX+AWNJlVLikgIASgAtVhw+dfrNXJK0B0gfJumyVqLWARXhqU3xljvzs7OclUk\n19SllOyH3M/22GpePe4Qt50LTbUmbYwxMaemaUz5vanmhkBqQ6EWVTpq6DKuhtaYikocjrxWVoZh\n6Lq1vnme59PTU2PM8+fPQTJkSqYI34iqD+SZmff7fYwRfgMwh5/WgGkOWOEQQtd1p6enZm2wgChd\njOM4jmOIqeu6ruvtAwvqLK1pJ+0Yi5GI2noYbs4AodVoT9yzztfBQGs06tU3L1UAYQvjO4TKFZQK\nVjJWA5bqkAslBJg9jENERGVKuhI9Rjj7OvCJmRH6ID+B02etPTk5yaXaDzEDLny1WkH7M/PV1RV4\n9lQMNEkIU8qFakh/5kLNoK4SNgjPiH1f6hwFOycFEqlxDKRov9+rZOpERL4/b1DdCzAh6d6pFdxu\nt2+88UaMEcNSnz17dn19rVCOVEZAvfbaa+M4rlar/+DP/7m/9V//zdXmZLvfOd9O842xbtU219fX\nxlhnjYiQ4LBbZnYrN47jMC1j6du2DSkh1QlL/+DBg/Pzc0QeMQgRYVNQGUGcCnHS9t5cyha5AN81\n1lQDsEbD3+H47Nmb3/7295xrpuG4Xp+QxNvb3eb0RGzeHw+XV1fG2advPXv7C58/TscHjx+uT05a\n7zebzYPzi5cvrnPOWLqc85e+9KXXX38dktB6m3M2i+6lnHNOMUm21ksxNnrebcVcKhXdzDIMQvNI\n2HWoNq4yWkv44l0MMco9hnlsJPSylAweaqE5Z4x1ws9csVYzMwQXl1qcbkpd17nWUyF209vdbDZU\nwlKYHDzVfByo+LCmKhfDwNShIu4WZqmeNqSro2ZMdUGsBjipjsB1NJ5TG6AOI5cJYFx597ZUcWvn\nF+YfX+orQidof31MGB5N1ORquEtKCTlJdR7x8QXnTXJ7e8sluaEPSCW7oipDb+x8c6I7W5slDW1j\nhQNOkq21XIELYukv0QAI6wYZmOf57OysdnKphI8QOXWcsU3jOLbtSm8VjhEzbzabWjJhHiB1mEMD\nFmQoI1cmJXIBU+j1Qwit88453QVocGMM1C6eRX2RWBFCK0xA7ofaqUKvcZU9qz1u+G1UAB06bLDv\ne7hE+ll13pWbQ6+ALcA0OVhTfBZh0M3NTb2Pucrp1RpcY/1UOu1UhcG81agBKrgbTFKHKarH/LwS\nx6vfqbkQU2U+qbCUKsRUf0lVijuX/DzCHUWo29JXUC8yjoMuFBw1PUrqhtvSi2Kro4GPvPHGG7e3\nt1dXV8MwwONB1Ns0DQZvY8E//PDDt99+++rFJ//v/+ZvN13/8ccfnz94eHN1fXp6vt/vb65v0Hos\nkkIIInd1a9/cAeH0dHvvrXdad4fTEEIgQU5sIaGAVVaHUmM7rcdL1WKhooId2d7cElHOtNmcPnjw\nYJqm3e1xnnLjbcq83R3mm9uYIXt5u9/5zq9Wq65vjCX11Pu+99zudtcYNnh+ft51XciYQmlTSrQE\ne4t0EbExJtzHV0sJi+V+akRE3OnpKWbf2jJT0hgDB01FVo+fb5t5SqnwztqqmKaHUM2AXcYxLXk8\nNRUY8/pvFQVjzTzPYu6xh+HWt9utHpVUGLq8901xBtXxRKYF2jneJ9gmotPTUw2VUpmm472/uroy\nVTld3V4sQq6yyfqvhhHq/IoIYho9hAqIQN1YPReuMk6aTKirwZpSQ1Su+Ulb8uC2ZOHx1LHAJfVP\nyNS9ePHCeo8TpU6xlE5MUxXncNkwTlShFUxJGij4VfNO1lom472narQEFXt8dXVlCy5O7wc8hyh7\nQumrgMKxNaV9BOcfYgMZwKGF1Vmv1zpPiwpkGfuONV+tVtBcOWccG2gxfTSkqpxzn3z03BVQoka0\neKfuqS+UBzFG5jvEhy0oG65mO+UCXXWFQYfqtEyF19crQFNrFSdXFMbaHaK0UnpY8HFwZnNBRiAG\nUu8qFWS2Zs9sVYbUqCuXlGyuCA/xOL6aSoeb0RNh7nPj0v1CrAoV7rPGWEqVO7VVg5GpmOK4Sk/p\nR9Sm1sY+V8xY6gVCrnBXWuHGymMR9vu9uZ8zx/1fX1/f3t6enZ0hFvzoo4+stZvNpus6xILWWswy\nfu2113747nvv//jHX//6T//5//CP/52/93durq5SCvvD/s23PnN9dWmtjXGepolKMDdNk3Xdq7YW\n1O/eKee9KSU3awyRGGN1WdQ2a9CpzjRexpJQkmxEBDRfkjll2WxOvW/Pz/znPmsuX15b4x03bEgk\n9OMqSTzMA1k6s2aKkzGUUsAWjeORMztn4AVSdMfj8cWLF7FqN74LEuDT5zv33RiTQwhlbKOrGg/U\ne1bzDA/P2arWp+6JVLBalf6cg6Lpc+Hhh03G4VfnC1mC/fWtSqSKNSRDpbByHkUPM93PV6hJsKVb\nYlG4+c7x1EupptaDracIpxp6Xw+D6secM9SWwqI0ZFEtUOsCVQRqmWAFsZiasc2FlFbuNznVgTbu\nEN4Amo20zzGXkhWAf64giYv/Jc65w+EA1Z9L0rJt26Zr61OtD6JulOpQXUBbEhf6S5UErtovFm1F\nwrzgZnTBYbFOT09V6ahfrJ4KV1VlU/Ua673FggGz1nZdp1dQqbWlaVdTl7j5WDBvtbijFiIVlhd+\nZVPoBNWjUg/MVDDF2vBoUkDXU50GVW2pBuzkO3dVf6n+L1Wxl26l/iaV8bW+0IyqCsYboCKx70p+\nWHtjoTDxq9dVSyAXyFmuUl4q6ho042hw6WRAHIZ3DsOAA2Wq1JBeJFc1GM1X16dJf8NVJlzPr1od\nKU60OtR6/HEFPC/fZ8ev7ZCKIu4qVeVMfVL89/T09N133728vESczcxt215fX7/99ttd183z/NFH\nH11cXGw2m+12+/HLF+//8IcPHjz4xV/8JRF++PhJ07jvffe7H3/8onF3csWVvg5hErkPVa36TBCM\nDsOAEJ8pM2XDd9V9qaov+ht1NYwxQinnnNOd3suJcs5d207TxImttZvNiXMe3s80H0OKEsiwZWPY\niW2684sz713TlPZ/WVz8xnvXNMYYpViUqqcipSTLtgozJ8mZxBinBwovqUA3saDAFuG/vb2NhW4O\n0E91plQs1IrQwmB/ly5QCbYVYhK/R3bOl7EuSHcyM1SDKc1MehJyzinF9XpN9q7mrHuGdnERQemV\nFFgRZ70TtYt1D019QpAZcKUhNxbkXq5qffk+i6I+o6ngWFTN4FEdoWeAKkdPQ1H099SLqQ4yFdRQ\nLgM7mqa5vb1FyiWVki++7pUEoL5sBWxVNR1SdM5xhS3UjVMrq0uNT530q1qbaA7nFVDvInxMxhip\nnr02SKr1an0HLYz0DgwDSkpIgEjl9sIGoJyDU4pvV3e+1vJ6SqGgD4cDWuXxwZubm77vsfXQKdM0\n7ff7nPPF6RllSSmxkGVjiCXllDIvQmKJiIVyTEREWUiIsuSYUogLNVTKbIykzJacsZYNZYkSwcEV\nQ1RNpKZLlYgqWVMAb3V6WYVHKrCrKVlE5E+welgcW7oG1VzplrnSeoxDVEu4LRz2fL9pFDe83+8R\nGqovQpVuhSUAFlwq0JQqAVX0Z2dnWtnVN7gCx9doIJZGN2QI8XIFQG+rjLqqMAgeAgs1gfgBtT25\n3ziB2z47O1P1kivg/ieffJJSOj8/R6ElpTQMw9XV1UcfffTs2bO33nrrwYMHqKn/3b/7d7/97W+f\nXjz4hT/+i77p/tjP/a/+h//xH4qkzenpOB1zTklKIQA5AMnwMpktm7verGWj8zIz4XA43N7ePn78\nuBy04AuiXfNPuk26a0oZE+LifzAxUaP6Kic67AcjSBGbcZxTQjNZL7vt4sTMKXHoN/1mszk5OTk5\n22DlvG3Y2TkGw945Av3b6ekpsgticD8558yL6iuGn0SrjyrSVHoPFmNct2TVZBuqhrRnRZ98Cfkl\nd+0a7JMqcKb0l6RC/mFKAWkcx3XTmft0vFwY+/P9uFuPQSoaVuXeltlCUlgXcyEwbu0d83ztBiIv\nX7s/uObNzZLS1VpCSgnlcfW5qEo1xPsDAHVlQ5mpoarQFuwDVc51LGDTWLW81DpXjwEVyEBtCF2Z\nXQTPALSV+hXqSzIzkmCYCYaK8TzPx3FomobumO1JT3UdB9SGRNetvrjuqZTMJLRhJvHepwoYqecE\nlXD47OoT6J3XRxHX1wkXdQbPWnt9vdUkD5QLFhNK0FczKVTxucLNg/vk0lkJN98UGrfFDzA2yR3V\ntCoyLSDVViHnLHI3feNOlZSV0fXU/+YQU6Eg05VkZsCCcunDMyXLVJsiGG/cGHbWew9riqKamhar\nudlSToCe0lYnU/J4rrTEqoVTMeN/W5VLTT7+66rOKhHBrM6mcCibanYq/C09PvAAIF21mfRlphzf\nR/ekCuygN6M3xlUEJhWogasMtpRYSs0k35/GkgoGTD/onLu4uIDwXF5ejuN4enr65MmTr371q4fD\nAb7R8Xh8+fLl2dkZM/+Fv/AX/upf/ave+x+//8Pf+70/ePnicr1ZrS9Wx2Hv2OaciIz33pplJfu+\nj9sD8Z3+FRFITyoOsU4iV3Wktr8+9bUV1xDWVQSDXGJokbuGxb7rnXOnp6c4mE3TiaT1et30TRf6\nw3i8vH1xeXn5wYcfvv3O52M8FWG8czlosoD7+75/8ODBQkkqFGNs/V1OxeAGxIjklJLWrTUrZu5z\nrOjmLmebmVEmhf9iqsyYanNmtoaHYYiyOCCmUnMoBZkyy1WlTU+RKoKcM+RSr1Av7jRNcYGg3CVz\nVJfpUVcby3SXsvdlRkiqIMJqWrgMTVcKyFxIUOCkw79wZeZ0bSZVNeu/mN4mFQwd96A1A1NgQiro\nKh/1U8O66FbZMhNIg1RbodTQpcgFXqEG1ZVx2po8pBJemBK71IeZiLbbrb5HoSVUTUWrPRo8US1A\ni0qy91SVvpCpg+rBdiBQRqCTq5hYbcBqtYJBwo4cDgc8UdP0UATY3FD4NOucGBd3KpUB3qg2Ax3Q\n9z3IqrHFCqjBC4Uiut+/pcpUn1eU9TLJK/GBnjGqgPL1FmQmXTQuQTw2FA8Vq6YcKqyM2AgldEc0\nqXKuhVjIDxIGesjVzqlQuYIg9dW0zFQVexQ9QZXjaApKIlacRnpZGCF8JJWqUq5SHblKCWLloTRV\nEUsJ96UKpvW46X/1nfrtfB81gwXJFUmHpmFiYWHOFUWQFBhLrBDetsxuhsnpuu7k5OTk5OTFixcA\n0MIODcNweXn55MkTxNls3O12vz3sf+1f/vp0PFxdM0s+OV3Pw5hyFgiqpHmeOSeMJBJeWIJ0EUTE\nmjtaGY1irbFN01hzx0ZYO4541YdXfTuVWCLCVKQYQQfuQ0iGnWQGA16SbI033okjbuxE04vLT54/\nf359fX12dmbtHTxyGIYUyUR/PB7B1OecOx6P7KyCgBZvpkBhDJuURJPaqidNIcuo9zrn7FLKx3Hw\n1vfrlSEzhdlad3J2srvdZcqUJaTIwkmyY0fCZI3JpCdN1R/WJaV0OByQQPDLxHEPHZEkWzau8d46\n46xN1reNty5JnsdpCjNlYWt819q7RmYSyYhqYkzw/4goRrD8uqZpckjCOWdha5xxwhTnOMfAhBnH\nJi8zZ8gaa5w57o+ZhIXHeZQkrnEsPMeZMsUcMQDAsEkSKJP1xjmXSSTlTCJZkmRKRIbDNLM1LJQJ\nQzwyZREmQ8zWELEwxRDnGCxb46y3PuYoMQuLZSuMq6UYk/VOhJIkErLesXCm3HV9zDGlLEw5S8zJ\nZ2GgPJimYYw5YfUMsXF2v925xjdNkyTv9/sk2RnrGj+VMJeqWIdLpo6qjA0kplv1zGzIZMpYk5xy\nkuR9kylKFjJCxGxN67xr3DDNIBwWkYyUFyM/HsdxTCk7ZxGPdV2/WvXG2HmeiKBNSCSHEHNOMaYQ\nZiKGmjUmGWNFpO/by8t92/brdX885mkaRBpm6ft1SmEc5xhn55qmQJVyzsMwYHQCMPo4M4fDASfB\nl+lTOAOHw9EY0/pGd1NEQBqWJEsSMuyNY2tYBJkHSLJx1lpbGu9zZ1vMyhOmO0lg9l37ihuonixm\nL+HeYCdcwbDlQmYIywQEtiJcqJSp4LRS6Q3Kpc0AmwvjPc8zrlwHqVJlwqH+NCY21UsKel7THnr/\nqG1olgL1JFtm4N4ppoq0Xj1CGB7NjiCtol2DsMSg4dHbUO9B485cgBW2YmyRAgtCGK0ecH0/uA6K\nBQgumVVfoxWs9d57w8fddjoeri4v33jjjXmeveHGmvb81Fp+6603u1U/z/OPP/jwM5/5zH/73/29\nj55/Yoj7VStkb292bedTzELZkMmJpmniLL4zrmlzkkQlJ2TJCGUhZ+3hMMQYjXdt07GxMZG1luiO\nRk8K+CgV+nMqmQb1AHR/c86S1TwYhp52nDlnE8Um11jfuoZ9lDSMh3me+3X3uQefe/DowjaOl/IB\n+KjSMEw55NbNDy5eH8N0HA7EwszjdFyZzelmdTgcJOWckqSckYs0xMSZhD/lZNSyd88azSG5prXs\ndoejEWOc73yXhNg4a6xj12/6F89fnJyfUKLDOKzXSxJzLpzHtiAllBix73t0Iex2O/yJUhbDxpgo\nWWLIKTTWjWGepomsabzrGpfmMKcYQmoax2zneYwxW8vGOGaJES1HiVmYrfdNjHm73fX9WtjkzOMc\nGstkjW+6KDFOUSjPMYUcvPG2sdMch/3QunaY5rPNme+7/e0+iRhhPLttrLN2CtFIFsONb9jxMI27\nwyHHuNpszk9PY87H/X5/PD568CCJGMMkkiSM89x63/b9T370websVFozHQ8SxXe+a7pMst0djDcS\nJVHqfBclpjmxY990vm1zlGGeLdk4T5TINnbdrSE7c5rjHMcw7XfDRy8+OTvZhJRONusk4oxhaw+7\n3WEYjLMzipnGCJN1vvE+FgYmLuDmULqVQdkH5xd7tNvtDofDkyevz/OEe+ub3jaNYclpnuYYJTt2\nxjkjJgZJiVKIItx1vbU+50iEg2Fyjtvt3jnTtr1zxvvWWo4x7/eHlGSzWTVNl1IyxomkGHNK0ftO\nhAAv8L611jBTCOPLly9DmDebzcuXL2JMfd+N4/H8/CzG+ebm+unTZ/M8vXjxcrNZp5SHYXj48LF2\n8ECbKyZYa9q5lNlEhKwxzpHhkFNjXdetKOUxzI11IaccYmYSpsxkvWu89T5NcTJCrm1CmucU2r7x\nXbu7uZ2nSCmTNa3zxjvOEufsvUeD88nJibX2cDggKso573Y7ZoaLjWwBWlaRxEPkhON6cnIyTRP4\n5WCB5nne7XYvXrxYr9emwrmpddntdvozfESk4/DVQHCcnp5O07Tb7UIhd3klLuGq8gojVKs/LgmV\nVFrlhmFArwzCICj9k5OT9Xr9/vvvu4rRx5dJtQA31uAL2M7Hjx8jdtHYC/uFZgBAKHMhDDsejw8e\nPEAMR6WMDasWC4XdPM/K9cfMx+NRdaLmu2KMcRo3q/aw3Q0pbvpV4/1Zv6I5fPDDd5umubr65I/+\n9E//yx//YJh3X3znnReXtyK9/eTqD77zg8994Svbm+tpPN5sj13vGnLGdSwh5zLht/ON74zJbN3x\nuB+nwbXOGIoxseGr65cnZxeJxDqfhF5e7s5Oz0XkcDwC8em8yTnHNGsAvWq6lNI4HtNxQdDILMip\nwHrB9yKhMIfLmxenm81+uNkddrvj9Wc//8b3v/dud9LFcbq5vUK+bpyHQHG12tzsrs9OL1jMZrU2\nxlDKp+tN33bWtNN8EM5znJrOW0MPL86Z7XG/YyJnKGYm1BetQ0bEe+/bOzJDEiJZRnFConJOZNga\n6xrvMO9LCA54lCjzHJccRSJu7DjOmWmelz67q6urOpBXSF6uqspcUsBJB9STsFCUbDOmHvKs48Dz\n4vukBasuITBRmmeEcs5aArnFfa8KSZ5VXuDtYsVEySabmKOITFHRqCYzGWGy7H2biQzbYZ5yzlGy\nEZOZ2rZH7/ed6U7pOI15iKvVCtAaa+0wTSLSr9cXDx/CFU1wcEAw6r33fnN2bq0lazbdKdYhSubM\nUXJDTkx2prGN52xFZhzIdBzh9p6drdbNCSocU1TeNiZrGu6oIaLcrzdyPESkubz33o/jKDGitob8\nUWQmkZhzrAiWUjUXSkTQ2Cslp58K30yMmcgYz8YYMUxk2FHr+nmeJXOQlGciIoxetWJTiilZ5lzo\nEe/9KyIpiTHJGG+tbVvMQJNhGKYplDQmt21vrW2azpgl3wjtyszr9draE6gtIpqmCf2k+O/xeJjn\nOWdtyL2Xcaq1c9d1tYtdpz7GccxMp5uNtXaaJjJ8fn5+fX1NRGSNZSb0dZWRQgvqhxf+00XmnXVM\nkSIzZyYq2SG8IcYIyiiuarQas6bCFam56FyA4HgQZobKHsfxWOaUY3GA50YyHO4g8pywIr5qYuOS\n+uaC5dNCDhKGXOUSqSqd6lppUEJVAj+VFjfoAb097eO+vb0FpwP+i5dmbPTjtmq7DiGguFvnY6X0\nFHLBU0iVR9UClYZxGmLaCgANiwUtWQuDlL7D6Xg47I+S88OHj463W9f1Z6enP/nJT7765a/85m//\n1ttvffbJkyfr9foLX3rn8uqFc93NzeGf/dpvnF2cD4fjBx/8/mrVn12cxwgOVkFmxjjv2bORJDnG\nTDmADhV3G1LkLE+ePmW2CJLYOCYzpyxR6uRTrCDdpiou2sIVkiu4oBbnRMTYZIlDDsR0cn7yYHpw\ns7uZ0nA43jrTXlxcpBSmPJeyJa3anip8Y2N91zVd2zHb6+vDfr+NcV6ve+cgydkYg9Flhlhwt1RK\nem4ZJ5ZLZl7dC41l1WTcsXbWeVsulQkEs3AukCIAPQbfb+KRQjoA9UqlzAC/jO+/IFLI72toqUKG\nPL4p5U1boah1S7TcraeIqm5qPT8qu/qApoBwENjhCInIZrOBL8klkwPllVIYhgE1lGmaAHnSMZp1\nJl3FGsM0QT1pSye55srr5ANeKSV0M0AUtOyBOUmqGsrnCP065j7qxBS+rxoKrBuvp1T/Vf2CAFkK\nVfNqtcKRV32keBZNwdf6qNhL0aBbL64jFeAixapnVmvvrnAPGmNg3VX8aEmOp5RS2za73Q7QjOPx\n2Pe9dgVhebWGr+UuqaoO0Fzb7daVJqdavR4Oh4uLC2vtJ598wsyoTj9//lxjBTxmKigYKlgb7QSC\nOQfXg5YbuWqUxmOC6g2Vv3SflyEXvBxQ2q/EOnWII/czYKag6lNpSoNkYn10Qerr+Ir4QMMa9DPZ\nQiKsWyz3odtqLXRhX5FPqVJzVKC5oRANqMzrp2oNoNfHV19dXeniL2kc55xzkBOcvlQa9Uw1tCUX\n2ipmDiHM8+gc/kp24QwUojxNg34wlSK0Mf7hwyciwuKYfNet9/vBEA/H+eL80Ze/9LXj8fDgwWuv\nP3nzrbc+/y/+xb/85u9/+0/98n+w7v3vffO3P/e5z33+858Ncfq1X/tnX/ji2689eGAMSUohzobY\ntJ6JQggnJ+chRWNMTCbkICII9djacZyFzOnpBcJfzpJybNvOVNVrqrKpsZrVonXBVPrK9XhiZZCs\nyjmv1+tHjx6hHTCEwAvKlEKY1+vVEMcYY7/uQDMGTdg3Xd+vG9dK5s1m8eSQ+EViGZSGrmqwU3mr\nb8xWBIOqjWtBcrbqt6pFjUrfdUppvV4j0ldwhRTi2FTI6qHW8YRUmH6ICPgQW0EzTWmEVMeqNlTI\nIGlpLhccnQrlKydE+ZqkcgCpYKbr79WlsaWTA91bKSUdLSiFp6C8Zu891tY5p2Ntj8cjfC5bIZFw\nPGDGULONZciCnnPVHbE0G6pZBUSqBndwwX/r9aWQ66zXay3PAjGvnNm2ICb03vQOdde4km8unuYS\n7Mtyk3p9rMnJyYkiIXWR5VODHqgi6zMV4CeXKj2gbqYMk0XjQqoYYvQOmZkoHw6HYSDVjJp1oeKP\nl9teWmH6fgEl6grjUjBmtqJ3wkY8fvx4u91aax8/fpxzfvnyZc754uICLf25SlihsIGCRC4ULOpS\naCdgrbLVOcM26ULpQdDlrdeQ76NA1djo4qQK+Q32z1xhlHHUY9V3ZUtvFgwnDqlUSDPd0Fc0gMqJ\nHi59hcKx7SqGxhACZk/E0i5GxXNXFmNTdQgoqiUXeK0p7Rm1DwpxAvUDsOy1quVCHKXWhQpsDz40\nPAZ1WxV7xiV0UNihtT4MabfbPTh/OI7T/nr32c9+9vz0rOtW4xBPT87/6T/552+/887v/d63/pu/\n/bc/+OCDN976zN/4G/+PP//n/9f/2X/2v/9bf+tvdY1j484vTuM8E2VrrTBzNEtLDFkiur69ISLn\njLCZp5gltmzJLznz9ebss5/93NnZWdP6nMgQuwq2rkqV7iOzVK2reH9aJQIOA/Ypa+3p6el6vZ6O\nwzge53ne7m9d6zanm2k7Hg6Hft2pX2uMda4pbpOsVistUqo6qs8sF1iTqTK6deCL+wfqpHatmNn5\nwndJ911mV8aLQQ6AN4Po186RFBglzidiDipVVhHZbDZ60lTg6tj5FUdby3TqKKnnqHU8/TisUa46\nybl0J2hmT0ollgoRS32ekWC11irzSir8gzHGlDDJeFkHRbLOZa4dzpImuHEF0KXAP1X2Rnw7Tmmq\nZuCGELTAjsLAOI5oZa2tXazYS9VUYBdSQazhDVKR96iscGF80HWGO5MrjB+u0zRLl6hU+XS49vpZ\n/KB7J/djLLxhHEclgFAzo8dDTQIVXxjavHZBoCS7rhvHAd1mWCKwfKaUwNylIQIXKnfd6FTxW5vC\n5xur3lJsPTgVb29vReTRo0cxxpcvX4JTgytYvOIkmzLwTe2oLS1Qug61LlCeMSjNnDMKP7U+pWr2\nqOpxXZ/aG1M3E3qWS7+ElBgLwq8ouFesS62quOTK4AKqCaTqpVZZJdZVXQemwvTjPeAI1xhRncJU\nkcHghSP2SgQvxatDBoJKW2UqZBzO3TnQtjQ5Oee0D09fuOxqteq6Fl+Y0rL1XdcWkGdUqQO5gbft\nPEcifvLa02/97h984xs/Nw3jo4ev3WxvD8PhZ37mG//4H/+T3/rN39mPexH+Z//s1/7kn/yTrz0+\nu729/Xf/vV86Wa9ee+21/8v/+f90fra6vr5crbvWN2BESLJEitb6zNT0ZZYmpY45zMn6drXqHz16\n9Prrr1s2krIzTbPpA1opCvUMF1rC2vxQyU9qKKxaPhfWc0XHHA4HZt5sNuv1+rjbT8O83W5fXr1Y\nn66TpA8/+nAcxwePLtBC0PnWGzeToyyWbBKTZf7kk0+ur6+hil3pY1tsUgHQGWPYMIRf2wz0RNSb\nrufFWutUL+sGq1wCN2xKO3osQ+lfkW/cB7S5Vh194aVG06seVCpBPd6v91S0DwOoo/aDii8TCrMy\nhBKOVX0nardUg9RughpCLnOyFRGL/dvv97WHWCyZm6apaTycYp10xxUVty4xzN7hMALHRSVTkUvy\nWnUBFQICmFhXNR6q7gsVUWyt41ar1X6/A+pfKWXRGKFGQpcuVR1U+Kt6UtAy+jhq5IjmVMoYWHks\nI7ogbcXZgfdrRrjeXFOR/+tX4ynwyxijqjn81ReaACipcpwySD+RSkI2mIjOz88vLy81LMDXIXVw\nOIyvrCTuGV6LfhciMyS1dIqltfbq6irGCCFUzasnok6DaKbeOYeLqyjqLktphZHCQxgKbw2sux5d\nU/qN6iNmqmQ4SkH6OFDT+X4VAUunaqg2KlxFG7Zyt6n0cauvoO+nkrHXx9Hd59JxmUoPA7ImsIJS\nEuyKauMqC5cKigRPCnrTurUrFQaK+mZqwc5VMlMfTX+jig/yM02RaHEx+77v+x4ZacBJ1DXhxV3O\nFyePvG9//5u/96f+1J96+PDhT37yk//hH/z3f+Wv/JW/9//7//63f+e/+y//y7/xD/7RP3x5+cnX\nf/ZnfumXfulLX/2Sc/ZHP35/u91+8uKjX/2H/+DJa6/93/9v/9f/6r/6f737/e83TdO3XdM0lklE\nUogxp+vbrQiv133btqvN6hv/zs9+4xvf2Gw2pxfnhq31jXftarUZx3GIoxsbLq6zOl61HOpZy6Uj\nWDfO3k9HgeMVGBYkV9br9VXjT5pOOI9psN4exwMCI3ChhjIHOaUUY2ZjDdHheIQahD2T0rHjEOjn\nKroojM9c0h65YpPSjaMq839njUyV5CGi3W4HOBByI3gehSqpVOlF4aCFwhWm/hF8cN312lVXlSFV\neVnvVc0JlW44qYJrLWtprk93RV0JtUBGp8OV1gocHpxDKKZ6uhoecJ7nGOezs7Om8VxoLrmiwFJf\nW0q3RAhBhPSX0Hf1sZH7wYFU9TYUpfBQfd/DVU8KA1kexLVtG2MwFTEdbJIt2LnatJuSWeIyn1DF\nFyRD6qRQ6b0NIaqUS2EtshXj3Cvaqg5Va29A8cSql9WB4CqY0C+qVaSaMaKMfjUU+RBbaBQLz8tU\nCFcpqcj8qSnv4CWLBYiMdYbfg1rRfr9v2xaxkTZj6XqqcrclCUZVBIan4E9l6qigFtN9SKvyNEoV\nuPP98Y+1tKvNUINUYvcEQ6hPrd+iUlH7Z8yM4a0ouNaKIN8vgqrx4PsBhz5pbb24dPKZKvyFKeKq\n4VR9wdpLUCi26oRasVhrVYFgo5XjnCvuhrpiYUsLMJZimqaUIpyVi4uL8/NznAJFLUlVxxKh8TC7\ng/nD732rX/k8h9/93d/cH26ub1785m/9K+uk7fzJyfrnf/6P/bn/zX/49OnTy5vLF88/mubhD37v\n9/7Yz/70zcuPf/CDH/zkJz/+yle/vN/ebrfbm5tra62reu271fo4DsdxmGNYbdaPH7/2+rM3mDnM\n0RiKccxeJJH3vm877/12u5cCW4e0SxXUquyp6tOshivMMmqrpESrXOi1NpvNhz/+AB0RcYgxhxDC\nxq6nGBTcaK0nMpyFmaxbCuG+8DInndKCmSx50VTMLKW2WvvHUmLfWiHrwVkGh6gLnwr7EH6A4sbx\nCxW7sCoaU/obgOlUn9oXssXtdqsomtrZ1MK+qgwqPfyxcHNx4X5WBKpeWSVeNZrmAXJVW8oVaRWX\nLtFQKPzAvIkV0HyaLQAVa+00ATUwmzLEBWUqIDvUKGLn8NVnZ2cIF5oysRjWBek4Peq62sjpoU9z\ns9mgnAYYK1WxHS9eLX/88cdEslqtkAJGcu/i4kJbR6WUpvFdczUQ01RFIyUFr+23cy6laKv0YCij\n5ZFypIr8GxnLk5MT1Qu5SiGqclHFBH0BpLJS8OGG53m+ubnB6aISDdvSCLzZrMH0k1K6vr4+OTm5\nvr62ZfK69qlgGY25i7FU0cQYHz586AoFHAQSP2w2G4TvAHGh98WXNupQGDdqT3+hvLo/HERd0Vyl\nTIlIETGxDPdKKR2Px5OTEy3BwtFxhR3KVKRZqQABTk9PY0EEqJQqUSFeVBVcEXOoaqCSzIHMqGHg\nQsQA+IytcEmqQfh+izSeEY+PlCl+sPepoep8AM6FHmG4a/BckaGVKkOOBzkcDqZgc/DUUAtnZ2dq\nBVGdtdZCqNQvVCklwlTJjC86PT3dnJykgn42xbXKmkJg433zyScfPn32+J/+s/9pd3X7+utP/uJ/\n/B//7f/P33z782/9p/+7/2R/uP0L/9Gfu7y5vrz6aLe7Pk5Hlvz8+fO33/7c+++/96f/9L//i7/4\nJ/7J//K/fOELX+AsP/jBD3743vvjOIYi2Nb7l1eXRPTo0aPXXnvtnXfe+amf+qk333zrxYsXZ2e9\nCMcYwUrXNE1KGfkD9dggtNA2ppq2rv5xKqSxelpzVQfBcsFKQc32ff+FL70TwrQ/7jMl21hhOjk/\nefPNN0Wytc4Yx0ISU0xMLjK525vd4XAApEv5VhCKEBG4siBdMaUQQr9eUZV7pzJFwRYWfFVZIsK/\n/Vv/JucM/KiUUAYnf7vd5pxBERjLFiIvjGVCVMHMUI5Uyra5jJO5urp6+PBhKNBYKlP/YOH0yEmV\nMkqlvAHzttlsvPeYqIGzp6V+vB+cCK60HTx58uTq6gr3YyrKAz11SC9gPsXV1VXOGVWxs7Mzay3y\ndWdnZyD/SClYa2MMKaVxHPu+B/oO2kpdRSpJ/xjjen2qKql2A6VMK1CNI2WesUY2UIt934PU63g8\nWmtRmpKFXmi+urq6uDiPMaLUARcPehYHW20hfHBTyjahdBpBINq2RbWgZqZwzhnj6X4pSGMCW0gQ\nMMEBkm0qUhZdCmzuyclJSglqBeZH/bV6u6UaPq0EGSU/Bs7TO8pOSALkE3ZItTyO3zwv9qzve23H\nSSWrDicAAnY8Hm9uboZhePDgAcKjWErr8CFSGXGEXYNh3m63YKbHX2FR1MyrVlVrVKjJFlAiEnSo\nOOIw26rmhEBB7Zwe9ToUUEnDRoDOHPKAe8bvkSGRKlejMWid+dF4FE/HpStL46oiFUZ3KhW+JVPo\nbhFx4hlBXpUKBB+GVqFG6qebAscw91MjufTSYsS1NsZCYwzDgI2AttW/6hFTiVWd2DRORH71V3+1\nbdu/+p//51eXl+fn58baqSh67z0bQ8tns2UhyinGGOeGPRsaj8fb25vnn3y82vQpye1he5zGw3QY\njlNmev3x63EO8zz/5Cc/emnlpgAAkzNJREFUmcax7/vdbnc8HsM4geDuww8//PDDD2+uruHNt31/\n8fDhF77whRjjZnP6y7/8yyL85S9/ebvdOts0zjEVSIIz1rj9MHJJCwORj03HmaWqcwvBLhQ4FYx0\nLLx/tky0gTfw7rvvvv/++/M8pxROzk7Pzk7Z0hjGkKJtbNs2Dx8+evz4sSU7HgfHThJJkn61+Re/\n8a9/9X/6R23b/pk/82e++PkvoIvu+vq6Q9c63/kr4LNuurt6vFRY0Ff0J/ZORw7e8T5RycA8ePAA\nz3N5ealBD5xTaHO04M3zvFqtwEoJpXM4HJDWg+PMFdGZ2iTNR2tgpKEJF5g1NOwrKD78XkNUzb1g\ns3Eyh2FQX1JTn+DUgg+lPEYoIaCqbCtsBYxHjDO8P1cQgzBmVF51sMmlnqwBAVdZjlDGPgGizQXC\n8Prrr2OqJtJEkDmMz8B2ILgE9cs8T/jBVtVLeBnX19eqH6HXhmFAV6Bz7nA4rNfrq6urBw8eoLE/\nVOyriL5BhXJ1dVufZ031xIKMUMdWRJoyORSB4FRmTcIX0WYA1W5N0+x2u1gNVVONBgQ28qVq6pwz\n2+12teo1T6hINoACVHJgy+d5xnQ+VeuQFmvtRx99hDGmVKaet2378OHDm5ub9Xqtc9m5lNBwmOsi\nhJTZM+rO46lBPuJLq5DKMO7tcDgA1Y3gGCEpkoGQRkRLGtaA7BU3mUqZRGMvfZsmOqD6qeRhfJnf\nAbfPl1m6KEpDkjVy1QyYL3RZUuUkNThLhc5RIw/cBkJM3QJ87+3tLXQinjqUuVZNmRKiBhu7htWo\ncyd4HY9HpJLUy5EqnauxoN6hL/1D5j7ibprC2dnZj370wTRNP/7RB595661pHCmktlshKgohEgEC\napmJTCZia6x1LbEhSYA6OU/rdd80zcmDlfEuEXo86PrldiIjQm3bsXDbdJOfYxMdG02oPHv2LISQ\nYxKmpusvLy+JqO/7p0+frtcnTHa3PVrTEHGKGeJGRFlS5AWcFQscSYEMmu+pAkGyZXIHl7qR5roU\nw4a3weWNMfbrDuw/iVLn+7XldtV1XWeMHfYHQ7axzapbS5LD9nD58uXz58+ttc+ePXv69Ck6tbGt\ni5rjmlp6AaHQfUymxiS16cGN3U0HeMWzGIZBObJwtvF4T548qb0hPNXFxQUOmzEGeQn8sFqtdrud\nSk9teNTsLTdejgFiLBTcYox42hgjeMZUQagon56eoiSAiMcYg75OyKgqR1NSUul+E2guxVjNzule\nFmmeUopwzWwhUEmp9FcXzkc9Hgg41A7pckM1qNU3Jdl9c3NjjMGpA8gbR10nrAOkoP4yAHvqnyrv\nC7oLc9VlpQwxyO0AYqv5k1wwwXq3MMDAjofCBZ4KzhhqVDcrlR5DqXLTtRlDQwOyKJpCQbnOlHqm\nlFQnXH7VJpoUkmW89OLWAcu+Wq0QG9W+f0oJjgg0GmrUAPVBesFcp+g+W6ANEBhNH+nWq/V1Zb64\ntjfALY1l8h7MHlAG6jPpCYxlap+SX0CegcvAO23V6BPLCCu5j55XDa6ZGQ0ytOlVlfs4jtBK5lPN\nFa6MmcmluQ2LgzoilVqRrUDhd9pFRMoQGiQqdBHwBi65O7g4UlKdsJq+kFGpI6/3pmlVFSHAGsES\nnQuYOJcqpi0VUE0PIpxV4Vdt5l17fXX7+pNnv/mbv/lf/82/9Zf/8l9++uzZx8+fX1wAsu+dNURk\nluskipGtUBbJmSlJjMMw7A9biMo0Dzf7XWYSQ8MwDMMs0Q6HeRzH4YAu7DTPMYY0z2EOMQn5tmv6\nLuec5hBC2A9H661vm7btV+uTOaST9erdd9//2pe/oovMtBDGZ74bomEquIr6Aaa0jqWK4lIlSuVH\nVW4uiWWECkTElowzTeNc61zjnTNiiIg634YQDFlIlCQ5Ho8//slHP/rRj6y1jx49AvUqih1d10k1\nRHHR9kRUzTrArqkw643VtsrZis5ZVSoOj9LUbzYbeP1zIeLNZVA3RB8mB2kubexQlwdaxhb8goYR\ntRHSF2y4ulGxTHpHrgzuPxXPEd6lVBVX9EVBAaXywldA5SEjR6UFJFes+NhdgNRNaVoahiHGpcaA\nf20hHdGlp6rAgy6/T9taOESwsurY5pxB7glI93q9RqIDOTr1x10FlZmmCasIawQJwypp+tQU7lpQ\nzuz3+4uLixcvXjx+/Pjy8hJFJgQNyM8giAEpZNet1QtWCyoi6Bvj0leYC6AfsabqNVPGbEsBWEJd\n5ipfpC+YEOR+dWK3wjrmeZ6mYb1eEy0pTWxZ27bIl6r1ooq3TcRoQ4ImA+Gf5pKm04gE9QYsl1Ym\ncBsw8+oozPO8Xq816IGC0B4XLIKpKjTqfj179gyGARNrtEYFA3A4HPxC54g041Iirj1fdY0hqDB+\nan5M6ROfyzg+nBRVW9hlaCsIm7tP4x3LfAr1nNQb0GOLV67ABVh/U9VrY2muTFWXrilVZPAPxQo6\n0bYtTDJXhMhcGHoePXoEw4kjDIFsqpmTWG1XON1rP0m0WytRc7rabnff+MbP/5t/8zv//J//y4uL\nx3/pL/2lGGmes3NsLBHZRecJhVkab4hArpYsGTauabpVf7o/Hg6H4fr6+ieffJhEfN/O8zyNwUi3\n3x5DCNvt1lqTIh+Po3ZcLAYgxnme52Ec5qlp26dPn/b9ahgmZjtNc+vjb/zGb3zx7S+WfGPMS1KU\nnXOGWUo7nRrsXOFWVNtIRYOLFxXoinpIuZD0Y5fZ0jiPlqwY69um71vnXGbJObe+9d57auYxHPYH\nx24a5hcff3z54sXF40eYGNA4rxBQPKzlu9ZyFtKzUOt/VVm1scRF7jDKdB9JuVqtcIrQ1aFn1RWK\nXIgRPHd10GoFgcMPLa+Onik1K7Sdxwo/ik8hCtEAqDaQeofqExlj1AeEltSE21z4EO/ZXufU0uBw\nYns0/oXaVSvlPbzIVDsX+GpftT5IFVZqq0cqBTDcgC4XF+59UzrvsHRq/+APWmvBLY8V0KY/EOEg\nHYfp3b5MVcC96bAZPca1byKFTBNxA1UAKt0mTTfZCpEF5StVf6KULleuXqrjlg7zUlBNBVdZV+y5\nlMdhZjQBi5vBLs/z3DQLvEdHgSjURbWVVo9yXiZK4JzQfVRbKNPn1CXSYkwuFU3Vfa4wo+ecp2mq\naRcAxKCSyhcR5PpUKetXHI9HlDdgTpQU7uHDh2rCUynJqCqpk5CwlIh9U0V7gzcod4mU8huVshlV\nbUB1wiRVczfUV9X0o1QZS6niFT25Gqgh+OaK8N4Ygxm+sDRUJqoQEVyEVIYuchX2UcE0mapX5vHj\nx1AytW2DnOg9p4rSwvu7eqeed8McY96sT3LOq36dk3zrD779q2f/6J133lmvNjFkTyZFjBdy1pJz\nXU4jZYpznKZgkhDnacyS3cMHrwvnw3423KaccrIknon323F/M8Y0z0N0zlgK8zHkTLvjgVmY1WHN\ntrEr150/uLCuGcdpDiHnfDwec5Qf/+gnIFrtmpYox3nMOaNcmoWEWFWuRkgIGVVWVRFppUB3jQvc\nTKrizSItzmyaDVkyBpMJo++axUsYZ2ut0JLG940fhuH5R58Mw/CVJ08eP34MsYQiCiHwkl2869NX\nREOt/GtFQRWlOl5LI5uUfgIkc2KZHUmlkxFOHPxEPAzS9LlAJ7fb7Xq9hr6YyqROU9C3tWaEXkOc\naKq+RdxlLoAcZLpx06nQTuhmQGvgUQH5BVkAlhJPoXZLzbKIYLj98vCFtULNsAL2NAXXNA2WDuuu\nlSF1OuR+wR9lIawMV908yNKq663O5tXVFbJPIQSkHNEVgbDmlQisaZrT09OUIswq3gMFfXp6ivRU\nrkDSUPEodD969Oh4PJ6engIzjXI60qE3Nzd40rOzM0UxYJsgDDlnaMO5jG+H/wFfGz9AZVcximiO\nRZ0yLjBIzXSlCqKKqXqxcG5qGcmVCQtqSKQUMKTkWmESnHPWNgojRCALv1spTFC6Q6EOJln1OHJQ\nVNx/W3oGuZS+cP7nMilDpRewjlxYpVMBTUCWzs/Pc84ILl977bV5noHF6LoOIJ3dbqfeRrrfSqIC\nbEtaWFWPuU+sog4c5BPpWVeGrHPJzWrflR6lWNCDekb021XF6xKpl6PexlRGwaKcibAez6vhkZo3\nvU/kmjS4VENOBS54eXkZK1RkbYnVIobCXqhiJpVjba0V5pxEJKckX/3qH/mn//Sfv/feD4/H+f33\nf/TOO19++PDi6dM3Hjw477qVSIrRMguLJeJpDDc3h3F3iDHO0zQMhyRZOF9eXj5/+XKKIUgchiHF\n3PuT7fUuJTTRs3W7/X5LlG/326Z1TePY5JwzkbStd41POad5Timt1yf7/f6Tjy9TyNvtdgEc2cQs\nkhmTgSjGlIXd0j6cKwykpt3gg3IpIKkpShVWBcfHFI4oLi3S1hvrrW3YNZ4oR0l6xhvrc6Zhwmxf\nvr3d/ei9H7333nunp6ef//zn33zzTbWFKSXvfalJ3GGkeZFMUk9Xs+tcylpyP8+/4K1zNWxGA2oq\nDIY5Z/VwP/74YwgiqpTDMMB/V9cG2TxfOC4L4dtdy5H6VrXcUxWZ4TZSod6C6sTpMhW2h6uywXa7\nPT8/hxOK44EsYixwZNVZm81Gkx5QUgiGoJWQQkEyUOsQ+FJU0YDV5oJ3141PFVkhVpkqIJNqLqpy\netBrbdseDgfEZ6enpygMfvDBB8+ePbPWIu+BInDXdSmFvu9DmH3h19FgAk8E5ILWBjTCQNYebG+Q\nUTw1lFEoo3S899fXW03Q8f38qq1afbkUeGr51vwSF3iVxog4DJrK01e+DwfXi6h7pNoZcoh705SO\nnk/Nx1pr4SfBwONmgIlQTzyX9KyebdVoqQAKcGXVjyq6TeGC44L4t9b2fV9Pz1MH0JSUqR5FV6Zn\ngetBnQYNPrRelQtuyJQUFt6pJjOXcT66dFLNJ6sXBNIiZepjbX6gCLC8/o4M5i4JxgVlRxWSAnuH\nk47mBC1lu9IGgBfuuU7AQCSmMh0D/isV4K+avd1uhzfg47FQS9ShrS0dI6Yaq0YljZFSysmQ0DBM\n1vi27acxXF5eDsfwwQcf/M5v//7DRxeff/uLn/3cZzbr05QDiWk7f7JaN42TlLfb7bDbz/OYYpzn\n6TAcs8jhcNhPh0QyhGGeZ2v8u+9/5/Z6K5xjjGyESA7HW++t8ewb65xhk7OI86bv267rjPW+63NK\n4zg+//CHH334ye319nAYnFsGhVjL1lrKKaUUxsTGOnvHcqlPFyu+FRVmJIH191KV6gFH1H0sXo4R\nScY0Xdc1jYty54B2vg0hjeM4TfNhN7z/g/e/9a1vHQ6Hn/uZn//MZz4DreX9QpHVdZ2B2Msdxwq0\nBqIlqYgR1D3V/+rLcZXLUu2pDin0LPBy4zheXl6iPRCeNYIhLBOY5HEwAO2XUizR8wnRlFLJpKod\nV1dN3aVcqJlsgUcjSJfSkgnRBAbp6urKGAPvG3sD24MHQSlLwbK2lMqwJbCsilCHgsAqh0BN44gk\nRgBJXd930zQz0zhOOWcRPJqxlpiN2jlda00poN8FLzWQwzBg4jjwF6bCK3/00Ufol06FpMtau92O\nL1++jDGsVuvj8ZCzjOPonPfe7/eHnFPTtN477xsiSQlJyAb/Hg6HpmnHcWyalhljIAwRdx173xjD\n1roQ4unpKTIwOWfEEDj/wzAgdlEvDGsLTYd4S5Mzc5k2QgUwgsIPL5m67FzjvWW2Mc4wECIyz2NK\nyRhqmsZ7S2RSSi9fvry4OPe+8d4bA6d7DCH0/SqEQMR4XmaOcaE82G63qnCxlYfDAdP/4IIAog33\nPN2ngMMTweew1u73+xpSASuSC5cHDN7xeDwej5q9VD8d1wTsEMEllCYipGmabm5udrsdYClnZ2fw\njXwZTaShgOogvT01lnrO1XjkglxwhUnLFTgoPt40TaiITtQem5JAU4cXZ1ZTMVSGLVHB3Op7NGya\n5xn9FavVCqm/+qVpz1A6jYBU9hVzeShTP9QAcykH5MKOYy031idK3ljXusY2KYUcsrA4tpkzZw4p\npDnNMc/zoe36T55/8Dvf/M0vvvPWd7/3/cPxNpPc3t7+6IMf/uAHPzg9uzDE4zytuv7i4oKIz87O\nNv0q55xTtIQYNE1TGObh6ub6dr87jofLqytkBeIUdze3ZE1KgVmIZRiGtnc5Z2OzMSyMoVNutVo1\nfQPLfXV1I5GH47hen9zc3BIZsoRpOw0Za20SHudxnudutRazwBOw6Sia1PMV62xNzpi2lqd5JpEs\n4p0T6FtmJhLORihTEkk5i28dZ5nHQZK33nW+7ZuOiHa3+5RknuM8h5cvrr7zne98+PHzh48uvvrV\nL5+dbg777fF43Dx8lJmDpMaZGCNlI7WBqbg8VA2+ovNfff3Wb/5rW+rVUNM4pW3bDsOAIAMO+Hq9\nvr6+hsjCDm232xcvXlhrHzx4ABWgjh6S4+v1ArdVleoKZQP6XZYor8DPkTl5+fLlycnJOI5I1HBB\nNMbCQ4NcVi7kaZD7WKY94venp6fb7Xa3273++uvI+B0OB2gEay2w6QjdNptNUwZHhsIAi3RfXnLu\nc85kDGHSknNN2/p5jtM0HA7D7e31V77ytY8++knXrfAVEBcoLE0a+NI1BYdaMyr7/f7x48dUhrFq\nKw+q+lIlfJG5YuZxPGLyk3MNzqwxlDOlFOY5em/btp+mIYTUdQ2zHcejMW6ex6bpNpvV8TiKJGt9\nCNMrz+WcQ2sb0N4QIGzQfr9Ppc9RSsMmMnLqvKui0e2G7wzpwnFqGtThuETzYq3z3qWUQ5iHYSQS\n75sYQ84CMQshzHPEHeJJY5y9b40h/GaawvG4F2EFgpvSFpMKGAleji9tSbk06iooIxbIFpecLWwq\njj14cjebze3tLQRGoQEQm81moyhqRNgajquBwdeZUuPRMCKXojR2+Xg8rtfrk5MTeFdoHpqroeNU\n+ttw2xhThLhfRJArg2eg2j+Vgk0qE+r0WMFuoV57PB7Pz8/3+z0R3dzcWGsvLi6oQFFsGZUEJnUo\nEM0XUem2xnabCluYyshXKTB0U8CiXFqakOyF5cZ9quRrWBZjtCQpR8pknGlcIywppDnOKaR+3Vu2\nmKJpvU0h7Q67KcW2byTRRx8/f+8H7/3wRx+8+PjldneYx5CJGtd2/dqym2PIMTNz166YrQoPZZmm\naZyOhh3bYkpzKp56SGnIOWI8IxYkaS6EhHkpiSUSZraOJU6rdZtSnoYRg1eapjnZnP21v/bX2rZt\nO+94iWuNIWutIduUAcG28E0odGuu6EMBmj05Pcfk0uM4dI33bTMc9/1qhQyaYY45jsdhmEZnbNc1\nxtJq1cFlcc513SpFORwO2+0+Z/ngxx9+/NEnH3744e///rfOT07/7J//s2+89aRpXEmqg21hqQgY\nWuBdYU7M3HWrtm3HeVD/PlZ9eLbiY9Rcrru4WAjyEByoZYKu0cyv+kf7/f7hw4fGmJubm3meHz16\npD4dQhDYRcCWrLWoAeh54JKyxFHn0lqs4J/r62uUdjQ1TGUWS9M0GL6A4Ezzh5qpZ2Y0FWGfvPeY\n1IDP4vl3u50tOCi4ZrnMvdacG9QH/kW+LpWmQufcPMfdDn2Rvutkv/eHw+F4HPt+jTKAepG1olE0\nBxXic2stYAi6tlJ6pKE0AZaFN60W13tvjGMOMeZ5PkoBv9V5DGMCkUFearu9zkuXVRZZGrPsgkV2\n1iqd6LzbHUQEDgQcUugdU6B0tqD7sMWh0GSYghtWF8eWiTvQIOp0xzjP89h1LZBsRRx1ns1StPDe\njyNCexHhnO+qncyYdwXJZKJlFhezRQr6+voa+973/enpKZJCEAApCA515/FQ6O5CTRQcXCcnJ7e3\nt6nUz2PBTKtWVV9Pwxcg9WEG1GnVbVXbo7lKrBtMi9bqNXuJ2hJy4DhEQPSp8dOaIg4dZAPQ1lDx\np+AZFTEEZ0hdrtqQIF1srQW8c57nhw8fQpghCVdXVzgUq9Xq4cOHl5eXuB9VJbA9MDNqO/k+5gjv\nQaL+cDjAe3Ole0SzJoCK1FkTtzRgsIToXWsqSAURtb6JHC0bZnLGZspAD3hvNxe9cSbG9Do/Wq26\nN996dn19u9vu/+APvns8jFdXty9+/FKE+75vmk5EDsejMU6dRWYOMUwx5DwVGV6od4goS8qUhCUJ\nTA+RSJKMZBW4loQNW7MkFzMxpe3twRjT96tpmq6vr58+ffqVr335hz9+f71eI1dPysnEbDN1hQpL\nq9rQUTDnqfAvEJHz/vb2Vpi8XRDLeI8QGeY5BCbxbWMtN42zbJxzbee7pkM8kKNMwxzmNBzG4TCE\nEH7ywQe//Vu/u9sdzs/Pv/KVrzx5/bE1lFMIM0l2RMawWGZDmHQsIkjgL3pARJQES9O/eIRQ8XDe\nWSNEG/gALqGhlvZIwk/MOUOstd6gVhozXpECBs4YEobTWHSfUXFU2dWzqjkuLgVkhGjKLoxSMP4E\n82kLTwGEEjlDjbd0cjuUkWbA9/s9MmA4gTHG9Xp9fn7+8uVLjWPqA6aVBji2cCQPhwNONfKHq9UK\npKW3t7dIUfL9eW5YwFjgEnnhJyUiAkM7cIlcmBQ2m8319bXGed57kAUcj0fEi9igVAqVSE8p/hVu\nlC0FGIUVQK3AdTg/P1frixsGlm8ubfZ62rEaKPvbQueqHroCW3RndftSxdFgl2Yje3Nz03Vt7d9Q\nwTjgG+E3QMbwsymFsbwwAS5T7KRKKbsyI0DJcrS6rsdYd4QrCtFUUHAa6OQCXseDuAo5ibhH/Qld\nfykjovG98Fj1UmpK8RSmmo0NV6zOjOH4SOFxsCW5rfOucil6qbrUtDCEyhdu2VyNEcGBhZbXbUqF\nWFJE4BiBxAQ2CSg4VBy7rkMuMYQAigG5T3mcSgPfxx9/7JzbbDbn5+eIIGMB+tuKFNGUVLxa6Fia\n0vApMBtpOFWcrdBaR3Rv0gcuiHOXSw1Mv7dx7RynOKe2aZ4+ef31154cj+N+f/jC2188HIYf/eiD\nH3z/vevrGyI6Ho9gnNLEbFEC2droHKAlSWTJfxpjRDjmJufoRTDVU0Q4pZyBppMslDOJELYoRnIc\nj0cMf3E5k7V+szl98uTpNAXnwjQFY1zRk0LLNI3CApxL5j8Tj7OIZGHnW9+oAbMhDMzsyKQQg2Q2\nJoUsnlxjAwUWYqEU8zyFxlu3XjNZISNkUqZ5DiGMwzAMw8jMH7/45Ic/+tHHL543Tffszaefffst\nY60QpxRTDi6JtR4GI4kYi2YyNtYYS0TExugAVbUIKvy6cbWyddpMqw4djjE8d1uaBKUAzEQE/jIU\nnJJzqBnjAhmIVbNeUw13wTFWQwLHE+qemZEZgPrWnDIRNU2z3++R9sEDiAhSCji3uDdfgNepoE1y\nqTzjnQrPhcii3I37NwW/rreqphdvtgXXpEkPvAHHmEtdXTWsVGPKMPrTVt21MUYQAWCtYDsVnoC7\nwhPpOkjFvW0K5AkOfq5qaeq7SRnAofhp+dQQWL0USso3Nze5QA9wG/C+0Y0rpZdIKSFshXHX+FK9\nePjjqvqda/BcuVSStMStJVYqaHLYp/Xa1cuYCp5KM5mqx9UpgaaA0yAigKUAr6iuBlXVYIgi/Bus\nP0roVFAqqiVf4YXT/B4WxJQO61jQ50iu6kPlCj4aC61ffTUuMAcqk5+ohAWpQM7URVDYZyw9eXoF\n/FUlXGUDzhlXRCHApiKHnKpiKkIWOEZIb6BmVh9kXUndAmb+yle+st/vYcaU0A9d8FRNx4A8K/FS\nLmRjSHIiNappVd0IZmFitfdoPlG3JlbYeikpwaWMGxMZZiI2pvVNXuXNak1s33zj6de//kdZyLdN\nCvkw7F+8+Bg6EOVAoLSwhlSSNGpHc85TiOrlJFmCp5SXinuEC5JTmFPO2RqyzOD9ijGenJw8ffr0\nyZMnwzBgRFlKCZH6shFsVl0X5yWMhpzUO6V3pRWW/XaH4w8vtuubnPMaun4BLpjddNze3HZ903fr\neU4xovOS5jnt93swG93e3n7nO9+5vLz8/Oc//+TJk8985jPganK+KV7IgjzKWYiIl2GvzBVDmHqN\nXLHxQgZ0Z1VbppQcmAugNfQD9ZFTD4gKQzhqaJqkJiIAhLBJYIWBKkEAUUutOuN1XVRrthrT4U9Q\nE6bUAGxppoEQw4FCZUutiyndMAiPuIw0BeTJGHNxcQH7h58hRi9fvoQPqPGEenzIkFLJ1E9lqiYW\nAcf7+vp6mqYHDx48ePDAfArXjzpQKi0dCF3hYqMYY6skPpoih2HQMIWIpmlSEsla6ahKVUeeK+AN\nZCUUvH4utXdoDb0NX/pAUbjCMAUceFgLiIQW4ZWzQMuqGj2YqutF9b4mo0IIzKIpx1x6nG1plMaz\n4LO4sb7vj8dRzb8t1alcKDk0RJAqC4e/wp1SfZ0LR7WtIMWqVvT+VatKFSQpIoCqsN5WEPOc883N\nDar3vhBZ6anLBQuLl65PSgm5uFyhTH3hqtDziIuYwgyrB4fLGLpYdYjjueA6cFXUwToD4I47h+5D\nAlB9mmEYUPhE4RbuERYWlTPE37hOvRSuzDuAX6u+ji5jvaq60VJ483B9qirbuaKzyyUvGuMsfEcw\npnGnMWa326VSYdLT4ZxLEltvV77PTDnEOUVDue+adbce57mx5L1JIcwxdI1drc/e+MwDKHZ0AkDD\n5JzR7QtFpJX5GPPt7ZCL7cmZwsKMgKHjMSQpqgMqjiSFvm+hrC4uLh4/foyEUyqTydShEREWWnfr\nVd8jvQFSOCh9YIZBnayJgdVqdX19Sykz83HYww8QScBipBQAzZWU4jxf7ff73cBmCUasteN4vLm5\nubm5GcfxO9/5zvX19dNnT77+9T/6+PHjk5OT9eok5YC0PTNbu3CUkFBiyXlxBYwxiJlA77ladWpc\n1fCodlJDhUvdsY5ThSijqr1Df4a9tdZuNhusYEn331FGUhV3m6ollkoGiQuS+PLyEs4mhFLdGSk1\nLvwVyhRVfZw3eCs4tNDpULUgxwNBlrqfkHUNONSshgqtYArXpC2dmLp26hprWBOq+TQwin3fhxBQ\nvtput5q5wqFSxYenVjnTQb+h0JPjB3zv8Xg8OzujwmatxXB0DplS8zCFx5dKt4fqqVhBCdTSq6uu\n0QaXVHgoXJmxUPXU7gwOmy0UgqYi9VEVXy+XlCZiaC48wjRNImg4WKDJ0JipEMlQGRekQWrTNIfD\n+IqbQqXARiUAtRW/2WazOR6P6MGEmxILtRWX0FxtNlQ5LP3p6SkRofSCRO4rsYu6wLWca0yv+lGq\nzhhV+vUH9ayF+/ykXBJ9mkzT6LPrOgwy1xKprgNMlK1IqkyZ9Y7cNbyHXEYA+4rGUOWw67rPfvaz\n4zh+/PHHzIwFgf7F0VOazuPxmAq1jNoJPbOmoFvhSbjSWwbvSs9sLK24uh3Y91zauZgZ0Y9+RTFI\ngZxv22a1WuGycPJwBu194lQpQ0xcY53vLEvOkubAQs67OE+SZmdps2pSNONE1phu1X7w0Y8zJWOc\nMdS01vnOmI1z5ng8MYZEGNgfopySxJAvX25jljDHkj6VkFNKicRE9DpxoclPZCyFceq6JROjrNPY\ncVMNS8W25pg6v9T5UsHjYBPVA6Mq7cnMp+vNndvEGeKNOGyaJmsZjD7W2qurq+urm8354xSFmZ03\nKD0eDruUErP94he/+NWvffnp06eLlDqWCG2GHAYbdmaxJQznU5a0sFV3TcM4DYNsRWiiShJK1SGD\nAa9ZFQ1e2kWYC9h6HEcMWYLIpoKOVX/NlEQ8jhayMerSpgJkcNUMLikE21KNhHGF10fLD0QEGjft\nPYIUAlyXCsoAt21KA7D3Hj5XLvk69O547xX5pi04tpqMolY5Fti+4lioMAZp00kscwpA/ak0B1IG\nj7rCqySlmRzRDFSn+vv1alxdXeE+a098qqYJ6FLjftSu6/XxyJhWh+fVndVb0ohEk3LX19dYWxhy\n9cGB/qj7P3AnsAp4xWr+m5QIGyvpF17OpWLPJVmkKGTUBRWjjxp+0zQnJ+dUceSo86RyRRVM2ZfZ\n5NjcqQyXMqXvr5YxzTipQGrgTlWPERXoICJvPf/4uL7Nlq4XfLUrM08RKOg9pIJtQyKOqyEOVHqG\n+r5HsRORWSoMRq5qe9RPpYKVsAWf0pbJUooUrbX/ZrPZbrdQ4mpi+75HAyZkDFKHrAlWRq0sFdJo\nql6p8Fww89OnT1NKx+MRqTlA74wxh8MB5yJVvYZS2Lmo+JTYWeccPAldcLtMZ05pmtWiqwmHx+kK\n+V4uiB5IV4xRnNjGUSIW2LcwjZPxxhubmSgHphSm8TjcPnv2esohJ8oS5ylO85CTGJZ137GRnMg7\ngl2RzEnIGB/mNE1hnueQYoo5pRQlG+PiUpFdUtaJ2BjDWTQohKDmnLtuhSbTkuly1mbnJEk8PT1f\nwl+iEHNMEmMMMQ/jrIApYz0byTlL5rOzC0nZWGoWmow5TDOLccaSb5hZciaRvu3X/Xrnjj98/8e3\nux3S1NbalCKz+Mb+7Dd+9rXXHj1+/DCldBwOSdIUpmmcrfWIF9u2Xa+XqSgxSWMtel+ZmXAqjbHM\n8zx+2vyoeqzPGhHdcV6Fwm+oYUqdAYBbjUT84XDQ98+FtTPnjCQM7hXnCoGk9q/EQtwbY0SiD+df\nj65UgbweIYQ7qfTAP3r0yFqrUFpmBtJBM4e4Meccmh72+z00F3hXlY4FTOSgMHj+/PnDhw/pftee\nnjqYOvw3VXMitMbw0UcftW37xhtvvPbaa7ABCHo0qUUlVeW9B6mB+uNdmfJX+wioyqCVCk4x6lJI\nJ5qCyADmDY7qo0ePdOO4dJvqCVc3XwNBgOM1HMwFrMHMWHC8B6oQvq1aMlVAcGK06KhqBUULqLZY\nMTQ3jWvbdhwHKoSEmp+8vb3F/SOIhNtYx9ZcYW+oDMJIBYkbC1M7ZsKifysVuBE0tSnlKy7tgTgJ\nDx480HwUknupKqppQMkla6qOTp3fQ/cJYmWpiHRVYLga2BoLSZct/TTaaq2qFsuC66xWKzTw+tL9\n40qDcyr97fM8b7dbfUackWmakMLCWYCpxkcAY1F/8fLyMqUE/rHz83OkGdBlAZQNQnNIBWjgTXnV\nsqHoGywdViMUJiopiWt1XjUctwUEjJOlvj8yY1Z5WCpAkJa6kTAwFUgKVdicM9g/mdkbZ71xzsU0\ni6TIY2OdUJ7HozHmdLMSkf2wzzHGhK2HtDnrWZ3CyDHnTCZbY9myzXRx1k1zxFLHmGNOKWLkHAqZ\nJEQ5UwgBIO9VuxxqBUBBgBGaU4XA7LqOxLCzhg0RMgpEJMwQYJqmaRzB6dwxk/cNbSTPQVJ2fpmH\ngrog3Kn1enFYoU/eeuutR4+ffimZT15c3tzc4Bvbzq/Xq81mRUTG0vE4EuWu7buuhWKZ57jbDsMw\nrFbJu967lgSZvxlv0KdQT0WTUlIBiNQTklLiIaIluxrLdBwUD3NBtSv0+fHjx+CPSdVcmVSBttV9\n1oqIMWaz2VxeXu73ewDBISjoKMRFYN7gPw7DgNI0Cqdc2uVCwRCjjKSBGs4STkguNAfqQeN+kMTY\n7XZnZ2e+zLtUuxtCuL29hVjEGFGuNBV0gqrxIepRgvIZewwV9uzZM2C79USppjOlcq7ZPD2HiDXx\ndBi9QSVVJSKY2aGZcXUIbm9v1+s1hi3hQcZxxMcBMg4hIP0C+wd3Aac3l/F0MMbf/e5333jjDdyJ\nDkUEQlpE8CnsVNd1kFeqSMrxsNDUseLchPLCduCwWWv3+z2CSKyYVkfwG/WVqDC/QaGo+5zKJGlr\nLcK+m5sb8BL1fT/PM6hgNVjRiFbNJFQAUu1PnjzBOvD93n6pGBCwsEiSxBixCAgZr6+vc84nJye4\nDWPMw4cP9/s9cOHAxUhBDXnvVa7gZOSK5w2RPW4GLheVeb7IsSCC1B+w5qakc29vb20pjyH4gJwj\no47vhd2KhQ5/GAZgSuG66cahXwr3CedDc7PII202G0Dp9vu9ZuFgA5pC2YdOKS4keDlneEtwLHRf\n1LfDbUOwVT/gmlqjhXyWXLFL5firCNmq8YCqWUrqzs6TfmlnrU2Zcxasv3XWLhXoA27A2S7FhSGl\na9bjIfSrFfZumqYsU2MtO4bkpByJaNW3bdMcC2HmMM37/d4aF4vqj2khrHOusdYz2b4z3kXDxtnG\n9U0IofFLB0LOybulmjuOo2QKlNl6wxKSEGUiE+eQM6HPVYTGOXpvOdP+eJyMscQ8MRFN8+yca9re\nekNE1ntmmacpTmD4FbaWxa5OTsk6Y2i9XnddIyKHcXLONMYZ440lMWaOSURiFmLXb05c21lrQ5Zh\nDtZaYWOMTTlTGeyZQBTCpP6TL5SGKjCaKrCF7mDpY9KapDpc0E04LW3b3t7eakJWD7BGRaEwW6eq\nygetAcyYelLIjIGSFfgZCDHQcVwx63CFzUgVO6f6rbbMDoBSDqWBA2EELcMgkuYrPp3m0ktpzVMP\ngyZAkNBQGx4K9lRJCnJpb8rV8ECp5gfiN+jtV+8PJGn6Trlfk4BOR+VM4wOoMOgRfNH5+flcRkxt\nt1tgc2Phn4aHoffPhboJKaCzszPYMzgH8Isxc4VLx+Xt7S3Mec5Z0R9YVU2LIYDTNFQu+WskIbGz\nMBjOOZE7FCKcfViR3W6nNRIVJOz7atXDMGiPAVbj7OwsFU68XICaWsPT/YVdxA+w2bi+9mUjIamo\nTlVkSFjhLGkSGDYb0nJ5eWmMgbDBVEPqAD1SqaNSYtH7rxNoL1++xEGFOlZFjEwXNGZTgPuhTGuE\n3wMSB5iQnDOI2GGBNDJQGy9lEgQWChfX1LEppSY9AkUzLvoiFiwZzm9buGXxILglKZAEDfFTQW9i\nQbC22GJXKCKR3tDFr33nfL8ClHMWSY21Oadckrq5aojUj/BdsTOvV13PllImY+c5hBwlSiJ2rhHD\nOedEYowhayRLSjKNcZoSScrJMHnvemtaZs7JkDimzJSZmImtca3zZMFfJcwsS0SbmqaZxjnGGHJa\nYoDCRCwiRHcsxq5Ay1zh8VL0ivfeWpeCjjhA2AGbbUWiCBMJKEtyzvMcJzats0KZsyQSS2wb2/nG\nNr5xBu11USKLZCaz9Bh0fWc0sRFCYhYmkzOlJESJo1hrs7XEOUURyZLJsGciyZSTMAkbQsXBuTsS\nI2OM95ZiMibVT6p5AvVfRSE/0CypMEflUu2EOUGb9/+/rDfrkSRZrsbM3D0it9q7e7rn4uqSDwQI\nAuT//wOC9ChI+EBIXD6JlxzO9PRSW1YuEe5uejhpJy17kryD6qrMjAh3c1uPHWMZQ513x0KxB14M\nCz8QR/izzRk2Ye2SF0IRrT8+PiIpNI7j/f198powjQ2tUUw0W+Aqho1hyUfDpFu0R6iPD6gONYby\nhSgQs9t7h40ZnbDuGBhL1TNap2jdgaSTk+FrmPRcHPnNc4VVvbu7Q/FGfSQwojHUS5qTz7vkCXQE\nz2Hx2XHPz8+IpfD4SKHgT9fX1+TmgYex2WyQusQXDk6IICKYYMszAI2DGj4dAiSLAPSHZ31/fz/4\nzCRYCAY6yWuY+FqGzoNTGrbW9vu3nHOt51w/wCkYLsy1YoBLDxcmUAI2ZLPZgMlXHUCPVaIlY565\nhPlDInJ9fQ2NjOh2DjQ55rF18qYC6HekemDylz6zdfTOawoeko3qFVZ0kmGGOhYf5pMFLcgegg8c\njeJ9oGyhZZYDxoMSwiB+9p6teLAZ5EUpwttw2KvD/bMD9CmrPGgQe84lQqTCDKE5wL35ODgGfC20\nEKhnj5sjEZLPdGfevgVKvaizsuOb+D2ttTIuWju39Jt3U+XQ2x8eRKdpSmUQbcd5mqdDl541mfZU\nRhOtvZqklLMm7da66WKxSmnMOatmULqDj2qeW++SUsE8YhFNSXNWs5YkNakppaSljEPOXTX19ioi\nUlO1XrIkPYW2U21Jc75swcxe80vO/di9NGhJxKfBXm50g0VjKsistz63qr13a732qiK5lOViKOOQ\nRPOQSsqp5KGkVLOYzbX3XptoPY0dORUgc9bWWi7xUMOxFjFEBTklmed2PML5O+2XSlJJQJyUUsyS\nBMBUNELcQYqcqhY4j6w/8zPJ2+XgbjefPRN1tDhcD6q5hJ5q5gdK4Iqnt4WYicj65sMlkc+hPqJs\nwRNHuAbPncwr4NCjwkphYhjKuYwEoaEwE7aGsXvoCefh11CloGEWj5zMyxh4OndhTjNJc4C6caEZ\nhA1OQpN86AvqWDGWYghI00sLrU4OhvACvuo8z6iRUC2O3qWEqg8eln43Fc3z8zNUHl1vhDLr9ZqV\ns+LdV8nhkZNz7YgzWkJ+qMGTd32CFGMYBkTA1JKttXlui8Vis9kcj8cvX76sVqv3798D7I6HomIi\npwDXuXp3GngR1ZM/FqjYqOPEgSQo1+GzDw8P8ANqre/fv//ll1+o+3ja1SEA3Dtx2h7qdKI51EfM\ngboXSJ9v377d3t4CgQavBUEtBdXMHh4exnFEwQmmneyrWLfk+XARgcGuzr/Hu5rnGclSODoIVXEJ\ndXCHXTJkm+cwi8MCq/fk4hKUZEiR+ugNSlF30jz6Xq4QjdF5dXwN7uH5+ZlyXgJTLaNquezkLaEf\nhQqk91O7Lr09vEopMNUWmLRERDU1k5xzLmmylnspJQ8pV2vz8WiiSbOkQaR3SZpSyUk1DyWnlJJm\nMR3KaGZJtbaqgvSWtNZMLOeUS25NEKtZV0tm7QSYVBEzNbOiyYZTyi6lYtJ5wOk90PdibsAVoKme\nR1z+sCD82c49OaXX2VR6EjPt1q23Y03VTqGkplOzfM5qZr2lt/0kksy01tNUa/oKIU1lXtcHwiKX\nPKZ8dtNzRu+8T12y5l+V6jzndGpUoGo1M0A6efRw/2f+fLpRUebe3t7u7u4A6alORy+BoQ9iwb/m\nQBuKq0LRU9TMDGloEQFyVFWRAIFdoVbtYURQ9gbJHODgeBuiAVTae+/o+TgNg3LflqkbwGfjljPr\nWAN3sgQo3dFnCtBU82xQs9PqiEjUX/S1YTZoM6JIHXwkKEIKRlrIp0cACFLwd3d3T09PADSCnXa5\nXKJ8DY0D5539IjAkxeFYBO7Dok/OSZO8Mjd4lTjmbFHNjhEqdpnaP8KmsQKsBKBZCjkZmLqUxqur\nK2hehIloDaaLnbzTYBgGJNyp7/Bm3BUtOp7lh4wTERx4ZPzTnHlIPG0NWz46CRvdHWAme++ES4zj\neHNz8/vvv3/8+HEcx8fHx/1+j+GNCLixngjass80weh3hE2TUyGAgw7xK9SEnVjClrOPWkdMxrwu\n++FgjLE14OaATJbA9o1vlsueWfVxHhomrWgYSd5D21P0uuiwYx3E0w80KnSDaGNiyJJ9/gg1Uff0\nONJ0uAGKFmQy5rGpvnvvh8OhtUrng3o8qjbzyQOa8nZ/WPTmvDhSxKZWpzq32oY8pDQmyb3NYppT\nGlf68vIylhOLq2cdJeUs5nGemFg3s5w0axqWQ2tN5zlbs6TpxJMqSUsSE+mqqaSh914NCi0BhpDO\njYmSUh7HRWut1vP8JxEV6XM1M+VTYiVURRObc8xMVJOopGRzm1VLSl0RNgmuq1OrHq2ex0yIpGlG\nJH0GvPVqc6uq2vrJWKaUTKwAQ9G7SQK8UMTgiWTT+fVlGIZlBbe1qGoB8alqSuecB38g6iEKW2Gu\nBocZDrU5SxsQaM3xoMkLwuq5KQSYo/e7aUgXQJk+Pz8DI5C9ajI6/RpNMYookGbMa4iGAZKx2+2Q\niUJLGrTbYrEgg0hkEjRHcsMLHk/8clOt9enp6fr6Gg0lsA1gMXl6emqBqkAuw6PkcF7eT/N+Rppz\n/DD7hGC6Pzn0b82Xo2Nba8DRmmckjj41EqNCa+CN7w5nUA9eUWzDvqBkgnQKdhp5NoDO6eYM3uEr\nIkABuFd1iv9+SNM1b1WG1UTXM7YDNobfxjSLOZs9cnSzN5Qwqss5wUTlnB8eHhDjdu+a4nriYVM6\nQ//5CIiZkneVMXFEhBgBAsi4IipCnxyuCzfo27dvkHDIHvoHcBvv3r2DwsU7EbqhTgYNi9onEsUI\nHO/v73/99deHh4fPnz/f39+DYjgFgg+oYEBDp2lCmyFPCtZEvHWsO+ECvoGzdyly2Oj379+TUF9V\nEVoB1t+8k0wcGbFer9mnRW/PPJMmzhHOI4wV6D5hEplJ2s6o9+E2Dd5IwOKWhXlIdM4mJ2qhJMeA\nADvLZzTPzKeURHrR08gcSgieBWkDulDuKVprDXt6cjqRV2xTyaOZmOSUxEzMTDSXnEX2qlbrpDrM\n84SVNNNxLK5JE1Jn4HgspZxosYt2hRstJefVamO2a9bFzl2frVnKyew8kUhDOzbIQulLwR/rXcDT\n+INtzs51UkNnt6qaaUqiquBx7U1gNzQn662LiUmvs7sLJecCT09Vcj6zUOYEmImKwDscc2boUugf\nqKpIElMzkPdDHZ3cnWlKi8Wi5DPrPw0Ecaoa8kCnTkmG4ZBgJriurq66l47HwK8THRYqsupwA54l\nuJPeeHVixkV2Aj3/yFNRcYgI2zPpK5nXGHLobivesdQdVQy5QT2GR5o+O4wBVAkyeKh5iAO4CUJr\nl/NMUWuxkJyMfhOPNEWKUQW9AN+Y0+AQXB2qjfnMOXQ14juxSoycsJjDMKBaiGPw9etXWnF0DDCl\n1hxO4gncE2EPUIuAvd3e3nYfAY4sKFTqD/dszknx9vaGsGzwsa2r1Qrj56FPi/eEM2tXnJxKnExa\nVefZZ6gsl0j36WnC+tmEd4ekl7KgxlSn3GUDED1iRCfAy3R/8QDTe4C7A1JBqE6gM6D3iUJGDoBV\nKHMAS60VwyaQLWitPT8/o5wGMOo4YnLHqXbSe8fMCFSGEMYBIY3QB4KnnouGOWSl05wED8fHAjvX\n6fQGLCJvsjvMLHltvzqsnEwi9A+4XzzdJwfZnxdiAG2Cu8KWNcdk0x7EjycvDs0+ISIWvSBsIkLy\nQ3rrzFswpGNUZ2a913EYaz0dw6gocLfUYFAsg443t7foQqUDLSKrvJ6maiLNRDVpUpijLnJ1tU5q\nb2+TppKLLlfjblfneSpDMjOTLto1WVJVNZHeaq+1t2YiqWgS4Ao0rddXtfbjVFsHZ6kWFck9+T4y\nv4KnAyqKooty7DjKUFYiJgJFd7ZGZoIlxw9yIhEXLQjgtHdrvXXrZl1EcsqSDPkds9ZqFZVcVM2S\nqOpZ44lkM4R5BVFXSqnkseQijo1UVU2nQC3nnJIsFotulaGOiM/0Gi44QaDKKITcxJNWV+dNiWE+\nj9P19fXb2xuUDo4fMmPFgQApsPiAnyoF6MHsHJcRVocrPj09gZCbwiQiyAq2gALozs7y7t07M9vt\ndgA7AQC93++vrq4QLfGRVqsVKtV4IoDu2d/z9vYGVi7x/lkJ4RTuv4Tm3BTS0N0LWox1GEfCqW9O\njicBCIR//vzzz0BwYBnJ0Aw3H2cb0R52AfB0c5o1Hryrq6vX11fkiIZhuLu7ExF0gF1fX19fX9/f\n32+328G5OPH4fAQYP47aw1OwIDEMAxJQREPALiJNB/0ClDPAdRGmqIHWAbGdiGy3W5BuQJbGcbnf\nv5n1zebq9vamtf709FhrWy4XORdsIFvvYU2goNSbdRCOzPN8f3+PHGzxTjgEiNh66CNoPahaiBYO\nP6gNYEVmZ3IjpgAaE9YRMkZXAPlSJMeen5/hW6SUAAlprX348OGXX375y1/+8ttvvyFH13tfrVav\nr68vLy/fvn1Dlg8+WXLs8tPT02q1ur29vb6+hnXf7XYgasK4qeS0wpBn8R7Vm5sbXFpV0SyBe95u\ntzc3N8W5lABbfXt7QxMFTCBOJVPHyHniIHC1Wzuj16rT4WA1Pn/+jM4wBi7qMVPM+LHuRQqGUgow\nlt1rjXTC8NIw1rZ7Sck9UelmXcyamYqaNnThJFmvNsf5mCTlIee5dLEkabFcvh2nWqt005x6bVOd\nhzwOw2Is2qxb61pyVu1q0q3OrajNre73+1xKSmm1XrfWOkBfrlNh/5NIk64B4ns6+CoiksRyzgq4\ngWjKqeQySmqB4i/63MMwbDYbqKPm46GHYZE09S69a2tCM6an7hdTlZSUMAdVS/lkCfiC7TgtYxpy\n0dZS7/A4h3meU04AWcCXSCmp5NZMs6p4A/uQU04islovPNBkYCeqmrJIVTHLScdxGE8dEWM97MVO\n3rA5Nk1Vwc3GE3e61f/9f/tfYRW6tzHD98RpxIu+aq0VkFY8Hg48syLV8VrdE8fFxwqw5Q3usHna\nF8kl6BFxan1cNDsiAA4j+iGYh1FHpqWUjsfjYrF4eHgws69fv4IVBlEdvU5xjGy0NJR+PSWFTiLS\nvXcPzl12zCHuE5dWVRZ4JSCsaq3X19dPT09QIq+vr4DhIsGVAhIaGxCBhRCyOQzIAPYXyQdo4e5z\nNGqtr6+v8C6Rg9putz/99BMUqJmhAwb3hrnOGMyD7Bkyot2JyeGaoUEYu4BYQT0ZgkXuvcOWA5sg\nImh+wjogDsBTU8uID3nDMXt5eVmtFovFqrV5tzu0Ni+X69VqcTzO6/VSJL28PGEyUylj9UYfGM4a\nZsZD4fIRnp6ePnz4QIx7d2ho9f4GTlOkoKKOBes7TdPDwwPaaDabDVKgRI0DmojiFnMGGuhIINgw\nz+ZZrO4jUTQQJjFeZKb3+/fvkI3FYvH6+opEAlLQGGeMNB2m/JmD33D68M4UkDsMiUCvAPFAyppn\nh1ERNX53NhN2FExhhixja+wjTPLsDa3MJ9PysTFrDpMv8FWDs0cCw4JQD/e2XC6BNGH+md5ePLDD\nMJg17dq1Z8nVap/71KYxj5ZsSINk6XM/zIcsOY9Dzvltt5unSVRzSiZSci7DkFM6HI/zNGlKOaVT\n8URE1eZ5Xi+WWvLudaslb5arwzwtytDErLapVWndko65aMn7/ZFZpdkZ1LAj89TmeYbNm+p82O33\n01yWq3oGWSjPSJ9PtYzj8WjtNAcLwylaQDowgqFzwH3EF3ar8ehFm7Q4jQo7wn2Z57mLlVIwpTWF\nl9h50LOr8UXOOYkOudRpOmm8lM3cxmQdUh6GU+NHLqp2RljoH2Lx6IjwJstPP/3UvLcG+QRI2+i9\nh4yvs9czkQ1LKbFphs51OU+EOyAjcXd3h09VB3QiXPj27dvNzQ3cATi8OXBtdSdyRRoKeCRsQ3dC\nSZyWzWaDg7rdbiGs9/f3WPoW0AS0pnj+mNSG+0YS/urUL4h4UHeh/8g7RNaL9vIUvHrfIuFzvD3M\nLqP8MRL9+PEj1QH+mr06hdtDKhluPt6DTvibm5s///nPeAO7ar5//w5pMB87nbzUhzYRRKXb7RaO\nLfQOHVhGvd1RwhIyhwACQDBKQBjCzqHzsdYKRSMhlxLFUVV7R7dsWi6XZmDF1lLKdrsrpdze3puz\neDBEYwSfHZF8dXW13++BVQHunEvHO2eCCLYW2hZ9Oc1rhGBQRhetmcEhQ7u0ePcx7hw4wMmpH8yx\nbdWx19i+4iDS4nNazdspojQmLyNtNhv4gsWbt+gwYV8ghwDfQwixd6MT6pvjv8UBUeIzlPFQcBqw\n1xxY5R7uqWYGEDwiM/hG1ZHozSEG8MPqqQ9srZfUlDxNSGDQfpgjR5jzTE6iYWbsTEe2AFoSXq94\n/ZXmXEIjmqqWYjnnNKQxJ5yrrqKmFUpcLaHDd56hrHAP8zzP05QWi+TGW0SsNTmfvtREtVkeFyml\nuVvvYinXaTocTsY15zynM3/KD6KObMF6reY1V92b2JiHcmjCo0H3V0S0B7xGcF+Goaj11kzaKSOH\n/6UsIpoM6T6lQSrpxLEdbZKIHJ0t15yZN+ciSVNJdsmrSdufHYSSyYCsul4s+1igYIdytlhW55xz\nyZHpqlm3biwvnck/s/MV0LicjgzywpBdIovEW5pj9BANWvIb5cln3YjxR7QugCrMTuWbUsIktMhl\nQm1IB9bCeAJo/OL4XfWgB6zDKSWUZ8mgU72jQgNymslK3gZPFDgi5bLpBItOzftDPKdOQgF3D2YY\nBgzpOEDRjk7gTU0UrTKsZnOa/exl2KgyaAPECUPneSY6g4WE9Xr9/PwMpOLxeESwhYiNwzqh7ECR\nMAbGPG6uea1i8rnd1DK4Sg9YFXN21MfHx7u7O+DNMIlHvM7M9Zx9foeegaGnRlfoesa+2acoJaeF\ntTB+HuuAbA+ThHjG7gg6XkK9WwVTw6vPaZyd5ALWhR9B3AO5gm8BvY/34wvJEcCJcOT1oSHheeHj\na+ClTinhbhc+gxF4geT8iljboxOe5pyRgcTdkiNRRIB2YX6bXs7Ly8v9/X3OGcxAuBCeXT0H3kLJ\nE1lHSNfr6ysMEn4Ds0HLaj5fA+5d9ylNOPtwC7hNUVRiTEaJGp1rXN0HxaORHThaNfPqd/dkVyzQ\nWuiU4j0gvp/DmCVekTLfQ303ezMJDpR50S5q0pjk4NnBq3spCEkRaFS6KbmkeqzqK5PlzL6Ylktx\n6KM175ewPs9zd9RGDrWWGnpI4qt43ycdCLygQygheN4yDqLaxGjMuOZ8Lt78OI6LMmyWK2knfE1O\nSoXQ55RSykmoVBFr5nQ+s7yEhmQsLy0iJSagWOeMPh0jRCwHkKZ0JKERUP7R0I6TfFwpV4RuCN62\n2WyQaII3x9XklnOfCPNjHpwGeRgG9s1w3bMPV2ZmwzxDElMo1bnC8HvcIc5SdGNx0lJiw/OpsD86\nGZd49wlGwnz9+vXp6QmMO0AcQHf86U9/al6lrI50Mh/RFG8Db6OxoflPZLotBTlSjIFH9evl5YWD\nM1Dt6w6yPxwO8Hk5VL4496D7mIWhMFSPOak2HQ4kDGEyxUEiZoYupdvb28+fPz88PHz58gWjrJFe\n4z5yrRAHcKPFczJggjgcDkhyjmGqLzVgDtO6UBtD1xHrVTTktAoscPL3kHs8DkAHeAPcKWh8mGE+\n7+DtnwBkI+VdnL8DH6ddoakzDxwp8xbgYaBGhZcGC40VwwHsAcaG74lLETUvuQRRt6dlZTSGfQRW\n83A4IL3Jw9VCpyrjeJhGninzKYjFAYHFSY2ZEeGxhRvEpnLeNn6IURS+5/3799+/f9/tdjc3N6vV\nCihHBNnZcaotcHxEk5CdBWr2URc09lR2ONHJ2w2Tt1JMPq6FWg7Hf5om4uyzZ31RMqSezGF2V9T4\nXC6eaN7VSRI0VzlUkeQamEF8ce4MEdHitTSxY501+NPR/EQtT0U9OO8o7SJeyG1YQHOc1KyqyJnD\ngqeM0cjsnLyLxeJ6vSmaknnDk3WKWT6ZtLMfoEArlDNEkz+YB5FcLvz+BHmCPAHnI4GiPHkHCb8r\nykR0CiDBDIeR8TCnADfv0jdPmkGbIMey3+8RmjChpyGygz/LBAjPEk4CSiP0ItFRBMBeDxUabjy3\nBDvavZQqDk1uPrsapwgpjtGJlcwRxj2gRKiwpmkCxIAFj81mg7/WwJxGVyt7qwoTLDjkXOocMLLM\npw2nsSXG4SviJJu4nDp4P3vt7f7+/vb2FiAO1NsYgxYnaYXfLY5AQY6I2j96lBRo7MLDw8Pj4+On\nT5++fv0KPsM4YJSigu+BLY+HmUKPdFMLHAFRFAkaxhseHx/Ra4XxgASAQHekMA8bCwJ5I1wN5twc\nKQonF64GTA72nbUZhrPJUdeqCiGBwCPGZemUQjWGQZTUUym0xTSv0qdQ1q7eNo4TEf16CnPzF7db\nQtIMGXVzBi9sAUZN4lN07Gj8YIaRa0Wikvx4PB0R/CnO7BB9uxY6h2hF8OUMPpi3GHzGyux8gDyt\nxTlVf1g01ESphaqzVeWAVYs3jHwv8n6QLmpY3mTcNWBTKat4XqC6NGTk8FwIEKkPo6MANku6wuk0\nfn5StSLJIXCqosAiWG9QKKroR1IRSSZAnaQwqhQLRbn6ozXq4UVrJO785TDCLeeccla7QJ9SFGlH\n4yulVJRlvECmcBH/4FoXy0LxpkdOeeBGnAaQqKeJ8DDqCRx6RlTcUFtQZ3gxYlVHVeEN6n50cyYC\n3CjEd3Q6S6CeIC45YE/lcopX9IaooOd5BtekqtKtw6VpMBiR4OoodMctwZ+AAaPFopEGioECak42\ngwYUSj+eGoOXkDzBmohPZ6gOXKRAm0dsNPnqY1izDzJg+MLgrIRZFWgmFa+s9N7BBGw+22bh859g\nIPHf5HN7uafqDia08+STRHit5MN7YoWJ+7jb7e7v779+/frp06fHx0dEYM0Zp+gNde+XMg+Meqi1\ngESntYZqHEvcKcwUiLYNE3fmecYIdjxRpJuDXaFiYqUQFwKoYXAe7mj2SgBV4/aiDz74i9JSHMVO\nB44fsQDCptZjUIJ/wgR2z2TCazkej0DeZ2eJRTsRvypKY3Yaveg+4lw0H7WgnraixmfwhwcBKLE7\nN796jnr2gV5UcNRrUZhZofzw4QP0Dm1b8ow3DNIPthnADZCUA3NBrUL/jzqOF8J7ktdEf7CseLUw\nkZZaiIoOoeQP30+lyTQyhTBarxbyutE0pss2qehZ4s3dNNfeYIv8ctT4FD9qJxGRkDHroWhCdcoT\nyiXlF6aQDeMjRHuzWCxa79kxeHwQCYMLoEmKd1tfrdZotKKVPW1Wq6paHCjeL5m99DJxjXCl+LBN\n3vyJu5DPQO+PiXvq6xSa1KIi45PDT+ExG8IgYQouHXmULojiI9MPUx+UM7xKqBglT02ifCLOtJ0c\n2RKVJjcJ93n08S1cMkg2uuUptZQA1gZSmLqEQ06VbV5Swg83NzcsSwAvAF+GeHfcpIWomTmEFIac\n4m00rngzMGzsruAJQQsL8HJT4HOCwXh7ewM5d/Yh05Q/8f6P7jNBehjfB+XIsEPci1dn4gAnNHQK\nsoWYghqtbHU2ZXOKXwkZaipoJKzSZc2JYsOgCooAZBMWIkgURbLPXqIEUmfRKUYmELBAzHPqYbY0\n1rz3Dohd8vay5jQEWHAIGw8ScqRRweFZUJmXMDUOf9psNkBCgo0J2wRjWZyumwcT3g8PWj7Pi0rf\nv3+nDuVVqkPP6UU1R21QiVB4+PHsleP9fv/8/Hx1dQXE+eDcV80BY+pd3txW80ho4cT2jIqwpMAK\nzmHAIE9ohAKRGAyBHY8tTRHx7hpIu5EtmJ00KKo/HByUxsWxr5S6eK5FpPpYej5y8aokH1YDNWUP\ntUx6IRKCJ3HLDQhMb/Lt8QlzyrtnmyxpF01DEZGMyD7U4+3S/DMNQ3UfjZC4UyuXL3NoNW1M9eaN\nufb8w/d0sW5jGVNKJZezyzL3w/GYRWU8aYOkUs4QZVjKH+F85ygwuNRROZ/XwawA1YbfbrdbtFNg\na/kw+K7iRCzF6eKRHxvHERUL8WYCdThQ97F1yZOBzdP3379/v76+xoh49EOYt+nRYzUfWI6YAEqT\n0tB9MBfehgIA/dboFzMw4j+r86AgTwVcH600b34OozzpXNMScEQQjBbgA9M0XV9fPz4+4tuA9IN2\niKaRR4VPLZ5+RD4BU9JR646uKLBVGrxg3B7qEOi+gmeNJzIfTgGoRfcgVUNAgLApewNmDYDd6uN6\nkeKrPjCXkQoOOQQApDj45cPDQwkF1fjULQA9oQKQrH94eBCRL1++zPMMxh000/SQxxPHi6PGWUqB\ncYUbxOIW3UxkuuCyaID7wxMCFpHnHH9FLwH6BOgNQInTWtP7UU+mNa+smFNR4LwAp8Mwi1oSSAG0\nUkRDwtI3Yn2IDSEDcDWwldgCPHK6HCfYe//y5Qu4S7oncOj60Eul05Zz/vDhAwRvHEdEtzDwKJKp\nh4b03NlZaJfttL/88ksL1FODtzHRu8KfkPvCyjw/P4OTFwhvVLIpPPTxsQLFIUU0eNhleGkRUE5h\nw0mk0MKF5Z7SMIsHBJyZgryIqu59WkQphT0quFyE+3KXcdzM4wCGZSr5enNVm00YzRdU8w8mhMYS\nYkCNFLWxXdb18SeIdwp8m7RV5pEls3xZU1mMXSx+Ff4L1USBOZ3i1o/Ho/bT0LukQoSB9pbQ+hS8\nHLlED4q7zqjzUQ6ZvtL/+e//im02j4SobdEbiM+QTIEquzlkVr1UC7o5Tk+pzonA9L2ZMQMDBSEh\nSsW2seUTnjKEHrBpepeQKoRig0Ndib9orQFoN/hEjew4C84TwqyEv/3bv/3ll1/+/u//frfbff36\nFf4yjRkwGhjil7zoxe18fHzE3o/OOorfM4dJOYCYgnubci8eHHRvDUEqY7lcfvv2DQoCB4z3gDQg\nNA74oW9ubqAsXl9fzbEnyPxw0gGod1j/uL6+zt5dD1WLzeq9Y6yU+OwDFmmiD4smSkQVzTmbr6+v\nR+f9xG621tCMmQP/oXlgVJzaDr4LjC46Une73bt378ZxfH5+lgC3Y1CPssH19fWvv/6KPjkgaFOY\nXUt/nIov5rvQNnR9ff39+3emfeZ5RoMaWotaGIsgIoA+D8OABcewrl9++QUjjqC2Hh8f/+Zv/gb4\naTg3xaknAXTE2uJPd3d3CD5wkxC2Ugo4SpY+JA27RsMzO3UInBvkM4dhwOMDMoOngA1gBMAzAgEz\nzxPWQDKCvWa4gH2EUAGhWnwmmXllCyj8n376CU4D/CQMrp580jnWP6U0+7RD8xBNPXY0z4w1Z5jF\nGSSWOgVmVQjSMAykt2heTGUyXLx1VwLNEq2XOrRHfSaOeQFPVeFQHn18xuCjzoirpBeF84sOkME7\nGmlicUxGHyYCbVnyWOsJPTjVUwrncDgcjsc0FHSdq6rmpKq742ExrqbpHBVEowXFGLW5xpHeAZlM\n3wj+hF4mA2uz3s8CQHcfIkQlD/GbpsNQ0mo86fyhZJTHaq1jTr33nE4Il2maxFopxSQRQBG9LloW\nSkXv/TyJfPBhcRoSuwRUVKcOgrZVJ09rzqqJqXfYPI65A+YYug90pd05SQenw6L7o56FaF6Foi3F\nN6RQQkyOjXl+fibGqXgh9+bmxkK5rHvFgnNUQWFwe3v722+/ffv2DeV3ZmnE88UI2zXAhcW7WODH\n9UD2hd9zO0cf5ganHj4O1KuFcit2hZ4mbTN9Hz4Isg0YCPTy8gLdjYd9//491Ld62gpm4Pb2tnp5\nOXknGY4iAiYRAYTkB5E1T0JGyzo4MQysO3xYtjohwGW2B1zpXPnmZBbQbnhA7tfd3R1p1EspuCUI\nMdUHLgeNAKNljoHGvry8vHz58gX1legP0qOEVYOixI0hxyienu2eZEueUqBKYudTrRVJM0SBg9OC\naJi8FbU8LAQEr9b69evXnPPnz5+BQ4FrhcoiN470d2gPgl+Cb4CCwwHBhQBMYLYAnzLvCsAGvb6+\nwvCzaYxHL+ZJ1HG9uBkewNFHT1FEIbqQcJou5AYPPtOaM3B7QA1o6KTB97P2iSODdc45Y5HzuXnl\nVPCAVagOBLfA6pY83xitUQ/pOLMzYWi6BGoxvoEIAXlIJP3gI2miO47307rTPmFh0TpmnvlIzmj1\n9vKmllW0pFzGrDlhBfaHQ3e2ve5sLwoWOFEGOniJI9dPIUVAH0TnvnslQj39rpcRmJkNw2lUVVTF\nfFHzwPzUaZKas5wSsL0r92U+7A38GK7c7ESmck41iffDJaffNc884eqF+oXuCdVoCY2QMfVPa5Eu\na5LqadPqcKnmL3MwFW+CveWUy+y8RDE/hjfUQIYPjQCLjTMWK96TD9mMLUclgFtgFNFMvt1u8Vcw\ntlETcVeinvrBp1AfpZoCnlhV0UdF35C2BM/bQ9W0BXgP/jv4dFqelqjdmuOYIWpw4sTn8qH/xpxm\nqXk/LyUVCqs4i/McOoix8jjS/BJcnXL58vIyDMPb2xtGGyA1Cv/UHLxETTRcdn22MI0bH2ytAbcC\n7x6FE2qKeNvNwSDVcWWQJdAS0lHIOcMykVUEJoc1WNB5qE/lgN2dwhiU7CUWqhUachgAPCB8RkD4\n1Mn6oB26Q+prqNy+vr4ul8vD4YAIsvf+8PBAE85HoDZJXkGhkhWHrtHzVU/BSxhkzPvHxvHLoxZL\nXoRrXkBytdJTKIP3UJOIeV2+U701Qr2pw8xo7PEUTLVVx2fyOP9wS3pZwcUbuK0aqMsow4OjPau3\nIWfPkkWvjgonOih4FuRsojeJFwx29rIrRIiEPdHkYA2hf2anfs8+Pmpwai4qRq6SdKu1VtyYSUqS\ns2qy4qQ3ppLzidegzv2EsQsv6gdzrER8aupkLkgKiTvx0i/+WXJJQmyRlpRzzkMuJWUtkvV0FTFL\nosMwqMtYrVWsM6uZTwr27J30piJikujZSEjZFUf3UB5E5DQD2Ly/RDwsgOtXvJOg+Qgiln9wSQgN\ny0hIOCAh3sNwLVpscZ7gHOai8m70PMjkZPAXPuuTarp7zM7Ce/Gqr3h7gYZRQOqhK34ArEDdU4ZO\nLA5d415y+ZB8g8CxAYheVbnsB0o+kAYPjpQLbumvf/1rVJ3dayFsfKHhwXdiUClqwtlLUzFMvLu7\nQ4IOaChYO9o55C2ZReyOFaRblL1Ivl6vkXECHyhScN1DZK45KyWAn2DvcuCxpT3D3RIqJk7cwIQG\nLAFjoxSqAnRFOTmecA9zGBi+9tu3b4P3gVVHiyI9S13GU4ovqbUif7jZbACCAAIwHm92gjNPwNwL\nvelaKzAIdEpAmTqHpgJqQwQuyBxgxYAgz15VxiWQS4hnMIXkMLQYHVUq9+Lj/qq/6NLl0CiGZ8Tj\nA+dSnTIOe2p/QJfRqjHHYqHURzETz1GrAxZKaFRQN7TinRVRWtTpjLm/NOcQy2i3ouYqlyDGFhCG\nEmK+FpoUo53GzUM8LMCv8ZGHhwceH0DDk6PsGMoXn6/RA2JCQ5hIDVm8betkZ47TkEdT670nEKFq\n72atN5x0kACZnmhfxnEUq6oprgO/jb+M9qYHzlw7z8w97x3v08xAT8foMIUMZPwIT3dKSXoFMzq1\nJXYBvAxmnW4T1yd54orHpzmfll2+Tt5o9U77FHoC8EqO4cE5h2NrzkI/e/8XI1bcyuDD8apzi9Gx\nyl5tiuur7mRR3adL5AzXmplo8Vl5C59LJiFNzKhOfPJFdYQu/wQ/Dn4NSlOs4UMUhsCuTyuIb0N5\ng2rULpGHyadDffnyBZQnf/rTn+gdUBNBW0F0YFQYIrAGA80++ARVFJaRQ6BOz94sQueAj0D1RwOP\njabPizdjs5hx1eAcJM+bm4PrhsuRo80T9EMYAtsdgMcEAtQrkuMoy9NAchKEOV87Sx08DMljUBhX\n5vEs5JNTSuDARrLFnAsHuLWc89vbG0JJRDnQNeK+M/ZxmqbRpwhmn9FpPrEbpHbsrUaoB6oLhIbQ\nZQxzx3FEWz7aVIdheH5+JqYA+wszzI4uKG5ywkIAFs46GiMq8y7sdJnOYlsVUxHVe4R/UNx8zc52\nPzgQkV4Xo1ImqyVAT7EXWCUOFaNDxiQKpSKRC4fVgpANprWAhHTHZFPMkABsPpgxO46DlowqFT9A\nYs1RD9TauE+m+LAF0cmGEJoZ0C7ExGYnMqDVSY7c46XpZuVApl5r7d3qcVLVZCe/OQ+lmc2tDosx\npXSc5xPAwZEFwzCI9/JEd4ELy2iS55GHjhpJvAkkhxnZePXe8QkJoZX5VBqwj8tpdHrJWaVLa6d1\nWK2WwJ2amfSmqmJCha/Szay289w4Sl1zchANMbeZnUcpc/8gtRifjIOXHMyawjQzon6hVXF6eZB+\nWDWGArybWNeiBY6HhKlGCf4OpZP2Epo6eUUBzzI5mVgL4yHMqyni6DXgAM0MqsQcrYCLMsoR9yJj\nPRyDFbLXfmlxJ58tBKuwXq/v7++ZGmqhaETvgD4mtHzyyejqbHvQsJS/7ETOSJQxxUpBpIBOPmEh\n+hn4COrtOMYI/q6vrzEPKYeRRUwWzc4vgIoOuB6IbYlf/oPSkRDOTtME9zyHYR/msGYwthXvYINr\nstlsRqfZHcLEPHgPUEmjz/lGdhQ/YEewmDnnw+GA5ULwBwp5CUE55QTLSwv6g5+xdAYX7Ff3+lMp\nBZGlev2G5goQRzwCetEAaqC24lLT62dxC5p6DrMzJDTwAzTUAtHwD54W7hDgncVigYx09lHFEpJy\n2flgckDw/6BEuA70qAYn5miXA1ZSoGujZcKFNHjcPNEaugyp5WGNsAJMzUUEPL+qhcE58SoaXj/Y\nRftDsydFvXihhS38YDXroabO1SYWl3/C1zJQnsMgSlVtvWVNSXVIWXLKKSNSKikPw2CqZRy0pXGx\nOFk1S+I0dNSQ3Dg+HdUjogILE9EYActloNl7t661nl2Z5FFRdeyihCpMSklVcilm59k37JDbLBc5\n56SlOiAuneZrnBvqzaltRp/aii8/WyO9JBimXzM4Zxo15tGHo1A1lNADBERs8swJpbZ4I5t6ytu8\nS5EPGcUd6jhKv4ZESvwNnpCNOMhZM3SL11XPluacv3//DhKaq6urUgpqvDEjnEIhhKYIaqKEdi0M\nFEjey4LT0ntHPg1ZkR6qTdzaaPvhlNHWsikV2Kfu9HTcjtn7q5AmQhZRVTknRi87n7EgXHzmZ3JI\nfOfQhN8cg5tC1So5ZQPucLvdQrciimK8yEOSvBpBXdadOCOlhE/Rp8NVcmBR9OKtdGfWEE8HmQM+\nVfXx8ZG5KY7fxuwiWCnUEpA0HseRiG3Yg5eXF3gVOXYaujYpzsdD1S/eoIZAHNtEFCzqXt2BiHgb\n/DZQgMOxwP3Dy2Z8j11DErg7XVvyAmfysIwHijpIHIXcvbMKRx1Bc/POkuQxDYuLFDweqOgaU68x\nNcI3EGy5cF2JcbfZ53UNgaSOfhKPKiWfHirdhSlMLtcwdlI8sKNUPz09Ra+FIsFYKoVZMMmzeZR2\n7nK0xxqGDdLeM0uM48+vUg+jaYTssruIxjVeFKtRNJWsyendemtmrVmf65yqivRxUVarRe99WC5U\nTVXbqUAhP9iSaHc1xDpRz/BhJWRlecOwRqpd9RxU8Bty6AsM1z3lNuHlMFZJKS0K1OMpea6qSU1E\nRj2DPsTLNOq1wOrFOVyiII/MvaGdRNVaROgnYg9IYzz5bDpxzw5mzByEwx2l1gOqxwKekgaAzhF8\nnxhRcoPpqFYfnQJfoDtkRUQQbo/jSAYzqmZc8d27d9CegDDgunhG3G3sqWTq6QdFKU7PSm8uB/hG\n8ZeFHmE0HoknlJI3Y45OOgIIHFRVc4ADDieDX+CM8TNA4cBGQyN0j0iy50KBNiTKmaGeqgJqjOQS\nFuH19fXp6enjx4+Dw1XpgzOHmXN+fX29u7ubpon80ObFags9/MUraj84BMMwQH7g8m+3WwQZyYkV\nAEPHOjw/Pz88PGBTsJ4APWMRkNaPAZz5rCmOKqavh+kMT09PqgpdhiCJYPfJWTxwzIDpokcVs4IW\naI1Y/KPsyWUo/9tvv93c3Oy3b4v1alGGWuv7+4ftfpdMqnVpvfeeRVNK2k9fCy8E3tLRp0cO3pCO\nTYRrhVVS1aJJl8sh5WG5kNab2Ga5OtZZWs/DsBzGY53nwxGNySlAHtRjCMb0UWeJlwyhfXa7HTYL\nacAcCEabV4iZL8HjF6eKYOYzecaVGpAWhW4f5E0DM1b19vDBpyEQ4cazhlf09rKDgXnSo4dEP0O8\nawoLrk7GD92IrobItU9fBy4F9Wm0T9F74DonTaZdnIshpZRKVkuWtOS8HBepZCxF0tTn2tpc8rKr\nJZOukkW7SjLpScecq3XtKP4kS6o9NbE2zZJT0dRLktbn3vpca61jLi0bPqvdWm/SejMdhtHsnCOl\n2WAJE5JGG9bazOxLnY6991zKcrV43e1hcE1S603EkpoFesnshdjujZ498ADgO/X/+b//GUediWko\nI/AYHo9HgJHM7OXlpTmTfDQk1dsSs8+uRucB1bH6EAQIPewHiLAoCvTEa2A2ZECGr7q5uYE2ZHYO\n+SXMrVDVp6cn5GpQM2CkD0O13+/3+/2nT58+f/58e3tLeBgccDT8Tj7WhQHNFIilk89hAt9rC3MW\noLCa83nj/qszRmfnksCdoymELZnABdBDjLkXJJ1qqPm31pBxYu8UtjmC0dVRJ9kxacj8wOCllNBA\nY86511pDJAf4gHkxjBEMbgMdteI445wzoATVCSVzzjjMV1dX2+2WYFzm3yn0q9WKXrw4pLB4ybB4\n6WsOpO8p1I1gC0UEN/Dp06fn5+evX78+PDww1KMJBCZqu90iIkdkDFONEhGEkF4OopmvX78y3qWD\nTK2NuAdrjpYAZOrwbQ8PD6gCHo/HNs0pJWu9jMNyXNTerPXVZl2nebleJdHdYW+t56H02t72O0un\nFIJ6DdzMjscjG+YwmAoL2HvXbuM4JtG51SSaSq7TvDvs3z+8O0zHxTAuVsv9225/PGRNmlOTM3dO\ntEYQJAxbQhYXAo8YBf0Mkzex4uBA8HD2WdoZAlMADQNWW0PCij4K+ruhsuO54y/PqjwlVUXdsXgr\nApV+SgkNefByEL09PT0lz1uw0EWvpflEIgn5j+PhzATG/JKI/NM//dPr6+u3b98IxMU2IVOXnY2e\nAR8XwTzaPn1ta3T9a63HeV4sFug8E5G5nVMy0zTtj4dmaipJzv9VE0lqrdfe1ERzUpNmXU1SyUmy\naEqiXUy64fddrKRce0uiw+IkLW2uknIznVtlVYleQgp5TgaaWVObUEDpfGTRUzpkOZ44qDSxIFTX\n46L3SjU1OeuYOn1BzEsVujn05vDD9fU1nF9KGwY3oH8oO0kaBJe09iQSxsQtSHDySUh4JLRbMt5s\nAWKA2/3w4QNqvxizNPqALyhlevcllAdRIkYoEB068fYgCBAIDrI3EqoTrWtInbHgpI75gZUdnbQb\nS4QYkUYIrjGMbnfcNnQ0Vv/Lly9kmmHU2D0Xx71n0EkHRB0TCGW98EGujCdgb9A3w6yC+DQmcWw0\nRroBL4D9haJpjkHAf0mUaU41lr1sC68cpx36cRxHTJP6+vXrNE1/+tOfDofDt2/fiD/sgS5scG43\nGm/xMnJzGDfdlxToMllCsID9hVt9d3cHM4COLvPsv3q2jd73hw8f2MUJXUYcB+Pd7og11GOSJ5Ho\n2VgoNkRdk72ehG+rjoZorZV0akU4uW5vb9DpgJaI9/8nL0odw2goCURt6AtEUJ7DqPte29SPZ68W\nqYjWP3/+nFJq6/UZwpfTDIYq/9p+mV8yh04x+21mhFBq4EBpgSYVAknxwBmMCQ84v1gfucwy0VzR\n5OQwTjqGmNVrrhL4Es0LB7QZjNLMcRlDaFovoSe9hTl+4umT7tlyBrjZq4m//vorM8Pds3DJE/U8\nwliE2Vt9+TjmEV7OWUmarLrwAA53mICx1gSVLiJdrF2umImJmUnPKqKSVEwsi6SchmE8HudTQi2s\n8MmlAxqim6lIN1U16apnohDeqjqUNB6NnLMoEoMJ/y8iJ/GRExasGRJFZ3ithNxvc9QbF/wHZ6ik\nS6gMNQLmizTHUs9O0AB/DacLEDVQMJFHK3vzSq31+fkZrNJy2ZBBXwlXjB+keNEeYI1+/vln7nR1\nqK6ZgU4G+pE5k947Tq+GBjHCnRGPJ89XICpCcMDyCX0ufBtwWVCyRKzVAETkmtLmwyK6j9A3mw0S\naxi7Bxqh6+vrz58/q6Mn1X35lBIyKjROVIur1SqOxuGFQGqAlaRXgVuCNoFdRJEMj4yEw0BuD9cd\nxSf2Mn+SnaaMgQ4KMFdXV7/88sunT5/MbLvdAj2Iqaz0hlqYAZNDNwZzX8SzVJ/lI4HLHDby9vYW\nlWRMnlXV7XYLdEApBQBrcEkwI8SlaM47MHlLPPdIvCJdHKXCIwD5xz8h5HgcMP1IAKox+sQZjonT\ncRwXqcB2IjI7+ux2ZrZxCVgmDLGmgeRNqmpMP8Ssw7hYVK/JibvnpRRE4cUpwLNT+bXWEB6dHVJ3\nX7JXRqn04fR0JzJIIfNpoXdQQ6sGmro0cJiK58H4TwltsJQ9agCq0Zgj4sFkhkAuq+4Il7FudMIQ\nxGPls1e1u4/704Ax490O4ylP2C/z6l+/foUfgwVp/uL92CWmIOpSC+MWCUfqDsiyy8IYnaSUkuaU\nSm5/oNzlFcVd6u6tgZvNprdzHpKqCYJnl92msPpD4BDqvSexrGIWy0W4N00J+CZ2DXczwXPnU2m8\ni6gIEC4lp6S9qZxTsrifErrKUgiXT5VA/ipmJLCdOEuzU5gcj8d3796VUkCug+z28/Mz+mOgDpoz\nMUMU1GsG3CSuHe+GuyWeUluv10gI4LR3p8XL3shpTpCMI4SPs3EHNAR4z+hDvtmrQYVozn0CYhUe\nleRJA3RZMj4YhgH5mebs1FRYKEVIaGWYfWKCOHIPqgSuEzRUdTaR5P0luCJkHSHUHGbbkHwMBwOg\nCTODLibyjbqSCVhEQsx3mzd5MLPXnGFldCaP2Wlezb1mHjmsXvLSLipe4sQKADsMDjKmbVBVMABR\nDOha1sABod5EklL66aefwEBDhXh3d4cxItvtFuhqLMXhcABtq4UxQtG5i1tmnqoGrpK6L3u3aQpQ\nGvhxCDJKKGgnB9FiraCnUkqQ3gqKzy58OuqaHOpnuBYMf5czGTPtTXaaNexvVKnjOC7HJWM+c3IH\nJN7pOPZQUZ+mCXqGz8slikpTHLPHj/PwYm1Hn39DtT44KL8F2iE6lFz8qLWjNUpOygxRTAGlKSEg\nPoapss1TbZBqrH91bJGIEOkOiWWgFuHFVH1Yc/5A1ZkuuaGzl/dxLQBYagBQJM9M0GjR0uTLlix1\nbuzmfR3RAOSci9hqs67BS6a80V3QgNForZkprFE0MNH89ABzV5GSTrNf/yhy0augYetBQwo7L7Ok\nhDSdUd313lV6n6vYxYgcphYoddzN8zwhdWSquqk8+uAvoulw0uhU8vTWWn///ffisO/Jp1Eknx6G\nP4kTtFDp0KFjAwe9leiGmE91g3OB4qGqAlTWvUVDvc+pB7QGZQXaBERtOKUpBNFEB1Ck8Hp8fOy9\nr9drIB3Yv/L+/XuqLarRFgZhdH9hPWFi8SAw2CklOEr4OG97CAOixHu5qF6h5VNKtPqqiloCljEF\nzHcP1SlCyIqP2qNCgZ22AENiGoR6HNUUONdY8N774+Pj9fX1t2/fIDbPz8+47r/927+BoJrJfZzh\nIWDx1SdyQllEwaP3pKp//etfoT6urq7Gcdzv94+PjyCuvrq6Qv/Qp0+fEDLe3d09PT3FL0kODiwO\njeET5dO46HXUQbTlKIzROxFH/CPsA7QdPhCiMYplcfBSOpGNnuJp1CZrrdvtFoELzgJCYWAo4NSa\n+/4UgJwzXJAa6BUgEsA1MVZQ7xnqvSNtjgchwrDWKj6tlCanexzPRu8cYETFER90EVi95xGm8UBZ\nhdaa2sfCK2p/+gdMZlK30DJhB2nPWFSm7uLpwPuZh0doqF62wV81TMKmPo0v2tp4P5vNpof0Zs4X\nOLRoh+IByYHgA19ORReDM+rl+CUppTGPKaVBNYlk1e63DY2KyjEfvNbam6gmy6fAJoXk0JCT5HOn\nF5yeZoIYioaTzyKBGD4amJSKdBPtOYmZJlWzppZ6bV0s5wzkeKsq1mfp0npOZ1+HtjOGRLRJ586p\nHlL8cPTQ9gVE02q1enh4YD1QRG5vb9U7425vb79//w4sUw1dAvM8393dIYJGKgmeCwMC+gLinjKA\nCVBkiKsQ7gyOCzxnzF1GZycJperRQFXSe4d1RLYHEwTi2UaOhdJG34T1ldmZYHAG4FwgVQhzYiEB\nitLR6HMz6XsioES5BdZlsVjc3Nz8/vvvyenAqTfRJ9RC3bV5pv7p6QlhKIbG4pfb7RZYQWphijir\nvt0zA/glVTBdUdw2+B1iyaqF2iz2juHpNE23t7fb7RYkCF++fBERIJGi3ONO8HHou+xVsR88R9qD\n5AETeHT2+z0G3WIjoPWwDs/Pz2b29evXr1+/gs+b2RUuHYoZNLdUENlhONWhzDztaI8dAlc3PB45\nJy5ORDWQusHnp0DU2QvcU6G/Il7Yw5oP3p7MxWmtq2oP99YD0gn3Qxfw5O3tdvSLNQyzr6Ejm9qt\ngE31cl/o6fM8MtABKS29q+o0PD2MQaLZiLWZfDmHDFW9GsY9RDvUAl/A4BTUsRREYVZPCUY93j1P\nkLyfxELjINmNuxcFs4O7KAaUT/WMaFTl5pQWrFfB4Rgc3ZedmzE6WJNPF4znF6cV11XPQNL34i/p\nFueca23I36YQrIjPm84OKWSYmHTEV0X55xGmnJwerdWkafYqU7osN9CTplbMqipmql4vgvbGt1Vg\n87hTp4eQM3MgrU58Ro0+KH8VDbiIwBtS538DyY06GUl3yBxQDCmlv/u7v9vtds/Pz9+/f5+m6f37\n96gD40vmeYYGBKSYwQTPsIVoPYcSKLdhDkxQOfQnvr297fd71N6bj17OOT89PUHvqwPM1Cvb0zTd\n3Nyg7I9/srLdPP+LUwdDRZOMe4ByT55dUfcf8SCQQq548u6l3377LfvAApBzA5inIaah4hMv1Zq3\n+4B8oTsTEjPj6jw6BKvQJHevltENic4+jzrtENb25eWFN//DGSC8InuFD9gz8W4GoAmQSeuh54Z7\nyrZZRiq0RmiZMidXRpULdguguOpl81orijqwx4CDQzssFgsYp+YV4xTAF+YlIiwCTjLx9BrmPUf9\nMk0TUmFsaYBZSqEli1uWUsKDiI+2QwITwPToMovzhrDV5nxW5cx9zpwtLXT3JjaecMLYaMPwvMBe\n8vGp8iwMbcvexEp8ZvFGveRYuB7KJDQwjDPwlTWwCPLUw2hBkjm2xgJ2QESAkpic6ZXfWS9J9sRT\nas1HM/9gC+ED4RHgTGMv0A+QPb1GpzZauGiVp2nmMeT+0k1huBDdBYo3tcfg1LQaXNvqjDgWGAKb\nt8S00HZjnh9OKVmrKqqiCq2i3nbZbchlMZyGmFjrJeWSsvVca+2t926aRVWlm3RbjqfZ8PQJem99\nrsNi2bWaWso/tAbT6IioqEpKklKyJpoM22LWRM5575SSSe/Wk0EMJKWc0ymOjAbPQsKcuywiZ5o1\nCQ3hrTXwcCNMwcdeX1/f3t4eHh5ubm66J77o8H7+/BkXAIYYXf3//d//fXd3l3MGihpnj3UXXNGX\n5hToXF1dwT1HfzvadOBs5jAil6KJGQGIf7GdUGGckofiClQbHKXZabOx5bXWzWZDXZACrBmKz3xY\nCxmjc86gzQZKWMIoQjx+8xZgnI1a61/+8hcU+emRwQwguwVwKi1NcxzgMAwo1E/Oco+u2+KwdTzy\n1dUV51BkT69Bs6DhcXb+dvHKENI4dEFaaxgIghtgEo86i44/1SukBUwTiO3IBwqugXyJF4hmu/iM\nInoA8Akk8J7RlcMvMWwX9Ujs6ePjo5khHAeUBt1X3Yk/8FdAGUtAY3bHNKaUUHWvDuKnhkLbA30O\n8UFtkxOtUmfhg0wKgX4bedTD4TDqCVMnjhNjKIanI1HCMAya036/NzllwxBM94C4RcIgeY631opY\nqXmJkQ4+sYXIvCHVfJiOq9WqyRl+xn2h2w7Zq+R3CcVUGnJsH9ts6a0vFgvCi7A+8AjFkVCE8jO8\nu7m5gfDQd+7ej0IjQXPYe3///n11lAFLv5OPkIexweL33sGOwTqohIFe8QFpM+wPAT1/czYPofqV\nHUtpDkDl00U7zfczHQ0PoDpgiolEXqt5qlYDut1CsNt9UAi3GE7e5mpV5z6HYRzRCejhdcqip1z7\nGSFJbyMujnkoY9bkPHL83K0l0lWTSe+Nh91SkiHlJp1CFVMIJfQjcpf1//o//w+uBR4pexWU/Fri\n3eb39/dQCsMwAH6NxFTzMgOfx0IRgmAwuGD7/X6e559++glHXZy7+uAT6aEgwKpAG5Yu2UTEnSaI\nOLQnhA/d+NV7YyEQsKD/8R//8f79e3QpFicWzKF9kt5i905j9egbqf/i+GYsIqbRsPXHnOB8dDJ/\nPAUMDOh+mxPDYAbEP/3TP2HsrLtmE+zKZrMBdxluFbYQ3/zy8gKb9+uvvy6Xy59//hk+IJlSkzM5\nDcMAHc1KHqV2u92ikhF3DY/89vaG8izwkNC2ODm73Q53hXILYPe4mZeXl947smeYfDiGOeJDYDiV\nkGen9MNgDIH5GHLIdgKUW3LOUMfJJ/qg8eD19RUeMbQDRkWY2devX2HOaaqPxyN4GWDGkkPp4IVA\nchaLBaz17e3t09OTmWGQBzEjlI3RiXRhOcyRNcguttZ+un83+oCfyacF5pzZvaCOr5nnuVkfhuEw\nT0wL49Q8Pz+3wHGuHrsfj8diCsJcZHexPjxWLdQweu/DYpymKY+n3iB1TndQjMO1olVunijGbyxw\nBprDJWi/uY90JsSjB3BkYM4WIww8eynl119/1dCt0ZxCghYlOXcDvh8c+faHyRHIgfO6WG1GsXBG\nuwNSICoIuPEp+GGHwyHp2ZZUB2Jkp79K3iNPr87MUEpn4q57zpPeTPPW4ORpntn7RrITKDfnY8s5\nv76+wpBP04Q0XfYpkSyViecz2b6iJ+LQE28LA01xCBUtOl3tudZjbc3LRdA/PKHDcCEnIlLnNuaR\n21Fr7Xbixsw5twbI0qnbsvferQ75jFKhTVJPfkRXoNaq//Pf/5XXxmnETGtozGEYqOK/ffuGaWB4\nNjhc4HacA0kBDTiuxNQHtgGuJco2yfPp5P4anFUTb+Yqz96+8/Ly8vj4CBUMwDQDvVorbpi+2PPz\nM3raGQJjbLZxTL1DV3OgWGWQDo1Dtp4fXMXuTApUQ6NP4qDzqN56gjAICIjqRBLr9fr9+/ccH3c8\nHhGP9t7fvXuHjBancKaUoOJLKS8vLzAksN+9999///3Tp09U7hImeeOgYoNywLaNzjpKPzF55hMb\nlFIC8gImjY4n04MIHCdvROW0N2SooNeopKIfhBugx5dCJrY5gp8pzb/+9a9vb2+3t7eIXzHVCRC+\nqKpilhWeAcKdaZpYxu+h+sgaJwhPxYEDaBoTkQ8fPkDjvL29zd5NiSMN2YjojOa4amw6Cq7Y9JvV\n5vHxcZ7n29tb0CEi3Gdlkc54KQVj1qp1yjN0xH6/v729pf+knhicpmnUjMMILwH2mzYVCw6zdDwe\nNadpmtJwCk1wCiDt8BHNmcToEU9ON66BcASrqk4oR5WdUgKaqTgFAwzh0WdfZQeUUwchS0FdT+MH\nOaTiY0K1OCEp9a95blA8T86wG5YGf42ITRxeJAmT5z/hgozDUi6LVT2AF6jH1eHHtBD8nmhxk1cl\n1eOt79+/r9drOHPweIAPIgzdAueniGAwawrIEXw/zxf1u99bH0LXNoOqHw4dHaBpbnM/HU8GJOqN\nzMnho3zSdgyAIO0exLPiewZDip4yij0kOWlNYcgpzBCkgi7O6uhnXHi5XD48PCADBkO1Wq1++ukn\naBbiPpl1of/VfDYrLVP2Olt3CAN9H73EyOIN2ck8oodCKSylXF1drddrdJ+8vLygbIAtp+mCdwA1\nFJXFMAycLlh8Aqk5kXAMaXnAcPPcPyqdmOelxWVsTis7ONHnNE0AUGw2GwYo4hUFJD1mbw3rvb++\nvmoAEWSnAtvv92ATwANCC9/e3jYnaac2x1IAQzh75xC0anecJPziyQfqJK8hId/19vaGtyHdV5wg\nhwamODfa4EPnxNMLqDsyVqDOZaGRv4Q8YIZm9qmGyRHwwzB8+PABcD5Vvb+/hxV5enpCKFCdjRHP\nDucDnnIK8y+y090WBwozT4h3ivcVYcgIgTxYVRgtDndXh2klL8zc3NywrrY4z8qc6rCIEBjzoeDk\nM+yXBYaXl5dhuWCQjRsDcQlzLHrJ7ti8Qs78QQpoaQ15ecNkCnW0bu9HH/vdLytnfMblcvn29gZq\niXEcUcO7vr7GLGPIP72NHLhfJfRLJWccxl+pOiHY6t3+o8+W7c6HMjhomyqMyqGEpqviYKXJyTV6\nALw1f0mgfGXGonoTAsWSb84Bi5FC1icHfqPZ6bv4p+woCV6Lti2GdFTQzdl+4dYjgEYAt1wu6/F4\n2nKT4khdM2tzTaIppSGXJs3MRFWT5CGVklW1iYko49paq6qoWBITs6wy5CQymKQk58o9tToz0nJZ\nyimLIaeENCREN6tmTa23nEQki4hKt26qmjX1U/WtY7nyHzoKaPXNrMClZfIBPv5isfjXf/3X3jvS\nNaUUNNiXUn7++Wck6/Ci2dRA5kHRx33MzhdAZ+Hl5aXWCp+U78Q2wMyoKpmEGBcjlf/zzz8D6YtU\nDLQb+pxYM4C0YcArSusIcRAbdSdblNDdFn327KXd5s2J4uGjhRoszipymDhax+OR/Hh8XhppHICr\nqyuqkre3N3xcvIxUfHw1fq+eeUBdYblcfvnyBcEfUN1mhhjrt99+izcZs/AS2HbxsAQjFO+pop+L\nAw+IhziFD91AJBma86QhQoIfw3oSbhuxNezi6Gzl8ECjEjd/0RQVz61jK0lb9/379+aZK0SlQ5j4\niY/D/OPLYfWRTO69f/jwAQSy2efy4QFHH7pBN4WSAFWI9urv378jWUrjgVvlVg7ezaqO20YnwOFw\nQJYYg89vbm5AA0OkKLXAPM/zVDebzbA8j5/A8hKMU70rnDYeSeMa+Oab54XMDM6EcLRHgZFodJsQ\nw8G/oV9YHfIqItvt9uPHj9vt9l/+5V9KKf/wD/+wXC7/67/+K3kjPBQWVqb3znpt92KPekcqHTUN\nL5YTSHdCsVFPas1hqDwcgsFZ/LuXZKCx4UzAWZx94Ce9TAusu/KHmYpUvlRcPeAMLRRUsjNYqhPp\nZkejRMskl4ki7Bd8nR7KPwBhcbA6jJB5LlQC0se8hIZn6V7KooKC5GcfgyIOLzIHSlSngPFNyaLa\n9ezEJJ/4g1iWj483DClfb65FEkpv84niyHrvomcIhtkF27UEGGoKCC9/8zntVDi/nRWa5qRk8KPV\nC4zQU9jOfslDxRCSv6c4Im3C+JrGFpaPfkcK2FCvg51vl4GneCMhhPLdu3cvLy/cDHpk5kBGcSik\n+uQYaHmmd+mesM4ZfQENFcIUiLqxSs2TsJSSWuv379/5Gw3l0Hfv3kHIOBwP9hUR92azgWrgUqOb\ndXDAK5LaR5/ggLwKiPuotfFZiDXaPiKxaRTl1hqsOBVrDoN5YG+YJ8G+UJu0kHbDsuApure4Z2fO\nbmEmiHhmaenTHSkhEJvb21vgYpBGKz6uWFUBj2Q0rKooDdKh7g4+HgNTfXWSQFj3L1++MGhG9S47\nz2wLYz7oAyJ2p7udHHEOy0rJpMx/+fJlsViwCGFmgHgUU15xdC7U1hqcCfWQlEtKxRdPbPe2bvHQ\nk45UnRslvwTy0Ljy5+cq5Xg8tn46cRogKtkb1PhfXP39+/f//u//bmb/+I//WGv953/+51rr3/zN\n30go/lFbySWJhlym6/lcFlLi7ZJulWetXHYUMcMWDxcVIhQ3jidToMW5N+OaUN4kFMb0EraAxek+\nTwB+T8RJRV+KeonCwIel10tvSUQwC3h0tjMc/9H5L1KICE/5lXHMPtlScXsioppgOE8DZE1EsmrJ\nWU+8PyY4CP684ziaSBJJ2KlTBkhKzv0UP2iyXBQZgrHPAGedTVG3Ll4G9qWQlE4I75zhRHYR3AIw\neNr7GWlJY0+NpCF7LyIF2hnKHQsBrQHigC9fvjw9PQ3D8P79e1R0I4lncrgtctY/WEL17le43kgm\nQFWhkxGlFNT5aU4GH3CXfXSFekIPzPzsSMeeDT5ONBoSLBkKALCyYMRB+pEGP4VJzBTZFpgzupeU\n+mVSju+ECZm9KZqXwzHrDglR7wzFmYfVYeWDyWs8Baq+ILfmE8GHMjNsDYgBUWabvJ8Om4hSE9PQ\n8HlLKbgxeBjIt/DA8DygsIE3QIcyqchViqnLWitw/KUUtHzhgOGs5kD6AEU5+9CXH1QS/ceYAwG0\nGg44RCg7a3VzoJ04LBMhQrTKYHISZ00FagABN6EZ0zSBWDPnfHt7S5+U+dXeO6qPzdm+22WfXHZm\n+u12W7wTTkISJmuGHGKoKBKSqJ/Tu6L6zjnvdjs7nHQ0c9Qx20NHEv8soatXvK+lODMQ/TyY59rb\nMAxJCu0cHTULE8U0UCN++/bt4eFBVV9fX2utHz9+NLPj8YiAjxpZPFXAAl66nLaAPeU59dijMzFb\nfR5gCXjRmDmEXqJGowNBXZad/aj7mDGKB563O6JKfd7uFIbwnkpTTndE05XCAHg607Q96sMRmvPu\n8yMWwineJOM/VWUBCS9ma+gQ7Ha7q/Waa0g7mi4heRLcTRoPC3gTRgXR8GPTNSW5XMzkxAK8lgR0\nH788WhHRrgoRPdsYO9Wwz3x91KsU4xTmdIjIyaJQhgaf/Ajur+vr60+fPiF9BKVA2SqBoKn6UIDi\nzUM9BEk5VNQ1NBPgkCAk53mjmeHZyKEjWpyDB9sMPU4gUPMhK5P3ulPbphDDsmhk7lyrT3yI5hqv\nwWk9GVHR51Jv1quhJy6aZLsc7UP2TOhK2BVERdDyMBjAcPN4J0+2IrEJqVr5VHIcIYQUuD2URrOP\nyGPAkR3vi9UGAkK8KI3cHeXmj9JzdDZPPqZ4elZDNXuaJkKMyOrdWiMZJVW2XXbAYT1jVNRD27mZ\nQaejDvT4+IhR5XRcUC5qrkrQq4htAnKp+czv2WdAwNIQxQdBQhPYYrF49+5daw009r13OG3IYPCk\nqeegxnGEdmY6FEcGCG9x7kE05FHgqSLPPrvYcrms1pHPARcfBTuqRfXE3aiZmp22sPhkhBwAk621\npNnMcnH2ZRFWXEqYB5a976I57R4zVNkbYxGdi08kyp7xRj6zeSWGRh0tYvF+cGqur6+j/vrhv/F+\n0h96kHk01BHYdBpSGM3XvAhEDUN1gTNIHRjU7HnWkTkGjwGleJWF99YCOFu9jvWD64ClAPho8mnO\nUFaxFzM7ET4Esi+XEpyb5pxJyQtsOeS9e+/DkEXUrKd0ahKCpwEzjwZTEUtJVDVpNk0WaHuibFNj\n00SVUtSytd7TWZwA+06irZ+KoKmcBVvTKSuWQuEtulP82czK07fvi/XqZnOlJfe5TrUmE0uq3Z6e\nnoqmT58+TfvDv//Hf7y7u3//8SeATaksoDHZsz04TzO3Z+kTygdvnTkej4ix7u/voZ3hiccUQTI5\nznOfqyUdczG15TB+/vqlTfPdu4f1YrmdJu12dXV1eNsd5nlIWUux2kopy2FsrY25bG6up/0Bs2RK\nKX2ur6+vq3ExLhbJ5Hm3O7ztJKer1XpcLaV1M0smmtOQchpKMsE84BgFigj4T7FVyOHguELarq6u\nUpLWDP6fWZtnmefj3d3DNB222+1qtbi6umlt3u8P7M/YLFdzb9vnl6nV+XDc3FxvlquushoXU6v1\nOHWVPtc8Du/vHw7TYfe6lSyrcbVeL+fDfDju14v1YjEUPf3fYjH0uU+tqkdpDGiw/XAvkE+bL7tA\njsfjcbfXkpPJcrkcUs4597l2laJpVtVuklMWTY4g3+12yKHlnJG4Px6PIO94eXlh5A2t2lrrc63W\nk4nkhJkrWIE2zW/HN2ldS16UYXlzsxzG3778nkzKOKzGxTzPfa739/fb55flZp1Fj/O0KMNqs5HW\nX9622k1E1ovlm9lqXHx/fmrT/HI8jrnkYSiaquqYy2q1snry6wmoob67vr4GC/Dd3R2CVEQt7AFv\n07w7HutxsqTLYZScrLbFejWkfKiHw9vOkl6t1ler9f3tHUtr19fXNzc3c+CrZWWRBmk7TU3s/f1D\nWYyHt52N4931TVmMz98fNefTwFDRrtKmubYu5Uy6o86nBY+bWBucRFzu8fmpLMYh5bk3zkPa9z6k\nPItgR7Tbsfd6nOZ5XpTT3AotaUjZVKf94e3tTVqfWl2UIY0j4FPS+jRNGXkb0VLKogxNDDN4pHVL\nijk92k1Vh5TNTFpPqhkJQ02TTdZPzWdUXszmlYBhYzzXnF+RXibFGDWqWieRc2G4ePM48gfqkBAz\nU8njeKZWSQ4Hn+eZ3OQ51OE1kJMxl0jLp4GfU72LCO8EKB+V7xSKfDnUQYk6o1Gk/Rscsm/OOpEc\nnzzPM3awqxRJTUzMqvVhGDBxCFO1oFc1D13MQvpXPGydvWOvOyy+lKIi8zzZKdLoqhk5HREpJama\nuzjneXVzPcPHGUxzbeXypf/yP/7HYrVsc53qvBwXeSjzcaq9DblI0l7bVOckWsZBTaY6a8n39/dQ\nzTQh6Pmgv0NjiJMGm388HlEbYAkEOr17tg2mqx6nlJJ0wzSOMg7Sbarz6/PL1c31clwcpuNu+9bF\nVovlYrUcy/C237W5DotxMYxzq7z/cbmQbrvDvtc2LheY8HG13pjKy9PzsBiP+8PD+3dtrnko+7dd\nF8PsEDWZW50Ox6nO42p5f3+/3++fn59vb2/RloHMpHkno/jgg3meVa21mnO5vb358uXr3d3tMIwi\ndjgca51V0zgOKeXj8TDP1cwWZZFSKilrPnE9jWVYrlfbl1ckgDERR3May1DGoc7HMpbVYjXV6fX5\nVbOul+sufT7OtVc1TSVJF/ycS8njghLQfWAgSu5o3UAQDLTh6+vr3fXNer221o/zNOTSxfZvu+M8\n/eXP/0uzXqf5OE+H3X6q82IYl+vV1E7E28TlV28wYpwBTx9G6+P7DyKCWTvSDVNY8PNhOkq3cbkY\ny4B9bNYPu/3D+3eH3X61WWdNTy/PQy6H6bhZrffHAyb6HPcHU1kvV2Ucbq9vvj89Zk2b66s6zdvd\nW53mZj1rWqyWh90+lYzV3qzWu8O+q0iI5nlCgAnsjp1lAcNqOx6PWdNqsy4pT3UuKa8268NurznV\naTaV682VqRx2JySCOdTqeDwCGcj0afdp7liiE59sUqyPtY71kaRtrppPcgKpkH5KJlNNM/UBVwO5\nyuK4c/XMeR4KdhaTb+o0T3XerNZv+91iGPfHA57renN1nKde22K1xDSd683V96fH9w/vnl6e8bxD\nLpyv02urva0WS/ymiyVRPMXcakn5NMggp6xJkiZRMzvu9ma2O55IF6GXy3jqNsHSNbE5UEFShrsT\nr0C5U/ZoBkopKcnhsIclAoDQezZ0mqZWz/QlDHQOhwMg14i5X19fGWvKH+qsq/UJdQUzCcMQx4CJ\n05viljA/qXtn1eiDBWgdiYPIOYNiGHicWitKp8CmV6dRr/U8PQgB0HGeoNMwvg97Bx2CuUfWuunp\nDBbvsGZ9QTy9ydROc9KpYRiGYeHJjzwMC5HzlCwJBGbZ8Rc0sRJqiuptTBLyfqUU/bd//ufqjaI5\nZ7S5wN6kQKAJbXucp8ViAcxPrRVUykDl4bwVHyTMnGMpBW4gx7WhNAUMLrMExYnRRj1BnmJkB4ea\njkn27qXj8chBVczg4dIgkkB1BL9ELyrgTJBIBtRAQjd/iTcM5aF8+/ZtdbWB05FCkWPhc4aoDnrv\n83w0s3me8PHn52dULKH0a2jpp9dzvbyugQCY/g4KDHzzKR61Oo7jfr9Tz3NiTYjDiZGviHSx3vRY\nZyZeqvd7qsPe6PJDV66HRXFCRtw8rgXv3sI8qpTSsBhXq9WxnrmEu9eT1aFltdaXlxfYvM1mM8iZ\nEZnui/n0M/FU3hSYQLEad3d36/Ua5TcRubm5ARAjqi0z+8///E+0xyGcxT0AjIBmBnUuhsVicZiO\nwzBgwkILk6rVU8fUUEjBmdkiFeSCONlBnatXneWMBU7cFWp7KF9hs2Ynd+clSpgyx6MroZ+J1fgf\nUhzM1TAGMoeubTabcRzx7OIJc/5AvYD3IwTc7XZ//vOff/vtNwyxXK/X6Ph+fHykSQPmm0deAhOa\nmS18UnsPBf/q6POogE7ZhZTN7HA8ms+2r9ZzzpLOvXrVOreYRWsNxZsWajaDMxT03kWA0DvxTPZ+\nqmbN89yatdaSngjuaq21wvNoqIZCjWJWDmsQuByeBfrn7v4GW48bIEwGH8+hwwSS3OqZgxFnJIe2\nPAuQXUjF6+vrEJifWBSoocv49M2tTdOk+Tw3SELC0wIJLOMqGlEL/bN2Od+IlyhhLC/crOgDYUNb\naMbiQdNLSmKeLwrwWesmxwRTsHBh5HnpDnRnkhh9/rx6l4B67yFUJ08LUx/Z+fO7A5y4DfTmGB6u\nrm9RrhydXkFEgEDjFbHNNCSMBKt3b6SU7u/vU0oYFdF94ida+lNKaJhABwnmVhBlQM9lnucutt/v\nD/ME2EUcccRjoA4P7b33DlJXY+0KLhXcmQjky45m3j5uqSDwYulLvGODK2mim82mtdp7HwNjNKQk\nex0IPlfvfZqOQ1kWMbr5ECmWQKt3mzMV0B3MA5vNG+BRwe2dIsKSc86roTCZOTkXuDmaSFWhHU7J\n+qnGOF09pc6VTD7BjHsByWlOFQHMNxGGlHVoh4eHB2SPuxPA9N4BYVCvpbOQhoPd7VykVC+BIDND\nEDkPDBMXrO3BdmK/ON9WA58mfGTcf3FwKXMgsUtsHEeUOrqPCYZhw5/aHyY10Jzw9qgXYEtoDHA2\nqwOizLuk+YD39/e///77X/7yl9773//93//1r3/98OFD935McNTO83x3d0eyIhpjcbKAFJpzo9Wx\ny9xXuyweUPIpNrXWMg5UYaLnovfks6PoVzUfuNy9dsBa4DxPPDviL/eAx5SSyrmiYz5p25yFgRau\n9whfNt68qgI0kQLpDBTXEGZLyiUxNm/VvIJOaVGv1rB6il3DscXKq49qRKiSQ4kXzzD4xDKiq36w\nTBKSAclL3XhJKCj+8M3R56BV+8G56QEugNfghCA9YCKixuO99d5L7x0cl6wSQ5R7qDNzHU+tHiUv\nAsc2TEu0DZSwdJkT55b33q+urrCRhAKbN9LHzSMoS7xIA3g31ov8ctH8dse2Zoe90labx0PgWm2c\n+OKfjcrxcDiYSs65XxJJQdaLNzNy9XvvrZlIbT6j7Pr6epomRG+w9xRuV8QKZY0FRLfpOI6wvjFW\n4y6inkHoI6GJ7PtDciY70mwoSyajKejZiWvLZb+RhioxZB0HAKt0NopBv7y9veVx4N7R4i6XSxpv\nuNjTNO12OyCek8NqAZ/9o3rKIdsOjIB6tKGqwP5pgEfT+1PVr1+/ppQeHh6wMuwuQi/U4IyWwoG2\n1lsAecdQQwJRAv7ZDlNwvYUGAMk3rAy7iBCaLHxmRLT9qoroCltmPjKO5wjRJOQWXQESKsyQRnMn\n0kJfC94JdAAmbkioW9BINO/oxF/BU/Xly5eHhwdM8QCrAtAcoHUYnHImXY4dwSsFbEvUADgazNgw\nCIDZSHoqj5u75FiEq+HMQ89TnBz5TTwRfo/bSw4GSw5HNLPNZnM8HuzEWWCwysVhjfN0dsggPMvl\nyWtp3tfFNCDNP+VkGAaRMyQVtwewEuGjVLvm/XZ/9L34/eqV3eR5dZjb7BxLyWlh+x9QEjTpXOdo\nZmgtaJb4qWitecCLg2UkkIj+IGPxny1Q2/FL6LpFd6Q78F2D14LvOXFaNx9Vh2MDPBItRCJgfCj0\nK7snbSkKzVO6WA56CjAwxKWopyNYKKYOXS6Xu5eTtoU5AZFPlBi6hzwetPMaMgPg0dEQZvJAwssY\nhmG32202G5zDd+/eTc7WTJWNsNeSkiEYSa3tdgunVdxZpjRA5dXaVNPNza2IbJykAAsffVtV/f/+\n9f/tXs7JYfASkOjFqfJhgw9HZNVO7Fjs6kWytAeefNqe3W6n5Tx3joKi7oXRY4XuW49LThLBqo7j\niLzNDxkS/BMxFkjk4MShN6C1htZg8XoybE8xpS6jgKZQ5GTGrAWIfEoJQQOkhblsdaguJTA73Jn6\nglIBy0T295RSstR773Yxlpuf5V3xrznnNBipFmgYcHty6YThaACvDyGBVUbGeBgGNCeBYQ99u+jg\nZvxE3xwlN45QojlvobPHQowrIpzgALsV0+m8TyoaeIdsGxi8La86dvn9+/dgo2DiBaES030SwjsN\n8wgodaMzCdFHRkqtT2f0ExMe1GunxQ+TbdGHJyIkeRNvmcclqIjEW+bnefJFUnV/C8toRYMcAg98\nAtqI91+n0F7Ns8NdmOvJQogzX9Dq85IpVE10PD0U1llVoX5jqpYbSt0SzUZx1qUSOC9wiIZhgGtF\nJRkD1qgn9TJgwn7xJHKb4ovGku5a89oPni4HUK4G1AZ3nAo5BifRDS0ArcKFR+0ODoWesqscKWgi\nIknX6/V+OjKNC5AiEA3qzkvxvhmYKxaBuKbJx9b90Lq4WCz2siU4O3lvo3igAyUIvw/fEHubqVh7\n75xcTjOGNUIGEmCKeZ6RyqdySSmB9eCUJhZ7fX1NQwGetThLf855cg58uhvcaZZAeu/DMLRacynH\nw+GP/mPv/ebmBohPGGN13p3iQ9ss5J0Bskfzc0rp+vr67u6u944xCj0QWdLm1Vpz0miB2iWogdKQ\nc16v1/PukB3/xqgIhVzeP6VHRMZxxBSvwQfpQlnDGyAIG+9cr9cyn6biNh/6gNugTHdvfqRSgE4E\nGPfu7g5c8uYw3+pYR2zK7e3tn/70J/hS2OvBuRt46mizqcTpcjEYBeGFBJoDqgPqGvNsJDwb8RYZ\nYnlaayByzAHlBTFrXurACA/2C+MLqUew4HDp8B48Qty1FGZbUCHiuvDT4bgg79ecZIHv786dD5zR\nf//3fwPX/uHDB7Ry995RR4kuP4VTQ2uqumtP7UbVxl6u7gVziBBoMCXkUeSyqaPWWq3zn+xvIzsi\nDmYLiUrsV0ppHIdv376ldAqeej8l3w6HwzBgAVM+1wvgKTaqLKgmAIZBUsXEOB6/lFLbxDM1O0Hi\n4XDgRHa8zNPXqM+pKvwPakVst3ilkGraHLvB9exeKRxCE4t47qtOx+5VFa4zTEXM5VC0aKXoWvH9\n9FQk9KvQOMUTxKJmfGc0V/SG+VzFu3Si2S7IxkTFmrwO0UL58fQnPT3e6DQwGihS9JIRKzsSMXmp\nmXeGbUBpkScW1QjExeYpCBbPo4iz4KY+fy9fjtAopfz22284jVDxKCAdDoeff/65++wsVYXLb2ao\nG43ON4OlrL3t9/tUTxR5CNQIC6TLU53vpHsNHxNakZ14fX1FKTi7zxs1wruPHzFNFiEpghIzu7m5\noZR0Z37LZQVZF48LkVPVS6e+B+xcyQmczVFiov9lTrw4OuMnCmNIzfXeUZItDitKntyfpukwHVNK\nw3LB0nFKCVkmc1LIhb+wVubaipmi7pWhEprVxFOFh8sBl/v9/uXlZXC2IWal6Up///59sViA25ca\nhEqhOFc0VJipmJm6REkoyNOIcpVgpMVOBA2MtuGXsHoPh+Dgo3uRXcHdAkSzXC6RvIU802BDACYf\nBsFbNedlR5EfNOrZGUa4p3zha7F9DG6wpxJoZvpl1qWUMo7j4+Pjp0+ffv31159//hmZg9fX1+4h\nAtLIJO+P5hnLy4KiXLatIDijkrHQfwqPobhenpzUwwKymSq7O7FevqQFqoEggDZSvb13uVy4e10X\nPpxMNatqb8Jz0RpgCCd0KNtUgYQCb6R4zMr7Qb+gOtULQ5yof3mfOefd28H+ABngaF0Js3LMezFx\nGKHougPneuix5fpkh8PQl8WzUDlwZfhBKk86NzRXdllnqk549oOxoAD8YNW6V5i4FHxemp902aBZ\npmlCB/XLywuyK6qKTEIPAcfJNyx5u91qyagS4yOwRpQwXhLy3QPNqIa8mYiA7xn5MZB7vr29XS1W\ncB/wWTA1wCWk3TavENDa0Xyax+AfP36E1kDclnMmriHn/OHDB4BVnp+f4Uiy5Ds7j1MpJQ9lvV5b\nUrhIq9UKMGg4aAzX4irX2uCMYyUhyovlsvkpRcgIUai12tQpOnCcN5vNzc3Nb7/9Bp07BOLINrXF\nYjHPE5Jg+/0ewxFQ1c+OjKg+enIYR5Wi5VT1bQEwQ/cKd4JL04EF1g4wMDxsD5il4sSjc6uMg5sj\nVrEONKv9Eoghc6OxTw7a0dCZgeITFF/ypDOWEQTYr6+vnz59QsMgsS3Zmxkxdwq039nxbBYqw8lb\nHXvvqWQzU5+6RAGmaqBmST7NLxWj41m8hUsuiaxgj2enh0eREr4w9xRfi0AcS7Tdbne7HdCANHWz\nt31Up257e3vD1uCrYJmi7cSdYBbwbrd7fX3NOaPwBpeLWiyFaRHDMDw+PuJEXF1dff78+fr6GjLT\newf2Z7/ff/z4Eby98LeKg9RrIESWUAmgv8zCW/IX1mr/us0+PYu2J4W6HTVG9jFOWAdWnYnvsADk\noxW8ublZr1dY1db6ZrMZxtF6f3nZttb2uyNcBPW8zvPzU3IyF/PZj7vd7qeffsqXbPGQopQF3rx5\nYo2RIqQoQqvUy1rIA4kPLkCRFV+CBcSL+pOyZN4S0zxHyhgAL8LKAashEhJo0qj9mfygF0htxhon\nHVy6gzVA2PiF3OvmI2OoD2N2roVCI9MhKeQ5/3+5jC+h+NPonQAAAABJRU5ErkJggg==\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 3
- }
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "cFHKCvCTxiff",
- "colab_type": "code",
- "outputId": "5a78c0ef-9ad8-4106-f699-81eec13f33f8",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 553
- }
- },
- "source": [
- "mask = Image.open('PennFudanPed/PedMasks/FudanPed00001_mask.png')\n",
- "# each mask instance has a different color, from zero to N, where\n",
- "# N is the number of instances. In order to make visualization easier,\n",
- "# let's adda color palette to the mask.\n",
- "mask.putpalette([\n",
- " 0, 0, 0, # black background\n",
- " 255, 0, 0, # index 1 is red\n",
- " 255, 255, 0, # index 2 is yellow\n",
- " 255, 153, 0, # index 3 is orange\n",
- "])\n",
- "mask"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi8AAAIYAgMAAADYxeTCAAAADFBMVEUAAAD/AAD//wD/mQBMHVIj\nAAAGkklEQVR4nO3dTZKbPBAGYHB9bNjrEpyCTfakytxH6+8UWk5xyhiPhfkRM1Kr5e7xvO8iiSdx\n+SnUagns4KpCEARBEARBEARBEARBEARBEARBEARBEARBEARBEARBEARBEARBEARBEARBEARBEARB\nEARBEARBEARBEARBEARBEARBEARBSmWy0oIll2manDTC52aZPqQRj8wHZpqkFY+0mjB3i5IS/hwl\nJRXcfWJ0VPD0iLRjTusxVlpSLaPEXzT1OI6JT7l4C3vRNDdMrwVjbphBC+ZmGa9KMHPJpBZNMUxz\nx/Q6MGZMH6dimHFMH6cnhrkFPzC9Bkyt6cg0mjAGGE5MBQwwPxrTlcGMeRjehfKdME4BplWJscCc\nYJwmjIbZ9NxDsGJ8B+6JGFsCMxAxThOGtWj8hjzxbFsnhrWC/XkTeQ9h5TFLo2Gt4AXTJz2tUAV7\nzJD2tDJFY2gV3BXBVLkYy4lprg2pgv1IOU4M8UpaqUv2DaWCnxPKsmLqPAzvnqamVHCpPU1N6cGF\nmrDH9FQM6zjVmT24xMqdhlldSiuxcqdVcLvCOH5MWgWvLKxF4zF9wnMumjDrUWKtYAqm22AsH8Zv\nygcyxmnCMBbNm2EYK5hyIre1MFbwu2EcMC/DpKyUwPxujPGYPvopF2CA0YcZgAEmERO/bLfA/G7M\nCMx3mPgNjWoM3/ktMIyYDpiTqBqm/aotitmfN8liuvKYPvo5LTC/GVMDA8ybYAZxjNGEGRVhahKm\nK4MxmjCjIkzNgmF6K85owoyKMLUmzGaUEi5DFMGMijA1FTMVwDSaMAaYk8yCP5owRglmnkxXTZhh\nXTSSmHlmV4owVxJmf7GIA3Mrl6HWgrlBejWYylwrEqYtgamH7fIkiqmqN8B0hTBGLaanYiwPZqRg\n9hZgCmNqCubQgIEpjNn0vNg+074CE7vtLIUh9byXYGKf1L0AM0hjxh+POVh4MLTri6/AxM7sY897\nQwxTz3t3TGzTO85sHoyhYI6WN8RsLJELZWAy6cK4d8PUijGDKKb58ZjQ1ObE/P38LXI9KITxPa9X\nhTGKMI/xir5cXwQz+uFJvANCWUwlj/E9b8jGWFaMSVgPAph8y9Jm+lyMY8RUHjMQMVYThsHi28w1\nF8Py8ZkVJq3rlTgyz8mkB9MvGOr5AYOl1ohZ/TnymV25nrfC9DSMZcNcNWGGFWYQwxiFmP7+QBoz\nHjGRXa8cZv2AhmFYm7Z3cdrIEjGWG2OomP85e96QibGc+7wtpk/GVC2DxWP6XAxLTAgzyGIejxpZ\nzLazaMTEdT12zG5ppGJ4Pli/wyTdVY8ds53ZaXfVK4XxD2UxRhNmVyNJd9UrhBl2j5MxjsNy2PSm\nLE7cmObw2gk3oC2EWf1EEGM0YY4NN+HWvGUww+FHEpjQGSQJYxkwx8mUcmF6KoLZ/EwMc5xMKRem\nmTHHySSHCV4BEcZsX9hEd70VJt8SnEwJt2rnPTKh+hXG7BpcE931VhiXjwlNJhomf6cXvpwYv1Ku\nMDkVXK8xfZCYiLEZmGH+NTiZiBhHx1R3QXAyETE5RWOeb48eqiN4vL7D5BSNmV8tOJmoGEvHzOXy\nNziZqBhHx3x1t44T4zEdV9F8gYleKdkwZsGc/FUqJqeCGwZMy1XByzgd+z4R4zIw5hTTxGK2n47L\nKZrVB1WCmNSVMm+3x4DZVrDNwDRnzS0ew1c0p28bx29o+IrmUcJnyqizbb6iqb/ERJ3gsrW9zxIO\nHIAmHsPX9u6vGsAYKsblYKpwbztbJr7F5J0iNOeTiYLJPMllxrgsTBN4Sb+eH5nfYjJP5QIYQ8dk\njtN/AV8GxuZp9nlujikYV8hCwpT46joypshX10Vu9Y4YK4/5KFM0iZjHhuZjOUJlvsO5j/rXHvPc\n2PBi4hR7TFeo05AwywbUKcAsh4a3aIiYQt8fSsMsJSx3aFaYVvzQ+MGZ/yx+aNaYZXY7BZhlnJi/\nkDcT4+Qxhb5tOyHrgVGFEa9gtZhWE0Z85d50FmDOMJ0mTKsJc9GEqVRhWk2YxzhZIUy3fXlVmE4U\nMynCXIA5SasJ02nCTEGMjEUV5nDpQRLT7jGtIKYD5iSTIoyv3+fprBxmGaQd5vWn2ps3+6UxrSbM\npAhz0YuxG4z71ZiTj1K2m0cvS3eOebnlC4zA5cXzPiOMcctPLyL1e/KfDi4i9Vs9h6Rdj4tI/Z5F\nFaaTfJNyn85KCxAEQRAEQRAEQRAEQRAEQRAEQRDk3fMPJ+0iGAT73hIAAAAASUVORK5CYII=\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 4
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "C9Ee5NV54Dmj",
- "colab_type": "text"
- },
- "source": [
- "So each image has a corresponding segmentation mask, where each color correspond to a different instance. Let's write a `torch.utils.data.Dataset` class for this dataset."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "mTgWtixZTs3X",
- "colab_type": "code",
- "colab": {}
- },
- "source": [
- "import os\n",
- "import numpy as np\n",
- "import torch\n",
- "import torch.utils.data\n",
- "from PIL import Image\n",
- "\n",
- "\n",
- "class PennFudanDataset(torch.utils.data.Dataset):\n",
- " def __init__(self, root, transforms=None):\n",
- " self.root = root\n",
- " self.transforms = transforms\n",
- " # load all image files, sorting them to\n",
- " # ensure that they are aligned\n",
- " self.imgs = list(sorted(os.listdir(os.path.join(root, \"PNGImages\"))))\n",
- " self.masks = list(sorted(os.listdir(os.path.join(root, \"PedMasks\"))))\n",
- "\n",
- " def __getitem__(self, idx):\n",
- " # load images and masks\n",
- " img_path = os.path.join(self.root, \"PNGImages\", self.imgs[idx])\n",
- " mask_path = os.path.join(self.root, \"PedMasks\", self.masks[idx])\n",
- " img = Image.open(img_path).convert(\"RGB\")\n",
- " # note that we haven't converted the mask to RGB,\n",
- " # because each color corresponds to a different instance\n",
- " # with 0 being background\n",
- " mask = Image.open(mask_path)\n",
- "\n",
- " mask = np.array(mask)\n",
- " # instances are encoded as different colors\n",
- " obj_ids = np.unique(mask)\n",
- " # first id is the background, so remove it\n",
- " obj_ids = obj_ids[1:]\n",
- "\n",
- " # split the color-encoded mask into a set\n",
- " # of binary masks\n",
- " masks = mask == obj_ids[:, None, None]\n",
- "\n",
- " # get bounding box coordinates for each mask\n",
- " num_objs = len(obj_ids)\n",
- " boxes = []\n",
- " for i in range(num_objs):\n",
- " pos = np.where(masks[i])\n",
- " xmin = np.min(pos[1])\n",
- " xmax = np.max(pos[1])\n",
- " ymin = np.min(pos[0])\n",
- " ymax = np.max(pos[0])\n",
- " boxes.append([xmin, ymin, xmax, ymax])\n",
- "\n",
- " boxes = torch.as_tensor(boxes, dtype=torch.float32)\n",
- " # there is only one class\n",
- " labels = torch.ones((num_objs,), dtype=torch.int64)\n",
- " masks = torch.as_tensor(masks, dtype=torch.uint8)\n",
- "\n",
- " image_id = torch.tensor([idx])\n",
- " area = (boxes[:, 3] - boxes[:, 1]) * (boxes[:, 2] - boxes[:, 0])\n",
- " # suppose all instances are not crowd\n",
- " iscrowd = torch.zeros((num_objs,), dtype=torch.int64)\n",
- "\n",
- " target = {}\n",
- " target[\"boxes\"] = boxes\n",
- " target[\"labels\"] = labels\n",
- " target[\"masks\"] = masks\n",
- " target[\"image_id\"] = image_id\n",
- " target[\"area\"] = area\n",
- " target[\"iscrowd\"] = iscrowd\n",
- "\n",
- " if self.transforms is not None:\n",
- " img, target = self.transforms(img, target)\n",
- "\n",
- " return img, target\n",
- "\n",
- " def __len__(self):\n",
- " return len(self.imgs)"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "J6f3ZOTJ4Km9",
- "colab_type": "text"
- },
- "source": [
- "That's all for the dataset. Let's see how the outputs are structured for this dataset"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "ZEARO4B_ye0s",
- "colab_type": "code",
- "outputId": "03974749-b9ba-4d03-b3a6-9a566078b320",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 326
- }
- },
- "source": [
- "dataset = PennFudanDataset('PennFudanPed/')\n",
- "dataset[0]"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "(,\n",
- " {'area': tensor([35358., 36225.]), 'boxes': tensor([[159., 181., 301., 430.],\n",
- " [419., 170., 534., 485.]]), 'image_id': tensor([0]), 'iscrowd': tensor([0, 0]), 'labels': tensor([1, 1]), 'masks': tensor([[[0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " ...,\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0]],\n",
- " \n",
- " [[0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " ...,\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0],\n",
- " [0, 0, 0, ..., 0, 0, 0]]], dtype=torch.uint8)})"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 6
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "lWOhcsir9Ahx",
- "colab_type": "text"
- },
- "source": [
- "So we can see that by default, the dataset returns a `PIL.Image` and a dictionary\n",
- "containing several fields, including `boxes`, `labels` and `masks`."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "RoAEkUgn4uEq",
- "colab_type": "text"
- },
- "source": [
- "## Defining your model\n",
- "\n",
- "In this tutorial, we will be using [Mask R-CNN](https://arxiv.org/abs/1703.06870), which is based on top of [Faster R-CNN](https://arxiv.org/abs/1506.01497). Faster R-CNN is a model that predicts both bounding boxes and class scores for potential objects in the image.\n",
- "\n",
- "\n",
- "\n",
- "Mask R-CNN adds an extra branch into Faster R-CNN, which also predicts segmentation masks for each instance.\n",
- "\n",
- "\n",
- "\n",
- "There are two common situations where one might want to modify one of the available models in torchvision modelzoo.\n",
- "The first is when we want to start from a pre-trained model, and just finetune the last layer. The other is when we want to replace the backbone of the model with a different one (for faster predictions, for example).\n",
- "\n",
- "Let's go see how we would do one or another in the following sections.\n",
- "\n",
- "\n",
- "### 1 - Finetuning from a pretrained model\n",
- "\n",
- "Let's suppose that you want to start from a model pre-trained on COCO and want to finetune it for your particular classes. Here is a possible way of doing it:\n",
- "```\n",
- "import torchvision\n",
- "from torchvision.models.detection.faster_rcnn import FastRCNNPredictor\n",
- "\n",
- "# load a model pre-trained pre-trained on COCO\n",
- "model = torchvision.models.detection.fasterrcnn_resnet50_fpn(pretrained=True)\n",
- "\n",
- "# replace the classifier with a new one, that has\n",
- "# num_classes which is user-defined\n",
- "num_classes = 2 # 1 class (person) + background\n",
- "# get number of input features for the classifier\n",
- "in_features = model.roi_heads.box_predictor.cls_score.in_features\n",
- "# replace the pre-trained head with a new one\n",
- "model.roi_heads.box_predictor = FastRCNNPredictor(in_features, num_classes) \n",
- "```\n",
- "\n",
- "### 2 - Modifying the model to add a different backbone\n",
- "\n",
- "Another common situation arises when the user wants to replace the backbone of a detection\n",
- "model with a different one. For example, the current default backbone (ResNet-50) might be too big for some applications, and smaller models might be necessary.\n",
- "\n",
- "Here is how we would go into leveraging the functions provided by torchvision to modify a backbone.\n",
- "\n",
- "```\n",
- "import torchvision\n",
- "from torchvision.models.detection import FasterRCNN\n",
- "from torchvision.models.detection.rpn import AnchorGenerator\n",
- "\n",
- "# load a pre-trained model for classification and return\n",
- "# only the features\n",
- "backbone = torchvision.models.mobilenet_v2(pretrained=True).features\n",
- "# FasterRCNN needs to know the number of\n",
- "# output channels in a backbone. For mobilenet_v2, it's 1280\n",
- "# so we need to add it here\n",
- "backbone.out_channels = 1280\n",
- "\n",
- "# let's make the RPN generate 5 x 3 anchors per spatial\n",
- "# location, with 5 different sizes and 3 different aspect\n",
- "# ratios. We have a Tuple[Tuple[int]] because each feature\n",
- "# map could potentially have different sizes and\n",
- "# aspect ratios \n",
- "anchor_generator = AnchorGenerator(sizes=((32, 64, 128, 256, 512),),\n",
- " aspect_ratios=((0.5, 1.0, 2.0),))\n",
- "\n",
- "# let's define what are the feature maps that we will\n",
- "# use to perform the region of interest cropping, as well as\n",
- "# the size of the crop after rescaling.\n",
- "# if your backbone returns a Tensor, featmap_names is expected to\n",
- "# be [0]. More generally, the backbone should return an\n",
- "# OrderedDict[Tensor], and in featmap_names you can choose which\n",
- "# feature maps to use.\n",
- "roi_pooler = torchvision.ops.MultiScaleRoIAlign(featmap_names=[0],\n",
- " output_size=7,\n",
- " sampling_ratio=2)\n",
- "\n",
- "# put the pieces together inside a FasterRCNN model\n",
- "model = FasterRCNN(backbone,\n",
- " num_classes=2,\n",
- " rpn_anchor_generator=anchor_generator,\n",
- " box_roi_pool=roi_pooler)\n",
- "```\n",
- "\n",
- "### An Instance segmentation model for PennFudan Dataset\n",
- "\n",
- "In our case, we want to fine-tune from a pre-trained model, given that our dataset is very small. So we will be following approach number 1.\n",
- "\n",
- "Here we want to also compute the instance segmentation masks, so we will be using Mask R-CNN:"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "YjNHjVMOyYlH",
- "colab_type": "code",
- "colab": {}
- },
- "source": [
- "import torchvision\n",
- "from torchvision.models.detection.faster_rcnn import FastRCNNPredictor\n",
- "from torchvision.models.detection.mask_rcnn import MaskRCNNPredictor\n",
- "\n",
- " \n",
- "def get_instance_segmentation_model(num_classes):\n",
- " # load an instance segmentation model pre-trained on COCO\n",
- " model = torchvision.models.detection.maskrcnn_resnet50_fpn(pretrained=True)\n",
- "\n",
- " # get the number of input features for the classifier\n",
- " in_features = model.roi_heads.box_predictor.cls_score.in_features\n",
- " # replace the pre-trained head with a new one\n",
- " model.roi_heads.box_predictor = FastRCNNPredictor(in_features, num_classes)\n",
- "\n",
- " # now get the number of input features for the mask classifier\n",
- " in_features_mask = model.roi_heads.mask_predictor.conv5_mask.in_channels\n",
- " hidden_layer = 256\n",
- " # and replace the mask predictor with a new one\n",
- " model.roi_heads.mask_predictor = MaskRCNNPredictor(in_features_mask,\n",
- " hidden_layer,\n",
- " num_classes)\n",
- "\n",
- " return model"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "-WXLwePV5ieP",
- "colab_type": "text"
- },
- "source": [
- "That's it, this will make model be ready to be trained and evaluated on our custom dataset.\n",
- "\n",
- "## Training and evaluation functions\n",
- "\n",
- "In `references/detection/,` we have a number of helper functions to simplify training and evaluating detection models.\n",
- "Here, we will use `references/detection/engine.py`, `references/detection/utils.py` and `references/detection/transforms.py`.\n",
- "\n",
- "Let's copy those files (and their dependencies) in here so that they are available in the notebook"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "UYDb7PBw55b-",
- "colab_type": "code",
- "outputId": "45309f6e-2fed-4c49-a2c0-381da0fb4aca",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 68
- }
- },
- "source": [
- "%%shell\n",
- "\n",
- "# Download TorchVision repo to use some files from\n",
- "# references/detection\n",
- "git clone https://github.com/pytorch/vision.git\n",
- "cd vision\n",
- "git checkout v0.3.0\n",
- "\n",
- "cp references/detection/utils.py ../\n",
- "cp references/detection/transforms.py ../\n",
- "cp references/detection/coco_eval.py ../\n",
- "cp references/detection/engine.py ../\n",
- "cp references/detection/coco_utils.py ../"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "fatal: destination path 'vision' already exists and is not an empty directory.\n",
- "Already on 'v0.3.0'\n",
- "Your branch is up to date with 'origin/v0.3.0'.\n"
- ],
- "name": "stdout"
- },
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 8
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "2u9e_pdv54nG",
- "colab_type": "text"
- },
- "source": [
- "\n",
- "\n",
- "Let's write some helper functions for data augmentation / transformation, which leverages the functions in `refereces/detection` that we have just copied:\n"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "l79ivkwKy357",
- "colab_type": "code",
- "colab": {}
- },
- "source": [
- "from engine import train_one_epoch, evaluate\n",
- "import utils\n",
- "import transforms as T\n",
- "\n",
- "\n",
- "def get_transform(train):\n",
- " transforms = []\n",
- " # converts the image, a PIL image, into a PyTorch Tensor\n",
- " transforms.append(T.ToTensor())\n",
- " if train:\n",
- " # during training, randomly flip the training images\n",
- " # and ground-truth for data augmentation\n",
- " transforms.append(T.RandomHorizontalFlip(0.5))\n",
- " return T.Compose(transforms)"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "FzCLqiZk-sjf",
- "colab_type": "text"
- },
- "source": [
- "#### Note that we do not need to add a mean/std normalization nor image rescaling in the data transforms, as those are handled internally by the Mask R-CNN model."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "3YFJGJxk6XEs",
- "colab_type": "text"
- },
- "source": [
- "### Putting everything together\n",
- "\n",
- "We now have the dataset class, the models and the data transforms. Let's instantiate them"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "a5dGaIezze3y",
- "colab_type": "code",
- "colab": {}
- },
- "source": [
- "# use our dataset and defined transformations\n",
- "dataset = PennFudanDataset('PennFudanPed', get_transform(train=True))\n",
- "dataset_test = PennFudanDataset('PennFudanPed', get_transform(train=False))\n",
- "\n",
- "# split the dataset in train and test set\n",
- "torch.manual_seed(1)\n",
- "indices = torch.randperm(len(dataset)).tolist()\n",
- "dataset = torch.utils.data.Subset(dataset, indices[:-50])\n",
- "dataset_test = torch.utils.data.Subset(dataset_test, indices[-50:])\n",
- "\n",
- "# define training and validation data loaders\n",
- "data_loader = torch.utils.data.DataLoader(\n",
- " dataset, batch_size=2, shuffle=True, num_workers=4,\n",
- " collate_fn=utils.collate_fn)\n",
- "\n",
- "data_loader_test = torch.utils.data.DataLoader(\n",
- " dataset_test, batch_size=1, shuffle=False, num_workers=4,\n",
- " collate_fn=utils.collate_fn)"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "L5yvZUprj4ZN",
- "colab_type": "text"
- },
- "source": [
- "Now let's instantiate the model and the optimizer"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "zoenkCj18C4h",
- "colab_type": "code",
- "outputId": "44c71ea4-7778-40ec-c838-99ee45aace4d",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 71
- }
- },
- "source": [
- "device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')\n",
- "\n",
- "# our dataset has two classes only - background and person\n",
- "num_classes = 2\n",
- "\n",
- "# get the model using our helper function\n",
- "model = get_instance_segmentation_model(num_classes)\n",
- "# move model to the right device\n",
- "model.to(device)\n",
- "\n",
- "# construct an optimizer\n",
- "params = [p for p in model.parameters() if p.requires_grad]\n",
- "optimizer = torch.optim.SGD(params, lr=0.005,\n",
- " momentum=0.9, weight_decay=0.0005)\n",
- "\n",
- "# and a learning rate scheduler which decreases the learning rate by\n",
- "# 10x every 3 epochs\n",
- "lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer,\n",
- " step_size=3,\n",
- " gamma=0.1)"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Downloading: \"https://download.pytorch.org/models/maskrcnn_resnet50_fpn_coco-bf2d0c1e.pth\" to /root/.cache/torch/checkpoints/maskrcnn_resnet50_fpn_coco-bf2d0c1e.pth\n",
- "100%|██████████| 178090079/178090079 [00:02<00:00, 61358754.67it/s]\n"
- ],
- "name": "stderr"
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "XAd56lt4kDxc",
- "colab_type": "text"
- },
- "source": [
- "And now let's train the model for 10 epochs, evaluating at the end of every epoch."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "at-h4OWK0aoc",
- "colab_type": "code",
- "outputId": "80d9fbf0-100b-46b5-ea7d-fad8bd8bd4e5",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 7517
- }
- },
- "source": [
- "# let's train it for 10 epochs\n",
- "num_epochs = 10\n",
- "\n",
- "for epoch in range(num_epochs):\n",
- " # train for one epoch, printing every 10 iterations\n",
- " train_one_epoch(model, optimizer, data_loader, device, epoch, print_freq=10)\n",
- " # update the learning rate\n",
- " lr_scheduler.step()\n",
- " # evaluate on the test dataset\n",
- " evaluate(model, data_loader_test, device=device)"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "stream",
- "text": [
- "Epoch: [0] [ 0/60] eta: 0:01:54 lr: 0.000090 loss: 3.5688 (3.5688) loss_classifier: 0.7563 (0.7563) loss_box_reg: 0.1544 (0.1544) loss_mask: 2.6350 (2.6350) loss_objectness: 0.0167 (0.0167) loss_rpn_box_reg: 0.0064 (0.0064) time: 1.9101 data: 0.4269 max mem: 3175\n",
- "Epoch: [0] [10/60] eta: 0:00:35 lr: 0.000936 loss: 1.5702 (2.1186) loss_classifier: 0.4521 (0.4978) loss_box_reg: 0.1846 (0.1915) loss_mask: 0.9227 (1.3971) loss_objectness: 0.0173 (0.0219) loss_rpn_box_reg: 0.0087 (0.0103) time: 0.7126 data: 0.0450 max mem: 4552\n",
- "Epoch: [0] [20/60] eta: 0:00:26 lr: 0.001783 loss: 0.8643 (1.4273) loss_classifier: 0.2400 (0.3407) loss_box_reg: 0.1589 (0.1740) loss_mask: 0.3977 (0.8806) loss_objectness: 0.0173 (0.0201) loss_rpn_box_reg: 0.0090 (0.0119) time: 0.5888 data: 0.0067 max mem: 4552\n",
- "Epoch: [0] [30/60] eta: 0:00:19 lr: 0.002629 loss: 0.5349 (1.1192) loss_classifier: 0.0967 (0.2569) loss_box_reg: 0.1289 (0.1610) loss_mask: 0.2496 (0.6734) loss_objectness: 0.0102 (0.0163) loss_rpn_box_reg: 0.0101 (0.0116) time: 0.6026 data: 0.0066 max mem: 5310\n",
- "Epoch: [0] [40/60] eta: 0:00:12 lr: 0.003476 loss: 0.4128 (0.9479) loss_classifier: 0.0634 (0.2091) loss_box_reg: 0.1078 (0.1524) loss_mask: 0.2095 (0.5601) loss_objectness: 0.0059 (0.0138) loss_rpn_box_reg: 0.0113 (0.0125) time: 0.6283 data: 0.0066 max mem: 5310\n",
- "Epoch: [0] [50/60] eta: 0:00:06 lr: 0.004323 loss: 0.3223 (0.8260) loss_classifier: 0.0453 (0.1783) loss_box_reg: 0.0899 (0.1395) loss_mask: 0.1734 (0.4838) loss_objectness: 0.0038 (0.0118) loss_rpn_box_reg: 0.0113 (0.0126) time: 0.6311 data: 0.0070 max mem: 5310\n",
- "Epoch: [0] [59/60] eta: 0:00:00 lr: 0.005000 loss: 0.2608 (0.7366) loss_classifier: 0.0390 (0.1564) loss_box_reg: 0.0574 (0.1245) loss_mask: 0.1512 (0.4334) loss_objectness: 0.0020 (0.0103) loss_rpn_box_reg: 0.0102 (0.0121) time: 0.6404 data: 0.0075 max mem: 5310\n",
- "Epoch: [0] Total time: 0:00:38 (0.6413 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:28 model_time: 0.3890 (0.3890) evaluator_time: 0.0042 (0.0042) time: 0.5795 data: 0.1848 max mem: 5310\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1158 (0.1223) evaluator_time: 0.0046 (0.0088) time: 0.1289 data: 0.0036 max mem: 5310\n",
- "Test: Total time: 0:00:07 (0.1421 s / it)\n",
- "Averaged stats: model_time: 0.1158 (0.1223) evaluator_time: 0.0046 (0.0088)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.682\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.982\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.872\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.406\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.693\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.311\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.742\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.742\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.700\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.745\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.704\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.982\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.910\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.434\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.717\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.323\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.748\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.750\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.688\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.754\n",
- "Epoch: [1] [ 0/60] eta: 0:01:04 lr: 0.005000 loss: 0.3601 (0.3601) loss_classifier: 0.0550 (0.0550) loss_box_reg: 0.1111 (0.1111) loss_mask: 0.1692 (0.1692) loss_objectness: 0.0032 (0.0032) loss_rpn_box_reg: 0.0217 (0.0217) time: 1.0794 data: 0.4107 max mem: 5310\n",
- "Epoch: [1] [10/60] eta: 0:00:37 lr: 0.005000 loss: 0.2678 (0.2754) loss_classifier: 0.0542 (0.0497) loss_box_reg: 0.0572 (0.0565) loss_mask: 0.1510 (0.1532) loss_objectness: 0.0016 (0.0019) loss_rpn_box_reg: 0.0096 (0.0142) time: 0.7499 data: 0.0436 max mem: 5310\n",
- "Epoch: [1] [20/60] eta: 0:00:28 lr: 0.005000 loss: 0.2345 (0.2438) loss_classifier: 0.0400 (0.0421) loss_box_reg: 0.0362 (0.0445) loss_mask: 0.1347 (0.1429) loss_objectness: 0.0014 (0.0022) loss_rpn_box_reg: 0.0095 (0.0121) time: 0.6846 data: 0.0068 max mem: 5310\n",
- "Epoch: [1] [30/60] eta: 0:00:20 lr: 0.005000 loss: 0.1942 (0.2286) loss_classifier: 0.0235 (0.0373) loss_box_reg: 0.0205 (0.0355) loss_mask: 0.1293 (0.1434) loss_objectness: 0.0005 (0.0017) loss_rpn_box_reg: 0.0068 (0.0106) time: 0.6301 data: 0.0066 max mem: 5310\n",
- "Epoch: [1] [40/60] eta: 0:00:13 lr: 0.005000 loss: 0.1951 (0.2253) loss_classifier: 0.0277 (0.0361) loss_box_reg: 0.0173 (0.0324) loss_mask: 0.1331 (0.1450) loss_objectness: 0.0005 (0.0016) loss_rpn_box_reg: 0.0074 (0.0102) time: 0.6304 data: 0.0066 max mem: 5310\n",
- "Epoch: [1] [50/60] eta: 0:00:06 lr: 0.005000 loss: 0.2011 (0.2242) loss_classifier: 0.0348 (0.0370) loss_box_reg: 0.0207 (0.0309) loss_mask: 0.1337 (0.1438) loss_objectness: 0.0007 (0.0016) loss_rpn_box_reg: 0.0080 (0.0109) time: 0.6441 data: 0.0068 max mem: 5310\n",
- "Epoch: [1] [59/60] eta: 0:00:00 lr: 0.005000 loss: 0.2162 (0.2248) loss_classifier: 0.0381 (0.0382) loss_box_reg: 0.0253 (0.0307) loss_mask: 0.1325 (0.1437) loss_objectness: 0.0008 (0.0016) loss_rpn_box_reg: 0.0085 (0.0106) time: 0.6245 data: 0.0067 max mem: 5310\n",
- "Epoch: [1] Total time: 0:00:39 (0.6548 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:17 model_time: 0.1625 (0.1625) evaluator_time: 0.0040 (0.0040) time: 0.3575 data: 0.1894 max mem: 5310\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1113 (0.1127) evaluator_time: 0.0037 (0.0072) time: 0.1226 data: 0.0034 max mem: 5310\n",
- "Test: Total time: 0:00:06 (0.1306 s / it)\n",
- "Averaged stats: model_time: 0.1113 (0.1127) evaluator_time: 0.0037 (0.0072)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.750\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.983\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.959\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.440\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.353\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.803\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.803\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.725\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.809\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.734\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.974\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.889\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.413\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.749\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.339\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.776\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.776\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.662\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.784\n",
- "Epoch: [2] [ 0/60] eta: 0:00:57 lr: 0.005000 loss: 0.2592 (0.2592) loss_classifier: 0.0457 (0.0457) loss_box_reg: 0.0357 (0.0357) loss_mask: 0.1604 (0.1604) loss_objectness: 0.0005 (0.0005) loss_rpn_box_reg: 0.0169 (0.0169) time: 0.9603 data: 0.4132 max mem: 5310\n",
- "Epoch: [2] [10/60] eta: 0:00:31 lr: 0.005000 loss: 0.1793 (0.1962) loss_classifier: 0.0260 (0.0358) loss_box_reg: 0.0164 (0.0199) loss_mask: 0.1189 (0.1288) loss_objectness: 0.0010 (0.0015) loss_rpn_box_reg: 0.0086 (0.0102) time: 0.6373 data: 0.0410 max mem: 5310\n",
- "Epoch: [2] [20/60] eta: 0:00:25 lr: 0.005000 loss: 0.2012 (0.2086) loss_classifier: 0.0270 (0.0358) loss_box_reg: 0.0164 (0.0226) loss_mask: 0.1226 (0.1372) loss_objectness: 0.0010 (0.0015) loss_rpn_box_reg: 0.0102 (0.0115) time: 0.6289 data: 0.0052 max mem: 5310\n",
- "Epoch: [2] [30/60] eta: 0:00:18 lr: 0.005000 loss: 0.1754 (0.1926) loss_classifier: 0.0270 (0.0320) loss_box_reg: 0.0133 (0.0183) loss_mask: 0.1226 (0.1313) loss_objectness: 0.0005 (0.0011) loss_rpn_box_reg: 0.0082 (0.0099) time: 0.6294 data: 0.0067 max mem: 5310\n",
- "Epoch: [2] [40/60] eta: 0:00:12 lr: 0.005000 loss: 0.1664 (0.1907) loss_classifier: 0.0313 (0.0322) loss_box_reg: 0.0121 (0.0178) loss_mask: 0.1240 (0.1294) loss_objectness: 0.0005 (0.0014) loss_rpn_box_reg: 0.0079 (0.0098) time: 0.6273 data: 0.0067 max mem: 5310\n",
- "Epoch: [2] [50/60] eta: 0:00:06 lr: 0.005000 loss: 0.1771 (0.1862) loss_classifier: 0.0285 (0.0308) loss_box_reg: 0.0145 (0.0170) loss_mask: 0.1263 (0.1278) loss_objectness: 0.0005 (0.0013) loss_rpn_box_reg: 0.0086 (0.0094) time: 0.6417 data: 0.0068 max mem: 5310\n",
- "Epoch: [2] [59/60] eta: 0:00:00 lr: 0.005000 loss: 0.1771 (0.1900) loss_classifier: 0.0257 (0.0316) loss_box_reg: 0.0158 (0.0180) loss_mask: 0.1269 (0.1291) loss_objectness: 0.0009 (0.0014) loss_rpn_box_reg: 0.0077 (0.0099) time: 0.6555 data: 0.0073 max mem: 5310\n",
- "Epoch: [2] Total time: 0:00:38 (0.6433 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:18 model_time: 0.1615 (0.1615) evaluator_time: 0.0041 (0.0041) time: 0.3662 data: 0.1992 max mem: 5310\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1143 (0.1142) evaluator_time: 0.0035 (0.0059) time: 0.1230 data: 0.0034 max mem: 5310\n",
- "Test: Total time: 0:00:06 (0.1307 s / it)\n",
- "Averaged stats: model_time: 0.1143 (0.1142) evaluator_time: 0.0035 (0.0059)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.803\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.958\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.474\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.814\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.363\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.840\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.840\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.846\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.764\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.922\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.474\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.776\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.345\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.803\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.803\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.725\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.809\n",
- "Epoch: [3] [ 0/60] eta: 0:01:31 lr: 0.000500 loss: 0.2188 (0.2188) loss_classifier: 0.0488 (0.0488) loss_box_reg: 0.0222 (0.0222) loss_mask: 0.1369 (0.1369) loss_objectness: 0.0002 (0.0002) loss_rpn_box_reg: 0.0106 (0.0106) time: 1.5300 data: 0.7803 max mem: 5310\n",
- "Epoch: [3] [10/60] eta: 0:00:35 lr: 0.000500 loss: 0.1462 (0.1512) loss_classifier: 0.0216 (0.0238) loss_box_reg: 0.0074 (0.0093) loss_mask: 0.1066 (0.1111) loss_objectness: 0.0005 (0.0006) loss_rpn_box_reg: 0.0048 (0.0064) time: 0.7073 data: 0.0738 max mem: 5310\n",
- "Epoch: [3] [20/60] eta: 0:00:27 lr: 0.000500 loss: 0.1462 (0.1572) loss_classifier: 0.0216 (0.0257) loss_box_reg: 0.0068 (0.0108) loss_mask: 0.1055 (0.1123) loss_objectness: 0.0004 (0.0007) loss_rpn_box_reg: 0.0052 (0.0077) time: 0.6362 data: 0.0049 max mem: 5310\n",
- "Epoch: [3] [30/60] eta: 0:00:20 lr: 0.000500 loss: 0.1587 (0.1656) loss_classifier: 0.0256 (0.0275) loss_box_reg: 0.0095 (0.0120) loss_mask: 0.1156 (0.1169) loss_objectness: 0.0005 (0.0009) loss_rpn_box_reg: 0.0082 (0.0083) time: 0.6555 data: 0.0066 max mem: 5310\n",
- "Epoch: [3] [40/60] eta: 0:00:13 lr: 0.000500 loss: 0.1624 (0.1694) loss_classifier: 0.0229 (0.0269) loss_box_reg: 0.0107 (0.0128) loss_mask: 0.1235 (0.1206) loss_objectness: 0.0007 (0.0010) loss_rpn_box_reg: 0.0076 (0.0082) time: 0.6545 data: 0.0068 max mem: 5310\n",
- "Epoch: [3] [50/60] eta: 0:00:06 lr: 0.000500 loss: 0.1547 (0.1647) loss_classifier: 0.0229 (0.0262) loss_box_reg: 0.0094 (0.0123) loss_mask: 0.1069 (0.1176) loss_objectness: 0.0003 (0.0009) loss_rpn_box_reg: 0.0057 (0.0077) time: 0.6276 data: 0.0068 max mem: 5310\n",
- "Epoch: [3] [59/60] eta: 0:00:00 lr: 0.000500 loss: 0.1461 (0.1655) loss_classifier: 0.0218 (0.0258) loss_box_reg: 0.0084 (0.0123) loss_mask: 0.1061 (0.1185) loss_objectness: 0.0003 (0.0009) loss_rpn_box_reg: 0.0056 (0.0079) time: 0.6126 data: 0.0068 max mem: 5310\n",
- "Epoch: [3] Total time: 0:00:39 (0.6519 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:18 model_time: 0.1630 (0.1630) evaluator_time: 0.0038 (0.0038) time: 0.3705 data: 0.2021 max mem: 5310\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1125 (0.1124) evaluator_time: 0.0037 (0.0057) time: 0.1215 data: 0.0036 max mem: 5310\n",
- "Test: Total time: 0:00:06 (0.1294 s / it)\n",
- "Averaged stats: model_time: 0.1125 (0.1124) evaluator_time: 0.0037 (0.0057)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.814\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.991\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.953\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.543\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.823\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.371\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.855\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.855\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.787\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.860\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.760\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.991\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.918\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.478\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.768\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.345\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.801\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.801\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.750\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.805\n",
- "Epoch: [4] [ 0/60] eta: 0:01:06 lr: 0.000500 loss: 0.1322 (0.1322) loss_classifier: 0.0270 (0.0270) loss_box_reg: 0.0052 (0.0052) loss_mask: 0.0926 (0.0926) loss_objectness: 0.0006 (0.0006) loss_rpn_box_reg: 0.0069 (0.0069) time: 1.1061 data: 0.5225 max mem: 5310\n",
- "Epoch: [4] [10/60] eta: 0:00:32 lr: 0.000500 loss: 0.1779 (0.1740) loss_classifier: 0.0281 (0.0279) loss_box_reg: 0.0109 (0.0119) loss_mask: 0.1205 (0.1249) loss_objectness: 0.0003 (0.0020) loss_rpn_box_reg: 0.0063 (0.0073) time: 0.6471 data: 0.0514 max mem: 5310\n",
- "Epoch: [4] [20/60] eta: 0:00:25 lr: 0.000500 loss: 0.1608 (0.1713) loss_classifier: 0.0286 (0.0280) loss_box_reg: 0.0116 (0.0126) loss_mask: 0.1129 (0.1215) loss_objectness: 0.0003 (0.0015) loss_rpn_box_reg: 0.0059 (0.0077) time: 0.6207 data: 0.0055 max mem: 5345\n",
- "Epoch: [4] [30/60] eta: 0:00:19 lr: 0.000500 loss: 0.1483 (0.1668) loss_classifier: 0.0242 (0.0268) loss_box_reg: 0.0076 (0.0124) loss_mask: 0.1040 (0.1189) loss_objectness: 0.0004 (0.0012) loss_rpn_box_reg: 0.0059 (0.0075) time: 0.6336 data: 0.0070 max mem: 5345\n",
- "Epoch: [4] [40/60] eta: 0:00:12 lr: 0.000500 loss: 0.1355 (0.1625) loss_classifier: 0.0154 (0.0258) loss_box_reg: 0.0067 (0.0115) loss_mask: 0.1040 (0.1165) loss_objectness: 0.0003 (0.0011) loss_rpn_box_reg: 0.0070 (0.0075) time: 0.6434 data: 0.0075 max mem: 5345\n",
- "Epoch: [4] [50/60] eta: 0:00:06 lr: 0.000500 loss: 0.1472 (0.1608) loss_classifier: 0.0202 (0.0249) loss_box_reg: 0.0074 (0.0112) loss_mask: 0.1040 (0.1161) loss_objectness: 0.0003 (0.0011) loss_rpn_box_reg: 0.0060 (0.0076) time: 0.6428 data: 0.0071 max mem: 5345\n",
- "Epoch: [4] [59/60] eta: 0:00:00 lr: 0.000500 loss: 0.1477 (0.1613) loss_classifier: 0.0225 (0.0251) loss_box_reg: 0.0092 (0.0113) loss_mask: 0.1126 (0.1163) loss_objectness: 0.0003 (0.0010) loss_rpn_box_reg: 0.0065 (0.0076) time: 0.6340 data: 0.0069 max mem: 5345\n",
- "Epoch: [4] Total time: 0:00:38 (0.6423 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:17 model_time: 0.1500 (0.1500) evaluator_time: 0.0040 (0.0040) time: 0.3557 data: 0.2002 max mem: 5345\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1121 (0.1121) evaluator_time: 0.0034 (0.0057) time: 0.1219 data: 0.0034 max mem: 5345\n",
- "Test: Total time: 0:00:06 (0.1286 s / it)\n",
- "Averaged stats: model_time: 0.1121 (0.1121) evaluator_time: 0.0034 (0.0057)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.820\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.991\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.953\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.537\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.831\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.376\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.860\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.860\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.775\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.866\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.769\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.991\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.910\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.447\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.779\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.347\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.806\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.806\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.738\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.811\n",
- "Epoch: [5] [ 0/60] eta: 0:00:52 lr: 0.000500 loss: 0.1502 (0.1502) loss_classifier: 0.0202 (0.0202) loss_box_reg: 0.0114 (0.0114) loss_mask: 0.1132 (0.1132) loss_objectness: 0.0002 (0.0002) loss_rpn_box_reg: 0.0052 (0.0052) time: 0.8670 data: 0.2655 max mem: 5345\n",
- "Epoch: [5] [10/60] eta: 0:00:32 lr: 0.000500 loss: 0.1636 (0.1717) loss_classifier: 0.0243 (0.0294) loss_box_reg: 0.0138 (0.0136) loss_mask: 0.1141 (0.1192) loss_objectness: 0.0003 (0.0006) loss_rpn_box_reg: 0.0084 (0.0090) time: 0.6526 data: 0.0301 max mem: 5345\n",
- "Epoch: [5] [20/60] eta: 0:00:25 lr: 0.000500 loss: 0.1494 (0.1601) loss_classifier: 0.0224 (0.0261) loss_box_reg: 0.0092 (0.0117) loss_mask: 0.1076 (0.1138) loss_objectness: 0.0003 (0.0005) loss_rpn_box_reg: 0.0083 (0.0080) time: 0.6330 data: 0.0066 max mem: 5345\n",
- "Epoch: [5] [30/60] eta: 0:00:18 lr: 0.000500 loss: 0.1496 (0.1594) loss_classifier: 0.0195 (0.0251) loss_box_reg: 0.0092 (0.0113) loss_mask: 0.1076 (0.1146) loss_objectness: 0.0002 (0.0005) loss_rpn_box_reg: 0.0075 (0.0079) time: 0.6204 data: 0.0066 max mem: 5345\n",
- "Epoch: [5] [40/60] eta: 0:00:12 lr: 0.000500 loss: 0.1606 (0.1639) loss_classifier: 0.0249 (0.0260) loss_box_reg: 0.0108 (0.0124) loss_mask: 0.1124 (0.1169) loss_objectness: 0.0003 (0.0005) loss_rpn_box_reg: 0.0072 (0.0081) time: 0.6338 data: 0.0067 max mem: 5345\n",
- "Epoch: [5] [50/60] eta: 0:00:06 lr: 0.000500 loss: 0.1578 (0.1641) loss_classifier: 0.0230 (0.0257) loss_box_reg: 0.0093 (0.0117) loss_mask: 0.1112 (0.1180) loss_objectness: 0.0004 (0.0006) loss_rpn_box_reg: 0.0055 (0.0080) time: 0.6592 data: 0.0070 max mem: 5345\n",
- "Epoch: [5] [59/60] eta: 0:00:00 lr: 0.000500 loss: 0.1517 (0.1626) loss_classifier: 0.0220 (0.0252) loss_box_reg: 0.0081 (0.0111) loss_mask: 0.1121 (0.1179) loss_objectness: 0.0003 (0.0007) loss_rpn_box_reg: 0.0053 (0.0078) time: 0.6494 data: 0.0070 max mem: 5345\n",
- "Epoch: [5] Total time: 0:00:38 (0.6447 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:17 model_time: 0.1581 (0.1581) evaluator_time: 0.0041 (0.0041) time: 0.3526 data: 0.1888 max mem: 5345\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1133 (0.1119) evaluator_time: 0.0036 (0.0058) time: 0.1216 data: 0.0035 max mem: 5345\n",
- "Test: Total time: 0:00:06 (0.1288 s / it)\n",
- "Averaged stats: model_time: 0.1133 (0.1119) evaluator_time: 0.0036 (0.0058)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.818\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.959\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.531\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.828\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.374\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.858\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.858\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.787\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.863\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.764\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.916\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.484\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.772\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.350\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.806\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.806\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.809\n",
- "Epoch: [6] [ 0/60] eta: 0:01:15 lr: 0.000050 loss: 0.1268 (0.1268) loss_classifier: 0.0136 (0.0136) loss_box_reg: 0.0076 (0.0076) loss_mask: 0.0992 (0.0992) loss_objectness: 0.0001 (0.0001) loss_rpn_box_reg: 0.0063 (0.0063) time: 1.2659 data: 0.4840 max mem: 5345\n",
- "Epoch: [6] [10/60] eta: 0:00:34 lr: 0.000050 loss: 0.1542 (0.1612) loss_classifier: 0.0221 (0.0240) loss_box_reg: 0.0120 (0.0117) loss_mask: 0.1061 (0.1164) loss_objectness: 0.0002 (0.0004) loss_rpn_box_reg: 0.0063 (0.0087) time: 0.6829 data: 0.0505 max mem: 5345\n",
- "Epoch: [6] [20/60] eta: 0:00:25 lr: 0.000050 loss: 0.1531 (0.1596) loss_classifier: 0.0212 (0.0233) loss_box_reg: 0.0076 (0.0108) loss_mask: 0.1123 (0.1169) loss_objectness: 0.0003 (0.0006) loss_rpn_box_reg: 0.0059 (0.0080) time: 0.6122 data: 0.0072 max mem: 5345\n",
- "Epoch: [6] [30/60] eta: 0:00:18 lr: 0.000050 loss: 0.1465 (0.1650) loss_classifier: 0.0202 (0.0256) loss_box_reg: 0.0058 (0.0120) loss_mask: 0.1123 (0.1186) loss_objectness: 0.0004 (0.0009) loss_rpn_box_reg: 0.0055 (0.0078) time: 0.5959 data: 0.0069 max mem: 5345\n",
- "Epoch: [6] [40/60] eta: 0:00:12 lr: 0.000050 loss: 0.1378 (0.1603) loss_classifier: 0.0256 (0.0268) loss_box_reg: 0.0068 (0.0109) loss_mask: 0.0993 (0.1142) loss_objectness: 0.0005 (0.0009) loss_rpn_box_reg: 0.0052 (0.0074) time: 0.6272 data: 0.0066 max mem: 5345\n",
- "Epoch: [6] [50/60] eta: 0:00:06 lr: 0.000050 loss: 0.1372 (0.1623) loss_classifier: 0.0256 (0.0264) loss_box_reg: 0.0075 (0.0115) loss_mask: 0.1033 (0.1161) loss_objectness: 0.0003 (0.0009) loss_rpn_box_reg: 0.0058 (0.0075) time: 0.6603 data: 0.0066 max mem: 5345\n",
- "Epoch: [6] [59/60] eta: 0:00:00 lr: 0.000050 loss: 0.1372 (0.1619) loss_classifier: 0.0204 (0.0260) loss_box_reg: 0.0082 (0.0116) loss_mask: 0.1074 (0.1159) loss_objectness: 0.0004 (0.0008) loss_rpn_box_reg: 0.0070 (0.0075) time: 0.6463 data: 0.0067 max mem: 5345\n",
- "Epoch: [6] Total time: 0:00:38 (0.6395 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:17 model_time: 0.1552 (0.1552) evaluator_time: 0.0040 (0.0040) time: 0.3581 data: 0.1974 max mem: 5345\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1129 (0.1116) evaluator_time: 0.0035 (0.0057) time: 0.1212 data: 0.0034 max mem: 5345\n",
- "Test: Total time: 0:00:06 (0.1282 s / it)\n",
- "Averaged stats: model_time: 0.1129 (0.1116) evaluator_time: 0.0035 (0.0057)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.820\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.960\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.596\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.831\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.378\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.861\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.861\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.787\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.867\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.767\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.916\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.462\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.776\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.349\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.809\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.809\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.813\n",
- "Epoch: [7] [ 0/60] eta: 0:00:53 lr: 0.000050 loss: 0.1048 (0.1048) loss_classifier: 0.0119 (0.0119) loss_box_reg: 0.0030 (0.0030) loss_mask: 0.0879 (0.0879) loss_objectness: 0.0000 (0.0000) loss_rpn_box_reg: 0.0020 (0.0020) time: 0.8976 data: 0.3350 max mem: 5345\n",
- "Epoch: [7] [10/60] eta: 0:00:31 lr: 0.000050 loss: 0.1401 (0.1356) loss_classifier: 0.0189 (0.0191) loss_box_reg: 0.0068 (0.0071) loss_mask: 0.1048 (0.1042) loss_objectness: 0.0002 (0.0003) loss_rpn_box_reg: 0.0039 (0.0049) time: 0.6264 data: 0.0366 max mem: 5345\n",
- "Epoch: [7] [20/60] eta: 0:00:25 lr: 0.000050 loss: 0.1401 (0.1490) loss_classifier: 0.0189 (0.0204) loss_box_reg: 0.0068 (0.0087) loss_mask: 0.1070 (0.1134) loss_objectness: 0.0003 (0.0007) loss_rpn_box_reg: 0.0044 (0.0057) time: 0.6145 data: 0.0077 max mem: 5345\n",
- "Epoch: [7] [30/60] eta: 0:00:19 lr: 0.000050 loss: 0.1424 (0.1498) loss_classifier: 0.0211 (0.0213) loss_box_reg: 0.0081 (0.0087) loss_mask: 0.1076 (0.1126) loss_objectness: 0.0005 (0.0008) loss_rpn_box_reg: 0.0058 (0.0065) time: 0.6514 data: 0.0081 max mem: 5370\n",
- "Epoch: [7] [40/60] eta: 0:00:12 lr: 0.000050 loss: 0.1435 (0.1523) loss_classifier: 0.0230 (0.0232) loss_box_reg: 0.0090 (0.0091) loss_mask: 0.1069 (0.1127) loss_objectness: 0.0004 (0.0007) loss_rpn_box_reg: 0.0057 (0.0065) time: 0.6590 data: 0.0071 max mem: 5370\n",
- "Epoch: [7] [50/60] eta: 0:00:06 lr: 0.000050 loss: 0.1519 (0.1545) loss_classifier: 0.0251 (0.0239) loss_box_reg: 0.0092 (0.0099) loss_mask: 0.1141 (0.1131) loss_objectness: 0.0003 (0.0007) loss_rpn_box_reg: 0.0056 (0.0069) time: 0.6489 data: 0.0068 max mem: 5370\n",
- "Epoch: [7] [59/60] eta: 0:00:00 lr: 0.000050 loss: 0.1533 (0.1590) loss_classifier: 0.0280 (0.0257) loss_box_reg: 0.0101 (0.0109) loss_mask: 0.1141 (0.1143) loss_objectness: 0.0003 (0.0008) loss_rpn_box_reg: 0.0084 (0.0073) time: 0.6595 data: 0.0072 max mem: 5370\n",
- "Epoch: [7] Total time: 0:00:38 (0.6479 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:18 model_time: 0.1607 (0.1607) evaluator_time: 0.0041 (0.0041) time: 0.3618 data: 0.1955 max mem: 5370\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1134 (0.1118) evaluator_time: 0.0037 (0.0058) time: 0.1218 data: 0.0036 max mem: 5370\n",
- "Test: Total time: 0:00:06 (0.1283 s / it)\n",
- "Averaged stats: model_time: 0.1134 (0.1118) evaluator_time: 0.0037 (0.0058)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.821\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.960\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.596\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.832\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.380\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.862\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.862\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.787\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.868\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.768\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.917\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.464\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.776\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.350\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.809\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.809\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.813\n",
- "Epoch: [8] [ 0/60] eta: 0:00:56 lr: 0.000050 loss: 0.1368 (0.1368) loss_classifier: 0.0151 (0.0151) loss_box_reg: 0.0078 (0.0078) loss_mask: 0.1098 (0.1098) loss_objectness: 0.0004 (0.0004) loss_rpn_box_reg: 0.0038 (0.0038) time: 0.9355 data: 0.2996 max mem: 5370\n",
- "Epoch: [8] [10/60] eta: 0:00:31 lr: 0.000050 loss: 0.1555 (0.1604) loss_classifier: 0.0233 (0.0258) loss_box_reg: 0.0086 (0.0107) loss_mask: 0.1098 (0.1175) loss_objectness: 0.0002 (0.0003) loss_rpn_box_reg: 0.0047 (0.0061) time: 0.6251 data: 0.0334 max mem: 5370\n",
- "Epoch: [8] [20/60] eta: 0:00:25 lr: 0.000050 loss: 0.1418 (0.1505) loss_classifier: 0.0192 (0.0216) loss_box_reg: 0.0067 (0.0087) loss_mask: 0.1037 (0.1131) loss_objectness: 0.0002 (0.0004) loss_rpn_box_reg: 0.0054 (0.0068) time: 0.6100 data: 0.0068 max mem: 5370\n",
- "Epoch: [8] [30/60] eta: 0:00:19 lr: 0.000050 loss: 0.1427 (0.1506) loss_classifier: 0.0195 (0.0224) loss_box_reg: 0.0062 (0.0088) loss_mask: 0.1037 (0.1120) loss_objectness: 0.0003 (0.0004) loss_rpn_box_reg: 0.0065 (0.0070) time: 0.6461 data: 0.0068 max mem: 5370\n",
- "Epoch: [8] [40/60] eta: 0:00:12 lr: 0.000050 loss: 0.1516 (0.1536) loss_classifier: 0.0240 (0.0236) loss_box_reg: 0.0096 (0.0103) loss_mask: 0.1037 (0.1117) loss_objectness: 0.0003 (0.0006) loss_rpn_box_reg: 0.0072 (0.0074) time: 0.6651 data: 0.0068 max mem: 5370\n",
- "Epoch: [8] [50/60] eta: 0:00:06 lr: 0.000050 loss: 0.1570 (0.1595) loss_classifier: 0.0253 (0.0244) loss_box_reg: 0.0110 (0.0114) loss_mask: 0.1060 (0.1156) loss_objectness: 0.0003 (0.0006) loss_rpn_box_reg: 0.0074 (0.0074) time: 0.6429 data: 0.0067 max mem: 5370\n",
- "Epoch: [8] [59/60] eta: 0:00:00 lr: 0.000050 loss: 0.1545 (0.1596) loss_classifier: 0.0253 (0.0247) loss_box_reg: 0.0092 (0.0111) loss_mask: 0.1118 (0.1157) loss_objectness: 0.0003 (0.0007) loss_rpn_box_reg: 0.0074 (0.0074) time: 0.6498 data: 0.0066 max mem: 5370\n",
- "Epoch: [8] Total time: 0:00:38 (0.6474 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:17 model_time: 0.1581 (0.1581) evaluator_time: 0.0041 (0.0041) time: 0.3566 data: 0.1928 max mem: 5370\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1125 (0.1125) evaluator_time: 0.0036 (0.0058) time: 0.1217 data: 0.0036 max mem: 5370\n",
- "Test: Total time: 0:00:06 (0.1290 s / it)\n",
- "Averaged stats: model_time: 0.1125 (0.1125) evaluator_time: 0.0036 (0.0058)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.826\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.960\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.596\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.837\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.382\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.865\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.865\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.787\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.870\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.772\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.917\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.458\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.782\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.352\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.812\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.812\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.815\n",
- "Epoch: [9] [ 0/60] eta: 0:00:52 lr: 0.000005 loss: 0.1495 (0.1495) loss_classifier: 0.0158 (0.0158) loss_box_reg: 0.0093 (0.0093) loss_mask: 0.1086 (0.1086) loss_objectness: 0.0054 (0.0054) loss_rpn_box_reg: 0.0105 (0.0105) time: 0.8829 data: 0.2796 max mem: 5370\n",
- "Epoch: [9] [10/60] eta: 0:00:32 lr: 0.000005 loss: 0.1645 (0.1607) loss_classifier: 0.0271 (0.0248) loss_box_reg: 0.0093 (0.0111) loss_mask: 0.1086 (0.1156) loss_objectness: 0.0007 (0.0020) loss_rpn_box_reg: 0.0077 (0.0072) time: 0.6560 data: 0.0323 max mem: 5370\n",
- "Epoch: [9] [20/60] eta: 0:00:25 lr: 0.000005 loss: 0.1444 (0.1535) loss_classifier: 0.0218 (0.0224) loss_box_reg: 0.0078 (0.0095) loss_mask: 0.1078 (0.1142) loss_objectness: 0.0004 (0.0013) loss_rpn_box_reg: 0.0036 (0.0060) time: 0.6136 data: 0.0072 max mem: 5370\n",
- "Epoch: [9] [30/60] eta: 0:00:18 lr: 0.000005 loss: 0.1361 (0.1559) loss_classifier: 0.0218 (0.0234) loss_box_reg: 0.0078 (0.0101) loss_mask: 0.1026 (0.1149) loss_objectness: 0.0004 (0.0010) loss_rpn_box_reg: 0.0052 (0.0065) time: 0.6150 data: 0.0069 max mem: 5370\n",
- "Epoch: [9] [40/60] eta: 0:00:12 lr: 0.000005 loss: 0.1613 (0.1622) loss_classifier: 0.0243 (0.0252) loss_box_reg: 0.0092 (0.0118) loss_mask: 0.1054 (0.1169) loss_objectness: 0.0003 (0.0010) loss_rpn_box_reg: 0.0072 (0.0075) time: 0.6652 data: 0.0075 max mem: 5370\n",
- "Epoch: [9] [50/60] eta: 0:00:06 lr: 0.000005 loss: 0.1473 (0.1602) loss_classifier: 0.0232 (0.0251) loss_box_reg: 0.0084 (0.0116) loss_mask: 0.1102 (0.1151) loss_objectness: 0.0004 (0.0009) loss_rpn_box_reg: 0.0070 (0.0075) time: 0.6760 data: 0.0074 max mem: 5370\n",
- "Epoch: [9] [59/60] eta: 0:00:00 lr: 0.000005 loss: 0.1391 (0.1572) loss_classifier: 0.0203 (0.0244) loss_box_reg: 0.0067 (0.0109) loss_mask: 0.1049 (0.1136) loss_objectness: 0.0004 (0.0010) loss_rpn_box_reg: 0.0066 (0.0072) time: 0.6440 data: 0.0068 max mem: 5370\n",
- "Epoch: [9] Total time: 0:00:38 (0.6447 s / it)\n",
- "creating index...\n",
- "index created!\n",
- "Test: [ 0/50] eta: 0:00:17 model_time: 0.1590 (0.1590) evaluator_time: 0.0039 (0.0039) time: 0.3443 data: 0.1797 max mem: 5370\n",
- "Test: [49/50] eta: 0:00:00 model_time: 0.1123 (0.1119) evaluator_time: 0.0035 (0.0057) time: 0.1212 data: 0.0034 max mem: 5370\n",
- "Test: Total time: 0:00:06 (0.1280 s / it)\n",
- "Averaged stats: model_time: 0.1123 (0.1119) evaluator_time: 0.0035 (0.0057)\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "Accumulating evaluation results...\n",
- "DONE (t=0.01s).\n",
- "IoU metric: bbox\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.828\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.960\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.596\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.839\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.382\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.867\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.867\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.787\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.873\n",
- "IoU metric: segm\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.771\n",
- " Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.990\n",
- " Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.917\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.458\n",
- " Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.780\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.351\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.811\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.811\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.762\n",
- " Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.814\n"
- ],
- "name": "stdout"
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "Z6mYGFLxkO8F",
- "colab_type": "text"
- },
- "source": [
- "Now that training has finished, let's have a look at what it actually predicts in a test image"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "YHwIdxH76uPj",
- "colab_type": "code",
- "colab": {}
- },
- "source": [
- "# pick one image from the test set\n",
- "img, _ = dataset_test[0]\n",
- "# put the model in evaluation mode\n",
- "model.eval()\n",
- "with torch.no_grad():\n",
- " prediction = model([img.to(device)])"
- ],
- "execution_count": 0,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "DmN602iKsuey",
- "colab_type": "text"
- },
- "source": [
- "Printing the prediction shows that we have a list of dictionaries. Each element of the list corresponds to a different image. As we have a single image, there is a single dictionary in the list.\n",
- "The dictionary contains the predictions for the image we passed. In this case, we can see that it contains `boxes`, `labels`, `masks` and `scores` as fields."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "Lkmb3qUu6zw3",
- "colab_type": "code",
- "outputId": "fe5616ea-7e27-4a29-d070-358bee6a1be8",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 527
- }
- },
- "source": [
- "prediction"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "text/plain": [
- "[{'boxes': tensor([[ 61.6491, 35.3001, 197.0657, 327.6245],\n",
- " [276.3604, 21.6470, 291.0668, 73.5886],\n",
- " [ 78.8921, 43.7346, 201.9858, 207.4100]], device='cuda:0'),\n",
- " 'labels': tensor([1, 1, 1], device='cuda:0'),\n",
- " 'masks': tensor([[[[0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " ...,\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.]]],\n",
- " \n",
- " \n",
- " [[[0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " ...,\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.]]],\n",
- " \n",
- " \n",
- " [[[0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " ...,\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.],\n",
- " [0., 0., 0., ..., 0., 0., 0.]]]], device='cuda:0'),\n",
- " 'scores': tensor([0.9995, 0.8236, 0.0713], device='cuda:0')}]"
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 14
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "RwT21rzotFbH",
- "colab_type": "text"
- },
- "source": [
- "Let's inspect the image and the predicted segmentation masks.\n",
- "\n",
- "For that, we need to convert the image, which has been rescaled to 0-1 and had the channels flipped so that we have it in `[C, H, W]` format."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "bpqN9t1u7B2J",
- "colab_type": "code",
- "outputId": "13b60c23-dce3-4a0c-fdf0-54eae39e5cc6",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 366
- }
- },
- "source": [
- "Image.fromarray(img.mul(255).permute(1, 2, 0).byte().numpy())"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAASQAAAFdCAIAAAAltoeyAAEAAElEQVR4nKT9WY8kS5YeCJ5FRBdb\n3D3Wm/fmnrV0sZpoNlmNwoDAzKDnnfOP5o/wX/CBj3wh0OipYgNk1nSxulhsMpfKvFvciHB3M1NV\nETnnzMNREVP3yCSJGcuLSHdzM1VRkbMv38H/1//z/yYiZsbMZqaqzNz3PREhor/jP4vIklIiA0RV\nVVVEjDGS/5oLAKABACCifwXRcs5IhoiICABWX35Z/xgAAMB6x3S9gn++lCIizAz1hZuXv29m7Vt+\nHWaOMXZdR0QiIiKIiAwAcJpOOecQAiKmlACg67qUkt/RPwwAIYQYY5kWVfXr+41ijH5lfwrfsRij\nmeWyIAiA+p3MLOe8zDnnHELcLJ4BYN1D6sxsXTlzWwAGRkTD9aYiklXMbODOH/zZ7pVS/M0Qgj9y\nSinnrDm3xfuHVdV3o73TzgUA0PD6JoKZCZj6k+L6joKte26UsyDy9rz81Zbni/d3kDmLQmDjOIk8\nXKaHaTLu4m748PFj7DsCBNQXh5uuDxERiOdFstgvfvXLEIIZ9H3/5u3bv/3bv6XYxRhLVhGJfUdE\nRGEcx4f337Vz9x0IIQzD8PDwsF1e28BSip+vP76fqX+gEbkvfhzHcRyZmZkRcVmW8/k8z7N/Bn7P\na/un0AixHUmj3WeM4d8UKbgyEq7caCYi4zCYGehKf06vZgIACOBE4HTgZ9CW2J6NiJiZNeScc86l\nFF+Gf1FVn3GaLymltCWm9joej6WUnHM7eCJCgJTSPM8i4gvIOTcWIqL2vO2HRijOnC6VQgjM7J93\nWeA3UlOmlYvagmOMzCyiG5ly3UAkbsffth0AhmEQkaLSltp1HSJaEv9AY5hnz97kjm+RVImwlRf+\nRM+Oe10tx/UzuB6NmKovDMA/R4CGgIhgRGT+OO2m2wVsT4qIgMhQlNAMrqQCiRITERoAwtgPKc9d\n3CsaKux2u8fz5Ke82+1DCO3IthySUsp5mqZJU8o5p5R8u5wxrtK2LqatzZ/x2f6oqh93+3BVHk+Y\n6tkD/ldfKxHjRu2oqpO7L8VX6XovlyKoXG+AAFgXd7lcAADtenKoBqix74mh8VhbcQihPWRjPESk\nDZ/7CfkXSymfcpST4LPn9yePMTaV6LoIERUkhIABnbsAwFmamf0It9u9vZ1rOd8QX9LlcvF3/Gj9\n8wZCAGqlSRAAMPXb+Tqpvr1emZmfnfT2jLdrABfGkdqmtUX6F7dSrF3neDyKiG/F9sMuRBqftxtB\n5TRfkiIgINXLIsDKZgCGAEYhIMCV1Nr5+hr84lcyNQvEgiAKDMiATIRIAMpECEBod8ebb7/56tCP\nYgpI47HjOfnTHY9HM8s5d103Ho4hhJxERChwKQUxE5FI8edlZqcNp2dfkuulpnKhCutPxVZT1J9S\n3faYnJk/5cPf+QqNoBuJuyhtstapfJUQqtSxf36rfImo7yIAEFxlABkg2XmaGlNtrZdGKI1oEDEg\nga7moj9J25etudgoBgB8ec82CBG/++47fz/G6NutqkXzfr/HakL4Xfzzbge26zttERHoupi2y77g\n/X7vwq+ZnWZmIJIz4MqQ/shpKTlnAGzXXznTzBQBr0RvGwab5xkRgVYx55LOzPbdCABbzvGv+D7Y\n5uXr36q1Jkxdcm+VQ7uOFpcaAADAxM42bnzWt1fjFgHMT+c5X/mtneidT6yaCTH0gAYGhNZFHq0T\nZOpjzmJqgfmw33+di0rRIoC0LAsAHA6H3W53c3NzOp0u09T3vZvNblOAFBFRtRjj/ubGz7qZ0y5W\n/NdmlTTCc6NpK7Z8u7a01DbzGUc1ZvsvMNj2rwE28mz7t2YmtV9d7RRGZkYAA3DrIiABU5qX9nUy\naMTHzH5pJHK9g4hgprn4LQIHI9vcnZ7ptPWadTFbPbBlM79a+0ozWds7ZhYxlFIMr9dpJl+Tgn61\nRjpZ5iaD2u4jojNDIzJXULksJoK0Gq5gVEpJKZdSxnH0M115DMDvb0/Zpj3OUjIi+ntblnAfYyuh\noOrztgPbbREpRkgUsD6FFVODrOt9DdrOGyIiEwA4EagrMURyHxhAfPmVqcHPC6xamObGDgKAikkB\n9U1TRARVUAETUwADQuyQC1sBAsMAWMyYqA8xEkMWzdmYTg+P3A+vX7/u+56Zl2U5nU5ElHK6+uR2\ntb+GYQghOIO50WEbL+BTa7BtV9Nv+IklvKW3ddMqGTSy/PQzv4PZ2tf8085UjdzbpddTVCVaDchm\nh7gDstUYAatdgZpSMtsI7w11uoG31ekAwNj5HjVTdvtUtnGorPo2uDEP2m7O8+y2k6/TP0MBd7vd\nVk217fBT2W7cVhtsN87vNY6j065bqs5sXDAyuxkJAAjc9/1utzoVIrKKIKN2tO5arJtQj5+IdAZV\ndTKC6vQSkSWBahFtCWK7Cds1b3nPqnGBzSx8SnkAEMIaJyuVp6D6tE4Lqopm4hofrDImwEavwkYm\nPlueGZCKISEYAYJaKYtkAjU0CdZpyYdxVJGyzNwPpRSMejgczOzx8fF0Os3zHEKI/TAMQxcHMxPT\n8/m8LNndgRY1cCpybdY0eduBT9f8jEka7z17v+3Jlhvxv6jf1r3tus7X4atsf2jRLdiYH2YGYsDm\nCooBUc1AAfEyL0QUiUMIwFwZVZlZ9apA2hk0T+xTomk8s7VUt2bPdmumaVoZqX7L328BEtrEZgx1\nWRZgj/RIi0TBRnNuX2bWEUNlMKiqz8zcR/WLQBVSakWq5QYAWIWOqjJHAANzNeDHxq4PmjWiT7kd\nEaFGd9u+CMiWST49Y/cCXMQAwJKXRiVQQ5EiEmP0CzZDaN1ZBTPQqqrUDLfCvvEwoLlR/dQg2orC\nrYhsJ67FCNAMIpIQECKoimYwRAACzCkd9vvT/YOKsFnf96mUQDjP84cPH0opLqBzzpfLZYIFAChw\nE9C7Lvoz+krcc3OJ7MLX1+NUoarzPH/KbI2RYPPszz6w/dmeBpx+3yfDMAzM3Mxrp5LmEuAnznop\nBUN121CheiAeLWCkRoKqaialFIXr1ZoUd97exoj84E2y1fB6u1Tbpu1jYDUvcWNPN2I9nU6+Bpcm\nMUa375kZGJ49Y/vh0231ZbihvxVJfpDNG0HPglAvJa0mN5EZlFKcCABIRNyMbE8AANM0uegFANkY\nh8UUEZGpqhQofkZFficdOH045/t2+aU4ciMmrNE51wDP/I0q+PUqWTfG0lVTrTcDMlBENDV4Eth0\nWbO13psXFIjJUAH8zAJYJGREAlQzREUySWnXDyf7oEXIYDcM0+NJk53P59Pp1Pf92PdmNqWcUpqn\nZGbDbmy06n5a4zQiGoah7/umMGBjJgDA6XRqqmlLCf9Vztmy6H9Bs20VWJjnuRG6f63pAXga4/J4\nfBei5DIvCQB4fToCgOUyIWKpvwIAqCk4h6w6zcUMGkgpBEiAaOCSlohijATIHTcFaJtojVM8VPPV\nj78J6b7v3emyjQe13+9djvj2hRCQoZRymS7udjsfOhPe3d1tPeOWe4xA/oGUkm+o2yfNDGth5a7r\nuq4rOflmqrZYCDHHtBQ3poiuCQ/fbVX19XD13c3s7vZOVYtePTp2E5Su3nxz8T0v2ihsG7lJJTVD\n3SVXYwAXH/M8N74VkRi6YgqfGIFtc3yFnupAg1LWFGjJ+So60ULVl8Ro62GVpaTDeIgQk5kSjX1c\nzHBJHAjUMMT9MB4Oh4j0x3/8x//+f/9rX95+v//tV1/e398DwDzPuZSUkiIhYoz9PM9uWM5zurm5\nWZZlHMcQwrIsTpxu4HhCtT2FO3u+XdsoQJNfWmOE+NTgxBrbW730nP3nbcjqd74QMTSOt83LJdN2\nBS4MANEdd6qhtnaP1YcOoXl9JmpGyOQf3B6zc5dzhduHUEMyzl3NEmvyw7NV0EI1lSWGYVgXsMnC\nwya63QIbACDmgcHVKJX6cnJvm+iUuu6yri5fU55OcG6+4saC9RXmdE3aVDHvxtsaomyqeDU/Am8d\ny3YEp9OpxVNWJgczsw6D1Jx7W1IppaVAmnjyPSzqApCeSa4tI7WnzioqRkYKYKpYicJZupkYUMku\nhgBAnn93bm9LeuYTrpSqNk0zMxdACBGAzHP4oB5s8SANEZgJERDBMHQauitRVRHQWEJVCbid+M3h\nMAyD6+32rRjjhw8fYGP4uDz6lCXsE9Pm/8/X9i5he8xaA/QAsCxLY+VmD4gqMBERIKpp8WNAJyAg\nREaKvCZ/BUREA7GHs1Zvu/6nIm44N1mOiGCWS966do2+22K2hGJml8ul2S0xxpa+8+BVO5jGMCGE\nGCLWqHFzoNvj+9XatuTL3I7t2fZtJUIpxbVTDG4R4JXl1POKXbNzzK6J70BXU3ArX24Pt85sjV6d\nxsuU/MPN0vYbtdB/Cwut1IO2Hpkv2KpWRBAwaum7EBAxKimZmKIqqoIaABBcpTu5+WpgBjVtagwG\nZmSKYOQZATMwRUD/rz2Uge33I4XOkCBE6GIhWgokk9P5TITAq8+S0tKkklzFxLr/zIxIWkPHbosx\nF6iBrpRSSsn3x8XrsyjAp+S0ZTP8XQ7Fup//DVHH3/d6zmztilyrt5o48RWrqG10KzN3IcYYVYSI\nAodmRhIRAJdSkK7XoZrdcofqmqFq5i+E5m80fbJdnn+l/dwoeGWkmnrmWt7VNg5dZsKag33Gt80t\nxJpd9NXu9/tmKjfV96m3o6p+hY1yqm5SCIjYTPcqc1au3ibTt0bL/f29mSlclaoz28Dd9qafCkSs\nsR/3DYoJbW7dbuR6GDeZA0Q0ACn5eugtL19F8Gqj6srSmkuzirf2iG7yeM+WCiAopRhAiJa7x/P5\nPJ2SXiVCsRKAL/MEZEY4paVYcbud6BpLa5YX1rRHo9vtiVu1X/CT2pGm8Bsx/P+g1toG/leZ0MzC\n77RNn5lw/nomG0QE1ZgphtB3nX+SAAEA1fMt6OYWMUClVK3FIrypA3xyF77Gr7Z2SMtRwiasLCKH\nw6EVQG5VU7ugX81VHwVMKWXNzXps1OAmuN8IEd0/ZOY0J9qEZJ1MoTqQbYVNytq6n0ZECFzFMD4+\nnt01bk/EFIlEbBNdrH9CxP1uNDPDa8mBgKnq/bsPvs4WSvUMyjAMbZ2NtjiEvJQaWVzrrZzQLpdL\nkyBW884iEmNnCK7TPBehHnZGBDNwfnZLxDxHd6WzRtD2ScCg2SZxGIEQ1IwDxG4wHVU7hNNlQiYF\nKaUI4+lyocDURVVVW6sT3TXaqiZrMdR69Nv8Km3ypcuybKsF/Wq8Kbht1LLlhd/5esZX/y06zV9h\n+x3aBB6XZdnetWkYItJGeQBQo8nrMauZmdv6AOA6jfhJ+YWTZotnPPMittJ6+2C2MfDc5fN33A9u\nHgXVmmkPPOCmikJV0VaScv++Zn5MVb0W0Z5qNlUdx3FLMU7Znl216n+2l5mFarv6qqGq3xoQ24h5\nRUBFIk9UQo3KrAfTd1BrNfwlpq6xG0HDmlRgIvIkhz97I8VVw1elBxvl+fLly60j5ztfSkmlIKz+\nE9pVcrOBRxpyzmSgqozEISwlw6ZgvZFvk3dYHQH/eZ5nIExqygHNsiQxVURkAkIRSSXHjqfl0g99\nP+wkDksBDyYTcaOBECIiMkWrUUcnA9+HFhGB6sTe3d2t6Z8a94enycAm4u33x/Hh92u/38dy28+H\nxuj0tPZkm27WGjBFonmeEYEMmAPwuomlFJOrMmmONaASALvtTqzVaTbCgGRmakZIVqvIpYqq7Vqv\nirQShG1Uv7+jNejiAt65zq/QSAoAFNaD96fb5jq9llI3ZWX+cwvW0RpjXBfgadbmL2mtmbRtYMB8\n98BM+76v2lRVwGpAoIra50GwtRaU1mpMAMgqWsuL/DMeSvW/utDBWs662k4i1DE8jaf5z/f392sU\nsRSrQTYR2R0O7cNrD4fXhqxZ1hrtNzNyWVOunAxIHlS6Fi2D26KerAOCw2EHHJKaccC+h2UuwIIw\np2yIYtrE3H6/7/f7gj0mrTVWz1MdvgONpvGT0iqsQTgPUbow0pqI25p1Tbj/VzXVp5/B329Gbl9X\nZgs1kNiWTpuWk9Xh9r+CG9h0tY+rv1wJB+qTiORMYBHJCAkIAwckAVNRRUAAIyRDAQNxye/SnQAU\ngDwooyAITAxqYKiIzJEIg3nFIICp5lL6rvOapSWloe9FFQHUrOS8pKQiHEKxYqiMgQi8kgOMACQt\nRTSDEQcM3BERGAW6Ng01Negq9P3799v9wRr6N+c6DE1ZeX3VNE3NxWfmEGIMPQfMkolWiUCCKmtN\nT1mS4tY/AXESkVJKQTXuIjObaUrZDFo6jp7WtWFVa2ZPUupDDSBpjE2WF5HWneCiENTMjGzl1DUl\n2Hy2YjF2uEkMeB4fkWIMz9gbAMxAtACaiqkpAi6X6fTwULzAC0wNMqgiCFHX94fxsGQ10KBKKgrV\n8mJaloWZGVhyFhEgTGmOkUuCEEKa52lZ+lKAyESA6N27d6Hr+hjFDM3cuBdXZf/thiAAACgAw1pB\no26O1Z/p6b+w0WyI+CR87GLSuc5ja1AzVB54AMTL5YJERqgILtWYOXLouq4ZMIhIRubCAyzlnCFX\nTSQZ0QAIkZgpsJkVlSJV2pswswKIFFXrukBAWTVwUCsioqgcAnVsBjmX0EUOgQEDGAMWUy2qCB6i\nRjWRlTSjRUXoKIY+oKJqIY6inviOl2kqJVkxQDVFAyEMMdDxuG/qrukxfzWbUzc5A2Rv1cGyllkx\nBZSshoBMXBMeRAToxfWZmJnYDIgC9WsuMcbDklLOBQCYGJFFpFgSs2EXIgcvYqxcREmKmQESeaw4\nZ2ImomWar5aLl314TSZZzqWRgjRDqPZtrAK32hDE7En3nHMrN1ewlASZiIiDF8EAACAFpACwRiyv\n5glIiIEC9sa56DwvXdYdhftlob77+Hh69dmb7nC4X9KbL36IHKfzvIfQI76I4eM3J+1i6LpUJHYD\nk6GZFulCLJpTLjGySEbEkjIxjvvBVNU0DrHr+3maDFVAioqKjN0uxLBcLkXVTNE2csGslNLH6CkJ\nNGAk1/MmqsxAaICAYIiGIKpA6Il+M9j+CzV+u2o2z9VudS48jZFsuXO1/p/6WqoqJEnW6nsiQlgD\n66WkYRgArh007cZSm1+2oX/X8gBQVFKqbgkqABRJXd/3w5BSmnOaszJz6IMlb6xcg/WtqIo2Zp5f\nRwAMgZERGRgAg5uFqkVk7WfDUJNaIoRIBDmL6pUo2zXdJvH4e4vcENGyiJeCbM2znPM4js0p30Rc\nhNzKQzVTM3RNLiIic845LZ4zjYhYipaSDseeCJgJqrW2KhPFdkD+KqaA0IXYogX4u+zJ7Q+G0AEJ\nGNRkJ2CtfZRrfJjgyj9EwUMuANTKSwAw5yf9Y2ulF9I0nzmEgEEF2WCMnQBZiN9NU+iiAj1Osywz\nDACk8ni+e/EaTDoFNHFLpLX/gHqAZrU+AMAIGUnEM7zVJPBUW21vA8TiSd21cGcT/dqw3Np6Y9fQ\nDgEqsxty3nkEhESkTIgoJgCbfoj1dNaQ4cpsXjbWjqERBNfOji3JqstyelIY1XybrS1anenEBlXl\nPnm11Naz42+BE0byalcGNA8rVX4PeA3kHI/HrS/XWjzd12pPtPruhK69GdBw9cEkFxNN03xVUNWT\nqX6fbvehHqJZdQW9i8e5vet2sKnSpm2h06bss9rmue8jVQsccJvnAKqFDl031O0qRRZvn/Bdc3pG\nxAjuA6+bWUrJKqWU7mlVe5N6uukvts2LCLH6W/4BX5MXxKxcCzWLaBBjNLx+uPG7VU9kK2Gxxmbr\naWP7vIgMh9HM0rJAKW5P6eqYXMXTds1gBvV5t7do7zgNt8PSmi5yTdDI5kp+NbBnNe3B1Q1uhLSl\n4a3K2d73iSDDT5htpakWCNlmizZ05j6H2vOLtu+2XOoqFwHGcXRm234YquTYerf+8kKT7bEhYkfB\nCEspaZrMrOu6GGNWyfPy7nHZ6kaPOHkgYXu79UKAeXWO14dqBqG3wPgJQa0+QbSu63z9zXF1v2X7\nq9+3Fn85aWproPLvTtPUKK9tqap++PCBuDIDMDO7Zuu6QVXB8FnDVTtdu2bhrvEA3hZwqCCi1m6G\nZ8rtma1RhalKSa7ZGnN60Xkr9PFtbMKLAulVoT3Z7S0JrqY4CIaNqFdT01JKWhY0IMC1jC4ERNzt\ndgcKRETNRK+vlTc2zGa2Fsdff31a9ONuTtMH7mADQKtWbcxWt+JJE81VyNYtayfYyOAZhZtHmDbu\nYGj5lmfMtg15b5ntdDoJXOV0Oy136rZc6rnf8/ns4AjPXo7hIZustG/oPE1E5E0R3rnoLoHXBLUI\nu9UEw35/aPnZFtKVWgm9xSxYyTEGqEmqLqzVyaqquZRSYOOGoQERLMvimk1r2bTHMNsyoOoxry43\n4+0Zb4vLnkjlVczjMHTXO66JCteriIgqJiLLMi0LiIiakFeUVqsPEUMAIppTISIOsXV59QjM/PD+\nfSP9tmCoec5nxOHP4r6uVdXk7lwkbsrB4MqxV41QL47VDm/8tmU2LYWZGQNCACBUk1y8+doQz+fz\nMAwYeZom2R/34whLoc0LiXCTczc1RLQa+cSnnSLbnW9t+1sShaoe1l+3mm1NZV1bKAoWLiVQbLl+\nRmIkIF4thXayzmmf0Pyal6BN6saq8bOVT2uMy5VyLWv4NIBpV52wNnD0Q/idZuSz8OuW2popixWG\nYE0073Z938/zvKTkrmaMsSFSQC1MMbOcc9/37V7tKXBjyGE1aZzyDuOulGKbukpnNkPwfrwWcPO1\nXS4XriW/jpjil/L326E2ymtmc1NNAEAUSkmtSHMlbrGU0vF4W5XKKsKICMxKSbXxDVyzmTmLmpm5\nIeo7IGDPdOl2N7aM0fZfwZ1e21o268L4mlBt+TcFU7GGSrSlVK11klRjQgCAgMXUvXoUE9OcZZ7n\n8+X84ovvw9g9XiZmDsTLNC/LUoC4FI7Pa+VcILTgqq0hiavIoK2GR2xiekta+LT0BGBN5fuLvTGl\nrMTceMHPrzkmTdCvsCCf1PQ9YTZ33HGDguQf/fjx41Z3Nc3WdZ1fx+/UCjq3BuGqeRARV83wjOgB\nrqHq9hXXNuMwAIDrEefCiEgdAQAjYUAX26oqlV23t6YKwrOVXr6/LhqylBCCu63DMKiqpExEaVma\nS2aywiggGjKp1mZQROdnZzA/whpl0Ro4idsQiD/U2tqzKfZvB9B1wYw8HF3dSwGA0+kE1cnZWhBE\n1DQbVGYwD1RspFhKKUlBxPi0NgB/F7LT9RQQAP0xK2F5llBV8WrKNhbVtVr5msRvLxfgrooapRJh\nxwEAHAjKFIiu1trh5ubDwyM6ETO7VUlZGZ8EulS1FGEMW2aDmiax5ljWYgY3Rg6Hg4j0fd/3vRv5\nblj2/dR2A68bA8s0TdOUdGns2gxAfOpk6dOq/Wd0/oTZ+r5vnOYv3VQtbbaJVBXdmmoQFczNz94K\n4GY5AEBg3vrB20XQJhgD1SlKtfreH8BN516NiFbILVq7rS+Xy/3DQ6Aeq/HQrs+buh6o7pwvVWoW\nuNl4itfuz1WHi1aO9f6RaxKZaonTy5cvG1gQ1bIgIprnshWWzmkppeZDbsW/meW8NO3hn/Flewc3\nPO2XNxM3S9df9XoXLxDbmhvBFBFLTco3Omgn9YztEdEQShYj9KqW9Sirtm/veDTyUwimxp/tLLZ3\nMTNAC54SADSinhlDfwTMgS/n891nr5lIRdHA5Xi5zCqmgbaU7d4Bx2C/y1TDp1Eol4wuHKXWFcHG\n43oiQWpOtW17S6ISkQKWUoYubni+pJRaO8unnIZYMwDObI1xWzINa9rNa3PaczJzH2POWXU1q7zL\n1YXEsixSO8f882vDZVmxABoL+ftbzeaP1NA1IjEAZBUiGvveJZCIIK/xwzTNRqiqQ99Pl+zu7zaI\n2hwGqwXgXskaYywpM9KuH4ioLElVmYiZ85JKWmt8UGuYlK9+rJNXM0GbPPP3G6k1Tm7vOBdN09Rq\nOH2XXP84VYW1WHmlVOaIFShla3kiIvMVSOcKdGW2G0dEdGC89XkRHMVoy2ztILZugm0sJSJSfG4T\nIqIUaRa+9wGEEBQMmKQW8VjtjKYaxGuuwfqrrRXSXJtiEGDo+z1hYL5cLsfjcUlJVQ/jLoaAXUdL\ndkdORCCGK+mrOo4iInJkCmQApZSx61sHrap6RdHlcnEKcdnnPzspns9TKzonWF07ADg/Pm4Me1FV\njuT552qAkG4yHsQsIqG2icWarO66zsMiRHQt0m/H4K9pmvweW7vff2WERn9aYQJ2u10TaVLBAszT\nHVVM8ga8oOGLtBNl5sDMrSIhWRZZlmW9lCtSuPqExbSUQti1lbdz9evb0w4u/9nTYk3oup9mZmM/\nXGtYrZZfkKVStHKXbQxUfGqeNakm8uRJm6jyU2/iGTatMc0S9pd/sayAP9B4u25vaHentVJ+xc9E\nRKr9Tarqof9QD7cxj7+2rpRdnUnwdqhtNsB/5o2v0RIMhlCy2lMP0C9Fm5yHtbCTaehCQCJgc0JF\nZpAo/P7hsSfo9vv379+PfXcWfXP7IvR4O+zm+TLZGRG90Z2IYowlCVUzUlXB0ACsdiTZU41NRG5c\ntJ9d+JrZd999yK3ttVY+IWL0wnS17dXWbqOnyQx/QI+Qi4iz1osXL25ubqZp+vjxY6OHK/jpM9Jx\n0xY3iRFEJG+nB2uU5ELdz4w2KZ16hA44sXZPt8r9UgFOGv2tUpMIRBnJwUmhIXs2lxSAAMUUAKIh\nkolBY6oq+xkRG/M/IwJUY+L1cRAJ12TAKZ9k7WNYw54qYqjIDHTtUG5E/2lrTOWNa8U2bjpB/KUb\nk8yX2sV+810kotgFZr5cVrenkbjTxO+6KQKA+OMTu24xM83JzLZmzIaDrG3vVukZbAmpsqj/u+3d\nrOaWAai6xUH0NBhjoF6vAgAGCrDGDFHNaL0oolfTiTe/IqKbSMf9ro/dbrez84R6dUCaoPKkn9k1\nKGKqUMOSLfSgmzZl+6SZ2M+xKX9/LqtNOiu1VLHSqBoRwcBxBgJxIFYUM8vLCi409gMRBeLdML64\nvXv37l2TsGEbom1HCNUfs01NRqMPqNFIrdW3rjH1GrxuegaHrvcKjCZypKIM+Hd1U/wRmMeu98SR\nF2eEECiu0XyqDfllBUgzIpqTbnewKWqHmvNbbOkMK8SiU0d78N1u5zWHTYgokaGGroPfBZ/ekub4\n9OW1gk2Bt6+0FW4DHmZW8hOAFmaGfFXIqusTaY0QtJB9oyd/P/Yj1KjVuoAYVHV6fNwK4HYvJ6at\nvY2ISOjlWlg/dv2u6Had68YSmoCDW7bzbTz5TL2YGYCaiRmCKq60vWY7b+/uckDJxc2tz16/YcBL\nSnKZS0lNtKlqKiUn6UK/SpqahDczpDVP3YRas2C7rtPqP0NNljqYwpXs9Yp6EPyJDLabLCKEG99+\nk2R3YI7Hx8f7+/svvvjipz/9aSnlr/7qr3BjRV/NyO3OAsD5fG62bFs3h+DZZKshh3b8jX2bPiGi\nELjv+1Kwkdp2oU2pNpMmtI5PAwLUKgsVIaXEzGrWkMlr2U5o5KKbyOSyLM6ubVXtvq612i54/dty\nma7mRJOOZK9vbhxJpRnJWKOpGz1xfRbEK3AybtREk4vurF4J0RCxZWydaLSUUtsRBACQLBBxiCKk\nssnEECKip2W9iqWJxXYEukWb3nSONJ95q//RK0XwulqqdrnhBg2lam8gZGBDNRPVJ6wFAB7SrI+v\n5JDHVRWv168uRs7ZODrO9MPDQ/fDH9/f31tK/QYe8/qt1WpAT0IYqvlntibMpgHCnqr3rXD0Q29s\no60UqcJtbL+43SjYoFH5Vh+Px3/2z/7ZP/2n//Tdu3f/6l/9q1//+tefffbZN+++bdoybCNgjWhs\nY321QwohcO2YtKfBnMY8ugn1MDMRnM9nkdyMlvbJZkB7VIOqLgBRrwYSkVSylxSoqhGGEMw1mwck\nCAGAwzUj17ZAa29VU8tUG2pAdDURr34XmFnktVvUrdlVOTPc3987OlhbrRvDW9zIdqJm5r5oU/jt\nUFt/XQvhmBkC7XaHJoCcTnJJIoJ4lVy8MdQX2WBprqg6tKUV90ZSSp7RariUlWuwEa5VCCAnF1Xn\nhyeazb9GtZwfWmHEyqgSQlC4OsbtFs+iZY1PzAxUHceECXXtybHz46mng5l1IX747tt5nqfz+eX+\ncDNySvMMU3NSuq6LAUsSRKSNz9K2cbOf0Ii5gSM008C1XMu1ejfDKvNaqz4gPvUAN1JJywbf/oc/\n/OEXX3xhZv/6X//rruv+0T/6R5999tm/+Tf/BmrpX9d1T2qatotr5Uut2tDJR1VRV9pq8cNm9rR1\nNJabc/LQubNB27J2PB4FdRmsImPoEFeMWy3ehGaqCkyNE6zmzYBQjFuJFtQony9vnuc2doNq1qUP\nMYZgvuNqIiJoiHi5XEQEzEII4o8gamRzychrEHV7ltt9b8ofavlPk1xYtZBrnqYhdS0Nc3htQh8e\ngyYiuaScszOyaiGi2HnJrJlB4K49Ea7Cy2MP1ohv5VJXmjWF82zl22KARk+qinB9lvWdWs9Q9RVd\nK0Y8n4zXrWivbdndltn8mloUgBEYwVw7eT9h6HsX0768vu+paJPFzVwEb2zbepsGLe22vVfbjWYw\nNybUtZljg3VtV4txdTHqY7UzBTUkQANTQ4Oh6/f7/c3NzdvXbwLxfJlU1d25H/3ghzHGv/zf/s3X\nX3/trcahVKz8LfX4UsRjSmZQIxBE1I0D2ooVB1Vli0gLpzbJDQCREUNkgu1yEVeQmTWiWlETc85S\nymWeIgcgVDCO67AYAXt4eGj6AVoghAl0zSXoFQ1KUK2LsbErBm6J5nmeubXJVodBVYf9zjsjuXqG\nUoqavbw5AhlR8HwpwFqbf7nMrePO4VbXMVEAACBqaoqbQTNudhYRR0ZQAwwMIRIUVXWgW4OV9OgK\nAbAGPEIkADBxXbdSC67Zf1BVCtGLesDQCBUpEEamy8MjgDGgETKgrniPUJYETAyoYGQgFUYcCdl5\nyA/LPXODXK5lU9isHsBlWQyVgP1foPVfNAIAAlYUAlYQAiYA5s5AsqoZAhOFENGi8bg/fvP4kZmm\n8+NuGAEAmHIp5XL2JgpCYEORksWKGFOtyQQR07VHqJa8ak3MSO0DDiEImJaiWBO80RGmU82jGiAQ\ng5e5B1xrQb2sREQUTPxMGdjYEEIIoYtvXr9589nbF7d3Hx8eIZW7ly+O+wMQd13/ox/95MPjpSh9\n9dVXRSmsTXiemd2YjjnnYio5NXsAmRBxSsvWemx6z82qJik92cJoOidQUVA31T1Y5wkBBVARKcVN\nL/8yMiUTh5ICgJwFANQsdh0xg4tqVbeUkMlw9VW8uVJrBKmoxRjjbiAicYm9CgIoOU/TZDVLCwBA\nWFRKNVA3mocjoOQCYDEys4cWiZnGMYjkhnrqLMchzqnGoUEJFLE2L5uRz/XKkrMoACsFTTldYhc6\nDmYKakjGHXNAVe27OJ0vj4/nQDOSmVkf4jB0sQuuOmSeAMCQwGxJczfuDHEWycWAGCgU03EcJSUE\niF0HZktKYNaFGPoVxF/NVIRU/eCdy7TZfiKAqKiEoFJKft6QyiFkAVUBRjMtJmSCgTQLMCqoooGY\ngCqoJxU8xmBERSUvl2QWGUSWl4fdXGQgjATzdOm6DiIKSNeFgbsh8LIkMo0YQqCliAZVAFEJSDEy\nIeZSTAuhYUAk09rlRJEEBRCREc3UZHUejIBVSgIEjpEo2FI8jbzGt40YHSidAdkQDJVjRIJlngPx\n93/4g+9//kUuOuz28vFxv9vfvXj98PHxs89/1HddUvkf/vGf3735/F/8i39xOp1C00gudxtrLSWb\nmfq4ETNAEFMw6GtqDp/G3FqqfmuuuPHJAMVqyNs1swEQtjb1dl+o18Xq3TaW2HoFzewGxFwKELKC\nmaEaAcb6OAFpHWHVmoPMYoyhDhOiTbELM5eutOiC1FJux+hHdIfQe7QAkVWTKpgVVfIGNoBMXDAO\nAAwm5nkf09pPeR0oowBiIFmyFAOBAt6GgL4kNVUduj7EOBrFbhiHgZlNFNFKuhCgd717j5YCKNiA\njDEWI/ASNtUCilJ6KOhm0rI0GtrCRjQRSZsqM9pW9Jrp0yAqbv5qBrjm/wkJgwISMnGpc8IAwMg8\nGsNIsIY9gxIWQFtHb+hFiqppKlKSql7mc+y7w81xTkvPbEVjjDEXNTACDCFXpEliZgQiQjBCkJRF\nhOMKeIGIcegRMXj3s3uqdo2WB4xmjl0uCCwiYEDELd7jPdfNEqbAAKAgiBb7bhi6EHuDPC95GIZh\n3INR7AbmKAqmfHt3czfl8yULxNBCjiKypNRCK+Ld4pvCNt/aLGsQ1uMNrRBTNvMKrOGHmexC5512\nZmYIBg4kD/Myu9ehLVrIRERapMUV1scjCiE4GKtVb7h59qpktlZfMjhQbLyCc7jkVvXRfog4LQmr\npPAnav0BTZtBLfXcqu51kfWLjililYf9Z2KeUxIzAjATNgXHZgT1sriAhIFDQDEsamIlZ8ggziGM\nxMzuST4+nLqu01UGoUPZmEoXEUStiIESIBGaWRZBMBVRYxUgQIqBIQDTPvbdUyAgf1iPPDVO41rp\n2t5pj3w1/qswhE0uqzlpVyOzWvvbaMRK3ICO0QJIQEiAjEhmDKhzKqaqxsy5yPl8Hsc9Nw7BmhL0\nxTx3fK5SY+h7DBz7ruu6NQncRQBY0hUZGqEFaR3ooat9KVQR9IE9xuM9qEYujptaaqTSYGxyzrvd\nzgsJD4cDIqaUqOsV8Hh7d7i5c/4PzZ9xd8s3a0rLqohaJNfDJPa8klVrzWFjBq0vNNnHvjmyrTJB\nEVY0qLp0M/MIYQvKt63kOrC3ma9NuIIKEQFhZGrMxnSVweLFspt6zr7rWlQOaqBcVff7vTWMjU0u\nzsvWtIbyG72eTqdmBUDrTuKgxLoWxCkBIJlHunXVXRSZgDo1XIqA6AKhihsMTAZMCIo43NxFDjln\nNODxQMyEi0he0pygqCo4JgWhiKacY4yKZMRAkbs+xA45EPTL6QPF6Ge/KvBSHDoNNl5Ds0ealQib\nqFKTKbChcgDAKoxgE0jDpzMH26Y5z6gZAhioKSqg4moBOAMj8TAMmEop5XS5uFmRimRVJBqG0a1R\nBRyGwRqFEJCBSkGmUooD0UptrSIVEfFA+nqIm9zGMk9u7zAzIquqZp+lGJgZVodnRSKNkT1k1Q69\npYuYyYtIQgi73aGUMk3T7W4vxfpu/KM//pO//du/DS7RsdZYuULwPI/vzlUsESLiwLEdgFTzzzav\njbxZg2MIYLiWEpiZgJla3/dST9GLSv1qoZ4TbKJkAPD4+Gg1eumqL8aITGKMTJ2nqtTF3pPCxXW1\nuArjj6fzltka9TQB75vQSHN/OKw18IhWCzXUrB+GusubQuQYLl5daQqgbIBoaECIqgJeyC1mAFlt\nmfOkmXbDaoeWkgENmIkMwymlQDZNkxaZxEIIZUlgMgYLQKpgSsQ+TYYAqOsGAVPz8kgoKbuBGWN0\nC0qrtezWhDezNrvRRAygVFi7Z+aMmYWK/bbaBcxIxGZEDExmhp5uVQVERcDATjRmVmM6xhtsPF1z\n0eDIKF2I7rkwc4zouH1FxZBECgB0XRfH2JvRUhbTEPtiamaRmAlANKeEhQEoIDBFBHQUMyCQYpfp\n3JIxG2azNReo3hoPZqbFSlbuVgdk/TN45Ys1aeL84uWEMcauG5pu2O/3j4+P0zTdAnRd13H4n/7s\nz/7q5z8Pm2KF1UfyX4dhZ3Yde4c1qtFKTvGpz9agAWRTjmhm8zyjqdXaVlcyZsYVko2ZY9dxxW90\n1AfXLS2gr5vMbGMMfzCEQIGjj6b3YJ1cEw+iolZbAutsANoIcq6tN9u8kG6i8w8PD63ABTftBc2q\nbK0AREQqsY9qRgqqSgZm3lMIfehUtSjlIqUsKZUlabJyuL2TgJKLx6ALKDMy4Hi4AYAMVFKG2FPX\nxW6ICOX8QAgczKVOIIwAveQY+6JqSAZYFFSKSkGyKV3mjfnQjN4WT99KtGatbH9tvNfOtOk9ADAi\nlOcVYVt23V6zgEXPfAIiAiEZGgEyQtcRpRnEc8oeqGRmLgCOg04UlKOJAGmLOroYQGLR5NKkGwci\nil23ShbE0HfM3I/Dxt65+v9pnkRLSaUVHqJgKQXdGPHZxqqqyqRq3HWhUb5d+5uo6zovioLNJInz\n42l6f//i1cuf/fCHf/DjHwQHD3W6GTa7v7Zj18yG6zJVlSzN1OTaPLe9d6kv34ssQrWfTcBW0jcT\n1wBMCObqFAN3EFqBTDP3/eKt8EJrWs+Pa+Vhd3nNrGZI/DNqekW3VwWAOWWuj4mbFthGWLZOQ89+\nHlKZaluRBHXAfHvfau3oZZoMlcSaZiNzQb4BzCGIMVLgjlBDxBDMcoY8pWRWYoxM9JgKIk7TlOdl\nyOLR3TEGR+iPTACqAoDIhEChaN0qZADNWcCAkbphFClNNW0V+NZubPvcOGrLbFsugo3lrKoYwgoy\nUU/HvyObosQmfKnZ4QCG4Hl9AzQCMgwhGFksea4SNpUsZoCgADnnaU6nlCZR5aAoqaw4IhZiyTl7\nzToHBC5iOefz+czMnVopBesUgeaGIiLxCogEQs5XMUQkBCAVV/ZeC+rPlUmAqGtPxBV9uOmDhj7q\nqeN333z1gx//6Iffe52T/N//6Z8Hn5bihxErMIOZrSnRTcujB9b3w6CbEnuo4YrHx0fc+FpUAST7\n0DmzKUJs7px3Q9HKFd4P4r7mcbf3nGlTGs7MbWJT89yYmQLnRUzcbAPUKwCOc4uaJ2OukRUn5fZc\n7d/t+IUmrkIIQ4y+mNYg4zpwTYJXAb/uSeBFE4Cyg70RuktJSI+XM2EgCoAEyHGIQ+iwHz6IGEcV\ny4ZTFhEJYiGE99++Y+ZpmuZ57rou9F0kHmJ4fdhrpKgMJqAWSCMCwTr5NXBA5CIFZFEDVRBJKS1+\n/FDrCtq8Mn81TntmOj7jrmdaTkSyCm9CL9d9QGwIzVtGtVbMYKRgAFTADEkQBCgSxy4mlZzSImXO\n6Xw+7zgSkgoUtcs8PU5LMgvDmNVSqZMu0US1GJhh4A6r+dqSbGb26uXLK2O0wnfm9999F0Lowqha\nmCMzS8rzPOclXdW4NkkGjTxEhDm20y+leEbUCcMBab75+svD2EVJf/EXf/HLX/4y+OCIlfiq2HM9\n4yfd5IGzn7tzXu3a9Ezj6Ta4bHW6TCmwR1nIxQOu4bzGNgKGhE3bXC4X0LXK3pWMm3Cei9vaJDln\nQ8iCse+iTxWqI06dN0RESvaxOFLDWTlnY261L22pbgksy+LDvqiO/gBEYGKiYkrmxX1sZrvjQTa9\nVW6Y9X1/Ws7TdGZADiipmBlhWEoS1aXMIQ4ce+QQ+oE4PM7L+2m+v0zneYJabCWXiZln1T7Gw6tX\nr/p+HEcKfDmdz/cfv37/8fWLm8Ouh7VjPzChSFHAkksWjVU61PI563ejbircVRUDixR3jpvZklW8\nBtU3qnV2NYZxkxsB1WHtCLvQEQcvelpHzDEvy+Lz4poV0E7Taqmtl4MCkAI4s2HsM9q39/fDMDw6\nujOREQIhKIS4Rgq6rmOih8sU+iGGnoiGYdj34+NjEZHYRdcQbii2BtwYoz9XCwc0WJoVPkO9kCA2\nvJlSrviF4To80T5+/Pizn/1kmqbHx8ecs5eGcAVdnqZpHMdhGN6/fz8Mw93N8d/+xf9S8hRj/N6r\nQ9h6yVXBGhFJycuy5DqNDQAa9AhugnIt/M0V474pN3/N84wVN1Lbt3yiuYHVWtKV1UXMwESbU9Qy\nE9rwveuLaDXrVdX3LqB7wKscfeY5+N4dDwferPAqFxD7vnd50dwzYp5zal+XTYfLVmxrLSdPJee8\nSMrAjIB6LZiUcdyfl5Oy7bs+Cdw/3CMFCz2EiFHK+fLw8FBKCZ3nLXR3vGFmQ5xSnlW7rqMYd7cv\np4f7j5dUjI6HfUdWctKigej+fAGV2q1HRMSAIdCSlgYz06SDbFo9/NV2Gzde8XaXwtOpFHUX0APF\nLWrlcci+7724vlmtra6oqT4AQARPEgqCWgKmVnXpd4zd0DNMUxIuoYswLUSIoWMuqiBaACAtfY6G\nyGAkItM0hRCQV0z/9mhPNPN1AbyGbhRsxTZHrwxtQQQRyVeho3/4hz978+bN/f29+5ZuEo7jWIqG\nEHbjrpTy8eNHVb25uZlO97/8xX8MWG5vb/nuLrTQbTO7sZpiXnzoO4WIXoSBRRtztpd+Uh65brRZ\nzpmcn1oVWJU6ax1eLXFad0GvNW/NYml2SPMMN3xCYppyyjl3PrBK1i4mVS2m6ggztbQSNxNnmucG\nAM2cboN8VdW7HLw4szkefuuUlpb4RkRkUpFSyuFwKKkPIXBARzcBgMucPjyeQt9j13/3+Dhl2e1v\nOXTvT49fvn8QpmVZimrs++PdrfN8KQWZRTXlLMsSUx72u3HoQ94TQA40iQLxOIwBjM1KnhADxy50\nAyIaYTCMkfsxzMvk0+q8r9HbxikwEbVZp1Kn1cVunfnmNfpt21crRGUrnU3MFOacItQ2YsKsQiru\n81eHmchTFLIys0+xMlMAUCAlWJVYO9bI3dAPwzAIfMzfmYa+7wFOzspRRNQrta4Tfd0p7bqBiMQU\nkRHXEq411EFejUmIxkyVAysN+oQ59OgahtCZmZmEEOipDfnw8OC2IiK7d9N13fl8n3MeX45mRhR8\ntvB379/df/wQsTBCZHoyFV43DchOjKEyG4CDt5An+P3z7VGbyU71tUoOI8kFQRv/UK0f5y6GxpbN\ntzYzvTJSU2WI6ArH9dhWw+ScFYx1TQqBi6bW2lxR96BecFkWrUzCG7AQ20Q4qdVtglf921bt+yd9\nsIa/+DpE2zMbpqqWUYp6SkIMkANwNxf5cL7M2XTYdyHMCqd5in0/DMP+5hhCAMR5WbyajGIgooIm\npiLZlrmIEdHdy1ek8vHdu0crP/jszWE/lMslMJAKhQCEaqZgDtnLsAKVus/m1vI0XVFu2nk1EbYV\nmm1b2g7QZsaDqha1BniKFdhra1ZspaRd4zSIak4JZCQIiqi1yDiEQEMfY1SE2HUiZqDDsFN7b0hA\ngTlyWCF3XSSJ4xPDim/p2VVXj0xPnqgJcQBQBVoLpHRNlXt5dM1a+bd4rVZFIvrqq688KGhmfR/d\nbxKRcRyXZck57/f7GHsPzn/77bdx6CWXx/mSP2hYURNrQKlJbiMUEccNXWnXZ4U9m4/lYqG2/Tc2\ng9aLoWa1mHo7fGMl8c1BChiomoiWK5hms04bTVvrsVcFkVKUY+j7LoQQiREx0jpCSVWTFG/6Fq+l\nROzDWpTQlKQbqMMwhJr3pOr1IuLxePRlw9OiCp8l63gvV0dcNNsiIkoKAFml75kjG9Krt5//n7/8\n1eOc+ps7I/n1N98Ou8OLl6/x23fLnIHCYdjHGE+XcylKsTufz+DFNExEwQBSllwmsHCLPPRdITyd\n593pkRnRJCIVUDSBnLTIsiwBA5Aty/l0PmFFQW/P3ipm8CkA63ZPrvtcUztaA7NUO+ViPxiCe8h+\nuEUldNH5yr/OIYQuohCX7H8C9bEABABgRIwFSM0kZ8Xgp19Mz+fzZ3f70HcC6y20YJnnXMqw6zsH\nR8u5lFIcLIdwmibmCEgx9B5y0zXFiohMtIGaRTQrzGyKqgLkJWxGRIRBJVcFZA4t7ls3jn0pxVFV\nvdDC5dTNzc39/X1KaRgGs2ReGBi7MOwELANJsiedl43ZzIw7n6Sx/ioiXsDV4XXg95a7GliQPunY\nU1Krda0rPAsAGKGmgoiN2VwloFqsKo1r51gTjVDddKqwOYbQ9zF0sfe4kKiIQJ1e7VKTajrdHy2E\nYJuSIqm4qy6SpaJcpZSWZSkiSQpuev61vjwG4DF0ayO/yECBgBhZQZlD1w+h75TCd/cPD5dpKiBL\nWgw1BB53PO5u7l4+frz32znCShz6F4fDvCw5ZwfeizGiF+wjZ7EPj6fbw368u0OED48nyfnuOIa+\nJ0RiCpEFMaoShdB1zIa0ng5vZs+3hm7YoBK1TXYFCADegN/s7eat+aEAE8fAmZtZ0ejYA2n8FOcP\nALIUM0NBM2MlAABkM4SwxpmkAAAoWErp8fFx2t32fV8UkaOIZMCczoUoxrjb7czscrlAybRieDIa\nDcPQ9X1TEnNOOWeskPVNXwGAisUYjMxQwW1ZMgAkorQ4cgcSEePVyd/tdufz2SnEy4x8J91E3+12\nfd+nVBwLCylQv2OCvh+7LlzNSGhxSBd+Maiqjw5YVbApEUXkluZq/NAOzKr/Vi09Xf013sAK4eoD\nNd7WytJkwIH1ikP4pIJhyxt+umLaxc5whVJyZvOMp0e3xV1fAB/I6LsPlWNX1wjRze5mbPhzrVha\nsI7sWZupvNwVaUoLORAVoaoRITGjWnqcAAiAipaiwCFntcfL9Ku//xK6uN8fZpWkuru53d+9yKY/\n+MEP7vfjw/kkmufHaZomAbtcTkg+T0fMMCsQERsDx2LyOE1ANsZAXZfycppnMNm/7ogodLGLnXAG\nAETmGMLAcez8SbmLTnxGGIc1+l9UrawJQw7RzFw8ef2uxyeRaKmpFzOzcm0FdvWuFTTf48Zurrc2\nRal9jKpuKq7MBivog5mBFSFGZjYiNUEfU57Su3fv4mYqNyKWnON+v7XqaR3UpqradV3f9/0w4NMU\nzhqTq2mtRquIHhEhALFaMmI1749IMcbIT7JcLq1SSmsgao39lMPh0IZCI+KyLB8e7jNx5p5DH7o+\nnJf5mgUPTJGZVmvYcEXtVKdaM1CFGMDQvOLPndq14mVttCNCRlhj+WAlJUZwdxwqEF8BpU1IsNZB\nAgKYMwxAJvKCHhUxgKHvcyk+jZm9fFkkF2VIIqa5oLthSMBro5rPxfUSbyvg4846DojIZu43FxGm\ndfxYEck5E3OsJ6nesFOeeGtuU0agQMHQACWJqGTDompdPzhkv0mQkrMBFHtcSuj7TKHb7cZxhMfT\neVnwfDoejx8f7rMUA8ol5SyKULLO80PXr642EaFRKQUEEPOSFg54PstFEoONsStp/ubD/e6w75mA\nCEhNdMoLKooVNECGtCwp58CsBqYaYlQjNZNSUi4qAohdLezKAogoRghYFIsiGoiRQxi0OgEzMgqA\nIVEw4ITGgMpBSEsYCmoJA4dYBEE0UcfAJUCIvYGpKKghEBABEyDPy0yxx65HRsgJjDz4/c379y+P\nt0AspuruIts4jpfLhUJQ1WmaOGBAWrSUlIupkKaKUhNCiH3fj+P9/X01BRXW6cRZLSuYR0QVDL09\ncXXRvYidTaQYgWbXMXcvblq41f0ODlhKefv27W53MJD3H94H7sbDXrXM8zxN05xmzycFGnotpauj\na1PJkU2K1jxVcQOj3+2cXwORVMSebCpSrJijIxFRDPHDhw9uXN3c3ChoCAFUQA3d5WNEAxMLMV4z\nOVVmaJFuPIx9p6WoADKKal6yIXYUSxZQoxBQQYqndNmKEEKIFQYHlIgCh2Wa7TqkGsCMVuUUvGwv\nqwBivxvJwOHsgKkfBmDynx1KbIgdejMyruET14p97N0hHpCOuyMi5pznnCF0gHxOy5LT3es3H+4/\nLlr+029/OxyO3PUWI4TY7w/L5TSlCSf+9puvEQCBtVIgUggRiQKpLks20b6PVixr6bqOywwFwULK\nWUrJsTuMu/2bm199+/GLt2+wQHeIzCzThUkVCDkKYAFKwKUABiaCS1HgXsAAosWB2IzQkBIgc8jB\n03EREQujdD0iLjqbGQISk4Coahe6Ybc755SHfVajYQfASTXcHqEbQneciSbRDLssSU5KgBCHZbEs\nUkohwBiJ2Xu3lhcvXk5Sjjc/+MWvf1UUOOsQBxGzEGTofvYHf5S6/5z+P/8eRcdxHIbd7YuXRZUC\n726PyzJlSYblND3eDmH/4ghAu/EAqjmV29sXy7JcpqWIQskhIJmmdFKT2JGRFtECBRgDkmpxpgoh\nlJI6Dhw4LcmbUVTFRPe73fl0yimZ6t3tSwBVUyMrVj48vN8fjkQUOrp/OJ0vH49jHKLO87ycTyFL\nLlIMjY2LFkQUH22ctk0lKIIA3vuYzdbBk7bB3rJN9R1XZC4RLfMcGWPskQkpqOSiVkrJWbxXiMjn\nj1mMPahdpily509LoevRo0Eoaz2EkQkAODY5IRwOx1InDGFFZGDmt5997gX7XjlutbxzGFep4VWk\nkpKogsHjNOHqbaz/H4ahG8fL/WMMwbNJvIU28vZHMxVJPlOulCTK3AtIIbLQfXh8zEC//M1vF8WX\nx7tCdEl5mad5yUtOQJyzFPVO02LrGAffTLe43AYzxLS2DhQhBMs5lZKLILIAzsUWSTnbb799/yd/\n8JNvPjx89vJ2PBwlTaHvH8/FkJWiMihgCGzEZGr9QGAiqiUvJc2XaVlSKin2Q9HCHMZxGIYxhBj6\nXYzh8Lo3c9XiSHQaY9cN3e7mOEs2UWRCQzVjDKGLoAjIoJCllCRiykgY+KJ5BdZCcK3LRF5PXVS0\n5L/75S8lKzGO/S6l1PUDdT33Yz/sOXbIMXDfhS5wNBQOARgBMUCHTHNaCpgxReqRyTBQxxCiJBFH\nCLB1FjEyoQlyICKktWvWazaJEAND8ko4JAqMBcgYEQBFzEqJfedtIufL47fffhtCePXmTSmPiBxj\nLCp2fng8P+52w+nhHZtENEULIMlKFs1GpCLMDKiaMyq7CYtEqF4JpURBzBgZGUFBVvwOREItCgCC\nAgpoCAqSRUsOXU8IQEEBVaGIFYWiEGPXgAbEEDwFyXh88YrqUOywG1VVpKjqbrezGKjORmgRlIfH\nx0taAGDHO0JachKREMLDN7Nusn9Q09DnXFoZgWdr0GNrIkRka/mpMjOFEPr+cn9igw4wGQSoiQqA\nfJlEpMgmQNf1gHTJBYkxcOyG83QpgN+8/3D3+vWccgGcSz4vqagSMwae59mbaOyTV6noy1764IH7\nUgoBlSKlFFMMHarCnBYtcv/dOzD5B3/8R5d5yQaimlVjCC+/eEtdh8gi2QvbvU6i70ciIArMq/Vk\nhqpl2O1zXkQMQL0D3QXiNC2q5VlnOga8pJSlmCgQgqKCEQiLkLEXfxQVR0EIzEgQiSFwYDQELWII\ngZgCaZEYWQM/fLwnNEANd7fnlG4Ot0xd4GEcj2ABISBEpn7o9lTympNFzIpQqCxGHasxcpcFTJGo\nS8WmJWVDh04wNAAqnv1BCoEQDcHLaNfEALPP8V0jbVTH3ptRjHGeK4AVhpzLPM8vX74EgPv7+7u7\nl59//vl3H97/23/7b7/68pvzeco5M61RgDDGEKCOVDaNgUNgKJl8WIGDzIEFz/mpAHAgRu4YsKAv\nKJhJCJ0foeYSY49qYzdiP2QVBcuiS1E0MUTquq7vuhANAdSyFCtijmQXw+Np8WBjjDEYAZJQVND7\ny9JwoDxAFyOwIXSDFDEz4QjMOZWkwmLupocQQ7+GNJ3rdrcvsaaDssxZ1LUUIla8W3I46QwsCoe3\nn3mQcH4KNcuqqIq18NqnMyOQGI3jKIbcRcnl17/+9ely6Zc0yX3sBkWwogDGIYBBTkXyOq+9xfGg\n1hZ6v+nq1hKpruXFIt6nYyZ1IJ7ai1dvugBf/OgHP/vZT24P48f336DK3avX788LD0PHXZIkSQSE\njBRVgZMVEClSGNjIIkWInHNWU1sd6BXSB82g783YjIwMzH1m05QR0WGKzQzQwAgIV2lFCISoDu0B\nHjB8PJ8oklwNIl3hyJlBYRiGLvIwDEQwjmNKJYQIFkwghl6yIaCgggABgxYAQCNQZCMUMjFGNiNA\nzkVVS9/3KUsRY09SoxmimahFJDBvFmn+OSCunsa2CurZDKY10JJS6iIh4uPjIxH9wR/1P/nJT77+\n+tt//s//+X/4j393PB67OPziP/+fdzdD38VVN+yGXrt1UG3OtM7d1Wd9TWZS3OvJRaHz9NcaYCcK\nHsWwFavIzMo8p743jnEppYCZmo+TJ+YYAjFPbgiq5iLmkj4G5G6GTEDFNIlZKqo6zUlVX7x4ASKa\nknhsK0YMQYgMTUJnZpmCICXkBQgV4rBDIiMSN/ZMi6qqdeZUBAUwc5AW1SEqtT+olJLzxT1Y6LpF\ntIFVcm10cC/Zm3N3t3e73W4cxy7EIQ4vbu8ezydg+vabd//Hf/7F9370Y+RwOk8QFH38mqpoghqF\nd3Mdap7dz9KxYWwDWLZ2G3o7LzASmmFJQswcKOWci/77//B3f/5P/nEyOyXpIz/mXGKwLhLHIlYM\niwEqCthxtycrkkQ1q4CRKRARpJSZHSTPgc0JgFQLUVh/NkFkM1IxyRZDiBYanB7Rmky6nN0s5xZD\nVjBDGMd+lWqrHPFYi5APPIphP/ZdF6fpoiUNMfShBwEr0sUouQTuTESyQFbICogYLAAj0RiHXTcS\nBRdAqopIgTtViLF3t4WIQiQA49AhWeRgOTEYu1NuFX6ZV+lmJqqsqgaiCIrg5WBDv0tL8Yllv/nN\nl7/4xa/+8n/7d4fD4fXr12b28sXreZ7vL/cvXrxI8ykwIxIihZzUyHoKCqqChQ0BsygZGQMbCygq\nCggDKJQCQQUCGmCgSFTzm0UWUQTRpEhgSTGpdYiFopI354kWkaKYkyHc3dyCqeaiQCaqhItizsbj\njmPwQa84jmQWQ0DEeweQBFBEHx2pIZjZ6XLJBmaQUwaALJp8aH0uv9OM/DAl2jQRsw+hDF0cho65\n7/vD4XA4HLyGNRtAF0utGFuDppX6cZOnWqv+1Kakg8FFDU3fPZx+8fe/+eL7P3z88L4bx3nxkHHJ\nIkSZOQI54s61AM1frniXOtAHKsihmXXk1WGMgCZaTCNACH3f8+Pj/W++/GrKhWIX97uuixkJux66\nzjiiInNEUFAALR8uZyBgZOo6gvo/sMghbFDiVbGUXEoh8hY4MAMwISIIgNCdzxdmRABRJWCO6vjw\n/TgAIQEXEQf0iCEwo+TkKq3ym7fkqIGlPOPkhVSiWkTK/rAbhi5nUytjF82E0EDFpHSBRdjMQEVK\nURBNCaUECGWecNgFMEIkVMmJCXK6oCPkOjDxarKhDy5wU9IA0TF3AJlXzWlmauUaiK5iIqW02+1C\nCOdpTimdLvPd3V3Xdd9+++08L8fj8f7+/v7jQ6Br7VH4eEnd0GEIGWySEoQUOUMEAzT06LaBiSEa\nArFRNERPyBMAA2gpDsCQp6kQQdd1w5ARoesWJOh6Q68gEkABMEYCpvePU1axIsUURAXMigjYuw8f\nu3FwHjgejx6W6PvuxedvmtSPMQ7D4GGY3X7fgIOcLmUzMXmbEmRmDBzC2hfXZvT4nxrCsaouqpdp\nFpFi0B2Pilcc3+pSqVeLWx2drQoiXgsoMF0UMYTw5XffQdcVAOOYiy55KqUQhYC0onwH4HidbtUq\nzV1LePLQozJurIYQTD0gbcaoKqWiU2eyOeVXr9/OpfQ2UjdCF1QsKVAuUkCsoINaCBTVftgpCBop\niCiIFBPwuPcIGAICYAiRajXp+/fvEQlxDU0xr8Jr2I3MTIBFBQ04BjQsIktKHmj3CXpqViQwcwBl\nAiL0wwFQD+8CwNj3RHRz3M/zHA67vgv7cewHLjKb5dgFpBKiiWSwhanE4L3OIpbMJJIMAQ67DkgP\nA/pkU8CyLGeOAdIFEMEiQuf5JAEzYjARKVrnq4C5WrQuUFKvWFrb2hCNCIZh58UPpRTX52B0d/sy\n9tO3336bUum6brfbPz6eHh4e37793sf3X0GthQgzRQqj9DstRQpSjNp1gGGeZyaWtQR5tXMMCELw\nSRcOFgI5uwzeibjxmnO+ubm5TNN9zqmUl68+07XImcLQ7cfxcDh4G0JzRt2nyjmnUiDE2HfOJw1/\npu/7aZpa5binKc2slPzu4bHfjQFpzgnVuItkMOXch6iISKzMqLaYYcqa825ceyiLgHg6AANQqKkB\nK2oigBjCMPRdhNgXQFP1ESoK5iAJWcDfAcTAgSJxBDORFBaTrhswhG8/fOh2u9O8AAJzlDmVosNA\nMcQVcmfRmxc3TT1uAyShjtJueAT+JpbaPWWsYFoE1BKu9dN/+g//+64fMQQoQTFwzyyGThOKgEDA\nAmICYs4FPvPRS+xDIF6mMwGCmlRWd8ulj93QD56zLqUwMTMDw3w5I6JW3N8A5qIhhIgEYAhazIzR\nq21xmaYueg1QWZbkYqsf4jzPIZBBQLTL5cSMHz++v8znn/30D5UWhYnCALQgJVAxm0o5qRQmYjbu\nLYR4gDB2sjvsReTtzUgUpOiUlrNdOht6KogcUIJlFcglq2hC9D5sx0E0z2urAWhcqxqu2Bxbe37c\n7fb7fd/39/f3PqdGRA6Hw263e3x8jF1/e3s7TdP9/T1z9IyymYUZh7TAfbqYmSrKtJjNAJBzIVKi\nteDNYxIhRh7CsBt9XqkrE+ecxjOtyMOrzsRq6/em+6uUInXgdxJdmz5DDF1XABczQDTmNepAVHLG\nGH32ngfcy1psyfFwEAAxE2I1sVyYiPoheYUKggEgoQG406vE1YAMWCtCyxoVAQMQJF13B0QsEBYR\nUEXmQJRFvC8hcgCTGFjMtBQMSIjnaVHQYezVSJHuH06iAGiO5IhMrJBS0lyIiNDUYJomzwdqbTlz\nmdIKMkTEuwodYOvQ79+9e393d/P4+Hhzeyip5Cx3L948PpYf//gnrqLP5+nmxe2yLCmVoe8R2GMD\na7YGQx8jACiqgABfy+4QLXSDipiUPgR0hE7RgDjGzopIETSLSCaqsi64mQ8N84cZOVApqRQ1E+KA\nCGaacy5WZPHRFtgNnYNAny7z5XJRLTnL/rhDhlKyF8Y+XL4DlinfL6dv//E/+dOvv/6WcJimh/sH\nffPmTRf4dDohCCEfdrsvvvc5I5GByJySktkI8PoYHx8/QnowoJKDIIpoTsIcQzec54XY9VstiwEV\nkaWUECgQI+JuPzTnues6wrAseRz3y5Jj7N+8eYOI4+E4DIMpdLFfUjKzly9fgxWTxdH6ACD8o//L\n/7VluszQA76INk0+npdUi7/PHCng/eWj91xhLYcBohJCqREztzDDOlVB3TqGFYzH0AwQteJqmW0a\napy+PTJooGuQdgWZ9DkbHu5aIZrU1rnKbq4gAYGYIZICmjniH5o/z2oIkj8MKiqYKYoJAQMZKxoq\nGhkZ+jsUKTAakBEAEjDW6BUigTqujUOfGXscmUgJDTmnJKofHu6TlH3slcmL5RzGzwDVCgEj2bIs\nXq9TKjR1s2abi9jcRQCY0kIEpZT9YSylxMiHw246PR534xeff3Z7cwixn+f548cHD5xaMQRBAFP1\nGRxXx2NtigAy8CIah/swUTIwVEYSVVLHMl1Rk9u/qKZoKhYCAQSRnNKsK8Q15TwBADOYoUhaPUDJ\nu3FQVStynhdJD0tZTDxGCklyWXw6McQh9qHHaJfl/jydBebI3eG2C/E1Ij3cnyTnwMKBxh0F9pkz\nRfNJi/p4PTQLXT/sh5v98fWL3duXNwIoxZalTJcliyIQhrjf74EDmRZTVOOwogdM05mIAjFUIIW6\naeTTTswM8Xl7Cji+m7JrFAKfa7d6H+HDnImBCYg9xmUIRgzY7wBVBYokKaZWUACt7F68QlxTBVRr\nTLP3dyIaYVFvZAIEMEUE6TEgoqi5a0ZERuwzMtsLAMBAzZDBCzZWZYPo2smcWdDbfxAAnPCzFCAg\nQPD+b1yBEEQNaK37qKlKQkSBNbov/jFAADQAJva0twEgoJGt0/oAEDyQhmsQQQHQGNFoxao3MARd\nAWFrNQwRnU4nIgJQL7lBRHdO1ByWVYAwleKdjlpB9aAWmjZmg80ra8bAonkYx8eHj7vdOPTh4eHy\n+tX3v//ZZyhimCOHyzzRuGdglWy41p6COS41EpIDL6HXRKH5lGsQRTA0NTWXbWgKZlhhI1vFKkG9\nKppDigCoG11eUZFyijH6nNSUp/P5PM+zSF7SCABaZE7TfFmyJARARjQomrUIBe5i5EiqKiVxwPPy\nuHyYDuOhG7EfdqZYNIHGYWREI6TdMBBBSrNptpy9v0ZEpMxsqR93oeeAAyBPU8rLAlpW2OxlFmBU\ntRU4TNFHomrpY0dE2OqC7cpviGyrTgFEZApEpGLZCnn7j1rO2ax0gQlDVTQWhv1hDeHXF21nHZEG\nDhQqpBRq0kIMDIxkBqxYDAN4LS6DKRqAeVuokYEGQCVkJCVUqdh4TOZgZo5LrrBqLazl5OvZrpEf\nrA2mVomvzj0AED9yQEBg4tZl7ANZPF3U/kVGIwQ0BDQWEAR2MFogYmTz+m9QE8goqtrH4EOlCAnJ\nyMzIiJAIGIAYzExQEVBNTYrCGqLsu46ZA5KILMviqGFEZCYqxQGLgdCzwfVZ1+dtqgw3gDz1pZ6H\nLSWpShdomc4//Pztn/zhTz//7M10PvXj7rAfRYQRp2kau8jVQnbaIaRVgMFqNGCN/eg6wVDNeQbQ\nTAAJQYGY/HBMjRBNAQlNkSxLklycSQwtL2meU5oXHWIMYcnz6fHx48P9Ms1ieplCk0elFFVBROKV\nSzlyiEyBiuZ5TlM+38VDAQG1uSxmFBAw8G7fEYYQQ1mSaM4ZiSCXhKZ9ZH9etSKGiqXIQhgNiZiJ\n2XFzY+zBUHJhrSCNaJ58ceNO3IXzFkttMW3tQ0dkWBG+26l4Z3oInTcBqLbWk6uFEpay0AbpoDHb\n9p1VvporH2GOzAHABBTB0Swp50KIRkAawKOGiKqGRGvVC7CqAgIieXi1ZlsM0Hyaia2tMLRpYH/+\nevYmIsOagq3gTWBmXlyzZmVhjSWioRKsXfHquMUA4Ial/7sK7lqIigZIhmpghuqIzgZmCEVFVJC9\nIHu1L8kxuAEQlEyPuzEti3f9r7rREBAEDdDMWR5snYX8/Lmw/YAb1B1XRAQwT5c+Yh9pyvOf/ZP/\n8fPPP39xe3j33YcA1nPoOaiC5AJddGCvdeW+WegSHMB8lEd9akBANbIWmjcy8AMit4W2/yqgackI\nFphUdbqcU1my4/TNS5iZiZaULufTZbpILgomEFte0Vmi5CKS9x5VDiwgOeVclpRKsfL+/qOhRu6L\nQclpMRz73fHm7nKaGtMuupSSckpEeMqlj6EfhxgjIGTVkhOKKIQAnNQE0UKPcQAgtgygPm7Ohx1w\nQANWVWIwW/vTK4OImSNGGjrEnZGqriZ4Nf5FRIpJMUUtrBSsagoIgcDI2EPyhkYYkIApIHmDmSL4\nDBRUK6alCIFj6K9DVSgQEqIBARlYoGAV10UY2BGmEFHRcdLXeg7vfUHE1Xo18EiqXmV8c1faBZ+J\nk3a19rGmGbbf3YoMwieYDrqZ6tbuiFcUIDQ0QzFAhQIQDMQAzSRnMRNkZEYgQDY3KGKIIsYGaVle\nvnjx1VdfmVnXdfNlEinepgRuhxMooMka7tfa6eyvLYNtWQ5ADX2SgI5jHwO/+f73/+Gf/ncfvvs4\nnU4RgVTn81lKCrG/Oe6lmpEGVqv1lZA4sKquws3nL6gBgaEpqVptwkBBAGIQEyCHMRYzNBQzBJOU\nl76PzOF0Or179+7h4SMAxM7xf5z4soioFQMDoHm5iK4qkogAtWjOJXdSDFUrPoP7frHvPzx+GIYO\nySAt0yWVnHed3N5gKUoUgEKII6iolrQUIprmS4xxjzh4sVspYhmoix0vOS0ZFsMMmBXAUIGwFMNq\nuqOqsa2IGE4/W5gPr6Wx7bk4DVntQEekUsqyeGaSUkqBVmQVRAyE6l6+oSEAEgUCZEjzpKsXBeae\nnKiqxthBXuPC5mjHqlIKNR/LEbSAALx54pqewqdZYHz6quxjCEo+Rn0FTHBd0l7WWM6VltZ5cVuF\nvC3Ram8iBgDwFjs18/mmYKvfRuilqnCVRd5/4fFHRANRK+4zKqqButJQBHeZi5UOOtOCBlrk888+\n++arr+pAYzTwdXroD6r6vK7ZKkbNVl48syEVhAFzWQ67wY/zf/zH/0MfA0h5/HAe9zegusxT5EAK\nfewuIGs/dJ1DDQgK6oPFHcYT3TNGEHRYcxUfJIBgoGDGSN6TZObt9GYOxWbqhcyzyOPDw/nxfr6c\nENEklpxTnlOanRCZEcwKaCpWYCsu1cyMbEpTUEfLzTlnB/8KFo04K6bLAqImlBZNl8c0l8N4MMkq\n2YoEpqJkEAxo2N8aQkGeFRChABoyMo+7/Zx0BpEQzUgsEHWBjWaMtMKVK3rnlyqi44XWYgPH4YMr\n6olezQ3HpHN8NxFx0FG4ugBcLUkM6BTmu2iGZsJA3l5pq2u8Nr2yF92SiEg2Q2UMyECAagWNlIzA\nZ4CtWrK1gW5r/5yqWiZg6yK6nvtUrTXV9Owd87Tlhqna7XA7h6WpNdPAT6wy/yMixMj1uyaitbtc\ng9cWqCgwg+sC9QmMYl6uhlpyFkDTnHOyRUR9Jujrt2+QKZXMSBxQdYWX8/WISBaLsUMCcxzFdTQR\nIhqoASmtUEnsghCIEISRlpSPL1+Wy2WZlz/+6R+c7x/evH3197/9qhv6ogA5d0O/zDLPM3esBH7s\n3iBJiK7rvJFTzJwcPBZ0HXRooKYG6mMozEWvgpq0fxEMkc+nk6Ntm+I47nXtFmUVTIsCKkJ0sslF\nKcZurfPMDpq0ElhEUgods5Eo5mRLzgLp5u5Wki5LDhR2wz7gsFyWnHBBmSXP06Raxq43MxEKHKdp\nSSWbiaPTIyLFLnYYOjif0+m8LElKJhWjMIwxBBAF9H0AMDVDQDEF86ijkwohIiGoWVEpK6wjuS1e\ntYL67BuRbFo4hi4ygBI20W0BkLA+PAB0XWeAuVxrI8GsyApgSkTecgDBQ1Xo8NGIXI/LnJYVFMGw\ntrg2+saNK9jKgtpoXDNz5HQiMvCWE09Nk2tIhK2YX032QAiEImqqzr4xBvCeTzDiGpZVAeaU541h\nUJOVRCHSWqMkxUBDZEQsJZclCQgIIDIx5WWRlIfdAQkZAwgg0Bh3Agaih+FooGI67sfL5fL9H/7g\n5etXHx/uQ/CCPUIiAxD3eYCYAVBSzgYMoQeKi1lQjBT6COf7D8MwHg/Hac5qSHHMOakpEx7jzk5p\nh/z/+J//Z70s4zio4ng83E9nih2N3ZQTUiAKosWs6SQj9EixFVFAIFiJCMDAAE1LypGJDC1LCJxz\nEZE4dGvvj4JJcZBStzYkSyqYhVLBnFf8ElVdliVnFenUJCVF0hhj1+3u7x+WnO7uXlBBzIYiHz58\n2O12+91gjLNmM+v74Wa4S5geHh5oGULg6fJxyqW7hfN5OZ/Pb16+IezPyzklCLGbsjlIAc16Pk3j\nfsfM9/eXeT4z8zAIxfwP/+TP9/vDixcvbm5fjOOemc0Q1P6Pf/+//+X/+y9UFQrO87w/7vKSOHSI\nbBmQrJElIsYYACSVCQmBzCPMQ98DQIxUyoJmN4fxQnaaLqRpfxgBE1ozI9d5a0rk/Eetc9qDCs1y\n8/fVY1RmVmENBNZsIJqnr2D916e7PYWRdELfGkvtzWY7bT/cfvCnbYFTrR107YLbq0HF/bPq7DWV\nSDX41N4BADNdlrm2q6mvRVVVC3MIQFJRxAOSUQhEYFez2dEv3RXxDHsqBYi6Yfjs88//03/6T/ZE\nRDx5ISIzCrIxiUApomBI0Jsd+/44dJbmdLpQNwz9gWIXmafzw7Hroug//Ad/cjPs7naHjJZ89Cmr\nEhOiEaMhgNsdzmu2WozYIrwGAJ76W61Cs/14wFqPQkTFSPKyGIQQTMFUTdzUJjf0z3NalpxSWZY8\nTdPlcvHpyn3f+5iEcRxLKQ8PDwBwPB6Pt4fvvv3w1W/eOTbOfr9Pk4HkspxbrcwcdO41pXS+TDHs\nkMrj+8vlcnn4cHp8fFyWJU3FYSxCCHve7/f727sV3uenP/lDv/KrV6886HI8Hl++fPnhwwesznlJ\nS64jr/7sz/7s5ubmL//yL7/++utu6HPOuI68dIK3zb9YQedW8ExiRfRBRSCaDXzvMUSKyb2GXBAd\nNxURr/O4nNS4Avc3uO9P6X4NZz19NdrFp2HM3+frb/EqsY51t4oL3b7Sfvazb9dp9SvtY20Nz3h4\ny+3MXDEs8dnatMLatIiLIzhw9HVebdEVqaWBOTzdihCCq/cYYxfCH/7sZ3/xv/6vV8W+WR5d94eZ\nomIQ9DyGooFKjmRDxzFGMBHlnpW7iIYyGVl59eLlH/z0R69e3qiVGEKuW2erlXgVJf/V19VwBDuf\nzwDqgWwiOp/Pj4+PALDf711lbfcWa6nQOI6vX7/ebmzXdTlnZt7tdszsF+z7/vH8kHM+Hm69HzfG\nOE0LM//4xz85HA4+QWGZ1xrAebkUkdiFaZpKKcMweDX2mzdv3r171yqWGu2VUnLSjx8/ppT8Kyml\n3/72t33fOzoIAHih3DRNrgyn6ecxxi+//PJyubx+/XpZFmfj6zTcjQRvrkp70vbSK0Q5+eAoL2fd\njfuW+w7N2/HPtcbKrZO3YRKfaP4kKdQExjOO2n7x2blCnTGttXbeq4q33LW5KWL1Gxu/NZZrxbvP\nlFXDl25f8btILtuLt6t5mT9WwMn2OE6C/oB1DV7lx8/UcltSDUyhqr59+xZqqPP30bqqqglSDCEQ\nCKkFKMEMS4pYfvDmLX3++eP5MiXjGObpobvd67T80U9+eLPrb4/7x48fbt+8ElnPqyWATNEjbIZP\nkHP99ezXtfbVtOu62vZiTr7n8znn7FCTzeGkih5Zi6hXec0ryhX+5je/8ZmAv/rVr8zM9dv9/f0P\nf/yDUsrjw3lZFkcKMnPJSx8+fHBMjc/efv7mzRszO50f1CxE9k+eTidPjjt4Y9d1ZjbPs5fR+qET\nriCzzo3MPM/z4+Pjd999F2NcPZQqSVX1dLp4z/XNzY1HOHyY1pZ4tgbXRjBdQwNQRz40+d5KW5P3\nVTKraXimQxrvPaPILWXgk0g0bBXjp1+smdz1RNtCQx2rs11isxK34qQxW3vU9nlE9Cqn9pVKNNfj\nf/b+M5ZuP4c6wqqtn4gQg6oyX0uosFqh263HTTgxpUS0jmJYSun7fuj6ZVmYGGC1ymlF0wQzQ2NV\nKVYCCq5obMBqPeNxHI9DOAz4+ffeYuzffXj8cP8xdbue96T2g89fH8Ze8yJpAlM3/OrkMXOz0cvq\n3XNu4Vknsu1+bjXbNE0A6mPHcs7ffPPNl19+Oc/z6XSCT0Q7IjKvEIZ+hdbBwMx3d3dezzkMwzAM\nMca+73/+858Pw7DfHd++ffv69euU0rt377/++uu//uu//ulPf/rnf/7nIvL3v/7tz3/+81JK14cP\nHz+KFldoiLgsy/l8VtX37987zLP3Ge/3e+c9H9DiVNT3vYOspZR+9rOfacV9Q0RvHOm67nKZ/+Zv\n/mYYBkR0He4qtMGu6dNeqi15b1UO10FIVi01XgHMAZiQAgYO2w5FqLXbW1H9jOVijIBXa60WbOnz\noGJ9bdnm01VuZOo1n95+3V7kWSi/sR9WI7Nd6hmX+l8bij1shPqWWxr60DMRNafFCXfzmISIKvpM\nMK1r8PmAtVI0xvj555//5je/Ab1u2vbRtl9HVVIFE7Jy3I0//d6rXQCZT8GWH33+/RfH/S9+nSKP\naPrZq9c3Y/fyZv/h/uNxv9MipSSPR9WYGhqhgQEYVwP22blsd6C9H2N0zeY66ng8OuP9g3/wD+Cp\nkPXv5ixOuC49U0punr148aLprpyz+3Ii8ubNG2Y+n6Zf//rX/nlEPp/P9/f3/+7f/bu/+qu/ijHG\n0Dt+VErp9vZ2SXPf9yGsmN5OpbvdDmsXFVQQeFUN3C/L4isnomVZiGi/3ztha40GN2Ov78f/8B/+\nw+Vy8cfx520OxTPys40t03QDr3jhBE+lPDOXUlLRLiBQx4FDo6H26S0r4ydm5LMdb2zTYhXP/iqf\njO1tbPYs2oFPVSV8olS3t2535AoD+uwzW525ZS1+itm8Eeqw3YeqhAFWEbDJH9CKWfJMuPhjolkg\nUp85TsxI33v72d//6tf+mVqzssYtDKAUIQyBIxKrKGjpIh3H8e2ru++9fsE2z48nXU7Tw7uA4Qdv\n7wKjSfns1R0ZoeYhcLfrT3lWVQtsyAjsZTpr3pQZ8cmTYu292G5L273z+YxoDYHUzNzpctnfpGEz\nw3a7g1MtALQJHsz85s2by+WSff6wqjMbIv79b3/95s2bt286R0E/n8+73WFZlmEYu65zdmJaAWQ5\nYD8M8zI1x8y1VkrJR2bbBrTXfx2Hgze5u5PmMJJ3d3feotW8pMY2fT/+yZ/8yd/8zd94UMcp0/lt\n+8mtf7jdrk9pHjY2dlGd52UACDxQH0PL1nMd9oc1XLG9Yvt5nmcH03xmibUkdbN3oYbmn3Faa0t7\nItSfRjK2/NZ+3gZIGulsbwcbqeMHv32EdQtqgMS/rrVuI9RZcNtmzVa1tH3SSk8VU73lYchbSL1P\nzJHP1CNjp9Pp5ubGH+yJ7DDQUsijIMglFSLadeH2Znh1e+iidcb7ux1D/uo3v+jHww9+9MOUlsDR\n8nK8ufv44dvXb7+YzJaUrD0+oBLQmk1FZqozobby4hpeeqZpb25uVAvWrigi6vt+GIatMG1b5+0/\nbeKmX9yZ8+HhwTfTI20+2f18Pn//+98/HA6X80xENzc3+/3+cLh5fHyMsXOQ48PhMA57twBjx0tK\nRTLX+WF+Fw9vtCv7RCg3Necp+2ofHh4Qcb/fM/PlchnHUSu0hB933/dd17179+7t27d//dd/Pc9z\n3/ePj48tvNG0CGzkaamjsJsx1QRWoxM/egBQhd142O0Px7vb/X6/uitUx/w1bmkb2g7Dd38Lc7s9\nJyev1tvWIlfeat3EYduUtr5QB6m4HGrSN4Tg0SqqSFiem6+Psfoe7U182ofqdsj2UmEzwvyZEHIT\nqC3SzT+Xsn3fu8bzFr5297a5VlFyV0FLRIBdiCa6H3dpXlyWVeBoQ1ttDJ9MMAyDqZJBWpaSFkJj\ngld3ty9ub24O+8/fvomBDkPcD/HV3T5dThGVUQjlcjnf3BzUCgCELsZ+4Nghk1bzxMyQ1imqfrgr\nNlF9wLCZAmWOQLwsKaXz+bwsiz+U1DEGLS6/5Ux/Jj9iJ4C7u7vdbueADn46TrV+7n4K7hT5X/3o\nX79+DQDf+973pmn67W9/+/Of/9wDFdM0tTEdMcYWrix18iAR+fWPx+M4ju4fXi4XX0mjBDPzFqeu\n6/zX8/n87t27L7/8ss1wu7m5EZHj8eihO4czayKmGYB/+qd/CgD7/d41oevncRx9E6h1fobgG/vd\nd9/F2H322fdev34TtIbUt0z1jCg31IlY61NoEyjXOjDen7zZKq5hmu7eUnk7tiY57GkYVzeVFi3c\nBNt1PI18PnvnmWa/2kvVEt4+wqc6s8otn8uRvZ3IP1l19XZzmkekVNsxRATqpDiuIwHaMDpEBMSA\nNM1zAeRSyCD2fSAjov1uCJFi4C7y3fGoIn2kQAgkBgoQEdHTOytAPIWcc1FVQvcwwdYFxhj9mZ7t\nQ7OI2vPqCvUpzUTcCvXm0NJTWH8ibnkCorVtj4geHh6cGdY24jpkrzjW/xohgnYjH2TlRI9r9T24\nNlMTRHSD0A1atx6dk93qm6bJNcE4jNM0+bE6M3hA1SpYk3NCixY6GHGjeXiqoz7li7/7u787nU4+\nWMMLIH2aNtYARBPBMcbdjn7y0z8Y9vvlMr17927lv0+ps0VXnvFbKcVpSDdxP38S24wLavk6rZW+\n24vYJnKKG6vVNgXHjfSf/fyMnZ5peaiRiWf7dWW2Tz5M1cd9dqNmJ7RH8Gv6V7z54hPORwAANTAD\nNW+C7mPcDYOnHAiQKmae94Mzc+QIYArWxc7yvEwpMPYhRuIQ6O7FzZdfftkNOzHVLCLQdRRiNKDi\nNdHAgFgUlKB4LaN5f4J4d3p7BKqJJuec7bZcH3bDb7aJPTphNdfFL+JpNNdjriIul4sL3NevX+ec\n53k+n8+Xy6XNTPz73/4aEQlD81xcHHsC2k1Q17Fm9vD48fs/+AGHVcZ5qAYR+75vNxrH0d1Ch2xJ\nizS539ZJRB7fh2rL+C3meT4cbs7ncxtI1jZnu0W6iaKr6s3NjRuljv/74sULfwR4WpY4DMM48E9+\n/OPLNL3/7ruHDx9Ck+7PqHPLeJ++tkqgMec21NM+8CkbwCZDvaXUpqm3/GCbOOSna8Dq6z9TYp+u\n/7rUJzLkSapk+1zPLHL4RFvqJv7ZhBmAmU/pq4cKNQC9qAEAw5NYERF1HLgLSwG3NtOiWbPLYKM1\nIXm5XBTIKBTVGKMhBx6IQIxBLRddiNWoKCjb2t9nAKhkYAKt6g1a5jfnBnD0bFe3TghUmWt1ZC5t\nYm68QjCc/dScOf3iZuYlI55N9pMtpUzTtGLPrKb0GttIKYlojNGJOMZ4PB4PhwN9DTnnb759fzqd\nvCjkcDh40o+IfEqZG/wA8P79+++++46pc+5aluVyubgH4bal1RBLS4S6rXg+n7ey+5nW2ZIQAFwu\nl2VZHh4e/Hy7rvujP/qjEMJvfvObraT2P8UYI2EM4bjbx7gOJHwSKLdNf8qndySiFvrfEihtIuaN\necwxajZpCnxald8+/zu1VrssAKTNFJVnH2tX2FpE2z3aWgJbbmnKuXFsu93WsnIuamLCZzZi7VN/\nSoIKqojrsj2f5n7aOovQq6ZkUyGtCqImJjmhQRdiRGDm0HeEGYCKwpLF5qVgVAeRE+iBCAMgm3FW\nyKoKqEimXjtigEA+codDrdFabf5mNn96iLgxyLenJmuj52pnukT3GMOXX3692+089O/er09X//bb\nb1X1eDzudjvnn9UhR805e5m3X8orSF69ej3Ps+fimPnrr78+n8/n8/mrr7/mQMfj8e7uzjPj8zx7\n/dfhcHB71RXjVkY0BBczO51O8zwfDof2gC3V5nO/AMAhjd3z3HIEbNo7/Z2bm5uf//znnl04n88P\nDw+n0+n29vb73//+NtRJNbUwT+mu617eHA0gbFn5GWtuGbqRrohghRxqOgRrnKOxTSOm5mttTbhn\nDKDXsB4++8Fq18nvkzf/ZTn0+16NLWEjp/Fp0SYRmaHm9DtZGuBqYVaIE7C1D3RdfyPTUso4jmYG\n4gGx6/N2XYdIkbUQ+egmALi/v6cvXiEyEOYi/TCKgQICReIeOYihABKQAYthMVNiIzTwqmIvXzQj\nw6di1Ko7jU9tgWdbuvXNWiTDg0ANl3prrbWgRSNfAHh8fDydToiYc3758uXnn3/uTt2yLCrQ930b\nhsrMh8PB5616sOHv/u7vAGDc9aL6eHrwybqllL7v37x58/bt2z/90z89Ho/zPP/yl7/8+uuvXYXG\nGAP3vmBXjykl/+4f/MEfUC2NajX3Xdd1XUbEzz77zO1kd/za6TShQ5vY+4cPH1zVe6pgt9t98cUX\n5/O5Gca2sVcDcYzR8cKfjJzc7v6ndH89rSsUhX26LN1Mtd9aHZ9qpCY4tc6Ppc1s9e1X2tnbJqnQ\n1rZdA2yMuk/5DTcW43Y9sAmWbO/+7CJbkbTdqCe3BvBRDf5NF0N93x93ezelUkoFNm3zJqpAHIua\naI5MUuSbr9/lP/hxH9Uw5pLuXr56OF1CN1CMYRgUQxLQJIJCDIXQ52it+GEItHbkKXmVAl4l2lY+\nbje5SZ8tN2JFbpvneRzHlstykvKA283NDSL6+ymly+XiVHi5XBzG1OPy5/P5m2++mef59sVNKSWn\nNQvqRt0wDM5p7V5e6nW82YvqkuZxHH/0ox99//vfJ6Jvv/32u++++5f/8l96ANBj0cfj8e3bty9e\nvMipNAIALzsuBQD+5m/+ppVruYzzWYpEFwB4/fr1isgE0Pf9M391e8QvXrwYx9FVyzzPLj5U1YPV\nz6wGROxjR2jedBaaYKbazwQrqA04rpWZIHpvz7pKYkQgA0ecVwQiRjAk9vJcL/c3phAClyz+SUBb\nxx4DARohMxMCFchSFMAQqIWtcNON9ow+nkni38lszYXAT+zh38k8jcnbX1eTyXSWrKqE0AFF8+R2\noYAcaCtngMlDUQYCYGCEUHqLjPg69N+L/Q31AnlBnLEsHAoVDLFjOr1/JNWu35MoWdmHHpDxdLFp\nAYgIXbalv31lAtoP2PUaBrWQC5LaQBYDCJKCMrABwDptDBxHRLxkvAZg20YxO9CWQG3PVRUzMRBD\nv4AaqsPJl5KWPH/99ddLTpILMjESBY4cQhdvjzeny1myciTJOqfpsDv2Y3c8HrMkRMyS5nkmJzQG\nR1N0KCSH6+jiMI7jj3/80xcvXuScfvGLb6B6VtM03d7dffb2e07Qv/7V33vC+uZ4++rla3cXncqn\nafr44X66zMOwa2Vcp9Npni/M/ObNq48fP7YkqpkBaM4LgIYQiOD29hjCSgO73a4lk7Z0AgCI7B7j\nfr+f5znn5fb29nDYvX79spUoOchCk2VM5FN8iCAQGqIDSIF/AEARITB6E7hb1wheTU5mpsVWJBFg\nQDRFEy0qpgpGagWBQ2Awyks2RSRgBwUS8OsRA4eAZggUKFAMasUUTawLq+NOdSaaqalKjBHIVDUQ\nNy3nLViBENE16jpxl4lMjLxXwu8IZuAtbS0+AbW0QkTEA8rulCKimXM7GQ4iplLANCoPoeuRCbjM\nJRKro4mZGKKwLarc2SIpTjqqHZHjZfn+Yn92fP3w3T2AFiLhYelpgnwuRXP6yeefldOlLBnGSGqa\nli7EoetPv/p2/OKtHEIcX36cJ93fwdDReNMNL0AC+Jg5ZkEWUwI1seCoYWYFTREyGIIGWnMnq/RE\nqIE7KMXxGxnJRLKAGCqypbQwk5biGHtZ8tvvvX379i3H4ICCf/+r3/zghz/sYvzu/fvAPB7HvJQl\nz6B4oJ1k/e7DO1DMkpZl4Uj92E3L5atvvjwcdjFyZOoCq2pJCwBoySrLxw9fd9Hu7u7ubsfT6ZTT\nXDIjhfO5R+j6LqpqYBl644DM/Pj42HU77wbKeUbEGHtEns4X09J1nUq5XC5mut8fxqHv375BRA/q\neEqgFmbQdPms5KWLDJG9WaHvgsdaQwieFpZ1wBPuxkMq+mq3y2XZ0VBkCQwlXwAgxo6ITGwcBy+H\n8OIyZJznpe+7YKZVoWHt37Zn/7oCWEWguDZQUIAVDcBL6QjcYTHHViREhDqNGQC8Rdg5n5BEBBUR\nHUFaW6oqpQyb9pCmfLZarkUCtxbdM11Hm+ThpwYhbKzHpsraD1tLIFJ0GCJWBCNQVAQzicTAgMQG\n5hhuhBgA8uU8BjyGuFcdL7O++8jfvB/e3Q9JFbUglGiTwYDWAQLSzSJoiCEGQEYiQAocYrSHie9K\nVwL0fR5jCBD3Y7e/fTgrUEDEwtyxJ5rBxIqJCbir6N3WWP1GsxXeAg0N17+arlNtlQwL+CQGQzMt\nagXVgWSgxTwYScwYiZFfvHjhV+77votRQUqQWAIacSTGIFYYw5JnyeponGIlchcjq+rQd7e3t7mk\ntOSUF1NAgoeHh91+HMcxRN7tdj51C4hVu8ADrx0GIg5nYvbjH/+Y14lCsDXeTDTl2bMRr1+/anUO\nMcauC94+k1ISKQBKFFWt6+JuN2JNjnkaowX8/E23mdVg6G/M7OPHh8NxQKLH00cA/eP/7g/v7z/0\nfS9Zl2XpePANBsRpunAMOScifJIp/tQ8s0/cnhZR3H7FatTxmePUrP/tdXxrrpXB1fPxHSOi38ls\nz0LSuqnhgI0xub3gMzMSN8nZ7Qq3Jj5sbAYAYIM9UK9a1IMPoGDJMgBA1wOiz+xGNDRjgCD2Grp9\ngXApcn/SjzOeptfU3bz54tvffq0m2WAp2huMiDsgUb5B7uKOiViBiXwKcQGbU5GP56n/rn95sz8M\n+75HC2lOXTcUjL6PyRF1QATEpwuuo2IUsYJkeIEYVqQaA0eI9GnI4nYMGJgYKJpDCgoYgv8Lq1EJ\nHFhEiFkEXty+nJfFEHbDvuTsLoiPbkKjGLqOu0Cx7/uSJEtiDLEPBFw0p5TGcSQK83y5XOZBMnNk\nxt3u8PLVq7uXr7ouVHxNkmKn88wMzIAIxEiCImRm03Rmxq7rPKDSggX9MHjkc+3dJvZKoGmapmm5\nXGZPMBBRSulyWUucvazZpym4EHGKcvPVw6QppZRL4IfdbndzczPNj5qTpyL+43/8jyHQMAwlCQAU\n1hBCyUIxpJTYNOccPuWQ/zKnAQCSVeiDJ5QNT0zbJxfcqpf2Gd60eLRvEWGMwZ5687/zFs9443f+\n+qla2y5gqwCvT7fZDSJCgyAggllQEQhQUbUan0Sub4UlBAQyCHP5zGiclnR/On/zXj6eh2yjYLc7\n3rxSEUlaFtAFdTFZQIuK5DTGnok0F1IYOJralNPY9/n+cp++2l/mux9+ftwdJeO7eeGbPlMBgLzG\nYEwIFBSVGBEMQAzNSB3iknCFt/WCE0AvYjFCREZVVHIXE1jBQZqJgE1BixpiTmlZ8nxZcCRTUITL\n+Xx78wI0MUVmTnN2/EgtVrKIiGbkgIsVDliy5lKoi13owSjn3Hfjbj8gsKqmRbuuOx5u94exZB2G\nHVMEQBUQkZzSsiyxH8xKStlb/93bJwYVIMYQOXaBGAEMCQIxogUMSOuJOyPt9/uf/vSnp9PpdDqZ\naQhRpKSUvfZlmianN08/elgVEVv/aynF04whhJvjjSfx+r4vYN6lut/vEU1Vl2XZ7XZes/Jw/9jv\nxmHoy7Kcz+dSyrWC5BlTfZpEhk0gfkufK52jurm5/lB/1hY/9MIKA7D/L2F/1iRJkqQJYnyIiKra\n5e7hceRVd1UfM01DtLO0WFrMw/4M/AcQAY94wiN+1r4BhAXNYgjonZ6Z6uqp6qqsjMw4/LRDDxFh\nZjywmoZlVC/BMsjJ0tzNTA9h4evj7yOwuRbiZTIf23fmqDPTzo/a9n7VFhtYbGZJ3uxcbL10uYtz\nu3xlEev4bCu5tE889wlZkYtxFVAVRmXQQEIgoAUqA0TAYJpMm2Ikthqkvd/vhlLHaX3SOqieRjmN\npzFfrdeimCtmg2pQkYpBAcgYEwYQq9VYIZgAABXlAFOVXAcMIWyPXbeOm464+T5P0DAiIzifowER\nMaHinG7rOb/2dkEkRidlNTNTqwhofmXmPzYwAAFURDQEOpNiMxigohaVLNhgpICGUz+VlCOFxFFE\nutQSYyUhgIIVCQjZdZ2QiIGAYhubTbdxfQ9kalLr+LIpChE0TbfqNk/TvhadpkJl1kMlCsyO/hOn\n1/YJBiIC0MPhyIylTNM0lzGJKMama7rTcTgej2bmonklP919fPjP/+m3XulHMqlGDF27fvny1ceP\nH9wIPdRar9felBeR6+trbyf66Pc0TYB0PGR3U44+d2zk/f191zV93w+ncbvdqoJ38Ffbzel06sfB\nR1fDJWLjs2UKFz5qWZ2XUeJfmuLlH+MFcvxyxX9WwbeLHExV3V3AX7jHxfN89l2f/YrOKOrF8D4z\nrUtoiF2Ud73nsxzhvN2IJkGoSs4jwaQBjVFAQTQgBoNGbaXSKnKWzWHcPp5W/WSlWq6GLBwy88QI\n/QlEgiqCJQBFULCCVlNjQABmlAiMjQCg5WYYa2yiEedjfv72h3rotzfXcrO5+vJFQoIQKloxGEWr\nVDEwJATGhRlGjYwUABXtPCJkZgAEIGAoMiOSfTWfLwggOk+bR/tBZOlABgCoRQi57/vVaoXIIhXA\nVEBVPd5xpCYAICoCERlAYGbn4GWgp/3e4cLM0Wc0/T60bRujT7h4+7F1GOTj8xOiMUdmJpqjHpFP\nbWiv/vu4d9d1AdNqNY8CL7X4BQ6Gs0CFqlgpQlRTajykdHj0arXybsHd3Z1XkmqtHz586Pu+7/sQ\nk0rwtsGUT9M07a7W+/3+H//xH7/88k3f99OQv/rqK4bosKHNZrNevz4NvQ+qBvuL+vhnIdlnj78s\nieKPWr3/cgiHfzFD9dnnLFYXQvzM5/ifLVOty19eprD+l4tVL/b8mWe7tPZLpJXfj8U9Xm4oCgZo\nQiYBlEHYKhuYWRUGagxX1TaTdEX4lLv96aqvaT/2fa+lImKD1K1WsFqN4wj6yQMDAIhOZAerkwkS\nUBNQzVV/gRmkEqAayJTHoX8+nYaHx7xpt/Iz3HTNao1tKoysOohk8Ja3ulIcmAGCzuI4FZWRvPcm\nc10EwAU0TOscg6inelhrdWl1QgzEQkyAaFCm3Pe9iKaUhr5PMVYuJlole8nBQ7IYI5yHevWsRDmN\noz+fcj6Np34cXF2JAmstuRYxpcAKNubJP6frOm8Zz7ABhy4ZEroYg8WQaq0qSEiE0XtZYPy8f/aZ\noFqrW0hKbdM0pcg0zb3s9XrbdY0r5iKZo73cdF1FyBeAN+V8HO6LL74QkW613m5u/x//8//z4eHh\n1esbVLm/v3/54vbf/tt/C6CllKeH56ZpyigpJQDo+15ViviGYgEuYqfPQqm/9B6LkeCPx88+s66/\nTJyWt3wWHH4WlH6WUF0a52Jm8GPvdPlevEAk1Qthwctv9DByCZKXrv9ibMuHICICahENWJwbhJwE\nH9gURBqDVYXtKNtB20Ho0Kf9yZ4O5XCqw5Cl6iwSg0Q0I0jU0IAMEEDQ2LRtkpaCAE2IWmUqUkUY\neNW01awUaZHaZmWB81RleHy738frq+s3L1cvXrSbdQiUCCfCQylGYsSoqF4tYQMEMSUzBN8hZj5M\nAEA0REOa5ebMLRTBTGYORVADcV7aKvl0kru7OwD66quvpmmcpmZJQMxcDzMTUYyuDjXry/kHl5Jz\nnmqtuZbVdpPrpFq98OI8hiI+EgUi1aVw/PCYY4qNQ+RqMQgWAseYYgRVy1lNzVxSAcwUpeJ6vXYy\nXGa+urpS1Vr1ArLcqGrf98fjMcYYI7fdnEk50Lnve58tojPpBhF5YOlL4vn52c6IMDPb7Xa73a5p\nmlKm1Wp1OvSllHHMzmiScwZwgRcQkcB/we0x7+g/RlosQZ2qMs9+YMEThBCIFs/gljbTdXQuETTH\ndfNivmwvns1q6dl/MuDldiKin/+CXbgwNlvA4x5Mw3n0Ey9YjOAMVVlCRAfm+K88r11QOfYJGKmY\nIHWrMpxOZdqENgSSsWeDLfGN0nrK8eEEDyc4lXAq3A9aM1jlxEFslFJqzbmKKY6HEAIjoVoi7po2\nREYgYk5MqlrViDC2DRSqtUoVJUTGQOS82In4OvALjuU5D0/fnuL361cvdl99watWrb65un7O02iZ\nmxZSnEodS0HAQBCbKC5UHxAISqnMPI2jkZlKkXK+1woGFGiVVrVWyVIkA1lswt3Dx+urFyExc6xa\nbm6vD4fD4/NTjPz999/f3NxcXV3trreHw6Hp0uFw6LquSDazmKKqOjqEmcF0Kr0inMYTRXr//n3b\ntlOdFPXrr7/Oks2sWTW+MLLkxIRKZmgGC1llDIGZ9/vD1dXVOE5mBBalCgD0/f72xQYRkIEImJHB\nhxVjjI1Pi3u0qaoqoGpOB/Ttt9+KyG638xlt35QfHh68dur4kt1uV2tlii9fvnz37p0H4d2q1Xk4\nkLque/PqCxGpazWzX//610Y4TSMQ+nBd+CwmhIvgEP6lx9K4WBzLArP6yw+Bz1KgvyDe+cy/nXfK\nfyEcvfzVpSu7LORcfrtXby+PHM8UXYv7cpiCrwO9mKNZ3mKEmWys04SKibRmEGsVdsjrqpuptvsR\nHw/x/pT63E0KOQNrBRO0SqBICqTM4PoUgQ3JRAshokaASW0SzWYqQua86IBMSCGAs5rPOhiooAhB\nQR9P25S2IY5m5cN+nCS+vFlvVkDDVRM3bdej7IfDIWcjbJrGEASzmghWAs46lTJpBUZUFEJTqqym\njglC0JwroIFVy16aQFRg+/DxbepWgfDp8DBHAkH6abi+2VCyXPpi4zSNxVpipWSSa7FKqkaAJApq\noGrFVLNkM7RDNqhTPubCuZym3H/99Zdv3nyJaKfTUGsOgZi9fAbnfu88KxBCurq62my2ZqDisK+U\nUlph261IxOfcaq1+TxGMpmlwuH+tut/vSyldu97u1jHF29tbdwar1crDPz+/7XbrFQffu9frdRUF\nS+M49n2/3d1aCPv9vkzzON8wDKdDj4iRGjM7HZ+ej4ef/eynVaXv+/1+Hz5bYUvQ9alLeLHoAYAI\nFiYlmNknjQjqDKJdwku7cIlz3LL8PJOlzd/gTNju1uis2/bZV18ezxKpLha4HN5iljxzG32eni3W\nvjhqO4Po8DzRg0upE61a7fOEiG2INk0B8IrCVnV1yu0p890ePjzh84kGZTEkKASFVNEU0ZAhICvP\nQsfMigjqwjCaa81mvZgLipEBuZQeIsw1N0OAGfCMrokKrVKTgYBag75IrkcQaoSGfuTrDeN6IgEp\njHUwm8Zh3STJODeXKQrkrIMhZFF1rV8QjyBds7JIBq/jW0EDQ6JkzYpP/ZgoQmBTKLOeqlYrKoIZ\nADpGwgBi41j6ehojp1wn1YzseDypRlMZ1u2GQJiDWd7umtPpWOp4PI0Pjx+6Fa03jaoMwxgChwhA\n8Pr1lyLoTQW/ty48XMdca/GBNQCQap5tjeOgNlMBEAZwkSET5sBEZjZN5Xjcn06nGA/9sHpxu0NE\nZwfyKr9vu86q4NUXJ/Pr+z6XenP95urq6nA4jONYp6lbdZHD8XiMkXPOZapEtG63y8jc4+NjahvH\npoVldV5a2mc+4dLqAD65o8VKL73cjzzDBZKDLyZEL0cK9IJhwStgn7mpS6P6yy+a7V6Wetr8jZcU\nd5dB8nJ2l0duF8Pml2enZFJBwLoQEwAVveH4wtge93yc6DDi/Z4OPQ8TViMIgFDMim8oTIjARgyg\n8Kkqa2QmmmutUovaoU6CNFsaUTCd+3sYzJnlbVYwMUJUWDXresol96FrdjENVfNTP02lrEIdhunw\nnNcxbtq24eNwun+8y9sVw1wZb9u2Sp7yRGcMl+P1AYADhhCY4lhGRDQDMefICNRoC/xF99IX9Gq1\nqbUeDodaZb1qnp+fVWskVjXikKWvOHk5I0ufhUigijq2Nst4uHtGtM1mV2u+vn5RpS9VxukYY/Pw\n+A5JUgrMsYGIk2Dm/cO+Vq1VSimu3+h76cvbVyFCqYMqqMA4jqIZSY7HD4h6HpZjM6y1SrXt9so9\nAWHY7Tbb7dbv9X6/L2V2TW4equrzaU3TrFarcRz3+72ZhRBE7T/+x/+43+9jjCFCYiK29+/f//3f\n/32MLCI1i6ombmOMUnUs+eHhfrPbOs4zXMZpy7K7tIfPHnrBu7jU2S9Rv/YvlVX+t0z30rD/xbDw\nf2sj0As2h2WMHy7coLcj+cxwtryRz2QsC8YHz6SRy3ct3xsIwKzh0AE2xVqhV9Rshrr//rHJEo8j\nncZYlRCJTEGFKINWL4ID8azhA+BuyTwaAjFQgVo0m1QRYDM/F9RqShUQEerikw1tBlup0amUqWQz\n65gDoEotUsYDhNud1JIHOp24TG1ZxdNwOBwfiEYzzTkjWhqSMw2nJnRdJ1pKLZ7cBmCjBCzFBgQ0\nQzEBA7JgZsDSrZpShAi5sdAG49Z5fm7S9nQ6Ikvfn5iDjTnE2K4bRLNcvc0qKAbKHBhhGk9d1wBX\nlczJ2nXosNndtOOYq41TPXWbXQjQT/tD/8zIXVwDEgfiMEsBMkfCIHJSaIkFyTiQWOWYES1GAvSC\nrCwIPCT4wx/+q2N9Q4gppcDJzGqtr17furEtC8+nFhyG4uBG5wXbbDZI/Ktf/u37u4+/+93vRI3B\nSi03Nzf/7t/9u6aJIlKmWmt1fH+eymkcXry44RimaXp+fv5Ujbxc9P+ieZwX/aeBy8X8loVuP6Zh\ngHMpYvmQS7QUXAC18MykUOu/zIO5VIQuj3bxTpeWtjixpaCyhIiXdnv5Icvo7l+edUAKbKlYk2VX\noc2T3e/p476lGIYpTJUBkUmt9lJFsRCJAiOhmbomzQzdAHUSVUI184MmBGa2QIGYAcHLlec/BoAZ\nFDIDwEHAHoYjhxg5ZtDxdMo5G2FsY6zmeofH/vhwuntiGdg0uMS0CBQwkDz55EsjDQUVkSpZVBDR\nNIAUxVBkhtGJiotp+JU5Pj13XUcW+seDk6JSSPv9nhmRtem4KofAVaYyjWLT9fU1shJZjBFIVCFG\nTJhSd7PdblX1eKxIpe0CIm42u+fnZ1VVG4cRfQgthHB1dfVw9wNRYHLukOjGhsBEoWlB1VJq22aV\nmma93hLB/rmc+4eOOe5iaJjD3/3d3wVOqjqOeZoyAAROxHA8Hg6Hgw/LXd739XrtSC6vf3hgEmL8\n+PGjNycQMTDnUg6Hw8ePH29urnLONQsidmmtqsfj8e7x4fr6SnJW1aZpAuLnFf9lRf6lpYEnWqhq\nnySqzoOKBq5pPuNHZiPx8jHALLvnz2eVWX/iItjzO35E63f+xk/l/ktP6OsghB8N0i6O1yuNfMHJ\n567s8nP8sVRNlq/7ZLSALQXNYkNOFVeVysfH8e3HZsjJhMaMWpnRmLJBtiIAWp3UWAERFAjQ1Mgg\nMIuYIhgjG2IFthltYUh8Ftr160vk0qwzZ4mZqZmoCsAUOHQNYcjDVKaB1CIxmdowhoZW626NAfp8\nGvdTQ7xNp764LlgIAdEUq1KmFPt89KDEwEX2qhTCitN5HgwApH5S9qomigkIs061FCoIhgKlimad\ndt12E9fr9Xq/3x8Oh/54il0Y6xBCiCHMm0gEZiqnEgIejwOADMMREfu+B5AYScRqnfb7cZqmUgpR\nW+v04nZNRCE4SD+AzcMoT4/33YoROSQhnyFQ0KqPT3e+2caQzJqlvPzu3febza5tVogWY2DmpmlD\nCNvtxo9hmiY/61KKz576Js7MKaVl2q1t2+vr67Ztj6cniCE1SVuJMe73e3XVEUSQOWhqmubh4UFM\nmbnrOi+QOKbKXCgXkRGtVgXQs5QbLT+JSEFAUVEJGMhFoxQUFZSMFJUxGBkDwzwpN/e+lp+f5WC6\n0CWwMUVXIP3Mj12a2cXuoEgRyeCccblyIzHQTGxpUqtaVVOfpYuJAVVVzy0KiJFTE4ahLE5o3jIQ\nzTQylSo29A12qwqHD/f1w/1Nu4E62TQZiiIrYyXNbAaoqqCggGSgBqLABmQzskwRLiEyRETmfFiq\nqibKgMARkUXFL5/vU6Ja1AoarFsNNEy5DD2W0qakxLlkGCkMFNfN9Xr9qiv7Mo51yrmejvuma9q2\nDavAIQYMQG0bVuM4Ok0m8cyGbmJqOJ5GwpnB29RAAYmZwsvXr1UVANftqpSSp4zA6/XWzGoRpqRo\nq26rYmA8TcNh3+c8dt3aEpiSikgFQrh/eu4261JKbJs2ptg249QbWZWMzJEZGFbrBEySyzA+50zM\nFEJ0/IcpiogqpKblRoiMmyp0PJwO42M+nU6kgYhjjAgtSM6nXvYm1QCw6LBZ71JKzNGIjkM/DnnV\nru/u7t6+fTsMw8I/54/n5+eFDdbJiwywbdP+6eF0eN5utimFu4/v9/tnFfjFL38VY0SDccx1FERO\nqeUYOdj+uHe9juDzTd7EIArOIGgmqpBSYJ6hj0QoolPOHIP52F/AgKFa1aJVlYkNEYANEZCNDJAB\nzc5zch5BLzPAcqHI4PT5gCiqVfLipi5/cpw5P2yWokNEJMRpGsCU0EwFXLbezBVfF39FCBwQHPch\nggzMKDLXncQgV1tvO9c9iSGG4ORFgmCnw56nfB34RWpO//Td45///FVcdQQ1T2ZCBAWtmo5SxlqA\niCmaqRoQgigQQzAfKS0QwMxqLUVFQF2BK2H0wACQldTMpGoGEZGmaXIuRWrbtlm1ZI27Naem73s8\njEmgia0SjmiVEFT1+dCJphe7N7ur78vjixebPzz+0K5WWqjbXUdKD3cPIrDd3ljlSNE7zTGG1WoV\nU3RC/1V6mXPePx5Xq5UZhtC8++HDF198cXjK9/f3RHQ6nYhos9kcj8fVeksxdKtrgNU01X//7//h\n5csXfT++efPq+flwc3P7+Ph8d/fx+vpF309ff/16GA9XV68en06g1pJu1l3bda+/+Or58JRiFKse\nLVWTJrYxxaxD0zUhhHEch3Fo23Z/eLq9vT3t94fD41P/oWmalAJ4yziEtl0d90Ob1kO1/FxDCG2z\nyjk/PT2n1L7WL45Tt1qtzGC/33fter266bDrVuuf/fwXi9pOjHG3293f3y+aAZvtbqY9lzIN/Yub\nbRMDqA2nnHjdRrna3gzH/JSfV6vVP/72n7784qfjWJtUAHSYnto2dl23f3oOIgURfZJT1SkhnQDH\nCV7yOdVhRAiRkMiXiSmqa+WamSJHRmACQGT3j0SEaKVMlzHhZZiKF42vC5dFlwHt5R8vj8XLqSmY\nmi1DcV5FRCKapmHxHstPABhLXsrc5JkdmpmMw6nWigBmIlVFFQGIuWuD5kxm9z+8g4cHGYY86XGY\nEpBBNWABzVomqWIKgKriYu9kwObCqMCI7IyRCEIeVXnQ6FEFAICCqZh4pR+sVFEsZqjEYxUBtBgF\nMNeaaw0iJqigypTBKiGilTEHCOsNTKdy+Pj0UGMRjYGGqe/3OaXgl+dpOqlW5kgEiCxTyf2JGZlj\nw6uxz6vV9vbrL3Ie3737cHOz2XY3T3f7V6+63FcA6tJaFe7ePYxjVgkQ4sPDqZQfvvnm65vr1/vn\n44cPH//87Q/MgQhfv34zDvoMPXP4X//+v6w3LWAOgYnoeX+8u3tYr7v1ep2acBrGaRq6rrm+2YEj\n8a0C4eF0dNxW06WmTXiiXKeqBRljGzhatexrOAYkljE/pwbXm20sdjgcT8+PbdO9fLNB5If999M0\n/eqXv7m5uTn0Y5/H0NAwdSHCimKMQGRqNk6H4cN+v9+v12tHcg1jfd7PohzbzcZ0msYeFNt208T2\n+fn522+/++LLWwA1K+PUG0hKIYREBI/PY9cl53pwlZYf9ak9t1nEdZYaBjNHiKJgrjyNRgBIYG5c\npuSEB2BonnV4/vYjs1mMyl/hC64L91ohkOo8Tkq08NSrqYIZmII5vv2TCikqqugy7EpMZMRw7l8b\nkhPfGxhhE9t5efvUFCIoiKiKeNMUjUxNxQgR0FBUa9EKb7/98/ZpbM9z4sWUyBBBVHIttVYFRSJV\nUVD05MvAZqlxsPMgrV0oSit8YiaQedtQVcctai05pZaQpqkYYYxhlDJWLFJhDsrUFJT9u2wcxwBk\nolJ16oe9HGDbfPz4kQKrgGjxOfoYmt3VZhqPapUwdKumbVZq9XjoT/3h8eH51etbBI6Jr3Y3T0/7\n79+++/kvfvrb//I7A2GKr17fBo4xNtvNTbPqhmmSqj+8fWeiqjBNw4vrW2Ychun5+fH7736oNU9d\nub7e9ceBCWPEFEIgKsWmvmjtTahtQ4yxazYphDoZImqFWkFVci7jaVa6WK2kPw5t6tq0bts0juP+\neGRGJ9563j999+0//fWv/2qapsPxkYhiRBEdp0OViYjadkUcTv0jcUUqTQql7g8nYlwho9hkRkCS\n68Gpu2JTgQZvYZuzKTfJIMcmAEHVoiAxRCDZH58Ov//YdpEI/vCnP4TETVqDNcxsIE2XHh8fr252\nYVnolzV3uGDXuozHEBF9VgYAFWY6EcRILCJo4AEeIICoIQIawcI8gujJuOMVAM/PDQ3E1ETFNHIw\nM1AzTyXI1X59jtip4cyzSwL0Komem3VwRv17UnuZ3c3eVWYcluf9erHLzH22C2xXVc2gAYXEoOjz\nw32TcRtjpEhVJRfkgC6NXcSLeGRWFcCP0MDMy4kIAIZoBoSkcwvfR89myhDPyhZjEzAMrKYYAwBM\n/cDAgXAqeQCoWgE0ABKCovkkDTt8VERrZQ3bpntXn0ktcmpXa+8geYs2hLBZX5keTqd6Go99P3Td\n5B2RwM3f/M3f/v73v++6rm2v37//oKoi+vv/+kdVffPmTc65P02qg6quOr67ux/GvN5tX9++JgqR\neL1e79a7sYyRms1m89v/9NurF1dlLB8+3F1trmKK+8NjzjWlEGMM3IHZw/3zOA65jLe3N0Q0jv3V\n9e7LL79sm9XpdECwUseU/PxC26zbZt113Xfffbder9arq2E83d09Nc3AzNvNddu2p9Px8fERAJy3\n+HDcHw6HL774cne1Isap7O2QkYzDKtciZihHLyA5rxbymNrarS3GQiRBc6gZANourFZRi67WTdsF\nMCplyLmPia5vNrcvN+tNW+tYZfjpz16tVrtpVKb4/Q/fNW0cxhOShcjo5Rc4s6w4snQxPSICA62i\nFQAA4ccSoUQ497nnBe2zU+4MwcCq2CxMfC7FeLDIrAZg9ukVf7MJmqJHV97NVQVVNFE1r1QigMqP\nHIT/m2sthqDA6OwMn9ubHwSoAfq4MiGh0afSi8M4gKGUUnOpkncca/8oU66FTLFggVIjkCIAWBUp\nZyi9qm8Pfpj+7ag4F1tdQtkQDEHVBEAB/J1mYIgKKmaCIGZMwUEfZlbRkFEZpVoxLaBMoIBCYAjq\nP1WbmFBhPPYWV7e76z/d7YehTCaHfnRS0dvbWwA8HE7T9JaZm6bZ7a6JyMUx2rZ98eLlx48ff/GL\nXx2Px++/f/fTn/40xvju3bvtdvv8/BxjMwxT3x+dlkMV7u8eu8368e7x5upFldKtVu2qeXp47sdT\nzfLi5c3N1YuXt7eH5+PhtB/7yczyJCpWizUttm0gw5JxHOSXv/rN1dX2cDhMo9TMz0/9MAyHwzMH\nUNWXL1+GQAiRsO1PNU+nq93t8bR/fHystb569erl7RtEfH5+ev/+fds2X3zxWlXbtnWUsIi8f/9+\nGI7H4/H25U3b8fP+cZr6lFrUPI3VsVpCqZSipnFFj8fvfHqAG05Ycs6nfBjz883mGzMpZeraJKL9\n6QRY2445KOBoOMamTvUxig5TAWNiQaoGWXSc1RLcLSwDmh5bukX5Tr+0rR3zQgZGGImN0DF1pKaE\nqGY4D3OzgRGS09sbABgCEswiwSYKCKbmrzMhATKhiRICuBK0qHszRLCz+Dq6gcLMdPqXzffFUy2v\nLEEsnaNfdly8aNXs/jYQuxB4RUAOQKi55H5MIKnh797+AKVYYUFUpOq0I2ZVtYiWWsXNScwAzRT9\nCqC7fz9z3wRM1YqKqCiYIAiY2hkHA1bRVEHBai3A1JepiAgCB6pglXE0UdOEoIQ+FKeAhiC1NiHQ\nUHI/YMu7dgW5FpHu5hpUr3YxBOraLYAGbj1DQzRTVjMVylOVOpnii5vXp9PhizffdO366Wk/jj0i\nf/xw3zTd/d3jOGYARYyIWrKtVpuu6X748H6dVqdxKH1WBC31zVdfPj88fnx/t+lW05BfXF1/8cUX\nv//dP9VaX9y8AJ7FTw773tsz69X1H37/XYw8jiMzEjan013f913XPD/vRQphU2vuTwXO0biIXF3v\nvvry57XmnPPHD89d1zXNCnTqug4R9/v96fR0PPaImPPYtu12uw2REHEYTyIlRhIpw+lYijAzch4z\neonf1VSqnsY8Zw2zGqO1m9XLcez3h8emaZpmNU6WS9kf7leb6/1hIpaQyqm/QyrDVKRCt9oCTutN\nqHIK3iw+Dwh+4gtZsLmXNQxG8gqjB3Ls878+SaGKnsspOHrWu2kBSWzGQIAZEjKgQ5INgTyDUXXA\nloARGBCxB7e1VlWHvUopCsDeoIDzpyOAKJoxoEsQLvkh2YX5LVACgGkciCgQow+ym5qoIYgVZPKA\nVqBQYK2CortVu2ua93/+840xGhAiBmYAMQXTWutYS1FzrmMtSkxz51ENDZBQ8NMFqWZVJEsVEXdx\nYmboVAamAGJggAKQRWIIwzQO05hiiwZ5yhmtmBiaEAoCgYn7RgMppQmEACSGYi0FrtqleBpLBosx\nhcCnU++kAKrwk5/8/P37d+/ff8h58oJRSoaI9/dPzATAIvXLL7/67rs/51z++q//9uHhsZScUjcM\nfQhxter6flC1WmW33nZNF0JkpA93H1dtN/Xj1fZqGMZpmE5Dv/nJTxPHzWrTj0MthlVFJOfiWlBE\ngIht7FIKVgERrdLpMPX91MV1FzfZRtI4HI4N5/VmpcUTAXu6O0xdXa+7dbMTkfv3T8fT84vbzf39\nIwCk5GDllUgxpcPh+ObNV227eny8Px0HDsgUx3FUlRAIEfr+uAgYqFYf2c55tDNAKqXUtnGaRk/Y\nch1DihyRqh3752qrU/+4Woduw9P0HIoKWjEj0acjcFOeT++DS2E46eRSEVnc3WJsS5lEpgIOjiBQ\nIAOVqmoSOAKaKjg/JJj5yhSXdDkXWnCmosF5xgaB1ERVah1LUZMQQggEHFVKzlWkCIUQaJoKoikF\nZgQKgQBxFuCbOwHn7JCQAU1FnbVCTZafgNbE1DRxs1qntmEkQ/D3Dac+pMhIVQXU3PColi3YFXA5\nDe36JlYve9aqSghmms2yVDFFIwCoYkQKhgSAiAIwNwDBEBnmdplUlWpiarN3UgMgBXP6IAWrYJWA\nAw1TOeRxk5JL3ZaAwv43IGjoNRWYJ+IFhQFiCMyhECegq9WWV93+4a6U3meIUmrN7Onp6be//S0R\nXV9fuyrn4+OjK0XFGJ3j+O7ufpoyAKaU/vSnbz0NXq/Xx+OxbcM33/zk7u7u48ePP/3mJyLy8PCQ\nx+nq6mq73my327dv33Zdd7Xb7fd7rfLw8PDP//zPr1+/HvN0eD4CoX/adnvFjOM4nvrjOObX3UvC\nut/vVQgxrrrtarV9//4dADI1hC1zAxaPh/3h8IyIMcauy0OfiUi0ElHbbFfd9em0r7U2sZUSnh6H\nvj9O0/DmzZuH++Ph8Bwjd+2uH47P+SgiV9td27a16tPTwzjmrmvadoVofT8iWowNM4pYKRMiA0CV\n3K2armtEZBh6VT1zxU77wwOFLibqh2eACkA51+f9/eHUrVfbKQ9h1bYOb9Fa4UJ8dDYPIikFltEY\nFhBBUwAiA0D2VqhprWrn4AQ8dCIiCqwlBw40A66nKU+uhKCL1ANolZJLdgb5tk1mrhuqiMDsWaGm\nFACUiEMgAFKtRBxC2J/2tVZTTE1Yr7ardcsUAXW7ufLutFpVAQNBYEarNRNRLWWY+sDsyoUcgoHW\nXL1LEENwTuMA1FTZpYTTFDq1Kk23VtGUooiIySRVACsgqBERp6bkCuR6uwaA3m0MSAZQTatJBa1g\nFTwSVuIoZDYDRFDUVEEQgGmUktWUeKiVEQzBAvVTH5kNg3g6S6iESEgxVJE1xUjcH3tqNl+9fP3W\ncuRwc307jqOpIbEK1CpN6q6vrn/44QcEfnrcM/ObN2+++/P/99/8m38zDMM4jiXLN1//9Hg8IvDd\n3d1utwspvf3uh81mIyITl3/+w59evXoVQ/P+/XuPg3a7nYv6fvjwwTkmnp6ezKxt21LKarU6HA5q\nKqKrZuO8/3ksIRAoOgfm8bkfx0mrabW2bXLOb799xwFjbE1wu7569/au61pm/vDDY7dqbm5uvvv2\n/Zs3r5yVdX86hkB5ksNx//T09PXXX3bdeDzuX716td2+/uM/v7u9vSFKUvVPf/xzCKSqbZv+6+/+\n089/8bPNehvienqefvLTr6Xqn7/79sXN7ak/pioxhXHIMcVNdwUQ/vz2h6vdy7HkkFYpxNM4ANZD\nf9pNTUjJCJtVc4275+fnWtUUKfJYc+2HrmvCQi0EZ2FitzcPWxfb8znRQNDEBLN6Ay7EyYjowQDO\nrPcGc6KmtdYiEpmdZMYQVTXX6gmP1jqVorUWEQIAhhCIYkgcgIkBgSkgYeA2JgHzV8igqDAgBr56\ncVVVtAoQBmIK7IRsh+MjxxCIPXxVsEAGzEysJsxMRiJChi4hv7veze2HT2MQGIqV56FmeLm7Ds6d\n4/qXosxcASpaBacrmq+UIdAF77qagakDosRUTKuqmLoTMwSBGSkpYKImpgJYwVTNkCaTDIoESqBq\noEohEgIYqpqYqWFVA9DIhPMctjHOFJQI8Pz8PJ5RO36XF6Dtq1evvETp8yDX19d93y/MwQsthxO/\nuVvzCMjLaXd3d/cPHxHx6uqqa9phGgnw6uYa1I79abNaTyWXKYupV561Cqi0IYVA5+iRZ5eMPI7D\narV5enq6vr5+fn5+cXPbn4a2WavJ48NjDM0XX3wh1/i8f1TNbds1qe3aDVxziqvj4WRnNqd3Pzzs\ndrvXL7fr1a7WOg72/t3T2+8+lJp/+P4BQL/88kuTRKHpuuarr79YdS/Gvq+5/+lPf1ozf/vH94j4\nzVe/+vjx4/FYAMpms1mttimlabRx7LfbXa3a9yNYn+I6cFNFD4cT2MsQkkjZ7/dmcnV1ZWauueFX\nUm0KTWQzWqLEJT2TMs0vMhMYoxFTCEHqjHVEcLZVRAIy9E7lgk6eEyfCqxdX5rFNCAhQaiVEYpZa\n1UxFPut61TJRwEDs/+9eAgilVFMBA2THzlsVAZEYI7D3jjXXWouCqCK0KXmnTUwBtJpqraZQyjQM\ngxNfOwcTM59OJ/3+zxdmNtMGt0P+OXaRuxebjT4eAwQCq6qKqoxVpYoW/cSxgwhmqEBADGqeiTIA\nElU1UStqVS2rORYOnALLky4zMRQDAa1mVU3NJpFiFhmRsQrUWpT9j9W5zhXQjHAeI5TzZuELGUCU\nCGNiz8BLKaWK17if94+bzabUqYsNEVXJbZfu7j8Q0brr1psuhFAlbHdr0RJCyGUMkZCsbZrT6dS0\n0V8PIWAgMRnLZFUmLSB6HPrVqqsmVWtR8RKaValqIcDpdDA7On+WSPGM6OrqKgT6yU9+8vj4+OrV\nq+fnZw9/Vt36cDjkXFUBkfNUc84iAE14eprVNpzXMaX0+LDv1qvt5oWZ3d/tn56eROrVVQSIx/3p\n9evXUx7efndXSvnmm28+frj/D//vf/j5r36mVnPOT/vJMVnTNH24OzRN03XrGGOuNj4NpexjjDe7\nm//17//h5vrNZr17eftmtdo9Pz/nPJ6O493d4zA+hlR2V+1m2zlhEQB9++0fAcDJKkM965TDjxFS\nXp/8y9HmtGpV1adEAzMxz0THRDO20oPI8yuTuIkgBg5IxgSiRlhFnO/fSyYCZqJVS0xshGZQvRGr\nAqIC1sZUVFANAzPgVIuWKqD1UN04DcE7dW6i43gqUqVUz9gUTKuIqaE+7x+dBvDu7g4RU0rPz88O\n8V6Ehf0WpkNOAyKu1iHdnwZo1nN/P8WstZgWFVnIhcDYUAzDJwoGcUE2Z7GuplWliMjcuUBDKFVc\n+KKaqmEBFTMlyKqKmE0qgQeKE2ipBQwIQIXVMQVIyITMZiimRUFEQInmdoyGECwG5lBrqRVr9eEJ\n7fvBTIlYVUSkFP9CAIBaSynFTMdxJMLT6dS2Ta0SAqta06RSynq9qlWur69O47A/PjsNKwY+9gc0\narr08PzkGFqxCooKQsBIsLva+uQlGiMAEkSedXEB7fr6+v7hbr1ePzw8vHjxwjn3N+stAn14/1FE\n2nYVQnp6esq5ylBEZJpKKQJATcPjmMeprLrNer02RRUwpWn0FU7ff/9eRL766itmlkrTqLvty+Nh\nun15AzY8PZ5evHjx8vbL+/v7h/tH1dnam6a5uroqpRyPjx/C85svvkHjpumeno4P96dSSrdKbbNL\ncXX/8C6Ucnt7w5QeH/aqykxNsyaCtm3X63X48ssvFwO7rOZdmt8i35hSEinVqhdMApEXuJ0cTMxQ\nzQHLhigKCiRIRWqtlbSiQZGqVRRs3a0MrIioGqhVlZpLkaxSFOaChlbJtUipVQUNci1o4MFhkVpz\nqSo59xxDChGZ3KiccTCFeBr64dQbQpsajkFKnepYQR6eHz2pcPxb13WHw8H7HL5VL35gc6qv4Kqv\nZeZAq0Vr8Spi9VKHiJjOTQUjR39WR8CIU3owhkgxlXEStWogBnXuqgEoVBVFUEMBUNCqqoAzi4CB\nIAhCBVSDClpVCBHgDFj7EfeEoXNwzs3GudA1jKcCxQv9APPcnEhZr1fH4/729tXpdChFQiAzffny\nxTBMqjXniblRlb4/DkPfdSkEDoFydtyslDKVIkbWdEmmykCc2KpBBQLkxONpDE1om8YoatFqNcyS\nNdQExvRJa9fDv6fHh+vr3Yd3P2xX3eP93Xa9Gk7H1Wp9Oh4RWETKWFJKu6tNrTUPo5R6tdtut1tE\nvL+/n8Yp7dJms9kfn5+eH0RLrRXJCMGD4Z+9+cXDw8PT01PJcpx6HzBr2rjWTSl3qhpCMOWH+/1h\nPyDEaex/9cufffnllznn77///vu3b1X166+vTqehP01q1LTrJq1r1XE8/vm7982K7u8PsdFuve+G\n5JQ5KYU3b74ep36apsen0yfh9suulA9f+nNviThNLBFw4qBBVcGsqppZVtWzfqdcaO0AgIKF1NYq\ntVaYHGwx64M8PDx4M33p5hGRh28Gn7iG5KwN7+gHAEhgEEFVi9Rcp6kMaFglKSoqCggDG9mqWe1P\n++E4KGqXOopUp9rnoWI99genMRvrGJGxorHE2IiUSaax9ucSLFOkFlIUQqlt04BYzhkN/UjMTEyr\nKQO6kIGYIcGslmsWfDIY0QBEz3kagHl7Tc0QqqkZCKCCiXkpEgygogEREKpqBTW1LLWqdBwZkJEY\niBErWBEBx+QsA3s4DxwysOY5376YtZ3HqwDg+nqXUnD5XE/Ru64ZR0O0EEJKARFTCqvV6nQ60VwW\nnszEU30IQMzX1zsznKZBQNfrDoBqzRgwRo5tRLTKitUQidmOp71pCZFjRCJExVrrlAsR+F2utTKj\n11pynmJofM04qWPJMow9c/BMzzed6+vr0+kUQpBBXlxfF3HGBHGpaRGNid+9/37VbXa7HSI3Tff1\n1z85nU7H475ZNYAWQiilDMPk0opdt+669ek0/OlPf845Hw4HMyQKp9OACv0pt+0KNJRsIobQlKyP\nDyeERmX64fv7puUXL667Lp2O4/f1o+dsABDY8+iztJ+jlvDMYOXYPw9/EFSEpn4S+6R97gbmTQI5\n63ctxiYAh+O7GTqo6mVPntm4Zh4VImqahkIDhIhwOBzmmTdPHUX8WH3GyatbLjo+DEPO4yQDEBCQ\noYGCgnrrYbvejnnMYza0E50MrUxlKFPcxGrFajUTC1hRhjoiW7ZSNVdR1YrIbMgci2CIGIH6cVw1\nrQ1ZVRm5SDUmL7urY67hrH3uaBXVeXSVSF2F3SdHAVyy0HQGHKvhzGd+rvvbJwkBUCAFnWoxgFyK\nqVgIHn4QLpol89vxzCYmZ8qaFNIqtKGNfjdrrZbFazalTt2qUasxMXFzPJar6+3T01MIQUSQLJdR\nrXZtFzOLFhc27VZN3/eb7arWmppEMTwdnxOnEGJsYtNx0yTmYKbPz/sQ2JWiIhNHNAMwjZFjE4nY\nFV0QOUZ25wMAXdd5jeTjx48hUq31xc3N6TQ4XQ8iOlKRmX2g8+lpj4hfffWFL6fn58ebFxsg2e5e\nAIAqlFJ++P79fv+squ/rezP7+qufANC7d++en5+ZMTQh19w0zfPzcwih1rrdbveHg4gM47her6dp\nuru7CyH88pe//MnXP7neXsfY3d58hZAeH/p3P3y4f/hY6lHhpNCIHodxP40yjVLL9PDwuNvtACCE\n2HVdeDzsvR7gfqbW7JmXh1K+1o/H4zAMABCbmLrkKPWlkODGtshSLsZm5quHikdbZ8KCpmm6rhuG\nYUkLfdBTVUVKlaw6k1r6x7qZrVYrd4OttKkkEen7fsgDMxmqz+AtP0H14/ODP2dGIQAwSBxDFKsU\nQ61VxEL0cHEMKZqKoWGihG30ac6qsQqVTCNNz/tdsy5QFJADK6A66yKAuiYdoc6MRqpmgIBMFAMw\nFXULNrc0RfANoaKJqiI5tto5Fmc0CZ7t1l1frQI2aUXTWqtQVEZltzeIjACAYkhmhBpAyYAsAbQE\nbWBcJUeK5pwhAsvc/U8pfXz66AXJnPOvv/n1w+HBgrWrNsbIgROl3c0OIhBTpJja1HVdgbJerw+H\nQ2oSBvzJy69PwxERnR9uv99btc1mc3270fMchg/Ci4iUOh1HCqQ6+8YmdcyMgUotm83m/vH+1as3\nT09Pr7548+7du9Wqg2Cx5anCaToKCAQLzcyjur3aitgwnIBpLNn34u12m+tQSnl+fhaxpmlqrWZ4\ne3v76tWr4/H0/HRQhV//+tfb7fa7777Nuf7zn/647larzer66mqcpq5tzWzVdfvD4bDfi2qZSq3y\n3bffvf3zDyDwcP8csBNFgoY4IFjVabWiIT+HUDe7ZtWl56eRMY+DNElLKbUOiHv8v/7f/k8L/qXW\nWmvxXMBFBuhCvU6kEFG7aigGb+SZmXOg55xdKMRp91xZfJqmfhh0lpWaM0APF+nMjnxZlUFEY1Ct\nhp9IFuw8npNzXjgh4Ywsc9kRERExAD1nJot042x+ZugzewISAoGDF91zzpGbpbZ5enpaNy1VXVHc\nYCz702/izf8Ob+OH03A8DcNUsrTrdWq6XEQI+mnMpSBDjNERKwSok8QQnA55t9mGEKZpqioCRszV\ndMxTFbFAilBqrYBVZwIVoAAAYlBMLdAktZpVtEl0KFlMg+F1SLvUrkMTAMggcQiRCHA4HlLkJsQY\nI68TpHCU6a2e/muXj2tGZhGZSp5KdlTperOZIxHPms604QKfonq8oKVZEEUuHOPpViklnyPqZZP1\nN/rO6LnxgpoHs3IqjDP8vZTiU40AUKu6Hk3J1cNaP7yuaVTVO++m6LNtMcb7+/tvvvkmpfa77767\nurpyVoWUQtexD+97nBk4OVql67qcc841xtikznOqq5vr3//+98C0W6+y5BfXV/dPj20MnCIDH4e+\njBmZEycjjhRjjNMw5qmUsYhxpICBUS1LAa2rbUsg66suBbx9fZuHccjD6y/elFLadvUf/sP/Eu6e\nHikQGk5lGoch14kxcKT+eOJIjJTrdDr0w9SbKpBRz75XzffGycREXFzc48ks2X9VrMbmklAVBAQN\nUX/EP7eEnWYGoAo/IhTxJ4rqBTYhvz9malUrIOpMD4cGgoCqxcyIHJCoAADofATeGdRFdfoc1wEg\njiWHJjVdR7mmilSkEdh1KY4aq0xq6LSKZoIkJAqkeEYVo3fxTc04MBKBR+eEYpprKSoxRkUQVVGt\nc2cO/QMVwWiGAgAhKiCgLF0/AgMAQqfTJwqEwQjVZnIJrkYgAYx92IjFB4pagJaoiTgEAUJgbWMM\nSIiumUEExpJMKxkxY6BIDKUqMBAF74M5nOG8ec13HtgEsyES+YE7mNxLY6IeGTUoUiEwgGI0BIWg\nViW1EQHACMQYiII5F0aMkdnJZJEjc5xZgBGUgWIbWOdqihUVkPVuvd5tzaxZNdWqEVbRSPjFm6+e\nnh9c2TRwEJCmaV+8uP3DH/6AiK6ey1SnaRrH8XQ6AVAkJgpUq4gyYIzNetWJmKpmZOc7MUNTqEXI\nkIzMDLQqGomIgkkxs/7QD+NpmtYxMVOqtVSo//kf/pGY37x5k+IqvP/4niOh0ZiH/nTKdUqhSW0c\n+4ECMpJYrVmqlrlHK8UIseDikdwYjuOJiJAQwEqtS6HlsvTy2f63vAjnCTfPEv+yYAMX9P2LWS6M\nWp5OAAA6SBlUTcEIAWdNRgBHhICvCVsWOyDNA3c5T13XBSJVQwMRaULYbDa5r2bimA/PqfyodGHO\nw08ngvCJ68Fj45ksTmpKSVzP3lRMQQFcSOCsAgk+8+BcKQYo1e3JjRAN2MEojEz+fE4TPUcMSGTg\n4qNsQGCEvE4pJQlBxYx8iiREBFK0YZoQIQYyCyBGjCFQjIGDOuTNpZvn+URQFeNATAHQW+fqf1VN\n5wtA5IBrV9cMIRRUv7qJyWeKKxr6yCMokjks2KWnfPKglJLznIl4qzMFD3p9YZiZihRVRUIzGccx\nBMp5bJqIaG2bvC9fstze3sYYj8ejiJfvb3iW4DgDD0WOx2NqO2+6qqqP6qsqc8x5WBKfEIIZzpzd\ncE5VQMxQHKlg0HUrMyGGly9fpxTW6/Zw2KPydrtFoq7rvvzyy/B8fPDaW661llytopgWqVpAICAp\nGUUIMaKagPgt/iz8AwAv0F1aFxExY5FPfbyF4GH5hAsbQ/dX5DbyL/HhLZcJzvAxPFPfXX4vnkUF\nPjtCt8YZ9i92+cdA6HpCZSqSc0eJkdZd061Xkz4YnEmOF/ginifjEGi+FOcRGwEAxfn0eakE2kUU\nYHAmhKbLXWYeTfLuGQOzf928znyxwRLgoSkZsKlvYgzIaIQQDFmVjANxE9Oqs2PMRcUQKaASitQq\n0rbRqRW9S4GIKcSU0uF0RERAmbEG838ArhFrs/0BwKycCBVsIbuA87ghzIN7CIjIAYiYCFUQVBAI\nEc4D9MQciKgfKhKmFFzsxWsBdYbSWJUsdWHRVp8qzmU69UckMNDNesOMTdPkWpi5261vb2/dopzF\n1QnAD4fDMAwI7C2fWutmt2uaCKCqjYEQzeSq+/2+lCrVQtC25RgSM5mhVkA093UzJpcQFKSqgRGF\ntu2ILOc6jhMR9mWoIsMwIGIoWswKARoqRYgYwKBqrlBMVdGnsdFQzxNrdrYT3+Btycfc2eCnh7my\nsIMl3F7wrNzmkJ8lkpx/Tabq3wWf/VbVhwfoPFPjGAxzPYcF++Kbj78bHKcFswrRYlpmQoBmjsoH\nREACl7IdS2a0yJSI2pCmaYpSzSSjZrQCGkwDmAHIWUfuci9YjpgBkUjAplqKihcD3cuZme8m7pZk\nNvlPHTMAQ8IQgiCoKqCJKQM6UGXmxvPmHiLDTPIYiBiQDCMSGWDVEKkNzKQ+jotEHFkIShEpapoN\nWYFU1VTQQKxmrMS6XD78RJKGolXU1PCiTwNmmhrn3oTz5T/LoYACVsBZH4jImMEUKdIcuC+nrCJW\nQyIvU5tZrVpKYQgtxDKVUgqAilZVjTE2bfSyiu+6IXDTxG7VAhqg9f2pioiOb3/43oVsmEORul5t\nmZmY265brTbM7Jlh27Zt25YyMXOV3DSNtw1KqaWUWrRWJYyEkchEHEXuIAlfcsv+TyqSc35+OlSZ\nQiDRabfbbq43qtWJgwKQKswj1oyoIKZSRVMM8zw12TwOg4CAqua6lUv27A9vt+vFVI6ZqVaaBePn\nooWZmPnzORNYeLt8As5AfmyAnx6XTmx5vvBMLgHtX4avF05SiZwSdU7bgOYpBA9KRaRLyfGLqQ1P\nhye2WkEKmv8LaBFN6RNZ5bL1uLExMRowsW+rXkpNTbOUbWfu/llj90dO3sxMDQjNgENgMAIgNBYv\nAPtygvPBKwMRIQsaGSMSQiBictrJChoJMedRuCISBvDeHAAbac5F57kDHzIyUYMiKTWLJPAlgYt5\nFxCQCJyECgDNNMbGDfOCKo08TmcGHybxmCbGwAhkpAozdY1vQGoi0q2S3yARqTXXWpg5NA1iABRm\nAhBEYwYAbloWsXE6AlZASykwW9uGUop7ML85OWc+K7HcP3zs2rXDprquybmO43hWYlFVjYktc4zB\nmaDW63XOeRyyKp09reWpQtFaVQRVHSSACAhIqkBEiVsi0uLXAgHg+++/b5o4juN2uw1G82imgqqa\ngoCrtQcOTASoYCZel0YiYr1URUMynKGVDETokyZAToBoQKhawQlA0HzQ0X/6kMzcawFCYs8lDGTx\nbJeRJCvOxAcMMNMjmHt292pmfpAesQBfsJ1f2h0AIM3VSJy5C1R1nsaJgdoU8+nQUXpxfdVyHe/u\nKqqQTWQVLaJVMASoOivAI/rpfZoKBwBF8GLjlLOaOfFgVVEzYAImnCv76MVAOzORqKrDTr0JgACo\nhgAEyDNdmal6/DZrbhChnvmQ3Mnbp4FgCoFCIENC8mxLESEytrstgNKZhpDBnJhQwO0KzWQOsYmJ\ngLCZN0TzCFOJAiKdN1CYB5wAfOtUhcCQUotoCEAEMQZlQoWl4wpGzCRsqrDdrkTm2LXr2mmaACDG\nOA0TUkopAosKxBhLKRQg11JqSW1S1Rgpy5BSWyT3U68z2WPbxtbIpmnKY3/oj8M0efR4Gk+n03A4\nHJjZTEIEt7ppGlMKIiUE6ro2hEAYaoUUmxhjKSKi5HdjHsO3+R4ADeMpRkbyEqt4fng8nkIINzc3\npZQ3b94EQ/WkRatUrYAaQgghTdPEOlM+1loNhDAwc+QG1VTxorxO3v73xNFMSvGRf0K0KmVZB+cV\ngQBuCT4i9CnuBDTVGYX0Wc52bpjMmgH+CCEQKSI6lY0KAioRcUDCYCA+YgNG82Aqqk+u+oD5udZp\naNCkBKKJQxfaIs9Nk7756qtuhH/644fKJmqVQQgK2jxwDf+y/3UuFpqpTeaiedu2p3H4VB8ikrNO\n2uXjfDgGHpGbgpx3EJ8ORDNQAVJUDzqMfMjB6ZbQKyfVVFQNakW6vrkqzSTVClQFQLdyBJMiIKhI\nYAGDkRmAiTDHCnoe6fAbYYgQgpegQ6055ypSEZGZcs6XjRZmJGIirlVDgJSiOytEC4HMMCDVWr3D\nSuQ1bQSAaZrUxJmPmyaG6K/UrmtjrF3XpcQiyszDoDFiiG3OtFnvnFrvdDqFwFVySs3xOORiqQlO\nyco8x2G11lKk1EyMgLLdrq+vrx/u7lS3vtfVmkMENwEAJcIQAhGkmFJqAApzdT4oIjWTiygbtpsr\ng9IPh+PxWCWntG3btm3T3dPHUsrhcIgx4v/+//DXl9EgnFVm6MyD77MzBqICKhKwWbwOczinKkrE\nAFZKLSUjUkoRAEvJjOj3CX/MLOTdejgzC80N7hRrza4YeyHKOnd+fnSci8fjea8VKaoQAjVNFyPv\n90ffiT2ddeO3eebFCDCgz62RIlRTRfj6iy+H58OWUxgqnab/y//x/3yNbXm///int/+v//v//Lvf\n/tN0HDexu929zNNU+qylIlrbpZSSOexdhIUDMxrc3Nyc9oenp6fXr18T0Yf7Oy/xKyPMwtcugn1h\n9epIAHTotoKJQUWrBlnqWIuV/Hp7FcG6kLqYWMRybZhWXQOm0zRxpO3VRgnv9w+H/vS80vbf/fIP\n+UPTdAoihrGLuSpH8s4kARMDAxMBAQOoIS3X02s3zJEZfXh3CfuX18cxM6MZljIBUIycUksEzNHx\nk+4DicDHFGcluLmvgUu4dd5vPCeMviREhIxULxfOUrl1FMQnEaKSRYoGiv4lzBxCWoBKtSgiTlNx\nEYhSip8RA4YQUuOtYzznIDRNU4qtY8aJ0jTWaSqE8eP3d01aO17Md1JEUK0xxmE8tF0k0tdvbq+u\nts/7x65LpQ6lTtvtdqYfX2I2O29piHxOSNSMAL0MomYGpHaeZ1OVc2621OVnLU8vp3IAED3nI7Jg\nU/xqm8knzAcoIhOjCMLZli6t61KV5tMVd/lMJAAgiufXVRWbJn6WvPlbnMQE1AISz/pXykiReRpH\nMBv7Ya306vZlCnEc8nE8NVfbf/3f/duf/vrXH797/+7btzKoqKviwmf8J8vRxhABYBFwnGpZYDdz\n0IgAAN55W957zuYwwKxH75fCxUrJQAD6adzEiClwCmxBGKaSy1BTE+M6xTYOZKfp2KOsX73YfX31\nAWXVtJxCroaIkYNqjjFasCVlnCkkvOhCQBQR0Sxc5sDTNPna8LsBc6RKzHP447uh18lUUdUb08td\nm8fJgQkROWCkCLYwA7iH9FQFkXQOz9GIlAMiBjNzOmSvzlcpZgZITnZIbCEiMaUQ9Fy3JDREZQZE\natvkoeA0TSIyjkoEqQlkEGNMKRCRzjUsAYCmiSlFqahqhBHB+bbDgso4X5z5nqpVIhcRL9M09QOK\nFOJ0ej7lMtZaU0oBLjaWMxMj4pnSw6MyRBeMBWRwGIf9qApvSJ5QITEiETMRAyIYECGoVVMBdNpT\nryUjGBEzYeCACKxmYAQETRMdR39OutRsVjO9sJpPDzfjJWGBeRRNAMyTDThXU2DRjps3SDMTZ2hU\nMI40jn0CUq1a8a9+86sU6DDuKwG1oXtx1W22pvhw93AaT0D4WRln6dpXUzIKKYrpWDIGxsBl6M/b\n2XICi2WCCxEuDx+1RARUY/SJUL87AACpbZCpz8Mw9QFolWK36VKIqjJanaDudtc/ff3N+nqHjI88\nfn/8567rQpNgHJDZD6xpGm/VwGJsjhNDcBbui3rjHEf47kln4ozLLY8XEe15p/9s/z1HWgCIWKUi\nExPDmU8TDFSVAn76yHOHHAFp1gFCMDBUAwUDJAyBl49VnY+TgcnYo3c9yygyMgDVoiERRzaUnJUF\nkWnVNpE5RnYSu3Hsay1ODx4in3NXQDJAMaiqcKYoh3P3YlmHldhjb8t57PuqVgC6aexFijBRikEv\nd1b0pJ1cpBcAEBgREMkXNIB5zLBcR4CZxX4pvtNZHs3MVGubAioa6jkiJXdOIZJZPB/oTGylFdq2\nRZ1FTO1CIeAyhbu0NXFhvgtApl1IWPnfL7EoAACxQ0tEjW3Ocg2s5oJshtw1TemPf/Obv5JSx2mC\nFE6n4e75wYba55FSDCkOh6OLZMwdr4uHqhlZjNEJ4lerFSLmWmZvhnM9Hc7uG889ussHmiuDIph3\nreYCCSDdPdzvdqur7S4xIYCAHcsk4+nqZnf94uX1q9tm03ZX2+uXLzY3V99s6H/5n/4QQ4gcaogh\nRQiccw5I07lROfcScO6nNTFxDAtCaInYXSBqsaXlRix6FG6fC+smnZWJ8Jyu+4ug6Nmnnk1kxsnM\nunznL0UfV7IQuNZaynSG3bpuVMBZNxJV7KxgSIgMAsHYzsGnmY/O4zCconilqYYIyQiA2lUElRiR\n2UQEUACFWMFF9KyogRkDCoCKFKkSAnkd6Ly61AwAFUCZ0aCEQBysyoRoouXFi+vlsgTGOVqYT2/e\ngYLquZYghkRgaAI+eOar6mJfWfTcbLmsqurhpifHRLB0ws6m7dV/uFSVEVO1sOhrm9lc8wPyvccP\n1WejP5m6iZprAHhlTw2UAyOBl8dobrW5VQo68TghiQFA4LnjjMTDcNquwzCcXr56MR2HEOnpMCpD\nZawmGqjbrvOpDOMYffZx6S7NRUKDc/85lwKEsUkXOGz02EhnNr9zkIY4N9Fm0/dwjh04AgCMqICM\nZEQVJJtkE0QIxDGlrmko8l//7V81mxZjKFZyw7kLum1pGyjFMRdiQ2TzTBGoVnVsTXAKdpvDawEL\ngZ1JE3Ruaru1FKvzi4if2DjBtBqee4boFJzm6sDzyA8CEhCYEytBCknhR57nXB1YWkRzDZnYk2t1\npRQGb/ezO95S5Bxie0/P64JmKOjVaCDPCT0maNcpNiwiiYmp6bQRkTY1JY+EhlTRJERACgjMHM2A\nMNWqYJxiQ0Q554IgAVXcac/bgoEAKBIQgaqkpl2tulIHQC1lur+72+12zrYUlrAQAM7uCzz18q3l\nHDyIg48Wd7GEkZ82rTNswsx8NokZNU+uWH+5I9L5McfxZ3BJtR8pEi53Yml3LiCpT8d8Mfy2oEaW\nKEj1U5PdzKqIN7gZiXBmgp1p+ZgD0mnKIw5dagiwlhJiPI5PbdvFrpmO42kaT9NYVYBJ6yc087Lj\nLMYmIsus/jiOlz7ZjdGLmYafXN3FSX26UL7VL8dszKvtpoIcxiOF7fXN9RdffPH111+9fPkirbup\nTofSKzbNbhWvNgcdn+/7Fy9f7d9/C9PEKdZaXVfIUwhEZJzBIQpqvscpiM3Nd9/y/GJ6GAnwqXB/\n3vh0uQILdnl50U95WTaGoOaqb7p0Ss9lal6MTXXZ9xVRYwwpLUHQfKGWwUgAYp/5JiKiMgqAIfmC\nRDP2Q91uO2bO2VSpaZKq5pyZzGO185pvzucbplGIuGRD5CY1RDSOk5mGANVoOSO1aia+XSGZlto0\nYbVuh7EACIC9fvPqxc0tM/d9HyJFMztLqOGc0BiEuFTlPZZjRS3oib7nUXQR1uM56gMiMAMv7MQY\ni1Tfiuxc5HAODDjHn37t5lDY1GzOmi+thc80e5cxm99L0TkxPa/UxeV+IhU/+9vZwfgL6hWfGYqJ\njmp3Kqi/+dWvSinuliHQWPNh6E/TsD8dnw57nGpKqZbJbeBHh2TuL9jnldarlSt3XcbAcImeOKNy\n5os4/+aTt7Sz95tZRpD68Wioq83NT3/5i1//6hc3Nzfr9apdNff7p+5q/frqJoPup/5hOoU2Nleb\nn/3iF28f3htA4JTLQEBN01URBnYWGZhblwJMZprSPEK12AOe23fnHa3OsC1AAIixudjUCIDcrC6j\nUJsrH4RkRap4pc3/3rHMiOQEHDbj7IgIkRmFUL2odg4i5ripac+RjhFeVMIwBfeZ52iL0IE4YJ8a\nPzYDwsWUw1z+I0amcN4vIEQvjRoRhkA1zCxvPu6gDuI9B5FIHjERoIZIMfKUIcSAiM+P+zY1ZjYM\nQwCoc0N1fuN5EYuejc27nL7d6dyoOV/fZVksIxjL4vOnGBgDIbNKFYdrBQ5NrFUMQdSKVi96o5Kq\nAJJodZQVzFB7BjTflefk7vxbQEMDptmYl6TcF0etVUwIKXBANDQCrUbAzIECGRiowsyjbopQ9brb\nSe3/9td/g4pMzal/7jjuj6f+eELEpmuRqaKzhgh45mwE81yP89m5Z7Naa4gNEo1T6brGsxH1zj8Q\nggCQV+4uCyQ4I4BQzVANwdCAUAOYoEXDN9evDqc9CjJzbBtKOFqupVy9vhrK9PD8CAGoiV1qIAUw\n+NmXX/9DbEcpXUzDMDBS07ZTzlMtiBYhOkg4EpoxA5QpGxkiq1ZVUK1eQ26azt2YSjExOFeSY2oA\nHFRR3GTMkAhijEtz3IwQjYiRQQEiLVnAp+DA526QUBHFGbeJiDmwmfmRLIuKQmAidp4Ku0hezCw0\nqZRipQoYmbnkpIBJLhSDmVUTVvQhQ4qggApiYIzOWG8iTtUaEAxUAAmjYjXjglQ5IFVFFE8y3WEg\nkCicq+KEZAK14cBMt69ebHdXfd/rOIQKE8yblOMQPiVjMNeKQHRO0hlQtII5FJpDYJgZSpRnnYta\ntTJzk2Zic0UrVkoRAzFCZFC0rDmX2rQxNDGRlCzm8WogAo5IAOR9MwRg9jgBzHTeN4nmrm/VNjaI\nDAroHM00u+Jaa0COMYBXWc0ScxuityKyCCCmlBSMOV5td5b1/oePbUq7q6v/5l/9ty3Fj48/MEQ9\nHJuiG04fDx+enh6VoWIVqhTJJg3MbUxjybUoYGMgJSt2PE6VUwMUpiqpXQ1lQg4YkP3kFESFlAxN\nbV5xvkv7RrfEFHPv34AAIjFigAkCdajh9//4u9/8zS8eh6cXL6+xpakeKMCaCJDFgfkChlan4b/5\nzV//+//Pf6AY8+m42a764VRMi1QAzZpJJUHoYmBg1bpbrSfNUs0YKQTi6JCAaZxCpIDMgTBwiITA\narWIIUJsElFaRnKgCczRVf4Wk3OdA44B4bKQqDMP8QKCMSKbtXxAoSoAuVszAJNzpudREhJ7DKqq\nVa3WyoJEHJowy61UJSDiQA0rWEhEYCaKTKFBBWtXK1V1iNZkBU2BAAjEynrdwqQlV8Vxqn2WI6XQ\ncmLC00lLHtBnMDipVY4sJoYshhRptW3AaoXaT+Xw8QMiYooB6VMaZnPKBEuUc/Zd59VgFigs9QCP\nXPE853QZ3Z1tVYkIAgQkRT5LepqAAWpRYVABC5EoBgYUERN1owuhcbYsDzpS4KpgooaEBsAhMphh\nBIa5jSMAhLOiAHZNe4alf0rzyHS97QBgKlkMmeM0TWUaR0TL+nK3o6p/97d/EwDH0xCIIVfIVYep\n9mOdsohULVWlamVV0HmSCIwUSQwUKDG6Oi5hAMIqTsVMisBAMMuQKBlV088aGpdXbwnh4tIkUEUj\nVGAxbGAq9fd//Od//W//1Sn367YNRIjmSrBms9YQKoDCzXq7Dk3k2ISYc1ZQAd3tNmZWS7Fco2EI\nISoKBtWK5uN44TJ4s6hn+AEiGnrXfW51+h7tgsTeUwEn7r7MrgEEgNpm46V5b2ggYAoJwqcKs6pW\nq54FmEGZxSs9CfdPUzNLqV3W51KiIww5F1Vb+mCuruphl+8EZGZsjsYwQiM0JORAZqSkVtEpvNXE\natEqoIZNbLnpohWCQWxWcgHPSUxNgaS6LTAF5sjBWE2qqqEakopDFJF+dMPdzuzTOMwSK86nlOJl\nCrvEjUuovZglABAgMhNjIHY5sdl41BgJ1FQVwZiYAJ1QSqsgA6LT/JKJo4gUAE3UnzEiIgciAAiE\naGKK5w6MZwsCIOhaNSZeVgMAQNgfn0IIiBSbtF51220HAl1q7n74uNu0h48Pf/1XPweb8nBErONw\nqjmP4zgMQx4nndMNXysSFyQkmJhXby00ySvRnpc6Us7MiH4k+/j/93EOmT5dXr+qhAHBRzzK7373\nX//1f/t3ucrKMePAzhhJFAyZgQ2hbdvNzfbm5gbaeMs2kQXGiDarq4oIgCtKGsHsRueyjY8PzS63\n6Zp5O6i+yADQZcPMCBTV5nKPw01NQPz5kpYDABj247AkpZcb+o+MrVZ3dwrWrFriuQKJZ1IpT9vc\nL6iqCqh4t+3zss2FI7HlMsI5ETXCPFUgw0/Rhat2WaRZU1s9TAwhpZSrqCIYmZ0V0xQByAmHXbZh\n5kfBpAqkut5sVUDEREq46IXj5ZEtBcNl8/DXFw+2vMvfUmtdni9ZEzOVMhE4UgPPKBU1NUCCWVXD\nnHxk/kxVNSvzvC/ovEVDLtU13IBcJNFh14pRzXRmiyWA82zjeXhl7jwu5zIMlRiKiEwjgFnVmkuP\ncbfqwPKmTbtNg1Jq6W2qQ7/XKmWcpnGs54nYT/ZA86yygBXH8wOEEEoe/UKp6lI0+2znutzflomb\ny99+9sd4DjkCBwhcwTimu/uHt29/ePnlS4E54wFvjQIDsBmiWd8PV6ukCnkciUgkU0xkKiLiIQsh\neD6L6CM0gIZq4gBNMI9HGoyKYCJZKog6X/U8CCtL+f7TAet5BOBypwDDkktw7oYzTM/3ps8K1P5Q\nMB0GcNFMIiZyYl9RTTF6kOo4mCpSS8mltG332UqeZwjdkM4Dx3PJh0lETAHRPP+fi8ouvut1TQqm\nM7nSOJWAjZoaBDB1DXgzM4RZYNpMQBwkSkyqwORNTANX1Li0dTx3yc4y17Pguj9RtTpNc+h4Dnv8\nZxvjsn/gWamUiKqZiSzVFIC54T9/HZEi1lqlViKKxIakqlqrF0acfhyYVKs7aWBapKqchZFIeN78\nEABEtNbqjsXZRugcTADh69cvMfA0lpxzZJZqdcoJA4vZmP/ub/66DQylWB2Hw4lU8jhM45i9ZgyA\nem7CIjoABhDFtJgIEsE8t+pxta+kJdJeKmaX9kYwa8V92unn0YRPWA2/pIEYiAhCYJzqQE0AgH/4\nL//5f/z6fxQR46gGEAiAnLfTENVQqjmdzGnMlLgJDcVIaGKVCSGwxsAGCRlFQYoPuOtcsDOFuf5z\nGgcgNNFcyyI8UlWY+aI7/+nhHZ0fubXzCSOj/1NV/99znwlnfl/zyjgyIKjP6VbnKXVXKmYKVGoF\nVSBKIaChVS1TcZauSz+5gBjPVUq3fDUjACYiF/YDsJlMmAgxOJSMmRE5MiNwjEnkFLzwYEV9VMXm\nzTKloFSkioMZihbACia19IjMgEwYYoyOjicGpohkUs2ZiGEuidUZLw+AZCqAZIQByMhInacRNTBX\nLSamIGQsICpiJirito3n1UaGquZBSgiMIRRDAWLmpmmk1nPH09xCZu/awnIRLzaFzBwAZnq8hRHI\nu3xmtgB55sBX8d27D7HpRERLTalJFBLHVUjj87Hl8G/+1b8mgzpO0zD2p8Mqrss05Zy11GXDVlUB\nY8/MmRTP4zaMRCymiOg79zQOPm0B50Yi/Dgxu3zgj391aWnLVsjA3poRMVOIsfn+7bucywyjIxVD\ndvC/oXNZdk1LRq9ffzG9fzuCUJMgEDOM1dDb6w53BQWQrCLncXHwzOw8fpfrONepEJF9PtkF9uyz\n7eOTxz4zal88qJb5THMeVQHRQkghkIiLQTgA2rzYCwCr1arW6rqznoy4rBcBGpuoISIjcWT2ps4Z\nE3dpcnhGtC/9DL+VaDPJEgCB+qgheydJBRAgppYoMHDg1LZtCAELI4ARn5PVeZiPYgAoVryjUNWq\nWQG1xMzMgYhjCEzgwGtGdJYaQ3PwB6ie8UwIoGAIJs5NwWAGhqbEGImB2aqYVFQgskioaFJKqVMT\nExLyma8OzpGDWwCYMAduoiozc0pReQ5IljDddyaPyi4DfVU0S4yqVk0N5LwwhEkBgUxVq3qE785B\nAUNqu7gRklFGKCxoCKrRgsXrzVWE8Hz3VA+9jLVOtUiWs1tOHCb69O1mZrDIERoAEDPHqGcKKq+I\n2gVCF8/r4FNE4AtwWaYX9qbO8Q6Alwg8QDWTCoiYSzHG2MTD8UhpKyIMQVWDb7YGAKgGDJzH6fXt\ny/d3H+8eP+CqGY/ZIlsAQFQTKZVAA7GJVs2iiMyR2eOiKuJYabFqAIGIHMNPRAAkPyJusguInN/r\n5ZXz8bNIQQRTNRD1GQNjJATR82BhVfXbSYiotZooqBET+1y9mRpEHwox9ESDmZtutdlshjqpVhEB\nAxUXpVh4lXyWkJbjMSBxaAsiz5uhw5cxRLYqiQMiS1EkCHRmcZrNTH34CBBQRbQaVEQLkZo2RmsA\n2USgKkJ1ntCgWs9rkYnEDJZXPBxYdCPmh1ZAFCwmBgAMDMyBgrAEIyBwxnwAGHAwrZEDETUhxrZJ\nHBShTnlCcloJrEoBI7GQkQErMLnVJdcBUlWnygvEYlBlJu49Ry1WstQqWqoiJA5GCALVdNOtVAlq\nlaom4MGzEo0ZIjMAQxE1IyMgRuBN3G6aqw9v73EqMNVd11rF0zh4gTaEoAhcFdhzUTabk0wvKeK5\nJCtToR/PBy3IG7xIzz7tGvYjG1v8m5zF8X4MHjBENNHQxkEHRb15eTtM48Y2C+gNAHCmHoJg2K5W\nk47XNy++ffvdu/uPIFqnCTXWLEKgKp64W2Rfc7VURjRnCjSrtTrDrKpGMwuBiMQsOEIaIIYA4Pxa\nAGqLcjoj+dixmtlZQdYhYRhiDMSQlERM0QfewDvlBgBMQBgYiZkTN6pKhhioCQkYrWqWIrk66H2q\nWUQQoVm17bqjEUqhSWcspe8BoNrE+Mm9LtBB4nGqiBgIiREds6KeyWI1DIwqWnMhYFMBcZ4QY7BK\nBlDRZ4dIaxmNK5KmFNZdC0xIalotVzRztYOwahMRiUjO2aQwcyBQcAVNUNUqM0FdjDHGWKZMM47W\nvb1JATQVET5T3JlURFx37WbVNRyIyJVoQA1MU+QQabNaVxXn8febxEjI1Pc9mo1TPfUHu2BZApgH\nDlxqRERijG3qplMJIay7GwpcpopEIfBU8tQbUmjiumu45jKVGohj1xE3w1RAtfa0att105Rjrxqf\n9of//m//O1T4+O7jOqRYOcXNaTxwiq11grS/uxuG8eb2xcfv3ociae6Vz73UcRzRbN20tdab9ZaI\nTqeTncskeIGXXwq54BQCZxgNXtRyPfhcjGcB0ziFQNe1+/5RW5hK/vLLL/tp7Mdhs2oFRISKlRAw\nUUBAMcWqIKIiv/zZz+8eHx6G/cvrm7v9E0YMhtVmrhFEFNUpD7HtVGXKwxzzMzRtZOac83q9Hoah\n7RIAnE6n9Xpdpkzs8f3cUwP12gAfDwdi9jTaWSgMrYoFik4QgUxNDC4lVWsJxCEwqFkRIOQYQE1E\nx+m4Wq3W3RrI8lhEagrN9XqTQjPmYTiNqXLkxJG02vPj/YtXL4/9iRB9v8YzJdTpdIILQNLMG1st\nsRQRrdWqgBMFiKpq5ACGUqoqEKjVoqU2KSZkGYXJmujxfDEwJEE0gRoYDs8PN1e/ydo/7x8kT9tu\nRYDkqdY0TXPloxaH5AMggPluAYAhcEopBHap2IkY0FBRUbWokTEQoLWpAfY8zlARCMhZomboGZh8\nKqX66pw3+HlCShXE8gyVXGKPZRNySmZXCXNepFqrVPn6y58MfQnMqWkgITKhYSp5PE1ioAXBOFLL\njaEiVN7vp1rrbr3p1qtN261XbeEhqjbdi013E0odu51M+f5xv0pN020Ox2NfpmEcFYybGFJKKTGK\n5jK3oUSXYpqq0gWq5jLdWgKtyyiBLnjsfhRenr3c7A/PDwSYq/QEzNiEiAxiMk1Dzh1DExjFAA0q\nIJsZGjAHZFZ6dfXiFz/5+f63//D44WFzs6lWhcznVGfUkdOzej1fTUHJwMw8dm5CRPS4U8ixmoAx\nRq/BoRoTRWJgQjUxWzWtF7fMlWAJUU0Mu9QJGOpMw6BoZCigZcwYCBXY5VoCMZCIpNCQAaHEEDfX\njV9kVQ2km7bpYhDp4Izk6FYRikSgEJsYIgOpqIM1tu3KLkv/hiKCIqvUVhUhFi0OmjEwMYVamEJk\nMoRKLo07jP0+K4xDFannjMCrzdAkmGqtMk6j9Kfn1IUXV7smhee7J0BgMmAOzIRkiEQcCEOIBEYx\nzfgAL5PQLJ1pUrOHtoSkCAAkIN5IbWJQ9F5t9RvgclJynpvCGfuBzC7XEB1A6IKjcEYPO+4O0dnO\n6NxdYe8LmalIDSGE0KhGqzyNErDtYtP34937uyz15c3L7dX1yy+/MGSrNuRJspyBQ/j6+uZ4PK5i\nB1pLL1MtOpQq9b//H/6HVVzd3f+AGDebdjwdfR9I607HUzaBwJEjBS5Sy5QboBBCJJ6GUas0MVKI\nWiUiLYn44pdCCPUveBA8YkT0sqpPk82BJcFMa0dILmu47EoA6GkPETRtA2S1lkN/2G5aQgtggNWL\nTEEEmTLW1EabSuriL7765u7+4+nbI04VgzFCMFQnTHetYW/YzL6XfLyEfKoXgQwYCUQBMHEIxBgT\n26IuFpqYkMm1h9q2WySU/acDvpuYRFWrFcm1VLHq3Cfb9dqN0l/hSASsquumFVEROUfvlrNUKVPN\nKaUUgxDUWk0rAkQEZm5D5zUCuJiucsbIZQubIwXTIqYGwl4jD6rixXMCLKVanaSoFIkx7dat3d6s\n0vXpOB2PvfN/FxFOHBOKlG6bYmp3N93VdpUaAtDURCxC88QDBo8KzAwx0XnwxmzWKPMeiO/RpU5S\naheSJ/WRGBkR4/kELCABQjT2KhbOava4lICWZhcink4nnRXqLzRrTIkIAxOgIhD6cClV06ZpslQt\ntZqqKgYmIgxBB5NSJEuM8Wc/+8Xt7W2K3fF4/PDhbrVaBW5lsnEsRNS27Sq1KiBcNrFDUJ1KwwEb\nCmBfvPwi96c8ToFgvV43MUjNuRZVyyYZlGJoQhNjUrCacwNtDIEAJRetNYWAHFyR1GyZsJozhPNI\nyBx7X9obnj0h/jhzg3PH4jJhMzNELXVSqGLIKVSTrFmnMuZtZGgY0Rgd62SGQqBBkaSIDEPq4r/6\nzV8j0e/+9LuwThU0IAIHRcV5RpOJADzqZwazKuIlACIEgyYl73cZABMhACsEQ0NjZOfSUyfNm0vt\nRr6HiCEiA1mVmUilitaCABwocEATFATQgIhobEBkgfDdD299eGKJDph51aVSSooUI4tA4KXmHBjI\nR90+G8mrPAs2+Qr3G6QI49gbBkwR8TxnAACgp/0pI1k1ZbAGV90mpWa8qVNfd6t22KZDH0+n0ziO\nZoYM2+31atetVmm7W23XjaHmnCXr7e4anCnaLDCCtzeRCA3szF7qJo6mjEDMZsYIQuggBSIkwmUp\ngA8XzpV6voiFKLatJ9kiUqSCzL2Xp6enlFLbtkshxPuYDjfzxqI4DYupmE7DFFJMXZsIpdRcS6mC\nYvv7p+vVi3a9rbXmcSpTrlnfv3uXYmuiRbLU6r7CBMqUy1h0Khoqo7GpTbmMA8eQx2NkvL7amEwC\nxUjSKlqFt9993J+OY61d0zTr1aZZrbabMQtNc91CREgsNswcipbEM0WkfkKvX6AC4EeW5v4K54m7\nufRLZwt0t4ZntwZqBIZEKhVIDSymiCQECgClDlVINLIZqBCogBIGRDo+71PbFJRh6l++vv3Xv/nr\np8P983hUMWOMISCD8mz5ZSqEFpAoEDn2qoqBMpCYtjFgYA8XJRd2BM9ZuslqUS8UMZmpSvVmr+er\nhBiZzMCRAIkJ2saLYSkl1wO4LGD41vyrn/9swVst/PbM/PDwAFKrCgAwogOWRSxQADGtRaQ6RYfn\nxtvVyj2wW1opWWo1xG3XORyMGZnorFaNzRdfmVnXrJrUASBzRKPTcQAMKbUxRlUdx/E09OM41pqn\naaDIVTKQcYAY2VYpxqYOFYF9tHseZtOzwJpftGVPvUwb/LhRF7DhJ2TA4qDn3vFF+rHMy/FMrjp/\nncvYAYDL38xOL7CXYA1MRRXAKswr1fEnCFJrLtkLJF27/upvfvrVy6+apvvjH//45z+/rbW+fPnq\n9vb2+vr6eOiHYWqabUoJgWqtWvSrl6/LOEmpY39s2jaRYcNfffkmMJHVmBAtoGklEy1P+8dDf8wq\nFFgJiTm1TdO2hY9zn00csgiMFAzN0GtIXgpbWn/n4dHzdOjMf3zBhXy+Mp+ttsVQL0Ig83FgYW3b\nhhmNA7EWLSKl1uykdOq9G5MYwvHxcHWDzabp++NwON7sdv/qr/7mP/7uP51kmLSqCjhjJyoiRuJ5\nASABQlCS80yj1hqa4CshpdRXCYTsUCe1Gd+DGIkpsIkiGwHGJgViBQvEqW2kqHMuiaqpAiKpaakN\nBzkr2hKimpEaIaQmlJKH00lVzECkTlOeprFtuyrVDIgwpSYmMgPMcr3aimiZclVhJOYAallLRHaM\nCAVmQ+EagEIK7aoh9gkvj9uXTSfXUkcxnUqtikgIPI4jM4+z9q2UUrzCwSxtS0Aqtaja6enUblrV\nOtF4s75diEfCpUV5WXKxLjzX0Bb3zURkoFU+rR67WD1nQ7rMTKZpmscZiGY1VwBVbdcr93hzMM3E\nTo5v6r0UR854AmcAbdsiYql17gSEEFPadKtffvPzvJ8e7z8w6i9//s3L29ebzW4YpuPhVPNIYOu2\n6brODyqFtL9/jIh5OE398fr2RZuILPz0mzfbdexPA2CJTUCD8ZD7ob9/+iikqWsBSESmWryeICIh\npNmtGTDizO5IFEJwY5uv2DloWYwNfvz4LJFboke4KEIuVxgRSykihUMKkZqmIaIQEFnVpNZSawkE\n7DQ4olUk2Aiq4zAAQzAcjidjev3y5TeHr+6OD4+nwwST9x781JqmMXGIzMwiEWg+CykV1GqtBEip\nYaQmpWgIOkO6lnKIIqQ2TLUwYOragJSlBqTYNEpaVKxKJQXRaiq5TDY1IYoKqrk8tCtxU6SSB6ch\nDJFSaLiNm9Xaud6QzDkJY2hiYlOUWANx5JiIx5zR7CySR2gGakzExDE5qpZS11SdiFym0MydI/hS\noTrplE+jnHKuTDGlRlXbtlUr4zj2wyQisW261AAzUQyJt5uuW7enw3G16YZhmKaCgHiewQsKoiAK\nSoiGMBOkEg5TH9y5nu0wpRA5kJFWWXKSpaI9TZOdUW1LmIRMRYrHVJdLx/vaMcbNZuMjwDPIpZRA\nPCcv6MLcCDDLnxNj4sANeqgGouPUj9NxLLnbNK+/ftXEFimoSEV6vb3d3GzAjDge94ePj/cEeHNz\n89PffHFzdV3zVPr+9e3L6fB0//7jetWUPDDBdrvuUnN3/+Hu7l5VQ0jU9zHGEnAYJ0C6CsWSUDD2\nJBNAiStbBCKDaJaIRxNQJQJGIgJVqFYBUGFhgEYAZSQxozNGegY9eVC0YOnNDEHQFM0QA6H0xaoy\nIAFwIiFVBmMNKBPWbBKVjQQggqpVHcqQUhyGYSjj1e0NIE77Y9g0v/zm5+19Q0TH0leQClJREHHV\ntaUUqzNvWqBARCFEERkBQLVMEwHgasXATUwRyURd67yNCXjuoG5X65AnBgxNIgPNQAYMGFKKZpY+\nccZ4cLhatb7tLhEjAITIx75v2i6l5Fziw6AxxrZtkecxtiWAFRHJdSi5iS0iVim11qBzcOGa1ArG\n6OwbUs2iSa2ZA7n2g8mnCgKlRERdl4hCzcUMEbhIfj48cIoxcLsJiDGEoKKlTIYaNFSVkDDXaU0d\nEpjJaTzhmWI69JoVVVErQEMRmbXKWCZ1VAGagUUKTePtuIrIhjrzHyPizBODwdjMRCucoUlqCmIp\nrZxfGgCQfJEYEqzWrVvylMscmTRtSslKJvNGB4uI1jrXGBBTCGY4lMIiKSVG1Jzfvv8OgVddZ5N1\nkKtKmbKYTvt8OB3HfvBqWAGVWp8/vvvt27+/udqu267DcLdfcbVtbLa7eHo+blddzen9+493Hw+k\nnVZplGI+Tjocg9jrdLDhj+Ofrr/e3P3zHwRod/vm9394m0VCCKu2gbHsupZywVIYLKUYGUuZ1DBE\nGqeiqDNocR4I8quLdr7BycNwYiAKKY4551oqmEZSw7Fk7TPvxy/evBoSfMz71WZTCbRBbtKguZYT\nAHTbLlALWa1AJD6VaSw1MiPRcX/gGChSrtpsupu4LauMR5ugWIPVaiklkK62Ttel01REpGmaVbd5\nenjafvEVUXh+fn716tV+v7/d3mw2q8PxWRFyLde7jZQaA1fV3fYK1AJEE/U+KgVuU9N13Wl/YpoZ\nFjx+Eyk55yplvVmJlNPpVGv28mOIK7WaC4lmRAyxCRGZGZn3z8+ImGKbUlKB0+mYcybA6+2OAprZ\nZrd2RERMARGrFgW5ubl5+/btq1evTsPxxfWLvj8Cw/+Prf8Msiw98/vA1x97z/Umva0s374b6AYG\nDRDEDMfPiAzFSMugOKFYaj8oYkmtUYREbVBciVzFygTJ1UYsudLSaCgG7Q5nMBjNAAMMgEaj0V3d\nXb6y0tvr3fHnvG4/nKwaULH3Q0VFZmRVxr3nNc//ef6//3g6KrDkaZwUZ4AQyrZty7QzzmXOKaVJ\nkqRp7ro2cQyIMRciyTKlFOJIKfWShgQAyKecUtob9qSUlJkKX7W7EEKEyxwUM6BACS2whqoAh2p1\nZc6WSsJciBwCIIU2CHt583lZVAAACjfAy8tnceJJAKUQGly152FhstFaaZWk/OU0FnhJDVHSJhAW\nUbhIQ/DS846U4lIU1xupodZKKKA0QLNgAgAKEjINJ+AFmgIhxBjjnEstgQRa66uQHYyBKQLpJ4FP\nFMiMEs6lu7AaRAHFKE3TKEizOIMKYECEhkBxA2KBBGRaMBnLjBBq2RBgQTBKkjhTAhLKbJfnwoTI\nM80wDpSUBGgMEUZAaKiLniW8gpfpF3MShfenuIQW8gSGqBBFAICFDQJiBIGWSqVa5lpioMuWbVEm\noSQEEUaBQYABgIks6sgojeKkm/RCYJuaEIkVBLRkaqAVKCJY9BUWGUgZ5xQgB5sps4GMJdCYYIJx\nyXWEyDnPIISOVWyIGEJdLXuEUK2gzLlJmbJcgrBWKsuyWq0KIcIYhZwTgvM8n04npmmBAleIkYKa\n51nAeZwmJrMEF1prTCDCtEiZRRhGQYQxRAiYJmOGrbXO81xDTHJajJEjhLS+IrfyXJbcstYaACSl\n4pxjTF3XpBSbJgNSCSGlFkorobhIeXFeGYbR7V8aFrvonhuGcX55hjH0yk61WrZtF2M4AyCOY8Ko\nV3GDIMCCU0YphAAgpik1mOmY82CuRaa1LgbktdYIQZMYUkrTNIpJziRJLNs2DCPLMgUEkEByyRUn\nCFwRyBguQhAgAABqTQjBRctIvMikV1oimef85XL66arjpUwCXsxAaK1FgU/CxaK/0lSA1ghqQhEh\nEEIoJdRaYwwQAkAhLvPCOa6hVlf2RKURIJgppSBEzKQvewmUEBOSYtpYyORl1D0mLElTCCF+4SWH\nSBBCKKM1t8Y5h7lAQhmGIfJ4cXGREKJzGUfxfB6maVpsDEUfBmKkIShkGyFyxCizTICgaVtRnGit\nEQSOZYbRGBETE1IMN/10k0PrqzSfn6b6aK3BTwn9Rfcfw6ufAghmeVaMrkklpZBC5EopDIBhUoC0\nUFxiiTEEGGoMINS1Wi1ncSaDNEix1IhYShPJNeAYaHzFYtCEKwWVhBJIrSCDtmVlkPNEpjoFGmBC\nEYBAayUlhFChl4ZRSRBBCEqtEAZScUIQhCDn3HFsSnGa5lGUTCazPHcxpqbJMEZKiSIoWkpd8JKV\nwjwThbjlMEtBlaRZmqZKyYXFjlJqNpvEccwYuYr2hth13WJmSAgBIS4ANtggk8nEMAxKDK31C4C3\n4lwxirMsEULoVBebb/GJEEJmwcyyLD/ybdv2I980TalVEAe2bSZ5opTIRBYmYZRGCgJIYJhEIAFC\niDhOCMG1Wr2YJC8+zf+Vhaper19cXMRx3G638zw/PT0FAJRKpdFk7nqlUqmEECIMEqA1UhBhaCB6\nNaylJCicTBpA9dJ2BgCARYQv/ikW58tt46eVySuFUykJCjD6la6gr3odSIgcgKvYe6211lfeSkyu\n5JmCza21BhAoqCVSQgkEEaMYAcyzQoFQAGiolZSqmBYnBFBKGEOUGhhDhIjWUggMAKXUoAbjUmmt\nDcYohZTQXIFyuZonHOQqSbI8z4v3kSuulBJa5JoroAqBRORcMQ0I0hhBhkTEMYZaKQyKeUVSnJ/4\nBSzxp2UPeGXs/1+/ri7JRdsE/gnuTylV2LqllDzPheAaI4oLQJPMJQdEEwo0hgppROBkPoVcKpHx\nPBZZKglnimZclE2EFQGFLFy0khTSCiKgKWUGZY424zxOkiuCShrHmGHTNMULLYpSgxASJ/HLjzhN\n08KAKxXPslgpYRjGysqK53lxHEdRxJhrWUaWgTiOi2KeEGJZhmEYeS7zPMcEYUo0AFxyDbVhsYPD\nQ8OkEEJmGp7nIoTiOM7zXMgcIew4DrhiKKhCVys6aZRhCLBlWUWlxzl3HAtCBYAppSimuDkXlJI8\n53EclUolrZXneVmW2ratNGcMYQLjxFdKGYbhunYURVl2Ffherzcty5rNZnEch2EwGPXK5TKltJAS\nC5WhEPkwxrVaLQiCvb090zSLIOLLfs9xPT4V8/kcAECIxkLmUmkoFVdYKyS5EiK3DbuAvQCltYZK\nSaigRprSwjRQtDWkUgVWWGcq/WllUr+4gxITaaWF+hOhsggHQVCiKzVfqqukW6SAxsQqomOB1kDK\n4izQAJg2AxxCCIlBIYQKa601wSwPUiiVlAoAzQhhjBJCAdBZlkuulNLFm44x0lLmeQoglVJDwy6E\ntWJppSpL47jYcTWGUiqdpUoLqVWupCpEGiU0kFJyiSB1jYTnCEKKcJ5ylec2o6bF4jzGGIOr7gV4\n2W2DL7hZL880/UIPpggjhAjCCF7dvQvDMYRQaS2ELLzeSAOCiYkZQkgjDZGkBjEsQxpEU44MPBkP\nTUgwUFxxzhUUmiNTA5iLnACFXqhcxf8BNJQ5x4JShQzCTGKaJBVQYkSSPKDUKLRWAAoznlZKaKQV\nVBBBwzazLIMAKa0lUHbJjeNwNpqlPC1oytSkXtVLkkRooZGGBCKImMGoSREhigsJFM/T/OpZzUzT\nLNmlpsEoxZxzIfNcCpnLKAmLOWWg/+TJLpKZEEIQ4iAO+ZwrqYuK62qaNBBRFBiGlaax1tA0mZTa\ntBkQwPWc6WxaqXiXvUvPc0eTkWVTp1QBUCugFFCEERshRCBjZrVanc/nQnE/zKMkRBjZjm1YDGPs\neCVKaZqmVAhCCOc8iqLecFAqlcIwdF232Wzu7+8btvXrf+7PhlFyeXl5enoahiGxiCkg4rlECgCu\nizMNCO1UXC14YQKTUguRawAA0oVkVLyKa1txar2cNfmTDxUhBKFlMAlkYSUopt4YIRBjg1JECAKA\nSwmUKti5UutMKA2LYxMUKVhaa4j0cDBVWrw8N66KTo1qdukFBw0ahlHMnkop6/VSsdUVK+oKUiBl\nmkkppRBccY2BduwSBMg0bX/oQ0QYpZzzLMuFkkJKroSAEpsUIYkgNJmhgOZalRqV8Dx2gKmBJACK\nLC/ZjmmaQRLDwlYMoXhBBHjRSfk3btovvvYnjq9i51ZXbl8NEJRSciUkF1ADRimjjBGiuRRaa6go\nxZRiCbXSEmrIGCEIU4ixrYXKlUbFyEthlpRKYaUUeOEZB5BLzdMMYIAYspkhlMOB0FhzSJQCMucK\n6KJVI4VO09S23WLvYIwlSaKukkHzycS3bZsxVlB0TdOcz+dHR0eO4xRtRsZYUXFJKZPMn07nEBGT\nGRgjpKESIOP5LPAJhnEOQn8ep4lj2aWyV2+0XNcdDAZAayQQIcS2bULI1Ukbp8X9EGNM8JVxGSJg\nUJLn1HGsAlxmGEae54ZhhGFIiOF5rm3bCwukUqk0mzlEejzpMUYoxULoIh/UNE3HcWaziZTSMCzT\ntEzTLA75JE+jKHGyxKAsFxwBaFgmQZgw+sUvftG0rR//6MPD46NyubyxtXlydPzDH33glSrFP0sp\nJTazADCUAQoKEkKAmAxjiAGWWgKlIURXXZgXOX4vhRD8AvKOEDIM4+WV8iUsvuh3CsWVkELJF/g5\noBXIc46pLty+WiqIJYZIAcgFLKROrYFWCLzIwXBMq5B51YvB7cIAGvgxQy+QrEIroa8+16igAMiX\nLS8pZc65YVtZmqFcQqERsTrtdhiGBqRXGo9SWZZHScw5V1pwKXKgHJNBmGCgTdNQGc+UdhvVYTc2\nEZBSupZFpLQZBUApIJXSxSgC+KmlBX6qn/byTCse+2JQ++pO/oJ1KYHWEEgpueBaa4NQYjBKKYZA\nQ6GhxhgRhiGBCohc5kQqCWQuJVAQM4RNwlOZqlxrxBAEGmGtuBAaQQYAAhgRhQAUuVAQEEAMTB1q\nJTzNZY4AJoRhjFUxs1pM/EiptQyCuZS60WhoqADSUgih5NrGOoQ6DEOIAUCaGqRc9RBCWZa9GG9Q\nRedfSJHnnFBq2FbJdphlAqniLM2SKM1TCxmYUNN2NCaEkCjJ5vMAAOXP5hjjYgFYliUUn0/8KIoM\nw5JSGsxyDUNpFUWRlJIxpjULk5gYLMkzrTUkeDafKQjOLy8syyqXy36/V6vV5mFAKZ1PpgBCBZVh\nW0TKIvbeMhyAIaIEEpzkSZRGCJHiUCmVSl6lyoUAWpuUFIUBM42KU9vde+64rlNyN7e20jyb9Hu2\n67z62muPHz91S25ncYEQQrCGmBoEYamVEhIR7Fi2aVtxGHENNb4yuRRiCSIw4ymm+GXmN3iBKy5i\ne4uvFAqB1kVGKYEKaAWhQgBcdVqFEAhhWKAUpVYKIIUAQlpDCkykCCqMg0BpoAFUEMLpaIoxVlpw\nzmFBoVMqS1JGMDYIokQpxZWGQBFS2No1RpQSJPBV80QrAeFVmh5G0MDMMexms/liYo5iTDOdxmmS\nJIkEWgIttcg1tzEoNhtGcJyqVCnXNaCBlQRaCtexdJojAIXIFQDFr/dSHQH/5np7WdBerTQAi0GN\n4ltFIIQo/OUASimVkAhBRqhBGMIYKUkIAUxRQ2OLUYMhVBDdNCJICwkptk0bmDALU50DgRSCGuqC\nTaeLpEOtIFaYGCQTXIAcEYgNjBUEQkslECGu7RiG5Yfz2dRXOmHUpJTmuQiCiHNeqVUJIQV9oNgy\nkiRWSpXL5SRJ0jSNosjzvFqtJoSIoqiYw2KMEUKowZjtQAhTnkdpUrwJQgEhhFmtA6CyjGutQXHn\nAQhC/fYXrg/7g2632+v1TNMslUqGYTLGwjDmnAONiuyxMAyL70KkceHNMA0EoOXYvu8LJTudTnuh\nE4dRqewNev3O4sL56VkQ+dWKE8WZUkBpGEcppgTBaOb7w/6g5FWKnCOMxGQ692dzarBXX3sjGA6T\nJKMU57kIQ99xSgsLbcO00zTVAFmWZdtuq90WQh0dnUyn04uLiyRJMMbEZIyZZjCfU8MwTVNqbZtm\nFMUYQmJZL/uGxfOICIzTKMuTLMuUvrpmaK0l54wQpZTJ2MuxMZ5lQKM8F4yZUkIpAcZYSSC4pNRC\nCAku0jSt1WpZlhFCgiAg2EAaS4VSzoUQXGTtdnswGJTL5TyQLzZKRBhh1EQYMdMslZwkSaIwLfR1\nQqRlWaZppmmqDJymcTEaJqVME2naZpbxLE5Mi2ioTo7PvvzWz8hMT+fzwA+BAooLCCFjNM5SzvNc\n5sQ2qGuwnGeSe57rWHY08j2vPqmMwunMotiEEGDsGGzij5lBsQbFyQAKGE7hRsEoTVP9clYHaIQQ\nwZginOc5QSgXgnOOCDZNE2oVp8k8CAghzGCUUsIohBBIBbUOo8CittCqWq1qLXOZQwNoAKjBEAWt\nSr1VbmQ+H14OoyDVEiRJDgjCGEGMgYJcSqCF1hpRooTMOZdA28h2LJdSSgSVIhCZGPbOTccslypB\nODcMSymRCYkQsl1nPB6nacoMI0lT13VPT09rtdpkMmu1OtPpHGNcrdYHg4GUejweLy8vR1GSZanW\nkDETIQgQyQX3A79YgVEUXb9+vdvtZrmY+1OCWXthkRJj9/nTZqMNtNzbO2AEA4CuXbteq9U++eST\ncrnq+/7iwvLBwUGlQpVSzWbLsuz5fN7tdpM0evudd/aeP8/ynBLClXS9UpbnJdedzmZJHPeGgziK\nqGk8evJ4c3tjMBrZri1EHEaxY9tBGAkhK9V6GCXMcrVUURLXKtXJdF72vHKlphQI4mTn2vXL7sXe\n0+frG2snZ+f90XBjfbPb6yZx2mo3IWbzMAj8kHNODTOdze+++lqv1yMIQINi6HmmyRgztZaW5Wgt\n81xgBDClRaaNVFxKKZSyLYtQVBwsLwQikee5bdtFdy9N0z+ZAMCMEhNBQ4hMCAUklBohzRBkQGrH\ndl0LSKV4muaQa4GFAC6zCTFylc7DeTSPIxLbyFmoLWCBKS1GuYsOOKGUQoRSkTYapCjVkiQJgiDP\ncwAQACgIovl8Tin1vIrj2BhThBQkiCDXwgbTjNQJxThMwjzlBFOAtFQ6l+IF7EACpDWD3VG/VHUq\nbjn0A2owr1GdDSKr4nIzhNNc8ZwBjLXSAAgpf9rP9vJAUy/YZMVXXsoVEEJKiXxRWBJCNIJSKPGi\neVDcGjBEsMCOKckYw5REyRyHQYOtdhqds/lls9mMk8igLAzj0WDXISVEMYc6z9KGV6WAAABzKaGQ\nFCKMKcaF5QQyzAimQME8ysIsCrIg0jGz6pVyNQzDkM9M09QaTKd+LgRlxvnFxbXrO6blDAaDW7fu\nDAa9crkqpcSY9vt9Sg0puet6o9EojtNOp3N2duE4Vr3e1Fp2OotK62d7zwmjUZhsbGw8fPjw+vXr\nve5gfW1rMpkMBsOF9eXADyxLryyvj8dj2zKbjTaCOgiiLMum07nnVcIwHI+mnfbiV77y/uXl5Xw+\nD4JgOp02m+3T85OFxeVvfvObW1vXWq3WfB5gjGczf3Gxc3R0Mhz2O51F358tLi5fXFxcv3Hr9ddf\nffL00Wg0sCyLEBbFeRznpunOZv7S8vr+/n693nSdytHxeblcPjm9KAdxbzCu1mvdbr/R7PzGb9y9\n99mni4vLu3vPS+7kxs07Fa98fnlxcnK2uLxkWY5tw/Pzc8ZMIRQhjFiMWiajmECktRQQ6TxP0zRG\nlGmklRZAKiH1S2+b0rlSSr2YjYQAYIgMyjBEEsBC4nupwimtGaVAIy2BElrjIqAZMmIYlHEpTGZo\nCCxqjacT22QGc2WC2/VOo1mHEPr+LM/zbvci9pOS7RaIAABUnudhGiKEiEFW1pb7o8FZ77SohhFC\nWqo4TizLKpe8pYVF27Ydx0nT1AcQIAkwskyKBCSKNhdbGOM0zVUuGCZKaAWuQOtXFgwEy/XqJJ9J\nIGWWB9GcShPYSCBVbtbzkznGEillYkogRBhwITCmVzotuKpslVZSqpdiJHxhurlak0IUDQPDMKjB\ncinSNC2OesIoxaTgSlyRhoSkJo2SmFisXC5nGTeAATGdBT4mKM0zLoVbKtuGN+6PYpE3Wo3JYGpA\nyhCjEBNAIIQMAg1QluUIX5E8ClHUYpZGsNubjOdHK6urreZiynMIITVIq9n56JOP33jjjbuvvPrk\n2dPLy0ti0MPjE9Mysow/f/7s1q07Z+cXy8urtXrz7PxyNJ5Saszmc8tyAMRn55eEoEePd997771q\ntb6/vz+dzHjGV5ZWoIZpnD5++MR13ZWlVaiJEtCfRUqp1eUNQlAaB0kaFxZQLtTC4vJoNKrWmgCh\nD370Y8uyJpPJ0tISgPijn3zSbjfjOElyPp37kOAwjOZhYFvOebc384Odm7cq5aofzOMoqTaaUqgf\nffSTOI6TJKNG6c4rr/3u73xzc3NTA3B2dr60tLK5fbPZbD9+/PjzB7sbG2uOXVlf2/n0888WVtaf\nPtvdUnA+i6TG3//Bhzdu32p3lk/Pe0M25Up2Fla41AeHp+Px+J233zQMI0mSPBfw//X3/rxh0EzI\nNI2VAohACHCYhAU+Wkot1JUmWYCHrir4P+mY/YlxSL3Ahr1E+gBNLKOEIMuy7GVyCgCAMVaMApim\nWailcRxjjNMwq5QWoURhFGRZZhjUcRylhGkxzvOCIM+MwsPCKaXMYrNggmhhGONRFHHOHccpl8v9\nfv9lG7BohhBCXNeiJiAE8yjHAt/eur2+sNY97lNFdK5EzvM8T7M4iIIoCYXIMyLstRqy4Hw2DJM5\ntCnXKhO6YVRrsd390a5xHLWEVWa26dq9dMaFoJoU7UEBdCFdCiVzJQEo4pYgQqgIagJaA6l4LBCA\npm1ZjiO1mgTzIIqUUrbrYIwZoYQQBAp2gJCSY6Ilk7xEOq+su9caPk5pw/B5MJ2Om/WGzlXvrM+I\neWvnTqvRyaPs8b0HNqYmswxEkERAKigQVNqgDCAICcQUEYMQkxKDaQPd23ukCFhcXLzsdafT6cb2\nJqZkOh1X6rXBcNhe6HCePXj8qFwuJUl248bO6fHx2trabDZbXFx8+PDh8vJyuVwWQsxms3v37m1t\nbTWbzWfPnn3lK185ODiQUjql0mw2azbb3W739u3bjx8/3djYCIJASeB53vn5RSFpKqWWl5eDwMdQ\nCpmVSldFoO/7z54+d13X87xGo4UxHg7HYRjO5/OVlRUFle/PGGOtVqsoH+bzeRzHo9GoWq3att3t\ndpeXl8/OzizLiuM4TdNyuay1Pjs76/UGX/3qVx3HGY1Gve6g1Wo1Gs35fN7v90ul0vPn+4ZhLCwu\nlmvVfr9fJLxnWWbb9nQ67XQ6juMUYvj5+Xm73VZKNRqNfr+vRF6v1k5PT23bJnEWpxwihPM8k1pT\nQKTMANRKCXVFeNQQF6AnrQAoSrKX1kDwgrr+om97Bca6wjYCZBsWw0xYVGtdKJbFIFma8k6raZrm\nwYEPVF6vlgghp8HlaNKnxFJaWJ7ZajUwxlmWxkkYZyEACmWIZEWvSOEcUw5znqR+rJSyLMtzHYxt\nIUQUTEoOm8/nPM8ZY8witokhhABJDbRWOkkixInjOFnKtYKU0iiJhLxi8b70TVHTkEqluQAAWAbD\nJkuAFFxyoCWBmiDTNGmCGMYyS7WWV0iI/39QOvhTna6C4ytFgSZAzGCWZSGEoiguZGKn5BYbEyqk\nYKWh0hhACFGSRgvLK89HJ7A/vPHVNz47eUiAZTCrs7R4fnLKoGGVvMvz3uCDD1rNBSQhD+OUMFco\nxzAtZBKMEMBAaUyJ1loqKTKeiYxIamiFkLG5tvmjTz+Jo9xybIJZ93LglNylpdWzywsp9Xwe1GqV\n8Xi6tbVlWs7RyfFoON47OPrlX/7lJ0+f3rrzyv7+/jyIdnd32+32v/Xn/u1vfetbnz94tL29Hcap\nhrhcrSRhBBUkkNiG3T3vbm9sK6WatWaW5jzn2xvbk8lEKWBZ1tH+SbvdHM8mWvNytTEYTarVaqlc\n3dq57rrus2fPzi76rusCAIfDYZqmy6trSup6rf35g8/cUnkwGNi2DQA4OTnZ2dkZj8dpxjFhGqDV\ntY3xeGzZbn8wqdZaYRitb+z83M/96uHh4dlZn3O+tLwBAADQ6A9mxyfd69e9en1BKRWF+f7hfcMy\n0zStVqvr6+tZlkk1f753VK/XPc9jjN26/arv+x988MHS0lKtUs0SHrKk1x/atk2E4EKIooMBlBRC\nhElMKUUYAwQRQQQRCKEEV/fDQm172bkqFk8xs/+yWYQxNgyDEIIAYgRiDACEAEBCIedKaS6FjpPg\n/CKyLIsylPNkMh1SSpltIGRixKKIz6KJnsicp6bJ8jx1PBtCrZTK81RyCZEGCqiM8zyult1KpQ4h\nDIIgCzPHcWr1yqNHj4QQnue5JZplWWEMV0rVW/Xi4EUCGIaRxImWSmOoJPiTdaaUUgIzbBisubb0\n5OCxiYFlu5eTvlEptRYXZpdTAaQCkhKEAMAAJnkmoXwZnI0xVlopdcXfhS+c1+hFLKuUUisFtS6V\nSoQQBGAcx2EYKqUs2/bK5WKW5Sp2VAOtQQEWX1xc3n2+T1vu+ubG2dmZ74e1zc5v/+43DQNvbm7e\nunkjCZMwTGrVVqe9NO6PBkGY8ExKzbMsI9wzLIsyZpAsy18sfqihVkrzXGikq+3ml9/7itRqOBwg\nRMq1shDi2d5+p9OxteBCWJbz7he/hCn67LP7X/jC22sr60KIH/zgg7W1tZOTM9f16vX6fB6EYXh4\nePwzP/O+67rFycOYOR5PodLzefDq3c5gMPrxjz76whff7fd6d1957XD/CCAch/sQEYKxVHoyGodh\naLkMIjkYjA4ODjqdTtmrcs4H/dGbb7z9O7/zu81mq9NZvHXrTp7nYRiWy45pG4ZhjUZTIdT+/pFl\nmbVaM8v4ZDJvNunZ2fmzZ8/znDca9VLJU0oLrtdWt2q1xje/+a1SqRTH8cry6tnp5WQyK5fLm5ub\n9VprOBy3WouHh4f1ZvmNN9+Z+9Ojw5NutxeF6Suv3rGt0ptvvpXEmVd2f/d3fu/Bg4f+PLx563rg\nxz/5ycfNarVaLY9GUwgnxC3ZYRgygyCEhJSc80zgcrkUp4lUSkrFFUAIAQSvaD7iChV+VbsjxAhF\nAEouXtKmCush1EDIXMhUqqyIJ1faVEpJlUEIl1dao9GIi2hlZUUpNZmQPM9r9c5gGmECYQFcZzLJ\nYkpQlqf+ZOo4NkIoySINpONYhmFohfgsC6Ncg6xUKpU8g6Y6DKfjSbezUEuSxLJMCPlsPkjTtNFo\nlMu1XCqdK4owZsy27Zk/L9pxxUuoouUthBCIIkRwqVImBkMyxxgTiqlBqcE0gsRgACGMIVAcQyAl\nB6RI3bmaz5YKaHnV8X9pC7wqCLNca00wZowVwlKSJEEU5lIU1vWXtwYEEbzaqSDUWmg9HA7XNtb7\n+Ww0nOzcuFuj6R//8R/XajWlBOfyonuJAaXM7Pb6Wa7Xl1c9w1ZpnkeZzHLBZZylWiKJCZCwSE0H\nGKICFwMhAGg0nKRAJknCmNG07FxygplXquSZaLYbp+dnP/rgw/d+5svNdvPs7DJJsjRO4jh+8423\ntdaHh4eW6Vycd7c2rw0Gg6dPdruXfUrpzs6OPw8RQkudJYLwaDA+PT5NoqTdbEONTGZ9+slnkgvb\nLT168PjazvW11dUkzVWuLs+6pYpRqrqmIVaW10qlEoQoTTMI0aeffvbWW+9kWRaFSZbyk5OTSqXy\n6OGTar3SWVwKw9jzykkmAFCm7X76+X3HKV10e7lQG1vbGNPRaNAfjpvNZrc/frp72Gg0Xn/zrc8/\nf/Ds2d7u8+Pt7e3tnRuPHz+e+fHi4iJhdhBljKLs8gABAABJREFUQqGdnRsKyG9961u/+Iu/vLe3\nqzW8OO+urq5fXvQuLrp5ngZBxBhxnBJG9OL8PAqTTr1JqfH6a2+4JYeEUTQcD9IsIxRpiIu+u+WY\nuRQii+Ms4zxDiFCDMGIQQkzTSOMsjmORc6WpYRiEYkwQM6hhmi/DeJVSec5FEnOVA6BSnmoNIQEY\nY0QxISTlmeXao9Hg9OKEUtpuN7vd7uNnnyVcU2blec4Y8yoNw3I9z5vO+HQa2g5BCGa5zPJESEA1\n0Fo0WnWeZVmeR8O+1ppSWiqVmp0WhFBOFKLYNM1as55lmWlZXEklIVcaY2oS0zacuQ4wJlpCJa50\nES5FLvNMCqAhgvLs4pwwCjPNmLWzdSMBcjgLkUaWZRGKEFIAKoQBhoS+uDwW90UAlIRAAS0h0AhK\nrQsavBBCcI40oJgyQjVUXOZRlmY8pYRZBgMAxP6cMRMhgBEihRNYyyJfuVDbG9eWFhcXnz59tvnO\nLeAyVjH39p632+1wHikhtreu80ycX/RPzy+IBCrPRCIglwakiGATAg0xZbhIWQBcF9EuVAMAgWk7\ni63m7t7zo8MDTVC1UfXq1XkQ1huNIMl7g5FTqh6fnH3445+88cYb9+/ft0zz4uICAGxZluuWKTXD\ncJznl1mWvf7aO4eHh8PB7PoOOz3pvvHGG6PxbNQfYGQfHl3cvn376ZNn52f9zc1N399/+OjpK6+8\n8vO/8IuGYURRgrG87HVbnXalXuZS9LrTSq16crw3HI8QQDdv3RoNZ73eDGoUROHO9rUo5ifHz1bW\nlqWAlHhSpMdHXc/zFhYWzs5ONzdu7O/vA6jW1tYeP959//33nz9/DgD4/PMH62tb6+ube88PJmP/\njTfe2tq8ee+TTxE0Tk+6737xq48ePfr9b333vffeq1QqnfbKwwfPtZZ3br/5rd/9Q8uxvvbVrx6f\nHs2ns0ar9d3vfM9y7K9/7U8/evJ4bWXddpzI55GfrW/emk+m00lyctwnAkrEsCYgk7llOaVSaTbz\np/MJY2bmJxXPk9LQGkogoVIIiEqlejQZNJp1SmmSptPptNFoRVEEIc5FJhQvis5ms9FeXProow+i\nbLa2ssy5Mx5PIFYaQqklAjAMgpWVlSfPHrquDZGezHsbG2uQqeWltcdPdwlxNjc3Hzz8fGlpSap5\nuUx3du7u7u6Wy7XZLC25bG19aXd3t1GtaQA6i4vD4bBwQJXL5TiOZ74PIcw4z4UACK2uryulBoOB\n7ZSGg+n5xeWNjRt5wIWQaZQ6xE6jVEmZpxlEUEGdyszwrHqrljE9GA4hw2mY1auNV2+9+g/+598i\nrvvnfvHX9n90v+w4XA2dSgkKSAEyFCMYMWZyITLBMy0zJSKZc60QwUopBCBSGgplMaNkWJZhYkrC\nPA6SOM0zbGDXtAxGtdAYIqYhLkhBiud5LrXAhDJmCJHVq5U0iVzX/fprrz3tHz188KzUqjaai+PR\nfNQdvfnam+fHvSRJ262Fp0+ftjrty15vubFUqZVBIhTXw7lvQtLwKkCpkmUKmVvMStKIISwzoUQi\nSXRjefN0/7CztPRP//W/+tO/+PPEsPdOz6rV8p3X3vi93/s9LcUv/cIvTvrTlc5qlCa2XZlMQs6n\nrVbnww8/W1hYkhIuLm4qZbhuKwjkxx8/LZUWPvjgwfHxseeWsywrlUrj6f3xeNhqtToZtEq19tL6\neW+YcLG6utpZaAEAAIUry2thJE7PL3efPd+8ZmNUybIAKjiZytEwn8xnZbfElTo9nXAlv/GNX03T\n9PHjp1niVyqtQIpJPzFwpDnrDkdLndWnTx8P6DCax9PRtFlrMsaWOiuD/rh/2Xctl1LDNpze+Wmj\n2nn08HGns3h5OibA+eqXfk4Icbh74ZXdNMkdp7R/tB/6MvDn/+R/+md2yWzWK6sbqxtra3Ga/4P/\n8R+sbWwSZT568qzd6FxczKLg88FgtLy8LKWEf/O//zOFTlgU8UUlZlnWeDyGL9AjaZoWGk63233v\nC++cn58XzbRmu8VzCSEMotAwLN/3CWOLi8tCiMvLy3K1IkS+s7V8eXlOCMsynsQ5IQwjuri4OJlM\n9vb27ty9Val4H/74h5TixcXOfD4HABX192QycV334ODgxo0bRRuq1WoFQVCtVofDYVElZlnmOuXp\ndM4539raGo/Hpmm6rnt5eQkhtG17aWlpNptdXFwUY+yzqb+yvgElCob+5tLWSn0ZJpr7PPYjHudB\nHHCZB2kwS2ZOxa626imW3XSWK940XX8+W1hYWNpYMVz7ePdw9vwieHxSvkxWUc1KSRxmKQKAMWqb\ncZ6leZYqkQqeSi6AhhhhiBQXQGsLU49ZFjMoRBKCrj8RQGMACcYWYQwVB466ojsDILTKpZBaQYIR\ngUCpUCTmUmXx1esjFEem1mU2TQPG2GAwsIjZrNT73YFBDMbMaqP+4PGDa9euhfPQY87zB0+a5eqd\nzRtUQxMjkWQUI56llaqnVF5M1hOzpBAmNju8PPveRz/SNoM2RSZ7+PQJQDBN0zdff6NeLV+cnZcd\nN8/zO6+93u33+v1+q9mZzWa93qBcLm9ubn3++eeVcm1lZcX3w9PT04WFhUql9uzpbprmAADGyK1b\nt5hBHzx4wBh57bVXDo/2gmAuFa9UvPF4/Nprr83n0zwDhJYHg/He3p7neQX4EADQaDQ2NzeLAV/L\nslZXV+M4ZowFfmRQWjgMLi8vpeSLSwtxHI7Hw+s3tsPQZwbhPGs0aq7rYoIEl7NZGIVJvz9stzs8\n16PR5Oz0Ms+U63pbW1tSqlKppJTq93uU0iAIpYBaa8PEi0vNweByabn1448++D/9n//Khx9++KX3\nfua3fut/Xl3ZQIhJASZjv1ZrfPLp/TAMr127Np/P4X/yf/tSqVQqaMdBEIzH46LkcBwnCILV1dX5\nfG5Zlu/7RXWRRjGE0HaccrlcrVaPjk78MKhWq/NZ4FUrcRwrBXLOXddFCE1nY8XDarW8s3ODEvbs\n2X7gR5VKRUqdZVnRnvaD2dJSGyLQ611+9atf/fTefSllp9M5Pj5+8803P/zww9u3b4/H416vt7q6\nenx8vLOzEwSBYRimaQZBNJ9FnudBCC8uLvI8tyzr6Ojo9ddf11pPJpNCIJrP52EYWpa1ubk9mc0N\nYqXT2Cb22zff7B5erDRXD58fQAEykXGZz+O5n/nIQhLqQTRlLY9rcXd9e6HT/vzzz1e2NvaODkeX\nvTWroU+m7bHuSBtMeTCPMwyBaVDL9JMojKJUcqGVVEpfgReRzDklpOp6JctWQvIkTQUfpyE2mG2Y\nDGEtFVIaQ0QgIoRIoKWUXEmhFUBQIwihhlpBh01ACtslUTN8KsqrTU7AfD5vtdrDbi+ahdev3bh5\n8/a9j+4dnZ5Qx/J9f9wf7qxtYgkRlw23CjJRL7kmJVXP43lqUpJm4ZVUAxk2zXKzrk2aAvXZ8yen\ng+7K1oYfR261rJQ6Oji8OD0DWpfdkmVZ5Vp1b39/aWlpMBi9+eab3/rW7+/s7CRxtr6+/vnnDwgh\nnc7idDpN07Td6ti2LYQaDAaTyWgymZxfDFst7+bN6+Px0Pd9t2SvrCwPh/08zwFUUsrZNGy116Mw\nK/xsWZa1Wq1Cf1paWlpaWjo/Px8MBsXmu7Ky8tZbb+Vp+vjxQ855tVqVknd7l0EwX1hov/7Gq+12\nazabZVnyow9/uLCwUC6XDMMCGvV6g3q9ATRizD47PU9TIYWm1LAsq9frFXV1msaUUt8PISBJkgCo\nNMg5TyybtNr14+PDX/3VX3311VcPD49dpzybhd/59vcwpvVa8/TivGBjz+dz+B/9tTdrtRpCqFqt\nZllWCKZCiFdfffXs7KyYuJnNZuVy+fj4mDGWJXm1XPEqZaVUHMeTyYwZRqPRuOwPTNOcTeeMsVxw\n27bjOEYI7uysMQLPTi8tyxFcEcJu3LhxedkNwzAIfEJIqeScnh03m1WtdZIkGBvVavXTe59/4Ytv\n81yurC7583A8GUKA4yQUXIWRH4VJq90YDSeGYVQqdULI8939O3dv8VymWbyyvHZxeWaZTq9/KbhC\nGNSqjVa7EfjRZDLJpWhV29PeZLm+2PaaFjBMZUwGkyzOJJBpnsySeQYyYOA4jy6ng3d+7mvHZ8dr\nzc750dHWte37Tx6V6tXlRvvoo8e0GyxMcSM38JxzrqFlKstIBZ+HwTwMrvLcMMLwKpYVA+g4TqVc\nRgCGcz/w/UwKZBu4cNcprXOhpKSYMEwMw8gE55wXBlyAr/iLaRqTkjWSEV2q6oZzGPTKq22z4jx9\nvnv37t2y7ZXd0k9+/PHJ0Wmz2WKGZZdLn352/7U7d5lG7Wrz8NlzIuGt7W0opWOwZrUieG6YOE9i\n2zG11kTRcq0eixxbxvrt6//V3/7vLsfDkPP908Hrb9/WWnc6neFwuP/8+dbGZuFrXllZOTo6+tKX\nvvTwweOtra1Hjx5pDWezWa3WKBwYQMMwDA3D2Nzcrtfr8/n84cP7UsrllaUiboUxMhgMtrY2dnd3\nTYtNJhPG6P7+8RfeeefRkwOey2azGUVRlmVra2tSyuJ8M02z3+9zzsvlsud5YRgmSeJYRpIkRUqW\n57mMMSE5IWg6Hb/++uuU4aWlpW9961uOY2OMoyjqdBb6/f7NG7fPzy8r5brvhxgZk8kkipKFhQUh\nBACKcz73p4ZhaAUFh2EYIgyCYOa4tN2pXXbP7t69vbCwMJnMPK/8yt3X/v7f/58a9fbXv/6Ne/fu\nAazyPHv69JltW/Af/c7/TkrZ7/cxxnEcv1xsxa++sbExnU5XVlaKTvRkNHLtUqGYzefz0Xjc6SxS\nSo+Ojrau7URR1B+OSqWSbdulUun47DSNQgQFgCrP1NLSUqvVGY8mYRgTQjY3N7e2tj7++KPJdJxl\nSaNROzg4+NrXvnZ5OZhN51pDpcTq6vrZ2cn6+uaHH37Q6SwmSfTKK689ffpYa1gul+bzoN1uP3u6\nzxhzHHd7e+vs7Lzf71HKTNPAmAwG/du37wSB/wd/8Ielknvz5q0oCjfW1qCGJjQNSdabK1QQEWR5\nlMVxKkQ+9ifzJCCe4TU9yFCkeWNjMc7S3/7H/5Qn8btfeu/NL7wz8mfj7pBOM3w29S4ya5rDaQYh\nhZaZUzhPUz+J4jCCSheBrwwTSkhhQjFNs/iMZ7NZnueIUatcKgIotJBaawQhI5RhQgjJBM/zXGiF\nECoWm9baYeYsD63lVv3m+rPpxRjGrWtr/flkMB7s7+9f29z60hfe+9Y3vxX40Z07d7r9QXcwzoT8\nwhtvPb7/wMamSDOXsa2VtWrJZQiVHVMrUa9XMJSGSXnCqUStVmc0n7bXVqZJPAhmp8Pet7797Xff\nf38eh0dn557nuY6XJAkCYDAYtNtNw6C9Xo9SOp3OzStMqCCEtJrtLMvCMDRNuwCHdjqd8Xic52mS\nJNevXy9qkyRJmq1GsTs/f/58PB7fuHHj6Oggy/j62sbZRT9N84WFhTAMi+5WMR6IECrUgcLHzTkn\nhERR0GrUKhXP9/3pdGrbtm3bWZbN/dm1a9eK5tDq6mq/369Wy4VjbTQaDYdDw7AQxHku1tY2kjgD\nAHHOGWNRFCCEHNcqphKzTFqm58/Dkuc8enS/0fQoQ3HiX7u2HUVRnueUsrXVrTfffPvRw6draxtS\n8g8++j7GejgcVyoeOTg4iuM4CALbtimlhmFRaliWozVcXV2v1Wqbm9uPHz92HMf3w+XlVR7no9HY\nMIxarZblkhAqBVAAn5/3KKVlrx6GYfdy6HkeMdjSysbZ0X7JK7/5+u1erxdHWbVaH41md+9e/+CH\nP37w4JFhUEqpY9NqpdXt/rh7Obr3yQPbcillrVbzs08fQQgQ7FpmGUHDtmgYZGmiHMcdDX3bdoaD\nWZ7p97/ylQ8++HA2ja7v3O20lz2v8vz5M9t2TcM9PDinFP87v/HvTSaj4+PTnZ3rlkHPjs42l9Zm\nw2l95/X+8QVVWAkpuSiG7gs5MU4yKYA20P/49//hzs1rt+++YmA0Hk//9e9+s7W8kvvh3fYm8JE5\n9bHvA6opopLgXGRRmmSCI4QYwRZhJqEGpgalJcctQH1+GMZ+oIU0LcuwLQBRJrjI8sJMbTKDYVJ0\nI5RS+ir8CYAi70aDJI41BOPBOLGwcuDq2vrJZf+wdyG0iMI0COKjk9P3vvQz9Wrj+9///jyIwjhf\nWFp+8nQvTngseKdR5xl/vLfHEFxdXLixvUkYiYXgeexCmwJQcRyRc9d2eJLyJNtcWX+2vw8luDy5\nAIy9dvvVT+59Gjv83Xff/ezT+0GU/rkvf/XZ7tOzs64QvN1azLKMlRjn/M0333z8+GkQRAUBrvCh\njUaTLEsZIxsbGwCAH/7wh4Zh7OzshGG4v3dEKZ1O/J1rN48OTzyvPhXTo6OzVmex8KRijC3LKv5O\nCNnY2Hjy5Emh/xbGgrW1tdXV5e/84f8iJQ+CoJAbwjDUWju2O5sG0+kUIcRzpbXudYeWZYVhWKtV\n5rPQtkGlUlleXtQKlkrlYk8MgiAI5mkWmxaxLCPLlVJXIU2e5ymlLMvRQPw7v/G/eb73DEKklPrJ\nR/dLbvXv/d3/d6vVOT0939hYwxjGSbi5tdbv9wnnMk1zy3IwJlpDreF8HjiOU63Wj49P4zi1bXt5\neXUymZimnaXCZBZCZDSeZrmYTGaBnzDT7rSXb9++/bu/900h5PLy8ta1G1rrLMts20waoeu6QoAo\nyvIM1KqtTnvx7PRifX3j8PBgbW1Naz2bT6pVfuf26/NZ8pWf+boUGkI8HPZr1U6vdzkeBRDSXnei\ntbw4H43Hw1qtgRDAyPb9cHlpo3s5evONL15env/Ov/79u3dvZymIwnw86vX73a2ta65rn532VleX\nK+X2xx9/dPP6NaXgD//4R++/86XBYFQtVwfHlyYxQskBgqRwsGg4Gg3nSQBdVm82Ly96PmQ/+6e+\n/uGHH1qu2+0OGqXys6f79iitjTIvkpZGhmFIg6KUp2mqoGaUOsx0qWFhahNmUGZgKoGO0jSLYi2V\n4zjENDSCaZ5pIQpuOSPUILRoyuUvsGpXczlXce/AsUutincaTZFGrVqr3Fr84cPPTdcxLBaG6eXF\nwHOqr7/y5mQ8+94f3yvXTICtLOVpLk3Xm48mg8ls0h/Wy2WRJrZXipUyCMJACwgVIVCjII4SEJeq\ntdlkurGzM0vjiuV16u2D3f3NnZ3To7NapRkn2Q9/8ONmq7O4tHZ8dn56cnZ2el4ulzFiWus8F0KI\n3/3d33NdD0I8GIyKyyeCZDC4rFbLlmWNRiPLsprN9mQyOTk5W1paklJTijY2tgBAjl3OUnHzxt0w\nDJOcl8tmASApxq8oNaSUDx8+FkLYtqbU0BoahjkeT9vtdqnk3L5zazKZXFxcYIxd14UQT6dTxkzT\ntB27NBqNtIZBENTrrNVcjJOQMdO23TBIFzrG48dPa7Ua54LzvNVqLSwsxEkYBPPRaCAkd50SwbZh\nGHEcW5a1v39Yq3l/42/83d/8zV/+9N7n77//Pn6XDgbDwn/EOX/06JFTZhfnl9VKrXvZg3/1//5n\nptOp4zgvaTlCiMXFxdPTU611vV53HKeY8Z1MJkmSWMxZXl6+vLy8uLjI0nx5bXU6nU+m02azCSF8\n8823x7PpbOpjjMvlstIinM9q1XIhLfZ6A9/37969e3Z2Vhh4FxcXx+Px+fkphPDmzZuPHj7b3r4+\nncyn03m3e/HKK6+laSyEqlbLhmFhDDGmp6fHk8mMEJRlHCGUpVcISggh57yYTL1+/Xq73Y7juNfr\n9Xq9wrsupbx952a7Xjs7PNy9/+QXvvazb91+PRr5KJFpHIdhKJQaRdNQppKhYTyLReq1q2atPJtM\nG3bp8uRs6gdetaIZowpUMlyeifZU23POYsUojbTszcbTJEEEu8wsW45LTQsRmzCbGcXuO4/CWRRA\ng9oVT0LgR6HMuVIKgmLs0yiqO6VUnKUAgBcsXaALr4AGMlU50vZKs3p97YcHj+lC5Q8/+dHKjU0A\noYKgf9k1GK165cXFxfl83htNlla3/TBsNdq7T59RiKpe+dHnD5YXOyrPCdY1r2QwfG1rrVb1So6d\nB9FaueZQg1ADG6ZA0KnV3Frtv/nbfycWfJ4kHCE/ihXCdsnlQhoGc2zGCBoOxwihQriqVquO4xTW\n5t3dXaXU66+/bhjGdDIvV0qlkvPw4f00TRcXF/NcIIRs2z04OHBdt9PpdC/71Wo1jtPiUaxWq1N/\nXq1WwzAMw7BSqXS7Xdu2gyCglG5sbBS8nel02m6379+/77pmGvvtTsv3fcdxXKc0HA4dp9TpLM5n\ngZRycXF5OBxhjKfTaRjEJc9Rijdb9X5vCCFEiMRxbJoWQsi2bSG4ELnSolotW5Yx92eCSwgspbRS\ncjabpFlcqXhS5WkaF06x4XC0tbXdarafP99PkmxtbYWa5PGT+2+88dZsNkFBmJa8WhTnw9EMIlau\nNCbTQEjYaC5Uqk0/SPwg4QLsPj8cT/z1te3u5eDo8PT46CyIUoiN8Wjuz8Ms40KAvYOTf/4vf3s6\n8SuVapJlQZgQbBnMLVdaUSx+/NFnP/n4My7AH3//h4ZpD4bj9770M0+e7uVcLy5t/NIv/9lHj/f2\nD05PTnqPHu8dHJ45bu3xk70sB2mmoljEiej1p1Lh5ZWt6zfuxol89733p7NoaXltYXFNabK0vFGr\ndx48fMYF/Ozzx892D3/ww482t240W0uWXVaaVKqt4WC2v3c8n0crKxvVSiOLc4aZ5JxiggAsuh22\nbY9n07OL8yBNJ34QRYnrenkuGo1WuVx944134igb9Mfd3rDZXgIIY0SLG4sQXEoJhPRMu1Yqu4Zl\nM8O1bAOTJIolF/PpLI2TUqlUqNi+7ysugJBUQ5Myx7Rsy2KUFryJqwNNA6A01AAjRBBmmJiUuaat\nctnvDrIkn0/mK4srMtO7uwfn55dRlCgNqGmOZ7Mkz4p2SMktp2m6tbWVSRUkaWdpOVe60m4lUhql\nUqbV0739mMtMAwFgbzSO4jSM0ziOsySNZv5sOP7Fn/szZcd1LXs6GFnUoAANun3LcrIsd11PCDUa\nTuIotUxHCj3oj+q1phQaaLSxsWEYRrfbPTk5yXna6/W63e7S0gpCZDSapGneaLTG4/Hq6upCZ+ns\n9AJjyrksZhrL5YoQotfrHR0dPHnyiFLsOFaaxp1OCwCFEAiC+fr6KsZQiPwP//AHlGLDMBhjOzvb\nq6urrVaLUtpsNre3t/f394tKEmPium6vO4AAM2bmmVAKjIYTAJCUmnOhlM4zYZpmoXDO5/PCv+I4\nThzHcRxPp1Ot9cLCwo0bNxYXFy3LajZarVbHdb1ms/3aa6+XXI9SwzTNcrlkWdbJyXm7tXx5MQyD\nDP7yn9969dW7vd7Asoxutz8Y9Ahhm5vrWsPT0+O33nrHNNnZ2UW73fT98P79+wZlX/vK1xAlP/nJ\nTzyvjDF2XPezzz5zy5VGo3Hr5p00TS97XQAAhNjzPMswz0+PKaVLSwvn5+emyWazGcZ4dXX1/Py8\n2MOuXbs2nwd5npuG+8EPf2zb7q1btwgho9Go1+t9/etf73a7ruuenZ0dHx97nieEaLVazWbz8vIy\nyzhGpFwuz+fzGzdufPvb3yaELC8v7+3t7ezsOI5Tq9UeP3789ttv379/3zKNyaCLpYSp/Et/4TcX\nvIZOsmAwToLI931im735MMOgF085g73ZGFl0OJ8iAGyN5+N5Z3ExSOKYq1//+V98+J0Pr5k152zm\nhbLN3DAM53kymE00wLVqtep6DGGqoYEI1kBywTlPslQADQ3KEYiypEAGwVwalDLTZKYBMcqlyPKc\ncy7BvxGQW5xvWAOisaZUlK3YIQ9GZ4GNWKsKXfPw9OTT+4dvvLbOGGm3Gv1h33EcgDBlbhLnhmH0\n+0OCcBBErmVHoU8gQBBkabjQbPAsrlcrr9y9jbJ80XDLhq2Uckolp1RGjGBmh1nyX/13/+3WjZvI\nsvZOTsrNZpSlYZouLCxgCDjP7t69++GHHx4cHGxsbCRJYtv2cDisVD1KabVa5Zzv7z9vNtu1WuXs\n7GxnZ+fo6EhrvbS08umnn37pS186OTmJwkQIsby8PBqNGDPjON7c3AzD8PnB8+vXr+3s3IjjsNvt\n12qV8/NLSrHrekoJrWEchxsbW9PpOAzjMJoxAisV76OPPt7e3u51+4uLi9VqnVLj+OgUIYIxOT09\nrdeajuNMp/NqraSUFCJP0xQAZFm2UiqOUiEEJrDVaikla7VKr3+eZYnruhhT16mZpmWaRpqms9kk\n56nWMssShMgrr9xZW1sLw3AymRVV93Q6HYwmBb4ljmP4H/5nP88YefToCQCqWq1/8Yvv7O7uHRzs\nDYdjQpBlOb4/W1hYunPnVr8/PHi+2261lpaWwiCuVqu9Qf/i4uK119545ZVXuv3hw4cPb96+9cEH\nH2xubM/nc6fkAgUsw8zzPOdZmsbVanVpaaHX611cnq2vrx8eHl7fuVmp1OI4jqJk0B9CiHvd0Ww2\nW1pa2tvbazQa1Wp1d3d3eXm52+2urKwghF62CE9OTvKcr6ys9bqD3/zN32w0Gn/9r//1PM+bzWal\nUonjeHFx0XGcomF4enqaJMnrd+9kcZAFwf7DJ3/1//gf00TpNIcpT6KYEPRw96nbLJ/Px6PMf3J8\nsP3qbeZaAurjvYPhyTkQutFsv/72O+Mg9Ewbj5PSOK0NEi/i6+Xm2dlZrPk8Ckxs1SqVsu0iCJWQ\nGMDC95llGQcKICghiHgWJTHXyiSUKOAw03IdTEkmRZpnKc+FlAWiq+h5FqGEBQ3IQVRAJKt2YNO9\ncHiUzJdu78x4NI0CBdWrd+8eHOwdHR202k2pNWH05PCi3mw16q1SyZvP52EYZ0lKKa1VvEGv12k1\noJL+dLK9tTGbjN995TUjSSuWkyRJpVJpNTtSK4gYIHhpbe0f/pN/8u0Pvv8bf+EvfPDxR7sHh9Sy\nLccOgqBcLtdqlW63SynN87zVbpRKpbOzM9u2j46Oms06xpjzbGFhKY7j+XyuNVxeXp5Op5ZlGYbh\n+z5CaD6fX1xc/NIv/dIf/dEfEcwMw0jT1LQYQAhhEIVJtVbGiHpldzb1FxbbB/tHlap3fecmF9nh\nwXGchPVaM+fp6vJC8bOEkH5vMBwOPa/ieZXJeCaEaLU6s9l8aWmp1+sdHZ7YjuF5LiYwz/MwiJUC\njuPalkspFUIkaXTr1i0IwYMHnwOo0jSt1+uOXSaEZlmaJAkAqoA6GwYlhA0GveFwWK1WX3/99R/9\n6Eenp4MbNzYNy/G8CoQwyzJyenL57rvvlr0+hPD05AyCz8rl8nyWrCxvPHny5PaXX//GN77x8ccf\n97rjd9/98uuvvf3g03tZKtvthel0vrV5/cnj50CTh4938zx//bW3Gq3m9Z3paDS5c+fVy2736OjI\npGZxlGnNPa9yeHjc6/XC0H/9tbebjYQx88GDR+PRZDyeltxqFEVxnFSrVYRonvM33nj7o48+NE1H\nKd1otAmhSoHJZPr48TOlxOrqhhDCMktpev63/tZ/f3HRW11dwpg+e7a/trYyHI5ff/3Ni4vubObH\ncfqzP/tnjo5OHjy4X3dtxDnPVae5MDvvZjnXWZ6EUa9/WfG8wWTSWmjJmFbj+ecPHrz95Xd7/R5m\n7N//3/4lfzyfz6PPHzz2Gg0e8mXDQ0RSA7AcF4AgDgUjtGbZLqRYalBwNyHQAHCgMiC5VkpqoVSS\np4ViCQCwqWGZpkmZugq8fZF5/4Kh8NKqU6w6DFEmcikIQbRRqx+dTnmeHx4dv/6FN+utZsVzf/CD\nP75165bGKs2ys7OzeqMMgSi5Zq9/4ZUqp6fH1WpVQzULA7dSOTo5azfrcZbvPt+fzybxzL+7vGos\nLyut0ywr0HEApQay/cnkP//P/urab/2jv/X//H+88+Uv18uuXalIoJMkKu4aCKHxeMwM4jjO7u6u\n53mOYy0tLdi2OZlMDJPFcRjHMecSIfT48ePFxcWi+ZYkSbfbbbfbrVbj7OxkbW2FENLv99c3lmez\n2c7NG8Nhf3e2F8dhq9U5ONhrNtulkrN9bZNS/ODh54XzuunWh8MhAKrfR+12e3t7++LiolqtFpal\n2WzCBX/y+HnBfj06Ory4uPA8r16vDkfdVqvVaHTiOJ1OAqV0kiSTyWRhYcGyrGdPn7fajVKpPB4P\nG/XWcDg8S7r1esM0DUqpZRlZluVZTik9PT197733yuXyd7/7nYISubBQzbLs9LxXqVQMZgKo4Z/6\n9RtxHK+trRXXths3bjx48KDgkN29e1drPRgMms0mAODg4ABCvbO5KRU/Oz/3vArGeDabKQBPTk48\nz6vU6u12+8mTJ4Zpa62Xl5cvLrpJEJ+cnKyvrydpqJSoVLx2p3V6enzr1h3G2P7ewZ07r/zgBx9o\nBefzcHl5OU3TTqcTRykm8OK865Xd7mVfaQEBHo0HCJI/8/M/e//zh4ZJFzpLH3/88Y0bd87OzoCG\nQnKMiJCcEoYwxIgQinvdfrVWmU3nAOpr2zsL7dbeowdMaxPgv/Nf/denj59G4xlIssD3mUlPe5cZ\nUd147kPhq9yqlWexH8TRa3funjzZP9w96PfCd9//wmDqW5i2gbkK7PWMNVIdnHe1EnORMELXvSZR\nSAGgIdAYaYK4kpngUZZyKXLBhVYFAJRSahFWMx2bGpCRnPMwS+I8kwhgQtQLCpDWuojVhQAQDW2E\nQp7JshOXzKhs/mD3QePG1qPj/fpCu9lpfvLJT1ZWF8IwWFhsC8VXV1f75z2EyNHJ6crq+mg0cVzv\n5OSsXm80m03Hsk8ODsqeq3PhlZyzw2MGVY3QL73xpmPZFON6tcEILQohZpmQsmt3bv6n/9f/PMgT\nr1FDlqER2t07UhqWy2XGWJrFs9ns8vLyvfe+6DjOyckRAKBc8XzfNwza6w1Mw6LUiqP0yn8MZKlU\niqLA9/2lpaXZbLK5tSGl9P2Z67pBEDBmCqUghEmSDgb9TmehUimfnJxijISQWZY2Gs1qtVJYZmzb\n6fd7oe/btp2leRRF4/F4bW3N932ESKfT2d3du379+nQ6VUr5vr+8tNpo1kolK+dZ4Ifn55fDwdSy\nHNO0/Hm4sLA0m80QQhcXZ7Vardmq9/v9SqVcRJ1NJpPZbAYAIIS0Wq1r17ZM0/zOH/0hhLBUKtm2\nGUWR41gXF13T9izLAgBJyZFtectL60ATCKjg4NN7D5KY93vjJOYf/fiekkgK+OMPP7n3yf0ozL7w\nhS+tbWwcH50GQXRycgohOj+/ME379u27r73xJs/lD77/wY3rt1zXi6Lk93//Dx49fDye+J32sut6\n49EsDGPLcirl6ubmNoRQK7CxsQUh/vKX3k+SHAJ8fHQ6Hk0/vff53t7ev/7tbw8Gg7JXdRwnibOt\nra31tc00TU9Pzlut1sV5t9frNZttQsi17Z3ZbGYwczgcAg3TNDWYWa1Wq5Wa67prq+urq6s7166P\nx+PvfOc7CJIs43fvvooRlUIjDSAAJmW9y26e56urq4eHh++///5593I4Gg0n05zLP/yD78ym/rVr\n1//t3/h1jKmU+vnz/aOjk/F4CiFElCRJQhihlDqmZWHKFES8oABCBXSmRCzyVItUiUSJTAqIkGlZ\ntm1bhmkZJoSwKOqKRYh+KkHh5Xp7kbirtVYGIRQjniUiSxGESIO1lVWCcBzHr7766uuvv14ulz/8\n6PPxdPTo0YMkDcJg6rnWbDpqtRpS8Ua7Uap4aZqeX16Yjt3rDmbzoOxV4zRDiIznvh9HUqtciIIP\nZ1KGNLANM5iNuhen//5f/PPXr22++sqtdr2CIOj1LhFC/X7/5PTo+Pi4Xq/evn3z7OwEQj2Zjv1g\nfnR0EEVBrVZjjAxHA8HV9es3TdNeWFgI/ChN02az+eabrzNG3n7nLQBUs1mlFOc8vn5jy7JoEM4r\nVW86nXhlN8+z1bXlTqcdxQHneavdME2Di2xpaTFJo6dPn4zH43q9XiAtCi7OeDwGAFiWEUXB8nIH\nQh0E00ajtrKyNBhe7u097fbOx+Oh0tK2TWaQQrKP47jb7S4tLRX8IscpnZ6cm4YdRfFkMvF93zCM\ndrtdrVaLEYXLy96nn34OAfZKlbt375ZKpa2tLcYYpbjVapTLJcYQhBq+/Y0NzrnneWdnZ4SQer1e\nsJRv3ryJEGo0GpPJ5OHDhxDCWq3Gs+zGzub5xanW2mDW1J9blpWmOWNMaX1ycmZYZhRFqytrSim7\n5EZ+dLh/4jiO41gIgc5Cs9e7jBP/jTfeODo6yvO8ezms15thkDQaLYSIbduTyeSrX/3q9773ve3t\nbd/3i6z6g4OD+Xx+8+bNgvz+7rvv/qN/9I8KqyUlhm07hQOt0WgMh0PDMIoHt16v12q1g4OD7e3t\nk5OTarWaBGHuhzwI/tp//J985c23T58+S6ez+WAYB6EEsjcbk7L12eEuqpV++OBefWXZKju1Wm33\n4eOgNzGQkXN957XXS/X6o0/vV3K0gZyfaW2Uwnx2eGpaVBmkYruVBFIOcqg1xTmBseKzLI54xoF6\nGZzNCLUN0zJNExJLI52LjOep5LmSEgKFgIRA/hSrHGmAIMQAIq1MDQUC3LO6KpWtyv3+mSw7uOKO\nwykg8PBov9GoPnnW39xy2wtNyQUDyPO8i25XARQnnBl2moutreuHB0crS0vj/pAgBIUCUhqEhtPR\nRrt1a3OjWipblNnMqLpeq1kXQiCMORDQoPXlBWQbf+8f/v3tGzuzOHEqrT/63h8HQfDaa6/96Ec/\nMk32jW9847d+6x9BCJlBt7a2+v1ulmVLSwthGO7tHTXry6Zpe54XRcHDh49+/hd+9sc//tHP//zP\n3fv0kyCYNxq1OAmjKNzc3DQMw3GcmR+tra3dv/+wWi0fH58uLy8mSRYE8yTJptNxo9GCULuuB6He\n3t6hlA66g8AP2+32aDRqNpu7u7tr66sFn2o0GvnzYDwZ3bh+s1qtnp+fU0aCYJrnuWE4aZINh1PH\nLlWrjThKGTMpNZaWlgq+RhDMkyQxTVbynDAMXvQGpJTSsizHsQ8ODprNuhACQFVAQ7Msqdfrjlcq\nMl7yPIfv/9IrmJI4jBDBnls6PD5YX1srujp/6T/4D/7O3/7baZ68+4X3/uh738EQ1Wo1gvSzZ89a\nrZZlWbbr2bZ9enrq+36r1T4+Pbl165YQYmN9CyF00b2cz+dZIpIkcSxbapFniVA5wbDRbFbK5b39\nfZNZi0urg96wUqtfnl9oCJr1Rn/Y0xJsbm8d7O0roJcXl45PTyQXtUa9XPJOz8+A0tV6rd1sDYZj\njMloNOGcLywsFOuKIDiZTQuA7uHh4c2bNyzHTtP0+Pj4T73/VRjz06d7//V/8V8aSh88uA+ixB+P\nFc+Hs4npuXOe/v6H369vrz/vnglGUskNgxkAdUq1i7PLzsJKfzxZWFtJ5mFDMWsQfKW9qc8GajJX\ngjutat31yCRhCgOKtUESLad5PE3COM8UhoRSgjGGiCFsG6ZlmCahKs3zNEvzLFdSQ6AQLJjnuoj/\nREXKFoQaFFHUDEIOtXDNIZbm2vLD4dneuA/K9jgONq9fsxxzNBqYJuMim00mXGRYK9d1DdOM43Rj\n61p/OMxyVaSUOJa7urIy6PaCyQxoOZlMKrb96s5WxbZNQj3LsQkrO26nXud5LqRsdBrD+VQAvfPK\n7X/22/8qzJJEyPt7+4CwKIrm8/m1a1tFzLRpGZTS6XRqWUaapowxy7Kq1fLBwUno82q9Fcxnmcja\nzbrQQmQpwPDVu7c/+uQjz3FTnnqu65ZLruVUajXHKZ2dXRSLhzH2xhtv/MEf/MFkMplOp7PZzHEc\nIcT6+vpgMPA8j1K61F5OkmQ4HBa++MKtDyF86623fv/3fz+KogJK4Hme74cAKNMyZrOZYzmOW5Fc\nYcKSKNt9vr+zff2y17VNC1OCIQiisN1szfzp6srSRfcCalgqe0pILgUCkEvuuaWTs+NatToY9bc2\n1k/OThcX2mmW5VKUy+WifYrmk/mwP2rVW4wYWuhf/eVfC2bB+emFyPL/6K/8lTyJb9+8+ZMPf8QI\nwRCcnRwfH1006gtpIoeDmcj0vZ98blIHaepankmdQXdMoNFudk6Pz/yJb2DDsewoCCM/CP3INuzx\nYF4tNarlJhB4sbM66k+H/VGtXDvcPxBZnsaJYxm97sX7P/OlZr1Wq3giz5IosE3Dc9xyyfMcr1qu\nVUqVPOUPPnsgchH6ich0OE8iP91c37o4uxx0B/Vqo3fZxRg3m43eoNsddDHDmcrdUmk+DqajuZZ6\nOp5UKhXCiIZKI23bphA5hLhWayqOmpXlemlhqbGBpUW0xaDdqiwggNdWVoMgsAzj+e4zQlCepAYi\nSMKS6ZaoI3KhCUI2xQ7LgfCTIIh8yXNKEENQ55lKUwvAVslrlzwXIB5FQkpBoKRYU6wIkghoBDHG\ntmXZzDAhYQoyoZnQjGtDIJ1LIKBMRd2pGAA13WqlVM7T3LLcXn+0u3tycTE1WZ3pCtNVkjue2+Yc\nR6Fg1Pnko3uO5Yos9WcjJdKFhdrnn/54Ouv78WTt2jKx4TybrWytNZfaI3/CSiYySZjHkcgQoxjj\nJM5WF1Y61Wb/8Pyrb76XjSKS6XqlXK7YaRZgop7tPvaDqWWzarXquq6UMkmyVqtTKpWVAhDSmzdu\nrW5sZjz3o7Bc9SSQYezfeuWmBPnqxvLWtU1ESalc+eJ7XymV6nGivvPtH+w9PxoPxnvP9vyp/91v\nf/f/8p/+F+PB2LVcDHClVDGpaRs2w8xi1nwy7533p9NprzcAAOW5SNOcEHMwmBwfn9+7d9/zalJg\nKbBtVRh18wzEkTg56GPtZCEI5+np4cV8EhHAGrVm9/zCZEbZdTBSjkUhENNxD0E1HY2BAjKX4+EI\nKs2znGEMlE7jsFIu2QZr1ms8yxzblDnHCJXcKsJGq70UxTncfqVp2/ZXv/rVo6MjSnEYhnN/SghZ\nXOxsb28/ffp4Np/2+/1ms/n1r3/tn/7Tfw4BgwA7jlNMmlUqlYuLi8KhU9zcAACe5x0dHRUmtLfe\nems+nxf+Yt/3G43G4eGhZVlKqXffffeDDz5wXffWrVvXrl377ne/izAYj8c///M/98knn5yfn//a\nr/1b9+7d832fUspzKaWsVGoF2no8HnMuXnv1jfsPn3qeNxyOIAT1ajVNYwi153mthdbZ2VkucsNi\nAKNf/7O/9j/8D/8fqjANdT6Nvv8Hvz+5vJxensbTSRrMeJ4ijAPBOSLPu5fPLnvSNGdpPo+CO7ev\n7z97amvcqNeeHx6sXdvqTUZQ8GXmXWPeWoStYeTkoOzYwGJCCCYVAVAAHfHMz+KE5xICRDDAyKTM\nZAZDmCgANWAII4znIs+V5FJwJXWRsQoBUBpjTAAkGuKiry0VUBpIZZdcjkEAdWzjOYN789GzWW8G\nhNmoIdOczgMAoGe6PM6zIKrVPObhjCdZnhQbvOd53e5Fs9lcXV2+d+/e4uLiyclJs9Uo5o8mg/6r\n1298/f2vfPzBh1ur6xW33ChViALNai1PeTj3K/VaEASthc48DLJc/Ks/+N2TZOzLxLFL9Xq9oNDv\n7x8KIWzbrdVqu7u7lNJKuYoxzvN8d3dv58adk9PzW7dvxLFvWpRSTBlECCVJLKWaTucIkvfe+/In\nn9wDGu1cu+ZPZ2kaD4fDYhS+KGiHwyGltFKpbG1tXV5eFmMl6+vrvV4vipIoigo6v5S6UqmYhm1Z\n1nw+55wPh+ONjY0kSV3Xnc1mnU7n2cOnnudZpqOUynNhGEalUu31eozR+XyeZQkzUK1Wy/K4GP6q\nVhr7+4d5nlNKi4lnzyu1Wq3+oMt5ZhiG0gIhBKE2DCNO80yJnMt6vd7v91EBMvjwww8QAsWgNADA\ntu1inno8HmNElpaWut3u4eHx5cXYsizGWKVSKYr4UqlU4H2CICh4+kVqTgFGN01zd3d3Op0uLCz0\n+/1qtRoEweLiYmGN++ijjyCElUrl0aNHu7u7hbZz586d+/fvX79+/Td/8zfv3btXKpWKsq3Qvuv1\numEY/X7ftu3Nzc3BYKCBtGyDMSpkrpRgjBiGgTEej8elUqlSqXheJU/yv/lf/jcil8E8sJhRr5SB\n0pZhlEqlWrXq2iUlQRynYRAnSWKaZjFKggnUWh4c7N2+fevs7DSO462trbk/zXmKEMjTGCoNpKIY\nNWoV17FknmVZAgDIpUiyNMuy4vkowJXFn5ZlEUK4FGnx4jmXMlMiFTyTItcyB4pDLQhMgUygSrCO\nKUgYjBmMGIgY6IWTURYEKk20SAEHBirXqp2VpShNuJIIoXajyTCyGcVaOZapuEjTFEESBldAIcdx\ner3eJ598KgriipRSylqtNpvNPM87uziP4pQLJTVg1AzD2PMqeS4qlQpjjGEihDCZhTRaXVm5detW\ns9lM4sz3w6Ojk93dvfF46vshQsSfB48fPYEAWabt+2G1Wg+CiHP57rtfaDYqUqTdy3ODkbLnBnM/\nDHwM8fHh0WQ0jsLwO3/47WdPnkohzs/Pj46OCGG1WsOyHIRIFCVpmtfrzUajNZ8Hh4fHnMt6vbm4\nuFyp1MrlarVax7iIDnWXl5c7nU6e5/v7+6en50mSKaWjKD47Oytu6ePxuOAsFQM9QojRaDybzWaz\n2XzuFzzPUqlU5BvOZjMhxGQyUUpVKpUsy+bzuRDi7Ozss88+K8StogUSx7FhWBDiJI2SJIriWRhN\nTQuTAmAqpXz27Jlt2/v7+wuL7TzP9/b2kiSJ47BUKjVbjZWVldPTU88ztdYI4UK6LRwTi4uLnPM7\nd+4U7gFCSBRFjuMUa68ACe7u7nY6nSJB23Gc8XhcLpd933///ffzPH/27FmWZe+8884ff/+7f/Ev\n/oW/+3f/7ng8vnfv3ttvf+Hw8LDwLzXqrel0Op/PK5XK0tLSdDotfNmFVSnnMaU4COZCiEJEWVxZ\nPD09NW0rGgy3t7dFLiazabNc2V7eenXrOoHIc0swCWPBY0IYY+VqxcyySZqms2kSRmo4CgXPeG4a\n+JNPfvKn/tSfGo8GSRo3GrXJ8cy2nWA6hV7LMpmVKoKgyPI0SShjWusiHxUzamEGKQEEI4KFVpKL\nMM2wBhQiTAnPeJolyjS4ErkUouhaEwQ01Agq9SJxBkIMigxWAJAuVVxoUEVQxkAORCqyJE8E1UoJ\nzjOEgVbcYFRrYBDsz+ZWzWw0Gq7rjsfjbu+ieAMty5pOp9vb2/1+t9VqZXm6vr7+8OGj3HXvXr/+\nz/7lv/jVX/iV3um5SczlZrs36C82Wnmem6YJISQQjUejLE0ffn7/i++8+/HRs2q1TinNsmw2m3Eu\nLcuilM6m86997Wuff/755ua2aZq+7y8uLq6vr+/t77baNSmF45ppGj958qDdbpuW0ag3v/jF946O\nTqIwaTZbjFlpklOSM2YOh8MsyzzPI4TEcVzwti8uLhhj4/HYsqxSqdTr9XzfX1tbOz4+Ld60YrrK\nsUuFs5tziTHWGhBCHMcpyPnj4aTwQJuGTQjjXCRJWrTmpJSe5xGCOgutOA4pJUE4p5QSzGzb9jzv\n8vISANVoNBhjGKMwiA2TAqApxVnKCSFaFcFpAhOttXRcgxCCLMsoJs0Nk9qOWViGINTFRREhNJ/5\nruvO/dnbb789GIzSNIdIO67luBYXmWUbNasynY273W4URaurq5WqZ5qGEMIru4NhL83iQurM8oRS\n6pVd2zGTJEEY/OTjHydJcvv27d3dXYh0lmXf/e53j4+P//Jf/st/82/+zePjY0rpcDhsNptxHJdK\npeFwmCRJEe44Go1t23ZdO47jarVcnHjEIJV6pdvt3rv32eLiIiNGdbE2GU1v7Nw8OTlpe9VwNv+z\nv/JrVa/Mw+ByHobTucyla7mj6RQaVGudpXxpaUkwZgJQblWHw17kc6UFACoO/YQnIuclzyEclEsu\nmwOtZJYmKudQKdNgIuMaAggRJURjpHARsya4knmSipwTjCE1aBFloSRXIpOKK82VKpLoJAQaAgm0\negGfxAgVaFeEdTSfUIMKiwlsQJNQ02AwR4yUPBdRCiGcTkYusWSSEYqTKFCMgwyenpzcunXrV375\nlz///NOPPvqo0Whc29oe9Aej4bDZaJiGMRqMdravXVycT/1AAPj88EhnvJmLk7OLO1s7s3kAShAj\nEoeJYVhxEEqgkzDiSXp50XNaNYSQa5cYMWzThhXo+z6G5OnjZ+1mZzQYP3z4cGtraz6fM5OWKq7j\nWqPx0LKMpaUFzrNiwuvBg0dbW1uGYbiOhzFDkMyDOQCo5FiTyQRjbBiWEMKyHIxxt9tlzGSMpWkK\nIbZtbdtuFEW7u3tLC8sFu6nIYSxSjShjm+urT58+RQCbzOq0Fi7Pu8UNLo3iIo8XYzweT9I0TeIM\nAECoCsMwioI4CRkj5bJHKQ2DuF63i3k013WLH0zTtFarFqzhQu63LMc0bABQpVwz8gASLYSSPCfn\n5+eO4xQZVvP53LbtXq8XRVGtVimXy1EUOI7T7XYLCqzBpoyx6XRedL0LB/fZ2dnm5ubS0pJhGFLK\nzc3N0Wg0GAwKM8HKykoQBDdu3Njf32eMFf3xyWRSXKiePz9YW1sudr44jj3Pe/bs2TvvvPMv/sW/\n4JyfnZ1Vq9Vms6m1NgyzQG4JIQodv9lsPX/+PEwi02ReuQQhRBg2mvVGo3F5ebm6uiqEyJO0Vq5l\nKh33Riud1Yv9gwW7vLG2orJsPpsFszkQUmtduBKp7TCRTdM8kOp8Mpr6c2LRuT9dXF7+5jf/8J23\n7kIIzy9OWytLi4udyfQwTZI0A0xrAhEkNNMySRIAIABAIaiVklrlXHIhhJLFHY9QAgHkUkgpEdDE\nNBKppFYS6KuCTakiaUAj+DJ0SgFAIIIIYozq9YYmMEUgxjAWKk/jOAiSNJznmVXyqtWqr6VUGVe8\nYjlCI6XUfOrfuHHjrbfeevr0abfb39jY8H3/6Oik3W4q1SruAtPptNVqSSkH43Gn2bocDFSSeYZ9\nc2t7NJ22yhUIoRQyjmPXdQ2HBVH4+iuvfvjgcwSA1vro6Li46lerMSUGgkRr3Wy279+/X6vVlpdX\np9O567rlcqk/OoOosrDQlkpwkZc8t9vtIkRarZbvhwiS1dW1k+MLSo3C6N3vDcuV0tLSEqX04OAA\nANBsNjHGxWTw0tJSq9Xa29vjnLuuq5SqVqu+7+d5XiqVSm4ZQjidTn0/8Lwy5xxCPBqNMMbDwbhS\nqdhll0Jacssz4Rf0GtM0i0HkJElsx2SMIaQIIRBCy7KARsfHxwAgjDFjzDTN4ltxnLhuqVwuK6XT\nNMGIxnGqJJBSe15FIzkdjTUhZH1jFWN8586dzz77rFqtPnz4cGVlyTDo6enpzs4OpcZgMEqSrFwu\nNxqNg4ODdntBKTWZTLIsKzx2YRgeHBzkeZ5lmZTy7Owsz/MkSYqKZTweh2H4/Pn+9evXRqPRr/zK\nrzx69KjIrb527drdu3chhOfn561WK8/zg4PDZrM2HA47nU4URUtLK+PxuBifu3Xzzt7eHiFsbW1t\nMBhMJhPbdkolV8p8eWnBq9Qwxo1GzXU9g5lra2urS6vf+973fukXfvneT+61Gk3OuT+cLrUXf/3r\nP5uE0azfH5yf8TSTWZLEcZblQoOYC87w0tLSXu/SoBQoDZQolUqfffbwlZtrS8sLBz/Yv3btmuG5\nWZYlSTLns7awEUJScKQ0hDpJU0qZBkBqUCj4XEmplIZA6qusDASgKkKrNVAAciUFULpAuAKgEcRa\nS60wwAACiCACEGNMEcYYUwjSWUAYARahhHk261SqRtVTJfve00dK8iQOLduUGScMZyoXSrx6+9W7\nr736R3/0R//qX/62W7J93x8Oh6+99sre3t6NGzeiKDo5OUniTAo9Go0QQlIB16sc7D5fbnXiND8+\nPXvt+p0wTrBGWkgh5Hzul0puEsUE4TzPEcRCSARJnqWFYjnLwmvXrjWb7SdPnhmGZVlOmuStZsc0\nTWaglZUlQmHxWFerVXNj84MPfnRyfHDz5u1Go3Xvk88JNMpeFSr85MnT5eVlx3EcuxSFiVIRggRC\nmCa5VnBlee3s7CzPBASYURNoFIVJnudHhyeFmpKmaRwnpmnatr20tNLt9l3XAxqFYSi1rtebxdMb\nB+FoNJrNfEIIxiTPhNZQCBEEAYDKca7yd/v9vgaSEkMp0Gw0MaJpktu2vbKy0mq1igCdUskJgmg+\n913X9eehlIpQmCGpgEqivF5vE8/zJpPJ8+fPC3z/rVu3MIaEkHfffffjjz9OkqSIS/Z9HwCws7Mj\npS6Xy4WEsL29fXp6ev369WfPntXr9TzPu93uwcHBVVcBISnlfD7vdDqc88KO/u1vf3tlZaVUKr39\n9tsQwmazeXx8fHJyIqV0XbfdbgFwlfTV6XS63S7GeHNzUyn14Y8++sIXvnB6ev7s2bOtra08zwsI\n++npcRxXkiyzbdu23ePjQ38eKaUuTi8WOp3ZeJZEcf1anWI8m0yZ1L/57/67Z/v7wWw2H0+yIBxc\nXkCgmu2m65X9NAaY1jvtYD7P0jTwZ3CAcp3fubXz/jtfzNL07t27iqKI50dHR23XIYpiQLjIh+M5\nhYh5DjMNLhUAQCiVC5FrqQGAGBGMEdBFsYExJggDCGXOk0RwBNRLjnIxOyKVBpACgiBECFGESREF\nDBGC2jNdyHCKQQyQlsDUyKUEO87Pf+NnLybD814fUzIbTk3bSMJIExSG4ePHj7Ms29raOj09pZSu\nrq4Swt54442Dg6NOpxOGYeFmXF5ZnM+ClbXKvU8fbK2sKQlG4ykSajAcV13Hs5FtG5ZpjgdDzkWB\nZH3ztTf+vz/+gU5luVwtotERYnme7OzcODo82dq81uv1JuM5Qqigzj59dtBs261O7fR0lCTZaDRa\nWVm1TOeVV17r90ZKYkKYZTqj0cTzyvVa8+LiYnl5iVI6nwdScq2h70+TJKtWq2dnF2+99RYA6Ozs\npNcbFMHjtVoNY5xlmVKaEFKr1Qghvh/OZkeWZSkJ8jyvVusFUmE2m9Xr9eJ2qrWO42RpcUXwCWOm\n1rpWq8VxHMOEENjuNIuwSggh53GhcRQO0cPDwyJxu/inAj/JMt5quVmWYawdx7ocXCgloih3rQoa\nj4fT6TiOw7W1FcexlpcXHz9+rLX+zne+s7297TilNM0vL3uzma813Ns7yPN0f//5o0f7lYo3nY7v\n3Lm1uNh57bVXJpPR3t7u5eV5u910XbtWq1Qq3mg02N7eFCKv1SqffPITpcStWzeePHl07drW4eH+\nBx/84OHD+w8f3r92bSvLEqXE+voqY6yohsvlsmVZtVrt4cOHBwcHb775JmPsy1/+8t27d6fTacFj\nllJub20xxoqro9SKmUZ7obO4uNjpdAzD6F5cXt/ZOdh9/vTzh08+f/A3/tpfPzs+8UfjcW+Qxkkw\n97VUCJIsycIwdpxSEATPnz+/ffNW9/LSMU3HNNfW1qIo4lwKrm7euXt6fq4ByLIsThOIMGE0l8Lx\nyk65EnIe5qmGQEIttYZXofQYvAjXBsVFUWuplVSKayWvMu4RhBgBjBWiCluQlZBZxlYZmlVteJK6\nHJcyZKfASgGNJU0VjkWN2DQHIOIWxD/+/g9P9w8//vFHUMu1tRXmGAIr7DBsGRpBmQuTGqP+4PVX\nXuUJf/705Df/wr9HIHnl9p3Dvf1WvWVQutBuY4Bd1/P9cHVjEyIiNZgFYX8wGg7H81mQpqlp2qcn\n50IrrXWr1Z7MprVmI0vyhdaCbdgriys/96d/bnN1c3Vx9Tv/y3d2nzwTGZe5aNaa48E4T/LnT5+3\nWwtxlB7sHXpu2XO9zfVtx/QYsY4OTpr1DiMWw1YcprZpR0EchWGz3sqyfDSaKKV9PxRC3r59d2lp\nOQii6XT29Onuo0ePHz9+muecMdN1S0mSZlmOAeIpxwATSNIoJYDUvFqj0sjiLJyHJjVQcdPgMosT\nKaXnVRDChfpiGFaR7IkxXVlZqdVqBeF7YWEBIbS2tl5o3UWkRsktp0n+5PGzNMnPTi/2nh/M50EU\nJo8fPT09OX/08Mn+3rFnV5EyRAqjeY4uLi6Wl5eDIIAQPn78+PT0tGBCrq6uFpfAa9eulcvl09PZ\ny8Th7e3ttbXm06dPi3HMy8vLBw8ePH/+vDjQ+v0+AGBhYaHZbNZqtcFgcOfOnb29vZs3b2qt//E/\n/udf+cpXDg8PLy8vy+Vy0TbodrutVosQsrS0tLa25nneeDwOguBlgkfh6ZzNZkmS9Hq9wpFdgC6X\nlpZKpRJU0DTtJElmU7/f74dhWCzIuT89PzqBUjKEiIYly5RxnPihPxn7k2kchpIrgqhp2Hmez2Yz\nAqnJDAQgVBJoPRz0/OnMoObTp7uVSiVNcsZM03a8Sm1377jWbBiOowgO8gwwYrmu4TgCaKn1S4Wj\nAIm/DNaAEGoENYLF+oIIFVaaFwMiGimNpMZSW4jYiFqImogYCkIuVZrzKNNcAq6xRnmU8TQTnE8H\nE5XJd956e3lxaTabnZychFGEMKYGK1XKec5HoxGE0DDM4XBo23ajXvrmN795dnZ2cHBULpdN09QK\nzmazNE3DMMxzQSCOopgSw/dDAND+/v7JyVkUJsRgtuucnl1wISzbRggNBgMI4enJOQR4NvUfPnhy\nenp2eHhUqzXzXEwmszQReSYIZgiSslcv2W6j0arXG3kuEWSBnxwdnfa6Y4LtwE+SOFdKx3Ha7w+n\n02lBMWWMGYbpOI7nlSmlSZLOZjPfL5A5LI5jzoXjOFKqIAgMyvZ3903TXl1dLeourSAAYD4PpNSG\nYViWXeBGMcYF6sYwzDRN4zgO/Ggymb186oqbZJ7nhmEpCcIwDsNoOp02m82iXOx2u9PptGjt5LmY\nzfwgiOI4LpXKnKsoSuv1Fufq0cPdfm8CJPHnCanVKlmW+P7s6OhgY2Ot8BEfHh62Wp0kySil9+7d\ns0zn2vZCGMS3b992Xfvjjz8q7OhayzSN19ZWLMsoclbH42EUBYZBu90LKaXjOIPB4I/+6NuVive9\n7/3EdcE777zywx9+P8uynZ3t09PT4+PDa9eu7e/vz+fzer1+cnLU6Szu7e212+1iMHJ7e/v4+PjG\njRvdbhchdHl5WXTSJ5NJtVqdTCY8l3kmKMXt9gKAkJBwNptjiOI45mmWJbEQYKnZzqPkF77xjSwI\nZoPhpN+bjcaJHyouMNQYQqiRa7mjyFeUxnHKswxq4JiGiPlsMrcNs98dPEKPyq1Wt9u/9frrhzO/\n3m5Cwxh3J3XHcZmb8GyaJLZraYIK/DpQsNB4r4LaECowBwpopaSWSkjBlc6F1hBBDQiACCBY+BUg\nCvyIYWIxw6CMWMRCSGuttYzSBBqY2SwFAlFmG+iwe8aYqTVEiPjzkJiW67q1Wk1K2ag2Jv0RApgR\ngjHOkowSUnLdTz/5rNNpnZ2cFr2TZrNpUsufBqfnF4CwqlsN5qEFmeDy8eOnr926k/KcGuZs6pcq\n5SCOZoFvuDY2jPFkFoYxgcQyrCzJQj/2PK/TWmg3O5PRNIlSqFGxnaVxRgjNMn456G5sLk/GPudC\nK1z2mhDgs7NztuaMR/50OnVd13GcklcqOAsIYyllqVSktSIIsOt4S4vUtgvGY2qZjuACI1pyy74f\neraXxhlQEGNsGbYUGgBgGU4URFprqNF86hdyIFBQ5JKZKIpiCLBpkqLlGMdpkiSEoCSJTIvZtsU5\nFzJnjBVeDdexOOez2cw0bUJImubT6YxSqpQWQnpeOY4yy7K+8IUvRFHEMzEej/u93sVpjywtL3a7\n3WLSeX19vTg0pJS2bc/n8/fee+/Zs2c8l1tbW8VxcXl5vr29rbUuBhE9z+t2u/P5nBACAOh0Oq1W\nq5i8jKIIAFDEao1Go9u311qt1uPHjwkhjUbj2bNnOzs7T58+PTk5KerglZWV/f39LDtZW1vr9XqO\n41QqtbOzs/fee8+yrGajfXh4uLW19fDhwyKsudfr1+v1fn8glDQM4XpenCYFQKLoRUZRVC6VXGaW\nLBub1v/hf/8fnu4+H55fzPrDaOZrpQiAECDOeZIkJoZaKg54FAQmM2qVCrVtaplBzj2vzOfh558/\nbC4vTsYBVzqME7dceX5wshShillmrp1ECCFoVyvRZAKVBvAqOEpfOdoAphQAIK8S45RQUmqlAHBd\nVwEINcAaFGOTRZFGLRMAkAOQaSGylHNeaJiO4wCAAAQTKYRtIMsYBj43wMMnTzOe2yWvXC4bhiE4\n7/f7WMJhr++55fl8WuR4+fOAi5wxVljjbdtOksz3/SLcY3l5eTj2Az8SuZRSK64IpvOZv76wjBGd\nzv3V1WUNQW8wZLbJbOvw7KTkloFln59fuq4rZT4YjOr1+u7urmU60+mUUiqlwpjEcWLbMJiHtuEK\nDqeT8Pr1m4xa/z++/jxItvS6D8S+7e55c63MWl69pVc00ARAYqNEkENSokBSKy1R9MCgTHEw0lCk\nFeOxPZaloGU5KIkehUWLIiUotDjGQ5EWBI04pEwFxaEJNBcQbKCBRqPX1/3WerXnnjfv+i3+45f3\nq1v1ms5AIKrrZWXe+92z/s7vnHN2NiaGve+933x8dEII6bT72iiUj6NWEASB63lZlmGuVpIkR0dH\n6/VaStnr9bAIrizLwWCQJMl8Ph9ubalCrdfr9XrteR5njtaaEIrIUGtdVaooCq1IkVeUUl7wvtfL\n8xwuNM9LTIDlnHuer5RS0kipVqu149J2u8sYu/POvd3d3SiKXNf1vMAYE0UtQigUtSrVfLZcrVZF\nUd2//9Ao/S0f/JBW6vx0nKymotvttlqto6OT0fbwG9/4xnQ6bbXaH/vYx95883a/339w/2C5SJ5/\n/vn79+8zJlzX+chHPnL79puMsW/+5m9+++23tdYYtlOWZafTuXnzpuM4d+/edV0X9TohxJ07d7Aq\nbr1ex3Ecx/HZ2dlTTz0lpfymb/qmXq8HfBJhMSQgiqLlctnp9LBlT0q5TlZSyt///d8nhHied3R0\n9C3f8iHf948PT7Qh6yRL83K2mG8Nh34QMeFwoydHp8HWSFXl+fzoE3/sjw867RfeflsvVtlqKYvc\n4ZwxxxgjS1Vm5ToviO9oLZVSrV6r3+/O0sTxfVeTVhivVkUctR89eNTtd26//U5RKpJWJ2n2TTfe\nly3y08XC4Zx43ixN+90ewwqMersvXst1QghhlBFClDGUc0apS5lwHGOoMQbzsypqFNWUmEpLxYim\nRHNKPEa4TzljjI2zQjNNuFw7TMS+6IW5y1nL/9obr2uHcuE4wmt50apc5Yu0CNPlfCFLpZRyHEcI\nBlKBVBVjrNcbGKMYY0qZIAgfPXq0txdd2752dHQSuIHvuLNCPvvUs0f37rHn2XQxH/Q6WZGv07TV\n7eRSnU3OXn3zdtzpnMyXWVZ0Or1Wqz0+nxZ5lWUZafEsyxnjVaU4d7TOtSZloZbr5f61G6Ebz8er\n5eJ0PJ70e1tx0L91/cmHDx+enZ4oXY1Gw04rZpyMZ1PH9ZFBYQl5VVVSaqXMc8+9T2v9Ld/y4cVi\n8dJLL6VpvrU1Wi1XW72t3e0dZEBAIzFLi1JelqVWWOjlYMqLUgrBMzEsy7KqUkEQGU2wjdFxHGNU\nmqZaq7gdCCFAH1mv1wCP0zTFvrQgCKaTOaU0DFt5nm9tjSjl77xzN45ab771OlFyezjgVIn79+/f\nvHlzNNr66Ec/WpXyF37hF4fD7VdfffUDH/jmr3/96+2422q1Hjx4oLXe398zRv3mb/7mt33bH0H6\nVFUV8IPZbPapT33qd3/3d7/61a/u7u4CigTKfOPGDQzBZYzt7e31+/0gCDB6CWU6qFYURS+//PKP\n/MiP/PZv/+6DBw8+9rGPvfTSS0qp0Wj08ssv93q9D33LR87OzgaDwXQ6Rap2eHjY723lWek4Dhde\nURWy0mA5VGU56PQC5nSjSCWZ04r+/J/906+8/HLgOquq1FIRrbUhul5wRQgJgqDiJMnWZV6sz860\nVEWaeVwsZsvVIh3FfUd4o+HOOFscH59GQcgMSbLs+Pz8phNzxrQ2q6JUVZEvFkJtlI00X3wTRqra\n31FGGeNVURioEWOUMSq44Uwx6kbtVJZJka3KLCmLTFWSGGZoO4gZYUVZkMjjpIocqkOfhT5VZeD7\nmhgtNSNs2OlV27vXdq9Nz2bJej0YDNCwvLOzE4bh7du3t3dGlNI8T4MgCMOw3+8/fOjO5/NBL+x3\n+8VqPZ8uQi+8ffudP/u93zsc9DGv+mtf+7oXRteu779z9+7v/8EXtecvtKkq+Z73vOfRo0dRGAMo\nppSiuiOltn16RV4JhxnNd3f3fa/zzjt3ilxe27vpON69uw+NMZSRra2RVLnrutPpNIz8VqvVitqz\nxVwpVRQFth+3Wi1K6Ze+9KW9vb1Hjx7N53OUvNAp5nkeBuDmea6UzvNcKZPnOfSHMQEtwihLQrTW\n2vd93wuhw57nVWVljGl3Ys9z8jwvynVR5GUh12x9fn6epQXcwPb2drvd7na7juO6rht8U2SM6XR6\nUsrBYBhF0dnp+fZoePfOW1v9LqiLYnt7eHZ2Aqbik08+6Ti82+3ev3//9ddfx9UvFovVaj0ajV59\n9dVOJ37yyVuHR4/G4/Hzzz9/enZKqPnIRz4y2h6+/sZrq2Q5HG194IPvPzk5eeONN+I4/vbv+Pib\nb76ZF1l/0HNdV2l5++23Tk/PP/axj1RVFYS+H3iHR49Q02t34hdffBH15bt37966dcsYeu/evSAI\nsBxjOBwmSbq/v4/x/XHcPjsdF0WlNYm9UBMSRXEQRJ7nrZNkMpnEbpAslqysnrj1ZOC7v/P//bxT\nSVdqahRE22BhoTRKGV+4Z5PztcoJIQf3HwghhqOBEd54mSeLhMYsz8vdm9eP7kxY4BWlzJP19Z2d\nl7/6Wu89H+gKHx2Wjid4ngvNoWnosAasn2SpVTZMX+WcU6IFD8ym/EYNoxWjkpqK6LfefDUjak1k\nTlTBiXG48YQrhFlkQoikzCPdlfm8Q/OpKkPj7Fzbj+O4LApdFuv5UjsuKaTJS991y7LstjtSyjIv\ntDTj8/MwCGRZOVzcunGTUpokSZHlH3z/N+d5ef/e8Wi4XcxXabIOmAhc77v+s+88OjxwKB1Ppw8O\nDp546tbRycnLr3z94aPD3u5uqqjwgk7cvZvf67XdbJ1lWXb46LDT6fluIKUudCmlJJoWRUmpFwSt\nL7/4NaMZIXxnZ38+W4zPz1AQ55xSalzX29u7Np9PijIzWpXFdDpfQD1839/e3gEdjFI6Ho8JId0u\nm81mnU7cbjv37ty9de3Wo4cHq9UqjuOoFa3Xa1XJ0A/SNHeE63vharVihIZ+EMdxKYvx9NwP3CiK\nylK6ro/JJVrr09PTra0+Bubt7Gz3+93tnWFVVYK7ZVlifpbWRkqJNZpRFGOXkxDCdTzP87qdgeuw\n4TDWMp/P51HLFa+++nqSJNf29lfL5CtffmlnZ+ett94qimqdFO12++HDR889996vfvVrhNAPfOCD\nq9VyvhgLQZaLVZGXnhuk60IrSom4f+8gSdKzs7ODraM4jne2r1FKW1FnMpkwId773ve+/fbbDx8+\n/PCHP3z3zr17d+87jrOzszOdLNbr9Y3rTxw+OhmNRqvVmnMnz5P1eh3HnUcHh8kqjcL46aduHB2d\nYD/9eDwGa7ssJ+l63QrCPC9UUWZ5VsoyT4tWFDA/NGmxPdjKZsvhdvuPfcd360LtDrbPHjysitIY\ng6ng4PVoKauqevTo0TsHDzrb/d7+Tnlwb7S367eC2TqjXswJn52PO73udDrtdbqJLLSpKCF/5s//\nhX938M+OdP724aOdnR3lMFXIDuOCEoJJxhS5G6WUsnYMiFIpVSlpjOHMoZzJSimiZaUKWRVVmZZF\nJstcSxZ6mSEZoSXjJSfEFdQROedGaM/hy0ozwdZlISrlBVEYtA8Pj29edwLHXZfFcrbKOEtXRZZW\ngR/Fvf5oZ6eqqmvXb5yfn8+Xiz/2x//ErVu37tx5O47j8XicrHOpyM7u9le/8jXOxORsoqTs9wd3\n33r7p3/qpw5OTxerNAq8krLW1sDtdP/Hz/7Ser3evfnkg+Njp9NbjKdGv31tb//555//jd/4jTju\ngDzV6XQwJ1wp5bqukqXneZUsFvMkiuIsS4JgM5K01WpVVRFFkee7WbZK03Q8nvq+u7+/P5kvQj/w\nXN8QzSgv82I+ma/TZGd7lxhDCVOVJIqUeRF64XPPvOfo6Ag0eq01cHUpyzRNCSFRFMTtKFkvGSdR\nFA62elmWvf8Dz3e63V6nnxV5vzvo9LqT87Hre4xQP/SW80UUh2HgpXnaigJtjCs8TYwrHEOpLCs/\nDPrdARdClmq1Tqgho53d5XxRympvZ+/4+JHntZLlFIQB+r6PDnZ2dqIorqrqwYOD2WzW7fQp5VIq\n3/dXy/Xzzz+/XCZZlnle8OjR/W4vRgtqURRlKRHadTqdNM1MvTCeUTEYDO7fv0+ZjnteVqx3Rrvb\n29tHR8f9fp8Q5gjv6NEj3wuX81W3260quVqtRqOd6XS8TFaMsSzL+v0+hhxhf0Kv1/N9v9Pp3Llz\nJ251sixrt9uz6dTRjuM4nudRxvKyKGTlO27cCs+PTr7vj33P3dferFbpv/zH/+Tgzp23Xnn9D37n\nhb1Bd9jrckqFEMzwZbJKknS2Wn704390WeXKdd45Ovi1L/zm4NpO3Ov67TiKO1/5yleJ0lLK7qC/\nWM2lVltbW+vF6iPv/+B6Mr/75u39nd2zs7Mgbp2dnIziQeiFVVWVRUEI0VorqTnnlHJlNPYtbnI5\nwzTVzBVFVSmlOOde4GN5jdSKMqYY2VQRGDH1aGTOGAbDPP9N38QccXh8lOU5KiiUUqN1URRGaYdT\nzhxCdW+4RTlDA9S1a9e+9rWv+b4/Ho9Ho5GUFcoqjNX8I9dPF+t2HCdJoiu5Wiw/+cn/5enJSRRF\ncRiNx+d379598OgAVAfOeWUUFZ4iBsR0xpjjOJRy/JxlGXJFNEorpQwhrusaij2qhlIqhOu6LiaK\nl2UpZck5Z4xQSl3X9QNXMKcs8zTN0zQpS0mpcV3fcbgxNAz9KIo5p0oZzmkUxWHoX9vdi1qh53nI\nZcCoUlJXVYXb3AwsY0wIwRhzHI9Q7rmu63mUkLKqKCHCcYgxaKFmnAtOCaNEG2W0QE1Um0ppLZUm\nRlWylBUjNCtyo7RwPGJMUZbEGMfhZZUZo46OjsqyFHkulaJFUWVpIbi7Pdr1/fDk5JRSGgatMGyd\nnY3TNPX9kBCSZcXTzzwZBP7JyWlZquvXb0RRSyuys33tnXfugqKVZZnWZLXKGHNvPXWj1eavv/mK\noQSbpSaTmdE0y4p+p19VVZaVUaQ581xHEcnKggRuywvcMGiBEtrpdMKg1WmXGDCmFel1B8hKp9Np\nmVeGmCovyrIMoyjwfGpIslxNzs77cefVV15zpZmdT7e39/S6/L3f/J1bN57QxZpSKoRYrVau429t\nbRE+P1vMNCX7N66fLOYnZ6eG0NU6/dC3/dG0KqpSdTrxYrHgjC8WM845Iablh0yTe0eP9vf3/+zH\nf/jf/Jt/47TdhUxNL54LnrusYqIginNOKVXScM6zLCeEaUaMYITUW3+pLrUioQsErKinjxjDN7PH\nGbWBKPRNM6O1dsOokMrjglPBCTfSMJcZbbQyRhGtSUWo1EppHSuzXicf/ehH33nnnUqZD3/0W199\n9dWt0Q4TwhUuchtjlOOQrEgnxbwXxWj9CsNwsDNapOnLr79+fn7e7/fzPM+yTGstwohwXipVSkNk\niVIh5w6Wh6DTBFi053mwAsVmVpeuqsr1PeiqMYZSY4wyhlaVKoq8KAoMF4PSuoIGbX9ntD0ajfr9\nfhiGlFKMwBD1CxaNEMI5F4JhkheW4wCABa8AyfwmN7Y/EMa5Y8zG3CilYAU457ha2YC4UDLVWuJL\nN6vXta6qCmA+slNAAPgnQkgY+lwwWRmljAiDVlWqIk+0JmHYCsNQCGc2m29vbx8fH2tFqqowxpRl\nGQTbYGZ96EMfwkmdnp5KKWWl33777fUaGw9cKTUOK8uyo6Oj686W1kRro5SOo7DbJbKQutLYAISW\nIU6okQqIi5RlUZWtVgsPgFJOKd/Z2ZtMJoQwrcsoiqVccO6AnEkrgzhBae0FPvZiV1JWSk7ns0Cz\nMIq+/vWXt+LuH/22b/vai7/f2uq8/JUvU0P6/X6v567SdZbnTz79lCb09jt3RadVav2Bb/7g8Xxy\ndHKsiDl4eJhlBaW82+0sFgvHcabTKbabP/vss2+++ebBwSHnTq83WC6Xucyp4IRRQwnljAlOKdVm\nw43cKA+hxLDNKB9GqaECnplS+D2Igq2DbwiV9UuqDfwFuUcTIITbvg3nTwihSt2+ffu93/T8f/yP\n/3Fvb48xdnx8fOvWrXfeeQd9iXg/Ajml1FqvqqoyWmN2gNb63r17SZKglpNlGVByfJHjYLGzh4Yg\nCB8UMk1TABIQ3yiKhsMh5nnG7TYgGVAg4MEgLfBF+Hz8E+ec0cYsFsawCchxHNCO7e9r+Zbb29va\nKBwLpRQaAm3H8ZI6RtBaG020JsCzQKaDQDLGoDngMFqXSAiRsrSfjFuGsuGL8BusAcE/SSl931XK\naGXod3zvB9frNRj3aCT1fT9JkvV6fXBwcOP6rX6/77rueDzGSLOT06MnnniCc95ut2/fvq21DoPW\n4eHh9vYu53wymRFCAPGv1+s4Dqgj4244Go1aUXs+m3U7/eNHx5PJRClDKRPM2d7eLtPy7OxMCDfP\n86AVzJeL7e1tQshqtcLVb29vT6dTkEqh+fCiDhfZMmUoalGCVWbgEy7H02GvTwt5Y7jzsQ98y4/+\nr354e7h999VX/+CF3xofP+r3+6enp+fn53Gro4gZ7e/t3bpFAvdrb72RE7V149r/53/+9Wff//yd\nu/eLrLScA7QAa63b7fZTTz2FJg7O+eHh4Xw+393dHZ+O4yj2Hb+qFJYYKaXyrDTGKHVhI4nZaIVm\nWjgOczgSG+xVgpDhRqwlJvWkLcoMuh+sDGHShjEG8dgmYIP0KOV4Yr5a3rp1C23OnU7n5Zdfvnnz\n5tHREd5cgxO8qqoizXwmBOe7u7sQqVarFYbhjRs3QBU6OTnJ8xyLoAghfhB4YQQwczQa7e3tYTgN\nDD+MBe7UBqsIeuHzEWJ4WGW0WdTmAvyA3GutW1EAIYZDs21+uHi7e8QYI6VUqnIcJ8tTpRSuHzpm\nSXNWfzY/SY1xadZN4VRx5rgGawIQdgrBYAuklPaj8DMeIhJUMJyyLGOMhWEIbqdQlSaacio4FVUh\ni6IgmhJNfdfrd3uOYMdHj8BJ6XXbVVWFfvDO7beVUs8991xVyCzLykwRTfM0a7fbRumdnZ135ndk\nIZlh+/s35sl56Pt5WixmjybjmbpGjTGDwXC1WCmlPOGaylSVAtV6452lMkoLIQTjWqoyL5LlSksl\ny4pH7PTsNAgCfF1RFFIrWAFNCa2qSklonR+FeVlGrnf/0YFg/I/cfeeN2299/EMffvMbvSJdu34Y\nxR0viOJ293wyrgxJ8ny5nM1XyRe/9hXeCpZltvjKV4XjiTq6QF8sNjbMZrMXX3wRkx0+//nPSymf\ne+45VF10sAlpLBW7zme41bXaXTEiiOO6lZZWtiCRTXG8EpaUZYGIoNVqZVkmpUSfrtYazqosy/V6\nvQkTlHrm2tOtVuvll77a7Xbx5uFw2O90n37iSc45mtnhZ3zfj8KQEZolG5uitV4ul1VV+b6/u7e3\ns7uL+TlQJ9/32+320ekZDAEUAJVSpNzIi6A/CL2MMVvDIUQTp7Qh2dQvQPxNiUdlHO4ODqcoCvh/\nfKBSCg4Eyqa1zvJUaw3jAn1APGm/wj4UrUwYtoyh+Cd72tBVq0iEkLJEMsmiKICmQY3t0wHF3Dpz\n/LmUMo47rusLXiilxHyWxHEc+LEQIpOZ4AZtCK7r4nK3t0f4rCxLl8slWFSA73w/DMNwtVz3+/2D\ng4Nut4tKn+u6zzzzDKxC6PmT8SyO4yRJut3+eDx1GPf9gFKaZUUmizwrKeUYx1AURZYVmFACth66\n9JIkQYqvlAI5AIa8qqre1qCqqizPS1nBAhljVCWjKGLacMqn2frw7OTXf+s33/vMs/L3Ms8P0jw7\nOjkWjnP9+k3huTxLwjhWnFJHvHb7TS8KjSsWk/F23F7nmSpKRijEJY5jJP3L5RLTu37xF//9T/zE\nf/Frv/Zry+Wy1Wp1Oh0rRrbOBk+ltbExIWfORs64MYRAXEDJsxaUNmYh25CSEILxw0qpb/u2b0PM\ns7W1pbUGywkG1Za2CCGaqHang95CKBuW/qzXa+z7C8MQp1oUhee6rTAS8UZJMIUKK3Ydx8E70R1j\njEEs1+71cYWMMfgobCdEXFqWJS4SN4UuEFw/TgNdnlmWRVHEGIOk4eLxs9ES8RgWakN5KKXI+uyf\nQNgIIY7DpapwpBaGsXGpNVsbl0hYkiSUcqts8IFQZmsBLa2EUloUGWIrKBsiRty+1X/wWiilSpnR\nMHIdl/OEGCaKvPTcilEuPMcRStfE2eFwOJmQ8Xh87dpenudKV71+x/OGjuOu11m7HZ2dnWnF8PBc\n1+31BpTydJ2dHJ9itsxwuH02OVksVtqQXrvX72xFUXTv3v3T4xNjTL/TJ5JQSrMs41TEcUwpK2mJ\nAreUEotF8rz0fR/ltaqqiqKKothxvDAknDtx3PG9IEnX6zTLitJxHMfzBeeM8nWW9dvdNFnv7O8z\nZe4cPPzQhz9y//iRk2Yf/aPfdjY+f+mll96+dy/sxOsin+b5073n/uBrXzNceL4bb/WMFxycHPX7\n/SBsE2OWyyXnTprmlHLfD13XXy6Xruv/o3/03/3bf/tvP/Wpv/T1r3/99u3b1/euzSYz7jrEMLOJ\nU7SmhAthlIalF0IwKuqcQVdSaqORzW/+tZGhmcYLeovR1uv1+tlnn0XENRgM0jRF9ILYyaoKIWSZ\nLCilg34fq3HjOJ7NZu12+9bNm9YGQzQBaRZZ3gpCyDRSL/QEwxtA6yB5+CdBKP4cbAwkbGiTw+QV\n6ANSPiRmkDHYHfxVnuez6RTJGN4AyCHLMmMU/BKOxbpBeBXcL2msHymKglKqlSnLjeeBprVaLcGF\nvRhiNn+e5yX0xL5s5gaFxNussklZWvOHpwb9xPHaS4Ieog2HEGoMoZTRZ56/iQXE165dk7KcTqeu\n5xijijLrdDrn56c7O9tpmvb6neFw+OD+wac+9cM//dP/3cbvUQGLMhgMlsukqqqqlGEYbm1t3bt3\nbzjc9gMnr1ZhHOlKSqnW6/VoNDKK7O3t3X/nPsLZ1WqVLNeu62ptiqIoZelHoVIKpRKtNWYihGGI\nTarAkTFZJQzDdZoRQgpZ2QE7hBAjVVWULT9YTmd7w21VViovoyD4gT/xfTf7/aeu7d27d//k9LTT\n742nkzffuTNPVjefeer2/fvH88lktQo6cSpLNwp8308m81YUzWazra2ts7MzIHXwQsYY0OR2dnZ8\n33dd9847dwUVrSgymsJXFEUhJRhtzDouYhiy6kqV0mjON4/TyhNkscn5ssomHEYIGY/Hn/nMZzzP\nQ581BpLCpUDabILuBS5is263yzkfj8fGmDiOl8ulDYdgvDdRU1l143aapghSQPdJkgQeFQ4NWeLG\nh7se/hDuixACEiOlFLtsIbsW5rG4jnUXzSiUUmrdMvyDMaoZZ+JtkHsbOEAxYBGqqkBCiyIbnK3N\nu0Dnx1pgzrnjeEoZfK/Vf7wBB2iP3XotraVFRyilFu1E9Av8Birtum4UxYK7rutNJpOqqkS+zsMw\nTNfJbDyhzMwmk06nHUWB4eLeO3eefvrJIs3iMKqySlfy/OQ0WSQuc4kkXuAppWRRDofb3bhLFD04\nOOh1B3ErXkwXH3j+A48ePUpkqak8O7t348aNG9dvHR8dnR6fhW74jdNvGGMcx0uTTCnlCpdTLmWR\npmkUt4gyDhNVXmKySrfT3d+9NplM1svEYcLljiIqaoWO4yRpeu3a9fPz87yScdwRQhRFYaRyAt9z\nfFPJdrcvDXH9IAxaoe9/+ZWvr/aueZ5zPJsNru0VVcnCcJnntx8+eOvwwG21WODF7U5SFkxwZhjV\n9P3v/0ArjKIoAjwThiEwYtBrlsslngr6L995+04lKzwiqRVh1PU9rgyl1BGbsLyqKhhdQ/B7h9ed\nb5B+ZCAWBLOP2cZdCLoseglcHmASVPiilEfIMlkIIaqqQmsSBOvw8BD5IRwLbAc+0HNczJnCJ+jZ\nFNLvBj7QoOli7jgOdmLgIQI6gn+w4T2IvwC0kGVtyL7rlNRIJqVUlhu43BjjhJwxqitZlSVjmG9E\nDGP2TiHNtusKr00RBZQdxhzHqyqplOLc4ZwoZQhRwMkdx2WMGUM9j4JDjCou2ZQNBC4VTokxBsON\n2HVzGloTomExLVoDK4mc0F4S9FZr7QYuaglZlombN28WReZ5jtY6DNArmUipq1Lt7+/fuHHL993D\nw8MsS0+Oz4wh/+k//SdjTLfbxSieOI4ZY0VRHB8f7+/vz2fLxWIxHA611r7vr5LF/s3rjuNVpTk4\nOFzM5lprxY1SZr1et9vcd72qqpI0Afrc7/cPj4+4s4mmqqpCyxxuCWkDrXl3+JMkzaIoarfbzBFU\nG7C/l/NFukqIMZwyTzhhEMRhxJVYV8Wjs5PhyWCarlgeMMb8bue7v/97v6/1Fwhn1BGSkKTI1kWu\niTFccGqKLPecTXgG6cdDguXG4AqcOya4VHnFOdeaQCeRyfi+r5WxObdNxBkjwnO1VrCmNlojhIAu\nYx3dJgHTmjKKQ7h37x7MP3KqsiytB2ja47AVwJwj1LQrWoHR4U8gKwAGyrywkm1vmXO+XC4BEQFv\ngJZKKcOQQpmtm8KrqGv6OAdcYZqmRF1cnlWbTSrLuX3QuHdKqaYbCbYoPH2sHGK1Bd9r/5bUxTF7\nMnizjS0R9ekGao8bJ4QgZGtmfTXmWTbTaVIDrfbNSqnGNxJGBaWbQEBUZZ6uV5zz+WymVXtra2te\nlJxz4JP37z7Y3h5Ox7NOJ07TdHu4c3Zy3ooiahinQjAnjtqz2Xxcjr/pfe+/ffu2lPIHfuAHirz6\njd/4jdFoxKg4Oz2njBpFCKH9Tt8Ys16n63U66A2UUmmSGmMwPmg5n09ms1Y7JtoYpQk3XDCLZTmO\nMxqNWq0W7AQGwYetKCuqMGwJIaRWRmlKaVmWZZZvbW0JxrVSUkpBmee4xhiVZXK1vPnEE63JpJTV\neDw+mz7av3H95t6eF/hEcENZhxgiuOO5jvAoM0WWWuCY1CUd/IxJoIjllFLtdvujH/3ob/6n32SM\n+X4IqKAoiqKoiqIgZhNyND9Ha12WpZQVAEbrzazoNKUEzxselRDy6quvuq4LnZxMJq1Wyz775mty\nvoZMI85xXRdpCY6x/jrGCDXGGKWJy40mUiu4pgvYo5CL1dJxnCAIuCMIo6WsyrIEGxBxF0wSdBty\nDyWELELlPOFY82G1C5cNMbXijtvngttcqIlD4D+begsVAn/FqoeqSymwEfA3VjG01gDedKPHF3+I\n/Bm/sWgT3oPrhMeDp4ETszdlrSQhzPcUpVrKSspKlGXu+54QTlWVQggpq1arFcexUgpNMZw7mI6y\nWmWMUQxvRTvQYDDA/cdxfOfOHUxT/Q//4T8sF8ne3t53fdd3/cp/+NWH9x76kU8p9zxnezj0/SAI\nwmvXrjFCu91uv9sDhhYEgec4BqfDL1JhewRI6xEjjUYj4H6U8kpq4bmEEFmUgL+jKPIcFxwIRmlZ\nloIyIUSaptPJeSv0+nvb3Z2hUmq0Svqnp9dv3doaDvM8p5xV2lRSEsKYs0l8V6U0psDF0AYFgXOe\nJMlisYDsInwfDAa+75dlqZTRWmN0IeypI1yUKCilWm8wKynLJEsJMVaekAzDdVzJVTZGlG6k7e7d\nu91ut9frDQYDjCprKlvT9DaFYFPsprTpRmyy1HRlyEzq2IkYYwAbBEFgJRWmDZpsPTlKdrgF1Sjy\nQnxdLkyjTMwa9WK8H4pKaljfbHpxdfOmaN0raO/XOpNmXAclJ5slzNKeoVUYXFvT6dkXohUoFfQf\n7/e8jdd1XbcJwNjUl9QxP76xrHKt9XK5nC+moijyVhyu10kY+Zw5i8Wi3W4zxra2hmVZLperd96+\nRzAjud3f2dmhlNgDiuP2crnsdrvD4fDw8DiKIt8LAZHneX7t2vXrN28YY7zQ05Wm1ARBkOe50Xpn\nZ0eWFZ5oVVValpvTEcJ1fcdzLccnSZLVapXn+Xd+53cTQjDyYDgcxnGcpmme52WlNlJIKIwNp8xz\n3bIojNaKkLIsS0Ic7aRFnmbZqsiPp1NNDGOskJXibLxcHpye4uCkMuB8UkMYY4bqbrdd6YuKqo3L\nIYWw6KZ+LRaLJ55+6uHDh/P5EpGbMQajDilljHNpdFmUICdIKcHOEUiiPc91XZxJ09BYOGFz7HzD\n5FqtVkgqQIkCLmLDJyuaHjwkMcJxbWaoCDXGICmi2hippFJVVZWyKmVlY0uEFSjfjcdjAG5AvSFJ\nrutqaegFeLCJx6xvsc7T/n+AqRP1GdJGvV4rbZQmGi4W/6801fYEaAMUgU42fAiBSsCQ4RitsuGp\nWQ+GcNH+bGMNXZNCYGguDFz9LZTSyWSCuh+tCZb4EDu3+4rhQNZKqDZGiU987/eEoT+bLTA3d7lc\nxq2OUgqenHNeVWpra6sqFWNMG5kkS89zKaVpmm5v7+R5vrW1JaV87rn3LZfLKIwRnTuO02q1oyja\n2dsWniuLEg/p+PgwzzIp5c7ODrBd3/dDvw0eKghBmlyweDAKU9a7wjAu4ujoyHJbXce3CYasKtjU\nPMsEZQCdMFXCcd2qqnJVTadj7jt5nrfbbWUIF1wSs8pSY4zLBWOCcx54wuVYOGPSrCjVJkUGAgHD\nbAXLhkPIgra2tg4PDy3ySykN/BCZFFDBLMvAaGM1+UiIC/ei6hKthemuBIeEGCCxeMxY+QcqVvNt\n1gMzc5EjsUZ9HJrDa2IXImFNiayUFTL4IvwnckJTF/E45/DAeVrYANLmUfB4sCCQS/t7XntmCzBY\ncbdB2kXaQ4xjuDTaumL83t6d1UDr6ABU2GizGRzZb2weaRNMsh9C6sKgMab5+UDCLAJp3RouuBky\n2L89PT31PEcp7XmO+I6Pf5vnO1Wp0MOrlMmyIs/zQX9La00pX6+zKIqMppTSZL0kRHq+u1qtjDGB\nHzLGPC84PT1dr5Lz0zO+I27cuHF+NvE8jxI6Ho+lVsaYJEnSNIF5C/zIEd6Xv/zlMAxDz1dKPUiS\nPM+5oL7vM+Hao2yGCkmSQNChzMgljDGcO6bmzgi6STBkUZ4cHbu+RynFdFRgX0VVMNdRlKZlGXF2\ncnKilPLdIM/zVtTOSEH1ZhE2p0xrXaqCe26lN2VZ68GacQ4GWvi+r+rxZpBgaBpMjB3eanlVcBeM\nEcdxbDnNxjN8Q9K95KPwjayOgmwIh2Z2U4NyVug3PyhtoQUbDVrnA/VWdQmYuw6nRFkHzpjSuqwq\nqZQhhHGO3xhCHNf1fJ/UiV8Tk8DH2ijOij7+H9VeCwhZxWvKqK0rUM4oNVA20sjrrI2wz8L+fCWq\ntHoLe4G4kdacSVbXxE2dK9pAFDGL/UZ7/ZReBL1WHpRSAAVtimv12XF41Ao5E4Zo4XmB77nDrc7J\nycl0Oncc7+HDh1Upv/7yKzdu3Lp+/abjOGenY6SSUpWPHt3v9jppmvb7/YcPDiilAC0o5b7vv/zy\nV09OjoIgklIul0vf909OjhzPJZpWqnSF4/v+cr64c+fO1qA3m82O16msqbeEakNplhVe4EdB6Poe\np0xqpSopteKUJenac1zHc40xUisuZVGVRbYIwpAzVlUVdV3uOkab2WyG7mfuOkzrSsr1el1UZZ6n\njJOiKgmjnU7n8PBwvV6XhQx8Py9So4jWWlDmu57jcFMZVSraqMA2LauUErANqCSu6yZJYozZBAiz\nuda6SLOsLDzhVFXFCGHCCVyPCh64nhuELheKKKWkql8wlnb0LakTDBukUUpbbktrmWVZlRdlllNK\nq7wAP9g0inLGKGOYMapSWiqpNWFMUcpRf5ay9LyAUGMYV8RIQyqtOHccJqqyVNpobRijqNxSygmh\nmLdnDMXsFMaEMbTMy6YBapohMBNQyQABknPuMF4UBdXEsq6aAm31FjpAKeWCKaWkrijllBpCWFUV\nxlDOoS3KGGqMQuwGNbA63ARI8JnIMmwEsbEC2iCUsO4LEYfruq7rILC37GfGGGUXJVB7X9ajIiKz\nsSUhhHMGRlRVVfRf/IufPTs7abXaCHtA1ALO6/uhNbRJkqC8E8fBZDrGPbTb7TAMQZ/TynQ6HUvf\nBn0uyzKljB8GRpEkXcVRC0XYyWRiWQ4w5zZIIIxWUnqum2ZZVZZcCCWlHwRVWTLOjdau5xFj8qJw\nhNDGOELkRSE4B/aA00G1ZD6fb29vz2Yz4TiMMfCG41aIEKjT6axWK4Tg6CgNwxbOKPR8e3bC83Hv\no9EIFg4rrLD0GY36yL+NMUIwXUnXE7/yy/9TXlSL+Txut8uiiFptz3EJ44xQbISSShutldaEU9MI\n86w93pj2OkzC/zNCYj9khEqtbIw02h09+9x7GCOcc8KZ1rpSUqkKIXEramutq0pVVUEIo9QoZcoy\nF8I1RlHKCdFKmVqIOaEbTBwpRxRFcRxrrWezmV1q8cQTT+A9ZZFrVRG1yX+sE7aaA+wEJQeYfN14\nmcaEP7hW+wn2DdpIQgylDP8PH0kpKcvKGE0p45xxLozRUiopK1uEsOYJBtF6clbzeHCFW/0BXJnF\nvfHnls9ZP9mNP2yG69Y0WN1uAj+UUoZ00WzORBweHq/X6+l0Ceabfeph2Foul/gZLrXX6xGiAXQK\n7pRVkazWSimtTBRFSmqgx57vGk2UllqBw+aqShZFoaWy0S0mseL+IVucc9/3fd8vqhIGT0pZSam0\nLsvS1O1DUkqRZYQQPBsbgodhiFlx2hjHcZTWjuuGUUQZc1wXJUjP86qyNIpIVRmlVRh5jttuxY7j\n5CJfLpdaI8Gl3OWO5xBCGBOEsCiKjDF5nkPN2IbHvcB+Ahume54Xhj4jJE+zD37wgy+++OJTTz11\nAVhp5GNKVZsMkwvhMFZWhaw9A87f5ug2QLJSyChlhFFDVCU38Bqj6/X67OT0qWeeTNM0WSdaa8cT\ntm62WC0ZE0gXkZ9Ak/M8h3lFNF6U1aa7hHJKqeN4WsuqAsYtpSyVMlJKrbFyOtdaMiZkVeTJktIL\nnWm+ELLCxtGaptwM9pqiyRhrVuShElyA3a+Ukubyq9VqwbEAWEIexRgLAs8WG3TNOLGkE9rgWKHk\ngejAahevX8BXaY3EWA9s+5JII0O2LrQRbW4emS98+35RFAVcGeAUlGjRKQg6KeIBVG8nkwljhBLm\nOJ7W2hiKphZKmOM4VVkoRnzfpYLneaqUYQxkC4yTcjDL0vfDOO5QmtRuk1AqlVIIToiRRpGqkGVe\nVZUUQhhFiKZR0CqKgpFN2ZRTo5SihBV54TgOin5KKRQAmeCc8dCPVKU5FUTTNMk8z0vTNPQDpTZO\nxXX9OEb0z9I0F8KtpYFJqQkhrkuMMfP5/ODgABjU1tZWkiTT6RSLqUwNdllsgDGmNb1169Zrr72G\n1V51QeaC92AtGmUMJtxm2KbG9CyU38yFCCGaGEYpEA7uCIc7RVGcn58/8dQtC65oLVUlDSVKmSKv\n4O0R1EFjKaNGSU2MllxzppQq86woCmMoYh6tlNaqLCslhayqqio5F0YrJZWSVbJaSFlRyozRvhCC\nX5DlLdgAFojRmlHqCGFL1TbE0vWdy6pCKITpfpQQR4gaXOFxHBNi4HmCILC7LBCdgpRD6sKJEKKs\ncotbWGWz0L/VJet8Oq34il3DD0EQ2PpHM+jQjSIBbeSo4PTQy2m2MYaai58FEg+QTS3tEBnqJkil\nFCNWYHiAT3JuKOWe53ues1qtl8skCKKqkgCTOHeMIYj1jdHIizzf4czJ8zxd54SQLC3KKmdU+IFL\nDCvLDLtFKRNFUTAmMBeJMYYjQtMR545SFapYRVE5DgdAUpaS0hxRiTGUEEMIcxwnz8GrIGmaMibW\nSTYccEo1pagyOYQQzh1K6XqdMcYYE1KWSZIqVVHKoyg6PDzEAyaEzOdzCDQhZLVakRoLgbZkWbZe\nsm6n47ri9PS01Wph0fNiseCcC+7aB29sP1VV2aTNAtw2ubc6eaHMlEopPce1QQuwvqIo3nnnHc65\nYVQplSSlMYYJLoRYLFaeu6nCWbtrPx9wBec8CAL4CuxAUkoqVSmlHIcJwYXwfD9kjCDf831PKaY1\ncQRTZcH5hSO1AMN8PocrwxHB/7Ca1ItyIgJLvA2UQry/QfyFWdQWFLG1fpT7bGRkI1LH5davWmCD\n84tKt3VxG+smNyBNMxLWdYXa1GV0q0U1t/iqZ0Nnun3ZPDZwggvPhjoA2lgwrRG9DGADZlm2Xq9h\n7aB+G+K2IkqZspCMsapUSkvBlTakKmWapoK7QehxxrRWruvmWblcruK4Fbe6ruMXRZmmKWO8yCtK\nEWVxrYjWMl3nhLGqKl0XGbkxhlaVzLKCc1WWVauFPquKECalApSXplmWleCZxHGLMccY7bqUUoID\n3GDOlFHKq1IxzgR3GRNGU60Jo5QQtoGXmSOJLPIyy9ecOUKI9XIVuF4cRpxzI5WgTGoD/4AwbDM8\nb0NoVLPZLAz9t956yxgDhj7kBvaY0g3bC66pklLpTf3O1IChlSH74C1gQCnVRDPGhOuwqrRCQAjB\nWsAgCKxdd7hwhOMKh1FjNFAozhnRWsmq6vc69ZcSrSqttdGcGOV7jtHSGEoI15p4HihypigqLoRm\nhLuCEu0IppTxPKfV7XiuAH6wEXfHwck0Cb4WLkcTkPXhtvbV6XRsPNn08GEY2GKA/b2uieCEkA2p\npa6UVLJ414jAxiBXwlEQHvAe635VY1QM9NPqD2hoVpfs529tbV3RNLxUoS6UDQYJWAVOBETv6XQa\nx7GpS0kIvl3XNZo6juv7/mpVrbM10sfAjwghlHClynSdE5JLGcJPlmUVBKHn+YyxoiiyLPc8nzGO\n5ouqqqRUxsiyrHCIlDMcpef5uJM8L/K8EELleR4EYVVtYnq0Y7muu16bssyqSgQB2axH02Y+n+ua\njMM5ZwyBxKZVT7skSwvOpTGG+lwrEoahIzxCiNG0qqp0nRuTEUIwpRC0LFhoBNgodq3XaxxaLfea\nEp2mGicWhmGapru7u2VZBn4IT2Zbs6S86A4mjb7sK8/yir2k1AYmG7YX22ClHrwuHiXssdYa7U60\nxgDAiEcArBt1c/AkKKWj0RbWGNWVFe66Qin17LPvDcMQDSKEELCN4ygySgO7s7EZ/JIlallfR+vo\n13oY6/poDUiax+qKUl4M6rE/UEpt94D9HMgqnIdpFELw8jzPqlzz3onS0CUbz0PTPM+z7bw2RyCE\ntNtt++f22RFC8jx/XNmoIa7wLpQNFG9E0hjEB0UH2RckdxSUlVL13lSKmSKwShhxjpyyKEqldFVV\nRVFCNAkp4zh2HGe1Wq1W6ywrokghCKwDfWmxV6VMEARGaQzx3cRdVHDGi6xYzJeMcCA0vu+nSWYU\nGY0iwRxFNaeCEU40VZWWUs2ni6IoBoNBnueu6xpFkuW6KspVzR4yDQo5yuu4DGiC/U9GtO+7QeBR\nSmezyWxGCCEYfI1nI2VJqeN5HiKcssi01teuXXv06FEYEjw2XTc4lqXEgFqttTEXTApWU8BogwlF\nLgcq+E/DaCGrvMhLJTnnWklOqOM4q+Wy3W577Xar1RLOJvJhdSHB0thxnVrrVquF3+ANpmblMkZR\nSECHKK4K/gcboZHbgxcaRVFVVHY8ZtPSG6qw6Yowbp2DlLLTH1xE0UppJVVZwUERY4gtDVsFI8Ya\nDllVsizxaa0wxBdZ86SU4pRSrJU0xhjDKCWGwK/BozZf9oJRNQF31KaUpiZzNt/JGCuy3Fyuc+CC\nBePkcra28aXqAuvaMABRkD06OgLOa4zBSBn0Ix0cHHie1+/3i6JwnQBN6Hk9TAITkUejkcWdtNbr\n9RrWzvMCzF5PkqTb7cIzYN1pt9vFFhWrV4wxNGhX9diPKIpgR9HWget2XRfzzMVm/tmGSIWJAHAd\nYEv166ZJYwza4ZTa9CMZY9CERghZr9emZsFxzrGtqqoqz3eqPINXR3+NEAJDB6wKWb8E25yla6z5\nm81maZrv7OzgbFGrtOMu8Cx03bdGG0x2+4FW2RoSTA25VKSyD7uSEjOIRqMR45usBjtlXdcRTGii\nqaHCFa5wCSP4DSOMCcYI00Q73BGucARbJQmjVDiO0Zoy5jqOIUQrFYShI5gfBGVReL5HjHId7tDN\ntHXaAOKMMZZ6Ri5nnjY1Arxh4QpLiWx6HjxWezI22MNTgKVw6okJUMIsWzdhDCvoTWfetGLoFUIi\nUJsbZn2darRo4P0QJ9rA/fG6QpezNyKEY39J/5v/5q/N5/MwDC0JaDweIzDo9Xqu667X6zzPWV0z\n4cy1xUHcKi7r7OwMnVGozDDG0JnLa14c0CTHccCoAIViNptJKUFoxoaELFmbmtuWpil6HEG0BR5o\n6qZ0CPrOzs75+Tl26CB9QhC/Xq9pzUk19YygoiikUVBvXCropDC6NhRBHUIIoY3M1wlnm8Oy8Jdp\ndFIARrcz2JRS/X7fGHN2dhYEEaX04cOHWut1giblixgDM1yVlrwOw0ydzplGZiLqaRaUUtd1maFS\nykqW9l8dzjjnjstxbT//8z9/dnZipxJ4nmuIopoaZgQVhhlOuCLKSKOpFlRQQR3mGGaIIoooI5U0\nmmpjGHUYN4xSbaTR+FlQZhhlhkij0SwjpeZ0I+g2nKYN9k/TlLDGuAdVz/DB2zAXw0aV9g9Jo+bW\ndBqQTMgDhtvDjhOiR6MRDOtwOMyybDab9Xo9YwwiPcSTgB5830/SNZw8NqKhzLNer6MoUjXzRtUM\nG8dxZFlx+i7NvrpB4GxqHWMXxCOBCGq9XnPO2+025AxKgv4lUsOgyFU4ZxaQybJsOp1C8VqtFo4J\n/TLGmO3t7X6//8YbbzBGAUuWZVkUeZpm63XSbt8KAl/rjpSV67qr1XI+X5RlwQljnLqORxnJ87wo\nc1BdkiQRDudMEGqqUkpVGU0oI4QQ4XDHcQzRVVVpo7IsS9arwA+VlkVREGooYZQR13Vdz0nzPAg3\nzcXCYdpIqSpCSNSKWM0V0lprI/OiVGVFjDT0QoYs/FDPjmdoctE1eyAIgiRJzs7OoijK83K5XBZF\nsV6vUSgihF15JJ7nsbqbwwofvZzZbxKADdhwQY9qWlAksWEY/vqv//qf/JPfh2logecaoxil+FpC\nNDOUUC0oE0E9h0vpSm16z3Bf/HK52VBD9YXXYoRSRj3KiSCUUmpYMzCzl8pq2NO6CIgjJpSFYWgH\nliCgyLIsjmNYWEop2oiSJGEN5j5+xp/ked7tdpfLJYYLwZiORiNCNDa2g3xblmW328VfAYMA0xAd\nSev1utvtYlIbknNkT+gpYQ0ccmNblXb4piSzgRga6Iv1yc3faF3apykcx7l27RoyflWPsmGMITTH\n3GZ7nwjbwKIUQnDOqqp0HAHUGPWQKAqzLDs/Pz89PZlOe57nUjTccuI6nnBYGIZxOzw/P4vbETGY\n1m0oM0JwLqiuFKecC8YYcVzh+67r+nEclWVJiCbUEKK5YIwLSjljZJ0mhGjHFZQaxxGcO1oTKctV\nsmSMOI7nCC6EC56EUlUYuUHg4aQAoGnt2oTecVwhIrfeTc6IDv3AFRsbxhqNG8jBOOegSlvFczz/\n937v9zDWZrFYTKdTY0xRFK7ja60BitBNaZVRSsMwJA0lV5cnwNnIx/5SGi2NVsZoYzjZ7DHV2pRl\n6fu+Kqsv/d4XP/lDf5EovVqt2u24LHMuLijI9mlWVUUJoYQScsFaJoRgzZKNtTZKyC74uMiCWK1O\n8/mc1ATcmuXkIrmglNY8Cm5vpNPZMRtOaY5YoNXClrN8uZwTQtB0slzOGWNxHOd5aVHBK/TU1WqF\n80/TVAiB5q/VamE3TqMuh4ALrl7XzeOIFKIokjWmAuQGFQjrymwRAg+dU2aUtsUZY9PuhtWjjf8n\nhAjhWrMloOWQACnlJuutKjtRDB4MhIMoipL1Eu4uagWEEMYJJUw4LM/yvEg5c/zADYKg3Wkt5qvJ\n9Hx3d1epqqzyKq0o3WiyUipqeY4D9NZUMiNE+4EIAm+2nhjjUGo458ZUjsOFIJQazg3nTAiwOggh\naARkQlDPi3CrnuehixkhhGVIINhAnTCMQy5YWVRKy8APuWCUMNdzAj8k1GhltFFGE4alhIwSbdya\nTWfMRbIOQAhfim8EGuEF4fHx8WQyMcbMZjNkkjY0skCI67qe53MhPM8taw5hE+6/7M0uYjDQiDcE\n9k0rKjIiKqUMo9bdu3fTNOWcG6WzLFOqEmYjpqqmICImtxrVDIqqEuHxhnNojGJMgIVIiLa/r9Mi\nbdE/vOCmWD33phlVQhYRNEEzcdfAFZVSWLUzmUw456PRiHM+nU7DsHUlVLP41nK5tFk0TOdqtUrT\n9dbWVlmWmFiBx8TqySII0xhjSL0stQhBps07kDfZM8ehEUIYoUqbi5zscnDRCB0vuh+KStp/FYyx\n9Xo9nU5d18XaUcbYbDY7OzvjnKPznxAi62lhQRBIWeZFSqjUmihVKVXO56XnBZSaLF/LcR5FcRQF\nrusWRVaWKduMttxM4cSDT9O0LHOyKeMqSk0Y+lEU7O89zwi1ABqpE2LAIbYVxVoTpHPQJXCCKaW2\nJ7+2LrUwMSI81xiV56XWMggiQrSUmnNaFBUlxnEdUG8pNUK4DuNFltvmJaUuaiY2y0IMaYtpUsrz\n83NANUmSgEKJakqTXiSE4FwQSitZ1n03Ek8XMJ19zLjZC2VQUimlMeyt4WEw1qrf6Uopjx4dPvHE\nE4Onny6rosgTx+FNmh8u1bbMbGRFScyJc0SAoAeLhyFBhLKqkpQyRhmhjBCqtcLp+v4FtE0aKBxa\n47XWSir7IIwxWipqCCOUUMoIFYwzsQmn59MZIaTf7VFKp+MJ57zb7WLSNuecUGK7ASC0g14/y7Jk\nuRr0+mmaTs7HcRz3967dfedOq9V64uat2Ww2n84A1k/Ox1grvVosKaWW8Nnt97DjOo5jUkNlURRZ\nw1fV044pxaEQ1uhXIo3ImVxGR8jjYAkhpCxLwMEWS2SM7e/vAxWEgiGt5JxbPqsxynW9Xq8DC5em\nueNgzFC2XKog8IRwKTW7e7uAxQBgWJY0PrBu6BI2CFmMp+bynDBccZIkvO72bSamrJ4LAmIHQALP\nc2GuyJU+LqIYY4QjC6W+H1ZVkeclY6TX61FqKOVayywrkmS5Xq+ZIa0wZnXtSNfdIhCjK1wh3NcX\nfvt3ptNpURSYwIOIRQjhOsJ13SCI7GCCNE3LqiLUpDW+Yr/FfpF9cX4RiZGr3ELKGHOdMAzDw8PD\nTqfzcz/3cz/2Yz8mpWScXt/fkZLZMteVhMq+arhC08Ch9NK/0os9GMymi9hGAL9t0ZEm/Gg7VvTl\nDBBTuhBlwB2hZ+LRo0e9Xo8Qgm3a/X6fUnp+fo4wzEqCqRtwYF8opcD0wSzH6WGqFx4QBB3Shdup\ncwettRZCyHIz+UvWrZ+4KeQI1mRvSpeGaKlszt1UKno5wbZGp0m7E+gmdl0XphEPFVpO6vmhlrLN\nOfX9yPNd1/GEwz3XD6NAcIdQE4Ut4XDBHeFwRjnjFP9flqXvb0Zl2LhIKQVUGlmQlCAHVev1ynUu\nHhihmlBKKCWERK3ASpiNTDaSxwxnzHEvNif41EXwYJtqpZRlqWQpGd+QSg3RZZmXVa618QN/nawY\nJ47whMN83xVOmzPHd93FeO4KB7VgUic8tEa38cnARYqimC3mv/Zrvwa3ppTyPA8JeqvVCgOEQ9Tm\n90VRVlJywWSDqKVrOl+tSKwZu8KgEEII2xyLtZqrVdLpdLIse88zzx4cPOh2u+04juNWkS0oIzVO\nKKyHaXo2SqlglAnuMKfKC8YuhjQSQiijlFFPeAT4aR1GMcoI1zxwDUFnbVXJwgbAdv4C4xTai8+c\nTM/xUDzfwR0tlplSqt1ppVlCKW13WoSQVbIgBBtAL3j3TWw2iiJMFfB9fzKZuK7b7/fn8/l6vd7f\n3y+KYrFYBEHQ7XZBeY/jGCg6HiXQSM/3siwLohDWHN/IOYdSNJtEYUqINoRt8rFmLbTpxGywgJ/z\nLLP/JFxXLBYLzqnj8F5v2O/3q6rqdrtpmiKqxKlZ410UWbsT2yZwSxsXQqC/E/i+bdTTVenUg27w\ntotoXm9G92hnM3ZbYVwZ28y+1w3ygTXt5DKah1Bb8M3H2j/xWy4+QVeSMeYw7vhBEARKVUzQspR5\nnmZVluep43hR4PW73aoqlDK6klJqY5Tru65wQj/w/Y1jJzX3CqIDFgWyWc55lmWnxyevvfKNJ55+\narlc+n7oed5isRgMBq7jB0GQ52WarjFPUhuCtqC0yBAeWyNqRap5R6Zu5icbNSDGaIPlTIRTSqJW\nW1b61q0nHxw86nZ7L33t5e/6z77z+OS03faZ1EYT65Rg1H3vggZFN9AIIYRl6Zpz0wxi0ckGGdVa\nw11ZcSrSnNALEoyN2JstM6aeu2rq4rJsTCAH2JYkCdB/vA1gb5EXvu8XRQVYEuUiWlftRqNRlmXz\n+RxceUw96ve7k8mk3W7v7++fnZ1JKbvd7ng8LooC9a3JZKK1RnVqPp11+73lckm0CaKQGrJYLDhl\nYStihDqei45KNKzIsqqqKvQD0gBXbYTfrOw1nZ5qpHj0V375F3BjIEDmeY5B0LYT9lIYprUQ3Bra\nJn+sKIq9vb3ZbGaMGQ6HmE/qui7TyhUOWvqgotg+oxqd8KQG+jjnShnruLS+eK6+74OBJYRAxQxC\nCToSaB+wZGDT8rogbnslsizLsvVwOEzWS1npqBVkaZEXaafdk6o8Ox1fv3FNSTOenAV+1OnGRV6t\nVqvQj/D4gbM1VQIPHreZJEm/3/9f/IU/n2cF5fBLG1pJmuer1VpqpdUFG1ARSrUxzBByQXVtxr1w\n+IQQ65nh4vK8wA5u2zRpU/lWEJZlifrNYDB4/vnnf/yv/dX55KQs1ki/Wd1kUFWVNR9Nq0wM831f\nKWPDPHs9lF7FBSilhGzgH+iPFRspZRBslJk0SB66bqfi9Vh8UzNXNuZXa5hpUpNC4jgG5wahIGBz\nFA/snzTlsClRrNH3DfJg0+3ozYsYSgTj3BHUEKkVNYQ7oshyx3MZoUVVUkMczzVKo96gbONpY3bQ\nFR/Q/Bbr5ejv/96vA37B6VdVhboeol573VYamraqqd8W5IFV01qjKdsXnBqCJRiTyWQ0GnW7XTBI\naI28NU2sEG4zW7OShHVNduEDtkmglg2Pigo7PsdxnH6//9Zbb8VxvLW1dXJyQgjBmO40Tbrd7unp\nKed8OByCyD8cDo0xx8fHmFeFscEgZ2u9GdOJlNKCNMiyTD1cbDKZzOfzv/k3/2YYtY0xldIAlyml\naV5mWVZW0ioq5u3gWRBCWL2ErXnarK7dWfhHb8aqkqaRss8YUSvkGHMyHMf5W/+n/3Z/1GdUo4TT\nbrdR6UZ/EP1Dsnlr5prGzuYe9quvyLSqlyEa02TJXIqpbDRo1cDUWTcIHKYBmZKahJ1lGeAoSCmG\nvgHDuKI/Nk8hlwnEuiYuN3zy5vdCuNqSvLW2nTiq7u0UjYHw9rlYJ2QaNBd7JrqmJTQPllIquu0O\nIUQwbiFs13GllLqmyVJKCTOcc+wWa4JLnDHH2TCmtVTnkzPow+HhoeM4o9Ho7OTk6SefWC2WAOUB\nu3meBz5UU29NnUOjraaZ0OMBWBxFKYWxYcaYxWJx69Yt2H6Imq7H8ty9excEgsPDw16vJ6U8PT1F\n4eXw8BDss/F4TCnd2dmZz+dFUezu7q5Wq8PDw62trTRNT05Oer0eipk2VLCsIkQ+gI5OTk6uXbv2\nC7/wC7u7u9owKWWaFyifKKUqZSyMuVEkah8MePfU2p3mE7WBn8X6OeeMOVZWmj/QmnAEA4Sxua+9\n9tozNz8xGZ+CFblYLLB6BmzsKzqGlw3/rIVV9dS3ppg29af5hprjunFZTSiL1mSrZoyKf7IP+nEX\nsVgsdnZ28jzH3mCoHLouLVJi0Sk8Kft19ovsD8071Y21NU3zYerkHJ5D1Kt5IGMAuq3c2tNrejDT\nQIZwzrgAAe4IsBdjjN1RCB4quRwDkHoWjTUGVmHAUXJdF7V5x3G2t7cZIYyxfr+PRVXb29tnZ2fH\nx8dPPfVUTcY1ulGyFEJofVFLhRmG/UP7D+ccZUcg6aAgQtnwrzAZCPEXi0Wr1XIcZzKZxHGMoSPd\nbns4HK5WK8yvT9N0Op3iEOfzOfLPk5MTjGeeTqetVtuGuKauZSOaRWAGwVoul2+//Xan05kvEgiB\nbRtFuqSNto9fU8u6gLgTKxNWKJtaZ5klxhhr3ViDRGKMAUsdf643Oy/D27dvLz7+rYPBAHMusJz5\n5OSk0+m8q6Y1dcxekrXf9j3NYKmpafY91lI0QdSmtFihtC9rzppSoZTqdrvz+bzX68VxPJ1OsfIK\nVAHaiG9pnTs9HsVZBb6iUTaiNnbxYoOnaho5s67JBshWmvrJGl2q9gbtoZE6IsDvxWg0Ap4hhECD\nBlJYFB9Yg/NmGvPxbIJL6hF5GFcKNBYpGfY8VVU5GG02GwZBgKIHav/2+mxEWpYldq7SOhpuaru1\nWPhbsJOXyyXOtGqM1CaEDAaDo6MjXafCWOk0Go2qqrhiceEJfd8H6QHTU5CBtFotWDJxeVsK5xxL\nQtAzcePGjTfeeMPzvNlspvTF+JrNQRPGOSeVvJBRavNpfGZTPC78Bq2RbkuYNMYw1pxefiFb7mb8\nq0Z8RQi5du3aN77xjXa7PZuNW61Wu92GWYGwQt+sINqv5o3eraaLuwBCL79QNLqigYwxWQ9FJXV2\n1Dx2+0sr+rRRbLC/h1T0ej3Uo7e3t9fr9enpKZZjwshau4Y435Yrr3wgvVzqsMqmVEXeLUjWWuNI\nmzO5UBIQNcmBEMLrbgarVI8bI/t7gWIaCGkg+FpDThtt5PbPrCUQdWsgr+euhWGICVPo4yqKwnGc\nVhhAtfr9Pg4CPwBXQIXXaqzWGvMIrCTZ1LkoijiOOedoJUaufHZ2tru7iyn2ljtCKW21WrPZbDAY\nrNfr1WpluXPdbtdx+Gq18n0/jmOEkcPhEEsnEEZOJhOMJVsul3EcC+E2iVTWBgOwgX/L8/zZZ589\nODgYDAZKXQz6bAYFVxxRU52avzeXQx1Vb7W0QqnqwS2sURWg9agMkGZgdzzPe/WV14ui2NnZWSwW\nq9Wq3W5rreHirPJcuYamUFplQ9xBHnNHxhgkaZReqt1RSh3nUrhrFaDpIZtnYong+nIfbRiGx8fH\n7Xa71+uBGoZAyfoAm/NbT8UbHW721ppppL0vQgjmrJgag4B488YSAjvqmDdGx7PGvHHrMMjlYLJp\nszbCDJyRaM2F8ByHEeI5DmPMwQR2QqgxBB+hNTUmT9OmBlK7AEFrLaVRinAuy1JVFfAfawNsfYNS\nGkWRrfnak8XnWJTMnhTuDX+In1EJtZmrNQq0HhyP/5zP56PRiDF2dna2tbU1Go3eeuutMPSvXbt2\nfn4+nU7hmk5PTzHC+fz8HP3Ch4eHw+Fwd3f3/v37165dR4eBFURVdwxMJpNut+u67ng8RpCzt7dX\nydymWLXn1MYYxi9m05v6ZuHZCLlI661wsAYD0xJK7ImRy6EarVs/Wq0WghQcNY4IZSjgPVjJC7zE\nnjNt+FZ6xc9efs/j/2rljNc9oPgZ7RTW7tiXTXqb5t/ejv1P+zTzPEf0i1wARrDJ8LDKYxoDXq1l\ntLLR/F7eIOxzfjFbUl8u+ttiFdQYN4XjZfX4ZGvsruiYffq8MWxXoC2K1V2GAMoB3TbNAK0rXbSR\nj6pGdx0wIjhcMFGiKCqy/NHDg/e9733T6fTBgwc7OzuMsdlsxhjrdrv4WByQPZSyrJrG1apTp9OZ\nz+e2UxgwQBRFSLQopUgLgbtg4LHneWhc6HQ6GLu/t7eX5+l0OsU7J5MJyuuz2azb7RJCFotFFEXX\nr1/H9pzt7e3VaoXnZNsukUQVRdHr9dAE1O/3//E//sfvec97lsul4wa0EU0heLdWtnYZNi9iqh5U\n+rgQm7q2ZhoJD30sHCKNkdecc3hyPMr9/f3pdNqKLlqKGGOo2DZV68p/NqXH/mwuOzobE+p6qrFV\nNlMzwq54EtqIg0jD19lbZu+GRsKjIiNdr9dhGAZBgBzHBofI9q2W4mot1EnrdTmkYZdtXhCGjh3p\nhf+3xFFbzAB2AJh3Nps1MyD7soBT06eZy1E6vffGVzDTl9eUTWPMcrn0PG8wGCwWC8QhWZZNJpNe\nryeEODw8xD2jjBhF0aNHj7a3t4UQs9lsf3+/LMt79+4hG1zOZ1ivjM1PAAbPzs6Gw6FNiIUQ8Htl\nWTqOR2p0xFZ7jDHoerAxhqkZRr1eD7vtsUkY8wugeyjQZ1lmdwgLIapqsysMCBDsgu/7WPgENTbG\ngF+7Xq/39vaTJEGyit/AjiilsJiTc/75z3/+s5/97Gg0Oj8/1waTGzet2VJKqYnWmtALwQLhh3PO\nGNrpLx6PlW/Q1dEw3pR4i0ZecTVWqgD6AysXzPzIJ//in/z+T6CxxXXd+XyOCp6lL9nvxUs0WpWb\n1wNgwObw1qIDXmaMgZIi6m1S6C1s2g7WaMokdRqMdEvWC+Ctz7Giz2sCatOZ2IuH/NiLpHU6LYQA\nZQSPdTQa2cIsbWymp5RKeTEbwgbtWmu0/+DrgA7gPe12G5KMIREQKpChCSGAPHTNPg+CYD6fW7NC\n77/5UlmWaFJAL1ZZlr1eT2s9mUz6/T6KSBhld3JyMhqN0MMG9aB1dF5VFTBlWIKiKDqdTp7nvU57\nPB4rpXq9Hq07MrC8zxpv3A9jMPMX0HDzKJvna4UAdno0GiVJsl6v+/2+UgphBjjg7XZbCHF+fo7r\nn06nxijEitgBYFUI+7IJIQBIEGgFQbBarUHFRhxrF8Rprfv9/qNHj1qt1s/8zM8cHR212+3ZbEaZ\nY4yRelNLVUpJTYwxqLNt7otuCNaMYT3sVRDfyndRXOyqrd9w0X5/5f9pPYHUzht1ONkddP6rv/rp\n97///Xm+6efHY9KPoYt4WdzL/gaPw0aeVj/tgwD9Gp8PxQOK0Hy/1VKbf9Zef6PSTZ1p+gc896YS\nssZStaZPxgt4EjRhNpt1Oh0k51mWgf8AY2r72cKwZb+xmf6ROs2DbluEgtbTIwHG4AKAFCBYWywW\ngOWMMSCU0RpdFwicsC8GWVaWZZ1OB0QNeGog6fhXMNlRIUC3HyIxjMvF9FVSt+LxemY6qXlV9md7\nQDYws6Gp9f42IbHBJKn7D0hdLUD5iHMOoAKEVOt/IK+o4da+S9uaiar3bmJqGKwGrhMKVpYluqQI\nIYgzEfWh4/D4+PiJJ5747Gc/a7M+3/ezHMMkN9fMOeeGEkKkSi8eqiH1070EhzSTFtuKTi9PTDDm\nIsB73L9ZiamjNfr222+/9NJLH/rQhwAjkTr4byqYPW1Sh2FNPdE1Ft/UahtfNAXdWsAmOmIu56LW\nc6p6KCCtoXbTKDDYSPUKDnHlux4/BPQWTiaTMAx3dnYmk8l4PN7a2hJCQA3Ql41VqZ1OpyylvQZ7\n1MZcbK7EBcjG1AYIRpqm4LLAB8ZxfHx8jBDMdV30WGGDufXYAs2qgHq01rD66/W61+vduHGjqiok\nppTSyWSCxGlrawvAo64rAajo4wYskol6/3Qy7nQ6lFIoAMqRgJ6te7UeDHGKDVFMA7S1VClSJ+UI\nM4IgODo6iqJoa2sLExzsRguQg3FT0LpOp1MUGZQNVTLbk2ZnUcAQ4OtgAkBahYm1Bh6B02Qy+eIX\nv4ib4pyjsEYI0eSie40SRhvAj1LK6EuRW9M2WwFtUpDsaTT16oqa2Zc1z5xzY1i/33/ttdfsrDEI\nnM2Fmn9u3dQV1cXLNJCDJipQ1eO+od4WCjc1pmJ10n6FfeimkXDauzONHI/WW2ZYg8VOa07244YG\n/2lx13v37vX7/d3d3XfeeafVaoFpNR6POefb29uU0vPz8yiKrWLTuuxubwT4hW01pDX4CStgK64I\nOFGKAPZuCVXWsymlxFZ/4HARdUNs3A0833Pc8XhslO51uvP5PC0rCCvitNAP0mQdBEG7FRdFUeaF\nEMLUm7VQn6WGEGNUJStC2+02wn1oLOIi9FlYxIk2cDYhLraZXHlIeOqs3l+MgCFN08FggO2+w+EQ\nzdFbW1vGmPF4jA3AtmtjvV4XRQbOJMYH2XCi1+uB940CFH6O43i1WiF/a4adyJKfeuqpv/23/zZg\nwOVy2el0lsslZQ6U7UIU0OTb8BiK2ElBF/Uf0nAaV/IQegkxenfP1pRRXdcttSZhHB4fH6/Xa9vc\nhKJQsw7W9CpYXc/ryTH4QBvFkbr8YK/HWgFVk11JnXE1HbKu90Kh5IPUjtS48bveEX7JOSePGQVV\nd1I3f4nXer3e3d0FRQFE2dls1u/3O53ObDZTSm1vbwNBQLBXFJV1aNaCkLoNvAnn4D9BzgyCALFM\nlmWqsX+UMYYsFNmm1ho+BlcoIKCEEMyvX61W2FWttZ7P5xgQAB5Qu93GNraTkxNgcfgssEKRKOMU\nWL0HJEmS4XBg3TGt8SjP85AgmZosZw0JiMikUbHFEdhI2r7ZgkjIhquqWi6XCCNRiEM5u6qLENaJ\nWUjX2mAYqib1Hv9qf0nrvilEF8gJx+PxK6+8ghDFcRzMn8kLSWrPtlEDqgkhqo4Ym76CEG3Nin0k\nujEc4YrZJn+4Z7MOx36LUkoxs1qtAt+BvUBIj6Ta/tUVlbMK1jx/8hgdyYaXgPibLH6bm135ZPzM\nGq1DpI4qZWMt6MYe1fEbwsKm2cWrqdvNI+r3+w8ePOj3+9evXz89PUVxFbIBEzybzfA2pdRkMmm1\n2qTxssduh3ZZg4IDwXgF2WjJC8MwiqLxeIxVEJ1OR2sNKu/W1tZ0OuU111cgrwWwQelmeScSFZhD\njDFC9RYLa+CsMLMV3VkIwFBoRgBmMyUMgVNKARHBIJfVaoW2iNpaX8w5BKhFGuETqxkMtJG90Hry\nLnxOq9VyXReDZeM4Rq805vJjhB66OTudjut6NnanlKIzNwxDDH4mhDRhkizLOHewYARhJ0AnNMJ+\n7nOf29nZQY2YELJYLFzXXacFIUSZBheBYOMHaQA/V2PIpkTaWogVvqbfI3+IByB1nkMaRFilTCGr\nQb/Da04prVvOeYPn3fSuFjC0CISuy7VWEJvZnWUd2Lh0k59c3gluGsyv5qBYXJiqF1bYK7FFal5v\nCDJ1lqgbFbamhuBGptPp9evXCSHHx8ecc8zVwv1OJhNKKRh50+mUENJqtWBD8V20UdhA0m7q2p2s\nd7jBiyDbh/Fy61UKOzs7YMwSQq5fv85qnqoNN8T5+fnW1hZUv9/vt1otNGgRQlA6hHiZumPv9PT0\n6aefXiwW4/F4e3sbDHrUdrTWCOoIIY8ePYrjuNvtLhYzPBIoJAIYHC7coPV4eJuq6S1N8bJPl10u\nxaBcAVURQgDkXK1Ww+FwuVyOx2NYndlsFgQBKIJVxdE6gHgJLQ4YrWezSlrPeEKCG8URp2KdpdSQ\nKG4RbVbrZDqdvvLqN4qiaLXjsizny4XnuvPF0hijCdX6Ql43HU31vDdCCCeUMMYM0ZRTrXSjamzl\nm9ddz7UmUUZQBP9Di3K0Dr8bH7VJmbA4hTYWJqnGErPaBGjTYBVbDWd1UYE8Fs6RTTXiYro4RJMQ\nApluYjz4XiBSpkah4UCANNh713Xt7oquWotg6hTaWhlbkEBTqed5GGQK4ABDUDHyA9a81+tBz0W9\nvtwevtUN60VJ3cFNCLELw0yNIyAPROWJ1Nn+2dkZNJw0Kor01Re/gInFdgQyRA1YPNZH2BLWaDSS\nskRzHiD1TqfT6XQePXrkOE6v1wN5DCkZPGkQRCcnJ0EQ9Hq99XoNWBZVwmZMb42iPVzrfEkdzlmZ\nsCGltQKIQ0RjbQXASfyhqSeURFE0mZzb6fzWzmHMkRUj3Xj5YVDKgmiqiYmCsKjK9SrpDfqf++y/\n+9KLf3B0cNTfGoR+MF8uVotlUZVaa8IZpRx5i1akXtJXMMYYxWBwjvE5miglSz/0kV6DFJ4VpVJK\nuE7T3BirZPrdw0hWNwpYCaCUuoIm07O/9MOf+st/+S8LIcbjMVoqEZvZk7TKgA9pcv9ssA3jaC5z\nduGEyGPhaPMKTSOJgCwCx4OAwb+JemgPihaysRINwTmtdzLZ0S/NANIaBUIIpRfczuZ7rH2x8qDr\nnjRVtw7g3HCGuCSllCW+11DQhiHJatAVfffi8uQvGwXY46WUCmuBcNBgnUH3wjAEBxSEDDjfwaCH\nGQrIEauqWq1Wo9FoMplgTIiUEksefN9fLpeMib29vSRJZrMZig8wA1bT7OOxitdUQpu9wBY0NYE0\nghZr53SNm8GDG2OgcjgylODgwexkQkIIBms3bTkOgXKWZonjuoQTqk1eFnmeR3Hr7OzsG6+9ulqt\nvMBXSi1Wy6qqvCB0/WCRLEgjDCNkYyA24Raps3BjtDGUkCiK0nRdVOVgMIDzXyZr3/ellPV7NxPh\nrFI1Jcz+bI0oaeDmnsMqL3j66achDYyxs7Mz5PTNVhre4MunaerUy2Kav7cENFIXu2o/8C5TLvF+\n+5umn7SdR1BdSC16gobDYVmWGBnseR5kEnLf1KvHFcl+CyGEsUscDntQwKXt6VnH1TQEpu7KI4Sc\nn59j1yfco7ViSLiQ+aM25jgOGgWbX2qV36bHxhgB2JoQ4tSjxSiluHl4Xqg4GrdA5wW8gYZrdGSP\nRqMwDAHc+b6/Wq2qqsKeAKyopzWGaw/RnqBNBqyONcNF/dhmg2aATmusljZYi00ptNGF1V7MV7Ta\nC0Qe2In9QGr7rGpWJ1AW7DbDINTj42NCCLw06t2cO0VReF5gEQ5GYe1AKeKEELIZaaqN0dBDYzRj\nZGe0vVqt0jxrtVpaVlo7SimqKeWbwYuUMYI1V5fHs14RQZvs2fPxff/ZZ5+FiENwwTJr3ikuGOII\nVppNjK/ElleO1xgDPMX+Z1MZrhhTXI+qubw2JIFPGI1Gjx49CsNwe3t7sVjM53MUe6148Jot2HxM\n9vabyvOuh2MTP+twmhfWvGzcaa/XOz8/V0ptbW3ZabCtVgt2EPUhUS8wUTUVkzR8Gl6mUT5BC9ml\nXmmtNZp5wQ/E8CPoz2AwWK0WaLzPssyO5QIlFzTCKIpAh8WHSKkBwWOuSavV2tnZmc1mzTrPFedr\nH5I9zSsq9/ipWQkjtVdBeZ02AkVKaRAESbKEggGyt0wuRDUW6rQHhKUCZVm6rmupZC+88IKlWdMa\nuUJPtxcGF2zGDU8PJH1ujNHqosMKL1g3Y1SWZVxwhAy61hkrvlpryhjRxvCLbPaKS7mSVmmty1L+\nxR/8QcjK/v4+pfTBgweYMYOR3bhf0RgjqWpyLakR/EbVzljP9q4C3RRZqJD1tORSpHeJYoYPPDw8\nfOKJJ1ar1YMHDwaDwXA4BIfTKucVIW7+3tR4srncDdi8tubhNE/VvtkGI1CHw8PDGzduhGF4fn6O\nbXv1VlDPXpWo1yw23Xjz1mijnEgpFQDfrE8DgJGm6fb2NuaQY57kbDZLkmR/f78sc8CPqGtzzhGY\ngVlSliWQRmMMSInAJDnnMAn2i0yDJkIakX0zbbOXqxvlXXLZUlo4i9YhJSqMQJDsk7b4GwboEkKQ\npOH2waOzD4DVUzEMJdpgJBvRmiCfXi6Ts7Nxt9PLi4JS6TgO51jATcIw1JRsfNrF+hU8Y8AkyhBV\nPxFNmcnTZDgcLFbzbreNeCFud5IkMRvTS4gx2hBKCdWKACGpTVLTNlk5tkqolCqr8lu+5VtA+Ueo\nAtLccrm0LotcdukWsbTVbXOZLNK0FJRSpS4txLAKaRMT2qgBNsWd1ik6+Kv7+/tvvvlmu91+9tln\nF4sFqBSoF9unb/Wc1QOFmjFLbYJJ846stFi+lZUu02j6JLV5rW9KPfPMM48ePUrTdGtra29vb7Va\noYOuqgqcJ2IBcCNBn7Bf19Rz3mAtM8tUsMeHL0NfBnhMcBSqph2iSQxvhoxiiFocx0EQIP3F7FTw\nNlC5B/LON2NuQ+tOLchrX6rRxGUaiMjjL3tjTYVkdakAywHtLCAspkGQjVoT7guuzw4bhFCidkkI\nQbuA1hqLDcqyfPjwIcbHk3qALBJXBKicc9fxPc8D8Vc09oE0L9vUGF0cx4vF4nOf+9w7d267nnBd\ndzabeJ7nNPKlpoj8YedgLuOZG2WraTSAJUDOBiyJ3mc7bRt3DYTWHrtuIChXHDJpVBqar6aU/2Ev\nq3WsMW/z5OTk6aefjuP44OCAc761tSXrllBbu6ONer190Nbi2KikaXGaB0IaUL6Vqys3Yj/28PBw\nZ2fnmWeeqarq6OiIEIIkHw0fEA9a91uqRq9N8ylYK4PLu9gNCUAcXx/HMSBOKAwaVTzPm06nvV4H\nOZvW2iIQ4CsDVEUaI6VEEgmKMwyYHeqg6g5Ia+HsNdnfNG0DazRKksdygKbK0cZoKtFoa7d2ERMs\nCCEWJmH1TsMrkq2UohXTimRZQSk3RhdFFQTRG6+/GQZRUVSua2vfxBhqDFXKUMIZ50JYsdhA4Uqh\nA7XhtBljjJZl9s//+T/jxPzU3/m//NTf/3utVrvX6U5m0yCIOCGGEmMuzbu+Eq3Ry+1kpMETwPn0\nej3o0nA4lFIeHBzM5/NnnnkGQZp99FbIdB062p+tjNJGGEIbcTu9HLmZBkLQfP8VJ6wbs8Q9z2u3\n20dHR47j7O7u5nmO7gRez0pg9YQFKxJXUBP7UuoCbLMiQWpamWk0p1rNtDduRVFrjV5HBHF25Inn\neYRsXDEuG8JsM88roak9DRiITf0eumRL1di8jozQtg+hWLFer7e3tyeTyWq1wk4p2PvBYHDv3j2n\nXvGOaX6u62q9GYgAKKzX63U6nZOTE5TjLG/aWjhcDGvU0/DMoKjNMAbPT15u62yGQACRMKMBsoUa\nPdwyYBI7kBCVa3a5JVkp5Xlekq4BsqBic+/evSzLsO0eJ4uRT5zzsiyLouJ8s4gMGLEt41hH1LC+\n5uMf/6M3b91QSn3nd37nL//yL59NxsvVPPB8iu1thujGzZLHWEtW0HmjSZHa8f1E/e7v/u4P/cU/\nv1qt7t27F0URME9gsE1RsB9r55eRmoZC6jEH7DJBsalpTYtuDZ+N06xW68vDESzOjswHTaJY7WJ7\nT22uAWnGRdoxas3AldTotPUwppGJgBBLGhGslR/ruq2x1lqfnZ3Fcex5HiICRECEkLKs8Kyti4NU\nWJlphgD2MjYffvvlL6IZDJ9OKb13794zzzyDlX8Y0goqIOrdjG3G3ZGaCOK67snJSbvdRgyptW61\nWohJOp2OMbSod4UiG3Rdt9vtAlp1XReYO0QfDaC22woQC7qw7CJMa4cgBJhIqeupb+LycHIbfzZk\nVIHmgnVeKKdaTgOpG0ZwJV7gF0Ultep2u1rrdZIyxv7W3/pbRVG4Lq6H26g1S4s8z1d1a2bDQ24G\ncW9vb4O9jUfIGPN991//wr/K1omU0gvCt9566//8k3+bEJaVBWcOYZwYyAdVxBhNCSGMX1jNK/8P\nObZBF2OMU+0Y9fM/94+wcqDf70PNTD3u154VqZHbw8NDpOvz+bwsS9RdkZCzeg+BEAIEi6qqpCyt\nN7A638TTmwbeSv/jL8TwNq2w7wSajYeCPM36cBvyXM4gLpSt6fEAPptGUylpNKc24wX77Gjd2QzW\nSFVVSZL4vmvVGH8LDwQuWDMuw37Cfr9vP1l0u93Dw0MoBqzF/v4+1jpKKTGtDT01oJgkydI+V1ZP\nK8BTpJSioxYMeuCZg8EQJsE6AUJIkiSYjEApxQRILD3EozV1DVrUi0U552iQMcZADbAODiYH+tnU\nLlKDy00jh3sej8cPHjzIsmx3d/f69etoZkUaiYcHW24H97bb7aIqLT03z/OHDx8+99xzqxWINZt8\nCUYuz3M71rth4QwhpNfrnZycrFarvb296XQ6HA6Pjo7+3J/5z0PfI6YqS7peLT/ykQ8l69XWYIhO\nR0KIoUAmqCBUc/z8LkigdVNNM49XkiS3b9/+wAc+wDlH0VwphdnA5jJCAGkG8SJNU3SmgZrT7XYh\nCbxuSLPC2uSOWL9HGrFl8z+bD+KKHloFYzWghQ9EzolrdhwHEUoURZZbSy5jlc008sp30QbkaB1m\nsw7WfD+p/SSpd5fDJRRFZqeAw1hzzjEW0fd95MMoooCde35+jpqtsLRaXTMttNZxHJ+entJ6gA96\ndZRSoBGiewc5N+ATQCNIwUFGQa8NAhKUU230jwAADQQIscRmqvlmc6eul6nj8+G4kAfioBHPgGrc\nPFabm10xpVb0ccqtVuupp54CaFGW5dnZGarzaZpaBWN1816RpVVVcSYU1VmaXbt2/R/8g3+wt7d/\ndjZGhy8xzD6MLMvzPKfcMYYYQ4yhhF5se0Lfx3A4WK1W3W47SZbvfe97/upf/S9PTg+W89lguPXM\ns0997atf39+7tk6zKIo2c2g0SJaEUo5qmzSaNKI1+/OV31iJCYLglVdeASaJQcg4dhvdNf0DMAmk\nKCDsdrtdxhiaIMfjsRBid3eXUgoJ2d7eTtPEiia57GbtlTQ9mG6UapouyGoar+fq4JKKogChYj6f\nG2OAUoAXgQ+32WZTT5qP3r6tqYHk8tS2x8/NZnQw/RDUKIqCwEuSBMbIti9UVYXRG5jMCUFSSiVJ\nsrOzY8VP3L59++mnn2aMoaSGUBDkj+3tbcCMVVUBVJjP591uW2uNFUf4PsTZ3W4XkzQR6aIHrN/v\nJ0kKNdObgb4bWiMSOV1zFOHx0jRFmc4y9I0xqHEJIeD97H5Kzjko0fryAGocvXxsRzNeg8Gmlcaa\nZFpnd/Y6aY16EUKWi9XWaJjn+c2bNz//+RfefPNN3/dPTk5AyLJ1M6UUZiA43LmQLHYhClVVKqWy\nTC6Xy9Fo9OSTT37qhz9ZVsVotHV9f/fhwaMsW1/b3/3Jn/xbP/Kj/8X+tetSSm0ogEZtOKUX80Cb\n99WU1MfdGiGk1Wq98sorrN6WiusBO5w0/A+tR/+Cd26Mwe5l7OkMwxDLcoUQaIsEg3Q8Hrvupl6q\nG0xl0hioaBroCLs8E795AU3da7opEOpV3emP+fbokDSNXiRSJ4F2tyt5zFlZZSaNELT5ZtpABFhd\nt7AEQFKvqoLWUUrRJRMEAaYDgjVFCMGUTt/3+/0+Ri1CBgRM1BNPPAG0EDgkvCHGmAIgAYMkSRLI\nJRQaxSvGWFVVoHchVUN6hjobMElaT0/Q9XhT9NKyBjuO1t1ukAPQrMBgIjXZ1JoofDsuxj7O5unT\nywmDfXjIa5VSSNU452hNGA6H8KJQQuRvvu+zwEnTNAxbr7/+5uc///l2u318fNpud/OslFJqVdUu\nc4PxKGOwE/4CHiRKax0EwWKxcBy+vb19dn7yv/6RH/7u7/7ut996vd+LFvMsDPzjw6PeYOu55577\nE3/8e37vi78fRTEjRMNlGZTXOKWbNm/rypr6dsVy41UUxenJIanXJtkeWdNottA1qZLXu+RNPfUV\nJ4/GpdVqxRjrdDrGmMViIYTY2tpKkmVTVZqG4MqVPK5dV+yFamxdpXUGPp1O0cyFb9zd3TXGgA9o\noxVTo7Jaa+tHm99lGtxuy0QjDQToyiWRmnRCG5N8AEIOh8Pz8/Pz8/NWq4XyyXq9Ho/Hg8FgPp+D\nRNXtdjF7YjweY6sjDlbcvHnztdde6/f7W1tbq9UKNU1EhggkUKrGrAQElmEYIuhH3Izgfjwe7+3t\nUUoxLKjVai2Xy+VyGUWbejFvjFsCAAgCCoIWgCigotkWKaRktG78gXe2dT+tNdJIa4fs6T8uc9ZE\nAfq3u/BgEUajEYwCBMvKn+f7jvDzsnjppZc+//nPz+dzeFTXdSnhCDgJIVIqaziVQdvlxTYSpeso\nQojBoL9YLL7ru77r/e9///n5+fb2dp4tVqvVU089E4bhq6+9HkXx3/ybf+OH/uInGWPGUEYIpRxL\nvQ2ExzBsjaHvFkY+7tmQIGAgHMqeQRBgRIe1UM3YCROslFIAmZEpoUsSO9Mw7gbzndBAaM2fjdlU\ng77UvJLHf/m4jbBmET8Mh0MscLV7SZVSzf6spvsyxhhzaeKD/SLV6HJomgP2WKnwihXQdXcCZHI6\nnQohhsMhr0eYcs7jOMaUNwS36/UanE80H1tzIG7cuHFwcGB3FwABR4iIhgjIFpLmOI7LMkfpDBN1\nrIuglGLOnOM4INGjG9X3N8tTYCYh8QBI0B0HogDYekBRgf7bWQPAqZIkEfUkOVOv/7Lo8JVDpI8l\n4vZVVUWapgBgkMJCzVTdUoW/ggwBATKU/NIv/VKr1UKhn9U4OK6NEMK5ss7T5V5DiC9+jx1li8Ui\nL9JPf/rTu7u7d+68vbu9FQXu3rPPfOP1N9rtbhSE1JD5Ym5FiBOGDlNjLtY0Py4QV2SuaWIEF51O\n54033viO7/gOKI81880/1HWhAuvOkDh4nrdcLhlj/X4f3YyEEDSnQE7iOJayvHLapjGU9l3lvvnO\nK/9v32aD0jRNQSGwHPyqqhCz0cZ+JVJnEKizXTFG9jO1vmSnyGVi95UrRBZj5Q1wvxBOURSwuSgP\nlmUJeTY1ZOK6LjZbgKOPXG6xWLAsy5544omyLMFXtGNM1us1OJBgIQMjQftMnucYUWR9t5QSHTRK\nKfCzwF1AKFInLRWpt/KiJkgpRb3VVk7B8ADpk9brOfFLrCCCFUAZACENeh+UuvAteInLLzC1Pc+J\n4ziMfMflhG6oKkDhrFnB+cJqaGkcx/mdF37X4SJPs07crQrpOW6e59Rs1lzBQCBe972QMWYIU5pU\nSpZlWcmiqiopq6oqoiiIWsGnPvXJwWDAOd3Z2cEBzldJu93eNFwJPhgMvvXbvlWpSmtpiNLUGFIZ\no7QulaoMUYaQK/97XFDsz0VVKm3+4MUvL1dJlhf9rQFhFIPWSIN5AygrSRIkEejnMMZg6xBUy3Yw\n4U8AO6Nf3oKHVufxFPjlF7tMs7gS7F3xaVbQ1+s1zATKD0KIwWDQ7EKwf94sNuLWcGEWelV1k7Ut\nfqr6pS+/TA29yHruHavXKTuOg5xttVotFguUyzHuwFawADRgYRNiy1u3btF7r/0B5/yNN97gnD/9\n9NOEEMCJlmSJKeJhGEIhR6MRSgJCCMwmQWBmLuN4qEGHYTibLbx6hbxqMPGgjaQugECX8KTRGYBa\nAgp6iG1sBxohBJ+PBd9NIdP11i+87V08m8ysRUcyjTcEfoRzFEIYQznnSZJwLn7tV3/t9dfePDg4\n8DyPCgfD/YMwJMYoaybZpoBTKVJWdJ3lnu+maUJNZYxap8vRaMsR7OHDh4PB4Hd/93dee+VVpPiE\nGlkkrucQQvKiIAQZAsuL6sd//MePT889z18uk36/nxdVURSuH5bKKMoQU7LNxRtaN4YzaoQQgeuB\nG02Mdl2xTleh5//rf/2vwzC8f//uaDQySkNV4nYrjuPFbIpwGlEJIQRQMEy47/udTuf09BRFGmS2\neIPWGvk8pRTlCoyItxA0XrQxKK3JYW6qio1HmrCElNKYS02u9s0YTgx4jDbGIUdRTBpNAPbzm4wT\nq+S0sfbJNMYn26ykWfRjjVVezYTFmgZaT6QkddIEjB0RU5qmDLDS+9///qOjI1wfWIVNt0Dq9iTU\nN4wxYISgHo1qmB3AAuAe3hnuFS0JsEngbgKBwGMDCAbzsLW15dXLu9vtdqfTAeAJwDeOY8SWYCFe\n2d9jLmNfcFn2XGDSyionhBBq58MRzqk1K4PBABeJCBmzAV95+RurRRL6ESO8zHIjFWOMYjdSg19r\nv8IwygQ/OzsTQqRFLjxnd3f3fHw6n8/DMPjBH/wLjx49evKpJ1bJEpXiTXDiOIPBwHXd2WyW5flo\ntPXX/jc/kayXQeB3OvEyWXBher1OXqSKGEWMoUQTo4xBl7cml2zKJkkghHOeFWUr7hwen375pa+N\nZ9Oda/tZlvlhwDm/efMmpfTs7Kzb7W5vb9s+f2gLpoP2ej3HcbDLAr+ERsEyFkWB7UVKqTiOkdKD\nAqIud5raq7Ju0HrCK0+wCXuQBsR1Rb6B1eka2gnqFwTM+q7m5zeF4V2/qPldtEESaMZHEHX7spER\nfm/q3Y44RoSKaCD0PI++9bXfQb1VSvn666//qT/1p7DQzMoQPtHUQ57tUjLLVUECbYwB7gmIxY6g\njOOOnZVrvZ8lvFBKnXqzJuebgQWwDc05u6hfo78YwSpyp7IshWDvGvSbi2SpgQJTzflVrJkxQQjJ\n0qLb7S4WKxQPy7Lc3t7+2tde/hf/9F9GYcwET9MUmLhhFE8JB0oIkXqz2qpSRGmxznLGKaWKcVJV\nOdEyannv3H77H/7D//uf+zN/5v79+2ma3rx5M1mtpaq6sV+UeVFWcO+O4xSlTJKECuenfuqnDh4e\nrtfreT12Ns1lRYQhjJKLSgAzMCCEMcYZYdhpjNWNDhbWVYHn7+7u/u/+9/9bz/O6cfv09DSOQsdx\nXM+RUlZFCe4NQnrE0mjZsv1+ePq0MWAcPgH/ROrNbM3+6yseqX5MFzHk4yGl9YT2u7SWjz0vLMS4\nmDkJNyI3I6gvHGnz2x+POe2fX/kN/hPD1K64L1p3bNlX8/pZg46DA0G4XqNokiE86/f7t27dunbt\n2p07d7A8rb5VDTXV9bg8QIWknoukGu1P1lyperiIEAKpIKo3mCAE8wPpwVV6nofFyvhe65qKogCA\nBoubJAnQZ0rparVC7m6Dcht5mwbZ0h63zR+MeffVQSA0WdwFSfkLL7wQhCGlFPYSRoTWFAFdTxoF\nWJfneVnl6/VKGxXHG56AnWn77d/+8W//9m+fTCbb29u2vjwcbAHQw3RBjL6FATJSfeITnzg/P2eM\ndbtdnIPrCmY0JZpcjsGuiOOFKJANo38wGLzxxhudTgdGbXd313Gc+XwOigyiQUII1pXACFpmICq2\nICrg6Rf1Gi3WGOFmhwXQes2SuvyyinTFJlr30gxPmtJssSgE+fgKJMm2j1vX/GnrhZqJ4uMvawis\nzOBlxQnDVHu9Xrfb7Xa7nU6n3W6Dtm5fzXSUNkAXU6e1uGy82fM8gYIAEvT3vOc9X/nKV0ajEakr\nOaamkNv7AWfX8qRU3WBvPRVCCCSIURSt1xmtayYWriWEzOdzW9Wx/s2ii/gEVY9MgRdu/rl9YMgc\nHn9CTmOW/YUJZdR+gDGGEGYMAf8Q4tJq+UVR9PuDxWLxpS/9wb27D3zHL4oKOsBdR9dnomFTlIRR\nqKpKEUMIldK0e/3pdOp6LFnMQ98d9Lv37t7+Z//0nypdLaYzrbvveebZO3fu9Lr9JEniuFPkGaW0\n3Yqlxi4BGccx5861nV30UnS73RRz3Y2hjHCrZjC69c+UEAwnJ5ejsuFw+8GDB57nff3lb3zwgx98\n4403PvrRjxKttre35/N5WVSj0WixWEwms8Fg4Ps+1n3BCNI6HULLL/gloKRjS87W1hYyC4xwg/MH\nsm3ji8t+7OIKm/9varxNNQbMKKUcZ1Mcsx+oa4qzfb6kLgY6jtOcGK0b7di8bue/clVXbJb92E0U\nc7kgQRv9KFfk0Eat1rhbNUNuqZRi8/m81Wo9fPgQ5u29733vF77wheZmSmB0Xr1EF/bAzj8xxqCM\nJmpCJ6+3Y+GM0OIhpUTGBScATBl2SGuNZkFU+bAvDi64akyiRYHIbvqDpSE14x7RrD3QK+H4xXmR\npjG6ZPPgdbXWqOy/+OKLn/vc50Q97QurAjjnm/Y2Y5RSpazsOdrvosxoLbWWRVFwwXq93gsvfP6T\nn/zPr+3vMsaeeuqp6XR6cnKCufC2Yx3kG0Yo+G7LxSJZrp5++ulPffKTs9kMY56LLBOCsStEi8bd\nNY0LNAQmT9XU4V/4hV8wxly7dv3OnTtg9qCxcDqdUkotig1iOqBgmGQcC8qnrJ6xGQQBeOSw8bIe\nmubWSyCaam9f1rFccXFXEiT2brS75g/0sVyO1ePo4e6aHqwZ4DU/x1wuA1z5ClYvTgADC+Xlx50k\n/ha5lbUyNsqDPDPGWq0WQ8Ea/m04HHY6nb29Pax1pw2sxuYngE9Q40PKaCM3G8dzzkFaBS0ICqk3\nK6E3hB10vhT1dmw0LwLSsJmDV4/sxg/QfFG3Y1pgQ1+GkqzD1DWuJepWgPpSmTGUEEYJZ1TgNj0v\niONOEISe508mky9/+cvTyVwIkWRpXpWFrNIix+yXLM8BRm86aIihgnN3E+G4rpunSSv0BSVR4OfZ\nejgc/vW//tfHp2fr5WpyPt7b2c2yjFEuS/XMU8+cHJ6EXrg72iWEnZ+fL+cLqpnr+Ag4v+/7PvGJ\n7/ljjGjhMEI1p4QzwhlllGz+Rzb/I43ohVJOKVfK4CLPzs62tkaEsPPzyde//vVut4s+2tlsgUrj\nbDZfr9M4buPpcM5hvKCuSAcWi0UQBFh4AGIqCnEI7IGpAKDHih+LrVuPYTH0K0bQGgt2uWXByj2i\npybyoRssLdKYuG5lrOmIoDBNJW9aKvt1F9FP/c4rV9h0XPSx+njzDcYY6y1sTEsIoa+++Fucc9D2\ne73e8fHxYDD4whe+8Ef+yB/h/FK3gsX37DTy5uQcGwdqreFq8jxfLBaDwRD5htbamj006UynUxTu\nUKmUdWcNMjRMZUaxG2xJ5BvNUaq+76/XqysHhDsHPQVqae9fa01ooy2dNFrWmaiqSggnSZJXX331\nM5/5TDvuLpfLstT2WTLGKGNSyrwsNuwzetGJh8fNuFOWZVnm/UFvncxPTo7+h//h//Xe970nXSW9\nXu/enbt7e3tVqReLRSuMpSqjwC2KDRFHU1IUhdHU8zzuiNVqVSm5tbX1oz/6o+fn561O++T4jHuB\n3vT+EzTd1E96I7KO47h802unlApDnzJilGaMYRP8k7du/I2/8TcYoUphDq/TjuPVapVlWa/X9Txv\ntVoA7wX4BkzL9/0kSVCDRXYNybY5Hly0VU7VIBuYRru95wXk3V6y3qxi9RDyGoZ+0wuxixLCpe4H\nWrfeYOKLVXWrS1e8VvMPyWX32/z946/mReL9uBKEnbzuarUAB0qUgCouaBAgWGF48K1bt7761a/i\nrIHyQxVxw4AxgOOTeqwslCGKIlCZy7Jst9tbW1sAZGwui8Ca1AtiEGSixg1OM1Yc4qu11ni0KKyL\neiIFHkwtTCGvh/uiOoeAB5BDnue4MGmX5Rpm/1cfFlHKrNcp5yJLC63If/jVXzN6s90KyUmaZXlR\nZHmOfGYTpKkN5lvKSmplKCGMZGkSt0JKzHq1TJLk5s2bH/3whw/uP2CErpbzrf4gTzOjda/bhQTE\nrQ41LM9LrYnLXbEZyLWZfJpn63S9+umf/nvPPfdska79wPUcrlXVCnyipCxz3xVES4dThzPB6l27\njBq2cYKO42RpLqWKohZoRFlafPaznwXS0+/3tSZlIcOghVInypsIPsFBBz6MR2Dpr2i8QoIAtUS8\nFEUR1BLhJaUUgTckz9TNU9YTWsqRHX9gAzPf9yEerJ5pyeppsDaQuQIowAeqBsPB6pItvl/JL5re\nzH4gb9BrIOo2SbEq18BLNU4MEk7rzBPGAuxiijmlD9/8CsyqDQhBzL1//77W+r3vfS9qBaARgB2i\nGlud7HXrupvGtvri+haLTcGK1CU4aDl0qfk5uGEEkIQQyLTVTNyh53mYc1zVK+c7nRgN5kqpdruN\nvlWMkeU13YHVjEdZNwc0PTZSdikV5zzwo3/4D//h22+/jQtYrzNCmJSyrOsfqm5gU6TmSQhuba3W\n2nPc+XzuusL1RLfb/umf/vtR4HU6ndOTo62tLU/4i8WiLFWr1XKEV+Z5niVxHDHGVutEKQWbUlRV\nkiTD7VG705rNZmmahlF0fHz8V/7KXwmijjJmMZsPRztgMFy/fvPw8ND3Q0IIYch5XCsZsii1lo4Q\nCOyF4L12ZzAYjM9PP/3pT1+/fv3mzeuzydQY0+21l8ulMZrSd6Evep5nCVOUUthZUHkwX9WWvO0T\ntKlj0yH4fogO42apFjkFvZxv19HdZlmpavTRyXrmBbtckmaM2Z3sTUWi9TQuqy3/f36wrybuT+qy\nhG37smEawkWnsVtc13tFRM3XJwBvcQrIRqx0xnH8nve8BzvgJ5PJ/v4+EGpS779CzoffwGagLIbr\nANsQzEmLCsI4IXBndW2E1K0uuCZbi9P1VFPb2wZCJqYGLZdLANbwxsYYO9YSQ5dd1wWPRmsNSyzr\nWe21YaNIdijlMIJ5VkZhzDl/8803hXAp5b4fBkEQhGEQhgCahetsGnN4Pe/aahohqKBnWdbrdRzO\nJ2fnP/5j/1W/246jltEyjlrZOt004wZhvk7zNG21Wo5wweyLglbghUoaCHS701ot56vFUim1XM5l\nVWyPtj784Q8LRoxS/W4nWS2ULONWOJ2ct1uxDausvDK6GVDnuj5nm+Ih56Isy6OjoywtfvEXf1Fr\nvVisEAKcnpzjxN4Vsod1830fSQFyZnwm8AMUeUGqIo3uW4Qzui4doU0eUQy6IoGykMegFBsN6vql\nLpOtrJo17cKV3IxczrUe16srOLZV0ebbmp4Q2206nQ4cBniLKAlciUjt6dmP3ex0LssSYCDeQSkN\nw/BDH/rQK6+8ghmD6Bkt6/1jpG7s1TWzDrYNBwe1RhzSarUQ4iNmsI1ApoZ6q3oZDWIVIQQQS5wa\nVIUQgr5vhCj7+/vn5+d43rAilmUymUzAT2d1Ca55terdtsPgmYE5+tu//dugrViyGKrD2NSD4YF+\nFCKIClsRolzSaPNxHF6UmeuK0WjrW7/1o1KWh0cHSil0pqRpagz1fd9xPK2ILKtOq8MMrerBwC62\nYZVl5Aec8/F47Arn2rVrqIP9/b/3U3/uz/5pTo3rup24VeUFmDRSXXDWdL1MS2tNDEOXE2NMSbvz\njRpjut0uMexnfuZn3nrrrTRN+/2+HZRAG0CfVTnw46xZhK3BeSJFx5+ALGpdioV8beEbf2sLNsAP\nms/FhnP4Q+vTaGMdtqWMW+WxOmbfYwPCdwU/mq8rkmAV+xLIXM9BQZvffD4HS3Fra8txnMViYVWL\n1DCmxfCsY6QP3/wKWDZgHqMVjTGG0PGFF17Y3d3d2dlR9ZhO65QQ2llcpCzL4XCIEA4YPYLyTqdn\nUUeYMdgD2D/75IB9obVH1lMiTGNiBPqXptPpzs7O+fk51mXEcRxFAcIbO3LH1LVB1ZgX1DBaTdTn\ngu3a7fS/8IUv/Pqv/wamlyZJ4ro+pbSSUpMLgFhrXchKSkn5ppWhqKqqXvzNCPEcka1X8/n0Z//x\nP3r6ySdu3Nx/8803t7b6RhHf91WpVsu147jdbt8oMp2OHcbbnRaeH+G00+koVY2nE9939/f3j8+O\n0eItpVxn6zCMjKEvvfTSP/n5z6R5duPGrcNHR0VRcdcpK8MYI4YaYxShnHPheK5wosBTSqlqMzDL\ncXnkB77vV0UxHA6nszFj7P/4f/hvr127FkXRfD4NQhfGs2nO8aBh9dBtaHe74qyMMTCj+D2adGxo\nDYlHtN/rDYAloAkYIShaPchjvB8cuQ3PrMOhlMp6VNTlNxNbx2u6O3J5J+Pj/2pvtvnDFX3Gy+5I\nM8aAhIDOGtwIpbTZlAzBhjuh6PtgjCFnk/XkAihGmqbPPffcvXv3GGNg5dCaV2V1jBACK4L8mDfq\n1KAjgKZgYUZbLYX6kcY+NFwlmlCDIABVD8UNfHhZlltbW9iPA1YEMn5cDLgOGBCNpjjawHavPMjH\n7dmrr776W7/1W6TOFUF715cNW9Nq4q9k7UbkZgqykaoUgn3v933iT//pP0kpPTg4eO65Z239kNVE\nbVxtEGyIo1prOAdMnu62O0mSnJ2dMcbgpbe2tq5du9brdR3Ovu8T3/sDP/ADRunJ+TiMAmOUJxyH\nXwpj4N+KqrTmDKOdlTQA0D3PWywWoD7+7M/+7N27dzG1qSY91XhS3bYLVMzGCzgHWEPr5a7wY0kj\n2yEXLTDv7tlMo05NHkulmjeFy2viz/QyFnIlsLwSH9LHcrPmm/Vjwzmb1EcwS6SU5+fnthfbdV38\n7NZLP/BMMV717Ozs5OTk+Pj46OiIHrz1Eq2hPDwDkIkAIc7n8+VyeXBw8OEPf3ixWAAgsdnXReaH\nvi9jIPe2W8wYs1wmQKt0PU4MABS4UVYNrHPP8xz2EpiH3SEC7gIqPGisRtCbJEtEqvhP3DAEwkIv\nzeeB+cT1s6Faa62IMeYzn/nMO++8c/36zUePHnHuwIZxKBWp1ymRzfNWSpWyIoRUjT2ATHDBqanK\nDzz/vr//03+vqgpO2WI5a4UBRC1Nc0FF3OpoqReLFWOi2+2qskiShHESx3Gl1GI5F4L1+30m6Hg8\nNswMh8OT0+OyLJXWW1tb1NBHjx7duHHr3/37//Fn/9HP7ezsdXv9hw8fCdfXmkiljTGGcUqwypu0\n/IBS6gpumWiCEcdx4jo06PV6Z6fHURT95E/+5GDQK6sMbXjWn1hQERAIHrR9LojA8eBM3WyBXgEL\ngDX1raouIBZKKd6GAVP4UvuNZgNubcgZvJ50SGoalGkMLKL1GFIwXa1SPa69VxxX84emW9M1swwq\nR+sA1R6LqrvDPM+zi5kgCQh5cNlYxQj3Qw/f/hrmyyNRMcYgtcV5Abh/4YUXPvjBD/b7fRSvZN1K\no5Sy6yl83z88PHRddzQaZVmGfu0wDKW8QFOMMXasHQY2okUVAQbqpPB++LmqKgzrRBd52ZiPi8cT\nBMF8PiWEIEdXdRUhiqKzszPM4bPYl4WzkUSwTdl041p/4id+Igxas9kM/TU40KKoolZr05lWVUop\naTb1IqkVY8xYij2l3HEEY4cP7774+19cJytjTL/fZZycHp8g38uyTJXKEZ7rekqZIstBrCmKrCgK\nQ7Tn+tzhSpZ5Wfi+yxibLRdCMLCizsbnnPN+d4BgwXX8f/8//fK//Jf/0lC2u7u7XKxKpZU0hjJG\nuWEbrIsS7gqBiqnDhed5wmGEkMD1OGdlWTFGQz8Af//T/+WP3ry1Z4zSWht1FbbN85xzpxX6WpF1\nuqKEt+KwlDrPU8YY2qwgQghqEFn5vm8MzYrc4QLsM4SjNoy0CKdVTqufSinH4damW2WzfMgryqa1\ndhzvDwtermja4/rWfJWX55Syy8viEYzghWtW9bh7p94BZE08UmXOOcOJCCEmk8lwOERx06unwEKy\nP/ShD33pS19CsNdud7UmYdjqdHpSatf1B4OhMZRzZzAYtlptrYnvh61Wm3PHGCqEsI05iC3zekM8\nWkvLejY4rBd4QLAT2IiNcwQ6jDfzukMH1+nUY7aMMaruFMTgA1R7nHqkF5odHJcToquq4JwSYtJ0\nnWVpux0TqsPIJ0QnyXI6HY/HZ+v16vjoaHx2vl4lVVGqSupKSqmkVMRQWamyrAihlVKO53lusF6v\nn7x5i1HSCqOqKF3hreZJK2orabK04Mxhwk2LfJUmhhkvcJkgeZkKV3iBZ6iWWjKHUc6yoigqJTWJ\nwhh8lyRJo6BFFD89mcStHjGCEPL93//93/ld33Hj+m5Zpq7Hta4clyqZO4KuV3OqleNwQ1Slq0or\naXQpqzTPsryspK4MqYzhnk8dJ5WVFnyarP4fP/fz9x89Eq6X5gUTjusHUps8LwlhnHBBBVFGS+MK\nNwpaTJPpeOYJN3ADqmmeplrruB0FoZcXaakK1/eY4EmaSaU73YHjBqdnk7Ks7KojDESxhVkbr8JJ\nQtbzvKwqhVqo1gR5EGPC/h7/BAyFMQFvA1wAwmzbYaAYthfGyhX4JXBHlqECMbPurizL6XR6dHR0\ndnYGmB0xmqUKorTb6XSAmVk2BcJmvIc+eOPLSPXgBwBLorS9tbW1WCzgZ05OTr7yla/80A/90Hy+\n3N7eXq1WKAxgaghUX9VD2PEdiK9A/vA87/z8fG9vbzabgUsOBjqIIHYIJEi3YJDBQSG9AZqHRwJ4\nEIpUVdVotIV9FBakQsyJFNZczq2NMa04RHcGIaQsZJIk2Ar7Yz/248YYrQ2g7aqqwM8oCkWQpG+S\nNGXZ0GVZtjrtoijKSmF7lu+J/9vf+cknn7glhAjD8Pj42Bjzvve978GDB3g8QM+Bu3LOW63WarUw\ndfsSTA8CeNtbhDwWlY92u02pGI/HN2/eWK0Wmpg0S/7r//qvj8fjuN3N85wJP0nWURQXeWUom81m\nQdSGmb/wwJzDqCH0AFZZG3jtO+Tv/t3/685w+87dd/qdvue7eZpxzo3UlFJOGSFES2mMaYVR3Gnf\nvX/fDwPP84zReZVrI33f9313tlgaY3yvFYZhller1SoIotHWcHx+nKZreEJSAy34Gc3OcRwTQkC8\nwGxc61uajog2hkA2PRKtG09RyLXwmM1ZrsBvvGZHqAYLrPnhtNHJigq+/aI/zBOyek+iblSSKaUM\nPX+q3neKWwVJajwewxcVRfHMM89EUXT79u12u41WH/S85fWOQtmYF2KhYa011ABtGrPZDJiVrofP\niXpOOCEEjg5WB/BxkiRKKaeeVIlgFToMEAUVBdyJbfFgdT9VM1vDC1eFd8K7Avz8yle+YqczYIAE\nrK/rulGrFYQh0k7uCCGE4wjX3Ugq7NRoOJjPJq04/P7v/35MaFyv15ixY8d0osiO8B18Wa01WlS1\n1jA0juMgF0KCiptCVIZJLXmer1arp5566o033gAA67rupz/96dFoZIxBmcQYs1wuMWVxd3e3mf+o\nmtaA6YN4AVKTdUdFlha/9Ev/78Vi5XtBu9ubzubCcV3PZ47QlEgtDTXcFdwVpSwns1kQhVRweE5W\nl3GzrEDcXpblYrGghgx6fVc4p6fH7XYbNhrWB53d4/G4LMvt7W2k4kVRDIdDbI1qXr8VcVUPQaM1\nIg/ZwGIT1uigaYaRFs23RyHrNi5bgLVvs42h0DorSPbT5OWXRUfsn8NFr+tXkiR0+uhNeA9EaAAh\ngVNhwg+th66UZfm5z33ue77nE5zzbrcLAodFGk09js5Wt3BGcIxaa4xeHg6HG4pTWcK8aa1RMccY\nLzuuSGuNSUZI3tC3D/BG1aNdtdar1QJHDCVkdUmnCY3wBrG1kgUOpSgK3wt7vd4Xv/jFX/3VXz04\nOATWSGsipay01poL36JSymBNBmiILEkS4W1UZTgcnk/Gv/rv/322mIyGW7PZDBaqLMt79+6B2oK0\nBwcCsHu1Wvm+yzdLAgoof1VVs9nM7kxBSgOTN5/Po6gdhqHWajw+8wJfOMzznBdffPHv/r2f9jzP\n8aLlcpXnZeBHmtCDg4Ph9p5pvEg9w1DWhEZbSPQ8z3F4y/e1llrKf/Wv/lWapuPxWRy1lKoiqEft\nK7RSsFmd/lBKKVVJKdYyGanKqqqkVp1OR3B3vc7yrHBdXwhXazmfTUajYRRFCPM456CSIFQxDc4Q\nfrYFcVo3aiHeQ8uVxU6sQlpEVF3mK5vLY6DsL9ljA3/MZcjEypL1IlfeibchCoO3sM4QULlVezYe\nj6uqcl1XSgnWBXQ0TdNr164xxhaLxfb2tp3R/8ILL4D1jz06URQ12wdlPRAB2CBaQlerFQoR/X7/\n/PwcR0Zr8hQOF6GgBTPhJ0U9xwKsM9AU8Z7FYoHBJKauxeGuqno6kAW1mpiSzfoc4Slp8KVf+tKL\ny2XiOC7n9dh3wxjdlEQ3No8SkEVstbQoc+FwarTvOpyze/fu/tAP/iClm3mm6AC6d+9ekiRbW1uE\nEJwzzBlaHAB7ABnq9Xrgl2LyGaIAPELXdbMsQ9kUk9Lu378/HA5B9UbB5tu//ds/+MEPSimPj49x\nCOPxOM/z/f19a4n1ZYoJHgGoebC7SZIkSTqfLw4ODvNS/uzP/ZM8K2/efML3QyHcsqq4EG7ga0qS\nLMnLzA+9nd3dJEmkVsJxuCOkVqWsmOCtdhwF4WqxXM4XURB2Ox1ZFbIsuu1Ov9+fz+eHh4e4u7Is\n0SZ3RdBtBm5/06wyQzPhlIC4LJfL6XQ6Ho+XyyVmp6Kd15JjkZvgPy2PwoaC7LHZRKgJA+2wUsTq\nkWG87j4RdY+yhdDI5d4cp/FiAOsAi4HAwRhDa5ONp5FITCaTj3/840EQnJ6ertdrqDIQCF2PW7LV\nM5uzITSy/g1AIj4WeRo4Pgg5wDjBe4p6Hh5i0cFgwOuatdsYrgrf2yyaw9U0ISk8IZg6u8au2+0O\nh8PJZIJhPqwmK1zQLwihlEspK3XRBm6V1pYlEfbcuLn/l/7SX0qSBKEBYr8sy4Cm4sIg06iBSimT\nJCmKAm9DIQTj0ODKsHoBwTPcYFmWQHRHo9HXv/51zLpcLBb4xr/zd/7Oxz72MRi7OI673S7kwEqD\nNT1NL2eTHyAKs9lsMV8Ffst1gt/7vS9+5jP/bDKeuV7Q6w20JlLKspLKaCFc4brKmFW6Fq6jNSmK\nqiw2qIOUEhZEa50kyWIxM0ZjcNP5+LTdjtG3AasPHgV0II5jVFBBUsfPtsSK/RVgX6zX68VigXBM\n1vRiUo/ZUQ0mxyZZujwL3UaDNjdrQovWHunLdT/e2FNlLr9IPXtPNJpc8flF40XvvvolSimwwfPz\nc5AAGWOr1Wo+n+/s7HS73ePjY4C2rVbr5OTs9u3bOzs7733ve1er1Xq9hvgio0ClS9RLq0y9pWky\nmWAUc6fTGY/HgB8RHDLG7MYMGG/oMBQSFbyyLHu9XlYvFrZVOyllFG0EkdQ0SwCVGBBvGjUWnCAy\nvaKosLPqV37lV37jN/7nPM/LQjYeUt3/RozSRBGCSL75PKIoODg46A368CT//X///5zNFu959unx\n8bEjOLQRfHZYhzAMsRem1WphVBnmwO3sjBaLBdpDrRQCEMJ+MGAYtlbT6fTRh9DrdZbJKgi9qio4\n53lR+b6f5vIP/uDFf/JPPnN+NnH9oKoq17/UXUYbaw2tQPBGE7RDxHA4PDk5abXCbrfLBf0X/+Kf\n52nieZ5SlZQl49R3Pc55mibLZbK9cz3P86LIGCO+51JqijLL89wo2e/3fT9cJ1m6SimlQRA6jnN8\ndjIajbD/FXv/ut0uSjUYxmq3C6h6AQgCnKIe+2VjH4v4We/EGAMob2vuNrNAEYzVq6dgT1ljSxt5\nN1akfTVDpKYqNt+M2ArGupkx2gSSzo9uHxwcbG9vw4jeu3dvb28PSoJFTTC9qInNZjPH8e7evbte\nr2/evLm/v49iuT2Csp5gh7I1Rt8h0Z/NZtevX0fp/P9X15vFWpad52Fr3NOZhzvVrSp2VXVzaJMS\nZ0IOY5IiZdkiTdgOElsRHNuyHCCSX5Q8JEBsP+TFgGHDseIIhiwlL0pix0IcIYAGimyalEWJYqgm\nm+wW2c3uGu9875nPPntYQx6+s/67q5o5aDTuvXXuuXuvvdY/fP/3fz/mErRaLWgPdbtd9BbALA2H\nw7IsocwFswdjiTIAZgt3u11r7WQySZKICqOAcwA8gItIy0EWHdsdXP5Hjx7943/8j6VUk8mEs+14\nYSEEWPOMMc+EiqLa2W0nzfUQdL/ZbPb390/OToVgv/RLv3T33nPz2dI702u12lnr4uKC9g1ysMFg\ngK8BhMC+5HkeRQoxPF2/9x4hBokQeu+Rl9Z1XVVWKTUaDafTKx1H4GHWda10XJZlf7hrrfvn//x/\n+uLvvbRYrXu93iovm1k07RjKrnnAJ7FEymtjTBSpvb09kKqff+HuP/gHf3+xWAjBbF2ui7VzLo6j\nOI6FkIvpKtJJFCvnTFVsnLdayzjRtq7yPFcq6vV6ksn1aqOU7vf7Qsujo6NFkDBarVZAntEq5UL/\nFNaEtFBZYPY083Mi5VWN5jo6YJQ14RgQCAlLDcPNAvhJWRy5QYoYfQNm45zjo5qBKAIHjNRAYEUX\nI4SAdsv20x689sftdvv09BQCL2VZnp6evuMd7xBCYD7Azs4ONiiCyTwvut3u17/+9fV6/fnPf342\nm4EPTlKBgAeppwaNcFEUwZCj3FnXNZj7SGDwyfj1o6MjCJzgBKJyLYLYCZJASP0g6Do9PR4Oh0gd\nYRSQUl5cXODcKqXOz88555g2vNmUYDx0Op2f//lfQMeEMcY7nMbruMJ77rxflUWSprhg560QQoRh\n2VVdeO8PDw/+0T/6R91upyyrWKuzk9P93T2EdkhWYYnOzs4wBtkErXU8m/l86pyDUQN2J6WEwA5Z\nYh40rYQQQsCWeyEYl0JIBqWEsjJpmq43tRBytcr/+l/7z1UUO+c2JRmI6wFIyNmaloh+HovEOZdl\nmbV1lMRS8vF4/PnPf+6nPvsXjanKTaFjlSTJ0fHj+/fvm9rdf/NRv99/xztu3Xv+Thpp522k5GR6\n2e92qqoypXHOCSY558Y4Y60L0hSUkuHRQ44B2lVlGLlEtRweBFHQzo8TiNjMOQdqRFmWeZ6DUwGY\nbduvFOY2QywQ7AgAzt77J0+etFotkGNgfeigNn0XAdrNKMmGl3NuMBggRWSM4XoQcCFDwRPkJ29+\nG9sRoZ1S6vLyEn5DCHF2dobWt3a7DUenVAQ28Be+8IXPfvazkFXdbDYwOYiCXKM7HUkFkg1CMtDB\nSqcfMScPAmbEDlmv1/CB1J2NFcQdBlpdTTUo7z0+FjEnpgLgrII1PxgMOJfT6TRJkm984xtf/OKX\niqLA/KG6AijMnjlspbPAgDnnSkvOua0rY4x1tRDs+Pj43/7b/7Ou6+Fw2G63N+u15MJUNaqLCB3B\nPoPvYoz1ej2tNTZNFEVCMGIY0BZ0zg2Hw/Pz87IsUf+Ef8uyjHPQMq1zxnrnvAG7SkeJ916oBPnF\nj3/qM+1uzzln3PU4ZRHmSNJh8w18Et9qoZnzjAnOfbvb0VoLwW7duvUP/+HfV7EWjG3K8vLq/M23\n3jo/O3OWtZKsrqqqKj/xif/4YG+nrHJvjZBstZjHcRzJyBhTFSjnpEmSrPOch74kGzov4dLR58U5\nuiK2ogy4a+89pvmBp4LiE6wqkALYd6XU6ekphk4XRXF1dVWWZa/XA/lpPp8Dm0AqYULjPxWQqNur\nDjJhdK54g7lGsWUz0+NBp5Wgb+xq+l2FhA8OGkYCjTogVnLOd3Z2Hjx4cPfu3cVigRpXFCX7+/tC\niB/7sR/75je/+ZGPfAQ9vOSLqTiLQAjIhwsMOlTAURJBeI0lI0wCv4vVR/YIVKduqACh5ktvw0PC\nE0I0C6AC6vzW2p2dHWstxIydM91u76233vqDP/ias6wqjbOsrqz33Ie5atv/HPOMKa3XZeGZj7R2\nDu1JrrZGK8mY++n/7K912+1er7dczn/w+vfe/yM/OpvM4Vf39/eRo6KOT6k/NpAJDUpRpAj4Rr0I\n0BYmeIFuJqVEfbIoCng2IbiUUgrFhUavp3WsLMssSax1WdYme2eqp0bD0JETjTmAT4VPjOk42mxK\nKbhzxjleO//Nb72ctjubopjPZg8fPXrzzTfzYjPo9TudznI6m0ynb91/sz/sjXc+uV6vleBScaBZ\nxldSiAQCLVw9IwJJfG4f6stxkNdHjAcnA8OEvU5JPuLDqsF4xqnDuTo9PUUBCcMur66uOOdwGzbM\neRdBhw/HDGcbXyPKIBvUBEVdgyBG9tF7D2QYO7AZSdK3nHOFM5aEIU9oVIE3BEERpD7U1tAcgXMF\ny/21r33tYx/7GC6aXDBvVNtw9rC36OLwfsKOgHngV6CgbK0FOI5zdXJyMh6PgWjByUgpUV0AikWc\nDOpbRSEY4zsgkQ39xqKo3/nOd/7Jn/xJWZZXV1ewAnmeJwkYJ9dAk3PeMV/X1wX6TZ4zxqIIGld+\nMpn81//NLx4dPR4MelLyGwd7l1fn3Ann2P7+/snJycHBwXq9HgwGl5eXiHtRnKTxCYyx1WoBk4Rb\nwzMD5Lu7uwuEgGoh1lrGkFwxa53njHG35Q0zgYzUGJCbtrxYz69lt30DgWzmsYS2cc65s3Gs67qM\notgYUzvb7XYZ5/cfPPj2t7/z+uuvL1d5mqY3bt1kXD98dFzm69ViPp3M3njjjR//1Cdqa1tpa7ma\nZ0lcVZWtayZlrNBQZ0tTO8e88TYMG6PLIAlqGFxiVBHFHBEKdg4FSlWQPBFhbpkMCpO4NeyWJEkg\nWERhJEhVnHOEZojLcHTJJJH/0A1ZxGdsEy0swDzWqO9hV4MWgxsRuJNut4toh0quCOGWy+Xh4eHR\n0RH+HpIo5FTGmLt3756dnc1mMxVETqj4iMAJEDy4Z9TZASyE8DoqwCO55JwD8YdFwXuIwBUFkVCy\ni8BL0J/fDCfqul4ul2CsoZAAHKXdbr/++uvf/c5rIhga1EWCQ/Pee2e9s1vEKc8LxgPfXAgdx7AX\n0+n0Z37mZ6SUBwcH3pk0iQ4PD9A2jiD21q1bYLSBg1YGlQfcKXWjEtsdLDvaH+PxGKOVodSCr9FL\nhpdotPwgLQSQyxhDrogCpm+8cEfNw/YM2iYEk0oYW1tnpORMMljobrf/K7/yq99+5bud7vDWc3ei\npHU1mV9cLTalOTk7n6+WjLHxeNdZlmUt5xg2iZQSN7jZrGezSVnkWkjKG3GiqDCNJAdoPowsPDyC\nLKB0IDYg8oLdB9aNW4vjGGk5iigwu9SLgPW8vLzUWgM8Q8W11+uJRvsCKpmQn7FB0YS2tAs1ff42\n0BIbuxlBwN7JwIzb8vHo5AGuQO4ISADAIEYGw7e2WnGapqvV6sUXX3z8+PHHP/7x11577cd+7MfI\n0bOgmOmDsDuVrWFjkJXh4BGyFLJ/cX5+TlQsBFrtdvvGjRuQdpKBEYaP8t5XVbFer4mTAR4GBqYi\nf8PYHSiuZVnWbvf+9b/+1xj+FAc98263W5b1M/vSe2/ZNkVGtSfLUs9svs6drz796U//wi/8wtXF\n2WDQs8YqFWFeNncCrSur1erGjRvHx8dAekQQ6yQjikFnsGuAgpEz4G2Hh4doBybdOOxOKdXWIFjn\nHePCM7bFxLTWq3ztnIdlUWDbmB8yPOmZY9a00Fz4osirqqjjOMkyY2y+2XAuprMFW+brTdUfjrTW\nVWHPz55cXZ5q7pmvW63Ohz70obIs40RfXZzv7gwE45J5eAYYEe6FZ1apmDPfLFrStqGUlYIXpF4I\nkQCQUJpHhqmJQ6JAl+c5TDABJIAbYJIQcMLw6aCcj48iD48acrNeR1vimeWiF9Xlyb/BlMAhc86N\nMQIEKOz+KIrA5mKMgTOJaO327dvodsGFAqTGVsYW+d73vgeWCqEd8DYIAlkQA6d1TIKmP1bKh8FW\nW8UvIUTQBkVDHWMMMAxdPTIfvA0kL1TPKdyH7cDGhbYmShRvvPHG97//feccpBn822YIPnPecDFl\nXRlneWgJuXfv3i/+4i+u1+vRaBRH0XagWSvTctsPf35+jtoJTh1ZFh/4rPDP4LuJINmNOi9CKeRs\nnU5ns9kAqUPzBDKT1Wo1mUzOz8+Pj4+fPHmCCXsoVV1eXoIMRK26lKfR17iSZ86bDwgb5z6OdVHk\niPBRod7f3z84OEjTVr4uLi9mT05Ol+t8Z/fGpiwWq+V73vtnUDHC4sN2MMaqqnTORlHUSjMtFbAm\nSnvo/PMwUUwF4ZkiDF2hQJryfHw4YG0btCJhgrF7OedEk0BTS5ZlCHPg/GH34WlQcIK/hR4HLKAP\nPSg8zKaB+3VPa5Y0D5t5m3qXEGI6nU6nUzwOAa2SMnReIlkCbHj79u0HDx7s7+/neX7r1q0333wT\npgL1LgiwVlX17ne/+8mTJ9j9zSuD9yTb0+S8IUokliPnHK4DDgq7kNwgbhLZDtAC5xyYBFh3KlPC\nOhpjlsu1tX4wGDEmptO5lBq9P86xr371q0iUcXKIOuP9VjfLee+Y95x5zrZBHWOCSSWk8NyUZjQY\nfvLPfaqdZt7a1WK5XC4PD24qIaeTGWGkaZqC2AmcBuQykGXBhEjTdGdnB3hxmqZ4Cijg9nq9fr9/\ndXVFFQ7OOYaeZln7yZPHJyfH4F6iInxwcHj79nNpklSV0ZIL5oe9Lvc2S+IsiSV3nHvJPOf476kA\nsvk17r40NeouxpjNpnCOWcs77UFR1NWmXC6Xq+WyKIrlbD65vFguJpwZZ8uPfvgD1pZppuu6Go+H\nq9VquZxjR2Gdp/PZpiyEkvlmhUSrmfwgQUDQiOgOpFkQlEEDAM0aYRcMEHAE4JM4jbu7u67BHSFX\no5QaDofz+fzk5IRzDjlq6O2BII7Ngw83xkwmExGG7+nGtLNm8kYnqmmm4UJwg3j07XY7SSKFlsKH\nf/pNxtjx8fGdO3fgH46Ojg4PD+Gyz87OUOBP0/T8/DxJEghaIS+ikbzHx8cPHjz4zGc+gzg1yzLU\ni0DUKsJkKZhzots2K/pkOVANd86hCocKCWMMGS0gu7quu90uJBzBX4FjhLBhWZbz+SJN0+FwuJiv\n5vP5c889hzz1n/2zf5avVrPZbL5cs1Dyd9u5Ktw464ytrbHmusayqWqlhDFGSMYYm82mO6PBb/7m\nvyvytTV1VRWeWcl4mOsrHBNoFobRUUohBb1///7+/n4cx5vN5vLyEpySNE0xk3J3dxeERiT6qqFA\nAdOATCbbThvPkeVClwUI0MHBwXqTo8fPWn9ycvLLv/zL3331tbTdGo52Vov11XRy8+bt1XIthFqt\nVmmr47333DHGuKD+aKYkZ4x5x611zCuloiztJEnW7vScc0oLmMLBoHd8fCS4ravZ5//ST/3En/90\nt9utNrnWOo4iYypbG0YTdsJ2dJ63Wp1NWdahnxi3hlSFiHJNi4Dyd7jxwoSeCaQM8EIySOjRoSVc\nEZ9fhRljdV1jJ6AAU5ZlXds4yD/D5eCM+adTXBaA/iio9DXTNh4kQpqxut9CiZYLz5kUkvHjH7xS\nVRU8Rr/fx+amcr73fjab7ezsIPyDEhv+ng0MaFziG2+8sbe3NxqNwAuBEAgsAd5AxVmsAjFoZEPN\nwgYZPBuadHzoWUC4m6bpycnJ4eEhLBmKKtC7nkwmSPCc87PZLE1aSqlWq+Oce/Dgwbve9a5vf/vb\nv/7rv+5MtVwuV/m1irPznDFWGUNlyirMdfPem9IYY4bD/uXl5XhnOJ1O/t4v/Fef/exf9NYZW7ra\neGalRHWFMSY8l3TYqkBdR5ADh2atbbfbUAfz3i+XS7QFIFPHUgBXQJRBPbLW2tVqlSQRov3ZbIZS\nDVZmOp0+99xzQghkevv7+2+++ebDx4/+1a/9L9959dVbt55TSi2WG6UUZ2p3d/dyMmOM0WHjfKuE\nJLxzljnnOZdKJlrHSsZCqCzLWq3W669/bzjsb4rc+3p/f9+a/J3vvPmxj3zgfe97HxJ+KaUS0hij\nhPTeM/vUyCXGGBPbGdwIm5EgtVqtR48ewYN570Hv4EFBowrT/2DifagN0KBMHupvAKiiMKiRIiys\nGOAKtF8AAgBWZRr9IpQHEReELr5Zn2wCIc0vyN01fmIxA917z4/e+DbuvCgKDCKhXAXW9+TkBFff\narUuLi7qut7b2wPMCt5GURT9fv/09PS11157//vfD8ODlYIjogIikcfquu71enC4jDHCDwHd4n6I\nVSgC32wwGMxmszRNr66ubt++DQc4n89BjUc+GkVRHCdCiOVifXl5ORiMDg4OlsvlSy+99KUvfck5\nV1VFURRbQF8rxhj8WG2t9x6qB6Z21lrjrLdOceHCbEtjq7/1t/7mf/E3fma1WiznC8+M8ExIprWM\nokgpwbmsjMNhc0ErxgXJ0bIsp9PpjRs3cOqAjA2HQxQtkC2Mx2NAU0hBGWNE1wq1oKIIwqbAe0Hn\nTdP04uJis9ncvXsXVY2iKFSk//Drf/xL/+JfCKF3dnY2hYnj+OJ8EkWR1PEzh40JxjmPJWqeXus4\nidtax9Y4Y1xRFEkSKS21lqvVot1JyrJsZ/rv/b3/cm9ngAlbW5CMcWOMlso5541tpr6ccy7jt4de\nWB9Cs/FmH6rJ5GRcmCVP2Rpr9L+QqaJDQsinDSpDPjArgJ/Xdc3YdnYhhVdEZnomUMS3VBKgGBXn\nigpuzficc9Qqt2dKoRBU13Wn01ksFpCj894DTgDd/vj4eG9vz3tPU+d5qANiday1o9EIIShK3vB+\nuCUVBtzQ/Zsg1Qronwp0QDto4eif4O42m81oNJrP551O5+TkBPV3MH0QdlZVNZlMlMqxZW/dulUU\n1XK5fPjw4R/90R+h3mBt7QIDdes5mSWdY1qp7T5gHlTGuq6NrRjzP/XZv2CtXa/X/UHXWmPrEnHB\nfD43pnKOqSgBJxYfZUP3AxzXvXv3njx5Aij/5s2bYK9jQgXtGNQGUKknlW8k0q1Wy9otI5nEy8Ba\nwvED8sY573Q63W73te/9KTC95TJfr9eMa1D4tNbGMc452xpmxjn3jEYrCc6l1jqOUKJlnhml+dXk\nfDDoGcvW+TxryySVH/3Yh59//q7kni6ec848IwCmWYxiDKnwU02GyDvKskRNEmxjEoypwmwK+BkT\nog/AGwRmIGoQgdEOHJ8OLQIoZCioZLLG0EYX2PqAxGEvENbxBvBIG0M2tBJYgzNJ39KxDNnjNUFH\noXYBKIKF7m7cEuqMqL2CQoW0Af01kI7ACUHc+MILL7z66qt3796t6xpy5UDweZjeRmUGJGZ46iy0\nVCJ0RoSN9VWhkwBQHpAlrDV6eCl1tmGOdpqmznmEas45kDb+5b/8l9ZakNm31ldJLgWdqC00ykOO\na52x2/whkrw2Za/fOz09+emf/uk8z+uyEoKdnp4KwbXkWIFrhNcxkswTQbjGBcVL1AMeP368v7+P\nfryqqtC6NhgMpJSQr4OUBbpIiD6yXq+vrq7SNEaCd3V1JYQANWk2m+GToyhCGDkajQ4ODnauLh3j\ni8UiyzrOOeeNUipNWnVdM9a0LNdpRlGUiKdwwp1z1sL52OGoe3Z2/NydW1K1k0T9+Z/8iY99+EOc\n87railJyzr13MPXMec654FtaffBgrqo2eNAIZLz3aZr2+/2LiwsgCjxwgLBZwakAHILsBpCjEAJd\n3oQ3CiGAr1DFkoKjXq9XhBnFcMLQEUmSJMu2wsYicJVArKM6QUi9rttMnzmEvtFiQ++hykEcax4I\nA0pKuVgsbt68OZvNut3uZDKBW0AxDVWg8Xh8cXEB24y+LCSRjDEExCQTcnh4eHl5+cILLyDegxUR\nQaoWaQwCcTxIH6qZMP8k5sMYQ1lTBKFCQmJu3bq1XC53d3ex28g6gCIwHA6tdXmeJzF4ie2XXnrp\n8vJyNBqdn5/boDsvGvJM23UJJ809TT+NsyRfLi8uzt/7vhf/5t/6G8vlnDEXRVErG3POBXPOOSi1\nwidzGT8TuOOBQX1sMBhcXV2BJ4Bixs7OTlEU5+fnq9WKemHn83mWZd1uF0C/tRZAGSo01JKIGgAK\nhvh8VGzTNH3w4AHKpO/5M+9NkqTT6QghLq/m4/E4X5eLxQIACWEX3nvPvHfMGoOmLWO2QBHgk+Vy\nfm/nrtL7s9llp9v+zE986mMf+8ig16mqijvf3GfbzYdoRVwPo8A6wGkQHob7Xa1WVChjjXoA7XIR\nGG3YtVB/qoOAJA+aNzxQHUzoz0BwCDyc6Cks0Duw92iLEnBPnpmyNboF+/TMAPJgb/8hXuRsBJwD\nsYHw/EzoQ0PVGGYD+A8+CA4HwDSWgODR27dvX15erlYroCMIOIkioEIHBCwWCxMSQAJkAXTB13UY\nFMw5Bx3BGHNwcHB1dQXTjv+jbI36CfBJgAeTyQRp4e/+7u8eHh6ORiO8QSgp1HaGkHHWOEshvvfe\neW9JQ0YKIdhmk1tXJ2n0yU9+MooiRICr1Wo+n6P704WBZtCBlm/r4cUdtVottKih0jAej3GzR0dH\neNLT6RT1NMDuwD8QJ6O71HsPsvVkMoFMMgAtvBP2DgBJmqY3b95EzvzgwYNPfOITAO42m83Z2Rn8\nnv9hsDV2NmfSO26Nd95gCnkUycGwu1xNo0g4X49GvR/50Re5sIhpm+E3gvNn9twWHuBcNGbZIBIG\nFeHq6orIn8hisP1wC/DtzSIqomvQ+WH3iTQLEVETenAImnJBzhBTddDhxYOIDkKnuq63+muNcbau\n8aJV8g3IEcaaNcTdiKShlOJcMias9cY4fnb/VbBDBoMBQGTAIVi12WyGogTnHNsX7nI6nTLGRqMR\nKDZoPQaXH4pfn/jEJ1arFQ5hHSRfvfdNIvJ0OrXWAuJfr9fk9LCmzjkCo9DfBUEu5xzU/GH1jTGI\ngfEY4jiWUhljik318OHDL3zhi2+++WYShhgNBoNNmUdRxLks663Mi6ldaeq6Npa8nGOWee+98E5w\n10rjv/JX/pOPf/zPSin393cfP3yUZom3TmsdaymlRBKMB2DcluZLjwSGGaakqiooaoLQAIIIyCKw\nLDhvstGyBSuOdUvT1DlDphpAFMAtSOgkSfLw4cP9/X18lIp0UdWdXu9Tn/rMjRs3ur3RfD4XXHvv\nLQoegEa4Y4xZb5nnWmjmg6zq9qRpHclOp3V6euyZ+bt/9+98+CMf9N5zztppK19tdHBfMDQcw9oZ\nZ4wJf+3e8Z7a+mfONqwwVOvpUdqGcDKWEW9jAcaMQrc+2JJZEIrFPlSh39SFVh1YRoSUnHOw0uM4\n1jomDwkAzwbWv2zI9JODJaYUPWL4w+b55E/rZ9OJFShYY9RoWZZ3796l+jpIj+CJobSFxjCQYuiP\nDQYDYNyAVu/evZskydnZGeE/yHHB8W+1WvQtTNdyuYQogFIKs399EBSBv4WiOC4PfxRuFhXw5XJ5\ndXU1m80ePXp0dXV1cnIym80uLi4mk0mWZefn57AdIogLxXHMBPd8OyfVem/Z9QCDsiw3VQk1f++9\n44xz/uDBWz/5kz+RpvFkcrlcLXr9Lgobm80a4AREC7Gm+FtNW+4bfcFRmFUPhBbQyOnpqfceXpEx\nBgAdp9QEfimyOGQy2JRVUDulAEwFFTNSYkfqe3Z29vM///Ow90ACYMUQXmJAO0jbcRwzLyBTqyPJ\nuddatdppliWPnzwYjfs/+7M/C/EF5xxiIu99Xdu6tugvYUwwL6TQSkZSaGg8YhIq/ovCDF46fjaM\nI2ahS53wQJKRJ8PqQ0JMWxzgGfJbrTVo5RAXAxEEhQSwZLXWED5DJQPFOmwkFhgX2BiwaKLRLIOk\nCaRT55wJs+ABaDUNR/PuhJCYFCKl4k9e/xZjDAKm4/EYzqeu6+FwiFvCfaJTEwcPHkYptVwucdLg\nUquq2t3dffPNN/v9/quvvnr79u1erweaGTEAoXk8mUygSoATj4smYAZXDIhPCIGcFV8ThOgDRNvt\ndjGS+969e0hg5vPFaDTSKv6d3/mdl17692UYWQqs3znjOZQ9bbEVcHfGoUnN1A6AsuCcM86lYNVm\nMR72/ud/8cubIm+326vVqi6rwWDAnM3znAWVT+ccY06paFPWZIzF0z1RhJfY0B+tGmMBCcJFBotu\nXYqaYG6KoqjrkpA0KpzooL9A+TAy/lanzaUSSv3Kr/zayy+/XFaOMaZkXJalpx4dITyzxpiyLq1x\nrbhjrbe2bneyNI3X+aLTab33vS/+pc9/bjabtNsZGluNMVLxYl2MhzsiqErDucU60lrb2vAwxATb\nA6tRPe0ZkJC7Rn+dfxrlQ5kxCpPQyFMh2sT+RtkANUnOOTUrE8EIFhxIGzhfi8VCKTUYDNbrDVGf\nEXdorRGygYyK56KC0ocLvaoANoEmoFzOGzdLEU2aZnSbCr44SZKrqysWWG1lWV5cXAyHQ+zp1WoF\nVstoNAL3HL+Mi6YYF49hMBhgVj0w7tlshqAI66WUGo1GAJfIKpvAV+52u9/97nejKEIFD3EmMn7M\nFuaBw1UGpXjk1nfu3OGcQ9MSPzy8MfjmN7+Jvwh9dSml9dtRHrXdjqKs67oy1jlXVTX8GOfcecYY\nE5wz5pbL+V/7T/9ybSrnTJYlxlSL2bTbbbezlve+3GzoSpBJy8bc8ObSR2HQh28MiEB/kAzEPKTH\nyHXBnOj1etRoDMgEnd2wQdiL2EOo3IDQBCcJPu5gNJZaHx4efuc73/GgGjOhtXZMUJrh/BZ6pSi6\n3+/XZvPgwf13vuv5v/pX//IHP/j+KNbe28VikedblMJuvDf+9OQ8CnUq7JYsSZMksbVRSkVSNQ7b\nVsnXP61B4N7G0mCNmgHcmmtUa5BHkC6LDy2bpBxhgjy+C4ME0zA+DvpUKozsRK2Yc45ug06nc3h4\nCGcAeBMEXaq/o9xFZo6uB5BhM1qmOyKiM2NMbTYbMFyhfwyvhZ9QJIoYNwozKzDXEwWi5XI5Go2S\nJJlMJlEUPX78+Pbt27PZbDgcPn78+Pz8/ODgAFkpdsD5+TmswtHREeHFuBk4ehFK2Kg6IPLE0rDG\nJBod+kfQoGCtBbMkTVPG+IMHD1bL/PHjx51OD2EGnmueb7hk1tqqtjW9jLXWVtZSzGBdeNjcaa0/\n/elP13WZZdnl5eXNmzfz1RqGJkkSyTnm2qHqled5HCeUT/OGlJUIxdBmCuecIwluOCtsI0i7wkDA\na9kwIQ1HEXaUcjaEGKiCYD9hytxkNt1sNvPz8x/90R/9jd/4jTTr5nm+XEz7/T4a95xDL9y281Ar\nIZhot7NNsb516/Dnfu7vvOO5w5OToz/42n9wzgnBqspwztMk854zxvqdbrFZp3EEMh02manq9Xqd\nJan3XrLrxjD8KxVdEYZRMlYFsV16A+Fq2N8y9PX7xugcGbjdOF3EskCSj3CJBQ4+sg+QVBEDLxaL\noqgGgwGwq3WYPYauERW0SREtUwBsA9UemxDlJRVkJuiFb6uqpLOn4AqklL1e78mTJ6C9UKEQ2eRo\nNEL/pdZ6Z2cHjId+vw/eBg4AIOzxeAwIG4HigwcPTk5Obt++DcWR0WiEwhGONBXsXUO5BAA3fo4s\nizEG5JOsCA8aJ9jlURTN5/PhcPjw4cPRaCSEfPHFF3/tV/9XzjmhnWjOrapKKF5ZU5Wmrus66NYh\nlmGMOeaNNcwLpRSXwnv34Q9/6Natw4uLiySBXojpD7pE+NRSYigCEgZiNrinx6uTheNBaRSWC7+I\nBwwDh7w0jmM0wqG8AXcHi9tqpXChqDQipgJlBGKVaE5FFtTr9axnSV0LYRGLGmOiyCilluuN9956\nwxhIMFpHWgqV6GRyNTu8eTAej1768he9t/1+1zOHiN1Z7xxrt2vOZBTFvbbUQZmYP11XZEnqn54y\nQ0tBbu0ZJ+Cf1lHFC2Ek0WWwOVGjSpIEaK0NSs9IutAUDzLxaDTinGMUCZo2oTFlQ0uBEIp4vEII\nBJ8IphBT8IBVWmtXqxVjDA8LGT7OOZJD8mkf9XAAAEVtSURBVGDNe9FaQ97GOaeEEHmej0YjMKBx\nwOAxJpMJLHGr1QL0TDb78vLy4OAgz3PQjgB1gDmFWi1QzePj4/e///337t2DjCaOGSAjWl8WBn/g\n+EVh+DUuWkpJlhsHDPevg9AsGqJRG4TopxDy4uLitdde6/V6RVEBSnFBCKmsitLUZVHXdY1ytnMe\nIZQQAiwKGEUmuKnrz33uc1BYcc51u93j4+Netyul5M6v1+s0jhHf4tGOx+MiLwgdkY1x7OTlKGOh\nNyAsQegPi06ynAiwqzB0AkA53AgSfc45mlDPz89nsxk+BOk05zxtZbV1SZL83u/9lrUW6kyc88vL\nSx2nlFcoLbTWKlJSqHyd33v+ThzHi8UizeI8X11cXNw4PKjr2tSWcxlFcbvV0zrmTDIvtY6lZOSU\ntNZaQmNENO+d/JuzjpwSawyeByKC9IR+BebVBbHkZiSJLk+EkfRDOEAcOUhpAHtDmRvYLywdfjFJ\nkihKAKi0Wi0we+fz+fHx8Xg8pgCKh1KbDEJAKNaJIL+N9IG2tG/UQqzx4AxwzhXyHGB9KGS7gK3j\ncEspF4sF+mQZY2gDq4JOOEk7tlotDCgdDoeo5EBT+f79+3VdQ3UcKUoShpvyIPSN50SmgtoECXIE\n0aYK8/jgCeEihsMhDMFyubxz587x8fH3v//6l7/85dVqRWp2cKdlUMYt66qotuK1jDHrg3EVnPvt\nTHouRV3X6/X6Qx/+QL5ZxnFcmxLZIIp+SnNjuW0MzYLlEypqLjfZuSg0FFO6jLcRloiL1IGoDtuB\nzlfqb+j3+5PJJeBcGHUsBR7EfD5HpkfNb8vlcmdvP0qSqqpGo1FVe2OMd2K9Xq83pZRSaqGUEpJR\neMYYI3KPtfbOnTu9Xmc2m+2Md+M45lwrGbXbPeZVVZnVsuj3IyVFEicqaMImURxFkUOB2HnvgciB\n62i54BQlstDd756WQyXnhiS2qZaFnQD5Q5xDgjEIZ6cBHWmags5GQ2NAQkTlCUt3cXE1Go2GwyFa\nBOHfwDfQgf6PMB5PRwateKVUHIbdwv02/QcdtqIsyaqqOI7R34Y7995DhxrKhyBerddrkFyEEN1u\nFwQ2yJJ77/v9/tnZGWJi2GlALEKIg4OD1Wp1dna2v78PKQ74jeYBM6EtFw8AtBV8AqwARHOBkTaT\nVMASUZzM5/P5Ynnz5s237j94+eWXv/rV/wDUdLFaW2uFkvPlotfrzRbz5XrFpdxOTPBOMu4FRwvI\nNpVynnEhGHfGF3m5nC867Z6pcls765y3Rb/XWy6XrVZLctFut+uihlYXhA/Ozs5292+4MHndBqVa\ngiLpYdAjAZzlnMMW6Xa7eMAAfraeJ5hPBN74p36/H8fxfD6fTqcoh+LRIEaCKmNebM4uLjZlobW8\nvLpK01ae5+v1RkntfC2YEjKWCsQIU9elMe7GjcN2u93pZOOdYbudOWestUi8hRDOMe+ktXUSx+12\nO1JMi7rdSdtpW2hRF7WxdV3Xnrk0To2pvfPeA/DgzjHvfRzF5MF8Y7IpydIQ88E0OiHpoYOTxDk/\nOjpC2Mw5hyfA7kcUAEPZarWQ11xcXKATF81foNfC6Gut0QFAYSQP0kBwD7JRz8TmhAPwoQ9YSgmy\nwdvdGuecC78NlrlTr732Gi4XKb4QAmx6KeX+/v4bb7wBM4BQ9cGDB3fu3MGiIIxBAA3rC2uBeBIw\n2mQyuXFjf7GYZVkC4BiDbOJYI4ni3Dtn6toqJZQSWZYsl8s41ozpKFJZljDmiiKPokhKnueFECLL\nkjjWy2VdVYWKNOMqSlrG8aKyV9PFb/3O70VRxIQsy7Kscs55UdZcqMl0XpZlWddFkXvGuOCCSe+4\ns6AF+DTN6rpWXFpjnLOM807SHr+j60pTbipbuazdkky62mVxy5TWcqdkpKII4irrzUYp1R8OLy7O\n+v1+lmUA9JVSSmn4rpClIJ681tatay8E73RaVVUVRa61juNIqe5qtUrTmDGnlOCcLxYzCOYhDIFq\nLWgGEDkHBIUdiYQky7L5OveCc8nzMq9d7b3XCc/zFdymlHI+n4IK2O124zQ5vLm7s7vbbqVVVZV1\nMRwOtiPyUJ0TylrrLFOqiiMdRypRseSsKgtW+0jFaZI5x8pyUzIex9pyvl4v87LodttKRaY2bvPs\nLF+Y2qajw0JFQXqUhzKAasCeNHFKBl3+9Xp9cnKSZe04joVQeZ7Xte31ep1OL47Ts7MzzmW73e73\nh0VRlGVlrcddI27HGcOpnk6n/X4fJ6quawx1iuN4OByC7BKHOVswf00zSuExfqI1CS55/uo3vkKV\nLuRLQFeAmuA60BaALiw0iYCp+OTJk/39fdBDJ5MJYwzRC9JQmJk41svl8vXXX/+RH/kR2BI4fdag\n81AhG+URF5hs2KNU6MC8aYol6rrmUrXaAy7148ePv/zlLx8fH2O0QhJ08ui5wlIaZzd14TkDvwGS\nrAwWV8XGGCm1MUYJLYRQMhoNWv/kn/wPcSRRP8BfR8qKVBZJFPW8UN8+UikR5BvQ0fhMjEHJANyX\nbU4MDv0QQEFgWQFd0oivyWSCh0KCYlgrArfqulaRrjnXSfyDH/zgt3/7t2ez2XQ6BfB9cXEhwrCl\nVqs1HA739vb6g0G73RZKQmNHS4WMOo5jD+UPJGXY8dZx7+8+9w5T1Qh0RVDI9d7T6FmgqWWYJmuf\nloWjYJ4OHmv0rVD2TlAKORCCCvGgERwqpS4vJyroBSH+BKzNOYdMEArToO8AzAOg7UOFeTAYIGQg\nr0sYXlVVe3t7eMTYlhRGIsd+5uHCx9JPtrq8OFTQY4A5gTcfDAa+MfZpOByCdWWtxYbwoUpGejtk\nk7CNNpsNym6np6fI9ZFGwzYABQKghCwZcChWUAftfsLoEG8AR4EjRQzw1ltvvfzyyw8fPsQgUhmY\n5lTOquvrWvPbE1kKoV1orPDe16bEdAsUTKfTKZrEsizb29sTQgCTFEHRmhJOFqZt+ID412EQebMY\n0ITpfKM+6wIDEFOjCPLGtxhPg0OCqBvnigXJzS3S01B6AxD3vve978UXX0T73NnZGcIZZNF37tx5\n17ve9a53ves973kPJAO1VEpsa+7Me2dtK0kjGcZKWAe2GlBB1IqQF9kgCoJWaGwnypGWyyU2tG9U\nrrcbMbxkGAOCXa4CxbSJYWJX2NCIrINSSFVV4IIAhMM2wyZxziHRbaYh5LuQGaGNlTEGeE82NGMA\nw6B4QNYfm1wphd8iF0Kv5vHz3vMnr38LZxqHHj0OeH4IM9ADsre3hzXFO0EEEUIsFovRaIQVWSwW\naPSA74J4Y1HkcH2vvPJKr9d77rnnkNALIQhypLsF9L9YLFBbB2qEui0tE6LzLTBTVvPFZjJb/Jt/\n82+I6mXD4GwbXvCf3nvPWWmNY5Z72EjhvYdnEx5PHUKlW2jrU3/uP/rZn/3rF+cnRRBXj+N4b29v\nMBhgo4MHlAQhvaqqcLO4bCklcfbwXAnOZY2aYdO0Yx9gQdChh21kwwxXwFQQgMD2xYNAiRI0A8YY\n/u56k0/X69LUMF7QcfHehwBy28LT7BZrdzo6jpzZRladTieJY+ec4lsxU6WUqWpwXMbD4XI+i3UE\nji/BWkj1URJEpAfDD11qUF6aft6H+fS0FPSiXeueJtdTOZv4tNiZnU6PggI4Me899jOKHzCLNsgf\nYG1Xq1W73e50Orh+1FFweHDY4OHhpRG18tC7zYL8lgicmCbA08zVBVG8ZEPrPAvDe2HIIVPDw0Q1\nRE2gLMJpIKGkAmIzVIDjKsvy5s2bZ2dnCLXrIHvsQ3ssHB22DsIPG2T3QJVAJonnhK0M17e7v/+9\n77/++MlRFCfW+dU6r431jBvrPONcSCEVF9Iz7jwzW+cmoBLpnMcZpAdvt/Rt672t6/Lgxt7Ozk63\n2x2Pxy+88MJ73vMe8mk4Y7xBfo3C8GEgN7hrPGYdemRZUw41CFa7MMbSB3Qbexq1TRVmO0JZeTwe\ng+CHwVRRmGPIGqwudJoi2ajC9BY8RJI9xxnA50spQZJE1pdEMWQ/tFKcMaR/W5EPLrIk7Xa7WZY5\nY6bT6e3btxF0ER0RWx/sH3yLlF5rvbu7i7lQCC+bh0o0+ITNA0Ze4hmngRAG6SuhhVRQBU+wDkpw\nYJaaMKaLyJDoBkAg7b2fTCaTyYRzjqEixGNOg845JLoQBlL7GLwRUTefMZ1P3SOEn3B2cXEUBFMh\nGAQrpHPYB1dXV9Bg2dvbg/Yl1qXf74O+jM5/7DAc0YODg93d3W9961sELhEOzoKGmQmC+EQ/xddY\nGtNoaIfWknPu6mqKkhp2NhA5osM1n59zztof0jRBjxb7nocKD+f85s2bZVmieIo340ouLi5gpCkn\ngXuhYbxVGOOKErMK2hCUolDU1LwAF5qplFK7u7s69F6AqIW7QNEPVAlcA+zUarW6vLzcbDYQdUVx\nkhy7lHIwGAyHw4ODAxR46KBiYWEWm3HNYDCAdjfggeFwSMq5cRwPBoMtkXdTaK17vR50qRB37O7u\n4t6xO5GqYZvRmjftC8o5b381o5JmPOZDKwnsCz5Naw17AWi+1WqhYQXxPAwE+U8Z5lrWQd0Ey0h/\nq9frwVziD6HLjNYKDw4xCPx20RjOSKeuudm891ulB3wccnps/X6/D+eGT1dKUcrovV8sFmdnZ0Tt\nOz09RSYKxhqx0QmuxZTgw8PDR48eocxAYZ6gGR9hYJJrCEjAYICJg2eJ5M17D5v9G7/xG/fv3xdC\nTCYTsAExP7b5wEx4WWu9Z94x+DSK6SiBgk/Df9bW4/EIZhK0YJhn0OQXiwUOGB4hfAgcL/kWmAnv\nPSRiWagvNYtLrjGvmXYSFkRrjcicAIblcon0IwnD3IqiIAos2ORxGPaNyPzw8BBldyhwol8OCQnn\nXIVmQlwPcBEppXdOSbmlWTJebYosSdtZ0HqpqiSKMLDi/Py8rutOpwOyEWAkit+wLBSqXF1dwZpX\nWwr49dmrwwzrZw6YC00rz3i/Mkh0UYgBshusErGQsT83YWQ5PJ4P4tlQr7HWwk0B3WWMoScQcIYP\nmotRFGEbc85RJeeBbgbXp4JqcvOZPnXYkB4gI8czxrewCtbaJElAgJxOp1EUXV5egjjy6NEjDEzE\nfG0EnKhXTCYTUD950B7HQtR1/cILL/zgBz8A5xoXocN4XsZYU45bBT1JLARJccAGIwgRXL788svI\nB+CNz87OKJ5uHrPmc/2hr6afocQDT8IHnKMoivl8jmtAkoD3kEQKGSYbqD2DwQAkb5zDZy7MNjR3\nm8E9HvBgMKAHVtf1cDjEJraB6Ue0yX6/j6oAD0UnGN3NZoOZEqhGIHr3132NHJQugPuwd6PRCMMK\nEV/t7+9jTPHFxYX3HpuVByJSK81QgEUrLbCioijOzs7g06AsiMIggFP4ExnGwQHVgMloPibK3JqB\nGVYJPyd4DIRGHsQUkB6D9IdyK6wJ/sk+raIFqgD8G+JGbLw4jhGsYQCq9x4MOBEGlYE5DEClKIqj\no6N2u42jK8N0RUQlTZ/M3/ruHz9+/PjevXvYr1VVPXny5N69eyA6futb33rxxRcBzjjnTk9Pb926\nhX7709NTCGsDnzk6Otrd3QUXBjVE51yaptbWzSUDSI0RArBYRVHs7OxMp1O4Y2iYIjVnjCEWgpYJ\nSEmYSYAH+e/+7//nt77474WKEZ45587OzqALhCNB4QrFh8Za651gnKg3SEuYddbaNI2LopBCQET1\nf/yn//T05GG/1zbGdDqdPM/RJ47EGj4cHFFEvzBSviF7TFvk7OwMeF0deOgw/PBCvoFcwV6ibtk8\nxjjVOPDAJ6SUMOEIqKKnB6N77/NiM8tzriR4AlUY3Qz4xIbhG9idiOEx3Vsynuc5TGcaJ5zzfLWC\n29zZ2VFC4q+kaZrGEeFYcB1wLCBChMa/Dc4hYAYEPjANqFig6kNgbBOQAKbQdPt08MhQNs/hZlNS\niN4M5GBrCKEgdhgADyoVbDYbhFF4uEhJ4O2xM1E2EGGINuEdsLxU3qB9S3IHzjn+4LX/F7nv7u4u\noCqML8SioHh648YN1M1wghFhCiHm8zkcoBACuSaoj0II4DlZlnlvaflgflDtuXXrFlKCKIpwmNGk\njGjNh2ZKGGkp5c7ODpQ5njx5At5aHMf/7X/333dGe+tNNZlMUOuADUZKSc7q2q0xJpSs69pbRxVS\nBJGJjjabTRzrsizbrdZ3vvPqr/3av/rohz+wWk5MVRKQhTUBlm2MgbdH5sM5h6Y8AirMZW+329CK\nBFiKXiEElowxJBjPbCO8bJjzgg1B6Q0yLqw/9TUjyKQyQxXGJDjmV1VVmhpvlkHfBbuNgjcYL2KK\nZVnWTreC7WVZKiGTJFFC0JlvpduJllVVDXrdZ7JNF/AeXC0MBHJ+3C+xzHAlyNV9EM5owpLIJkSj\nLbAZUvpGoktLBxrctTMJYC9iKNVQKFFhdlLdmCjoQlN20pA5cY0GHyKR2DA+js42gkTvPeQe6jC6\njAJgUVUVVGhEGNKBVl9kXxjI4gMsAe8MuAn/B9GTc07lXR5GoUKMDUEp3R6yglardXp6CllVSmHB\nXgMSjeeBiBGJ6Ww2w86DDI4Q4pVXXtFad9pdxqWxvqrtfLEqK6OjRKqoNq6qbVmZsjK1ccZ65znb\nyhULa30AULYVubou0zQGIbWqyps3D9797ndVVUVKEMBgMVu8CiLqANzroFAEdJ5QLNp5jDFI7mA1\nXID+mz7wmSiXkHRKa7GkwDZwPTBwcAt0Jqmsgu1OkTn2ExygCDNs4yCaj4tM0zTRka22hc00TpTY\nTmhQSnW73SxJy00B5KydtSKlm9mptXY6nSKhQL0UVFKwW4AS+YZUhAj8LMRNVVURXvqMt2+aIfb/\n88Kv0HG9zpSCLOIzOSHWFoE9om4XehR8I5f2oVprw3wPoJqgyMLeoXUjiiJA9Ph1hOii0TEsyGoi\n9sV1z+dzVMnquh6Px1dXVyi4Id0EG7AoCmradaFLD/9UliUYlWht8IGXLYRAOX88HhdFcXx8XNc1\nulERUOFmIFCHsB4+PcsyVEIQKFtrv/a1r/3qr/5qt98bDocu9HdD2dsYg4oqD4VOWinaZOLpKgV2\nJzIBY2ul1M/93M9dXl4iOMQ2AjhhjIHLPTs7g3sBc+3q6goWClPgsHq4NtC4kW4xxk5PT6+urpDW\nw789s13c0y9KAESY5EpxF2X2yKNEoGjboCwgtoN72nCwOP8Iz1hQX4P5U2EsLVA4dGnAFSOUxc2C\nqWSMKYNSJawJrCosJmpI4LXHcUy5E/w/giC081K05r0HYwHXT60rUZAl9m+rBDQrTDwAyJT3NtcT\nL1S34QAYY7CDVEEh4ICABjr5QKqwPmj1ovNjgq4poPvpdEoq4BcXF8j6kqDXaIwROBuDwQCFEQpg\nICJCJwoxOkzUdDrFJoA9w7e4RDrlqKUAoEvTlDTqAJEh80aUjM9hgXHiGtK2VRhOh52KdlXO+f7+\n/sOHDy8vLwmAYWHqlQpjvshqUnCyjSctE1xpHUt5rVCN9VqtVvsHeyhAfeYzPy4lN6YC2APDj5Ix\n6ul4ctQaYxrFdwSNiMl1UHcCfoDduQmjNCnZEE9XmXBhNnQGYGOxMJoHew7MWhW0e1UQoibJDUrM\ndJhXRgcMABo2NwuELFgcmGQtVVVsu7mSKFJC1GVVbrY32Eoz5rYScQjX4XKVUsPhMI7j5XIJJXD4\nVawbcjwWhNlhFOA2iUQPAFA0aCV0Wpqn6O3ACQ/8koA5XzcQNPEkohbRZ1IUSj+kR+kaSq/0Au6V\nhSk5yGwBe4owoAYxDpaF4n+lFD958zugR5yenoJqif335MmTvb09GMLJZAKmCGIDTNhAaStJkocP\nH47HY4DjgHd3dnawxc/Pz9M0RoUXS4wdg4AQruP27duwkchNcdRh4Uzoh4XROjo66vf7u7u7q9Xq\nlVde+cIXvjBf5RWLitIC8kIijuhFh04kHqrG+MCs1WGMCc6dc1VVGGO0EkmScGerqkqzREp5cXb6\npS99ab1e1+VmNr28sb+HJQKBA6LRKuil9/t9pdRiscCTBu0D5JJ2u402WTSSAYdgjCGZTpIEbY68\nQfyjl2uozdDBg3FZrVbWWpANsDOa4CQkXwGfFFWZGyO0UoFKT7as3W7DzIugKoXlqouy3W5rqYow\nxCtSylrLnIctTpIkS7azPqqqUkrgoFLwLALeDfguC/O6bFCXYSGxRBiGb3lDBo+cGP4cOZNmPNl0\nX83/Iy94Zj1p1wE1qBoayXT4WZDBh0/DphVBLR+BPRw1GQJgj9gV/X6fXDoLissmEIkQTWyHFDPG\ncFoQkiHYm8/neH6IQAB3itBlUwaRZ7SKusAe5qEdC+giKkXAOXyjyoxrLYpiOp0iJaBgqek2ZWB5\nc857vR4c7NHR0fPPPw8E9cGDR6v1xljvmZAqcp5bx9qdntKxVBEXyjPBhRJSSxVJFUHviTU4pj4A\n0FmWIWDe39+nNCyKIkRBiGZdYCHDaaxWK2QpuH5U+QDKAQTHWsMFQbEQgTE5xmZ09EwIRBUC1ygP\nUMxD1C3ZGHuPUwTME6uqgwinCW1N2HA4ZlFDSEcFlcW6rKy1cRy3s0wF1RAsBffMVFsBrEgqya7h\nRFTSptMp8f5g9bA4lLNh3ydhNKEPmXwzMhSBJwXewjMBZHOtnvE8tK0R+FHMDMtIH05xYB2GCooA\nt7DQOuwawxDxAiIC57wJ2jMUNl9dXQHdQLQJbU8TmqS3eRbqJ+jXsKEGjaSL7A1jDFNS8XWSpVrr\nyWwax/FyvRqPx8v1arVaMcGLougN+ovFwjGP1mz7tGwlzD8RzLrd7tXVFULZKIgsmNC6GwXVk7qu\nEUMOBoPT09MbN270+/2PfvSjn/rEJ2/e2OG8ms3OGCvH406WalNvODNpEknFnbWo6XvPtY6zrL21\nnd57xqTUUkrPRG0ck8oLORjtPnx8/Lm/9JfzTbUpai+j7mB3ttxYprhKZJRxFV3NFjpKmZBpq522\n2lhKFIs7nc5isSqKKo7Tfn/ImLi8nMznyzhOu90+Y2KxWC2XayFUlrW951dXU0A1KKwzJhgTpPrm\nHMM/CaG0jpWKlIo2m02Spb1ez3OW57lxNsuy3qBf13VlaqVUq9OO47ioyrIshdLddkdrzax3zkVS\nx3GsuKzrejGdW2sTHSulmPXWWu6Y8KzT6pRlOZ8vnHNZ2orj2DtmjGFcZFmWZi3r3Wqdl3Uloyhp\nZVrr6XR6cnKCmlUWZtZCJGo8HldVdXZ2tl6vsURw+ybI+JF5onYBiuoJYaIXTiO+NsYYZwF7cSmk\nVvjPva2+Sr8CSAlwKNG4UThBWIjPhyYF4ZawlbAd8/kcvgeTLSaTCZonbt68iUhhtVq1Wq29vT1k\nE7hNIvrzb3zlt2EL4XOOjo5u375NsS/qSIh5ECl1et3FajnsD45OjnudbpTEVVFa76ZXk/HuDnPe\nMX91cdkb9JnzWmvm/DqMMkWYC8/pg87kycmJc+7w8BBBC4AW2DyxrZxslsslgB0CkbefZspX//S7\n3/3T137/P3xtsVhIqauqjtNWFCXLRZ61OtyLsnLeQ9nTSi20VrXbClB7Y4tiWy0BxrC7u/vcc8/9\n7b/9s2hFuXHj4PLyst1u/+AHr49Ho93dMWcuSaJvv/wnN28cCMk6WbpeLWeTqyiKslbSafdm8xXs\nGRhe0Cw7ODiA37OhrZOqNMYYIIQuSNyxRv8yoZRkgI2tty1CggvG8bXnjDlvnLW1ccxzz6x3tja1\nNTpOmODcC8esM95zp4TmklVFXdtKMKljpYSuTFmXxtq60+lFkapru1zOpdTDYT+O06oqlsu14ixN\nW1mWWOvX6yVjIkkiyZzzhnrJMd4RXcLD4RCnC1WQbreLhmgC07HrAEsg5xGNgbree85kVVWQY9Ra\nCyUpMrLWYlolBZDWe8GYMzZSW1kU8khEsqEQgDL8PF/xIOhASEFd1wj4m351G2bXW/CJB9Z10/MX\nRQHYfDwex3EMiOUa3/rm7/+uUgp7FzCRcw6FWiQDbCvE64qiWK5Xo9EoSmIEpsYYHdRUifEJKiAm\n3CqlFBOATLClfGiwQ5qBhqKvfOUrH/jAB1C+I7DEBXzcBiI8JKioKTOKIiHdYj1hwt9/6+Hvf+0P\n/+gPv26tHw7H5xeTQX+nrO1mUwmusqztPM/zjTG1UNxxCgy8915wqbVGbuAcK4riAx/4kPf+xo0b\n9+7dM9Yu1ovL8/NOK7vzjtuHhwd7u2PryquzMyk9t84zY2vjrclaSSvrbIq6qgy1JgAm9t6j+Q0A\nErByGfpEKCFBzOOcw/JSKsKugW9vnGX8h4zGlo1ZdhT/cM7zoo6D7iLVBqgOiwgQ2AkWGd/K0PyP\n8gC1BQDXobasutj0ui3mLUBFE4h1aZqSzqdo1KOdc6jmN1MvHwCh69yGhIMsK4rqGkOS15mbY54x\n1mwg85xxz1jjsPEG/4b+HG0tJBFVVTSXOqwzh0vAOuBQhJR7W35EpiPDxBj8FqA4ZLNATQCobD/5\njW//4WazAdkEyNvR0dHBwQECUyHEcrnEQDbO+cXVZRzHu/t75+fn6FqFT8ANwIfiYRwfH6Pym6jt\nJEjGGB6bCAg1okchxPe+972yLN/3vvcBCnONEgcBAxAjADBI8yWyVlSa5XI5X61Wd59/wVn267/+\nv7/00pcr48oCPEghhPKe19YpFaVZtikrHwop0GOzdlv13tnZSeK0LMs4TqWUIIMzwVerVa/T7XRa\nw34vjvViPlWafeaTn+z324vJNM2iLElns0kcKc5kmnU8F2BOQqRpvV6j7QWDCwE3i8CooGcDZ4jw\nhpJA0Wij3O4xxnDY6BzSLmGNFj7kYEqpxWqjgqhb01WCSFWFsQ/4KABoQgg8KaT7MjQHAEcFKgam\nSLFeCc603FbMkZTGcYyUBPRFQj6RZAJPbuZIOEiuocNFIKRzDk1P2+PKr+93KwH69GFjzruqjpSm\n1ROh7QU/4aFnh12DZ4be06ytUzsivvXeA1nB3iDb5EPTMxJU7z38FuwajBpFtvz4B69QkzXMHmQh\nZZg8ihAOvzadz6qq6g36oGugjEYuC0z8/f19XCjoFP12F14R8C6KVHRXgLyyLPuDP/iDwWDwvve9\nj1pCgHEBQmRh5gZuG84tiqKsFenIrTbz1WLtvI/jeO/gxsXZ5a//b//HH/3R11d5IaXOWh3mWFGV\npnbGM+OkYwIXoLWOY+hOG/CwvWMANsbjMefSex/HcVkXvU43SeNYSc/sbHLFvP2pv/CT73zn3cuL\ni1YaDXr9yeQy0nKdF+1Ov9XqlGWJmkwUJg+h6hKFoUTgE8MP4LDR8YBZVaGzpvlizAkhyLM1X7CG\nPsx5uI481XboBHAIbHpQq0RDdN0EbSWqmAHtZIwRQgPnX4Tp51EUacHLYiOYJwYzPtxaC1kOciME\nRxELl3AveD9SE6MNAC+H6ANb0bFraAQHz9I/OYf4mVsHeS/6o9g8CFnF0wRUxpj3ltIWG2TGGWMA\nmVxoscGNbzYb7zk5dpRwkAFiryIzgtE0xhCmiHvn91/9BphsWZah2qa1XiwWe3t7gONRTADlz3pX\nVVVZV8BLOOcoEVLXHQhczjn4ybIsd4djQGfo1KDeyiQMwhqNRmVZnp+fv/HGGx/60IfwcxfatG1g\n07Cg90B4mjHGs9rzfGdnOLm4sszv7Oys8yJfr4XU8/lS6Vhr/daDhy998YvfeuUVxkSadUsjhYzo\nxAqhoihSckvozvMCMOzOzo6USmoND1xVlVRCMm9drQRfrxY/+ROf+ehHPzifzbw3/W63rstup7Vc\nrI1l7XYX8Fcdesx7vd50OsUwB5AMiNpD5HHcKQtVL9sgv+OkSSk5jhl/dswsC53m5KAopEyyDq6E\nNWZTuEBCoDJMFWTuQVOi1JpK5wgRiSWIrtN2mrRbWVVtzyeIuVhb35hv3ITOCYDljVYmFnqsKGVC\nzSBN0/UyJwTSsWsrI5REnvbUvzofS6WEJFdJh42M1zNhLedPdab6QO4D9M/D3BJs3VarVRRVGVRZ\nYX3KIC+ZhWFPFGQibaMnpYBNI+IHHJSm6dXVFRpqUCpB2YExlrVbjLHZYo44EGcMlgw2cjgczmYz\nzEMaDAYXFxc2lNhd6AWGc9dan52d3bx5E/gnqOX3799/73vfKwLbiLwZJSHYT6gprVar5So/PBgy\ny3u9wWq1euuNtwbj0Z3n7p2dnbGOX67zuJV+/M9+7IPvf98bb7zx0kv//ne/9OXaxlmr2+l0oqi9\nWuXr9do5kyRsU6wFV+12NhoNQA+o6zrlzFsTxZoLxpirijxfLQX3s9k0jjVjLMsS8EWUEsyLOE3s\nuiyC3g5ECJElg6WxXC5B8wELrEnDhem1YXINEanJA3jvOWfWWg6x5qc83nV81YydnHMQ88HxbnZ5\ny9B4gm4dim+RpKVpSmKmOGMo3kDZGjhWVVXLfK2V5JzB8ENTENt0sVhUYSwR+U/iCZH5oK1PKrci\nMDyBHHL/VIWNDArMh3tKtoRxwaSQgj/VrMSeDrnJePmgWQrL4txW0JLyW8QaSChggIwxadqiAhXy\nTCFEU4oGbQSgDQkhwC5EEWir9Qf/DpVV732/34c+JOwcuKQ4x/Atl5eX1J3NgziXCOVRWLJWq9Xp\ndDb5BlYtCmPveWOqahzHFxcXqO3evn0bvBA0XMHeEPkDewhejnaAtfV6Ve3ujKerqavl7cN7XIrp\n5dQYd/Pm7cdHT8qyvLq8lFK+8PzznXZ7/8bh//WbX1gsN2frVZqmURQnsXbOeWuU4EJw58xiPnW2\n9oJppaNILZfz/MkqSZJNsa6KMo51lsYvvvgiY+zq6qrXbUdRVG5yY9xsMdc6VkpV1m7y0jKfZZkX\n3Hi3LjZxHAut0nbL57yyZlOVWus4S/Oy8NYwK6Io0knM6toyv6lKx5kXnHMJvQbOOePccy+8IM/W\nPGOsQUZrYgBlvS26UO2IBf28uqEMhYeCfUYhJSILH7hUgHMQOAFTresSPMkoijqd2BiT50VVAf6B\nphiKLppzYa2pKiMEAR68ri3n5OI0OKve8/C1M6ZEz8H2ePDrA+Os41tH35BYZj/kdf3rwZs1nRtt\nSAq84WxdIEyCDoKUbLFYMCZQRYQHAxCCw7ZpCFpDNwR1QvIQ/P6r38ARmkwm8/kc6sWdTuf09FQp\nhV4VIcRkMul0OnGaWGvLujo+Pn7hhRd4oBHgKCLil1JOp1Mw31ut1tHDx2DBNYFEFDHB/FJhBBlj\n7K233lqtVrdv3x6Px6YhkIwcgzFGtCCS3ZxenIP4F8fx6enp2dnJcDzq9TpFXa3X6zhNOGdFUSCF\neOMH97vj/S9+6Stf/epXF4tFlrXFltywRaKt8SKQHjab0hiTZOlsNrt37956vSw3Ra/f8dZ+8EPv\nt1XZ6/Xe+cK9LMvW65WtayFY2upoHdW1xSqjAIp8CYcBwT3at5MkAQUc3gwgBKwg/S5to7BznGSc\ncjbfqINv92+gy1A6VNtt7AR6hA9aKYhKfBCDcIGToLVGqYY0ThDzU9NAHibs4VvhXV1tS1XWWigx\nk+ZX80qwiTE0Igq61z4AEiQHIsKIehwMU9Vk032YDuu9BzL5djSyFSeSi+Ypah4zCl/JJBVF3gSQ\nfMBO0DcEbyaCzLuUcr3ePHMmCaTFmcSoPaKYFkGDWWvN//Sbv48SFkrgaICDfzw6Orpz5w5ljcfH\nx3fu3XXOMcGPj4+R3GPdz87OUBYEpXg+n9+6dWsymbRaLWbc8fHx4eFhGaa9PHny5ODgAKeOYmsR\nuC3gZ9y6dasM+pgIhJBR1HVN5LQ4jp3zxXLjw0ytsizX6yUTPE2TVrfz+PHDOE14GHYTxWoync83\nJZfqm9/85ksvvTSfLQNt34YAhlOWKIVGvAcgZ7GcJVF8797d559/fjDstdNkvV7HiR6Px1KKxWxu\nbNVudRnjOto249gwo4hzvlwuVWjpRS95FEUQDnKNzh1qwIEzkYHLh/2qJBeeeXZd+RGBYEkZP6Ul\n2/eIbQW1+UMy8Dw0s7Igpu3CizFGIc8mjAFSYRwheb9qk/ugbYE3wOQDRaBvESURmEylIBQYkIBs\nzUnwyVrrSOmy2LbkpmmatjIyVXGaGGOqRmICQet+uwNbRBEjlhHbrxl1s9DtYRpzJylJgzmQDbkA\noNOrVU7VasDpWB/YGtiRzWaDmtbu7i4S9S1k9Y2v/Pbu7i7MGzh7QDjwJ7334/EYT2i1WsVpIoQw\nztKCAjipquri4gJQB44ECgZVVUVCwZipQKIFTIem3eZhg+NWSn3xi1/8yEc+Aow4SZJ1GPTOGmU3\n4EtRFLuKVcVW1YxzXpmyKIrKVt1utzJbuavz8/NWO8vzfJGv7z95dHF59ejRI2jC5XlR17VWsQhk\nVsxOEkIkSRrH8dnZGZTeRqOhYFxI1m632+1MeFYUhfMmTdMkib33dVVY45kQadLSpGwZ6lSMMXgJ\noAgAJOFyVaO/Cx4DGQ5ZUHILXHhhffOwkesj9PgZDACHTTRawlxoPGnGWvRz3Zi+6UKjEPJ2eKEo\nyMPAL7XThCCW8FAiJITi6TobPp+yCUJNcOpOT09JmIPKj1rrSCtn7Hazyi1s6JwrqlJrLUOi65zj\nUigh20kqGOehO4k1SgsUVbKnqnzbKu5TsGFA/mTo0COEaTgcw3dNJhOl1HA4BDAOhw8DhAgFAhCH\nh4fXxguRJVVgF4sFGiURQ96/f38wGADWzLLs9Pzs4OBAMD8ajU5PT4G6IIYkf4ho5OzsDEQK2DBk\ng0opxLhXV1cYtkj22IdidxRF73rXu/74j//4c5/73MXFBZ49mvBs4HAxxpCvcy6YVVXQJmm1WlGa\nVdYV6xXniCH9fLk6OTuPptFyuVzmy9lqfnz0ZJOvR8NBWZZXfrJhnnNmzDaXkIIrKZMk6XUHrVbr\ng+9/f7/f39nZgcLUplgTD1DFqizLoqq4Eri7xWJh61qKbaiMRSdvg9ox7CLiOsBLOI1A6orG0BYX\nOCWKerS8oU+jdcMLLSSEs18DA0I1LboPimv0wg7zoZEUEZQKSp42DPsjhICQbhhZy7xUMoq0Zd6U\nzjIvtIqTxHhnjKmdlTx0ddR1VZauZp1OJ+K8XiyKzYZJob3jzspI52VR1BXwG815nufLyWR/bxe3\nb4wp6y21Moqisq580C/dLkjwihRXN3M29fSwRfonISQPQpQEg+OWQebinEPjFa0b0+l0MBhgsAS6\n5m/evMk5x+yBKoxrhN8jtQgcYAUeFuYewpZAFgb/jASMGFsAVdJWhhOPiBE30Ol0oOmP/bG7u3t5\neTkej73fFiuRxqhAOCa0RwRuO+4/z/M7d+7MZrOvfOUrH//4xyeTyf7+/snJCX6RAiFY06IolEy8\ncN67TVU47nWsqqooqnK9ybkUaRofn51WVfX4+EgIsVjNjSmFYK0WeAxuZ3fMGJtNt03+7Xa73e6C\nWDQe70JZHWbV2CprJVkrstuBBDFA0c1m470zxmghW63WJq9Mg+vNAoEVQDZuHCPCcKjAwyb3ZUJT\nOfJYGyajb7EyIZWWgl0fMyoPaK3xfh9obtt4SVzX61ijvmTM9bnlYSI2C/gzMTlgLoEi8jCdmJLA\nOI5BdyI0ld5PDrCJ2iGel0EwHNYWBC6MRAMEEAUJVMbYer3WUuG8JTLxoS8GwxXyMNVEaw2GWlVV\nzIWoO6BrLlTMn3HmjDFirsgwx9wGwjFOAUIGzjmOUFWZ73//+3fv3gXgHEXRo0ePbt68SbEGAmMs\nCBwYpQP89W997eTk5ObNmyIU9U9PT2/fvl0HcZizs7Nbt24h5zs6Od5sNvs3DrCH0Dk6HA4RPxwd\nHcVxDJkaKeX9+/d7vV43a+O5zudzzjliVOQwMjRlI3Og3YOt9lu/9VsYN4VxgWWYNF2FTmdgCa1W\nyzGfr/LZYlZsSs9ZXVZ5scnzvDR1mqbrTZ7Gyen5mRCCMR8nEo4Fi9LvDVut1ny+HeotpWRsOx9I\ncCWE6HQ6xpiiqBjbyr8URXE1uYjTFGVfa+1qvdVF73Q6xaYmoi1N8arrGuWQUNwT8Hs+MO554I+7\nRgnYNyrU8CexlpKL5mFrhn9NaOQ6ShS6GT6RXSefwEKTGxw7YgRsTRhc5CT9fr9J6uVBYWo+n2Pd\nKABDitGsH9rQjAfbBNoKpu3gzUgftmemobmSxVFZbDBaKIoiZDHYmd1+zxhT1jULxCsmOBgktt4y\nFigmh4HgodggGqXtstw0c1oblBeNMejJRE4EZ9NqtZxjzrnHjx/v7+9j2mun07m6umoiTFRERS2N\nB2zzqWgHsCFSOoQlYOXjW/x5hI4w1d57UOCwJ3Z2dtDbBvO2u7u7XC596qWUkGSownBUAKNkcmSo\nPDLG4iCC+YlPfOLrX/86ul1I5MMGUmmgWbplPhOC1a6qXb4q5lVpGGNeSCesjuVkdjkYDIyxo93x\nfD7vdttFvtJaRtE2WQcUNh4P5/MlCyCBlNcQFhAUtM/CYEex6vf7VRCBTJLEgoPunJSy2922YOAR\nRkEsjIanNVGBKDSeUlERsSW5Hcpmr70Qu7bPPNC1WWg9JuN97cf4U7kZvYEAEgpH8SBgjKsgY67C\na71ei9CPiwvGTgBv1gZ2rw5al+hOBDvPN/pfDw4OIGiHn/AgzYCchx6BD8rWWZLWVYnnLtQ2WOCc\no/gUpykLsnYq0kkUe8+UkC40IlMoVDam5JBdEKFERhZNBWES4BcoPKZB/RYItrX2ne9859HREZDz\n9XqNuWUIRJGFwpozxiDOhWfK77/6DZQvYZiRGgLewMO4vLysqgqzNTyKqlLANqNdgoJ4pRQkt7DD\nUBx3lUEZACFiWZaABGDjXRA59oEGiWNZlmWn03nzzTcfPnz4mc98ZjqdAgp3DXaftdbYYr668twx\nxoqqWq/XeV5wznWUGGNUHF1cXCZJ4h2Pkng2m7Wzlrd1HOZUsG1tVMRx7B231nrPRZB5s9YaY01l\nu91ummWIJGWQG6jCYIM0Tbm8buHrtHqIQ0CDoEgSjSQoT4FzIIM4OQv9izJMJ6LWBwp+8K0SLNYR\n909J3FBOQpEMmW3nnOfPjp9lQXmJDh7FlmQdgBnwAJ3DMGMH4/wQgpJmGVlb3hg0A3ND6QpFvCjq\nYH3qIMKLbBY8FaS7jLH1ep2vl/ujHe9C68PWLQnO+XK9iuNYBaUW55zUSksVCanlVvC3avTp1Y0B\nAzxAlEIIrbfRI2/mxs5573EulFLguOZ5PpvNLi8nN27c8N7LMHZiMBhAcIm4ZjCaMrRi4sUh+EN6\nrD4MH0FrthACE54QWhhjuGda6/l8zpwvy9JblyRJkW+01oLxxWJxeHDj8vJyvVwppaqi7LTaYKIA\n6cbvwh+qRseuaSjegM2JC4WK7dHREdwLTGMU2mNBUIBnVkq1s6zX6XSyVhRFkZZxHCc62t/ZLfPN\naNCLtDzY2W2lsZbRsD9oZx3uWayTfnfQSrNI6SSOI60F45KLJIo7rXa/2xv0eoNuJ1ZScK8kZ85v\n1uuqKJUQ3XZbS1EVRVVssige9PupjvLFstyslWBZEknuy8263KyZM5ES+7tj5szk8rzcrPvd9u54\nmMa6KnIteaeVdttZEinurRIsiVQrjZNIRUpESiSRypIo1pJ7W24KxJCBtsU450pIKaW3znvP3PW/\neuucc97UzBpvavoP3yrOuLPMGuGd4kxx5k1d5usyXzNrEq1iJb2pTVkwa7TgnSyNpMD7szhqp0ka\nac49VXTolMLDo+ejDjrzcOlSygcPHlR10W63o1hZa42tnHPGVpxzpYVSinFnjLGuRul8la+Ns1Ir\noWRl6rzYlHXlmB+Px0KpTZiTCIIOMgsbZHwgPgcPjJifokp4IXiwKsgQ+UbDLkW2dV1PJpPpdMo5\nHw6H73jHO66urhaLhdYaApunp6cQrkOHERwj7CbyXvKo27pKEqaBwu6ORiP0yGDfZ1mG2BTnod/t\nPXn0+B13nhNCcM9baXZxdr473mmlmWA81lG5KfRoVJuKcw5aIIgpiBKvrq7G4zGcGM425xxatqvV\nCojJcrkyptrZGa1Wi9PT49Fo4L3n3FtrokhdXEyUUox5JdNEt6XYkpW7raydDnEOyXTt9sfWWmMt\n94JxF42Sdb5MVdI/6NSVraoqFhEgU+/9lmxaVzqGtrFYlpWzhluZpmkkRCGY98xVJWO8n2WZispy\nU61WnV53p9fLlFqtcutZkiSjTreM4qIohLFayETIQatd6Uhz4ctKCZEpbbngtanMOo7jnV4fsZkw\nttNqAdqq65o7rzRGWKla+SJfJ0kSaV2Z2hkjmPTee8e4Zwy9bd4z55133jrGvJS6CU42rfs2fHKW\nASyNdKRVXdfOGil4HGnOfFVVzDsltZSilaVFUZTFxjvbbrfTJPbMbcqqrDZS8VY7lQVfLBa1KeGx\n40Qz7larlXV1v9+PE+28GY0HdV2t1os4jgbD3nq9ct54zz2zUaQZq8uy4pxnSRpFvCy5rU1hjGEs\nTdNYqbIsrWeO8cpYLqUCIbgsS0y4F5I7hzgI2meQafLeo6gggzogIbecP9UwQZ4fzooUH4iloJTo\n97tVVRVFzrmPIjUaDeq63mzWjLk4jjFSb71e1nUZx3Eca1icoqj5d77+ZR+m5qDQgXQCgASIF6DV\naa1RckUnBcJOvBnQPEgJVLIEGIpqEnB5xthqtYLNgPxWmqaYRo22wjiOra1F4EZKKa21l5eX5+fn\nzz///HA4lFJiiPZkMiGRIor+RaNKS+CYD0UFOEDEJwjQ66DCu9lsIH2FdXCBJsdDQYkxRgAGFaCi\nMK2PhcksWBxYKB30LeCQiaNAsZMKnGDW4Kf70NYhGnXqZrBH2R0FwwjtWAMy8U+j24SCEFzJAqhA\nJTLcMowvwjmwRhAQFkWB8hEeDTiTaZpm7da6rKpAoYCSVB1mdJFuLKEFURQ5t50uQo8D/gcBNtYQ\njQViy3rReEa0aFuTFPqA6P2MMSVkr9Xy1tGc97quARDQ2ESia4YC4PWAOCwdjiLegxWG+UYg2ul0\noO+G+XjdbhezYiCUxhsKsJAOgfIPlk4hcoNWJCYy+1DZRNMa0jkcMEiyeu+x0UHCwsJhjhSaxlF/\ngPIc4QGMMcDqaDKgIJCFCn0AAziEB/GZo9EojuMnT548ePBgMBgguJ1MJnEcI4VVoXOJNSTNKCcR\n4SUbFFBsTQTucPr4WB7gXSLgEGkd10/lRDB6qauSOinwgLFZZVCzAZwtGlMByqCzi63jGwoiuiFa\nSo8NRV4cD6DnrDHBSARFURderIHpk1vDSTNh5oMNdAf8hBB/LA5iM0Ln6YXsn3MOFI1z3kpTFcbl\nsChqpamL46X3zhjmnBIibbWUEKvVylRVpBTEgoqiWC2WwGOyJBWMG2NKY5nzcRwrIfNyzRiTXCgh\nY60lpgVVlZZSCVGhFM0YA6bvvbiGPVvYNpeXl3Vd7+3tIXoCc982NKrDmdeUU/EwVwhPHz8XYcIj\nqI+IJ2GJsIwo93e7XRJ+RwCJsJlEH5IkUXhUUHqC6CcOCTwvEbfBTMFZohQWLEoUtWlHYq9ba+fz\neRS6uWAvo9DGW1XVcrnc3d2FyHGe56enp3t7e2VZxrGmQT64+jiOAf5Mp1Mc15OTE1wttKt8gMht\ng3aEDa2CrLwLIyrJmdhACESRtA7DE7DFAZYCMCA8F6uG6B+fT6QeBK5kDmEFZKhVgsWPDySxDTxs\n0Lvr0IxDgASdCnJNePaE/lGCJJ6WEngGC6EPwfYi1BtsMtMUWgt7EaA8TiAOGNqOXKD4AAODRIWO\nEx1FkFoDLQarhBp9FZqGsUTAkLCkuGWa/UnNXDYMf8IDms1mkPGAZTHGUA2QelvIxXlrj4+PDw9u\nrFarg4MDY8z5+floNJpMJmizwMuEMe5aa8aeav/DasM6E5SABw37uFwugUtDcgbdRrhm+N6qqmgc\nVxLmn2xjEJwu7z3G7aCbBn8bit9YJnQHQrgTVQGU2BFZgfiMYjnWF28mEl0cxwhIsClRNiDdxSho\nYgI+BiCJjilg7oPBYG9v7+WXX8Yu6fV6+NN44VA16yeccxwJOjwhZvB42IjFkU+bIJSNwK+Z0hRh\nChy4ziz0sIJyJUMXLG5fBnFvcESj0FWklOp0OjqMKVOBMo9bhj+hBlyqSlPYyQJngipv0OF0QT1B\nhuocb9C76H5hg5pAJd4Gl06doLChNiixNQEPhNwoyiOZEUL0+/1erycD8QIHkmifLszZgRODsccS\nLRYLnNterweu32KxwExwLBpsOtYQRpP6kogEhwgTBwC2BkcOcrQnJydQtnfODYfD4+Nj1JNEKNar\nRh83jh/AVYoV+dM18Tqo33HOb9y4AS4RJUTgQlxcXJD2M5WvcKdlWc7n8/PzcwEOGOHOpP+MQ4V4\nnURLEExyznFI8GxoQ8DwAH0CZ5zKF2kYJwelCvzk6uoKIkTI2dABAL4SbGQUVN8QHK9Wq9dff51E\nFxFJkzkXDWIbYjAeNNvKsrRhfIkN2ok6zIYWQQefvAoPxR+yO+TEYK0ppnehM1KHicQ4jUmQanNB\nBB/GHleIeiaxt8gE4Pzj8MuGpggL0D+8DYUPBGGzt70o8OPhxZ4mnYCb6oOmIpwDZVxU1UiD5mwU\nRRDPcs7hIULyGakEkmS8AXldFXqWReAPkJEyxsAQR2FMAt6AIy2EgFWC/2nOdqN+cBsUmpFB4Ugj\nM2y32/v7+48fP7bWKqUWi8WNGzfgtGmdYVVR4qKdwxtyQCx0KsNPUMCClIfkQAFC4tOAvpqgcovn\ni8il1Wr1er3RaKSMMRD6Q9Tuvb+8vITwKFAQIt0jygLzAwYyTVNoHxSBNYPDDauZZRn2DSyEDpNd\nbeAuwHtQbr2N+5mjChV2OTal1vqDH/zg48ePb9++DWQZOTqVj2m9fCChN8Mk2nB16PtGbOwC+QtG\ngX4Fh43CLaRz4umGOmqGxwHTjQmPeD/2PSJYYjzCNqNiAa4JZdU6jICiY8BCuYyckg0KJdgErtFz\n/Uww2VwWHoAi+igc5mbIKkIHEM4bHiiitToMsEYGgXgvSZIoiT1HE0BVbqxSqtdpwVLbuhTMRVrr\nTgsBjrcQeB1ESq3X6yLPufdpHEcB86gxUa3Vwk/qshRCdNtZpERVVbYurWCxVl4J732ebwRzkkda\nChEpY4wz1Xpd9zr9clMcHh5ibUEUxnTI5sqIoLghJacyNz0+LAIF3rS2zrnlconzA8NEtaudnR2Y\nDOJ/oYcAYluINQTnHOQACtCRayFKRCyugzQ8glREGs45xIowRTAqiDHwhJDI2UDSl6HSx7Y0mbLf\n70O6HJ8wGo1QjkN2DhCJqIN5nt+9e7fX6z158qTT6Tx58gS1fxkIOOLptj/sM9jOJIhaw+rgzYhD\nYFZhI5IkQYSMJfMBtaOqC3RaVWiwR6QkG9w52Gk8FUQKFD9ba5GvbjYbSHPDt+BqTUNBlQ4DxTx0\nd4Re4KHAWJAiC2WJ2EwEt9CvU8gNu0CpGpIfHHJcFQ86bYiKSZQfASGe7Gq12qxzU9Wwa4vFgiah\nwhVgF2ICaBRU0621GPYAJ4ZwEcASorhOp7O/v48YFdsG2ZG1lhrbEZTCv8HH9vv9OI7rsjo/PUOA\nOhwOEW1hQAX+HAITilyQ++Dem24fkQv2RtEYKQq3BouJkNUEbhqOAJ44D2UVHnBgbCH+p9/8fYKe\nCD9A1QuMGyEEWtbRWiaE2Gw2g8HAB7WGxWLR7XbjIJuBzA1IOmMMuotCCCguwxPin+I4RjgxHo/R\nSmOtXS7n+/v7LKgXIfZoupff/M3ffM973nP37l16GDw0ApK3RAyDjeW9R6EzCXLfZVCVigK9HUcL\na+eDPAmUDOE5yfCjyonDiYOEo1JVFeoZUkrE3jwMPwB7G5Ls9AwQfmdZhiUtwyhaBBSEDVIeRdYK\n6RAicEziA1DGQnGCgmofVKWagSVr0CMJUheNMSM0GLEKLTMwVdiRsL/YatPptK7r/qhHUqewpOT9\niKCH4+e9rytrjKOeIxg1shrNkxCFuTar1YJxh/FjwLHhCbA48LEwzd771TLXMsJ2hWgVbhMwGwv4\nPv5uHMetVmu9XlJtJg4DD2C8+NMMG3J6b4/MfaDjpY1pUthL1A2w2WwUBR6EdEOkdjgcRqG31wXi\nNh4MbP+1cxQCl96MUig2Q+wEOq/3HvsD502FPnwWoAsR+hfxLW/gznjAFxcXH/jAB9588813v/vd\nKLvXQVXKB0DJB/I1RXRs2yZYg9xIAV4zToDZJugJl+eDIA99vg/Zc7NmpYLKA6ID4mrBh6DPFVCq\nCr3SeRiwBseFnU0OGVAe/VHKymxoAmgikLgAfAKdKBFKjv7pmhstCKEp9Ga8YDV46ElxDRavCGpc\nNnQJaa2pNVsGaS0egD78lguMTc650hjWZbE+FKEBqdaNkQN2243KlVKebdeZSotA2kAw4mjGWS61\n1lGsJNv6cxgsXAMOAA94I0FKgHaoKGKD5g0CHFo09sNe/mngF0Gjb9B94QAgo6qUarfb19MG4ENE\ngwkuAgBKZg+3gUgmCl0VKjBTsVIysMuwIWCQ4NAZY4ijRCgB0a3SPkM4AcwNOQwxgKBLqZQajUYP\nHz5Et4ENIqe0jUSjQIxDC2QC542SXWxNF8RxyT2ShYaTxA7wYYKeCROwqqCxx4OkClxxFIbLwZ75\nQG+lcjkPSJdr9J6o0D9maHKVMfREaUnpZnVomsQt4NOa6yAarJHmjml+IRrDYugs1UHhi9wCXDc2\nExyUC0MztNarzRLhaxTUdVnoW2kGHbhyIYRS24lnhJpSCCOD2I4JfbdCsFarVZvShynYAAJAk0Bs\nT3VzPFwht5uqDvOJyAe6pzsq+LbUsbXy5ukhbE3zSivW9HXN5WVhrhj9FgtNq/DVeCnKy3EEkeH0\n+30UTKS8bq3zoc1Wh1m1lJnAaQD85dfzTbbCG0nQisKewPspbYBFRMCD4wcIERmLaTBo6roeDofr\n9fr5559/5ZVXIHRBZ4OWEu+XoTeMB4IplpIMHgtIIFYA2DeWBsuEw0BukIUeMMp/EKfJLZ9V01pj\n09ShlxkXgDpPVVVxHPd6PUjD01HBwsIcilCCZ41IQTSVDhq7AVFGFAbSE9ZKx4kyh2f2Cv2keTJF\n0OHAjavAXwUghEC6eZxQ1UCtyQcJbnxLubEIEGu4U+Uco3AaK+kCL0c927XIWu1UWWFD7RgSqDDE\n2GaofBIYLnyl1LXqFP5PoYFpTOriW3S3pAL0M5fadFzNuPGHeja834dewTr0puBfkbkI2FHV6MxF\nfgXVYRdgfRZkQEWDHIT3I5NBOKGDoiWSELwHbTs8FA+QOPkAS8owt625jeiem+gQVSeBRj569AhX\nTjayabax8xDY0EdR/kM71TXmlYlQdaHVpHukWDeEN9swiT6BrmG5XFL5C1sNOQmwYLLfELoDbQCw\nDaJNHvr5dUPD2DaK9bi2JKgaMsaofwLPuA4UW7ry5tGizfGMx6M3kEgRWQFcBoG0zXjHe99KMyV4\nXRblJmfORkpGSgrmq2JjqpJ7p6XQUnDvvDXMecmFlkpy4YytitLWRnIRKe2tq8uqKkpvneRCcsGc\n99bZ2ijBk0gL5stNjr8Sa5VE2ltTbnJTlXhDEulIaWrbJXyIiul8OyesgvcWT1euZai2w4vSDvHh\nRavk3/bijfwCTrIMA7Tw0I0xeZ7/fyQiwhh406bpAAAAAElFTkSuQmCC\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 15
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "M58J3O9OtT1G",
- "colab_type": "text"
- },
- "source": [
- "And let's now visualize the top predicted segmentation mask. The masks are predicted as `[N, 1, H, W]`, where `N` is the number of predictions, and are probability maps between 0-1."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "5v5S3bm07SO1",
- "colab_type": "code",
- "outputId": "502433ff-ac0d-4388-d79c-1d94cf26dc38",
- "colab": {
- "base_uri": "https://localhost:8080/",
- "height": 366
- }
- },
- "source": [
- "Image.fromarray(prediction[0]['masks'][0, 0].mul(255).byte().cpu().numpy())"
- ],
- "execution_count": 0,
- "outputs": [
- {
- "output_type": "execute_result",
- "data": {
- "image/png": "iVBORw0KGgoAAAANSUhEUgAAASQAAAFdCAAAAACPv085AAAqs0lEQVR4nO1daXsTyc6VVEtXL7YT\n7tz3///AO0Bid3et0vuh2k6ALIZ4CRANM/NAjOM+OTqlUqkkgA/7sA/7sA/7sA/7sA/7sA/7sA/7\nsA/7sA/7sA/7sA/7sA/7sA/7sA/7sA/7sA/7sL/M8IrfGgG///YCAAICco0P9KxdByREQFRKK73/\nEAggAiIswoULy3sCSl/heyIgEqK1trH1DxARRESkcOGcU84F4P2gdAWQEACJiEzbti0CVJCQRZhL\nziVFQhaRd4PRVZgEiEiKrOuHAQEACJGQmZlTyikScBYWfDcoXR4kBAQkUsq2w3pTQSIiLMycY4rR\nA+dU8P1gdB13QyRFyrb95hZhcT4qpXAOIQTFORGBvB+YriLciEhKWzesbwkAgBQpLKWU5L03mJNX\nJFcMTr63q2jS3t36BSSllMKSS07zZDQkbxTiDzHU9ewa7oaIREofQEKllKKcc47WGCW+MYqE/2aQ\nEAAQlVLGDZtbAgRQWivKKadotKIyNZroHWF0eZCQlFLWOec266HvCABAK60o62yUAEAOIUSKAZjf\nSTx5eZC0McZ1Xdt92gxtc9AkQlQKWQA5pcJmJMnyTmKli4NEyrimG/ph+LRZdXuQSCGprEgASXJh\nUSTZ/71MUta1w3q1Xt1uhgUkUkRUiioESAoKC6JkTwjvYwN3BXezrhvWm83NzYFJRERIqrBCUgZZ\nkCR5S+/D2a7CJNN0q/XN7e1mPbQNIgAQEqJiZk1aGxIkxX40hPguiHQFTdLW9cP65tN/Vv3QNQgI\nNXPCLFyUNlYjKZ13d5bgnVDpKprUDevN7X/6tm1dzZwgAgqLcDYlG1LapLvWEsL72L9dIwRw3bC6\n+fRPa61tYMlLIggsSTertGnCv635mzXJum5Y33z6j1vStzXvVlPbwiJJm8bNq9bSe9m/XUW4225Y\nrTaWkPBRln1/CGBIGXPfOU3vBCOgS39DJGWs1YoQ6zbu4Sv73yEiESHRe0kFXAEkra0xivCHkxrc\nw4SIhIR48Q/3jF2NSQoXLfrxFYhEFaX3QaTLgwSktLVGE+KPINTfVnd7RyhdnklKG2O0oqcfH+v5\nEi6SdOEP94xdGiR8JNzPQkBERIjvBqUrCvePyg2wD8Cprm9Pv+Tidi3h1lTj7O+/Cg9r2xOadSW7\nMEgIQMrsmfTcS6pwvx9Ruo67Wa3oicIb2HsbLhC9E3e71uHkc64kIFxSjD6kIu+l/ubyezeoRTZP\nP70ICOfg/ehDKszvAqMLuxseMAJ4CiYBEOEU53GaQy78TupvrrI9et6NRERKDvM4zn8tkwDgwKSn\nvgIgIpzCvBvnmP5WJiHUDOTzMIlwjn4cfUjM7wOjqzAJnoGo5iaFU3W3XOSdoHTxvRsAvLC0L6vb\nXpPeB0aXBalGRtXZfnx8Wb7KOc7jNMdU3ou/XWN1e16S6uq2uNv70aTLBpP7UHuh1Dcxt4AACxfO\nKczTFGIu/GQwdXm7KEhIRFrrmnMTQXm0NRMRYc4552n2IaRU+JIf7UW7JEhIpMgsiUmQhUl7rggz\nlxRTmqbZh5gLv5Od28WZpJQ2xhitCUHqkeRi9T5AjCHMsw8x5fJOEIILMwlJaa21tkYhiOwhqv9l\nLiWn4Odp9j7ElN/JngQuzyRdmaQIRZaoqX5NhEvJMczzNPuwyPY78bfLapIiddAkOMi2AFR3yzkF\nP03zHGJK5f0w6bLBZHU3Y0xl0v70HwAAFibt3S3/nSDVyxKLu+GyOTk4m7BwSZVJe3d7J952hdXt\nECeBSNWkRb65lJxiZVJMqbyPQBLgsu6GVJmk95oE8AgjYc45Bj/N83wQ7vdhF2DScpeElGlb1677\nttGKDqfcD9VsiESklNHGGmuzejd1pZcAiUgpZY2xtnXO3a66Ri3VEPXrFSYkJKWNdbGb527OnCPi\n33MjALXWpnWudY1r3O26s3o5eEQAFFyUqd5cso3r5qmbU46B3ovDXYJJyhjX9/3QNk3T3Ky6Rqkf\njh4RkBQr06Qc2272MfpawfQeYDo/SEhKN65fb9a9tbZZr7tGER4qa3C/O8HF3UqaZ++9t/pvqr4l\nbazr17e3gzXWrFZdo+nbsppa80ZE2tjCqZv9PM9GEbwT5b6EJilj3bC5/WdtjDb9urOKEAlhodIC\nBJISMY1A9rOf59FoRHgfyn0ZTWrafn37z8Zord3QN/pbRUIAAUQSJYYFy9z5eWqsor9ndUNS1d3+\nuVVaaevaZqngwkc0AkEkABFUpfPej43R+D4uTVxKkxrXr2//+aRUTbrVCi7Yd3IBgeUSTl3jvPe+\ndebFisGL2plBQgSlbeO6YbW+uSVFpKiG248fH5e8CVWQXNt2nXPWpALyHjLd5wVJKaXMarW5uVl1\nTi/VawcCPbZ6KCCISGSsa7thtRl1DPE9ZHHPCxJpa5rVenNzs+oarR6qt56qcZOaTRGlrev6YbUe\naUJO7yDsPjOTTOPaYb2uINWS2ucxWgpvlbEu9cNqmgH5XWzgzswk07T9ar25uRm6Rte9yLN1kCgA\nQABK26b4YT175ujfg3SfH6Rh0aTG0JNXJR5Z7RqktC3SD7MPOfnxPeRLzu5u3TDsmXTQpCdhQkFB\nBBIyRSAOPsQ47/RfwCRd3W2z6bpG153IC09dsyZKN0jZh5T96PR7SAVcgEmr9frmpmkqSE9dA1gM\nQRBQBAyiKiHlPN01fz6TkIxr+2G1ubnRWmsFT4ZIj14PAIAIpFhiLjz2jXkPW5OLMGlzc3PkRREE\nBCARgVRY7jun8R00BzgjSFgvJQ+da4z+mfsPCAjK2Ma5xhpdGK59THk+kBAQlXFd3zb6Jw+uUGok\nYK0xppRr6/ZZmYSo7B6kn9VfJG2MNcaYfP1N7hmZhIjaNN3QWvPzR6ALk6wx6frd3c52gosAj5j0\n04+JpIw19qXrupezM7ubcd3w85oEKEDKFGuM0bpcHaTz1QIgImrbdH1rfxokAFRaG2vtn84kQFLG\ntX3b/LwmIZIyYq2xfzRIiLh0uLG/srdAUgLW/A2apE3T9Vr/iruRRvzj3Q2JtDKNcy2R+gWQkAD1\ni80oLmdnA4mstc3QWv2GcyFSSluj1R8LkjJt2/atVb+IUW3UrY01mq7dIuiMTHL9anBW/erdfkRE\npcx7YNLZfkjKtMN6aK16Ic32mlUmXV+TzgeSdf2mb61+Q5cIJKXfg3KfDSSyC5PecJ6PSi/udl2U\nzuhurt9UkH4FpqWGQr0L4T6ju7XDurrbS2ntFwyBSO9DgKtS6Xyrm3FDZdKvPOBStaTUny7cbb9f\n3X7Vljjp6iidh0kIcFiYfuUBl6Q2KtO0rWsayyxXPA04C0h4uCrxa3uS/fUl0qZpu7Z1ruQC5dQf\n82g7E5P2Dcd+yVEWjKSmWtqubV1CuOJpwHmYtHSK/EVng9rPBGqr/K5tnSPg6xHpLCAhPBDpVyVJ\nAJbi5rZtWwdc0ok/5U/Y2TSJ8FfdrXZRAoDqbl3bulZKumJEeTZNQiJ6Q7QNIgKkTdN1Xdu6nK6Z\nCjiXJhERqV8Ublgavggq67htW+dS+IXs5snsrEw6aNLPDGuTh/+hNg66tm1dMOqKd5bOItx7TfrV\n1W3fYImUBeo655w316zmOo+7kdJKKUVU7yMvfUmONBHZj8ElZalxbdfVkW/X6jhxDpBIWWNdU3u3\nCh/K246CSUBKLkUAAbkwizKuX6fgJ8/M17kfcBZ306ZxrjF7kGqt/1I2+rpJySkKEpIwC5Bp+030\nczuVnOUqIeV5mGSa1jU1ySEMCDXbcCRKUlIIQkRKRETIuD74aWxdulal0lmYpKxr28bWLkkVJDi+\njks4R89KqRoakXVDnsada0C4XGWJOwuTtGnax+4GgAwkeEQoIJVJnrXWTIiAZFzmcde1jXC+Tpnp\neZj0g7shiRwbLUnJ0RdjWCtCQmVaod22ax2XhHANlM4AEi5Mso+ZBMfQCAAAREqKMzOLCCkUMoLm\nvu/aJqcrRZRn0qSmdY1ZmFQXN5GjA++SgmdmANGIRJZMXg29cylcaQN3epAQSJkq3IoQuN5rRxI5\nSpQW4S68BO5CpEFWfdc2wajrzMU7V5z0SLhr6QMfvUGVkoIvy86GgRQpWg1d21itEOUKMJ0cpGXO\nvSYpyZNaapPQGvz+evJTVhsEpzDnknOy1tpkjCFSpumGFGPIzJfvY3ZqkHCfloSS5p1SihQAALGg\nUse8gUjJMcwxxWBt09imaRgIdNOtck6p5IT50mH3GTSpJgCkxNkqpSo0JKjMEbvc2ts1hjlEY3TT\nNE3TFiGNqumGlFLMES9/bHJ6Ji1DfqBEr7TSFSRF2vAxwi0sJSc/z1op1TTONQXIWNBNt0ophoxS\nLh4HnINJiEQEJc6glltuoJRp+Ji1bc+kiYjIuhBaIW3dAlIISThdPA44MUgPByVQIhStTQVJmyaz\nvL7DXWYEhHlEBLRtjAmNdQVV0+UYQogl6YvHAedxNyIFJZaktdEaAEA3MbMch1HJyc+TCIiNMSZl\nXSqgbScxBB+uEVGeS7hJSkEwRhsNAGDalPn5hu4HE9kziZm5iTFl04ZUQDWAwQfvw6wv3jLoXEwi\nKIWLNcYYAQDTx8wAr+9MKkh+nnIpuYkp56b3qYAGpYP38zzby2e7Tx9MLjBJiSlFa6wBAbA+5mMm\ntQgIl5zCPOaUUpNyzu0qpIJK2Sb4eZ5Ge/m9yRmYRKSUUoVz9LnkbEAAso+5HIWSiJQUvY8xxSTM\nMkw+RCJSyjZt2zbWaCWXLcQ59eqGpLRWWmsgAuAk9QyfQ8qF8Zh2tlibvBdmLjlH7afdticihCmx\napxr21QKX7J/8BlAqt3bRSEKS6k7Ng4xFUZ69bEQoTZ5Zy5cctJhnsZtS0QEcxRlG9d2KacsIBeT\n71O7W50nobRmIoBSK2gAJcRc+HWMAGBp8l4KM+ek0E+7zhESYUiimsa1bYoILH8Ak5gQgQsXRsAF\nJH41VMKDuzEzl5II5mncWiJCKkWUda7tEgpnkos53MmFm5RWWmtdFIFwTjkjIkI4durP4m7V4TIi\n+GnXmGWiOWlonOsScFblcq06T80k2jMpEyKUHENCRAKfcinqmIfCxd2YGTOC+KmxigiJrG0UNa5t\nY8kpEF8sEDjb6lazkin6gISExzKpFqEs7gYAzLM1mpAIVYdGKefaLuYUau3TZXA6LUgISKSrcitC\nKDn4GYkI62SEIyIlPAh3YQEpxRitgJBIoWmVbVzrYwqaSC52CHc2d1OECJzjPBERUhXuI91tCZOE\nBZGUIhQkJG1aUU3ThhC91QpJLnUKd1KQEADVItyKqLrbRESkjhbuBSWuKAECEUohJDTtSlTjQhvD\nbCuTLmSnBAkR1FJQYjTh4jRFRKDic/RT1RZlIgACJaeoEQlLiDElJtPGGGNWKaV0mZsCJwQJEVEZ\n67q2aYwiFM77UbZLSHn0Oy2932qFKZccCZEkeD/bDMaVnBlMCCHkcombAicFiVDpxrWts0YTSMnV\nwxYnO7oUd99BcD+IKudEiMgx+LnJoFssDGjmWWPMeAEqndbdqDLJ2YVJpTCDCIjIi304f3gnOkwT\nBOGSCQlRQvBzg6iNYkEyRqEgXqKs63QgYe1f37h61kogJeeqRXsmHY3RQrrqbqVkxIVJ3htrTFMD\ne5TCwvn8C9xp3Y2Usa7tXGM0oZRcY53loshzXW+feKPH7iZcMiAicgh+dmi1IyRlNEpJhfMF6rvP\n525Q3U1+QZRqB/MFJeYCggioovdza0C3mpSxWkoMKUc6f5PFUzNJV3dbhDsz83ItC37iBsWCUTXh\nIoKwMMm3YNpGm8apHMMc0i80i/lpO6UmLUxqW9c8CLfAnknHr261r9ACrrAQAyKoGLz3GbTrjW1a\nSmF2Pig6/+7kpO5GpExT3W1hUjmEALifnfCayQ/CjYyAgCUEP88FTdtbFxP5aVe/0dnthCCRUsba\npl0qAekwd/PRXPdjctz1TOrAunoNAAFUCsGHWEBZUjrn/lCXeW47GUioTOPcMHSta6zWpI09XFMT\n5lJKyUoddRJQ98g/XnCTkmLw87hTzIVzAVJa0YPEn81OBBICkm7afui7pVpSaetazpEQRKBwyVWh\nXnmfqmz6qXvg9UTOT+NWiYAkBtRKKaKzV7+dikkIZJpuWPXd4m3K2KbNURPsE0Q569dAwv3Bnf6+\nGYAgAJcc/TyNO4WImFlIa6V+GybhwqRh6KtSaKWMdW30mhBEkLmUfExGCfcjhdWPtwC5pBj8NG5J\nKVKZgZTWv5G7ASKZphuqJhmt6gYlzA9MyuUId6uOq5T+wd0ERerE5XGntDY6F0Ct1aMV4mx2UpDa\nxd2UVqS0bdrJasI6v73sA4KX3wYA6eBu3ykNlxzDPI1bsrbYxLIXbjlz0H1S4e6GKtx1DKd1rTO6\nznKtmnRE/hYREZ8UbgEuibSfRqeawlAY9pr0ewSTuGfS0Hets4SI2ljXNlarWuLHnHM5KsuNe3ej\n7zPYUjKqeR4bygwkBbCmid/Qf/A4OxWT8BGTDACAMk3TNkbTw/HHMZOkEWUv3D88OZcM5KfGEAMp\nZCClLoHRCSNuZZp2WA1957SIiNLWtc4qWphUSs7lmCnJDyHAj3ESMPjJaBJShh5CgHPDdKoQAJeV\nmxCEhYVzTimm5bBNOEc/zda9docWBQWVsa6xTzQCEMaSYpg1EaLKKeWYchE4pvDpLXa61a0WcAOX\nLMzMwc/TOIe0oFSiH3e2za8Xl9Zpp86aH/xN9vcFjEIQlXPKk09H1Ya9zU63utWprSAlMzOXuICU\n6/31HOdx1y6Fk6+8lzLWuaeaeIvUSfAKQZhKLnkOMfPZUToJSMtuAqkyCZkLh/ANk3Kcx3EI+bX7\nkyjLxUv7RM98EZGSoyKQUqiUUiYf8+9yWrJ3NkKRkrEULgd3WzQp+HG3jvn15U32TPrhvo6gLIdw\nzDmpwoWn/Tc4yWM8ZyfVJCIE5gyllBK9n8bJx1zvQJY473ZzyPxqlTKi0k3rnhpRISBcEiFwSZGY\nhb2P+bjD87fYCSPuuhRLyVJK+Y5J1d3meIRwL5kpq5/ak4mUjMA5RUMsIsHHfGSJwRvsdBE31p5S\nXLLkkksI8zR9q0m7KRwj3PSsuwEAlySck9YaQUTy8lM4yVM8a6eLuKu7iZTMueQcD0xiEaghwBxe\n1yTA54UbRKiAlKxIKQQQKCnl85eYni59W4UbuCTJOeXg52n0YblSIjnMqp9jfvU+Fwoq/VwIAMDC\npX4nREDgpdbrVE/xtJ0uM1nLr0G4cE45z/M8TymmipGUFNTkY2J++RgXBZBqz5wnM/wiUADrLVZE\nFJbz6/apQBLmHObdV1ZKKc455+3oUzlUAApzzjnFGBMRvXwZt1YUvpKXlarql+modBqQRIRLnLZ3\nZQGp5PtxjuWh9Ea45JRSilGrF+4GogBCPS2pWbfnU0WCh2PPc9up3E2khHn7NSmlSHLJ5X70sTBL\nHYgsUkpKKcaYAF5kEgqi0sYsKccnQRAUlAt2CDgJSCLCmOO0a6JSpKTkUu7HOdaCCRAQZC45xZRi\nQlSv7EyI1L4y9QUeVQDPv/7DSd0tzFsdFCklpZSyHX11t9rKVjhTpRK+VvK+nLstZ0ov+dulbuCc\nTLghx0ljsweJx6pJS58/4EK5upt6MT+JggtKy0n3M/4GUgXrIqJ0KiaBlKCx2AoSF54nH8tD5Y1w\nwUW4yytRd8XoZXcTBBCUCy1vp2IScIlYkl5AYg4hxFybIdYCmiyVSfnlHC7KchCgEF9QZ9lfv/mN\nmASCGTh5pUgRMDPnlNNDZlUYRHJKMab8CpMQkTQbTa+FAHCh+wAnZJIIJ0Q6gCSH5b++gIVTSinF\n189MFibtQ4AXkPidQgAAABBBAGJikrpZ+HZxlrpcH1egREoZ27hYSr5MuPiynbLSTfChYOvpR6t5\n8NcOgBCJtLGuSykJw4U7JTxhJ+8LIMJQK26/PX1dmpbRD8dpT9i+QjWSlHx9jE4LkmDF5tnwBfcl\n2i8aEpMytu0ClPwHTnkX3N+3eSoThoD0+mAkRCRRpnGd5xSfjygvZ6cFSVCAqfraj/nppUD7dX9D\nrGW8c75W08Rv7fRdb4RrBP7Ej39JKb72DogE2ti2m4JRf6K77f/74ur2ypvgnkntbNR1ut1+a6df\n3R79+73t8+CvZrlJltuFRj2bVLqgnRqkl08u9hn8lw0Bq3C3zR/KpGds33tKHTGlAwGgljdVJl0d\npouBpIisNVrrI4IAAEClbdMYTXj+kshX7UIgYR2ObB4yjq+8HklbZ+31Z+ACXI5JpIxurDFP1fk9\nZaiMqZfCz14R+bpdavgOKm2ttcYcxyRApa1rjFbH39w9n10IJCSlrTVVk45RbiRtm3qMe32ULsUk\nUtrYn3K3Ktx/E5MAlbHWHi3ctXDS1tXt7B/uNbugu5nGWv3DHa2nXw50cLfrY3RJd7PWGGOOHPqG\nSpsq3HB9mC4YAlR308f5z6Ng8ie65ZzJLgNSvTG46pw5UmOwTnhvmrYVSlec7goAlwGpzvoZ1pvB\n/Vjm/9zfIaWNadquBw/XnFwKcBGQEBCVcf1mM7SWjpQYJFLaNq4bBDie+yO+YhdhEiLZdlhvemcI\njpQYVFrbpu36XKK68hb3UiAtTDLHtjo4dNAZUvLqysmSy7gbkXH9ejM4c+yYN0Sl2TSu64N/4m7A\nZe1CTFK2HaomHbvLIMXGNm03zM4cNRXmjHaRH1J1t4MmHfVXiBZN6hpDVw6VLuFuVZOGzcb9hCah\nAjSN64Zdc3UmXUy42369MeZ4eSFAtq7t+rb5CzQJSWnduLYb+u8zAMvRijyRM0IgQWOatnPNJVok\nvWhnBgkB0Trnbm8Gp78VbamTk+vURFI/6g4CqlrRfe2jgHMzCVHZbhj+c9M79XjbJgBSmOsvow38\nMEwYpeYzj8qtnNfOCxIiITX9+uY/N4PTj2olBASYcym5lMzW1vab3xXBHzop/enuhqhst/70z83Q\n6MdZDwHhUlJOOefaUwu+9TeU/S63Hitd0+POzSQkarrNp38WJj18SURKTinFlDKQsvKjJgmSrq1d\nzvohX7ezM4nIdutP/2wGpx6XJokIl5xjjCEm1LbUw+xvVYn2jcvO+yFftUsId7/+9M9N7x6v5FKv\nwKUUQvBJ26bIUuX/8DcF8K8AaXG39ad/VkOjH9LVta6ylBSj9z6YptbFf6fbsmjSHw4SIKGy3fo/\n/7StU4/DpOpuKYYwz8HFzFynCX/zl5GU+UuYZLvNp3+MMY/nsi3ulmPwfvJtSPt2ON/ghKpe6rp2\njdIZQUJA0zRNv151zupHTiNQcsppHqdxnKdp8tYaDVprpembAyek/WkAc+HrHQecDSRERGy6vl/f\nDt8ckgiIZO99mMZpHGc/z0Er4GSttUYb/ahpAmLNc3dDTumKZybnYxIike3Xm9vbVasf17izSPLj\nOI7TOI3e+xAIuUTXOtc0DEoO0lWZ5Np+5Qk4n+2jvmZnZBKpGkferlrzyIlEhLMf7+/GaZwmH0JI\nKCWHrutTEVBGPQgTKW0a1/YDAafr6dIZmUSkmn796b+3q/aRu4kIcwrj3ZfdOE1TiDEmLin4IeQi\nQIYftLtWELiuH4DzxSdNPtg5mUSq6daf/rn5lkkgzNmP95+30zRNMaWUSw5+DokFlWketaFCUpqt\na/uBk79ievJ8TCJSyvabT//dC/cjKmU/3lWQUs6ppOinKRWgZfDyHiYkpaFxXTckb35oO3k5O+fq\nVpn039Ui3MsXFndbmJRLLhz91IwVo2+6viEpQevafhVmc8UTyjO7W7/+9N+2bc03jdqrcH+5m6dp\nKlyYjTXWAWnrulgEHpY3UkiNa/th2l0z0X1O4VYVJGPM4zNJqZp09/lumuaJWYS1VtqRtq7rQ/5G\nuIHIuq4fdo2hF68tn9XOA9K+cqbtV5vNN7cAhEtK0U+77d3dPM2TiIAoIjU3ruuHyfuYDmE3AgHZ\nxnVD56ym566snN3OARIiEbq+67rboTX47a42zfPs/73bzSlnXq57iwhLjvN475w1yVhjloJSFCDd\ndEPfd11buDBfA6azgKQUqbZfr1ZLsL38uTAzx3m72/37dTfH2gpX9gPKcpxH56ym7NoW4RBZkWna\nvu/a1uWMWeRiM0sf7CwgkdK6HTY3N7crZx7VGAsXjtP2692/d7s55sOeVUSAc5h31mqFZcVoCKie\nC6AyTTv0fde2EeEPYhIpY9ph/ek/3zIJhEuJ0/brv/9+3c6ptntb2isB5+hHYxQBM2inYJ+hI920\nse+6tkVgArzCFfjzgKS1dcOm7ki+CbVLDvP2y//27ra0e0EQkBxmpRQCM2qXC+LiiGSarvRd1znh\nnPAPcjdj22Hz6b83Q2seJQCES47T9uv/9u62b4kDAJzjjIjARYwbUlOQAABQlG6K9H3XtpxTbdB5\naSqdR7i1sW2/+fTf9erxQZJIKTlO2y//+3e7nVOuXUuW3jWcI4oA5wSu3+SCSzYXyTSCfde1LqdY\nQ4M/w92UNm7YfPq/tmsfCzdzyXHefv3f53maY+Z9h8jKpCAlc84R+43PhfZtX8gI6r7vujYFtbR6\nvTCVzutuxlr9aHETLjlM2y//+xJjiCyHmZqCAllKjCVFT5udTw8NbUmjLn3Xti6Y2lnwj9AkIL2A\nVC9vH6xq0v3X/30thb/pNSUgkhFVjn5Wn0afi+Ll8ESRlqpJvl41eUSl36t/0sGQEJu2Gzarvm3M\ngUXCpZQ0TfN0v5vmkJbx5I9NQACSIpqn3f2ddk5wGVKOAqbphlUpLIpZuPZn2veN+V26Ax4MFZFy\n3Wpzu+6bR+8tKYbop2maPt9P8dlOrPUwbt7d/QtDFjRUz9xQlG2HDaDSbWHmkutgptrJ6vzx5ckH\nmGulXbfa3G569yiXKGmep2mcxvHz/VTTIU+aMJfod3f/YmYyoJfK11q9S0rbjguXnGJMqU6CLyBn\njy5PDpIyxvXD5nbdNfpReiT73XY7juP4ZWHS08+1MOlrS0KmwUN1sLbt4JW2TV9K4eR98DHnlLEA\nnL8N1emZZOyT7uZ3d3e7cTd+3k6Bn+uvJMJc0ry7awh10ymk5XWq6YakbePmUkqJ8zRpX6Mm4Rfa\nCJ/IzsCkpu1X69tN3+h9KY0AJz/efdltd7uv91N8vvOdcMHod1aRcX00pJYUnLLtim3j2pBLLmE0\nmigQygLSmWE69epWmTRsPq17px+lI7Pf3X3ebbe7+/spPj+PRaRAmncKVNOtglVmzyTbFmic70Mu\nOQerCZBQWJjLbzV2GqCWOBzcbX+3TQAk+fHrl+32frsbX9AkEQZIs4KsuvUUnC4PIIFqQwgp55xn\nTcCCtTT1xT7Cp7GzaFK/2tz27pEmiSS/u/tyf7+9n3yIzzesZxCJCnLQ65s5JFu4slFbULbWDuaU\nJwLODFxyKfvGpue0M2iSdd2wuXVGfyPc8+7u8/39/Z0vuTw/dkoYWSCHSd/8Z4rpMN1GNdqWnHNJ\nOeU0AeeYueSUMv1eE5URltF3XT8MK0u4LN8sIin6cXt/d39/H15u6SsCwjkot91Ns7e1US4CobJS\nSikl5ZRMisEnLjnlkhUJ/x7jFAGAFCnVrzabm03v9ul/AZGcS95td7MP6ZjJnFAD7zhtvxoyTQHY\nHwkAIgmREmNd2yVhYQAuGcvvM5JDGWuG1frmdt03upZsiwhwiiHeb8fJv9pB+WBLM32rXZdhz8hl\nHqWIaOvaPrMIC5ecROS8tUsnHBasm6YZ1pubm009/AfYH/zP8/12nH08chCLCEqJ0+5r4/pYiHg5\nhUMkECEl2jZtLHUAYY6Rl1jpbHbK6aXWdcNqvbnd9E4/eBunMO3utuMUwjFDJ5eGniXO269tv4qF\noIbde39TANq4Lpc6ozEFXbj8FiABAlaQNje3694Z3DOJS/Lj9n53YNIx/lZBarrVHIs6jC9BBCQR\nAGObto7aKzE0ppQz1+eeauAUIGnbLkwa3IMmMSc/be+2u8nH9Pq0YICKSAlTY/qbOWaFuKcSAjEB\ngrausDBzScFbk/NvAVJtx25dP6zXN7ePV7fqbtv77Tj7kHM57u0ESpw1Drs5FOb9LhcBgAAQxRYG\n4MIlemdNPHel9+lCAFR7dxtaVzPbIsJ7Jo2Tj+W40YcCKCVOwKtxjuUh240A9VqcWAGCUkoJ82TP\nXw5/uhCgMmm13tx2xpqHuraSwliZFPmYicoAIAA5IqfNbo6HcxMEQUAhEUIB1FBKKX5qfh+QEAGr\nJm1ubtqHzuQPmjROIT6ba/veBEoocb7ZVSYt5YHLtbc6bskgcyneOXtUm7g32ZtBQkAgpZUeVqth\n6DtnjYalibakGMO83e3GyYdcfioZzQUk+Gl3z65InVS2pP1FSkopTeM0ex9jnUf81sd40d4OEhKq\nxlq7vt2sV73bH7QJiEicp3n39W43+fiTGAmASPHj/ZfcdUBISMiy/FNCCGHabrfb7W72KZ17yutb\nQUIkRca1bbu+2axXfXvokMQinObd9v7r/a5ODf65dxaQHKb7z6UIKUVExIWZuTAnP8/zuNvtdvfj\nFOJLaYWT2NuZpJQyrh+Gze1mveqcVfvFn4XjvLv78vV+O/mQjty27a3OYBzvvwCgtkotc6xKKVzi\nOE7jOI67cbuba/j11sd40d4IEiKRUsb1683NzWY9VHeD5dZ/ifPu6+ev97tpjumnf9oiJYz3nxFV\n02oWUTnnkksuJey2u+04TuO0Gydf6wrPaW8DCWvnFeP61c3tzc161R+YVMva5u3d5y/3u9GHnwWp\nMmm6b5Vu2p4NAOS83P72u/v7u908TfNU3e19M6ne3beuX99+2mzWq761CqBuUqWeDlUmhfTaMK4f\nTDiH8d5o2/ZRABBKSjHllNO8vf/6ZTfPfp5n72N615qEAECktHH9+vZ2vV4PnTMHd2PmOO++fr6/\n300+5Z97EEEByH40ZNthjgCIkOvJbUrj7v7r55333vsYQsrvfHVb5h65fn3zaTWsBleLiwEAmLnE\neXf3ebfbjf6nV6Bll0vS9GsfAZAwpxhjjDFNu/uvn7chBJ9SyqkcGcj/sr19ddsz6VPfD72l/RZB\nRBYmTdM0efn5BxHIgTi163GOiKQw5xRDiDFMu/uvX+5DjCFzKeefO/0WkHDpJmJd1w3rddf13cO1\ndhEWzmEat/PsffzpLHTd5SLn7W6cZmYR3vtXHHfb+7v7FGMqIucfqPw2kIhIu64f1kPvrNEK96V/\n9VM/3r3/ggnuSwPuv9jGWhN88CHGGHfjHPIyifgSZVxvAkkpZdt+tdqsutZqrfYZe3kAaHnlL36H\nWokz3n+xxhodQ4ghpZjG3RxTOeQU3vUxd63X7ob1ZuicrY3tH51sf5vz/5WTMREulPx474zRRqUY\nY8wppfk3YtK+8eq6bmyXoay4DL49FB//si1Rux/vjdZaq+WYOyc/zmEZ/P09Z89ib2OSMrZdmNQY\npR4aJH1/cvQLPBIEYC6Y5tEopZSinHJOJecSxnoz5QKaDQBv1SRtal571VdNetz6Bx4mc/2yJAlj\niX5HQKQIy7J1K3F+YNK7dzfSpnnQpIcEoQicQE4FQRgheYKChIQ1BcCFUwjhwKQLoPRmJrUHkOhR\nGz/5TrZ/UbdFikSSEhEQgfdWUkp5Pxv9DQ9wrL1xdTON61brmiIhIoRHBVVvh0mEURKUOMNyGlx/\nMZdSGC7kbG9d3Wox0nrTdm09IMF9GPlobcZfFyVGBCmRqL5hXTaXxfOClyfeuLppY+ryvOiRiECt\nQM9L47+3RDJ1RHlhwgeQLuRh39gbQEIkpZYzLxERlPoswoVLyTnlFOpRxpsmtNUrgwdqXgGjNzOp\ncugQNtaSoVJySTmlHFNtGPFGiPYR4+XhqfYmkJCUVupRcATCzFJyzimnlNKxJRLPmewLSg4qdBWc\n3pRPIqW13jddrQ/DzFxyWuz4YptnbcFJ5NBz+S3v9mv2Rnd7YFL9/CwVoxhTSnHPpDd5G0g9276G\nGC32xnzSw7q2/LyZSyk5xRhTTOntZ9CyFGkfgq5rIHUC4V6ItAQxzCXnFENMMcWQ8ltPxB6hdDXl\nPoG7PTCpYrT4WyXT26sZ9uX+V3O2t65uSn/TP1IOuh3DcrCR36ZJAFdFZ7G3nruhcMlJKVIsIlJS\nzin4eZ5jjDGG+LaQ+53YW0DiFObRaoW5cU2jRQRKzjkH72cfU4ppN4eUj61ve7/2JpBynEetkGNj\nG6uWpr8lRx+CTymntJt8PKRZT/aZL25vAamk4EdCKcFaY5WACJdSSowhxpRzyrt9BvF3huhNIAnn\nMGuUkubatk1AmEvhFFNMOZecxyk8Ovr5be1tmhRnkpKC00ZrqhMkmDmnlFMpJZdx9mlpbvM74/Qm\nd8uBoKTgrVZK436Du+9tUJhryc1fziQCTmG2RpFSCAJQs6ullNr/IfiwVKv/1jC9bXVDzsForYiW\nXEBNujFzzUanlNKSdvud7S1V4qSUIkWkcN9ta8lpLAZSCv8BGL1tuBwu/3z/Lg+Jyt9csT/swz7s\nwz7swz7swz7swz7swz7swz7swz7se/t/2Uw49KD+rS4AAAAASUVORK5CYII=\n",
- "text/plain": [
- ""
- ]
- },
- "metadata": {
- "tags": []
- },
- "execution_count": 19
- }
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "0EZCVtCPunrT",
- "colab_type": "text"
- },
- "source": [
- "Looks pretty good!\n",
- "\n",
- "## Wrapping up\n",
- "\n",
- "In this tutorial, you have learned how to create your own training pipeline for instance segmentation models, on a custom dataset.\n",
- "For that, you wrote a `torch.utils.data.Dataset` class that returns the images and the ground truth boxes and segmentation masks. You also leveraged a Mask R-CNN model pre-trained on COCO train2017 in order to perform transfer learning on this new dataset.\n",
- "\n",
- "For a more complete example, which includes multi-machine / multi-gpu training, check `references/detection/train.py`, which is present in the [torchvision GitHub repo](https://github.com/pytorch/vision/tree/v0.3.0/references/detection). \n",
- "\n"
- ]
- }
- ]
-}
\ No newline at end of file
diff --git a/_static/tv-training-code.py b/_static/tv-training-code.py
deleted file mode 100644
index d520b2437..000000000
--- a/_static/tv-training-code.py
+++ /dev/null
@@ -1,165 +0,0 @@
-# Sample code from the TorchVision 0.3 Object Detection Finetuning Tutorial
-# http://tutorials.pytorch.kr/intermediate/torchvision_tutorial.html
-
-import os
-import numpy as np
-import torch
-from PIL import Image
-
-import torchvision
-from torchvision.models.detection.faster_rcnn import FastRCNNPredictor
-from torchvision.models.detection.mask_rcnn import MaskRCNNPredictor
-
-from engine import train_one_epoch, evaluate
-import utils
-import transforms as T
-
-
-class PennFudanDataset(object):
- def __init__(self, root, transforms):
- self.root = root
- self.transforms = transforms
- # load all image files, sorting them to
- # ensure that they are aligned
- self.imgs = list(sorted(os.listdir(os.path.join(root, "PNGImages"))))
- self.masks = list(sorted(os.listdir(os.path.join(root, "PedMasks"))))
-
- def __getitem__(self, idx):
- # load images and masks
- img_path = os.path.join(self.root, "PNGImages", self.imgs[idx])
- mask_path = os.path.join(self.root, "PedMasks", self.masks[idx])
- img = Image.open(img_path).convert("RGB")
- # note that we haven't converted the mask to RGB,
- # because each color corresponds to a different instance
- # with 0 being background
- mask = Image.open(mask_path)
-
- mask = np.array(mask)
- # instances are encoded as different colors
- obj_ids = np.unique(mask)
- # first id is the background, so remove it
- obj_ids = obj_ids[1:]
-
- # split the color-encoded mask into a set
- # of binary masks
- masks = mask == obj_ids[:, None, None]
-
- # get bounding box coordinates for each mask
- num_objs = len(obj_ids)
- boxes = []
- for i in range(num_objs):
- pos = np.where(masks[i])
- xmin = np.min(pos[1])
- xmax = np.max(pos[1])
- ymin = np.min(pos[0])
- ymax = np.max(pos[0])
- boxes.append([xmin, ymin, xmax, ymax])
-
- boxes = torch.as_tensor(boxes, dtype=torch.float32)
- # there is only one class
- labels = torch.ones((num_objs,), dtype=torch.int64)
- masks = torch.as_tensor(masks, dtype=torch.uint8)
-
- image_id = torch.tensor([idx])
- area = (boxes[:, 3] - boxes[:, 1]) * (boxes[:, 2] - boxes[:, 0])
- # suppose all instances are not crowd
- iscrowd = torch.zeros((num_objs,), dtype=torch.int64)
-
- target = {}
- target["boxes"] = boxes
- target["labels"] = labels
- target["masks"] = masks
- target["image_id"] = image_id
- target["area"] = area
- target["iscrowd"] = iscrowd
-
- if self.transforms is not None:
- img, target = self.transforms(img, target)
-
- return img, target
-
- def __len__(self):
- return len(self.imgs)
-
-def get_model_instance_segmentation(num_classes):
- # load an instance segmentation model pre-trained pre-trained on COCO
- model = torchvision.models.detection.maskrcnn_resnet50_fpn(pretrained=True)
-
- # get number of input features for the classifier
- in_features = model.roi_heads.box_predictor.cls_score.in_features
- # replace the pre-trained head with a new one
- model.roi_heads.box_predictor = FastRCNNPredictor(in_features, num_classes)
-
- # now get the number of input features for the mask classifier
- in_features_mask = model.roi_heads.mask_predictor.conv5_mask.in_channels
- hidden_layer = 256
- # and replace the mask predictor with a new one
- model.roi_heads.mask_predictor = MaskRCNNPredictor(in_features_mask,
- hidden_layer,
- num_classes)
-
- return model
-
-
-def get_transform(train):
- transforms = []
- transforms.append(T.ToTensor())
- if train:
- transforms.append(T.RandomHorizontalFlip(0.5))
- return T.Compose(transforms)
-
-
-def main():
- # train on the GPU or on the CPU, if a GPU is not available
- device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
-
- # our dataset has two classes only - background and person
- num_classes = 2
- # use our dataset and defined transformations
- dataset = PennFudanDataset('PennFudanPed', get_transform(train=True))
- dataset_test = PennFudanDataset('PennFudanPed', get_transform(train=False))
-
- # split the dataset in train and test set
- indices = torch.randperm(len(dataset)).tolist()
- dataset = torch.utils.data.Subset(dataset, indices[:-50])
- dataset_test = torch.utils.data.Subset(dataset_test, indices[-50:])
-
- # define training and validation data loaders
- data_loader = torch.utils.data.DataLoader(
- dataset, batch_size=2, shuffle=True, num_workers=4,
- collate_fn=utils.collate_fn)
-
- data_loader_test = torch.utils.data.DataLoader(
- dataset_test, batch_size=1, shuffle=False, num_workers=4,
- collate_fn=utils.collate_fn)
-
- # get the model using our helper function
- model = get_model_instance_segmentation(num_classes)
-
- # move model to the right device
- model.to(device)
-
- # construct an optimizer
- params = [p for p in model.parameters() if p.requires_grad]
- optimizer = torch.optim.SGD(params, lr=0.005,
- momentum=0.9, weight_decay=0.0005)
- # and a learning rate scheduler
- lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer,
- step_size=3,
- gamma=0.1)
-
- # let's train it for 10 epochs
- num_epochs = 10
-
- for epoch in range(num_epochs):
- # train for one epoch, printing every 10 iterations
- train_one_epoch(model, optimizer, data_loader, device, epoch, print_freq=10)
- # update the learning rate
- lr_scheduler.step()
- # evaluate on the test dataset
- evaluate(model, data_loader_test, device=device)
-
- print("That's it!")
-
-if __name__ == "__main__":
- main()
diff --git a/_templates/layout.html b/_templates/layout.html
index a6fa24075..22a295435 100644
--- a/_templates/layout.html
+++ b/_templates/layout.html
@@ -11,11 +11,14 @@
{%- endblock %}
+
{% block footer %}
{{ super() }}
{% endblock %}
diff --git a/advanced_source/coding_ddpg.py b/advanced_source/coding_ddpg.py
new file mode 100644
index 000000000..7dd3acf23
--- /dev/null
+++ b/advanced_source/coding_ddpg.py
@@ -0,0 +1,1218 @@
+# -*- coding: utf-8 -*-
+"""
+TorchRL objectives: Coding a DDPG loss
+======================================
+**Author**: `Vincent Moens `_
+
+"""
+
+##############################################################################
+# Overview
+# --------
+#
+# TorchRL separates the training of RL algorithms in various pieces that will be
+# assembled in your training script: the environment, the data collection and
+# storage, the model and finally the loss function.
+#
+# TorchRL losses (or "objectives") are stateful objects that contain the
+# trainable parameters (policy and value models).
+# This tutorial will guide you through the steps to code a loss from the ground up
+# using TorchRL.
+#
+# To this aim, we will be focusing on DDPG, which is a relatively straightforward
+# algorithm to code.
+# `Deep Deterministic Policy Gradient `_ (DDPG)
+# is a simple continuous control algorithm. It consists in learning a
+# parametric value function for an action-observation pair, and
+# then learning a policy that outputs actions that maximize this value
+# function given a certain observation.
+#
+# What you will learn:
+#
+# - how to write a loss module and customize its value estimator;
+# - how to build an environment in TorchRL, including transforms
+# (for example, data normalization) and parallel execution;
+# - how to design a policy and value network;
+# - how to collect data from your environment efficiently and store them
+# in a replay buffer;
+# - how to store trajectories (and not transitions) in your replay buffer);
+# - how to evaluate your model.
+#
+# Prerequisites
+# ~~~~~~~~~~~~~
+#
+# This tutorial assumes that you have completed the
+# `PPO tutorial `_ which gives
+# an overview of the TorchRL components and dependencies, such as
+# :class:`tensordict.TensorDict` and :class:`tensordict.nn.TensorDictModules`,
+# although it should be
+# sufficiently transparent to be understood without a deep understanding of
+# these classes.
+#
+# .. note::
+# We do not aim at giving a SOTA implementation of the algorithm, but rather
+# to provide a high-level illustration of TorchRL's loss implementations
+# and the library features that are to be used in the context of
+# this algorithm.
+#
+# Imports and setup
+# -----------------
+#
+# .. code-block:: bash
+#
+# %%bash
+# pip3 install torchrl mujoco glfw
+
+# sphinx_gallery_start_ignore
+import warnings
+
+warnings.filterwarnings("ignore")
+from torch import multiprocessing
+
+# TorchRL prefers spawn method, that restricts creation of ``~torchrl.envs.ParallelEnv`` inside
+# `__main__` method call, but for the easy of reading the code switch to fork
+# which is also a default spawn method in Google's Colaboratory
+try:
+ multiprocessing.set_start_method("fork")
+except RuntimeError:
+ pass
+
+# sphinx_gallery_end_ignore
+
+
+import torch
+import tqdm
+
+
+###############################################################################
+# We will execute the policy on CUDA if available
+is_fork = multiprocessing.get_start_method() == "fork"
+device = (
+ torch.device(0)
+ if torch.cuda.is_available() and not is_fork
+ else torch.device("cpu")
+)
+collector_device = torch.device("cpu") # Change the device to ``cuda`` to use CUDA
+
+###############################################################################
+# TorchRL :class:`~torchrl.objectives.LossModule`
+# -----------------------------------------------
+#
+# TorchRL provides a series of losses to use in your training scripts.
+# The aim is to have losses that are easily reusable/swappable and that have
+# a simple signature.
+#
+# The main characteristics of TorchRL losses are:
+#
+# - They are stateful objects: they contain a copy of the trainable parameters
+# such that ``loss_module.parameters()`` gives whatever is needed to train the
+# algorithm.
+# - They follow the ``TensorDict`` convention: the :meth:`torch.nn.Module.forward`
+# method will receive a TensorDict as input that contains all the necessary
+# information to return a loss value.
+#
+# >>> data = replay_buffer.sample()
+# >>> loss_dict = loss_module(data)
+#
+# - They output a :class:`tensordict.TensorDict` instance with the loss values
+# written under a ``"loss_"`` where ``smth`` is a string describing the
+# loss. Additional keys in the ``TensorDict`` may be useful metrics to log during
+# training time.
+#
+# .. note::
+# The reason we return independent losses is to let the user use a different
+# optimizer for different sets of parameters for instance. Summing the losses
+# can be simply done via
+#
+# >>> loss_val = sum(loss for key, loss in loss_dict.items() if key.startswith("loss_"))
+#
+# The ``__init__`` method
+# ~~~~~~~~~~~~~~~~~~~~~~~
+#
+# The parent class of all losses is :class:`~torchrl.objectives.LossModule`.
+# As many other components of the library, its :meth:`~torchrl.objectives.LossModule.forward` method expects
+# as input a :class:`tensordict.TensorDict` instance sampled from an experience
+# replay buffer, or any similar data structure. Using this format makes it
+# possible to re-use the module across
+# modalities, or in complex settings where the model needs to read multiple
+# entries for instance. In other words, it allows us to code a loss module that
+# is oblivious to the data type that is being given to is and that focuses on
+# running the elementary steps of the loss function and only those.
+#
+# To keep the tutorial as didactic as we can, we'll be displaying each method
+# of the class independently and we'll be populating the class at a later
+# stage.
+#
+# Let us start with the :meth:`~torchrl.objectives.LossModule.__init__`
+# method. DDPG aims at solving a control task with a simple strategy:
+# training a policy to output actions that maximize the value predicted by
+# a value network. Hence, our loss module needs to receive two networks in its
+# constructor: an actor and a value networks. We expect both of these to be
+# TensorDict-compatible objects, such as
+# :class:`tensordict.nn.TensorDictModule`.
+# Our loss function will need to compute a target value and fit the value
+# network to this, and generate an action and fit the policy such that its
+# value estimate is maximized.
+#
+# The crucial step of the :meth:`LossModule.__init__` method is the call to
+# :meth:`~torchrl.LossModule.convert_to_functional`. This method will extract
+# the parameters from the module and convert it to a functional module.
+# Strictly speaking, this is not necessary and one may perfectly code all
+# the losses without it. However, we encourage its usage for the following
+# reason.
+#
+# The reason TorchRL does this is that RL algorithms often execute the same
+# model with different sets of parameters, called "trainable" and "target"
+# parameters.
+# The "trainable" parameters are those that the optimizer needs to fit. The
+# "target" parameters are usually a copy of the former's with some time lag
+# (absolute or diluted through a moving average).
+# These target parameters are used to compute the value associated with the
+# next observation. One the advantages of using a set of target parameters
+# for the value model that do not match exactly the current configuration is
+# that they provide a pessimistic bound on the value function being computed.
+# Pay attention to the ``create_target_params`` keyword argument below: this
+# argument tells the :meth:`~torchrl.objectives.LossModule.convert_to_functional`
+# method to create a set of target parameters in the loss module to be used
+# for target value computation. If this is set to ``False`` (see the actor network
+# for instance) the ``target_actor_network_params`` attribute will still be
+# accessible but this will just return a **detached** version of the
+# actor parameters.
+#
+# Later, we will see how the target parameters should be updated in TorchRL.
+#
+
+from tensordict.nn import TensorDictModule
+
+
+def _init(
+ self,
+ actor_network: TensorDictModule,
+ value_network: TensorDictModule,
+) -> None:
+ super(type(self), self).__init__()
+
+ self.convert_to_functional(
+ actor_network,
+ "actor_network",
+ create_target_params=True,
+ )
+ self.convert_to_functional(
+ value_network,
+ "value_network",
+ create_target_params=True,
+ compare_against=list(actor_network.parameters()),
+ )
+
+ self.actor_in_keys = actor_network.in_keys
+
+ # Since the value we'll be using is based on the actor and value network,
+ # we put them together in a single actor-critic container.
+ actor_critic = ActorCriticWrapper(actor_network, value_network)
+ self.actor_critic = actor_critic
+ self.loss_function = "l2"
+
+
+###############################################################################
+# The value estimator loss method
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+#
+# In many RL algorithm, the value network (or Q-value network) is trained based
+# on an empirical value estimate. This can be bootstrapped (TD(0), low
+# variance, high bias), meaning
+# that the target value is obtained using the next reward and nothing else, or
+# a Monte-Carlo estimate can be obtained (TD(1)) in which case the whole
+# sequence of upcoming rewards will be used (high variance, low bias). An
+# intermediate estimator (TD(:math:`\lambda`)) can also be used to compromise
+# bias and variance.
+# TorchRL makes it easy to use one or the other estimator via the
+# :class:`~torchrl.objectives.utils.ValueEstimators` Enum class, which contains
+# pointers to all the value estimators implemented. Let us define the default
+# value function here. We will take the simplest version (TD(0)), and show later
+# on how this can be changed.
+
+from torchrl.objectives.utils import ValueEstimators
+
+default_value_estimator = ValueEstimators.TD0
+
+###############################################################################
+# We also need to give some instructions to DDPG on how to build the value
+# estimator, depending on the user query. Depending on the estimator provided,
+# we will build the corresponding module to be used at train time:
+
+from torchrl.objectives.utils import default_value_kwargs
+from torchrl.objectives.value import TD0Estimator, TD1Estimator, TDLambdaEstimator
+
+
+def make_value_estimator(self, value_type: ValueEstimators, **hyperparams):
+ hp = dict(default_value_kwargs(value_type))
+ if hasattr(self, "gamma"):
+ hp["gamma"] = self.gamma
+ hp.update(hyperparams)
+ value_key = "state_action_value"
+ if value_type == ValueEstimators.TD1:
+ self._value_estimator = TD1Estimator(value_network=self.actor_critic, **hp)
+ elif value_type == ValueEstimators.TD0:
+ self._value_estimator = TD0Estimator(value_network=self.actor_critic, **hp)
+ elif value_type == ValueEstimators.GAE:
+ raise NotImplementedError(
+ f"Value type {value_type} it not implemented for loss {type(self)}."
+ )
+ elif value_type == ValueEstimators.TDLambda:
+ self._value_estimator = TDLambdaEstimator(value_network=self.actor_critic, **hp)
+ else:
+ raise NotImplementedError(f"Unknown value type {value_type}")
+ self._value_estimator.set_keys(value=value_key)
+
+
+###############################################################################
+# The ``make_value_estimator`` method can but does not need to be called: if
+# not, the :class:`~torchrl.objectives.LossModule` will query this method with
+# its default estimator.
+#
+# The actor loss method
+# ~~~~~~~~~~~~~~~~~~~~~
+#
+# The central piece of an RL algorithm is the training loss for the actor.
+# In the case of DDPG, this function is quite simple: we just need to compute
+# the value associated with an action computed using the policy and optimize
+# the actor weights to maximize this value.
+#
+# When computing this value, we must make sure to take the value parameters out
+# of the graph, otherwise the actor and value loss will be mixed up.
+# For this, the :func:`~torchrl.objectives.utils.hold_out_params` function
+# can be used.
+
+
+def _loss_actor(
+ self,
+ tensordict,
+) -> torch.Tensor:
+ td_copy = tensordict.select(*self.actor_in_keys)
+ # Get an action from the actor network: since we made it functional, we need to pass the params
+ td_copy = self.actor_network(td_copy, params=self.actor_network_params)
+ # get the value associated with that action
+ td_copy = self.value_network(
+ td_copy,
+ params=self.value_network_params.detach(),
+ )
+ return -td_copy.get("state_action_value")
+
+
+###############################################################################
+# The value loss method
+# ~~~~~~~~~~~~~~~~~~~~~
+#
+# We now need to optimize our value network parameters.
+# To do this, we will rely on the value estimator of our class:
+#
+
+from torchrl.objectives.utils import distance_loss
+
+
+def _loss_value(
+ self,
+ tensordict,
+):
+ td_copy = tensordict.clone()
+
+ # V(s, a)
+ self.value_network(td_copy, params=self.value_network_params)
+ pred_val = td_copy.get("state_action_value").squeeze(-1)
+
+ # we manually reconstruct the parameters of the actor-critic, where the first
+ # set of parameters belongs to the actor and the second to the value function.
+ target_params = TensorDict(
+ {
+ "module": {
+ "0": self.target_actor_network_params,
+ "1": self.target_value_network_params,
+ }
+ },
+ batch_size=self.target_actor_network_params.batch_size,
+ device=self.target_actor_network_params.device,
+ )
+ target_value = self.value_estimator.value_estimate(
+ tensordict, target_params=target_params
+ ).squeeze(-1)
+
+ # Computes the value loss: L2, L1 or smooth L1 depending on `self.loss_function`
+ loss_value = distance_loss(pred_val, target_value, loss_function=self.loss_function)
+ td_error = (pred_val - target_value).pow(2)
+
+ return loss_value, td_error, pred_val, target_value
+
+
+###############################################################################
+# Putting things together in a forward call
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+#
+# The only missing piece is the forward method, which will glue together the
+# value and actor loss, collect the cost values and write them in a ``TensorDict``
+# delivered to the user.
+
+from tensordict import TensorDict, TensorDictBase
+
+
+def _forward(self, input_tensordict: TensorDictBase) -> TensorDict:
+ loss_value, td_error, pred_val, target_value = self.loss_value(
+ input_tensordict,
+ )
+ td_error = td_error.detach()
+ td_error = td_error.unsqueeze(input_tensordict.ndimension())
+ if input_tensordict.device is not None:
+ td_error = td_error.to(input_tensordict.device)
+ input_tensordict.set(
+ "td_error",
+ td_error,
+ inplace=True,
+ )
+ loss_actor = self.loss_actor(input_tensordict)
+ return TensorDict(
+ source={
+ "loss_actor": loss_actor.mean(),
+ "loss_value": loss_value.mean(),
+ "pred_value": pred_val.mean().detach(),
+ "target_value": target_value.mean().detach(),
+ "pred_value_max": pred_val.max().detach(),
+ "target_value_max": target_value.max().detach(),
+ },
+ batch_size=[],
+ )
+
+
+from torchrl.objectives import LossModule
+
+
+class DDPGLoss(LossModule):
+ default_value_estimator = default_value_estimator
+ make_value_estimator = make_value_estimator
+
+ __init__ = _init
+ forward = _forward
+ loss_value = _loss_value
+ loss_actor = _loss_actor
+
+
+###############################################################################
+# Now that we have our loss, we can use it to train a policy to solve a
+# control task.
+#
+# Environment
+# -----------
+#
+# In most algorithms, the first thing that needs to be taken care of is the
+# construction of the environment as it conditions the remainder of the
+# training script.
+#
+# For this example, we will be using the ``"cheetah"`` task. The goal is to make
+# a half-cheetah run as fast as possible.
+#
+# In TorchRL, one can create such a task by relying on ``dm_control`` or ``gym``:
+#
+# .. code-block:: python
+#
+# env = GymEnv("HalfCheetah-v4")
+#
+# or
+#
+# .. code-block:: python
+#
+# env = DMControlEnv("cheetah", "run")
+#
+# By default, these environment disable rendering. Training from states is
+# usually easier than training from images. To keep things simple, we focus
+# on learning from states only. To pass the pixels to the ``tensordicts`` that
+# are collected by :func:`env.step()`, simply pass the ``from_pixels=True``
+# argument to the constructor:
+#
+# .. code-block:: python
+#
+# env = GymEnv("HalfCheetah-v4", from_pixels=True, pixels_only=True)
+#
+# We write a :func:`make_env` helper function that will create an environment
+# with either one of the two backends considered above (``dm-control`` or ``gym``).
+#
+
+from torchrl.envs.libs.dm_control import DMControlEnv
+from torchrl.envs.libs.gym import GymEnv
+
+env_library = None
+env_name = None
+
+
+def make_env(from_pixels=False):
+ """Create a base ``env``."""
+ global env_library
+ global env_name
+
+ if backend == "dm_control":
+ env_name = "cheetah"
+ env_task = "run"
+ env_args = (env_name, env_task)
+ env_library = DMControlEnv
+ elif backend == "gym":
+ env_name = "HalfCheetah-v4"
+ env_args = (env_name,)
+ env_library = GymEnv
+ else:
+ raise NotImplementedError
+
+ env_kwargs = {
+ "device": device,
+ "from_pixels": from_pixels,
+ "pixels_only": from_pixels,
+ "frame_skip": 2,
+ }
+ env = env_library(*env_args, **env_kwargs)
+ return env
+
+
+###############################################################################
+# Transforms
+# ~~~~~~~~~~
+#
+# Now that we have a base environment, we may want to modify its representation
+# to make it more policy-friendly. In TorchRL, transforms are appended to the
+# base environment in a specialized :class:`torchr.envs.TransformedEnv` class.
+#
+# - It is common in DDPG to rescale the reward using some heuristic value. We
+# will multiply the reward by 5 in this example.
+#
+# - If we are using :mod:`dm_control`, it is also important to build an interface
+# between the simulator which works with double precision numbers, and our
+# script which presumably uses single precision ones. This transformation goes
+# both ways: when calling :func:`env.step`, our actions will need to be
+# represented in double precision, and the output will need to be transformed
+# to single precision.
+# The :class:`~torchrl.envs.DoubleToFloat` transform does exactly this: the
+# ``in_keys`` list refers to the keys that will need to be transformed from
+# double to float, while the ``in_keys_inv`` refers to those that need to
+# be transformed to double before being passed to the environment.
+#
+# - We concatenate the state keys together using the :class:`~torchrl.envs.CatTensors`
+# transform.
+#
+# - Finally, we also leave the possibility of normalizing the states: we will
+# take care of computing the normalizing constants later on.
+#
+
+from torchrl.envs import (
+ CatTensors,
+ DoubleToFloat,
+ EnvCreator,
+ InitTracker,
+ ObservationNorm,
+ ParallelEnv,
+ RewardScaling,
+ StepCounter,
+ TransformedEnv,
+)
+
+
+def make_transformed_env(
+ env,
+):
+ """Apply transforms to the ``env`` (such as reward scaling and state normalization)."""
+
+ env = TransformedEnv(env)
+
+ # we append transforms one by one, although we might as well create the
+ # transformed environment using the `env = TransformedEnv(base_env, transforms)`
+ # syntax.
+ env.append_transform(RewardScaling(loc=0.0, scale=reward_scaling))
+
+ # We concatenate all states into a single "observation_vector"
+ # even if there is a single tensor, it'll be renamed in "observation_vector".
+ # This facilitates the downstream operations as we know the name of the
+ # output tensor.
+ # In some environments (not half-cheetah), there may be more than one
+ # observation vector: in this case this code snippet will concatenate them
+ # all.
+ selected_keys = list(env.observation_spec.keys())
+ out_key = "observation_vector"
+ env.append_transform(CatTensors(in_keys=selected_keys, out_key=out_key))
+
+ # we normalize the states, but for now let's just instantiate a stateless
+ # version of the transform
+ env.append_transform(ObservationNorm(in_keys=[out_key], standard_normal=True))
+
+ env.append_transform(DoubleToFloat())
+
+ env.append_transform(StepCounter(max_frames_per_traj))
+
+ # We need a marker for the start of trajectories for our Ornstein-Uhlenbeck (OU)
+ # exploration:
+ env.append_transform(InitTracker())
+
+ return env
+
+
+###############################################################################
+# Parallel execution
+# ~~~~~~~~~~~~~~~~~~
+#
+# The following helper function allows us to run environments in parallel.
+# Running environments in parallel can significantly speed up the collection
+# throughput. When using transformed environment, we need to choose whether we
+# want to execute the transform individually for each environment, or
+# centralize the data and transform it in batch. Both approaches are easy to
+# code:
+#
+# .. code-block:: python
+#
+# env = ParallelEnv(
+# lambda: TransformedEnv(GymEnv("HalfCheetah-v4"), transforms),
+# num_workers=4
+# )
+# env = TransformedEnv(
+# ParallelEnv(lambda: GymEnv("HalfCheetah-v4"), num_workers=4),
+# transforms
+# )
+#
+# To leverage the vectorization capabilities of PyTorch, we adopt
+# the first method:
+#
+
+
+def parallel_env_constructor(
+ env_per_collector,
+ transform_state_dict,
+):
+ if env_per_collector == 1:
+
+ def make_t_env():
+ env = make_transformed_env(make_env())
+ env.transform[2].init_stats(3)
+ env.transform[2].loc.copy_(transform_state_dict["loc"])
+ env.transform[2].scale.copy_(transform_state_dict["scale"])
+ return env
+
+ env_creator = EnvCreator(make_t_env)
+ return env_creator
+
+ parallel_env = ParallelEnv(
+ num_workers=env_per_collector,
+ create_env_fn=EnvCreator(lambda: make_env()),
+ create_env_kwargs=None,
+ pin_memory=False,
+ )
+ env = make_transformed_env(parallel_env)
+ # we call `init_stats` for a limited number of steps, just to instantiate
+ # the lazy buffers.
+ env.transform[2].init_stats(3, cat_dim=1, reduce_dim=[0, 1])
+ env.transform[2].load_state_dict(transform_state_dict)
+ return env
+
+
+# The backend can be ``gym`` or ``dm_control``
+backend = "gym"
+
+###############################################################################
+# .. note::
+#
+# ``frame_skip`` batches multiple step together with a single action
+# If > 1, the other frame counts (for example, frames_per_batch, total_frames)
+# need to be adjusted to have a consistent total number of frames collected
+# across experiments. This is important as raising the frame-skip but keeping the
+# total number of frames unchanged may seem like cheating: all things compared,
+# a dataset of 10M elements collected with a frame-skip of 2 and another with
+# a frame-skip of 1 actually have a ratio of interactions with the environment
+# of 2:1! In a nutshell, one should be cautious about the frame-count of a
+# training script when dealing with frame skipping as this may lead to
+# biased comparisons between training strategies.
+#
+# Scaling the reward helps us control the signal magnitude for a more
+# efficient learning.
+reward_scaling = 5.0
+
+###############################################################################
+# We also define when a trajectory will be truncated. A thousand steps (500 if
+# frame-skip = 2) is a good number to use for the cheetah task:
+
+max_frames_per_traj = 500
+
+###############################################################################
+# Normalization of the observations
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+#
+# To compute the normalizing statistics, we run an arbitrary number of random
+# steps in the environment and compute the mean and standard deviation of the
+# collected observations. The :func:`ObservationNorm.init_stats()` method can
+# be used for this purpose. To get the summary statistics, we create a dummy
+# environment and run it for a given number of steps, collect data over a given
+# number of steps and compute its summary statistics.
+#
+
+
+def get_env_stats():
+ """Gets the stats of an environment."""
+ proof_env = make_transformed_env(make_env())
+ t = proof_env.transform[2]
+ t.init_stats(init_env_steps)
+ transform_state_dict = t.state_dict()
+ proof_env.close()
+ return transform_state_dict
+
+
+###############################################################################
+# Normalization stats
+# ~~~~~~~~~~~~~~~~~~~
+# Number of random steps used as for stats computation using ``ObservationNorm``
+
+init_env_steps = 5000
+
+transform_state_dict = get_env_stats()
+
+###############################################################################
+# Number of environments in each data collector
+env_per_collector = 4
+
+###############################################################################
+# We pass the stats computed earlier to normalize the output of our
+# environment:
+
+parallel_env = parallel_env_constructor(
+ env_per_collector=env_per_collector,
+ transform_state_dict=transform_state_dict,
+)
+
+
+from torchrl.data import CompositeSpec
+
+###############################################################################
+# Building the model
+# ------------------
+#
+# We now turn to the setup of the model. As we have seen, DDPG requires a
+# value network, trained to estimate the value of a state-action pair, and a
+# parametric actor that learns how to select actions that maximize this value.
+#
+# Recall that building a TorchRL module requires two steps:
+#
+# - writing the :class:`torch.nn.Module` that will be used as network,
+# - wrapping the network in a :class:`tensordict.nn.TensorDictModule` where the
+# data flow is handled by specifying the input and output keys.
+#
+# In more complex scenarios, :class:`tensordict.nn.TensorDictSequential` can
+# also be used.
+#
+#
+# The Q-Value network is wrapped in a :class:`~torchrl.modules.ValueOperator`
+# that automatically sets the ``out_keys`` to ``"state_action_value`` for q-value
+# networks and ``state_value`` for other value networks.
+#
+# TorchRL provides a built-in version of the DDPG networks as presented in the
+# original paper. These can be found under :class:`~torchrl.modules.DdpgMlpActor`
+# and :class:`~torchrl.modules.DdpgMlpQNet`.
+#
+# Since we use lazy modules, it is necessary to materialize the lazy modules
+# before being able to move the policy from device to device and achieve other
+# operations. Hence, it is good practice to run the modules with a small
+# sample of data. For this purpose, we generate fake data from the
+# environment specs.
+#
+
+from torchrl.modules import (
+ ActorCriticWrapper,
+ DdpgMlpActor,
+ DdpgMlpQNet,
+ OrnsteinUhlenbeckProcessWrapper,
+ ProbabilisticActor,
+ TanhDelta,
+ ValueOperator,
+)
+
+
+def make_ddpg_actor(
+ transform_state_dict,
+ device="cpu",
+):
+ proof_environment = make_transformed_env(make_env())
+ proof_environment.transform[2].init_stats(3)
+ proof_environment.transform[2].load_state_dict(transform_state_dict)
+
+ out_features = proof_environment.action_spec.shape[-1]
+
+ actor_net = DdpgMlpActor(
+ action_dim=out_features,
+ )
+
+ in_keys = ["observation_vector"]
+ out_keys = ["param"]
+
+ actor = TensorDictModule(
+ actor_net,
+ in_keys=in_keys,
+ out_keys=out_keys,
+ )
+
+ actor = ProbabilisticActor(
+ actor,
+ distribution_class=TanhDelta,
+ in_keys=["param"],
+ spec=CompositeSpec(action=proof_environment.action_spec),
+ ).to(device)
+
+ q_net = DdpgMlpQNet()
+
+ in_keys = in_keys + ["action"]
+ qnet = ValueOperator(
+ in_keys=in_keys,
+ module=q_net,
+ ).to(device)
+
+ # initialize lazy modules
+ qnet(actor(proof_environment.reset().to(device)))
+ return actor, qnet
+
+
+actor, qnet = make_ddpg_actor(
+ transform_state_dict=transform_state_dict,
+ device=device,
+)
+
+###############################################################################
+# Exploration
+# ~~~~~~~~~~~
+#
+# The policy is wrapped in a :class:`~torchrl.modules.OrnsteinUhlenbeckProcessWrapper`
+# exploration module, as suggested in the original paper.
+# Let's define the number of frames before OU noise reaches its minimum value
+annealing_frames = 1_000_000
+
+actor_model_explore = OrnsteinUhlenbeckProcessWrapper(
+ actor,
+ annealing_num_steps=annealing_frames,
+).to(device)
+if device == torch.device("cpu"):
+ actor_model_explore.share_memory()
+
+
+###############################################################################
+# Data collector
+# --------------
+#
+# TorchRL provides specialized classes to help you collect data by executing
+# the policy in the environment. These "data collectors" iteratively compute
+# the action to be executed at a given time, then execute a step in the
+# environment and reset it when required.
+# Data collectors are designed to help developers have a tight control
+# on the number of frames per batch of data, on the (a)sync nature of this
+# collection and on the resources allocated to the data collection (for example
+# GPU, number of workers, and so on).
+#
+# Here we will use
+# :class:`~torchrl.collectors.SyncDataCollector`, a simple, single-process
+# data collector. TorchRL offers other collectors, such as
+# :class:`~torchrl.collectors.MultiaSyncDataCollector`, which executed the
+# rollouts in an asynchronous manner (for example, data will be collected while
+# the policy is being optimized, thereby decoupling the training and
+# data collection).
+#
+# The parameters to specify are:
+#
+# - an environment factory or an environment,
+# - the policy,
+# - the total number of frames before the collector is considered empty,
+# - the maximum number of frames per trajectory (useful for non-terminating
+# environments, like ``dm_control`` ones).
+#
+# .. note::
+#
+# The ``max_frames_per_traj`` passed to the collector will have the effect
+# of registering a new :class:`~torchrl.envs.StepCounter` transform
+# with the environment used for inference. We can achieve the same result
+# manually, as we do in this script.
+#
+# One should also pass:
+#
+# - the number of frames in each batch collected,
+# - the number of random steps executed independently from the policy,
+# - the devices used for policy execution
+# - the devices used to store data before the data is passed to the main
+# process.
+#
+# The total frames we will use during training should be around 1M.
+total_frames = 10_000 # 1_000_000
+
+###############################################################################
+# The number of frames returned by the collector at each iteration of the outer
+# loop is equal to the length of each sub-trajectories times the number of
+# environments run in parallel in each collector.
+#
+# In other words, we expect batches from the collector to have a shape
+# ``[env_per_collector, traj_len]`` where
+# ``traj_len=frames_per_batch/env_per_collector``:
+#
+traj_len = 200
+frames_per_batch = env_per_collector * traj_len
+init_random_frames = 5000
+num_collectors = 2
+
+from torchrl.collectors import SyncDataCollector
+from torchrl.envs import ExplorationType
+
+collector = SyncDataCollector(
+ parallel_env,
+ policy=actor_model_explore,
+ total_frames=total_frames,
+ frames_per_batch=frames_per_batch,
+ init_random_frames=init_random_frames,
+ reset_at_each_iter=False,
+ split_trajs=False,
+ device=collector_device,
+ exploration_type=ExplorationType.RANDOM,
+)
+
+###############################################################################
+# Evaluator: building your recorder object
+# ----------------------------------------
+#
+# As the training data is obtained using some exploration strategy, the true
+# performance of our algorithm needs to be assessed in deterministic mode. We
+# do this using a dedicated class, ``Recorder``, which executes the policy in
+# the environment at a given frequency and returns some statistics obtained
+# from these simulations.
+#
+# The following helper function builds this object:
+from torchrl.trainers import Recorder
+
+
+def make_recorder(actor_model_explore, transform_state_dict, record_interval):
+ base_env = make_env()
+ environment = make_transformed_env(base_env)
+ environment.transform[2].init_stats(
+ 3
+ ) # must be instantiated to load the state dict
+ environment.transform[2].load_state_dict(transform_state_dict)
+
+ recorder_obj = Recorder(
+ record_frames=1000,
+ policy_exploration=actor_model_explore,
+ environment=environment,
+ exploration_type=ExplorationType.MEAN,
+ record_interval=record_interval,
+ )
+ return recorder_obj
+
+
+###############################################################################
+# We will be recording the performance every 10 batch collected
+record_interval = 10
+
+recorder = make_recorder(
+ actor_model_explore, transform_state_dict, record_interval=record_interval
+)
+
+from torchrl.data.replay_buffers import (
+ LazyMemmapStorage,
+ PrioritizedSampler,
+ RandomSampler,
+ TensorDictReplayBuffer,
+)
+
+###############################################################################
+# Replay buffer
+# -------------
+#
+# Replay buffers come in two flavors: prioritized (where some error signal
+# is used to give a higher likelihood of sampling to some items than others)
+# and regular, circular experience replay.
+#
+# TorchRL replay buffers are composable: one can pick up the storage, sampling
+# and writing strategies. It is also possible to
+# store tensors on physical memory using a memory-mapped array. The following
+# function takes care of creating the replay buffer with the desired
+# hyperparameters:
+#
+
+from torchrl.envs import RandomCropTensorDict
+
+
+def make_replay_buffer(buffer_size, batch_size, random_crop_len, prefetch=3, prb=False):
+ if prb:
+ sampler = PrioritizedSampler(
+ max_capacity=buffer_size,
+ alpha=0.7,
+ beta=0.5,
+ )
+ else:
+ sampler = RandomSampler()
+ replay_buffer = TensorDictReplayBuffer(
+ storage=LazyMemmapStorage(
+ buffer_size,
+ scratch_dir=buffer_scratch_dir,
+ ),
+ batch_size=batch_size,
+ sampler=sampler,
+ pin_memory=False,
+ prefetch=prefetch,
+ transform=RandomCropTensorDict(random_crop_len, sample_dim=1),
+ )
+ return replay_buffer
+
+
+###############################################################################
+# We'll store the replay buffer in a temporary directory on disk
+
+import tempfile
+
+tmpdir = tempfile.TemporaryDirectory()
+buffer_scratch_dir = tmpdir.name
+
+###############################################################################
+# Replay buffer storage and batch size
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+#
+# TorchRL replay buffer counts the number of elements along the first dimension.
+# Since we'll be feeding trajectories to our buffer, we need to adapt the buffer
+# size by dividing it by the length of the sub-trajectories yielded by our
+# data collector.
+# Regarding the batch-size, our sampling strategy will consist in sampling
+# trajectories of length ``traj_len=200`` before selecting sub-trajectories
+# or length ``random_crop_len=25`` on which the loss will be computed.
+# This strategy balances the choice of storing whole trajectories of a certain
+# length with the need for providing samples with a sufficient heterogeneity
+# to our loss. The following figure shows the dataflow from a collector
+# that gets 8 frames in each batch with 2 environments run in parallel,
+# feeds them to a replay buffer that contains 1000 trajectories and
+# samples sub-trajectories of 2 time steps each.
+#
+# .. figure:: /_static/img/replaybuffer_traj.png
+# :alt: Storing trajectories in the replay buffer
+#
+# Let's start with the number of frames stored in the buffer
+
+
+def ceil_div(x, y):
+ return -x // (-y)
+
+
+buffer_size = 1_000_000
+buffer_size = ceil_div(buffer_size, traj_len)
+
+###############################################################################
+# Prioritized replay buffer is disabled by default
+prb = False
+
+###############################################################################
+# We also need to define how many updates we'll be doing per batch of data
+# collected. This is known as the update-to-data or ``UTD`` ratio:
+update_to_data = 64
+
+###############################################################################
+# We'll be feeding the loss with trajectories of length 25:
+random_crop_len = 25
+
+###############################################################################
+# In the original paper, the authors perform one update with a batch of 64
+# elements for each frame collected. Here, we reproduce the same ratio
+# but while realizing several updates at each batch collection. We
+# adapt our batch-size to achieve the same number of update-per-frame ratio:
+
+batch_size = ceil_div(64 * frames_per_batch, update_to_data * random_crop_len)
+
+replay_buffer = make_replay_buffer(
+ buffer_size=buffer_size,
+ batch_size=batch_size,
+ random_crop_len=random_crop_len,
+ prefetch=3,
+ prb=prb,
+)
+
+###############################################################################
+# Loss module construction
+# ------------------------
+#
+# We build our loss module with the actor and ``qnet`` we've just created.
+# Because we have target parameters to update, we _must_ create a target network
+# updater.
+#
+
+gamma = 0.99
+lmbda = 0.9
+tau = 0.001 # Decay factor for the target network
+
+loss_module = DDPGLoss(actor, qnet)
+
+###############################################################################
+# let's use the TD(lambda) estimator!
+loss_module.make_value_estimator(ValueEstimators.TDLambda, gamma=gamma, lmbda=lmbda)
+
+###############################################################################
+# .. note::
+# Off-policy usually dictates a TD(0) estimator. Here, we use a TD(:math:`\lambda`)
+# estimator, which will introduce some bias as the trajectory that follows
+# a certain state has been collected with an outdated policy.
+# This trick, as the multi-step trick that can be used during data collection,
+# are alternative versions of "hacks" that we usually find to work well in
+# practice despite the fact that they introduce some bias in the return
+# estimates.
+#
+# Target network updater
+# ~~~~~~~~~~~~~~~~~~~~~~
+#
+# Target networks are a crucial part of off-policy RL algorithms.
+# Updating the target network parameters is made easy thanks to the
+# :class:`~torchrl.objectives.HardUpdate` and :class:`~torchrl.objectives.SoftUpdate`
+# classes. They're built with the loss module as argument, and the update is
+# achieved via a call to `updater.step()` at the appropriate location in the
+# training loop.
+
+from torchrl.objectives.utils import SoftUpdate
+
+target_net_updater = SoftUpdate(loss_module, eps=1 - tau)
+
+###############################################################################
+# Optimizer
+# ~~~~~~~~~
+#
+# Finally, we will use the Adam optimizer for the policy and value network:
+
+from torch import optim
+
+optimizer_actor = optim.Adam(
+ loss_module.actor_network_params.values(True, True), lr=1e-4, weight_decay=0.0
+)
+optimizer_value = optim.Adam(
+ loss_module.value_network_params.values(True, True), lr=1e-3, weight_decay=1e-2
+)
+total_collection_steps = total_frames // frames_per_batch
+
+###############################################################################
+# Time to train the policy
+# ------------------------
+#
+# The training loop is pretty straightforward now that we have built all the
+# modules we need.
+#
+
+rewards = []
+rewards_eval = []
+
+# Main loop
+
+collected_frames = 0
+pbar = tqdm.tqdm(total=total_frames)
+r0 = None
+for i, tensordict in enumerate(collector):
+
+ # update weights of the inference policy
+ collector.update_policy_weights_()
+
+ if r0 is None:
+ r0 = tensordict["next", "reward"].mean().item()
+ pbar.update(tensordict.numel())
+
+ # extend the replay buffer with the new data
+ current_frames = tensordict.numel()
+ collected_frames += current_frames
+ replay_buffer.extend(tensordict.cpu())
+
+ # optimization steps
+ if collected_frames >= init_random_frames:
+ for _ in range(update_to_data):
+ # sample from replay buffer
+ sampled_tensordict = replay_buffer.sample().to(device)
+
+ # Compute loss
+ loss_dict = loss_module(sampled_tensordict)
+
+ # optimize
+ loss_dict["loss_actor"].backward()
+ gn1 = torch.nn.utils.clip_grad_norm_(
+ loss_module.actor_network_params.values(True, True), 10.0
+ )
+ optimizer_actor.step()
+ optimizer_actor.zero_grad()
+
+ loss_dict["loss_value"].backward()
+ gn2 = torch.nn.utils.clip_grad_norm_(
+ loss_module.value_network_params.values(True, True), 10.0
+ )
+ optimizer_value.step()
+ optimizer_value.zero_grad()
+
+ gn = (gn1**2 + gn2**2) ** 0.5
+
+ # update priority
+ if prb:
+ replay_buffer.update_tensordict_priority(sampled_tensordict)
+ # update target network
+ target_net_updater.step()
+
+ rewards.append(
+ (
+ i,
+ tensordict["next", "reward"].mean().item(),
+ )
+ )
+ td_record = recorder(None)
+ if td_record is not None:
+ rewards_eval.append((i, td_record["r_evaluation"].item()))
+ if len(rewards_eval) and collected_frames >= init_random_frames:
+ target_value = loss_dict["target_value"].item()
+ loss_value = loss_dict["loss_value"].item()
+ loss_actor = loss_dict["loss_actor"].item()
+ rn = sampled_tensordict["next", "reward"].mean().item()
+ rs = sampled_tensordict["next", "reward"].std().item()
+ pbar.set_description(
+ f"reward: {rewards[-1][1]: 4.2f} (r0 = {r0: 4.2f}), "
+ f"reward eval: reward: {rewards_eval[-1][1]: 4.2f}, "
+ f"reward normalized={rn :4.2f}/{rs :4.2f}, "
+ f"grad norm={gn: 4.2f}, "
+ f"loss_value={loss_value: 4.2f}, "
+ f"loss_actor={loss_actor: 4.2f}, "
+ f"target value: {target_value: 4.2f}"
+ )
+
+ # update the exploration strategy
+ actor_model_explore.step(current_frames)
+
+collector.shutdown()
+del collector
+
+###############################################################################
+# Experiment results
+# ------------------
+#
+# We make a simple plot of the average rewards during training. We can observe
+# that our policy learned quite well to solve the task.
+#
+# .. note::
+# As already mentioned above, to get a more reasonable performance,
+# use a greater value for ``total_frames`` for example, 1M.
+
+from matplotlib import pyplot as plt
+
+plt.figure()
+plt.plot(*zip(*rewards), label="training")
+plt.plot(*zip(*rewards_eval), label="eval")
+plt.legend()
+plt.xlabel("iter")
+plt.ylabel("reward")
+plt.tight_layout()
+
+###############################################################################
+# Conclusion
+# ----------
+#
+# In this tutorial, we have learned how to code a loss module in TorchRL given
+# the concrete example of DDPG.
+#
+# The key takeaways are:
+#
+# - How to use the :class:`~torchrl.objectives.LossModule` class to code up a new
+# loss component;
+# - How to use (or not) a target network, and how to update its parameters;
+# - How to create an optimizer associated with a loss module.
+#
+# Next Steps
+# ----------
+#
+# To iterate further on this loss module we might consider:
+#
+# - Using `@dispatch` (see `[Feature] Distpatch IQL loss module `_.)
+# - Allowing flexible TensorDict keys.
+#
diff --git a/advanced_source/cpp_cuda_graphs.rst b/advanced_source/cpp_cuda_graphs.rst
new file mode 100644
index 000000000..90c5cbd70
--- /dev/null
+++ b/advanced_source/cpp_cuda_graphs.rst
@@ -0,0 +1,193 @@
+Using CUDA Graphs in PyTorch C++ API
+====================================
+
+.. note::
+ |edit| View and edit this tutorial in `GitHub `__. The full source code is available on `GitHub `__.
+
+Prerequisites:
+
+- `Using the PyTorch C++ Frontend <../advanced_source/cpp_frontend.html>`__
+- `CUDA semantics `__
+- Pytorch 2.0 or later
+- CUDA 11 or later
+
+NVIDIA’s CUDA Graphs have been a part of CUDA Toolkit library since the
+release of `version 10 `_.
+They are capable of greatly reducing the CPU overhead increasing the
+performance of applications.
+
+In this tutorial, we will be focusing on using CUDA Graphs for `C++
+frontend of PyTorch `_.
+The C++ frontend is mostly utilized in production and deployment applications which
+are important parts of PyTorch use cases. Since `the first appearance
+`_
+the CUDA Graphs won users’ and developer’s hearts for being a very performant
+and at the same time simple-to-use tool. In fact, CUDA Graphs are used by default
+in ``torch.compile`` of PyTorch 2.0 to boost the productivity of training and inference.
+
+We would like to demonstrate CUDA Graphs usage on PyTorch’s `MNIST
+example `_.
+The usage of CUDA Graphs in LibTorch (C++ Frontend) is very similar to its
+`Python counterpart `_
+but with some differences in syntax and functionality.
+
+Getting Started
+---------------
+
+The main training loop consists of the several steps and depicted in the
+following code chunk:
+
+.. code-block:: cpp
+
+ for (auto& batch : data_loader) {
+ auto data = batch.data.to(device);
+ auto targets = batch.target.to(device);
+ optimizer.zero_grad();
+ auto output = model.forward(data);
+ auto loss = torch::nll_loss(output, targets);
+ loss.backward();
+ optimizer.step();
+ }
+
+The example above includes a forward pass, a backward pass, and weight updates.
+
+In this tutorial, we will be applying CUDA Graph on all the compute steps through the whole-network
+graph capture. But before doing so, we need to slightly modify the source code. What we need
+to do is preallocate tensors for reusing them in the main training loop. Here is an example
+implementation:
+
+.. code-block:: cpp
+
+ torch::TensorOptions FloatCUDA =
+ torch::TensorOptions(device).dtype(torch::kFloat);
+ torch::TensorOptions LongCUDA =
+ torch::TensorOptions(device).dtype(torch::kLong);
+
+ torch::Tensor data = torch::zeros({kTrainBatchSize, 1, 28, 28}, FloatCUDA);
+ torch::Tensor targets = torch::zeros({kTrainBatchSize}, LongCUDA);
+ torch::Tensor output = torch::zeros({1}, FloatCUDA);
+ torch::Tensor loss = torch::zeros({1}, FloatCUDA);
+
+ for (auto& batch : data_loader) {
+ data.copy_(batch.data);
+ targets.copy_(batch.target);
+ training_step(model, optimizer, data, targets, output, loss);
+ }
+
+Where ``training_step`` simply consists of forward and backward passes with corresponding optimizer calls:
+
+.. code-block:: cpp
+
+ void training_step(
+ Net& model,
+ torch::optim::Optimizer& optimizer,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss) {
+ optimizer.zero_grad();
+ output = model.forward(data);
+ loss = torch::nll_loss(output, targets);
+ loss.backward();
+ optimizer.step();
+ }
+
+PyTorch’s CUDA Graphs API is relying on Stream Capture which in our case would be used like this:
+
+.. code-block:: cpp
+
+ at::cuda::CUDAGraph graph;
+ at::cuda::CUDAStream captureStream = at::cuda::getStreamFromPool();
+ at::cuda::setCurrentCUDAStream(captureStream);
+
+ graph.capture_begin();
+ training_step(model, optimizer, data, targets, output, loss);
+ graph.capture_end();
+
+Before the actual graph capture, it is important to run several warm-up iterations on side stream to
+prepare CUDA cache as well as CUDA libraries (like CUBLAS and CUDNN) that will be used during
+the training:
+
+.. code-block:: cpp
+
+ at::cuda::CUDAStream warmupStream = at::cuda::getStreamFromPool();
+ at::cuda::setCurrentCUDAStream(warmupStream);
+ for (int iter = 0; iter < num_warmup_iters; iter++) {
+ training_step(model, optimizer, data, targets, output, loss);
+ }
+
+After the successful graph capture, we can replace ``training_step(model, optimizer, data, targets, output, loss);``
+call via ``graph.replay();`` to do the training step.
+
+Training Results
+----------------
+
+Taking the code for a spin we can see the following output from ordinary non-graphed training:
+
+.. code-block:: shell
+
+ $ time ./mnist
+ Train Epoch: 1 [59584/60000] Loss: 0.3921
+ Test set: Average loss: 0.2051 | Accuracy: 0.938
+ Train Epoch: 2 [59584/60000] Loss: 0.1826
+ Test set: Average loss: 0.1273 | Accuracy: 0.960
+ Train Epoch: 3 [59584/60000] Loss: 0.1796
+ Test set: Average loss: 0.1012 | Accuracy: 0.968
+ Train Epoch: 4 [59584/60000] Loss: 0.1603
+ Test set: Average loss: 0.0869 | Accuracy: 0.973
+ Train Epoch: 5 [59584/60000] Loss: 0.2315
+ Test set: Average loss: 0.0736 | Accuracy: 0.978
+ Train Epoch: 6 [59584/60000] Loss: 0.0511
+ Test set: Average loss: 0.0704 | Accuracy: 0.977
+ Train Epoch: 7 [59584/60000] Loss: 0.0802
+ Test set: Average loss: 0.0654 | Accuracy: 0.979
+ Train Epoch: 8 [59584/60000] Loss: 0.0774
+ Test set: Average loss: 0.0604 | Accuracy: 0.980
+ Train Epoch: 9 [59584/60000] Loss: 0.0669
+ Test set: Average loss: 0.0544 | Accuracy: 0.984
+ Train Epoch: 10 [59584/60000] Loss: 0.0219
+ Test set: Average loss: 0.0517 | Accuracy: 0.983
+
+ real 0m44.287s
+ user 0m44.018s
+ sys 0m1.116s
+
+While the training with the CUDA Graph produces the following output:
+
+.. code-block:: shell
+
+ $ time ./mnist --use-train-graph
+ Train Epoch: 1 [59584/60000] Loss: 0.4092
+ Test set: Average loss: 0.2037 | Accuracy: 0.938
+ Train Epoch: 2 [59584/60000] Loss: 0.2039
+ Test set: Average loss: 0.1274 | Accuracy: 0.961
+ Train Epoch: 3 [59584/60000] Loss: 0.1779
+ Test set: Average loss: 0.1017 | Accuracy: 0.968
+ Train Epoch: 4 [59584/60000] Loss: 0.1559
+ Test set: Average loss: 0.0871 | Accuracy: 0.972
+ Train Epoch: 5 [59584/60000] Loss: 0.2240
+ Test set: Average loss: 0.0735 | Accuracy: 0.977
+ Train Epoch: 6 [59584/60000] Loss: 0.0520
+ Test set: Average loss: 0.0710 | Accuracy: 0.978
+ Train Epoch: 7 [59584/60000] Loss: 0.0935
+ Test set: Average loss: 0.0666 | Accuracy: 0.979
+ Train Epoch: 8 [59584/60000] Loss: 0.0744
+ Test set: Average loss: 0.0603 | Accuracy: 0.981
+ Train Epoch: 9 [59584/60000] Loss: 0.0762
+ Test set: Average loss: 0.0547 | Accuracy: 0.983
+ Train Epoch: 10 [59584/60000] Loss: 0.0207
+ Test set: Average loss: 0.0525 | Accuracy: 0.983
+
+ real 0m6.952s
+ user 0m7.048s
+ sys 0m0.619s
+
+Conclusion
+----------
+
+As we can see, just by applying a CUDA Graph on the `MNIST example
+`_ we were able to gain the performance
+by more than six times for training. This kind of large performance improvement was achievable due to
+the small model size. In case of larger models with heavy GPU usage, the CPU overhead is less impactful
+so the improvement will be smaller. Nevertheless, it is always advantageous to use CUDA Graphs to
+gain the performance of GPUs.
diff --git a/advanced_source/cpp_cuda_graphs/CMakeLists.txt b/advanced_source/cpp_cuda_graphs/CMakeLists.txt
new file mode 100644
index 000000000..76fc5bc67
--- /dev/null
+++ b/advanced_source/cpp_cuda_graphs/CMakeLists.txt
@@ -0,0 +1,31 @@
+cmake_minimum_required(VERSION 3.18 FATAL_ERROR)
+project(mnist)
+set(CMAKE_CXX_STANDARD 17)
+
+find_package(Torch REQUIRED)
+find_package(Threads REQUIRED)
+
+option(DOWNLOAD_MNIST "Download the MNIST dataset from the internet" ON)
+if (DOWNLOAD_MNIST)
+ message(STATUS "Downloading MNIST dataset")
+ execute_process(
+ COMMAND python ${CMAKE_CURRENT_LIST_DIR}/../tools/download_mnist.py
+ -d ${CMAKE_BINARY_DIR}/data
+ ERROR_VARIABLE DOWNLOAD_ERROR)
+ if (DOWNLOAD_ERROR)
+ message(FATAL_ERROR "Error downloading MNIST dataset: ${DOWNLOAD_ERROR}")
+ endif()
+endif()
+
+add_executable(mnist mnist.cpp)
+target_compile_features(mnist PUBLIC cxx_range_for)
+target_link_libraries(mnist ${TORCH_LIBRARIES} ${CMAKE_THREAD_LIBS_INIT})
+
+if (MSVC)
+ file(GLOB TORCH_DLLS "${TORCH_INSTALL_PREFIX}/lib/*.dll")
+ add_custom_command(TARGET mnist
+ POST_BUILD
+ COMMAND ${CMAKE_COMMAND} -E copy_if_different
+ ${TORCH_DLLS}
+ $)
+endif (MSVC)
diff --git a/advanced_source/cpp_cuda_graphs/README.md b/advanced_source/cpp_cuda_graphs/README.md
new file mode 100644
index 000000000..cbe368d1e
--- /dev/null
+++ b/advanced_source/cpp_cuda_graphs/README.md
@@ -0,0 +1,38 @@
+# MNIST Example with the PyTorch C++ Frontend
+
+This folder contains an example of training a computer vision model to recognize
+digits in images from the MNIST dataset, using the PyTorch C++ frontend.
+
+The entire training code is contained in `mnist.cpp`.
+
+To build the code, run the following commands from your terminal:
+
+```shell
+$ cd mnist
+$ mkdir build
+$ cd build
+$ cmake -DCMAKE_PREFIX_PATH=/path/to/libtorch ..
+$ make
+```
+
+where `/path/to/libtorch` should be the path to the unzipped _LibTorch_
+distribution, which you can get from the [PyTorch
+homepage](https://pytorch.org/get-started/locally/).
+
+Execute the compiled binary to train the model:
+
+```shell
+$ ./mnist
+Train Epoch: 1 [59584/60000] Loss: 0.4232
+Test set: Average loss: 0.1989 | Accuracy: 0.940
+Train Epoch: 2 [59584/60000] Loss: 0.1926
+Test set: Average loss: 0.1338 | Accuracy: 0.959
+Train Epoch: 3 [59584/60000] Loss: 0.1390
+Test set: Average loss: 0.0997 | Accuracy: 0.969
+Train Epoch: 4 [59584/60000] Loss: 0.1239
+Test set: Average loss: 0.0875 | Accuracy: 0.972
+...
+```
+
+For running with CUDA Graphs add `--use-train-graph` and/or `--use-test-graph`
+for training and testing passes respectively.
diff --git a/advanced_source/cpp_cuda_graphs/mnist.cpp b/advanced_source/cpp_cuda_graphs/mnist.cpp
new file mode 100644
index 000000000..97c5fb80c
--- /dev/null
+++ b/advanced_source/cpp_cuda_graphs/mnist.cpp
@@ -0,0 +1,372 @@
+#include
+#include
+#include
+#include
+
+#include
+#include
+#include
+#include
+#include
+
+// Where to find the MNIST dataset.
+const char* kDataRoot = "./data";
+
+// The batch size for training.
+const int64_t kTrainBatchSize = 64;
+
+// The batch size for testing.
+const int64_t kTestBatchSize = 1000;
+
+// The number of epochs to train.
+const int64_t kNumberOfEpochs = 10;
+
+// After how many batches to log a new update with the loss value.
+const int64_t kLogInterval = 10;
+
+// Model that we will be training
+struct Net : torch::nn::Module {
+ Net()
+ : conv1(torch::nn::Conv2dOptions(1, 10, /*kernel_size=*/5)),
+ conv2(torch::nn::Conv2dOptions(10, 20, /*kernel_size=*/5)),
+ fc1(320, 50),
+ fc2(50, 10) {
+ register_module("conv1", conv1);
+ register_module("conv2", conv2);
+ register_module("conv2_drop", conv2_drop);
+ register_module("fc1", fc1);
+ register_module("fc2", fc2);
+ }
+
+ torch::Tensor forward(torch::Tensor x) {
+ x = torch::relu(torch::max_pool2d(conv1->forward(x), 2));
+ x = torch::relu(
+ torch::max_pool2d(conv2_drop->forward(conv2->forward(x)), 2));
+ x = x.view({-1, 320});
+ x = torch::relu(fc1->forward(x));
+ x = torch::dropout(x, /*p=*/0.5, /*training=*/is_training());
+ x = fc2->forward(x);
+ return torch::log_softmax(x, /*dim=*/1);
+ }
+
+ torch::nn::Conv2d conv1;
+ torch::nn::Conv2d conv2;
+ torch::nn::Dropout2d conv2_drop;
+ torch::nn::Linear fc1;
+ torch::nn::Linear fc2;
+};
+
+void stream_sync(
+ at::cuda::CUDAStream& dependency,
+ at::cuda::CUDAStream& dependent) {
+ at::cuda::CUDAEvent cuda_ev;
+ cuda_ev.record(dependency);
+ cuda_ev.block(dependent);
+}
+
+void training_step(
+ Net& model,
+ torch::optim::Optimizer& optimizer,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss) {
+ optimizer.zero_grad();
+ output = model.forward(data);
+ loss = torch::nll_loss(output, targets);
+ loss.backward();
+ optimizer.step();
+}
+
+void capture_train_graph(
+ Net& model,
+ torch::optim::Optimizer& optimizer,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss,
+ at::cuda::CUDAGraph& graph,
+ const short num_warmup_iters = 7) {
+ model.train();
+
+ auto warmupStream = at::cuda::getStreamFromPool();
+ auto captureStream = at::cuda::getStreamFromPool();
+ auto legacyStream = at::cuda::getCurrentCUDAStream();
+
+ at::cuda::setCurrentCUDAStream(warmupStream);
+
+ stream_sync(legacyStream, warmupStream);
+
+ for (C10_UNUSED const auto iter : c10::irange(num_warmup_iters)) {
+ training_step(model, optimizer, data, targets, output, loss);
+ }
+
+ stream_sync(warmupStream, captureStream);
+ at::cuda::setCurrentCUDAStream(captureStream);
+
+ graph.capture_begin();
+ training_step(model, optimizer, data, targets, output, loss);
+ graph.capture_end();
+
+ stream_sync(captureStream, legacyStream);
+ at::cuda::setCurrentCUDAStream(legacyStream);
+}
+
+template
+void train(
+ size_t epoch,
+ Net& model,
+ torch::Device device,
+ DataLoader& data_loader,
+ torch::optim::Optimizer& optimizer,
+ size_t dataset_size,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss,
+ at::cuda::CUDAGraph& graph,
+ bool use_graph) {
+ model.train();
+
+ size_t batch_idx = 0;
+
+ for (const auto& batch : data_loader) {
+ if (batch.data.size(0) != kTrainBatchSize ||
+ batch.target.size(0) != kTrainBatchSize) {
+ continue;
+ }
+
+ data.copy_(batch.data);
+ targets.copy_(batch.target);
+
+ if (use_graph) {
+ graph.replay();
+ } else {
+ training_step(model, optimizer, data, targets, output, loss);
+ }
+
+ if (batch_idx++ % kLogInterval == 0) {
+ float train_loss = loss.item();
+ std::cout << "\rTrain Epoch:" << epoch << " ["
+ << batch_idx * batch.data.size(0) << "/" << dataset_size
+ << "] Loss: " << train_loss;
+ }
+ }
+}
+
+void test_step(
+ Net& model,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss) {
+ output = model.forward(data);
+ loss = torch::nll_loss(output, targets, {}, torch::Reduction::Sum);
+}
+
+void capture_test_graph(
+ Net& model,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss,
+ torch::Tensor& total_loss,
+ torch::Tensor& total_correct,
+ at::cuda::CUDAGraph& graph,
+ const int num_warmup_iters = 7) {
+ torch::NoGradGuard no_grad;
+ model.eval();
+
+ auto warmupStream = at::cuda::getStreamFromPool();
+ auto captureStream = at::cuda::getStreamFromPool();
+ auto legacyStream = at::cuda::getCurrentCUDAStream();
+
+ at::cuda::setCurrentCUDAStream(warmupStream);
+ stream_sync(captureStream, legacyStream);
+
+ for (C10_UNUSED const auto iter : c10::irange(num_warmup_iters)) {
+ test_step(model, data, targets, output, loss);
+ total_loss += loss;
+ total_correct += output.argmax(1).eq(targets).sum();
+ }
+
+ stream_sync(warmupStream, captureStream);
+ at::cuda::setCurrentCUDAStream(captureStream);
+
+ graph.capture_begin();
+ test_step(model, data, targets, output, loss);
+ graph.capture_end();
+
+ stream_sync(captureStream, legacyStream);
+ at::cuda::setCurrentCUDAStream(legacyStream);
+}
+
+template
+void test(
+ Net& model,
+ torch::Device device,
+ DataLoader& data_loader,
+ size_t dataset_size,
+ torch::Tensor& data,
+ torch::Tensor& targets,
+ torch::Tensor& output,
+ torch::Tensor& loss,
+ torch::Tensor& total_loss,
+ torch::Tensor& total_correct,
+ at::cuda::CUDAGraph& graph,
+ bool use_graph) {
+ torch::NoGradGuard no_grad;
+
+ model.eval();
+ loss.zero_();
+ total_loss.zero_();
+ total_correct.zero_();
+
+ for (const auto& batch : data_loader) {
+ if (batch.data.size(0) != kTestBatchSize ||
+ batch.target.size(0) != kTestBatchSize) {
+ continue;
+ }
+ data.copy_(batch.data);
+ targets.copy_(batch.target);
+
+ if (use_graph) {
+ graph.replay();
+ } else {
+ test_step(model, data, targets, output, loss);
+ }
+ total_loss += loss;
+ total_correct += output.argmax(1).eq(targets).sum();
+ }
+
+ float test_loss = total_loss.item() / dataset_size;
+ float test_accuracy =
+ static_cast(total_correct.item()) / dataset_size;
+
+ std::cout << std::endl
+ << "Test set: Average loss: " << test_loss
+ << " | Accuracy: " << test_accuracy << std::endl;
+}
+
+int main(int argc, char* argv[]) {
+ if (!torch::cuda::is_available()) {
+ std::cout << "CUDA is not available!" << std::endl;
+ return -1;
+ }
+
+ bool use_train_graph = false;
+ bool use_test_graph = false;
+
+ std::vector arguments(argv + 1, argv + argc);
+ for (std::string& arg : arguments) {
+ if (arg == "--use-train-graph") {
+ std::cout << "Using CUDA Graph for training." << std::endl;
+ use_train_graph = true;
+ }
+ if (arg == "--use-test-graph") {
+ std::cout << "Using CUDA Graph for testing." << std::endl;
+ use_test_graph = true;
+ }
+ }
+
+ torch::manual_seed(1);
+ torch::cuda::manual_seed(1);
+ torch::Device device(torch::kCUDA);
+
+ Net model;
+ model.to(device);
+
+ auto train_dataset =
+ torch::data::datasets::MNIST(kDataRoot)
+ .map(torch::data::transforms::Normalize<>(0.1307, 0.3081))
+ .map(torch::data::transforms::Stack<>());
+ const size_t train_dataset_size = train_dataset.size().value();
+ auto train_loader =
+ torch::data::make_data_loader(
+ std::move(train_dataset), kTrainBatchSize);
+
+ auto test_dataset =
+ torch::data::datasets::MNIST(
+ kDataRoot, torch::data::datasets::MNIST::Mode::kTest)
+ .map(torch::data::transforms::Normalize<>(0.1307, 0.3081))
+ .map(torch::data::transforms::Stack<>());
+ const size_t test_dataset_size = test_dataset.size().value();
+ auto test_loader =
+ torch::data::make_data_loader(std::move(test_dataset), kTestBatchSize);
+
+ torch::optim::SGD optimizer(
+ model.parameters(), torch::optim::SGDOptions(0.01).momentum(0.5));
+
+ torch::TensorOptions FloatCUDA =
+ torch::TensorOptions(device).dtype(torch::kFloat);
+ torch::TensorOptions LongCUDA =
+ torch::TensorOptions(device).dtype(torch::kLong);
+
+ torch::Tensor train_data =
+ torch::zeros({kTrainBatchSize, 1, 28, 28}, FloatCUDA);
+ torch::Tensor train_targets = torch::zeros({kTrainBatchSize}, LongCUDA);
+ torch::Tensor train_output = torch::zeros({1}, FloatCUDA);
+ torch::Tensor train_loss = torch::zeros({1}, FloatCUDA);
+
+ torch::Tensor test_data =
+ torch::zeros({kTestBatchSize, 1, 28, 28}, FloatCUDA);
+ torch::Tensor test_targets = torch::zeros({kTestBatchSize}, LongCUDA);
+ torch::Tensor test_output = torch::zeros({1}, FloatCUDA);
+ torch::Tensor test_loss = torch::zeros({1}, FloatCUDA);
+ torch::Tensor test_total_loss = torch::zeros({1}, FloatCUDA);
+ torch::Tensor test_total_correct = torch::zeros({1}, LongCUDA);
+
+ at::cuda::CUDAGraph train_graph;
+ at::cuda::CUDAGraph test_graph;
+
+ capture_train_graph(
+ model,
+ optimizer,
+ train_data,
+ train_targets,
+ train_output,
+ train_loss,
+ train_graph);
+
+ capture_test_graph(
+ model,
+ test_data,
+ test_targets,
+ test_output,
+ test_loss,
+ test_total_loss,
+ test_total_correct,
+ test_graph);
+
+ for (size_t epoch = 1; epoch <= kNumberOfEpochs; ++epoch) {
+ train(
+ epoch,
+ model,
+ device,
+ *train_loader,
+ optimizer,
+ train_dataset_size,
+ train_data,
+ train_targets,
+ train_output,
+ train_loss,
+ train_graph,
+ use_train_graph);
+ test(
+ model,
+ device,
+ *test_loader,
+ test_dataset_size,
+ test_data,
+ test_targets,
+ test_output,
+ test_loss,
+ test_total_loss,
+ test_total_correct,
+ test_graph,
+ use_test_graph);
+ }
+
+ std::cout << " Training/testing complete" << std::endl;
+ return 0;
+}
diff --git a/advanced_source/cpp_frontend.rst b/advanced_source/cpp_frontend.rst
index 23751e77a..09281630f 100644
--- a/advanced_source/cpp_frontend.rst
+++ b/advanced_source/cpp_frontend.rst
@@ -1210,9 +1210,6 @@ C++ 프론트엔드는 개별 텐서뿐만 아니라 모델 및 옵티마이저
.. code-block:: python
- from __future__ import print_function
- from __future__ import unicode_literals
-
import argparse
import matplotlib.pyplot as plt
diff --git a/advanced_source/ddp_pipeline.py b/advanced_source/ddp_pipeline.py
index 53b6dfd35..6dff4c38f 100644
--- a/advanced_source/ddp_pipeline.py
+++ b/advanced_source/ddp_pipeline.py
@@ -1,6 +1,6 @@
"""
분산 데이터 병렬 처리와 병렬 처리 파이프라인을 사용한 트랜스포머 모델 학습
-=======================================================================
+=============================================================================
**Author**: `Pritam Damania `_
**번역**: `백선희 `_
@@ -241,7 +241,7 @@ def get_batch(source, i):
######################################################################
# 모델 규모와 파이프 초기화
-# ---------------------------
+# --------------------------------
#
@@ -333,7 +333,7 @@ def get_total_params(module: torch.nn.Module):
######################################################################
# 모델 실행하기
-# ---------------
+# -----------------
#
@@ -436,7 +436,7 @@ def evaluate(eval_model, data_source):
######################################################################
# 평가 데이터셋으로 모델 평가하기
-# ---------------------------------
+# -----------------------------------
#
# 평가 데이터셋에서의 결과를 확인하기 위해 최고의 모델을 적용합니다.
diff --git a/advanced_source/dispatcher.rst b/advanced_source/dispatcher.rst
index 1a8034a62..0b5fd3c8a 100644
--- a/advanced_source/dispatcher.rst
+++ b/advanced_source/dispatcher.rst
@@ -129,7 +129,7 @@ for debugging in larger models where previously it can be hard to pin-point
exactly where the ``requires_grad``-ness is lost during the forward pass.
In-place or view ops
-^^^^^^^^^^^^^^^^^^^
+^^^^^^^^^^^^^^^^^^^^
To ensure correctness and best possible performance, if your op mutates an input
in-place or returns a tensor that aliases with one of the inputs, two additional
diff --git a/advanced_source/neural_style_tutorial.py b/advanced_source/neural_style_tutorial.py
index 711ebbf05..5accb2988 100644
--- a/advanced_source/neural_style_tutorial.py
+++ b/advanced_source/neural_style_tutorial.py
@@ -43,8 +43,6 @@
# - ``torchvision.models`` (미리 학습된 모델 불러오기 및 학습)
# - ``copy`` (모델을 복사; 시스템 패키지)
-from __future__ import print_function
-
import torch
import torch.nn as nn
import torch.nn.functional as F
@@ -54,7 +52,7 @@
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
-import torchvision.models as models
+from torchvision.models import vgg19, VGG19_Weights
import copy
@@ -68,6 +66,7 @@
# 또한 ``.to(device)`` 메소드는 텐서 또는 모듈을 원하는 장치로 이동하는데 사용됩니다.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
+torch.set_default_device(device)
######################################################################
# 이미지 불러오기
@@ -242,7 +241,7 @@ def forward(self, input):
# 일부 계층은 훈련하는 중 평가와 다른 동작을 하므로, 네트워크를 ``.eval()`` 를 사용해 평가 모드로 설정해야합니다.
#
-cnn = models.vgg19(pretrained=True).features.to(device).eval()
+cnn = vgg19(weights=VGG19_Weights.DEFAULT).features.eval()
@@ -253,8 +252,8 @@ def forward(self, input):
# 이미지를 네트워크로 입력하기 전에 정규화하는데 사용합니다.
#
-cnn_normalization_mean = torch.tensor([0.485, 0.456, 0.406]).to(device)
-cnn_normalization_std = torch.tensor([0.229, 0.224, 0.225]).to(device)
+cnn_normalization_mean = torch.tensor([0.485, 0.456, 0.406])
+cnn_normalization_std = torch.tensor([0.229, 0.224, 0.225])
# 입력 이미지를 정규화하는 모듈을 생성하여 쉽게 ``nn.Sequential`` 에 넣을 수 있습니다.
class Normalization(nn.Module):
@@ -289,7 +288,7 @@ def get_style_model_and_losses(cnn, normalization_mean, normalization_std,
content_layers=content_layers_default,
style_layers=style_layers_default):
# 모듈 정규화
- normalization = Normalization(normalization_mean, normalization_std).to(device)
+ normalization = Normalization(normalization_mean, normalization_std)
# Content / Style 손실이 반복적으로 접근할 수 있도록 하기 위해
content_losses = []
@@ -345,8 +344,10 @@ def get_style_model_and_losses(cnn, normalization_mean, normalization_std,
######################################################################
# 다음으로 입력 이미지를 선택합니다. Content 이미지 사본이나 백색 잡음을 사용할 수 있습니다.
#
+# .. code-block:: python
+#
+# input_img = torch.randn(content_img.data.size())
-input_img = content_img.clone()
# 만약 화이트 노이즈(white noise)을 사용하려면 아래 주석을 제거하세요:
#
# ::
@@ -398,6 +399,9 @@ def run_style_transfer(cnn, normalization_mean, normalization_std,
# 모델의 매개변수를 제외한 입력을 최적화해야 하므로
# 이에 맞춰서 requires_grad 값을 갱신합니다.
input_img.requires_grad_(True)
+ # 또한, 모델을 평가(eval) 모드로 전환하여
+ # 드롭아웃(dropout) 및 배치 정규화(batch normalization)와 같은 특정 레이어가 올바르게 동작하도록 합니다.
+ model.eval()
model.requires_grad_(False)
optimizer = get_input_optimizer(input_img)
diff --git a/advanced_source/pendulum.py b/advanced_source/pendulum.py
new file mode 100644
index 000000000..38524cfff
--- /dev/null
+++ b/advanced_source/pendulum.py
@@ -0,0 +1,930 @@
+# -*- coding: utf-8 -*-
+
+"""
+Pendulum: Writing your environment and transforms with TorchRL
+==============================================================
+
+**Author**: `Vincent Moens `_
+
+Creating an environment (a simulator or an interface to a physical control system)
+is an integrative part of reinforcement learning and control engineering.
+
+TorchRL provides a set of tools to do this in multiple contexts.
+This tutorial demonstrates how to use PyTorch and TorchRL code a pendulum
+simulator from the ground up.
+It is freely inspired by the Pendulum-v1 implementation from `OpenAI-Gym/Farama-Gymnasium
+control library `__.
+
+.. figure:: /_static/img/pendulum.gif
+ :alt: Pendulum
+ :align: center
+
+ Simple Pendulum
+
+Key learnings:
+
+- How to design an environment in TorchRL:
+ - Writing specs (input, observation and reward);
+ - Implementing behavior: seeding, reset and step.
+- Transforming your environment inputs and outputs, and writing your own
+ transforms;
+- How to use :class:`~tensordict.TensorDict` to carry arbitrary data structures
+ through the ``codebase``.
+
+ In the process, we will touch three crucial components of TorchRL:
+
+* `environments `__
+* `transforms `__
+* `models (policy and value function) `__
+
+"""
+
+######################################################################
+# To give a sense of what can be achieved with TorchRL's environments, we will
+# be designing a *stateless* environment. While stateful environments keep track of
+# the latest physical state encountered and rely on this to simulate the state-to-state
+# transition, stateless environments expect the current state to be provided to
+# them at each step, along with the action undertaken. TorchRL supports both
+# types of environments, but stateless environments are more generic and hence
+# cover a broader range of features of the environment API in TorchRL.
+#
+# Modeling stateless environments gives users full control over the input and
+# outputs of the simulator: one can reset an experiment at any stage or actively
+# modify the dynamics from the outside. However, it assumes that we have some control
+# over a task, which may not always be the case: solving a problem where we cannot
+# control the current state is more challenging but has a much wider set of applications.
+#
+# Another advantage of stateless environments is that they can enable
+# batched execution of transition simulations. If the backend and the
+# implementation allow it, an algebraic operation can be executed seamlessly on
+# scalars, vectors, or tensors. This tutorial gives such examples.
+#
+# This tutorial will be structured as follows:
+#
+# * We will first get acquainted with the environment properties:
+# its shape (``batch_size``), its methods (mainly :meth:`~torchrl.envs.EnvBase.step`,
+# :meth:`~torchrl.envs.EnvBase.reset` and :meth:`~torchrl.envs.EnvBase.set_seed`)
+# and finally its specs.
+# * After having coded our simulator, we will demonstrate how it can be used
+# during training with transforms.
+# * We will explore new avenues that follow from the TorchRL's API,
+# including: the possibility of transforming inputs, the vectorized execution
+# of the simulation and the possibility of backpropagation through the
+# simulation graph.
+# * Finally, we will train a simple policy to solve the system we implemented.
+#
+
+# sphinx_gallery_start_ignore
+import warnings
+
+warnings.filterwarnings("ignore")
+from torch import multiprocessing
+
+# TorchRL prefers spawn method, that restricts creation of ``~torchrl.envs.ParallelEnv`` inside
+# `__main__` method call, but for the easy of reading the code switch to fork
+# which is also a default spawn method in Google's Colaboratory
+try:
+ multiprocessing.set_start_method("fork")
+except RuntimeError:
+ pass
+
+# sphinx_gallery_end_ignore
+
+from collections import defaultdict
+from typing import Optional
+
+import numpy as np
+import torch
+import tqdm
+from tensordict import TensorDict, TensorDictBase
+from tensordict.nn import TensorDictModule
+from torch import nn
+
+from torchrl.data import BoundedTensorSpec, CompositeSpec, UnboundedContinuousTensorSpec
+from torchrl.envs import (
+ CatTensors,
+ EnvBase,
+ Transform,
+ TransformedEnv,
+ UnsqueezeTransform,
+)
+from torchrl.envs.transforms.transforms import _apply_to_composite
+from torchrl.envs.utils import check_env_specs, step_mdp
+
+DEFAULT_X = np.pi
+DEFAULT_Y = 1.0
+
+######################################################################
+# There are four things you must take care of when designing a new environment
+# class:
+#
+# * :meth:`EnvBase._reset`, which codes for the resetting of the simulator
+# at a (potentially random) initial state;
+# * :meth:`EnvBase._step` which codes for the state transition dynamic;
+# * :meth:`EnvBase._set_seed`` which implements the seeding mechanism;
+# * the environment specs.
+#
+# Let us first describe the problem at hand: we would like to model a simple
+# pendulum over which we can control the torque applied on its fixed point.
+# Our goal is to place the pendulum in upward position (angular position at 0
+# by convention) and having it standing still in that position.
+# To design our dynamic system, we need to define two equations: the motion
+# equation following an action (the torque applied) and the reward equation
+# that will constitute our objective function.
+#
+# For the motion equation, we will update the angular velocity following:
+#
+# .. math::
+#
+# \dot{\theta}_{t+1} = \dot{\theta}_t + (3 * g / (2 * L) * \sin(\theta_t) + 3 / (m * L^2) * u) * dt
+#
+# where :math:`\dot{\theta}` is the angular velocity in rad/sec, :math:`g` is the
+# gravitational force, :math:`L` is the pendulum length, :math:`m` is its mass,
+# :math:`\theta` is its angular position and :math:`u` is the torque. The
+# angular position is then updated according to
+#
+# .. math::
+#
+# \theta_{t+1} = \theta_{t} + \dot{\theta}_{t+1} dt
+#
+# We define our reward as
+#
+# .. math::
+#
+# r = -(\theta^2 + 0.1 * \dot{\theta}^2 + 0.001 * u^2)
+#
+# which will be maximized when the angle is close to 0 (pendulum in upward
+# position), the angular velocity is close to 0 (no motion) and the torque is
+# 0 too.
+#
+# Coding the effect of an action: :func:`~torchrl.envs.EnvBase._step`
+# -------------------------------------------------------------------
+#
+# The step method is the first thing to consider, as it will encode
+# the simulation that is of interest to us. In TorchRL, the
+# :class:`~torchrl.envs.EnvBase` class has a :meth:`EnvBase.step`
+# method that receives a :class:`tensordict.TensorDict`
+# instance with an ``"action"`` entry indicating what action is to be taken.
+#
+# To facilitate the reading and writing from that ``tensordict`` and to make sure
+# that the keys are consistent with what's expected from the library, the
+# simulation part has been delegated to a private abstract method :meth:`_step`
+# which reads input data from a ``tensordict``, and writes a *new* ``tensordict``
+# with the output data.
+#
+# The :func:`_step` method should do the following:
+#
+# 1. Read the input keys (such as ``"action"``) and execute the simulation
+# based on these;
+# 2. Retrieve observations, done state and reward;
+# 3. Write the set of observation values along with the reward and done state
+# at the corresponding entries in a new :class:`TensorDict`.
+#
+# Next, the :meth:`~torchrl.envs.EnvBase.step` method will merge the output
+# of :meth:`~torchrl.envs.EnvBase.step` in the input ``tensordict`` to enforce
+# input/output consistency.
+#
+# Typically, for stateful environments, this will look like this:
+#
+# .. code-block::
+#
+# >>> policy(env.reset())
+# >>> print(tensordict)
+# TensorDict(
+# fields={
+# action: Tensor(shape=torch.Size([1]), device=cpu, dtype=torch.float32, is_shared=False),
+# done: Tensor(shape=torch.Size([1]), device=cpu, dtype=torch.bool, is_shared=False),
+# observation: Tensor(shape=torch.Size([]), device=cpu, dtype=torch.float32, is_shared=False)},
+# batch_size=torch.Size([]),
+# device=cpu,
+# is_shared=False)
+# >>> env.step(tensordict)
+# >>> print(tensordict)
+# TensorDict(
+# fields={
+# action: Tensor(shape=torch.Size([1]), device=cpu, dtype=torch.float32, is_shared=False),
+# done: Tensor(shape=torch.Size([1]), device=cpu, dtype=torch.bool, is_shared=False),
+# next: TensorDict(
+# fields={
+# done: Tensor(shape=torch.Size([1]), device=cpu, dtype=torch.bool, is_shared=False),
+# observation: Tensor(shape=torch.Size([]), device=cpu, dtype=torch.float32, is_shared=False),
+# reward: Tensor(shape=torch.Size([1]), device=cpu, dtype=torch.float32, is_shared=False)},
+# batch_size=torch.Size([]),
+# device=cpu,
+# is_shared=False),
+# observation: Tensor(shape=torch.Size([]), device=cpu, dtype=torch.float32, is_shared=False)},
+# batch_size=torch.Size([]),
+# device=cpu,
+# is_shared=False)
+#
+# Notice that the root ``tensordict`` has not changed, the only modification is the
+# appearance of a new ``"next"`` entry that contains the new information.
+#
+# In the Pendulum example, our :meth:`_step` method will read the relevant
+# entries from the input ``tensordict`` and compute the position and velocity of
+# the pendulum after the force encoded by the ``"action"`` key has been applied
+# onto it. We compute the new angular position of the pendulum
+# ``"new_th"`` as the result of the previous position ``"th"`` plus the new
+# velocity ``"new_thdot"`` over a time interval ``dt``.
+#
+# Since our goal is to turn the pendulum up and maintain it still in that
+# position, our ``cost`` (negative reward) function is lower for positions
+# close to the target and low speeds.
+# Indeed, we want to discourage positions that are far from being "upward"
+# and/or speeds that are far from 0.
+#
+# In our example, :meth:`EnvBase._step` is encoded as a static method since our
+# environment is stateless. In stateful settings, the ``self`` argument is
+# needed as the state needs to be read from the environment.
+#
+
+
+def _step(tensordict):
+ th, thdot = tensordict["th"], tensordict["thdot"] # th := theta
+
+ g_force = tensordict["params", "g"]
+ mass = tensordict["params", "m"]
+ length = tensordict["params", "l"]
+ dt = tensordict["params", "dt"]
+ u = tensordict["action"].squeeze(-1)
+ u = u.clamp(-tensordict["params", "max_torque"], tensordict["params", "max_torque"])
+ costs = angle_normalize(th) ** 2 + 0.1 * thdot**2 + 0.001 * (u**2)
+
+ new_thdot = (
+ thdot
+ + (3 * g_force / (2 * length) * th.sin() + 3.0 / (mass * length**2) * u) * dt
+ )
+ new_thdot = new_thdot.clamp(
+ -tensordict["params", "max_speed"], tensordict["params", "max_speed"]
+ )
+ new_th = th + new_thdot * dt
+ reward = -costs.view(*tensordict.shape, 1)
+ done = torch.zeros_like(reward, dtype=torch.bool)
+ out = TensorDict(
+ {
+ "th": new_th,
+ "thdot": new_thdot,
+ "params": tensordict["params"],
+ "reward": reward,
+ "done": done,
+ },
+ tensordict.shape,
+ )
+ return out
+
+
+def angle_normalize(x):
+ return ((x + torch.pi) % (2 * torch.pi)) - torch.pi
+
+
+######################################################################
+# Resetting the simulator: :func:`~torchrl.envs.EnvBase._reset`
+# -------------------------------------------------------------
+#
+# The second method we need to care about is the
+# :meth:`~torchrl.envs.EnvBase._reset` method. Like
+# :meth:`~torchrl.envs.EnvBase._step`, it should write the observation entries
+# and possibly a done state in the ``tensordict`` it outputs (if the done state is
+# omitted, it will be filled as ``False`` by the parent method
+# :meth:`~torchrl.envs.EnvBase.reset`). In some contexts, it is required that
+# the ``_reset`` method receives a command from the function that called
+# it (for example, in multi-agent settings we may want to indicate which agents need
+# to be reset). This is why the :meth:`~torchrl.envs.EnvBase._reset` method
+# also expects a ``tensordict`` as input, albeit it may perfectly be empty or
+# ``None``.
+#
+# The parent :meth:`EnvBase.reset` does some simple checks like the
+# :meth:`EnvBase.step` does, such as making sure that a ``"done"`` state
+# is returned in the output ``tensordict`` and that the shapes match what is
+# expected from the specs.
+#
+# For us, the only important thing to consider is whether
+# :meth:`EnvBase._reset` contains all the expected observations. Once more,
+# since we are working with a stateless environment, we pass the configuration
+# of the pendulum in a nested ``tensordict`` named ``"params"``.
+#
+# In this example, we do not pass a done state as this is not mandatory
+# for :meth:`_reset` and our environment is non-terminating, so we always
+# expect it to be ``False``.
+#
+
+
+def _reset(self, tensordict):
+ if tensordict is None or tensordict.is_empty():
+ # if no ``tensordict`` is passed, we generate a single set of hyperparameters
+ # Otherwise, we assume that the input ``tensordict`` contains all the relevant
+ # parameters to get started.
+ tensordict = self.gen_params(batch_size=self.batch_size)
+
+ high_th = torch.tensor(DEFAULT_X, device=self.device)
+ high_thdot = torch.tensor(DEFAULT_Y, device=self.device)
+ low_th = -high_th
+ low_thdot = -high_thdot
+
+ # for non batch-locked environments, the input ``tensordict`` shape dictates the number
+ # of simulators run simultaneously. In other contexts, the initial
+ # random state's shape will depend upon the environment batch-size instead.
+ th = (
+ torch.rand(tensordict.shape, generator=self.rng, device=self.device)
+ * (high_th - low_th)
+ + low_th
+ )
+ thdot = (
+ torch.rand(tensordict.shape, generator=self.rng, device=self.device)
+ * (high_thdot - low_thdot)
+ + low_thdot
+ )
+ out = TensorDict(
+ {
+ "th": th,
+ "thdot": thdot,
+ "params": tensordict["params"],
+ },
+ batch_size=tensordict.shape,
+ )
+ return out
+
+
+######################################################################
+# Environment metadata: ``env.*_spec``
+# ------------------------------------
+#
+# The specs define the input and output domain of the environment.
+# It is important that the specs accurately define the tensors that will be
+# received at runtime, as they are often used to carry information about
+# environments in multiprocessing and distributed settings. They can also be
+# used to instantiate lazily defined neural networks and test scripts without
+# actually querying the environment (which can be costly with real-world
+# physical systems for instance).
+#
+# There are four specs that we must code in our environment:
+#
+# * :obj:`EnvBase.observation_spec`: This will be a :class:`~torchrl.data.CompositeSpec`
+# instance where each key is an observation (a :class:`CompositeSpec` can be
+# viewed as a dictionary of specs).
+# * :obj:`EnvBase.action_spec`: It can be any type of spec, but it is required
+# that it corresponds to the ``"action"`` entry in the input ``tensordict``;
+# * :obj:`EnvBase.reward_spec`: provides information about the reward space;
+# * :obj:`EnvBase.done_spec`: provides information about the space of the done
+# flag.
+#
+# TorchRL specs are organized in two general containers: ``input_spec`` which
+# contains the specs of the information that the step function reads (divided
+# between ``action_spec`` containing the action and ``state_spec`` containing
+# all the rest), and ``output_spec`` which encodes the specs that the
+# step outputs (``observation_spec``, ``reward_spec`` and ``done_spec``).
+# In general, you should not interact directly with ``output_spec`` and
+# ``input_spec`` but only with their content: ``observation_spec``,
+# ``reward_spec``, ``done_spec``, ``action_spec`` and ``state_spec``.
+# The reason if that the specs are organized in a non-trivial way
+# within ``output_spec`` and
+# ``input_spec`` and neither of these should be directly modified.
+#
+# In other words, the ``observation_spec`` and related properties are
+# convenient shortcuts to the content of the output and input spec containers.
+#
+# TorchRL offers multiple :class:`~torchrl.data.TensorSpec`
+# `subclasses `_ to
+# encode the environment's input and output characteristics.
+#
+# Specs shape
+# ^^^^^^^^^^^
+#
+# The environment specs leading dimensions must match the
+# environment batch-size. This is done to enforce that every component of an
+# environment (including its transforms) have an accurate representation of
+# the expected input and output shapes. This is something that should be
+# accurately coded in stateful settings.
+#
+# For non batch-locked environments, such as the one in our example (see below),
+# this is irrelevant as the environment batch size will most likely be empty.
+#
+
+
+def _make_spec(self, td_params):
+ # Under the hood, this will populate self.output_spec["observation"]
+ self.observation_spec = CompositeSpec(
+ th=BoundedTensorSpec(
+ low=-torch.pi,
+ high=torch.pi,
+ shape=(),
+ dtype=torch.float32,
+ ),
+ thdot=BoundedTensorSpec(
+ low=-td_params["params", "max_speed"],
+ high=td_params["params", "max_speed"],
+ shape=(),
+ dtype=torch.float32,
+ ),
+ # we need to add the ``params`` to the observation specs, as we want
+ # to pass it at each step during a rollout
+ params=make_composite_from_td(td_params["params"]),
+ shape=(),
+ )
+ # since the environment is stateless, we expect the previous output as input.
+ # For this, ``EnvBase`` expects some state_spec to be available
+ self.state_spec = self.observation_spec.clone()
+ # action-spec will be automatically wrapped in input_spec when
+ # `self.action_spec = spec` will be called supported
+ self.action_spec = BoundedTensorSpec(
+ low=-td_params["params", "max_torque"],
+ high=td_params["params", "max_torque"],
+ shape=(1,),
+ dtype=torch.float32,
+ )
+ self.reward_spec = UnboundedContinuousTensorSpec(shape=(*td_params.shape, 1))
+
+
+def make_composite_from_td(td):
+ # custom function to convert a ``tensordict`` in a similar spec structure
+ # of unbounded values.
+ composite = CompositeSpec(
+ {
+ key: make_composite_from_td(tensor)
+ if isinstance(tensor, TensorDictBase)
+ else UnboundedContinuousTensorSpec(
+ dtype=tensor.dtype, device=tensor.device, shape=tensor.shape
+ )
+ for key, tensor in td.items()
+ },
+ shape=td.shape,
+ )
+ return composite
+
+
+######################################################################
+# Reproducible experiments: seeding
+# ---------------------------------
+#
+# Seeding an environment is a common operation when initializing an experiment.
+# The only goal of :func:`EnvBase._set_seed` is to set the seed of the contained
+# simulator. If possible, this operation should not call ``reset()`` or interact
+# with the environment execution. The parent :func:`EnvBase.set_seed` method
+# incorporates a mechanism that allows seeding multiple environments with a
+# different pseudo-random and reproducible seed.
+#
+
+
+def _set_seed(self, seed: Optional[int]):
+ rng = torch.manual_seed(seed)
+ self.rng = rng
+
+
+######################################################################
+# Wrapping things together: the :class:`~torchrl.envs.EnvBase` class
+# ------------------------------------------------------------------
+#
+# We can finally put together the pieces and design our environment class.
+# The specs initialization needs to be performed during the environment
+# construction, so we must take care of calling the :func:`_make_spec` method
+# within :func:`PendulumEnv.__init__`.
+#
+# We add a static method :meth:`PendulumEnv.gen_params` which deterministically
+# generates a set of hyperparameters to be used during execution:
+#
+
+
+def gen_params(g=10.0, batch_size=None) -> TensorDictBase:
+ """Returns a ``tensordict`` containing the physical parameters such as gravitational force and torque or speed limits."""
+ if batch_size is None:
+ batch_size = []
+ td = TensorDict(
+ {
+ "params": TensorDict(
+ {
+ "max_speed": 8,
+ "max_torque": 2.0,
+ "dt": 0.05,
+ "g": g,
+ "m": 1.0,
+ "l": 1.0,
+ },
+ [],
+ )
+ },
+ [],
+ )
+ if batch_size:
+ td = td.expand(batch_size).contiguous()
+ return td
+
+
+######################################################################
+# We define the environment as non-``batch_locked`` by turning the ``homonymous``
+# attribute to ``False``. This means that we will **not** enforce the input
+# ``tensordict`` to have a ``batch-size`` that matches the one of the environment.
+#
+# The following code will just put together the pieces we have coded above.
+#
+
+
+class PendulumEnv(EnvBase):
+ metadata = {
+ "render_modes": ["human", "rgb_array"],
+ "render_fps": 30,
+ }
+ batch_locked = False
+
+ def __init__(self, td_params=None, seed=None, device="cpu"):
+ if td_params is None:
+ td_params = self.gen_params()
+
+ super().__init__(device=device, batch_size=[])
+ self._make_spec(td_params)
+ if seed is None:
+ seed = torch.empty((), dtype=torch.int64).random_().item()
+ self.set_seed(seed)
+
+ # Helpers: _make_step and gen_params
+ gen_params = staticmethod(gen_params)
+ _make_spec = _make_spec
+
+ # Mandatory methods: _step, _reset and _set_seed
+ _reset = _reset
+ _step = staticmethod(_step)
+ _set_seed = _set_seed
+
+
+######################################################################
+# Testing our environment
+# -----------------------
+#
+# TorchRL provides a simple function :func:`~torchrl.envs.utils.check_env_specs`
+# to check that a (transformed) environment has an input/output structure that
+# matches the one dictated by its specs.
+# Let us try it out:
+#
+
+env = PendulumEnv()
+check_env_specs(env)
+
+######################################################################
+# We can have a look at our specs to have a visual representation of the environment
+# signature:
+#
+
+print("observation_spec:", env.observation_spec)
+print("state_spec:", env.state_spec)
+print("reward_spec:", env.reward_spec)
+
+######################################################################
+# We can execute a couple of commands too to check that the output structure
+# matches what is expected.
+
+td = env.reset()
+print("reset tensordict", td)
+
+######################################################################
+# We can run the :func:`env.rand_step` to generate
+# an action randomly from the ``action_spec`` domain. A ``tensordict`` containing
+# the hyperparameters and the current state **must** be passed since our
+# environment is stateless. In stateful contexts, ``env.rand_step()`` works
+# perfectly too.
+#
+td = env.rand_step(td)
+print("random step tensordict", td)
+
+######################################################################
+# Transforming an environment
+# ---------------------------
+#
+# Writing environment transforms for stateless simulators is slightly more
+# complicated than for stateful ones: transforming an output entry that needs
+# to be read at the following iteration requires to apply the inverse transform
+# before calling :func:`meth.step` at the next step.
+# This is an ideal scenario to showcase all the features of TorchRL's
+# transforms!
+#
+# For instance, in the following transformed environment we ``unsqueeze`` the entries
+# ``["th", "thdot"]`` to be able to stack them along the last
+# dimension. We also pass them as ``in_keys_inv`` to squeeze them back to their
+# original shape once they are passed as input in the next iteration.
+#
+env = TransformedEnv(
+ env,
+ # ``Unsqueeze`` the observations that we will concatenate
+ UnsqueezeTransform(
+ unsqueeze_dim=-1,
+ in_keys=["th", "thdot"],
+ in_keys_inv=["th", "thdot"],
+ ),
+)
+
+######################################################################
+# Writing custom transforms
+# ^^^^^^^^^^^^^^^^^^^^^^^^^
+#
+# TorchRL's transforms may not cover all the operations one wants to execute
+# after an environment has been executed.
+# Writing a transform does not require much effort. As for the environment
+# design, there are two steps in writing a transform:
+#
+# - Getting the dynamics right (forward and inverse);
+# - Adapting the environment specs.
+#
+# A transform can be used in two settings: on its own, it can be used as a
+# :class:`~torch.nn.Module`. It can also be used appended to a
+# :class:`~torchrl.envs.transforms.TransformedEnv`. The structure of the class allows to
+# customize the behavior in the different contexts.
+#
+# A :class:`~torchrl.envs.transforms.Transform` skeleton can be summarized as follows:
+#
+# .. code-block::
+#
+# class Transform(nn.Module):
+# def forward(self, tensordict):
+# ...
+# def _apply_transform(self, tensordict):
+# ...
+# def _step(self, tensordict):
+# ...
+# def _call(self, tensordict):
+# ...
+# def inv(self, tensordict):
+# ...
+# def _inv_apply_transform(self, tensordict):
+# ...
+#
+# There are three entry points (:func:`forward`, :func:`_step` and :func:`inv`)
+# which all receive :class:`tensordict.TensorDict` instances. The first two
+# will eventually go through the keys indicated by :obj:`~tochrl.envs.transforms.Transform.in_keys`
+# and call :meth:`~torchrl.envs.transforms.Transform._apply_transform` to each of these. The results will
+# be written in the entries pointed by :obj:`Transform.out_keys` if provided
+# (if not the ``in_keys`` will be updated with the transformed values).
+# If inverse transforms need to be executed, a similar data flow will be
+# executed but with the :func:`Transform.inv` and
+# :func:`Transform._inv_apply_transform` methods and across the ``in_keys_inv``
+# and ``out_keys_inv`` list of keys.
+# The following figure summarized this flow for environments and replay
+# buffers.
+#
+#
+# Transform API
+#
+# In some cases, a transform will not work on a subset of keys in a unitary
+# manner, but will execute some operation on the parent environment or
+# work with the entire input ``tensordict``.
+# In those cases, the :func:`_call` and :func:`forward` methods should be
+# re-written, and the :func:`_apply_transform` method can be skipped.
+#
+# Let us code new transforms that will compute the ``sine`` and ``cosine``
+# values of the position angle, as these values are more useful to us to learn
+# a policy than the raw angle value:
+
+
+class SinTransform(Transform):
+ def _apply_transform(self, obs: torch.Tensor) -> None:
+ return obs.sin()
+
+ # The transform must also modify the data at reset time
+ def _reset(
+ self, tensordict: TensorDictBase, tensordict_reset: TensorDictBase
+ ) -> TensorDictBase:
+ return self._call(tensordict_reset)
+
+ # _apply_to_composite will execute the observation spec transform across all
+ # in_keys/out_keys pairs and write the result in the observation_spec which
+ # is of type ``Composite``
+ @_apply_to_composite
+ def transform_observation_spec(self, observation_spec):
+ return BoundedTensorSpec(
+ low=-1,
+ high=1,
+ shape=observation_spec.shape,
+ dtype=observation_spec.dtype,
+ device=observation_spec.device,
+ )
+
+
+class CosTransform(Transform):
+ def _apply_transform(self, obs: torch.Tensor) -> None:
+ return obs.cos()
+
+ # The transform must also modify the data at reset time
+ def _reset(
+ self, tensordict: TensorDictBase, tensordict_reset: TensorDictBase
+ ) -> TensorDictBase:
+ return self._call(tensordict_reset)
+
+ # _apply_to_composite will execute the observation spec transform across all
+ # in_keys/out_keys pairs and write the result in the observation_spec which
+ # is of type ``Composite``
+ @_apply_to_composite
+ def transform_observation_spec(self, observation_spec):
+ return BoundedTensorSpec(
+ low=-1,
+ high=1,
+ shape=observation_spec.shape,
+ dtype=observation_spec.dtype,
+ device=observation_spec.device,
+ )
+
+
+t_sin = SinTransform(in_keys=["th"], out_keys=["sin"])
+t_cos = CosTransform(in_keys=["th"], out_keys=["cos"])
+env.append_transform(t_sin)
+env.append_transform(t_cos)
+
+######################################################################
+# Concatenates the observations onto an "observation" entry.
+# ``del_keys=False`` ensures that we keep these values for the next
+# iteration.
+cat_transform = CatTensors(
+ in_keys=["sin", "cos", "thdot"], dim=-1, out_key="observation", del_keys=False
+)
+env.append_transform(cat_transform)
+
+######################################################################
+# Once more, let us check that our environment specs match what is received:
+check_env_specs(env)
+
+######################################################################
+# Executing a rollout
+# -------------------
+#
+# Executing a rollout is a succession of simple steps:
+#
+# * reset the environment
+# * while some condition is not met:
+#
+# * compute an action given a policy
+# * execute a step given this action
+# * collect the data
+# * make a ``MDP`` step
+#
+# * gather the data and return
+#
+# These operations have been conveniently wrapped in the :meth:`~torchrl.envs.EnvBase.rollout`
+# method, from which we provide a simplified version here below.
+
+
+def simple_rollout(steps=100):
+ # preallocate:
+ data = TensorDict({}, [steps])
+ # reset
+ _data = env.reset()
+ for i in range(steps):
+ _data["action"] = env.action_spec.rand()
+ _data = env.step(_data)
+ data[i] = _data
+ _data = step_mdp(_data, keep_other=True)
+ return data
+
+
+print("data from rollout:", simple_rollout(100))
+
+######################################################################
+# Batching computations
+# ---------------------
+#
+# The last unexplored end of our tutorial is the ability that we have to
+# batch computations in TorchRL. Because our environment does not
+# make any assumptions regarding the input data shape, we can seamlessly
+# execute it over batches of data. Even better: for non-batch-locked
+# environments such as our Pendulum, we can change the batch size on the fly
+# without recreating the environment.
+# To do this, we just generate parameters with the desired shape.
+#
+
+batch_size = 10 # number of environments to be executed in batch
+td = env.reset(env.gen_params(batch_size=[batch_size]))
+print("reset (batch size of 10)", td)
+td = env.rand_step(td)
+print("rand step (batch size of 10)", td)
+
+######################################################################
+# Executing a rollout with a batch of data requires us to reset the environment
+# out of the rollout function, since we need to define the batch_size
+# dynamically and this is not supported by :meth:`~torchrl.envs.EnvBase.rollout`:
+#
+
+rollout = env.rollout(
+ 3,
+ auto_reset=False, # we're executing the reset out of the ``rollout`` call
+ tensordict=env.reset(env.gen_params(batch_size=[batch_size])),
+)
+print("rollout of len 3 (batch size of 10):", rollout)
+
+
+######################################################################
+# Training a simple policy
+# ------------------------
+#
+# In this example, we will train a simple policy using the reward as a
+# differentiable objective, such as a negative loss.
+# We will take advantage of the fact that our dynamic system is fully
+# differentiable to backpropagate through the trajectory return and adjust the
+# weights of our policy to maximize this value directly. Of course, in many
+# settings many of the assumptions we make do not hold, such as
+# differentiable system and full access to the underlying mechanics.
+#
+# Still, this is a very simple example that showcases how a training loop can
+# be coded with a custom environment in TorchRL.
+#
+# Let us first write the policy network:
+#
+torch.manual_seed(0)
+env.set_seed(0)
+
+net = nn.Sequential(
+ nn.LazyLinear(64),
+ nn.Tanh(),
+ nn.LazyLinear(64),
+ nn.Tanh(),
+ nn.LazyLinear(64),
+ nn.Tanh(),
+ nn.LazyLinear(1),
+)
+policy = TensorDictModule(
+ net,
+ in_keys=["observation"],
+ out_keys=["action"],
+)
+
+######################################################################
+# and our optimizer:
+#
+
+optim = torch.optim.Adam(policy.parameters(), lr=2e-3)
+
+######################################################################
+# Training loop
+# ^^^^^^^^^^^^^
+#
+# We will successively:
+#
+# * generate a trajectory
+# * sum the rewards
+# * backpropagate through the graph defined by these operations
+# * clip the gradient norm and make an optimization step
+# * repeat
+#
+# At the end of the training loop, we should have a final reward close to 0
+# which demonstrates that the pendulum is upward and still as desired.
+#
+batch_size = 32
+pbar = tqdm.tqdm(range(20_000 // batch_size))
+scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optim, 20_000)
+logs = defaultdict(list)
+
+for _ in pbar:
+ init_td = env.reset(env.gen_params(batch_size=[batch_size]))
+ rollout = env.rollout(100, policy, tensordict=init_td, auto_reset=False)
+ traj_return = rollout["next", "reward"].mean()
+ (-traj_return).backward()
+ gn = torch.nn.utils.clip_grad_norm_(net.parameters(), 1.0)
+ optim.step()
+ optim.zero_grad()
+ pbar.set_description(
+ f"reward: {traj_return: 4.4f}, "
+ f"last reward: {rollout[..., -1]['next', 'reward'].mean(): 4.4f}, gradient norm: {gn: 4.4}"
+ )
+ logs["return"].append(traj_return.item())
+ logs["last_reward"].append(rollout[..., -1]["next", "reward"].mean().item())
+ scheduler.step()
+
+
+def plot():
+ import matplotlib
+ from matplotlib import pyplot as plt
+
+ is_ipython = "inline" in matplotlib.get_backend()
+ if is_ipython:
+ from IPython import display
+
+ with plt.ion():
+ plt.figure(figsize=(10, 5))
+ plt.subplot(1, 2, 1)
+ plt.plot(logs["return"])
+ plt.title("returns")
+ plt.xlabel("iteration")
+ plt.subplot(1, 2, 2)
+ plt.plot(logs["last_reward"])
+ plt.title("last reward")
+ plt.xlabel("iteration")
+ if is_ipython:
+ display.display(plt.gcf())
+ display.clear_output(wait=True)
+ plt.show()
+
+
+plot()
+
+
+######################################################################
+# Conclusion
+# ----------
+#
+# In this tutorial, we have learned how to code a stateless environment from
+# scratch. We touched the subjects of:
+#
+# * The four essential components that need to be taken care of when coding
+# an environment (``step``, ``reset``, seeding and building specs).
+# We saw how these methods and classes interact with the
+# :class:`~tensordict.TensorDict` class;
+# * How to test that an environment is properly coded using
+# :func:`~torchrl.envs.utils.check_env_specs`;
+# * How to append transforms in the context of stateless environments and how
+# to write custom transformations;
+# * How to train a policy on a fully differentiable simulator.
+#
diff --git a/advanced_source/privateuseone.rst b/advanced_source/privateuseone.rst
new file mode 100644
index 000000000..5b5b37c20
--- /dev/null
+++ b/advanced_source/privateuseone.rst
@@ -0,0 +1,309 @@
+Facilitating New Backend Integration by PrivateUse1
+===================================================
+
+In this tutorial we will walk through some necessary steps to integrate a new backend
+living outside ``pytorch/pytorch`` repo by ``PrivateUse1``. Note that this tutorial assumes that
+you already have a basic understanding of PyTorch.
+you are an advanced user of PyTorch.
+
+.. note::
+
+ This tutorial only involves the parts related to the PrivateUse1 mechanism that facilitates the integration of new devices,
+ and other parts will not be covered. At the same time, not all the modules involved in this tutorial are required,
+ and you can choose the modules that are helpful to you according to your actual needs.
+
+
+What is PrivateUse1?
+--------------------
+
+Prior to Pytorch 2.0, PyTorch provided three reserved dispatch keys (and their corresponding Autograd keys)
+for prototyping out-of-tree backend extensions, the three dispatch keys are as follows:
+
+* ``PrivateUse1/AutogradPrivateUse1``
+* ``PrivateUse2/AutogradPrivateUse2``
+* ``PrivateUse3/AutogradPrivateUse3``
+
+After the prototype verification is passed, you can apply for a private key for the new backend, such as CUDA, XLA, MPS, and so on.
+
+However, with the rapid development of PyTorch, more and more hardware manufacturers are trying to
+integrate their backends into PyTorch, which might cause the following problems:
+
+* Every new backend integration involves a lot of file modification
+* There is currently a hard limit on the number of Dispatch Keys (``DispatchKeySet`` 64-bit limit)
+
+.. note::
+
+ There is also a problem with integrating the new backend into PyTorch through the PrivateUse1 Key, as it is impossible
+ to integrate many backends at the same time. Fortunately, these out-of-tree backends are rarely used simultaneously.
+
+
+In view of the above reasons, the community began to recommend new backend to be integrated
+into the PyTorch via ``PrivateUse1``.
+
+However, the previous ``PrivateUse1`` mechanism is not fully capable of integrating with the new backend, because it
+lacks some related support in certain modules, such as Storage, AMP, Distributed, and so on.
+
+With the arrival of Pytorch 2.1.0, a series of optimizations and enhancements have been made
+for ``PrivateUse1`` in terms of new backend integration, and it is now possible to support the integration
+of new devices rapidly and efficiently.
+
+How to integrate new backend via PrivateUse1
+--------------------------------------------
+
+In this section, we will discuss the details of integrating the new backend into Pytorch via ``PrivateUse1``,
+which mainly consists of the following parts:
+
+1. Register kernels for the new backend.
+2. Register generator for the new backend.
+3. Register device guard for the new backend.
+4. Register serialization and deserialization functions for new backend metadata.
+5. Other Modules.
+
+Register kernels for the new backend
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+The new backend may have some high-performance implementations of operator, which can be registered to the dispatcher
+by ``TORCH_LIBRARY_IMPL`` API described in `Registering a Dispatched Operator in C++ `_. This involves
+several situations:
+
+1. Register all the forward operators supported by the new backend to the dispatcher, and register the fallback
+ at the same time, so that when the new backend does not support some operators, these operators can fall back
+ to the CPU for execution to ensure the availability of functions.
+
+.. code-block:: cpp
+
+ at::Tensor wrapper_Custom_Tensor_add(const at::Tensor & self, const at::Tensor & other, const at::Scalar & alpha) {
+ // Implementation of add kernel in new backend
+ ...
+ }
+
+ TORCH_LIBRARY_IMPL(aten, PrivateUse1, m) {
+ ...
+ m.impl("add.Tensor", TORCH_FN(wrapper_Custom_Tensor_add));
+ ...
+ }
+
+ void custom_cpu_fallback(const c10::OperatorHandle& op, torch::jit::Stack* stack) {
+ // Add some hints about new devices that do not support and need to fall back to cpu
+ at::native::cpu_fallback(op, stack);
+ }
+
+ TORCH_LIBRARY_IMPL(_, PrivateUse1, m) {
+ m.fallback(torch::CppFunction::makeFromBoxedFunction<&custom_cpu_fallback>());
+ }
+
+2. Register kernels from ``torch::autograd::Function`` to the dispatcher by ``AutogradPrivateUse1``, if it is necessary for
+ new backend to override ``PyTorch Autograd layer``, the dispatcher and autograd system will automatically call the forward and
+ backward implementations of these operators.
+
+.. code-block:: cpp
+
+ class CumtomSeluFunction : public torch::autograd::Function {
+ // Implementation of selu kernel in new backend
+ }
+
+ at::Tensor wrapper_AutogradCumstom__selu(const at::Tensor & self) {
+ return CumtomSeluFunction::apply(self);
+ }
+
+ TORCH_LIBRARY_IMPL(aten, AutogradPrivateUse1, m) {
+ ...
+ m.impl("selu", TORCH_FN(wrapper_AutogradCustom__selu));
+ ...
+ }
+
+3. Register kernels which want to support `automatic mixed precision (AMP) `_ and
+ fallback mechanism to the dispatcher by ``AutocastPrivateUse1``, the autocast system will automatically call these kernels when needed.
+
+.. code-block:: cpp
+
+ TORCH_LIBRARY_IMPL(aten, AutocastPrivateUse1, m) {
+ ...
+ KERNEL_PRIVATEUSEONE(, )
+ ...
+ }
+
+ TORCH_LIBRARY_IMPL(_, AutocastPrivateUse1, m) {
+ m.fallback(torch::CppFunction::makeFallthrough());
+ }
+
+What needs to be added is that if you want to support AMP in a new backend, you need to register a new ``BackendModule`` by
+``torch._register_device_module("backend_name", BackendModule)``, and the ``BackendModule`` needs to have the following APIs:
+
+* ``get_amp_supported_dtype() -> List[torch.dtype]``
+ get the supported dtypes on the new backend in AMP, which might support one more ``dtype``.
+* ``is_autocast_enabled() -> bool``
+ check the AMP is enabled or not on the new backend.
+* ``get_autocast_dtype() -> torch.dtype``
+ get the supported ``dtype`` on the new backend in AMP, which is set by ``set_autocast_dtype`` or the
+ default ``dtype``, and the default ``dtype`` is ``torch.float16``.
+* ``set_autocast_enabled(bool) -> None``
+ enable or disable AMP on the new backend.
+* ``set_autocast_dtype(dtype) -> None``
+ set the supported ``dtype`` on the new backend in AMP, and the ``dtype`` be contained in the ``dtypes`` got
+ from ``get_amp_supported_dtype``.
+
+Register generator for the new backend
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+It is necessary to support generators corresponding to new devices. Currently, ``PrivateUse1`` can dynamically
+register custom generators, which are mainly divided into the following steps.
+
+1. Inherit the ``GeneratorImpl`` class to implement the generator class corresponding to the new backend,
+ and implement various general methods.
+2. Define a new backend ``builder`` with a single parameter: ``device index``.
+3. Call ``REGISTER_GENERATOR_PRIVATEUSE1`` macro to complete dynamic registration.
+
+.. code-block:: cpp
+
+ struct CustomGeneratorImpl : public c10::GeneratorImpl {
+ // Implementation of generator in new backend
+ }
+
+ at::Generator make_custom_generator(c10::DeviceIndex device_index) {
+ return at::make_generator(device_index);
+ }
+
+ REGISTER_GENERATOR_PRIVATEUSE1(make_cumstom_generator)
+
+Register device guard for the new backend
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+PyTorch provides functionalities related to device, stream, and event switching via ``DeviceGuard``.
+This function is also applicable to ``PrivateUse1`` Key.
+
+1. Inherit the ``DeviceGuardImplInterface`` class to implement the various general methods corresponding to the new backend.
+2. Call ``C10_REGISTER_GUARD_IMPL`` macro to complete dynamic registration.
+
+.. code-block:: cpp
+
+ struct CustomGuardImpl final : public c10::impl::DeviceGuardImplInterface {
+ // Implementation of guard in new backend
+ }
+
+ C10_REGISTER_GUARD_IMPL(PrivateUse1, CustomGuardImpl);
+
+Register serialization and deserialization functions for new backend metadata
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+PyTorch is currently able to dynamically register serialization/deserialization functions to support the serialization and deserialization
+of new backend additional metadata named ``backend_meta_`` in class ``TensorImpl.ExtraMeta``. You can refer to the following steps:
+
+1. Inherit the ``BackendMeta`` class to implement ``CustomBackendMetadata`` corresponding to the new backend and
+ various fields of the new backend can be customized in the class.
+2. Implement the serialization and deserialization functions of the new backend, the function signatures are
+ ``void(const at::Tensor&, std::unordered_map&)``.
+3. Call the ``TensorBackendMetaRegistry`` macro to complete dynamic registration.
+
+.. code-block:: cpp
+
+ struct CustomBackendMetadata : public c10::BackendMeta {
+ // Implementation of backend metadata in new backend
+ }
+
+ void for_serialization(const at::Tensor& t, std::unordered_map& m) {
+ // Implementation of serialization
+ }
+
+ void for_deserialization(const at::Tensor& t, std::unordered_map& m) {
+ // Implementation of deserialization
+ }
+
+ TensorBackendMetaRegistry(c10::DeviceType::PrivateUse1, &for_serialization, &for_deserialization);
+
+Other Modules
+^^^^^^^^^^^^^
+
+In addition to the above-mentioned parts, there are some other modules that can be expanded through ``PrivateUse1``,
+such as ``distributed collective communication``, ``benchmark timer``, and others, which will be added in the future.
+One example about ``PrivateUse1`` integration is `Ascend NPU `_.
+
+
+How to Improve User Experience with Privateuse1
+-----------------------------------------------
+
+The primary goal of integrating new devices through ``PrivateUse1`` is to meet the basic functional requirements,
+and the next thing to do is to improve usability, which mainly involves the following aspects.
+
+1. Register new backend module to Pytorch.
+2. Rename PrivateUse1 to a custom name for the new backend.
+3. Generate methods and properties related to the new backend.
+
+Register new backend module to Pytorch
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+Some CUDA-related interfaces in PyTorch can be called through the following form: ``torch.cuda.xxx``. Therefore, in order to
+comply with user habits, the new backend implemented through the ``PrivateUse1`` mechanism should also provide similar interfaces.
+
+For example, using ``Ascend NPU``:
+
+.. code-block:: python
+
+ torch._register_device_module('npu', torch_npu.npu)
+
+After doing the above operations, users can call some exclusive APIs of ``Ascend NPU`` through ``torch.npu.xxx``
+
+Rename PrivateUse1 to a custom name for the new backend
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+``PrivateUse1`` Key is the internal mechanism of the new backend integrated into PyTorch. For users, compared with ``PrivateUse1``,
+the custom name strongly related to the new backend should be more friendly.
+
+Taking the ``Ascend NPU`` as an example, the first usage will be more user-friendly.
+
+.. code-block:: python
+
+ torch.rand((2,2),device='npu:0')
+ torch.rand((2,2),device='privateuse1:0')
+
+Now, PyTorch provides a new C++/Python API for the self-named ``PrivateUse1`` backend, which is very simple to use.
+
+.. tab-set-code::
+
+ .. code-block:: python
+
+ torch.rename_privateuse1_backend("npu")
+
+ .. code-block:: C++
+
+ c10::register_privateuse1_backend("npu")
+
+Generate methods and properties related to the new backend
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+After renaming ``PrivateUse1`` to a custome name, automatically generate properties and methods related to the new backend name
+in the ``Tensor, nn, Storage`` modules for the new backend.
+
+Here is an example for ``Ascend NPU``:
+
+.. code-block:: python
+
+ torch.rename_privateuse1_backend("npu")
+ unsupported_dtype = [torch.quint8]
+ torch.utils.generate_methods_for_privateuse1_backend(for_tensor=True, for_module=True, for_storage=True, unsupported_dtype=unsupported_dtype)
+
+Then, you can use the following methods and properties:
+
+.. code-block:: python
+
+ torch.Tensor.npu()
+ torch.Tensor.is_npu
+ torch.Storage.npu()
+ torch.Storage.is_npu
+ ...
+
+Future Work
+-----------
+
+The improvement of the ``PrivateUse1`` mechanism is still in progress, so the integration method of ``PrivateUse1``
+of the new module will be added in turn. Here are a few items that we are actively working on:
+
+* Add the integration method of ``distributed collective communication``.
+* Add the integration method of ``benchmark timer``.
+
+Conclusion
+----------
+
+This tutorial walked you through the process of integrating new backends into PyTorch via ``PrivateUse1``, including but not limited to
+operator registration, generator registration, device guard registration, and so on. At the same time, some methods are introduced
+to improve the user experience.
diff --git a/advanced_source/rpc_ddp_tutorial.rst b/advanced_source/rpc_ddp_tutorial.rst
index 42293a6e5..d59395f5d 100644
--- a/advanced_source/rpc_ddp_tutorial.rst
+++ b/advanced_source/rpc_ddp_tutorial.rst
@@ -1,6 +1,6 @@
분산 데이터 병렬(DDP)과 분산 RPC 프레임워크 결합
=================================================================
-**저자**: `Pritam Damania `__ and `Yi Wang `__
+**저자**: `Pritam Damania `__ and `Yi Wang `__
**번역**: `박다정 `_
diff --git a/advanced_source/semi_structured_sparse.py b/advanced_source/semi_structured_sparse.py
new file mode 100644
index 000000000..38c2c6878
--- /dev/null
+++ b/advanced_source/semi_structured_sparse.py
@@ -0,0 +1,651 @@
+# -*- coding: utf-8 -*-
+"""
+(beta) Accelerating BERT with semi-structured (2:4) sparsity
+=====================================================
+**Author**: `Jesse Cai `_
+
+"""
+
+####################################################################
+# Overview
+# --------
+#
+# Like other forms of sparsity, **semi-structured sparsity** is a model
+# optimization technique that seeks to reduce the memory overhead and
+# latency of a neural network at the expense of some model accuracy. It is
+# also known as **fine-grained structured sparsity** or **2:4 structured
+# sparsity**.
+#
+# Semi-structured sparsity derives its name from its unique sparsity
+# pattern, where n out of every 2n elements are pruned. We most often see
+# n=2, hence 2:4 sparsity Semi-structured sparsity is particularly
+# interesting because it can be efficiently accelerated on GPUs and
+# doesn’t degrade model accuracy as much as other sparsity patterns.
+#
+# With the introduction of
+# `semi-structured sparsity support `_,
+# it is possible to prune and accelerate a semi-structured sparse model
+# without leaving PyTorch. We will explain this process in this tutorial.
+#
+# .. image:: ../../_static/img/pruning_flow.jpg
+#
+# By the end of this tutorial, we will have sparsified a BERT
+# question-answering model to be 2:4 sparse, fine-tuning it to recover
+# nearly all F1 loss (86.92 dense vs 86.48 sparse). Finally, we will
+# accelerate this 2:4 sparse model for inference, yielding a 1.3x speedup.
+#
+
+#####################################################
+# Requirements
+# ------------
+#
+# - PyTorch >= 2.1.
+# - A NVIDIA GPU with semi-structured sparsity support (Compute
+# Capability 8.0+).
+#
+# This tutorial is designed for beginners to semi-structured sparsity and
+# sparsity in general. For users with existing 2:4 sparse models,
+# accelerating ``nn.Linear`` layers for inference with
+# ``to_sparse_semi_structured`` is quite straightforward. Here is an example:
+#
+
+import torch
+from torch.sparse import to_sparse_semi_structured, SparseSemiStructuredTensor
+from torch.utils.benchmark import Timer
+SparseSemiStructuredTensor._FORCE_CUTLASS = True
+
+# mask Linear weight to be 2:4 sparse
+mask = torch.Tensor([0, 0, 1, 1]).tile((3072, 2560)).cuda().bool()
+linear = torch.nn.Linear(10240, 3072).half().cuda().eval()
+linear.weight = torch.nn.Parameter(mask * linear.weight)
+
+x = torch.rand(3072, 10240).half().cuda()
+
+with torch.inference_mode():
+ dense_output = linear(x)
+ dense_t = Timer(stmt="linear(x)",
+ globals={"linear": linear,
+ "x": x}).blocked_autorange().median * 1e3
+
+ # accelerate via SparseSemiStructuredTensor
+ linear.weight = torch.nn.Parameter(to_sparse_semi_structured(linear.weight))
+
+ sparse_output = linear(x)
+ sparse_t = Timer(stmt="linear(x)",
+ globals={"linear": linear,
+ "x": x}).blocked_autorange().median * 1e3
+
+ # sparse and dense matmul are numerically equivalent
+ # On an A100 80GB, we see: `Dense: 0.870ms Sparse: 0.630ms | Speedup: 1.382x`
+ assert torch.allclose(sparse_output, dense_output, atol=1e-3)
+ print(f"Dense: {dense_t:.3f}ms Sparse: {sparse_t:.3f}ms | Speedup: {(dense_t / sparse_t):.3f}x")
+
+
+######################################################################
+# What problem does semi-structured sparsity solve?
+# -------------------------------------------------
+#
+# The general motivation behind sparsity is simple: if there are zeros in
+# your network, you can optimize efficiency by not storing or computing those
+# parameters. However, the specifics of sparsity are tricky. Zeroing out
+# parameters doesn’t affect the latency / memory overhead of our model out
+# of the box.
+#
+# This is because the dense tensor still contains the pruned (zero)
+# elements, which the dense matrix multiplication kernel will still
+# operate on this elements. In order to realize performance gains, we need
+# to swap out dense kernels for sparse kernels, which skip calculation
+# involving pruned elements.
+#
+# To do this, these kernels work on sparse matrices, which do not store
+# the pruned elements and store the specified elements in a compressed
+# format.
+#
+# For semi-structured sparsity, we store exactly half of the original
+# parameters along with some compressed metadata about how the elements
+# were arranged.
+#
+# .. image:: https://developer-blogs.nvidia.com/wp-content/uploads/2023/06/2-4-structured-sparsity-pattern.png
+# :align: center :width: 80%
+#
+# Image sourced from `NVIDIA blog post `_ on semi-structured sparsity.
+#
+# There are many different sparse layouts, each with their own benefits
+# and drawbacks. The 2:4 semi-structured sparse layout is particularly
+# interesting for two reasons:
+#
+# * Unlike previous sparse formats,
+# semi-structured sparsity was designed to be efficiently accelerated on
+# GPUs. In 2020, NVIDIA introduced hardware support for semi-structured
+# sparsity with their Ampere architecture, and have also released fast
+# sparse kernels via
+# CUTLASS `cuSPARSELt `__.
+#
+# * At the same time, semi-structured sparsity tends to have a milder
+# impact on model accuracy compared to other sparse formats, especially
+# when accounting for more advanced pruning / fine-tuning methods. NVIDIA
+# has shown in their `white paper `_
+# that a simple paradigm of magnitude pruning once to be 2:4 sparse and
+# then retraining the model yields nearly identical model accuracies.
+#
+# Semi-structured exists in a sweet spot, providing a 2x (theoretical)
+# speedup at a much lower sparsity level (50%), while still being granular
+# enough to preserve model accuracy.
+#
+# +---------------------+-------------+--------+------------+-------------+
+# | Network | Data Set | Metric | Dense FP16 | Sparse FP16 |
+# +=====================+=============+========+============+=============+
+# | ResNet-50 | ImageNet | Top-1 | 76.1 | 76.2 |
+# +---------------------+-------------+--------+------------+-------------+
+# | ResNeXt-101_32x8d | ImageNet | Top-1 | 79.3 | 79.3 |
+# +---------------------+-------------+--------+------------+-------------+
+# | Xception | ImageNet | Top-1 | 79.2 | 79.2 |
+# +---------------------+-------------+--------+------------+-------------+
+# | SSD-RN50 | COCO2017 | bbAP | 24.8 | 24.8 |
+# +---------------------+-------------+--------+------------+-------------+
+# | MaskRCNN-RN50 | COCO2017 | bbAP | 37.9 | 37.9 |
+# +---------------------+-------------+--------+------------+-------------+
+# | FairSeq Transformer | EN-DE WMT14 | BLEU | 28.2 | 28.5 |
+# +---------------------+-------------+--------+------------+-------------+
+# | BERT-Large | SQuAD v1.1 | F1 | 91.9 | 91.9 |
+# +---------------------+-------------+--------+------------+-------------+
+#
+# Semi-structured sparsity has an additional advantage from a workflow
+# perspective. Because the sparsity level is fixed at 50%, it is easier to
+# decompose the problem of sparsifying a model into two distinct
+# subproblems:
+#
+# - Accuracy - How can we find a set of 2:4 sparse weights that minimize
+# the accuracy degradation of our model?
+#
+# - Performance - How can we accelerate our 2:4 sparse weights for
+# inference and reduced memory overhead?
+#
+
+#####################################################################
+# .. math::
+#
+# \begin{bmatrix}
+# 1 & 1 & 0 & 0 \\
+# 0 & 0 & 1 & 1 \\
+# 1 & 0 & 0 & 0 \\
+# 0 & 0 & 1 & 1 \\
+# \end{bmatrix}
+#
+# The natural handoff point between these two problems are zeroed-out
+# dense tensors. Our inference solution is designed to compress and
+# accelerate tensors in this format. We anticipate many users coming up
+# with custom masking solution, as this is an active area of research.
+#
+# Now that we’ve learned a little more about semi-structured sparsity,
+# let’s apply it to a BERT model trained on a question answering task,
+# SQuAD.
+#
+# Intro & Setup
+# -------------
+#
+# Let’s start by importing all the packages we need.
+#
+
+# If you are running this in Google Colab, run:
+# .. code-block: python
+#
+# !pip install datasets transformers evaluate accelerate pandas
+#
+import os
+os.environ["WANDB_DISABLED"] = "true"
+
+import collections
+import datasets
+import evaluate
+import numpy as np
+import torch
+import torch.utils.benchmark as benchmark
+from torch import nn
+from torch.sparse import to_sparse_semi_structured, SparseSemiStructuredTensor
+from torch.ao.pruning import WeightNormSparsifier
+import transformers
+
+# force CUTLASS use if ``cuSPARSELt`` is not available
+SparseSemiStructuredTensor._FORCE_CUTLASS = True
+torch.manual_seed(100)
+
+
+######################################################################
+# We’ll also need to define some helper functions that are specific to the
+# dataset / task at hand. These were adapted from
+# `this `__
+# Hugging Face course as a reference.
+#
+
+def preprocess_validation_function(examples, tokenizer):
+ inputs = tokenizer(
+ [q.strip() for q in examples["question"]],
+ examples["context"],
+ max_length=384,
+ truncation="only_second",
+ return_overflowing_tokens=True,
+ return_offsets_mapping=True,
+ padding="max_length",
+ )
+ sample_map = inputs.pop("overflow_to_sample_mapping")
+ example_ids = []
+
+ for i in range(len(inputs["input_ids"])):
+ sample_idx = sample_map[i]
+ example_ids.append(examples["id"][sample_idx])
+ sequence_ids = inputs.sequence_ids(i)
+ offset = inputs["offset_mapping"][i]
+ inputs["offset_mapping"][i] = [
+ o if sequence_ids[k] == 1 else None for k, o in enumerate(offset)
+ ]
+
+ inputs["example_id"] = example_ids
+ return inputs
+
+
+def preprocess_train_function(examples, tokenizer):
+ inputs = tokenizer(
+ [q.strip() for q in examples["question"]],
+ examples["context"],
+ max_length=384,
+ truncation="only_second",
+ return_offsets_mapping=True,
+ padding="max_length",
+ )
+
+ offset_mapping = inputs["offset_mapping"]
+ answers = examples["answers"]
+ start_positions = []
+ end_positions = []
+
+ for i, (offset, answer) in enumerate(zip(offset_mapping, answers)):
+ start_char = answer["answer_start"][0]
+ end_char = start_char + len(answer["text"][0])
+ sequence_ids = inputs.sequence_ids(i)
+
+ # Find the start and end of the context
+ idx = 0
+ while sequence_ids[idx] != 1:
+ idx += 1
+ context_start = idx
+ while sequence_ids[idx] == 1:
+ idx += 1
+ context_end = idx - 1
+
+ # If the answer is not fully inside the context, label it (0, 0)
+ if offset[context_start][0] > end_char or offset[context_end][1] < start_char:
+ start_positions.append(0)
+ end_positions.append(0)
+ else:
+ # Otherwise it's the start and end token positions
+ idx = context_start
+ while idx <= context_end and offset[idx][0] <= start_char:
+ idx += 1
+ start_positions.append(idx - 1)
+
+ idx = context_end
+ while idx >= context_start and offset[idx][1] >= end_char:
+ idx -= 1
+ end_positions.append(idx + 1)
+
+ inputs["start_positions"] = start_positions
+ inputs["end_positions"] = end_positions
+ return inputs
+
+
+def compute_metrics(start_logits, end_logits, features, examples):
+ n_best = 20
+ max_answer_length = 30
+ metric = evaluate.load("squad")
+
+ example_to_features = collections.defaultdict(list)
+ for idx, feature in enumerate(features):
+ example_to_features[feature["example_id"]].append(idx)
+
+ predicted_answers = []
+ # for example in ``tqdm`` (examples):
+ for example in examples:
+ example_id = example["id"]
+ context = example["context"]
+ answers = []
+
+ # Loop through all features associated with that example
+ for feature_index in example_to_features[example_id]:
+ start_logit = start_logits[feature_index]
+ end_logit = end_logits[feature_index]
+ offsets = features[feature_index]["offset_mapping"]
+
+ start_indexes = np.argsort(start_logit)[-1 : -n_best - 1 : -1].tolist()
+ end_indexes = np.argsort(end_logit)[-1 : -n_best - 1 : -1].tolist()
+ for start_index in start_indexes:
+ for end_index in end_indexes:
+ # Skip answers that are not fully in the context
+ if offsets[start_index] is None or offsets[end_index] is None:
+ continue
+ # Skip answers with a length that is either < 0
+ # or > max_answer_length
+ if (
+ end_index < start_index
+ or end_index - start_index + 1 > max_answer_length
+ ):
+ continue
+
+ answer = {
+ "text": context[
+ offsets[start_index][0] : offsets[end_index][1]
+ ],
+ "logit_score": start_logit[start_index] + end_logit[end_index],
+ }
+ answers.append(answer)
+
+ # Select the answer with the best score
+ if len(answers) > 0:
+ best_answer = max(answers, key=lambda x: x["logit_score"])
+ predicted_answers.append(
+ {"id": example_id, "prediction_text": best_answer["text"]}
+ )
+ else:
+ predicted_answers.append({"id": example_id, "prediction_text": ""})
+
+ theoretical_answers = [
+ {"id": ex["id"], "answers": ex["answers"]} for ex in examples
+ ]
+ return metric.compute(predictions=predicted_answers, references=theoretical_answers)
+
+
+######################################################################
+# Now that those are defined, we just need one additional helper function,
+# which will help us benchmark our model.
+#
+
+def measure_execution_time(model, batch_sizes, dataset):
+ dataset_for_model = dataset.remove_columns(["example_id", "offset_mapping"])
+ dataset_for_model.set_format("torch")
+ batch_size_to_time_sec = {}
+ for batch_size in batch_sizes:
+ batch = {
+ k: dataset_for_model[k][:batch_size].cuda()
+ for k in dataset_for_model.column_names
+ }
+
+ with torch.no_grad():
+ baseline_predictions = model(**batch)
+ timer = benchmark.Timer(
+ stmt="model(**batch)", globals={"model": model, "batch": batch}
+ )
+ p50 = timer.blocked_autorange().median * 1000
+ batch_size_to_time_sec[batch_size] = p50
+
+ model_c = torch.compile(model, fullgraph=True)
+ timer = benchmark.Timer(
+ stmt="model(**batch)", globals={"model": model_c, "batch": batch}
+ )
+ p50 = timer.blocked_autorange().median * 1000
+ batch_size_to_time_sec[f"{batch_size}_compile"] = p50
+ new_predictions = model_c(**batch)
+
+ return batch_size_to_time_sec
+
+
+
+######################################################################
+# We will get started by loading our model and tokenizer, and then setting
+# up our dataset.
+#
+
+# load model
+model_name = "bert-base-cased"
+tokenizer = transformers.AutoTokenizer.from_pretrained(model_name)
+model = transformers.AutoModelForQuestionAnswering.from_pretrained(model_name)
+print(f"Loading tokenizer: {model_name}")
+print(f"Loading model: {model_name}")
+
+# set up train and val dataset
+squad_dataset = datasets.load_dataset("squad")
+tokenized_squad_dataset = {}
+tokenized_squad_dataset["train"] = squad_dataset["train"].map(
+ lambda x: preprocess_train_function(x, tokenizer), batched=True
+)
+tokenized_squad_dataset["validation"] = squad_dataset["validation"].map(
+ lambda x: preprocess_validation_function(x, tokenizer),
+ batched=True,
+ remove_columns=squad_dataset["train"].column_names,
+)
+data_collator = transformers.DataCollatorWithPadding(tokenizer=tokenizer)
+
+
+######################################################################
+# Establishing a baseline
+# =======================
+#
+# Next, we’ll train a quick baseline of our model on SQuAD. This task asks
+# our model to identify spans, or segments of text, in a given context
+# (Wikipedia articles) that answer a given question. Running the following
+# code gives me an F1 score of 86.9. This is quite close to the reported
+# NVIDIA score and the difference is likely due to BERT-base
+# vs. BERT-large or fine-tuning hyperparameters.
+#
+
+training_args = transformers.TrainingArguments(
+ "trainer",
+ num_train_epochs=1,
+ lr_scheduler_type="constant",
+ per_device_train_batch_size=32,
+ per_device_eval_batch_size=256,
+ logging_steps=50,
+ # Limit max steps for tutorial runners. Delete the below line to see the reported accuracy numbers.
+ max_steps=500,
+ report_to=None,
+)
+
+trainer = transformers.Trainer(
+ model,
+ training_args,
+ train_dataset=tokenized_squad_dataset["train"],
+ eval_dataset=tokenized_squad_dataset["validation"],
+ data_collator=data_collator,
+ tokenizer=tokenizer,
+)
+
+trainer.train()
+
+# batch sizes to compare for eval
+batch_sizes = [4, 16, 64, 256]
+# 2:4 sparsity require fp16, so we cast here for a fair comparison
+with torch.autocast("cuda"):
+ with torch.no_grad():
+ predictions = trainer.predict(tokenized_squad_dataset["validation"])
+ start_logits, end_logits = predictions.predictions
+ fp16_baseline = compute_metrics(
+ start_logits,
+ end_logits,
+ tokenized_squad_dataset["validation"],
+ squad_dataset["validation"],
+ )
+ fp16_time = measure_execution_time(
+ model,
+ batch_sizes,
+ tokenized_squad_dataset["validation"],
+ )
+
+print("fp16", fp16_baseline)
+print("cuda_fp16 time", fp16_time)
+
+import pandas as pd
+df = pd.DataFrame(trainer.state.log_history)
+df.plot.line(x='step', y='loss', title="Loss vs. # steps", ylabel="loss")
+
+
+######################################################################
+# Pruning BERT to be 2:4 sparse
+# -----------------------------
+#
+# Now that we have our baseline, it’s time we prune BERT. There are many
+# different pruning strategies, but one of the most common is **magnitude
+# pruning**, which seeks to remove the weights with the lowest L1 norm.
+# Magnitude pruning was used by NVIDIA in all their results and is a
+# common baseline.
+#
+# To do this, we will use the ``torch.ao.pruning`` package, which contains
+# a weight-norm (magnitude) sparsifier. These sparsifiers work by applying
+# mask parametrizations to the weight tensors in a model. This lets them
+# simulate sparsity by masking out the pruned weights.
+#
+# We’ll also have to decide what layers of the model to apply sparsity to,
+# which in this case is all of the ``nn.Linear`` layers, except for the
+# task-specific head outputs. That’s because semi-structured sparsity has
+# `shape constraints `_,
+# and the task-specific ``nn.Linear`` layers do not satisfy them.
+#
+
+sparsifier = WeightNormSparsifier(
+ # apply sparsity to all blocks
+ sparsity_level=1.0,
+ # shape of 4 elements is a block
+ sparse_block_shape=(1, 4),
+ # two zeros for every block of 4
+ zeros_per_block=2
+)
+
+# add to config if ``nn.Linear`` and in the BERT model.
+sparse_config = [
+ {"tensor_fqn": f"{fqn}.weight"}
+ for fqn, module in model.named_modules()
+ if isinstance(module, nn.Linear) and "layer" in fqn
+]
+
+
+######################################################################
+# The first step for pruning the model is to insert parametrizations for
+# masking the weights of the model. This is done by the prepare step.
+# Anytime we try to access the ``.weight`` we will get ``mask * weight``
+# instead.
+#
+
+# Prepare the model, insert fake-sparsity parametrizations for training
+sparsifier.prepare(model, sparse_config)
+print(model.bert.encoder.layer[0].output)
+
+
+######################################################################
+# Then, we’ll take a single pruning step. All pruners implement a
+# ``update_mask()`` method that updates the mask with the logic being
+# determined by the pruner implementation. The step method calls this
+# ``update_mask`` functions for the weights specified in the sparse
+# config.
+#
+# We will also evaluate the model to show the accuracy degradation of
+# zero-shot pruning, or pruning without fine-tuning / retraining.
+#
+
+sparsifier.step()
+with torch.autocast("cuda"):
+ with torch.no_grad():
+ predictions = trainer.predict(tokenized_squad_dataset["validation"])
+ pruned = compute_metrics(
+ *predictions.predictions,
+ tokenized_squad_dataset["validation"],
+ squad_dataset["validation"],
+ )
+print("pruned eval metrics:", pruned)
+
+
+######################################################################
+# In this state, we can start fine-tuning the model, updating the elements
+# that wouldn’t be pruned to better account for the accuracy loss. Once
+# we’ve reached a satisfied state, we can call ``squash_mask`` to fuse the
+# mask and the weight together. This will remove the parametrizations and
+# we are left with a zeroed-out 2:4 dense model.
+#
+
+trainer.train()
+sparsifier.squash_mask()
+torch.set_printoptions(edgeitems=4)
+print(model.bert.encoder.layer[0].intermediate.dense.weight[:8, :8])
+
+df["sparse_loss"] = pd.DataFrame(trainer.state.log_history)["loss"]
+df.plot.line(x='step', y=["loss", "sparse_loss"], title="Loss vs. # steps", ylabel="loss")
+
+
+######################################################################
+# Accelerating 2:4 sparse models for inference
+# --------------------------------------------
+#
+# Now that we have a model in this format, we can accelerate it for
+# inference just like in the QuickStart Guide.
+#
+
+model = model.cuda().half()
+# accelerate for sparsity
+for fqn, module in model.named_modules():
+ if isinstance(module, nn.Linear) and "layer" in fqn:
+ module.weight = nn.Parameter(to_sparse_semi_structured(module.weight))
+
+with torch.no_grad():
+ predictions = trainer.predict(tokenized_squad_dataset["validation"])
+start_logits, end_logits = predictions.predictions
+metrics_sparse = compute_metrics(
+ start_logits,
+ end_logits,
+ tokenized_squad_dataset["validation"],
+ squad_dataset["validation"],
+)
+print("sparse eval metrics: ", metrics_sparse)
+sparse_perf = measure_execution_time(
+ model,
+ batch_sizes,
+ tokenized_squad_dataset["validation"],
+)
+print("sparse perf metrics: ", sparse_perf)
+
+
+######################################################################
+# Retraining our model after magnitude pruning has recovered nearly all of
+# the F1 that has been lost when the model was pruned. At the same time we
+# have achieved a 1.28x speedup for ``bs=16``. Note that not all shapes are
+# amenable to performance improvements. When batch sizes are small and
+# limited time is spent in compute sparse kernels may be slower than their
+# dense counterparts.
+#
+# Because semi-structured sparsity is implemented as a tensor subclass, it
+# is compatible with ``torch.compile``. When composed with
+# ``to_sparse_semi_structured``, we are able to achieve a total 2x speedup
+# on BERT.
+#
+# .. table::
+#
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Metrics | fp16 | 2:4 sparse | delta / speedup | compiled |
+# +====================+========+==============+=================+===========+
+# | Exact Match (%) | 78.53 | 78.44 | -0.09 | |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | F1 (%) | 86.93 | 86.49 | -0.44 | |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=4) | 11.10 | 15.54 | 0.71x | no |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=16) | 19.35 | 15.74 | 1.23x | no |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=64) | 72.71 | 59.41 | 1.22x | no |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=256) | 286.65 | 247.63 | 1.14x | no |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=4) | 7.59 | 7.46 | 1.02x | yes |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=16) | 11.47 | 9.68 | 1.18x | yes |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=64) | 41.57 | 36.92 | 1.13x | yes |
+# +--------------------+--------+--------------+-----------------+-----------+
+# | Time (bs=256) | 159.22 | 142.23 | 1.12x | yes |
+# +--------------------+--------+--------------+-----------------+-----------+
+#
+# Conclusion
+# ==========
+#
+# In this tutorial, we have shown how to prune BERT to be 2:4 sparse and
+# how to accelerate a 2:4 sparse model for inference. By taking advantage
+# of our ``SparseSemiStructuredTensor`` subclass, we were able to achieve a
+# 1.3x speedup over the fp16 baseline, and up to 2x with
+# ``torch.compile``. We also demonstrated the benefits of 2:4 sparsity by
+# fine-tuning BERT to recover any lost F1 (86.92 dense vs 86.48 sparse).
+#
diff --git a/advanced_source/static_quantization_tutorial.rst b/advanced_source/static_quantization_tutorial.rst
index fe24050e0..2a6ef89ad 100644
--- a/advanced_source/static_quantization_tutorial.rst
+++ b/advanced_source/static_quantization_tutorial.rst
@@ -59,8 +59,8 @@
- 신경망의 처음과 끝에 ``QuantStub`` 및 ``DeQuantStub`` 삽입
- ReLU를 ReLU6로 교체
-알림: `여기 `_ 에서
-이 코드를 가져왔습니다.
+알림: 이 코드는 `여기 `_
+에서 가져왔습니다.
.. code:: python
@@ -207,14 +207,15 @@
# 양자화 전에 Conv+BN과 Conv+BN+Relu 모듈 결합(fusion)
# 이 연산은 숫자를 변경하지 않음
- def fuse_model(self):
+ def fuse_model(self, is_qat=False):
+ fuse_modules = torch.ao.quantization.fuse_modules_qat if is_qat else torch.ao.quantization.fuse_modules
for m in self.modules():
if type(m) == ConvBNReLU:
- torch.ao.quantization.fuse_modules(m, ['0', '1', '2'], inplace=True)
+ fuse_modules(m, ['0', '1', '2'], inplace=True)
if type(m) == InvertedResidual:
for idx in range(len(m.conv)):
if type(m.conv[idx]) == nn.Conv2d:
- torch.ao.quantization.fuse_modules(m.conv, [str(idx), str(idx + 1)], inplace=True)
+ fuse_modules(m.conv, [str(idx), str(idx + 1)], inplace=True)
2. 헬퍼(Helper) 함수
----------------------
@@ -426,16 +427,19 @@ ImageNet 데이터
print(myModel.qconfig)
torch.ao.quantization.prepare(myModel, inplace=True)
- # 첫 번째 보정
+ # 첫 번째 보정(calibrate)
print('Post Training Quantization Prepare: Inserting Observers')
print('\n Inverted Residual Block:After observer insertion \n\n', myModel.features[1].conv)
- # 학습 세트로 보정
+ # 학습 데이터셋으로 보정(calibrate)
evaluate(myModel, criterion, data_loader, neval_batches=num_calibration_batches)
print('Post Training Quantization: Calibration done')
# 양자화된 모델로 변환
torch.ao.quantization.convert(myModel, inplace=True)
+ # 모델을 보정해야 한다(calibrate the model)는 사용자 경고(user warning)가 표시될 수 있지만 무시해도 됩니다.
+ # 이 경고는 각 모델 실행 시 모든 모듈이 실행되는 것이 아니기 때문에 일부 모듈이 보정되지 않을 수
+ # 있다는 경고입니다.
print('Post Training Quantization: Convert done')
print('\n Inverted Residual Block: After fusion and quantization, note fused modules: \n\n',myModel.features[1].conv)
@@ -533,7 +537,7 @@ x86 아키텍처에서 양자화를 위한 권장 설정을 그대로 쓰기만
.. code:: python
qat_model = load_model(saved_model_dir + float_model_file)
- qat_model.fuse_model()
+ qat_model.fuse_model(is_qat=True)
optimizer = torch.optim.SGD(qat_model.parameters(), lr = 0.0001)
# 이전의 'fbgemm' 또한 여전히 사용 가능하지만, 'x86'을 기본으로 사용하는 것을 권장합니다.
diff --git a/advanced_source/super_resolution_with_onnxruntime.py b/advanced_source/super_resolution_with_onnxruntime.py
index 5fdf00cf4..52e01ff7b 100644
--- a/advanced_source/super_resolution_with_onnxruntime.py
+++ b/advanced_source/super_resolution_with_onnxruntime.py
@@ -1,23 +1,38 @@
"""
(선택) PyTorch 모델을 ONNX으로 변환하고 ONNX 런타임에서 실행하기
========================================================================
-이 튜토리얼에서는 어떻게 PyTorch에서 정의된 모델을 ONNX 형식으로 변환하고 또 어떻게 그 변환된 모델을
-ONNX 런타임에서 실행할 수 있는지에 대해 알아보도록 하겠습니다.
-ONNX 런타임은 ONNX 모델을 위한 엔진으로서 성능에 초점을 맞추고 있고 여러 다양한 플랫폼과 하드웨어(윈도우,
-리눅스, 맥을 비롯한 플랫폼 뿐만 아니라 CPU, GPU 등의 하드웨어)에서 효율적인 추론을 가능하게 합니다.
-ONNX 런타임은 `여기
-`__ 에서
-설명된 것과 같이 여러 모델들의 성능을 상당히 높일 수 있다는 점이 증명되었습니다.
-이 튜토리얼을 진행하기 위해서는 `ONNX `__
-와 `ONNX Runtime `__ 설치가 필요합니다.
-ONNX와 ONNX 런타임의 바이너리 빌드를 ``pip install onnx onnxruntime`` 를 통해 받을 수 있습니다.
-ONNX 런타임은 버전 3.5에서 3.7까지의 Python과 호환됩니다.
-``참고``: 본 튜토리얼은 PyTorch의 master 브랜치를 필요로하며 `링크 `__ 에서
-설치할 수 있습니다.
+
+.. Note::
+ PyTorch 2.1부터 ONNX Exporter에는 두 가지 버전이 존재합니다.
+ * ``torch.onnx.dynamo_export`` 는 PyTorch 2.0과 함께 출시된 TorchDynamo 기술 기반의 최신(이지만 아직 베타 버전의) ONNX Exporter입니다.
+ * ``torch.onnx.export`` 는 PyuTorch 1.2.0부터 지원 중인 TorchScript 백엔드에 기반한 ONNX Exporter입니다.
+
+이 튜토리얼에서는 TorchScript 기반의 ONNX Exporter인 ``torch.onnx.export`` 를 사용하여
+PyTorch에서 정의한 모델을 어떻게 ONNX 형식으로 변환하는지를 살펴보도록 하겠습니다.
+
+이렇게 변환된 모델은 ONNX 런타임(Runtime)에서 실행됩니다.
+ONNX 런타임은 다양한 플랫폼과 하드웨어(윈도우즈, 리눅스, 맥 및 CPU, GPU 모두)에서
+효율적으로 추론하는, 성능에 초점을 맞춘 ONNX 모델을 위한 엔진입니다.
+
+`여기 `__
+에서 설명한 것처럼 ONNX 런타임을 활용하면 여러 모델들의 성능을
+상당히 높일 수 있다는 것이 증명되었습니다.
+
+이 튜토리얼의 진행을 위해 `ONNX `__
+및 `ONNX 런타임(Runtime) `__ 의 설치가 필요합니다.
+
+ONNX 및 ONNX 런타임은 다음과 같이 설치할 수 있습니다:
+
+.. code-block:: bash
+
+ %%bash
+ pip install onnx onnxruntime
+
+ONNX 런타임은 최신 버전의 PyTorch 런타임을 사용하는 것을 권장합니다.
+
"""
# 필요한 import문
-import io
import numpy as np
from torch import nn
@@ -166,7 +181,7 @@ def _initialize_weights(self):
import onnxruntime
-ort_session = onnxruntime.InferenceSession("super_resolution.onnx")
+ort_session = onnxruntime.InferenceSession("super_resolution.onnx", providers=["CPUExecutionProvider"])
def to_numpy(tensor):
return tensor.detach().cpu().numpy() if tensor.requires_grad else tensor.cpu().numpy()
diff --git a/advanced_source/usb_semisup_learn.py b/advanced_source/usb_semisup_learn.py
new file mode 100644
index 000000000..421282854
--- /dev/null
+++ b/advanced_source/usb_semisup_learn.py
@@ -0,0 +1,253 @@
+"""
+Semi-Supervised Learning using USB built upon PyTorch
+=====================================================
+
+**Author**: `Hao Chen `_
+
+Unified Semi-supervised learning Benchmark (USB) is a semi-supervised
+learning (SSL) framework built upon PyTorch.
+Based on Datasets and Modules provided by PyTorch, USB becomes a flexible,
+modular, and easy-to-use framework for semi-supervised learning.
+It supports a variety of semi-supervised learning algorithms, including
+``FixMatch``, ``FreeMatch``, ``DeFixMatch``, ``SoftMatch``, and so on.
+It also supports a variety of imbalanced semi-supervised learning algorithms.
+The benchmark results across different datasets of computer vision, natural
+language processing, and speech processing are included in USB.
+
+This tutorial will walk you through the basics of using the USB lighting
+package.
+Let's get started by training a ``FreeMatch``/``SoftMatch`` model on
+CIFAR-10 using pretrained Vision Transformers (ViT)!
+And we will show it is easy to change the semi-supervised algorithm and train
+on imbalanced datasets.
+
+
+.. figure:: /_static/img/usb_semisup_learn/code.png
+ :alt: USB framework illustration
+"""
+
+
+######################################################################
+# Introduction to ``FreeMatch`` and ``SoftMatch`` in Semi-Supervised Learning
+# ---------------------------------------------------------------------------
+#
+# Here we provide a brief introduction to ``FreeMatch`` and ``SoftMatch``.
+# First, we introduce a famous baseline for semi-supervised learning called ``FixMatch``.
+# ``FixMatch`` is a very simple framework for semi-supervised learning, where it
+# utilizes a strong augmentation to generate pseudo labels for unlabeled data.
+# It adopts a confidence thresholding strategy to filter out the low-confidence
+# pseudo labels with a fixed threshold set.
+# ``FreeMatch`` and ``SoftMatch`` are two algorithms that improve upon ``FixMatch``.
+# ``FreeMatch`` proposes adaptive thresholding strategy to replace the fixed
+# thresholding strategy in ``FixMatch``. The adaptive thresholding progressively
+# increases the threshold according to the learning status of the model on each
+# class. ``SoftMatch`` absorbs the idea of confidence thresholding as an
+# weighting mechanism. It proposes a Gaussian weighting mechanism to overcome
+# the quantity-quality trade-off in pseudo-labels. In this tutorial, we will
+# use USB to train ``FreeMatch`` and ``SoftMatch``.
+
+
+######################################################################
+# Use USB to Train ``FreeMatch``/``SoftMatch`` on CIFAR-10 with only 40 labels
+# ----------------------------------------------------------------------------
+#
+# USB is easy to use and extend, affordable to small groups, and comprehensive
+# for developing and evaluating SSL algorithms.
+# USB provides the implementation of 14 SSL algorithms based on Consistency
+# Regularization, and 15 tasks for evaluation from CV, NLP, and Audio domain.
+# It has a modular design that allows users to easily extend the package by
+# adding new algorithms and tasks.
+# It also supports a Python API for easier adaptation to different SSL
+# algorithms on new data.
+#
+#
+# Now, let's use USB to train ``FreeMatch`` and ``SoftMatch`` on CIFAR-10.
+# First, we need to install USB package ``semilearn`` and import necessary API
+# functions from USB.
+# If you are running this in Google Colab, install ``semilearn`` by running:
+# ``!pip install semilearn``.
+#
+# Below is a list of functions we will use from ``semilearn``:
+#
+# - ``get_dataset`` to load dataset, here we use CIFAR-10
+# - ``get_data_loader`` to create train (labeled and unlabeled) and test data
+# loaders, the train unlabeled loaders will provide both strong and weak
+# augmentation of unlabeled data
+# - ``get_net_builder`` to create a model, here we use pretrained ViT
+# - ``get_algorithm`` to create the semi-supervised learning algorithm,
+# here we use ``FreeMatch`` and ``SoftMatch``
+# - ``get_config``: to get default configuration of the algorithm
+# - ``Trainer``: a Trainer class for training and evaluating the
+# algorithm on dataset
+#
+# Note that a CUDA-enabled backend is required for training with the ``semilearn`` package.
+# See `Enabling CUDA in Google Colab `__ for instructions
+# on enabling CUDA in Google Colab.
+#
+import semilearn
+from semilearn import get_dataset, get_data_loader, get_net_builder, get_algorithm, get_config, Trainer
+
+######################################################################
+# After importing necessary functions, we first set the hyper-parameters of the
+# algorithm.
+#
+config = {
+ 'algorithm': 'freematch',
+ 'net': 'vit_tiny_patch2_32',
+ 'use_pretrain': True,
+ 'pretrain_path': 'https://github.com/microsoft/Semi-supervised-learning/releases/download/v.0.0.0/vit_tiny_patch2_32_mlp_im_1k_32.pth',
+
+ # optimization configs
+ 'epoch': 1,
+ 'num_train_iter': 500,
+ 'num_eval_iter': 500,
+ 'num_log_iter': 50,
+ 'optim': 'AdamW',
+ 'lr': 5e-4,
+ 'layer_decay': 0.5,
+ 'batch_size': 16,
+ 'eval_batch_size': 16,
+
+
+ # dataset configs
+ 'dataset': 'cifar10',
+ 'num_labels': 40,
+ 'num_classes': 10,
+ 'img_size': 32,
+ 'crop_ratio': 0.875,
+ 'data_dir': './data',
+ 'ulb_samples_per_class': None,
+
+ # algorithm specific configs
+ 'hard_label': True,
+ 'T': 0.5,
+ 'ema_p': 0.999,
+ 'ent_loss_ratio': 0.001,
+ 'uratio': 2,
+ 'ulb_loss_ratio': 1.0,
+
+ # device configs
+ 'gpu': 0,
+ 'world_size': 1,
+ 'distributed': False,
+ "num_workers": 4,
+}
+config = get_config(config)
+
+
+######################################################################
+# Then, we load the dataset and create data loaders for training and testing.
+# And we specify the model and algorithm to use.
+#
+dataset_dict = get_dataset(config, config.algorithm, config.dataset, config.num_labels, config.num_classes, data_dir=config.data_dir, include_lb_to_ulb=config.include_lb_to_ulb)
+train_lb_loader = get_data_loader(config, dataset_dict['train_lb'], config.batch_size)
+train_ulb_loader = get_data_loader(config, dataset_dict['train_ulb'], int(config.batch_size * config.uratio))
+eval_loader = get_data_loader(config, dataset_dict['eval'], config.eval_batch_size)
+algorithm = get_algorithm(config, get_net_builder(config.net, from_name=False), tb_log=None, logger=None)
+
+
+######################################################################
+# We can start training the algorithms on CIFAR-10 with 40 labels now.
+# We train for 500 iterations and evaluate every 500 iterations.
+#
+trainer = Trainer(config, algorithm)
+trainer.fit(train_lb_loader, train_ulb_loader, eval_loader)
+
+
+######################################################################
+# Finally, let's evaluate the trained model on the validation set.
+# After training 500 iterations with ``FreeMatch`` on only 40 labels of
+# CIFAR-10, we obtain a classifier that achieves around 87% accuracy on the validation set.
+trainer.evaluate(eval_loader)
+
+
+
+######################################################################
+# Use USB to Train ``SoftMatch`` with specific imbalanced algorithm on imbalanced CIFAR-10
+# ----------------------------------------------------------------------------------------
+#
+# Now let's say we have imbalanced labeled set and unlabeled set of CIFAR-10,
+# and we want to train a ``SoftMatch`` model on it.
+# We create an imbalanced labeled set and imbalanced unlabeled set of CIFAR-10,
+# by setting the ``lb_imb_ratio`` and ``ulb_imb_ratio`` to 10.
+# Also, we replace the ``algorithm`` with ``softmatch`` and set the ``imbalanced``
+# to ``True``.
+#
+config = {
+ 'algorithm': 'softmatch',
+ 'net': 'vit_tiny_patch2_32',
+ 'use_pretrain': True,
+ 'pretrain_path': 'https://github.com/microsoft/Semi-supervised-learning/releases/download/v.0.0.0/vit_tiny_patch2_32_mlp_im_1k_32.pth',
+
+ # optimization configs
+ 'epoch': 1,
+ 'num_train_iter': 500,
+ 'num_eval_iter': 500,
+ 'num_log_iter': 50,
+ 'optim': 'AdamW',
+ 'lr': 5e-4,
+ 'layer_decay': 0.5,
+ 'batch_size': 16,
+ 'eval_batch_size': 16,
+
+
+ # dataset configs
+ 'dataset': 'cifar10',
+ 'num_labels': 1500,
+ 'num_classes': 10,
+ 'img_size': 32,
+ 'crop_ratio': 0.875,
+ 'data_dir': './data',
+ 'ulb_samples_per_class': None,
+ 'lb_imb_ratio': 10,
+ 'ulb_imb_ratio': 10,
+ 'ulb_num_labels': 3000,
+
+ # algorithm specific configs
+ 'hard_label': True,
+ 'T': 0.5,
+ 'ema_p': 0.999,
+ 'ent_loss_ratio': 0.001,
+ 'uratio': 2,
+ 'ulb_loss_ratio': 1.0,
+
+ # device configs
+ 'gpu': 0,
+ 'world_size': 1,
+ 'distributed': False,
+ "num_workers": 4,
+}
+config = get_config(config)
+
+######################################################################
+# Then, we re-load the dataset and create data loaders for training and testing.
+# And we specify the model and algorithm to use.
+#
+dataset_dict = get_dataset(config, config.algorithm, config.dataset, config.num_labels, config.num_classes, data_dir=config.data_dir, include_lb_to_ulb=config.include_lb_to_ulb)
+train_lb_loader = get_data_loader(config, dataset_dict['train_lb'], config.batch_size)
+train_ulb_loader = get_data_loader(config, dataset_dict['train_ulb'], int(config.batch_size * config.uratio))
+eval_loader = get_data_loader(config, dataset_dict['eval'], config.eval_batch_size)
+algorithm = get_algorithm(config, get_net_builder(config.net, from_name=False), tb_log=None, logger=None)
+
+
+######################################################################
+# We can start Train the algorithms on CIFAR-10 with 40 labels now.
+# We train for 500 iterations and evaluate every 500 iterations.
+#
+trainer = Trainer(config, algorithm)
+trainer.fit(train_lb_loader, train_ulb_loader, eval_loader)
+
+
+######################################################################
+# Finally, let's evaluate the trained model on the validation set.
+#
+trainer.evaluate(eval_loader)
+
+
+
+######################################################################
+# References:
+# - [1] USB: https://github.com/microsoft/Semi-supervised-learning
+# - [2] Kihyuk Sohn et al. FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence
+# - [3] Yidong Wang et al. FreeMatch: Self-adaptive Thresholding for Semi-supervised Learning
+# - [4] Hao Chen et al. SoftMatch: Addressing the Quantity-Quality Trade-off in Semi-supervised Learning
diff --git a/beginner_source/Intro_to_TorchScript_tutorial.py b/beginner_source/Intro_to_TorchScript_tutorial.py
index 832536a74..bfe78618a 100644
--- a/beginner_source/Intro_to_TorchScript_tutorial.py
+++ b/beginner_source/Intro_to_TorchScript_tutorial.py
@@ -31,9 +31,9 @@
"""
-import torch # This is all you need to use both PyTorch and TorchScript!
+import torch # PyTorch와 TorchScript를 사용하기 위해 필요한건 이것이 전부입니다!
print(torch.__version__)
-
+torch.manual_seed(191009) # 재현을 위해 시드값(seed)을 설정합니다.
######################################################################
# PyTorch 모델 작성의 기초
@@ -113,7 +113,7 @@ def forward(self, x, h):
# 모델을 간결하고 읽기 쉽게 작성할 수 있습니다.
#
# 여러분은 출력된 내용에서 ``grad_fn`` 을 확인하셨을 것입니다. 이것은
-# `오토그라드(autograd) `__
+# `Autograd `__
# 라 불리는 PyTorch의 자동 미분 방법의 세부 정보입니다. 요컨데, 이 시스템은
# 잠재적으로 복잡한 프로그램을 통해 미분을 계산할 수 있게 합니다. 이 디자인은
# 모델 제작에 엄청난 유연성을 제공합니다.
@@ -155,9 +155,9 @@ def forward(self, x, h):
# 대한 미분값을 명시적으로 정의할 필요가 없습니다.
#
# .. figure:: https://github.com/pytorch/pytorch/raw/main/docs/source/_static/img/dynamic_graph.gif
-# :alt: 오토그라드가 작동하는 방식
+# :alt: Autograd가 동작하는 방식 방식
#
-# 오토그라드가 작동하는 방식
+# Autograd가 작동하는 방식
#
@@ -295,7 +295,7 @@ def forward(self, x, h):
# 새로운 입력
x, h = torch.rand(3, 4), torch.rand(3, 4)
-traced_cell(x, h)
+print(scripted_cell(x, h))
######################################################################
@@ -373,6 +373,7 @@ def forward(self, xs):
#
# 더 읽을거리
# ~~~~~~~~~~~~~~~
+#
# 튜토리얼을 완료했습니다! 관련 데모를 보려면 TorchScript를 사용하여 기계 번역
# 모델을 변환하기 위한 NeurIPS 데모를 확인하십시오:
# https://colab.research.google.com/drive/1HiICg6jRkBnr5hvK2-VnMi88Vi9pUzEJ
diff --git a/beginner_source/PyTorch Cheat.md b/beginner_source/PyTorch Cheat.md
index d0aacadb5..f67d69903 100644
--- a/beginner_source/PyTorch Cheat.md
+++ b/beginner_source/PyTorch Cheat.md
@@ -102,7 +102,7 @@ See [math operations](https://pytorch.org/docs/stable/torch.html?highlight=mm#ma
### GPU Usage
```
-torch.cuda.is_available # check for cuda
+torch.cuda.is_available() # check for cuda
x.cuda() # move x's data from CPU to GPU and return new object
x.cpu() # move x's data from GPU to CPU and return new object
diff --git a/beginner_source/README.txt b/beginner_source/README.txt
index 2b73514ee..c49532c9f 100644
--- a/beginner_source/README.txt
+++ b/beginner_source/README.txt
@@ -23,4 +23,4 @@ Beginner Tutorials
6. transformer_translation.py
Language Translation with Transformers
- https://tutorials.pytorch.kr/beginner/transformer_tutorial.html
+ https://tutorials.pytorch.kr/beginner/translation_transformer.html
diff --git a/beginner_source/basics/autogradqs_tutorial.py b/beginner_source/basics/autogradqs_tutorial.py
index a9f162aad..5142f7459 100644
--- a/beginner_source/basics/autogradqs_tutorial.py
+++ b/beginner_source/basics/autogradqs_tutorial.py
@@ -35,7 +35,7 @@
######################################################################
# Tensor, Function과 연산그래프(Computational graph)
-# ------------------------------------------------------------------------------------------
+# --------------------------------------------------------------
#
# 이 코드는 다음의 **연산 그래프** 를 정의합니다:
#
@@ -64,7 +64,7 @@
######################################################################
# 변화도(Gradient) 계산하기
-# -------------------------
+# --------------------------------------------------------------
#
# 신경망에서 매개변수의 가중치를 최적화하려면 매개변수에 대한 손실함수의 도함수(derivative)를
# 계산해야 합니다. 즉, ``x``\ 와 ``y``\ 의 일부 고정값에서 :math:`\frac{\partial loss}{\partial w}`\ 와
@@ -91,7 +91,7 @@
######################################################################
# 변화도 추적 멈추기
-# ------------------------------------------------------------------------------------------
+# --------------------------------------------------------------
#
# 기본적으로, ``requires_grad=True``\ 인 모든 텐서들은 연산 기록을 추적하고 변화도 계산을
# 지원합니다. 그러나 모델을 학습한 뒤 입력 데이터를 단순히 적용하기만 하는 경우와 같이 *순전파*
@@ -126,7 +126,7 @@
######################################################################
# 연산 그래프에 대한 추가 정보
-# ------------------------------------------------------------------------------------------
+# --------------------------------------------------------------
#
# 개념적으로, autograd는 데이터(텐서)의 및 실행된 모든 연산들(및 연산 결과가 새로운 텐서인 경우도 포함하여)의
# 기록을 `Function `__ 객체로
@@ -209,6 +209,6 @@
#
#################################################################
-# 더 읽어 보기
+# 더 읽어보기
# ~~~~~~~~~~~~~~~~~
# - `Autograd Mechanics `_
diff --git a/beginner_source/basics/data_tutorial.py b/beginner_source/basics/data_tutorial.py
index fffc79000..2baef464a 100755
--- a/beginner_source/basics/data_tutorial.py
+++ b/beginner_source/basics/data_tutorial.py
@@ -145,7 +145,7 @@ def __getitem__(self, idx):
#################################################################
-# __init__
+# ``__init__``
# ^^^^^^^^^^^^^^^^^^^^
#
# __init__ 함수는 Dataset 객체가 생성(instantiate)될 때 한 번만 실행됩니다.
@@ -168,7 +168,7 @@ def __init__(self, annotations_file, img_dir, transform=None, target_transform=N
#################################################################
-# __len__
+# ``__len__``
# ^^^^^^^^^^^^^^^^^^^^
#
# __len__ 함수는 데이터셋의 샘플 개수를 반환합니다.
@@ -181,7 +181,7 @@ def __len__(self):
#################################################################
-# __getitem__
+# ``__getitem__``
# ^^^^^^^^^^^^^^^^^^^^
#
# __getitem__ 함수는 주어진 인덱스 ``idx`` 에 해당하는 샘플을 데이터셋에서 불러오고 반환합니다.
@@ -205,7 +205,7 @@ def __getitem__(self, idx):
#
-#################################################################
+######################################################################
# DataLoader로 학습용 데이터 준비하기
# ------------------------------------------------------------------------------------------
#
@@ -220,7 +220,7 @@ def __getitem__(self, idx):
train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=True)
-###########################
+######################################################################
# DataLoader를 통해 순회하기(iterate)
# ------------------------------------------------------------------------------------------
#
diff --git a/beginner_source/basics/optimization_tutorial.py b/beginner_source/basics/optimization_tutorial.py
index 67ade9650..d6d9ce9f7 100644
--- a/beginner_source/basics/optimization_tutorial.py
+++ b/beginner_source/basics/optimization_tutorial.py
@@ -49,7 +49,7 @@
class NeuralNetwork(nn.Module):
def __init__(self):
- super(NeuralNetwork, self).__init__()
+ super().__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28, 512),
@@ -149,26 +149,34 @@ def forward(self, x):
def train_loop(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
+ # 모델을 학습(train) 모드로 설정합니다 - 배치 정규화(Batch Normalization) 및 드롭아웃(Dropout) 레이어들에 중요합니다.
+ # 이 예시에서는 없어도 되지만, 모범 사례를 위해 추가해두었습니다.
+ model.train()
for batch, (X, y) in enumerate(dataloader):
# 예측(prediction)과 손실(loss) 계산
pred = model(X)
loss = loss_fn(pred, y)
# 역전파
- optimizer.zero_grad()
loss.backward()
optimizer.step()
+ optimizer.zero_grad()
if batch % 100 == 0:
- loss, current = loss.item(), (batch + 1) * len(X)
+ loss, current = loss.item(), batch * batch_size + len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
def test_loop(dataloader, model, loss_fn):
+ # 모델을 평가(eval) 모드로 설정합니다 - 배치 정규화(Batch Normalization) 및 드롭아웃(Dropout) 레이어들에 중요합니다.
+ # 이 예시에서는 없어도 되지만, 모범 사례를 위해 추가해두었습니다.
+ model.eval()
size = len(dataloader.dataset)
num_batches = len(dataloader)
test_loss, correct = 0, 0
+ # torch.no_grad()를 사용하여 테스트 시 변화도(gradient)를 계산하지 않도록 합니다.
+ # 이는 requires_grad=True로 설정된 텐서들의 불필요한 변화도 연산 및 메모리 사용량 또한 줄여줍니다.
with torch.no_grad():
for X, y in dataloader:
pred = model(X)
diff --git a/beginner_source/basics/quickstart_tutorial.py b/beginner_source/basics/quickstart_tutorial.py
index fb36ac1b2..2f19ac676 100644
--- a/beginner_source/basics/quickstart_tutorial.py
+++ b/beginner_source/basics/quickstart_tutorial.py
@@ -149,9 +149,9 @@ def train(dataloader, model, loss_fn, optimizer):
loss = loss_fn(pred, y)
# 역전파
- optimizer.zero_grad()
loss.backward()
optimizer.step()
+ optimizer.zero_grad()
if batch % 100 == 0:
loss, current = loss.item(), (batch + 1) * len(X)
diff --git a/beginner_source/basics/saveloadrun_tutorial.py b/beginner_source/basics/saveloadrun_tutorial.py
index cff004d14..60943e320 100644
--- a/beginner_source/basics/saveloadrun_tutorial.py
+++ b/beginner_source/basics/saveloadrun_tutorial.py
@@ -62,3 +62,4 @@
# 관련 튜토리얼
# -----------------
# :doc:`/recipes/recipes/saving_and_loading_a_general_checkpoint`
+# :doc:`/recipes/recipes/module_load_state_dict_tips`
\ No newline at end of file
diff --git a/beginner_source/basics/tensorqs_tutorial.py b/beginner_source/basics/tensorqs_tutorial.py
index 04c4fd50c..fae9f189c 100644
--- a/beginner_source/basics/tensorqs_tutorial.py
+++ b/beginner_source/basics/tensorqs_tutorial.py
@@ -132,7 +132,7 @@
######################################################################
# **텐서 합치기** ``torch.cat`` 을 사용하여 주어진 차원에 따라 일련의 텐서를 연결할 수 있습니다.
-# ``torch.cat`` 과 미묘하게 다른 또 다른 텐서 결합 연산인
+# ``torch.cat`` 과 미묘하게 다른 텐서 결합 연산자(tensor joining operator)인
# `torch.stack `__ 도 참고해보세요.
t1 = torch.cat([tensor, tensor, tensor], dim=1)
print(t1)
diff --git a/beginner_source/bettertransformer_tutorial.rst b/beginner_source/bettertransformer_tutorial.rst
index 96249d886..60ffa52ea 100644
--- a/beginner_source/bettertransformer_tutorial.rst
+++ b/beginner_source/bettertransformer_tutorial.rst
@@ -8,11 +8,11 @@ In this tutorial, we show how to use Better Transformer for production
inference with torchtext. Better Transformer is a production ready fastpath to
accelerate deployment of Transformer models with high performance on CPU and GPU.
The fastpath feature works transparently for models based either directly on
-PyTorch core nn.module or with torchtext.
+PyTorch core ``nn.module`` or with torchtext.
Models which can be accelerated by Better Transformer fastpath execution are those
-using the following PyTorch core `torch.nn.module` classes `TransformerEncoder`,
-`TransformerEncoderLayer`, and `MultiHeadAttention`. In addition, torchtext has
+using the following PyTorch core ``torch.nn.module`` classes ``TransformerEncoder``,
+``TransformerEncoderLayer``, and ``MultiHeadAttention``. In addition, torchtext has
been updated to use the core library modules to benefit from fastpath acceleration.
(Additional modules may be enabled with fastpath execution in the future.)
@@ -32,7 +32,8 @@ To follow this example in Google Colab, `click here
Better Transformer Features in This Tutorial
--------------------------------------------
-* Load pre-trained models (pre-1.12 created without Better Transformer)
+
+* Load pretrained models (created before PyTorch version 1.12 without Better Transformer)
* Run and benchmark inference on CPU with and without BT fastpath (native MHA only)
* Run and benchmark inference on (configurable) DEVICE with and without BT fastpath (native MHA only)
* Enable sparsity support
@@ -48,9 +49,9 @@ Additional information about Better Transformer may be found in the PyTorch.Org
1. Setup
-1.1 Load pre-trained models
+1.1 Load pretrained models
-We download the XLM-R model from the pre-defined torchtext models by following the instructions in
+We download the XLM-R model from the predefined torchtext models by following the instructions in
`torchtext.models `__. We also set the DEVICE to execute
on-accelerator tests. (Enable GPU execution for your environment as appropriate.)
diff --git a/beginner_source/blitz/autograd_tutorial.py b/beginner_source/blitz/autograd_tutorial.py
index de1b4ad41..0288988b8 100644
--- a/beginner_source/blitz/autograd_tutorial.py
+++ b/beginner_source/blitz/autograd_tutorial.py
@@ -149,7 +149,7 @@
######################################################################
-# 선택적으로 읽기(Optional Reading) - ``autograd`` 를 사용한 벡터 미적분(calculus)
+# 선택적 읽기(Optional Reading) - ``autograd`` 를 사용한 벡터 미적분(calculus)
# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
#
# 수학적으로, 벡터 함수 :math:`\vec{y}=f(\vec{x})` 에서 :math:`\vec{x}` 에
@@ -258,7 +258,7 @@
z = torch.rand((5, 5), requires_grad=True)
a = x + y
-print(f"Does `a` require gradients? : {a.requires_grad}")
+print(f"Does `a` require gradients?: {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")
@@ -309,5 +309,6 @@
# 더 읽어보기:
# ~~~~~~~~~~~~~~~~~~~
#
-# - `In-place operations & Multithreaded Autograd `__
-# - `Example implementation of reverse-mode autodiff `__
+# - `In-place operations & Multithreaded Autograd `__
+# - `Example implementation of reverse-mode autodiff `__
+# - `Video: PyTorch Autograd Explained - In-depth Tutorial `__
diff --git a/beginner_source/blitz/cifar10_tutorial.py b/beginner_source/blitz/cifar10_tutorial.py
index ae84a8c67..637345b53 100644
--- a/beginner_source/blitz/cifar10_tutorial.py
+++ b/beginner_source/blitz/cifar10_tutorial.py
@@ -1,7 +1,7 @@
# -*- coding: utf-8 -*-
"""
분류기(Classifier) 학습하기
-============================
+===============================
지금까지 어떻게 신경망을 정의하고, 손실을 계산하며 또 가중치를 갱신하는지에
대해서 배웠습니다.
@@ -9,7 +9,7 @@
이제 아마도 이런 생각을 하고 계실텐데요,
데이터는 어떻게 하나요?
-------------------------
+--------------------------
일반적으로 이미지나 텍스트, 오디오나 비디오 데이터를 다룰 때는 표준 Python 패키지를
이용하여 NumPy 배열로 불러오면 됩니다. 그 후 그 배열을 ``torch.*Tensor`` 로 변환합니다.
@@ -114,7 +114,7 @@ def imshow(img):
########################################################################
# 2. 합성곱 신경망(Convolution Neural Network) 정의하기
-# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
# 이전의 신경망 섹션에서 신경망을 복사한 후, (기존에 1채널 이미지만 처리하도록
# 정의된 것을) 3채널 이미지를 처리할 수 있도록 수정합니다.
@@ -289,7 +289,7 @@ def forward(self, x):
# 이러한 신경망들을 GPU에서 실행하려면 어떻게 해야 할까요?
#
# GPU에서 학습하기
-# ----------------
+# -----------------------------------------
# Tensor를 GPU로 이동했던 것처럼, 신경망 또한 GPU로 옮길 수 있습니다.
#
# 먼저 (CUDA를 사용할 수 있다면) 첫번째 CUDA 장치를 사용하도록 설정합니다:
@@ -331,12 +331,12 @@ def forward(self, x):
# - 이미지를 분류하는 작은 신경망을 학습시킵니다.
#
# 여러개의 GPU에서 학습하기
-# -------------------------
+# -----------------------------------------
# 모든 GPU를 활용해서 더욱 더 속도를 올리고 싶다면, :doc:`data_parallel_tutorial`
# 을 참고하세요.
#
# 이제 무엇을 해볼까요?
-# -----------------------
+# -----------------------------------------
#
# - :doc:`비디오 게임을 할 수 있는 신경망 학습시키기 `
# - `imagenet으로 최첨단(state-of-the-art) ResNet 신경망 학습시키기`_
diff --git a/beginner_source/blitz/neural_networks_tutorial.py b/beginner_source/blitz/neural_networks_tutorial.py
index bed2d8e4c..52330c763 100644
--- a/beginner_source/blitz/neural_networks_tutorial.py
+++ b/beginner_source/blitz/neural_networks_tutorial.py
@@ -1,7 +1,7 @@
# -*- coding: utf-8 -*-
"""
신경망(Neural Networks)
-=======================
+==========================
신경망은 ``torch.nn`` 패키지를 사용하여 생성할 수 있습니다.
@@ -53,6 +53,34 @@ def __init__(self):
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
+ def forward(self, input):
+ # 합성곱(Convolution) 레이어 c1: 입력 이미지 채널 1, 출력 채널 6,
+ # 5x5 정사각 합성곱, 활성 함수로 RELU 사용 및 (N, 6, 28, 28)의 크기를
+ # 갖는 Tensor를 출력 (N은 배치 크기)
+ c1 = F.relu(self.conv1(input))
+ # 서브샘플링(Subsampling) 레이어 s2: 2x2 격자, 순전히 기능적인 레이어로,
+ # 이 레이어는 어떠한 매개변수도 가지지 않고 (N, 6, 14, 14) Tensor를 출력
+ s2 = F.max_pool2d(c1, (2, 2))
+ # 합성곱(Convolution) 레이어 c3: 입력 채널 6, 출력 채널 16,
+ # 5x5 정사각 합성곱, 활성 함수로 RELU 사용 및 (N, 16, 10, 10)의 크기를
+ # 갖는 Tensor를 출력
+ c3 = F.relu(self.conv2(s2))
+ # 서브샘플링(Subsampling) 레이어 s4: 2x2 격자, 순전히 기능적인 레이어로,
+ # 이 레이어는 어떠한 매개변수도 가지지 않고 (N, 16, 5, 5) Tensor를 출력
+ s4 = F.max_pool2d(c3, 2)
+ # 평탄화(flatten) 연산: 순전히 기능적으로 동작하며, (N, 400) Tensor를 출력
+ s4 = torch.flatten(s4, 1)
+ # 완전히 연결된 레이어 f5: (N, 400) Tensor를 입력으로 받아서
+ # (N, 120) Tensor를 출력하며, 활성 함수로 RELU 사용
+ f5 = F.relu(self.fc1(s4))
+ # 완전히 연결된 레이어 f6: (N, 120) Tensor를 입력으로 받아서
+ # (N, 84) Tensor를 출력하며, 활성 함수로 RELU 사용
+ f6 = F.relu(self.fc2(f5))
+ # 가우시안 레이어 출력: (N, 84) Tensor를 입력으로 받아서
+ # (N, 10) Tensor를 출력
+ output = self.fc3(f6)
+ return output
+
def forward(self, x):
# (2, 2) 크기 윈도우에 대해 맥스 풀링(max pooling)
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
@@ -153,7 +181,7 @@ def forward(self, x):
# 이제 ``.grad_fn`` 속성을 사용하여 ``loss`` 를 역방향에서 따라가다 보면,
# 이러한 모습의 연산 그래프를 볼 수 있습니다:
#
-# ::
+# .. code-block:: sh
#
# input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
# -> flatten -> linear -> relu -> linear -> relu -> linear
@@ -172,7 +200,7 @@ def forward(self, x):
########################################################################
# 역전파(Backprop)
-# ------------------
+# -----------------------
# 오차(error)를 역전파하기 위해서는 ``loss.backward()`` 만 해주면 됩니다.
# 기존에 계산된 변화도의 값을 누적 시키고 싶지 않다면 기존에 계산된 변화도를 0으로 만드는
# 작업이 필요합니다.
diff --git a/beginner_source/blitz/tensor_tutorial.py b/beginner_source/blitz/tensor_tutorial.py
index 2e893f1a8..714d36f20 100644
--- a/beginner_source/blitz/tensor_tutorial.py
+++ b/beginner_source/blitz/tensor_tutorial.py
@@ -1,6 +1,6 @@
"""
텐서(Tensor)
---------------------------------------------
+=============================================
텐서(tensor)는 배열(array)이나 행렬(matrix)과 매우 유사한 특수한 자료구조입니다.
PyTorch에서는 텐서를 사용하여 모델의 입력과 출력뿐만 아니라 모델의 매개변수를 부호화(encode)합니다.
diff --git a/beginner_source/chatbot_tutorial.py b/beginner_source/chatbot_tutorial.py
index ef00d6305..5d63c5278 100644
--- a/beginner_source/chatbot_tutorial.py
+++ b/beginner_source/chatbot_tutorial.py
@@ -95,11 +95,6 @@
# 그 다음에는, 몇 가지 필요한 도구들을 import 하겠습니다.
#
-from __future__ import absolute_import
-from __future__ import division
-from __future__ import print_function
-from __future__ import unicode_literals
-
import torch
from torch.jit import script, trace
import torch.nn as nn
diff --git a/beginner_source/colab.rst b/beginner_source/colab.rst
index 07bf5fbcc..02b410f37 100644
--- a/beginner_source/colab.rst
+++ b/beginner_source/colab.rst
@@ -7,7 +7,7 @@ Google Colab에서 튜토리얼을 실행할 때, 튜토리얼이 제대로 동
성공적으로 실행하기 위해 다양한 설정을 구성하는 방법에 대해 설명합니다.
Google Colab의 PyTorch 버전
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
공개(release)된지 얼마되지 않은 PyTorch 버전을 사용하는 튜토리얼을 실행하는 경우,
해당 버전이 아직 Google Colab에 반영되지 않았을 수 있습니다.
@@ -48,15 +48,15 @@ Colab에서 파일이 열리게 됩니다.
이를 해결하기 위해, 필요한 파일들을 Google Drive에 복사하겠습니다.
1. Google Drive에 로그인합니다.
-2. Google Drive에서 **data** 라는 이름의 폴더 및 이 아래에 **cornell** 라는 하위
+2. Google Drive에서 ``data`` 라는 이름의 폴더 및 이 아래에 ``cornell`` 라는 하위
폴더도 생성합니다.
3. Cornell Movie Dialogs Corpus에 방문하여 movie-corpus ZIP 파일을 내려받습니다.
4. 로컬 머신에 압축을 풉니다.
-5. **utterances.jsonl** 파일을 Google Drive에 생성한 **data/cornell** 폴더 안에 복사합니다.
+5. ``utterances.jsonl`` 파일을 Google Drive에 생성한 ``data/cornell`` 폴더 안에 복사합니다.
이제 Google Drive 상의 파일을 가르키도록 Colab의 파일을 편집해야 합니다.
-Colab에서 *corpus\_name* 으로 시작하는 코드 섹션의 윗 부분에 다음 내용을 추가합니다:
+Colab에서 ``corpus\_name`` 으로 시작하는 코드 섹션의 윗 부분에 다음 내용을 추가합니다:
::
@@ -66,8 +66,8 @@ Colab에서 *corpus\_name* 으로 시작하는 코드 섹션의 윗 부분에
이제 다음과 같이 2줄을 변경하세요:
-1. **corpus\_name** 값을 **"cornell"** 로 변경합니다.
-2. **corpus** 로 시작하는 줄을 아래처럼 변경합니다:
+1. ``corpus\_name`` 값을 ``"cornell"`` 로 변경합니다.
+2. ``corpus`` 로 시작하는 줄을 아래처럼 변경합니다:
::
@@ -85,3 +85,11 @@ Colab에서 *corpus\_name* 으로 시작하는 코드 섹션의 윗 부분에
이 예제가 Coalb에서 보다 복잡한 튜토리얼을 실행하는데 있어서 좋은 시작점이 되길
바랍니다. PyTorch 튜토리얼 사이트에서 Colab을 더 활용하여 사용자들이 더 쉽게
사용할 수 있는 방법을 찾아보겠습니다.
+
+CUDA 활성화(Enabling CUDA)
+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+일부 튜토리얼은 CUDA-지원 장치(NVIDIA GPU)가 필요하며, 이런 경우 튜토리얼을
+실행하기 전 런타임(Runtime) 유형을 변경해야 합니다.
+Google Colab에서 런타임을 변경하려면 상단 드롭다운 메뉴에서 **Runtime** 을 선택한 뒤,
+**Change runtime type** 을 선택하세요. **Hardware accelerator** 에서 ``T4 GPU`` 를
+선택하고 ``Save`` 를 클릭하세요.
diff --git a/beginner_source/data_loading_tutorial.py b/beginner_source/data_loading_tutorial.py
index 3d485b2bf..253782709 100644
--- a/beginner_source/data_loading_tutorial.py
+++ b/beginner_source/data_loading_tutorial.py
@@ -4,8 +4,8 @@
사용자 정의 Dataset, Dataloader, Transforms 작성하기
==========================================================
-**저자** : Sasank Chilamkurthy
-**번역** : 정윤성
+**저자** : `Sasank Chilamkurthy `__
+**번역** : `정윤성 `__, `박정환 `__
머신러닝 문제를 푸는 과정에서 데이터를 준비하는데 많은 노력이 필요합니다.
PyTorch는 데이터를 불러오는 과정을 쉽게해주고, 또 잘 사용한다면 코드의 가독성도 보다 높여줄 수 있는 도구들을
@@ -20,7 +20,6 @@
"""
-from __future__ import print_function, division
import os
import torch
import pandas as pd
@@ -54,9 +53,9 @@
# 적용한 데이터셋입니다.
#
#
-# 데이터셋은 아래와 같은 특징을 가진 CSV 파일이 포함되어 있습니다.
+# 데이터셋은 아래와 같은 식으로 작성된 ``.csv`` 파일에 포함되어 있습니다:
#
-# ::
+# .. code-block:: sh
#
# image_name,part_0_x,part_0_y,part_1_x,part_1_y,part_2_x, ... ,part_67_x,part_67_y
# 0805personali01.jpg,27,83,27,98, ... 84,134
@@ -71,8 +70,7 @@
n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:]
-landmarks = np.asarray(landmarks)
-landmarks = landmarks.astype('float').reshape(-1, 2)
+landmarks = np.asarray(landmarks, dtype=float).reshape(-1, 2)
print('Image name: {}'.format(img_name))
print('Landmarks shape: {}'.format(landmarks.shape))
@@ -116,7 +114,7 @@ def show_landmarks(image, landmarks):
#
# 데이터셋의 샘플은 ``{'image': image, 'landmarks': landmarks}`` 의 사전 형태를 갖습니다.
# 선택적 인자인 ``transform`` 을 통해 필요한 전처리 과정을 샘플에 적용할 수 있습니다.
-# 다음 장에서 전이 ``transform`` 의 유용성에 대해 알아보겠습니다.
+# 다음 장에서 변형 ``transform`` 의 유용성에 대해 알아보겠습니다.
#
class FaceLandmarksDataset(Dataset):
@@ -144,8 +142,7 @@ def __getitem__(self, idx):
self.landmarks_frame.iloc[idx, 0])
image = io.imread(img_name)
landmarks = self.landmarks_frame.iloc[idx, 1:]
- landmarks = np.array([landmarks])
- landmarks = landmarks.astype('float').reshape(-1, 2)
+ landmarks = np.array([landmarks], dtype=float).reshape(-1, 2)
sample = {'image': image, 'landmarks': landmarks}
if self.transform:
@@ -164,9 +161,7 @@ def __getitem__(self, idx):
fig = plt.figure()
-for i in range(len(face_dataset)):
- sample = face_dataset[i]
-
+for i, sample in enumerate(face_dataset):
print(i, sample['image'].shape, sample['landmarks'].shape)
ax = plt.subplot(1, 4, i + 1)
@@ -182,37 +177,39 @@ def __getitem__(self, idx):
######################################################################
# Transforms
-# ------------
+# ---------------
#
-# 위에서 볼 수 있었던 한가지 문제점은 샘플들이 다 같은 크기가 아니라는 것입니다.
-# 대부분의 신경망(neural networks)은 고정된 크기의 이미지라고 가정합니다.
-# 그러므로 우리는 신경망에 주기 전에 처리할 과정을 작성해야 합니다.
+# 위에서 볼 수 있었던 한 가지 문제는 샘플들의 크기가 같지 않다는 것입니다.
+# 대부분의 신경망(neural networks)은 고정된 크기의 이미지를 입력으로 받는 것을 가정하고 있습니다.
+# 그러므로 몇 가지 전처리 코드를 작성하도록 하겠습니다.
#
-# 3가지의 transforms 을 만들어 봅시다:
+# 다음의 3가지의 변형(transforms)을 만들어 보겠습니다:
#
# - ``Rescale``: 이미지의 크기를 조절합니다.
# - ``RandomCrop``: 이미지를 무작위로 자릅니다.
-# 이것을 data augmentation이라 합니다.
-# - ``ToTensor``: numpy 이미지에서 torch 이미지로 변경합니다.
-# (축변환이 필요합니다)
+# 이것을 데이터 증강(data augmentation)이라 합니다.
+# - ``ToTensor``: NumPy 이미지에서 torch 이미지로 변경합니다.
+# (축 교환(axes swap)이 필요합니다)
#
-# 간단한 함수 대신에 호출 할 수 있는 클래스로 작성 합니다.
-# 이렇게 한다면, 클래스가 호출 될 때마다 전이(Transform)의 매개변수가 전달 되지 않아도 됩니다.
-# 이와 같이, ``__call__`` 함수를 구현해야 합니다.
-# 필요하다면, ``__init__`` 함수도 구현해야 합니다. 다음과 같이 전이(transform)를 사용할 수 있습니다.
+# 이러한 변형 과정을 간단한 함수들로 작성하는 대신, 호출 가능한 클래스로 작성하도록 하겠습니다.
+# 이렇게 하면 클래스가 호출될 때마다 매번 변형(Transform)의 매개변수를 전달하지 않아도 됩니다.
+# ``__call__`` 함수만 구현하면 이렇게 할 수 있으며, 필요 시에는 ``__init__`` 함수까지도 구현해야 할 수 있습니다.
+# 그런 다음 다음과 같이 변형(transform)를 사용할 수 있습니다:
#
-# ::
+# .. code-block:: python
#
# tsfm = Transform(params)
# transformed_sample = tsfm(sample)
#
-# 아래에서는 이미지와 랜드마크(landmark)들을 어떻게 적용하는지 살펴보도록 하겠습니다.
+# 이러한 변환 과정을 이미지와 랜드마크(landmark)들에 어떻게 적용하는지를
+# 살펴보도록 하겠습니다.
+#
class Rescale(object):
"""주어진 크기로 샘플크기를 조정합니다.
Args:
- output_size(tuple or int) : 원하는 출력 크기가
+ output_size(tuple or int) : 원하는 출력의 크기.
tuple인 경우 해당 tuple(output_size)이 결과물(output)의 크기가 되고,
int라면 비율을 유지하면서, 길이가 작은 쪽이 output_size가 됩니다.
"""
@@ -237,17 +234,19 @@ def __call__(self, sample):
img = transform.resize(image, (new_h, new_w))
+ # 이미지의 경우 x와 y가 각각 axis 1과 0이기 때문에,
+ # 랜드마크의 경우 h와 w가 바뀌어야 합니다.
landmarks = landmarks * [new_w / w, new_h / h]
return {'image': img, 'landmarks': landmarks}
class RandomCrop(object):
- """샘플데이터를 무작위로 자릅니다.
+ """샘플 데이터를 무작위로 자릅니다.
Args:
- output_size (tuple or int): 줄이고자 하는 크기입니다.
- int라면, 정사각형으로 나올 것 입니다.
+ output_size (tuple or int): 원하는 출력의 크기.
+ int 값 입력 시 정사각형으로 잘립니다.
"""
def __init__(self, output_size):
@@ -264,8 +263,8 @@ def __call__(self, sample):
h, w = image.shape[:2]
new_h, new_w = self.output_size
- top = np.random.randint(0, h - new_h)
- left = np.random.randint(0, w - new_w)
+ top = np.random.randint(0, h - new_h + 1)
+ left = np.random.randint(0, w - new_w + 1)
image = image[top: top + new_h,
left: left + new_w]
@@ -276,19 +275,20 @@ def __call__(self, sample):
class ToTensor(object):
- """numpy array를 tensor(torch)로 변환 시켜줍니다."""
+ """NumPy의 ndarray 형태의 샘플을 Torch Tensor로 변환합니다."""
def __call__(self, sample):
image, landmarks = sample['image'], sample['landmarks']
- # swap color axis because
- # numpy image: H x W x C
- # torch image: C x H x W
+ # NumPy 이미지와 Torch 이미지의 색상 축(axis)을 교환해야 합니다:
+ # NumPy 이미지의 모양은 H x W x C 이고,
+ # Torch 이미지의 모양은 C x H x W 이기 때문입니다.
image = image.transpose((2, 0, 1))
return {'image': torch.from_numpy(image),
'landmarks': torch.from_numpy(landmarks)}
######################################################################
+#
# .. note::
# 위 예시에서, `RandomCrop` 은 외부 라이브러리의 난수 생성기(random number generator; 이 경우, Numpy의 `np.random.int` )를
# 사용하고 있습니다. 이는 `DataLoader` 가 예상치 못한 동작을 하도록 할 수 있습니다.
@@ -296,16 +296,15 @@ def __call__(self, sample):
# 실제 상황에서는 `torch.randint` 와 같은 PyTorch가 제공하는 난수 생성기를 사용하는 것이 안전합니다.
######################################################################
-# Compose transforms
-# ~~~~~~~~~~~~~~~~~~
#
-# 이제, 샘플에 전이(transform)를 적용해 봅시다.
+# Compose transforms
+# ~~~~~~~~~~~~~~~~~~~~~
#
-# 이미지의 가장 짧은 측면을 256개로 rescale하고,
-# 그후에 무작위로 224개를 자른다고 가정합시다.
-# 다시 말해, ``Rescale`` 과 ``RandomCrop`` 을 사용해봅시다.
+# 이제, 샘플에 변형(transform)를 적용해보겠습니다.
#
-# ``torchvision.transforms.Compose`` 는 위의 두 작업을 하는 간단한 호출할 수 있는 클래스입니다.
+# 먼저 이미지 중 짧은 쪽의 크기를 256으로 변환(rescale)하고, 그런 다음 224 크기의 정방형으로 무작위로 자르도록 하겠습니다.
+# 이를 위해 ``Rescale`` 과 ``RandomCrop`` 을 사용합니다.
+# ``torchvision.transforms.Compose`` 클래스를 사용하여 위의 작업들을 간단하게 할 수 있습니다.
#
scale = Rescale(256)
@@ -313,7 +312,7 @@ def __call__(self, sample):
composed = transforms.Compose([Rescale(256),
RandomCrop(224)])
-# Apply each of the above transforms on sample.
+# 각 변형들을 샘플에 적용합니다.
fig = plt.figure()
sample = face_dataset[65]
for i, tsfrm in enumerate([scale, crop, composed]):
@@ -331,7 +330,7 @@ def __call__(self, sample):
# 데이터셋을 이용한 반복작업
# -----------------------------
#
-# 전이(transform)를 적용한 dataset을 만들기 위해서 만들었던 것을 다 집어넣어 봅시다.
+# 변형(transform)를 적용한 dataset을 만들기 위해서 만들었던 것을 다 집어넣어 봅시다.
#
# 요약하자면, 데이터셋은 다음과 같이 샘플링 됩니다.
#
@@ -352,9 +351,7 @@ def __call__(self, sample):
ToTensor()
]))
-for i in range(len(transformed_dataset)):
- sample = transformed_dataset[i]
-
+for i, sample in enumerate(transformed_dataset):
print(i, sample['image'].size(), sample['landmarks'].size())
if i == 3:
@@ -362,26 +359,26 @@ def __call__(self, sample):
######################################################################
-# 그러나, 데이터 상에서 반복하는 ``for`` 문은 많은 특징(features)를 놓칠 수 있습니다.
-# 특히, 아래와 같은 것을 놓칠 수 있습니다:
+# 하지만 단순한 ``for`` 루프를 반복하여 사용하는 경우 많은 기능들을 놓치게 됩니다.
+# 특히, 다음과 같은 과정들을 놓치고 있습니다:
#
-# - 데이터를 묶는 과정
-# - 데이터를 섞는 과정
-# - 병렬처리 과정에서 ``multiprocessing`` 을 사용할 때 데이터를 불러오는 것
+# - 데이터를 묶는 과정(batching)
+# - 데이터를 섞는 과정(shuffling)
+# - ``multiprocessing`` 워커를 사용하여 데이터를 병렬로 불러오기
#
# ``torch.utils.data.DataLoder`` 는 위와 같은 기능을 모두 제공해주는 반복자(iterator)입니다.
-# 사용되는 매개변수(Parameters)는 명확해야 합니다.
-# ``collate_fn`` 는 흥미로운 매개변수(Parameters) 중 하나입니다.
-# ``collate_fn`` 을 이용하여 샘플들을 정확하게 배치하는 방법을 명시할 수 있습니다.
-# 그러나, 대부분의 경우에 대해서 정확하게 작동해야 합니다.
+# 여기에 사용되는 매개변수(parameter)들은 명확해야 합니다.
+# 관심있게 살펴볼 매개변수 중 하나느 ``collate_fn`` 입니다.
+# ``collate_fn`` 을 사용하여 샘플들을 어떻게 일괄적으로 처리해야 하는지를 지정할 수 있습니다.
+# 하지만 대부분의 경우에는 기본 함수가 잘 동작합니다.
dataloader = DataLoader(transformed_dataset, batch_size=4,
shuffle=True, num_workers=0)
-# 배치하는 과정을 보여주는 함수입니다.
+# 데이터 묶음(batching) 과정을 보여주는 헬퍼 함수(helper function)
def show_landmarks_batch(sample_batched):
- """Show image with landmarks for a batch of samples."""
+ """샘플 묶음(batch)에 대해 랜드마크가 표시된 이미지 보여주기"""
images_batch, landmarks_batch = \
sample_batched['image'], sample_batched['landmarks']
batch_size = len(images_batch)
@@ -398,15 +395,15 @@ def show_landmarks_batch(sample_batched):
plt.title('Batch from dataloader')
-# Windows를 사용 중이라면, 다음 줄의 주석을 제거하고 for 반복문을 들여쓰기 합니다.
-# ``num_workers`` 를 0으로 변경해야 할 수도 있습니다.
+# 만약 Windows를 사용 중이라면, 다음 줄의 주석을 제거하고 for 반복문을 들여쓰기 해주세요.
+# 또한, 위쪽의 ``num_workers`` 값을 0으로 변경해야 할 수도 있습니다.
# if __name__ == '__main__':
for i_batch, sample_batched in enumerate(dataloader):
print(i_batch, sample_batched['image'].size(),
sample_batched['landmarks'].size())
- # observe 4th batch and stop.
+ # 4번째 배치까지 살펴보고 멈추겠습니다.
if i_batch == 3:
plt.figure()
show_landmarks_batch(sample_batched)
@@ -417,13 +414,15 @@ def show_landmarks_batch(sample_batched):
######################################################################
# Afterword: torchvision
-# ------------------------
+# --------------------------
#
-# 이번 튜토리얼에서는, 데이터셋 작성과 사용, 전이(transforms), 데이터를 불러오는 방법에 대해서 알아봤습니다.
-# ``torchvision`` 패키지는 몇몇의 일반적인 데이터셋과 전이(transforms)들을 제공합니다.
+# 이번 튜토리얼에서는, 데이터셋 작성과 사용, 변형(transforms), 데이터를 불러오는 방법에 대해서 알아봤습니다.
+# ``torchvision`` 패키지는 몇몇의 일반적인 데이터셋과 변형(transforms)들을 제공합니다.
# 클래스들을 따로 작성하지 않아도 될 것입니다.
# torchvision에서의 사용 가능한 일반적인 데이터셋 중 하나는 ``ImageFolder`` 입니다.
-# 이것은 다음과 같은 방식으로 구성되어 있다고 가정합니다: ::
+# 예를 들어 다음과 같은 방식으로 구성된 데이터셋이 있다고 가정해보겠습니다:
+#
+# .. code-block:: sh
#
# root/ants/xxx.png
# root/ants/xxy.jpeg
@@ -435,9 +434,11 @@ def show_landmarks_batch(sample_batched):
# root/bees/nsdf3.png
# root/bees/asd932_.png
#
-# 여기서'ants', 'bees'는 class labels입니다.
-# 비슷하게, ``RandomHorizontalFlip`` , ``Scale`` 과 같이 ``PIL.Image`` 에서 작동하는
-# 일반적인 전이(transforms)도 사용 가능합니다. 이와 같이 데이터로더(dataloader)를 사용할 수 있습니다: ::
+# 여기서'ants'와 'bees'는 class labels입니다.
+# 비슷한 방식으로 ``RandomHorizontalFlip`` 이나 ``Scale`` 과 같이 ``PIL.Image`` 에서 동작하는
+# 일반적인 변형들(transforms)도 사용 가능합니다. 다음과 같은 방식으로 DataLoader에서 사용할 수 있습니다:
+#
+# .. code-block:: python
#
# import torch
# from torchvision import transforms, datasets
diff --git a/beginner_source/dcgan_faces_tutorial.py b/beginner_source/dcgan_faces_tutorial.py
index 624e47b3f..5086627cf 100644
--- a/beginner_source/dcgan_faces_tutorial.py
+++ b/beginner_source/dcgan_faces_tutorial.py
@@ -11,10 +11,10 @@
######################################################################
# 개요
-# ----
+# -------
#
# 본 튜토리얼에서는 예제를 통해 DCGAN을 알아보겠습니다. 우리는 실제 유명인들의 사진들로 적대적 생성 신경망(GAN)을 학습시켜,
-# 새로운 유명인의 사진을 만들어볼겁니다.
+# 새로운 유명인의 사진을 만들어보겠습니다.
# 사용할 대부분의 코드는 `pytorch/examples `__ 의 DCGAN 구현에서 가져왔으며,
# 본 문서는 구현에 대한 설명과 함께, 어째서 이 모델이 작동하는지에 대해 설명을 해줄 것입니다.
# 처음 읽었을때는, 실제로 모델에 무슨일이 일어나고 있는지에 대해 이해하는 것이 조금 시간을 소요할 수 있으나,
@@ -22,48 +22,66 @@
# 추가로, GPU 1-2개를 사용하는 것이 시간절약에 도움이 될겁니다. 그럼 처음부터 천천히 시작해봅시다!
#
# 적대적 생성 신경망(Generative Adversarial Networks)
-# ----------------------------------------------------
+# ------------------------------------------------------
#
# 그래서 GAN이 뭘까요?
-# ~~~~~~~~~~~~~~~~~~~~~
-#
-# GAN이란 학습 데이터들의 분포를 학습해, 같은 분포에서 새로운 데이터를 생성할 수 있도록 DL 모델을 학습시키는 프레임워크입니다.
-# 2014년 Ian Goodfellow가 개발했으며, `Generative Adversarial
-# Nets `__ 논문에서 처음 소개되었습니다.
-# GAN은 *생성자* 와 *구분자* 로 구별되는 두가지 모델을 가지고 있는것이 특징입니다.
-# 생성자의 역할은 실제 이미지로 착각되도록 정교한 이미지를 만드는 것이고,
-# 구분자의 역할은 이미지를 보고 생성자에 의해 만들어진 이미지인지 실제 이미지인지 알아내는 것입니다.
-# 모델을 학습하는 동안, 생성자는 더 진짜같은 가짜 이미지를 만들어내며 구분자를 속이려 하고,
-# 구분자는 더 정확히 가짜/진짜 이미지를 구별할 수 있도록 노력합니다.
-# 이 ‘경찰과 도둑’ 게임은, 생성자가 학습 데이터들에서 직접 가져온 것처럼 보일정도로 완벽한 이미지를 만들어내고,
-# 구분자가 생성자에서 나온 이미지를 50%의 확률로 가짜 혹은 진짜로 판별할 때, 균형상태에 도달하게 됩니다.
-#
-# 그럼 이제부터 본 튜토리얼에서 사용할 표기들을 구분자부터 정의해보겠습니다. :math:`x` 는 이미지로 표현되는 데이터로 두겠습니다.
-# :math:`D(x)` 는 구분자 신경망이고, 실제 학습데이터에서 가져온 :math:`x` 를 통과시켜 상수(scalar) 확률값을 결과로 출려합니다.
-# 이때, 우리는 이미지 데이터를 다루고 있으므로, :math:`D(x)` 에는 3x64x64크기의 CHW 데이터가 입력됩니다. 직관적으로 볼때,
-# :math:`D(x)` 는 :math:`x` 가 학습데이터에서 가져온 것일 때 출력이 크고, 생성자가 만들어낸 :math:`x` 일때 작을 것입니다.
-# :math:`D(x)` 는 전통적인 이진 분류기(binary classification)으로도 생각될 수 있습니다.
-#
-# 이번엔 생성자의 표기들을 확인해봅시다. :math:`z` 를 정규분포에서 뽑은 잠재공간 벡터(laten space vector)라고 하겠습니다
+# ~~~~~~~~~~~~~~~~~~~~~~~
+#
+# GAN이란 학습 데이터들의 분포를 학습한 뒤, 동일한 분포를 갖는 새로운 데이터를
+# 생성하도록 딥러닝 모델을 학습시키는 프레임워크입니다.
+# GAN은 2014년 Ian Goodfellow가 개발했으며,
+# `Generative Adversarial Nets `__ 논문에서
+# 처음 소개되었습니다.
+# GAN은 *생성자(Generator)* 와 *구분자(Discriminator)* 라는 두 개의 서로
+# 다른(distinct) 모델들로 구성되어 있습니다.
+# 생성자(Generator)의 역할은 학습한 이미지들과 같아 보이는 `가짜(fake)`
+# 이미지를 만드는 것이고, 구분자(Discriminator)는 이미지를 보고 이것이
+# 실제 학습 데이터에서 가져온 것인지, 또는 생성자에 의해 만들어진 가짜
+# 이미지인지 판별하는 것입니다.
+# 모델을 학습하는 동안 생성자는 더 진짜 같은 가짜 이미지를 만들어내며
+# 구분자를 속이려 하고, 구분자는 진짜 이미지와 가짜 이미지를 더 정확히
+# 판별할 수 있도록 노력합니다.
+# 이러한 과정은 생성자가 마치 학습 데이터에서 가져온 것처럼 보이는
+# 완벽한 가짜 이미지를 생성해내고, 판별자는 항상 50%의 신뢰도로
+# 생성자의 출력이 진짜인지 가짜인지 판별할 수 있을 때 균형 상태(equilbrium)에
+# 도달하게 됩니다.
+#
+# 그럼 이제부터 본 튜토리얼에서 사용할 표기들을 구분자부터 정의해보겠습니다.
+# :math:`x` 는 이미지로 표현되는 데이터라고 하겠습니다.
+# :math:`D(x)` 는 구분자의 신경망을 나타내며, 실제 학습 데이터에서 가져온
+# :math:`x` 를 통과시켜 확률 값(scalar)을 결과로 출력합니다.
+# 여기에서는 이미지 데이터를 다루고 있으므로,
+# :math:`D(x)` 의 입력으로는 3x64x64 크기의 CHW 이미지가 주어집니다.
+# 직관적으로 :math:`D(x)` 는 :math:`x` 가 학습 데이터에서 가져왔을 때 출력이 크고(HIGH),
+# 생성자가 만들어낸 :math:`x` 일 때는 작을(LOW) 것입니다.
+# :math:`D(x)` 는 전통적인 이진 분류기(binary classification)로도 생각할 수도 있습니다.
+#
+# 이번엔 생성자의 표기들을 살펴보겠습니다. :math:`z` 를 정규분포에서 뽑은
+# 잠재공간 벡터(laten space vector)라고 하겠습니다
# (번역 주. laten space vector는 쉽게 생각해 정규분포를 따르는 n개의 원소를 가진 vector라 볼 수 있습니다.
# 다르게 얘기하면 정규분포에서 n개의 원소를 추출한 것과 같습니다). :math:`G(z)` 는 :math:`z`
# 벡터를 원하는 데이터 차원으로 대응시키는 신경망으로 둘 수 있습니다. 이때 :math:`G` 의 목적은 :math:`p_{data}`
# 에서 얻을 수 있는 학습 데이터들의 분포를 추정하여, 모사한 :math:`p_g` 의 분포를 이용해 가짜 데이터들을 만드는 것입니다.
#
-# 이어서, :math:`D(G(z))` 는 :math:`G` 가 출력한 결과물이 실제 이미지일 0~1사이의 상수의 확률값입니다.
+# 이어서, :math:`D(G(z))` 는 :math:`G` 가 출력한 결과물이 실제 이미지 여부를
+# 나타내는 0~1 사이의 확률 값(scalar)입니다.
# `Goodfellow의 논문 `__
-# 에 기술되어 있듯, :math:`D` 가 이미지의 참/거짓을 정확히 판별할 확률인 :math:`logD(x)`를 최대화 시키고,
-# :math:`G` 에서 생성한 이미지를 :math:`D` 가 가짜로 판별할 확률인
-# (:math:`log(1-D(G(z)))`)를 최소화 시키려는 점에서, :math:`D` 와 :math:`G` 는 최대최소(minmax)게임을 하는 것과 같습니다.
+# 에 기술되어 있듯이, :math:`D` 와 :math:`G` 는 일종의 최대-최소 게임(minimax game)을
+# 하고 있는 것과 같습니다. 이는 :math:`D` 는 이미지가 진짜인지 가짜인지 여부를 판별하는 확률인
+# :math:`logD(x)` 를 최대화하려고 하고, :math:`G` 는 :math:`D` 가 가짜라고 판별할 확률인 :math:`log(1-D(G(z)))` 를
+# 최소화시키려고 하기 때문입니다.
# 논문에 따르면, GAN의 손실함수는 아래와 같습니다.
#
# .. math:: \underset{G}{\text{min}} \underset{D}{\text{max}}V(D,G) = \mathbb{E}_{x\sim p_{data}(x)}\big[logD(x)\big] + \mathbb{E}_{z\sim p_{z}(z)}\big[log(1-D(G(z)))\big]
#
-# 이론적으로는, 이 최대최소게임은 :math:`p_g = p_{data}` 이고, 구분자에 입력된 데이터가 1/2의 무작위 확률로 참/거짓이 판별될때 해답에 이릅니다.
-# 하지만 GAN의 수렴 이론은 아직도 활발히 연구가 진행중이고, 현실에서의 모델들은 이론적인 최적 상태에 도달하지 않는 경우도 많습니다.
+# 이론적으로는, 이 최대-최소 게임의 답(solution)은 :math:`p_g = p_{data}`
+# 일 때이며, 이 때 구분자는 입력이 진짜인지 가짜인지를 무작위로 추측하게
+# 됩니다. 하지만 GAN의 수렴 이론(convergence theory)에 대해서는 아직도
+# 활발히 연구가 진행 중이며, 실제 모델들을 학습할 때에는 항상 이러한
+# 이론적인 최적 상태에 도달하지는 못합니다.
#
# 그렇다면 DCGAN은 뭘까요?
-# ~~~~~~~~~~~~~~~~~~~~~~~~
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~
#
# DCGAN은 위에서 기술한 GAN에서 직접적으로 파생된 모델로, 생성자와 구분자에서
# 합성곱 신경망(convolution)과 전치 합성곱 신경망(convolution-transpose)을 사용했다는 것이 차이점입니다
@@ -81,14 +99,13 @@
# 다음으로, 생성자는
# `convolutional-transpose `__
# 계층, 배치 정규화(batch norm) 계층, 그리고
-# `ReLU `__ 활성함수가 사용되었습니다. 입력값은 역시나
-# 정규분포에서 추출한 잠재공간 벡터 :math:`z` 이고, 출력값은 3x64x64 RGB 이미지입니다. 이때,
-# 전치 합성곱 신경망은 잠재공간 벡터로 하여금 이미지와 같은 차원을 갖도록 변환시켜주는 역할을 합니다 (번역 주. 전치 합성곱 신경망은
-# 합성곱 신경망의 반대적인 개념이라 이해하면 쉽습니다. 입력된 작은 CHW 데이터를 가중치들을 이용해 더 큰 CHW로 업샘플링해주는 계층입니다).
+# `ReLU `__ 활성함수가 사용되었습니다.
+# 입력값은 역시나 정규분포에서 추출한 잠재공간 벡터 :math:`z` 이고, 출력값은 3x64x64 RGB 이미지입니다.
+# 이 때, 전치 합성곱 계층(strided conv-transpose layer)은 잠재공간 벡터로 하여금 이미지와 같은 차원을 갖도록 변환시켜주는 역할을 합니다.
+# (번역 주. 전치 합성곱 신경망은 합성곱 신경망의 반대적인 개념이라 이해하면 쉽습니다. 입력된 작은 CHW 데이터를 가중치들을 이용해 더 큰 CHW로 업샘플링해주는 계층입니다.)
# 논문에서는 각종 최적화 방법이나 손실함수의 계산, 모델의 가중치 초기화 방법등에 관한 추가적인 정보들도 적어두었는데,
# 이 부분은 다음 섹션에서 설명하도록 하겠습니다.
-from __future__ import print_function
#%matplotlib inline
import argparse
import os
@@ -113,30 +130,41 @@
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
+torch.use_deterministic_algorithms(True) # 결과 재현을 위해 필요합니다
######################################################################
-# 설정값
-# ------
+# 설정 값
+# ---------
#
-# 몇 가지 설정값들을 정의해봅시다:
+# 몇 가지 설정 값들을 살펴보겠습니다:
#
-# - ``dataroot`` - 데이터셋 폴더의 경로입니다. 데이터셋에 관한건 다음 섹션에서
+# - ``dataroot`` - 데이터셋 폴더의 경로입니다. 데이터셋에 대해서는 다음 섹션에서
# 더 자세히 설명하겠습니다.
-# - ``workers`` - DataLoader에서 데이터를 불러올 때 사용할 쓰레드의 개수입니다.
-# - ``batch_size`` - 학습에 사용할 배치 크기입니다. DCGAN에서는 128을 사용했습니다.
-# - ``image_size`` - 학습에 사용되는 이미지의 크기입니다.
-# 본 문서에서는 64x64의 크기를 기본으로 하나, 만일 다른 크기의 이미지를 사용한다면
-# D와 G의 구조 역시 변경되어야 합니다. 더 자세한 정보를 위해선
-# `이곳 `__ 을 확인해 보세요.
-# - ``nc`` - 입력 이미지의 색 채널개수입니다. RGB 이미지이기 때문에 3으로 설정합니다.
-# - ``nz`` - 잠재공간 벡터의 원소들 개수입니다.
-# - ``ngf`` - 생성자를 통과할때 만들어질 특징 데이터의 채널개수입니다.
-# - ``ndf`` - 구분자를 통과할때 만들어질 특징 데이터의 채널개수입니다.
-# - ``num_epochs`` - 학습시킬 에폭 수입니다. 오래 학습시키는 것이 대부분 좋은 결과를 보이지만, 당연히도 시간이 오래걸리는 것이 단점입니다.
-# - ``lr`` - 모델의 학습률입니다. DCGAN에서 사용된대로 0.0002로 설정합니다.
-# - ``beta1`` - Adam 옵티마이저에서 사용할 beta1 하이퍼파라미터 값입니다. 역시나 논문에서 사용한대로 0.5로 설정했습니다.
-# - ``ngpu`` - 사용가능한 GPU의 번호입니다. 0으로 두면 CPU에서 학습하고, 0보다 큰 수로 설정하면 각 숫자가 가리키는 GPU로 학습시킵니다.
+# - ``workers`` - ``DataLoader`` 에서 데이터를 불러올 때 사용할 워커 쓰레드의
+# 수입니다.
+# - ``batch_size`` - 학습에 사용할 배치 크기입니다. DCGAN에서는 배치 크기를
+# 128으로 사용했습니다.
+# - ``image_size`` - 학습에 사용하는 이미지의 크기입니다.
+# 이 튜토리얼에서는 64x64의 크기를 기본으로 하나, 만일 다른 크기의 이미지를
+# 사용한다면 D와 G의 구조 또한 변경되어야 합니다.
+# 이에 대해서는 `여기 `__ 를 참고하여
+# 더 자세한 정보를 확인할 수 있습니다.
+# - ``nc`` - 입력 이미지의 색상의 채널 수입니다. RGB 컬러 이미지의 경우
+# 이 값은 3입니다.
+# - ``nz`` - 잠재공간 벡터의 원소들의 수입니다.
+# - ``ngf`` - 생성자를 통과할 때 만들어질 특징 데이터의 채널 수입니다.
+# - ``ndf`` - 구분자를 통과할 때 만들어질 특징 데이터의 채널 수입니다.
+# - ``num_epochs`` - 학습시킬 에폭(epoch) 수입니다. 학습을
+# 길게하는 경우 대부분 좋은 결과를 보이지만, 이러한 경우 시간 또한
+# 오래 걸립니다.
+# - ``lr`` - 모델의 학습률(learning rate)입니다. DCGAN 논문에서와 같이 0.0002로
+# 설정합니다.
+# - ``beta1`` - Adam 옵티마이저에서 사용할 beta1 하이퍼파라미터 값입니다.
+# 논문에서와 같이 0.5로 설정했습니다.
+# - ``ngpu`` - 사용 가능한 GPU의 개수입니다. 0인 경우에는 코드는 CPU에서 동작합니다.
+# 만약 이 값이 0보다 큰 경우에는 주어진 수 만큼의 GPU를 사용하여 학습을
+# 진행합니다.
#
# 데이터셋의 경로
@@ -178,7 +206,7 @@
######################################################################
# 데이터
-# ------
+# ---------
#
# 본 튜토리얼에서 사용할 데이터는 `Celeb-A Faces
# dataset `__ 로, 해당 링크를 이용하거나 `Google
@@ -188,7 +216,7 @@
# 압축 해제 후, 위에서 정의한 ``dataroot`` 변수에 방금 만든 ``celeba`` 폴더의 경로를 넣어주세요.
# 위의 작업이 끝나면 ``celeba`` 폴더의 구조는 다음과 같아야 합니다:
#
-# ::
+# .. code-block:: sh
#
# /path/to/celeba
# -> img_align_celeba
@@ -227,6 +255,7 @@
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))
+plt.show()
######################################################################
@@ -339,7 +368,7 @@ def forward(self, input):
######################################################################
# 구분자
-# ~~~~~~
+# ~~~~~~~~~
#
# 앞서 언급했듯, 구분자 :math:`D` 는 입력 이미지가 진짜 이미지인지 (혹은 반대로 가짜 이미지인지)
# 판별하는 전통적인 이진 분류 신경망으로 볼 수 있습니다. 이때 :math:`D` 는
@@ -452,7 +481,7 @@ def forward(self, input):
######################################################################
# 학습
-# ~~~~
+# ~~~~~~~
#
# 드디어 최종입니다. GAN 프레임워크에 필요한 부분들은 모두 가졌으니,
# 실제 모델을 학습시키는 방법을 알아보겠습니다. 주의를 기울일 것은, GAN을 학습시키는 건
diff --git a/beginner_source/ddp_series_fault_tolerance.rst b/beginner_source/ddp_series_fault_tolerance.rst
index 2bc63d7ec..7a4e3cc8c 100644
--- a/beginner_source/ddp_series_fault_tolerance.rst
+++ b/beginner_source/ddp_series_fault_tolerance.rst
@@ -1,7 +1,9 @@
-`Introduction `__ \|\| `What is DDP `__ \|\| `Single-Node
-Multi-GPU Training `__ \|\| **Fault
-Tolerance** \|\| `Multi-Node
-training <../intermediate/ddp_series_multinode.html>`__ \|\| `minGPT Training <../intermediate/ddp_series_minGPT.html>`__
+`Introduction `__ \|\|
+`What is DDP `__ \|\|
+`Single-Node Multi-GPU Training `__ \|\|
+**Fault Tolerance** \|\|
+`Multi-Node training <../intermediate/ddp_series_multinode.html>`__ \|\|
+`minGPT Training <../intermediate/ddp_series_minGPT.html>`__
Fault-tolerant Distributed Training with ``torchrun``
@@ -61,8 +63,8 @@ Why use ``torchrun``
don't need to. For instance,
- You don't need to set environment variables or explicitly pass the ``rank`` and ``world_size``; ``torchrun`` assigns this along with several other `environment variables `__.
-- No need to call ``mp.spawn`` in your script; you only need a generic ``main()`` entrypoint, and launch the script with ``torchrun``. This way the same script can be run in non-distributed as well as single-node and multinode setups.
-- Gracefully restarting training from the last saved training snapshot
+- No need to call ``mp.spawn`` in your script; you only need a generic ``main()`` entry point, and launch the script with ``torchrun``. This way the same script can be run in non-distributed as well as single-node and multinode setups.
+- Gracefully restarting training from the last saved training snapshot.
Graceful restarts
@@ -84,48 +86,43 @@ For graceful restarts, you should structure your train script like:
save_snapshot(snapshot_path)
If a failure occurs, ``torchrun`` will terminate all the processes and restart them.
-Each process entrypoint first loads and initializes the last saved snapshot, and continues training from there.
+Each process entry point first loads and initializes the last saved snapshot, and continues training from there.
So at any failure, you only lose the training progress from the last saved snapshot.
In elastic training, whenever there are any membership changes (adding or removing nodes), ``torchrun`` will terminate and spawn processes
on available devices. Having this structure ensures your training job can continue without manual intervention.
-
-
-
Diff for `multigpu.py `__ v/s `multigpu_torchrun.py `__
------------------------------------------------------------
Process group initialization
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
- ``torchrun`` assigns ``RANK`` and ``WORLD_SIZE`` automatically,
- amongst `other env
- variables `__
-
-.. code:: diff
-
- - def ddp_setup(rank, world_size):
- + def ddp_setup():
- - """
- - Args:
- - rank: Unique identifier of each process
- - world_size: Total number of processes
- - """
- - os.environ["MASTER_ADDR"] = "localhost"
- - os.environ["MASTER_PORT"] = "12355"
- - init_process_group(backend="nccl", rank=rank, world_size=world_size)
- + init_process_group(backend="nccl")
+ among `other envvariables `__
+
+.. code-block:: diff
+
+ - def ddp_setup(rank, world_size):
+ + def ddp_setup():
+ - """
+ - Args:
+ - rank: Unique identifier of each process
+ - world_size: Total number of processes
+ - """
+ - os.environ["MASTER_ADDR"] = "localhost"
+ - os.environ["MASTER_PORT"] = "12355"
+ - init_process_group(backend="nccl", rank=rank, world_size=world_size)
+ + init_process_group(backend="nccl")
torch.cuda.set_device(int(os.environ["LOCAL_RANK"]))
-Use Torchrun-provided env variables
-~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+Use torchrun-provided environment variables
+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-.. code:: diff
+.. code-block:: diff
- - self.gpu_id = gpu_id
- + self.gpu_id = int(os.environ["LOCAL_RANK"])
+ - self.gpu_id = gpu_id
+ + self.gpu_id = int(os.environ["LOCAL_RANK"])
Saving and loading snapshots
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
@@ -133,20 +130,20 @@ Saving and loading snapshots
Regularly storing all the relevant information in snapshots allows our
training job to seamlessly resume after an interruption.
-.. code:: diff
+.. code-block:: diff
- + def _save_snapshot(self, epoch):
- + snapshot = {}
- + snapshot["MODEL_STATE"] = self.model.module.state_dict()
- + snapshot["EPOCHS_RUN"] = epoch
- + torch.save(snapshot, "snapshot.pt")
- + print(f"Epoch {epoch} | Training snapshot saved at snapshot.pt")
+ + def _save_snapshot(self, epoch):
+ + snapshot = {}
+ + snapshot["MODEL_STATE"] = self.model.module.state_dict()
+ + snapshot["EPOCHS_RUN"] = epoch
+ + torch.save(snapshot, "snapshot.pt")
+ + print(f"Epoch {epoch} | Training snapshot saved at snapshot.pt")
- + def _load_snapshot(self, snapshot_path):
- + snapshot = torch.load(snapshot_path)
- + self.model.load_state_dict(snapshot["MODEL_STATE"])
- + self.epochs_run = snapshot["EPOCHS_RUN"]
- + print(f"Resuming training from snapshot at Epoch {self.epochs_run}")
+ + def _load_snapshot(self, snapshot_path):
+ + snapshot = torch.load(snapshot_path)
+ + self.model.load_state_dict(snapshot["MODEL_STATE"])
+ + self.epochs_run = snapshot["EPOCHS_RUN"]
+ + print(f"Resuming training from snapshot at Epoch {self.epochs_run}")
Loading a snapshot in the Trainer constructor
@@ -155,14 +152,14 @@ Loading a snapshot in the Trainer constructor
When restarting an interrupted training job, your script will first try
to load a snapshot to resume training from.
-.. code:: diff
+.. code-block:: diff
- class Trainer:
- def __init__(self, snapshot_path, ...):
- ...
- + if os.path.exists(snapshot_path):
- + self._load_snapshot(snapshot_path)
- ...
+ class Trainer:
+ def __init__(self, snapshot_path, ...):
+ ...
+ + if os.path.exists(snapshot_path):
+ + self._load_snapshot(snapshot_path)
+ ...
Resuming training
@@ -171,34 +168,35 @@ Resuming training
Training can resume from the last epoch run, instead of starting all
over from scratch.
-.. code:: diff
+.. code-block:: diff
- def train(self, max_epochs: int):
- - for epoch in range(max_epochs):
- + for epoch in range(self.epochs_run, max_epochs):
- self._run_epoch(epoch)
+ def train(self, max_epochs: int):
+ - for epoch in range(max_epochs):
+ + for epoch in range(self.epochs_run, max_epochs):
+ self._run_epoch(epoch)
Running the script
~~~~~~~~~~~~~~~~~~
-Simply call your entrypoint function as you would for a non-multiprocessing script; ``torchrun`` automatically
+
+Simply call your entry point function as you would for a non-multiprocessing script; ``torchrun`` automatically
spawns the processes.
-.. code:: diff
+.. code-block:: diff
- if __name__ == "__main__":
- import sys
- total_epochs = int(sys.argv[1])
- save_every = int(sys.argv[2])
- - world_size = torch.cuda.device_count()
- - mp.spawn(main, args=(world_size, total_epochs, save_every,), nprocs=world_size)
- + main(save_every, total_epochs)
+ if __name__ == "__main__":
+ import sys
+ total_epochs = int(sys.argv[1])
+ save_every = int(sys.argv[2])
+ - world_size = torch.cuda.device_count()
+ - mp.spawn(main, args=(world_size, total_epochs, save_every,), nprocs=world_size)
+ + main(save_every, total_epochs)
-.. code:: diff
+.. code-block:: diff
- - python multigpu.py 50 10
- + torchrun --standalone --nproc_per_node=4 multigpu_torchrun.py 50 10
+ - python multigpu.py 50 10
+ + torchrun --standalone --nproc_per_node=4 multigpu_torchrun.py 50 10
Further Reading
---------------
diff --git a/beginner_source/ddp_series_intro.rst b/beginner_source/ddp_series_intro.rst
index 9aea8b247..527a3cc1c 100644
--- a/beginner_source/ddp_series_intro.rst
+++ b/beginner_source/ddp_series_intro.rst
@@ -1,7 +1,8 @@
-**Introduction** \|\| `What is DDP `__ \|\| `Single-Node
-Multi-GPU Training `__ \|\| `Fault
-Tolerance `__ \|\| `Multi-Node
-training <../intermediate/ddp_series_multinode.html>`__ \|\| `minGPT Training <../intermediate/ddp_series_minGPT.html>`__
+**Introduction** \|\| `What is DDP `__ \|\|
+`Single-Node Multi-GPU Training `__ \|\|
+`Fault Tolerance `__ \|\|
+`Multi-Node training <../intermediate/ddp_series_multinode.html>`__ \|\|
+`minGPT Training <../intermediate/ddp_series_minGPT.html>`__
Distributed Data Parallel in PyTorch - Video Tutorials
======================================================
@@ -34,9 +35,9 @@ You will need multiple CUDA GPUs to run the tutorial code. Typically,
this can be done on a cloud instance with multiple GPUs (the tutorials
use an Amazon EC2 P3 instance with 4 GPUs).
-The tutorial code is hosted at this `github
-repo `__. Clone the repo and
-follow along!
+The tutorial code is hosted in this
+`github repo `__.
+Clone the repository and follow along!
Tutorial sections
-----------------
diff --git a/beginner_source/ddp_series_multigpu.rst b/beginner_source/ddp_series_multigpu.rst
index 5d25bfa62..5d3993c86 100644
--- a/beginner_source/ddp_series_multigpu.rst
+++ b/beginner_source/ddp_series_multigpu.rst
@@ -1,6 +1,9 @@
-`Introduction `__ \|\| `What is DDP `__ \|\| **Single-Node Multi-GPU Training** \|\| `Fault
-Tolerance `__ \|\| `Multi-Node
-training <../intermediate/ddp_series_multinode.html>`__ \|\| `minGPT Training <../intermediate/ddp_series_minGPT.html>`__
+`Introduction `__ \|\|
+`What is DDP `__ \|\|
+**Single-Node Multi-GPU Training** \|\|
+`Fault Tolerance `__ \|\|
+`Multi-Node training <../intermediate/ddp_series_multinode.html>`__ \|\|
+`minGPT Training <../intermediate/ddp_series_minGPT.html>`__
Multi GPU training with DDP
@@ -49,7 +52,6 @@ Along the way, we will talk through important concepts in distributed training w
Diff for `single_gpu.py `__ v/s `multigpu.py `__
-----------------------------------------------------
These are the changes you typically make to a single-GPU training script to enable DDP.
@@ -60,22 +62,24 @@ Imports
- The distributed process group contains all the processes that can
communicate and synchronize with each other.
-.. code:: diff
+.. code-block:: diff
- import torch
- import torch.nn.functional as F
- from utils import MyTrainDataset
+ import torch
+ import torch.nn.functional as F
+ from utils import MyTrainDataset
- + import torch.multiprocessing as mp
- + from torch.utils.data.distributed import DistributedSampler
- + from torch.nn.parallel import DistributedDataParallel as DDP
- + from torch.distributed import init_process_group, destroy_process_group
- + import os
+ + import torch.multiprocessing as mp
+ + from torch.utils.data.distributed import DistributedSampler
+ + from torch.nn.parallel import DistributedDataParallel as DDP
+ + from torch.distributed import init_process_group, destroy_process_group
+ + import os
Constructing the process group
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+- First, before initializing the group process, call `set_device `__,
+ which sets the default GPU for each process. This is important to prevent hangs or excessive memory utilization on `GPU:0`
- The process group can be initialized by TCP (default) or from a
shared file-system. Read more on `process group
initialization `__
@@ -83,30 +87,29 @@ Constructing the process group
initializes the distributed process group.
- Read more about `choosing a DDP
backend `__
-- `set_device `__
- sets the default GPU for each process. This is important to prevent hangs or excessive memory utilization on `GPU:0`
-.. code:: diff
+.. code-block:: diff
+
+ + def ddp_setup(rank: int, world_size: int):
+ + """
+ + Args:
+ + rank: Unique identifier of each process
+ + world_size: Total number of processes
+ + """
+ + os.environ["MASTER_ADDR"] = "localhost"
+ + os.environ["MASTER_PORT"] = "12355"
+ + torch.cuda.set_device(rank)
+ + init_process_group(backend="nccl", rank=rank, world_size=world_size)
- + def ddp_setup(rank: int, world_size: int):
- + """
- + Args:
- + rank: Unique identifier of each process
- + world_size: Total number of processes
- + """
- + os.environ["MASTER_ADDR"] = "localhost"
- + os.environ["MASTER_PORT"] = "12355"
- + init_process_group(backend="nccl", rank=rank, world_size=world_size)
- + torch.cuda.set_device(rank)
Constructing the DDP model
~~~~~~~~~~~~~~~~~~~~~~~~~~
-.. code:: diff
+.. code-block:: diff
- - self.model = model.to(gpu_id)
- + self.model = DDP(model, device_ids=[gpu_id])
+ - self.model = model.to(gpu_id)
+ + self.model = DDP(model, device_ids=[gpu_id])
Distributing input data
~~~~~~~~~~~~~~~~~~~~~~~
@@ -116,27 +119,27 @@ Distributing input data
- Each process will receive an input batch of 32 samples; the effective
batch size is ``32 * nprocs``, or 128 when using 4 GPUs.
-.. code:: diff
+.. code-block:: diff
- train_data = torch.utils.data.DataLoader(
- dataset=train_dataset,
- batch_size=32,
- - shuffle=True,
- + shuffle=False,
- + sampler=DistributedSampler(train_dataset),
- )
+ train_data = torch.utils.data.DataLoader(
+ dataset=train_dataset,
+ batch_size=32,
+ - shuffle=True,
+ + shuffle=False,
+ + sampler=DistributedSampler(train_dataset),
+ )
- Calling the ``set_epoch()`` method on the ``DistributedSampler`` at the beginning of each epoch is necessary to make shuffling work
properly across multiple epochs. Otherwise, the same ordering will be used in each epoch.
-.. code:: diff
+.. code-block:: diff
- def _run_epoch(self, epoch):
- b_sz = len(next(iter(self.train_data))[0])
- + self.train_data.sampler.set_epoch(epoch)
- for source, targets in self.train_data:
- ...
- self._run_batch(source, targets)
+ def _run_epoch(self, epoch):
+ b_sz = len(next(iter(self.train_data))[0])
+ + self.train_data.sampler.set_epoch(epoch)
+ for source, targets in self.train_data:
+ ...
+ self._run_batch(source, targets)
Saving model checkpoints
@@ -146,14 +149,14 @@ Saving model checkpoints
more on saving and loading models with
DDP `here `__
-.. code:: diff
+.. code-block:: diff
- - ckp = self.model.state_dict()
- + ckp = self.model.module.state_dict()
- ...
- ...
- - if epoch % self.save_every == 0:
- + if self.gpu_id == 0 and epoch % self.save_every == 0:
+ - ckp = self.model.state_dict()
+ + ckp = self.model.module.state_dict()
+ ...
+ ...
+ - if epoch % self.save_every == 0:
+ + if self.gpu_id == 0 and epoch % self.save_every == 0:
self._save_checkpoint(epoch)
.. warning::
@@ -173,7 +176,7 @@ Running the distributed training job
- ``world_size`` is the number of processes across the training job. For GPU training,
this corresponds to the number of GPUs in use, and each process works on a dedicated GPU.
-.. code:: diff
+.. code-block:: diff
- def main(device, total_epochs, save_every):
+ def main(rank, world_size, total_epochs, save_every):
diff --git a/beginner_source/ddp_series_theory.rst b/beginner_source/ddp_series_theory.rst
index 963f8f9c6..bd77ed13c 100644
--- a/beginner_source/ddp_series_theory.rst
+++ b/beginner_source/ddp_series_theory.rst
@@ -1,7 +1,8 @@
-`Introduction `__ \|\| **What is DDP** \|\| `Single-Node
-Multi-GPU Training `__ \|\| `Fault
-Tolerance `__ \|\| `Multi-Node
-training <../intermediate/ddp_series_multinode.html>`__ \|\| `minGPT Training <../intermediate/ddp_series_minGPT.html>`__
+`Introduction `__ \|\| **What is DDP** \|\|
+`Single-Node Multi-GPU Training `__ \|\|
+`Fault Tolerance `__ \|\|
+`Multi-Node training <../intermediate/ddp_series_multinode.html>`__ \|\|
+`minGPT Training <../intermediate/ddp_series_minGPT.html>`__
What is Distributed Data Parallel (DDP)
=======================================
@@ -13,7 +14,7 @@ Authors: `Suraj Subramanian `__
.. grid-item-card:: :octicon:`mortar-board;1em;` What you will learn
* How DDP works under the hood
- * What is the DistributedSampler
+ * What is ``DistributedSampler``
* How gradients are synchronized across GPUs
@@ -37,15 +38,17 @@ ensures each device gets a non-overlapping input batch. The model is replicated
each replica calculates gradients and simultaneously synchronizes with the others using the `ring all-reduce
algorithm `__.
-Why you should prefer DDP over DataParallel (DP)
--------------------------------------------------
+This `illustrative tutorial `__ provides a more in-depth python view of the mechanics of DDP.
+
+Why you should prefer DDP over ``DataParallel`` (DP)
+----------------------------------------------------
`DataParallel `__
is an older approach to data parallelism. DP is trivially simple (with just one extra line of code) but it is much less performant.
DDP improves upon the architecture in a few ways:
+---------------------------------------+------------------------------+
-| DataParallel | DistributedDataParallel |
+| ``DataParallel`` | ``DistributedDataParallel`` |
+=======================================+==============================+
| More overhead; model is replicated | Model is replicated only |
| and destroyed at each forward pass | once |
@@ -66,3 +69,4 @@ Further Reading
API `__
- `DDP Internal
Design `__
+- `DDP Mechanics Tutorial `__
diff --git a/beginner_source/deep_learning_60min_blitz.rst b/beginner_source/deep_learning_60min_blitz.rst
index ee9643a96..0c5b598d4 100644
--- a/beginner_source/deep_learning_60min_blitz.rst
+++ b/beginner_source/deep_learning_60min_blitz.rst
@@ -21,11 +21,11 @@ PyTorch는 Python 기반의 과학 연산 패키지로 다음 두 가지 목적
- 높은 수준에서 PyTorch의 Tensor library와 신경망(Neural Network)를 이해합니다.
- 이미지를 분류하는 작은 신경망을 학습시킵니다.
-아래 튜토리얼을 실행하기 전에, `torch`_ 와 `torchvision`_ 패키지가 설치되어 있는지 확인하세요.
+아래 튜토리얼을 실행하기 전에, `torch`_, `torchvision`_, 그리고 `matplotlib`_ 패키지가 설치되어 있는지 확인하세요.
.. _torch: https://github.com/pytorch/pytorch
.. _torchvision: https://github.com/pytorch/vision
-
+.. _matplotlib: https://github.com/matplotlib/matplotlib
.. toctree::
:hidden:
diff --git a/beginner_source/deeplabv3_on_android.rst b/beginner_source/deeplabv3_on_android.rst
index c9cd70802..955ec82a0 100644
--- a/beginner_source/deeplabv3_on_android.rst
+++ b/beginner_source/deeplabv3_on_android.rst
@@ -16,7 +16,7 @@ PyTorch의 의미론적 이미지 분할에 사용하는 `DeepLabV3 모델 `_ 을 확인하고, PyTorch 안드로이드 예제인 `HelloWorld `_ 앱을 실행해 보십시오. 이 튜토리얼은 대게 처음으로 모바일에 배포하는 모델인 이미지 분류 모델을 넘어선 다음 단계를 다루고 있습니다. 이 튜토리얼을 위한 전체 코드는 `여기 `_ 에서 확인 가능합니다.
+.. note:: 이 튜토리얼을 진행하기 앞서 `안드로이드를 위한 PyTorch 모바일 `_ 을 확인하고, PyTorch 안드로이드 예제인 `Hello World `_ 앱을 실행해 보십시오. 이 튜토리얼은 대게 처음으로 모바일에 배포하는 모델인 이미지 분류 모델을 넘어선 다음 단계를 다루고 있습니다. 이 튜토리얼을 위한 전체 코드는 `여기 `_ 에서 확인 가능합니다.
학습 목표
---------
@@ -103,7 +103,7 @@ PyTorch의 의미론적 이미지 분할에 사용하는 `DeepLabV3 모델 `_ 를 따라해 봅니다. 이 튜토리얼의 DeepLabV3과 PyTorch HelloWorld Android 예제 내부의 MobileNet v2 둘 다 컴퓨터 비전 모델이기에, `HelloWorld 예제 저장소 `_ 에서도 손쉽게 모델을 읽고 입출력을 처리하기 위한 코드 수정 방법을 찾을 수 있습니다. 이 단계와 4단계의 목표는 1단계에서 만들어진 `deeplabv3_scripted.pt` 모델이 안드로이드에서 확실하게 동작하는지 확인하는 것입니다.
+첫 번째로 모델을 안드로이드 스튜디오 프로젝트에서 PyTorch Mobile과 함께 쓰기 위해 `안드로이드 레시피를 위한 모델 준비 <../recipes/model_preparation_android.html#add-the-model-and-pytorch-library-on-android>`_ 를 따라해 봅니다. 이 튜토리얼의 DeepLabV3과 PyTorch Hello World Android 예제 내부의 MobileNet v2 둘 다 컴퓨터 비전 모델이기에, `Hello World 예제 저장소 `_ 에서도 손쉽게 모델을 읽고 입출력을 처리하기 위한 코드 수정 방법을 찾을 수 있습니다. 이 단계와 4단계의 목표는 1단계에서 만들어진 `deeplabv3_scripted.pt` 모델이 안드로이드에서 확실하게 동작하는지 확인하는 것입니다.
이제 2단계에서 사용한 `deeplabv3_scripted.pt` 와 `deeplab.jpg` 를 안드로이드 스튜디오 프로젝트에 더하고 `MainActivity` 내부의 `onCreate` 메소드를 이와 유사하게 수정합니다:
@@ -122,7 +122,7 @@ PyTorch의 의미론적 이미지 분할에 사용하는 `DeepLabV3 모델 `_ HelloWorld 프로젝트의 입력 처리를 위한 코드를 재사용 합니다. `MainActivity.java` 파일의 `50번째 줄 `_ 과 73번째 줄 사이의 코드를 아래와 같이 변경합니다:
+이전 단계에서 모델을 읽어들인 이후 입력값이 잘 동작하는지, 예상한대로 출력값을 생성하는지 확인해 봅시다. DeepLabV3 모델을 위한 입력은 Hello World 예제 내부의 MobileNet v2에서 쓰는 이미지와 동일합니다. 그래서 `MainActivity.java `_ Hello World 프로젝트의 입력 처리를 위한 코드를 재사용 합니다. `MainActivity.java` 파일의 `50번째 줄 `_ 과 73번째 줄 사이의 코드를 아래와 같이 변경합니다:
.. code-block:: java
@@ -211,7 +211,7 @@ PyTorch의 의미론적 이미지 분할에 사용하는 `DeepLabV3 모델 `_ 을 확인하고, PyTorch iOS 예제인 `HelloWorld `_ 앱을 실행해 보십시오. 이 튜토리얼은 대게 처음으로 모바일에 배포하는 모델인 이미지 분류 모델을 넘어선 다음 단계를 다루고 있습니다. 이 튜토리얼을 위한 전체 코드는 `여기 `_ 에서 확인 가능합니다.
+.. note:: 이 튜토리얼을 진행하기 앞서 `iOS를 위한 PyTorch 모바일 `_ 을 확인하고, PyTorch iOS 예제인 `Hello World `_ 앱을 실행해 보십시오. 이 튜토리얼은 대게 처음으로 모바일에 배포하는 모델인 이미지 분류 모델을 넘어선 다음 단계를 다루고 있습니다. 이 튜토리얼을 위한 전체 코드는 `여기 `_ 에서 확인 가능합니다.
학습 목표
-------------------
@@ -105,7 +105,7 @@ iOS에 모델을 배포하는 첫 단계는 모델을 `TorchScript `_ 의 단계 3을 따라합니다.
-이 튜토리얼의 DeepLabV3 모델과 PyTorch HelloWorld iOS 예제 내부의 MobileNet v2 모델 둘 다 컴퓨터 비전 모델이기에, `HelloWorld 예제 저장소 `_ 를 모델을 읽어 들이고 입출력을 처리하는 본보기로 삼아 시작할 수도 있습니다.
+이 튜토리얼의 DeepLabV3 모델과 PyTorch Hello World iOS 예제 내부의 MobileNet v2 모델 둘 다 컴퓨터 비전 모델이기에, `Hello World 예제 저장소 `_ 를 모델을 읽어 들이고 입출력을 처리하는 본보기로 삼아 시작할 수도 있습니다.
이제 단계 2에서 사용한 `deeplabv3_scripted.pt` 와 `deeplab.jpg` 를 Xcode 프로젝트에 추가하고 `ViewController.swift` 를 이와 유사하게 수정합니다:
@@ -134,7 +134,7 @@ iOS에 모델을 배포하는 첫 단계는 모델을 `TorchScript `_ HelloWorld 프로젝트의 입력 처리를 위한 코드를 재사용 합니다. `TorchModule.mm` 안의 `predictImage` 메소드 구현을 아래와 같이 변경합니다:
+이전 단계에서 모델을 읽어들인 이후 입력값이 잘 동작하는지, 예상한대로 출력값을 생성하는지 확인해 봅시다. DeepLabV3 모델을 위한 입력은 Hello World 예제 내부의 MobileNet v2에서 쓰는 이미지와 동일합니다. 그래서 `TorchModule.mm `_ Hello World 프로젝트의 입력 처리를 위한 코드를 재사용 합니다. `TorchModule.mm` 안의 `predictImage` 메소드 구현을 아래와 같이 변경합니다:
.. code-block:: objective-c
@@ -226,7 +226,7 @@ iOS에 모델을 배포하는 첫 단계는 모델을 `TorchScript `__
and the `launching script `__,
if the application needs to scale across machine boundaries.
-5. Use `torch.distributed.elastic `__
+5. Use multi-GPU `FullyShardedDataParallel `__
+ training on a single-machine or multi-machine when the data and model cannot
+ fit on one GPU.
+6. Use `torch.distributed.elastic `__
to launch distributed training if errors (e.g., out-of-memory) are expected or if
resources can join and leave dynamically during training.
@@ -131,9 +134,21 @@ DDP materials are listed below:
4. The `Shard Optimizer States With ZeroRedundancyOptimizer <../recipes/zero_redundancy_optimizer.html>`__
recipe demonstrates how `ZeroRedundancyOptimizer `__
helps to reduce optimizer memory footprint.
-5. The `Distributed Training with Uneven Inputs Using the Join Context Manager <../advanced/generic_oin.html>`__
+5. The `Distributed Training with Uneven Inputs Using the Join Context Manager <../advanced/generic_join.html>`__
tutorial walks through using the generic join context for distributed training with uneven inputs.
+
+``torch.distributed.FullyShardedDataParallel``
+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+
+The `FullyShardedDataParallel `__
+(FSDP) is a type of data parallelism paradigm which maintains a per-GPU copy of a model’s
+parameters, gradients and optimizer states, it shards all of these states across
+data-parallel workers. The support for FSDP was added starting PyTorch v1.11. The tutorial
+`Getting Started with FSDP `__
+provides in depth explanation and example of how FSDP works.
+
+
torch.distributed.elastic
~~~~~~~~~~~~~~~~~~~~~~~~~
@@ -150,7 +165,7 @@ throws an exception, it is likely to lead to desynchronization (mismatched
adds fault tolerance and the ability to make use of a dynamic pool of machines (elasticity).
RPC-Based Distributed Training
-----------------------------
+------------------------------
Many training paradigms do not fit into data parallelism, e.g.,
parameter server paradigm, distributed pipeline parallelism, reinforcement
@@ -202,5 +217,5 @@ RPC Tutorials are listed below:
PyTorch Distributed Developers
------------------------------
-If you'd like to contribute to PyTorch Distributed, please refer to our
+If you'd like to contribute to PyTorch Distributed, refer to our
`Developer Guide `_.
diff --git a/beginner_source/examples_autograd/polynomial_autograd.py b/beginner_source/examples_autograd/polynomial_autograd.py
index 004c4b75b..ebaadb2dc 100755
--- a/beginner_source/examples_autograd/polynomial_autograd.py
+++ b/beginner_source/examples_autograd/polynomial_autograd.py
@@ -1,7 +1,7 @@
# -*- coding: utf-8 -*-
"""
PyTorch: 텐서(Tensor)와 autograd
---------------------------------
+-----------------------------------
:math:`y=\sin(x)` 을 예측할 수 있도록, :math:`-\pi` 부터 :math:`\pi` 까지
유클리드 거리(Euclidean distance)를 최소화하도록 3차 다항식을 학습합니다.
@@ -16,23 +16,23 @@
import math
dtype = torch.float
-device = torch.device("cpu")
-# device = torch.device("cuda:0") # GPU에서 실행하려면 이 주석을 제거하세요
+device = "cuda" if torch.cuda.is_available() else "cpu"
+torch.set_default_device(device)
# 입력값과 출력값을 갖는 텐서들을 생성합니다.
# requires_grad=False가 기본값으로 설정되어 역전파 단계 중에 이 텐서들에 대한 변화도를
# 계산할 필요가 없음을 나타냅니다.
-x = torch.linspace(-math.pi, math.pi, 2000, device=device, dtype=dtype)
+x = torch.linspace(-math.pi, math.pi, 2000, dtype=dtype)
y = torch.sin(x)
# 가중치를 갖는 임의의 텐서를 생성합니다. 3차 다항식이므로 4개의 가중치가 필요합니다:
# y = a + b x + c x^2 + d x^3
# requires_grad=True로 설정하여 역전파 단계 중에 이 텐서들에 대한 변화도를 계산할 필요가
# 있음을 나타냅니다.
-a = torch.randn((), device=device, dtype=dtype, requires_grad=True)
-b = torch.randn((), device=device, dtype=dtype, requires_grad=True)
-c = torch.randn((), device=device, dtype=dtype, requires_grad=True)
-d = torch.randn((), device=device, dtype=dtype, requires_grad=True)
+a = torch.randn((), dtype=dtype, requires_grad=True)
+b = torch.randn((), dtype=dtype, requires_grad=True)
+c = torch.randn((), dtype=dtype, requires_grad=True)
+d = torch.randn((), dtype=dtype, requires_grad=True)
learning_rate = 1e-6
for t in range(2000):
diff --git a/beginner_source/fgsm_tutorial.py b/beginner_source/fgsm_tutorial.py
index 175965f59..7c1548195 100644
--- a/beginner_source/fgsm_tutorial.py
+++ b/beginner_source/fgsm_tutorial.py
@@ -66,7 +66,6 @@
# 이제 본 튜토리얼의 동기가 명확해지길 바라며, 구현으로 넘어가 보겠습니다.
#
-from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
@@ -75,13 +74,6 @@
import numpy as np
import matplotlib.pyplot as plt
-# NOTE: 아래는 MNIST 데이터셋을 내려받을 때 "User-agent" 관련한 제한을 푸는 코드입니다.
-# 더 자세한 내용은 https://github.com/pytorch/vision/issues/3497 을 참고해주세요.
-from six.moves import urllib
-opener = urllib.request.build_opener()
-opener.addheaders = [('User-agent', 'Mozilla/5.0')]
-urllib.request.install_opener(opener)
-
######################################################################
# 구현
@@ -91,7 +83,7 @@
# 정의한 다음 공격을 코딩하고 일부 테스트를 실행합니다.
#
# 입력
-# ~~~~~~
+# ~~~~~~~~~~~~~~
#
# 이 학습서에는 입력이 3 개이며 다음과 같이 정의됩니다:
#
@@ -102,7 +94,7 @@
#
# - ``pretrained_model`` - `pytorch/examples/mnist `__
# 를 통해 미리 학습된 MNIST 모델의 경로.
-# 튜토리얼을 간편하게 하려면 `여기 `__ 에서 미리 학습된 모델을 다운로드하세요.
+# 튜토리얼을 간편하게 하려면 `여기 `__ 에서 미리 학습된 모델을 다운로드하세요.
#
# - ``use_cuda`` - CUDA 를 사용할지 말지 정하는 이진 플래그.
# 본 튜토리얼에서는 CPU 시간이 오래 걸리지 않으므로 CUDA를 지원하는 GPU 의 여부는 중요하지 않습니다.
@@ -111,11 +103,12 @@
epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "data/lenet_mnist_model.pth"
use_cuda=True
-
+# 재현을 위해 랜덤 시드(seed)를 설정합니다.
+torch.manual_seed(42)
######################################################################
# 공격을 받는 모델
-# ~~~~~~~~~~~~~~~~~~
+# ~~~~~~~~~~~~~~~~~~~~~
#
# 앞서 말한대로, 공격받는 모델은 `pytorch/examples/mnist `__
# 와 동일한 MNIST 모델입니다. 본인의 MNIST 모델을 학습 및 저장하는 방식으로 하거나 제공된 모델을 다운로드 해 사용하는 식으로 진행할 수 있습니다.
@@ -127,37 +120,45 @@
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
- self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
- self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
- self.conv2_drop = nn.Dropout2d()
- self.fc1 = nn.Linear(320, 50)
- self.fc2 = nn.Linear(50, 10)
+ self.conv1 = nn.Conv2d(1, 32, 3, 1)
+ self.conv2 = nn.Conv2d(32, 64, 3, 1)
+ self.dropout1 = nn.Dropout(0.25)
+ self.dropout2 = nn.Dropout(0.5)
+ self.fc1 = nn.Linear(9216, 128)
+ self.fc2 = nn.Linear(128, 10)
def forward(self, x):
- x = F.relu(F.max_pool2d(self.conv1(x), 2))
- x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
- x = x.view(-1, 320)
- x = F.relu(self.fc1(x))
- x = F.dropout(x, training=self.training)
+ x = self.conv1(x)
+ x = F.relu(x)
+ x = self.conv2(x)
+ x = F.relu(x)
+ x = F.max_pool2d(x, 2)
+ x = self.dropout1(x)
+ x = torch.flatten(x, 1)
+ x = self.fc1(x)
+ x = F.relu(x)
+ x = self.dropout2(x)
x = self.fc2(x)
- return F.log_softmax(x, dim=1)
+ output = F.log_softmax(x, dim=1)
+ return output
# MNIST 테스트 데이터셋과 데이터로더 선언
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(),
+ transforms.Normalize((0.1307,), (0.3081,)),
])),
batch_size=1, shuffle=True)
# 어떤 디바이스를 사용할지 정의
print("CUDA Available: ",torch.cuda.is_available())
-device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")
+device = torch.device("cuda" if use_cuda and torch.cuda.is_available() else "cpu")
# 모델 초기화하기
model = Net().to(device)
# 미리 학습된 모델 읽어오기
-model.load_state_dict(torch.load(pretrained_model, map_location='cpu'))
+model.load_state_dict(torch.load(pretrained_model, map_location=device))
# 모델을 평가 모드로 설정하기. 드롭아웃 레이어들을 위해 사용됨
model.eval()
@@ -190,6 +191,24 @@ def fgsm_attack(image, epsilon, data_grad):
# 작은 변화가 적용된 이미지를 리턴합니다
return perturbed_image
+# 텐서를 원래 스케일로 복원
+def denorm(batch, mean=[0.1307], std=[0.3081]):
+ """
+ 텐서 묶음(batch)을 원래 스케일로 변환합니다.
+ Args:
+ batch (torch.Tensor): 정규화된 텐서 배치(batch)
+ mean (torch.Tensor or list): 정규화시 사용했던 평균(mean)
+ std (torch.Tensor or list): 정규화시 사용했던 표준편차(standard deviation)
+ Returns:
+ torch.Tensor: 정규화가 적용되지 않은 텐서 묶음(batch)
+ """
+ if isinstance(mean, list):
+ mean = torch.tensor(mean).to(device)
+ if isinstance(std, list):
+ std = torch.tensor(std).to(device)
+
+ return batch * std.view(1, -1, 1, 1) + mean.view(1, -1, 1, 1)
+
######################################################################
# 테스팅 함수
@@ -238,18 +257,24 @@ def test( model, device, test_loader, epsilon ):
# 변화도 값을 모읍니다
data_grad = data.grad.data
+ # 데이터를 원래 스케일로 복원합니다
+ data_denorm = denorm(data)
+
# FGSM 공격을 호출합니다
- perturbed_data = fgsm_attack(data, epsilon, data_grad)
+ perturbed_data = fgsm_attack(data_denorm, epsilon, data_grad)
+
+ # 정규화를 다시 적용합니다
+ perturbed_data_normalized = transforms.Normalize((0.1307,), (0.3081,))(perturbed_data)
# 작은 변화가 적용된 이미지에 대해 재분류합니다
- output = model(perturbed_data)
+ output = model(perturbed_data_normalized)
# 올바른지 확인합니다
final_pred = output.max(1, keepdim=True)[1] # 로그 확률의 최대값을 가지는 인덱스를 얻습니다
if final_pred.item() == target.item():
correct += 1
# 0 엡실론 예제에 대해서 저장합니다
- if (epsilon == 0) and (len(adv_examples) < 5):
+ if epsilon == 0 and len(adv_examples) < 5:
adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
else:
@@ -260,7 +285,7 @@ def test( model, device, test_loader, epsilon ):
# 해당 엡실론에서의 최종 정확도를 계산합니다
final_acc = correct/float(len(test_loader))
- print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))
+ print(f"Epsilon: {epsilon}\tTest Accuracy = {correct} / {len(test_loader)} = {final_acc}")
# 정확도와 적대적 예제를 리턴합니다
return final_acc, adv_examples
@@ -337,9 +362,9 @@ def test( model, device, test_loader, epsilon ):
plt.xticks([], [])
plt.yticks([], [])
if j == 0:
- plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
+ plt.ylabel(f"Eps: {epsilons[i]}", fontsize=14)
orig,adv,ex = examples[i][j]
- plt.title("{} -> {}".format(orig, adv))
+ plt.title(f"{orig} -> {adv}")
plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()
@@ -364,3 +389,7 @@ def test( model, device, test_loader, epsilon ):
# NIPS 2017 경쟁에서 소개된 다양한 공격 방법을 직접 구현해 보고, FGSM 과 어떤 점이 다른지 연구해 보세요.
# 그리고 나서 직접 만든 공격으로부터 모델을 방어해 보세요.
#
+# 그 외에도 다른 방향으로는, 사용 가능한 자원이 있다면 위의 각 ``epsilon test()`` 루프에서
+# 한 번에 하나씩 공격을 처리하는 대신 일괄(batch), 병렬(parallel) 또는 분산(distributed)으로
+# 작업을 처리하도록 코드를 변경해 보세요.
+#
\ No newline at end of file
diff --git a/beginner_source/finetuning_torchvision_models_tutorial.rst b/beginner_source/finetuning_torchvision_models_tutorial.rst
new file mode 100644
index 000000000..39eba2064
--- /dev/null
+++ b/beginner_source/finetuning_torchvision_models_tutorial.rst
@@ -0,0 +1,10 @@
+Torchvision 모델 미세조정하기
+=================================
+
+이 튜토리얼은 https://tutorials.pytorch.kr/intermediate/torchvision_tutorial.html 로 옮겨졌습니다.
+
+3초 뒤에 자동으로 이동합니다.
+
+.. raw:: html
+
+
diff --git a/beginner_source/former_torchies/parallelism_tutorial.py b/beginner_source/former_torchies/parallelism_tutorial.py
index ac7c8ec83..5dc58e33d 100644
--- a/beginner_source/former_torchies/parallelism_tutorial.py
+++ b/beginner_source/former_torchies/parallelism_tutorial.py
@@ -52,7 +52,10 @@ def forward(self, x):
class MyDataParallel(nn.DataParallel):
def __getattr__(self, name):
- return getattr(self.module, name)
+ try:
+ return super().__getattr__(name)
+ except AttributeError:
+ return getattr(self.module, name)
########################################################################
# **DataParallel이 구현된 기본형(Primitive):**
diff --git a/beginner_source/hta_intro_tutorial.rst b/beginner_source/hta_intro_tutorial.rst
new file mode 100644
index 000000000..5562c879b
--- /dev/null
+++ b/beginner_source/hta_intro_tutorial.rst
@@ -0,0 +1,390 @@
+Introduction to Holistic Trace Analysis
+=======================================
+
+**Author:** `Anupam Bhatnagar `_
+
+In this tutorial, we demonstrate how to use Holistic Trace Analysis (HTA) to
+analyze traces from a distributed training job. To get started follow the steps
+below.
+
+Installing HTA
+~~~~~~~~~~~~~~
+
+We recommend using a Conda environment to install HTA. To install Anaconda, see
+`the official Anaconda documentation `_.
+
+1. Install HTA using pip:
+
+ .. code-block:: python
+
+ pip install HolisticTraceAnalysis
+
+2. (Optional and recommended) Set up a Conda environment:
+
+ .. code-block:: python
+
+ # create the environment env_name
+ conda create -n env_name
+
+ # activate the environment
+ conda activate env_name
+
+ # When you are done, deactivate the environment by running ``conda deactivate``
+
+Getting Started
+~~~~~~~~~~~~~~~
+
+Launch a Jupyter notebook and set the ``trace_dir`` variable to the location of the traces.
+
+.. code-block:: python
+
+ from hta.trace_analysis import TraceAnalysis
+ trace_dir = "/path/to/folder/with/traces"
+ analyzer = TraceAnalysis(trace_dir=trace_dir)
+
+
+Temporal Breakdown
+------------------
+
+To effectively utilize the GPUs, it is crucial to understand how they are spending
+time for a specific job. Are they primarily engaged in computation, communication,
+memory events, or are they idle? The temporal breakdown feature provides a detailed
+analysis of the time spent in these three categories.
+
+* Idle time - GPU is idle.
+* Compute time - GPU is being used for matrix multiplications or vector operations.
+* Non-compute time - GPU is being used for communication or memory events.
+
+To achieve high training efficiency, the code should maximize compute time and
+minimize idle time and non-compute time. The following function generates a
+dataframe that provides a detailed breakdown of the temporal usage for each rank.
+
+.. code-block:: python
+
+ analyzer = TraceAnalysis(trace_dir = "/path/to/trace/folder")
+ time_spent_df = analyzer.get_temporal_breakdown()
+
+
+.. image:: ../_static/img/hta/temporal_breakdown_df.png
+
+When the ``visualize`` argument is set to ``True`` in the `get_temporal_breakdown
+`_
+function it also generates a bar graph representing the breakdown by rank.
+
+.. image:: ../_static/img/hta/temporal_breakdown_plot.png
+
+
+Idle Time Breakdown
+-------------------
+
+Gaining insight into the amount of time the GPU spends idle and the
+reasons behind it can help guide optimization strategies. A GPU is
+considered idle when no kernel is running on it. We have developed an
+algorithm to categorize the `Idle` time into three distinct categories:
+
+* **Host wait:** refers to the idle time on the GPU that is caused by
+ the CPU not enqueuing kernels quickly enough to keep the GPU fully utilized.
+ These types of inefficiencies can be addressed by examining the CPU
+ operators that are contributing to the slowdown, increasing the batch
+ size and applying operator fusion.
+
+* **Kernel wait:** This refers to brief overhead associated with launching
+ consecutive kernels on the GPU. The idle time attributed to this category
+ can be minimized by using CUDA Graph optimizations.
+
+* **Other wait:** This category includes idle time that cannot currently
+ be attributed due to insufficient information. The likely causes include
+ synchronization among CUDA streams using CUDA events and delays in launching
+ kernels.
+
+The host wait time can be interpreted as the time when the GPU is stalling due
+to the CPU. To attribute the idle time as kernel wait we use the following
+heuristic:
+
+ | **gap between consecutive kernels < threshold**
+
+The default threshold value is 30 nanoseconds and can be configured using the
+``consecutive_kernel_delay`` argument. By default, the idle time breakdown is
+computed for rank 0 only. In order to calculate the breakdown for other ranks,
+use the ``ranks`` argument in the `get_idle_time_breakdown
+`_
+function. The idle time breakdown can be generated as follows:
+
+.. code-block:: python
+
+ analyzer = TraceAnalysis(trace_dir = "/path/to/trace/folder")
+ idle_time_df = analyzer.get_idle_time_breakdown()
+
+.. image:: ../_static/img/hta/idle_time_breakdown_percentage.png
+
+The function returns a tuple of dataframes. The first dataframe contains the
+idle time by category on each stream for each rank.
+
+.. image:: ../_static/img/hta/idle_time.png
+ :scale: 100%
+ :align: center
+
+The second dataframe is generated when ``show_idle_interval_stats`` is set to
+``True``. It contains the summary statistics of the idle time for each stream
+on each rank.
+
+.. image:: ../_static/img/hta/idle_time_summary.png
+ :scale: 100%
+
+.. tip::
+
+ By default, the idle time breakdown presents the percentage of each of the
+ idle time categories. Setting the ``visualize_pctg`` argument to ``False``,
+ the function renders with absolute time on the y-axis.
+
+
+Kernel Breakdown
+----------------
+
+The kernel breakdown feature breaks down the time spent for each kernel type,
+such as communication (COMM), computation (COMP), and memory (MEM), across all
+ranks and presents the proportion of time spent in each category. Here is the
+percentage of time spent in each category as a pie chart:
+
+.. image:: ../_static/img/hta/kernel_type_breakdown.png
+ :align: center
+
+The kernel breakdown can be calculated as follows:
+
+.. code-block:: python
+
+ analyzer = TraceAnalysis(trace_dir = "/path/to/trace/folder")
+ kernel_type_metrics_df, kernel_metrics_df = analyzer.get_gpu_kernel_breakdown()
+
+The first dataframe returned by the function contains the raw values used to
+generate the pie chart.
+
+Kernel Duration Distribution
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+The second dataframe returned by `get_gpu_kernel_breakdown
+`_
+contains duration summary statistics for each kernel. In particular, this
+includes the count, min, max, average, standard deviation, sum, and kernel type
+for each kernel on each rank.
+
+.. image:: ../_static/img/hta/kernel_metrics_df.png
+ :align: center
+
+Using this data HTA creates many visualizations to identify performance
+bottlenecks.
+
+#. Pie charts of the top kernels for each kernel type for each rank.
+
+#. Bar graphs of the average duration across all ranks for each of the top
+ kernels and for each kernel type.
+
+.. image:: ../_static/img/hta/pie_charts.png
+
+.. tip::
+
+ All images are generated using plotly. Hovering on the graph shows the
+ mode bar on the top right which allows the user to zoom, pan, select, and
+ download the graph.
+
+The pie charts above show the top 5 computation, communication, and memory
+kernels. Similar pie charts are generated for each rank. The pie charts can be
+configured to show the top k kernels using the ``num_kernels`` argument passed
+to the `get_gpu_kernel_breakdown` function. Additionally, the
+``duration_ratio`` argument can be used to tune the percentage of time that
+needs to be analyzed. If both ``num_kernels`` and ``duration_ratio`` are
+specified, then ``num_kernels`` takes precedence.
+
+.. image:: ../_static/img/hta/comm_across_ranks.png
+
+The bar graph above shows the average duration of the NCCL AllReduce kernel
+across all the ranks. The black lines indicate the minimum and maximum time
+taken on each rank.
+
+.. warning::
+ When using jupyter-lab set the "image_renderer" argument value to
+ "jupyterlab" otherwise the graphs will not render in the notebook.
+
+For a detailed walkthrough of this feature see the `gpu_kernel_breakdown
+notebook
+`_
+in the examples folder of the repo.
+
+
+Communication Computation Overlap
+---------------------------------
+
+In distributed training, a significant amount of time is spent in communication
+and synchronization events between GPUs. To achieve high GPU efficiency (such as
+TFLOPS/GPU), it is crucial to keep the GPU oversubscribed with computation
+kernels. In other words, the GPU should not be blocked due to unresolved data
+dependencies. One way to measure the extent to which computation is blocked by
+data dependencies is to calculate the communication computation overlap. Higher
+GPU efficiency is observed if communication events overlap computation events.
+Lack of communication and computation overlap will lead to the GPU being idle,
+resulting in low efficiency.
+To sum up, a higher communication computation overlap is desirable. To calculate
+the overlap percentage for each rank, we measure the following ratio:
+
+ | **(time spent in computation while communicating) / (time spent in communication)**
+
+The communication computation overlap can be calculated as follows:
+
+.. code-block:: python
+
+ analyzer = TraceAnalysis(trace_dir = "/path/to/trace/folder")
+ overlap_df = analyzer.get_comm_comp_overlap()
+
+The function returns a dataframe containing the overlap percentage
+for each rank.
+
+.. image:: ../_static/img/hta/overlap_df.png
+ :align: center
+ :scale: 50%
+
+When the ``visualize`` argument is set to True, the `get_comm_comp_overlap
+`_
+function also generates a bar graph representing the overlap by rank.
+
+.. image:: ../_static/img/hta/overlap_plot.png
+
+
+Augmented Counters
+------------------
+
+Memory Bandwidth & Queue Length Counters
+^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+
+Memory bandwidth counters measure the memory copy bandwidth used while copying
+the data from H2D, D2H and D2D by memory copy (memcpy) and memory set (memset)
+events. HTA also computes the number of outstanding operations on each CUDA
+stream. We refer to this as **queue length**. When the queue length on a stream
+is 1024 or larger new events cannot be scheduled on that stream and the CPU
+will stall until the events on the GPU stream have processed.
+
+The `generate_trace_with_counters
+`_
+API outputs a new trace file with the memory bandwidth and queue length
+counters. The new trace file contains tracks which indicate the memory
+bandwidth used by memcpy/memset operations and tracks for the queue length on
+each stream. By default, these counters are generated using the rank 0
+trace file, and the new file contains the suffix ``_with_counters`` in its name.
+Users have the option to generate the counters for multiple ranks by using the
+``ranks`` argument in the ``generate_trace_with_counters`` API.
+
+.. code-block:: python
+
+ analyzer = TraceAnalysis(trace_dir = "/path/to/trace/folder")
+ analyzer.generate_trace_with_counters()
+
+A screenshot of the generated trace file with augmented counters.
+
+.. image:: ../_static/img/hta/mem_bandwidth_queue_length.png
+ :scale: 100%
+
+HTA also provides a summary of the memory copy bandwidth and queue length
+counters as well as the time series of the counters for the profiled portion of
+the code using the following API:
+
+* `get_memory_bw_summary `_
+
+* `get_queue_length_summary `_
+
+* `get_memory_bw_time_series `_
+
+* `get_queue_length_time_series `_
+
+To view the summary and time series, use:
+
+.. code-block:: python
+
+ # generate summary
+ mem_bw_summary = analyzer.get_memory_bw_summary()
+ queue_len_summary = analyzer.get_queue_length_summary()
+
+ # get time series
+ mem_bw_series = analyzer.get_memory_bw_time_series()
+ queue_len_series = analyzer.get_queue_length_series()
+
+The summary contains the count, min, max, mean, standard deviation, 25th, 50th,
+and 75th percentile.
+
+.. image:: ../_static/img/hta/queue_length_summary.png
+ :scale: 100%
+ :align: center
+
+The time series only contains the points when a value changes. Once a value is
+observed the time series stays constant until the next update. The memory
+bandwidth and queue length time series functions return a dictionary whose key
+is the rank and the value is the time series for that rank. By default, the
+time series is computed for rank 0 only.
+
+CUDA Kernel Launch Statistics
+-----------------------------
+
+.. image:: ../_static/img/hta/cuda_kernel_launch.png
+
+For each event launched on the GPU, there is a corresponding scheduling event on
+the CPU, such as ``CudaLaunchKernel``, ``CudaMemcpyAsync``, ``CudaMemsetAsync``.
+These events are linked by a common correlation ID in the trace - see the figure
+above. This feature computes the duration of the CPU runtime event, its corresponding GPU
+kernel and the launch delay, for example, the difference between GPU kernel starting and
+CPU operator ending. The kernel launch info can be generated as follows:
+
+.. code-block:: python
+
+ analyzer = TraceAnalysis(trace_dir="/path/to/trace/dir")
+ kernel_info_df = analyzer.get_cuda_kernel_launch_stats()
+
+A screenshot of the generated dataframe is given below.
+
+.. image:: ../_static/img/hta/cuda_kernel_launch_stats.png
+ :scale: 100%
+ :align: center
+
+The duration of the CPU op, GPU kernel, and the launch delay allow us to find
+the following:
+
+* **Short GPU kernels** - GPU kernels with duration less than the corresponding
+ CPU runtime event.
+
+* **Runtime event outliers** - CPU runtime events with excessive duration.
+
+* **Launch delay outliers** - GPU kernels which take too long to be scheduled.
+
+HTA generates distribution plots for each of the aforementioned three categories.
+
+**Short GPU kernels**
+
+Typically, the launch time on the CPU side ranges from 5-20 microseconds. In some
+cases, the GPU execution time is lower than the launch time itself. The graph
+below helps us to find how frequently such instances occur in the code.
+
+.. image:: ../_static/img/hta/short_gpu_kernels.png
+
+
+**Runtime event outliers**
+
+The runtime outliers depend on the cutoff used to classify the outliers, hence
+the `get_cuda_kernel_launch_stats
+`_
+API provides the ``runtime_cutoff`` argument to configure the value.
+
+.. image:: ../_static/img/hta/runtime_outliers.png
+
+**Launch delay outliers**
+
+The launch delay outliers depend on the cutoff used to classify the outliers,
+hence the `get_cuda_kernel_launch_stats` API provides the
+``launch_delay_cutoff`` argument to configure the value.
+
+.. image:: ../_static/img/hta/launch_delay_outliers.png
+
+
+Conclusion
+~~~~~~~~~~
+
+In this tutorial, you have learned how to install and use HTA,
+a performance tool that enables you analyze bottlenecks in your distributed
+training workflows. To learn how you can use the HTA tool to perform trace
+diff analysis, see `Trace Diff using Holistic Trace Analysis `__.
diff --git a/beginner_source/hta_trace_diff_tutorial.rst b/beginner_source/hta_trace_diff_tutorial.rst
new file mode 100644
index 000000000..608d29ea3
--- /dev/null
+++ b/beginner_source/hta_trace_diff_tutorial.rst
@@ -0,0 +1,66 @@
+Trace Diff using Holistic Trace Analysis
+========================================
+
+**Author:** `Anupam Bhatnagar `_
+
+Occasionally, users need to identify the changes in PyTorch operators and CUDA
+kernels resulting from a code change. To support this requirement, HTA
+provides a trace comparison feature. This feature allows the user to input two
+sets of trace files where the first can be thought of as the *control group*
+and the second as the *test group*, similar to an A/B test. The ``TraceDiff`` class
+provides functions to compare the differences between traces and functionality
+to visualize these differences. In particular, users can find operators and
+kernels that were added and removed from each group, along with the frequency
+of each operator/kernel and the cumulative time taken by the operator/kernel.
+
+The `TraceDiff `_ class
+has the following methods:
+
+* `compare_traces `_:
+ Compare the frequency and total duration of CPU operators and GPU kernels from
+ two sets of traces.
+
+* `ops_diff `_:
+ Get the operators and kernels which have been:
+
+ #. **added** to the test trace and are absent in the control trace
+ #. **deleted** from the test trace and are present in the control trace
+ #. **increased** in frequency in the test trace and exist in the control trace
+ #. **decreased** in frequency in the test trace and exist in the control trace
+ #. **unchanged** between the two sets of traces
+
+* `visualize_counts_diff `_
+
+* `visualize_duration_diff `_
+
+The last two methods can be used to visualize various changes in frequency and
+duration of CPU operators and GPU kernels, using the output of the
+``compare_traces`` method.
+
+For example, the top ten operators with increase in frequency can be computed as
+follows:
+
+.. code-block:: python
+
+ df = compare_traces_output.sort_values(by="diff_counts", ascending=False).head(10)
+ TraceDiff.visualize_counts_diff(df)
+
+.. image:: ../_static/img/hta/counts_diff.png
+
+Similarly, the top ten operators with the largest change in duration can be computed as
+follows:
+
+.. code-block:: python
+
+ df = compare_traces_output.sort_values(by="diff_duration", ascending=False)
+ # The duration differerence can be overshadowed by the "ProfilerStep",
+ # so we can filter it out to show the trend of other operators.
+ df = df.loc[~df.index.str.startswith("ProfilerStep")].head(10)
+ TraceDiff.visualize_duration_diff(df)
+
+.. image:: ../_static/img/hta/duration_diff.png
+
+For a detailed example of this feature see the `trace_diff_demo notebook
+`_
+in the examples folder of the repository.
+
diff --git a/beginner_source/hyperparameter_tuning_tutorial.py b/beginner_source/hyperparameter_tuning_tutorial.py
index 3d4b57601..2593412d7 100644
--- a/beginner_source/hyperparameter_tuning_tutorial.py
+++ b/beginner_source/hyperparameter_tuning_tutorial.py
@@ -1,7 +1,7 @@
# -*- coding: utf-8 -*-
"""
-Ray Tune을 이용한 하이퍼파라미터 튜닝
-======================================
+Ray Tune을 사용한 하이퍼파라미터 튜닝
+=========================================
**번역**: `심형준 `_
@@ -33,11 +33,12 @@
설정 / 불러오기
-----------------
-import들로 시작합니다.
+필요한 라이브러리들을 불러오는 것(import)으로 시작해보겠습니다:
"""
from functools import partial
-import numpy as np
import os
+import tempfile
+from pathlib import Path
import torch
import torch.nn as nn
import torch.nn.functional as F
@@ -45,31 +46,42 @@
from torch.utils.data import random_split
import torchvision
import torchvision.transforms as transforms
+# sphinx_gallery_start_ignore
+# Fixes ``AttributeError: '_LoggingTee' object has no attribute 'fileno'``.
+# This is only needed to run with sphinx-build.
+import sys
+if not hasattr(sys.stdout, "encoding"):
+ sys.stdout.encoding = "latin1"
+ sys.stdout.fileno = lambda: 0
+# sphinx_gallery_end_ignore
from ray import tune
-from ray.tune import CLIReporter
+from ray import train
+from ray.train import Checkpoint, get_checkpoint
from ray.tune.schedulers import ASHAScheduler
+import ray.cloudpickle as pickle
######################################################################
# 대부분의 import들은 파이토치 모델을 빌드하는데 필요합니다.
-# 마지막 세 개의 import들만 Ray Tune을 사용하기 위한 것입니다.
+# 가장 마지막의 import만이 Ray Tune을 사용하기 위한 것입니다.
#
# Data loaders
-# -------------
+# ---------------------------
# data loader를 자체 함수로 감싸두고 전역 데이터 디렉토리로 전달합니다.
# 이런 식으로 서로 다른 실험들 간에 데이터 디렉토리를 공유할 수 있습니다.
def load_data(data_dir="./data"):
- transform = transforms.Compose([
- transforms.ToTensor(),
- transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
- ])
+ transform = transforms.Compose(
+ [transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]
+ )
trainset = torchvision.datasets.CIFAR10(
- root=data_dir, train=True, download=True, transform=transform)
+ root=data_dir, train=True, download=True, transform=transform
+ )
testset = torchvision.datasets.CIFAR10(
- root=data_dir, train=False, download=True, transform=transform)
+ root=data_dir, train=False, download=True, transform=transform
+ )
return trainset, testset
@@ -93,7 +105,7 @@ def __init__(self, l1=120, l2=84):
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
- x = x.view(-1, 16 * 5 * 5)
+ x = torch.flatten(x, 1) # 배치(batch) 차원을 제외한 모든 차원을 평탄화(flatten)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
@@ -105,20 +117,29 @@ def forward(self, x):
# 흥미를 더해보고자 `파이토치 문서의 예제 `_
# 일부를 변경하여 소개합니다.
#
-# 학습 스크립트를 ``train_cifar(config, checkpoint_dir=None, data_dir=None)`` 함수로 감싸둡니다.
-# 짐작할 수 있듯이, ``config`` 매개변수는 훈련할 하이퍼파라미터를 받습니다. ``checkpoint_dir`` 매개변수는 체크포인트를
-# 복원하는 데 사용됩니다. ``data_dir`` 은 데이터를 읽고 저장하는 디렉토리를 지정하므로,
-# 여러 실행들이 동일한 데이터 소스를 공유할 수 있습니다.
+# 학습 스크립트를 ``train_cifar(config, data_dir=None)`` 함수로 감싸둡니다.
+# ``config`` 매개변수는 학습할 하이퍼파라미터(hyperparameter)를 받습니다.
+# ``data_dir`` 은 여러 번의 실행(run) 시 동일한 데이터 소스를 공유할 수 있도록
+# 데이터를 읽고 저장하는 디렉토리를 지정합니다.
+# 또한, checkpoint가 지정되는 경우에는 실행 시작 시점의 모델과 옵티마이저 상태(optimizer state)를
+# 불러올 수 있습니다. 이 튜토리얼의 아래쪽에서 체크포인트(checkpoint)를 지정하는 방법과
+# 체크포인트의 용도에 대한 정보를 확인할 수 있습니다.
#
# .. code-block:: python
#
# net = Net(config["l1"], config["l2"])
#
-# if checkpoint_dir:
-# model_state, optimizer_state = torch.load(
-# os.path.join(checkpoint_dir, "checkpoint"))
-# net.load_state_dict(model_state)
-# optimizer.load_state_dict(optimizer_state)
+# checkpoint = get_checkpoint()
+# if checkpoint:
+# with checkpoint.as_directory() as checkpoint_dir:
+# data_path = Path(checkpoint_dir) / "data.pkl"
+# with open(data_path, "rb") as fp:
+# checkpoint_state = pickle.load(fp)
+# start_epoch = checkpoint_state["epoch"]
+# net.load_state_dict(checkpoint_state["net_state_dict"])
+# optimizer.load_state_dict(checkpoint_state["optimizer_state_dict"])
+# else:
+# start_epoch = 0
#
# 또한, 옵티마이저의 학습률(learning rate)을 구성할 수 있습니다.
#
@@ -156,33 +177,45 @@ def forward(self, x):
# 특히 Ray는 `fractional-GPU `_ 도 지원하므로
# 모델이 GPU 메모리에 적합한 상황에서는 테스트 간에 GPU를 공유할 수 있습니다. 이는 나중에 다룰 것입니다.
#
-# Ray Tune과 소통하기
+# Ray Tune으로 통신하기
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~
#
-# 가장 흥미로운 부분은 Ray Tune과의 소통입니다.
+# 가장 흥미로운 부분은 Ray Tune과의 통신입니다:
#
# .. code-block:: python
#
-# with tune.checkpoint_dir(epoch) as checkpoint_dir:
-# path = os.path.join(checkpoint_dir, "checkpoint")
-# torch.save((net.state_dict(), optimizer.state_dict()), path)
+# checkpoint_data = {
+# "epoch": epoch,
+# "net_state_dict": net.state_dict(),
+# "optimizer_state_dict": optimizer.state_dict(),
+# }
+# with tempfile.TemporaryDirectory() as checkpoint_dir:
+# data_path = Path(checkpoint_dir) / "data.pkl"
+# with open(data_path, "wb") as fp:
+# pickle.dump(checkpoint_data, fp)
#
-# tune.report(loss=(val_loss / val_steps), accuracy=correct / total)
+# checkpoint = Checkpoint.from_directory(checkpoint_dir)
+# train.report(
+# {"loss": val_loss / val_steps, "accuracy": correct / total},
+# checkpoint=checkpoint,
+# )
#
# 여기서 먼저 체크포인트를 저장한 다음 일부 메트릭을 Ray Tune에 다시 보냅니다. 특히, validation loss와 accuracy를
# Ray Tune으로 다시 보냅니다. 그 후 Ray Tune은 이러한 메트릭을 사용하여 최상의 결과를 유도하는 하이퍼파라미터 구성을
# 결정할 수 있습니다. 이러한 메트릭들은 또한 리소스 낭비를 방지하기 위해 성능이 좋지 않은 실험을 조기에 중지하는 데 사용할 수 있습니다.
#
-# 체크포인트 저장은 선택사항이지만 `Population Based Training `_
-# 과 같은 고급 스케줄러를 사용하려면 필요합니다. 또한 체크포인트를 저장하면 나중에 학습된 모델을 로드하고 평가 세트(test set)에서 검증할 수 있습니다.
+# 체크포인트 저장은 선택사항이지만,
+# `Population Based Training `_ 과 같은 고급 스케줄러를
+# 사용하기 위해서는 필요합니다.
+# 또한, 체크포인트를 저장해두면 나중에 학습된 모델을 로드하고 평가 세트(test set)에서 검증할 수 있습니다.
#
-# Full training function
+# 전체 학습 함수
# ~~~~~~~~~~~~~~~~~~~~~~~~
#
# 전체 예제 코드는 다음과 같습니다.
-def train_cifar(config, checkpoint_dir=None, data_dir=None):
+def train_cifar(config, data_dir=None):
net = Net(config["l1"], config["l2"])
device = "cpu"
@@ -195,30 +228,33 @@ def train_cifar(config, checkpoint_dir=None, data_dir=None):
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=config["lr"], momentum=0.9)
- if checkpoint_dir:
- model_state, optimizer_state = torch.load(
- os.path.join(checkpoint_dir, "checkpoint"))
- net.load_state_dict(model_state)
- optimizer.load_state_dict(optimizer_state)
+ checkpoint = get_checkpoint()
+ if checkpoint:
+ with checkpoint.as_directory() as checkpoint_dir:
+ data_path = Path(checkpoint_dir) / "data.pkl"
+ with open(data_path, "rb") as fp:
+ checkpoint_state = pickle.load(fp)
+ start_epoch = checkpoint_state["epoch"]
+ net.load_state_dict(checkpoint_state["net_state_dict"])
+ optimizer.load_state_dict(checkpoint_state["optimizer_state_dict"])
+ else:
+ start_epoch = 0
trainset, testset = load_data(data_dir)
test_abs = int(len(trainset) * 0.8)
train_subset, val_subset = random_split(
- trainset, [test_abs, len(trainset) - test_abs])
+ trainset, [test_abs, len(trainset) - test_abs]
+ )
trainloader = torch.utils.data.DataLoader(
- train_subset,
- batch_size=int(config["batch_size"]),
- shuffle=True,
- num_workers=8)
+ train_subset, batch_size=int(config["batch_size"]), shuffle=True, num_workers=8
+ )
valloader = torch.utils.data.DataLoader(
- val_subset,
- batch_size=int(config["batch_size"]),
- shuffle=True,
- num_workers=8)
+ val_subset, batch_size=int(config["batch_size"]), shuffle=True, num_workers=8
+ )
- for epoch in range(10): # loop over the dataset multiple times
+ for epoch in range(start_epoch, 10): # loop over the dataset multiple times
running_loss = 0.0
epoch_steps = 0
for i, data in enumerate(trainloader, 0):
@@ -239,8 +275,10 @@ def train_cifar(config, checkpoint_dir=None, data_dir=None):
running_loss += loss.item()
epoch_steps += 1
if i % 2000 == 1999: # print every 2000 mini-batches
- print("[%d, %5d] loss: %.3f" % (epoch + 1, i + 1,
- running_loss / epoch_steps))
+ print(
+ "[%d, %5d] loss: %.3f"
+ % (epoch + 1, i + 1, running_loss / epoch_steps)
+ )
running_loss = 0.0
# Validation loss
@@ -262,27 +300,39 @@ def train_cifar(config, checkpoint_dir=None, data_dir=None):
val_loss += loss.cpu().numpy()
val_steps += 1
- with tune.checkpoint_dir(epoch) as checkpoint_dir:
- path = os.path.join(checkpoint_dir, "checkpoint")
- torch.save((net.state_dict(), optimizer.state_dict()), path)
+ checkpoint_data = {
+ "epoch": epoch,
+ "net_state_dict": net.state_dict(),
+ "optimizer_state_dict": optimizer.state_dict(),
+ }
+ with tempfile.TemporaryDirectory() as checkpoint_dir:
+ data_path = Path(checkpoint_dir) / "data.pkl"
+ with open(data_path, "wb") as fp:
+ pickle.dump(checkpoint_data, fp)
+
+ checkpoint = Checkpoint.from_directory(checkpoint_dir)
+ train.report(
+ {"loss": val_loss / val_steps, "accuracy": correct / total},
+ checkpoint=checkpoint,
+ )
- tune.report(loss=(val_loss / val_steps), accuracy=correct / total)
print("Finished Training")
######################################################################
# 보다시피, 대부분의 코드는 원본 예제에서 직접 적용되었습니다.
#
-# Test set 정확도(accuracy)
-# -----------------
-# 일반적으로 머신러닝 모델의 성능은 모델 학습에 사용되지 않은 데이터를 사용해 테스트합니다.
-# Test set 또한 함수로 감싸둘 수 있습니다.
-
+# 테스트셋 정확도(Test set accuracy)
+# -------------------------------------------
+# 일반적으로 머신러닝 모델의 성능은 모델 학습 시 사용하지 않은 데이터를
+# 테스트셋으로 따로 떼어낸 뒤, 이를 사용하여 테스트합니다.
+# 이러한 테스트셋 또한 함수로 감싸둘 수 있습니다:
def test_accuracy(net, device="cpu"):
trainset, testset = load_data()
testloader = torch.utils.data.DataLoader(
- testset, batch_size=4, shuffle=False, num_workers=2)
+ testset, batch_size=4, shuffle=False, num_workers=2
+ )
correct = 0
total = 0
@@ -297,24 +347,25 @@ def test_accuracy(net, device="cpu"):
return correct / total
+
######################################################################
# 이 함수는 또한 ``device`` 파라미터를 요구하므로, test set 평가를 GPU에서 수행할 수 있습니다.
#
# 검색 공간 구성
# ----------------------------
-# 마지막으로 Ray Tune의 검색 공간을 정의해야 합니다. 예시는 아래와 같습니다.
+# 마지막으로 Ray Tune의 검색 공간을 정의해야 합니다. 예시는 다음과 같습니다:
#
# .. code-block:: python
#
# config = {
-# "l1": tune.sample_from(lambda _: 2**np.random.randint(2, 9)),
-# "l2": tune.sample_from(lambda _: 2**np.random.randint(2, 9)),
+# "l1": tune.choice([2 ** i for i in range(9)]),
+# "l2": tune.choice([2 ** i for i in range(9)]),
# "lr": tune.loguniform(1e-4, 1e-1),
# "batch_size": tune.choice([2, 4, 8, 16])
# }
#
-# ``tune.sample_from()`` 함수를 사용하면 고유한 샘플 방법을 정의하여 하이퍼파라미터를 얻을 수 있습니다.
-# 이 예제에서 ``l1`` 과 ``l2`` 파라미터는 4와 256 사이의 2의 거듭제곱이어야 하므로 4, 8, 16, 32, 64, 128, 256입니다.
+# ``tune.choice()`` 함수는 균일하게 샘플링된 값들의 목록을 입력으로 받습니다.
+# 위 예시에서 ``l1`` 및 ``l2`` 파라미터는 4와 256 사이의 2의 거듭제곱 값인 4, 8, 16, 32, 64, 128, 256 입니다.
# ``lr`` (학습률)은 0.0001과 0.1 사이에서 균일하게 샘플링 되어야 합니다. 마지막으로, 배치 크기는 2, 4, 8, 16중에서 선택할 수 있습니다.
#
# 각 실험에서, Ray Tune은 이제 이러한 검색 공간에서 매개변수 조합을 무작위로 샘플링합니다.
@@ -332,7 +383,6 @@ def test_accuracy(net, device="cpu"):
# config=config,
# num_samples=num_samples,
# scheduler=scheduler,
-# progress_reporter=reporter,
# checkpoint_at_end=True)
#
# 파이토치 ``DataLoader`` 인스턴스의 ``num_workers`` 을 늘리기 위해 CPU 수를 지정하고 사용할 수 있습니다.
@@ -349,34 +399,30 @@ def main(num_samples=10, max_num_epochs=10, gpus_per_trial=2):
data_dir = os.path.abspath("./data")
load_data(data_dir)
config = {
- "l1": tune.sample_from(lambda _: 2 ** np.random.randint(2, 9)),
- "l2": tune.sample_from(lambda _: 2 ** np.random.randint(2, 9)),
+ "l1": tune.choice([2**i for i in range(9)]),
+ "l2": tune.choice([2**i for i in range(9)]),
"lr": tune.loguniform(1e-4, 1e-1),
- "batch_size": tune.choice([2, 4, 8, 16])
+ "batch_size": tune.choice([2, 4, 8, 16]),
}
scheduler = ASHAScheduler(
metric="loss",
mode="min",
max_t=max_num_epochs,
grace_period=1,
- reduction_factor=2)
- reporter = CLIReporter(
- # ``parameter_columns=["l1", "l2", "lr", "batch_size"]``,
- metric_columns=["loss", "accuracy", "training_iteration"])
+ reduction_factor=2,
+ )
result = tune.run(
partial(train_cifar, data_dir=data_dir),
resources_per_trial={"cpu": 2, "gpu": gpus_per_trial},
config=config,
num_samples=num_samples,
scheduler=scheduler,
- progress_reporter=reporter)
+ )
best_trial = result.get_best_trial("loss", "min", "last")
- print("Best trial config: {}".format(best_trial.config))
- print("Best trial final validation loss: {}".format(
- best_trial.last_result["loss"]))
- print("Best trial final validation accuracy: {}".format(
- best_trial.last_result["accuracy"]))
+ print(f"Best trial config: {best_trial.config}")
+ print(f"Best trial final validation loss: {best_trial.last_result['loss']}")
+ print(f"Best trial final validation accuracy: {best_trial.last_result['accuracy']}")
best_trained_model = Net(best_trial.config["l1"], best_trial.config["l2"])
device = "cpu"
@@ -386,54 +432,51 @@ def main(num_samples=10, max_num_epochs=10, gpus_per_trial=2):
best_trained_model = nn.DataParallel(best_trained_model)
best_trained_model.to(device)
- best_checkpoint_dir = best_trial.checkpoint.value
- model_state, optimizer_state = torch.load(os.path.join(
- best_checkpoint_dir, "checkpoint"))
- best_trained_model.load_state_dict(model_state)
+ best_checkpoint = result.get_best_checkpoint(trial=best_trial, metric="accuracy", mode="max")
+ with best_checkpoint.as_directory() as checkpoint_dir:
+ data_path = Path(checkpoint_dir) / "data.pkl"
+ with open(data_path, "rb") as fp:
+ best_checkpoint_data = pickle.load(fp)
- test_acc = test_accuracy(best_trained_model, device)
- print("Best trial test set accuracy: {}".format(test_acc))
+ best_trained_model.load_state_dict(best_checkpoint_data["net_state_dict"])
+ test_acc = test_accuracy(best_trained_model, device)
+ print("Best trial test set accuracy: {}".format(test_acc))
if __name__ == "__main__":
- # sphinx_gallery_start_ignore
- # Fixes ``AttributeError: '_LoggingTee' object has no attribute 'fileno'``.
- # This is only needed to run with sphinx-build.
- import sys
- sys.stdout.fileno = lambda: False
- # sphinx_gallery_end_ignore
- # You can change the number of GPUs per trial here:
+ # 매 실험당 사용할 GPU 수를 여기에서 변경할 수 있습니다:
main(num_samples=10, max_num_epochs=10, gpus_per_trial=0)
######################################################################
-# 코드를 실행하면 결과는 다음과 같습니다.
-#
-# ::
-#
-# Number of trials: 10 (10 TERMINATED)
-# +-----+------+------+-------------+--------------+---------+------------+--------------------+
-# | ... | l1 | l2 | lr | batch_size | loss | accuracy | training_iteration |
-# |-----+------+------+-------------+--------------+---------+------------+--------------------|
-# | ... | 64 | 4 | 0.00011629 | 2 | 1.87273 | 0.244 | 2 |
-# | ... | 32 | 64 | 0.000339763 | 8 | 1.23603 | 0.567 | 8 |
-# | ... | 8 | 16 | 0.00276249 | 16 | 1.1815 | 0.5836 | 10 |
-# | ... | 4 | 64 | 0.000648721 | 4 | 1.31131 | 0.5224 | 8 |
-# | ... | 32 | 16 | 0.000340753 | 8 | 1.26454 | 0.5444 | 8 |
-# | ... | 8 | 4 | 0.000699775 | 8 | 1.99594 | 0.1983 | 2 |
-# | ... | 256 | 8 | 0.0839654 | 16 | 2.3119 | 0.0993 | 1 |
-# | ... | 16 | 128 | 0.0758154 | 16 | 2.33575 | 0.1327 | 1 |
-# | ... | 16 | 8 | 0.0763312 | 16 | 2.31129 | 0.1042 | 4 |
-# | ... | 128 | 16 | 0.000124903 | 4 | 2.26917 | 0.1945 | 1 |
-# +-----+------+------+-------------+--------------+---------+------------+--------------------+
-#
-#
-# Best trial config: {'l1': 8, 'l2': 16, 'lr': 0.00276249, 'batch_size': 16, 'data_dir': '...'}
-# Best trial final validation loss: 1.181501
-# Best trial final validation accuracy: 0.5836
-# Best trial test set accuracy: 0.5806
-#
-# 대부분의 실험은 자원 낭비를 막기 위해 일찍 중단되었습니다. 가장 좋은 결과를 얻은 실험은 58%의 정확도를 달성했으며, 이는 테스트 세트에서 확인할 수 있습니다.
+# 코드를 실행하면 결과는 다음과 같이 나올 것입니다:
+#
+# .. code-block:: sh
+#
+# Number of trials: 10/10 (10 TERMINATED)
+# +-----+--------------+------+------+-------------+--------+---------+------------+
+# | ... | batch_size | l1 | l2 | lr | iter | loss | accuracy |
+# |-----+--------------+------+------+-------------+--------+---------+------------|
+# | ... | 2 | 1 | 256 | 0.000668163 | 1 | 2.31479 | 0.0977 |
+# | ... | 4 | 64 | 8 | 0.0331514 | 1 | 2.31605 | 0.0983 |
+# | ... | 4 | 2 | 1 | 0.000150295 | 1 | 2.30755 | 0.1023 |
+# | ... | 16 | 32 | 32 | 0.0128248 | 10 | 1.66912 | 0.4391 |
+# | ... | 4 | 8 | 128 | 0.00464561 | 2 | 1.7316 | 0.3463 |
+# | ... | 8 | 256 | 8 | 0.00031556 | 1 | 2.19409 | 0.1736 |
+# | ... | 4 | 16 | 256 | 0.00574329 | 2 | 1.85679 | 0.3368 |
+# | ... | 8 | 2 | 2 | 0.00325652 | 1 | 2.30272 | 0.0984 |
+# | ... | 2 | 2 | 2 | 0.000342987 | 2 | 1.76044 | 0.292 |
+# | ... | 4 | 64 | 32 | 0.003734 | 8 | 1.53101 | 0.4761 |
+# +-----+--------------+------+------+-------------+--------+---------+------------+
+#
+# Best trial config: {'l1': 64, 'l2': 32, 'lr': 0.0037339984519545164, 'batch_size': 4}
+# Best trial final validation loss: 1.5310075663924216
+# Best trial final validation accuracy: 0.4761
+# Best trial test set accuracy: 0.4737
+#
+# 대부분의 실험은 자원 낭비를 막기 위해 일찍 중단되었습니다.
+# 가장 좋은 결과를 얻은 실험은 47%의 정확도를 달성했으며,
+# 이는 테스트셋에서 확인할 수 있습니다.
#
# 이것이 전부입니다! 이제 파이토치 모델의 매개변수를 조정할 수 있습니다.
-#
+#
\ No newline at end of file
diff --git a/beginner_source/introyt.rst b/beginner_source/introyt.rst
index d2a4d880a..4a64b89b8 100644
--- a/beginner_source/introyt.rst
+++ b/beginner_source/introyt.rst
@@ -9,13 +9,13 @@
PyTorch 소개 - YouTube 시리즈
========================================
-Authors:
+Authors:
`Brad Heintz `_
-번역:
+번역:
`김태형 `_
-이 튜토리얼은 YouTube `파이토치 초보자 시리즈 `_ 와 함께 이어집니다.
+이 튜토리얼은 YouTube의 `파이토치 초보자 시리즈 `_ 와 함께 이어집니다.
`이 튜토리얼은 파이썬 및 딥러닝 개념에 대한 기본적인 지식이 있다고 가정합니다.`
@@ -24,7 +24,7 @@ Authors:
이 튜토리얼은 몇 가지 방법으로 실행할 수 있습니다:
- **클라우드에서 실행하기**: 이 방법이 가장 쉽게 시작할 수 있는 방법입니다! 각 섹션은 맨 위에 Colab 링크가 있으며, 이 링크는 완전히 호스트된 환경에서 코드가 있는 notebook 파일을 엽니다. 전문가 팁: GPU 런타임과 함께 Colab을 사용하여 연산 속도 향상시키기 *런타임 > 런타임 유형 변경 > GPU 선택*
-- **로컬에서 실행하기**: 이 옵션을 사용하려면 먼저 로컬 컴퓨터에서 PyTorch 및 TorchVision을 설정해야 합니다(`설치 가이드 `_). notebook 파일을 다운로드 하거나 자신이 좋아하는 IDE에 코드를 복사하세요.
+- **로컬에서 실행하기**: 이 옵션을 사용하려면 먼저 로컬 컴퓨터에서 PyTorch 및 TorchVision을 설정해야 합니다( `설치 가이드 `_ ). notebook 파일을 다운로드 하거나 자신이 좋아하는 IDE에 코드를 복사하세요.
.. include:: /beginner_source/introyt/tocyt.txt
diff --git a/beginner_source/introyt/autogradyt_tutorial.py b/beginner_source/introyt/autogradyt_tutorial.py
index a2ed238e5..abf75a7d2 100644
--- a/beginner_source/introyt/autogradyt_tutorial.py
+++ b/beginner_source/introyt/autogradyt_tutorial.py
@@ -213,7 +213,7 @@
#########################################################################
# Recall the computation steps we took to get here:
#
-# ::
+# .. code-block:: python
#
# a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
# b = torch.sin(a)
@@ -250,9 +250,9 @@ class TinyModel(torch.nn.Module):
def __init__(self):
super(TinyModel, self).__init__()
- self.layer1 = torch.nn.Linear(1000, 100)
+ self.layer1 = torch.nn.Linear(DIM_IN, HIDDEN_SIZE)
self.relu = torch.nn.ReLU()
- self.layer2 = torch.nn.Linear(100, 10)
+ self.layer2 = torch.nn.Linear(HIDDEN_SIZE, DIM_OUT)
def forward(self, x):
x = self.layer1(x)
@@ -456,10 +456,10 @@ def add_tensors2(x, y):
# .. note::
# The following code cell throws a runtime error. This is expected.
#
-# ::
+# .. code-block:: python
#
-# a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
-# torch.sin_(a)
+# a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
+# torch.sin_(a)
#
#########################################################################
diff --git a/beginner_source/introyt/captumyt.py b/beginner_source/introyt/captumyt.py
index 2ff8e9e70..abf2391d2 100644
--- a/beginner_source/introyt/captumyt.py
+++ b/beginner_source/introyt/captumyt.py
@@ -98,21 +98,28 @@
Before you get started, you need to have a Python environment with:
- Python version 3.6 or higher
-- For the Captum Insights example, Flask 1.1 or higher
+- For the Captum Insights example, Flask 1.1 or higher and Flask-Compress
+ (the latest version is recommended)
- PyTorch version 1.2 or higher (the latest version is recommended)
- TorchVision version 0.6 or higher (the latest version is recommended)
- Captum (the latest version is recommended)
+- Matplotlib version 3.3.4, since Captum currently uses a Matplotlib
+ function whose arguments have been renamed in later versions
To install Captum in an Anaconda or pip virtual environment, use the
appropriate command for your environment below:
-With ``conda``::
+With ``conda``:
- conda install pytorch torchvision captum -c pytorch
+.. code-block:: sh
-With ``pip``::
+ conda install pytorch torchvision captum flask-compress matplotlib=3.3.4 -c pytorch
- pip install torch torchvision captum
+With ``pip``:
+
+.. code-block:: sh
+
+ pip install torch torchvision captum matplotlib==3.3.4 Flask-Compress
Restart this notebook in the environment you set up, and you’re ready to
go!
@@ -155,7 +162,7 @@
# now.
#
-model = models.resnet101(weights='IMAGENET1K_V1')
+model = models.resnet18(weights='IMAGENET1K_V1')
model = model.eval()
diff --git a/beginner_source/introyt/introyt1_tutorial.py b/beginner_source/introyt/introyt1_tutorial.py
index 2255cbb4c..91aeb4789 100644
--- a/beginner_source/introyt/introyt1_tutorial.py
+++ b/beginner_source/introyt/introyt1_tutorial.py
@@ -276,7 +276,7 @@ def num_flat_features(self, x):
transform = transforms.Compose(
[transforms.ToTensor(),
- transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
+ transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2470, 0.2435, 0.2616))])
##########################################################################
@@ -284,11 +284,30 @@ def num_flat_features(self, x):
#
# - ``transforms.ToTensor()``는 Pillow 패키지를 사용하여 불러온 이미지를
# PyTorch tensor 형태로 변환합니다.
-# - ``transforms.Normalize()`` 는 tensor의 평균이 0이고 표준 편차가 0.5가
+# - ``transforms.Normalize()`` 는 tensor의 평균이 0이고 표준 편차가 1.0이
# 되도록 tensor의 값을 조정합니다.
-# 대부분의 활성화 함수는 약 x=0에 강한 기울기 값을 가지고 있어 데이터를
+# 대부분의 활성화 함수는 x = 0 부근에서 강한 기울기 값을 가지고 있어 데이터를
# 중앙으로 집중화하여 학습 속도를 높일 수 있습니다.
#
+# 변환(trnasform)에 전달되는 값들은 각각 데이터셋에 있는 이미지들의 RGB 채널별
+# 평균값(mean)들(첫번째 튜플)과 표준편차(standard deviation)들(두번째 튜플)입니다.
+# 아래 몇 줄의 코드를 실행하여 직접 이 값을 계산해 볼 수 있습니다:
+# ```
+# from torch.utils.data import ConcatDataset
+# transform = transforms.Compose([transforms.ToTensor()])
+# trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
+# download=True, transform=transform)
+#
+# #stack all train images together into a tensor of shape
+# #(50000, 3, 32, 32)
+# x = torch.stack([sample[0] for sample in ConcatDataset([trainset])])
+#
+# #get the mean of each channel
+# mean = torch.mean(x, dim=(0,2,3)) #tensor([0.4914, 0.4822, 0.4465])
+# std = torch.std(x, dim=(0,2,3)) #tensor([0.2470, 0.2435, 0.2616])
+#
+# ```
+#
# transforms 는 cropping, centering, rotation, reflection를 포함하여 더 많은
# 변환이 가능합니다.
#
@@ -536,9 +555,9 @@ def forward(self, x):
#
# 루프의 나머지 부분은 epoch 횟수, 학습 루프를 통해 수집된 손실 값을 출력합니다.
#
-# **위 셀을 실행한다면** 다음과 같은 값이 표시됩니다:
+# **위 셀을 실행하면** 다음과 같은 출력이 나타날 것입니다:
#
-# ::
+# .. code-block:: sh
#
# [1, 2000] loss: 2.235
# [1, 4000] loss: 1.940
diff --git a/beginner_source/introyt/modelsyt_tutorial.py b/beginner_source/introyt/modelsyt_tutorial.py
index 8126ce841..2ce66ebca 100644
--- a/beginner_source/introyt/modelsyt_tutorial.py
+++ b/beginner_source/introyt/modelsyt_tutorial.py
@@ -342,7 +342,7 @@ def forward(self, sentence):
# the 6x6 input.
#
# **Normalization layers** re-center and normalize the output of one layer
-# before feeding it to another. Centering the and scaling the intermediate
+# before feeding it to another. Centering and scaling the intermediate
# tensors has a number of beneficial effects, such as letting you use
# higher learning rates without exploding/vanishing gradients.
#
diff --git a/beginner_source/introyt/tensorboardyt_tutorial.py b/beginner_source/introyt/tensorboardyt_tutorial.py
index 8e3263204..80bac7bcb 100644
--- a/beginner_source/introyt/tensorboardyt_tutorial.py
+++ b/beginner_source/introyt/tensorboardyt_tutorial.py
@@ -24,12 +24,16 @@
To run this tutorial, you’ll need to install PyTorch, TorchVision,
Matplotlib, and TensorBoard.
-With ``conda``::
+With ``conda``:
+
+.. code-block:: sh
conda install pytorch torchvision -c pytorch
conda install matplotlib tensorboard
-With ``pip``::
+With ``pip``:
+
+.. code-block:: sh
pip install torch torchvision matplotlib tensorboard
@@ -64,6 +68,13 @@
# PyTorch TensorBoard support
from torch.utils.tensorboard import SummaryWriter
+# In case you are using an environment that has TensorFlow installed,
+# such as Google Colab, uncomment the following code to avoid
+# a bug with saving embeddings to your TensorBoard directory
+
+# import tensorflow as tf
+# import tensorboard as tb
+# tf.io.gfile = tb.compat.tensorflow_stub.io.gfile
######################################################################
# Showing Images in TensorBoard
@@ -207,13 +218,14 @@ def forward(self, x):
# Check against the validation set
running_vloss = 0.0
- net.train(False) # Don't need to track gradents for validation
+ # In evaluation mode some model specific operations can be omitted eg. dropout layer
+ net.train(False) # Switching to evaluation mode, eg. turning off regularisation
for j, vdata in enumerate(validation_loader, 0):
vinputs, vlabels = vdata
voutputs = net(vinputs)
vloss = criterion(voutputs, vlabels)
running_vloss += vloss.item()
- net.train(True) # Turn gradients back on for training
+ net.train(True) # Switching back to training mode, eg. turning on regularisation
avg_loss = running_loss / 1000
avg_vloss = running_vloss / len(validation_loader)
@@ -237,7 +249,7 @@ def forward(self, x):
#
# TensorBoard can also be used to examine the data flow within your model.
# To do this, call the ``add_graph()`` method with a model and sample
-# input. When you open
+# input:
#
# Again, grab a single mini-batch of images
diff --git a/beginner_source/introyt/tensors_deeper_tutorial.py b/beginner_source/introyt/tensors_deeper_tutorial.py
index 188aa48b7..4562b66e4 100644
--- a/beginner_source/introyt/tensors_deeper_tutorial.py
+++ b/beginner_source/introyt/tensors_deeper_tutorial.py
@@ -9,6 +9,7 @@
Pytorch Tensor 소개
===============================
+
번역: `이상윤 `_
아래 영상이나 `youtube `__ 를 참고하세요.
@@ -33,10 +34,10 @@
#########################################################################
# Tensor 생성하기
-# ----------------
+# ------------------
#
# tensor를 생성하는 가장 간단한 방법은 ``torch.empty()`` 를 호출하는 것입니다:
-#
+#
x = torch.empty(3, 4)
print(type(x))
@@ -45,7 +46,7 @@
##########################################################################
# 방금 무엇을 한 것인지 들여다봅시다:
-#
+#
# - ``torch`` 모듈에 있는 수많은 메소드 중 하나를 사용해서 tensor를 만들었습니다.
# - 이 tensor는 3개의 행과 4개의 열을 가진 2차원 tensor입니다.
# - 객체가 반환한 type은 ``torch.Tensor`` 이며 이는 ``torch.FloatTensor`` 의 별칭입니다.
@@ -54,18 +55,18 @@
# - 생성한 tensor를 출력하면 아마 무작위 값을 볼 수 있을 것 입니다.
# ``torch.empty()`` 는 tensor를 위한 메모리를 할당해 주지만 임의의 값으로 초기화하지는 않습니다
# - 그렇기 때문에 할당 당시에 메모리가 가지고 있는 값을 보는 것입니다.
-#
+#
# 간략하게 tensor와 tensor의 차원 수, 그리고 각 tensor의 용어에 대해 알아봅시다:
-#
+#
# - 때로는 1차원 tensor를 보게 될 것인데 이는 *vector* 라고 합니다.
# - 이와 마찬가지로 2차원 tensor는 주로 *matrix* 라고 합니다.
# - 2차원보다 큰 차원을 가진 것들은 일반적으로 그냥 tensor라고 합니다.
-#
-# 코딩 하면서 주로 tensor를 몇 가지 값으로 초기화하고 싶을 수가 있습니다.
-# 일반적인 경우로는 모두 0으로 초기화 하거나, 모두 1로 초기화 하거나,
+#
+# 코드를 작성하며 주로 tensor를 몇 가지 값으로 초기화하고 싶을 수가 있습니다.
+# 일반적인 경우로는 모두 0으로 초기화하거나, 모두 1로 초기화하거나,
# 혹은 모두 무작위 값으로 초기화 할 때가 있는데,
-# 이때 ``torch`` 모듈은 이 모든 경우를 위한 메소드를 제공합니다:
-#
+# ``torch`` 모듈은 이러한 모든 경우에 대한 메소드를 제공합니다:
+#
zeros = torch.zeros(2, 3)
print(zeros)
@@ -81,15 +82,15 @@
#########################################################################
# 이 모든 팩토리 메소드들은 우리가 기대하던 것들을 모두 수행합니다 - 0으로 모두 채워 진 tensor,
# 1로 모두 채워 진 tensor 그리고 0과 1사이의 무작위 값으로 채워 진 tensor를 얻었습니다.
-#
+#
# 무작위 Tensor와 Seed 사용하기
-# ~~~~~~~~~~~~~~~~~~~~~~~~~~
-#
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+#
# 무작위 tensor에 대해 말하자면, 바로 앞에서 호출하는 ``torch.manual_seed()`` 를 눈치채셨나요?
# 특히 연구 환경에서 연구 결과의 재현 가능성에 대한 확신을 얻고 싶을 때,
# 모델의 학습 가중치와 같은 무작위 값을 가진 tensor로 초기화 하는 것은 흔하거나 종종 일어나는 일입니다.
# 직접 무작위 난수 생성기의 seed를 설정하는 것이 다음 방법입니다. 다음 코드를 보며 더 자세히 알아봅시다:
-#
+#
torch.manual_seed(1729)
random1 = torch.rand(2, 3)
@@ -111,17 +112,17 @@
# 이 각각 서로 동일한 결과가 나온다는 것을 볼 수 있습니다.
# 무작위 난수 생성기의 seed를 수동으로 설정하면 난수가 재 설정되어 대부분의 환경에서
# 무작위 숫자에 의존하는 동일한 계산이 이루어지고 동일한 결과를 제공합니다.
-#
+#
# 보다 자세한 정보는 다음 문서를 참고하세요 `PyTorch documentation on
# reproducibility `__.
-#
+#
# Tensor의 shape
-# ~~~~~~~~~~~~~
-#
+# ~~~~~~~~~~~~~~~~~~~~~~
+#
# 두 개 혹은 그 이상의 tensor에 대한 연산을 수행할 때, tensor들은 같은 shape를 필요로 합니다
# - 다시 말해서 차원의 개수가 같아야 하고, 각 차원마다 원소의 수가 같아야 합니다.
# 그러기 위해서는 ``torch.*_like()`` 함수를 사용합니다.
-#
+#
x = torch.empty(2, 2, 3)
print(x.shape)
@@ -148,14 +149,14 @@
# 위쪽의 코드 셀에 있는 것들 중에 첫 번째는 tensor에 있는 ``.shape`` 속성을 사용했습니다.
# 이 속성은 tensor의 각 차원 크기에 대한 리스트를 포함합니다
# - 이 경우에, ``x`` 는 shape가 2 x 2 x 3 인 3차원 tensor입니다.
-#
+#
# 그 아래에는 ``.empty_like()``, ``.zeros_like()``,
# ``.ones_like()``, and ``.rand_like()`` 메소드를 호출 합니다.
# ``.shape`` 속성을 통해서, 위의 메소드들이 동일한 차원값을 반환한다는 것을 검증할 수 있습니다.
-#
+#
# 여기서 다루는 tensor를 생성하는 마지막 방법은 PyTorch collection
# 형식의 데이터를 직접적으로 명시하는 것 입니다:
-#
+#
some_constants = torch.tensor([[3.1415926, 2.71828], [1.61803, 0.0072897]])
print(some_constants)
@@ -171,15 +172,15 @@
# ``torch.tensor()`` 는 이미 Python tuple이나 list 형태로 이루어진 데이터를
# 가지고 있는 경우 tensor를 만들기 가장 쉬운 방법입니다.
# 위에서 본 것 처럼 중첩된 형태의 collection 자료형은 다차원 tensor가 결과로 나옵니다.
-#
+#
# .. note::
# ``torch.tensor()`` 는 데이터의 복사본을 생성합니다.
-#
+#
# Tensor 자료형
# ~~~~~~~~~~~~~~~~~
-#
+#
# tensor의 자료형을 설정하는 것은 다양한 방식이 가능합니다.
-#
+#
a = torch.ones((2, 3), dtype=torch.int16)
print(a)
@@ -197,24 +198,24 @@
# ``dtype=torch.int16`` 자료형으로 설정했습니다. ``a`` 를 출력할 때,
# ``1.`` 대신에 ``1`` 로 가득 찬 모습을 볼 수 있습니다
# - 파이썬에서 아래 점이 없으면 실수 자료형이 아닌 정수 자료형을 의미합니다.
-#
+#
# ``a`` 를 출력할 때 또 한가지 주목할 점은,
# ``dtype`` 을 기본값 (32-bit 부동 소수점)
# 으로 남길 때와 다르게 tensor를 출력하는 경우
# 각 tensor의 ``dtype`` 을 명시한다는 것입니다.
-#
+#
# tensor의 shape를 정수형 인자의 나열, 즉 이 인자를 tuple 자료형 형태로
# 묶는다는 것을 발견할 수 있습니다. 이것은 반드시 필요한 것은 아닙니다
# - PyTorch에서는 첫 번째 인자로 tensor shape라는 값을 의미하는 라벨이 없는 정수 인자를 여러개를 받습니다 -
# 하지만 선택 인자를 추가했을 때, 이 방식은 코드를 더 읽기 쉽게 만들 수 있습니다.
-#
+#
# 자료형을 설정하는 다른 방법은 ``.to()`` 메소드랑 함께 사용하는 것 입니다.
# 위쪽 셀에서 평범한 방식으로 무작위 실수 자료형 tensor ``b`` 를 생성합니다.
# 이어서 ``.to()`` 메소드를 사용해서 ``b`` 를 32-bit 정수 자료형으로 변환한 ``c`` 를 생성합니다.
# ``c`` 는 모든 ``b`` 의 값과 같은 값을 가지고 있지만 소수점 아래 자리를 버린다는 점이 다릅니다.
-#
+#
# 가능한 데이터 자료형은 다음을 포함합니다:
-#
+#
# - ``torch.bool``
# - ``torch.int8``
# - ``torch.uint8``
@@ -225,16 +226,16 @@
# - ``torch.float``
# - ``torch.double``
# - ``torch.bfloat``
-#
+#
# PyTorch Tensor에서 산술 & 논리 연산
-# ---------------------------------
-#
+# -----------------------------------------
+#
# 지금까지 tensor를 생성하는 몇 가지 방식을 알아봤습니다…
# 이것을 가지고 무엇을 할 수 있을까요?
-#
+#
# 먼저 기본적인 산술 연산을 알아보고,
# 그 다음 tensor가 단순 스칼라 값과 어떻게 상호작용 하는지 알아봅시다:
-#
+#
ones = torch.zeros(2, 2) + 1
twos = torch.ones(2, 2) * 2
@@ -256,9 +257,9 @@
# 이러한 연산의 결과는 tensor가 될 것이기 때문에,
# ``threes`` 변수를 생성하는 줄에서 처럼
# 일반적인 연산자 우선순위 규칙과 함께 연산자를 연결할 수 있습니다.
-#
+#
# 두 tensor 사이 유사한 연산도 직관적으로 예상할 수 있는 방식으로 동작합니다:
-#
+#
powers2 = twos ** torch.tensor([[1, 2], [3, 4]])
print(powers2)
@@ -273,33 +274,33 @@
##########################################################################
# 여기서 주목해야 할 점은 이전 코드 cell에 있는 모든 tensor는 동일한 shape를 가져야 한다는 것 입니다.
# 만약 서로 다른 shape를 가진 tensor끼리 이진 연산을 수행한다면 무슨 일이 일어날까요?
-#
+#
# .. note::
-# 다음 cell은 run-time error가 발생합니다. 이것은 의도한 것입니다.
+# 다음 cell은 run-time error가 발생합니다. 이것은 의도한 것입니다.
#
-# ::
+# .. code-block:: sh
#
-# a = torch.rand(2, 3)
-# b = torch.rand(3, 2)
+# a = torch.rand(2, 3)
+# b = torch.rand(3, 2)
#
-# print(a * b)
+# print(a * b)
#
##########################################################################
# 일반적인 경우에, 다른 shape의 tensor를 이러한 방식으로 연산할 수 없습니다.
# 심지어 위에 있는 cell에 있는 경우처럼 tensor가 서로 같은 개수의 원소를 가지고 있는 경우에도 연산할 수 없습니다.
-#
+#
# 개요: Tensor Broadcasting
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-#
+#
# .. note::
# 만약 NumPy의 ndarrays에서 사용하는 broadcasting 문법에 익숙하다면,
# 여기서도 같은 규칙이 적용된다는 것을 확인할 수 있습니다.
-#
+#
# tensor는 같은 shape끼리만 연산이 가능하다는 규칙의 예외가 바로 *tensor broadcasting* 입니다.
# 다음은 그 예시입니다:
-#
+#
rand = torch.rand(2, 4)
doubled = rand * (torch.ones(1, 4) * 2)
@@ -311,35 +312,35 @@
#########################################################################
# 여기서 무슨 트릭이 사용되고 있는 것일까요?
# 어떻게 2x4 tensor에 1x4 tensor를 곱한 값을 얻을 수 있을까요?
-#
+#
# Broadcasting은 서로 비슷한 shape를 가진 tensor사이 연산을 수행하는 방법입니다.
# 위의 예시를 보면, 행의 값이 1이고, 열의 값이 4인 tensor가
# 행의 값이 2이고, 열의 값이 4인 tensor의 *모든 행* 에 곱하게 됩니다.
-#
+#
# 이것은 딥러닝에서 중요한 연산입니다.
# 일반적인 예시는 학습 가중치 tensor에 입력 tensor의 *배치* 를 곱하고,
# 배치의 각 인스턴스에 곱하기 연산을 개별적으로 적용한 이후
# 위의 (2, 4) \* (1, 4) tensor연산의 결과가 (2, 4) shape tensor인 것처럼 -
# 동일한 shape의 학습 가중치 tensor를 반환하는 것입니다.
-#
+#
# Broadcasting의 규칙은 다음과 같습니다:
-#
+#
# - 각 tensor는 최소한 1차원 이상을 반드시 가지고 있어야 합니다 - 빈 tensor는 사용할 수 없습니다.
-#
+#
# - 두 tensor의 각 차원 크기 원소가 다음 조건을 만족하는지 확인하며 비교합니다. *이때 비교 순서는 맨 뒤에서부터 맨 앞으로 입니다;*
#
# - 각 차원이 서로 동일합니다, *또는*
-#
+#
# - 각 차원중의 하나의 크기가 반드시 1입니다, *또는*
-#
+#
# - tensor들 중 하나의 차원이 존재하지 않습니다.
-#
+#
# 이전에 봤던 것처럼,
# 물론 동일한 shape를 가진 Tensor들은 자명하게 “broadcastable” 합니다.
-#
+#
# 다음 예제는 위의 규칙을 준수하고
# broadcasting을 허용하는 몇 가지 상황입니다.
-#
+#
a = torch.ones(4, 3, 2)
@@ -362,37 +363,37 @@
# - 모든 열은 3개의 원소값 모두 동일합니다.
# - ``d`` 에 대해서, 연산이 이전과 반대로 모든 계층과 열에 대해서 수행합니다
# - 이재 모든 *행* 이 동일합니다.
-#
+#
# broadcasting에 대한 더 많은 정보는, `PyTorch
# documentation `__
# 에 있는 주제를 참고하세요.
-#
+#
# 다음 예시는 broadcasting 시도가 실패한 사례입니다:
-#
+#
# .. note::
-# 다음 cell은 run-time error가 발생합니다. 이것은 의도한 것입니다.
+# 다음 cell에서는 run-time error가 발생합니다. 이것은 의도한 것입니다.
#
-# ::
+# .. code-block:: python
#
-# a = torch.ones(4, 3, 2)
+# a = torch.ones(4, 3, 2)
#
-# b = a * torch.rand(4, 3) # 차원은 반드시 맨 뒤 원소부터 맨 앞 원소로 차례대로 맞춰야 합니다.
+# b = a * torch.rand(4, 3) # 차원은 반드시 맨 뒤 원소부터 맨 앞 원소로 차례대로 맞춰야 합니다.
#
-# c = a * torch.rand( 2, 3) # 세번째와 두번째 차원 모두 서로 다릅니다.
+# c = a * torch.rand( 2, 3) # 세번째와 두번째 차원 모두 서로 다릅니다.
#
-# d = a * torch.rand((0, )) # 비어있는 tensor는 broadcast 할 수 없습니다.
+# d = a * torch.rand((0, )) # 비어있는 tensor는 broadcast 할 수 없습니다.
#
###########################################################################
# Tensor를 사용하는 다양한 연산들
-# ~~~~~~~~~~~~~~~~~~~~~~
-#
+# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+#
# PyTorch tensor는 tensor들 끼리 수행할 수 있는 300개 이상의
# 연산을 가지고 있습니다.
-#
+#
# 다음 작은 예시는 주로 사용하는 연산 종류 몇 개를 보여줍니다:
-#
+#
# 공용 함수
a = torch.rand(2, 4) * 2 - 1
@@ -454,18 +455,18 @@
#
# Tensor의 값을 변경하기
# ~~~~~~~~~~~~~~~~~~~~~~~~~
-#
+#
# 대부분 tensor들의 이진 연산은 제3자의 새로운 tensor를 생성합니다.
# ``c = a * b`` ( ``a`` 와 ``b`` 는 tensor)연산을 수행할 때,
# 새로운 tensor ``c`` 는 다른 tensor와 구별되는 메모리 영역을 차지하게 됩니다.
-#
+#
# 그럼에도 불구하고 tensor의 값을 변경하고 싶은 순간이 있을 수 있습니다 -
# 예를 들어, 중간 연산 결과 값을 버릴 수 있는 각 원소 단위 연산을 수행하는 경우가 있습니다.
# 이런 연산을 위해, 대부분의 수학 함수들은 tensor 내부의 값을
# 변경할 수 있는 함수 이름 맨 뒤에 밑줄 (``_``)이 추가된 버전을 가지고 있습니다.
-#
+#
# 예시:
-#
+#
a = torch.tensor([0, math.pi / 4, math.pi / 2, 3 * math.pi / 4])
print('a:')
@@ -482,7 +483,7 @@
#######################################################################
# 산술 연산에서, 비슷한 행동을 하는 함수가 있습니다:
-#
+#
a = torch.ones(2, 2)
b = torch.rand(2, 2)
@@ -504,13 +505,13 @@
# (e.g., ``torch.sin()``)처럼 ``torch`` 모듈의 메소드가 아니라
# ``torch.Tensor`` 객체의 메소드인 점에 주목해야 합니다.
# ``a.add_(b)`` 와 같은 경우처럼, *메소드를 호출하는 tensor는 값이 변경됩니다.*
-#
+#
# 이미 존재하고 있는 메모리에 할당된 tensor에 계산 결과값을 저장하는 또 다른 옵션이 있습니다.
# tensor를 생성하는 메소드 뿐만 아니라 지금까지 이 문서에서 봤던 수많은 함수나 메소드는
# 결과 값을 받는 특정 tensor를 명시하는 ``out`` 이라는 인자를 가지고 있습니다.
# 만약 ``out`` tensor가 알맞은 shape와 ``dtype`` 을 가지고 있다면,
# 새로운 메모리 할당 없이 결과값이 저장됩니다:
-#
+#
a = torch.rand(2, 2)
b = torch.rand(2, 2)
@@ -531,11 +532,11 @@
##########################################################################
# Tensor를 복사하기
-# ---------------
-#
+# -------------------
+#
# 파이썬의 다른 객체와 마찬가지로 변수에 tensor를 할당하는 것은
# 변수가 tensor의 *label* 이 되고 값을 복사하지 않습니다. 다음 예시를 보시죠:
-#
+#
a = torch.ones(2, 2)
b = a
@@ -547,7 +548,7 @@
######################################################################
# 하지만 만약 우리가 작업할 별도의 데이터 복사본을 원하면 어떻게 해야할까요?
# ``clone()`` 메소드가 당신이 찾던 해답이 될 것입니다:
-#
+#
a = torch.ones(2, 2)
b = a.clone()
@@ -564,7 +565,7 @@
# 만약 source tensor가 autograd를 가진다면 clone이 가능합니다.
# **이 부분은 autograd와 관련된 동영상에서 더 깊이 다룰 것 입니다.**
# 하지만 만약 자세한 내용을 간단히 알고 싶다면 계속 설명하겠습니다.
-#
+#
# *대부분의 경우에서 이것이 바로 여러분이 원하는 것입니다.*
# 예를 들어, 만약 여러분의 모델이 그 모델의 ``forward()`` 메소드에 여러 갈래의 계산 경로가 있고
# 원본 tensor와 그것의 복제본 *모두* 가 모델의 출력에 기여를 한다면,
@@ -572,11 +573,11 @@
# 만약 여러분의 source tensor가 autograd를 사용할 수 있다면
# (일반적으로 학습 가중치의 집합이거나, 가중치를 포함하는 계산에서 파생된 경우),
# 여러분이 원하는 결과를 얻을 수 있습니다.
-#
+#
# 반면에 원본 tensor나 그것의 복제본 *모두* 가 변화도를 추적할 필요가 없다면,
# source tensor의 autograd가 꺼져있다면
# clone을 사용할 수 있습니다.
-#
+#
# 그러나 *세번째 경우* 가 있습니다:
# 기본적으로 변화도가 모든 것을 위해 켜져있지만 일부 지표를 생성하기 위해서
# 스트림 중간에서 일부 값을 생성하고 싶어 하는
@@ -584,7 +585,7 @@
# 이 경우에는 변화도를 추적하기 위해서 source tensor의 복제본을 원하지 *않을* 수 있습니다
# - 성능이 autograd의 히스토리 추적 기능을 끄면서 향상됩니다.
# 이 경우를 위해서는 source tensor에 ``.detach()`` 메소드를 사용할 수 있습니다:
-#
+#
a = torch.rand(2, 2, requires_grad=True) # autograd를 켭니다.
print(a)
@@ -600,7 +601,7 @@
#########################################################################
# 여기서 무슨 일이 일어나는걸까요?
-#
+#
# - ``a`` 를 ``requires_grad=True`` 옵션을 킨 상태로 생성합니다.
# **아직 이 선택적 인자를 다루지 않았지만, autograd 단원 동안만 다룰 것입니다.**
# - ``a`` 를 출력할 때, ``requires_grad=True`` 속성을 가지고 있다고 알려줍니다 -
@@ -611,27 +612,27 @@
# - ``a`` 를 ``c`` 에 복제를 하지만 ``detach()`` 를 먼저 호출을 합니다.
# - ``c`` 를 출력합니다. 계산 히스토리가 없다는 것을 확인할 수 있고,
# ``requires_grad=True`` 옵션이 없다는 것 또한 확인할 수 있습니다.
-#
+#
# ``detach()`` 메소드는 *tensor의 계산 히스토리로 부터 tensor를 떼어냅니다.*
# 이 메소드의 의미는 “메소드 뒤에 어떤 것이든 와도 autograd를 끈 것처럼 작동하라.“ 라는 뜻입니다.
# ``a`` 를 변경하지 *않고* 이 메소드를 수행합니다 -
# 마지막에 ``a`` 를 다시 출력할 때, 여전히 ``a`` 가 가진 ``requires_grad=True``
# 속성이 남아 있다는 것을 확인할 수 있습니다.
-#
+#
# GPU 환경으로 이동하기
-# -------------
-#
+# ---------------------------
+#
# PyTorch의 주된 장점중 하나는 CUDA가 호환되는 Nvidia GPU에서의 강력한 성능 가속화입니다.
# (“CUDA” 는 *Compute Unified Device Architecture* 의 약자이며,
# 병렬 컴퓨팅을 위한 Nvidia의 플랫폼입니다.)
# 지금까지 모든 작업을 CPU에서 처리했습니다. 어떻게 더 빠른 하드웨어로 이동할 수 있을까요?
-#
+#
# 먼저 ``is_available()`` 메소드를 사용해서 GPU가 사용 가능한지 아닌지 확인해야 합니다.
-#
+#
# .. note::
# 만약 CUDA가 호환되는 GPU가 없고 CUDA 드라이버가 설치되어있지 않다면
# 이 섹션에서의 실행 가능한 cell은 어떤 GPU와 관련된 코드도 실행할 수 없습니다.
-#
+#
if torch.cuda.is_available():
print('We have a GPU!')
@@ -647,10 +648,10 @@
# 계산에 필요한 *모든* 데이터를 GPU장치가 접근 가능한 메모리로 이동해야 합니다.
# (평소에는 “GPU가 접근 가능한 메모리로 데이터를 이동한다“
# 를 “데이터를 GPU로 옮긴다“ 라고 줄여서 말합니다.)
-#
+#
# 목적 장치에서 데이터를 가져오는 다양한 방법이 있습니다.
# 객체를 생성할 때 데이터를 가져올 수 있습니다:
-#
+#
if torch.cuda.is_available():
gpu_rand = torch.rand(2, 2, device='cuda')
@@ -664,15 +665,15 @@
# ``device`` 선택 인자를 반드시 명시해줘야 합니다.
# 새로운 tensor를 출력할 때, (만약 CPU에 존재하지 않는다면)
# PyTorch는 어느 장치에 객체가 있는지 알려준다는 것을 확인할 수 있습니다.
-#
+#
# ``torch.cuda.device_count()`` 를 사용해서 GPU의 개수를 조회할 수 있습니다.
# 만약 1개보다 많은 GPU를 가지고 있다면, 각 GPU를 인덱스로 지정할 수 있습니다:
# ``device='cuda:0'``, ``device='cuda:1'``, 와 같이 말이죠.
-#
+#
# 코딩을 할 때, 어디에서나 장치 이름을 문자열 상수로 지정하는 것은 상당히 유지 보수에 취약합니다.
# CPU 하드웨어나 GPU 하드웨어 어떤 것을 사용하는지에 관계없이 여러분의 코드는 잘 작동해야 합니다.
# 문자열 대신에 tensor를 저장할 장치 핸들러를 생성하는 것으로 유지 보수가 쉬운 코드를 작성할 수 있습니다:
-#
+#
if torch.cuda.is_available():
my_device = torch.device('cuda')
@@ -687,7 +688,7 @@
#########################################################################
# 만약 한 장치에 tensor가 있을 때, ``to()`` 메소드를 사용해서 다른 장치로 이동할 수 있습니다.
# 다음 코드는 CPU에 tensor를 생성하고, 이전 cell에서 얻은 장치 핸들러로 tensor를 이동합니다.
-#
+#
y = torch.rand(2, 2)
y = y.to(my_device)
@@ -696,35 +697,35 @@
##########################################################################
# 2개 혹은 그 이상의 tensor를 포함한 계산을 하기 위해서는
# *모든 tensor가 같은 장치에 있어야 한다* 는 것을 아는 것이 중요합니다.
-# 다음 코드는 GPU 장치가 사용 가능 하다는 것과 관계없이 runtime error를 발생할 것입니다:
-#
-# ::
-#
+# 다음 코드는 GPU 장치의 사용 가능 여부와 관계없이 runtime error를 발생할 것입니다:
+#
+# .. code-block:: python
+#
# x = torch.rand(2, 2)
# y = torch.rand(2, 2, device='gpu')
# z = x + y # 오류가 발생할 것입니다.
-#
+#
###########################################################################
# Tensor의 shape 다루기
# --------------------------
-#
+#
# 때로는 tensor의 shape를 변환할 필요가 있습니다.
# 아래에 있는 몇 가지 흔한 경우와 함께 tensor의 shape를 다루는 방법에 대해 알아볼 것 입니다.
-#
+#
# 차원의 개수 변경하기
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
-#
+#
# 차원의 개수를 변경할 필요가 있는 한가지 경우는 모델의 입력에 단일 인스턴스를 전달할 때 입니다.
# PyTorch 모델은 일반적으로 입력에 *배치* 가 들어오기를 기대합니다.
-#
+#
# 예를 들어, 3개의 색깔 채널을 가진 226픽셀 정사각형 이미지인 3 x 226 x 226 개 데이터와
# 함께 작동하는 모델을 가지고 있다고 상상해보세요.
# 이미지를 불러오고 tensor로 변환하면 ``(3, 226, 226)`` shape를 가진 tensor가 됩니다.
# 그럼에도 불구하고 이 모델은 ``(N, 3, 226, 226)`` shape를 가진 tensor를 입력으로 기대합니다.
# 이때 ``N`` 은 배치에 포함된 이미지의 개수입니다. 그렇다면 어떻게 한 배치를 만들 수 있을까요?
-#
+#
a = torch.rand(3, 226, 226)
b = a.unsqueeze(0)
@@ -737,11 +738,11 @@
# ``unsqueeze()`` 메소드는 크기가 1인 차원을 추가합니다.
# ``unsqueeze(0)`` 는 새로운 0번째 차원을 추가합니다
# - 이제 한 배치를 가지게 되었습니다!
-#
+#
# 이게 *un*\ squeezing이면, squeezing은 무슨 뜻 일까요?
# 여기서는 차원을 하나 확장해도 tensor에 있는 원소의 개수는 변하지
# *않는다* 는 사실을 이용하고 있습니다.
-#
+#
c = torch.rand(1, 1, 1, 1, 1)
print(c)
@@ -753,10 +754,10 @@
# 출력 값의 shape는 ``(N, 20)`` 라고 기대할 수 있습니다.
# 이 뜻은 입력으로 단일 배치가 들어왔을 때,
# ``(1, 20)`` 의 shape를 가진 출력 값을 얻는다는 것 입니다.
-#
+#
# 만약 그저 20개의 원소를 가진 벡터와 같이
# - *배치 shape가 아닌* 연산 결과를 얻고 싶으면 어떻게 해야할까요?
-#
+#
a = torch.rand(1, 20)
print(a.shape)
@@ -778,31 +779,31 @@
# 위에 있는 cell의 결과를 자세히 보면
# 추가적인 차원을 가졌기 때문에
# ``a`` 를 출력하는 것에서 “추가” 대괄호 집합 ``[]`` 을 볼 수 있습니다.
-#
+#
# 오직 차원의 값이 1인 경우에만 ``squeeze()`` 를 사용할 수 있습니다.
# ``c`` 에서 크기가 2인 차원을 squeeze 하려고 하는 위 예시를 보면,
# 처음 그 shape로 다시 돌아온다는 사실을 알 수 있습니다.
# ``squeeze()`` 와 ``unsqueeze()`` 를 호출하는 것은 오직 차원의 크기가 1일 때만 작동합니다.
# 왜냐하면 이 경우가 아니면 tensor의 원소 개수가 바뀌기 때문입니다.
-#
+#
# ``unsqueeze()`` 는 broadcasting을 쉽게 하는 경우에도 사용합니다.
# 다음 코드를 보고 이전 예시를 떠올려 보세요:
-#
-# ::
-#
+#
+# .. code-block:: python
+#
# a = torch.ones(4, 3, 2)
-#
-# c = a * torch.rand( 3, 1) # 3번째 차원 = 1, 2번째 차원은 다음 코드랑 동일합니다.
+#
+# c = a * torch.rand( 3, 1) # 3번째 차원은 1이고, 2번째 차원은 a와 동일합니다.
# print(c)
-#
+#
# broadcast의 순수한 효과는 차원 0과 차원 2에 대한 연산을 broadcast해서
# 무작위 3 x 1 shape의 tensor를 ``a`` 의 원소 개수가 3인 모든 열에 곱하는 것이었습니다.
-#
+#
# 만약 무작위 벡터가 오직 3개의 원소만을 가지면 어떻게 될까요?
# broadcast를 할 능력을 잃어버리게 됩니다, 왜냐하면 마지막 차원이
# broadcasting 규칙에 맞지 않기 때문입니다.
# 하지만 ``unsqueeze()`` 가 도와줍니다:
-#
+#
a = torch.ones(4, 3, 2)
b = torch.rand( 3) # a * b를 시도하는 것은 runtime error가 발생합니다.
@@ -814,7 +815,7 @@
######################################################################
# ``squeeze()`` 와 ``unsqueeze()`` 메소드는 tensor 자체의 값을 변경하는
# ``squeeze_()`` 와 ``unsqueeze_()`` 또한 가지고 있습니다.
-#
+#
batch_me = torch.rand(3, 226, 226)
print(batch_me.shape)
@@ -831,7 +832,7 @@
# 이후에 있는 선형 계층은 입력 값으로 1차원을 기대합니다.
# 여러분이 요청한 차원에 입력 tensor가 가진 원소와 같은 개수를 생성하는
# ``reshape()`` 를 여러분을 위해서 제공합니다:
-#
+#
output3d = torch.rand(6, 20, 20)
print(output3d.shape)
@@ -850,35 +851,35 @@
# 하지만 shape가 메소드의 첫번째 인자라면 - 연속된 정수라고 속여서 사용할 수 있습니다.
# 여기에서는 메소드에게 이 인자가 진짜 1개 원소를 가진 튜플이라고 알려주기 위해서
# 편의상 소괄호와 콤마를 추가해야 합니다.
-#
+#
# ``reshape()`` 는 tensor를 바라보는 *관점* 을 변경합니다.
# - 즉, 메모리의 같은 지역을 바라보는 서로 다른 관점을 가진 tensor 객체라는 뜻입니다.
# *이 내용은 정말 중요합니다:* source tensor에 어떠한 변화가 있으면
# ``clone()`` 을 사용하지 않는 한, 해당 tensor를 바라보고 있는 다른 객체 또한
# 값이 변한다는 뜻 입니다.
-#
+#
# 해당 소개의 범위를 벗어난 조건 *들* 이 있습니다.
# 그것은 ``reshape()`` 가 data의 복사본을 가진 tensor를 반환 해야 한다는 것 입니다.
# 더 많은 정보는 다음 문서를 참고하세요
# `docs `__.
-#
+#
#######################################################################
# NumPy로 변환
-# ------------
-#
+# ----------------
+#
# 위에 있는 broadcasting 부분에서, PyTorch의 broadcast
# 문법은 Numpy와 호환 가능하다고 말했었습니다
# - 하지만 PyTorch와 NumPy 사이 유사성은 우리가 생각한 것 보다 더욱 깊습니다.
-#
+#
# 만약 NumPy의 ndarrays에 저장되어 있는 데이터를 사용하는
# 머신 러닝 혹은 과학 분야와 관련된 코드를 가지고 있다면,
# 같은 데이터를 PyTorch의 GPU 가속을 사용할 수 있고
# 머신 러닝 모델을 만드는데 필요한 효과적인 추상화를 제공하는
# PyTorch tensor로 표현하고 싶을 수 있습니다.
# ndarray와 PyTorch tensor끼리 바꾸는 것은 쉽습니다:
-#
+#
import numpy as np
@@ -892,9 +893,9 @@
##########################################################################
# PyTorch는 NumPy array와 같은 shape의 tensor를 생성하고, 같은 데이터를 포함합니다.
# 심지어 NumPy의 기본적인 64비트 실수 데이터 자료형을 유지합니다.
-#
+#
# PyTorch에서 NumPy로 변환은 다른 방식을 사용해서 쉽게 할 수 있습니다:
-#
+#
pytorch_rand = torch.rand(2, 3)
print(pytorch_rand)
@@ -907,7 +908,7 @@
# 이러한 변환된 객체들은 해당 객체의 source 객체가 위치한
# *메모리의 같은 공간* 을 사용한다는 점을 아는 것이 중요합니다.
# 이것은 한 객체가 변하면 다른 것에 영향을 준다는 의미입니다:
-#
+#
numpy_array[1, 1] = 23
print(pytorch_tensor)
diff --git a/beginner_source/introyt/tocyt.txt b/beginner_source/introyt/tocyt.txt
index f956671c1..24b47e489 100644
--- a/beginner_source/introyt/tocyt.txt
+++ b/beginner_source/introyt/tocyt.txt
@@ -5,4 +5,3 @@
5. `PyTorch TensorBoard Support `_
6. `Training with PyTorch `_
7. `Model Understanding with Captum `_
-8. `Production Inference Deployment with PyTorch `_ (video only)
diff --git a/beginner_source/introyt/trainingyt.py b/beginner_source/introyt/trainingyt.py
index 84750da77..84d08a98b 100644
--- a/beginner_source/introyt/trainingyt.py
+++ b/beginner_source/introyt/trainingyt.py
@@ -290,15 +290,19 @@ def train_one_epoch(epoch_index, tb_writer):
model.train(True)
avg_loss = train_one_epoch(epoch_number, writer)
- # We don't need gradients on to do reporting
- model.train(False)
running_vloss = 0.0
- for i, vdata in enumerate(validation_loader):
- vinputs, vlabels = vdata
- voutputs = model(vinputs)
- vloss = loss_fn(voutputs, vlabels)
- running_vloss += vloss
+ # Set the model to evaluation mode, disabling dropout and using population
+ # statistics for batch normalization.
+ model.eval()
+
+ # Disable gradient computation and reduce memory consumption.
+ with torch.no_grad():
+ for i, vdata in enumerate(validation_loader):
+ vinputs, vlabels = vdata
+ voutputs = model(vinputs)
+ vloss = loss_fn(voutputs, vlabels)
+ running_vloss += vloss
avg_vloss = running_vloss / (i + 1)
print('LOSS train {} valid {}'.format(avg_loss, avg_vloss))
diff --git a/beginner_source/knowledge_distillation_tutorial.py b/beginner_source/knowledge_distillation_tutorial.py
new file mode 100644
index 000000000..4601352ff
--- /dev/null
+++ b/beginner_source/knowledge_distillation_tutorial.py
@@ -0,0 +1,738 @@
+# -*- coding: utf-8 -*-
+"""
+Knowledge Distillation Tutorial
+===============================
+**Author**: `Alexandros Chariton `_
+"""
+
+######################################################################
+# Knowledge distillation is a technique that enables knowledge transfer from large, computationally expensive
+# models to smaller ones without losing validity. This allows for deployment on less powerful
+# hardware, making evaluation faster and more efficient.
+#
+# In this tutorial, we will run a number of experiments focused at improving the accuracy of a
+# lightweight neural network, using a more powerful network as a teacher.
+# The computational cost and the speed of the lightweight network will remain unaffected,
+# our intervention only focuses on its weights, not on its forward pass.
+# Applications of this technology can be found in devices such as drones or mobile phones.
+# In this tutorial, we do not use any external packages as everything we need is available in ``torch`` and
+# ``torchvision``.
+#
+# In this tutorial, you will learn:
+#
+# - How to modify model classes to extract hidden representations and use them for further calculations
+# - How to modify regular train loops in PyTorch to include additional losses on top of, for example, cross-entropy for classification
+# - How to improve the performance of lightweight models by using more complex models as teachers
+#
+# Prerequisites
+# ~~~~~~~~~~~~~
+#
+# * 1 GPU, 4GB of memory
+# * PyTorch v2.0 or later
+# * CIFAR-10 dataset (downloaded by the script and saved in a directory called ``/data``)
+
+import torch
+import torch.nn as nn
+import torch.optim as optim
+import torchvision.transforms as transforms
+import torchvision.datasets as datasets
+
+# Check if GPU is available, and if not, use the CPU
+device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
+
+######################################################################
+# Loading CIFAR-10
+# ----------------
+# CIFAR-10 is a popular image dataset with ten classes. Our objective is to predict one of the following classes for each input image.
+#
+# .. figure:: /../_static/img/cifar10.png
+# :align: center
+#
+# Example of CIFAR-10 images
+#
+# The input images are RGB, so they have 3 channels and are 32x32 pixels. Basically, each image is described by 3 x 32 x 32 = 3072 numbers ranging from 0 to 255.
+# A common practice in neural networks is to normalize the input, which is done for multiple reasons,
+# including avoiding saturation in commonly used activation functions and increasing numerical stability.
+# Our normalization process consists of subtracting the mean and dividing by the standard deviation along each channel.
+# The tensors "mean=[0.485, 0.456, 0.406]" and "std=[0.229, 0.224, 0.225]" were already computed,
+# and they represent the mean and standard deviation of each channel in the
+# predefined subset of CIFAR-10 intended to be the training set.
+# Notice how we use these values for the test set as well, without recomputing the mean and standard deviation from scratch.
+# This is because the network was trained on features produced by subtracting and dividing the numbers above, and we want to maintain consistency.
+# Furthermore, in real life, we would not be able to compute the mean and standard deviation of the test set since,
+# under our assumptions, this data would not be accessible at that point.
+#
+# As a closing point, we often refer to this held-out set as the validation set, and we use a separate set,
+# called the test set, after optimizing a model's performance on the validation set.
+# This is done to avoid selecting a model based on the greedy and biased optimization of a single metric.
+
+# Below we are preprocessing data for CIFAR-10. We use an arbitrary batch size of 128.
+transforms_cifar = transforms.Compose([
+ transforms.ToTensor(),
+ transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
+])
+
+# Loading the CIFAR-10 dataset:
+train_dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transforms_cifar)
+test_dataset = datasets.CIFAR10(root='./data', train=False, download=True, transform=transforms_cifar)
+
+########################################################################
+# .. note:: This section is for CPU users only who are interested in quick results. Use this option only if you're interested in a small scale experiment. Keep in mind the code should run fairly quickly using any GPU. Select only the first ``num_images_to_keep`` images from the train/test dataset
+#
+# .. code-block:: python
+#
+# #from torch.utils.data import Subset
+# #num_images_to_keep = 2000
+# #train_dataset = Subset(train_dataset, range(min(num_images_to_keep, 50_000)))
+# #test_dataset = Subset(test_dataset, range(min(num_images_to_keep, 10_000)))
+
+#Dataloaders
+train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=128, shuffle=True, num_workers=2)
+test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=128, shuffle=False, num_workers=2)
+
+######################################################################
+# Defining model classes and utility functions
+# --------------------------------------------
+# Next, we need to define our model classes. Several user-defined parameters need to be set here. We use two different architectures, keeping the number of filters fixed across our experiments to ensure fair comparisons.
+# Both architectures are Convolutional Neural Networks (CNNs) with a different number of convolutional layers that serve as feature extractors, followed by a classifier with 10 classes.
+# The number of filters and neurons is smaller for the students.
+
+# Deeper neural network class to be used as teacher:
+class DeepNN(nn.Module):
+ def __init__(self, num_classes=10):
+ super(DeepNN, self).__init__()
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 128, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.Conv2d(128, 64, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ nn.Conv2d(64, 64, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.Conv2d(64, 32, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ )
+ self.classifier = nn.Sequential(
+ nn.Linear(2048, 512),
+ nn.ReLU(),
+ nn.Dropout(0.1),
+ nn.Linear(512, num_classes)
+ )
+
+ def forward(self, x):
+ x = self.features(x)
+ x = torch.flatten(x, 1)
+ x = self.classifier(x)
+ return x
+
+# Lightweight neural network class to be used as student:
+class LightNN(nn.Module):
+ def __init__(self, num_classes=10):
+ super(LightNN, self).__init__()
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 16, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ nn.Conv2d(16, 16, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ )
+ self.classifier = nn.Sequential(
+ nn.Linear(1024, 256),
+ nn.ReLU(),
+ nn.Dropout(0.1),
+ nn.Linear(256, num_classes)
+ )
+
+ def forward(self, x):
+ x = self.features(x)
+ x = torch.flatten(x, 1)
+ x = self.classifier(x)
+ return x
+
+######################################################################
+# We employ 2 functions to help us produce and evaluate the results on our original classification task.
+# One function is called ``train`` and takes the following arguments:
+#
+# - ``model``: A model instance to train (update its weights) via this function.
+# - ``train_loader``: We defined our ``train_loader`` above, and its job is to feed the data into the model.
+# - ``epochs``: How many times we loop over the dataset.
+# - ``learning_rate``: The learning rate determines how large our steps towards convergence should be. Too large or too small steps can be detrimental.
+# - ``device``: Determines the device to run the workload on. Can be either CPU or GPU depending on availability.
+#
+# Our test function is similar, but it will be invoked with ``test_loader`` to load images from the test set.
+#
+# .. figure:: /../_static/img/knowledge_distillation/ce_only.png
+# :align: center
+#
+# Train both networks with Cross-Entropy. The student will be used as a baseline:
+#
+
+def train(model, train_loader, epochs, learning_rate, device):
+ criterion = nn.CrossEntropyLoss()
+ optimizer = optim.Adam(model.parameters(), lr=learning_rate)
+
+ model.train()
+
+ for epoch in range(epochs):
+ running_loss = 0.0
+ for inputs, labels in train_loader:
+ # inputs: A collection of batch_size images
+ # labels: A vector of dimensionality batch_size with integers denoting class of each image
+ inputs, labels = inputs.to(device), labels.to(device)
+
+ optimizer.zero_grad()
+ outputs = model(inputs)
+
+ # outputs: Output of the network for the collection of images. A tensor of dimensionality batch_size x num_classes
+ # labels: The actual labels of the images. Vector of dimensionality batch_size
+ loss = criterion(outputs, labels)
+ loss.backward()
+ optimizer.step()
+
+ running_loss += loss.item()
+
+ print(f"Epoch {epoch+1}/{epochs}, Loss: {running_loss / len(train_loader)}")
+
+def test(model, test_loader, device):
+ model.to(device)
+ model.eval()
+
+ correct = 0
+ total = 0
+
+ with torch.no_grad():
+ for inputs, labels in test_loader:
+ inputs, labels = inputs.to(device), labels.to(device)
+
+ outputs = model(inputs)
+ _, predicted = torch.max(outputs.data, 1)
+
+ total += labels.size(0)
+ correct += (predicted == labels).sum().item()
+
+ accuracy = 100 * correct / total
+ print(f"Test Accuracy: {accuracy:.2f}%")
+ return accuracy
+
+######################################################################
+# Cross-entropy runs
+# ------------------
+# For reproducibility, we need to set the torch manual seed. We train networks using different methods, so to compare them fairly,
+# it makes sense to initialize the networks with the same weights.
+# Start by training the teacher network using cross-entropy:
+
+torch.manual_seed(42)
+nn_deep = DeepNN(num_classes=10).to(device)
+train(nn_deep, train_loader, epochs=10, learning_rate=0.001, device=device)
+test_accuracy_deep = test(nn_deep, test_loader, device)
+
+# Instantiate the lightweight network:
+torch.manual_seed(42)
+nn_light = LightNN(num_classes=10).to(device)
+
+######################################################################
+# We instantiate one more lightweight network model to compare their performances.
+# Back propagation is sensitive to weight initialization,
+# so we need to make sure these two networks have the exact same initialization.
+
+torch.manual_seed(42)
+new_nn_light = LightNN(num_classes=10).to(device)
+
+######################################################################
+# To ensure we have created a copy of the first network, we inspect the norm of its first layer.
+# If it matches, then we are safe to conclude that the networks are indeed the same.
+
+# Print the norm of the first layer of the initial lightweight model
+print("Norm of 1st layer of nn_light:", torch.norm(nn_light.features[0].weight).item())
+# Print the norm of the first layer of the new lightweight model
+print("Norm of 1st layer of new_nn_light:", torch.norm(new_nn_light.features[0].weight).item())
+
+######################################################################
+# Print the total number of parameters in each model:
+total_params_deep = "{:,}".format(sum(p.numel() for p in nn_deep.parameters()))
+print(f"DeepNN parameters: {total_params_deep}")
+total_params_light = "{:,}".format(sum(p.numel() for p in nn_light.parameters()))
+print(f"LightNN parameters: {total_params_light}")
+
+######################################################################
+# Train and test the lightweight network with cross entropy loss:
+train(nn_light, train_loader, epochs=10, learning_rate=0.001, device=device)
+test_accuracy_light_ce = test(nn_light, test_loader, device)
+
+######################################################################
+# As we can see, based on test accuracy, we can now compare the deeper network that is to be used as a teacher with the lightweight network that is our supposed student. So far, our student has not intervened with the teacher, therefore this performance is achieved by the student itself.
+# The metrics so far can be seen with the following lines:
+
+print(f"Teacher accuracy: {test_accuracy_deep:.2f}%")
+print(f"Student accuracy: {test_accuracy_light_ce:.2f}%")
+
+######################################################################
+# Knowledge distillation run
+# --------------------------
+# Now let's try to improve the test accuracy of the student network by incorporating the teacher.
+# Knowledge distillation is a straightforward technique to achieve this,
+# based on the fact that both networks output a probability distribution over our classes.
+# Therefore, the two networks share the same number of output neurons.
+# The method works by incorporating an additional loss into the traditional cross entropy loss,
+# which is based on the softmax output of the teacher network.
+# The assumption is that the output activations of a properly trained teacher network carry additional information that can be leveraged by a student network during training.
+# The original work suggests that utilizing ratios of smaller probabilities in the soft targets can help achieve the underlying objective of deep neural networks,
+# which is to create a similarity structure over the data where similar objects are mapped closer together.
+# For example, in CIFAR-10, a truck could be mistaken for an automobile or airplane,
+# if its wheels are present, but it is less likely to be mistaken for a dog.
+# Therefore, it makes sense to assume that valuable information resides not only in the top prediction of a properly trained model but in the entire output distribution.
+# However, cross entropy alone does not sufficiently exploit this information as the activations for non-predicted classes
+# tend to be so small that propagated gradients do not meaningfully change the weights to construct this desirable vector space.
+#
+# As we continue defining our first helper function that introduces a teacher-student dynamic, we need to include a few extra parameters:
+#
+# - ``T``: Temperature controls the smoothness of the output distributions. Larger ``T`` leads to smoother distributions, thus smaller probabilities get a larger boost.
+# - ``soft_target_loss_weight``: A weight assigned to the extra objective we're about to include.
+# - ``ce_loss_weight``: A weight assigned to cross-entropy. Tuning these weights pushes the network towards optimizing for either objective.
+#
+# .. figure:: /../_static/img/knowledge_distillation/distillation_output_loss.png
+# :align: center
+#
+# Distillation loss is calculated from the logits of the networks. It only returns gradients to the student:
+#
+
+def train_knowledge_distillation(teacher, student, train_loader, epochs, learning_rate, T, soft_target_loss_weight, ce_loss_weight, device):
+ ce_loss = nn.CrossEntropyLoss()
+ optimizer = optim.Adam(student.parameters(), lr=learning_rate)
+
+ teacher.eval() # Teacher set to evaluation mode
+ student.train() # Student to train mode
+
+ for epoch in range(epochs):
+ running_loss = 0.0
+ for inputs, labels in train_loader:
+ inputs, labels = inputs.to(device), labels.to(device)
+
+ optimizer.zero_grad()
+
+ # Forward pass with the teacher model - do not save gradients here as we do not change the teacher's weights
+ with torch.no_grad():
+ teacher_logits = teacher(inputs)
+
+ # Forward pass with the student model
+ student_logits = student(inputs)
+
+ #Soften the student logits by applying softmax first and log() second
+ soft_targets = nn.functional.softmax(teacher_logits / T, dim=-1)
+ soft_prob = nn.functional.log_softmax(student_logits / T, dim=-1)
+
+ # Calculate the soft targets loss. Scaled by T**2 as suggested by the authors of the paper "Distilling the knowledge in a neural network"
+ soft_targets_loss = torch.sum(soft_targets * (soft_targets.log() - soft_prob)) / soft_prob.size()[0] * (T**2)
+
+ # Calculate the true label loss
+ label_loss = ce_loss(student_logits, labels)
+
+ # Weighted sum of the two losses
+ loss = soft_target_loss_weight * soft_targets_loss + ce_loss_weight * label_loss
+
+ loss.backward()
+ optimizer.step()
+
+ running_loss += loss.item()
+
+ print(f"Epoch {epoch+1}/{epochs}, Loss: {running_loss / len(train_loader)}")
+
+# Apply ``train_knowledge_distillation`` with a temperature of 2. Arbitrarily set the weights to 0.75 for CE and 0.25 for distillation loss.
+train_knowledge_distillation(teacher=nn_deep, student=new_nn_light, train_loader=train_loader, epochs=10, learning_rate=0.001, T=2, soft_target_loss_weight=0.25, ce_loss_weight=0.75, device=device)
+test_accuracy_light_ce_and_kd = test(new_nn_light, test_loader, device)
+
+# Compare the student test accuracy with and without the teacher, after distillation
+print(f"Teacher accuracy: {test_accuracy_deep:.2f}%")
+print(f"Student accuracy without teacher: {test_accuracy_light_ce:.2f}%")
+print(f"Student accuracy with CE + KD: {test_accuracy_light_ce_and_kd:.2f}%")
+
+######################################################################
+# Cosine loss minimization run
+# ----------------------------
+# Feel free to play around with the temperature parameter that controls the softness of the softmax function and the loss coefficients.
+# In neural networks, it is easy to include to include additional loss functions to the main objectives to achieve goals like better generalization.
+# Let's try including an objective for the student, but now let's focus on their hidden states rather than their output layers.
+# Our goal is to convey information from the teacher's representation to the student by including a naive loss function,
+# whose minimization implies that the flattened vectors that are subsequently passed to the classifiers have become more *similar* as the loss decreases.
+# Of course, the teacher does not update its weights, so the minimization depends only on the student's weights.
+# The rationale behind this method is that we are operating under the assumption that the teacher model has a better internal representation that is
+# unlikely to be achieved by the student without external intervention, therefore we artificially push the student to mimic the internal representation of the teacher.
+# Whether or not this will end up helping the student is not straightforward, though, because pushing the lightweight network
+# to reach this point could be a good thing, assuming that we have found an internal representation that leads to better test accuracy,
+# but it could also be harmful because the networks have different architectures and the student does not have the same learning capacity as the teacher.
+# In other words, there is no reason for these two vectors, the student's and the teacher's to match per component.
+# The student could reach an internal representation that is a permutation of the teacher's and it would be just as efficient.
+# Nonetheless, we can still run a quick experiment to figure out the impact of this method.
+# We will be using the ``CosineEmbeddingLoss`` which is given by the following formula:
+#
+# .. figure:: /../_static/img/knowledge_distillation/cosine_embedding_loss.png
+# :align: center
+# :width: 450px
+#
+# Formula for CosineEmbeddingLoss
+#
+# Obviously, there is one thing that we need to resolve first.
+# When we applied distillation to the output layer we mentioned that both networks have the same number of neurons, equal to the number of classes.
+# However, this is not the case for the layer following our convolutional layers. Here, the teacher has more neurons than the student
+# after the flattening of the final convolutional layer. Our loss function accepts two vectors of equal dimensionality as inputs,
+# therefore we need to somehow match them. We will solve this by including an average pooling layer after the teacher's convolutional layer to reduce its dimensionality to match that of the student.
+#
+# To proceed, we will modify our model classes, or create new ones.
+# Now, the forward function returns not only the logits of the network but also the flattened hidden representation after the convolutional layer. We include the aforementioned pooling for the modified teacher.
+
+class ModifiedDeepNNCosine(nn.Module):
+ def __init__(self, num_classes=10):
+ super(ModifiedDeepNNCosine, self).__init__()
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 128, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.Conv2d(128, 64, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ nn.Conv2d(64, 64, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.Conv2d(64, 32, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ )
+ self.classifier = nn.Sequential(
+ nn.Linear(2048, 512),
+ nn.ReLU(),
+ nn.Dropout(0.1),
+ nn.Linear(512, num_classes)
+ )
+
+ def forward(self, x):
+ x = self.features(x)
+ flattened_conv_output = torch.flatten(x, 1)
+ x = self.classifier(flattened_conv_output)
+ flattened_conv_output_after_pooling = torch.nn.functional.avg_pool1d(flattened_conv_output, 2)
+ return x, flattened_conv_output_after_pooling
+
+# Create a similar student class where we return a tuple. We do not apply pooling after flattening.
+class ModifiedLightNNCosine(nn.Module):
+ def __init__(self, num_classes=10):
+ super(ModifiedLightNNCosine, self).__init__()
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 16, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ nn.Conv2d(16, 16, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ )
+ self.classifier = nn.Sequential(
+ nn.Linear(1024, 256),
+ nn.ReLU(),
+ nn.Dropout(0.1),
+ nn.Linear(256, num_classes)
+ )
+
+ def forward(self, x):
+ x = self.features(x)
+ flattened_conv_output = torch.flatten(x, 1)
+ x = self.classifier(flattened_conv_output)
+ return x, flattened_conv_output
+
+# We do not have to train the modified deep network from scratch of course, we just load its weights from the trained instance
+modified_nn_deep = ModifiedDeepNNCosine(num_classes=10).to(device)
+modified_nn_deep.load_state_dict(nn_deep.state_dict())
+
+# Once again ensure the norm of the first layer is the same for both networks
+print("Norm of 1st layer for deep_nn:", torch.norm(nn_deep.features[0].weight).item())
+print("Norm of 1st layer for modified_deep_nn:", torch.norm(modified_nn_deep.features[0].weight).item())
+
+# Initialize a modified lightweight network with the same seed as our other lightweight instances. This will be trained from scratch to examine the effectiveness of cosine loss minimization.
+torch.manual_seed(42)
+modified_nn_light = ModifiedLightNNCosine(num_classes=10).to(device)
+print("Norm of 1st layer:", torch.norm(modified_nn_light.features[0].weight).item())
+
+######################################################################
+# Naturally, we need to change the train loop because now the model returns a tuple ``(logits, hidden_representation)``. Using a sample input tensor
+# we can print their shapes.
+
+# Create a sample input tensor
+sample_input = torch.randn(128, 3, 32, 32).to(device) # Batch size: 128, Filters: 3, Image size: 32x32
+
+# Pass the input through the student
+logits, hidden_representation = modified_nn_light(sample_input)
+
+# Print the shapes of the tensors
+print("Student logits shape:", logits.shape) # batch_size x total_classes
+print("Student hidden representation shape:", hidden_representation.shape) # batch_size x hidden_representation_size
+
+# Pass the input through the teacher
+logits, hidden_representation = modified_nn_deep(sample_input)
+
+# Print the shapes of the tensors
+print("Teacher logits shape:", logits.shape) # batch_size x total_classes
+print("Teacher hidden representation shape:", hidden_representation.shape) # batch_size x hidden_representation_size
+
+######################################################################
+# In our case, ``hidden_representation_size`` is ``1024``. This is the flattened feature map of the final convolutional layer of the student and as you can see,
+# it is the input for its classifier. It is ``1024`` for the teacher too, because we made it so with ``avg_pool1d`` from ``2048``.
+# The loss applied here only affects the weights of the student prior to the loss calculation. In other words, it does not affect the classifier of the student.
+# The modified training loop is the following:
+#
+# .. figure:: /../_static/img/knowledge_distillation/cosine_loss_distillation.png
+# :align: center
+#
+# In Cosine Loss minimization, we want to maximize the cosine similarity of the two representations by returning gradients to the student:
+#
+
+def train_cosine_loss(teacher, student, train_loader, epochs, learning_rate, hidden_rep_loss_weight, ce_loss_weight, device):
+ ce_loss = nn.CrossEntropyLoss()
+ cosine_loss = nn.CosineEmbeddingLoss()
+ optimizer = optim.Adam(student.parameters(), lr=learning_rate)
+
+ teacher.to(device)
+ student.to(device)
+ teacher.eval() # Teacher set to evaluation mode
+ student.train() # Student to train mode
+
+ for epoch in range(epochs):
+ running_loss = 0.0
+ for inputs, labels in train_loader:
+ inputs, labels = inputs.to(device), labels.to(device)
+
+ optimizer.zero_grad()
+
+ # Forward pass with the teacher model and keep only the hidden representation
+ with torch.no_grad():
+ _, teacher_hidden_representation = teacher(inputs)
+
+ # Forward pass with the student model
+ student_logits, student_hidden_representation = student(inputs)
+
+ # Calculate the cosine loss. Target is a vector of ones. From the loss formula above we can see that is the case where loss minimization leads to cosine similarity increase.
+ hidden_rep_loss = cosine_loss(student_hidden_representation, teacher_hidden_representation, target=torch.ones(inputs.size(0)).to(device))
+
+ # Calculate the true label loss
+ label_loss = ce_loss(student_logits, labels)
+
+ # Weighted sum of the two losses
+ loss = hidden_rep_loss_weight * hidden_rep_loss + ce_loss_weight * label_loss
+
+ loss.backward()
+ optimizer.step()
+
+ running_loss += loss.item()
+
+ print(f"Epoch {epoch+1}/{epochs}, Loss: {running_loss / len(train_loader)}")
+
+######################################################################
+#We need to modify our test function for the same reason. Here we ignore the hidden representation returned by the model.
+
+def test_multiple_outputs(model, test_loader, device):
+ model.to(device)
+ model.eval()
+
+ correct = 0
+ total = 0
+
+ with torch.no_grad():
+ for inputs, labels in test_loader:
+ inputs, labels = inputs.to(device), labels.to(device)
+
+ outputs, _ = model(inputs) # Disregard the second tensor of the tuple
+ _, predicted = torch.max(outputs.data, 1)
+
+ total += labels.size(0)
+ correct += (predicted == labels).sum().item()
+
+ accuracy = 100 * correct / total
+ print(f"Test Accuracy: {accuracy:.2f}%")
+ return accuracy
+
+######################################################################
+# In this case, we could easily include both knowledge distillation and cosine loss minimization in the same function. It is common to combine methods to achieve better performance in teacher-student paradigms.
+# For now, we can run a simple train-test session.
+
+# Train and test the lightweight network with cross entropy loss
+train_cosine_loss(teacher=modified_nn_deep, student=modified_nn_light, train_loader=train_loader, epochs=10, learning_rate=0.001, hidden_rep_loss_weight=0.25, ce_loss_weight=0.75, device=device)
+test_accuracy_light_ce_and_cosine_loss = test_multiple_outputs(modified_nn_light, test_loader, device)
+
+######################################################################
+# Intermediate regressor run
+# --------------------------
+# Our naive minimization does not guarantee better results for several reasons, one being the dimensionality of the vectors.
+# Cosine similarity generally works better than Euclidean distance for vectors of higher dimensionality,
+# but we were dealing with vectors with 1024 components each, so it is much harder to extract meaningful similarities.
+# Furthermore, as we mentioned, pushing towards a match of the hidden representation of the teacher and the student is not supported by theory.
+# There are no good reasons why we should be aiming for a 1:1 match of these vectors.
+# We will provide a final example of training intervention by including an extra network called regressor.
+# The objective is to first extract the feature map of the teacher after a convolutional layer,
+# then extract a feature map of the student after a convolutional layer, and finally try to match these maps.
+# However, this time, we will introduce a regressor between the networks to facilitate the matching process.
+# The regressor will be trainable and ideally will do a better job than our naive cosine loss minimization scheme.
+# Its main job is to match the dimensionality of these feature maps so that we can properly define a loss function between the teacher and the student.
+# Defining such a loss function provides a teaching "path," which is basically a flow to back-propagate gradients that will change the student's weights.
+# Focusing on the output of the convolutional layers right before each classifier for our original networks, we have the following shapes:
+#
+
+# Pass the sample input only from the convolutional feature extractor
+convolutional_fe_output_student = nn_light.features(sample_input)
+convolutional_fe_output_teacher = nn_deep.features(sample_input)
+
+# Print their shapes
+print("Student's feature extractor output shape: ", convolutional_fe_output_student.shape)
+print("Teacher's feature extractor output shape: ", convolutional_fe_output_teacher.shape)
+
+######################################################################
+# We have 32 filters for the teacher and 16 filters for the student.
+# We will include a trainable layer that converts the feature map of the student to the shape of the feature map of the teacher.
+# In practice, we modify the lightweight class to return the hidden state after an intermediate regressor that matches the sizes of the convolutional
+# feature maps and the teacher class to return the output of the final convolutional layer without pooling or flattening.
+#
+# .. figure:: /../_static/img/knowledge_distillation/fitnets_knowledge_distill.png
+# :align: center
+#
+# The trainable layer matches the shapes of the intermediate tensors and Mean Squared Error (MSE) is properly defined:
+#
+
+class ModifiedDeepNNRegressor(nn.Module):
+ def __init__(self, num_classes=10):
+ super(ModifiedDeepNNRegressor, self).__init__()
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 128, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.Conv2d(128, 64, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ nn.Conv2d(64, 64, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.Conv2d(64, 32, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ )
+ self.classifier = nn.Sequential(
+ nn.Linear(2048, 512),
+ nn.ReLU(),
+ nn.Dropout(0.1),
+ nn.Linear(512, num_classes)
+ )
+
+ def forward(self, x):
+ x = self.features(x)
+ conv_feature_map = x
+ x = torch.flatten(x, 1)
+ x = self.classifier(x)
+ return x, conv_feature_map
+
+class ModifiedLightNNRegressor(nn.Module):
+ def __init__(self, num_classes=10):
+ super(ModifiedLightNNRegressor, self).__init__()
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 16, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ nn.Conv2d(16, 16, kernel_size=3, padding=1),
+ nn.ReLU(),
+ nn.MaxPool2d(kernel_size=2, stride=2),
+ )
+ # Include an extra regressor (in our case linear)
+ self.regressor = nn.Sequential(
+ nn.Conv2d(16, 32, kernel_size=3, padding=1)
+ )
+ self.classifier = nn.Sequential(
+ nn.Linear(1024, 256),
+ nn.ReLU(),
+ nn.Dropout(0.1),
+ nn.Linear(256, num_classes)
+ )
+
+ def forward(self, x):
+ x = self.features(x)
+ regressor_output = self.regressor(x)
+ x = torch.flatten(x, 1)
+ x = self.classifier(x)
+ return x, regressor_output
+
+######################################################################
+# After that, we have to update our train loop again. This time, we extract the regressor output of the student, the feature map of the teacher,
+# we calculate the ``MSE`` on these tensors (they have the exact same shape so it's properly defined) and we back propagate gradients based on that loss,
+# in addition to the regular cross entropy loss of the classification task.
+
+def train_mse_loss(teacher, student, train_loader, epochs, learning_rate, feature_map_weight, ce_loss_weight, device):
+ ce_loss = nn.CrossEntropyLoss()
+ mse_loss = nn.MSELoss()
+ optimizer = optim.Adam(student.parameters(), lr=learning_rate)
+
+ teacher.to(device)
+ student.to(device)
+ teacher.eval() # Teacher set to evaluation mode
+ student.train() # Student to train mode
+
+ for epoch in range(epochs):
+ running_loss = 0.0
+ for inputs, labels in train_loader:
+ inputs, labels = inputs.to(device), labels.to(device)
+
+ optimizer.zero_grad()
+
+ # Again ignore teacher logits
+ with torch.no_grad():
+ _, teacher_feature_map = teacher(inputs)
+
+ # Forward pass with the student model
+ student_logits, regressor_feature_map = student(inputs)
+
+ # Calculate the loss
+ hidden_rep_loss = mse_loss(regressor_feature_map, teacher_feature_map)
+
+ # Calculate the true label loss
+ label_loss = ce_loss(student_logits, labels)
+
+ # Weighted sum of the two losses
+ loss = feature_map_weight * hidden_rep_loss + ce_loss_weight * label_loss
+
+ loss.backward()
+ optimizer.step()
+
+ running_loss += loss.item()
+
+ print(f"Epoch {epoch+1}/{epochs}, Loss: {running_loss / len(train_loader)}")
+
+# Notice how our test function remains the same here with the one we used in our previous case. We only care about the actual outputs because we measure accuracy.
+
+# Initialize a ModifiedLightNNRegressor
+torch.manual_seed(42)
+modified_nn_light_reg = ModifiedLightNNRegressor(num_classes=10).to(device)
+
+# We do not have to train the modified deep network from scratch of course, we just load its weights from the trained instance
+modified_nn_deep_reg = ModifiedDeepNNRegressor(num_classes=10).to(device)
+modified_nn_deep_reg.load_state_dict(nn_deep.state_dict())
+
+# Train and test once again
+train_mse_loss(teacher=modified_nn_deep_reg, student=modified_nn_light_reg, train_loader=train_loader, epochs=10, learning_rate=0.001, feature_map_weight=0.25, ce_loss_weight=0.75, device=device)
+test_accuracy_light_ce_and_mse_loss = test_multiple_outputs(modified_nn_light_reg, test_loader, device)
+
+######################################################################
+# It is expected that the final method will work better than ``CosineLoss`` because now we have allowed a trainable layer between the teacher and the student,
+# which gives the student some wiggle room when it comes to learning, rather than pushing the student to copy the teacher's representation.
+# Including the extra network is the idea behind hint-based distillation.
+
+print(f"Teacher accuracy: {test_accuracy_deep:.2f}%")
+print(f"Student accuracy without teacher: {test_accuracy_light_ce:.2f}%")
+print(f"Student accuracy with CE + KD: {test_accuracy_light_ce_and_kd:.2f}%")
+print(f"Student accuracy with CE + CosineLoss: {test_accuracy_light_ce_and_cosine_loss:.2f}%")
+print(f"Student accuracy with CE + RegressorMSE: {test_accuracy_light_ce_and_mse_loss:.2f}%")
+
+######################################################################
+# Conclusion
+# --------------------------------------------
+# None of the methods above increases the number of parameters for the network or inference time,
+# so the performance increase comes at the little cost of calculating gradients during training.
+# In ML applications, we mostly care about inference time because training happens before the model deployment.
+# If our lightweight model is still too heavy for deployment, we can apply different ideas, such as post-training quantization.
+# Additional losses can be applied in many tasks, not just classification, and you can experiment with quantities like coefficients,
+# temperature, or number of neurons. Feel free to tune any numbers in the tutorial above,
+# but keep in mind, if you change the number of neurons / filters chances are a shape mismatch might occur.
+#
+# For more information, see:
+#
+# * `Hinton, G., Vinyals, O., Dean, J.: Distilling the knowledge in a neural network. In: Neural Information Processing System Deep Learning Workshop (2015) `_
+#
+# * `Romero, A., Ballas, N., Kahou, S.E., Chassang, A., Gatta, C., Bengio, Y.: Fitnets: Hints for thin deep nets. In: Proceedings of the International Conference on Learning Representations (2015) `_
diff --git a/beginner_source/nlp/README.txt b/beginner_source/nlp/README.txt
index c1ea17a75..2d588c1e3 100644
--- a/beginner_source/nlp/README.txt
+++ b/beginner_source/nlp/README.txt
@@ -1,6 +1,28 @@
Deep Learning for NLP with Pytorch
----------------------------------
+These tutorials will walk you through the key ideas of deep learning
+programming using Pytorch. Many of the concepts (such as the computation
+graph abstraction and autograd) are not unique to Pytorch and are
+relevant to any deep learning toolkit out there.
+
+They are focused specifically on NLP for people who have never written
+code in any deep learning framework (e.g, TensorFlow,Theano, Keras, DyNet).
+The tutorials assumes working knowledge of core NLP problems: part-of-speech
+tagging, language modeling, etc. It also assumes familiarity with neural
+networks at the level of an intro AI class (such as one from the Russel and
+Norvig book). Usually, these courses cover the basic backpropagation algorithm
+on feed-forward neural networks, and make the point that they are chains of
+compositions of linearities and non-linearities. This tutorial aims to get
+you started writing deep learning code, given you have this prerequisite
+knowledge.
+
+Note these tutorials are about *models*, not data. For all of the models,
+a few test examples are created with small dimensionality so you can see how
+the weights change as it trains. If you have some real data you want to
+try, you should be able to rip out any of the models from this notebook
+and use them on it.
+
1. pytorch_tutorial.py
Introduction to PyTorch
https://tutorials.pytorch.kr/beginner/nlp/pytorch_tutorial.html
diff --git a/beginner_source/nn_tutorial.py b/beginner_source/nn_tutorial.py
index 8243f895f..85e5d1084 100644
--- a/beginner_source/nn_tutorial.py
+++ b/beginner_source/nn_tutorial.py
@@ -76,6 +76,11 @@
import numpy as np
pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
+# Colab이 아닌 경우에만 ``pyplot.show()``
+try:
+ import google.colab
+except ImportError:
+ pyplot.show()
print(x_train.shape)
###############################################################################
@@ -92,8 +97,8 @@
print(y_train.min(), y_train.max())
###############################################################################
-# ()``torch.nn`` 없이) 밑바닥부터 신경망 만들기
-# -----------------------------------------------
+# (``torch.nn`` 없이) 밑바닥부터 신경망 만들기
+# -------------------------------------------------
#
# PyTorch 텐서 연산만으로 첫 모델을 만들어봅시다.
# 여러분이 신경망의 기초에 대해서 이미 익숙하다고 가정합니다.
@@ -317,7 +322,7 @@ def forward(self, xb):
# 이전에는 훈련 루프를 위해 이름 별로 각 매개변수(parameter)의 값을 업데이트하고 다음과 같이
# 각 매개 변수에 대한 기울기들을 개별적으로 수동으로 0으로 제거해야 했습니다:
#
-# ::
+# .. code-block:: python
#
# with torch.no_grad():
# weights -= weights.grad * lr
@@ -330,7 +335,7 @@ def forward(self, xb):
# ``nn.Module`` 에 대해 PyTorch에 의해 정의됨)를 활용하여 이러한 단계를 더 간결하게
# 만들고, 특히 더 복잡한 모델에 대해서 일부 매개변수를 잊어 버리는 오류를 덜 발생시킬 수 있습니다:
#
-# ::
+# .. code-block:: python
#
# with torch.no_grad():
# for p in model.parameters(): p -= p.grad * lr
@@ -405,7 +410,7 @@ def forward(self, xb):
#
# 이렇게 하면 이전에 수동으로 코딩한 최적화 단계를 대체할 수 있습니다:
#
-# ::
+# .. code-block:: python
#
# with torch.no_grad():
# for p in model.parameters(): p -= p.grad * lr
@@ -413,7 +418,7 @@ def forward(self, xb):
#
# 대신에 이렇게 말이죠:
#
-# ::
+# .. code-block:: python
#
# opt.step()
# opt.zero_grad()
@@ -476,7 +481,7 @@ def get_model():
###############################################################################
# 이전에는 ``x`` 및 ``y`` 값의 미니 배치를 별도로 반복해야 했습니다:
#
-# ::
+# .. code-block:: python
#
# xb = x_train[start_i:end_i]
# yb = y_train[start_i:end_i]
@@ -484,7 +489,7 @@ def get_model():
#
# 이제 이 두 단계를 함께 수행할 수 있습니다:
#
-# ::
+# .. code-block:: python
#
# xb,yb = train_ds[i*bs : i*bs+bs]
#
@@ -521,7 +526,7 @@ def get_model():
###############################################################################
# 이전에는 루프가 다음과 같이 배치 ``(xb, yb)`` 를 반복했습니다:
#
-# ::
+# .. code-block:: python
#
# for i in range((n-1)//bs + 1):
# xb,yb = train_ds[i*bs : i*bs+bs]
@@ -529,7 +534,7 @@ def get_model():
#
# 이제 (xb, yb)가 DataLoader 에서 자동으로 로드되므로 루프가 훨씬 깨끗해졌습니다:
#
-# ::
+# .. code-block:: python
#
# for xb,yb in train_dl:
# pred = model(xb)
@@ -774,8 +779,7 @@ def __len__(self):
return len(self.dl)
def __iter__(self):
- batches = iter(self.dl)
- for b in batches:
+ for b in self.dl:
yield (self.func(*b))
train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
diff --git a/beginner_source/onnx/README.txt b/beginner_source/onnx/README.txt
new file mode 100644
index 000000000..e9b1e74e6
--- /dev/null
+++ b/beginner_source/onnx/README.txt
@@ -0,0 +1,14 @@
+ONNX
+----
+
+1. intro_onnx.py
+ Introduction to ONNX
+ https://tutorials.pytorch.kr/onnx/intro_onnx.html
+
+2. export_simple_model_to_onnx_tutorial.py
+ Exporting a PyTorch model to ONNX
+ https://tutorials.pytorch.kr/beginner/onnx/export_simple_model_to_onnx_tutorial.html
+
+3. onnx_registry_tutorial.py
+ Extending the ONNX Registry
+ https://tutorials.pytorch.kr/beginner/onnx/onnx_registry_tutorial.html
diff --git a/beginner_source/onnx/export_simple_model_to_onnx_tutorial.py b/beginner_source/onnx/export_simple_model_to_onnx_tutorial.py
new file mode 100644
index 000000000..895be83cf
--- /dev/null
+++ b/beginner_source/onnx/export_simple_model_to_onnx_tutorial.py
@@ -0,0 +1,212 @@
+# -*- coding: utf-8 -*-
+"""
+`Introduction to ONNX `_ ||
+**Exporting a PyTorch model to ONNX** ||
+`Extending the ONNX Registry `_
+
+Export a PyTorch model to ONNX
+==============================
+
+**Author**: `Thiago Crepaldi `_
+
+.. note::
+ As of PyTorch 2.1, there are two versions of ONNX Exporter.
+
+ * ``torch.onnx.dynamo_export`` is the newest (still in beta) exporter based on the TorchDynamo technology released with PyTorch 2.0
+ * ``torch.onnx.export`` is based on TorchScript backend and has been available since PyTorch 1.2.0
+
+"""
+
+###############################################################################
+# In the `60 Minute Blitz `_,
+# we had the opportunity to learn about PyTorch at a high level and train a small neural network to classify images.
+# In this tutorial, we are going to expand this to describe how to convert a model defined in PyTorch into the
+# ONNX format using TorchDynamo and the ``torch.onnx.dynamo_export`` ONNX exporter.
+#
+# While PyTorch is great for iterating on the development of models, the model can be deployed to production
+# using different formats, including `ONNX `_ (Open Neural Network Exchange)!
+#
+# ONNX is a flexible open standard format for representing machine learning models which standardized representations
+# of machine learning allow them to be executed across a gamut of hardware platforms and runtime environments
+# from large-scale cloud-based supercomputers to resource-constrained edge devices, such as your web browser and phone.
+#
+# In this tutorial, we’ll learn how to:
+#
+# 1. Install the required dependencies.
+# 2. Author a simple image classifier model.
+# 3. Export the model to ONNX format.
+# 4. Save the ONNX model in a file.
+# 5. Visualize the ONNX model graph using `Netron `_.
+# 6. Execute the ONNX model with `ONNX Runtime`
+# 7. Compare the PyTorch results with the ones from the ONNX Runtime.
+#
+# 1. Install the required dependencies
+# ------------------------------------
+# Because the ONNX exporter uses ``onnx`` and ``onnxscript`` to translate PyTorch operators into ONNX operators,
+# we will need to install them.
+#
+# .. code-block:: bash
+#
+# pip install onnx
+# pip install onnxscript
+#
+# 2. Author a simple image classifier model
+# -----------------------------------------
+#
+# Once your environment is set up, let’s start modeling our image classifier with PyTorch,
+# exactly like we did in the `60 Minute Blitz `_.
+#
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+
+class MyModel(nn.Module):
+
+ def __init__(self):
+ super(MyModel, self).__init__()
+ self.conv1 = nn.Conv2d(1, 6, 5)
+ self.conv2 = nn.Conv2d(6, 16, 5)
+ self.fc1 = nn.Linear(16 * 5 * 5, 120)
+ self.fc2 = nn.Linear(120, 84)
+ self.fc3 = nn.Linear(84, 10)
+
+ def forward(self, x):
+ x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
+ x = F.max_pool2d(F.relu(self.conv2(x)), 2)
+ x = torch.flatten(x, 1)
+ x = F.relu(self.fc1(x))
+ x = F.relu(self.fc2(x))
+ x = self.fc3(x)
+ return x
+
+######################################################################
+# 3. Export the model to ONNX format
+# ----------------------------------
+#
+# Now that we have our model defined, we need to instantiate it and create a random 32x32 input.
+# Next, we can export the model to ONNX format.
+
+torch_model = MyModel()
+torch_input = torch.randn(1, 1, 32, 32)
+onnx_program = torch.onnx.dynamo_export(torch_model, torch_input)
+
+######################################################################
+# As we can see, we didn't need any code change to the model.
+# The resulting ONNX model is stored within ``torch.onnx.ONNXProgram`` as a binary protobuf file.
+#
+# 4. Save the ONNX model in a file
+# --------------------------------
+#
+# Although having the exported model loaded in memory is useful in many applications,
+# we can save it to disk with the following code:
+
+onnx_program.save("my_image_classifier.onnx")
+
+######################################################################
+# You can load the ONNX file back into memory and check if it is well formed with the following code:
+
+import onnx
+onnx_model = onnx.load("my_image_classifier.onnx")
+onnx.checker.check_model(onnx_model)
+
+######################################################################
+# 5. Visualize the ONNX model graph using Netron
+# ----------------------------------------------
+#
+# Now that we have our model saved in a file, we can visualize it with `Netron `_.
+# Netron can either be installed on macos, Linux or Windows computers, or run directly from the browser.
+# Let's try the web version by opening the following link: https://netron.app/.
+#
+# .. image:: ../../_static/img/onnx/netron_web_ui.png
+# :width: 70%
+# :align: center
+#
+#
+# Once Netron is open, we can drag and drop our ``my_image_classifier.onnx`` file into the browser or select it after
+# clicking the **Open model** button.
+#
+# .. image:: ../../_static/img/onnx/image_clossifier_onnx_modelon_netron_web_ui.png
+# :width: 50%
+#
+#
+# And that is it! We have successfully exported our PyTorch model to ONNX format and visualized it with Netron.
+#
+# 6. Execute the ONNX model with ONNX Runtime
+# -------------------------------------------
+#
+# The last step is executing the ONNX model with `ONNX Runtime`, but before we do that, let's install ONNX Runtime.
+#
+# .. code-block:: bash
+#
+# pip install onnxruntime
+#
+# The ONNX standard does not support all the data structure and types that PyTorch does,
+# so we need to adapt PyTorch input's to ONNX format before feeding it to ONNX Runtime.
+# In our example, the input happens to be the same, but it might have more inputs
+# than the original PyTorch model in more complex models.
+#
+# ONNX Runtime requires an additional step that involves converting all PyTorch tensors to Numpy (in CPU)
+# and wrap them on a dictionary with keys being a string with the input name as key and the numpy tensor as the value.
+#
+# Now we can create an *ONNX Runtime Inference Session*, execute the ONNX model with the processed input
+# and get the output. In this tutorial, ONNX Runtime is executed on CPU, but it could be executed on GPU as well.
+
+import onnxruntime
+
+onnx_input = onnx_program.adapt_torch_inputs_to_onnx(torch_input)
+print(f"Input length: {len(onnx_input)}")
+print(f"Sample input: {onnx_input}")
+
+ort_session = onnxruntime.InferenceSession("./my_image_classifier.onnx", providers=['CPUExecutionProvider'])
+
+def to_numpy(tensor):
+ return tensor.detach().cpu().numpy() if tensor.requires_grad else tensor.cpu().numpy()
+
+onnxruntime_input = {k.name: to_numpy(v) for k, v in zip(ort_session.get_inputs(), onnx_input)}
+
+onnxruntime_outputs = ort_session.run(None, onnxruntime_input)
+
+####################################################################
+# 7. Compare the PyTorch results with the ones from the ONNX Runtime
+# ------------------------------------------------------------------
+#
+# The best way to determine whether the exported model is looking good is through numerical evaluation
+# against PyTorch, which is our source of truth.
+#
+# For that, we need to execute the PyTorch model with the same input and compare the results with ONNX Runtime's.
+# Before comparing the results, we need to convert the PyTorch's output to match ONNX's format.
+
+torch_outputs = torch_model(torch_input)
+torch_outputs = onnx_program.adapt_torch_outputs_to_onnx(torch_outputs)
+
+assert len(torch_outputs) == len(onnxruntime_outputs)
+for torch_output, onnxruntime_output in zip(torch_outputs, onnxruntime_outputs):
+ torch.testing.assert_close(torch_output, torch.tensor(onnxruntime_output))
+
+print("PyTorch and ONNX Runtime output matched!")
+print(f"Output length: {len(onnxruntime_outputs)}")
+print(f"Sample output: {onnxruntime_outputs}")
+
+######################################################################
+# Conclusion
+# ----------
+#
+# That is about it! We have successfully exported our PyTorch model to ONNX format,
+# saved the model to disk, viewed it using Netron, executed it with ONNX Runtime
+# and finally compared its numerical results with PyTorch's.
+#
+# Further reading
+# ---------------
+#
+# The list below refers to tutorials that ranges from basic examples to advanced scenarios,
+# not necessarily in the order they are listed.
+# Feel free to jump directly to specific topics of your interest or
+# sit tight and have fun going through all of them to learn all there is about the ONNX exporter.
+#
+# .. include:: /beginner_source/onnx/onnx_toc.txt
+#
+# .. toctree::
+# :hidden:
+#
\ No newline at end of file
diff --git a/beginner_source/onnx/intro_onnx.py b/beginner_source/onnx/intro_onnx.py
new file mode 100644
index 000000000..b5cbafc1c
--- /dev/null
+++ b/beginner_source/onnx/intro_onnx.py
@@ -0,0 +1,80 @@
+"""
+**Introduction to ONNX** ||
+`Exporting a PyTorch model to ONNX `_ ||
+`Extending the ONNX Registry `_
+
+Introduction to ONNX
+====================
+
+Authors:
+`Thiago Crepaldi `_,
+
+`Open Neural Network eXchange (ONNX) `_ is an open standard
+format for representing machine learning models. The ``torch.onnx`` module provides APIs to
+capture the computation graph from a native PyTorch :class:`torch.nn.Module` model and convert
+it into an `ONNX graph `_.
+
+The exported model can be consumed by any of the many
+`runtimes that support ONNX `_,
+including Microsoft's `ONNX Runtime `_.
+
+.. note::
+ Currently, there are two flavors of ONNX exporter APIs,
+ but this tutorial will focus on the ``torch.onnx.dynamo_export``.
+
+The TorchDynamo engine is leveraged to hook into Python's frame evaluation API and dynamically rewrite its
+bytecode into an `FX graph `_.
+The resulting FX Graph is polished before it is finally translated into an
+`ONNX graph `_.
+
+The main advantage of this approach is that the `FX graph `_ is captured using
+bytecode analysis that preserves the dynamic nature of the model instead of using traditional static tracing techniques.
+
+Dependencies
+------------
+
+PyTorch 2.1.0 or newer is required.
+
+The ONNX exporter depends on extra Python packages:
+
+ - `ONNX `_ standard library
+ - `ONNX Script `_ library that enables developers to author ONNX operators,
+ functions and models using a subset of Python in an expressive, and yet simple fashion.
+
+They can be installed through `pip `_:
+
+.. code-block:: bash
+
+ pip install --upgrade onnx onnxscript
+
+To validate the installation, run the following commands:
+
+.. code-block:: python
+
+ import torch
+ print(torch.__version__)
+
+ import onnxscript
+ print(onnxscript.__version__)
+
+ from onnxscript import opset18 # opset 18 is the latest (and only) supported version for now
+
+ import onnxruntime
+ print(onnxruntime.__version__)
+
+Each `import` must succeed without any errors and the library versions must be printed out.
+
+Further reading
+---------------
+
+The list below refers to tutorials that ranges from basic examples to advanced scenarios,
+not necessarily in the order they are listed.
+Feel free to jump directly to specific topics of your interest or
+sit tight and have fun going through all of them to learn all there is about the ONNX exporter.
+
+.. include:: /beginner_source/onnx/onnx_toc.txt
+
+.. toctree::
+ :hidden:
+
+"""
diff --git a/beginner_source/onnx/onnx_registry_tutorial.py b/beginner_source/onnx/onnx_registry_tutorial.py
new file mode 100644
index 000000000..dfb54d609
--- /dev/null
+++ b/beginner_source/onnx/onnx_registry_tutorial.py
@@ -0,0 +1,468 @@
+# -*- coding: utf-8 -*-
+
+"""
+`Introduction to ONNX `_ ||
+`Exporting a PyTorch model to ONNX `_ ||
+**Extending the ONNX Registry**
+
+Extending the ONNX Registry
+===========================
+
+**Authors:** Ti-Tai Wang (titaiwang@microsoft.com)
+"""
+
+
+###############################################################################
+# Overview
+# --------
+#
+# This tutorial is an introduction to ONNX registry, which empowers users to implement new ONNX operators
+# or even replace existing operators with a new implementation.
+#
+# During the model export to ONNX, the PyTorch model is lowered to an intermediate
+# representation composed of `ATen operators `_.
+# While ATen operators are maintained by PyTorch core team, it is the responsibility of the ONNX exporter team
+# to independently implement each of these operators to ONNX through `ONNX Script `_.
+# The users can also replace the behavior implemented by the ONNX exporter team with their own implementation
+# to fix bugs or improve performance for a specific ONNX runtime.
+#
+# The ONNX Registry manages the mapping between PyTorch operators and the ONNX operators counterparts and provides
+# APIs to extend the registry.
+#
+# In this tutorial, we will cover three scenarios that require extending the ONNX registry with custom operators:
+#
+# * Unsupported ATen operators
+# * Custom operators with existing ONNX Runtime support
+# * Custom operators without ONNX Runtime support
+#
+# Unsupported ATen operators
+# --------------------------
+#
+# Although the ONNX exporter team does their best efforts to support all ATen operators, some of them
+# might not be supported yet. In this section, we will demonstrate how you can add
+# unsupported ATen operators to the ONNX Registry.
+#
+# .. note::
+# The steps to implement unsupported ATen operators are the same to replace the implementation of an existing
+# ATen operator with a custom implementation.
+# Because we don't actually have an unsupported ATen operator to use in this tutorial, we are going to leverage
+# this and replace the implementation of ``aten::add.Tensor`` with a custom implementation the same way we would
+# if the operator was not present in the ONNX Registry.
+#
+# When a model cannot be exported to ONNX due to an unsupported operator, the ONNX exporter will show an error message
+# similar to:
+#
+# .. code-block:: python
+#
+# RuntimeErrorWithDiagnostic: Unsupported FX nodes: {'call_function': ['aten.add.Tensor']}.
+#
+# The error message indicates that the fully qualified name of unsupported ATen operator is ``aten::add.Tensor``.
+# The fully qualified name of an operator is composed of the namespace, operator name, and overload following
+# the format ``namespace::operator_name.overload``.
+#
+# To add support for an unsupported ATen operator or to replace the implementation for an existing one, we need:
+#
+# * The fully qualified name of the ATen operator (e.g. ``aten::add.Tensor``).
+# This information is always present in the error message as show above.
+# * The implementation of the operator using `ONNX Script `__.
+# ONNX Script is a prerequisite for this tutorial. Please make sure you have read the
+# `ONNX Script tutorial `_
+# before proceeding.
+#
+# Because ``aten::add.Tensor`` is already supported by the ONNX Registry, we will demonstrate how to replace it with a
+# custom implementation, but keep in mind that the same steps apply to support new unsupported ATen operators.
+#
+# This is possible because the :class:`OnnxRegistry` allows users to override an operator registration.
+# We will override the registration of ``aten::add.Tensor`` with our custom implementation and verify it exists.
+#
+
+import torch
+import onnxruntime
+import onnxscript
+from onnxscript import opset18 # opset 18 is the latest (and only) supported version for now
+
+class Model(torch.nn.Module):
+ def forward(self, input_x, input_y):
+ return torch.ops.aten.add(input_x, input_y) # generates a aten::add.Tensor node
+
+input_add_x = torch.randn(3, 4)
+input_add_y = torch.randn(3, 4)
+aten_add_model = Model()
+
+
+# Now we create a ONNX Script function that implements ``aten::add.Tensor``.
+# The function name (e.g. ``custom_aten_add``) is displayed in the ONNX graph, so we recommend to use intuitive names.
+custom_aten = onnxscript.values.Opset(domain="custom.aten", version=1)
+
+# NOTE: The function signature must match the signature of the unsupported ATen operator.
+# https://github.com/pytorch/pytorch/blob/main/aten/src/ATen/native/native_functions.yaml
+# NOTE: All attributes must be annotated with type hints.
+@onnxscript.script(custom_aten)
+def custom_aten_add(input_x, input_y, alpha: float = 1.0):
+ alpha = opset18.CastLike(alpha, input_y)
+ input_y = opset18.Mul(input_y, alpha)
+ return opset18.Add(input_x, input_y)
+
+
+# Now we have everything we need to support unsupported ATen operators.
+# Let's register the ``custom_aten_add`` function to ONNX registry, and export the model to ONNX again.
+onnx_registry = torch.onnx.OnnxRegistry()
+onnx_registry.register_op(
+ namespace="aten", op_name="add", overload="Tensor", function=custom_aten_add
+ )
+print(f"aten::add.Tensor is supported by ONNX registry: \
+ {onnx_registry.is_registered_op(namespace='aten', op_name='add', overload='Tensor')}"
+ )
+export_options = torch.onnx.ExportOptions(onnx_registry=onnx_registry)
+onnx_program = torch.onnx.dynamo_export(
+ aten_add_model, input_add_x, input_add_y, export_options=export_options
+ )
+
+######################################################################
+# Now let's inspect the model and verify the model has a ``custom_aten_add`` instead of ``aten::add.Tensor``.
+# The graph has one graph node for ``custom_aten_add``, and inside of it there are four function nodes, one for each
+# operator, and one for constant attribute.
+#
+
+# graph node domain is the custom domain we registered
+assert onnx_program.model_proto.graph.node[0].domain == "custom.aten"
+assert len(onnx_program.model_proto.graph.node) == 1
+# graph node name is the function name
+assert onnx_program.model_proto.graph.node[0].op_type == "custom_aten_add"
+# function node domain is empty because we use standard ONNX operators
+assert onnx_program.model_proto.functions[0].node[3].domain == ""
+# function node name is the standard ONNX operator name
+assert onnx_program.model_proto.functions[0].node[3].op_type == "Add"
+
+
+######################################################################
+# This is how ``custom_aten_add_model`` looks in the ONNX graph using Netron:
+#
+# .. image:: /_static/img/onnx/custom_aten_add_model.png
+# :width: 70%
+# :align: center
+#
+# Inside the ``custom_aten_add`` function, we can see the three ONNX nodes we
+# used in the function (``CastLike``, ``Add``, and ``Mul``), and one ``Constant`` attribute:
+#
+# .. image:: /_static/img/onnx/custom_aten_add_function.png
+# :width: 70%
+# :align: center
+#
+# This was all that we needed to register the new ATen operator into the ONNX Registry.
+# As an additional step, we can use ONNX Runtime to run the model, and compare the results with PyTorch.
+#
+
+
+# Use ONNX Runtime to run the model, and compare the results with PyTorch
+onnx_program.save("./custom_add_model.onnx")
+ort_session = onnxruntime.InferenceSession(
+ "./custom_add_model.onnx", providers=['CPUExecutionProvider']
+ )
+
+def to_numpy(tensor):
+ return tensor.detach().cpu().numpy() if tensor.requires_grad else tensor.cpu().numpy()
+
+onnx_input = onnx_program.adapt_torch_inputs_to_onnx(input_add_x, input_add_y)
+onnxruntime_input = {k.name: to_numpy(v) for k, v in zip(ort_session.get_inputs(), onnx_input)}
+onnxruntime_outputs = ort_session.run(None, onnxruntime_input)
+
+torch_outputs = aten_add_model(input_add_x, input_add_y)
+torch_outputs = onnx_program.adapt_torch_outputs_to_onnx(torch_outputs)
+
+assert len(torch_outputs) == len(onnxruntime_outputs)
+for torch_output, onnxruntime_output in zip(torch_outputs, onnxruntime_outputs):
+ torch.testing.assert_close(torch_output, torch.tensor(onnxruntime_output))
+
+
+######################################################################
+# Custom operators with existing ONNX Runtime support
+# ---------------------------------------------------
+#
+# In this case, the user creates a model with standard PyTorch operators, but the ONNX runtime
+# (e.g. Microsoft's ONNX Runtime) can provide a custom implementation for that kernel, effectively replacing the
+# existing implementation in the ONNX Registry. Another use case is when the user wants to use a custom implementation
+# of an existing ONNX operator to fix a bug or improve performance of a specific operator.
+# To achieve this, we only need to register the new implementation with the existing ATen fully qualified name.
+#
+# In the following example, we use the ``com.microsoft.Gelu`` from ONNX Runtime,
+# which is not the same ``Gelu`` from ONNX spec. Thus, we register the Gelu with
+# the namespace ``com.microsoft`` and operator name ``Gelu``.
+#
+# Before we begin, let's check whether ``aten::gelu.default`` is really supported by the ONNX registry.
+
+onnx_registry = torch.onnx.OnnxRegistry()
+print(f"aten::gelu.default is supported by ONNX registry: \
+ {onnx_registry.is_registered_op(namespace='aten', op_name='gelu', overload='default')}")
+
+
+######################################################################
+# In our example, ``aten::gelu.default`` operator is supported by the ONNX registry,
+# so :meth:`onnx_registry.is_registered_op` returns ``True``.
+
+class CustomGelu(torch.nn.Module):
+ def forward(self, input_x):
+ return torch.ops.aten.gelu(input_x)
+
+# com.microsoft is an official ONNX Runtime namspace
+custom_ort = onnxscript.values.Opset(domain="com.microsoft", version=1)
+
+# NOTE: The function signature must match the signature of the unsupported ATen operator.
+# https://github.com/pytorch/pytorch/blob/main/aten/src/ATen/native/native_functions.yaml
+# NOTE: All attributes must be annotated with type hints.
+@onnxscript.script(custom_ort)
+def custom_aten_gelu(input_x, approximate: str = "none"):
+ # We know com.microsoft::Gelu is supported by ONNX Runtime
+ # It's only not supported by ONNX
+ return custom_ort.Gelu(input_x)
+
+
+onnx_registry = torch.onnx.OnnxRegistry()
+onnx_registry.register_op(
+ namespace="aten", op_name="gelu", overload="default", function=custom_aten_gelu)
+export_options = torch.onnx.ExportOptions(onnx_registry=onnx_registry)
+
+aten_gelu_model = CustomGelu()
+input_gelu_x = torch.randn(3, 3)
+
+onnx_program = torch.onnx.dynamo_export(
+ aten_gelu_model, input_gelu_x, export_options=export_options
+ )
+
+
+######################################################################
+# Let's inspect the model and verify the model uses :func:`custom_aten_gelu` instead of
+# :class:`aten::gelu`. Note the graph has one graph nodes for
+# ``custom_aten_gelu``, and inside ``custom_aten_gelu``, there is a function
+# node for ``Gelu`` with namespace ``com.microsoft``.
+#
+
+# graph node domain is the custom domain we registered
+assert onnx_program.model_proto.graph.node[0].domain == "com.microsoft"
+# graph node name is the function name
+assert onnx_program.model_proto.graph.node[0].op_type == "custom_aten_gelu"
+# function node domain is the custom domain we registered
+assert onnx_program.model_proto.functions[0].node[0].domain == "com.microsoft"
+# function node name is the node name used in the function
+assert onnx_program.model_proto.functions[0].node[0].op_type == "Gelu"
+
+
+######################################################################
+# The following diagram shows ``custom_aten_gelu_model`` ONNX graph using Netron:
+#
+# .. image:: /_static/img/onnx/custom_aten_gelu_model.png
+# :width: 70%
+# :align: center
+#
+# Inside the ``custom_aten_gelu`` function, we can see the ``Gelu`` node from module
+# ``com.microsoft`` used in the function:
+#
+# .. image:: /_static/img/onnx/custom_aten_gelu_function.png
+#
+# That is all we need to do. As an additional step, we can use ONNX Runtime to run the model,
+# and compare the results with PyTorch.
+#
+
+onnx_program.save("./custom_gelu_model.onnx")
+ort_session = onnxruntime.InferenceSession(
+ "./custom_gelu_model.onnx", providers=['CPUExecutionProvider']
+ )
+
+def to_numpy(tensor):
+ return tensor.detach().cpu().numpy() if tensor.requires_grad else tensor.cpu().numpy()
+
+onnx_input = onnx_program.adapt_torch_inputs_to_onnx(input_gelu_x)
+onnxruntime_input = {k.name: to_numpy(v) for k, v in zip(ort_session.get_inputs(), onnx_input)}
+onnxruntime_outputs = ort_session.run(None, onnxruntime_input)
+
+torch_outputs = aten_gelu_model(input_gelu_x)
+torch_outputs = onnx_program.adapt_torch_outputs_to_onnx(torch_outputs)
+
+assert len(torch_outputs) == len(onnxruntime_outputs)
+for torch_output, onnxruntime_output in zip(torch_outputs, onnxruntime_outputs):
+ torch.testing.assert_close(torch_output, torch.tensor(onnxruntime_output))
+
+######################################################################
+# Custom operators without ONNX Runtime support
+# ---------------------------------------------
+#
+# In this case, the operator is not supported by any ONNX runtime, but we
+# would like to use it as custom operator in ONNX graph. Therefore, we need to implement
+# the operator in three places:
+#
+# 1. PyTorch FX graph
+# 2. ONNX Registry
+# 3. ONNX Runtime
+#
+# In the following example, we would like to use a custom operator
+# that takes one tensor input, and returns one output. The operator adds
+# the input to itself, and returns the rounded result.
+#
+#
+# Custom Ops Registration in PyTorch FX Graph (Beta)
+# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+#
+# Firstly, we need to implement the operator in PyTorch FX graph.
+# This can be done by using ``torch._custom_op``.
+#
+
+# NOTE: This is a beta feature in PyTorch, and is subject to change.
+from torch._custom_op import impl as custom_op
+
+@custom_op.custom_op("mylibrary::addandround_op")
+def addandround_op(tensor_x: torch.Tensor) -> torch.Tensor:
+ ...
+
+@addandround_op.impl_abstract()
+def addandround_op_impl_abstract(tensor_x):
+ return torch.empty_like(tensor_x)
+
+@addandround_op.impl("cpu")
+def addandround_op_impl(tensor_x):
+ return torch.round(tensor_x + tensor_x) # add x to itself, and round the result
+
+torch._dynamo.allow_in_graph(addandround_op)
+
+class CustomFoo(torch.nn.Module):
+ def forward(self, tensor_x):
+ return addandround_op(tensor_x)
+
+input_addandround_x = torch.randn(3)
+custom_addandround_model = CustomFoo()
+
+
+######################################################################
+#
+# Custom Ops Registration in ONNX Registry
+# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+#
+# For the step 2 and 3, we need to implement the operator in ONNX registry.
+# In this example, we will implement the operator in ONNX registry
+# with the namespace ``test.customop`` and operator name ``CustomOpOne``,
+# and ``CustomOpTwo``. These two ops are registered and built in
+# `cpu_ops.cc `__.
+#
+
+
+custom_opset = onnxscript.values.Opset(domain="test.customop", version=1)
+
+# NOTE: The function signature must match the signature of the unsupported ATen operator.
+# https://github.com/pytorch/pytorch/blob/main/aten/src/ATen/native/native_functions.yaml
+# NOTE: All attributes must be annotated with type hints.
+@onnxscript.script(custom_opset)
+def custom_addandround(input_x):
+ # The same as opset18.Add(x, x)
+ add_x = custom_opset.CustomOpOne(input_x, input_x)
+ # The same as opset18.Round(x, x)
+ round_x = custom_opset.CustomOpTwo(add_x)
+ # Cast to FLOAT to match the ONNX type
+ return opset18.Cast(round_x, to=1)
+
+
+onnx_registry = torch.onnx.OnnxRegistry()
+onnx_registry.register_op(
+ namespace="mylibrary", op_name="addandround_op", overload="default", function=custom_addandround
+ )
+
+export_options = torch.onnx.ExportOptions(onnx_registry=onnx_registry)
+onnx_program = torch.onnx.dynamo_export(
+ custom_addandround_model, input_addandround_x, export_options=export_options
+ )
+onnx_program.save("./custom_addandround_model.onnx")
+
+
+######################################################################
+# The ``onnx_program`` exposes the exported model as protobuf through ``onnx_program.model_proto``.
+# The graph has one graph nodes for ``custom_addandround``, and inside ``custom_addandround``,
+# there are two function nodes, one for each operator.
+#
+
+assert onnx_program.model_proto.graph.node[0].domain == "test.customop"
+assert onnx_program.model_proto.graph.node[0].op_type == "custom_addandround"
+assert onnx_program.model_proto.functions[0].node[0].domain == "test.customop"
+assert onnx_program.model_proto.functions[0].node[0].op_type == "CustomOpOne"
+assert onnx_program.model_proto.functions[0].node[1].domain == "test.customop"
+assert onnx_program.model_proto.functions[0].node[1].op_type == "CustomOpTwo"
+
+
+######################################################################
+# This is how ``custom_addandround_model`` ONNX graph looks using Netron:
+#
+# .. image:: /_static/img/onnx/custom_addandround_model.png
+# :width: 70%
+# :align: center
+#
+# Inside the ``custom_addandround`` function, we can see the two custom operators we
+# used in the function (``CustomOpOne``, and ``CustomOpTwo``), and they are from module
+# ``test.customop``:
+#
+# .. image:: /_static/img/onnx/custom_addandround_function.png
+#
+# Custom Ops Registration in ONNX Runtime
+# ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
+#
+# To link your custom op library to ONNX Runtime, you need to
+# compile your C++ code into a shared library and link it to ONNX Runtime.
+# Follow the instructions below:
+#
+# 1. Implement your custom op in C++ by following
+# `ONNX Runtime instructions <`https://github.com/microsoft/onnxruntime/blob/gh-pages/docs/reference/operators/add-custom-op.md>`__.
+# 2. Download ONNX Runtime source distribution from
+# `ONNX Runtime releases