You have to write three functions namely - PNum, GPNum and SPNum (JS, Coffee), p_num, g_p_num and s_p_num (Python and Ruby), pNum, gpNum and spNum (Java, C#), p-num, gp-num and sp-num (Clojure) - to check whether a given argument n is a Pentagonal, Generalized Pentagonal, or Square Pentagonal Number, and return true if it is and false otherwise.
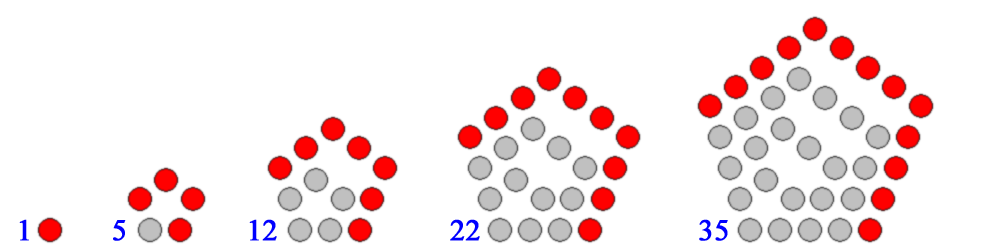
Pentagonal Numbers - The nth pentagonal number Pn is the number of distinct dots in a pattern of dots consisting of the outlines of regular pentagons with sides up to n dots (means the side contains n number of dots), when the pentagons are overlaid so that they share one corner vertex.
First few Pentagonal Numbers are: 1, 5, 12, 22...
Generalized Pentagonal Numbers - All the Pentagonal Numbers along with the number of dots inside the outlines of all the pentagons of a pattern forming a pentagonal number pentagon are called Generalized Pentagonal Numbers.
First few Generalized Pentagonal Numbers are: 0, 1, 2, 5, 7, 12, 15, 22...
Square Pentagonal Numbers - The numbers which are Pentagonal Numbers and are also a perfect square are called Square Pentagonal Numbers.
First few are: 1, 9801, 94109401...
- Pn = Nth Pentagonal Number
- Gpn = Nth Generalized Pentagonal Number
^ ^ ^ ^ ^
P1=1 P2=5 P3=12 P4=22 P5=35 //Total number of distinct dots used in the Pattern
Gp2=1 Gp4=5 Gp6=12 Gp8=22 //All the Pentagonal Numbers are Generalised
Gp1=0 Gp3=2 Gp5=7 Gp7=15 //Total Number of dots inside the outermost Pentagon