Presentación.qmd

---
title: "Onboarding Neurociencias LaSalle Bajío"
author: "Alberto Barradas"
format: 
    revealjs:
        slideNumber: true
        center: true
        controls: true
        progress: true
        history: true
        # transition: 'slide'
        # theme: 'black'
        theme: 'white'
        width: 1920
        height: 1080
        margin: 0.1
        # hash: true
        # separator: '^\n---\n'
        # verticalSeparator: '^\n--\n'
    beamer: 
        aspectratio: 169
        theme: "default"
        colorlinks: true
    pdf:
        number-sections: true
        colorlinks: true
    html:
        code-fold: true
code-fold: true
jupyter: julia-1.10
bibliography: references.bib
---

## Temario

:::: {.columns}

::: {.column width=50%}
- Variables y Procesos Aleatorios
- Muestreo y Distribución Probabilística
- Estadísticas Descriptivas
- Esquema de Tests de Hipótesis
- Modelado y variables latentes
- Modelos Jerarquicos o Mixtos
:::

::: {.column width=50%}
- Probabilidad Condicional
- Teorema de Bayes
- Actualización de creencias con base en evidencias
- Tests bayesianos de hipótesis, Factor de Bayes, y JASP
- Meta-Ciencia, Ética, Bibliometría, SNA, PM, KM, Mindfulness and Cognitive Flexibility
:::

::::

## Variable Aleatoria
:::: {.columns}

::: {.column width=50%}

En Probabilidad y Estadística, una variable aleatoria es **una función que asigna un valor numérico al resultado de un experimento aleatorio**.

La variable no tiene un solo valor numérico, sino que puede tomar varios valores numéricos, cada uno con una cierta probabilidad.

Una forma de describir esa probabilidad es mediante una función de probabilidad, que asigna a cada valor numérico posible de la variable aleatoria una probabilidad.

:::

::: {.column width=50%}

```{julia}
#| echo: true
#| output: slide
#| label: alg-var
#| fig-cap: "Variable Algebraica vs Aleatoria"
# using WGLMakie
using GLMakie
using Distributions, Random, HypothesisTests
N = 100
x = rand(Normal(0, 0.5), N)
y = rand(Normal(0, 1), N)
fig = Figure(size=(800, 600));
ax = Axis(fig[1, 1])
density!(ax, x)
density!(ax, y)
stem!(ax, mean(x), 1, color=:red)
fig
```

:::

::::

---

## **Ejempos**:

::: incremental
- El número de caras que aparecen al lanzar una moneda 3 veces.
- La cantidad de tiempo que un estudiante tarda en completar un examen.
- La cantidad de veces que un estudiante se enferma durante un año.
- La presencia o ausencia de un comportamiento especifico en distintas personas.
:::

---

## __Definiciones__

:::: {.columns}

::: {.column width=50%}
Para distinguir una variable algebraica de una variable aleatoria, se suele utilizar letras mayúsculas para las variables aleatorias y letras minúsculas para las variables algebraicas.

Por ejemplo, si $X$ es una variable aleatoria, $x$ es un valor posible de $X$. Y la probabilidad de que $X$ tome el valor $x$ se denota como $P(X = x)$.

:::

::: {.column width=50%}
**Ejemplo**:
La variable X que representa las probabilidades de los valores de un tiro de dado, puede presentar seis distintos valores: 1, 2, 3, 4, 5, 6. 

La probabilidad de que X tome el valor 1 es P(X = 1) = 1/6.

:::

::::

## Visualización de una variable aleatoria

### Animación
```{julia}
#| echo: true
#| output: slide
#| label: random-var
#| fig-cap: "Variable Aleatoria"
N = 10000
x = Observable(rand(N))
fig = Figure(size=(1800, 600));
ax = Axis(fig[1, 1], subtitle="Variable Aleatoria")
scatter!(ax, x)
ylims!(ax, -1, 2)
ax = Axis(fig[1, 2], subtitle="Distribución")
# density!(ax, x)
hist!(ax, x, bins=100)
xlims!(ax, -1, 2)
button = Button(fig[2, 1:2], label="Generar Nueva Muestra")
l = on(button.clicks) do b
    x[] = rand(N)
end
fig
```

## Muestreo

:::: {.columns}

::: {.column width=50%}
Generalmente no es posible estudiar cada posible probabilidad de cada valor de una variable aleatoria, por lo que se puede tomar una muestra de la población para su estudio.

A las funciones que nos permiten agregar información de una muestra a la población se les llama Estadísticas.
:::

::: {.column width=50%}
```{julia}
#| echo: true
#| output: slide
#| label: static-sample
#| fig-cap: "Muestreo de una población"

U = 1000
N = 10
X = rand(U)
t = sample(1:length(X), N)
x = X[t]
fig = Figure(size=(800, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:teal)
scatter!(ax, t, x, color=:coral, marker=:xcross, markersize=20)
fig
```
:::

::::

## **Ejemplo**:
- La media de una muestra de una población $\bar{x}$ se puede utilizar para estimar la media de la población $\mu$.
- Lo mismo se puede hacer con la varianza, la moda, el rango, la mediana, la correlación, la covarianza, etc.

__Definiciones__:

::: incremental
- **Población**: Conjunto de todos los elementos de interés. (Universo: U)
- **Muestra**: Subconjunto de la población. (N)
:::

## **Ejemplo**:

::: incremental
Tomamos una muestra de 20 personas de una población de 100,000 estudiantes entre 18 y 30 años en México. Se extrae una estadistica de la muestra para estimar la media de la población. Esa estadistica será representativa, en medida de que la muestra sea representativa de la población.

Pregunta: ¿Cómo se puede saber si una muestra es representativa de la población?
Generalmente se utiliza el muestreo aleatorio simple, donde cada elemento de la población tiene la misma probabilidad de ser seleccionado.
:::

## Visualización de muestreo

```{julia}
#| echo: true
#| output: slide
#| label: sample
#| fig-cap: "Muestreo de una población"
# Muestreo de una población
U = 10000
N = 10
X = Observable(rand(U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:teal)
scatter!(ax, t, x, color=:coral, marker=:xcross, markersize=20)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X, color=:teal)
hist!(ax, x, color=:coral,  normalization=:pdf, bins=100)
button = Button(fig[2, :], label="Tomar Nueva Muestra")
l = on(button.clicks) do b
    t[] = sample(1:length(X[]), N)
    x[] = X[][t[]]
end
# sg = SliderGrid(fig[2,1],
#     (label="N", range=1:1:N, startvalue=N),
# )
# sliderobservables = [s.value for s in sg.sliders]
# bars = lift(sliderobservables...) do N
#     t[] = sample(1:length(X[]), N)
#     x[] = X[][t[]]
# end
fig
```

## Distribución de Probabilidad

Hemos utilizado distribuciones uniformes, como las de aventar un dado. Estas variables aleatorias pueden tomar cualquiera de sus valores con la misma probabilidad, pero esto no tiene que ser así. Si un dado está cargado, la probabilidad de que salgan ciertos numeros es mayor que otros.

Una distribución de probabilidad describe cómo se distribuyen los valores de una variable aleatoria y la probabilidad de que la variable aleatoria tome un valor específico.

Recomendamos que memoricen dos distribuciones de probabilidad con sus parámetros:

```{julia}
#| echo: true
#| output: slide
#| label: distributions
#| fig-cap: "Distribuciones de Probabilidad"
U = 8000
N = 30
X = Observable(rand(Normal(0, 1), U))
# X = Observable(rand(Uniform(0, 1), U))
# X = Observable(rand(Exponential(1), U))
# X = Observable(rand(Binomial(10, 0.5), U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:teal)
scatter!(ax, t, x, color=:coral, marker=:xcross, markersize=20)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X, color=:teal)
hist!(ax, x, color=:coral,  normalization=:pdf)
button = Button(fig[2, 1:2], label="Tomar Nueva Muestra")
l = on(button.clicks) do b
    x[] = sample(X[], N)
end
fig
```

## Distribución uniforme

El ejemplo más común cuando se habla de una distribución aleatoria es la distribución uniforme. En una distribución uniforme, todos los valores posibles de la variable aleatoria tienen la misma probabilidad de ocurrir. Por ejemplo, si lanzamos un dado, la probabilidad de que salga un 1, 2, 3, 4, 5 o 6 es la misma.

```{julia}
#| echo: true
#| output: slide
#| label: uniform
#| fig-cap: "Distribución Uniforme"
U = 10000
N = 10
X = Observable(rand(Uniform(0, 1), U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:seagreen)
scatter!(ax, t, x, color=:crimson, marker=:xcross, markersize=20)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X, color=:seagreen)
hist!(ax, x, color=:crimson,  normalization=:pdf)
button = Button(fig[2, 1:2], label="Tomar Nueva Muestra")
l = on(button.clicks) do b
    t[] = sample(1:length(X[]), N)
    x[] = X[][t[]]
end
fig
```

---

Una distribución uniforme puede ser completamente descrita por dos parametros: `a` y `b`, que representan el rango de valores posibles de la variable aleatoria. Cambiando los valores de `a` y `b`, podemos cambiar la forma de la distribución:

```{julia}
#| echo: true
#| output: slide
#| label: uniform-params
#| fig-cap: "Parámetros de la Distribución Uniforme"
U = 10000
N = 10
A = Observable(0.0)
B = Observable(1.0)
X = Observable(rand(Uniform(A[], B[]), U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:seagreen)
scatter!(ax, t, x, color=:crimson, marker=:xcross, markersize=20)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X, color=:seagreen)
hist!(ax, x, color=:crimson,  normalization=:pdf)
sg = SliderGrid(fig[2,:],
    (label="a", range=0:0.01:1, format="{:.2f}", startvalue=0.0),
    (label="b", range=0:0.01:1, format="{:.2f}", startvalue=1.0),
)
sliderobservables = [s.value for s in sg.sliders]
bars = lift(sliderobservables...) do a, b
    X[] = rand(Uniform(a, b), U)
    t[] = sample(1:length(X[]), N)
    x[] = X[][t[]]
end
fig
```

## Distribución normal

No todas las distribuciones aleatorias tienen la misma probabilidad de ocurrencia. La distribución normal es una de las distribuciones más comunes en estadística: es simétrica y tiene una forma de campana. También es una distribución continua, lo que significa que puede tomar cualquier valor en un rango continuo.

```{julia}
#| echo: true
#| output: slide
#| label: normal
#| fig-cap: "Distribucion Normal"
U = 10000
N = 10
X = Observable(rand(Normal(0, 1), U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:mediumaquamarine)
scatter!(ax, t, x, color=:lightcoral, marker=:xcross, markersize=20)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X, color=:mediumaquamarine)
hist!(ax, x, color=:lightcoral,  normalization=:pdf)
button = Button(fig[2, 1:2], label="Tomar Nueva Muestra")
l = on(button.clicks) do b
    x[] = sample(X[], N)
end
fig
```

---

La distribución normal puede ser descrita por dos parametros: `μ` y `σ`, que representan la media y la desviación estándar de la distribución. Cambiando los valores de `μ` y `σ`, podemos cambiar la forma de la distribución:

```{julia}
#| echo: true
#| output: slide
#| label: normal-params
#| fig-cap: "Parámetros de la Distribución Normal"
U = 10000
N = 10
μ = Observable(0.0)
σ = Observable(1.0)
X = Observable(rand(Normal(μ[], σ[]), U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X, color=:mediumaquamarine)
scatter!(ax, t, x, color=:lightcoral, marker=:xcross, markersize=20)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X, color=:mediumaquamarine)
hist!(ax, x, color=:lightcoral,  normalization=:pdf)
sg = SliderGrid(fig[2,1],
    (label="μ", range=-10:0.1:10, format="{:.2f}", startvalue=0.0),
    (label="σ", range=0.1:0.1:5, format="{:.2f}", startvalue=1.0),
)
sliderobservables = [s.value for s in sg.sliders]
bars = lift(sliderobservables...) do μ, σ
    X[] = rand(Normal(μ, σ), U)
    t[] = sample(1:length(X[]), N)
    x[] = X[][t[]]
end
fig
```

## Estadísticas Descriptivas
Las estadísticas descriptivas son métodos para resumir, organizar y visualizar datos. Estas estadísticas se pueden utilizar para describir las características de los datos y para resumir la información contenida en un conjunto de datos.

```{julia}
#| echo: true
#| output: slide
#| label: descriptive
#| fig-cap: "Estadísticas Descriptivas"
U = 100000
N = 100
# X = Observable(rand(Normal(0, 1), U))
# X = Observable(rand(Exponential(5), U))
# X = Observable(rand(Uniform(0, 1), U))
X = Observable(rand(Binomial(5, 0.1), U))
t = Observable(sample(1:length(X[]), N))
x = Observable(X[][t[]])
means = Observable([])
experiments = Observable(0)
fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
scatter!(ax, X)
scatter!(ax, t, x, color=:red)
ax = Axis(fig[1, 2], subtitle="Distribución")
density!(ax, X)
hist!(ax, x, color=:red,  normalization=:pdf)
ax1 = Axis(fig[1, 3], subtitle="Media de Muestras")
push!(means[], mean(x[]))
scatter!(ax1, means[], color=:red)
ax2 = Axis(fig[1, 4], subtitle="Distribución de la media de Muestras")
density!(ax2, means[], color=:red)
# hist!(ax2, means[], color=:red,  normalization=:pdf)
button = Button(fig[2, 1:4], label="Tomar Nueva Muestra")
l = on(button.clicks) do b
    x[] = sample(X[], N)
    push!(means[], mean(x[]))
    scatter!(ax1, means[], color=:red)
    empty!(ax2)
    density!(ax2, means[], color=:red)
    experiments[] += 1
end
fig
```

## Pruebas de Hipótesis
Una prueba de hipótesis es un procedimiento estadístico que se utiliza para tomar una decisión sobre una afirmación acerca de un parámetro de una población. La afirmación que se está probando se llama hipótesis nula (H0) y la afirmación alternativa se llama hipótesis alternativa (H1). La prueba de hipótesis se basa en la probabilidad de obtener un resultado tan extremo como el observado, si la hipótesis nula es verdadera. Si la probabilidad es baja, se rechaza la hipótesis nula.

```{julia}
#| echo: true
#| output: slide
#| label: hypothesis
#| fig-cap: "Pruebas de Hipótesis"
U = 100000
N = 1000
μ1 = Observable(0.0)
σ1 = Observable(1.0)

μ2 = Observable(0.0)
σ2 = Observable(1.0)

μ3 = sum([μ1[], μ2[]])
σ3 = sqrt(σ1[]^2 + σ2[]^2)

x = range(-10, 10, length=U)
y1 = Observable(pdf(Normal(μ1[], σ1[]), x))
y2 = Observable(pdf(Normal(μ2[], σ2[]), x))
# y3 = Observable(pdf(Normal(μ3[], σ3[]), x))
α = Observable([quantile(Normal(μ1[], σ1[]), 0.95)])
β = Observable([quantile(Normal(μ2[], σ2[]), 0.20)])
p = Observable(pvalue(SignedRankTest(y1[], y2[])))

fig = Figure(size=(1600, 600));
ax = Axis(fig[1, 1])
l1 = lines!(ax, x, y1, color=:teal, linewidth=10)
l2 = lines!(ax, x, y2, color=:coral, linewidth=10)
# l3 = lines!(ax, x, y3, color=:orchid, linewidth=10)
lα = vlines!(ax, α, color=:black, linestyle=:dash, linewidth=1)
lβ = vlines!(ax, β, color=:red, linestyle=:dash, linewidth=1)
Legend(fig[1, 2], [l1, l2, lα, lβ], ["H0", "H1", "p=0.05", "Power=.80"])
lab = Label(fig[2, 2], "p=$(round(p[], digits=4))")
fig

# SliderGrid
sg = SliderGrid(fig[2,1],
    (label="μ1", range=-5:0.1:5, format="{:.2f}", startvalue=0.0),
    (label="σ1", range=0.1:0.1:5, format="{:.2f}", startvalue=1.0),
    (label="μ2", range=-5:0.1:5, format="{:.2f}", startvalue=0.0),
    (label="σ2", range=0.1:0.1:5, format="{:.2f}", startvalue=1.0),
    (label="N", range=10:10:U, format="{:.0f}", startvalue=N),
)
sliderobservables = [s.value for s in sg.sliders]
bars = lift(sliderobservables...) do μ1, σ1, μ2, σ2, N
    # μ3 = μ1 + μ2
    # σ3 = sqrt(σ1^2 + σ2^2)
    y1[] = pdf(Normal(μ1, σ1), x)
    y2[] = pdf(Normal(μ2, σ2), x)
    # y3[] = pdf(Normal(μ3, σ3), x)
    α[] = [quantile(Normal(μ1, σ1), 0.95)]
    β[] = [quantile(Normal(μ2, σ2), 0.20)]
    p[] = pvalue(SignedRankTest(sample(y1[], N), sample(y2[], N)))
    lab.text[] = "p=$(round(p[], digits=4))"
end

fig
```

---

## Problemas de reproducibilidad en ciencias cognitivas

- The Open Science Collaboration (2015) https://osf.io/82fth: 36% de los estudios replicados tuvieron resultados significativos, comparado con 97% de los estudios originales. @open2015

The Many Labs Project (2014) https://osf.io/wx7ck/:  10 de 13 estudios replicados tuvieron resultados significativos, comparado con 13 de 13 estudios originales. @klein2013

## Prácticas questionables en investigación

John, L. K., Loewenstein, G., & Prelec, D. (2012). Measuring the prevalence of questionable research practices with incentives for truth telling. Psychological science, 23(5), 524-532. [https://www.cmu.edu/dietrich/sds/docs/loewenstein/MeasPrevalQuestTruthTelling.pdf] @john2012


1. In a paper, failing to report all of a study’s dependent measures.
2. Deciding whether to collect more data after looking to see whether the results were significant.
3. In a paper, failing to report all of a study’s conditions.
4. Stopping collecting data earlier than planned because one found the result that one had been looking for.
5. In a paper, “rounding off” a p value (e.g., reporting that a p value of .054 is less than .05).
6. In a paper, selectively reporting studies that “worked”.
7. Deciding whether to exclude data after looking at the impact of doing so on the results.
8. In a paper, reporting an unexpected finding as having been predicted from the start.
9. In a paper, claiming that results are unaffected by demographic variables (e.g., gender) when one is actually unsure (or knows that they do).
10. Falsifying data.


## Modelado y Variables latentes

Cuando los verdaderos parametros de una población no son observables, se pueden utilizar variables latentes para describir el comportamiento verdadero de la población. Estas son variables que no se pueden observar directamente, pero que se pueden inferir a partir de evidencias. Esta forma de pensar nos permite conceptualizar cada experimento: no como eventos independientes, sino como un muestreo de una variable latente.  Así, cada nuevo experimento produce evidencia en contra o a favor de nuestras creencias sobre los parametros que describen la distribución de la población. A esto le llamamos modelado estadistico.

:::: {.columns}

::: {.column width=50%}
```{mermaid}
%%| fig-width: 6.5
graph TD
    A(Variable Latente) --> B[Observación 1]
    A --> C[Observación 2]
```
:::

::: {.column width=50%}
```{mermaid}
%%| fig-width: 30
graph TD
    A(Alimentación) --> B[Estatura]
    A --> C[Peso]
    B --> D[IMC]
    C --> D
```
:::

::::

Este tipo de modelado requiere el manejo explicito de creencias sobre las distribuciones de parametros en la poblacion a estudiar. También nos permite modelar otras posibles variables ocultas (o de confusión) que puedan influin en los resultados de nuestros experimentos.

---

## **Ejercicio**
Hagamos un ejercicio para desarrollar intuicicón. Infiere la distribución de la que provienen las siguientes muestras:

```{julia}
#| echo: true
#| output: slide
#| label: latent
#| fig-cap: "Modelado y Variables Latentes"
U = 100000
N = 50
distributions = [Normal(0, 1), 
                Exponential(1), 
                Uniform(0, 1), 
                Binomial(10, 0.5),
                Poisson(5),
                Gamma(2, 1),
                Beta(2, 7),
                Cauchy(),
                LogNormal(0, 1),
                Weibull(1, 1),
                Pareto(1, 1),
                ]
dist = sample(distributions, 1)[1]
X = Observable(rand(dist, U))
x = Observable(sample(X[], N))
means = Observable([])
experiments = Observable(0)
fig = Figure(size=(1200, 600));
ax = Axis(fig[1, 1], subtitle="Muestra de Población")
# scatter!(ax, X)
scatter!(ax, x, color=:teal)
ax = Axis(fig[1, 2], subtitle="Distribución")
# density!(ax, X)
hist!(ax, x, color=:teal,  normalization=:pdf)
ax1 = Axis(fig[1, 3], subtitle="Media de Muestras")
push!(means[], mean(x[]))
scatter!(ax1, means[], color=:coral)
ax2 = Axis(fig[1, 4], subtitle="Distribución de la media de Muestras")
density!(ax2, means[], color=:coral)
# hist!(ax2, means[], color=:coral,  normalization=:pdf)
button = Button(fig[2, 1:4], label="Tomar Nueva Muestra")
l = on(button.clicks) do b
    x[] = sample(X[], N)
    push!(means[], mean(x[]))
    scatter!(ax1, means[], color=:coral)
    empty!(ax2)
    density!(ax2, means[], color=:coral)
    experiments[] += 1
end
fig
```

::: {.callout-tip collapse="true"}
## Solución
```{julia}
println(dist)
```
:::

## Modelos Jerarquicos
Así como podemos inferir la distribución de una variable aleatoria a partir de una muestra, también podemos inferir la distribución de los parametros de una distribución a partir de una muestra. A esto se le llama inferencia jerarquica. Aqui los parametros de una distribución son variables aleatorias que siguen una distribución. Este tipo de modelado nos permite inferir la distribución de los parametros de una distribución a partir de una muestra, y nos permite modelar la incertidumbre en nuestras creencias sobre los parametros de una distribución.

```{mermaid}
%%| fig-width: 6.5
graph TD
    A(Variable Latente) --> B[Parametro_1]
    A --> C[Parametro_2]
    B --> D[Observación_1]
    C --> E[Observación_2]
    C --> D
```
A su vez, estos parametros pueden representar variabilidad entre grupos de muestras. Por ejemplo, si tomamos muestras de dos poblaciones distintas, podemos inferir la distribución de los parametros de cada población, y la variabilidad entre las poblaciones. A esto se le conoce también como modelos mixtos. Estos son el estandard de oro en la inferencia estadistica. Prof. Nan Laird obtuvo el premio internacional de stadisticas por su descripción de estos modelos [@laird2004].

## Probabilidad Condicional

Como hemos visto, no todos los eventos son independientes. La probabilidad de que ocurra un evento puede depender de que ocurra otro evento. A esto se le llama probabilidad condicional. La probabilidad de que ocurra un evento A dado que ocurra un evento B se denota como $P(A|B)$. La probabilidad condicional se puede calcular como el cociente de la probabilidad conjunta de $A$ y $B$ entre la probabilidad de $B$. $P(A|B) = P(A ∩ B) / P(B)$.

__Definiciones__:

- **Independencia**: Dos eventos son independientes si la probabilidad de que ocurra uno no depende de que ocurra el otro. $P(A|B) = P(A)$.
- **Dependencia**: Dos eventos son dependientes si la probabilidad de que ocurra uno depende de que ocurra el otro. $P(A|B) ≠ P(A)$.
- **Probabilidad Conjunta**: La probabilidad de que ocurran dos eventos simultáneamente. $P(A ∩ B)$.
- **Probabilidad Marginal**: La probabilidad de que ocurra un evento sin importar si ocurre otro evento. $P(A)$.

## **Ejemplo**:

La probabilidad de que un estudiante apruebe un examen de matemáticas es de 0.7. La probabilidad de que un estudiante apruebe un examen de matemáticas y física es de 0.5. La probabilidad de que un estudiante apruebe un examen de física es de 0.6. ¿Cuál es la probabilidad de que un estudiante apruebe un examen de matemáticas dado que aprobó un examen de física?

::: {.callout-tip collapse="true"}
## __Solución__
- P(A) = 0.7
- P(A ∩ B) = 0.5
- P(B) = 0.6
- P(A|B) = P(A ∩ B) / P(B) = 0.5 / 0.6 = 0.8333
:::

## Teorema de Bayes
El teorema de Bayes es una regla para actualizar creencias con base en evidencias. Nos permite calcular la probabilidad de una hipótesis dada una evidencia. La probabilidad de una hipótesis $H$ dado un conjunto de evidencias $E$ se puede calcular como el producto de la probabilidad de la evidencia dado la hipótesis $P(E|H)$ por la probabilidad de la hipótesis $P(H)$ dividido por la probabilidad de la evidencia $P(E). P(H|E) = P(E|H) * P(H) / P(E)$.

![VisualBayes](https://upload.wikimedia.org/wikipedia/commons/c/c9/Bayes_theorem_visual_proof.svg)

$$
P(H|E) = \frac{P(E|H) * P(H)}{P(E)} = \frac{P(E|H) * P(H)}{P(E|H) * P(H) + P(E|¬H) * P(¬H)}
$$

## **Ejemplo 1**
Sabemos que la probabilidad de que un estudiante de cierta escuela tenga TDA es del 0.1. También sabemos que la proporcion de hombres y mujeres es del 50%. También sabemos que entre los estudiantes diagnosticados con TDA, el 60% son hombres. ¿Cuál es la probabilidad de que un estudiante tenga TDA dado que es hombre?

## __Solución__
$P(A) = 0.1$ es la probabilidad de que un estudiante tenga TDA.
$P(B) = 0.5$ es la probabilidad de que un estudiante sea hombre.
$P(B|A) = 0.6$ es la probabilidad de hombres entre los estudiantes con TDA.

Para encontrar $P(A∣B)$, primero necesitamos calcular $P(B∣A)$ y $P(B)$ como se ha dado, y luego encontrar $P(A∩B)$ usando la fórmula de probabilidad condicional. Esta es la probabilidad de que un estudiante en esa escuela tenga TDA Y sea Hombre.
$$
P(A ∩ B) = P(B|A) * P(A) = 0.6 * 0.1 = 0.06
$$

Por lo tanto, la probabilidad de que un estudiante tenga TDA dado que es hombre es:

::: {.callout-tip collapse="true"}
$$
P(A|B) = P(A ∩ B) / P(B) = 0.06 / 0.5 = 0.12
$$
:::


## **Ejemplo 2**
Hicimos un experimento, en el que el 30% de nuestros participantes reportaron reportaron dormir mal. Sabemos que el 50% de las personas que reportaron dormir mal, también reportaron tener ansiedad. También sabemos que el 20% de las personas que no reportaron dormir mal, reportaron tener ansiedad. ¿Cuál es la probabilidad de que una persona tenga ansiedad dado que reportó dormir mal?

::: {.callout-tip collapse="true"}
__Solución__:

- $P(D) = 0.3$
- $P(¬D) = 0.7$
- $P(A|D) = 0.5$
- $P(A|¬D) = 0.2$
- $P(A ∩ D) = P(A|D) * P(D) = 0.5 * 0.3 = 0.15$
- $P(A ∩ ¬D) = P(A|¬D) * P(¬D) = 0.2 * 0.7 = 0.14$
- $P(A) = P(A ∩ D) + P(A ∩ ¬D) = 0.15 + 0.14 = 0.29$
- $P(D|A) = P(A|D) * P(D) / P(A) = 0.5 * 0.3 / 0.29 = 0.5172$
:::

## **Ejemplo 3**
Un laboratorio produce pruebas de detección de un trastorno. La prueba tiene una sensibilidad del 99% y una especificidad del 95%. La enfermedad afecta al 1% de la población. ¿Cuál es la probabilidad de que una persona tenga la enfermedad dado que la prueba dio positivo?

__Solución__:
La sensibilidad se refiere a la probabilidad de que la prueba sea positiva dado que la persona tiene la enfermedad. La especificidad se refiere a la probabilidad de que la prueba sea negativa dado que la persona no tiene la enfermedad.
Ambas se pueden obtener de una matriz de confusión, y describen completamente el desempeño de una prueba de detección.

|          | Enfermo | Sano |
| -------- | ------- | ---- |
| Positivo | TP      | FP   |
| Negativo | FN      | TN   |

---

En este caso:

|  %  | Enfermo | Sano |
| --- | ------- | ---- |
| +   | 0.99    | 0.05 |
| -   | 0.01    | 0.95 |

::: {.callout-tip collapse="true"}

- $P(D) = 0.01$
- $P(¬D) = 0.99$
- $P(+) = P(+|D) * P(D) + P(+|¬D) * P(¬D) = 0.99 * 0.01 + 0.05 * 0.99 = 0.0585$
- $P(D|+) = P(+|D) * P(D) / P(+) = 0.99 * 0.01 / 0.0585 = 0.1684$

:::

## Más material

Para desarrollar una intuición sobre el teorema de Bayes, sugiero los videos de Grant Sanderson en 3Blue1Brown:

- [Bayes Theorem](https://youtu.be/HZGCoVF3YvM)
- [Bayes Theorem Proof](https://youtu.be/U_85TaXbeIo)
- [Bayes Theorem Examples](https://youtu.be/lG4VkPoG3ko)

## Actualización de creencias con base en evidencias

Como pueden ver, el teorema de Bayes nos permite actualizar nuestras creencias con base en evidencias. A diferencia de un test de hipotesis, donde nuestra N debe ser muy bien definida, con el teorema de Bayes podemos actualizar nuestras creencias con base en cada nueva evidencia que obtenemos. A medida que obtenemos más evidencias, nuestras creencias y certidumbre sobre ellas se refinan. Esto es lo que se conoce como inferencia bayesiana. En la inferencia bayesiana, las creencias se representan como distribuciones de probabilidad.

[BeliefUpdate](https://en.wikipedia.org/wiki/Belief_revision#Contraction,_expansion,_revision,_consolidation,_and_merging)

## Tests bayesianos de hipótesis

El marco de test de hipótesis no excluye el análisis bayesiano. De hecho, el test de hipótesis es un caso especial de inferencia bayesiana. En el test de hipótesis, se calcula la probabilidad de obtener un resultado tan extremo como el observado, si la hipótesis nula es verdadera. En la inferencia bayesiana, se calcula la probabilidad de que la hipótesis nula sea verdadera dado el resultado observado. A esto se le conoce como factor de Bayes. Si el factor de Bayes es mayor a 1, la hipótesis nula es más probable. Si el factor de Bayes es menor a 1, la hipótesis nula es menos probable.

![BayesFactor](https://www.researchgate.net/profile/Johnny-Van-Doorn/publication/330569075/figure/fig3/AS:723795040034816@1549577593137/A-graphical-representation-of-a-Bayes-factor-classification-table-As-the-Bayes-factor.png) [@van2021jasp]

## Herramientas

![JASP](https://jasp-stats.org/wp-content/uploads/2024/07/front.page_.0.19.0.0-site.png)

La herramienta que utilizamos para hacer estos tests es JASP. JASP es un software de código abierto, desarrollado por la Universidad de Amsterdam, que permite hacer análisis bayesianos de forma sencilla. Pueden descargarlo de [aquí](https://jasp-stats.org/).

## Meta-Ciencia

El método cientifico se puede aplicar a la ciencia misma. Lo que llamamos meta-ciencia es el proceso de analizar los métodos y prácticas del laboratorio a travez de **análisis estructurado y crítico**. Aunado a la inferencia bayesiana, existen otras herramientas que nos permitirán mantener un manejo **explicito** de nuestros conocimientos cientificos.

Lectura sugerida: @hofstadter1999.

**Pregunta:** ¿Cuál es el rol del cientifico en la sociedad?

## Manejo y gestion del Conocimiento

El manejo del conocimiento es el proceso de adquirir, almacenar, compartir y utilizar el conocimiento. El conocimiento es un **activo intangible** que puede ser difícil de cuantificar y medir.

__Definiciones__:

 - Conocimiento Tácito (Implicito): Conocimiento que no se puede expresar en palabras, pero se puede demostrar a través de acciones.
 - Conocimiento Explicito: Conocimiento que se puede expresar en palabras y se puede compartir con otros.
 - Institución: Conjunto de creencias que se expresan en el comportamiento de un grupo de personas.
 - Conocimiento institucionalizado: Conocimiento que se ha convertido en parte de la estructura de una organización.
 - Conocimiento tácito institucional: Conocimiento institucional que no se puede expresar en palabras.

**Pregunta:** ¿De que formas explicitas se maneja el conocimiento cientifico? ¿Qué formas implicitas de conocimiento cientifico conocen?

## Pirámide del conocimiento

La pirámide del conocimiento es una representación visual de la jerarquía del conocimiento. 

![DIKW](DIKW.jpg)

Img: @flood2016

## Sesgos Cognitivos

El pensamiento humano falla comunmente de formas predecibles y sistemáticas. A estos fallos sistemáticos del pensamiento se les conoce como sesgos cognitivos. Los sesgos cognitivos pueden afectar la toma de decisiones y la interpretación de la información. Algunos de los sesgos cognitivos más comunes son:

- Sesgo de **confirmación**: Tendencia a buscar, interpretar y recordar información que confirma nuestras creencias preexistentes.
- Sesgo de **anclaje**: Tendencia a depender demasiado de la primera información que se recibe.
- Sesgo de **disponibilidad**: Tendencia a sobreestimar la importancia de la información que se recuerda con mayor facilidad.
- Sesgo de **representatividad**: Tendencia a juzgar la probabilidad de un evento en función de lo bien que se ajusta a un prototipo.
- Sesgo de **atribución**: Tendencia a atribuir los éxitos a factores internos y los fracasos a factores externos.
- Sesgo de **sobrevivencia**: Tendencia a centrarse en los éxitos y a ignorar los fracasos.

[![Codex de Sesgos Cognitivos](https://upload.wikimedia.org/wikipedia/commons/6/65/Cognitive_bias_codex_en.svg)](https://upload.wikimedia.org/wikipedia/commons/6/65/Cognitive_bias_codex_en.svg)

## Técnica de Lectura de Artículos Científicos

- Proposito: ¿Para qué estoy leyendo este artículo? ¿Qué información necesito obtener de él?
- Busqueda: ¿Cómo puedo evitar el sesgo de confirmación?
- Título: ¿Existe una relación con lo que busco? ¿Es relevante?
- Autores: ¿Quiénes son los autores? ¿Son expertos en el tema?
- Resumen: ¿Qué se investigó? ¿Cuál es el objetivo del estudio? ¿Cuál es el resultado que presumen?
- Resultados: ¿El resultado del resumen está respaldado por los datos presentados?
- Si los resultados parecen congruentes con el objetivo, entonces pasamos a:
- Métodos: ¿Cómo se realizó el estudio? ¿Qué técnicas se utilizaron? ¿Qué datos se recopilaron?
- Discusión: ¿Los resultados son consistentes con la literatura previa? ¿Tiene sentido el estudio? ¿Qué implicaciones tiene el estudio?
- Mis conclusiones: ¿Qué aprendí de este artículo? ¿Respaldó mi hipótesis? ¿Qué preguntas me quedan?

## Bibliometría

La bibliometría es el estudio **cuantitativo** de la producción, difusión, interconectividad, y uso de la información científica. La bibliometría se puede utilizar para evaluar la calidad de la investigación, identificar tendencias en la investigación y evaluar la eficacia de las políticas de investigación. Generalmente depende de las publicaciones en revistas científicas.

__Definiciones__:

::: {.columns}
::: {.column width=50%}

 - [Factor de Impacto](https://en.wikipedia.org/wiki/Impact_factor): Medida de la frecuencia con la que los artículos de una revista científica son citados en un año determinado.
$$
  IF = \frac{\text{Citas}}{\text{Publicaciones}_{2 años}}
$$

:::
::: {.column width=50%}

 - [Índice H](https://en.wikipedia.org/wiki/H-index): Medida de la productividad y el impacto de un científico basada en el número de citas que recibe un científico. Un autor con un dado indice H ha publicado H artículos que han sido citados al menos H veces.
:::
:::
## Redes Sociales

Una de las formas de medir la interconectividad de la información científica es a través de las estructuras sociales e individuos que la producen. El análisis de redes sociales es una técnica que se utiliza para analizar la estructura de las relaciones entre individuos y organizaciones. Se puede utilizar para identificar patrones de colaboración, identificar líderes de opinión y evaluar la eficacia de las políticas de investigación.

![ResearchRabbit](https://images.squarespace-cdn.com/content/v1/5dee82c56fcd7b0290640db5/1628479532521-VKCC2DKYPJ7W20MN3W0C/Picture3.png)

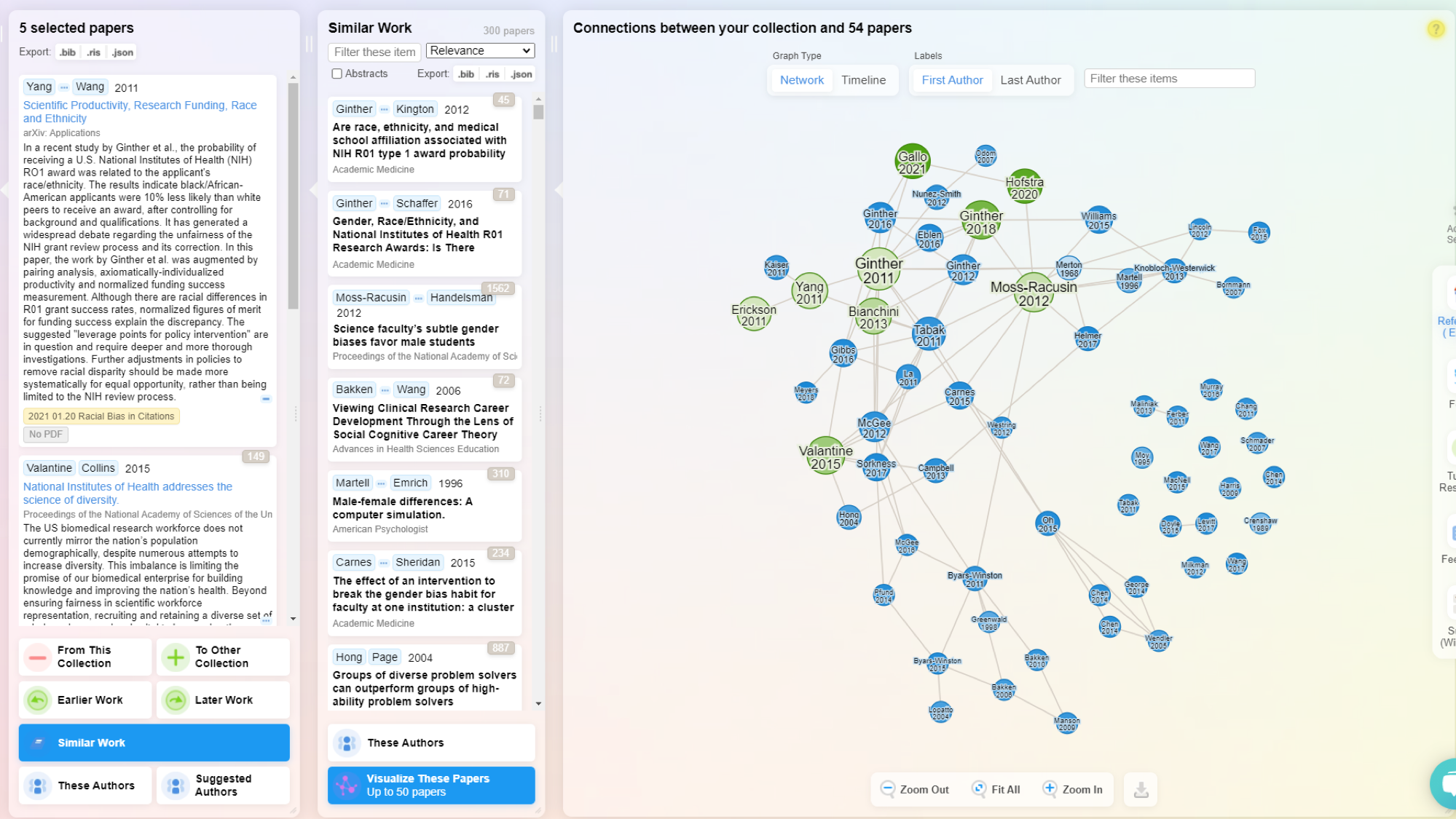
## Manejo de Proyectos

El manejo de proyectos es el proceso de planificar, organizar, dirigir y controlar los recursos para lograr un objetivo específico. El manejo de proyectos es esencial para la investigación científica, ya que permite a los investigadores planificar y ejecutar sus proyectos de manera eficiente.

En la ciencia, comunmente debemos identificar el entorno y los recursos necesarios para llevar a cabo un proyecto. Para esto les presentamos una herramienta conceptual que servir como referencia:

![cynefin](./cynefin.png)

img: @snowden2007

## Herramientas

### Buscadores

- [**Google Scholar**](https://scholar.google.com/): Motor de búsqueda de literatura académica. (Google scholar button)
- [**PubMed**](https://pubmed.ncbi.nlm.nih.gov/): Base de datos de literatura médica: National Library of Medicine USA.
- [**Semantic Scholar**](https://www.semanticscholar.org/): Motor de búsqueda de literatura científica y académica.
- [Web of Science](https://www.webofscience.com/): Base de datos de literatura científica para la que se requiere una suscripción.
- [Scopus](https://www.scopus.com/): Base de datos de literatura científica de Elsevier.
- [Crossref](https://www.crossref.org/): Base de datos de referencias y citas (Libreria de metadatos).
- [Clarivate](https://jcr.clarivate.com/jcr/home): Base de datos de literatura científica para la que se requiere una suscripción.
- [Paperpanda](https://paperpanda.com/): Motor de búsqueda de literatura científica.
- [ConnectedPapers](https://www.connectedpapers.com/): Herramienta de visualización de referencias y citas.
- [IOP Publishing](https://iopscience.iop.org/): Base de datos de literatura científica.
- Otros: Tenemos accesso a algunos otros buscadores cientificos.

---

### Datos y pre-processamiento 

::: {.columns}

::: {.column width=50%}
- [OpenNeuro](https://openneuro.org/): Base de datos de datos de neuroimagen.
- [Wikidata](https://www.wikidata.org/): Base de datos de conocimiento libre y abierta.
- [Academic Torrents](https://academictorrents.com/browse.php): Tecnología de datos distribuidos para la comunidad científica.
- [Kaggle](https://www.kaggle.com/): Base de datos de todo tipo, para competencias de ciencia de datos.
- [Zenodo](https://zenodo.org/): Repositorio de datos y software científicos.
- [Open Science Framework](https://osf.io/): Repositorio de proyectos científicos.
:::

::: {.column width=50%}
- [**MNE y tutoriales**](https://mne.tools/stable/auto_tutorials/index.html): Herramienta open source para procesamiento de señales EEG y MEG. Incluye muy completos tutoriales.
- [**LabStreamingLayer (LSL)**](https://labstreaminglayer.readthedocs.io/index.html): Herramienta para connectividad de dispositivos usando TCP/IP.

Toolboxes de Matlab:

- [Brainstorm](https://neuroimage.usc.edu/brainstorm/): Procesamiento de señales EEG y MEG.
- [FieldTrip](https://www.fieldtriptoolbox.org/): Procesamiento de señales EEG y MEG.
- [EEGLAB](https://sccn.ucsd.edu/eeglab/index.php): Procesamiento de señales EEG.
- [SPM](https://www.fil.ion.ucl.ac.uk/spm/): Procesamiento de señales de neuroimagen.

:::

:::

---

## Manejo de citas

::: {.columns}

::: {.column width=50%}
- [Zotero](https://www.zotero.org/): La herramienta que yo uso.
- [Mendeley](https://www.mendeley.com/): La herramienta que la Dra. Sanchez Gamma usa.
- [EndNote](https://endnote.com/): La herramienta de microsoft: tal vez ustedes tengan acceso o experiencia con ella.
- [Paperpile](https://paperpile.com/): Herramienta alternativa de gestión de referencias y citas.
:::

::: {.column width=50%}
- [LaTex](https://www.latex-project.org/): Herramienta de escritura de documentos científicos.
- [Overleaf](https://www.overleaf.com/): Herramienta de escritura colaborativa de documentos científicos.
- [GoogleScholarButton](https://addons.mozilla.org/en-US/firefox/addon/google-scholar-button/): Complemento de exploradores para buscar literatura científica.
- [ScienceResearchAssistant](https://chromewebstore.google.com/detail/science-research-assistan/ceacgaccjcomdbnoodjpllihjmeflfmg?hl=en&pli=1): Complemento de Chrome para buscar literatura científica.
- [OpenAccessButton](https://openaccessbutton.org/): Herramienta para encontrar artículos de acceso abierto.
:::

:::


## Análisis

::: {.columns}

::: {.column width=50%}
- [**JASP**](https://jasp-stats.org/): Herramienta de análisis estadístico frequentista y bayesiano.
- [JAMOVI](https://www.jamovi.org/): Herramienta de análisis estadístico basada en R.
- [R](https://www.r-project.org/): Lenguaje de programación estadística.
- [R Studio](https://rstudio.com/): Entorno de desarrollo integrado para R.
- [Julia](https://julialang.org/): Lenguaje de programación de alto rendimiento para la ciencia.
- [Python](https://www.python.org/): Lenguaje de programación de propósito general.
- [SPSS](https://www.ibm.com/analytics/spss-statistics-software): Herramienta de análisis estadístico: Aquí no promovemos la pratería, así que no la usaremos con ustedes. Existen suficientes herramientas adecuadas como para obligarlos a usar esta.
:::

::: {.column width=50%}
- [ResearchRabbit](https://www.researchrabbit.ai/): Herramienta de exploración de redes de referencias.
- [Elicit](https://elicit.org/): Herramienta AI de análisis de literatura científica.
- [Consensus](https://consensus.app/): Herramienta AI útil para preguntas "Si o no".
- [Python Scholarly](https://pypi.org/project/scholarly/): Herramienta de búsqueda de literatura científica en Python, usando google scholar.
- [PyBibliometrics](https://pypi.org/project/pybibliometrics/): Herramienta de análisis de literatura científica en Python, principalmente scopus.
- [Python SemanticScholar](https://pypi.org/project/semanticscholar/): Herramienta de búsqueda de literatura científica y autores en Python.
- [Padron del SNII](https://conahcyt.mx/sistema-nacional-de-investigadores/padron-de-beneficiarios/): Lista de investigadoras/es en México.
:::

:::

## Gestión de Proyectos

- [ClickUp](https://clickup.com/): Herramienta de gestión de proyectos. Mi única herramienta que aún no es abierta. Estamos buscando alternativas.
- [Asana](https://asana.com/): TODO list con colaboración.
- [Trello](https://trello.com/): Común entre desarrolladores de software, diseñadores y equipos de marketing, usa metodo Kanban (Basado en pizarroncitos).
- [Notion](https://www.notion.so/): Herramienta de gestión de proyectos muy poderosa, para quien no sabe programar.
- [Obsidian](https://obsidian.md/): Originalmente para tomar notas, pero programada en javascript, así que tiene extenciones para todo.
- [Logseq](https://logseq.com/): Llegó despues de Obsidian, pero es gratis y open source.
- [Vikunja](https://vikunja.io/): Herramienta de colaboración sencilla que se puede mantener en tu propio servidor.

### Comunicación

La universidad de LaSalle tiene una licencia de Microsoft Teams. Hemos estado usando WhatsApp.
Teams está hecho para solucionar nuestro tipo de problemas.

## Habilidades Cognitivas

La **flexibilidad cognitiva** es la capacidad de cambiar de pensamiento o de acción en respuesta a un cambio en el entorno. Es esencial para la resolución de problemas, la toma de decisiones y la adaptación al cambio. Se puede entrenar a través de la práctica y la exposición a nuevas ideas y experiencias.

La atención plena, o **mindfulness**, es la capacidad de prestar atención propositivamente a las experiencias del momento presente sin asignar juicios de valor. Es una herramienta de meta-cognición que procuramos desarrollar en nuestro laboratorio.

Si les interesa este tema, con gusto podemos discutir sobre las habilidades cognitivas (o **herramientas de pensar**) que utilizamos en el laboratorio, pero consideramos estas dos ser las más generales y relevantes. Lectura sugerida: @dennett2014.

## Ejercicio Ético

El ejercicio ético de la ciencia requiere de análisis crítico y reflexión sobre las implicaciones de nuestras acciones. Es un **proceso continuo** y **activo** de **auto-evaluación** como **individuos** y como **institución**, aunado al **dialogo** y la ejecución de acciones que promuevan los valores éticos en la ciencia.

Con esta slide buscamos establecer el continuo dialogo sobre la ética en la ciencia en un ambiente de **confianza y respeto**.

## Referencias
::: {#refs}
:::