diff --git a/README.md b/README.md
index 0f38fa3..bff97b8 100644
--- a/README.md
+++ b/README.md
@@ -1,14 +1,20 @@
# Photon Reflection #
-Photon starts moving to the right from point `(0.50, 0.26)` in a grid lattice with a circular mirror in each point (`R=1/3`) - see [Visualization](https://github.com/LMesaric/PhotonReflection#visualization).
-The speed of a photon is `1 point per second`. Where will the photon be located after `20 seconds`?
+Photon starts moving to the right from point `(0.50, 0.26)` in a grid lattice with a circular mirror
+in each point (`R = 1/3`) - see [Visualization](https://github.com/LMesaric/PhotonReflection#visualization).
+The speed of the photon is `1 point per second`. Where will the photon be located after `t = 20 seconds`?
-Solving this problem comes down to calculating the reflected line after interaction with the circle. All calculations must be done with very high precision.
+Solving this problem comes down to calculating the reflected line after interaction with the circle.
+All calculations must be done with very high precision - see
+[Result dependency on precision](https://github.com/LMesaric/PhotonReflection#result-dependency-on-precision).
+Algorithm used in this project does **not** use any trigonometric functions nor angles between lines.
+The only _problematic_ part is calculating the square root, but that can easily be done in arbitrary precision.
-## Photon reflections and final result ##
+## Points of reflection and final result ##
-Calculating with `100` significant digits, these are the points of reflection (except for 1st and 18th) rounded to `6` decimal places.
+These are the points of reflection (impact), except for 1st and 18th point,
+rounded to `6` decimal places. All decimal places are correct.
1. (+0.500000, +0.260000) - START
2. (+0.791407, +0.260000)
@@ -37,9 +43,14 @@ Calculating with `100` significant digits, these are the points of reflection (e
## Result dependency on precision ##
-Final points calculated with different values of `N` are listed below. `N` is the number of significant digits used in all calculations.
+Final points calculated with different values of `N` are listed below.
+`N` is the number of significant digits used in all calculations.
-It is important to notice that a `double` variable can store up to `15` stable decimal places, meaning that for values in range `<-100, 100>` it can store only `17` significant digits. That is the exact `N` at which a large computation error occurs. For this kind of calculations, one must use data types capable of storing numbers in very high precision, such as `BigDecimal` used in this project.
+It is important to notice that a `double` variable can store up to `15` stable decimal places,
+meaning that for values in range `<-100, 100>` it can store only `17` significant digits.
+That is the exact `N` at which a large computation error occurs.
+For this kind of calculations, one must use data types capable of storing numbers in very high precision.
+_Java_'s `BigDecimal` type was used in this project.
N = 50000 => (+4.094557, -0.360327) - correct result
N = 24 => (+4.094557, -0.360327) - correct result
@@ -54,10 +65,25 @@ It is important to notice that a `double` variable can store up to `15` stable d
N = 15 => (+6.551874, +1.408657)
N = 14 => (+5.776366, -4.158442)
+A small error in locating the impact point will make an error in the equation of the reflected line,
+which will propagate to the next collision with a lever arm of the free path. Even with exact mathematical equations,
+numerical errors will occur due to limited calculation precision. These errors will soon accumulate resulting in
+critical errors such as completely missing a mirror which should have been hit.
+Using symbolic calculations might seem like a good solution at first, but after just a few reflections
+the expressions become incredibly complex and calculations are slowed down. Evaluating the final expression on its own
+might result in large errors due to possible numerical instability.
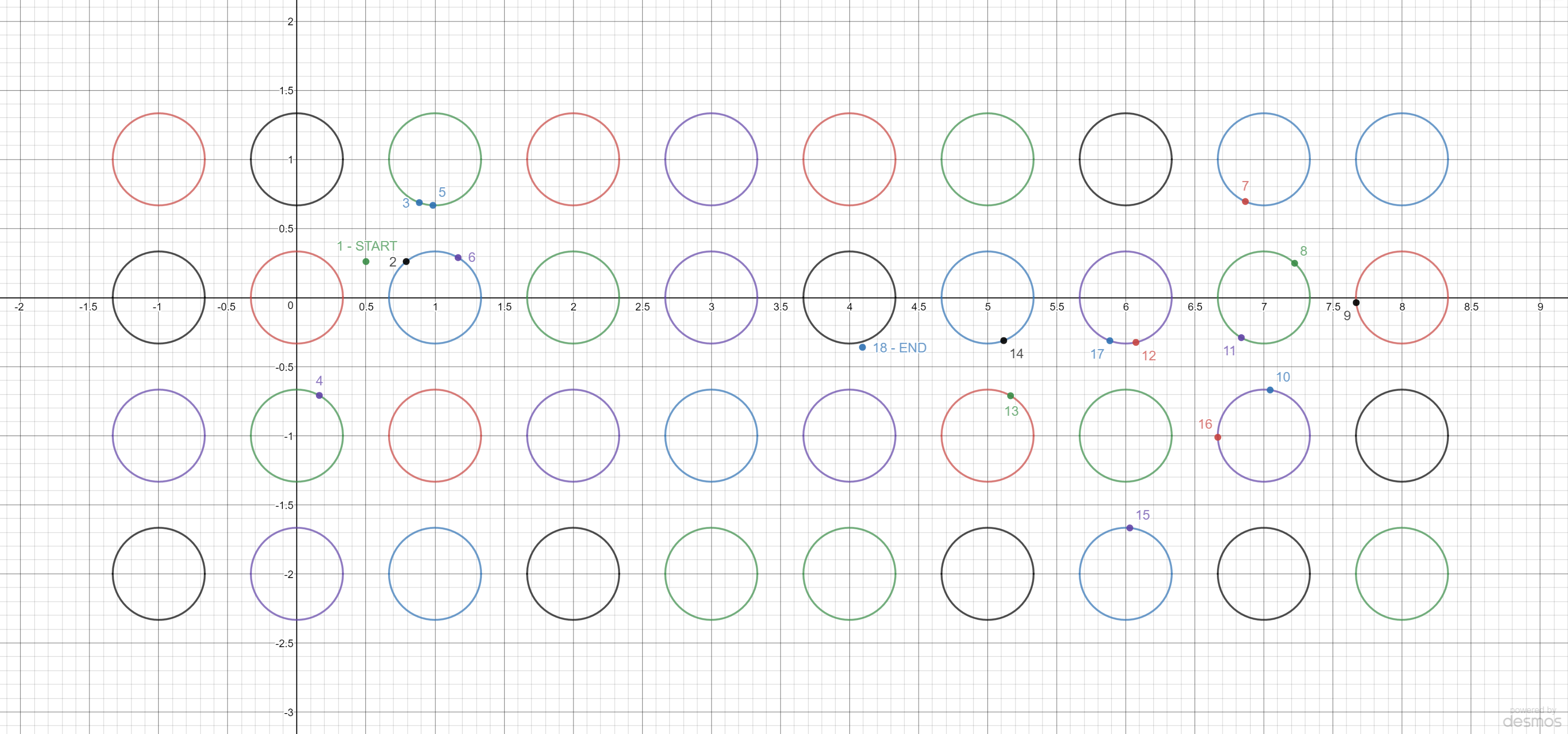
## Visualization ##
-Image below illustrates the entire problem and solution. Each of the reflection points is labeled with a number, from `1` to `18`. Connect the dots to get the photon's trajectory.
+Image below illustrates the entire problem and solution for `t=20s`. Each of the reflection points is
+labeled with a number, from `1` to `18`. Connecting the dots in order will give you the photon's trajectory.
+
+## Increasing the time frame ##
+
+Let us increase the time frame from `t=20s` to `t=200s`, keeping all other parameters the same.
+At that exact moment the photon will be positioned over point `(-15.454298, -7.616898)`.
+This result will be consistently achieved for `N=140` and higher. It is quite obvious that using double precision
+will produce completely unpredictable outcomes.